Справочник проектировщика промышленных, жилых и общественных зданий и сооружений. Книга 2 - Уманский А.А.

Автор: Уманский А.А.
Теги: строительство инженерных сооружений строительство строительные материалы строительное проектирование строительство зданий
Год: 1973
Похожие
Справочник проектировщика промышленных, жилых и общественных зданий и сооружении. Расчетно-теоретический
Справочник проектировщика промышленных, жилых и общественных зданий и сооружений. Каменные и армокаменные конструкции
Справочник проектировщика промышленных, жилых и общественных зданий и сооружений. Основания и фундаменты
Справочник проектировщика. Типовые железобетонные конструкции зданий и сооружений для промышленного строительства
Текст
                    Под редакцией
д-ра техн, наук. проф. А. А. УМАНСКОГО
Рассмотрен и одобрен
Центральным научна-исследбеателъским институтом... строительных конструкций
им, В, Л. Кучеренко
ИЗДАНИЕ ВТОРОЕ. ПЕРЕРАБОТАННОЕ И ДОПОЛНЕННОЕ
В ДВУХ КНИГАМ
УДК 624 04(031)
Справочник проектировщика промышленных, жилых и общественных зданий и со-
оружений. Расчетно-теоретический. В двух книгах. Кн. 2. Под ред. А. А. Уманского.
Изд. 2-е, перераб. и доп. М., Стройиздат, 1973, 416 с.
Вторая книга расчетно-теоретического тома «Справочника проектировщика про-
мышленных, жилых и общественных зданий и сооружений» дополняет расчет стержней
и стержневых систем, приведенный в первой книге, вопросами устойчивости, динамики
и предельных состояний.
Во второй книге даны примеры расчета пластин и оболочек, рассмотрены вопросы
взаимодействия сооружений с грунтом, основные принципы моделирования, применения
метода конечных разностей.
Справочник предназначен для проектировщиков, научных работников и студентов
13)303.
Табл. 230, ил. 507, список лит. 487 назв.
ОГЛАВЛЕНИЕ
Стр.
Стр.
Предисловие ко второму изданию....... в
РАЗДЕЛ 12
УРАВНЕНИЯ И ФОРМУЛЫ ТЕОРИИ
УПРУГОСТИ, ПЛАСТИЧНОСТИ
И ПОЛЗУЧЕСТИ
И. И, Голъденблат, В. А. Копнов
12.1.	Основные уравнения теории упругости . ,	9
12.1,1,	Уравнения равновесия .	у
12,].2. Уравнения совместности деформаций ..... Ю
12.1,3.	Определение перемещений по составляющим
тензора деформаций .....	......	И
12.1.4.	Физические уравнения теории упругости н тер-
моупругости ............	....	12
12,1.5.	Уравнения теории упругости в напряжениях . .	13
12.1,6.	Уравнения теории упругости и термоупругости
в перемещениях (уравнения Ляме)	13
12.1,7.	Потенциальная энергия деформации	Ь
12J.8. Общие принципы теории упругости . , .	.	.	14
12.2.	Плоская задача теории упругости . .	.	.	14
12.2.1.	.Плоское напряженное состояние	14
12,2,2.	Плоская дефорглация	.	15
12.2	3 Функция напряжений Эри ....	....	15
12,2,4.	Функция Эри для плоской задачи анизотропного
(ортотропного) тела	15
12,2,5.	Плоская задача в полярных координатах . - .	15
12,2.6.	Сведение плоской задачи к задаче об изгибе
пластинки ...... а ............ .	16
12.3.	Вариационные методы решения задач теории
упругости	17
12,3.1,	Метод Ритца . .	. . , . 6 , , 5 . , е .	18
12.3,2,	Метод Бубнова — Галеркина .........	19
12.3.3.	Метод Треффца (метод смягчения граничных
условий).......................................  of)
12.4.	Сводка некоторых решений теории упругости 21
12.4.1.	'Чистый изгиб	й .	21
12.4,2.	Поперечный изгиб консоли	21
12	413. Поперечный изгиб балки	21
12.4.4.	Изгиб кривого бруса (задача	X. С.	Головина)	22
12.4,5.	Клин, сжатый сосредоточенной	силой	. ,	.	.	22
12	4.6. Толстостенный цилиндр и сферический	сосуд	.	.	23
12.4.7.	Упругая полуплосткость и упругое полупростран-
ство	я ч о	.	23
12.5.	Концентрация напряжений .......	24
12.5.1,	Концентрация напряжений при растяжении . .	24
12.5.2.	Концентрация напряжений при изгибе ...	25
12.6.	Элементы теории упругости, учитывающей
моментные напряжения .........
12,6	1. Основные положения моментной теории упругости 26
12.6.2.	Уравнения равновесия и несимметричный тензор z
напряжений в двухмерном случае ...... ,	26
12.6.3.	Деформации, вызванные действием силовых и
моментных напряжений	э » и 07
12,6.4,	Закон Гука	?	2’7
12	6 5. Условия совместности деформаций . . . . . о	28
12,6,6,	Функции напряжений . =	......... 2«
12.6.7.	Некоторые результаты расчетов по моментной
теории упругости ...................... ......	- 2g
12.7.	Основные уравнения теории пластичности и
термопластичности	28
12.7,1. Общие свойства пластической деформации . .	29
12 7,2. Основные	положения	теория	к‘асигческого
течения , . .  ....................... .......	29
12.7,3. Основные	уравнения	теории	пластического
течения .......	. ......... .	29
12,7,4. Деформационная теория пластичности — частный
случай теории пластическою течения	30
12,7.5. Идеально упруго-пластическая среда ...	31
12 736, Метод характеристик решения задач теории
пластичности	31
12.7 7. Напряжения под жестким	штампом	.	,	.	д	.	32
]2 7 8. Плоское напряженное	состояние	.......	33
12 7,9. Пластические деформации вблизи круглого от-
верстия в пластине	34
12.7 10. Упруго-пластическое кручение ,	.....	35
12.7.11. Пластическое кручение стержня с растяжением	35
12.8. Ползучесть и релаксация	36
12 83. Основные понятия . я	4	.	36
12.8.2. Релаксация ................	37
12.8.3. Ползучесть	.	...	37
12.8.4, Особенности процесса ползучести некоторых
строительных материалов	. * . .	......	38
12 8 5. Реологические модели ...... < , * » *	38
12,8.6 Теории ползучести ............	39
12,8 7. Наследственная теория ползучести бетона
Н. X. Арутюняна , , . в ........ .	41
12.8 8, О ползучести металлов ...	.......	4 3
12.8.9. Ползучесть при изгибе балок и кривых стержней 43
12,8.10. Ползучесть при кручении .........	45
Литература , » . . » в , ,	. . . . . , я а	45
РАЗДЕЛ 13
УПРУГИЕ ТОНКИЕ ПЛАСТИНЫ
(ПЛИТЫ И БАЛКИ-СТЕНКИ)
А. Л, Китов ер
13Л. Общие термины, обозначения	46
13.1.1	. Основные обозначения ...........	46
13.1.2	. Определение упругих характеристик конструк-
тивно ортотропных пластин	... .....	47
13.1.3	, Связь между усилиями и напряженьями , . .	47
13.2,	Прямоугольные пластины	.......	48
13,2.1. Прямоугольные изотропные	плыы .....	48
Нагрузка равномерно распределит-я по всей пло-
щади плиты (48). Нагрузка, раомшдолекная по
гидростатическому закону (49) Нагрузка, рас-
пределенная равномерно по части площади плиты
(50). Нагрузка в виде трехгранной призмы (50). На-
грузка, распределенная вдоль прямой линии
(51). Нагрузка в виде силы, приложенной в цен-
тре плиты (51). Квадратная плита на упругих
опорах под равномерно распределенной нагрузкой
(51). Определение	сосредоточенных	реактивных
сил в углах плиты, свободно опертой по перимет-
ру (52).........................с	.	52
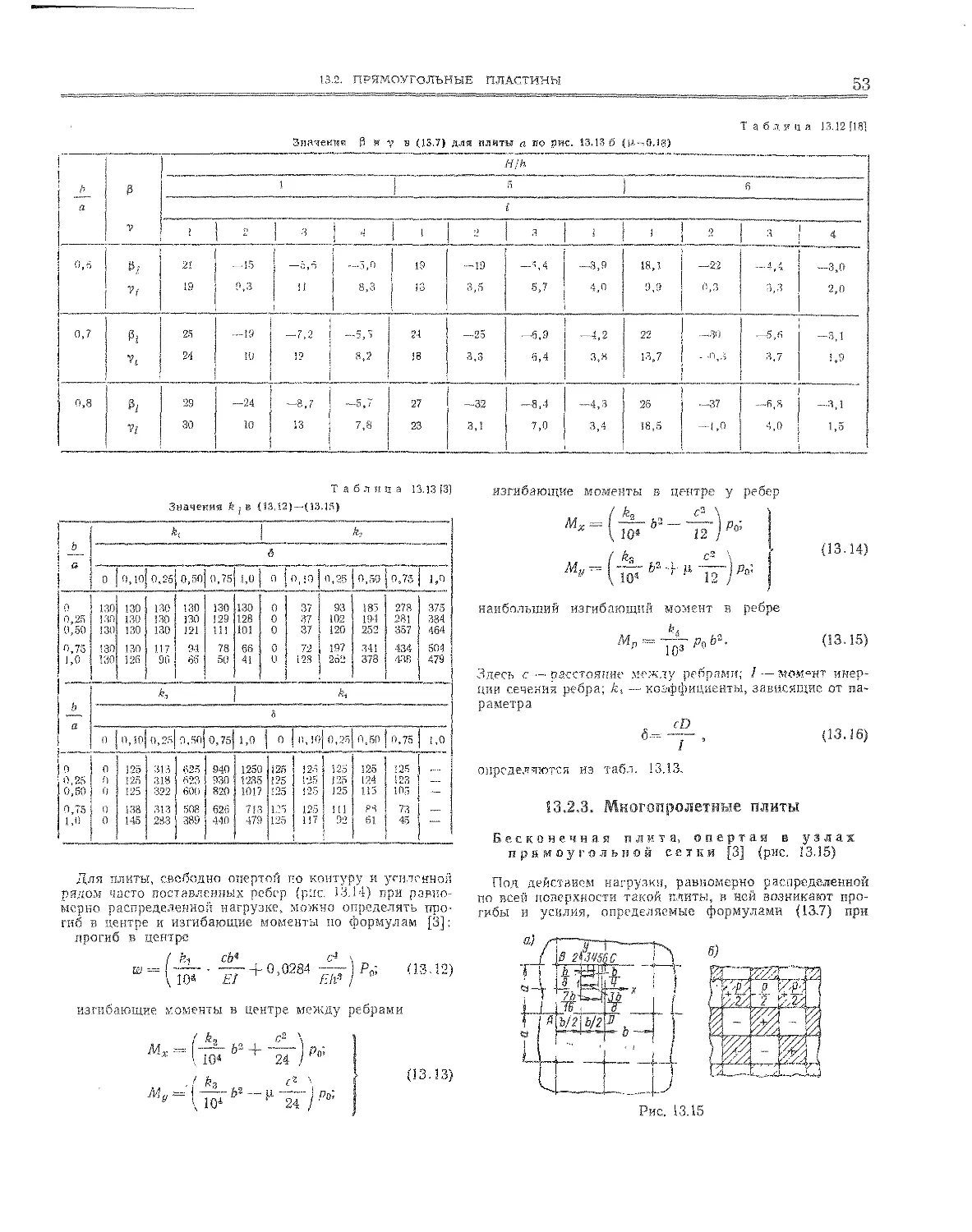
]3 2.2. Ребристые плиты
13.2 3. Многопролетиые	плиты ..............  53
Бесконечная плита, опертая в узл 1х прямоугольной
сетки (53). Квадратная плита, шенст кон-
туру и поддерживаемая колоннами (М). Приближен-
ный способ расчета неразрезных плит	54
13.2,4, Плиты на упругом основании . . „ 9 . , .	65
13 2.5. Балки-стенки.............................  90
13.3,	Круглые и кольцевые пластины.................. 61
ОГЛАВЛЕНИЕ
Стр.
Стр,
13.3.1	. Осесимметричная задача расчета изотропных
плит ...................
Плоское напряженное состояние (61). Плиты на
жестких опорах (62), Круглые ‘ плиты с кольце-
выми ребрами (65). Плиты на упругом основании
(66). Бесконечные плиты (66). Круглые и кольце-
вые плиты (69) ...........................
13.3.2	. Изотропные круглые плиты под произвольной
нагрузкой . .	........... ........
Круглая плита с защемленной кромкой (69). Круг-
лая плита со свободно опертой кромкой (69). Сво-
бодная круглая плита иод действием статически
уравновешенной нагрузки (70) .........
13.3,3	. Круглые и кольцевые ортотропные пластины , ,
Плоское напряженное состояние (70). Изгиб круг-
лой и кольцевой плиты (70)............  .
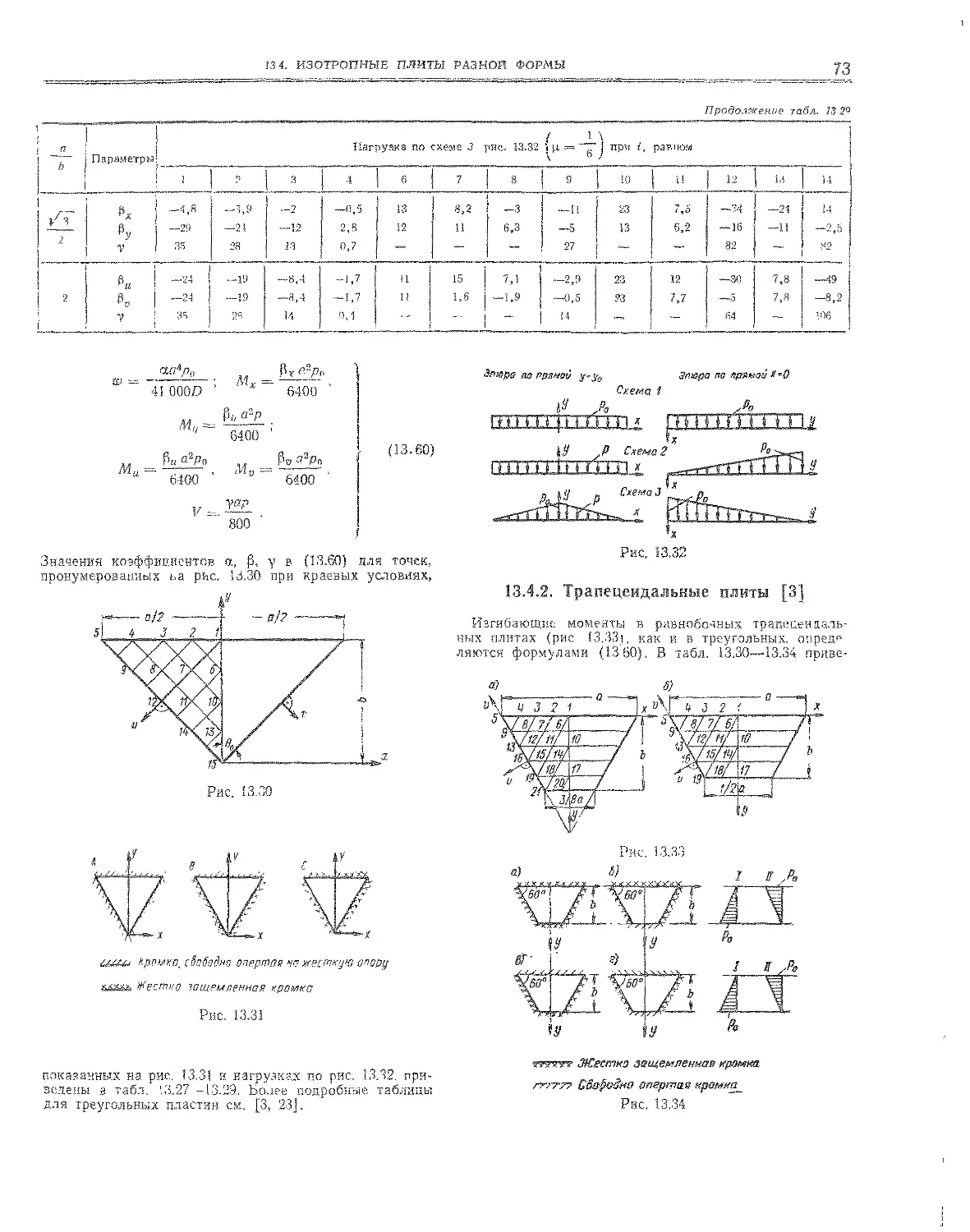
13.4.	Изотропные плиты разной формы . . « .
13.4.1	Треугольные плиты	*
13.4.2.	Трапецеидальные плиты • * - я	.
13.4.3.	Эллиптические плиты.......« . . ,
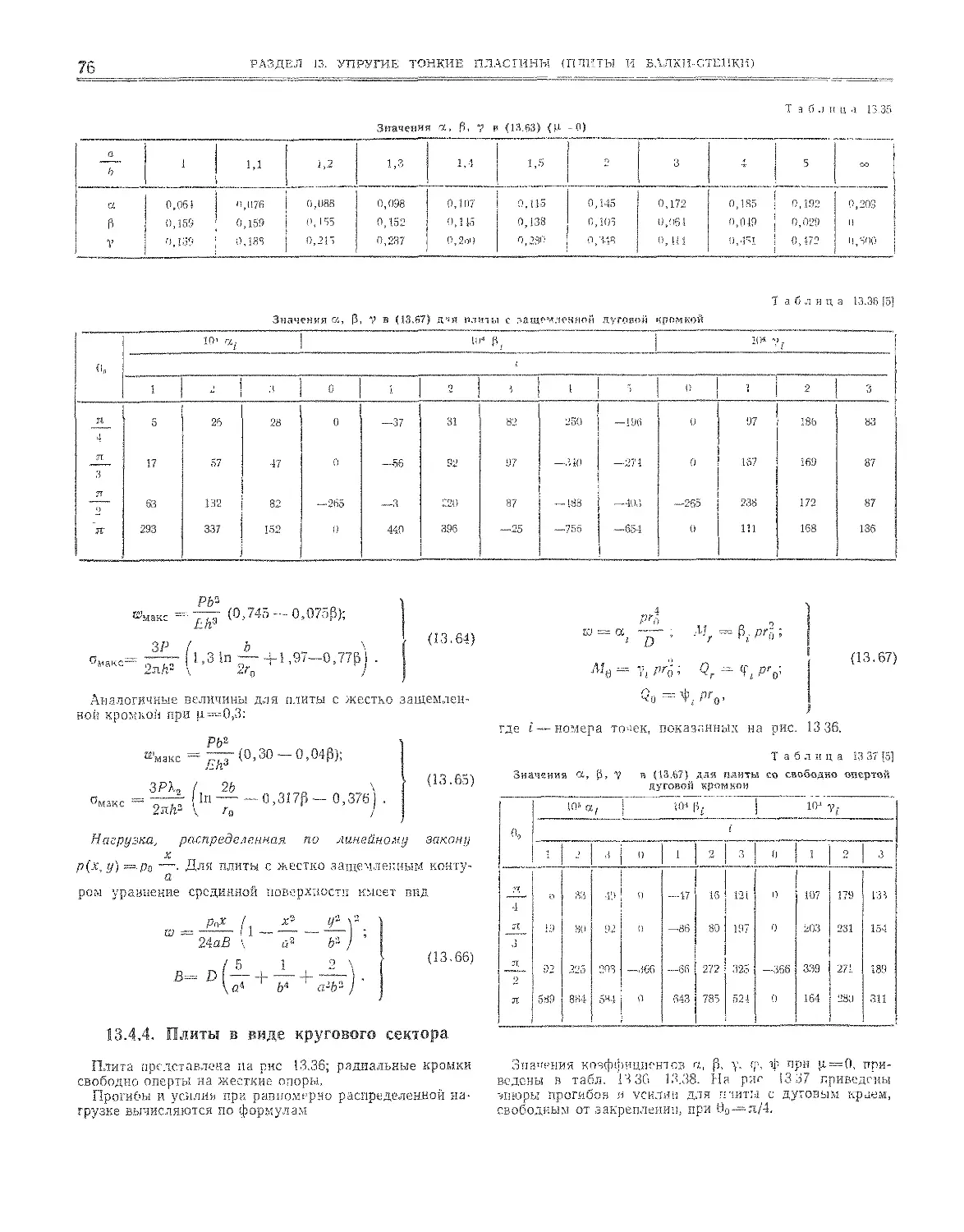
13,4,4.	Плиты в виде кругового сектора .......
13.5.	Температурные напряжения в пластинах
13.6,	Обзор таблиц по расчету плит . . . . .
13.7.	Краткие сведения об аналитических методах
определения усилий и перемещений при изгибе
тонких упругих плит
Литература , # . , я . s ч ?	а * *
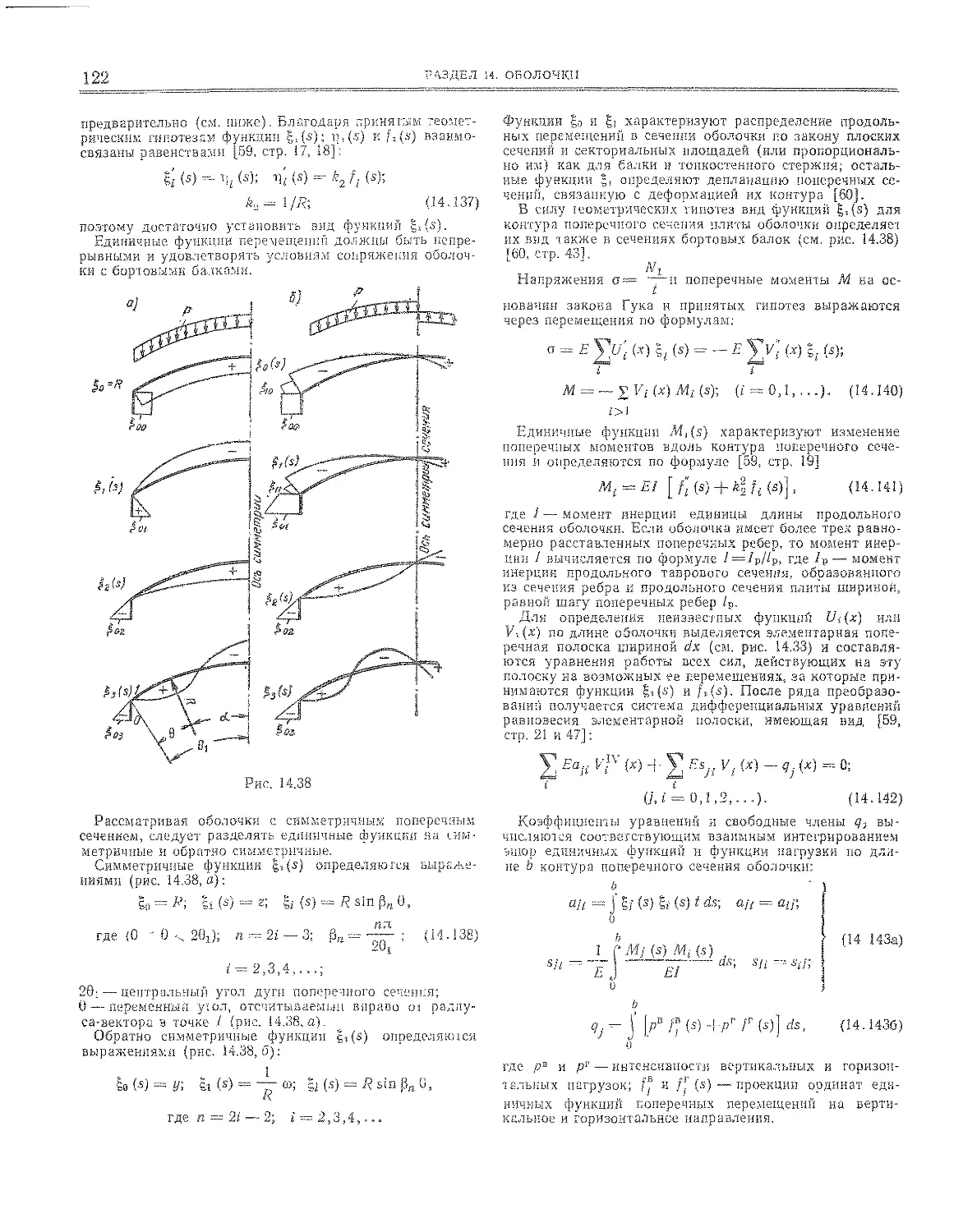
14,5.1.	Определение, формы срединной поверхности и
П	граничные условия ...	.........	101
14.5.2,	Усилия и перемещения пологой оболочки. Осо-
бенности расчета .......................... 107
14.5,3.	Формулы и таблицы для расчета пологих оболо-
_чек, прямоугольных в плане . , . .	....	109
69	14.5.4. Круговые цилиндрические оболочки открытого
профиля .............	..... Ш
70	14.5.5. Дифференциальные уравнения пологих сфериче-
ских оболочек в полярных координатах - . . . , 1И
14.5.6.	Некоторые решения нелинейной теории пологих
оболочек..............................      117
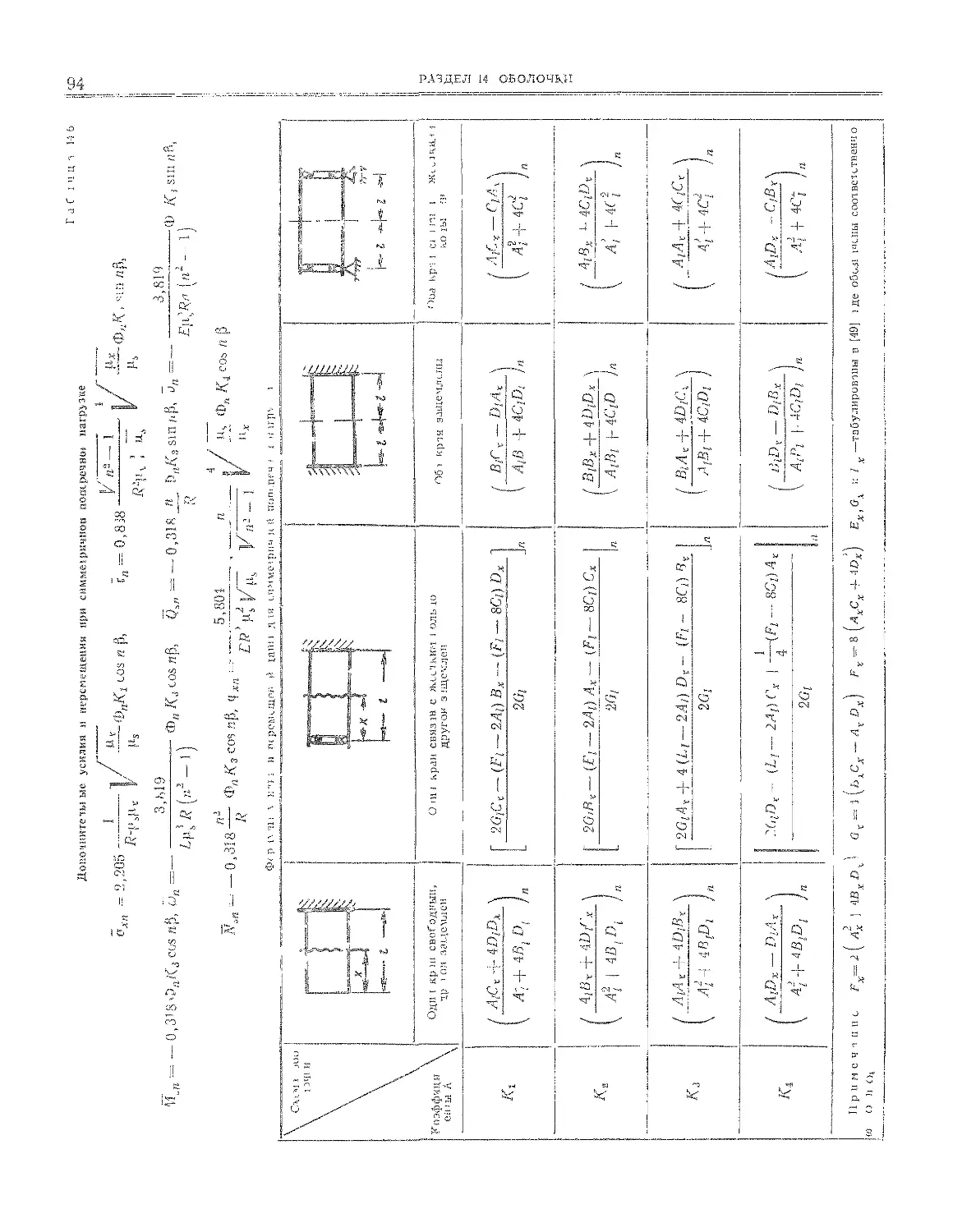
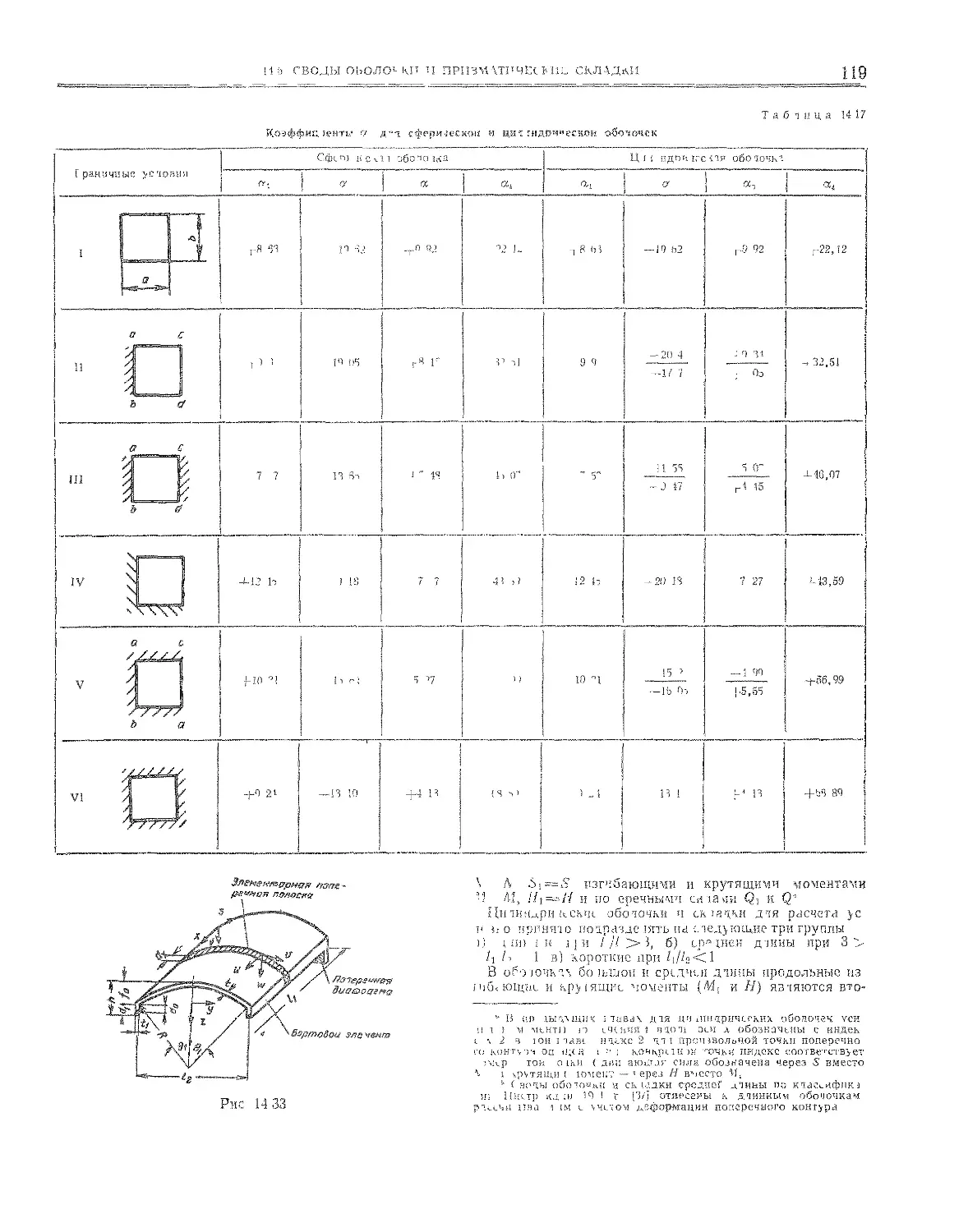
79	14.6, Своды-оболочки и призматические складки
(И. Е. Милейковский)......................  ng
70	14.6.1, Основные обозначения и классификация сводов-
оболочек . . . . ,..............	.	118
71	14.6.2. Расчет оболочек и складок средней длины До-
пущения и гипотезы................................120
71	14.6,3, Расчет диафрагм-оболочек и складок средней
73	длины ,	.................	135
75 Литература , , . . . . , , , . , „ „ ч я ,	136
76	РАЗДЕЛ !5
77 МЕТОД СЕТОК В ПРИЛОЖЕНИИ
К РАСЧЕТУ ПЛАСТИН И ОБОЛОЧЕК
78	П. М. Варвак, Д. В. Вайнберг
15.1. Основы метода сеток .........	138
РАЗДЕЛ 14
ОБОЛОЧКИ
П, А.Лукащ, И. Е. Милейкоаский,
А. Г. Иммерман, Л. Б. Львин
14.1.	Классификация оболочек и качественная ха
рактеристика их работы (П. А. Лукаш) . .
14.1.1.	Общие положения	а
14.1,2.	Тонкостенные оболочки 1 ...... а «
14,1.3,	Общая характеристика работы оболочек	, .
14.1,41	Характеристика теорий расчета оболочек	. .
14.1.5,	Условия применимости безмоментных теорий
14.1.6,	Основные постановки задач теории оболочек
14.2.	Замкнутые круговые цилиндрические оболоч
ки (Л. Г. Иммерчан)
14,2.1.	Основные условные обозначения.........
14,2,2.	Общие дифференциальные зависимости теории
цилиндрических оболочек.......................
14.2,3.	Оболочка под действием осесимметричной на
ipy^KP Безмоменткая теория .......
• 14.2.4. Оболочка под действием осесимметричной на
грузки; Моментная теория
14,2.5.	Сопряжение оболочек. Осесимметричная нагрузка
14.2.6.	Оболочка под действием нагрузки, не обладаю
щей осевой симметрией . , -...................
14.2.7.	Особые ;случаи нагрузок и расчета оболочки
14,3,	Оболочки вращения (П. Л.' Лукаш} , з
14.3.	L Определение и основные обозначения . .
14,3.2.	Усилия и перемещения в оболочках по безмо
ментной теории при осесимметричной нагрузке .
14	3 3. Безмоментные сферические оболочки при верти
калькой осесимметричной нагрузке .....
14.3.4.	Оболочки вращения под действием равномерно
распределенного нормального давления . , .
14.3.5.	Расчет оболочек вращения по безмоментной тео
рин на несимметричную нагрузку . . .	,
14,3	6, Учет изгибающих моментов . .	, . я < .
J4.4. Циклические (моментное) напряженное
" состояние оболочек вращения, сопрягаемых
между собой (Я, Б. Львин) . , . . . . .
14,4.1. Выделение циклического воздействия и его рас-
пределение. Общий поочдок расчета ......
14 4 2. Едини" ые (краевые) реакции оболочек . .	.
14 13 Измен нье у< илий вдоль меридиана каждой
оболочки , . . ‘А....................  .	, , . .
14.4,4, Кольцо, Единичные реакции и внутренние усилия
14.5. Пологие оболочке (Л. А. Лукаш) . . , .
15.2. Плоская задача
80
80
81
81
81
87
83
83
83
15.2.1	. Плоская задача а напряжениях. .......	139
15.2.2	. Двойной итерационный процесс решения плоской
задачи..................................  139
15.2.3	. Решение в перемещениях. Вариационный метод
построения разностных уравнений (ТО. А1. Стру-
гацкий) .	................ . . ,	141
15.3.	Изгиб пластин ........... из
15.3.1.	Основные уравнения и граничные условия . ,	143
15.4.	Устойчивость и колебания пластин ....	157
15.4.1. Уравнения устойчивости пластин	......
15,4.2. Собственные колебания пластин	......
15.5. Оболочки ................................
15.5.1. Основные уравнения и граничные условия для
пологих оболочек . . . ......	. ... .
Литература . . . . . . . . . . .	, . .
gs	РАЗДЕЛ 18
g5	МОДЕЛИРОВАНИЕ
85	А. Я. Александров, М. X. Ахметзянов,
86	3 В. Б. Геронимус	
157
159
Ш
164
168
89	16.1. Основные положения теорий подобия и раз-
93	мерности .......... г .... . не
93	16.2. Простое подобие статических упругих со-
93	стояний. Метод анализа размерностей .	.	.	ДЗД
16.3. Расширенное подобие в сгап'чесяих задачах
95	теории'упругости. Анализ уравнений	. .	.	.	ИЗ
9g 16.4, О влиянии коэффициента Пуа&она на рас*
пределение напряжений , . .	. сш,,,'* 174
97	16,5, О моделировании Объемных сил . .	Д./й3 174
98	16,6. Подобие в динамических задачах теории
99	упругости.............  СТ:.	Ср . т.СЕДШ П5
16.7.	Подобие в задачах термоупругости	. . .	176
16,8.	Моделирование больших деформаций . . .	176
16.9.	Подобие в задачах пластичности ....	и?
0	16,10. Подобие в задачах ползучести	, . л	177
16.11. Моделирование некоторых видов конструкций 177
jo® 16.12. Вопросы подобия при исследовании состав-
ных систем ....................;	. с, С) ЖХ.,. ш
1®	18.13. Таблица критериев подобия и уравнений свя-
Оз зи между масштабами в задачах статики и ди-
106 намики .	:.7: ;igg
ОГЛАВЛЕНИЕ
5
Стр.
' 1е5
185
186
Вп
186
187
Ь8
188
189
190
КО
к о
191
192
192
192
ЬЗ
191
194
194
195
199
200
200
203
204
200
206
206
208
211
213
213
214
216
218
219
219
220
221
222
Й22
222
Стр.
16.14. Таблица критериев подобия температурных
полей
Литература . . . . , ...... . . . . . <
РАЗДЕЛ 17
УСТОЙЧИВОСТЬ СТЕРЖНЕВЫХ СИСТЕМ
С. И. Лейтес
17.1.	Основы теории устойчивости стержневых си-
стем со сжатыми элементами.......................
17.1.1.	Понятия устойчивости и неустойчивости. Устой-
чивостъ равновесия деформируемых систем . . ,
17J.2. Консервативные и неконсерва гпвные системы.
Методы исследования устойчивости равновесия , .
17.1.3.	Потеря устойчивости при разветвлении форм
равновесия.....................................
I7.L4.	Потеря устойчивости при достижении предельной
нагрузки . . ..................................
17.1.5.	Устойчивость линейно мпругой системы с конеч-
ным числом степеней свободы ...................
17.1.6.	Собственные значения и собственные функции ,
17,1.7.	Энергетический критерий качества равновесия^
I7JJL Потенциальная энергия центрально сжатого" лм'-"
нейио упругого стержня ........................
17,1.9.	Задача Эйлера .........................
17.1,10.	Равновесные состояния сжато-изогнутого ли-
нейно упругого стержня...........................
‘ 17,1.11. Об’ анализе больших перемещений сжатых и
сжато-изогнутых стержней.........................
17,1.12.	Устойчивость «в большом» и явление перескока
17.1.13.	Идеальные и нендеалъные системы. Начальные
несовершенства реальных стержней...............
17.1.14.	Свободная длина и гибкость стержня . . . -
17.2.	Линейно упругие сжатые и сжато-изогнутые
стержни постоянного сечения..................  .
17.2.1.	Линейно упругий материал. Обозначения , . .
17.2.2.	Уравнение упругой линии стержня в форме ме-
тода начальных параметров.................
17.2.3.	Критические силы центрально сжатых стержней
с различными условиями закрепления концов . .
17,2.4.	Внецентренно сжатые стержни .......
17.2,5.	Сжато-изогнутые стержни ...............
17.2.6.	Принцип независимости действия сил. Принцип
взаимности перемещений
17.2,7,	Растянуто-изогнутые стержни . . , . е . . ,
17,2.8.	Большие перемещения внецентренно сжатых
стержней
17.3,	Линейно упругие стержнеаые системы. Мето-
ды расчета ...............
17.3.1	Основные положения расчета по деформирован-
ной схеме	* ......... .
17.3.2.	Метод сил ,
17,3,3.	Метод перемещений - ч ...... а .
17,3.4,	Расчет неразрезных балок ..........
17.4.	Линейно упругие стержневые системы. Опре-
деление критических нагрузок .......
17.4.1.	Постановка задачи об устойчивости линейно уп-
ругой стержневой системы ...................
17.4,2.	Лн.тлш критических состояний методом сил и ме-
тодом перемещений . .............................
17.,4.3	. Примеры исследования устойчивости методом сил
j и методом перемещений	..........
17,4.4,	Качественный анализ устойчивости линейно упру-
гих стержневых систем . ....................
17,4,5.	Устойчивость однопролетных стержней с упруго
закрепленными концами .........................
17.1.6.	Устойчивость неразрезных балок на упруго пере-
мещающихся опорах....................... . . . .
17.4.7.	Устойчивость неразрезных балок на упруго вра-
щающихся опорах .	. .................. , ,
17А.8. Устойчивость рамных систем ........
17.4,9.	Устойчивость стержня в упругой среде , . , ,
17.4ДО.	Справочные данные для определения свободных
длин ....... * .......... .
17.5.	Линейно упругие сжатые стержни составного
сечения. Стержни с переменными по длине жест-
костью и сжимающей силой ........
17.5,1.	Сжатые стержни составного сечения .....	2’2°
17,5.2.	Сжатые ступенчатые стержни ........	223
17.5.3.	Сжатые и сжато-изогнутые стержни с непрерыв-
но изменяющейся по длине жесткостью............... 224
17 5.4, Сжатые стержни, жесткость которых изменяется
по степенному закону .............	226
17.5.5.	Сжатые стержни с переменными по длине жест-
костью и сжимающей силой	227
17.6.	Линейно упругие стержни, сжатые следящи-
ми силами	228
17.6.1,	Стержень, сжатый следящей	силой общего типа	228
17.6.2.	Динамический критерий устойчивости равновесия.
Три вида собственных движений стержня ....	228
17,6.3.	Гармоническое колебание стержня, сжатого сле-
дящей силой  ...................................   229
17,6.4,	Критические состояния стержня, сжатого следя-
щей силой	230
17.6,5.	Области устойчивости и неустойчивости невесомо-
го стержня, несущего сосредоточенную массу и сжа-
того следящей силой . , . .......................  231
17.6.6,	Области устойчивости и неустойчивости весомого
стержня, сжатого следящей силой .......	232
177, Нелинейно упругие сжатые и сжато-изогну-
тые стержни	233
17.7.1	, Нелинейно упругий материал	233
17.7,2	. Устойчивость центрально сжатых стержней	.	.	234
17.7,3	. Изгиб и устойчивость сжато-изогнутых стержней 234
17,7.4	, Аналитическое исследование равновесных и кри-
тических состояний внецентренно сжатого стержня
с двухточечным профилем ............	234
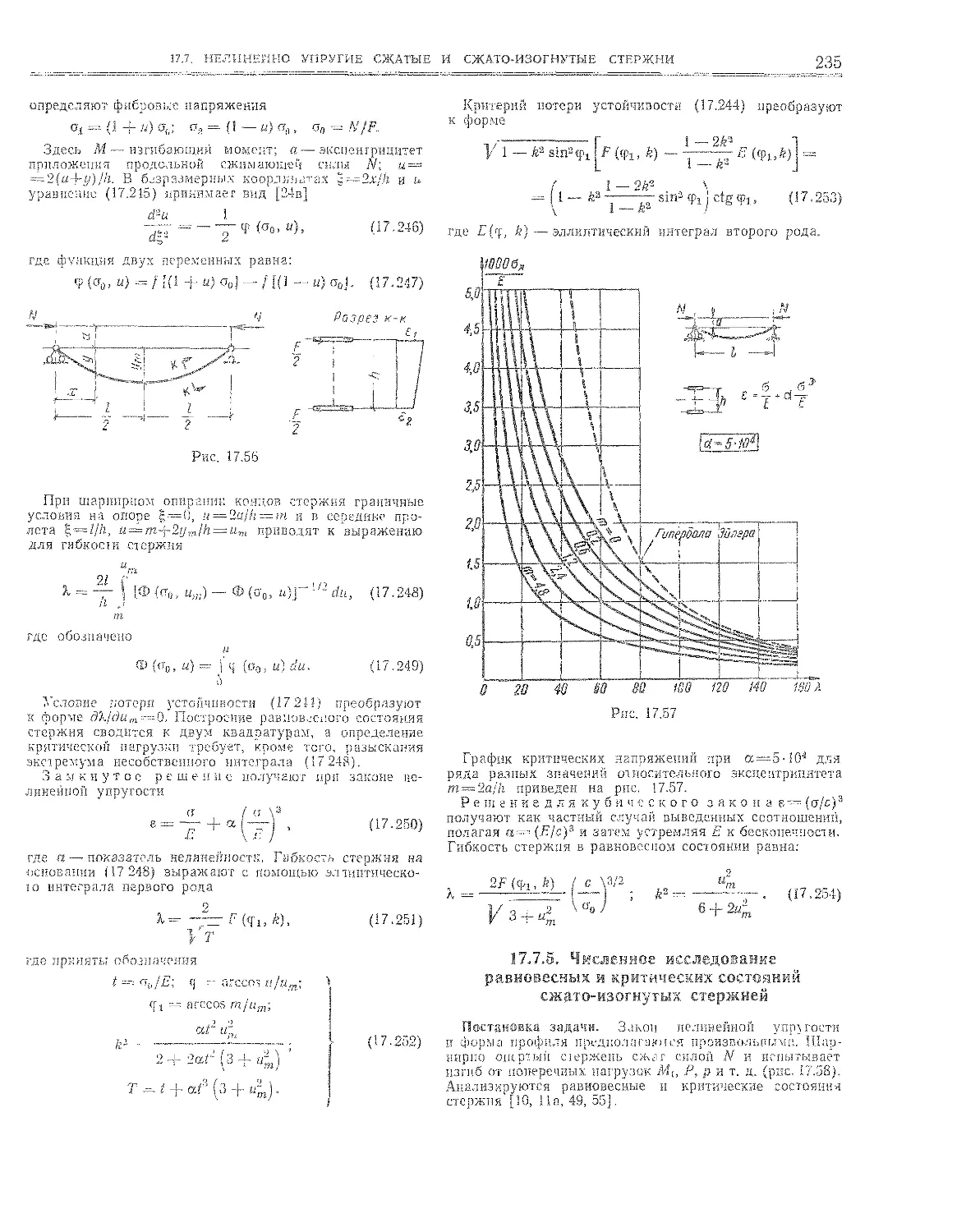
17.7,5	. Численное исследование равновесны?* и критиче-
ских состояний сжато-изогнутых стержней . . .	235
17.7.6	. Приближенное определение критической силы вне-
цеш-ренно сжатого стержня......................... 236
17.7.7	, Качественный кршерий устойчивости сжато-изо-
гнутых нелинейно упругих стержней ......	237
17,8.	Упруго-пластические сжатые и сжатснизогиу-
тые стержни	237
17.8.1.	Упруго-пластический материал. Обозначения , .	23/
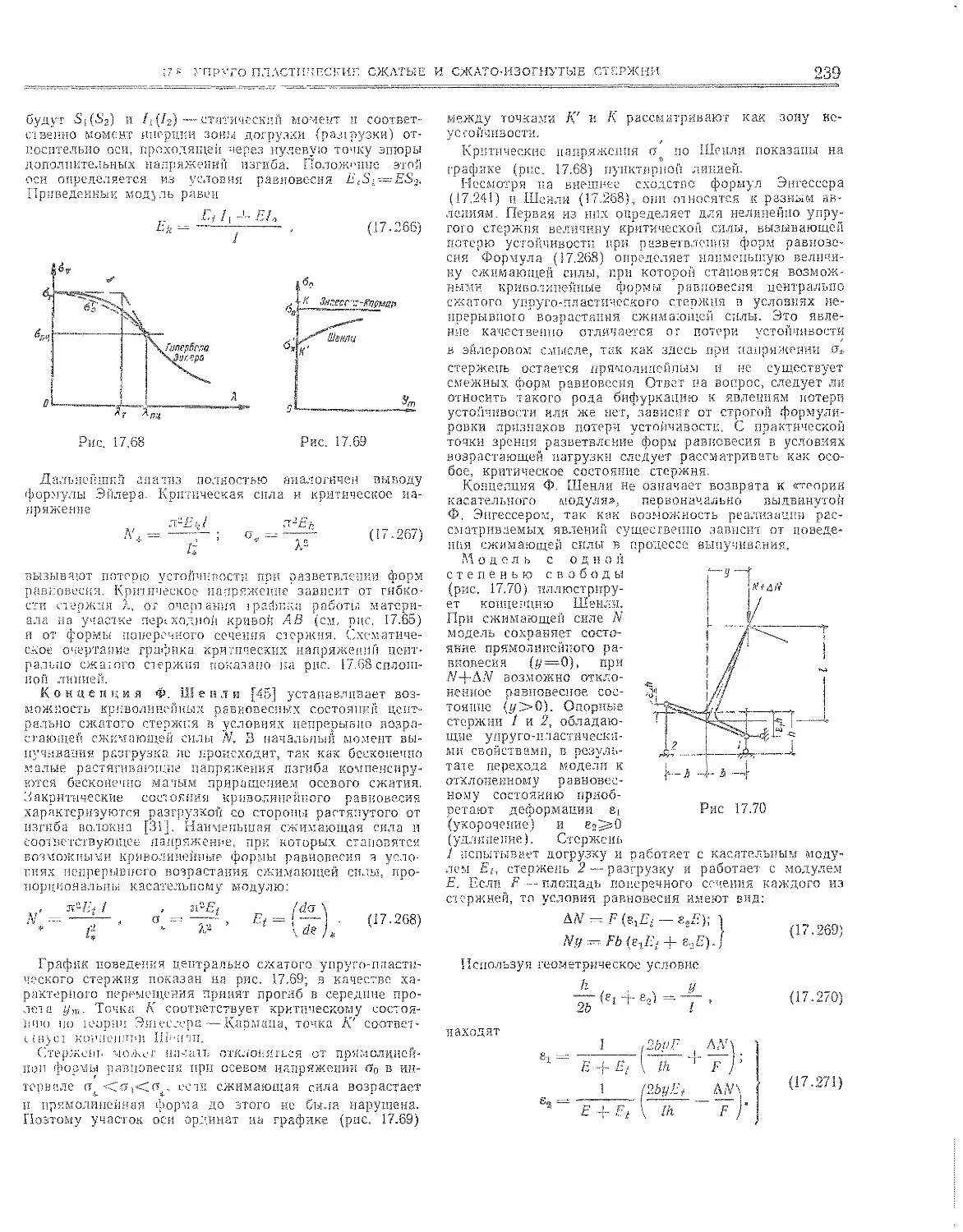
17.8.2.	Устойчивость центрально сжатых стержней . .	238
17,8.3.	Изгиб и устойчивость сжато-изогнугых, стержней	240
17.8,4,	Сжато-изогнутые стержни из идеального упруго-
пластического ?латериала ...........	240
17.8.5.	Приближенное исследование устойчивости вне-
центренно сжатого стержня прямоугольного сечения
из идеального упруго-пластического материала . .	242
17,8.6.	Влияние формы поперечного сечения на устойчи-
вость внецентренно сжатых стержней из,идеально-
го упруго-пластического материала . ц . . . .	244
17,9,	Подбор сечений сжатых и сжато-кзогнутых
стержней	244
17.9.1.	Основные положения подбора сечений сжатых и
сжато-изогнутых стержней . .... . _ .... ,	2-Н
17,9.2.	Расчет центрально сжатых стальных стержней
по нормативной методике .	‘.	'--45
17	9.3. Расчет сжато-изогнутых стальных стержней по
деформированной схеме	245
17.9.4.	Расчет сжато-изогнутых стальных 'стержней по
нормативной методике ............	246
17.9,5.	Расчет сжато-изогнутых стальных .стержней по
критическому напряжению . ..........	247
17.9,6,	Сопоставление результатов расчета внецентренно
сжатого стержня ио трем различным методикам	248
17.10.	Линейно упругие тонкостенные ’ сжатые и
сжато-изогнутые стержни . . ,	  249
17,10.1.	Дифференциальные уравнения равновесия тон-
косюниьш стержней......................	249
17,10.2.	Изгиб и кручение тонкостенных сжато-изогну-
тых стержней . ...............................     250
17.10,3.	Расчет тонкостенных сжато-изоп#утых стержней
ио деформированной схеме . . . д . ,	...	250
17.10,4.	Изгиб, кручение и устойчивость тонкостенных
внецентренно сжатых стержней	......	,	250
17,10.5,	Устойчивость тонкостенных центрально сжатых
стержней ............ я . .... .	251
17.11.	Нелинейно упругие стержневые системы.
(А. В. Геммерлине) ................................  jsi
17,11.1.	Постановка задачи об устойчивости нелинейно
упругих стержневых систем « . е . « . 3 » « .	-:51
ОГЛАВЛЕНИЕ
Стр
17.11.2.	Основные	аналитические	зависимости	.	«	.	»	252
17.11.3.	Алгоритм	«Сечение»	а	..♦	«
17.11.4.	Алгоритм	«Стержень»	« % , <,	.	.	«	.	«	•	2эЗ
17.11.5.	Алгоритм	«Рама» ....«,	в	.	*	•	2оЗ
17.11.6.	Предельное состояние системы	*j4
17.12.	Устойчивость линейно упругих колец и арок.
(А. Б, Мореаевский)	254
17.12.1.	Постановка задачи. Поведение нагрузки » ® »	254
17.12.2,	Устойчивость круговых колец .......	255
17.12.3,	Устойчивость круговых арок в их плоскости	256
17.12,4.	Устойчивость параболических арок в их пло-
скости . .	2^6
17.12.5.	Устойчивость пологих двухшарнирпых арок в
их плоскости  ....................................  ^6
17.12.6.	Устойчивость одиночных арок из их плоскости 257
17/13. Местная устойчивость профилей сжатых
стержней (А. Г, Иммерман)........................... 256
17Л4. Устойчивость плоской формы изгиба балок,
(Г.	М. Чувикин] . . . ...... . . .	262
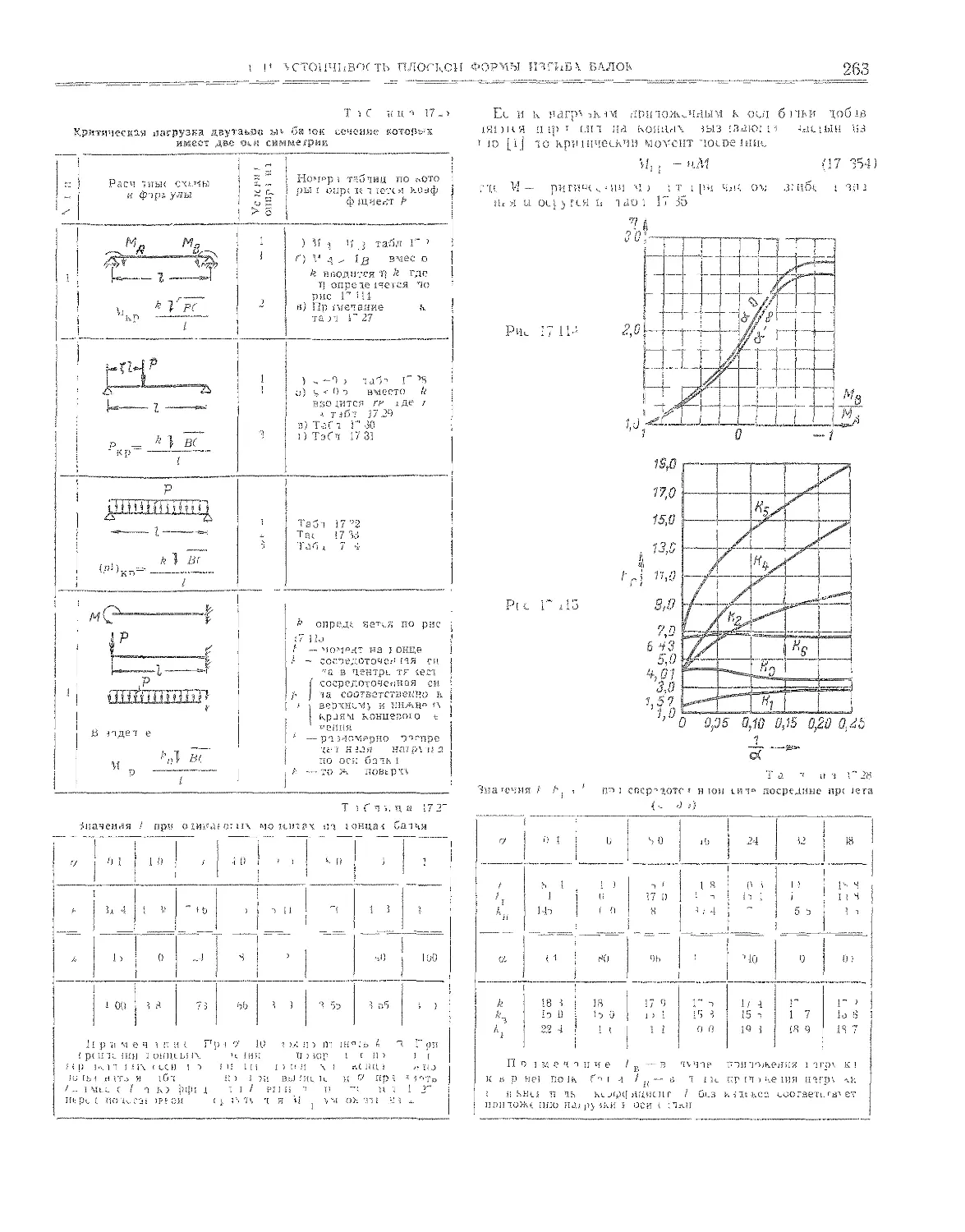
17.14,1. Устойчивость двутавровых балок ...<•<	262
Учет прогиба балки в плоскости изгиба (264). Кри-
тические напряжения (265). Балки с продольными
связями (265). Влияние перехода критических на-
пряжений за предел пропорциональности (265).
17.14,2. Устойчивость стальных двутавровых балок . »	265
Балки с сечением, имеющим две осн симметрии
(266), Переходные коэффициенты для сталей разных
классов (267), Двутавровые балки с сечением, имею-
щим только одну ось симметрии (267).
Литература », ©.гол» «.ваявшее 268
РАЗДЕЛ 18
устойчивость ПЛАСТИНОК и оболочек.
РАСЧЕТ ГИБКИХ ПЛАСТИНОК
В. Л. Агамиров, А. С. Вольмир
18,1.	Определение и основные обозначении ... это
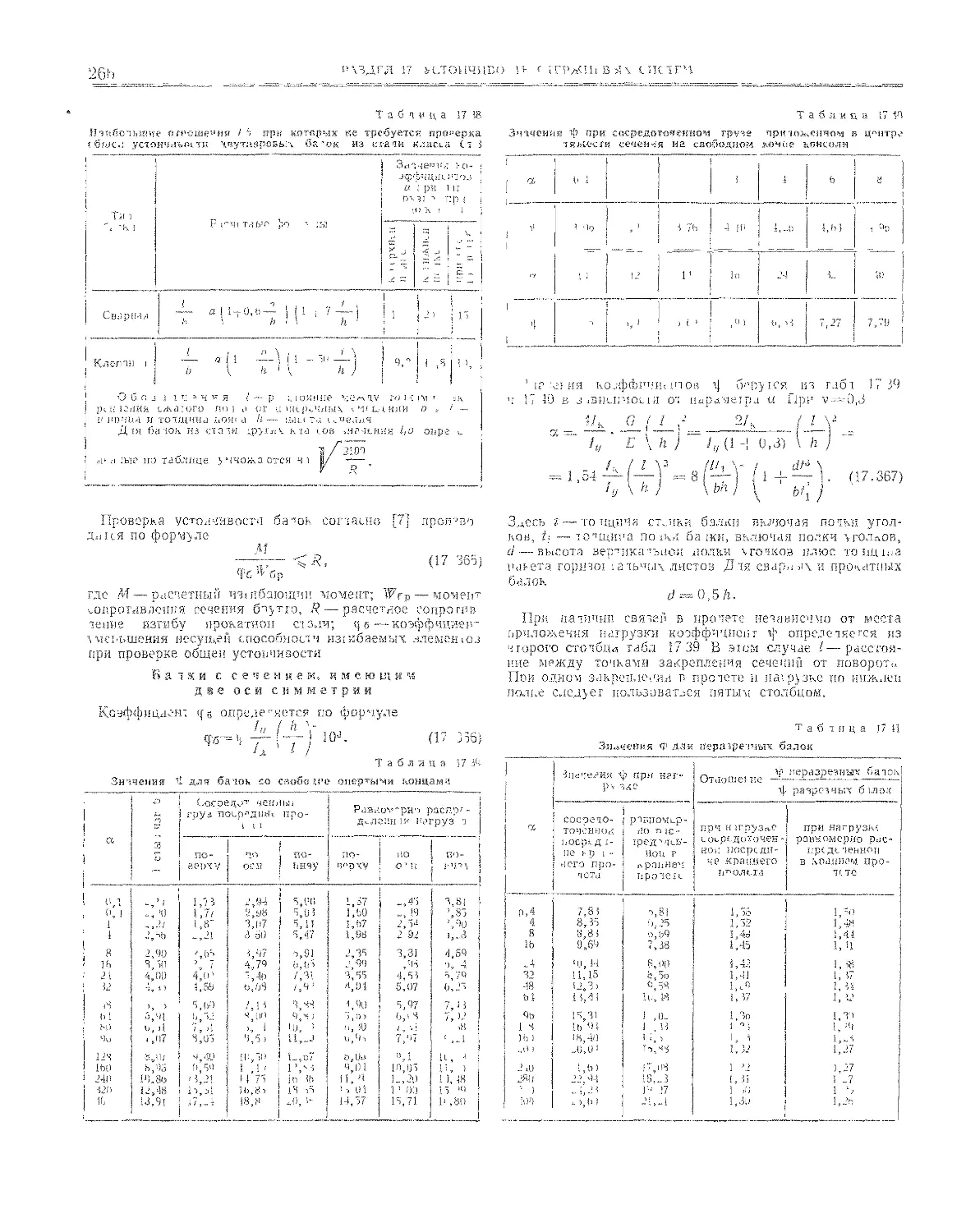
18.2.	Устойчивость пластинок в пределах упругости 270
18.2.1.	Прямоугольные пластинки .........	270
18.2.2.	Прямоугольные и квадратные пластинки, под-
крепленные ребрами . . . . . , .... > . .
18.2,3.	Несущая способность подкрепленных ребрами
прямоугольных пластинок после потери устойчиво-
сти при сжатии, сдвиге и чистом изгибе. Редукци-
онные коэффициенты  ............• »»,.«	277
18.2,4,	Непрямоугольные пластинки	. . . » . а » .	277
18.3.	Устойчивость незамкнутых оболочек (пане-
лей) в пределах упругости ........	279
18,3,1.	Цилиндрические панели , . « . я » г . * »	279
18.3.2.	Конические панели	о ....... .	281
18,3.3.	Сферические панели . * ....................  281
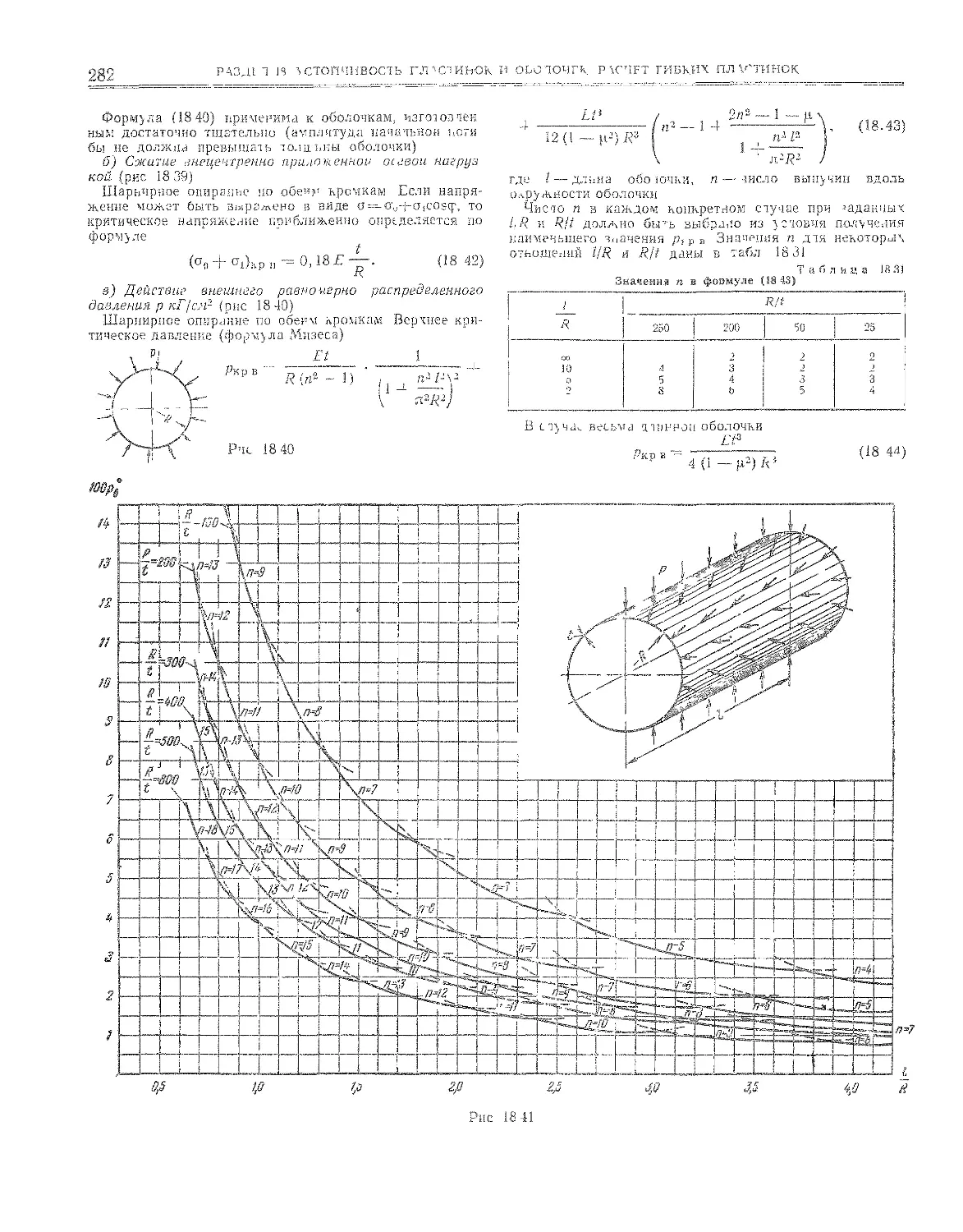
18,4.	Устойчивость замкнутых оболочек в преде-
лах упругости ............	281
18,4.1.	Цилиндрические	круговые оболочки . . ,	»	„	281
18.4.2.	Цилиндрические	эллиптические оболочки .	»	.	285
18,4,3.	Усеченные конические круговые оболочки	.	.	285
18.4.4.	Усеченные конические круговые подкрепленные
оболочки . . . .	.............	.	?86
18.4.5.	Усеченные конические эллиптические оболочки 286
18.4.6.	Сферические оболочки	287
18.4.7.	Эллипсоидальные оболочки . 4	.	287
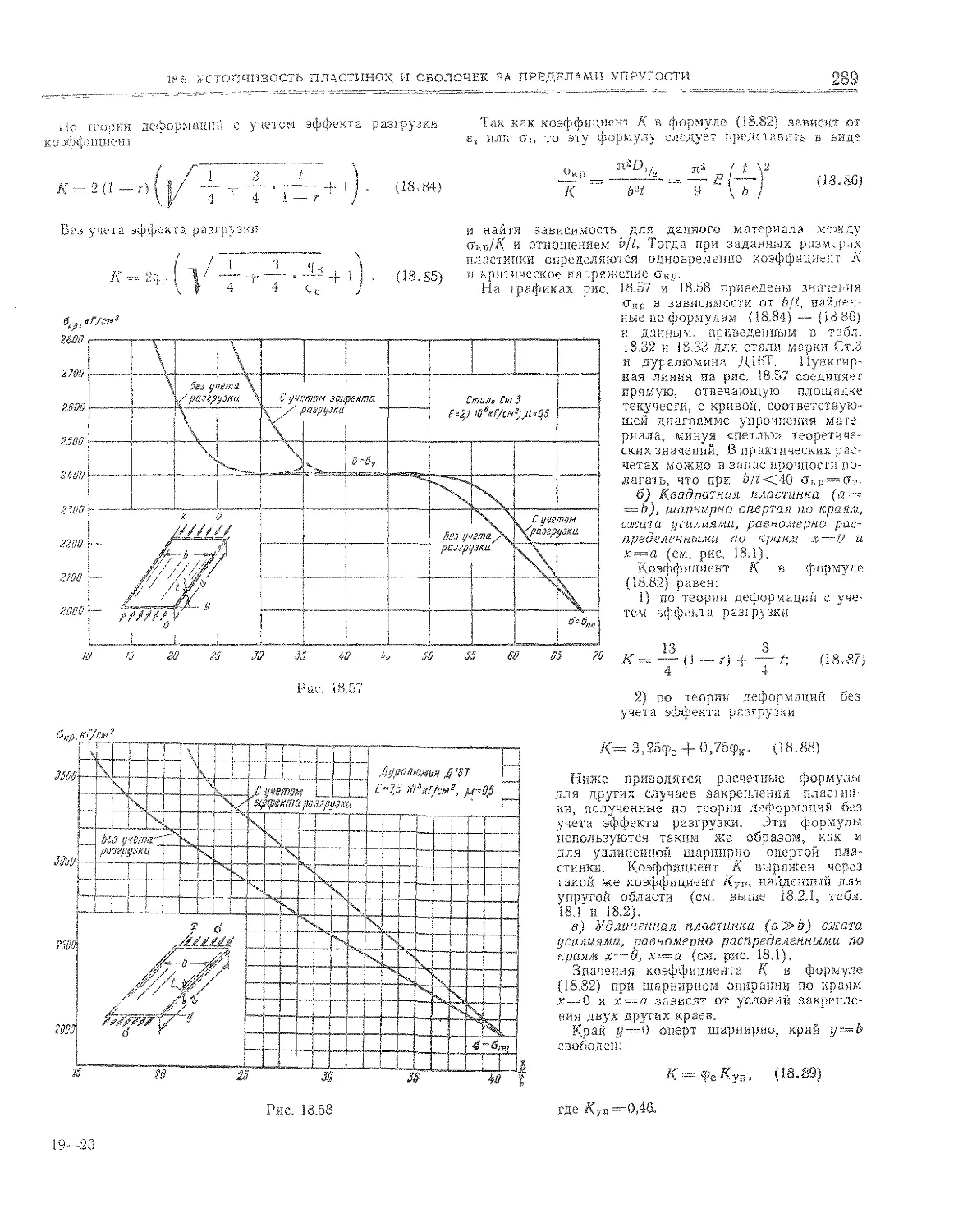
18.5.	Устойчивость пластинок и оболочек за пре-
делами упругости ...........	238
18.5.1,	Общие положения	я а ,	288
18.5.2.	Прямоугольные пластинки .........	288
18.5,3.	Цилиндрические оболочки	290
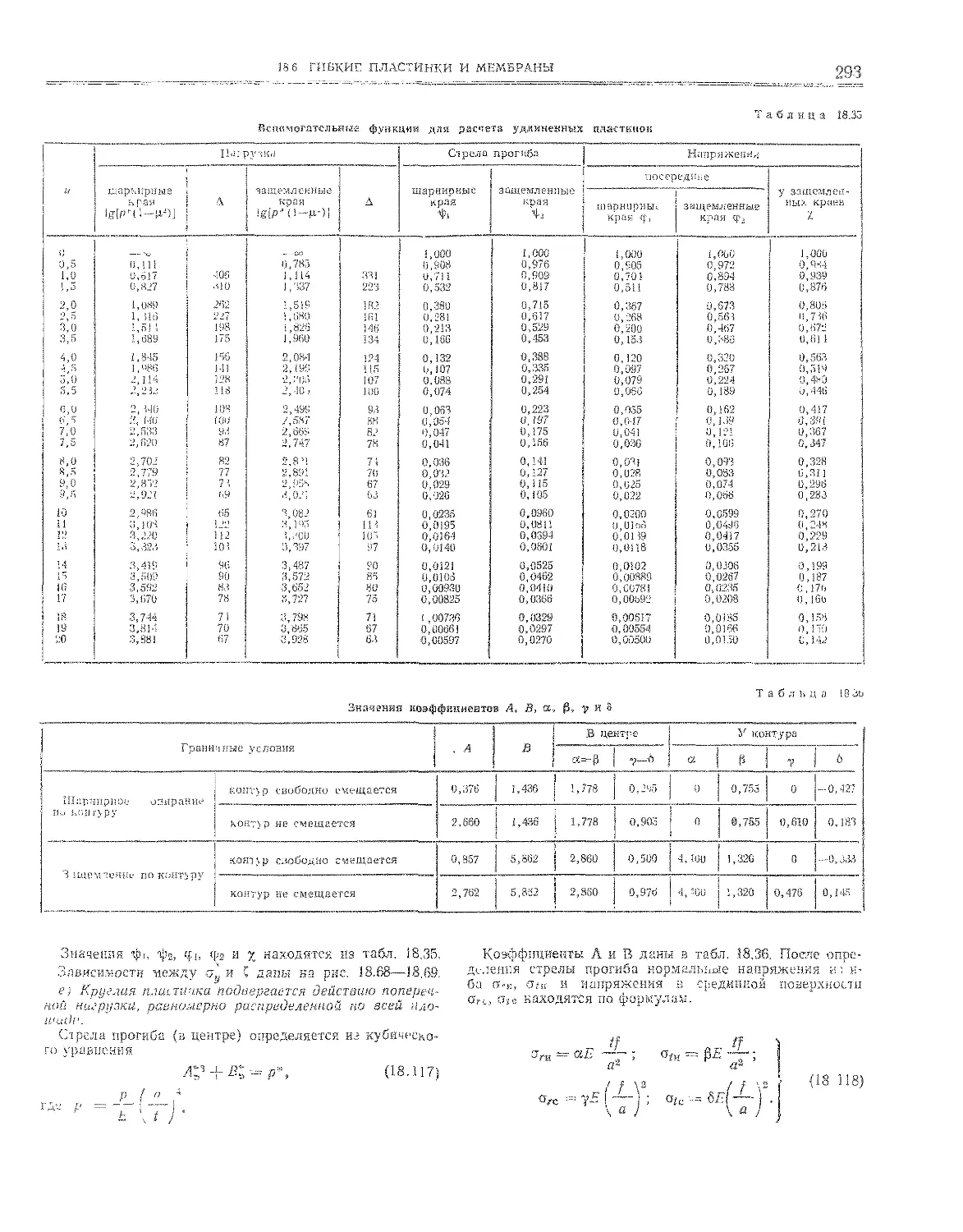
Ш6. Гибкие пластинки и мембраны ......	299
18.6.	L Гибкие пластинки e « . , „ .......	290
Стр.
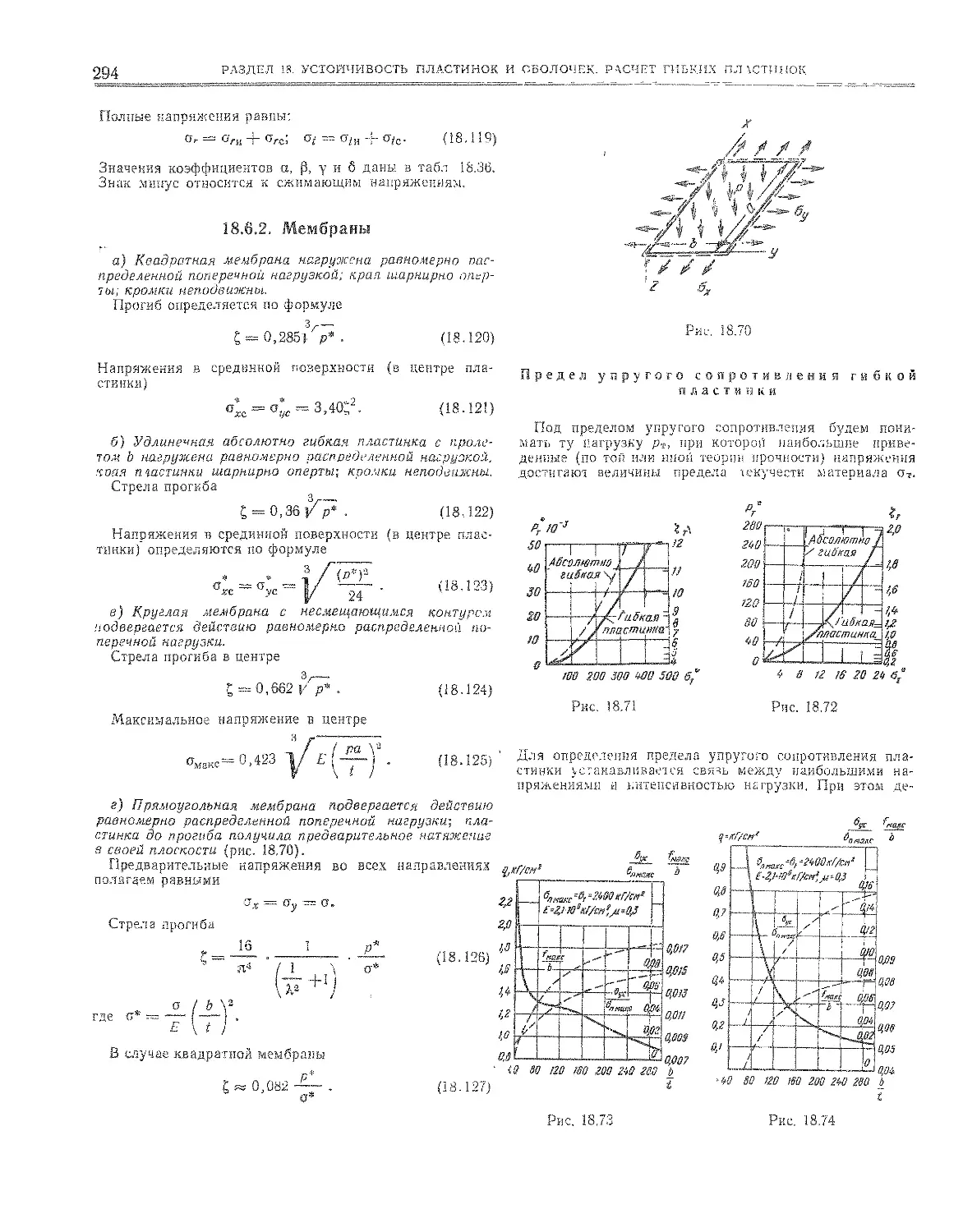
18.6.2.	Мембраны	........ Е	s 0 .	292
Литература . , « . . . . . ► . , . „ в . . 9	29о
Р А 3 Д Е Л 19
РАСЧЕТ СООРУЖЕШШ,
ВЗАИМОДЕЙСТВУЮЩИХ С ГРУНТОМ
М. С. Бернштейн, Г, К- Клейн, А, П, Синицын
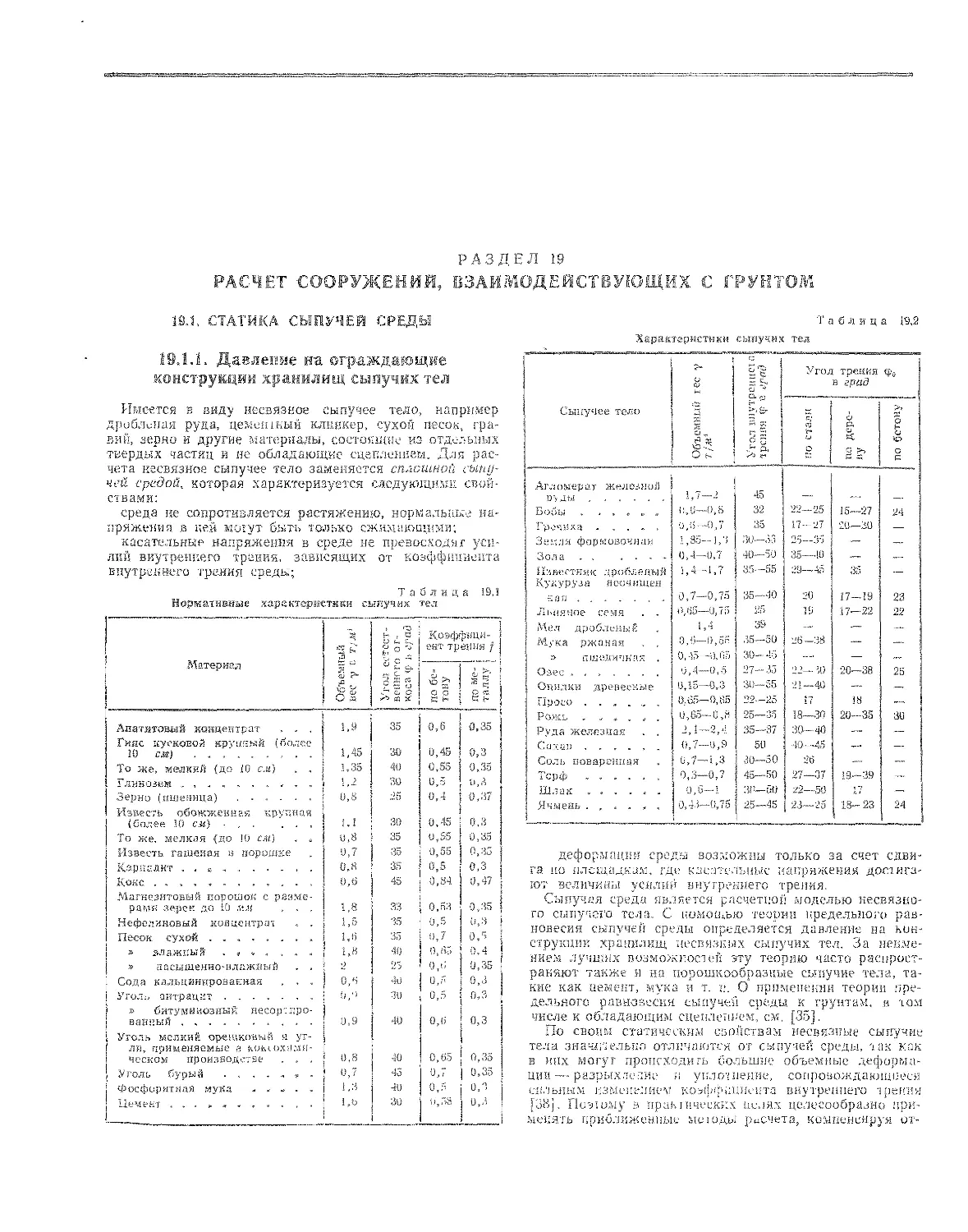
19.1.	Статика сыпучей среды (М С. Бернштейн) 295
19.1.1.	Давление на ограждающие конструкции храни-
лищ сыпучих тел	296
19.1,2.	Предельное равновесие сыпучей среды. Строгие
и приближенные решения плоской задачи . . . .	297
19.1,3,	Давление сыпучего тела на массивную стенку.
Теория Кулона. Строгое решение для частного
случая	299
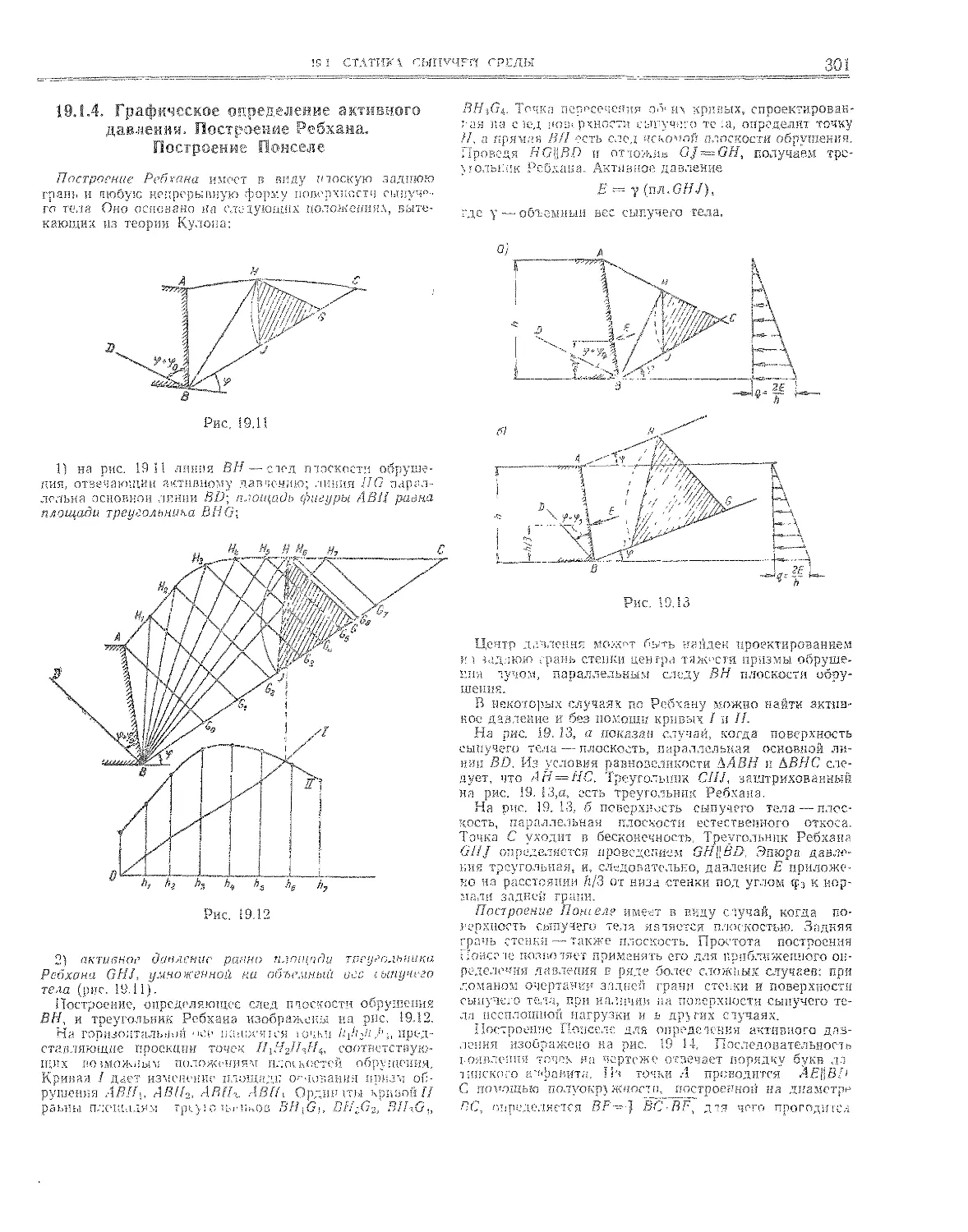
19,1.4.	Графическое определение активного давления.
Построение Ребхана, Построение Понселе . . . .	301
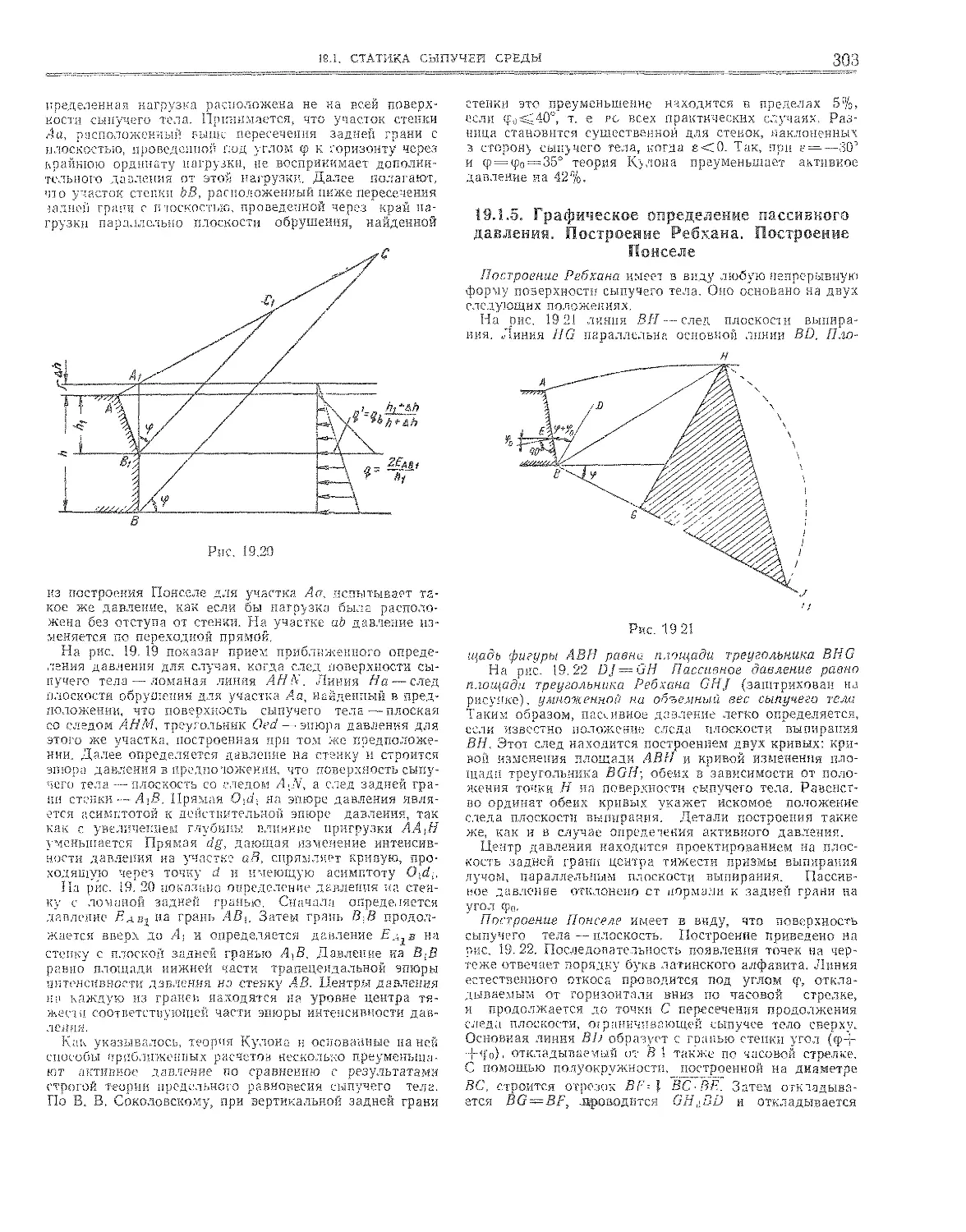
19.1.5.	Графическое определение пассивного давления.
Построение Ребхана. Построение Понселе ....	303
19,1,6.	Давление сыпучего тела в бункерах и силосах 304
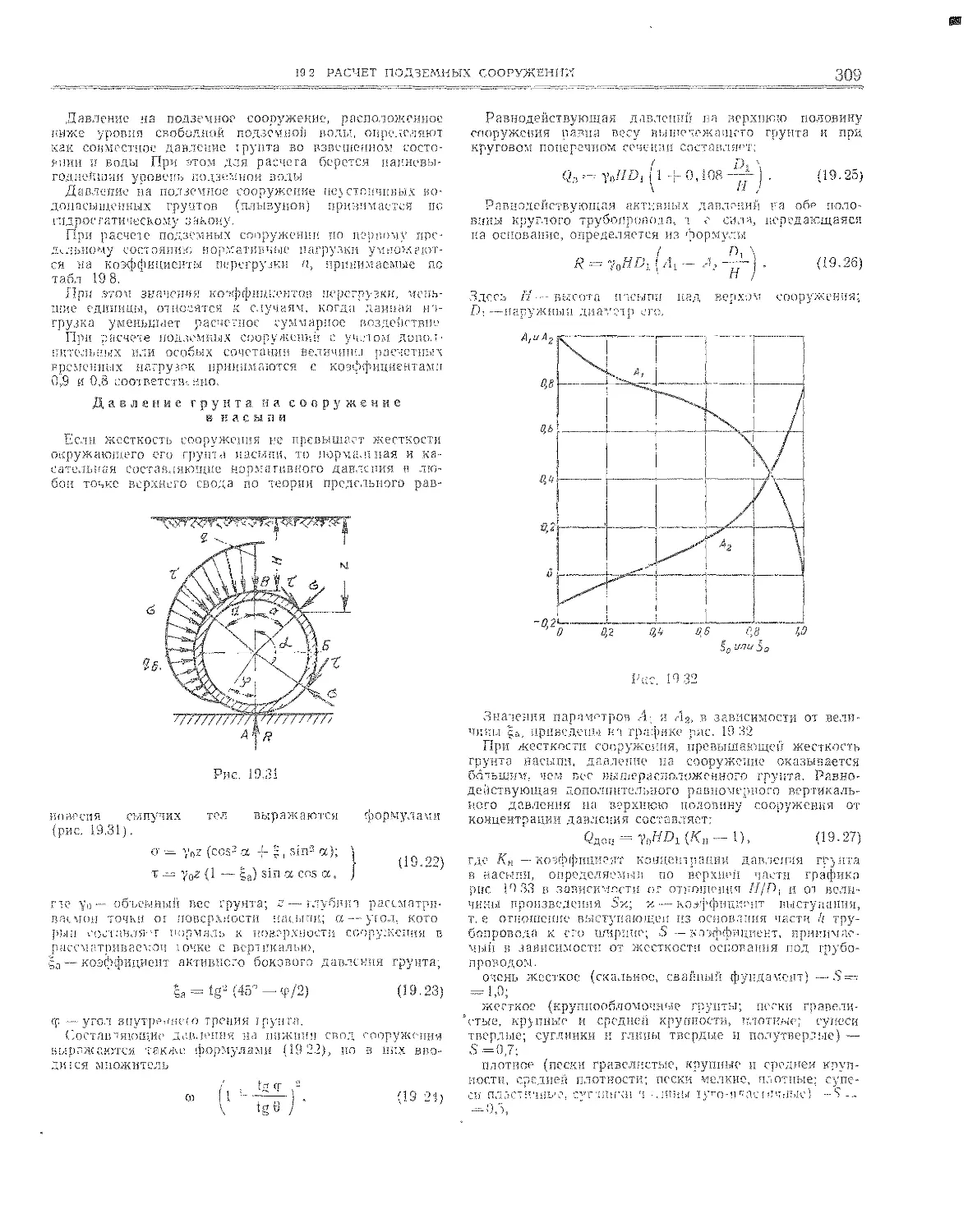
19.2.	Расчет подземных сооружений (Г» К- Клейн)	ш
19.2.1. Физико-механические свойства и характеристики
грунтов ...................	305
Виды и составные части грунтов (306). Напряжения
и осадки грунта (ЗОБ). Расчетные механические мо-
дели грунтов (307). Прочность грунтов (307).
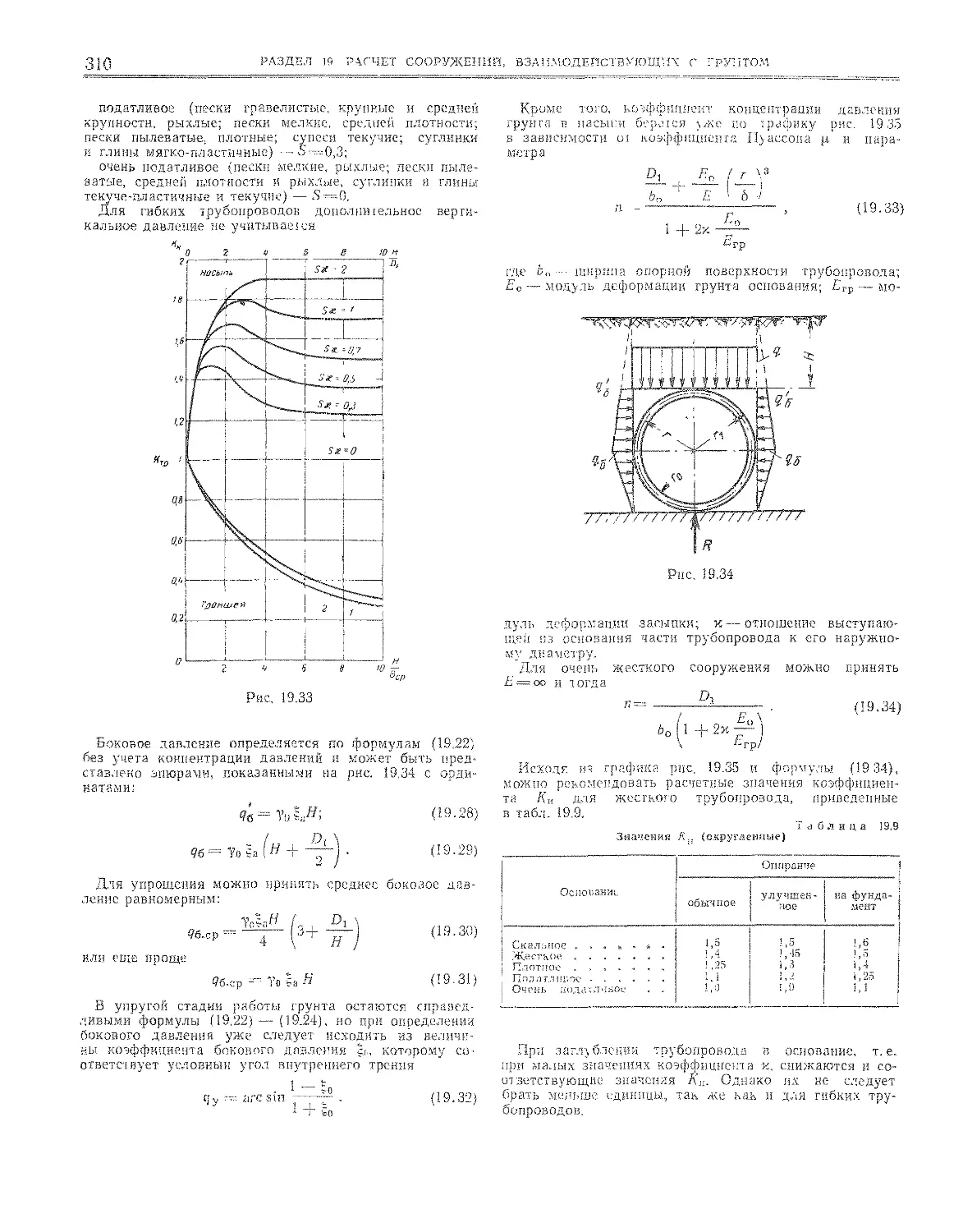
19.2 2. Давление грунтов на подземные сооружения « «	308
Напряженное состояние грунтов до и после прове-
дения выработки (308), Давление грунта на соору-
жение в насыпи (309), Давление грунта на сооруже-
ние в выемке (траншее) (311). Давление грунта на
крепь выработки и обделку туннеля (311). Давление
грунта в пространственной задаче (312). Давление
ни сооружение от наземных нагрузок (313).
19,2 3. Расчет жестких подземных сооружений кругового
поперечного сечения .............	314
Распределение опорных реакций (314), Внутренние
усилия в сооружении от различных нагрузок (315),
Приведение расчетных нагрузок к двум эквивалент-
ным сосредоточенным сидам (315). Деформация по-
перечного сечения сооружения (317).
19.2.4. Расчет подземных сооружений с учетом отпора
грунта . ,  .................................,	320
Общие соображения (320), Способ Метропроекта
(320). Способ О. Е. Бугаевой (322), Совместное дей-
ствие на подземное сооружение нагрузок и внутрен-
него давления при учете упругого отпора грунта
(322), Несущая способность сооружения по условию
прочности (323), Расчет сооружения на упругую
устойчивость и жесткость (324).
19.2.5. Расчет сооружений с учетом пластичности мате-
риалов .......................................  324
Выравнивание изгибающих моментов в стенках соо-
ружений (324). Пластическая стадия работы под-
земного сооружения при совместном действии внеш-
ней нагрузки и внутреннего давления (324). Пре-
дельное состояние сборной туннельной обделки
(325).
19 2.6. Расчет сооружений некругового поперечного
сечения...............	> .......... ,	326
Расчет туннельной обделки в виде пологого свода
(326). Расчет обделки подземного сооружения в ви-
де свода, опирающегося на массивные стенки (326).
19.3.	Балки и плиты на упругом полупространстве
(Д. П„ Синицын) . . . 4 . а . . , . .	327
19.3.	L Выбор расчетной схемы s	в 327
19.3.2.	Бесконечно жесткая балка	328
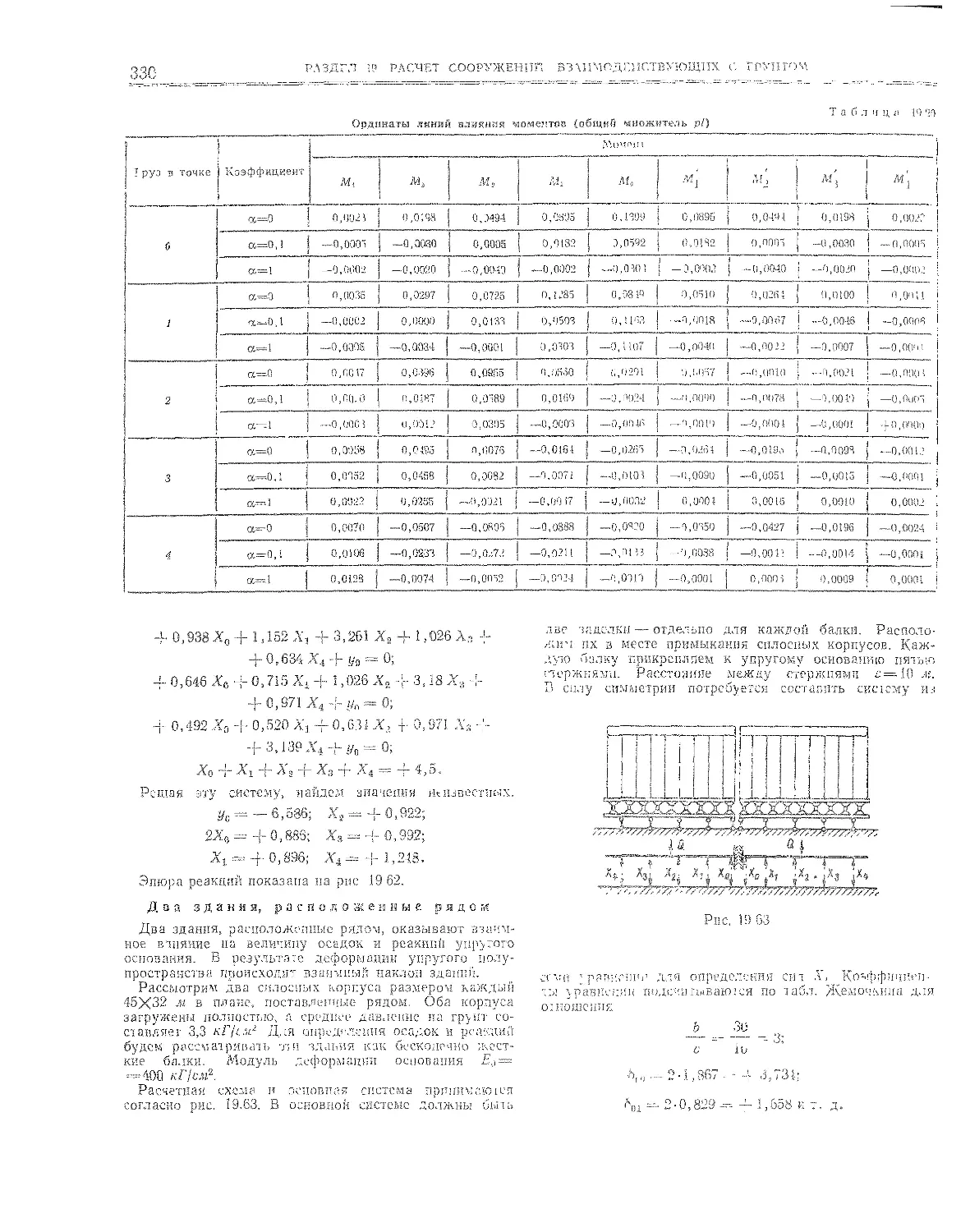
19.3.3.	Гибкая короткая балка ...........	329
Двухслойное основание (329), Два здания, располо-
женные рядом (339).
19.3,4.	Балка за пределом упругости	331
Определение наибольшей нагрузки в упругой стадии
Распределение реакций за пределом упругости (332).
Величина пределыюй нагрузки (333).
19,3.5.	Расчет плит за пределом упругости . . » . ,	333
Бесконечно-протяженная плита (333). Влияние мест-
ных и общих деформаций (334). Нагрузка на краю
плиты (335). Расчет слоистой плиты (335). Опти-
мальная толщина плиты (337).
Литература я я а « - » в с - - а * © © . ь о 338
ОГЛАВЛЕНИЕ
7
Cip.
РАЗДЕЛ 20
ДИНАМИКА СООРУЖЕНИИ
В. Г. Коренев, В. И, Сысоев
20.L Элементы теории колебаний	гзо
20J.1. Кинематика колебательного движения	....	33:'
20.1.2	Колебания системы с одной степенью свободы 2>0
Свободные колебания при О1С}тстпш1 сил сопротив-
ления (340). Свободные колебания при наличии сил
сопротивления (340). Вынужденные колебания при
отсутствии сил сопротивления. Резонанс (341). Вы-
нужденные колебания при наличии сил сопротивле-
ния, пропорциональных скорости колебаний (342).
Вынужденные колебания при затухании по теории
Е, С. Сорокина (342).
20.1.3	. Колебания системы с несколькими степенями
свободы......................................  34.3
Свободные колебания при отсутствии сил сопротив-
ления (343). Свободные колебания при наличии сил
сопротивления (344), Приближенные способы опре-
деления основной частоты свободных колебаний
(345). Вынужденные колебания при отсутствии сил
сопротивления (345).
20.1.4	. Колебания систем с непрерывно распределенной
массой......................................... 345
Продольные свободные колебания стержней (345).
Свободные колебания балок (346). Цзгибные коле-
бания пластинки постоянной толщины (347). Вынуж-
денные колебания балок (348)„
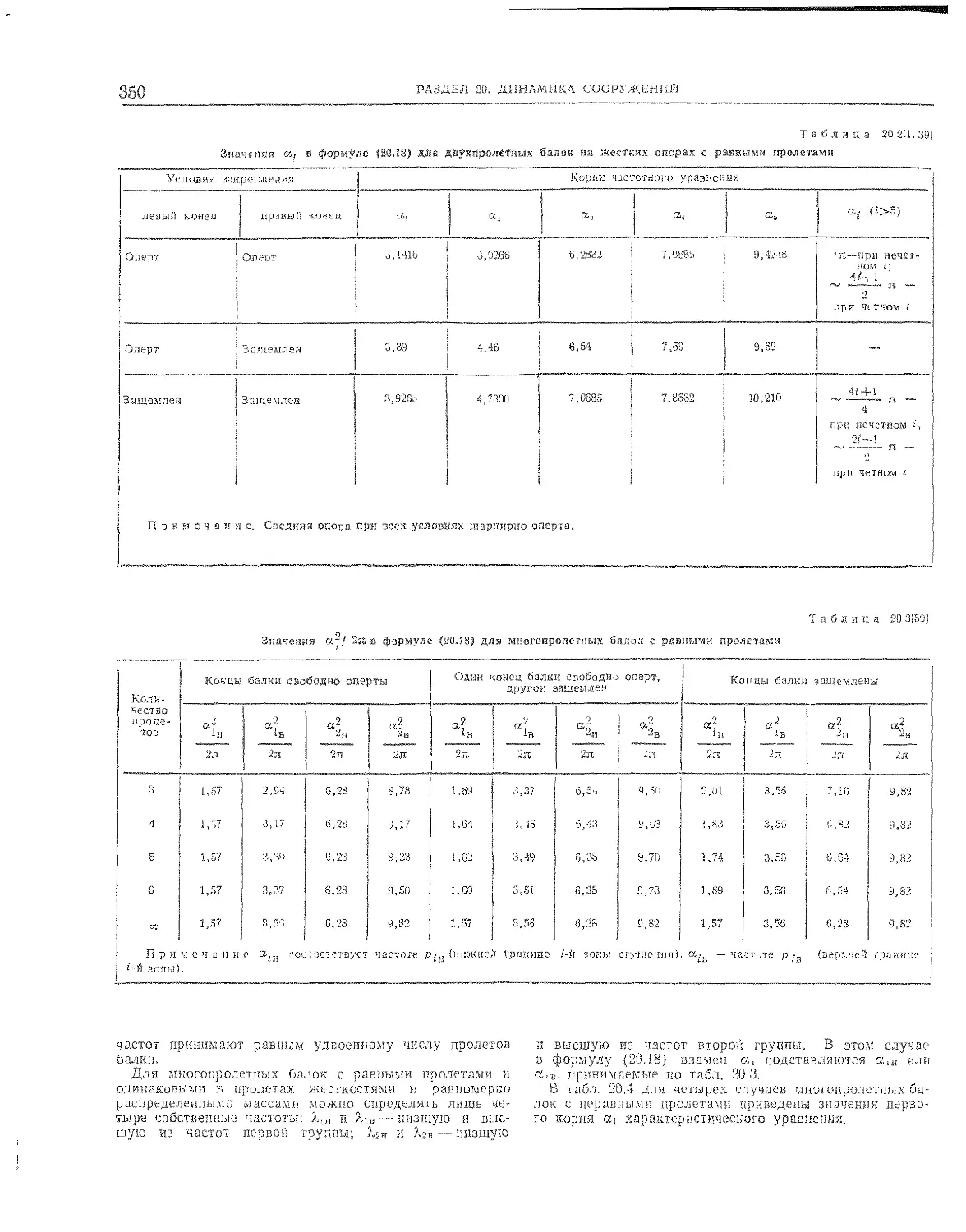
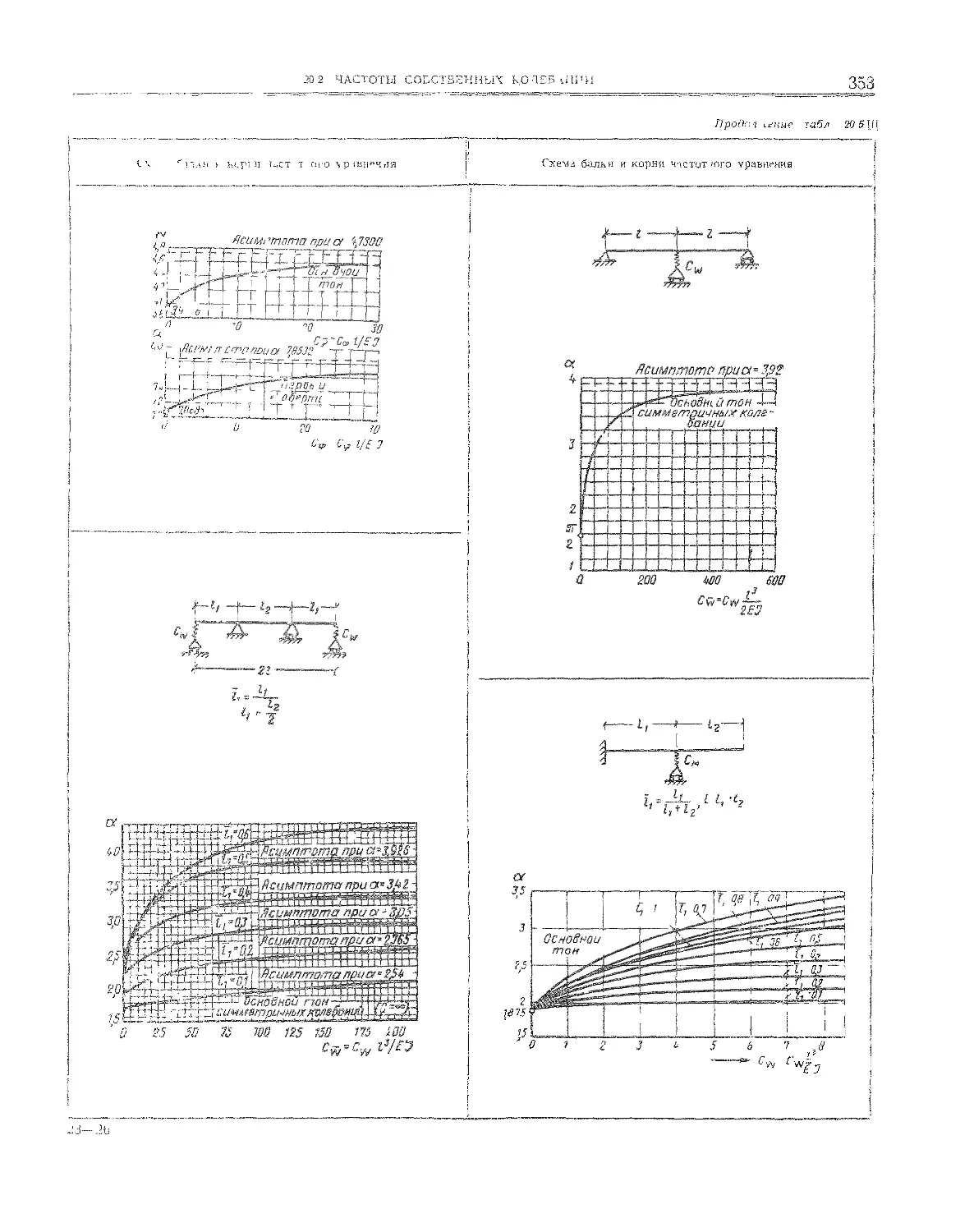
20.2,	Частоты собственных колебаний . . . , .	349
20.2.1,	Балки	на	жестких опорах	349
^0.2,2. Балки	на	упругих опорах	..........	351
20.2.3.	Балки с распределенными и сосредоточенными
массами............................................ 351
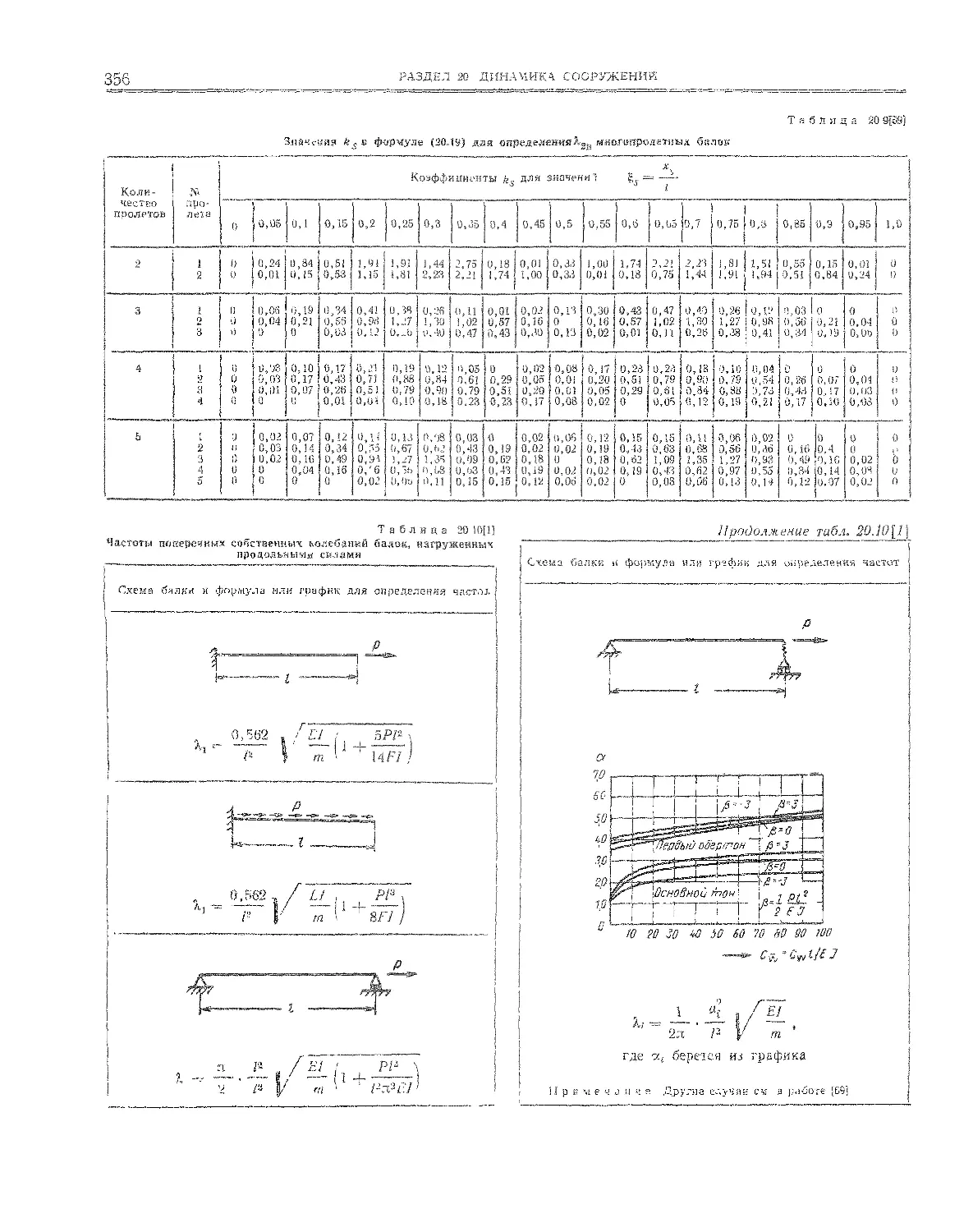
20.2.4.	Балки,	нагруженные продольными	силами	351
20.2.5.	Рамы	 .......................... 357
Рамы без сосредоточенных масс (357). Рамы с со-
средоточенными массами (358).
20.2.6.	Фермы	359
Метод Польгаузена (360). Метод наложения (360).
Метод эквивалентной балки (360).
20,2.7.	Арки, длинные своды, кольца.................  360
Круговые арки и своды постоянного сечения (360).
Параболические симметричные арки переменного
сечения (361). Круговые кольца (362).
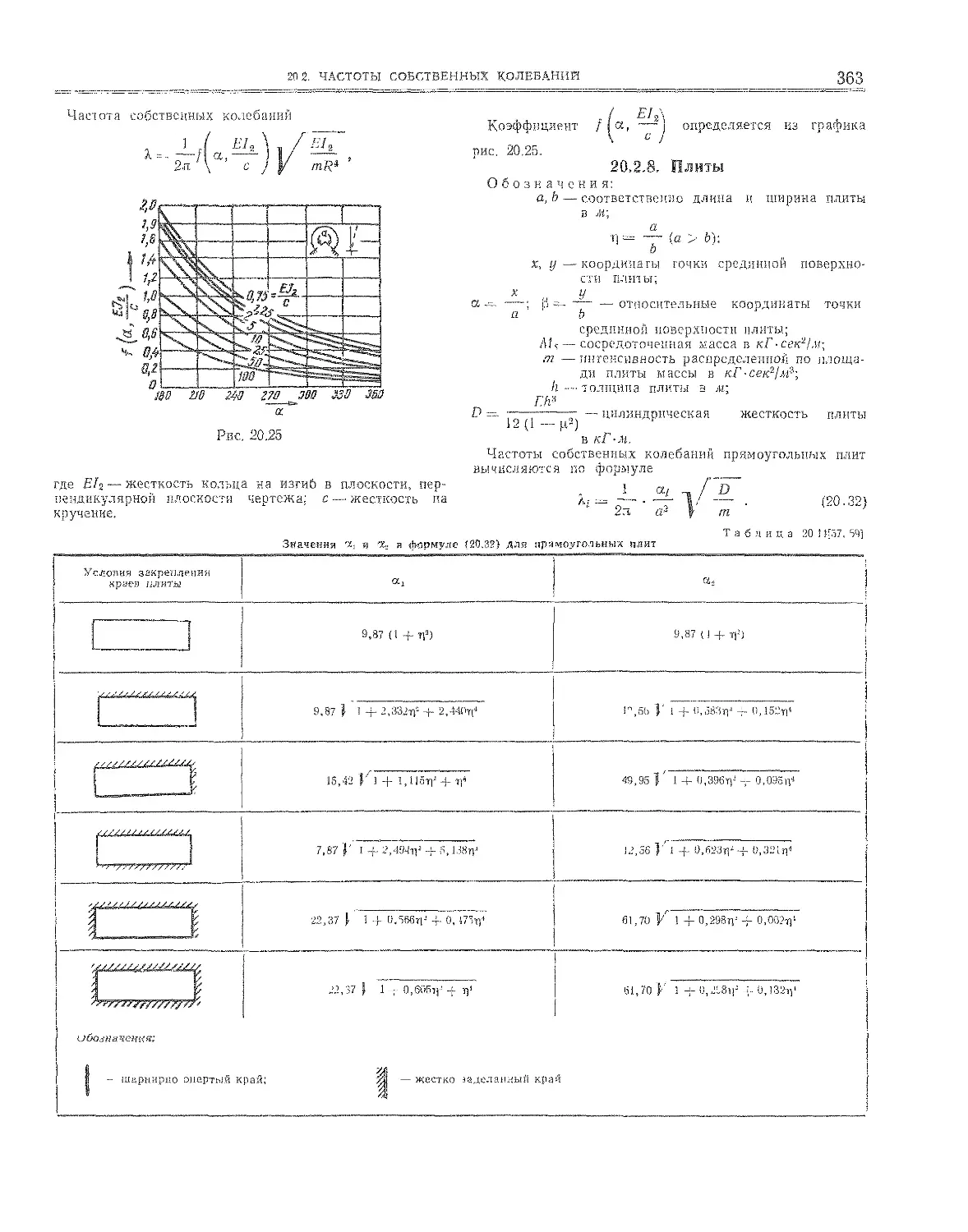
20.2,8.	Плиты	а ,	363
20.2.9.	Стержни переменного сечения.................  365
20.2.10,	Крутильные и продольные колебания стержня.
Колебания струны . . . ........................... 368
20,2.11.	Колебания жидкости в резервуарах .....	369
20.2.12,	Колебания трубопровода, по которому движет-
ся жидкость .....................................  370
20.3.	Динамические характеристики строительных
материалов и конструкций ........	370
20.3,1.	Динамическая жесткость ........	37G
20,3.2.	Внутреннее поглощение энергии колебаний (зату-
хание) в конструкциях и материалах сооружений 370
20,3.3.	Выносливость строительных материалов , . ,	871
20.4.	Динамические нагрузки от машин ....	371
20,4.1.	Машины с конструктивно неуравновешенными
движущимися частями ............	372
20.4.2.	Машины с номинально уравновешенными, а фак-
тически неуравновешенными движущимися частями	372
20.5,	О динамическом расчете перекрытий и карка-
сов зданий .............
зтз
20 5.1. Расчетные схемы .................	. а . ,	373
20.5.2.	Частоты и формы свободных колебаний . . .	374
20.5.3.	Результаты динамическою расчета и норматив-
ные требования ..................................  375
20,6. Виброизоляция и другие способы борьбы с
вибрациями...................................... 3'6
20.6.1. Виброизоляцпя..........................  376
20.6,2. Принципиальная схема работы i-шбронполирован-
ной установки^ Конструктивные схемы вябронзоля-
Стр.
п, ни и виброизоляторов. Содержание и задачи
расчета ....................................... 376
20.оЗ Расчет виброизоляции ......................  377
Активная вибрация при периодических нагрузках
20 6 4 Другие способы борьбы с вибрациями строитель-
ных конструкций ..............................  378
20.6.5. Мероприятия по уменьшению вынужденных коле-
баний, передаваемых машинами	379
20.6 6. Мероприятия по уменьшению колебаний при про-
хождении через резонанс ...........	380
Литература а * 9 . » . , „ , , а . , . . я .	380
РАЗДЕЛ 21
РАСЧЕТ КОНСТРУКЦИЙ (СТЕРЖНЕВЫХ,
ПЛАСТИНОК И ОБОЛОЧЕК)
ПО ПРЕДЕЛЬНОМУ РАВНОВЕСИЮ
И УЧЕТ ПОЛЗУЧЕСТИ
А. М. Проценко
21.1.	Основные положения по расчету конструкций
в состоянии пластичности ........	382
21,1,1. Поведение конструкций в пластической стадии	382
21.1 J. Основные положения теории предельного равно-
весия .	............................... . .	383
21.1.3. Основные ограничения теории . . а . а , 5 .	384
21.1.4. Типы нагрузок и классификация задач . а . а	384
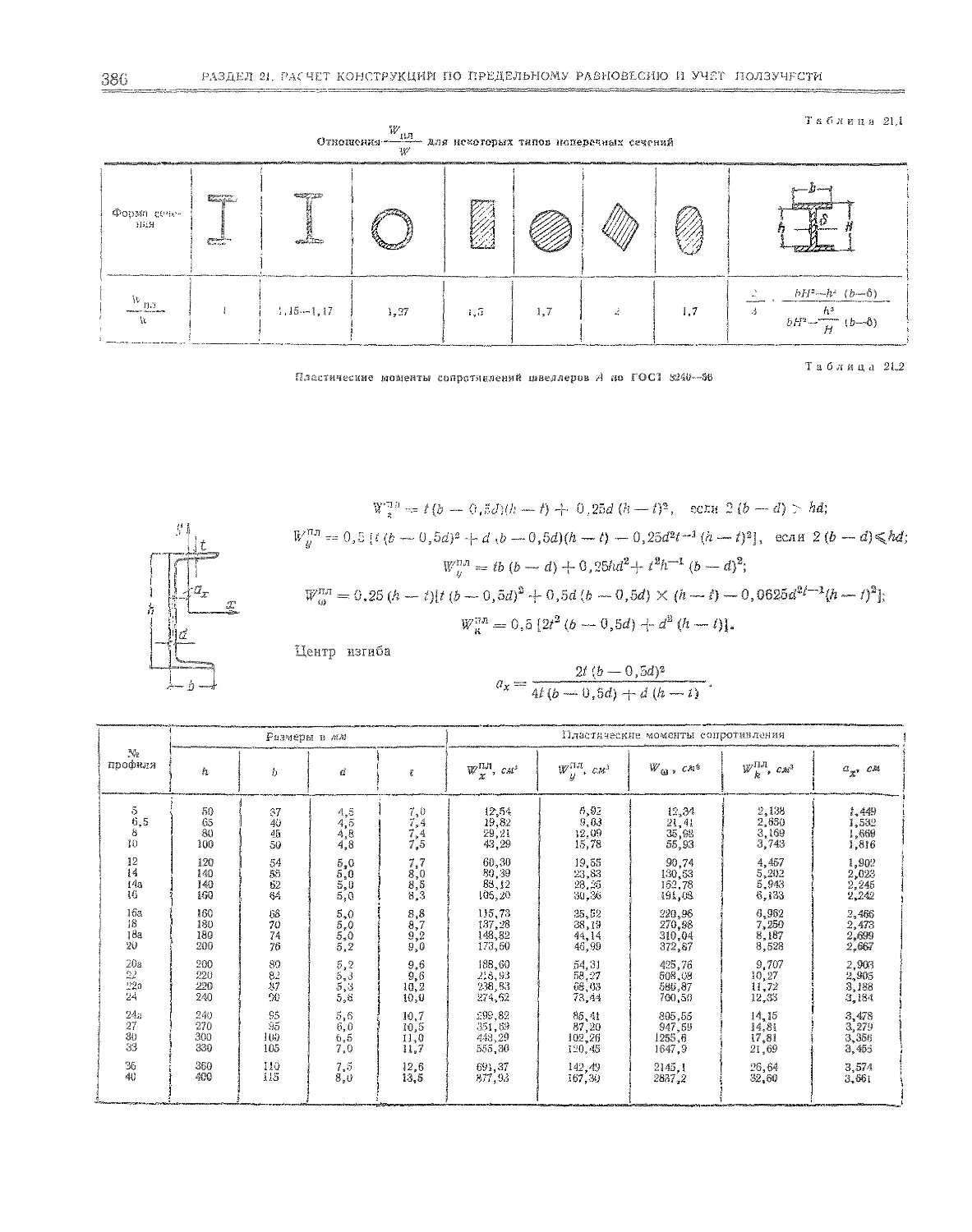
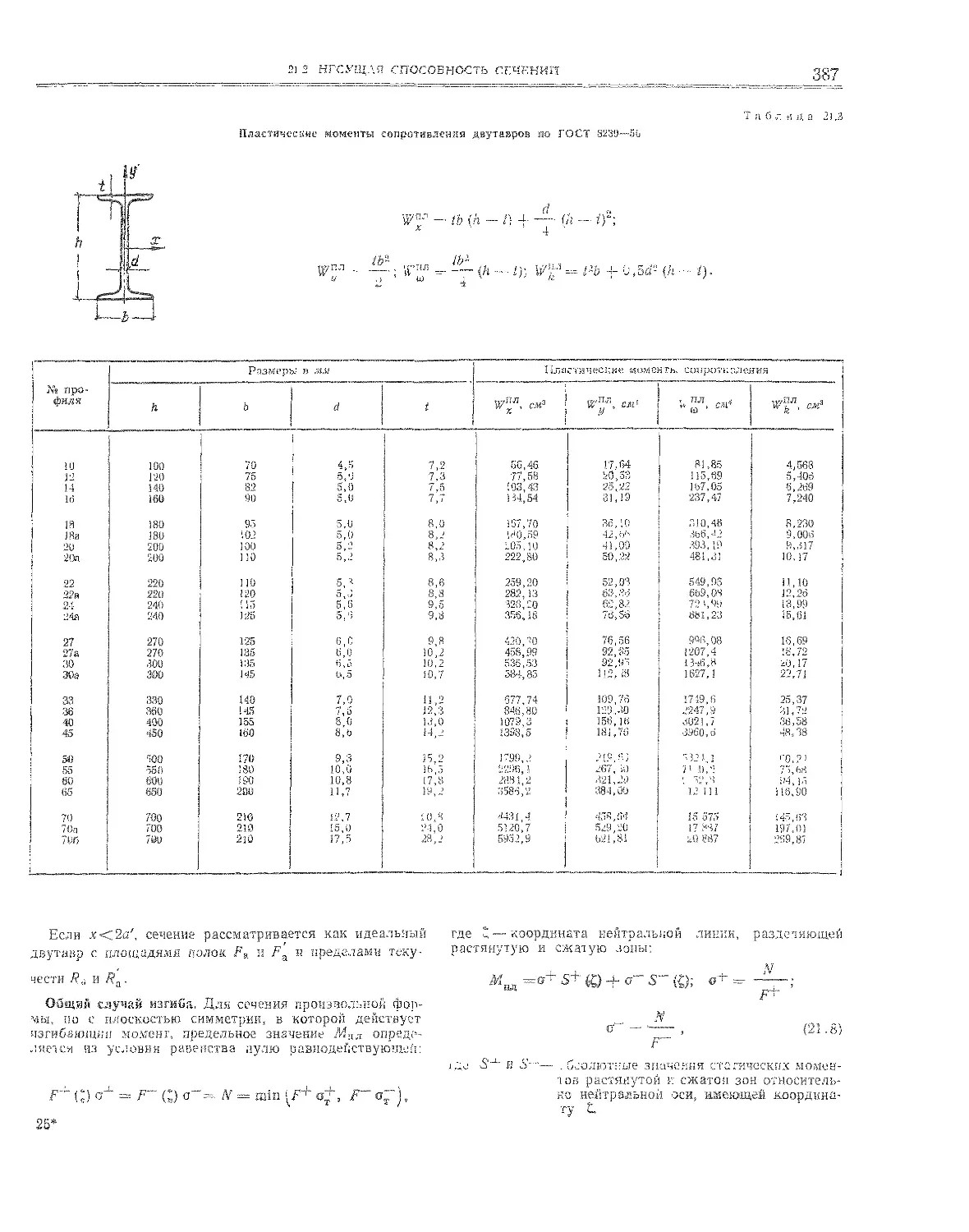
21.2,	Несущая способность сечений . . . « .	385
21	2.1. Чистый изгиб сечений в плоскости симметрии	.	385
21.2	2. Косой изгиб стержня ...........	388
2L2 3. Вис-центрепное растяжение (сжатие) в плоскости
симметрии ....... - ....... . , .	388
21.2	4. Учет поперечной силы при изгибе	389
21.2.	6. Предельные состояния сечения при кручении . .	389
21,2.	6. Условия пластичности для изгибаемых плит . .	396
21.2.	7. Несущая способность плиты пои совместном дей-
ствии изгиба is плоского напряженного состояния	391
21.2.	8. Ассоциированный закон пластического течения
для конструкций	.	391
21.3. Расчет плоских стержневых систем . . , ,	392
21.3.1.	Пластические шарниры в стержневых системах 3.92
21.3.2.	Расчет статически определимых стержневых
систем . .	392
21.3.3.	Расчет неразрезных балок ........., . .	393
21.3.4.	Расчет статически неопределимых рам . , я .	‘'95
21А Предельное равновесие пластинок , » , ,	398
21.4	.1. Общие положения расчета	398
21.4	.2. Кинематический способ определения несущей спо-
собности плит ..............................   Збо
21.4	3. Статический способ определения несущей способ-
ности плит ....................... ..........	399
21	4.4 Некоторые частные решения для пластинок, за-
груженных сосредоточенной силой, при шарнирном
опирании ..................	^80
21.4.	5. Пластики, загруженные равномерно распреде-
ленной нагрузкой ..................... ......	401
21.4	6 Предельное равновесие пластинок, защемленных
ал контуру .......................... .......	1W
21.4	7. Пластинка с отверстием при равномерно распре-
деленной нагрузке '............................404
21.5.	Предельное равновесие оболочек . . . ,	406
21.5.1.	Общие положения расчета оболочек . , . . ,	405
21.5.2.	Расчет осесимметричных оболочек ...... ФН
21.5.3.	Некоторые типы оболочек вращения .....	407
21.5.4.	Пологие оболочки с отверстием .......	Ю9
21.6.	Методы решения задач ползучести ....	409
21.6.1.	Уравнения состояния для задач ползучести - . .	4(Н
21,Ь 2. Методы решения задач линейной ползучести 411
21.6.3.	Методы решения задач нелинейной ус'пшошш-
чиейся ползучести ...........................  412
21.6	4. Расчет стержневых систем при нелинейной пол-
зучести	443
Литература , й « « э . e е о v s „ , . , , .	414
ПРЕДИСЛОВИЕ КО ВТОРОМУ ИЗДАНИЮ
При составлении второго издания Справочника мы
воспользовались советом mhoihx читателей—разделить
содержащийся в Справочнике обширный материал на
две книги, облегчив тем самым пользование им..
В первую книгу вошли разделы:
1.	Математика
2.	Теоретическая механика
3.	Напряжения, деформации, прочность материалов
4.	Материалы для строительных конструкций. Мето-
ды расчета
5.	Строительная механика упруюю стержня и стерж-
невых систем
6.	Матрицы, Численные методы строительной меха-
ники
7,	Таблицы геометрических характеристик сечений
стержней
8.	Таблицы и формулы для расчета балок, рам п
арок
9	Стержни, очерченные по дуге круга, и круговы»
кольца
1U Фермы
11.	Вантовые и пневматические конструкции
Во вторую книгу вошли разделы:
12.	Уравнения и формулы теории упругости, пластич-
ности и ползучести
13.	Упругие Тонкие пластины (плиты и балки-стен
ки)
14.	Оболочки
15.	Метод сегок в приложении к расчету пластин и
оболочек
16.	Моделирование
17.	Устойчивость стержневых систем
18.	Устойчивость пластинок и оболочек Расчет гиб-
ких пластинок
19.	Расчет сооружений, взаимодействующих с грун-
том
20	Динамика сооружений
21.	Расчет конструкций (стержневых, пластинок и
оболочек) по предельному равновесию и учет ползучести.
Первая книга, наряду со (строительными нормами и
правилами (СНиП), а также со специализированными
io нами «Справочника проектировщика.», должна удов-
летворять практическую потребность инженеров, зам
гы.х расчетом прежде всего стержневых конструкций
Вторая кита предназначена для инженеров, решающих
более сложные задачи, в частности, по расчету оболочек.
Разделы 6, 11, 15, 16—новые, написанные специаль-
но для второго издания. Разделы 17 и 21 коренным об-
разом переработаны по сравнению с соответствующими
разделами первого издания. Остальные разделы пере-
работаны частично и дополнены краткими сведениями
о расчетных методах, развитых в последнее десятилетие.
Раздел «Нормы ншрузок и 1абарлтов» исключен как
дублирующий официальные нормативные издания.
Раздел 12
УРАВНЕНИЯ И ФОРМУЛЫ ТЕОРИИ УПРУГОСТИ,
ПЛАСТИЧНОСТИ И ПОЛЗУЧЕСТИ
В разделе справочника «Напряжения, деформации и
Прочность материалов» даны определения тензора иа-
иряженпй и тензора деформаций (см. 3.1.5 и 3.2), а так-
же различные формы записи закона Гука для изотроп-
ных и анизотропных тел (см. 3.3,1 и 3.3.2). Здесь даются
основные уравнения и формулы теории упругости, плас-
тичности и ползучести.
Соотношения (12.3) носят название граничных усло-
вий Тензор напряжений в цилиндрической системе коор-
динат г, 0, z (рис. 12.4)
/О Ггй Щ\
I V °н Tfte •	<I2-4>
\EZ Де ° J
12,1. ОСНОВНЫЕ УРАВНЕНИЯ
ТЕОРИИ УПРУГОСТИ
Здесь:
12.1.1. Уравнений равновесия
Составляющие тензора напряжений
(рис. 12.1)
(12.1)
Or -- норматъное напряжение на площадках, перпендику-
лярных радиусу-вектору г; — нормальное напряжение
в меридиональных сечениях, проходящих через ось л
и раднус-ьсктор г\ т()2—касательное напряжение на
пющадке, перпендикуляппоп оси 2, напращтешюе по ка-
сательной к окружности r — cohst в сторону увеличения
угла 0; Trz — касательное напряжение на той же плен
являются в общем случае функциями координат..
Здесь: о», о»,	— нормальные напряжения па площад-
ках, перпендикулярных соответственно осям х, у и z.
В обозначениях касательных напряжении первый ин-
декс соответствует направлению напряжения, второй —
направлению оси, перпендикулярно которой расположена
р асом ат р и в ае м а я пл о; падка.
Для тела, находящегося в равновесии, чти функции
должны удовлетворять уравнениям равновесия:
+	Эт,..
дх ду ' дг
К,* , дОу г?т,
дх ду д.
5т,,	Д,„	до,
« + + г + /г=0.
ох	ду	дг
(12.2)
Здесь X, У, Z — составляющие вектора объемной силы,
т. е. внешней силы, отиесенпои к единице объема. Такой
объемной силой является, например, собственный вес
единицы объема твердого тела.
Внешние напряжения (рис. 12.2) рхх, Рнч, p2V , дейст-
вующие в какой-либо точке поверхности тела с внешней
нормалью
у границы
V, связаны с внутренними напряжениями
тела (Ji, Тц,. .... су (рис. 12.3) формулами:
р„,. = о /-г-д тДт п;
,1	' хи 1 хг
P„v — т I + r> т+ t п;
' их	их	 у уг
р„,, == т /-Г-т т т о п.
ozv	2Х	’ гу	! г
(12.3)
Здесь
I ~ cos (х, V); т = cos (у, v); п = cos (г, v).
10
РАЗДЕЛ .12. УРАВНЕНИЯ И ФОР.Ш'ЛЫ ТЕОРИИ УПРУГОСТИ. ПЛАСТИЧНОСТИ И ПОЛЗУЧЕСТИ
щадке, направленное здо1ь радиуса-вектора г, т;г— ка-
сагетпное напряжение па площадке, иерпенцжулярной
радиусу-вектору г п направленное по осп г; — каса-
тельное напряжение па тон же площадке, направленное
по касательном к окружности /' = const в сторону уве-
личения утла 0; луд —касательное напряжение в мери-
диональной се-кпип с внешней нормалью в сторону уве-
личения угла 0, направленное вдоль оси г; тщ, — каса-
тельное напряжение в том же сечении, по направленное
вдоль радиуса-вектора г.
Рис 12.1
Уравнения равновесия в ци.пшдричсекнх координата:::
Здесь /?, Q, Z—составляющие обьемной силы в направ-
лениях г, 0, z соответственно.
12.1.2, Уравнения совместности деформаций
Составляющие тензора деформаций в декартовых коор-
динатах (рис. 12 5)
Рис. 12.5
должны удовлетворять уравнениям совместности Сен-
Бриана.
	
. -	-L- 	1
	дх2
	д-е.г
	
дг2	dy2
	
дх2	1 дг2
д : f	ду,г
	
дг Ох	ду
+	ду а/
Ох \ ду	дг
д СЪ’ге ,	дУцг
ду 'с дг 1	Ох
	1	
дхду = diy‘J2  дудг д3угх		
дхдг о д'^ .		•	(12.7)
дг У	дхду дУуг \ _ „ д'^х дх ]	дудг оу /	дхдг		
12 1 ОСНОВНЫЕ УРАВНЕНИЯ ТЕОРИИ УПРУГОСТИ
11
В случае плоской деформации (ш = 0) система урав-
нений совместности деформации (12.7) заменяется одним
уравнением
д~е ( ( Э-f,,. _ д2ух[1
ду~ 1 дх°- дхду
(12.8)
Тензор деформаций	в цилиндрических координатах:
/ ег	1 _L \ 9	1 гО	9	5
J 9 1 Ог 8 ( \ Т Ъг	1 ₽0	VT0-’		(12.9) 1	j 'У Tzo	к- /
Если через 2 обозначить радиатьнос, через ц—тап-
геицпалы.ое и ырез и—аксиальное перемещения
(рис 12 6), то компоненты тензора деформаций в цилин-
дрических координатах могут быть вычислены по фор-
мулам-
оф	I	Эр	у	Эи
ег ~~~ ;	—	• то- +	; cz ==	:
dr	г	<10	г	дг
Составляющие вихря перемещения характеризуют
вращение бесконечно малого элемента в рассматривав-
ди UV
мой точке Так, ухи == — + ~ (рис. 12.7) характери-
зует сдвиг, т. е уменьшение прямою угла в рассматри-
ваемой точке между направлениями, первоначально па-
раллельными осям Ох и Оу-, разноыь этих углов
ди dv
<вг = —- — дает удвоенный угол поворота вокруг
оси Ог биссектрисы угла между этими двумя направле-
ниями.
Зависимости между составляющей тензора деформа-
ции и составляющими вихря вектора перемещения:
до>г дх	ду. г Эу	дУп, 1 Эг'’
дои.	Эщ-	
		_ о —Ч .	)
ду	f/Z/	/}г’ ’	(12.14)
Э<» г	де-	
			2—=-	
дг	ду	Эх ’ |
8ц	ц	1	Э2
7 гв ~ П~ ~г ' згГ ’
дг	г	г	о0
1 Эи Эр	Эд дш
г 0Q дг >,л дг Г дг
! (12.10)
1
Уравнение совместности деформаций в случае плоской
деформации (ы=0)
/ 1 Э- 1 Э 2 \
I    • ----- —	•	—J— ~~ I F г -4—
\ Г-’.	т дг'гМ
/ <У	1	д-	2 \	1	d2Trf)
\дг2	г2	ФР	С- /	г	дгод
12.1.3. Определение перемещений
по составляющим тензора деформаций
Coci авляющне гечзора деформаций связаны с состав-
ляющими вектора перемещения и, v и и дифференциаль-
ными зависимостями — уравнениями Коши (рис. 12,7):
t)u		!е	ди	1	
Е v ~	’ дх	- -	ду '	<дг		
ди	d?j	dw i	ди		
ухц = ~ -	с)х		' дг ’	I (	(12.12)
да ди
— с —
дх ' дг	।
1
Составляющие вектора nepi мощения и, v и w и со-
ставляющие вихря вектора перемещения кы, ми и нм
связаны cooiношениями
ди дг'
=- — — — ;
ду дг
ди дш
со и	— —-
дг дх
ди
ду
(12.13)
Пусть составляющие вектора перемещения и вихря
вектора перемещения то-пкп /11о(л-о, у», гп) тела (рис 12 8)
имеют значения: и(,, v0, <щ и св”, ш" соответственно
Составляющие вектора перемещения любой другой
точки Mi(xi, iji, Z]) могут быть вычислены но формулам
“1 =. и0 -ф- — <Ф’ (zj — г0] —
9 ’ ш2 ( У{ Ус] Т-
+ f {Ux dx и- Uijdy -ф- иг dz,
М.Ж
°i = и + кг ®" (xi - М -
I п ,	,	I
- V“x(2—K))+	!	(12.15)
-J- (КX dx 4~ Vу dy Щ рс,	|
м\м,	I
I л г 1 I
Ю1 = »о + V ®х I У[ “ Ус) - I
1 "I Ь I
- 7' ШЛ xi ~ -о) +
+ ( (Wxdxd-Wudy + W2dz).
aiLvi,	’
Здесь
Ci 'Д 1 V X Щ 1 i
2	\ оу
1	I дс,.	дуг,\
ф — (Z1 — z) 2 —- —
2	\ дг Ох !
12
I АЗДРП 12 УРАВНЕНИЯ И ФОРМУЛЫ ТЕОРИИ УПРУГОСТИ, ПЛАСТИЧНОСТИ И ПОЛЗУЧЕСТИ
Рис. 12.8
этого тела как функции координат. Таким путем может
быть, например, решена задача о смещении ючек верх-
ней поверхности полупространства и другие аналогичные
задачи
12.1.4. Физические уравнения теории
упругости и термоупругости
Физические уравнения теории упругости, связывающие
компоненты тензора напряжений с компонентами тензора
деформаций, для избранного тела в пространственном
случае (для нормальной температуры) имеют вид, пред-
ставленный в 3.31 и 3.32
В случае наличия неравномерного поля высоких тем-
ператур эти связи между напряжениями и деформациями
принимают вид
7 = К — В (У) (ои + 7)1 т- « (Т) (Т - Т„);
пли при "аписи напряжения через деформации
ох = 2G (7) [7 7  ——— „ __
L 1 - 2ц (7) р
1 + Р (7)
1 — 2ц (7)
а (Г) (Г - Т„)
G (7) ’
— G ( Г) уЛ7у
Формулы (12.15) носят название формул Чсзаро
В этих формулах выражения для Vx, Vv, Vz и 1, й"„,
№г получаются из приведенных выражений для UXy
Uz круговой перестановкой букв х, у, г. Криволинейные
интегралы в формулах (12.15Й могут быть вычислены
по любому пути между точками Мо и Лф.
Обычно в теории'упру: ости интересуются только отно-
сительными смещениями точек тела относительно друг
друга, а не движением тела как целого, поэтому для
точки Лф Uo = T'o = ®o = 0 и 0'1= wj= fflz=0. Формулы
Чезаро дают возможность найти перемещения точек те-
ла, если известны составляющие тензора деформации для
В случае анизотропного тела физические уравнения
теории упругости имеют вид, приведенный в 3.3 2. В .плос-
ком случае для ортотропного тела в технических обозна-
чениях физические уравнения имеют вид, приведенный
в 3 3 1.
При наличии неравномерного поля высоких температур
для анизотропного тела физические уравнения обобща-
ются, в них так же, как для изотропного тела, добав-
ляются температурные слагаемые. Причем поскольку ко-
эффициенты линейного расширения для анизотропного
тела будут, как и другие физико-механические характе-
12 1. ОСНОВНЫЕ УРАВНЕНИЯ ТЕОРИИ УПРУГОСТИ
13
ристики, зависеть от направления, необходимо ввести
в'рассмотрение тензор коэффициентов линейного расши-
рения «иДЛ-
= -(1 + Ji)
'dZ	дХ \
Д + _
дх	дг /
12.1.5. Уравнения теории упругости
в напряжениях
где о — ах 4- п„ + оу,
3= г)з уз
! =-------I---------!	------ .
Зх= Зг/= дг"
В теории упругости в основном приходится иметь дето
с двумя типами задач. В задачах первого типа на по-
верхности исследуемого тела задаются внешние силы
Требуется начти напряжения и смещения любой точки
тела под действием стих сил. Иногда в задачах этого
типа помимо поверхностных сил задается еще объемная
сила (например, собственный вес тела) В задачах дан-
ного типа для 15 неизвестных функций, а именно
шести составляющих тензора напряжений ах, ov, а2,
Х%Х, Xyz> Хх Уу
шести составляющих тензора деформаций 8-х, е„, ег,
1	1	_ J_
2 Vzx’ g ^уг’’ о "'’ХФ
Таким образом, получается система из девяти уравне-
ний (12.2) и (12.16) для шести неизвестных функций
<Д.т, оу, аг, т1г, Та:,/, т. е. сверхопределенная система.
Доказательство того что эта система не противоречива
и допускает единственное решение при заданных на по-
верхности тела усилиях, см., например [11],
12,1.6. Уравнения теории упругости
и термоупругости в перемещениях
(уравнения Ляме)
трех составляющих вег.тора смещений «, ш. с, имеется
15 уравнений- три уравнения равновесия (12 2); шесть
уравнений, связывающих составляющие тензора дефор-
маций с составляющими вектора перемещении (12 12);
шесть уравнений закона Гука (см. 3.3.6).
Эти уравнения должны быть решены таким образом,
чтобы на поверхности тела удовлетворялись граничные
условия (12.3). Для решения задач теории упругости
в напряжениях нужно использовать уравнения равно-
весия (12 2) и уравнения совместности деформаций
(12.7), выраженные через напряжения с помощью урав-
нений закона Гука (см. 12 1 4) Эти уравнения совмест-
ности деформаций, выраженные через напряжения, носят
название уравнений Бельтрами — Митчелла:
о=о	дХ
_2(1 щ г!)
дх-	дх
/ ^Х	ду	dZ\
- ± .
' ох	ду	дг /
д"п
(1 + М) Д ~7Т -= ~ 2 (! х Н) -------------
Зу-	ду
__ -1 + !‘У / дХ д. dY -
1 — ]л \ дх ду ' дг Г
(1 + Ц)	=
дг-
ц (1 + jt) (ЗХ
д7.
— 2 (1 ф- у.) ----
(
В задачах второго типа, решаемых в теории упруго-
сти, на поверхности тела задаются смещения Требуется
найти напряжения и смещения в любой точке тела.
В задачах этого типа за основные неизвестные прини-
мают три (.оставляющие вектора смещения и, о и w.
Чтобы получить три уравнения для нахождения и, v
и ю, удобно в уравнения закона Гука (см. 12,1.4) под-
ставить формулы, связывающие составляющие тензора
деформаций с составляющими вектора смещения (12.12),
и затем полученные выражения для напряжений подста-
вить в уравнения равновесия (12.2). В результате поу-
чаются три уравнения для трех состав
смещения — уравнения Ляме [16]:
36
(I + G) + 6Д« 3- X =
ох
2G (1 + у) 3
= —1—. (аТу
1 — 2р Зх
3ft
(X + G) Д GV=o + У =
ду
2(1 (1 + р) 3
= _ (аГ).
1 - 2р ду
бб
(Я, 4. С) — + Gy% + Z =
02
2G(I ^-Ц)	3 , __
= _____---- , .— (ъГ)-
1 — 2р. дг 7
вектора
!
!	(12.17)
д"-а
(1 + Р)	" =
дхду
= -(1 Т
дуд-
дгдх
1
(12.16)
!
— : второй
2р) р
Здесь 6= 4	4- е2; 7 =
коэффициент Ляме G——~~~—-—const совпадает с
2(1 4-Р) .
модулем сдвига (pt = constкоэффициент Пуассона).
Должно быть найдено такое решение этих уравнений,
которое удовлетворяет граничным условиям, т. е. необ-
ходимо найти три такие функции координат
и ~ и (х, у, г), v — v(x,y,z), w = w {x,y,z),
которые, удовлетворяя уравнениям Ляме (12.17), в то
же время на поверхности тела принимали бы заданные
значения составляющих вектора смещения.
14
РАЗДЕЛ 12 УРАВНЕНИЯ II ФОРМУЛЫ ТЕОРИИ УПРУГОСТИ, ПЛАСТИЧНОСТИ И ПОЛЗУЧЕСТИ
Точное решение уравнений теории упругости для боль-
шинства задач, выдвигаемых практикой, неизвестно, по-
этому большое значение приобретают приближенные ме-
тоды решения этих задач.
12.1.7. Потенциальная энергия деформации
Потенциальная энергия деформации может быть вы-
числена либо через компоненты тензора напряжений, ли-
бо через компоненты тензора деформаций:
= f J.( И +	+о1-2н (ох <3,^ а2 + «2 о J +
V °
4- 2 (1 + у.) ( iX!l -ф- т“г -J- т(}2)] dxdydz; (12.18)
”^Ш01!-;+2+'1+г4фг«=+
V
+ v (€ы/ + т“г+тУ]л^г- <12-19)
Интегралы (12.18), (12.19) распространяются на весь
объем гола В случае плоского напряженного состояния
при ог = т!1 = тг#=0 выражение (12.18) принимает вид
у = j j +
+ 2(1 + и)тЦ dxdy,	(12 20)
в случае плоской деформации выражение (12 19) прини-
мает вил
МР Н+';++
+	dXdy'	С12.21)
12.1.8, Общие принципы теории упругости
Принцип возможных перемещений Лагранжа форму-
лируется в таком виде: работа всех внешних и внутрен-
них сил на любом возможном (т. е. совместном с геомет-
рическими связями) перемещении для любой снег* мы,
находящейся в равновесии, должна быть равна пулю
|( 1А + + Убо + Zbw) dxdydz +
+ f [ (+,. 8и + Yv So + Zx fe) dS — 5F = 0.
Вариационное уравнение Лагранжа представляет собой
равенство нулю первой вариации полной потенциальной
энергии системы. Составляя вторую вариацию полной
потенциальной энергии всей системы, можно показать
[10], что эта энергия принимает минимальное значение.
Это составляет содержание принципа минимума полной
потенциальной энергии деформации' в состоянии устой-
чивого равновесия полная энергия деформации должна
принимать минимальное значение.
Из этого вариационного уравнения могут быть получе-
ны дифференциальные уравнения равновесия в напряже-
ниях и статические граничные условия £10]. Это урав-
нение лежит в основе ряда широко используемых вариа-
ционных методов приближенного решения задач теории
упругости, в частности в основе методов Ритца и Буб-
нова— Галеркина (см. 12 3).
Принцип Кастплиано предполагает такое изменение
напряженного состояния тела, прп котором удовлетво-
ряются дифференциальные уравнения равновесия и ста-
тические граничные условия, т. е, исходное напряженное
состояние тела и вариации этого состояния явтяются
статически возможными. При этом вариационное урав-
нение Кастплиано имеет вид [10]:
6Э1 = 0,
где
— (р—	+ vYу + ixjZv ) 4S,
т. е, среди всех статически возможных напряженных
состояний в действительности имеет место то, для кото-
рого величина имеет стационарное значение.
Составляя вторую вариацию 6ПЁ, увидим, что полная
энергия деформации в этом случае принимает минималь-
ное значение.
Из вариационного уравнения Кастплиано можно по-
лучить уравнения неразрывности деформаций. Оно ис-
пользуется при приближенном решении в напряжениях
ряда конкретных задач теории упругости.
12.2.	ПЛОСКАЯ ЗАДАЧА ТЕОРИИ УПРУГОСТИ
12,2.1.	Плоское напряженное состояние
Рассмотрим случай, когда топкая плоская пластинка
находится под действием сит, приложенных по контуру
параллельно ее плоскости и равномерно распределенных
по толщине (рис. 12,9). Допустим также, что объемная
сила Z равна нулю, а силы X и Y являются функциями
h
только х и у. Поверхности пластинки г=±+р свободны
от внешних сил, и компоненты напряжений oz, tz;Zjtzs
здесь равны нулю Если пластина тонкая, то без сущест-
венной ошибки можно принять, что эти компоненты рав-
ны нулю по всей толщине пластинки и что три другие
компоненты — ах, о„, т1у — практически остаются посто-
янными по толщине пластинки. В таком случае имеет
место плоское напряженное состояние, для которого
qz = tzi = tZ!, —0, а ох, <+ и xxv являются функциями
только х и у.
Средние по толщине пластины напряжения оу, оч
и х-су связаны с действительными напряжениями сщ, ау
и соотношениями
12,2, ПЛОСКАЯ ЗАДАЧА ТЕОРИИ УПРУГОСТИ
15
Jz.	А
2	2
°* -= Y f A •*; О.у = у [ A dz-,
т	А
л
1 I* -
ТЩ/ =-=	' J хху dz,
' h
12.2.2.	Плоская деформация
Пусть длинный цилиндр находится под действием по-
перечной нагрузки, равномерно распределенной вдоль
осп (рис. 12.10). Пусть составляющая объемной силы Z
равна нулю, а X н У являются функциями только х и у.
Рис. 12.10
Pxv~ °х cos A. А 4~ хл1/ cos (v, у);
PyV = Cos О А ± cos (v, у).
Положив
д'~ц>	д2ф	д~Ф
1Д ? Gy ~	~ у—	4х >
ду^ дх-1 и дх ду
(12.23)
(12.24)
легко убедиться, что первые два уравнения системы
(12.22) удовлетворяются тождественно, я третье приво-
дится к бигармоническому уравнению
<Лф	Дф <Ар
—L _< 2------! । —L = 0	(12.25)
дх* дх* ду* ду*	v ’
функция у (х, у) носит название функции напряжений,
или функции Эрп. Контурные условия (12.23), выражен-
ные через функцию Эри:
ЗИр	/ д'-ф	\	)
Дт = “ДГ CQS А - А — —— — qx cos (у, т);
dy-	их ду /
/ Лр \
1 (12.26)
<Пф
+—COs(y,v).
Итак, при заданных на контуре напряжениях плоская
задача теории упругости приводится к интегрированию
уравнения (12.25) при условиях (12.26),
В этом случае деформация значительной части тела, на-
ходящейся на некотором удалении от торцов, не зависит
от координаты д, а перемещения и и v являются функ-
циями только х и у. Если торцы цилиндра не могут
смешаться в направлении оси г, то перемещение а?=0.
Из симметрии следует, что в средне?.! сечении также
а?=0. ?Ложно приближенно допустить, что и в любом
поперечном сечении тела ш = 0. Тогда компоненты тен-
зора деформаций йх, ev и \’*v будут функциями х и у,
а компоненты е£, уед, yzll — равны нулю; компоненты
тензора напряжений ах, oxh <т2. хху будут функциями
только х и у, а компоненты x,jz и т-х — во всех, точках —
равны нулю. Такое напряженное состояние носит назва-
ние плоской деформации.
Допустим, что торны цилиндра могут свободно сме-
щаться. Тогда можно предположить, что продольная де-
формация е2 представляет собой постоянную величину.
Такое напряженное состояние называют обобщенной
плоской деформацией.
12.2.3.	Функция напряжений Эри
Если объемные силы постоянны (к постоянным объем-
ным силам относится, например, собственный вес), то
как для плоского напряженного состояния, так и для
плоской деформации основные уравнения теории упру-
гости (12.2) и (12.16) приводятся к виду
АДд ед	Эт-та	0.	dzVx	дау	_ == 0.	1
дх	ду	’ дх	ду	’	1
У2(Рх4-о'д) = 0,	J
(12.22)
где q — объемный вес.
На контуре тела, согласно (12.3):
12.2.4.	Функция Эри для плоской задачи
анизотропного (ортотропного) тела
Для данного случая введем функцию напряжений ф
следующим соотношение!!:
ГЛ-Г21. С-’Щ
Здесь — компоненты обратно симметричного тензора
второй валентности
( 0 1\
\—1 01 ,
т, е.
Ф; = 0;	~ 1; и„ 5 =— 1; Хоо = 0.	(12.28)
Легко установить, что при подстановке выражений
(12.27) в (12.2) при отсутствии массовых-сил уравнения
равновесия удовлетворяются тождественно.
Из закона Гука (см. 3.3.4) следует
«ед	дух 1	Д’ф	р,-и	6-ф
Ех	Еу	У Ех	ду*	Еи	дх*
8у ——	— О’г -4-     —~— •	—А
У Ех Еу Ех ду*
± ДА	°2’295
+ Еу ’ дх* '
I . __	1	гАр
Gxy'lx,J^~ GXII' дхду '
Если подставить формулы (12.29) в бигармоинчеекое
уравнение (12.25), то получим
16
РАЗДЕЛ 12. УРАВНЕНИЯ И ФОРМУЛЫ ТЕОРИИ УПРУГОСТИ. ПЛАСТИЧНОСТИ И ПОЛЗУЧЕСТИ
Ех ду* \ GxtJ Еу ) дх2 ду2
Таким образом, функция напряжений в плоской задаче
теории упругости анизотропного тела должна удовлетво-
рять уравнению (12.30).
Из сопоставления уравнений (12 25) и (12,30) можно
записать условия эквивалентности напряженных состоя-
ний изотропной и анизотропной пластан:
— = 1;	(12.3!)
2'— — ^) = 1.	(12.32)
Exi, Е,, ,
Упругие характеристики многих анизотропных мате-
риалов не подчиняются условиям (12.31) и (1232), и ре-
шение плоской задачи для таких материалов более слож-
но. В частном случае изотропного тела условие) 12.31)
выполняется автоматически, а условие (12.32) приводит-
ся к известному соотношению между упругими констан-
тами:
2(1 + ц)
Исключением является ряд простейших напряженных
состояний, характеризуемых функцией Эри, например
вида
Ф = Сх3 + Dus + Ex" у 4- Fxy2 + Gx2 + Ну" + Кху.
Этц напряженные состояния будут одинаковы как в изо-
тропных, так и в анизотропных пластинках, так как все
производные четвертого порядка от <р равны нулю
и уравнения (12.25) и (12.30) обращаются в тождества.
12.2.5.	Плоская задача в полярных
координатах
Уравнения равновесия (рис. 12.П):
ст,	1 ^Tzf) ° г ~		
	+ 	 ,	. 	 + R = Г);	
дг	Г	дв	г	(12.33)
1	'"Ч	2т. й	
		— + -— +Q-0.	
г	дв	дг	г	
Если ввести Функцию напряжений ф(г, б) и положить
(при отсутствии объемной силы) /? — Q — Q
1	Лр	I		r?3q:
°7 ~ г	дг	г2		““ дг2
	д /	1	Эср \	
дг \ г дв2 I ’
(12.34)
то уравнения равновесия (12.33) удовлетворяются тож-
дест нешто.
Функция напряжений <р должна удовлетворять диффе-
ренциальному уравнению
5=	1	д	1	д2 '	1/ 53Ф ,
	U »--» 							-  
. дг2 г	дг	и	<№ ,	В дН
1	дсу	1	д2ср \	
4“	—	+ ~Г 		= 0.	(12.35)
В частном случае, если напряженное состояние сим-
метрично относительно оси, проходящеп через начало
координат перпендикулярно плоскости чертежа (плоско-
сти деформации),
\в = 0;
4
о> == — ф- В (1 +2 In г) + 2С;
А
Of) = ~ ~Т + в (3 + 2 In г) + 2С.
г-
Постоянные А, В, С определяются из условий на кон-
туре.
12.2.6.	Сведение плоской задачи к задаче
об изгибе пластинки
Для решения плоской задачи можно прибегнуть к сле-
дующему приему [5]. Разыскивается функция ф(х, у}
таким образом, чтобы на контуре выполнялись условия
Ф-тЬ	(Дф
р = cos (Х; v) _ cos {у, v).
ду“	дх ду
<)ДЬ
(12.36)
Функция ф(х, у) при этом вовсе не должна удовле-
творять уравнению (12.25) и может быть задана без
затруднений, например, в виде полинома с достаточным
числом неопределенных коэффициентов. Эти коэффи-
циенты следует подобрата таким образом, чтобы хотя
бы приближенно удовлетворять условиям (12.36), Воз-
можны и другие формы задания функции ф(х, у).
Функцию Эри ищут в виде
<р = ср(х, у) =ф(х, у) ф-ш(х, у}.	(12.37)
Поскольку на контуре, согласно (12.26):
52<р
р _ ——- cos та та — —-------- cos (у та;
ду2	дхду	’
г)2®	сРф
р _—---------cos та та д_-----cos та та
 vv дхду	’ дх3
3. ВАРИАЦИОННЫЕ МЕТОДЫ РЕШЕНИЯ ЗАДАЧ ТЕОРИИ УПРУГОСТИ
17
то функция w должна удовлетворять условиям
d~w	г)2ш
— cos (х, v) —------------cos (у, у) = 0;
ду2	дх ду
d~tt>	d"w
— cos (х, у) + cos (у, у) = 0.
дх ду	дх-
(12.38)
Подставив (12.37) в (12.25), получим
I	д* д4 \
\дх* 5х2 ду"- ду* Г ’
Следовательно:
гМш д*еа
-— + 2--------
дх* дх- ду"
д*ю
ду*
(12 39)
Задача сведена к задаче об изгибе полностью защем-
ленной пластинки (см. раздел 13). В самом деле, если
на контуре пластинки удовлетворяются условия
w = 0 при х = 0; х = [• у == 0 и у = /г;
дю	дю
 = 0 при л- = 0, * = I и-----= 0 при у — 0, у = /г,
дх	ди
то должны удовлетворяться также вытекающие из
(12.25) условия. В результате приходим к формулам
д2ю / \2х2	Г2х	\	/дю
Q . .. । 0- . ।	.	—.. j р _i	.
ду2	v \ h2 h	J	дх2
d"zo
^^ITdy >
где
Р{х, у)
Ж1	Д'Щ
дх* ду2	ду* ) ’
(12. 10)
Р
Рис. 12 12
т. е, известная нам функция.
Итак, плоская задача сводится
к задаче об изгибе пластинки
при контурных условиях (12.38)
(см. раздел 13).
Так как решение последней
задачи во многих случаях из-
вестно, указанный прием может
оказаться весьма полезным для
решения ряда задач.
Отметим, что для полной
аналогии с задачей об изгибе
пластинки необходимо поло-
жить
Ь------1
lllrilllHIIKIIIIIIIIlllllllll
Рис 12.13
где w — функция прогибов полностью защемленной пла-
стинки, находящейся под нагрузкой 24р/й2.
Для балки, нагруженной согласно схеме, показанной на
рис. 12.13, примем
Эго Даст

др
/г3
(12.43)
Р(х, у) =
Р(X. у}
D
6г>	, х=
ду*
где п(х, у} — действующая на пластинку нагрузка; Л —
цилиндрическая жесткость.
В случае прямоугольного диска контурные условия
(12.38) принимают вид
(те ! у3	у2 \	д2Ю
Щ ( ДГ	2 h]	<h.s ’
6л	д2ю
Пу =— 7Д- (У3 — У1)	
/г3	дх ду
d-w
----= 0 при х = 0 и х = У
ду2
32Ш
—— = О при у = 0 и у = k; I (12 41)
d2w
—----— q — вдоль всего контура.
дх ду
Для прямоугольного диска, нагруженного согласно
рис. 12.12, возьмем функцию ф в виде
/ х*	2	\
ф= -7---л3-1,5х2 у. (12.42)
\ /г2	/г	/
Продифференцировав (12 42) дважды по х, получим
Все условия
стве w взять
на контуре удовтетворяются, если в каче-
функцию прогибов прямоугольной, пол-
ностью защемленной на контуре пластинки, находящейся
.. 6Р ]2Р	„	.
под нагрузкой ———р-у. положив	где
п'- hx
'12р
го2 —прогиб пластинки от нагрузки у, а —прогиб
п3
бу
пластинки от нагрузки — , можем воспользоваться го-
товыми решениями.
Изложенный прием дает возможность при надлежа-
щем выборе функции ф использовать решения задач
о защемленной пластинке для плоских задач теории уп-
ругости.
G
у —
И?
12х
12.3.	ВАРИАЦИОННЫЕ МЕТОДЫ РЕШЕНИЯ
ЗАДАЧ ТЕОРИИ УПРУГОСТИ
Подставив в (12.25)	получим
54ш д*ш d*w 24п
— 4- 2---------4- ----=— --- .
дх* 1 дх2 ду2 ду* й"
2—26
Вариационные методы решения задач теории упруго-
сти имеют ботьшое практическое значение, так как они
в большинстве случаев лают возможность получить
сравнительно просто приближенное решение тех задач
( ро П С ;то 1
18
РАЗДЕЛ 12 УРАВНЕНИЯ И ФОРМУЛЫ ТЕОРИИ УПРУГОСТИ, ПЛАСТИЧНОСТИ II ПОЛЗУЧЕСТИ
теории упругости, для которых точное решение неизвест-
но я.ш слишком громоздко. Ниже излагаются основные
вариационные методы решения задач теории упругости,
12.3.1.	Метод Ритца
Метод Ритца основан на использовании начала Ka-
ro плиало При решении задачи этим методом для дан-
ной конкретно!! задачи выбирается система функций:
(12.44)
(12.45)
удовлетворяли как уравнениям равновесия
Do f	бт х:/ 8т е?
_1„	— -L — О’
дх ду c)z
^их	.	dOi/	8tvz__
дх	ду	'	дг
дог = о
дх	ду	1	дг
так и условиям на поверхности тела:
и-- + ^2п = Pxv-, ay>i^n + д№ „ о.
Гх 1 + °'Лит + "4 П = Рух- 4* 1 т + Ггг ” = °
44 1 + Чд т П~ "с п “ Pzv; Т’Х) ~П rtl + п °’
Что касается других уравнений теории упругости, то
они, вообще говоря, пе будут удовлетворены выбранной
системой функций (12 44). В самом деле, подставив вы-
ражения (12.44) в уравнения закона Гука (см. 3,3.1), най-
дем составляющие тензора деформаций ех, tv, sz, уыу, ...
Подставив затем эти составляющие тензора деформаций
в уравнения (3 23) (см. 3 2.1), получим шесть уравнений
для составляющих вектора перемещения (и, о, ш):
ди	dv	dw
.	,	__ g .	__ g .	___ g .
дх	ду и дг
ди	dv	dv	dai	dw	ди
,	"5 ) Уху ~V~~ 4” 'У'" = У yz, ~ 4“ П = Уих
ду	дх	дг	ду	дх	дг
Однако если выражения (12 44) пе являются точными
решениями уравнений теории упругости, полученная си-
стема уравнений будет неразрешима, так как определен-
ные вышеуказанным способом составляющие тензора де-
формаций не будут удовлетворять уравнениям совмест-
ности деформации Сен-Вепапа (127).
Тем пе менее, согласно Ришу, можно, исходя из вы-
ражений (12.44), получить приближенное решение урав-
нении 1еории зпртгости, опреде П1В неизвешпые коэффи-
циенты иа из уравнений
dW
---- -- 0 при к = 1, 2, 3,...,	(12 46)
дау
где У7 — выражение для потенциальной энергии дефор-
мации (12 18) или (12.19).
В случае тоскою напряженного состояния выра-
жение для потепцчалыгой энергии принимает вид (12 20).
Воспользовавшись функцией Эри (12 24) и принимая
у—0, преобразуем уравнение (12.20) к виду
1 (‘ Г (। Ч’ V i Ф I3 1 д'2 Ф V
Т ----- ---------2- -у-------ф2 (---— | 4-
2 с JJ I. бх2 , ду- ) дхду /
[/ д- гр д- <р б3фЧ)
щ2и ГщчН	—V-\\dxdy. (12.47)
р\ охду j дх- ду- JJ
Выберем теперь систему функции
<Уо(х,У}, Ч1(х,У), <f2lx, у), . ..
таким образом, чтобы удовлетворялись следующие кон-
турные условия:
д- фп	д- фо
~Т7Г cos (П Н — — Т~ cos (у, V) = р ;
оу-	дхду
д2 фп	д2
_^COS(XJV)+^COS({/1,,)=^.
д" ф/,	б2 ш
——- cos (х, v) — —— cos (у, а) = 0;
дуи	дхду
д2	д2
— cos (-х’	+ “ПТ- cos (У’ v)=0 (й = 1, 2, 3...).
дхду	дх-
Положив далее
т
Ф Фо + S фй (х, у)э
можно найти коэффициенты из системы уравнений
(12,46), используя для Ж выражение (12.47).
Пример 12.1. Найти распределение напряжении и пря-
моугольном диске, ограниченном прямыми х=~а, у —
= ±.Ь и нагруженном на кромках х = +а напряжениями
Граничные условия:
при х а
т:ху = 0;
при У=±Ь ау = 0, гху ^0.
Это дает для функции Эри:
при х = Ш а
при у = + Ь
б2ф	/ у2\	сЭф
ду"	\ Ь- /	дхду
д~ св	б3 ср
—24 = 0; ------= 0.
дх-	дхду
12 3 ВАРИАЦИОННЫЕ МЕТОДЫ РЕШЕНИЯ ЗАДАЧ ТЕОРИИ УПРУГОСТИ
19
Положим
<₽ = Фо (х, lJH ак Ф* (х < У) = ~7Г УЦ1— —) 4-
Vassal	Z \ ЬО" /
k
+ Voj Vk (х-У)-	(12-48)
k
Все граничные условия будут удовлетворены, если
в качестве функции (р.(х, у) принять выражения:
ад (х,	у} = (х2	—	а2) (у2	— Ь2)\
<Д (х,	у) = (х2	—	с2) (у-	-- Ь°) х2;
цу (х,	у) = (г'2	—	а") {у2	— 4>2) у2-,
фз (х,	У) =-= (х'2	—	а2} (у-	— Ь2) х4;
Подставив (12.48) в интеграл (12.47), произведя инте-
грирование и потребовав выполнения соотношений
(12.46), получим систему уравнений для коэффициентов.
В первом приближении можно все ак, кроме су, поло-
одно-
жить равными нулю, и задача сведется к решению
dW
го уравнения ~~— = 0, из которого
Р___________________1_______________
ц4 Ь2 64	256 ft2 64	64
7 + 49 а2 + V ’ а4
12.3.2. Метод Бубнова — Галеркина
Выбирается такая система функций
иа(х,у,г); fk(x,y,z)-,	1
Ф) (х, У, г); <pk(x,y, г);	(12.49)
Ц-’п (х, у, z); ^к(х, у, г) (й= 1,2,3.. .), |
чтобы выраженные с ее помощью составляющие вектора
перемещения
и = и0 + S ak h:, V = о0 + S bk ФФ
k	/г
w = wB + ^ck^k>	(12.50)
k
где as, bk, Ck—пока произвольные постоянные, удов-
летворят!! некоторым изложенным ниже условиям.
С помощью составляющих вектора перемещения мож-
но вычислить составляющие тензора деформации:
8х = е2+4П1 ф=Е"+8^ 1 s2=fz+fin;
^Ху = V =т"у +t!V ; К2=?22+Щ;
л; — п Ж-Д1!
7 г/г “ ТУ2 + • г/г ,
В частном
=— 0,0-’2 33,
а4
будут:
случае квадратной пластинки а{~
и составляющие тензора напряжений
/	и2 \	/	Зу2 \ !	X2-’
Sj=p 1-ч- -0,1702,о 1--“	1- —
\	Ь2 /	\	а2 1 \	ц3
оу=—0,1702р 1
Зх2
а2
у2 V"
а2 / ’
XI/ /	Х“
хы =— 0,6805р -ф- 1 — ~
а2 \	а2
9ип дх			ду	0 dw^ дг			-2k k	dfk дх
е(1) =	k	bk	df2k ~ ду	е(П =	V k	ск'	d^k _ 9г	
= i XU	ди0 ду	4-	дУу _ дх	/ . i Х2	дг	' 4~	dwa дх	
Для получения более высокого приближения можно
принять й = 3. Это приведет к системе трех уравнений
с тремя неизвестными
В частном случае квадратной пластинки
аг = 0,04040 — ; а2 = а, = 0,01174	,
aQ	а3
а для пластинки с отношением сторон а/Ь^.2
at = 0,07983	 а» =0,1250—~ ;
eft Ь3 *	а6
а3 = 0,1826 —Л— .
а0 о-
Имея значения a!t as, аз, с помощью формулы (12 48)
получаем приближенные значения функции Эри, что,
в свою очередь, даег возможность подсчитать по форму-
лам (12.24) возникающие в диске напряжения.
2*
Имея составляющие тензора деформации, можем по
формулам закона Гука (см 3,3.1) вычислить состав-
ляющие тензора напряжений:
ах = +<4’ ’ J ау =ау 1
°г = °г +°Г ’ 1 \д = 4 +т^>;
Щ=1л-г+тГг; ^г =^г +гй>>
(12.51)
20	РАЗДЕЛ 12 УРАВНЕНИЯ И ФОРМУЛЫ ТЕОРИИ УПРУГОСТИ, ПЛАСТИЧНОСТИ И ПОЛЗУЧЕСТИ
где
Для того чтобы выражения (12.51) действительно
представляли собой приближенное решение соответст-
вующей задачи теории упругости, И. Г. Бубнов пред-
ложил определять входящие в них коэффициенты а>,
и сь. (*=1, 2, 3 ...) из системы алгебраических уравне-
ний, которая получается после подстановки выражений
(1251) в уравнения
TV ’txy’
.....................................  •	' I
Составляющие тензора напряжении (12.52) должны
удовлетворять из поверхности тела условиям:
<( 4-4 m+
ali)z +тЯ’т + T1V 'i =- °;
4z + ^m + 4« = /V
(12'53)
1 + т + 4п = pZv’
Tzx Z "Т rzff m + 4’’ n = °’
Для этого исходная система функций (12 49) должна
быть выбрана таким образом, чтобы на поверхности тела
удовлетворялись 'условия:
2(1 —р.)	dfk	д^
---------- ------14-------пг = 0:
1 — 2р.	r'x	ду
2p	Эф;-	Лрд	йф^
--------, ---- I -------- ф_ ------- п = Q.
1 — 2р	ди	дх	дг
2о	64ц.
1 — 2р	ду
дг ' 1 1 — 2р
1
>(	дах дх +	дххл,	Этг, \	1 	у	] dxdydz = 0; ду	дг }
	1, дх !	дди	дх,,, \ 	 —|		 dxdydz =- 0; ду	дг )
		дх,,, dtx, \ , ,
[ 1 j1 ф/г	”4 + ( дх			 д_	] dxdydz --- 0 ду	дг /
	(k	= 1,2, 3...)
(12.55)
с последующим вычислением приведенных интегратоп
Эффективность метода Бубнова — Галеркина зависит
от того, насколько удачно выбрана исходная система
функций (12.49). Опыт показывает, что при удачном
выборе этих функций можно добиться необходимой точ-
ности решения, ограничившись в рядах (12.50) двумя
или тремя членами, т. е. приняв
а = «(, + afy,
V = п0 4- 6<Pi;
w = wB 4- ctfy;
илп
а - ап -у- аг fy 4- <4 /4 1
о = v„ J- bi <р, 4 b, <р,; I
а) = а.,04'с1 Ф1 + са фа.
(12 56)
----- т !
дг
—— / 4- —— г
дх ду
JiLl+
ду
1 — 2р.
Э<Га /;j_ 2(1 — 10 dtfk
дх ' ‘ 1 — 2р ду
4 ~V~' п = 0;
ду
dfk
•----п — 0:
дх
д^ь .
. .---п __ Q.
— 2ц ду
, 2 (1 - и) оф;,
4 ----;„ ==
дг
-2р
dfk
 ---т = 0;
дх
+ —:— Ч	0;
ду
УГГ.1,
- т 4----- я = 0
1 — 2р ду дг
(*=1,2,3...).
2ф
1 — 2р.
.-------т
0;
J
(12.54)
Заметим, что эти условия на поверхности теля могут
быть легко удовлетворены, если систему функций (12 49)
выбрать в виде полиномов достаточно высокой степени
с надлежаще подобранными коэффициентами.
12,3.3. Метод Треф-Лчя
(метод смягчения граничных условий)
Выбирается система функций
и/г(х,у,г), од, (х,	2); wk(x,ty,z) (12.57)
(k = 1, 2, 3...)
таким образом, чтобы ряды
v	1
и= i akUk(x, у, г);	.
&	I
o=E*H^4,y,a);	(12.58)
k
w = S CfetOfe (x, y, z)
k
1
удовлетворяли уравнениям Ляме (12 17). Функции
(12 57) рассматриваются как составляющие вектора пе-
ремещения точек упругого тела и по формулам п. 12,1
вычисляются составляющие тензора деформаций ех,
8г, Уху, Ухг, Yyz-
После этого по формулам закона Гука вычисляются
составляющие тензора напряжений ах, ov, ог, т.хУ,
Тхг, Tyz.
Полученные составляющие тензора напряжении будут
автоматически удовлетворять уравнениям равновесия
(12 2), поскольку функции (12.57) удовлетворяют урав-
12 4. СВОДКА НЕКОТОРЫХ РЕШЕНИИ ТЕОРИИ УПРУГОСТИ
21
нениям Ляме, но граничные условия при этом не будут,
вообще говоря, удовлетворены. Однако при надлежащем
выборе неопределенных коэффициентов as, bk, ch гранич-
ные условия удовлетворяются приближенно Для этой
цели следует подставить выражения (12 58) в уравнения
П’(пл 1+ т + гх*'г~рЧ иk dF = °;
'р
Н ( т I Л- а т + т п — р ) V , dF -= 0;
JJ \ у# ' у uz F W4 k
F
И ( т I 4- т т 4- а	dF ~ 0
,1,4 гх 1 zu 1 z г <4 k
(12.59)
и решить полученную систему линейных алгебраических
уравнений относительно неизвестных коэффициентов
треугольной нагрузкой. Напряжения вычисляются по
формулам
х3 у	р /	6
ах = р -у ф. — —2ху> Д ~ с2 ху
4са	4<4 \	5
Зпх2	р
Ы/ = уу- ч - ч - Ч - У1) -ь
12.4. СВОДКА НЕКОТОРЫХ РЕШЕНИИ
ТЕОРИИ УПРУГОСТИ
12.4.1. Чистый изгиб
Пластинка, имеющая поперечное сечение в виде узкого
прямоуготышка, нагружена по торцам нормальными на-
пряжениями (рис. 12,14), сводящимися к двум парам
Рис. 12.15
Рис. 12.14
с моментами ,14. Решение теории упругости совпадает
с элементарным решением сопротиатения маи’риалов:
М
ох^ У, ° у - °-
Рис. 12.16
Рис. 12.17
12.4.2.	Поперечный изгиб консоли
а)	Консоль, имеющая поперечное сс-чсппе в ваде узкого
прямоугольника, нагружена на копие поперечной ситои
(рис 12 15). Если распределение касательных напря-
жении но торцовому сечению следует закону
Q (h~ -- 4фф
г. — ------------
то точное решение теории упругости совпадает с элемен-
тарным решением сопротивления материалов:
М Рхц
ах^ — у == -у- ; о,, = 0;
QS _ 44уЫ4
T*i7 lb	8/
Если касательные напряжения по торцовому сечению
распределены но какому-либо иному закону, то в соот-
ветствии с принципом Сен-Велана, на расстояниях от
торца балки, равных примерно высоте ее сечения, мож-
но с достаточной точностью пользоваться приведенными
формулами.
б)	Консольная балка, имеющая поперечное сСчелИе
в виде узкого прямоугольника (рис. 12.16), нагружена
Решение справедливо, если по торцовому сечению бу-
дут ипствовать нормальные и касательные напряжения,
получающиеся из приведенных формул при х = 1.
12.4,3.	Поперечный изгиб балки
а)	Действие собственного веса (рис. 12.17). Распреде-
ление напряжений:
Зу ,	/2	\
Оу =	IF
3	/,	У" \
Ю =--у	—
Здесь у — объемный пес материала Решение справед-
ливо, если по торцовым сечениям действуют касательные
и самоуравновешенные нормальные напряжения, полу-
чающиеся из приведенных выражений (при х^^Ы),
6)	Действие поперечной нагрузки (рис. 12,18), Распре-
деление напряжений:
Ю_ (/:
2/ х
р 2	2	\
х2) У +------- — У’ — — с- у ;
’	2! \ 3	5 Г
-) ,	P\ U П Р М’\Г Ш il’in I <1 орцс дщ ТГОГИП У П1 У ГОС^И ПТ'СТИ I Ж Г т И ПОТ’' ЧГСЛ I
Рис 12 18
а . =— p — (ф ch ay — a-i у sh ay) —	(b4 sh ay
а„ у ch ay) sin ax
d-
(a c sh ay — щ у ch аг/)
a, у sh ay) coa ax
3 lecn
a ac —
ac ci ac — sh ac
ac ch ac. sh ac ~
sh 2ac 2a
— (a4 c ch ay —
4,
a ch ас — a,
ac sh at — ch ar — 6,
ar sh ar p ch ac - 6,,
sn ac — lac — d,
Dcme шс спр 1ВсД шво при ус ю ши что па ’оонах ба а
кч вштмг 1 icmninii nipwins по у1 ающиесч
из приведенной форму i i при л~=0 и х = 1
12 4 4 Изгиб кривого бруса
(задача X С Головина)
Брас имеет круговую осевую шпию рипуса г и по
У Д\
3!л
~Г
сюяшюе "oiicpi, пос сечение в виде уi\ого прямою отв
пика Брус иг иб 1 тсч в птослостч свое i крчвпзгы па
рюш сиг 21 прптол in mi по кои гам Р icnpeie тение
напряжен ш в го яр i щ коор гпн it щ гстся форму нами
ог
(р Ь" Ь
I-------.in —
в0
г- а
г	а \
Ь In — -r а ш — ,
Ь	г )
Рис 12 19	Рис 12 20
есчи по торцам
теш о справе чтиво
еатетьшп. ч Сзмоуравновешенн ie
есичя поучающиеся из приведенных
ют
про
е = + /
в) При переменном попсрс том
Распреююиш нанря пенни
ба тки депству
иорматы-шс
форму а
сюепи и
(рис 12
Л!/
В
7
tgsp


па гтубипс л
на
при
19)
31 I у 1 — 1ЧВ1СП1 води
пня е ниш цы объема
Решешк спрашд'ыво при
се кпию деиствуют норм i тьныс и касатспяпи папря
жегпи no iy чающие си чз пригкдешшх форму а при
УС1ОВИ1 ЧТО
q — собствен
по торцовом'
i) Из1иб б ики с шусощатопоп 'кмру’кои (рчс 12 20)
— ny сп аг/ - а} у sh аг/) — (о sh an
г/j	d2
у ch ay) 1 sin ах
~ и in — - b — а'
2	\ — (Ь — а ) — 4а b [ 1р —
\ а
Зтесп а о —соотвстм-венно внутр ппии и наружный ра
иди от г
Эти тгошмгшя яв тяю ся ТОПП.1М рнишкч задачи
а ш in тор I гм брус! р шире ie т тис нор I 1 н hi lx папря
Ж НИН С И I впр 1Жс1 ИЮ I 1Я о
12 4 5 Клин, сжатый сосредоточенной силой1
(рис 12 21)
Р а т I г 1 not тагря/Мпш в по шрных координатах [21]
В11 ПК ЯС I по форму тс
Рс 10
a ] —- sm 2a
Пзив о I < 'в 12 11—1 4 р пиния с 1ра зе чивы как ;то
вьин з мечато I юико .ц i rupt к. шип закон а д паспретете
и 1 ио’) in hi х з hi it аь x напр шин ^орцэв ш с<че
н в ток Пр! тр I их п к ли тепе тн х расгрспепс
пнях ор 1 I nix I I а in (них niip i сиз пп горцотш сече
Н1ям	ги р л с и'I ост нт1Я гост! опо гопы и rfa рас
стоштх от тонн, равны пр впр о по ови те высоты баткз
12 4 СВОДКА. НЕКОТОРЫХ РЕШЕНИИ ТЕОРИИ УПРУГОСТИ
23
Распределение нормальных и касательных напряжений
в прямоугольных координатах дается формулами
== or sin2 0;
Ра п-2 — Рь Ь"
ох = or cos2 0;
1
тлд = ду г sin 20.
Решение является
точным, если распреде-
ление нормальных и
касательных напряже-
ний по торцовому се-
чению следует приве-
денным формулам.
12.4.6. Толстостен-
ный цилиндр
и сферический сосуд
При осесимметрич-
ной деформации толсто-
стенного цилиндра или
диска (рис. 12,22) рас-
пределение напряжений
в полярной системе ко-
ординат с началом в
центре дается форму-
лами
(Ра — Pb) а2 Ь-
г2 (62 — а2)
(Рл — Рй) а'2 Ъ2
т2 {Ь2 — а2)
Здесь Oi — норм ильное напряжение па площадке, плос-
кость которой проходит через ось трубы; ог — нормаль-
ное напряжение на площадке, перпендикулярной ра-
диусу г.
Рис. 12.22
При полярпо-симметричиой деформации толстостенно-
го сферического сосуда (рис. 12,23) распределение на-
пряжений в сферической системе координат [21] дается
формулами
а3 (2г3 -ф &3) Ь3 (2г3 -ф Ь3}
?г3 (Ь3 — а3)	2r'3 (63 —	л3)
а3 (г3 — Ь3)	Ъ3 (а3 — г3)
г3 (Ь3 — а3)	+	г3 (Ь3 — а3)
Рис. 12.23
В приведенных формулах ра— внутреннее и ръ — внеш-
нее давления.
12.4.7. Упругая полуплоскость и упругое
полупространство [21]
Дана сосредоточенная сила, приложенная к точке пря-
молинейного края полубескопечпой пластинки
(рис. 12.24). Распределение напряжений в плоскости тп
Рис. 12 24
па расстоянии .г от прямолинейного края дается фор-
мулами
2Р cos3 0 2Р х3 1
сц——•------ • -----=--------• -------------;
л г	л (х2 -'г д2)2
2Р
Sin2 0 cos2 0;	(	(12.60)
2Р . п .... 2Р х2у	|
tw =—------sin 0 cos" 0 --— — •----------.
лх	л (Н-фу2)2	I
Здесь Р — сосредоточенная сила Угол 0 — см. рис. 12.21.
При сосредоточенной силе Р действующей на тон-
кость, ограничивающую полубескопечное тело
(рис, 12.25), распределение напряжении в цилиндриче-
ской системе координат дается формулами
24
РАЗДЕЛ 12 УРАВНЕНИЯ И ФОРМУЛЫ ТЕОРИИ УПРУГОСТИ. ПЛАСТИЧНОСТИ И ПОЛЗУЧЕСТИ
N	N
где о0 = — = ———— номинальное напряжение, огнесен-
F	2Ьо
ное к площади брутто.
Для овальных отверстий коэффициент концентрации
напряжений может быть вычислен по формуле
«».«»
где р — радиус кривизны дна отверстия; t — половина
ширины отверстия.
12.5. КОНЦЕНТРАЦИЯ НАПРЯЖЕНИЙ1
12.5.1. Концентрация напряжений
при растяжении
а) V отверстий. ГЬ рис. 12 26 даны эпюры распреде-
ления напряжений по поперечным сечениям растянутой
4
Рис 12.26
Рис 12.27
полосы, ослабленной отверстиями различной формы.
При приближении к краю отьерсгия напряжения резко
возрастают (эффект концентрации напряжений). Коэф-
фициент концентрации напряжений
/Макс
о0
3 Уточнение решений может быть получено на основе мо-
ментной теории упругости (см, 12.6.7).
При круговом отверстии k~3.
б) У выточек. На рис. 12.27 и 12.28 даны эпюры
распределения напряжений по поперечным сечениям
растянутых стержней, ослабленных выточками, а на
рис. 12 29 — у выкружек. Максимальное напряжение
°макс —:
где
„ Л Р
а°~” К “ 2а8 ‘
Таблица 12'1
Отношение а/р	Поперечное сечение стержня		
	по рис. 12.27	по рис. 12 23	
		ДЛЯ С;	для о.
0	1	1	1
10	4,1	3,3	1,05
20	5,6	4,6	1Л
30	7	5,6	...
Таблица 12?
б'р	1	С/р			
	I 10	5	1	2
1	)	1,70	1, Ь6	1, зо	13’
.<	1	1,55	1,81	О	1,9’
3	1	2,09	1,91	1,79	—
4	2,15	1,99	! ,Н	—
5	2,17	2,02	1Л1	—
Коэффициент концентрации напряжений k определя-
ется: у выточек по табл 12,1, у выкружек (рис, 12 29)
по табл. 12.2.
12,5. КОНЦЕНТРАЦИЯ НАПРЯЖЕНИЯ
25
12.5.2. Концентрация напряжений
при изгибе [15]
Балка с круглым отверстием (рис. 12.30)
а)	Чистый из1иб (рис, 12.31, а). Для балки с круг-
лым отверстием, центр ксюрого расположен произволь-
но по BLieoie балки, напряженке
Л1г
о0 -------(sin 0 — sin 39) —
—------ц—2 cos 29).	(12,63)
/ г
Рис. 12.31
Здесь Л? — изгибающий момент; Д — момент инерции
сплошною сечения балки относительно нейтральной оси,
г — радиус отверстия; 0 — полярная координата точки
контура; h — расстояние от центра отверстия до ней-
ipa.ibiioH оси балки; расстояние h считается положи-
тельным, когда центр сиверстия расположен в сжатой
тоне.
б)	Поперечный изгиб при действии сосредоточенной
силы (рис. 12,31,6), Центр отверстия расположен про-
извольно по высоте балки. Напряжения но контуру:
Л1
Од =- — —— [г (sin 0 — sin 39) -Ц А (1 — 2 cos 20)] —
Р
— —— [г- (sin 20 — s:n 49) ~~ rh (cos t) — 3 cos 30) —
— 2 (с2 —Ц) sin 20],	(12.64)
в)	Поперечный изтиб под действием равномерно
распределенной нагрузки (рис. 1231, а). Центр отвер-
стая лежит на нейтральной оси балкя. Напряжения по
контуру
Рис. 12.32
.41 — изгибающий момент в сечении по центру отвер-
стия
При построении миоры контурных напряжений значе-
ния аоткладываются на радиусах
Эпюра, построенная по формуле (12.65), показана на
рис. 12.20
Балка с отверстием квадратной формы
(рис. 12.32)
Таблица 12.3
0 в граи	0	15	30	45	53	I5	80	90 ,
$ в грач	0 i	9° •)!)'	24° Л)'	45'’	Ь5°&1'	Ь0°2Ь'	83°40'	90° :
У в граР	100	IU5	120	135	150	165	180
в гр аО	96°20'	99'41)'	Ш°10'	135й	153“50'	17О°20'	180°
Центр отверстия лежит на. нейтральной оси балки.
Решение дано для квадрата с прямолинейными старо-
26
РАЗДЕЛ 12 УРАВНЕНИЯ И ФОРМУЛЫ ТЕОРИИ УПРУГОСТИ, ПЛАСТИЧНОСТИ И ПОЛЗУЧЕСТИ
нами и закругленными углами. Две стороны квадрата
параллельны центрально!! оси балки.
а)	Чистый изгиб (см. рис. 12.31, а). Напряжение
М	г 1/~2	Г
=- у- 	-------г 1 185 (sin 9 +
х 2 | 0,9 — — cos 40 )
\	2	/
+ cos 0) Д- (sin 30 — cos 30) +
+ (sin 50 4~ cos 50)j.	(12.66)
Здесьr= (flo’+bo). где an—половина стороны квад-
рата; ba — половина диагонали квадрата; 0 — полярный
угол в преобразованной области; 0 — полярный угол
в плоскости балки.
Задаваясь углом 0, получаем гд — напряжения по
площадкам, перпендикулярным контуру отверстия.
Для построения эпюры контурных напряжений нужно
в плоскости балки откладывать соответствующие углам
0 углы 'в. Пересчет углов производится по табл. 12,3,
б)	Поперечный изгиб под действием сосредоточен-
ной силы (см. рис. 12.31,6). Контурные напряжения
~-------------------1,185 (sin 0 + cos 0) Д-
2/х (0,9 — — cos 40 j L
\	3	)
+ (sin 30 — cos 30) Д — • (cos 50 Д- sin 50)~j —
P	f Г
	Дз q §34 cos 20 Д- sin 40 4-
/	2	\ 1
1 x i 0,9 — — cos 40
\	3	1
113	]
-J-—- cos 60 — cos 20 .	(12.67)
Эпюра ol(, построенная по этим формулам, показана
па рис. 12.32.
При построении эпюры значения (^откладываются по
нормали к контуру. Отсчет углов О ведется от линии
Д —0, составляющей с горизонтальной осью балки угол
а ==45°.
Формулы п. 12.5.2 выведены для бесконечной полосы
прямоугольного сечения, но они могут быть применены
с достаточной для практических расчетов точностью для
балок ограниченных размеров si любого сечения. Точ-
ность результатов зависит от величины отверстий. Фор-
мула для чистого ш-гиба дает хорошее совпадение
с опытными данными, если наиболее близкая к краю
балки точка отверстия отстоит от этого края на расстоя-
ние, не менее наибольшего полудиаметра отверстя;
в случае изгиба сосредоточенной силой — не менее 3—
4 диаметров отверстия.
Наличие нескольких отверстий изменяет картину рас-
пределения напряжений в балке; но для практических
расчетов и в этом случае могут быть использованы те
же формулы при условии, что расстояние между цент-
рами отверстий больше двух диаметров отверстий.
Пластические деформации вблизи круглого отверстия
см. [19].
12.6. ЭЛЕМЕНТЫ ТЕОРИИ УПРУГОСТИ,
УЧИТЫВАЮЩЕЙ МОМЕНТНЫЕ НАПРЯЖЕНИЯ
12.6.1.	Основные положения моментной
теории упругости
Действительная прочность некоторых материалов за-
висит ог градиента деформаций или напряжений. Кро-
ме того, распределение напряжений при резких градиен-
тах (например, в условиях концентрации напряжений)
в большинстве случаев не соответствует решениям, по-
лученным в классической теории упругости. Дело в гом,
что в классической теории упругости, начиная с Коши,
считают, что воздействие одной части тела на другую
по некоторому произвольному сечению может быть све-
дено к распределенной нагрузке — нормальной и каса-
тельной. При этом возможная распределенная момент-
ная нагрузка не учитывается. Не учитывается и дефор-
мация малых элементов, вызываемая моментной на-
грузкой.
Моментные напряжения (рис. 12.33J учитывает тео-
рия упругости, разработанная Косеера [13].
12.6.2.	Уравнения равновесия
и несимметричный тензор
напряжений в двухмерном случае
Уравнения равновесия, выражающие, что суммы про-
екций всех сил, действующих на выделенный элемент,
на оси х и у равны нулю, имеют обычный вид (при от-
сутствии объемных сил и моментов]
дох	дтх„
—5_ I ----М.
дх	ду
дХух i Угу
. л---------
дх ду
Уравнение, выражающее равенство пулю суммы мо-
менлов всех сил, действующих на выделенный элемент,
имеет вид (рис. 12 34)
дтх
дх
дт{,
ду
— 0 
Следовательно, вообще говоря, тензор напряжений (см.
3.1.5) не симметричен, т. е. тха=Дтух.
12 6 ЭЛЕМЕНТЫ ТЕОРИИ УПРУГОСТИ УЧИТЫВАЮЩЕЙ МОМЕНТНЫЕ НАПРЯЖЕНИЯ
27
Наряду с приведенными деформациями существуют
еще деформации изменения кривизны элемента
Несимметричный тензор напряжений
/ ° г Хху \
ау /
можно представить в виде суммы симметричного и ко-
сосимметричного ынзоров
да>,
у= (рис. 12.36).
s OX
дбх
л дх Ох
Обозначим:
Рис. 12.34
12.6.3.	Деформации, вызванные действием
силовых и моментных напряжений
Деформации е», cv, у-с1, и жесткий noeopoi ы2 нахо-
дятся по обычным формулам.
Рис. 12 36
ди	дю	dv ди
= __ = ------, = + ~~
1 / dv	ди \
= —---------—------
2 \ дх	ду )
Деформация е», ву, учу и жесткий поворот <ог пнхо-
вае1 обычны,! сдв'и, анидцм месячная (тд)—неурав-
новешенное вращение (рис. 12,30).
12.6.4.	Закон Гука
В теории упругости, учитывающей моментные напря-
жения, закон Рука имеет вид (в двухмерном случае пзо-
ipomioiо тела)
1 + ц
ег = —— [<Д — g (Д + аф];
РАЗДЕЛ 12 Г. РАВНЕНИЯ И ФОРМУЛЫ ТЕОРИИ УПРУГОСТИ, ПЛАСТИЧНОСТИ И ПОЛЗУЧЕСТИ
в„ 	1о„ — и (ог + оу,)];
с
ла к I не чико, эффект влияния моментных напряжений
невелик. Однако при наличии градиента деформации в
том случае, когда размер тела приближается к I, мо-
ментные напряжения могут существенно влиять на ре-
зультат расчета.
1 1
4В ' 4В у
Здесь Л -- новая константа упруюсти материала, нося-
щая название модуля кривизны; множитель 'В вв> ден
для удобства.
12.6.5.	Условия совместности деформаций
В двухмерном случае условие совместности линей-
ных и угловой деформаций имеет обычный вид
О-Гг д~еи______д"Уху
Оу'-- ' дх"	дх ду
Кроме того, должно иметь место условие совместности
кривизн:
О'Л t д'Лу
Оу дх
Условия совместное гн деформаций и кривизн имеют вид
____ду и/	дгх _ деу 1 духу
х 2 их ду ’ У дх 2 ду
12.6.6.	Функции напряжений
Если ввести две функции напряжений у (х, у)
и ty(x,y}> то можно у доь.'.е творить всем уравнениям
равновесия, положив
<92<р	82ф	32ср <Э2ф
х ду" дх ду ’ lJ дх" дх ду
Фф 32ф	32ф	! Фф
ху Ох ду ду" ' ух дх ду дх2
д^	аф
----; т„ =	.
их	ду
Причем обе функции у и ф должны удовлетворять си-
стеме уравгг или
- (Ф - I"2Ф) — 2 (1 ~ ,ii) Р у Ч);
дх	ду
~~~	о (1 — ц) I- ~ у 2ф,
Оу	дх
а каждая в отде.тыюсгл — уравнениям
у Др = 0 и
V24'--Pr^ = O (V4 = vV)-
В последних Формулах 1 — I /
F о ’
где В — модуль кривизны, G — модуль сдвига.
От величины I зависит степень влияния моментных
напряжений. Если отношение наименьшего размера те-
12.6.7.	Некоторые результаты расчетов
по моментной теории упругости
В 12 0.1 отмечалось, что при одноосном растяжении
iriaCTnin.i с круглым отверстием радиуса I коэффициент
концентрации k=-‘3. Это действительно имеет мт-Сто во
всех случаях, когда г/1>10. Однако, при уменьшении
Рис. 12.37
Рис. 12.38
t/l уменьшается и коэффициент концентрации. Зависи-
мость коэффициент коньентрштии or отношения t/l при
разных значениях коэффициента Пуассона ц покатана
на рис. 12 37.
Зависимость коэффициента концентрации напряжений
около круглого отверстия от отношения /// в случае чи-
стого сдвига показана на рис. 12.38 (с.м. также [19]),
12.7. ОСНОВНЫЕ УРАВНЕНИЯ
ТЕОРИИ ПЛАСТИЧНОСТИ
И ТЕРМОПЛАСТИЧНОСТИ
В настоящем разделе используются обозначения (по-
мимо введенных р.днее)
1
о = “ (о.е + оф + сг2);
1
о; "= — X
I 2
X /	ст _ aja ж (о; ~ 0J+
+ 6 1T.W + TXZ + ф-’)
(интенсивность напряжений);
1
£е-р = з (Ас + £у + И)!
V~2
е‘ ~ з х
х| (ел	НФ,- ФГ г .
12.7. ОСНОВНЫЕ УРАВНЕНИЯ ТЕОРИИ ПЛАСТИЧНОСТИ И ТЕРМОПЛАСТИЧНОСТИ
29
Н” 9 [уху Г Чу? ' Чгх}
(интенсивность деформаций).
Уравнения равновесия (12.2), геометрические урав-
нения связи между вектором перемещения и тензором
деформации (12,12), а также уравнения неразрывности
деформаций (12.7) полностью сохраняются при реше-
нии задач пластичности и гермопластичности.
Граничные условия (12,3) в деформационной теории
пластичности полностью сохраняются; в теории пласти-
ческого течения они изменяются.
12.7.1.	Общие свойства
пластической деформации
Перечислим свойства упруго-пластического упрочня-
ющегося материала.
1,	Пластическая деформация носит необратимый ха-
рактер. Эта необратимость проявляется как в остаточ-
ных деформациях, так и в ходе изменения температуры
образца при деформировании.
2.	В пластической области между напряжениями и де-
формациями не существует какой-либо однозначной
связи. Пластическая деформация зависит от программы
или истории нагружения.
3.	Полные приращения составляющих /деформации de
аддитивно складываются из приращения составляющих
упругой деформации Феу и пластической деформация
den, т, е. de = фщ-гЕгп
4.	Составляющие упругой части полной деформации
описываются законом Гука (3.3.1), если среда изотроп-
на, или (3.3 2), если среда анизотропна.
5,	Разгрузка из любого состояния происходит упруго,
подчиняясь тому же закону упругости (3.3.1) или (3.3.2).
6.	Повторное нагружение по пути разгрузки может
быть проведено почти без петли гистерезиса. Поэтому
в теории пластичности принимается, что петля гистере-
зиса отсутствует
7,	Для многих металлов и сплавов пределы текучести
и пропорциональности практически совпадают, как это
следует из опытов. Поэтому в теории пластического те-
чения принимается, что они в точности равны друг
Другу.
8.	Опыт показывает, что при деформировании метал-
лов и сплавов в широком диапазоне скоростей вязкость
проявляется весьма слабо. Поэтому в теориях пластич-
ности материал предполагается невязким. В теориях
пластичности пренебрегают также деформациями пол-
зучести, что вполне допустимо, если рассматривать де-
формацию на относительно небольших отрезках време-
ни. Таким образом, при указанных условиях кривая
а—г не зависит от скорости нагружения и эффектов
ползучести.
9.	Пластическая деформация упрочняющегося упруго-
пластического материала — есть равновесный процесс,
следовательно, как и в случае упругого материала, ско-
рости деформаций должны быть однородными функция-
ми первого порядка скоростей напряжений.
10.	Напротив, в случае деформации идеально пласти-
ческого материала скорости пластических деформаций
являются функциями напряжений, Тем не менее идеаль-
но пластическая среда имеет глубокие отличия от вяз-
кой среды Так, для вязкой среды не существует поня-
тия разгрузки, в то время как для идечлоно пластиче-
ской среды при разгрузке деформации становятся чисто
упругими. Есть н друпде различия.
12.7.2.	Основные положения теории
пластического течения
Теория пластического течения является более общей,
чем теория малых упруго-пластических деформаций, так
как в случае простого нагружения теория течения при-
водит к гем же результатам, что и теория малых упру-
го пластических деформаций. Вместе с тем теория тече-
ния относительно лучше описывает процесс сложного
нагружения, чем теория малых упруго-пластических де-
формации.
Теория пластического течения упрочняющегося мате-
риала основывается на предположении, что существует
замкнутая поверхность в пространстве напряжений —
начальная поверхность текучести, отделяющая чисто
упругую область от пластической области.
В процессе нагружения начальная поверхность текуче-
сти деформируется так, что изображающая напряжен-
ное состояние точка в пространстве напряжений никогда
не покидает эту поверхность.
В теории пластического течения задается закон де-
формации этой поверхности при нагружении (закон
упрочнения).
В теории пластического течения формулируется закон
пластического течения, ассоциированный с функцией те-
кучести (или функцией нагружения),
Основные уравнения теории пластического течения
получаются из постулата Д, Друккера [20], утвержда-
ющего, что в процессе приложения к первоначально
напряженному элементу тела дополнительных напряже-
ний внешнее воздействие совершает неотрицательную
работу; работа внешнего воздействия за нотный цикл
приложения и снятия дополнительных напряжений так-
же неотрицательна.
Из постулата Друккера вытекают следствия:
1)	поверхность текучести ( = 0 выпукла;
2)	вектор скорости пластической деформации ортого-
нален к поверхности текучести f =0,
3)	между скоростями пластической деформации и ско-
ростями изменения напряжений должны быть линейные
связи.
Наконец, важным положением теории пластического
течения является условие непрерывности, в соответст-
вии с которым напряжения и деформации в пластиче-
ской области согласуются с напряжениями и деформа-
циями в упругой области, koi да изображающая напря-
женное состояние точка движется по поверхности те-
кучести.
12.7.3.	Основные уравнения теории
пластического течения
Дтя упрочняющегося материала физические уравне-
ния теории пластическою течения записываются следу-
ющим образом.
ёР = 0	при	/	0 или	I
df	.	I
при	/	--	0; I --	Д—	ОД	-< 0;	ц
ё," = h — f при f = 0; / ой > 0,
’	йоц-
(12.68)
I де й— скалярная функция, зависящая от пластических
деформаций, напряжений и программы нагружения,
РАЗДЕЛ 12. УРАВНЕНИЯ II ФОРМУЛЫ ТЕОРИИ УПРУГОСТИ, ПЛАСТИЧНОСТИ И ПОЛЗУЧЕСТИ
30
В случае идеально пластической среды скорости пла-
стического течения отличны от нуля при постоянных на-
пряжениях. В этом случае физические уравнения тео-
рии пластического течения принимают вид

df
доц '
где X = 0 при ф=0, а также
Ф .
при / = 0; / = — ои- < 0;
доц
df .
X > 0 при f = 0; f =-- ай = 0,
ctoz/
где X—скалярная величина.
(12.69)
J
Можно отметить, что приведенные в 12.7.1 свойства
пластической деформации получают полное отражение
в теории пластического течения.
Следует подчеркнуть, что теория пластического тече-
ния отражает фундаментальное свойство пластической
деформации — зависимость ее от программы нагруже-
ния. В этом заключается большое преимущество теории
пластического течения перед деформационной теорией.
12.7.4.	Деформационная теория
пластичности — частный случай теории
пластического течения
Деформационная теория пластичности является те.м
частным случаем теории пластического течения, в кото-
рый последняя переходит при простом (пропорциональ-
ном) нагружении.
Деформационная теория (или теория малых упруго-
пластических деформаций) основана на предположении,
что между напряжениями и деформациями существует
однозначная связь как для процессов нагружения, так
и для процессов разгрузки.
Тепловое расширение в деформационной теории пла-
стичности учитывается точно так же, как в теории упру-
гости. Таким образом, основные уравнения деформаци-
онной теории термопластичности для случая нагружения
записываются в виде
Если вместо составляющих тензора деформации еы,
и ez ввести составляющие
= гх — а (Т — Т0У 1
sy = ey—^(^ — TQ); >	(12,72)
~	а (7 —- 7\j), J
то уравнения термопластпчностп и уравнения деформа-
ционной теории пластичности формально ничем не бу-
дут отличаться.
Уравнения (12.70) справедливы для многих материа-
лов только в тех случаях, когда все напряжения растут
пропорционально времени (простое нагружение) или
при нагружении, близком к пропорциональному. Следо-
вательно, для обоснованного использования уравнений
(12.70) должна быть решена задача об общих условиях
внешнего силового и теплового нагружения, при кото-
рых для материала с заданным законом упрочнения
(12.71) процесс нагружения каждого элемента объема
был бы простым.
В общем случае для любого закона (12.71) эта задача
не имеет решения. Частный случай этой задачи, когда
отсутствует тепловое нагружение и закон упрочнения
имеет вид	исследовался А. Л. Ильюшиным [8].
Процесс разгрузки элемента описывается обычными
уравнениями термоупругости. При этом пластические
деформации могут быть подсчитаны как:
;е" =Е - Ед;е" = ег 8Г-	1
} (12.73)
о п -— -v  	—лл . рП «0  1
ху i ху »ху t/Z iyZ » yZ’ ZX ZX *2X'J
Здесь e", e" и т. д. — пластические и соответственно еу,
е‘у .... и т. д. упругие деформации
В случае плоского двухосного напряженного состоя-
ния уравнения деформационной теории пластпчпошн
для несжимаемого материала могут быть записаны в
виде
(12.74)
где
«х = “ + CD (о,) (ах — о) + а (Т — То);
Тхд = 2® (ф)
(12.70)
ai = V °; ж	°у + Зтцх;
Решая уравнения (12.74) относительно о,, и ff,j, получим
Здесь К— модуль всестороннего сжатия и Ф(оф—мо-
дуль пластичности, связанный с г, зависимостью
sz== уф (at) at.
(12.71)
°д =
3
(12.75)
В общем случае модуль пластичности Ф зависит не
только от он, ио и от Т, т. е. Ф = Ф(с>1, Т).
Для нормальных температур (Т~Т0) уравнения тер-
мопластичности (12.70) превращаются ь уравнения де-
формационной теории пластичности.
Для перехода к уравнениям тсрмопластичности нуж-
но воспользоваться соотношениями (12.72).
Функциональная связь at=f{ег,Т] может быть по-
лучена на основе экспериментов на растяжение при раз-
личных температурах.
13.7. ОСНОВНЫЕ УРАВНЕНИЯ ТЕОРИИ ПЛАСТИЧНОСТИ И ТЕРМОПЛАСТИЧНОСТИ
31
Пример 12.2. Рассмотрим прямоугольную пластинку,
жестко закрепленную по контуру. Начальная температу-
ра пластинки То. При равномерном нагреве До темпе-
ратуры Т в пластинке возникнут сжимающие напряже-
ния, которые и нужно определить
Запишем уравнения (12.72) с учетом (12.74) в виде
е( /'	1	\
ех = ех — а (Т — 7 0) =- ох	о у );
0{ 1	2	;
El !	1	\
ЪУ = 6Д ~ а № ~ Хд ~=' “	9
Так как пластинка защемлена по контуру и нагрев рав-
номерен, то всюду в пределах пластинки должно быть
gI = e,J = 0. Учитывая эю, получим
1	<7
а _ а а (Т .
2	в,
ах 4 а„ =— к (Т — 7'0)	,
2
откуда
о,-
Ох -= Оу	2а (Т —- То) — .
В рассматриваемом примере
е. = 2 ]/+	+ Ц =
V з
2 , г-------------
= —г V За2 (Т - Т оуг = 2а (Т - То) .
Гз
Величина о, =/(е1, 7) =f [2а(7—Tt),T] может быть
найдена для данной температуры Т по эксперименталь-
ной кривой.
Окончательно напряжения
ох^Оу = ~~Ц2а(Т-То), Т].
Все рассмотренные выше закономерности относятся к
упрочняющимся упруго-пластическим материалам.
12.7.5.	Идеально упруго-пластическая среда
Как показывают эксперименты, некоторые сплавы,
полимеры и другие материалы характеризуются упру-
гими деформациями в начальной стадии нагружения
и после достижения предельного напряженного состоя-
ния— бсзтрапичным возрастанием пластических дефор-
маций. Переход от одной стадии деформации к другой
определяется условием пластичности. В пластической
стадии деформирования инварианты девиатора деформа-
ции могут принимать любые значения, Наоборот, ишза-
риаторы девиатора напряжений в этой стадии сохраня-
ют постоянные (предельные) значения. Соотношения
компонентов девиатора деформации сохраняются неиз-
менными. Изменением объема тела по сравнению с пла-
стическими деформациями пренебрегают.
Такие материалы, для которых упругие п пластические
деформации проявляются раздельно па разных шадпях
нагружения, называют идеально упру; о-пластичеекими
материалами.
В упругой области связь между напряжениями и де-
формациями выражается законом Гука (3.3.1) или (3 3.2);
в пластической области эта связь выражается уравнени-
ями (12.70) н условием пластичности. Причем в этих
уравнениях модуль плашичлосги Ф принимает постоян-
ное значение. В качестве условия пластичности для изот-
ропных пташнческнх материалов иснолщуют условие
Губера — Мизеса — Гонки либо условие Сеп-Веиана
[2,22] Для анизотропных материалов пли изотропных
материалов, получающих заметную анизотропию в про-
цессе деформирования, может бьыь использовано усло-
вие пластичности Мизеса — Хилла [22]
Применительно к строительной шали лучшее соответ-
ствие с опытом дает условие пластичности Сеи-Венаиа,
12.7.6.	Метод характеристик решения задач
теории пластичности
Рассмотрим плоскую деформацию идеально упруго-
пластического тела в пластической стадии. Это напря-
женное состояние определяется уравнениями равнове-
сия
do,	dtru	дг,,,	да,,
”Т£ + -щ-^-0; -^-. + ^-4 = 0	(12.76)
ох	ду	дх	ду
и соответствующим условием пластичности, например1
по Сен-Венан)
1	+	=	О2'77)
ИЛИ
по Губеру — Генки — Мизесу
оф - Ох оу + о • + зЩ = о; .
Подстановка в уравнения (12.76) выражений
ох = <т -|~ та sin 2<f; ‘
Оу = о — tT sin 2<р;
Хху =— Тт cos 2ф
приводит к системе уравнений
до / д<р	д<т \
----2тт cos 2<р—— + sin 2<р-------- = 0;
дх	\	дх	ду	)
до	7	дер	ду>	(	(
—- + 2тт sin 2w — — cos 2ф -------- = 0,
ду	\	дх	ду	)
(12.78)
(12.79)
(12.80)
обеспечивающей тождественное выполнение условия пла-
стичности (12.77) или (12 78). В формулах (12 79)
и (12.80) о — среднее напряжение, <р — угол наклона
площадки Тмл,i к оси х
Характеристические линии (характеристики этой си-
стемы) совпадают с линиями скольжения, т, е. линиями,
которые в каждой своей точке касаются площадок мак-
симальных касательных напряжений.
Линии скольжения образуют два ортогональных се-
мейства кривых д и Р В локальной системе координат,
образованной касательными к линиям скольжения а не-
которой точке пластического тела, вместо (12.80) полу-
чается система уравнении
(о Д 2тт <р) 0; --Д- (ст - 2тт ср) О,
СЖр
й д
где фдр- и • — производные вдоль линий скольже-
ния и р Эги дифференциальные уравнения выражают
равновесие бесконечно малого элемента скольжения
32
РАЗДЕЛ 12 УРАВНЕНИЯ И ФОРМУЛЫ ТЕОРИИ УПРУГОСТИ, ПЛАСТИЧНОСТИ И ПОЛЗУЧЕСТИ
пластической среды, образованного сеткой линий сколь-
жения, Вдоль семейств линий скольжения о, и (3
-у—~ tg ip; + <г = const =	(12.81)
dx	2тт
du	о
—-— ctg ср; ~— — ср --= const =- г],	(12.82)
Здесь | и q — параметры, меняющиеся при переходе
о: одной лишш семейства к другой того же семейства
(« или р).
Если известно поле линий скольжения и их парамет-
ры fj и ip то из уравнений (12,81) и (12 82) находят
о — а(х1у) и ф = ф(х, у) и затем с помощью соотношений
(12.79) компоненты тензора напряжений а:с(х, у), аа(х,у)
н Хху{х, у).
Пусть имеет место равномерное напряженное состоя-
ние, когда o = const и <p = const и уравнения линий
скольжения имеют вид
у = X cig ф 4- С1 и у х ctg Ф + Са.
Им соответствуют два
ортогональных семейства
прямых (рис. 12.39).
Случай т] —const харак-
теризует простое напряжен-
ное состояние, при котором
Ф = const, и одно семейство
линий скольжения определя-
емое уравнением у—xtg<p =
— const.
Это семейство линий яв-
ляется пучком прямых, за-
висящих от двух парамет-
ров ф и С. Вдоль каждой
прямой этого семейства среднее напряжение о = 2гт (q—
—Ф) сохраняет свое постоянное значение.
Второе семейство линий скольжения представляет
семейство кривых, ортогональных прямым первого се-
мейства (рис. 12.40).
Граничные условия, определяемые нормальной Оп(з)
и касательной т„(з) составляющими напряжения, задан-
ными на контуре, ограничивающем пластическую зону,
учитываются с помощью соотношений:
°п (s) = о + тт sin 2 (<р — а);
хп (s) ==— гт cos 2 (<р — а),
(12.83)
где а — угол между нормалью к элементу контура А
и осью абсцисс (рис. 12,41),
Зная уравнения кривой контура х—x(s), у=у($},
а также заданные иа контуре напряжения on(s)
и xn(s), можно определить из (12.83) о — о(з) и тр —
= ф(4):
о (s) = tjn (s) + тт sin 2 (ср — а);
1	тй (s)
<р (s) = « (s) ;£ — — arccos —— + тл.
(12.84)
Зуесъ т — произвольное щ лое число, а под арккосину-
сом понимается его главное значение. Знак выбирается
исходя из конкретных механических условии задачи.
В частном случае, когда на контуре с» —0, вмесго
(12,84) получаем формулы
<р (s) = a (s) ±	+ тл;
4
a (s) =	(з) зр тт;
«I (s) = ап (s) + 2тт.
(12.85)
Для свободной прямолинейной границы (х — 0) имеем
а = 0 и (ь) =- с« (s) =0; следовательно:
л
Ф (з) =± ~~ + тл; о (з) •= у тт;
ох = 0; Оу ~ = гр 2тт.
По полученным величинам граничных значений ср(.з)
и о(з) переходим к параметрам §(з) и i](s) с помощью
вторых равенств (12.81) и (12.82).
Параметры | и q, сохраняющие постоянное значение
вдоль линий скольжения, вообще говоря, изменяются
вдоль граничного контура.
12.7,7, Напряжения под жестким штампом
На рис, 12,42 показаны штамп и пластическая зона
вблизи его. Линия контакта штампа со средой предпо-
лагается симметричной относительно оси х и неизмен-
ной вследствие жесткости штампа. Она характеризуется
уравнениями
х = х (а) — х0; у = у (а).	(12.86)
Кривая контакта в месте пересечения с осью х может
иметь перелом. Свободная граница пластической среды
представляет собой горизонтальную прямую (а — 0).
Пластические перемещения предполагаются малыми.
Трение между штампом и средой отсутствует, т. е.
1» (з) =0.
На свободном участке границы
сгп (з) = -сп (з) = 0.
С учетом (12.85) можно записать:
<₽ (Д = ±	+ Ж
4	)	(12.87)
a (s) = Т тт. ]
Вдоль контакта T7!(s)=0, a o71(s) неизвестно; следо-
ВсИельно, вдоль линии контакта
а (5) = ПяИ + 'Ч»
Из последних формул видно, что линии скольжения
примыкают к граничной линии под углом л/4 как вдоль
контура, так и вдоль свободной границы. Предполагая,
12 7. ОСНОВНЫЕ УРАВНЕНИЯ ТЕОРИИ ПЛАСТИЧНОСТИ И ТЕРМОПЛАСТИЧНОСТИ
33
что вблизи свободной границы среднее давление имеет
огрицательиые значения, принимают для этой части гра-
ницы
ф(Д------— o(s) = — тт (я = 0).	(12.88)
т. е. в областях AGD и ВЕГ напряженное состояние
равномерное, В областях ADH и BFJ, в которых Е,—
— const ==|в, возникает центрированное поле, характери-
зуемое наличием пучков прямых, сходящихся в точках А
и В. Вдоль прямых AD и BF g = so и 1] = Цо, а вдоль
прямых АН и ЕМ g = g0, но Ч = ф-
В областях АСН и BCJ также 5 = 5о и имеются се-
мейства прямолинейных характеристик, а также семей-
ства характеристик, являющиеся продолжением характе-
ристик соседних областей. При подходе к лилии контакта
3
кривые этих семейств образуют о осью х угол а-|-—я,
4
Поэтому для линия контакта
Ф (s) = a (s) + л;
4
а(з) = оп (s) + гт.
(12.90)

а,, (s)	1	3
?{j)=^TOAJ.+	+в(5)+ л. (12.91)
2от	2	4
В то же время в областях АСН и BCJ
»	.	1л
ё = g0 ы — -—то-—- [см. формулу (12 89)].
Из сопоставления формул (12 89) и (12 91) следует
<j„(s) =~ — И (2 + л -ф 2а).
Равнодействующая давлений под штампом
“к
Р =-= 2 [ ап (з) Р (s) cos ackx,
«о
где В— радиус кривизны профиля штампа; а0 и ак —
начальное и конечное значение ц на концах профиля
штампа.
3—26
В случае плоского штампа а —0. Нормальное давление
на поверхности штампа составляет
оп = — тт (2 + п)
(решение Прандтля).
На рис 12 43 показано поле линий скольжения под
плоским штампом.
S 2.7.8. Плоское напряженное состояние
Напряженное состояние идеального упруго-пластиче-
ского тела в пластической стадии при плоском напряжен-
ном состоянии определяется, как и при плоской дефор-
мации, двумя дифференциальными уравнениям» равно-
весия и соответствующим условием пластичности,
например Сен-Венана (12.77) или Губера — Генки—1
— Мизеса (12.78).
Последнее выполняется, если положить
О; == 2тт cos ((о
л \
6 J ’
л \
о /
(12.92)
а2 — 2тт cos
где щ и а2—главные напряжения, а <а(х, у) — неизве-
стная функция (О ш 2л).
При этом
at = тт (Wees <о ф- sin и cos 29); I
= тт (Vs cos <а— sin а» cos 29); |	02. „3.
'My—'M sin ® sin 20,	I
Здесь 0 — угол между первой главной осью и осью абс-
цисс. Компоненты тензора напряжений ограничены
пределами
J | < 2тт; | ву ] < 2тт; | т^ I ч Д
Дифференциальные уравнения равновесия, выражен-
ные через введенные функции ы и 0, имеют вид
(/з sin оз cos 20 — cos <а) -—
? дх
, „да>	дв
3 sm со sin 29 —• — 2 sin ш — ~ 0;
дг/	ду
(12.94)
'Уз sin со sin 20 —- —
34
РАЗДЕЛ 12 УРАВНЕНИЯ И ФОРМУЛЫ ТЕОРИИ УПРУГОСТИ, ПЛАСТИЧНОСТИ И ПОЛЗУЧЕСТИ
— (У.З sin to cos 20 4- cos to)
Условие пластичности возьмем по .Мизесу:
(12 94)
°, °е+ ег£ = Зт~.
(12.97)
4- 2 sin to — = 0.
dx
При — < to < — или — <o -------------система (12.94)
6	6	6	6
л	5	7	11
гиперболическая; при со ==— , ~~р л, -—л, — л
6	о	о	6
— параболическая; при 3—4cos2<o<0 эллиптическая.
Если система (12 94) является гиперболическом, то
уравнения семейств характеристик а и Д принимают
соответственно вид
дц
у—= tg(0 —ф),
с)х
ди
7“ = tg (6 + Ф),
дх
Q (со) — 0=const = 1;
Q (to) 4- 9 = const м г;.
(12.95)
Здесь
га
1	С I (to)
2	(<в) = — — I--------------da,
2 J sin to
л
6
--------- cfg Щ
4 cos2 © ; 2ф = л —' arccos ~—ущ-
Линии характеристик пересекаются под углом 2ф
и образуют неортогональную сетку кривых, не совпада-
ющих с линиями скольжения.
Если система уравнений (12.94) параболическая, то
S(to)==0 и Я(ш)= 0. Вдоль каждой характеристики
угол 0 постоянен. Уравнение одного из семейств харак-
теристик записывается в виде
2/ = xtg(0—-ф) + Ф(0),
где Ф(0)—произвольная функция, определяемая из
граничных условий:
5	11
ф — 0 при и = —- я и — л;
6	6
л	1	7
ф = — при со — — л и — л.
1	2 г 6	6
Вдоль каждой характеристики напряжения постоянны.
При небольших давлениях р в упругой стадии работы
в пластине возникает напряженное состояние чистого
сдвига. Пластическая деформация появляется на краю
отверстия при р = тт. При Д>тт пластическая дефор-
мация возникает в зоне	где с — подлежит оп-
ределению.
Для напряженного Состояния в пластической зоне
справедливы уравнение равновесия (12,96) к условие
пластичности (12.97).
На границе пластической и упругой зон, т. е. при
г —с, должно быть о,—а = от.
и
Положим
аг = 2тт cos
Од = 2т cos со — —
0 т I 6
и подставим в уравнение равновесия (12.96).
В результате получим уравнение
(УТ4- etg to) da 4- 2 -у = 0.
я
Решение этого уравнения при ® = —р~ и г = с дает
12.7.9.	Пластические деформации вблизи
круглого отверстия в пластине
С V
— = е
sin to
Пусть в пластине имеется круглое отверстие, по краю
Которого приложено равномерно распределенное дав-
ление р (рис. 12 44). Эта задача осесимметричная и ре-
шается в полярных координатах.
Уравнение равновесия имеет вид
dar ar ~~
dr	г
(12.96)
где оу и а, — радиальное и тангенциальные напряжения.
6
л
Полагая здесь г = а, получим <оа >- ~ при данной вели-
чине с. Давление по краю отверстия р==ог находится из
/	я \
формулы Or = 2ТТ COS СОД”-----При (i)=toa.
'	6 /
При увеличении давтения со., растет и достигает зна-
5
чения coa = ~g”я п₽и максимальном значении Дьикс =
= 2тт.
12.7. ОСНОВНЫЕ УРАВНЕНИЯ ТЕОРИИ ПЛАСТИЧНОСТИ И ТЕРМОПЛАСТИЧНОСТИ
35
12.7.10. Упруго-пластическое кручение
В случае чистого кручения стержня из идеального
упруго-пластического материала напряженное состояние
в пластической стадии (так же, как и в упругой стадии)
удобно представить с помощью мембранной аналогии
Прандтля. Вводится функция напряжений соотноше-
ниями
Крутящий момент, воспринимаемый стержнем с круг-
лым сечением в упруго-пластической стадии,
Ж = (4ДЭ — д3) тТ)
6
где а — радиус упругого ядра сечепия.
^хг —
дер
ду"’
Чуг = -
дер
дх
при этом дифференциальные уравнения равновесия удов-
летворяются тождественно. Крутящий момент, возника-
ющий в стержне, М = 2 i epdF, т. е. равен удвоенному
F
объему, ограниченному поверхностью функции <р (по-
верхность мембраны) и плоскостью поперечного сечения.
В пластической стадии кру-
чения поверхность ср представ-
ляет собой поверхность равно-
го ската (рис. 12.45), так как
касательные напряжения, рав-
ные тангенсу угла наклона
плоскости, касательной к по-
верхности функции напряже-
ний, в пластической стадии ра-
боты всегда равны тт.
В табл, 12.4 приведены предельные крутящие момен-
ты, воспринимаемые различными сечениями в пластиче-
ской части работы Мпп. Для сравнения в этой же таб-
лице помещены крутящие моменты Муп, соответствую-
щие упругой стадии работы стержня к началу появления
пластических деформаций в наиболее напряженных точ-
ках сечения. В табл. 12.4 введены обозначения: Q — пло-
щадь, ограниченная срединной линией замкнутого профи-
ля (рис. 12.46); а—коэффициент, приводимый в спра-
вочниках для различных отношений Ь/а.
В случае тонкостенного поперечного сечения стержня
с переменной толщиной стенки 8 пользуются той же
формулой, что и при 6 = const, вводя минимальное зна-
чение биин-
При упруго-пластической работе стержня, когда не все
его сечение перешло а пластическую стадию работы, для
упругой части сечения следует применять дифферен-
циальное уравнение мембраны
Рис. 12.46
Относительный угол закручивания определяется по уп-
ругому ядру сечения
aG
12.7.11. Пластическое кручение стержня
с растяжением
а) Круглый цилиндрический стержень. В поперечном
сечении действуют только напряжения az, xxz и xyz.
Условие пластичности по Губеру — Генки — Мизесу име-
д2<р д2<р
—- 4-—ж- = 20'0,
ду2
где 0'— относительный угол закручивания.
Для пластической зоны следует применять поверхность
равного ската.
Рис. 12.47
ет вид
°1+3 ( < М т|2) -	(12.98)
по Сен-Венану
«г + 4 [ С +	=“ V
Плоские поперечные сечения в
процессе деформирования остают-
ся плоскими, поворачиваясь по-
добно жестким дискам вокруг оси
стержня. Продольная деформация
е.== const.
Используя зависимости между
Тхг и Тцг и соответствующими де-
формациями упруго-пластического
тела, а также между сдвигами и
относительным углом закручива-
ния 0', с учетом условия пластич-
ности, например (12.98), получим
значения напряжений в сечении:
Т а б л и ц а 12.4
м	Типы сечений					
	круг радиуса /?	квадрат дХо	прямоугольник аХ b (Ь а)	тонкая полоса дхй-	кольцо (наружный радиус—внутрен- ний радиус—г)	тонкое кольцо и тонкое замкнутое сечение
пл	— ЛЯ3Т 3	1	1	— я! (ЗЬ - а) те 6	т		~ Л (R-’ - Ы) тт	2£ЖТ
«УЧ	— л№те 2	г	0,209 а»Чт		у-	~ (Rt _ zS) т 2R	2£ЖТ
3*
36
РАЗДЕЛ 12 УРАВНЕНИЯ И ФОРМУЛЫ ТЕОРИИ УПРУГОСТИ ПЛАСШЧПОС Ш И ПОЛЗУЧЕСТИ
Здесь г — расстояние рассматриваемой почки сечения до
центра сечения;
Эпюры ог и г приведены на рис 12 47 Соответствую-
щие этим напряжениям предельные значения продоль-
ной си ы и крутящего момента равны
(12.99)
Определив из выражения для А’цр
ИА-Пу	- - пр
А пр
и подставив в выражение для А4цр, получаем уравнение,
связывающее предельные значения Афр и Maj>:
С
27ло„
3 о» ни-

где Wan=~—л/?3 — пластический момент сопротивления
3
при чистом кручении
Предельные”зиачения М и N по упругой стадии работы
стержня в момент достижения касательно! о напряжения
тт в наиболее напряженных точках находятся из урав-
нения
12Л43
л2 R4 а'4 л2 Rb а;
б) Тонкая полоса. Для тонкой полосы депланацчей по-
перечного сечения можно пренебрегать только для сдви-
гов yxz. С учетом этой особенности получены формулы
напряжений и уравнения, связывающие предельные зна-
чения А/др и Мир:
(12.100)
1

1
6Ьат
кГф
(12100)
В этих формулах А— толщина, Ъ — ширина пластинки;
у — измеряется в направлении толщины пластинки.
Уравнения (12 100) приводятся к виду
Уз	lz3^vnp
	Щ/2 ьр	
b--------------6Ьо 1
ли+^==
ф
Величина ф определяется пи Л'ар из первого уравнения,
а величина Л1др но ф и Л’ар — из второго уравнения.
12.8. ПОЛЗУЧЕСТЬ И РЕЛАКСАЦИЯ
12.8.1.	Основные понятия
Равновесные и неравновесные процессы деформации.
Равновесным состоянием тела называют такое состояние,
в котором тело может находиться неограниченно долго;
при этом размеры гола его гомпература и величины
внешних нагрузок, приложенных к нему, остаются посто-
янными Равновесный процесс деформации — это беско-
нечно медленный процесс, когда тело проходит через ряд
равновесных состояний, непрерывно вытекающих одно из
другого.
Есин процесс состоит из ряда неравновесных состоя-
ний, следующих одно за другим, то это будет неравно-
весный процесс. Пример равновесного процесса — упру-
гая деформация; пример неравновесного процесса — де-
формация ползучести
Равновесный процесс деформации может протекать
и в обратном направлении, т. е. равновесные процессы
обрапмы Неравновесные процессы необратимы. Следо-
вательно, процесс ползучести необратим.
Квазиравновесные процессы. Упругая деформация
и вязкое течение. Равновесный процесс деформации твер-
дых упругих тел является примером обратимого процес-
са Такого рода процессы в случае малых деформаций
и линейной связи между напряжениями и деформациями
изучаются в классической теории упругости. Близкими
к ним являются почти равновесные или квазиравновес-
ные процессы деформации.
Если Же рассматривать тело в состоянии текучести, то
его сопротивление воздействию сдвигающих сил опреде-
ляется не деформациями, а характером изменения ско-
ростей деформаций Такие сопротивления называют вяз-
кими сопротивлениями.
12.8. ПОЛЗУЧЕСТЬ И РЕЛАКСАЦИЯ
37
Большая часть строительных материалов, обладающих
аморфной структурой (или имеющих аморфную фазу
в своем составе), проявляет одновременно свойства уп-
ругости и свойства текучести. К таким материалам от-
носятся, например, бетоны, смолы и др. В зависимости от
длительности наблюдения процесса деформации упруго-
вязких тел на первый план выступает свойство либо уп-
ругости, либо текучести.
12,8.2.	Релаксация
Представим себе стержень из упруго-вязкого материа-
ла, сжатый двумя продольными силами Р до некоторой
определенной величины относительной деформации
А/
в== — , где I—’Первоначальная длина стержня; А/—
укорочение, вызванное силами Р. Подобное состояние
деформации стержня будет состоянием неравновесным,
и для поддержания деформации в, неизменной во вре-
мени, необходимо постепенно снижать силы Р, Этот
процесс уменьшения величин внешних сил (или напряже-
ний) при неизменности во времени вызванной ими де-
формации называется релаксацией.
Время, в течение которого внешние силы (или напря-
жения) ослабевают в е = 2,72 раза, называется време-
нем релаксации.
Простейшая релаксационная теория упруго-вязких тел
(теория Максвелла) дает закон деформирования в виде
уравнения
dv	dya dyn	1	do	а
dt	dt	'lit	G	dt	ц	'	’
Здесь G— модуль сдвига; ц — коэффициент вязкости
по Ньютону; и у,. — соответственно обратимая (упру-
гая) и необратимая части деформации сдвига. В основе
закона (12.101) положена линейная зависимость (Гука)
упругой деформации от напряжения и линейная зависи-
мость (Ньютона) скорости деформации ползучести от
напряжения.
dy
При остановке деформации ~~ =0, и, следовательно,
at
1	do	о	JPp
— .—-==О, откуда а=а0 е л , т. е. напряже-
G	dt	Jj
иие а снижается с течением времени (релаксация) по
экспоненциальному закону (рис. 12.48). Время релаксации
~ Т]
в данном случае равно f — ~—1 . В табл. 12.5 приведены
G
данные о коэффициентах вязкости в пуазах (1 пз—
— 1 дн-сек/см2) и времени релаксации для некоторых ма-
териалов.
Максвелловская теория является наипростейшей из
возможных В более общем случае уравнение, описыва-
ющее поведение упруго-вязкой среды под нагрузкой,
представляется в виде
dn а	dn-i a
df‘	dt"-1
__ gft	gog
dtk
или даже в виде нелинейных соотношений между раз-
личными производными напряжений п деформаций по
времени.
Табл и ц а 12.5
Материал
Асфальт при 20° С ...........
Лед .........................
Исландский шпат при 18° С . . .
Зеленогофенский известняк . . .
В /23
* в сек
время
Рис, 12.48
Рис 12,49
12.8.3.	Ползучесть
Под термином «ползучесть» обычно понимают нерав-
новесный процесс развития деформаций материала во
времени без увеличения нагрузки. В зависимости от ве-
личины приложенных сил деформация ползучести либо
стремится к некоторой постоянной величине, либо не-
ограниченно увеличивается вплоть до разрушения. Пола-
dy ов
гая в (12.101) о=Оо=const, получим ~	, от-
ер,
куда у = фо + — А Таким образом, деформация ползу-
чести материала, подчиняющегося уравнению (12.101),
а0
происходит с постоянной скоростью “ . На рис. 12.49
Рис. 12.50
дана типичная диаграмма
ползучести. Как видно из
рисунка, процесс ползучести
можно разделить на три ста-
дии. Первая стадия харак-
теризуется переменной ско-
ростью деформации ползу-
чести (неустановившаяся
ползучесть), вторая — по-
стоянной скоростью (уста-
новившаяся ползучесть).
третья — резким нараста-
нием скорости деформации ползучести (стадия разру-
38
РАЗДЕЛ 12. УРАВНЕНИЯ И ФОРМУЛЫ ТЕОРИИ УПРУГОСТИ, ПЛАСТИЧНОСТИ И ПОЛЗУЧЕСТИ
Явление отставания деформации от напряжения назы-
вается последействием. Если напряжение растет быстро
(неравновесный процесс), то полная деформация, соот-
ветствующая конечному напряжению, наступит спустя
некоторое время. То же явление наблюдается при раз-
грузке. На рис. 12,50 отражены один процесс нагруже-
ния и один процесс разгру-жи, На рис. 12.51 участки Д
II и III соответствуют деформациям под действием сил
РА <_Pg <Рв, приложенных в моменты времени Д, Б
и В. Участки IV, V и VI соответствуют мгновенной раз-
грузке.
12.8.4.	Особенности процесса ползучести
некоторых строительных материалов
а)	Ползучесть гипса. Гипсовые конструкции, хорошо
работающие в воздушно-сухом состоянии, обнаруживают
ползучесть при увлажнении. На рис, 12.52 показаны ти-
пичные кривые ползучести
гипса. Они получены на ос-
новании изучения изгиба
гипсовых призматических
брусков постоянного сече-
ния. Кривая I относится к
Рис. 12.52
Втивеительное сжатие,%
Рис. 12.53
работе образцов в воздухе. В этом случае деформация
остается постоянной, т. е. ползучесть отсутствует. Кри-
вая II относится к случаю ползучести при обильном
смачивании образцов водой и кривая III— при смачи-
вании их 10—30% водным раствором СаС%.
б)	Пластичность и ползучесть каменных материалов.
Хрупкие каменные материалы обнаруживают способность
к значительным пластическим деформациям и деформа-
циям ползучести в условиях высокого всестороннего сжа-
тия. На рис. 12.53 показаны кривые деформации песча-
ника при всестороннем сжатии. Исследования показыва-
ют, что механизм и характер пластической деформации
каменных материалов отличаются от механизма и харак-
тера пластической деформации металлов.
в)	Ползучесть дерева. Величина деформации дерева
в высокой степени зависит от продолжительности дейст-
вия нагрузки. Если приложенные напряжения не превос-
ходят известных пределов, деформация ползучести иосит
затухающий характер; в противном случае опа нараста-
ет со временем вплоть до разрыва (рис. 12.54). На
рис. 12.55 показано изменение со временем деформаций
упругого последствия в опыте с изгибом деревянного
бруска.
Отмеченные особенности процесса ползучести некото-
рых строительных материалов имеют весьма важное зна-
чение, так как они показывают, что процесс ползучести
зависит не только от свойств самого материала, но и от
условий среды, особенностей нагружения и т. д.
Рис. 12.54
12.8.5.	Реологические модели
Законы деформации различных сред можно иллюстри-
ровать посредством простых механических или, как их
в настоящее время называют, реологических моделей.
Деформация чисто упругой среды, подчиняющейся за-
кону Гука о —Ее., иллюырируется деформацией пружи-
ны (рис. 12.56). Деформация вязкой среды, подчиняю-
сь
щейся закону Ньютона о — 1) —, может оыть проиллю-
cll
стрироваиа при помощи модели, состоящей из поршня,
двшающсгося в цилиндре с вязкой жидкое 1ью
(рис. 12.57).
12.8. ПОЛЗУЧЕСТЬ И РЕЛАКСАЦИЯ
39
Деформация жестко-пластического тела, которое при
напряжениях ниже предела текучести <гт совсем не де-
формируется, а при напряжениях, большил sy, переходит
в состояние течения, может быть проиллюстрирована при
описываются некоторыми интегральными соотношениями,
К такого рода средам принадлежит, например, среда
Больцмана, деформация которой описывается уравнением
t
a (t) ~ Ее (t) + f ф (t — т) е (т) йт.
о
12.8.6. Теории ползучести
Рис. 12.63
Рис. 12.64
помощи модели, состоящей из двух пластинок, по пло-
щади контакта которых развивается кулоново трение
(рис. 12.58),
На комбинациях этих исходных моделей можно иллю-
стрировать процессы деформации сред, обладающих бо-
лее сложными свойствами чем упругая, вязкая или же-
стко-пластическая среда. Так, модель на рис. 12.59 изоб-
ражает упруго-пластическую среду; на рис. 12.60 пока-
зана модель упруго-вязкой среды, деформация которой
описывается уравнением
а = £е 4- п —
di
Если тело, расположенное в среде с постоянной темпе-
ратурой, находится в равновесии под действием прило-
женных к нему сил, то между возникающими в теле на-
пряжениями а, деформациями в и температурой Т долж-
ны существовать соотношения ф(<т, в, Т)=0, называемые
уравнениями состояния. Примером уравнений состояния
являются уравнения, выражающие закон Гука в теории
упругости.
Связь между всеми переменными, входящими в урав-
нение состояния: напряжением, деформацией, скоростя-
ми их изменения и временем, устанавливается на основе
той или иной принятой гипотезы, в зависимости от кото-
рой и различаются существующие теории ползучести.
Теория упруго-вязкого тела. Эта теория рассматривает
среды, обладающие упруго-вязко-пластическими свойст-
вами. В общем виде уравнение состояния таких сред име-
ет вид
/ц Е '^18 ~f” Ее йдСТ -р Е,: а = 0,
где kt —реологические параметры. В работах [9 и 18]
рассмотрено это уравнение в виде закона линейного де-
формирования упруго-вязкого тела:
Ег-ЕТ-рЕ^ё^а+Т^а, (12.102)
Т|
где Tv~—~———-—время релаксации; т; — коэффициент
£1 + Es
вязкости; Ei — начальный модуль упругости, характери-
зующий мгновенную деформацию; Е2—модуль эласти-
ческой (упруго-вязкой), развивающейся во времени де-
формации; с = ------— —конечный модуль упругости,
+ £«
характеризующий конечную, предельно длительную де-
формацию.
Из (12.102) при а = const получается закон деформи-
рования (последействия) в виде
__t__
е (t) —	— (ек е0) е п 5
Модель на рис. 12.61 изображает среду, деформация
которой подчиняется уравнению Максвелла:
de	1	da	а
— = — • -—4-—ж
di	Е	dt	т)
На рис. 12.62 показана модель, изображающая вязко-
пластическую среду; на рис. 12.63—’Модель среды, де-
формация которой описывается уравнением
<7
где ев = ~ ' конечная, стабилизировавшаяся деформа-
с
о
t-ч-оо); е0= — —начальная мгновенная де-
£1
£j л
(при 7 — 0); Уп = Трвремя после-
т. е. время, за которое разность sK-—е0 умеиь-
ция (при
de
£1е + TJi —~ =
dt
da
dt
формация
действия,
шается в е = 2,72 раза.
Из (12.102) при е — const получается закон релаксации
Деформация среды с более сложной структурой изо-
бражается моделью, показанной на рис. 12.64, и т. д.
Можно рассматривать также модели сред с непрерыв-
ным распределением параметров, характеризуемых одно-
типными элементами. Законы деформаций таких сред
а/ -=	+ (а0 — ок) в
где ffo = £i8 — начальное напряжение (при 7=0); ок =
— Ее — конечное напряжение (при 7-*оо); Гр — время
релаксации.
Частными случаями уравнения (12.102) являются бо-
4Q	РАЗДЕЛ 12, УРАВНЕНИЯ И ФОРМУЛЫ ТЕОРИИ УПРУГОСТИ. ПЛАСТИЧНОСТИ И ПОЛЗУЧЕСТИ
лее простые законы —закон Гука, закон Ньютона, урав-
нение релаксации Максвелла (12.101) я др.
Теория упрочнения. Эта теория предполагает наличие
функциональной зависимости между деформацией, ее
скоростью и напряжением:
ф (г, 8, <т1 — 0.
Указанная зависимость исходит из подобия кривых
ползучести (упругая деформация обычно не учитывает-
ся) и принимается в виде
.	/ (а)
8П — г , Г' >
Ь 18п)
гае е-в — деформация ползучести, а вид функций /(ст)
и /?(еп) принимается различным.
Так Ф. С, Чуриковым и Ю Н, Рабогновым предложено
F (8П) = f (ст) = аеь , откуда
о — b In —------ при l?8a! а,
a
а =-= 0	при |88а! < а.
При о = const
i	п 1
еп = [о (а + !)c+1 exp [ —,
! b (а -+ i) J
где а, а, с, b — параметры
Уравнение релаксации в данном случае имеет вид
। р	ab—a
о (t) =—— ! (о0--с>)е b da.
аЕ'^л J
п
Теория течения. По этой теории уравнение состояния
имеет вид ф(о, в, () =0. Принимая, что полная скорость
деформации складывается из скорости упругой деформа
ции t,v и скорости деформации ползучести ея, получим
8 Г) = П + 8П.
Скорость упругой деформации
Скорость деформации ползучести при подобии кривых
ползучести можно определить как произведение функции
напряжения F{a} и функции времени х(():
?1J = F(a)x(f),
В теории ползучести часто применяется зависимость
F(o)=0n; тогда
„	1 da
г = ст"х (() + —  — -
b at
При большом значении t или при пренебрежении зату-
хающей деформацией	— согЫ. Уравнение ре-
лаксации по теории течения записывается в виде
1
ст = стД1 + о -1)	<о]
где ао — начальное напряжение, а
г
— \n(i)dt
b
Теория старения. По этой теории время явно входит
в уравнение состояния:
ф (о, е, /) = 0.
Рассматривая деформацию как сумму упругой де-
формации и деформации ползучести имеем
е(ф = еу + еВ!
а
где 8у = — , a gn — некоторая функция напряжения и
времени, например, если кривые ползучести подобны, то
можно принять
вп И) = F (о) «W
При степенной зависимости между напряжением и де-
формацией полная деформация
8(!) = -^ + <j«Q(/).
Функция Я (7) отражает изменение свойств материала
во времени, его старение. Отсюда и название теории
Уравнение релаксации по теории старения
а9 = а + a”EQ (t).
Линейная теория наследственной ползучести. Теория
наследственной ползучести исходит чз того, что дефор-
мация в данный момент времени зависит не только от
величины напряжения в этот же момент, но и от истории
предшествующего деформирования При этом учет пред-
шествующих деформаций производится на основе прин-
ципа суперпозиции (наложения).
Уравнение состояния в теории наследственной ползу-
чести имеет вид
t
a (t)	f
е (/)=———+ I f( (t — т) а (т) dx, (12.(03)
Co	J
0
где первый член правой части отображает мгновенную
деформацию е9 в момент ф вызванную напряжением о(/),
а второй член — развивающуюся во времени деформа-
цию. вызванную переменным во времени напряжением
ст(т).
Разрешив уравнение состояния относительно напряже-
ния а, получим
ст (!) — £’о8 (!) — j R (t — т) 8 (т) dx, (12,104)
о
где первый член отображает начальное напряжение в мо-
меш t, а второй — изменение напряжения во времени
при изменяющейся во времени деформации е
При o = const уравнение ползучести по данной теории
имеет вид
t
при 8 = const получаем уравнение релаксации
t
o(t) =8[£0- |>(!)а!].
12 8, ПОЛЗУЧЕСТЬ И РЕЛАКСАЦИЯ
41
Функция К(б—т) в (12 103) --ядро ползучести— ха-
рактеризует влияние на деформацию в момент t нагруз-
ки, приложенной ранее, в момент т; функция R(t—т)—•
ядро релаксации — характеризует влияние па напряже-
ние в момент t деформации, возникшей в момент т.
Рис. 12.65
в)
Дифференцируя уравнения (12 103) и (12 104), полу-
чим
Л'(0 = “
о
d?
dt ’
R (t) = -
8
da
Id '
Следовательно, функция K(t)—есть скорость деформа-
ции при о = 1; функция R(t)—напряжение, необходи-
мое для поддержания деформации е=1. Функция А'(1)
может быть определена по кривой скорости деформиро-
вания при o=const, a R(t) —по кривой скорости релак-
сации при 8 = const.
Уравнения наследственной ползучести отличаются боль-
шой общностью и при соответствующем выборе ядра
K(t) приводятся к рассмотренным выше законам ползу-
чести.
Нелинейная теория наследственной ползучести. Учет
нелинейной зависимости между о и е достигается введе-
нием в уравнения (12.103) и (12.104) не самих напряже-
ний и деформаций, а их функций У(о) или <p(s), харак-
теризующих связь между а и е. В зависимости от вид.э
семейства кривых о—8 могут иметь место три случая,
1) Кривые а—е для разных t не подобны, каждая из
них описывается своим законом ф,(е) (рис. 12.65, а).
Уравнение для напряжений имеет вид
t
о (t) -= ф0 [в (г!)) — [ R (о; /— т) о (т) 4т;
о
уравнение для деформаций
г
е (0 — [а (£)] + (О (о; / — т) f fa (т)] dx.
о
Здесь фо(е)=ао н /=0(о) = в0—мгновенные напряжения
и деформации. В частности, при степенной связи между
напряжением и деформацией функции ср(е) и /(о) могут
принять вид
I
Ф (е) = Aft”1; f (о) = j ',!i.
2) Кривые а—в подобны для всех моментов времени,
за исключением начального (рис. 12 65, б). Функции
Ф(е) и ((а) имеют два значения: if0(e) и (п(<т) при 1=0;
<р(в) и f(a) при 0<t<oo. Сравнение для напряжений
принимает вид
t
о (0 = Фо [s (01 — )’ R (t — т) Ф [8 (T)j фт;
о
уравнение для деформации
t
8 (0 = (0 (о О + f Q (1 - Т) / [О (Т)] dt.
о
Здесь
da 1	de 1
R (t — т) = —--------------; Q (t — t) =-------•-------- .
x J dt cf(s) ’	’ dt f{a)
3) Все кривые о—e для любого	являются
взаимоподобными, т. е описываются единой функцией
<;(₽) (рис. 12,65, в). Уравнение для напряжений имеет
вид
t
о (t) = ф [е (!))•— f А (/ — т) Ф [е (т)( dt. (12 105)
о
Это уравнение можно разрешить относительно ф(е):
t
Ф [е (ЛИ — о 4)4 ( К (I — х) а (т) dx. (12.106)
"о
При o^const и в— const уравнения (12,105) и (12.106)
принимают соответственно вид
сф) = Ф(8) [1 — [ A (t)dtj;
0
f
ф [« (01 = а U 4 Г 4 (0 Л].
о
12.8.7.	Наследственная теория ползучести
бетона Н. X. Арутюняна
В основу этой теории положены три предпосылки:
1) рассматриваемый материал однороден и изотропен;
2) деформация и напряжение связаны между собой ли-
нейной зависимостью; 3) для деформации ползучести
принимается закон наложения. Вторая предпосылка для
ряда материалов справедлива при напряжениях, не пре-
вышающих примерно половины предела прочности мате-
риала. Построенная на этих предпосылках теория ут-
верждает, что если на сооружение действуют только
внешние силы, то напряженное состояние в элементах
сооружения при некоторых условиях (если коэффициент
поперечной деформации ползучести цп равен коэффици-
енту упругой поперечной деформации р.у и Кп = р.у =
=const) остается неизменным и при наличии в них явле-
ния ползучести. В этом случае ползучесть не меняет на-
пряженного состояния, а влияет только на деформации
сооружения. В задачах подобного типа обычные методы
строительной механики позволяют учесть влияние пол-
зучести. Необходимым условием этого является следую-
щее: относительная деформация ползучести C(f, т) от
единичной нагрузки при одноосном напряженном состоя-
нии (мера ползучести) должна быть пропорциональна
деформации ползучести <а(), т) при чистом сдвиге, т. е.
С (t, т) =-|- a(t, т),
Е
где t—момент времени, в который определяется дефор-
мация; т — возраст бетона в момент загружения, Е и
42
РАЗДЕЛ 12 УРАВНЕНИЯМ ФОРМУЛЫ ТЕОРИИ УПРУГОСТИ ПЛАСТИЧНОСТИ И ПОЛЗУЧЕСТИ
G — соответственно модули упругости мгновенной дефор-
мации и сдвига
Если же напряжения изменяются вследствие цефор
мании ползучести, то последняя сказывается и на напря
женном состоянии и на деформациях Н X Арутю-
нян [1] составил уравнение упруго ползучей среды счи
тая, что закон изменения меры ползучести бетона мо
жет быть представлен следующим выражением
C(t, т) = /со+ [1	,	(12 107)
\ т ]
где Со—предельная мера ползучести при Л{ и
у — постоянные
С учетом этого закона изменения C(t т) (подтверж
дающегося экспериментами) получаются следующие
уравнения для напряжении
t
*	С « д г 1
+ С(г?э т) Lk (t = 1Э 2, 3),
i
С д
aik (о = ал W + W д~ ° « X
,/	О’ ь
’(12 108)
X 4-и(т)1 dr
[б (г) J

!
где Oik(t)—напряжения для упруго мгновенной задачи
Для случая изменения C(i, т) по закону (!2 107) и при
условии что модуль мгновенной деформации £(т) изме
няется во времени незначительно так что его можно
принять постоянным, уравнения (12 108) приводят к
решению
.	Г /А 1
°« (0 = аи (Ь) 1 - ?£о — + со X
L	\Т1	/
f ___
Хт’Д1 f *
• ' -Д
(12.109)
Задачи термоупругого состояния с учетом ползучести
разбивают на три этапа 1) определение температурного
поля, 2) решение термоупругои задачи, 3) определение
напряженного состояния с учетом ползучести бетона
Для определения напряжения в любой момент време
ни представим уравнение (12 109) в виде
°li (Д) Я1 (X П)> где

X [Ф(Д,р) —Ф(гд,р)] —
коэффициент затухания
Здесь приняты обозначения Оц(т) — термоупругое на-
пряжение в теле для данного температурного режима,
£о — модуль мгновенной деформации, г = у(1+£оСо) —
параметр, характеризующий с физической точки зрения
ползучесть бетона в старом возрасте, р=уА1£0— пара
метр, характеризующий меру ползучести бетона в моло
Таблица 12 6
Время в днях	Возраст оетоиа т, в днях						
	7	14	28	45	60	90	360
7	1						
14	0 584	1	,	.									
28	0 25	0,47	1				—	_—
45	0,134	0,297	0 487	1			—	—
60	0 105	0,252	0 259	0,535	1	—	——
<ю	0 092	0,232	0 301	0,323	0 334	—	_—
130	0 092	0,232	0 301	0,323	0 334	0,34	1
—	0,092	0,232	0 301	0,323	0 334	0,34	0 355
дом возрасте, Со = lim C(t, д)— предельное значение
меры ползучести для данного материала, Aj и у —опыт-
ные коэффициенты, характеризующие интенсивность из-
менения меры ползучести бетона, необходимые для опре-
деления С (7, Т]) по формуле
С(1, Д) = [се +	[1 -	Ч.
Функция Ф(е, р) определяется по формуле
Ф(й, р)
Значения этой функции протабулированы и приводят-
ся, например, в [6]
В приводимых ниже примерах приняты следующие ха-
рактеристики бетона (по данным экспериментальных ра-
бот)
А1 = 4,82-10~®, Со = О,9-Ю~®, у = 0,026;
£0 = 2-10® кГ/см\ р = 0,25, г = 0,073.
Для этих постоянных коэффициент затухания (t, ri)
приведен в табл 12 6
Пример 12.3. Определить напряжения в толстой бетон-
ной плите при возрасте бетона д=7 дней (рис 12 66),
торцы которой не могут перемещаться, т е «1 и «2 рав-
ны нулю Плита равномерно нагревается от нуля до
Т = 25° С
В данном случае термоупругие напряжения равны
,	£о®
Он (д) = <д2 (д) = — ------Т.
1 — Ц
Остальные напря/кения, как и перемещения «1 и иг по
осям 1 и 2 равны нулю Перемещение по оси 3 (и3)
равно
1 -т- ц m
«з ==а -----Г-
1 — р
где а — коэффициент линейного расширения для бетона
(а. = 0,000012), р, — коэффициент Пуассона для бетона
(р='/б) Тогда Оц (г,) =о22(Т|) = —43 2 кГ/см.2, а напря
жения с учетом ползучести бетона будут tJu(f) — Ozzit) —
= —43 2£/1(zl, тф В табл 12 7 приведены значения на-
пряжении для различных моментов времени
Пример 12 4 Бетонный брус, один конец которого за-
щемлен, а другой свободно оперт (рис 12 67), подвергает-
ся неравномерному нагреву, его верхние волокна имеют
температуру 77 = 15° С, а нижние— 7.2=5° С.
12 В. ПОЛЗУЧЕСТЬ И РЕЛАКСАЦИЯ
43
Таблица 12 7
Термоупругая задача для такого бруса известна при
следующем законе распределения температуры по высоте
сечения:
1 Г	2х I
7 = " [(7, + Тг) + (7Х - г2) Y] 
Максимальные напряжения по этому решению будут
в сечении х = 1, т. е. в защемленном сечении.
Напряжения по сечению будут определяться форму-
лой (для Т[>Т2)
3	2х
Он (И) = — — (Ti — 7г) аЕй .
4	h
Величины упругих и упруго-ползучих напряжений для
бетона в возрасте Т] = 14 дней соответственно будут
равны:
°имакс П1) = ± 36 кГ/сжг; о11макс(0 =
мин	мин
= +36Д.(7 14).
В табл. 12.8 приведены значения о+макс(0 Для различ-
МИН
ных моментов времени.
Т абл ица 12.8
Время в днях	14	28	45	60	90	ООО	3 года	со
мякс мин к Г [см1	±35	+17,25	±10,7	±0,1	±8,4	±8,4	±8,4	±8,4 	
Из таблицы видно, что уже к 90-му дню напряжения
за счет ползучести бетона уменьшаются более чем
в 4 раза.
12.8.8.	О ползучести металлов
Явление ползучести металлов и сплавов становится за-
метным при повышенных температурах. Так, для угле-
родистых сталей и чугуна ползучесть начинает сказы-
ваться при 300—350° С, для легированных сталей — при
350—400° С, для цветных металлов — при 50—150° С
и т. п.
Некоторые металлы, например свинец, испытывают де-
формации ползучести и при обычной комнатной темпе-
ратуре.
Расчет на ползучесть конструкций основан на резуль-
татах экспериментального исследования металла глав-
ным образом на постоянную нагрузку. На основании экс-
периментальных данных предложены многочисленные
формулы эмпирического и полуэмпирического характера.
Для установившейся стадии ползучести применяется
следующая зависимость между скоростью ползучести и
напряжением
еп= kon,
где k и п— коэффициенты, зависящие от температуры
испытания и свойств материалов [6].
Максимальное напряжение, не вызывающее деформа-
ций ползучести больше допускаемых для данных усло-
вий работы, называется условным пределом ползучести
материала по допускаемой суммарной деформации ползу-
чести.
Расчетное условие ползучести при одноосном напря-
женном состоянии имеет вид
е = 8у + % + % = е0 + kontc < [е],
f \
где еу — относительная упругая деформация! е =
£т — модуль упругости при данной температуре; еп и
£По — относительные деформации неустановившейся и ус-
тановившейся ползучести; [е] —допускаемая деформа-
ция за время службы конструкции; Д — срок службы
конструкции.
Деформацией неустановившейся ползучести (еп,)
иногда можно пренебречь. Тогда для <т получается урав-
нение
+ kantc = [ej.
*'т
Если пренебречь и упругой деформацией, то расчетное
условие принимает вид
»а I—
I Мс /
Пренебрегать упругой деформацией и деформацией не-
установившейся ползучести можно только тогда, когда
эти деформации малы по сравнению с деформацией уста-
новившейся ползучести.
12.8.9.	Ползучесть при изгибе балок
и кривых стержней
Рассмотрим некоторые задачи по расчету балки, сече-
ние которой имеет две оси симметрии, на изгиб для слу-
чая установившейся ползучести. Изгибающий момент
44
РАЗДЕЛ 12. УРАВНЕНИЯ И ФОРМУЛЫ ТЕОРИИ УПРУГОСТИ, ПЛАСТИЧНОСТИ И ПОЛЗУЧЕСТИ
действует в вертикальной плоскости уОг (рис. 12.68).
При решении задач установившейся ползучести считают,
что спустя известный промежуток времени после загру-
жения напряжения в сечении не изменяются и скорость
деформации постоянна.
Определим закон изменения нормального напряжении
по сечению и прогиба балки во времени. При решении
„	пренебрегают касательными напря-
жениями и предполагают справед-
ливость гипотезы плоских сечений.
М -
Ог= У п °
Для прямоугольного сечения
h
Рис. 12.69
Рис, 12.68
п
о
dy -=
2 п
2п
Следовательно, напряжения для бруса с
сечением будут
2пД- 1 /2*А.- 6Ж
о, =-------—.----------
Зп \ h bh3
Ь’п
прямоуг ольным
! Чистый изгиб (рис 12,69). Примем закон
в форме
ползучести
а.
dez V
где ~ — скорость деформации.
dt
Из условия равенства момента внутренних
сил
и внешних
h
4 f огуЬ [у) dy --= М,
(12.110)
6М
Величина —— равна максимальным упругим нормаль-
fl я-
ным напряжениям
УЬР гмакс
Следовательно, максимапьное напряжение установившей-
ся ползучести при чистом изгибе в брус,, с прямоугопь-
/	h \
ным сечением будет (полагаем у j
_ 2ft 1 ц
«гмакс — ‘ дя «гмакс*
Так как п всегда больше единицы, то о.
меньше Огмакс • Для малых прогибов
d3y
~~~ .
d’y
m __-----
всегда
а на основании гипотезы плоских сечений
at
на.111)
(12.111),
по t
предваритель-
и используя
Тогда
пг = А " (ту)" ,
пе т — скорость изменения кривизны
в рассматриваемом сечении.
Подставляя
(12.112)
изогнутой оси
(12,112) в (12.110), получим
М—mn k п!п,
(12.113)
где
й
!п = 4j b (у) у
dy.
Из (12.111)
и (12,113) следует
.	Мп
k—~y.
dt	In
(12.114)
выражение для т из (12 113)
в
(12.112),
Подставляя
получаем закон распределения нормальных напряжении
при чистом изгибе в случае установившейся ползучести:
dm
dz" ’ dt
dm
Подставив выражение для —- в
at
но продифференцировав (12 111)
(12.114), получим выражение для определения скорости
изменения прогиба балки при ползучести:
сРу [М \п
UJ
Интегрируя и учитывая граничные условия:
при г — 0 у =0;
I dy
при г = —----- = 0,
г 2 dz
получим величину полного прогиба в момент t (с учетом
упругого прогиба):
МР	Р	(М \п
у Н) =---- у---- k — t.
8Е/	8	\fn
(12.115)
2. Поперечный изгиб балки, загруженной сосредото-
ченной силой Р в середине пролета. Условия (12.115) бу-
дут такими же, как и при чистом изгибе. Максимальный
прогиб во времени определится по формуле (с учетом
упругого прогиба)
k
РР
ИмЗКС (0 ,.rr 4“	,, . I 1,
48£7	2'" (и+,) (я Д-2)
рар+-2
-------L
12 8. ПОЛЗУЧЕСТЬ И РЕЛАКСАЦИЯ
45
3.	Поперечный изгиб консольной балки, нагруженной
сосредоточенной силой Р на свободном конце. Гранич-
ные условия имеют вид:
/ бу
при г == —	= 0;
при г = I у - 0.
Максимальный прогиб во временя (с учетом упругого
прогиба) будет
рр р Рп 1п+“
Умякс (0 =----ГО -------- ------t-
нмакс I > ЗЕ1 ~Г п 2
4.	Поперечный изгиб балки на двух опорах с равно-
мерно распределенной нагрузкой интенсивности q. Бал-
ка выполнена из иикельхроммолибденовой ста ти и нагре-
та до Г=450°С. При этой температуре п==2.
_ _5_ дИ 299_ уЧ«
Гмаке (6 ~ Т84  £/ У 23070 М
5.	Поперечный изгиб консольной балки, нагруженной
равномерно распределенной нагрузкой интенсивности q:
qH l kqn l1 <П+1)
g£/ +	2„£J t-
12.8,10. Ползучесть при кручении
При решении конкретных задач кручения с учетом
ползучести применяется теория старения, основанная на
теории малых упруго-пластических деформаций, или
обобщенная теория вязкого течения.
Решения многих задач, в том числе и задач кручения
см, [9].
ЛИТЕРАТУРА
I, Арутюнян Н. X. Некоторые вопросы теории ползу-
чести. Гостехизлат. М. — Л , 195:2
2. Безухов Н. И. Основы теории упругости, пластично-
сти и ползучести. Изд-во «Высшая школа---, 1961.
3, Безухов Н. И. и др. Расчеты на прочность. устойчи-
вость и колебания в условиях высоких земператур. М-пигмз, 1965,
4. Вялов С, С. Прочность и ползучесть мерзлых грунтов
и расчеты ледогрунтовых ограждений. Изд-во АН СССР, 1962,
5. Го л ьд ен б л а т И. И. Ра счет и конпру прова нмс желе-
зобетонных балок. Госстройпздаг, ZM. — Л , 1940.
6, Гольденблат И. И,, Николаенко Н. А. Тео-
рия ползучести строительных материалов и ее приложения,
Стройиздат, I960.
7. Гол ь д ен бл ат II. И, и £о ппов В А, Обобщен-
ная теория пластического течения аниjoiропных сред. В сбл
«Строительная механика». Стройиздат, 1966,
7а. Г о л ъ д е и б л а т II. И. и Копнов В. А. Критерии
прочности и пластичности конструкционных материалов. «Маши-
ностроение», 1968.
8. И лью ш и п А. А. Пластичность. Изд-во АП СССР, ИКС,
9. Качанов Л М Теория ползучести. Фгвмтгнл, !С!6О.
Щ. Лейбензон Л. С. Курс теории упругости. ОГИЗ,
ГИТТЛ, 1947,
И. Ляв А. Математическая теория упругости ОНТИ
ЖГИ, М — Л.. ГМ5.
Г2. М а л и н и и Н, Н. Основы расчетов на ползучесть.
Мяшгю 1918,
13.	Миндлия Р. Д. Сборник переводов «Механика».
«Мир», М 1 {мн), мы
И. А1 у с х о л и ш в н л и И, И. Некоторые задачи теории
упругости. Пзд-во АН СССР, 1956.
15.	И е й м а н ДА. И. Напряжения в балке с криволинейным
отверстием. Труды ЦАРИ, А? 313, Л., 1937.
16.	П ипко в и ч П, Ф. Теория упругости. Оборонгиз. 1939.
17.	Р а б о I в о в Ю. Н, Ползучесть элементов конструкций,
«Наук,о , !9и6,
18.	Ржаницын А. Р. Некоторые вопросы механики сн-
егом. риформирующихся по времени. Гситехиздат. М. — Л., 1949,
19, С а в и н Г, Н. Распределение напряжений около отвер-
сгип. Ищ-вп «Нтикова дуиа», Киев. 1968,
у). Сборник статей «Гео.-гогня•>. НИЛ, М.. 1902,
21.	Ф и л о н о н к о~Б о р о д и ч М. М. Основы теории vnpv-
гт'ти Г-п'техизла г. 11)56,
22	Хилл Р, Математическая теория пластичности. ГИТТЛ.
1956.
РАЗДЕЛ 13
УПРУГИЕ ТОНКИЕ ПЛАСТИНЫ (ПЛИТЫ И БАЛКИ-СТЕНКИ)
13.1 ОБЩИЕ ТЕРМИНЫ, ОБОЗНАЧЕНИЯ
Пластиной (рис. 13.1) называют цилиндрическое тело,
толщина которого /z = const мала по сравнению с дру-
гими размерами (сторонами прямоугольника, диаметром
и т. д.). Плоскость, параллельную основанию и делящую
пополам толщину пластины, называют срединной плос-
костью. К тонким относятся пластины, у которых h не
превышает 0,2 наименьшего размера основания.
Рис, 13.1
Пластины, подвергающиеся изгибу, называют плита-
ми. Прямоугольные пластины, находящиеся в плоском
напряженном состоянии, называют балками-стенками.
От тонких упругих пластин следует отличать гибкие
плиты (плиты, у которых максимальный прогиб больше
VPi; методы их расчета изложены в разделе 18) и пла-
стины, в которых возможны пластические деформации
(см. раздел 21).
Приведенные критерии деления пластин на толстые,
тонкие и гибкие условны и могут быть использованы
в качестве первого приближения.
13.1,1. Основные обозначения
X, у, z—прямоугольные координаты (рис. 13.1, а);
плоскость ху совмещена со срединной плос-
костью пластины;
г, Q, г—цилиндрические координаты (рис. !3.1,б);
плоскость Г0 совмещена со срединной плос-
костью пластины.
Размеры (рис. 13.1), нагрузки (рис. 13,2)
h— толщина пластины;
Н—высота ребра;
а, b— размеры прямоугольной пластины, радиу-
сы круглой и кольцевой пластины;
Р— сосредоточенная сила;
М°х, Ai”, Л4® — сосредоточенные пары,, вращающие во-
круг осей х, у, г;
р— интенсивность нагрузки, распределенной
по площади;
р — то же, по линии;
тх, тг—интенсивность моментной нагрузки, рас-
пределенной вдоль линии и вращающей
вокруг осей х, г.
Рис. 13.2
Индекс у Р, р, р показывает направление силы. Так,
Рх, рТ означает, что Рх направлено вдоль оси х, а рГ—
вдоль радиуса.
Компоненты напряжений и усилий (см. рис. 13.2)
ах, суп т. д. — нормальные напряжения по площадке
с нормалями х, г и т. д.;
тлд> тег—касательные напряжения. Первый индекс
указывает направление напряжения,
а второй — нормаль к площадке, по ко-
торой действует напряжение;
Л'—нормальная (продольная) сила;
Q—поперечная сила (направлена перпенди-
кулярно срединной плоскости);
V—-приведенная поперечная сила или реак-
тивное усилие;
5— сдвигающая сила (расположена в сре-
динной плоскости);
Л1 — изгибающий момент;
Л1К—крутящий момент;
Н—сосредоточенная реактивная сила в уг-
ловой точке прямоугольной пластины.
Индекс у усилия означает направление нормали к еди-
ничной площадке, по которой действует усилие. Так,
например, Мх — изгибающий момент по площадке с нор-
малью х; Mhr — крутящий момент по площадке с нор-
малью г.
Перемещения
w — перемещения точек срединной плоскости
при изгибе по направлению оси г;
13 1. ОБЩИЕ ТЕРМИНЫ, ОБОЗНАЧЕНИЯ
47
»j,arHT. Л — перемещения точек срединной плоскости
при плоском напряженном состоянии по на-
правлению оси х, радиуса г и т. д.;
&х, fiy, —угол поворота при изгибе волокна, направ-
ленного вдоль оси х, у, г.
а) для ребер, расположенных симметрично относи-
тельно срединной плоскости пластины (см. рис. 13.3):
(и- -1- Ь“) sin 2а
2abh0 бс
(13.4)
Упругие константы и характеристики жесткости
б) дтя ребер, расположенных по одну сторону от
пластины:
Ег, Г.2, G—модули упругости;
р3, }‘-2—коэффициенты Пуассона;
Щ — 1 — д; А, — 1 -ф Л — 3 -ф д;
А; --- i -ф Зр; Л5 — 5 ~ф ц; А6 — 5 — Зд.
А, = 7 -ф Зщ
(13.1)
(а2 -ф b~) sin 2а
1^Мб~фмУ” '
Значения 6С и 6И в (13.4а) равны:
„	/ a b \
бс == 1,21 ——- -ф	I
\ Pi )
Fp —
(13.4а)
Et hs
Dt== ~~~7.-----—жесткость плиты (i=l, 2).
12(1— Pi pi2)
ah [ Ь i a
24 (1 -фу.) \ /nz Лг
(13.46)
13.1.2. Определение упругих характеристик
конструктивно ортотропных пластин
Пластины, усиленные часто поставленными ребрами,
Здесь Ан и Z2z —моменты инерции сечений ребер, парал-
лельных осям х, у относительно центральных осей, пер-
пендикулярных плоскости х, у.
Если конструкция состоит только из перекрестных ба-
лок, то в (13.2) следует положить h—Q, а (13.3) заме-
нить на
а также решетки, состоящие из перекрестных балок,
жестко сопряженных между собой, часто заменяют при
Go — Fp G.
(13.4в)
определении усилий и пере-
мещений эквивалентной ор-
тотропной пластиной. Ниже
приводятся формулы, по ко-
торым можно определить
упругие характеристики эк-
вивалентной пластины.
Предполагается, что рас-
сматриваемая конструкция
выполнена из изотропного
материала, характеризуемо-
го константами Е, д, G.
Обозначим толщину эквива-
лентной ортотропной пла-
стины йо. Она может быть
Если пластина усилена ребрами в одном направлении,
то в (13.2) следует положить либо Fь либо F2 равными
нулю, а в (13.3) принять йр=0.
Жесткости плиты при изгибе Di и Вг можно опреде-
лять по формулам
Phs .
12(1—фф a ’
Eh? , Ehx
12(1 — ц2) b
(13.5)
задана произвольно сооб-
разно с удобством расчета.
Следует иметь в виду, что замена действительной
конструкции эквивалентной пластиной неизбежно свя-
зана с неточностями при определении усилий и дефор-
маций в основной конструкции. Эти неточности резко
Здесь 71р и /2х —осевые моменты инерции сечений ребер,
параллельных осям х и у относительно центральных осей,
параллельных осям х, у.
Коэффициенты Пуассона можно либо принять равны-
ми нулю, либо определять по (13.2).
Жесткость при кручении для эквивалентной плиты D*
вычисляем по формуле [6].
пп СЛ3 , Лк
возрастают по мере увеличения расстояний между реб-
рами.
Для пластины, снабженной рядом перекрестных ребер
(рис. 13.3), модули упругости и коэффициенты Пуассона
эквивалентной пластины можно определять по фор-
мулам
где
S = 1
Д” 7щ (о7.2К — АЛк)
6/2к (a- Др -ф й- /ЗЛ)
(13.5а)
(13.56)
Здесь Цк и Hi; — моменты инерций сечений ребер, па-
раллельных осям х и у при кручепип, а 7ь, и /2-с—осе-
вые моменты инерции тех же ребер относительно цент-
ральных осей, параллельных осям х, у.
13.1.3. Связь между усилиями
где F] и F2 —'площади сечений ребер, параллельных осям
х, у.
Модуль упругости при сдвиге эквивалентной пласти-
ны Ga вычисляется по формуле [6]
G() =-= (1 -ф Ар) G.	(13.3)
Коэффициент Fp в (13.3) равен:
и напряжениями
а) Задача изгиба (г — расстояние точки от срединной
плоскости)
12г М
и ~ —-—-
* й3
!2zMt/
°У	' дз
(13.6)
48
РАЗДЕЛ 13 УПРУГИЕ ТОНКИЕ ПЛАСТИНЫ (ПЛИТЫ И БАЛКИ СТЕСКИ)
(13.6)
ц от р.т Для уточнения значений изгибающих моментов
можно применять приближенную формулу.
м1==
—— j(i — w\) м] + (и —	Ж|,
1 рт
(13.8)
б) Плоское напряженное состояние
Nx	Ny
=	= о2 = 0;
Sx _ Sy
txu - h h
(13.6a)
Для полярной системы координат индексы х, у, заме-
няются на г и 0.
13.2. ПРЯМОУГОЛЬНЫЕ ПЛАСТИНЫ
13.2.1. Прямоугольные изотропные плиты
Для расчета прямоугольных изотропных плит, опертых
одним из указанных на рис 13.4 способов, можно ис-
пользовать следующие формулы:
« Ро а*
10‘ ' D
3
Мх — ——- р„ а~;
103 f °
Y
Му= ~ Ро а~; Vx = ФА, а;
Уу=^рйа.
Здесь ро — максимальная интенсивность распределенной
нагрузки;
X
Кромка, свободно опертая на
жесткую опору
/Кесткд 'защемленная кромка
— Кромка, свободная от усилии
Рис, 13,4
a = at; |3 = р,; у=у<; <p==q>i; ф = ф,—коэффициенты,
используемые при определении значения прогибов или
усилий в указанной на схеме А (рис. 13.4) точке i;
а. = а1;, (3 = ^,3, у—— коэффициенты, используемые
при определении максимального из значений, которые
принимает прогиб или усилие на отрезке прямой с кон-
цами в указанных на рис. 13.4 точках i и /.
Все перечисленные коэффициенты определяются по
приведенным ниже таблицам или графикам. Таблицы
коэффициентов а, Д, у составлены при фиксированных
значениях pi=p,i. При значительном отличии заданных
где Д42 = Л1ю если Mi=-Mx и М2 — Мх, если Аф—ЛД;
<МТ— значение момента, определенное с помощью таб-
лицы.
При необходимости рассчитать плиту на нагрузку, ли-
нейно зависящую от указанных в таблицах, следует ис-
пользовать принцип суперпозиции.
Нагрузка, равномерно распределенная
по всей площади плиты
Коэффициенты р, у
эффнциенты i(1A и ф1й.
(13.7)
находятся по табл. 13.1, а ко-
(здесь k — помер схемы на
рис. 13.4) — по графикам
рис. 13.5.
Пример 13.1. Определить
стрелу прогиба и усилия в
плите, представленной на
схеме 7 рис. 13.4 при следу-
ющих данных: а=1,8 м;
Ь~3 м; р = 1 Цм2; ц=0,15.
а	1,8
Для ~~ — ——- = 0,6 по
о	3
габл. 13.1 находим а,5= 38;
₽5=15; у5==43; р]==—77;
у4 = —102.
По формулам (13.7) на-
ходим прогиб и изгибающие
моменты в центре плиты:
гц	рМ	38 1-1,8“’ИО7	4-Ю5
щ — —— , ----------—----------------------------— см.
IO1	D	IO4 D	D
fi-; 15
Мх = -'-~па2 =--------1 -1,8- « 0,049 Т-я/м; (
103	103	1
у.	4.5
pefl =	1 П ,8= « 0,146 Т-м/м.
1
Рис. 13.6
Здесь 107 — переходный! множитель, связанный с пере-
ходом i -м- в кГ’СМ-.
1 i.2 ПРЯМОУГОЛЬНЫЕ ПЛАСТИНЫ
49
В'ЛД, ^^’табляца 13.1 [10]
Значения а, 0. V для Чшределения w, Мх,
при равномерно распределенной нагрузке ( и =0,15)
а b	Схема 1			Схема 2				а5	(хема 3		
	j	! t	М	X	г*.	ъ			р.	%	р.
0,5	101	17	96	49	6	58	121	( '1	20	&	122
0,6	85	1’4	82	45	10	54	116	7 с.	27	71	117
0,7	73	30	68	41	18	J9	109		31	ЧП	но
Р,8	60	33	56	37	19	J3	КО.	4Ь	32	32	102
0,9	50	36	46	32	22	37	92	36	32	v>	93
1,0	41	37	37	28	24	32	85	28	32	24	85
Схема 6
Схема 4
Аналогично вычисляем изгибающие моменты в точке 1'.
К	77
XL рйз ==_ J. [ ,8а«—0,250 Т-м/м-
Ю3	' ’	(в)
Mv = [1/Ид. «—0,037 Т-м/м.
На рис. 13 6 приведены эпюры для задачи об изгибе
свободно опертой квадратной плиты равномерно рас-
пределенной нагрузкой [23],
Нагрузка, распределенная
по гидростатическому закону
а
b		&
0,5	26	Г)
0,6	25	1
0,7	24	8
0,8	23	10
0,9	21	14
1,0	1»	16
Схема 7
,"V2
Схема 5
Прогибы и усилия находим по формулам (13,7). Зна-
чения коэффициентов приведены в табл. 13.2 и 13.3 для
схем нагрузок, представленных на рис. 13.7, Коэффициен-
41
10
38
35
32
29
85
84
82
78
74
70
М
46
26
19
29
80
60
44
16
Ш
ПС
90
80
7о
47
42
зф
:п
28
7
14
17
23
76
50
13
23
78
78
75
71
67
10*
88
67
Схема 9
Схема 8
и
ь	ОК,	Рв	То	-Р1	—4К	а5	р.	%	-р>	“V2	«в	₽6	Тв	-Р,	“Уг
0,5	15	10	54	78	111	25	3	41	56	81	25	4	40	55	82
0,6	38	15	15	77	102	24	6	Ж	56	81	23	8	37	56	78
/) ,	<г>	20	37	74	89	22	9	33	56	77	21	12	32	5«	72
0,3	26	о ?	29	70	76	20	12	31	56	72	18	14	27	55	65
0,9	20	23	22	65	64	18	15	О 7	55	66	15	16	22	53	58
1,0	16	23	17	60	54	16	17	23	54	60	13	18	18	51	51
Схема 10
a
ь	«г,	Р,	У 5	а,	У	аг,	Рв	V&	PsKvs) «>			I "А	-V.
0,5	35	16	32	62	58	9		12	5П	34	18	27	71
0,6	45	18	41	77	72	П	4	|7	FC	12		53	80
0,7	54	20	5»	89	85	И	6	'Ч	54	19	2ч	38	84
8 8	62	21	5В	97	92	16	Я	Q-1	фт	Рю	9'5	И	8,5
0,9	71	20	67	108	104	18	9	°6		62	27	43	Я-,
1,п	78	20	74	116	111	13	8	28		65	ПЯ	14	85
1,2	89	18	>И	125	120	92	8	3?	56	73	23	41	85
1,5	102	14	47	1.32	126	2Л	5	36		76	?8	45	85
2,0	114	9	ПО	137	132	25	3	40	56	ъЗ	29	45	84
ты <р и ф для некоторых схем можно определить по
графикам на рис. 13.8 (коэффициенты ф и ф для нагру-
зок по схеме рис. 13.7, а; <р и ф для нагрузок по схеме
рис.
13.7,6, где р—ра
а b	Схема /7						СхемхЗ 12						
		Рв	•А,	-р.	Т..	V,	П; j Рв		Vs		aj	Р,	
0,5	13	—3	н	77	32	21!	15	К)	22	56	21	3-3	85
0,6	21	1	Ю	90	48	11	17	К)	’’5	61	26	411	85
0,7	30	5	9 -i	101	64	•/!	18	10	28	66	26	43	85
0,8	39	9	.4.1	109	78	74	20	10	32	71	?7	45	8,5
0,0	47	12	44	115	90	8^	о	5)	31	74	27	44	85
1.5	55	11	51	118	100	9 7	Ю	7	35	77	28	41	Яч
1,2	1)9	и	65	121	ИЗ	110	/1	о	38	80	28	45	85
1,5	86	16	82	123	128	КЗ	Г} 1	3	10	83	23	45	84
2,0	105	12	101	125	136	131	27	1	42	83	29	45	84
Изгибающие моменты в точке 4 (схема .4 рис. 13 4):
у,	102	I
Л1 = -0-0. „в2	---- 1.1 gs 0,323 Т-м/м,
v 10s Р 10s	(б)
М.х = [iMy —— 0,049 Т-м/м,	1
Таблица 13.2 [10]
Значения «, f>, у в (13.7) для иагрщки, изображенной
на рис, 13,7, а (Д —Я,1в)
а b	Схема 1					Схема 9							
	а6	р,	V,	Ри	7’>4			Vs	Й.И	Уи	—V.j-Vi	-₽1	1
0,5	51	ч	48	12		12	2	20	5	20	49 32	28	29
0,6	43	12	41	И	41	12	4	18	5	18	17 31	28	30
0,8	30	17	23	17	31	ч	7	14	7	14	41 24	28	2'1
1,0		18	13	П		0	9	9	9	10	33 18	26	27 1
а		Схема 2					Схема 7						
b	сх6	fir,		р...	м		Г/'<3	i	1	Ps<	7м	чъ	
0,5	22	а	27	5	27	65	20	4	25	6	61 25	36	36
0,6	20	5	26	7	26	63	17	7	22	7	56 22	36	36
0,8	17	ф	21	9	21	56	К’	10	И	10	И 14	33	33
СО	13	11	16	It			7	И		11	34 К)	32	31
а	Схема 4						Схема 5						
b		Рв	V-,	Р=4	Угг	—'П	1 2 ; I		fir,	ъ	flrr ) З’.ч	—03	
0,5	13	1	21	4	21	51	31	42	12	40	12 42	61	61
0,6	13	9	20	5	20	56	38	32	11	зо	11 33	55	56
0,8	11	5	13	7	1.8	47	31	18	16	16	16 20	45	48
1,0	10	8	14	8	15	43	26	10	И	Я	U 13	35	33
4-26
50
РАЗДЕЛ 13. УПРУГИЕ ТОНКИЕ ПЛАСТИНЫ (ПЛИТЫ II БАЛКИ-СТЕНКИ)
1 а б л и ц а 13.3 ЦО]	’
Т а бли д а 13.4 [5]
Значения а5, $5, ?6 в <13,7) дли нагрузки, изображенной
на рис. 13.7, б (Ц^-0,15)
а	Схема 1						Схема 9												
b	&& Ро		п		Р.» | Тп		ай	₽» 1 V»			₽о		?!'. — Р»|—Р. —А»						
0,5 0,6 6,8 1,0	51	9 43 12 30 17 20 18		50 41 28 18		21 22 23 22	51 42 28 18	14 12 9 6	2	20 4 18 7	14 9	9			9 9 10 10		22	45	11	41 20	43	14	39 14	38	17	33 9	33	18	25					50 46 36 27	
а	Схема 3							Схема 8											
b	ГХ5		?>		А,	Ъэ	-р»				Те j		₽|» V:, —					-То»	
0,5 0,6 0,8 1,0	45 П 36 14 22	17 13 16		42 34 20 11		17 17 17 16	42 34 20 11	84 76 61 50	2 20 3 19 7 15 9 11			20 19 15 И		9 23 45 41 9 20 43 , 40					50 46 37 29	
													У	;5 38 35					
													10 П 31 29						
а b	Схема 4									Схема 5									
			7s		е»	У.»	—?2	—		а»		&		Р,3	У.<3		-е.		-ft.
0,5 0,6 0,8 1,0	16 15 13 10	1 2 5 8	21 20 19 18		8 10 12 13	25 23 21 19	42 42 39 35	57 51 44 38		42 32 18 10		12 1б 16 14	40 30 16 8	17 18 18 15	40 30 16 8		37 36 32 27		84 75 53  43
а	Схема 10								Схема И										
h	сс5	, Р5				ctj	Ъ		«5 !		р»		Тз	-0»				7»	
0,5 0,6 0,8 1,0 1,2 1,5 2,0	13 17 24 31 37 45 53	9 11 13 13 13 11 7		11 15 22 29 35 42 51		20 24 31 34 34 32 28	19 23 39 33 33 31 28		4 7 13 20 27 36 47		2 4 " 8 И 12 12 9		3 6 12 18 25 34 45	29 36 48 57 65 75 85		9 13 .21 26 30 30 27		8 12 20 i 25 29 29 27	
b а	Схе?ла 12							Схема 13							
	|р6| у„			-?=|г4.		V,	-у,	(% 5	р»	То	-Те	-Р»| «>		Р.	-То
0,5	6	8	8	24	8	12	21	3	9	4	12	пщ	4	7	24
0,6	 7	8	10	75	8	12	20	4	3	5	17	26	6	8	17
0,8	9	8	13	33	у	И	16	7	6	9	°?.	29	6	10	15
1,0	11	6	16	36	6	10	11	В	7	12	30	34	5	10	12
1,2	11	5	18	40	5	8	я	10	7	14	35	38	о	8	10
1,5	Г2	3	20	41	4	()	7	12	4	16	38	41	4	6	7
2,0	12	1	2!	42		4-	5	12		19	41	45		1	5
t м -	1
Нагрузка, распределенная равномерно
по части площади плиты
В табл. 13.4 и 13.5 приведены значения р и у для оп-
ределения изгибающих моментов от нагрузки, распре-
деленной равномерно с интенсивностью р по заштрихо-
ванной площади (рис, 13.9), Моменты при этом опреде-
ляются по формулам (13.7) с заменой в них ра2 на рав-
нодействующую приложенной к плите нагрузки. Это дает
возможность использовать табл. 13.4 и 13,5 в частных
случаях — при Д]=0 или 6i=0. т. е. при нагрузке, рас-
пределенной вдоль линии у = а!2 или х — Ьр,.
Значения 0.»  Т» в (13.7} для плиты, опертой по всему контуру
(схема 4 рис. 13,4) и нагруженной по рис. 13,9 при Ц ~ В
b	Ъ,„		р	при й;/а					V.-.	при aja			
а	а	0 I	0.2 |	0,4	0,6 :	0,8	1,0	0	0.2	0,4	0,6	0,8	1 i
	0			256	196	160	133	ПО		175	121	93	72	59
	0,2	175	165	114	123	104	88	256	165	117	90	72	58
1,0	<1,4	121	117	109	96	8'1	69	196	1-14	109	84	67	оа
	0,6	9'1	90	81	76	67	56	160	123	96	76	61	50
	0,8	72	72	67	61	51	44	133	104	83	67	5-1	43
	1,0	59	5В		50	43	37	по	88	69	56	44	37
	0		218	184	147	122	101			201	153	119	98	80
	0,2	100	150	131	111	96	79	234	194	147	119	96	79
1,4	0,4	79	78	i V	85	57	48	195	158	130	107	88	72
	0,6	19	48	16	12	36	31	147	125	104	88	74	61
	0,8	40	39	37	34	30	26	129	110	93	79	66	54
	1.0	34	33	32	30	20	22	пз	96	82	68	57	47
	0			228	175	139	115	95			221	168	133	ПО	90
	0,2	98	94	87	76	65	66	246	193	155	127	105	87
2,0	0,4	51	49	47	42.	37	30	188	159	134	114	95	79
	0,6	28	28	27	25	21	18	1.53	133	114	98	83	69
	0,8	19	18	17	15	14	11	125	110	96	82	70	59
	1,0	14	14	13	12	11	9	103	90	79	69	58	48
Т а б л и ц а 13.5 [5]
Значения ps. ','s в (13.7) для плиты по схеме 4 (рис. 13.4)
с иагрумой по рис. 13,9 при g = О
ь . а	flj ь	05 при bjb				щ при bjb				—Т> .<ри bs jb			
		. о	0,2	0,6	1,0	0	0,2	0,6	1,0	0	0,2	0,б|1,0	
	0		210	123	83			231	143	97	85	83	72	54
	0,4	233	182	П7	79	101	98	80	58	86	85	74	55
0,5	1,2	139	119	87	60	33	32	28	21	RH	99	85	63
	2,0	Г-0	78	57	40	18	18	16	12	120	108	84	60
	0			172	91	г,1>		2-10	149	102	140	138	119	88
	(’,4	196	143	81	57	по	107	87	61	142	139	Н9	88
0,7	0 8	136	108	69	46	63	62	53	38	146	142	120	87
	1,4	85	68	46	30	36	ЗГ>	30	22	150	133	101	71
ь	6.	05 при aja				у5 при aja					при aja		
а		°	Л 2	С6	1,0	0	0.2	0,6	1,0	0	0,2	0,6	1,0.
	0			129	55	32	—	239	144	98	166	162	136	98 ।
	ол	211	121		30	177	Н8	108	77	166	162	135	97
1,0	1.2	117	31	39	21	77	75	62	45	165	159	125	90
	2,0	75	5Л	25	16	47	46	39	28	163	140	101	70
	0	__	197	Т.09	70		161	80	49	169	169	167	164
	0,-1	68	67	49	32	186	132	74	47	156	155	148	121
1,1	1,2	28	27	20	13	129	ИХ)	62	38	127	126	115	89 i
	23*Л	10	10	7	5	83	66	42	27	86	85	76	58
	0		196	109	61			161	79	51	168	168	167	164 i
	0,4	68	Л	43	32	185	134	73	46	155	154	1 17	121 1
	1,2	111	8	6	4	97	79	51	32	99	98	88	67 i
	2,0	1.	1	1	1	63	51	32	24	61	62	56	42 :
Нагрузка в виде трехгранной призмы
В табл. 13.6 даны значения «у. у5 для определения
по формулам (13.7) прогибов и изгибающих моментов
в центре опертой по контуру плиты под нагрузкой, по-
казанной па рис. 13.10. Коэффициенты <р и ф в (13.7)
J 3 2. ПРЯМОУГОЛЬНЫЕ ПЛАСТИНЫ
51
Рис. 13.10
схема /1), то прогибы и усилия можно определять по
формулам (13.7) с заменой в них рйа?- на Р.
Коэффициенты р5 и у5 для плиты, опертой по контуру,
определяем по формулам [23]:
103
103 /
=	In
4л \
2л	\
—— -У ц ф- б3
лс	у
(13.9)
Т а б л и ц а 13.6 [5]
Значения а5, 03, в (13,7) для плиты, свободно опертой
по контуру, с нагрузкой в виде трехгранной призмы (Н*=0)
Нагрузка Ъ а	По схеме а на рис. 13-10			По схеме б на рис. 13.10		
		&	fr,	а,	fe	ъ
1,0	26	24	27	26	27	24
1,2	36	22	37	37	27	34
1,4	46	19	46	46	25	43
1,6	53	16	54	оо	23	52
1,8	60	14	60	6*2	99	59
2,0	65	И	65	65	20	6о
3,0	78	4	78	78	12	89
Таблица 13.8 [23]
Значения а-> и в (13,7), а также 6] и б2 в (33.9)
для нагрузки в виде силы Р в центре плиты
ь а	Плита, опертая по контуру (схема 1 на рис. 13.4)			Плита с жестко за- щемленным контуром (схема 9 на рис. 13.4)	
	«5	6,	1	щ	«г,	-7)
1,9	116	0,565	0,135	56	126
1,2	115	0,350	0,115	65	П9
1,4	Н8	0,211	0,085	69	160
1,6	157	0,125	0,057	71	165
1,8	162	0,1)73	0,037	72	167
2,0	165	0,012	0,023	72	167
со	16’)	0	0	—,	—,
для определения приведенных поперечных сил можно
находить по графикам на рис. 13.11 (коэффициенты ф,
и ф, для нагрузки по схеме a, a ф, и ф, для нагрузки
по схеме б на рис. 13.10; i — номер точки на рис. 13.10).
Нагрузка, распределенная
вдоль прямой линии
Если нагрузка распределена равномерно вдоль прямой
линии у=а!2 или х = 6/2 (рис. 13.4), то при опорных
закреплениях по схемам 1 и 4 на рис. 13.4 можно опре-
делять изгибающие моменты по табл. 13.4 и 13.5. Про-
гибы в центре плиты от подобной нагрузки, действую-
щей на плиту, свободно опертую по периметру, можно
определять по первой формуле (13.7), заменив в ней про-
изведение роаг равнодействующей нагрузки, приложенной
к плите.
Рис. 13.12
Таблица 13.7 [23]
Значения ая в (13.7) для плиты, свободно опертой по контуру
и равномерно загруженной по линии х = Ь>‘2 или у^а/2
Ь а	По линия х = Ь!1				По линии у — а/2			
	1.0	1,2	1.5	2,0	1,0	1,2	1,5	2,0
а, । 67,4		95,3	125,1	162,9	67,1	79,9	91,1	98,7
Значения 6162 и для рассматриваемой плиты при-
ведены в табл. 13.8. В ней же приведены значения ag
и уз для плиты с жестко защемленным контуром, загру-
женной силой Р в центре.
На рис. 13.12 приведены эпюры некоторых усилий для
квадратной плиты со свободно опертым контуром, за-
суженной силой в центре [23]. Из эпюр следует, что
если углы плиты не могуг перемещаться, то там возни-
кают не только сосредоточенные силовые реакции Н, но
и реактивные моменты.
Квадратная плита на упругих опорах
под равномерно распределенной
нагрузкой
Нагрузка в виде силы,
приложенной в центре плиты
Если положить, что сила Р распределена по площади
малого круга радиуса с с центром в точке 5 (рис., 13,4)
Прогибы и изгибающие моменты находим по форму-
лам (13.7). Значения а, (3 и у приведены .в табл. 13,9
для следующих плит (схема А рис. 13.4):
1) плита, у которой кромки х=0 и х=й оперты на
упругие балки, а остальные кромки — на жесткие опоры
(плита а);
4*
52
РАЗДЕЛ П УПРУГИЕ ТОНКИЕ ПЛАСТИНЫ (ПЛИТЫ И БАЛКИ-СТЕНКИ)
Значения о, fi V в (13.7) для плит, опертых полностью
или частично на упругие балки (Ц^О,25)
EI aD	Плита а.				Плита б			
	а-	а, \		Уз	|	cq	й-ГОТн	
	41	0	46	46	41	0	46	0
ЮН	41	0	46	46	41	0,3	46	0
50	41	0,4	46	46	42	0,7	46	0
25	42	1,4	47	46	43	1,7	17	0 2
10	43	1,2	48	45	47	4,4	48	2. 1
5	46	8,5	50	45	52	9,9	49	6,5
4	48	И)	52	44	,55	11	50	Я,а
3	50	14	53	44	59	15	52	12
.2	53	20	57	б	67	21	54	18
1	6-3	36	65	30	87	38	60	И
0,5	76	58	77	37	117	62	69	56
0	130	144	123	23	257	175	111	053
2) плита, у которой все кромки оперты на упругие
балки (плита б).
Принято, что все опорные балки имеют одинаковую
жесткость Е1.
При / = 0 по табл. 3 3.9 можно рассчитать плиту, опер-
тую только в вершинах (плита б}, и плиту, свободно
опертую по двум кромкам, при условии, что две другие
кромки свободны от усилий (плита а).
Определение сосредоточенных
реактивных сил в углах плиты,
свободно опертой по периметру
Если углы плиты, свободно опертой по периметру, не
могут перемещаться в направлении оси г (см. рис. 13.3),
то у вершин возникают реактивные сосредоточенные
силы
(13. !0)
где 6, следует брать в зависимости от нагрузки из
табл. 13 10 (i — номер точки на схеме А рис. 13.4).
Реактивные силы в вершинах плиты вызывают появ-
ление у вершин распределенных изгибающих моментов.
Максимальное значение этих моментов по единичной
площадке, наклоненной к сторонам плиты под углом
45°, равно:
(13.11)
13,2,2. Ребристые плиты
На рис. 13,13 представлены следующие ребристые
плиты:
а)	прямоугольная плита, свободно опертая по трем
кромкам и снабженная ребром по четвертой кромке; не-
распределенная;
Т а б 7 и ц я 13 И [13]
Т а б л и ц а 13,1п [23]
Значения ф. я (13.19) для разных нагрузок
Нагрузка	Г	Ь/а					
		м	!,2	',4	1,6	1.8	2,0
Равномерно распределен- ная	б-	63	74	83	86	90	92
Гидростатическая 1рис. 13 7,6)	(Ь	26 39	31 43	35 18	37 49	38 52	10
Гидростатическая (рис. 13.7,а)	б, б,	26 39	27 17	30 53	27 59	27 63	26 66
Сосредоточенная сила Р в центре плиты	, б,	122	И6	103	88	74	60
Для сосредоточенной силы в центре плиты следует
(13.10) заменить ppP на Р.
б)	прямоугольная полюса, свободно опертая по краям,
параллельным оси х, снабженная рядом ребер, распо-
ложенных на равных расстояниях друг от друга; нагруз-
ка показана на рис. 13 13, б.
Изгибающие моменты для точек, показанных на
рис. 13 13, определяются по формулам (13.7), Значения
р и у привгдсцы в табл. 13 11 и 13,12.
13.2. ПРЯМОУГОЛЬНЫЕ ПЛАСТИНЫ
53
Т а б л и ц а 13.12 [181
Значения 0 и в (13.7) для плиты а по рис. 13.13 6 (Н--0Л8)
ь	0	H/h											
		1	1	5							1	s				
а		i											
	V	!		1 ;i 1		I	•)		I	!		3	4
0,6		21	— 15	—5,6	—5,0	19	— 19	—	—3,9	18,1	—22	-4,4	—3,0
		19	с.з	11	8,3	13	3,5	5,7	4,0	9,9	0,3	3,3	2,0
0,7		25	— 19	—7,2	—'5,5	.2-1	—25	—6,9	—4,2	22		-5,5	—3,1
	Vl	24	ю	12	Я,2	18	3,3	6,4	3,8	13,7	- .0,3	3,7	1,9
0,8	h	29	—24	—8,7	-5,7	27	—32	—8,4	—4,3	26	—37	—6,8	—3,1
		30	10	13	7,8	23	3,1	7,0	3,4	18,5	— 1,0	4,0	1,5
Таблица 13.13 13]
Значения k в (13.12)—(13.15)
К	|
b a	6													
	0	0,10	0,25	0,50	0,75	1,0	0		0,10 |		0,25	0,50	0,75	!,0
0 0,25 0,50 0,75 1,0	130 130 130 130 130	130 130 130 130 126	130 130 130 117 96	130 130 121 94 66	130 129 111 78 50	130 128 101 66 41	0 0 0 0 0		37 37 37 72 128		93 102 120 197 262	185 191 252 341 378	278 281 357 434 438	375 384 464 504 479
b a	k.					A.								
	5													
	n	0,10	0,25	0,5o| 0,7s| 1,0 | 0						O,io| 0,25		0,50	0,75	1.0
0 0,25 0,50 0,75 1,0	0 0 0 0 0	125 12.6 125 138 145	313 318 322 313 283	625 623 600 508 389	940 930 820 626 440	1250 1235 101? 713 479		125 125 125 125 125		125 125 125 125 117	125 125 125 111 92	125 1.24 115 86 61	125 123 105 73 45	III II
изгибающие моменты в центре у ребер
/ k„	с" \	)
Mr, = Ь" — —- Рп, |
\ 10*	12 ) °
/ с3 \ (
му= ! То*"&3 g Тг”/ Рв' I
наибольший изгибающий момент в ребре
ki
(13.14)
(13.15)
Здесь с—расстояние между ребрами; I — мом°ит инер-
ции сечения ребра; ki — коэффициенты, зависящие от па-
раметра
<5-= 22.
(13.16)
определяются из табл. 13.13.
13.2.3. Многопролетные плиты
Бесконечная плита, опертая в узлах
прямоугольной сетки [3] (рис. 13.15)
Для плиты, свободно опертой по контуру и усиленной
рядом часто поставленных ребер (рис. 13.14) при равно-
мерно распределенной нагрузке, можно определять про-
гиб в центре и изгибающие моменты по формулам [3]:
прогиб в центре
! kt cbf	с4 \
Под действием нагрузки, равномерно распределенной
по всей поверхности такой плиты, в ней возникают про-
гибы и усилия, определяемые формулами (13.7) при
изгибающие моменты в центре между ребрами
/ й, с3 \
63 +	) Ро;
(13.13)
Рис. 13.15
54
РАЗДЕЛ 13. УПРУГИЕ ТОНКИЕ ПЛАСТИНЫ (ПЛИТЫ II Б'.ЛКИ СТЕНВД1)
Т а блица 13.14 13]
Значения а, Р, у в (13.7) для плиты по рис. 13.15
(ц =о.зо)
а b	сч	Сб2		h	(%	(6		°?		г		Г	 г	
1	58	44	36	50-	40	11	52	123	36	13	21	48	111	181
1,1	49	40	37	41	35	5,7	51	114	29	19	26	48	10/	173
1,2	43	38	38	35	28	4,8	49	106	24	24	31	54	106	1о7
1,3	39	36	39	30	24	2,4	47	100	21	28	35	56	пи	159
1,4	36	35	39	26	21	—0,4	45	95	19	32	38	58	КН	153
1,5	34	33	39	23	17	-1.5	44	90	17	36	41	60	102	119
9	30	29	41	и	5,5	-6,7	39	74	13	48	50	66	97	132
	26	26	42		— 25	—25	25	25	13	83	83	83	83	83
значениях а = а,, |3 — у = у> (i — номер точек на
рис. 13.15, а) по табл. 13.14,
При размещении равномерной нагрузки не по всей
плите, а лишь на некоторых панелях, наииевыгоднейшей
является загрузка в шахматном порядке (например, за-
грузка панелей, заштрихованных на рис. 13.15,6), При
такой загрузке напряженно деформированное состояние
любой панели может быть определено суммой двух со-
стояний: первого, возникающего при загружении всей
плиты равномерной нагрузкой интенсивности 1/2 р0,
и второго, возникающего при нагрузке, показанной на
рис. 13.15,6 (заштрихованные и незаштриховаппые па-
нели загружены нагрузкой одинаковой интенсивности
J/2 р0, но разного знака). При втором загружении каж-
дую панель .можно рассматривать как свободно опертую
по контуру, и, следовательно, определять в ней усилия
и прогибы с помощью табл 13.1 (схема l), Иначе гово-
ря, максимальные прогибы и усилия в панели при шах-
матном расположении нагрузки можно определять по
(13.7), полагая а, |3, у равными среднему арифметиче-
скому значений, определенных по табл. 13.1 (схема 1)
и табл. 13.14.
Пример 13.2. Определить максимальный прогиб в цент-
ре квадратной панели безбалочного перекрытия при а —
= 3 ж, ро = 0,8 Т1м2. По табл. 13.1 (схема 1) и 13.14
и формулам (13.7) находим
1	а рп cfi
а = — (41 + 58) «50; ш = -— •	=
2	'	’	W D
50-0.8-ЗМ07	3,24-10®
_ _—————.—___ -----------. „„
Здесь 107—переходный коэффициент от Т-м2 к кГ-см2.
К в а д р а.т н а я пл и та, опертая по контуру
и поддерживаемая колоннам и (рис. 13.16)
Для плиты, опирающейся на четыре колонны и по пе-
риметру на жесткие опоры, можно определять изгибаю-
Т а б л и ц а 13.15 [23]
Значения V в (13.7) для плиты по рис. 13.16
=0,23 И -0,2)
щие моменты по формулам (13.7). В табл. 13.15 приве-
дены значения р, у для равномерно распределенной на-
грузки по заштрихованным областям плиты на рис.
13,16,	а, б, в (i—номера точек по рис. 13.16, а).
Приближенный способ расчета
и ера з резных плит [23]
Цели неразрезная плита состоит из панелей примерно
одинаковых размеров и одинаковой жесткости, то при-
ближенно максимальные
Рис. 13.17
ных сечениях иеразрезпой
арифметические значения,
ных панелей.
значения опорных моментов
можно определить следую-
щим образом. Каждая па-
нель рассчитывается как
изолированная плита, за-
щемленная по линиям со-
пряжения с соседними па-
нелями (остальные кромки
закреплены заданным спо-
собом). За действительные
значения моментов в опор-
плиты принимаются средне-
найденные из расчета смеж-
Пример 13.3. Определить расчетные моменты на опорах
плиты (рис. 13.17), засуженной по заштрихованной об-
ласти равномерно распределенной нагрузкой. По внеш-
нему периметру плита свободно оперта.
Так как пролеты панелей одинаковы, то достаточно
вычислить осредпенные значения коэффициентов |3 из
(13.7) в опорных сечениях 1—1 и 2—2, показанных на
рис. 13.17. В сечении I—1 от нагрузки левой панели на-
ходим по схеме 3 табл. 13,1 значение р' =—85. В сече-
ниях /—1 и 2—2 от нагрузки средней панели получим по
схеме 5 табл. 13.1 значение Р" =—70.
Для расчета принимаем для кромки 1—1
+=—	(85 + 70) «-78.	(а)
По аналогии для кромки 2—2
+=—-у (70 + 0) =—35.	(б)
Точные значения этих величин [5] равны:
+ =—80,4; +=—33,9.	(в)
Рис. 13.16
13.2. ПРЯМОУГОЛЬНЫЕ ПЛАСТИНЫ
55
13.2.4. Плиты на упругом основании [26]
Ниже приводятся таблицы для расчета плит бесконеч-
ных размеров в одном и двух направлениях, лежащих
на упругом основании и загруженных сосредоточенными
силами Р.
Предполагается, что интенсивность реакции основания
р* определяется по формуле (гипотеза Винклера)
p* = ta>,	(13.17)
где k — модуль основания или коэффициент постели (см.
[16, 26] и разделы 5, 19).
на рис. 13.2041=0,2 6; /!4 = 0,2а; Z15=0,6a.
Пример 17.4. Определить прогибы и усилия в точках
И и 1 для плиты на упругом основании, загруженной
колоннами, расположенными в вершинах квадратной сет-
ки (см. рис. 13.19).
Дано. Расстояние между колоннами 2а = 500 см. Вы-
лет консольной части плиты [=125 см Толщина плиты
h=60 см. Нагрузка на средние колонны Р=240 Т; на-
грузка на крайние колонны Pi = 160 Т. Модуль упруго-
сти плиты £=2,1'105 кГ/см?. Коэффициент постели грун-
та k = 2 кг!см?.
Жесткость плиты (ji = 0):
Рис. 13.20
Д =
Eh3
12
2,l-10g-603
12
= 37,8-Ю8
кГ-см.
(а)
Определяем параметр tj по (13.18)
//" k - 2
Д ~2°° у 37,8-10s
(б)
Таблица 13.16 [26]
Значения а, 0, у в (13.7) для центрального поля
бесконечной плиты при одинаковой нагрузке
от всех опирающихся на нее колонн (рис. 13.18) (р. = 0)
	аг			1	105					10“ Д	
9	1									
	1	2	3	6	1	2	3	6	2	3
0,8	625	623	609	603	—189	—116	—29	29	—45	57
1,2	135	133	119	113	— 188	— 115	—29	27		56
1,6	52	50	36	31	—185	—113	—27	25	—42	53
2,0	29	26	14	9	—182	— 108	—23	21	—39	49
2,4	20	17	6	2,2	-174	-101	— 19	17		43
Расчетные величины определяются по формулам (13.7)
с заменой р0а2 на Р.
Значения а, (5 и у даны в зависимости от параметра
т] = а
(13.18)
где а — величина, определяющая расстояние между си-
лами Р.
Рассматриваются следующие расчетные схемы:
а)	бесконечная плита, загруженная равными силами Р,
расположенными в вершинах прямоугольной сетки
(рис. 13,18);
б)	полубесконечная плита, загруженная равными си-
лами Р, расположенными в вершинах прямоугольной сет-
ки (рис. 13.19);
в} полубесконечная плита, загруженная равными си-
лами Р, расположенными с шагом 2a вдоль оси х
(рис. 13.19);
г) плита в виде бесконечной полосы, загруженная ря-
дом равных сил Р, расположенных по оси симметрии
полосы (рис. 13.20).
Для определения моментов и прогибов в точках, ука-
занных на рис. 13.18—13 20, по формулам (в) на стр. 57
следует пользоваться значениями коэффициентов а, (3, у,
приведенными в табл. 1,3.16—1.3 19 (эти значения вычис-
лены при ц=0). При этом следует иметь в виду, что
расстояния между точками i и / (4'1), приведенными на
рис. 13,18—13.20, приняты равными:
на рис. 13.18 — /12 = 114=0,2 а-,
на рис. 13J 9 -—фл = Zzy = йт = Z73 = 0,2с: ^2 = 0,2 f;
Таблица 13 17 [261
Значения a,Р, ув (13.7) для крайних полей и консольной
части полубесконечной плиты при одинаковой нагрузке
от всех опирающихся на нее колонн (рис. 13,19) (|4=0)
а					Юэ				
	*1				i				
		1	3	5	7	10	11	12	13
	0,8 1,2 1,6 2,0 2,4	1189 309 128 68 41	1106 271 107 65 34	805 142 37 12 4,3	659 124 47 27 19	643 108 31 12 5,6	757 136 31 6,9 0,3	1018 247 83. 33 14	1162 283 102 44 20
Vs	0,8 1,2 1,6 2,0 2,4	945 221 81 38 20	867 194 72 37 23	706 128 36 13 5,4	641 130 50 28 20	625 114 35 14 5,8	700 122 31 8,5 1,8	848 175 54 20 7,5	930 205 67 25 8,7
3Л	0,8 1,2 1,6 2,0 2,4	730 150 46 17 7,1	711 154 59 32 21	649 121 37 14 5,8	637 135 52 29 20	620 119 36 14 5,9	643 119 32 10 2,3	693 137 42 16 6,8	721 139 38 10 1,4
1	0,8 1,2 1,6 2,0 2,4	543 90 21 4,6 0,3	614 136 55 31 21	618 124 38 14 5,9	00 СО СО СЪ © : Cg СО csj СЧ	622 122 37 14 5,9	619 119 33 10 2,4	597 120 39 16 6,9	538 85 17 1,1 -2,4
56
РАЗДЕЛ 13, УПРУГИЕ ТОНКИЕ. ПЛАСТИНЫ (ПЛИТЫ И БАЛКИ СТЕНКИ)
Продолжение табл. 13.17
а	103 P i													
	0	1	1												
		1 | 2 j 3			4	5	6		8	9	10	11	1 I2	13
	о,я	182	201	198	135	32	106	149	46	80	—57	-35	1-92	-105
	1,2	180	200	197	133	31	105	148	45	79	—56		1—90	— 103
	1,6	176	196	193	во	29	103	146	43	76	—51	—27	—89	-99
	2,0	167	188	185	123	25	98	141	40	70	—49	—23	—79	—91
	2,4	155	176	174	11°	20	91	134	34	61	-43	— 18	-6$	—79
	0,8	89	151	164	ИЗ	30	106	149	46	57	—57		-69	—69
	1,2	88	150	162	W	29	[05	148	45	56	— 57	—28	—63	—66
7 а	1,6	81	117	.159	1 0"	27	102	146	43	53	-53	—?5	—65	—63
	2,0	78	141	158	105	24	'1.8	141	40	49	— 19		22	„„GO	—57
	2,4	68	1 ']	144	97	20	91	134	34	42	—В	-17	—52	—48
	0,8	46	125	153	108	29	106	149	46	49	—59	-27	—60	-40
	1,2	44	129	152	107	23	105	148	45	48	—56	—26	—59	—39
т.	1,6	42	129	149	105	26	102	146	43	46	—53	—24	—57	—3.6
	2,0	38	ио	144	100	23	98	141	40	42	— 19	—21	—52	—32
	2,4	31	107	137	93	18	91	134	34	36	—43	-16	—45	—25
	0,8	24	106	150	106	29	106	149	46	46	—56	—27	—57	—22
	1,2	93	105	149	105	28	105	148	45	46	—66	-26	-56	—21
1	76	21	103	146	103	26	102	146	43	44	—53	—25	—54	—20
	2,7	18	РО	И1	98	23	98	141	39	40	-19	—21	-49	—18
	2,4	И	92	Вп	91	18	91	134	34	34	—43	—16	—43	— 13
Продолжение табл. 13.17
	/ . а	1У7г.											
		1										
			3	4		6	7	1 8	! 9	1 W	ч	12
	0,8	75	111	61	-185	—63	ВО	28	46	—68	— 15!	—27
	1,2	73	147	50	-137	1,4 30	195	82	30	—, >	1	— 104	—23
	1,6	80	151	40	-К)!		218	122	53	21	—м	—19
	2,0	81	154	31	—74	37	222	119	56	25	—43	— 15
	2,4	82	156	23	—54	34	215	113	59	21	—20	— 12
	0,8	6R	187	—8	—122	— 10	179	76	86		—91	—2
	j 2	/ я	193	3	—92	25	214	111	92	15	—61	4
Л	1,6	75	198	12	—71	37	223	120	96	25	—41	9
	2,0	76	199	17	—57	38	?'? 1	И9	98	24	—28	И
	2,4	75	200	19	—45	33	214	112	98	20	— 19	13
	0,8	72	227	37	—74	27	213	ЦП	125	14	— 14	31
	1 2 Г, о	72	228	40	—’64	38	223	120	126	24	—35	33,
		71	227	40	—57	40	224	123	125	26	—29	30
	2,0	67	223	37	—51	37	220	115	121	24	—24	29
	2,4	60	216	32	—44	32	214	111	114	19	-18	23
	0,8	80	261	74	—39	53	236	133	159	36	-10	63
	1,2	73	252	64	— W	43	227	125	150	28	—21	54
1	1,6	64	242	53	—53	40	224	121	139	26	—25	44
	2,0	лз	г['р	13	—50	37	220	11?	128	23	—2.3	34
		41	218	,44	— И	32	2 В	111	116	20	— 18	24
Таблица 13Л8[26]
Значения а, v в <13-7) для крайних полей и консольной
части полубесконечной плиты при загрузке только крайнего
ряда опирающихся на нее колонн (рис. 13.19)
f а	1Ыа/								
	11	£							
		1	|	3		S	7	10	1 "	! 12	13
	0,8	1201	1056	509	150	150	505	1032	1075 I
	1,2	338	28.3	82	—3,6	-3,8	79	259	311 \
7*	1,6	13Э	112	18	—5 8	—6,0	15	71	ИЗ i
	2,0	71	57	4,7	—2,3	—2,5	2,0	35	47
	2,4	42	34	1,4	—0,7	— 1,1	—6,4	14	21 ; j
	0,8	1008	809	407	131	131	404	789	99° ?
	1,2	252	196	67	3,2	3,0	64	218	237 i
7г	1,8	90	74	17	—2,2	—2,4	15	56	76
	2,0	40	38	6,1	— 1,2	— 1,4	3,7	21	27
	2,4	20	24	2,5	—0,5	—0,6	—0,7	8,1	9
	0,8	828	637	344	126	126	341	620	819
	1,2	178	150	63	8,9	8,7	51	120	170
7,	1,6	53	59	19	—0,3	-0,5	16	•12	45
	2,0	19	32	7,1	—0,9	-1,0	7,6	17	И i
	2,4	7,1	21	2,9	0,5	0,6	1,3	7,3	1,4
	0,8	665	524	308	128	128	305	470	660
	1,2	118	128	63	13	13	60	112	И4
1	1,6	26	55	20	1,0	0,8	18	39	22
	2,0	5,1	32	7,5	—0,8	—0,9	5,3	17	16
	2,4	0,2	21	3,0	—0,5	—0,6	0,3	7,,5	—2,5
Продолжение табл. 13.13
№0.
	п	!| 2		3	4	5	7	9	10	11	12	В
	0,8	181	200	197	132	18	1,2	79	— 1,2	— 17	—91	—104
	1,2	179	199	195	132	17	1,1	78	— 1,2	-16	-89	— 103
7.	1,6	175	197	191	128	16	1,0	75	— 1,0	— 15	—85	-98
	2,0	169	187	18)	121	14	0,7	69	—0,7	— 13	-79	—93
	2,4	155	176	173	112	И	0,4	61	—0,4	— К)	—68	—79
	0,8	89	149	162	ИЗ	16	1,1	56	—и	-15	—68	—67
	1,2	87	149	161	112	15	м	55	—1,1	— 14	—67	--66
7г	1.6	84	146	158	109	14	0,9	52	—0,9	— 13	.—64	-63
	2,0	78	НО	152	104	12	0,6	48	—0,6	— И	—59	-57
	2,4	68	131	144	96	10	0,3	41	—0,3	—9	-51	-48
	0,8	45	12)	152	106	15	1,1 1,0	48	— 1,1	— 14	—59	—40
	1,2	44	123	151	10b	14		47	— 1,0	— В	—58	—39
Т.	1,6	42	120	148	103	13	0,9	45	—0,9	— В	—55	—.36
	2,0	37	115	144	99	12	0,6	41	—0,6	— И	—51	—38
	2,4	31	1(17	136	92	9	0,3	36	—0,3	—8	— 15	—26
	0,8	24	106	149	63	14	1,0	45	— 1,0	—В	—56	
	1,2	23	105	148	103	14	ИО	45	-1,0	— В		-1D	—21
1	1,6	21	102	145	101	13	0,8	43	—0,8	— 12	—53	—29
	2,0	18	98	1'11	97	и	0.6	39	—0,6	— 11	-49	— 17
	2,4	14	92	134	91	9	0,3	<31-	—0,3	—Я	—43	—12
Продолжение табл. 13.18
f а	10’^			
	п	i		
		2	3 I 4	5	7 | 9 1 10 1 11 | 12
7г	0,8 1В	76 79	144 —62 Ц9 1 - 45	—206 —194	47 -192 —187	—28 — 129 —72 I 52 | — 70 1—1В
13 2. ПРЯМОУГОЛЬНЫЕ ПЛАСТИНЫ
57
Продолжение табл. 13.18
г, а	1UJ^									
	л	i								
		2	3	4	5	1	9	W	п	12
	1,6 2,0 2,4	8? 83 S3	153 156 157	—34 —2-5 —20	—81	—23 —5,5 -3J	56 58 60	-21 —4,1 —0,7	—62 —34 — 17	ш 1	—* ОТ- ОО
Ч--	0,8 1,2 1,6 2,0 2,4	70 77 79 79 76	189 200 204 204 201	4 14 23 25 23	1 1 1 1 1 ГС СО >и _ ,U ОТ ОТ GC .ОТ	— 143 -51 — 18 —6,3 — 1,7	88 98 103 102 100	—.	— ОТ i тот от -,4-Г ’ 1 и "и	— 124 —62 —32 -18 — И	ТГ1Г5 Т 77777
	0,8 1,2 1,6 2,0 2,4	76 81 78 70 61	232 241 237 229 218	! от слепив ОТ СП ОТ ОТ	ас от г- с,- ; оо -9 го cj ci I 1 II II	I 1 1 1 1 -".ДДЗ	130 133 135 126 116	1 1 1 1 1 ОТ Ui —- ОТ от го	от	—73 — 31 — 18 — 13 — 10	35 44 41 34 2о
1	0,8 1,2 1,6 2,0 2,4	89 86 72 57 42	273 270 255 237 220	86 86 71 53 38	1 1 1 1 1	Iftft 1Д f	170 168 152 114 118	77711	777 i7	72 64 56 39 26
Продолжение табл. 13.19
10-0
а	л	i							
		1 | 2		3	4	5	6	7	8
	0,8	286	284	247	146	—85	— 163	— 163	—162
	1 с)	283	181	243	143	,—34	— 160	— №	— 159
’/>	1,6	274	,?7'J	235	Ыб	—81	— 152	— 152	— 151
	2,0	259	256	220	124	—7ч	—137	— 137	—186
	2,4	236	234	197	106	—69	— 115	— 115	— 111
	0,8	181	167	97	69	—48	-86	—83	—75
	1,2	380	165	95	69	—48	—35	—82	—74
7,	1,«	175	161	90	65	—16	— 79	—77	— /0
	2,0	168	] S3	83	6'1	—44	—71	—70	—62
	2,4	155	141		50	— 10	—60	—69	—б)1
	ОФ	157	128	47	5’2	—41		(fti	—58	„4]
	1,2	156	126	46	51	—40	—63	-57	—40
7.	1,6	15в	123	43	49	—,й	—60	—54	-37
	2,0	147	118		44	—38		„49	—33
	2,4	138	108	31	37	-35	—16	—41	—26
	0,8	150	107	-Т.1	17	—38	—58	- 16	GO
	1,2	149	106	о ?	46		эд	—59		55	—22
1	1,6	147	loo	21	44	—37		-42	—20
	2,0	142	99	ы	40	—36	— 5и	—39	—17 .
1	2,4	135	9’2	14	35	—34	— 43	—32	—13
Таблица 13.19 (26J
Значения а, 7 а (13.7) для плиты в виде бесконечной
полосы, загруженной равными силами по оси симметрии
(рис. 13.20)
b						1	1о’д							
													
а	'П												
		1	3	5	6		8	1	2	4	5	6	7
													
	0,8	2463	2462	2435	2422	2423	2423	142	69	51	6,1	1,9	1,7
	1,2	504	502	476	464	464	464	142	69	51	6,1	1,9	1,7
7.	1,0	173	172	146	155	185	135	142	69	51	6,1	1,9	1,7
	2,0	82	80	56	46	46	46	142	69	51	0,1	1,9	1,6
	2,4	47	46	25	16	16	16	142	69	51	6,1	1,8	1,6
	9,8	1235	1227	1219	1212	1212	1210	199	75	98	29	20	15
	1,2	205	248	239	233	233	2 31	197	73	97	29	20	15
Ч,	1 ,ъ	89	82	74	68	68	66	197	72	96	29	19	15
	2,0	44	37	29	24	24	9 9	197	71	94	28	19	15
	2,4	26	19	13	8,3	7,9	6,8	195	70	94	26	16	13
	0,8	829	810	816	811	809	802	236	77	134	57	43	32
	1,2	176	157	163	158	156	149	235	76	133	56	42	32
7/	1,6	65	48	53	48	46	10	239	73	130	56	40	30
	2,0	35	18	22	18	17	10	227	08	125	49	35	27
	2,4	•JO	7,1	11	7,8	6,6	1,4	218	61	116	42	29	22
	0,8	п32	394	620	615	610	590	269	85	167	87	71	48
	1,2	142	105	129	125	120	101	265	81	162	81	67	4,)
1	1,6	58	25	UJ	42	37	21	255	72	153	73	57	
	2,0	33	5,2	21	18	14	1,7	240	58	138	59	44	29
	2,4	21	0,2	И	7,5	5,0	-2,5	220	42	118	41	ц	19
Формулы для прогибов и усилий (13.7) принимают вид
г_ =	а"	—
w = [а,- Р — аг (Р — РЛ\ ~ ~ (240 а,- —
=.	10s-2502
—80а/)----------= 1 ,224 (За,- — а,) мг;
’ 37,8-10“
МХ=--^Р~- ft(P — Рд =	(В)
= 80 (3ft - ft) Т-см/см;
MtJ = ft Р у/ (Р - РЛ =
= 80 (3-у;- — ft) Т • см/см.
Здесь a, ft у определяют ив шбл. 13.17, а а, ft у—•
из табл, 13.18.
При Ца—1/2:
для точки И
w = 1,224 (3 -0,122 — 0,064) « 0,4 =«;
Мх = — 80 (3-0,028 - 0,014) « —5,6 Т-с.п/см;
Aft =—80(3-0,061 —0,062)	9,7 Т-см/см;
для точки 1
V) = 1,224 (3-0,221 —0,252) яв 0,56 см; |
Мх = 80 (3-0,088 — 0,087) = 14 Т-см/см; Му=0. /
Давление плиты на основание:
Рц = kwu = 2-0,4 = 0,8 кГ/см~;
р\ — йау — 2-0,56 = 1,1 кГ/см",
58
РАЗДЕЛ 13. УПРУГИЕ ТОНКИЕ ПЛАСТИНЫ (ПЛИТЫ И БАЛКИ-СТЕНКИ)
Т а бл иц а 13,20 [3]
Значения о., 6, v в (13.19) для схем нагрузок по рис. 13.21
(г — номера точек на схеме A, f — номера точек на схеме В)
Схема В а^Ь\ с=0,075д
i	1	2	3	4	5
а! 0	-43	1,2 — И	34 —21	83 0	100 142
		Схема 2: a	-г>- c=0,Ia		
1	1	1	2	3	|	4	6	7	11	12	13	14
«г	-49	—21	—15	— 18	;	—12	26	127	—16	„13	— 17	122
рг	—к»	—94	—79	—50	—30	—53	0	—65	—43	— 19	0
i	18	19	20	21	23	26	|	27	j 28	—	— ~
~“8	-11	0,9	79	0	0	0	0	—	
₽г	-88	—94	„.,qo	0	—117	— 175	:	—257	—400	— 1	
		Схема	3'. a~b		
i	1	2	|	3	4	|	5	6	|	7	|	/	4 j 10	18	25
а,-	-28	—24	|	—31	—37	|	—26	•39	|	184	|	4	:	—52	—63	—116	—181
	Схема 3’ a —2b			Схема 4' a — 1,5 b	
/ 1	2	|	3	|	4	5	i • I	2	|	3	4 j 5
ау	—258	— 123	|	—116	—117	|	302	ay	—123	—66	|	—28	50	211
Схема 5\ а^Ъ					
i	1	2	|	3	|	4	1 5 1 6	7	:	8	9	10	11	12 j 13 | 14
аг	—319	— И	„4	I —3	|	57	207	—64	-56	—21	—18	— 13	38	205
₽г > -	—345	—Hl	—10	3	-43	—1,8	— —	-95 ' —109	—86	—48	— Ц	—
	- — —		— —	75	63	52	44	23 ; —
I	15	16 j 17	।	18	19	|	20	21	23	24	25	26	27
az	1,2	—2fi	— Г	— 17	—24	—7	181	— —• —	™ | —
	—33	—71	—96	—105	—78	—	1,2	•	—49	—134	—253 \	—419	
т.	30	49	59	—67	—61	„	j	— —
		Схема	5: a~b		
z J 1	2	3	|	4	|	5	|	6	7	I .	4	11	)	18	25
a*	—54	—39	—55	—7Q	—67 |	25	475		B£ |	99	50	—36	|	—128
Схема 7: a~b					
i	1 9	10	11	12	13	|	14	|	— —
a(-	j	206	52		0,4	-8,4	—32	|	—68	—93	~ j ”
ПРЯМОУГОЛЬНЫЕ ПЛАСТИНЫ
Схема 10:
60
РАЗДЕЛ 13. УПРУГИЕ ТОНКИЕ ПЛАСТИНЫ (ПЛИТЫ И БАЛКИ-СТЕНКИ)
Продолжение табл. 13.20																												
с j					1=2	|	7=3	|	1=4																1^6	|	i^7							
—а	—35	„н	5	7,8 6	|																6,8					5,7				7,4			
Схема 11: а^Ь; значения																												
с	Z —1	2		3			4		5		ь						8				9		10				11	
0 6 	1 ь 3 1 ь 2	-591 —302 —99 —5,6	- 304 —262 —145 —60		s 5 i § ill!			—3,6 —61 —135 —203		27 — 13 —62 — 136		40 13 — 13 —60			67 41 26 —5,6			—660 —280 -77 0,2				—281 —682 — Hl —51		—76 — 141 —238 —133				2,6 -51 -132 —234	
£	|	12	13		н			15		lu		17			18			19				20		21					
0 1 ь 6 J ь 3 —6 2	26 —20 —'56 — 133	33 13 —6,5 —51		53 33 —22 0,2			—862 —190 —22 13		-188 —237 — 107 —27		—24 —105 —Ж —100			И 	Р5 —101 —.359			16 ~1,8 -27 — 101)				16 —7,3 —27		20 15 15 13					
Схема 11: значения «у																												
а - Ь/2 при 1, равном											а =25 при /, равном																	
	*	2		3			4		5					3			/				3		3				10	
и — 6 4 2	—533 —м 16	1 ND	Ю •— W	о jb		1 i 8 s s			3,4 2,7 —23		1 3,5 16		0 ±,ь 4 J-b !)			— 1592 —898 —324			1 1	1 й & ! 	 1				1 1 1 I § g		126 — 122 —395				582 128 —324	
Схема 11: а=^2Ь; значения <zy при /, равном																												
с	11		12			13		14		15		16				17			18			1				20		
и -*-6 -1 2гь	। 1 и § S I 1		—802 —780 —379			—22U —379 —622		108 —100 —379		444 108 —220		-2388 —526 —62				—524 —1043 —287			1	1 1 СО	ND CD 2	S'1			83 —49 —287				205 80 —62 j		
13.2.5. Балки-стенки [3] На рис. 13,21 приведены 11 схем различного загру- жена прямоугольных балок-стенок. Предполагается, что все нагрузки отнесены к пластине с толщиной /г=1. При этом усилия, действующие на единичную площадку,										где в зависимости от нагрузки р* равно: Р	Ма Р*х=Ро< р*-=— ", Р* = —д .	(13.20) а	а- Т а б л иц а 13,21 [3] Значения 5 в <13.21) для схем нагрузок по рис. 13.21																		
численно равны напряжениям. Усилия и напряжения определяются по формулам а	В !02,”*-. Gg~Ny~ wap- т	(13.19) тж„ = S = —— р*, ХУ	1Q2 1											Схема		<5 при i, равном															
													!		*			3		4		5		3				7
											1 2 a €		0,144 1,014 2,135 0,515		0,153 0,866 2,052 0,545			0,183 0,729 1,364 0,568		0,244 U ,624 1,123 0,762		0,346 0,560 1,006 0,989		0,486 0,532 0,965 1,545				0,608 0,495 0,907 1,845
13 3. КРУГЛЫЕ И КОЛЬЦЕВЫЕ ПЛАСТИНЫ
61
Значения коэффициентов а, Р, у из (13.19) в точках,
занумерованных на схемах А, В рис. 13 21, для всех рас-
четных схем сведены в табл. 13.20. В этой таблице индекс
г обозначает номер точки на схеме А, а индекс j—но-
мер точки на схеме В, для которой определяются усилия
или напряжения.
Рнс. 13 22
Рис. 13.21
костью симметрии), В силу этого Qe — Л1К =	=0;
фг=У,. при изгибе плиш и 3-,—Uy =0 при плоском на-
пряженном состоянии пластины.
Вее остальные компоненты усилий и перемещений за-
висят только от переменной г (рис. 13.1) или безразмер-
ной координаты
р = г)а,	(13.22)
где а — радиус одной из кромок пластины.
Плоское напряжениое состояние
На рис. 13.22 показаны эпюры ох, ау и тХу для харак-
терных сечений некоторых схем нагрузки, предоавлен-
ных на рис. 13,21 (пунктирные линии показывают закон
распределения напряжений по формулам курса сопро-
тивления материалов).
В табл. 13.21 приведены значения коэффициента 6,
(i— номер точки на схеме А), позволяющего определять
значения вертикального перемещения иу для некоторых
схем нагрузки, показанных па рис. 13.21, по формуле
Формулы для усилий и перемещений:
_	 ДР
“у — £ > «s= £ -
(13.21)
13.3. КРУГЛЫЕ И КОЛЬЦЕВЫЕ ПЛАСТИНЫ
13.3.1, Осесимметричная задача расчета
изотропных плит
Если нагрузка и граничные условия не зависят от угла
0 (см. рис, 13,1), то имеет место осевая симметрия (лю-
бая плоскость, проходящая через ось г, является плос-
Постоянные с, в (13.23) для первых двух схем, показан-
ных на рис, 1,3.23, находим но формулам.
схема и
Г -1 V4 "”7	С2 = 0:
ro;fl = -y	1₽Г°:
схема б
1 - 1 -
r < r0; = — p v; c2 =—- — p Vb“;
r > Л) rcy = 4" p (v — A.J; c2 =-—
— -у P^b'-Hj.
(13.24)
62
РАЗДЕЛ 13 УПРУГИЕ ТОНКИЕ ПЛАСТИНЫ (ПЛИТЫ И БАЛКИ-СТЕНКИ)
Здесь принято
(13 24а)
а
Используя (13.23), нетрудно получить решение для дру-
гих схем, аналогичных показанной на рис. 13,23 а.
Пример 13.5. Определить реактивные усилия р'г для
схемы на рис. 13.23, в при а = 6 м- Ь — 3 м; р—1 Т/м и
р=0,15.
По (13.1) находим + =0,85; Х2 = 1,15. Постоянные с,
от нагрузки р находим по (13.24) для схемы б при гд>
>га — Ъ (Ь/а=0,5):
1,15+0,85-0,53	)
у= ----------------= 1,81;
1 — 0,52
+ =—(1,81-1,15) =0,33 7+ I, (а)
с2=— — З2 (1,81+0,85)==-— 12Т/м.
2
Затем по (13.23) определяем иг для г = й = 6 м:
а /	12 \	а
и ----- 0,85-0,33 + 1,15 —- =0,67-—- .	(б)
Eh \	6” /	Eh	' }
Постоянные с, от реактивных сил р* находим по (13,24)
/ b	\
для схемы б при г<г0=а!— =0,5 :
\ а	)
1,15 + 0,85
v = -—+-л— = 2,67;
1—0,52
р*	—
Г1 ==— -у 2,67 = — 1, ЗЗр* 7/м;	(в)
р*
с2= — 2,67-33 = 12р* Т/м
2	1
и по (13.23) определяем ит для г = а~6 м:
ар*	12 \	ар*
йг = —++1,33-0,85 — 1,15 — =—1,51 — . (г)
E/i	36 /	Eh	v ’
Суммируя (б) и (г), найдем полное перемещение ur
точки г —а и приравняем его нулю:
ur= ++0,67- 1,51 + ) = 0,	(д)
Eh
откуда
0,67
+ =-—-= 0,44 7/.Ш	(е)
I ,01
Плиты на жестких опорах
Решение осесимметричной задачи об изгибе изотропной
плиты на жестких опорах методом начальных парамет-
ров см. [12]. Здесь приводятся готовые решения задач
об изгибе плит, показанных па рис. 13,24, Во всех этих
задачах, как и в любой осе-
симметричной, поперечные
силы в сечении г=го можно
определить по формуле
где Р—проекция па ось z
равнодействующей всех сил,
расположенных в области
0< г < г0.
Для определения W, 7ИГ,
Mq в задачах, показанных
на схемах /—5, следует
пользоваться формулами
табл. 13.22. В этой таблице
помимо обозначений (13.1)
принято:
(13.25а)
При решении задач, показанных на схемах 6—18, следует
пользоваться следующими формулами:
W = (Cj + +3 + С3 In Р +
ро4
+ +"“lnp)+ —РФ
<7©	1 Г	Сд
= + = —. 2сар + — +
dr	a L	Р
1	ра3
+ с41о (2 In р + 1) + ++ Р3;
I	1ЫР
М,
> (13.26)
1	Лэиа2
+ с4 (2Л.г 1п р + Л3) | — — р3;
J	16
D Г .	+.
Д4д ——	- 2лгсг + са +
а- [	р2
„ ,	„ 1 Tipas
+ + (2а2 In р + Х4)-------——— р2.
J	1о
4c4D	ра
I
1
где с, — коэффициенты, отражающие граничные условия;
они определяются по табл. 13.23, 13.24 (для схем 6—11)
и 13.25 (для схем 12—18), в которых, как и в табл. 13,22,
используются обозначения (13.25а).
Наибольшие напряжения и прогибы в плитах, изобра-
женных на схемах 12, 12а, 13, 16а, 17а, 19—21, опреде-
ляются по формулам
_ 2L
°макс — 71	'
Рг2
__ Г °
+1аке Уз г,,
(13.27)
13 3. КРУГЛЫЕ И КОЛЬЦЕВЫЕ ПЛАСТИНЫ
63
где Yi и Vs берук'я по графикам рис. 13 25, и и 13 25,6,
а Р и Го определяются так.
|ра2—схема 73;
pb“—схема 12а, 16а, 19, 20;
яра—схемы 13, 21;
лрЬ—схема 17 а;
_ f а— схемы 72, 13;
т»"~ j Ь — 12а, 16а, Па, 19, 20, 21.
Рис. 13.24
Пример 13.6. Для плиты по рис. 13.24 (схема 6) дано:
с = 4 м; Ь — 2 м, р—1 Т/м2; р—0,15. Требуется опреде-
лить прогибы и усилия в точках г —0, г = '2 м, г —-3 м.
Вычисляем вспомогательные величины по (13 1): Д =
=0,85; 7.2=1,15; Л3 = ЗД5; 1Д=1,45; Х7 = 7,45; й/а = 0,5,
По табл 13.23 определяем иосюяпиые для загружен-
ною участка плиты:
Cj =-£—(4-3,15 —7,45-0,5“ +
1 с л 1 П s	’	1
Д 4-1,15-0,52 1п0,5)-0,52 = 2,161 ----;
64D
па4	}
= —— (861,15 1п0,5 -ф-
64X2D v
+ 2-0,85-0,52 — 8) 0,52 =— 3,033 2—
'	640 j
(а)
Т а б л ица 13,22
Значения w, Мг, /Ид для схем 1—5 рис, 13,24
о и	W	мг	Mq
1	(Д - - 64Z, D — 2%эр-’ + Х2 р4)	(I _Pd i6		(V-pJ) lb
2	(I -P!)i 6 ID	16	(Д- wi 16
	(1 -рОД 16лХ2 D + -Ф, р- In р]	р 	In р 1Л	p ( P-1   1П p) 4л
; 4	ра~ 	In р) 1ьл£>	Р 	(l-i-k. In р) 2/т	p — 	 111 p) 4л
. 5	2Х. D	—m	—m
Т аб л иц а 13.23
Значения для схем 6—11 (рис. 13.24) при r<h (с
Схема	Общий множитель	64?v„Z)c1	|	fa-alvaD Cq	Схема	Общий множитель	6TkJJct	647.2Ос.
6	pa‘pJ	-— X-JS" -j- 4- 4k,{3” In 3)	8 (Д In p — 1) + 27.Tr	у	8Л2р(23&	(1 - pJ) Д2рцп р	1 — р^ -р 2 In Р
7	l-.pa^O	4 _	+ 4|3• hi P	4 (2 In 3 — P“) i	1(1	32та-	(?-' In р — 1) gJ	— (%j 4' kifH) 2
S		(] - P4 Д + 4- 2?..,p; bl [5	?.., (2 In P - 1 + P-)	Г1	13та-	2?.;PJ In р	(1	Р)“
G4
РГЦ11 В М1Р1ГИЕ ТОНКИЕ ПЛАСТИНЫ (Г ТИТЫ И ЬТТКИ СТЕНКИ)
Т 1 б 1 и I I 3 13 24
Значения сд дтя схем 11 (оис 13 2^) при г>Ь					
Схема	Общий множите ь	1 » Dl	М? De	1« Ос,	11?
6	л,ри р	р + ?	If		1?
7	27 | ра*	Т F	О’ р 3 )	хр	1
)	rpt	/ ? ]	I- 0 - к	/ (3	?
О	<Р pit b	1 -т 1	(1 в р)	0	2
п	1Гт (5	—	1 1 L	2.	2	и
D	1 та р		1	6 2 {	и
=f (12,1319 20 21)
С $ (12а 16а 17а)
os
/-.(J
По форсив (13 _3) н во i.i 1
w = В 4 с„(" п	ра1 ' MD Р ~	ла4 1,46 	 iAD
22 ,Ж		ра-
Л Г1 ID	16	— 3,78 64
а) аля г - f о	J			
2 161д 4	м,	И к‘У	2Х,ПС,	6 98ло
4V	L 1 -— 1	с4О			(2	Ы ’ (б)
2л Рс,	1йпа2с>2	ра	j
-------- -  --------- - 5 83 1------
а-	16	6г
р<2()	ра
б) для г ” 2 л, р 0 5

'’начения с дтя с^ем
’Я (рис 13 2л)
С <ема	Общи) МНОлъ iT и-	1) м	De		Ы/ De	Ы?tDr	o4> Lc,
1 а	ра4	>	1 (’	It	1и 3	-° !? (1- Г ) Л »	В 61	4р	(А -г 6 V In |3)	
/ / а	8? J а 1	/	Vln ₽		2у li р	'—	) 1	7 In р X.	2
П pta	7 та		-1		>	-j Ao b	0
/ 1 а	и	1			„I	-2 — p К	0
16 16а	X Сра*	! -% 6 --В	Р4—к/	₽4 In !.	3/ 0 In I5 - 2 - ! - к 6 ’	- <₽	-^4Л P In pj	
Г'	ЗА. ра b	2 - ? 0	р ах р	In [5	-?;-/₽	7 0 111 Ji	P (I + X In P)	J
1S 16 а	32 ТпЪ				- 1	2	и
13 3. КРУГЛЫЕ И КОЛЬЦЕВЫЕ ПЛАСТИНЫ
65
Для ненагружениого участка плиты с, находим по
табл. 13.24:
с3 =
2ра^(\“	рс^
г, =— с„ = (2+ — Z+-) -4—1- = 2,63 2— ;
S1 2 я 11 64А2Р	640
2ра*$~	1 ра^
-—— +.+ —---------;
64А2О	'	4 640
2ра4 63 „ ра2
_±_Ю.4Ао==2Л— .
4	64+D	‘	640

Затем по (13.26) для г=3 м и р=0,75 находим:
ш = ——[2,63(1 — 0,752)4- ——In 0,75 +
640 L	4
Ipe9
= 0,77—-;
64D
ра-
Мг =
64
_0^________
4-0,75“
— 2 (2.1,15 1п 0,75 + 3,15)]= 1,39	;
0,85___
4-0,75“
.	рсР
— 2(2-1,15 In 0,75 + 1,45) = 4,23—— :
(г)
(е)
Л4„ = — 2.1,15.2,63
64 I
I
I
4с4О	8ра*О	ра
а3р	Ь4Ои3-0,75	6
Круглые плиты с кольцевыми ребрами
Если кольцевое ребро (рис. 13.26) отделить от плиты,
то при осесимметричной нагрузке усилия, передающиеся
на нею ог цлшы, сведутся к равномерно распределен-
ным силам и парам, по-
казанным на рис. 13.26,6.
Чтобы получить расчет-
ные усилия, следует си-
5—26
лы р перенести в средин-
ную шоскость плиты и
плоскость, проходящую
через нейтральную ось
сечения ребра. Это вы-
полнено на рис. 13.26, в.
Обозначим угол поворота
и радиальные перемеще-
ния сечения плиты г~га
(рис. 13.26) соответствен-
но ра и иа, а угол пово-
рота сечения ребра и ра-
диальные перемещения
его точки, отмеченной на
рис. 13.26, в крестиком,
назовем |3Р и др. Тогда
уравнения совместности
деформаций, из которых
определяются р и т, за-
пишутся так:
Зп —' Др1 + — + •	(13.28)
Величины |3Я и «Е находятся по формулам (13 23)
и (13 26).
Для ребра имеем (поворот по часовой стрелке счи-
таем положительным)
р 4
рр==_	„р==	+^рЯь (13_29)
h-/р	t г р
где и /р — площадь и момент инерции сечения ребра
относительно нейтральной оси х (рис. 13.26), a — рас-
стояние от оси х до верхней кромки ребра.
Упрощенный расчет основан на пренебрежении дефор-
мациями плиты от сил р. При этом второе уравнение
совместности деформаций (13.28) заменяется условием
равенства нулю_«р (£3.29). Отсюда можно найти зави-
симость между р и пц.
Для ребра прямоугольного сечения получим
(д)
6 _ _	/	h
р^-~~ ,И1; гпд =	4 4- 3 —
п	\	п
(13.30)
Величина пр определится из первого уравнения (13.28).
Пример 13.7. Рассмотрим плиту, представленную на
рис. 13.26, при следующих данных: а = 4 м; г0 = 2 м;
/1=10 см; b — lQ см; И = 20 см; ,а = 0,15. Равномерно
распределенная нагрузка р=1 Т/м2.
Находим отношение жесткостей ребра н плиты:
£7„	/ Н V Ь
~+Г= Т — (1-ц“)^ 0,364.	(а)
raD \ h ) rQ
По формуле (13.29) находим угол поворота сечения
ребра:	_
5,5тг
т1 го	пц г п
=—2,75—--—
(б)
D
£/р	D
Прогибы плиты запишем в виде
w — w0 +
где а>о — прогибы от нагрузки, а и, — прогибы от
ствия реактивных пар т0.
Угол поворота сечения га — 2 м от нагрузки найдем по
схеме 2 табл. 13.22 (р = г(1/а=0,5):
, ра3
W°=~^D2(1 “Р2)2Р =
(в)
дей-
1-43-0,75-0,5	1,5	„
—-------------=— — ра+
16Z?	D
(г)
Для определения угла поворота того же сечения от
действия т0 находим для схемы 11 табл. 13.23 значения
Ci и с2 (Р — bja — 0,5) и используем (13.30):
16m0nU8(l — Р2)
I	10\-
4Ч1-0,5£ 4 + 3—- К	-
\	20 / __	16,5m!
40	~ Ъ ’
____16т0а22+Р3 In Р _
С1	64Дле
!	<0'1-
42-0,5Мп0,514 + 3—' mt
1	20)	_ 3,8ffli
4Д	~ D ’	,
66
РАЗДЕЛ 13. УПРУГИЕ ТОНКИЕ ПЛАСТИНЫ (ПЛИТЫ И Б UtK.II С ГЕНКИ)
Затем по (13 26) прп г = г0-=2 м найдем
2с2р 4,12h’i
<е)
Следовательно, полный угол поворота сечения плиты
(Зи равен:
,	,	4,12т,—1,5
)Зп = и,, + ду =------------.	(ж)
Приравнивая правые части (б) и (ж), найдем
тг = 0,155 Т-м/м.	(з)
Зная ГП\, можно вычислить прогибы и усилия в любой
точке плиты.
К примеру прогиб п изшбающии момент в центре пли-
ты от па-рузки находим по табл. 13.22 (р=0; Х2 =
= Пр=-1,15):
да4	1	/м2Х.,	_ „
к, =----= ___ лг y.j — ——ы. — j дэ Г-мм.
640	D	16
+ U'1] + Вл[^и’,-иЛ tp.l-Lu', -му?; )
-• Р	/	4 V	> 1 I
Л'ф,	+11(7? 4 I
+ Pm Р21 и\ - 14? 4 В; f 17' I- пи ? 4 i
v Р	!	1 Р	7	(13.34)
4 5 4;-ВХ).	j
При пользовании форму теми (13 31) стедуег иметь
в виду, что при р—0
1 1
-у21(р)=0; — U2({) — -—0,5.	(.13.35)
Те же величины oi пр находим по (13.26) и (д):
3,841!
0,589
О
2?.„-16,5/Я!
Мп
0“
= 0,363 Т-м/м.
Постоянные В, из (1,3 32) и (13.34) в общем случае еле-
дуе1 определять по заданным краевым условиям; в не-
которых частных случаях можно во.’шегьтеьаться при-
веденными ниже готовыми формулами [15].
Следовательно, ребро снижает прогиб в центре плвы
в 2,43 раза, а изгибающий момент в 1,46 раза.
Бесконечные плиты
Плиты на упругом основана и
Рассматриваются пластины, расположенные на осно-
вании типа Винклера, характеризуемом коэффициентом
постели k Реакции основания сведутся к вертикальной
распределенной нагрузке (см. разделы 23, 6)
А=--/ги.	(13,31)
Общее решение для осесимметричной нагрузки имеет
вид [15]:
щ = BJ7t (р) 4 £,[72 (р) + б3?73 (р) + 34С74 (р) 4 — ,
я
(13.32)
где р—интенсивность распределенной нагрузки;
В[ — произвольные1 постоянные;
U t—цилиндрические функции аргумента р, опреде-
ляемого формулой
р = -qr; Ц =		(13.33)
Значения функций U, и их первых производных Иt —
d
=---— Ui приведенные в табл, 13.26, позволяют вычис-
лит1, не только прогибы, но также углы поворота 6,-
н усч шя по формулам
В,. а/ = (Bjt/'j + B,U\-ф е/А + Ви\} ; 1
уЪ - (BiUs - ZU/, 4- В.ли, — BJUB В2,
(\ »У = I,’’ I В,и’, —	+ B,U\ — ВЛ J;
Мг == Dr-p I В, р-2 и' -- и ?! + В, [ и , + j
L \ р У Ч р "	}
/эф == В2 =.4 = 0;
а) Сила Р, сосредоточенная в начале координат:
Р
4 гр 2)
б) Силовая нагрузка, распределенная по
радиуса а с интенсивностью р-
при г <; а; р < ру р0 == qa
п_______п ! \.
Ч~ 21]3D Ро^
4?я =

при г > а; р > р0; рс == ра
Вг = В. = 0; В~, = ^’5- С (р );
1 1М'’
s4 = -
Cs (р0),
2ipD
(13.36)
окружности
(13.37)
(13.38)
в) Моментная радиальная нагрузка, распределенная по
окружности радиуса а с ичхчсппосыю
при г <. а; р < р„; р„ =
р „ ЛТ2! и' i	1
51-	?? ) Ps ) ) 9
2<Г-0
1 (13.39)
13 3. КРУГЛЫЕ II КОЛЬЦЕВЫЕ ПЛАСТИНЫ
67
Т а б лица 13.26
Значения Е’; и У в (13.32)
р	vl		-%	-~U2	«3		“В	
0,00	1,0000	о.оооо	о,оооо	0,0000	°,5000	ее	о.оовд	
0,02	1,0000	0,000!	0,0000	о.споо	0, /97	2,5643	0,0288	3!,828
0,04	1,0000	0,0004	0 О’УЮ	(1,0200	0 J-989	2,1282 1,8653	0,0438	13,01В
0,06	1,0000	0,0009	0,0()fH	0,9300	0,1978		0,0655	10,595
0,08	1,0000	0,0916	0,0000	0,0400	0,4963	1,6825	0,0800	7/378
0.10	1,0000	0,0025	0,0091	0,0500	9,494 >	1,7409	0,0929	6,84 В
0,12	1,0000	0,1'036	0,9001	0,0600	6,4926	1,4254	0,1046	5,2754
0,14	1,0000	и,оош	0,0002	9,0700	0,4904	1,3279	0,1152	4,5126
0,16	1,0000	0,0064	0,0003	0,0800	0,408'1	1/436	0,1248	3,9394
0,18	1,0000	0,0’ ’81	0,0004	(5,0900	0,4851	1,1695 1,1033	0,1337	3,4925
0,20	1,0000	0,0100	0,9005	0, юти	0,4826		0,1419	3,1340
0,22	1,0000	0,0121	0,0007	0,1100	0,4797	1,0437	0,1495	2,8400
0,21	0,9999	0,0114	0,0009	V, 1200	0,4767	0,9894	0,1565	2,5941
0,26	0'9999	0,0)69	0,001.1	0,1300	0,4735	0,9397	0,1630	2,3854
0,28	0,9999	0,0106	0,0014	0,1400	0,4761	0,8938	0,1680	2,2059
0,30	0,9999	0,0225	0,0017	0,1500	0,4667	0,8513	0.1746	2,0498
0,32	0,9998	0.П256	0,0020	0,.(60з	0,1-51°	0,8117	0,1798	1,9127
0,34	0,9998	0,0280	0,0025	3,1700	0,45%	0,7707	0,1840	1,7912
0,36	0,9997	0,0324	0,0029	0,1800	0 %%	0,7409	0,МН	1,6828
0,38	0,9997	0,0361	0,0034	0,1900	0,452 )	0,7073	0,19(2	1,5854
0,40	0,9996	!),040и	0,0040	0,2000	0,148 ’	0,6765	0,!970	1,4974
0,42	0,9995	0.Щ41	0,0046	о,2100	0,1-В!	0,6473	0,2006 0,2038	1,417-1
0,44	0,9994	0,0484	0,0073	0,2200	П 1400	0,6198		1,3443
0,46	0/993	0,0529	0,006.1	0,22.79	0,4 ’>59	<>,593о	0,2058	1,2773
0,48	0,9992	0,0576	0,0069	0,239°	0,43В	0 5686	0,20%	1,2156
0,50	0,9990	0,0625	0,0078	0,2,99	0,4275	0,5449	0,2121	1,1585
0,52	0,9989	0,0676	0,0088	0,2599	0,42 Г.	0,5223	0,2141 0/165	1,1956
0,54	0,9987	0,0729	0,0098	0,2<j0Q	0,4110	о,5006		1,0о61
0,56	0,9985	0,0784	о,оно	0.2799	!), 11%	0,4800	0,2184	1,0105
0,58	0,9982	0,0841	0,0122	0,2398	0,40В	0,4602	0,2201	0,9675
0,60	0,9980	0,0900	0,0135	0,2998	0,4, >58	0,4413	0,2217	0,9273
0,62	0,9977	0,0901	0,0149	0,3098	0,4014	0,1231	0,2230	0,8891
0,64	0,9974	0,1024	0,0164	0,ЗЮ7	0,3969	0,4057	0,2242	0,853В
0,66	0,9980	0,1089	0,0180	0.3297	0,39'24	и.3389	0,2252	0,8201
0,68	0,9967	0,1156	0,0198	0,3396	0,2x879	( ,3729	0,2261	0,7883
0,70	0,9962	0,1224	0,0214	0.3496	0,3834	0,3574	0,2268	0,7582
0,72	0,9958	0,1295	0,0233	0,3595	0,3783	0,3425	0,2274	0,7296
0,74	0,9953	0,1368	0,0253	0,3694	0,3743	0,1282	0,2279	0,7024
0,76	0,9948	0,1443	0,0274	0,3793	0,3697	(’,3144	0,2282	0,6766
0,78	0,9942	0,1520	0,0296	0,3892	0,3651	ЮТ! 1	0,2285	0,6о20
0,80	0,9936	0,1599	0,0320	0,3991	0,3606	0,2883	0,2286	0,6286
0,82	0,9929	0,1680	0,0344	0,4090	0,3560	0,2760	0,2286	0,0061
0,84	0,9922	0,1762	0,0370	0,4180	0,351 1	и, /141	0,2285	0,5817
0,86	0,9915	0,1847	0,0397	0,4288	9, И69	(’,2526	0,2283	0,5642
0,88	0,9906	0,1934	0,0426	0,1336	0,31В	0,2415	0,2279	0,5146
0,00	0,9898	0,2023	0,0455	0,	0, В77	Р,!Г08	I), 2270	0,5?лЗ
0,92	0,9888	(1,2111	0,0436	0,4581	(),33°2	о .1-L05	0,2271	0,5077
0,01-	0,9878	0,2206	0,0519	0,1681	О, 1283	0,2105	0.2265	0,1904
0,05	0,9067	0,2301	9,05'3	0,1770	О,32И	0,2008	0,2259	0,4737
0,98	0,9856	0,2397	0,0588	0/(870	0, «93	0,1915	0,2261	0,4576
1,00	0,9841	0,2496	0,0621	0,4971	0,3151	0, В25	0,2243	0,4422
1,10	0,9771	0/017	0,0831	0,5458	0,2929	0,1119	0,2193	0,3730
1,20	0,9676	0,3587	0J078	0,5835	0,2713	0,1076	0,2129	0,3149
1,30	0,9551	6,4201	0,1370	0,6403	0,251/	0,0786 0,6542	0,2054	0,2656
1,40	0,940}	0,4867	0,1709	0,6860	0 S1O2		0,1971	0,2235
1,50	0,92 И	0,5576	0,2100	0,7302	0,2110	0,0337	0,1882	0,1273
1,60	0,8979	0,6327	0,2545	0,7727	0 1926	0/166	0,1788	0,1560
1,70	0,8700	0,7120	0,3048	0,8131	{?, 1752	0,0023	0,16.92	0,1290
1,80	0/367	9,7953	0,3612	0,8.50')	о, 1588	0,01/4	0,1594	0,1056
1/4)	0,7975	0,8821	0,4238	i’,8357	0,1 вз	0,0189	0,1493	0,0854
2,(?	0,7517	0,9723	0,4931	0/170	0 LB4	0,02%	0,1399	0,0679
2,2	0,6377	1,1610	0,6520	0,9661	0,1023	0,0 571	0,1210	0,0397
2,4	0 , 4890	1,337=1	0,8392	0,8911	0,08(Ч	0,04/	0,1032	0,0189
2,6	0,3001	1,5569	1,0552	0,69В	0,1)614	(',0416	0,0868	0,0039
2,8	»,06Я|	1,7529	1,2993	0,9589	0,0455	0,0417	0,0718	0,0066
3,0	"“9			1,9376	1,5'698	0,880'1	0,0326	0,0427	0/0586	0,0137
3,2	0,5644	2,1016	1,8636	0,7199	0,0220	0,0394	0,0470	0,0180
3,4	0,9680	2.23М	2,1755	0,5577	0,0137	0,0356	0,0369	0,0204
_____________________ (Продолжение таблица/, на след. стр.)
68
РАЗДЕЛ 13 УПРУГИЕ ТОНКИЕ ПЛАСТИНЫ (ПЛИТЫ И БАЛКИ-СТЕНКИ)
Продолжение табл, 13 2(>
р	V1	-и.		—tn	и3		-у3	U4
								
з,ь	1	2,3199	2,4983	0,2935	0,0072	О,Oil 1	0,0284	0,0213
3,8	1,9674	2,3459	2,8221	0,052b	0,0022	0,0260	0,0212	0,0210
4,0	2,5634	2.2927	3,1346	0,4912	0,0014	0,0230	0,0152	0,0200
4,?	3,2195	2,1422	3,4199	1,0318	0,0039	0,0192	0,1)104	0,0185
4,4	3,9383	1.8726	3,6587	1,6833	0,0056	0,0056	4,9065	0,0168
4,о	4,678 1	1,4810	3,828!)	2.4520	0,0066	0 0125	0,0035	0, и 148
4,8	3.4531	0,8837	3,9006	3,3422	0,007!	0,0097	0,01'12	0,0129
3,0	6,2301	0,1160	3,8454	4,3542	0,0071	0,0073	() ,9003	0,0109
5,2	6,98(13	0,8658	3,6270	5,4835	0,0069	0,0053	О,(ИД7	0,0091
5,4	7,6674	2,0845	3,2063	0,7198	0,0065	0,01)37	0,0025	0,0975
5,6	8,2-166	3,5597	2,5109	8,0453	0,0059	0,0023	0,(И)30	0,0060
5,8	8,6644	5,3068	1,5856	9,4332	0,0053	0,0012	0,0033	О,|Н)47
Ь,0	8.8583	7,3347	0,2931	10,34b	0.UO46	0,0001	0,003'3	0,0036
Примечание; Табличные значения, расположенные ниже жирных горизонтальных линий,							отрицательны.	
при г > а, р > р0; ро =
Определив
^ = ^ = 0;
(13.40)
р0 = Т]а -= 1,08;
Рр0 200-1,08
“"2-3-10М
и найдя по табл, 13 26 для р0 = 1,08
9,08
— м
103
(б)
г) Нагрузка интенсивностью р, распределенная по пло-
щади круга радиуса а
при г < а; р < р0; р0 = рд
иг = 0,979; У2=—0,291; П3 = 0,297;
U4 = —0,150;
</ = — 0,079; U'2^=— 0,536;
(в)
fi!=“
ЛРРо
2k
У4 (Ро) '
U3 = — 0,220; П4 = 0,387,
S==“^ir^W; fi3 = B4 = 0;
при Г > а; р > р0; ра = Т)«
В — В = 0; В = — СДа и' С р ) ;
1 а ’ з 2А 2 \ f °'
.84=-->^Рй);
(13.41)
(13.42)
вычислим по (13.41) и (13.42) постоянные В,:
а)	для участка г<2 м (В3 = В4 = 0)
35,1
В, = — AU, = — — - м-
1	4	10“
б)	для участка г >2 м
48,5
Л - — AV., =	- м-
з	-	!04
Затем по формулам (1332), (13.34), (13,35)
определим для центра плиты (т = р—0)
2000
3.14-23-3
б, = -ж/3=.
(В, =В2-=0)
19,9
----- м
(г)
Пример 13.8. Плита весьма значительных размеров
в плане и толщиной й. = 60 см загружена нагрузкой Р =
— 20 Т, распределенной по площади круга радиуса
а = 2 м. Коэффициент постели основания k — 3-10J 77л3.
Упругие константы платы р—0,15; Aj —0,85; Е~
= 2-106 кГ]смг.
Приняв центр нагрузки за начало цилиндрической си-
стемы координат, определить прогиб и усилия в плите
для г=0 и г = 3 м,
Вычисляем. D и т) (13.33):
7,14
----№
10J
и табл. 13.26
(д)
£) =
2-108-0,63
12(1 — 0,15-)
= 3,64-104Т-м-
3-103	1
------_ 0 538 — .
3,64-104	м
(а)
1Q4 (
18,3
------.и — 0,183 см
10’
Л1Г = — 0,5382-3,64 [— 35,1-0 —
— 19,9(1—0,85-0,5)1 « 12Т-л/л;
Л4е = — 0,5382-3,64 [— 35,1-0 —
— 19,9 (0,15 + 0,85-0,5)] « 1?Т-л/,и.
(е)
(ж)
(в)
Определив затем по табл. 13.26 для ро= 1,62 (г=3 л)
В3 = 0,186; £/.] = —0,011; В3 = —0,175;
t/' = 0,145,
(и)

J
13 3. КРУГЛЫЕ И КОЛЬЦЕВЫЕ ПЛАСТИНЫ
69
вычислим ио тем же формулам для г — 3 л:
w --=	(48,5-0,186 — 7,14-0,011) «
10*
4,9
~------м - 0,049 см;	(к)
10*
Г	/	0,85	7
М, = — 0,538'--3,64 48,5 —0,011 +---------- 0,175 —
L	\	1,62	J
!	0,85	71
— 7,14 (0,186 + -Л— -0,145 ~ —2,35 Т-м)*; (л)
1,62	/]	'	'
Л1е = — 0,538‘-.3,64 ^48,5 (—0,15-0,011 —
0,85	\4
—	0,14t> I ре 4,59 7-лг/л;	(м)
Qr = — 0,5383-3,64 [48,5-0,145 ф- 7,14-0,175] «
а 4,7 Г/м,	(н)
Круглые и кольцевые плиты
Решение ищется в виде суммы
w -= -у ш*,	(13.43)
слагаемые которой определяются из расчета бесконеч-
ной плиты: первое — аг°—из расчета на заданную на-
грузку по формулам (13.32)— (13 42); второе — д'*—.
из расчета на компенсирующую нагрузку, выбираемую
так, чтобы условия в сечениях бесконечной: плиты, сов-
падающих с краями рассматриваемой кольцевой пли
круглой плиты, были тождественны заданным, Расчет
на компенсирующую нагрузку ведется по формулам
(13 32) — (13,34) при р~3 и сводится к определению
произвольных постоянных (i= 1, 2, 3, 4,). В частно-
сти, для сплошной плиты следует принять В3=В,[ =
=0, а В* и Bq определять из граничных условий.
Пример 13.9. Плита из примера 13.8 имеет по окруж-
ности г==3 м кромку, свободную от усилий. Определить
прогиб в центре плиты.
Слагаемое ш° в (13.43) было найдено в примере 13.8.
Соответствующие усилия в сечении г = 3 м равны [см.
формулы (л), (н) из примера 13.8]:
Мщ= — 2,35Т-м/м, Q°r = 4,7T/M.	(а)
При расчете бесконечной плйты на компенсирующую
нагрузку В3=В4 = 0. Используя значения (и) из при-
мера 13 8, а также (13.34), найдем М' и Qr в сечении
г — 3 м.
М[ = rfD (fl,51В* — 0,48В3)
Q* = 514 D (0,78В* — 0,27В*)
(б)
Из заданных в сечении г=3 м граничных условий
Mr -= M°r +	= 0; Qr =- Q[’ + О; =- и (в)
получим
»	50,3	,	36,1
В, =.	; в, = ——
1	D	~	D
(С
Прогиб в центре плиты (см. пример 13 7)
18,3	50,3	32,2
----р-----------------------,!г — Q уро см,
10*	3,64-10*	10*
(д)
Если бы плита была абсолютно жесткой, ю прогиб в
центре был бы равен:
92
3,14-З'-З
24
------0,24 см
10*
(с)
13.3.2. Изотропные круглые плигы
под произвольной нагрузкой
Круглая плита с защемленной кромкой
На плиту действует следующая нагрузка:
1) сила Рг приложена в точке В (рис. 13 27):
Рг
16л£>
(13.44)
2) пара Мд, действующая в радиальной плоскости,
приложена в точке В (рис. 13.27) и стремится выгнуть
центральную часть плиты вверх:
-И1’
”Т>
8 л D
-ф (а — г cos 6) fl -i- 2 In j —
\	«Кг ]
~7~ [ar — pjcose)
Щ В)
(13.45)
В (13,44) и (13 45) принято (рис. 13 27)
Р" = г* ф- а2 — 2 cos 0;
, В)	2ro г
Й7 = г- 4- — —-------- cos 0;	(13.46)
а“ а
Круглая плита со свободно
опертой кромкой
Прогиб от действия силы Р, приложенной в точке В
(.см. рис. 13.27),
70
РАЗДЕЛ 13. УПРУГИЕ ТОНКИЕ ПЛАСТИНЫ (ПЛИТЫ II БАЛКИ CTI HKiI)
Гц ( Гц— SracosO) S 2 dS Xj Q
rj S~ r a~ — 2,ф arS cos О	К °
+ 23=ln^ .	(13.47)
°A1 J
Свободная «ругмя плита
под действием статически
уравновешенной нагрузки
пендикулярные плоскости упруго» симметрии, из кото-
рых одна проходит через ось г (см. рис. 13.1), вторая
параллельна срединной плоскости, а третья перпендиау-
лярна первым двум (плита отважна к цилиндрическом
системе координат г, 6, г). Птаыипу, обладают}ю та-
кими свойствами, будем называть цл ындрически орю-
троппой. Упругие свойства такой пластины харакн'ри-
зуют величины £'ь рц (для волокна, совпадающего с ра-
диусом) и Ег, рц (для волокон, перпендикулярных г).
Модуль упругости сдвига G при осеснммшричнон де-
формации не испол: зуетея.
В последующем приняты обозначения
Г	-т /
Р=—; 8=1/ А-	(13.50)
а	|
а)	Вдоль кромки плиты действуют п равных сил Р,
расположенных па равных расстояниях друг от друга
и уравновешенных равномерно распределенной вдоль
тон же кромки нагрузкой р (рис. 13.28).
Рис. 13.28	Рис. 13.29
Прогиб в центре плиты
ZdL
2лХ3 D
(13.48)
где	а — 0,139;	Ь — 0,195	при	п = 4
а = 0,296;	3 = 0,378	»	п = 3
а = 0,773;	6=1,128	»	л = 2
б)	Вдоль хромки плиты действуют п равных сосредо-
точенных пар Л4ц (рис. 13.29).
Прогиб в центре плиты
(13.49)
где а и I. равны:
а = — 2;	6 = 5,545	для	п	=	2;
а = — 1,179;	b == 2,950	для	п	=	3;
д =— 0,858,	6 = 2,035	для	д	=	4.
13.3.3. Круглые i: кольцевые ортотропные
пластины
Рассматривается осесимметричная деформация круг-
лых я кольцевых пласгнп из ортотропного материала.
Ь каждой точке пластины существуют три взаимно пер-
Плоское напряженное состояние [17]
Усилия и перемещения определяются по формулам
Nr = B1Pk^ - Sa(>-A-!;
Лф = 8(А P^ + Mp^1);
a	,	(13.51)
«г = PT I (8—ja) pA 1 +(% + и2) p k ;
Постоянные В, в (13.51) определяются из граничных ус-
ловий на кромках плаепшы и из условии сопряжения
смежных участков. Приводим зпш синя постоянных В,,
для кольцевой пластины, загруженной по внешней или
внутренней кромке равномерно распределенными ради-
альными усилиями (а и b — радиусы внешней и внут-
ренней кромки, р0 = а/6).
а)	По внешней кромке действуют растягивающие уси-
лия с интенсивностью р<:
- 2Й
Р1
77 = -—^; Вг=,-------------	(13.52)
1-Р,7	1-Ро‘
6)	По внутренней кромке действуют растягивающие
(направленные к центру) усилия с пнтжижвноыъю /г>
рА;+1
-----— .	(13.53)
1 — п-,г
1 Ри
Изгиб к р у 1 л о й и кольцевой пл и ты [17]
Уравнения срединпоя нов. рхноети и формулы для
усилий при осесиммеграчнох! нагрузке имеют вид
W =	"Т 1 1 ~Ь ^4	“I" ~J“ Pr'k
о
«г=	= 2В„/ -5(1+ fe) Bsr‘ ф
dr
4	(13.54)
+ (i^Z’)/’Afc+P7 A;
Mr = — Dii w‘ -ф — ш' I:
И r ]
13 4. ИЗОТРОПНЫЕ ПЛИТЫ разной формы
71
мв = — D2 + — w'j;
Qr = ~D J®"' -+ —	— w'j ; I (13.54)
A =-----—-------- .
(9 - k2) D,
Постоянные Вг в (13.54) определяются из граничных
условий на кромках плиты и из условий сопряжения от-
дельных участков плиты.
Сплошная плита должна содержать изотропный сер-
дечник, для которого
га =	+ В2Г“,
(13.55)
Приводим формулы для прогибов и усилий в круглой
плите, загруженной сосредоточенной сплои в центре и
сплошной равномерно распределенной нагрузкой.
а) Плита радиуса а загружена силой Р в центре.
Внешняя кромка жестко защемлена (k=p 1):
Ра2	г w = 		—		 1 — k + 4л (1 — k2) (1 4- k) Dt l + (1 +k) ps--2P1+fe];	
мг =	L_ [/£ ж „ j p*~i _ 2л (1 — feS) n ‘	
~(i +ps)];	(13.56)
p Же^"2М1-^) [0 + адрА	
J	
б) Плита радиуса а загружена силой Р в центре.
Внешняя кромка шарнирно оперта (йдМ):
PCA	r W = 				£		 и „ k _ 8(9-Ы)(1	1 -4p1+fc + (i +й),А;	
r 2 (9 —	1 ” ' 27	
-(3+ ;<_,) p2];	(13.58)
P^2	Г	l.-_1	
A - 0{gAA) HA + OP -	
- Й-Ч + 1)P2],	
2	
г) Плита радиуса а загружена равномерно распреде-
ленной нагрузкой интенсивностью р. Внешняя кромка
шарнирно оперта на жесткую опору (/г=АЗ; k=pl):
рай	Г (3 — й) (4 + й ж р„) ~ '
8(9-^)D1'[ (1+7)^ + !Н) ~
Н-1щрЛ.
(1+W+1M Г
2 (9 - РР) • ‘
(13,59)
___жЛй2 Г(3-Н(.) (1 -1 рл-А к_л
2 (9 — й2) [ Ни ’Р
— (1 ~р Зр1) р2].
13.4.	ИЗОТРОПНЫЕ ПЛИТЫ РАЗНОЙ ФОРМЫ
13.4.1.	Треугольные плиты [3]
Прогибы и усилия в треугольных плитах (типа пока-
заний на рис, 13.30) можно определить ло следующим
формулам:
Таблица 13 27
Значения сх, у в (13,00) для пл1зт, опертых по схеме Д
рис, КЗ,31, ппи 60 -^303 (равносторонний треугольник) (ц=(Ц
Ра2	ПЗфН ц2) (1 — й) ,	
4л (1 — k~) Di [ (1 +4)2 + !-Ц) 4-p2	 (1 + k) (к + p2) 	]’ лп=^1+Ак(р^1); 2л (1 — #,2) Q .. JL. 2.v Pk"	НЖчННуХ!) Д-.1	(13.57)
AM -	s	p ° 2л (1 — A2) 1. k + iu	
- (1 + Ml) ] •	
5 5	ai	|	6l/l	|								A	}	X		
a	i										
	33	10	1 6	j la	10 1	6	j ?3	j 10 |	6	-	1 1? ;
/ 1	50 ?	397	23?	98 i		71		38 |	09	A17	297 ;
2	26 1	122	159	51 :	68	47	—30	18 j	73	166	129 
в) Плита радиуса а загружена равномерно распреде-
ленной нагрузкой иншисшшмтью р. Внешняя кромка
жестко защемлена (1г =АЗ; й=?Н);
Т а б лица 13 28
Значения a, j3, V в (13,60) дл? плит, опертых по схеме В
рис. 13.31 ври 0J---3O (равносторонний треугольник) ( Ц—(Ъ
§ у. “г | Рщ | А [ Рщ | Р
	13	10	Q	1.5	10	ь	1.5	10	G	12 j И П		
1	12	79	79	О 3	60	48	-10	4	L3	-1’7	1Ж	2 A
2	4	48	88	8	36	33	—13	—3	48	—39	rio	1 ’2
72
РАЗДЕЛ И. УПРУГИЕ ТОНКИЕ ПЛАСТИНЫ (ПЛИТЫ И БАЛКИ-СТЕНКИ)
Т j б л я ц а 13 29
Значения а, {3, у а (13,(Ю) для плит, опертых по схеме С рис, 13.31
а				Нагрузка		по схеме	7 ня рис	13. 32 j.	, jnp-И 1. рапном					
b	Параметры													
		1	2	3	4	6	7	«	9	н.	1 И	1 12		14
		0	0	0	О	322	262	m	0	102	63	U	Г2	9
	₽х	„—, >9	— 19		12	—3,5	126	90	- 24	.-220	75	23	— 1'> 1	23	-29 i
0,5	₽v	— 134	— 116	—70	—21	57	45	9	-47	1,5	—7	—31	о 2	—У .
	У	266	239	159	46	—	—	—	288	—		208	—	190 :
	а	0	0	0	0	199	162	74	и	98	О1	О	11	п
	|3„	—23	—20	—12	—3,4	82	60	— 11	— 132	73	23	— 135	21	-34
(1,75		—140	— 120	—71	—21	67	57	24	—Об	4,9	-6,8	3,9	-5,5	— 12 ;
	У	244	218	143	44		—		218		—	224	—	102 ;
	о,	0	О	и	и	118	95	42	0	82	51	0	12	0
		—21	— 18	— 10	—3	53	38	—b	—67	62	20	—110	21	—к
1, и	V	— 125	— 107	—62	18	59	51	25	—26	16	1,3	—43	— 11	— 18
		222	197	129	48	—	-	—	159	—	—	220	—	111	.
	i о-	у	0	0	0	45	Зо	15	0	45	28	О	U	0
	h	— 15	— 13	—7,2	—2	25	17	—2,4	— 19	38	12	—53	19	— к ;
	У	—92	-77	-43	— 12	38	34	20	—11	27	12	—38	— 11	-30 .
		182	160	106	48	—	—	—	78	—	—	—	—	13У ;
	а	0	0	0	о	20	15	6		и	14	0	7.2	0
		— И	-9,1	—4,9	-1,3	13	8,2	—0,7	—6,3	22	6,5	—24	13	—26 ;
2, U	‘0	—66	—-55	—30	—8	24		14	— 3	25	13	—26	1,7	—34
	7	151	132	89	45	—	—		47		—	122		144
а Ъ	Параметры				Нагрузка по схеме 2 на рис. 13.32					при i, равном				
		1	2	з 	4 i	6	7	|	8 1	0 1	10 )	11	!2	13	14
	сс	0	0	0	и	245	203	90	0	54	34	и	2,9	0 
0,5		1 L	—16 —97	! i СЛ <£> ос	—2,9 —17,7	95 43	68 34	— 17 5,8	—177 —36	39 Н	11 7,9	7 ।	-1,1	1 ! I<j СС о >)ы
	У	239	П8	152	56		—	—	222	—	—	)<18	—	25	'
	а	и	0	и	0	147	120	55	0	56	35	0	2,9	0
0,75	₽х	1 1.	—16 —96	—9,7 —58,4	—2,9 -17,6	60 51	45	-6,3 18	- 1 Сю	41 -3,2	—9,3	—81	4,8 -4,7	4 L f с
	у	211	191	133	51	—			168	—	—	125	—	25	;
		0	о	0	О	84	68	31	0	48	30	0	3,7	и
	к	•"™* 16	—14	—8,3	—2,5	37	28	45	-51	35	И	—68	0,6	
1	₽'у	—98		—49	15	45	39	39	—195	4,4	-3,7	—27 :	— 8,8	—7,8 1 32	|
	V	185	167	117	51	-	—-	—	!19	—.	—.	Ш	—	
		0	0	0	0	30	24	И	I)	2b	16	0	4,5	о i
		—11	-9,4	-5,5	— 1,6	16	12	—0,3	—14	21	7	—3]	7	—2о ]
	fj У	—66	—57	—33	—9,6	28	26	15	—8,5	13	4,6	—24	9,9	— 15
	V	145	131	94	47	—	—	—	'	63	—	—,	103	—	53
		0		0	0	13	10	4,3	о	13	8	0	3,3	О
		—7,7	—5,5	—3,7	—1,1	8,2	5,8	0,3	—4,/	12	3,8	—15	о, 4	— 14
*•	₽v	—46	—39	—22	-6,5	18	17	И	—3	13	:	61	— 17	-6,3	—18 !
I	У	117	105	77	43	—	—	—	39	—	—	75	—	61
13 4. ИЗОТРОПНЫЕ ПЛИТЫ РАЗНОЙ ФОРМЫ
73
Продолжение табл. 13 2®
а b	Параметры	Нагрузка по схеме 3 рис- 13.32							54	j при Z, равном				
		1	)	?	|	3				6	7	8	9	1°	11	12	13	14
		—4,8	—3,9	—2	-0.5	13	8,2	—3	1 — н	23	7,5	—34	—21	14
2	5 V	—29 35	—21 28	13	2,8 0,7	12	н	6*3	27	13 -	6,2 -	— 16 82	—11	—2,5 82
		—24	—19	—8,4	— 1,7	11	15	7,1	-2,9	23	12	—30	7,8		49
2	р0	—24	—19	—8,4	-1,7	И	1,6	— 1,9	—0,5	23	7,7	—5	7,8	—8,2
	V	35	28	14	м		—	—	14	—-	—	64	—	Ю6
--_----- - Л1у =.------
41 000D	6400
..	Pu ^ра
М„ —------,
“	6400
6400 ’
,. Pt? л2рп
,И„ = ------
6400
fap
800
(13.60)
Эпюра по прямой	Эпюра т прямой % •(}
Схема 1
Рис. 13.32
Значения коэффициентов а, Р, у в (13.60) для точек,
пронумерованных ьа рис. 13.30 при краевых условиях,
Рис, 13.30
13.4.2. Трапецеидальные плиты [3]
Изгибающие моменты в равнобочных трапецеидаль-
ных плитах (рис 13.33), как и в треугольных, опредр
ляются формулами (13 60). В табл. 13.30—13.34 приве-
Apwra свободно опертая на жесткую опору
Жестко защемленная кромка
Рис. 13.31
Рис. 13.33


показанных на рис. 13.3! и нагрузках по рис. 13.32. при-
ведены в табл. 13.27 -13.29. Более подробные таблицы
для треугольных пластин см. [3, 23J.
гигет? Жестко защемленная кромка
гггтта СвороЗно опертая кромка
Рис. 13.34
74
РАЗДЕЛ 13 УПРУГИЕ ТОНКИЕ ПЛАСТИНЫ (ПЛИТЫ И БАЛКИ СТЕПКИ)
Значения Зу s (13ЛзО) для пшьы а (рис. 13.34)	—
Схема плигы по рис. 13.33	। Нагрузка	1 3	j	1	:									
			1 1 J 2		1 5 1 1		6	I 7	8	9	10	И
	/	1 с	'1 7	—5,7 —' И	1 в	о ~	4,9 - 1,1	1,6 0,2	-3,2 1,7	”. 7 7	17 22	12 19
	И	j У 1 У	—н	Ь 1 У К 1 ~ I	— ц,9 И	—1,9 — 11	8,3 И	6,3 1 м	0,2 И	I 7	19 32	15 28
б	/	! у У	— У)	-5,1 — И		1 1 О1 с;	4,1 4,0	3,0 4,1	L 7	7 7	И 25	11 21
	П	1	у 1	у-	—19	- 7,5 —-И	7 7	- 1,6 	0,3	6,2 16	6J 15	2,0 12	00	S'-	1 25	10 22
Сх^ма п чю ы							/					
по рис. 13 33	Нагрузка		12	13	и		16	17	1й	19	:Ю	21
&,	/	У- У		о 7 7	20 25	4,1 13	7 7	14 9,3	3,8	-36 -17	1 1 О1 СК со	7 7
	И	У У	1,1 15	-из	17	5,1	7 7	8,5 ; -5,4 :	2,9 —7,7	L 7	—35	-12 — 12
	1	У Ру	12	7 L	(3	7,0 8,5	—11	—7,8 -17	-39	—14 —14	—	—
О	II	р„ с	12	—21 —W	\7	3,4 1,1	1 7 о to 		1 1 J1 <J! • СО	4  СО У- со	2 I	—	—
Табл и ц а 13.31
Значения 3(, в (13.Ш для плиты б (рис, 13.34)
Схема плиты т,	_	м по рис- 13. 33 j Нагрузка	Э			i								
			1	2	3	|	4	|	6	|	7		8	I 9	18
а	1 1 У		—7,7 —46	1 1 QQ	'	-6,2 —19	—П38 — 1,6	5,5	1,5 —0,3	—3,9 1,3	I 7	20 2°
	1	у i	sJ г "	| у		— 12 —60	:	—10 —60	-37	-1В — И	i 8,7 В	6,1 13	-0,3 И	У	21 32
6	/		tn Г-.	(г. ! 1	— 19		.тгз	—о, 9 —5,8	5,3 1В	2,9 2,8	5,5	— 4, 1	и
	и	3 1 У	;	-9,4	—3, 1 —50	L 4	— 1,7 -В	15	6,1	0,9 И	! 1 СО со	15 X)
Схема плиты по рис. 13. 33	Нагрузка		I								
			и	12	13	14	и	(6		18	19
а	)	1		13 19	— 1,1 11	- 17 —8,1	29	2,7	- 17 — В	25 27	15 В	— 48 	JO,
	II	У	I	113 Ру	!	28		0,2 15	—27 —В |	21 20		—40 — 19	— 16 6,2	7,3 0, 1	— 18 - И :
б	/	Ру	14	(1 11	~~14 -8,о	В	10	|	—31 19	।	-В		0 0	0 0	0	 1}
	.11	у	13	*•• у1 1:	-И1	) 9	, 1	-~-1 1	0	1	0
13 4 ИЗОТРОПНЫЕ ПЛИТЫ РАЗНОЙ ФОРМЫ
75
Таблица 13 32
Знатен'я f х, ц( ц (Ь 60) шя п 1ьты s (рис 13 34)
1г1
ПЛИТЫ 110 рис	Н i руз		; j 7 | ь | j				10 | 11		К j 13	
а			12 j 5,ч | — >Д 17 1 Ъ j 7 b			-6,9 — 3,3	23 28	lb 24	—3,3 !—35 I —17	
	/7	бу В	JO J5	1 38	1	1 1	.8 38	37	U В	7 i 1
( хом а плиты ПО Р ’С 13 И	3	р	I							
			14 j 1 1		( 7	17	18	19	д0	2(
а	/	Вл С	21	1,0 25 j h		1 1	lo 6 2	9,5 b,2	1 X	1 1 Сл ц; ui - ю	—20 —20
	II	Рх С	23 18	4, >	I I 1	M — 15	M —13	i_ 1^	^7 : -—42	7 7
Таблица 33 33
Значения (ф, Ру в (13 60) чая платы г (рис 13 34)
Схема i гли^ы по рис 13 33	ГЧ£^ 1 ПЩ	в							
			0	|	/		8	9	10	п	В
а	7	к 7,	1 1 f 1 1 !		ч	I । !	В 29	в	D, D 13
	fl	к р-	5 j (3		—2,2.	ф L i k w 	32 41	2 4 38	14
Схема плиты по рис 13 33	| II !гр>зка 	в	l						
				! 1	15	10	17	18	()
а	1 к 1 5 7			И Ю	-, 1 В	ь 5} ! !	5	Id 13	! i i| КЭ СП 1
	П	Те	- 3 20	0	2,8 > 1	—2/	20 а	8,5 —3 8	! 1
дечы значения коэйфидиеитов и |3В для точек пли-
ты проиумерог а’ гы>\ ла рис 15 ’1 грч краевых усло-
виях и нагрузка р(4.) У)=р{у}, показанных на
рис 13 34
13.4.3. Эллиптические слиты (рис. 13.35)
Нагру^ь. 1 (инг> чг i >еост ее п) раено черно распреде-
ленная по осей пго1"ади о пп.ы Для птьтыс жестко за-
щемленной кромкон (и = 0)
Таблица 13 34
Значения а (13 60) для плит рис, 13 34
Схема плиты ПО ПЙС 13 33	Нагрузка	п	ита а при		, оачаюм		Плита о		три i	равном	
		9	13	16	19	21	9	13	1b		21
	J	—4,4	—20	—40	—42	— 18	—»,ь	—22	—д7	—60	0 j
а	11	—11	—34	—Кб	—38	—р	-11	—35	—51	—48	0
	1	—5,0	— 14	-10	—П	—	—1,6	—21	— к	!)	—
	ч	™10	—26	—27	— й	—	— 1,2	™1	— к	— 18	
Схема		Плита		при	/, равном		Плита с. при t			равном	
плиты по оис 13 33	Нагруз	9	13	16	19	21	9	к	lb		
	, ./	—8,7	—б0	—31	—J„	—20	__д ?2	—» у	— рЭ	—70	0,
а	И	—10	—52	—Ь5	„19	— И	— 1ч	— 1	—7i	—62	0
1
/ 3	3	2
л = SD — + — + —у
1 at	od	g-’g-
м^ = -	4pD	/ з«-		1 '
	А	\ а'	а2Ьг а“	
	4pD	/ Зу-	X2	1 \
Му 		Я		а-Ь“ Ь- /	
j
Изгибающие моменты в центре плиты
1Лаьиых осей алллпсо pas ты
MD
(Жх)х=0, д=0 = ~^Г ’
ЬрО
Аа“
4рР
Ао“

’	(13.61)
и на концах
(13 62)
fipD
= - ~76т
Для плиты с кромкой, шарнирно опертой на жесткую
опор,, гропп и И31 ибепошие моменты в центре плиты
при ц = 0 определяются по формулам
МН
w = (X , Л’ ( ~ &pb:, Мц = урб- (13 63)
Значения коэффициентов
«, р, у даны в табл 13 35
Нагрузка Р распределен-
ная в центре п гиты по кру-
<у самого радиуса г0 Мак-
сима дные з щчения проги
ба и ноомалыюго напряже-
ния в центре плит я кром
кои, шарнирно опертой на
жесткую опору определи
Ю”ся по формулам (у.=0,3,
Р = Ь/ц)
76
РАЗДЕЛ 13. УПРУГИЕ ТОНКИЕ ПЛАСТИНЫ (ПЛИТЫ И БАЛКИ-СТЕНКИ)
Т а б л и ц а 13,35
Значения а, р, у в (13,63) (Ц -0)
а h	1 1 1,1		3,2	1,3	|	1,4		1,5	Г)	3	4	5	оо
а	0,061	о,И76	0,088	0,098	0,107	0,115	0,145	0,172	0,185	0,192	0,209
р	0,159	0,159	0, 155	0,152	0,115	0,138	0,105	0,061	0,049	0,029	0
V	0,139	0,188	0,215	0,237	0,2о0	0,28°	0Д18	о,ш	0,4-1	0, 472	0,500
Т а б л и ц а 13.36 |5]
Значения а, 3, у в (1,3,67) д^я плиты с защемленной луговой кромкой
	10. с/.		1	Н				4 |				10* у-		
	L												
			,3	о		*		t		0		2	
л 4	5	26	28	0	—37	31	82	250	—196	0	97	186	83
3	17	57	47	0	—56	92	97	—340	—274	0	167	169	87
о	63	132	82	—265	—3	220	87	— 188	—402)	—265	238	172	87
П'	293	337	152	0	440	396	—25	—756	—654	0	111	168	136
«'макс =777 (0,745 — 0,07оЗ);
Eh3
ЗР / Ь
Жкс= уТГ И .3 In ~ +1,97—0,77fi
(13.64)
Аналогичные величины для плиты с жестко защемлен-
ной кромкой при р =0,3:
Ргп
ы = « уу ; Ч = р. рг0 ;
Л)й = Tt prl; Qr = prv
Qu = VV
где i — номера точек, показанных на рис. 13 36.
Таблица 13 37 [5]
(13.67)
РЬ"
«макс = 777 (0.30 —— 0,04р);
Eh-3
ЗЯ /26
омжс =777 In— — 0,317fS —- 0,376
у	ГQ
(13.65)
Нагрузка, распределенная по линейному закону
х
р(х, у) =.р0 •—. Для плиты с жестко защемленным конту-
а
ром уравнение срединной поверхности имеет вид
(13.66)
Значения <х, 3, V в (13.67) для плиты со свободно опертой
дуговой кромкой
	ЮБ	j				101 р(			Ю-* 7,-			
О,	i										
		>	3	0			3	0	I	2	3
		33	49	о	—17	16	121	0	107	179	кв
4											
	19	80	92	О	—86	80	197	0	203	231	154
3											
о	92	226	203	—366	—66	272	325	—366	339	271	189
л	589	884	584	0	643	785	521	0	164	280	311
13.4.4. Плиты в виде кругового сектора
Плита представлена на рис 13.36; радиальные кромки
свободно оперты на жесткие опоры.
Прогибы и усилия при равномерно распределенной на-
грузке вычисляются по формулам
Значения коэффициентов а, р. у. <р, ф при р = 0, при-
ведены в табл. 13 3G 13.38. На рис 13 37 приведены
эпюры прогибов и усилии для птиты с дуговым краем,
свободным от закреплении, при 60 = л/4,
13 5 ТЕМПЕРАТУРНЫЕ НАПРЯЖЕНИЯ В ПЛАСТИНАХ
77
Таблица В 35 [5]
Рис 13,36
13.5.	ТЕМПЕРАТУРНЫЕ НАПРЯЖЕНИЯ
В ПЛАСТИНАХ
При неравномерном распределении температуры
в пластинах могут появляться усилия.
Ниже рассмотрен случай, когда изменение температу-
ры зависит только от координаты г (см. рис. 13.1 и
13.2).
Пусть температура нижней поверхности пластины
(г-=й/2) изменилась на Д С, а верхней поверхности
[г — —й/2)—на fj С. Тогда, определив
, _ / __
‘° “	2	’	”	2
(13.68)
найдем, что средняя температура try вызывает плоское
напряженное состояние, a t — изгиб пластины.
Если пластина любого очертания в плане жестко за-
креплена по контуру, то при воздействии температурно-
го поля (13.68) она останется плоской и па ее контуре
возникнут продольные силы N и изгибающие моменты
А1ПЭГ, определяемые по формулам
/V
aEtfjh
atDK
’> Л4иЗГ “	,
h
(13.69)
где а — коэффициент линейного расширения.
Таким образом, задача сводится к построению реше-
ния для пластины с заданными опорными закрепления-
ми от нагрузки, приложенной по кромкам и определя-
емой (13.69). Это может быть выполнено при помощи
формул, приведенных в 13.31.
Пример 13.10. Определить деформацию круглой плиты
радиуса а, свободно опертой по кошуру, от действия,
( = ----------
2
Используя (13.26)
и положив с3 = с4 = 0, получим для
кромки пластины
	w = ci + о = 0;			
	D Mr ~ ~	^‘SC2		аШХ2 — = 0. h	(а)
Откуда	с1 =		'ztcfl 2h	(б)
Рис. 13.37
Следовательно,
a to2
ш=—--(1—р®).	(в)
13.6.	ОБЗОР ТАБЛИЦ ПО РАСЧЕТУ ПЛИТ
Приводим некоторые сведения о наиболее распростра-
ненных монографиях, содержащих таблицы для опреде-
ления прогибов и усилий в плитах.
1.	Вайнберг Д. В., Вайнберг Е. Д. Пластины,
диски, балки-стенки. Стройиздат УССР, 1959. В рабо-
те содержится весьма обширный справочный материал
(формулы, таблицы, графики, примеры) по определению
усилий и деформаций в круглых, прямоугольных и дру-
7S
РАЗДЕЛ 13 УПРУГИЕ ТОНКИЕ ПЛАСТИНЫ (ПЛИТЫ И БАЛКИ-СТЕНКИ)
гой формы плитах под сосредоточенными и распределен-
ными нагрузками.
2.	В арвак П. М. и др. Таблицы для расчета пря-
моугольных плит Изд АН УССР, 1959, Даны таблицы
коэффициентов дчя определения прогибов и усилий
в прямоугольных плитах с разнообразными опорными
условиями от равномерно распределенной и сосредото-
ченной нагрузок. Таб.нпгы составлены при помощи чис-
ленною интегрирования, в связи с чем возможна по-
грешность при определении расчетных величин, которая
(по мнению авторов) в большинстве случаев ие превы-
шает 10%.
3.	Г а лер кии Б Г. Упругие тонкие плиты. Гос-
стройиздат, 1933. Содержит таблицы по расчету прямо-
угольных, секторных, треугольных плит с разнообраз-
ными опорными условиями под распределенной и сосре-
доточенной нагрузками.
4.	Панков и ч П. Ф. Строительная механика кораб-
ля, ч. II. Судиромгиз, 1941. Приведены таблицы для
определения усилий и прогибов прямоугольных плит, а
также таблицы для расчета круглых плит под осесим-
метричной нагрузкой на опорах и упругом винклеров-
ском основании.
5.	К а л м а н о к А. С. Изгиб тонких прямоугольных
плит, Машстройиздат, 1950 Таблицы по определению
прогибов и усилий в прямоугольных плитах под трапе-
цеидальной нагрузкой.
6.	Коренев Б. Г. и Черниговская Е, И. Рас-
чет плит на упругом основании. Госстройиздат, 1962.
Приведено большое количество табулированных функ-
ций, которые существенно облегчают расчет прямоуголь-
ных и круглых плит на упругом основании.
7.	Смотров А. Решение плит, нагруженных сплош-
ной нагрузкой, по закону трапеции. ОНТИ, 1936. При-
ведены таблицы для прямоугольных и треугольных плит.
8.	Т и м о ш е и к о С. П., Во п н о в с к я й - К р и -
rep С. Пластинки и оболочки. «Наука», 1963. Даны
таблицы для определения усилий в прямоугольных пли-
тах под разнообразной нагрузкой. Имеются также таб-
лицы, формулы и графики для расчета эллиптических,
круглых и треугольных плит,
9.	Шехтер О. Я. и Винокурова А В, Расчет
плиг на упругом основании. Госстройиздат, 1936 Содер-
жит таблицы по определению усилий и прогибов в бес-
конечно большой плите и плите в виде бесконечной по-
лосы, опирающейся на упругое винклеровское основание
и загруженной сосредоточенными силами, расположен-
ными в углах прямоугольной сетки, либо по оси сим-
метрии бесконечной полосы.
10.	Шиманский Ю А, Изгиб пластин. ОНТИ,
1934. Содержит таблицы по расчету прямоугольнь х
плит под разной нагрузкой.
13.7. Краткие сведения об аналитических
методах определения усилий и перемещений
при изгибе тонких упругих плит
Задача об изгибе «упругой тонкой плиты сводится
к определению функций прогибов ®, зная которую, мож-
но вычислить усилия и углы наклона касательной
к срединной поверхности плиты по формулам
-0-
лд.-=
д-ш
В) ~;
дхду
д-о	д-&>	д
У 2-Ю = —- Д	Q v	— D —- V2W.
дх-	ду-	дх

(13.70)
х дх у ду
Функция прогибов должна удовлетворять дифференци-
альному уравнению в частных производных четвертого
порядка (разрешающее уравнение) н граничным усло-
виям на кромках плиты. В частности, для плиты по-
стоянной толщины из изотропного материала разреша-
ющее уравнение в декартовых координатах имеет вид
[5, 19, 23]
сН	д&	di \	р
~о -------- J- ~— ю =	_
дх*	дх-ду-	ду* /	D
(13.71)
Соответствующие уравнения для плиты из анизотропно-
го (в частности, ортотропного) материала приведены
в [17], для плиты переменной толщины — в [3, 23], для
плиты на упругом основании — в [4, 16, 23]. Соотноше-
ния (13.70) и (13.71) в декартовых координатах целе-
сообразно применять для бесконечных пластин, загру-
женных нагрузкой, распределенной по площади прямо-
угольника; для полубесконечпой плиты, ограниченной
прямолинейной кромкой; для бесконечной (или полубес-
коиечиой) полосы с параллельными кромками и, нако-
нец, для плит, имеющих форму прямоугольника, парал-
лелограмма, треугольника или трапеции. Для круглых
и кольцевых плит, а также для плит, имеющих (форму
сектора или кругового прямоугольника, целесообразно
использовать полярные координаты (соответствующие
.-.ависимости см. [5, 12, 17, 20, 23]). Для плит, имеющих
форму эксцентричного кольца, кругового сегмента ми
круговой луночки, целесообразно применять биполяр-
ные координаты [24]. Другие возможные системы ко-
ординат см. [5, 23].
Как правило, решение задачи об изгибе плиты ищут
в виде суммы
К! = шо-фа1*,	(13.72)
где удовлетворяет только (13.71) при заданной на-
грузке, a w" удовлетворяет (13.71) при р=0 и подби-
рается таким образом, чтобы погасить искажения гра-
ничных условий на кромках плиты, вызываемые ш°.
Слагаемое W* называют однородным решением.
Оба слагаемых (13.72) компонуют из элементов (й =
= const)
Fn = h (п, kx) (n ,ky)	(13.73)
в следующих формах:
/д°ш
мг = -о
\ ох*
а2а, \
Ф2 / ’
д'2ш \
ан j ’
(13.70)
w ~ [ ДДя.
i)
(13.74)
(13.75)

B.S. ОБЗОР ТАБЛИЦ ПО РАСЧЕТУ ПЛИТ
79
Отлетим возможные варианты.
а)	Задавая /2 или /3 в (13.73) в виде
Д, = щ cos nky + cs sin nku (13.76)
и используя (13.74), можно получать решения большо-
го количества задач в виде ряда Фурье [3, 5, 20, 23j.
б)	Используя (13.76) и (13.75), можно получать ре-
шения в виде ингеграла Фурье. Такие решения исполь-
зуются обычно для плит бесконечных размеров [3, 14,
20, 23, 24, 25].
в)	Придав /2 или ft в (13.73) в виде
/2 = с^У с^пк<>	(13.7'7)
и подобран соотвегствуюш.им образом параметр п, мож-
но определить ряд однородных решений, удовлетворя-
ющих заданным граничным условиям па кромках пла-
стины у=0 и tj — ii, Такне решения принято называть
функциями Попковича—Фадля. Они могут быть исполь-
зованы для расчета прямоугольных секторных плит и
плит в виде кругового прямоугольника [11, 20].
г)	Задав ?, и [3 в (13.73) в виде степенных функ-
ций, можно, суммируя конечное число элементов Fn, по-
лучить решения в виде степенных полиномов, удовлет-
воряющих (13.71). Такие полиномы могут быть исполь-
зованы при решении задач об изгибе прямоугольных
пластин [13],
д) Ряд эффективных решений задач об изгибе плиты
в виде полосы, круговой луночки и кругового прямо-
угольника может быть получен в форме (13,75) путем
применения интегральных преобразований Фурье, Мед-
лина [25].
Если удается получить решение задачи, используя ко-
нечное число элементов (13.73), или найти аналитиче-
ское выражение для суммы ряда (13.74) или значения
интеграла (13,75), то говорят, что задача допускает
замкнутое решение. Так, например, замкнутое решение
для усилий может быть получено в задачах об изгибе
бесконечной плиты, ограниченной прямолинейной кром-
кой (защемленной, свободно опертой пли свободной от
закреплений) под действием сосредоточенных сил или
пар.
В тех случаях, когда задача не имеет замкнутого ре-
шения, имеется большое число приемов, позволяющих
облегчить вычисления путем усиления сходимости ряда
(13.74) (см. первое издание справочника). Приемы, об-
легчающие вычисление несобственных интегралов
(13.75), см. [25j.
В ряде задач слагаемые Fn в (13.74) могут быть най-
дены независимо друг от друга. В этом случае можно
говорить о точном решении задачи. Однако’в большин-
стве задач слагаемые Fn в (13.74) определяются с точ-
ностью до множителей сп. Эти множители могут быть
найдены из бесконечной системы линейных уравнений.
Хотя и в этом случае решение может быть получено
с любой степенью точности, будем такие решения на-
зывать приближенными.
К группе прибтиженных решений следует отнести ре-
шения, основанные на принципе минимума потенциаль-
ной энергии деформации. В этих методах компонуют
решение в виде ряда (13.74) при условии, что каждое
из слагаемых Fn задано с точностью до постоянного
множителя сп я удовлетворяет заданным граничным ус-
ловиям. Множители са определяются из бесконечной
системы алгебраических уравнений [30, 21, 23].
В заключение приведем ссылки на литературу по не-
которым аналитическим решениям задач об изгибе плит,
которые могут представлять интерес для проектиров-
щиков:
а)	метод начальных параметров для осесимметричной
деформации круглых и кольцевых плит [12];
б)	осесимметричная деформация круглых и кольце-
вых плит переменной жесткости [1, 3, 23];
в)	некоторые решения по неосесимметричной дефор-
мации круглых плит [3];
г)	некоторые решения по изгибу прямоугольных плит
переменной жесткости [3, 23];
д)	изгиб прямоугольных и круглых плит из анизот-
ропного материала [17];
е)	метод начальных параметров для осесимметричной
деформации круглых и кольцевых плит на упругом ос-
новании типа Винклера [15];
ж)	задачи об изгибе плит на упругом основании
с двумя упругими характеристиками [4, 16];
з)	решения, некоторых задач об изгибе плит в виде
треугольника, сектора, кругового прямоугольника, эл-
липса, кругового сегмента [3, 20, 23, 25J.
ЛИТЕРАТУРА
L Биргер И. А. Круглые пластинки и оболочки враще-
ния. Оборонив,
2. В а р в а и П. М, и др. Таблицы для расчета прямоуголь-
ных плит, Изт. АН УССР. 1959.
3. Вайнберг Д. В, и Вайнберг Е. Д. Пластины,
диски, бал'ки-сгенки. Госстройиздат УССР, 1959.
4, В л а с о в В, 3. и Леонтьев Н. Н, Балки, плиты и
оболочки на упругом основании. Физматгиз, 1960.
5. Г а л ер к и и Б. Г. Упругие тонкие плиты, Госстройиздат,
1933.
6. Гасте в В. А. я 1< я т оз с р К- А. К определению уп-
ругих характеристик ребристых пластин, «Строительная меха-
ника и расчет «щоружсинЖ, 1961, № 6,
/. Горбунов-Посадов М. И. Таблицы для рз.счеда
тонки?; упругих нлнт на упругом основания. Госстройиздат, 1059.
8. Г о р б у и о в - П о с а д о в М, И. Расчет конструкций на
упругом основании. Госстройиздат, 1953,
9. Ж е "ч очки и Б. И, и С и я и ц ын А, П. Практиче-
ские методы расчета фундаментных балок и плит на упругом
основании Гны ТШ.Ю7ЫН Винклера. Госстройиздат, 1962.
10. К а л м а и о к А. С. Строительная механика пластин,
чат, 19Ж
И.Китонер К. А. И сгиб тонких прямоугольных пластин.
В об ; ^Расчет пространственных конструкций», вып. 2. Гос-
стройнздат, 19Ж,
12. К и ? о в е р К- А. Круглые тонкие плиты. Госстройдз-
дат, 1953.
13. Китов ер К- А. Применение степенных полиномов к
решению задач об иннбе ортотропных плит. В сб.: «Расчет про-
странственных конструкций», вып. V. Госстройиздат, 1959,
14,	Китовер К. А. Об упругом равновесии тонких беско-
нечных пластин из орт О’1 р-.иного материала. «Инженерный сбов-
иик» АН СССР, т, XXX, 1960.
15.	Коренев Б, Г. Некоторые задачи теории упругости
и теплопроводности, решаемые в бессолевых ф-ункдг.пх, Физмат-
гиз, 1960.
16.	К о р е н е в Б. Г. и Чер г иго в ск а я Е. И. Расчет
плнт на упругом основщши, Госстройиздат, 1962.
17.	Лехи и ц к и й С. Г. Анизотропные пластинки. Гос. изд.
те.хнико-теор. лиг., И57.
18.	Мал пев А. С. Исследование изгиба ребристых плит,
вын. 1, ВВМИСУ, 1939.
19.	Папкович П. Ф. Строительная механика корабля,
ч. П. Схдпромгиз, 1941.
20.	Папкович П. Ф. Теория упругости. Оборонгиз, 1939.
21.	Пратусевич Я. А, Вариационные методы в строи-
тельной механике. Гостехщщат, ЗУМ.
22.	Смотров А, РешенЕ'»' плит, загруженных сплошной
нагрузкой по закону трапеция. ОНТИ, 1936.
23.	Сладкопевцев А. А. К вопросу о расчете пластин
средней толщины. В сбл «Нелинейные задачи строительных
конструкций», Под ред. И, С. Цуркова. МПСИ, 1970-
24.	Уфлянд Я- С. Биполярные координаты в теории уп-
ругости. ГТТИ, 1950.
25.	Уфлянд Я. С. Интегральные преобразования в зада-
чах теории упругости. «Наука», 1967.
26,	Шехтер О. Я. н В ин о куров а А. В, Расчет плит
иа упругом основании. Госстройиздат, 1936.
27,	Шаманский Ю. А. Изгиб пластин. ОНТИ, 1036.
РАЗДЕЛ 14
ОБОЛОЧКИ
14.1. КЛАССИФИКАЦИЯ ОБОЛОЧЕК
И КАЧЕСТВЕННАЯ ХАРАКТЕРИСТИКА
ИХ РАБОТЫ
14.1.1. Общие положения
Оболочка представляет собой тело, ограниченное дву-
мя криволинейными поверхностями, расстояние между
которыми, называемое толщиной оболочки (1), мало по
сравнению с другими размерами. Толщина оболочки
может быть переменной величиной. Поверхность равно-
отстоящая от ограничивающих криволинейных поверх-
ностей, называется срединной поверхностью. В зависи-
мости от характера этой поверхности различают глад-
кие оболочки и складки. У гладкой оболочки (рис, 14.1)
срединная поверхность плавная, без выступов и перело-
мов. Складка составлена из отдельных пластинок, так
что ее срединная поверхность представляет собой не-
верность многогранника (рис. 14.2). Кривизна срединной
поверхности гладких оболочек или повсюду постоянна,
или плавно изменяется от точки к точке; у срединной
поверхности складок она сосредоточена в местах сопря-
жения граней; во всех остальных точках она равна
пулю.
Встречаются оболочки смешанного типа, состоящие из
частей гладких оболочек, соединенных между собой под
некоторыми углами (рис. 14.3), а также комбинации из
гладких оболочек и складок.
В зависимости от знака гауссовой кривизны различа-
ют три класса оболочек:
1)	оболочки положительной гауссовой кривизны
(сферическая, эллиптическая и т. п.) (рис. 14.1, а);
2)	оболочки нулевой кривизны (цилиндрические и ко-
нические) (рис. 14.1, бив);
3)	оболочки отрицательной гауссовой кривизны (на-
пример, в форме гиперболического параболоида и т. п.)
(рис. 14.1, г).
Часто встречаются оболочки смешанной кривизны,
у которой гауссова кривизна имеет различные знаки на
различных участках, например торообразная оболочка
и др. (рис. 14.4).
Оболочки, срединная поверхность которых представ-
ляет собой поверхность вращения, г. е. поверхность, об-
разованную вращением плоской кривой около непо-
движной прямой (оси вращения), называются оболоч-
ками вращения.
Оболочки, срединная поверхность которых образова-
на поступательным перемещением плоской кривой по
некоторой другой плоской кривой (плоскости обеих кри-
вых перпендикулярны), называются оболочкой перено-
са или трансверсальной оболочкой.
В зависимости от соотношения между толщиной обо-
лочки t и ее генеральными размерами в плане L раз-
личают.
толстые оболочки
тонкие (тонкостенные) 1/200	1/8 Амин и очень
тонкие (<21/200 Амин.
Рис. 14.2
Конструктивно оболочки могут быть оформлены как
сплошные, сетчатые или ребристые.
Рис, 1.4,3
В зависимости от при-
меняемых материалов
различают анизотропные
и изотропные оболочки.
К анизотропным оболоч-
кам относятся многослой-
ные (например, двух- и
трехслойные оболочки),
слои которых могут со-
стоять как из изотроп-
ных, так и из анизотроп-
ных материалов (напри-
мер, стеклопластиков).
Если оболочка сделана
из изотропного материала, но по разным направлениям
конструктивно оформтена различно, то говорят о ее
конструктивной анизотропии.
It 1 КЧУССПФПКЩИЯ ОБОЛОЧЕК И КАЧЕСТВЕННАЯ ХАРАКТЕРИСТИКА ИХ Р ЛЕОТИ
81
Края оболочки могут быть свободными, шарнирно
опертыми (подвижными или неподвижными) либо за-
щемленными как по всему контуру, так и по части кон-
тура или же в отдельных точках, а также могут иметь
упругие опоры в виде гибких диафрагм пли ба ток.
Участок ндпсдой кривизны
Участок отрицательной кр':Ри№ы
.^-Участок попо.кительнои кривизны
Рис. 14.4
14.1.2, Тонкостенные оболочки
Тонкостенные оболочки, применяемые в покрытиях
и перекрытиях, разделяются на: 1) купола; 2) своды,
своды-оболочкп, волнистые своды; 3) пологие оболочки;
4) призматические складки и шатры; 5) висячие обо-
лочки.
Куполами перекры
или имеющие форму
Рис. 14.5
вают помещения, круглые в плане
правильного многоугольника. Они
бывают: гладкие, ребристые и
многоугольные.
Гладкие купола имеют фор-
му оболочки вращения.
Ребристые купола в своей
основе имеют решетку, состав-
ленную из ребер, направленных
по паратлелям и меридианам
Многоугольные купола состав-
лены из пересекающихся частен
оболочек вращения (рис, 14.3,6).
Сводами называю п я обо ючки, очерченные по цилинд-
рической поиерхноши. Они применяются в качестве по-
крытий помещений, прямоугольных в плане. Края сво-
дов (параллельные образующей) могут опираться на
сплошные непрерывные опоры. В этом случае размера-
ми, характеризующими свод, будут: пролет I (расстоя-
ние между опорами) и подъем свода fn. Отношение
для сводов не меньше 1/6. Своды, опирающиеся на
жесткие поперечные диафрагмы и на продольные бор-
товые элементы, называются сводами-оболочками (рис.
14.5). Они характеризуются гремя размерами: расстоя-
нием I] между поперечными диафрагмами (пролет обо-
лочки), расстоянием, между бортовыми элементами 12
(длина волны) и подъемом /о-
Если /|//2>1, ю свод-оболочка называется длинной
(практически это отношение достигает 3—4). Подъем/0
принимается не меньше J/in Л и не меньше '/6Z2. Длин-
ные своды-оболочки бывают однопролетные (опираю-
щиеся па две диафрагмы), мпогопролетпые (опирающие-
ся на ряд диафрагм), одноволновые и многоволно-
вые (состоящие из нескольких параллельных оболочек,
связанных общими бортовыми элементами).
При С/4<1 свод-оболочка называется
короткой;
подъем короткой оболочки
1
/о > "у ^2-
Волнистыми сводами называются своды, имеющие в
продольном разрезе волнистое очертание (рис. 14.6).
Форма поперечного сечения волнистого свода может
бьпь криволинейно» или складчатой — треугольной или
трапециевидной
Пологие оболочки (см рис. 14.25) имеют небольшой
6—26
подъем ДДчн) Близкими к пологим оболочкам
по характеру работы и притщиению являются слегка
ненарушенные птиты и ступенчаю-вспарущецлые пане-
ли, у которых верхняя поверхность делается плоской,
а нижняя представляет собой криволинейную или стч-
пенчатую поверхность.
Призматические складки 1см. рпс. 14 2,6) и шатры
(с?,г. рис, 14.2, а) применяются для тех же целен, что
и своды-оболочки или полотне оботочки Шатры имеют
форму у сеченной пирамиды; бо.т е подробно они описа-
ны в [37]. Описание складок ст;. {37, 12, 59].
Висячие оболочки применяются в покрытиях больших
пролетов, они создаются на основе пространственных
сеток из вант (см. раздел И).
14.1.3.	Общая характеристика работы
оболочек
В оболочке в отличие от плиты, кроме изгибающих
и крутящих моментов и поперечных сил, возникают про-
дольные (осевые) и сдвигающие силы. При определен-
ных условиях величина первой группы сил, связанных
с работой оболочки на изгиб, относительно мала, по-
этому оболочка работает в основном на продольные си-
лы (сжатие или растяжение), а не на изгиб и кручение.
Эго определяет эффективность конструкции типа обо-
лочек, поскольку материал используется более выгодно,
чем в плитах или балках.
Вследствие кривизны оболочки проекции продольных
и сдвигающих сил на нормаль к поверхности оболочки
создают подобие «упругого» (фиктивного) основания
под оболочкой. Можно сказать, что оболочка работает
как плита, под которую подведено упругое основание.
Этим объясняется увеличение прочности и жесткости
оболочки по сравнению с плнтои. Большое влияние на
работу оболочки оказывают условия ее опирания.
14.1.4.	Характеристика теорий расчета
оболочек
В основу различных технических теорий оболочек по-
ложена гипотеза Кирхгофа—Лява: прямолинейные во-
локна оболочки, перпендикулярные к ее срединной по-
верхности до деформации, остаются после деформации
прямолинейными и перпендикулярными к срединной по-
верхности и пе изменяют своей длины.
Исходя из этого, построены две группы теорий рас-
чета оболочек: линейные и нелинейные.
Линейные теория описывают напряжспно-деформчро-
ваниое состояние оболочек, выполненных из матерна ы,
подчиняющегося закону Гука. Кроме того, предполага-
ется, что перемещения оболочки, возникающие пп.и ее
деформации, малы и ие могут вызвать существенного
82
РАЗДЕЛ 14. ОБОЛОЧКИ
перераспределения усилий. Линейные теории относи-
тельно просты, но имеют сравнительно узкую область
применения, ограниченную предпосылками, на которых
они основаны.
Исчерпывающие представления о работе оболочки на
всех этапах нагружения можно получить с помощью
нелинейных теорий. Различают три вида нелинейности:
физическую-—обусловленную нелинейной связью между
тензорами напряжений и деформаций (материал не под-
чиняется закону Гука), геометрическую—-определяемую
нелинейной связью между деформациями и Перемеще-
ниями и конструктивную, связанную с возможными из-
менениями расчетной схемы оболочки в процессе нагру-
жения.
При определенной величине напряжений почти все
строительные материалы перестают следовать закону
Гука, так что диаграмма, определяющая зависимость
между напряжениями и деформациями, становится не-
линейной, Кроме того, возникают пластические дефор-
мации. В тех случаях, когда требуется и тучищ иаиря-
женпо-деформироваппые состояния оболочки при на-
пряжениях, превосходящих предел пропорциональности
(например, в тех случаях, когда изучается работа обо-
лочки при нагрузках, близких к разрушающим), необ-
ходимо учитывать физическую нелинейность. Наиболее
просто учитывает физическую нелинейность теория пре-
дельного равновесия, основанная на понятии жестко-
пластического материала.
Если перемещения, возникающие в оболочке (напри-
мер, прогибы), настолько велики, что могут вызвать
существенное перераспределение усилий, то необходимо
учитывать геометрическую нелинейность. Такие случаи
встречаются, например, при работе тонких, очень поло-
гих оболочек.
Нелинейные теории значительно сложнее линейных, и
расчеты по ним весьма трудоемки. Поэтому важно
в каждом конкретном случае решать вопрос о выборе
теории. Можно руководствоваться следующим крите-
рием.
1.	Подсчитывается вся нагрузка <?, действующая на
оболочку вместе с коэффициентами перегрузки, и опре-
деляется характерное перемещение fa (например, про-
гиб) по линейной теории.
2.	Это значение прогиба подставляется в формулу,
устанавливающую связь между нагрузкой и прогибом
по нелинейной теории, и определяется величина рн> со-
ответствующая прогибу f.i.
3.	Если разница между и а будет больше необхо-
димой точности расчета, например 5%, го расчет обо-
лочки необходимо производить по нелинейной теории.
Иногда в процессе нагружения могут изменяться гра-
ничные условия, исчезать некоторые связи или появ-
ляться новые. В этих случаях оболочка ведет себя как
конструктивно-пелшгеппая система.
В силу некоторых, упомянутых ниже, особенностей
оболочки изгибающие и крутящие моменты могут быть
настолько малы, что их можно отбросить без особого
ущерба для точности расчета, В соответствия с этим
все теории оболочек (как линейные, так и нелинейные)
можно разделить на моментные и безмоментвые. Безмо-
ментиые теории значительно проще моментных, поэтому
практически важно знать условия их применимости.
14.1.5. Условия применимости безмоментных
теорий [29]
Эти условия зависят от ряда факторов, влияющих
на работу оболочки:
1) гауссовой кривизны;
2) наличия на поверхности оболочки линий искаже-
ния напряженного состояния, т, е. линий, вдоль которых
могут произойти возмущения напряженного состояния.
Эю те места, где геометрические или физические свой-
ства оболочки (или характер нагрузки) изменяются
скачком- а) края оболочки, б) линии, вдоль которых
нагрузка (итч ее производные) или геометрические па-
раметры оболочки (кривизна или толщина) изменяются
скачком. Вблизи этих мест во шикают дополнительные
напряжения, вызываемые краевым эффектом (см. 14.3.6).
Для характеристики работы оболочки большое зна-
чение имеет показатель изменяемости нагрузки, опреде-
ляемый следующим образом. Назовем коэффициентом
изменения нагрузки (или вообще какой-либо функции)
число у, равное отношению среднего значения производ-
ной функции к среднему значению самой функции (на
некотором интервале). Например, для разномерно рас-
пределенной нагрузки у —0; для треугольной нагрузки
Р Р
(рис. 14.7) у = ——	=2; для сосредоточенной силы
у=оо. Показателем изменяемости нагрузка назовем
число S, связанное с у соотношением
1 t \-S
у = ------
\2R )
где t —- толщина оболочки; R. — некоторый характерный
радиус кривизны поверхности оболочки,
Из этой формулы получим
t
Для равномерно распределенной шшрузки показатель
изменяемости равен — оо, для сосредоточенной силы
+ =».
По безмоментиой теории могут быть рассчитаны обо-
лочки, удовлетворяющие следующим условиям.
1. Линии искажения напря-
женного состояния должны
быть расположены на поверх-
ности оболочки достаточно ред-
ко — так, чтобы зоны затухания
возмущений напряженного со-
стояния, возникающие около
р 14 у	этих линий, не покрывали цели-
ком срединную поверхность
оболочки. Например, оболочки,
подкрепленные часто расположенными ребрами, не мо-
гут быть рассчитаны по безмоментиой теории.
2. Нормальная кривизна срединной поверхности обо-
лочки па любой линии искажения не должна обращать-
ся в пуль ни в одной точке. Например, цилиндрическая
оболочка с краями, расположенными вдоль образующей,
или та же оболочка, имеющая отверстие, или замкнутая
цилиндрическая оболочка с ребрами, расположенными
вдоль образующих, не могут быть рассчитаны по безмо-
мептной теории.
3. Показатель изменяемости внешних поверхностных
и краевых нагрузок не должен быть слишком большим.
Для поверхностной нагрузки по всем направлениям
должно быть Эгф’/а, для краевой нагрузки 5гДф3 (для
оболочек по вокительной и отрицательной кривизны) и
SskJ/j (для оболочек нулевой кривизны). На сосредото-
ченную нащузку, показатель изменяемости которой ра-
вен фоо, оболочки не могут рассчитываться но безмо-
ментпой теории.
4 Срединная поверхность пе должна обладать неко-
торыми особыми свойствами. Например: а) коническая
14.2. ЗАМКНУТЫЕ КРУГОВЫЕ ЦИЛИНДРИЧЕСКИЕ ОБОЛОЧКИ
83
оболочка не должна содержать вершину конуса;
б) срединная поверхность оболочки не должна касаться
плоскости по замкнутой кривой, как в горообразной
оболочке (см. рис. 14.20).
5. Срединная поверхность оболочки не должна дефор-
мироваться без растяжений (сжатий) и сдвигов. Иными
словами, по безмоментной теории можно рассчитывать
только такие оболочки, в которых изгиб и кручение воз-
можны лишь при растяжении (сжатии) или сдвиге эле-
ментов срединной поверхности.
Указанные пять условий применимости безмоментной
теории являются достаточными, но не необходимыми.
Иногда можно рассчитывать оболочки но безмоментной
теории и при нарушении одного или нескольких из этих
условий.
Например, призматическая складка (см, рис. 14.2),
пластинки которой соединены шарнирами, нагруженная
в местах шарниров сосредоточенной нагрузкой, может
быть рассчитана по безмоментной теории, хотя при этом
нарушаются второе и третье условия. Оболочку поло-
жительной гауссовой кривизны, нагруженную сосредо-
точенной силой, можно рассчитывать по безмоментной
теории, так как возмущения, вызванные сосредоточен-
ной силой, быстро затухают.
Концентрации напряжений, вызванные возмущениями
напряженного состояния около линий искажения, могут
не приниматься в расчет, если пластические деформации
и изменение формы оболочки не приводят к снижению
ее несущей способности; в оболочках, выполненных из
хрупкого материала, учет концентрации напряжений не-
обходим.
Поэтому вопрос о применимости той или иной теории
должен решаться в каждом отдельном случае. Для обо-
лочек положительной кривизны второе и четвертое ус-
ловия всегда выполняются.
14.1.6.	Основные постановки задач
теории оболочек [48]
Имеется несколько постановок задач расчета оболо-
чек. Для полного описания напряженно-деформирован-
ного состояния оболочки необходимы четыре функции:
1)	функция Fo, описывающая срединную поверхность
при начальном нагружении <?о (эта функция описывает
заданную поверхность оболочки);
2)	функция F, описывающая срединную поверхность
при расчетном загружении q. Эта функция выражается
через перемещения оболочки и, следовательно, зная ее,
легко вычислить деформации и напряжения;
3)	функция q, описывающая нагрузки (или другие
факторы, например, температуру), переводящие оболоч-
ку из состояния, выраженного функцией Рй, в напря-
женно-деформированное состояние, выраженное функ-
цией Р',
4)	функция f, устанавливающая связь между напря-
жениями и деформациями, т. е. функция, описывающая
свойства материала.
В зависимости от того, какими функциями задаются
и какие разыскиваются, различают следующие постанов-
ки задач расчета оболочек.
1.	Заданы начальная поверхность оболочки (функция
/ф), нагрузка q и материал (функция f). Требуется оп-
ределить напряженно-деформированное состояние обо-
лочки (функцию F).
Это так называемая прямая постановка задачи. Ее ре-
шение получается путем интегрирования сложной си-
стемы дифференциальных уравнений, выполняемого при-
ближенными методами, Большинство решенных задач
относится к прямой постановке.
6*
2.	Заданы начальная поверхность (Уф), напряженно-
деформированное состояние, выраженное функцией Р,
и материал (функция f). Требуется определить нагруз-
ку q.
Это обратная постановка задачи. Ее решение не тре-
бует интегрирования уравнений и сводится к дифферен-
цированию известных функций. Эта постановка позволя-
ет получить точные решения. К обратно:; постановке
прибегают в тех случаях, когда решение задачи в пря-
мой постановке становится очень громоздким. В лите-
ратуре описано сравнительно мало задач, решенных
в такой постановке.
3.	Заданы нагрузка q, напряженно-деформированное
состояние оболочка (F) и материал (f). Требуется оп-
ределить начальную форму оболочки. Решение этой за-
дачи позволяет получить наиболее экономичные формы
оболочек. Задачи в такой постановке почти не решались.
4.	Возможна четвертая, малоисследованная постанов-
ка: заданы начальная (Ро) и деформированная форма
оболочки Р, а также нагрузка д. Требуется подобрать
материал, т, с. определить функцию f. Эта постановка
может найти применение при расчете многослойных обо-
лочек.
14.2. ЗАМКНУТЫЕ КРУГОВЫЕ ЦИЛИНДРИЧЕСКИЕ
ОБОЛОЧКИ
14.2.1. Основные условные обозначения
Геометрические параметры (рис. 14.8)
Д — радиус срединной поверхности стенки
или обшивки оболочки;
I — длина оболочки;
с'./=Д12— относительная длина оболочки;
х—расстояние вдоль образующей от неко-
торого начального поперечного сечения
до какой-либо произвольной точки на
срединной поверхности;
о;=з R —относительная величина л;
s — расстояние по дуге окружности средин-
ной поверхности от некоторой начальной
до какой-либо произвольной точки на
той же поверхности;
fj=s R —. относительная величина s (центральный
угол);
ах — расстояние между кольцами жесткости;
as — расстояние между продольными ребрами
жесткости;
1	— момент инерции всего поперечного сече-
ния оболочки (пустотелой балки) отно-
сительно нейтральной оси;
S	— статический момент части поперечного
сечения относительно той же оси;
Fx — площадь поперечного сечения продоль-
ного ребра с примыкающей к нему
частью обшивки;
/5 — момент инерции сечения s=const коль-
ца жесткости с примыкающей к нему
частью обшивки;
/s — погонный момент инерции продольного
сечения s = const;
! х — момент инерции поперечного сечения
x=const продольного ребра жесткости
с примыкающей частью обшивки;
/у — момент инерции сечения s = const конце-
84
РАЗДЕЛ 14. ОБОЛОЧКИ
вого кольца жесткости относительно оси,
параллельной образующей оболочки;
+ — погонный момент инерции сечения х =
= const;
E(~FX — приведенная толщина оболочки в по-
перечном сечении х —const;
рR --относительная величина /щ
7/ 12/;
/5 = I/	—'— — приведенная толщина оболочки в
’ я х
продольном сечении s=-const;
[R — ts R— относительная величина t,;
t — толщина гладкой стенки безреберной
оболочки;
|i— t R— то же, относительная ветчина I;
Рис, 11.8	Рис. 14.9
Нагрузка
р — величина вектора внешней удельной па-
!рузки (на единицу поверхности изи на
погонную единицу);
р^, Pv, ps~~ проекции вектора внешней нагрузки на
ось х, на нормаль и на касательную к
контуру поперечного сечения срединной
поверхности оболочки.
Напряжения и усилия (рис. 14.9)
ах, F'х, Qx, Мх—нормальные напряжения, нормальные
(продольные) силы, поперечные силы
и изгибающие моменты, действующие
в поперечном сечении (х = const) обо-
лочки;
O's, ,VS, Qs, Ms — нормальные напряжения, нормальные
(продольные) силы; поперечные силы
и изгибающие моменты, действующие
в продольном сечении (s = const) обо-
точки;
N3x — \'.x —сдвигающие силы;
т — касательные напряжения;
М, Q, /Ик — изгибающий момент, поперечная сила
и крутящий момент в пустотелой
балке.
П е р е м е щ е н и я и д е ф о р м а ц и и
w, и, v—перемещения точек срединной поверхности
оболочки в радиальном, продольном и тан-
генциальном направлениях;
фк — угол поворота образующей оболочки;
7ж> "X? — деформация изгиба в продольном и попереч-
ном направлениях;
Ха-с — относительная деформация кручения;
Е — модуль упруюсти;
G — ыорупъ сдвига;
v — коэффициент Пуассона *;
Fд, fs— относительное, удлинение в продольном и
кольцевом направлениях;
ц, — относительный сдвиг.
14,2,2. Общие дифференциальные
зависимости теории
цилиндрических оболочек
Основные зависимости теории топких цилиндрических
оболочек, выведенные исходя из допущений двухосною
напряженного состояния и сохранения прямых норма-
лей, в общем случае имеют следующий вид,
Дифференциальные уравнения равновесия:
алл да		5ЛГ« + RPx = др	0.		1	
d\R	dN^	п . п			0;		
др	до	^5 “Г				
+	dQx да	dOt + ir+/?Pv		0;		 (14.1
дМхз да,		дМ, оф	0;			
dMs		дМг - QxR = да	0.			
Уравнения неразрывности деформаций:
дХз _	0.
да сф
др ' ~~ да ~ Rdfi + Rda ~ ’
Хх _ д П _ двхх ~ д^\ ]
R R"da '2 др да ) ~Г
I д I т „ 1 * *	'i = 0
+ W(3 \ бф 2 ’ да /
(14.2)
Связь между усилиями и деформациями:
(gz V8sj.
1 — V"
Et
+ V8*);
Et
Д7	= -—---------- Sr z
2(1+ -v)
1 Коэффициент Пуассона обозначается обычно через ft; здесь
он обозначен через v , так как через J-L обозначена относитель-
ная толщина оболочки.
14 2 ЗАМКНУТЫЕ КРУГОВЫЕ ЦИЛИНДРИЧЕСКИЕ ОБОЛОЧКИ
85
Связь между деформациями и перс мощениями:
Т а б л и да 14 1
Усилия в оболочке и ее перемещения при осесимметричной
нагрузке (?w оеамомеитнои зелрнн)
Вид нагрузки
Расчцгш-т формулы
1	*/	1 i dv \
R да s R \ <Д 1
1 / ди	ди \	1 дга>
— ------- <------- ..—,-------------
R \ др	да )	л R- да2
1 д [ дш \
у = — . — -----------г о ;
Ль в- ар \ ар	/
1 а / dw	\
Xxs ~~~ R2 ' да \ ар '
} (14.4)
!. Собственный вес £ в кГ'с'л и
равномерно распределит,! и по
периметру нагрузка гр в
2. Равномерное внутреннее дав-
ление pv в кГ!1-М'‘
14.2.3. Оболочка под действием
осесимметричной нагрузки.
Безмоментная теория
Безмомснтная (мембранная) теория приложима
к расчету цилиндрических оболочек при выполнении об-
щих условий, указанных в 14.1.5. Следует лишь отме-
тить. что при осесимметричной нагрузке в безмомент-
ной цилиндрической оболочке отсутствуют не только
изгибающие и крутящие моменты и поперечные силы,
но и сдвигающие силы.
Дифференциальные зависимости-
а) уравнение равновесия
Д^+^Р,==0; ..V+«pv=0;	(14.5)
лгу. -	ь
б) перемещения
R
и = АД = —~ (Р — Л'ст);
dw 1 dw
=	04.6)
Усилия в оболочке и ее перемещения при различных
нагрузках даны в табл, 14.1.
14,2.4. Оболочка под действием
осесимметричной нагрузки.
Моментная теория
Исходят из гипотез общей теории оболочек. При осе-
симметричной нагрузке отсутствуют крутящие моменты,
сдвигающие силы и поперечные силы в продольных се-
чениях.
Моментная теория применяется для определения уси-
лий краевого .эффекта и для расчета коротких оболо-
чек, когда длина обо ючки не превышает длины участка
действия краевого аффекта.
3. Гидростатическое давление
жидкости с удельным весом у в
k:Jcm}
.	0; Л73 - 7^;
МДД lf
Et	Et
Коэффициент трения грунт
по стенке принят равным
нулю
Г Давление грунта с объемным
весом 7рр и нг/слб и пригрузка
Рв в hf/CM2
5, Равномерное нагревание обо-
лочки на iQ
V , -= ..V -= д
Д.।
86
РАЗДЕЛ М ОБОЛОЧКИ
где
Дифференциальные уравнения равновесия:
dE\	dQ,_	)
фТф + Rpx = 0; -ту ф Ф ф АХ = 0; аа	аа	'	j
,,,	(П.7)
dMx	j
—r-AQs=0.
da	J
__ЕР___
12 П -Л) ;
Связь между усилиями и деформациями:
		
11, у .	(< r —i~ * c J, j \ < — 1	1 ",u /'s 1 — V2 ' X 1 ih	4	1 — VS		
>< (Ф + « x);		(14.8)
лл	EE		
cVl Y		/ «г, *	12(1 -- A2)	J	
EP		
‘ *s	~ 12(l-v2) ' f-x'		
Связь между деформациями и перемещениями:
<Px =	dw Rda ’		1 R	da da	
	Ф =	ГЛ) R			’ (11.9)
1	d-w		I	d’-'ia	
/ж- R,	da3	Ъ		dfi3	
Выражения усилий порез пер: метение ’v:
/ б7 ,	1
— С — j р, dx; = J Лфм— щ — j ------ ;
u ________ЕР___ Лю _
!2(1 —л-) Л2	I (П.Ю)
Л1, ДИД
ЕР	cPw
Q v ~	—--------~ ‘	,
12(1—v2)	ах3
Основное дифференциальное уравнение:
J rf3 Г °!
РР ' "da3 [ 12(1 —V2)
d-w ]
dad ]
+ v
А
R
(Н.П)
При 1 —const уравнение (14.11) принимав г вид
Лю 4	R*	V, \
--- -j- 4пХ = — п. ф- v —	(11.12)
dad 1	11	D ф ' 1 R /	v 1
ИЛИ
(П.12)
Уравнения (14.12) или (14 13) того же вида, что и
уравнение балки иа упругом основании. Общее решение
уравнения (14 13):
w = ет'л (Cj cos ух + С2 sin qx( + e~~ ц'г (Cs cos qx ф-
+ C.s sin qx) 4- f(x),	(14.14)
Здесь
/(x) — частное решение уравнения, зависящее
от поверхностной нагрузки;
С,, CR, С3, Cj— произвольные постоянные, определяемые
по граничным условиям (габл, 14.2).
Т а б л иц а 14.2
Характеристика гршшшшх условий
Край оболочка защемлен	= 0; ®	0
Край оболочки свободен	рл=,0; Лф;=0
Кран оболочка шарнирно зак- реп тан	ет ~ 0;	0
Если выражение для перемещений w решением урав-
нения (’14.13) получено, то все усилия и деформации
могут Сыть определены по формулам (14Д0), (14.9) и
(14 8).
В табл. 113 приведены усилия и перемещения при
различных нщрузпцх.
14.2.5. Сопряжение оболочек.
О сеси м м етр и ч н а я на груз к а
В местах сопряжения двух оболочек вращения раз-
личной формы (цилиндрической, конической, сфериче-
ской и т. п,), в местах перелома меридиана или скачко-
образного изменения ею радиуса кривизны или ступен-
чатого изменения толщины оболочки, а также в местах
подкрепления кольцами к усилиям, определяемым по
безмоментной теории, добавляются усилия и моменты,
вызванные изгибом (см. тюке 14.3.8).
Расчет сопряжения ведется обычными методами строи-
тельной механики, а) методом сил с использованием ус-
ловия совместности деформаций сопрягаемых элементов;
б) методом перемещении с использованием условия рав-
новесия усилий, дг йствующпх иа сопряжение; в) смешан-
ным методом Ришоиальная основная система, допуска-
ющая расчет на действие нагрузки по безмоментной
шории, может быть образована в простейшем случае
(рис. 14.10, а) методом сит, в более сложных—смешан-
ным методом (рис. 14.10,6, в).
В общем случае (рис. 14.10, в) иа лиши сопряжения
оболочек ити на осевой линии кольца в каждой точке
накладываю тел две смет — радиальная и противовра-
щательная, реакции которых обозначены (сила) и R?
(пара); соответствующие перемещения Zt (радиальное)
14 2 ЗАМКНУТЫЕ КРУГОВЫЕ ЦИЛИНДРИЧЕСКИЕ ОБОЛОЧКИ
§7
4
Усилия в оболочке и ее перемещения при осе''мм'петр!шной пагоу^ке (по моментной теории) 71 = |/
(з.лпцл а е> л	U. V, Г, Т приводятся в 5.5 6)
нагрузки
ЕР
Расчсгяые формулы
1 . Равномерно распределенная по
кругу нагрузка pv в кГ/см
Pv
при х = О
(тр:); при x
Pv
Р.
маке
Й7]Ц)
4р
-Е т (Пх).
Формулы справедливы при I > —•


М
3 Цилиндр с защемленными кра-
ями под равномерным внутренним
давлением pv в кГ/см1
2. Равномерно распределенные по
контуру радиальная нагрузка о0 в
[r|AI,U (ipO + QFT (гр-')];
hMoW' (туз + Q«v(ж)!; А1
Формулы справедливы при I
__ р.
зКж- М--= —
Р,
Л
Прогибы и усилия в любом промежуточном сечении оболочки ча расстоянии х определяют-
ак сумма случая 2 этой таблицы и случал 2 табл. П L
Если давление на торцы не передается слепкам, то в табл. 14.1 надо принять v = О
4 Цилиндр со свободно опер-
тыми краями под равномерным
внутренним давлением pv в кГ/см-
Прогиб и усилие в любом промежуточном сечении оболони на расстоянии г определяются
сумма случая 2 этой таблицы и случая 2 табл 14.1
Если давление на торцы не передаемся стенкам, ю в табл. 14.1 надо принять у = 0
5. Цилиндр, подкрепленный
кольцами шириной с и* поперечным |
сечением Е^, под, равномерным внут- |
ренины давлением pv в кГ/см1
MQ -£\304pv Rt
При jc — 0 (сечение у края кольца)
FK ~~ d
3t 1 Rt
Е‘ — ct
(?0 = 0,78pv ( Rj	:
F -/ 1 ,obi | Rt
v
У сил не
в кольце
Л
Е; Л
Формулы справедливы при a ~А
1]
88
РАЗДЕЛ U ОБОЛОЧКИ
Предо tveeHt е тагм 14 3
Вид нагрузки
Расчетные формулы
!э Цтичдп с тоски i днпшр^
поц равномерным внутренним д-ю
"ением pv в к!/см*
у +	х*2А>ду
4Лд(! + V> 'ч,1	— — "j |ГГд+2/?Дц (1 —
2ti , эд<рц Уа*
а Dn(l+V) £(д + 2Дц^ fi(l-v)
Ру *
1Од (1 + V)
После вычисления Мп и Qn перемещения и усилия в цтинтре опргдр тяются суммирование я
репизии дтя случая 2 той таб ины и случая 2 табт 14 1 В днинщ напряжения определяются,
как в пластинке с нагрузкой pv 9 MQ и Q® Формулы справедливы при длине цилиндра I >
> зУЖ
7 Ци ш-гдр ГО сфери-lfc! им днищем
под внутренним давлением pv в
кГ/ся?
р% IP (2 - V) - (1 ~ у)] (1 —
———~	—.    ^.,-n,..,n,.l
л„2	(1-« -2(нУТ)(н/И)
д
В цилиндре перемещения и усилия определяются по вычисленным М-. и О» суммированием
вели тин для случая 2 этой таблицы и случая ’ табт 14 1 Ь сферическом днише перемещения и
\С1 лт определяются i лк я сферической оболочке с нагрузкой pv , MQ и Qo Формулы спрл
р^длияы при I ^Vht
8 Резервуап с гшем^ыы п
стенками псд гидросттти юским дзв
лением жидкости удель-зым весо <
у в кг/елд
Форму ы справедливы при А/ ^Vflt
14 2 ЗАМКНУТЫЕ КРУГОВЫЕ ЦИЛИНДРИЧЕСКИЕ ОБОЛОЧКИ
§9
и 2г (угловое) образуют первую
I руппу основных неизвестных.
Между примыкающими к кольцу
оболочками и кольцом (с нало-
женными на него связями) в ос-
новной системе сохраняются толь-
ко связи-стержни меридионально-
го направления. Дополнительные
к безмоментному состоянию сило-
вые взаимодействия оболочек с
кольцом и наложенными связями
(радиальные усилия Х}, Х3, пары
Хо, Х4) образуют вторую группу
основных неизвестных.
Матрица уравнений смешанного
метода для случая, когда сопря-
жение оболочек усилено кольцом
массивного профиля высотой 2с,
имеет вид
Свободные члены Rip, R2P— радиальная и моментная
реакции в наложенных связях — и AUJ,  А4Р— ради-
альные и угловые перемещения контура оболочек — оп-
ределяются расчетом безмоментною состояния. Коэффи-
циенты Гц, Г22 — радиальная и моментная реакции от
единичного растяжения и единичного закручивания коль-
ца— зависят от жесткости последнего; •••> 644— ра-
диальные и угловые перемещения контура оболочки от
единичных радиальных усилий и единичных моментов —
зависят от очертания и толщины оболочки. В побочных
квадратах матрицы — элементарные выражения коэффи-
циентов смешанного метода, удовлетворяющие условию
Г ik——fiftl-
При решении системы уравнений целесообразно вы-
разить Хц ..., А'4> используя уравнения II группы, и под-
ставить в уравнения I группы; это приводит к двум
уравнениям метода перемещений относительно Zb Z2,
Если кольца нет, но меридиан имеет излом (см. рис.
14.10, б), то Г];— Гз2™0; С — 0;	Xi “Хд-р/фр;
й(2 = %4. Исключая Z], Z2, Аф, Х2, получим систему двух
уравнений метода сил относительно Х3, Х$.
Если к тому же и меридиан не имеет излома (см.
рис. 14.10, а), то А?!р=0, Х;=Х3 (соответствующую си-
стему уравнений метода сил можно составить непосред-
ственно).
Формулы и графики для расчета сопряжений цилинд-
рических оболочек с оболочками других видов и с коль-
цами жесткости см, [45].
Рис. 14.10
14.2.6. Оболочка под действием нагрузки,
не обладающей осевой симметрией
При действии нагрузки, не обладающей осевой симмег-
риеи, оболочка рассчитываемся на основе тпогез iexi-ш-
ческои (полубезмомешион) теории В 3 Власова: в урав-
нениях упругоы и не учгиываюгся крутящие и продоль-
ные изтбающие момешы, щвиг, растяжение (сжатие)
Рис. 14,11
в кольцевом направлении. Ниже дается способ расчета
[36], основанный на указанных гипотезах. Он распрош-
раняется на юнкостенные гладкие и ребристые оболочки,
последние приближенно заменяются ортотропными Раз-
личная жесткость ортотропной оболочки в продольном
и кольцевом направлениях оценивается введением в рас-
чет различных приведенных толщин стенки. Расчетные
формулы, даваемые ниже, справедливы при следующих
соотношениях	между	длиной	оболочки и	ее	толщиной.
1	1
а/ — 5; ц щ ; а> =10- ц. С —;
‘	f ’	30	50
1
ai = 20; ц .
f 100
При промежуточных значениях щ предельную относи-
тельную толщину ц можно определить шиерполяцпен.
В ребристых оболочках отношение	должно бьыь
не более соогветшвующих значении у?.
В дальнейшем рассматриваются нагрузки, симметрич-
ные относительно некоторого диаметра оболочки
(рис. 14.11, а), что отвечает большинству практических
случаев 6 За начальную итчку для отсчета дуговой коор-
динаты Р принимается точка Оь лежащая на указанном
3 Расчет а случае неелммбнричной ншзрузки см. ЦЬ], где
в формуле (13)
90
РАЗДЕЛ 14 ОБОЛОЧКИ
Табл и ц а 14 4
Кольцевые изгибающие моменты, поперечные и нормальные силы, грузовые коэффициенты для некоторых нагрузок
Схема нагрузки	Кольцевые усилия в первом состоянии	Грузовой коэффициент
Неравномерно Р л, q ^0 i	е радиальное давление, заданное тригонометрическим рядом р\^=Ра X»,X ^=Роя	rpj cosjS ~ЬР'> cos2|3 »» Ф —0
р - > ’о,	। ' п р ' >	' 1 ь У 1'jii ХдХ ~Pj№sp 'О' _й> / *	М® = 0, Q° =0, W°=P1 я cos з	Ф = 0
Р = 0; ? = 0 Pv = Ptl cos Л0 про п >2	n	Рп R1 AI® =_ ___. cos пр7 п	прп 0° ——. —~	— sin пр, *5	П‘ — 1 М° — „X созпр-	n	ио	a	A n~ — i
V 4 Л ~ Ч /М 1-/'-=- -«у М"' лХмЛ f ХуГм р=7Г2д, q v .JL si-n р 2	Давпение нидкости с з-делоным весом 7 в лг,счэ 0<Р< —; 2 Л0 —	f	'	1-0,25 cos	3 -j- 0,25 3 sin fll	7Я1, s	\	п	) Q® =— 0,250 cos pv.P3, = (0,25 3 sip ₽ + 0,75 cos 3) V«2, — < 3 < -, 2 МП =	f	1	o,25 cos 3 — 0,253 sin 3 + —	sin 0^	чР3, 4	\	Л	4	J Q® =— 0,25 (n — 3) cos 3vP2, Д ® ~ 0,25 (cos 3 — p sin 3 -1- n sin 31 7Д3	ф —	cos	у Fc, (n - 1)	2 при n — 2 Ф2 =— 0,2222'; Ц",
14 2 ЗАМК1П1НЕ Круговые ЦИЛИНДРИЧЕСКИЕ ОБОЛОЧКИ
диаметре. За начало отчета предо м»>й координат «
принимается поперечное сечение, совпадающее с одии
из краев оболочки или с плоскостью симметрии, обще»
для оболочки и натрузкп
Напряженное и деформированное состояние слагается
из. 1) элементарного напряженною и деформированною
состояния пустотелой балки, коюрая является в данном
случае основной системой, и 2) дополнительного напря-
женного и деформированною состояния, отражающего
статическую неопределимоеп> оболочки и характер!!дую-
щего в сочетании с первым дейегшнельцую работу обо-
лочки.
Усилия в пустотелой балке и ее перемещения (их обоз-
начениям присвоен верхний нулевом индекс) определя-
ются элементарными методами сопротивления мате-
риалов.
1.	Продольное нормальной и касателы^ напряже-
ния— как в обычной балке кошцевшо сечения.
о т
ст.. -=------cos	к Г !с
О
т° = —— sin В кГ/см",
лЯ1х н
где М и Q— изгибающий момент и поперечная сила
в балке ьоЛпЦевою сечения от данной на-
грузки.
2 Изгибающие моменты, нормальные и поперечные си-
лы в продольном сеченьи s = co’ist и соответствующие
перемещенья — как в кольце от загаппои пюрупси,
уравновешивав мой (рис. 14.il, б) поверхностными каса-
тельными силами:
Р
q~ ~—Рт^ кГ/слР,
где Р — равнодействующая внешней нагрузки на обо-
лочку в данном сечении в кГ1с,л.
Выражения кольцевых моментов, нормальных и по-
перечных сил для нагрузок, задаваемых нроешми анали-
тическими формулами, можно ср;щ найти г. замкну юн
форме, подобной привод,.иней в табл 14.4 для трубо-
провода, наполовину заполненного жидкостью Аналогич-
ные выражения для шкоырщ др)1их нашу -,ок имеются
и в [45]. Однако в ряде случаев шпртзку не те. ообраз-
по раскладывать в кольцевом направлении в тршоио-
метрический ряд, приведенный в табл. 14 1 При -ном
все силовые факторы в продольных сечениях пуш отслои
балки (Л4А, (Г, Ар1) определяются тоже рядами, обра-
зующимися из разложения
S°= I SX	(14.15)
72—0
после замены буквы S соответствующим искомому фак-
тору обозначением (Л4, Q, AZ). В частости, этот прием
удобно применять при расчете вертикальных цилиндри-
ческих сооружений на ветровую нагрузку, распределенье
коюрой в кольцевом направлении соыасно СНиП,
задастся численно,— аэродинамическими коэффициен-
т амл с, определяющими давление па единицу поверхно-
сти оболочки.
Усилия и перемещения дополнительного состоянии
(они обозначены буквами с чертой наверху) определя-
ются по следующим формулам:
Ш 16)
В этих формулах все величины под знаками суммы
выражаются через продольное напряжение и его про-
изводные ];
Р
-y-a^sin nS);
fl
-^-^-^COSnP;
R'P, _
АУС
a.' =—--------— о,, cos нН;
PVx - . „
v = - - ————— a sin nK-
n ЕЦпЦп2—Ip xn
R4X
ixn	El-JI- {rP—Vp m
(14.17)
Полные усилия и перемещения вычисляются по форму-
лам 2:
тте. = о” ф оА. ; т — т’! у т;
Лф -- Л11; + Д , Qs =	-г- Qs;
^ = Л" + Щ	(М.18)
щ = Д cos р -ф -isfi w;
v f  sin р ф- д° -ф- v ; I
Чф -=• <(.* cos р, + ф” И фА. .	)
Здесь f и у*— прогиб и угол поворота простой бал-
ки кольцевого сечения ог ладанной ншрузки.
Значения аХп и тто производных определяются из диф-
ференциального уравнения, совпадающею по своей ма-
! При косоФИммстр 1чнои нагрузке тригонометрические думк-
цип циклически за^ечяюп ч сп$ п 0 на sin п р а ып a 1j
л os п |3.
2 При нагрузке, н-оигошнон вдоль обра р/ющещ
92
РАЗДЕЛ 14 ОБОЛОЧКИ
тематической форме с уравнением балки на упругом
основании
+ 4"Фн °лП = еп фп 	(14.19)
Здесь
а , л‘ \п' — If 1'	Д f,2^ 1)
f . C/i
<1>; - f 41',’cos Дi сф.
Последнее выражение — грузовой член — связывает
напряжение о1п и ею производные с внешней нагруз-
кой. Для нс ко < орых видов нагрузки его значения даны
в табл. 14 4.
Уравнение (14.19) решается в начальных параметрах
точно так же, как уравнение для балки па упругом
основании Искомая функция и ее производные выража-
ются через началыпле параметры в общем случае сле-
дующим образом:
Гиперболо-круговые функции, входящие в (14 20),
ш ch Фп х cos ф„ х;
1
Бл -= --- (ch фп х sin фф х ф- sh ф,; с cos фл х);
sh ф„ х sin ф,
,Dt --— (ch ф„ xsin ф„ к—sh фП xcos фл х),
4
табулированы в 5.5.6.
В качестве начальных параметров в (14.20) входят,
криле начальных значений искомой функции и ее произ-
водных, обобщенные деформации, которые связаны
с производными искомой функции п грузовым членом:
___Д’Д_______
~ ~ Z7, п- — 1) п
, .
г ДД гБ (п- — 1)" °лп '
/у4/ -
~ LI„ п- (Д — 1) Ф,! +
xtR' il
_L ————    - — Q
Через начальные параметры выражаются и
ные деформации:
(14 21)
обобщен-
(14.22)
Входящие в (14 20) и (14.22) члены с интегралом
представляют собой частные решения дифференциаль-
ною уравнения и зависят от характера нагрузки. Не-
известные начальные параметры определяются из гра-
ничных условий согласно табл. 14 5,
При нагрузке, постоянной вдоль образующей оболочки,
Ф„ =0, и решение упрощается, В табл. 146 приведены
для этого случая готовые формулы для усилий н пере-
метцений дополнительного сосюяния в зависимости от
граничных условий.
3. ОБОЛОЧКИ ВРАЩЕНИЯ
93
Таблица 14 5
Граничные условия
Условия на краях оболочки	Нагрузка постоянна вдоль образующей	Нагрузка постоянна или меняет- ся вдоль образующей (общий слу- чай)
1, Жесткая за- делка края	п- (п- — 1) .. у ™ —А—	J-. ф ХП	31$J t х	н ft" = 0 хп	и» -=0;	~0 ^п ’ *хп
2. Свободный край	o'" =0; о' =0 хп	хп	G — 0; хп а' —0 хп
3 Край связан с абсолютно же- С1Л.НМ кольцом	г,	П~ (П2— 1 ) О ~0; о == —А	-Ф хп	хп nA-iх п 1	X гУ
4 Край связан с упругим иеза- тр\женным коль цом	ел в 4-	। * г	л	Г	а, а 1	н	1	г? S '	= уб +	
5. Условия на краях симметрич- ны; распределен- ная нагрузка По- стоянна вдоль об- разующей; за на- чальное принима- ет ея среднее се- чение оболочки	q' =0: </ 2=0 хп	хп	—
Имея решения для оболочки с одним защемленным,
краем, а другим свободным и для оболочки с одним за-
щемленным краем, а другим, связанным с абсолютно
жестким кольцом, можно получить все усилия в обо-
лочке, у которой один край защемлен, а другой под-
креплен упругим кольцом:
Syn.K = SCB 4- (Зж Зев) Куп.
Здесь Sya к — усилие в оболочке, имеющей упругое коль-
цо; Зя,—усилие в оболочке с жестким кольцом; Зсв —
усилие в оболочке со свободным краем;
„ - Шса
Ауп —	.	>
Щуп -|- Шсв
где шсв— перемещение свободного края оболочки;
шуп— перемещение упругого кольца от сил взаимо-
действия оболочки и абсолютно жесткого
кольца (в обоих случаях — амплитудные зна-
чения перемещений).
Приближенное определение продольного изгибающего
момента. Продольные изгибающие моменты Мх в сече-
ниях, удаленных от краев, при неосесимметричной по-
перечной нагрузке невелики и практически могут не учи-
тываться, Вблизи защемленных краев продольные из-
гибающие моменты могут определяться по формуле
Pv V
= ——тггдддщщг-- е (cos цх --sin 'qx),	(14.23)
У 12 (1 - у")
где
pv — наибольшая интенсивность поперечной нагрузки
в месте защемления й кЦсмР.
При х = 0
(см. случай 3 табл. 14,3).
14.2.7. Особые случаи нагрузок
и расчета оболочки
Расчет замкнутой тонкостенной цилиндрической обо-
лочки на дейезвие произвольной сосредоточенной нагруз-
ки, приложенной к шпангоуту, можно найти в [94]. Дей-
швие сосредоточенных и локальных нагрузок непосред-
ственно па оболочку рассмотрено в [3, 5, 6].
Оценку дополнительных напряжений в цилиндрической
оболочке вследствие начальных отклонений от правиль-
ной формы см. [96].
Расчет круговых цилиндрических оболочек с косым
срезом см, [56, 106].
14.3. ОБОЛОЧКИ ВРАЩЕНИЯ
14.3.1. Определения и основные обозначения
Рассматриваются оболочки, срединная поверхность ко-
торых в цилиндрических координатах г, Д г (рис. 14 .12)
задается уравнением r = r(z). Линии пересечения этой
поверхности с вертикальными плоскостями p = const на-
зываются в дальнейшем меридианами или образующими
Рис 14.12
(поверхность рассматриваемых оболочек может быть об-
разована вращением такой линии вокруг оси г). Линии
пересечения поверхности оболочки е горизонтальными
плоскостями д==соиь1 называются параллелями или на-
правляющими.
Основное внимание уделено расчету оболочек враще
ния по безмоментной теории при наиболее распросгра-
О'
Допочнитеи! ые усилия и перемещения
при симмефичмон поперечное нагрузке
Г а С I 1ИП 14 Ь
И
0,3’8 cos пр,
1
= 2,205 ---------
lC-pj.1
1/ — «уС-сози^,
F |Ц
3,819
Ф„ /О cos п(3,
iip
— Фп/С3 cos n(3, 4xn
[/ n" — 1
t„ = 0,838-----------—
LI
Q,„ = — 0,318 JL PP Sin np,
, _—------—’-------ф [r sinnB,
E^Rn [n1 - 1}
5,801
4 / ---------
tl , / us ф,
K'j COs n [3
)Z;1’ _ ]
Ф< pi's'll! \ И’1! I и перемещен Й U11I1! Д1Я СПММС’РПЧ Ilil гюперсч 1 I nupv 1
+1	/ AiC\ + 4DiDx \	Г 2GlCv~(Fl~2Al)Bx~(F1~~8Ci)Dx 1		( B^x — D.Ax X	k 4 + 4q’ )n
	1 л^м/^d, jn	L	26/	J/2	AiB 4" 46/D/ / n	
	/ 4/ВтЧ-4О/гг \	Г 2G>P	(-(Ei~~-2Ai) Ax- (Ft-BC^Cx I	(	-|-4D/Dx	f Ai_Bx ^ACjDx X
А3	\ -4 । 4В+Л В	L	\п		A,Rt \-4C,D )n	I 4 и4 jn
	/ Ар4г -{- 4DiBx \	Г 2GHt	+ 4(Li~~2Ai)	(В/ - 8G)	|	I BiAx + ^iCx X	( AiAx А iCx \
Аз	\ 4-i ^pt л	L	2Gr	jn		i. AtBi+KtDi )	G + 4G in
Л4	/ Арх -— ПгЛг X	1 26zDy	-	2A,RCx 1 -—-(Fi-BCRAx |	( EtDx-DPx X	/A,J)X ~CiBr\
	\ 4j + 4BzD, )п	I	In		\	h 4G/D/ /h	l, А4 t 4cc lrl
11 р и м е ч	11111 с fx=4 4 1 ‘1вхо.	’ Gv = 1	- At dJ F.=-8 (axCx + Wx)	и x —табулированы в [49	i де обоз’ В’опы соответственно
« О И <)1					
РАЗДЕЛ 14 ОБОЛОЧКИ
113. ОБОЛОЧКИ ВРАЩЕНИЯ
95
пенной на!рузке — oeecmmтричиой (симметричной и тю-
бом сечспия $ —const) FL ш-осесимметричных нагрузок
рассмотрены односторонняя снеговая и ветровая Белее
подробные сведения о расчел обо.юткк вращения по без-
мометной теории па песимметршшые нагрузки можно
найти в книге В
3.
Власова 116]; в частносш, в иен
приводятся формулы и табли-
цы, позволяющие рассчитывать
сферические и эллиптические
сад.пиши под действием силы,
лниложадиой в произвольной
точке, а также сферическую
оболочку, ограниченную двумя
щриетыикулярнымп сторонами,
под длшгвием собственного
веса.
Рассматриваются также
практические методы опреде-
ления дополнительных момент-
ных напряженных состояний,
воыинадошпх вблизи опорных
сечений оболочек (краевой эф-
фект) и, в частности, цик.Шче-
состошшй возникающих, например, при
или нескольких сопрягаемых оболочек
ских моментных
опирании одной
через кольцо иа рад равноотстоящих по окружности
колоть
Некоторые вопросы расчета оболочек вращения за пре-
делом упругости материала освещены в разделе 21,
В дальнейшем наряду с используемыми ранее обо-
аначеппями, применяются следующие (см рис, 14.12):
а — угол между нормалью к поверхнооти обо-
лочки и осью г;
а — угол широты;
1 — толщина оболочки;
₽1 — радиус кривизны меридиана (образую-
щей);
Фх—кривизна меридиана;
1?2— радиус кривизны нормального сечения
поверхности оболочки, перпендикулярно-
го меридиану в рассматриваемой точке,
йа==1Д2—соответствующая R2 кривизна;
r=/?3sin а—радиус параллели;
р — величина вектора внешней удельной на-
грузки (на единицу площади);
Рг, Р^—соответственно величина вертикальной,
нормальной и тангенциальной составляю-
щей вектора внешней нагрузки;
Qz— величина вертикальной составляющей
равнодействующей внешней нагрузки,
действующей на часть оболочки, распо-
ложенную выше сечения z = const;
Оц — меридиональное напряжение — напряже-
ние в нормальном сечении поверхности
(B = const;
A'jy-aji — меридиональное усилие;
о2—кольцевое напряжение — напряжение в
сечении (3 = const;
Аф—сгД— кольцевое усилие;
A’ls — сдвигающее усилие;
Н — распор;
Q — поперечная сила;
Al; — меридиональный момент, приходящийся
па единицу длины параллели;
ЛД — кольцевой момент — момент в слепни
Р = const па единицу длины меридиана,
Лфа—крутящий момент;
и, и, — соответственно проекции вектора переме-
щения на касательную к меридиану (по-
ложительное направление вниз), нормаль
к поверхности оболочки (положительное
направление наружу) и радиус паралле-
ли г (рпс 14 13);
О — угол поворота касательной к меридиану;
оп положителен, если увеличивает угол «;
Ej, f2 — соответственно относительные удлинения
меридиана и параллели, определяемые
формулами
И.3.2. Усилия и перемещения в оболочках
по безмоментной теории
при осесимметричной нагрузке [70]
Моменты Лф и М2 принимаются равными пулю; кро-
ме того, в силу осевой симметрии нагрузки Л/и = 0 Уси-
лия Л, и ,М определяю!ся из системы уравнений:
Q2 Лф , N.,
2nrsina ’ R, т
(U.24)
Здесь первое уравнение выражает условие равнове-
сия (Зс = 0) части обоючки, лежащей выше рассмат-
риваемого сечения г = сопз1. Второе уравнение (уравне-
ние Лапласа) есть условие равновесия элемента оболоч-
ки (сумма проекций всех сил, приложенных к элементу,
па ютрма.ть к срединной поверхности оболочки равна
пулю)
Величина Qz в общем случае определяется по фор-
муле
Q2 = J pz2nr у l+f“) dz. (14 24а)
Для сферической оболочки с радиусом R
а
Qz =- 2лД2 ( рг sin a d а.
о
Для прямой конической оболочки (рис 14 14)
(г
фг =- 2 л cos а ] рг Idl.
0
Для сферической оболочки Д1 = У2~;Д, второе урав-
нение (14,24) принимает вид У;-|-А/2 = р2У.
Для конической и цилиндрической оболочек ф[ = оо
и Дф=.рв^2.
Перемещения (рис 14.13) рассматриваемых оболочек
определяются следующими формулами:
•л 4- w	dw
---------шг ~ р.,Д, sin «; w — -------------.
“ "	da
Здесь величина и определяется:
для сферических оболочек из уравнения
и’ — и cfg а = — (Лф—Аф)(1 ф- V);
(14 25)
(14.26)
96
РАЗДЕЛ 14. ОБОЛОЧКИ
ДЛ!1 конических оболочек (см, рис. 14.14)
1 (' N1 — viV„
w=-------- —2------------
L ,) t
и
где С—постоянная интегрирования, определяемая гра-
ничными условиями
Так как в копнческпх оболочках перемещения вдоль
Сг = 2лЯ
1де До—вес на
Й1 — <о же,
(14.27)
О
Рис. 14 17
—cos «)-(-
So St .	,]
--------(1 4~ sin а — cos а) ,
единицу площади в
в
Л/1
ключе;
Qg
2nr sin а
пяте;
14.3.3. Безмоментные сферические оболочки
при вертикальной осесимметричной
нагрузке [70]
Ns = R & +
So — Si \
-------а । cos а —
ав )
_ etg «
2лД sin а
Ng
(14.31)
а) Равномерная нагрузка на горизонтальную проек-
цию оболочки (рис. 14.15) интенсивпощью рг кГ/см2.
л\ =- рг д Ay = р? Rcos Ж
1
распор Я= —- р.Дсоза.
(14.28)
Нулевая точка (Дг = 0) при а —45°
Для незамкнутон оболочки (рис 1116):
Если толщина оболочки постоянная
Q_z = 2лД2^ (1 — cos а);
R.S
Ni = —--------; N2 = Rg cos а — Ng
1 Д cos а
д °rctga
2лД sin а
(д.=До==Д), то
1
(14.32)
0=----
ft
sin- а-Д
sin*1 а / ’
1 sin2 од
д; п /у CUS2 а ~ — 4. —----------------
\	2 sin2 а
1	/	sin2 од)
fj — ,, р cos а 1 — .--------------- .
2	л	\	sin2 а /

sin a cos од-
R sin а
wr -= —jj- (ЛД -• vNt).
б) Нагрузка от собственного веса (рис.
па оболочки меняется по закону
I
«о
I
1
(14.29)
(14.30)
14 17). Толщи-
Нулевая точка (ЛД — О) при а = 51°49'.
Для оболочки в виде сферического пояса
толщины (обозначение од см. на рис. 14.16):
Q, = 2nR-g (cos од — cos а);
Rg ,
=  ---— (cos а,—cos а);
sin2 а
==/?£-АД;
.Rgcosa
д	——-------/cos а — cos а) _
sin2 а
N
ПОСТОЯННОЙ
1
(11.33)
Перемещения для рассмотренных оболочек
ной толщины:
/ 1
12 1 ——

пос гояи-
w =
1
sin а;
(14.34)
R sin а
Et
1
14,3. ОБОЛОЧКИ ВРАЩЕНИЯ
97
в)	Нагрузка жидкостью (рпс. 14.18) Объемный вес
жидкости у, высей а жидкости над вершиной купола и
(рис. 14 18); шпенсивность нагрузки
р-, -= у (а + z) = у [а + R (1 — cos а)ф j
Рг ~ Т 1а "К R 0—cos a)] cos а; ।	(14,35)
Pi - О,	J
Усилия:
Г	2	) 1
Qz = яуД2 (a -i~ R) sin2 a R-—R (cos3 а — 1) .
L	з	j
yR Г , r 2R (1 — cos3 а) ]
А1 =-----a R- R —--------------------;
2 L	8 sin-а j	(14.36)
Г 1	/I — cos3 а	VI
N о = уД — (л + R) 4 R---------------— cosa ;
[ 2	\ jsin-a	jJ
Н = Ni cos a.
yR
При u = 0 A'i (a=i>) ~ ^2 (a=O) “	,, °-
Pnc. 14.18
Для оболочки в виде сферического пояса (обозначе-
ние а, и ci по рис. 14.16; высота а на рис. 14.18 может
быть 04рпца|СЛ1>на, ио всегда ос —Zj):
( 1
ф2 =- 2луД2 — (а + R)(siп2 a — sin2 op) ф-
ф- _.	(cos3 a — cos3 ajj j .
yR Г 1
Лф =---------— (a + R)(sin a —
sin2 a 2
— sin2 ay) ф- — R (cos3 a — cos3 op)]
Лф = yR [a + R (1 —- cosa)J — Лф;
H = Лф cos a.
Перемещения определяются по формулам, одинаковым
для оболочек типа сферического сегмента и оболочек ти-
па шарового пояса:
yR2	R sin a
О » —- sin a; wr — -——— (Аф — тЛф) •	(14.38)
Для оболочки, находящейся под внутренним давлением
столба жидкости высотой а, выведенные формулы со-
храняют силу при перемене знака на обратный (у опре-
деляемых величин).
г)	Нагрузка в виде постоянного внешнего давления:
Рг -- P-о cos a -- Р cos a-
Для оболочки типа сферического сегмента:
Q2 = рлД3 sin2 a;
л,- рК н pR
ж = N о = ------- ; л = -— cos a.
2	2
(14,39)
Для оболочки типа сферического пояса (обозначение
а, по рис. 14.16):
Qz — TtRRp (sin2 а — sin2 ay); 1
pR. / sin2 op
Лф —	1
2 \ sm~a
Л 2 —- o	. >
2 \ sm- a
„ P-R /, sin2 op
и = -—- cos a  1 — —-—
2	\ sin2 a
Перемещения:
(14.40)
„	R sin a
e = 0'wr = —~— (Аф — мЛф). (14.41)
д)	Оболочка в виде сферического пояса под вертикаль-
ной нагрузкой (обозначение ср по рис. 14 16), распреде-
ленной вдоль контура меньшего основания с интенсив-
ностью р (единица силы/единица длины);
<Зг = 2лД sin агр = 2лгр;
sin a,	sin а,
Ni = р	—. Ni =_ р	.
Sin2 a	Sin2 GS
sinai cos а
п = р ----------------=
sin2 а
(14.42)
14.3.4. Оболочки вращения под действием
равномерно распределенного
нормального давления [16]
Рассматриваются в основном оболочки, образующая
(14.37)
является кривой второго порядка
(эллипс, парабола, гипербола).
При направлении оси z, показан-
ном на рис. 14.19, нормальные си-
лы в таких оболочках, загружен-
ных нормальным давлением рв —
= д —const, определяются приво-
димыми далее формулами.
а) В эллиптической оболочке
(уравнение образующей
а'2
Г2 ^Ьг — г2),
Рис. 14.19
где a, b—полуоси эллипса)
/V1	р	+ а2 (] „ р2)Ъ
а
=— р ——-----------— X
2 Z 26(1 Ф-1Д
v 2	+ 2,2 П — P2d — (] +
У 462р2 V а2 (1 — р2)2
(14.43)
7—26
98
РАЗДЕЛ 14. ОБОЛОЧКИ
гдер="|/ •	(14.44)
При г = 0 (р = 0) и г = 2Ь (о =оо)
аа
Л'-< = Л-., —— р —
1	3	2Ь‘
При г = Ь ((> = 1)
а	а (2Ь- — а2)
Мг	N3 =--- р	.
б) В сферической оболочке (a = b — R)
R
— р .	(14.45)
При 2 -= С (р = 1)
рс Уз
1
N.2~
2 V 3
д) В горообразной оболочке (рис 14 20)
(14.48)
в) В оболочке вида нижней полости двухполостного
гиперболоида вращения с образующей
as
г2 ~ (2Ьг + г2);
а 1Г4б3р2 + О3П +р2)2
Большое количество формул для расчета оболочек вра-
щения см {68].
Рис. 14.20
2 [4Ь2ра + аа (1 + Ра)21 — а3П — Р2)3
(1 “ Р2) /Sv+^oTp3?2
где р=~|/
При г =- 0 (р = 0)
N^NS^P^.
/ 1 \
При г ~ Ь I р ~ ——
\ Кз /
14.3.5. Расчет оболочек вращения
по безмоментной теории
на несимметричную нагрузку [37]
Снеговая нагрузка (рис, 14.21). Расчет сферической
оболочки на вертикальную нагрузку типа снеговой при
одностороннем загружении снегом производится по фор-
мулам:
нормальная составляющая снеговой нагрузки
Ри = 0,4р2 (1 + sin a-sinif), (14 49)
Лф = р -~р К3&2 + 4а--
а 6Ь- + 7а2
N3 = р — • ——------— .
26 Кзй2 + 4 а3
При г — со (р = 1)
Л\ = Na = ОО.
г) В параболической оболочке вращения
образующей гг = 2сг)
N1 = P — УТ+УУ
с 1 + 4р2
Л , ~ р--—---------- ,
2 У 1 + 2,о2
г УТ ,/т
Где т°
При г — 0 (р = 0)
где рг — нагрузка на единицу площади горизонтальной
проекции поверхности оболочки;
соответствующие усилия
Г 1 cos а
Л'т^О.4/^ T + ?;-^(2 4-cosa)X
1
(уравнение
(14.47)
cos-a)2 sin ф ;
( 1 Г
Л’а == 0,4рг /? < — + sin а —
cos а
щ— (2 + cos а) (1 — cos а):
3 sin-’ а
„	0,4рг₽
12	3
(2 + cos а) (1 — cos а)3
.---------------------cos .
sin3 а
(14.50)
14 3. ОБОЛОЧКИ ВРАЩЕНИЯ
99
Ветровая нагрузка на оболочку вращения прини-
мается нормальной к ее поверхности и определяется сог-
ласно [37], т. е. как произведение скоростного напора q
на эпюру аэродинамических коэффициентов Св=0,5 sin2a
(0,85з1пф—0,15 sin Зф)—cos-Д (рис. 14.22). Норма-
тивные н расчетные значения скоростного напора ветра
определяются в соответствии с указаниями СНиП.
Можно также пользоваться упрощенной формулой:
р = рв sin a sin ф,
(14.51)
где р0 — давление ветра на вертикальную площадку,
перпендикулярную его направлению (при а =
= Ф = 90°).
Меридиональные и сдвигающие усилия АД и NK нахо-
дятся из условий равновесия сегмента оболочки, отсе-
каемого параллелью, проходящей через точку, в которой
определяются усилия; они имеют значения:
М 51пф
лг2 sin а
is —
---------cos ф.
лг" tg а )
(14.52)
Здесь И— равнодействующая ветровой нагрузки, при-
ложенной к сегменту оболочки; М— момент этой нагруз-
ки относительно диаметра отсекающей параллели, пер-
пендикулярного направлению ветра. При очертании ме-
ридиана, заданного уравнением r = r(z):
К
Н = лр0 ] г sin adz-,
u
Л
Л1 — Hh — лрй ] (rz sin « г2 cos a) dz,
о
(14,53)
где h — высота сегмента; координата г отсчитывается
сверху вниз (см. рис. 14 19).
После определения АД кольцевое усилие опреде-
ляется из уравнения Лапласа (14.24).
Для полусферы величины усилий определяются по
[25, табл. 15, стр. 115]. Если закон изменения нагрузки
7*
задается согласно (1451), то усилия определяются ио
формулам:
cos а Г 2
A'l = PoR ——~ — — cos а -к
sitf a L i
1 1
j_ __ ссвз а sin,|;.
[	cos a I 2
'"a = Po S sin « — — -—' —* —- cos a +
[_	sin- a \ 3
(14.54)
,,	R I 2
A'i2 = Po	~ — cos а +
sm3 a \ 3
-]~ — cos3 a cos ф
пли же по таблице Дпшипгера [33, стр. 49]
а	+Ni	—N>,	X'12
0		0,0000	0,0000
10°	0413	1334	0419
20а	0840	2580	0894
30°	1187	3913	1371
40°	1455	4973	1900
50°	1615	6043	2510
60°	1605	7 OSS	3210
70°	1409	7958	4 (23
80°	0909	8943	5200
90°	ООО!)	1,0000	Обо”
				
Л‘1—A\ р, R sin ij-	N,~N^p, R sin ip, jVj2 — A'jnp		К <. os Ц-
14.3.6, Учет изгибающих моментов [41]
Около мест прикрепления оболочки к опорному кольцу
возникают изгибающие моменты (краевой эффект), ко-
торые быстро затухают по мере удаления сечения от
края.
Эти моменты и их влияние па нормальные п попереч-
ные силы (которые надо предварительно определить по
безмоментной теории) при осесимметричной нагрузке
приближенно учитываются следующим образом.
Вычисляется коэффициент затухания.
,/3(1— V2)
й=Д11/ -—-у-,	(14.55)
F 7Д Г
который при переменной кривизне является переменным.
Для сферической оболочки
k = iZу- У	(14.56)
Усилия, моменты и угол поворота касательной к ме-
ридиану определяются по формулам:
100
РАЗДЕЛ 14 ОБОЛОЧКИ
Лф = ~— ctg аСе ta cos (kas -1- 6);
4 .Rg
, = JLLEkL. kCe-k^ sin [kb3 4- 5 4---4 ;
4^	'	* 1
Q = ---- G?~*“cos (kw 4- 6);
X (ka + 6).
(14.57)
Здесь А'к — кольцевое усилие в оболочке в зоне, непо-
средственно примыкающей к кольцу, определяемое по
безмомеитной теории.
Величина 6 зависит от условий связи оболочки с коль-
цом. при полной заделке 6 = 0, а при шарнирном соеди-
нении 6 = п/4. При указанных значениях 6 формулы
(14,58) значительно упрощаются. По ним легко могут
быть определены усилия, моменты и углы поворота при
любых значениях параметров а и со, в частности в месте
сопряжения оболочки с абсолютно жестким кольцом
(ш=0 и а = а0— см. рис. 14.12)
Задача определения краевого эффекта в оболочке, со-
прягаемой с кольцом конечной жесткости или с другой
оболочкой вращения при осесиммегрнчиои нагрузке яв-
ляйся частным случаем задач, рассмотренных ниже и
может быть решена ио формулам, приведенным в 14 4
14.4. ЦИКЛИЧЕСКОЕ (МОМЕНТНОЕ)
НАПРЯЖЕННОЕ СОСТОЯНИЕ
ОБОЛОЧЕК ВРАЩЕНИЯ,
СОПРЯГАЕМЫХ МЕЖДУ СОБОЙ
Эти формулы выведены для постоянного k, ио с извест-
ной точностью ими можно пользоваться и при перемен-
ном k. Угол широты w отсчитывается от нижнего края
до того сечения, где определяются усилия (см. рис. 14.12).
Постоянные интегрирования С и б определяются из ус-
ловий прикрепления оболочки к кольцу.
При абсолютно жестком кольце формулы (14.57) при-
обретают вид
14.4.1. Выделение циклического воздействия
и его распределение. Общий порядок расчета
Когда одна или несколько монолитно связанных обо-
лочек вращения опираются через бортовое или объеди-
няющее их кольцо на ряд
________Pi ctg «
]/г (?2festn fe
1
г k(a cos (few 4~ S);
g—Aw
/V 2 = Л' к	t
sin <
sin I few + 6 + “1 >
Ri
Q =	__
У 2 R,k sin | 6 + —
X e—to cos (few -J- 6);
(14.58)
равноотстоящих по окружно-
сти колонн (рис. 14.23) или
поддерживают стойки фона-
ря, радиальные ребра, стяж-
ки и т. п„ их напряженное
состояние можно разложить
на осесимметричное состоя-
ние и циклическое состояние.
Для выделения осесиммет-
ричного состояния следует
рассмотреть действие осе-
симметричной нагрузки сов-
местно с уравновешивающей
ее реакцией, принимаемой
также за осесимметричную,
г. е, равномерно распреде-
ленную ио осевой линии
кольца. Для выделения цик-
лического состояния надо
рассмотреть действие проти-
M, = —NK
2P,2k2 sin
' ka cos (few 4- <5 -J- — ;
\	i
Et3 ctg a
M	. _щ_ 0 4. vM
12 (1 — v2) R,
XSV~2~
e= ,vK
EtPx sin ( 6 4- —-
\	4 ,
X sin (few 4- 6).
воположно направленного давления, равномерно распре-
деленного по осевой линии кольца, совместно с урав-
новешивающими его реакциями колонн (рис. 14.23).
Основная трудность при расчете оболочек на цикли-
ческое воздействие — в его распределении, т. е. в опре-
делении контактных усилий между сопрягаемыми элемен-
тами (кольцом и оболочками). Эта задача решается раз-
ложением циклического воздействия в тригонометриче-
ский ряд, число воли в гармониках которого п кратно
числу колонн п0 (п = п0, 2п0, Зио, --) Каждый член та-
кого ряда вызывает в рассматриваемых оболочках
и в кольце независимые от других членов ряда гармо-
нические циклические состояния, при которых усилия
и перемещения в кольцевом направлении изменяются
пропорционально cos/ф или sinn(3, где (3 — угол широты.
Число членов ряда, которые необходимо учитывать при
практических расчетах, зависит от числа колонн и отно-
шения жесткостей кольца и оболочек, С ростом а одно-
101
14 4. ЦИКЛИЧЕСКОЕ (МОМЕНТНОЕ) НАПРЯЖЕННОЕ СОСТОЯНИЕ ОБОЛОЧЕК ВРАЩЕНИЯ
..........—--- - •;..... ...1.—............. ...:п.. ....................  -т----------
сительиая жесткость кольца увеличивается, поэтому мож-
но принять, что гармоники циклической нагрузки с чис-
лом волн больше некоторого п воспринимаются только
кольцом. При достаточно жестком кольце можно при
расчете оболочек ограничиться первым членом ряда
(n = «o).
Ниже под циклическим состоянием подразумевается
гармоническое состояние с произвольным числом волн п.
Поскольку для такого состояния закон изменения уси-
Для унификации размерностей символами У) и Z2
(Х!2, R!2, R2, Р2) обозначены углы поворота (моменты),
умноженные (разделенные) на соответствующие радиусы
rj или г0.
Связь между перемещениями и усилиями Z; и RI, с од-
ной стороны, и У! и XI, с другой, вытекает из их опре-
деления и геометрии сопряжения оболочки с кольцом:
И = [я] И N 
И = [<[< И 
(14.59)
(14.60)
где матрицы и [/ф определяются параметрами,
указанными на рис. 14.24:
лий и перемещений в кольцевом направлении известен,
задача сводится к отысканию лишь их амплитудных зна-
чений.
Для сокращения записи дальнейшее изложение ведет-
ся в матричной форме что потребовало использования
следующих обозначений:
j— порядковые номера сопрягаемых элементов
(у’ = 0 относится к кольцу; /= 1, 2... —- к обо-
лочкам);
i, k~ 1, 2, 3, 4 —индексы направлений переме-
щений и усилий; 1— нормальное к средин-
ной поверхности (для оболочки) или ради-
альное (для кольца); 2— вращательное
в меридиональной плоскости (для углов по-
ворота и моментов); 3 — меридиональное
(для оболочки) или осевое (для кольца);
4 — касательное к параллели (тангенциаль-
ное);
гв—радиус осевой линии кольца;
Д— радиус линии контакта срединной поверх-
ности /-Й оболочки с кольцом (рис. 14.24);
Z; и У1— амплитудные значения перемещений точек
осевой линии кольца и линий контакта сре-
динной поверхности у'-й оболочки с кольцом;
R[ и X!—амплитудные значения контактных усилий,
действующих между кольцом и у-й оболоч-
кой, заданные соответственно в координат-
ных направлениях кольца и оболочки;
Pi и 7?j— амплитудные значения внешней цикличе-
ской нагрузки, приведенной к осевой линии
кольца и нагрузки, действующей на изоли-
рованное кольцо.
1 Матричные символы:	|[ — прямоугольная матрица; [ ] —
квадратная матрица. ( } — матрица-столбец (вектор); *— знак
транспонирования матрицы.
Кроме того, для каждого изолированного элемента
(оболочки или кольца) между усилиями и перемещения-
ми может быть установлена связь вида
И==17У!у0
КЫ'УКЬ (14.62)
где [ф] (у = 0, 1,...)—матрицы единичных реакций, оп-
ределяемые формулами из 14.4.2 и 14.4.4.
Из приведенных соотношений ясно, что если перемеще-
ния кольца Z,- известны, остальные факторы находятся
весьма просто: У1 из (14,59), X! из (14.61). Для опреде-
ления Zi используется уравнение (14.62) вместе с очевид-
ным соотношением:
= N - s И) 
(14.63)
Замена {Д1} в (14.63) выражением (14.60) приводит
на основании (14.62) к системе канонических уравнений
метода перемещений относительно неизвестных Z,:
trik\*{Zi\ = (ЛЬ	(14-64)
где
Ы’ЧФ 2 [<[<[>»
у=1, 2,...
(14.65)
После вычисления контактных усилий изменение на-
пряженного состояния каждой из сопрягаемых оболочек
в меридиональном направлении может быть определено
по формулам (14.4.3). '
102
.РАЗДЕЛ 14. ОБОЛОЧКИ
14.4.2. Единичные (краевые) реакции
оболочек
Дополнительные обозначения*
---------- £/2	£/3
Х=У 12(1—V2) ; B^-Et-
л	X
гы =	п“ (4Гц	+ 4ц),	гд8 ~	4)	п2 Ги,
ri2 =	п (4Гц>	412);	г34 —	Л;	п" Гз,;
/"аз = .43 (4Г32 +	432);	гм ==	/ц	п- Г33;	(14.66)
Дз =	п~ d^'	п°
г за = 4а nd23;	г„л = А3 nd„A.
Здесь:
жесткости;
г
и - —отношение главных кривизн (х=0 для ко-
bRi
иической и %—1 для сферической обо-
лочки);
Ьг
р=----- — приведенный радиус;
4 — Г33 Г44“ гзФ
413 = Г34 Г14—Г44 Гщ; 4ц = Г14 dti—Гц 413;
4ц — Гзз Ги — Г34 Г1э; d13 = Гм424 — Tjg 423 =
= Г24 413 — Г2з dis't
42з — Г34 Г24 — Г44 Газ;
4й4= Г33 Г24 — Г34 Г231 422 = Г24 d^ — Г23 di3.
(14.67)
щ ™ дф + у 1Д-1 ; ду —	ф*1 Н~ 1;
z—	п
т„ = ]/ 2ф = — ;
s
для переменных величин вводится значение на линии
сопряжения с кольцом.
Для каждой из сопрягаемых оболочек элементы мат-
рицы [r-f, ] определяются по следующим формулам (ин-
декс / далее опускается):
Для г,* справедливы условия взаимности г^ — гщ и,
кроме того, дополнительные тождества: а) для кониче-
ской оболочки Гзз = Д|4; б) для сферической оболочки
гзз = г44; Г)з = —г]4; Г23=—Гц-
Выражения входящих в (14.66) — (14.67) коэффициен-
тов Г,* приводятся ниже для оболочек, замкнутых в по-
люсе или образующих пояс, достаточно широкий, чтобы
пренебречь взаимным влиянием условий на отдаленных
краях. Формулы приближенные, порядок их погрешности
1 : п2. Для оболочек, отличных от конической и сфериче-
ской, для упрощения опущены также члены порядка
а : п.*
41 Более полные данные см. {54].
Таблица 14.7
ik	а№	vifl	Ik	alk	hk
11,22	т	Коничес 1 —g _ 1 + V	<ая обо 13	кочка 1	2 -4- jp
33Р44	т	1 £? + ) «	24	т 1	2^3 k1
12 34 И, J2	1 4- т —	 п S 1 — V 	.		 п 3 т.\ -J- т.	2s	s m	1 — k “Г ”— n	4n m	1 — k - । n	An Сферичес 1 + V C—	14 23 кая обо 12	т п 0 почка	2'1js 4mn 1 + & 4mn m.	1 	
33,44	т1 + т2	s ?1_1+г+дд>	34	— vm,	n	s . m\ 1 J V» + —— -1		
13,14	-Т-+ — 772^	772^	8	П ъ + — фз	23,24	1 т,	n	s Ъ
Здесь: V;
3 4" 2<pJ <— пъ (\
1 тх J
144. ЦИКЛИЧЕСКОЕ (МОМЕНТНОЕ) НАПРЯЖЕННОЕ СОСТОЯНИЕ ОБОЛОЧЕК ВРАЩЕНИЯ
103
Таблица 14 8
Тип обо- лочки	tk	a'ik	4		ъ
						11				1
	12	1 v		> 	n
Сферичес-	22	2	- (1 + T)		n2
кая и ко-	33	2	L — V		
ническая	34	1 — V	2	1	'°i	1 (3—v) (1-Щ)
	44	2	1 — V		J
	13	4—8v		s	в,ь	
	14	144 4V	3 — 5v	J	3rn	
Коничес-					(3-v)(Hv)
кая	23	2— Lv	3 — v		
	24	4	3 — v	/	3rrr	
	13	—. 3	.9	)	B.b	
	14	3	2	J	L?/2	
Сфери-				в b	3—v
ческая	23	— 1	—2		
	24	1		)	2r;z-	
а) Коническая и сферическая оболочки:
Значения коэффициентов
Таблица 14.9
Значения ф		Уровень	: погрешности	!
для конической оболочки	для сферической оболочки	
>5	>9	<0,01
>4	>7	<0,02
>3	>5	<о,оз
Относительная погрешность при этом оценивается с по-
мощью табл. 14.9.
б) Круглая и кольцевая пластинки. Формула (14.69)
и табл. 14.8 в предельном случае 6 = 0, а== — 1 дают точ-
ные значения г,ь для круглой пластинки, а также при-
ближенные значения для достаточно широкой кольце-
вой пластинки, нагруженной по наружному краю. Пре-
дельный случай 6 = 0, а=ф-1 также соответствует коль-
цевой пластинке, но нагруженной по внутреннему краю.
В обоих случаях г — радиус нагруженного края,
в) Оболочки вращения других очертаний. Исходя из
г
отношения главных кривизн % — —— на контуре оболоч-
ки (табл. 14.10), определяются вспомогательные вели-
чины:
; atk h afiik
(14 68)
приведены в табл. 14.7.
При достаточно больших значениях параметра *ф мож-
но, минуя определение Г,л, определить непосредственно
значения
^ = Бт(а« + а₽У-
б] =2ф(рг+ 1);	?! = 1 + 2фца,
приведенные в табл 14 8.
после чего находятся входящие а (14.66), (14 67) выра-
жения {14 71):
Таблица 14 10
Тип оболочки вращения	Уравнение меридиана	Екпомогагельиыг. параметры	
Эллипсоид	Р	q-	— - !- — р*	Q*	1 q2 а
Двуполостный гиперболоид	Р	Н. Р‘	Q1		q-d
Однополостный гиперболоид	-й_ - X. = ! р-		__ 1 q^ d
Параболоид	ГР-М = с (р + 1) г	Г.Р	S ф ф*1
Тороидальная 1	г = К «f-2*	— я/	
,	2 Катеноид (антисфера)	т ~~ с сй с 1 Л — расстояние от оси оболочки до центра кривизны меридиана.		—	
104
РАЗДЕЛ 14. ОБОЛОЧКИ
14.4.3.	Изменение усилий вдоль меридиана
каждой оболочки
Нормальные и касательные усилия определяются через
функцию
Ф (a.) ==с4Д (а) — с2/, (п) +с3 f3 (а.) Д с4 Д(а) (14.72)
и ее производные по а по формулам:
1
— -- (аф' — л2 Ф);
г
(ф"ф-аф'—	Ф); .	(14.73)
АД = — пФ'.
г
Изгибающие и крутящие моменты и поперечные силы
определяются через аналогичную функцию
й? (а) =с2Д (а) Д-Сз Д (а) -4- f3 (а) — с3^ (а)	(14.74)
и ее производные по а по формулам:
Mi =	[17'' + (1 + v) aW — vn1 W];
V
Л1„ = [vft7" + (1 + v) aW' — rfi ft7];
V
Л412 =------(1 — -v) nW';
Q	(W"" Д. aW" — n- ft7' — on7 ft7);
V-
tn
q2 -------+ 2aW' - Л2 W).
Определение постоянных Ci, аргумента а и функций
f, (а) излагается далее.
С удалением от граничной параллели усилия цикличе-
ского состояния имеют тенденцию к затуханию. Затуха-
ние может начаться непосредственно от границы или для
части усилий ему может предшествовать некоторое воз-
растание по сравнению со значением на границе. Для
практических целей достаточно установить начало зату-
хания и оценить его интенсивность. В связи с этим вы-
ражения fi и правила их дифференцирования определя-
ются здесь лишь приближенно.
а) Определение постоянных с,. Постоянные с, связаны
с краевыми перемещениями У;, У2 и усилиями А'ь Х2 че-
рез параметры од L, следующим образом:
(14.76)
(14.77)
[ Ф* ]	j	iS32 633 634
I. 04 J	I	642 643 644
ir
4
7-3
L-i
(14.78)
Значения 6щ зависят от типа оболочки. Для кониче-
ской н сферической оболочки значения
«м = 4 + -7'^	(14'79)
приведены в табл. 14.11.
Для оболочек других типов дополнительно к форму-
лам (14.70) — (14.71) определяются вспомогательные ве-
личины:
б) Определение аргумента а. Аргумент а, (безразмер-
ный) определяет положение точки на меридиане. В об-
(14.75)
(14.80)
(14.81)
щем случае
(14.82)
14 4, ЦИКЛИЧЕСКОЕ (МОМЕНТНОЕ) НАПРЯЖЕННОЕ СОСТОЯНИЕ ОБОЛОЧЕК ВРАЩЕНИЯ	105
Таблица 14. И
			
i Ik		’'ik	Обозначения
I			Коническая оболочка
31		—1 + Pl — р.	
33		-А, - Р>	
			т3 1	тэ 4- I	_	1 — k2 п	k3
33	—а	—Pi — 3.1	а, = —-— : а,	—X—., р, =,	 g, = _А_ _
34	1	-3« + 3.1 4 3.,	2т	‘2т	4	16ф
	41	.,	QT	1 — 3, — р..	
			1 4- k	о 1 — /г	т2 + 1	т- — 1
42	1	Эр — 3*	
			4m	4	4фт	4фт
43			”3, т- Рз	
41	1	-3- - 3, + 3,	
			Сферическая оболочка
31	m2 аг	--31 3,	
32	tZj	”3. Зи	
33	—а, с/.	— 31 04 Г7?.->	
34	а2	т- 3. 3.		1	о	а3	n	2>”i — w-2 (Xi — = m, 4- i-n^;	= •— ; pj—	; p2 = 			 j тг	2g	m-i
41	—tZj а,	”31 3; У	
			q =sa	4“ “L“IJ IJ j	3=3 “h
42	—сс.	_р, р. 2	«h	ЧЖ
43	т2»!	—31	
44		3. р; —	i	
		т2	i	
Таблица Н.12
Тип оболочки
a	Тип оболочки
Цилиндрическая
Коническая
Катеноид вращения
(антисферплеская)
Сферическая
Параболоид вращения
степени р-Н
Эллипсоид вращения
вы тянутый
То же, сплюснутый
Г иперболоид вращения
однополостный
То же, двухполостный
Тороидальная
L — ]Ч* arc tg Ч" а]®
L + [Ч- Ar th 4'a]g
L Ж П' Аг с th Ч-
Обозначения (см, ыкже табл, 14 10): 4
— ; / полюсное расстояние;
7
У /_Д. + _1иТ
L“in’ ----; [ ]“ = [ |и - ! ]0.
1д (_Д + _Ц
(индекс а, относится к исследуемой точке, индекс 0 —
к граничной параллели).
В табл, 14,12 приведены выражения а для оболочек
различных типов.
У сферической оболочки а можно определять по
табл. 14.13, содержащей рачности Аа = а(у)—а(у—В)
при изменении у от 1’ до 90° (в табл. 14.13 у —<р+й).
У параболоида вращения второй степени (р=1) а
можно определять по табл. 14.14, в которой приведены
значения переменных геометрических параметров поверх-
ности, в том числе разностей Аа при различных значени-
т
ях отношения <р = ~~~ < 3.
РАЗДЕЛ 14. ОБОЛОЧКИ
106
Таблица 14.53
ф	8					
	0°	15“	30“	45“	60°	73“
0°	175	181	203	249	35-1	697
1°	175	182	205	253	366	748
	175	183	.207	258	378	807
3°	175	184	209	263	391	876
4°	175	185	212	269	405	959
5°	175	186	214	274	421	11)58
6°	176	187	217	280	438	1182
7°	176	189	220	287	436	1339
8°	176	190	223	293	47 6	1545
9°	177	192	226	301	199	1826
10° 11°	178	193	230	308	523	2234
т 90	178	195	233	316	550	2878
13°	179	197	237	325	580	4056
14°	180	198	241	334	6X5	6932
	180	201	245	344	653	Q-J
ГГ р я м е ч а Щ“4.	и и е.	"абличн	ie зи а*	ения у	множат	на
Т а б л и и а 14.14
г Ф -= —•	ь	а	X	Дсх
3,0	~Г 0,9487	0,3162	~Б 0,1000	0,211
2,8	9417	3363	1131	
2,6	9333	3590	1289	
2,4	9231	3846	1479	
9 О	9104	4138	1712	218
2,6	8944	4472.	21)00	
1,Я	8742	4856	2358	
1,6	8480	5300	2809	
1,4	8138	5^12	3378	241
1,2	7682	6402	4098	
1,0	7071	7071	□ООО	300
0,8	6247	7809	6098	
0,6	5115	8575	7353	350
0,4	.1714	9285	8621	453
0,2	1961	9806	9616	72,1
0,0	0000	1,0000	1,0000	
Значения а, определяются путем сложения значений
Да нарастающим итогом от граничной параллели до рас-
сматриваемой.
Значение а и Ь см. рис. 14.24.
в) Определение функций /у (а) и их производных.
Функции ]’,(а) — затухающие:
6 = е (а) cos р2 (а); /3 = е р"(а) cos/ц (а); 1 (ц83)
= е^Р1<а) sin р2 (а);	= e~~'p=(a) sjn	j
В первом приближении можно положить р,(а)==
= sita,, приняв Ьг по табл. 14.15,
Производные от функций /, линейно связаны с теми же
самыми функциями, В первом приближении
f'l = — s (&i b + Ьч AA
f-2 = — s (i-j. 6 — C
h- - 4b3 b + A Aj;
4 = -s {ba ft ~ bt AA
(14.83a)
Табл и u a 11.15
ф.	Ко(шческая оболочка	Сферическая оболочка	Другие типы оболочек
	т -6 1		ПЛГ.',!
			
	2		2
6 О	т ~ I	1	Г22 + Г24
	2/п		
	т — 1	п	Г.„- г14
		т. — ——	
ь.	.2	S	2
	т — 1		^22	^24
Ь-,		0	
	2т		
14.4.4.	Кольцо, Единичные реакции
и внутренние усилия
Формулы относятся к случаю кольца нетонкостенного
профиля; одна из главных центральных осей инерции се-
чения предполагается лежащей в плоскости осевой ли-
нии кольца.
Обозначения:
EF л	л EJ*
2 ’ А1~~	4	; As~- 4 ;
го	го	го
О/к
г0

жесткости, отнесенные к радиусу осевой линии (при
продольной деформации, при изгибе в плоскости осевой
линии, при изгибе около этой плоскости и при кручении).
Единичные реакции определяются по формулам:
гц —= Ав (п-	I)2 Ар, г22 — Л2 4- п2 Лк,
ги = пАр,	ip3 = nA А„ ф- п" Лк,
г44 = и2 Лц	гэз = гг4 Л2 4- и2 Ак;
(14.84)
г12 — г18 — г-24 — г34 — 0.
Продольные силы, изгибающие и крутящие моменты
и полеречные силы в сечениях кольца определяются че-
рез Z,:
Л = [Ад — (п2—1) .41] Гд Zi nA0r0Zp,
= (я3 ~ 1) A r0Zp
А2 ф., + n2Z3);
z/ = n.V3(za + zA
п.	п	1
Qi — All; Q* = — 44= + — W,
И	Гд	Гд
(14.85)
14.5. ПОЛОГИЕ ОБОЛОЧКИ
14.5.1.	Определение, формы срединной
поверхности и граничные условия
Оболочка, имеющая небольшой подъем, называется
пологой. По В. 3. Власову, к пологим относятся обо-
лочки со стрелой подъема, не превышающей 7S иаи-
14.0. ПОЛОГИЕ ОБОЛОЧКИ
107
меньшего размера опорного плана. Это простое опреде-
ление требует уточнения. Обозначим уравнение средин-
ной поверхности пологой оболочки до нагружения
(рис. 14.25) через z = Eo(;c, у). Для пологой оболочки
должно соблюдаться условие; в любой точке срединной
d/’o dFv
поверхности частные производные —долж-
ны быть величинами первого порядка малости, так что
их квадратами при вычислении кривизн поверхности
Рис. 14.25
Рис. 14.26
Рис, 14.27
можно пренебречь. Иными словами, для пологой обо-
лочки характерно, чю в любой точке кривизны и круче-
ние поверхности можно отождествлять со значениями
вторых производных, т. е. определять по формулам:
.	h	ь d"Fo
Rx~- дх> :	ду* ху~~ дхду-
(14.86)
Если это условие не соблюдается хотя бы в одной
точке, то оболочка перестает быть пологой.
Например оболочка, изображенная на рис. 14.26, не яв-
f« , 1
ляется пологом, несмотря на то, что у нее ~ <.	,
I 5
так как в средней части при вычислении кривизн нельзя
пользоваться формулами (14.86). Из этого определения
пологой оболочки следует, что линейный элемент ее
срединной поверхности ds можно считать равным
ds— ) ДД-р-ДД; это означает, что метрика срединной
поверхности пологой оболочки приблизительно совпа-
дает с метрикой плоскости. Такое допущение положено
в основу технической теории пологих оболочек. Поло-
гие оболочки могуг быть любой гауссовой кривизны:
положительной, нулевой и отрицательной. Вследствие
пологости срединной поверхности разница между теми
или иными поверхностями одного гнпа кривизны несуще-
ственна. Г. конструктивной точки зрения наиболее при-
емлемы поверхности переноса (например, для оболочек
положительной кривизны эллиптический параболоид,
круговая поверхность переноса). Кроме того, могут
быть использованы сфера, эллипсоид вращения и дру-
гие поверхности второго порядка (или более высоких
порядков). К категории пологих оболочек относятся так-
же слегка искривленные пластины («вспарушенные» пли-
ты). Опорный контур может быть плоским или выпук-
лым (рис. 14.25, а, б). Оболочки с прямоугольным планом,
опирающиеся на плоский контур, имеют в централь-
ной части положительную, а вблизи углов — отрицатель-
ную гауссову кривизну. Если плоский контур не обяза-
телен по архитектурным или иным соображениям, то ре-
комендуется применять оболочки с выпуклым опорным
контуром, что обеспечивает повсюду внутри контура по-
ложительную кривизну.
Пологие оболочки могут располагаться отдельно
(рис. 14.25) или входить в состав многоволнового покры-
тия (рис. 14.27). Отдельно стоящие оболочки могут опи-
раться на бортовые диафрагмы, выполняемые в виде ба-
лок, арок или ферм, или же непосредственно на стены.
Опоры считаются шарнирными, если оболочка опирает-
ся на стены или диафрагмы, достаточно жесткие в своей
плоскости и гибкие из плоскости диафрагмы. Средние
волны многоволнового перекрытия считаются защемлен-
ными (в отношении углов поворота) по контуру.
14.5.2.	Усилия и перемещения пологой
оболочки. Особенности расчета
В пологой оболочке возникает система усилий Nx, V„,
Nxv (рис. 14.28, а) и изгибающих и крутящих моментов
Мх, Му и Мху (рис. 14.28,6). Перемещения характеризу-
ются тремя компонентами: uj]x; ®||z.
Связь между перемещениями и деформациями уста-
навливается формулами:
dv	1
е = _ k w +
оу	2
ди	dv
z-xii — ~~	+ ~	w 4-
ду	Ox	v
dw dw
+ __ , — ,
dx dy
O-W
Xx = ' Xl/ '
d-w
Xxy ~ Ox dy '
(14.87)
Здесь Ei и fv — относительные удлинения; exy—’Дефор-
мация сдвига; ух, уу—’Приращения кривизны; %ху —
приращение кручения срединной поверхности.
Для оболочки из линейно-упругого материала усилия
и моменты (положительные направления которых ука-
заны на рис. 14.28) согласно закону Гука равны:
108
РАЗДЕЛ 14. ОБОЛОЧКИ
ЕЛ
Nx =	+ w^);
1 — V*1
Et
Ny^Y^^&u + ^x}'
Et	(14.88)
{'ху 2 (1 + v) Сху’	
Мх = — D (%х 4- v%y);
Му = — D (%у 4- v%xy,
Мху = 4 D(1 — v) x^-
Здесь t — толщина оболочки; v — коэффициент Пуассо-
ЕЕ
на; Е — модуль упругости; D =	~ — цилинд-
13(1	V")
рическая жесткость.
Для оболочки из нелинейно-упругого материала уси-
лия определяются согласно [48].
Условия равновесия:
24 = 0;	dNx dNXy -7 + ~~~ + Рх = 0; дх	ду	
2У = 0;	ду + дх + Ру~°’	
22 = 0;		-Л.	о ~4- дх-	“ дх ду	(14.89)
4-	д*М„ ~jl + Nx {kx + Xx} + ду-	
4- Nу (ky	4- Ху) + 2NХу (kXy 4- Хху) 4"	
	4 Рг = 0 	
Здесь рх, Ру, Рг. — проекции внешней нагрузки на оси
х, у, г. В наиболее часто встречающемся случае верти-
кальной нагрузки рх = Ри —0, т. е. когда тангенциальные
составляющие поверхностной нагрузки равны нулю, нор-
мальные и сдвигающие силы выражаются через функцию
напряжений по формулам:
Первое уравнение (14.91) —уравнение неразрывности
деформаций — получено из первых трех выражений
(14.87) путем исключения из них перемещений и. и v
и замены деформаций усилиями по формулам (14.88)
и (14.90). Второе уравнение (14.91) получено из третьего
уравнения (14.89) после подстановки в него значений
усилий через перемещения и функцию напряжений по
формулам (14.87), (14.88) и (14.90). Система уравнений
(14.91) описывает поведение пологой оболочки в самом
общем случае с учетом моментов и конечных перемеще-
ний; иными словами, это есть уравнения моментной не-
линейной теории пологих оболочек. Отбросив в этих
уравнениях нелинейные члены, получим дифференциаль-
ные уравнения линейной моментной теории пологих обо-
лочек:
1	d~w d-w
d"-w
— 2kxt/ = 0;
J дх ду
d-w d"wy
(32Ф
+ ^хи ' — — рг = 0-
 дх ду
(14.92)
Если в уравнениях (14.91) положить £> = 0, т. е. пре-
небречь работой моментов, то получим дифференциаль-
ные уравнения безмоментной нелинейной теории пологих
оболочек; если исключить работу моментов в уравнениях
(14.92), получим уравнения безмоментной линейной тео-
рии пологих оболочек:
1	д-w	d-w
“7-7" V2V'“4> + kx ——“ + ky —
Et	ду-	dx-
d*w
- 2kxy = 0;
дх dy
<Дф <4®
82rp
(14.93)
В этом случае дифференциальные уравнения пологой
оболочки можно записать в следующем виде [16 и 21]:
1	d*w d-w
Et V * ду- у дх*
д-w	d*w	d*w
ху дх ду	дх-	ду-
' d*w у
дх ду)
— kx -	д* ф	<4<р <7 “ kv ^дхЛ
r4tp + 27 —— у дх ду	<4ф d-w ду- дх-
д-у d-w	d'2 w d-w 4 2 —— • — - дхду дх ду
дх- ду-	
— Рг(х,у) = 0;	о _ д3-  , д2.  дх* "и ду*
•	(14.91)
4- Pz — 0.
Уравнения (14.93), (14.92) и (14.91) отличаются раз-
личной точностью и сложностью. Поэтому практически
необходимо решить, какие уравнения целесообразно по-
ложить в основу расчета заданной оболочки.
Особенно важен вопрос о пределах применимости ли-
нейных теорий. Следует иметь в виду, что пологая обо-
лочка, например положительной гауссовой кривизны, ра-
ботает аналогично плите, находящейся па некотором
фиктивном упругом основании, создаваемом кривизной
оболочки с коэффициентом упругости, равным (для сфе-
рической оболочки):
где R — радиус кривизны. По мере нагружения оболоч-
ки радиус кривизны увеличивается (оболочка выпрям-
ляется), а это приводит к уменьшению коэффициента
упругости фиктивного основания. Это означает, что с уве-
личением прогибов конструктивная схема пологой обо-
И5, ПОЛОГИЕ ОБОЛОЧКИ
109
лочки ухудшается. Поэтому расчет по нелинейной тео-
рии для полот их оболочек необходим для выяснения
действительною коэффициента запаса, который при
расчете по линейной теории получается завышенным.
Влияние нелинейных членов в уравнениях (14.91) на
величину усилий зависит от подъема оболочки: чем
меньше подъем, тем эго влияние значительнее Для обо-
лочек положительной или нулевой кривизны при подъе-
ме	линейная теория может дать погрешность
в отношении прогибов в пределах 5%.
Для заданной конкретной оболочки положительной
или нулевой кривизны вопрос о целесообразности расче-
та по нелинейной теории можно решать следующим об-
разом: подсчитывается вся нагрузка q, действующая на
оболочку (вместе с коэффициентами перегрузки), и по
формулам линейной теории определяется максимальный
прогиб (л. Это значение прогиба подставляется в фор-
мулы нелинейной теории, по которым определяется вели-
чина нагрузки уя, соответствующая прогибу fn. Если
окажется, что уп существенно меньше q (например, на
5%), то данную оболочку необходимо рассчитывать по
нелинейной теории.
Для оболочек отрицательной гауссовой кривизны во-
прос о применимости линейной теории подробно не об-
следован. Но вследствие того что эти оболочки могут
обладать мгновенной изменяемостью, расчет их должен
быть проверен с помощью нелинейной теории.
Область применения моментной теории для пологих
оболочек может быть определена следующим образом:
пологие оболочки отрицательной и нулевой гауссовой
кривизны должны рассчитываться по моментной теории
при всех видах нагрузок. Оболочки положительной кри-
визны, нагруженные распределенными нагрузками, мож-
но рассчитывать по безмоментиой теории при достаточ-
но большом подъеме оболочки (например, при Д/фУ-20).
При этом необходимо учитывать изгибающие моменты
у опорных участков Указанные границы применимости
отдельных теорий намечены ориентировочно, в порядке
первого приближения, и подлежат уточнению.
14.5,3.	Формулы и таблицы для расчета
пологих оболочек,
прямоугольных в плане
Для шарнирно опертой оболочки (см. рис. 14.25) в си-
стеме главных координат (kxv = Q) с граничными усло-
виями, определяемыми формулами:
при х = 0 х -= а; у = 0; у — b , w = 0;
д- w д- ш
а
д2 ®	(’
при х = 0; х — a; Nх — —— = 0; I Nхи dx — 0,
о
ь
д2 ф Р
при у = 0; у = &; N4~ —— = 0; 1 Nxl/ dt/ = 0;
о
усилия и прогибы в точке с координатами х, у определя-
ются по формулам [16]:
V	V / пл V
Nx=— У > — атп F (х, у);
4яия/ tes-ssi \ о /
т=1 п=1
со со
Ny=— J1 Рг а’™ F (х>
VI	VI ^пл3
~	;	(х > У)’	(14.94)
т=1
V	vr/mnv /ил\31
ЛД = D / ,	+ ДТ/ \bmnF(x, ff);
m~l я==1
m—1
f	—-'j 1 bmn F (x, y);
\ a / J
мху = D 0 — Д 2„ 2j bmn F^x>
m=l ri~l
zEj IEj ^mn F (%, y).
n~ 1
F(x, у) = мп—— sin -—™ ; Fx(x5 y) = cos------------cos —-----
c b	a b
(14.95)
но
РАЗДЕЛ 14 ОБОЛОЧКИ
k\ и k2—главные кривизны; m= 1, 3, 5,	п=1, 3, 5, ...
Эти формулы получены путем интегрирования системы
уравнений моментной линейной теории пологих оболочек
(14.92) методом Бубнова—Галеркина в форме, предло-
женной В 3. Власовым [16]. Чем больше кривизна обо-
зочки, тем больше членов ряда необходимо брать в вы-
ражениях (14.94). Один член ряда дает удовлетвори-
тельную точность для очень пологих оболочек
<0,8), для которых по существу линейная теория не-
приемлема. Для оболочек с подъемом ДД>6 необходи-
мо брать 4—5 членов ряда (по каждому направлению).
Если в формулах (14.94) и (14,95) положить D — 0, по-
лучим выражения для усилий пологой безмоментной
оболочки. На основе этих формул В. 3. Власовым со-
ставлены таблицы для определения усилий, моментов
и прогибов пологой сферической оболочки на квадрат-
ном плане с подъемом 0 ' fa!t< 10, нагруженной равно-
мерно распределенной нагрузкой [16]. При больших
подъемах рекомендуется пользоваться таблицами, со-
ставленными В. В. Дикович [33], а также Инструкци-
ей [37].
Усилия по безмоментной теории для оболочки с пря-
моугольным планом, очерченной по поверхности эллип-
соида под действием сплошной и односторонней равно-
мерно распределенной нагрузки, можно определять по
таблицам, вычисленным методом конечных разностей
А. Р. Ржаницыным [83].
В работе В. М. Никиреева и В, Л. Шадурского [68]
приводятся многочисленные формулы для определения
усилий, моментов и перемещений для оболочки положи-
тельной кривизны при шести случаях закрепления обо-
лочки тангенциальными связями. Там же имеется боль-
шое количество формул для расчета многоволновых
оболочек и оболочек отрицательной кривизны.
Л, С. Гараниным составлены таблицы для расчета
прямоугольных в плане пологих оболочек, нагруженных
равномерно распределенной нагрузкой Pz = p =
= const [22].
_ Таблицы_дают значения безразмерных величин Nx, Уч,
NxV, Мх, Му, Мх„, и, v и го, через которые действитель-
ные значения усилий, моментов и перемещений опреде-
ляются по формулам:
АД = /?Д2 АД; Мх = ps° Мх; и = •"—щ— о;
Et
Ng = Ng- M,J =ps- Mv; ~~ v-
ill
Nxu = pRv N xifi Ntx1J — ps“ Mxy-
pRi _
ш
Et
Таблицы составлены для различных значений пара-
метров
- Ь	- R,	- s
а=—. r = „—, s==_i	(14.97)
а Д1 J
М
г ~ —
о2
fs
Рнс, 14.29
При выводе формул (14.98) принято:
а2 «
(14.98)
(14.96)
Безразмерные коэффициенты подсчитаны для узлов
сегки прямоугольного плана оболочки (рис. 14.30) при
двух вариантах граничных условий. В обоих вариантах
кромки х = 0; х — а шарнирно-подвижны; граничные ус-
ловия на кромках:
которые в свою очередь могут быть выражены через гео-
метрические характеристики оболочки, и, b, R2, Ri (при-
ведены на рис. 14.29) и
(ш = Мх	и)х_^-=: 0.
х~~а
з = 0,76 Р Д21 .
(14 97')
Параметры г и s также выражаются через стрелки
подъема контурных диафрагм по формулам:
В первом варианте граничных условий края у-==- ±:Ь/2
тоже шарнирно- по д в и ж ны
(w= Му = Ny = и) h =0.
У = ± —
2
14 5. ПОЛОГИЕ ОБОЛОЧКИ
Ш
Во втором варианте края у= ±bj2 полностью защем-
лены
w — и — 93 — V— О,
где 0а— угол поворота касательной к срединной поверх-
ности оболочки.
При отсутствии табличных данных для расчета поло-
гих оболочек, прямоугольных в плане, можно пользо-
ваться методом сеток (см. раздел 15).
14.5.4.	Круговые цилиндрические оболочки
открытого профиля
Уравнения моментной линейной теории пологих оболо-
чек можно применить к расчету круговых цилиндричес-
ких оболочек открытого профиля (не полших). Поло-
жим в уравнениях (14.92)
ki = 0; й2= —-; х — aR; у ~ рЛ),
R
где а и ₽ — безразмерные координаты (рис. 14.31).
Уравнения примут вид:
I	5® w
— V2 V2 Ф + Р —т = 0;
Et	даг
(14.99)
где рг в отличие от предыдущих параграфов обозначает
нагрузку, нормальную к поверхности оболочки
Усилия и моменты выражаются через функции у, и щ
следующим образом:
_ 1 а®Ф
А 1  	9 ——™—-
R?-	9£2
D / д3 w 5s w \
Я2 \ ба2 9р )
I д" гр
N, = ---- . ——У- ;
R- да?
D / д" w дг w \
М, = ____ ------.
R2 \ др ба2 /
ю_______,_1	а2Ф
12	R2	’	бабр	’
_	Et3	d2w
12(1 +	v)P2 ’	dadfi
(14.100)
Подстановкой w — у® у2 Ф;
б2 Ф
ф = REt ——— получаем
ба2
из уравнений (14.99) одно дифференциальное уравнение
восьмого порядка
1	v«. gt ф pi
WW * + -yr	O’-1»»
где
F
C2= —
12Р2
Рис. 14.31
усилия и моменты выражаются через
ба®
бэФ
Перемещения,
разрешающую функцию Ф следующими формулами:
б3 ф ба Ф
й= —-—
дадр
б3Ф
др +	"’да°д$ J’
щ = у® у® ф-
б«ф
о=—
Et
N = .
R
Et
N -------
2 R
di Ф
да? 95
ба4"’
Л'-
да3дР '
_ _££
12 ~~ R
м
_ D Г б8 б2 ~
= R2 [ да? +V б₽2
D Г б2 б2 ~
4. = ---- ------- 4-v---
Я2 [ ба2
угу2Ф; (14.102)
V2 V2 Ф;
Г) '	О2
=— — (1 — v) —— Vs V® Ф;
R“	бабр
о г б®	а® ;
<? =—7Г 7Т + 2(1“1')-Т^Д8 Vs Ф;
R‘3 I ба3	бабр“ J
. D Г д3	д3 1
R3 др '	’ ба3 65
Здесь Q| и Q2 —' обобщенные поперечные силы (в смыс-
ле Кирхгофа), необходимые при формулировке гранич-
ных статических условий.
Однородное уравнение (14.101) (рг=0) может быть
разложено на четыре независимых уравнения:
дФг 1
V3 Фх + у (1 + i)——== 0;
да
дФ„
—	+ I) ~~ = 0;
да
дФ, f
Vs Фз + vd - г) ^- = 0;
да
t дФ4
=0,
(И. 103)
П2
РАЗДЕЛ 14. ОБОЛОЧКИ
где
Полное решение однородного уравнения
Ф = Ф1 + Ф3 + Фв + Ф4.	(1.4.104)
Оболочка, свободно опертая по контуру. Нагрузка
считается положительной, если она направлена по внеш-
ней нормали (на рис. 14.31 нагрузка pz отрицательна).
Граничные условия:
I
при а — 0 и а = aj = — и — w — N\	= 0
при (3 = 0 и {3 = pi и — w = А?г = М2 = 0.
Нагрузка рг и разрешающая функция представляют-
ся в виде двойных тригонометрических рядов.
Окончательное выражение для разрешающей функции
имеет вид:
Ф(а, Р) = — X
шла nnfJ
”	“	Втп sin -—-sin——
х V V	а1	;
^«а .aej Г//ПЛ\2 /ПП \314	1 — № //ПП\4
Я=1	+ J +	j (14 J o5)
4 Г Г	тпа	nnR
В,пп =——	1 Рг(а, 3) sin— sin— dfida,
«1Р1 J J	®i	Pi
о о
где
t2	n	„ b
C? ~ ------ - а — -- • Я .
12R2	R	R
a) Случай радиальной сосредоточенной нагрузки Р,
приложенной в произвольной точке с безразмерными ко-
ординатами а = | и |3 = т] и направленной по внешней
нормали вниз
4Р
Втп==~ a>1S3
4а:ХцР
Ф = —------- X
/п=1 П=1
тла	плВ
sin — sin—— F(g, л)
И1______Pi_______
(tn? + Ш2)4 4- jim4
Перемещения и усилия в любой точке срединной по-
верхности в соответствии с формулами (14 102):
_	4?-llf> У1 VI rn- (vm~ — ?-Ф2)
а3л£/ -4J	(т2 R Л2п2)4 -j- p.m4 А
772 = 1 Г2-—1
шла	лл(3
X cos-------sin------ F (j, p);
ai	Pi
4XpP уч "y n (F-n-‘ -1- 2 (1 [- v) m2]
(m2 4-2,2n2)4 4-pm4
in—1 n— I
тм	/inf!
X sin ----sin------F (t, i]);
“i	Pi
co co
4?е3цР чп п?п?
Л ’ а( R 2-.' (т~ + ВРРр 4- рщ* Х
т —1 72 — 1
щла	плй
X sin-----sin — F (5, n);
“1 Pt
N = _ 4>-рР VI____________________mi x
‘ a(R 2j 2-i (w2 + ^2»2)4+ gm4
m—1 я-I
. тгл . nnp
X sin —-----sm —— F (g, n);
»i Pi
N =^42cH£.vi	-——-x
13 a( R Zj Ai (m2 + X2»2)4 4- gm4
m— 1 n— 1
тм	„
X cos-------cos —-y~ F (c, tj); (14.10/)
«1 Pi
a2P
w = ~ (w0 —wk);
441 P (i^io /И3д);
Л42 = P (Mlo - Afife);
Ali> = P (ЛА’ -
Здесь дм, ЛФо, Лу0 п Л4 {?--прогиб и моменты от силы
Р==1 в плоском пластинке со сторонами а и Ь:
(14.106)
К'о =
4Х уч
л4
in — 1
(т2 + Х^2)2
72=1
где
mns	?гпт)
F (g, П) = sin ----------- sin —- ;
«1	₽i
т2 -у мХ3«2
I — T3. ai_______12 (1 — v3)	a*_
С2 л4 ~ n4 ' R2t3 '
тла.	nnf>
X sin —— sin ——' F (?, т|);
«1	Pi
14 5 ПОЛОГИЕ ОБОЛОЧКИ
113
.. U V V V * * * *"2 + Vfn'2
AU — ~---- 7 У-----------Т~--- X
“° я3 ^J(m" -г №п~)'2
tn=l п—1
тла плВ
X sin ~—- sin—— F (s, n);
ai	Pi
= ll(1,„v) у	у—
12 п"	4-J	(tn2 4~ №п-)
т~1	п—1
тиа	пя(3
X cos -----cos —— F (с, т|).
ai Pi
тла нлр
X sin------cos----;
Pi
„Т 16Х2р, VX VI тп
л 1 = — —~ кр у; у;—
я-	4», Стп
.V. —
—
т
тп
тла пяй
sin---sin
тла ллр
sin---- sin -д— ;
Ш.и
—— Rp X
и3
(14.108)
Величины !ВЙ, Mik, Мгк, М^ связаны с кривизной
оболочки:
тяа млр
cos --cos--;
4Хц
wk = ——
л4
ра^
w =	— Mj. ри2 (Л11о — М1к);
т— 1 п— 1
шла пя£
ти, sjn ---sin —-—
_______________________Pi ________ Е
(m2 + X2n2)2 [(га2 4- ?Xn2)4 + jim4] F
М2 = РМ (Mi0 - ЛЬ.);
М,2 --- ра2 (Л^'Р — МУУ\,
Стп ~ (п2 + Х'Ь3)4 + ртХ
4fyi
wlfe= -4-
n2
Здесь
m=l n— 1
m4 (m2 + v^2n2) sin---------sin------
________________________«1 Pi
(m3 4- ^2«a) [(tri2 4- ?.3n3)4 +
X
т=1 п~1
тла	плр
sin------sin------
a-t Pi
тп {m" 4- Л3п2)3
Mw --=
16 V V m34-vX2n3	тла	пяВ
— У , 7 ,-------------;-----sin------sin —— ;
п-i 4J 4=1 тп (m2 4- Z.2n2)3 ax	f4
m~ 1 n=[
шла	плВ
mi (Xsn2 4- vmz) sin----sin-------
«1	Pi	rr
(m2 + W3) [(m2 + X2n3)4 + ptra1 lS’
lb, 413u
Л< = —“О — 'OX
n,2
mm	nnp
mbn cos--cos---
«1 Pt
“ ” (тз + X2n2) [(tn2 + Vn2)4 +
m— Jz2=J
f (s, 4)-
б) Случай равномерно распределенной поверхностной
нагрузки pz — const.
Усилия и перемещения:
_ j6B %аР V V Vm“ ~~ ^2д2 х
’ Et Ъ Д пСтп Х
т—\ п=1
тла	ллВ
X cos *---sin----;
«1	Pl
__16Д Rap Y1 V хзла + 2 (1 + у)
л3 Et Д тСтп
т~ I п — t
pn 16X
M 4 = -—(1 -v)
n.J
тла	nrep
-------cos-------
«1 Pi
(tn2 4- W3)2
16n V VI m’3	. тяа nnfi
Wk __  !™ ------------------------------—. Sin ------ sin    »
n {tn~ + X‘M2) Cmn	Pl
лг=1
i6p y y m?’ (m2 v'miim
t> 4J n (tn2 + K2n2)2 Cmn
m—1 zz—i
mna /2 rep
sin---sin-—
»1 Pl
18;t Y m3 (4-я3 4-'VM2)
n*! zb n (tri2 4- Л2»2)2 Cmn
m~l n=l
mna	r?ap
X sin —-— sin----------:
ai	Pi
8-26
114
РАЗДЕЛ 14. ОБОЛОЧКИ
mna	nnfi
X cos —— cos ——
«1 ₽i
В этих формулах индексы т и п — нечетные числа на-
турального ряда (т=1, 3, 5,	я=1, 3, 5, ...).
Для круговых цилиндрических оболочек со свободны-
ми криволинейными краями при отношении толщины
к радиусу 1/А = 0,01 и коэффициенте Пуассона м—О
А. Л. Гольденвейзер [29] составил графики, позволяю-
щие определять усилия Л'ь АД Л'|2 и М2, и таблицы для
определения вертикальных перемещений при равномер-
но распределенной нагрузке.
Если круговые цилиндрические оболочки оперты по
всему контуру (с различными вариантами граничных
условий), то для определения усилий, моментов и пе-
ремещений следует пользоваться таблицами, составлен-
ными В. Д. ЖеМочкиной и М. М. Микшисом [35].
Это уравнение аналогично уравнению плиты на упру-
гом основании; таким образом, сферическая пологая
оболочка работает так же, как плита, лежащая на упру-
гом основании с коэффициентом упругого основания
с = £1/Ж
Рис. 14.32
14.5.5. Дифференциальные уравнения пологих
сферических оболочек
в полярных координатах [16]
Дифференциальные уравнения моментной линейной
теории в полярных координатах г и |3 (рис. 14.32) имеют
вид [2, гл. IX, § 9]:
———- V2V2<T + V2® = 0;
п DR
V" Ф — “V
Изгибающие и крутящие моменты определяются по
формулам:
.<•	' г '	/(14 113)
Ч =- D ( Хр + vXa);	= D (1 - v) уир. ]
Здесь
1 d2tv	1 / 1	1 dw 4
Ха ' да? ’х₽ = Д 'а3 "	+	’
I ! 1	й2®	1 dw 4
Zafi = ТУ ~ 77'‘
(14.109)
А)
В этих уравнениях: <р — функция напряжений; ® —
прогиб срединной поверхности; R — радиус кривизны
оболочки; D — цилиндрическая жесткость:
Это уравнение следует применять только для свобод-
но опертых оболочек. Для оболочек с другими граничны-
ми условиями подстановка (14.110) может привести
к ошибкам, потому в этих случаях следует исходить из
системы (]4 109).
Нормальные и сдвигающие силы определяются по фор-
мулам:
Efl
fl
D = -— ----— ; Га ~ ..
12(1—Я	12(1 — м"-)Д2
Дифференциальный оператор V2 имеет вид
1	д'1 1	г
а др Г где ®	‘
Нагрузка pz и прогиб w считаются положительными,
если они направлены по внутренней нормали (на
рис. 14.32 — сверху вниз).
Подстановкой
Л1 = -Р
гб
б2ф
"др
<1ф
Л'
Vs =
го
д2(р
да2
(14.114)
12
азФ
да дв
I
а3
ш = у2у2Ф и
или через функцию Ф
Eh
R \ а2 ’
Л’-
по формулам
д2
Eh
R
д2
да, Эр
эр;
j
)
Etr~
Ф =-
(14.ПО)
А
системы (14.108) приводится к виду
Д2
77^°
или с учетом первого равенства (14.110)
у-у’-ш Д- w — ——- рг = 0.
at
Eh / I
второе уравнение
д2
ба2'
I
у-2ф;
д
(14.115)

-’г 1)\Ч2Ф-
(14.111)
(14.112)
Осесимметричные задачи [2,
матричных задачах нагрузка зависит
радиальной координаты а, поэтому напряженное состоя-
ние будет также зависеть только от одной переменной в.
Оно будет полностью симметрично относительно оси
гл IX, § 10].
только
В
осесим-
от одно»
вращения.
14.5 ПОЛОГИЕ ОБОЛОЧКИ
115
Уравнения (14.109) превращаются в обг	якновснные
дифференциальные уравнения четвертого порядка:	
/ 42	1	d \!rl"w	1	dw \ (	1_		.			 —	-ф .  	+ \ da,"	a	da /\ da'2	a	da /	' ,	R“ г	Et		(14.116)
Id2	1	d \/4аФ	1	ФФ\ 1	~Ф "•  ® — i [	,	 1 а \ аа2	а	da /\ da2	a da ) Крутящий момент и сдвигающая сила равнь	нулю, все
прочие моменты и усилия определяются по	формулам:
D /d2w	1	dw \ М, =— —- 	-ф v —	 • р \da2	a	da 'о	' D ( 1 dw	d2w \ r2 \ a da г da2) D d fd"~w 1 dw \ Ql = ——. — /	 _ф—.— • r2	da ( da2	a	da j 1	1	йф	1	d2ip д/ 		 ,	• Дф —	. -	. 2	а	da	J	r~	da" ro	+	 (14.117)
Общий интеграл первого из уравнений (14.	116) имеет
ВИД
w (к) = г!,/, 4" /L/2 4“	“4 44/4 4"' ^4 (®)  (14-113)
Здесь fflP(a) —частный интеграл неоднородного урав-
нения; /1, /2, ф, Д — некоторые функции а, представляю-
щие частные интегралы однородного уравнения.
Значения функций Н и их первых производных приве-
дены в табл 14.16 Значения вторых производных вы-
числяются по формулам:
/	=—-	/2	—	— /j ;	/2	= /j —	—.	/	;
а	а
1	' г” _	+ к
0 _ /4 —	/3; /4 —— /3— а 14 .
(14.119)
Значения постоянных А,, А%, Аз и At, определяются из
граничных условий.
Частные случаи. 1. Сферическая оболочка находится
под действием сосредоточенной вертикальной силы Р,
приложенной в верхней точке (полюсе). На опорной па-
раллели, имеющей радиус Ь, оболочка закреплена шар-
Т аб л иц и 14.16
Значения функций /5. /2, /ъ Ц и их первых производных
а				2
0	-4-1,0000	0	0	П
6,1	-hl, 0000	+0,1X125	—0,0001	+0,0590
0,2	-pl,0000	+9,0100	—0,0095	+о 1СЧЮ
0,3	+0,9999	+0,0225	—0,0017	-LOJ500 :
0,1	-[-0,9996	+0,0400	—0,0040	+0,2000
0,5	4-0,9990	+0,0625	—0,0078	4-0,2499
0,6	+0,9980	4-0,0900	--0,0 035	4-0,2998
0,7	4-0,9962	+0,1224	—0,0211	-l-о ,з+б
0,8	-J-0,9936	+0,1599	—0,0320	4-0, 1992
0,9	4-0,9898	+0,2023	—0,0455	-1-0,4485
1,0	4-0,9844	+0,2495	—0,0624	-[41,4974
1,1	4-0,9771	4-0,3017	—0,0831	-+,5458
1,2	+0,9676	-(-0,3587	—0,1078	4-0,5935
1,3	4-0,9551	-J-0, 1201	—о, 1+п	4-0,6403
1,4	+0,9401	+0,4867		+0,6860
1,5	+0,9211	+0,5576	—0,2100	+0,7302
8:
Продолжение табл. 14.16
а	h ‘	а	/	/
1,6	+0,8979	+0,6327	—0,2545	+0,7727
1,7	-90,8700	+ 0,7120	— 0,3018	4-0,8131
1,8	-00,8367	+0,7953	—0,3612	+0,8509
1,9	-[-0,7975	+0,8821	-0, 1238	+0,8857
2,0	-[-0,7517	+0,9723	—0,4931	+0,9170
2,1	+<1,6987	4-1,0654	—0 5690	+0,9442
О ')	-(-0,6377	+ 41610	—0,65’20	+0,9666
о 3	+0,5680	+ 1,2585	—0,7490	+0,9836
2,4	-1-0,4890	+1,3575	—0,8392	+0 9941
2,5	+0,4000	-(-1,4572	—0,9436	+0,9983
2,6	4-0,3001	+ 1,5559	—1,0552	+0+942
2,7	+0,1887	+ 1,6557	—1,1738	+0,9814
2,8	+0,0651	+ 1,7529	— 1,2992	+0,9590
	—0,0714	+ 1,8172	— 1 4314	+0,9256
3,0	—0,2214	4-1,9376	— 1,5698	+0,8804
3J	—0,3855	+2,0223	— 1,7141	+0,8223
3,2	-0 5641	4-2,1016	'—1,8636	+0,7499
3,3	—0,7584	+2, 1723	—2,0177	+0,6621
3,1	—0,9680	++2331	—2,1755	+0,5577
3,5	— 1,1936	4-2,2832	—2,3361	+0,4353
3,6	— 1,4353	+2,3199	—2,4982	+0,2936
3,7	— 1,6933	+2,3413	—2,6608	+о, 1052
3,8	— 1,9674	+2,3454	—°, 8222	—0,0526
3,9	—2,2576	+2,3300	—2,9808	—0,2596
4,0	—2,5634	4-2,2927	—3,1346	—0,4912
4,1	—2,8843	+2,2309	—3,2818	—0,7482
4 +	—3,2195	+2,1422	—3,4200	—1,0318
4,3	—3,5679	+2,0286	—3 5466	— 1,3432
4,1	—3,9283	+ 1,872:1	- 3,6588	— 1,6832
4,5	—4,2991	+ 1,6860	—3,7536	—2,0526
4,6	—4,6784	+ 1,4610	—3,8280	—2,4520
4,7	—5,0639	+ 1,1946	—3,8782	—2,8818
4,8	—5,4531	+0 8837	—3,9006	—3,3422
4,9	—5,8129	+<) 5251	—3,8910	—3,8330
5,0	-6,2301	+0,1160	—3,8454	—4,3542
5,1	—6,6107	—0,3467	—3,7589	—4,9046
5 +	—6,9803	-0,8658	—3,6270	—5,4835
5,3	—7,3344	— 1 4443	—3,4446	—6,0892
5,4	—7,6671	—2,0845	—3,2064	—6,7198
5,5	—7,9736	-2,7890	—2,9070	—7,3729
5,6	—8,2466	—3,5597	—2,5410	— 8,0454
5,7	—8,1791	—4,3986	—2,1024	— 8,7336
5,8	—8,6644	—5,3068	— 1,5856	— 9,4332
5,9	—8,7937	—6,2854	—0,9844	—10,1394
6 0	—8,8583	—7,3347	—0,2931	— 10,8462
Продолжение табл. 14.16
а	!3	0	3	
0,0	+о, 5000	— ее	0	+со
0,1	+0,4955	—1,5409	—0,09293	-г6,34!3
0 2	+0,4826	— 1,1034	—0,1419	—3,1340
0,3	+0,1667	—0,8513	—0,1746	--2,0498
0,1	+0,4480	—0,6765	—0,1970	--1,4974
0,5	+ 0,4275	-0,5449	-0,2121	— 1,1585
0,6	+0,4058	—0,4413	—0,2216	+0,9273
0,7	4-0,3831	—0,3574	—0,2268	+0,7582
	+о, 3608	—0,2883	—0,2286	+0,6286
0,9	+0,3477	—0,2308	—0,2276	+0,5258
1,0	+0,3151	—0J825	—0,2213	+0,4422
1,1	+ 0,2929	—0,1419	—0,2193	+0,3730
1,2	+0,27 +	—0,1076	—0,2129	+0,3149
1,3	+0,2501	—0,07859	—0,2054	+0,2656 <
1,4	+0 2302	—0,05419	—0,1971	+0,2235
1,5	+0,2Ш)	—0,03370	—0,1882	+0,1873
1,6	+о, 1926	—0,01657	—0,1788	+0,1560
1,7	+0,1752	—0,00235	—0,1692	+0,1290
1,8	+0,1588	+0,00936	—0,1594	+0,1056
L9	4-0,1433	+0,01888	—0,1496	+0,085.39
2,0	J 0,1289	+0,02651	—0,1399	+0,06786
(Прпдо	лжение та(	лицы на с	лед. стр.)	
116
РАЗДЕЛ И ОБОПОЧКИ
Прадо iter Нис та/л Л 16
а	О	6	73	4
0 9	+ ,W2b	+0,03712	—0,1210	40,03+8
2,1	+0,08039	+0,0+90	—0,10’2	_L+<)1442
2,5	+0,0613b	+0,04463	—O,08b75	-rti.noan
2,8	-00,04553	у 0,0 1471	—0,07186	—0,1 Ob 32
3,о	+0,03256	4 0,04267	—0,05860	—0,01 6/
3,2	: 0,02202	+0,03941	—0,0 1697	—0,O189>
3,4	+0,01 366	-60,03557	—0,03692	—0,02011
3,6	+0,007162	L.0,03139	—0,02836	—4 02127
3,8	+0,002151	-j-0,02 05	—0,(12117	—0,O2V)',
4,0	—0,001398	4 0,0230-1	—0,01522	—0 02004
4,2	—0,00 3043	+0,01017	—0, Ц039	—0,01855
4,4	—0,005620	+0,015bl	—0,006522	—0 01675
4,6	—0,005608	40,01248	—0,00 3497	—0,01 18’
4,8	—0,007066	4 0,00971	—o+iii+o	—0 01 8!
5,0	—0,007122	-^0,007 ’09	+0,0005218	- 0,01(105
5,2	—О,ПОп893	—0,005 325	40,001735	CT),0O 4 17
5,1	—0,00645b	-j 0,00 3661	-i 0,00’546	—0,00719b
5,6	—0,005892	' 0,002312	+0 0030 3b	- 0 005011
5,8	—0,005257	J-0,0012 13	1-0,003276	—0 001711
6,0	—0,004591	J-0,0004166	-+,00 >32o	—0,003585
нирно Граничные условия при a = az=b/r0, w—Г),
Mi =0
Из условии, относящихся к полюсу оболочки, следует,
что
л ₽Г'! Л
~ и Л4 = 0.
Вследствие отсутствия распределенной поверхностной
нагрузки частный интеграз wp(a) — 0
Отсюда согласно (14 119) прогибы и моменты опре-
деляются по формулам
р,5	1
гг0
w = АО 4" Аг12 4“	 !8,
Гели коэффициент Пуассона v = 0, то
2 1 а ?кс оболочка, защемленная по опорной парал-
те т I
b
Граничные условия при п = «2 =—; ш=0; w'— 0
Прогибы и моменты и в этом случае определяются по
формулам (14 120), постоянные А и А2 при v —0 равны
4^; ha+ + ++;
1
(14 120)
3 Сферическая оболочка под денствием нормальной
нагрузки р, равномерно распределенной по всей поверх-
ности Коэффициент Пуассона х—0 В данном случае
из условии у полюса оболочки Дз = Л4 = 0 Частный ин-
теграл
(14.123)
При защемленном крае
R2 ~ 4 (+ !\ (“) +4 ( /1: (А 4 ( 6 6, —
1
!
5. ПОЛОГИЕ ОБОЛОЧКИ
117
4.	Кольцевая пологая сферическая оболочка под дей-
ствием вертикальной равномерно распределенной на-
грузки р, приложенной по верхнему основанию.
Если по иижнему основанию оболочка имеет шарнир-
ное закрепление, то граничные условия будут:
при а = аг =--- Мр = 0;	= — р sin у;
Го
Ь
при а = аа =---- ®о=0; ЛД = 0.
гв
Здесь у — угол наклона к оси вращения касательной
к меридиану в точке а. Величина w определяется по
формуле (14.118), в которой надо положить шР (а) =0.
Для определения коэффициентов А, А, A, Ai необхо-
димо решить систему уравнений:
L	J
Ы]~
L	J
+ At [ }3 (а1) +	;4 (“а)] = °;
L	J
^1^2 (а1) — А2 Л(а1) А(ч (а1) +
Рг0
4-	(а Л = — — sin у;
4 3V и D *’	(14 125)
А; Л (а) + f2 (аг)+ -л-з h (а) +
А Ад /4 (а2) = 0;
+ Л4 [ Z3 (%)
Моменты определяются по формулам (14.117); для их
определения необходимо вычислить с помощью выраже-
ний (I4.it 19) и (14.120) вторые производные от аэ.
5.	Та же оболочка под действием собственного веса
g кГ1м2.
Прогиб ю определяется по формуле (14.118), в кото-
рой надо положить
Для определения коэффициентов Ait А2, А3, Ад необ-
ходимо решить систему уравнений:
AiJi (аД А-А^з (®i) + -4а^з (A) ~г 1
R2
-т-Д4/4 (а2) + g — 0;
} (14.126)
Z2 (a)	Аз^4(а)~Ь
4~ Л4 /3 ( a2j = 0.
Во всех приведенных случаях нормальные силы Ni
и Л'2 определяются по формулам (14.117).
Функция <р связана с функцией w уравнением
rf3q>	1 dtf	Etrl
da"	a da	Д
Общий интеграл этого уравнения имеет вид
<Р = —— (А 1па + <рет).
л
(14.127)
(14.128)
Здесь Лд— новая постоянная интегрирования, опреде-
ляемая из граничных условий; срш — частный интеграл
неоднородного уравнения
d2qw
da"
da,
(14.129)
которое при известной функции ш легко интегрируется.
14.5.6. Некоторые решения нелинейной теории
пологих оболочек [21]
Ниже приводятся некоторые формулы, полученные
в результате решения общих нелинейных уравнений
(14 91) приближенными методами.
Шарнирно опертая по четырем сторонам пологая па-
нель, прямоугольная в плане и нагруженная равномер-
но распределенной нагрузкой (см. рис. 14.25).
Обозначим безразмерные величины:
f	kra"		
g	.	k	_— . t	x	t »	l-./b2	. a ky=. -r- 1=T;			
. Pz 	 	; 1 E	, _pxb" Px EE ’		(14.130)
Ру " Efi
118
РАЗДЕЛ 14 ОБОЛОЧКИ
Здесь рх— нормальные напряжения на кромках х = 0,
х = а; ру — нормальные напряжения на кромках у = 6,
у~Ь При этих обозначениях зависимость между безраз-
мерными нагрузкой и прогибом выражается формулой.
яь / 1	„ V
п» =----В3 —
р 256 \ X2 /
—	( Рх + Ру} т + kx Рх + ку Ру +
п6 / 1	. \2
+------------- —+ М В- (14 131)
192 (1 — v«) V- /
Частные случаи: 1, Края оболочки свободно смещают-
ся в плане. В уравнении (14.131) надо положить рх~=
=PV =0. Для квадратной в плайе оболочки (Х=1) со
стороной Ь при v=0,3 получим
р4 = 7,5g3 —2,06g2 + (0, № + 22) 1,	(14.132)
где А=Д‘+Д‘.
Для цилиндрической панели шириной Ъ и радиусом R
k — b/Rt, для сферической k = <2b'2IRi.
2. Края панели не смещаются. В этом случае:
Р*у ~8~ щЗГуз	+ VM Х
Для квадратной цилиндрической панели при м=0,3 из
формулы (14.131) получим
р* = 28,9g3 —	+ (0,51г2 ф- 22) g. (14.133)
Края оболочки в плане свободно смещаются и либо
шарнирно оперты, либо защемлены. Зависимость между
нагрузкой и прогибом в центре опорного плана оболоч-
ки выражается формулой [48]
Р —а1 gJ + а2 go 6” + я.з 1б + ®i g (14.134)
Здесь go = }0/i—отношение начального подъема оболоч-
ра*
ки к ее толщине; р
где а —- ширина опорного
плана.
Коэффициенты аь а21 аз и а< приведены в табл 14 17
для квадратом в плане оболочки со стороной а для ше-
сти случаев граничных условий, обозначенных в табли-
це римскими цифрами I—VI. Штриховка на рисунках,
помещенных в таблице, означает, что соответствующий
край защемлен относительно углов поворота; отсутствие
штриховки означает, что край шарнирно оперт.
В таблице приведены коэффициенты для сферической
оболочки и цилиндрической панели. Коэффициенты а?.
и аз, стоящие в числителе (для граничных условий II,
III и V), относятся к цилиндрической оболочке, у ко-
торой края ab и cd криволинейны; значения ttj и а3,
стоящие в знаменателе, относятся к цилиндрической обо-
лочке, у которой края ас и bd криволинейны. Коэффи-
циенты подсчитаны при v = 0,3; при других значениях
коэффициента Пуассона необходимо величину ач умно-
fl,91
жить на отношение ----—; значения ai, а2 я а3 не из-
1 — Vй
меняются
Следует иметь в виду, что в случаях II, Ш и V в таб-
лице указаны величины, относящиеся к прогибу в цент-
ре плана оболочки, а не к максимальному прогибу.
Формула (13 134) может быть использовала для пред-
варительной оценки влияния геометрической нелинейно-
сти на величину ншрузки для заданной конкретной обо-
лочки, иными словами, ее можно использовать при ре-
шении вопроса о выборе теории для расчета заданной
оболочки (см. 14.14). Для этого подсчитывается наи-
большее значение всех нагрузок (р*'), действующих на
оболочку (вместе с коэффициентами перегрузки). Далее
по формуле |л = р*/а4 подсчитывается значение прогиба
|л, определяемое линейной теорией Это значение про-
гиба подставляется в формулу (14.134), по которой вы-
числяется соответствующее значение нагрузки ра и под-
считывается относительная разница между ря и р :
Р» —Р	“j	%	«з 2
----;--- = — (р*Д + — g0 р4 +-------g0.
Р	ОЦ	«4
Если эта разница не велика (например, меньше 5%), то
расчет заданной оболочки можно производить по линей-
ной теории.
14.6. СВОДЫ-ОБОЛОЧКИ
И ПРИЗМАТИЧЕСКИЕ СКЛАДКИ
14.6.1. Основные обозначения
и классификация сводов-оболочек
Своды оболочки и складки (см. 14 1) вдоль криволи-
нейных краев опираются на диафрагмы, а вдоль прямо-
линейных краев окаймляются бортовыми элементами
Расстояние между опорными диафрагмами называется
пролетом оболочки или складки и обозначается Ц. Рас-
стояние между бортовыми элементами называется дли-
ной волны и обозначается 12 Стрела подъема оболочки
(без бортовых элементов) обозначается Д (рис. 14 33).
Для расчета сводов-оболочек и складок приняты сле-
дующие обозначения координатных осей: ось, параллель-
ная образующим поверхности оболочки, называется про-
дольной и обозначается х; горизонтальная и вертикальная
оси в плоскости поперечного сечения оболочки — у и г;
криволинейная ось, направленная вдоль контура попе-
речного сечения оболочки, — s; нормаль к поверхности
оболочки — v
Опорные диафршмы при расчете оболочек и складок
условно рассмазриваюзся абсолютно жесткими в своей
плоскости и абсолютно гибкими из плоскости.
В общем случае напряженное состояние оболочек
и складок определяется десятью силовыми факторами
(рис. 14.34, а), нормальными и сдвигающими силами
11b СВОДЫ ОКОЛО1- КП и ПРИЗМАТИЧЕСКИЕ СКЛАДлИ
119
Коэффициенты О' д,”з сферической и цил шдои»’ес>юи оболочек
Таблица 14 17
Граничные условии					1	Сфщм и с г п обо то пса				Ц f I идеи зге-ия оболочка			
					1	ПД	|	О'		’	а	«4		(У		«*
I	а		l3		ГЯ 51	Р 52	op	Л? в	8 Ы	— В Ь2	г9 92	г22,12
я И 4 й				f	11 ’	14 05	ГЧ 1г г 1	В з]	9 9	-20 4 — 1/ 7	J 9 31 1 <Ь	32,51
III	9		£?		Л 7	7 7	13 (Ъ	j " 13	Ь (Г	5"'	]1 55 - 9 47	5 Щ г4 45	3-40,07
\ \ iv X				1	Д-12 b	) 18	7 7	В в	12 Ь	-20 В	7 27	U3,59
G	Г. V b	а					Но ’1	Ь Г1			10 °!	— 1Ь <Ъ	„щ ЯП 1-5,55	щ-56,99
V1 4 v					21	--^П W		+4 В	(3 м	1.1	13 1	Д 13	+Ь8 89
Рис 14 33
\ Л 6i=S изгибающими и крутящими моментами
Д Л1з //,=/-/ и ио еречнымп силами Qi и Q"
Цнлиндри дскщ оболочки и ск тачки дня расчета ус
и чо приняло подразде тять па следующие три группы
1) иш 1 и ]}и / // Д> 3, б) сринеи длины при 3>
Л Л 1 в) короткие при Л//2<1
В оболочках бо щщои и средней дтины продольные из
ноющие и крутящие моменты (М( и Я) являются вто~
,f- В по 1ылмцих ! завах для ди гинцрнчегких оболочек vch
и 1 } м ментп so счения 1 влом оси л обозначены с нндек
с \ 2 в юн I заве ндекс 2 дз1 произвольной точки поперечно
го конт\оз оп щен 1 п I коньщлi-пи 'т,очки индекс соответствует
cvitp той о 1ки ( дин аюлег сила обозначена через S’ вместо
\	1 днтящи 1 iO3ieiiT — ’ ерез Н вместо Mi
*• ( волы обозлили и скидки средней длины по классифпка
in Ннстр кд in Щ 1 г [3/] отнесены к длинным оболочкам
рпссчм ива -1 IM с числом деформации поперечного контура
120
РАЗДЕЛ 14. ОБОЛОЧКИ
ростепенными и могут быть отброшены. В коротких обо-
лочках влияние поперечных моментов (М) резко падает,
а продольных {№[) возрастает.
В длинных свободно висящих оболочках и складках
деформация контура и поперечные моменты мало влия-
ют на величину и характер распределения продольных
напряжений в поперечном сечении.
В соответствии с классификацией и характером рабо-
ты цилиндрических оболочек и складок вводится ряд
гипотез и допущений, позволяющих упрости гь их расчет.
Длинные своды-оболочки и складки со свободно ви-
сящими продольными краями при симметричном сечении
и нагрузке рассчитываются как балки, а при несиммет-
ричном сечении или нагрузке — как тонкостенные стерж-
ни, но без учета жесткости при чистом кручении [37,
стр. 51—-76]. По длине оболочки нагрузка либо постоян-
на, либо медленно изменяется. Поперечные моменты М,
соответствующие им поперечные силы Q и нормальные
силы поперечного направления N определяются из рав-
новесия полоски единичной ширины, выделенной в про-
лете, в месте наибольшего значения продольного балоч-
ного момента. По длине пролста изменение М и Q при-
ближенно можно принять таким же, как изменение про-
гибов в балке, с той же схемой опор, а изменение N —
как нагрузки.
Напряжения в коротких оболочках невелики, поэтому
при обычных пролетах и нагрузках такие оболочки рас-
считываются упрощенно [37, стр. 91 —102].
нако, как показали экспериментальные и теоретические
исследования, в ряде частных случаев это взаимное
влияние незначительно и для упрощения расчета им мо-
жно пренебречь [37, стр. 47—51].
Средние волны мпоговолновых складок с поперечными
сечениями, приведенными на рис. 14,35, при /1/4^2, на-
груженные равномерно распределенной нагрузкой
Рис. 14.36
(рис. 14 36, о), могут рассчитываться в продольном на-
правлении, как балки корытообразного сечения
(рис. 14.36, s).
Для определения поперечных моментов в средних
волнах по длине складки выделяется полоса шириной
1 м, которая рассчитывается как неразрезная балка
с опорами по ребрам складки (рис. 14.36, а).
14.6.2. Расчет оболочек и складок средней
длины. Допущения и гипотезы
В общем случае оболочки средней длины рекомендует-
ся рассчитывать с учетом взаимного влияния продоль-
ных усилий и поперечных изгибающих моментов Од-
Рис 14.35
Средние волны многоволновых бесфопарных и фонар-
ных с распорками цилиндрических оболочек с симмет-
ричным поперечным сечением, со свободно висящими
продольными краями, при li//2>2, нагруженные равно-
мерно распределенной нагрузкой (рис. 14.37, а), могут
быть приближенно рассчитаны как балки корытообраз-
ного сечения подобно длинным оболочкам (рнс. 14.37,-а).
Одноволновые и многоволновые оболочки с попереч-
ными ребрами высотой не менее '/жй и числом более
трех, нагруженные равномерно распределенной нагруз-
кой, могут в продольном направлении также рассчиты-
ваться как балки корытообразного сечения. За расчет-
ное поперечное сечение, воспринимающее продольные
усилия, принимается сечение между ребрами.
После определения продольных нормальных напряже-
ний o = NJt и сдвигающих усилий 5 поперечные момен-
ты М, поперечные силы Q и нормальные силы попереч-
ного направления N в ребристой оболочке определяют-
ся как в длинных оболочках. При этом в пролете обо-
лочки выделяется поперечная полоса шириной, равной
шагу поперечных ребер [37, стр. 70—76].
Одноволповые складки и оболочки и крайние полу-
волны мпоговолновых складок и оболочек средней дли-
ны. промежуточные волны многово.таовых оболочек при
и оболочки, опертые по контуру независимо от
14.6, СВОДЫ-ОБОЛОЧКИ И ПРИЗМАТИЧЕСКИЕ СКЛАДКИ
Ш
длины, рассчитываются с учетом деформации поперечно-
го контура и взаимного влияния продольных нормальных
сил и поперечных изгибающих моментов. При этом крап-
ине полуволны многоволновых оболочек и складок со
свободно висящими продольными краями можно при-
ближенно рассчитывать как полуволны одноволиовоп
оболочки или складки с симметричным сечением
(рис. 14.36, б и 14.37,6).
Одним из распространенных практических методов
расчета цилиндрических оболочек средней длины произ-
вольного сечения является метод заменяющей складки,
при котором цилиндрическая поверхность заменяется
вписанной складчатой системой. Для оболочек кругового
сечения такая замена не обязательна (см. ниже),
В общем случае для расчета цилиндрических оболочек
и складок средней длины обычно вводятся следующие
гипотезы:
а)	геометрические — деформации сдвига и удлинения
поперечного контура срединной поверхности оболочки
принимаются равными нулю, деформации изгиба конту-
ра поперечного сечения учитываются;
б)	статические —‘ учитываются продольные нормаль-
ные усилия N\, сдвигающие 5, поперечные моменты М,
поперечные усилия Q и нормальные усилия по продоль-
ным сечениям N; при этом усилия N\ и моменты М на-
ходятся из рассмотрения деформаций оболочки, а ос-
тальные из уравнений равновесия. Не учитываются рас-
четом продольные моменты А4L и крутящие Н. Система
учитываемых расчетом усилий на единицу длины сече-
ний оболочки приведена на рис. 14.34,6, Указанное на-
правление усилий принято за положительное.
Складка представляет собой многократно статически
неопределимую систему. Определение усилий по ее реб-
рам может быть выполнено методом сил 1 (за лишние
неизвестные принимаются усилия), смешанным методом2
(за неизвестные принимаются частично усилия и частич-
но перемещения) и методом перемещений (за неизвест-
ные принимаются перемещения). Метод сил в форме
[73, 74] приводит к системе 12-членных уравнений, он
удобен для расчета складок с небольшим числом гра-
ней. Смешанный метод в общем случае приводит к бо-
лее компактной структуре восьмичленных, обыкновенных
дифференциальных уравнений. Этот метод подробно из-
ложен в первом издании справочника [87] и в работах
[14, 15, 16, 19, 37]. Вариант этого метода с весьма прос-
тои структурой выражении коэффициентов уравнений,
позволяющий рассчитывать также складки, имеющие
кривизну в продольном направлении, см. в [62а],
В методе перемещений3 почти вдвое сокращается чис-
ло расчетных уравнений, даже если учесть продольные
и крутящие моменты; он применим для расчета оболочек
средней длины и коротких [37, 42, 59]. Этот метод удо-
бен, если заранее составить выражения коэффициентов
уравнении, особенно для цилиндрических оболочек кру-
гового очертания.
В последнее время с учетом использования ЭВМ были
разработаны: а) в МИЙТе — метод расчета в перемеще-
ниях многопролетных в одном направлении плитпо-ба-
лочных и призматических складчатых систем с шарнир-
ным опиранием на поперечных краях [85]. Решение
строилось на основе интегрирования бигармопическпх
’ Метод сил расчета призматических складок разработан
И, Л. Пастернаком [73 , 74 , 76J
z Смешанный метод расчета призматических складок разра-
ботан В. 3. Власовым (И, 15, 16, 19).
3 Метод перемещений дли цилиндрических оболочек призма-
тических складок и складок, имеющих кривизну в продольном
направлении разработан И Е. Милейковсьим [42, 37, 59, 6Д,
В основу был положен вариационный метод В, 3. Втасоаа [16, 19].
уравнений плоского напряженного состояния и изгиба
пластинки (как элемента основной системы) в одинар-
ных тригонометрических рядах; б) в ЦНИИСКе— метод
расчета складчатых систем [63а], а также пологих пря-
моугольных в плане многопролетных в одном и шарнир-
но опертых в другом направлении оболочек складчато-
го типа, поверхность которых вписывается в поверхность
переноса положительной, пулевой и отрицательной гаус-
совой кривизны [636]. Решение строилось путем приве-
дения исходных уравнений пологих оболочек на основе
некоторой модификации метода Власова — Канторовича
сразу к нормальным системам обыкновенных дифферен-
циальных уравнений первого порядка, составленных от-
носительно четырех групп обобщенных перемещений и
четырех групп обобщенных усилий. Интегрирование
этих уравнений выполнялось методом Рунге — Кутта
в сочетании с методом Годунова [28]. По этому мето-
ду в ЦНИПИАСС на языке АЛГОЛ составлена про-
грамма «РОСТ» (расчет оболочек складчатого типа)
для ЭВМ. Учтена совместная деформация обо-
лочек с промежуточными диафрагмами и диск-
ретное расположение ребер жесткости и переломов
поверхности в одном из направлений. При разработке
метода и программы «РОСТ» не вводилось никаких
дополнительных гипотез, помимо основных гипотез тон-
ких оболочек Кирхгофа — Ляна. В результате оказыва-
ется возможным избежать разделения складчатых систем
на длинные, средние и короткие.
Расчет круговых цилиндрических оболочек средней
длины методом перемещений (вариационный метод)
[59, 60]. При расчете цилиндрических оболочек кругового
сечения с радиусом дуги К = const проще не использо-
вать метод заменяющей складки, а сохранить исходную
поверхность. Продольные перемещения и (х, з), танген-
циальные перемещения (по касательной к контуру)
v (х, s) и перемещения по нормали w (х, s) любой точки
срединной поверхности оболочки (см. рис, 14.33) пред-
ставляются в виде конечных рядов:
a(x,s) = J]6;(x)^(s);
I
фЗ) = Р'г(х)Ш	(м135)
I
aa(x,s) -= v; Vt- (x)ft (s).
i
Каждый член ряда образован из произведения двух
функций, одна из которых зависит от продольной коор-
динаты х, а вторая — от поперечной (тангенциальной)
координаты 5.
Функции ТА (х) и Vi(x), зависящие только от коорди-
наты х, это неизвестные функции обобщенных продоль-
ных и поперечных перемещений, подлежащие опреде-
лению.
На основании принятых геометрических гипотез эти
функции связаны между собой зависимостью (которой
подчиняются угол поворота и прогиб оси обычной балки)
U. (х) = — V't(x).	(14.136)
Поэтому для расчета достаточно определить или функ-
ции Ut (x) или V,(x). Функции g> (s); г), (s) и K(s) назы-
ваются элементарными пли единичными (а также коор-
динатными). Они определяют соответственно изменение
продольных и поперечных (по касательной и по нормали)
перемещений точек контура сечения оболочки при Vi — 1
и характеризуют единичные деформированные состояния
расчетной модели. Вид этих функций устанавливается
122
РАЗДЕЛ 14. ОБОЛОЧКИ
предварительно (см. ниже). Благодаря принятым геомет-
рическим гипотезам функции (s); р, (s) и ДД’) взаимо-
связаны равенствами [69, стр. 17, 18]:
ё- (з) = Д- (з); Д (•’) =- Е, fi (з);
Д=1/Д;	(14.137)
поэтому достаточно установить вид функций |i(s).
Единичные функции перемещеппп должны быть непре-
рывными и удовлетворять условиям сопряжения оболоч-
ки с бортовыми балками.
Рис. 14.38
Рассматривая оболочки с симметричным поперечным
сечением, следует разделять единичные функции на сим-
метричные и обратно симметричные.
Симметричные функции ^(з) определяются выраже-
ниями (рис. 14.38, а):
si (Д = а; Д (s) = Д з1п[Д 0,
пл
где (0 ' 0 с, 20J; п = 21 — 3;	; (14.138)
20!
1 = 2,3,4,...;
29j — центральный угол дуги поперечного сечения;
О — переменный угол, отсчитываемый вправо oi радиу-
са-вектора в точке 7 (рис. 14.38, а).
Обратно симметричные функции £г(з) определяются
выражениями (рис. 14.38,6):
1о($) = У; ё1(«) = -фгш; Д (s) = Дз1п[Д О,
А
где я = 21 — 2; I = 2,3,4,...
Функции i|o и gi характеризуют распределение продоль-
ных перемещений в сечении оболочки по закону плоских
сечений и секториальных площадей (или пропорциональ-
но им) как для балки и тонкостенного стержня; осталь-
ные функции Д определяют депланацию поперечных се-
чений, связанную с деформацией их контура [60],
В силу геометрических гипотез вид функций ДД) Для
контура поперечного сечения плиты оболочки определяет
их вид также в сечениях бортовых балок (см. рис. 14.38)
[60, стр. 43] .
Аф
Напряжения о = поперечные моменты М на ос-
новании закона Гука и принятых гипотез выражаются
через перемещения по формулам:
о = еYp’i	« Ф- (Д;
i	I
А4 = —21ф(х) АДД); (1 = 0,1,...). (14.140)
1>1
Единичные функции ЖДз) характеризуют изменение
поперечных моментов вдоль контура поперечного сече-
ния и определяются по формуле [59, стр. 19]
A4f = El [ (s) + k2 (s)],	(14.141)
где /— момент инерции единицы длины продольного
сечения оболочки. Если оболочка имеет более трех равно-
мерно расставленных поперечных ребер, то момент инер-
ции 1 вычисляется по формуле l = lvllv, где 7Р—• момент
инерции продольного таврового сечения, образованного
из сечения ребра и продольного сечения плиты шириной,
равной шагу поперечных ребер Д.
Для определения неизвестных функций lh(x) или
1Л(х) по длине оболочки выделяется элементарная попе-
речная полоска шириной dx (см. рис. 14.33) и составля-
ются уравнения работы всех сил, действующих на эту
полоску на возможных ее перемещениях, за которые при-
нимаются функции Д(з) и (а). После ряда преобразо-
ваний получается система дифференциальных уравнений
равновесия элементарной полоски, имеющая вид [59,
стр. 21 и 47]:
X Еап (х) Д J Es.. (х) - q. (х) = 0;
i	£
(у, 1 = 0,1,2,...).	(14.142)
Коэффициенты уравнений и свободные члены д} вы-
числяются соответствующим взаимным интегрированием
эпюр единичных функций и функции нагрузки по дли-
не b контура поперечного сечения оболочки:
b	' ?
ail = j Sj (s) 11 («) t ds; an = ац;
6
1 CMj (s) AMs) .
- ds; sn^su;
u
b
q. = j f® (s) +дг Г (s)] ds,
о
где ps и Д — интенсивности вертикальных и
тальных нагрузок; f® и /J' (s) — проекции ординат еди-
ничных функций поперечных перемещений на верти-
кальное и горизонтальнее направления.
(14 143а)
(14.1436)
.14 6 СВОДЫ-ОБОЛОЧКИ И ПРИЗМАТИЧЕСКИЕ СКЛАДКИ
123
Таблица 14.18
Коэффициенты разложения нагрузки в ряд по фундаментальным функциям
Вид нагрузки	Род закрепления		л	А,	А,	
	край л	-^0	j	крах				
	Оперт	| Оперт	1,2732	°	0,424-1	0
Постоянная р — 1	Защемлен	| Защемлен	0,8161	°	0,3639	°
		| Свободен	0,57-18	0,4119	0,2542	0,1819
	>->	| Оперт	1,2168	—0,1169	0,1729	—9,06198
		! &	0,6366	—11,3183	6,2122	—0,1591
По закону треуголь-	»	| Защемлен		0,4082	-0,1902	0,1818	—0,1215
ника р=> —~	»	| Свободен	0,4176	0,09245	0,03239	0,01654
		j Оперт	0,5377	-0,3436	0,2499	—0,1958
В силу ортогональности тригонометрических функций
s3i = 0 при /¥=г.
Решение уравнений равновесия (14.142) для оболочек
средней длины выполняется с помощью разложения пе-
ремещений Vi(x) и свободных членов q,(x) в ряд по
фундаментальным функциям свободных колебаний
балки:
Ь (х}" S {х}’ (« =1 -2 > • - 
т
wW = S„. z ы
4Jm \ЛЬ
т
(14.144)
Функция Zm удовлетворяет дифференциальному урав-
нению:
6)	= Zm (х);	.	(14.145)
Общие выражения функций Zm(x) и параметров цт
для различных схем опирания однопролетных оболочек
на криволинейных краях и значения этих функций и их
производных для первых четырех членов ряда приведены
в работах [19, стр. 81—86 и 37, стр, 280], а для последу-
ющих четырех членов в [61].
Если эпюра поперечной нагрузки по длине оболочки
постоянна [р (х) = const] или имеет вид треугольника
[р(х) =рх/1}] с максимальной ординатой р, то коэффи-
циенты определяются выражением
•фт = ф'Лт.	(14.146)
Коэффициенты Ат для первых четырех членов разложе-
ния нагрузки приведены в табл. 14.18. Если нагрузка ме-
няется по трапеции, то коэффициенты .43-т получаются
линейной комбинацией для первых двух схем; q, опреде-
ляется по формуле (14.1436).
При расчете на сосредоточенную вертикальную нагруз-
ку Р® (й) , приближенную к бортовой балке или к попе-
речным ребрам в точке k сечения х~а:
ч1 (a) Zm (а)
qi<n =--------—-;
р^а}=Р*(а)^,	(14.147)
где коэффициенты Вт определяются из табл. 14.19.
Таблица 14.19
Схема граничных условий на торцах		В,	B.		sm>4
tl 		 X	0,500Л	0,500 lt	0,500 lx	0,500 I,	0,500 lt
	1,0369 h	0,9984 h	l,	A	h
"TL	0,4996 1.	0,4999 I,	0,4999 Д	0,5002 1,	0,5 A
	5,8556 h	0,9640 1,	1,0051 ?!	0,9999 4	I,
124
РАЗДЕЛ 14. ОБОЛОЧКИ
Таблица 14.20
Матрица алгебраических уравнений при симметричной вертикальной нагрузке
№ уравнения	^0		уО	у0 3	Свободные члены
0	Л 4 °00 Лт	а01 Кп	а02	°03 '^т	0
1	е	Д! С			
2	О	О	°22	+ «2 2	°23	К
3	е			°33	+ s33	£ 98
Дифференциальные уравнения (14.142) после подста-
новки (14.144) преобразуются в алгебраические; при этом
для каждого из первых членов ряда (при т=1, 2, 3, 4)
эти уравнения можно разделить на совместную систему,
состоящую из четырех уравнений, определяющих пара-
метры U^m и V°im при i=0, I, 2, 3 и независимые урав-
нения:
ац + s7y) /ги ~	Чjm’,
(i = / > 3).
(14.148)
Такая возможность обусловливается резким увеличе-
нием главных членов уравнений, содержащих коэффи-
циенты зц. Независимые уравнения (14.148) уточняют
значения поперечных моментов; при этом для практиче-
ского расчета цилиндрических сводов-оболочек, загру-
женных распределенной нагрузкой, достаточно ограни-
читься учетом одного из уравнений (14.148) при /=4.
Для оболочки с симметричным сечением совместные
уравнения в форме матрицы (по Власову) для расчета
на симметричную нагрузку приведены в табл. 14.20 и в
табл. 14.21 для расчета на обратно симметричную на-
грузку (индекс т при неизвестных параметрах опущен).
Не указанные в этих таблицах побочные коэффициен-
ты, относящиеся к нижней левой половине матрицы,
отмечены точками и определяются из условия симметрии
на основании равенств, приведенных в формулах
(14.143). Для получения какого-либо уравнения нужно
коэффициенты одной строки умножить на неизвестные,
выписанные над ними в верхней строке матрицы, приба-
вить свободный член этой строки и результат прирав-
нять нулю.
Для оболочек с соотношением /1г >1,5 последнее
уравнение табл. 14.21 уместно решать независимо от
остальных, подобно уравнениям (14.148).
Таблица 14.21
Матрица алгебраических уравнений при обратно симметричной вертикальной нагрузке
№ уравнения		vo	V2	уО	Свободные члены
0	fl00	й0! Кп	а02	й03	0
1	®		*12^	а13	1 Чз*
2	О		й22	4" s22	С я	,-^т Е 42
3	О			°33 Кп + S33	Е qs
146 СВОДЫ-иЬОЛОЧКИ И ПРИЗМАТИЧЕСКИЕ СКЛАДКИ
125
1 аблпца 14 22
Выражения коэффициентов а^. " сА Лд =	ЛЕ
при симметричной нагрузке
ii	A A	4
00	I	1
01	“1	1 ~ V6 Cj + vec0
02	1 Ka	fij sin 0! —VCC1				 —AV’oPiSin Oj
03	_L0o 3 «02	3fl02
и	a-2	1	->	9 9 •y v6 ci -T ^6 7
12	cos Oj (Pf-i)Mi	„ Pj sin 0j -7‘1	3	— — + Cq Pl sin 0J
13	cos 9j (₽3~1) Ml	Зй j q
22	72	9 Pf sin2 0] v6 7 '	3 	 + + + coPisin 91
23	0	3a22
33	72	9(7 22
jj>33 П р и в лаб. 0 < feo Fo + = &2==1-	7a м e ч а н и e Выраж i. 14 22—14 28, 6 < 0jj « = 0j — = 1)R-, L^2R0r = tROi, Fx = hdi, Fi V6 = —- ; Гб AF0	Mt = v~; V1= T" A	Fa s 4),Scos 20!—0,75-	(2/ - 3)2 4 5НИЯ	величин,	ВХОДЯЩИХ 0;	17 = A; c, = d.JR; c0 -=: d0/R; Fa = F\ + А/7! Д Af0; 37, стр, 69] sin 0t ax cos 9j	; U1 n 20i	sin 20] 0i ;	Оз-1-0Д ei .
Таблица ТА23
Выражения коэффициентов а . — ( tP. 4- A. F„\ R~
it \ н 0 1 jt 6}
при обратно симметричной нагрузке
ji	4	a'd
00	1 — «3	sin2 0j
01	— Я1	v6 sin 0l(2014-c1 sin 0,.) + A^OiA'A-TVo bin 0i) sin 01
02	P, sin tp f pj — I) ot	p, sin2 t), 'Wl 	p-	 + ^o6Ofl-3 ЗШ2 0!
03	P4 sin 0, ( Pl-l)«i	2ffg,
11	-E02 3 1	Ve ^02 + C[0 , sinS; + । 1	2 • ° <л \ i _L 	 c S1R- Q	I з	1	4 + vo ( °i + cosin °1)2 + 7 01
12	i Ps	vg —- p.2 sin 01(301+2c1 sin 0i)+ 6 + v0c0p2 sin O^Qx -r c0 sin 0J
13	— Д 2 12	2n12
22	1 2	pf sin2 0| + 7	;	+ + co Й311,2 01»
23	0	2a22
33	1 2	4й22
ii' 33	1 2	(j  1)" a-22
126
РАЗДЕЛ 1.4. ОБОЛОЧКИ
Коэффициенты s --= з*^. —
Симметричная нагрузка		Об р ат н о с и м ме т р и ч н а 51 нагрузка
//	4	А
22	рад ад2	рад ад2
33	ад - А	рад ад2
//.''33	рад-ад п — 2/ — 3	₽ад ад2; п = 2ф — 1)
Таблиц а 14 2”>
Свободные
" °!
П г» / л
члены q. q. Rp | cos (А — cos-------- 1 и q. =
соответственно при вертикальной равномерно
распределенной нагрузке р и полосовой вдоль бортовых балок р}
Симметричная нагрузка		Обратно симметричная нагрузка	
- 1	0	0	0	(J
1 1	ф	ф	q	pi
О,
1
— 1
cos 03
sin О
cos 0.
о

В табл. 14.22—14.24 приведены выражения коэффи-
циентов а„ и Sjj и входящих в них множителей: и^',
ajt и s°.. для одной половины поперечного сечения.
Выражения некоторых общих величин в табл. 14.22—
14.28 приведены в примечании к табл 14.22.
Бортовые балки рассматриваются состоящими из пря-
моугольной стенки площадью F1 = i'1d1 и утолщений
(стрингеров) по концам с площадью сечений A.F0 и Aj/~3
(рис. 14.39).
В табл. 14.25 приведены выражения свободных членов
для двух случаев вертикальной нагрузки (равномерно
распределенной по сечению оболочки р и полосовой
вдоль бортовых балок ps) также для половины шик реч-
ного сечения.
i
Р1

* Второе слагаемое в
симметричной нагрузки
скобке отлично
нуля для обратно
В табл 14.26—14.28 приведены единичные функции
перемещений, моментов и углов поворота бортовой балки
при симметричной и обратно симметричной по сечению
нагрузках. Двойными индексами помечены значения этих
функций в нижней и верхней точках {0 и 1) сечения
бортовой балки; первый индекс здесь и в последующих
фюрмулах обозначает номер точки поперечного сечения,
второй — номер единичного состояния.
После решения уравнений табл. 14.20 и 14.21, уравне-
ний (14.148) и определения параметров U® и V°( переме-
щения и усилия для каждого члена ряда вычисляются по
следующим формулам (индекс т при неизвестных пара-
метрах. при функции Z и ее производных опущен):
а) нормальные, вертикальные п горизонтальные про-
гибы точки k
Wk (Д = уО fki z w.
i
= fuz A
i
A(*) = JA? fki'ZAx)-,
i
б) изгибающие моменты в точке k
Mk (x) = - А б? Mk. Z (x)-
(14.149)
(14.150)
в) продольные нормальные напряжения в ючке я от
симметричной пш'рузки
14 6. СВОДЫ-ОБОЛОЧКИ И ПРИЗМАТИЧЕСКИЕ СКЛАДКИ
127
Таблица 14 26
Ординаты эпюр единичных функций перемещений при симметричной нагрузке
i	51 («)	’ll (^)	fi (s)	fl (s)	f't (s)
0	£0 = Я Bio = Soo = R	0	0	0	0
1	Si	R (cos а — — COS 0j) loi = di	Л1 =~—	^0 == Пп	i	fi =- cos a; /ni = fn = 0	/f = 1; 1	fl = fl=f^o
2	12 = 7? sin 5os = Pidi sin	T)«= Pl cos pjO; %2= Ъ = Pi sinO,	f.> = ~“ Pi sin PA /12 = Pl cos 0iJ /ог = Pi [cos 4~ +aMp?-!)]	/? — Pj (P, sin Pjflx X cos a+cos Ptfl sin a); /02 = /12 — Pl sin ei	ff, =Pi (cos pj fl cos a— — Pi sin p!0 sin a); /12 = f12> /02 = /02
3	?3 = R sin f>30; los = ~~ Рз<4 sin Oi	Пз — Рз cos p30; ilos = ilis== PasinOj	/3 Рзsin P:A /гз = Рз cos fl,; /03 == Pa [cos flj 4~	/3 =— Рз (Рз sin PiA< Xcos a -(-cos p30 sin a); /оз = /?3=- Рз8Ш0!	/3 = P3(cos Рз0 cos a-— — Рз sin p30 sin a); /Тз = /igi /оз = /оз
гХЗ	11 = R sin P„ 0; lol =—	sin 0j	’ll = p„ cospf! fl; sin Sj	/1=-рДпрд- /и = Pc cos 0Х; /oi = P« [cos 0i + + di *2 (P« —• 0]	ft	P« (P«sin X cos a + + cos fin в sin a); A = A=-P„sinei	/ir=PH(cos PA cos a“ —- pn sin P„0 sin a); /11 = fu 1 f‘ot ~ fot
Таблица 14.27
Ординаты единичных функций перемещений при обратно симметричной нагрузке
i	h (л	П1 (s)	ft C)	fl. А	fits)
0	|„ =— R sin a; ^00	510 ~ R .sin	40 — cos a; ^loo ” П10 ~ 0	f(! — sin a; /co — /10 = 1	/оо=/?1 = /о = 0	f()0 /01 = /0 = *
1	It =— Ra; In =- M; s«i =— (-Rfli + R- sin 04	41 = i; П01 = ’In = sin ei	/1 = 0 fn = cos flt; f01 — cos Sj — fe.dj	=— sin a; /01 = fn =- sin ei	/[ = cos a; ?n /ц; /51 = /01
2	§2 — sifl IM; g02 —	'^^2 SIU	Tfe = p2 cos p30; 002 = 1112 = = p2 sin 0! (.Пр	/2 =— fl sin Д2®; /12 = Рг cos (A /02 Рг [cos A 4" + A k2 (pfl 1)] одолжение таблицы на след	fa2 — З2 sin p,e X Xcos a-j-cos PA sin a); /Й2 = /?2 =- Plsin 6I . стр.)	f.=P?(cos PA cos a — — p2 sin pa0 sin a); fni^-fvR /oj=/o2
128
РАЗДЕЛ 14 ОБОЛОЧКИ
Продолжение таб г 14 27
i	(*)	41 (s)	/- (s)	/Г (S)	/f (s)
3	h = R. sin p40; ёоз =— Mi sin °1	T]3 = |34 cos |340; flos = Pis = = p4 sin 0J	/3 =— Й sin ftA /13 — Pl C0S ®1’ fol ~ Pl [C0S ^1 + +	( p4 — I У]	/з=—Р-Ж sinp40x Xcos a-f-cos p40 sin st); /оз /”з == P4sin 6]	/J=₽4(cos Рч0 COS a~~ — p4 sin p40 sin a); /13 = /13’ /оз = /03
г>3	ы = R sin p„6; U =~“ P« sin °i	Д = cos РД), %=П11=Р« sin °t	/i=-P«sinPn°; /n = (3„ cos 01; foi = Pn [C0S + + dl^(₽2-l )]	sin ₽„0X Xcos a-|-cos p„9 sin a);	/[=P„(cos p„0 cos a — —P„ sin	sin a); fu~fli’ fui ~ ft)i
Таблица 14.28
0	2
Ординаты эпюр единичных моментов Мг “ M^Elk^ в плите оболочки и угла поворота Ч ц бортовой балки
M,, <[];	Сим м етр ич п а я нагрузи а	।	Обратно симметричная нагрузка
	Pl (Pi — 1) sm pj 0	1) sin p20
M3	Рз (Рз“ sin Рз°	p4(pi — l)sin|340
M'l	p2(^l)Sin₽„0	
41'1		a2
Ф12	^2 Pl (Pl 1)	— k2 p2 (Pg — 1]
‘Pis	— ^2 Ps (Ps — 1 )	-А2Р4(РЖ 1)
*4	Ж’РДРл-П;	-*2 РДРл-‘}
n — 2i — 3		П = 2(i- 1)
(х) = - Е [u° |w + S V° tki) z” (х)- (14.151а)
1>U
от обратно симметричной нагрузки
(%) = -£ 2 V^lkiz" (х);	(14.1516)
i
г)	для вычисления сдвигающих усилий дугу окружно-
сти произвольного поперечного сечения можно заменить
вписанным (не обязательно равносторонним) ломаным
контуром из восьми — двенадцати участков (рис. 14 40).
Сдвигающие усилия в вершине k ломаного контура
о, , Д о. Z'"{x)
S. (х) = S, j + t, d.	---LL, (14.152)
k \ / A-l -г ti к 2	Z"(%i)	‘	’
где th и dk -—толщина и длина й-го участка вписанного
ломаного контура, предшествующего А-ft вершине
(рис. 14.40); значение Z"(x-i) принимается для сечения,
в котором вычислялись напряжения сь (xQ;
д)	суммарные сдвигающие усилия Т\(х) по А-му
участку вписанного контура
h dk	Zm(x)
Tk (x) = Sw (x) + — (2ci_1 -b a J	(14.153)
Gh — напряжения в k-& вершине;
14 о СВОДЫ-ОБОЛОЧКИ И ПРИЗМАТИЧЕСКИЕ СКЛАДКИ
129
е)	нормальные силы по продольным сечениям (вне
точки 1 поперечного сечения)
таблиц [37, стр. 279—283], Для шарнирно опертой обо-
лочки (табл. 14.19, схема 1) коэффициент равен:
Nk [S fe2 & Vх? Mk. Z± (х) + Rpv\, (14.154)
g.==	=J;23.
О
(14.1566)
где pv — интенсивность нормальной нагрузки; в точке 1
Л’г « Ipi—Ti (0) ДДЛДвш&п (14.155)
где щ и Т[ — соответственно полосовая распределенная
нагрузка и суммарное сдвигающее усилие в опорном се-
чении, действующее в плоскости бортовой балки. Форму-
лы (14,154) и (14.155) относятся к случаю расчета обо-
лочки на равномерно распределенную нагрузку.
При расчете оболочки на нагрузку, равномерно рас-
пределенную по длине, достаточно в разложениях
(14.144) ограничиться одним первым членом ряда, решая
уравнения табл 14.20 и 14.21 и уравнения (14.148) при
гп-~\, Значения о', Мише достаточной степенью точ-
ности определяются этим расчетом Влияние последую-
щих членов ряда на значения S и Т может быть учтено
умножением их на коэффициент
В формуле (14.155) значения Д и Д относятся к пер-
вому члену разложений (14.144).
При расчете сводов-оболочек, нагруженных сосредо-
точенными по ребрам или не-
равномерно распределенными по
длине нагрузками, напряжения о
(и сдвигающие усилия S) следует
определять с точностью пяти —
семи первых членов ряда в раз-
ложениях (14.144). Если оболочка
и нагрузка по длине имеют ось
симметрии, то расчет следует про-
изводить с точностью трех-четырех
членов ряда (т = 1, 3, 5, 7). При
отсутствии поперечных ребер для
определения поперечных моментов
Л4 можно ограничиться одним, а
при наличии ребер первыми дву-
мя-тремя (m—l, 2, 3,) членами
ряда [37, стр. 251], производя
расчет по табл. 14.20 и 14.21 и
уравнениям (14,148), Для опреде-
ления напряжений о (и усилий
S), соответствующих последую-
щим членам ряда, расчет можно
производить как для безмоменг-
ной оболочки по табл. 14,20 и
14.21, отбрасывая в них коэффи-
циенты s„.
Упрощенный расчет сводов-обо-
лочек на сосредоточенные попереч-
ные и продольные силы, включая
предварительное напряжение, и
указания о расчете неразрезных
сводов-оболочек изложены в рабо-
тах [87], [37] и [42]. Методика
учета кручения бортовых балок
изложена в работе [60]; обобще-
ние метода на оболочки поло-
жительной кривизны см. [626].
Пример 14.1. Рассчитать сборную оболочку конструк-
ции Ленинградского Промстройпроекта (рис. 14.39, а).
Бортовые балки двутаврового сечения (рис. 14,39, б)
имеют небольшую кривизну по верхнему поясу (для сто-
ка воды). Стенка балок имеет отверстия. При расчете
предполагается, что балки имеют постоянное сечение
с приведенной высотой d'o и что стейка воспринимает
только сдвигающие усилия. Площади сечения нижнего
и верхнего поясов бортовой балки обозначены соответст-
венно через АГ0 и Аг,- Оболочка имеет поперечные реб-
ра, расположенные через 3 м (рис. 14.39, е). Схема по-
перечного сечения оболочки приведена на рис. 14.39, б.
А-1 lzi (И
(14.156а)
равный отношению площади эпюры равномерно распре-
деленной нагрузки к площади эпюры нагрузки в виде
первого члена ряда.
Значения и Zl при х—0_и х = 1 принимаются из
* Приведенная высота может быть определена по жесткости
приравниванием максимальный прогибов заданной' балки пере-
менного сечения и эквивалентной балки постоянного приведен-
ного сечения при нагружении их одинаковой равномерно распре-
деленной нагрузкой Прогиб балки переменного сечения может
быть определен, например, графо-аналитически (87, стр 2341
или согласно работе Г. И Бердичевского «Расчет деформаций
предварительно напряженных железобетонных двускатных балок
нерешенной высоты» («Бетон и железобетон», 1961, Дь &),
130
РАЗДЕЛ 14, ОБОЛОЧКИ
Основные геометрические данные (расчет производит-
ся в К Г И СМ) .
(),’= 28“ 29'; Ofад = 0,497128;
1	а
R- 1258,42 см- k„--------- 0,79465-ЮЖ
К
R 2400 см; 12 = 1200 см-, cla = 96 см-
1 — 4 см; i\Fu — 900 см"; ЛЕф — 390;
7\ =- 0; Eg 5F0 + AFj + f j = 1290 см";
Р„ = +1ф = 2502,38 см-;
F,	АРа
тс =-- — = 0; V,. = —= 0,69764;
Рб	/Д
сй	= 7,62861 • 10~2;
R
АР1
тг--------- = 0,302325.
Рб
Погонный момент инерции продольного сечения
(рис, НЗЭ. ь’)
Модуль упругости бетона £ = 3,1-10’ кГ/см2.
Расчет на симметричную нагрузку
Схема нагрузки показана на рис. 14.39, б и состоит из
равномерно распределенной по поверхности нагрузки
р = 393 кГ/м" и полосовой Р: = 323 кГ/м, действующей
вдоль бортовых балок.
Система расчетных уравнений приведена в табл. 14.20.
Решение выполняется с точностью до первого члена ряда
Коэффициенты и свободные члены этих уравне-
ний вычисляются по табл. 14,22—14.25,
Вспомогательные величины, входящие в эти коэффи-
циенты, вычисляя на основании выражений, приведен-
ных в примечании к табл, 14,23:
sin (ф = 0,47690; cos 9t 0,87896;
sin 20, = 0,83835; cos 2Оф = 0,54513;
„ sinO,
O[ = cos (ф— —-— = — 0,080350;
sin 2(3,
a„ = 1 + 0,5 cos 20, — 3/4 ——— = 0,007775;
O1
p, = — = 3,15974; p3 = 38ц = 9,47922;
21ф
P=- 5Pj = 15,7987; ff( = 9,98398;
P/= 89,8556; (3/= 249,598.
Значения угла 0, sin |3n0, a, sin a и cos a в точках се-
чения 1, 2, 3, 4, 5 (рис. 14.40.6) приведены в табл. 14.29
Оболочка однопролетная, на поперечных краях свободно
оперта (;абл 14,19, схема 1), при этом фундаменталь-
ные функции совпадают с тригонометрическими, т. е.
х
— sin Pm j >
где 11т=П1Л при Щ = 1, р,,|=Я,
?•! --= о, 130899- Ю”2;
4
Т а б л н д а 14 29
'1 ршономст ричрские величины	A’ V>4+!				
	1 i 2	]	,3			•1	| 5	
е	0	1 8 U 1	l/ th	'6 «!	
а=0,—0	fl,	7« (8	l>,	'/ - 8i	0
sin a	o, 47(590	0,		0,16^)5	0
cos a	O,S7S96	0,01390	0,9 IW	О/Ж29	1
sin 9	0	0,0588	‘/2	0,866	1
sin	0	0,707	1	0	—1.
sin	0	0,9659	7-	0,066	I
Ц 0, 171348- 10
4=0,29360-10~11.
По табл 14 22 вычисляем;
= (2502,38 -Ф
+ 1290) 1258,42а-0,29360-10~11 = 17,6327-10
a10 X* = at Fo -фх'о + Е6) R~ 4 =
=(—0,08035-2502,38 + 0,697674-7,62861 -1О”"2 -1290) X
X1258,42s-0,2936-10~11 =•— 0,615598-10~3;
aQ2 = 6,925968-10”3; а03 4 = 1,025965-10^4
an 4 = 0,107449- 1(Г~3; л,, 4 =— 0,761366-10"’3;
=— 0,134506-10~3; а„ X3 = 5,872714-10 ”3;
% 4^ 0J65882-10~"3; адэ л3 = 6,315066-Ж”3;
с444 = 7,199768-10^3.
По табл. 14 24 вычисляем:
/«1 .3 й4 ( Я2 ,>2_ 144,67-0,497128	,
Х(0,79465-10~3)3.9,9839573 (9,983957 — I)2 =
= 0,145504-IO"-’3; s33 = 1,152 9 06; sM = 69,632321.
По табл. 14.25 вычисляем:
д4 =дМФ + Р1 = 0,0393-1258,42-0,497128 ф
+ 3,23 = 27,8354 кГ/см2;
Р ) “Т"1
q„ = — Р, “+-----pR cos (ф — р4 р4 sin (ф =
1 (ф-1
10,98396
=— 3,15974 —---------0,0393 -1258,42-0,87 «96 -
8,98396
НС, СВОДЫ ОБОЛОЧКИ И ПРИЗМ ТТИЧГСКИЕ скллдки
131
Т j 6 " TI и з ’ 1 30
[	1 шдн : 1	- il L d \ «х 	С О	у0	0!		Свобдд- 1 ыс члены, М1ЮЖД - 1 тель — L	Контроле шде с}ГЛ- МЬ.1
0	1,76327	—0,06156	0,6926'1	0,102596	0	2, 196906
1	—0,06156	0,010745	—0,076137	—0,013451	—35,44106	—35,58110
	D.692 К)	—0,076137	0,001822	0,016588	'220,01254	221,217."'
3	0,102596	-0,013451	0,016588	115,922107	555,04953	671,07737
£	2, W6906	—0,140403	1,234873	116,02784	739,62101	858,97779 858,97770
— 3,1597-1.3,23-0,47690= — 172,7987;
9з-=—435,933; <?4 = 716,627.
Вычисляя суммы о.C-i+sj; и умножая свободные чле-
ны па /1| = 4/л, окончательно получаем числовую матри-
цу уравнении, приведенную в табл, 14,30, При этом коэф-
фициенты при неизвестных увелнчнпы в 100 раз. Пятое
уравнение выделено согласно (14.148) в качестве неза-
висимого;
69,6414- ДЛ -912,11^ = 0.
Окончательные значения корней уравнений;
4 =215,549-IO2 — , V® = 1739,306-102 --р-
уг> =— 393,468-102 4г ; Г? =- 4,721  102 — ;
£	3	Е
К"=— 0,13-102~~- .
Усилия п прогибы вычисляются по форму там (14 14°) —
(14 153). Предварительно по табл, 14.26—1428 1гд<- </
заменяется на Ф,) вычисляем ординаты единичных функ-
ций для точек 0—5 поперечного сечения (рис. 14.40,6).
Например:
= — 31 4 sin 0Х =— 3,15974-96-0,47690 =— 144,7;
л	0,	1
Д> = Д sin —  — =1258,42 — = 629,2 и т. д.;
20,	3	2
,M32 = £/^f(p;_I)sin2.A =
Значения ординат единичных функций приведены
в 1 аб 1 1131.
а)	Нормальные напряжения в среднем сечении
Ь = 0,5ф; Zj(0,5/j)=—7,2]:
о(, (0,5 4,) =П (У2 ф,0 Д V« Е0] + Vg en2 + О’ с03) ?.2 =
= (0.21555-1258,42-4-1,73931 -964-0,39347- 144, Д 0.00472Х
>(433,5)0,17134 = 85,19 кГ1см" (параметр У2 ьо малое»!
и" влияет па напряжения п);
щ = 4б,48 кТ/с.н2; оч = 0,42, п3 = — 20,99; <щ=—67,03;
щ =-84,78.
Таблица 14 31
Значения функций gp fp Л1;/£
фикции	.V точки					
	0	1	i 2	3	4	5
"Ао	1233,12	1258,1258,42		1238,42	1258,42	1258,42
			-41,0	—80,6	—134,3	—152,3 
’/2	—144,5	0	325,67	629,2	1089,8	1258,42
	—434,0	0	889,3	1258,42		-1258,12
Оч	-723,3	0	1215,5	62') ,2	—ins; ,8	1258, 12
he		0	—	0,94	0,98	1,0
hi	4,91	2,78	—	— 399	—8,64	—9,98
Оз	72, Щ	0,33		—89,§п	0	89,86’
0л	114,71	13,89	—	- 124,8	216,1	—249,5
	—		0,212-10“”“	0,11.10“”2	О.ТЫО"”2	4.82-10““2
~Г-Уз		—	0,515	0,726	0	—0,727
	—	—	5,56	2,83	-4,99	5,76
Эпюра нормальных напряжений, построенная по вы-
численным значениям, приведена на рис... 14.40, а
Для контроля эпюры напряжений о проверяется усло-
вие равновесия продольных сил, действующих в попереч-
ном сечении при я =0,5 I:
hi
АД Со ~г АЛ Сд Д . (<т1 “г 2о» ф- о3) 4-
4
Г.  144,67-0,79465:
•9,98396-8,98396— =
2
+	' Лз -г 2<Ji Д Oj) = 0,
= 0,410-10~2Д
cos03 = 3,15974.0,87896 = 2,78;
л 0,	1
/32	- ₽? sin ' “у” — 9,98396— =—4,99.
9*
где 3 = /?01/3 = 208.53 сел.
Подставляя числовые значения и суммируя отдельно
все положительные и отрицательные члены, получаем.
109 292 ж 100 026. Расхождение около 0,3%.
б)	Сдвигающие усилия S в опорном сечении (х = 0;
Z; (0) : Zs (0,5 ()=?Д. Дуга окружности сечения за-
132
РАЗДЕЛ 14 ОЬО Точки
I J б I и ll л 1г 32
Тригономе^рпчесьис пе+нчпны				Д11			
	il	2			1	V	
е	0	’/« 0i	ys e,	7 e.	-! 0,	д'» 0s	
	e,	’/<, 0,	7s 9,	‘/й	/, 0	7„ 0.	0
sin а	0,47690	0,4^591	0, 73971	0,21587	0,16505		0
cos а	0,87896	0,91390	0,94303	0,96930	0,98629	0,9 ) 1566	1
ьга Р,Й	0	0,2588	72		0,8b6		1
sin	0	0,5	0,8bo		0,866	0,5	0
cos 3.0	J	(\86b	0,5	0	-0,5	--0,866	=4
	0	0,707	1		0		
яп p,e	0	0,8oo	0,866	n	—0,8bo	-n),86o	0
cos (ЗЩ	]	0,5		—1	—0,5	0,5	1
sin pjp	0	0,9659		—	—-0,8ob	—	1
cos p3 0	—				—	—	—
меняется вписанным ломаным контуром (рис. 14 40,6
пунктирная линия), при siovi длина участка контура
приближенно принимается равной d
So(O) = S11,(0) = A^ff0X1 =
= 900-85,193-0,1309++' = 100,4 юГ/с,и;
+ =- S« + AF0 cr.L \ =124,09 кГ/см-,
td / cr, + ср \
S„ = + +-----—£_+—+ } = i36 g
1	2 \	2	)
+ =131,28; S4 = 83,23 кГ/см + « 0.
в)	Суммарные сдвигающие силы в опорном сечении
(х = 0). Так как бортовая грань сквозная, го
+ = ds + = 96 •100,37 = 9635,1 кГ;
+ +	г (0,5+)2
7 2 =	(2о, + +) 7^ = 13824,6 кГ,
Ъ
Т, = 14 082,4 hr, Т„ = 23 239,7 кГ, + = 9051,6 +.
Проверка равновесия оболочки, отделенной от диа-
фрагм (внешняя нагрузка должна равняться сумме про-
екций суммарных сдвигающих сил на вертикальную ось);
проверка выполняется для *4 части оболочки
V Тk sin 4’fe = ф- pj	.
4.J	л ti-2
k
Сумма части внешней нагрузки, определяемой первым
членом ряда
8!г
(pRlR -р Р1)---- = (0,0393-1258,42-0,49713 +
л‘--2
4-2400
4-3,23)--------= 27055,8 кГ.
3,14"
Коэффициент 8/л2 учитывает нагрузку только от перво-
го члена ряда [формула (14 1566))
Сумма проекций суммарных сдвигающих сил на вер-
тикальную ось
+ 4- Т2 sin ф2 4- Тфзшфз 4- Т4 з1’пф4 ф Т-, з1пф5 =
=9635+13824-0,44024-14082-0,36433 + 23240-0,24587+
+ 9051,6-0,0828 = 27321 кГ.
Здесь: ф-, = 01/6; ф4 = ф5+0]/3; ф3 = фд4 0j/4; ф2 = фз+
+006 Расхождение меньше 1%
г)	Значения Зя с учетом коэффициента (14.156):
S()=S« = 123,8 кГ/сш; Sf = 153,1; +=168,9, +=162,
+ =102,7.
Эпюра сдвигающих усилит! приведена на рис 14 40,6.
д)	Поперечные моменты в среднем сечении + = 0,5 4):
луо+у =— (И М,, + V] /+, + К'1 4+) =
(—393,5-0,212 40—2 — 4,72-0,515 —
— 0,13-5,56) НО2 -- 398,8 к Л
7И3 = 540,8, М, = 214,5; М -, = 54,8 к'Г-см/см.
Эпюра моментов приведена на рис 14 40, г.
Пунктирной линиеи показана эпюра мометов только
от равномерно распределенной нагрузки /7=393 кГ)м2.
е)	Нормальные прснибы в среднем сечении
% = ®О = *7 /щ + *Ш /(J3 + V4 /« =
14 6 СВОДЫ-ОБОЛОЧКИ И ПРИЗМАТИЧЕСКИЕ СКЛАДКИ
133
=. —10~5(—393,5-4,94 - 4,72-72,69 —
3,1
— 0,13-314,71)10= =—0,75 см;
к1, =	=—0,37 см; ш„= 0,78; w„ =1,09;
J -	«3	4
ш5 = 1,14 см
Эпюру прогибов см. рис. 14 40,8.
Расчет на обратно симметричную
нагрузку
Нагрузка, равномерно распределенная по каждой <
метричиой половине оболочки интенсивностью
= 100 кГ),;?, обратно симметрична относительно
сим-
р=
оси
По табл. 14,23 вычисляем;
aea = ( <4 Fu 4- а'м F&) R~ = (0,0784035 • 2502,38 +
Г 0,227434)1258,42s-0,29359-Ю^11 = 2,276304-КГ3;
ам Х1 = (0,08035-2502,38 + 0,249184) 1258,422Х
X 0,29359  10" ‘1 = 2,429354  10'
+2 M — 1 - 352706 -10^3;
an Xf = 2,59757-IO""3;
al3 ^ = 0,105972-10“3;
а23	= 0,442356-1 О'""3;
В) WS,e»(x=^5L}
д) 6,лГ]сиг^.--0^'С)
23,64
Рис. 14 41
а03 4 = 0,0289598-10~3;
а12 7^ = — 1,3278-КГ"3;
а22 4= 6,038403-10—3;
а33 ?4 = 6,701948-10-3.
По табл. 14.24 вычисляем:
/К
2
18,0442-10“:
X 1594,87 (39,9358— I)2 =
= 18,0442- 10~~9 -2,41782Х
X Ю8 = 43,6276-10'
sS3 = 11,60325.
Система расчетных уравнений при-
симметрии сечения Система расчетных уравнений при-
ведена в габ.1. 14 21. Решение выполняется с точностью
до первого члена ряда (/и=1). Коэффициенты и свобод-
ные члены этих уравнений вычисляются по табл. 14.22—
14 25. Вспомогательные величины, входящие в коэффи-
циенты, вычислены на основании выражений, приведен-
ных в примечании к табл. 14.22:
(32 = 2+= 6,31948;	= 4!= 12,63896;
Р 5 = 39,9358;	= 159,74 33;
fjj = 1594,868; Р4 = 0,255178 • 10s;
sin 20i	0,83835
аэ = 1 - 0,5——— =1 — 0,5—------------- = 0,156807.
(ф	0,497128
При расчете па обратно симметричную нагрузку по
сравнению с расчетом на симметричную введены допол-
пиге.тьные точки 3' и 4', показанные на рис. 14.41.
Значения используемых ipm онометрических величин
приведены в табл, 14.32.
= q° Rp cos 62 =
По табл. 14.25 вычисляем сво-
бодные члены:
/} _ —] Rp cos Oj =
, COS Oj /
= (1 —-----------'j 1258,42-0,01 -0,87896 = — 1,52319;
\	0,87896 /
?2------Рз
Rp cos 8j —
2л (
cos---1
40,9358
= —6,31948------------ 1258,42-0,01
38,9358
= — 157,10089;
(0,87896 + 1) =
р3 = — 12,6531-12,5842 (0,87896— 1) = 19,4941.
Вычисляя сумму fljj/q+s), и умножая свободные чле-
ны на Л] = 4/я, окончательно получаем числовую матри-
2
134
РАЗДЕЛ 14 ОБОЛОЧКИ
Таблица 14-33
№ урав- нения	0	С		1 3	Свободные члены (множи - тель 1/£)
0	2/276304	2,4'29351	— 1,352706	0,0289548	0
	2,429354	2,59757	—1,32780	0,105972	1,939386
	—1,352706	- 1,32780	49,6660	0,442356	200/12710
3	0,0289598	0,105972	0,442356	И 609,95	—24,82067
цу уравнений, приведенную в табл. 14.33. Коэффициенты
при неизвестных увеличены в 1000 раз.
Окончательные значения корней уравнений следующие:
Г,® = 337,910-10® ~ ;
® £
о	1
У; = —318,481-Ю3 — 
1
У| = — 3,338599-103	;
1/ = 0,0043292-103 — .
3	Е
Усилия и прогибы вычисляются по формулам (14.149) —
(14.153). Предварительно по табл. 14.27—14.28 (где
заменяется на d0) вычисляем ординаты единичных функ-
ций для точек 0—5 поперечного сечения (рис. 14.41,6),
например:
1о3 =---РЛ S’n 4
= — 6,31948-96-0,47690 - - — 289,321;
50,
/, = — sin----1 = - 0,40594;
21	6
/2 ™ — Р2 ( Р„ sin 3» cos ai + cos С Osin ttj) =
= —6,31948 (6,31948-0-0,87896 ф- 1-0,47690) =
= - 6,31948-0,47690 = —3,01376;
Ж22 = 7И® Elk/, = р| ( pf — 1) sin p, 02 Elk/ =
= 39,9538-38,9538-0,5-144,67-0,631464-10^E
= 0,07102447.’ и т. д.
Значения ординат единичных функций приведены
в табл. 14.34,
а)	Нормальные напряжения в среднем сечении:
= Е (У® еи + У® + У® /2 + У® Х|;
сг0 = [337,910 (— 600,14) + (— 318,481) (— 671,378) ф-
4- (— 3,338599) (— 289,321)
ф~ 0,0043292 (—578,642)] 103-0,171345• 10~~5 =
= 20,5 кГ/см2;
Oj = — 6,1 кГ/см2;	о2 —. — 12,38 кГ/см2;
оз = — 15,71 кГ/см2;	а3, = — 15.75 кГ/см2;
о4= — 12,64 кГ/слф	сгг = — 7,01 кГ/см2;	*
о5 = 0.
Значения функций (ф Е ; tyJE
Таблица 14.34
Функции	Дэ точки							
	0	1	2	3	3’		4?	5
4о	| —600,14	—600,14	—506,539	—409,465	—309,584	—207,589	— 104,147	0
1	^41	—671,378	|	—625,596	—521,329	—417,063	—312,798	—203,531	— lfC,266	0
^ke,	—289,321	1 °	629,21	1089,79	1258,42	1089,79	6.29,21	fj
’to	-578,612	0	1089,79	1089,79	0	—1089,79	— 1089,79	0
flo	0	o	:	0	0	0	0	0	(1	;
fa	—0,47690	—0,47690	—0,40594	—0,32538	—0,24601	—0,16496	—0,082760	0
fa	—3,01376	—3,01376	,	—20,48169	—33,7305	—38,6657	—33,5894	—19,4465	0	'
fls	-6,02749	—6,02749	—129,179	—128,753	3,10931	137,484	137,339	0	:
	—	0	0,0710244	0,1230144	0,142049	0,1230144	0,0710244	
	—	0	1	2,006142	2,006142	0	—2,006142	—2,006142	0 i
1И) СВОДЫ ОЬО.’ЮЧКИ И ПРИЗМАТИЧЕСКПГ склхдки
135
Эпюра напряжений приведена на рис. 14.41, а,
б)	Сдвигающие усилия S (в опорном сечении); контур
сечения принимается в виде ломаной линии:
So = AFoa^-.900-20,5-0,130899.10^‘ = 24,1;
S'/ = 24,1;
S? = 504~ЛР1<%^ = 24’1 +
4 390 (— 6,1) • 0,130899 • 1(Г2 = 20,82 к.Г/см;
Id / оу 4- сг„ \ я
52 = 5i + "у	= 1О178;
53 = 8,11 кГ/см; S3, =— Q,48 кГ/см
S4 = — 8,23 кГ/см, SA, = — 13,59 мГ/см;
34 = — 15,01 кГ/см,
в)	Суммарные сдвигающие силы:
Ti = Зо80 = 96-24,1 = 2313,36 кГ/см;
= 1937,610 кГ/см;
Т3 = 1261,271 кГ/см; Т3, = 398,095 кГ/см;
Т4 = —468,796 кГ/см; Tv = — 1164,431 кГ/см;
Тф = — 1549,965 кГ/см.
Проверка равенства нулю суммы проекции суммарных
1_двш ающих сил на горизонтальную ось:
Т„ Cos % + Т3 C0S + Ti' COS ^8 + Т4 C0S ^4 +
4-	Т4, cos 44, + "g cos ф. = 0;
1937,61 -0,8980 + 1261 ,271-0,93137 4- 398,095-0,9583 —
— 468,796-0,9786 — 1164,431-0,9923 —
— 1549,965-0,99910 = 3299,0 — 3160,0 « 0.
138,0-100
Погрешность	—3]6О~7Г = 4,4°0‘
Проверка равновесия оболочки, отделенной от диа-
фрагм: полный внешний крутящий момент Л1кр равен кру-
тящему моменту суммарных сдвигающих сил р отно-
сительно центра дуги поперечного сечения оболочки
(проверка выполняется для ]/4 части оболочки);
Л%р 4" Тг1, 4~ 2 Ti, (R cos <(/,) = 0;
k
0,
cos = cos —— = 0,9992;
*	12
fflKp (j 2	4 4q\Rli
44r„--. —-— - — • — =----------------
*p 2 л л rC
4 (— 1,523191 1258,42-2400
= —9------!--------’-----------= — 1864454,3 кГ см,
9,86959	‘ ’
где шкр = qtR;
TJg 4- S Tk (/( cos ду.) = 2313,36-600 +
k
4 (1937,61 4-1261 ,271 = 398,095—468,796—
— 1164,43 - 1549,965) 1257,41 = 1935976,0.
71521,7-100
Ошибка составляет	—;------—~-- = 3,80%.
1 864 454
Значения сдвигающих усилим с учетом коэффициента
Ш.156 6): So =5)' =29,64 кГ/см; Sf =25,61; S,= 19,40;
Ss = 9,97, S3,=—0,59; St = —10,12; 5],= —16,71; S5 =
= — 18,16.
На рис. 14.41,6 приведена эпюра сдвигающих усилий S
п показано направление действия суммарных сдвньт-
ющпх усилии Т со стороны торцового сечения оболочки.
г)	Поперечные изгибающие моменты в среднем сечении
(рис 14 41, в):
44=0; М, (0,5<?s) = —	Д-Д3<>3]==
= — (— 3,338599-103-0,0710244 Д-
4-	0,0043292 • 10J • 2,006142) = 228,437;
А13 - 402,009; Му = 474,245;
М = 419,379; М ,= 245,807.
д)	Вертикальные прогибы в среднем сечении
(рис, 14.41, а):
= Л, + п^ + ФТз =
= 0,323-Ю-5 ((— 318,481 ПО3) (— 0,4769) +
+ (— 3,335199-103) (— 3,01376) 4
4- 0,0043292-103 (— 6,02749)] = 0,523 см;
ш/ = 0,637;	д>) = 0,700;
щ,, = 0,670;	w. = 0,530;
Шу, = 0,293;	= 0.
Л'Т и к1® для правой половины сечения имеют обратные
зпакп (рис. 14.41, в, г).
14.6.3. Расчет диафрагм-оболочек
и складок средней длины
Диафрагмы рассчитываются как плоские стержневые
лонструкции на нагрузку от собственного веса и опор-
ного давления оболочки, передаваемого в виде сдвигаю-
щих сил. Для расчета диафрагм арочного типа удобно
згчйвпь геометрическую ось арки ломаной линией, по-
добной ломаному контуру, которым заменяется опорное
сечение оболочки при вычислении сдвигающих усилий.
После этого полученные из расчета оболочки значения
усилий Т-Л в опорных сечениях каждой грани следует
сосредоточить в узлах ломаного контура оси арки и раз-
ложить их на вертикальные Р'1/ н горизонтальные состав-
ляющие P/g Так как срединная поверхность оболочки
не совпадает с осью арки, то, помимо сил и Р^, сле-
дуем приложить узловые моменты тк. Значения этих сил
и моментов определяются формулами:
P"k = V (Tksin + ГШ1sin ’h+i);
^'ГШС05%н);	(14.157)
тс. = — ~ (ГРс 4~ Т'щуг) е0.
136
РАЗДЕЛ 14, ОЬОЛОЧКП
Экецеитрпшпп! определяется по формуле
где Ла и t— соответственно высота сечения арки и тол-
щина оботички. Злак плюс берется, когда оболочка при-
мыкает к арке ио нижнему краю, знак минус — когда
оболочка примыкает к арке но верхнему краю.
Расчет диафрагм коротких оболочек см. [37] и [25].
Расчет диафрагм длинных оболочек см, [30] и [37].
Расчет цилиндрических оболочек и складок с учетом
влияния на пх напряженно-деформированное состояние
конечных жесткостей реальных диафрагм [71а, 716, 8й,
89, 104J.
Л И ТЕР А ТУРА
1	. А. б о в с к и й Н. П., Аз ар хин А. М., Шесто-
пал Б. М., Кириллова Л. И. Программа расчет поло-
1 их ребристых оболочек для ЭЦВМ. Красноярский подтеки,
алит (учебное пособие). Красноярск, 1964.
2	, А м б а р д у м я и А, С. а) К. вопросу построения при-
бшженных теорий расчета пологих цилиндрических оболочек.
РМ?А, Pj54, А-? 3: б) О пределах применимости некоторых гипотез
юшдгх цилиндрических оболочек, Извеснш АН СССР, Огд. техн,
наук, 1454, М> 5.
3	А и о х и и а С, И, Применение тригонометрических рядов
к расчет) цилиндрических оболочек на сосредоточенную яагруз-
щ,. СБ. трудов ЛПИХ'1а «Исследования по строительной меха-
шп,.е» , вып. 190, Л., 1962.
А Б артсне в В. С. Практический метод расчета покры-
тий в виде железобетонных круговых цилиндрических оболочек,
['("-ринк трудов М11С11 им. Куйбышева, Al? 11. А\., Сгройиздат,
5.	Бнйлард П П. Напряжения от локальных иагрхзок
г. и и л и ч лричсь ких сосудах давления. Сб. переводов «Вопросы
пулнтп! цилиндрических оболочек». ИЛ., I960,
6.	Вайлара II. II, Напряжения от радиальных нагрузок
и внешних момш-пов в цилшщрическнх сосудах давления. Там
7.	В о б р о в п и к А. Е. К расчету оболочек методом сил.
С грол / ел иная механика и расчет сооружений», 1962, А7 4.
У В а й н f?e рг Д. В., Синявск и й А. Л- Дискр-етиый
анализ в теории пластин н оболочек. Д1., «Наука», 1966
9	Вайнберг Д. В.., С и ня вс к и й А. Л. Расчет обо-
лочек. Госстройиздат УССР, Диез, 1961,
10.	Вайнберг Д. В., Ройтф арб Н. 3. Расчет пла-
стин и оболочек с разрывными параметрами. Сб. «Расчет про-
странственных конструкций», вып. X, Стройиздат, 1965.
11.	Вас я л ь к о в В. С. Расчет коротких цилиндрических
ободочек с учетом трещпнообразоваипя. «Строительная механи-
ка и расчет сооружений».
12.	Васильков Б. С. Расчет оболочек с несимметрич-
ным сечением М,, Госстройиздат, 1962.
13.	Васи л ь к о в Б. С., М и л о й к о в с к и й И. Е. Экс-
пер именталыно-теоретическое исследование сборной желе зобе-
тонной оболочки. Сборник ЦНИИСК АСиА СССР «Эксперимеи-
нлъные и теоретические исследования по железобетонным обо-
лочкам». М., Госстройиздат, 1959.
14.	Власов В. 3. Новый метод расчета тонкостенных приз-
матических складчатых покрытий и оболочек, М., Госстройиздат,
19.13.
15	Власов В. 3. Строительная механика оболочек.
О1ГШ, 1936.
16.	Власов В. 3. Общая теория оболочек. ГПТТЛ. 1949.
17,	Власов В. 3. Избранные труды, т. I, Изд. АН СССР.
1Ш2.
18.	В л а с о в В. 3, Избранные труды, т, II. Изд. АН СССР,
1уоЗ,
19.	Власов В. 3. Избранные труды, т. Ш, «Наука», 1964.
20.	Власов В. 3., Мрощи некий А. К. Контактные
•>плачи по теории цилиндрических оболочек, подкрепленных про-
.а явными ребрами. Сборник ЦНИПС «Исследования по вопро-
< м теории и проектирования тонкостенных конструкций». М,,
I ..гстрийнздат, НПО.
21'	. В о л в м и р А. С, Гибкие пластинки и оболочки, ГИТТЛ,
Ад
22	Гаранин Л. С. Расчет пологих оболочек, Стройи’,дат,
20	Гвоздев А. А. К расчету тонкостенных цилиндриче-
(-1.их оболочек. «Строительная промышленность», 1932, Ху 1.
21-	Г в о з д о в А. А. Еще о безмоментной теории оболочек.
Гт рос Ы'льная промышленность», 1933, М> 2,
23.	Г воздев А. А., Мурашей В. И., Г о р н о в В. И ,
Б л а с о .в В. 3. Инструкция по проектированию si расчег-,
чш-'i 11 i I ч I j х тонкостенных покрытий я перекрытий, ЦНИПС,
О111И М>, Стройиздат, 1937я
26	Г п л ь м а н Л. С. К рш-чсну желе>обе.гинных цилиндри
ческих оболочек. 1руды Ленпш радыми о и.нс.ыиу1а янженгрно-
ПрОМЫШЛеНИО! 0 ШриИ ! ОИп ЫИ1, выи. 193ч.
27.	Г ил ь м а н А. С. К pacueiy изогрош’ых цилиндрических
оболочек под проиочильной нглрузкон. Цпды Высш, военно-
морск. инж.-cip. училища РКМФ. 1939
28	Годунов С. К. О -численном решении краевых задач
лля систем линейных ооыкноиенных дифференциальных уравне-
ний «Шпеки матсм. наук», т, Х\"1, вып. 3, ("Я,
29,	Г о л ь д е и в е и з е р А. Л. Имран упругих тонких обо-
лочек. М,, Гостехт сориздат, 1933,
30	Г о р е и ш I е й н Ь. В. Формулы и трафики для усилий
в цилгшдрцческих оболочках и диафрагмах, «Шроительная ме-
ханика и расчес сооружений», 1964, АЗ 1.
31,	Г р и г и р с н к о Я. М , Б е » полова Е. И., Вас и-
тонко .А. П. и др. Численное решение краевых задач в ста-
тике ортотропных слешеtwx. оболочек вращения иа ЭВМ тина
ЭМ-220. Методическое пособие. Киев, Шау^ова думка», I97L
32.	Д а р е в v н и В М. Решение некоторых вопросов тео-
рии цилиндрических оболочек, ПММ. г. XVI, вып. 5, 1952.
33.	Дикович В. В. Подот'ис прямоугольные а плане обо-
лочки вращения. М,, Гоестрийи nvai, iW1.
34.	Дишингер Ф. Оболочки, тонкосюишче железобетон-
ные купона и своды. М., Госстройиздат, 1932.
35	Ж е и о ч к и н а В. Д., М ь к ш и с М. М. Таблицы для
расчета средней длины цилинщшческих крутовых и призматиче-
ских оболочек, опертых но всему конуру. М.., Стройиздат, 1967.
36,	И м м е р м а н А. Г, Расчел ортгрошюй цилиндрической
оболочки на поперечную нагрузку. Сб. «Расче! пространственных
коис'рукш'й;-, вып. 111. М., Госстрощы тат, 1955.
37,	Инструкция по проектирован?!.о желеюбетоиных тонко-
стенных пространслвенны.х попраний и перекрытий. АСиА СССР,
ШП1ЖБ и ЦНИИСК М.. Госстрой;! ;да1. 1961,
38.	II т ц х а к и Д, Расчет при нса:ическнх и цилиндриче-
ских оболочек покрытий. М., Восприми щат, 1963.
39.	К а л ь м е й е р А. Ф, Аль'ритм и программа расчета
пологих ребристых оболочек е переломами средкшпш цовср.хш’-
сги. В со.: «Организация и .ш толика строительного проектиро-
вания с применением 5шчнелнтельнт) и оргапи ищнонной техии-
М1», ГИПРО1ИС. Реферативная информация. Серия X, въш, 7,
М., 1971.
40-	Каи С, II. Строительная механика обаточек. «Маши-
ностроение», 1966, Ab 1.
-Н. Кол кунов И, В. Основы расчета упругих оболочек,
«Высшая школа», 1972.
ч2.	Кузьм и н И. Л., Л у к а ш П, А., М I. леЙков
ск ий И. Е. Расчет конструкций из тонкостенных стержней
и оболочек. М., Госстройнздаг, 1960.
43.	К У л а г и а А. А., К о р м « р Б. Г. Расчет пологих обо-
лочек покрытий с учетом действптедыюй жесткости контурных,
элементов. Сб. «Строительное проект ированне промышленных
предприятий», 19е8, А'у 2.
44.	Ла ул ь X. X. Расчет цилиндрических оболочек с кри-
волинейными частями, очерченными по окружности. Труды
Таллинскою политехническою инсымута, .Аз 50 Таллин. 1953.
45.	Л е с с и г Е. IE, Л и л ее в А. Ф., Соколов А. Г»
Мет аллические листовые конструкции. М., Сгройиздат, 1970.
46.	Лес си г Е. Н. Расчет конюльных иилпндрическшх обо-
лочек на неосегимметричныс пепсуи-чные нагрузки. Сб, трудов
МПСП им. Куйбышева, ,М 43, I ос. н:р, чно-т i \и. изд. лиг. по гор-
ь-.)му делу, 19р2.
47.	Л и п н ицкп й М. Е., Горен ш т е й н Б. В,, В и я о-
грпдов Г. Г. /Келеитбетоияые прострашчвенпые покрытия
зданий.
•18. Л у к а ш П, А. Расчет пологих оболочек н плит с уче-
том физическом м геометрической шх-ишшшости. Сборник «Рас-
чет конструкций, работающих в упруго-пластической стадии». М.,
Госх-гройнздат. 19bl.
49.	Jl у и и н В. С. Балки посюхимого п опер с 4)1 от о сечения,
лежащие на упругом основашти, «КУЬУЧ», 1933.
50.	Лурье А. И. Концентрация напряжений в области от-
верстия на поверхности кругового цилиндра, ПММ, т. X, вып. 3,
19 А.
51.	Лурье А. 11. Статика тонкоыснных упругих оболочек,
М , Госсгройиздаг, 1917.
52.	Л ь в и н Я. Б. Сопротивление сферической оболочки
краевым циклическим воздействиям, Сб. «Расчет пространствен-
ных кошчрукний4, вып. V. М., Госстройиздат, 1959,
53	Л ь в д и Я. Б, Сопротивление конической оболочки крае-
вым циклическим воздействиям. Сб. «Расчет !.<рошранственных
КО!!, Трукций- , ВЫ!]. VI. zM., Г\ К'СТр ой из л а г, 1961.
51.	Л ь в и н Я. Б. Сопротивление оболочек 'вращения крае-
вым циклическим воздействиям Сб «Расчет пространственных
конпру кшг1Г', вып. VIE М., Гос. гронт! з,- ат , 1962.
55, Ляв А. Математическая т_орн;1 '-пруюш.и, ГТТИ, 1935
(перев. с англ.).
,')6. Мальков В. М. Расчет цилиндрической оболочки
с коы.гд срезом, Ленинградец, гос. унинертитег нм. Жданова,
Л кследовашн! п? с яры ос, и и пл аш ичшктн», ьып. 3. Изд. ЛГУ,
Л , ИМ
"7. .М и л е й к о в с к и й И Г Некоторые практшшскш’ за-
дачи По рас-иду siuKpuin.H ыш_ цилиндрических оболочек, В сб.
ЛИТЕРАТУРА
137
ЦНИПС «Исследования по вопросам теория и проектирования
тонкостенных конец?} кцтш», М., Госсгро/шщдг, 1950,
58.	М и л е йков ск и й И. Е., Вас и л ь к о в Б. С. Рас-
чет покрытий и норокрь.-’Лй из пологих выпуклых оболочек двоя-
кой кривизны. Сб. ЦНИПС «Экспериментальные и теоретические
исследования тонкое генных пространственных конструкций». М„
Госстройпздат, 1952.
39.	М плей к о в с к и й П. Е. Расчет оболочек и складок
метолом перемещений М , Госсгройиздаг, 19150,
(А Милейковскнй И. Е. Расчет железобетонных ци-
линдрических сводов оболочек. 61., Госстройиздат, 1963.
61.	М и л е й к о в с к и й П, Е., Доренб ау м И, В. Ме-
тод расчета покрытий на оболочек, очерченных по поверхности
гиперболического параболоида. Сб. «С ipo тельное проектирова-
нне промышленных предприятий», 19(35, № 3.
62.	М и л е й к о в с к и й IE. Е. а) Новый вариант х-равнопий
смешанного метода расчета складок и оболочек. «Строительная
механика». М., Ст рой щ, л ат, 1966: б) Практические методы рас-
чета оболочек и складок покрытий. Сб. ЦПИИСК нм. Кучерен-
ко М., СтроТшчдац 19/0.
63.	М и л е й ковскпй П, Е., Золотов О, И. а) 1< рас-
чету складчатых систем на ЭЦВМ. Сб. ЦНИИСК им, Кучеренко
«Строительные копит рхкпип», вып. 6. Расчет ободочек, 197г). Ро-
тапрннтное издание/ 6} Вариационный метол пехотных мраппе-
Ш1Й при расчете складок и особенности напряженного состояния
оболочек екладчанло типа Сб «Пространственные конструк-
ции тдаипй и сооружении», ДЕ, Стройиздат, 1972,
61.	М н ш о и о в М. К теории пологих оболочек. ПММ, XXII,
вып. о, 1958.
65.	М р о щ и и с к ч й Л. К. Расчет цилиндрической оболоч-
ки на сосредоточенные силы. сб. «Пластинки и оболочки». М.,
Гощ тройне дат, 12 У).
НЕ HaiapoB \ Л. Основы теории и методы расчета по-
логих оболочек. М, Сгройшдат, 1966.
67.	Ники ре ев В М. Раздольное применение белмомент-
ной и моментной -и оряй к расчету пологих оболочек Трмды
IV Всесоюзной конференции по теории оболочек и пластин. Ер —
ван, 21— Я октября 1962 г. Изд-во АН Армянской ГСР.
68.	Н и к и о с с в В М.. Hi а д v р с к и и Б. ТЕ Практиче-
ские методы расчета оболочек. Сгройизлат, 1966.
69.	Ново ж и л о в В. В. Теория тонких оболочек. 2-ц изда-
ние, Гос. союзное издательство судостроктельной промышленно-
сти, Л., 1962.
70.	Овечкин А, М. Расчет железобетонных круглых ре-
зервуаров. М., Сгройиздаг, 193(6
71.	Одинцов М И, а) Расчет цилиндрической оболочки
с учетом упругой податл-ипосги опорных диафрагм «Строитель-
ная мсхашжл и расчет соору/кеяий», 1962, № 5; 61 К расчет v
диафрагм цилннлричеч них оболочек. «Строительная механика
ч расчет гоорУЖ’пий», ИМ. А1- 5.
72.	П а в и’л а й н е я В. Я, Распет многовотповых покры
тин. Сб. «Расчет иросгогшывениых конструкций-, вып, ХШ.
ЛЕ, С (ройищат, НПа.
73.	Пас1”р н а к П. Л. Практический расчет складок
и цилиндричщг.их оболочек с счетом изгибающих моментов.
Информационный бюллетень НКТП, 1932.
74.	Паттерна к ГЕ Л. Практик скнй расчет складок и ци-
линдрических оболочек с учетом изгибающих моментов «Проект
и стандарт1-', 1933. М 2.
75.	Пастер и а к П. Л. Оболочки двоякой кривизны
в гра/кданехом и промышленном строительстве. Известия ЛСп.Х,
196’), № 3,
76.	Пастер и а к П Л. и др . Железобетонные конструк-
ции. Сщциалыгын кзре. М . IV ’трсчшздат, 1961.
77,	Пирогов И. ЛЕ Гасир’деление напряжений около си-
верстия в шизнилри’инжой <160,704x0 при действии сосредоточен
рых сил. Ил?. АП СССР, О1Н, Сер. мох. и маш № 2, 6959.
78-	Попов И, Г. Приближенный расчет длинных цилиид
ричсских ободочек «Расчет пространственных конструкций'',
вьш. VI. М . Госсгройшлат. 1961
79.	И щ е и и ч и о в Г. И. Расчет сетчатых цилиндрических
оболочек Пн. АН СССР, 1961.
80.	Р ж а я и п i.i я Л. Р. Об определении тенториальных гео
метрических х<?р <кг<’рш"тпк сечениа ..-онкое?ошю'1 о сгержчя
роч произвольных -и юр). Труды лаборатории строительной меха-
ники ЦНИПС, М, Пропищат. HU1.
81.	Ржаннпыл Л. Р. Расчет тонких безмоментных обо
дочек врлиочгия м итой криви ыы hi ярой цюдьпмю нагружу. Тру-
ды лаборатории сци-игидыюи механики Ц1ИП1С. АЕ, Строщп
цат, 1949,
82.	Рж а н ицы н А. Р, Безмоментные пологие оболочки. Сб„
«Расчет пространственных конструкций», вып, HI. М., Гож
изд-во литературы по строительству и архитектуре, 19о5„
83,	Ржаннцыв А. Р. Пологие оболочки и волнистые на-
стилы (некоторые вопросы теории и расчета). Научное сообщение
ЦНПИСК АСиА СССи, вып. 14. ЛЕ, Госстройиздат, 1969.
8Е Слез пнг ер II. И. Решение основных уравнений по-
лу безмо.ментной теории цилиндрических оболочек, «Строительная
механика ц расчет сооружений», 19и6, № 1.
85.	С м ир нов А. Ф., А л ександров А. В., Шало ги-
н и к о в П. Н., Я а щ е н и к о в Б. Я. Расчет сооружений с при-
менением вычислительных машин. М,, Стройиздаг, 1966.
86,	Строительная механика в СССР 1917—1967 гг. Ра/дел
«Расчёт оболочек и других тонкостенных конструкций». Строй-
изд ат, 1959.
87.	Справочник проектировщика промышленных, жилых и об-
щественных зданий и сооружений Расчетно-тсорегическнй, Под
род. проф, А. А, Уманского, М., Госстройиздат, 1961.
8а, с у ругацк и й 10. М. Некоторые вопросы расчета
призматических складок по полубез.моментной теории. Сб. «Рас-
чет пространственных конструкций», выл, IX. М., Госстройнз-
дат, 1964.
89.	Стругацкий Ю. М. Расчет ортотропных цилиндриче-
ских оболочек в главных координатах. Сб. «Расчет просчранст-
вениых конструкций», вып. XII. М., Госстройиздат, i960.
99.	С у м б а к Л. А. Расчет предварительно напряженных
цилиндрических железобетонных оболочек с учетом жесткостей
крччепия и юризонтального изгиба бортовых элементов. «Тру-
ды Таллинского политехнического института», К? 161. 1959.
91.	С v м б а к А. А. Экспериментальные исследования пред-
варительно ианря/кеяных цилиндрических оболочек. «Труды Тал-
линскою политехническою института», № 163. 1939,
92.	Т и и ошенко С. П, Пластинки и оболочки. ОГИЗ Гос-
техыдат, 1918.
93.	Т й м о ш е н к о С. ГЦ Бойцовски й - К р и rep С.
Пластинки и оболочки. Физматгиз, 1963.
91	Гюленев Л. И. Расчет цилиндрической ободочки
и шпангоута на сосредоточенную нщрузку. Сб, «Расчет про-
странетвеиных'. конпрукций», вып, V. ЛЕ, Стройиздат, 1959.
9а. Труды VII Всесоюзной конференции по теории оболочек
п пластинок. Обзорные доклады. М., «Наука», 1976.
96.	Ф и н к е л ь ш т е й н Р. ЛЕ О напряженном состояния
круговой цилиндрической оболочки, имеющей нал а линию откло-
нения од правильной формы; Лен?щградск. гос. университет
им. Жданова. «Исследования по упругости и пластичностью,
сб. 1. Изд. ЛГУ, Л., 196Е
97.	Ф дюгге В, Статика и динамика оболочек (пер с не-
мец-) 5Е, Госстройиздат, 1961,
АЗ. Филин А, П. Элементы теории оболочек. М., Строй-
издаг, Л., 1Жо,
99.	Пере и и и а В. С. Статика тонкостенных оболочек вра-
щения «11аука’->, 1968.
19/)	Черных К. Ф. Линейная теория оболочек. Изд. Л1У.
Части 1, 1962, част. И, 1961.
101.	LH акра м а н о в Г. С. Расчет тонкостенных цпличдри-
ческих оболочек по обобщенным формулам. АН ГрузССР. Треды
научных корреспондентов ин-ia строительного дела, т. 1, Тбили-
си, 1935.
192. 1П т а с р м а н М. Я- Основные идеи современной 'гес.пии
куполов и сводов. Труды Всесоюзной конференции по бег оду
и жслезобсгону. 1932.
163. Ш т а е р м а н П, Я.. Расчет купола как арки ка упру-
гом щновашш. «Проект и стандарт», 1933, № 9.
101 1Н т е л п б е р г М, В. К расчету неразрю.ных идпинтри-
ч-’ских оболочек, «Строительная механика и расчет сооружо-
шш -. 19(Е,	6,
Кб. Щопотьев А. С, Экспериментальные исследования
жслегобхгенной цилиндрической оболочки. «Проект и стандарт*,
193о, А'<= 11.
]|)и. э стр ни М. И. Расчет цилиндрической ободочки, юы
чреплениой по косому контуру. И-.в. АН СССР. OIH мех. и ма-
шиностр.. г. 2. 1932.
107. Э стр и и лМ. П. Р-зсчег цилиндрической оболочки, за-
«рстенной по косому контуру. Изв. АН СССР. ОТН. Стр. мех.
и маш. Ав 2, 1959.
108 Второй международный конгресс по топкостенным обо-
лочкам покрытием (пер с англ,, франи. и нем.) под р.'дакптшй
А, А. Гвоздева. М , Госстройиздат, I960.
Ш9. Симпозиум пл проблемам взаимосвязи проел?чроваипя
р вощеде'нця оболочок для проп щодс:венных и общеегвеншзх
зданий с большими продел амщ ЛЕ, Госстройиздат, 1966.
РАЗДЕЛ 15
МЕТОД СЕТОК В ПРИЛОЖЕНИИ К РАСЧЕТУ ПЛАСТИН
И ОБОЛОЧЕК
15.1. ОСНОВЫ МЕТОДА СЕТОК
Аналогично (рис. 15.1,6):
Метод veroK, или метод конечных разностей, нашел
широкое применение при решении различных, задач ме-
ханики. Этому за „оследине годы способствовало внедре-
ние в практику электронных вычислительных машин.
Основная идея метода состоит в замене точных значе-
нии производных их приближенными значениями через
конечные разности или дискретные значения функций.
Пусть, например, дана функция двух переменных
F = F(x, у) и надо вычислить частную производную
дР(дх в узле i (рис, 15.1, а).
rl"F
йу-
Fn 2Fi + Fm
Запишем еще третью и четвертую производные:
dAF _ Ft — 2 (Ft — Ffl) — F,
(15.3)
rVF F, — 4F'i + 6Ft — 4Fk + 4
=--------------(15.5)
X
Аналогично
+ .4FCT+Fa
Рис, 15,1. К замене производных разностями
Для смешанных производных:
дхду	44 Ру	’	( °’ }
(FF 1
7	=	j4F/ _ 2 (Fn щ Р/ + р + р } щ
да+у- Л
X ^у
+ (F9 + Fp + PrA~F0)l-	(15.8)
Если АВ есть касательная к поверхности F = F(x, у)
в узле I, параллельная плоскости ху, то точное значение
производной равно тангенсу угла (tsya) наклона прямо»
к оси х. Приближенное значение для производной можно
получить, если вместо прямой АВ рассмотреть прямую
/1|В]; тангенс угла наклона прямой Л,В1 приближенно
представит первую производную в точке i:
OF
дх
F, -- Fh
2лх
Аналогично
В некоторых случаях необходимо применять уточнен-
ные н односторонние производные. Уточненные значения
первой и второй производных з точке ::
dF 1
ь ps + 8FA_8^ + Fi), (15.9)
(JX	i & Лд»
Пли
(PF 1
“ =--Д—- [(4 + 4) - (4 + Ад]; (15.9а)
р-р 1
ь 4 щ +4 _ 30F. +
12Л®
dF JFn-Fm
ду 2Л,.
где кх, ку — шаги сетки.
Вторые производные можно получить, записав в числи-
теле разность первых разностей, т. е. вторую разность,
а в знаменателе — квадрат шага сетки:
o2F (Ft — Рр — (F, — Fxi	F< — 2F, 4- Fi,
AX- У - p • TO)
+ 164-4].	(15.10)
Односторонние производные в узле i мо<ут быть пред-
ставлены следующим образом:		(15.11)
dF d.t	Fl - Ft Ат	
Л ти dF <1х	А, - 4 ЛА-	(15.12)
(15.1)

15 1 ОСНОВЫ МЕТОДУ СЕТОК
139
Уточненные значения односторонних производных в уз-
ле k:
._J^(^3Fk + iFi ^plY
дх | k дх
(15.13)
Также
у-	(- 3FS - lOFk + ISFi -
OX l/г 12лс
— 6F/ — F/);	(15.14)
d2F I I
~~T -----------(11FS - 20 F R + 6FS +
U	12л~
+ 4F/--F0-	(15.15)
Замена точных значений производных конечными раз-
ностями сводит задачи, описываемые системами диффе-
ренциальных уравнений, к задачам решения систем алге-
браических уравнений. Общие методы их решения зцесь
не рассматриваются. Некоторые из них можно найти
в разделе 2,2, а также в специальной литературе [8, 10,
29]. Здесь основное внимание уделено построению раз-
ностных уравнений и формулировке граничных условий
в задачах расчета пластин и оболочек. Рассмотрены так-
же некоторые частные способы решения систем раз-
ностных уравнений, существенно связанные с особенно-
стями исходных дифференциальных уравнений или со
спецификой самого метода сеток.
15.2. ПЛОСКАЯ ЗАДАЧА
15.2.1.	Плоская задача в напряжениях
Для решения плоской задачи теории упругости исходят
из бигармонического уравнения
cFF д*Р	fPF
----4 2-------l--------
дх* ' дх2дуг ду*
(15.16)
Покажем, как методом сеток найти интеграл уравне-
ния (15.16) при заданных на контуре значениях F
и dFjdn,
Используя ('15.5), (15 6) и ('15,8), можно уравнение
(15.16) для узла i (см. рис. 15.1,6) записать так:
Д (6а5~г 8<х0+ 6) — 4 (Fп ~(-anFi -I- Рm -]--a0Fj,) (a0 ф- 1)
-+ 2atl (Fq + Fp 'r Fr + Fo) Д F,. F^-P
+ F!lF-F,ap ---0.	(15.17)
Через u обозначена величина
a,r lyj -	(15.18)
В случае квадратной1 сетки (а=1) уравнение (15.17)
упрощается:
20F, - 8 (Ffe т FS ;- F„, 1 F„) Д 2 (F„ Д Fp +
4" Fq i Fr) -J- F., -p F( -•]- Fu -J- Fv - 0.	(15.19)
В качестве примера рассмогрим ход решения задачи
о плоском напряженном состоянии квадратной балки-
стенки (рис. 15 2, а), находящейся под действием силы
посередине Найдем па контуре области значения F
и dF/dn, исполыуя рамную аналогию будем контур бал-
ки-стенки рассматривать как замкнутую раму. Разрежем
раму внизу посередине (рис 15 2,6’) и для этой основной
системы построим эпюру изымающих моментов (пока-
зана сп тошной линией) и эпюру продольных сил (пока-
зана пунктиром). Значение функции напряжении F на
контуре балки-стенки равно изгибающему моменту,
а нормальная производная 5Р!дп равна продольной си-
ле в соответствующем сечении рамы.
Правило знаков сформулируем следующим образом
Будем откладывать изгибающий момент со стороны рас-
тянутого волокна; тогда изгибающий момент, построен-
ный внутри области, соответствует положительному зна-
чению F, а построенный вне — отрицательному значению
F, Продольную силу считаем положительной при растя-
жении; положительная продольная сила соответствует
положительному значению дР/дп.
Из (15.1) следует, что
F;=-F/U27.V.	(15.20)
Выберем сетку, изображенную на рис 15 2,'.’ с шагом
7 = 1/6. Неизвестними являююя щаченпя F в отдель-
ных узлах, В силу симметрии количество неизвестпых
значений функции F при выбранной сетке равно пятиад-
ца-1 и.
Значения F на контуре легко находим из эпюры 'VI
(см, рис. 15 2,6):
PI.	Р1
=	Fjj = ,ИП ;
140
РАЗДЕЛ 15. МЕТОД СЕТОК В ПРИЛОЖЕНИИ К РАСЧЕТУ ПЛАСТИН И ОБОЛОЧЕК
о
р
12 .
F;V = Fv =- FV! = ,.. = Fxni = 0;
dF	I _	dF	I	_	dF	I
dy	|1	dy	In	dy	lin
dF	|	_	OF	I _	_	dF	| _
dx	lv	dx	|vi	’	’	dx	|ix
На основании (15 20) запишем выражения функции
напряжений F во внекоптурных узлах cti, an и др Они
нужны при составлении уравнений в предконтурных уз-
лах. Имеем:
F = Г •
г
= F(
Fa- Ш
3
I
F„ =хР~2 —
“VI «	6
р = р •
“11	2’
I
6
Р__
2 ’
2
И т
Д-
F,,	— F
“XI- ?15
Составим уравнения для характерных.
области (см. рис. 15.2, я):
для узла 7
20F, - 8 (2FS + F4 4- Fln) 4- 2 (2F5 + 2FU) +
узлов сеточной
торые особенности Они заключаются в том, что по за-
данной нагрузке функция напряжении на контуре обла-
сти определяется с точностью до слагаемого вида
(-1 + Fax С3у	(15.23)
В случае односвязной области константы Ct могут
быть заданы произвольно и, в частности, приняты рав-
ными нулю, так как уравнения Сен-Венапа, устанавлива-
ющие связь между компонентами относительных дефор-
маций Ба:, е„ и yXi), выражают необходимые и достаточ-
ные условия сплошности плоского односвязного тела.
Если тело ограничено миогосвязной областью, то эти
уравнения недостаточны для удовлетворения неразрыв-
ности деформаций. Должны быть выполнены дополни-
тельные условия. Этот вопрос рассматривается в рабо-
тах [28, 31]. Трудности решения плоской задачи теории
упругости для неодносвязных областей можно обойти,
если пользоваться уравнениями в перемещениях. Боль-
шие возможности решения плоской задачи, а также дру-
гих задач теории упругости открывает метод сеток в со-
четании с конформным отображением. Используя
различные системы ортогональных криволинейных, коор-
динат, можно достаточно точно исследовать поле напря-
жений плоских областей сложного очертания, включая
неодиосвязные области. Указанный метод изложен в ра-
ботах [14, 28].
15.2.2.	Двойной итерационный процесс
решения плоской задачи
для узла 5
20F5 — 8 (F4	F6 ф- Fe Ц- Fs) 4- 2 (Fj 4" F? 4" F4 4*
Pl
+ f9) f5 + Fn + ~ = 0;
о
для узла 2
Р1
6
Pl	Р1 \
_i_ ——-- _р f6 4- .	4- F? 4- Fs 4- F2 = 0 •
12	4 /
Таким образом можно составить систему 15 уравнений,
решить их и найти значения функции F во всех узлах
сетки После этого составляющие напряжений находят по
формулам:
Для решения систем алгебраических уравнений наря-
ду с методом Гаусса представляется целесообразным
в случае матриц высоких порядков прибегать к итераци-
онным методам, особенно учитывая специфику современ-
ных цифровых машин. С этой точки зрения оказалось
'удобным при решении плоской задачи разностным мето-
дом заменить бигармоническое уравнение относительно
функции напряжений
Ц2Ц2Е = 0
системой двух уравнений второго порядка:
52F	d"F
+	= f(x,y);
дх2	ду2
d2f	d2f
—I —= о
дх2	ду2
(15.24)
(15.25)
(15.26)
d2F	d2F
л dy2 v дх2 '
d"-F
где
(15.21)
итч на основании
в }з.ю I равны:
’' дхду
(15.2), (15.3) и (15.4). Напряжения
F/-2F, + Fk
Представим уравнения (15 25) и (15 25)
форме, приняв квадратную сетку с шагом
(см. рис. 15.1,6).
Уравнение Пуассона
Fk 4- F, 4- Fm + Fn- 4Ft
”	= /о
разностной
Хх  !j ~~~~ К
(15.27)
*	7.3
Fn — 2F,- 4- F,
О// —	,
уравнение Лапласа
7,2
= 0.
(15.28)
(Fn + Fp) - (Fg + F4
i и —
(15.22)
этих систем
4Т.2
При решении плоской задачи для неодносвязных обла-
стей, например пластин с отверстиями, возникают неко-
Двойной итерационный процесс решения
уравнений сводится к следующему. Во всех внутренних
узлах сеточной области задают произвольные начальные
значения F и находят первые приближенные значения f.
Эта операция состоит из двух частей. Вначале опреде-

74
в
а
15 2. ПЛОСКАЯ ЗАДАЧА
 ,  J41
ляют контурные значения 4<-,п.г, подставляя в форму-
ты (15 27) соответствующие начальные шаченяя пред-
контурных ординат и известие на контуре я в его окре-
стности контурные и законтурные значения функции
напряжении F. Законтурные значения функции напряже-
нии находят по экстраполяционной формуле
, I дР 1
^зак ~ 5koIlT26 I -	1	.	(15,29)
\ оп г<хи’п~г
При известных па контуре значениях [кпнт находят
значения во внутренних узлах сетки, решая задачу Ди-
рихле для уравнения Лапласа (15 26) по формуле
гП~Г1 1 ГП ! Ш. рт+1
(15,30)
Индекс п относится к первоначальным значениям f,
а п+1—к исправлшшнм.
Численное решение этот уравнения может быть вы-
полнено с помощью иi«рационного метода верхней ре-
лаксации [10, 33, 39].
После решения уравнения Лапласа переходят к ис-
правлению первоначально принятых значении F при по-
мощи формулы
f (п+1) + р(П) + рЛ)	р(« + 1) _ }2
Операция (15.31) совершается однократно Далее, ис-
пользуя исправленные значения	в предконтур-
ных узлах сетки, находят новые значения Ефаят на кон-
туре, затем итерационным путем решают уравнения Лап-
ласа и 1. д.
Процесс повторяется до тех пор, пока сумма квадра-
тов разностей (л)-го и (п+1)-го прибтижении по всей
области не оказывается меньше заданного числа. Эти
значения функции считаются окончательными, и па ним
находят напряжения в узловых точках пластины,
Для ускорения процесса итераций при решении урав-
нения Пуассона используется метод нижней релаксации
[33, 39).
Описанный двойной итерационный процесс решения
плоской задачи лето реализуется с помощью ЭВМ
В настоящее время имеются типовые программы, позво-
ляющие решать таким способом задачи о плоском на-
пряженном состоянии для областей, вписанных в сетку
с числом узлов бо ice 1000.
15.2.3.	Решение в перемещениях.
Вариационный метод построения
разностных уравнений
Решение тоской задачи для
иеодпосвязиых областей
во многих случаях упрощается при использовании урав-
нении в перемещениях:
дЛ.	1 — V	д211	1 С- V	дх	1
дх~	2	' diF	1	2	дхду	
	1 4- v	дЛ t	дЧ>	1 — V	дХ> dXi +
	в.)	дхду	' <HF	2	
			Тг-°’		(15.32)
где
Eh
и, v — компоненты вектора перемещений, направленные
соответственно вдоль осей х и у, X и У — компоненты
массовых сил; В — жесткость.
Хотя в (15 32) число неизвестных удваивается, полу-
чение их копс’шо-разиостного аналога благодаря понч-
жеиию порядка уравнении упрощается. Кроме того, ре-
шение в перемещениях особенно удобно для вывода раз-
ностных уравнений вариационным методом. Этот метод
вывода сеточных уравнений отличается от обычно ис-
пользуемого тем, что конечными разностями заменяются
производные не в уравнениях (15.32), а в выражении
потенциальной энергии Л, представленной функционалом
В	1 — v Г/ ди V | ди	ди
2	2	[\ ду / ' ~ ду	дх
— (Хи ф- Yv)\ dx dy,
(15.33)
где S — рассматриваемая плоская область.
После замены в (15.33) производных конечными раз-
ностями сеточные уравнения находятся как необходимые
условия минимума потенциальной энергии. Матрица ко-
эффициентов этих уравнении всегда (независимо от гра-
ничных условии и формы контура рассматриваемой об-
ласти) симметрична и позволяет применять для решения
системы наиболее эффектвцые численные методы, легко
реализуемые на ЭВМ.
Рассмотрим описанный способ составления сеточных
уравнении подробней [11, 12, 13, 25, 26].
Наложим на рассматриваемую плоскую область S пря-
моугольную сетку с шагами 7,х и X,, (рис, 15 3, а') и бу-
дем искать перемещения ее узловых точек.
Введем вспомогательную сетку с шагами 4/2 и ?.„/2
(рис. 15.3,6). Присвоим каждой ящике этой сетки но-
мер ее нижней левой угловой точки j (например, на
рис 15 3,6 прямоугольнику idha присваивается номер 1}
и назовем 5, его пересечение с S Ес.нт обозначить через
П; значение функционала (15.33) при S—S?, можно за-
писать:
S-=VSy;	+	(15.34)
1	I
Заменим диффереициалышс выражения в функционале
П, конечными разнос!я'ш Считая основную сетку доста-
точно мелкой, можем принять для областей S,, 5,, Sr, Si,
(па рис 15,3,6 заштрихованы наклонными линиями):
и(х,у] ty; и(х,у) = иу
для областей S(, S„, S,, S(на рис, 15 3,6 заштрихова-
ны вертикальными линиями):
ди	и;—11 i	ди v, — V/
дх Хх ’ дх К г
для областей Sr, Sg, Sri, S, (на рис 15 3,6 заштрихова-
ны горизонтальными линиями):
ди	U; — и„ ди	О; —- 1>п
ду Хи	’ ду 7,а
Кроме того, истинную нагрузку е компонент,эш; Y р
(включая и контурные силы, которые можно рысчац i
142
РАЗДЕЛ 15 .МЕТОД РЕЗОК В ПРИЛОЖЕНИИ К РАСЧЕТУ ПЛАСТИН И ОБОЛОЧЕК
вать как частный случай массовых) заменяем статически
эквиватептяой с компонентами А' и Г, так чго в области
S“ = St+S<+.S/4~'SfJ (на рис. 15.3,6 она заштрихована
наклонными линиями):
dv	и/ — и i
ух dy = р . Л Л
'Зу	К
X(x,y)-.Xi; Y{x,y)-=~YU
где
11 A' udx dy =--= \ X и dx dy =~ F\ X[ ui
e.)	(Л)
Рис. 15.3. К. выводу разностных уравнений вариа-
ционным методом
И T 11.
После замены дифференциальных выражений конечны-
ми разностями необходимые условия минимума ночной
энергии сводятся к системе алгебраических уравнений.
д'П _ дПу дП yi дП/
<Jul Хял ищ ' ovi ZJ dvi
i	1
(15.35)
где / пробегает все узлы, а г —только основные.
В л<1л»дое уравнение системы (’5.35) входят значения
неизвестных перемещений лишь в девяти узлах. В этом
нетрудно убедиться, приняв во внимание, что значения
неизвестных в узле г входят в выражение потенциаль-
ной энергии только четырех окружающих ее ячеек основ-
ной сетки или 12 ячеек вспомогательной сетки. Таким об-
разом, систему (15,35) можно записать и так:
Z -ф Е 4®^ =	
ф	ф
Коэффициенты из (15.36)
быте определены по (формуле
(15.36)
в общем случае мотут
У "Я,-
(13.37)
/
где / — индекс, пробегающий 12 значений (j—d, I, a, g,
,	, 4Fi
с, k, s, i, t, m, b, e); Aj= ~~~~ —отношение площади
,	Xе -V
ооласти к площади ячейки вспомогательной сетки
(очевидно, что ОС ky g 1, причем крайние значения соот-
ветствуют расположению j-i'i ячейки вспомогательной
сетки целиком впе ичи внутри области S, а промежуточ-
ные— пересечению ]-й ячейки контуром области S);
—коэффициенты с такими же верхними индексами,
как и у определяемых /ф(р [здесь и в (15.37) они опуще-
ны], значения которых находятся по табл. 15.1. В этой
таблице приняты обозначения.
<.--rS

Таким образом, нагрузка, перемещения и их пронзвод-
ньы в любой точке области S определяются лишь их зна-
чениями в узлах основной сетки. Соответственно только
эти значения войдут и в выражение энергии, отдельные
слагаемые которого примут вид:
1Ц	U l
к
(si)
Рассмотрим несколько примеров определения коэффи-
циентов уравнений (15.36) по формуле (15,37). Соста-
вим, например, сеточные уравнения (15,36) для точки 11
области S, показанной па рис. 15.4. Наложим сетку
рис. 15.3, б на область 5 так, чтобы узел I совпал с рас-
сматриваемой точкой 11. Тогда коэффициенты к} опре-
делятся следующим образом:
t	|1 при / = Ф, г, a, g, и, k, т, Ь, в
J	[О при / = s, f ,1
1S.3. И31 ИБ ПЛАСТИН
143
Умножая каждую строку табл, 15.1 на соответствую-
пиш коэффициент k, и складывая в соответствии
е (15.37), найдем искомые уравнения:
— 2^ип — a uk ф- 3(« •+ (J) at — 2 а щ —
— 2yvq 2yvr — 2&у 4- 2yvt 4- 2iivm —
3	,
- 2yvp = — mA;;
— 7f>un —	— а щ — 6рцт 4- (9 а ф- 13 ]3) 14 —
1 — v
— (1 -T v) vq — vvn + (l — v) °C — 4T'H + ~ vl +
+ (1 + V) v0 + 2vvln — (1 — v) Vp = 5Z; ©;
1 — v
— (It v) uq — -y-	4“ 2wy — 4yuc vut 4-
— 2yuq -7 2уи,. 4- 2buk 4 2ущ — 2дит —
— 2уир — 2ao„ — p vk -7 3 (a 4- p) v{ — 2 p ty —
3
— acm = — - шУ/.
Аналогично можно записать уравнения (15,36) и для
любой другой точки, приведенной иа рис, 15.4. Посколь-
ку этими схемами охватываются все возможные вариан-
ты, возникающие при совпадении контура области S
с отдельными .межузловыми отрезками сеточных прямых,
в табл, 15 2 приведены уравнения (15.36) для любого из
пронумерованных на рис, 15.4 узлов.
В качестве примера составления разностных уравне-
ний при несовпадении контура области S с сеточными
прямыми рассмотрим узел g на рис. 15,3, а. Наложив
сетку рис, 15,3,6 так, чтобы ее узел i совпадал
лучим;
Т (1 4- А-) Up + (1 — V) ит — 2vup - 7a.vn —
— 8 Р vk 4- (13 а 4- 9 р) Vi — ~$0i — 6ao,ft = 5Угсо.
На рис. 15.5, а показана квадратная пластина с цент-
ральным квадратным отверстием, сжатая сосредоточен-
ными силами вдоль оси симметрии. На рис. 15,5,6 пока-
заны эпюры напряжений в некоторых характерных сече-
ниях пластины. У узлов помещены величины коэффици-
ентов k-c и kv, входящие в- формулы для найденных на-
пряжений:
Р , Р
ах^К а& ’	у ab’
где Р— величина действующей нагрузки; а, 6 — сторона
и толщина пластины,
C g, no-
0 при i = b, e, a
kj = ;0,5 при j = i
1 при j = d,g,c,k,t,f,s>m
указанные в j-x
15.1, на коэффициенты k3 и складывая в
с (15.37), найдем:
Умножая значения
габл,
ствии
строках
соотвег-
15.3.	ИЗГИБ ПЛАСТИН
15.3.1.	Основные уравнения
и граничные условия
Функция прогибов w пластины определяется из реше-
ния краевой задачи для бигармоилческого уравнения
<94 ш 6* а/ д4ш а
~7~Г т 2 ТТГТЛ т ~7~, = "77	(15.38)
дх'1 dx-dU“ dtp D
при удовлетворении граничных условии.
Выше обозначено:
А/г3
Z? =----;---— — цилиндрическая жесткость
12 (1 — V2)
пластины; у— интенсивность нормальной на-
грузки.
Используя центральные разности, предста-
вим уравнение (15.38) в конечных разностях
для узла I сеточной области (рис, 15.1,6):
20 и/ — 8 (wk 4- wt 4- wm + и„) 4- 2 (ш0 4-	--
Рис, 15.1. Обозначения типовых узтов сеточной области
4- wq + ®г) 4- ws 4- Wt+Wp -7- w,j = ~т— , (15.39)
| ? №
Рис, 15.5, Сжатие квадратной пластинки с отверстием
сосредоточен и ы м и с и л а .м и
144
РАЗДЕЛ 15 МЕТОД СЕТОК В ПРИЛОЖЕНИИ К РАСЧЕТУ ПЛАСТИН И ОБОЛОЧЕК
Т а б ища Г5 1
Коэффициенты при перемещениях узлов и свободные ч’тены
Z		Utl					!l UV aiq>l	1									Vp
		л j k |	i			J	m	d	n	r	k	t	/	|	0			m	p 1	
d		-23		23				V—1	1— V						i	
/		—23		2(a+3)	—2a			2v				1—V				2m
а				2a	—2a				2v			—2v				
%		-23		23			V—1	1— V								
с		-23	—2a	2(a+fi)	1			—2v		V— 1	8V					2 m
k			—2a	2a			—2v			2v						
ч				23		—23							1— V	v—1		
f			—2a	2(a-}~.3)		-23					—-87			2v		2m
t			—2a	2a j	1	1				—2V			2v			
tv				23		-23								1— V	V—1	
b				2(a4-3)	—2a	-23					8?	v—I		—2v		2 m
				2a	—2a							2v			-2v	
		a™. j(p;									avv гф/					-2Т
			n		k		l 1	0 1	m	p 1	n.	k		1	m	
			~~2v	2v							—2a		2a			
			1— V			—87	2v				—2a		2(a+fi)	-"3		2m
--				I			У”^—1						23	-23		
			2v								—2a		1 2a			
c			v—1		—2v	Sf					”™"~a	-23	2(a+3)			2fi>
/		V— 1			1 — V							-23	23			
s								'2V	™2v				2a		—2a	
)					2v				1— V			—23	2(a+3)		—2a	2m
1					1 v—1			1—V				-23	2fJ			
m									2v	—2y			2a		—2a	
P						8y	| —2v		v—1		1 1		| 2(«+3)	—2?>	—2a	2m
										V—]			23	-23		
15 3 ИЗГИБ ПЛАСТИН
145
Таблица 15.2
Разностные уравнения плоской задачи теории упругости s узлах сетки, указанных на рис, 15,4
г р яв- нсния	Узлы	и	V	1														
		1	j	1	I	Ы n	k	i	I	m	q	| n	r | k	I	I	о | m	p 1	।	1														
Первое	/ 3 4 5 6 7 8 9 10 II 12 /3	4(«+₽.)	— 4a —1g	?V 3v—I	1— 3v	— (MO	2<a _4a	4(a+P)	—40	1—3v —87	Ц-v 3v— 1	?m —40	4(a+g)	—4a	3v—i i p4	—8v	1—3v	2<a														
																
		—4a	8(a+g)	—4a — 8₽ ;	1 —lv	3v—! \ 1+,	— Ml) 4m —1f5	8(a+g)	—8a —4g	3v—1 1 gv	I—3v —' MD 4<o —4g —8a	8(<Mg)	—4g f — (MD 1—3v	1 H 3v—! 1	4“ —8g —4a	8(a4-g)	—4a	t — (v+l)	1+v 3v—1	1—3V	4m —8g	—8a	16(a+0)	—8« —8g 1 — (vfl)	1+v	1 H	\ HMD Bra														
		—Bp	—8cz		2(и+3)	—Ip — (v-p)	1-yv	- -8v	1—3v : 1-yv 3v—I	603												
		—8g —4a	12(a+3)	—8«: — 1g  -MO	Mv 8v— i 8-y i— 3v 	1—3v -(v-J-l) 6<a — Ig	—8a	12(a+g)	—4a —8g	— (vp!)	1—3v	87	3v_]	1+v	— (Ml)	6<i) — 1g	—4a	!2(a+₽)	—8a —8g	3v—1	l^v 1— 3v	—8?	H-v	—МН)	S®														
	Узлы	u.									V					r
		q	n		k	i	I	0	m |	p		П	k	I		m	
Второе	/ 2 3 4 5 6 7 3 9 10 11 /2 13	-(Ml) -(Ml) -(v+1) -(MI) -(Ml) -(Ml) -(MD	J— 3v 3v--1 1— 3v 3v—j 3v—I ]— 3v	l-p 1M IM IM Mv 1+v 1+v	3v—1 1— 3v 3v—I l—3v i— 3v 3v—1	87 -87 -3? 87 -87 87 87 -87	1—3v 3v— ? 3v 3v—1 3°y— 1 l—3v	1 + v 1+v l+7 1+v 1+v 1+v 1 + v	3v—1 1—3v 3v—1 l-3y l-3v 3v— 1	л dr	dr	dr T	T T	T T T I	M 1 1 i f 1 i !	11	1 aBspsssS-	я я	-4g -4g -4|3 -8j3 -4g Mg -8g —4g —8g -8g	4(aM) 4(a+g) 4(a+g) 4(a+g) 8(a Pg) 8(a+g) 8(a+g) 8(a4-g) 16(a+g) 12(a gg) 12(a+g) 12(a M) 1+M g)	-4(5 -+ -4g -80 -4g -8g -4g —8g —4g -8 g	1 1 1 t 1 III	11 CO И Д Л 00	M 03	M £	9	9 Й S	R &	£	9	8	2(0 2(3 2<o 2® 4© 4(0 4(i) 4® 8(0 6(1) 6(0 6(0 6(0
Приводим выражения для интенсивности усилий:	Д изгибающие моменты	Qx = — мт iwt — М + wr — М> +	— 2>^ Г)	— wq — 4 (wi — ад)};	(15.43) Мх = —	2wt+w[)+v (wm — 2wi+wn)]; (15.40)	D Xa	Qg = — ~ {wv — wu + wq — w0 + wp — My^-^{{w„l~-2wi+wn)+v(Wk--2wi+wiyi-, (15.41)	- м - 4 (®л - мг)} 	(15.44) А4*	Если на рис, 15Л,о ось у принять за правый край пла* стины, то полная интенсивность реакции или обобщенной крутящий момент	поперечной силы в узле 1 может быть представлена D л - v)	0 виде: (15.42) поперечные силы	+ (2— v) [wr — wB~\~wp — wq — 2 (wi — М)1Ь (15-45)																
10—2S
146
РАЗДЕЛ 15 МЕТОД СЕТОК В ПРИЛОЖЕНИИ К РАСЧЕТУ ПЛ АСТИН И ОБОЛОЧЕК
Разностные уравнения
злы (рис. 15.6, (А7)	W							
	V		п	р		k	1	
1							0,5 a2	
2		0,5 v			0,5 а2	— (а2-Ч)	0,5 a2	
3	0,5 а2	0,5 v	— (a2+v)	0,5 v			0,5a2	
4				0,5 v			0,5 a2	
1 ")							a3	
6'				V			a.2	
7		V			а2	— 2 (a3 -,Lv)	a2	
8	а3	V	— 2 (a24~v)	V			a2	
9			— (a3~6v)	V		— (a34''v)	3 (a24®2)44	
10		V	— (а2 4- v)		а2	— 3 (а2-гу)—4(1—v)	3(a34a3)+4	
11	а2	V	—3(а2Жу)—4(1 — v)	4—2 v		— (a2~j-v)	3 (a4az)+4	
12	а2	4—2 v	—3(а2—v)—4(1-v)	V	а2	— 3	—4(1—v)	3 (a2+a3)+4	
13		0,5 V	— 2 (а'-Ч vl	V	0,5 а2	— 3 (a24vl—4(1— Vj	5,5 a2+6a2-J-8	
14		V	—2 (а24 а)	0,5 v	а2	--4 (a24-l)	5,5 a2-r6a2~[-8	
1	15	2а2	4—1.5 v	—6 (а2-Ч)—8 (1—у)	4—v	0,5 а2	— 3 (a24~v)—4(1—vl	5,5 a24-6a2+8	
№	2а2	4—v	—6 (а24'У)—8 (1—v)	4—1,5 v	а"-	— 4 (a24-l )	5,5 a2-|-6a2-)-8	
17	0,5 а2	0,5 v	—З(а24-А!) — 4 (1—у)	4—1,5 v		— 2 (a24 v’l	6 a24-5,5 a2-|-8	
18	0,5 as	4—1,5 v	— 3 (a=4v)—4 (1— v)	0,5 v	2 а2	— 6 (a2~6v)—8(1—v)	6 a2-po, 5 a2-'-8	
19	а2	V	— 4(а2-Н)	4—v		— 2 (а2 Ч a)	6 a2-p5,5 a2 (-8	
20	а*	4—т	—4(а2-|-1)	V	2 а2	— 6(a2'}-v)—8(1—v)	Oa2-] 5,5 a2-j-8	
21			— 2 (а2-су)	V	а2	— 4 (a2~rl)	6 (a24-a2)4-8	
15 3 ИЗГИБ ПЛАСТИН
изгиба пластин
			cJ			Правая часть Z
1	t	О	т	1	r	u	
		0,5 v	—(a2+'v)	|	0,5 v	0,5 a2	
		0,5 v				
						
'— (a2 -J- v)	0,5 а2			0,5 v		
		V	— 2 (а-Ч~т)	V	a2	
— 2 (а2 4- v)	а2	;			V		
		V				
						
—3(aa-f-v) — 40 — v)	а3	V	— 3 (а2 v) — 4(1 —v)	4—2 v	a2	1 	8 2
—(a2-f-v)		4—_о v	— 3 (a4-'rv) — 4 (I—v)	V	a3	1 2 8
— 3 (a2+v) —‘ 4 (1—v)	а?		— (a2 + v)	v		1 .— g 2
— (а® -f- v)		V	— (a2+v)			1 _ g	. 2	
— 4 (а2	1)	а2	4—1,5 v	— 6 (a2^v) 4~ 8 (1 — v)	4—v	2as	s	
— 3 («®+v) — 4 (1 — v) :	0,5 а® )	4—v	— 6 (a24”T) — 8 (1—v}	4—1,5 v	2a2	8
— 4 (а2+1)	а3	0,5 v	— 2 (a2+v)	V		8
— 3 (а2-)-^)—4(1 —v)	0,5 а2 |	V 1 )	—' 2 (a24-v)	0,5 v		8	i
— 6 (агфт) — 8(1 —v)	2 а3	V	— 4 (a" + 1)	4—v	a3	8	;
— 2 (а2+ v)		4—v	— 4 (a® + I)	V	a2	8
— 6 (a34~v)—8 (1—v)	2 а3	0,5 v	— 3 (a2+v) — 4 (1—v)	4—1,5 v	0,5 a3	8
— 2 (a24-v)		4—1,5 v	— 3 (a2-,-v) — 4 (1 — v)	0,5 v	0,5 a2	8
™" 4 (ex —j- 1)	а2	4—v	— 6 (a2 >-t) — 8(1 — v)	4—v	2a3	8
		(flpwo veep'	(' 7<7U 1.	HC C led ltd}			
10'
148
РАЗДЕЛ 15 МЕТОД СЕТОК В ПРИЛОЖЕНИИ К РАСЧЕТУ ПЛАСТИН И ОБОЛОЧЕК
Узлы (рис, 15,6, 15 7)	W						
	V	ч	n	1 p 1 s i	k			i
22	а?	V	— 4 (a2 4- 1)	4—v		— 2 (a,2-|“'v)	6 (a?+a2)+8
23	а2	4—v	— 4 (a3+l)	V	2a3	— 6 (a2+v)—8(1—v)	
24	2а°	4—v	—6 (a24"'v)—8(1—v)	4—v	a2	— 4 (a24-l)	6 (a24-a=)+8
25	а2	4—2v	—6(a?4-v)—8(1— v)	4—v	a2	— 6 (a2+v)-8(l—v)	11 (a24-a3)+16
26	а2	4—v	—6(а24-^) — 8 (1—v)	4—2v	2 a3	-8 (a3 4- 1)	11 ( CZ216
27	2а2	4—v	-8(a24~ 1)	4	a2	— 6 (a2+v)—8(1—v)	11 (a24-a2) + 16
28	2а2	4	— 8(a24-I)	4—v	2 a3	— 8(a34-l)	11 (a3-4-a2) -j- 16
29	а2	4'—v	—6(а2-Н)— 8(1—v)	4—v	| 2a3	— 8(aa+l)	12 a2+H a2-f-16
30	2а2	4—v	— 8(a2+l)	4	a2	— 6 (a2+v)—8(1—v)	11 a2+12 a?4-16
31	2а2	4	-8(а2+П	4—v	2cc2	-8(a2+l)	11 a2+12o?4-16
32	2а2	4	- 8 (a*+l)	4	2 54	-8(a3+l)	12 a2+ll a?+16
33	2а2	4	— 8(a24~l)	4	2 a,2	-8(a2+l)	12 (a2 + a?) + 16
34	2а2	4	— 8 (a? 4~ 1)	4	0 5 2	— 8(SH-1)	12 a24-ll,5 a3+16
35	2а2	4—0,5v	— 8(a3+l)	4	1,5 a2	— 7 (a24-v)—8(1—v)	11,5 a2+12a34-16
36	2а2	4	-8(a3+l)	4—0,5v	2«=	— 8(a24-l)	11,5 a34~12a“+16
37	1,5 а2	4—0,5v	— 7 (a24-v)—8(1—v)	4—0,5v	2 a,3	-8(a2+l)	12a24-ll,5a34-16
38	2а3	4	— 7 (a24-v)—8(1—v)	4—v		— 7 (a2-|-v)—8(1—v)	9 (a3 4-a2) 4-12
39	2а2	4—v	— 7 (a24*v)—8(1— v)	4	a2	— 5 (a3-j-v)—4(1—v)	9 (a24-a2) 4- 12
40	а2	2v	— 5 la3—v)—4 (1—v)	4—v	a2	— 5 (a3-r'v)—4(1—v)	9 (a34-a2) 4- 12
41	а2	4—v	— 5 (a24-v)—4(1—v)	2v	2a2	— 7 (a2-(-v)—8(1—v)	9 (a34-a3)4-12
42	2а=	4—0,5v	— 6 (a2 4’4—8 (1 —v)	4—v	1,5 a2	— 5 (а3-И)—4(1—v)	6,5 a24-6a24~8
43	2а2	4—v	— 6 (a2-j~v)—8(1—v)	4—0,5v	a3	— 4(a2+l)	6,5a34-6a24-8
"		Л3‘ I	(z/x,? qsij	D'nrrbc-joj. апнэжггодос!ц) (a+=»)S —	|	A		e»s‘l	(л— Of—(л+s®) S —
3		X	(л+г®) 5	л S‘ 1	8^	(l+E”f) i> —
35	г®о	Л—-fy	(л—0g—(a+z»)Z —	Р		(a— Of—(л+г®) S —
3X £	E^G	f	(a—08—(a+s®) L —	Л—	C»6	(л—1)8—(A~h®) Z —
5 3 — e	s®	A,—f	(л—I) f— (л+гю) д —	Л5	г» 5	(a— 08—(a+c®) Z —
z 9 	 £	EZ)	AS	(a—Of—(a+e®) S —	Л		E 7)	(л— Of—(a+s»)2 —
35	s®5	f	(Н г»)8 —		г»5	(l+c®)8 —
35	s®8	л g‘Q—f	(1т- г») g —	р	Е» S ‘ I	(л—08—(a+s®) Z —
3g			(Ис») 8 —	А9‘0—V	г» 5	(l+c®)8 —
35	c ‘ |	& 9 ‘ 0—f	(л--j)8 — (л-Ь») Z—		s»5	({_j-sa)8 —
3g	z^Z	f	(Н с») 8 —		s®S	(l+s®)8 —
35	s»	Л—	(л—1)8—(л+г») 9~		5» Z	(l+г®) 8 —
35	C®5	Л—f	(Иг») 8—			(л—08—(a+e®)9 —
3g	E®6	f	(l-Ьг’л) g —	л—i’	0	(l+г®) 8 —
35	c'®5	f	(г+т») 8 —		г®3	(l+г®) 8 —
35	u*-'	Ag—f	(л—1)8—(л+г»)9 —	Л/—f?	г®	(a— 08—(a+e®)9 —
3g	s®	A—f	(л—1)8—(^:®) 9 —	Ag—1>	г® 5	(l+г») 8 —
35	г»5	л—ф	(1+г»)8 —	’f	г»	(a— 0 8— (a+cz>)9 —
35		f	(1 + г») 8 —		e®5	(l+c®)8 —
3		A,	(л + г») 5 —	Л,	Е»	(i+e”£) f —
3	г»	Л	(I + г») —	Af		(a+s®) 5 —
3	E®	Л,	f	(I 4~г») > —	Л,	г® 6	
7 ЧГЗЕЬ ИЕ0Л?Цц	a	! 4		0	7	L
	<a					
g gi vyoj. атп-ож^о^ос/ц
6H
HHDVUII ЗИ1ЕИ esi
150
Р-ХЗДРП !5 МЕТОД CFTOK В ПРИЛОЖЕНИИ К РЗОЧЕТУ ПЛД1Ш1 и оьоточек
Узлы	w
.... иг с .....  -----------------------------------------------—.............—— --------------:----------------—   .......:------------------—..............
(рис 15 6, 15 7)	V	1	*7	1	я	1 р	j 5	k	1	1
44		1,5 v	|	— 2 (а2 рк)		j 1,5а2	— 5 (a2 f-v)—4(1 — v)	6,5 a?2 + 6a2 + 8
45		V	— 2 (а2 V)	1 ,0V	a2	— 4	1)	6,5 a2+6a24-8
46	1,5а2	4—0,5v	— 5 (а2 4 v)— 4(1 — v)	1,5 v	2a-	— 6 (a24~v)—8( 1—v)	6a2-J-6,5 a2-j-8
47	1,5а2	1,5 v	— 5 (а2-рг)—4(1™ v)	4—0,5v		— 2 (a2-^v)	6 a2-}-6,5 as-4~8
48	а2	4—v	— 4 (а2-1-!)	V	2 a2	— 6 (a2~4v)—8(1—v)	6 a3+6,5a'24-8
49	а2	V	|	— 4(а," ; 1)	(4—v)		— 2 (a2 2 v)	|	6 a2—6,5a24~8
59	а~	2v	— 2 (а2 (л)	V	a2	— 2 (a2^v)	a2 + a3
51	а2	V	— 2 (а2—v)	2v			a3 as
52		V			a2	— 2 (a2-f-v)	a2 -j- a"	;
53				V			а2 Д- a3
54							0,5 a3
55							0,5 a2	j
Ж				V			0,5 a2
57		V			j		0,5 a3
58							0,5 a'2
59					1		0,5 a2
60				V	(		0,5 a2
61		V					0,5 a3
62		\	— 2 (a24-v)	V			7 a2 -p 6a2 -p 8
63		V	— 2 (а2 pv)	!	V	a2 |	— 4 (а2ч-1)	7 a2-p6a24~8
64	2а3	1		— 6 (а2-2 V)—8(1—v) |	4—i	j		7 a24-6a24-8
65	2а-	4— v	— 6 (а2 4 v)—8( 1 —т)		a2 1 i	— 4 (a2 rl)	7 a2 ; 6a2 p8
66		V	|	1		I	— 2 (a2—v)	6аЦ7а24 8	,
1т 3 ИЗГИБ ПЛАСТИН
1И оОа псение табт. 15 1
W						Правая часть Z
।	1	|	t	j	о	)	m	1	r						
— 4(a=+l)	a3	4—0,5 v	— 6 (a3-!-^)—8(1 —v)	4—\	2a3	1 6
— 5 (a3-|-v)—4(1—v) I	1,5 a3	4—v	— 6 (a3+v)— 8(1— v)	1—0,5 v	2 a3	I	8
— 2 (a2-^)		4—v	-— 4	1)	V	a3	s
— 6 (ct2-j~v)—8(1—v)	2 a3	V	— 4 (as4-l)	4—v	.	fV «	e
— 2 (ct2-f-v)		4—0,5 v	— 5 (a3-[-v)—4(1 — v)	1,5v	1,5a2	s
— 6 (a2-j-v)—8(1—v)	2 a2	l,5v	— 5 (a3-J-v)—4(1—v)	4—0,5 v	1,5a3	8
		V				
	a3			V		
		2v	— 2 (a3-L-v)	V	a2	
2 (схл-р'у)	a-	V	— 2 (a2-(-v)		a2	
				V		
		V				
						
						
				V		
		V				
						
						
- 4 (a- (-I)	a3		— 6 (a3p-v)—8(1—v)	4_v	2a2	8
		4—v	— 6	—8(1 —v)		2 a3	8
4 (a2-r 1)	a2	A	— 2 (a3 ; v)	V		
		V	— 2 (a3 - v)	A		
— 6 (a3 pv)—8(1—V)	2 a2 j	v	j (Проба i c		- 4(a3 -1)	|	4— v ujx та ) 'иц> ai t 1 i> i [n )		a2	;	&
91 4 (г» 4 г 4 ft	(l4=4 8 —	г»г		(I 4 г») 8 —	f	г» 5	SS
91 4 (г» 4 г») fl			f	(I 4=o)8-		c»S	fS
91 4- (г» 4 г») fl	(l4г») 8 —	г» 8					£8
91 J (г» 4 г») fl							S8 :
914г» Н4г® SI	(14г») 8 —		f	(l4s»)8 —	f	г»8	IS
914г» Sl4c» fl	(l4c»> 8 —	о О		(I 4 г») 8 —	f	c»S	08
914с» SI 4г» fl			f	(l 4 г») 8 —		7^4	SI
914г» fl4c» 81	(l4E»)8 —	г» ь					81
91 4 г»Итг» II	([4г») 8 —	г»8	Л.—	(l 4 г») 8 —	f	г»3	U
91 4 s»fl4c» II	(л—1)8—44г») 9 —			(14г») 8 —	Л—	s»S	M
91 4 s»f 14г» Il	(l4r4 8 —	г» г					SL
9l4-»fl4c»II	(л—1)8—4+г») 9 —						tl
914г» ll'4s»fl	(l4г») 8 —	г» 6		(l 4 г») 8 —	f	4>6	\ CL
914г» Il4s»fl			f	(14г») 8 —			и
9l4r»Il4s»fI	(14г») 8 —	г» 5		(л— l)g—44г») 9 —	Л—		| и
91 4 г»1 14г» fl			Л-—t	4—1)8—44г») 9 —		г»	1 | OL
84г»/4г» 9	(л—1)8—44г») 9 —	г» 8	Л	(14г») f —		[ E»	69
84г»/4г» 9	44г4 г —			|	(14г») f —		г»	|	89
84г» 84г» 9	4—1)8—44г4)9 —	г» 8	Л.	1			| L9
I	7			!	1	|	b	|	a		(L QI ‘9'C[ -ЗИЙ)
Hire
xahoirogo и HHiDvifu Aiahovd x иинзжо1ги<ш а ЯО13Э iroiaw si iratrsvd
SSi
15 3 ИЗГИБ ПЛАСТИН
153
Продолжение табл 15.3
	W						Правая часть ;
	1	\	t		о	|	m	|	г			и	
	— 2 (а-+^)		4—v	4 (oAf-l)	V	а2	
	— 6 (cAf-v)—8(1—v)	2 а2	V				
	— 2 (а3+^)				V		S
	— 8 (а2+1)	2 а3		— 8 (а3 + 1)	4	2 а2	2в
			4	— 8 (а2 В		2а2	2е
	— 8 (а2+1)	2 а3		— 6 (а2~г"Р) — 8 (1—V)	4—v	а3	28
			|	4—v	— 6 (a2-|-v) — 8(1 — v)		а3	28
	— 8 (а24~1)	2 а2	4—v	— 8 (а- + 1)	4	2а3	2е j
	— 6 (ex'3—f~-v)—8(1—v)	а2	4	— 8 (а2 4- 1)	4—v	2а3	2е
	— 8 (а24~1)	2 а3					28
	— 6 (a2+v)—-8(1—v)	а2					2е
	-8(а=Ч-1)	2 а2	4	— 8 (а2 + 1)	4	2 а2	2е
	— 8 (а2-3-!)	2 а2		— 8 (а2 -!г 1)	4	2а.2	2е
			4	— 8 (а2 А 1)		2а2	2е
	— 8 (а2+1)	2 а3					28
	— 8 (а2-|~1)	2 а2		— 8 (а2+1)	4	!	2а2	28
			4	— 8 (а34”1)		2а2	28
	— 8 (аг-[-1)	2 а3				1	28
							2в
154
I П 1,Г ' I M	I UPHJOa I РИИ к PW4H' ПЛ'( Till! II ОЮЛОЧ1 к
^4? J
P1K 1"6 1’ I JBblv \ I 1Ы i 31 (16 IP Olin JlliilM
13 3 IHI ИЬ ПЛАСТПН
3}

Шарнирно впертый
край пластины
Честно защепленный
край пластины:
Рис, 15.7, Типовые узлы изгибаемой пластины
156
РАЗДЕЛ 15 МЕТОД СЕТОК В ПРИЛОЖЕНИИ К РАСЧЕТУ ПЛАСТИН И ОБОЛОЧЕК
Аналогично, принимая на рис 15 1,6 ось х за нижний
край пластины, найдем
D
ац = — ^7. М — ИД — 2 (ш„ — щт) +
решения составленной системы разностных уравнений
найдены прошбы в узловых точках области. По ним вы-
числены внутренние усилия в узлах. Результаты пред-
ставлены в виде формул:
щ = w* 103; Мх = M,fq№-lO.
+ (2 — V) [wq — wa ~{-Wp — wr — 2 (wn — wm)]}. (15.46)
Разностные уравнения изшба пластин удобнее всего
формировав вариационным методом
В табл. 15 3 приведены эти уравнения для сеточных
узлов одно- и многосвязных из!ибаемых пластин, фраг-
менты которых изображены на рис. 15.6 и 15.7, где пока-
заны условные обозначения граничных условий.
Табл. 15 3 содержит коэффициенты при искомых узло-
вых перемещениях в разностных уравнениях, относящих-
ся к типовым узлам, пронумерованным на рис 15 6
и 15 7. В таблице принят следующие обозначения.
ст ТГТТСТ ЩЕШ 1W
Eh?
12(1 -ст2)’
К
D
где h — толщина пластины; Е, х— модуль упругости,
коэффициент Пуассона; у — интенсивность поперечной
нагрузки; Z— правая часть разностного уравнения.
Составим разрешающее разностное уравнение для уз-
ла 17, лежащего на свободном контуре пластины вблизи
угла, к которому подходит шарнирно опертая сторона
(см. рис 15 6) Совместив узел i сеточного шаблона
рис. 15.1,6 с соответствующим узлом пластины и поль-
зуясь табл 15 3, можем записать из строки 17.
0,5 а3 Шр ф- 0,5 vw4 — (3 (а2 + м) ф 4 (1 — v)] ьу,, ф-
ф- (4 — 1,5 т) wr — 2 (а2 ф v) ф- (6а2ф-5,5 а3 ф- 8)шг —
— [6 (а2 ф v) ф 8 (1 — v)] Wi ф 2 а2 ay ф хз/а —
— 4 (а2ф-1) wm ф- (4 — v) Щрф-а3 wu = —.
В качестве примера рассмотрим задачу изгиба пласти-
ны с тремя отверстиями, опертой продольными краями
и неопергой вдоль коротких сторон, находящейся под
действием нагрузки интенсивностью у (рис. 15,8).
На область пластины нанесена квадратная сетка с ша-
гом а/12. При решении задачи использована симметрия
относительно осей х и у
С помощью табл 15 3, сеточного шаблона из
рис 15 1,6 и обозначении типовых узлов на рис 15 b
и 15,7 сформирована матрица уравнений В результате
Рис 15 8. Изгиб пластины с квадратными отверстия-
2 у?.4
ми прогибы w = w"‘ ——IO2 и изгибающие моменты
Мх~ Мх q/7-W в характерных сечениях.
На рис. 15.8,6, в построены сплошной линией кривые
прогибов w и изгибающих моментов Мх в пластине.
Пунктирной кривой показаны результаты экспериментов,
проведенных на железобетонной плите. Обнаруживает-
ся исключительная близость результатов
16 4. устойчивость и колебания плхстин
157
15.4. УСТОЙЧИВОСТЬ И КОЛЕБАНИЯ ПЛАСТИН
15.4.1. Уравнения устойчивости пластин
Исходное дифференциальное уравнение для решения
задач устойчивости пластин имеет вид:
dsw d*w	d*w 1 / йЧа
Ox* ^2dx^dyi+ ду* ~~ D \ х 6?"+
+ 2Nxy	+ Nу ТОТ = 0 ’	(16 •471
дхду * ду* )
где
Nx = axh; Ny = ovh; Nxy = xxyh. (15.48)
Введем обозначения:
ол = РС; ау=уС; -сху = 6С.	(15.49)
При распределенной нагрузке величина С равна ин-
тенсивности этой нагрузки: С — р. При сосредоточенной
силе Р величина С — Р/а, где а — характерный размер
пластины.
Уравнение (15.47) в конечных разностях для узла i
прямоугольной сетки (рис. 15.1,6) имеет вид [6, 17, 38,
39]:
Рис. 15.9. Расчетная схема к задаче о потере устойчи-
вости квадратной пластины, сжатой в одном направ-
лении
<?Wi + <Н + ^1) + фз <ыт + а>„) +
-тФЧ Н~ ы0) 4- ф5 (wq + wr) + <рв (ш6 + wt) +
4~ Wy 4~	™ 0,	(15.50)
где
Ф1 = 6 4~ Sm 4- 6«а 4“ 2 (m3 4~ ?) k;
% = —4т — 4т2 — mfik;
Фз = — 4 — 4т — yk;
ф4 = 2/п — 0,5 ~^т 8k;
Фо = 2т 4- 0,5 |Кт 8k;
фв = т2;
в
т~ ’ ° ’
k — параметр критического состояния.
Полагая й==1, для квадратной сетки (т — 1)
(15.51)
получим.
44 = 20 + 2 (Р 4-Y)
% ’ 213-§-
Рз - 8 — yk; ср4 = 2 — 0,5бй;
ф3 = 2 4~ 0,5б&; <р6 = 1.	(15,52)
Обозначим
(C7i)Kp Укр = Ккр "~~у~ >	(15.53)
о-


 &а^5а е,5а
n’i
где b — ширина пластины, Ь = п%, Ккр=-------kKV,
л3
Ход решения задачи При действии на пластину в ее
плоскости системы сил необходимо в общем случае ре-
W5
D

Рис. 15.10. Величины кри-
гнческпх сосредоючен-
ных сил для квадратных
иласшн с отверстием
158
РАЗДЕЛ 15 МЕТОД СЕТОК В ПРИЛОЖЕНИИ К РАСЧЕТУ ПЛАСТИН II ОБОЛОЧЕК
шить плоскую задачу и найти составляющие напряжений
или усилий. Эти значения надо подставить в (15 47),
после чего можно перейти к разысканию параметра кри-
тической нагрузки.
В некоторых случаях первый этап может отпасть
Так, например, для пластины, равномерно сжатой с двух
сторон, имеем однородное напряженное состояние, и зна-
чения составляющих напряжений в любой точке могут
быть записаны сразу:
== — р; ох ~ тХ1/ ~ О-
При сжатии пластины сосредоточенными силами необ-
ходимо решить плоскую задачу и найти составляющие
напряжений в выбранных узлах сетки. После этого вы-
числяются коэффициенты (15.51) и для каждого узла
составляются уравнения (15,50) с учетом граничных ус-
ловий изгиба. Определитель полученной системы урав-
нений дает возможность найти критическую нагрузку,
D
Коэффициент k в формуле .4,.,,= k для критических нагрузок
Пример 15.1. Рассмотрим свободно опертую квадрат-
ную пластину (рис. 15.9), равномерно сжатую в одном
направлении. В этом случае (см, 15,3.3): а = Ь; у——1;
Р = б=О. Принимаем шаг сетки Х==&/4.
Запишем граничные условия. Для узла /: ®i = 0;
— 4,1 для узла //: шп=0; а.ф = — и т. д.
Коэффициенты уравнений из (15 52) равны:
(fj = 20	21г,	==	3; <р3 = 8 + k;
<?4 = 2;	=-= 2; <р6 = 1.
Составим уравнение для узла /:
(20 — 2k)	— 3 (Д>3 +	;) + (— 8 Д- k) (w2 Д
Д 2 (ш4 + иф ) 4- 2 (ш4 + ay )	— ^ = 0.
Аналогично составляются другие уравнения.
Таблица 154
прямоугольных пластан при различных условиях на контуре
Схема контурных закреплений			Сх см а н а г р у ж с и кг п																
					1 р а^-				a/i>		У			Г			... 1г		
													р		Р				
			f р											6			А	t и	
			Густота сетки																
			4X4 j 6x6 | 8x6 |						4X1	8x8 j 4			4X1	8X8		*	4X4	8X8	
			51,2	59,18		5% 6		70,S	54,3	73,5		79,8	32,9	33,2		36,03	66,6	86,4	92,97
																			
																			
			35, 1	43,2		45,05		46,6	51,7	69,8		7'4,0	8,7	11,3		1’2,2	66,8	86,4	92,90
																			
																			
	1		32,0	45,2		46,3		46,7	47,1	56,4		59,5	22,9	24,6		25,2	62,2	77,6	82,8
																			
			Л ,)	26,9		26,26		26,6	21.7	36,0		39,1	12,2	15,2		16,2	54,9	75	81,7
																			
																			
		5	12,2	В,12		16,2		16,7	2% 4	2(60		4,2	6,65	9,1		9,9	51,9	75	81 ,7
																			
																			
																			
По экстраполяции порядка л’.
15.4. УСТОЙЧИВОСТЬ И КОЛЕБАНИЯ ПЛАСТИН
1S9
Решение задач устойчивости пластин при деиствии со-
средоточенных сил, наличии отверстий и других сосре-
доточенных источников возмущения силовою поля прин-
ципиально не отличается от рассмотренною примера, по
требует более густой сетки. Поскольку заранее опреде-
лить необходимую густоту сетки очень сложно, а иногда
и невозможно, оказывается полезным следующий способ
уточнения приближенного значения параметра критичес-
кой нагрузки k: если известны его два значения k, и А,,
вычисленные при сетах разной густоты соответственно
при К у Кх -- К,х. и при Kv - - Г). \ -
= cji^x- (cfi то уточненное значение
можно определить по формуле
(15.54)
Приложение метода сеток к задачам устойчивости
пластин позволяет составлять программы счета на
ЭВМ, применимые при расчете пластин самой различ-
ной конфигурации под любой нагрузкой и при смешан-
ных граничных условиях. Примеры результатов таких
расчетов приведены на рис. 15.10 (критические силы для
пластин с отверстиями) и в табл. 15.4 (значения нара-
„ D
метра k из формулы Psp = k—, позволяющие опреде-
а
лить критические силы для квадрадаой пластины при
различных условиях опирания и комбинациях нагрузок).
15.4.2. Собственные колебания пластин
Эта задача связана с нахождением собственных зна-
чений следующего дифференциального уравнения [8, 13,
27, 37, 38, 41]:
<4ш d*w daw
(15.55)
Круговая частота определяется по формуле
®т = 3,-и]/	,	(15.56)
У 1гУч
ho
где ------—плотность на единица поверхности; гп —
9
номер частоты.
Для узла i прямоугольной сегки (см, рис. 15.1,6)
уравнение (45.55) примет вид:
(« + 1) hk + i»z) 4
-j- 1 + — {wmA Wn) 4 2 {wa + wp J- wq + wr +
Т a (w, -I- wt) j- —- (wK -J а'„) — и,„	-= 0,
а
где частотный параметр
(П5.57)
Ах Joy
Для квадратной сетки а=1 и (15.57) упрощается:
20»г -- 8 (шд ф- wi ф- wm ф- w„) ф-
+ 2 (ш0 + wp ф- wq ф- iur) 4 ws Д wt 4- ®„4-
4- wv—Kmwi^=0.	(15.58)
Для узла i сетки (рис. 15.11, а), состоящей из разно-
сторонних треугольников. уравнение (15.55) примет вид:
2 [2 (и 4- ip ф- А2 ]- В2 (- 4] Wi - 2 [2u (u 4 4 —
- АВ] (w0 + wr) - 2 [24 (и А П —Ви] (wp -ф шф -
— 2 ]2В (и А 1) — 4Д (ш? + ay) + A ]wm + w,,) ф-
ф- 2 4u (wn Wf) ф 2Ви (wd ф- шА -т 42 (wa ф- w4) ф-
ф- В2 (wc шу) ф- 24В (шу Wk) — An Wi = 0, (15.59
Параметр (3„ определяется-по формуле
(45.6©)
В ряде случаев удобно для решения задач применить
параллелограммную сетку-(рис. 15.11, б).
Для узла I (рис. 15.11,6) такой сетки уравнение
(15.55) примет вид
[4 (1 -j- г3)2 ф- 2 ф 2г1 ф- A cos ф] Wi --
— 4г2 (1 ф г-} (wln 4 wn) — 4(1 ф Д) (шв Д wt) —
-- 2г (г2 cos ф ф- cos <j— г) (wq ф wr) А
-}- 2r (A cos <р cos ф 4- г) (ш0 -ф wp) ф-
4 (1 — 0,5г2 cos <[) ф wt) — A cos q (шя ->г аф) ф-
А {А — 0,5 cos2 Ф) (юи -4- wA \ A cos <р (wc wd)
Рис 15.11. Различные
OlCleMH сеток
160
РАЗДЕЛ 15 МЕТОД СЕТОК В ПРИЛОЖЕНИИ К РАСЧЕТУ ПЛАСТИН И ОБОЛОЧЕК
Безразмерные параметры
а? ^частот свободных колебаний прямоугольных пластин
Таблица 15 5
Схема пластины					a ₽,	а=₽.	a-3.	0'3,	0'3,
		C p;- L///2rC"	fl M U j Cj		21,49 22,13	49,36 49,66	53,17 54,55	81,09 Ы 9 2	96 J8 96 Л6
		* II 3 IJ lJx_.							
'«I'M П	i! 3 к* сз 3	11					24,38 27,0b	.52,70 58,50	59,44 60,10	85,79 92,03	101,9 104,8
					28,82	53,13	86,07	106,6	138,7
-®МС НЕ- х	С = в/3 Ся а!2					32,00 34,25	62,78 65,53	83,85 94,25	102,3 109,9	132,9 140,3
а12^_ о	|					3,603	7,145	14,31	24,94	27,26
Л , J ЛЛ УУ/'j					6,5Ы	14,47	26,96	32,47	51,64-
L« ty 1 I Q U-					7,137	15,80	19,20	38,53	43,67
. 					10,45	20,44	23,71	47,72	50,16
I CrZZZZZZZZZZM					17,43 19,17	24,45 31,30	36,19 51,66	50,73 52,24	53,58 64,04
СЧ / §	z				i Ь/а я 2 I Wa = ff5					
									
			Wif=2		18,95 19,73	24,35 31,64	36,79 52,47	51,95 52,60	55,74 65,42
									
									
15 4, УСТОЙЧИВОСТЬ И КОЛЕБАНИЯ ПЛАСТИН
161
Продолжение табл 15.3
Слома пластаны	|	и f5s	j				и-р,	“Ъ	a-fe
г	Ыа = 2 ь/а-!35	15,42 18,3b	25,83 34,48	36,60 48,43	43,76 55,26	55,05 66,82
'77^7?;:.							
ь > Я	k о/а -- 2 Yjl,	у Ъ/а U		17,38 20, 10	24,51 34,22	36,35 51,60	50,07 56,70	52,29 64.83
Таблица 15.6
Безразмерные параметры а2 частот свободных колебаний треугольных пластин
Схема пластины	Ci, град	й-р,	o-tC	a ga j		aJPs
Ъ// т //\ zc \\\	45 60	49,34 52,63	98,36 122,7	128,0 209,8	059,9 226,9	189,6 329,0
	.у ,	45 60	60,09 66,06	112,3 141,6	142,5 142,6	Г/2,4 232,9	205,1 250,2
А	45 60	65,49 66,06	И8,7 341,6	152,1 142,6	178,3 232,9	Л6,с 250,2
	45 60	72,0а 81,15	125,9 162,0	157,6 162,7	184,3 '56,3	219,5 273,2
А	45 60	77,53 81,15	132,9 162,0	166,7 162,7	190,1 25b ,3	-31,1 273,2
АА	45 60	90,68 98,17	146.7 185.4	184,4 А5,0	АО.О 302,7	244,8 412,2
АА ТАНА—А	45	9,787		—		
	45	29,40	—			—
(Продолжение таблицы на след стр.)
П—26
162
РАЗДЕЛ IS МЕТОД СЕТОК В ПРИЛОЖЕНИЕ К РАСПЕТА ПЛАСТИН И ОБОЛОЧ1К
Пр )дол7С!знпе табл /5 5
Схем! пластины	а, гяа 1	a33i	я0^	аД,	0’0,	аД1
*/\ ”	45 60	b,308 lp599	—					—
.л X 1 	, 		45 »0	6,164 и, 618	>3,59 28 17	—	—	—
Таблица 157
Безразмерные параметры а2 час гот свободных колебаний трапецеидальных пластин
( \ ч } ; пасти 1ы		а ара)	Д0,	а 3	а 63	а 34	
» 1—7Г—Д\ У ’			45 60	57,21 72 0'5	97 , 12 1 1	151 4 209,3	121,5 238,1	199,3 277Л	;
		45 60	71,Х 87.10	м _> J 13 >	> 1	200,5 Ч),9	225,8	; 502,1
		4Э Ы	, 105,1	1'31 , 1- 1U ' I'/ j U 7,н	1H.J 11 -' Ьо,3 215	225,3 279,4	227,2 303,1
		60				2S7 5 к.1 319. /	325,0
/Л//Л// 1Л		45 60	103,9 127,5				264,1 335,0
		45 60	110,ч 133,4	1 т < 200 J	0 ) | /О >	257 И 312 0	и>,9 377,0
1	t		1 / \ ,/ \ ; р и ч еча ins Пр? а 4	45 (>0 1 = -—-Н при	4.509 5,703 Н а “60 h ——	_	—	—	—
15.4, УСТОЙЧИВОСТЬ II КОЛЕБАНИЯ ПЛАСТИН
163
Таблица 15.8
Безразмерные параметры а2 частот свободных колебаний
ромбических пластин
Схема пластины			агР,		
фф—11	24,70	52 ,58	71,02	83,40	121,4
а	29,71	58,67	79,19	ЭД, 61	127,8
а	33,81	65,43	84,79	97,81	136,6
LJ	34,19	65,26	85,49	97,71	135,8
О	36,51	63,40	89,57	97,8:.’	132,8
	-10,05	71,38	98,73	105,0	142,9
	45,67	80,12	m ,5	115,4	156,8
— Г COS ф (ш/ + Wf) 4- Г COS ф (®й ~г И/j) +
-4- 0,25г2 cos2 Cf (wa - 4 Шр + и; ф-ау,) —
~ *„Л;=0’	(15.61)
где
А
г ~	.
Частотный параметр:
|С-~~ЭД--	(15.62)
лт sin’ ф
11”
Таблица 15.9
Безразмерные параметры a2 f>m частот свободных колебаний
параллелограммпых пластин
Приближенное собственное значение (3,„ может быть
уточнено, если известны его два значения: (3,,,., опр ае-
ленное при сетке с шагами Хл_, и > определен-
ное при сетке с шагами X* =fe.. h. и X, =k.. ~J.
Г	i/ /< i, !Ъ и Ф
(4н<1). Уточненное значение определяется формулой
р2 __ Рж/
(15.63)
Пример 15.2. Квадратная пластина (см., рис. 15.11, в)
свободно оперта по контуру. Принято ix~j.!/ = a,lri.
При п — 3, записав для каждого узла уравнения
(15.49) с учетом граничных условий (они выписаны на
рисунке), получим систему уравнений, определитель ко-
торой равен:
18—X; —8;	— 8;	2
—	8;	18 —х; 2;	— 8
—	8;	2;	18 — х; —8	°'
|	2;	—8;	—8;	18 —х
Найденные собственные значения.: Xj=4; х> = хз=П6;
х4 = 36.
Используя формулу (15.57), вычисляем: а.3р; = 18;
а2р2 = а2|33 = 36; а2[ф = 54.
При п~4 частотные параметры, сооюетсгвующие 1-ем
же формам колебаний, имеют значения: и2^ = 18,744;
a a fj2 = а2р3 = 41,372; аДф == 64.
164
РАЗДЕЛ 15 МЕТОД СЕТОК В ПРИЛОЖЕНИИ К РАСЧЕТУ ПЛАСТИН II ОБОЛОЧЕК
Уточняя по (.15,63), получим
aspi = 19,66.
Аналогично уравнение (1.5 65) прямее вид:
(6a3 ф' 8a ф 6) гр, — 4 (1 а) (фт + cap-, -ф <р„ ф- дар;) -L
Аналогично: а2р2 = «23з = 47,39; a;’|j.j — 74,92.
В табл. 15,5—15.9 приведены безразмерные значения
a*’pm Для пластин' прямоугольных, треугольных, трапе-
цеидальных, ромбических и параллелограммных при
смешанных граничных условиях.
15.5. ОБОЛОЧКИ
15.5.1.Основные уравнения и граничные
условия для пологих оболочек
ф 2а (ф0 ф ср., ф- Цр ф- ip,) ф ф, ф а'3 ф, + ф0 ф- a3 cpz —
а _ \ _	_
—s	—- Т7 kU	Wn + ^г) +
А	Г /
а — —	— К а -
+ !iy (ЕЕ + wz) — Дфф" ^ху \wt> 4-
р-	2р
-ф Шр — Шр — ыр) = Rn2 10,0625 (ш0 -ф шр —	— wr)2—
— (ш* — 2wl + to;) (to,,J — 2to, 4- top) j.	(15.69)
Дифференциальные уравнения для пологих оболочек
с учетом геометрической нелинейности записываются
следующим образом:
с
д-rj;	д-w
дх2	ду2
1	, ,	,,	д2ш
— V~V“<₽ + А?	'
Eh	4 V	k	дх2
д2
V* ~~ ky ^Х2 ~ ^Ху
д"г	д
kx =	; kXy =
yjva	t v
<92ш	2 Д3ф А3к>
дх2 * дхду дхду
-рг=~-0;	(15.64)
5‘-а>	/ d2w \ з
. ----__ — = 0.
ду2	фАиф/
о3 д2
дхду J ду2
!z	д2г
у; ky= — .	(15.65)
flu	dtl“
Линейные уравнения (15.66) п (15 67) в конечных раз-
ностях имеют такую же форму, как (15.68) и (15.69),
только правую часть нужно положить равной нулю.
В этих уравнениях введены безразмерные функции на-
пряжений ф и функция прогибов ш, которые определя-
ются соотношениями.
о:Ф
ф== —Ш.
п2
афо2 _
10» f
(15.70)
Здесь:
й«р7 __
------- ш>
10“ D
(15.71)
При небольших прогибах оболочек можно исходить из
линейных дифференциальных уравнений:
Z)V‘V’to — V* Ф — Pz ~= °1	(15,66)
а — меньшая сторона плана оболочки, параллельная оси
х; р = 6/гт — соотношение сторон оболочки; ф = 12(1 —
—V2)).2 — коэффициент вспарушепности оболочки; л =
= //й — вспарушенность оболочки; / — стрела нодьема
оболочки в центре; 7?—12(1—v2) 10-4S — коэффициент
Pz : а \*
гибкости; S =-----( —-	—гибкость оболочки;
А’Л 1 h /
1 Q Q
у уН А^ш = 0.
(15.67)
Рассмотрим пологую оболочку положительной гауссо-
вой кривизны с прямоугольным планом. В конечных
разностях для узла i (см. рис 15 1,6) прямоугольной
сетки уравнение (15.64) может быть записано [4, 5, 13,
15, 22, 36, 42—44]:
/—	а ~ \	_ —	—
2 Мд + ~ ky <ф —	(ф;;1+фл) —
\	Р2 1
k у (фд + Ф1) +	„ kxtJ (q0 ф- фр — фр — <рг) -ф
ар
_2i_
а3ф
[(6a3 + 8a -у 6) W[ — 4 (1 ф- а) (ш„, ф- ашу, ф-
-ф wn -ф a wi) ф 2а (ш0 -ф wp +wq + wR +
_	- IO4
-ф	а3ш4 -ф a3toy] — —— =
= Rn2 [(ф„д — 2(рд- -ф фг!) (we — 2шг ф-toy) —.
— 0,125 (fi(1 -ф фр — ipp — фг) (ш0 ф- top —	— и,-) ф
-ф(фе — 2ф + (ф) (ш,„ — -ф ш„)ф (15.68)
безразмерные параметры кривизны оболочки.
Приводим выражения оiносите,,тьпых деформаций “е-
рез функцию напряжений:
tx =-	1 Eh	( 52 гр \ оу~	д2 <р \ —V  		 ; дх'* J	(15.72)
	1	( О2 ф \ дх2	О2 ср \ —-V	 : Оу- )	(15.73)
Уху —	2(1 + v)		0- ф	(15.74)
		Eh	дхду	
Нормальные и сдвигающие силы равны:
д2 О)	О2 ср	д2 <р
Лф=--.4П;	,V	(!5.75)
ду2 J дхду а дх^
Они могут быть представлены в виде безразмерных
величин:
а2 р, _
(15.76)
A'rl/=---^r4/Vly;	(15.77)
103 h
15 5. ОБОЛОЧКИ
165
Запишем выражения Л\, Nxll и Nv в конечных разно-
стях дня узла i (сеточная схема на рис. 15,1,6):
Лф = — 0,122(1 ~т2)(фш-2Чг + фД (15-79)
Nи =-— 0,122 (1 — v3)(tp.; —- 2срг J- qy);	(15.80)
Л'I,, = 0,032 V а(1 — v3) (ф(, 4- фр — <р0 — <рг).	(15.81)
Мембранные напряжения по
предел яюз с я равномерно,
толщине оболочки рас-
-Л/ XI/
(15.82)
h
II
и
h
Мимешные усилия равны:
/ О3 w	д2 а \
Mx~~—D-----------В-------;	(15.83)
\ дх'2	ду'2 /
при	Ш, = 0; А.г = 9; (N х у М 0) -
Из статических н кинематических краевых условий
b
следует, что при у —Ж ~ф" 
д~w	д" д
w — 0; -—— = 0; q =0; ----------— — 0;	(15.93)
ду2	ду2
а
при X = ±—
д2 w	д2 Ф
Ш = 0; ------= 0; <р = 0;-------= 0.	(15.94)
дх2	дх'2
б) Шарнирно неподвижное закрепление оболочки па
жестком контуре характеризуется наличием распора, а
перемещение точек контура отсутствует. Имеем.
Л4,„ = - D(1 - v) -Й-Д- .	(15.85)
дхду
Опп могут быть также предел авлены в виде безраз-
мерных параметров
ii" рг —
Мх	Мх;	(15.86)
10*
а- р, —
/АА, >	/АН, /.
103	и
а2 р? —
Л1,,; ------------- Мхи-
/У 10., ХУ
(15.87)
(15.88)
Запишем статические условия:
Ь
при у = 2 — Л1/; = 0; (Л'й +- 0);
2
при х =1	М,, --= 0; (N х 4 0).
Из этого для кромки, параллельной оси х, вытекают
следующие условия:
Запишем их в конечно разностной форме для узла I:
—	п'2 f	,
/VI = —--------а (sy, — 2wi + wd 4-
л 10> а I	‘ 1 и т
+v (»m — 2®z + кД ];	(15.89)
Mt,	\(wm — 2wl +Д)];	(15.90)
10- а
— п2 (1 — v)	.
/ИЛ1,=----------— 6»0 -j шр — др — wr). (15.91)
4-Ю3 I а
д'2 ф д'2 01
—-----—у--------= 0;
ду2 Ох2
1 Г д3 ф	Э3 ср
Eh [ ду3	’ дх2 ду
dw
ду
Аналогично для кромки, параллельной оси у:
д2 <р д2 ср
дх2 ду'2
(15.95)
Изтибпые напряжения определяются по формулам:
(15.92)
Рассмотрим некоторые характерные случаи граничных
условий.
а) Шарнирно подвижное опирание соответствует за-
креплению краев оболочки в тонкие диафрагмы, жест-
кие в своей плоскости и гибкие из плоскости. Кинематн-
жекие краевые условна з этом случае запишутся:
Ь
для кромок у =+ ~	= 0; и = 0; (и =4 0);
а
для кромок х =^4г — :ьа = О; v =~- 0; (гтд^О).
Статические краевые условия:
при у = ± Му =. 0; А у == 0; (N Лу =f= 0);
1 [ д3 <р
Eh [ дх3
(2 -ф v)
д3 <р
дхду2 ]
-9.
(15.96)
в) Жесткое защемление харшыершзуется иа.щчщм
распора на контуре оболочки я оюутсшшм иовороюа
опорных сечений.
b	dw
При и ± —	“ = v = w --= 0; —" = 0;
г У 2	ду
а	дш
ппи х ~ д- — и — v — w — 0; 	— 0»
’ 2	чх
Из этих четырех кинематических условии вьнекаег,
что для кромки, параллельной оси х
„—. V,	-- V
ду	ду2 дх'2
д'3 ф
5у3
+ (2 + V)
д3 ф
dx2 ду
(15.9/)
166
РАЗДЕЛ 15 МЕТОД СЕТОК В ПРИЛОЖЕНИИ К. РАСЧЕТУ ПЛАСТИН И ОБОЛОЧЕК
и для кромки, параллельной оси у.
w = 0;----=0;	---— —V----- = 0;
дх	дх~ ду“
0s ф	д3 ф
+ (2 + V) = °-	(15.98)
ох-	дхду“
Для каждого внутреннего узла составляется ио два
основных уравнения (15.68) и (15.69); таким образом,
общее количество неизвестных равно удвоенному коли-
честву узлов, если не учитывать симметрию системы или
нагрузки
При написании основных уравнений (15.68) и (15.69)
для предконтурных или контурных узлов в эти уравне-
ния в качестве неизвестных войду! значения w и ф
в первых или вторых законтурных узлах.
Приведенные выше граничные условия и представля-
ют собой те дополнительные уравнения, которые могут
быть включены в основную систему для нахождения
всех неизвестных, включая и законтурные. С другой сто-
роны, можно на основании граничных условий записать
выражения дтя внеконтурпых неизвестных w и ср, вы-
разив их через внеконтурные или контурные неизвест-
ные. Напишем выражение для внеконтурпых значений
функции на основании приведенных (раничных условий.
При шарнирно подвижном опирании кромки на осно-
вании (15 93) найдем: если иа рис. 15.1, б ось х совпа-
дает с верхней кромкой плана оболочки, то
Фи = —(15.99)
wn =—wm,	(15.100)
если на рис. 15,1, 6 ось у совпадает с правой кромкой
плана оболочки, то:
Ф/= —Ф4	(15.101)
глу = —.	(15.102)
При шарнирно неподвижном закреплении кромки- ес-
ли па рис. 15.1,6 ось х совпадает с верхней кромкой
плана оболочки, to:
щ„ = --й,л;	(15.103)
Фп = 2(1 — ш) фг 4- av (% + фг) — фт; (15.104)
ф0 = 2 [2 (1 + 2a) — 3a2 v (2 ф- v) j cpz —
— 4а [1 — av (2 ф- v)] (Г ф-фД — 4 [1 ф а (2 ф- v)] х
><	+ 2а (2 + v) + фг) — аЧ- (2 ф- v) X
X (ф5 + Ф/)+фг1 — fex(mn —ш,га): (15.105)
если на рис 15.1, б ось у совпадает с правой кромкой
плана оболочки, то:
оу — wk-,	(15-106)
Ф/ = 2	— ф-j ф, + ~ (фпг + Ф„) - Фа; (15.107)
Г /	2 \ 3v -4
Г v	1—2	—.	—
X 1 —	(2 + v) ф/г 4	(2 4- V) (<р0 4 ЧД)
V	-	—	-	1
— Т 12 4- v) ,<р„ -у фа) ф-
а-	ар-
X (ш/— wk).	(15.108)
При жестком закреплении оболочки:
если на рис. 15.1,6 ось х совпадает с кромкой, то
wn=.wm,	(15.109)
если на рис. 15.1,6 ось у совпадает с кромкой, то
ау=ЩА-	(15.110)
Функции напряжений в первых внеконтурпых точках
[сравним (15.95) п (15.97)] определяются, как и при
шарнирно неподвижном закреплении, по формулам
(15.104) п (15.107), а во вторых внеконтурпых точках—.
по формулам (15.105) и (15.108),
Выпишем для иллюстрации уравнения совместности
деформаций (15 65) для предконтурных и контурных
точек без включения внеконтурпых, которые исключают-
ся иа основании (15 104), (15 107), (15.105), (15.108).
Если ось х на рис. 15.1,6 совпадает с верхней кром-
кой плана оболочки, уравнение (15.65) для узла i мо-
жет быть представлено в виде:
2 [ 1 ф- о. (3a -L 4) ф- av ( 1 — 3av) j	—
-- 4a ](1 4- a) + v (1 — av)] (?p& 4- фг) —
— 4 [1 4- a (2 + v)]	+ 2a (2 4- v)(ф0 ф- фг) ф-
+ a- (1 — v2) (<ps 4. фф 4 2 <p„ 4- 2kx wm —
Га	_
— kxy (w0 4- wP — w0~ wr) =
= Rn" (0,0625 (w0 4- wa — <jdq — a>)2|.	(15.111)
Для узла i, смежного с угловым на рис. 15.1,6, гра-
ница плана оболочки проходит по узлам s, A, i, I, г,
уравнение может быть записано так:
[2 4~ a (5a 4” 8) + «V (3 —- 5a)] ф/ —
— 2a (1 4-v)[2 4-a(l —-v)]9; — 4|1 4- a (2 4- у)]фт —
— 4a (1 4- v) [1 4. a) (1 — v)]lfk 4-
4- 2a (2 4- v) (% + <p,.) 4. 2 4- a2 (1 — v2) <ps +
= Я,пг [0,0625 (to,, — кф)2|.	(15.112)
Аналогично (15.111) и (15 112) могут быть записаны
уравнения для узла i. если кромка оболочки иа рис.
15.1,6 изображается отрезком оси у.
Пример 15.3. Рассмотрим оболочку типа эллиптиче-
ского параболоида с квадратным планом (а = й)
и с шарнирно неподвижным опиранием. Нагрузка —
равномерно распределенная. Уравнение срединной по-
верхности оболочки
г = — ф -Jp (х- 4-62)j-	(15.113)
Безразмерны^ параметры кривизны приняты равными:
Ах —4; Av = 4; А^у^О.
Вспарушенность 7=10. Коэффициент Пуассона v =
= 0,17,
Ъ
= — = I.
а
35 5. ОБОЛОЧКИ
167
Выбираем квадратную сетку (а=1) с шагом
(рис. 15.12)
ЛХ — '-у — С •
Решим задачу в линейной
Ввиду симметрии оболочки и
постановке, приняв R~ 0.
нагрузки уравнения мол-
Рис. 15.12. Сеточная область на оболоч-
ке типа эллиптического параболоида
но составить для '/в части. Запишем для узла / уравне-
ние (15.69):
20 7 — 8 (2ф, + <р4 + cpj) + 2 (2ф54-2фп) +
+ 2 Ф3 + (pg + Фр — 2 (4-R4) ffiij Ц- 4	4 Wy j 4“
4 4 (и(2 4 ws) = 0.
Используя (15,103) и (15.104) для исключения epi и
wi, получим окончательно такое уравнение:
19 (fl — 16 ф.2 4 2 <р3 — 8 ф.! 4 4 (р5 ф6 —
— 6,34 cpj 4 4,34 Фи — 16 Ш; 4“ 8ш2 + 4 u’j = 0.
Аналогично записывают остальные уравнения. В ре-
зультате решения системы уравнений найдены величины
прогибов и функции напряжений в узлах сетки.
По этил значениям вычисляют мембранные и изгиб-
ные усилия, пользуясь формулами (15.79) —' (15.81) и
(15.89) — (15.91).
Например, для узла 6 (см. рис. 15.12)
NXc = — 0,12-10 (1—0,173) (2(Д —2ф6) = 1 ,277 и т. д.
В табл. 15.10 приведены значения безразмерных ко-
эффициентов прогибов, усилий и моментов в центре рав-
номерно нагруженной оболочки при шарнирно подвиж-
ном и шарнирно неподвижном закреплениях по конту-
ру для различных соотношений сторон в диапазоне
всиарушениости оболочки от 1 до 25.
Г а б л к ца 15 10
Безразмерные коэффициенты прогибов и усилий л центре							
	оболочки типа		эллиптического		зараослоида		
							
к ,	S я	Шарнирно подвижней.			Шпрририо неподвнж-		
go			опирание		 Юс	закрепление	
							
4 £ у	>иве рОМ( ус Ik		соотношение -		1'фОН оболочки		
£ о о СО Й =5	cgs	!	м	2	>	1,5	
	w	26,623	55.609	84,329	29,461	37,190	45,895
		15,210	1,6ЬЗ	2,522	7,706	12,111	14,176
		6,210	И, 194	12,774	7,706	7,282	6,779
		2,668	5,241	7,841	2,015	3,509	4,253
	51 D	2,6(58	2,756	2,754	2,015	I 735	1,285
		1'2,867	29,57.)	а 1,262		13,970	15.477
	~'x	5,998	1,783	.’,133	6,118	9,105	10,318
		5,393	12,007	16, я7!1	6, ИЗ	5,525	3,057
		1,144	2,640	1,934	0,704	1,257	у 492
		1,144	1,331	У 718	0,704	и, 502	0,327
	w	Ь,ь9»	16,314	1,8(>1	1,792	6,501	1,166
	Nr	4,678	1,811	2,870	1,470	с, 134	Н, i 71
		1, 678	10,034	15,417	1, 170	1, 321	1,673
		0,488	1,357	2,968	и,272	0.519	0,1^5
		0,483	0,653	1,014	0,с72	0,Ш	0 119
	w	3,881	9,687	2.2,063	/, ИВ	1,709	i 12i1
	Nx	3,618	3,026	2, 189	3, 398	1 /42	Р>7 i
4		3,618	8,142	13, 1-17	О, 148	1, 2*5	_ 8 12 ;
		О, 21 1	0,718	i, S18	0,Н2	8, г%	= 1, 17')
		0,214	0,156	0,064	<1, 112	6,1)69	'.on. ;
	w	2,462	6,474	15,149	l,3O(J	'JO	’ F7>
		2,869	2,459	2,136	2,6%	22 !	
з	Ny	2,869	В, 8[Ю	11,3<>7	2,6°)		,24>
	mx	0,094	0,401	1,181	‘ J.ti 17	",hi	o,_ о
		0,091	0.212	0,415	9,0.17	'МШ	1), 1J ,6
	w	1.674	4,506	ГМ88	0,868 .	1, 796	1, J59
		2,342	2,058	1,853	2,217	У 2о5	1,U<9 
6	Ny	2,342	5,602	Ю,(Ш	2,217	2,162	1,912
		0,040	0,234	и,782	0,019	(1.199	0,H5 '
		0,040	0,136	6,31!)	О,0Ю	9,(118	0,i L'n
8	w	0,904	2,493	6,243	0,459	0,669	1,U5 ’
	Nx	1,685	1,540	1,ШЗ .	1,829	2,444	2.787 :
	(Продолжение таблицы на след cip.)						
168
РАЗДЕЛ 15. МЕТОД СЕТОК В ПРИЛОЖЕНИИ К РАСЧЕТУ ПЛАСТИН II ОБОЛОЧЕК
Продолжение табл. 15.10
Вспарушен- ность обо- лочки	Приведенные перемещения и усилия	Шарнирно подвижное опирание			Шарнирно неподвиж- ное закрепление		
		соотношение сторон оболочки					
		1	| 1,5 j 2			|	1	| 1.5		2
	д	1,685	4,142	7,698	1,629	1,605	1,427
8	ч	0,082	0,078	0,359	0,001	0.043	0,078
	М	0,932	0,066	0,165	0,901	9,007	0,014
	W н	0,562 1,310	1.558 1,237	4,067 1,290	0,280 1,277	0,542 1,954	9,682 2,334
10	7р,	1,310	3,240	6,349	1,277	1,246	1,131)
	Лр	—0,004	0,020	0,165	—ООЗ	0,020	0,0-13
	S	—0,004	0,036	0,096	—0,003	0,903	0,098
	C2I	0,242	0,669	1,676	0,120	9,231	и, 289
	V	0,846	0,824	0,817	0,83.9	1,304	1,495
(5	V	9,841)	2, "60	3,958	9,839	0,808	0,731
	Ж	—0,003	—0,013	0,004	-0,901	0,004	о, 012
	Ж	—0,003	0.012	9,030	—0,091	0,001	0,003
	U’	“Д35	9,361	0,927	9,067	0,127	9,157
	н	9,628	0,618	0,615	0,627	0,978	1,123
29	N и	0,628	1,592	2,860	0,627	0,566	9,535
	м	—о.гки	—9,001	—0,028	—9,001	0,091	0,004
	лц	—0,001	<) ,<ж	и,оп	—0,901	0,009	0,091
Продолжение табл. 15.10
Шарнирно неподвиж-
ное закрепление
1 j 1,5
1,5 |	2
0,081	и 227
0,501	0.494
0,501	1J 82
—0,01)1	—",05
—0,0 И	0, п0 1
0,552	0,012
0,492	0,501
2,221	0,591
0,031	9,000
0,005	0,900
0,п80	0,098
0,783	9,899
0,456	0,420
0,000	9,001
0,000	0,001
П р п м t ч а и и е. При расчете прямоугольной оболочки
при "1/> мсш.шая сторона ..телилась на че1ырс части, а
большая — ли шесть чщгей
В оболочь-у с соотношением сторон 13 =--2 меньшая сторо-
на делилась па чгшре части, а большая--на восемь ча-
стей,
В заключенье изложим ход решения геометрически
нелинейных задач деформации оболочек. В этом случае
правые части уравнений 15.68), (15.69), (15.111) и
(15.112) нелинейны.
Записав уравнения для всех внутренних узлов сетки,
а также для контурных узлов, получим систему нелиней-
ных алгебраических уравнений, которую можно решить
методом последовательных приближений, учитывая гиб-
кость оболочки. В качестве первого приближения прини-
мается решение линейной задачи. По значениям функ-
ций ф и w первого приближения вычисляются нелиней-
ные правые части уравнений. Решив полученную линей-
ную своему, найдем значения функций <р и а> второго
приближения. По значениям ф и w второго приближе-
ния вычисляются новые правые части, а после решения
системы уравнений получаем третье приближение.
Процесс повторяется до тех лор, пока значения п-го
и (п-Н)-го приближений не будут практически совпа-
дать.
Процесс последовательных приближений может быть
реализован на электропцо-иычиелнкльвой машине.
ЛИТЕРАТУРА
1.	А б о j? г к и й Н. П,, С а м о л ь я н о в И, II,, П а с ь-
ко Д, А, Расчет пологих оболочек в матричной форме методом
сеток, Красноярск, 1965-
2,	А б о в с к и й I-!, П„ Е ндж невский Л. В. Дискрет-
ные методы расчета пластинчатых систем, Красноярск, 1965.
3,	Безухов II. И. Основы теории упругости, пластичности
и ползучести. «.Высшая школа», 1968.
4.	Б е р ез о в с к и й Л. Ф. О граничных условиях при рас-
чете пологих оболочек методом конечных разностей. В сб. науч-
ных работ института строительства и архитектуры АН БССР,
выгг 3. Минск, 1960,
5.	Березовский Л, Ф, К вопросу о расчете тонкостен-
ных пологих оболочек. Инж,-физ. жури,, т. III, № 5, I960.
6,	Боже нов А. Ш, Устойчивость квадратной пластинки
переменной толщины, сжатой в двух направлениях. «Приклад-
ная механика», т, X, вып, 6. Изд. АН УССР, 1961,
7.	Б о ж е н о в А Ш, Устойчивость прямоугольных пласти-
нок за пределами упругости. В сб.: «Сопротивление .материалов
а теория сооружений», вып. I. «Буд1вельник», 1965.
8.	В аз о в В., Форсайт Дж. Разностные методы реше-
ния дифференциальных уравнений с частных производных. ИЛ,
1963.
9.	В а й я б е р г Д. В., В ай н б с р 1 Е. Д. Пластины, ди-
ски, балки-стенки. Гоестройнздат УССР, 1959.
10.	В а й н б е р г Д. В., С и и я в с к и й А, Л., Д е х т я-
рюк Е. С, Итерационные алгоритмы и численные задачи тео-
рии пластин и оболочек Труды IV Всесоюзной конференции по
теории обо.ючек и плаепш, Ереван. 1Ьд. АН АрмССР, 1964.
11.	Вайнберг Д, В,, Ге р а ш е н к о В. М., Р о й т-
ф а р б П. 3., С. и и я в с к и й Л. Л. Вывод сеточных уравнений
изгиба пластин вариационным методом В сб,: «Сопротивление
материалов и теория соорУженигЬ-', зып. I. «Буд1велъник», 1965.
12.	В а й и б е р г Д, В,, В о р о ж к о П, И., Ройт-
фар б И. 3., С и п я в с к и и А, 51, Ра июсгные уравнения кон-
тактов задачи изгиба пластин. В сб : ' Сопротивление материа-
лов и теория сооружений', иып 11, ЛЛдшсльнмк», 1965.
1.3. В а й п б е р т Д. В , С и и я в с к п й А Л. Дискретный
анализ в теории плашин и оболочек Материалы VI Веесоюз-
ЛИТЕРАТУРА
169
гои конференции по теории оболочек и плзсти! «Нтукэ»
1366
И Вайнберг Д В Гуляев В И Конформное ото
брлжение и разностный мслод в з гачах о концен ран. ш напря
>1 ний В со < Конце нтрация и i чряжени > i i II «Пскова
2,\мка» 1967
h В а и п б с р г Д В I / а я ев В И Д е \ т я р ) к г С
Краевые -7апачи по югих а оя1 с к нпк их out ю к взаимол^и
ствующпх с опорными К НСТр}лЦИЯМИ В Ы <Р L пркграп
ственных конструкций» вып X] I Стройи пат 14 b
16	В а р в а к П М Рывит с и 1рил тис мстот сетол
к расчету ппасти юк i 1 II с АН АССР 1919
17	Варнак П М Устои трость тает о: пот де !ствием
сосредоточенных сил Доклады АН ЪССР V о Iе-’ )
18	В а р в а к П М Развитие и приложе ! ю метода сеток
к расчету пластнт ок ч II Пп АН ^ССР 19 2
19	Варнак	П М I у <	р м a i	И	О И иб кзалрат
чон пластинки с	различными леювиями	на	кртях В сб <11н
q орм	материалы	института ст	л it мех	АН	АССР» 19 7	10
90	В арв а к	П М I н	ео ч ан	Л	О М i р о н н и
ченко М. М П р е т. т е I с н с к и и Н Д Таб лицы тля рас
чета прямоугольных п in	!Ш АН УССР	!%9
1 Варвар А П	Пря ю7 го льны	плиты	ia угру	о 1
основании переменной серк ти ДАН АССР V К) 1953
22 В а р в й к П И	Рассказов	А О	Покрытие	из
оболочек в форме иперболического параболоида В сб «Про
стр лиственные конструкции в Крас ю> рслом ip^e» зып Ш
Изд Красноярского политехи нт та Р68
23 Василь в В В Oce.cn тметричнос xnpvro плас"И ie
ское состояние оболочек вращения «Пр (кл мех т VII вып 3
196]
24 Васильев В В К решению здда11 о концентрации
напряжении возле кр гового отверстия в ^фер t иСлОй оболочке
в упруго пластической стад in Труды IA Всесоюзной конферен
ции по теории оболочек и пласт 1 Нэд АН Ар 1 ССР Ере
ван 1964
2э В о р ош ко П П Сатаров А С Побх лова рюни
цевих р1вня ib теори пружиост! та ix одержавши на ЕОМ В сб
«Ошр матерзаюв i теорш слоруд вып IV БуД1вепьник> 1966
26 Геращенко В М П юбченьо С Н Складаиня
рюницених piB 1ЯН1 п ocsoi таори прул-л octi за дочомогою ва
рзащиного метолу В сб «Ошр млтерлалш i теор1я споруд»
вып V «.Ьущвелыпп » 196о
27 Г о н т к е в и ч В С Собственные колебантя пластинок
и оболочек «Наукова думка» 19о4
28 Г у л я е в В II О емм лннои задаче плоской теории
упругости В сб «Сопло ивле	I ie	мазер и	лов	и	теори я	соору
жений вып И «Буди ел ник	12	5
29 Гу л я е в В Н Дех	я	р 1 к	г	С	Програм	та ма
тричной прогонки д->я смете 1	ур	is ~н	и	Пул	IV7 Всссоюз
ной конференции по применению ЭЦВМ * строительной махани
хе мапгиг остроенин и строителю ом пр i водслв0 Киер 196о
39 I у л я с в В I Р о м а и и к о Ф О С п ня в
с ь к и и О Л Нюский пшрхжении стан 1 ctihkictb пластин
при зм июни грани ш ix м из х В сс «Ошр матер|ал1в j тео
р1Я гжрх1-» В11Л \ «Будве. ншк 191
31 Дту! ач АА И Мелоц сеток в смешанной плоской за
да ie теории хпрхгоеы- «Hi koi л) мк i 19бл
V I ы к шин А А П ласти iHocTi Гостехизцат 19^8
В К и с л о о I ий В Н
I епцние задач динамики пластин
числснн! ми се отлми В rf < Сопроы в ление матер илов и тео
рия соорх/кщми вып VIII Ьх д|веп1 ник» 1969
34 К ломиец И А Р течет т нк ix г'рпмощолыьх тил
заще’* пен mix в упруги koit>p Сб научных трудов в.-in
КИСИ |9(_
Зо Кору икни В С О растете ппямоу) опьных плит
на xnpyroi основании «Прикладная механика» т III вып 1
19о7
6 Пастернак П Л Основы нового метола рас юта
фундаментов на упруюм основания при помощи двух коэффи
циелтов постели Госс ройпздат 1954
37 П1скунов В Г До впзьакжя частот власних ко
ваш прямому "’них пласти юк
«Поив яехлнща» i X вып 1
при mi нних граничячх умовах
1J6I
38	П и е к 7 н о в В Г К за лат о колебаниях и устойчиво
сти параплеаогра imhux пластинок и м мешан «Прикладная ме
ханика> т I вып 3 19ьо
39	Романенко Ф О С и и л в с ь к и й О Л Инеем
не розвъязанпя узагальнено] задач пр вллсш значения В со
<Onip матерпив 1 теорш спорхд вып IV «Ь\Д1вел1 ник» 19ор
40	Сальз адори М Дж Численные методы в технике
ИЛ 19ээ
41	Филиппов А П Котебання механических к. ictgm
«Намкова демка 196о
42	Шевченко В Д Оо pai нениях для расчета поло
гих обо ючек «Прикладн я механика т VIII вып 4 19л2
43	Шевченко В Д О влиянии некоторых геометрию
ских пар1метров иа напряженно деформированное состояние по
аогих оболочек «Прикладная механика» т IX вып 4 1963
44	Шевченко В Д Нелинейная задача изгиба пологой
оболочки «Прикладная механика» т I вып 2 1965
45	Розин Л А Расчет гидротехнических сооружений на
ЭВМ Метод конечных элементов «Энергия» 1971
46	Филин А П Приближенные методы математического
анализа используемые в механике твердых деформируемых теп
Л Строииздат 1971
47	Справочник по теории упругости (для инженеров тропе
пси) Под ред П М Варвака и А Ф Ряоова «Вудшспьн ik» ,
1971
РАЗДЕЛ 16
МОДЕЛИРОВАНИЕ
16.1.	ОСНОВНЫЕ ПОЛОЖЕНИЯ ТЕОРИИ
ПОДОБИЯ И РАЗМЕРНОСТИ
Различают следующие виды моделирования:
1)	физическое моделирование, когда исследование ве-
дется на моделях (конструкциях, установках или уст-
ройствах), сохраняющих физическую природу изучаемо-
го явления. При этом соответствующие величины, харак-
теризующие явление, в прототипе (натуре) и модели
отличаются лишь количественно. Частным видом физи-
ческого моделирования является масштабное моделиро-
вание, когда модель изготовлена из того же материала,
что и прототип, но отличается от последнего размерами;
2)	математическое моделирование — это исследование
явлений на моделях иной физической природы, однако
имеющих такое ясе математическое описание, что и про-
тотип (электро-, гидроаиалогии и т. и.).
В настоящем разделе рассматривается только физи-
ческое моделирование У
Условия подобия, лежащие в основе моделирования,
устанавливаются путем анатаза размерностей величин,
характеризующих исследуемое явление (п. 16.2), или
анализа уравнений задачи (п. 16.3). В п. 16.13 приведе-
ны для различных задач критерии подобия и формулы
пересчета, полученные при помощи этих методов.
Напряженно-деформированные состояния двух тел
называются подобными, если напряжения, деформации,
и.’ремепишия и другие величины, характеризующие изу-
чаемое явленье, в сходственных точках этих двух тел
в сходственные моменты времени связаны соотношениями
вида
(16-0
З.	ъсь ап и —значения рассматриваемой величины
соответственно дтя натурного обт.екта п модели; та—'
масштаб этой величины
Вопросы теории подобия связаны с теорией размер-
ностей Размерность дшшоч величины записывается сим-
волически с помощью букв,, прнсво- иных основным еди-
ницам измерения Так, например, ес.та Р означает еди-
ницу силы, a L—единицу длшчз то размерность напря-
гкения выражается формулой
Размерносги нескольких пассмаз рпваемых величин
могут быть нз'щмно зависимыми и независимыми. Неза-
висимость размерностей ошачает, что формула, выра-
жающая размерность однон из величин, не может быть
представлена как комби.’,.и 'я в виде степенного одно-
члена из размерностей других рассматриваемых вели-
чин. Например, р;ымер1и>' ; (I л-шны (А), скорости
[ЕТ~^] и напряжения [PI ’3) ш шгисимы, так как
при плых значения а и р. Раз-
мерности длины [/.], изгибающего момента [РЕ] и на-
j[ пряжения [РА"3] зависимы, так как можно подобрать |
такие значения показателей степени а и Р, при которых
( справедливо соотношение L—(PL)a (PL-rf (в данном
" случае «='/3, $ = -—фз).
Кроме размерных величин могут быть безразмерные.
При переходе от одной системы единиц к другой числен-
ные значения размерных величин изменяются, безраз-
мерных — не меняются.
। Будем различать простое и расширенное подобия. При !
(простом подобии масштабы всех безразмерных величин 1
•равны 1, а все величины, имеющие одинаковую размер-
Тюсть (например, напряжения, модуль упругости и на-
грузка, распределенная по поверхности), моделируются
в одном и том же масштабе. При расширенном подобии
безразмерные величины могут моделироваться в мас-
штабе, не равном единице, а разные величины одинако-
вой размерности могут иметь и отличные друг от дру-
га масштабы.
Расширенное подобие, в свою очередь, может быть
двух видов: аффинное ч нелинейное [1], Аффинное—‘
это такое расширенное подобие, при котором масштабы
всех величин постоянны в пространстве и во времени.
Нелинейное — эго такое расширенное подобие, при ко-
тором масштаб хотя бы одной величины изменяется в
пространстве или во времени.
При простом подобии безразмернысрстепенпые кошь
лексы, составленные из величии, характеризующих со-
стояние В сходственных точках и в сходственные момен-
ты времени, соответственно друг jipyry равны. Это по-
ложение составляет содержание так называемой первой
теоремы подобия.
Так, например,
где о — напряжение; Е — модуль упругости; р. —> коэф-
фициент Пуассона; и — перемещение; х — координата;
е — относительная деформация.
Для удобства (особенно, когда рассматривается ие
два, а группа подобных состояний тел) зависимости
(16.2) принято записывать в виде
— = idem*; р. = idem**; — — idem; idem. (16.3)
£	х
Если величины, входящие в критерии подобия, заме-
нить соответствующими масштабами т, то получим
1 По Bonpocav электрического моделирования см. [2, 5, 9, 12].
* idem (лат.) означает «одинаковый», «один и тот же®,
’* Критерий подобия Пуассона.
16 1- ОСНОВНЫЕ ПОЛОЖЕНИЯ ТЕОРИИ ПОДОБИЯ И РАВНОМЕРНОСТИ
171
степенные комплексы, которые в теории подобия назы-
ваются индикаторами подобия;
«о
—; т„
тх
; т.
tnF ’ '"и ’
Из первой теоремы подобия вытекает, что для подоб-
ных состояний тел все индикаторы~йодобия равны еди-
нице:
тд
-~~г~ = 1;	= 1; — = 1; т„ =1.	(16 4)
тЕ	u тх	Ех	'
Из уравнений связи между масштабами (16.4) следу-
ем, что в случае простого подобия все безразмерные ве-
личины натуры и модели должны быть соответственно
равны (например, коэффициенты Пуассона ц, компо-
ненты деформации е и у) Масштабы остальных (т. е.
размерных, величии должны удовлетворять уравнениям
(16 1). Поскольку этих уравнений в общем случае мень-
ше, чем входящих в них масштабов, часть масштабов
выбирается произвольно, а остальные определяются в
соответствии с (16.4). Вопрос о том, какими именно
масштабами задаться, решается в каждом конкретном
случае в зависимости от содержания задачи.
Существует несколько путей получения критериев по-
добия. Один из них основан на знании размерностей
всех величии, характеризующих исследуемое явление.
В общем случае из величии, характеризующих сосюя-
ние тела, можно образовать множество безразмерных
комплексов (критериев подобия). Однако известно впол-
не определенное количество независимых критериев по-
добия, с помощью которых можно получить все осталь-
ные безразмерные комплексы.
Согласно так называемой л-теоречс количество неза-
висимых критериев подобия п определяется выражением
п =- «1 4~ щ — п3,	(16.5 )
где «| — количество размерных величин; щ— количест-
во безразмерных величии; п, — количество величин, об-
ладающих независимыми размерностями (щ^щ).
Изложенный подход к определению критериев подо-
бия называется методом анализа размерностей. До-
стоинство э1ого подхода в том, чю он позволяет иаиги
критерии подобия без привлечения уравнений рас-
сматриваемой задачи. Важно лишь знать все величины,
характеризующие изучаемое явление.
Метод анализа размерностей применим только для
простого подобия.
Второй способ получения критериев подобия основы-
вается на использовании уравнений, описывающих ис-
следуемое явление. Для этого обе части каждого из
уравнений делятся на один из членов-слагаемых. По-
лучаемые при этом в виде слагаемых степенные комп-
лексы и есть критерии подобия. Кроме того, критерия-
ми подобия являются аргументы всех трансцендентных:
функций, входящих в уравнения.
Сопоставляя полученные критерии подобия, в каждом
конкретном случае можно определить, какие из них
независимые.
Например, одно из уравнений обобщенного закона
Гука
1 ,
д --ук'-й (Од 1 д)]
может быть преобразовано к виду
1 - 0Г  И Д' _ Р’П
чх Е ел. Е ех Е ’
откуда находим критерии подобия:
----= idem; ’—— = idem; ------- = idem.
ед £	'е‘х E	ел E
Ести уравнение содержит дифференциальные или ин-
тегральные операторы, то перед lev. как производить
деление на один из членов-слагаемых, знаки дифферен-
циалов и интегралов надо опустить. Например, гз урав-
нения
получаются следующие критерии подобия:
т4( х	.Хх
—-—	idem; — — idem,
Д У	<Е.
а из уравнения
ду- 1 дх~ дх dy
получается
У хи У ,,
-э---= laem;-------idem.
ед. х2	ez х
До сих пор рассматривались соотношения между т.-
личинами в заведомо подобных состояниях тет Рас-
смотрим теперь обратную задачу — какие условия ц-'об-
ходимо и достаточно выполнить, чтобы тОСЮЯИИЯ тет
были подобны. Согласно третьей теореме подобия (тео-
реме М. В. Кирпичева — А. А. Гухмана [6]) эти усло-
вия таковы:
1) сосюянля обоих тел описываются уравнениями
одинакового типа;
2) для обеих тел соответственно равны дпуг другу
независимые критерии подобия, которые составляются
из величии, входящих в условия однозначности (г. е.
единственности) рассматриваемых состояний. Крите-
рии подобия, составленные из величин, входящих в ус-
ловия однозначности, называются определяющими.
Рассмотрим оба эти требования.
Осиовиы.ми уравнениями, определяющими тог или иной
класс задач механики сплошной среды, являются диф-
ференциальные уравнения равновесия (движения), урав-
нения связи деформаций и перемещении (или уравне-
ния совместности деформации), условия однозначности
перемещений для многосвязных тел, а также уравне-
ния связи напряжений с деформациями н с их скоро-
стями. Все уравнения, за исключением последних, явля-
ются общими для всех задач мехапи’гч тпгопшой сре-
ды. Уравнения связи напряжений с деформациями фор-
мулируются по-разному для упру тих задач при малых
и бо гьших деформациях, для задач вта^гнчлостч, пол-
зучести и т. п. Поэтому для выпо.тпепия первого усло-
вия третьей теоремы подобия щ обходимо, чтобы урав-
нения связи напряжений с деформациями для материа-
лов модели и натуры имели одни и гот же вид.
Единственность (однозначность) решения пити оп-
ределяется граничными и шшалыплии условиями, а так-
же нагрузками, распределенными по объему. Граничные
условия определяют нагрузки или перемещения Нч гра-
ницах тела, а начальные условия — состояние в началь-
ный момент времени.
172
РАЗДЕЛ 16 МОДЕЛИРОВАНИЕ
Таким обпазом в условия однозначности должны вхо
дить следующие параметры и зависимости
1)	геометрические характеристики тела или системы
тел—безразмерные геометри теские параметры Р (углы
и др) и линейные паоаметры lt = ^ I где cpzz,(i=l
2	)—безразмерные коэффициенты с помощью кото
рых любой размер тела выражается через один харак
торный размер I
2)	физические характеристики материалов образую
ших рассматриваемую систему (поскольку первым тре
бовапием третьеи теоремы подобия установлена иле!
тичность вида уравнении но не численное совпадение
входящих в них параметров) коэффициент Пуассона р
модуль упругости Е плотность р предел текучести От
"редел пропорциональности <тПц модуль упрочнения Е*
коэффицю! т линейного расширения а удельная тепло
емкость с коэффициент теточроводнос’и Лит п,
3)	вели ш№ входящ! е в граничные услов тя сосредо
точенные силы Д, = ср(/)Д моменты А4,=рр(М| /И на
грузки распределенные по линии q =ср,(<7^ (злись <щ—
безразмеовые коэффициенты с помощью котор 1.x каж
дая на1рузча может быть выражена церез один хаоак
тернын параметр — соотзе'”'гвеино силу Р момент Л1
или интенсив гость q) нагрузки распределенные по го
верхности X Y Z заданные перемещения на контуре
Ui vK
4)	нагрузки распределенные по объему X Y Z
5)	начальные условия в которых искомые фут кции
задаются в исследуемом обдатои в начальный момент
времени
Во всех приведенных вьше рассуждениях имелось
в виду так называемое полное л шейное подобие когда
условия подобия (16 1) соблюдаются для всех в< личин
характеризующих исследуе гое явление
О’нако условия полного подобия олазыв ютСЯ вссь
ма жесткими Соблюдшие их пр i моделнро! ни и го
многих ступях сопряжено с больпими трудностям! и
н все гд 1 нес бходгого Поэгочс hi практике часто при
бегают к моде ироааиию основанному п неполном ио
добии В эт!х случае х условия io юо я соблюдаются нс
для всех вс шчин характернаюн их исс едуемое явле
ние а гол!ко для яекэюрых i л хоте веипых точках
натуры и голе ш пене шо pa iiimi iro шнмаются кри
mj ни подобия со тавле гн те из в 1ичи i относительно
tvoiopn стремятся соблюсти под one При этом созиа
ТсТ но илу1 на го что относите лы о других величин
пот.ооие оу д г нлрхшшо Однако г г oi подход трсбуе-
осторожности в ясного по шмалю существа здлач
Room н полного часто иеголюзустея приближенное
1годоби С\щпог'л,ь его состоит в отк и от учета н°ко
топых ф 1к оров егит ит ию в 1НЯЛЩ тх I а напряж н
цо I с ne I нов г по° состоя! и тел i in] и гор во мио
гну \ । ч г 1 с у 1 о едя соеспп и ш i вес тс ia и т п )
16’ ПРОСТОР ПОДОБИЕ СТАТИЧЕСКИХ
VHP'ТИЧ состоянии
МЕТОД АНАЛИЗА РАЗМЕРНОСТЕЙ
Опр делим истов 1я подобия напряженно десрормиро
ванн х состояние олгорошых тзотроппых упругих гоа
в спх к малых сфориаши при з ща ших in контуре
пт ст г тчеслих нагрузках или перемещен !я\
°а । I мае тезрз м пн го гтоичнни всходящие в ус
ловил однозначности и являющиеся критериям i подо
бия
(ф = idem <p(Z) ~ idem ц =
ет у (Р) - idem
<р£(Л1) idem ср^' = item
(16 6)
Запицюм все входя ц ie в ус говия одиозна шести j гз
мерные в wiiiiii с их р пмерпост тми /[/	/ \Р1 *•]
Р[Р] М [KE] q[Pl 1] ~X[PL 2] Т]££ ’] 7|Д/ 2]
и [Е] vhlL] ш [и] ' A[W-3] У [Pl 3] 7[PL 3]
Всего размерных bctihih 14 из них две зс i iniHii
ironp пн р I и £ имеют шзагтсихые разм рности Таким
ооразом доп тнитсльно к (16 6) можно поручить 14 —
—2=12 независимых критериев подобия
Р	Л4	q	X ,
— = idem1, — — idem----------------= idem — = idem
— = idem — = irem —— = idem —— = i em |
L	F	I	I
XI	УI	71
---— idem — = idem —— iem —1 = i lem
/--Г	Г	Г	I
Критериям подоб ия (16 6) — (16 7) соответствуют еле
дующге уравнения связи между масшт1бами соответ
стгующ ix величин
т- ~ т = т~ п — гг — т
1	7 к	к
— mz ,	(16 9)
а шесп ураннспи i с 1язи
тР ; m w ( та = j
т т]	тг n’i	~rF т
т-r	'Р i	m-i т,
Л = 1	= 1	= 1
ОТ/	«	тЕ
(16 10)
содержат восемь масштабов Зил шт любые дв 1 маси та
ба могут быть RHooaiii фоизволпо а остальные
шесп м 1спп 1бо опрс готяются из уравнении (16 10)
Таким образом псоолоихпв и и достаю гными ус го
виями простого подобия пространственной задачи тео
pin хпрхгосги являются следуютie
1)	модел! и про тог in должны бить геометрически по
добннми
2)	коэФфипплцт ’ Пуассона ддя маторг ала vov 1
и л tipia л прототипа долил н оыть равны Прт э ом
Кпитерий петпбия Г хп
16 3 РАСШИРЕННОЕ ПОДОБИЕ В СТАТИЧЕСКИХ ЗАДАЧАХ ТЕОРИИ УПРУГОСТИ
173
выбор материалов обусловливает и масштаб модулей
продольной упругости ту,
3)	все нагрузки, действующие па модель, должны на-
ходиться в таком же отношении одна к другой, как и
соответствующие нагрузки, действующие па прототип;
4)	поскольку выбор материала для модели определя-
ет масштаб то для пр->чтиольного выбора остается
только один масштаб: либо масштаб /ьч, либо масштаб
одного из видов нагрузки, например сосредоточенных
сил тР.
В случае произвольного выбора масштаба т, нагруз-
ки должны моделироваться в масштабах mr~mynj;
myi — mr.mp т^ — тцтг, т^=ту = т^-~тр
т х = Mr = "б ~ т tdni(, а заданные перемещения на
контуре — в масштабах т«к = лгек = т-,тл ^тп., При
этом напряжения будут моделироваться в масштабе,
равном гпц, перемещения — в масштабе т , а деформа-
ции в модели будут равны соответствующим деформа-
циям прототипа.
При .произвольном выборе масштаба т;, лиш.лЬгый
1/
масштаб модели оказывается равным mi -= |/ — ,
' Е
нагрузки должны моделироваться в масштабах т и ~~
_____2_
= тР тп ; т„=у т т ; ш- ~tn-. = tn- =-т ; т —
Е	р , д t Е р, д.	7 Е, *
з I
=-тх =rnz~m тр~, а заданные перемещения па_«ои-
т/ р
туре — в масштабах тц ~ т,: = try, — I/ — .
lx	К	77/ jjp-
В этом случае папряж< пня будут моделяровиться в мас-
штабе, равном ту, m ремещеинч — в масштабе =
/~ га р
= mv = mw—~l/ ------ , а деформации в модели будут
У ш i
равны соответствующим деформациям прототипа.
16.3.	РАСШИРЕННОЕ ПОДОБИЕ
В СТАТИЧЕСКИХ ЗАДАЧАХ
ТЕОРИИ УПРУГОСТИ. АНАЛИЗ УРАВНЕНИИ
При моделировании может быть поставлена задача
определения не всех величин, характеризующих явление,
а только некоторых. Например, часто требуется опреде-
лить только компоненты напряжений. В связи с этим
возникает вопрос, можно ли упростить моделирование,
обеспечивая подобие по напряжениям и не заботясь
о соблюдении подобия по деформациям и перемещени-
ям. Разумеется, такая постановка задачи возможна
лишь при малых упругих деформациях, когда изменени-
ем конфигурации тела п перераспределением напряже-
ний в процессе деформирования можно пренебречь.
Выявление условий расширенного подобия проиллю-
стрируем па примере первой основной задачи теории
плоского напряженного состояния.
в этом случае определяются уравие-
упругости для
Напряжения
ниями:
(16.11)
Здесь рх = const; р,( = const.
В случае неодносвязного тела к уравнениям (16.И)
должны быть добавлены условия однозначности пере-
мещений:
"sl2>
Здесь интегрирование распространяется на любой
замкнутый контур, не пересекающий контур тела; s —
длина дуги этого контура. Пользуясь формулами Коши,
можно подынтегральные выражения записать через де-
формации, а последние заменить напряжениями, вос-
пользовавшись законом Гука. В результате можно
прийти к следующим выражениям однозначности пере-
мещений:
ф j\or+ov) cos (sx)+y ~ (ох + оф ds = j
= —(1+В)Лн	|	(16.13)
ф (ОД+<Ф cos (57)—-х ----- <оф- о„) ds = j
J [	рп	 J	I
= (1+р)ф.	’
Здесь п — нормаль к линии интегрирования; Rx, Rv —
составляющие равнодействующей усилий по замкнутому
контуру.
Рассмотрим сначала одиосвязное тело или многосвяз-
нос тело, у которого главный вектор внешних нагрузок
по каждому замкнутому контуру равен нулю. 3 этом
случае в условия однозначности рассматриваемой зада-
чи входят только геометрические параметры тела н на-
грузки Значит, материал модели может иметь произ-
вольные упругие постоянные, а сама модель должна
быть геометрически подобна прототипу, причем линей-
ный масштаб mi может быть выбран произвольно Так
же произвольно можно выбрать масштаб одного из ви-
дов нагрузки, например сосредоточенных сил тР Дру-
гие вилы нагрузки должны моделироваться в соответ-
тр
ствуюшпх масштаба.х т.« =тРт,; та = — ;
mi
т р	Pip
т- = т- = т„ — т„ = —т-.
X V т] рх ри т[
При соблюдении этих условий компоненты напряже-
ний будут моделироваться в масштабе та = т„ =
л щ
тр
= т = —у.
XI/ ГГГ[
Выясним, как при обеспечении подобия только по на-
пряжениям будут моле тироваться деформации и пере-
мещения.
Записав закон Гука для материалов модели и прото-
типа, после ряда преобразований получаем выражения
для масштабов компонентов деформаций тп , т_
И		/72g —	trip	^Х, м		Ф,м			
			тЕ mi		|ф	%,М			
			тР						(16.14)
		,ПУ -	mEm2i	ф,м		°Х.м ’			
		m - vxy	тр тЕ	1 Ч~ М-н 1 + Вм					
174
РАЗДЕЛ 16 МОДЕЛИРОВАНИЕ
Таким образом, при соблюдении указанных выше ус-
ловий подобия полей напряжений в первой основной
плоской задаче теории упругости поля углов сдвига
У»» будут аффинно подобными, а масштабы те и тг
будут функциями координат, т, е. поля относительных
продольпы.х деформаций ел и е„ будут нелинейно по-
добными.
Если же к рассматриваемым условиям расширенного
подобия добавить требование о равенстве коэффициен-
тов Пуассона материалов прототипа и модели, то поля
относительных продольных деформаций ех и е„ ока-
жутся аффинно подобными и все компоненты деформа-
ций будут моделироваться в одном масштабе
/Лр
т„ ~ т„ =- тг ~~ -----:
х ~ч тЕт^
При моделировании, когда тг, = 1,
Ир
т„ = т„ = mv = —ф- .
х и Пл т2
Для масштабов перемещений можно получить зависи-
мость
т =	тл <
«	X	" 1
т =--	т,, |
в	Д 1 J
(36.15)
т с. поля перемещений будут нелинейно подобными
при
При равенстве коэффициентов Пуассона материалов
прототипа и моде ш компоненты перемещений будут
моделироваться в масштабе
тр
ти =-= mv = ------------------- ,
а при тг — 1 т --= т — -—- >
1	£	и V П11
Отметим, что при Ци^Цм от напряжений в модели
может быть совершен непосредственный переход к на-
пряжениям в прототипе. При этом масштаб напряжений
равен масштабу нагрузки, распределенной по поверх-
ности. Переходить в этом случае от деформаций и пе-
ремещении модели непосредственно к деформациям и
перемещениям прототипа нельзя, так как масштабы де-
формаций и перемещении переменны в исследуемой об-
ласти,
Если моделируется многосвязное те то, у которого
имеется хотя бы один замкнутый контур, где главный
вектор внешних нагрузок не равен нулю, то кроме уже
рассмотренных величин в условия однозначности дол-
жен войти коэффициент Пуассона р [из условий одно-
значности перемещении (16.13) ]. В этом случае условия
подобия полей напряжений должны быть дополнены
требованием равенства коэффициентов Пуассона мате-
риалов прототипа и мотели. Аналогичное требование
должно выполняться и при исследовании второй основ-
ной и смешанной задач теории упругости.
Толщина плоской модели может быть выбрана неза-
висимо от линейного масштаба т,. Однако чрезмерно
большой толщину пршщмпь не следует во избежание
появления отклонении от плоскою напряженного состо-
яния, т. е. возникновения неравномерности распределе-
ния напряжений От, <т,. ч т,, по юлщине модели и воз-
никновения во внутренних слоях модели напряжений
Щ, Тх; И тих.
16.4.	О ВЛИЯНИИ КОЭФФИЦИЕНТА ПУАССОНА
НА РАСПРЕДЕЛЕНИЕ НАПРЯЖЕНИЙ
Во МНОГН.Х случая.х распределение напряжений в упру-
гих телах зависит от величины коэффициента Пуассона.
Поэтому при моделировании, строго говоря, необходи-
мо подбирать материал модели так, чтобы соблюдать
равенство этих коэффициентов у материалов прототипа
и модели. Практически это условие часто трудно выпол-
нить, поэтому возникает вопрос о величине возможных
погрешностей, вносимых несоблюдением критерия Пуас-
сона, и о путях соответствующей корректировки резуль-
татов исследования.
При исследовании плоски задач принципиально воз-
можна корректировка результатов исследования при по-
мощи испытания второй модели с другим коэффициен-
том Пуассона Тогда для определения напряжений в на-
туре можно воспользоваться выражением
_ тР, 1 Q ^141) (Д,-Им,.?) _
°Х’Я^ ml\ (1 ~Ин)(.11м,1 ~-Нм,2) J*M’!
, «У, (} -11m,2)(Eh~Em,i)
------------------------- ff я (16.16)
т1,2 (! -Ан)(Мм,2- Мм,1)-л’2
Здесь индексом «1» отмечены величины, относящиеся
к первой модели, а индексом *2» — относящиеся ко
второй модели.
По аналогичной формуле можно опред чтить и другие
компоненты напряжений аВ1Н и Тх,л!1.
Формула (16.16) записана для случая плоской дефор-
мации, Если имеет место обобщенное плоское напряжен-
ное состояние, то соответствующий коэффициент Пуас-
сона должен быть заменен в (16.16) на величину
(16.17)
1 -Ни
Практическая реализация этого подхода связана
с трудностью точного определения значений коэффици-
ента Пуассона. Поскольку значения коэффициентов Пу-
ассона модельных материалов находятся в довольно
узких пределах, то гошоегь определения напряжений
при помощи выражения (16.16) обычно невелика.
Часто при исследования плоских задач влияние раз-
личия коэффициентов Пуассона на величины напряже-
ний незначительно. Однако в некоторых случаях оно
может быть большим (например, для плоской задачи
о нагружении бесконечной плоскости сосредоточенной
силой).
Менее изучено влияние коэффициента Пуассона на
распределение напряжений в пространственно-напря-
женных телах. Известно, что оно зависят от характера
изменения суммы нормальных напряжений по точкам
объема тела. Чем более плавно изменяется величина
этой суммы, тем меньше погрешность, вызванная раз-
личием коэффициентов Пуассона, В частности, в ци-
линдрическом теле, подверженном чистому кручению,
когда сумма иормалы!Ы.х напряжений постоянна (рав-
на нулю), распределение напряжений не зависит от ко-
эффициента Пуассона Как правило, наибольшая по-
грешность, вызванная различием коэффициентов Пуас-
сона, получас гея при определении меньших по абсолют-
ной величине главных напряжений.
16.5.	О МОДЕЛИРОВАНИИ ОБЪЕМНЫХ СИЛ
Выбор для модели материала, у котового коэффици-
ент Пуассона такой же, как и у материала прототипа,
предопределяет масштабы модулей продольной упру-
16 6 ПОДОБИЕ Б ДИНАМИЧЕСКИХ ЗАДАЧАХ ТЕОРИИ УПРУГОСТИ
175
гости ms и объемного веса гр. А это, в свою очередь,
означает, что для все.х остальных величии масштабы
уже не могут быть выбраны произвольно, и каждые из
этих масштабов определяется величинами щЕ и т^. При
этом линейный масштаб модели
mF
=	(16.18)
Может оказаться, что линейный масштаб модели, опре-
деленный по формуле (16.18), будет неудобным или
технически трудно осуществимым. В этом случае мож-
но произвольно выбрать линейный масштаб модели т;,
но тогда в соответствии с выбранным nil надо будет
обеспечить и соответствующий масштаб объемных сил
__ тЕ . что может быть достигнуто с помощью
"у mi
центрифуги.
16.6.	ПОДОБИЕ В ДИНАМИЧЕСКИХ ЗАДАЧАХ
ТЕОРИИ УПРУГОСТИ
Из основных уравнений динамики упругого тела вы-
пишем величины, входящие в условия однозначности,
и их размерности: X[PL~a], плотность р[Р£-4Тг],
ФИ. р[1].
К этим величинам надо добавить величины, входящие
в граничные и начальные условия, которые рассмотрим
применительно к трем основным задачам.
а)	Первая основная задача. Па поверхности S тела
во все моменты времени начиная с t0 заданы нагрузки
Х = Д; Y=fi Z=-f3,	(16.19)
а в области V, занятой телом при t = ta, начальные ус-
ловия
/ du \
«=«о. v = v0; w = ш0;	и0=- — 1
\ dt /о
а0 =-
\ Л Д
(16.20)
Здесь f|, fs, — функции, заданные на поверхности те-
ла и зависящие также от времени; и0, v0, wa, u0, су, ®0—
заданные функции от х, у, г
Выпишем все величины,
значности первой основной
£р£-* 2], g[i], ?[Р] п
М7.Т-1].
Отсюда можно получить
добия:
Р
ti = idem; ---=-= idem;
ЕР
pF ш
— •= idem;
ЕР
входящие в условия одно-
задачи: АД Ию3], р[А£-4ГД,
1[Ц, время ДА], »о[£],
определяющие критерии по-
ЛР	и,
— = idem; — = idem;
Р	I
= idem,	(16-21)
* В целях единообразия записи__критсрисв подобия вводится
сосредоточенная сила Р вместо Л' (У, Z), поскольку масштабы
,->тих величин связаны мелзду собой зависимостью
nip
~ ------------.
2 “1
которым соответствуют
между масштабами
следующие уравнения связи
пц
тР г yvy
тр m"t ml
1.	(16.2 b)
В зависимостях (16.21) первые четыре критерия по-
добия — это уже полученные ранее критерии подобия
для статической задачи, остальные два — специфические
критерии подобия динамической задачи.
б)	Вторая основная задача отличается от первой
только тем, что граничные условия (16 19) заменяются
следующими условиями на поверхности S:
Щ. = О: = Л; шк=-Е3,	(16.22)
где Д, F2, Fs — заданные функции на S, зависящие так-
же от времени.
Для второй основной задачи в условия однозначно-
сти войдут следующие величины: .YjlPZ.-3]; р[Р£-№];
£[Р£-Д; р[1]; Щ£]; /[£]; ДГ]; <]; фП1]-
Отсюда можно получить определяющие критерии по-
добия
«к	., ХР
ц = idem; — = idem.; —— — item;
I	Е
Un	f>P	Unt
—p = idem; pp = idem: — -idem, (16.23)
которым соответствуют следующие уравнения
между масштабами
связи
«ЧК тх	тио
т = 1; ------= 1; ------= 1; ----- = 1;
и	тЕ	Ш
(16.24)
в)	Смешанная задача, где на части поверхности да-
ются условия (16.19), а на другой части — условия
(1622).
Для этой задачи в условия однозначности войдут все
те величины, которые входили в первые две задачи Из
них можно получить следующие определяющие крите-
рии подобия:
Р	ХР
и. = idem;----= idem; — = idem;
и	ЕР	Р
—р = idem; р~ ~ idem;
(16.23)
рР ш Ut>t ж
— = idem; — —idem,
ЕР	I
которым соответствуют уравнения связи между масшта-
бами
тр	т„к
ЯД = 1; -------- = ];--------— 1;-------= ];
тЕ m~i	тр	т1
^=1- т" 1 т“п mt
тЕ tn“t mi
(16.26)
176
РАЗДЕЛ 16 МОДЕЛИРОВАНИЕ
Зависимости (16.20), (16.23) и (16 25) свидетельству-
ют о том, что при моделировании динамической задачи
необходимо соблюдение уже встречавшихся ранее кри-
териев статического подобия [это первые четыре кри-
терия в (16.20), первые четыре — в (16 23), первые
пять — в (16.25)|. Сверх того в динамических задачах
надо обеспечить соблюдение еще двух критериев. Эти
дополнительные динамические критерии одинаковы для
всех трех краевых задач:
рр » uat ..
	— idem ;	— idem
Et~--------------I
При малых упругих деформациях мо/кно отказаться
от соблюдения требования тъ— \.
16.7.	ПОДОБИЕ В ЗАДАЧАХ ТЕРМОУПРУГОСТИ
При экспериментальном решении шдач термоупруго-
сги необходимо для моделей и проготипа обеспечить
подобие температурных полей и по-ей напряжении,
деформаций и перемещений
Условия подобия нестационарных пмпературных по-
лей в геометрическн подобных телах получаются из
рассмотрения уравнения теплопроводности Фурье. Для
твердого однородного тела при наличии в системе внут-
ренних источников тепла это уравненье inicei
вид
(16.27)
ат =
где Т[Го]—температура; /[7] —время;
X
—	[L27’~i]—коэффициент температуропроводности;
?,[Р7ф17 ~~"1 J — коэффициент теплопроводности;
c\L'lp} '] — удельная теплоемкость; у [Д'/--3]—удельный
вес; y[L], z[L]—координаты; qr [PL-~T~ *[ —
плотность внутреннего источника тепла (количество теп-
ла, выделяемого источником в единицу объема за еди-
ницу времени)
Здесь и в дальнейшем в формулах размерности сим-
вол Т соответствует единице времени, То — единице
тем перату ры
Если состояние тела стационарное, то
(16.27) принимает вид
уравнение
(16.28)
Потаг-нм, что физические
не зависят от температуры.
Путем анализа уравнения
подобия
ОуП .
-А- — idem ;
харамеристики материала
(16.27) получаем критерии
=. idem. (16.29)
В (16.29) записаны не все критерии подобия, а толь-
ко те, которые понадобятся в дальнейшем При этом
ввиду соблюдения геометрического подобия координаты
замен чы характерным линейным размером I.
Дтя го: о чтобы полностью решить вопрос об условиях
подобия температурных полей, необходимо в дополнение
к уравнению (16.27) рассмотреть граничные условия,
которые могут быть трех видов.
* Критерий тюяобяя Коши.
Критерий ГОМОХРОННОСТИ
Критерии подобия Фурье (критерий тепловой гомохрон-
ности)
Граничные условия первого рода характеризуются
тем, что на поверхности тела задается температура Т
как функция пространственных координат и времени.
Граничные условия второго рода определяются зада-
нием на поверхности тела удельного теплового потока
/, дТ	\
А —, где п — нормаль , как функции пространст-
\ fA's	]
ВСНПЫ.Х координат и времени.
Граничные условия третьего рода задаются в виде
температур сред, окружающих твердое тело, и коэффи-
циентов теплоотдачи ат от этих сред к поверхности
тела
Заметим, что все величины, входящие в граничные ус-
ловия первого и второго рода, фигурируют в критериях
подобия (16.29) и только граничные условия третьего
рода добавляют к величинам, входящим в условия од-
нозначности, новую величину <1т[РТ~~[Т	.
Следовательно, при моделировании задачи на основе
граничных условий третьего рода к (16,29) добавляется
еще один критерии подобия
I
—г—	idem*’.
(16.30)
Обратимся теперь к вопросу о подобии полей напря-
жений, деформации и перемещении при уже обеспечен-
ном подобии температурных полеп прототипа и модели.
При простом подобии в условия однозначности зада-
чи войдут величины- /[А], ц[ 1 ], E[PL~~Z], Z’fZ'nJ и ко-
эффициент линейного расширения а[Г^1 ]. Отсюда мож-
но получить два критерия простого подобия
р — idem; аТ = idem.	(16.31)
Рассмотрим теперь условия расширенного подобия
Для простращтвепноп задачи остаются в cine обычные
уравнения равновесия и .зависимости зижду перем-ще-
ииями и деформациями. Закон Гука имеет вид
Е
(16.32)
-----г
Е
уравнений (16 32) получаем критерии по-
р =- idem
Из анализа
добня по напряжениям:
пх
-----= idem;
ЕаТ
Условия (16.33) в сочетании с требованием геометри-
ческого подобия определяют подобие по напряжениям
для пространственной задачи термоупругости.
Аналогичным образом, проведя анализ общих уравне-
ния термоупругости, можно доказать, что для плоской
задачи достаточно обеспечить только геометрическое по-
добие
Если кроме изменения температуры на тело действуют
и нагрузки, то, наряду с критериями и условиями тер-
моупругого подобия, должны быть учтены критерии и ус-
ловия подобия, соответствующие нагрузкам.
(16.33)
16.8.	МОДЕЛИРОВАНИЕ БОЛЬШИХ ДЕФОРМАЦИЙ
Для определения связи деформаций с напряжениями
в качестве одного из возможных соотношении восполь-
* Критерий Био (критерий краевого подобия).
16 9 ПОДОБИЕ Б ЗАДАЧАХ ПЛАСТИЧНОСТИ
177
.дтчся рядом Муни [3]. Если улсроать дня тепа это-
го ряда, то ho.ij.4Hti
, 2а,	,	1
о = 2.4, V - --у- + 4/Ц В - 4.В,	+ р
}~	'
(j 1,2,3),	(16.34
где о, — главное напояженис; f..j — степ; ль удлинения:
тсрнстики среды.
В условия однозначности рассматриваемой задачи
входят те же величины, чго и в случае малых деформа-
ции, за исключением Е и у, вместо которых здесь всхо-
лят другие физические .характеристики среды:	”2],
B2\PL-aj, .44[РЕ-‘’], В4]АЛ-В. Соыветствующие этой
задаче условия (критерии) подобия укатаны в табл.
16.13 При соблюдении этих условий будь: сохраняться
геометрическое подобие прототипа и модели и в дефор-
мированном состоянии, что при больших деформациях
является обязательным (в отличие от малых).
В некоторых случаях условие равенства деформаций
модели и прототипа необходимо соблюдать и при малых
деформациях Сюда относится, например, тот класс кон-
тактных задач, где поверхность контакта существенно
изменяется в процессе нагружения.
16.9.	ПОДОБИЕ В ЗАДАЧАХ ПЛАСТИЧНОСТИ
В задачах пластичности в условия однозначности вхо-
дят следующие величины и зависимости.
1)	геометрические параметры тела;
2)	физические характеристики матерна ш Еф-РСТ2],
ц[1], кривая зависимости n,-=f(r,A, г.ш г, интенсив-
ность напряжений; с,—интенсивноегь деф ,'рмаций; фи-
зические характеристики материала фигурируют в рам-
ка.х классических теорий пластичности, деформационной
и теории течения Рейсса;
3)	история нагружения. В классической деформацион-
ной теории история нагружения не находит прямого от-
ражения, а предопределяет лишь области ее примени-
мости.
Следовательно, для обеспечения подобия при модели-
ровании задач пластичности требуется соблюдение гео-
метрического и силового подобия, равенство коэффи-
циентов Пуассона для прототипа и модели, а материал
модели должен характеризоваться кривой о,— ((е1),
которая подобна аналогичной кривой, описывающей ма-
териал прототипа, т <?. в сходственных точках этих кри-
вых с, м; а. п^=тй)1 -ч. Для обеспечения подобия
истории нагружения необходимо, чтобы все критерии
силового подобия были соответственно равны в сход-
ственные моменты времени.
Аналогично могут быть получены условия подобия и
для ряда других теорий пластичности.
16,10.	ПОДОБИЕ В ЗАДАЧАХ ПОЛЗУЧЕСТИ
Определение критериев подобия при моделировании
ползучести производится на основе теории ползучести
и общих уравнении механики сплошной среды,
В основе теории старения лежит предположение
о связи между напряжениями, полной деформацией и
временем, которую можно представить в виде [10]-
et = Д~ (6 - ГСТГа W 7 И-'0'); (16.35)
20 \	* М" /
12—26
здесь я — среднее напряжение; ср — функция инвариан-
тов тензоров напряжений и деформаций, характеризую-
щая состояние материала,
В те.х случая.х, когда кривые ползучести подобны,
функция <р может быть представлена в виде
Ф = Мофф (0.	(16,36)
Здесь f — функция интенсивности напряжений; ф—
функция времени.
Функция f может иметь вид:
экспоненты	/ (о/) = exp Ьпр	(16.37)
степенной	f (erj — ЛоП	(16.38)
или какой-либо другой (например, гиперболический си-
нус) .
Если вид функции /(о.) одинаков для материалов
прототипа и .модели, то для обеспечения подобия в рас-
пределении напряжении необходимо подбирать матери-
ал так, чтобы 6И = ЬЧ (16,37), либо m, = mM (16.38)
и т. п Можно показать, что величина А не влияет на
обеспечение подобия.
Существенно, что функция времени ф(ф может иметь
разную форму для материалов модезн и прототипа.
Сходственные моменты времени находятся из условия
Cfi фи (Ст) “ фл( (1М).	(16.39)
Это позволяет значительно сократить время испытания
специальным подбором материала
При отыскании критериев подобия влиянием коэффи-
циента Пуассона на распределение напряжений обычно
пренебрегают, так как оно несущественно.
Более удовлетворительные результаты получаются на
основе теории упрочнения, которая может быть поло-
жена в основу рассмотрения вопросов моделирования
ползучести.
Уравнение кривой ползучести по одному из вариан-
тов теории упрочнения имеет вид [10]:
па
е = е0 (о) -ц Bf1 exp — .	(16.40)
При моделировании статических задач и в тех слу-
чая.х, когда начальная деформация является линейной
функцией от напряжения, необходимо обеспечить вы-
бором материала и температуры испытания выполнение
условия
-- п,м.	(16.41)
16.11.	МОДЕЛИРОВАНИЕ НЕКОТОРЫХ
ВИДОВ КОНСТРУКЦИИ
Моделирование комбинированных конструкций, со-
СТ0ЯЩИ.Х из оболочек, пластин, стержней и г. п., осно-
вывается на изложенных выше общих условиях подо-
бия, При этом, если элементы конструкции выполнены
не из одного материала, коэффициенты Пуассона в про-
тотипе и модели при простом подобии должны быть
соответственно равны, а отношение модулей упругости
материалов прототипа должно быть равно отношению
соответствующих модулей упругости материалов мо-
дели.
В те.х случаях, когда нас интересует не картина на-
пряженного состояния каждого элемента, а перемеще-
ния характерных точек или распределение усилий меж-
ду' элементами, можно отказаться рэт строгого геометри-
ческого подобия и моделировать’ для всех или для
отдельных элементов какие-либо интегральные характе-
178
РАЗДЕЛ 16. МОДЕЛИРОВАНИЕ
ристики (например, соответствующие жесткости). Ука-
жем на некоторые особенности моделирования отдель-
ных видов конструкций, имея в виду их работу в пре-
делах упругости.
Тонкие пластинки постоянной и переменной толщины
должны моделироваться с соблюдением геометрическо-
го подобия в плоскости пластинки в произвольном ли-
нейном масштабе mi. Толщина пластинки может моде-
лироваться в масштабе тд, в общем случае отличном
от m.i. Масштаб нагрузки тР также произволен.
В этом случае при равенстве коэффициентов Пуассо-
на материалов прототипа и модели (ря = цм) напря-
жения будут моделироваться в масштабе
та
т.р
mh
деформации — в масштабе
прогибы — в масштабе
mprrij
-----ф
тЕ m'h
При Р-н ць)
1
1 1
--- Ж. цы-_
*'х,
тР 1“Пф .
т	= —у  -------
1ПР ’-Вн
(36.42)
(16.43)
(16.44)
(16.45;
(16.46)
1 — р;
mw ~~	,	„ •
m'h 1 — рм
(16.47)
I 1
Здесь ~, — — кривизны срединной поверхности де-
(Н Рд
формированной пластинки в рассматриваемой точке в на-
правлении осей х и у соответственно.
Для формул (16.45) — (16.47) координатная пло-
скость совпадает со срединной плоскостью пластинки.
При моделировании напряженных состояний безмо-
мептных оболочек постоянной толщины срединная по-
верхность модели должна быть (ео.шчрячески подобна
срединной поверхности иащры. ,'Пшенный масштаб сре-
динной поверхности пц может быть произвольным.
Масштаб толщины оболочки пи, может быть отличным
от гщ. Коэффициенты Пуассона материалов натуры и
модели должны быть равны
Для соблюдения простого подобия напряженных и де-
формированных состояний масштаб сосредоточенных сил
должен быть равен тР = mEm.itnh. При расширенном
подобии (подобии по напряжениям) масштаб тР может
быть произвольным.
Другие виды нагрузок должны моделироваться в сле-
дующих масштаба.х; нагрузки, распределенные по линии,
/72р
; нагрузки, распределенные по поверхности,
mi
тр
т— — т~ — т- = —нагрузки, распределенные по
A Y Z 2
Ш;
объему, — т-у = mz — —; сосредоточенные мо-
ml mh
менты — т.м = тртр
При соблюдении всех указанных условий подобия все
компоненты напряжений будут моделироваться в масш-
тр
табе та — ———t деформации—-в масштабе тЕ =
/72 р
~~	перемещения — в масштабе ти = тя = ягг.
772р- '!!' (>!
В некоторых случаях моделирование безмоментных
оболочек можно осуществить при произвольном выборе
многих масштабов. Так, при моделировании напряжен-
ного состояния безмоментных оболочек вращения масш-
табы «и,	, ту т/,, тР могут быть выбраны произ-
вольно.
Рассмотренные условия могут быть использованы и
при моделировании оболочек с небольшими моментными
зонами, однако в последнем случае подобие будет при-
ближенным.
Для моментшдх оболочек постоянной и переменной
толщины следует соблюдать условия полного геометри-
ческого и силового подобия пространственной задачи
теории упругости.
Пространственные стержневые системы могут иссле-
доваться на модели с соблюдением полного геометриче-
ского подобия или же на модели с сохранением подобия
лишь в соотношениях жесткостных характеристик отдель-
ных: элементов и поперечных сечений. При этом должно
сохраняться одно и то же соотношение для основных
жесткостных характеристик: на изгиб в обеих главных
птопкостях инерции и на кручение.
Если влияние продольных сил на деформацию мало,
то масштабы жесткостей всех подобно расположенных
элементов пространственной рамы должны удовлетво-
рять условию
1 + Им
тЕ1 = тЕр=—~ та1 .	(16.48)
1 + Цн к
В тех случаях, когда деформациями от продольных сил
в элементах пренебрегать нельзя, соответствующие же-
сткости дотжпы быть дополнительно [кроме (16.48)]
связаны зависимостью
(!6-49)
т1
Здесь/| и П — моменты инерции поперечных сечений
относительно главных центральных осей инерции; /к—
момент ширдчи поперечною сечения на кручение; F —
площадь поперечного сечения.
Для изучения сложных рамных конструкций, где
трудно оценить влияние отдельных жесткостньгх .харак-
IS 12. ВОПРОСЫ ПОДОБИЯ ПРИ ИССЛЕДОВАНИИ СОСТАВНЫХ СИСТЕМ
179
теристик. модель целесообразно выполнять полностью
подобной по всем жесткостяым характеристикам или по
всем размерам и форме натурной конструкции.
Итак, для обеспечения подобия в распределении уси-
лий и перемещений:
1)	модель в осях должна быть геометрически подобна
прототипу в произвольном линейном масштабе т,\
2)	одну из жесткостей поперечных сечений (например.
ЕЦ) можно выбрать произвольно в масштабе т , а
масштабы остальных жесткостей — в соответствии с
(16.48) и (16.49);
3)	сосредоточенная нагрузка моделируется в произ-
вольном масштабе тР (другие виды нагрузки — в соот-
тр
ветствующих масштабах, например 'mq ------, и т. д.).
При соблюдении указанных условий перемещения бу-
тРт1
дут моделироваться в масштабе ти — rnv — mw — ——,
т ЕЦ
а изгибающие моменты — в масштабе т-к^—т-ргщ.
Плоские стержневые системы в последнее вРёмя мо-
делируются все реже, особенно в связи с использованием
для расчетов ЭВМ. Однако когда к моделированию та-
ких систем все же прибегают, то учитывают, в отличие от
пространственных систем, жесткость поперечных сечений
на изгиб в одной плоскости. Остальные зависимости по-
добия — те же, что и у пространственных рам.
При моделировании плоских стержневых систем,
имеющих в своем составе криволинейные элементы,
должно соблюдаться также условие (16.49).
В общем случае комбинированных систем должны
учитываться все указанные выше условия подобия от-
це льны.х элементов в соответствии с характером работы
этих элементов.
16.12. ВОПРОСЫ ПОДОБИЯ ПРИ ИССЛЕДОВАНИИ
СОСТАВНЫХ СИСТЕМ
Пусть па упругое тело А, находящееся в контакте
с телом В, действует нагрузка. Требуется посредством
моделирования определить напряжения, деформации и
перемещения в теле А.
Рассмотрим отдельные возможные здесь случаи.
1	. Материалы тел А и В упруги.
В этом случае должны соблюдаться рассмотрен-
ные выше условия подобия упругой задачи. Важно лишь
подчеркнуть, что соответствующие критерии подобия
должны быть численно равны в сходственных точках
натуры и модели.
Если у патупы Е т,пЭ>£л,п, то необходимо, чтобы и в
модели было Е'д.мОЕ'в.м, и тогда приближенно можно
'учитывать только три определяющих критерия подобия:
р,л = idem; aB = idem; -------- idem, (16.50)
которым соответствуют следующие уравнения связи
между масштабами:
mJ*
=	=	(16 51)
2	Материал тела Л— упругий, тела В — сплошная
пластичная среда.
В условия однозначности рассматриваемой задачи
входят: ([£], Ел , JAa [1], Es[PL~~2]t jab[1], кри-
вая зависимости о'1,в=(в(е1,е), история нагружения.
Здесь должны быть соблюдены условия подобия, полу-
ченные для случая, когда оба материала упруги, и, кро-
ме того:
а)	материал в модели должен характеризоваться
кривой о,-в ~/в lri в	которая подобна ана-
логичной кривой, опчсыва.ющсн материал натуры о; в =
= !B(i ^bJ’
б)	история и характер нагружения должны быть в
натуре и модели одинаковыми.
3	Материал тела А —упругий, тела В — сыпучее тело
без сцепления.
Здесь в условия однозначности вондмг величины:
/[L], EA[PL~2], ид [1], PiP], объемный вес yB]Wm3],
а также угол внутреннего трения л[1] и угол трения
по поверхности контакта Maiepnaia В но материалу А
<ГЛА [1].
Из этих величин по 'учим следующие независимые
определяющие критерии подобия-
Цд == idem; (рв idem; <fB4 -= idem;
	= idem; 	= idem, (16.52)
Р---------------------Р
которым соответствуют следующие уравнения связи
между масштабами
Г'М "V
щ,. л = 1; т,- = Г; т r = 1;------------= 1;
НЩ	Св	Гузл	тР
Если для модели взят такой Ж" материал (тело В),
что и в натуре, то . =1 и t,iy =1 и необходимо
В	в
соблюдение зависим oi теш
т р т‘;	щ?
= 1;	= I; -----^=1;	——•=!.
тцА трвл	,пР	тР
(16.54)
Отсюда вьпекают ш-лбходч:(ые и достаточные условия
подобия в случае, когда тело В является сыпучим телом
без внутреннего л рения-
а)	коэффициенты Пуассона материалов упругого те-
ла А для натуры и модели должны быть равны (ул,в =
= Рл,ч);
б)	углы трения грунта по поверхности контакта натуры
и модели должны быть рав"ы (ф вл,п=®вл,ч);
в)	масштаб модулей упругости материала упругого
-его 4 го 1>гСп быть равен линейному геометрическому
масштабу, т. е. =
С.юдовагедьтго, можно либо произвольно выбрать
масштаб тр — т, (и тогда тР — тЕ), либо произвольно
2,-------------------------------------------------
выбрать масштаб нагрузки тР (и тогда /И( = у тР),
При соблюдении указанных условий напряжения бу-
дут моделироваться в масштабе тл, перемещения—
в масштабе т/, а деформации модели будут равны со-
ответствующим деформациям натуры.
4. Материал тела /4 —упругищ тело 5 — сыпучее тело
со сцеплением.
В этом случае к условиям подобия (16.52) — (16.54)
добавляется критерий подобия
—р—^idein,	(16.55)
где с в — удельное сцепление, и соответствующий ему
индикатор подобия

16 13. ТАБЛИЦА КРИТЕРИЕВ ПОДОБИЯ И УРАВНЕНИЙ СВЯЗИ
МЕЖДУ МАСШТАБАМИ В ЗАДАЧАХ СТАТИКИ И ДИНАМИКИ
Общие условия для всех зачащ
1 Модель и прототип до гжиы быть геометрически потобпы (линейный масштаб мотели )
г (Р)	(М)
’ Все нагру ?ки, действующие на модель Сосредоточенные епты PL = фг Р, сосредоточенные момен.ы Фу И naip\ пси роспределонпыс по линии qt =
нагрузки раенрече <епные по гн верхносги V, К, Z, iiaipjaRii, распределенные по объему, 1, У Z), должна находиться в тахом же отношения одна к друю^!
кш и соответствующие нагружп, действующие нт прототип
фО,*,!!, q,(A!S = idem = idem -^-=-|-= llle™ 2L = 3-= dem,
L	V Z	\ Z
nX mY mx' mx
=	тч(И)-1,	=	— = l, Щ = i,-----1 _= t,--d _ 1}.
1	1	‘	mY mz my mz
3 Мишыбы pdshbix bh юз пиpvЮк должны у ювтетворятъ зависимостям
т/5	тр
4 Заганные пс-речешдния на конторе гоажчы уюл_творять завш имостям
П ]	Н шоснование 31ДТЧИ	Вид 1 р ши шых условии И Ч I тип 3 1Д л.и	Необходимые а достпочнью у V ТОВИЯ п щэбил (в дапол- 1Ы 1ИС К ! бщи 1 условиям подоби! дл1 всех задач)		Возмож- ные пари шгы выб 1П 4 чшеша зб из	Масштабы переходi от J 1Дч * к па 1 уре			Примечания
			оиреде тлю 4,17 ЪрИТсРИ! иодзбия	у р 1Ы1СНИ i СНЯ3 ! А V Я ДУ лкхш тбами		дая напряасний	для деформаций	для пер! mi щеишт	
1	у	3	4	5	b	7	8	ь	U)
1	Прострапсл вен чая у пру г щ и а ’.плоская пзои-р мическая задача ДЛЯ II атропных чет (малые де шормадил)	а) ГКрч > I )с ловная ш ’-л	it — нет	1 (1==!	r‘l z 7 2 Д тр	-щр "7		п' п	Хпало1 ичные i с товия спр-звед т вы для момент- ных оболочек
							ртг	т т 1 Е	
		б) Вт< ! )Я ос ночная , щ 1ч 1	н. = k’cin	п	1	f"fc • "V Вс	тг т>, 	 ‘ /ук mj	т 1 ‘ к	11 к	
		В1 С\Ц ИЧЧИ' ш > i гача	U = teem, 	 ^tJem /е«|(	/р<} ~’1 т р	'Де "р’ mi	т Р m~t	,ПР т [ т~.	тр т, т 1 1	При абсолют по жестких свя ЗЙХ и отсутствии до>гих з тданных перемещений см п 1 а
					т1 ' т i	Ргр ти т1	;”»к т	ти 11 к	
				П1 (П/Ш .					
2	II ЮСКАЯ А ИрУ гая статическая и ^термическая за гача тля изо I ройных rc i (ма лыс деформ щяи)	а) Псрв 11 оь нонче я i । г i I j При ВЫПО Шенин усювий Леи!1 — Уи-гчет та	-	-	т1‘ "'Н‘ т , т , L тр	тр т, т, 1 h.	С М ф ф му ты 10 11	пр mt	h — то шиша те та Ана логичные \с^ория (праве д ТПВЫ ДТЯ ULHft<O МОН I ГР 'X )Гн ЛОЧСК
 I п	Н 1НМС KOI ШИ 3 1Д 1 ill	Вид 1РН1ИИ1ЫХ у^ ЮВИН ПЛИ I ип з щз ш	Необходимые и достаточные усчовия подоби г (в доггол наше к общим хсювиям	
			подобия Д I 1	всех задач)
			о тредсляю щне I рите рии яодоби]	yp пшеви i CBHiil Me RTy М1СШЧ тбчми
i	2	*	1	5
		б) Вторая ос ювная и 1ча	1.1 _= idem	m — 1
	Пчоекая упру гчя сз пическая изотермическая лдз чз пя и ю 3 Р ШНЫХ 111 ( '1 Ilk иформзщп )	в) Смс ванная и Н ч а	и = idem	in “1 &
		) Ikpbifl л !и 1 1J5I	За Дача	ц — idem U 	— idem	m — 1 U m\ml _=1 ml
			и U , 	 —idem	m m, m к E i
			гэ	mp
			- -—• —idem	mp’t
	Упругая дина п чс кая изо;ер мичи кая > 1 т, 11 1 1,зя насир зпннх		f t Hu =idin	? Н/П f 111 n U 1 .-!
	ii (мз тые до Форм Ш.Ш1)		a	u
		о) Вторая Ov □ни з пача	H = idem	ni ( ~ 1
			—— —idem	m m<
				) i t
				Idem,	и ni
			-—- _ idem	n
				m 11
			via t 	— — uc rn	Li	[
			IL	m
BO3V ож ные В ФИЗНТЫ выбора м кши бив	МэеШГ'бы ПЧкХиД! DT модели к натуре			Приме ипия
	для папря I ешш	дня деформаций	пере ?е’.цс шш	
	/		5	10
тчк nh	т~т у £ ик т1	т т1	,,1нк	Alia погичные НЮ!НЯ справед ливы при из1 ибе и ч кишок
	тр	тр	П1р	При тою полно ЛчССТКНХ связях И ОТСУТСТВИИ др} гик здцшнык пе р^мешешш	на
т. rn „ h Р	т, т 1 !	т т т 1	! h.	,ПЕ mh	
Ш, , 171 , L 1 п	ак	т r ти	т	т “ к	контуре при вы ПОЗНИШИ уе 10ВИЙ
	т	i		Певи — Мит it т та ем п ’ а и примечание КП ’’о
П1 771 i	р	тр	тр		
ОТР- «	пЧ	111L ’4	tn , т L 1	ws — перемеще пне в печатный / da , момент н0= —1 VP / f — время	р — плотность матери iaa
т , , пг , Z	р	muvml	т		
и	т «к /	n’l	!nt	4in	
16 13 ТАБЛИЦА КРИТЕРИЕВ ПОДОБИЯ И УРАВНЕНИИ СВЯЗИ МЕ'АДА МАС1ПТ W\М1!
л п	Il HiMcikih i не зада и	Вид Гришиных условий ИЛИ тин задачи	Необходимые и доела!очные условия подобия (в допол непие к обидим условиям подобия для всех зада 0		Воз моле ные варианты выбор 1 масштабов	
			определяю 1ЦИС критерии подобия	уравнения связи между масштабами		
1	2	3	4	5	6	
		в) Смешанная за j зча	ц — idem W 	— пет Р и FI -Р	=idcm Р "о — —idem, р/ 	— idem, ГН и / —— = idem	тн =1  т X т} ”'р т,, т, т !ih L / П1 р т‘‘, тj т, т т ти„	т „ т Е р тР mt	
					mL Ш/, т L их-.	
4	Пространствен нйя температур пая упругая за чача ря одно родных и зотроп иыч гет (матые it формаця 0	а) Прошраяст	u— 'dem	т --1 венная задача			тЕ- см также примеча пне	
		б) Плоское на	—	— пряжечное сост о янш.			гп г. , £ СМ 1 Ж с иримочт И! с	1
		в) Птоикое де формированное ioi 1оянпе			см пкже прнмоча шю	
						
Млдтнабы перехода от модели к и И}ре			Примечания
,ля напряжений	для деформации	для псреме щений	
7	8	q	1 0
тр /7Я	тр	тр	
	т	т т ь i	
т»к тЕ т1	т 11к т1	ти&	
тьтатт	т т _ а Т	татТт1	а— коэффициент линейною расши рения 7 тем пература Масштаб (ши та ) при па линии внутренних источников тепла до икей быть со пасован с уело внчми подобия температурных полей (см 16 7 и 1G 14) Линейный мае ипаб геометриче скоро поюбия mi должен быть со jтасован с уело впчмн подобия юмперат^риых потей во всех слу чаях (за исключе пнем подобия ста ционарных темпе рагурных полей при отсутствии внутренних иной пиков ген та и граничных уело внях	первою и второ! о рода когда т j можег быть произвоть пым)
тг. та тт	1 т-7-—- т т 1 + к ?	1 7< —“*— т т т„ 1^-ц	1 а 1 hM	
£ i" Д 2 )	(* < 700 - 7J sz	«с 7	
	(' -i Ц,)(‘ " 1’..) Х№« "т		
Упр}1ая сгятг,' j ческая и оюрми ! чсская задач! пя И301р0ПнЪ1* ОДНО родных П J при ботыппх Д; фор маниях		1, — I dtni Ч В, 	— ~1 н i —— —! Ч m д —-1— —idem	—i, HI 1 m -1-	„ i m —-	i !"‘ь mp II. n, l	'Ц mp		'nA			1	; / n>p 1	Г m A	'J |	— физические xa - рактерпстики mj lepuana (из \рзв нения связи re Формаций с на пряжения v - В	4 - д- г 1л4 ?; - л;		X — 4В1	~ н р \ — Д	j 1	/ сч IG 8
				"' A rnt		rn		J	,lll	
Snpjio laciii чсская пютермц eci ая статье {.кая зада за д ы Псрзонач t ILHO О ( породных	изо тропны* ГС 1		- iUlIll 1 —— — idem LI Ci да лс	M-1 " p 1 ;7 n 1 ци^ш	( ! !	n\ mp "/ Д	1 1 j i		i	i J i		j/ ДД ml	Кривде доъ-.’Ы быть по добпичи для ia repiuTOB пр ю UILI-j и модели 3 leib	— и I ей х ши и ’-ь п шря жепиГ1	1 тен nsiocib	е формаций	Все крн СПИН подош я ДО 1ЖНЫ быы to ответственно рав нъ в сходствен пые момешы врс шни
ho iooul j а ачн и<гь5чс II	!	—-— =масш h = dtn (’.! Ш m = j de ni) C i lip \ <_Ч Ш I	a . 1 ) mj rn П	II! D	1 - f/b z^O	П!Г ,n!> inp 1 1 1	i I inL	j 1 1 !		1 1 1 i		f / ¥	”‘b 11	В рамках ио рии ci зрения Кривые ПО I 5V ‘ LC1 ( 4-l(0t)'.lil> 10 1ЖПг! 6ЬП^ ЦО доСи [ !н Злее- -(ЬПДЦПЯ ин 1 1рипнюв тензо Г в 1 inp J 1Ш1Й и ш )ор ищи Xi ) ш пшющая С( оянш I пери п 1 дог) - ф ш Ц 1Я ТО 1ЬКО И I он шшив	напр I I v шй	т| (О — (i)\ И	шя	1О1ЬКО 1 De it Ш	Д 1Я фы	ин	нс П T!	IOTCI	3	1ВЧ имо тя /1 а ) — — i \п 60	и Н! т ™	ШОР М 1 (Д !1И I И /( <5 ) ДО III быт! 0 Of паке вой чтя ма ТЧ рПД-’ОВ про отн I а и мо и ш	1
184
РАЗДЕЛ 16 МОДЕЛИРОВАНИЕ
16.11. ТАБЛИЦА КРИТГРИ1В ПОДОБИЯ ТЕМПЕРАТУРНЫХ ПОЛЕЙ
(ОБЩИМ УСЛОВИЕМ ПОДОБИЯ ЯВЛЯЕТСЯ ГЕОМЕТРИЧЕСКОЕ ПОДОБИЕ НАТУРЫ И МОДЕЛИ)
	Тип задачи	Внутренние	Вид граничных условии	Необходимые и достаточные условия подобие (в дополнение к геометрическому подобие)		Возможные варианты произвольного вы- бора масштабов
nzn		ИС ГОЧЯИНН тепла		Определяющие кри- терии подобия	Уравнение связи между масштабами	
1	Нестациопар not поле	Есть	Первого и вто Doi о рода	пр t — idem, °Z) ~-r-r^~ = idem	m т. a? i mi mq, m‘i -—S.-— i m, m r Л /	т^, , т • тл, тл а? Л’ i т„ , т. , т,, аТ’	/ Qv ту т1' тТ  т. ; т., tn , m а Т л 1	1
		Есть	Третьего рода	ат t —•	— idem, I1 idem, ат1 	 — idem А	T ml	nt m1 —_щ±=ь m\	m\, mj ' maT ml —		1	т. , т. т	, а Т	I"	а Т mr, ’	m	i °-у	A	a f	1
		Нет	Первого и его рого рода	ат 	— — idem	ma mt m'l	m i m , m af	Л	I ; m. , tn a j4	A	t
		Нет	Третьего родт	ат 1 — — idem, 1- ат ! —		 -- и’сш.	maT mt m7 ma ml 	 = 1	ma ' rr,a тл a	Uy
2	Стационарное поле	Есть	Первого и второго рода	4t>г'	, ——	— idem	ml ,PT	m, m m, % nv I m. , m к I i ,p}.' тт
		Есть	Третьего рода	7 у 1 		 —idem, Л./ 1 —	 — idem X	m mr (k> I	j my. my mvT ml Л	n’aT' m4v , гп~ к	{J-'f	1
		Нет	Первого и второго род I	—	—	mr mt m>.
	П р и м с ч а н и е ко 'ффицнент тепло	Нет а? — коэфф’щ провотностп, Т	Третьего рода ?ечг течпер^ттропр — темпеоат^ ра а	а? 1 ——~—- ~~ ’(’ст ОЫ-ППОСГП, - kowtrnimimiT теплоотда	ma.f mi m. Л - плотность внутреннего	maT> источника тепла,
литератора
ЛИТЕРАТОРА
1 A j н \ ч е в П М Герок и "1 д с В Б М. и н s с
в и Ч I М ЩсгОВЦОВ Ь А ГирНЯ ПО оии» И ри ер
НО1 ОЙ Л ) [, -ПфОВД Но <131 ill 1Я ШКОТ 1 Ю
~ Вии? о в В А к > я додоГия и мс сшрэ ui п_ при
ML 1ИГО (I ДО к кЪЧ 1 1 i^kip HtplLilkl < В ы L LI d Я I IKO Э 1Ч(Ь
3 1р! 1 А Адк Не Да Ь)1ьши дприие д bop ia
цни и но'[ in (Hi о тынка тошней среди <Мир 19ээ
н Г хм ан А А Введение я теорию по ;оби i «Bjicuai
пл о I 1	1%J
к р о п я и к к Ч е г о т и и П М Э (смричеслое о
К яро! ине ; елроюедъной пс^анике Гоилромчз'и! 1ЛЗ
6 I нрпич’и М В Теория подобия И1Д^о АН СССР
ВЫ
7 Наваро А Г О ме \ ли 1ч сном по u i ин и ср и i
<| up ирчомые и (к l^opil I МОДР JHpUBJii 1 I) Издво АН
Ар 1 ССР LptB и 19Ьо
& Пчт мок Д А Ней типе строитель! их конструкций
lid МОДС (ЯХ Сгр)ИДЗ .[.Л 1J7
q 1 v х о ?з Г , I Р к и т I- е п Ь В ( i е п з н о в Ah,
А о I 1 р с в и О Н Э актр !4tckoe по хстиповнн I *ати ! строи
£ I f )И МО Шк! Пзщо ШИ1Р к; (	1Ш>3
10 Р юс гн и IO Н Цо
И \ г 1	1 )ЬЬ
П С -(Ой Т И Mlto-i.u
UIRC «II I', I !-> 1J
2 Г с 1 е т ъ б и у м II М
Фиш 1ПИ ll) 4
Ф И И 1 Р О О U X X
фор иции Лишив 1%1
'1 ХЧССГЬ ) 1С U1I си ьонорукний
пособи I и oHMtpfo in в геха
Этск райское моделирование
1Ь шренис напряжений и де
РАЗДЕЛ 17
УСТОЙЧИВОСТЬ СТЕРЖНЕВЫХ СИСТЕМ
ПЛ. ОСНОВЫ ТЕОРИИ УСТОЙЧИВОСТИ
СТЕРЖНЕВЫХ СИСТЕМ
СО СЖАТЫМИ ЭЛЕМЕНТАМИ
17.1.1.	Понятия устойчивости
и неустойчивости. Устойчивость равновесия
деформируемых систем
Понятия устойчивости и неустойчивости играют боль-
шую роль во многих разделах естествознания и техни-
ки. Предположим, что в некоторой системе изучается
зависимость между «причиной» и «следствием» Если
малому изменению причины соответствует столь же ма-
лое изменение следствия, то говорят, что система
устойчива. Если же малое изменение причины вы-
зывает большое изменение следствия, то система неус-
тойчива.
Строгая математическая формулировка этих понятий
была дана впервые А, М. Ляпуновым (1892 г.).
Одной из задач строительной механики является изу-
чение устойчивости равновесия деформи-
руемых систем, т. е. стержней, рам, пластинок,
оболочек и т. д. Теория устойчивости равновесия ведет
свое начало от Л. Эйлера, который впервые определил
критическую силу центрально сжатого прямолинейного
упругого стержня (1744 г.).
Параметр нагрузки и, принимающий различные значе-
ния, характеризует состояние системы. В процессе не-
прерывного изменения этого параметра система может
перейти от состояния устопчпвого к состоящие неустой-
чивого равновесия. На границе между устойчивым и не-
устойчивым состояниям!! система попадает в крити-
ческое состояние; соответствующее значение парамет-
ра нагрузки и.,, также называются критическим.
Явление потеря устойчивости при и~и, характеризу-
ется мгновенным переходом от устойчивых состоящий
системы к неустойчивым в процесс!, изменения параметра
нагрузки и и представляет собой качественный скачок,
переход от одного качеств равновесия к другому.
Понятия «критическое состояние» и «критический пара-
метр нагрузки» относят не только к явлению потери ус-
тойчивости, но также и ко всем другим состояниям, из-
меняющим степень нечетсйчивости системы (см. 17.1.6;
17.4.2; 17.4.4).
В настоящем разделе рассматриваются изгиб и устой-
чивость сжатых п сжато-ист путах стержней, а также
систем, содержащих тесте сер”л:и. Вопросы теории из-
лагаются применительно к стержневым системам [3, 8,
19, 21а, 32, 35, 36, 39, 41, 46ф.
17.1.2.	Консервативные и неконсервативные
системы. Методы исследования
устойчивости равновесия
Консервативная система обладает следующим свойст-
вом: работа внешних и внутренних сил системы, совер-
шаемая при переходе из одного состояния в любое дру-
гое, определяется только этими состояниями и не зависит
от траектории движения.
Понятие «система» объединяет деформируемую конст-
рукцию (стержень или совокупность стержней) и нагруз-
ку, поведение которой должно быть задано.
Отсюда следуют два необходимых и достаточных усло-
вия консервативности системы: 1) упругость деформиру-
емой конструкции, т е. обратимость деформаций, и
2) консервативность нагрузки, т. е. независимость со-
вершаемой ею работы (при перемещении из одной точки
пространства в другую) от траектории движения.
Консервативная система характеризуется замкнутым
энергетическим балансом — рассеивание энергии (дисси-
пация) в ней не происходит. Из условия равенства ра-
боты внешних сил (нагрузки) и работы деформации
следует существование для консервативной системы
потенциальной энергии. Потенциальная энер-
гия определяется рассматриваемым напряженным н де-
формированным состоянием системы и не зависит от ее
предшествующих состояний, т. е от программы нагру-
жения.
Потенциальная энергия системы обладает эк стр е-
м а л ь п ы м и свойства м п, которые позволяют сна-
чала выделить равновесные состояния системы из мно-
жества неравновесных, а затем оценить качество равно-
весия (устойчивость пли неустойчивость) каждого
равновесного состояния.
Для исследования устойчивости равновесия консерва-
тивной системы достаточен статический ме-
тод, основанный па рассмотрен;'!! равновесного состоя-
ния системы и на оценке его ущойчивости с помощью
энергетического критерия.
Системы, не обладающие свойствами консервативно-
сти, относятся к классу н е к о п с е р в а т и в и ы х си-
стем.
Неконсерватиьпость системы может определяться по-
ведением нагрузки, в то время как стержень или сово-
купность стержней обладают упругими свойствами. В
этом случае исследование устой швосги выполняется
динамическим методом, основанным на изуче-
нии характера возмущенного двпже шя системы. Здесь
возможны явления, не наблю !.аемые в сиэтемах консер-
вативных (см 17.6).
Более сложными являются случаи, когда неконсерва-
тигшость системы определи гея необратимостью
деформаций материала. Анализ устойчивости
стержневых сисмем, выло ш-ппых из упруго-пластиче-
ского материала, требует yaesa разгрузки и остаточных
17,1. ОСНОВЫ ТЕОРИИ УСТОЙЧИВОСТИ СТЕРЖНЕВЫХ СИСТЕМ СО СЖАТЫМИ ЭЛЕМЕНТАМИ
187
деформации в тех случаях, когда они возникают. Труд-
ности решения подобных задач обычно обходят, рассмат-
ривая однократное па1ружекие системы в условиях
активной деформации. При таких предпосылках упруго-
пластический материал можно рассматривать как нели-
нейно упругий (см. 17.8).
Устойчивость равновесия деформируемой системы
удобно изучать с помощью графика поведения,
изображающего совокупность всех возможных равновес-
ных состояний системы. По оси абсцисс откладывают
характерное перемещен н е, которое должно,
по возможности, отобразить деформированное состояние
системы в целом По оси ординат откладывают пара-
метр нагрузки и или величину, одновременно с ним воз-
растающую,— сжимающую силу, осевое напряжение
и т. п.
Особые точки графика (например, точки экстремума
и точки разветвления) соответствуют критическим со-
стояниям системы.
17.1.3.	Потеря устойчивости
при разветвлении форм равновесия
Модель с одной степенью
рирует рассматриваемые в
Рис. 17.1
свободы (рис 17.1) иллюст-
настоятцей главе явления.
Бесконечно жесткий стер-
жень длиной 1 сжат силой
Л, приложенной с эксцен-
трицитетом а. Малому от-
клонению у верхнего конца
стержня от вертикали про-
тиводействует упругая опо-
ра, создающая горизонталь-
ную реакцию И.
Отклоняющий момент от-
носительно опорного шар-
нира, создаваемый силой У,
равен М]==У(а+у). Ему
противодействует удержи-
вающий момент М2=Ш,
Упругие свойства опоры
характеризуются зависи-
мостью
Н = f (У) = v (у — pys),
(17.1)
где v>0 и pt^O. Условие равновесия Лф—Л12 = 0 право-
дит к соотношению
/V (а + у) — vl (у — ц/Л) -= 0.	(17.2)
Линейно упругая опора (ц = 0). В частном случае
при у=0 нелинейно упругая опора вырождается в ли-
нейно упругую. График поведения модели представлен на
рис. 17.2. По оси абсцисс отложено характерное переме-
щение у, по оси ординат отложена сжимающая сила А'.
а)	Центральное сжатие. Уравнение равновесия (17.2)
при р = 0 и я = 0 приводится к виду y(vl—N) =0. Не-
отклоненная форма равновесия у=~0 возможна при лю-
бом значении N. Отклоненные формы рапновесия с про-
извольной величиной у возможны только при jV = vZ.
В случае N <л'1 (os резок ОК на графике) неотклонен-
ная форма равновесия устойчива, ибо ври отклонении
у удерживающий момент больше отклоняющего: Л12>
>Л4,. Малое возмущение (например, малая горизон-
тальная сила) вызовет малое отклонение модели вер-
тикали. Наоборот, в случае (отрезок A’/V на гра-
фике) вертикальное равновесное состояние неустойчиво,
так как при отклонении у удерживающий момент меньше
отклоняющего М2<уМ,, Здесь малое возмущение пов-
лечет за собой дальнейший рост отклонений.
Значение сжимающие» силы
AA---V1	(17.3)
является к р и т и ч е с к и м, ему соответствует состояние
безразличного равновесия (прямая RKS на
рис. 17.2) с произвольным по величине и по знаку от-
клонением у.
Рис 17.2
Потеря устойчивости здесь характеризуется раз-
ветвлен и е м (бифуркацией) форм равновесия- поми-
мо неотклонеиной формы у = 0 при Л' = А, становятся
возможными смежные отклоненные формы равновесия
У ¥=0.
Точка К на графике (рис. 17.2), соответствующая кри-
тическому состоянию системы, называется точкой
разветвления (бифуркации)
Потерю устойчивости при разветвлении форм равно-
весия называют часто потерей остойчивости эйлерова
типа (или в смысле Эйлера). В строительной механике
стержневых систем принят также термин: потеря
устойчивости первого рода.
Характерный признак этого явления — существование
смежных форм равновесия при критическом значении
нагрузки.
б)	Внецентренное сжатие. Анализ зависимости (17.2)
при ц = 0 и а'р>0 прежде всего показывает существова-
ние первичных равновесных состояний (кривая ОА
на графике поведения, рис. 17.2) при у>0, N<Zvl. Эти
равновесные состояния возникаю: в процессе естествен-
ною возрастания нагрузки.
Существуют также в т о р и ч н ы е равновесные состоя-
ния (кривая PQ) при у<0, N>xl. Система может быть
«заброшена» в эти состояния только искусственным об-
разом Обе кривые равновесных состояний при а>0,
ОА и PQ имеют своей асимптотой прямую RKS, парал-
лельную оси абсцисс и проходящую через критическую
точку К.
Анализ качества равновесия с помощью энергетиче-
ского критерия (см. 17.1.6) показывает, что первичные
равновесные состояния устойчивы, вторичные неустой-
чивы.
188
РАЗДЕЛ 17. УСТОЙЧИВОСТЬ СТЕРЖНЕВЫХ СИСТЕМ
Асимптотическое поведение, связанное с неограничен-
ным ростом отклонения у по мере приближения сжи-
мающей силы 1V к критическому значению, характерно
для линейно упругих сжато-изогнутых стержней. Пред-
ставление о неограниченном росте отклонений является
следствием геометрически линейной постановки задачи —
учет больших перемещений (см. 17.2.8) показывает, что
по мере приближения сжимающей силы к критическому
значению отклонения быстро растут, по остаются огра-
ниченными по величине.
В реальных конструкциях быстрый рост перемещений
приводит к достижению предела пропорциональности,
после чего начинается стадия упруго-пластической рабо-
ты материала.
17,1.4.	Потеря устойчивости
при достижении предельной нагрузки
Для иллюстрации явления используется рассмотренная
выше модель с одной егеш'ш.ю свободы (см. рис. 17.1),
ио при значении парамо!ра жесткости упругой опоры
Нелинейно упругая опора (ц>0). График поведения
модели представлен па рис. 17.3.
а)	Центральное сжатие. Уравнение равновесия (17.2)
при а = 0 приводится к виду
у [А —• vl (1 — gy2)] = О,	(17.4)
откуда следуют два решения:
1)	у=0 при любом значении N (пеотклонепная форма
равновесия, отрезок OKN оси ординат на рис. 17.3);
2)	jV = v/(1—у.у~) прн A'Cvl (отклоненная форма рав-
новесия, кривая RKS па рис. 17.2).
Потеря устойчивости при разветвлении форм равно-
весия вызывается критической силой (17.3).
Анализ качества равновесия с помощью энергетиче-
ского критерия (17,1,8) показывает, что неотклоиеииые
равновесные состояния при Д'сАД устойчивы, при
•А>АД неустойчивы. Также неустойчивы отклоненные
состояния уэ^О.
Здесь в критической точке К наблюдается мгновенное
состояние безразличного равновесия. При A' = A4 стано-
вятся возможными бесконечно близкие смежные формы
равновесия. Касательная к кривой RKS в критической
точке параллельна оси абсцисс. Эю обстоятельство
позволяет классифицировать рассматриваемое явление
как потерю устойчивости эйлерова ища.
б)	Внецеитрениое сжатие. Уравнение равновесия (17.2)
при и>0 приводят к виду
а + У
Кривая OAjSA2 на графике поведения (рис. 17.3) изоб-
ражает первичные равновесные соскшшш системы прн
у>-0, кривая PQ— вторичные при у <0. Предполагает-
ся, что а | у < 1.
Характерной особенностью поведения модели в про-
цессе естественного возрастания сжимающей силы явля-
ется наличие экстремальной точки В, соответствующей
максимуму сжимающей силы N. Прн сжимающей силе,
превышающей это предельное значение Ам.1Ке, первич-
ные равновесные состояния невозможны.
Анализ качества равновесия с помощью энергетиче-
ского критерия (17.1.8) показывает, что устойчивыми
являются только первичные равновесные состояния,
изображаемые восходящей кривой 0/1,В графика пове-
дения. Первичные равновесные состояния, соответству-
ющие нисходящей ветви ВА2 графика, а также все вто-
ричные равновесные состояния (ветвь PQ) неустойчи-
вы. Отсюда следует, что наибольшее (предельное)
значение сжимающей силы
(17.6)
является критическим.
Критической силе Л\. соответствует критическое от-
клонение у,,.. Каждому значению сжимающей силы
А-щЛ'* соответствуют два равновесных состояния, из
которых первое, с меньшим отклонением У)<уЛ, устой-
чиво, а второе, с большим отклонением у2>у.., неустой-
чиво (рис. 17.3).
Необходимым условием максимума силы N, рассмат-
риваемой как функция характерного перемещения у, яв-
ляется равенство нулю первой производной или, как го-
ворят, условие стационарности:
Здесь наблюдается потеря устойчивости прн
до ст и ж с а н и и р е дельно й п a i р у з к и или., как
принято говорить в строительной механике стержневых
систем, потеря устой ч и вести второго р о д а.
Это явление отличается от потери устойчивости эйлеро-
ва типа, обусловленной разветвлением форм равновесия
в критическом состоянии.
Экстремальная точка В на графике поведения
(рис. 17.3) называется предельной точкой.
Потеря устойчивости при достижении предельной на-
грузки характерна для сжато-изогнутых стержней из
нелинейно уируюго или упруго-пластического материала.
17,1.5.	Устойчивость линейно упругой
системы с конечным числом степеней свободы
Положение системы характеризуется обобщенны-
ми координатами уь у2, . . уп, число которых
равно числу степеней свободы п. Пусть при любом зна-
чении параметра нагрузки и возможно неотклонепиое
равновесное состояние системы, когда все уд=О. При
значении и<и,г неотклонепиое состояние является един-
ственно возможным. Требуется найти крппгческое значе-
ние параметра нагрузки, и*, при коюролт становятся воз-
17 1. ОСНОВЫ ТЕОРИИ УСТОЙЧИВОСТИ СТЕРЖНЕВЫХ СИСТЕМ СО СЖАТЫМИ ЭЛЕМЕНТАМИ
189
ножными смежные отклоненные формы равновесия
(потеря устойчивости в эйлеровом смысле).
Условия равновесия системы имеют вид линейных
однородных алгебраических уравнений! относительно
обобщенных координат:
У11У1 1 Т12ЙЙ2
"b Via Уп 0;
Т.1У1 У^У-г +  • • + У-ел уп = 0;
(17.8)
УтУ1 + Уп?У« + " ' ’ + Упп Угг~0-
Коэффициенты этих уравнений у >л зависят, вообще
говоря, or геометрических размеров исследуемой систе-
мы, жесткости ее упругих связей и параметра нагруз-
ки и.
Условие существования нетривиальных (ненулевых)
решений системы (17.10) заключается в равенстве пулю
определителя (детерминанта):
D (и) ж | I 0.	(17.0)
В простейшем случае коэффициенты у, я являются
линейными функциями параметра нагрузки и, т. е.
УНг = '-У:к Д bih и.	(17.10)
При этом алгебраическое уравнение n-й степени (17,9)
имеет ровно п корню!
, . . . , /3.1,,	(1.-11)
определяющих критические состояния системы.
Если исследуемая система коиеервшпвна, то матрица
коэффициентов обладает свойством симметрии (или
взаимности) У1Л=у/н. В этом случае все критические
значения параметров и,у будут вещественными.
Потеря устойчивости происходит при достижении па-
раметром нагрузки и наименьшего из критических зна-
чений:
н41 =	.	(17.12)
Индекс 1 у наименьшего из критических значений
опускается в тех случаях, когда это не может вызвать
недоразумений.
17,1,6.	Собственные значения
и собственные функции
Теория собственных значений является аналитической
основой исследования явлений потери устойчивости при
разветвлении форм равновесия. Ниже в самом сжатом
виде формулируются основные положения эюй теории
применительно к рассматриваемой линейной задаче.
Дано линейное однородное уравнение
L,i Ф] = О,
(17.13)
где Lu—оператор, содержащий параметр и. Для систе-
мы с бесконечно большим числом степеней свободы
у — у(х}—искомая функция непрерывного аргумента,
оператор Lu имеет интегральную или дифференциальную
форму. В этом последнем случае уравнение (17.13) до-
иолнепо однородными граничными условиями. Для систе-
мы с конечным числом степеней свободы » неизвестен',!
является вектор
У — (У1, У-2,  • - > Уп)',	(17.14)
оператор L,, имеет матричную структуру и уравнение
(17.13) приводи1ся к виду (17.8).
Однородное уравнение (17.13) при произвольном зна-
чении параметра и имеет тривиальное решение у = 0.
С о б с т в е и ы м з н а ч е и и с м и,t. называется такое
значение' параметра и, при котором' уравнение (17.13)
имеет отличное от нуля (нетривиальное) решение.
Для задач устойчивости равновесия каждому собст-
венному значению u.t,j соответствует критическое состоя-
ние системы, связанное с разветвлением форм равнове-
сия. Возникающая при этом смежная форма равновесия
характеризуется собственной формой (или соб-
ственной функцией) у4/-, определенной с точностью до
постоянного множителя. В рассматриваемой задаче
(17.8) это будет собственный вектор
У*/ = (Л, Уз,---, Уп),	(17.15)
одна из координат которого выбрана произвольно, а все
прочие определены из уравнений (17.8) при ы = и*/.
Все собственные формы уц/ являются формами
отклоненного равновесия. В случае систем
с бесконечно большим числом степеней свободы их назы-
вают также формами криволинейного р а в-
н о в.е сия или крив ы м и в ы п у ч и в а и и я.
Первая собственная форма у,. ~yti является ф о р-
м, ой потер и у сто и ч и вое г и.
Совокупность всех чисел и,/ образует с и е к т р с о б-
с т в е и п ы х з н а ч е п и й (17.11).
Потеря устойчивости системы происходит при первом
критическом состоянии системы, г. е. при наименьшем
критическом значении параметра нагрузки и.,, = «*!.
Собственные формы системы с бесконечно большим
числом степеней свободы (сжатый стержень постоянного
сечения длиной /) обладают свойством обобщенной
ортогональности
? „ '
j ytiy'jdx^ f y^y^clx^-0	(17.16)
b	b
Для системы с конечным числом степеней свободы
свойство ортогональности выражается в равенстве нулю
скалярного произведения двух любых (не тождествен-
ных) собственных векторов
= 0 (1 ¥=/)	(17.17)
Бесконечное множество собственных функций yt) (х‘)
или совокупность собственных векторов y.ty обладают
свойством полноты. Для рассматриваемых в настоящем
разделе задач любое отклоненное состояние системы у,
вызванное произвольной нагрузкой, может быть пред-
ставлено в виде разложения по собственным формам
(векторам)
п
(17.18)
/=1
где Пт — коэффициенты разложения.
Рассмотрение высших критических значений параметра
нагрузки и.,.,г,	. дает возможность ответить па
вопрос о ста п е н и неус т о й ч и вести системы.
Говорят, что при параметре нагрузки и система имеет
сишепь неустойчивости V, если
u,.v и	(17.19)
Система е конечным числом степеней свободы п нахо-
дится в состоянии полной неустойчивости,
если и>ч,2П.
190
РАЗДЕЛ 17 УСТОЙЧИВОСТЬ СТЕРЖНЕВЫХ СИСТЕМ
17.1.7.	Энергетическим критерий
качества равновесия
Потенциальной энергией упругой системы называют
работу, совершаемую внутренними и внешними силами
системы при переводе ес из деформированного сошояиия
в начальное, недеформировапное.
Общие методы исследования равновесия и устойчиво-
сти консервативных систем основаны на экстремальных
свойствах потенциальной энергии.
Здесь в качестве начала отсчета принято недеформи-
рованное (пеотклоисиное) состояние системы. Предпо-
лагается, что перемещения (о1клонснчя) системы убыва-
ют от рассматриваемого значения до нуля; величина
нагрузки при этом остается без изменения.
Для системы с бесконечно большим числом степеней
свободы потенциальная энергия представляет собой
функционал
Л,
П=( F (х, у, у', у",...) dx, (17.20)
1«
который в частном случае линейно упругой системы бу-
дет квадратичным.
Для системы с конечным числом степеней свободы
потенциальная энергия представляет собой функцию
обобщенных координат
П = II (pi, у3, .. . , у„),	(17 21)
а в частном случае линейно упругой системы — квадра-
тичную форму.
Выражения для потенциальной энергии системы
(17.20), (17.21) содержат параметр нагрузки и.
Теорема равновесия. В состоянии равновесия потенци-
альная энергия системы имеет стационарное значение.
В частности, это условие может определять экстремум,
когда в состоянии равновесия потенциальная энергия
достигает наименьшей или наибольшей величины по
сравнению с неравновесными состояниями, близкими к
рассматриваемому равновесному.
Теорема равновесия требует обращения в нуль первой
вариации потенциальной энергии
<5П = 0.	(17.22)
Это условие стационарности эквивалентно принципу
возможных перемещений Лагранжа, так как первая ва-
риация потенциальной энергии системы 6П представляет
собой элементарную работу всех сил системы на возмож-
ных (виртуальных) перемещениях
Для системы с конечным «истом степеней свободы
в нуль должен обращаться полный дифференциал, отку-
да следует равенство нулю всех частных производных
дП
—— = 0 (/= 1,2, ..., п).	(17.23)
ду{
Как известно, условия стационарности (17.22) или
(17.23) являются необходимыми, но не достаточными
условиями экстремума.
Для системы с бесконечно большим числом степеней
свободы условие (17.22) приводит к уравнению Эйлера —
Пуассона
dF	d	dF d2	dF
	__	 	щ------------ 	—•.=0,(17.24)
dy------------------------dx-dy'-' dx“-dy"	’
т. e. к дифференциальному уравнению равновесных со-
стояний системы.
Теорема качества равновесия. В состоянии устойчиво-
го равновесия потенциальная энергия системы имеет ми-
нимальное значение по сравнению с неравновесными
состояниями, близкими к рассматриваемому равновес-
ному. При несоблюдении этого условия система неустой-
чива, если отсутствие минимума определяется членами
второго порядка в разложении потенциальной энергии.
Первую часть теоремы (критерии уш ойчивости) сфор-
мулировал Лагранж (1788 г.), строгое доказаюльство
дали Ф.Миндииг (1838 г.) и Г. Лежек-Дирихле (1846 г.).
Вторая часть теоремы (критерий неустойчивости) при-
надлежит А. М. Ляпунову (1892 г.).
Условие устойчивости требует положительности вто-
рой вариации потенциальной энергии
й2П ; 0.	(17.25)
Для устойчивости системы с конечным числом степе-
ней свободы положительным чои.ен быть второй пол-
ный дифференциал
Потенциальная энергия модели с одной степенью сво-
боды, рассмотренной выше (см. рис. 17.1), равна;
и
П = j v (У — IB/3) dy — N
(17.26)
Анализ этого выражения подтверждает выводы о ка-
честве равновесия модели, сделанные выше.
17.1.8.	Потенциальная энергия центрально
сжатого линейно упругого стержня
Рассматриваются малые изгибные перемещения пря-
молинейного центрально сжатого стержня, материал
которого следует закону Гука. Потенциальная энергия
такого стержня равна:
I
П = -у j (£7у"2 — A’//"2) dx, (17.27)
о
где х, у — координаты точки на упругой кривой; I —
длина стержня; EI — жесткость стержня при изгибе;
А/ — продольная сжимающая сила.
Выражение для потенциальной энергии (17.27) осно-
вано на технической теории изгиба стержней; такую
постановку задачи устойчивости называют геометри-
чески лине й и о й.
Уравнение Эйлера — Пуассона (17.24) в данном слу-
чае приводит к линейному однородному дифференциаль-
ному уравнению четвертого порядка
ElyW-FNy" =0,	(17.28)
определяющему равновесные состояния стержня.
При обозначении
а2 = А/£/	(17.29)
общий интеграл уравнения (17.28) имеет вид
у = С, sin ах ф- С2 cos ах ф- Cyt ф- С4,	(17.30)
где Ск — постоянные интегрирования.
17.1.9,	Задача Эйлера
Л. Эйлер впервые рассмотрел тад.тчу об устойчивости
центрально сжатого линейного упругого стержня с шар-
чытиш! опнршшем концов (17 44 г.).
Граничные условия
у = 0, у" = 0 при х = 0 и х = I
17.1. ОСНОВЫ ТЕОРИИ УСТОЙЧИВОСТИ СТЕРЖНЕВЫХ СИСТЕМ СО СЖАТЫМИ ЭЛЕМЕНТАМИ
191
приводят к системе уравнений относительно постоянных
интегрирования Ck:
С„ + С4 = 0;
— С.,а2 = 0;
(Д sin al + Csl = 0;
— (Да2 sin al — C2a2 cos al -= 0.
Рассмотренное явление потери устойчивости характе-
ризуется разветвлением форм равновесия при критичес-
ком значении сжимающей си ты N = Nf: этой силе соот-
ветствует начальная, прямолинейная форма и смежная,
криволинейная форма равновесия.
В этом случае говорят также о потере устойчивости
в эйлеровом смысле или о потере устойчивости первого
рода.
Параметром нагрузки для сжатого стержня служит чи-
сло нулевой размерности
и = al -=
(17.32)
— /.
Е!
Условие существования ненулевых решений системы
линейных однородных уравнении
0
0
sin и
i —a2 sin и
Отсюда находят
D (и) у
0
и
0
0
I
0
(17.31) юнее г вид
1
0
войт u=0. (17.33)
—a2 cos
спектр собственных значений
«*7 = /я (/=1,2,...).	(17.34)
Этим критическим значениям параметра нагрузки со-
ответствуют критические силы
)2л2Н
д, _
)2
(17.35)
и собственные формы
. 1ях
У*/ = I); sin -j- ,
(17.36)
где r|j — ордината упругой линии в точке с абсциссой
Х-—1/2), произвольная по величине.
При ] = 0 возможна только прямолинейная форма
равновесия у(х)^0; следовательно, значение и = 0 не
является собственным, хотя оно и удовлетворяет урав-
нению (17.33).
Наименьшее значение критической силы из ряда (17 35)
при ) = 1 соответствует потере устойчивости. Эта крити-
ческая сила
л2В/
Аф. = А'э = --—	(17.37)
называется эйлеровой силой. Первой собствен-
ной формой, или формой потери устойчивости, будет
лх
у3! (х) = т] sin — ,	(17.ЗЯ)
где т] — прогиб в середине пролета, произвольный по
величине.
Выражение для критической силы (17.37) носит назва-
ние формулы Эйлера.
Анализ устойчивости с помощью энергетического кри-
терия показывает, что прямолинейная форма равновесия
устойчива только при A1C.N
Упругая линия у(х), вызванная произвольной нагруз-
кой, может быть представлена в виде разложения по
собственным формам типа (17.18):
ео
у(^ ]СЛ/3'П	’	(17.39)
1=1
17.1.10. Равновесные состояния
сжато-изогнутого линейно упругого стержня
Сжато-изогнутым называют стержень, сжатый про-
дольной силой N и нагруженный некоторой поперечной!
(вызывающей изгиб) nai ру.зкой р(х), в составе которой
могут быть сосредоточенные силы Р, внешние изгибаю-
щие моменты (пары сил) М\ и равномерно распределен-
ные нагрузки р (рис. 17.4, а). Частным случаем сжато-
изогнутого стержня является внецентренно сжатый стер-
жень (рис. 17.4, б) с концевыми эксцентрицитетами на
левой опоре а и на правой опоре ka.
Пусть будет Л4 — изгибающий момент в точке с абс-
циссой х, вызванный одной только поперечной нагрузкой
р(х), без учета влияния продольной силы N. Полный
изгибающий .момеггг равен
Ж = Ж + Уу.	(17.40)
В случае линейной упругости материала и постоянной
жесткости стержня дифференциальное уравнение изтба
имеет вид
A/yIV + A'y’ = p(x).	(17.41)
Это уравнение четвертого порядка эквиваленте систе-
ме двух уравнений второго порядка
Ely" + М + АД = 0;	|
_	}	(17.42)
М"=—р(х),	J
Другая эквивалентная система имеет вид
ЕШ" + А’Л1 Е1р (х); 1
}	(17.43)
Ely"—— Al.	J
Весьма удобным является решение дифференциально-
го уравнения (17.41) в форме метода начальных
пар а м е т р о в (см. 17.2.2).
Сжато-изогнутый стержень испытывает деформации
сжатия и изгиба с самого начала нагружения. Под воз-
192
РАЗДЕЛ 17. УСТОЙЧИВОСТЬ СТЕРЖНЕВЫХ СИСТЕМ
действием продольной сжимающей силы рост перемеще-
ний (и напряжений в сечениях стержня) опережает рост
нагрузки.
В процессе естественного увеличения нагрузки проги-
бы сжато-изогнутого стержня неограниченно возраста-
ют по мере приближения сжимающей силы к критиче-
скому значению N* в эйлеровом смысле, т. е. первичные
равновесные состояния определяют асимптотиче-
ское поведение стержня. При	возможно
существование вторичных, равновесных состояний стерж-
ня. График поведения стержня подобен ранее рассмот-
ренному графику для модели с линейно упругой опорой
при а>0 (см. рис. 17.2).
17,1.11.	Об анализе больших перемещений
сжатых и сжато-изогнутых стержней
Геометрически нелинейная постановка задачи устойчи-
вости основана на учете больших перемещений системы.
При анализе стержневых систем используют точное вы-
ражение для кривизны при изгибе
1 <Ру Г (dy\21“ —
р " dx2 [ + \ dx j J
<&у г ___ / dy yq- —
ds2 _	\ ds / J
(17.44)
и учитывают сближение концов стержня. Во втором из
выражений для кривизны, предложенном Ф. С. Ясинским,
независимым переменным является длина дуги упругой
линии s [47].
Анализ больших перемещений преследует цели изу-
чить поведение системы при нагрузке, близкой к крити-
ческому значению, исследовать механизм потери устой-
чивости, описать закритическое поведение системы.
Определенная в результате такого исследования вели-
чина критической силы совпадет с результатом решения
задачи в геометрической линейной постановке, если
предкритическое (невозмущеиное) состояние стержня
является недеформировапным (пример — центрально
сжатый линейно упругий стержень, задача Эйлера).
В противоположном случае, когда стержень испытывает
деформацию (изгибается) до потери устойчивости, учет
больших перемещений вносит поправку в величину кри-
тической силы. Решение ряда частных задач (см. 17.2.8)
показало, чго величина этом поправки незначительна
(порядка десятых п даже сотых долей процента).
Отсюда следует, что практические расчеты стержней
и стержневых систем могут быть основаны на геометри-
чески линейной постановке задачи.
17.1.12.	Устойчивость «в большом»
и явление перескока
В некоторых более сложных задачах (например, при
исследовании закритического поведения стержня в гео-
метрически нелинейной постановке) при одном и том же
значении сжшмающей силы возможно не одно, а два или
более равновесных состояний, не смежных между собой.
Динамический процесс перехода от одного равновесного
состояния к другому, устойчивому через ряд неравно-
весных состояний, называется перескоком.
Исследование явления перескока требует, как правило,
геометрически нелинейной постановки задачи.
Простейшим примером системы, в которой реализу-
ется это явление, служит так называемая «ферма Мизе-
са» (рис. 17 5). Спшема образована двумя шарнирно
соединенными стержнями из линейно упругого магериа-
ла. Стержни могут испытывать значительные продоль-
ные деформации, не разрушаясь и не изгибаясь Нод
воздействием силы /фузел В фермы перемещаемся .в го
Рис. 17.5
ку В' (рис. 17.5, а). При достижении силой Р критиче-
ского значения этот узел мгновенно, перескоком, перей-
дет в новое положение В" (рис. 17.5,6). В этом новом
положении стержни фермы растянуты, система устойчи-
ва [53а]. Более подробны!! анализ задачи см. [31].
В других задачах возможность потери устойчивости
с перескоком зависит от меры возмущения, которая
должна иметь определенную конечную величину.
17.1.13.	Идеальные и неидеальные системы.
Начальные несовершенства
реальных стержней
Идеальным называют линейно упругий стержень, на-
груженный так, что упругая линия изгиба у(х) ортого-
нальна первой собственной форме ут(х), т. е. кривой
выпучивания при потере устойчивости з смысле Эндера.
Для стержня постоянного сечения это условие ортою-
налыюсти записывается в виде
I
у (х) У). (х) dx = 0.	(17 45)
о
Отсюда следует, что в разложении упругой линии по
собственным формам (17.39) коэффициент Ai равен
нулю.
Стержень называется неидеальным, если он на-
гружен так, что условие (17.45) не выполняется.
Простейшим примером идеального стержня служит
центрально сжатый шарнирно опертый стержень
(рис. 17.6, а), для которого у(х)=0. В момент потери
устойчивости становятся возможными смежные формы
равновесия ys(x), стержень выпучивается по полуволне
17 1 ОСНОВЫ ТЕОРИИ УСТОЙЧИВОСТИ СТЕРЖ'ЬИВЫХ СИСТЕМ СО СЖАТЫМИ ЭЛЕМЕНТАМИ	193
синусоиды (17.38). Кривая выпучивания показана на
рис 17 (>, и пунктиром.
Очевидно, что идеальными являются также централь-
но сжаше стержни с любыми другими закреплениями
концов
Внеценipenno сжатый стержень постоянного сечения
с равными по абсолютной величине, но противотю-
Рис 17.7
Рис 17 8
ложно направленными концевыми эксцентрицитетами
(рис. 17 b, б) изгибаемся по S-образноп (ансисиммстри н
нои относительно середины пролета) упругой линии //(лц,
которая ортогональна первой собственной форме щ(т).
Критическое состояние при эйлеровом значении сжима-
ющей силы Аф характеризуется разветвлением форм
равновесия, на антисимметричную упругую линию if{x)
иакладынае гея симметричная кривая выпучивания
у, [у) — полз полна синусоиды (17.38) с произвольно!!
но величине н знаку наибольшей ординатой т]. График
поведения этого идеального стержня представлен на
рис. 17.7, в качестве характерного перемещения выбран
угол поворота на опоре 0. Отрезок кривой ОК при
А’<А'.( соответствует устойчивым состояниям стержня,
отрезок KS при А’>Л'Э —неустойчивым. Точка Л' гра-
фика определяет критическое состояние стержня, свя-
занное с разветвлением форм равновесия.
Идеальным будет также любой lOKaio-nsoniyiwii стер-
жень постоянного сечения, упрушя линия коюрою
антпеиммечрнчна относительно середины пролета (см.
рис. 17.6,0).
Обобщение условия ортогональности по отношению
к первой собс 1 вепнон форме (17.45) на систему стере.-
неи приводит к понятию идеальной системы.
Примером такой системы служит П обргкзная рамп,
обладающая вертикальной осью симметрии и нагружен-
ная равномерно распределенной по рстелю нагрузкой
(рис 17 8). Сплошной линией показано очертание рамы
в состоянии и.31иба, вызванного пагручкой; пунктирной
линией показана кривая выпучивания при потере устой-
чивое! и в эйлеровом смысле.
К неидеальным системам относятся все системы, форма
изшба которых не ортогональна первой собственной
форме
Идеальные системы испытывают потерю устойчивое!п
при ра щегвлегщн форм равновесия, когда сжим<1Ю1К..я
ен ta доснп’не'1 критического значения.
Для неидеальных линейно упругих систем характерно
асимпимическос поведение, т. е. неограниченное возрас-
тание перемещения но мере приближения сжимающей
силы к критическому значению (пунктирная кривая
ОЛ,£ ин рис. 17.7).
Все реальные стержни имеют начальные искривления
и, кроме предусмотренных проектом эксцентрицитетов,
13—26
также начальные (случайные) эксцентрицитеты прило-
жения сжимающих сил. Начальные искривления и слу-
чайные эксцентрицитеты объединяют понятием и а -
ч а л ь н ы х н е с о в е р ш е н с т в.
Вопрос о необходимости учета начальных, несовер-
шенств при расчете сжатых и сжато-изогнутых стержни1!
следует рассматривать отдельно для стержнем с идеаль-
ной и неидеалыюй расчетной схемой.
При расчете неидеалытых стержней учет начальных
несовершенств вносит количественные коррективы, про-
порциональные мере этих, несовершенств. В большинстве
случаев изгибающие моменты, вызванные начальными
несовершенствами, мальмю сравнению с изгибающими
моментами, вызванными поперечной нагрузкой р(х) или
проектным эксцентрицитетом а приложения сжимающей
силы А', В этих случаях влиянием начальных несовер
шепств можно пренебречь.
При практическом расчете идеальных стержней не-
обходим учет начальных несовершенств, нарушающих
идеальную схему и создающих качественно другие усло-
вия работы стержня. Роет напряжений и перемещений
по мере приближения сжимающей силы к критическому
шачению вызывает развитие неупругих деформаций
материала.
Для учета начальных несовершенств идеального стерж-
ня па него накладывают начальное малое искривление
z/Дх) или дополнительную малую нагрузку, вызываю-
щую упругую линию причем в обоих случаях фор-
ма Уо(Л’) не должна быть opioiопальной первой собст-
венной форме у,, (х). Мера начального несовершенства
и его направление особой роли не играют, так как самое
малое нарушение идеальности в ту или иную сторону
переводит кривую OKS на графике поведения в положе-
ние ОС (см. рис. 17.7),
17.1.14.	Свободная длина
и гибкость стержня
Понятие свободной длины было введено Ф. С. Ясин-
ским [47] с целью обобщения формулы Эйлера (17 .’>71
па сличай центрально сжатого линейно упругого стерж-
ня с произвольным закреплением концов.
—
К
Зцесь свободная длина стержня
lt - Р/
(17.46)
(17.47)
представляет собой произведение коэффициента
свободной длины р на геомецшчеекую длину А
Величину р выбирают в соответствии со схемой закреп-
ления концов стержня
Запись критическоц силы
(17.48)
удобна для задач о потере устойчивости при разветвле-
нии форм равновесна, так как позволяет результат ре-
шения записать в виде одного числа — коэффициента
свободной длины Р, не зависящего от геометрических
размеров стержня.
В случае стержня переменного сечения £/ = /(%) за-
пись в форме (17.48) становится условной, поскольку
величина р зависит от выбранного частного значения
EI в (17 48).
194
РАЗДЕЛ 17. УСТОЙЧИВОСТЬ СТЕРЖНЕВЫХ СИСТЕМ
Гибкостью стержня называют отношение его свобод-
ной длины к радиусу инерции поперечного сечения:
17.2.2. Уравнение упругой линии стержня
в форме метода начальных параметров
(17.49)
Дифференциальное уравнение малых изгибных ;iepc-
мощений сжато-нзогну ioro стержня с произвольными ус-
ловиями закрепления концов имеет вид
Здесь I — момент инерции; F — площадь поперечного
сечения стержня.
Нормативная методика расчета сжатых и сжато-изо-
гнутых стержней основана на понятиях свободной (рас-
четной) длины и гибкости стержня (см. 17.9.2; 17.9.4).
diy d-y р (х)
Н~	—
dx^ dx- г/
(17 50)
где сР — А'ДУ; р(х) —поперечная нагрузка.
17.2. ЛИНЕЙНО УПРУГИЕ СЖАТЫЕ
И СЖАТО-ИЗОГНУТЫЕ СТЕРЖНИ
ПОСТОЯННОГО СЕЧЕНИЯ
17.2.1. Линейно упругий материал.
Обозначения
Рассматриваются прямолинейные массивные (не тон-
костенные) стержни постоянного сечения. Материал
стержней линейно упругий, т. е, существует прямая
пропорциональность между напряжением а и деформа-
цией е, выражаемая законом Гука а = Ее..
Силовая плоскость совпадает с плоскостью одной из
главных осей поперечного сечения. Сохранение плоской
формы изгиба считается обеспеченным. Не учитываются
деформации осевого обжатия и деформации, вызванные
касательными напряжениями. При анализе изгибных де-
формаций принимается гипотеза плоских сечений.
Общие положения см. 17.1.3; 17.1.9; 17.1.10; 17.1.13;
17.1.14.
Основные обозначения;
I — длина стержня;
х, у —координаты точки на упругой линии;
ут — прогиб в середине пролета;
z—абсцисса точки приложения нагрузки;
Q—dy'dx —угол поворота;
М — изгибающий момент;
(? — поперечная сила;
Н — проекция поперечной силы Q и продоль-
ной силы iV на направление, перпенди-
кулярное первоначально прямолинейной
оси стержня;
£7 —жесткость стержня при изгибе в силовой
плоскости;
N — продольная сжимающая сила;
Л'„ — наименьшее критическое значение сжи-
мающей силы;
Л’э — эйлерова критическая сила для шарнир-
но опертого стержня;
р—распределенная поперечная нагрузка на
стержень;
Р — сосредоточенная внешняя сила;
АД —внешний момент, пара сил;
и—уЕ ЕН—параметр нагрузки для стержня;
и*/ — j-e критическое значение параметра на-
грузки;
—наименьшее критическое значение пара-
метра нагрузки.
Общий интеграл этого уравнения равен сумме общего
шпшрала (17.30) однородного дифференциального
уравнения (17.28) и любого частного интеграла у'*(х)
полного уравнения (17,50).
у = Ct sin ах +- С2 cos ах Д С3х Д С4 + Д (х) . (17.51)
Наиболее удобным является решение уравнения
(17.50) в форме метода н а чаль н ы х парам е т-
р о в. Под начальными параметрами понимают величи-
ны Уо, 0О1 АД, На в начале координат при х = 0
(рис. 17.9). Здесь Н— проекция поперечной силы Q и
продольной силы Л' иа направление, перпендикулярное
первоначально прямолинейной оси стержня. Из условия
равновесия (рис. 17.10) Q = 77cos0+Asin0жЯ-уЛ'0 сле-
дует
H = Q — Л70; (17.52)
Решение уравнения
ных параметров имеет
, sin ах
У ~ Уо +	——— 
До == ф() ЛД0 (17.53)
в форме метода началь-
(17.50)
вид
АД
1 — cos ах. 1
а Е1
ах — sin ах
£7
dy	АД sin ах
0 = — = 0„ cos ах —---------• --------
dx	EI а
1 — cos ах
------.---- у 0ц.
До
£7
d-u
Л4 =— 77 —ж = 0 £/а sin ах у
dx2
,	sin ах
+' АД cos ах Но -------------J- Л1“;
Я = Но~~ НЕ
Здесь зависящее or нагрузки слагаемое равно
(х) = j [а (х — |) — sin а (x--g)j р (17.55)
Na J
г
17 2. ЛИНГГШО УПРУГИЕ СЖАТЫЕ И СЖАТО-ИЗОГНУТЫЕ СТЕРЖНИ ПОСТОЯННОГО СЕЧЕНИЯ
195
Таблица 17.1
Метол начальных параметров. Слагаемые, зависящие от нагрузки
I
j Вид нагрузки
— cos а (х — г)]
0“	р Г	sin а (х — г) 1 —(х — г) —	'	~ Ala2 [	a	j	р 	1 — cos а (х — г) 1 £/а2	л	ЛФ. —	 sjn а (х — Е! а
лГ	Р — — П — cos а (х — г)] а2	Р —	 sl‘n а (х —, Ct	Мг cos а (х —- г)
Q"	Р . — — sin а (х — г) а	— Р COS ГХ (X — 7)	Л1х а sin а (х — г)
Н" Примеч	— р (х — г) п и е При х<_г aie слипаемые от нагру-’.м	— Р , приложенной в точке с абсциссой	0 г, принимаются равными н\лю,
причем 5 — вспомогательная переменная, которая после
интегрирования и подстановки пределов исключается,
с — абсцисса начальной точки приложения нагрузки
р(х). При х<уг функцию г/н(х) и все ее производные
принимают равными пулю.
Аналитические выражения для зависящих, от нагруз-
ки слагаемых
du»	d-у»
у» (х); 0» =---; Л1Н ==— £7	;
dx	d х2
d3u»
QH £/ -TO_  fpi = OH _ Л/0»
dx3
(17.56)
приведены в табл. 17 1
ной нагрузки p = const,
1яжеиин стержня правее
Для равномерно распредслен-
воздеиствующеп па всем про-
точки г, из (17,55) следует
У11-	г).
где ф у н к ц и я в л и я и и я
(г — г)”	1 — cos а (х — г)
т И, И =	-------------------------
2	а-
(17.57)
(17.55)
Выражения для у» от сосредоточенной силы Р и от
лары сил (внешнего момента) Лф, приложенных в точ-
ке с, получаю! дифферснитрованием функции влияния
ао ж ременной г;
Р /)	М, д2
Т(х, г).	Тр,г). (17.59)
5г	Л	иг-
13*
Выражения для 0я, М», Q® получают из (17.57) и
(17.59) дифференцированием функции влияния ЧДх, г)
по переменной х в соответствии с (17.56).
Преимущество решения (17.54) по сравнению с дру-
гими возможными формами: а) из четырех подлежащих
определению величин у0, Йо, Л10, Яо две известны по ус-
ловиям закрепления левого конца стержня; б) влияние
поперечной нагрузки р(х) учитывается добавлением сла-
I аемых у», 6я, ... при х>2 без изменения предшествую-
щих членов.
17.2.3.	Критические силы центрально
сжатых стержней с различными условиями
закрепления концов
Решение задачи устойчивости (в эйлеровом смысле)
для одцонролетпого стержня при произвольных закреп-
лениях концов удобно основывать на соотношениях ме-
юда начальных, параметров (17.54), в коюрых следует
положить ул = 0ь = Л7н==Л,я==О. Из четырех начальных
параметров yr>, On, Mj, Нп два известны по условиям за-
крепления левого конто стержня при х = 0 Coci являют
два уравнения, отражающие условия закрепления пра-
вого копна стержня Эш уравнения буду! линейными и
однородными относительно двух начальных параметров,
иг щвишхея ней местными, коюрые здесь обозначены
(.нинолами Zb Zy
ш__
1 И юичиви^ь <hPAH ЬЫХ СЖ ILM
Собственные фермы и !рнимеские параметры waipy ня для гмагых линейно упругих стержней
( xe'i J стержнт и форм.! поте; л у с гоичиностн вторая <_ Жженная форма треть! соботвеннзя формз		\piHiTLU е Прут 04 1И !l!ri ((. ГОСТ Bet ноя , р 1Ь)	Уравнение пратяч ow о о сто>ния 1) («жО, 1 - 1 Л// 1 1 Об це< pt исгне уо !ине< и i /JU)-- >	Первые три лря1и it мн знач нитт I jpj-мец j сгрузки		Кри ГНЧ1 Спая : СИ Id Л я (..БобоДНиН длина
—	W	JJ _px=mU—	1 Р® ..£ —— —~зн	L Jl 1'	S ! и — -j	ия	- л =-	!41h	 ы L
3
172 ЛИНЕЙНО V’lpilllb СЖАТЫЕ И ( Ж VI0 ИжЛ Ч VIЫЕ СТЕРЖНИ ПОСТОЯННОГО СЕЧЕНИЯ	197
Пподоллсение табл /
Схема стера ня и форма потери устойчивости	Сравнение упругой ти пап (собственной Формы)	й равнение t-ригического со- стояния />(«)—0, и~У	1	Первые три f ритическш значения параметра на!рузчи и	Критическая сила Л* и свободная длина
вторая собственная форма		Общее решение сравнения b U) (		
третья собс1веинвя форма				
!/// и it. J t г 1Г _ць Hi: :. Ill 17р )
198
РАЗДЕЛ 17 УСТОЙЧИВОСТЬ СТЬРЖПГВЫХ С1К Т! '1
Коэффициенты этих уравнений у1ь=="у к(и) являют я
функциями параметра ншрузки
и = al = Vn/EH	(17 61)
Условие существования ненулевых решений системы
117 60) заключается в равенстве ну ио определителя
О (и) о I 711 712 |0,	(17 62)
I 7 22 I
который стедует рассматривать как функцию параметра
нагрузки и
Условие критического состояния (17 62) приводит
к трансцендентному уравнению относительно и, корни
которою образуют бесконечный спектр собственных зна
ченнй параметра ла1рузки
ил, «*,,	(17 63)
Для у-й критической си ты имеем
trFl
(/=1,2,...) =	(17.64)
Наименьшее критическое значение параметра нагруз-
ки /•/_— и*! соответвует потере устойчивости ыержня
при разветвтении форм равновесия Критическая сила,
вызывающая потерю устои швости равна
и~Е1
(17 65)
Для построения собственной формы у*7 используют
первое из уравнений мето щ начальных параметров
(17 54) при z/ = u„/, соотношение между двумя неиз-
вестными начальными параметрами Z\ и Z2 определяют
из уравнении (17 60) коюрые при и = иг/ становятся
эквиватеитиыми друг друi у
Любые две собственные формы z/t; и у,, обитают
свойством обобщенной ортогона шносю (17 16)
Из сравнения двух значении критической силы (17 49)
и (17 65) определяют своботдую ттииу стержня
I* - (У — I,	(17 66)
и т
где p=T/us.—коэффициеш свобо гноя типы.
Рис 17 11
17 2 ЛППГППО УПРУГИЕ СЖАТЫЕ И СЖАТО-ИЗОГНУТЫЕ СТЕРЖНИ ПОСТОЯННОГО СЕЧЕНИЯ	(QQ
Табл. 17.2 содержит результаты исследования устой-
чивости одионро. ie i пых сюржней для пяп1 едем с раз-
личными условиями закрепления концов Показаны
схема стержня, начальная недеформированная его ось,
форма потеря устойчивости, вторая и третья собствен-
ные формы, уравнение упругой линии с произвольным
множителем С, уравнение критического состояния
П(п)=0 и общее выражение для /-го корня этого урав-
нения, первые три критических значения параметра на-
грузки и„л, и*-,, формула для наименьшей критиче-
ской силы Л\, свободная длина 1*.
Если подобрать длины стержней I для каждой из
схем так, чюбы критическая сила была во всех случаях
одинаковой, то формы потери устойчивости можно рас-
сматривать как дуги одной и той же синусоиды (рис.
17.Н)
пх
y = sin—.	(17.67)
ч
При этом свободная длина 1„ равна расстоянию меж-
ду двумя смежными точками перегиба, т. е. полуволне
синусоиды.
17.2.4.	Внецентренно сжатые стержни
Общий случай — неравные концевые эксцентрицитеты.
Концевой эксцентрицитет равен а на левой и ka на пра-
вой опоре (см рис. 17.4,6). Предполагается, что j k15^ 1.
Условия па левом конце стержня даю! уо — 0. M0~Na.
Из условия равновесия определяют величину
Л0=--у-(1-^) У.
Воспользовавшись первым из уравнений (17.64) и под-
чиняя решение [раничному условию на правом конце
стержня (1/ = 0 при х~1), определяют единственный не-
известный начальный наражчр
0О = -—' |с(гг)4-Ь(ц)],	(17.68)
£/
где приняты обозначения для ф у н к ц и й Н. Е. Жу-
ковского [15]:
С(И) = _1.Л	=	(17.69)
и2 \ tg и /	и2 \ sin и j
Уравнение изогнутой оси стержня после преобразова-
ний приводят к форме
а ( и	, , .	,
у = — 1-----— [sin (и — ах) 4~ « sin ах] —
и Isinw
— [(и — ах) -ф- (гах]| .	(17.70)
Таблица 17,3
200
РАЗДЕЛ 17. УСТОЙЧИВОСТЬ СТЕРЖНЕВЫХ СИСТЕМ
Ниже рассматриваются частные иучш (шещнтрен-
но сжатого стержня.
а) Равные по абсолютной величине и по знаку конце-
вые эксцентрицитеты. В штучае Л«-1 уравнение 117.70)
1гринимае'| вид
(17.71)
прог 1’6 Б середине пролетз рлюн.
(17 72)
График поведения стержня представлен и таил 17 3 а
Сплошная линия соогиегствует ус.опчивып ПтрвианьП!
состояниям равновесия при А;<Л „ (/т>0. нуНК 1 Ир
пая-- тшустончивым вторичным при Д’>Л >. д1л <--2п.
Формы равновесия па схеме стержня и п.1 (рафике по-
ведения отмечены цифрами I я 2.
Для первичных равновесных состояний характерно
асимптотическое поведение — неограниченное возраста-
ние пропчба у,„ по мере приближения сжимающей си-
лы N к эйлерову значению
б) Равные нулю концевые эксцентрицитеты — цен-
трально сжатый стержень. При и — 0 возникает задача
Эйлера, рассмотренная в п. 17.1,9. График поведения
стержня представлен в табл. 17.3, б. Прямолинейная
форма равновесия у шО устойчива при N<Na и не-
устойчива при А'>ЛЛ. Точка К па (рафике соответству-
ет потере устойчивости при разветвлении форм равно-
весия
в) Равные по абсолютной величине, но противополож-
но направленные концевые эксцентрицитеты. В с.тучю
k ——1 уравнение упругой линии (17 70) принимает вид
(17.73)
Уюл недорога на левой опоре при х = 0 равен:
График поведения представлен в табл. 17.3, в; по оси
абсцисс отложено характерное перемещение во, по оси
ординат отложена сжимающая сила <V. Форма изгиба
по S-образной упругой линии ортотопальна первой соб-
ственной форме (17.38), стержень является идеальным.
Соответствующие этой упрут ой линии равновесные со-
стояния устойчивы при N<zNa и неустойчивы при об-
ратном знаке неравенства. Разветвление форм равнове-
сия (точка Л' на графике) характеризуется наложением
полуволны синусоиды (17 38) на S-образную упругую
линию (17.73), В критическом состоянии Л' = Лд, и, =
= я, 04=2в//,
17.2.5.	Сжато-изогнутые стержни
Сжато-изогнутые стержни разделяются на идеальные
и непдеальпые, примеры тех и других даны в крапаем
правом столбце табл. 17 3. Качественные особенности
поведения соответствуют рассмотренным выше случа-
ям «из п «г» внецентренио сжатого стержня
Если стержень не является шарнирно опертым, то эй-
лерова сила Л', должна быть заменена критической си-
лой .V„ по данным табл. 17.2.
бабл. 17.4 содержит справочные данные для шарнпр-
Щ) опертого стержня, нагруженного в точке z~kl внеш-
ними силами р, Р и Лф. В таблице даны, выражение
для прогиба у в точке х — ml при ш.<й (первая строка)
и mp>k (вторая строка); ана.тот никое выражение для
угла поворота 0; значения Оо и О, на левой и соответ-
ственно на правой опорах; выражение для титибаюшего
момента Лф абсцисса точки в которой тигибзющий
можнг достигает наибольшей величины Дшн; ттыра
жеште для тИчаис.
Табл. 17 5 содержит аналитические выражения для
усилий н перемещений сжато-изогнутых стержней с раз-
лшшыми условиями закрепления концов
Зависимость усилия (или перемещения) < жато-изо!-
нугою стержня от величины сжимающей ит.н.1 выража-
емся приближенным соотношением
S =
(17 75)
где 3 — соответствующее усилие (перемещение), опре-
деленное без учета влияния продольной сжи-
мающей силы.
17.2.6.	Принцип независимости действия сил.
Принцип взаимности перемещений
Принцип независимости действия сил (принцип суттер-
потиции) для сжато-изогнутых линейно упругих стерж-
не» применим в специфической трактовке- сжимающую
силу .V следует исключить из понятия «натру зка» и от-
нести к свойствам стержня [19, 21aj.
/Етнейноеть дифференциальною уравнения (17.50)
даег возможность наложить два решения р1 и у2, вы-
званных натру жами рф.т) и соответственно Дз(л'), если
величина и остается постоянной. Эю значит, что при
фиксированной величине сжимающей силы Л реше тие
у~у}±ц3 будет отражать воздействие нагрузки р =
=-й|+Р2
Использование принципа суперпозиции позволяет с по-
мощью табл. 17.4 и 17.5 получить решение ряда более
сложных задач, когда на сжато-изоптутый стержень од-
новременно воздействуют несколько поперечных на-
грузок
Для сжаю-изогиутого стержня, как и для любой) ли-
нейно у другой системы, справедлив тт р и и и н п в з а и м-
н о с т и работ (принцип Макешлла)
(17.76)
Здесь .Pi.Pa — сила первого и соответственно второю
состояния; — перемещение по направлению силы
Р„ вызванное силой 7Д
Под силами Pt, РА следует понимать поперечные на-
грузки, продольная гили .V одинакова как t> первом, так
и во втором состоянии.
Если силы Р, и Рц равны между собой по численной
величине, например в частном случае единичных сил
ПИЧГИНО snpvEHF СЖТТЫР il СЖИТО ИЗОГНУТЫЕ СТЕРЖНИ ПОСТОЯННОГО СЕЧЕНИЯ
201
Усилия и перемещения лииепно jnp*rorp сжато-изогнутогс шарнирно опертого стержня
	сг’ Г1 COS (1 — ‘) и	Pl’ fsin fl - к) и sin mu	1	V Р	'
к	11и~ [	a- мл п т	1 - Y(!-Aq	I lu- j_	и sin II — m d - fe)~j	f Em Г	cos d —'if ^!n t	i a. —	     -i-	m 1	мп и	j
	р/4 Г (т — МП т>	PF | sin Ln sin d - mt n	П,/ r(o« 'n s'n (i m) i
4"	f/u’t	2 чп/w s п)!—т) и оз кп - sin и | umiiui	1	f hi- [_	и sin и — r (1 — m	> la- L	sin и - (1 - m} j
	гГ’ Г (1 -М	Pl- ( sir d - s) n (Os m i	
к	Г1и*1	2	1 I — COs (1 — k) U	1 -г	cos mu imnvi	j	i 1л- [	sin и	Llu- Г л £r^ (1 — и	mj	1 _	__	~ r 1 1	Sin I	I
к	pF Г 1 -L- к- —' 2m Elu2[_	2 cos tn i — cos (1 — mt и cos k Л	PL " x rJ u“ f sin ku Ws (1 — m) и , ]	mi Plu- x Г и cos ku ros (1 — m) i	1
	1	U Sin и	j	[	sin и	1	*	—	T i [	чп a	j
	pF | । co (1 'И и alll- {	U «1П «	Pl-	d _ r) „	1	’И/ Г «cnsd - hi	1
	_ ji	j-q	T , I	) 1 Li i~ [	w u	j	1 —	-j-” 1 El a2-1 [	-><п и	j
	rp j I OS I- u LOs M Lin- [	ц «in и 1 V ]	Гr' «1П Pl	] Fla- L «с и	J	И,/ Г i сочки	1 	1— - —	- 1 Liu- [ sm»	J
	d	d !?} U	«И1 ! 1 /И и «1Г1 mil	(Os Ы к} U Sin ! w. dMl t
	im	и мпи	t i и 5Ш и	
К	рЦ E	t s n / 4 sin ( 1 - I ’ 1 I	1 i 4i d — m} н
	sin CM Sind -W) «COS kri— in и sin и	и мп a	^.i sin и
ч	1 — COS и (.Os ku — jrit^	 n	sin и cos А и	1 j	k	
	pl- uz	«in Pi m (1 — 4) ti	
к	I 1-2 cos и cos ku-r cos- few	u sm и	
202
РМДГ 1 17 РСЮИЧИВОС ТЬ . II P/KII1 ВЫХ ГДТГЧ
Т а б 1 и ц а 17 5
Усилия и перемещения линейно упругих сжаго изогнутых
стерт шеи
Cximi	j Усилия и перемещения
1
Момент в середине upoiva
Прогиб в серед! че про <ста
Угол поворота на опоре
Момент под грузом
Прогиб под грузом
РР / - и _ 1> \
2EhP \	2	2
Угол поворота пи опоре
М мент н М	сере 1 М	не про гм а
	2 cos	
I poi l6 в	ссрсдн	е проле
М„1	/	
2 Liu	1 COS	и	|
гол поворота на дева/ оюр
,. Мп1 .-
А = ~—----(1 — и ct г и)
Пи?
Угол поворота ча правой
опоре
о -	( а ~ \
Z 1и \ мт, и )
Продол пенис таг//I П •>
Схема			Усилия и перемещения
			Момент в за телке
			,,	р£ М =.		—•• )< 2и
	Р		2 — и чп и -- 2 cos и
			
		! N	S 11 U	U	Д
1^,		X *< -»	Угол поворота на левой опоре
	К-		9 = EL л Ии'
			(° — и sin " — 2 cos и)
			2 (sin и — и cos и)(1 — cos и)
			Реакция правой опоры
			_ Sin ku - ku cos и P = P	 sin n — U COS и
			Момент пот грузом
			м = Pl	ШУ	х bin и — и cos и
			л. ^сэз	и—
			sin (1 - /у ч	Д1
			«	j
			Момент в заделке
	мм	1 -	,,	sm ku — k sin и И	Pl 	—	 sin и — и СОэ и
			Пр гиб пол грузом
L	С t Г-1®- 1 —		р/’ г у —	1 л i(->m 1ш -k sm и.} р L/u )
			/	ЧП АмХ 1 НАМ/? cos и	 ,	1 —• со> (1 — /?) и
			xlll и — и СОэ и
			(1 — k ) и — S 1 п (1 — R ) и
			sm ti — и со> и
			\дот поворота на левой опоре
			„ Р1 е =	х Е/и‘
			' [А[ {и —'ли и) — А2 (1—cos и)]
Реакции правой опооы
Момент в серетине пролета
ч
cos----
Поотиб В город 1НР ПР0Щ1 -1
и и
----------- СОЗ и
Момент по 1 грузом
М - Р1
(M0^Na)
Угол поворота на опоре
Sin —----
2
]7 2 ЛИНЕЙНО УПРУГИЕ СЖАТЫЕ II СЖАТО ИЗОГНУТЫЕ СТЕРЖНИ ПОСТОЯННОГО СЕЧЕНИЯ
203
Схема
М-
!] ~

силия I перемещения
Момент э заделке
—• cos —
Pl
Прогиб ПОД ipyiOM
Pl	A
Liu3
и

опор®
2
а
R
Момент в заделке
\ г I поворота на левой
опоое
Ч — М
Р акция правой опоры
Мп и (1 - со-. «)
вверх
протега
17.2.7.
ц —
1.РР1
в сере.
dx*
где с.с
пролета
но
направлены вниз Положить
ное направление углов полорота
на опооах соответствует поло
жителыюму направлению оп >р
в заделке
Р1 4 и
шт в середине пролета
pl !	“	I '\
Момент в за гетке
Продог шиле таРл 17 о
Усилия я перемещения
Прогиб
COs Li-r-Ll sin и
Момент в заделке
рР
левого конца
Ыи
Момент в заделке
М =— Р1
тезою конца
г Ш
поворота левого конца
РР / 1
поворота
р!
£7z? \ соь и
Положи
ре 1КЦПИ направлены
Положительные момен
ягивают нижнее во юк
оложигелъные прогш н
Рг^Р^ 1 то
ц и п в з а и м
Бетги)
Прогиб левого конца
Момент в заделке
левого конца
М
из соотношения (17 76) следует прян
ности перемещении (принцип

(17 77)
Растянуто-изогнутые стержни
Дифференциальное уравнение мазых язгибных пене
мещении растянуто изогнутого стер/кня (рис 17 12) име
ст вид
р (Л
dx-
7/
V/Z7 \—растя! зшаюпря сила
(17 78)
4
204	Г- ' ГТППЧИВОСТЬ СТЕРЖНЕВЫХ (IKTfVt
Оощии интеграз зтого уравнения
у — С\ sh ал - С ch ах г ( эл — С4 у уА (л)
иим! гиперботическис функции с i можсг бит ipe
б] s ir in к форме метод i нач i гы ых пар >м тров
От. t iko шт необходимости в развергнвапии ш»ти
I tux 1 пиггческих зщисимостси так как форме ты mi
шин; и перемещении р ытяну io изотутого сгержия
ею хт бытт поте юны и соответствующих Форме * тя
ci по и отчего о те pa । я (ттот 174 17 Н нт о юье
простою преобр пор шия Парпнтр нагрузки рас; ту
ю изогнутою стержня
о - V \ /Ы1	(1/ 76)
( т. \ - растягивающая ( i т) стяжан с парт трот нт
грхзки и сооп ош пп м и'— — <.' Отсю и йоте 1ают
и tyютил устовия I ер хорт
с ж по изо1 ;утн 1 стерженв и sin и сох •/ tg и
растянуто изогнутый стержень 'о i ьп v ch v i th v
Ь резутьтате преобразования тюбом из формуя сии
вот мнимои единицы ;-= J, —1 исключается
Перемещения растянуто изогнутого стержня растет
м сине нагрт ок Потеря усгсчивости растянутою
с г ржия невозможна
пс s — тина дут *пруюи iinnin отешгываемая or
тевоп опоры Н — pt ыцги опор напртвti ишп перпен
тикхтярнт нс Деформирован; ои оси стер дня
При обозна гениях
а" - \ /Е1 у - Н/\	(И 81)
[ ш ине того ур 1 зпеипя зшисыгают в rip пи три; хон
q; рчс
2х	|
у —-----(1 — у")1 4 cos <f — ул — а
а
ч
1 f _ rf<f
а 0	I-)1 4	1 — и sm <т
ЧЛ>	1 а
1 Г	J (17 Я2)
х------------ Оиу(лоэ cfo -comp)
«(1 -г У)3 1 1-
Г
1	1 — „X ЧП3 <г
г V 1 — л sin' «
I П
Зт"сь <, —вспомогттстьная переменны (параметр)
гг —(зпа 1ечие до i переменной при л = 0 s—0) и ч ;с
то а(|/|<1) —постоянные ш тегриров щия
оор<ыс 1 1 ы 1
1 iob It a in I
амптитудои ср
ipMIUHOH Форк
pi первого и второю рода
ф
dtp
17 2 8 Бодмине перемещения внеиентренио
сжатых стержней
^тсеь рассматпивтются ботьшие и пены п т<> пн
ЦП ВЦ 1Ю1ТТ“ННО сжатого ТИЧСИЯО 1 ipyrn Т pz 1
О смысте и цсти талого юстедования см 17 1 11
''Ии ий стучат* - неравные концевые эксцентрицитеты
(рис 17 13) Дифф Олнщ атьнос хравненис изгиб! име
л! 11’1
/ hu^rr
— V (гт — г/) —/7л = О, (17 80)
) Г1Н 401 > Г OilTb П)
1 1ИПТИ И СК IX Ш-ntI {
с мод>аем / и
0	1 — X2 sin2 (р
== 7'(ф,х)
• (17 83)
к)
п И 1 — / ып ср
I
Из грани пп х устовии
у — 0 при л = 0 т — 0 ф — qy,
у — 0 при л — т — I гр ф}
и зелтвгя равенства тио изгибающего момента на про
нои опоре му = а(1 -k) находят
1 — 2/ Sin3 (Р
= 2^ (<Г Г
cos ф]
(17 84)
BioDot и третье соотношения (17 82) при if - epi
дэют
(17 851
С оответствхющии рассматриваемому равновес -тому
состоянию параметр наррузки равен
и - а/ -	С------. (17 86)
и— ми!/4 ’ т/:
I ’ ДИНРЫНО СПГХГИГ ГА'ТЪ1Е II сяотп хгопг ТЫК СТЕРЖНИ ПОСТОЯННОГО •'РЧЕ’ШЯ	205
Д1Я тангенсов углов поворота подучают
tg 0
dl)
dx
у (1 - 2хг sin’ ер) 2х чп и 1 1 л .in" q
1 — r>V." sin- ф г '’/у sin ф 1 — И’ Sin- ф
(17 87)
при ф—фп отсют.1 опредетяют тангенс угла поворота
из тевои опоре tgOt
Основанный нз г ведантах авчеимоетях выдели
гнныи алгоритм позволяет построил равновесное со
стояние стер/ ня го заданным значениям a/l k <pQ
Ниже рассматриваются частике случаи висценгр«.нно
СЖ 1ТО1 О СТСр/ НЯ
а)	Равные по абсолютной величине и по значу кличе
вые эксцентрицитеты В д г>е 7—1 у — 0 основное рас
ч тиое соотношение (17 8о) принимает вид
/ cos <)0 у- f (с(„ и)	(17 88)
Решения этого сравнения при потожитетыгнх зняче
днях мотеля / и nj> 1 <(п<п/2 соотщ 1с>гуют первичным
равновесным состояниям стержня Вторичны р ibhib с
ныс состояния onpi а шются решениями уравнг зчя
(17 88) при и-л'О и q >л/2 [22]
Наибольший ППО1ИО в середине длины стержня past н
Выражение (17 86) для параметра назрузки привозят
к виду
и=т2Г(ф0 х)	(17 90)
График поведен 1я стержня при больших гнстоеще
ниях представлен в забз 17 3 1 Первичные равновес
шк состояния (сгтоштя 1ииия OLS ia графилс) вот
можпы кал пр I V<V так и при М>\ прогибы по
тож ыетьнь и ограничены по вртичине А 1атиэ каче^т
ва равновсс ih с помощью энергетического критерия по
кпывает что перни шые равновесные состояния устои
ч авы
Втори шые равновесные состоят я при V>Va i/ra <
<—2а разте яюгся на устойчивые (сплошная линия)
и hovctoihhbi с (пунктир на 1Р1фике) Тожа Т на
графике служит границей между чегоичнвоп и нсустои
чивои йлтвями этон точке соответствует транс ери
ти чес кое течение сжимающей силы Ут>Лл Гпи
\ < \ т возможны только п°рвИ1ные равновесные со
стояния Каждому значению \>УТ соответствуют три
р вновесных состояния одно усюичивое первичное и
дай вторичных из которы устойчиво только одно с
ботыпим по а(солкипог веттипе прогибом у п
Переход вш [ентренно сжатого тержня оз первччнои
формы равновесия ко вторичной v ожст нроито ти тоть
го путем перескок!
По мере хоывания л сиептршш i та а тики I г 7 hi
графике сгпсмялся к одно i и то 1 же тоже с коорд! а
ТОМИ (0 У а)
б)	Равные нулю концевые эксцентрчинтеты - ней-
трально сжатый стержень При а —0 з уравнения
(17 88) ечепует ерп — ч/2 Расчетные зависимости (17 89)
и (17 90) преобразуются к виду
л!
.-2/-(и),	(17 91)
где Р(и)—поднь и ттипти щеки I чнтегт 1 и рпого ро
з (а тот w та гг — т/2)
График поведения стержня при бошпчх таремеидаш
я\ тая i табт 17 3 А Прямо шпени 1я форт р ibhobi
сия у = 0 устойчива при	и неустойчива при
Представют е о безраз дичком состо нпи ра
(овесия 1ри Г — Уф с допрете юпным i го ; ш-шне и пл
Hiai у прог п гм х tj - С sin (лх/ф я0зятог’я следствием
потатрюе ки I i геиноч пост нов и тин Ье щаззи 1
i ое состояние равнов сия на саз ом дс е яв1Я(1ся мтоо
венным так ка> при Ь — \ сущее вуют тшш беско
ie ню бтизкю формы равновесия смежные с прямоти
неииси формой yssQ
Дтя К1КД0Ю зпачеш я \ > V, по шмо нет стон пито!
прямотииеинои формы существуют две у тон ивы к и
водиц mi it формы равновесия ю строю определю
ми равными по абсолют юн величине ио протовопо
ложно направTCHHiPin I poi гбами Не >пре i тен iocti
устойчивых равновсс шх СОСТОЯ!!!!! пр ! 9>"Vo з Ж 1Ю
1астся в вьв. пре >ип[ гвтп тя изгиб I
Крита i ovm ситу У стедуст рас маытивато как ниж
иии предет трапскрнтичсскои сити '
lim У — Л э	(1" 92)
атО
Разветвление фор ’ равное сия гр дс'згтяет собо!
предотьиын стужи явтения гсреск i i -шрсскок ну
вон длины
В рассмотр! ’ноп iсометрн iect i не шне нои зздз i
спектр собстж 1 них j гач ши ирг У Тщ ячтяггся и
прерывным
''пруюю шгию нентратию сж лого стержня Ч1СТЗ
на !Ь в 1ют э г а с т и к о и
в) Равные по абсоиотнои величине по противоподож
но направленные концееые эк центрицитеты [201 1 рафик
поведения скрлкня пр i 7— — 1 представте 1
в табд 17 3 В щаыерны i п ремещением служ.ит т ш
юно ' за поворот г ьа ивой < п др 9 Стер к“Нп явтяст
(ч пдепып а П рвоизшт1Н1я 9 оиразрая форма рае
новесия с и Biaxt в то про ином р середиш дтины
ст ржня (i/m 0) ccioiiutai при УЩаЛз и пеусгопчивз
при А, д> \з Г1< им этой и усгопишои формы каждо
му зчзг uno У 2> У со >тг тствуют две тстопчивые фор
мы рты озе 1 в которых обрат! >я симметрия перво
и ч 1 н ноп S горю юн упр'лои ши и нарушена проги
И1 I/ „ ОТ 1И II I ну 1Я
Г1отерс ус с । пр cii I ри ia вегвтешп Форм равно
шчч coo" ciciisyer тэ вне t i поворота на опоре
1рф = 2а В I pniHietKo i состоя ши ф0 = л/2 и урав
ШИПЯ (17 чг) II] 1ВОДЯГ к ви„у
хГ1 у” -у/хИЗя , [2Г (х) - F (х)]	(17 93)
рз г (а) / ( ) — ПО a J шг КИЛ штогразы
В] итидс rai i ис I ара кт] i i t ny г
2/ (/)
“s 7------ю	(17 31)
\1 i )
зависит от в типы эксш птрипитота а и оказывается
лскотькз у "himithv л о-ч1"1 о раз ш то b°covi мачо и
составдяят тишь сельв дот t проп.“чта по тому У4«У,
В рассмотрение! г задач" предкрити кшкое (невозмх
п иное) состояни ярзяется т<форчир "энным в от ш
гае от стечдя центра тане сж того того ня Это обстоя
ТРТЬСТВО Г! Ж’тпришно ПС"ОВПа гения РИТИЦРСКИХ П"
pavmpoa опредрден ня из "натиза м тых i бодью гх
и гиГныл перемещении стержня
20(5
РАЗДЕЛ 17. УСТОЙЧИВОСТЬ СТЕРЖНЕВЫХ СИСТЕМ
17.3.	ЛИНЕЙНО УПРУГИЕ
СТЕРЖНЕВЫЕ СИСТЕМЫ
МЕТОДЫ РАСЧЕТА
17.3.1,	Основные положения расчета
по деформированной схеме
Рассматривается линейно упругая плоская стержневая
система, элементы которой испытывают продольные уси-
лия и нагружены поперечной нагрузкой, лежащей в пло-
скости системы. Каждый из элементов системы удовлет-
воряет условиям, сформулированным в 17.2.1. Кроме то-
го, приняты следующие допущения:
а)	обеспечено сохранение плоской формы изгиба как
для каждого элешчна, так и для всей системы я целом;
б)	система находится в состоянии устойчивого равно-
весия;
в)	величина продольных усилий в элементах системы
задана; приращение этих усилий, вызванное узловыми
моментами, или приближенно учитывается заранее, или
совсем не учитывается;
г)	наибольшее фибровое напряжение в самом напря-
женном сечении системы не превышает предела пропор-
циональности, который в большинстве случаев условно
принимают равным пределу текучести
°макс У ^Т’	(17.95)
Более точное определение продольных усилий; с учетом
влияния узловых моментов возможно па основе метода
последовательных приближений, т.е. требует выполнения
расчета несколько раз [19].
Расчет по деформированной схеме основан на пред-
положении о линейно упругой работе материала и учи-
тывает влияние продольных сжимающих сил. В качестве
предельного состояния здесь условно принимается опас-
ное состояние, соответствующее достижению фиб-
ровой текучести: щ1к[ = в7.
Аналитической основой этой методики является обоб-
щение канонических методов расчета статически неопре-
делимых систем на случай действия продольных сжима-
ющих сил, Возможность такого обобщения опирается
на принцип независимости действия сил (в его специ-
фической трактовке) и на принцип взаимности переме-
щений (см. 17.2.6) [19, 21а, 36, 44].
Ниже излагаются два основных канонических метода:
метод сил и метод перемещений, Отдельно рассматрива-
ются наиболее эффективные приемы расчета неразрез-
ных балок.
17.3.2.	Метод сил
Основная система. Заданная система п раз статически
неопределима. Основную систему метода сил (геометри-
чески неизменяемую) получают исключением п связей.
Неизвестные метода сил Аф должны заменить воздейст-
вие исключенных связей.
Рассматривают п единичных состояний Хь = 1 и для
каждого состояния строят две эпюры изгибающих мо-
ментов: а) эпюру Мк— моменты определяют с учетом
влияния продольных сил; б) эпюру — моменш опре-
деляют без учета влияния продольных сил.
Строят также эпюру моментов в основной системе /Ио,
вызванную поперечной нагрузкой; при этом учитывают
влияние продольных сил.
Перемещения в основной системе. Символом бы
(/, )=1, 2, п) обозначено перемещение в основной
системе по направлению неизвестного Xi, вызванное еди-
ничным неизвестным Аф = 1; символам Si а — перемеще-
ние в основной системе по направлению неизвестного Аф,
вызванное поперечной нагрузкой,
Единичные перемещения удовлетворяют принципу
взаимности (17.77). Вследствие устойчивости системы
тоавные перемещения положительны: 6i,.k>0.
Формула Мора для перемещений. Перемещения в ос-
новной системе определяются обобщенной формулой
Мора [21а]
Sc ли мк t v С л/и мк
J	= 2j J -Jjy— dx = 6Ai-. (17.96)
Здесь El — жесткость стержня при изгибе; dx—эле-
мент длины стержня, Интегрирование расирострапясчся
на всю длину стержня, суммирование — на все стержни
системы.
Формула (17.96) справедлива также н для перемеще-
ний от нагрузки; в этом случае
Фо =
Ml мп
EI
dx.
(17.97)
Несмотря на внешнюю простоту обобщенной формулы
Мора (17.96), практическое использование ее затрудни-
тельно, поскольку закон изменения изгибающих момен-
тов М(х) неизвестен, пока неизвестно уравнение изогну-
той оси у{х),
В практических расчетах для вычисления перемещений
могут быть использованы данные табл. 17,6, а также
табл. 17.4 и 17.5.
Канонические уравнения. Для определенна ней шест-
пых метода сил А'ь служит система линейных алгебраи-
ческих уравнении
-^1 + Фт Аф 4- Ал + 6W — 0;
621 A.J ф- 6,22 Аф б2)2 Хп + 62о = 0;
(17.98)
Фи Ад + 8tls Хг + • •+ Snn Хп -ф- 5Л0 —0.
Так как исследуемая стержневая система устойчива,
то детерминант матрицы уравнений (17.98) существенно
положителен, т. е. отличен от нуля, и все неизвестные
могут быть однозначно определены.
Усилия в заданной системе. Эпюру моментов в задан-
ной системе строят на основе зависимости
7И — Л1 j Аг -ц At2 Л з -4- •  - -ф- /Ил А л - А .VIо. (17.99)
Подобным же образом определяют поперечные силы
в элементах системы.
Дальнейший ход расчета зависит от результата про-
верки условия (17.95).
Практические рекомендации. В практических расчетах
выбор основной системы подчинен тем же соображениям,
которые определяют выбор основной системы при обыч-
ном расчете рам.
УлДачный выбор основной системы характеризуется
сл е ду ю щи м и п р и з н а к а м н:
а)	возможно большее число взаимно нулевых (ортого-
нальных) состоянии! Яф = 1;
б)	удобство анализа основной системы; возможно
большее число ненагруженных стержней в состояниях
Лф = 1;
в)	возможность использования готовых материалов,
таблиц или результатов другого расчета.
Использование симметрии системы. Для симметрии си-
стемы необходимы: а) симметрия геометрического кон-
тура; б) симметрия опорных закреплений и шарниров;
в) симметрия жесткостей; г) симметрия сжимающих
(растягивающих) сил.
17 3 ЛИНЕЙНО УПРУГИЕ СТЕРЖНЕВЫЕ СИСТЕМЫ. МЕТОДЫ РАСЧЕТА
Интегралы Мора f Af. dx
Таблица 17 6
с)тора М	Эпюр-з		
	1	"Щ1	$ г~~п?
Расчет симметричных систем может быть упрощен на
основе разложения поперечной нагрузки на симметрич-
ную и антисимметричную составляющие.
При расчете по методу сил возможно использование
сложно» (статически неопределимой) основной системы.
Пример 17,1. Заданная рама (рис, 17.14) дважды ста-
тически неопределима. Основная система ^метода сил
и эпюры единичных сосюяний Mi, Л4р,	Л40 дока-
заны на рис. 17.15.
Сначала должны быть приближенно определены сжи-
мающие силы в стержнях системы
Л4 = ~ + ~, Л1а«|Хв|
с учетом их приращения от узловых моментов Пусть по-
сле вычислении параметры нагрузки оказались равными
«I = VnJeiT4=1; дг= F 4 = 0,4-
208
РАЗДЕЛ 17 УСТОЙЧИВОСТЬ СТЕРЖНЕВЫХ СИСТЕМ
Восгюльзовтвшись таб 1 17 6 и обозначая k — Ll^JEhJ-z,
щ,ходят
5 /j tcj Щ , /7	1 — u-t de и?
”и "=-	'	4“ 77” • —— о	-=
7-71 Ui i 7 2 и-
0
(1,5574 + 0,3369*);
7/!
Z,
=—	Р^-0,06354*. б.о = О,
ЬЦ
Канонические уравнения метода сил имеют вид
(1,3574 4- 0,3369*) Xj +0,85087,? lt = Pls-0,0b35ik;
0,8508X4 + 0,5574Х2 Д 0,
откуда
Pl,k _
4,073 + 5,302*
Xs =— 1,5278 — .
71
Дальнейший ход расчета пояснений не требует.
Этот же результат получается прн меньшем объеме
вычислении, если выбрать статически неопределимую
основную систему (рис. 17.16) и воспользоваться дан-
ными табл. 17,5.
17.3.3.	Метод перемещений
Основная система. Заданная система п раз кинемати-
чески неопределима Основную систему метода переме-
щений образуют т заданной введением закреплений,
препятствующих поворотам и линейным перемещениям
т J ил; (рис 17,17), Неизвестными явциотся угон пово-
рота и линейные перемещения уз тон А’л (*--=1, 2, . , с)
Строя! и эпюр Мк единичных состоянии .+ = 1 и эпи>
ру ,И„ от щи|щзпи в основной системе, учитывая во всех
случаях влияние продольных, с/кимающих сил.
Рис. 17.17
Реакции основной системы. Символом (/. *-=1, 2,...
, . , н) обозначена реакция в основной системе, разви-
вающаяся во введенной ди связи от единичного переме-
щения Л",,==1; символом г10 — реакция, развивающаяся
в ди спязи от на1 рузки,
Реакции связен основной системы удовлетворяет прин-
ципу взаимности
rik^^kl-	(17.100)
Вследствие устойчивости системы главные реакции
положительны. Гль>0.
Единичные состояния и реакции основной системы
метода перемещений для стержней постоянного сечения
представлены в табл. 17.7. Для шести различных схем
указаны усилия в опорных закреплениях и уравнения
упругой линии Реакции основной системы выражаются
при посредстве девято функции + («) параметра нагруз-
ки и= J P'/El I, В таблице приведены также разложе-
ния этих функций в ряд Маклорепа; первые члены раз-
ложений дают значения Д7(г)), равные известным коэф-
фициентам метода перемещений при отсутствии продоль-
ных сил [19а, 21а].
График первых шести функций ЛДи) представлен на
рис, 17 18.
Численные значения функций имеются в источ-
никах, перечисленных в табл, 17.8, В этой же таблице
сопоставлены различные обозначения, применяемые для
реакций основной системы.
Для определения реакций основной системы от нагруз-
ки можно пользоваться данными табл. Г7.5.
Реакции основной системы метода перемещений для
стоек, упруго защемленных в основании, приведены в
табл. 17.9, Здесь вместо функции Lj(u) используют
функции R;(u, т), где параметр упругого защемления
т = ц.1!Е1-, ц — коэффициент жесткости опоры.
Канонические уравнения. Неизвестные метода переме-
щений Хь определяют из системы линейных алгебраиче-
ских уравнений
41 А-i +	Х5 +• • •+ г1п Хп +	/До = 0;	|
r21 -Xi +	+  —г г2п +	г30 = 0;
... .....	...	...	} (17-101)
rni -+ + гп2 Х2 +  • • + гт Хп + гп о == 0.	I
Так как рассчитываемая стержневая система устой-
чива, то определитель этой матрицы существенно поло-
жителен, т. е. отличен лт нуля, и все неизвестные X*
могут быть однозначно определены.
Единичные состояния и реакции основной системы метода перемещений для линейно упругого стержня
Т 1 q (цт
	Схема стержня	еичня в опорных закреппениях	Схема стержня	Усилия н опорных si рыи’сшых	Резкцш’ основн к < iltl ?ы		
		i нише упругой липни		Урнши не упругой 'шнии	£7 (и)	ачзпиии кос ibipax иис	р ит ’ i ц ь -ы Ч 1 Ж pt 1
! milin \ II.I 1 П1г ( тгг -кнгчыг
210
РАЗДЕЛ 17 УСТОЙЧИВОСТЬ СТЕРЖНЕВЫХ СИСТЕМ
Т а б л и ц а 17,8
Обозначения реакций основной системы и ссылки на. таблицы численных значений
Автор	Функция								
	L,	о	о	Е	О		С	с	Е,
Н. В, Кормоухов 119а] .	. .	2а	2Р	2(а-Ц₽)		а	v	и tg Ч	и зш а	и 1g и
В. Г. Чудноэский |44] . . . .	а		У		аэ	Г	—	___	
Д Ф. Смирнов [36]......	Ф.			12щ	Зф;	Зц.	—	—	—
Примечания: 1. Сокращенные таблицы см. в «Справочнике проектировщика. Расчета i теоретический том», 1-е над,
стр. 801 —803,
2 Таблицы для растянутых стер/кней см в [19а], [44].
Таблица 17.9
Реакции основной системы метода перемещений для линейно упругого сжатого стержня с упругим защемлением одного конца
(и= ) N/E! I; т
Схема				При наличии сжимающей силы (Ц>0)				При отсутствии сжимаю шеи сиды («-0)			
				обозначение	общий случаи	задел- ка	шарнир (m=U)	обоз- наче- ние	общим случай	задел- ка (m=:co)	шарнир (m=0)
				Я, (и)					З-ут		
			1		L). ^1'4_?гг				4-рп		
	ц	\	1	/?2 («)	г	7’i Е,	£	n		2 т		0
					-’-^2 Ej-pri				4Дт		
											
	1	22 R.ful —		R, («)	, ЕЕ	Lq			6 ~-т~т_ -!4-т	6	3 ;
			' 4 ”		L^-m						
	I		{		, EL,		0	/	6m	6	0
	1 1	V	1	/?3				г3	4-f т		
			\ 1		Li						
			А л	7?4(О1	r				р, l-CTl		
7					‘-a L^j-m	la	L,		4-f-m	12	
Эпюру моментов в заданной системе строят на основе
зависимости (17.99),
Практические рекомендации. Метод перемещений весь-
ма аффективен для расчет рамных систем, не имеющих
наклонных -j.ie.McHTов
При расчете симмстрн'шых систем может быть исполь-
зован прием разложения нагрузки на симметричную и
антисимметричную составляющие.
Возможно использование сложной основной системы,
элементами которой являются не отдельные стержни,
а группы стержней. В этом случае необходимо предвари-
тельное определение реакции основной системы для каж-
дой ИЗ Э1ИХ групп
Предварительное определение реакций основной си-
стемы позволяет рзспрос-рашпь пени перемещении на
системы, содержащие стержни переменной по длине
жесткости, в частности ступенчатые стержни (17.5),
Пример 17.2. Заданная рама (рис. 17.19) трижды ки-
нематически неопределима. Основная система метода
перемещений и эпюры единичных состояний показаны
на рис 17 19. Сжимающие силы в стойках Nt и зада-
ны; продольным усилием в ригеле можно пренебречь,
положив и3~0.
Реакции основной системы определены по табл. 17.7
(единичные реакции) и табл. 17.5 (реакции от нагрузки):
ЕЦ ,	,	Е13
ги =- ~Т (uj) д- 4 -	;
ч	Е
Е!3	Г/,
Си С -- 2 —— ;	г13 = г31 =------у- Е3 (иг);
4	7
Р1-,	2 — sin u-f — 2 cos zp	Ф
о ~~	;	— ~~~ ’	‘
2 тщ (sin tii — 14 cos Uj) PLj (nJ
гги —	. l-i {ui) д- 4 	;
Щ	h
17 а ЛПНЕГШО упругие слержнгвые системы методы расчета
211
1
Дальнейший ход расчета: определение неизвестных ,У*
и, решения системы трех уравнении, построение эпю-
ры -VI в заданной системе и т. д.
17.3.4.	Расчет неразрезных балок
Постановка задачи. Многопролетиая перазрсзная бач-
ка на жестких (не перемещающихся) опорах является
простейшей из статически неопределимых систем Для
расчета неразрезной балки по деформированной схеме
могут быть использованы методы сил и перемещений,
а также и метод частных решений, удобный для реали-
зации на ЭВМ.
Принятые обозначения (рис. 17.20):
п—общее число пролетов балкн;
k—номер опоры (Д==0, 1, 2, . . ., п) и номер пролета
(А = 1, 2, . . , п);
Д —' длина пролета;
£7у—жесткость балки при изгибе в силовой плоскости,
постоянная в пределах длины пролета;
V[, — сжимающая сила в пролете;
Цц—параметр нагрузки для пролета.
Уравнение трех моментов. Основная система метода
сп I — совокупность однопролегпых шарнирно опертых
балок. Неизвестными являются изгибающие моменты
pl*
Рис. 17.19
14*
212____________
РМ”РП 17 CTOl ит-T'l гт PVHEBb’X СИСТЕМ
В опорных С₽ТГН!1ЯХ /М 5 р ’ Не НИ" ЛрСХ ЧОМ1.М1ОВ ни
ет ВИД
Рис 17 26
Здесь б/,п — взаимный у гол поворота в шарнир" о
иовиои системы на олоре k вызванный нагрузкой (ci
табл 17 4 17 5)
Функции Н Е Жуковского с(и) и т(и) быт’ оппет
ле лы выш<” [см фор у ты (17 59)] Графт я» Генк
ции представлен на рис 17 21, таблицы те (19 4-1]
а такие" р 'Сгпаво пик проектировщика» 1 е изд
стр 800 —80
Чисто расчетных угиенщч р"в о листу неизвестньх
опорных мом нтов Л„ 5 рят?! еяи 1 гмю-от стандартную
трехчленную струн еру 11/102) а включением две
уравнении (первого и плследнего) о гр а лающих, усл^ьия
закрепления гонцов па ши
Уравнение трех зг-юв чст-гнют’ О юг лт пгет"«>з i
тода 1 р > иг/ и с 1 j г I сы од ю"]	за
и мл лм яд "емя концами бают Неизвегт лыми явт =
гт уг’’и иорооо-га опор inх сыении Ж Урав лелие
т к уггоз поворота лмеет лид
rh+i
+»йН(17 103)
гвД-1
Зле ь г п — суммарный момент в основной систему
в спортом защемлении k, вызванный нагрузкой
Ж "Жл 175)
Чис io расчетных уравнений равно числе неизвестных
углов поворота Ж Уравнения имею" стандартную трех
-тленную структуру (17 103) зз иск печением двух урав
/кчип (первого а последнего) отраж лющих. условия за
кр/чтения концов балки
Метол частных решении 16 уравнении метода начать
них плраметров (17 54) при y«-i = yx=O v — lk, ali,==
~ U), следует
31П/Щ —life COS «fe
щ, ~ — ’у—I ~~~	~г
к	uk~~^muk
1ь — Ub sin 1Jl. ~~ cos ui.
uk (uk — sin uk)
лн l!k
— —------------------- э
lh uk — vnuR
1
(17
104)
Ik ‘Ik - ein life
sin iJh — u/г rrK Uh
U-k — sin UR
'Жа i ния i/‘a О* Мп см гэбл 17 1
Pr in [>pi hthi re con ношения (1’104) позволяют в/
ш ti-iti по /сто mt Л! но все начеяия 0, W щли га
ion t чтщл ипе параметры 0 W на опоре 0 Из этих
Т х I типи одна повести например 0ц~9 пр->
щ 1Т"нии из опоре 0 (ищ М 0 при ппрппрюм опи
Г чи) чрупя величина Z М„ (ши Z 0п) и и"ве"т
4 1 и потлелпг определенно
П(113О 1ЛСТН0С П I !СЧИ гтрояг при И" ill ШХ П 1ра
у тра' On 0 7- Ио 1 (или 7— Q — 1 И —0) В ю
ул1т"т₽ после лов TI < т ,ного применения формул (17'011
при уа = 0н—И =0 определяют значен ля 0Д и М„ на
OI ощ п
Второе частное решение строят при нулувпх начать
ных значениях Ж О 'ИР-=-0 учитывая зав геящил от
налрузкл слтгте,’Ь‘’ ра 6я Мн I’ форма таз (л" 101)
В результате огред "я-от зил гелия 0^ и Мп на опоп г
На юже те чвчд частчыл мешении дает
О 70„	0, М	— и
//22г
(17 105)
I 4 1ИНГШЮ HPeHIF CTi-P/KHfFHH <"I« Tl '1 J ОПТ! I Д III! К ПТ П I ИХ И'ГГ'ПО!
213
Испотъзея условие 0„=0 (защезстение из опоре ti)
пти И —0 (шарнирное oi ирание право о конца б
км) опре" яют вези шну Z
Рекеррипн ie зависимост! (17 104) юпозь уюз t
тип pi гр 1 1ачазышх параметрах 0 М у о гн 1я
ciai темьн oi иатрузеи В процессе i п ш мин oupi i
зяюг истизин зназения уззов поворота 0; и покипи
Mk на опо( ах
Г 4 ЛИНЕГ1НО УПР'* I ИГ
СТЕРЖНЕВЫЕ СИСТГ ИЫ
ОПРЕДЕЛЕНИЕ КРИТИЧЕСКИХ НМРУЗО’х
17 4 1 Постановка задачг? об устойчивости
линейно упругой стермневои системы
Обобщение аичеровои задачи Разе т пр ib i< i ч in
неичо зпрмая нзосеая стер-к вы онг и л опт i
лоторои цыпразьно сжать (ин рзстяпуты) о iajiiiu
цементов спетом 1 удовлетворят уезовияз) itjopiyin
рованпнм з ’7 2 1 а систем 1 в щ том — ус юв 1ям сф
ме зирова шиз в 17 3 1 за исклю кзштсм пре тпозожсп 1я
об устотчвосли рассматриваемого pai повести о со
стояния
Вызывающая и-либ попер чиая нщрузка оз су теп у з
систем! ЯВ1ЯСИЯ итезинои
И с с а с д о в а н и с у с т о ч т и в о с т з спеша
потном объеме предпотагает решешы стсдующи-, то х
частных за пч
а) Построение спектра критических значений пара
метра нагрузки рая иссзедуемои системы Обы шо о ра
ничиваюгея вы течением нескоиких первых э-ем иов
спектра Наименьшее из этих критиюсквх значении со
ответствует потере устойчив о ст з ин.тс in
при р а з в е т в 1 е н и и Л о рм равновесия т i
ряту с первопа'- азьнои прямозипсино t форно' ращовс
сия ста золится возможной смежная кпи<_ о шш ин зя фор
ма Говорят также о потере уиоитво"зи в эи кров з 1
смысте изи о потере устои -птвости черзого рощ
б) Построение собственных форм (форм к[ проз шеи
кого равнонеси) соответствующих в t i изи i лль
ким найденные критическим значение пар змсточ нт
грузки бтн формы могхз быт! опредстещ с то-то
СТЬЮ ТО про-UBOT3 НО! О ПОСТОЯННОЮ МНОЖИЗС1Я Нерп -1 1
из собственных форм явзястся фор мои потери
устойчивости (кривой выну«звания)
в) Определение степени неустойчивости системы пр i
затзином значении параметра нагрузки (см 17 1 b) Оп
ретечяют место испытываемого чиста ь смотре цнги
чсских значении
Задача-минимум В практике проестчр звания ii то
ограничиваются onpi теч<нтм праого (имчшж о)
критическою зна юния параметр! нзгрюки "оотвеи ву
ющею позере устои швосгн при ра иста к ши фор i и зв
новесия
О б о з и а 1 с и и я ( охр тпяю-ся ОС1ЮВН1 Те обо31 3 с
ния принятые в 17 4 11од симвозас п /у Н V но шм ног
ся изгибине факторы возникающие ь кр т > деком со
стоянии системы
Дзя сжатою стержня системы с номером k приюты
следующие обозначения
Ik — дтина стерж тя
El h — жесткость стер кня,
' k—сжимающая си та
' Я Г рто plfl -ЮТ кос ан? СНТ Л1!ЗК11 1 ИЗ
дн параметр нагрузки дзя ст р т ля
и И 1ИМ И I! 11 кр) Til UKH1I 1Н!11М<Тр нагрузки
1 1 р ы
( исте ii i цсаом х р кгершуетт i i тувдтщми щра
м трамп
U 1) ЩШ1 II ip МСТр 11 1Г[ I и
и-,/ - р еоосп ное 1 к пшмстп нз рт
КП IU ОСТ 01 10 СП I
Ды — j с яз Юс epi in сек с ш 11 I пс пяоамезра
натрузк1Д язщшиопис mi
Да/ /С 1 pim 1СТГ0 И ПТ II Гр" НЗГр>
I и Л I? з 11 и ш । пек с I
ii - п тмин шее rni чи ю ni не г-’раметра
и ирз 31 и т м ia Hi	I
Устое [Я горю- Г1Ч СЖИМ irf ЦИС ci" О)Т1 по пр т
ПО з !О ИГ Г police epi ХО 1 е <1 М'I от устои 11
ГОТО С0"1 1ЯППЯ К	II ус	III <	U	13 ЗЮ1 1ПС	сиза
в стс [.mu 7	\ о р	in	от	ш	с {о тзошешю
Отсю I 1 е I I I про 0| шо I I 11 ( I М СЖИМ 1-0 I и
мн епт in i п щ хо пом (з,<	oi	ни	)	< i	чнтш н	крп
пиритом с стопит j	шт рн	у с	то	в	ют	i
(17 106)
В( зм< I О пуп	Г(П( 1ПОЗ I опт 3
С 111 1Я I Г О I К	TH 1 I ell 1 1 ГПЯ
I то ipi мя i\ii\ труп е и 1 ох ши>
Ill 1 И, Т -1 10 |р знт ( ж П	3 11
1 п "in к 1 еж. п п 1 1 он о u I за I
СИ см
Ведущий пар тетр нагрузки 11з з"
дз т стержня /г "тужит чисто
11 тктере возрз
т I 1 возрастзет
постоянную ве
1 1ВЮП0 >обно и
ст устои швостн
гетре ст натру’ки
«А	I	(17 107)
Оз nt ii с/кзтпх е p?i i i системы межно рассмотри
Г1 к н тут ст П ст з ’ачеиия 7 fl I (без интек
сов) от iochtct к bi ту и ч тт рж! ю и -ц аметр н тгруз
UI дзя JTO о ст р/Kin и бз UT Вс "у ц т тр п трем д тя
С ЮТ! Ш! В ЦО ОМ
Bl. 1 1СТГ11 I р-ТПО Ю КО! 1Я О шогор ионаTI пом воз
[ ста ПИ Сл\1 I 1ЮЩИХ С Т7 inpiw р 11 рз I’ ття зюбо
ГО 113 С1 pcKTll.ll СИ ТЕМ! j) IBU1
Т, / Ж П If.
uR &ги ык 1	- р- -у ,	(Г" 108)
У 3 е 11 I
I де ffle — 1ОСТ31И пи ш та i зв ппе с ctmoi о ’азаза
[1 !С И Т!
Ollp! 3UT I !₽ 1 П! 1П К ЗВ 14 зртмстр чагруз
1н в тан I ни м oi уекзптся етш ио н может приве
сти к не юр тзу т ниям
Сопостав юнце двух расчетных !аддч 1) рзстет по
теФорм ров пню I сх мс 2) опр тх п критически т
и и ре ли т но в гзб 1 17 К)
Несзютря нт терiтт тхотствз в х ишх чретпосыт
I 1х обо I нениях и ni iciinix icto i\ i ti и ли раз
iiihii ю с/щи зву В ш рт он з и ме iicv ie тустся н шря
?кенто состояние ттюз мп в it 11 in епруто i работы
з пер низ — co зоянпе ио puirnui > в патере Нес i
lyt"! !1 ВО ЗГОТЮН W-И КрТ MIL I СОСТОЯНИЯ НС МО
тут быть рея 1 I ов тит но твум при mi ei 1) чдстшпте
U СТС ты в тшурс нс стщсствуюз о) кпизтисские 13
тручки онрстщ енннт в прег ютож ши упругой р ч >ты
мзгериата стачают в ест шях обы-пю применяемых
стер-кис т ч 1 тон и е р т к н юоко -и ипряжештч гж иия
зч I оттеи по ит вшпавдщщ ир и i пре порш п п ноет з
4 i I нз и ч! тых I ei <>з ртш urn ii line i о i i i г н ix
FfiUB матер mi p i мят e i1 жт [ p зоот i си
cite i co сАШ in 1СЗЦ из I
214
РАЗДЕЛ 17 УСТОЙЧИВОСТЬ CTrpXHFBbU СИСТ1 М
Таблица 17 10
Сопоставление двух задач расчета линейно упругой стержневой системы
Элементы сопоставления	Расчет по деформированной схеме	Определение критической нагрузки (задача минимум)
Сжимакщие сизы V Ар	Заданы рщкеирова? чьи. значения	3 1дзно с отношение между ситам? N N К} из ? ie кис зная ния \	V # неизвестны
!	JL Осевое напряжение <J =	Не превосходят претста пропорционаат ногти (текучести)	Может достигать любой ветичи ?ы
.	А Фибровое напряжение &=•	__ —— F r й		Не мене быть )предезенз
Ордината }п»угой пнян	Орди гата изогну он ос з вы i аннои i в мшннм деисгвиьА потере 1чнх г а р зок И Предельных СИЛ Пр(ЩТЯ€ТС1 OX	I ю	О]дин ы кривой выпучивания (первой соб с диной ф рмы) во^ииз ан цеи в момент по Те 1 уез ШИВССТН 1? зс ?я т я с точи м_тью 40 пр И -ВОЧЬЯ О МН /КИТЕЛЯ
Неювнлиш расчстного ml	X а также црмие in ябные факт ръ — \ны поворо а 9 изгибающие момсн ты М	И-зпиннЕ }jikiopii вызванные сзвмесг шш действием пошл) гнпх нагрх^ок и про 1. ) 31 1ЫХ t 1 I	Изгиб ше <р 1ктс рз 5 возникающие в момент позер? ылойчивости и характеризующие пер в ю собственную форм}
Расчетные равнения	Неоднородные	О w родные
И-.КОМЬП 0РТИЧИН1?	Неизвестнее X опрндезяем! t решением расчетных уравнен?й	Наи 4 ньший параметр нагрузки прн кото ром рас гстные уравнения имеют неиу ев? СП НИЯ
Цель расчета	Анализ устои шаого напряженного состоя НИЯ	Определен?е критической кагртэки в эйлеро ? м емнете
Форма представления р е з у льт a л з д i я
зада ш миниму м Если известно критическое знашиие
ведущею пар (метра нагрузки ut то критический пара
метр нагрузки для сжатого стержня с номером k на ос
нова ши (17 108) равен «/«—<u;u4.
Критическая сиза для этою стержня

Uk 1.
Л- \
(17 109)
о) ветчина Ц, характеризует влияние продольной
юты на усилия п перемещения в ynpyroi стадии раоо
ты стержня Приближенная зависимость (17 75) показы
вдет что ветчина хараюеризуе"1 влияние продеть
нои сжимающей силы на напряженное состояние стерж
ня в упру;0 1 стации работы независимо от возможности
рсализии! /гои критической нагрузки
в) веллчин! позволяет опредешта свободную
длину стержня которая необходима для выпо тения
рас юга по нормативной методике СНиП (см 17 9)
ГДе Коэффициент С В О б О Д 11 О И ДЛИНЫ
	
д
шки^
(17 110)
17 4 2 Анализ критических состояний
методом сил и методом перемещении
Здесь понять коэффициента свобогнои длины р„ не
полыуелся г 1Я компактной записи резутьтатоь месте до
вання устои низости систем! i
(вобошая шипа ыержня = J3«(j прсцсгавдяет со
оои д шну юпратьно сжаюю шарнирно опертого
ыержня юн же жесткост ЕЕ который но устойчиво
ста эквивакинн рассматривасмочу
Истолкование результата для агат минимум Кри
тишскую ы п, \ k* по IV itmivio а результате решения
обоощешюи in кроной зап и ш 1ья понимал как ре
альную крпгпчс кую плрезке t citiyei ршемпри
ват как упругую характерней!! х оценивающею инну
СГерЖПЯ СЮ Ж1С1КОС1Э и свял от ожня с сиси, мои
Опрсдс геши аршине окон пат резки \ у* в эи деревом
смысле может иметь следующее пракычыское значение
а) вс ли шп 1 \к). представляет собой верхнюю гр i и
цу рсалнюи кри in щекой сиды Выше уже указываюсь
что эта оценка стишком груба
Три этапа исследования Пощроыпш спектра крити
ческих зпатшч исряиевои сисими методом сип или
метоюч rip мещенпч р юив идея на ipn этапа
1) пос poi них LHCK1 ли собственных зиакшш парамст
ра плюузли п гя о новно i системы
2) построение citKipi iBinix критических значении
nimvcTpi ишруж! i ля м iaiu ои гииош
1) нот л pot и н и> ною ют ipi криличссмх щаченпи
пар 1М< лр 1 п г рх от I 1я 11 шпион ей г mi который фол
шрл, с си и	ы- pi	unit г >о hi in м в некого
J u X С iy 1 1Я 01 ЮЛ Н 111 МСН )0 ПСЫ р 1 Э1 1 1 I I
СоГ гвеиные значения параметра ширузки для ос-
новной системы Оиюптя unit ia ме юда сил (тюре
I щенгя) ора х я и 1 нашили уелраж шем (ввело
ним) свяжи В обпитом с тл iai i oi та othoi |я ыют
хал hi пился сложной oi а слали шы и (кинсмаппс
лк л) сплрют ли ia
17 4 ЛИНЕЙНО УПРУГИЕ СТЕРЖНЕВЫЕ СИСТЕМЫ. ОПРЕДЕЛЕНИЕ КРИТИЧЕСКИХ НАГРУЗОК
215
Основная система обладает бесконечным числом сте-
пеней свободы и имеет бесконечный спектр собственных
значений параметра нагрузки:
исн>	,.. . , «о/, ...
Уог> Уог> •   > У tri >   •
(17.111)
Каждому собственному значению zznj соответствует
собственная форма yOj основной системы. Спектр
(17.11!) можно построить, приравняв нулю определи-
тель некоторой системы уравнений, характеризующих
равновесные состояния основной системы:
О0(и)= 0.	(17.112)
Корни этого уравнения образуют спектр (17.111), оп-
ределяющий критические состояния основной системы
(в эйлеровом смысле).
Для основной системы метода перемещений имеем
, иь !	и/,
Da (и) II sin ( sin —- —
— —cos
о
Uk\
2 /

П (sin iik — Uk cos iik) = 0,
(17.113)
где первое произведение распространяется па все сжа-
тые стержни, защемленные двумя концами, а второе —
па все сжатые стержни с одним защемленным и другим
шарнирно опертым концом (см табл. 17.2).
Анализ устойчивости основной системы метода сил
часто связан со значительными трудностями.
Среди элементов спектра (17.111), расположенных
в порядке возрастания, необходимо различать к р а т-
п ы е собственные значения. Собственное значение ищ
имеет кратность г, если
"о, /—1 С w0, = ао, /4-1=‘'	1У\ jy-r—i '~ип, i-ur-
В этом случае основная система распадается на г не-
зависимых частей, одновременно достигающих критиче-
ского состояния при U — llOj.
Все собственные формы ум основной системы взаим-
но ортогональны независимо от наличия кратных собст-
венных значений в спектре (17.111).
Явные критические значения параметра нагрузки для
заданной системы. Неизвестными метода сил (перо
мещепий) являются силовые факторы (перемещения)
V;, АП,..., Л’„ Рассматривая п единичных состояний
АВ, = 1. вычисляют перемещения (реакции) основной си-
стемы y,h{i, k—\, 2. .... н), причем у,А=й,й(==г1Л)
в случае применения метода сил (перемещений). Кано-
нические уравнения линейны и однородны относительно
неизвестных Л';,-:
X Л'Лу,7; = 0 (i=, 1, 2,..., п).	(17.114)
k— 1
Коэффициенты этих уравнений рассматривают как
функции ведупвно параметра нагрузки у./, =у,к (п).
Условие существования ненулевых решений однород-
ной системы (17.114) заключается в равенстве нулю
определителя [ 19, 21а, 30, 44]:
1’ст Унг
Упп.
Корни, этою трансцендентного
(17.115)
относительно и урав-
нения образуют бесконечный спектр явных критических
значений параметра нагрузки для заданной системы:
Kti, «д-з, , uxj,
УXI > Ух% , •  •  l)xj у
(17.116)
Каждому явному критическому значению uxs соответ-
ствует явная собственная форма (кривая выпучивания)
y.-.j. Термин «явная» и обозначение ijXj подчеркивают
тот факт, что рассматриваемая собственная форма за-
данной системы определяется отличными от нуля зна-
чениями неизвестных А'*.
Для метода сил iio-.<2iixy для метода перемещений
знак неравенства следует изменить на обратный.
Построение явных собственных форм. Среди неизвест-
ных Л'г, есть по крайней мере одно, которое можно при-
нять равным единице, например ЛА = 1. Тогда все осталь-
ные неизвестные однозначно определяются из уравне-
ний (17.114) при u = nXj. Ордината собственной формы
в произвольной точке системы равна:
п
Ух7= 'Х yii-'k.)
4=1
(17.117)
где у-,. — соответствующая ордината единичного состоя-
ния А'а = 1 при u = Ui,. В случае применения
метода перемещений значения уь можно опре-
делить по табл. 17.7.
Полный спектр критических значений параметра на-
грузки для заданной системы. Спектр явных критиче-
ских значений параметра нагрузки и.*, (17.116) отра-
жает только те формы криволинейного равновесия, для
которых по крайней мере одно из неизвестных А\ от-
лично or нуля. В некоторых случаях возможны такие
формы криволинейного равновесия заданной системы,
когда все неизвестные равны пулю: Л'?1 = О(А = 1, 2,...
..., п), Очевидно, что эти так называемые скрытые
формы следует искать среди собственных форм основ-
ной системы, соответствующих спектру (17.111). Если
скрытые формы криволинейного равновесия существу-
ют, то основную систему называют несовершен-
ной. Основную систему называют ложной, если
скрытая форма криволинейного равновесия соответству-
ет первому критическому значению параметра нагрузки
для заданной системы, т. с. эта скрытая форма являет-
ся формой потери устойчивости [36]. Скрытые формы
криволинейного равновесия ортогональны по всем еди-
ничным состояниям Л'= 1.
Потный спектр критических значений параметра на-
грузки для заданной системы
“ст> ««=•= "ст=-- 1	(17J18)
У*1 > У> - • • , У*/,  • - J
включает следующие элементы:
I.	Все элементы uXj спектра явных критических зна-
чений для заданной системы (17.116).
2.	Собственные значения для основной системы Unj,
ортогональные всем единичным состояниям Хе—\ (k —
= 1, 2, . . ., п); в этом случае определитель Г>х(и0}) име-
ет ограниченную (не равную бесконечности) величину.
3.	Кратные собственные значения для основной систе-
мы пщ — itn,j.r । = ...= и0,j 1если можно подобрать
не все одновременно равные нулю числа Ai, А2, .... Ar та-
ким образом, чтобы линейная комбинация соответствую-
щих собственных форм
У = -J0j + Ч'"о,(+1 Ч- -  • + \(17.119)
была ортогональна всем единичным состояниям /С,--!;
крапюсть критического значения u.j,j==uaj равна числу
216
РАЗДЕЛ 17 УСТОЙЧИВОСТЬ СТЕРЖНЕВЫХ СИСТЕМ
линейно независимых комбинаций типа (17.119), удов-
летворяющих условию ортогональности.
Определенные таким обратом элементы uit спектра
(17.118) располагают в порядке их возрастания.
Если скрытые формы кризолинейного равновесия т
сугствуют. то спектр явных критических значение
(17 116) совпадет с полным спектром критических зна-
чений (17 118)
При решении задачи-минимум, когда методом переме-
щений определяют перво" (низшее) критическое значе-
ние параметра нагрузки, критерием потери устойчивости
МОЖеТ служить условие (17.115)
Спектральная функция. Прон шедсние определите.!’ й
S(u)=^D„(u)Dv(u)	(17.120)
•обладает свойствами спектральной функции,
а именно'
а)	функция S(n) непрерывна и имеет непрерывную
производную
б)	корни сравнения Е(/;)=0 прн и>0 образуют нот-
ный спектр критических значении заданной системы
(17.118)
Выбор метода расчета и основной системы. При вы-
боре расчетного метода и основной системы следу?! ру-
ководствоваться общими указаниями п. 17.3
Простота ocHOBHoii системы и удобство ее анатаза яв-
ляются существенными признаками удачного решения
расчетной задачи При лом на второй план отступает
стремление получить решение с наименьшим числом не-
известных.
По указанной причине для анализа критических со-
стояний стержневой системы чаще используют метод
перемещений, ио не метод сит
В случае использования метода сил может быть при-
менена статически неопределимая основная система, по-
лученная из заданной исключением части лишних свя-
зей При использовании метода перемещении основная
система может быть обращвава введением закреплений
не между отдельными стержнями, а между i руппами
стержней.
Приметпио "аких сложных основных систем сни-
жает число № известных Xtl и соответственно уменьшав
порядок п определителя Г\(и}, но усложняет анаши
основной системы и затрудняет построение опрщп’зчт"
ля D0(u} и разыскание собственных значений основной
системы
Во вы. х стучаях сопоставления и опенки разлиншех
вариантов выбора основной системы необходимо учиты-
вать суммарную сложность и трудоемкость расчета на
всех его этапах.
Использование симметрии системы. Опреде юнце сим-
мегрии системы ем 17 3 2
Для симметричной системы все собственные формы
или симметричны, или антисимметричны Возможно ра
дел»вое построение спектров критических значений л ;я
симметричных и апти"имметричных форм криволитиио-
го равпопесия с поет-чующим объединением критюю-
еких значении параметра нагрузки в один общин сгвьтр
(17.118).
17.4,3. Примеры исследования устойнигости
методом см и методом перемещений
Пример 17.3. Треб’-ется псе теловатп оитичощчщ со-
стояния двухпрол'-тно"' г>"г1"’ярчгш балки, обошачстшч
ясны из рис 17 22 Задача решается тремя разным!5
способами
PaputWT а-- ч.^тог1 гц О-ризп т- гтд-.ц „щнпч-
ное состоянш noi,m’-i!i на pic 17 „2, г7.
Для основной системы — однопролетной балки дли-
ной 21 — имеем
Dn (и) з- sin 2и — 0,
откуда щ, — sin /л/2 и спектр собственных значений для
основной системы начинается элементами
л Зл 5.д
— , л, — , 2л, — - , 3л., ...	(17.121)
Заданная пстеми
а) Мтсд сил Зснодноя система
6) Метод сил 0с'1е!''чя етстена
Смтгтче Х.-1
д'! Метод
Елшщчно-’ перемещение основной системы определено
по табл 17.3
Р
°п ^2£ПР (iS-U ~ U]-
Условие критического состояния
Ог(«) л tg и — « = 0	(17.122)
приводит к значениям
1	2	13	1
и-1:! ~~	~ дут ~~	:	|
/ j	1 (17.123)
П; ЛИНЕЙНО УПРУГИЕ C"FPXHhBL’F
СИСТЕМЫ ОПРЕДЕПАНЯГ КРИТИЧЕСКИХ ИА! РУЗОК
§17
с И’ДЗШК W0 первые iptl ЭЗЗЯЛПа CIicC ipa Я1Ч1!\ Is.pi
1ическ1 =1 .jnii hhi для juanwd iHikMU буду t
4 4Q34 7 /2o3 10 90,1	(17 124)
ЛГ01 LlttKIp ДС Alli Olllb I.OI OHriCH ЭАИеНЮМИ Cl CAT
pa (1/12.1) onpc A laiOniH и крысьи формы кр тьо 1
ПСИНОЮ Ю liDBtci Я 1 р 1ф1<1 II ф'1 KL.S1 1 12 («) (10 1 1
ШНИЯ) И П,1«) (ЖИрЕВЯ ПИТИЯ) ПОЗЛЗчНЫ ria
рты 17 23 а

Рис 1 / 23
Дня соб in швы значений основной системы
им 2 i ii,b— t и i д oi pc ic im<_ it	имеет ко
ночную .tie шину Полому ука hi 1 юементы s'oiiu
В ПО mill Akhip КрзШЧЛКДА UlalUfflJl ыя JIJJHHOU сП
сП МЫ
I ! F3) 2 1 7 72oi Si 10 9041	(’" 125)
3iuo оспотая сисиуи яв тогся южной но oipow
нию по юс I аги нс 1 имстрзт нт форзам витии ты
ЭгИ ф(10М1 Н.1Х0 1ЯГ среда сОЫЛВ ых дору IX но
НО I LHl.lC.Mb
Bipuaui о lerod сиг Основная лдснм i ср тч
ное состояние Hoi аза ш ii рис 17 22 о
Оыюьндя ти. им! распинается in те пи дипп
чаши xpi ичюкие сосюянчя хоюрых оное и зяюп.а о т
ними и iitm и. юбывеннь ми значениями 11а рык
ния
Do (u) airmni - 0	(F 12.J
находят СП Tip у Которою Bet з СМЛ’АТ
несть 2
л, л 2 1, 2л, Зл, Зл
НМ < ЮТ к1Ю1
(17 127)
’ омозлыруя соб щепные формш соош. iciayro цис
Аден парс равныс coociB иных зча юнип потучнел
II 1 1М 1 р 1 1 Г) КЗ крыл орююн ПАЮ НН 14 )
с линию \i = i Слетова с 1ьно спектр (П ' j
ДОП П 1 ПН I ПЛЛр крЗШТЧесКИХ ИАН НИ I А 131 га
IJ1 I >.И с I с 111
1 шил 1 и 1 юн е основной 1.41 гены
<	21
ьп —(1 - иа^и)
Ыих
ч -з у т 1
D (и)	1 — и Др и п (17 123)
Эю урате. ин. и не! рсакнпя (1712т) обра рщи
тир u))cibUiiw\ зианш 117 121) I рафт i 1л ж
ти 2Д(и) и 1К{п} юказаиы на рнс 17 2с о
По lit in спи р критических зп тчениц (К 125) при
СГ1В1ЯШ собой су мчу cl Ki pa с joe I венш х цианиды
о ювнон системы 117 127) и ciieKipa ивны мини с
сых значении д ы за данной сисюмн (П 124)
3 1СЛ ОСНОВНАЯ СИЛ Ч а 1 1Кл1 Я0ТЯСТСЧ TllAiOIl IO 01
УШКНТЮ К 1НТНСН I leipil нят формам ЫПУЧИВ 1H1IH
Ии формы зоотв 1С1“ЗО| собшвенным q три 1м о 1л
31031 системы
Варен не в— lerod пер кшении Оснот и зя система
। с ’иии пюс Соломине показаны на рис 1 ?2 е
Основная система распаДееЗся ia тзс п,. авт лз 1Ыс
с 1 тн кршичюкие состояния коюрых опре тс имелся од
ними I юн 1 же Looci ьсииимл Aia-ieni ? 1ч Из jp и
аЛШЯ
Do (и) (ып« — «сотп)(в1пи— и cos и) —0 (17 129)
нахзля1' лскгр /обе ГВЗ.Н1Ю х значс пш осколзоп -~н и
мы юс З1ем ши калорию тмекл кранк) <и 2
1,9)4 1 1934 7 72/3 7 7253 109941 10 9041	(17 13)(
Комбинируя соб изенные формы спз звеюгв^юсти,
а-кюз нар, равных w6liHAim\ з^зачлкп’ ио yiao
химмстри знузо кривую о’зто! т awiyio дчизз пюме со
юяпшо 2) — 1 С зедоьазе юно спекзр (17 130) b\)mii
в I о зныи спектр крипечз них значении д 1Я з тан он с и
СТ Mil
НЛ0Д1 ж pt з t дде 1141 по
и и и
all! « U Юь U
f OMIOBUO I C/CUMH
Ю 17 7 piBFa
2£(	2tJ
-- /Д«)
д d ii II nl M i
о 1 &у д<1
sin и
D((.v}	—------------- о (17 131)
-ни и — ti cos и
Корчз лою урзансиия oupaJiHai iiik р
л, 2 г Зл,	(Fl И
1 р |фики функций 1В(и) и D.c(u.} I ок 13 TH I и
me 17 2з t
П ) in in сиекзр критических значении (17 125) п[лд
т с лет собой сумму СП к 1 р 1 собствт чпз \ значении А 1Я
о ювнон еаетсуп (17 110) и ,псзлр 1 явз ix. кршич
кнх значении ды за тайной илюмы (17 I д2)
Здль основная ежлмт явпзется лож ю । по отноше
। ню к <чмштрч-ш !М |>орм 14 выпучив шия hit формы
I IB IClByiOl юбезвлы II ф )р v М OCHOjlJll сИСГ“МЫ
( ш кзра iniiaa функция , из весе грс	з ip антов а
। ii- пни и > и ын. I о тш п юг а вит
.S (u) — DB (U) D J («) — alii и (Ы 1 и — и со л), (17 133)
218
РАЗДЕЛ 17 УСТОЙЧИВОСТЬ СТЕРЖНЕВЫХ СИСТЕМ
если исключить не влияющие на результат множители.
График спектральной функции представлен на рис.
17,23, а. Корни уравнения S(u) — 0 (исключая корень
и = 0) образуют полный спектр критических значений
(17.125).
Пример 17.4. Рама со сжаты-
ми стойками (рис. 17.24) пред-
ставляет собой упрощение и иде-
ализацию (в смысле исключения
вызывающих изгиб нагрузок) си-
стемы, рассмотренной в п. 17 3.3.
Исследование устойчивости выпол-
няется методом перемещений. Ос-
новная система и единичные со-
стояния показаны на рис. 17.19.
На основании (17.113)
и / и и и \
Dn (и) = sin ~I sin	cos — I (sin и—и cos uJ—q j
откуда получают спектр собственных значений основ-
ной системы
1,4303л; 2л; 2,4590л; 2,8606л; .
Условие критического состояния заданной системы				
	is + 4	2		
Ох (и) =	2	Li + 4	£s	-= 0.
	L-„	Г3	Z.e L 4	
Задаются рядом последовательных значений пара-
метра нагрузки и и вычисляют определитель ОДи)
Задано произвольное положительное число и, требу-
ется определить:
1)	степень неустойчивости системы v при параметре
нагрузки и—г (е — малое число), т. е. число элемен-
тов полного спектра критических значений (17.118),
расположенных в ожрытом интервале
2)	кратность q критического значения и<,} = и, равно-
го испытываемому числу и, в полном спектре (17.118);
при с/ = 0 число и в этот спектр не входит;
3)	степень неустойчивое:и системы v' = v+p при па-
раметре нагрузки нф-е, т. е. число элементов полного
спектра критических значений (17.118), расположенных
в закрытом интервале 0
Качественный анализ устойчивости позволяет отве-
тить на эги вопросы, не прибегая к построению полного
спектра критических значений (17.118). Если известен
спектр собственных значений для основной системы
(17.111), то решение задачи требует однократного вы-
числения определителя Dx(u).
Пусть для испытываемого числа и известны:
v — число пройденных собственных значений для ос-
новной системы (включая каждое из кратных значе-
ний), т. е. число элементов спектра (17 111)', заключен-
ных в интервале О<Ио3<а;
г — кратность собственного значения и в спектре для
основной системы (17.111); при г = 0 число и в этот
спектр не входит.
Прямой ход алгоритма Гаусса приводит симметрич-
ный определитель £>»('/) к треугольной форме:
Ол (и) -	7u Via ’ 7ai Та-? ’	’ Tira ’ 72/2			Р-1 Р12 ‘ 0 R 	‘ М1/2 ’ Ма/г
	7/21 у п-2. '	° 7/2/2		0 0--	
= рц ц2. .. ц„.
(17.135)
Коэффициентами устойчивости называют числа Ц|,
Нз, Рп, расположенные по главной диагонали тре-
угольного определителя. Эти коэффициенты выража-
ются через главные миноры А, определителя Dx(u) сле-
дующим образом:
А2
Р-i — Ты — Aj > Р-з =	, •  •
ДА
____________________ Рх (''•‘О
'	= А„_, ~ X.
А;
(17.136)
с помощью прямого хода алгоритма Гаусса. График
спектральной функции S(n) =D„(u). Dx(u) представ-
лен на рис. 17.25. Критические значения параметра на-
грузки равны:
0,6697л; 1,2332 л; 1,6806л;...	(17.134)
Скрытые формы криволинейного равновесия в дан-
ном примере отсутствуют. Потеря устойчивости проис-
ходит при критическом значении сжимающей силы
Е1
Ntt = (0,6697я)2 —- ,
17.4.4. Качественный анализ устойчивости
линейно упругих стержневых систем
Анализ устойчивости стержневой системы предпола-
гает в числе других частных задач также определение
степени неустойчивости системы [27, 29, 36],
Среди коэффициентов устойчивости различают нуле-
вые. конечные, положительные, отрицательные и беско-
нечные значения. Пусть будет: v0 — число нулевых зна-
чений; г- — число конечных отрицательных значении;
V» — число бесконечных значению
Степень неустойчивости определяют с помощью соот-
ношении [30]:

число	метод сил	метод перемещений	
V—		v _у v_ -Му	
q=	г -Г v0 -	г + т—Ж	(17.137)
x' — v — q —	\	г—V___—V	v-J-ry-voJ V	
1
17 t. ДШ1ЕП1Ю УПРУГИЕ СТЕРЖНЕВЫЕ СИСТЕМЫ ОПРЕДЕЛЕНИЕ КРИТИЧЕСКИХ НАГРУЗОК
219
Отсюда следует, что если при некотором значении
параметра шпрузки /1 основная система устойчива (и<.
<lu-n, v = 0) и нее коэффициенте: устойчивое:и конечны
и положительны (v> = v. =v, =0), то и заданная си-
стема усюичива.
В случае применения метода перемещений потеря
устойчивости системы (критическое состояние при нап-
меньщем значении ш) характеризуется следующими
тремя признаками: а) основная система устойчива
(u„<CT,t); б) все коэффициенты устойчивости конечны
и положительны, кроме последнего: р, X) (/=1, 2,
п --1); в) последний коэффициент устойчивости цп=0.
Качественный анализ эффективно используют также
для отделения корней уравнения Z2;C(«) =0 при пост-
роении спектра критических значений, а также и при
решении за.тачи-миннмум.
Пример 17.5. Качественный анализ. Рама со сжатыми
стойками (ем. рис. 17.24) была исследована в примере
17 4 методом перемещений. Прн п = 1,5л определитель
равен:
26,207
Dx (1,5л)
22,207
2
3,298
3,308
22,207
3,308
—15,59
26,207 2	22,207
=	0	3,145	1,614
0	0	—35,23
= 26,207-3,145 '—35,23) — 2904.
Здесь v,, = v»=(); v_ = l. Число пройденных собст-
венных значений основной системы v=l, так как
1,5л. 1,4303л =- ип; г — 0.
Степень неустойчивости системы равна:
v'- =-= v --= х г ф-	—v_= 1 ф- 0 ф- 0 + 1 = 2,
получаюг критерий потери устойчивости:
D,t (и)
Рис. 17.27
Обычно побочными реакциями пренебрегают, полагая
их равными пулю: р„ = р(, =0. Прн этом (рис. 1.7.27, а)
число параметров жесткости можно уменьшить до трех,
принимая

VIs
п —------
Е1
(17.140)
т. е. испытываемое значение параметра нагрузки и ле-
жит между вторым и третьим критическими значения-
ми: п*2< 1.5л<«»з. Эта оценка подтверждается сопо-
ставлением со ciieKipoM (17.134).
17.4.5. Устойчивость однопролетных стержней
с упруго закрепленными концами
Стержень а—Ь, входящий в состав упругой системы,
можно рассматривать как однопролетный стержень с уп-
Рис. 17.26
ругими закреплениями концов
(рис, 17.26). Связь стержня с
системой в узле а характери-
зуется тремя коэффициентами
жесткости )i„, vn, од. При по-
вороте узла а па угол !)<, = ! в
упругой опоре во шикает мо-
мент цд и перпендикулярное
первоначальной оси стержня
усилие ра. Линейное переме-
щение узла а — 1 вызывает
в упругой опоре усилие v„ и
момент ро. Подобным же об-
разом коэффициенты жестко-
сти Li*, СТ и (>,. характеризуют
связь стержня с системой в уз-
ле Ь.
и рассматривая эквивалентные по устойчивости схемы
(рис. 17.27, б, а).
Критерий потери устойчивости преобразуют к виду
та (7-4 ст п) -ф- {та ф- ть) Lx (L& ф- к) ф-
ф-£4 (я — и2) = 0	(17.141)
или к виду
та mt, [2(1 — cos и) — A sin и] ф (та -ф ть) и (sin и —
— A cos и) ф- Аил sin и — 0; А = и (1—н-/п)- (17.142)
Если стержневая система, включающая исследуемый
стержень и—Ь. содержит также и другие сжатые эле-
менты, то коэффициенты жесткости ц, v, р должны быть
предварительно определены на основе расчета по дефор-
мированной схеме. Прн отсутствии в системе других сжа-
тых элементов коэффициенты жесткости определяют
обычными методами.
Задачу решают методом перемещений. Вводя безраз-
мерные параметры жесткости
mt —-----
El
nt =
К Р
El
р,- Р
г1=п~Г (i=-a’b)’ (17-138)
17.4.6. Устойчивость неразрезных балок
на упруго перемещающихся опорах
Методы исследования устойчивости. Свойство упруго
перемещающейся опоры характеризуется соотношением
(17.143)
где Rk — реакция опоры;
Уь.— ее линейное перемещение;
Дф — коэффициент жесткости.
220
РУЗДГЛ 17 УСЮПЧШВОСТЬ СТЕРЖНЕВЫХ СИСТЕМ
Рсшенне задачи методом сил приводит к уравнению
пяти моменюв Возможно применение метода пергмеше-
ияй или же смешанного метода
Ниже излагается метод решения, особенно удобны»
длч реализации па ЭВМ
Метод частных решений. Обозначения
рис 17 28 Расчет основан па многократном
шш рекуррешиых завшимоетеп
ясны И 5
исио.нчова-
крепления концов балки и безразмерного параметра
лег I кос । и
мР
m------.
El
В случае бесконечно большого числа пролетов (п = оо)
условия закрепления концов балки роли tie играют Кри-
гпапское значение параметра нагрузки и» определяю! из
у равнения
(17.146)
9,	— (Т.
IE k
Л1,- '
k
2«2 (1 — cos и)
т =---------—-------_
(17.147)
h'
sm и
У к =	I
Н „ х .
1 '^*-1
'у “у
/7а + \ Wfe"
(17.144)
Задача И. Г. Бубнова. Для регулярных балок суще-
ствуй! нребеланое значение параметра жесткости упру-
гих опор ш0, при ко юром критическое значение пара-
метра на!рузки сгановится равным ut — л Каждый
«юг вынучяваегся по полуволне синусоиды, улрупге
про-
опо-
где обозначено
L/д иъ	1ь	_
Вк =--	Q - Н, , Т - С А,__ , Р (17 145)
Д	ик
Из уравнении (17 144) первые два представляю г собой
соотношения метода начальных параметров, трете урав-
нение выражает условие равновесия пролета 1к, четвер-
тое уравнение — условие упругости опоры k.
Пусть левый конец стержня шарнирно закреплен, тог-
да уо — М0 — О, величины Оо и Н, неизиесты 1йрвое
частное решение сгроя! при начальных значениях
=- АД -= (Д 0; /Д = 1.
Последовательное применение рекуррешиых формул
(17 144) при А —1, 2, . , п приводит к значениям у, . йф,
Л1„ н Нп^-\. Второе часшсе решение основано на зна-
чениях
Уо ~ 7И(] — Ht — 0; 0О — 1.
Вычисления по формулам (17.144) позволяют г,пр* п
лить величины уп, 0п, Мп, Нпх \
Полное решение строя! ыш сумму двух чайные ре-
шений
=	+ у"п 0О;
ит.д.
Критерий потери устойчивости составляют в тит т-
С1вии с условиями закрепления правою конца (.галки
Регулярные балки При Е — 1, Elp — Ll, Vt	\
xi, \ балка бу де! регулярной Кри i ич. скин парам.’ip
нацэузки ц. зависти от числа лро.шчов я, условии да-
ры ведут себя как абсолютно жесткие Дальнейшее уве-
личение жеечкосчи упрутх опор (iny>rna) ул-.е не повы-
шаем устойчивое 1 и системы [6]
Предельное значение параметра жесчкостп упругих
опор равно [21 а].
т0 =-2ла 11 + cos —— ),	(17.148)
\ п т /
где т==!/2, если жесюой является только одна крайняя
опора, или г — 0, если обе крайние опоры жепкие
17.4.7. Устойчивость неразрезных балок
на упруго вращающихся опорах
Методы исследования устойчивости. Свойство ynpvio
вращаюшешя опоры хараглеризусчсн сот ношением
(17.149)
где АЦ — момент в сечепил над опорой fe;
(Д—роз поворота этого сечения,
— коэффициент жесткости
Решение задачи методом перемещений приводит
к уравнению ipex углов поворота (рис 17 29)
-у--—Д.(Щ-щ) Щж=о	(17 150)
174 ЛИН1ЛН0 M1PMHL СП-РЖЧЕВЫГ ( {1СП МЫ O1 iPf ДЬЛКЬИЕ О И I H4f i КД1Л НАГР330К 221
Ниже из ai l гея метод pi шю ая особенно усобный д 1я рса тиш щи та ЭВМ Метод финальных отношений Левое фоки ншие ш НкШечп- определяют по рюуроешнон форму те [2 а|			М<сь обозначь	₽f °’ [ 1 110 (/’ — ЧИе	0,5 k k о про leiuu)	(17 157)
и - , у	— 1			ГЬ1 k — к - I нр	-тД, v п 4	1	117 1Б8)
74	/	i («д J-. ГРк	(Г 15П	Рамы с упруго	защемленными в основании		стойками
I Де обозные но
рД,	h Ti
mr ~r --------:—Г
Начале ное эвачеНДь левою фокальною
раВпО
к-	1 } г / , < ио Щ
L‘2 (Ul) L	J
(Г Г2)
(ЯНЫМИ 4
(17 153)
При жесткой зале тле нт крайнем левой опоре и0= оо
и (• ,=—оо, в случае шарнирною опирании р0 = ')
I loo гедоч 1те ibHOt вычисление Д <Д г „ по..воысг
сие ави.ь критерии ишерч устойчивости
D (и} - Г, Fn — 1 = 0,	(17154;
тде правое Локальное о 1 ношение равно
Д(W,J
В случае жесткой задепки на правой опоре тп — оо,
/- _=— с®, й условие (17 154; иринимаег более прошил
вид
D (и) - ~ F„ ~= 0.	(17 15М
Полагая все р л—0, получают решение задачи об
усюнчивосги балки на жесглчх опорах
17.4.8 Устойчивость рамных систем
Методы исследования устойчивости 1ля определения
вршических нардмыров нагрузки рамной системы ре-
кояендуется ме.од перемещений, ка тещ венный анализ
и построение спектральной функции
Одноэтажные многопролетные регулярные рамп
Стоики в основании защемлены, сжиыиощт о> ты р ш
преде юны произво тьно (рис 17 30)
Коэффициент свободной длины для t й СГОЙпЧ при
ближенно равен
й Ч 5Л  /лфГ
В/ =	---— 8/ —— но lK менее
1 ф 5Л у Л
<л ржн й с о/ину мирую зч" чтенчью концом шт
в I 0 1 1 ( 4
Р i ш со ыуиен шми чоиками Сшлкл, образован-
ную НС Ш1 !>< Ш1 У llclhaMT iOlJWuHuil ЖРСТлОШЦ, МОА-
Рис 17 30
но рассм тгривать как несколько однопро к гных стерж-
ней сел 1 при образовании исношюи сишсмы Mei эда не
р^мещений ввеш 1 на 1ранпцах учаыков доиолшпельные
укрепления, препятствующие иопорогу течения и юри-
зонгальиому нерюкщенцю (ри^. 17 31) При шом уве-
ШЧИВаПСЯ ЧИСЛО Д’ЯЗЬССГНЫХ Xк и юрядок определи
i ш Dx(u)
Другая возможношь здлзючаегся в предвари тельном
я,.следовании сгупенчаюй сюнкп По ле определения
рс 1кцяи от чиненною перемещения и иоьорота верхнего
222
РАЗДЕЛ П. УСТОЙЧИВОСТЬ СТЕРЖНЕВЫХ СИСТЕМ
конца стойку можно рассматривать как однопролетпый
элемент основной системы метода перемещений
(рис. 17.32).
Рамы со стойками, жесткость которых непрерывно
изменяется по длине (рис. 17.33). При некоторых зако-
нах изменения жесткости EI (х) реакции основной си-
стемы метода перемещений выражаются в замкнутой
форме (см. 17.5.3).
Рис. 17.34
Высокие узкие рамы (рис. 17.34). Расчет устойчиво-
сти, основанный на пренебрежении осевым обжатием,
дает удовлетворительную точность только в том случае,
когда высота рамы Н превышает ее основание В не бо-
лее чем в шесть раз.
Методы исследования устойчивости высоких узких рам
с учетом осевого обжатия см. в [19].
Здесь обозначено:
Шарнирно опертый стержень (рис. 17 36). Подчиняя
решение (17.161 ) граничным условиям у —М = 0 при
а=0, х-=1 и приравнивая определитель уравнении ну-
лю, получают условие критическою состояния
D (и) = sin ty sin v.2 = 0.	(17,163)
Отсюда находят
ty* = пгт, — пл (п — 1, 2, ...); (17.164)
следовательно, квадрат критического параметра нагруз-
ки равен:
«МиН- — .	(17.165)
4	(пл:)2
Целое число п должно быть выбрано так, чтобы ве-
личина и] была наименьшей, следовательно.
0	т 4л*	п	= 1
4л4	,	т	< 36 л4	п	= 2
36л4	т	< 144 л4	п	= 3
17.4.9.	Устойчивость стержня в упругой среде
Дифференциальное уравнение задачи и его общий ин-
теграл. Линейно упругая среда противодействует щ-
гибу стержня, создавая на стержень (рйс. 17 35) на-
грузку
-~Р = су,	(17 159)
где с — коэффициент жесткости среды.
Рис, 17.35
Рис. 17.36
Дифференциальное уравнение изгиба сжатого стержня
имеет вид
Е1уп -4- Ny" -Есу = 0.	(17.160)
В рассматриваемом случае говорят также о б а т к е
па упругом (в и н к л е р о в о м) основании
с коэффициентом постели с.
Если жесткость EI, сжимающая сила N и коэффици-
ент жесткости с постоянны по длине I стержня, <>
общим решением однородного уравнения (17.160) при
и2>2) т будет
у =- Сх sin
-V- , „ Ф*
— + С» cos-----------
I	!
сух
I
]- С4 cos ~
(17.161)
Если рассматривать и~ как функцию непрерывного
аргумента п, то из условия минимума и" можно найти
t? = 2j/»T.	(17.166)
Это приближенное решение задачи дает, вообще го-
воря, заниженные значения ut, но в отдельных точках
пои щ==л\ 16л4, 81л4... совпадает с точным решением
(17.165).
Другие схемы опорных закреплений могут привести
к случаям, когда	т и решение уравнения
(17 160) имеет вид, отличный от (17.161). Анализ ряда
схем см. в [35]. Там же исследована устойчивость бал
ки на упругом основании более общего вида.
17.4.10.	Справочные данные для определения
свободных длин
Формулы, таблицы и графики для определения свобод-
ной длины сжатого стержня, входящего в состав упру-
гой стержневой системы, имеются во многих изданиях,
например в [2, 3, 12, 19, 21, 27, 36, 44], а также в «Спра-
вочнике проектировщика*, 1-е изд, стр. 784 и далее.
Большое число графиков для определения свободной
длины содержится в [216J.
17.5. ЛИНЕЙНО УПРУГИЕ СЖАТЫЕ СТЕРЖНИ
СОСТАВНОГО СЕЧЕНИЯ.
СТЕРЖНИ С ПЕРЕМЕННЫМИ ПО ДЛИНЕ
ЖЕСТКОСТЬЮ И СЖИМАЮЩЕЙ СИЛОЙ
17.5.1.	Сжатые стержни составного сечения
Влияние поперечной силы па критическую нагрузку
цешралыю сжаюго линейно упругого шарнирно опер-
17 5 ЛИНЕПНО УПРУГИЕ СЖАТЫЕ СТЕРЖНИ СОСТАВНОГО СЕЧЕНИЯ
223
того стержня оценивают приближенно!: формулой
(Ф Эшессер, ДД
Ale Fi, Fo — площади поперечных сечений ветвей; с —
расстояние между цен I рами тяжести ветвей; Т — сдви-
гающее усилие на единицу д пшы, б — деформация
вышиною сдвш а смежных волокон, принадлежащих
ракитным ветвям, в месте соединения связями.
Здесь .V, — энтерова критическая сила; G — модуль
едина, /' — площадь поперечного сечения, а—коэффи-
циент зависящий от формы поперечно!о сечения стержня.
Пусть /г— гибкость стержня с произволь-
ными условиями «крепления концов; /„— свободная
длина; г — радиус инерции поперечного сечения. Тогда
кршичес'кое напряжение стержня
пй Е
о’.„ =—рю	(17.168)
Кр
Здесь Е — модуль упругости, а приведенная
гибкость определятся соотношением
\р= |./ X" ф-л2 a£/G.	(17.169)
Для сплошных (монолитных) стержней поправка, вно-
симая вторым слагаемым под знаком радикала, прене-
брежимо мала
Составные стержни. К стержням составною сечения
0ПЮСЯ1 (рис. 17.37): а) стержни на шпонках, б) решег-
Рис. 17.37
чатые стержни, в) рамные стержни (стержни на план-
ках). Здесь воздействие поперечной силы, воспринимае-
мой н₽ по всей длине стержня, как в случае сплошного
стержня, а в отдельных точках, требует обязательного
учета.
Самое простое, решение основано на формуле (17.168),
где приведенная гибкость составною стержня
X =1/х‘-фЛ'.
пр * U 1
(17 170)
Выражения для А2 в отдельных частных случаях см.
в «Справочнике проектировщика», 1-е изд, стр. 765 и да-
лее, а также в СНиП.
Стержень, состоящий из двух ветвей (пис. 17.38).
Более точное решение задачи [35] приводит к выраже-
нию для критической силы
Если пренебречь жесткостями отдельных ветвей БЕД
но сравнению с жесткостью всего сечения EI, го выра-
жение для критической силы (17.171) стаповшся сгрук-
1урно подобным формуле (17.167).
17.5.2.	Сжатые ступенчатые стержни
Ступенчатым стержнем называется однопролетный
стержень с прямолннениои осью, сосюящий из конечного
числа участков с поеюянион жесюостью и с по-
сюяш’.ои по длине участка сжимающей силой. Предпо-
лаюстся линейно упрушя работа материала. Для каж-
дого из участков в отдельности справедливы допущения,
принятые в 17.2.
Сжимающие силы при южены по оси стержня, система
являе1ся идеальной. Ставится задача определения крити-
ческой нагрузки в эйлеровом смысле
Приняты следующие обошачения (рис. 17 39);
п — общее число участков;
k—номер узла (.6 = 0, 1, 2, п) и номер участка
(6=1, 2, .., п);
Д — длина участка,
Е1 к — жесткость участка;
i\'i: — продольная сжимающая сила на участке;
ц„. и,,—коэффициенты жесткости упругих защемлений
на концах стержня.
Параметр ншрузки для участка k равен:
л2£/ ф -J- 1
' ^+E17wk’
(17.171)
где El — жесткость на изгиб всего сечения, рассматри-
ваемого как сплошное; 2Д/ь = £/[-[-Д/2— сумма жест-
костей на изгиб каждой ветви относительно ее центра
тяжести.
Коэффициент ф вычисляют по формуле
Метод фокальных отношений. Один из концов стержня
предполагают линейно подвижным в направлении, пер-
пендикулярном оси стержня (см. рис. 17.39). Основная
„л ( с~ ц 1	1 \ т
я2\2Е1к FFi + EFJ 6 ’
рекуррентная зависимость для лев
шения имеет вид [23а]:
г.	, k lk+^
Fk-pl = cos “н-i -t- "pi i
L1k+1 lk
o;o фокального oiho-
. /Vln uH-i x
uk+x sin “fe
(17.172)
( 1 ’
У I cos uk — —
(17.174)
22£
РАЗДЕЛ 17. УСТОЙЧИВОСТЬ СТЕРЖНЕВЫХ СИСТЕМ
Начальное значение левого фокального оыюшншя
F; — cos ztj
sin Aj 1Ц1
(17.175)
При go —0 (шарнирная опора) Fr—cc>i ut Если —oo
(жесткая задом), то /4== та
Критерием потерн устойчивое!!! служит уравнение
D (и) л FnF'n - 1 -=• 0,	(17.176)
где начальное значение правою фокального 01 ношения
Для случая свободного втрхнего конца р,, =0, Если
ц„ = оо (жесткая подвижная заделка), ю кршерий по-
тери устойчивости (17,176) приводя! к болта простому
виду
Г)(и)~Еп 0	(17.178)
Здесь н— ведущий параметр имрущи. Наименьший
корень и, уравнения (17.176) или (17.178) является кри-
тическим значение',I эюю параметра (см 17,4.1; 17.4,2).
Мето д ч я с I. ii ы х р е in е н и н, изложенный в 17.4 б,
позволяет исследовать устойчивость ступенчатого стерж-
ня при любых опорных закрешышях концов. В рекур-
рентных cooi ношениях (17.141; елсдус-г положить Vi — о,
Нк = Н.
Справочные данные ио определению критических на-
грузок и свободных длин ыупенчатых стержне!! см
в «Справочнике проекшровщпка», 1 е изд, стр. 752.
17.5.3.	Сжатые и сжато-изогнутые стержни
с непрерывно изменяющейся
по длине жесткостью
С ж а т о - и з о г и у т ы п линейно упругий стержень
с переменной но длине жтсткосгыо РЦх) иеныiывает 13-
гиб с самого начала нагружения. Дифференциальное
уравнение изгиба имеет вид
ф- \’и -! М 0,	(17.179)
dx-
где х, у — коердшшгы точки на изогнутой о,И шержня;
N — постоят.а,1 по длине сжимающая сила, А1 — изги-
бающий момеш иг поперечной нагрузки р(Х) без учета
ВЛИЯНИЯ Про lOJLHOil силы.
Это линейное уршшшше второго порядка с перемен-
ным коэффццшпюм при щаршем чдещ, може! быть про-
интегрировано численно, чыоды решения задачи устои
чпвости указана и 17.5 5.
Ниже рш. см a I f .ьвается ранение задачи в том частном
случае, кшда щ авпеиит (17.179) инымрируе 1ся в замк-
нутой форме.
Общее решение уравнения. Пусть ф 1 (х) -— решение
однородного уравнения, получающегося из (17 179) при
.-И —0, Второе линейно независимое решение однородно-
го уравнении определче 1 ся по формуле Лиувилля
ЖДсД-жжщД)	(17,180)
о
где w — постоянное число, равное вронскиану сис'емы
фундаментальных функции цДх) и <щ(х)
4l 4-2
?! ГП
Общее решение уравнения (17.179) имеет вид
у --= С\ ф, {х) ж Сг <ра (х) + г/“ (х),	(17.181)
где С|, С2— постоянные, ук—'Частное решение уравне-
пня, зависящее от нагрузки.
Пусть на участке стержня x>z действу?'! равномерно
распределенная нагрузка р, тогда
(17.182)
где функция влияния равна:
Чфо (х, Z) = --” + — j ФОи(х, ДйД (17,183)
Д W J
2
Здесь обозначено
Фоп(«Л) = ф1(х)ф;!(;)-ф2(х)Гр1(1).	(17 184)
Частные производные функций ЧД0(х, z) и Фоа(л, 7)
в тальн(яшем обозначают! символами
P+“
-----; (х> г) _ Vik (х_
дх> 1>г’	(17.185)
Р'-п к
-	, X) „„ (х , р),
dx‘ Ozp
Воздействие равномерно распределенной натрузки р,
сосредоточенно!! силы' Р, и лары сил (внешнего момен-
та) АД, приложенных в точке с абсциссой г, дает
гф (л) =-. -у- Чфо (х, г) — ~ Ф01 (х, г) —
л	л
-^Р Ф0,(х, г),	(17.186)
Решение в форме метода начальных параметров полу-
чаю!, выражая постоянные интегрирования С[ и С2 че-
рез начальные параметры 60—(Фу/Зхщ (см 17 2 2),
У = У,} - Фоо Ч, 0) - Чф2 (х, 0) -ф
w	А
+ Y V01 (X, 0) 4^н-	(17.187)
Для дифференцирования по х достаточно прибавить
единицу к первому индексу функций Ч и Ф 4 помощью
того правила из (17.187) получают выражения для
0 = у' и А1 = —£/(х) //'.
Метод перемещений. Реакции основной системы мето-
да перемещений для. стержня переменною сечения при-
ведены в табл. 17 11. Приняты обозначения (I — длина
ыержня)
Ф,/,- Ф,А (I, 0), D = 2w 4 Ф!0 — Фо; 4- /Фц- (17.183)
Задача устойчивости. Центрально сжатый стержень
с переменной по длине жесткостью является Идеальной
сиетмюь, для которой вожожна потеря устойчивости
щш разветвлении форм равновесия. Критическую силе
иаходю, приравняв нулю определитель системы одно-
родных уравнений, выражающих условия равновесия
ст с ржня
Устойчивость однопролет них стержней с упруго за-
крепленными концами )рис, .17,10), Обобщается аа слу-
17 5 Л1ПЧГШЮ HP'IIir t4V 1Г CTFP I I 11 ГОСПВНОГО СГЧГНИЯ
225
T l и ц ч 1 11
чан стержня переменной жесткости задача, рассмотрен
ная в 17 45 Кршерин потери устойчивости имеет вид
•J- -j (2w , Ф1о - Ф01 + ВФЦ) +	Ф00-^Ф01) Ь
~г ~ТГ (— Ф«о Ч- y®io) а®оо — О»
N
(17 189)
15—26
г те обозначено
v = l—h'/v	(17190)
Табл 17 12 содержит критерии потери устойчивости
для стержней переменного сечения с раз нашими уело
виями закреп чения концов Эти уравнения получают из
(17 189) придавая коэффициент у к седости ynpyiiix
закреплении ра, рь и v зга гения 0 и оо
226
РАЗДЕЛ 17. УСТОЙЧИВОСТЬ СТЕРЖНЕВЫХ СИСТЕМ
Т а б л и ц а 17 12
Критерии потери устойчивости для линейго упругих сжатых
стержней переменного сечения с различными условиями
закрепления концов
Схемп стержня					Ц.,	V	Критерий
					со	со	D 0
J. -				жо		0	Фи 0
/				л	0	с-а	1 Ф()1 у- Фсц U
		—-			0	0	Фи = 0
1 i-	j- । 1				0		со	ф«« — /®1, = о
4-		ж	1				В	Ф.,ь 0
1 1 1 	i-s-X- — 11				0	0		Фао “ У
Рис. 17.40
17.5.4. Сжатые стержни, жесткость которых
изменяется ио степенному закону
Закон изменения жесткости. Пусть жесткость стержня
изменяется по степенному закону (рис. 17.41)
[ х
л/ (х) 71/макс 1 j э
\ ° !
(17.191)
где х—абсцисса точки на оси
стержня, отсчитываемая от по-
люса о; а, b — абсциссы концов
етержия (8>-а); £7Макс — наи-
большая жесткость стержня
(при х = Ь).
Общий случай а=А2. Решение
дифференциального уравнения
(17.179) выражают с помощью
цилиндрических функций перво-
го и второго рода
Рис. 17.41
Яд (х) =-У х 4 W; (х) У х УДх) /17.192;
с индексом г = 1/\ а—2| и аргументом
2—п	______
Вронскиан системы функций уч, (|ц равен ш== (2—а)/л.
Функция
• Fti (a,b) = Jt (a)Y/ (b) — У( {a)Jil7 1T)
зависит от двух аргументов:
2— а
а = bk 2
2иг
l—k’
(17.195)
индексы i, j принимают значения г, s—-T-l-sign(a--2).
Критерий потери устойчивости (17 189) для ежзкно
стержня с упругими закреплениями (см рис. 17 40) при-
нимает вид
Г а~1 о	а	1
n\amb j 4k 2 (1 — й)—— л. —k - Fr—AFy, -)
L	J
( У	\ ж
~~ maii \k “ Frr 4- ЛР.1Г I -ф туи k ~ {Frr — AFrs) ф~
а
-у Au-k 2 Frr=- 0,
(17 liGj
17 5. ЛИНЕЙНО УПРУГИЕ СЖАТЫЕ СТЕРЖНИ СОСТАВНОГО СЕЧЕНИЯ
227
где обозначено:
Pal	Hbl . „ .7, N\ ,Лю
та =	—т.п =	------, I 1 _ — . (17.19/)
-'•--'макс	-^Лмакс	\	/
Особый случай а ~ 2. Полагая, что 2i£> 1—к, т. е. что
величина критической силы не слишком мала, находят
Ф, (х) = 1 Гх cosx, ф2 (х) = х sinx, (17.198)
где обозначено:
У/ и V	1
----- ——- . (17.199)
V — к/	4
Критерий потери устойчивости (17.189) для сжатого
стержня с упругими закреплениями имеет вид:
['—	/ 2и \	1
4р У k — 2р (1 +й) cos X + 1—k—А--- sin X М-
\	1—k)	J
[Q.ktl	"J
-—— sin X У Л (sin X — 2р cos X) -f-
1 —я	j
г 2и	1
+ гпь ки ----sin % — A (sin X Эр cos X) +
У — k	J
-[ А -—-sinX = 0; 7. = —pink. (17.200)
Случай 2и<1—k рассмотрел в [35].
Справочные данные. Большое число задач устойчи-
вости упругих сжатых стержней, жесткость которых из-
меняется по степенному закону, рассмотрено в трудах
А. Н. Диниика [14] и А Р. Ржаницына [35]. Графики
для определения свободной длины таких стержней даны
в [236].
17.5.5. Сжатые стержни с переменными
по длине жесткостью и сжимающей силой
Дифференциальное уравнение изгиба. Прямолинейный
стержень переменного сечения Е1 (х) сжат сосредото-
ченной силой S и равномерно распределенной продоль-
ной нагрузкой s(x) (рис. 17.42). Сжимающее усилие
в точке с координатой х будет равно
х
Л'+	(17.201)
6
а изгибающий момент
X
AI = Л40 + //а.¥ д Sy -ф f s (|) [у - р (У] <
о
(17.202)
Дифференцируя дважды по х обе части соотношения
Д1 (х) = - EI (х) у"	(17.203)
и принимая во внимание, что
X
М' (х) = До Щ Sy' у ф i s (у—Г]) d'i ” r/y-.V (х) у',
ах J
и
получают дифференциальное у равнение ищ иба
[ЕЦх)у” f H4VU)z/'f -о (17,204)
или в развернутом виде
Ely™ + 2EI'у" Д- (£7" -ДА) у Д-У’ у’ = 0.	(17.2051
Задача устойчивости возникает при отсутствии по-
перечной нагрузки на стержень н при однородных гра-
ничных условиях. Заменяя продольные нагрчзки S через
kS и s(x) через ks(x),, разыскивают кршическое зна-
чение параметра нагрузки К, соответствующее потере
устойчивости в эшкровом смысле. Ниже описываются
два метода решения этол задачи.
Численное интегрирование уравнения с использовани-
ем метода частных, решений. Из четырех начальных па-
раметров t/0, у(|, //j и //,, два известны по условиям за-
крепления левого конца стержня; остальные два началь-
ных параметра обозначают символами Z; и Z2, Уравне-
ние (17.205) при иекоюром фиксированном значении к
численно инте/рируют по методу Рунге-Кутта дважды:
при Zi = l, Z2 —0 и 2^=9, Z2=l. Наложение этих двух
частных решений позволяет сформулировать граничные
условия на правом конце шержпя в виде системы двух
уравнений относительно Z-t и Z2. Условие потери устой-
чивости заключается в равенстве нулю определителя этих
уравнений: D(k)=Q Критическое значение параметра
нагрузки k,,, удовлетворяющее этому условию, находят
методом попыток (направленного поиска).
Другой способ решения задачи. Длину стержня /
разбивают на п учатлоъ таким образом, чтобы в про-
Рис 17.43
делах длины каждого участка жесткость Е1 и сжимаю-
щую силу /V можно было считать постоянными с по-
грешностью, ие превышающей допустимой величины.
Устойчивость полученного таким образом ступенчатою
стержня (рис. 17.43) исследуют одним из методов, изло-
женных в 17.5.2. Способ позволяет учитывать также скан-
кообразиое изменение жесткости и сжимающей силы.
15
228
РАЗДЕЛ 17. УСТОЙЧИВОСТЬ СТЕРЖНЕВЫХ СИСТЕМ
17.6.	ЛИНЕЙНО УПРУГИЕ СТЕРЖНИ,
СЖАТЫЕ СЛЕДЯЩИМИ СИЛАМИ
17.6.1.	Стержень, сжатый следящей
силой общего типа
Следящая сила общего типа. Рассматривают линей-
но упругий стержень длиной I с защемленным нижним
и свободным верхним концом. Пусть будет 0 — угол по-
ворота, б — линейное перемещение верхнего конца стерж-
Рис. 17,45
Рис. 17.44
ня (рис. 17.44). Стержень сжат продольной силой N,
точка приложения и угол наклона которой изменяются
в зависимости от перемещений верхнего конца стержня.
С д в и г 6“ и в р а щ е и и е 0« такой следящей силы
общего типа определяются соотношениями:
6 ”-=	01 + /г12 б;
9 — А210ф-/г22	,
(17.206)
где ф3 (г, /=1. 2)—коэффициенты ориентации [52а].
Схемы стержней, сжатых следящей силой. Частные
случаи, возникающие при различных значениях коэффи-
циентов ориентации, представлены на рис. 17.45,
Схема а, Ап=4=0, Д2 = £21 =А22 = 0, сдвиг бн пропорцио-
нален углу поворота 0.
Схема б, А12=/=0, Ац = &2| = Аи = 0, сдвиг 5й пропорцио-
нален линейному перемещению б. В частном случае
А1а= 1 стержень сжат продольной силой с фиксирован-
ной линией действия; критическую нагрузку такого стер-
жня на основе динамического критерия устойчивости
впервые определил Б. Л, Николаи (1939 г,).
Схема в, А214АО, k\. —ki2 = А22 = 0, вращение 0“ про-
порционально углу поворота 0, коэффициент А21 назы-
вают коэффициентом преследования. Устой-
чивость стержня для случая k2i — 1 (строго следящая
или тангенциальная сжимающая сила) иа основе дина-
мического критерия впервые исследовал М. Бек [48].
Схема а, йи=й=О, йц = й12=Ам=0, вращение 9я про-
порционально линейному перемещению б. При йц<()
сжимающая сила N направлена на фиксированную точку
первоначально прямолинейной оси стержня. Расстояние
от полюса до верхней точки этой оси равно /) =—
При k22~l полюсом служит основание стержня.
Условие консервативности нагрузки. Следящая сила
общего типа создает иа верхнем конце сгоржня момент
М и горизонтальную силу Id:
М = Аб" = N (ka 01 ф- kl2 б); '
/	б \	(17.207)
Я = (V 0 = А7 US104~АЮ — 1.
Работа силы А на виртуальных перемещениях dA~
— N	будет полным дифференциалом, если
дб 60 ’
Отсюда следует, что необходимое и достаточное усло-
вие консервативности нагрузки заключается в симметрии
матрицы коэффициентов ориентации [25]
(17.208)
17.6.2.	Динамический критерий устойчивости
равновесия. Три вида собственных
движений стержня
Недостаточность статического крите-
рия у сто й чи вост и следует из того факта, что кон-
сервативность нагрузки в общем случае следящей силы
не обеспечена.
Динамический критерий устойчивости
оценивает качество равновесия в соответствии с видом
собственного движения, которое совершает стержень
[4, 31].
Для некоисервативных систем при определенных усло-
виях становятся возможными такие явления потери
устойчивости, которые не могут быть обнаружены на
основе статического критерия.
Дифференциальное уравнение собст-
венных движений стержня, основанное на до-
пущениях, сформулированных в 17.2 для задач статиче-
ского изгиба, имеет вид
d-y(x.t) d"y{x,t) d~y(x,t)
+	+	(И.209)
где x — абсцисса точки на оси стержня; у(х, 1) — орди-
ната этой точки в момент времени t; Ё1—жесткость
стержня; ц— масса единицы длины стержня.
Решение уравнения ищут в форме (метод Фурье)
y(x,t) = yf(t),	(17.210)
где у зависит только от х, [ — только от t.
После подстановки (17.210) в (17.209) переменные х
и t разделяются
= (17s211)
ИУ	f
Здесь — параметр разделения, постоянная величи-
на, равная квадрату частоты в случае гармонического
колебания.
Три вида собственных движений с те р -
ж н я определяются величиной со2:
L Гармоническое колебание — параметр
разделения со2 положителен, частота со имеет веществен-
ное значение. Равновесное состояние стержня устойчиво.
2.	Апериодическое д в и ж е и и е с возрастаю-
щими по времени отклонениями (дивергентное движе-
ние) — параметр разделения ш2 отрицателен, частота со
17 6 ЛИНЕЙНО УПРУГИЕ СТЕРЖНИ, СЖАТЫЕ СЛЕДЯЩИМИ СИЛАМИ
229
шест чисто мнимое значение. Равновесное состояние
ггсржия неустойчиво — наблюдается апериодичес-
кая неустойчивость (дивергенция).
3.	Сложное колебательное движение
: возрастающими по времени отклонениями (флагтерное
цзижеиие)—параметр разделения ы2 и, следовательно,
lacioia и — величины комплексные. Равновесное состоя-
ine стержня неустойчиво — наблюдается колеба-
тельная неустойчивость (флаттер).
17.6.3.	Гармоническое колебание стержня,
сжатого следящей силой
Уравнение движения
f+©2/ = 0	(17.212)
при ш2>0 имеет решение
f = Сщ1'^ + С„ e~iai = A cos (m/ф-ф), (17.213)
где ы — частота собственных колебаний; ф— сдвиг фа-
зы; Сь С2, А от времени не зависят.
Стержень совершает гармоническое колебание
у (х, t) = у (х) cos (at -}- <p).	(17.214)
Уравнение изгиба стержня определяет амплитудные
значения у(х')
ТХ7 Г''-	,	V
У' + ~ У —-77-7 = 0.	(17.215)
Здесь I — длина стержня; параметр нагрузки
и н параметр движения v равны:
Общий интеграл уравнения (17.215) nwvr вид
щх	tyx	и„х
у — sh -j- С» ch ~— + С3 sin —j— -ф.
и„х
ф С4 cos - ,	(1/21/)
где обозначено
Таблиц а 17.13
Реакции основной системы метода перемещений для сжатого линейно упругого стержня, совершающего гармоническое
колебание
Единичное состояние	Реакции основно i системы
Угол поворота
0=1
ЕЗ
Линейное перемещение
а, f-y
фФ ТЕ
и .•
V }
— (иг ch «j sin — u2 sh «j cos и A
L 2	v ~-jj- (ti2 sh — Ui sin z/2)
Гз	1 | U"	1 — 1 ~~ и.ли2 — ch cos u2) + sh щ sin u21 1/	J
4	QOS uz)
	u-j^u^V (u2 ch sin u2 4* sh cos
L\	tiiUnV sin ^2 4“ Щ u'l)
N
Ei
~ЁГ
Обозначе-
ния
U = uiiii (1 — ch щ cos u2) — -7— sh 1ц sin i/2
230
РАЗДЕЛ 17. УСТОЙЧИВОСТЬ СТГ.РЖЙЕБЫХ СИСТЕМ
Метод перемещений основан на выборе обобщенных
координат
О (/) = 0 cos [tat 4“ ф), 6 (1) — 5 cos {wt -[- q>).	(17.219)
Единичные состояния амплитудных величин 0 = 1
и 6=1 вызывают реакции основной системы, показанные
в табл. 17.13. Эти реакции определяются с помощью ше-
сти функций Ej(«i, Дз), которые при ш = 0, ц = 0 вырож-
даются в функции L3(u) для статической задачи (см.
табл. 17.7).
Канонические уравнения метода перемеще-
ний для амплитудного состояния стержня, сжатого сле-
дящей силой, имеют вид:

] (17.220)
Здесь т — сосредоточенная масса на верхнем конце
стержня; /т — полярный момент инерции массы (см.
рис. 17.44).
Частотное уравнение получают, приравняв
нулю определитель системы уравнений (17.220)
D (и, V) н.
|L1-.W = z0 Ь3 — кыи~ 1=0>(17.221)
I Ls — k^ifl Li — k22u- — т I
где приняты обозначения
к =
pZ3
т
(17.222)
Если параметр нагрузки и фиксирован, то из уравне-
ния (17.221) определяют спектр собственных значений
параметра движения v, Каждому собственному значе-
нию параметра движения v соответствует собственная
форма — упругая линия стержня, совершающего свобод-
ное колебание.
17.6.4.	Критические состояния стержня,
сжатого следящей силой
Состояния потери устойчивости стержня определя-
ются переходом, от гармонического колебания к аперио-
дическому движению (дивергенция) или к сложному ко-
лебательному движению (флаттер). Соответствующие
таким состояниям критические параметры нагрузки и,
исследуются ниже на основе выведенных в 17.6.3 анали-
тических зависимостей, описывающих свободное гармо-
ническое колебание стержня.
Исследования всех возможных критических состояний
стержня, а также построения упругих линий для всех
трех видов собственных движений должны быть основа-
ны на решениях дифференциальных уравнений (17,211)
пе только для гармонического колебания (ш2>0), но
также и для случаев дивергентного (ш2<0) и флаттер-
ного движений (о)2 = аф-(Е) [25].
Классификация явлений потери устойчивости. Схема-
тический график зависимости параметра движения v
(пропорционального квадрату частоты ш) от параметра
нагрузки и (ряс. 17.46) показывает возможность трех
различных явлений потери устойчивости стержня.
а. Переход к апериодической неустойчивости, тип щ
Сплошными линиями на i рафике показаны дна первых
корня V, и со уравнения (17.222). По мере возрашапия
параметра нагрузки а параметр движения (мепыиии ко-
рень) vt убывает и становится отрицательным, переходя
через нуль. Значение щ=0 характеризует шт рю устой-
чивости стержня при критическом значении параметра
нагрузки и =па.
Такой тип потери устойчивости характер-п для копсер-
вативных систем, по может всгршигься 1акжс и в :ом
случае, когда нагрузка проявляет слабые печонссрватив-
ные свойства.
Обращение в нуль определителя (17.218) при одновре-
менном равенстве пулю частоты собственных колебании
(со = О) эквивалентно статическому критерию потери
устойчивости. Рассматриваемый случай потери устойчи-
вости относится к эйлерову типу (разветвление форм
равновесия). Критический параметр нагрузки и ~uri
может быть определен с помощью статического критерия.
р. Переход к апериодической неустойчивости, тип р.
Штрихпунктириая линия на графике (рис. 17 46) пока-
зывает другой случаи перехода параметра движения щ
от положительных значений к стрицазельпым. Функция
v(u) испытывает разрыв непрерывности от о = -роо до
v =—оо при критическом значении параметра ширушег
Этот тип потери устойчивости характерен дчя пекои-
сервативпых систем с одной степенью свободы. Стати-
ческий критерий не дает возможности обнаружить рас-
сматриваемое явление.
у. Переход к колебательной неустойчивости. Два пер-
вых значения параметра движения О] и су по мере роста и
сближаются ио величине (пунктирная линия на графике).
В критической точке у при критическом значении пара-
метра нагрузки и —и^ корни уравнения (17.218) стано-
вятся кратными (двойными): 0| = п2. При дальнейшем
увеличении параметра нагрузки эти корни принимают
комплексные значения.
1/6 ЛИНЕЙНО УПРУГИЕ СТЕРХИИ СЖАТЫЕ СЛЕДЯЩИМИ CHTVHt
231
Тагоп тип потри устойчивости характерен для некон-
ссрватнвных систем с числом степеней свободы не менее
Д1 1
К 1 юснфикацчя рассмотренных явлении потери устой
чивости дана на рис 17 47
Рис 17 47
17.6.5.	Области устойчивости
и неустойчивости невесомого стержня,
несущего сосредоточенную массу
и сжатого следящей силой
D (и, ы) ~
Частотное уравнение для невесомого стержня полу
чается из (17 221) при и=0 Параметром движения
служит ветчина
ml3©2
w = —(17 223)
El
коэффициенты хит принимают значение 'А = 1т1тР,
т = 1 При этих обозначениях
— ^иа3 —	— ki2u~
Lg ТЩЦ"	Е±и:" W
= aw” + bw -j- с = О,
где
а = %, Ь (и) = — х (£4 — k21u”) —'
- (к - brlu”},
с (и) = (Z-! — kiiuE) (Ц — йми2) —
— (£з —	(7,3 — k21u2)
Отсюда определяют параметр движения
— Ь ~ V^fe2 — 4ас
ГО! — .......   -	_
(17 224)
(17 223)
(17 226)
Критерии потери устойчивости Статический критерий
потери устойчивости (ы—0)
Ра (и) - с (и) -= 0	(17 227)
' '’рактериз' ет переход к апериодическому движению
(дивергенции), тип а
Переход к апериодическому двоткепию (ототр ыщии),
тип р, опреде тяготя кошер it i
1
D __ -------- = о	(п ppg)
1 w (и)
Критерий перехода к фчаттерпому двиАешно з'ато
чается р равенстве иутю дискриминанта кштр того
уравш ыя (17 224)
Dy(u) - b2 — 4ос-0	(17 229
Исследование схемы а Негр зка явдя тся консер
вативио! Статически,! кршерин потери устойчивости
(17 227) приводят к виду
Исследование сопряженных схем б ч в Cxi. >ы я”
ляются сопрч/кепны Vi i тал как при гсростами к° ко/ф
фициеютов ориентации k12 и встотп! отредеттелч
О (и и,) но изменяет i (тапчеекют крлтернi потри
устойчивости (17 227)
cos и
= 721 = - ~-------- (17 231)
1 — cos и
определяет переход к дивергентному движению тдц а
Критерий перехода к дивергентному движению тип (3,
(17 223) при и~0 (инерция поворота массы т нс учи
тывается) приводит к уравнению
sin и — acosu = 0,	(17 232)
которое не содержит коэффициентов ориентации Наи-
меньший корень этого уравнения у =4,4934 д^ет дтя
критической силы постоянное значение
г 20.19И
(17 233)
На графике (рис 17 48) показана зависимость от
коэфФнкчеюта ориегпад/ш /г12 (ыи /и) обтащи тсто
чивостп заштрихованы Кривая	достгоспд по
уравнению (17 231), прямая l\LM тост тствуст кргич
ческоп си те (17 233) При й12<10 5 степы < пъ ^ржет ' стой
чивостс в эитерово ! схтысте критч ютчая сита завис! т
от ветчины k2 В случае АцОО 5 пот ря у стоиоттьости
не может быть установлена с номо ц>ю статччеслого
Рис 17 48
232
РАЗДЕЛ 17. УСТОЙЧИВОСТЬ СТЕРЖНЕВЫХ СИСТЕМ
критерия; критическая сила (17.233) постоянна по ве-
личине.
Эта критическая сила (17.233) по величине совпадает
с критической силой постоянной ориентации, вызываю-
щей потерю устойчивости (в смысле Эйлера) центрально
сжатого стержня с нижним защемленным и верхним
шарнирно закрепленным концом (см. схему 2
в табл. 17.2).
Представленные на рис. 17.49 для схем б, в формы
изогнутой оси стержня, совершающего собственное коле-
бание в критическом состоянии, совпадают с формой
потери устойчивости упомянутою выше стержня, верх-
ний конец которою закреплен. Верхний конец шержня
не перемещается в горизонтальном направлении, 6=0,
но инерционная сила R — nm‘2S имеет конечное, отличное
ог нуля значение, так как одновременно с убыванием 6
до нуля возрастает до бесконечности частота собствен-
ных колебаний со. Неопределенность типа 0-оо может
быть раскрыта.
Рис. 17.49 показывает, что при совпадающих формах
изгиба условия равновесия (в смысле Даламбера) гори-
щипальных сил для схем б и в различны.
Исследование схемы г. Нагрузка является консерва-
тивной Статический критерий потери устойчивости
(17.227) приводят к виду
и. COS и
_	(17.234)
sin и — и cos и
17.6.6.	Области устойчивости
и неустойчивости весомого стержня,
сжатого следящей силой
Частотное уравнение при отсутствии сосредоточенной
массы получают из (17.221), полагая т—0.
Области устойчивости для каждой из четырех схем
лежат ниже соответствующих кривых на графике
(рис. 17.50), изображающих зависимость критического
параметра нагрузки и, or коэффициентов ориентации
Сплошные линии на графике соответствуют потере устой-
чивости, связанной с переходом к апериодическому дви-
жению (дивергенции), тип а. Эти кривые построены на
основе статических критериев потери устойчивости
(17.230), (17.231) и (17.232).
Исследование сопряженных схем б и в
показывает, что при й12р=зб,354 (или й21^0,354) воз-
можна также потеря устойчивости, связанная с перехо-
дом к сложному колебательному движению (флаггеру);
соответствующая этому случаю кривая показана на
рис. 17.50 пунктиром.
Рис, 17,50
17 7. НЕЛИНЕЙНО УПРУГИЕ СЖАТЫЕ И СЖАТО-ИЗОГНУТЫЕ СТЕРЖНИ
233
Частотное уравнение для рассматриваемой задачи при-
водят к виду:
D (и, и) д uf — U] и2 ( и2, — и2) sh sin ц„4-
4- { и{ 4- и2) ch иг cos и2 ] + А1з [[ и.7 — и\]2 4-
+ 2и1 и, ( uf — и() sh sin 1/., —
— a~2 — u\ J2 ch cos u, ] = 0,	(17.235)
Рис. 17.51
или, для частного случая ki2—\ (Л21 = 1)(
D {и, о) = U;1 4- и\ + и, и2 ( ul — «yj sh и± sin и^
4- 2а] uj ch ut cos — 0.	(17.236)
Условие колебательной неустойчивости заключается
в равенстве между собой двух наименьших корней Vj
Рис. 17.52
(17.237)
стержня, совершающего коле-
устойчивости при критической
и t’o уравнения (17 235) или (17 236) Для частного слу-
чая /г2| = 1 (строго следящая или тангенциальная сила)
критическую силу определил М, Бек (1952 г.)
20,0547
Nt =
Формы изогнутой оси
бание в момент потери
силе (17.237), показаны на рис. 17.51 Несмотря на сов-
падение критических сил, формы эти для схем б и в раз-
личны.
Влияние распределения масс. Анализ устойчивости
весомого стержня, несущего сосредоточенную массу, для
схемы в при коэффициенте преследования й21 = 1 (стро-
го следящая или тангенциальная сила) показывает, что
критические силы для крайних значений т = 0 (17.237)
и 1.1 = 0 (17.233) отличаются мало (А, Пфлюгер, 1955 г,).
График зависимости от коэффициента распределения
масс представлен на рис. 17.52; для промежуточных зна-
чении т2>0, р>0 критическая сила снижается и может
составить приблизительно 80% от наибольшей величины.
11а этом же графике дано решение задачи при 7г21=О,8
и й21=0,6.
17.7.	НЕЛИНЕЙНО УПРУГИЕ СЖАТЫЕ
И СЖАТО-ИЗОГНУТЫЕ СТЕРЖНИ
17.7.1.	Нелинейно упругий материал
Закон нелинейной упругости. Деформации материала
полностью обратимы, напряжение и относительное уд
линение связаны нелинейной зависимостью o — g(e.)
или е = ((а), В общем случае эта зависимость для
сжимающих (о>0) и рас-
тягивающих (о<0) напря-
жений может быть различ-
ной (см. схематический
график работы ма-
териала на рис, 17,53).
Функция а = 4(e) одно-
значна, т. е, каждому значе-
нию е соответствует только
одно строго определенное
значение а. Закон нелиней-
ной упругости может быть
задан или аналитически,
или в форме таблицы, содержащей достаточно большое
число пар точек е, а.
Начальный модуль упругости
£ =
(17,238)
определяет наклон касательной к кривой графика в на-
чале координат, при е = 0, о = 0.
Касательный м оду л ь
do
Et=^—- = g'
du
(17.239)
определяет наклон касательной к кривой графика ра-
боты материала в произвольно!! точке с текущими ко-
ординатами « и <j = g(s).
График работы нелинейно упругого материала может
включать прямолинейные участки. Часто рассматрива-
ют материал, который в начальной стадии работы, до до-
стижения предела пропорциональное? и о1)ц
обладает свойством линейной упругости о = 4в; при даль-
нейшем развитии деформации эта зависимость заменя-
ется другой.
Энергетические теоремы сохраняют свое значение для
нелинейно упругих стержней, поскольку деформации об-
ратимы и силы упругости имеют потенциал.
Исследование изгиба и устойчивости нелинейно упру-
гих стержней основано на анализе малых изгибных пе-
ремещений. Используется гипотеза плоских сечений.
Предполагается сохранение плоской формы изгиба как
в устойчивых, так и в неустойчивых состояниях стерж-
ня. Влияние касательных напряжений не учитывается.
23-1
РАЗДЕЛ 17. УСТОЙЧИВОСТЬ СТЕРЖНЕВЫХ СИСТЕМ
17.7.2.	Устойчивость центрально
сжатых стержней
Центрально сжатый стержень представ-
ляет собой идеальную систему и до потери устойчиво-
сти сохраняет первоначальную прямолинейную форму.
Потеря устойчивости связана с разветвлением форм рав-
новесия Критическая сита шарнирно опертого
стержня равна (Ф. Энгессер, 1889 г.):
а" Гу!	Ida \
ЛЦ-—Е{— ~ =£'(еД,	(17.240)
СТ	\ U8 /,
где I — длина стержня; !— момент инерции поперечного
сечепяя.
Другие условия закрепления концов
стер ж н я учитываются с помощью понятия св обод-
ной длины E (см. 17.1.14; 17,2.3). Критическое на-
пряжение. равно
'da \
, Аг Ц
ными длинами I в критическом состоянии будет нахо-
диться самый длинны!! стержень, т. е. тог, для которого
dl
Аут
Качественная характеристика явления дана в 17.1 4.
Идеальной системой будет сжато-изо! нутый
(17 214)
Рис. 17.55
Д. =
F
7,2
(17.241)
где 1.~Е v F/I — гибкость стержня; F— площадь по-
перечного сечения.
График критических напряжений, изо-
бражающий зависимость <щ от л, удобно строить по фор-
муле
я2 /da \
\ Фе / *
(17.242)
задаваясь значением от и вычисляя соответствующую
гибкость
17.7.3.	Изгиб и устойчивость
сжато-изогнутых стержней
Процесс нагружения сжато-изогнутого нели-
нейно упругого стержня иллюстрируется графиком
поведения (рис. 17.54), по оси абсцисс откладывают
характерное перемещение —
прогиб в середине пролета
ут, по оси ординат —' сжи-
мающую силу N. В точке В
сжимающая сила Л', рас-
сматриваемая как функция
прогиба у,-,,, достигает эк-
стремального (максималь-
ного) значения. Это макси-
мальное значение ЛЦ акс =
-= Nis является к р и т и ч е-
ским; оно определяет со-
стояние потери устой-
чивости при дости-
жении предельной
нагрузки. В строительной механике стержневых си-
стем говорят также о потере устойчивости второго
рода.
Критерий потери устойчивости сводится
к условию стационарности функции Л' — Е(ут')
d.N
----
Adm
(17.2'1-3)
если фиксирована длина стержня I. Другая возможная
постановка задачи предполагает фиксированной сжи-
мающую силу Л/; тогда из множества стержней с раз-
стержень, нагруженный так, что форма изгиба ортого-
нальна форме ’потери устойчивости. Примером служит
антисимметрично нагруженный шарнирно опертый стер-
жень с S-образной упругой линией (см. рис. 17.5).
В этом особом случае потеря устойчивости при развет-
влении форм равновесия может произойти до достиже-
ния предельной нагрузки.
При слабой нелинейности в некоторых случаях воз-
можно также асимптотическое поведение стержня (пун-
ктирная кривая на рис. 17,54), характерное для линейно
упругих стержней (см. 17.2.4; 17.2.5), Предельное (асим-
птотическое) значение сжимающей силы зависит от
графика работы материала, от длины стержня, формы
и размеров его поперечного сечения.
Дифференциальное уравнение изгиба
имеет вид (рис. 17,55)
Д2Д. = _ е* ~е°	_	/17щ45)
Фх3	h	ft
Здесь х, у—координаты точки па оси стержня;
€1> 8з—удлинения крайних волокон сечения;
ai, ai — соответствующие фибровые напряжения;
h—высота сечения.
В общем случае, при произвольной форме профиля
стержня н при произвольном законе нелинейной упруго-
сти, возможно только численное решение уравнения
(17.245) (см. 17.7.5).
17.7.4.	Аналитическое исследование
равновесных и критических состояний
внецентренно сжатого стержня
с двухточечным профилем
Внецентренно сжатый стержень с двухточечным про-
филем (рис. 17.56). В этом простейшем случае уравнение
(17.245) интегрируется в квадратурах. Из условий рав-
новесия
Fh
М = АЦй + {/)=(<?! — «И)---;
4
F
N =. a0F = (01 ф. ог2) — ,
пл. нелинейно упругие сжатые и сжато-изогнутые стержни
235
определяют фибровые напряжения
Ш = (1 + и) а(1; ог =. (1 — «) оп, аа -= N/Р.
Здесь 1А — изгибающим момент; а—эксцентрицитет
приложения продольной сжимающей силы /V; и =
= 2(аф-у)//г. В безразмерных координатах г-Зф/i и ь
уравнение (17.215) принимает вид [24в]
Р-и 1
(17.2-16)
где функция двух переменных равна:
q)(c0,u)=/I(l +u)a0J-/I(l -U)o0j. (17.247)
Разрез к~к
При шарнирном опирании концов стержня граничные
условия на опоре g = 0, и —2alh = m и в середине про-
лета ’Z. — l/h, u = m~'r2y,n/h = um приводят к выражению
для гибкое!и стержня
и
| [Ф(л0, М-®((j0) и)Г' - du, (17.248)
il „'
т
где обозначено
и
Ф (<т0, и) = ] q (су, и) du. (17.249)
п
Условие потери устойчивости (17 211) преобразуют
к форме 5X/dum=0, Построение равновесного состояния
стержня сводится к двум квадратурам, а определение
критической нагрузки требует, кроме того, разыскания
экстремума несобственного интеграла (17 248).
Замкнутое решение получают при законе не-
линейной упругости
ст ( а \а
е = — + «(—-) ,	(17.250)
где «— показатель нелинейности. Гибкость стержня на
основании (17 248) выражают с помощью элтиптическо-
ю интеграла первого рода
7 = -М-р (фъ у),	(17,251)
1'т
где приняты обозначения
t~ab/E; q --агссоз и/иГЛ\ 1
Pi =- arccos
k> ..-------------------- .	(17.252)
2 3- 2aH (3 4- iQ'j
T ^l + at:i{d + iQ).
Критерий потери устойчивости (17.244) преобразуют
к форме
-----------г	;__1
V 1 — (г2 sin2ф! F (фь k) — -—Фу Е (фьй) =
L.	1 —«“ J
f	l-2ks	\
= 1 —й3-------sins срх etg срт,	(17.253)
\	1 — k“	J
где £(q, k)—эллиптический интеграл второго рода.
График критических напряжений при а = 5-1СИ для
ряда разных значений относительного эксцентрицитета
m = 2afh приведен на рис. 17.57.
Р е ш е н и е д л я к у б и ч е с к о г о з а к о н а в = (о/с)3
получают как частный случай выведенных соотношений,
полагая п— (Е/с)3 и затем устремляя Е к бесконечности.
Гибкость стержня в равновесном состоянии равна:
К =	(17.254)
]/з + ^ xaJ 6 +
17.7.5.	Численное исследование
равновесных и критических состояний
сжато-изогнутых стержней
Постановка задачи. Закон нелинейной упругости
и форма профиля предполагаются произвольными. Шар-
нирно ощртын шержепь сжаг силой N и испытывает
изгиб от поперечных нагрузок Mi, Р, р и т. д. (рис, 17.58).
Анализируются равновесные и критические состояния
стержня [10, На, 49, 55].
236
РАЗДЕЛ 17. УСТОЙЧИВОСТЬ СТЕРЖНЕВЫХ СИСТЕМ.
Ниже описывается один из оптимальных алгоритмов
численного решения задачи с помощью ЭВМ.
Процедура наложения. Пусть действующие в сечении
усилия М и N известны; требуется построить эпюру нор-
мальных напряжений о. Задача решается наложением
сечения па график работы материала (рис. 17.59). Удли-
нение крайнего волокна с вогнутой (выпуклой) стороны
равно ai(Ee); удлинение 0 центре тяжести сечения — е0.
Рис. 17.58
Высоту сечения h необходимо преобразовать так, чтобы
она стала равной длине (ei—Ег) в масштабе графика.
Условия равновесия имеют вид:
\vodF = M. (17.255)
f	F
Текущая координата v отсчитывается от центра тяже-
сти сечения; соответствующее напряжение равно:
о
о = У(е), в = е0 + — (&1~- е2).	(17.256)
Неизвестные величины si и находят методом двой-
ного направленного поиска или на основе итерационного
процесса (см. 17.11.3).
Процедура интегрирования. Дифференциальное урав-
нение изгиба
=	---V) (17.257)
dx*	h
численно интегрируют методом Рунге — Кутта при на-
чальных условиях г/ч=О и уо = 0о В общем случае гра-
ничное условие на правом
силы N определяют методом
конце у„— 0 не выполнено.
Одну нз двух величин
N или Оо следует изме-
нить так, чтобы это ус-
ловие было удовлетво-
рено.
Равновесное состояние
стержня. Целесообразно
зафиксировать Оо и ис-
кать значение N, удов-
летворяющее гранично-
му условию па правом
конце стержня. В этом
случае при рассмотрении
первичных равновесных
состояний стержня ис-
ключается двузначность
решения, свойственная
обратной постановке за-
дачи.
Величину сжим ающей
направленного поиска, пос-
ле чего становятся известными напряжения и перемеще-
ния каждой точки стержня.
Критическое состояние стержня. Построив несколько
равновесных состояний, наносят соответствующие точки
на график поведения стержня. Критическое состояние
стержня соответствует точке максимума; ордината этой
точки определяет критическую силу А/,.
17.7.6.	Приближенное определение
критической силы
внецентренно сжатого стержня
Постановка задачи. Разыскивается приближенное
значение критической сипы внецентренно сжатого стерж-
ня, Не преследуется цель
Рис. 17.60
анализа напряженного состоя-
ния стержня как в крити-
ческом состоянии, так и в
равновесных состояниях,
предшествующих потере ус-
тойчивости при достижении
предельной нагрузки.
Метод коллокации осно-
ван на задании формы изги-
ба стержня и требовании,
чтобы условия равновесия
выполнялись в п фиксиро-
ванных сечениях по длине
стержня, Задача сводится к исследованию изгиба и ус-
тойчивости системы с п степенями свободы.
В простейшем случае шарнирно опертого стержня при-
нимают форму изгиба в виде полуволны синусоиды
(рис. 17.60)
л,х
V = Ли sin — .
(17.258)
Напряженное состояние стержня полностью определя-
ется условиями работы одного сечения в пролете; систе-
ма обладает одной степенью свободы (л = 1).
Дифференцируя дважды по х соотношение (17.258),
полагая затем x = Z/2 и используя зависимость (17,257),
находят
Здесь
Ут=4-^(ЛДД)-	(17.259)
М = Д(а+ут) —изгибающий момент
в сред-
нем сечении стержня.
Для построения равновесного состояния стержня целе-
сообразно фиксировать величину ут и после ряда нало-
жений подобрать значение
N, удовлетворяющее одно-
временно уравнениям
(17.258) и (17.259). Крити-
ческое состояние выделяет-
ся с помощью условия
(17.244) [21а, 33, 51].
Оценка погрешности. Ме-
тод коллокации приводит к
несколько преувеличенным
значениям критической си-
лы
Графики критиче-
ских напряжена й для
стержней с различными фор-
мами профиля с помощью
метода коллокации постргюпы в работе [55]. Матерна i
обладает свойством линейной упругости при в<еПд,
г><Опц; при р.>епц закон нелинейной упругости выра-
жается суммой четырех экспонент. Условный предел
17 8 УПРУГО-ПЛАСТИЧЕСКИЕ СЖАТЫЕ И СЖАТО-ИЗОГНУТЫЕ СТЕРЖНИ
237
текучести принят ат = 2сПц, асимптотическое напряжение
аа г = 1,2 От (рис. 17.61).
Один из графиков критических напряжений (для дву-
таврового профиля) представлен на рис. 17,62. Он со-
держит семейство кривых, соответствующих ряду значе-
ний относительного эксцентрицитета m-aF/W, где IV—
момент сопротивления сечения. По оси абсцисс отложе-
на относительная гибкость л = ?.Дт, Хт = п E/g?.
17.7.7.	Качественный критерий устойчивости
сжато-изогнутых нелинейно упругих
стержней
К а ч е с т в е и н ый критерий устойчивое т и
сжато-изогнутых нелинейно упругих стержней в отли-
чие от экстремальных критериев (17.243) или (17.244)
не требует вычисления производных d.Nidym или dlfdym.
Он позволяет оцепить устойчивость одного рассмотрен-
ного равновесного состояния стержня; такая оценка с по-
мощью экстремальных критериев (17 243) или (17.241)
невозможна [5а, 11а]
Качественный критерий устойчивости основан на свой-
ствах заменяющего стержня,
Анализ равновесного состояния сжато-
изогнутого нелинейно упругого стержня определяет на-
пряжение в каждой его точке а = о(л", о), где х—абс-
цисса, указывающая место сечения, v—координата,
определяющая положение волокна в сечепии (см.
рис. 17.55). После этого, пользуясь графиком работы
материала (или аналитическим законом нелинейной уп-
ругости), находят касательный модуль соответствую-
щий напряжению о(х, о), и вычисляют коэффициент
ffi>< 1
Et	1	Уст
ffl(X;a)=^.= (i7.260)
Ь	Е	№
Сечение заменяющего стержня получают заме-
ной ширины каждого волокна Ь (у) шириной b(vi
ы(х, о). Площадь сечения заменяющего стержня равна:
Fa = j b (о) <а (х, о) dv.	(17.261)
Символом /(1) обозначают момент инерции площади
заменяющего стержня Еа относительно центра тяжести
этой площади.
Заменяющий стержень получают, нанизывая
центры тяжести всех сечении FPI на прямолинейную ось,
длина которой! равна длине исследуемого стержня I.
Разыскивают критическую силу при разветвлении форм
равновесия N,u заменяющего стержня, рассматривая его
как центрально сжатый линейно упругий стержень с пе-
ременной жесткостью Е1а (см. 17.5).
Для шарнирно опертого стержня приближенно можно
принять
(17-262)
где Efm —жесткость заменяющего стержня в середине
пролета; 5— коэффициент, учитывающий переменность
сечения по длине, В случае решения по методу колло-
кации обычно полагают 5=1.
Критерий устойчивости. Если jVffl><V, то исследуемый
стержень находится в устойчивом состоянии, т. е. ;V<.V*.
При обратном знаке неравенства равновесное состояние
стержня неустойчиво, следовательно, Ny>Nf,. Если
то исследуемый стержень находится в крити-
ческом состоянии; условие
А = Аи = АД	(17.263)
является признаком потери устойчивости при достиже-
нии предельной нагрузки
Кривую зависимости критической силы заменяющего
стержня от характерной деформации ут исследуе-
мого стержня показывают на графике поведения
(рис. 17.63). Точки А и А' соответствуют границе ли-
нейно упругой стадии работы материала (фибровое
напряжение достигает предела пропорциональности апц),
точка В является критической для исследуемого стержня.
Удобно также строить зависимость Nm от N
(рис. 17.64). Ветвь кривой, лежащая выше биссектрисы
координатного угла, соответствует устойчивым, ветвь,
расположенная ниже биссектрисы,— неустойчивым со-
стояниям исследуемого стержня.
17.8.	УПРУГО-ПЛАСТИЧЕСКИЕ СЖАТЫЕ
И СЖАТО-ИЗОГНУТЫЕ СТЕРЖНИ
17.8.1.	Упруго-пластический материал.
Обозначения
Упруго-пластический материал характе-
ризуют следующие три основные свойства:
а)	нелинейность зависимости между напряжением а
и деформацией е в целом; на отдельных стадиях эта
зависимость может быть линейной;
238
РАЗДЕЛ 17, УСТОЙЧИВОСТЬ СТЕРЖНЕВЫХ СИСТЕМ
б)	текучесть материала, определяющая рост деформа-
ции при постоянном (или почти постоянном) напряже-
нии;
в)	необратимость деформаций, связанная с возникно-
вением остаточных деформаций при разгрузке.
При упруго-п диетической деформации часть энергии
расходуется па изменение кристаллической решетки ма-
териала; диссипация (рассеивание) энергии делает си-
стему исконсерватявной. Энещетические теоремы, осно-
Рис. 17.65
ванные на свойствах потенциальной энергии системы,
в этом случае неприменимы.
Схематический график работы упруго-
пластического материала (рис. 17.65) показывает: стадию
упругой работы при e<enJ!, о<аш, (прямая 0/1), когда
связь между деформацией е и напряжением а линейна
о' — Ее (Е — модуль упругости); переходную кривую АВ,
соединяющую г,редел пропорциональности (ецц, аяц)
с пределом текучести (ет, стт); площадку текучести (пря-
мая ВС), характеризующую быстрый рост деформации
при постоянном (п.ш почти постоянном) напряжении <гт;
стадию самоупрочнення (кривая СО) с напряжениями
о >от.
Разгрузка происходит по линейному закону (пунктир-
ная линия PQ на рис. 17.65) с модулем разгрузки £'«£.
Исследование изгиба и устойчивости сжатых и сжато-
изогнутых упруго-пластических стержней основано на
анализе малых изгибных перемещений, используется ги-
потеза плоских сечений. Предполагается сохранение плос-
кой формы изгиба как в устойчивых, так и в неустой-
чивых состояниях стержня. Влияние касательных напря-
жений не учитывается.
В практических задачах обычно принимают во внима-
ние не все свойства упруго-пластического материала,
а только некоторые из них. Если используют предполо-
жение об актив иости деф ормаци и, то разгруз-
ка не происходит, и упруго-пластический материал мож-
но рассматривать как нелинейно упругий
(см. 17.7).
Идеализация свойств материала позволяет существен-
но облегчить решение задач изгиба и устойчивости.
Матери а л с линейным у п р о ч н е н и е м
(рис. 17.66, а) обладает упругими свойствами при
е<ет, с-Сот. В случае еу>?т, а>ат линейная зависи-
мость между напряжением и удлинением определяется
модулем деформации фЕ<1Е при догрузке
а — ат = фЕ1 (е — ет), а = фЕе + (I — ф) <JT (17.264)
или модулем упругости Е при разгрузке.
И д е а л ь п ы ii упруго- п л а с т и ч е с к и й ма-
териал обладает свогством неограниченной текучести
при е>г’т. ff = or (график Прандтля, рис 17.66,6). Раз-
грузка определяется модулем упругости Е.
О с и о в н ы е о б о з и а ч е н и я:
N — сжимающая сила;
АР. — критическая сила;
F—площадь поперечного сечения;
7 — момент инерции поперечного сечения;
<тв = А’/Е — осевое напряжение;
<з* = Аф/Е— критическое напряжение;
I — длина стержня;
ф — свободная длина стержня;
X — гибкость стержня.
Рис. 17.66
17,8.2. Устойчивость центрально
сжатых стержней
Центрально сжатый стержень представляет собой иде-
альную систему и до потери устойчивости сохраняет пер-
воначальную прямолинейную форму. В основу исследо-
вания устойчивости положен график работы материала,
представленный на рис. 17.65.
Потеря устойчивости в упругой обла-
сти возможна для стержней высокой гибкости
где граничная гибкость равна Хпи = л VЕ/олц. Кр ити-
ческая сила и критическое напряжение на основании
обобщенной формулы Эйлера (17,47) равны:
л-Е1
л2Е
д -------
* №
(17.265)
При этом критическое напряжение о* не превосходит
предела пропорциональности одч.
Потеря устойчивости в упруго-пласти-
ческой области была исследована Ф. Энгессе-
ром [50] и Т, Карманом [52] на основе концепции
Эйлера. В формировании теории большую роль сыграл»
критические замечания Ф. С. Ясинского [47]. На-
ложение поперечного сечения произвольной фор-
мы на график работы упруго-пластического мате-
риала показано на рис. 17.67. Изгибные деформации
стержня в начальный момент выпучивания определяют-
ся; в зоне догрузки — касательным модулем Et—dojde,
а в зоне разгрузки — модулем разгрузки Е'—Е. Пусть
17 S УПРУГО ПЛАСТИЧЕСКИЕ СЖАТЫЕ И СЖАТО-ИЗОГНУТЫЕ СТЕРЖНИ
239
будут Sj(S2) и /;(/»)—статический момент и соответ-
ственно момент инерции зоны догрузки (ращрузки) от-
носительно оси, проходящей через нулевую точку эпюры
дополнительных напряжений изгиба. Положение этой
оси определяется из условия равновесия EtSi — ESz.
Приведенный модель равен
Дальнейший аиатпз полностью
аналогичен выводу
между точками Д' и К рассматривают как зону не-
устойчивости.
Критические напряжения а* по Шенли показаны на
графике (рис. 17.68) пунктирной линией.
Несмотря па внешнее сходство формул Энгессера
(17.241) и Шенли (17.268), они относятся к разным яв-
лениям. Первая из них определяет для нелинейно упру-
гого стержня величину критической силы, вызывающей
потерю устойчивости при разветвлении форм равнове-
сия Формула (17.268) определяет наименьшую величи-
ну сжимающей силы, при которой становятся возмож-
ными криволинейные формы равновесия центрально
сжатого упруго-пластического стержня в условиях не-
прерывного возрастания сжимающей силы. Это явле-
ние качественно отличается ог потери устойчивости
в эйлеровом смысле, так как здесь при напряжении а*
формулы Эйлера, Критическая сила и критическое на-
стержень остается прямолинейным и не существует
смежных форм равновесия Ответ на вопрос, следует ли
относить такого рода бифуркацию к явлениям потерн
устойчивости или же нет, зависит от строгой формули-
ровки признаков потери устойчивости. С практической
точки зрения разветвление форм равновесия в условиях
возрастающей нагрузки следует рассматривать как осо-
бое, критическое состояние стержня.
Концепция Ф. Шенли не означает возврата к «теории
пряжение
(17.267)
касательного модуля», первоначально выдвинутой
Ф. Энгессером, так как возможность реализации рас-
сматриваемых явлений существенно зависит от поведе-
ния сжимающей силы в процессе
вызывают потерю устойчивости пои разветвлении форм
равновесия. Критическое напряжение зависит от гибко-
сти стержня от очертания 1рай>ика работы матери-
ала на участке периодной кривой АВ (см, рис. 17.65)
и от формы поперечного сечения стержня. Схематиче-
ское очертание графика критических напряжений цент-
рально сжатого стержня показано на рис. 17.68 сплош-
ной линией.
Концепция Ф. Шейл и [45] устанавливает воз-
можность криволинейных равновесных состояний цент-
рально сжатого стержня в условиях непрерывно возра-
стающей сжимающей силы N. В начальный момент вы-
пучивания разгрузка не происходит, так как бесконечно
малые растягивающие напряжения изгиба компенсиру-
ются бесконечно малым приращением осевого сжатия.
Закритические состояния криволинейного равновесия
характеризуются разгрузкой со стороны растянутого от
изгиба волокна [31]. Наименьшая сжимающая сила и
соответствующее напряжение, при которых становятся
возможными криволинейные формы равновесия в усло-
виях непрерывного возрастания сжимающей силы, про-
порциональны касательному модулю:
,	I , zt"Ef	Ida \
N	о=—р£	=	-	(17.268)
Модель с одной
степенью свободы
(рис. 17.70) иллюстриру-
ет концепцию Шенли.
При сжимающей силе N
модель сохраняет состо-
яние прямолинейного ра-
вновесия (у=0), при
М+ДМ возможно откло-
ненное равновесное сос-
тояние (у>0). Опорные
стержни 1 и 2, обладаю-
щие упруго-пластически-
ми свойствами, в резуль-
тате перехода модели к
отклоненному равновес-
ному состоянию приоб-
ретают деформации е(
(укорочение) и e2^s0
(удлинение). Стержень
выпучивания.
Рис 17.70
1 испытывает догрузку и работает с касательным моду-
лем Ei, стержень 2 — разгрузку и работает с модулем
Е. Если F— площадь поперечного сечения каждого из
стержней, то условия равновесия имеют вид:
= Р {ZyEt — еа7Г); |
Ny = Fb + е.Ш). J
(17.269)
График поведения центрально сжатого упруго-пласти-
ческого стержня показан на рис. 17.69; в качестве ха-
рактерного перемещения принят прогиб в середине про-
лета ут- Точка К соответствует критическому состоя-
нию но кюрии Эшессера — Кармана, точка Д'' соответ-
ствует кошгеппии Ш'чгш.
Стержень мо/Кег начать отклоняться от прямолиней-
ной формы равновесия при осевом напряжении а0 в ин-
тервале су <а,<сф, естп сжимающая сила возрастает
и прямолинейная форма до этого не была нарушена.
Поэтому участок оси ординат на графике (рис. 17.69)
Используя геометрическое условие
h
— (и + м
£
1
(17.270)
находят
1___АЛК
Е + Et \ th + F Г
1 IZbyEf AN_\
Е + Et \lh ~~~ F [
(17.271)
240
РАЗДЕЛ 17. УСТОЙЧИВОСТЬ СТЕРЖНЕВЫХ СИСТЕМ.
Второе из условий равновесия (17.269) преобразуют
к виду
461/	EN I 1
— D =------ —
lh	" "
где обозначено
F \Et
£
Ё
(17.272)
Линия LKTS на графике определяет критические на-
пряжения стержня, теряющего устойчивость по теории
Энгессера — Кармана при /.<7,*..
На рис. 17.71 показаны также графики поведения
стержня, основанные иа решении задачи в геометриче-
ски линейной постановке. Символом у0 обозначена наи-
D —
(17.273)
при W = 0,
определяют
(17.274)
силе Энгессера — Карма-
Nlh \	1 \
462F	£ )
Потеря устойчивости в эйлеровом смысле,
возможна только в случае Ь = 0, откуда
п р и в е д е п и о-м о д у л ь и у ю критическую силу
4b2F
N^=-~1T ’
lh
соответствующую критической
на (17.267).
Далее определяют сжимающую силу N, при которой
становятся возможными отклоненные формы равнове-
сия, если ДД>0, Найдя у из условия (17.272), приво-
дят второе из уравнений (17.271) к виду
AN Г Et / 1
Е =  ------__—. —. .—
F (Et + Е) [2D Et
(17.275)
Наименьшее значение сжимающей силы N, при кото-
ром то имеет неотрицательную величину, находят, при-
равнивая нулю выражение в прямых скобках Отсюда
находят касательн о-м о д у л ь и у ю критическую
силу
‘ lh
(37.276)
соответствующую критической силе Шенли (17.268).
И с ч е р п а н и е несущей с п о с о б н о с т и при
<т0 —сгт теоретически возможно для стержня из идеаль-
но упруго-пластического материала (рис. 17.66,6) при
малой гибкости ?.<ДТ, где граничная гибкость ?^т =
= л]/д/ож График критических напряжений для тако-
го стержня показан на рис. 17.68 штрихпуиктирной ли-
нией.
Устойчивость центрально сжатого
стержня из л п и е й и о - у п р о ч н я ю щ е г о с я
материала (см. рис. 17.66, а) требует специального
рассмотрения, так как площадка текучести, строго гово-
ря, отсутствует и критическое напряжение может прев-
зойти предел текучести оу. Три характерные точки на
оси абсцисс графика критических напряжений
(рис. 17.71) определяются граничными гибкостями:
(17.277)
большая ордината кривой выпучивания при критическом
напряжении дальнейший рост прогиба у сопровож-
дается возрастанием (при	или убыванием (?„)>
>7*) осевого напряжения а0.
17.8.3. Изгиб и устойчивость
сжато-изогнутых стержней
Сжат о-и з о г и у ты й с т е р ж е и ь в общем слу-
чае представляет собой неидеальиую систему. Исклю-
чением является, например, особый случай стержня, ис-
пытывающего нэп б по S-образной кривой (см. 17,7.3).
Процесс 1[ а 1 р у ж е н и я обусловлен возрастани-
ем сжимающей силы N. Предполагается, что упруго-
пластическая деформация является активной в каж-
дой точке стержня, т. е. что нормальное напряжение а
нигде не убывает. При этих условиях разгрузка не про-
исходит и упруго-пластический материал ведет себя
как нелинейно упругий [Иа, 33, 49, 51].
Потеря устойчивости при достижении пре-
дельной нагрузки определяется теми же условиями, что
и дчя стержней из нелинейно упруюю материала, Со-
храняют силу критерии устойчивости, изложенные
в 17,7.3 и 17.7.6.
М е т о д ы исследования изгиба и у с т о п-
ч ив ости рассмотрены в 17.7.3 и 17.7.4. Для прибли-
женного определения критической силы может быть ис-
пользован метод коллокации (см, 17.7.5).
В случае непрерывно возрастающей нагрузки крити-
ческие напряжения стержня соответствуют линии
QPTS; разветвление форм равновесия по Шенли про-
исходит при критическом напряжении
(17.278)
17.8.4. Сжато-изогнутые стержни
из идеального упруго-пластического
материала
В интерваде гибкостей	критическое на-
пряжение постоянно и равно а,= от.
И д е а л ь н ы й упруг о-п л а с т и ч с с к и п м а т е-
риал (см. рис. 17.66,6) обладает свойством ireoipaHH-
ченпон текучести при е>ет. ст = о’т. Это свойство, с од-
ной стороны, определяет возможность исчерпания несу-
щей способности сечения вследствие образования
17 S УПРУГО-ПЛАСТИЧЕСКИЕ СЖАТЫЕ И СЖАТО-ИЗОГНУТЫЕ СТЕРЖНИ
241
пластического ш а р н и р а, с другой стороны,
упрощает аналитическое решение задачи. Эти два об-
стоятельства обусловливают целесообразность специаль-
ного рассмотрения изгиба и устойчивости сжато-изогну-
тых стержней из идеального упруго-пластического ма-
териала [21а, 51].
Сохраняет свою силу допущение об активности де-
формации, принятое в 17.8,3,
Три стадии работы сечения произвольной
формы определяются эпюрой напряжений- упругая ста-
дия (рис. 17.75, а), стадии односторонней (рис, 17.75, б, в)
и двусторонней текучести (рис. 17.75, г),
Сечение по высоте разбивается на зоны текуче-
сти (о = ат) и упругое ядро (а<ют).
Исчерпание несущей способности сечения. Развиваю-
щиеся в сечении усилия — сжимающая сила N и изги-
бающий момент М достигают предельной величины,
когда в сечении образуется пластический шарнир
(рис. 17.72). Напряжение в каждой точке сечения рав-
но (по абсолютной величине) пределу текучести от; при
дальнейшем росте усилия N и М уже не могут быть
восприняты сечением.
Конечное соотношение между усилиями N
и М определяется условием: если г>0— осевое напряже-
ние, то сжимающее напряжение от изгиба равно
(<тт—о0), растягивающее — (оуй-ор). Положение нуле-
вой точки на эпюре напряжений от изгиба определяют из
условия равенства нулю главною вектора этой эпюры.
Отсюда получают конечное соотношение между усилия-
ми N и 44 s предельном состоянии
Ф(М, N) = 1.	(17.27 >
Для прямоугольного сечения (h — высота, b— шири-
на) это уравнение имеет вид [35]
444
4й2ат
(17.280)
соответствующая кривая взаимодействия по-
казана на рис. 17.73.
Исчерпание несущей способности стержня возможно
в том случае, когда стержень статически определим и
пластический шарнир образуется раньше, чем стержень
потеряет устойчивость при достижении предельной на-
грузки, например, шарнирно опертый стержень, сжатый
продольной силон N и нагруженный опорным моментом
Мо значительной величины (рис. 17.74). Предельную на-
грузку находят из условия (17.279); опа не зависит от
длины стержня.
16-26
Дифференциальное у р а в н еи ие
стержня из идеального уируго-птастического
имеет вид
d-y _ _ Дт
dx'2 Ес
и з г и б а
материала
(17.281)
где х, у — координаты точки па изогнутой оси; с — рас-
стояние от нулевой точки эпюры напряжений до бли-
жайшего волокна, в котором напряжение равяо пределу
текучести от.
Процедура наложения сечения на график
работы материала сводится к построению эпюры напря-
жений по заданным усилиям Л' л 41. Приняты следую-
щие обозначения, при односторонней (рис 17.76, а) и
двусторонней (рис. 17.76,6) текучести
Д, (из)— расстояние от шныра тяжести сечения до
крайнего вогнутого (выпуклого) волокна;
и— текущая координата по высоте сечения,
отсчитываемая от шштра тяжести (направ-
ление к зоне птастическою сжатия сшпа-
стся положительным);
Ь (v)—ширина сечения в точке с координатой о;
и—координата ближайшего к центру тяжести
волокна в зоне пластического сжатия;
u=u — 2с — координата ближайшего к центру тяжести
волокна в зоне пластического растягксния.
Расстояния Д| и с'з считаются положительными; коор-
динаты и и и подчинены правилу знаков, установленно-
му ДЛЯ V.
Задача определения параметров с и «, соответствую-
щих известным усилиям М п Л', решается методом на-
правленного поиска. В процессе решения приходится
многократно вычислять усилия М и N по заданным зна-
чениям с и и.
242
РАЗДЕЛ 17, УСТОЙЧИВОСТЬ СТЕРЖНЕВЫХ СИСТЕМ
Алгоритм определения М и А основан на
вычислении функций
?	г
f (г) = | b (v} d.v, s (г) = — \ b (о) vdw,
At>,	—о,
1 (z)-- j b(v}v"dv,	(17.282)
представляющих собой статические характеристики ча-
сти сечения, лежащей ниже волокна с координатой г:
I — площадь; s — статический момент (по абсолютной
величине); I—момент инерции.
Качественный критерий устойчивое т и,
рассмотренный в 17.7 7 применительно к нелинейно уп-
ругим стержням, сохраняет свою силу также и для уп-
руго-пластических стержней при условии отсутствия раз-
грузки. Для идеального упруго-пластического материала
<ь=0 в зонах текучести и ы=1 в упругом ядре сече-
ния. Поэтому момент инерции заменяющего стержня
равен моменту инерции упругого ядра /я относи-
тельно центра тяжести этого ядра (рис. 17.77) [Па].
Прямоугольное сечение. Если It — высота, b — ширина
сечения, то относительная высота сжатой зоны упруго-
го ядра в случае односторонней текучести равна [21а]
главный вектор эпюры нормальных
9
8 (от — о0)3
Д А,
(17.285)
В случае двусторонней текучести
1 тайный момент и
напряжений равны:
Замкнутое аналитическое решение за-
дачи об изгибе и устойчивости сжато-изогнутого стерж-
ня прямоугольного сечения для некоторых простейших
нагрузок получил К. Ежек [51], Эта же задача для ма-
териала с линейным упрочнением рассмотрена в [33].
Л1 = у- Ет [гд (г) ф- i (г)];
A — а± уг .у. s ,
с
Статические характеристики упругого ядра
ют по формулам:
(17.283)
вычисли-
/я - St! (г) - [Sts (z)]3/fa,	= St/ (z). (17.284)
Каждая из сумм в соотношениях (17,283) и (17.284)
содержит по два слагаемых; в первом слагаемом при-
нимают т = -Н. z — v, а во втором т =— 1, z = u.
Критерий потери устойчивости при до-
стижении предельной нагрузки имеет вид условия экст-
ремума (17,243) или (17.244).
йлругое ядро, и-1
Изменение жесткости упругого ядра.
17.8.5	. Приближенное исследование
устойчивости внецентренно сжатого стержня
прямоугольного сечения из идеального
упруго-пластического материала
Внецентренно сжатый стержень прямо-
угольного сечения сжат силой Л' с эксцентрицитетами
на концах а и /га(’|Й| е£1). Изогнутую ось стержня в кри-
т пческом состоянии аппроксимируют дугой синусоиды
(рис. 17.78)
y=.ymsin—,	(17.287)
’’я \ПР> ГО П.ПСТИЧЬСКШ. С/К ОГЫГ И ОК.ТТО’ПОГНУТЫ! СП Р i 114
___________243
Рис 17 79
Рис 17 82
Рчс 17 81
Рис 17 84
16!
244
РАЗДЕЛ 17 УСТОЙЧИВОСТЬ СТЕРЖНЕВЫХ СИСТЕМ
где ут — наибольшая ордината, L — длина полуволны
синусоиды. Абсциссу х отсчитывают от начала коорди-
нат, расположенного на расстоянии х0 левее левой
опоры.
Принимая, длину стержня равной l = uL/n, где и —
число, подлежащее определению, из сопоставления за-
висимостей (17 281) и (17.287) находят [40]
от
(17.288)
Относительная гибкость стержня ?. равна отношению
его гибкости R к граничной гибкости материала 1т =
= л1/ГЕ/ст; для стержня с прямоугольным сечением:
I
л/i
(17.289)
Равновесные состояния стержня. Обозначая ф =
= <7o/o't==.V/Wi<tt> z = 6y,n//i и используя зависимости
(17.276), (17 277) для стадии односторонней и соответ-
ственно двусторонней текучести, находят
4я2 (1 — ф) \	1 — ср )
(17.290)
Величины «из связаны геометрическим условием.
Так как
лхп	sm и	1 х—————'— ------
sin—- =------; /(и) = У 1 Ж k- — 2 k cos и , (17,291)
L	f (u)
то, принимая обозначение для относительного эксцентри-
цитета m = &a!h, находят
г—mf (u)/sin и.
(17.292)
Критические состояния стержня в об-
щем случае 4=4— 1 определяют из условия экстремума
[24г]
---= 0,	(17 293)
dz
а в особом случае 4 =—1—из условий и — п, z=m.
При k — — 1 стержень теряет устойчивость в упругои
области, если 4=1/ V" rp> I 1-у-т.
График критических напряжений для
стержней из стали марки Ст. 3 представлен на рис. 17.79.
Три кривые на графике для одного и того же значения
относительного эксцентрицитета т соответствуют слу-
чаям k —— 1, 4=0 и 4=1.
Сравнение результатов с данными более точного ре-
шения на ЭВМ показывает, что погрешность прибли-
женных значений ф положительна при 4=1 и отрица-
тельна при k =— 1.
17.8.6	. Влияние формы поперечного сечения
на устойчивость внецентренно сжатых
стержней из идеального
укруго-пластического материала
Метод коллокации. Для оценки влияния формы про-
филя на критические напряжения внецентренно сжатого
шарнирно опертого стержня с равными концевыми экс-
центрицитетами удобно использовать приближенное ана-
литическое решение, основанное на методе коллокации
(см. 17 7.5).
Испозьзуя соотношение (17.281) для сечения в сере-
дине пролета., находят [51]
р = — Сут.	(17.294)
Исследуя напряженное состояние этого сечения, по
лучают аналитическую зависимость, связывающую пере-
менные с и i/m или непосредственно или же с помощью
всиомо! ательпого параметра. Критерием потери устой-
чивости служит уравнение
d
~~Г~(сут)^ 0.	(17.295)
dym
В результате определяют аналитическую зависимость
1= Т(т, oj,	(17.296)
связывающую гибкость стержня X с относительным экс-
центрицитетом m = aF/W и критическим напряжением
о* (F— площадь сечения, W—момент сопротивления
сжатого от изгиба волокна).
Выражение для функции 'F содержит также парамет-
ры материала £, от и параметры формы профиля.
Графики к р и т и ч е с к и х и а п р я ж е н и й по-
строены для стержней из стали марки Ст. 3 с пределом
текучести от = 2400 кГ/смг и модулем упругости Е —
= 2,1-10G кГ/с.и2 [246]. Кривые зависимости критиче-
ского напряжения сщ от гибкости 4 соответствуют отно-
сительным эксцентрицитетам
аР
т = -- = 0,2; 0,6; 1,2; 2,4 и 4,8.
Симметричный двутавровый профиль (рис. 17,80).
Площадь каждой из полок Га, площадь стенки FCT =
= aFn, где а — параметр формы.
Симметричный двутавровый профиль, изгиб в плоско-
сти, параллельной полкам (рис. 17.81). Параметр а име-
ет тот же смысл, что и в предыдущем случае. Результа-
ты применимы также и для крестового профиля.
Тавровый профиль, изгиб в сторону стенки (рис. 17.82)
й в сторону полки (рис. 17.83). В последнем случае па-
раметр формы a=FrT/Fn весьма существенно влияет
на величину критических напряжений.
Сплошное круглое и тонкостенное кольцевое сечения
(рис, 17.84),
17.9.	ПОДБОР СЕЧЕНИИ СЖАТЫХ
И СЖАТО-ИЗОГНУТЫХ СТЕРЖНЕЙ
17.9.1.	Основные положения подбора
сечений сжатых и сжато-изогнутых стержней
Здесь рассматривается только расчет по первому пре-
дельному7 состоянию — по несущей способно-
сти. Основное расчетное неравенство имеет вид
N < АЩед,	(17.297)
где N—сжимающая сила в стержне от расчетного со-
четания нагрузок; А/пред — предельное значение сжи-
мающей силы, пропорциональное расчетному сопротив-
лению R материала.
Подбор сечений основан на сравнении нескольких ва-
риантов. Задаются подходящим сечением, удовлетворя-
ющим конструктивным требованиям (материал, габари-
17 9 ПОДБОР СЕЧЕНИЙ СЖАТЫХ И СЖАТО-ИЗОГНУТЫХ СТЕРЖНЕЙ
245
ты сечения, сортамент и пр.), и вычисляют его несу-
щую способность, т. е. предельную нагрузку 1Уаред при
заданных условиях работы. Из нескольких сечений,
удовлетворяющих расчетному неравенству (17.297),
выбирают наиболее экономичное (по затрате материа-
ла, трудоемкости изготовления и т. п) [об, 32, 38].
Величина предельной нагрузки зависит от вы-
бора критерия, характеризующего предельное состоя-
ние конструкции, т. е. от принятой методики расчета.
При проектировании строительных конструкций, за
редкими исключениями, применяют нормативную мето-
дику расчета сжатых и сжато-изогнутых стержней,
предписываемую соответствующими главами СНиП.
В технической литературе рассматриваются также
и другие возможные методы расчета ежато-изогпутых
стержней, в том числе расчет по деформированной схе-
ме (см. 17.9.3) и расчет, основанный на анализе крити-
ческого состояния стержня в упруго-пластической ста-
дии работы материала (см. 17.9.5).
Ниже рассмотрены принципиальные основы подбора
сечений сжатых и сжато-изогнутых стержней в предпо-
ложении, что плоская форма изгиба сохраняется как
в равновесных, так и в критических состояниях. При-
меры расчета даны для стальных стержней
(СНиП П-В.З-бЗП Стальные конструкции. Нормы про-
ектирования) .
Более полные практические указания по подбору се-
чений и необходимые для этого таблицы следует искать
в главах СНиП, нормирующих проектирование сталь-
ных, алюминиевых, деревянных, железобетонных, бетон-
ных и каменных конструкций, а также в других томах
Справочника, посвященных этим конструкциям.
Расчет тонкостенных стержней см. 17.10.
17.9.2.	Расчет центрально сжатых стальных
стержней по нормативной методике
Центрально сжатый стержень относится к идеальным
системам, при расчете которых учет начальных несо-
вершенств обязателен (см. 17.1.13).
Основное расчетное неравенство имеет вид
N^tfFR,	(17.298)
где F— площадь поперечного сечения стержня; ср —
= о*/от— коэффициент снижения расчетного сопротив-
ления при центральном сжатии, равный отношению кри-
тического напряжения а, к пределу текучести материа-
ла от; R—-расчетное сопротивление материала.
Коэффициент ср является функцией гибкости
стержня
^-=1.
(17.299)
где /» = р1—-свободная (расчетная при проверке устой-
чивости) длина стержня; I—геометрическая длина
стержня; (3— коэффициент свободной длины (см. 17.1.14,
17.4.1); г — радиус инерции поперечного сечения; /—
момент инерции поперечного сечения стержня.
Для стальных стержней критическое напряжение о»
соответствует потере устойчивости при достижении
предельной нагрузки внецентренно сжатого стержня
той же гибкости Л с относительным начальным (слу-
чайным) эксцентрицитетом
F
т0 = Нд-.	(17.300)
где Ог> — плечо силы N, IV— момент сопротивления по-
перечного сечения стержня.
Вычисление о, основано па предсгавтсиии об идеаль-
ном упруго-пластическом материатс (см рис 17 66,6)
и прямоугольной форме поперечного сечения стержня.
Рис. 17.85
График зависимости т0 и <р от гибкости 1 для стали
марки Ст.З представлен на рис. 17.85.
Табл. 17.14 содержит нормативные значения коэффи-
циента ср для сталей разных марок.
Пример 17.6. Сжатый по-
яс фермы образован из двух
равнобоких уголков 125X14
по ГОСТ 8509—57 (рис.
17.86). -Материал — Ст. 3,
расчетное сопротивление
/? = 2100 кГ/см2. Свободные
длины стержня 1хХ — 3 м,
1*у = ё м. По сор1аменту
площадь поперечного сече-
ния Г = 2-33,4 = 66,8 сл2; ра-
диусы инерции гх = 3,80 <ж,
гу = 5,60 см. Гибкости стер-
Рис. 17.86
жпя равны:
300
Л,- =-------= 79; Д, =
'	3,80	v
600
-----=107.
5,60
По табл. 17.14 для Ст.З и гибкости 1=107 находят
ф = 0,544, следовательно, предельная нагрузка стержня
равна:
Д/пред = еррр = 0,541-66,8-2,1 = 76 т.
17.9.3.	Расчет сжато-изогнутых стальных
стержней по деформированной схеме
Рассматривается стержневая система со сжатоизог-
нутыми элементами. Предполагается линейно упру-
гая работа материала вплоть до достижения наиболь-
шим фибровым напряжением предела текучести [16, 19]
Длакс“°т-	(17.301)
Определение напряжений производится на основе
246
РАЗДЕЛ 17. УСТОЙЧИВОСТЬ СТЕРЖНЕВЫХ СНГ ГЕМ
Т •! бли li а 17 14
Коэффициенты ф продольного изгиба центрально сжатых
элементов
	Зн<1Ч1ния ф для элементов из стали марок		
Гибкость X	Ст. 3	„	„ Ст, 4	С г. г»	11Г2. 10Г CI 1 эХСНД	10ХСНД
0	1,00	И 00	1,00	1,00
10	0,99	0,98	0,98	0,98
70	0,97	0,96	0,95	0,95
•в0	0,95	0,93	0,92	0,92
40	0,92	0,89	0,89	0,88
50	0,89	0,85	0,84	0,82
00	0,86	0,80	0,78	0,77
70	0,81	0,7 4	0,71	0,68
80	0,75	0,67	0.63	0,59
90	0,59	0,56	0,54	0,50
100	9,60	0,30	0, 1b	0,41
ио	0,52	0,41	0 , VO	0,36
но	0, 15	0,37	0,33	0, И
130	0,40	0,32	0,29	0,27
141)	0,36	0,28	0,25	0,23
150	0,32	0,25	0,23	0,20
160	0,29	0,23	0,21	0,18
170	0,26	0,21	0,19	0,16
180	0,23	0, И)	0,17	0,14
ISO	0,21	0,’.7	0,15	0,12
200	0,19	0,15	0, 13	0,11
210	0,17	0,11	0,12	0,10
220	0,16	0, 13	0,11	0,09
Гибкость стержня в силовой плоскости 7 =
= 1420/22,8 = 62.
Относительный эксцентрицитет
аР	19,3-150
т -----=-------------=. j _
Г 2890
а)
S)	в)
По данным табл. 17 5 находят изгибающий момент
в середине пролета
расчета по деформированной схеме с учетом влияния
продольных сжимающих сил (см. 17.2, 17.3).
Основное расчетное неравенство для одного из сжа-
то-изогнутых стержней системы можно представить
в виде
.V фвнР7?,	(17.302)
где (pB1‘ = Ouu/o'r — коэффициент снижения расчетного
сопротивления при внецентреииом сжатия; ооп — осе-
вое напряжение в стержне, соответствующее наступле-
нию фибровой текучести в наиболее напряженной точ-
ке системы.
Прн расчете идеальных систем по деформированной
схеме неустойчивоеть равновесного состояния не может
быть обнаружена. Например, сжато-изогнутый стер-
жень, нагруженный антисимметричной относительно се-
редины пролета нагрузкой, изгибается по S-образной
кривой (см. рис. 17.6,6). Равновесное состояние стерж-
ня, соответствующее точке Л) на графике поведения
(см. рис. 17.7), неустойчиво, так как N>N«, но можно
допу сыпь, что напряжения ни в одной точке не пре-
вышают предела пропорциональности. Учет даже само-
го малого по величине несовершенства нарушает иде-
альную антисимметричную форму изгиба и приводит
к точке Л2 (см. рис. 17.7), для которой У’<У,.
Поэтому при расчете по деформированной схеме
идеальных систем учет начальных несовершенств обя-
зателен.
Пример 17.7. Шарнирно опертый стержень длиной
/—14.2 м сжат продольной силой Л’, приложенной
е равными концевыми эксцентрицитетами «=19,3 см.
Сечение стержня показано на рис, 17.87, а. Материал —
cia.ii> марки Ст 3
Основные геометрические характеристики сечения:
площадь F—150 с.и2, момент инерции / = 78 000 см\
момент сопротивления 1^ = 2890 см3, радиус инерции
г ==22,8 см.
Приравняв напряжение в среднем сечении пределу
текучести
N . Л1 и" Е / т у
u = -у т TF ~~№~~ I1+ I= °т’
I COS------I
\	2 /
при модуле упругости Е = 2,1-Юв кГ/см3, от =
= 2400 кГ/см2 находят после нескольких попыток и =
= 1,383, следовательно.
и-П	,	1043
ооп =	= 1043 кГ/см"- фв-ч =	- = 0,435.
А“	J4vU
Эпюра напряжений в среднем сечении стержня в мо-
мент достижения фибровой текучести представтена на
рис. 17.87, б.
Предельная нагрузка стержня при 7? = 21ОО кГ^см?
равна:
Лшгед = 0,435-150-2,1 = 137 т.
17.9.4.	Расчет сжато-изогнутых стальных
стержней по нормативной методике
Нормативная методика расчета сжато-изогнутого
стержня, входящего в состав стержневой системы, ос-
нована на приведении его к эталонному шарнир-
но опертому виецептрепно сжатому стержню прямо-
угольного сечения.
Расчет распадается на следующие этапы:
а)	Расчет стержневон системы классическими мето-
дами (без учета продольных сил) и определение рас-
четных усилий для ещржпя Л’ и hi.
Расчетный изгибающий момент М определяют в со-
ответствии с указаниями СНиП в зависимости от очер-
17 9 ПОДБОР СЕЧЕНИИ СЖАТЫХ И СЖАТО-ИЗОГНУТЫХ СТЕРЖНЕЙ
247
Таблица 17 15
Коэффициенты Т] влияния формы сечения тля вычисления приведенного эксцентрицитета т
тания эпюрч изгибающих моментов па длине стержня,
В частном случае внецентренно сжатого стержня с рав-
ными концевыми эксцентрицитетами а расчетный мо-
мент равен Л1 = Л'а.
б)	Определение свободной длины для каждого из
сжато-изэтн;, тых стержней системы с помощью мето-
дов, описанных в 17.4. Гибкость стержня л находят по
формуле (17 299),
в)	Определение приведенного эксцентрицитета
«1=4^7 ,	(17.303)
где р — коэффициент влияния формы сечения (значе-
ния р для стальных стержней даны в табл. 17.15),
г)	Определение коэффициента снижения расчетного
сопротивления при впецентренном сжатии фвн = о'1/ат,
зависящего от гибкости стержня }. и приведенного экс-
центрицитета ОТ|.
Для стержней сплошного сечения из стали марки
Ст.З эта зависимость дана в табл. 17.16. Положенное
в основу таблицы критическое напряжение а„ соответ-
ствует потере устойчивости при достижении предель-
ной нагрузки эталонного стержня, т. е. внецентренно
сжатого стержня той же гибкости 7. с относительным
эксцентрицитетом т<. Сечение стержня принято прямо-
угольным, материал — идеальным упруго-пластическим.
Для сквозных (решетчатых) стальных стержней ко-
эффициент qC’1 определяют по другой таблице, осно-
ванной па критерии фибровой текучести (17.301).
В этом случае коэффициент tp“a зависит от приведен-
ной гибкости стержня (см. 17.5.1).
д)	Оценка несущей способности сечения по Форму-
ле (17.302).
Оценка погрешности нормативной методики
для сжато-изогнутых стержней, входящих в состав
сложной системы (рамы), затруднительна.
Для шарнирно опертых внецентренно сжатых сталь-
ных стержней с симметричным относительно нейтраль-
ной оси профилем погрешность нормативной методики
невелика. Эта погрешность становится более значитель-
ной для стержней с несимметричным сечением.
Пример 17.8. Стержень, рассмотренный в примере 17.7
(рис. 17.87, а). Гибкость стержня 7=62. По табл 17.15
находят для двутаврового профиля коэффициент влия-
ния формы поперечного сечения
г] = 1,45 -—0,0037= 1,264.
Приведенный эксцентрицитет
= v,m = 1,264-1 = 1,264.
По 7 = 62 и <711=1,264 с помощью табл, 17.16 полу-
чают <рви = 0,487.
Предельная нагрузка стержня
Л?пред = 0,487-150-2,1 = 153 га.
17.9.5.	Расчет сжато-изогнутых стальных
стержней по критическому напряжению
Несущая способность сжато-изогнутого
стержня в подавляющем большинстве случаев ограни-
чена потерей устойчивости при достижении предельной
нагрузки в стадии нелинейно упругой или упруго-плас-
тической работы материала.
Методы определения критической нагрузки для изо-
лированных стержней рассмотрены в 17.7 и 17.8, для
стержневых систем — в 17.11.
Решение задачи л ребус г значительного объема вы-
числений, поэтому практическая реализация расчета
предполагает применение ЭВМ.
Пример 17.9. Стержень,_ рассмотренный в примерах
17.7 и 17.8 (рис. 17 87, а). Расчет выполнен с помощью
248
РАЗДЕЛ 17 УСТОЙЧИВОСТЬ СТЕРЖНЕВЫХ СИСТЕМ
Таблица 17 16
Коэффициенты ФВН для сплоишостенчатых стержней из стали марки С.т.З
Гиб- кость ?.	Значения 1000 ср ви при приведенном эксцентрицитете mt																									
	0,1	0,25	0,50	0,75	1 ,о| 1,25		1,50 j 1,75		2,0	| 2,5	3,0	3,5	) 4,(>| 4,5		5, Г	5,р| 6,0		6,5)7,0 |з,0 |э,0 | 10,0 | 12,0 j 1 1,0 | 17,0 | 21',0								
10	957	920	847	781	721	667	618	574	535	468	414	370	333	303	285	256	235	220	205	182	162	147	123	106	(18.9	075 i
20	959	887	800	729	673	623	577	536	601	139	390	349	315	288	263	243	225	210	196	174	157	141	120	102	085	072
30	942	868	773	699	641	592	550		178	420	373	335	303	277	254	234	218	203	!91	[169	152	138	117	100	084	071
40	920	846	743	668	608	560	520	484	453	399	355	320	290	265	243	226	210	196	184	164	148	135	514	098	083	070 ।
50	890	820	711	634	574	528	490	456	427	377	338	304	277	253	234	216	201	189	177	159	143	130	111	096	081	069
60	860	78Я	674	598	540	495	459	428	402	355	319	289	263	241	224	207	193	182	171	153	138	126	107	094	079	068
70	810	749	634	560	505	463	429	401	377	334	301	273	249	230	213	198	185	174	164	147	134	122	504	091	077	066
80	750	701	591	521	471	432	400	371	353	314	283	258	236	218	203	189	177	167	157	142	129	118	101	089	075	065
90	690	648	546	483	436	401	372	348	329	294	266	243	224	207	192	180	169	160	151	136	124	Ш	098	087	073	063
100	600	590	500	444	403	371	345	324	305	275	250	229	251	197	183	172	161	153	144	13!	120	550	095	084	071	052
по	520	520	456	407	371	342	320	301	284	257	234	216	200	186	173	163	154	146	138	126	115	106	092	081	069	060
120	450	450	413	372	341	316	296	279	264	239	221	203	189	176	165	155	147	138	132	120	ИО	102	089	079	067	059
130	400	400	374	339	312	291	273	258	245	224	206	191	178	166	156	М7	Ю9	132	126	115	106	098	086	076	065	057
ИО	360	360	338	309	287	268	253	240	228	209	193	180	168	158	149	140	133	126	121	110	102	095	084	074	063	055
150	320	320	306	282	263	248	234	222	212	195	182	169	1,58	149	141	033	126	120	115	106	099	091	080	071	062	054
160	290	290	277	257	241	128	216	206	197	182	170	159	149	141	134	127	гю	Ц5	110	101	094	087	077	069	030	053 j
170	260	260	252	237	222	211	200	192	184	170	159	150	144	134	127	120	114	ПО	105	097	090	084	074	067	059	052
180	230	230	229	216	204	194	185	178	171	159	149	141	133	126	120	114	109	104	ЮО	093	086	080	072	065	057	051
190	210	210	210	199	188	180	172	166	160	149	141	133	126	120	114	109	104	099	096	090	083	078	070	063	055	049
200	190	190	190	132	174	167	160	154	149	140	132	125	119	Ш	107	ЮЗ	099	095	092	086	079	075	067	061	053	048 |
метода коллокации (см. 17.7.5 и 17.8.6) в предположе-
нии, что материал стержня идеальный упруго-пласти-
ческий с пределом текучести От=2400 дГ/с.и2. Толщи-
на полок двутавра принята пренебрежимо малой по
сравнению с высотой профиля.
Эпюра напряжений в среднем сечении стержня в мо-
мент потери устойчивости при достижении предельной
нагрузки представлена на рис. 17.87, а. Сечение испы-
тывает одностороннюю текучесть. Критическое напря-
жение о =1080 кГ)см2, следовательно, <рви = о /от =
= 0,450.
Предельная нагрузка стержня
А'пред = 0,45-15-2,1 = 142 т.
17.9.6.	Сопоставление результатов расчета
внецентренно сжатого стержня
по трем различным методикам
Сравнение результатов расчета внецентренно сжато-
го стального стержня в примерах 17.7, 17.8 и 17.9 дано
на схематическом графике поведения (рис. 17.88).
Масштаб выдержан только в направлении оси ор-
динат.
Расчет по критическим напряжениям дает наиболее
точный результат. Расчет по деформированной схеме
приводит к некоторой недооценке несущей способности
стержня. Для двутаврового профиля разница в вели-
чине предельных нагрузок, найденных по этим двум
17 10. ЛИНЕЙНО УПРУГИЕ ТОНКОСТЕННЫЕ СЖАТЫЕ И СЖАТО-ИЗОГНУТЫЕ СТЕРЖНИ
249
методикам, невелика; в рассмотренном случае она со-
ставила всего 3,5%- Для прямоугольного сечения эта
разница будет более значительна.
Нормативная методика в данном случае привела
к преувеличению несущей способности стержня на 7,8%
по сравнению с предельной нагрузкой, вычисленной на
основе анализа устойчивости стержня. Этот частный
результат не может быть распространен на другие слу-
чаи, для которых погрешность, связанная с примене-
нием нормативной методики, может отличаться от най-
денной выше не только по абсолютной величине, но
и по знаку.
17.10.	ЛИНЕЙНО УПРУГИЕ
ТОНКОСТЕННЫЕ СЖАТЫЕ
И СЖАТО-ИЗОГНУТЫЕ СТЕРЖНИ
17.10.1.	Дифференциальные уравнений1
равновесия тонкостенных стержней
Основные положения теории линейно упругих тон-
костенных стержней см. раздел 5.
Рассматриваются сжатые и сжато-изогну-
тые стержни с открытым тонкостенным
поперечным сечением, постоянным по длине
пролета.
Стержень длиной I сжат продольной силой N и не-
которой вызывающей изгиб и кручение нагрузкой, ко-
торая возрастает пропорционально увеличению силы N
(рис. 17,89) Дифференциальные уравнения равновесия
тонкостенных линейно упругих стержней были впервые
получены В. 3, Власовым [7]:
Ely g” Д- -ж (Мх ф ау N) <р> = Му,
Е1Х + АВ] 4" (А7?/— j Аг) ц> -=— Л1_г;
(Жг + N) l + ах N) i)+£/ffl <₽" +
4- (г2 N + 2<3Х~Му - 2<3;/ Мх - G/д) <р = 0.
Здесь Е, G — модуль упругости и модуль сдвига;
1-., 1У — моменты инерции сечения относительно глав-
(17.304)
пых осей; /л — момент инерции сечения при кручении;
/ш —бимомент инерции сечения (векториальный мо-
мент); F — площадь поперечного сечения; т]—ли-
нейные перемещения точки па оси стержня с абсцис-
сой г; х, у — координаты точки сечения; ф — угол за-
кручивания сечения с абсциссой г; Мх, Mv — изгибаю-
щие моменты от поперечной нагрузки, вычисленные без
учета влияния продольной сжимающей силы; ах, Qy —
координаты центра изгиба.
Геометрические характеристики г, и |3S вычисляют
по формулам:
2	2,2,2	2 О + О .
г = г0 ~рах +ау, ги -=---—- ,
J х (Г- + у") dF — ах;
У О2 + dF ~ аУ
• (17.305)
Уравнения (17.304) должны быть дополнены шестью
граничными условиями, отражающими опорные закреп-
ления концов стержня.
Система трех линейных дифференциальных уравнений
второго порядка (17.304) интегрируется в замкнутой
250
РАЗДЕЛ 17. УСТОЙЧИВОСТЬ СТЕРЖНЕВЫХ СИСТЕМ
форме для некоторых простейших случаев нагрузки и
простейших поперечных сечений. В общем случае эти
уравнения решают численно.
Приближенное решение уравнений (17.304) основано
на аппроксимации кривых изгиба и кручения известны-
ми функциями, удовлетворяющими условиям закрепле-
ния концов стержня. Затем требуют, чтобы дифферен-
циальные соотношения (17.304) удовлетворялись в от-
дельных сечениях на длине стержня (метод колло-
кации). Другая возможность заключается в использо-
вании процедуры Бубнова — Галеркниа.
Уравнения (17.304) являются приближенными; обзор
более точных постановок задачи см. [1].
17.10.2.	Изгиб и кручение тонкостенных
сжато-изогнутых стержней
Если сжато-изогнутый стержсшь находится в состоя-
нии устойчивого равновесия, то система уравнений
(17 304) имеет строго определенное и конечное по ве-
Рис. 17.90
личине решение. Здесь исключается случай однородных
уравнений с однородными граничными условиями, рас-
смотренный в 17.10.5.
Схематический график поведения стержня представ-
лен на рис, 17.90. По оси абсцисс отложено характерное
перемещение (например, прогиб рГ1 в середине пролета
стержня), по оси ординат — сжимающая сила N.
Кривая ОАС на графике показывает асимптотическое
поведение стержня — характерное перемещение неогра-
ниченно возрастает по мере приближения N к значе-
нию Дас.
Это асимптотическое значение Nао, зависящее от ви-
да поперечной нагрузки на стержень, приближенно оп-
ределяют следующим образом. Уравнения (17.304) варь-
ируют, заменяя | через g+<5S, г] — через р-ф-йр, ср — че-
рез <р+б<.р. Из полученных уравнений вычитают исход-
ные уравнения (17.304) и для шарнирно опертого
стержня полагают:
6с = A sin —— , I
1 |
6p=Bsin-y-,	(17.306)
„	лг
Оф = С sin .
Варьированные уравнения при г = //2 дают систему
линейных однородных уравнении относительно постоян-
ных Л, В, С:
да Е1и\	,
У-----\ ЛД (мл.т ш. йу N) С = 0;
л;2 £7 Д .
У - —	\ В+ (мут — а. Л') С - 0;
+ Оу А) А Д {М!/т — ах Л') Е Д
Д (в2 N Д 21Д Му.п — 2ру Мхт —-
(17.307)
_3десь Млт, AI,,m— значения изгибающих моментов
М-с и соответственно 7Д в середине пролета при г-=112-
Условие существования нетривиальных (ненулевых)
решений системы уравнений (17.307) заключается в ра-
венстве нулю определителя D(N) этой системы Асимп-
тотическая нагрузка N sx представляет собой наимень-
ший корень уравнения
Д(Д) = 0.	(17.308)
17.10.3.	Расчет тонкостенных сжато-изогнутых
стержней по деформированной схеме
В качестве характеристики предельного с о с т о -
я н и я принимают достижение фибровой текучес-
ти в наиболее напряженном сечении стержня — точка
В на графике поведения (с.м. рис. 17.90)
N	Л-11.	М1Г	В
ш==От= (17.309)
F !х	1Ц	1«>
Здесь ЛД, Му — изгибающие моменты, вычисленные
с учетом влияния продольной силы /V; В—бимомент;
х, у — координаты рассматриваемого крайнего волокна;
со — секториальная площадь; от — предел текучести
(или предел пропорциональности при более точной по-
становке задачи).
Соответствующая состоянию фибровой текучести
продольная сжимающая сила Й/Он условно считается
предельной нагрузкой, ограничивающей несущую
способность стержня.
Другое возможное предельное состояние стержня свя-
зано с достижением предельного по величине перемеще-
ния т|ПрРд (или бчред, фпред) —точка А иа графике по-
ведения (см. рис. 17.90).
Поведение стержня при развитии упруго-плас -
т и ч е с к и х д е ф о р м а ц и й иллюстрируется участком
кривой BDE на рис, 17.90. Экстремальная точка D ха-
рактеризует потерю устойчивости при до-
с т и ж е и ии пред е л ь п о й н а г р у з к и. Соответ-
ствующая критическая сила Nx лишь немного превы-
шает величину Noa,
17.10.4.	Изгиб, кручение и устэйчизость
тонкостенных внецентренно сжатых стержней
В нецентр е и и о сжатый стержень в общем
случае двухосного эксцентрицитета е», еу при
Мх=— Ney-, My — Nex	(17.310)
17 11. НЕЛИНЕПНО УПРУГИЕ СТЕРЖНЕВЫЕ СИСТЕМЫ
251
с самого начала нагружения испытывает кручение и из-
гиб в плоскости каждой из двух ктавпых осей инерции
поперечного гечення Поведение стержня качественно
не отличается от рассмотренного выше поведения сжа-
то-изогнутою стержня.
В двух частных случаях внецентренно сжатого стер-
жня возможна потеря устойчивости в эйле-
ров о м с м ы с л е.
А. Сжимающая сила приложена а центрах изгиоа
торцевых сечений еа = ау, ех = ах. Уравнения (17 295)
приводятся к виду:
blei 4 A'l- ал N;
EIд Г]" -{ Nc\ = аи N;
Е!ш ф” Д [( гЧ^х ах+2Цу ^N-EQ ф=.О,
(17.311)
В устойчивом состоянии стержень испытывает изгиб
в двух главных плоскостях, кручение отсутствует. По-
теря у с т о 5 чи в о с ти при р а з s е т в л е н и и
форм р а в н о в е с и я характеризуется возможностью
возникновения крутильных перемещений при критичес-
кой силе Nt, которую определяют из третьего уравне-
ния системы (17.311).
Б. Сечение имеет ось симметрии, сжимающая сила
расположена в плоскости симметрии. Если ось х — ось
симметрии, то a,; = p,j=0, Мх=0, Al,j==.Vex и уравне-
ния (17.295) принимают вид:
Е1Х 1]" -1- Л'П + А (сг — Дг) <р = 0;
Е (^~«,У'г'сЕ1ац" + |(7-Ч2Рлйл)Л'^	{17-312)
~-G/J<p = O.
В устойчивом состоянии стержень испытывает изгиб
в плоскости симметрии. Потеря устойчивости
при разветвлении форм равновесия харак-
теризуется нарушением плоской формы изгиба и воз-
можностью возникновения изгибпо-крутильных переме-
щений. Соответствующую кртпическую силу Лф опреде-
ляю! из второго и третьего уравнений системы (17.312),
17.10.5.	Устойчивость тонкостенных
центрально сжатых стержней
Сжимающая сила приложена в центрах тяжести тор-
иевых сечений; ЛД=0, А4в=0. Однородные уравнения
(17.304) при однородных граничных условиях имеют
тривиальное решение Е, = 1) = ф = 0, следовательно, в со-
сюянии устойчивого равновесия изгибные и крутильные
перемещения отсутствуют, стержень является иде-
альиым. Потеря устойчивости при разветвлении форм
равновесия характеризуется возможностью возникнове-
ния изгибных, крутильных или изгибно-крутильиых пе-
ремещений в зависимости от условий задачи.
Ниже приводятся формулы для критической силы
центрально сжатого шарнирно опертого стерж-
ня. Опорные сечения закреплены от линейных перемеще-
ний в направлении осей х, у и от вращения относитель-
но продольной оси стержня (| = т] = ф. = 0), но имеют
возможность свободной депланации.
Поперечное сечение с двумя осями симметрии. Потеря
устойчивости произойдет при достижении сжимающей
силой N наименьшего из следующих трех критических
значений:
л2 £7 г	л2 Ely
(17.313)
Первые две критические си «ы соответствуют изптбной
форме, третья—крутильной форме потери устойчивости
Поперечное сечение с одной осью симметрии. Если
ось симметрии — ось у, то из трех критических сил
Аф N х'.
___________________________| (17.314)
-р ]/(.У/;4-Л/(о)'2?^4;УцЛ'ите7й] I
первая соответствует пзгионой, две последующие — из-
гибно-крутильиой форме потери \ ctoiP'hboctii.
Поперечное сечение не имеет оси симметрии, Значения
трех критических сил определяют из кубического (от-
носительно Л) уравнения
(А'Л Щ (Ny - N) (Аф, - Л') г1 - № [(£•; - ,V) С2 4-
4	~ Л) 4] -- 0,	(17.315)
Потеря устойчивости характеризуется нагибно-кру-
тильными перемещениями стержня и произойдет при
наименьшей нз трех критических сил ЛИ.
17.11. НЕЛИНЕЙНО УПРУГИЕ
СТЕРЖНЕВЫЕ СИСТЕМЫ
17.11.1.	Постановка задачи об устойчивости
нелинейно упругих стержневых систем
Рассмотренная в 17,7.5 задача численного исследова-
ния равновесных и критических состояний сж,ато-изо-
гиутого стержня из нелинейно упругого материала в
настоящей главе распространяется на плоскую стержне-
вую систему (раму), составленную из таких стержней.
Свойства материала характеризуются нелинейной за-
висимостью <т=у(е) между напряжением <т и деформа-
цией е (см. 17.7.1).
Для упруго-пластического материала принимается
предположение об активности деформации в
каждой точке конструкции (см. 17.8.3). При этом раз-
грузка нс происходит и упруго-пластический материал
можно рассматривать как нелинейно упругий.
Исследование малых изгибных перемещений системы
основано на гипотезе плоских сечений и использовании
приближенного выражения для кривизны. Предполага-
ется сохранение плоской формы изгиба как в равновес-
ных, так и в критических состояниях системы. Влияние
касательных напряжений не учитывается.
0 дополнение к обычному расчету принимаются во
внимание вертикальные перемещения узлов рамы, вы-
званные сближением концов стоек вследствие изгиба и
осевого обжатия. Благодаря этому исключается необ-
ходимость специального рассмотрения особых предель-
ных состояний системы, связанных с потерей устойчи-
вости одного отдельного сжатого стержня или же с ис-
черпанием его несущей способности вследствие образо-
вания пластического шарнира.
252
РАЗДЕЛ 17 УСТОЙЧИВОСТЬ СТЕРЖНЕВЫХ СИСТЕМ
Предполагается, что вес нагрузки (как продольные,
так и поперечные) возрастают пропорционально одному
параметру к. Регутыаш исследования равновесных
состояний представлены на графике поведения
системы
(рис. 17.91)
4
Рис. 17 91
; по оси абсцисс отложено харак-
lepnoe перемещение [ (прогиб у
или угол поворота 0 в одной из то-
чек системы), по оси ординат—
параметр нагрузки k.
В подавляющем большинстве
случаев несущая способность сис-
темы определяется потерей у с-
т о й ч и в о с т и при достижении
предельной нагрузки—точка В на
графике поведения (см. рис, 17.91).
Аналитическим критерием поте-
ри устойчивости является у с л о -
в и е
мегра
dk
If'
стационарное т и пара-
пет рузки k.
-- о,
(17.316)
рассматриваемого как функция характерного переме-
щения /.
17.11.2. Основные аналитические зависимости
Исследование малых нзгибных перемещений одного
нз сжаю-изогнутых стержней системы основано на по-
нятии приведенной жесткости EI х сечения, зависящей
от развития деформаций в этом сечении (см. 17.11.3).
Дифференциальное уравнение изгиба имеет вид
(см рис, 17.9)
d- у	„
Г/-‘	+ Л' (у - .%) + Мй + Но X + Л7 = 0.(17.317)
Процедура наложения в общем виде описа-
на в 17.7.5; алгоритм «Сечение» решает эту задачу на
основе эффективного итерационного процесса [18].
Относительное удлинение (укорочение) волокна с ко-
ординатой v (рис. 17.92) выражается формулой
е = е0 ж т,	(17.320) Д
где У. — кривизна. Напряжение этого волокна
Здесь х, у— координаты точки на изогнутой оси стерж-
ня; N — продольная сжимающая сила; На — опорная
реакция на левом конце стержня при х = 0; NE —
опорный изгибающий момент; AfH — изгибающий мо-
мент, вызванный поперечной нагрузкой.
0 процессе интегрирования уравнения (17.317) не
учитывают различие между абсциссой х и длиной ду-
ги изогнутой оси s. После интегрирования определяют
сближение концов стержня по приближенной формуле
С !	0= \
Д/=	£„+— dx,	(17.318)
I)	\	1
где I— длина стержня; — относительное удлинение
(укорочение) оси стержня в точке с абсциссой х; 0 —
угол поворота этого же сечения.
Численное исследование равновесных состояний нели-
нейно упругой стержневой системы предполагает приме-
нение ЭВМ. Итерационный процесс решения задачи
основан па трех алгоритмах, описанных ниже [116].
17.11.	3. Алгоритм «Сечение»
Целью алгоритма является наложение сечения на
график работы материала, т. е. построение эпюры на-
пряжений и эпюры удлинений по заданным усилиям в
сечении — продольной сжимающей силе N и изгибающе-
му помещу
М = N (у — уа) + Л40 Нйх 7ИН. (17.319)
О=£ре,	(17.321)
где Е — модуль упругости; т] — относительный секущий
модуль; отсюда
о____g(e)
Ее Ее
(17.322)
Условия
площадью
авновеспя для рассматриваемого сечения с
записывают в виде:
Л' = J odF = Е ( е0 7% +	);
Л7 = fandF = £(eBS11 + x/T1) .
/
(17.323)
Здесь характеристики первого расчетного се-
ч е н и я равны [11а]:
P^^dF,
P
Sn = ) lyvdF,
J ’Ц2 dF‘
Из уравнений (17.323) следует:
£0 —	,,	>
£ (S^—- 7^ 7.J
х=—---------------- .
£ F^ 7^)
(17.324)
(17 325)
17 11. НЕЛИНЕЙНО УПРУГИЕ СТЕРЖНЕВЫЕ СИСТЕМЫ
253
Каждый шаг итерационного процесса основан на ис-
ходных значениях ео, и. Разбивая сечение но высоте на
достаточное число тонких полос, находят для каждой
полосы удлинение и относительный секущий модуль г;
ио формулам (17.320), (17.322). Далее численно опреде-
ляют характеристики сечения F^ ,	и находят е0,
и по формулам (17.325). Эти значения во, 7. являются ис-
ходными для следующего шага итерации. Процесс про-
должается до тех пор, пока не будет достигнут ipeoye-
мая степень точности.
17.11.	4. Алгоритм «Стержень»
Алгоритм «Стержень» предназначен для исследования
отдельного элемента системы (стержня рамы), В про-
цессе реализации алгоритма многократно используется
описанный выше алгоритм «Сечение».
Требуется найти интеграл дифференциального уравне-
ния (17,317), удовлетворяющий перемещениям концов
стержня, определенным из предыдущей итерации рас-
чета рамы.
Для численного решения этой краевой задачи по
длине стержня выбирают достаточное количество рас-
четных сечений. Алгоритм «Сечение» позволяет для
каждого расчетного сечения определить кривизну х и
продольную деформацию оси стержня е0. После этого
находят приведенные жесткости сечения на изгиб и иа
сжатие, В качестве первого приближения можно при-
нять
М	N
Е1Х =— — , EFX= —- .	(17.326)
и	е0
Более полные рекомендации даны в [Па].
При итерационном решении задачи целесообразно
дифференциальное уравнение (17,317) привести к виду
~~7Т~ =— [А (у — у0) ф- < ф-
ах2
+ Нах+ МИ\/Е1Х,	(17.327)
предполагая правую часть известной из предшествую-
щего шага итерации. В результате двукратного интегри-
рования находят:
d.w
» — 0Q /Ио Hq u-xx
— N (iox — ув uQX) — wax,
У = Уо + х ф- Л70 (и1х — хаОх) ф-
До (И2Л Хи1х) Ф~ А (Ах Х!>ох)
— F'tJo (ulx — Xuox) + wix — Xwox-
(17.328)
Здесь приняты обозначения для интегралов:
г е; М1'^
w, г =------—
в 5

“ J £’А
(i = 0,1,2).	(17.329)
Эти же интегралы, взятые по всей длине стержня,
обозначают соответственно щ, 1, и а.
Изгибающий момент Мв и реакцию Но на левой опо-
ре выражают через перемещения концов стержня
Do, 0/, у0 = Ь0, &i (рис. 17.93) следующим образом:
Жо - [0О us ф- 0/ (д I — и.2) ф- (6q	^1) и15~
+ 'v (IE 5. 'А А) — Ф) “а Д Ш1 “d/Д;
До ~ [ф щ ф- 9/ (и01 — иЕ ц- (60 б/) ua ф-
Ф Л (11! ф Ио ф) ф- К’о 111	>
(17.330)
где обозначено
О = Ц0и2-гф.	(17.331)
Из выражений (17.330) определяют реакции основ-
ной системы метода перемещений Л10, До, Л1г, Ht как
для единичных состояний, так и от нагрузки.
Выполнив ряд итераций, получают с необходимой
точностью искомые прогибы и углы поворота во всех
сечениях стержня, а также реакции Лл, г1а основной си-
стемы метода перемещений. Если две смежные итерации
отличаются одна от другой не более чем на 5%, то та-
кую точность можно считать достаточной для практи-
ческих целей.
17.11.	5. Алгоритм «Рама»
Алгоритм предназначен для построения равновесного
состояния исследуемой стержневой системы (рамы).
В процессе реализации алгоритма многократно использу-
ется описанный выше алгоритм «Стержень».
Канонические уровне и и я метода перемеще-
ний имеют вид:
х
S rikXk + rio = O, (1 = 1,2,	и),	(17.332)
k=i
где п—число неизвестных (степень кинематической не-
определимости системы); Йф— неизвестные перемеще-
ния (линейные горизонтальные и вертикальные, углы
поворота); Гц— реакции основной системы, вызванные
единичными перемещениями; — реакции основной си-
стемы от нагрузки.
Нелинейность системы уравнений (17.332) определяет-
ся тем обстоятельством, что коэффициенты этих урав-
нений fl*., По зависят от величины неизвестных Хф.
Пример выбора основной системы. Для одноэтажной
двухпролетноп рамы, изображенной па рис. 17.94, а, ос-
новная система (рис, 17.94, б) образована введением се-
ми дополнительных связей. Число неизвестных метода
перемещений равно семи: одно горизонтальное переме-
щение, три вертикальных и три угла поворота. При
этом сближение концов ригелей не учитывают, так. как
продольные усилия в ригелях незначительны.
Построение равновесного состояния стержневой си-
стемы. Задаются некоторым фиксированным значением
254
РАЗДЕЛ 17. УСТОЙЧИВОСТЬ СТЕРЖНЕВЫХ СИСТЕМ
параметра нагрузки я, определяют сжимающие силы во
всех элементах рамы и решают систему уравнении
(17.332) методом итерации до определения всех неиз-
вестных Xh с требуемой точностью. Сходимость итера-
ционного процесса обеспечена, пока рама находится в
а)
сосюянии устойчивого рав-
новесия— параметр нагруз-
ки /г, меньше критического
значения kf.
В результате однократной
реализации алгоритма «Ра-
ма» строится напряженное и
деформированное состояние
системы при заданном зна-
чении параметра нагрузки
к, находится характерное
перемещение /. Пара значе-
нии А, /’ определяет точку
на графике поведения си-
стемы (см. рис. 17.91).
Рис. 17.94
Поведение нагрузки в процессе деформиро-
вания системы влияет на величину критической нагруз-
ки. При анализе устойчивости арки в ее плоскости раз-
личают четыре основных типа нагрузок (рис. 17 95):
а) следящая нагрузка, направленная всегда
под углом у к деформированному элементу дуги;
17.11.	6. Предельное состояние системы
По мере приближения параметра нагрузки k к кри-
тическому значению k * сходимость итерационного про-
цесса ухудшается. Состояние потери устойчивости при
достижении предельной нагрузки — точка В на графике
поведения (см. рис. 17.91) не может быть пошроено
с помощью описанного алгоритма. Поэтому за крити-
ческую (предельную) нагрузку прини.мают наибольшее
значение k, для которою итерационный процесс сходит-
ся. Такое предположение создает небольшой дополни-
тельный запас прочности.
17.12.	УСТОЙЧИВОСТЬ ЛИНЕЙНО УПРУГИХ
КОЛЕЦ И АРОК
17.12.1.	Постановка задачи.
Поведение нагрузки
Общие положения расчета криволинейных стержней,
колец и арок см. разделы 5 и 9.
Здесь предполагается линейно упругая работа мате-
риала. Ось арки или кольца во всех случаях считается
несжимаемой [14, 28, 36, 39, 44, 46].
Для криволинейных стержней и арок характерны три
случая потери устойчивости.
1.	До потери устойчивости изгибные перемещения от-
сутствуют. Потеря устойчивости при разветвлении
форм равновесия определяется появлением изгибных пе-
ремещений.
2.	До потери устойчивости имеются изгибные пере-
мещения. Потеря устойчивости при разветвлении форм
равновесия определяется появлением изгибных переме-
щений нового типа, ортогональных к начальным.
3.	Потеря устойчивости определяется перескоком
(прощелкиванием), т. е, мгновенным переходом к равно-
весному состоянию нового типа.
б)	гидростатическая нагрузка, направлен-
ная всегда по нормали к деформированному элементу
дуги (частный случай следящей ншрузки при у = л/2);
в)	полярная нагрузка, направленная всегда
к фиксированному полюсу;
г)	гравитационная н а г р у з к а, сохраняющая
постоянное направление, не зависящее от перемещении
системы (например, собственный вес арки).
В случаях «а», «б» и «г» пред-
полагают, что точка приложения
нагрузки перемещается вместе с
а темен юм дуги.
При анализе устойчивости ко-
лец и арок из плоскости кривизны
полеречные сечения предполагают-
ся массивными (не тонкостенны-
ми). Различают два случая пове-
Рис 17 96 дения нагрузки:
а) нагрузка остается параллель-
ной плоскости недеформированпой
арки (рис. 17,96, а);
Р) нагрузка поворачивается вместе с сечением, со-
храняя направление вдоль главной оси сечения
(рис. 17.96, б).
В обоих случаях точка приложения нагрузки пере-
мещается вместе с элементом дуги.
17.12.2.	Устойчивость круговых колец
Круговое кольцо, подверженное равномерному
внешнему давлению д, в начальной стадии нагружения
испытывает только кольцевые сжимающие усилия.
Потеря устойчивости в пл о с к о ст и к о л ь-
ц а характеризуется появлением изгибных неремещепни
в этой плоскости Критическая нагрузка равна:
Е1>:
(17.333)
/У
где £7Г—жесткость кольца при изгибе в его плоскости;
Д — радиус кольца.
17.12. УСТОЙЧИВОСТЬ ЛИНЕЙНО УПРУГИХ КОЛЕЦ И АРОК
255
Коэффициент К равен: для гидростатической нагруз-
ки К=3; для полярной — /( = 4,5.
Потеря устойчивости из плоскости
кольца характеризуется появлением изгибных пере-
мещений, перпендикулярных этой плоскости. Если на-
грузка сохраняет направление, параллельное плоскости
недеформированного кольца, то критическая нагрузка
f/y 9
№	4 + EljGld ’
(17.334)
где Ely — жесткость кольца при изгибе в направлении,
перпендикулярном его плоскости; Gid — жесткость
кольца при кручении.
17.12.3.	Устойчивость круговых арок
в их плоскости
Круговая арка, нагруженная радиальной на-
грузкой (рис. 17.97), в начальной стадии работы испы-
тывает только кольцевые (окружные) сжимающие уси-
лия, постоянные по длине арки.
Критическая н а г р у з к а, вызывающая потерю
устойчивости арки в ее плоскости, определяется по фор-
муле (17,334). Значения коэффициента К для гидроста-
тической и полярной нагрузки приведены в габл 17.17
в зависимости от угла раствора арки 2а. Схемы арок,
формы потери устойчивости (кривые выпучивания),
Рис. 17 97
Рис 17.99
Таблица 17 17
Коэффициенты К для круговых арок при гидростатической
и полярной нагрузке
	Нигр>зкд гидростатическая			Нагрузка полярная	
2а, град	бесш_п- пирпая	дьл хшар- нйрпая	ТрсХ- шаряирная	бесшар- пириая	двухшар" н при а я
ао би 90 120 150 180	294 7 V .2, 1 18,1 П,5 8	с>	108 27,6 12 6,75 4,32 3	296 75,2 34,3 20,1 13,9 10,6	148 36 16 9,1 6,02 4,5
Таблица 17.18
Кривые выпучивания и условия потери устойчивости для круговык
арок при гидростатической naipjjKc
а также аналитические условия потери устойчивости от
гидростатической нагрузки приведены в табл. 17.18,
Для случая упругого защемления концов арки опорный
момент М и угол поворота опорного сечения |3 связаны
соотношением М = рф, где р,— коэффициент жесткости.
Критическую нагрузку определяют из уравнения
табл. 17.18 или по графику рис. 17.98.
Если вертикальная гравитационная нагрузка изменя-
ется по длине пролета арки в соответствии с законом
(рис. 17.99)
q = qa/casO,	(17.335)
где — интенсивность нагрузки в замке, 0 — централь-
ный угод то критическая нагрузка в эйлеровом смысле
определяется по формуле (17.333). Значения коэффи-
циента Л’ Для бесшарнирной арки даны в табл 17.19.
Круговая арка, нагруженная вертикальной равномер-
но распределенной вдоль пролета гравитационной на-
грузкой (рис. 17.100), испытывает изгиб по симметрич-
ной (относительно середины пролета) упругой линии.
Потеря устойчивости в эйлеровом смысле характеризу-
Таблица 17 19
Коэффициенты .К для круговых арок при гравитационной
нагрузйц
Вид арки, характер нагрузки	2 а, град	i				
	30	«о	90	120	189
Бесшарннрная, нагруз- ка переменная	291	73	31,2	16,4	
Двухшаонирная, на гр уз к а р а в но м ер н а я	-	36	16,2		3,72
256
РАЗДЕЛ 17. УСТОЙЧИВОСТЬ СТЕРЖНЕВЫХ СИСТЕМ
ется наложением ашисиммецщчцой кривой выпучива-
ния на симмшрнчную линию ижиба. Значения коэф-
фициента К, в формуле (17 333) для двухшарпириой
арки даны в табл, 17.19.
Рис. 17.100
17.12.4. Устойчивость
параболических арок
в их плоскости
Параболическая арка, несущая вертикальную
равномерно распределенную но длине пролета н-агрузку
(рис. 17.101), испытывает только сжимающие усилия,
возрастающие от замка к пене.
Критическая нагрузка, вызывающая потерю
устойчивости арки в ее плоскости, равна

(17.336)
Таблица 17 20
Коэффициенты К для параболических арок
Характер нагруз- ки. Закон изме- нения жесткости	111	Арки			
		бес- шар- киряая	дву.х- шар- нирная	| трехшарнирная Форма потери устойчивости	
				обратно- симмет- ричная	симмет- ричная
Следящая	0,1 0,2 0,3 0,4 0,5 0,6 0,8 1	60,7 101 И5 111 97,4 83,8 59,1 43,7	28,5 45,4 46,5 43, У 38,4 30,5 20 14,1		22,5 39,5 47,3 49,2 38 28,8 22,1
Гравитационная	0,1 0, 2 0,3 о, 1 0,0 1	—	28,8 46, I 48,4 45 31,7 15,4		22,7 40,2 49,8 54,5
Следящая J cos13^	'),! 0,2 0,3 0,4 0,0 о,8 1	65,5 134 204 277 441 587 700	30,7 59,8 81,1 101 142 170 193		24 51 83 118
Следящая д. 1 (6)-—— Л	С OS и	0,1 0,2 0,3 0,4 0,0 0,8 I	(12,3 112 154 152 133 118	29,5 4У 57 52 44 37		23,2 43,6 59 68 70
где I — длина пролога арки; Е1°х—жесткость сечения
арки в замке при изгибе в ее плоскости.
Значения коэффициента К для арок постоянного
и переменного сечения приведены в табл. 17.20 в зави-
симости от отношения j/l ([— стрела подъема) при
различных типах нагрузок.
Формы потери устойчивости двухшарнирных и бее-
шарнирпых параболических арок, соответствующие наи-
меньшей критической нагрузке, аналогичны указанным
в табл. 17.18 для круговых арок. Для пологих трех-
шарнирных параболических арок с f<0,3 I наименьшая
критическая нагрузка соответствует симметричной фор-
ме потери устойчивости. У более крутых трехшарпир-
иых арок наименьшей критической нагрузке соответст-
вует антисимметричная форма потери устойчивости по
двум полуволнам, как у двухшарнирных арок. В этом
случае коэффициенты Л’ для двухшарнирных и трех-
шарнирных арок, соответствующие антисимметричной
кривой выпучивания, совпадают.
0 запас устойчивости параболические арки при любых
нагрузках можно рассчитывать по таблицам, составлен-
ным для следящей нагрузки.
17.12.5.	Устойчивость пологих
двухшарнирных арок
в их плоскости
Пологая двух шарнир на я арка может по-
терять устойчивость в эйлеровом смысле, выпучиваясь
Рис 17.102
по антисимметричной относительно середины пролета
кривой ADB (рис.17.102). Критическая нагрузка
f El
32л2_Ц.^.	(17.337)
I
Арка может испытать также п роще л кив анпе
с мгновенным переходом в новое равновесное состояние
АСВ (рис. 17.102). Соответствующая критическая на-
грузка	л6		ЕЦ
-	4	1	
(1 —/п)3
т2
(17.338)
где F — площадь поперечного сечения арки; 1Х— мо-
мент инерции сечения относительно оси, перпендикуляр-
ной плоскости арки.
Расчешым является меньшее из двух значений кри-
тической нагрузки.
Если арка нагружена сосредоточенной силой Р
в замке, то прощелкивание становится возможным при
нагрузке
2Z ,
Р qt-	(17.339)
® л *
Вследствие пологости арки очертание ее оси, а также
и поведение нагрузки не оказывают существенного
влияния на величину критической нагрузки.
17 13 МЕСТНАЯ УСТОЙЧИВОСТЬ ПРОФИЛЕЙ СЖАТЫХ СТЕРЖНЕЙ
257
17.12.6.	Устойчивость одиночных арок
из их плоскости
Пространственная устойчивость одиноч-
ной арки обеспечивается заделкой ее пят, препятствую-
щей поворотам из плоскости арки, и не заиисит or
способности опор к поворотам в ее плоскости. Арки,
закрепленные в пятах цилиндрическими шарнирами,
можно считать защемленными относительно поворота
из плоскости арки.
а) Круговая арка сжата равномерно распреде-
ленной по длине дуги внешней нагрузкой, сохраняющей
направление, параллельное плоскости недеформирован-
ной арки (см. рис. 17.96, а). Критическая нагрузка
=	(17.340)
Коэффициент Kt находят из трансцендентного урав-
нения:
где а — половина центрального угла; Е1У — жесткость
арки при изгибе в направлении, перпендикулярном его
плоскости; Gia—жесткость арки при кручении.
В табл. 17.21 приведены значения коэффициента Kt
для некоторых частных случаев.
Таблица 17 21
Коэффициенты К, для круговых арок при нагрузке, сохраняющей
направление А
2ос, град	А					
	ЬЛ )		5	10	20	30
90	13.8	18,3	12, I	10,86	9,25	7,9
121)	7,05	0,7	5,88	5,01)	3,94	3,3
б) Параболическая а р к а нагружена верти-
кальной равномерно распределенной по длине пролета
травит анионной нагрузкой, приложенной в центре тя-
жести сечения. Критическая
нагрузка, вызывающая нару-
шение плоской формы арки
(рис. 17.103, план).
Значения коэффициента К} в
зависимости от А и /// даны в
табл. 17.22.
67 „
9*-«тСТСТ' (17.342)
г1
Таблица 17 22
Коэффициенты
/<! для параболических арок
111	Harpy жа
	1 поворачива- сохраняет направление	1 ется с сече- |	и и ем
	А
	U,7 i I 1	2	|	1
0,1	28,5	28,5	28	31,7
(1	41,5	41	40	Ьо
0,3	4D	38,5	36,5	137
17—-26
17.13.	МЕСТНАЯ УСТОЙЧИВОСТЬ ПРОФИЛЕЙ
СЖАТЫХ СТЕРЖНЕЙ
Под местной потерей устойчивости тонкостенных про-
филей понимают выпучивание пластинчатых элементов,
составляющих профиль. Длина полуволны выпучипы
зависит в основном от условий иа неиагруженных
краях профиля, т. е. от его формы, и не зависит от ус-
ловий на нагруженных краях, т. е. or концевых условий,
если отношение длины профиля к наибольшей ширине
достаточно велико. Местная потеря устойчивости про-
филя может предшествовать общей потере устойчивос-
ти стержня или происходить с ней одновременно. Под
критическим напряжением местной устойчивости пони-
мается напряжение, до которого исходное равновесное
состояние пластинчатых элементов, составляющих про-
филь, является устойчивым. Для профилен, образован-
ных из очень тонких пластинок, местная потеря устой-
чивости не обязательно означает полное разрушение:
в закритической области стержень может еще иногда
нести некоторую возрастающую нагрузку до полного
разрушения или до общей потери устойчивости.
В пластинках, теряющих устойчивость за пределом
упругости н при распределении напряжений, близком
к равномерному, предельная нагрузка приближается
к критической. Поскольку местное выпучивание элемен-
тов профиля обычно ведет к быстрой общей потере ус-
тойчивости, в большинстве практических расчетов вы-
пучивание не допускается. Некоторое исключение мо-
жет быть сделано лишь для пластинок-степок с оперш-
ий продольными кромками (для которых закритичес-
кия стадия значительна) и только при действии
статической нагрузки [5].
Критические напряжения местной потери устойчивос-
ти профилей зависят от соотношения геометрических
размеров, взаиморасположения пластин, образующих
профиль, физико-механических свойств материала и ха-
рактера распределения напряжения по загруженным
кромкам. Простейший прием теоретической оценки кри-
тических напряжений состоит в расчленении профиля
иа отдельные пластинки с последующим определением
для каждой из них своих критических напряжений при
подходящих основных граничных условиях. За крити-
ческое напряжение при этом принимается наименьшее
критическое напряжение, полученное из расчета всех
пластинок.
Однако этот прием дает достаточно точный резуль-
тат только для тех профилей, граничные условия эле-
ментов которого четко выражены: для тонкостенной
квадратной трубы, крестообразного сечения с равными
полками, равнобокого уголка без утолщений в сопря-
жении полок. В этих случаях сопряжение пластин про-
филя может рассматриваться как шарнирное. Для про-
филен, состоящих из нескольких связанных между со-
бой пластинок разной ширины и толщины, граничные
условия закрепления сложнее (упругое защемление по
линиям сопряжения) и значения критических напряже-
ний определяются с учетом взаимодействия элементов
профиля.
С целью повышения критического напряжения
местной устойчивости тонкостенных профилей может
применяться подкрепление его полок отбортовками или
бульбами (утолщение краев). При достаточно широкой
отбортовке линия сопряжения ее с подкрепляемой пол-
кой при потере устойчивости мало отклоняется от пря-
мой и отбортовка сама играет роль полки, а подкреп-
ляемый ею элемент может рассматриваться как стенка
с упруго защемленными краями.Приближенно, на осно-
Р\’Д1Л 17 УСТОЙЧИВОСТЬ С гГРЛ\НГг Ь1\ < -1СТГМ
вании данных а сшрч i шов с п н i ппофи i и у i
tun IL 0 oopiol JO МОЖНО P 1LCM tpiffiiri 1 «. К L1LI11 I
i Tli 1Ц 1 OU-Н IK If Oil I 1 Mil IO ИМИ о бортовки И Mi И I
mipuii не мене 0	0 1 iiinpiHii читмои ciopoi i
При шчьших [><hwih\ огоорювол их еждует pacev ш
j шаги i ак оу шоы сюроны «шпоры ом подкрепи
Рис 17 104
>Г КОК ЧНТК1 При рзсгростои ши в о~бортовках пта
и it ид к<Ьор 1 a i ш их эффективность падаю [2]
ч 1 втия! гя оутьб pi смо’реп в [3 7] отбортовок в
(2 3 10]
Цетеюобра iho чтобы участники составляющие про
фиш стержня и стержень в цепом бытя равноустоичч
к При вырочпепии устовия равноустоичавости необ
садимо принт матт во вилхпнве возможность неравно
мерною распреде-'енчя напряжен in в отдетьньн
II СI ИНК IX И ушном р-НУ. 1	"1 11111 1 И Oil'll пр 1
ПЩ.Щ И ipcui II ПО рп Ц IHpl	)	41 Ь П 1 I
I м I Т I К OI 1 OI..K TOI I I 1(1 Я 11 И1 Л II 1М Н 1 I 1 II
III! Нлривкш 1 счркы 0100» Jl'iWlH
в <. НиГ1< п])н на накипи ко <уфи ikbh <1 введен к i
начпьного относи it I.>iioi о жошпримп’-а т в i ibh
симосди от гибкости ыержня едя стами 1х лсмсн
юв — по графику рис 17 101 мя сюмшн -iriviy во
АМц М АМг М т,)==000/о / [4] дш оопэню т
О 0037
Пач ильное искрив к. и те и вин юно 1м черычом о
-юс распре ie шине i шр ia hi-i i m t> i попрнтч io i -« i ,n
aieiCH на честноп ш >и ih о th о ok профит inn
у 1СЧСТС коюрых СТСДМТ IIIHIIB U um LTBUHIO yi
ш кине напряжени i la свооо п о i кун но ср m i 11 ю
io родним напряжением сжатя [5|
Ниже приняты стедующчс ОСНОВ! нс обо П К НИЯ
х, у — оси чаиртв ,щшн, соответственно
ВДОТЬ И иомрск IT 1ННОИ ПТ 1СТИН
К11 III 11 о КООр ПШ I.T со СТОПОПН
наибм шт! ) с/к mi я
t— 1ОП1НН1 1 I НИШ И С IL М НО I 11
(cP С 1) III LOT 1ОВ1 Ч про} П
Ф) b Р К КИПЯ I 1 ipliin ПТ И. 11111л 1 СП 1K.U
И TH 11 11 Ч ( в С 1)
7о ширин! OIOOPIOW-I
Ffl
F— ~~~————НИ IHHTpll КСК 1Л H1K0LTI ПТ11.1И
12 (1 —
НОЛ
Cj и ох—ьаибошшее и и им гшес ычря/лс
пия на кр н и 1 шинки п ее ере
динноп ’НОСКОСТИ (г >0 1 о2>0—
ежа’ ie)
е — от носите тьно„ цижшк вють
оси л
а—параметр хаоаюер шющии ра пре
де 1сние нтцряж шт к 1 —
— ь(б)/с(О) им (готько в jnpxioH
стадии) а—1—<т2/о	с(й) — питч
ние е при у = й с (0) - ip, // — О,
пои равномерном caithi а-=-0 юи
чистом изгиое «—2 при тон ють
ном р тирс де тении н цтя-кенш а —
л 0J- 1 з ф
Рис 17 ЮЗ
i? В МЕСТНАЯ VGTOmilBOCTb ПРСФИЛГП СЖГГЫХ СТГРТИГЙ
259
элсмешов
Предельные отношений hjt для стенок, не имеющих свободных крочок, центрально и внецентренно сжатых
Центральное сжатие н внсцсптр'.лн.)' еждзне при а.';.0,5	Внецентрешюо сжатие при с/ -'1
1 Стенка, не подкрепленная ребром. Двмавр (рис
I7.1P5, а, л)
Швеллер, прямоугольная тоубт (h — большая иоронз) я
коробчатое сечение (рис. 17.103, б, ж, //, о, п>
0,2Л-
Каалратная труба (рис. 17.105, е). По формуле (б), но с
уменьшением на 20%.
Во всех случаях /ьД не должно превышать 75 При нелшиа
лряженшз элемента отношение ЛД MCvRti бъпь увеличс-ш я
RFq>
раз, но не более чем до 90
3. Стенка, не подкрепленная ребром. Двутавр
О — наибольшее сжимаюиде ПыПря'Кеппе у расчетной Гранины
щепки без учета Фвн, %% £'Ч=; » формуле (в) О - а TfCM-.
г>' — напряжение у противоположной границы стеакщ
т - гред.чье касательное напряжение в рассматриваемом отсек’
-£, (	1	| 1,4	1.5	
%	[ 2/22	2,67 j 3,26	I -	5,23 I б,,5
В интервале П^ж.а,<1 отношение А „7 определяе; ей линейной пи-
шюляцией между значениями при». .-0.5 и т, i“l.
Прочие сечения — по формуле (в), но с с ченыпением на 25%
- Стенка, подкрепленная посередине продольным ребром.
А , t увеличивается ь fl-раз	_______________
/р/0.42 1	о j 1	о	*	|	6	|
3’	1	1	| 1,4	1.6	
Ф Стенка, подкрепленная посередине продольным ребром. Пр.,
условии 1 рфз за Ао принимается наиболее напряиозниая часть
’Генки между поясом и осью ребра- Если ребро распото’жено е от
| ной стороны стенки, /р вычисляется oiиосигельно оси, совмещенной!
с ближайшей гранью стенки
/р — момент пиершш сечения ребра
б. При необеспеченной устойчивости в расчет вводится часть стенки шириной по nt, считая от границ расчетной вытопи п
Класс стали	С38/23	С44/29, С46/33	С52/44	С 60/45	С70/60	С35/73
п	15	14	13	12,5	12	11
ст и о.,,, — физический и условный предел те-
кучести маюрпала;
fi — расчетное сопротивление;
и — коэффициент Пуассона;
Г, Д, Л\ — модуль унрусостн, касательный и се-
кущий модули;
А — расчетная гибкость стержня;
Для наиболее распространенных профилей из стали
разных классов и различных алюминиевых сплавов с
учетом сказанного выше в СНиП установлены пре-
дельные соотношения между толщиной и шириной (вы-
сотой) стенок и полок. Соответствующие данные дли
стальных профилей приведены в табл. 17.2,3. 17.2-1. Ана-
логичные 1абл1шы для алюминиевых сплавов приводят-
ся в [15]. Расчетные ’размеры профилей даны па рпе,
17.105, I при отсутствии плапок — <а, Щ10..2 Ь).
В других случаях проверка местной устойчивости мо-
жет быть выполнена с использованием решения для бес-
конечно длинной полосы, находящейся в одноосном на-
пряженном состоянии [11, 12].
17*
В упругой стадии критическое краевое напряжение:
л2 D	л2 Е ! t V
or k ------------ ~ к,.-------------------1
’ р е lb- 12(1 — pH Ь )
(17,343)
где Е—коэффициент, зависящий от граничных усло-
вий и параметра «,
Для полосы с обоими защемленными или шарнирно
опертыми краями k,. принимается по графикам
рис. 17,106 и 17,107, для полосы с одним свободным
краем и вторым защемленным—по рис, 17.108, а для по-
поем с одним свободным, а други и шарнирно опертым
граем — по рис. 17.109,
Для промежуточных стучаов упругого закрепления
полок коэффициенты к,, даются в табл. 17,25 [13].
Таблица составлена при ц=г0,32, наибольшее сжима-
ющее напряжение на свободном крае полки; иара.Мс-гр,
характеризующий жесткость ;акреплепия,
(17.344)
2G0
н it ч 1
СТ ТИЧИВОСТп Cl ГРАШ ВЬ X СИ( 11 Cl
j - i m j
Вреде дные отдо 1еиия / / в центрально й bi «цеитреино сжатых и изгибае дьи ста <ьных алсме»п i\
				КЛиСС С											
ЪЧД CBCCd ПОТКИ					т да							10D		По	
11 окаЧм к пн 1	й	пи j j з 11 и 1)	а р 1	( ( С С	8 } 41 Ю 0 4а /С ( 8 ”о	( 4о j3		14 1 10 0 ч Н 5	U П 1 ’ ~>			13 Т 1S 17 1Ъ т 10 ) 4		о -> 0 18 о К В	В 14 0 В ) 1 а b		
11сс 1 им и_ я по 1 а ] и <_ У	On I	1 И I С 1	к pi ей (рз и 17 10а в н. р)	Ф j ТВ	С ( с с с	S я) О ) i "0 0J 8>_> о	С 4b 33		I 1 I К) S 0	I 1 1 П а И 10			1 3 1 П 4 В а В 11 5		в 1! 1 ы 13 э	0 18 ч 1 о В В 1 > 0		
Неокаих hhhih л^шая по кд 1 Г эк го jrori	ituk i м тег н i р т tpa (рис 1 10 б )	н р в по iha					11о п с 5	с	ill IU ЮМ		•= 10%					
j ш	гн>	Пр у. т М ШП11	)С НОМ (01 ор ов эй) 1 10 on с)	ок а и ( ЭЯ	с с : С	8 3 41 ) > 41 bj 4 а	С 4fj j3		>0	30 ж 8 1 ) 0 17 о			3 г о о 3		п 8 а 2^ 1	*0 э b		
о С ин и пот эк 1ни.т проср лей пс 1Ы^ рс ром и jt 1 шгые птанке	окай /и					По п 1 таот с с h		17.0 ЧИН1 .1	1утсм ю reran uni в формуя/ 						) ,
6 Нео аи й 1ен гь й свес потки тавра (р с I 10э J)						По П !\<АММ‘		-) .( 1 IC	нй	п I 1 и 2					
7 Стенка тавра (рис 17 10а д)	;		1				Пре тм ьнх cb (шци -I	/2	опре (,с !|—1—0 1		1 1 £	1	с. >мяо/ксниеи J?o			а
8 1В элаям те 1ь и <л	по ik з в (ниюа ши емкита )	JUTK X	с ( ( с с	8 44 4 П Я ™0 ’	<' u/33						1о В 11 11) о К) 9					
Прит е ч т н и е И i те i зпр HhJfJl 1 г_ш. К j 1И	Л Ш X	/л 111 I	кх сП а о А/ 7		LU V где	I &// монет го * — Hdf 1	ггтть уветичено в гшая из зс 1ичи г р q			R/c 1Нз	р и но ф иН.	не более чем ипю 1ьзо1 анных			за °-	о U
и и пр л,е эпс v о о иве м к ilh а М	1 Mv	МУ( | 	и-ш о—	В, 	У 4 К	1 <<	< 1	a i ru-ivMbn лот ах				о — ио ишая из ве i j шъ										
где 3—котффицпенг заде ik i пр’ним it ши с iotri
тсчпои степенью прнбп’шния [1] я ноли
швеллера по формуле
f1 h	1
th '	I i
1—0100------
X b
двуччнрз —• уцво 1ШО11 Б II ЧШ1
(17 34а)
для св
т 1Ври
ст
1>
(<"
it mi
b -
г<_
1 bu
1—0106 -—
и ширина у ру 1 о закрепленного
о ИНН 1
h и (>т—юицина и илрача закрсглч
ющпо этемепт 1— ст нки umniipi им твугшрв хве
са нотки тавра
Форматы (17 315) (17 346) дсипвиш гны ири ною
/ нс ibiiom з ас iiai тс
Зп в пня k дтя упруго з нерешенной citHMi при рав
iioitpiOM сжатии ci в [1] кр пн чей ис напряжения
ip 1 нер iBiioMt рном сжшш (в упруго t епдии)—
а [И] Данные i 1я тровепки м стнои устойчивости про
(Юк! в не юр в унррон егт ши при рииошрном ежа
1ии 1М(Ю1ся г 19 10]
В упруго 1П Л П [ССКОИ СГПИ1 CO! I 1CHO нриб IHAtH
1 ому решило [11 12] олюмнпок на рядг уироще
л I и гопу! I ги 1 риги ! с ос {t pt ктыкх) наиряи I
НИ! ОН It S Т« !(Я IO! Же Лопму IO1I (1 1 3 13) НО ВМС 10
Г ВВОДИ I СТ
Дт Ч^а>
(17 347)
I'H МГСТНУЯ УСТОЙЧИВОСТЬ ПРОФИЛЕЙ СЖАТЫХ стержней
2G1
где — редукционный коэффициент. При этом прини-
ышя, что loxpinически* деформации в срединной
инн ио., in ion я-. Кои и в упругой era ши, выражаю,
..л .паи иным н.ьоиом
t = tj 11—а—],	(17.348)
' \ b J
Таблица 17’’)
где Е| = е(О) —удлинение крайнего наибо ,ес сж iro'o
волокна, а а. по-прежнему изменяв геи в црсде ,ах 01 О
То 2
Из уравнений (17 343) и (17 347) при заданном кр i
вом напряжении Сцр требуемая толщина пластик.
(17.239)
Редукционный коэффициент q зависит о, граничшях
условии, параметра и и о.ношеннй EJE и ЕфГ л 14
наибо а t ирного кр 1Я (д .я и пери .ла, п,дующщ>
диаграмм.. Прандтя Lt/E — 3)
Дш 17 110
Для полосы с обоими З.ШМ1 питии краями
I, = 0,46 a Es/E -J (1 — 0,46 а) ф, (17 330)
а коэффициент q0, соответствующий а —0, принимав
ся по I рафику рис 17 ПО (сплошные линчи нацюфшс)
/1 ,я полосы с обоими шарнирными краями в (17,370)
лоаффнциенг 0,36 заменяется на 0,3, а ф принимает,-
по рис 17 111.
Для защем lemioil полосы полки
’1 = ))и"г(0,37сг -ф 0,575 а’ —0,255 д’) х
'<(£/£—р0)	(17.351)
коэффициент р0 принимается по рис 17 110 (пущ шр
на графике)
262
РАЗДЕЛ 17. УСТОЙЧИВОСТЬ СТЕРЖНЕВЫХ СИСТЕМ
Для шарнирно опертой полосы-полки
= (i!ri 2- 2,6 £?	(А3 А- Л).	(17.352)
Здесь А] — площадь между действи тельной кривой OPQ
диаграммы материала (рис. 17.112) и пря-
мой OQ;
А...— площадь между кривой OPQ и ломаной
ORQ-,
дается графиком рис. 17,113;
р ------------—.
с 2 + 2р. Д Зй
е = E/Es -- I.
Для материала, следующего диаграмме Прандтля,
£ -
Рис. 17.111	Рис. 17,112
Практически расчет по приведенным данным сводит-
ся к следующему; по действительному эксцентриците-
ту или относительному начальному эксцентрицитету,
соответствующему гибкости рассчитываемого стержня
!по приведенным выше выражениям та для алюминие-
вых сплавов пли рис. 17.104 для стали), определяют
параметр а и соответствующий ему коэффициент k,p
затем для данной гибкости и сечения стержня опреде-
ляют ширину (глубину) пластической зоны в проверяе-
мом элементе еечсиия и нулевую точку эпюры напря-
жения и соответственно им устанавливают значения
EJE и £//£ для наиболее сжатого края элемента; по
эгнм значениям и параметру а с помощью приведен-
ных выше уравнений н графиков находят редукцион-
ный коэффициент р. Далее, при известных размерах t
и Ь определяют критическое напряжение ио формуле
117.343), где k,, заменено на йил, или отыскивают по
формуле (17.349) толщину t. В первом случае критиче-
ское напряжение не должно быть ниже R, а во втором
н (17.349) вместо о1ир подставляется R.
При упругом закреп тении края 'редукционный клчф-
фшшс'пт приближенно жжс1 опрещлягься как сред-
няя величина для шарнирного и ыщсмленшн о
пли более осторожно приниматься напменышгл
Ширину зоны распространения пластической дефор-
мации и нулевую точку в полках 11-образных сгалы.ых
профилей при эксцентрицитете в плоскости, штра.т.ттль-
иой полкам, можно определять по данным, имсн-щичея
в [8|, в стенке тавра и полках швеллера — по данным
других работ того же автора.
Об устойчивости стенок в сжато-изотнутых и итги-
баемых элементах см. [6],
17.14.	УСТОЙЧИВОСТЬ ПЛОСКОЙ ФОРМЫ
ИЗГИБА БАЛОК
17.14.1.
Устойчивость двутавровых балок
Балка, нагружаемая силами, действующими в плос-
кости ее наибольшей жесткости, являющейся плос-
костью симметрии, вначале деформируется только
в этой плоскости. При достижении нагрузками крити-
ческих величин плоская деформация перестает быть
устойчивой и дальнейшее увеличение нагрузки сопро-
вождается изгибом в плоскости наименьшей 7K<cikocih
и кручением.
Ниже рассматривается такая балка посюяшюго се-
чения. Прямолинейная ось балки принята горизонталь-
ной, плоскость действия нагрузок остается вег время
вертикальной. Приведены формулы для определения
критических нагрузок. Расчет стальных балок двутав-
рового сечения, имеющего две или одну ось симметрии,
см. 17.14.2.
Критическая нагрузка двутавровых балок, сечение
которых имеет две осп симметрии, определяется по
формулам табл. 17.26,
В табл. 17.26 I — пролет балки; У — расстояние точ-
ки приложения нагрузки от ближайшей опоры; В —
= £/,,— жесткость при изгибе з плоскости наиболь-
шей гибкости (в горизонтальной плоскости)-, Е—модуль
упругости; 1 у — момент инерции сечения относи
дельно оси у, C — GE;—жесткость при чистом круче-
нии; G—модуль сдвига; I к —- 0,433 2Д£; b и /- соот-
ветственно ширина и толщина элементарных прямо-
угольников, образующих сечение Значения коэффици-
ентов k приведены в табл. 17.27—17.34 и зависимости
от вида нагрузки, места се приложения, условий за-
крепления кшшов балки н от величины коэффициента
где v — коэффициент Пуассона.
Рассматриваются стедующие услоз.ня опирания.
1.	Шартшрпое опирание. Опорные еччепия мотут сво-
бодно поворачиваться относительно своих главных осей
(х и у), перемещаться вдоль оси балки и депланиро-
вать, но они закреплены от смещений в своей плоско-
сти и от поворота вокруг продольной оси балки,
2.	Конны закреплены от вращения относительно вер-
тикальной оси у (от поворота в горизонтальной плос-
кости). Деплаттацня исключена.
3,	Дополнительные связи посредине пролета шарнир-
но онер!ой балки препятствуют повороту сечения бал-
ки относительно продольной оси.
\CTCH4hBOCТЬ плоской ФОРМЫ ИЗГИБ! БАЛОК
Т И и и 17
Критическая нагрузка двутаыэо ьп ба юк сечение которых
имеет две оиз симметрии
1 “	।	Расч 1пы( схемы и фора улы	Q £ > о	Но’жр1 таблиц по лото ры 1 onpi. зх 1 1етч. я новф ф щнеят >
1	.-Л/? Ф»	A A7W, о	г	J v- г£?г кг ' i	1 2	) V < И з табл Г' ’ О V Ж Ijg вмес о вводится Я & где Я опрете 1чется по рис ГШ в) Пр гмечание	к та л 1" 27
	А-— г — р 	 I В( кр 1	1 1 3	) .-О 1 ыФ Г о) е> < О о вместо k взо ;ится гр 1Де ? -> т w т j 7.29 в)ТаГч Г 30 О ТаГч 17 31
	р — 1 , .	k } IjC И?3 )КП~ — 			— 1	3	Табт 17 °2 Та< 17 33 Таб л 7 4
	j U—г л 	,р	 ШхШх^ПШб' Г В зпдет е « ы *г р		k опредс яет'1_я по рис ыш	i А —момент на 1 онце ; / - сосредоточен ий сп г,а в центре тя сест < Г сосредоточенная си ' Р 1 та соответственно к : t । верхнем} и ннжнл n i краям концевого с ! «енпя i —ртзчомррио п^пре тот нш натрхзга по оси банк ! к - тол поверх}
Т н" ч и ц а
Значения / при <з хина? oi п\ мо кипах нт юнца-с Сатчи								
		1 0	/	П) 1 i ) Mt ] ’				1 1
	И 4	1 It	.4	3	о !1 5		1 5	
	1)	0					ъО	100
1 | 1 °° 11 р н м I р< Н Чс (Ш Н Р 1 -ч П I .( Ю 1Ь 3 ;1 ITj ! ~ I ML С С Z IKpt 1 ПО Tv		Ч 1 п I ОНП, !Х t CCJ Я 16 7 31 )РГс	7 3 1 о П Ы IX. 1 о и	ьь •[ 7 R IH 1 П 11 И -> 1 1 1 / Г 1\ тх	1 ) U 1 зя I	П 1)1?! ОИ ВЫ I РЫ п 7 Я 31	3 55 3 П1 11Ы юр 1 IL Н И п \ м о	1Ь П п Г П > а НЦ 1 С/ пр ? (. м "1 X ТО 1 Н 1	5 ) Г рп по ' ПТо : 1 2" i
Ес и к i'<arpcA-nt дан юж,иным к oui б пьи юбы
1Я1ШЯ nip i un на концах шз iBasoiu шныи из
мо [1| то крмнчеекчн movoht косое тис
И, f - -Ml	(17 364)
Г'Ц М ... рИГИ«<к-..НЧ М .1 1Т 1 р'Н Час OVl 31H0t 1 ЗН 3
н, я и оц j гея н паи 1 17 35
Зна’ечия / h
nn ] соср^ютс’ и юн сич» посредине пре iera
(Оз)
Г/	1) 1	0	3 0	ф	24	12	в
t 4	t 1 1 14т	1 ) 0 ( п	17 0 8	1 з i 4	0 1 О 1	1 ) 5 р	1- ч Z
а	~~~	30	%		жо	0	0>
k п к в р I и к П П1П0>	18 1 Ъ D 22 4 1 м е ч nei по (ь, ни п чк 6Д ШЮ Не	18 Ь 0 1 < и и е го [ Л КС оцн i 13 зки t	17 9 1 ) 1 1 1 в га 1 и ~ 6 ИНЖII г ОСИ I п	Г О 15 3 п Г) чхчче 4 ilt Z без Ю1	1/ 4 15 5 10 1 пои чиже ПГ П) Ч€ 414 кеа	1 7 (Я 9 И ИЯ п 1ИЯ пчг соогветг	г > 1о 8 18 7 рх К 1 р\ -Л1 гвт ет
264 _
х хьо 1/ уооичиьостъ (Прлтвых сиспй
Гас иц
Г 9Ц
Отношения криги зеск тх си ; и напряжена t нои с, 0 э
и при южп i и сосредоточь тон н н к аз Ou чя ( — отнэи t те
расстояния то хх приложения ситы л опооы к расчетному
ipoieTv /)
		зг j Г'		1	10 |	0 0	0 1э	) 0
/	 г	(	1 1	(1.11	1 Г 13	1 1	h	1 10
	П р и		! D ЧИР	1 1 1 ( 111 11 1 1 1) 1\ ч р Ьпц те ТТН увптитс1ия			1 1 1 КРИТ	I
5	1 Ш X	PD I	0 1 р* га ш	ц т меде I снь	1 р эй 7 \ ЦК I I р / Т М	Р 0'1 н	TJT '1	Чр
a f 7 и 1 1" )
Зиатешя 1 при сосредоточенно) сите я центре сечения
ре 1ИНС про Нал оатки с концам 1 ihptn JCili пмн от позолота
а зори шгальноз а пкк'п
Т а С а и ц а ”31
Змч« яия / при оертдоточе но 1 сите в центре сечения
niсред* не jpoTt'fw ни с н 1р зионо лероами концами при
ополнитлтьзых связях пнре цше прочета
1 Z	) 1	4	Й	16	1	9Ь	Р8	00	40
	1	1 1	Н 1			4 3	я	П 8	1 4 ’
Т a f 7 i ц а 1 32
Значения / Лв k в ciy?at птвношрно р кпредсл иной
UipjJhK и uapt ирных опор баи i (сл примечи ihc к raoi 1	3)
а j 4 1		4	8		1	1	18
/ Л Zi	141	1	1 8 1	f 1	31 8 ( / 4 1	4) I	31 3
	(	30	1 8	0		ibO	ю :
/ > b	J 3	1	{ 1 1	i	1	8 I 1	8 J : ( 0 8 ;
3} тения * р случае равюмепно распредетеяно i нагрузки
но оси оа тки при закреп тении концов от поворота
в зориментальной плоскости
П 1 ()	8 0	11 I
Т а ( л и ц а 1	-1
Значения &в р1 в случае оавномерно распределенной
нагрузки и шар ирных опор при дополнительных связях
посредине пролета
4	4		8	। U	| 1 1	cfo	1 8	
k	17	2 1	Um	1 (	8		7b 4	7 8
^t,	o80	14	1	Ш	1	4		bc
		4	8ч	.14		8	81	1
Т а б 7 я ц ’ 17 За
Зна тения и
ГО Ct I II 1Я о
г 14 УСТОЙЧИВОСТЬ Плоско I ФОР'1Ы ИЗГИБУ БХВОх
Учет прогиба балки в плоскости
и з । и б а [ 1 ]
В i iv « пятого чмибз твут вровои бтткч кр и I.
нскпя моче и с унтом iponiba опре 1с тястся in уопз
Я( ния

Зтесъ V— уровень понта i ния ’-югрузкз а )—уро
вень птоскости связен in о но о паи
Fc ти связ 1 расноао । chi bi а с он б пк i ooat i i
11 0 47 с то потеря стоп iHBoi г потоки i гоа з i
acTKix меж i.y хз пп связ н фпвпи i ?кс осп on
hi PB0 ГЯТС l "О знаком мпцф
Т а а
где
п" т И
Р	;---
6/Л F1 ,
про
сту
ИГ А
т( пиритного опппания ionics (п
приводит к ’ вощению ритпыскою
1) М г
10 1 г
/п
(17 ФРр
31Р юн? я коэф	? в пмзе ни того изпн
I т ц з 17
Пои
обоих концов п = 2
ж е н и я
итические напря
ерити lecKiie напря ми ия i
К р
Напошнп
Отр(тствхкиш I п шбе тынсму моменту вн
с н дующим форма тм
в с ауч ie
нс
и пни
Я")ТСЯ
'кр —
дУр 9у
ЩИсТЗПЯ " оментоз
Л p~Vа
/ h
Е
нт
концах
k V"«
,1
(17 Зо7)
где
Л'
/
(17 358)
9нар ?! чозффг ? гт и сту тл гр^т тозешт сити
оергд j шок та
При
со ретото епноп
сите
посредине г ротетт
р
Р
21
---РФ
16
(17 ЗУ))
то газ ij полсеипя грез!
па id а ьп
OHOpl I
ни <
ыI поч грхj ’ 1
1ХОТИТС7
II шряя
в т пагсто
I ИС В СС и
г
----РФ.
4
(1 — С)
(1/ 160)
При рэп О И оно
р
спрет течнеи Н ГрузК'
РФ
(17 В1)
В 3 7Д"Тхс консо ти
(17 362)
Балки с продольными
с в я а п ии
11
2]
Нот продотпгпми СВЯЗЯ1 ПОН IV 1 ТСЯ горизонта чь
пая ферма попрс пяюцп oaaix в ат мппх то к х
(т з 1\) При С1П1ЯХ 1 п ос ос 1 га	н того г зя \
ияние уч зпп п я с шююи i ирамстр i о
ВнЗЙШЯ 1офЛииНС1Г! угезпдпия ЛППТ 11ИЮЧ на
грюки У СМ В 7 10 I 1 / 36 II 17 3”
В I ичте рпзпохцрно р icnm I ai niioi ни[)ю мо-к
io пои юр ат ся форма ао 1 [3 и 4|
О 81 — — 1 7) -
1	/г
пропорционапностн
Нш вишяж ши щрехо ит за пре т т пропор то
пинки о 1 рг< н тмю н 1 разку мо/ но расе витать
пр и имя in о юс зяпегз моду п х npvrocni Е п
ромнп моим 1 —ц/ ннримср ктсатъ ни мо
1\ ь и и мо пи Эшессс} i Кармин з гесь р козф
г] 1 rai I з пт щи 1 оа п прядения I С III I ричять 1ТО
МО IX П СТПИГ1 131НШ1 а- 1 нроиорипо! ЗЧЫ10 М0ДТТ1Г
ipo опп и е р гос ч то ш in 1 кри 1 ескон нагрх i
хи oi ре i in т in по форме m г-пп 17 6 в стх ас п
тихом Н11ПЯЛ.С1НИ за I р 11 ПроНОР U1O1I3 7Ы1ОСТИ ТО!
ЗИП! CIITI ХМИО CH I I К) (1чЦ1аП 1]
Ес т I ж( in cciMBi in рюхптатет к кричентзть
П X pi ОТ |5 И 1)] MT I И 1Ы1 X 3101 IHIfBl X О1
01 принят щм ВИГ ГО<ТОЯ11ПЧ ГО П пр 1Г0
it I I ко [фиш п х 1ты 1 н ни пер хо г кри п ескнх
н 1гря?1 ни 3 1 in "ст пр iijniiio атьио i-i
X 1 11	(17 364)
17 14 2 Устойчивость стальных
двутавровых балок
Со"тзс1 о CH1 П II В 3 62 [7] то зеркз oot ни устой
I зо гп inn) е требхе ся I стетхюнчх ст пят.
l)	1 I 11 П II ПП Н1С7Н13 10 О" 1 1М И7И М0П0 7И 0 3
' зое мп it n г 1 и нощи ся n caiii по ic 1
Il Ill ПЯТС ГВТ! Щ1 X 1101 О] оту ИГИИИ 07 ток
) при 0ТП31 1 ШЯ С1000Т7 0И Т 1111 II С/К7Т0Т0 ЮЯеЗ
п Х7 1в cot он б -1 I к с "о 1 пр ине н прев tinqio i ix з ii
II И пр! I Ш( X .Г [7] Bo TCI TO ио простым
tn ши 1/;	ip i min ио форму im tip 17 "
в) проги pi	TITO IBO l Щ0Г010ТЗ I ЗИ H ТОНН 31
poi e и "p t yi тс	i ос г япщи nrpx ki
I П70 о IT! 1 ПП П1Т1.Я [Темпом I И ПР
И 7Ь II I 1 X ( тр 3 11 3X1
26b
Р\ЗДГЛ 17 УСТОЙЧИВО И <ГГРл<ШВЧ\ Ш1ГЧ
Т а б т н ц а 17 38
Нзиботмпие огроше!!ия I Ь при которых не требуется проверка
< биен устокчиьоети тпутаззровых ба"ок из стати класса ii 3
Т а б л иц а 17 1П
Значения ф при сосредоточенном грузе приточенном в центре
тямесги сечения иа свободном кочне консоли
I
Р i-'Tit Trlb’O Д) т ш
Зятче^ня I-O-
ОффчЦЖНТОВ
С> I pH 1 И
m и * пр i
to к । i
О б о з 1 з ч 5 ч v я Z — р и з о я н не мем tv г о i < i м ’ ? к
римения сжатого по! a or ii шроыых < и< ь t нни о х f -
и ип’ша и толщина поя! a h — ши та тлепач
Дтя батон из стати других кта сов течения 1>о опре v
а	V 1			5	1	6	Й
V	3 По		5 7Ь	4 Н!	1,-b	!,М	1
г/	1 )	12	11	ь	.2-4		ю
ч	-			, ч )	ъ,	7,27	7,79
’ ir let ия ксифЛиши in ов ф бтауита из rjoi 17 34
ч 17 W в в.виецмостч от пиримстра и При v = 0,3
Ук . О И 7	24	П¥
it) £ \ h / 1ц (1 Ф 0,3) \ h /
(17.367)
Проверка устойчивости базой согтасно [7]
д.< I ся по формуле
ЛТ
"^77-
Фс, ”< бр
прои’во
(17 365)
где М—расчетный чз/ибающии момент; Жгр — момент
сопротивления сечения бэутго, R — расчетное сопрогив
челне изгибу прокатнон стали; ре—коэфф чинен-
лмсььшения несущей способности изтбаемых элемен.ов
при проверке общей устойчивости
З.щсь г — то чцича стстжи балки включая потки угол-
ков, 7; —тотщипа поли ба ли, включая полки тголлов,
d — высота вертикальной полни уголков плюс тонн ста
навета горизот iaibl4j\ листов Д та сварках и прокатных
балок
d = 0,5 h.
Б а т к и с сечением, вм ею щи м
две оси симметрии
При па лички связей в прочете независимо от места
приложения нагрузки коэффициент ф определяемся из
второго столбца табл 17 39 В этом случае I—расстоя-
ние между точками закрепления сечешш от поворот,.
Пои одном закреплении в пролете и натррзье по ннжиеи
полке следует пользоваться пятым столбцом.
Коэффициент Це определяется по формуле
<Гб~=’} у- {~Д~ I ЮК	(17 356)
* л /
Таблица Г/ З'з
Значения U для бачок со свобогно опертыми концами
а	Q JEh J !4L3 [	Сосредо"г чеинъп Груз ПОиретД1Ш«. про-			Рдвгюы^рнп pacnpf- д^лгиц in дагруз в		
		по- вепху	по осп	цо- цичу	по- в^рху	ио СГ 11	пп- н’т
4,1	’ j	1,7 8	2,94	5,90	1,37	.,45	3,81
0, .1	>0	1,7/	‘2,У8	зщз	1,00	19	‘,87
1	' !	1,8"	3,07	В и	1,Ь7	2, 5^	
•1	2,3()	~,21	3 511	5,47	1,98	2 92	9-3
8	2,90	(Л	1,97	%91	2,33	3,31	4,59
И)	з,щ	2	у	4,79	0,Ь5	2 99	,48	-> 4
21	4,00	4,11'	7,40	/’,31	3,55	4,51	5,79
42	4,	4,59	Ъ,08	/,Ч-	л, О'!	5,07	9,25
18		5,00	7,11	3,88	Т.Ои	5,97	7, В
b 1	3,91	Ь,“>2	стцо	Ч,Л	5,0?	b,i 8	7, )2
Ы1	u, J1.	7, 3		щ, >	о,	/,	>8
Ж)	< ,(17	8,05	9,5?		о.Ч,	7,ь7	' ,-1
128	8,11/	м,40	10,10	1_,о7	Ъ,1М	«,1	11. J
lb()	M5	0,59	1 ,1 г	1 ’г-*	‘>,1)1	10,95	и, )
249	10,80	> 5,21	U 73	! п (Ь	11, >1	ЩЛ)	1 1, 18
82D	12,48	Г\Я	1b, 8?	18 г	’ о 01	1 1 00	15 ’»
щ	18,91	1 /, _ 4	18,8	л>, 1-	14,57	15,71	Р ,8о
Таблица 17 И
Значения <Г для неразрезчых балок
1 сс	Значения ”ф прн нгг- р\ оде		ф неразрезных бачок	
			\jз цошег яе 4 разрезных б клок	
	сосрецо- точеичод оосрхд 1- пе в р i - него про- чета	рТВИОМср- rlo MJ.C- зред тхи- ной ? пра.11Неы протеи.	при н (грузде сосредоточен- ной посреди- не крайнего пролета	при нагрузке равномерно рас- пре де теннои в кранном про- тс те
0,4	7,8 5	а,81	1,55	1,5о
1 4	8,35	о, 25	1,52	1,48
8	8,81	ОДЛ	1,4э	1,41
1b	а, бч	7,38	1,45	1. п
.4	Ч>, 14	8,0(1	1,42	1, 18
32	11,15	8,5о	1,41	1, 17	>
i 48	> ь	0,58	l,v9	1, 51
bl	В?41	10, 18	1,37	1, 12
! %	15,3'1	1 ,0-	1, Зо	1,30
1 8	1b 91	1 , Ч	! -1	1,)!? ;
 lb )	Ж, 40	1	1, 1	1,СТ	>
-О)	Л),0 >	Ь,м8	1, 32	1,27
210	1,Ь)	17,пЗ	1 J2	1,27	i
i 2Я0	22,94	18,_3	1, 31	1 _7
1 )	.121	1‘* 27	1 >1)	1 Ъ
.	109	. \Ь 1	21,-1	1,31)	1,2п
1 И УСТОЙЧИВОСТЬ плоской ФОРМЫ ИЧГИЬА БАЛОК
2Ь7
Тля шрпре инх бпил I ющлх три или более р^в
лих ирлчегч I л iro петы 1 шляется нагрузка только в
i j ihlm про и е Кому с гх i о соо ветслвуют значения
U pi Л ЮПИ I I 1 f т 5 JI
Ели по фор л it (i ’66) q >0 85 то учитывая пере
viHiipa шш 1 шит 1 ропорпио I юьчоии в расчет
И < Фоому и (17 366) слеш в imo <рв подставить <[0,
опр I 1Ж 11 по 61 Г' 42
Таблица 17-12
Г	/ь, Л
р7 = О 43 — О 065 (-у I (2л - 1) h,
I—-расчетная длина балки,
А/а ,
~— п2 — векториальным момент инерции сече
‘и
ния
Ik------ Ф 6г (ф— моме it инерции пр i кручении,
bi и 6( — ширина н толщина «теме иарчь х пря
моуго мима образующих сменив,
7=1, 3 — для двумврого сечения у = 12—-для
таврового сечения (для двутавровое
сечечия с отпои осью сих метр ш при
нимаегся промежуточно'' зп mei ie у),
Gl
/J__y
L/v ’ h /
E G — моду ib упругости модель сдвига
Для однопро летной свободно оперто! о i« i в х другой
ст i ши работы козффиц тент у соответствующий иочь
игему поясу определяется по формуле
Переходные коэффициенты
д 1 я старей разтих классов
фб= 4
2/vhhi.
1ХЕ
10J,
Т161П I iiihiii у loci в Юнн пя балок из стале!
I in >в ( г с о ц i пр л1 теку eci I 2 4 т/см" Дм
I ) ipx ix fo ii I весов ш ) 1еиия i| определи
л i т ю i 1 о9 — 1”41 до 1жны блть умножены 1
21 (I)
7?
h\ — расстояние центра ^яжести сечения большого пояса
от центра тяжести всего сечения
h
При сжатии меньшего пояст ербк — <fc Т—
fh
Кооффицис it ф вычисляется 1 о Форму те
ф= 4 [в^Ув2 гс]
Дв V тa fо о гыбалки с сечением
мою ш. им тот 1 одну о t » симметрии
(рис 17 116)
/	tn iitpuii соогв тственно бо i
Шт > 1	1 11,3 11ЫО ПОЯСОВ ОТНОСИТМЬ 10
ОСИ СИМ 11 ШИ Сл 1СПИЯ
/
л---------к() ; , IItl!r ian летри 1 сечения,
А 4
Формулы для вычисления параметров 4 В и С приве
цены в табл 17 43 и 17 4<1
При чистом изгибе вызывающем сжатие большего
„ Pi
пояса В == при чистом тзгиое вызывающем растя
h
жение оотьиего пояса о =---,—
h
Коэффициенты ф чтя бллоч тлвртвл о еченчя при
действ! ii сосредото юннои или р<.вном°рно распределен
Рю 1 116
Т a f т и 1х а 17 43
«^ориуча дтя впчмкчечия 4 и С
Тиг нагрузки	А	С	
		двутавровое сечешь	тав posoe сеч 1 ие
Си 7"1 сосредото jch пая в середин0 про ста	3 (5	9 п у—п} (9 8	0 08
Рави мерно р 1и етени я нагр	5	J 'll п (1 л) (Ч н о. )	} 1
Чисть Й ИЗГ К)	л ЗП	0 111/2(1 п) ( ) 8 a J	0 0’ а
268_______
РАЗДЕЛ 17. УСТОЙЧИВОСТЬ СТЕРЖНЕВЫХ СИСТЕМ
Формула для вычисления В
Таблица 17.44
Су-ма сечения
и мостя прило-
жения натрузки
т
силе, сосредоточен-	равномерно расппс-
нои в середине	деленной нагрузке
пролета
ной нагрузки в случае а<40 должны быть умножены на
0,8+0,004». При п>0,9 значения Т определяются .-шлей-
ной интерполяцией между значениями if, вычисленными
при л =0.9 и и= I.
Таблица 17.43 для вычисления коэффициентов ф со-
ставлена для стали марки Ст.З с пределом юкучести
Ог=-2,4 т!смг и расчетным сопротивлением Я = 2,1 г/с.и’.
Для сталей других марок коэффициенты ф , определен-
ные из таблиц, должны быть умножены на отношение
2,4 От или 2.1/7J,
В случае перехода за предел пропорциональности
критических напряжений в меньшем поясе пли, кроме то-
го, и в большем, т. е. при <[г, п>0,85 пли, кроме того, при
1 1 т т	н — 1 -ь 0,7337 ^у7г	1 + М-Р y/h
1 1	1 __ п _ П,73,37 (Д/ft	1 __ п __ и 145 3^/^
1,0> фб>0,85, в формулу
ляется или <рб н , определяемые
мулам:
при сжатии большего пояса
Фб = Ч'б п
вместо Фб подстав-
по следующим фор-
-----ф (1 — П)
*+ ,н
при сжатии меньшего пояса
Фб.н'
Значения фй и (рбл( определяются по табл. 54 СНиП
П-В,3-62*
ЛИТЕРАТУРА
1.	Г> е й л и н Е, А. Общие уравнения деформационного рас-
чета и устойчивости тонко! генньIX стержней. «Строительная ме-
ханика и расчет сооружений». 196$, Ks 5.
2.	Ь и ргер И. А.. П а новко Я. Г. (реп,) Прочность,
v-i онч иное гъ, колебания Справочник, т, 3, «Машиностроение»,
3.	Ь.тейх Ф( Устойчивость металлических конструкций
(пир с англ.). Физмаииз, 1950.
4.	Болотин В В Ыокомеерватявные задачи теории уп-
ругой хщошшгпе гп, Фп'.матпв, 19(51.
5. Б р оу де Б, М. а) О линеаризации уравнений устойчиво-
сти равмовсйня ппсцентронно сжатого стержня. В сб.: «Исслс-
ювання по теории сооружений», вып. 8. Госстройпздат, 195D,
б) Теория устойчивости и принципы расчета конструкций В сб ,
«Проблемы устойчивости а строительной механике», Стройнз-
дат, 1963.
6	, Б у б и о в И, Г, Строительная механика корабля, т, 1.
Петербург,
7	. Власов В. 3, Тонкостенные упругие стержни (Проч-
ность, устойчивость, колебания). 2е изд, Фи.зматги.з, 1959.
8	В о т ь и и р А. С,, Устойчивость деформируемых систем,
2^' и зд «Паука»', 197
9	Г а л с и л и н 15. Г. Собрание сочинений, т. 1. Изд-во АН
СССР. 1952.
И). Тар г м а н Ф Устойчивость инженерных сооружений
(пер. с нем.), ГосстроЙи зда.1, 1939.
11.	Г е м мер л и и г А. В- а) Несущая способность стсрж-
нглых стальных конструкций. ЦН1П1СК. Госщройиздат, 1958.
б) Общий метод расчета рам и: упруго-пластического материа-
ла, «Строительная механика и расчет сооружении», 1968, № 3
12.	Г о л ь л е н б л а т И. И , С и з о в А. М. Справочник
по расчету строительных когтструкций на устойчивость и коле-
бания, Госстройиздат, 1952.
13.	Горбунов Б. П. Расчет устойчивости стержней и арок
при помощи последовательных приближений. В сб.: «Исследо-
вание по теории сооружений», Госстройиздат, 1936,
М.Дцнник А. И, Избранные труды. Изд-во АН УССР.
Киев, т, 1,2, 1952; т. 3, 1956.
15.	Жуковский И. Е. Исследование устойчивости кон
ггрукции гюропзаяов, Труды авнац. расчстно-испытат. бюро,
рь’ш. 5, 1918.
16,	3 а в р и с в К. С. Расчетные формулы прочности в осо-
бых глхча-ч. (УЧТИ НКТП Ш35
17.	Кпср;|<"В В А Строительная механика, Специальный
кхж- (Джюмика и устойчивость сооружений). 2-е изд. Строй-
и.дат, 19.(1,
18.	Коломиец В П. Метод определения напряжений
и деформаций в со'ипми билли при сложном на’ру/Кенич с уче-
том действительной диаграммы (a, Р). Шзв. вузов, авиац. тех-
ника», № 1, 1%б.
19.	Ко р « о у х о в И. В. а) Прочность и устойчивость стерж-
невых систем. Госстрой из л ат, 1949. б) Избравшие труды по
строительной механике. II зд во АН УССР, Киев, 1963,
2$. Косых Э. Г О статической устойчивости сжато изо-
гнутого упругого стержня. «Известия вузов, стр-во и арх»,
N5 4, 1968.
21. Лейтес С. Д, а) Устойчивость сжатых стальных
стержней- Госстрой!! щат, 1954. б) Справочник по определению
свободных длин элементов стальных конструкций. «Нроект-
сталъконст ру кция», 1967.
22. Лейтес С. Д. Формы равновесия упругих сжатых стерж-
ней и природа точек разветвления. В сб.: «Исследования по тео-
рии сооружений», вып 8. Госстройиздат, 1959,
23 Л”ейчес С Д. л) Применение метода угловых фокаль-
ных отношений к задачам устойчивости стержневых силен.
В сб,: «Исследования по теории сооружений», вып, 9. Госстрой-
издат, 1969, б) Устойчивость сжатых стержней, жесткость кото-
рых изменяется по степенному закону, В сб : «Материалы по
металлическим конструкциям», вып, 6 Госстройиздат, 196'2,
21. Лей гее С. Д, а) Устойчивость и упруго-пластические
деформации внецентренно сжатого тонкостей ней о двутавра.
В сб. сПсследовашгя по теории сооружений», вып 12. Госстрой-
издат, 1963. б) Поведение и устойчивость цг?нгрально и вне-
центренно сжатых стальных стержней В сб,- «Материалы по
металлическим конструкциям», вып. Ю. Слройцздат, 1%5.
в) Игстедоваине работы внецентренно сжатых стержней из не-
линейно упругих материн зов. В сб.- «Проблемы устойчивости
в строительной механике». Стройнздат, 1965, г) Приближенно!?
решение задачи об устойчивости внеценгрешно ц/катогп стерж-
ня. «Строительная механика и расчет соор; женнй», 1970, М> 3.
2,5, Л е й I с с С. Д. а) Собе таенные движения л критические
тпюа.метры упругих стержней при некою ервагиеной нагрузке.
«Прикл. мех.», т. 4, вып.. 11, 1959, б) Собственные дви/кения
п устойчивость упругого сжатого стержня. В сб : «Материалы
но металлическим конструкциям», вып. 14. Строппздат, I960,
в) Об устойчивости упругого стержня иод воздействием иа'-р\ з-
ки. ориентация которой зависит от деформаций стержня. В сб.:
^Исследования по теории сооружений^, вып. 18. Стройны
лат, 1979
26 Л е и т я с С Д,. Р а з д о л ь " к и й А. Г Иг.гзедова-
нне устойчивости внецентренно сжатых упруго-пластических
ЛИТЕРАТУРА
269
стержней. «Строительная механика ц расчет сооружений», 1967,
1,
М а т е в о с я н Р, Р. Устойчивость сложных стержневых
тем (качественная теория). ЦН1ШСК, вып, 3, Госстрийиздат,
1%!.
28, Моргаевски й А, Б. а) Об устойчивости двух- и
грсчшариирных арок с учетом поведения нагрузки. «Вестник
инж. я техн.-», № 1, 1938. б) Устойчивость арок при неплоской
деформации. «Прикл. маг. и мех», т. 2, вып. 3, 1939.
29. Н у д е л ь м а я Я. Л. Методы определения собственных,
частот и критических сил для стержневых систем. Гостехтеориз-
лат. 1949,
Ю. И у д е л ь май Я. Л., Л яхо в и ч Л. С. Уточнение
критерия, определяющего место заданного *исла в спектре соб-
ственных частот и критических сил упругих систем. В сборнике
тредов Томского ияж.-ыроит. ии-та ^Исследования по строи-
тельным коне! р>кцвям*-, !Вд во Томскою ргтд, 19ь8.
31.	П а н о в к о Я. Г., Г у б а н о в а И. И. Устойчивость
и колебания хпругих спычм Современные концепции, парадок-
сы и ошибки. 2-е изд, «Наука», 1967.
32,	П и к. о в с к и й А. А. Статика стержневых систем со
сжатыми элемешами, Фю.магпп, 1961,
33.	П и и а д ж я н В. В, Некоторые вопросы предельного
состояния сжатых ’-леменгов стальных конструкций. Изд-во АН
АрмССР, Ереван, 193и
34.	Попов Е, II, Нелинейные задачи статики тонких
стержней. Гостехи’.дат, 19 Н.
15.	Рж ан и ц ы н А, Р. Устойчивость равновесия упругих
систем. Госгех'тегуризлат, 1955.
36.	Смирнов А, Ф. а) Статическая и динамическая ус-
тойчивость сооружений. Траяежелдориутят, 1947. б) Устойчи-
вость и колебания соорт/керий. Трангжелдлртвдат, 1953.
37.	Снитко Н. К. а) Устойчивость стержневых систем.
Глсстройи-щат, 1932. б) Устойчивость стержневых систем в уп-
pyi о-пласт индской области. Стройиздат, 1968.
38.	С т р е т с ц к и й Н. С Материалы к курсу стальных
конструкций. Вып. 2, ч. 1. Работа сжатых стоек. Госсгропизлаг,
1959
39.	Тимошенко С- II. л) Вопросы устойчивости упру-
гих систем. КУВУЧ. 19И, б) Устойчивость упругих систем (пер.
с англ,), 2-е изд, Гостехиздат. 1953.
49.	Фридман А. М Несущая способность стержневых
систем. В сб : «Материалы по металлическим конструкциям*,
вып 12. Строиичдат, 1967.
41.	Хофф Н. II. Продольный изгиб и устойчивость (пер с
англ ), 1 Рид во ПЛ, VD5
42.	Циглер Г. Основы теории устойчивости конструкции
(пер. с англ.) «Мир», 197Е
43.	Чу вики и Г, М, Устойчивость рам и стержней Гос-
гтройиздат, ГЕЛ.
•И Ч у д и о в с к и й В, Г. Методы расчета ктобанпй и
тстсФчмвосги стержневых пмцы П-щ-во АН УССР. Енов, 1952.
15.	Ill V Н Л И Ф Ъпрпя К'-ИОНПЫ ОТ ППОД-ХТОМ УПШГОГЫ!
(пер. с англ.). В сборнике переводов «Механика (ПЛ)», № 2,
1951.
49,	Ш татр м а н И Я . II и к о в с к и й А- А. Основы
теории устойчивости строительны \ конструкций, Госс!ройп5да г,
1939.
47.	Я с и и с к и й Ф. С а) Устойчивости деформаций и ста-
тика сооружений, 2-е изд., Спб,, 1992. б) Избранные работы по
устойчивости сжатых стержней Гостехтсори 1дат, 1952.
48.	Beck М. Die Knicklast des cinseitlg eingespannte. tan-
gential gedruckten Stabes «Zcitschr. angew. Math, und Phys,»,
№ 3. 1952,
49.	G h w alia E. Theone des aufJcrmittig gedrfickten Stahes
aim Baustahl. «Shihlbau», № 21, 22, 21 1934.
50.	Engesser F. Vber Knickfe.sdgkeit gerader Sfabe.
«Zeitschr. Arch.- und logon, in Ilannoxer», Bd. 35, I88D.
V
,5k	.1 e z e k K. Dio Eestigkeit von Druckstaben aus Stahl.
Springer, Wien, 1937,
52	К а г hi a n Th Dntersuchnngon uber Knickfesfigkeit. Mif-
tcihingon iiher E’or.x-hungsarbeiten ain dem Gf-Mete des Inge-
r).iniinve*ens «Zmtsrhr VDD, №81. ’919
52a Korda s 7. SEatec znosc cprezyscie uf и icrdznncgo pre-
ta ы пюш’Ц!-) xv ogblnym przvpadkii z.cchou ania silo obciazcni.i.
«Rozprayy Inzynier-Aie», № 3, 1963.
53	Mises I? . Ratzm-dorler J a’ Die Knicksichcr-
heit Ю! f-ach", 11 ken №ik,hr жю. 4,11ч innl Mecli », № 3,
lr)23 b) Die Knu-kMchtrhi-it vjii RdhmvrHraguerken. «Zcibi.hr
ang-ew, M-r,th tmd Meeh / , № 3. 1926
51, Pilugpf A, btabilriatsprobl’Mne dor ElastostMik. Zxcci-
te A’bgabe, ^pitnger, Wien. 1№1.
55 Weinhold J a) Zur nahoenng-v. ы-'оп Рюш hniing
ПгцскЬшцеыаЬю in Lcion'.inetzillban  Мытным ibusselckr'E,
•У. К), Ю; № 1, 197E. b) Era юр шшл’цеп юн DniokhicgcWiheb
ль AE'ininniny. «Aluminium (Du-.-e[clorf)>-, A? 3, 1938.
Лоно /ним ibiiyio линр-nvp) /'m. в i м 1ьдл/<ц1 ^Слграыюни
ка проектировшдка». чтр. 4)8 и след.
К. И. 17.13
I.	В л о й х Ф. Устойчивость металличюких кот тракции
(пер ‘ чем.). Физмитгик 1959.
2,	Борисов Е. В. Уклончивость оюим цчшы< ребрами
по 1ох тонкостенных профилей С.МРС. Рыб, № 2.
3.	Ьрьуде Б. М. Об усюйчивосы! с/Катых полок профи
лен, усиленных бульбами. Сборник НИНИСК, «Псследование гь>
мегалличеч ним конструкциям-’.. I построив щи, ГДЕ.
Е Ь р о у л с Б. М. и Ч у в и к и н Г. .М. Обоснована ьц
которых ыпхобов расчета на югойчивоею в CEI 113-60, Сборню,
мыей '•-Строительные колегрккции ш алюминиевых сплавов ,
Госспрогш 1дат EJ62.
5.	Ъ роуд е Б. М, Тюрин устойчивости и принципы рас-
чета конструкций. Сборник .-окладов ^Проблемы у стойчпвос'д и
в crpniri сливой механике- I отчройнздат, ЕбЦ,
Н. Б р оу де Б, Ж Пр^д^льныс согг'очиц.ч стальных балок
Госегройиздаг, 1951.
7.	И «мер м а я А. Г. и М оживит и н В, С- Экспгри-
м>'!:га гьиыс исследования местной ссюйчнвоети уголковых про-
фи юй in сплава ДИ-Т. Сборник статей ^Строительные конст-
рукции из алюминиевых силанов». Госсгройн 1даг, 1962,
8,	Леитое С. Д, Устойчивость внецснтренно-с/.катогг> уп-
руго-тастнчсчкого стержня 11 обратного сечения. •сМатерни-ты
по металлическим конструкциям», вып. 11. Госстройнздат, 1966.
9,	М > е к в и т в н В. С. Практический способ расчета сжа-
тых страной из алюминиевых ытлавовна местную устойчивость,
РПК, вып, 9, Стройнздат, 1964.
И; Хертель Г. 1 пнкостениые конструкции (пер. с нем).
«Матиносгроонне» > 1965,
!! В i j 1 а а г d Р. Theory of plastic buckling of plates and
аррЕюЧот] io sjmp.lv supported plaios subjected to bending or
eccentric eompres-Jon in their plane, «Journal of applied mecha-
nic1'», lrSA, № I, J956.
12 В 1 j 1 a < r d P Buckling of pkafos under nnn-homogc-
инти .tress, -Tree amor. -дс. ^ivil eng.c, «Journal of the eng.
mech div » EM-3, 1957.
is 1) n •, j d s о n J Flange bucklingin a bent I-sedion
he'im, v.loHrnU of die mcehmic-' ami phvsic' oi snlicE,, London,
X E № 1, 1951.
I L S и t I e r K. Tho Joe d btickhng of aluminium plate de
пцп’Е, «Sheet rnetal пиЕтИт.-о № 1. I’M)
E5. СНиП П-В..3-70 Стал>.пыс конструкции. Нормы проекти-
рования Стройиздат, 1971
1о.	СНиП П 13 5-14 Д -цоминисчые кокы'рт кцнн. Нормы про-
ектирования. Стройиздач 19'эЗ,
К п. 17,14
1	Б р суде Б, <М, Предельные состо-п-нт стальных ба ток.
Строки здат, 1953,
2	. Вл асов В.. 3. Тонкостенные упругие стержни. Госстрои-
издат, 1941).
3	. DIN 4IH, Richtlinien-
4	N vlan dor H.r AbhadL Schwerk Ingemeurv. is-, Akad ,
Bd 174, Stokholm. 1943.
5	. Жуков A. M., Работнов Ю. IE Исследование
плапичсеких деформаций стали при сложном нагружешш
vIIh/K сборник;, .№ is, 195-Е
6	S t u s ьМ F. Die GnindLagen dec iTxithcmad-mhen PlaHH’-
iMstheone und VerMieh, ZmHt'hr. fiir angew. Math, und Phvsik,
voL L Ease. 4, EM).
7	, СНиП, II-B'1624 Стальные конструкции, Нормы проек'.и-
ровашы. Стройнздат, 1969,
РАЗДЕЛ 18
УСТОЙЧИВОСТЬ ПЛАСТИНОК и ОБОЛОЧЕК.
РАСЧЕТ ГИБКИХ ПЛАСТИНОК
18.1. ОПРЕДЕЛЕНИЯ И ОСНОВНЫЕ
ОБОЗНАЧЕНИЯ
Критическим напряжением для пластинок называют
напряжение, до которого исходное равновесное состояние
является устойчивым. Если выпучивание пластинки как
э гемента конструкции считается недопустимым, то напря-
жения от расчетной нагрузки должны составлять извест-
ную часть от критических Для пластинок, закрепленных
по краям и подвергающихся деиствш-о сжатия ити сдви-
га, потеря устойчивости не связана с разрушением; в за-
критической области пластинка может нести возраста-
ющую нагрузку.
При расчетах оболочек на устойчивость следует раз-
личать верхнее и нижнее значения критического напря-
жения. Под верхним критическим напряжением подразу-
мевается напряжение, до которого исходное равновесное
состояние является устойчивым «в малом», т. е. по от-
ношению к весьма малым возмущениям.
Нижним критическим напряжением называют напря-
жение, до которою исходное равновесное состояние яв-
ляется устойчивым <'В большом», так что исключен пере-
скок от начального состояния к другому состоянию,
характеризуемому большими прогибами.
В реальных конструкциях оболочки обычно имеют на-
чальные прогибы, сравнимые с их толщиной; выпучива-
ние оболочек происходит при напряжениях, лежащих
между верхним и нижним критическими значениями.
В практических расчетах оболочек на устойчивость
следует определять как верхнее, так и нижнее значения
критических напряжений. Напряжения от расчетной на-
грузки должны составляю известную долю от верхнего
критического напряжения [б, 1967 г., стр. 544]. Выпучи-
вание оболочек обычно сопровождается резким хлопком,
в процессе которого возникают пластические деформа-
ции; потерю устойчивости оболочек надо считать равно-
сильной разрушению. Более подробно см. [6].
При расчете гибких пластинок (см, 18.6) рассма:ри-
вается действие нагрузок, перпендикулярных срединной
плоскости. Подобные нагрузки вызывают изгиб пластин-
ки и деформируют срединную плоскость в срединную
поверхность. Если при этом в срединной поверхности пе
появляется значительных растягивающих или сжимаю-
щих напряжений, то пластинка называется жесткой пла-
стинкой или плитой, а в случае если эти напряжения
значитетьпы •—гибкой пластинкой, Если растягивающие
напряжения в срединной поверхности столь велики, что
по сравнению с ними wui.no пренебречь напряжениям:!
от изгиба, то нласшпкр шыываюг мембраною Переме-
щения точек срединное цщскости по перпендикуляру к
ней при деформации называют прогибами пластинки ч
обозначают через к! Принято считать, что теория гибких
пластинок применима при / —	- 6 Пластинка,
4
в которой прн ее нагружении напряжения пе превосхо-
дя; предела упругости, называется упругой. Здесь будут
рассмотрены упрутие тонкие гибкие пластинки.
Основные обоз паче н и я:
I—юлщииа пластинки или оболочки;
а. — сторона прямоугольной пластинки; радиус
круглой пластинки;
6--сторона прямоуго’пшои пластинки; внутрен-
ний радиус кольцевой пластинки;
R — радиус срединной поверхности круговой ци-
линдрической или сферической оболочки;
I — длина цилиндрической оболочки;
х, у—координаты точек срединной плоскости пря-
моугольной пластинки вдоль сторон а и Ь;
р—интенсивность поперечной нагрузки (прило-
женной по нормали к поверхности);
f—стрела прогиба (наибольший прогиб);
f ,
. -- — —безраз?<1ер.1ая стрела проптоа;
ох, — нормальные напряжения в срединной плос-
кости пластинки (в расчете гибких пластинок
различают нормальные напряжения изгиба
и растяжения срединной поверхности, обоз-
начая их дополните тьиыми индексами «и»,
«с», например: о\и, О’1)г);
т —• касательные напряжения в срединной по-
верхности;
Е, G—-модули упругости материала при растяжении
(сжатии) и сдвиге;
р, — коэффициент Пуассона;
ЕР
7г(Т^ст
— цилиндрическая
жесткость.
18.2, УСТОЙЧИВОСТЬ ПЛАСТИНОК
В ПРЕДЕЛАХ УПРУГОСТИ
18.2.1. Прямоугольные пластинки
а) Сжатие усилиями, равномерно распределс'жыии по
прайм х — 0 и х = а (рис, 18,1).
Критическое напряжение
л2О
л-Е
12(1 -- рф
(18.1)
Коэффициент К зависит от граничных устовии и от-
ношения сгорои пластинки. Значения коэффициента Д'
Л :я рамшчных трашпшых условий приведены в табл,
18.1—18.5.
На рис. 18 2 приведены графики но которым можно
опреде шть значения К при опюшшшях а/b, не поме-
щенных в табл, 18.1 — 18,5.
182 УСТОЙЧИВОСТЬ ПЛАСТИНОК В ПРЬДЕЛУХ ' ПРУГООТИ
о) Еигир' ни ромяш раснрсде leHHoi'iu вбочь
крае г ~0 л х = а (рис 18 3) по шнтнону зако'у
а
а
b
К ритп I
1>О[ чу
KOI I, 1
кое
(В 1)
я
ьи. ир
и inp 1/кечие (о 0);п опредетяется по
ia (опия Koabipi ц шита К дтя с р, 1ая
пени и шпнрио оперю, приведена!
и
а
лР 12 В
В ।

'У
Рис 18 1
6
1 1я едчая vnpyioro ззщемтсют по
И ипшшрноео опирания OCTrf 1Ы1НХ
И ( У
котфЛи’шонгы А даны в юбт 18 9
з Снапп ch н ч сосредоточь снычи сенат при ю-
iuimni в серединах бог^шнх сюрсн (рис 18 4)
Крита и ск я сп ia.
Lt'3
(1 — и-3) о
(18 2)
11Я С I}1 <я
nitnrli ЗН 1ЧСПИЯ
В iae 3t пн
КО1ДЭ вс«
К I ши в тает А 19
пения всех xp<es и пеппыи
~Г/!	/ о \
крв п петиции
шарнирно
Чр 1 ш яси ш
оиир лч I по краям
Рк О — ,
и
—-------ПрИ ---- о
(1 upb \ Ь
по кр ям л - 0 г -а
и — 0 у — b
ЕР
а
, при —
(1 — р-) b \ Ь
(18 3)
И цпрырно,!
(18 4)
Таблиц] 18 1
Значения коэффициента А в формуле (18 0
а/ b
гран мт m в^я	0	° j	0 о	) h । 0 7	0 3	0 0	00	1 1	1	! 5	I 1	! а	i 1	1		От
Все края n^KTiiki 1 пр .s 1рн( опеп 1	27	nJ? 11	6 25	! 5,14 । 4 53	4,2	1,04	4 0	1 01-	4 В	4 28	4 47	1 И	4 „	4,08	4 Пэ	1 9
Значения коэффициента А в формуле (48 П
Т а Г I : ц а 1^2
	1 p-H I	Ш I	Т0ЙИЯ			и/Ь									
						0 6	0 я	1,0	1,2	1 4	1,6	I я		О 0	
3 е края та пи		И1	n rH_ л ы				—	9,4	9,3	в	8, з	8 э		S	7 0
Зашл пне ( м опщшп	ГН крэ I / I т Ш НЫХ		0 И 17 Ktsae?	п тпч	ар -п р	7 Оэ	7 О	7 69	7,15	7		7 Оз	7 )		7,
8 -1 Hl ( f Hl Ц 1 HI p 11И1	П h.p 1	U 14	(1 И X spiel	i при	ринр	1 8	b ”	Ь 74	5 М	- 1,	М		1 S	1 В	1 0
Ш дрш p i J 3 IИ	J	I p in M	1 ) ! (!	чраim г и при	0 j 3	1 I	и а 1 кр 1			1 7	1 7	1 4	1 1	1	1, 3	1 зь	i 1
Ш рн ip НрИ П’О ш	ИТ ф 1H hp	no / h	краям л	0 А	и (/-О	5 О	„ 1	1 И	1 И	М5	FU	п 7о	0 7	п эо	О 46
272
РАЗДЕЛ IS УСТОЙЧИВОСТЬ ПЛАСТИНОК и ОБОЛОЧЕК РАСЧЕТ ГИБКИХ ПЛАСТИНОК
г) Касательные ушлая, равномерно распределенные
по hie I ораче (рис 18 5)
Критическое напряжение сдвша (при а/Ь)
zE Е ( t У
1л₽ ~ К 12 (1 — (Р) \ Ъ ) ’
(18 5)
При шарпирчем опирании всех краев К 5,344-
Зиа кчшя коэффициента К для других граничных ус-
ловия нрг^едсоы в табл 18 11
Рис 18 3
Т а б л я ц а 18
Значения коэффициента К в формуле (18 1) для случая
одинакового упругого защем пения по краям а 0,
и шарнирного опирания остальных краев
а	6/к/7Ж					
	0 25	'>,5	1,0	2 0	10	10,0
( Ф /6	6,8 1	i, 09	7,51	7, I? и, 64	7,37	7,61
	□до	п, 1 ‘	ь, В		b 85	b,9b
0 7	5.U	5,61	6 Об	1 ’	6 i 7	6 86
0,8	1/ы	5, 12	л,97	6, И	ьдп	7,08
0,9	/81	э, 56	д,99	h h 2	“ • )	7 5
1 0	/79	5, б	6 14	ОД '		7,6 i
Табыщ а .18 6
Значения коэффициента К в формуле (18 I) для случая
шарнирною опирания всех краев
Рис 18 4
Рис 18 5
Значения коэффициента А' в формуле (18 I) для случая упругого
заедем лечня края /-=0 и шарнирного опирания остальных краев
а	Ч2°»						
h	0/6	ОД	1,0	2,0	’°	6,0	1(\0
ОД	6Д2 5, /	6,63 5 ДМ	о,71 5,70	6,77 5,79	6,41 5,45	6,82 5,87	6,83 5,89
	1Д5 4, io	5, оз 1,75	5,10 1,06	5, 52 5,В	5, 10 5,25	5, И 5, 10	5,4ь 5Д 1
: U1	//	4, hl 9 ,64	/80 /95	5,11 5,21	5,28 5,43	5, 10 5,52	5 Ю 5, <41
	- уке~ТК( Нн’М кр	к ть н з кг1 чеяш Ребра, ко (\1ршнрчгет степет-			примы ь заще=*	сающегс 1ЛС51И Я)	к за
Таблица 18 3
1 а б 1 иц а 18 1
Таблица 18 7
Значения коэффициента К в формуле (18 1) для случая
шарнирного опирания siex краев при а 5
a 0	0 ‘8	0,31	0, Ю	o, u	0, in	0,52	ОД8	0,64
Л	b3,11	0\Ы)	1,32	53,28!	3 5Д/	51ДЗ	57,02	60,03 
Значения коэффициента К в формуле (18J) для случая упругого
мления края х 0 и шарнирного опирания остальных краев
6 а	G/JDn					
	0,25	0.5	1,0	2,0	4,0	10
0, 55	4,08	4/И	4,10	4,11	4,11	U!
0,5	4,16	0,19	4,21	4,23	4,24	1,21
/9	1,42	1, 16	о,Ы1	1,70	4,77	4Д2
д>	5,10	5, 19	5,7 b	6,1.1	6,4b	6,7.
/6	<- , 70	7 До	7,60	6 26	дод	9,68
	6,47	н,28	4,0 1	10,89	f /по	1 1, Т>
А1	11,50	1 ,02	12,77	В/Ч	15 Г	17, 0
Таблица 18 Я
Значения коэффициента К и формуле <18 t) для случая
шарнирною опиоания всех краев при а - 4
a b	одо	0,25	0,30	0, Й	0Д5	0,45	0/48
к	И6,о	(П/h	97, 3	06,2	96,3	103 Д	Ю7Д
18 2 УСТОЙЧИВОСТЬ ПЛАСТИНОК В ПРЕДЕЛАХ УПРУГОСТИ
273
Таблица 18 О
Значения коэффициента К в формуле (18 О для случая упругого
защемления по краям у—О, у г> и шарнирного опирания
остальных краев
	а Ь	С/К/Де					
		0,23	0,50	1,0	2.0	-1,0	10,0
	0,5	12 8?	13,37	1 5,86	14 23	14,46	14,62
	о о	11,03	11 69	12,33	12,87	13,23	13,48
	0 7	10,22	10,86	И 72	12 14	12,96	13,35
	0 R	ч 60	10,50	Н 55	12 55	13,26	13,83
	0 ')	0 11	10, 12	11 h*	12,<14	13,93	14,74
	1 0	0, 10	10,52	1J 90	13 54	14 16	14,62
	0,1	И 05	16 01	37,70	40,0 5	39,80	10,3’
	0,5	зо аз	32,85	55,17	17 01	38,24	39 10
2,0	0,0	20, * 1	31,00	51 42	37,52	30, 35	10 72
	0,7	20,00	32 17	55 01	30 41	12 06	44 14
Таблица 18 10
Значения коэффициента К в формуле (18 2)
Граничное условия	а/Ь			
	1,0	2,0	з.о	-о
Все края пластинки шарнирно оперты	1,49	1,03	1,00	1,00
Таблица 18 11
Значения коэффициента Л в формуле (18 5)
Грачи шые условия	a h					
	1,0	15	2 0	2 5	’° 1 -	
Все края пласгинки	1 1 ЗА	11,90	1 0 On	10,85		8,99
Ш эпннрчо^ опирд нис по крым Л 0 и						
х — а защемление по краям у-0 п (/-0 Зещем чение	по краям л—0 и л а	12,28	11,12	10,21	9,81	61	8,00
шармгрное опирание по краям у=-0 и и=-Ь	12	7 7?	6 70	6, -10	6,17	5,35 	
Таблица 1812
Значения коэффициента А для случая шарнирного опирания
всех краев
а b						
	0,2	0, 1	0,6	0,3	1,0	2.0
1 0	3, 36	2 85	.,50	2,22	2 00	1,33
2 0	3, 7b	2, (0	1,84	1,40	1,25	0,60
3,0	3,21	4 >	1,71	1,36	1,11	0,58
№	3,20	2, 40	<>67	1,25	!, 00	0,50
На рис 18 6 приведены графики с помощью которых
можно определять значения /( при отношениях а/b, не
помещенных в таблицах
д)	Одновременное скатив усилиями, равномерно рас-
пределенными в двух направлениях (рис 18 7).
Отношение сжимающих усилии задано
Критическое напряжение определяется по форм), да
(18 1) Значения коэффициента К для случая шарнир-
ного опирания всех краев даны в лтбл 18 12
Рис 18 7
Для случая, когда все края плдатлнкп тори 1рно опер-
ты, рекомендуется также пользоьагь..я форм), юи
in- я3	Et- tm- п- \
<М “ +	““ = 0,823 ~-----~ ~Г + ДТ • 08 6)
a- b-	(1 — Ц-) \ а- Ъ- )
где tn и п—числа полуволн г направлении > и у соот-
ветственно
Если ох удовлетворяет неравенству
/	а4 \	/	о" \
с 1-4 77	<Е. с 5 - 2-уг ,	(18 7)
\	о4 /	\	Ь- )
где
0,823 rt^
с~' (ГТиС’
то для нахождения гт„ кр при заданной гшччине <тг под-
ставляют в формулу (18 6) т~ 1 и п = 1
Если <3х велико и не удовлетворяет неравенству
(18 7), в формуле (18 6) берут п=1, а величина т опре-
деляется из условия
/	а“ \	I	а~\
с 2т- — 2т+Н-2 — охх с\ 2т-^'2т ф 1 -ф 2 — .
\	Ь~ J	\	Ь- )
Если Ох мало и да удовлетворяет неравенству (18 7),
в формуле (18 6) берут и=1, а величина п определяет-
ся из условия
Г,	°4 1 Г	а1 ]
с 1—и2 (п —I)3--- о\ с 1—ч- (о - I)2— .
18—26
274
РАЗДЕЛ 18. УСТОЙЧИВОСТЬ ПЛАСТИНОК И ОБОЛОЧЕК. РАСЧЕТ ГИБКИХ ПЛАСТИНОК
Для случая, когда все края пластинки защемлены,
формула для определения критического напряжения
имеет вид
(18.8)
По заданному одному из двух напряжений находится
значение второго напряжения, при котором пластинка
Рис. 18.8
Рис, 18.9

теряет устойчивость. Уравнение что приближенное н да-
ет хорошие результаты для квадратной пластинки и при
<7,т Яе О’
е)	Совместное действие усилий сжатия (растяжения),
равномерно распределенных по краям х — 0, х — а, и ка-
сательных усилий, равномерно распределенных по всем
краям (рис. 18.8).
Все края пластинки шарнирно оперты. Формула для
определения критического напряжения имеет вид:
где (То и тц — критические напряжения сжатия и сдвига
для пластинки заданных размеров и граничных условий
при раздельном действии усилий сжатия и сдвига.
По данному уравнению могут быть найдены критиче-
ские напряжения, если задано отношение <>кр/ткр или
задана одна из этих величин.
В случае растягивающих усилий первому члену в ле-
вой части уравнения должен быть придан знак минус.
ж)	Совместное действие равномерно распределенных
по всем краям усилий сжатия (растяжения) и касатель-
ных усилий (рис. 18.9).
Если все.края пластинки шарнирно оперты [19]:
(18.10)
Для случая, когда все края пластинки защемлены [19]:
В обоих случаях
0,823 Е I I V
с ~ -—'—~	.
1 — р." \ b J
При растяжении оу и о,, отрицательны.
з)	Совместное действие изгибающих усилий по кра-
ям х — 0, х—-а и касательных усилий по всем краям
(рис. 18.10).
Рис. 18.10
Если все края пластинки шарнирно
тнческие напряжения определяются из
оперты, то кри-
зависимости:
(18.12)
(ткру
1 bJ
где о„ и То—критические напряжения изгиба и сдвига
для пластинки заданных размеров и граничных, условий
при раздельном действии изгиба и сдвига.
По данному уравнению могут быть найдены критиче-
ские напряжения, если задано отношение Окр/ткр пли
одна из этих величин. Можно пользоваться также фор-
мулой (18.1), где Л' зависит от т/то (отношение действи-
тельного напряжения сдвига к критическому напряже-
нию сдвига при отсутствии изгибающих усилий) и отно-
шения а/b. Коэффициент Л' отклоняется менее, чем на
10% от значений, данных в табл, 18.1 и 18.2 для величин
а/b, равных 0,5—1. Для а/Ь=1 значения коэффициен-
та Л’ приведены в табл. 18.13.
Т а б л и ц а 18.13
Значения коэффициента А' при и>--1
2	9	0.2	0,3	0,4 । 0,5	0J)	9,7	0,8	0,9 ।	1.0
к	25,6	24г8	23,8	22,5 । 21,5	19,5	17,0	14s5	9,95 ।	о
18.2.2	. Прямоугольные и квадратные
пластинки, подкрепленные ребрами
Сжатие усилиями, равномерно распределенными по
краям х = 0 и х~а.
и)	Одно продольное ребро, делящее пластинку попо-
лам (рис. 18.11).
Все края пластинки шарнирно оперты. Критическое
напряжение определяется по формуле (18.1). Коэффици-
ент
(1 4-6-)--;-2у
₽=(1-%2б) ’
(18.11)
Рис. 18.11
132 УСТОЙЧИВОСТЬ mXCTIIIIOK В ПРЕДЕЛАХ УПРУГОСТИ
275
Таблица 18 14
Значения коэффициента К для случая одного продольного ребра
				у — 19			у ~ 15			? = 20			Т = 25		
0	о	2	о	1/0	о	о	о	2	О	О	о	О1			°
		II	°	II	И	о 1	т	II			р	1”	II	°	°
	«г	о					3	ю	-о	-	о	ю	ю	г-	-О
	16,5	16,5	16,5	16,5	16,5	16,5	16.э	16,5	16,5	16,5	16,5	16,5		16,5	16,5
0,8	15,1	14,0	13	16,8	16,8	16,8	16,8	16,8	16,8	16,8	16,8	16,8	16,8	16,8	16,8
1,0	12	11,!	9,72	16	16	15,8	16	16	16	16	16	16	16	16	16
1,2	9,83	9,0о	7,88	15,3	14,2	12,4	10,	16,5	16,5	1В, 5	16,5	16,5	16В	16,5	16,5
1,4	8,62	7,91	6,82	12,9	12	10,3	16Л	15,7	1 1,6	16,1	16,1	16,1	16 1	16,1	16,1
1,0	8,01	7,28	6,32	11,4	Ю, 5	9,05	11,7	13,6	11,8	16,1	16,1	1 1 1-	16,1	16,1	16,1
1,к	7,84	7, 19	6,16	10,6	9,7	8,35	1.5,2	12,2	10,5	15,9	14,7	12,6	16,2	16.2	14,7
2,0	7,95	7,29	6,2 1	10,2	9,35	8,03	12, 1	11,4	9,8	14,6	13,4	11,6	16	15,4	13,3
	8,28 Я 79	7,68	6,5 6,91	10,2	о, >.	7,99	12	11	9,45	13,9	12,7 12,4	10,9	15,3	14,5	12,4
2, i		8.05		10, 1	Ч, }'.)	8,15	11,4	10,9	9,37	13,5		10,э	15,1	13,8	11,9
-М	9,27	8 5	7,28	10,8	».8>	8,48	12, 1	11,1	9,53	В,5	12,4	10,6	14,8	13,6	11,6
2,8	8,63	7,91	6, И	И, 1	19, 4	8,94	12,5	I ‘ ,5	9, Во	В,7	12,6	10,8	14,8	13,6	11,6
3,0	8,31	7,62	6,53	12	11,1	Г) ДО	13, 1	12	10,3	П,1	13	11,1	15,2	13,9	11,9
о )	8,01	7,28	6,32	11.1	10,5	<’,05	п, 9	12,7	10,9	14,8	13,5	11,6	15,6	14,3	12,3
3,6	7,84	7,19	6,16	Ц),п	9,?	«,55	1 3,2	12,2	10,5	15,9	1 в 7	12,6	16,2	15,7	13,5
1,0	7,96	7,29	6,24	U), 2	9, 15	8,0^	12,4	11,4	9,8	11,6	13, 1	11,8	16	15,4	13,3
Таблица 18 15
Значения коэффициента К для случая двух продольных ребер
|3	V =	10 3	у = □		у	20 3	у — 10	
	6=0,05	б— 0,1	8=0,05	6—0,1	6=0,05	6=0,1	6=0,05	6=0,1
: 0,6	28,6	24,1	36,4	33,2	36 1	36,4	36,1	36,4
 0,8	16,9	15	23, 3	20,7	.9,4	2о,3	37,2	37,1
1,0	12,1	10,7	16В	14,5	20,5	13,2	28,7	25,6
1,2	9,61	8,о1	12,6	11,2	15,5	13,8	21,4	19
1,4	8,32	7,36	10,5	9,32	12,7	п,.з	17,2	15,2
1,6	7,7	6,81	9,4	8,31	11,1	9,82	14,5	12,8
1,8	7,51	6,64	8,85	7,83	10,2	9,02	12,9	11,4
2,0	7,6!	6,73	8,7	7,69	9,78	8,65	11,9	10,6
Все края пластинки шарнирно оперты. Критическое
напряжение определяется по формуле (18.1), коэффи-
циент
(1 -ф 6=Р + 3?
К Р(1+Зб)
Значения коэффициента К для некоторых величии
Р, у и б приведены в табл. 18.15.
я) Число
Вее края
напряжение
продольных
пластинки )
>ис. 18.13).
ритическое
= 3,38
Рис. 18,13
Рис. 18.14
(18.13)
где с—расстояние между продольными ребрами; пред-
полагается малым по сравнению с а.
г) Одно поперечное ребро,
(рис. 18.14).
делящее пластинку пополам


где
„	а	В	,	F
Р _	—-	—	р =	—,
b	b.D	Ы
В — жесткость при изгибе ребра; F— площадь сечения
ребра; D — цилиндрическая жесткость пластинки.
Вычисленные значения коэффициента К даны в табл.
18.14.
Значения Л’, стоящие в таблице над величинами, по-
казанным» жирным шрифтом, те же, что и для свобод-
но опертой пластинки с шириной, равной 6/2.
б) Два продольных ребра, делящих пластинку на три
равные части (рис. 18.12).
1Г
Рис. 18.16
Дк. 18.15
Все края пластинки шарнирно оперты. Критическое
напряжение определяется по формуле (18.1), причем

(1 Д °ф2Щ27фЗ
276
РДЗДГЛ 18 УСТОЙЧИВОСТЬ ПЛ4СТИНОК И ОБОЛОЛГк PTC4FT ГИБКИХ ПЛАСТИНОК
В табл 18 18 чаны предельные значения у при кото
рн\ выпучнванит пдастинк? не сопровождается потерей
устойчивости ребер
д) Три одина^оныт хюперечных ребра распо wwcn
ных на одинаковых раглточниях (рис 18 15)
Все кр п тастички ппрнирчо оперты Крили i слое
итпряжсичс ОПр.-ДСЛЯСТсЯ формулой (18 1)
л <1 R- 1 2у[Ф
(Ф
Предельные шот лм у приведены в табл 18 17
Таблица 18 17
Все края тастиши шарнирно оперта Критическое
иапряж.еши определяется по формуле (181) В табл
18 20 даны предельные значения Л
г) Енндратнач (пряпорготьнач) пшетинка, подарен
юнная диагоналъныч рхбром (рис 18 20)
Все стороны шарнирно оперта Криптасдое папрч-ке
нис для каждой из треугольных панелей
Et" д’
(18 15)
3,07 а2 (1 — р2)
Предельные течения у ччя с зуччя трех поперечных р»бер
₽	0 (э	0 о	|	1		1 2	1, 1
V ;	101	15 л	21 7	12 4	",71
е) Чигш г оперенных.
Ви края птастинки
напряжение
сдр~ 0
ребер ею тыне трех
шарнирно оперты
(рис 18 10)
Критическое
(18 14)
где с предпо пгается малым по сравнению с Ь
Действие касательных усилий,
равномерно распределенных по всем
кромкам
Т а б а и ц а 18 18
Предельные значения у для глучач одного поперечного ребро
а Ъ	2	1 9	1,^	1
В ? ~ — D а	0 83 j 2 Q		6,3	В
Таблица <8 13
а)	Одно поперечное ребпо, дс тчщее пыас-'ннку нопо
iav (рис 18 17)
Ви края пласн’икч ш цтнирио оперты
При Никоторые пре то шных ша юниях жесткости В
ре бр i каждая потомка п •‘анютки бу дот выну шпат! с л
кал прямоугольная плас пиша рапирами а/Ч п b со све
бо ню отертыми краями а ребро осг,к гея прямым Со
ответствующис значения у таны в табл 18 18
Предельные значения у для случая двух поперечных ребер
а	3	2 5	9	1 8	1 2
В у ~ Г) а	о , Ь4	1 °7		Ю 7	22,1ч
Нагибная жесткость диагонального ребра должна
удототегворять неравенству [17]
0,5806
У
Рис 18 19
аО Е
12(1 -Й
при этом ребро сохраняет свою прялюлинейную форта/
вплоть до выпушванпя треугольных панелей
б)	Два поперечных ребра /Ытацтпх птастпнкр на т)ч
ранные чагти. (оа 18 18)
Вы кр ш пластинки иирчирпо ошрта Предельны
знач< ния у даны в таб i 18 19
н) Тюннач, прчаор, о ынат п ш гпткн с несношкичи
предо in ил tu реорачи (рис 18 19)
Чистый изгиб
а) Одно предо тьное ребро на расстоянии К пт сжато-
го края (рис 18 21)
Все края прямоугольном пластинки шарнирно оперты
Прибтиженпая формула дтя наибольшей возможной вс
18 2. УСТОЙЧИВОСТЬ пластинок б пределах упругости
277
личины ур при заданных ЬДЬ и А' может быть представ-
лена в виде [1]
•’р = 7р
+ 6с,
(18.16)
где
F
б = —
Ы
Значения у^ даны в табл. 18 21.
Таблица 18 21
Значения -А
ЬрЬ			0,25	
к	50	50	ЪО	70
V1'	3	2,6	3,0	7,3
р				
с	36	56	92	107
Для указанных в таблице значений ф/6 и К величи-
на F/bt не превосходит 0,06.
Кроме того, можно пользоваться следующими при-
б л п ж е ш I ы м и ф ° р м у л а и и •’
если К=80
(18.16')
(18.16")
Граничные кривые для комбинации чистого изгиба
с чистым сдвигом для пластинок, укрепленных продоль-
ными ребрами, а также о влиянии упругого защемле-
ния продольных сторон пластинки на критические уси-
лия см. (1].
18.2.3.	Несущая способность подкрепленных
ребрами прямоугольных пластинок
после потери устойчивости при сжатии,
сдвиге и чистом изгибе.
Редукционные коэффициенты
Прямоугольная пластинка шарнирно оперта на ребра,
Жесткие по отношению к изгибу.
а)	Сжатие в направлении стороны а (а'щ Ь)
В этом случае после потери устойчивости пластинка
может нести возрастающую нагрузку, превышающую
значение критической нагрузки.
С увеличением нагрузки закон распределения напря-
жений в срединной поверхности меняется. В то время
как в центральной части пластинки напряжения мало
отличаются от критических, в краевых полосах, приле-
гающих к продольным ребрам, напряжения пропор-
циональны (в пределах упругости) относительному сбли-
жению нагруженных кромок е:
ор = Ее.	(18.17)
Эпюра сжимающих напряжений по ширине пластин-
ки приведена на рис. 18.22.
Нагрузка, воспринимаемая пластинкой после потери
устойчивости, определяется по формуле
Этот коэффициент определяется по следующим форму-
лам:
— при проверке прочности перекрытий, состоящих из
значительного числа смежных наиелеи обшивки, под-
крепленных жесткими иа изгиб ребрами;
ф_|/щ	(13.20)
—при проверке прочности изолированных панелей и
конструкций, состоящих из обшивки, подкрепленной от-
носительно небольшим числом ребер.
В формулах (18.19) и (18.20): окр— критическое на-
пряжение для пластинок заданных размеров; ар — на-
пряжение в подкрепляющих ребрах.
Несущую способность пластинок определяют обычно
из условий прочности и устойчивости подкрепляющих
ребер,
б)	Действие касательных усилий т (рис. 18,23).
Пластинка может нести после потери устойчивости
возрастающую нагрузку, во много раз превосходящую
критическую В случае тонкой длинной и частники (а ДЬ)
при значительной деформации образуйся диагональное
поле растяжения с ярко выраженными наклонными
складками.
Напряжение растяжения
Щ =	'(18.21)
sin 2а
где а— угол между направлением складок и длинной
стороной (близкий к 40°).
Главными напряжениями сжатия а2 можно прене-
бречь.
18.2.4.	Непрямоугольные пластинки
а) Круглые пластинки под действием сжимающих ра-
диальных усилий, равномерно распределенных по кон-
туру
1) Сплошная пластинка (рис. 18.24), При
шарнирном опирании по контуру
л3 Е / t V
Окр—0,425	----у — .	(18.22)
12(1 -- Ц“) \ а ]
При защемлении по всему контуру коэффициент К в
формуле (18,22) вместо 0,42,3 равен 1,49.
2) Круглая пластинка с отверстием
(рис. 18.25). Критическое напряжение определяется по
278
РАЗДЕЛ 18 УСТОЙЧИВОСТЬ ПЛАСТИНОК И ОБОЛОЧЕК РАСЧЕТ ГИБКИХ П 1АСТИНОК
формуле (18,1), Для случая опирания по внешнему кон-
туру при свободно смещающемся внутреннем контуре
значения коэффициента К приведены в табл. 13 22 и
18,23.
б) Эллиптическая пластинка под действием г''нимаю-
щих усилий, равномерно распределенных по контуру
(рис 18.26).
Рис. 18.26
Табл и ц а 18.22
Значения коэффициента К при шарнирном опирании
но внешнему контуру
1 а b	0		1		2		3	
1 к	0,425		0,4		0,265		0,328	
	Продолжение табл 18.2'2							
а b	4	5		6		7	|	8		9
к	0,28	0,256		0,231		0,219	0,207		0, 195
Таблица 18 23
Значения коэффициента К при защемлении по внешнему
контуру
ь а	0	0,1	0,2	0,3	0,4	0,5
к	I, 19	1,43	1,35	1, и	1,79	2,5'2
При ущемлении по всему кошуру кршическое напря-
жение определяется формулой (18,1). Значения К при-
ведены в табл 18 24
а) Равносторонняя треугольная пластинка под дей-
ствием равномерного сжатия со всех сторон (рис, 18 27).
Таблица 1Я 24
Значения коэффициента К для эллиптических пластинок,
защемленных по всему контуру
а b	I	1,1	1,2	|	1,3		5
к	1,49	1,38	1,30 j 1,23	1,12	1,15
Шарнирное опирание по всему контуру, Критическое
напряжение
я-Е I t V
<18-23)
?) Косоугольные пластинки; шарнирное опирание по
всем кромкам
Рис. 18.27
Рис. 18 28
1)	Равномерное сжатие в направлен и,
параллельном двум сторонам (рис. 18,28).
Критические напряжения относятся к меньшей из сто-
рон а и Ь, которая обозначается через
л= Е I ! К
0KD = /C -----—---- ----
12 (1 — Д-) \ с !
(18.24)
В табл. 18 25 приведены значения коэффициента К.
Табл и ц а 18.25
Значения коэффициента К в формуле (18.24)
ср в град	а b		
	П j !/> j 2->, i ! 1	2	1	зс
90	1	1,5о . 2,08	4	4	4	4
50	1,31 : 1,95 ' 2,?1	. 4,99 : 4,54	4,В	4
45	1,8b	2, 18 ( 3,2	5,94  5	4,25	4
3()	2,71	3,28 ;	; 5,63	5,б	4, 13	4
2)	Действие касательных сил, равно-
мерно распределены ы х по всем к р о м к а ,м
(рис, 18 29), Критическое напряжение определяется по
формуле (18 24). При сдвиге существенную роль играет
направление касательных усилий. Значения К даны в
табл, 18 26—18,27,
Рис. 18.29
18.3, УСТОЙЧИВОСТЬ НЕЗАМКНУТЫХ ОБОЛОЧЕК (ПАНЕЛЕЙ) В ПРЕДЕЛАХ УПРУГОСТИ
279
Таблица 18 26
Значения Д для «положительного» сдвига (рис. 18.29, а)
Ь/а	в ЕраО				
	90	|	75	60	15	|	39
1	9,34	13,78	20,58	<31,'1	53,5
0,7	7,2о	10,6	15,52	23, Н	•Й,7
0,4	6,2	6,9	12,7	18,91	30,65
0	5, Зо	7,61	10,9	16,1	25,9
Таблица Is 27
Значения К для «отрицательного» сдвига (рис. 18.29, б)
Ь/а	а ераа				
	90	75	60	45	«)
1	Q 2 4	6, м	4,74	3,58	I'1
0,7	? ,20	э 2Э	Ф уч	2,59	
0,4	6,2	4,1	3,21	2.17	1 , '!
0	э’”	3,78	2,6}	1,79	1,11
3)	Равномерное сжатие в иаправл-енип,
и а р а л л е л ь и о м двум сторонам, и сдвиг
усилиями вдоль двух других сторон
(рис. 18.30). Если тД и о]’р— критические напряжения
при изолированном действий сдвига и сжатия, то кри-
18.3. УСТОЙЧИВОСТЬ НЕЗАМКНУТЫХ
ОБОЛОЧЕК. (ПАНЕЛЕЙ)
В ПРЕДЕЛАХ УПРУГОСТИ
18.3.1. Цилиндрические панели
а)	Под действием сжимающих усилий, равномерно
распределенных вдоль кромок х = 0 и х = а (рис. 18.31).
При шарнирном опирании панели ио всем кромкам
верхнее критическое напряжение [6]
Е -А.	{18.27)
ДЗ(1-И2) Л
Рис. 18.31
Рис. 18.30
Формула применима при условии
гпческие напряжения ткр и <7кр при совместном их дей-
ствии определяются по следующей приближенной фор-
муле [12]:
^-(1-^ = 1, (18,25)
TL.„	о, „
где
cos ф
1 cos2 ср '
При «положительном» сдвиге (ф<90°) С положитель-
но, а при «отрицательном» сдвиге (или при Ф>903) —
отрицательно.
При заданных напряжениях тио запас устойчивости
п определяется как положительный корень квадратного
рравнения
При меньших значениях утла а, если отношение
а
----целое число, критическое напряжение
л2 Е ( t 1	lb \2
----—----- ,—	।----р —
3 (1 — р2) \ b )	4л2	\ R ) ’
(18.27')
Верхние критические напряжения для квадратной па-
нели при шарнирном опирании по всем кромкам приве-
дены в табл, 18 28.
1 а бл и ц а 18.28
ь1 RI	0	0		18	24
% ДУ Е /	9,6	1 п,з	ЮЛ	15,8	20,6 :
Ап- ф- вп —1=0,	(13.26)
Для панели с а/Ь — 1 нижнее критическое напряжение
определяется формулой [6]
22,2 , / ’о \-
он = оа—.	(18.23)
гН \ R J
ь
РНДГ1 IS УСТОЙЧИВОСТЬ ПТХСГИНОК И ОБОЧОЧГК РХСЧГТ ГИБКИХ плтстинок
Нижние критические напряжения для удчинеипых пи
не чей [6J
В-i края мне ти з<ищх<ч< пь Верхнее лритвческог на
пряж сине
8 т/ / I ф 3	! Ь V
о —-----------—	----£—	(18 31)
9	1-|Д 6 1	16ч“ \ R]
В табт 18 29 прше сны Теркине критические напряла
ния дуя квадрапюи цптиндричсской панели при всех
зацдмчснных краях
в) Под действием равномерного внешнего давления р
(рщ 18 35)
Края x = i//2 а = 0 и ая= b/R шарнирно закреплены
в направтснии пормати к пане ш
б)	Под деиствш- i рщ начерно nt cnpi.rie'i 'чнях по
вес i кроикач па ж ч 'ы риши (рпе 18 32)
Рис 18 32
Всл I ржи •( наш чу шарнирно очпта Верх w копти
ческой н ч г о- н i
тв = 0,10/ --- 5/Ц—р, (18 32)
где
п / h V3
(3—1 ; 0,80^-- (а й)
Вс кромки панели защемлены Верхнее KpHTiiwwe
напряжение
тв — 0,1 П —— -j-7,5 £ (—-У	(18 33)
R	\ b /
Рис 18 34
Можно пользоваться 1зкж< графическими зависимо
стями прудстав ~f иными на рис 18 33 и 18 34
Пнтечсчвпость нижних критических касательных 1 "н
та-	j а
чин Т’ь ~~ 11Я шарнирно опертой панели ( ~	1
9\дот определят ся de ijпщихш приближенны и (юр
”У Will
Рис 18 35	Рис 18 36
w 8 -> (при 0 ср — < 101,
н ! Н pt I
7,3—0 1 — I при 10 < —	25
PH \ Rf
Приближенные формулы для
критического давчепия [8]
2п 1С
Ркр з - П---~	РУ
з/б (1-у)0Ъ
определения верхнего
t
I
/ / \3/2
' R )
(18 31)
IB 4 УСТОЙЧИВОСТЬ ЗАМКНУТЫХ ОБО ПОЧТЕ В ПРЕДЕЛАХ О ПРО ГОСТИ
281
естн т,,	1
I Г и П \	Ь'1 1
Р,ра 1 R 112 (1 - ц ) \ b j i Р /4]	8 "°
ю ш т st: 1 I и
V-------, /а	,4 / R	Ь
тг 2 77 М - Г [/	|/ - -
Ь — 1 ШИТ др И ПЯНС 1 I
Форму 1Ы н гоафпк! 11я опреденния ниленсю трит
ясского гав июня см [о]
Щ1М в предегах oi КО ло 2 00) и с ом о юта 0 от 40
до 120“ можно рскомгндов и ск_ лисю акспсритен
I a it ию Форму п [0]
Ррее I 0 3 ЛА j	(18 38 )
гц коэффициент
(	0° — 40° \ /	Р \
Л - 1—0 17а —;---------11 - 0 07 ------ (18 38 )
’	40'	\	4Ш'	’
1 i t и и а
18 За
Значения коэффиц fen гов л /
Л / в фопмуче (14 JS)
18 3 2 Конические панели
Кони/секач пинечь под Оеиси нем. равномерного внеш
Hi о дашенич. р (рис 18 Jo) Кр гя пане 1и закрепило,
в н шрга книц норма ш
Ириогиженшк форме ия для опреде гения верхнею
критическою дав тонн! [8]
2т A	t / / V/2
Ркр в —	~	() /	1 Id ’
з|/Г	(1-г)°7	1
глти п г 1
I р хничныс ус юн а
При шарнирном опирай ш п
3 1 Арф свободно СМ Щ Hi
vc? о своей п оск ости (pauioi
При шарнирном оп ран ш т
>нгуру не смещат и сл я
Ко нту!
Контор а зщем сн и Fe с тещ
1 И
)4(Г
Ь
о
00 )
Кг
о
0
07

191
ес ш т гф 1 где
184 УСТОЙЧИВОСТЬ ЗАМКНУТЫХ ОБОЛОЧЕК
В ПРЕДЕЛАХ УПРУЮСТИ
Дср ,
cos а ’
R*
2а — угол конусности
18 3 3 Сферические панели
Сферические панеи под действием равномерного
внешнего дав шнич р (рис 18 3/)
Рис 18 37
В рхнее критическое дав тенив
1Р\	Р / А
й = ",л	'7 Л’ д
/ Я, VA
(18 38)
Коаффициен ii Л Л Аз Аз зависят аг "рп-пиных
ус oihi I приведена! в ио 1 18 30 (принят и — 0 3)
Дтя сферических паПсюи с отношением R/t тела
18 4 1 Цилиндрические круговые оболочки
а)	Равно нрнос осевое ежатис (pic 18 38)
Шарнирное опирая it по ооенм кромкам Верхнее кри
ТИЧЮКОС Напряжение [6 1967 г] В СТуЧДе X сеТНОИ по
тсви усюиывости
р в ” ~ т/т’т'/ттю: Г ~р~	(18 39)
|3 (1 - К )
Рие 18 38
Р 1с 18 г9
Ирин 0 2а-0 32
er t ~ 0 Г I —
1	Р
(J.8 40)
rhlKHCe бтджнсес критич I.IO- н ip гл IIII Щ
о щ/ —
°кр в ~~
(г8 41)
282
Р43Д11 IS УСТОЙЧИВОСТЬ ГЛ'СЛИВОК И ОБОДОЧКУ PVCIFT ГИБКИХ ПЛУ'ТИНОК
Формула (18 40) применима к оболочкам, изготовлен
ным достаточно тщательно (амплитуда начальной ноги
бы не должна превышать тонн.ины оболочки)
б)	Сжатие мецечтренно приложенном осевой нагруз
кой (рис 18 39)
Шарьчрное опирание но обеим кромкам Если напря-
жение может быть В1>1ра/лено в виде o=-o„-f-Oicos(p, то
критическое напряжение приближенно определяется по
формуле
(ао+<Е)кРн-О,18£—.	(18 42)
К
в)	Действие внешнего равномерно распределенного
давления р кГ[сл~ (рис 18 40)
Шарнирное опирание по обеим кромкам Верхнее кри-
тическое давление (формула Мизеса)
Lt* /	2/1-—
——----------/ ^2 — j 4 •
12(1 - у-) У	,
1 — ц \
шугЛ (18'43)
п~ I-
Л'Д- J
где I — длина обо ючки, п — число выпучин вдоль
олружности оболочки
Число п в каждом конкретном случае при заданных
Z,R и Rjt должно бьг-ь выбрано из условия получения
наименьшего значения /Ура Значения п для некоторых
отношений 1/R и R/t даны в табл 18 31
Таблица 183]
Значения п в формуле (18 43)
		R/t			
		250	200	50	25
10		Л	2	2	
О		S	4		3
2		8	b	5	4
В стуча,, весьма длпнноп оболочки
ЕР
Ркр в ~	д~т~,
4(1— И ГУ
(18 4Л)
юоР;
Рис 18 41
1Н-» ХСТОИ П1Р0 ТЬ 3\'1КШТЫ\ ОпОТОЧРК, Р ПР! ДЕЛАЛ УПРАГОСТИ
283
Эл форме 1 т верна в тон мере в к ткои допустим
считав ратите R ттрытсбрежт мо литым по ердвиетию
о д типо ооотошт I _1ля ооо точек средней д тины при
1гСФ^С.4 можно потьзоваыся ириотижениои формутон
Е R / t V
'- 0 86 (Т^м- ММ (184S)
Зн 1 тения в ркних критических дзвлиин высчитан
них. по форму с (iS 43) три 1-1 = 0 3 д тя некоторых ра^
меров обою тек приведены на рис 18 41 ю р^ —
Рв ( R
=	[ j II 1 р т то 42 д-тны jii тч нн т ттижипх крч
тижских дав тенин здесь
Рн / Е ?
г)	Д^штвие thp /чигаюцих пар по торса > (рис 1843)
Д р-2д(?-(т
тд т— р дт яя ат. и т па .юсаю таното Ни ряженая
Края обо точки шарнирно закрещены Верхнее крити
ее 01 значение тюмент т
L R Е
^кр в 2д •	2 8 ।
1— I
L
(18 46)
Рис 18 43
Согласно экспериметтгатьным санным реаты-ье зн^че
ния ршЧчМл напряжении составляют ь трееНс 711 -
~г->а от з“ачении вычистечных но (Ьорзутам тичеи той
сории Теоретическое решение а нелинейной пос ановке
?84
г у щ л ж устойчивость mостинок и оболочек расчет гибких пласт, под
даст ci с ющис р хыа и В стучат оиюсиг шно ко
ненного решения [17] На графики п— ыезо вь пучин
возникающих при noiepe vcioh4ibociii
д) Совместное действие рас юг ернпо осе Oi.o ст агат.
и скручивающих пар по торцам, (рис 18 1л)
Шарпирио“ опирание по торцам Расчепаая формуй
1
(18 49)
Зд°сь в0 и т —критические напрял о шя с 1Я случая
простого сжатия и простого кру гния Вс ш пн i к ica
тельного напряжения в формую (18 19) сщгастся ii
данной Соогноше тот (1849) р„сг рос (ранях к.я шиле
на нижние критические напряжения
е) Сов местное действие равномерного осевого сжита i
и внешней равночерно распределенной поперечной ни
грузки (рис 18 46)
Шарнирное опирание по торцам Для оболочек ср< с
ней длины (1 sg l/R. sg: 4) верхнее критическое на щчжесше
[12(1 -р2)]0 1
1 753
(18 50)
Ннжнее критическое напряжение при шарнирном ош
ранни кромок опреде тяе гея врио П1 кенкоп форму юи
акр и=0> 18£ ДГ (1 ~ —— Y	(18 50 )
к \ Ркр и /
Р
L
/
ва возр стает Дгп непп длинных оболочек решение
nt дас! у сов I тгопи с ин 1х резу тьтатов
Края обо точки защемлены Верхнее критическое зна
чение момента
£
1 — В
где р„-р н определяется из графиков на рис 18 42
ок) Согнестное действие равнощрносо осевого сжатие
и снутреннеи равно серно ра npe.de генной попер мои
на ру ки
Шарнирное опирание по <орц1М Нилисе критическое
напряжение определяется по прибтил еннои формуле
ЛДП в—2т.
С
4 6-J-
(18 47)
Рис 18 Ь	Р то 18 46
окр н-=0,18£(1-L14 6 р"),	(18 50 )
А
4___р / R_\2
где р”	,
£ \ t /
Формула (18 50') справедлива пр i р 00 17 При
t
р^Р>0 17 С1едуег прин гч itd о , н—0 60о£ ~j~
з) Действие изгибающих пар нежащие в Оси имрать
нои плоскости (рнс 18 47)
Рис 18 Г
К 1я i ни п с
раз нс п о с у о hi
чщ ГО МОМсШ I
то I сто ия закрептопич на сонгх
I ь । \исе кр п 1 (ест ое значение кру
1 Р
J(l^p )°
V Ri
(18 48)
3 (кон р определения пор и шнп напряжет и в по
перечных сечениях до noi pu дюцшвипч озоточм
имеет вид
г/ М у
Цто расч( u oomo i 1ро1звоа>нои д шны даны
i Mpi I । н рис 1о 14 noLipo гпше на основании у (Оч
(Jy — СГП ССЬ--------QJ —..
« iR-t Ч
18 4 УСТОЙЧИВОСТЬ ЗАМКНУТЫХ ОБОЛОЧЕК В ПРЕДЕЛАХ УПРУГОСТИ
Координата у отсчитывается от точки срединной по-
верхности, расположенной в плоскости действия пары.
Шарнирное опирание по торцам. Верхнее критическое
напряжение определяется по формуле (18 39).
Судя по опытам над точеными образцами, находящи-
мися в условиях изгиба парой сил, реальные критиче-
ские напряжения составляют 68-3-75% ог окр в и имеют
сравнительно слабый разброс. При изгибе образцов, из-
готовленных менее тщательно, критические напряжения
Длина контура оболочки с малым эксцентриады, i о j
приближенно равна
/ 1 \
s == 2 ла fl—-— F 1 ,	(18.. 57,)
У'гггтт
тле R-----------------— эксцентрицитет.
а
Минимальная критическая нагрузка ₽К1, равна произ-
В1.депию минимального напряжения (верхнего или ниж-
нею) па площадь поперечною сечения оболочки.
-Ркр.в
2л
j,
£7Д
(18.58)
ГЕЪ ,	1
PKp.„--- 1,13 —— 1 — — 4%.	(18.59)
а '	4	/
составляют 40—70% от аКр в. Исходя из эксперимен-
тальных данных, для определения нижнего критического
напряжения рекомендуется формула
акр.н = 0,22Е	.	(18.S1)
и) Изгиб поперечной силой (рис. 18.48).
Защемление на одном торце, второй торец свободен.
Для длинных оболочек реальные значения критических
напряжений на 8—10% выше, чем при чистом изгибе,
Верхнее критическое напряжение
Офо.в = —====Г Е 	(18 52)
'	/3(1-ФД
Нижнее критическое напряжение
окр.н = 0,242Д	.	(18.53)
А
Формулами (18,58) и (18 59) определяется та кри-
тическая нагрузка, при достижении которой в зонах
оболочки наименьшей кривизны начинается образова-
ние первых аыиучин по длине
Вследствие наличия иа поверхности зон, поддержива-
ющих ослабленные участки, критическая нагрузка, при
которой начинается волнообразование по всей поверх-
ности, будет несколько превышать ту, которая опреде-
ляется формулой (18 59).
18.4.3. Усеченные конические
круговые оболочки
а) Равномерное продольное сжатие (рис. 18 50).
Шарнирное опирание но кромкам. Верхняя критиче-
ская сила
2л
—1-----------ЕР cos- а,
Р 3 (1 - р-)
(18.60)
Для относительно коротких оболочек критическое на-
пряжение приближенно принимается равным критиче-
скому напряжению кручения для оболочек тех же раз-
меров. Критические напряжения для оболочек длиной
1—2 диаметра определяются по приближенной формуле
Е
5,4 I
Скп — 0,3 ------77" | '	)
кр (1-р2)/а\д; д
(18.54)
18.4.2. Цилиндрические
эллиптические оболочки
Оболочка с небольшим эксцентрицитетом под действи-
ем равномерно распределенного осевого сжатия
(рис. 18.49).
Шарнирное опирание по обеим кромкам. Верхнее кри-
тическое напряжение определяется по формуле
Рис, 18.51
1 Etb
Дкр.в =	---'-----1	1	(18.5а)
/з(1-д=) ai
нижнее — по приближенной формуле
(18.56)
71“
Нижняя критическая сила опреде тис-гея по прибли-
женной формуле
Укр.н — 1 ,13277- cos2 а.	(18.61)
б) Внешнее равномерное давление (рис 18 51).
286
РАЗДЕЛ 18 УСТОЙЧИВОСТЬ ПЛАСТИНОК И ОБОЛОЧЕК РАСЧЕТ ГИБКИХ ПЛ УСТПНОК
Шарнирное опирание по кромкам. Верхнее кригоче-
ское давление [3]
Ркр-1. —
'П Ч 4п3 -2 е) ~|-
(n2g го k)(n
ЗдеСЪ П ~~~ ЧИСЛО ВЪГП ПИИ.
5 сюичивос гн;
A t й И . ,,	Г<-
О — — ; р--------• у „ ------
П I г.
%- т; — rI2s J
возникающих
1
2(1 — р2) ’
£6 cos а
(18.62)
с =. 0,4 --
i> = 1,41(Р р—-
(1 — уя)(1 — у)
— 0,203  ---Щ'-З—МЛ
боковая поверхность, подвергаются действию давления.
Эта же формула используется п для открытых конусов
при выполнении условия
[_____Р_____1‘П (рЩг . Г И
112Г (1 - ц2)] ДМ LW (1 - Ц3) j
В этом случае возникающее меридиональное усилие
значительно дальше отстоит от своего критического зна-
чения, чем окружное усилие.
Также несущественно, на каком из краев открытой
оболочки уравновешивается осевая сила (создаваемая
давлением из-за наклона образующей), так как связан-
ное с этим сжатие или растяжение оболочки в меридио-
нальном направлении сравнительно мало влияет на ее
устойчивость.
Если в формуле (18.65) пренебречь величиной V2 по
сравнению с п2 (считая с!<лф), получается простая
формула для р1:р,в:
(1 — у)2
g^= 1 - 0,305 2----i-7
е-= (1 %- -у2)(32,4₽'~ го 138(1-sirf- a) % 32,4ф%%
1 Л. -.2 -ф у4
fe= 2,3В2--------!—L-
1 4 у2
/'	3	1 — у2,
f = 0,575р3 cos2 а (1 — у2)2 Н - — • фу-щ; h
л = si,ар-
(18.63)
где
Я<,=
1?ср
cos а
Из формулы (18 66) следует, что при углах конусно-
сти 2u<C40J р,,р в для конуса отличается от ркр в для
цилиндра длиной I и радиусом, равным /%р конуса,
не больше чем на 10%. Поэтому и в других случаях
загружения (осевыми силами, крутящим моментом
п т. д.) можно без большой погрешности рассчитывать
конус при сравнительно небольшом «, как цилиндриче-
скую оболочку длиной I и радиусом, равным /?ср конуса
При а-М) и Го/'г,-^! выражение (18,62)
в формулу (18.43) Мизеса для кругового
в случае всестороннего сжатия. Полагая в
(18.63) у = 0, т. е. го = О и щ¥=0, получаем формулу для
определения критического
ской оболочки:
ьг1 cos а
Ркр.в = ~С~7,	д7~
2(1 — U2) fj
Переходи
цилиндр .1
(18.62) п
давления замкнутой кониче-
18.4.4. Усеченные конические круговые
подкрепленные оболочки
Равномерное всестороннее давление (рис, 18 52).
Шарнирное опирание по кромкам Для ребер жестко-
сти, установленных на оболочке достаточно часто, прп-
1,41 sin2 а %- 0,2л2
---(п4 у- 12,8зи2 sin2 о: 4- 170 sin4 а.) а
6П
н2 -А 63,5 sin2а 1
+ 0,57a sin2 а cos2 а--------------------—— -------I .
n4 У 8,35,ч2 sin2 а %- 46,5 sin2 а. ]
(18.64)
Число вылучин п в записанных выражениях варьиру-
ется до получения (щ,р в) ЧьИ Приближенная формула
для указанного случая имеет вид [8],
Et cos3 а £а (v2 — Ш)-ж v4
Ркр.в — ф ’ '~П	“ .	(18.65)
'СР	-А (V2 + П2)2
где
Рнс 18 52
Рис, 18 53
%	О •)	)	’ V	7
12 (1 — рл) £)peos~a	1
Эта формул? выведена в предположении, что конус
закрыт с обеих сторон дисками, которые, так. же как и
читается, что жесткость
но.мерпо распределяется
кость обшивки на изгиб
на изгиб каждого нз них рав-
но пролету. При этом жест-
ио направляющей оболочки во
18 4 УСТОЙЧИВОСТЬ ЗАМКНУТЫХ ОБОЛОЧЕК В ПРЕДЕЛАХ УПРУГОСТИ
287
много раз меньше аналогичной жесткости ребер и ио
этому не учитывается Прн этих допущениях верхнее
кри гическое давление
Е cos a 1 1 cos а
Ркр.в -= ;---у- I ------(Ш -2 dn- I- е) 4-
b + n-c i
t	ri2 -C h	1
4/ —-------------------------------—-----(18.67)
2 (I — p2) щ (n-g + k)(n2 4 m) — n2s j
где /—момент инерции подкрепляющего ребра с при-
соединенным поясом обшивки; lt — расстояние между
ребрами.
Значения постоянных параметров определяются из
формул (18.63).
Этому напряжению соответствует давление
бкр-в —	----------Е
У з (I - нН
Нижнее критическое
формуле
напряжение определяется >ю
18.4.5. Усеченные конические эллиптические
оболочки
(18.73)
Более подробные расчеты па
устойчивость сферических обо-
лочек сад, [7]„
Оболочка с, небольшим эксцентрицитетом под действи-
ем равномерного продольного сжатия (рис 18.53).
Шарнирное опирание ио кромкам. Верхнее критиче-
ское напряжение
18.4.7. Эллипсоидальные оболочки
1 ГЛЬ
Оьр.п'-• ' „ cos а.
V 3(1-— Р)
(18.68)
а} Вытянутая эллипсоидальная оболочка (рис. 18 55)
под действием, внешнего равномерно распределенного
давления р, Верхнее критическое давление
Нижнее критическое напряжение приближенно опре-
деляется но формуле
ЕГо
акр.н=--0,18—p-cosa.	(18.69)
U"
Ра -
2Е
/3(1^У
—------ 1,21Е —— ,
2й2 — а'2	2Ъ~ — а2
(18.74)
Здесь « — угол между высотой конуса и образующей,
проходящей через вершину большой полуоси эллипса',
Гоч относится к сечению оболочки, где определяются
параметры а и Ь. Эксцентрицитет считается малым. Ми-
нимальная выпучивающая сила, действующая перпенди-
кулярно плоскости основания, определяется аналогич-
но тому, как для цилиндрической оболочки эллиптиче-
ского сечеиня:
где а, b — полуоси эллипса. Появление вмятин следует
ожидать в топе экватора.
2 л	ЕП I	1	4
Ркр-в	“——;— ------ • ——— 1 1 —--k2 cos- а; (18.70)
Уз(1-р2) а '	4	'
i^b /	1	Ч'
Ркр-и = 1,13--- 1-------№ I cos- а. (18.71)
а \	4	'
Рис. 18.55
Рис. 1856
Формулами (18.70) н (18 71) определяется га критиче-
ская нагрузка, прн достижении которой в зонах оболоч-
ки наименьшей кривизны начинается образование пер-
вых вынучин по длине.
Вследствие наличия на поверхности зон, поддержива-
ющих ослабленные участки, критическая нагрузка, при
которой начинается волнообразование по всей поверх-
ности, несколько превышает ту, которая определяется
формулой (18 71).
б) Сплющенная эллипсоидальная оболочка (рис. 18.56)
<им дейс твием внешнего равномерно распределенного
дивленич р Верхнее критическое давление
18.4,6. Сферические оболочки
Появление вмятин следует ожидать в зоне полюсов
А и В
н) Сплющенная эллипсоидальная оболочка при а>
2 под действием внутреннего давления р. Верхнее
критическое давление
ч'кр.н 0,1562?	.
Равномерное внешнее давление р (рис. 18 54).
Величина равномерного сжимающего напряжения в
этом случае равна
pR
а —-----.
21
Верхнее критическое напряжение определяется по
формуле (18,39),
2Е	F	f2
----------- , ----------- j 21 f---------.	(18.76)
Появление вмятин следует ожидать в зоне экватора.
Нижнее критическое давление рп для эллипсоидаль-
ных оболочек составляет примерно такую же долю от
рв, как и для сферических оболочек; практические рас-
четы надо вести по величине рь.
288	Р 23ДЕЛ 18 УСТОЙЧИВОСТЬ ПЛАСТИНОК и оболочек расчет гибких пластинок
18,5. УСТОЙЧИВОСТЬ ПЛАСТИНОК И ОБОЛОЧЕК
ЗА ПРЕДЕЛАМИ УПРУГОСТИ
18.5.1. Общие положения
Приведенные выше формулы применимы при условии,
что критические напряжения лежат в пределах действия
закона Гука; это означает, что интенсивность напряже-
нии в любой точке пластинки или оболочки, определя-
емая, как для плоскою напряженного состояния, не дол-
жна превышать предела пропорциональности материала
Овщ (считаем его равным пределу упругости oyD):
о* — <Д % +	+ Зт2 < опц. (18.77)
Для расчета пластинок и оболочек на устойчивость за
пределами упругости имеется несколько методов [6],
1.	Расчет но теории упруго-пластических деформаций,
предложенный А. А, Ильюшиным [9]. Этот метод ана-
логичен расчету на усюичпвосгь сжатых стержней с
применением резу.чыирутощего модуля Кармана. Здесь
учнтывашся эффект разгрузки для волокон, располо-
женных при выпучивании стержня на стороне выпукло-
сти; принимается, что для этих волокон связь между
напряжением и деформацией ошечает начальному мо-
дулю упругости материала.
2.	Расчет по теории jпруго-пластическнх деформаций
без учета эффекта разгрузки. Этот метод отвечает рас-
чету на устойчивость с.катых стержней с применением
касательного модуля (метод Шенли — Работнова),
3	Расчет по теории пластического течения.
Ниже приводятся данные для расчета по теории де-
формаций как более близкие к результатам экспери-
ментов. При этом расчет без учета эффекта разгрузки
приводит к значениям критических напряжений, лежа-
щим ниже экспериментальных; учитывая же эффект
разгрузки, получаем критические напряжения, лежащие
несколько выше экспериментальных.
В расчетные формулы входят некоторые величины, оп-
ределяемые по дишрамме о,—е, для данного материа-
ла; эта диаграмма связывает интенсивность напряжений
о, с интенсивностью деформаций ьц, причем
s, ==^ + е^ + е2+±?2.	(18.78)
Если счшать коэффициент Пуассона р равным 0,5, то
диатрамма ст,— е, совпадает с кривой о(е), полученной
при одноосном растяжении (сжатии) образцов из рас-
сматриваемого материала. Введем обозначения: Еа для
секущего модуля, йф — для касательного модуля, Т —
для результирующего модуля; прн указанном допущении
o'	do	4ЕЕК
Ес = — ; £„ = —; Т - -—--------——
ь ай (н + lz£K)"
Кроме тою, обозначим
(18.79)
(18.80)
Таблица 18,32
Расчетные параметры для стали марки Ст.З
3 В	и а кГ/смя		'Рк |		г
U,095	2000	1	1	1	; j
0,10	2100	”,Ч9	0,68	0,8>	0,005
0,11	2200	0,95	0,47	0,66	0,025
9,12	2280	0,90	0,32	0,50	0,057]
0,13	2340	0,80	0,22	0,41	0,075
0,14	2380	0,81	0,12	0,26	0,11
0,15	2390	0,76	0,062	и, 16	0,15
0,16	2-100	0,71	i ,029	0,094	0,19
0,18—0,40	2400	0,63—5),	и	0	0,33—0,71
0,45	2410	0,26	0,0 И)	0,033	0,61
0,50	2420	0,23	0,019	(|,01й	0,о0
0,00	2x570	0,20	0,У2Ч	0,07]	0,63
0,70	2520	0,17	0,024	0,071	0,65
0,80	2575	0,15	0,024	0.071	0,08
0,90	2630	0,14	0,02 1	0,071	0,70
1,00	2685	0,13	0,02 1	0,071	0.71
1 ,р)	2740	о. 1з	о ,0Ы	ч,и71	0,73
1,20	2795	и, н	9,424	0,071	0,74
Т а б лица 18.33
Расчетные параметры для д^ралюмина ДИзТ
В в %	а а кГ/см*	<рс		1	
0,27	2000	1	1	1	0
0,30	2200	0,98	0,79	0,88	0,01
0,35	2460	0,94	0,54	U, 73	и,оз
0,40	2640	0,87	0,50	0,66	О,Об/
0,45	2780	0,82	и, я	0,51	0, 10
0,50	2900	0,77	и, 27	U,-И	6,1 3
0,60	3080	0,68	0,20	11,33	0,19
0,70	3200	0,61	0, 16	0,27	0,2 I
0,80	3320	0,55	0.11	0,23	(1,29
0,90	3400	0,49	0,11	0,20	11,33
1,00	3450	0,46	0, л	0,00	0,35
1,10	3560	0,43	'Л	0,20	0,38
1,20	3640	0,40	0.11	0,20	0,40
В табл. 18 32 и 18 33 приводятся значения безразмер-
ных параметров <щ, <щ, t и г в зависимости от интенсив-
ности деформации е, и напряжении ст, для стали марки
Ст.З (табл, 18.32) при о,и. = 2000 кГ/см1-, от =
= 2400 кГ/см1, Е = 2,1-101‘ кГ/см2, р. = 0,3 и для дуралю-
мина Д16Т (табл. 18.33) при о(,1( = 2000 хГ/сш2, сщ2 =
= 3050 кГ/см-, £ = 7,5-10J кГ/слГ, ;.i = 0,32. Участок
0,18% =Сб=С0,4% для стали относится к площадке теку-
чести,
18.5,2.	Прямоугольные пластинки
а) Удлиненная пластинка (ар>2Ь), шарнирно опертая
по краям, сжата усилиями, равномерно распределенны-
ми по краям х—-0 и х — а (см рис, 18 1).
Критическое напряжение
Здесь при р. = 0,5
П3

(18.82)
(18 83)
18 S УСТОЙЧИВОСТЬ ПЛАСТИНОК и оболочек за пределами упругости
289
По теории деформаций с учетом эффекта разгрузки
коэффпциеш
Так как коэффициент К в формуле (18.82) зависит от
е, или о,, то эту формулу следует представить в виде
д' = о (I — г)
(18,84)
qKp __
/Г~
b-t
тЭ / t V
— Е —
9 \Ь
(18.86)
Без учет эффекта разгрузки
и найти зависимость для данного материала между
акр/К и отношением bit. Тогда при заданных размерах
пластинки определяются одновременно коэффициент А'
(18.85) и критическое напряжение оКр.
На 1 рафиках рис. 18.57 и 18.58 приведены значения
аИр в зависимости от b/t, найден-
Рис. 18.57
ные по (формулам (18.84)—-(1886)
к данным, приведенным в табл.
18.32 и 18.33 для стали марки Ст.З
и дур алюмин а Д16Т. Пунктир-
ная линия на рис, 18.57 соединяет
прямую, отвечающую площадке
текучести, с кривой, соответствую-
щей диаграмме упрочнения мате-
риала, минуя «петлю» теоретиче-
ских значений. В практических рас-
четах можно в запас прочности по-
лагать, ЧТО при Й/КЙО Оьр = С5т,
б) Квадратная пластинка (а=-
— Ь), шарнирно опертая по краям,
сжата усилиями, равномерно рас-
пределенными по краям x — !J и
х — а (см. рис. 18.1).
Коэффициент К в формуле
(18.82) равен:
1) по теории деформаций с уче-
том эффекта раз!ррки
13	3
/<= — (1 -Н + ~-~t;	(18.87)
4	4
2) по теории деформаций без
учета эффекта разгрузки
К=3,25фс4-0,75фк.	(18.88)
Ниже приводятся расчетные формулы
для других случаев закрепления плаш ин-
ки, полученные по теории деформаций без
учета эффекта разгрузки. Эти формулы
используются таким же образом, как и
для удлиненной шарнирно опертой пла-
стинки. Коэффициент К выражен через
такой же коэффициент Куп, найденный для
упругой области (см. выше 18,2.1, табл.
18,1 и 18.2).
в) Удлиненная пластинка (at3>b) сжата
усилиями, равномерно распределенными по
краям. х=0, х=а (см. рис. 18,1).
Значения коэффициента К в формуле
(18.82) при шарнирном опирании по краям
х=0 и х = а зависят от условий закрепле-
ния двух других краев.
Край у=0 оперт шарнирно, край у = 6
свободен:
К=ФсКуп, (18.89)
где КуП = 0,46.
19—26
290
РАЗДЕЛ 18 УСТОЙЧИВОСТЬ ПЛАСТИНОК И ОБОЛОЧЕК РАСЧЕТ ГИБКИХ ПЛАСТИНОК
Край у —О защемлен, а край у~Ь свободен:
(18.90)
где КуП = 1,33.
Края у = 0 и у~Ь защемлены:
/	1	/~ 1	3	<рк
Л’= <рс 0,648 j/ —- + — • — -ф 0,352 ДуШ(18.91)
\	Г 4	4	фс	/
1 Де К у д — 1,0.
Ориентировочные расчеты для любых граничных усло-
вии можно провести по «формуле секущего модуля»:
Д = фсДуп.	(18.92)
18.5.3.	Цилиндрические оболочки
/ Круговая замкнутая оболочка, шарнирно опертая
по торцам, сжата осевой нагрузкой (см. рис. 18.38).
Приближенно верхнее критическое напряжение равно
скр.в= 0,6£фс4- .	(18.93)
л
Для практических расчетов эту формулу следует
представить в виде
-^Д- = 0,6Д —	(18.941
Фе	R
и определить зависимость оКр от отношения R/i, поль-
зуясь диаграммой о(в) для данного материала (см. вы-
ше 18.5.1).
Деформация, отвечающая «ближнему» нижнему кри-
тическому напряжению, определяется но формуле
___ 1
Екр.в — Q “ ^кр-в*
о
(18.95)
Соответствующее напряжение
°кр.н ™ Ее ®кр.н=	(18.96)
Во всех других случаях нагружения оболочек крити-
ческое напряжение можно приближенно найти по анало-
гичной «формуле секущего модуля»:
°кр — о15р.уп фс-
(18.971
Здесь под (Щр уЛ понимается критическое напряжение,
найденное по данным 18 4 1 для упругой области.
2. Круговая замкнутая оболочка, шарнирно опертая
по торцам, подвергается действию равномерно распре-
деленного внешнего давления р (см. рис, 18.40),
Приближенно безразмерный параметр верхнего крити-
ческого давления равен:
3. Круговая замкнутая оболочка подвергается дейст-
вию скручивающих пар по торцам (см. рис, 18,43).
Верхнее критическое напряжение равно:
0,888£s
L j \ R
(18.99)
Зависимость (18.99) получена для оболочки средней
длины Для оболочек большой длины
/ h VA
rD = 0,272 (0,75)— л F.s ^-1
/ h дм
0,326£s I—	.
\ R /
(18.100)
18.6.	ГИБКИЕ ПЛАСТИНКИ И МЕМБРАНЫ
Полные нормальные и касательные напряжения в
каждой точке гибкой пластинки складываются из напря-
жений в срединной поверхности (пли цепных, мембран-
ных напряжений) и напряжений собственно изгиба.
18.6.1.	Гибкие пластинки
а)	Прямоугольная пластинка шарнирно оперта по
контуру; контур не смещается; поперечная нагрузка рав-
номерно распределена по всей площади (рис. 18.59) [4].
Стрела прогиба (в центре) определяется из уравнения
+ < =
16
Для центра пластинки
г W	рг <
= «д — • ~лт;
С?"	о-
rPf\~ KrPf'\2
= уЕ ; nl/c = 6Д .
\ b /	\ b J :
Дгп “ °ги Д' Фтс! ™	“г- Сур
(<ЬЯ и (Туп — полные напряжения).
(18.101)
(18.102)
Коэффициенты А, В, а, р, у и б даны в табл. 18 34.
Для квадратной пластинки имеется уточненное реше-
ние [6], которое дает зависимости для определения стре-
лы прогиба, напряжений в срединной поверхности и на-
пряжений изгиба, представленные на рис, 18.60 и 18.61,
б)	Прямоугольная пластинка шарнирно оперта по
контуру; края пластинки свободно смещаются, попереч-
ная нагрузка равномерно распределена по всей площади
(см, рис. 18.59).
18 6. ГИБКИЕ ПЛАСТИНКИ И МЕМБРАНЫ
291
Таблица 18.31
Значения коэффициентов А, В, а, Щ у и 6
alb	-1	В	а	е	V	6
М	1,82	1 ,зз	1,643	1,645	0,615	0,615
и	1,53	1,11	1,416	1,587	0,518	0,60i :
1,2	1,34	0,96	1,242	1,544	0,448	0,592
1/1	1,21	0,84	1,107	1,510	0,7:92	0,584 ;
1,4	1.11	0,76	1,000	1,484	0,351	0,581
1,?	1,05	0,7	0,913	1, -162	0/315	0,574
1,ь	1,00	0, 65	0,84 3	1, !Н	0,^88	0,571
1,7	0,95	60	0,781	1,429	0,263	0,568
1.S	0,93	0,67	0,735	1,417	0,246	0,567
1,9	0,90	0 54	0,693	1,-107	0,230	0,566
2,0	0,88	0,52	0,658	1,398	0,217	0,566
Приближенная формула для определения стрелы про-
гиба имеет вид
Рис. 18.60	Рис. 18,61
1 а
где А = ——
b
Напряжения в срединной поверхности o1Jf будут наи-
большими по абсолютной величине у кромок (х = 0,
х = а) и по средней линии пластинки (х = й/2):
Максимальные напряжения изгиба будут в центре пла-
стинки
Л2	tf /	11 \
„	—---------- £_П	, (18.105)
уа 2(1 — р2)	\	л2/
Наибольшие полные напряжения равны;
Oj,n = -ф ауи.	(18.106)
Для квадратной плиты стрелы прогиба напряжения
в срединной поверхности и напряжения изгиба по за-
данной величине поперечной нагрузки определяются со-
ответственно из рис. 18.62 и 18.63, полученных с по-
мощью уточненного решения. Буквой С обозначен центр
пластинки, А — угол.
в)	Прямоугольная пластинка находится под действи-
ем поперечной нагрузки, равномерно распределенной по
19*
поверхности пластинки, и защемлена по контуру; края
пластинки неподвижны (рис. 18.64).
Кубическое уравнение для определения стрелы проги-
ба имеет вид
(18.103}
Для определения напряжений в срединной поверхно-
сти следует величины оАС и аус> определенные по m>i-
симостям (18 110), сложить соответственно с рх и
которые находятся по формулам:
(18. 108)
Напряжения изгиба определяются по формулам теории
жестких пластинок.
Уточненное решение для случая а — Ъ приводит к за-
висимостям, данным на рис 18.65—18.67. Буквой В обоз-
начена середина стороны пластинки .
г)	Прямоугольная пластинка защемлена по краям и
находится под действием поперечной нагрузки, равно-
мерно распределенной по поверхности пластинки; кром-
ки пластинки свободно смещаются (см. рис. 18,64),
Рис. 18 64
Е ( t
чоо
300
200
100
о
О, ц О, в 1,2 1,6 2$
Рис. 18.65
292
РАЗДЕЛ 18. УСТОЙЧИВОСТЬ ПЛАСТИНОК. И ОБОЛОЧЕК РАСЧЕТ ГИБКИХ ПЛ ЕСТ ИНОК
Стрела прогиба определяю ся из кубического уравне-
ния (при ц = 0,3).
I
6,48 ~т+1
\ А‘=
12,18 1	Г / 1	\
----ш----у + 8,98 3 Стт 1 +
' (1 + ^)- J	L \ л4	/
О ->
ст к = р*
(18.109)
Максима юные напряжения в срединной поверхности
(в центре пластинки) равны:
о
— ° ус
.Максимальные напряжения изгиба для нижних воло-
кон посередине пролет
,	3	, -
о^и == “~ (1 --Р“) Д 41 (шарнирно опертые края);
(18.114)
оуи ~ -—(1 — 1СТ) р* тр, (Защемленные края). (18.115)
Максимальные папрчлщния изшба для верхних воло-
кон у опор
Ода = у(1--~рв)р*х.	(18.116)
Здесь
Напряжения изгиба определяются по формулам тео-
рии жестких пласгинок.
д) Удлиненная гибкая пластинки пролетим b находит-
ся под действием равномерно распределенной попереч-
ной нагрузки р.

Рис. 18,66
Рис. 18.67
Рис. 18.68
Прогибы определяются по формулам:
5
6, = —у-р* (I — р2)Ф1. (шарнирно опертые края);
(18.111)
С = _р» 0 _ psja (защемленные края). (18.112)
Максимальные напряжения (в плоскости, параллель-
ной длинным ыкршм краям) в срединной поверхности
равны.
U3
3 ‘
(18.113)
18 6 ГИБКИЕ ПЛАСТИНКИ И МЕМБРАНЫ
293
Таблица 18.35
Вспомогательные функции для расчета удлиненных пластинок
	Нагрузка				Стрела прогиба		Напряжения		
	шарнирные края	Д	защемленные края Igfp-’ (1—ц,-)|	Д	шарнирные края Чн	защемленные края	посередине		у защемлен- ных краев Z	<
							шарнирные края д,	защемленные края <р2	
0		-yj		—— оо		1,000	1	1,000	1,000	1,000	1,000	;
0,5	0,111		0,783		0,908	0,976	0,905	0,972	0ДН4
1,0	0,517	406	1,114	331	0,711	0,909	0,701	0,894	0,939
1,5	0,827	310	1, '>37	223	0,532	0,817	0,511	0,788	0,876
2,0	1,089		1,519	182	0,380	0,715	0,367	0,673	0,806
о	1, Л 6	227	1,680	161	0,281	0,617	0,268	0,563	0,716
3,0	1,51 1	198	1,826	146	0,213	0,529	0,200	0,467	0,672
3,5	1,689	175	1,960	134	0,166	0,453	0,153	0,386	0,61 1
4,0	1,845	156	2,084	124	0,132	0,388	0,120	0,320	0,563	<
4,5	1, «86	141	2,199	115	0,107	0,335	0,097	0,267	0,519
5,0	2,114	128	•2,206	107	0,088	0,291	0,079	0,224	0,4*0
5,5	2,212	118	2,-10)	100	0,074	0,254	0,066	0,189	0,446
0,0	2, 140	108	2,499	93	0,063	0,223	0,055	0,162	0,417
6, 5	2, -140	1(Ю	2,587	88	0,054	0,137	0,047	0,1.19	0,391
7,0	2,533	93	2,669	82	<1,047	0,175	0,041	0,121	0,367
7,5	2,620	87	2,747	78	0,041	0,156	0,036	0,106	0,347	<
3,0	2,702	82	2,84	71	0,036	0,141	0,03>	0,093	0,328
3,5	2,779	77	2,891	70	0,032	0,127	0,028	0,083	0,311
9,0	2,852	7 1	2,95s	67	0,029	0J15	0,025	0,074	0,296
9,5	2,921	09	8,071	63	0,026	0,105	0,022	0,066	0,283
10	2,W)	65	3,082	61	0,0235	0,0960	0,0200	0,0599	0,270
11	3,108	122	3J	11 1	0,0195	0,0811	0,01об	0,0496	0,248
12	3,220	112	1,300	106	0,0164	0,0394	0,0119	0,0417	0,229
13	3,323	КН	3,397	97	0,0140	0,0601	0,0118	0,0355	0,213
14	3,419	96	3,487	90	0,0121	0,0525	0,0102	0,0306	0,199
15	3,509	90	3,572	85	0,0106	0,0462	0,00889	0,0267	0,187
16	3,592	83	3,652	80	0,00930	0,0410	0,00781	0,0235	0,176
17	3,670	78	3,727	75	0,00825	0,0366	0,00692	0,0208	0,16о
18	3,744	71	3,798	71	(,00736	0,0329	0,00617	0,0185	0,158
19	3,814	70	3,865	67	0,00661	0,0297	0,00554	0,0166	0,150
20	3,881	67	3,928	63	0,00597	0,0270	0,00500	0,0150	0,142
Таблица 18 Зь
Значения коэффициентов А, В, и, ₽, у и 8
Граничные условия		, Л	в	В центре		У контура			
				а=3	у—6	а	₽	V	6
Шарнирное опирание по коатхру	norm р свободно смещается	0,376	1,436	1,778	0,245	0	0,755	0	— 0,427
	коятхр не смещается	2,660	1,436	1,778	0,903	0	0,755	0,610	0,183
3 1 щемление по контору	когтр свободно смещается	0,857	5,862	2,860	0,500	4,100	1,320	0	—0,333
	контур не смещается	2,762	5,862	2,860	0,976	4, 4J0	1,320	0,476	0,145
Значения у, ч|з2, ф(, ф2 и у находятся из табл. 18.35.
Зависимости между ау и С даны на рис. 18,68—18,69.
е) Круглая пластична подвергается действию попереч-
noii нагрузки, равномерно распределенной по всей >йго-
панд’.
Стрела прогиба (в центре) определяется из кубическо-
го уравнения
Коэффициенты А и В даны, в табл. 18,36. После опре-
деления стрелы прогиба нормальные напряжения и: и-
ба п-и, о»п и напряжения в срединной поверхности
Ore, Огс находятся по формулам.
AZ3 +
(18.117)
if
= аЕ
ал
\ j
а2
/ / г
б£ — .
\ а )
(18 И8)
294	РАЗДЕЛ 18. устойчивость пластинок и оболочек, расчет гибких пластинок
Полные напряжения равны:
о, == а™ + оге; Ст/ = о/и + oic. (18.119)
Значения коэффициентов а, р, у и 6 даны в табл 18.36.
Знак минус относится к сжимающим напряжениям.
18.6.2.	Мембраны
а)	Квадратная мембрана нагружена равномерно пас-
пределенной поперечной нагрузкой; крал шарнирно опер-
ты; кромки неподвижны.
Прогиб определяется по формуле
зл—
С = 0,285].' Р* 	(18.120)
Рис. 18.70
Напряжения в срединной поверхности (в центре пла-
стинки)
< = < = 3.<2.	(18.121)
б)	Удлиненная абсолютно гибкая пластинка с проле-
том Ь нагружена равномерно распределенной нагрузкой,
коая тастинки шарнирно оперты; кромки неподвижны.
Стрела прогиба
£=0,36]/р* .	(18,122)
Напряжения в срединной поверхности (в центре плас-
тинки) определяются по формуле
°« = V =		(!8J23)
в)	Круглая мембрана с несмещающимся контуром
подвергается действию равномерно распределенной по-
перечной нагрузки.
Стрела прогиба в центре
з—.
£ = 0,662 V р* .	(18.124)
Максимальное напряжение в центре
Предел упругого сопротивления гибкой
п л а с т и н к и
Под пределом упругого сопротивления будем пони-
мать ту нагрузку р.с, при которой наибольшие приве-
денные (по той или иной теории прочности) напряжения
достигают величины предела текучести материала ат.
Рис. 18.71
амакс— 0,423
ра
£ .
k t
(18.125)
упругого сопротивления пла-
г) Прямоугольная мембрана подвергается
действию
равномерно распределенной поперечной нагрузки; пла-
стинка до прогиба получила предварительное натяжение
в своей плоскости (рис. 18.70).
Предварительные
полагаем равными
напряжения во
ал. — Оу — q.
Стрела прогиба
£= — —-
п« / 1
где
g / Ь\-
Е \ t )
В случае квадратной мембраны
£ « 0,082	.
О*
' Для определения предела
станки устанавливается связь между наибольшими на-
пряжениями и интенсивностью нагрузки. При этом де-
всех
Р_
о'
Рис. 18.73
Рис. 18.74
18.6, ГИБКИЕ ПЛАСТИНКИ И МЕМБРАНЫ
295
формации считаются упругими на всем участке до пре-
дела текучести.
Пример 18.1. Квадратная гибкая пластинка находится
под действием равномерно распределенного по поверх-
ности пластинки поперечного давления; кромки пластин-
Ч.кГ/сн’
Рис. 18.75
Рис, 18.76
ки шарнирно оперты; края не смещаются. На рис. 18.71
и 18.72 изображена зависимость между от и рт для
малых и значительных прогибов чт. Дана «предельная»
нагрузка, полученная при том же условии для абсолют-
но гибкой пластинки, которая оказалась равной
р* = 9,63 (o*p’s.	(18.128)
В практических расчетах надо вычислить сц. по фор-
муле
и найти р* из графиков рис. 18.71 и 18,72,
Пример 18.2. Удлиненная гибкая прямоугольная пла-
стинка пролетом b находится под действием равномер-
но распределенной поперечной нагрузки. Кромки пла-
стинки шарнирно закреплены; края не смещаются. Гра-
фик предельной нагрузки из условия достижения наи-
большим напряжением предела текучести оа,манс =
— От представлен на рис. 18,73 сплошной кривой [Н].
Верхняя пунктирная кривая показывает возрастание от-
носительного прогиба /макс/й с увеличением b/t, Ниж-
няя пунктирная кривая характеризует рост роли цепных
напряжений. Аналогичный график предельной нагрузки
для пластинки с защемленными кромками приведен на
рис. 18,74. Коэффициент Пуассона р — 0,3.
Нагрузка на пластинку ограничивается также усло-
вием достижения предельного прогиба. Кривые постоян-
ного значения	представлены на рис. 18.7а (пла-
стинка с шарнирно закрепленными кромками) и на рис.
18.76 (пластинка с защемленными кромками). Принято
р.” 0,3.
ЛИТЕРАТУРА
I.	Броуде Б. М. Устойчивость пластинок в элементах
стальных конструкций. Машстройиздат, 1949; Предельные со-
стояния стальных балок. Гос, изд-во лит, по строительству и ар-
хитектуре, 1953.
2.	Бубнов И. Г. Труды по теории пластин, Техтеоретиз-
дат, 1953.
3.	Буиич Л. М., Палий О. М, и П п с к о в и т и-
н а И, А, Устойчивость усеченной конической оболочки, нахо-
дящейся под действием равномерного внешнего давления. «Ин-
женерный сборник», 1956, № 23,
4,	В а р в а к П, М. Приближенный расчет пластинок сред-
ней толщины. Труды Киевского инженерно-строительного инсти-
тута, вып. 3, 1936,
5.	Вл асов В. 3, Общая теория оболочек. Гостехиздат,
1949.
6,	Вольмир А, С. Гибкие пластинки и оболочки. Тех-
теоретиздат, 1956; Расчет пластинок. Справочник машиностроите-
ля, т, 3. Машгиз, 1956; Устойчивость пластинок при пластиче-
ских деформациях, Изд. ВВИА имени Жуковского, 1959; Устой-
чивость деформируемых систем, Физматгиз, 1967; Устойчивость
пластинок, Устойчивость оболочек. Справочник «Прочность,
устойчивость, колебания», т. 3. «Машиностроение», 1968.
7,	Гениев Г, А., Чаусов Н, С, Некоторые вопросы
нелинейной теории устойчивости пологих металлических оболо-
чек, СтроЙнздат, 19-54.
8,	Даревскяй В. М., К арташ кин Б. Д. Методи-
ка расчета на прочность и устойчивость корпусов турбореактив-
ных двигателей, Оборонгиз, вып. 5, 1956.
9.	И л ь ю ш и н А, А. Устойчивость пластин и оболочек за
пределами упругости. «Прикладная математика и механика»,
вып. 5, 1944 и вып, 5—6, 1946: Пластичность. Техтеоретиздат, 1948,
10,	Корнишин М. С., Исанбаева Ф, С, Гибкие
пластинки и панели, «Наука», 1968.
11,	Лейте с С. Д, Упругий и упруго-пластический изгиб
длинных прямоугольных пластинок. Сб. «Расчет пространствен-
ных конструкций, вып. VIII, Гос. изд-во лит, по строительству
л архитектуре, 1962.
12,	С аченков А. В. Приближенное определение нижней
границы критической нагрузки при продольном сжатии тонкой
конической оболочки. Известия Казанского филиала АН СССР,
серия физико-математических и технических наук, 1955, Кэ 7.
13.	Субботин К- И. Прочность и устойчивость косо-
угольных свободно опертых пластинок, автореферат диссертации,
издание МАИ, 1953.
14.	Тимошенко С. П. Пластинки и оболочки. Техтеорет-
издат, 5948; Устойчивость упругих систем, Техтеоретиздат," 1946.
15.	Феодосиев В. И, Упругие элементы точного прибо-
ростроения. Оборонгиз. 1949,
16.	В u г g е С, G., Structural principles and data. Hand-
book of Aeronautics, ,№ 1, 1952.
17,	Sturm R. G,, Stability of thin cylindrical shells in tor-
sion, ASCE, vol. 73, Л'Ь 4, 1947.
18.	J о J 1 c Ko s a r a, Diagonal stiffening of a simply sup-
ported square plate submitted to shearing stresses. Pubis Inst.
Acad, serbe Sei., 1953, 5.
59.	Roark J., Formulas for stress and strain, 1943.
20.	Kempner J., Postbuckling behaviour of axially comp-
ressed circular cylindrical shells, Journal of the Aeronautical
Sciences. № 5, 1954.
21.	Nash W. A., Effect of large deflections and initial im-
perfections on the buckling of cylindrical shells, J, Aeron Set,
As 4, 1955.
22,	11 s u Lo Gr ate H, and S c h w a r t z E. B„ Buckling of
thinwalled cylinder under axial compression and Internal pressu-
re .NACA TN 2021, 19.50.
РАЗДЕЛ 19
РАСЧЕТ СООРУЖЕНИИ, ВЗАИМОДЕЙСТВУЮЩИХ С ГРУНТОМ
10.1, СТАТИКА СЫПУЧЕЙ СРЕДЫ
19.1.1. Давление на ограждающие
конструкции хранилищ сыпучих тел
Имеется в виду несвязное сыпучее тело, например
дробленая руда, цемешный клинкер, сухой песок, гра-
вий, зерно и другие материалы, состоящие из отдельных
твердых частиц и не обладающие сцеплением. Для рас-
чета несвязное сыпучее тело заменяется сплошной сыпу-
чей средой, которая характеризуется следующими свой-
ствами:
среда не сопротивляется растяжению, нормальные на-
пряжения в ней могут быть только сжимающими;
касательные напряжения в среде не превосходят уси-
лий внутреннего трения, зависящих от коэффициента
внутреннего трения среды;
Таблица 19.1
Нормативные характеристики сыпучих тел
Материал	Объемный вес у a	Угол естест- венного от- коса <р ь град	Коэффици- ент трения f	
			по бе- тону	по ме-  таллу :
Апатитовый концентрат . . .	1,9	35	0,6	0,35
Гипс кусковой крупный (более 10 елг) .... 		1,45	30	0,43	0,3 ;
То же, мелкий (до 10 см) . .	Г 35	40	0,55	0,35
Глинозем , ........ ,	м	80	0,5	0,3
Зерно (пшеница) ......	0,8	8.5	0,-1	0,37
Известь обожженная крупная (более 10 см}  , .	. . ,	1,1	30	0,45	0,3
То же. мелкая (до 10 см) . .	0,8	35	0,55	0,35
Известь гашеная в порошке	U,7	85	0,55	0,35
Карналит	0.8	35	0,5	0,3
Кокс .	.	0,6	45	0,84	0,47
Магнезитовый порошок с разме- рами зерен до 10 мм	. . .	1,8	33	0,53	0,35
Нефелиновый концентра"! . .	1,5	35	0,5	щз .
Песок сухой ........	1,8	35	0,7	0,5 .
» влажный	1,8	40	0,6-5	0,4
» насыщенно-влажный , .	2	25	0,0	0,35
Сода кальцинированная , . .	0,6	40	О.,5	0,3
Уголъ антрацит , 		ощ	30	0,5	0,3
» битуминозный несортиро- ванный ..........	0,9	40	0,0	0,3
Уголь мелкий орешковый и уг- ли, применяемые в коксохими- ческом производстве , . ,	0,8	40	0,05	0,35
Уголь бурый	0,7	43	0,7	0,35
Фосфоритная мука , . , . .	1,8	40	0,5	0,3
"Цемент , . . > , ..... .	ЦО	30	1 >, 58	0,3
Таблица 19,2
Характеристики сыпучих тел
Сыпучее тело	Объемный г ее у 7/лС 					Угол инутрспнс?G трения Ф в град	Угол трения <р0 в град		
			ио стали | _—J	по дере- ву	Я* о ©
Агломерат железной					
РАДЫ		1,7—2	45	—	,—,	—.
Бобы .	. . 4. - ,	51,6—0,8	32	22—25	15—27	24
Гречиха .....	0,3—0,7	35	17-27	20—30	—
Земля формовочная	!,85-1,:’>	:ю—36	25—35	г—	—
3 од а . ,	....	0,4—0,7	40—50	35—Ю	—	—
Известняк дробленый Кукуруза неочищен	5,4—1,7	35—55	29—45	35	—
нал 			0,7—0,75	35—40	20	17—19	23
Льняное семя . .	0,65—0,75	25	19	17—22	22
Мел дробленый	1,4	39	—	—	—
Мука ржаная . ,	0,6—0,55	.35—50	26—38	—	—
» пшеничная .	0,45—0,55	30-45	—,	—	—
Овес .......	0,4—0,5	27—35	22— Я)	.20—38	25
Опилки древесные	0,15—0,3	30—55	21—40	—	—
Просо .	0,65—0,85	22—25	17	18	—
Рожь . , * , , .	0,65-0,3	25—35	18—30	20—35	30
Руда железная . .	2,1-2,4	35—37	30—40	—	—.
Сахао ......	0,7—4,9	50	40—45	—	—
Соль поваренная	0,7—ЦЗ	30—50	26	—	—-
Торф ......	0,3—0,7	45—50	27—37	19-39	—
i Шлак ......	0,6—1	ЗР—50	22—50	1.7	—
Ячмень	0,43—0,75	25—45	23—25	18— 23	24
деформации среды возможны только за счет сдви-
га ио площадкам, где касательные напряжения достига-
ют величины усилий внутреннего трения.
Сыпучая среда является расчетной моделью несвязно-
го сыпучего тела. С помощью теории предельного рав-
новесия сыпучей среды определяется давление на кон-
струкции хранилищ, несвязных сыпучих тел. За неиме-
нием лучших возможностей эту теорию часто распрост-
раняют также н иа порошкообразные сыпучие тела, та-
кие как цемент, мука и т. п. О применении теории пре-
дельного равновесия сыпучей среды к грунтам, в том
числе к обладающим сцеплением, см. [35],
По своим статическим свойствам несвязные сыпучие
тела значительно отличаются от сыпучей среды, так как
в них могут происходить большие объемные деформа-
ции— разрыхление и уплотнение, сопровождающиеся
сильным изменением коэффициента внутреннего трепня
[68]. Поэю.му в праыически.х нолях целесообразно при-
менять приближенные мы оды расчета, компенсируя от-
19.1 СТАТИКА СЫПУЧЕЙ СРЕДЫ
297
клонение расчетных величин от действительных запа-
сами устойчивости и прочности.
Сыпучее тело характеризуется двумя величинами: обь
емным весом у и углом внутреннего трения или прини-
маемым равным ему углом естественного откоса ф. При
решении расчетных задач необходимо также знать ко-
эффициент f или угол <ро трения сыпучего тела по по-
верхностям ограждающих его конструкций. В табл. 19.1
приведены нормативные характеристики различных еы-
rviHX тел согласно [39]. Эти характеристики можно при-
нимать также при расчете бункеров и ограждающих
стен складов для сыпучих тел
В габл. 19.2 приведены характеристики некоторых сы-
пучих тел по данным литературы [18], которые могут
быть использованы при расчете хранилищ для этих ма-
териалов.
19.1,2. Предельное равновесие сыпучей среды.
Строгие и приближенные решения
плоской задачи
Статика сыпучей среды есть статика ее предельного
равновесия. Принимается, что в этом состоянии дефор-
мации сдвига происходят только при условии, что по
некоторым площадкам кагате тьиые напряжения т и нор-
мальные напряжения о связаны зависимостью
т = a tp ф,	(19.1)
где <р — угол внутреннего трения.
Непосредственно из предельного круга Мора
(рис. 19.1) видно, что в каждой точке сыпучей стыды
имеются две такие площадки, где соблюдается условие
(19.1). Огибающие этих площадок дают липин скольже-
ния. Нормали к указанным площадкам наклонены к
большему главному
90 + ф
углами-------- и
нормальному напряжению со
90 тФ
_ -----. Отношение г Таиных.
под
нор-
мальных. напряжении равно:
(19 2)
(19 31
Взаимное расположение надрав тений главных нор-
мальных напряжений и площадок скольжения в точке
среды изображено на рис 19 2. Переходя от элемента к
массиву, напряжения стедуег рассматривать как функ-
цию координат точки. В той зоне сыпучей среды, где
имеет место состояние предельного равновесия, в усло-
виях плоской задачи возникают два семейства линий
скольжения: наклоненные к траекториям большего
Рис. 19.2
главного нормального напряжения о. под углами
+ ^4а——j и —^1о—~-у и пересекающиеся друг с
другом под углом 190—ф).
Для решения задач о плоском предельном равновесии
сыпучей среды разработаны строгие и приближенные
методы.
Рис. 19.3
Строгие методы основываются на условии предельно-
го равновесия элемента < ыпучей среды (рис. 19.3). Для
.того элемента могут быть написаны три совместных
рашишия, связывающих между собой три неизвестные
Ьтнкции координат — напряжения <тд, и т. Первые
два уравнения — известные дифференциальные уравне-
ния равновесия:
д<\	дг	гИ,	От
дх	дг	дг	дх
где у — обы мнып вес среды.
(19.41
298
РАЗДЕЛ 19 РАСЧЕТ СООРУЖЕНИИ, ВЗАИМОДЕЙСТВУЮЩИХ С ГРУНТОМ
Третье уравнение связывает между собой компоненты
напряжений ах, oz и т и записывается следующим об-
разом:
(av —	+ 4т3 = (аг + ауу sin2 <j>.	(19.5)
Строгий метод решения системы уравнений (19.4) и
(19.5) разработан В В, Соколовским [34]. Для некото-
рых частных случаев получены замкнутые решения.
В других случаях решения отыскиваются численными
методами. С. С. Го.тушкевич предложил для этих целей
графический метод [7].
Строгая теория предельного равновесия в пространстве
разработана только для случая осевой симметрии.
Приближенные методы исходят из упрощающих допу-
щений об очертании линий скольжения. Большей частью
предполагается, что линии скольжения являются пря-
мыми.
Приближенный метод, предложенный Репкиным, ис-
ходит из предположения, что в состояние предельного
равновесия переходит вся сыпучая среда и что полное
напряжение по вертикальным площадкам параллельно
верхней прямолинейной границе среды, а полное напря-
жение по площадкам, параллельным этой границе, вер-
тикально и равно ус cos (3, где у — объемный вес сыпу-
чей среды (рис. 19.4).
Это предположение эквивалентно допущению, что ли-
нии скольжения и траекгории главных напряжений явля-
ются прямыми. Величины напряжений по любым площад-
кам находятся с помощью круга Мора (рис. 19.5). Преж-
де всего определяются напряжения по площадке, парал-
лельной верхней границе среды, которые в соответствии
с рис. 19.4 равны:
<т = yz cos (3; т = уг sin (3 cos р.
Эти величины определят на диаграмме Мора точку F.
В угол, образованный двумя прямыми, проведенными
под углами +<Р и —<р к оси о, вписывают окружность,
Рис, 19.6
проходящую через точку F. Задача имеет два решения.
Малая окружность с центром С отвечает случаю сполза-
ния сыпучей среды — активному давлению. Большее
главное напряжение равно меньшее главное напря-
жение равно ода. Одно семейство прямых линий сколь-
жения параллельно прямой EaD, другое — прямой EaD'.
Большая окружность с центром Cj отвечает случаю над-
вигания сыпучей среды — пассивному давлению. Большее
и меньшее главные напряжения соответственно равны
а-[Р и Огр. Семейства прямых линий скольжения парал-
лельны прямым EpDf и EpD^
Метод Репкина в настоящее время применяется только
для решения таких задач, как определение давления сы-
пучего тела на стенки и воронки бункеров (см. далее
п. 19,1.6), на криволинейные ограждающие поверхности,
когда иных методов решения не имеется, а значительные
отклонения от действительности в величине и распреде-
лении давления не имеют существенного значения.
Наибольшее применение в практических целях пока
имеют приближенные методы решения задач статики
сыпучей среды, в которых линии скольжения предполага-
ются прямыми, а их положение задается с точностью до
одного параметра, который определяется из условия
экстремального значения давления сыпучей среды на
ограждающие конструкции.
Эта идея Кулона лежит в основе его теории давления
сыпучего тела на массивную стенку (см, далее 19 1.3).
Деформации сыпучей среды определяются сдвигами,
возникшими в результате преодоления внутренних уси-
лий трения. Поэтому можно считать, что диаграмма ма-
лого перемещения А обобщенной силы Р, приложенной
к сыпучей среде, такая же, как идеализированная
диаграмма сдвига при сухом трении твердых тел
(рис. 19.6, а). Пока Р<Рмакс, перемещение равно нулю,
а при Р = Рма!:с оно может неограниченно расти. Воз-
можность проявления так называемой псевдопластично-
сти [2], когда переход в предельное состояние сопро-
вождается внезапным падением силы, вызывающей сдви-
ги, и Рпр1;д<'Рмаис (рис. 19.6,6) не принимается во вни-
мание.
Считается, что сыпучая среда ведет себя как жестко-
пластичное тело и, следовательно, подчиняется положе-
19 I. СТАТИКА СЫПУЧЕЙ СРЕДЫ
299
ниям, определяемым следующими экстремальными тео-
ремами о предельном равновесии таких систем [1, 6].
1.	Величина нагрузки заданной конфигурации, вызы-
вающая переход в состояние предельного равновесия сы-
пучей среды в целом или только ограниченной ее части —
так называемая разрушающая нагрузка — является наи-
большей из величин статически возможных, т. е. уравно-
вешивающихся нагрузок той же конфигурации. Это по-
ложение непосредственно вытекает из диаграммы, изо-
браженной на рис. 19.6, а.
2.	Разрушающая нагрузка есть наименьшая из нагру-
зок, способных вызвать пластическую деформацию сыпу-
чей среды, т. е. наименьшая из кинематически возможных
нагрузок заданной конфигурации. Это положение лежит
в основе кинематического метода определения разруша-
ющей нагрузки. В сущности именно такая задача при-
ближенно решается при определении пассивного давле-
ния сыпучей среды на стенку. Сила, надвигающая стенку
на сыпучее тело, получается наименьшей при наимень-
шей величине пассивного давления.
3.	Величина реакции подающейся связи, ограничиваю-
щей сыпучую среду и вызывающей в ней своим переме-
щением состояние предельного равновесия, есть наи-
меньшая из всех статически возможных и наибольшая из
всех кинематически возможных. Типичный пример пода-
ющейся связи — стенка, ограждающая сыпучее тело.
Определение активного давления на стенку по теории
Кулона есть отыскание кинематическим методом при-
ближенного значения реакции подающейся связи.
19.1.3. Давление сыпучего тела
на массивную стенку.
Теория Кулона. Строгое решение
для частного случая
Теория Кулона лежпт в основе приближенных методов
определения давления сыпучею тела на массивные слеп-
ки. Имеется в виду бесконечно длинная стенка, так что
задача решается как плоская. В расчет вводится стенка
длиной, равной единице. Задняя грань щенки плоская.
Верхняя граница сыпучего тела имеет произвольное очер-
тание. Давление на стенку определяется для момента
перехода ее в состояние предельного равновесия. Если
этот переход вызван перемещением в сторону от сыпу-
чего тела, стенка воыфишпгает активное давление или
распор сыпучею тела. При перемещении стенки в проти-
воположном направлении на нее действует пассивное
давление или отпор сыпучего тела. Перемещение стенки
создает состояние предельного равновесия в ограничен-
ной зоне сыпучей среды, непосредственно примыкающей
к стенке и имеющей форму призмы. Граница между этой
зоной и остальной частью сыпучей среды является пло-
скостью. Наклон плоскости определяется из условия
экстремума давления сыпучей среды на стенку,
Случай активного давления изображен на рис. 19,7.
Зона сыпучей среды, находящаяся в состоянии предель-
ного равновесия, называется призмой обрушения, ее гра-
ница— плоскостью обрушения. Фигура АВН—основа-
ние призмы обрушения. Прямая ВН — след плоскости
обрушения. Призма обрушения сдвигается по плоской
трани стенки АВ и плоскости обрушения ВН, Реакции
этих двух плоскостей наклонены к нормалям плоскостей
под углами трения соответственно ср0 и <р.
При заданных размерах и угле е наклона задней грани
стенки к вертикали, очертании поверхности сыпучего те-
ла, объемном весе у и углах грения ср и ср0 реакция стен-
ки является функцией одной переменной — угла 0, опре-
деляющего положение плоскости обрушения. Из тре-
угольника сил получаем:
sinCO — ф)
i-r — (j ——	———.
sin (ф + 0 — ср)
(19.6)
где G— вес призмы обрушения, равный уХ(пл ЛВг/)Х
XI, и угол ф = 90—-е—ф0.
Активное давление равно максимальной величине Е.
При непрерывных Е и dEjdQ угол наклона 9 плоскости
обрушения может быть найден из условия 4Е/вГ0 = О.
Величина активного давления находится нз выражения
(19.6).
Очевидно, что активное давление по теории Кулона
есть реакция в подающейся связи, определяемая прибли-
женно кинематическим способом. Погрешность делается
в сторону преуменьшения, т. е. не в запас прочности.
Поэтому в некоторых случаях приходится отыскивать
более точное решение.
Случай пассивного давления изображен на рис. 19.8.
Зона сыпучей среды, находящаяся в состоянии предель-
ного равновесия, называется призмой выпирания, ее гра-
ница— плоскостью выпирания ФигураАВН — основание
призмы выпирания. Прямая ВН — след плоскости выпи-
рания. В этом случае:
sin (0 -а ср)
£ = U--------------~,
sin (ф + в 4- ср)
(19.7)
где G — вес призмы выпирания, равный уХ(пл. АВН)'рА\,
и угол ф = 90—е+фо.
300
РАЗДЕЛ 19 РАСЧЕТ СООРУЖЕНИЙ ВЗАИМОДЕЙСТВУЮЩИХ С ГРАНТОМ
Пассивное давление равно минимальной величине Е
При непрерывном £' и dE/dO угол наклона 0 плоскости
выпирания может быть .найден из условия dE/dQ =0
Величина пассивного давления находится из выражения
(19 7)
Определение пассивного давления по теории Кулона
эквивалентно приближенному определению кинсиатпч
ским методам разрушающей величины силы, надвигаю
щеп стенку на сыпучее гело (рис 19 9) и, следовательно,
дает погрешность в сторону преувеличения, т е не в
запас прочности Поэтому в некоторых случаях прихо-
дится искать более точное решение [34].
Распределение давления по высоте стенки — закон из-
менения ею интенсивности и положение центра давления
в теории Кулона остаются неопределенными Для устра-
нения этой неопределенности полагают, что давление на
верхнюю чаете стенки, расположенную выше некоторого
уровня, ие зависит от того, перемещается или не переме-
щается нижняя часть стенки, расположенная ниже того
же уровня С помощью теории Кулона можно построить
кривую полных давлений на стенку, каждая ордината
которой равна величине давления на ту часть стенки,
которая расположена выше ординаты Интенсивность
давления находится как производная кривой полных дав-
лении по длине Применяют также и другой прием —
вентр давления находят проектированием на заднюю
грань стенки центра тяжести призмы обрушения или
призмы выпирания лучом параллельным следу соответ-
ственно плоскости обрхшения или плоскости выпирания
Опыт строительства и сп циалыю поставленные экс-
перименты показали что теория Кулона в большинстве
случаев удовтетчорчтел „к согласуется с деиствителЕ-
чост ю [29] Особенно >ю относится к случаю активно
го давления Определять величины дав тения по фор
мулам (19 6) и (19 7) целесообразно только в простел
Unix случаях Для абсолютно падкой вертикально»
дички н горизонтальной поверхности сыпучей среды
(ргс 19 10) Кутой получил следующие выражения
активное давление
F == у #s tg“ Й—f )	П9.8)
пассивное давление
Т т б т и цт 10 3
Коэффициенты А для определения по форси тс (10 г) иоргте тьнои
составляющей I} активного дарения (в -эпитете)
и пассигного дазюшзя (s шамепатече)
					В	spat			
ф	Фа								
 гра 1	зрид		—20	— 10	0	10	20	10	40
		>->	(п	( ь7	9,7)	0,74	0 8^	'ДР	1 1 1
			1 75	1 57	1 42	Д Р	I, Р	1,3 )	1 5
		0 0	1 (И	1) 9 3	0 Ьб	0 7 }	0,8п	0 и	1 0)
i 1	э	2 17	1	1 Ь'г	I 5э	1, 17	1Д1/	1 47	1 58
		0, V	0 ~ )	0 X)	0,3	0,09	0 71	0 90	1 07
	Н)	2,51	2 0?	1,7'	1,01	1 31	IE		1ДР
			G 1)	п	( 40	0 55	0,b5	0 ы>	10.
		1 3	_ 1 1	17	2,Q^	дьз	1,	1, 4	
		И ?1	п 3	»>	0 И	0,51	0 hl	0 7”	0 О1
0	1)						- ——*	——-•		j.—•—	• 1
		1 Д		5	2,51		2,0>	1 <ь	1, с
		) ’)	0 5	1 4э	0 41	0 Р	0,58	1 71	0 Р
	20	5, лэ	I, д	4 Р	2,(15	2, Ю	2,2е)	Д17	415
		0 1S	о ’ >	0,27	0,03	0, и	0 51	0 Г	0,89
		7,01	5,05	3,7b	3,00	2,4о	Д17	1,09	1
		ОД 5	0 ’ •)	0 21	0,29	0, 17	0 -18	0 6?	0 8’
30	15	Ц 7	11	5,80	Д Ь	ДкО	3,08	.,08	3,1/
		0 I 4	0 17	О ;1	, 7	0 и	0 И	57	0 7-
	40	РД	10,5	7 51	>,57	Д48	>,77	ч 2 4	2 !э
		П 1)3	0 1	1 1 >	0 ’	О Of)	9 41	) э >	П
		.д, >	Д	, 15	1 W	Д №	2,	„ Ь	2, 40
41		9 1) з	0 10	0 1 1	3 1 )	9 2>	( 47	ОД]	0,Р
		•>5, >	21 0	1 , 1	о 0)	0,5b	5,05	4,08	4,34
		0 05	1 14	0 1 5	0 ч	I) 4	0 4	0 18	О 70
	4 )	57 1	1 .	21,0	1 1 0	0 71	7,	5 55	1 73
методы спреде тения активного и пассивного тан'кипя
основанные На теории Кутана (см пп 19 1 4 и 10 I 5)
Для чайного случая подпорных с.еиок с плоской мт
1юп гранью при горизонта шпон новг рхаости тасьшлг
удобно полетовзтгея резг, штатам» р счегоь Е В ( око
товского и 3 Н Буцко по строгой теории прнведечны
ми в ттбг 19 3 В jToh таблице даны коэФфнцпенгы 7
дтч определения норм гльноп составтяющеи Еа актив
пою и пассивною давления на стенку по следующей
формуле
yh“
Еп = д-^-.	(19.10)
Эпюра давления — трещим них, центр давления надо
дш г па расстоянии 7/3 от юга стенки
Чтя более слот нт (тучхв имеются аналитически
выр же гия mmii 1 давления [33] Удобны графические
Кастете пая гост излаю пая Г„ вычисляется умпоке-
ине'.1 £я на ксысрфициснг aptния
= Еь tg <ро
(19 Л)
19 I СТАТИКУ СЫПМЧЕП СРЕДЫ
301
19.1.4. Графическое определение активного
давления. Построение Ребхана.
Построение Понселе
Построение Ребхана имеет в виду тоскую заднюю
грань и любую непрерывную форму поверхности сыпуче-
го тела Оно основано иа следующих положениях, выте-
кающих из теории Кулона:
1) на рис. 19 11 линия ВН—стед гпоскости обруше-
ния, отвечающий! активному давлению; линия IIG парал-
лельна основной линии SZ5; площадь фигуры АВИ равна
площади треугольника BHG;
Рис. 19.12
2) активное Заиление равно площади треугольника
Ребхана GHJ, умноженной ни объемный вес сыпучего
тела (рис. 19.11).
Построение, определяющее след плоскости обрушения
ВН, и треугольник Ребхана изображены на рис, 19.12.
На горизонтальной оси наносяiся гонки /гфиг,бь пред-
ставляющие проекции точек НсНщПфЕЦ, соответствую-
щих во(можцым положениям плоскостей обрушения.
Кривая I дает изменение площади основания призм об-
рушения АР>Н\, ABI7-2, АВН->„ ABHi Ордитты кривой П
раьны площадям трщ>о шгшюв ВНИИ, ВН;(щ, ВНИИ,
ВНсСщ. Точка пересечения о>'т их кривых, спроектирован-
ная па с кд поверхности сыпучего те :а, определит точку
//, а прямая В‘1 сеть след искомой плоскости обрушения.
Проведя HG'PPiD и отложив GJ^=GH, получаем тре-
угольник Ребхана. Активное давление
Е = у (pji.GHJ),
где у — объемный вес сыпучего тела.
Рис. 19.13
Центр давления может быть найден проектированием
н 1 шдаюю грань стенки центра тяжтеп! призмы обруше-
ния лучом, параллельным следу ВН плоскости обру-
шения.
В некоторых случаях по Рсбхану можно найти актив-
ное давление и без помощи кривых / и //.
На рис. 19. 13, а показан случай, когда поверхность
сыпучего тела — плоскость, параллельная основной ли-
нии BD. Из условия равновеликости с\АВН и ЕВНС сле-
дует, что АН = НС. Треугольник CHJ, заштрихованный
на рис. 19. 13,а, есть треугольник Ребхана.
На рис, 19. 13, б поверхность сыпучего тела — плос-
кость, параллельная плоскости естественного откоса.
Точка С уходит в бесконечность. Треугольник Ребхана
GHJ определяется проведением 6//Ц5Д, Эпюра давле-
ния треугольная, и, следовательно, давление Е приложе-
но на расстоянии Й/З от низа стенки под углом <ро к нор-
мали задней грани.
Пост роение Понселе имеет в виду случай, когда по-
герхпость сыпучего тела является плоскостью. Задняя
грань стенки — также плоскость. Простота построения
Понсе те позво ляет применять его для приближенного оп-
ределечия давления в ряде более сложных случаев: при
ломаном очертании задней грани стенки и поверхности
сыпучего тела, при наличии иа поверхности сыпучего те-
ла иссплошной нагрузки и ь других случаях.
Построение Понселе для опредетения активного дав-
ления изображено на рис. 19 14. Последовательность
появления точек на чертеже отвечает порядку букв лл
тинского алфавита. Из точки А проводится АЕ\\В1>
С помощью полуокру жностп, построенной на диаметре
ВС, определяется BF-~) BC-BF, дтя чего проводится
302
РАЗДЕЛ !9 РАСЧЕТ СООРУЖЕНИИ, ВЗАИМОДЕЙСТВУЮЩИХ С ГРУНТОМ
ГЕА.ВС. Затем из точки В откладывается BG — BF и из
точки G проводится GH\\BD. Прямая ВН есть след плос-
кости обрушения, Откладывая ог точки G отрезок GJ =
= GH, получаем треугольник Рсбхана GHJ. Активное
давление на стенку
Е = у (пл. GEM),
где у — объемный вес сыпучего тела.
Активное давление приложено в точке, расположен-
ной на расстоянии /i/З от низа стенки, и наклонено под
углом <р0 к нормали задней грани стенки.
А'. Таким образом, высота стенки увеличивается
Величина h0 может быть вычислена по формуле
1
h' = Ло----------------------~.
1 + tg Ф tg р
Построение выполняется для стенки высотой
Эпюра давления имеет форму трапеции, заштрихован-
ной на рис. 19.17, Центр давления лежит на уровне цене-
на h0-
(19.13)
hA-hn-
Рис. 19.14
Рис. 19.16
На рис, 19.15 дано измененное построение Понселе
для случая, когда точка С расположена далеко справа,
и построение, согласно рис. 19. 14, оказывается неудоб-
ным. Компактность построения достигается параллель-
ным переносом характерных точек.
На рис. 19, 16 изображено построение Понселе для
случая, когда АЕЦВО проходит выше следа плоскости,
ограничивающей поверхность сыпучего тела. В этом
случае из точки С проводится CFCl.BC и определяется
ВА=)ГВС-ВД Дальше построение продолжается так
же, как на рис. 19. 14.
При наличии на поверхности сыпучего тела равномер-
но распределенной нагрузки (рис, 19. 17) интенсивностью
р она заменяется эквивалентным слоем сыпучего тела
высотой
ha =
(19.12)
Поверхность сыпучего тела «приподнимается» на ве-
личину hrj. Задняя грань стенки продолжается вверх до
пересечения с новой поверхностью сыпучего тела в точке
ра тяжести этой трапеции. Верхняя ордината эпюры
<7я дает интенсивность активного равномерно распреде-
ленного по высоте стенки давления, вызываемого рав-
номерно распределенной нагрузкой р.
Ниже описываются некоторые частные случаи, когда
построение Понселе удастся использовать только для
приближенного, ио практически приемлемого решения за-
дачи.
На рис. 19, 18 изображен прием приближенного опре-
деления давления для случая, когда равномерно рас-
39.1, СТАТИКА СЫПУЧЕЙ СРЕДЫ
303
иределенная нагрузка расположена не на всей поверх-
ности сыпучего тела. Принимается, что участок стенки
Аа, расположенный выше пересечения задней грани с
плоскостью, проведенной под углом ф к горизонту через
крайнюю ординату нагрузки, не воспринимает дополни-
тельного давления от этой нагрузки.. Далее полагают,
•по участок стенки ЬВ, расположенный ниже пересечения
задней грани с и топкостью, проведенной через край на-
грузки параллельно плоскости обрушения, найденной
Рис. 19.20
из построения Понселе для участка Аа, испытывает та-
кое же давление, как если бы нагрузка была располо-
жена без отступа от стенки. На участке ab давление из-
меняется по переходной прямой.
На рис, 19, 19 показан прием приближенного опреде-
ления давления для случая, когда след поверхности сы-
пучего тела — ломаная линия АНН. Линия На — след
плоскости обрушения для участка Аа, найденный в пред-
положении, что поверхность сыпучего тела — плоская
со следом АНМ, треугольник Oed — эпюра давления для
этого же участка, построенная при том же предположе-
нии. Далее определяется давление на стенку и строится
эпюра давления в предположении, что поверхность сыпу-
чего тела —плоскость со следом A^N, а след задней гра-
ни стенки — А>,В. Прямая ОД1 на эпюре давления явля-
ется асимптотой к действительной эпюре давления, так
как с увеличением глубины влияние пригрузки АА>,Н
уменьшается Прямая dg, дающая изменение интенсив-
ности давления иа участке аВ, спрямляет кривую, про-
ходящую через точку d и имеющую асимптоту ОД1.
Па рис. 19. 20 показано определение давления иа стен-
ку с ломаной задней гранью. Сначала определяется
давление Cabj на грань АВ|, Затем грань BtB продол-
жается вверх до Ai и определяется давление Елгв на
стенку с плоской задней гранью Л,В. Давление иа BtB
равно площади нижней части трапецеидальной эпюры
интенсивности давления на стенку АВ. Центры давления
на каждую из граней находятся на уровне центра тя-
жести соответствующей части эпюры интенсивности дав-
ления.
Как указывалось, теория Кулона и основанные на ней
способы приближенных расчетов несколько преуменьша-
ют активное давление по сравнению с результатами
строгой теории предельного равновесия сыпучего тела.
По В. В. Соколовскому, при вертикальной задней грани
стенки это преуменьшение находится в пределах 5%,
если	т. е гс всех практических случаях. Раз-
ница становится существенной для стенок, наклоненных
в сторону сыпучего тела, когда е<0. Так, при г = —30’
и ф = фо = 35° теория Кулона преуменьшает активное
давление на 42%.
19.1.5. Графическое определение пассивного
давления. Построение Ребхана. Построение
Понселе
Построение Ребхана имеет в виду любую непрерывную
форму поверхности сыпучего тела. Оно основано на двух
следующих положениях.
На рис, 19 21 линия ВН — след плоскости выпира-
ния. Линия HG параллельна основной линии BD. Пло-
Рис. '19 21
щадь фигуры АВН равна площади треугольника BHG
На рис. 19,22 DJ=GH Пассивное давление равно
площади треугольника Ребхана GHJ (заштрихован на
рисунке), умноженной на объемный вес сыпучего тела
Таким образом, пассивное давление легко определяется,
если известно положение следа плоскости выпирания
ВН. Этот след находится построением двух кривых: кри-
вой изменения площади АВН и кривой изменения пло-
щади треугольника ВОН- обеих в зависимости от поло-
жения точки Н на поверхности сыпучего тела. Равенст-
во ординат обеих кривых укажет искомое положение
следа плоскости выпирания. Детали построения такие
же, как и в случае определения активного давления.
Центр давления находится проектированием на плос-
кость задней грани центра тяжести призмы выпирания
лучом, параллельным плоскости выпирания. Пассив-
ное давление отклонено ст нормали к задней грани на
УГОЛ фо.
Построение Понселе имеет в виду, что поверхность
сыпучего тела — плоскость. Построение приведено на
рис. 19. 22. Последовательность появления точек на чер-
теже отвечает порядку букв латинского алфавита. Линия
естественного откоса проводится под углом ф, откла-
дываемым от горизонтали вниз по часовой стрелке,
и продолжается до точки С пересечения продолжения
следа плоскости, О1раничивающей сыпучее тело сверху.
Основная линия BI) образует с гванью стенки угол (ф+
+<fo). откладываемый от В 1 также по часовой стрелке.
С помощью полуокружности, построенной на диаметре
ВС, строится отрезок ВЕ--1 ВС-ВЕ. Затем откладыва-
ется BG=BF, .проводится GH,\BD и откладывается
304
РАЗДЕЛ 19 РАСЧЕТ СООРУЖЕНИЕ, ВЗХИМОДГНСТВМОЩт Г ГРУНТОМ
GJ — GH. Треугольник GH1, заштрихованный на
рис. 19. 22, — треугольник Ребхана. Пассивное давление
Е = у (пЯ-GHJ),
где у — объемный вес сыпучего тела.
Эпюра интенсивности давления имеет треугольное
очертание, как показано на рисунке. Следовательно,
пассивное давление приложено в точке, удаленной от
низа стенки на й/3; оно отклонено от нормали к задней
грани иа угол <рп.
Построение Понселе может быть использовано для
определения пассивного давления и в некоторых других
случаях, например при наличии на поверхности сыпучего
тела равномерной нагрузки. Для этих целей применяют-
ся те же приемы, которые применяются для определения
активного давления.
Как указывалось, теория Кулона и основанные на ней
приближенные способы расчета приводят к некоторому
преувеличению пассивного давления по сравнению с ре-
зультатами строгой теории предельного равновесия сы-
пучей среды
Разница между величинами пассивного давления, по
Кулону и по В В. Соколовскому, для вертикальной зад-
ней грани дана а табл. 19 4.
Таблица 19 4
Разница в процентах чежду величинами пассивного давления,
определенными по теории Калона и по строгой теории
ф, еД СЕ'		° 1	0	30	
(£?.. ер аг	1	г> J 10	Щ	15	30
Разного !•		5 j	15	8	50
Терца гв считает, что пассивное давление можно опре-
десять по теории Кулона только, если	[38].
19.1.6. Давление сыпучего тела
в бункерах и силосах
Бункером называется хранилище цилиндрической или
призматической формы для сыпучего тела с отношением
высоты вертикальной стенки к наименьшему размеру
поперечного сеченчя меньшим 1,5. Если это отношение
равно или превышает 15, хчдшлишо называется сило-
сом. Этой условной границе отвечает значите юная раз-
ница в расчетной величине и распределении давления сы-
пучего тела па ограждающие поверхности хранилища.
При определении давления в бункере исходят из упро-
щающих предпотоженид, что хранящееся в кем еып', чее
тело, ограниченное сверху горизонтальной плоское» ю.
целиком находится в состоянии предельного оавновесия-
при этом вертикальное ов и горизонтальное ог напряже-
ния на гл; бипе у равны:
/ гр
°и =- у у и сг	у у tg3 145——-
Вертикальная стенка бункера испытывает только нор
малыше давление, распределение по линейному замшу
(рис. 19. 23), так что нормальное давление
c/iu = "\’>E tg2 Йо——}	(19.14)
Давление на наклонные » н менты норочки имеют нор-
мальную и касательную составляющие, определяемые по
известным формулам напряжении по паклсшшлм пло-
щадкам:
о = ffB cos2 а -ф or sin3 а;
°г.	1 'Щ
т =------------sin 2а.
О
Эпюра нормального давления на лактонный элемент
воронки трапецеидальная (рис. 19. 23), нормальные дав-
ления равны:
Qw = Щ cos2
(19.15)
q;in = yfftj -J- h,,) cos3 v. -j- tg3 145—— sin3 a
(19-16)
Эпюра касательной составляющей давления на наклон-
ный элемент зороики также трапецеидальная.
Давление на стенку силоса определяется по теории
Янсена—Кенена, согласно которой предполагается, что:
а) все сыпучее тело в сплосе находится в осесиммет-
ричном напряженном состоянии предельного равно-
весия;
б) главные п лошадки вс всех точках сыпучего те та
вертикальны н горизонтальны;
в) отношение между главными нормальными напряже-
ниями — горизонтальным и вертикальным — во всех точ-
ках сыпучего тела
<?г
9в
°2
/ ф ''
= tga(45—J;
г) давление на сгенку имеет две составляющие— нор-
мальную gr—-а2 и вертикальную к кате iw\ рншмо
где ти — коэффициент трения сыну чего дыа по
стенке,
19 1 СТАТИКА СЫПУЧЕЙ СРЕДЫ
305
Очевидно, что предположения «бч и «г» противоречат
друг Друг;,.
Вели шна и распределение давления на стенку силосз
оиреде ппотся из решения дифференциальною уравнения
равновесия слоя сыпучею тела, имеющею форму круг-
лого диска толщиной dy (рис. 19.24):
Fdc/}, yFdy щ Udy,
где F — птощадь поперечного сечения силоса; U — пери-
метр диска.
Рис. 19.24
Интегрирование дает следующее выражение для нор-
мального давления:
<?г = У "7" (I — В.	(19.17)
/о
где
F
Р =	; /0 = tд- <г„;
f« ♦ » Л- Т’ \
= У---- tg 14о_	.
Р \	2 /
Нормальное вертикальное давление на любом уровне
Общий характер эпюры давления изображая на
рис. 16.25 Наибольшие значения давления получаются
при у~~^оо>:
ТР
^г-махс ~ с
/о
20- 26
Т а б л я ц а 19 5
К вычислению норма илюго	д пп формуле (19.17)
П	к		k	П	k
г), 02	ПЩ.О	0,50	(),3 )3	0,08	0,625
0,04	0,033	0,6’	0, юз	1,00	0,632
0,0 9	0,063	0,3 4	0, 1.17	В')	0,667	
0,05	0,077	л, ,)	0, 1.29	1,20	0,699
0,10	0,0 4	0,58	<5, !«	1 30	0,727
0,12	о,Ш	Л,бЛ	И, 41	1, ю	0,753
0,14	0,131	0,6 ’	0, 42	1,50	0,777
0,16	D ,143	0,61	ы,473	1,60	0,798
0,18	л, 165	0,66	0, 183	1,70	0,817
9,20	0,181	0,68	0, Н’>	1,80	0,815
0,22	0,Ш7	0,70	0,503	1,0()	0,850
0,24	0,21	0,72	9,51 3	2,00	0,865
0,27	0,220	0,71	0,523	2,20	0,889
0,28	0,2Н	0,76	0,532	2, Ю	0,90 5
0,60	0,259	0,78	0,3'<2	2,60	0,920
0,32	0,271	0,40	(5,551	2,80	0,939
0,34	0,288	0,82	0,559	3,00	0,059
О 36	0,302	'\81	0,568	3,20	0,95 1
0,38	0,316	0,86	0,577	3, Н)	0,967
0. Ю	о/ш	0,88	0,585	3,60	t',973
0, 42	0,313	0,00	0,591	3,80	0,978
0,4	0,356	0,92	0,601		0,982	;
0,46	0,369	0,91	0,60 )	5,00	0,993
0,4й	0,381	0,96	0,617	6,00 8,00	0,948 1,000
И
г/в,„чс уР t,;J f45 Ф Pyj .
Л)	~ f
Для обтегчення раслеточ с помощью формулы (19. 17)
в табл, 19. 5 приведены величины
k 1 — е ф
Измерения в натуре, » ою'чшности проведенные в
И»38 -1939 гг. С Г, Тахтамышевым на зерновых сило-
сах элеватора в Баку, а так/ее лабораторные экспери-
менты показа in, что формула (19. 17) дает удовлетвори-
тельные результаты лини, для случая, когда сыпучее тело
в силосе находится в покое. Как только открывается вы-
пускное отверстие р днище силоса, величина и распре-
деление давления по вертикали и периметру силоса
в большинстве случаев лначнтелыю отличаются от полу-
чаемых по теории Янсена — Кенена. Максимальные ве-
личины горизонтального давления могут превосходить
теоретические в 2—3 раза.
Учитывая опытные данные, к формуле Янсена — Кене-
на вводят поправочные коэффициенты, большие единицы.
По [39] при расчете нижней зоны стенок силосов на про-
тяжении 2/3 высоты стенки горизонтальное давление, вы-
численное по формуле (19. 17), умножается на поправоч-
ный коэффициент, равный двум; на такой же коэффици-
ент умножается вертикальное давление при расчете
днищ.
В силосах для всех видов продовольственного зерна
при расчете днищ и нижней зоны стснок высотой, равной
0,15 высоты силоса, а также при расчете стенок сило-
сон для угля по всей высот поправочный коэффициент
не вводится,
фая получения расчетных нагрузок нормативные дав-
ления умножаются па коэффициент перегрузки п= 1,3.
306
РАЗДЕЛ 13 РАСЧЕТ СООРУЖЕНИИ, ВЗАИМОДЕЙСТВУЮЩИХ С ГРУНТОМ
19.2,	РАСЧЕТ ПОДЗЕМНЫХ СООРУЖЕНИЙ
19.2.1.	Физико-механические свойства
и характеристики грунтов
Виды и составные части грунтов
Грунтами называются горные породы верхних слоев
земной коры. Грунты разделяются на скальные и на-
скальные (дисперсные).
Скальные грунты обладают жесткой связью между
частицами, спаянными или сцементированными между
собой, и залегают в виде сплошного массива или трещи-
новатого слоя.
Нескальные грумы состоят из твердых минеральных
частиц (скелет грунта), между которыми имеются про-
межутки (поры), заполненные водой или газами. Физи-
ко-механические свойства нескальных грунтов зависят
от свойств этих компонентов, их количественного соот-
ношения и взаимодействия.
Нескальные грунты разделяются на следующие ос-
новные виды:
крупнообломочные—несцементированные грунты, со-
держащие более 50% по весу обломков кристаллических
или осадочных пород крупнее 2 мм-,
песчаные — сыпучие в сухом состоянии грунты, не
обладающие свойством пластичности и содержащие ме-
нее 50% по весу частиц крупнее 2 мм;
глинистые —- связные грунты, обладающие свойством
пластичности.
Скальные грунты подразделяются по происхождению
(изверженные, метаморфические и осадочные), по сте-
пени трещиноватости, по временному сопротивлению
сжатию и по степени растворимости и размягчаемости
в воде,
Крупнообломочные грунты подразделяются в зависи-
мости от их зернового состава на щебенистые (галечни-
ковые) и дресвяные (гравийные), а пески—на гравели-
стые, крупные, средней, крупности, мелкие и пылеватые.
По степени влажности песчаные грунты могут быть
маловлажными, влажными и насыщенными водой.
В зависимости от величины коэффициента пористости
песчаные грунты разделяются на плотные, средней плот-
ности и рыхлые,
Глинистые грунты в зависимости от числа пластич-
ности lFn относятся к супесям (1 IFH О 7), суглинкам.
(7<61Fn<17) нли глинам (ТРаУИ?). По консистенции
глинистые грунты могут быть твердыми, пластичными,
и текучими. Суглинки и глины могут быть еще полутвер-
дыми, туго-пластичными, мягко-пластичными и текуче-
пластичными. Численные критерии, характеризующие ви-
ды и состояния грунтов, приведены в СНиП П-Б.1-62'.
Напряжения и осадки грунта
Зависимость между осадками s поверхности нескаль-
ного грунта и действующей здесь местной нагрузкой р
имеет вид кривой, показанной на ряс. 19. 26. Кроме оса-
док непосредственно под нагрузкой наблюдаются еще
осадки за пределами загруженной площади, которые
с удалением от нагрузки затухают более интенсивно,
особенно при песчаных грунтах, чем расчетные верти-
кальные перемещения поверхности упругого однородного
и изотропного полупространства.
Криволинейный график зависимости между давлением
р на грунт и его-осадкой s под нагрузкой можно условно
разделить на три участка, соответствующие трем ста-
диям сопротивтения грунта (рис. 19.27). На первом
участке 0—1 в стадии уплотнения грунта зависимость
между s и р близка к линейной. На участке ]—2 — в
стадии преобладающего сдвига грунта—зависимость
между s и р носит отчетливо выраженный криволиней-
ный характер. Третья стадия, начинающаяся от точки 2,
называемая стадией разрушения, в которой сдвиги грун-
та получают еще большее развитие, обычно оканчивает-
ся выпиранием грунта из-под загруженной площади.
Рис, 19,26
При разгрузке осадки частично сохраняются, особенно
в пределах загруженной площади. За ее пределами осад-
ки почти полностью исчезают.
Повторные нагружения поверхности грунта возрастаю-
щей с каждым циклом нагрузкой
изображаются графиком с петлями
гистерезиса (рис. 19.28, а), Полные
осадки складываются из восста-
навливающихся и остаточных, а
график полных осадок s может
быть преобразован и представлен
в виде суммы ординат двух кривых
(рис. 19 28, б), одна из которых со-
ответствует восстанавливающимся
осадкам sB, вторая — остаточ-
ным д0.
Кривые последующих нагружений в диапазоне ранее
приложенных нагрузок почти прямолинейны н боле*е по-
логи, чем кривая первого нагружения, благодаря упроч-
нению, связанному с разрушением острых контактов
Рис. 19.28
и увеличением общего их количества при переходе струк-
турных элементов грунта в более устойчивое положе-
ние. Упрочненные грунты при нагрузках, ие превышаю-
щих предыдущие, характеризуются относительно мень-
шими остаточными деформациями и по своим механи-
ческим свойствам приближаются к упругим телам.
19 2 РАСЧЕТ ПОДЗЕМНЫХ СООРУЖЕНИИ
307
Расчетные механические модели
грунтов
Для определения напряжений и деформаций грунта
путем расчета вместо самого грунта рассматривается его
расчетная механическая модель, которая должна отра-
жать основные механические свойства грунта, но сво-
бодна от второстепенных деталей, не играющих сущест-
венной роли для поставленной цели.
Разнообразие грунтов и их свойств, связанное с ус-
ловиями их формирования и существования, породили
несколько расчетных моделей — модель сплошной среды
(упругой или неупругой), модель зернистой среды, мо-
дель местнодеформируемой поверхности (модель Фус-
са — Винклера) и различные комбинированные модели.
При расчете оснований и подземных сооружений
в большинстве случаев используется модель Фусса —•
Винклера или модель упругого однородного изотроп-
ного полупространства, приводящие в большинстве слу-
чаев к наиболее сильно отличающимся друг от друга
результатам. В первом случае в качестве расчетной ха-
рактеристики грунта используется коэффициент упру-
гого отпора k (коэффициент постели), во втором слу-
чае— модуль деформации Ео и коэффициент Пуассо-
на р0.
Расчетную величину коэффициента упругого отпора
k скального грунта в первом приближении можно прини-
мать в зависимости от величины коэффициента крепос-
ти / по формуле
й = 50а/.	(19.18)
где а. — коэффициент, учитывающий степень трещинова-
тости скального грунта, принимаемый равным 0,8, 1
и 1,2 для грунтов соответственно значительной, средней
и малой трещиноватости.
Ориентировочные значения k и Ео для различных
грунтов приведены в табл. 19.6.
Т а б л и ц а 19 6
Ориентировочные значения характеристик деформируемости
грунтов
Г руит	Модуль деформации Еп в кГ!смг	Коэффици- ент лб'стели /?. в к Г /см'
Базальт . ... 		75. Ю<—95.10'	К)П— ’200
Гранит, порфир, диорит - . •	50-104—80-10*	500—900
Гнейс . . . - 		•ю ю*—ад-ю4	350—500
Песчаник , . . 		70-103—30-10*	80—250
Известняк (плотный), доломит.		
песчаный сланец ......	15 - ID3—70- КГ*	40—80
Глинистый сланец ......	30-10=—-40- 1(Р	20—60
Туф			1000—10-103	10—30
Крупноблочный грунт ....	500—1000	5—10
Песок крупный и средней круп-		
ности , . 		  .	.	330—460	3—5
Песок мелкий	240—370	2-4
* пылеватый 			100—но	1-1,5
Глина твердая 		1000—2000	10—20
Глинистые грунты пластичные	80—350	1-1
Коэффициент Пуассона Щ принимается равным:
для скальных грунтов................................  о,2П
»	крупнообломочных грунтов........................  0,27
*	песков и супесей...................................фзп
»	с ji линков...................................    0,35
» глин
Для насыпных грунтов расчетные значения модулей
деформации и коэффициента постели должны быть
снижены в 2—3 раза и более. Для грунтов, лежащих
иа значительных глубинах и испытывающих большие
давления от веса вышележащей толщи, значения Ео
и Цс могут быть более высокими, чем приведенные
в табл. 19.6.
Прочность грунтов
Прочность нескальных грунтов зависит от их сопро-
тивления сдвигу, которое определяется величиной коэф-
фициента среза, или коэффициента крепости грунта.
Последний представляет собой величину отношения
между предельным касательным тлр и нормальным а
напряжениями, действующими по данной площадке:
Тп и	С
f= -^- = tg4) + — ,	(19.19)
о	о
где ф — угол внутреннего трения грунта; с — удельное
сцепление.
Для несвязных грунтов с = 0 и / = tgcp.
Для скальных грунтов величины коэффициентов кре-
пости зависят от их пределов прочности прн сжатии
и принимаются равными /=0,01 Rrik. Расчетные
значения уо, Ф и / для различных грунтов приведены
в табл. 19.7.
Таблица 19.7
Ориентировочные значения характеристик горных пород
Грунт	Объемны"! вес в т/м'	Угол внут- реннего тре- ния ф в град	Коэффициент крепости f
Наиболее крепкие базальт, квар- цит, порфирит и габбродиорит . .	2,8—3	87	20
Очень крепкие гранит, кварцевый порфир, кварцит, кремнистый сланец, наиболее крепкие песча- ники, известняки .......	2,6—2,7	85	15
Крепкий гранит, очень крепкие пес- чаник, известняк и конгломерат	2,5—2,6	82°30'	10
Некрепкий гранит, крепкие песча- ник, известняк и мрамор, доло- мит, колчеданы 			80	8
Обычный песчаник	.	2,4	75	6
Песчанистый сланец, сланцевый песчаник ...... 		2,5	72°30Л	3
Крепкий глинистый сланец, некреп- кие песчаник и известняк, мягкий конгломерат , ........	2,8	70	4
Некрепкий сланец, плотный мер- гель, разрушенный песчаник . .	2,5	70	3
Мягкие сланец и известняк, мел, гипс, каменная соль, мерзлый грунт, антрацит, мергель, сцемен- тированные галька и хрящ, каме- нистый грунт		. .	2,4	65	2 
Разрушенный сланец, крепкий ка- менный уголь, слежавшиеся галь- ка и щебень, щебенистый грунт, твердая глина . . 			1.3-2	60	1,5
Средней крепости каменный уголь, плотный глинистый грунт ., . .	1,8	60	1
Мягкий каменный уголь, гравий, глинистый грунт, лёсс ....	1,6	10	0,8
Слабый глинистый грунт, сырой пе- сок, растительный грунт, торф	1,5	30	0.6
Песок, мелкий гравий, насыпной гр)нт, добытый уголь .....	1,7	27	0,5
Разжиженные грунты . ... .	1,5—1,8	9	0,3
308
РАЗДЕЛ РЛСЛГТ СООРУЖЕНИИ ВЗ 11!ЧОДГПГ'ТВУ1ОГЦИХ С ГРУНТОМ
Для связных грунтов величина / является перемен-
ной, так как зависит от действующего напряжения <т
Однако в практических расчетах величину f принимают
постоянной.
19.2.2.	Давление грунтов
на подземные сооружения
проводы водоснабжения, каиа тнзационные коллекторы,
водоето, и и др ;
сооружение, р,о^р,'денио‘’ закрытым способа и
(рис. 19 30, н), при котором массив грунта не наруша-
ется с говерхиоети. этот способ прим*чяск я при строи-
тельстве туннелей и при бестраншейной прокладке тру-
бопроводов.
Напряженное состояние грунтов до
и после проведения выработки
До проведения выработки и до возведения подземно-
го сооружения грунт s неограниченном массиве и,т;о-
.чится в состоянии естественного или гсостатнческого
равновесия при деиствии собственного веса. При этом
Рис. 19,29
на глубине г в массиве грунта (рис. 19 29) действуют
следующие сжимающие напряжения (давления):
вертикальные
«г =- уог;	(19.20)
горизонтальные
= ay = gfiy„?,	(19 21)
где у0 — средний объемный вес вышел- жапшх грунтов;
So— коэффициент бокового давления гррпа в условиях
естественного залегания.
Проведение открытой или подземной выработки tn-
меняет условия равновесия массива грунта и приводи г
к возникновению в нем деформаций и к перераспреде-
лению напряжений.
Давление грунта на подземные сооружения оказы-
вается иным, чем давление в нетронутом массиве на
той же глубине, так как, во-первых, сооружены обла-
дает другой жесткостью, чем грунт, во-вторых, пер- чи-
щения грунта успевают произойти в период врем ни
между разработкой грунта и возведением сооружения,
наконец, в третьих, между сооружением и массивом
остаются зазоры, допускающие некоторые перемещения
грунта
Давление, оказываемое грунтом на сооружение, за-
висит от глубины заложения и жесткости последнего;
влажности п степени уплотнения грунта над сооружени-
ем и особенно рядом с ипм и от способа возведения
сооружения Следует различать три основных случая
возведения сооружения:
сооружение в насыпи (рис. 19.30, я), возведенное шш
уложенное непосредственно иа поверхности земли или
в очень небольшом по сравнению с шириной вы-мчи
углублении с последующей засыпкой; так обычно соору-
жаются водопропускные трубы под дорожками на-
сыпями;
сооружение в выемке или траншее (рис, 1930,6),
когда оно возводится или укладывается в открытой вы-
работке, имеющей небольшую по сравнению с гаубинои
ширину и ограниченной бол.-е или пенсе твердыми стоп-
ками; пространс.по рядом с со< рушением и над ним
заполняется грунтом; так обычно укладываются трщю-
Рис. 19.30
Давление грунта на подземное сооружение не оста-
ется постоянным, а меняется вследствие изменения
температурно-влажностных условий и ползучести грун-
та, В большинстве случаев давление на сооружение по-
степенно нарастает с течением времени, достигая наи-
большей величины через некоторый промежуток време-
ни, с последующим иногда уменьшением.
Для определения давления иа подз’мные сооруже-
ния от грунта последний рассматривают либо в качестве
упругой, либо в качестве сыпучеи среды.
Первая расчетная модель применима в тех случаях,
когда напряжения в массиве грунта после проведения
выработки значительно меньше разрушающих Ьсти же
в панбэтее напряженных областях грунта наступает
разр>, in-'чис, то почто шп.’п расчетная модель сыпучеи
среды, находящейся в состоянии предельного равнове-
сия.
Табл и ц а 198
	Значения коэффициентов 'перегрузи		
		Нагрузка	п	1 5
	Собственный вес конструкций: а)	сборные . . . , . , . . л . . » б) ?юнолят,ных Давление поды Вертикальное давление грунта. а) па тун ноли желетр’лпр^жп ью п лито дорожные при сводообра зопанчи б)	то ж?, от веса всей налегающей толщи .......	. . , в)	на городские транспортные и пешО' уоднън туннели и трубопроводы в ндыпях или тряшпечх	 Гори 'юятальяоо активное давление грунта а) на jуыъ ти	.....	, . . б) на трубопроводы в вагыпяк или ,	траншеях я	, 	 Под’зцжпал Horpi заз на лол ррмюгта; а) от ьо Юнн автгжрян!тр15 .	, . о) от ко'ц,яых и ~т',шг1ны\ h-itpvtok в) от подвшы'гно состава w.ii’jiwx дорог	.	.......... г)	от пешеходов	1,1 1,2 Ми 0,9 1,5 I,1 и 0,9 1,2 и ОД 1,2 и 0,8 1,2 1; 0,9 1,-1 м 1,3 м	
19 2 РАСЧЕТ ПОДЗЕМНЫХ СООРУЖЕНИИ
309
Давление на подземное сооружение, расположенное
ниже уровня свободной подземной воды, определяют
как совместное давление 1рупта во взвешенном состо-
янии и воды При этом для расчета берется иапневы-
годнейшии уровень подземной воды
Давление на подземное сооружение пе\стончцвых во-
донасыщенных грунтов (плывунов) принимается по
гидростатическому закону.
При расчете подземных сооружении по первому прс-
гклытому состоянию нормативные нагрузки умножают-
ся на коэффициенты перегрузки гг, принимаемые по
табл 19 8.
При этом значения коэффициентов перегрузки, мень-
шие единицы, относятся к случаям, когда данная на-
грузка уменьшает расчетное суммарное воздействие
При расчете подземных сооружений с учетом допол-
нительных или особых сочетании величины расчетных
временных нагрузок принимаются с коэффициентами
0,9 и 0,8 соответственно.
Давление грунта на сооружение
в насыпи
Если жесткость сооружения не превышает жесткости
окружающего его грунта насыпи, то нормам!пая и ка-
сательная составляющие нормативного давления в .по-
бои точке верхнего свода по теории предельного рав-
Рис, 19,31
новесия сыпучих тел выражаются формулами
(рис, 19,31).
О' = yoz (cos3 а ф- у, sin3 а);
т — Vo-г (1 — Sa) sin а cos а<
(19.22)
гте у’о — объемный вес грунта; с — глубина рассматри-
ваемом точки ог поверхности насыпи; а — угол, кото
рым состанля'’т нормаль к поверхности сооружения в
рассматриваемой ючке с вертикалью,
уа — коэффициент активного бокового давления грунта;
Ь = tg“ (45"	<₽/2)
(19.23)
ср ___ угол виутрргикчп трения грунта.
Составляющие давления на пижиип свод сооружения
выражаются также формулами (19 22), ио в них вво-
ди 1ся множитель
03
(19 2-1)
Равнодействующая давлений на верхнюю половину
сооружения равна весу вышележащего грунта и при
круговом поперечном сечении составляет:
(19.25)
Равнодействующая активных давлений на обе поло-
вины круглого трубопровода, т е сила, передающаяся
на основание, определяется из формулы
I	~ 91 \
/? = у0ЯО1(Л1-	•	(19.26)
Здесь И — высота птсынн над верхом сооружения;
Dt —наружный диаметр его.
Значения параметров .Д и Л2, в зависимости от вели-
чины |а, приведены нт графике рис. 19 32
При жесткости сооружения, превышающей жесткость
грунта насыпи, давление на сооружение оказывается
большим, чем вес вышерасположенного грунта. Равно-
действующая дополнительного равномерного вертикаль-
ного давления на верхнюю половину сооружения от
концентрации давления составляет:
(Здог^ДЛАСК,,--!).	(19.27)
где Кн — коэффициент концентрации давления грунта
в насыпи, определяемы!! по верхней части графика
рис И 33 в зависимости ог отношения H/Dj и от вели-
чины произведения Sz; z — коэффициент выступания,
т. е отношение выступающей из основания части h тру-
бопровода к его ширине; S — коэффициент, принимае-
мый в зависимости от жесткости основания под трубо-
проводом.
очень жесткое (скальное, свайный фундамент) —5 =
= 1,0;
жесткое (круппообломочные грунты; пески гравели-
стые, крупные и средней крупности, плотные; супеси
твердые; суглинки и глины твердые н полутвердые) —
5=0,7;
плотное (пески гравелистые, крупные и средней круп-
ности, средней плотности; пески мелкие, плотные; супе-
си пластичные, с^гтшиш ч типы i що-пчас t шыые) -5 __
= 0,5,
310
РАЗДЕЛ 19 РАСЧЕТ СООРУЖЕНИЙ, ВЗАИМОДЕЙСТВУЮЩИХ С ГРУНТОМ
податливое (пески гравелистые, крупные и средней
крупности, рыхлые; пески мелкие, средней плотности;
пески пылеватые, плотные; супеси текучие; суглинки
и глины мягко-пластичные) —5 = 0,3;
очень податливое (пески мелкие, рыхлые; пески пыле-
ватые, средней плотности и рыхлые, суглинки и глины
текуче-пластичные и текучие) — 5 = 0.
Для гибких трубопроводов дополнительное верти-
кальное давление не учитывав;ся
Боковое давление определяется по формулам (19,22)
без учета концентрации давлений и может быть пред-
ставлено эпюрами, показанными на рис. 19,34 с орди-
натами:
Яб ~ Vo Sa^l
96 — То Sa
(19,28)
(19.29)
Для упрощения можно принять
ленис равномерным:
?б.ср —
или еще проще
9б.ср То Sa Д'
В упругой стадии работы грунта остаются справед-
ливыми формулы (19.22)— (19.24), но при определении
бокового давления уже следует исходить из величи-
ны коэффициента бокового давления Ф„ которому со-
ответствует условный угол внутреннего трения
Чу
= arc sin ------- .
1 ~г So
(19.32)
Кроме того, коэффициент концентрации давления
грунта в насыпи берыся уже по iрафику рис. 19 35
в зависимости oi коэффициента Пуассона р, и пара-
метра
где Ьп — ширина опорной поверхности трубопровода;
Ео — модуль деформации грунта основания; £гр — мо-
Рис. 19.34
дуль деформации засыпки; х—отношение выступаю-
щей нз основания части трубопровода к его наружно-
му диаметру.
Для очень жесткого сооружения можно принять
£ = оо и тогда
D,
г' =	----.	(19.34)
601 +2х-^
\	'-гр/
Исходя из графика рис, 19.35 и формулы (19 34),
можно рекомендовать расчетные значения коэффициен-
та Л’и для жесткого трубопровода, приведенные
в табл. 19.9.
Таблица 19.9
Значения (округленные)
среднее боковое дав-
(19.30)
(19.31)
Основание	Опирание		
	обычное	улучшен- "ное	на фунда- мент
	1,5	1,5	1,6
.Жесткое .......	1,4	1,45	1,5
Плотное .......	1,25	1,3	1,4
Под атлнпоо ......	1.1	; ‘	1,25
Очень податливое . ,	1,0	1,0	и
При заглу бдении трубопровода в основание, т. е.
при малых значениях коэффициента и. снижаются и со-
ответствующие значения Лф. Однако их не следует
брать меньше единицы, так же как и для гибких тру-
бопроводов.
19.2. РАСЧЕТ ПОДЗЕМНЫХ СООРУЖЕНИИ
311
Давление грунта на сооружение
в выемке (траншее)
Равнодействующая нормативного вертикального дав-
ления грунта на сооружение в траншее определяется
по формуле
Qb = То HBKtp ф,	(19.35)
где Н — высота засыпки над верхом сооружения;
Лтр — коэффициент вертикального давления грунта
в траншее, зависящий от отношения H/Bav и опреде-
ляемый по нижней части графика рис. 19.33; при этом
Рис. 19.35
чае расчетное давление на сооружение в траншее опре-
деляется по формулам для насыпи.
Давление грунта на крепь выработки
и обделку туннеля
Возникновение областей пластических деформаций
и разрушения в некоторых породах, преимущественно
пластичных, приводит к оседанию всей толщи пород,
находящихся над сооружением, особенно при большом
его пролете. В этом случае, как показывают измерения
Рис. 19.36
кривая 1 соответствует песчаным грунтам, а кривая
2—глинистым; В — ширина траншеи на уровне верха
сооружения; Вср — средняя ширина траншеи; ф— ко-
эффициент, учитывающий совместность деформаций
трубопровода и грунта, находящегося между его стен-
ками и стенками траншеи:
Вгр (В -	/_£_\3
EkDi	\ 6 J
(19.36)
Здесь 6 — толщина стенки трубопровода; г — радиус
срединной поверхности трубопровода; v.~коэффи-
циент выступания трубопровода из основания; Е—мо-
дуль упругости материала трубопровода; £Гр — мо-
дуль деформации засыпки, принимаемый по
табл. 19.10.
Таблица 19.10
горного давления на сооружения, заложенные на глу-
бине 25—50 м от поверхности, вертикальное давление
в глинистых грунтах может доходить до полного веса
всей налегающей толщи, а в прочных породах состав-
ляет 70—80% этого веса.
В других грунтах, например в песчаных, область
нарушения может не доходить до поверхности, так как
над сооружением образуется естественный разгружаю-
щий свод, очертание которого принимается параболи-
ческим (рис. 19.36).
Давление на сооружение в этом случае считается пе-
редающимся от грунта, занимающего область внутри
разгружающего свода, ограниченную с боков плоско-
стями скольжения.
Пролет L свода давления и его высота h; лад верх-
ней точкой выработки определяются по формулам
М. М. Протодьяконова:
L = Dp -% 2/i tg 45°
Значения модулей деформации грунтов плотной засыпки
Грунт засыпки	ггр, кГ/ем-
Пески крупные и средней крупности . . » мелкие ......... « , . . » пылеватые	. Супеси 1:1 суглинки ......... Глины . . .............	170 120 50 60 40
(19.37)
Боковое давление грунта в узких траншеях или сов-
сем не учитывается или при хорошем уплотнении «па-
зуха учитывается в размере до 20% вертикального.
Вертикальное давление грунта на сооружение в ши-
рокой траншее не может превышать соответствующего
давления на сооружение в насыпи. В противном слу-
где Dt — ширина или диаметр выработки в h — вы-
сота пли диаметр выработки в м; ф — угол внутренне-
го трения грунта в град; f — коэффициент крепости
грунта (горной породы), учитывающий его внутреннее
сопротивление разрушению, а также характер напла-
стований, степень трещиноватости и способ сооружения
туннеля.
Нормативное горное давление на крепь или на тун-
нельную обделку принимают равномерно распределен-
ным, и его равнодействующие определяют по фор-
мулам:
для вертикального давления
Фв —“ Ти/б ^11	(19.38)
Н
312
РАЗДЕЛ 10 РТЕЧЕТ СООРУЖЕНИИ, ВЗ ШМОДЕР1СТВУЮЩИХ С ГРУНТОМ
для горизонтального давления
Q.6 уо 7о Д) (^1 ”Г tg" ^-,5  —у '	(19.39)
где у0— объемный вес грунта.
Значения характеристик уп, ф и f различных грунтог
приведены в табл. 19 7.
Расстояние от вершины свода давления до дневной
поверхности или до контакта со слабыми породами
должно быть не меньше высоты свода давления
В противном случае, а также при невозможности сво-

дообразоваиия, нормативное вертикальное давление
принимают равным весу всей шири грунт,) над тупее
дем, а равнодействующую горизонтального давления
определяют по формуле
/ <г \
<2б = То ffofttg" (45’—--L	(19.10)
где На — высота толщи грунта, пасполо>ле”нои выше
оси туннеля, приведенная к объемному весу слоя у0
грунта у оси туннеля, в м.
Горное давление на обделку нараллеюных (упнелен
при возможности образования над Кижтой 'выработкой
самостоятельного свода давления определяемся для
каждой выработки в отдельности. Если же при задан-
ных размерах каждой выработки, целика между ними
и физико-механических свойств породы образование
самостоятельного свода над каждой выработкой не-
возможно, то давление на обделки определяется исходя
из предположения существования над ними общего
свода давления.
Активное давление грунта со стороны подошвы вы-
работки («дутье»1, направленное снизу ш>'р\, глщт.ъ
ет в результате выпирания грунт г) из-под стен об.ы тки
под воздействием вертикальной нагрузки и гобст..очно-
го веса обделки (рис, 19.371.
Равнодействующая сил давления грунта со стороны
подошвы вырабожи
где q— давление стены на основание.
Для определения активного давления иа кпепь оди-
ночной выработки КруГОВОГО ПОПерСЧНОГО С‘ ЧС'ППЯ Н !
основе теории предельного равновесия К. В. Руппе-
нейтом предложена формула
? — гаИТоДо + д^- |ехр (-л tg(f)	, (19.12)
\	tg Ф /	tg Ф
где На — глубина заложения центра выработки от по-
верхности грунта; у0 — объемный вес грунта; ср — угол
виутршшего трения грунта; с —	сцепление;
К — коэффициент концентрации давлений, принимае-
мый равным: для песков 1,0—1,3; для глин 1,8—2,0;
для станцев 1,5—1,8.
Дач тепле принято равномерным и действующим нор-
мально к поверхности сооружения.
Давление грунта на подземное сооружение может
быть определено из решения контактной задачи теории
упругости для полуплоскости с подкрепленным отвер-
стием.
При горизонтально!! крупой выработке, центр кото-
рон находится ка гтубипе На от поверхности, нормаль-
ное давление на обделку равно:
То Дп (1 г . г. . / I ,
+-—-j cos 20	(19.43)
j щ Еп L+i Ра 1 Д” 21<- .
1	С ‘ 1+}10 ’’	1—Р2	’
В 1 -Г .------------------------------------- . —
ь (1 + 1‘-е)(5 — бМо) (1 — р2)-
5 — 6;,10 ; Е„ 1 + 9	___ О________ _
4 —6р0 1 Е ' (1 Д р0) (4 — 6р.о) ’(1—.рз)4 ;
D = 3 — g Д 4 (3 — 4р) р’“ — 6 (1 — 2р.) р4 —
— 4рв — (5 — 6р.) рв,
где 0 — лотчршын угол, отсчитываемый от вертикаль-
ного диаметра, Д—коэффициент бокового давления;
Е и р — модуль упругости и коэффициент Пуассона ма-
приата сооружения; В,, и ц0 — модуль упругости и ко-
эффициент Пуассона ,-ругзта; р = гр/г(.
При достаточно топкой обделке давл) нис на н»е вы-
раачгтамга и может быть принято равномерным по
длине окружности:
уНв(1 д0)
(19.44)
Давление грунта
в пространственной задаче
Принимается, что при осадке кровли песчаного грун-
та наг подюмным сооружением крупной формы
в плане над ним образуется естественный купол и что
на сооружение оказывает давление вес грунта, находя-
иу-тося внутри этого купола, имеющего форму пара-
болонта вращения (рис 19 38, а), Наиботшпая иитсп-
спвность вертикального давления на сооружение по оси
купола
у„ а
qB = --4^- ,	(19 45)
где п — радиус купола, который может быть больше
радиуса сооружения; f — коэффициент крепости, берет-
ся по табл, 1’9,7,
Потная нагрузка на сооружение, равная весу грунта
в объеме, ограиисениом поверхностью купола
луп о3
&=-=	(19-46)
19 2 РАСЧЕТ ПОДЗЕМНЫХ СООРУЖЕНИИ
давление грунта qt> на стенки вертикальных
выработок 1шл1) определяется как давление в масси-
ве до выработки или активное давление по теоош!
предельною равновесия с учетом объемного веса к уг-
ли внутреннею трения грунта каждою слоя. При атом
Рис. 19 38
учитывается неравномерность распределен™ бшавого
давления по сдеме, изображенной на рис. 19.38, б.
Давление деушовоп воды принимается равномерным
и нормальным к иоверхпоыи сооружения.
Давление на сооружение от на з«»и-лкы х
нагрузок
При расчете туннелей и трубопроводов, укладывае-
мых под автомобильные дороти, временную вертикаль-
ную ншрузку ог транспорта следует принимать от ко-
«1Ы1ЛЫ авюмобплей по схеме П-30 иди от одной транс-
портной единицы на юолес.чом ходу по схеме НК-80.
Д.ы трубопроводов, укладываемых в местах, где воз-
можно движение автомобильного транспорта, следует
принимать нагрузку от колонны автомобилей по схеме
Н-18 или гусеничную нагрузку НГ-60.
При заглублении верха сооружений на 1,2 м и бо-
лее нормативную вертикальную нагрузку от колонн ав-
|омоб!11еи разрешается принимать равной 2 Tjw-,
Для трубопроводов, укладываемых в местах, где
движение автомобильного транспорта невозможно, при-
нимается равномерная нагрузка от пешеходов бООкГ/лт2.
Для сооружений, укладываемых под железнодорож-
ными путями, в качестве нормативной следует прини-
маю нагрузку, соответствующую классу данной же-
лезнодорожной линии, но не ниже С14.
Динамический коэффициент подвижной наземной
нагрузки при высоте засыпки 0,7 м и более (при нали-
чии покрытия 0,5 м и более) принимается равным еди-
нице, а при высоте 0,25 ж—1,3. Для промежуточных
Рис. 19.39
314
РАЗДЕЛ 19 РАСЧЕТ СООРУЖЕНИИ ВЗАИМОДЕЙСТВУЮЩИХ С ГРУНТОМ
высот засыпки значения динамического коэффициента
берутся по интерполяции,
Для определения давления, передающегося через
грунт от нагрузок, приложенных на поверхности зем-
ли, применяется способ распределения давления под
углом 30° к вертикали или, что предпочтительнее, фор-
мулы теории упругости для вертикальных напряжений
в полупространстве.
На рис. 19.39 приведен график, позволяющий найти
наибольшую интенсивность вертикального давления
для разных глубин заложения верха сооружения от
различных нормативных подвижных нагрузок. Влияние
дорожного покрытия учитывается приведением его
к эквивалентному слою грунта.
19.2.3.	Расчет жестких подземных сооружений
кругового поперечного сечения
Распределение опорных реакций
Внутренние усилия, возникающие в стенках сооруже-
ния при действии тех или других нагрузок, зависят
также от распределения опорных реакций, которое оп-
ределяется способом опирания сооружения на осно-
вание.
При укладке сооружения на плоское грунтовое осно-
вание (рис. 19.40, а) опорную реакцию принимают со-
средоточенной вдоль нижней образующей.
Если сооружение уложено на жесткое спрофилиро-
ванное по его нижней части грунтовое основание
с центральным углом опирания 2« (рис 19.40,6), то
опорную реакцию принимают равномерно распределен-
ной по всей ширине опорной поверхности интенсив-
ностью
7?
q =---------- ,
Dj sin а
(1Э.47)
где R — равнодействующая нагрузки; £>| — наружный
диаметр трубопровода.
При ширине ложа 6o=0,6Di угол 2а лк 75°.
При опирании круглого трубопровода на основание
из слабого грунта распределение опорной реакции мож-
но принять по треугольнику (рис. 19 40, в) с наиболь-
шей ординатой
9	.	(19.4Я)
Djsina
Если жесткое сооружение имеет плоскую подошву
шириной Ьо, то эпюра реакций имеет седловидную
форму. При этом разница между крайними и средними
ординатами тем больше, чем большей связностью
и плотностью обладает грунт (рис. 19.40, а).
Для песчаного и пластичного глинистого основания
можно принять распределение опорной реакции равно-
мерным
Трубопровод, уложенный на фундамент (рис. 19.41, я),
может рассматриваться ь качестве свода с заделанны-
ми пятами (рис. 19.41,6) лишь в том случае, если
в действительности обеспечена связь между трубопро-
водом и фундаментом и если сам фундамент достаточ-
но жесткий. В противном случае при деформации тру-
бопровода он оказывается как бы шарнирно опертым
по двум образующим у краев опорной поверхности
(ряс. 19.41,в).
Если контакт между трубопроводом и фундаментом
сохраняется на всем протяжении опорной поверхности,
но фундамент недостаточно жесток для обеспечения
полной заделки, то обычно принимают опорные реакции
направленными радиально (рис. 19.41, а) и распреде-
ленными по закону
47? cos 0
(sin 2а + 2а)
(19.49)
Рис 19.40
Рис. 19.41
19 2 РАСЧЕТ ПОДЗЕМНЫХ СООРУЖЕНИИ
315
Распределение опорной реакции по подошве жестко-
го фундамента такое же, как и по плоской подошве
самого трубопровода.
При приближенном расчете туннельных обделок ре-
акцию принимают равномерно распределенной по дли-
не диаметра сооружения.
Внутренние усилия в сооружении
от различных нагрузок
Сооружение достаточно большого протяжения в оди-
наковых условиях работ, испытывает плоскую дефор-
мацию, и для расчета можно выделить учасюк соору-
ную кривизну оси поперечного сечения, а окружные
силы положительны, если они создают растяжение.
Учитывая, что радиус осевой линии поперечного се-
чения трубопровода г меньше радиуса ty внешнего кон-
тура, к которому приложены внешние силы, можно
еще ввести в формулу (19.50) при определении изги-
бающих моментов от давления грунта и временных на-
грузок коэффициент, равный rh'\. При опирании на об-
разующую этот коэффициент не вводится.
Основное давление грунта на сооружение, уложен-
ное в насыпи, вызывает следующие изгибающие момен-
ты и окружные силы:
Рис. 19.42
М = Qa г I.M + т -^М « A4QB г;
\ н ]
N = QB (.V + я NQB,
\ п /
(19.52)
(19 53)
где Qa—yHD^.	_ _ _ _
Значения коэффициентов М, т, N и п, зависящих ог
величины | — коэффициента бокового давления грунта
засыпки, приведены в габл. 19.12.
Кроме того, должны быть еще учтены изгибающие
моменты и окружные силы от дополнительного равно-
мерного давления, вызванного концентрацией давлений
у жесткого сооружения.
От неравномерного нагревания стенки сооружения
с круглым поперечным сечением возникают изгибающие
моменты
жения длиной, равной единице. При этом расчет соо-
ружения сводится к расчету кольца, находящегося
в равновесии при действии нагрузок и реактивных сил.
Расчет кольца производится методом сил (см. раз-
дел 5) с переносом неизвестных для их разделения
в уравнениях в упругий центр, совпадающий с геомет-
рическим центром кругового кольца. При нагрузке,
симметрично!! относительно вертикальной оси, из трех
неизвестных остаются только йф и Х2 (рис. 19.42).
Кольцо считается опертым в нижней точке А, что
равносильно жесткой заделке полукольца в этом сече-
нии. Расчет кольца можно производить отдельно на
каждый вид нагрузки и на действие опорных реакций,
а затем ал!ебраически складывать внутренние силы от
тех или других внешних воздействий.
При этом равнодействующие нагрузки и соответству-
ющей ей опорной реакции должны быть равны между
собой и направлены в противоположные стороны.
Окончательные формулы для изгибающих моментов
и окружных нормальных сил в любом сечении стенки
круглого жесткого сооружения приводятся к виду:
М = MR;r,
N = XR,
(19.50)
(19.51)
где R — равнодействующая той или другой нагрузки;
г—средний радиус трубопровода; М и N — коэффици-
енты, зависящие ог распределения нагрузки и опорной
реакции и от положения взятого сечения.
В табл. 19.11 —19.16 приводятся значения коэффици-
ентов М и N для различных нагрузок при разных усло-
виях опирания. Коэффициенты относятся к трем харак-
терным сечениям кольца: к подошве, (Л), к бокам (5)
и шельне (В), При этом изгибающие моменты считают-
ся положительными, если они уменьшают первоначаль-
Л1Л— МБ -- Мн	,	(19.54)
где й — толщина стенки сооружения; Е — модуль упру-
гости материала сооружения; а;—коэффициент линей-
ного расширения; ф и t\—температура у внутренней
и наружной поверхности соответственно.
Для сооружения с плоской подошвой, имеющего по-
вышенную толщину стенки 6д у подошвы, распределе-
ние внутренних усилий оказывается другим, чем в со-
оружении с постоянной толщиной стенки 6. Например,
при подошве с углом 2а = 60° и —^-=1,7 для
о
равномерной вертикальной нагрузки МА = 0,359; Л4С =
= —0,0875; Мв =0,091.
Приведение расчетных нагрузок
к двум эквивалентным
сосредоточенным силам
Для облегчения сопоставления различных нагрузок,
действующих на трубопровод, и их сочетаний с несу-
щей способностью труб, а также для облегчения рас-
четов принято при расчете трубопроводов приводить
все нагрузки к двум эквивалентным линейным нагруз-
кам, действующим по вертикальному диаметру
(рис. 19 43).
Принимается, что в упругой стадии работы трубопро-
вода эквивалентными являются такие нагрузки, кото-
рые вызывают одинаковые по величине наибольшие
ядровые моменты. Наибольший ядровый момент воз-
никает в том же сечении трубопровода, в котором
действует наибольший изгибающий момент, а этим се-
чением в большинстве случаев оказывается сечение А
(лоток).
316
гпздгл 19 РАСЧЕТ СООРУЖЕНИЙ, ВЗАИМОДЕЙСТВУЮЩИХ С ГРУНТОМ
Значения коэффициентов М и N для различных нагрузок,
действующих на сооружение круговою сечения, опертое на нижнюю образующую
Табл и ц а 19Д1
Наг ру зкэ	Схема нагружения	Ко^ффиЦие{1Т					
		«А	M Б	мв	NA А		Л'в
Собе 1 ВЕЩНЫЙ ВВС	рО 6 wZi	® 3 ff= 2Tfr^	0,239	—0,091	0,080	—0,080	—0,250	0,080
Вес жидкости при нанолне НИИ	j	В JTy = У/г_г ।	f	0,239	—0, (Hl	0,080	0,398	0,07)	0,239
Верткальндя равномерная	цп-^ 5 Wa" " 2	0,291	—0,154	0,150	—0,031	-0,500	0,051
Горизонтальная равномср- ная	в 8-^—	—Г^""|) Н р о Ч1 л ни 1 TH pfi А-J		QU И 4f/?=0 и	—0,125	0,125	—0,125	—0,500	0,000	—0,500
Сосредоточенная	p Б	I 0,318	-0,182	0,318	0,000	—0,500	0/000
Приведенная к двум сосредоточенным силам эквива-
лентная нагрузка
Р = f>f> --- л (м,1МС + Л' R,
\	6г /
(19,55)
где R. — равнодействующая той или иной активной
нагрузки; (3 — коэффициент приведения нагрузки;
Л1магс — максимальный табличный ко'.ффициент, соот-
ветствующий данной нагрузке с учетом действительно-
го распределения опорной реакция; \ — i иблн-шый ко-
эффициент для окружной Тилы в еечешш с наиболь-
шим изымающим моменгом.
Если толщина степки 6 трубопровода мала по срав-
нению с радиусом г его срединной поверхности, то
можно принять |3—лМ.Лакс.
Для практических расчетов и средних грунтовых ус-
ловий можно рекомендовав следующие значения ко-
эффициентов Р для давления грунта с учетом бокового
давления и для наземных нагрузок:
при укладке па плоское основание — 0,75;
при укладке на спрофилированное основание, а так-
же для труб с плоской подошвой — 0,45;
при укладке на фундамент — 0,3.
Для собственного веса и веса жидкости, наполняю-
щей трубопровод, соответственно 0,75; 0,4; 0,2.
13 2 РАСЧЕТ Г О.ЦЗЕЛТНЫХ СООР ЖЕНИН
317
Рис, 19.43
Деформация поперечного сечения
сооружения
Перемещения с гонки сооружения могут быть найдены
путем интегрирования дифференциальною уравнения
упругой линии кольца или (при наличии эшоргл изги-
бающих моментов от нагрузок и опорных реакций) по
способу Мора.
Прогиб круглого поперечного ссчепия сооружения,
без учета отпора груша, равный удвоенному радиаль-
ному перемещению по вертикали, может быть выражен
следующей общей формулой
МШЛ=/
Д(1 ~ц3)
Е
у? 7 р\
i> ) 4рл
(19.56)
Таблица 2922
'Зваче-гия коэффициентов ЛЬ ш, N и п чДЯ давления грунта
в насыпи, действующего на сооружение кругового сечения,
оиергое на образующую
Коэффициент 601кВОГО ДПГ н-пия §	Коз, рициент	i					
	В в	31 fel СИ to	ч 4 |S- M i—_____	na ~ПА	n , 1 Hl	"в
•	од’*ц 0,037	—0,154 —0,014	0, WQ 0,002	-0,051 - 0,00 5		0,041 | 0,005 ;
	0,282 O.OlO	—0,100 —0/Ю1	9, 1 4 —Oj'lO	— OJlro —0,0 4	’> JO 0,051	—0,050 0,034
0,4	И, I ’ - 0,011	-0. 10 5 0,ni2	li. 100	- 0.177 -0,072	—0,500 —0,054	—0,161 0,072
036	0, —0,044	J. I 0,0 В	1.0 '>	-0,201 — 0,128	—0,500 —0,054	—0,263 0,228
0,8	0J0 1 —0.0J8	ijl 0.851	4,111, •),!<! >	—0, Ш —0,_04	—0,500 —0,054	—0,375 0,204
1,0	0,000 —0,187	0,000 j O,!)0<) 0,072 | - 0.1Ю5		- 0,500 - -0, 51 1	-o.wo -0,054	—0,500 0,313
где R — равнодействующая ion или иной нагрузки;
Е и р. — модуль упругости н коэффициент Пуассона
материала трубопровода; / — коэффн тент, зависящий
от распределения нагрузки и опорной реакции
(табл. 19.17).
Т а б л и ц а 19.13
Значения коэффициентов М и N для опорных реакций сооружения на грунтом основааии
Схема нагружения	Центральный yi ал За в град	Ко ффьцаюп					
		МА	Ais	мв			NB
в	0	0,000	0,000		0,090	0,008	0,000
	I	30	—0,036	0,002	—6,00?	0, 0 Ц	0,009	—0,004
	i	6Й-	—а ,пц	о, ои7	—0,007	0,013	0,000	-0,0В
							
	УО	—0,136	0,014	—0,013	0,027	0,00)	—0,027
Олтв	120	-0,155	0,021	-0,019	0,0 Ю	о.ооо	—0,040
	150	-0,163		—0,02.5	0,050	0,000	—0,050
ПЛОТНЫЙ rpJHT	280	—0,169	0.029	—0,025	0эО5 5	ojjou	-0,053
|в	U	(1,000	6,0210	0,003	0,000	0,009	0,000
	.»	—0,040	0,н01	—0,001	:	0J 01	0,900	—0,00!
	60	:	—л, и 7 5	0,00 5	—0,00 3	0, UI)?	0,000	—0,007
- -X—“ - h £	но	—0,098	0,007	—2), 00 3	0,0В	0,000	—0,013
	120	—0,114	и,010	—0,020	0,022)	0,000	—0,020
	1&0	-о, су	0,01 ’	—0,012	0,0.5	0,000	—0,025
	18U	—0,227	0,01 1	-0,0В	15,027	0,000	—0,027
1	слабый грунт							
318
РАЗДЕЛ 19. РАСЧЕТ СООРУЖЕНИИ, ВЗАИМОДЕЙСТВУЮЩИХ С ГРУНТОМ
__	__	Таблицами
Значения коэффициентов М и N для опорных реакций сооружения на фундаменте
Коэффициент
Схема нагружения	Центральный угол 2а в град	№а	мв	мв	мд	na		N о £5
в								
	0	0,000	0,000	9,000	0,000	0,000	0, 000	0,000
	30	—о,пз	0,005	—0, 005	0,016	0,010	0,000	—0,010
54^'7’\“"Г5	60	—0,190	0,020	—0,019	0,055	0,040	0,000	—0,040
	90	—0,232	0,042	—0,038	0,098	0,080	0,000	—1,080
2 1	2	120	—0,249	0,065	—ri,055	0,124	0,119	0,000	—0,119
	150	—0,250	0,083	—0,0 )Ь	0,127	0,149	0,000	—0,149
1 я	180	—0,250	0,091	—0,0о8	0,091	0,159	0,000	—0,159
с отрывом от фунда-								
мента								
в	0	0,600	0,000	0,00	—	0,000	O.OOJ	9, ООО
	30	—0,052	0,002	0,012	—	—0,075	0,000	0,008)
S	'	\ с J—_. —Х—  —4— 5	60	—0,119	0,008	0,010	—	—0,137	0,000	—0,001
	90	—0,180	0,016	- 0,00 4	—	—0,176	0,000	—0,018
								
	120	—0,179	0,027	—0,019		—0,205	0,000	—0,046
	150	—0,190	0,036	—0,0 40	—	—0,226	0,000	—0,036
без отрыва от фунда-	180	-0,195	0,04-1	—0,036			—0,239	|’,000	—0,079
мента								
Таблица 1915
3начения коэффициентов М и А/ для разных нагрузок при различных условиях опирания
Нагрузка	Коэффи- циен г	Способ опирания сооружения					
		па плоскость i'a—0	на плотное основание	на слабое основание	на плоскую подошву 2а=60°	на фундамент 2а—120°	туннель 2а — 180°
			2а-	75°			
Собственный вес сооружения		0,239	0,119	0,152	0,134	0,060	0,070
		—0,091	—0,081	—0,086	-0,084	—0,064	—0,063
	-«В	0,080	0,070	0,075	0,073	0,061	0,055
	na	—0,080	—0,060	—0,070	-0,067	—0,285	-0,277
	nb	—0,250	—0,250	—0,250	—0,250	—0,250	—0,250
	Со	0,080	0,060	0,070	0,067	0,034	0,027
Вес жидкости при наполне-	МА	0,239	0,119	0,152	0,134	0,060	0,070
ням сооружения							
		—0,091	—0,081	-0,036	—0,084	—0,034	—0,032
	йв	0,080	0,070	0,075	0,073	0,061	0,055
		0,398	0,418	0,408	0,411	0, О)’	0,451
	NB	0,069	0,059	0,019	0,069	0,069	0,059
	N В	0,239	0,219	0,220	0,226	0,193	0,186	
19 2 РАСЧЕТ ПОДЗЕМНЫХ СООРУЖЕНИЙ
319
Продолжение
Нагрузка		Коэффи- циент	Способ опирания сооружения					
			иа плоскость	на плотное J основание	на слабое основание	1 на плоскую подошву 2сс—30°	на фундамент “2рб —120°	туннель 2а=180°
				2 а ~	75°			
Основное при £о=О тикальная грузка	давление грунта и Н D\ или вер равномерная на	".4	0,294 -0, 154	з, 171 —9,141	0,208 - 0,149	0,189 - 0, ! 17	0,115 - 0,127	0,125 —0,125
			0,150	о,но	0,145	0,1 г>	0,131	0,125
		М	—0,053	- [),0Р	- 0,(Ш	—9,010	-9,258	0,000
		Л'В	—0,50)	—0,500	— 0,500	- 0,309	- 0,500	-0,500
		Ав	0,053	0,03)	0,043	0,040	0,001	0,000
Основное	давление iрунта		0,23Ь	0, 1 12	0,170	0,154	0.0 4(1	—
в насыпи	при So — —• и Н > 3	*Б	-о, из 0,110	—0,104 0,102	—0,109 0,105	—0,107 0,101	—0,091 0.095	—
		Л.4 Ъ:Б	—0J50 —0,500	—0, ГМ -0,500	—0,142 —0,500	—0,140 —0.50л	-0,314 —0,500	—
		лв	—0,110	—0,126	—0, 118	-0, 120	-0,147	—
: Основное	давление грунта	Л14	0,19!	0,101	0,129	0,111	0,010	—
в насыпи	при £о 		И И > 2	«5	—0.053	-0,082	—0,085	—0,034	—0,059	
> Di		мв	0,083	0,076	0,079	0,076	0,039	—
		Х А	- 0,219	—0,212	—0,212	—0,209	—0,370	—
		’^Б	—0,500	—0,500	—0,500	—0,500	—0,500	
			—0,212	-0, 227	—0,219	—0,222	—0,246	
Та б л и ц а 19 16
Значения коэффициентов Л1 и М для бесшарнирного кругового свода при равномерной нагрузке
Схема нагружения	Коэффи- циент	гол охвата трубопровода фундаментом 2 а в град									
		0	20	40	60	80	100	120	140	160	180
	ГЛА	0,294	0,285	0,240	0,200	0,172	0,150	0,120	0,095	0,070	0,054
ШАШШТ*											
	мд	-0,150	—0,135	—0,120	-0,100	-0.087	—0,072	-0,055	—0.050	-0,014	—0,024
/ \	ЛД, ь	0,150	0,130	0,120	0,100	0,087	0,072	0,055	0,050	0,034	0,024
\ /											
мГ J %?		—0,500	—0,500	—0,500	—0,"00	—0,500	—0,500	—0,500	- 0,500	- 0,500	—0,500
	Л' В	о, озз	0,025	0,020	- 0,015	—0,090	-0, 125	—0,160	—0,200	—0,240	-0,280
320
РАЗДЕЛ 18 РАСЧЕТ СООРУЖЕНИИ, ВЗАИМОДЕЙСТВУЮЩИХ С ГРУНТОМ
Т а б л и ц а 19 17
Значения коэффициентов ]'
В<лпчина
3EJ ___ Е /М3
иа (1 — Д) 4(1 — р2)\ г /
(19.57)
является критическим внешним равномерным нормаль-
ным давлением для сооружения круглого поперечного
сечения по М. Леви, т. е. без учета отпора грунта.
Для сооружения, стыки которого допускают про-
дольные деформации, принимается ц —0.
При действии на сооружение двух сосредоточенных
сил по направлению вертикального диаметра
(рис, 13.43) f=l,8. Соответствующий коэффициент для
определения укорочения горизонтального диаметра
равен: Д = 1,632.
Если учитывать ползучесть грунта, то прогиб, под-
считанный по формуле (19.56), следует увеличивать
в 1,25—1,5 раза.
19.2.4.	Расчет подземных сооружений
с учетом отпора грунта
Общие соображения
Грунт, в котором находится сооружение, не только
создает нащузку, но и, оказывая сопротивление пере-
мещениям стенок, снижает изгибающие моменты и по-
вышает несущую способность сооружения.
Для расчета сооружений с учетом отпора грунта су-
ществует несколько различных методов, отличающихся
положенной в их основу расчетной моделью цэунтовой
среды и по форме.
Способ Метро проекта
Сооружение рассматривается как круговое кольцо
в сплошной упругой среде, механические свойства ко-
торой характеризуются коэффициентом постели; среда
способна оказывать только однозначный отпор, направ-
ленный в сторону сооружения.
Для расчета кольцо заменяется вписанным в пего
16-угольником, а сплошная упругая среда — отдельны-
ми упругими опорами, расположенными во всех вер-
шинах 16-угольника, кроме грех верхних, попадающих
Рис. 19.44
в безотпориую зону. Направления опорных реакций
стержней принимаются по соответствующих радиусам
кольца, а при учете сил трения — с отклонением иа
угол трения между грунтом н обделкой.
При переходе к основной системе метода сил во все
вершины многоугольника, кроме двух, вводятся шар-
ниры, а в качестве неизвестных принимаются прикла-
дываемые в этих сечениях изгибающие моменты 41ь
ТИз,.... Ms. При этом моменты М}, Mt.Mg, приложен-
ные в симметричных сечениях, будут групповыми неиз-
вестными (рис. 19.44).
Типовое каноническое уравнение метода сил, состав-
ленное для опоры п, имеет следующий вид:
Мп^ М Мп^ Д бпп Мп 4-
+ 6„,п+1 AJn+I Д М,^.2+- • Д\.р = о. (19.58)
Коэффициентам» при неизвестных и свободными
членами уравнений являются перемещения основной
системы по направлению этих неизвестных от единиц-
19.2. РАСЧЕТ ПОДЗЕМНЫХ СООРУЖЕНИИ
321
них моментов и от заданной нагрузки соответственно.
Для их определения нужно предварительно найти co-
ot ве1С1вуюшне усилия.
Верхняя часть основной системы (рис. 19.45), нахо-
дящаяся в безотпорной зоне и не подверженная дей-
ствию упругого отпора грунта, рассматривается как
1рехшарнирная арка, опорные реакции которой от на-
реакции упругих опор
2 ctg ва

____1
г sin 9fi
В остальных элементах основной системы этот еди-
ничный момент усилий не вызывает. Единичный момент
М3. приложенный на опоре трехшарнирной арки, вы-
зывает следующие усилия:
нормальные силы в звеньях
«о
г cos—-
2
реакции упругих опор
I
Rfi —	~  a
Г sin 0,
Определение перемещений основной системы произво-
дится с учетом влияния нормальных сил и перемеще-
ний упругих опор.	_
Так, например, перемещение по направлению Ж» от
единичного неизвестного М«
грузки и единичных моментов передаются с обратными
знаками на нижележащую шарнирную цепь. Усилия
в звеньях шарнирной цепи опреде.ляются из условий
равновесия последовательно вырезанных ' узлов
(рис. 19.46), Из условия равновесия n-го узла при
действии заданной нагрузки определяются:
Окружная нормальная сила в звене между узлами я
и п~Н
,1	, n	sin 0„	cos 0„
л; = Сл + Yn ----------------Хп	;	(19.59)
cos — cos —_
2	2
реакция упругой опоры в узле п

— Yn cos 0„ — XnsinQn, (19,60)
где Уп — сосредоточенная вертикальная сила в узле п
о: заданной нагрузки; Хп—сосредоточенная горизон-
тальная сила в узле п от заданной нагрузки; 0„—цен-
тральный угол, заключенный между вертикалью и ра-
диусом, проведенным через точку л; 0О — центральный
угол, заключенный между радиусами, проведенными
через соседние вершины многоугольника; для 16-уголь-
ника 0о = 22°ЗО'.
От единичного момента Мп, приложенного в узле л,
возникают следующие усилия:
нормальные силы в звеньях
Nfl~[
2/ cos -—
2
„ V f Мп
e"” = 2j —'*+
+ V	+	(19.Ы|
Т ЕР Т kab
Здесь Мт и Мп—изгибающие моменты в произволь-
ном сечении звеньев от соответствующих единичных
моментов; Nm и IV» — нормальные силы в звеньях от
соответствующих единичных моментов; Rm и fin — ре-
акции в опорных стержнях от соответствующих еди-
ничных моментов; £/ и EF—жесткости продольных
сечений обделки на изгиб и сжатие; a — длина сторо-
ны многоугольника; b— выделенная для расчета шири-
на кольца обделки; k — коэффициент упругого отпора
породы.
После определения восьми неизвестных из системы
восьми уравнений окончательные усилия определяются
по формулам:
^=.л/° + 2^гж.:
+	Л4.;
Rn = < х 2 Я„г Mi.
(19.62)
„	.,0 !<«
Здесь N/v мГ1 и /?л—усилия в основной системе от
заданной нагрузки; Nni, и Rni—усилия в основ-
ной системе от единичных узловых моментов; Mt —
найденные значения неизвестных.
Правильность вычислений контролируется выполне-
нием условий равновесия отдельных частей обделки
21—26
322
РАЩЕЛ 19 РАСЧЕТ СООРУЖЕНИИ, ВЗАИМОДЕЙСТВУЮЩИХ с ГРУНТОМ
и равенством нулю приводе иной 1т. е деленной иа Е1)
площади окончат.плюй -/шоры изгибающих моментов.
АиалогнччЫ|| мсюл расиста с использованием в ка-
честве уцрушх харамеристик грунта ею модуля уп-
ругости Ln и коэффицпетп <i Пуассона рщ разработан
С. А Орловым
Для приближенных расчетов трубопроводов обычно
испольтрется следующая зависимость между коэффи-
ннешом упругою сжатия k и модулем деформации
ipy.nra Л'1Р:
1'Р
7 (1 Щ.р)
юте ц,р — коэффициент Пуассона грунта.
Способ О. Е. Бугаевой
(19.63)
Грунтовая среда, окружающая сооружение, характе-
ризуемся коэффициенто.м у npyi oi о отпора к. Отпор
принимается радиальным и девствующим на нижнюю
часть сооружения с центральным углом 270°. На про-
тяжении верхней душ с щ тральным углом 90° прини-
ма..тея беаошориая зона (рпс. 19.47).
Рис. 19.47
Упругая линия кольца аппроксимируется уравне-
ниями:
для 45° •' 0	90° w = ду, cos 20;
для 90°	0 <' 180° w w А cos- 0 ф- wL sin2 0,
где 9—угол наклона сечения к вертикали; w А и да д —
ординаты упругой линии в сечениях А и Б.
Изгибающие моменты и окружные нормальные силы
в характерных сечениях кольца определяются ио сле-
дую щи м ф о рмула м:
от собственного веса сооружения
Л1 р = 0,070Rr (1—0,059л);	1
Лф =—0,02777(1 —0,040л);
Mb = — 0,063>(l —0,066/г);
(19.64)
Л’ь = — 0,2507? (1 ф- 0,011л);
Лф = 0,055X1 —0,064/г);
Л'в = 0,0277? (1 — 0,040л);
от веса жидкости, наполняющей сооружение,
Л'1А 0,0707?/ (1	0,050л);	)
Лф -9,151/7(1— 0,056л), j
Al/, — - 0,0631?/(1 —0,0'оЬлг, J
АЛ - 0,0687? (1 — 0,042л),	|
Хф - 0,0557?/ (1 — 0,064щ;
Л д =- 0,1867? (1 -- 0,056/1), j
01 вертикальной равномерной iiaipyinn
йф - 0,125/<г (1 — 0,067л):	1
Л, --ОАШп;
Aly ~ — 0,125/?/ (1 — 0,066/г),
Лф =—0,500,ф (1 4-0,012л);	)
Мь = 0,1257?/ (1 — 0,56л),
Лф = —0,021 Rn, j
(19.66)
где 7? — равнодействующая соотвеюгвующей иструзки;
1
п =	=
0,06416 -1- ---
Am4
(19.67)
£ ( b /
0,0641b + ------ —
’	!	hr \ г
Е— модуль упругости материала сооружения; 1—мо-
мент инерции продольного сечения стенки иа единицу
длины сооружения.
При £7=оо или при 4 = 0 п = 0, и формулы (19.64) —
(19.66) переходят в соответствующие формулы, не
учитывающие отпор грунта.
При наличии безотпорной зоны опасным сечением
сооружения оказывается шелыга (сечение В), так как
здесь отсутствует отпор грунта.
Для этого сечения можно принять коэффициент сни-
жения изгибающих моментов жесткою трубопровода
при учет упругого отпора груша, равный
Ф = 1 — 0,056л =-------------------,	(19.68)
0,143/Щр ф- ря
где д.1 — критическое внешнее давление для иезасы-
паниого трубопровода ио формуле (19.57);	=
= 0.1674/— параметр, учитывающий однозначный уп-
ругий отпор ipyirra; k — коэффициент oitiopu груша,
который для сооружений, улотшшых открытым спосо-
бом, берется для нарушенною грунта засыпки.
Если упругие свойства засыпки выразить модулем
упругости Его и коэффициентом Пуассона pirp, то па-
раметр, учшывакмции в формуле (19.68) упругий от-
пор грунта,
Ргр=ХХ---------y-XXX- (19.69)
6 U Г Цгр)
Совместное действие на подземное
сооружение нагрузок
и внутреннего давления
при учете упругого отпора грунта
Внутреннее равномерное давлении р др«.шелop 1 ируе~
мой жидкости или газа вызывав в стенках сиоруже-
19 2 РАСЧЕТ ПОДЗЕМНЫХ СООРУЖЕНИИ
323
ния кругового поперечного сечения только
норматыше си гы:
N = рг0
РЕО,
окружные
(19.7'01
где Го и Г| — внутренний и наружный радиусы попереч-
ного сечения трубопровода; г—радиус срединной по-
верхности трубопровода.
Эти нормальные силы должны быть дополнительно
учтены при подборе толщины стенки сооружения или
при проверке ее несущей способности.
При начальной овальности поперечного сечения со-
оружения или при деформировании его нагрузками,
действующими извне, внутреннее давление оказывает
расправляющее действие и кроме нормальных сил
(19 70) вызывает еще изгибающие момеГпы. Если ап-
проксимировать начальную овальность или упругую
линию кольца одним членом ряда w — wA cos 29, со-
ответствующим действию равномерной нагрузки
(рис. 19.48), то совместное действие отпора грунта
и внутреннего давления может быть учтено умножени-
ем расчетных прогибов и изгибающих моментов или
приведенных расчетных нагрузок на коэффициент
ОПГгр -г Рл
При этом внутреннее давление р считается пош'жи-
щжщым, а внешнее— отрицательным.
Рис, 19.49
График значений коэффициента С для стальных труб
и разных значений Erv при р=0 приведен на рис. 13,49.
Болес строгое решение дано в работе (5).
Несущая способность сооружения
по условию прочности
Из условия прочности по продольному сечению на-
порного подземного сооружения кругового поперечного
сечения, работающею в упругой стадии, при совмест-
ном действии внешней приведенной нагрузки Р и внут-
реннего давления р можно получить допустимую внеш-
нюю приведенную нагрузку Р при данном расчетном
внутреннем давлении р и при учете отпора грунта:
(19.72)
где
8
-= mRp —;
го
л	8
ря — Пср (у — ~ Q, 524р°8
6	г
(19.73)
Рр — расчетное сопротивление материала сооружения
при растяжении; т — коэффициент условий рабош
трубопровода; С — коэффициент, определяемый форму-
лой (19.7'1).
Величина Р° в (19.73) дает допустимое значение
внешней приведенной нагрузки при отсутствии внутрен-
него давления и устанавливает связь с величиной р°.
являющейся допустимым внутренним давлением при
отсутствии внешней нагружш
Кривые отношений Р/Рп в зависимости от отношений
р/р° дтя стальных труб с b/i' = 0,02 при разных величи-
нах тЯр и £гр показаны иа рис. 19.50. Чем жестче
юоружение, тем ближе его график к прямой, отсекаю-
щей на осях координат отрезки р//30=1 и р/р°=.\.
Расчетное сопротивление материала трубопровода
при растяжении Rv и коэффициент условий работы т
принимаются по СНиПу,
21
324
РАЗДЕЛ 19 РАСЧЕТ СООРУЖЕНИИ ВЗАИМОДЕЙСТВУЮЩИХ С ГРУНТОМ
Если для растяжения при изгибе установлено другое
расчетное сопротивление А’из, чем при окружном растя-
жении, то в формулы (19.73) вместо Ар вводится Акз.
При совместном действии внешней приведенной на-
грузки Р и внешнего нормального давления /щ напри-
мер гидростатического или атмосферного при образо-
вании в трубопроводе вакуума, коэффициент С полу-
чается из формулы (19.71) при отрицательной величи-
не р, а знак минус в знаменателе формулы (19.72) ме-
няется на плюс.
В этом случае вместо в формулы (19.73) входит
расчетное сопротивление материала трубопровода при
сжатии Ас ж.
Расчет сооружения на упругую
устойчивость и жесткость
При некоторой критической величине внешнего нор-
мального давления р поперечное сечение подземного
трубопровода круговой формы теряет устойчивость
и оп уже не в состоянии нести никакой внешней на-
грузки Р.
Критическая величина внешнего давления, соответ-
ствующая любому числу полуволн упругой линии, и при
Рл
Акр — 7 г Рл Ргр
п„ Рл
При Ргр <	- дкр — рл.
4
(19.74)
(19.75)
Кроме того, следует считаться с тем обстоятельством,
что при деформации кольца нагрузка от грунта может
оказаться нормальной к стенке и общее расчетное
внешнее давление окажется равным:
Р
2гхР"
(19.76)
При расчете сооружения на упругую устойчивость
должен быть введен коэффициент условий работы
ту < 0,6.
Расчет сооружения на жесткость или по деформаци-
ям сводится к определению прогиба поперечного сече-
ния по формуле (19.56) с учетом отпора грунта коэф-
фициентом t> определяемым по формуле (19.71), При
этом расчет ведется по нормативным нагрузкам, без
приведения их к двум сосредоточенным силам.
Предельно допустимая величина отопительного уко-
рочения вертикального диаметра f/2r установлена рав-
ной для стальных трубопроводов 0,03, а для трубопро-
водов из полиэтилена и твердого поливинилхлорида
0,05
19.2.5, Расчет сооружений с учетом
пластичности материалов
Выравнивание изгибающих моментов
в стенках сооружений
Благодаря многочисленным опытам со стальными
и железобетонными трубами установлено, что действи-
тельная разрушающая нагрузка всегда оказывается
значительно выше расчетной, найденной из рассмотре-
ния трубы как упругой системы. Это позволяет исполь-
зовать скрытые резервы прочности стальных и безна-
порных железобетонных труб при расчете их по методу
предельного равновесия с учетом пластичности мате-
риала.
Применение этого метода для расчета напорных же-
лезобетонных и других трубопроводов шраничено не-
обходимостью их расчета на трещинойойкость в упру-
гой стадии сопротивления материала при эксплуатации,
но может быть полезным для объяснения нх поведения
при разрушении от совместного действия внешней на-
грузки и внутреннего давления.
Предельные нагрузки для трубопровода из идеально
упруго-пластического материала могут быть определе-
ны из условий предельного равновесия механизма,
в который обращается кольцо при образовании в нем
четырех пластических шарниров, два из которых воз-
никают на концах вертикального диаметра, а два дру-
гих — в сечениях, близких к концам горизонтального
диаметра (рис. 19. 51).
Если принять, что при образовании пластических
шарниров нормальные окружные усилия остаются та-
кими же, как и в упругой стадии работы кольца, то
при одинаковых несущих способностях всех четырех
сечений изгибающие моменты оказываются равными:
М. — 2МБ
МА.пр= - ^£.пр= А^.пр--------(19.77)
где Мд, Мб, Мв,— изгибающие моменты в упругой
стадии работы кольца при нагрузке
данного вида.
Пластическая стадия работы
подземного сооружения при совместном
действии внешней нагрузки
к внутреннего давления
При совместном действии на трубопровод круглого
поперечного сечения двух сосредоточенных нагрузок
19? РАСЧЕТ ПОДЗЕМНЫХ СООРУЖЕНИИ
325
Рпр и внутреннего давления ряр из условий предельно-
го равновесия расчетной схемы деформированного коль-
ца получается следующая зависимость между проги-
бом f и действующими нагрузками (рис. 13.52):
f =	.	(19.78)
2Дпр г ~~ 0,5Рпр
Нормальные растягивающие силы в сечениях Л и £
равны;
=	(19.79)
?/ь = РпР^ + °>5Л-0,5Рпр.	(19.80)
Формула (19. 78) может быть использована для об-
работки результатов экспериментов с трубами при
совместном действии раздавливающей нагрузки на
прессе и внутреннего давления.
Для начала пластической стадии работы жесткой
трубы можно принять f~0 и тогда формула (19.781
переходит в формулу (19.77) при МА=Мв. В этом
случае зависимость между внешней сосредоточенной
нагрузкой Рар и внутренним давлением рир выража-
ется формулой, полученной, исходя из эпюры нормаль-
ных напряжений, показанной на рис. 19.53:
\ Рпр / \ я^пр /
где РПр —предельная сосредоточенная нагрузка при
отсутствии внутреннего давления;
п 417т ат
=	(19.82)
Уравнение (19 81) выражает нелинейную зависимость
между Рвр/Р®вр и Рпр/^ир (рис. Г9.54), связанную
с физической нелинейностью деформирования. При на-
личии еще геометрической нелинейности, обусловленной
расправляющим действием внутреннего давления на
гибкий трубопровод, кривизна графика возрастет.
В зарубежной практике такие графики для чугун-
ных и асбестоцементных труб на основании экспери-
ментальных данных принимаются параболическими.
Предельное состояние
сборной туннельной обделки
Предельное состояние туннельной обделки из арми-
рованных бетонных блоков может наступить при об-
разовании в ее верхней части трех пластических шар-
ниров (рис. 19 55).
Предельная интенсивность равномерной вертикальной
наг рузки
(19.83)
где г — радиус срединной поверхности обделки; fj —рас-
стояние по вертикали между центрами пластических
шарниров; (— геометрическая стрела подъема свода
между сечениями D и В; ев — эксцентрицитет нормаль-
ной силы (распора Я) в сечении fi; Nd— нормальная
сила в пластическом шарнире В;
Nd = 0,67тШсж;
Здесь т—коэффициент условий работы; 5 —толщина
блока; b— ширина блока; /?Сж — расчетное сопротивле-
ние блоков при сжатии.
Угол ап, определяющий положение пластических
шарниров, находится из условия минимума величины
предельной нагрузки.
Нижняя часть обделки, являющейся опорой свода
с тремя пластическими шарнирами, рассчитывается как
упругая криволинейная балка на упругом основании.
При этом можег бьиь использован способ, изложенный
в п. 12.3.
326
РАЗДЕЛ i9. РАСЧЕТ СООРУЖЕНИИ, ВЗАИМОДЕЙСТВУЮЩИХ С ГРУНТОМ
19.2.6. Расчет сооружений некругового
поперечного сечения
Расчет туннельной обделки
в виде по л оiо г о свода
Обделка в виде несущего свода, опирающегося на
прочный скальный грунт, может быть применена а без-
Рис, 19.56
напорных туннелях при отсутствии бокового давления.
Расчет такого свода производится методом сил с уче-
том упругой заделки пят ь грунт (рис, 19.56) (см. так-
же раздел 5)
При переходе к основной системе неизвестные Xlt
Хг, Х3 переносятся в упругий центр 0 при помощи бес-
конечно жестких консолей, длина которых с овределя*
ется из условия, что побочное перемещение обраща-
ется в нуль. При ьтом:
s/2
и
С ~~	S/2
Г & , а
J Е1 +Ь
у _ лщ + Рр
1 ~	+ Рт ’
Лор ~~Р Рр (f ~ с) ~4~ Лр
+ Р1 (/ — с)" 4- б2
(19.84)
(19.85)
(19.86)
Здесь
s/2
. С МР dS
A+ = j ТЁГ
и
I* Мр yds
J Е!
р Л'р cos ц ds
j EF
n
A2/j---
где f — стрела подъема свода; s — длина дуги свода;
</i — ордината оси обделки по отношению к горизон-
тальной оси, проходящей через замок свода; у — орди-
ната оси обделки по отношению к горизонтальной оси,
проходящей через упругий центр; <р —угол наклона ка-
сательной к оси свода а произвольном сечении но от-
ношению к горизонту; а — угол наклона касательной
к оси свода в пяте по отношению к горизонту; йд —-
толщина свода в пяте; /д—момент инерции про-
дольного сечения обделки в пяте; / — момент инерции
сечения обделки в произвольном сечении; Л4Р и Л'р —
изгибающий момент и нормальная сила в произволь-
ном сечении основной системы; М d и — изгибаю-
щий момент и нормальная сила в пяте основной си-
стемы.
Для свода постоянной толщины hj, очерченного по
дуге окружности, при а = 60° и при действии равно-
мерной нагрузки у неизвестные выражаются форму-
лами:
у МО,2310+0,3867п-Д0,0440т+
' 1 ” и (М302 +1,0019л + 0,3001/п +
+ 0,1136/дл) + 0,2165л]
+ 0,7750mn) + 0,25п ’	(	' 
X _ qri 1632 ~~ 0,6092л + 0,2354ш
m (1,6302 + 1,0019л+ 0, 100.1m +
— 0,2267m,л) — 0,375л]
--------'----------— ,	(19.88
+ 0,7750тл) + 0,25п
kr	f h \г
где т~ ~ ; п = — 
Е	\ г 1
г — радиус срединной поверхности обделки.
Изгибающие моменты и нормальные силы в замке,
четверти пролета и пятах определяются соответствен-
но по формулам:
Л1С= Ах —0,173++ у
Хс = А'.у
М1/4 = X,— 0,074+J—0,094?+;
Л/2/1 = 0,901 Xg + 0,1875pr;
+ 4 = 2J + 0,327гХ2 — 0,375у+;
Na = 0,5+, +0,75^.
ч _ ... .1
hAk
J
kl
cos® а;
622 —
Рр- шА 
л
Дд = "mJ cos а=
2	s/2
1 y2ds С cos® cpd<j
ИГ + J ~~ЕЕ
Расчет обделки подземного сооружения
в виде свода, опирающегося
на массивные стенка
По предложению 60. С. Давыдова расчет такой кон-
струкции (рис. 19.57) производится с учетом совмест-
но]! работы отдельных ее элементов и с учетом упру-
гою отпора груша но наружным iраням и подошвам
(' ds
J еГ ’
u
IP3. ВАЛКИ И ПЛИТЫ Н\ УПРУГОМ ПОЛУПРОСТРАНСТВЕ
327
стенок. При этом ipym сбоку и снизу от стенок рас-
сматривается в качестве упругих сжимаемых слоев
толщиной Дг н Яц, а непрерывный контакт между
стенками и грунтом заменяется 10 стержневыми свя-
зями, усилия в которых принимаю1ся в качестве не-
известных.
Кроме того, при переходе к основной системе сме-
шанного метода и прн введении связей против пере-
мещении Степок прикладываются еще два неизвестных
Рис. 19.57
перемещения и сдвигающая сила по подошве. Наконец,
неизвестными являются еще три усилия в упругом цент-
ре свода.
Для определения неизвестных составляются две не-
зависимые системы уравнений, Коэффициентами при
неизвестных силах являются осадки сжимаемых толщ
ipynra. Эти толщи определяются из условия, что допол-
нительные давления на их границах от перемещений
сооружения составляют 20% природных давлений в
грунтовом массиве.
Этот расчет может быть упрощен, если рассматри-
вать грунт в качестве местнодеформируемой среды
с коэффициентом постели
5пДс, Ь
%о И — Ии)
(19.89)
где h — размер стены в плоскости, для которой оты-
скивается й; b — длина стены, выделенная для расчета;
Г:„ и у,, — модуль деформации и коэффициент Пуас-
сона ipyimi; yu — максимальная осадка упругого слоя,
зависящая от его толщины Н,
При //=-0,2/1; 0,4/г; 0,6й; 0,8/г ц большем h соответ-
ственно имеем у,; ==2,4; 3,8; 4,6; 5,2 и 5,6,
19.3.	БАЛКИ И ПЛИТЫ НА УПРУГОМ
ПОЛУПРОСТРАНСТВЕ
19.3.1.	Выбор расчетной схемы
Фундаменты сооружений очень часто располагаются
на грунтах естественного сложения; в этом случае их
рассчитывают как балки или плиты, лежащие па сплош-
ном упругом основании.
Если фундамент располагается на плотных грунтах,
то основание рассматривается как упругое полупрост-
ранство. Взаимодействие между балкой п упругим по-
лупрогчранством осуществляется через нормальные
и касательные усилия, возникающие по площади кон-
такта балки и упругого основания. Для определения
контактных напряжений между балкой и упругим по-
лупространством вводятся связи, усилия в которых
представляют собой равнодействующие напряжений.
В такой постановке задача о расчете балки или плиты

Упругое полупространство
Рис. 19.58
I Р
Рис, 19.59
на упругом полупространстве сводится к определению
усилий в связях, т. е, К расчету обычной сташчески
неопределимой системы (способ Б. Н. Жемочкина).
Касательные напряжения, возникающие по подошве
балки, в большинстве случаев оказывают незначитель-
ное влияние на результат и поэтому в расчете ими мож-
но пренебрегать. Тогда основная расчетная схема для
балки принимается согласно рис. 19.58. Между балкой
и полупространством поставлены упругие связи, позво-
ляющие учесть наличие разрыхленного слоя грунта,
расположенного непосредственно под подошвой фунда-
мента. В предельном случае упругие связи переходят
в жесткие нерастяжимые стержни.
В основной системе (рис. 19,59) балка отделяется от
упругого полупространства и к ней добавляется задел-
ка. За неизвестные, принимаются усилия Аф в связях-
пружинах, осадка ув и угол поворота заделки <тт>. Для
определения сил Xh Х2, ... составляется система кано-
нических уравнений:
•5ц	-J- 615 Х? Хз 7- А4 +
~г • • • 7~ о?. Йо ~г Ajp = 0;
<5.51 Aj “Г 7' ЙоЗ Хд -% »\4 Х4 ~т
-г--- +?ф + дл’о +	= °;
бщ-Л ёз<>. А'г <%з	634 А4 -I-
+ • •  + у0 -7 о, ср0 Л Азр = 0;
S..n Хг + %?2 Х2 ф- Зл3Х3 7- 8Ы X, 7-
+ •••+%> 7'%ДРЙ 7-Л„Р-0;
АгЛХ2 + Лф7— —ЗЛ==0;
од Аф 7' «а Аф 7" аз Аф Д   < — 1 ЛЦ = 0.
(19,90)
328
РАЗДЕЛ 19. РАСЧЕТ СООРУЖЕНИИ, ВЗАИМОДЕЙСТВУЮЩИХ С ГРУНТОМ
Через щ обозначено расстояние от заделки до силы
Л',; 2ft и 2Л4,— равнодействующая и момент внеш-
них сил.
Физический смысл первой группы уравнений (19.90)
состоит в том, что перемещения в основной системе по
направлению каждого неизвестного ft, Хг и т. д. от
всех сил равны нулю. Таких уравнений надо составить
столько, сколько имеется неизвестных сил А',-. Послед-
ние два уравнения являются уравнениями равновесия.
Рис. 19.60
При вычислении коэффициентов 6;л канонических
уравнений приходится учитывать как прогиб балки
см, так и осадку упруюго полупространства ylfl ос
единичных сил (рис. 19.60):
Stk^Vih-i-yik;	(19 91)
£и —модуль деформации полупространства; — зна-
чение функции.
Подставив значения и т/щ в формулу (19.91),
получим.
са	1	ц.~	1 (ft
S.A	w.k щ. ------F, =- (£zft rj^lk) ------ (19.94)
ЬЕ1 z.oc:t	1.осл
Щ Е„ 71
а^--------------.	(19.95)
6 [1^) Е1
Общий множитель (1.—Цц)/£осл одинаков для всех
коэффициентов 6,8, и поэтому при выполнении расче-
тов его можно учитывать в конце.
Ординаты р, эпюры реакций упругого полупростран-
ства вычисляются путем деления сил на соответст-
вующие им площади подошвы балки.
(19 96)
где с —расстояние между связями; Ъ — ширина балки.
19.3.2.	Бесконечно жесткая балка
При расчете бесконечно жесткой балки пользуются
уравнениями (19.90), но при вычислении коэффициен-
тов канонических уравнений учитывают, что деформа-
Т а б л и ц a 19 18
Значения реакций для бесконечно жесткой бдлки
п и п ш м	1	IHI
£J = OO	Чй	
ft й
Прогиб пщ вычисляется по обычным формулам как
прогиб в сечении I балки, заделанный одним концом,
ос силы ft=l, приложенной в сечепии k (рис. 19.61):
Мк	ak i	ak
U1Ъ ~ \------dX •=----1 Я, — —
1 J El	2EI \	3
6 £7

(19.92)
где El — жесткость балки;
с—расстояние между связями (см, рис. 19 59).
Осадка упругого полупространства вычисляется по
формуле Б. Н, Жемочкииа [14]:
(3 — к)
(19.93)
я£о с
где щ — коэффициент Пуассона полупространства;
Ы1	Ч/С	Реакции р^				
		Ро	р>	Р;		А
Ь/1—QQ	( 0,00	1) ,688	0,68.5	0,732	0,852	1,892
	| 0,5(1	0,704	0,720	0,790	0,950	1,680
Плоская	1 1,00	0,730	0,760	0,8’20	0,980	1,551)
задача	; 1,35	0,760	0,770	0,810	1,002	1,509
о,зз	0	0,799	0,8 32	0,858	У,’>07	1,
0,22	0	0,846	0,855	0,88]	0,927	Мда
0,11	0	0,889	0,890	0,919	0,961	1,298
0,07	0	0,900	0,905	0,928	0,973	1,247
Примечание, 1 —- пролет балки, Ъ ~ ширина балки, йо — толщина слоя. €—’7,9						
19.3, БАЛКИ И ПЛИТЫ НА УПРУГОМ ПОЛУПРОСТРАНСТВЕ
329
Та б л и ц а. 19 19
19.3.3	Гибкая короткая балка
Ординаты эпюр М и Q бесконечно жесткой балки
Усилия		b.'l					
		плоская задача Ь/1^™	0,33	0,22	0,11	0,07	общим мн ожи- тель
|	Моменты	I	М,	4-0,1-м	4-0,136	4-0,134	40,131	40Д29	Р1
	м.	40,098	40,087	40,085	40,082	40,081.	
	м2	4-0,057	40,048	40,046	40,044	4-0,043	
	м3	4-0,094	40,019	40,013	40,on	40,015	
	м,	40,004	4-0,003	40,003	+0,002	40,002	
Поперечные силы j	Qi	—0,500	—0,500	—0,500	—0,500	—0,500	Р
	Q-.	—0,424	—0,W	—0/104	—0,402	-0,400	
	0,	—0,345	—0,314	—0,308	—п.302	—0,298	
	р4	—0,257	—0,216	—0,208	-0.Ю7	—0,192	
		-0,105	—0,083	—0,078	—0,072	—0,069	
Примечание. Моменты и поперечные силы укъ нзны
на 1 пог. м ширины балки.
пчя балки должна быть равной нулю, и поэтому фор.
мула для 6,й будет состоять из одного члена, равною
перемещению упругого полупространства:
1 — /
----— Elk-	(19,97)
жЕ0
Изгибающие моменты и поперечные силы зависят от
закона распределения внешней нагрузки, так как момент
внешних сил зависит от положения нагрузки по длине
балки. При обратно симметричной нагрузке ординаты
эпюр реакции будут пропорциональны моменту равно-
действующей внешних сил, вычисленному относительно
зачетки. В тзбл. 19 18 указаны ординаты эпюры реак-
ции, а в табл, 19.19 — ординаты эпюры моментов А1
и Q,
Балка должна рассчитываться как короткая и гиб-
кая, если справедливо неравенство
Г Е
/>0,8/гэ 1/ — ,	(19.98)
У 7?о
где I—продет балки; й—высота балки; Е — модуль
упругости балки; Бы — модуль деформации основания.
Ординаты линий влияния моментов даны в табл. 19 20,
Двухслойное основание
Найдем распределение реакций основания для беско-
нечно жесткой балки, расположенной на двухслойном
основании.
Расчетная схема и основная система показаны па
рис. 19.62,
Рис 19.62
Упругий слой, подчиняющийся гипотезе пропорцио-
тльпости, расположен между балкон и упручим полу-
пространством, и его толщина + =12,5 я-.
,	12,5-3,14(1—0,35=)
<+ = 2 • 1,867 + 2 —------------------ = 6,030;
3-10
би= 1,867 + 0,469 + 1,148	3,484;
</ = 1,867 + 0,246 + 1,148 = 3,261;
6за = 1,867	0,165 + 1,148 = 3,180;
в44= 1,867-4- 0,124 + 1,148 = 3,139.
Побочные коэффициенты вычисляют по формуле
(19.94), значение Еги — по таблицам Жемочкина [14]
+ 6,030 Хе + 1,658 Аф - 0,938 Аф + 0,646 Хэ /
+ 0,492 Xv -- 0;
ф- 1,658 Х0 + 3,184 X, + 1, 152 X, 0,715 Аф +
-у- 0,320 Аф т у0 — 0,
РЛЗДГЛ W РАСЧЕТ СООРУЖЕНИИ ВЗМПЮДП1СЛВУЮЩНХ С ГРУНТОМ
Т а б л л ц а 10 20
Ординаты линий влияния моменте?, (общин множитель р/)
Момрш
Труз в точке	Коэффициент 1	Mi	м.	Ж	X	Л1„		Л!.', "		М\
	а=0	1	0,0021	0,0148	0,0494	0,0895	OJ309	0,0895	0,0401	0,0198	0,002?
в	(X=0J	|	—0,0005	—0,0030	0,0005	0,9182	0,0592	0,0182	0,0005	-0,0030	j — 0,0005
	С6™1	|	-=□,0002	—0,0020	— 0,0049	—0,0002	—0,0101	— 0,0'412	-0,0040	—0,0020	—0,0<Ю2
	а—0	|	0,0035	0,0297	0,0725	0,1285	0,081»	0,0510	0,0261	0,0100	0,0ч И
7	а—0,1	|	—0,0002	0,0000	0,0133	0,0503	0,11-13	—0,0018	—0,0067	—0,0046	, —0,0006
	а=1	|	—0,0005	-0,0034	—0,0001	0,0503	—0,1107 :	—0,0040	—0,00 22	—0,0007	—0,0(1-л
	а—0	|	о, поп	0,0396 :	0,0955	'1,0560	(),0291	0,0'157	—ОДЮН)	—0,0021	—0,00(1!
2	а—0,1	|	0,0(12)	11,0187	0,0589	0,0169	—0,0024	—0,0040	—0,0078	—9,00 К	—0,(11105
	а.—1 j	—0,0001	0,0012	0,0305	—о.оооз	—0,0046	—0,01)1')	—0,0001	—0,(1001	Д 0,0'100
	а—0	|	0,0058	0,0195	0,0076	—0,0161	—0,0265	—0,026 4	—0,019ч '	—0,0098	—0,0(112
3	а=0,1	|	0,0052	0,0458	0,0032 '	—0,0071	—0,0101	—0,0090	—0,0051	—0,0013	—0.0001
	а— 1	j	0,0022 i	0,0265 i	—0,0021 !	—0,0017 j	—0,0032	0,0001	0,0016	0,0010	0,0002
	а“0 j	0,0070	—0,0507	—0,0805	—0,0388	— 0,0820	—0,0550	—0,0427	—0,0196	—0,0024
4	а—0,1	|	0,0106	—0,0233	—0,0.172	—0,0211	—Г>,01 в	—0,0038	—0,0012	—0,0014	—0,0001
	ос—-=-1	|	0,0128 !	—0,0074	—0,0052	—0,0024 (	—0,00 Г) !	—0,0001	0,0001 ;	0,0009	о,оот
0,938 Хо 4~ 1 з ^2 Л4“ »261 Xg 1,026 Ад -j-
+ 0,634 Х4 + уо = О;
+ 0,646 Хо + 0,715 А\ + 1,026 Хф + 3,18 Х3 +
+ 0,971 Х4 + уп = 0;
+ 0,492 Хв + 0,520 Xj + 0,63i X, А 0,971 Х3 +
+ 3,139Л'4 + + = °;
Хо + Х4 + Х2 + Х3 + Х4 = + 4,5.
Решая эту систему, найдем значения неизвестных.
у0 = — 6,586; Х2 = + 0,922;
2Хв = + 0,886; А'з = + 0,992;
Х4 = + 0,896; Х4 =- + 1,248.
Эпюра реакций показана на рис 19 62.
Два здания, расположенные рядом
Два здания, расположенные рядом, оказывают взаим-
ное влияние па величину осадок и реакций упругого
основания. В результате деформации упругого полу-
пространства происходит взаимный наклон зданий.
Рассмотрим два силосных корпуса размером каждый
45X32 м в плане, поставленные рядом. Оба корпуса
загружены полностью, а среднее давление на грунт со-
ставляет 3,3 кГрлХ Для определения осадок и реакций
будем рассматривать ли здания как бесконечно жест-
кие балки. Модуль деформации основания + =
=400 кГ/ыХ.
Расчетная схема н основная система принимаются
согласно рис. 19.63. В основной системе должны быть
лве заделки — отдельно для каждой балки. Располо-
жим пх в месте примыкания силосных корпусов. Каж-
дую балку прикрепляем к упругому основанию пятью
стержнями. Расстояние между стержнями с — 10 м.
В силу симметрии потребуется составить систсму из
Рис. 19 63
дни ; равнеипн для определения сит А', Коэффициен-
ты уравнении подсчитываются по табл. /Кемочыша для
OI ношения
+,- 2.1,867 = ф 3,731;
+ = 2 -0,829 = + 1,658 нт. д.
19 3 БАЛКИ II ПЛИТЫ ПА УПРУГОМ ПОЛУПРОСТРАНСТВЕ
331
Решая систему уравнений, находим значения неиз-
вестных при Q=l:
<р0 =	0,0663',
.% = - 1,284;
А’о = 3-0,1318;
А\ = + 0,2133;
X., = 4- 0,1973;
Х3 = + 0,1892;
A’t = + 0,2684.
А 41 -= 0,2133-1+0,1973-2+0,1892-3+0,2684-4 = 2,249.
На практике очень важно знать разность осадок раз-
личных точек одною и того же корпуса. Эту разность
можно найти двумя путями; умножить полученный
угол наклона rfo па расстояние между точками, раз-
ность осадок которых требуется определить, или вы-
числил, независимо осадки той п другой точки, прини-
мая во внимание, что силы, приложенные к упругому
полуцроираиству, теперь известны.
Найдем разность осадок точек 0 и 4, умножая угол
noBopoia <jo на 4:
А у = +() = — 4  0,0663 = — 0,265.
Определим осадки уц и га по табл. Жемочкина:
у0 = (1,867-0,1318 + 0,829-0,2133 + 0,469-0,1973 +
+ 0,323 -0,1892 -1 0,246-0,2684) 2 = + 1,285;
у4 = 1,867-0,2684 Ж 0,829-0,1892 + 0,469-0,1973 +
+ 0,323-0,2133 -9 0,246-0,1318-2 + 0,197-0,2133+
+ 0,165-0,1973+0,142.0,1892+0,124.0,2684 = + 1,017;
Ду = 1,017 — 1,285 = —0,268.
Сравнивая результаты, вычисленные разными спосо-
бами, замечаем, что расхождение оказалось в пределах
точности подсчетов Полученные величины у0 и Ау,>
определены для ф=1; в действительности Q = 32-45X
X 33 = 47 500 г.
Для получения действительных осадок надо умно-
жить полученные величины, согласно формуле (1,9.93),
иа величину
1 — Во Н — 0,352) 47 500
------Q = -----------------= 0,332.
.лЬос	3,14-4000-10
Тогда потучаем действительную осадку7 в точке 0:
гы = 1,285-0,332 = 0,43 м = 43 см.
Разность осадок точек 0 и 4:
А,,	= 0,268-0,332 = 0,09 м = 9 см.
“Действ
Различная осадка вызывает взаимный наклон зданий,
19.3.4. Балка за пределом упругости
Определение наибольшей нагрузки
в у п р у г о й с т а д и и
Рассмотрим ба н.р прямоугольного сечения, нагру-
женную еосрелотош иной силой Р в середине длины
(рис/ 19 64).' Определим значение +, при котором
н краплем волокне опасного сечения балки напряжения
будут достигать предельной величины <тПг>. Это значе-
ние силы будет наибольшим для упругой стадии рабо-
ты балки при условии, что упругое основание сохраня-
ется линейно-деформируемым.
В сечении под грузом изгибающий момент будет
равен:
Р
АД=-уте0.	(19.99)
Расстояние с0 от середины пролета до центра тяже-
сти эпюры реакций зависит от закона распределения
реакций по /длине пролета балки и вычисляется з ре-
зультате решения задачи в упругой стадии.
Эпюра реакций
Рис, 19.64
В зависимости от соотношения жесткости балки
и упругого полупространства величина св изменяется.
Чем больше жесткость балки, тем больше с0. При рав-
номерном распределении реакций упругого основания
с0 = 0,25/, т. е. равнодействующая реакций проходит
Д четверти пролета балки. Для гибких балок величина
с0 становится меньше 0,25 I (табл. 19 21) Для беско-
нечно жестких балок <?0 становится больше 0,25 /,
Для определения Ро приравняем Ме моменту внутрен-
них сил; тогда получим;
+ = 2аПрГ/с0.	(19.100)
Табл и ц а 14 21
Значение м
а	|	Ь'с=-3	Ь‘С='2	Ь/^1
0,0	0,2793				
0,1			0,1421
1,0	|	0,030 >	0,0э57	0,0731
332
РАЗДЕЛ 19. РАСЧЕТ СООРУЖЕНИИ, ВЗАИМОДЕЙСТВУЮЩИХ С ГРУНТОМ
Если а—ОД и Ь/с~=2, в табл, 19,21 найдем значение
Со—0,128 /; тогда для прямоугольной балки получим:
bh? I
(19Л01)
Распределение реакций
за пределом упругости
Выясним распределение реакций упругого основания,
если внешняя сила Р будет больше Ра. Теперь балка
будет работать за пределом упругости в упруго-пласти-
ческои стадии, а ее жесткость изменится.
Рис. 19.65
Для упрощения задачи исключим из рассмотрения
процесс перехода балки в упруго-пластическую стадию
и будем считать, что в результате образования пласти-
ческого шарнира балка разбивается* на два участка,
которые находятся в упругой стадии.
Выразим силу Р через Ра по формуле
Р=пР0.	(19.102)
Множитель п в этой формуле будет больше единицы.
Для всех значений расчетная схема балки име-
ет вид-, указанный на рис, 19.65. Особенность этой рас-
четной схемы состоит в том, что с увеличением Р мо-
мент А1Пр остается постоянным, сохраняя свою вели-
чину. Для данной расчетной схемы разрешим две вспо-
могательные задачи, для Л4=1с и 4=2, как это пока-
зано на рис. 19,65,
Для определения реакций упругого основания соста-
вим такие две системы уравнений, которые различают-
ся в уравнениях равновесия правой частью:
6,0 Ха Д б01 Хг -f- бов Х2 Д- <3ОЗ А'3 Д- 601 Ха -ф
+ М0 сФп = 0
W ~Ф ДI ~Ф <^15, Хг 4- й1а Х3 -j- йи А 4 Д
+ Фо + Wo = 0
й20 Хо + Xt Д &№ Х-2 + <5„3 АД + йи Xt Д
-|- 1у0 -ф2«р0 = О
бзо Д б31 АД Д- (532 X, -ф 6з3 Х3 -ф- 634 Х4 -ф
~Ф Фо ~Ф Зсф0 = 0
Ха -ф S41 Хг -ф 34,, X, -ф (\в А'з -ф й44 -ф
-ф ф0 -ф 4стря = О
1 Аф Д IX, Д IX, -ф 1Х3 4 IX, 4-04-0=0
ОХ0 -ф IX, 4- 2Аф -ф ЗХ3 ф IXi 4 0 + 0=1
= 0;
= 0;
= 0;
= 0;
= 0;
= 1;
= 0-
Если к балке будет приложена сила Р~пР0 (при
nb> 1) и момент
,« уФ о 25о
*''Фр = t аса —	Л10,
где 2Sn — пластический момент сопрогивлепчя. равно-
действующие реакции упругого основания будут най-
дены с помощью чисел влияния по формулам:
х0 = х0 2 Ро ; Хо г0 PQ;
(19,103)
Значения A't- и Аф даны в табл 19 22 и 19,23. Для
вычисления интенсивности реакции необходимо поде-
Таблиц а 19,22
Числа влияния от Р=-2
Числа влия- ния			Ь/с=2		1	
	гх—0,1	а=1	j	а—1	й=0,1	
+	4-0,5256	+0,7342	+0,5738	40,8026	+0,6155	+0,8453
л-;	+0,4849	+0,3568	+0,4880	+0,2770	+0,3999	+0,2232
Х2	+0,2139	+0,0218	+0,1844	—0,0014	+0,1597	—0,0118
4	+0,0177	—0,0490	+0,0219	—0.0376	+0,0210	-0,0282
	—0,2417	—0,0634	—0,2181	—0,0403	—0,1957	—0.0238 ;
до	—4,8191	—5.8739	—3,6613	—4,3304	—3,0222	-3,4746
	+ 1,6438	+3,2195	4-1,2366	+2,2352	+1,0090	41,7557
Таблица 19323
Числа влияния от АГ-^1 с
Ч мхлф влия- ния					?з/с=3	
	1	а—1	а=0,1	а—1	I.	!	а—1
х.;	—0,2389	—0,5693	—0,2907	—0.6880	-0,3383	—0,7718
+	—0,0746	+0,2392	—0,0225	+0,4184	+0,0249	+0,5565 .
Xj	+0,9409	+0,2259	+0,0681	+0,2125	+0,0913	+0,185! !
А'.	+0,0951	+0,1064	+0,0939	+0,0720	+0,0944	+0+458
+	{-0,1770	— 0,0026	+0,1510	—0,0149	+0,1274	—0,0162
7!)	+1,6439	+3,2190	+1,2366	+2,2852	+1,0095	+1,7550
с Фо	— 1,3468	—5,8207	— 1,1375	—4,8426	-1,0117	—4,2427
лить силы X, па соответствующие нм площади F,„ На-
пример, дтя bjc==3 и а = 0,1 получим:
ЛД =	со=0,118 — / = 0,059 Р9/.
Дтя прямоугольно"! балки	поэтому Afnc —
IE
= 1,3 Al0 = 1,5- 0,059 Ро/=О,О885 Pal.
19 3 БАЛКИ И ПЛИТЫ НА УПРУГОМ ПОЛУПРОСТРАНСТВЕ
333
Теперь подсчитаем значение реакций; если Р — 2Ро,
получим:
= 0,6155 — — 0,3383 —= 0,3461 Ро.
2	с
Интенсивность реакций в точке П ра равна:
Ро
2Х„
2-0,3461 Р„
1/9 У
= 6,29%;
%— среднее давление на основание от Рп.
Для Р = 3 Р о и м е е м.
Хо = i0,6155 ------0,2694j Рв 0,654 Р„;
% = 0,654 • 18 % — 11,772 %.
Рис 19.66
Рнс. 19,67
Аналогично вычисляем значения реакции в других
точках балки. На рис. 19.66 показаны эпюры реакций
при работе балки за пределом упругости. График по-
строен при относительных ординатах, Из графика вид-
но, что после образования пластического шарнира под
сравнению с балкон иа двух опорах без упругого ос-
нования. Как известно, исчерпание несущей способности
балки на двух опорах наступает тогда, когда в одном
из сечений балки образуется пластический шарнир
и балка превращается в механизм. Балка на упругом
основании может воспринимать нагрузку и после того,
как возник пластический шарнир. Для такой балки пре-
дельное состояние лимитируется наибольшим прогибом,
который является предельным для данной балки по ус-
ловиям ее эксплуатации. При увеличении нагрузки
после образования пластического шарнира величина
прогиба под грузом определяется с помощью чисел
влияния. Для определения Рпр необходимо задать пре-
дельный прогиб уПр в долях от наибольшего прогиба
у0, соответствующего концу упругой стадии Уп-р — kyp
/ f 1	 Sl\ С„ \
где прогиб иод грузом от Р0 = 2;
у0— то же, от М = 1 г.
После преобразовании найцем:
р ^.р	.^<2— 	 — Р
Уо Ув W с
Учитывая, что уо^у^Рц, получим:
й = fiE. = 2k — 2 — • — 	.
Р° у'о Уо W С
Sn
Для таких числовых данных й=3;	=0,75;
= 1,01; с = -~ = 0,11; % = -- 3,02; у’о = 1,009;
гп 0,118; а — 0,1 и Ь/с-3
по тупим:
грузом изменяется эпюра распределения реакций меж-
ду упругим основанием и балкой. С ростом нагрузки
п ~
наблюдается более интенсивное увеличение ординат
реакций под грузом. Так, например, увеличение нагруз-
ки в три раза (я=3) вызывает увеличение наиболь-
11,77
шей ординаты эпюры реакций в -^-р—=4,75 раза,
^ПР __ о
  1 - сЭ
Ро
1,01-2
3,02
1,009-2
+ -у------0,75
3,02
0,И8
0,11
а это значит, что при переходе балки за предел упру-
гости зависимость между внешней силой и наиболь-
шей реакцией основания становится нелинейной.
На рис. 19.67 показан график изменения р-иакс в зави-
симости от Р. Если P/Pq^XI, то балка работает в упру-
гой стадии и между умакс и Р имеется лииенная зави-
симость, С увеличением Р в балке образуется пласти-
ческий шарнир и поэтому необходимо сделать
специальный расчет для определения рЫакс—линейная
Этот результат показывает, что после перехода бал-
ки за предел упругости прогибы под грузом растут.
Оценим влияние жесткости балки на величину Рпр.
Для этого сделаем расчет еще для а = 0 и а=1.
При а=0
^пр
---— - Q
ре
0,555
1,56
1,009
1,56
0,75
0,2798
'о?н
1,398.
При « = 1
Рпр 1,6	1,756	0,06
ДФ = 3----------- +-------о ,75 —
Ро	3,474/2	3,474/2	0,11
экстраполяция в данном случае приводит к преумень-
шенному значению. Это видно из графика, на котором
такая экстраполяция изображена пунктиром. Здесь
важно отметить, что упругое основание в дайной за-
даче остается линейно-деформируемым и полученная
нелинейность возникает в результате того, что балка
переходит за предел упругости.
Сопоставление полученных величин показывает, что
величина предельной нагрузки зависит от соотношения
жесткостей балки и упругого основания.
Величина предельной нагрузки
В тайной з?лччс понятие о предельной несущей спо-
собности балки приобретает несколько иной смысл по
19.3.5, Расчет плит за пределом упругости
Бесконечно-протяженная плита
При переходе плиты ;а прелет упругости образуется
упруго-пластическая область, жесткость плиты изменя-
ется, а это вызывает перераспределение реакции осно-
вания и моментов в плите.
334
РАЗДЕЛ 19. РАСЧЕТ СООРУЖЕНИИ. ВЗТИ.МОДЕПСТВМЮЩИХ С ГРУНТОМ
Для расчета за пределом упругости процесс дефор-
мирования птиты разбивается на интервалы. Сначала
делается расчет пс упругой стадии и определяется воз-
можное расположение линейных пластических шарни-
ров в плите. Затем выполняется новый расчет для ос-
повпой системы, в которой изменяется расчетная схема
плиты и учитывают! образовавшиеся пластически"
шарниры. Перемещеш’я, входящие в уравнения, вычис-
ляются для новой расчетной схемы плиты, поэтому
после решения уравнений будут найдены новые значе-
ния реакций основания и по ним построена эпюра мо-
ментов в упруго-пластической плите.
В данной задаче понятие «предельная нагрузка» при-
нимает несколько Иной смысл, так как образование
в плите одного или даже нескольких линейных пласти-
ческих шарниров еще не приводит к исчерпанию несу
щен способности в силу того, что плиту поддерживает
угфугое основание, которое работает в упругой стадии.
Чаще всего предельная несущая способность определя-
ется путем нормирования величины наибольшего про-
гиба плиты. После образования пластических шарни-
ров для жестких плит наблюдается интенсивное увели-
чение прогибов, которое зависит от соотношения гео-
метрических размеров плиты и упругих характеристик
плиты И основания,
Для гибких плит образование первого пластического
шарнира не влечет за собой значительного увеличения
прогибов.
Упругий слой, расположенный между пли гоп и полу-
пространством. оказывает влияние на распределение
реакций упругого основания, в результате чего проис-
ходит снижение концентраций реакций к краю плиты.
При переходе плинт за предел упругости происходит
увеличение прогибов плиты за счет деформирования
слоя.
Для плиты бесконечных размеров, нагруженной со-
средоточенной силон, величина предельной нагрузки
может быть определена приближенно с учетом образо-
вания линейных пластических шарниров по образую-
щим конуса и кольцевого шарнира на контуре его ос-
нования Для этого приравняем работу внешней силы
Р„р сумме работ моментов в шарнирах и реакций ос-
нования. Получим:
(19.104)
Наименьшее значение Ряр подучим:
(^пр)мин = 2лЛ1пл — ~jpj- ЛГ“ (Щмкс ' йг) "Л
(19.105)
где Мл.> — момент иа единицу длины пластического
шарнира (имеет размерность сплир, г—расстояние от
груза до кольцевого шарнира; а-илге— интенсивность
реакции упругого основания под грузом; — интенсив-
ность реакции упруюю основания на расстоянии г.
Для балочной плиты, нагруженной сосредоточенной
си той в середине пролета, величину Р,1р найдем для
разных значений наибольшего предельного прогиба упр,
выраженного в безразмерной форме уРР1уР через наи-
больший прогиб у», который соответствует концу упру-
гой сгаднп работы пли гы.
Зависимость между Рир и илр пощчаетоя ш1 тинейтюн
п зависит от соотношения физических постоянных плиг
и упругого основания, которое характеризуется пара-
метром
До I ! I V з
•’ттЫ"...............1	<19-™
гд" Е„—'Модуль деформации основания; Е — моусоъ
упругости плиты, I и b— пролет п ширина плиты; Л —
тотщипа плиты;
Р;10-^==(0,14А О.вОа1-’)^)2^.	(19.107)
1 о
Формула (19.107) получена при соблюдении условия
2 4Д,р:5.	(19.108)
После образования первого пластического шарнира
наблюдается изменение эпюры реакций основания.
Распределение реакций зависит от соотношения жест-
костей плиты и упругого основания, а также от вели-
чины внешней силы — в этом случае задача становится
нелинейной.
Влияние местных
и общих деформаций
В прямоугольных плитах во шикает комбинированная
схема разрушения, состоящая иг местных и общих де-
формаций. Если плита достаточно узка, то ее схема
разрушения при грузе, расположенном в середине про-
лета, будет похожа иа балочную схему. Под грузом
образуется пластический шарнир, распространяющийся
на всю ширину плиты, как это показано иа рис. 19.68, а.
Для широкоп пли гы механизм разрушения будет при-
ближаться к случаю бесконсчно-протяжшшой плиты
(рис, 19,68,6). Эта две формы разрушения возникают
в каждой плите (рис. 19 68, л),
В результате наложения обоих эффектов конфигура-
ция местного конуса. д> формаций изменяется. Наличие
ба,ю того линейного шарнира сокращает размер плас-
тического конуса в направлении линейного шарнира.
В результате этого основание пластического конуса из
круга превращается в стпюснутую кривую, изображен-
ную на рис 19 68, п, Длина кругового пластического
шарнира, соответствующего основанию конуса, а также
и длина образующих конуса ’уменьшается; поэтому пре-
дельная нагрузка Р теперь будет меньше Рп для бес-
конечной птйты и больше, чем для балочной плиты Рг,:
Рб *Р Рп-	(19-109)
Для бесконечной плиты величина предельной на-
грузки определяется по формуле
Рп 4лЛ1пл	—~~ № (умакс дг) -~
-;--улд9;..	(19.1Ю)
Е этой формуле щрвы" два слагаемых представляют
собой работу пластических моментов в круювом шар-
нире н и шарнирах, возникающих по образующим ко-
ЯЗ Б1ПКП И ПЛИТЫ Т-И УПРУГОМ ПОЛУПРОСТРАНСТВЕ
335
нуса Последний член равен работе реакций основания
в пределах пластического конуса.
Дтя балки ветичина предельной нагрузки определяет-
ся по формуле
Р6 - 2/Ипл	,	(19.111)
где Гт — расстояние до равнодействующей реакции ос-
нования. Применяя общие теоремы предельного состоя-
Рис. 19.68
ния, получим величину предельной нагрузки для комби-
нированной схемы образования пластических шарниров,
Рассмотрим птиту с отношением сторон Ь// = 0,5.
Определим для нее величину балочной предельной си-
лы Pi>, предполагая, что шарнир образуется в середине
пролета по всей ширине плиты:
Pty=Mwc0.	(19.112)
Эта сила соответствует образованию пластического
шарнира в середине пролета плиты при условии, что
по всему поперечному сечению плиты в середине проле-
та изгибающий момент распределяется равномерно.
В действительности этого не получается—-изгибающие
моменты под склон растут быстрее, чем по краям пли-
ты, поэтому пластическая область будет образовывать-
ся сначала в непосредственной близости от внешней си-
лы, а затем уже распространяться в стороны. Предель-
ные размеры пластического конуса, образующегося под
силой, можно определить из формулы (19.110) для Рп,
сети в иен сделать изменения, учитывая, что основа-
ние пластической области будет теперь представлять
собой кривую, похожую иа эллипс.
Пластическая область под грузом теперь будет
уменьшена па коэффициент, который равен отношению
площадей й = 0,7. Таким образом, предельная сила, со-
ответствующая комбинированной схеме разрушения,
Рк - 0,7Рп-+ (
Рб-
(19.1
Величина Р* не может быть больше Ря, следователь-
но, эта формула справедлива, если
Рй(б-2г2) . 0,ЗД,,	(19.114)
где Ь — ширина плиты; гг — малый радиус конуса плас-
тичности.
На Iр у з к а на краю плиты
Когда сосредоючсшшйп i руз располагается вблизи
края достаточно протяженной или полубесконечной
плиты, то обращены характерный мехаиитм разруше-
ния плиты В отныне о г бесконечной плиты взамен
кольцевого шарнира п imuoio пластического конуса
воишкаст по ювшш конуса, основанием которого слу-
жит иолу эллипс, Очертание кривой, по которой распо-
лагается пластический шарнир, соответствующий сече-
ниям с отрицательными моментами, приближается
в плане к полуэллипсу, у которого размер вдоль края
плиты вдвое больше поперечною.
Линейные пластические шарниры, соответствующие
образующим конуса, заполняют всю область, и работа
пластических моментов в пределах всего конуса будет
подсчитана аналогично тому, как это было сделано для
бесконечной плиты, Теперь боковая поверхность плас-
тической области будет почти в два раза меньше, Так-
же уменьшится и работа пластических моментов в коль-
цевом шарнире, длина которого будет меньше, чем по-
ловина полуокружности, построенной на большем диа-
метре пластического конуса.
Реакции упругого основания, которые совершают ра-
боту при деформировании плиты, могут быль подсчи-
таны достаточно точно. Вдоль края эпюру реакции
можно получить, выделяя из плиты полосу и рассмат-
ривая се как бесконечную балку. В направлении, пер-
пендикулярном краю, выделенная полоса будет пред-
ставлять собой полубескопечную балку, натруженную
силой на конце. Из условий равенства прогибов для
бесконечной и полубесконечной балок в точке приложе-
ния груза получим формулу для распределения внеш-
ней нагрузки между продольной и поперечной балками.
Для определения границ, через которые проходит коль-
цевой шарнир, используются эпюры моментов, возни-
кающие в балках. Кольцевой шарнир образуется в том
сечении, где возникает наибольший отрицательным мо-
мент.
Работа, совершаемая в линейных шартшпах, равна
1,25 зтМпл. Такое же выражение получим для работы
моментов в кольцевом шарнире. Работу реакции упру-
гого основания можно подсчитать, предполагая, ч:п
основанием конуса пластичности является окружность.
Тогда получим:
1 , 1
р ^макс 7r) + g Fqr>
F будет представлять собой площадь основания кону-
са пластичности, причем F = 0,5 лгф
Ймакс — 0,123 Рпр
Тмяко
Теперь можно подсчитать величину предельной силы'
2,5 л Ип,
^₽ = Т^м'Г = 2’92лМпл-	(12Л15)
Полученное решение показывает, что нагрузка, при-
ложенная к краю плиты, значительно раньше вызыва-
ет разрушение плиты, чем нагрузка, приложенная
в центре ее. Соотношение этих нагрузок зависит oi
жесткости плиты и основания. Для жестких плит раз-
ница будет больше, чем для гибких Если плита имеет
небольшие размеры в плане, то необходимо также рас-
смотреть возможность разрушения ее по комбинирован-
ной схеме, когда кроме пластического конуса еще об-
разуется линейный иластическип. шарнир, соединяю-
щий пластический конус с незагруженной стороной
плиты.
Расчет слоистой плиты
Рассмотрим трехстопную плиту, состоящую из двух
плит разной жесткости, разделенных: упругой прохлад-
336
РАЗДЕЛ-19. РАСЧЕТ СООРУЖЕНИИ, ВЗАИМОДЕЙСТВУЮЩИХ С ГРУНТОМ
кой, Плита расположена на упругом основании и на-
гружена сосредоточенной силой Р; размеры плиты
в плане примем достаточно большие для того, чтобы
ее можно было считать бесконечно-протяженной. Рас-
пределение сил в такой плите зависит от соотношения
жесткостей всех элементов, из которых образована
плита. Изменение жесткости одного элемента, например
упругого основания или упругой прокладки, вызывает
перераспределение сил во всей системе. Это обстоя-
тельство значительно усложняет задачу о расчете сло-
истой плиты, хотя для выполнения такого расчета мож-
но применить прежние методы,
Для расчета в упругой стадии составим два диффе-
ренциальных уравнения равновесия для каждой плиты
в отдельности:
/ д* d4 w, д*- ©< \
D, __L । 2 ——L । -—-X. <
\ дх‘1 дх3ду2 dyi J
+ D3 (Wi — Ш2) = Qi (х, у);
/ д* 9 О* ©2 б4 ©И __
2 \ dxi г“ дх° ду" ' ду^ }
— D3 (Wi — ш2) = —ц» (*, у),
где ©1 и w3— прогибы верхней и нижней плит соответ-
ственно;
Р1(х, У)—внешняя нагрузка на верхнюю плиту;
(х, у)—реакция упругого основания;
и Ds—жесткости верхней и нижней плиты;
D3— жесткость упругой прокладки, которая
подчиняется гипотезе пропорционально-
сти.
Если связи, размещенные между плитами, будут аб-
солютно жесткими, то ©i = ©2 и, складывая оба урав-
нения, получим:
/ б4 ш д- ш di w \
\ бх1	дх* ду* г бу4 }
= <h(%, y)-~<h (х, у).
Это значит, что систему в целом можно рассматри-
вать как одну плиту, имеющую суммарную жесткость.
В этом случае усилия распределяются между плитами
пропорционально их жесткостям. Изгибающие моменты
будут равны:
М! = — М; = — М; D = Di -{- Ж,
D	D
где и АД— изгибающие моменты в верхней и ниж-
ней плитах соответственно;
М—общий момент, воспринимаемый обеими
плитами, т. е. момент в монолитной
плите с жесткостью, равной суммарной
жесткости двух плит; в упругой стадии
величину М определим, как для одно-
родной плиты, имеющей суммарную
жесткость.
При увеличении нагрузки за предел упругости будет
переходить первой та плита, в которой напряжения бу-
дут больше: сначала верхняя плита, если ее толщина
будет больше. При дальнейшем увеличении нагрузки,
после того как в верхней плите образуется пластиче-
ский шарнир н момент стабилизируется и будет равен
Мп, в нижней плите изгибающий момент будет быстро
нарастать, так как
= Afo •
После того как в обеих птитах образуются пласти-
ческие шарниры, суммарный момент, воспринимаемый
обеими плитами, будет равен:
Л1В — /И01 ф- гИч2.
Таким образом, схема разрушения стоистой шчты
может быть принята такой же, как и в однородной
плите с образованием пластического конуса, по* обра-
зующим которого располагаются линейные пластиче-
ские шарниры, а в основании конуса в сечении с наи-
большим отрицательным моментом возникает крщовои
пластический шарнир Величину предельной силы в этом
случае получим по формуле
1 1
Рп 4лЖпл -j-	я/'“ (?макс	Щ) 4“ —g ‘lr“ Уг
Входящие в последнюю формулу величины вычисля-
ются, как было указало выше. Для Рп:
Рп= 1,395-4лЛДл =. 1,395-4Л (/Ио1 ф- Маз)
Более сложный случай получим, если будем учиты-
вать упругость прокладки, расположенной между пли-
тами, В этом случае процесс деформирования слоистой
плиты в упругой стадии можно рассматривать состоя-
щим из двух этапов: сначала возникают прогибы и уси-
лия в плите, имеющей несжимаемую прокладку, т, е.
прогибы обеих плит будут одинаковыми и внешний мо-
мент распределится между плитами пропорционально
их жесткостям; затем определяется величина деформа-
ции упругой прокладки — эта деформация зависит не
только от соотношения жесткостей всех трех слоев, но
также и от модуля деформации основания.
Прогиб слоистой плиты при жестких связях следует
рассматривать как среднюю величину между прогиба-
ми верхней и нижней плит прн упругих связях, поэто-
му для получения истинного прогиба верхней плиты
к среднему прогибу необходимо прибавить половину
разности прогибов; если же от среднего прогиба отнять
эту величину, то получим прогиб нижней плиты.
Изгибающие моменты, возникающие в каждой от-
дельной плите, из которых составлено слоистое покры-
тие, можно рассматривать, как результат сложения
двух моментов:
I),	IX
ЛД = ж АМ и = М _ дМ.
Из этих формул видно, что при упругих связях мо-
мент в верхней плите будет больше, чем в нижней,
если даже их жесткости будут одинаковыми. В прак-
тических случаях жесткость верхней плиты обычно бы-
вает больше, чем нижней, поэтому в верхней плите бу-
дет раньше возникать первый пластический шарнир,
чем в нижней. Можно было бы найти формулу для ве-
личины АА4 путем интегрирования соответствующего
уравнения, но в этом нет особой надобности, так как
для дальнейшего этот момент не потребуется. После
того как образовался пластический шарнир под грузом
в верхней плите за счет податливости прокладки, нач-
нется образование пластического конуса с кольцевым
пластическим шарниром, расположенным на расстоя-
нии П от груза. Величина и зависит от соотношения
жесткостей верхней плиты и упругой прокладки и со-
ответствует сечению, в котором отрицательный момент
будет наибольшим по абсолютной величине. Для вы-
числения г, можно использовать формулу
19 3 БАЛКИ И ПЛИТЫ НА УПРУГОМ ПОЛУПРОСТРАНСТВЕ
337
то тогда величина внешней силы, при которой в верх-
ней плите образуется пластический конус,
1,34.4дЛ101.
При этой величине внешней силы пластическим кощс
образуется только в яерхнси плите, нижняя шита бу-
дет находиться в упругой стадии и поэтому несущая
способность слоистой пипы еще не будет использова-
на, Верхняя плита будет передавать избыток нагрузки
на нижнюю плиту, а в ре гультаге этого эпюра нагрузки
па нижнюю плиту будет состоять из двух частей: or
силы Рп эпюра будет приближаться к равномерно рас-
пределенной на площадке радиуса гь а от приращения
нагрузки эпюра будет представляться сосредоточенной
силой. Благодаря этому кольцевой шарнир в нижней
плите образуется иа расстоянии г2 от точки приложе-
ния нагрузки, причем г3>г\. Вторая часть нагрузки
Рп, воспринимаемая нижней плитой, подсчитывается
аналогично, но величина г2 определится из формулы
_ л/
г2 = 1,о-2,о В/ ————— ,
4
Поэтому Рп равно:
Р^= 2,77-4лЛ4вз.
Таким образом, полная несущая способность трех-
стопной плиты определяется величиной нагрузки
Рп = К + Р'п = 4л (1,34Л401 + 2,77Жад) .
При наличии упругой прокладки несущая способность
слоистой плиты будет выше, чем при жестком соеди-
нении плит. Например, если слоистая плита состоит из
двух одинаковых плит, то
Мо1 = Л102 = О,5Мо.
Прн жесткой прокладке
Рт 1,395-4л (Л1о1 4- Л1М) 1,395-4лЛ40;
при упругой прокладке
Рп1 = 4л (1,34МО1 4 2,77Л1ог) = 4лЛ1й-2,055;
„ ,	2,055
Рn\JPпа—1 ", „о_ — 1,48.
1,39о
При наличии упругой прокладки несущая способность
плиты увеличилась в 1,48 раза. Оценивая благоприят-
ное влияние упругой прокладки, размещенной между
плитами, следует иметь в виду, что толщина ее долж-
на быть достаточно большой для того, чтобы произош-
ла полная приспосабливаемость конструкции; в против-
ном случае величину внешней силы следует уменьшить.
Полученные формулы позволяют определить ту умень-
шенную толщину слоистой плиты с упругой проклад-
кой, при которой эта плита будет способна выдержать
ту же самую внешнюю силу, как и плита с жесткой
прокладкой; для этого надо принять Pno — Pni и из
полученного уравнения найти искомую величину. На-
пример, при 7141 = ^02=0,5 Л40 была определена внеш-
няя предельная сила Рп0= 1,395-4 л.Мп. Теперь опреде-
лим, насколько можно уменьшить момент в нижней
плите для того, чтобы воспринять ту же силу, но при
наличии упругой прокладки и сохранить толщину верх-
ней плиты. Имеем уравнение
/	-<п	\
1,395.4лЛ10 = 4я 11,34 -у-4 2,77Л1ОП
или 7ИЙЗ = 0,262Л4о.
22—26 "
Эго значит, что путем включения упругой прокладки
т, / 0,5
можно снизить толщину иижнеи плиты в I/ — —— =
У 0462
—-1,38 раза или, если сохранить толщину нижней пли-
ты, то можно соответственно снизить требования
к прочности материала нпжпеп пли гы.
Оптимальная тол щ и на плит ы
Для определения оптиматыюю соотношения в тол-
щинах слоистой пл’пы с ynpyioii прокладкой служит
i рафик, показанный на рис. 19,69. В общем случае ве-
личина предельной силы будет определяться как
Рп - ИЛ401 -г ВЛ4„.
Для данной величины 73,,, изменяя .4 и В, которые
зявисят от соотношения жесткостей элементов, полу-
чим семейство прямых, которые, образуют многоуголь-
ник на координатной плоскости Л101—Мог, как это по-
казано жирной линией иа рис. 19.69. Полная толщина
плиты равна сумме толщин плит, а каждая из этих
толщин пропорциональна корню квадратному из момен-
та. Поэтому
Параметры С и D зависят от прочности материала,
из которого сделана плита, т. е. это будут постоянные
величины, поэтому для данного значения h получим
кривую, которая связывает .Л1о, и М,2. При изменении
величины h — h^JigChs получим семейство кривых,
которые показаны на рис. 19.69 пунктиром. Наимень-
шее значение толщины плиты определяется кривой А,
которая касается многоугольника. В данном случае
это будет кривая 4. Хотя кривые 4 и h2 соответст-
вуют меньшему значению толщин панты, но они рас-
положены левее многоугольника, ограничивающего ве-
личину РГ1, поэтому величина Р„ для плиты толщиной
hi и 4 будет меньше требуемой по условиям задачи.
Толщины hi и hg, соответствуют значению предельной
несущей способности, которое больше требуемого. Тол-
щина h;„ полученная из графика, представляет собой
суммарную толщину слоистой плиты и отвечает вполне
определенным значениям предельных изгибающих мо-
ментов, которые должны быть восприняты верхней и
нижней плитами; из. значение возьмем из графика
рис. 19.69 для точки, в которой линия 4 касается много-
угольника. По этим моментам можно подобрать толщину
верхней и нижней плит. Толщины плит будут разные,
338
РАЗДЕЛ 19, РАСЧЕТ СООРУЖЕНИИ, ВЗАИМОДЕЙСТВУЮЩИХ С ГРУНТОМ
так как в данном случае Моз>Мл-
Изложенный способ, основанный на общих принци-
пах проектирования сложных систем наименьшего ве-
са, позволяет определить оптимальную толщину слоис-
той плиты, состоящей из двух плит, соединенных упру-
гой прокладкой, которая передает нормальные напря-
жения и позволяет свободно скользить верхней плите
по нижней при деформировании плиты. Влияние каса-
тельных напряжении, возникающих в упругой проклад-
ке, можно также учесть, но при этом задача значи-
тельно усложняется и объем вычислении возрастает»
Касательные напряжения, возникающие в упругой про-
кладке, оказывают второстепенное влияние на распре-
деление сил и определение несущей способности, поэто-
му они существенных изменений в полученные резуль-
таты нс вносят.
ЛИТЕРАТУРА
Г, ЯернштеЙ и М. С. Расчет конструкций с односторон-
ними связями, Госстройиздат, 1Щ7.
2.	Ьурдзгла Н. Л. Статический расчет гидротехничес-
ких тоннелей. Госстройиздат, 19Ы.
З.	’Бялер И. Я. К вопросу о расчете несущих конструк-
ций многопролетных станций метрополитена. Изд, АН СССР,
ОГИ, М> 7, 1934.
4.	Волков В, П. Гоннсли Иа автомобильных дорогах.
Автотранснзда i. 1957.
5,	Г а б б a l о в Р. Ф., К л е й н Г. К„ О расчете подзем-
ных напорных груб с учеюм геометрической нелинейности.
«.Строительная механика и расчсг сооружений», 1966, А'11 э,
6.	Гвоздев А. А, Расчет несущей способности конструк-
ций по методу предельного равновесия. Госстройиздат, 1949,
7,	Г о л у ш к е з и ч С. С, Плоская задача теории предель-
ного равновесия сыпучей среды. Госзехиздат, 1948.
8,	Гор б у fi о в По с а д о в М, И. Расчет конструкций на
упругом осповашш, Госстройиздат, 1953.
9,	Давыдов С, С. Расчет к проектирование подземных
конструкций, Госстройиздаг, I95O-.
П\ Дан дуров М. И, Тоннели. Трансжелдориздат, 1952.
II.	Егоров К.. Е. К вопросу деформации основания ко-
нечной толщины, Сборник трудов Ке 34 НИИ оснований и под-
земных сооружений, Госстройиздат, 1958.
12.	Емельянов Л, М. О расчете подземных трубопрово-
дов по теории упругости. «Строительная механика и расчет со-
оружений», 1961, Аз ц
'13	. Жсмочкин Б. Н. Расчет круглых плит на упругом
основании. Изд, ВИА, 1939
14,	Демочкин Б. И., Синицын А. П. Практические
методы расчета фундаментных балок и плит на упругом осво
вании без гипотезы Винклера. Госстройиздат, 1947, 1962.
15.	Камер штейн А, Г„ Рождественский В. В,
Р у чим с к и й М. В. Расчет трубопроводов на прочность.
Гостоптехнздат, 1963.
16.	Клейн Г. К. Расчет подземных трубопроводов.
Стройиздат, 1969.
17,	Клейн Г. К. Проблемы строительной механики под-
земных трубопроводов. «Строительная механика и расчет соору-
жений» , 1967, № 4.
18.	Клей н Г. К. Строительная механика сыпучих тел.
Госстройиздат, 1956.
19.	Клейн Г. К. Расчет балок иа сплошном основании.
Сб. трудов МИИГС, вып. 3, 1954.
29. Коренев Б. Г. Штамп, лежащий на упругом полу-
пространстве. Доклады АП СССР, т, 112, Л? 5, 1957.
21.	К р а ш е н н н о ков а Г, В, Расчет балок на упру-
гом основании конечной глубины. «Энергия», 1964.
22,	Кузнецов В. Й, Упругое основание. Госстройиздат,
1952.
23.	Л и м а и о в Ю, А. Осадки земной поверхности при со-
оружении тоннелей в кембрийских глинах. ЛИИЖТ. 1957.
24.	Л ьв и и Я- Б. Расчет балок на упругом полупростран-
стве и полуплоскости Методом сил, В сб.: «Исследования по
теории сооружений», вып. 5, Госстройиздат, 1951.
25,	Орлов В. В., Гудзь А. Г. Сборник примеров и
задач по механике iирных пород п крепи, Госгортехиэдат, 1961.
26.	Орлов С, А. Методы статического расчета сборных
железобетонных обделок тоннелей. НИИ оснований и подземных
сооружений. Госстройиздат, 1961.
27.	П а щ с в с к и й Д. П. Приближенное определение соб-
пчрйных частот колебаний балки, лежащей иа упругом полу-
пространстве. Вестник ВИА. № 106, 1957.
28.	Прево Р. Расчет на прочность трубопроводов, зало-
женных в грунт. Сгройиндат. 1964.
29	Прокофьев П, IE Давление сыпучих тел и рас-
чет подпорных стенок. Госстройиздат, 1917; Физматгиз, 1?6Л.
31)	. Р у п п с н »• й т К, В, Некоторые вопросы механики гор-
ных пород. Углетнхиздат, 1954.
31,	С и н и ц ы п А, П. О распределении напряжений у осно-
вания плотин треугольного профиля. Вестник ВИА, № 20, 1937.
32.	С и н и ц ы и А, ГЕ Расчет балок и плит на упругом ос-
новании за пределом упругости. Стройиздат, 1964а
33,	С и п и п ы н А. П, О распределении напряжений в под-
порных стенках ломаного профиля. В сб.: «Исследования по
теории сооружений». Вып. 4. Госстройиздат, 1949.
34.	Соколовский В. В. Статика сыпучей среды. Изд.
3-е. Гостехиздат, 1955.
35.	Справочник проектировщика. Основания и фундаменты.
Стройиздат, 1964.
36.	Строительные нормы и правила: гл, П-Б.1-62, «Основания
зданий и сооружений»; гл, П-Г.3-62, «Водоснабжение»; гл,
11-Г.16-62, «Тепловые сети»; гл, П-Д.7-62, «Мосты и трубы»;
ы, П-Д 8-6'2, «Тоннели железнодорожные и автодорожные:
гл. П Д.Щ-62, "Магистральные трубопроводы»; гт. П-М.4-62,
«Подземные горные выработки предприятий по добыче полезных
ископаемых». Госстройиздат, 1962.
37.	Теплиц к и й Е. И„ Давление породы на подземные
сооружения. «Вопросы расчета и методы возведения подземных
сооружений», Сб. № 41. НИИ оснований и подземных сооруже-
ний, ГогсгроГшздат, 1959.
38,	Терца г и К, Теория механики грунтов, Госстройиздат,
Ю6Е
39.	Технические условия проектирования силосов для сыпу-
чих тел (ТУ 124-56). Госстройиздат, 1956.
40.	Ф и л о н е я к о - Б о р о д и ч М. М. Некоторые прибли-
женные теории упругого основания. Ученые записки МГУ, вып
46, 1940.
41.	Черкасоа И. И, Механические свойства грунтовых
оснований при деформации вдавливания, В сб.: «Определение де-
формаций грунтов». Автогранснздат, 1955,
42.	Шахтер О. Я. Расчет бесконечной плиты, лежащей
на упругом основании конечной и бесконечной мощности. Сб.
трудов научно-исследовательского сектора Фундамент строя,
Л» 10. Госстройиздат, 1939.
43.	Э р й с т о в В, С. Расчет обделки напорных туннелей
в анизотропных породах. «Гидротехническое строительство»
1967, № 5,
РАЗДЕЛ 20
ДИНАМИКА СООРУЖЕНИИ
Динамические нагрузки, в зависимости от закона их
изменения во времени и пространстве, обычно делятся
на: 1) периодические, 2) импульсивные, 3) случайные
и 4) подвижные.
Расчет сооружения на действие динамических нагру-
зок имеет целью:
1)	проверку прочности, выносливости и. в отдель-
ных случаях, динамической устойчивости конструкций;
2)	проверку допустимости вибраций с точки зрения
их воздействия на людей;
3)	проверку допустимости вибраций для нормального
хода технологического процесса, работы измерительных
приборов и т. д,;
4)	проверку динамической жесткости конструкций,
например элементов покрытий, определяемой предельно
допускаемой амплитудой колебаний при данной частоте.
При проектировании междуэтажных перекрытий
я каркасов зданий технологические требования и ука-
зания санитарно-гигиенических норм обычно более
жестко ограничивают колебания, чем требования проч-
ности. Наоборот, в процессе расчета высоких и гибких
сооружений на действие ветра и при расчете всех кон-
струкции на сейсмические воздействия н действие взры-
вов основную роль играют требования прочности.
Динамические расчеты при равных требованиях
к точности описания работы конструкций расчетной
схемой сложнее статических, При их проведении поль-
зуются общими методами динамики сооружений, из-
ложенными в литературе. Порядок динамического рас-
чета и его содержание в значительной мере регламен-
тируются нормативно-инструктивными документами,
содержащими также ряд вспомогательных п справоч-
ных материалов.
Основные вопросы динамического расчета и соответ-
ствующие нормативные документы следующие:
определение динамических нагрузок от машин [25];
определение динамических воздействий ветра и рас-
чет гибких сооружений на действие ветра [18, 19, 23,
52, 67];
расчет несущих конструкций зданий на действие пе-
риодической нагрузки от машин, а Также па периоди-
ческие нагрузки, передаваемые через грунт [18, 19, 52];
расчет конструкций на действие импульсивных на-
грузок [26];
расчет фундаментов под машины с динамическими
нагрузками [61];
расчет сооружений на действие сейсмических нагру-
зок [22, 53, 65];
расчет покрытий промышленных зданий на действие
гармонических нагрузок [66];
вибооизоляция и другие меры борьбы с вибрациями
[20, 27];
специальные мероприятия по снижению уровня виб-
раций на заводах сборного железобетона [21];
санитарно-гигиенические требования [79];
22'
нормирование усталостных напряжений [54].
Вопросы расчета сооружений па действие гармони-
ческих ншрузок являются основными для этого разде-
ла, при составлении которого были учтены основные по-
ложения инструкции [19].
Целью динамического расчета конструкций, который
носит поверочный характер, является определение Уров-
ня вибрации и установление допустимости этих вибра-
ций с точки зрения требований, сформулированных во
введении. Если технологические или санитарно-гигие-
нические требования ие удовлетворяются, необходимы
специальные мероприятия по снижению уровня вибра-
ций; если же не выполнены требования прочности,
нужны меры либо по уменьшению динамических уси-
лий, возникающих в рассматриваемой конструкции, ли-
бо по ее усилению. Вопросы расчета конструкций зда-
ний и сооружений на сейсмические воздействия здесь
ис рассматриваются (см. [ГО, 22, 24, 31, 35, 36, 41, 42,
46, 49, 53, 63, 65, 71]).
20.1. ЭЛЕМЕНТЫ ТЕОРИИ КОЛЕБАНИИ
20.1.1. Кинематика колебательного движения
Если механическая система имеет одну степень сво-
боды и закон изменения обобщенной координаты во
времени можно представить в виде
х(Ц =х (И1 Ц-О-
гле k — произвольное целое число, то движение назы-
вается периодическим, а величина Т — периодом коле-
бании.
При гармонических колебаниях
х = a sin (ai Ц- фр),	(20.1)
где а— амплитуда колебаний; (iK+фо— фаза колеба-
ний; фо — начальная фаза; т = 2л/Т—круговая часто-
та колебаний; Т — in/2л — период колебаний; = 1/Т —
частота, число колебаний (циклов) в единицу времени
(обычно Т выражается в секундах, при этом ?. выра-
жается в герцах).
Удвоенная амплитуда называется размахом коле-
бании.
Скорость v и ускорение ш при гармонических колеба-
ниях равны:
dx
и—------ _ аю cos	ф0);
ett
dv
а/= ~dt =— a<ii”	Фо) =— X'
Колебания, представляющие сумму нескольких гар-
монических колебании, называются полигармоиичс-
скими.
340
РАЗДЕЛЯЯ. ДИНАМИКА СООРУЖЕНИИ
Если x(t) — случайная функция времени, колебания
называются случайными.
Колебания, которые представляют сумму двух гар-
монических колебаний с близкими частотами (биения),
называются колебаниями с периодически возрастающей
и убывающей амплитудой.
20.1,2. Колебания системы с одной
степенью свободы
Свободные колебания
при отсутствии сил сопротивления
Дифференциальное уравнение малых свободных ко-
лебаний системы с одной степенью свободы, например,
груза на пружине, прикрепленного так, что возможны
)	перемещения лишь в направлении
оси х О’ис- 26.1) имеет вид
х
Зу г	т Д- сх = 0,	(20.2)
'	яг-
и
.Г
Рис. 20.1
где т —• масса; с — квази-упругий коэффициент (для
системы, изображенной на рис. 20 1 жесткость пру-
жины).
Решение этого уравнения при начальных условиях
dx I
х(О>==хо и —-	==о0 имеет вид
Л к=о
с„
х-~ — sin at ст xn cos at,
(Л
или
х — a sin ((в? -А. ф0)(
где
«мы
Фа = arctg--------;
^0
Статическая осадка пружины, вызванная весом
груза,
mg
хст ’*»
с
5
поэтому >	~~—'jz - где Хрт—в гм- X — в тернах.
10с/
Очевидно, чго при вращатетьных колебаниях
где с (кГм!рад) — величина вращающего статического
момента, вызывающего единичное угловое перемеще-
ние; 7г — момент инерции массы относительно оси вра-
щения.
Зачастую система с одной степенью свободы имеет
параллельное (рис, 20.2) или последовательное (рис. 20.3)
соединение упругих элементов. Общая жесткость с
определится формулами: при параллельном соединении
с ~ ci +	T • •  ф~ СП1
Рис. 20.3
Рис. 20.2
при последовательном соединении
Свободные колебания при на лич-и и
сил соироти в леи и я
Если сила сопротивления F—Qx. пропорциональна
скорости то дифференциальное уравнение колебаний
имеет вид
d'2 х	dx
------4- 2а -------+ ®® х — 0; ® =
df1	di
Р
2я= —	(20.3)
tn
и при &>п система совершает затухающие колебания
по закону
х =- Ав e~nt sin (fflj t + ф0); ®г — уЛо3 — па;
Аг'
(ио 3 пхоГ.
,	*0 ®3
Фо = arctg-----~—
4- пхв
Если w 3> я, то ®i ях ®,
Быстрота затухания характеризуется логарифмиче-
ским декрементом колебаний б (логарифмом отношения
двух последовательных амплитуд, взятых через проме-
жуток времени, равный периоду), равным 6-=п7.
График движения см, рис. 20,4.
Если сопротивление вызывается только силами сухо-
го (кулонова) трения, которые сохраняют постоянную
величину и все время остаются направленными в сторо-
ну, противоположную движению, то сила трения
F =— /TV sign х.
Здесь f — коэффициент трения; Л' — нормальная ре-
акция; символ sign х означает знак скорости.
Для решения задачи о свободных колебаниях нужно
по отдельности рассматривать движение для участков
времени, иа протяжении которых знак ялы трения не
’ Напр«’.«сг, г”та слтоотчвтстчя вязкой среды (воздуха,
жидкости) при не очень больших скоростях.
20 1. ЭЛЕМЕНТЫ ТЕОРИИ КОЛЕБАНИЯ
341
меняется, и воспользоваться условиями сопряже-
ния [14].
При свободных колебаниях с сухим трением ампли-
туда колебаний убывает по лпиеиному закону. На час-
тоту свободных колебании сопротивление сухого трения
не ока ллваег влияния.
Если сопротивление вызвано силами внутреннего
трения, описываемыми комплексной гипотезой, то зату-
хание колебаний происходит по закону
at §
к = ae * sin (и/ -ф <р), у = — ,
л
где а, ф—постоянные, определяемые из начальных ус-
ловии.
Вынужденные колебания
при отсутствии сил сопротивления.
Резонанс
Дифференциальное уравнение колебаний при дейст-
вии внешней силы Р sin pt имеет вид
dr х
m л- сх =. Р sin pt,	(20.4)
где р — круговая частота нагрузки (р#-<в).
Решение уравнения (20.4) имеет вид
Р
х = A sin <г4 4- В cos a>t Ц- ———--— sin pt.
с ]— — 1
\ со’2 /
Первые два слагаемых — это общее решение одно-
родного дифференциального уравнения; третье слагае-
мое— частное решение неоднородного уравнения; если
имеются даже небольшие силы сопротивления, то сво-
бодные колебания быстро затухают, поэтому представ-
ляет интерес рассмотрение частного решения, которое
описывает чисто вынужденные колебания:
хст
х _ ------sin
1 — v«
р	Р
где	, хС7~ — ; называется статическим
О)	с
перемещением (оно представляет перемещение, вызван-
ное силой, равной по величине амплитуде динамической
силы); его нельзя смешивать с /Ст, вызванным собствен-
ным весом системы.
Амплитуда вынужденных колебаний
хгт
<ао.5)
Отношение аД'ст называется динамическим коэффи-
циентом.
График а!х^-, представлен на риг 20.5 кривой п1сг>~
~0. Совпадение частот вынужденных и собственных,
колебании носит название ре шнапса (хотя слово резо-
нанс имеет и другое значение); в naciматриваемом слу-
чае при резонансе V---1 и формую. (20.5) теряет смысл.
Если считать, что соиротип tncy гл вуст, то ампли-
туда колебании при резонансе растет пропорционально
времени, а закон движения ирг. пулевых иачатьных
условиях имеет вид
При v<l фазы возмущающеи силы и перемещения
спстечы совнадш-от, при vP>l они отличаются на 180°,
Еста на систему действует сада, изменяющаяся по
закону P(t'), то решение задачи принимает вид
i
ту	ю (‘
х= -— sin cat ф- х0 cos a>t~ — Р sin (n (t g) dp,
ш	с J
о'
при нулевых начальных зезовиях и Г((ф =0
г
® Г	, P(t)
— Р (g) sin со {t — с) аф ----------—
С ,1	с
о
f
— — F' (g) cos (t — g)
b
Первое слагаемое — это статическое перемещение;
второе слагаемое мало, если сила Р изменяется доста-
точно медленно.
Если возмущающая сила есть заданная периодиче-
ская функция времени, то решение задачи можно по-
лучить иначе, разложив эту функцию в ряд Фурье;
каждый из членов ряда представляет силу, изменяю-
щуюся по гармоническому закону. Действие такой си-
лы было разобрано выше, и поэтому решение сразу
можно представить в виде ряда Фурье. Однако этот
ряд может сходиться медленно, и тогда желательно
представить периодическую часп, решения в замкнутом
виде. Если P(t] — P(t+kT} , где k — целое число, Т —
период возмущающей силы, го чисто вынркдеиные ко-
342
РАЗДЕЛ 20 ДИНАМИКА СООРУЖЕНИИ
лебания представляют
риодом Т; поэтому
периодическое движение с
пе-
Динамический коэффициент а/хст в этом случае
равен;
х (0) = х (Т);
dx

и периодическое решение имеет вид
1 ( соТ \
-р з2 cos со/ —
2<о
1	!	тТ \
--- s, — а» cig------ sin и/ 4-
2w \ *	' ь 2 /
a 4s,
о
где
т
— I Р (J) cos ар А
m J
о
7
S., „= ---- |
m J
о
Вынужденные колебания при наличии
сил сопротивления, пропорциональных
скорости колебаний
Дифференциальное уравнение колебаний
d~ v	dx	Р
	-й 2п 	Д со'- г --= —sinp/ /20,6)
dP--------dt-m
Рис. 20.6
имеет решение
х -= Ae~nt sin (fflj) -L ф0)
+------5-------------------sin [pt — f),
На рис 20 5 приведены графики отношений амплиту-
ды чисто вынужденных колебании к статическому про-
гибу Хет в зависимое гн от отношения n/ы, а иа
рис. 20.6 графики величины а, характеризующей изме-
нение фазы вынужденных колебаний в зависимости от
частоты возмущающей силы.
У (1 — vs)2 + 4б¥-
Максимального значения коэффициент достигает при
т= \/ 1—2 <5ф так как обычно 2йф4,1, то и в этом
случае считают резонансом случай v—l. При резонан-
се, определенном таким образом, динамический коэф-
фициент не является максимальным, однако для ма-
лых п он практически не отличается от максимального.
Если на систему действует возмущающая сила Р =
—-P(t), то при <х>>п
х (t) = Ae~ni sin (<£)}/ Д <Ро)+
t
+	( Р (1) е—sin ffll (t - g) 41.
mfflj J
i)
В отличие от случая, когда сопротивление отсутству-
ет, приведенные решения справедливы при любых от-
ношениях р/w. Амплитуда колебаний при р/& — \, на-
зываемая резонансной амплитудой, определяется по
формуле
л 1
яр?з = ~Г Аст —	;
б	(йрез
таким образом, коэффициент резонансного увеличения
iz/xCT зависит от резонансной частоты шреа. При зату-
хании, вызванном внутренним трением в строительных
конструкциях, полученная выше формула для резонанс-
ной амплитуды не подтверждается опытом.
В практике расчета строительных конструкций и нор-
мативных документах принята другая феноменологиче-
ская теория, называемая часто теорией внутреннего
трения, или комплексной теорией, или теорией Е. С. Со-
рокина.
Вынужденные колебания при затухании
по теории Е. С. Сорокина
При расчете строительных конструкций используется
теория затухания, в основу которой положено пред-
ставление о «поглощении энергии-».
Рассмотрим движение системы с одной степенью сво-
боды по гармоническому закону х = х0 sin pt. На диа-
граммах рис. 20 7. 20.8 показана зависимость между
силой, действующей на систему, и перемещением, Если
сопротивление отсутствует, то при нагрузке и разгруз-
ке па рис. 20.7 ветви диаграммы совпадают; при нали-
чии сопротивления ветви нагрузки и разгрузки ие сов-
падают и график (рис. 20 8) представляет замкнутую
кривую (петлю гистерезиса).
Площадь петли гистерезиса равна работе Дш, совер-
шаемой силами неупругого сопротивления за цикл; пло-
щадь заштрихованного треугольника есть наибольшее
за цикл значение энергии упругих деформаций, равное
работе упругих сил за четверть цикла w0.
:\w
Отношение ф = называется коэффициентом по-
глощения.
При гармонических колебаниях
хп	Rn
ф -=- 2 л — - = 2 л — ,
*'о	s„
где хп — амплитуда пеупругой деформации, равная по-
ловине ширины петли гистерезиса; х0 — амплитуда
20 1. ЭЛЕМЕНТЫ ТЕОРИИ КОЛЕБАНИИ
343
упругой деформации; — амплитуда силы иеупругого
сопротивления; s0—амплитуда упругой силы.
Энергия системы с одной степенью свободы, совер-
шающей затухающие колебания, равна:
где x(t} —ордината огибающей эпюры затухающих ко-
лебаний; с — жесткость. По определению коэффициен-
та поглощения
I
Используя приведенное выше выражение дтя w,
можно записать
t+T
dx	х Ш
ф =—	2 — =2 In------!----= 26.	(20.7)
J х x(t-\-T)
--t
При динамических расчетах можно считать, что ко-
эффициент поглощения:
П не зависит от статических напряжений
2)	практически остается постоянным и равным ф
при амплитудах динамических напряжений ад>о0,
I ^ст I ,	,
где о0 = ———; | ffCT | —соответствующее допускаемое
статическое напряжение; при од<о'о коэффициент по-
(Тд
глощеиия можно принимать равным —-ф;
3)	не зависит от коэффициента асимметрии цикла,
равного
ост
41 в диапазоне частот, с которыми приходится встре-
чаться при расчете строительных конструкций, не зави-
сит от частоты колебаний.
При вынужденных гармонических колебаниях системы
с одной степенью свободы, коэффициент поглощения
которой равен ф, амплитуда колебаний
20.1.3. Колебания системы с несколькими
степенями свободы
Свободные колебания при отсутствии
сил сопротивления
Рассматривается случай системы с тремя степенями
свободы (рис. 20,9). Используя принцип Даламбера,
Рис. 20 9
приходим к дифференциальным	уравнениям	движения
трех точек: .	d‘2x-i _	d~ х. X ~— Оп/Ят 			 — ОП/7Ъ 		 1 at*	к - di*	&13rh3	, dt*	
a’Cq	ddx2 4 ~ Ь-'т'г ’ dt*	dt-	- о»3Щз ~ ; at-	(20.8)
.	d-x2 *3 “	^/7?!	О32/722 at*	at-	^xi ^33т3	,,, • at-	
Здесь б,, обозначает перемещение точки i при статиче-
ском действии единичной силы в точке j.
Решение этой системы имеет вид
Xi = ai sin (ffl( -ф- <jy) ; х.2 = а2 sin (ctrf -f- гр„)
х3 = as sin (&t 4- <f0).
Амплитуды a2, аг подчинены однородной системе
линейных уравнений:
~ щ -4- п.брэ, Д	0;
\	ш‘- j
+ (m2522 — ~М а2 + msS23a3 = 0;
\	to-/
лдбзтПт + Щ2632а2 -j- (,'К3б3з —	.'j а3 =-= 0.
Существование отличных от нуля амплитуд возможна
только в том случае, когда определи гель, составленный
из коэффициентов при амплитудах, равен пулю:
Ф
где у ———коэффициент неупругого сопротивления
Раскрывая определитель и решая полученное уравне-
ние, находим три значения частоты свободных колебаний.
Каждому значению г<> соответствует одна определенная
однородная система уравнений, из решения которой на-
ходятся значения а;, аг, а3 с точностью до постоянного
344
РАЗДЕЛ 20. ДИНАМИКА СООРУЖЕНИИ
множителя, т. е. каждому значению со соответствует
одно определенное соотношение между щ, а2, а2, опре-
деляемое, например, числами aja^. При этом пред-
полагается, что уравнение не имеет кратных корней.
Если координаты xI; х2, х3 выбраны так, что 6!2~
= б21 = б23==632 = б13 = 631 = 0, то система дифференци-
альных уравнений (20,8) распадается на три независи-
мых отдельных уравнения. В этом случае координаты
%1, х2, х3 называются главными координатами.
Если при i—0
Xj == х3 = х (О'); щ ~= v„ = 0,
то колебания будут симметричными с амплитудами «! =
= а2 = х(0).
При начальных условиях х
Х1 =— х2 = Xj (0); vt = оа = 0
Рис. 20,10
возникают обратно симметричные колебания с амплиту-
дами о.[ ==п2 = Х1(0).
В частном случае, когда отношение (щ/(£>2 мало отли-
чается от единицы, возникают биения; например, если
при 1 = 0
x1 = l, х2 = 0, о1 = 0, у3 = 0,
1 1
*1 = — cos ffljl 4 — cos <ва(;
Рассмотрим пример: к невесомой балке (рис 20 10)
в третях прочета прикреплены равные массы яч = т2=от,
тогда й„ — 622.
Дифференциальные уравнения:
1 1
X3 = COS ffljl---------------------— cos (ОгП
=— бицг
iPx-i
di*
. d-x2
— о^т-------
“ di3
d3x,	,Px.
x 612m	— d22m —— .
aP	dP
и колебания носят характер биений, При вынужденных
колебаниях биения обычно возникают в случае, когда
правая часть дифференциального уравнения представ-
ляет сумму двух гармоник с близкими частотами.
Полагая jci = Oi sin (e(-hq>o); x2=a2 sin (<в(4фо), по-
лучим:
тйп ал+тЬ12а2=&;
4 ^пбп —	] а2 =0.
Приравнивая нулю определитель, составленный из ко-
эффициентов при неизвестных, получим (при условии,
что 5ц=б22 и учитывая, что бы^б,;) уравнение частот
--ш"6|2 = 0
ИЛИ
_ А /7^хЛfт6Х1 -А	0s
1	to2	Д	(йа	J
откуда
ZZjZZZ. ю _ t/ZZZTZZ
m (бп 4 6J2) I m (6U — 61S)
Свободные колебания при наличии
сил сопротивления
Рассмотрим систему с тремя степенями свободы и
учтем силы сопротивления, пропорциональные скорости;
в этом случае при движении массы т( возникают силы
сопротивления, равные c,xt, и дифференциальные урав-
нения движения при с2=0, с3 = 0 примут вид:
Xj. —	^12/ц2х2	— 6-|3C|Xi;
х2	— б„2/паха ба3из3ха —
Xg = —-	Sgg/HgXg - бдд/ЦдХд .
(20.9)
Решение полученной системы дифференциальных урав-
нений будем искать в виде
Xj = а^1; х3 = xs =	,
где 5 — комплексное число, действительная часть кото-
рого определяет скорость затухания, а мнимая — круго-
вую частоту свободных колебаний.
Приравнивая нулю определитель системы
Так как ftnOfin. то второй корень, так же как и первый,
действителен, при этом щОв; будем нумеровать часто-
ты в порядке их возрастания. Внося в уравнения для
определения я, и а2 вместо <л величину получим
а1 = <г2, т. о обе массы движутся так, что их амплитуды
одинаковы и фазы совпадают. Этот первый тип колеба-
ний назовем симметричным; при т —с>2 имеем а.\ =—аг,
т. е при втором типе колебаний, который назовем обрат-
но симметричным, амплитуды колебаний обеих масс
одинаковы, но фазы противоположны (отличаются друг
от друга на 1?0"),
511т1
S“
®31^1

fll4^sa®sas'r
найдем три комплексных корня sb s3, s- Частоты коле-
баний равны коэффициентам пои мнимых частях указан-
ных корней, а действительные части их характеризуют
скорость затухания колебаний соответствующей частоты.
20 1 ЭЛЕМЕНТЫ ТЕОРИИ ЕОЛЕЕАНИИ
345
Приближеяные способы определения
основной частоты свободных
колебаний
Уравнение час ют в случае системы с п степенями сво-
боды имеет вид.
(	1	- Л)	J J) . • • а »	/4 J, fl
4 ц	(“4 22 A) . . a a a
4,It	3/22 а а а а а	/.)
1
где Aik =- <\k mA A = ~ 
w-
Приближенные значения А можно получись с помощью
следующих формул1.
1)'формула Дункерлея
А31 -L- А32 -}- • --А- А,1п,
которая дает грубое приближение снизу для первой
частоты;
2) формула П Ф. Иапковича

где
п	п
д __ v л(~т. я _ v ди.
я(2г) — _ Ajj , Air) — AJ; ,
1=1	/=1
А'2г,-~ элементы главной диагонали матрицы МП2’’
(/=!, 2, ..., п; г=1, 2, 4, 8);
3) формула С. А. Бернштейна
jZ ^(f)- lZ2A<2f) -A2	<
< ]Z %) +/_
Вынужденные колебания при
отсутствии сил сопротивления
Положим, что к первой массе системы с тремя степе-
нями свободы приложена сила Pt sin pt; будем искать
решение задачи о чисто вынужденных колебаниях в
виде
Xi =- Oj sin pt; хг -= sin pt; xs =- «а sin pt;
сокращая левые и правые части дифференциальных
уравнений колебаний на sin pt, получим:
«3.61301 + т,б.23а2 Д (ж>3д33 -- ~~ А3 =
i Р- 2
р
-а13-~А.	(20,10)
п~
Эти уравнения имеют только одну систему решений ср,
и2, а2. Исключение представляет случай р — <иг, тде ы,—
одна из трех частот свободных колебаний; в этом послед-
нем случае имеем явление резонанса. Если внешняя сила
приложена так, что она не совершает работы при какой-
либо форме колебании, то амплитуды, соответствующие
этой форме, при резонансе со временем не возрастаю!.
20.1.4. Колебания систем с непрерывно
распределенной массой
Продольные свободные колебания
стержней
Уравнение движения элемента стержня (рис. 20.11)
при продольных колебаниях имеет вид
/	ON	\	д2и
— N А- ((у л--фх = рр —— Jx,
\	дх	)	дг-
Рис 20 11
Здесь и — продольное перемещение; р — плотность; F —
ди
площадь поперечного сечения; Л’ — £/• ——-- цродоль-
дх
ная сила; Е — модуль упругости.
Если площадь поперечного сечения постоянна, то
д~и
<Fu
01“ ’
а-
(20.11)
Полагая и (х, t) = X (х) 7 ((')
ные, получим два уравнения
и разделяя перемек-
Т ф- <ш2Т = 0; X"
которые имеют следующие решения:
«Ап — ,, j С1 4" «‘АаТ» + «Аз^з — 'Sn „
р- /	р-
«1б1а«1 + и2622 — — <за -f- №3бмаа = Si2 — ’>
\	Р- /
Т = A* sin cot -J- ft* cos wt, X = C sin '— x -f-
a
CD
-J- D cos — x.
a
' См. А А Яблонский и С. С Норейко. Курс
рии колебаний «Высшая шклла», 19Ь6, § 30-
Функция A(x) называется формой колебаний; <в — кру-
говая частота свободных колебаний Для определения
постоянных С, D и ш нужно воспользоваться граничны-
346
РАЗДЕЛ 20 ДИНАМИКА СООРУЖЕНИИ
ми а для определения А ' и В' начальными условиями1 *.
Ее ш концы стержня защемлены, то из граничных усло-
вии и(0)=0, ы.(/) =0 получаем систему уравнении D=-~
<о
= 0, С sin —- 1 =0, откуда
а
Следовательно,
пла
<вя = —-— , п= 1,2,3..
Формой колебаний является отрезок синусоиды, содер-
жащий целое число полуволн. Если начальные условия
и(0, х) — F}(x), и(0, х) —F3(x) представить в виде
и (0, х) = у А„ sin —~ х; и (0, х) = 7 , В„ sin ~ х,
а	ХяА	а
Л=1	Я=1
что можно сделать для весьма широкого класса функ-
ций, то для определения Ап, Вп, Сп получаем следующие
Уравнения поперечных колебаний стержня, работающе-
го на едвчг, крутильных колебании стержня и колебаний
струны имеют вид, аналогичным (20 11).
Свободные колебания балок
Дифференциальное уравнение nonepe-шых колебании
балки постоянною сечения имеет вид
дау	д2у
EI Д m----------= 0.	(20.12)
дх*	дР
Полагая у = А(х) Т (!), получим для функций X и Т после
разделения переменных обыкновенные дифференциаль-
ные уравнения
Т + Ш8Т=0; XIV — -АА. А- = 0.
EI
Решение первого из этих уравнении приведено на
стр 3-15, решение Biopolo уравнения'
X = Сф sin kx -J- С2 cos kx ф- C3 sh kx ф- C4 ch kx,
4
k = l
уравнения:
Ап sin -у х = У В’ С„ sin х*
Z2—1	П=1
где
это решение удобнее записать в виде
X = Ш Ш + D,B [g] ф- D3C (g) ф- D.D (Е); I = kx,
Отсюда
Вп = ^п' А А. = Ai
где
- „ 1 1
.4 (g) = —- (ch g -ф- cos £,), В (I) = ~~ (sh g ф- sm g);
С (I) = (ch g — cos g); D (g) = ~ (sh g — sin g)
Таким образом,
/ Вп	\	<вп
и(х ,t) = У -—- sin / ф- Л.j cos an t sin — x.
\ a>rJ	j	a
n=l
Рассмотрим другой случай граничных условии, считая,
что один конец стержня защемлен, а агорой свободен,
и, таким образом, п(0)=0, и'(/)=0.
Из граничных условий имеем
ю /	to	со \
D = 0, — С cos — I ф~ D sin — I = 0.
а \	а	а ]
Эти функции обладают свойством единичной матрицы1:
ф	А		с	D
Ф(0)	1	0	0	0
Ф (0)	0	I	0	0
Ф (0)	0	о	1	0
Ф (й)	0	0	0	i
Для определения со получаем трансцендентное урав-
и связаны друг с другом
ними зависимостями:
следующими днфференциаль-
нение
<о
cos — I = 0,
а
Д (g) =
dB Й)
d g
В <a =
dC (I)
Eg
стл/да. со =
-у-), л-1, 2, 3, ...
С (g) =
dD (E)
di
5(1)
dA (E)
Eg
3 Очезидйо, что по слщестй’ вычисляется не пять а четьюе
неизвестных, так чан, на Hapv.i ая общности, можно, например
,	„ /	о	, Ь	Ш	У
положить А — С мп — х Ц--------cos — х , а затем считать
\	и С	а	)
А*С = А„ В‘-С = 13,, Л = sin — х Ц- Di cos — х,
и	а
Воспользовавшись граничными условиями иа концах
балки, получим частотное уравнение, из коюрого можно
напти частоты свободных колебании шп (п = 1, 2, . . .)
Заметим, что А'п(х) представляет соответствующую
форму свободных колебании
Покажем на примерах, как составляется частотное
уравнение.
1'Де Dt=~.
С
1 Фтнхцич Ид). j3(H, С(д) /?(д) легко ио.щчшж с помо-
щью таблиц раздела I (табл 133).
20,1. ЭЛЕМЕНТЫ ТЕОРИИ КОЛЕБАНИЙ
347
Пусть балка длиной I шарнирно оперта по концам;
тогда
у (0) = 0; у'1 (0) = 0; у (L) = 0; у” (^) = О,
где5!=Н
Первые два граничные условия дают D,=-0; ЕФ = 0;
из двух других получаем
ОД (1J + ДД (St) = 0; Д2Д (I,) + ДА (SJ = 0.
Так как одновременно Д2 и Д< не могут бьпь равны ну-
лю, то должен равняться нулю определиjель полученной
однородной системы, т. е.
5 (Sr) =0
5(Ц) В (5!)
После очевидных упрощений имеем sh|;sincji=O и,
следовательно, kl—пл., где и=1, 2, 3, ... .
Частота свободных колебаний
Соответствующую форму колебаний А'я получим исходя
из того, что при заданном любое из двух граничных
условий на правом крае дает возможность найти отноше-
ние DJD^, после чего форму колебаний можно считать
известной. Результаты вычислений сведены в многочис-
ленные таблицы, с помощью которых можно иайги ча-
стоты собственных колебаний [26]. Определение движе-
ния балки по начальным условиям у(0, х), г/(0, г), задан-
ным начальными смещениями и скоростями, производит-
ся как в предыдущем пункте, и приводит к тем же фор-
мулам для В'п и Дг; отличие заключается в том, что
Ап и Вп представляют в этом случае коэффициенты
Фурье разложения начальных условий в ряд по функ-
циям Хп (см. раздел I). Таким образом;
I _	1
( У (0, х) X„(x)dx	(у (0, х) Хп Д) dx
X;t (x) dx
и
Если вдоль оси балки действует постоянная сжимающая
продольная сила Р, то дифференциальное уравнение
колебаний принимает вид
д^у	, Р <Ру т	* д"у _ Q
дх4	*	Е/	' ох2	1 El	’ дР ~~
В этом случае функция Х{х) удовлетворяет уравнению
Xiv+asAT_fe4x=0. к3 Р
EI
решение которого имеет вид
X = Q sin stx -ф Cs cos SjX -ф C3 sh s3x -ф C4 ch s3x.
Здесь
Если оба конца балки шарнирно оперты, то
лфг2
св,, —---
Р
РР
nEPEl
При растяжении знак Р меняется на обратный.
Дифференциальное уравнение поперечных колебаний
балки переменного сечения имеет вид
д" [
dxa I
Е1 (х)	® W П~ = 0-	(20.13)
dxi J	оР
С помощью подстановки y = X(x)T{t) получим для Х(х)
уравнение
д’-	д~х \
-ДТ (£/ (х)	- m (ж)	= 0.
dx»	dx* j
Это уравнение с переменными коэффициентами для
некоторых случаев и, в частности, когда брус имеет фор-
му клипа и Конуса, допускает точное решение в бессе-
левых функциях |33ф Обычно задачу о колебаниях бал-
ки переменного сечения решают каким-либо из прибли-
женных способов.
Изгибные колебания пластинки
постоянной толщины
Дифференциальное уравнение свободных колебаний
пластинки постоянной толщины в прямоугольных коор-
динатах имеет вид
<Д Г W d^W ph ds IF
dx1 dxsdya ду‘> ОдР	’
где h — толщина; D — цилиндрическая жесткость пла-
стинки. Используя замену W = w(x, y)T(t) по-прежнему
получим Т (t) — A sin at -ф В cos <вф причем функция
w(x,y) удовлетворяет уравнению
d’te	Ли	phtsP
dx" т дх2ду*	ду*	D
Если пластинка шарнирно оперта по всем сторонам, то
прогиб можно разыскивать в виде
оо со
/72JU ппу
У , Атп sin--sin-----,
' а Ь
т--=Л п—1
где а V. Ь — длины сторон пластинки.
Эго решение удовлетворяет всем граничным условиям;
внося его в дифференциальное уравнение, получим для
частоты ш»,я формулу:
__ n‘h 1 /'ZZUZZZ v,
шж== 2 |/ 3(1_азЦ Х
/ Г/ т Y / п V] Ди = 1, 2, 3,.. А
a j	\ Ь / J \л = 1, 2, 3,...
Полагая т = 1, л=1, получим частоту основного тона
я2/г _ [ Е /1	1 \
и =----Д /---------------- — _ф — 1 .
2 F 3 (1 — а2) р \	1 b° }
В случае, когда две стороны пластинки (например х—0,
х=ф шарнирно оперты, а по двум другим (^=0, у-~li}
условия опирания произвольны, полагаем
ЖД	ппу
W У}== 2-1 Fa яп 
/25=1
348
РАЗДЕЛ 50. ДИНАМИКА" СООРУЖЕНИИ
Для Fn (у) получаем линейное дифференциальное урав-
нение
п2ла й,аДга /я«л4
-—Д _ з  -----. —2 ।---------
dtp F dy* \ F
р/г<а2
£« = О,
которое интегрируется так же, как и уравнение попереч-
ных колебаний балки.
Для круглой пластинки задачу удобно рассматривать
в полярных координатах; дифференциальное уравнение
свободных симметричных колебаний круглой пластинки
имеет вид
Id*	1	d \*	ph&*
---- _L -- ,--- w-------
\ dr*	г	dr j D
(20.15)
Если пластинка без отверстия и не имеет опоры в центре,
то решением уравнения будет
ш= Л40 (Ат)4-6/0 (foj,
где 7(7) —функция Бесселя нулевого порядка?
/0(7)—модифицированная функция Бесселя нуле-
вого порядка;
Если пластинка шарнирно оперта по контуру радиуса
R, то граничные условия записываются в виде
й2®	1	dw |
©(У = 0; ---+----------- =0,
dr-	г	аг р=д
откуда В—0, и для определения частот получаем транс-
цендентное уравнение:
Jo(kR) = O-
Вынужденные колебания балок
Дифференциальное уравнение вынужденных колебаний
балки постоянного сечения при действии внешней нагруз-
ки q(x) sin pt имеет вид
й4ц д*ц
£/-т~-4-я-ц-Д = 9 (х) sin рД (20.16)
Решение уравнения (22.16) ищется в виде y(x,t)~
= ш(х) sin pt-, для функции w(x) получается следующее
дифференциальное уравнение
d®w
El —— — mp*w — 9 (х),
которое отличается от уравнения изгиба балки дополни-
тельным слагаемым — mp2w в левой части. Граничные
условия, как правило, такие же, как и в статической за-
даче для балки, за исключением случаев, когда на сво-
бодном конце находится точечная масса, а на шарнирно
опертом или свободном конце имеется элемент, облада-
ющий моментом инерции масс. В этих случаях взамен
условий равенства нулю поперечной силы и момента
получим
Ди 1
ах
где т i — масса на конце; гта — момент инерции этой
массы.
Для интегрирования уравнения (20.16) воспользу-
емся методом начальных параметров. Обозначив
для случая, когда q(x) — const, имеем
ш(х) =waA © + 0О -у' +
+ж°	+ Qo ¥е/	+
+ (^	[Jd)^].
0 (х) = wokD © 7 0ОЛ © + Л10 77 S(=) +
kLi
+ Qo 777 C (i) 4- я {тррт Р
k‘E!	Ik* El i
M (x) = w0Elk*C © + 0oE/W © 4-
— Qo — q —
+ Л1ол (1)4-^6(1)4-77 4 0
(20.17)
Q (x) = waEIk3B © 4- 9aElk*C (1) 4-
4- M^D © 4- Q0I (i) 4-7-6 (I),
где 1,-kx- ш(х), 0(x), M(x) и Q(x) — амплитуды пере-
мещений, угла поворота, изгибающего момента и попе-
речной силы; Wo, 0о, 7Иа, Qo — значения этих амплитуд на
левом Конце балки; Л|, Sg, и <О§ — функции, приве-
денные выше.
Рассмотрим примеры.
1. Концы балки, имеющей длину /, защемлены; нагруз-
ка q распределена по всей длине балки; граничные ус-
ловия: ®(0) ==t®o==O; 0(0) =0о=О; w(l) =0; 0(1) =0.
С учетом условий на левом конце получим для w вы-
ражение
© = -^ С ® 4- 77“ D © + -J- [А (|) - 1];
k*Ef hAFi	1BEI
из условий на правом конце получаем систему двух ал-
гебраических уравнений
- С (/г) + ~~ D(lx) 4- (Л ft) — 1] = 0;
k*El г й«£/ v k4t! 1	1
— В (У 4- —— С (ZQ у —— D (IА = 0,
Ш	k3Ef 11 k*El ' 17
решая которую, находим Л40 и Qo,
2. Концы балки защемлены, в сечении х = а приложена
сила Р sin pt. Обозначим ka = u; если Ka, то
Aio	Qo н ,е,
ш = ш	С 7	_ D р .
‘ k2Ef	kJEl
при 5Э5Я нужно к функции Wt добавить такое слагае-
мое, которое, удовлетворяя однородному дифференциаль-
ному уравнению в точке 5 = а, не нарушит непрерывно-
сти а>, w' и М, но даст в поперечной силе Q скачок на
величину амплитуды сосредоточенной силы Р,
Из свойств функций А (5), 8(|), C(t), .0(g) следует,
что этим слагаемым может быть только функция
—а); постоянную Л* подберем так, чтобы скачок
поперечной силы имел нужную величину; нетрудно по-
казать, что
Р
А k3Ef
20 2 ЧАСТОТЫ СОБСТВЕННЫХ КОЛЕБАНИЙ
349
и окончательно:
С помощью этого приема можно рассмотреть задачу
о балке с присоединенными массами (для чего, восполь-
зовавшись принципом Даламбера, нужно учесть дейст-
вие инерционных сосредоточенных сил, равных тр2х>)
и задачу о неразрезной балке.
Указанная схема и результаты непригодны в случаях,
когда р совпадет с одной из частот свободных колеба-
ний стержня; при этом имеет место резонанс, и при ре-
шении задачи следует учесть затухание.
Решение задачи о вынужденных колебаниях балки
можно получить иначе, разложив решение в ряд по фор-
мам собственных колебаний [37].
Рассмотрим балку, шарнирно опертую по концам. При-
мем начало координат на левом конце и представим
решение в виде
. пях
w = Xj’,'iSin ~г'
п-~\
Подставляя общий член этого ряда в дифференциаль-
ное уравнение форм вынужденных колебаний
d4o;
---------- — __ „
dx*--4
и разложив нагрузку у(х) также в ряд по синусам
ппх
Ч(х) = A Snsin — s
получим
вп
A =
Если на балку действует нагрузка
ю
q0 sin — sin pt,
то =	Bn=0, и, следовательно:
Ро .
w =	sln — .
п4л4	I
—— _ bi
I*
В задачах о колебаниях балки, лежащей на упругом
винклеровом основании, сохранякмся схемы расчета и
выкладки, приведенные выше. Отличие заключается
в том, что дифференциальное уравнение имеет вид
d*w
El ~dx* ~~~	W== q'
где k<s — коэффициент постели (см. раздел 5.5,6
табл 5 5), b — ширина балки; поэтому, применяя метод
начальных параметров и метод разложения в ряд по
собственным функциям, нужно вычислять k по фор-
муле
— фф
£7
Вопрос о вынужденных колебаниях в системе с зату-
ханием, пропорциональным скорости, разобран в рабо-
те [68]; для затухания, ие зависящего oi величины
скорости, описываемого комплексной гипотезой Е, С. Со-
рокина, решение задачи дано в работе [58].
20.2.	ЧАСТОТЫ СОБСТВЕННЫХ КОЛЕБАНИИ
20.2.1.	Балки на жестких опорах
Частоты собственных поперечных колебаний балок по-
стоянного сечения на жестких опорах определяются по
формуле
(20.18)
где а, — характеристические числа (корни частотного
уравнения); для однопролетных балок а, принимаются
по табл. 20.1; для двухпролетных балок с равными про-
летами н одинаковыми в пролетах жесткостями и равно-
мерно распределенными массами а, принимаются по
табл, 20.2.
Частоты собственных колебаний многопролетных ба-
лок с равными пролетами и одинаковыми в пролетах
жесткостями и равномерно распределенными массами
образуют бесконечное число так называемых зон сгуще-
ния. В каждой зоне имеется столько частот, сколько про-
летов имеет балка.
При динамическом расчете неразрезных балок на пе-
риодические нагрузки число определяемых собственных
Таблица 20.1 [37, 47. 59]
Значения ai « формуле (20.J8) для одиопролетиых балок на жестких опорах
Условия закрепления		Корни частотного уравнения					
левый конец	правый конец	Ki	а 2			И5	а.[ (1>5)
Защемлен	Свободен	1,8751	4,6941	1,8548	10,996	14,137	2i-l ~		 л 2
Оперт	Оперт	j	3,1416	|	6,2832	|	9,4248	|	12,566	13,708	1	/я
Оперт (оперт)	Защемлен (свобо- ден)	3,8266	7,0585	10,210	13,352	16,494	~-А±я 4
Защемлен (свобо- ден)	Защемлен (свобо- ден)	4,7М;	7,8532	10,996	14,137	17,128	2/4-1 —А— п 2
350
РАЗДЕЛ 20. ДИНАМИКА СООРУЖЕНИИ
Таблица 20 2Н. 39]
Значения оу в формуле <20.18) для двухпролетных балок на жестких опорах с равными пролетами
Условия закрепления				Корни частотного уравнения			
левый коней	правый конец	а.		Йа		।	аэ	Sj- (г>5)
Оперт	Опеот	3,141b	А ,02.66	6,2832	7,0685	9,4248	’Л—при нечет- ном i; 4i-rl при четном t
Оперт	Защемлен	3,39	4,46	6,54	7.59	9,69	
Защемлен	Защемлен	3,926о	4,7300	7,0685	7,8532	10,210	414-1 ~	 п — 4 при нечетном К при четном t
П р нмеча ние, Средняя опора при всех условиях шарнирно оперта.
Таблица 20 3[50]
Значения ат/ 2л в формуле (20Л8) для миогопролетных балок с равными пролетами
Коли- чество проле- тов	Концы балки свободно оперты				Один конец балки свободно оперт, другой защемлен				Концы балки защемлены			
	1» 2 л	д 2л	гД 2н 2л	«:] 2в 2 П	а.2 *Н 2л	К 1в 2л	а~ 2н 2л	«5 -В	и| 41 2 л	‘в 2л	в2 “В !л	А 2 л
3	1,57	2,94	6,28	8,78	1,69	3,37	6,54	9,50	2.01	3,56	7,16	9,82
4	1,57	3,17	6,28	9,17	1,64	И 45	6,43	9,ьЗ	.1,83	3,56	0.82	9,82
5	1,57	3,34	6,28	9,38	1,62	3,49	6,38	9,70	1.74	3,56	6,64	9,82
6	1,57	3,37	6,28	9,50	1?60	3,51	6,35	9,73	1,69	3,56	6,54	9,82
	1,57	3,56	6,28	9,82	1,57	3,56	6,28	9,82	1,57	3,56	6,28	0,82
При l-Й зоны)	м е ч а н и	е а/н t?oui зет сгвует		частоте р	•ti (нижней границе		Кй зоны	сгущения)	“.в ~ча	ст„те р,-в	(верхней	границе
частот принимают равным удвоенному числу пролетов
балки.
Для многопролетпых балок с равными пролетами и
одинаковыми в пролетах жесткостями и равномерно
распределенными массами можно определять лишь че-
тыре собственные частоты: л(н и Aiaнизшую и выс-
шую из частот первой группы; Хан и Хав — низшую
и высшую из частот второй группы. В этом случае
в формулу (20.18) взамен аг подставляются агн или
скв, принимаемые по табл, 20 3.
В табл. 20,4 для четырех случаев многопролетпых ба-
лок с неравными пролетами приведены значения перво-
го корня он характеристического уравнения.
20 2 ЧАСТОТЫ СОБСТВЕННЫХ КОЛЕБАНИЙ
351
'I i б л и 11 а 20 W 30 j
Значения в формуле (20,16) лля мишопроде'ишк балоь
на жестких опорах с неравными пролетами
Схема бальи я первый корень частотною уравнения
20.2.2.	Балки на упругих опорах
Частоты соб< 1ВСПШ.1Х поперечных колебаний балок на
;.нррл\ опорах вычисляются но формуле (20 18); при
Э1ом а, принимается ит 1абл. 20 5 в зависимости от
условии закрепления концов балки
Обозначения, принятые в табл 20 5,
бц. — жесткость в кГ/см опоры относительно по-
перечных перемещений;
Сч --жесткость в кГ/см опоры относительно утло-
вых перемещении;
— опора, у приют отиоешельпо поперечных и
жесткая относите пято ттловых перемещений;
— шарнирно подвижная опора, упругая от-
носительно поперечных перемещении;
А А		A Л	
I	1,50592	1/6	3,11752
3/4	1,00170	1/7	3,12bf,’
1/2	2,51395	i	1/8	3,13143
1/3	2,94042	i	1/9	3,13449
1/4	3,05881	1/10	3,13641
1/5	3,09975	|	0	Я
при А < Д
1	9
—шарнирно подвижная опора, улрутая отно-
/зГ сителыю угловых перемещений.
20.2.3.	Балки с распределенными
и сосредоточенными массами
Частоты собственных поперечных колебаний балок
с равномерно распределенными массами т и сосредото-
ченными массами А1 вычисляются по формуле (20.18).
При этом а, принимается но табт 20 6.
Для однонролетттых балок, имеющих различные гра-
ничные условия, и для мнот опролетиых балок с шарнир-
ным опиранием и с равными пролетами при наличии со-
средоточенных масс ,Л14, расположенных па расстоянии
х4 ог ближайшей левой опоры, можно приводить сосре-
доточенные массы к эквивалентной равномерно распре-
деленной массе тп по формуле
s«
A VksMs, (20.19)
где А' — количество пролетов; тв— равномерно распре-
деленная масса; s0 — количество грузов на балке; п—
номер частоты колебании.
Коэффициенты ks определяются: а) для однопролет-
ньх балок и при определении частот Ди и 9.2Я многопро-
легиых балок — по табл, 20,7; б) для многопролетных
балок при определении частот ?«1в — по табл 20,8; в) для
мнот опролетиых балок при определении частот Л2и— по
табл. 20 9.
20.2.4.	Балки, нагруженные
продольными силами
Для балок, нагруженных продольными силами, ча-
стота поперечных собственных колебаний вычисляется
по формулам и графику табл. 20.10. Прн сжимающем
продольной силе знак силы Р в формулах табл. 20.10
меняется на обратный.
352
РАЗДЕЛ 20 ДИНШИДА СООРУЖЕНИИ
’’чачение "(в формуле (п0 18) для балок на упругих опорах
Т a G л л j j ’ll ДН
Схема балки и корни частотного урав! пья
Су = tfe
’-и ,2?
И/
Схааа балки и корчи частотного хрипения
Ясемптота при а~ л
Симметричные м.ге5ания
5	присх.
13SS уит1^-Д^^--тг—^нтис^мвгпри-ми1е киле/йан to
'-Ргимптота при а
Симметрии капеОин л
V" «
I
0 Ю 1 и 10 ч0 50 ео Ю во so юо
е.:~е f/f
Г Vioi'unm^f^ij rp> tp~№~~\
^вирзТи обертон
LED
r->o
C-mCwtCf 1
20 2 ЧАСТОТЫ СОБСТВЕННЫХ КО НЕБ ШРИ
353
Г/росНи ^ние табл 20 5 V!
<х 1 гИлИ > KA.pl И -UCT Т ОГО \р1ВНАЧЯЯ
Схема балки и корни частот иго уравнения
С& 1/£ 3
РАЗДЕЛ 20 ДИНАМИКА СООРУЖ1 ПИП
Значения & в формуле (20 18) для весомых балок с сосредоточенными массами
Таблица 20 ДП
Схема ба тки и корни частотного уравнения
Схема бз-ки и коони частотного уравнения


Прямей а и и е Дрл' ип случаи см в dt6oi? [П
20 2. ЧАСТОТЫ СОБСТВЕННЫХ КОЛЕБАНИИ
355
Таблица 20 7[591
Значения & л а формуле (20J9) для приведения сосредоточенных масс к разномерно распределенной
массе в однопролетных и многопрол<ыных балках при определении л1н -Ч X2JJ
Условия закрепления		1 W Q	Коэффициенты										’ для значепп :			К? =	х						
левый конец	правый конец	гЬ о 2* £4 к О 1	0	0,05	0,1	0,15	0,2	0,23	0,3	9,35	0, 1	0,45	0,5	0,55	0, 6	0,65	0,7	0,75	0,8	0,85	0,9	0,95	1
		А1и	0	0	0	0,1	0,02	0,04	0,06	о/ы	0,21	0,32	0,40	0,61	0,85	1,10	1,38	1,73	2,10	2,52	2,97	3,47	4
Защем-	Свобо-	1Н																					
лен	Ден	и,	0	0	0,03	0,14	0,36	0,70	1,11	1,61	1,37	2/)0	2,01	1,80	1, 19	0.88	0,40	0,07	0,02	0,34	1,10	2,32	4
			0	0,05	0,19	0, 11	0,69	1,00	1/И	1,59	1,81	1,95	2,00	1,95	1,81	1,59	1,31	1,00	0,69	0, 41	0,19	0,05	0
Оперт	Оперт																						
			0	0,19	0,69	1,31	1,81	2,00	1,81	1,31	о, go	и,1у	0	0,19	0,159	1,31	1,81	2,(XJ	1,81	1,31	0,69	0,19	0
		Хы,	0	0,08	0,31	0,66	1,07	1,49	1,86	2,13		2,25	2,09	0,81	1,46	1,08	0,72	0,42	0,21	0,08	0,02	0	0
Оперт	Защем-	АН																					
	лен	Х2н	0	0,24	0,84	1,51	1,94	1,91	1,44	0,75	0, 18	0,01	0,33	1,00	1,71	2,21	2,23	1,81	1,15	0,53	0,15	0,61	0
Защем-	Защем»	Ль.	0	0	0,04	0, 15	 0,37	0,74	1,20	1,69	2,12	2,42	2,52	9,42	2, 12	1,69	1,20	0,74	0,37	0,16	0,04	0	0
																							
лен	лен	в	0	0,02	0/21	0,72	: 1,46	2,09	2,27	1,86	1,07	0,31	0	0,31	1,07	1,86	2,27	2,09	1,46	0,72	0,21	0,02	0
Таблица 20 8[59]
Значения k$ в формуле (20,19) для определения К^многопролетных балок
Коли-	XT									Коэффициенты для значение						»s	/						
честно пролетов	про- лета	0	0,05	0,1	0,15	0,2		0,25	0,3	0,35	0,4	0,45	0,5	0,55	0,6	0,65	0,7	0,75	0,8	0,85	0,9	0,95	1
2	1	0	0,08	0,31	0,66	1,07		1,49	1,86	2,13	2,27	2,25	2,09	1,81	1,46	1,08	0,72	0,42	0,21	0,08	0,02	0	0
		0	0	0,02	0,08	0,21		0,42	0,72	1,08	1,46	1,81	2,09	2,25	2,27	2,13	3,86	1,49	1,07	0,66	0,31	0,08	0
3	1	0	0,02	0,06	0,13	0,20		0,28	0,34	0,37	0,37	0,35	0,30	0,23	0,16	0,10	0,05	0,02	0	0	0	п	0
	О	0	0,01	0,06	0, 17	0,36		0,61	0,90	1,20	1,44	1,62	1,68	1,62	1,44	1,20	0,90	0,61	0, 36	0, 17	0,06	0/Н	0
	3	0	о	0	0	0		0,02	0,05	0J0	0,16	0,28	0,30	0,35	0,37	0,37	0,34	0,28	0,20	0, В	0,06	0,02	п
4	1	0	0,01	0,04	0,08		9,13	0,18	0,21	0,23	0/22	0,20	0, 16	0,12	0,08	0,04	0,02	0	0	0	0	0	0
	2	0	0,01	0,05	0,13		0,25	0,40	0,58	0,75	0,87	0,94	0,93	0,86	0,73	0,56	0,39	0,24	0,12	0,05	0,01	0	0
	3	0	0	0,01	0,05		0,12	0,24	0,39	0,56	0,73	0,86	0,93	0,94	0,87	0,75	0,58	0,40	0,25	0,3,3	0,05	0,01	0
	4	0	0	0	0		(5	0	0,02	0,04	0,08	0,12	0,16	0,20	0,22	0,23	0,21	0,18	0,13	0,08	0,04	0,01	0
5	1	0	0,01	0,02	0,05	0,08		0,10	0,12	0,13	0,12	0,11	0,09	0,06	0,04	0,02	o,oi	0	0	0	0	0	0
	2	0	0,01	0,03	0,09	0, 18		0,28	0,40	0,50	0,37	0,60	0,69	0,53	0,43	0,32	0,25	0,12	0,05	0,02	0	0	[’
	3	0	0	0,02	0,08	0,18		0, 13	0,51	0,69	0,86	0,97	CU9	0,97	0,86	0,69	0,51	0,38	0,18	0,08	0,02	0	0
	4	и	0	0	0,02	0,05		0, Г2	0,21	0,32	0,43	0,53	0,59	0,60	0,57	0,50	0,40	0,28	0,18	0,09	0,03	0,01	0
	5	0	0	0	0	0		0	0,01	0,02	0,01	0,06	0,01	0,11	0,12	0,13	0,12	0,10	(К 08	0,05	0,02	0,01	0

356
РАЗДЕЛ 20 ДИНАМИКА. СООРУЖЕНИЙ
Т а блиц а 20 9(50]
Значения ks а формуле (20Л9) для определения Л2в многопролетных балок
Коли- чество пролетов	.V про- лета	Коэффициенты kc ДЛЯ значений	е =		 5	*	1																				
		О	0,05	0,1	0,15	0,2	0/25	0,3	0,35	0.4	0,45	1 0,5	0,55	0,6 | 0,б5		0,7	0//5	0,8 । 0,85		0,9	0,95 | /0	
о	1	0	0,24	0,84	0,51	1,91	1,91 :	1,44	2,75	0/8	0,01	0,33	1,00	1,74	2,21 0,75 	2,23 /44	1,81	1,51	0,55	0,15	0.01	0
	2	О	0,01	0,15	0,53	1,15	1,81	2,23 ;	2,21	/74	1,00	0,33	0,01	0,18			1,91	/94	0,51	0,84	0,24	0
3	1	9	0,06	0,19	0,34	0,41	0,38	0,26	0,11	0,01	0,02	0,13	0,30	0,43	0,47	0,40	0,26	о,к>	о.оз	0	0	0
	2	0	0,04	0,21	0,56	0,98	1.27	1,30	5,02	0,57	0/16	0	0,16	0,57	1,02	1,30 0,26	1.27	0,98	0,56	0,21	0,04	0
	3	0	0	0	0,03	0,12	0,_6	4,40	0,47	0,®	0,30	0,13	0,02	0,01	0/1		0,38	0,41	0,34	0/9	0,06	0
4	1	0	0,03	0,10	0,17	0,21	0,19	0, Г2	и, 05	0	0,02	0,08	0,17	0/23	0,23	0,18	0,10	0,04	0	0	0	0
	о	0	0,03	0,17	0,43	0,71	6,88	0,84	0,61	0,29	0,05	0,01	0,20	0,5 J	0,79	0,90	0,79	0,54	0,26	0,07	0,0'1	О
	3	0	0,01	0,07	0,26	0,51	0,79	0,90	0,79	О.а!	0,20	0,01	0,05	0,29	0,61	0,84	0,88	0.73	0,4,3	0,17	0,1)3	0
	4	4)	0	0	0,01	0,01	(МО	0/18	0.23	0,23	0,17	0,08	0,02	0	0,05	0.12	0,19	0,21	0,17	0/0	0,03	0
6	1	0	0,02	0,0?	0,12	0,11	0,13	0,98	0,03	0	0,02	0,06	СМ2	0,15	0/5	0,11	0,06	0,02	0	0	0	0
	2	о	0,03	0,14	0,34	0,55	0,67	0,62	0,43	0,19	0,02	0,02	0,19	0J3	0,63	0,68	0,56	о.лб	0/6	0,4	0	
	3	0	0,02	0,16	0,49	0,9Ji	М7	1,35	и, 09	0,6?	0,18	0	0,18	0,62	/09	1,35	1,27	0,93	0,49	6,16	0,02	0
	4	9	0	0,04	0,16	0/6	0,3b		0,03	0,43	0,19	0,02	0,02	0/9	0,43	0,62	0,97	0,55	()»34	0,14	0,08	0
	5	0	0	0	0	0,02	0,0и	0.11	0/5	0.1S	0/2	0,06	0,02	0	0,03	0,06	0/3	0,14	0,12	0,07	0,02	С)
Таблица 20! 0Ц]
Частоты поперечных собственных колебаний балок, нагруженных
продольными силами
Продолжение табл. 20д0[Г]
___________ ______ ______ .
Схема балки и формула или график для определения частот
I Схема балки и формула или график для определения частот
— ------------______—_____
где сс берется ид графика
И р и м е ч а я и е Другие случаи см в работе (69]
JO 2. ЧАСТОТЫ СОБСТВЕННЫХ КОЛЕБАНИИ
357
20.2.5. Рамы [1]
Рамы без сосредоточенных масс
Здесь приняты индексы- стойки—1, ригеля — 2.
Для П-образной симметричной рамы с жестко защем-
ленными стойками (рис. 20.12) частоты собственных из-
гибных колебаний вычисляются по формуле
(20.20)
где ац — корни уравнения частот.
Антисимметричные
колебания
Л/Ы/Ч Ы77/Ж	/ в
колебания
где
А* (а) = ch a sin а + sh a cos а;
Д'* (а) = ch и cos а + 1;
8* (а) = 2 sh a sin а.
Для трехпролетной симметричной рамы (рис. 20.13)
частоты собственных изгибных колебаний вычисляются
по формуле (20.20).
А/ипиа1^ея(шчные
колебания
Рис. 20.13
При симметричных колебаниях Ян определяются из
уравнения частот:
Рис. 20.12
k \№ (а8/) — Н (а5;)] 4- F (а1г) —
Уравнение частот при симметричных колебаниях име-
ет вид
У £7д (ай) ~ у £/,
где
В* (а) = ch а sin а — sh а cos а;
С* (а) — 2 ch а cos а — 1
Di(a)-=ch а cos а—1
С"' (g??j
При /],=/„ = /; £/. —£/,=£/ и 7Я1=га2==Дн «п —а2г- =
= а, уравнение частот симметричных колебаний имеет
вид
S* (а,-) = С* (аг).
Корни этого уравнения:
яр =-= 1,2326; «9 = 4,3906; а3 = 7,5322;
51 — 3
а, = 10,6738; а3 =13,8154; а,-= —— п (г > 5).
Уравнение часто! при антисимметричных колебаниях:
где
___У-П3 (а.д)______
f (аиН kF (ай)
sin а ch а — sh а cos а
F («) = -------------------7-------«;
1 — cos а ch а
sh а —- sin а
Н (а) = —-----------——- я.
1 — cos а спа
Уравнение частот при k — \ и а;,- = ао1 = а<
Я2 (а,)
ЗД(а1-)=//(аП-~.£-р? = 0.
2F (аг)
Наименьший корень, соответствующий основному то-
ну симметричных колебаний, равен а;=3,473.
При антисимметричных колебаниях ан определяются
из уравнения частот:
all	Г2 (“1/) {2Д (а1г) 4-
ai/
4-Л[ЗД(я2П-Я(а2г)П ] = Q
4- k [2F (аи-) 4- Н (а3/)]} — *2Я3 (ая-) j
где
«1! Д* (Кд-) — В* (аи)
ЕЦ D’’ (ац) Д- /1’ («и)
V т2 Д’, (ДД
/ Е/„ В* (яа/)
1 ,5/ZZg /а
ц= ---------- .
h m-s
sin а ch а 4- sh а cos а ,
= —---------_2__—--------аз.
1 — cos а ch а
sh а sin а
L (й) = -------——
1 — cos а ch а
а3.
358
РАЗДЕЛ 20. ДИНАМИКА СООРУЖЕНИИ
Уравнение частот при k=l и ai = a2 имеет вид
а4 - — (а 1	|
‘ р (.	2Р(щ)13Р (at)+H (аг-)]-№(аг-) J
= 0.
Наименьший корень, соответствующий основному то-
ну антисимметричных колебаний, сс.^1,70.
Яиягисинме/приыые
колебания
Рис. 20.14
Симметричные
колебания
Янтиеинметричмые
колебания
Рис. 20.15
Для Т-образной рамы (рис. 20.14, 20.15) частоты соб-
ственных изгибных колебаний
1	«/ т, /~ЁГ
1*1	™ 8 / в
2я Рут
Если стержни рамы шарнирно закреплены по концам
(рис. 20.14), то при симметричных колебаниях
«1 = 3,9266; «2 = 7,0685; а3 = 10,210;
41 + I
а4= 13,352; а5 = 16,494; аг » —— л (г > 5);
4
при антисимметричных колебаниях: а, = 1я (г=1. 2, ...).
Если стержни рамы жестко защемлены по концам
(рис. 20.15), то при симметричных колебаниях
04 = 4,7300; а2 = 7,8532; «3 = 10,996; «*=14,137;
21 + 1
а5 = 17,279; а/ « —— я (г > 5);
при антисимметричных колебаниях:
«! = 3,9266; а2 = 7,0685; а3= 10,210; а4= 13,352;
4i + 1 ,
а-, = 16,494; а, «------ я(1 > 5).
Рамы с сосредоточенными массами
Частоты собственных изгибных колебаний
где «о определяется из уравнений частот, приводимых
ниже. В этих уравнениях приняты обозначения:
где 10— соответственно половина или одна треть про-
лета ригеля (см. рис. 20.16—20.18); £— длина стойки;
4 — длина ригеля; <?i— погонный вес стопки; д2— по-
Рис. 20.16
тонный вес ригеля; М—присоединенная масса; /м —
момент инерции присоединенной массы Al; f—амплиту-
да колебаний массы М; f' — угол поворота при колеба-
ниях массы М; u=f+f'l;
sin a ch а — sh а cos а
р =  ----- —.—--------------а;
1 — cos а сп а
sh а — sin а
Н (а) = -----------------—- а;
1 — cos a ch а
£(«) =
sh а sin а
1 — cos а ch а
ch а — cos а
N (а) = -------------~~
1 — cos а ch а
п а ch аД sh s cos
(а) =--------------------------- а3:
1 — cos а ch
П (а)
sh а -!- sin а
--------------------------яз,
1 — cos а ch а
2	cth а -4 ctg а
— --------— ------- а. G {а) — --------л :—
cth (а) — ctg а	cth а — ctg а
С(«)=
tg а — th я
20 2. ЧАСТОТЫ СОБСТВЕННЫХ КОЛЕБАНИИ
359
Для П-образной симметричной рамы с защемленны-
ми стойками и присоединенной в середине ригеля массой
(рис. 20.16, а) уравнения частот имеют вид:
при симметричных колебаниях (рис. 20.16,6)
4	^9з Гп \	(«о) ___1 _
К° Mg L °)	(a) + kF(a(l) ]
при антисимметричных колебаниях (рис. 20.16,0)
2fe№ («,,)
+	J,- — X
e„ «,/.
Для П-образной симметричной рамы с шарнирно
опертыми стойками и с присоединенной посередине ри-
геля массой (рис. 20.17) уравнения частот:
при симметричных колебаниях
[Ф (a) + kF к (%) -	(afl)= 0;
I.	42 ‘о J
при антисимметричных колебаниях
2fe№(afl)
ф(а) + ЙЛао)_-------
2^)^.^
x[2Q(a)__a.J!£±^i
L	41 h
— 2G3 (а) = 0.
Для П-образной симметричной рамы с защемленными
стойками и двумя присоединенными массами (рис. 20.18)
уравнения частот:
при симметричных колебаниях
а щ k {b — 2Н (а)] — —у— [ab — kN3 («□)] = О,
А/‘ (а0)
где
а = F (а) -+ kF («.„);
, os-/ , о, .	4 Mg Р2 .
Ь = 2Д (а0) — И (а0) — а0 ——  — ;
9s 4	1'1
. Mg
с = ® (%) ~ ^ (%) ^ а0 Ту
при антисимметричных колебаниях
----~— [ab — A.V2 (а0)] = О,
А'3(а0)	аП ’
а + k \b + 2Н (аД]
где
2L3 (а)
а = F (а) + kF (а0) — —----------—-------~----------Г~ 1
„ „ , .	, Mg + <?2 /2
2Д (а) — к1 -------------
91 4
Ь=2Д(а9) + Л(%)-а^.^.
4 W
С = 2Д(а0)4-/7(а0)-а0 ур.
9s го
Частоты свободных горизонтальных колебаний много-
этажных рам можно вычислить по приближенным фор-
мулам (см. «Справочник проектировщика. Сборные же-
лезобетонные конструкции», Госстройиздаг, 1959,
табл. XXV.2).
20.2.6. Фермы
Обычной расчетной схемой фермы является система
с конечным числом степеней свободы. При этом предпо-
лагается, что масса стержней фермы сосредоточена в ее
узлах и узлы соединены между собой упругими неве-
сомыми стержнями, шарнирно связанными на концах.
Масса каждого узла равна половине масс сходящихся
в данном узле стержней и массе узловой нагрузки.
Число степеней свободы фермы принимается равным
удвоенному числу узлов за вычетом числа опорных
стержней:
(Р t)k
™ fan sin
“TOTO =— 2 Nkn c°s akn,
aP n
где mit — масса, сосредоточенная в А-м узле; АДЯ —
усилие в стержне, соединяющем узел k с каким-либо
другим узлом п;	— угол наклона стержня kn к оси
х; Xh, уа — горизонтальная и вертикальная составляю-
щие перемещений узла k при колебаниях.
Усилия Mtn выражаются через перемещения х^, Ук
по формуле
EFhn
Ntm = ТО—' l(xk — хп) cos akn + (Уь — 9л) sin аы],
где Е — модуль упругости; Fhn — площадь сечения
стержня, соединяющего узлы k и п; Еп — длина этого
стержня.
Решения дифференциальных уравнений колебаний ра-
зыскиваются в виде
Xfe= Uk. sin (It + <p); yk= VhSin(M-М $).
Для определения амплитуд колебаний иь и получа-
ются алгебраические уравнения:
vk X3 р
П
mk Uk У3 V „
"""ТО--= 2j skn “в aka,
n
360
РАЗДЕЛ 20 ДИНАМИКА СООРУЖЕНИИ
где Sfe„= \(tik — и„) cos akn + (vk —• в„) sin akn],
^kn
Приравнивая нулю определитель, составленный из ко-
эффициентов при амплитудах иц и vk, и раскрывая его,
получим уравнение относительно №, которое даст воз-
можность определить частоты собственных колебаний
фермы, число которых равно числу степеней свободы.
Метод Польгаузена
где

(20.26)
В формулах (20.25) и (20.26):
Е—длина стержня k; Ек — площадь поперечного се-
чения стержня k: Е — модуль упругости; т,—масса
г-то узла; А'йг— усилие в стержне k oi единичной си-
лы, приложенной в узле i.
Формула (20 25) дает несколько преуменьшенное зна-
чение частоты.
Этот метод позволяет найти частоты собственных ко-
лебаний ферм путем последовательных приближений не-
посредственно из уравнений (20.21). Для этого SK7J рас-
Метод эквивалентной балки
Частота определяется по формуле
сматриваются
Полагая
как некоторые усилия.
получим
-pk X2
g F-g
(20.27)
где
Pfeofeips--= X Sk„slnakn‘
n
= Ssfecos akn.
(20.22)
к
h
EFk
(20.23)
Уравнения (20.22) выражают условия равновесия уз-
лов фермы, несущей в узлах вертикальные и горизон-
тальные СИЛЫ PhV),.^ и Рд-и^ф2-
В качестве нулевого приближения задаются значени-
ем ф2=1, а за систему перемещений «ь, принимают
перемещения узлов от единичного груза, приложенного
в середине пролета, находя их из построения диаграммы
Виллио, По первым приближениям узловых нагрузок
/Дщф2 и Рци>^2 определяют Sftn, например, с помо-
щью диаграммы Кремоны, По этим усилиям находят
новые значения перемещений узлов ик, vk путем по-
строения новой диаграммы Виллио.
Первое приближение для ф2 определяется из формулы
-у = 1/	(20.23)
ф[ r k	к
Принимая за новые узловые нагрузки величины
Р), Ф) и находя из новой диаграммы Кремо-
ны отвечающие им усилия Skn, из очередной диаграммы
Виллио определяем следующие приближения перемеще-
ний ик, v-R . Второе приближение для ф2 будет
^ = ]A(P^+S(Pa0")2	(20.24)
V2 Г fe	k
н т. д.
При достаточно хорошем совпадении приближений
частоту определяют через величину ф
7 = ф VEg .
Поскольку влияние горизонтальных смещений на ча-
стоту незначительно, часто упрощают метод, для чего
а формулах (20,23) и (20.24) не учитывают члены, со-
держащие перемещения ик, uk, и}, и т. д.
Метод наложения
Частота определяется из формулы
(20.25)
В формулах (20,27) и (20.28):
—усилие в стержне k от действительной нагрузки
Р; Nk —усилие в стержне k от единичной силы, прило-
женной в середине пролета фермы; 1ц—длина стерж-
ня k\ Fц — площадь поперечного сечения стержня k;
Е-—модуль упругости; g— ускорение силы тяжести.
Формула (20 27) позволяет заменить эксперименталь-
ное определение частоты колебаний существующей фер-
мы более простым определением ее прогиба под какой-
либо нагрузкой. Так, если экспериментально измерен
прогиб фермы ог какой-либо распределенной нагруз-
ки д, а действительный погонный вес фермы с нагруз-
кой равен р, то
Методы Польгаузена, наложения и эквивалентной
балки применяются для определения частоты основно-
го тона колебаний фермы,
Частоты основного тона колебаний и одной-двух пер-
вых гармоник определяются приближенным способом,
изтоженным в приложении 7 [19а].
Для определения всех частот многомассовой системы
применяется метод, изложенный, например, в приложе-
нии 3 [19а].
20.2.7. Арки, длинные своды, кольца
Круговые арки и своды постоянного
сечения [57, 62]
Обозначения:
R — радиус оси арки (или свода);
Ф — центральный угол;
F — площадь поперечного сечения.
За поперечное сечение свода принимается поперечное
сечение вдоль образующей на единицу длины.
Малые колебания арок и длинных сводов могут про-
исходить как за счет изменения длины оси арки или сво-
да'(рис 20 19, а) (радиальные колебания), так и вслед-
ствие изгиба (рис, 20.19,6) (изгибные колебания).
20 2, ЧАСТОТЫ СОБСТВЕННЫХ КОЛЕБАНИЙ
361
Частоты радиальных колебаний арок
Частоты изгибных козебаний арок
ah \
-----(1= 1,2,3,...). (20.29)
ср1/?- F/
—2,3, ...).	(20.30)
Рис 20.19
1 kl
----.
2л/?2 ср2
Коэффициенты а, и k, приведены в табл. 20.11—20 12,
При вычислении частот собственных колебаний длин-
ных сводов необходимо в формулах (20 29) и (20.30)
Е'1
жесткость EI заменить через ~—1——, где р, — коэффици-
I — }.!“
ент Пуассона,
Параболические симметричные арки
переменного сечения (рис. 20.20) (Э]
Таблица 20 П
Значения а* в формуле (20.29)
Ус овия закреп- ления		Корни харалтеристического сравнения						
левый конец	правый конец		а.	а.	a.	«5	al	ii>5>
Оперт	Оперт	3,1416	15,2832		12,666	15,708		in
Защем- лен	Защем- лен	4,7300	7,8532	Ifl,996	14,137	17,-79		
Обозначения;
ls — момент инерции сечения в замке;
1Х — то же, на расстоянии х от замка;
<рА “ угол между касательной к оси арки и го-
ризонта лью и сечении с абсциссой х,
Таблица 20.12
Значения коэффициента k в формуле (20,30)
Рис. 20.20
Условия закрепления	,,
и формы колебаний	Коэффициент *
f—стрела подъема арки;
;s = ~^/>Г ~~ —радиус инерции сечения в замке;
Fs — площадь сечения в замке
Момент инерции поперечного сечения изменяется по
закону
1Х = /, sec грл.
Частоты антисимметричных собственных колебании
Значения а,:
а, = 3,9266; а2 = 7,0685; а, = 10,210; а, =13,352;
4г -б 1
а^ 16,494; а,	- л.
Частоты симметричных собственных ко тесаний
Значения а,, найденные и; уравнения частот
(ch а — (Jr) sin а -ф (cos а — yr) sh a = 0,
приведены в табл. 20 13.
120,31)
362
РАЗДЕЛ 20 ДИНАМИКА СООРУЖЕНИИ
Таблиц а 20 >3
Значения а,-в формуле (20.31) для определения частот
изгибных симметричных колебаний арок
		<Х2		CZj	cz2
20 19,5 19 18,5 18 17,5 17 16,5 16 15,5	5,05 5,04 5,03 5,01 4,99 4,97 4,94 4,91 4,88 4,81	9,00 7,67 6,84 6,46 6,26 6,12 6,02 5,95 5,89 5,85	15 14 13 12 11 10 8 6 4 2 0	4,79 4,69 4,5, 4,44 4,29 4,12 3,76 3,36 2,93 2,55 2,36	5,81	\ 5,75 5,71 5,b7 5,61 5,6.1 5,57 5,54 5,52 5,51 5,50
изгиба из плоскости, при которых наряду с перемеще-
ниями, перпендикулярными плоскости кольца, происхо-
дит его закручивание.
Частота любого вида собственных изгибных колеба-
ний в плоскости кольца
Рис. 20.21
Рис. 20 22
Величины р, у и г определяются формулами
1,33 Г	/	3 \	3
р =----- — 1 -г —' sh а. -ф- —- ch а
a3 |_	\	a- j	а
1,33 Г/	3 3	3
у =------ 1 — — sin a -j---------- cos а
а3	а3 /	а
Круговые кольца
Здесь приводятся формулы [62, 14] для колец посто-
янного поперечного сечения, одна из главных централь-
ных осей инерции которого расположена в плоскости оси
кольца.
Обозначения:
R— радиус осевой линии кольца:
т— масса кольца на единицу длины;
i—число волн по окружности кольца;
I х— момент инерции поперечного сечения относитель-
но оси х (рис. 20.21);
1р — полярный момент инерции поперечного сечения;
F —площадь поперечного сечения кольца;
I — момент инерции поперечного сечения относитель-
но главной оси, расположенной под прямым уг-
лом к плоскости кольца;
и — коэффициент Пуассона.
Частоты радиальных колебаний кольца
1 Г EF
=	о=1,2,3, ...).
2п г
Первая частота собственных крутильных колебаний
для любого поперечного сечения кольца
1 2л У mR3 '
Частоты высших тонов колебаний в случае кругового
поперечного сечения кольца
I , f~EF
FT 1/	(Р+1) = I 2- 3,   )
2л у 2m/?3
Нагибные колебания кругового кольца разделяются на
два вида: колебания в плоскости кольца и колебания
При /=1 л=0, т. е. кольцо движется как твердое те-
ло. При !=2 кольцо колеблется по основной форме; при
1 — 3 и / = 4—по высшим формам колебаний. Крайние
положения кольца при этих формах колебаний показа-
ны на рис. 20,22, а, б, в сплошными линиями.
В случае изгибных колебаний из плоскости кольца
кругового поперечного сечения, при которых наряду с пе-
ремещениями, перпендикулярными плоскости кольца,
происходит закручивание стержня, частоты главных
форм колебаний
х- = JL1 / лЕЗЕтЕНзЕ”
' 2л У mR* ' i3 + р. + 1
Неполное кольцо. Рассматривается случай, когда
часть кольца с углом а защемлена на обоих концах
(рис. 20.23).
Рис. 20.23	Рис. 20.24
Частота собственных колебаний
Значения коэффициента /(а) при а от 180° (полу-
кольцо) до 360° (полное круговое кольцо, защемленное
в одной точке) для колебаний по основному тону при-
ведены па графике рис. 20.24.
Если кольцо имеет малые размеры в направлении,
перпендикулярном его плоскости (направление осн ци-
линдра), то возможны колебания из этой плоскости.
Система, приведенная на рис. 20.25 (вверху, справа), мо-
жет рассматриваться как балка высотой h, защемлен-
ная на нижнем конце.
20 2. ЧАСТОТЫ СОБСТВЕННЫХ КОЛЕБАНИЙ
363
Частота собственных колебаний
Рве. 20.25
где Е/з — жесткость кольца на изгиб в плоскости, пер-
пендикулярной плоскости чертежа; с — жесткость на
кручение.
/ Е!2\
Коэффициент f <х, — определяется из графика
рис. 20.25.
20.2.8. ПЛИТЫ
Обозначения:
а,Ь — соответственно длина н ширина плиты
в м;
0= V (а > 6);
о
х, у—координаты точки срединной поверхно-
сти плиты;
х	У
—; [3 —	— относительные координаты точки
а	Ь
срединной поверхности плиты;
— сосредоточенная масса в кГ-сек'2/м;
т —интенсивность распределенной по площа-
ди плиты массы в кГ -секУм3-,
h — толщина плиты в лц
Eh?
D „ ---------_. _ цилиндрическая жесткость плиты
12 (1 — ц2)
в кГ • м.
Частоты собственных колебаний прямоугольных плит
вычисляются по формуле
. !
Д- ™	, -
2л а2
(20.32)
т
Табл и на 20 ! 1[57, 59]
Значения	в формуле
(20.32) для прямоугольньзх плит
Условия закрепления краев плиты	CZ.J	а3
	9,87 (1 + п=)	9,87 (1 Щ ц')
Г 2,440ц4
12.37J 1 + 0.56611' 4- 0, 175ц'
61,70 V 1 + 0,298ц' + 0,0С2-Ц1

’7777777'
22,37 )	1 - 0,605ц'Д- ц'
(51,70 У 1 А
Обозначения:
шарнирно опертый край;
— жестко заделанный край
364
РАЗДЕЛ 20 ДИНАМИКА СООРУЖЕНИИ
Значения в формуле (20,32) для определения частот собственных колебаний квадратных и прямошм^ых плит
Условия закрепления краев плиты			Дополни- тельным пара- метр плиты	«1	л.	а-.	Ct.s	а	а
ft	|	1 1—			.......	3,49	8,55	21,44	27,45	И, 16	—
ft А	о			6,96	24,03	26,79	48,0э	ЬЗ, 1 1	—
° «> j | 1	_J м			~~	19,73	49.33	78,95	93,67	128,28	-67,
Z2 ft	1			~~	23,65	51,68	58,64	86,12	то, ж	113,
4?	& jy 1	J и ^7?'"'1			—	8,94	о4,74	и	9 1,37	102,19	129,
° О '! а у*”			--	и, Эд	73,40	!08,28	131,58	132,28	165,
а			1 т}-= — Т]™5	з,зи 3,49 3,47 3,45	а, 58 8,55 К 92 34,73	21,95 21,-44 21,60 21,52	10,2d 27,45 94,47 1D \ ’	.4,85 31J6 43,71 Н!	;	! I 1	1 |	! I i 	1	1 !
|м ч		 1							
ft а	1/V й		0—15° 6-20 0=45*	3,60 3,96 4,82	8,87 10,19 И,75	—		—	
20 2, ЧАСТОТЫ СОБСТВЕННЫХ КОЛЕБАНИЙ
365
Значения	2) принимаются по табл 20.14
и 20.15.
Если прямоугольные птаты имеют сосредоточенные
массы А1,, то приведенная равномерно распределенная
масса Иприв вычисляется по приближенной форму-
ле [59]
«привел: 4 Ц- V Ад (as) ks (Rs) ЛД,
ao
где s0—число масс на плите; as, ps — относительные
координаты массы Afs.
Коэффициенты kt(aa) и А,(|эа), зависящие от номера
определяемой частоты, значении относительных координа г
х,	у,
массы as =	—	и	—	и способа закрепления краев
а	Ь
плиты (рис. 20.26), определяются по табл 20.7 так же,
как и для однопролетных балок.
Для определения частот собственных колебаний пря-
моугольных плит по формуле (20..32) при отношении
сторон а/6=0,2; 0,4; 0,6; 0,8; 1,0; 1,25; 1.6; 2,5; 5 и раз-
личном закреплении сторон плит (шарнирное опирание,
жесткая заделка и свободный край) в работе [70] при-
ведены таблицы значений коэффициентов а1; где они
обозначены через [, Подробные сведения (формулы
и таблицы) о частотах и формах собственных колебаний
пластинок можно найти также в справочном посо-
бии [82].
Для многопролетных шарнирно опертых плит с коли-
чеством полей в направлении осей х и у соответственно
(Уж>4 и A'(j>4 частоты собственных колебаний вычис-
ляются по формуле (20 32), в которую взамен «г под-
ставляются а1Я или сщв (см. 20.2.3), принимаемые по
формулам [59]:
а1в = 9,87 (1+0; «1В = 22,37	;
аан = 9,87 (4 4 +); а5в = 22,37 V7,57 4 2,27+4+
Частоты собственных колебаний круглых плит опре-
деляются по формуле
(20.33)
2лг3 V m
где а, (г = 1, 2, ..) принимаются по табл, 20.16 в зависи-
мости от условий закрепления краев плиты и от числа уз-
ловых диаметров и; число узловых окружностей равно
Д-1.
Т б л и ц а 20 16р6'
Значения ом в формуле (20.33) для круглых плит
Условия закрепления плиты	n	a.	j a-	C4i
		10,212	39,787 ; 88,917	—
	1	21 224	61,000 , 120,56	—
	2	34,847	88,36''’ ’ 158,76	
/ vA	0	5,779	39,47(5 )	74,89	139,05
I	i	1	14,684	49,224	103,49	177,50
	2	26,368	70,846 ( 135,02	218,92
J	3	40,692	95,558	569,44	263,22
	h	3,760	-0.914	6(1,695	119.72
44				
20.2.9. Стержни переменного сечения
Частоты собственных колебаний имеют вид
к =
2л.Ч
(20.34)
где 70, Fo — момент инерции и площадь поперечного се-
чения стержня в начале координат.
Клинообразная консоль [16, 74] (рис. 20.27). Высота
поперечного сечения 2А(х) пропорциональна расстоянию
26
от вершины 26= -ух, где 26 — высота в заделке; шири-
на консоли постоянна.
Значения коэффициентов а, при 1фЗ см. далее
в табл. 20.1.9; при z>3
«»• =
(2t 4 I)3 я
32
Эта формула применима к пустотелому конусу со стен-
кой постоянной толщины
Консоль в виде кругового конуса [16, 74] (риг,
20 27, б). Момент инерции и площадь поперечного сече-
ния изменяются по законам
nd*	nd“
/о ~ ~кл'	~7"’
64	4
12П
«1=1,39; аг = 3,52; аг-= —-(:> 2).
РАЗДЕЛ 20 ДИНАМИКА. СООРУЖЕНИЙ
366
Формула (20 34) применима к пустотелому конусу со
стенкой, толщина которой меняется с высотам по ли-
нейному закону В этом случае
Ь4	4
Первая частота собственных колебании усеченного
конуса (рис, 20 27, е ) вычисляется [77] как
1 т. /ПЛ
7= — 1/ —- ,	(20.35)
CZ- > pF.
где постоянная
£ Г	/1	£ V
С = 0,719+ 1,069 — 10,14 — 2,24 — — —-
L L	' 2 L
или определяется по табл 20 17
Для консольного стержня, момент инерции и площадь
поперечного сечения которого изменяются по .чиненно-
му закону,
х
Т;
Л
X
1 “ П у

значения а, приведены в табл, 20 18. Начало координат
принято в защемленном конце
По табл 20 19 (см [76]) определяются для раз-
личных случаев сюржнеи переменною сечения.
Таблица 2017
Значения коэффициента С в формуле (20 35)
А.,	0 (конус)	0,264	0,501	0,754	1,00 (цилиндр)
L					
с	0,719	1,101	1,368	1,695	1,788
Таблица 20 18
Значения <zs в формуле (20.34) для консольного стержня
переменного сечения
п	«!	Ц	«з	i
0	0,560	0,6	0,7 30
0,2	0 597	0,8	0,869
0, 1	0,552	1.0	1,140
Табл и ц а 20 19
Значения в Форма ле (20	различных консольных стержне»
Конструкции балки		/ b	b h,	«1	«3	а3
2?	,-aJ	Клинообразная ко'коть	1	х/1	0,85	2,42	4,78
	Четырехгранная пирамида	хГ1	X/L	1,29	3,37	6,12
«Ы—4Г'	 I <Г	Четырехгранная пирами и < T0AAV1 ВЫП1 h 1ЫМ41	1р<1 ня ми	Гт	л/	1,10	..,88	5,44
	Уцененная	клинообразная пОНСОЛ!	”Т	1	0,75	3,85	10,20
20 2 ЧАСТОТЫ СОБСТВЕННЫХ КОЛЕБАНИИ
367
Табл и ц а 20 20[П
Значения fl( я формуле (20,37) для крутильных колебаний стержней постоянного сечения
Схема стержня и корпи частотною уравнения
л=Л т_
2 G^p

£$кр

368
РАЗДЕЛ 20 ДИНАХ ИКА СООРеАРНИИ
JJ рог)) по ни т г i "Ч/ /)
Схемт бруса ж корни частотного уравнения
1де т](л, 1} — продольное перемещение стержня или
20 2.10. Крутильные и продольные колебания
стержня. Колебания струны
Крутильные и продольные колебания стержней и ко
лебаппя струн приводятся к рассмотрению одного и
того же дифференциального уравнения вида
б2т]
др U дх2
(20 36)
троса, или уют закручивания секция ещрлчя в точке х
или поперечное отклонение толи струны с абш ис
б Г)
сой х, а2— коэффициент, равный	—— —для крутите
ных колебаний стержнем, £/р— для нродолпных коле
бании стержней N/pF— для колебании стоун б/к0—
жесткость поперечного сечения стер/ь тя при кру шипи
/р — тнтратьшш полярный чтинг инерции поперечно
’о сечения скркчя р - п ютносп материала А — то
шадь поперечного селения, N ищяжспие трупы,
рА — Д’
20 2. ЧАСТОТЫ СОБСТВЕННЫХ КОЛЕБАНИИ
369
Частоты собственных крутильных колебаний стержней
(20.37)

Значения коэффициентов
табл. 20.20 Обозначения:
ps принимаются по
Рис. 20.29
Рис. 20.28
Рис. 20.30

г — жесткость опоры при кручении стержней в кг-сч;
г ~ г ——— относительная жесткость опоры при круче-
Сг/кр
нчг: (для симметричных брусьев принимается половина
г); П,— момент инерции сосредоточенной массы в
кГ • сек2 • см.
Некоторые случаи определения частот свободных кру-
ти тьинх колебаний стержней силовых установок мето-
дом трех крутящих моментов и методом деформаций
(методом углов закручивания) можно найти 8 рабо-
те [69].
Частоты собственных продольных колебании стерж-
ней определяются как
1 а , ГеР
1 / _ ;	(20.38)
2л I у т
где EF — жесткость па растяжение.
Коэффициент а зависит от условий закрепления и
имеет следующие значения:
1)	элемент, закрепленный на одном конце
(рис. 20.28, а):
[	1 \
а = \ п 4- — л,
\	2 )
где п — 0, 1, 2, 3 ... — число узлов в форме колебаний.
2)	элемент с обоими закрепленными концами
(рис. 20.28,6): а==дл, где п — число полуволн в форме
Колебании;
3)	элемент со свободными концами (рис. 20.29): а—
-ст, где Л--1, 2, 3 . —число узлов.
24—20
Частота собственных поперечных колебании струны
с закрепленными концами
где n = 1, 2, 3 ...
На рис. 20,30 показаны три первые формы поперечных
колебаний струны.
20.2.11	. Колебания жидкости в резервуарах
[72, 73, 75]
Прямоугольный резервуар [72]
Частота основного тона собственных колебаний жид-
кости определяется формулой
1 1 / Г 5 е /т|/~5 h \
Ут-тЧКт-у).
где I — половина длины той стороны резервуара, вдоль
которой происходя г колебания;
h — глубина жидкости.
Цилиндрический резервуар
По Лэмбу частоты собственных колебаний жидкоеги
определяются формулой
X; == — 1/ a/-~th \'Zi
2л | R \
(20.39)
где at имеет значения:
«г = 0,586 л; «„= 1,697 л; «3 = 2,717 л;
R — радиус резервуара.
Рис. 20.31
Рис. 20.32
Первые три формы свободных колебаний жидкости
в цилиндрическом резервуаре представлены на
рис 20.31; вверху даны контурные линии (горизонта.т).
370
РАЗДЕЛ 20 ДИНАМИКА СООРУЖЕНИЙ
Резервуар, имеющий в плане форму,
изображенную на рис, 20.32
Частота собственны.'!: колебаний жидкости по перво'!
форме относительно малой оси определяется формулой
где
Ж Оу т г,ь
(20.40)
/ Ц ст	R
-ф 0, 197 1— 4-0,131 — ф- 0,166
20.2.12	. Колебания трубопровода,
по которому движется жидкость
Частота собственных малых поперечных колебаний
гибкого трубопровода, по которому течет жидкость
вычисляется по формуле
V (ш0 ~г т) И — т0 mv°
т0 + т
--------;,
гп0 т
где I — длина трубопровода; т0 — погонная масса тру-
бопровода; т — погонная масса движущейся жидкости;
v — средняя по сечению скорость течения жидкости;
Я — продольное натяжение в трубопроводе, предпола-
гаемое ввиду малости колебании постоянным.
20.3.	ДИНАМИЧЕСКИЕ ХАРАКТЕРИСТИКИ
СТРОИТЕЛЬНЫХ МАТЕРИАЛОВ И КОНСТРУКЦИИ
20.3.1.	Динамическая жесткость
Жесткость элементов строительных конструкций,
вводимая в динамический расчет, определяется исходя
из упругой стадии работы. Исключение представляют
расчеты па действие мощных ударных и импульсивных
нагрузок, при которых допускается появление пласти-
ческих деформаций.
При динамическом расчете стальных и деревянных
конструкций модули упругости принимаются равными
статическим. При рассмотрении горизонтальных колеба-
ний кирпичных зданий модуль сдвига кирпичной клад-
ки принимается равным 0,3jS, где Е—модуль упругости
пои сжатии кирпичной кладки, принимаемый по
СНиП П-В.2-62*.
Жесткость изгибаемых элементов монолитного или
сборно-монолитного железобетонного каркаса щапст!.
а также железобетонных конструкций перекрытии и по-
крытии. плит и балок, лежащих на упругом основании,
днищ и стенок резервуаров и других монолитных и
Предполагается, что течение ламинарное.
сборно-монолитных железобетонных конструкций мож-
но определять по формуле
Bk -= Еб I,
где Е-, — модуль упругости бетона; I—момент инер-
ции поперечного сечения без учета продольной арма-
туры.
20.3.2.	Внутреннее поглощение энергии
колебаний (затухание) в конструкциях
и материалах сооружений
Вследствие неупругих свойств материала, излучения
энергии колеблющейся конструкцией и т. д. происходит
явл< ине затухания свободных колебаний конструкции.
Для поддержания вынужденных колебании постоянной
амплитуды необходимо непрерывно производить рабо-
та 6 л и ц а 20 21
Материал	Коэффициент 7	
	пря динами- ческой на- грузке I и II категории	при динамиче- ской нагруз- ке III и' IV категории
Жетезобетон обычный . , Железобетеш предварительно	С, 050	0,100
напряженный . ,	...	0,025	0,050
сталь ...»	0,010	0,025
Кирпичная ктадка . . ,	0,040	0,080	i
Дерево . . 		0,030	0,050
ту, компенсируя ту энергию, которая рассеивается при
колебаниях. Роль внутреннего поглощения при динами-
ческом расчете конструкций очень велика, так как от
нее зависят амплитуды колебаний в резонансном ре-
жиме.
В практических расчетах значение коэффициента He-
lp	6
упругого сопротивления у = ~— == — рекомендуется
2л	л,
принимать в соответствии с табл. 20.21.
Очевидно, что коэффициент у не зависит от катего-
рии динамической нагрузки; смысл дифференциации за-
ключается в том, что она в соответствии с нормами
приближенно учитывает зависимость у от величины ди-
намических напряжений. Как показывают эксперименты
пря весьма малых напряжениях, у линейно зависит от
амплитуды динамических напряжений и начиная с оп-
ределенного значения напряжений у практически оста-
ется постоянным.
В случае составных, многослойных и комбинирован-
ных конструкций, выполненных из различных материа-
лов, рекомендуется коэффициент у определять по фор-
муле
т
V Л
" Ап ип	т
где у„ — коэффициент неупругого сопротивления я-го
элемента или составной части; Dn — жесткость я-го
элемента или составной части; D — суммарная (полная)
жесткость конструкции; т — число элементов или со-
ставных частей.
20 4. ДИНАМИЧЕСКИЕ НАГРУЗКИ ОТ МАШИН
371
Жесткости составных частей для монолитного сечения
определяются относительно нейтральной оси всего се-
чения; для немонолитпого — относительно своей ней-
тральной оси.
20.3.3.	Выносливость строительных
материалов
При оценке прочности конструкций, на которые дей-
ствуют одновременно статические и динамические на-
грузки, различают два основных случая: первый соот-
ветствует учету периодической нагрузки, действующей
в течение длительного периода эксплуатации сооруже-
ния, во втором учитываются динамические нагрузки,
сравнительно непродолжительные (эпизодические) с ма-
лой повторяемостью. В первом случае на прочность влия-
ют явления выносливости.
Предел выносливости представляет наибольшую по
величине сумму статического напряжения и амплитуды
динамического напряжения, при которой материал спо-
собен выдержать без разрушения бесконечно большое
число циклов нагружения.
Расчетные сопротивления материала конструкций, под-
вергающихся одновременному действию статических и
систематических динамических нагрузок, вычисляются
путем умножения статических расчетных сопротивлений
на понижающий коэффициент kQ: зависящий от отно-
шения р наименьшего по абсолютной величине напря-
жения в рассчитываемом элементе оЧ11И к наибольшему
напряжению оМ8КР (каждое напряжение со своим зна-
ком) и определяемый согласно СНиП. Величину р мож-
но определять по формуле
рмян 1 s
Р ~ 0	_ls ’
омакс 1 1 й
где s — отношение абсолютной величины наибольшего
динамического напряжения (усилия) к статическому на-
пряжению (усилию).
20.4,	ДИНАМИЧЕСКИЕ НАГРУЗКИ ОТ МАШИН
Различаются .машины с конструктивно неуравнове-
шенными движущимися частями и машины с номиналь-
но уравновешенными, а фактически неуравновешенными
движущимися частями. Для первых определение дина-
мических нагрузок производится по кинематическим
схемам на основе расчета, для вторых (в этом случае
неуравновешенность носит случайный характер)—по
величинам эксцентрицитетов, коэффициентов и т. д., по-
лученных на основе экспериментальных данных.
Ниже приведены данные для определения динамиче-
ских нагрузок, взятые из инструкции [25].
Нормативная динамическая нагрузка развивается ма-
пшноп в ес нормальном состоянии, отвечающем техни-
ческим требованиям по эксплуатации машин. Расчетная
динамическая нагрузка вычисляется путем умножения
нормативной динамической нагрузки на коэффициент пе-
регрузки, который для машин первого типа принимает-
ся равным 1.3 и для машин второго типа — 4; в каче-
стве исключения для впброннерциопных грохотов и ков-
шовых элеваторов коэффициент перегрузки принимается
равным 2.
Деление машин на группы по частотности, на катего-
рии по динамичности и па классы по чуветвите 1ьносги
к колебаниям производится ио действующим инструк-
тивным материалам.
24*
Отнесение машин к той или иной категории по дина-
мичности производится на основании ориентировочных
данных табл. 20.22.
От динамических нагрузок, возникающих в машине
и заданных амплитудами главного вектора и главного
момента динамических сил, по формулам табл. 20.23 де-
ляется переход к динамическим нагрузкам, передающим-
ся на опоры.
Динамические нагрузки большинства машин непре-
рывного действия изменяются по гармоническому зако-
ну, а в отдельных случаях выражаются некоторыми пе-
риодическими негармоническими функциями времени.
Таблица 20 22
Ориентировочное деление машин на категории по динамичности
Категория машин по дннамлчпостц	Динамичность машины	Наименование машин
I	Малая	Станки и автоматы фрезерные, зуборезные, зуборезьбошлифовальные, сверлильные, ре- вольверные, расточные и доведенные; шлифо- вальные станки с весом шпинделя и камня менее 20 кг, токарные стачки по металлу с ве- сом шпинделя 20 кг, деревообрабатывающие станки; прядильные машины, упаковочные автоматы кондитерской, пищевой и вкусовон промышленности; пагшросонабнвные и другие автоматы табачных Фабрик; автоматы для точки лезвий бритв; швейные машины; элек- тромашины весом менее 100 кг, ротационные насосы весом менее 50 кг и т. п.
II	Средняя	Шепинги и другие строгальные станки; то- карные станки с весом шпинделя ботес 20 кг; шлифовальные станки с весом шпинделя и кам- ня более 20 кг, но менее 100 кг; точильные камни; маломощные поршневые насосы; не- уравновешенные одноцилиндровые двигатели, произведение веса поршня которых на радиус кривошипа меньше 250 кгем, горизонтальные и вертикальные центрифуги с весом заполненно- го барабана менее 100 кг; гребнечесальные ма- шины прядильных фабрик; гладильные бара- баны швейных фабрик, трансмиссионные пере- дачи; вентиляторы с весом ротора менее 30 кг; электромашины весом более 100 кг, но менее 1000 кг и т. п,
III	Боль - шая	Центрифуги с весом заполненного барабана более 100 кг, но менее 300 кг; вентиляторы с весом ротора более Зп кг, но менее 100 кг; ткацкие станки: штампы п прессы с весом пол- зуна менее 200 кг; типографские машины; шлифовальные станки с весом шпинделя кам- ня более 100 кг, электромашины весом более 1000 кг; неуравновешенные одноцилиндровые двигатети, произведение веса поршня которых на радиус кривошипа более 250 кгегл, но мень- ше 730 кгем; поршневые насосы средней мощ- ности и 7. п.
IV	Очень боль-	Штамп- и пресс-автоматы с весом ползуна более 200 кг (например, прессы шарикопод- шипниковых заводов, штампы бисквитные); сотрясательные сита крахмальных и сахарных наводоа, рассевы, дробилки; внбросголы и грохоты обогатитепьных и других фабрик и за- водов; вентиляторы с весом ротора более РЮ кг; центпифуги с весом заполненного ба- рабана более 3<Ю кг; неуравновешенные одно- цилиндровые двигатели, произведение веса поршня которых иа радиус кривошипа больше 750- кгеи; мощные поошневые насосы п т. п.
372
РАЗДЕЛ 20 ДИНАМИКА СООРУЖЕНИЙ
«ема действия на конструкцию инерционных сил машин
Таблица 20 23
Схема лействтинцпх иа конструк-
цию ТСИЮзР Прл опирании 'IWT’.bl
в двух точках
Схема действующих на, конструк-
цию усилий при сплошном опира-
ет
нии машины или при'Д~<0,2 О-—
пролет)
При вращении ротора неуравновешенность приводит-
ся к центробежной силе /? = отеш2 и к моменту
= meb(i)2 (т — масса ротора; е — расчетный эксцентри-
цитет центра масс; b — расчетное плечо пары сил; m —>
круговая частота вращения), постоянных по модулю, но
переменных по направлению.
При возвратно-поступательно движущейся массе ди-
намическая нагрузка в общем случае может быть пред-
ставлена тригонометрической суммой
R = S (ay cos kcat -ф- bk sin kcut),
h
в которой си a bk — коэффициенты Фурье.
Кратковременно действующие (импульсивные) на-
грузки по характеру действия во времени делятся иа
кратковременный импульс и мгновенный импульс. Крат-
ковременный импульс определяется величиной, формой
и продолжительностью действия; мгновенный импульс
определяется только своей величиной.
20.4.1.	Машины с конструктивно
неуравновешенными движущимися частями
К числу таких машин относятся машины с кривошип-
но-шатунными и кривой,шпио-кулпснымн механизмами:
поршневые компрессоры, метал,лообр 1батывающис стро-
гальные, плоскошлифовальные и тому подобные станки,
щековые дробилки, вибрационные центрифуги, ткацкие
станки, штампмашияы, поршневые насосы, плоскопечат-
ные типографские машины и т. и.
Динамические нагрузки от машин с кривошипно-ша-
тунными и кривошипно-кулисными механизмами, щеко-
вых дробилок, ткацких станков, штампмашин, металлоре-
жущих станков с гидроприводом и типографских машин
можно найти в [25],
20.4.2,	Машины с номинально
уравновешенными, а фактически
неуравновешенными движущимися частями
К числу этих машин относятся центрифуги, метал-
лообрабатывающие токарные, точильные, шлифоваль-
ные и тому подобные станки с вращающимися шпин-
делями и камнями, вентиляторы, электромашины, тур-
бины и т. п.
В таких машинах возникают динамические нагруз-
ки, определяемые величиной центробежной силы
Д = теса2,
где R — нормативная амплитуда динамической на-
грузки; т — масса движущихся частей машины, е —
20 5. О ДИНАМИЧЕСКОМ РАСЧЕТЕ ПЕРЕКРЫТИИ И КАРКАСОВ ЗДАНИИ
373
Таблица 20 24
Значения е для некоторых машин
№ п- п.	Виды машин	е	Примечание
1 3 4 5 6 7	Грохоты Центрифуги Молотковые дрен илкн Металлорежущие станки с главным г- р а щ а г е л ь п ы м л г, и ж е н и е м Веитиляторы t горизонтальной осью, располагаемые на междуэтажных пере крытиях Электромашины Турбины	а 5 D ЮОО t мм d 10 п»5 мм ы) во 350Д-Щ2	а — амплитуда колебаний коробов в соответствующем направлении D — диаметр ротора, Для вычисления амплитуды мо- мента берется плечо силы, равное половине длины ротора За расчетную амплитуду силы от молотковых дробилок принимается увеличенная в 4 ра-?а центробежная сила, во-шикающая при отрыве одного молотка Для вычисле- ния нормативного моменга (при рабочем режиме дробил ки) борется плечо силы, равное потовинр расстояния междл осями подшипников; для вычисления расч'пнш’о : динамического момента (в аварийном режиме) следует принимать плечо силы, равное половине расстояния меж- ду крайними рядами молотков d — диаметр обрабатываемой детали пли инструмента, сила считается приложенной к центру тяжести вращаю- щихся частей, динамический момент не учитывается	; В вентиляторах, рабочие колоса которых подтюрштнсь лини, статической балансировке, ууитывается динамиче- < кнй момент, вычисляемый при чкс"’’Ч грицитете, равном е. ==0,34-0,001 Ь, где D — диаметр ротора в мм, и при ши- рине ротора b п — число оборотов глазного вала машины в 1 сек
эксцентрпшпет движущихся масс; со — круговая ча-
ст от а.
Величина т представляет собой условную массу вра-
щающихся частей: в грохотах это масса коробов и 25%
массы обрабатываемого материала, находящегося одно-
временно па ситах грохота, в центрифугах — масса
барабана н вала вместе с заполнением, в металло-
режущих станках с главным вращательным движени-
ем (токарные, сверлильные и т. п.) — масса вращаю-
щейся заготовки или инструмента со шпинделем, в вен-
тиляторах, электромашинах и турбинах — масса ротора
и вала.
В табл. 20.24 приводятся значения величины е для
некоторых машин.
20.5.	О ДИНАМИЧЕСКОМ РАСЧЕТЕ ПЕРЕКРЫТИЙ
И КАРКАСОВ ЗДАНИЙ
20.5.1.	Расчетные схемы
При расчете на действие периодической нагрузки
предварительно определяются частоты свободных ко-
лебаний конструкций сооружения. При этом обращает-
ся внимание на. то, чтобы расчетная схема по возмож-
ности хорошо отражала действительную работу кон-
струкции. В частности, для оценки частот свободных
колебаний перекрьпий следует правильно учесть усло-
вия опирания и ш тки отдельных элементов. Для
монолитных перекрытий вследствие большой крутиль-
но-изгиб.чой жесткости балочных элементов, обрамляю-
щих миш, пшшгдшю следует считать защемленными
по тем сторонам, где плита примыкает к балкам. Ба-
лочные элементы обычно рассматриваются как разрез-
ные или неразрезные балки без учета сопротивления
колонн и тгибу или балок — кручению.
Для сборных элементов условия заделки плит и ба-
лок зависят от степени и надежности замополичивания
и условий эксплуатации. Опыты показали, что в не-
которых случаях плиты, недостаточно надежно замоно-
личенные, имели в начале эксплуатации частоты, близ-
кие к условиям заделки, а затем, с течением времени,
частоты снижались за счет того, что условия заделки
под действием нагрузки изменялись.
При расчете покрытий и перекрытий рекомендуются
расчетные схемы, приведенные в табл. 20.25.
Болес подробные сведения о расчетных схемах пере-
крытий можно найти в инструкции [19].
При определении частот свободных колебаний об-
ращается внимание па величину п расположение полез-
ной нагрузки, так как в отдельных случаях значитель-
ное изменение (в том числе и снижение) полезной на-
грузки может быть причиной появления резонансных
колебаний,
При определении частот горизонтальных свободных
колебаний зданий рампо-каркасного типа, можно пре-
небрегать массой стоек, присоединять массу заполнения
к массе соответствующего перекрытия и считать каж-
дое междуэтажное перекрытие абсолютно жестким
в своей плоскости. Жесткость перегородок, степ, лест-
ничных клеток и т. д. может значительно (иногда во
много раз) увеличить жесткость каркаса, поэтому нуж-
но по возможности принимать во внимание жесткость
всех элементов здания.
В связи с этим рекомендуются следующие расчет-
ные схемы по табл 20. 26.
374
РАЗДЕЛ 20 ДППАМ1 IK 3 ГООРГЖЕНИИ
Т а б л и ц а 20 25
Типовые расчетные схемы для динамического расчета перекрытий и покрытий
Тип конструкций	Элементы, для которых определяю 1ся частоты	Расчетные схемы	Возможная ПО1рсшкость определения частот
1. Плиты и настилы по бал- кам железобетонным, стальным и деревянным	Главные и вспомогатель- ные балки Плиты с дроле том более 1,5 м	Однопролетные или неразрезные многопролетные балки, Однопролстные или неразрезпые балочные плиты (в зависимости от фактических условий)	U, 25
2. Железобетонные ребристые перекрытия	Главные и вспомогатель- ные балки. Плнлы с проле- том более 2 щ	Перазрезные многопролетные балки или рамы с несмещающим ися узлами. Неразрезные балочные плиты	0, 30
3. Железобетонные крупнопа- нельные плиты по стальным или железобетонным ригелям	Прогоны, плигы	Моразрезные многопролетные балки или рамы с несмещающимчся узлами. Неразрезные ммоюпро- летные плиты по перекрестным балкам. Однопро- лстные плиты	0,35
4, Безбалочные перекрытия	Безбалочная плита	Плита, подпер гая в точках, с учетом жесткости колонн и капителей	03 35
5 Покрытия по фермам	Фермы	Система с конечным числом степеней свободы	0,15
6. Железобетонные покрытия по балкам и фермам	Плиты и балки	Мнсп опролотные и однопролетные балки, одно- пролетные плиты	0,15
Таблица 20 26
Типовые расчетные схемы для расчета зданий на горизонтальные колебания
Типы зданий	Расчетные схемы	Возмож- ная по- грешность определе- ния частот
1. Каркасные здания с нежестким стено вым заполнением (например, со сплошным остеклением стен), без внутренних несу- щих стен. Каркасные площадки под ма- шины 2. Каркасные здания с тяжелым стено- вым заполнением и внутренними стенами Здания с несущими стенами и монолитны- ми перекрытиями	Этажерка с неподвижным основанием и недеформнруемыми перекры- тиями. с которыми жестко связаны вертикальные стойки. Перекрытия могут поступательно перемещаться и поворачиваться в своей (горизон- тальной) плоскости. При si ом стойки считаются работающими на попе- речный изгиб ч кручение Коробка с недеформпруечыми перекрытиями, с которыми жестко свя- заны вертикальные стойки Перекрытия могут поступательно переме- щаться в своей (горизонтальной! плоскости При этом стойки считают- ся работающими на поперечный изгиб, а наружные и внутренние стены иа сдвиг в своей плоскости	0,25 0,30
При определении изгибной жесткости моменты инер-
ции рекомендуется принимать следующим образом:
для балок при немонолитном настиле — момент инер-
ции поперечного сечения балки;
для балок при монолитной железобетонной плите —
сумму моментов инерции сечений балки и плиты; при
этом расчетная ширина сечения плиты принимается
равной расстоянию между осями балок, по не более
половины пролета балки;
для балок ребристого монолитного перекрытия (по-
крытия)— момент инерции монолитного таврового се-
чения с шириной плиты, указанной выше; если сталь-
ные балки обетонированы железобетонной плитой по-
верху или понизу, перекрытие рассматривается как
ребристое монолитное;
для балочных плиг — момент инерции поперечного
сечения плиты,
При расчете крупнопанельных плит, плит безбалоч-
ных перекрытий и т, д, определяется цилиндрическая
жесткость или гы.
Если постамент под машину или установку монолит-
но связан с перекрытием, он учитывается при определе-
нии жесткости соответствующего элемента перекрытия.
20.5.2.	Частоты и формы
свободных колебаний
Определение частот свободных колебаний составляет
существенную часть динамического расчета.
При расчете сооружений на действие периодической
нагрузки часто раскладывают решение в ряд по соб-
ственным функциям; определение частот своботных ко-
лебании предшествует рассмотрению вынужденных ко-
лебаний Если при расчете сооружений на действие
нагрузки изменяющейся по гармоническому закону,
непосредственно определяется частное решение неодно-
родного уравнения, определение частот свободных ко-
лебаний формально не нужно, однако и в этом случае
рекомендуется определять частоты свободных колеба-
ний с целью выяснения вопроса о том, насколыко ве-
роятны явления резонанса, что в свою очередь зависит
от cooi ношения частот свободных и вынужденных ко-
лебаний.
При расчете сооружений на действие импульсивной
нагрузки необходимо определять несколько частот сво-
бодных колебаний по указаниям инструкции [26].
20 5. О ДИНАМИЧЕСКОМ РАСЧЕТЕ ПЕРЕКРЫТИИ И КАРКАСОВ ЗДАНИИ
375
Как правило, при расчете на периодические нагруз-
ки всегда определяется частота основного тона и не-
которое число высших частот; при этом следует учи-
тывать, насколько близки частоты свободных колеба-
ний к частоте вынужденных колебаний; как правило,
в практических расчетах определяется следующее число
частот и форм собственных вертикальных колебаний
несущих конструкций: для однопролетиых балок —2;
для однопролетиых нлит —4; для неразрезных ба-
лок—2N, для ферм — согласно инструкции [66], по ко-
торой число определяемых частот и форм определяется
верхней границей той резонансной зоны, которая за-
ключает в себе частоту возмущающей силы. Здесь
N — число пролетов балки.
Для регулярных неразрезных балок, неразрезных
плит и безбалочных перекрытий можно определять
лишь четыре собственные частоты, соответствующие
верхней и нижней границам первой и второй зон сгу-
щения.
В практических расчетах можно не определять соб-
ственные частоты, большие, чем 1,5 Нт (где пп — часто-
та динамической нагрузки) и соответствующие формы
собственных колебаний. При этом минимальное число
определенных частот должно быть не менее 2.
Определение частот свободных колебаний связано
с неминуемыми погрешностями, возникающими вслед-
ствие того, что расчетная схема всегда является доста-
точно грубым приближением к действительности; зна-
чения параметров, от которых зависят жесткости,
задаются неточно и т. д.; к тому же свойства конструк-
ции могут существенно меняться в процессе ее эксплуа-
т ации из-за раскрытия трещин в железобетоне, изме-
нения масс и закона их распределения по конструк-
ции и т, д. В то же время это изменение может ока-
зывать большое влияние в тех случаях, когда одна
или несколько частот свободных Колебаний близки к ча-
стоте вынужденных колебаний.
Указанная погрешность учитывается вводом частот-
ных зон, границы которых определяются по формулам
n'== (1—е) n”; nr = (1 4- е) п® (20.41)
и т. д., где Д—r-я частота собственных колебаний
элемента, определенная в результате расчета; пг —ле-
вая граница частотной зоны; пг — правая граница ча-
стотной зоны; в—расчетная погрешность в определе-
нии частот, определяемая по табл, 20.25 и 20.26.
Для конструкций, имеющих зоны сгущения частот,
частотные зоны увеличиваются путем уменьшения низ-
шей и увеличения высшей частоты каждой зоны по
формулам:
Ф = (1-?)Д	= (1 + е) п\;
0	,	.	(20.42)
п.2 = (1 — в) Д; n2 = (1 + е) д2,
о * о ,?-
где Мр Пр ?г2, п<2— низшая и высшая частоты соответ-
ственно первой и второй зоны сгу-
щения, полученные в результате
расчета.
Для ферм эти рекомендации уточнены в инструкции
[66].
Определение частот свободных колебаний может
производиться с помощью методов и таблиц этой гла-
вы, материалов нормативного характера, нормативных
документов [19, 26, 65, 66, 24, 49] и многочисленных
материалов, опубликованных в литературе,
20,5.3.	Результаты динамического расчета
и нормативные требования
После определения динамических усилий и переме-
щений необходимо выяснить, являются ли полученные
значения допустимыми. Допускаемые с физиологиче-
ской точки зрения амплитуды скоростей и перемещений
(табл, 20 27) определяются в соответствии с санитарны-
ми нормами (СН 245-71).
Таблица 20 27[50Т
Предельно допустимые амплитуды перемещений и скоростей
при гармонических колебаниях рабочих мест в производственных
помещениях
— частота в гц; — амплитуда (пикойое значение)
перемещения в мм)
п	| а.	п	щ	ч	
1,1	3,11	5,6	0,13	22,1	0,02
1,6	2,22	6,3	0,09	25	0,018
2	1,28	н	4,056	'31,5	0 014
2^	0,73	10	0,045	40	0,0113
2,8	0,61	И,2	0,011	45	0,0102
3,2	0,44	12,5	0,036	50	0,009
4	.	0,28	16	0,028	63	0,0072
5	0,16	20	0,0225	80 90	0,0056 0,005
1,4 5,6	Среднеквадратичное значение скорости: при частоте от				
	до 2,8 гц — 11,2 мм'сек, до 90 гц — 2 мм/сек.		от 2,8 ло 5	,6 гц — 5 мм/сек и от	
Более детальная классификация кинематических па-
раметров гармонических колебаний по характеру их
действия на людей содержится в табл, 20, 28.
Таблица 20 28
Характеристика воздействия колебаний на людей в зависимости
от скорости и ускорения гармонических перемещений
с амплитудой не более 1 мм
Характеристика воздействия колебаний на людей	Продельное ускорение колебаний ®> в мм/сек’-	Предельная скорость колебаний и в мм'сск
Не ощутимы ....... Слабо ощутимы . , . . . Хорошо	»	..... Сильно ощутимы (мешаю-1-) Вредны	прн	длительном воздействии ...... Безусловно вредны . - .	Для частот от I до 10 кол,сек 10 40 125 9 9 1000 Более 1000	Для частот от 10 до 100 кпл'сск 0,16 0,64 2,0 6,4 16 Более 16
Кинематические характеристики колебаний могут ог-
раничиваться с технологической точки зрения; эти ог-
раничения должны регламентироваться технологами;
для ориентировки в этом вопросе можно пользоваться
табл, 20. 29.
Таблица 20 29
Классы машин и приборов по чувствительности к гаррдоническим
колебаниям основания
Класс машин и приборов	Характеристика машин и приборов по чувствитель- ностн к гармоническим колебаниям	Допускаемая амплитуда	
		ускорения и»; в мм'сек3 для частот 4—40 гц	скорости va в мм'се к для частот 40—400 гц
1	Высокочувствительные . .	6,3	0,1
II	Средно‘п вствительные . .	63	1
III	Малочмвствптетъные . . .	250	4
п	Нечувствительные . . .	Более 250	Более 1
376
РАЗДЕЛ 20 ДИНАМИКА СООРУЖЕНИИ
Проверка изгибаемых элементов на прочность произ-
водится по формуле
AIP ф Л1Р < М?;
проверка нт вынос швость производится по формуле
мвын,
где М — изгибающие моменты: Ж" — от расчетной ста-
тической нагрузки; Л1” — от нормативной статической
нагрузки, Л1₽ — от расчетной динамической нагрузки;
№ — предельный момент, воспринимаемый сечением,
определяемый по СНиП П-В. 1-62Д Мвыи— предель-
ный момент, определяемый согласно СНиП по рас-
де;ному пределу выносливости.
В отдельных случаях, когда динамические перемеще-
ния малы, проверку на прочность (с учетом динамиче-
ских воздействии) и на выносливость не производят.
В частности, для изгибаемых элементов перекрытий,
площадок и г. п. не учитываются динамические на-
грузки от мантии и установок всех категорий дина-
мичности, если наибольшее динамическое перемещение
от расчетных нагрузок за вычетом перемещений опор
не превышает	пролета элемента; для колони
и степ зданий, а также сюек площадок и этажерок от
машин я установок всех категорий по динамичности
проверку на прочность и выносливость не производят,
если разность горизонтальных динамических перемеще-
ний нижнего и верхнего концов колонны (стены, стойки)
в пределах этажа от расчетных нагрузок не превыша-
ет фзоооо высоты этажа.
Если полученные в результате расчета динамические
параме;ры колебаний или усилия недопустимы, то в
тех случаях, когда превышение невелико, может ока-
заться возможным получить удовлетворительные ре-
зультаты, изменив размеры сечений; это относится глав-
ным образом к тем случ, ям, когда нс выполнены тре-
бования прочности
Однако в большинстве случаев такой подход нельзя
считать правильным, и нужно разрабатывать бозсе ра-
дикальные и эффекте -ые и в конечном итоге ботее
экономггчныс методы с’ггжения уровня вибрации
(см. 20.6),
20.6.	ВИБРОНЗОЛЯЦИЯ И ДРУГИЕ СПОСОБЫ
БОРЬБЫ С ВИБРАЦИЯМИ
20.6.1.	Виброизоляции
Виброизоляция — одно из наиболее простых и эф-
фективных конструктивных решений, уменьшающих
вредное влияние вибраций.
Задачей активной впброизоляпчи является сущее;вен-
ное уменьшение динамической составляющей сил, ш -
редаваемых неуравновешенной машиной на опорную
коишрукцивд. в результате чего уменьшатся вибрации,
передаваемые изо тируемыми машинами на сооруже-
ние. При проемировании и расчете активной виброню-
ляцпи важную роль играет характер динамического
возденетвия маппшы
Пассивная виброи’отшшя предназначена для изоля-
ции то-шых приборов, ппеппзиоиных станков, рабочих
помосгщ и т л от вредного мпяшщ колебании под-
держивающих гонг трупшш. При расчете пассивно >
вибропзотяпни цгобюэлчмо -щать характер колебании
подд.р.А':. л; 1 го -румити.
20.6.2.	Принципиальная схема работы
виброизолированной установки.
Конструктивные схемы виброизоляции
и виброизоляторов.
Содержание и задачи расчета
Если в состав машины входит направленный верти-
кальны;! вибратор с массой вращающихся частей ть чис-
лД
лом оборотов в 1 мин. N (круговая частота р = ~— \ экс-
0V
цеятрицитето.м вращающихся частей г?, то амплитуда
силы, передаваемой вибратором, равна Рд==т;р2е.
В вес виброизолированной установки P = mg включает-
ся полный вес машины, опорной рамы и постамента или
блока. Постаментом или блоком называется часть фун-
дамента под машину, жестко с ней связанная и соеди-
ненная с опорной конструкцией системой гибких опорных
элементов — амортизаторов или виброизоляторов. Если
суммарную жесткость виброизоляторов в вертикальном
направлении обозначить через Сг, то круговая частота
собственных колебаний виброизолированной установки
ч /^7
будет (0= а/ ---- . При проектировании виброизолнро-
F !П
ванной установки круговая частота m выбирается так,
р
чтобы отношение у—----было достаточно большим —
й
порядка 4—5 и более. В этом случае при работе вибрато-
ра колебательная система «установка — опорные пру-
жинит будет находиться в зарезонансном режиме, и со-
гласно формуле (20 5) получаем, что пружины передают
на основание силу, амплитуда которой, если пренебречь
влиянием затухания, равна:
Рд
(20.43)
у- — 1
Так как уменьшение амплитуды силы, передаваемой
на опорную конструкцию, в основном определяется от-
ношением частотных характеристик, то для достижения
доажного эффекта виброизолягоры должны быть до-
статочно податливыми.
При проектировании виброизоляции следует учиты-
вать прохождение через резотне в процессе пуска или
остановки машины.
Для уменьшения амплитуд колебаний при прохож-
дении через резонанс нужно применять виброизолято-
ры, имеющие достаточно большое затухание (например,
комбинированные — .металлорезиновые или резиновые
виброизолягоры). Затухание обычно мало сказывается
на качестве гшброиэоляпии в эксплуатационном режиме,
Виброизолированная установка может быть выпо ще-
на в опорном (рис 20.33) и подвесном варианте
(рис. 20.34 и 20 35), В первых двух щучаях чиброию-
ляторы работают на сжатие, в третьем — на растя-
жение (рис 20 35).
Если отметка основания блока ниже уровня пола, то
он опирается па днище железобетонного короба, назы-
ваемого взшгой (рис. 20,36).
Конструкция внброизояяторов г гибкими ет.лтьрыми
пружинами показана на рис, 20 37, Дтя демпфирования
колебании в процессе пуска (остановки) нецел! зуютс-.г
вязкие демпферы — системы, состоящие щ поршня ко-
торый при колебаниях движется в сосущ, наполненном
вязкой жидкостью (рис. 20 38); элементы в которых
возникает cvxoe трение, например рессоры (рис 20 39),
цсзиногыс элементы.
20 6 ВИБРОИЗОЛЯЦИЯ И ДРУГИЕ СПОСОБЫ БОРЬБЫ С ВИБРАЦИЯМИ
377
Все демпферы включаются в конструктивную схему
параллельно гибким опорным элементам.
В качестве гибких элементов могут быть приняты и
резиновые виброизоляторы; в этом случае необходимое
сопротивление для уменьшения амплитуд колебаний
Рис. 20.33
Рис 20.34
Рис. 20.35	Рис. 20.36
Рис. 20.37
Рис. 20.38	Рис. 20.39
в процессе пуска и остановки получается за счет внут-
реннего поглощения в материале влброизолятора.
Для нормальной работы виброизоляции необходимо,
чтобы все примыкания трубопроводов и других соедини-
тельных элементов были достаточно гибкими, для чао
применяются гибкие вставки.
Под расчетом виброизоляции подразумевается опре-
деление основных параметров виброизолировапной уста-
новки— массы блока, моментов инерции массы блока,
жесткости виброизоляторов, их количества и располо-
жения в плане, установление необходимых параметров
затухания. Расчет вибронзо.тяции обычно проводится но
проверочной схеме. До расчета задаются ориентировоч-
но чпеленш.гни значениями сооишг ицющих конструк-
тивных ьаргшстров, т жнем лгюгц> йог, насколько пра-
вильно оы.'Ш заданы эти значения.
Расчет виброизоляции состоит из проверки работы
виброизоляции в двух режимах: а) эксплуатационном и
б) переходном.
Для проверки виброизоляторов па прочность и подат-
ливость определяются напряжения и перемещения в гиб-
ких элементах; в необходимых случаях проводится про-
верка пружин на устойчивость.
20.6.3.	Расчет виброизоляции
Активная виброизоляция при
периодических нагрузках
При расчете активной виброизоляции необходимо оп-
ределшь, в какой степени уменьшается величина ампли-
туды силы Рв, передающейся на поддерживающую кон-
струкцию, по сравнению с амплитуде.» заданной дина-
мической нагрузки Рл Эффективность активной вибро-
изоляции определяется коэффициентом передачи силы
Обычно р принимается равным Дгз—’До. Если из тех
или иных соображений задается щ то v определяется
из формулы (20.44).
Изгоювление виброизоляторов, обеспечивающих ча-
стоту свободных колебаний установки ниже 2 гц, за-
труднительно, поэтому виброизоляция наиболее эффек-
тивна и проста в изготовлении для машин, число обо-
ротов которых превышает 500 об/мин. В диапазоне
350—500 об/мин можно в качестве исключения допу-
скать увеличение коэффициента и, однако так, чтобы
Частота собственных колебаний установки не опреде-
ляет однозначно размеров постамента и жесткости ьиб-
роизоляторов.
После определения необходимой частоты свободных
колебаний виброизолированыого фугдамепта основные
параметры виброиэоляцин — масса установки т и об-
щая жесткость виброизоляторов с — определяются ис-
ходя из допускаемой амплитуды колебаний блока, ко-
торая назначается иа основании технологических требо-
ваний.
Подсчет амплитуды вертикальных колебаний произ-
водится но приближенной формуле
' Рг
дв„ = —----- ,	(20.45)
тр"
В тех случаях, когда нужно учитывать горизонталь-
ные и вращательные колебания фундаментов, амплиту-
ды горизонтальных колебаний центра тяжести блока
ерх, ими определяются по формулам:
Рх	Рц
авх-^------ ;	— •	(20.46)
тр- ‘ то-
Амплитуды углов поворота <рок, рпу. цщ, возникаю-
щих при вращательных колебаниях, находятся по при-
б л и ж е н н ы м ф о р м у л а м.
«?ог, “	;	(20.47)
‘Цу/ р
7 nn
(12 Р"
Принятые обозн"дЧ-Я1Шн
?л, Ру И Р2— d	„;ы Л п ЯВЛЯЮЩИХ В03\\Ш2Ю-
щеи силы в яанраплении осел х/.
И <’о в кГ;
378
РАЗДЕЛ 30, ДИНАМИКА СООРУЖЕНИИ
Мш, Maj,, Mf)Z— амплитуды возмущающих моментов
относительно осей х0, у0 и г0
в кГ • см;
JBX, Д и Д—моменты инерции массы изолиру-
емой установки относительно осей
х0, У о и z0 в кГ-см-сек2;
т-=О g— масса всей установки, равная сум-
ме масс изолируемой' машины и пос-
тамента, в кГ-секУ-см-1;
р~2'Л.н„ — круговая частота возмущающей си-
лы;
«0=7/60—частота возмущающей силы в гц;
N — число оборотов (циклов) машины в
1 мин.
Оси Хо, Уо, г0 являются главными центральными ося-
ми инерции виброизолируемой установки.
Ориентировочная величина амплитуды горизонталь-
ных колебаний наиболее удаленной от плоскости
точки (точки с максимальной амплитудой горизонталь-
ных колебаний) изолируемого обьекта в направлении
осей х0 и Уо определяется по одной из формул:
ах = айх + ц>у уг; ау-= айу + флц2, (20.48)
где гц— расстояние (в направлении оси z0) между
плоскостью хуОуо и наиболее удаленной от этой плос-
кости точкой изолируемой установки.
Амплитуду горизонтальных колебаний г-й точки уста-
новки, для которой задано допустимое значение этой
амплитуды, подсчитывают по формуле (20.48) с подста-
новкой вместо v2 величины v22, равной координате г-й
точки на оси га.
Приближенные значения амплитуд колебаний J-й точ-
ки установки, вызванных только вращательными коле-
баниями последней относительно осей х0, и До (без
учета поступательных колебаний центра тяжести уста-
новки), допускается определять по формулам:
ajx ~ фох и!х", aiy ~ Уоу uiy'i aiz = Фог и/г>
где и1х, Ujy и Uj2 — расстояния от соответствующей оси
вращения х0, у0 и г0 до наиболее удаленной от нее /-Й
точки установки.
В случае, когда вычисленные по формулам (20.45),
(20.46), (20.47), (20.48) амплитуды колебаний установки
окажутся больше допустимых, необходимо увеличить
массу пг и моменты инерции путем устройства специаль-
ного постамента или увеличения его размеров, если по-
стамент был ранее предусмотрен.
Величина коэффициента неупругого сопротивления
6В	Фв	,
ув = ---= ——' , характеризующего демпфирующие
л	2л
свойства (затухание) в виброизоляторах, определяется
по графику (рис. 20.40) в зависимости от углового уско-
рения е (в гц/сек) и отношения максимальной амп-
литуды колебаний установки при пуске или остановке
машины «яак0 (в см) к амплитуде вертикальных коле-
баний установки при рабочем режиме машины а02
(в см), где По — частота свободных вертикальных коле-
баний в гц.
Зная величину е и задавшись отношением Дмакс/Дог,
по графику определяют величину минимально необходи-
мого значения уы. Если найденная по графику величи-
на ув^0,03, то можно применять виброизоляторы из
одних стальных пружин. При ув>0,03 необходимо при-
менение резиновых виброизоляторов или комбинирован-
ных внброизоляторов, состоящих из стальных пружин
и резиновых элементов,
Виброизоляция вентиляторов может выполняться с по-
мощью одних пружин, так как гибкие патрубки, соеди-
няющие вентиляторы с воздуховодами, обеспечивают
достаточное затухание.
Пассивная в и бро изол яци я
При проектировании пассивной виброизоляции необ-
ходимо знать частоту колебании основания <и0. Для оп-
ределения частоты свободных колебаний виброизолиро-
ваннон установки иг задаются коэффициентом передачи
ц, равным отношению амплитуд перемещений установки
и основания, после чего находят отношение
= |у —. Обычно	коэффициент
неупругого сопротивления принимается равным у аг
аг 0,04=0,05. Расчет виброизоляции подробно рассмотрен
в руководстве [49а].
20.6.4.	Другие способы борьбы с вибрациями
строительных конструкций
В тех случаях, когда при проектировании сооружений
полученные в результате динамического расчета харак-
теристики колебаний строительных конструкций не удов-
летворяют требованиям норм с точки зрения прочности,
воздействия на людей или влияния на приборы или ма-
шины, следует уменьшать расчетный уровень колебаний
в запроектированном сооружении.
Имея в виду трудности, возникающие при борьбе с
вибрациями в эксплуатируемом сооружении, необходи-
мо обратить внимание на учет динамического фактора
при проектировании, В случае, если вибрации возникли,
то всякие меры по борьбе с ними возможны только пос-
ле тщательного обследования, сопровождаемого инстру-
ментальным замером величин, характеризующих колеба-
20 G ВИБРОИЗОЛЯЦИЯ И ДРУГИЕ СПОСОБЫ БОРЬБЫ С ВИБРАЦИЯМИ
379
ния, и внимательного изучения источников колебаний
и динамических характсришик стропы.тьиых конструк
ций. Нельзя дать общих правил для выбора наилучшего
мероприятия по борьбе с вибрациями. В каждом отдель-
ном случае паилучший способ будет найден в результа-
те инженерного анализа, учитывающего как теоретиче-
скую, так и практическую сторону дела, т. е. эффектив-
ность, простоту и экономичность рекомендуемых меро-
приятий.
Выбор мероприятий сопровождается динамическим
расчетом, позволяющим в ряде случаев надежно уста-
новить, насколько уменьшатся при измененных условиях
величины, характеризующие колебания (амплитуды, ско-
рости, ускорения и т. д.). Во многих случаях речь идет
главным образом об уменьшении амплитуд перемеще-
ний, так как обычно нас интересуют колебания с задан-
ной частотой.
20.6.5.	Мероприятия по уменьшению
вынужденных колебаний,
передаваемых машинами
Один из способов уменьшения колебаний — снижение
амплитуды динамических нагрузок. В тех случаях, ког-
да машины принадлежат к числу номинально уравно-
вешенных, для уменьшения колебаний рекомендуется
провести балансировку, в первую очередь статическую.
В машинах с конструктивно неуравновешенными дви-
жущимися частями рекомендуется динамическое уравно-
вешивание, а также спаривание (или страивание) отдель-
ных кривошипно-шатунных механизмов. Если колебания
сооружений вызваны работой близко расположенных
мощных низкочастотных компрессоров, спаривание мо-
жет быть эффективным средством борьбы с вибрациями
только при проведении жесткой синхронизации работы
машин для исключения возможности возникновения
биений; рекомендуется также устройство антивибраторов.
При ярко выраженном резонансном характере колеба-
ний можно попытаться изменить число оборотов маши-
ны (уменьшить или увеличить), если это допустимо по
технологическим соображениям, избегая совпадения но-
вой частоты возмущающей силы с другой частотой соб-
ственных колебаний конструкции.
Виброизоляция наиболее эффективна для машин
с числом оборотов в минуту 500 и более; степень эф-
фективности растет с числом оборотов. В отдельных
случаях применение правильно рассчитанной виброизо-
ляции не дает положительных результатов. Причиной
этого могут быть дефекты конструирования и монтажа,
приводящие к тому, что жесткость виброизоляторов бу-
дет значительно выше проектной. Например, при резино-
вых виброизоляторах любые боковые обоймы
(рис. 20.41) или стенки резко повышают жесткость виб-
роизоляторов, так как пе дают резине возможности рас-
ширяться в поперечном направлении; при пружинных
виброизоляторах сильная предварительная затяжка мо-
жет полностью ликвидировать податливость, т е. нару-
шить основное условие работы виброизоля гора. Нако-
нец, отсутствие или малая подаiливоегь птбжпх вставок
в местах примыкания труб и других конструктивных эле-
ментов к изолируемой машине также может быть причи-
ной плохой работы виброизоляции.
Вертикальные колебания перекрытия могут быть
уменьшены, если машины, передающие вертикальные
динамические нагрузки, поместить вблизи опор. Гори-
зонтальные колебания здания можно уменьшить, рас-
положив машины так, чтобы горизонтальные дипампш-
ские силы были ориентированы а том направлении, ко-
торому соответствует большее значение произведения
<(1—v~), где с — жесткость, равная 1/6,,; 6„— стати-
ческое перемещение каркаса от единичной силы на от-
метке перекрытия; м— отношение частоты вынужден-
ных колебаний к частоте собственных.
При изменении расположения машин на перекрытии
изменяется спектр частот; при приближении машин
к опорам частоты свободных колебаний перекрытия по-
вышаются.
Рис. 20.41
Увеличение жесткости сооружения служит при опре-
деленных условиях одним из эффективных способов
борьбы с вибрациями, поскольку при этом возможно
также существенное уменьшение колебаний за счет из-
менения частоты свободных колебании, при которой
конструкция выходит из состояния резонанса.
Частоты основного тона междуэтажных перекрытий
обычно составляют 8—15 гц, что соответствует часто
встречающимся числам оборотов машин (480—
900 об!мин).
Для предупреждения резонансных колебаний можно
в отдельных случаях увеличивать жесткость балок, с тем
чтобы частота основного тона свободных колебаний ста-
ла значительно выше частоты вынужденных колебаний
Для того чтобы изменение жесткости было достаточно
большим, рекомендуется в случаях, когда это возможно,
уменьшить пролет, например путем устройства дополни-
тельных опор, применения легких порталов или усиле-
ния шпреигетями (рис. 20 42). При стальных балках
возможно увеличение жесткости путем приварки допол-
ни типи элементов или обетонирования. В железобе-
нишых бачках для увеличения жесткости рекомендует-
ся обетопнрование, а если уменьшение высоты помеще-
ния нежелательно — устройство больших вутов по кон-
цам балки па протяжении ее крайних третей (о недостат-
ках метода см. стр. 376).
В отдельных случаях, когда машины стоят на пере-
крытии и их пос гамет имеет значительную протяжен-
ность по сравнению с пролетом балки, связь этого поста-
мента с балкой может заметно повысить жесткость.
При гори тотальных колебаниях рамного стального
или железооеюппого каркаса следует учесть, что в этих
сравпшельно низкочастотных конструкциях (порядка
380
РАЗДЕЛ 20 ДИНАМИКА СООРУЖЕНИИ
3—5 гц) колебания мтут возникать вследствие работы
сравнительно низкочастотных машин с горизонтальными
инерционными силами, установленных на перекрытиях
или близлежащих фундаментах. В ряде случаев очень
хорошие результаты дает применение крестовых связей
в плоскости рам (рис. 20,43), которые резко повышают
частоту, увеличивая общую жесткость здания.
Колебания, о которых идет речь, при проектировании
усиления обычно имеют весьма малую амплитуду. По-
этому прикрепление всех усиливающих элементов —
крестов, порталов и др. — должно быть жестким, без ка-
ких-либо малейших зазоров или люфтов; рекомендуется
эти элементы приваривай,, хорошо обетонироиащ сты-
ки и т, д.
В отдельных случаях, когда колебания носят ярко
выраженный резонансный характер, с большим коэф-
фициентом резонансного увеличения, можно уменьшать
жесткость, с тем чтобы поньмачься перевести конструк-
цию в зарезонансный режим. Однако этот вариант тре-
бует особо тщательной прош-ркн, так как возможные ре-
зонансы с обертонами будут более опасными, чем в не-
измененной конструкции, и, кроме того, может ухуд-
шиться работа конструкции на действие статических на-
грузок; в этом случае необходим расчет на прохождение
через резонанс.
20.6.6.	Мероприятия по уменьшению
колебаний при прохождении через резонанс
Для уменьшения колебаний при прохождении через
резонанс рекомендуется:
повышать скорость прохождения через резонанс, ко-
торая характеризуется значением углового ускорения
в момент, когда угловая скорость равна частоте соб-
ственных колебаний. Обычно скорость прохождения при
остановке значительно ниже, чем при пуске; ее можно
повысить устройством тормоза — механического, осно-
ванного на трении, или электрического, основанного на
использовании контртока в момент остановки;
применять демпфирующие приспособления. Наряду с
демпферами сухого и вязкого трения желательно ис-
пользовать устройства, включающиеся в работу только
во время прохождения через резонанс я не влияющие на
работу в эксплуатационном режиме. К числу этих уст-
ройств относятся
1) ударные и динамические гасители колебании, на-
строенные на частоту собственных колебаний;
2) демпферы сухого и вязкого трения, включающиеся
при больших амплитудах и не принимающие учшчпя
в колебаниях при небольших амплитудах в эксплуата-
ционном режиме; демпферы можно включать последо-
вательно через упругий элемент.
ЛИТЕРАТУРА
I,	Ананьев Н В Справлччик по расчету собственных
колебаний упругих стилем- ОГИЗ Гостехиздаг, 194о.
2.	Андронов А. А., Хайкин С, Э, и Витт В, И,
Теория колебаний, Госгогошдат, 1958,
3.	Баркан Д, Д. Динамика оснований и фундаментов
Стройвсеимориздш, 1948.
4.	Безухов Н. П Динамика сооружений в задачах я
примерах, Госстройиздат, 1947.
5.	Белоус А А, Метод деформаций в динамике рамных
конструкций, Сб, «Исследования по теории сооружений», вьш, 3.
Госстройиздат, 1939,
6,	Б е л о у с Л. А Колебания и статическая устойчивость
плоских и пространственных рам. Сб. «Расчет пространственных
конструкций», вып. ПГ Гос. изд, лит. ро стр. и арх,, 1955.
7.	Бернштейн С. А. Основы динамики сооружений.
Госстройиздат, 1911.
8,	Болотин В. В, Динамическая устойчивость упругих
систем. Гостехтеоретиздат, 1956,
9,	Бондарь ГЕ Г. Устойчивость и колебания параболиче-
ских арок. «Инженерный сборник», т. ХШ, АН СССР ОТН, 1952.
10.	Быховскпй В. А.„ Карапетян В. К, Библио-
графический справочник по инженерной сейсмологии и сейсмо-
стойкости сооружений Ереван. Изд-во АН Арм.ССР, 1964.
И.	Власов В. 3. Тонкостенные упругие стержни. Гос,
изд. строительной литературы, 1940.
12,	Гол ь денбл ат И. И. Динамический продольный из-
гиб тонкостенных стержней, «Инженерный сборник», т. V АН
СССР, 1948.
13,	Г о ль де иб л ат И. И., Сизов А. М, Справочник
по расчету строительных конструкций на устойчивость и коле-
бания. Гос, изд. лит., по стр, и арх , 1952.
14,	Д е п - Г а рто г Дж. П. Теория колебаний. Перевод со
второго американского издания А. Н. Обморшева. Гостехтеорег-
издат, 1942.
15,	Динник А. Н. Устойчивость упругих систем. Изд. АН
СССР, 1950.
16,	Динник А. Н. Избранные труды, т. И, Киев, 1955,
17.	3 авриев К. С. Динамика сооружений. Трансжелдор-
издат, 1946,
18,	Изменение № I к разделу СНиП И-А.11-62. («Бюллетень
строительной техники» № 4, 1965).
19.	ЦНИИСК им, В. А, Кучеренко Инструкция по расчету
несущих конструкций промышленных зданий и сооружений на
динамические нагрузки. Сгройизда!, 1970.
Г9а. Инструкция по расчету покрытий промышленных зда-
ний, воспринимающих динамические нагрузки. ЦНИИСК
им. В. А„ Кучеренко Госстроя СССР. Стройиздат, 1967.
20,	Инструкция по проектированию и расчету виброизоляции
машин с динамическими натре .нами и оборудования, чюютвм-
тельного к вибрациям (И-2(М^55/МСПМХП) Минметаллургхи?л-
строй, ЦНИПС, Гос. изд, лит. ио стр. и арх , 1956.
21,	Инструкция по устранению вредных воздействий вибраций
рабочих мест на предприятиях железобетонных изделий
(СН 190-61), Госстройиздат, 1962,
22,	Инструкция по определению расчетной сейсмической на-
грузки для зданий и сооружений. Госстройиздат, 1962.
23.	Инструкция по проектированию железобетонных дымовых
труб. Стройиздат, 1962 (НИИЖБ АСиА СССР. Теплопроект Мин.
стр-ва РСФСР).
24,	Инструкция по расчету жилых, гражданских, промышлен-
ных и сельскохозяйственных зданий и сооружений на сейсмиче-
ские воздействия, Стройиздат, 1963.
Инструкция по определению динамических нагрузок от
машин, устанавливаемых на перекрытиях промышленных зданий.
Стройиздат. 1966 (ЦНИИСК им, Кучеренко Госстроя СССР).
F 26 Инструкция по расчету перекрытий на импульсивные .на-
грузки. Стройиздат. 1966 (Ц'НИЙСК им, Кучеренко Госстроя
СССР).
27.	Инструкция по мерам борьбы с вибрационными воздейст-
виями технологического оборудования прн проектировании зда-
ний и сооружений промышленности нерудных строительных ма-
териалов, Стройиздат, 1963.
28.	II о р и ш Ю. И. Измерение вибраций. Машгиз, 1956,
29,	Карман Т< и Био М. Математические методы в
инженерном деле. Перевод с английского, Гостехтеоретиздат,
1946.
30,	Кац А, М, Вынужденные колебания при прохождении
через резонанс. «Инженерный сборник», т. 3, вып. 2. Изд. АН
СССР, 1947.
31.	К и р н о с Д, П, Некоторые вопросы инструментальной
сейсмологии. Изд. АН СССР, 1955,
32.	Коренев Б. Г., Сысоев В. И. Метод гашения
колебаний сооружений башенного типа «Бюллетень строитель-
ной техники», 1953, М 5.
33.	Коренев Б. Г. Некоторые задачи теории упругости
и теории теплопроводности, решаемые в бесселевых функциях,
Физматгиз, 1960,
Я Коренев Б. Г„ Пановко Я. Г. Динамический
расчет сооружений, В кн,: «Строительная механика в СССР
1917—1967». Под ред. И. М. Рабиновича. Стройизлащ 1964
35,	Коренев Б, Г. Расчет промсооружечиЙ на действие
эксплуатационной динамической нагрузки «Строительная меха-
ника и расчет сооружений», 1962, № 4
36.	Корчи некий И, Л Расчет строительных конструк-
ций на вибрационную нагрузку, Стройиздат, 1048.
ЛИТЕРАТУРА
381
37,	Крылов А. Н. Вибрация судов, т. X, Изд. АН СССР,
194 В.
33.	Лойцянский Л. Г. и Лурье А. И. Курс icnpe-
тической механики, т. II, Готехгсоретиздат, 1955.
39.	Лурье А. И, Методы динамического расчета соору-
жений. Снрзвочиз-ж. инженера-проектировщика промсиоружений,
1, И, расчетно-теоретический. Госстройнздат, 1934.
40.	М а к а р и ч е в В. В Фундаменты под турбогенерато-
ры, Госэнергоиздат, 1У5Е
41.	Медведев С. В. Инженерная сейсмология. Госстрой-
издац 1900
42.	М ед в е дев С, В. и др, Сейсмические воздействия на
здания и сооружения Стройиздат, 19b8.
43,	Пановко Я. Г. Основы прикладной теории упругих
колебаний Машгиц 1957.
44.	П а новко Я. Г, Состояние и перспективы проблемы
учета гистерезиса в прикладной теории колебаний. Труды иауч-
но-техя. совещания по изучению рассеяния анергии при колеба-
ниях упругих тел. Киев. 1958.
45,	Подольский В, Г. Вибрация конструкций при су*
хо.м трения между элементами. Харьков, изд. «Прайор», Г97О.
46.	Поляков С. В. Сейсмостойкие конструкции зданий,
«Высшая школа», 1969,
47,	П ф е й ф ф е р ГЕ Колебания упругих тел. Гоштехтеорет-
издат, 1934.
48.	Рабинович И, М., Синицын А. П., Тере-
я и и В. М Расчет сооружений на действие кратковременных
и мдновешшх сил, Изд. ВИА, ч. I, 1956, ч. П, 1958,
49,	Расчет каркасных зданий на сейсмические воздействия
с учетом высших форм колебаний (таблицы и графики), М,.
1964. Напечатано на ротапринте.
49а	. Руководство по проектированию виброизоляции машин
и оборудования. ЦНИИСК им. В. А. Кучеренко Госстроя СССР.
СтроЙиздат, 1972.
50.	Санитарные нормы проектирования промышленных пред-
приятий (СМ 245-71), Стройиздят, 1972.
5L Смирнов А. Ф Устойчивость и колебания сооруже-
ний. Трансжелдоризда!, 1958. См, также «Теория сооружений»,
г. Ш. Грансжелториздат, 1948.
52 СНиП II-AJ1 -62. Нагпузки и воздействия.
Г>3, СНиП II-А. 12-62 Сейсмостойкое строительство.
51,	СНиП II-B.l-u2*. Ьетониые и железобетонные конструкции.
55.	Рекомендации по экспериментальному определению ди-«
намических характеристик машин предприятиями машиностоои-
тельной промышдезтности. ЦНИИСК. им, В. А. Кучеренко. Гос-
строя СССР Стройищат, 1972
56.	Солодовников В. В. Введение в статистическую
динамику систем автоматического регулирования. Гостехпздат,
1952.
57.	Сорокин Е. С. Динамика междуэтажных перекрытий,
Госстрой из д а 'г, 1941,
58,	Сорокин Е. С, Метод учета неупругого сопротивле-
ния материала при расчете конструкций на колебания. Сб. «Ие-
•ле.тования по динамике сооружений». Сзройизды, 195).
59.	Сорокин Е, С Динамический расчет несущих кон-
струкций здании. ГосшройпздиТ, 1956,
60.	Стрелков С, ГЕ Введение в теорию колебаний Гос-
т&Х1еоретизда1, 1950,
61,	СНиП И-Б 7-70. Фундаменты машин с дннамичщжимй
нагрузками. Строки щат, 1971.
Щ', Г и м о ш е и к о С. 11. Теория колебаний в инженерном
деле. Гос, научно-юхпнч, изд., 1932.
63.	Указания но определению сейсмической нагрузки для
вертикальных аппаратов и примеры расчета. Стройиздат, 1961,
С4 Указания по проектированию конструкций крупнопанель-
ных жилых номов (СН 321-65). Стройиздат, 1966.
65.	Указания по проектированию конструкций крупнопанель-
ных жилых домов, строящихся а сейсмических районах
(СН 328-65). Стройиздат, 1966.
Ьб, Инструкция ио расчету покрытий промышленных зданий,
нос1'ринимающ1!.< динамические нагрузки. Стройиздат, 1967,
67.	Указания по расчету на ветровую нагрузку технологичес-
кого оборудования лолонного типа к от крытых этажерок. Строй-
издат, 1963.
68.	Ф и л и л п о в А. П. Колебания деформируемых систем.
«Машиностроение» , 1070.
69.	Чуд новей нй В. Г. Мыоды расчета колебаний и
устойчивости стержневых систем, Киев, Йзл. УССР, 1952.
70.	Чуковский В. Г. Исследование колебаний и
устойчивости пластинок. Сб. «Расчет пространственных конст-
рукций» иод род. С. А. Алексеева, В. В., Новожилова,
А, А. Уманского. Вып. XI. Стройиздат, 1967.
71.	Byegly Perry, Seismology, New York, Prentice—Hall,
Inc.. 1912.
72.	Honsner G., Dynamic Pressures on Accelerated Fluid
Containers, Bulletin of die. Seismological Society of America,
47, № 1. January, 1957.
73.	Jacobsen L, S. Impulsive Hydrodynamics of Fluid
Inside a Cylindrical Tank and of a Fluid surrounding a Cylind-
rical Pier. Bulletin of the Seismological Society of America,
vol. 39, 1949.
74,	Kirchhoff G Liber die Transversalschv, Ingungen eines
Stcibes, Wied. Ann, 10. 501-612, 1880.
75.	Lamb H.. Hydrodynamics, Cambridge University Press,
1932, or Dover Publications, New York, 1945.
76.	M a c d u f f Y. N. and Pel gar I?. P,, Vibration Frequen-
cy Charts, Machine Design, February, 7. 1957.
77.	Mononobe N., Zeitschrift fur angew. Math. Bd. L
S, 444, 1921,
78,	Рекомендации no уменьшению вредных вибраций рабочих
мест на предприятиях железобетонных изделий ЦНИИСК им.
В. А. Кучеренко Госстроя СССР, Стройиздат, 1972.
79,	Санитарные нормы проектирования промышленных пред-
приятий СН 245 71 (Госстрой СССР). Стройиздат, 1972.
80.	Справочник по динамике сооружений Под ред. Б. Г. Ко-
ренева и Й. М, Рабиновича, Стройиздат, 1972,
81.	Коренев Б. Г., 3 е в и н А. А., Резников Л, М„
Сравнительный анализ зффектившгсти динамического !А ударно-
го гасителей колебаний. «Строительная механика и расчет соо-
ружений», 1972, № 3,
82,	Гонткевич В, С. Собственные колебания пластинок
и оболочек. Справочное пособие. Киев, «Няукова думка.», 1964.
РАЗДЕЛ 21
РАСЧЕТ КОНСТРУКЦИЙ (СТЕРЖНЕВЫХ, ПЛАСТИНОК И ОБОЛОЧЕК)
ПО ПРЕДЕЛЬНОМУ РАВНОВЕСИЮ И УЧЕТ ПОЛЗУЧЕСТИ
21.1. ОСНОВНЫЕ ПОЛОЖЕНИЯ
ПО РАСЧЕТУ КОНСТРУКЦИЙ
в состоянии ПЛАСТИЧНОСТИ
Учет неупругих свойств материалов позволяет надеж-
нее оценивать поведение конструкции под нагрузкой
и в большинстве случаев получать более экономичное
решение по сравнению с расчетом конструкции как уп-
ругой системы.
Отклонения от идеально упругих свойств связаны
с образованием остаточных пластических деформаций и
развитием деформаций ползучести (см. раздел 12). Рас-
чет с учетом пластических деформаций в первую очередь
связан с оценкой несущей способности элементов кон-
струкций или всей конструкции в целом. При этом ос-
новное внимание уделяется определению максимально
возможной нагрузки, которую еще может нести кон-
струкция без разрушения, а развивающиеся к этому мо-
менту деформации имеют второстепенное значение.
По современным строительным нормам определение
несущей способности является расчетом по первому пре-
дельному состоянию.
Предельной нагрузкой на конструкцию называется
такая нагрузка, которую конструкция может выдержать
без разрушения ее основных элементов.
Напряженное состояние всех элементов конструкции
в такой стадии называется состоянием предельного
равновесия,
В конструкциях, в которых предельное равновесие
определяется свойствами пластичности, исчерпание не-
сущей способности означает возможность развития
чрезмерных деформаций при постоянной предельной на-
грузке.
Основным объектом приложения теории предельного
равновесия являются статически неопределимые кон-
струкции из различных материалов — строительных ста-
лей, железобетона, синтетических материалов. Эта тео-
рия применяется для определения несущей способности
самых разнообразных конструкций: от простейших
стержневых систем до сложных оболочек.
21.1.1. Поведение конструкций
в пластической стадии
До тех пор, пока напряжения во всех элементах кон-
струкции не превосходят предела текучести от, зависи-
мость нагрузка—деформация практически линейная
и конструкция рассматривается как упругая, С появле-
нием напряжений, равных пределу текучести, рост на-
грузки отстает от роста деформаций. На рис. 21.1 пока-
зана балка, загруженная увеличивающейся равномерной
нагрузкой. До нагрузки	напряжения по
сечению распределены линейно и кривизна изогнутой
оси балки постоянна по длине (l/p = qlEl). С увеличе-
нием нагрузки распределение напряжений все более от-
личается от линейного, и зоны пластичности (участки
сечения с напряжением ст) увеличиваются. При этом
на участке, охваченном пластическими деформациями,
кривизна увеличивается (линия 2 на рис. 21.1). Часть
Рис. 21.1
При малых значениях §
сечения между зонами пластичности называется упругим
ядром, которое с ростом нагрузки уменьшается; кривиз-
на изогнутой осн обратно пропорциональна высоте это-
I	От
го упругого ядра: -— = ~—
Р	<- =
кривизна становится очень большой величиной, а изги-
бающий момент незначительно отличается от момента,
который может воспринимать все сечение, находящееся
в состоянии пластичности (состояние 3 на рис. 21.1).
Несмотря на то что полного состояния пластичности
достичь не удается, однако при нагрузках, очень близ-
ких к такой теоретической величине, развиваются
столь значительные деформация, что конструкция прак-
тически выходит из строя. При этом размеры упругого
ядра так малы, что зоны пластичности заполняют тре-
угольники acb и a'cb\ а развившиеся в среднем сечении
пластические деформации приводят к прогибам, очень
близким к тем, какие были бы при переломе оси балки
в среднем сечении. В такой стадии работы балка не
в состоянии воспринимать дополнительную нагрузку,
и происходит движение балки с переломом оси в середи-
21.1, ОСНОВНЫЕ ПОЛОЖЕНИЯ ПО РАСЧЕТУ КОНСТРУКЦИЯ В СОСТОЯНИИ ПЛАСТИЧНОСТИ
383
не и увеличением учла 0. Эта картина такая же, как
движение кинематическою механизма, состоящего из
двух жестких дисков, соединенных шарниром в точке С,
только в балке на месте шарнира в точке С действует
(тт h"
постоянный изгибающий момент М-ал =--------, Поэтому
4
в предельном состоянии балка, или любая другая кон-
струкция, называется пластическим кинематическим
механизмом. Нагрузка, приводящая к образованию та-
кого пластического механизма, называется предельной.
Превращение жесткой конструкции в пластический
кинематический механизм, состоящий из жестких дис-
ков, соединенных пластическими шарнирами, сопровож-
дается исчерпанием несущей способности конструкции из
упруго-пластического материала.
21.1.2. Основные положения теории
предельного равновесия
Теория предельного равновесия конструкций основана
на следующих положениях, в определенной степени
идеализирующих свойства материала и условия работы
отдельных элементов конструкций.
а)	Элементы конструкций обладают идеально упруго-
пластическими свойствами, что выражается в зависимо-
сти сила — перемещение, показанной иа рис. 21.2, а. Та-
кая зависимость называется диаграммой Праидтля.
Под термином сила следует понимать любое усилие:
от продольной силы до изгибающего или крутящего мо-
мента. Термин перемещение соответствует деформации
по направлению действия силы от линейного удлинения
до изменения кривизны оси или закручивания.
б)	Деформации упругого характера достаточно ма-
лы, чтобы не учитывать их в изменениях геометрических
размеров конструкции (геометрическая схема не изме-
няется), ио деформации пластичности могут быть любой
величины, необходимой для реализации перераспределе-
ния напряжений.
Это предположение о так называемых идеально жест-
ко-пластических свойствах фактически приводит к идеа-
лизированной диаграмме напряжений (рис. 21,2,6),
когда считается, что при усилиях	никаких де-
формаций нет (0 = 0), а при усилии /V=.zVn;t могут
быть любые деформации. Усилий N^>Nna быть не мо-
жет!
Строго говоря, подобная идеализация находится
в противоречии с действительными физико-механиче-
скими свойствами элементов конструкций. Тем не менее
опа существенно упрощает исследование стадии исчер-
пания несущей способности, и дает результаты весьма
близкие к экспериментальным, получаемым для конст-
рукций из различных материалов.
В статически неопределимой копмрукции возможны
различные равновесные (удовлетворяющие уравнениям
равновесия) распределения внутренних сил. Если степень
статической неопределимости к, то будет к линейно не-
зависимых распределений внутренних сил, уравновеши-
вающих внешнюю нагрузку.
Любое равновесное напряженное состояние, уравнове-
шивающее заданную внешнюю нагрузку, называется
статически аоз.ношным.
Для идеально упруго-пластической системы все внут-
ренние силы ограничены условиями пластичности
(прочности).
В обш,ем виде эти условия, отражающие природу ма-
териала и его физико-механические свойства, задаются
в виде одного неравенства или системы неравенств, ко-
торые могут быть линейными или нелинейными:
Фв(Д1;...,лу щО (а=1,. ...0,
где Л0, N!r. — внутренние силы.
Если для некоторого набора внутренних сил NJ;
N m все неравенства выполняются строго, т. е.
Фа (Л") <0 (а=1,	0, то это означает, что пластиче-
ские деформации не образовались и конструкция может
рассматриваться как идеально упругая.
Если для некоторого набора внутренних енл Аф, ...,
Nm часть неравенств обращается в строгие равенства
Фв(Д//)=0 (a=i, ..., Ф), а остальные неравенства бу-
дут строгими Фр (N") <0 (р = ф-Н, ..., 0, то это озна-
чает, что в конструкции частично или полностью разви-
лись пластические деформации, а часть или даже все
внутренние силы достигли предельного значения.
Статически возможное распределение внутренних сил,
удовлетворяющее условиям пластичности (прочности),
называется статически допустимым.
Любое деформированное состояние системы, не нару-
шающее условий закрепления, называется кинематиче-
чески возможным, Принимается, что при исчерпании не-
сущей способности жесткая система превращается в ки-
нематический механизм (перемещения всей системы оп-
ределяются перемещением одной характерной точки)
пли кинематическую цепь (перемещения всей системы
определяются перемещениями нескольких характерных
точек). Кинематически возможные перемещения, образу-
ющие кинематический механизм или цепь, называются
кинематически допустимыми.
Кинематический механизм предполагает образование
достаточного числа пластических шарниров, в которых
выполняются уравнения пластичности и вследствие это-
го известны действующие в шарнирах усилия А'лл
(i — помер шарнира). Определение нагрузки, сообща-
ющей перемещения механизму с k шарнирами, произ-
водится приравниванием вариаций работы внутренних
k .	t
(dU=2 Л'51Л60г) и внешних сил (64=S Pfiuj). Здесь
1=1 д /=1
0:— перемещения в шарнирах по направлению действия
силы Uj — перемещения по направлению силы Ру
Когда все силы пропорциональны одному параметру
Pj — Pkj, тогда из уравнения 64=617 определяется зна
384
РАЗДЕЛ 21 РАСЧЕТ КОНСТРУКЦИИ ПО ПРЕДЕЛЬНОМУ РАВНОВЕСИЮ И УЧЕТ ПОЛЗУЧЕСТИ
челне параметра нагрузки Р, соответствующего выбран-
ному кинематическому механизму:
я
J зог-
Р-= -у---------- 	(21 1)
D kj fill}
i= i
Три основные теоремы
предельного равновесия
I.	Предельная нагрузка не ниже той, которую может
уравновесить статически допустимое распределение
внутренних сил.
II.	Предельная нагрузка не больше той, которая мо-
жет быть определена из рассмотрения кинематически
допустимого распределения перемещений (кинематиче-
ского механизма).
III.	Предельная нагрузка является максимальной из
всех нагрузок, которые могут бьпь уравновешены ста-
тически допустимым нолем напряжений, вместе с тем
предельная нагрузка является минимальной из нагру-
зок соответствующих всем пластическим механизмам.
Первые две теоремы определяют два основных мето-
да теории предельного равновесия — статический и ки-
нематический.
Статический -метод заключается в установлении рас-
пределения внутренних сил N, уравновешивающих
внешнюю нагрузку Рст и нигде не нарушающих усло-
вий пластичности	Первая теорем?, утвержда-
ет, что РстОР’У где Р"'— предельная нагрузка.
Кинематический метод. По этому методу назначается
кинематический механизм с k пластическими шарнира-
ми, в которых действуют внутренние силы jVJI/1(i==l, 2,
..., k}, удовлетворяющие уравнениям пластичности
ф(Л/]1л)==0. Из уравнения (21.1) определяется нагрузка
Р КИН) £ из второй теоремы следует, что P’’^/’кин- Этот
метод полу чип широкое распространение благодаря
своей наглядности при выборе схем разрушения.
Третья теорема устанавливает, что если некоторое
равновесное распределение N' в необходимом числе то-
чек образует пластические шарниры (выполняются усло-
вия	0, а в остальных точках Ф(Л,')г^0, то на-
грузки Пет и Рг.ш равны предельной Р". Для произ-
вольных статически допустимых распределений внутрен-
них сил и кинематических механизмов Нс т=Д.РДлин.
При применении кинематического метода всегда следует
иметь в виду, что получается верхняя оценка предель-
ной нагрузки, а при статическом методе — нижняя
оценка.
При ассоциированном законе пластического течения
(см. раздел 12), если принять статическую формулиров-
ку в качестве исходной, кинематическая формулировка
получается как производная, и, наоборот, если принять
в качестве основной кинематическую формулировку, ста-
тическая получается как производная [21, 32].
21.1.3.	Основные ограничения теории
Наиболее важные результаты теории предельного рав-
новесия следующие.
Любое самоуравиовешенное распределение внутрен-
них сил не влияет па величину предельной нагрузки. Са-
мруравновешенпыли внутренние силы называются тог-
да, ’"огда они удовлетворяют уравнениям равновесия
при оп.'утсгвнн внешней нагрузки. Частные случаи са-
моуравиовешенной нагрузки — температурные усилия
и усилия в основной системе от лишних неизвестных.
Отсюда следует, что предварительное напряжение не
сказывается на несущей способности, так как создает
самоуравновешенную систему внутренних сил.
Недостаток теории предельного равновесия состоит
в полном игнорировании деформаций, которые играют
существенную роль при оценке геометрических эффек-
тов деформирования и исчерпания предельной дефор-
матвноыи. В [21] делается попытка устранить лаг
недостаток.
Важной проблемой в теории предельного равновесия
является у становление действительных условий пластич-
ности (прочности), некоторые примеры которых см.
в разделе 12. Создание этих условий требует большой
экспериментальной и теоретической работы, и не для
всех материалов и конструкций такие условия имеются.
21.1.4.	Типы нагрузок и классификация задач
Теория предельного равновесия применяется с больши-
ми или меньшими усложнениями для определения несу-
щей способности конструкций, подверженных действию
следующих внешних нагрузок.
Нагружение, пропорциональное одному параметру.
В этом случае все внешние силы Р, (1=1, 2,	1) из-
меняются пропорционально одному параметру Р и мо-
гут быть представлены в виде Р1 = Р/г, (1=1, 2,	1),
где k,—интенсивность силы Р,. В этом случае силы
своей ориентации не изменяют, а изменяется их вели-
чина,
Нагружение системой внешних сил, зависящих от не-
скольких параметров Р1, Р'1, ..., PJ. Каждая группа сил
в таком случае задается в виде PJk,, тар j — номер
группы сил, зависящих от одного параметра Р1 (/=!,
2,	s), a k.—интенсивность 1-й сиды в этой группе
(1=1,2, .... Д),
Внешние силы пропорциональны одному параметру Р,
но происходит многократное изменение этого параметра;
однако число таких изменений не столь велико, чтобы
приводить к усталостному разрушению.
Внешние силы зависят от нескольких параметров
Р> (/=1, 2, ..., s), которые могут многократно изменяй-
ся, не вызывая усталостного разрушения,
Динамическое приложение внешней, нагрузки, приво-
дящее к рассеиванию энергии вследствие образования
пластических деформаций.
Характер внешней нагрузки определяет задачи, кото-
рые могут быть поставлены в рамках теории предель-
ного равновесия:
определение максимальной несущей способности за-
проектированной конструкции (основная задача прове-
рочного расчета);
определение невыгодного распределения внешней на-
грузки, зависящей от ряда параметров Обычно эта за-
дача решается при дополнительных условиях, что на-
грузка задана в виде ресурса или на нее наложены
какие-то особые ограничения;
определение наивыгоднейшего распределения внешней
нагрузки, заданной в виде какого-то ресурса. Это зада-
ча оптимального распределения нагрузки;
определение границ приспособляемости конструкции
при многократно изменяющейся нагрузке;
оптимальное проектирование конструкций под задан-
ную нагрузку, Такая задача не всегда решает проблему
проектирования, так как в строительных конструкциях
очень часто размеры определяются вторым и третьим
предельным состоянием, а не первым (несущей способ-
ностью).
2, НЕСУЩАЯ СПОСОБНОСТЬ СЕЧЕНИИ
385
21.2. НЕСУЩАЯ СПОСОБНОСТЬ СЕЧЕНИИ
21.2.1.	Чистый изгиб сечений
в плоскости симметрии
Прямоугольное сечение. При чистом изгибе в плоско-
сти симметрии на крайних гранях возникают напряже-
ния: о+ на нижней грани и <г~ на верхней. До тех пор,
пока о+<от и —от, напряжения можно опреде-
Рис. 21.3
сопротивления материалов
лить
О—
по обычной формуле
Mi)
•—~ . При	на крайних гранях напряжения
будут равны пределу текучести (рис. 21.3). Увеличение
изгибающего момента сверх этой величины сопровож-
дается образованием зон пластичности высотой
Средняя часть сечения высотой (1—Qh называется уп-
ругим ядром. Момент, воспринимаемый таким сечением,
Л1.=
от й2 Ъ
4

Г	2	1
И (2 - 0 + -- (1 - О2
।	J
При £=0 в состоянии пластичности находится только
верхняя и нижняя грани. При £ — 1 в состоянии пластич-
h2b
ности все сечение. Величина Л4пл = От —:—называется
4
предельным пластическим моментом сечения, для ко-
торого широко используется запись
Мпл — ^пл,	(21.2)
Идеальный двутавр. Идеальным двутавром называет-
ся условная модель двутавра с материалом, сконцент-
рированным только в его полках площадью Е+ a F~.
При чистом изгибе продольные усилия в полках равны:
Al = min(<k F+;	F~), т. е. N равняется меньшей из
величин о+ F+ или F~. Напряжения в полках равны:
, N	А
сю =-----. 0 _, —_ . одно из этих напряжений равно
F+	р-
от с соответствующим знаком,! е. илна+ = од
==Щ~, или	|о~|=о~ Равенство о+ = о.,1:
|о~~ | = оД возможно только при К+ : Е'~ = оД:ок-
Для двутавра высотой h пластический момент Л1ПЛ —
~Nh-,	F+, я~ F-).
Для симметричного двутавра при	Maa = a<i:Fh,
где F — площадь полки.
Железобетонное прямоугольное
сечение
Деформирование н характер разрушения при изгибе
железобетонного стержня существенно отличаются от
поведения под нагрузкой стержней из других материа-
лов. Однако исчерпание несущей способности железобе-
тонных (не переармированиых) стержней можно опреде-
где 1Рпл==М2/4 — пластический момент сопротивления.
Кривизна изогнутой оси стержня при чистом изгибе
определяется высотой упругого ядра:
1 2от
у =
С уменьшением высоты упругого ядра кривизны стре-
мятся к бесконечности. Когда $=1, сечение становится
пластическим шарниром с моментом MBS и вся изгибае-
мая балка может вращаться вокруг центра этого сече-
ния без изменения момента.
лять теми же методами, что и однородных пластических
стержней, так как это состояние для железобетонных
стержней определяется достижением текучести в армату-
ре. Схема сечения в предельном состоянии показана на
рис. 21.4. Высота сжатой зоны определяется из условия
л а 1 а
х= ----
ДИЬ
(21.4)
Прямоугольное сечение с различными
пределами текучести
при сжатии и растяжении
Пусть ак и а~ — пределы текучести при растяжении
и сжатии. Предельная несущая способность прямоуголь-
ного сечения определяется из условия равенства нулю
равнодействующей напряжений в сечении: /г+ик=/1-с>Д
где А+ и h~ — высота растянутой и сжа-
той зон сечения. Предельный момент определяется сле-
дующим образом:
«к
М = о Й? ; с=2------------.	(21.3)
ПЛ т пл S	_1_ ,	_ v /
+°т
Если x=glO,55/io, то это не переармированное сечение,
в котором разрушение происходит при напряжениях в бе-
тоне, равных пределу прочности при изгибе RB и на-
пряжениях текучести в арматуре ка. Предельный мо-
мент сечения
А4ал — Ra Fа ко *"
ДаЛЛ
2Дай/
(21.5)
Для сечения с двойной арматурой высота сжатой зоны
определяется из тех же условий:
Ra ~ Ra
х= ----_----------
(21.6)
25—26
Rub
Если оказывается, что х^2а', предельный момент
Ял = «а bX (ho - °’5Х) + < к (к -а')  <21 -7)
38G
РАЗДЕЛ 21, РАСЧЕТ КОНСТРУКЦИИ ПО ПРЕДЕЛЬНОМУ РАВНОВЕСИЮ И УЧЕТ ПОЛЗУЧЕСТИ
Т а б л и ц а 21,1
Отношения------ для некоторых типов поперечных сечений
W
.. 	,			 Форма сече- нии	J	1					0	j-»-* гидТ ft _Й2- H
?.2d_		1,15—1,17	1,27	1,5	1,7	-	1,7	MP—h- (Ь-б) .1	A3 &H5-— (b—fl) n
Таблица 21.,2
Пластические моменты сопротивлений швеллеров А но ГОС1 8240--5й
Г™ = 7(6 — 0,Ы)(6 — 0 + 0,253 (А — IP, если 2 (b — d) > hd;
F™ = 0,5 К (b — 0,5d)2 4- d (b— 0,5d)(h ~ t) — 0,25d2FJ (A — 7)2], если 2 (b — d)^hd;
= a {b _ d) + o,25ftd2+ ish~l (b — d)2;
F”'1 = 0,25 (h — t)\t (b — 0,5d)2 + 0,5d (6 — 0,5d) X (A — i) — 0,06253г/_1(Л — tf];
F™ = 0,5 [2t2 (b — 0,5d) + d2 (h - 01-
Центр изгиба
2t (b — 0,5d)2
°x 4t (b — 0,5d) 4- d (A — 0
№ i профиля	Размеры в мм				Пластические моменты сопротивления				
	ft	6	j	<1	Г	W™, С№'	IF™, cjkj	• сл‘	У™, см- R	см
5	50	37	4,5	7,0	12,54	6,92	12,34	2 Л 38	Ц4®
	6,5	65	40	4,5	73	19,82	9,03	21,41	2.650	1,532
i	a	80	45	4,8	7,4	29,21	12,09	35,08	ЗЛ69	1,669
5 w	100	50	4,8	7,5	43,29	15,78	55,93	3,743	1,816
12	120	54	5,0	7,7	60,30	19,55	90,74	4,457	1,902
1 И	140	S8	5,0	8,0	80,39	23,83	130,53	5,202	2да
14a	НО	62	5,0	8,5	88,12	28,25	152,78	5,943	2,245
16	160	64	5,0	8,3	106,20	30,36	191,®	6,133	
16a	160	68	5,0	8,8	135,73	35,52	220,36	6,962	2,466
18	180	70	5,0	8,7	137,28	38,19	270,®	7,250	2,473
18a	180	74	5,0	9,2	148,82	44,14	310,04	8,187	2,6^
20	200	76	5,2	9,0	173,60	46,99	372,87	8,528	2,667
20a	200	80	5,2	9,6	188,60	54,31	425,76	9,707	2,903
	220	82	5,3	9,6	218,93	58,27	5®, 08	10,27	2,905
i 22a	220	87	5,3	10,2	238,83	68,03	586,87	11,72	3,188
24	240	90	5,6	10,0	274,62	73,44	700,50	12,аз	3,184
24s	240	95	5,6	10,7	299,82	85,41	805,55	14,15	3,478
i	27	270	95	6,0	10,5	351,69	87,20	947,59	14,81	3,279
;	80	300	100	6,5	11,0	443,29	102,26	1255,6	17.81	3,356
33	330	105	7,0	11,7	555,30	120,45	1647,9	21,69	3,455
36	360	110	7,5	12,6	691,37	142,49	2145,1	26,64	3,574
40	«ю	115	8,0	13,5	877,93	167,30	2837,2	32,60	3,661
21 2 НЕСУЩАЯ СПОСОБНОСТЬ СЕЧЕНИИ
387
Пластические моменты сопротивления двутавров по ГОСТ 8239—56
^пл
w и
tb-
W™- tb (/1-гн™(ад
А	4
Лл8 про- филя	Размеры э мм				Пластические моменты сопротивления			
	h	Ъ	d	1	ГД, c.v.3	|		U™, мй	»'^л, с,и3
10	100	70	4,5	7 2	56,46	17,И	81,85	4,568
]>	120	75		7,3	77,58	20,53	115,69	5,405
14	140	82	5,0		103,43	25,22	167.05	6,269
16	160	90	5,0	7,7	134,54	31,19	237,47	7,240
1R	180	95	5,0	8,0	167,70	36,10	310,46	8,230
]8а	180	102	5,0	8,2	ДО,39	42,6'^	Зоб,J2	9,00п
°0	200	100	5,2	8,2	2(Ь,10	41,00	393,19	9,317
20а	200	110	5,2	8,3	222,80	50,22	481,3!	10,17
22	220	ИО	5, А	8,6	259,20	52,03	549,96	11,10
•??я	220	120	5,3	8,8	282,13	63,36	609,08	12,26
24	240	115	5,6	9,5	326,20	62,82	72 ад	щда
24а	240	125	5,6	9,8	356,18	76,56	881,23	15,61
27	270	125	6,0	9,8	420,г0	76,56	903,08	16,69
	270	135	6,0	10,2	458,99	92,95	1207,4	18,72
30	300	135	6,5	10,2	535,53	92,95	I 3-41,8	20,17
30а	300	145	6,5	10,7	584,85	112,18	1627,1	22,71
33	330	140	7,0	11,2	677,74	109,76	1759,5	25,37
36	360	145	7,5	12,3	846,80	129,30	2247,9	31,72
40	400	155	8,0	13,0	1079,3	156,16	6021,7	38,58
45	450	160	8,0	14д	1393,5	181,76	3960,о	48,38
SO	500	170	9,3	15,2	1799,2	219,6!	адм	ГОДЫ
55		180	10,0	16,5	2296,1	267, 10	И 0,2	75,68
60	600	190	10,8	17,8	2881,2	321,29		94,15
65	650	200	11,7	19,2	3586,2	384,00	12 Ш	116,90
70	700	210	12,7	10,8	ад, 4	Д56,64	1S 575	145,63
	700	210	15,0	24,0	5120,7	529,20	17 837	197,01
70П	700	210	>7,3	28,2	5952,9	621,81	20 887	269,87
Если х<2а', сечение рассматривается как идеальный
двутавр с площадями полок Еа и Еа и пределами теку-
чести Л?,1 и /?а.
Общий случай изгиба, Для сечения произвольной фор-
мы, по с плоскостью симметрии, в которой действует
чзгибаюгщщ момент, предельное значение Л4ДЛ опреде-
ляется из условия равенства нулю равнодействующей:
Г Q = Е~ Q 0^=- N = min	оД),
25*
где ч — координата нейтральной линии, разделяющей
растянутую и сжатую зоны:
=ff+ s+ & Т S" & «+ =- ~~ >
F 1
сГ-------,	(21.8)
1Де S*" и S~~— абсолютные значения статических момен-
тов растянутой и сжатой зон относитель-
но нейтральной оси, имеющей координа-
ту U
388
РАЗДЕЛ 21 РАСЧЕТ КОНСТРУКЦИЙ По ПРЕДЕЛЬНОМУ РАВНОВЕСИЮ И УЧЕТ ПОЛЗУ ЧЕСТИ
21.2.2.	Косой изгиб стержня
В тех случаях, когда плоскость действия изгибающего
момента не совпадает с осью симметрии сечения, положе-
ние нейтральной оси определяется из решения системы
уравнений, фактически являющихся уравнениями стати-
ческого равновесия:
tg 0 =	, tg 0 = — ;	=- Г.
Mv	Sy
Здесь Мх и М„ — изгибающие моменты, отнесенные
к некоторой системе координат х, у, F~ и Е+ — площади
сжатой и растянутой частей сечения; S, и Sy — стати-
ческие моменты сечения, определяемые с учетом знака
напряжений; 0 — угол между выбранными осями коор-
динат х, у и нейтральной осью. В новых осях координат
х' и у', направленных вдоль и перпендикулярно нейтраль-
ной оси, предельный изгибающий момент определяется по
формуле

gt Fh
где F— площадь сечения; h — расстояние между цент-
рами тяжести сжатой и растянутой частей сечения.
Пластические моменты conpoiявления двутавров, сог-
ласно [28], определяются следующим образом:
при угле между горизонго.жной осью и плоскостью из-
гиба 0 от 5° до 20°
r i (h — f)2 d
«фл(0) =	4tg0 +
4 cos и L 
где h — высота двутавра; Ь — ширина полки; d — толщи-
на стенки; t — средняя толщина полки;
при 0>2О°
Г	t	1
ф Ж, — F — {b — 0,5d) cos 9;
I " d	]
£= — sin 0 — cos 0 ;
\ d	J
F = 2t (b — 0,5d) -ф d (h — /);
WA = t(b — O,bd) (h — t) -ф 0,25d (h — I)2.
21.2.3.	Внецентренное растяжение (сжатие)
в плоскости симметрии
Прямоугольное сечение. Предельное состояние пря-
моугольного сечения при внецентреином растяжении
(сжатии) и при различных пределах текучести на растя-
жение и сжатие показано на рис. 21.5. Положение ней-
Рис 21.5	Рис. 21.6
тральной оси (величина J) определяется из уравнения
равновесия относительно продольной оси
о+ h'Q — h (1 — □ = — .
Ь
Величина изгибающего момента определяется из урав-
нения равновесия моментов относительно центра сечения
где h, b, d и t имеют те же значения, а величина и яв-
ляется положительным корнем кубического уравнения
2,027ц3 -ф и2 ] 1,04b3 -ф 2 iji — f)] -ф
( ,	Г 5d (h — t) '!
-фм (h — i) tg 0 Ь-ф----—-L — 0,48b2
I	I 6i
— 0,2467b3 = 0.
Пластические моменты сопротивления швеллера опре-
деляются по формуле
1Ппл(0Ьу Оф
(b — 0,5rf)
В этой формуле вспомогательные величины следующие-
t Г	F	1
G =— — Фф-ф — (h — t) j sin 0 -ф
d I	2	j
Исключая из этх двух уравнений величину у и счи-
тая, что изшбающий момент может бьиь как положи-
тельным, так я отрицательным, получим предельное усло-
вие для IV и М:
I 2М 1	/ /V \‘2 N	о+ — а~ о+ о~~
j Ыг2 о I 1 \ b/io / bho о	о2
g = o+-L<j~.	(21,9)
Если оу’=оф", условие пластичности имеет вид
(21.10)
показа-
1 /114 л л;
где Л4ПЛ определяется по (21 4), a iVnn = ovbh.
Графическое представление зависимости (21,9)
но иа рис. 21.6, где по осн М введен масштаб
/Ипп определено по (21.4); на положительном луче оси
N введен масштаб 1//V+ и на отрицательном луче—
масштаб I/.V~" (А'+ —а + ь/г; N~ — o~bh). Это две пара-
болы, выделяющие выпуклую область. Если в сечении
действуют Ф и А1 и точка и, определяемая этими коор-
динатами находится внутри области, ограниченной пара-
212 ИССУШАЯ СПОСОБНОСТЬ СЕЧЕНИИ
389
ботами, сечение не достигло предельного состояния Ес-
ли с — точка с координатами Л’ и М— находился на
параболах, сечеиие иаходиюя в предельном состоянии.
Значения -V и Af, задающие точку Ь вне области, oipaira-
чеиной параболами, не имеют смысла.
Двутавровое сечение. Условие пластичности для
идеальною двутавра с предо чами текучести о+ и оу
и пютцадями полок 1-\ и 1'2 определяется четырьмя не-
равенствами:
2
— Ж<V 'УД,-
h	1
М — N < оДД2;
(21.11)
—	ЛНЛ’<йД F,.
п
Сечеиие будет находиться в состоянии пластичности
тогда, когда хотя бы одно неравенство npi вращается
в строгое равенство.
Область, ограниченная этими условиями, является
прямоугольником, показанным пунктиром па рис. 21 6.
Для симметричною двутавра при о 1 =о3 условия
(21.11) упрощаются:
десь А4пл— оуЕ/з; Дил—2g^F.
Сечение железобетонного внецентренно
растянутого (сжатого) элемента
Предельные состояния железобеюнн-ч о внецентренно
растянутою (сжатого) сечения определяются поверх-
1ЮС1ПЮ фшуры, показанной па рис 21.7. Точки па осях
координат М+ и М~ соответствуют ирсде.'пщому момен-
iy при чистом изгибе; <V+ и Л'~
соответствуют центральному рас-
тяжению и сжатию. Точки а и а'
разграничивают несущую способ-
ность сечения по первому и вто-
рому случаю. Точки Ь и Ь' соот-
ветствуют случаю, когда высота
сжатой зоны равна 2а'. За исклю-
чением двух параболических уча-
стков ab и а'Ь', соответствующих
первому случаю с высотой сжатой
зоны более 2а', остальные участ-
ки линейные. Если сечение арми-
Рис. 21.7
роваио симметрично, точки г и с'
лежат на оси N. Замена параболических участков ab и
а'Ь' прямыми вносит погрешность порядка 5%, которая
идет в запас прочности. Потому несущая способное^
гпецептренпо растянутого (сжатого) железобетонного
сечения может быть описана шестью неравенствами вида
РЧ М + Vi N + k[ < 0 (i=-1, 2,	, 6). (21.13)
Значения коэффициентов pt,, v, и kt зависят от рас-
сматриваемого участка. Считается, что сечение нахо-
дится в предельном состоянии, если хотя бы одно из
шести неравенств (21.13) превратилось в строгое равен-
ство для некоторых Л'” и М, а остальные неравенства
не нарушаются. Максимальное число равенств может
быть два, что соответствует угловой точке мпогоуюль-
пика па рис. 21.6, например точка а. При любых реаль-
ных значениях Л' и Л1 ни одно неравенство (21.13) не
может быть нарушено. Более подробно по этому во-
просу ем. [9, 20].
21.2.4.	Учет поперечной силы при изгибе
Если в сечении действует изгибающий момент М и по-
перечная сила Q, то при оф = оД = от удобно исполь-
зовать условие пластичности Мизеса: о'24~Зт2-= оу , При
отсутствии изгибающего момента (о = 0) предел теку-
чести па сдвиг тт = От/ ] 3. В прямоугольном сечении
касательные напряжения распределены по параболе
Рис 21,8
Рис. 21.9
с максимальным напряжением в середине сечения
В этом случае максимальная величина поперечной силы
Сил _ bho^.,
V' 4
Распределение касательных напряжений возможно
только в пределах упругого ядра (рис. 21 8). Уравненщ-
пластнчносгн для изгиба с поперечной силой имеет вид
(по Н. И. Безухову) [22]
| М I	4 / Q V	j Q I
+	, Д_ =	,	{21 14)
|А1ПЛ|	о \Чпл /	(Упл I
Область прочности для этих выражений показана на
рис, 21.9,
21.2.5.	Предельные состояния сечения
при кручении
Чистое кручение. Напряженное состояние сечения при
чистом кручении характеризуется только касательны-
ми напряжениями, а нормальные напряжения равны
нулю.
Применительно к задачам предельного равновесия
предельной величиной касательных напряжений явля-
ется тт = от/ Ц 3 при условиях пластичности Мизеса
и tT = cv/2 при условиях Треска.
Предельный крутящий момент можно вычислить как
удвоенный объем, ограниченный поверхностью равного
ската, построенной на сечении (табл. 21.4).
Для тонкостенного открытого профиля с постоян-
ной толщиной отношение Mnn/7HylIp= 1,5 (Л4упр =
= ТтИ7Крупр), а для замкнутого профиля Л4дп/Л1у1,р= 1.
Совместное действие кручения и продольной силы.
Продельное равновесие круглого сечения при кручении
и центральном растяжении (сжатии) приближенно оп-
ределяется уравнением
N у f Л4 '2
7 пл /	А1л”
2л
МчЛ=ПД^'с Лпл = ол-лД“. (21.15)
.390
РАЗДЕЛ 21. РАСЧЕТ КОНСТРУКЦИИ ПО ПРЕДЕЛЬНОМУ РАВНОВЕСИЮ И УЧЕТ ПОЛЗУЧЕСТИ
Таблица 214
Предельные крутящие моменты для некоторых типов сечений
Тип поперечного сечения	Предельный крутящий момент
	Ь- {За — &) Тт т	6
у ‘"ТО	0,5-щ (d2A + 2M6)	,
.а	а3 тт — т 12
1	2 — тт л (R3 —г3) О
Тонкостенная труба	2тт лб (R — б)3
Тонкостенный замкнутый профиль	2тт бй, где Q — площадь, ограни- ченная средней линией про- филя
&	2 — тт л (а3 — 4,5а&2 ф- 4й3) д
	1 — тт J б2 (s) ds
i	1	V —- тт ab- 2 т
Более точное предельное условие имеет вид
___ + _ + Л12=т^т;. <21Л6>
Предельное равновесие полосы при кручении и нор-
мальной силе устанавливается уравнениями
/з' ,, J/iTw j п
—— ib/i—sh I  ----- I = 0;
6	\ 6fetfT J
N boy h /	1
M + — — —2— 1/ 1 + — TO3 = 0.
ф ф Г 12
Из первого уравнения определяется ф(А1), подстановка
этого значения во второе уравнение дает уравнение пла-
стичности.
Совместное действие изгиба и кручения. Для тонкой
полосы предельное равновесие определяется уравне-
нием
12 М2И + 12 М2 = ат b1 h2.
Предельное равновесие двутавра при изгибе с круче-
нием определяется уравнением
где
/Мк
(21.17)
= «т	~ Ч И b).
Здесь h — высота стенки; d — толщина стенки; Ь — ши-
рина полки; 6 — толщина полки.
Уравнение (21.17) может быть использовано для при-
ближенной оценки предельного равновесия произволь-
ного сечения при изгибе с кручением.
21.2.6.	Условия пластичности
для изгибаемых плит
Изгиб плиты в двух направлениях. В изгибаемой
в двух плоскостях плите действуют в общем случае
три момента — два изгибающих Мхх и Mvv я крутя-
щий момент АП,,.
Условия пластичности формулируются для этих мо-
ментов, отнесенных к единице длины сечения плиты
плоскостью, нормальной к срединной поверхности. Та-
ким образом, размерность моментов равна размерности
силы, например кГ см/см = кГ.
Для плит, выполненных из однородного материала
с изотропными свойствами, условия пластичности ана-
логичны рассмотренным в разделе 16.
Условия пластичности Мизеса. Условия Мизеса для
пластинки имеют вид
Мхх - ЛЛЮ + -С +	, (21.18)
А3
где Мпл=ст—у—пластический момент единицы дли-
4
ны поверхности пластинки.
Это уравнение задает поверхность эллипсоида враще-
ния с осью вращения, лежащей в плоскости М11О.М!/В
и равнонаклоненной к обеим осям.
В осях главных моментов, в которых крутящий момент
равен нулю, уравнение (21.18) описывает эллипс, пока-
21 2 НЕСУЩАЯ СПОСОБНОСТЬ СЕЧЕНИИ
391
занный на рис. 21.10. Главные оси эллипса равнонакло-
нены к обеим осям.
Условия пластичности Треска. Это условие формули-
руется в главных значениях моментов
max (Wil, |Ма|, ИД - Ж2|) = Мпв. (21.19)
Здесь Лф ii Л43— главные изгибающие моменты. Усло-
вия Треска задает шестигранник, вписанный в эллипс
Мизеса (рис. 21.10). В общем случае условия Треска
в произвольной системе координат записываются зна-
чительно сложнее условий Мизеса.
Условия Иогансена. Эти условия следует рассматри-
вать как условия прочности, а не пластичности
(см. 212.7):
Фх = W.W	71ДЛ Ml 9;	1
ф2 = (Д/Д	мпл < °;	1	(21.20)
Ф3= <д“ф1ф2<°-	)
При превращении хотя бы одного неравенства в стро-
гое равенство ФДМ)=0, для остальных условий дол-
жно выполняться условие ФДЛ4)з£0 (J=W).
Неравенства (21.20) описывают фигуру типа конусов,
сложенных основаниями (рис. 21.11). В главных осях
MMS — это прямоугольник. Из условий (21.20) следует,
что если |Л4Ях| = Л1пл или = Л4пл, то обязательно
Л1о=0. Если	—Л'1Пл, тогда М1Х= 0 или Al!PJ=0.
21.2.7.	Несущая способность плиты
при совместном действии изгиба
и плоского напряженного состояния
В оболочках плита находится не только в состоянии
изгиба по двум плоскостям, но на нее действуют нор-
мальные и касательные напряжения в срединной по-
верхности.
Задача существенно осложняется, если главные на-
правления плоского напряженного состояния (мембран-
ные) не совпадают с главными направлениями изги-
бающих моментов. Общее условие пластичности Мизеса
записывается для такого случая двумя уравнениями:
пхх “ пхх пуу + пуц + тхх + -'”да +
+ Зп2ху +
з (И.Г.Г пхх + ПХ!) -L. т,.,. пш) — mtx п.(х —
™УЬ пУУ W'xx пуу	9,
где
Различные упрощения для этих условий состоят
в следующем (26, 27].
Мембранные и изгибающие усилия разделены:
пхх пух Щ Д :3п~_у = v;
m« - тхх тии + ;пп + Зтху = И-
Наиболее простое представление при v = p=l. Более
сложное при v+p.= l и условиях, что v>0 и р.^0 или
И+у.2= 1.
Модификация условий Треска для сложного напря-
женного состояния ПЛИТЫ В 1Л3311ЫХ осях плоского и на-
гибного напряженного состояний заключается в удов-
летворении неравенств
maxdMjl, 1;VS|, JAM — A7S|1 < M'1 (v > 0);
maxO./Wj], |ЛЦ, |АД--/11г!) •; aT h? p. (u .> 0)
4
при дополнительном требовании v2+p2==l.
Можно для v и |j. предложить условия, аналогичные
условиям Треска: max (v, ц, |v—itj)~ 1, что несколько
нарушает предыдущее условие. По этому вопросу см.
[27].
Для осесимметричных железобетонных оболочек, в ко-
торых действуют меридиональные усилия М„ и .V,, по
параллелям принимается, что действуют только растя-
гивающие усилия Nci , а изгибающие момешы равны
нулю (Мф=0). Усилия NSj , если они растягивающие
воспринимаются арматурой по параллелям и, следова-
тельно, не оказывают влияния на предельные усилия по
меридиану. Поэтому для меридиональных усилии сохра-
няют силу условия (21.13), а усилия по параллелям
ограничены условием
Й -	Fа <2 .Vq. <1	Fа ,
гае /щ — площадь арматуры иа единицу длины сече-
ния в плоскости меридиана; /г — толщина оболочки.
21.2.8.	Ассоциированный закон пластического
течения для конструкций
Действующие в сечении и в самой конструкции си-
лы, изгибающие и крутящие моменты в общем слу-
чае объединяются термином «обобщенные внутренние
силы», которые обозначаются A'i, <V2, AM.- Условия
пластичности задают некоторые уравнения для этих
сил а виде Ф,- (Ni, Nm)—0 (1=1, 2, .... п). Если при
некоторых значениях A], Nit А'^ справедливо равен-
ство для какого-то i-го уравнения пластичности Ф1 = 0,
то состояние пластичности характерно для обобщенных
сил, входящих в это условие, Если выполняются нера-
венства Ф,<0 для всех г=1, 2, .... п, то конструкция
не достигла еще состояния пластичности. Неравенств
типа ФгД>0 быть не может.
Основные положения теории идеальной пластично-
сти, называемой также теорией жестко-пластического
тела, состоят в следующем.
1, Если в конструкции выполняются условия Ф,<0
для всех г = 1, 2, п, то конструкция находится в жест-
ком состоянии, которое является идеализадиеи упру гон
392
РАЗДЕЛ 21. РАСЧЕТ КОНСТРУКЦИИ ПО ПРЕДЕЛЬНОМУ РАВНОВЕСИЮ И УЧЕТ ПОЛЗУЧЕСТИ
конструкции при малых упругих деформациях.
.2. Условия Ф,==С0 выделяют некоторую выпуклую об-
ласть в пространстве обобщенных внутренних сил N.
3, Перемещения конструкции могут быть только орто-
гональными к огибающей поверхности, заданной усло-
виями Ф.=0 (г—I, 2,	п), т. е. перемещение по на-
правлению действия силы ,V3 определяется как
.4J	JA- j
1=1
где Ц>0, если Ф1(.У) = О, п %, =0, если Ф1(А')<0.
В итоге перемещения конструкции могут быть опреде-
лены с точностью для некоторого, общего для всей кон-
струкции, множителя или группы множителей. Поэтому
величину 0j называют обобщенной скоростью переме-
щения по направлению действия силы Лф.
Функции Ф,(Л') по аналогии с теорией упругости (см.
раздел 12, теорема Кастильяно) называют пластически-
ми потенциалами, а уравнение (2121) называют урав-
нением ассоциированного закона пластического течения
Например, для прямоу; олъпого сечения с одинаковыми
пределами текучее!и при растяжении и сжатии условие
пластичности (2!,10) переходит в следующее:
I М I IN \3
Ф(М, Л)= -т- +	—1<0
l-^nal Л пл /
Скорости линейных деформаций 0Л- и угловых 0,и
определяются при условии Ф(Л', А1) =0:
0,.^-“%—^-, если М 0;
V
0м — 0, если М = 0; 0N -= 2Х -у-,
‘^лл
Таким образом, если уравнение пластичности выпол-
няется, то Лй>0. В ряде случаев может оказаться, что
выполняется уравнение пластичности и при этом Х = 0.
Поэтому общим случаем следует считать Л1Д=О при
Ф(Л\ ЛЦ=0 Расстояние мгновенного центра вращения
от центра тяжели сечения будет c = 0.v/9,w =
~2NM.TlaIAi^li. Как видно, эта величина не зависит от
неопределенного множителя Если в предельном со-
стоянии N—0 (чистый изгиб), то мгновенный центр
вращения совпадает с центром тяжести сечения, Если
(Й = 0, тогда 0м=0 и вращения пет, а происходит толь-
ко поступательное перемещение, всего сечения по на-
правлению действия силы.
В любом случае определяются только скорости пе-
ремещений, а не их действительные значения.
Кроме того, теория идеальной пластичности рассмат-
ривает только такие скорости перемещений, которые вы-
зывают скорости деформаций в пластических областях,
а в жестких областях скорости деформаций равны нулю.
21,3. РАСЧЕТ ПЛОСКИХ СТЕРЖНЕВЫХ СИСТЕМ
21.3.1. Пластические шарниры
в стержневых системах
Основные внутренние силы, рассматриваемые при рас-
чете плоских стержневых систем, это титбающие мо-
менты (М), продольные силы (/V) и перерезывающие
силы (Q). В расчетах статически неопределимых систем
учитываются только М и п, д 1я которых составляются
основные уравнения.
В соответствии с этими внутренними силами рассмат-
риваются «шарниры» пластичности в стержневых систе-
мах в виде вращательного и линейного шарниров.
Вращательный шарнир. Если в каком-либо сечении
стержня действует только изгибающий момент М = МПл,
то это сечение рассматривается как шарнир, вокруг ко-
торого возможно вращение остальных частей стержня,
рассматриваемых как жесткие диски. Центр вращения
располагается в центре тяжести сечения.
Линейный шарнир. Если в каком-либо прямом стерж-
не действует только продольная сила .V —Лфя, прило-
женная в центре тяжести сечения, весь стержень счи-
тается линейным шарниром, допускающим только сбли-
жение концов стержня,
Рассматривая стержень достаточно малой длины, при-
ходим к определению сосредоточенною линейного шар-
нира как предела линейных шарниров с уменьшающейся
длиной стержня.
Сосредоточенный линейный шарнир может возникать
в криволинейном стержне. Последовательность сосредо-
точенных шарниров может целиком охватывать криво-
линейный стержень.
Смешанный шарнир. Эго комбинация вращательного
и сосредоточенною линейного шарниров, сообщающая
сечению вращение и поступательное перемещение. Сме-
шанный шарнир можно рассматривать как вращатель-
ный шарнир относительно мгновенного центра враще-
ния (см 2128).
21.3.2. Расчет статически определимых
стержневых систем
В статически определимой стержневой системе все
внутренние силы являются линейной функцией нагрузки
N (х, Р) = P.V11 (.г), М (х, Р) = дли (х), (21.22)
где Р— параметр изменения нагрузки; №(х) и М°(х) ~
продольная сила и изгибающий момент от единичной
внешней нагрузки в сечении, определяемом координа-
тами х.
Предельная нагрузка определяется как решение урав-
нения пластичности Ф(А/, М) =Ф[Р№(х), РМ°(х}]~0
о । носительио параметра Р /Минимальное значение па-
раметра Р’! как корня такого уравнения есть предель-
ная нагрузка.
Пример 21.1. Рама (рис. 21.12) составлена из элемен-
тов прямоугольного сечения с площадью F.
Усилия в ригеле Мр(х, Р)~Рх; Np(y, .Р)=0. Усилия
в стойке М„ (х, P')=Pl, Nc{y, Р)~—Р. Уравнение пла-
стичности имеет вид (21.10). Для ригеля это уравнение
°х	Л1П1
-щ— =1, откуда Pi= --------- и минимальное значение
/Ипл	х
р* —
‘ 1 '' I ‘
Для стойки уравнение пластичности принимает вид
Р! f Р л
Л1ал +' рпл !	1'
откуда
3 РАСЧЕТ ПЛОСКИХ СТЕРЖНЕВЫХ СИСТЕМ
393
Учитывая (21 12) получаем
о- Sh2
pi== ___
Оывитно Р] <Р* ( м юватеды о, npt к л пы нюру”
ка Р — mir(j°7, Р;) и прстетыюе равпэвсси,. ли порук
ции о ределястся про1-пошью стопки
Рис 21 12
23.3.3.Расчет неразрезных балок
Кинематический метод Расчет кинематическим мето-
дом многопролетнои неразрезпои балки заключается
в исследовании возможных пластических механизмов
в которых действуют изтбающие моменты Л1, = Л1г1Л
где г — номер пластического ширнипа Некоторые воз
можные схемы пластических мехшчзмов для трехпро
тетиой неразрезпои быки показаны па р ?с 21 13 Гс ш
сообщить каком) нпбмдт шарниру порезы цени и то
углы перелом 5 во всех шарнирах определяюшя кал
0,3=0^ Работа внутренних ыл
и = и 5 ,л11П, (А,
где щ iK /И, г i соответствует знаку 0^ Работа внеш
них сил ив 1ястся функцией и — А =-иР'Р.ррг^, где Р— па
пгштр измерения внешней нагрузки Рр)—у я внешняя
силл п®— перемещение под си гои Рр, при «=1
Из уравнения U—4=0 определяется паоамегр
Р = S И1ПЛ0°/ХР/«“,	(2123)
I	I
соответствующий выбр твой схеме кинематического ме
хлннлма
Рассматриваются вс., возможные схемы образования
п астических шарниров и для каждого опреде гяется
сита PR (&=1 2 т) пг — чис-’о пластических че
х нгазмов Предел! ная нагрузка является минимальном
из всех этих сил Р =гшп (Pi Рг Рт)
В табл 21 5 представлены предельные нагрузки для
защемленных балок
Статическим метод Определение предельной нагрл з
ки производится в соответствии со стапгпесхои теоре
мои по которон ищется ст -юн лески допустимое распре
деление моментов Пусть требуется пасс тт 1ть двух
доотетчую перазро’иую балку (рчг 21 14 п) Для ес
расчета строятся шпорь протечных мом шов в пр^д
положении разрезности по всем пролетам Затем строит
ся эпюра моментов Af-t от опорного момента А = 1
Эпюру Мл увеличивают во столько раз, чтобы она кос
нулась в тоже b эпюпы пластических моментов /Иф'.,
!\ полученном таким образом эпюре моментов «подве
шиваите эпюру АР и уведнчиваюг ее коорлиналы в Р
Рис 21 14
раз так чтобы получающаяся в итоге эпюра коснулась
э поры предельных моментов М пф, но не пересекла ее
Получающееся значение параметра Р есть предельное
его значение Р4 Касание «подвешенной» эпюры РМ'1
с эпюрой произошло в точке а Эта точка опре-
деляет положение пластического шарнира с положитель-
ным изгибающим моментом, а точка Ь — вторая точка
образования пластическою шарнира —с отрицательным
моментом
В самом общем случае для k пролетной балки строят
эпюры гИ° и системv эпюр W , от единичных опорных
моаентов Необходимо чтобы выполнялось условие
- Л1~ РАЛ - S А, А1и < Л1ф, (21 24)
—i
Т 1 б л и ц а 215
Пр'СД^тьны*? naipv^Ki дтя защемленных пачок
О	на оэ п (	Ц 71	3	4- ’Гр 3Ari
		V , (!	21
	А	AU - s)
	7 —		
	Р	
	1	0 ипп
Г			у		AU - J
р		2,58-Ип.,
		
3		
4	— д —	P
Р		16 «пл A
		
7		
394	РАЗДЕЛ 2! РАСЧЕТ КОНСТРУКЦИИ ПО ПРЕДЕЛЬНЫМ} 1>\ВНОНЕСИЮ И УЧИ 110,133 ЧГ.С1И
при любых допустимых значениях лишних неизвестных
X, (4 = 1, 2, .... k — 1).
В ряде случаев такая задача решается графически
[22], но лучшее решение может был. ночучепо с по-
мощью аппарата линейного программирования.
Может оказаться такой случай, когда решение будет
не единственным для распределения моментов, по един-
ственным для предельной ншрузки Р Па рис 21.11,6
показана чрехпролечная балка, з которой предельное
Рис. 21.15
Нг --	уу	h'll Дз Дз Дн	j
		h,lf ni-i % nt
Это симметричная трехдиагональная матрица вторых
разностей, диагональные элементы которой /г‘(=-1//] +
n-l/ljni, а элементы слева и справа	1,у ~
Полная кинематическая матрица И составляется из
блоков г/1 и дополнительных k—1 строк;
состояние образовалось в левом крайнем пролете —
в точках а и о возникли пластические шарниры. При
недостаточно большой шпшеивностп равномерно рас-
пределенной нагрузки в среднем пролете может не ока
заться предельного состояния (линия /) или может об-
разоваться пластический шарнир в точке с. Однако его
образование пе отразится на схеме пластического ме-
ханизма балки. В любом случае как для эпюр, соответ-
ствующих линиям 1 или 2, величина предельной на-
грузки Р* неизменна, гак как ома определена из условия
разрушения левого крайнего пролета.
Использование линейного программирования. Расчет
сложной многопролетной неразрезной балки со сложной
формой внешней нагружп и неравномерном распреде-
лением материала требует очень большого объема вы-
числений, которые врушую реализовать невозможно.
Привлечение ЭВМ требгч т специальных подходов, ко-
торые для неразрезиоп балки выглядят следующим об-
разом.
Пусть неразрезпая бачка имеет k пролетов с опорами,
пронумерованными от ну и до k. Номер прочета счи-
таем по номеру правой опоры На рис. 21 15 показан
г-й пролет балки, в котором назначены пг опасных про-
летных сечений и два сечения над опорами I—1 и I. Там
же показаны распределения положительных и отрица-
тельных предельных моментов А4+ и Вся нагрузка
собирается в выделенные сечения в виде сосредоточен-
ных сил Рг\, Рг’, Рг'п_. Число и расположение опас-
ных сечений назначается из следующих соображений:
а) под точками приложения сосредоточенных сил;
б) вблизи места резкого изменения предельных момен-
тов яти A.i~7 ; в) для пролета с равномерной нагруз-
кой по всей длине расстояние между всеми сечениями
одинаковое и их число можно принять п, = 8=10, при
этом =llnt {i, s=l, 2, ..., nJ.
В итоге для i-го пролета можно составить векторы
/ = и, и, 4.)ии^=(7И];л, мгпл, ... муил) и
wnt	Лгмт • Дупл)- Затем Составляется
матрица размером ngg.11*-
1
k — 1
В первой дополнительной строке иа месте под стыком
матриц /2] и Я2 расположены элементы —	и —1/1].
Во второй строке под стыком матриц //2 и Н$ располо-
жены элементы —	— l//f (см. пример 21.2) и чак
далее.
Уравнение равновесия имеет вид
Н’т — Рг^О.	(21.25)
Здесь И' — матрица транспонированная к Н, а т —
вектор неизвестных моментов в выбранных сечениях для
k
всей балкч’, причем первые п = Р.пг компонент-—это про-
летные моменты, упорядоченные по пролетам, и затем
k—1 опорных моментов;
= И-	от^, да™,...
~~п	——-	'	'
Вектор г составляется из k векторов г1- г — (г1, г2,
rfl) и имеет всего п компонент.
Если есть постоянная нагрузка G, то она, так же как
временная нагрузка Р, собирается над сечениями в виде
сил £P~(g{, g\, .... gn,) и из них составляется вектор
g=(g', <s, ..., l?’1)' Уравнение равновесия записывается
так:
Н’ m~Pr — g = 0.	(21.25а)
Условия пластичности для Его пролета записываются
так: —Эги же условия можно распрост-
ранить на все моменты, составляющие вектор от;
-АГ[,	(21.26)
где векторы А1]]д и М~~п составляются нз и Л/'и~:
М-- =- 1AI1, Д12~,..., Мк лДЧ..., АД-!±).
пл 1 "пл • 'пл ’	’ пл ’ оп ’	’ "оп
Задача предельного равновесия заключается в опреде-
21 3 РАСЧЕТ ПЛОСКИХ СТЕРЖНЕВЫХ СИСТЕМ
395
„гении максимального значения Р* = тах Р(т) при усло-
виях (21 25) или (21 25а) и (21 26) Такая задача ре
шлется методами шнечного программирования
Пример 21 2 Трехпротетная неразрезная балка
(рис 21 16) имеет одинаковые по длине предельные мо
менты Л1Г^ и
ПТГТПТПТТТТГ^
Рис 21 16
Для этой балки
вектор неизвестных
fill	293»	з	j о ' '
tn — I тj, т,>, тА , zHj, ли,, m3, m 5 , rr^ ,	, mtm ।
m1	ma	mon
вектор интенсивностей внешней нагрузки r'~(k, 0 0, Ац
feb kj, 0)', ky — qLyb,
векторы пластических моментов
м+	 м~^{муя, . , м~Х
ИЛИ
ИГ = ЖГЛ(1. .пз	, 1)'
Матрица И имеет вид
4	Я	4
L1	Lt	Li
4	Я
0----- —
h	h
О
о
4
°
ООО
10 Li	5 £2	0	0
5	10	5	
—2	£2 ~~ 5 10	£?	0 0 ! 5
0 —		5	Z7 10
0	0 —	l„	i 2 J £n
5 ~ £s	0	0	0	0 5	2 j
0	0	0	~ ~ )
Число строк матрицы Н равно десяти — по числу ком-
понент вектора т, а число столбцов (восемь) равно чис
лу пролетных сечений и размерности вектора г В итоге
уравнения равновесия (21 24) состоят из восьми урав-
нений относительно десяти неизвестных В любой нераз-
резнои балке с А пролетами будет таких «лишних» не-
известных k—I по чшту статической неопределимости
системы
Если каждый про 1ет разбивается равномерно и, сече-
ниями, то можно ввести матрицы Нг по правилу
Матрица Н будет составляться из однотипных матриц
Решение сформулированном задачи возможно, как при
вч ю с помощью ЭВМ по стандартным программам за
да 1 линейного программирования Рекомендуется ис-
пользовать программы, учитывающие слабую заполнен
иость матрицы Н непутевыми элементами
21.3,4. Расчет статически неопределимых рам
Расчет рам, как правило должен проводиться с уче
гоч возможности образования воащаэетьных и линейных
пластических шарниров Если рама составлена только
из вертикальных стоек и горизонтальных ригелей, то
можно не учитывать возможность образования линей
пых пластических шарниров а ограничиться только вра
щательными шарнирами (рис 21 17, а) При более стро
юм расчете необходимо учитывать образование ланей
ных пластических шарниров (рчс 21 17 б) Это имеет
особое значение д 1я рам с наклонными элементами
Кинематический метод Э10г метод применяется для
расчета рам только с вращательными шарнирами В ра
ме назначается несколько схем пластических механнз
мов для которых по формуле (21 23) определяется на
1рузка, соответствующая этим механизмам Меньшая из
нагвузок принимается в качес’’ве предельной
Пример 213 Портальная рама нагружена силачи
РУ и Рк3 (рис 21 18) Очевидно что если стойки в рп
гель имеют постоянные сечения то пластические шарни
ры moijt образоваться в отмеченных на рис 21 18 а ше
ели сечениях Нч рис 21 18 б в г показаны три п-’асти
ческих лсхапчзча из которых можно образовать любой
пластшеспип механлзм с шарнирами в токах 1 —Ь Эти
механизмы называются баз геными Писю в слойках
ус юаня пласти игости и'^пт вил —Т
а в ригеле —Л'ЧгфМчб Ир Р«бола "ipTntunn и влек
них св 1 определится дтя каждой из схем следующим
образом
/	1	/1	1 X
Pk2 и„ = АД — 4-yfJ — ж _ 1 ।
“	’ h \ h ' Н —~h'~
4- М, —Ц 'j ug =	0! -	0, + М3 03
п — п
I 3	/ 1	1 \	1 \
Pki Их = 443	1 -у М4 I	-у ~——- -j- aWj ——— ц,з~
\ а \ а I — а ' I — а }
= М3 03 r Midi гмл,
Я?8 —~ (-Vi ф Vlj 4Д । ЛД)иг =-
Mi M3 0з -j-
396	РАЗДЕЛ 21. РАСЧЕТ КОНСТРУКЦИИ ПО ПРЕДЕЛЬНОМУ РАВНОВЕСИЮ II УЧЕТ ПОЛ'МЧГСТИ
В этих уравнениях Мг (7=1, 2, 6) равны Мст или
Alp и их знак совпадает со знаком угла перелома оси
—0,. Сокращая в уравнениях и и решая их относительно
Р, получаем три различных значения Pi, Р% я Р?„ соот-
ветствующих схемам б, в или г.
Предельная нагрузка будет минимальной из трех Р* =
= п11п(Р1, Pi, Р;,), и этой нагрузке будет отвечать одна
из приведенных выше схем, Если окажется, что Р*---
Рис. 21.17
Рис. 21.18
= Р| = Р2> то схема пластического механизма будет со-
стоять из комбинации схем бив (рис. 21.18). Такой
подход учитывает только изгибающие моменты, дейст-
вующие в раме. В этом методе весьма сложно учесть
влияние продольных сил.
Метод основной системы. Этим методом можно рас-
считывать любую статически неопределимую раму, в ко-
торой назначено т опасных сечений, где действуют про-
дольные силы Ni, N%, Nm и изгибающие моменты
Mi, М2, .... Мт.
Можно учесть и влияние поперечных сил Qi, Q2,
Qm, однако это приведет к чрезвычайно сложным вы-
числениям и не даст существенных уточнений.
Статически неопределимая система превращается
в статически определимую отбрасыванием лишних свя-
зей. Число отброшенных связей равно з —• степени ста-
тической неопределимости. Усилия в отброшенных свя-
зях обозначаются X], Х2, Хв.
Усилия и моменты в сечениях образованной статически
определимой основной системы записываются в виде
Лу = PM? + S Л'; N’i;
,==1	(21.27)
М = РА1р + S X М>
I	11	7	1
(I = 1, 2, ..., да).
Здесь М? и — усилие в i-м сечении от единичной
внешней нагрузки; A/j и —усилия в i-м сечении от
единичного усилия Xj—l.
Фактически Л'?, МР, :V f и м\— это ординаты единич-
ной грузовой и единичной эпюр от ;-г0 неизвестною
в г-м сечении.
Уравнения (21,27) удобно записывать в матричной
форме:
N=PNP+NX\ М = РМРМ MX, (21.28)
где №=(Л'Р, Л/Р, .... уР У, А1?=(М? ,М. AfP)'~
это векторы-столбцы. X=(Xi, Х2, ..., Х'а)'—вектор-стол-
бец неизвестных
Устюш; 11 частичности в общем виде записываются для
каждою сечения в оiдельности:
Ф/ (Nt, М{) <0 (1=1,2, ... ,т).	(21.29)
Можно в каждое такое условие подставить соответ-
ствующее выражение, Л/, и М, через Р и Л' и получить
условия пластичности относительно этих величин:
(PNi + S х, Ni; рм?м z х, < 0.
/=1 ,=1
Когда условия пластичности линейные и, в частности,
имеют вид (21,12), тогда каждое условие (21,29) запи-
сывается так:
| Л, I 1 Mi 1
, ---- +	j щ о (1=1,2, ... , т). (21.30)
1У/пл I шЪпл 1
Введя две диагональные матрицы
Уц/л	!
дг-1 = м‘2цл	! •
\
М71 I
можно все т условий пластичности (21 30) предста-
вить в компактном виде:
- 0-	(21-31)
где [1]т — вектор с компонентами, равными единице.
В итоге получаем следующую сншему условии относи-
тельно -S-Н неизвестных Р и А'ь .... Х„.
\^Jp^ -bvxjjo
4- РМр + МХ}\^[1\т .. 0.	(21.32)
213 РАСЧЕТ ППОСКИХ СТЕРЖНЕВЫХ СИСТЕМ
397
Эти условия записываются иным образом при помощи
четырех неравенств
РР-|-С‘Х-[1)т ТО; ^РР^МХ~П],п 0у|
рр тС-Х-[1 ]т <- 0; -PU-C- Л'-I 1 \т - 0J U'' °
где = Л'",1 -Vp Я Мр; l~ Л'^ Л+ - Л! АЯ -
векторы размерности т; С1 = Л 4- Л1~^ М,
С2 = N"n^ V — Л!ЯдМ — матрицы размером mXs Вы-
числение этих матриц особого труда „с
В итоге для s-f-1 неизвестного Р,
Xi, Х2, ..., Х„ имеется 4m неравенства
(21.33) и требуется определить мак-
симальное значение Р‘, удовлетворя-
ющее этим неравенствам. Это зада-
ча линейного программирования, ко-
торая с успехом может быть решена
с помощью ЭВМ.
Пример 21 4. Рассмотренную выше
раму (рис. 21 18) заменим основной
системой (рис 21.19) с тремя неиз-
вестными силами А'ь Х2, Х3. Запишем:
представляет.
Рис.
Мг = P{k, а 4- k2 й) — Хг - Н - Х3 а )
,М2 = Р (k}_ а) — А’г — Хг (И — А) — Х3 ар
М3 = Pkt а —	— Х3 а;
м4= 4-Лр
м- = + A'j — x:i (I - о);
Ale —	А'., Н — Х3 (I — н);
= Pki — А,;* .V, - Pki ~ А'3;
Х3 = Pk3 — А'з (по стойке);
Nц — Х2; Л'§ — Х3; Лд -= А3.	)
(21.34)
Матрицы п векторы, входящие в (21.33), имеют вид
0 0 — 1
0 0—1
0 0—1
" О 1	0 ’
о 0 1
0 О 1
1 — 1 — (H—h)	—а
! —1	0	—а
| —1	0	0
j —1	0	+(.( —а)
[ —1 И (I — а) |]
Ус ,овня (21.33) показаны далее в таблице, которую
следует читать сначала с верхними шаками, что соот-
ветствует первому условию (21.33), затем ео вторыми
знаками, что соответствует второму условию, и так
четыре уровня знаков. Такая система имеет четыре не-
известных Р, А'ь Х2 и +>„ д.гя которых имеется 4-6 = 24
ограничения в виде нер ibuktb.
Решение этой задачи, например, симплекс-методом
приводит к так называемому оптимальному плану Р*,
Ар Ай, Xj. Здесь Р*— оптимальное значение пара-
метра внешней нагрузки, a A’s — значения лишних не-
известных. Определение моментов и продольных сил
в предельном состоянии производится подстановкой
Р'- и Xs в выражения (21.28).
Подобным образом могут быть решены задачи с бо-
лее сложными условиями пластичности, например для
железобетонной рамы [9].
Любые выпуклые условия пластичности вида
Ф(Л',, AlJjgrO можно с достаточно высокой степенью
точности и по крайней мере безопасно заменить системой
вписанных линейных условии Так, условия (21,12') явля-
ются линейными и вписанными в условия (21, 10). Всег-
да одно нелинейное условие пластичности может быть
заменено системой t линейных условий a,NМ~Ь3М,. —
р		Л\	X,.	
+ k3 + 4ат 4 h	-у 1	- н	—	1	а	— 1 <0 -1 <0 — 1 <0 — 1 <0 — 1 <0 — 1 < 0
± Л'пл + Чл + йг + ki п	. с —< 1-11- и	ч А: 1 + 1 1 -	4 +j|! 4 Н _ 1 _	1 1-1 ня	; & 1	!	
— '"’'пл + ^пл + k-i -Е k3 а	i X. ~ 1	± <л		
ьи a 1 ь j	- 1 1 -1 - —‘ □"А-	0 + 1	пл — тпл	
0	Ж м1 —	ил - 1	1 + 1 a i-	0 -г 1 -г 1 — а	
0	<- -в ЛМ Т 1	0 - я	+ А/ ’	“ ЛЯ — 14 пл Д-  11л 7	1	t	а	
0	2: мр	ш л,6 — L1 пл	_ N<\ 1 4- пл	1 пл	
398
РАЗДЕЛ 31 РАСЧЕТ КОНСТРУКЦИИ ПО ПРЕДЕЛЬНОМУ РАВНОВЕСИЮ И УЧЕТ ПОЛЗУЧ! GT1I
— 1 гфО(/ = 1, 2, .... I) я эти условия будут достаточно
полные и самое главное безопасные, если задан мно-
гогранник, вписанный в область, ограниченную по-
верхностью пластичное ги.
21.4. ПРЕДЕЛЬНОЕ РАВНОВЕСИЕ ПЛАСТИНОК
определяемый по нормали к линии шарнира А1!!л—
пластический момент в шарнире, вектор которого на-
правлен вдоль касательной к линии шарнира
На рпс. 21,21 показана многоугольная плита, нагру-
женная в точке а сосредоточенной силой Плита шар-
нирно оперта по кошуру. Линии al-y-ab—линейные
21.4.1. Общие положения расчета
Предельное равновесие пластинок при их изгибе под-
чиняется общим теоремам предельного равновесия
и может рассматриваться со статических и кинематиче-
ских позиции.
Для успешного применения статического метода оп-
ределения предельной нагрузки существенную роль иг-
рают условия пластичности (а. 2.8).
Фактически для решения этой задачи необходимо
определить поле изгибающих и крутящих моментов
Мхх, Муу и Мх„, удовлетворяющее уравнениям равно-
весия п условиям пластичности и сообщающее пара-
метру нагрузки Р максимальное значение:
Рис, 21.21
Рис. 21,22
fl-
дх1 1 дхду 1 ду'“
щ Р'У (а , У) = 0;
Ф (Млл, Мк,„ < 0
(21.35)
При этом поле моментов должно удовлетворять
граничным условиям, зависящим от способа опирания
пластинки.
Эта задача в редких случаях имеет единственное ре-
шение для поля моментов, тогда как для экстремальной
нагрузки Р" задача всегда имеет единственное ре-
шение.
Использование кинематического метода основывается
на ащмизе различных схем излома пластинки, пре-
вращающих эту систему в пространственный кинемати-
ческий механизм из дисков, соеди-
ненных линейными пластическими
разозавшнйся вдоль
шарнирами.
Линейные пластические шарни-
ры в плитах — это аналог враща-
тельного шарнира в стержневых
системах и характеризуются тем,
что на некоторой линии изгибаю-
щие моменты вдоль нее удовлетво-
ряют уравнениям пластичности,
т. е по величине равны пластиче-
ским моментам
На рпс, 21.20 показан прямоли-
нейный пластический шарнир, об-
липши ab. Линейные гиастическне
шарниры могут образовываться как на прямых, так и на
кривых .линиях Широко используется название «криво-
линейный пластический шарнир».
21.4.2. Кинематический способ определения
несущей способности плит
По этому методу выбирается некоторый кинематиче-
ский .механизм или группа механизмов, для которых оп-
ределяется работа внутренних и внешних сил:
Й=[ Л4ПЛ 0dL; А = Р J uq (х, у) dx, dy, (21,36)
Здесь и — перемещение точек поверхности пластинки;
у(х, у) — интенсивность нагрузки; 0 — угол перелома,
пластические шарниры, позволяющие этой плите пре-
вратиться в пирамиду с вершиной в точке а' и высо-
той и. При такой схеме жесткие диски вращаются
вокруг опорных шарниров и линейных пластических
шарниров. Так, диск 1а2 повернулся на некоторый
угол вокруг опорного шарнира 7—2, вокруг шарнира
а] относительно диска 6а1 и шарнира 2а относитель-
но диска 2аЗ, Линии шарниров стали вершинами дву-
’ ранных углов. Величина этих углов определяется ио
следующей формуле (рис, 21.22):
6= у (cig ® + etg (?) и,	(21.37)
где и — вертикальное (из плоскости чертежа) переме-
щение точки а Приняв обозначения и нумерацию уг-
лов по рис. 21,21 и обозначив через /, длину шарнира
a.Ji (1=1, 2,	6), получим выражение для работы
внутренних сил
6
и	s (etg af: + etg PJ.
Работа внешних сил А = Ри. Отсюда предельная на-
грузка по формуле (21.22)
6
>пл s (cig ai + etg pz). (21.38)
Ь'=1
Для правильной многоугольной плигы, имеющей k
сторон, предельная нагрузка
P* = 2A4nJJMg™.	(21.39)
я
Криволинейные пластические шарниры. Образование
криволинейною пластического шарнира с появлением
по контуру шарнира изгибающих моментов с век-
тором, направленным по касательной к шарниру, вы-
зывает в области, ограниченной криволинейным шарни-
ром, появление пластических моментов	вектор
которых направлен к вершине конуса пластического ме-
21.4, ПРЕДЕЛЬНОЕ РАВНОВЕСИЕ ПЛАСТИНОК
399
ханпзма (рис. 21,23), Работа внутренних сил иа пло-
щади, ограниченной криволинейным шарниром:
/ г' V4 1
/—. _ — Мед_
\ Г } г J
[ [14- [~ур-
ё. L
(21.40)
Это выражение записано в
полярных координатах
(г, 0), центр которых поме-
щен в вершину конуса;
г(9) — уравнение криволи-
нейного шарнира. Для замк-
нутого шарнира интегриро-
вание проводится в преде-
лах от 0 до 2л. Подынтег-
ральные выражения 0
(21,40) можно упростить и
записать как
{/== «л+мм) ( 6, -90) + «, - 0,5М~)х
4(0,0
. г (0Д
г (01) ) + ^пл + Жпл^ Х
Г >	м
]    аи.
г(0)
(21.41)
Если криволинейный шарнир определен по кругу,
тогда г'(0)=О и Д== (Мпл+АГ;Л ) (0,—0О).
Для произвольно расположенного шарнира оптималь-
ной формой, сообщающей U максимальное значение,
является логарифмическая спираль г(0) =/?оес!).
21.4.3. Статический способ определения
несущей способности плит
Применение статического способа расчета тесно свя-
зано с методами линейного программирования и ис-
пользованием ЭВМ, Дифференциальное уравнение рав-
новесия плиты (21.35) заменяется какой-либо конеч-
ной системой линейных уравнений. Например, это мо-
жет быть конечно-разностное уравнение, составленное
для какой-либо сетки на плиге (рис. 21.24).
Плита разбивается прямоугольной сеткой со сторо-
нами пх = а[п и nv — b/m. Для каждого узла сетки
составляется конечно-разностное уравнение, которое
для внутреннего узла 1/ имеет вид U— номер узла ио
горизонтали; / — номер узла по вертикали):
— ЛЕД41' +2414^-
_____j_
А-
т.	_	, -	-	-f -
"%
щ	-- Д
+ Ptfl = 0,
где ql) — интенсивность нагрузки в точке fj. Таких
уравнений будет (п—1)  (т—1)—-число, равное коли-
честву внутренних точек.
При необходимости к этим уравнениям добавляют
уравнения граничных условий (см. раздел 15). Для это-
того вводятся «законтурные» точки, обеспечивающие
надежный учет граничных условий.
Введя вектор неизвестных в виде М—(М‘"'}Г , М“'Н.М^,
М.^,	, Mnxf ) и обозначив коэффициенты ко-
нечно-разностных уравнений как элементы матрицы А,
получим матричное представтение дифференциальных
уравнений равновесия
AMA-Pq--=0.	(21.42)
Присоединяя к этому уравнению условия пластич-
ности, составленные для каждой внутренней точки сет-
ки, получаем полную систему условий задачи
®{С- <,	<0
(1 = 1,2,..., п — 1, ; = 1,2,..., п — 1). (21.43)
Можно каким-либо способом линеаризовать эти усло-
вия, представив нелинейные условия пластичности в ви-
де системы линейных неравенств:
<0
(й= 1,2,..., t).	(21.44)
s>
Здесь t — число линейных условий, приближенно пред-
ставляющих условия (21.43); оно зависит от выбранной
точности линеаризации.
В первом приближении можно считать, что |аД =
= |ЬД=.ИПЛ н ]сд = (АД.дКз) ~1, это задает так на-
зываемый вписанный симплекс в условия пластичности
Мизеса. Здесь ( = 8—по числу октантов трехмерного
пространства моментов Знаки ак, Ък и ск назначаются
из следующей таблицы:
400
РАЗДЕЛ 21 РАСЧЕТ КОНСТРУКЦИИ ПО ПРЕДЕЛЬНОМУ РАВНОВЕСИЮ И УЧЕТ ПОЛЗУЧЕСТИ
Условия спастичности (21.44) в матричиои форме
записываются так:
1 1 1/УТ
1 —1
-1 —i 1/]/з
— 1 1 1/Уз"
1	1	I#/
1 -1 l/j/з
-1 --4 1/JZ3
— 1 —1 i/j/з
1
1
1
1
1 -°
1
1
1
Из матриц Р, как из блоков, составляется б точная
система условии пластичности всей задачи
(21-45)
21.4.4. Некоторые частные решения
для пластинок, загруженных
сосредоточенной силой,
при шарнирном опирании
Прямоугольные пластинки. Основная схема пласти-
ческого механизма
доточенной силой,
пиров, идущих от
Рис. 21.25
для пластинки, загруженной сосре-
приннмается в виде линейных шар-
точки приложения силы (точка с)
в углы пластинки (рис, 21.25).
Из уравнения работ для такого
механизма получается значение
предельное нагрузки
(21.46)
Для квадратной пластинки с силой, приложенной
в центре, Р' =8Л1ПЛ.
С приближением точки с к одной из сторон пластин-
ки получается Р”-» со при или у >0. В таком слу-
чае возможно образование местных криволинейных
шарниров, показанных на рис. 21.26.
Блочно-диагональная матрица имеет {п—1)(т—1)
блоков и весьма удобную форму записи; вектор [1]
имеет 8(п—l)(ffl—1) компонент, и все они равны еди-
нице. Поэтому хранение всех таких условий в памяти
ЭВМ не обязательно, так как матрица условий имеет
регулярную структуру, всего заполнено нулевыми эле-
ментами около 10%, среди которых фигурируют только
два числа: Мпп и Мал/ I' 3.
Если известно, что в результате решения всей задачи
моменты Мхх и М,,„ только положительные, то число
условии можно сократить, исключая в матрице р
строки 2, 3, 4, 6, 7, 8. Тогда
Рис, 21 26
11 1 Уз
1 1 — 1 J/з
Объем условий (21.45) при этом сокращается в 4 ра-
за, но добавляются такие условия, как М^х > 0
и	которые только облегчают решение задачи
методами линейного программирования.
Матрица А в уравнениях равновесия (21.42) имеет
удобную ленточную структуру. Поэтому ее хранение
полностью также не обязательно. В итоге оказывается,
что, несмотря на кажущийся очень большой числовой
материал для задачи в целом, можно обойтись перера-
боткой на ЭВМ сравнительно небольшого объема чис-
ловой информации, обрабатывая только ненулевые зна-
чения исходных матриц.
Решение задачи статического метода заключается
в определении Р’* = гпахР(Л1) при ограничениях (21.42)
и (21.45). Такой подход практически не зависит от
формы пластинки и наличия в ней разного рода отвер-
стий, Так же просто учитываются неоднородные и ани-
зотропные свойства материала пластинки.
Механизм разрушения будет как па схеме а тогда,
когда окружность радиусом и S' 2 не пересекает смеж-
ной стороны пластинки. По схеме а криволинейный
шарнир образуется по окружности; по схеме б криво-
линейный шарнир — логарифмическая спираль. В до-
полнение к этому шарниру образуется линейный шар-
нир cl, выходящий в угловую точку пластинки. Пре-
дельная нагрузка для обеих схем вычисляется по фор-
мулам
11,42МПЛ;
1
ч.	/ и	и	\
'^ПЛ Н" ' “ Т С I ’
J \ V	и	/
(0,5л % а 4- рр ф- [In--
„ 1 v
с = 2--------------------------------
0,5 л 4~ Д $
(21.47)
J
Окончательно предельная нагрузка определяется как
М =rniri(₽p В.,), если имеют место схемы, показанные
на рпс. 2125 и 21.26, а, или Р* — rnin/Bj, Р6 ), если
возможны схемы рис, 21.25 и 21.26,6.
21.4. ПРЕДЕЛЬНОЕ РАВНОВЕСИЕ ПЛАСТИНОК
401
Пластинки со свободным опиранием по контуру. Та-
кое опирание допускает возможность приподнимания
краев пластинки над опорами, что существенно сказы-
вается иа схемах пластических механизмов и предель-
ной нагрузке. На рис. 21.27, а показана прямоугольная
пластинка, нагруженная сосредоточенной силой. Пунк-
тиром показаны участки контура, которые приподни-
маются над опорами.
Определение точек выхода пластических шарниров
на контур пластинки определяется по формуле [4]
ш
/ =
(21.48)
Все обозначения показаны на рис. 21.27,6, где с —
точка приложения сосредоточенной силы; сВ— биссек-
триса угла/ kcl — перпендикуляр к биссектрисе сВ;
с/ и ccl — линии пластических шарниров.
Рис. 21.30
В горизонтальной плоскости остается только контур,
отмеченный цифрами 1—4. Внутренняя часть контура
опускается вниз, а внешняя приподнимается вверх. Для
центрально нагруженной квадратной пластинки Р* =
^б.бЗЖпл.
На рис 21.28 показана прямоугольная пластинка
с отношением сторон 2<Za/b <1, нагруженная в цент-
ре, у которой разрушение происходит так же, как
у квадратной пластинки, тоже нагруженной в центре,
но в которой невозможно приподнимание контура;
п Р*=8Мп.1.
Здесь происходит вращение частей 1—2—3—4 и
Г—З'—З'—4' вокруг осей 1—2 и 1'—4'.
Бесконечная пластинка, шарнирно опертая ио двум
параллельным сторонам. Схема разрушения такой
пластинки показана иа рис. 21.29. Здесь образуются
кольцевые пластические шарниры; предельная нагрузка
Pf = 10,28 А1ПП.
Кинематический механизм прямоугольной пластинки
при свободном опирании. Для прямоугольной пластин-
ки с отношением длинной стороны к короткой меньше
3 (а/b 3) при свободном опирании контура возможно
приподнимание в углах по схеме, аналогичной
рис. 21.27.
Для сосредоточенной силы, приложенной в произволь-
ном месте и при условии, что механизм не образуется
по схемам ряс. 21.26, пластический механизм показан
на рис. 21.27, Пластинка превращается в восемь жест-
ких дисков Диски I—IV вращаются вокруг осей 1—1,
2—2, 3—3 и 4—I, а диски V—VII— вокруг осей 1—2,
2—3, 3—1 н 4—1, лежащих на контуре пластинки.
Внешние участки, отсекаемые осями вращения 1—1~~
4—4, приподнимаются над опорным контуром.
26—26
После определения положения осей вращения 1—14-
4—4 пластинка может рассматриваться как многоуголь-
ник с шарнирным закреплением по всему контуру и без
возможности приподнимания краев. Предельная нагруз-
ка для такого многоугольника определяется по форму-
ле (21,38).
Частные решения для квадратной пластинки с распо-
ложением сосредоточенной силы на четверти диагонали
(т) = (1=0,25, см. рис. 21.25) дают Р4‘=8,4 7ИПЛ.
Треугольная пластинка. Схема пластического меха-
низма треугольной шарнирно опертой пластинки пока-
зана на рис. 21.30, а, а со свободным шарнирным опи-
ранием— на рис. 21.30,6.
В первом случае образуются криволинейные шарни-
ры, очерченные по логарифмической спирали, а во вто-
ром случае — только линейные шарниры с возмож-
ностью вращения жестких дисков и приподнимания уг-
лов. В этом случае положение лчнеиных шарниров оп-
ределяется в соответствии с формулой (21.48). В част-
ном случае для равносторонней пластинки по схеме
21.30,а Р*=9,14Л4ПЛ, а для свободно опертой по схе-
ме 21.30, б Р* = 6,92 7ИПЛ.
21.4.5.	Пластинки, загруженные равномерно
распределенной нагрузкой
Схемы возможных пластических механизмов шарнир-
но опертых пластинок при равномерно распределенной
нагрузке со свободным и несвободным опиранием прак-
тически одинаковы и погрешность составляет 5—7%.
На рис. 21.31 показан ряд возможных схем образова-
ния пластических механизмов.
Пример 21.5. Расчет прямоугольной пластинки при
шарнирном опирании и равномерной нагрузке Р про-
изводится следующим образом. Приняв схему пласти-
ческого механизма (рис, 21,32), определим прежде все-
го объем призмы со скошенными гранями, получаю-
щуюся при опускании точек с и с' на единицу:
В = 4-06(2 + 0-	(21.49)
6
Работа внешней нагрузки будет равна A — PV. Затем
определяем работу внутренних сил, считая, что в пласта-
402
РАЗДЕЛ 21. РАСЧЕТ КОНСТРУКЦИИ ПО ПРЕДЕЛЬНОМУ РАВНОВЕСИЮ И УЧЕТ ПОЛЗУЧЕСТИ
веских шарнирах действуют изгибающие моменты ;ИПЛ
U = Мпл (4 ctg а 4- 4 ctg р + ObQ. (21.50)
Углы а и Р определим из условий
ctg а = —----: ctg р = -—- .	(21.51)
a	ctg а
Угол 0 = 4/а — двухграиный угол в шарнире сс'.
Теперь требуется определить минимальное значение
Р(С) при О О 1, т. е. определить положение точек
с и с', при которых Р(С) минимальное. Для этого до-
статочно решить уравнение
4
что приводит к квадратному уравнению
Рис. 21.32
с решением
2l + k2 _	.
Я“
Подставляя это значение в /(С), получаем
Р*=	/(:*) = min Р(й- (21.55)
аЬ £
Для квадратной пластинки (fe=l)g=0 и Р* =
—24 7Ипл/а2. Условие С4 = 0 приводит к схеме пласти-
ческого механизма, показанного на рис. 21.31, б.
Для правильной многоугольной плиты с k сторонами
схема пластического механизма показана на
рис. 21.31, в. Объем пирамиды с высотой, равной еди-
нице,
1	2л
V = — Riksm— ,
о	k
где R — радиус описанной окружности.
Работа внутренних сил на системе радиальных пла-
стических шарниров
U = Жпл 22 ctg а = 27ИМ k tg .
Предельная нагрузка после простых преобразований
приобретает вид
pt___	544пл
Ricos —
k
Введем отношение k = bja и запишем
U = 4Л4пл
Г( 1 - й k + -— 4- kZ 1 =
L	(i-o a	л
= 4Л4пл Й4
 1
(21.52)
Нагрузка определяется из уравнения U—Ai
1
Й4-——
D ... 24/Ипл (1 - 0 k
——ГГГ“-
Обозначим
1 _L ^2 —
f © = п—к©—дд;
(1 — Ь) (2 -г о k
Гз
Для равностороннего треугольника	•—-— {а—
сторона треугольника) и
р* = ДЯ™ .
fl2
Для квадрата получается приведенный выше резуль-
тат. В пределе для круга (k
R2
тогда
Р© =
24А4ПЛ
ab
/©
(21.53)
(21.54)
Определение схем, показанных на рис. 21.31, г и д,
сложнее. Для треугольника можно ввести две коорди-
наты точки пересечения шарниров (точки с) и и а. Как
функции этих переменных можно определить объем пи-
рамиды V(и, о) и работу внутренних сил на линейных
шарнирах и =	а). Тогда предельная нагрузка
будет функцией двух переменных
I- (и, V)
21.4. ПРЕДЕЛЬНОЕ РАВНОВЕСИЕ ПЛАСТИНОК
403
Положение точки с (координаты ч* и о») найдем
как решение системы двух нелинейных уравнений
dL !и, г’) L (и, V] дУ (и, о)
---------— ---------- . --------. Q.
iu	V (и, v) ди
dL (л, н) L (и, v) д'У (и, V)
dv V (и, v) dv
Аналогично решается задача для трапеции. В этой
задаче уже три переменных. Две—координаты точки
с(щ о)- В силу того что точка с' находится на прямой
са, достаточно ввести одну координату для этой точки
(ш)—расстояние точки с’ от с или а, В вертикальной
плоскости точки с и С лежат также па прямой ас, сле-
довательно, в качестве характерной точки можно взять
только точку с. Если ее перемещение приравнять еди-
нице, то перемещение точки с‘ будет ас'/ас.
Объем усеченной пирамиды для такой фигуры будет
функцией трех переменных V(и, о, w), точно так же,
как работа внутренних сил па углах переломов в пла-
стических шарнирах и=МалЦи, v, щ). Координаты
/П, v\ ай находятся из решения нелинейной системы
трех уравнений
L (и, v, w) L (и, о, w) ОУ (и, и, w)
Для плиты с защемленным контуром, на: ружепной
сосредоточенной силой, предельная нагрузка
2л
р = 2ИПл + Чл j	(21.56)
б
Для защемленной пластинки при Мп,, = Л1ПЛ работа
радиальных предельных моментов равна работе момен-
тов по криволинейному шарниру. Очертание криволи-
нейного пластического шарнира — это логарифмическая
спираль с уравнением г(0) =Доесе .
Для любой пластинки, защемленной по всему конту-
ру и нагруженной сосредоточенной силой, предельная
нагрузка Р4=4лМпл,
Пластинки, защемленные по контуру
и нагруженные равномерно
распределенной нагрузкой
Прямоугольная пластинка имеет схему пластического
механизма, показанную на рис. 21.34. В дополнение
к линейным пластическим шарнирам в поле пластинки
образовались пластические шарниры вдоль защемлений.
Работа внешних сил определяется с учетом (21.49). Ра-
бота внутренних сил по формуле (21.52) должна быть
дополнена работой контурных пластических шарниров
Решение такой задачи без использования вычисли-
тельной техники требует больших затрат времени, в ос-
новном на простые алгебраические операции.
21.4.6.	Предельное равновесие пластинок,
защемленных по контуру
где k=-b ,1а.
АЕ =- 4Л'/'1Л4
Рис 21.34
Образование пластических механизмов в пластинках,
кон гур которых целиком или частично защемлен, про-
исходит с образованием пластиче-
ских шарниров около защемлен-
ных частей контура. Должен обра-
зоваться замкнутый криволиней-
ный пластический шарнир (рис.
21.33), для того чтобы образовал-
ся пластический кинематический
механизм. Этот шарнир может
быть расположен целиком внутри
пластинки, но может касаться кон-
тура пластинки.
Рис 21 33	В радиальных шарнирах текуче-
сти работа внутренних сил
2л
где г(0)—уравнение контура криволинейного шарнира
в полярной системе координат с центром в точке с.
Работа в криволинейном шарнире
2л
= (i +
h
где Мпл—предельный момент в криволинейном шар-
нире.
26*
Общее уравнение для предельной нагрузки:
Это уравнение практически не отличается от уравнения
(21.54) для шарнирно опертой плиты, за исключением,
слагаемого Л1ПЛ — предельного момента у защемления.
Из этого следует, что положение точек с и С Ее зави-
сит от способа опирания пластинки. Если Л1ПЛ=Л4ПЛ,
то работа изгибающих моментов на линейных пластиче-
ских шарнирах внутри пластинки равна работе изгибаю-
щих моментов на контуре. Последние имеют знак, об-
ратный моментам по линейным шарнирам внутри
пластинки.
Общий случай. Предельная равномерная нагрузка
на защемленную по всему контуру пластинку определя-
ется из формулы
2л
?=6ЛДЛ--------------------.	(21.57)
( r^dQ
о
404
РАЗДЕЛ 21 РАСЧЕТ КОНСТРУКЦИИ ПО ПРЕДЕЛЬНОМУ РАВНОВЕСИЮ И УЧЕТ ПОЛЗУЧЕСТИ
Таблица 21.6
Предельные нагрузки для круглых и эллиптических пластинок
Схема пластинки	Предельная нагрузка	Схема механизма и примечания
2г £rnTfrn~pj р		_ 1
1	2/?	i	R- -И г Я — 2Р	
nrrrd 1 tenn> Р ,	2И	1	^пл		
2г tpiri-h-JT] р 	2Р	г- (з — 2 —У \	Р / При г R R"	р определяется кац решение уравнении г >0,606Р 3—2 — /1 ™ Р \ —- In	— 0, Р / г < 0.606Z? I 4- 1п ™ - Р - зХ in Ра	г Ч(д-'! 4J
'— 2R -	"яМрп Д /дТЦЦЗ	§
	-Л1пл ‘я~~ Р 51п	Шарнирное опирание на часть контура
—{ -е		2яМа ь	Сила в одном из фо- кусов. Формула дей- ствительна при — < у Г ь
Продолжение табл, 21 6
Схема пластинки	Предельная нагрузка	Схема механизма и примечания
			„А!	О’+Ь’ пл ab При равномерной наг- рузке 2М 	1У X Зау х(р,+зС+1)	Формулы действи- тельны при 24<1 + УТ 19
т'га-ЦшШНШ Р	Р* — min (Pi, Р2); Pi - 6А4 J 1	——1 ил i г(1-я)! _ Яа(1—3CJn) Р41 "• 3;а 4- 2с,3)	1 1
Уравнение линейного пластического шарнира
ch \Ь (0 + а)]
где & и а — постоянные;
Криволинейный шарнир проходит вдоль контура; при
этом
Если знак неравенства обратный, то криволинейный
шарнир отходит от защемленного контура.
Равносторонний 6-угольник, описанный вокруг окруж-
ности радиуса R, имеет ту же предельную нагрузку,
что и круглая пластинка радиусом защемленная по
контуру:
Эта нагрузка в два раза выше предельной для шар-
нирно опертой пластинки.
В табл. 2!.6 приведены предельные нагрузки для не-
которых типов пластинок.
21.4.7.	Пластинка с отверстием
при равномерно распределенной нагрузке
Квадратные пластинки
с квадратными отверстиями
Пластинки с отверстиями рассчитываются так же, как
пластинки без отверстий, — выбираются схемы пласти-
ческих механизмов, для которых определяется нагрузка.
21.4. ПРЕДЕЛЬНОЕ РАВНОВЕСИЕ ПЛАСТИНОК
405
В квадратной пластинке с центральным отверстием
(рис. 21 35, и) предельная нагрузка
24Л©
7- - — А (?);
пластинки (рис. 21.35, а), определяется также сравне-
нием двух схем:
где
а-
(21-58)
24Л4кл
—Г5©© ©
а-
Функция л) определяется при помощи функции
Н) и Ы9 ф), П) — min 19, /5(С, т9],
где
/1 ©
2?
Г,а
Если отверстие расположено
Рис
21 35
f г___________________(1,5-Ц-?)_______________
5 Л 1-3?2(1 -?)-(2т| + ?-!)= (2- 4т] + ?) ’
Если пластинка защемлена по контуру, то учитывается
работа изгибающих моментов в защемлении.
Предельная нагрузка для
отверстием (см. рис. 21.35, а)
пластинки с центральным
24Л4пл
Р* =-----хп h {0
а-
(,у
О /б
1
1 — зр + 2?3 ’
Предельная нагрузка для пластинки с отверстием
между диагоналями (см, рис. 21.35,6)
2Шплг
„ I е (9 •
р#==Д<Н?
а2
Предельная нагрузка для пластинки с отверстием на
диагонали, но не перекрывающим центр пластинки, оп-
ределяется как минимальная из двух:
24Л4 „	24/ИП7т
Р1 _ -фг f3 л) +	- h (?, n);
а2
1
схемы для пластинки без отверстия
247ИПЛ
^ = ©©4©; П© = . . _•
а-	1 — 1,о?2
В случае, когда отверстие расположено на диагона-
ли и не пересекает центра плиты (рис. 21.35, в), воз-
можны две схемы пластических механизмов: с центром
в точках с и с'. Действительная предельная нагрузка
определяется по формуле
24МПЛ
Р* =-----(?, Л),
а*
где
F-i (?, Л) = min [/3 (?, ц),
r v	1—0,5?
fa (?, Ч)= --77Г-7-ТГ ;
1 _ 6nt- + Д
1 Г
-	у,, =	-------- q — ;
1—3?2+2?Ц
0,5(1 - С) [1 - 2П)£-Л) - ? 0 ™ 0,5?)]
Л(1 __ о,б? (1 -0,5?)
Функция f3© ц) соответствует первой схеме с цент-
ром в точке с, функция (©> д) —второй схеме с цент-
ром в точке С.
Предельная нагрузка для пластинки с отверстием,
расположенным на диагонали, но перекрывающим центр
1
Т]) — ! _ j-з ’
24 ЛН-,	24 Л1П1
Р5 - —А П. © + —h © Ш
а2	а2
1
/8Й’ Л) ©1 -ti)(1 -3« + 20:
Р* = min (Рг, Рг).
Предельная нагрузка для пластинки с отверстием, пе-
рекрывающим центр (см. рис. 21.35, а):
а-
24 М„я	24М'
Pi = —Ь © Ч) + —h © ©
а-
ч) = П +з?(1 -э-
X (2-©-?)]
24 Л1ПЛ	24 А1пл
© ,=	22 п (С> л) +--- q (L л);
аи	а*
Р* = min (J\, ©).
В тех случаях, когда не все стороны пластинки за-
щемлены, Л© учитывается с коэффициентами 0,25; 0,5
или 0,75, если защемлены соответственно одна, две или
три стороны.
406
РАЗДЕЛ 21, РАСЧЕТ КОНСТРУКЦИИ ПО ПРЕДЕЛЬНОМУ РАВНОВЕСИЮ И УЧЕТ ПОЛЗУЧЕСТИ
Круглая пластинка с круглым
отверстием (рис. 21.35, 4)
Предельная нагрузка определяется как минимальная
из двух.
6Л4ПЧ
Pi = (L л);
644 пл
Ра= дн/и (0.
[2*2	1
J _	- (1-ЗУ лГ3;
(1 - ф J
/н (О —
__ 1—£
1	3£- + 2£3 ’
Р-1 = min (Plt Ps).
Первая нагрузка соответствует пластическому меха-
низму в виде конуса в центре пластинки, вторая нагруз-
ка соответствует конусу с вершиной в центре отверстия
Если края пластинки защемлены, то Pi и Pz опреде-
ляются с добавочными членами
6М	6ЛД„
п-™пл ....	, , пл г ,
-р-(&> л) + —рр hi (ь. ч);
А"	А“
1
а> ч) —, Qf.„
1 — q
6ЛДл бЛ-f
- -ppp кг (S) + -пл- Аз (□;
ц-
1
/1з€)== j _ Зна
2
R-
Р* = min (РД Р2).
21.5.	ПРЕДЕЛЬНОЕ РАВНОВЕСИЕ ОБОЛОЧЕК
21.5.1.	Общие положения расчета оболочек
Определение несущей способности оболочек связано
с большими трудностями вычислительного порядка. Точ-
ные решения могут быть получены и представлены в ко-
нечном виде только для ограниченного числа простей-
ших оболочек. Например, определение предельной
нагрузки для пологой оболочки на прямоугольном пла-
йе при равномерной нагрузке связано с очень большими
вычислениями
В целом общая задача точного расчета может быть
сформулирована так: определить максимальное значе-
ние параметра внешней нагрузки Р при выполнении
дифференциальных уравнений равновесия оболочки для
внутренних усилий с одновременным соблюдением усло-
вий пластичности в виде неравенств.
Большинство решений проводится следующим обра-
зом: задаются системой дифференциальных уравнений
равновесия оболочки (см. раздел 14) и уравнениями
пластичности Ф(Л', Л4) =0. Часто эш уравнения назы-
вают конечными соотношениями. Затем задаются воз-
можными полями скоростей перемещений, согласуй их
с ассоциированным законом пластического течения, Со-
вместное определение внутренних уравновешенных сил
и скоростей перемещений, связанных с ассоциированным
законом пластического течения, дает предельное их рас-
пределение (третья теорема предельного равновесия).
Безмоментные оболочки. Для безмоментной статиче-
ски определимой оболочки задача решается просто.
3 этой оболочке действуют только нормальные силы
, Др и перерезывающие силы Т (см. раздел 14). Эти
силы могут быть определены как функции параметра
внешней нагрузки Na^=-PN°a, N $ = РЗ'^, Т = РТи.
Подстановка этих выражений .в какие-нибудь усло-
вия пластичности даст предельное условие
Ф(Р, .V^, Л’р ,Т°)гР0- Фактически задач а заключается в
решении алгебраического уравнения Ф(Р) =0, корень
которого Р‘ дает величину предельной нагрузки.
Моментные оболочки. Расчет оболочек прежде всего
должен проводиться с учетом, возможных разрывов
внутренних сил и скоростей деформаций. Если на ка-
кой-то линии происходит разрыв сил, то деформации
должны быть непрерывными и, наоборот, разрыв дефор-
маций может происходит только по линии, где внут-
ренние силы непрерывны.
Возможен приближенный расчет оболочек кинематиче-
ским методом. Для этого по каким-либо соображениям
выбирается схема пластического механизма, для кото-
рого определяется соответствующая нагрузка. Основ-
ными соображениями по выбору пластического меха-
низма являются данные эксперимента. Однако следует
иметь в виду, что пластический механизм оболочки яв-
ляется пространственным в отличие от стержневых си-
стем и пластинок. Наиболее удачные результаты полу-
чены для цилиндрических, конических и пологих обо-
лочек.
21.5.2.	Расчет осесимметричных оболочек
Общие уравнения. В осесимметричной оболочке (обо-
лочка вращения) при осесимметричной внешней нагруз-
ке действуют внутренние силы, показанные на рис. 21.36.
Уравнения равновесия следующие;
~(/Л')'~ — S + ~Q4-P<?«=0;
г	г	Rs
(г Q)' —	3' — ~п~ 3 4- Pqm ~ 0;
г	Rs
1	1
— (гМ)' — ----7 —Q — 0.
г	г

(21.59)
1
Здесь Р — параметр внешней нагрузки; qu и qw —
интенсивность внешней нагрузки по касательной к обра-
зующей и по нормали к ней. Исключение из этой сисзде-
21 э ПРЕДЕЛЬНОЕ РАВНОВЕСИЕ ОБОЛОЧЕК
407
мы перерезывающей силы Q приводит к системе двух
травнения
(/nV)' — г' S + ~ [(гМУ — r'T] -щ Prqu = 0;
z?s
(г МУ'-у(гТу-—г + т п-sj + Prfe = 0.
' As	Аф у
(21.60)
Граничные условия могут быть такие: шарнирное опи-
рание М.(Р( =0, скользящая заделка N (R) =0, защем-
ленный край — граничные условия произвольные.
Обозначим и (а) и тц(з) скорости перемещения по ка-
сательной к образующей (вдоль и по нормали
(вдоль /„). Скорости деформаций, соответствующие си-
лам А', Ж, S и Т, выражаются через скорости переме-
щений так:
(21.61)
Граничные условия для перемещений: шарнирное опи-
рание и защемление — u(R) = w(R) =0, скользящая за-
делка w ((?) =0, шарнирно подвижное опирание
u(R) cosa-pw(R) sina = 0.
Совместное решение систем (21,60) и (21.61) невоз-
можно, так как отсутствует связь между силами и ско-
ростями перемещений.
Большинство задач решается в предположении, что
по всей поверхности оболочки выполняются уравнения
пластичности и ассоциированного течения:
Это нужно для составления 2п уравнений в конечных
разностях для точек 0, 1, .... п — 1.
Уравнения равновесия (21.00) приводятся к эквива-
лентной матричной форме
(21 63)
Подматрицы А, В, .... V являют-
ся конечно-разностными аналогами
дифференциальных операторов, со-
ставляющих уравнения (21,60):
+ =(Д°г.	->
С“‘ )
Рис. 21 37
По конкретным граничным условиям вводятся допол-
нительные уравнения. Например, при шарнирном опира-
нии Мп — 0.
Условия пластичности записываются для каждой точ-
ки отдельно. Например, условия Треска записываются
для каждой точки в матричной форме
10	10
1	0—1	0
: о	1	о	1
но	1	о	-1
io “1 0-1
io	-1	0	1
у”	?
В ряде случаев такая задача может быть решена.
Произвольное распределение нагрузки вдоль образую-
щей обычно приводит к весьма сложным исследованиям
ре/кимов течения, описываемых формулами (21.62).
Решить задачу можно, ограничившись статической
постановкой в виде уравнений равновесия (21.60), со-
ответствующих граничных условии и условий пластич-
ности в виде неравенства Ф(Д, М, S, 7)^0. Определе-
ние предельной нагрузки Р- —это задача математиче-
ского программирования.
Приведение к задаче математического
программирования
Па образующей оболочки назначается п+1 точка,
лучше всею с одинаковым расстоянием между ними
А (рис 21.37). Уравнения равновесия запнсывакнся и
конечных разностях. Для этого вводятся векторы неиз-
вестных А'=(.¥о, .... АД)', S=(S0,	М=(М0,
М„)', Т—(Т0, .... Тпу. Вектор всех неизвестных состав-
ляется из этих векторов X'=(N', S', М', Т'). Всего век-
тор А имеет 4(«+1) компонент. Дополнительно вводит-
ся точка Г, усилия в которой равны усилиям в теаке 1.
X Pj — ( X 0.
! Ml J I  /
\Ti f \ I /
Объединение таких условий для точек 0,
дает блочную форму матрицы условий
(21.64)
1, п—1
(21.65)
В итоге вся необходимая информация сформулирова-
на в виде линейных равенств и неравенств (21,63) ч
(21.65), Определение предельной несущей способности
сводится к нахождению Р’ = максР(Х) при условиях
(21.63) и (21.64). Это задача линейного программиро-
вания.
21.5.3.	Некоторые типы оболочек вращения
Сферическая оболочка при равномерном внешнем
давлении [27]. Схема оболочки показана на рис. 21 38.
Безмоментное решение в соответствии с уравнениями
(21.60) будет
М = Т = 0; А< = — S; Р' = — .
R
408
РАЗДЕЛ 2J РАСЧЕТ КОНСТРУКЦИИ ПО ПРЕДЕЛЬНОМУ РАВНОВЕСИЮ И УЧЕТ ПОЛЗУЧЕСТИ
Решение с учетом изгибающих моментов имеет вид
8/ИП1 Г ( h з]1/2
Р* .= —— 1 Д--------------,	(21.66)
Rh L
где h — толщина оболочки;
S (а) =
sin а
— 1
К	0	1	2	3	4	5	6	6,7
у	1,877	1,891	1,955	2,048	2,178	2,355	2,565	2,743
р	0,73	0,70	0,728	0,728	0,723	0,715	0,702	0,681
Рис. 21.39
Пологая коническая
оболочка (рис. 21.41)
При обозначениях
₽ =	я = Р0/Д
п
Пологая оболочка вращения с шарнирным опирани-
ем. Для пологой оболочки отклонения от сферической
формы несущественно сказываются иа величине пре-
дельной нагрузки. Предельная нагрузка для оболочки,
показанной на рис. 21.39,
предельная нагрузка
Р* = 2лА4плф(а, 0),
где
здр (1 а) (1 -фа _ баз+Згхф
ф (а, 0) =---------------------------
(21.68)
8
3
41пл
h

Я
— i 2 (г) dr.
R J
о
Решение А Р. Ржаниныпа [21] для пологой оболоч-
ки, поверхность вращения которой задана уравнением
(21.67)
4р
г (г) = Л 1 - — .
\ R 1
Предельная нагрузка (верхняя оценка) для сосрсдо
точенной силы, приложенной к вершине,
: 2п	h \
Р”-= n/Vnq/щ; (А'пп = атЛ).
, п — 1	/ /
Для равномерно распределенной нагрузки
= Ж,л / / 2/1
3 (1—a) (l-j-tg3 ср)
Если окажется, что ф(а, 0)<1, то следует принимать
ф(а, 0) = 1.
Решение А. Р. Ржаницына для такой оболочки [24]
(верхняя оценка при ^о==0) дает
/ А \
Для равномерно распределенной нагрузки
Р* _ f j +
Д2 \ f )
Несущую способность пологой сферической обо точки
при действии сосредоточенной силы, приложенной в вер-
шине, можно оценивать по следующим формулам (верх-
няя оценка)
а) шарнирно неподвижное опирание (рис. 21.41)
Р* = от (0,5 -ф 0,09 49;
R-
Рис. 21 40

6) шарнирно подвижное опирание:
= От ЛЙ2 (1 4- pH ;
Р* = от л/р
1	2	4 l-z2
Ж — ж-------------=
4	5	Л 1 г
4о ) Т]
Пологая оболочка с защемленным краем (рис. 21.40)
Пластические шарниры образуются по радиусу pRi. Для
Д?
?=4——=46,7 предельная на
J.\ll
оболочки с размерами
в) защемленный опорный контур
1	(	у(4 — бу — ЗуД',
Р* ---<ут nh" 1 +  -—1—Х2
грузка
Параметр у определяется как решение уравнения
Р>
6МПЧ „
тф = —------
2(1—2у)
21.5, ПРЕДЕЛЬНОЕ РАВНОВЕСИЕ ОБОЛОЧЕК
409
Пологая оболочка на прямоугольном плане с шар-
нирно подвижным опиранием при действии равномерно
распределенной нагрузки. Обозначив отношение боль-
шей стороны к меньшей и=Ь!а, получим уравнение сре-
динной поверхности
г(х, + ^44+^.
Главные кривизны можно приближенно определить как
f	k > k V Ц"
4 т =	; kv ~	; 4 = ~—
а2	и2	h
Пусть приведенная нагрузка определяется в виде
Р — —— , где М*— предельный момент вдоль оси х,
Л+
пл
а Л^л — предельный момент вдоль оси у. Введем па-
раметр ортотропии
	и	и,1	0,2	0,3	0,4	0,5	0,6	0,7
ф.	1,72	1,73	1,77	1,82	1,щ	2,10	2,34	2,87
ф,	2,0	1,98	1.9С	1,82	1,68	1,50	1,28	1,02
X	0,4	0,5	0,5	0,6	0,6	0,6	0,7	ОД
Аналогично возможны две схемы пластических меха-
низмов для оболочки на круглом плане (рис. 21.42, в, г),
для которых
Ре -= 8лЖял -у- Ф3, Р.= ^Млл 4 Ф4  (21  70)
h '	п
Здесь Р — суммарная нагрузка на оболочку.
При условии, что	12+2-1 —, предельное значение
Р
приведенной нагрузки:
~ 6 (и2 + р") + 2«р (2fe + 3)
3ua
и
Если Ajs 12+24 —— , то (при р = 1) предельное значе-
Р
ние
80 (fe)2
ПФ _ _______________
^ +12^+324 '
fe	0	0,1	0,2	0,3	0,4	0,5	0,6	0,7
+	0,458	0,461	0,463	0,420	0,429	0,5	0,527	0,565
ф,	1,0	0,99	0,96	0,91	0,84	0,75	0,64	0,51
£	0,8	0,8	0,8	0,8	0,8	0.8	0,8	0,8
21.6. МЕТОДЫ РЕШЕНИЯ ЗАДАЧ ПОЛЗУЧЕСТИ
21.5.4. Пологие оболочки с отверстием [7]
На рис, 21.42 показаны пологие оболочки на квадрат-
ном плане и сферические, Оболочку на квадратном пла-
не примем в виде эллиптического параболоида с урав-
21.6.1. Уравнения состояния для задач
ползучести
В тех случаях, когда деформации ползучести линейно
зависят от напряжений, уравнение состояния имеет вид
i
Г	о (т)
s (t) = + (1) + £ (t, т) —ат, (21.71)
J	4 (+
4
нением срединной поверхности z=f(x2+y2)/а2, где 2}—
высота оболочки в вершине. Схемы пластических меха-
низмов могут быть такие, как на рис. 21.42, а и б. Пре-
дельные нагрузки, соответствующие схемам а и б,
определяются по формулам
Ра = 32 Л4ПЛ Фъ Р6 = 32 MUll ~ Ф,. (21.69)
h	п
Здесь Р — суммарная нагрузка па оболочку, предель-
ное значение которой выбирается как меньшее из Ра
и Рц.
где е+0 =о"(1)/Е(9—упруго-мгновенные деформации;
выражение £(), т) называется функцией влияния и в за-
висимости от конкретного типа теория ползучести имеет
различный вид.
Для уравнения состояния упруго-вязкого тела
(£(7) = const)
£ (t, t) =
Е—Н

exp
Н (t — т)
АП
(21.72)
где Е — мгновенный модуль упругости; Н — длительный
модуль упругости; р — коэффициент вязкости.
Ползучесть многих полимерных материалов удовлет-
ворительно может быть описана функцией влияния
(£(1) = const):
£(£т)=7Г:4)-(0<а<1).
(21.73)
430
РАЗДЕЛ 21, РАСЧЕЛ КОНСТРУКЦИИ ПО ПРЕДЕЛЬНОМУ РАВНОВЕСИЮ И УЧЕТ ПОЛЗУЧЕСТИ
Это так называемая функция со слабой особенностью:
при т = / L[t, т) = ос .
Для железобетона наиболее широко распространено
представление функции влияния при помощи другой
функции:
д Г 1	1
Ш т) = 7? (т) — 4СД, т) .	(21.71)
dr L Р- (т)	1
Здесь Е(т)—переменный модуль мгновенных деформа-
ций, который часто принимается в виде
Е (т) = Едл (1 - ае-'^) (0 - а<1).
В начальный момент, когда т=0, начальный модуль
деформаций равен: Е(0)=ЕДл (1—а), при очень боль-
ших т (старый бетон) Е — Едл.
Функция С(£т), наиболее удачно описывающая свой-
ства линейной ползучести бетона, предложена А. В. Яши-
ным:
С (4 т) = Аг —	0 —
\ т 1
+ А3 ё~'/г'1 (1 - е~^	).
Функция £(фт), которая определяется видом теории
ползучести, отражает влияние на деформации ползуче-
сти приращений напряжений Ао(т), приложенных в мо-
мент	, эффект от которых наблюдается в мо-
мент времени t.
Функция С(фт), определяемая из функции £(?, г):
1 I' L И, т)
С(4т) = -—=+	(21.75)
Е (т) J Е (т)
называется мерой ползучести материала и имеет раз-
мерность (слЕ/кг), обратную размерности модуля де-
формаций. Физический смысл этой функции виден иэ
уравнения (21.71), если считать напряжения постоян-
ными а(т) = о(4) —const и обозначить деформации
ползучести как
еп (4 = а (4) С (I,	(21.76)
Здесь еп(1)—деформации ползучести; е(4) — мгновен-
но-упругие деформации, образовавшиеся в момент при-
ложения напряжений о(4). Обычно принимают C(t, ф =
= 0. Тогда функция С(1, 4) ==en(4/°'(4) равна дефор-
мации ползучести в момент if, приходящейся на единицу
напряжения, приложенного в момент
Испытаниями материалов на ползучесть может быть
определена только мера ползучести C(t, т). Часто ис-
пользуется эквивалентная мере ползучести величина,
называемая характеристикой ползучести:
«НА 4) = Е(4)С(/, 4).	(21.77)
Характеристика ползучести — это отношение деформа-
ций ползучести, проявившихся ко времени t от напря-
жения, приложенного в момент времени t0 к упругим
деформациям, образовавшимся в момент 4 от этих же
напряжений. Деформации ползучести при помощи ха-
рактеристики ползучести записываются как
е« (if) = 8 (4) ф (t, 4).
Как правило, решение задач линейной ползучести свя-
зано с решением уравнения состояния (21.71) относи-
тельно напряжений. Это уравнение называется интег-
ральным уравнением Вольтерра второго рода. Его
решение в общем виде записывается при помощи резоль-
венты ЙД т), определенным образом связанной с функ-
цией £(f, т), которая в математике называется ядром
интегрального уравнения:
о НУ	(*
——- = е>(4 + 1 Л (4 т) а>'(т) А. (21.78)
К (4	J
А
Ядро и резольвента связаны уравнением
t
L (t, х) — R {t, r) =. j L (t, s) R (s, x) ds.
Во многих случаях решение этого уравнения затруд-
нительно и возможно только для относительно простых
выражений.
В тех случаях, когда £(1,т) есть функция только раз-
ности t—х—времени выдержки под нагрузкой, наибо-
лее удобно пользоваться преобразованием Лапласа для
нахождения резольвенты. Преобразование Лапласа для
ядра выглядит таким образом:
£*(.s)= f L(0)e“L9d0,
t
В этом выражении 6 = 0 при одностороннем преобра-
зовании, Ь = — то при двустороннем преобразовании.
Изображение резольвенты записывается так:
/?* (S) =
L*(S)
1 - I* (S) '
Более подробно о применении преобразования Лапласа
см. [6, 7].
Задача релаксации Эта задача решается для посто-
янных деформаций е°, вызывающих мгновенные напря-
жения <7° = Ее°. С течением времени эти напряжения
уменьшаются (релаксируют) по закону
t
а(4 = o°fl ~ «101; р(4=Е (0 f Л (4 т) А. (21.79)
4“
Функция р (4 называется функцией релаксации. Для
упруго-вязкого тела с ядром (21,72) функция релаксации
имеет вид
Если мера ползучести имеет вид C(t, т)=С0(1 —
— ё~W —т1), то ядро интегрального уравнения такое:
L (I, т) =
Его резольвента R{t,x) также имеет вид экспоненты
R (t, т) =— ЕС0 yf-Vd+EC.lE-T).
Величина ЕС0 обычно обозначается как предельная
характеристика ползучести фоо =£С0. Функция релак-
сации при этом такая:
Р(4 =	(21.80)
1 + ЧА
Подстановка ее в (21.79)
сации напряжений
дает выражение для релак-
о (4 = о0
1
1 + ЧА
-? (На,)*
1 + Ч’со
21.6. МЕТОДЫ РЕШЕНИЯ ЗАДАЧ ПОЛЗУЧЕСТИ
411
Для времени t= со
О(со) =
О'0
1 X Фте
(21.81)
Такая зависимость достаточно хорошо описывает раз-
личные законы релаксирования и может быть нсполь-
зовона при приближенных оценках решений задач ли-
нейной ползучести.
Обобщенная задача релаксации. Если деформация
являются вынужденными и изменяются во времени по
закону е(/), то определение напряжений является зада-
чей обобщенной релаксации. Напряжения находятся по
формуле (21.78).
Для ядра (21.72) при е°(1) = е°) равномерное увеличе-
ние деформаций
г	/	__t И
п (t) = е» [ш -ф- ф (Е — Н) \1 — е T‘/j.
Задача обобщенной релаксации чаще всего встречается
при определении температурных напряжений, когда рас-
пределение температуры T(t) вызывает температурные
деформации e(t) ~aT(t).
Линейная теория старения. Эта теория постулирует
параллельность кривых, иллюстрирующих меру ползуче-
сти С (t, т). Суть ее в следующем: если известна кривая
C(t, ф), то кривая C(t, t2) при может быть получе-
на как разность С(1, 4)—С(4,4), т. е. кривая C(f, f2)
получается из уравнения кривой	при помощи па-
раллельного переноса (рис. 21.43). Заштрихованные на
этом рисунке площади одинаковы и кривые ab и а'Ъ' по-
добны. В* этой теории часто оперируют характеристикой
ползучести как функцией одного аргумента ф(П —
EC(t, t0). Уравнение состояния по этой теории такое:
Эта теория достаточно проста в части математических
решений, но в ряде случаев опа не в состоянии правиль-
но описать явление ползучести, в частности при резко
изменяющихся напряжениях или деформациях.
Нелинейные теории ползучести. При расчете строи-
тельных конструкций часто попользуются интегральные
уравнения состояния типа (21.71), но учитывающие не-
линейные свойства ползучести.
Уравнение не чиненной ползучести в теории Маслова—
Арутюняна:
t
o(i)	Ё
е(/)=	т)ф)<т(т)] А. (21.83)
X; (?)	,/
in
Здесь <р(сг)—нелинейная функция напряжений. Напри-
мер, ф(о)=сг™ при т = 1 приводит к обычной линейной
ползучести.
Уточненная нелинейная зависимость для бетона исполь-
зует нелинейную меру ползучести С(/, т, о) =ф(о, t—т) X
ХС0)!, т), где q(o,)—т) —функция, зависящая от уров-
ня напряжений; с увеличением длительности действия
напряжений (ростом А—т) эффект нелинейности сглажи-
вается.
Уравнение состояния
8(О = а	+ сО(4)]] +•
L A Vo)	1
t
, Г	4о(т)
+ I С (t, т, а) --- dx.
J	dx
in
Нелинейное уравнение состояния по Ю, Н, Работнову
Hi]:
I
ф [8 (0] = 0 W + f Ь 0" — т) о (т) dr .
in
Другие типы теории ползучести приведены в разделе 12,
21.6.2. Методы решения задач линейной
ползучести
Е(/) =
o(t)
Е
4<Р (?)
dx
dx.
Расчет статически определимых систем производится
при условии, что напряжения от ползучести не изменя-
ются о(1)=о°, где о13 — начальные напряжения или
напряжения, изменяющиеся во времени. Учет ползучести
производится только для деформаций по формулам:
если с0 —const, то
u(t) == и°(1 + Ф (0),
Обычно это уравнение приводится к дифференциальному
вида
de	1 / do ,
Г™ ——— I	-т- Q
dtp	Е Ыф
где — начальные деформации, определяемые упругим
расчетом;
если Со функция времени, то деформации определяются
вычислением интегралов
В это уравнение вместо переменной t вводится новая
переменная <р, играющая роль условного времени. Реше-
ние относительно напряжений будет:
в (/) .1
Х(г)
В (х)
dx.
a (t) ~ Ее (0 — Е
f
С - Л.
J	' dx
t.
Уравнение релаксации	const] имеет вад
а(0 = а»(1 —(2L&i)
Здесь N(t)—изменяющееся во времени усилие; B(f) —
жесткость; £(/, т)—функция влияния.
Расчет статически неопределимых систем. Перерас-
пределение усилий в статически неопределимой системе
ог действия внешних сил возможно только тогда, когда
система составлена из элементов с различными свойст-
вами ползучести (неоднородная система).
412
РАЗДЕЛ 21 РАСЧЕТ КОНСТРУКЦИЙ ПО ПРЕДЕЛЬНОМУ РАВНОВЕСИЮ II УЧЕТ ПОЛЗУЧЕСТИ
В однородной системе при действии внешней нагрузки
перераспределения внутренних сил не происходит.
В однородной статически определимой системе уси-
лия от вынужденных деформации (температура, осадка
опор) релаксируют по закону
(1 р (О,
где Л7 (/0) — начальные усилия; р(/) —функция релакса-
ции
Применительно к железобетонным конструкциям эго
означает, что перераспределение внутренних сил возмож-
но в основном вследсызие неодинакового армирования
отдельных элементов,
Устойчивость стержня при ползучести [40, 42]. Для
однородного стержня устойчивость при ползучести мо-
жет быть оценена по формуле
РДл<гДю--	(21.84)
I т оо
Здесь Ра — критическая сила по Эйлеру.
Устойчивость армированного стержня при линейной
ползучести материала и идеальной упругости арматуры
см. [40].
мящаяся к некоторому пределу В?.. В случае В(В)—Н и
гп~ 1 получается уравнение ползучести Максвелла.
Задача о релаксации при постоянных вынужденных
деформациях е0 имеет решение
о Г) = оа [1 — р(0Г У
где о0 = £еи — начальные напряжения;
р (() = (1 - m) (1) оЩ1
t
йт а) = !' Bi (т) л.
о
Эта формула обычно дает некоторое занижение релак-
сированных напряжений для металлов по сравнению с
экспериментальными данными.
В теории старения принимается такое уравнение состо-
яния, которое записывается относительно деформаций,
а не их скоростей.
е (/) =	(!) а™ -1-
(21.90)
(21.91)
21.6.3. Методы решения задач нелинейной
установившейся ползучести
Основные уравнения. Уравнения состояния для
сплошного тела записываются относительно скоростей
деформаций ползучести и имеют вид
1
Сгх = “ / (Ю К —Л; •  ; еху = f (о;) оху(21.85)
” 1
где о = — (ои+оуу+огг) — гидростатическое давление;
Oi — интенсивность касательных напряжений; ехх, . .
exv, . . .— компоненты тензоров скоросюй деформаций
ползучести.
Обратное представление уравнений состояния такое:
Фм- — о = 2g (е,-) ехх,.... оху = g (et) ехд,... (21.86)
где et — интенсивность скорости деформаций сдвига.
Функции f(ст,) и g(e,), как правило, определяются экс-
периментально при одноосном растяжении или сжатии и
в ряде случаев при кручении. Например, из одноосного
растяжения (сжатия) получена зависимость для устано-
вившейся ползучести
«•.„-модг	<21-87)
В уравнениях состояния (21.85) фукция /(о,) будет
иметь вид
т-Н
адтсш	<г,а8’
Одноосное напряженное состояние. Уравнение состоя-
ния установившейся ползучести для скоростей полных
деформаций (упругих и ползучести) имеет вид
°
д(^=В1(0о'?г(О+-Щ.	(21.89)
£
Здесь е — скорость деформаций ползучести и упругих;
б|(ф—монотонно убывающая функция времени, стре-
i
flj (t) = | Bi (т) dt.
0
(21.92)
Такое уравнение можно использовать только при по-
стоянных или очень плавно изменяющихся напряжениях.
Релаксация напряжений определяется из решения не-
линейного уравнения
«Г (0 о” фс - о„.
(21.93)
Решение этого уравнения приводит к несколько боль-
шим значениям напряжений, чем решение по теории
течения (21,90).
Теория старения существенно проще теории течения
и наиболее широко используется в приложениях. Особен-
но это oiносится к методу изо-
хронных кривых [41]. Изохронная
кривая — это зависимость напря-
жение — деформация, построен-
ная для некоторого фиксирован-
ною времени. Фак пиески это есть
зависимость а—е по (21.90) прн
Qi(l) —const На рис. 21.44 пока-
зала серия изохронных кривых,
где первая кривая (1 = 0) есть
кривая упруго-мгновенных дефор-
маций, которая для идеально ли-
нейно упругого материала будет
прямой линией, показанной на рис. 21.44 пунктиром.
Пользуясь изохронными кривыми, задачу ползучести
для каждого момента времени ф можно решить как не-
которую нелинейно-упругую или упруго-пластическую
задачу. Для каждого момента времени будет своя не-
линейная зависимость о—е. Существенно уменьшаются
сложность задачи и объем вычислений, если изохронные
кривые подобны, т. е. справедлива зависимость в(/) =
Тогда задача может быть решена как не-
линейно-упругая с зависимостью е=В(о), а деформации
будут функцией времени. Постоянные нагрузки не будут
вызывать изменения напряженного состояния установив-
шейся ползучести, тогда как деформации будут изменять-
ся пропорционально функции f (t).
Сложное напряженное состояние. Задача ползучести
при сложном напряженном состоянии может быть реше-
21 6. МЕТОДЫ РЕШЕНИЯ ЗАДАЧ ПОЛЗУЧЕСТИ
413
на вариационными методами, весьма близкими к вариа-
ционным методам нелинейной теории упруюсти и дефор-
мационной теории пластичности.
Пусть скорости перемещений точек объема обозначены
как компоненты трехмерного вектора их, иу, иг. В этих
обозначениях мощность внешних сил, приложенных к
части поверхности,
А == ^(Хих 4- Yuy + ZiQ dS,
где So — площадь поверхности, на которой действуют
внешние силы X, У, 2.
Удельная мощность, т. е. мощность, приходящаяся на
единицу объема, рассеиваемая внутренними силами,
вследствие деформаций ползучести
J	1 + ц
<1
1
М = — •
т
Полная мощность системы внутренних и внешних сил
£/(и) = |‘WW —Л.	(21,94)
V
Скорости перемещений являются кинематически воз-
можными, если они удовлетворяют на некоторой части
поверхности кинематическим условиям. Наиболее часто
это условие несмещаемости.
Первый вариационный принцип: из всех кинематически
возможных распределений скоростей действительные
скорости перемещений их, иу, иг сообщают полной мощ-
ности минимальное значение
U (u*) = min Д (и).
Удельное дополнительное рассеивание мощности внут-
ренними силами при степенной зависимости в уравнении
состояния имеет вид
aJ
П (о) = ( ег d<Jt =	a«+*.
J	т 4-1
u
Мощность, дополнительно рассеиваемая телом объе-
мом V,
t (а) = \ П (<з) dV.	(21.95)
V
Второй вариационный принцип: действительное напря-
женное состояние о* является статически возможным и
сообщает минимальное значение мощности дополнитель-
ного рассеивания Т(а*) =пт1п Т(ст).
В задачах ползучести существует обобщение теоремы
Кастилиано на случай установившейся ползучести ста-
тически неопределимых систем:
а)	если в s раз статически неопределимой системе вы-
делены неизвестные Х[, Х%, . . Xs, го уравнения стати-
ческого метода запишутся так:
dt
= О (1 = 1, 2, .... Д; (21.96)
б)	скорость перемещения по направлению действия
силы Pk равняется частной производной дополнительной
мощности рассеивания по этой силе, т, е.
(21.97)
Приближенное решение задачи. В некоторых случаях
можно достаточно просто получить решение задачи ери
тех же граничных условиях, но в предположении упругой
работы — линейной или нелинейной. Обозначим это ре-
шение а0. Пусть о" решение задачи с позиций идеальной
пластичности при тех же граничных условиях. Например,
это может быть решение по методу предельного равно-
весия, хотя нагрузка нс предельная. Тогда о’- это какое-
то статически допустимое поле напряжений. Решение за-
дачи ползучести разыскивается в виде линейной комби-
нации этих двух решений
о (X) = 7.0» 4- (1 — X) а*.	(21.98)
В этом выражении 0=ДХ:Д1, а оптимальное значение
Xs' определяется на основании второго вариационного
принципа о минимуме мощности дополнительного рассеи-
вания:
clt (а (ЗД
—4—^ = 0.	(2Ь99)
дЛ
Другой прием приближенного решения заключается в
использовании упругой аналогии, koi да распределение
напряжений при ползучести приближенно представляется
как сумма решений задач нелинейной унруюстй с зара-
нее заданной степенью нелинейности:
о = Щ ст (отг) 4- с2 а (да2) +  -ф- сп а (пгп), (21.100)
где от, (1=1, 2, . . ., и) —различные показатели нелиней-
ности.
Коэффициенты с, определяются и соответствии со вто-
рым вариационным принципом
дТ (о)
—— = 0 (г = 1,2, ..., а).	(21.101)
ОС^
Возможно также применение вариационных методов,
аналогичных методам Ритца и Галеркина, применяемых
в теории упругости.
21.6.4. Расчет стержневых систем
при нелинейной ползучести
Статически определимые фермы. Напряжения в ста-
тически определимой форме находят обычным статиче-
ским расчетом. Скорости деформаций находят из урав-
нения состояния
е (!) = sign (о) Вг (!) рт|га. (21,102)
Деформации (перемещения) конструкции определяют
интегрированием
t
е (!) — f sign [о (т)] Bj (т) I о (T)lm di-
о*
При постоянной нагрузке
е (1) = sign (о) fa;!п Qj (1);
I
Qi(i)= АД(т)Л.
о
(21.103)
Пусть в ферме имеется k стержней с усилиями
Дг(1=-1, 2, . .	k). Дополншельно рассеиваемая мощ-
ность
к
Г = -4- Bi (!) l>dm+S (21.104)
m 4-1 Z_i F?
i=i
414
РАЗДЕЛ 21. РАСЧЕТ КОНСТРУКЦИИ ПО ПРЕДЕЛЬНОМУ РАВНОВЕСИЮ И УЧЕТ ПОЛЗУЧЕСТИ
где F. и I, — площадь поперечного сечения и длина i-го
стержня.
Систему внешних сил, действующих на ферму обозна-
чим Pi, Рг, , . Рп. Усилие в каждом стержне это ли-
п
нейная функция этих сил ./Vi = Sa,jP,-, где —усилие
в i-м стержне от j-й внешней силм, равной единице
(Р}=1)г Выражение дополнительной мощности рассеи-
вания
А (Р
m -j- 1
Т (Р) =
п
V ар
i^l
. (21.105)
(21.108)
где .Vf—усилие от внешней нагрузки; Xj (/=1, 2, . .
s)—лишние шизвсииые; з—степень статической не-
определимости.
В соответствии с выражением (21.96) составляется не-
линейная система уравнений для скоростей деформаций
ползучести. Это система, как и в методе сил, соответству-
ет отсутствию перемещений по направлениям лишних
неизвестных. После сокращения па Bi система уравнений
приобретает вид
Перемещение точки приложения силы по направле-
нию действия этой силы определяется в соответствии с
обобщением теоремы Кастилиано:
fc=i
aii = 0
или
4=1
аа
(21.106)
(/= 1, 2,..., з).
(21. 1С9)
k
а; =~ Д (ф S ац Ц
/=1
(21.107)
где <j(. = Аы/У, — напряжение в г-м стержне.
Статически неопределимые фермы. Расчет статиче-
ски неопределимой фермы в условиях ползучести начина-
ется так же, как и расчет упругой фермы, с выбора ос-
новной статически определимой системы. Естественно,
что расчет производится методом сил. Усилия в стержнях
основной системы записываются как линейные функции
внешней нагрузки и лишних неизвестных
Решение системы ? 5, . . X, приводит к распреде-
лению внутренних сил при установившейся ползучести.
Полное решение задачи дает Х = .У°+А"', где Р — реше-
ние упруго-мгновенной задачи.
Система (21.109) может быть решена приближенным
способом (см. 21.6.3). Более подробно см, [37],
Рекомендуемая точность различных приближенных ме-
тодов может быть ограничена 5—10%. Решение сложных
задач возможно только с помощью ЭВМ. Поэтому бла-
годаря невысоким требованиям к точности с успехом
можно применить методы случайного поиска. Эти методы
рекомендуется применять не для непосредственного ре-
шения системы нелинейных уравнений метода сил, а для
отыскания минимального значения дополнительной мощ-
ности рассеивания.
ЛИТЕРАТУРА
К п. 21.1—21,5
1.	Ахвледиани Н. В. Ц расчету железобетонных арок
по методу предельного равновесия. «Строительная механика и
расчет сооружений», 1962. JV? 2.
2,	В арв а к М, Ш., Дубинский А. М , Д ехтяр ь А, С.
Предельное равновесие оболочек, подкрепленных ребрами.
«Прикладная механика», 1966, вып. 9, т 2.
3.	Гвоздев А. А. Определение величины разрушающих
нагрузок для статически неопределимых систем, претерпеваю-
щих пластические деформации. Труды конференции по пласти-
ческим деформациям. Изд. АН СССР, 1938.
4.	Гвоздев А. А. Расчет несущей способности конструк-
ций ко методу предельного равновесия. Госстройиздат, 1949.
а. Гениев Г. А. Вариант деформационной теории пла-
стичности, «Бетон и железобетон», 1969, № 2.
6	Дехтярь А. С., Дубинский А, М. Несущая спо-
собность пологих железобетонных оболочек с иерастяжимым
контуром. «Строительная механика и расчет сооружений», 1966,
Ле 4.
7.	Д е х т я р ъ А, С., В арвак М. Ш. Несущая способность
пологих оболочек с центральным отверстием. «Прикладная ме-
ханика», 1968, вып. 3, т. 3.
8,	Д у б иис ки й А. М. Расчет несущей способности же-
лезобетонных плит. Госстройиздат, УССР, 1961.
9.	Власов В. В. Расчет железобетонных конструкций,
работающих по второму случаю внецентренного сжатия.
«Строительная механика и расчет сооружений», 1969, № 2.
10.	Купман Д„ Ланс Р. О линейном программирова-
нии и предельном равновесии. «Механика», 1965, № 2.
11.	Л петрова Ю. П., ПотаповВ, Н, Рудис М. А.
Предельное равновесие некоторых оболочек вращения, выпол-
ненных нз материала с различными пределами текучести при
растяжении и сжатии. МТТ, 1969, № 1,
12.	Мирзабекян Б. Ю. К определению нижней гра-
ницы несущей способности оболочек. «Строительная механика и
расчет сооружений». 1968, Лб 3,
13.	М и р з а б е к я и Б. Ю., Рейт м а я М. И. Опреде-
ление несущей способности оболочек при помощи линейного
программирования. МТ Г, 1968. № I,
14.	Нем др оа ский IO. В , Р аботнов Ю. Н. Пре-
дельно? равновесие подкрепленных цилиндрических оболочек,
Изд. АН СССР ОТН. Серия механика и машиностр., 1963, № 3.
15.	Овечки и А, М. Расчет железобетонных осесиммет-
ричных коистоукций, Госстройиздат. 1961.
16.	Ольш а к В., С as ч у к А. Неупругое поведение обо-
лочек. «Мир», 1969,
17.	Пльюшня А. А. Пластичность. ОГИЗ, 1948.
18.	Прагер В,, Ходж Ф. Теория идеально пластиче-
ских гел. ИЛ , 1956.
19.	Проценко А. М. Статический метод предельного
равновесия и связанные с ним задачи оптимального проектиро-
вания. Сб. НИИЖБ «Особенности деформаций бетона и /Келезо-
бетона я использование ЭВМ». Стройиэдат, 1969.
20.	Про ц е и к о А. М., Власов В. В. Применение ли-
нейного программирования к расчетам железобетонных стати-
чески неопределимых конструкций. «Бетон и железобетон»,
1969, № 6
21.	Проценко А. М. Некоторые вопросы теории предель-
ного равновесия строительных конструкций. «Строительная ме-
ханика и расчет сооружений», J970, Ле 2.
22:	Ржаницын А. Р. Расчет конструкций с учетом пла-
стических свойств материалов. Госстройиздат, 1934.
23.	Р ж а и и ц ы и А. р. Расчет оболочек методом предель-
ного равновесия. Сб ЦНИИСК «Исследования по вопросам тео-
рии пластичности и прочности строительных конструкций»,
Стройиздат. 1968.
24.	Ржаницын А. Р. Пологие оболочки и волнистые на-
ЛИТЕРАТУРА
415
стилы. Научное сообщение ЦНИИСК, вып. 14. Госстройиздат,
1960._
25.	Ржа н ицыи А. Р. Расчет цилиндрических сводов-обо-
лочек методами линейного программирования. «Строительная
механика и расчет сооружений», 1966, № 4.
26.	Розеиблюм В. И. Об условиях пластичности для
тонкостенных оболочек. ПММ, I960, № 2.
27.	Р озе н б лю м В. И. О расчете несущей способности
идеально-пластических осесимметричных оболочек. Сб. «Иссле-
дования по упругости и пластичности». Изд. ЛГУ, 1965, Ле 4.
28.	Стрельбицкая А. И. Информационное письмо
Ин-та строительной механики АН УССР, 1957, № 20; 1958, К? .29.
29.	X и л л Р. Математическая теория пластичности. ИЛ.,
1956,
30.	X о д ж Ф. Расчет конструкций с учетом пластических
деформаций. Машиздат, 1963.
31.	Соколовский В. В. Теория пластичности. «Наука»,
1969.
32.	Чир ас А. А. Методы линейного программирования
прн расчете упруго-пластических систем. Стройиздат, 1969»
33.	G г е е п b е г g Н,, Prager W. On limit design of
beams and frames. Trans, ASCE, 1952, П7, 447.
34,	Massenet Ch„ Save M. Calcul plastlque des const-
ructions, v. П, Bruxelles, 1963.
35.	N e a 1 B. The plastic method of structural analysis. New
York, 1956.
К П. 2L6
36.	Арутюнян H, X. Некоторые вопросы теории ползу-
чести. Еосгехнзда-1, 1953,
37.	К а ч а и о в Л. М, Теория ползучести. Физматгиз, I960..
38,	А! а л и и и н Н. Н. Основы расчетов на ползучесть.
Машгиз, 1918.
39.	Прокопов» ч И. Е. Влияние длительных процессов
на напряженное и деформированное состояния сооружений. Гос-
стройиздат, У9иЗ.
49.	Проценко А. М. К расчету железобетонных стерж-
ней с учетом линейной ползучести бетона. Сб. НИИЖВ «Проч-
ность и жесткость железобетонных конструкций». Стройиздат,
1968.
41, Работнов IO. Н. Ползучесть элементов конструкций.
«Наука», 1966.
42. Р ж а и и цы н А, Р, Теория ползучести. Стройиздат,
1968.	-
В книге 1-й «Расчетно-теоретического справочника проектировщика промышленных, жилых и
общественных зданий и сооружений» дополнительно обнаружены следующие опечатки:
Стр-	Строка	Напечатано	Должно быть
219	Правый столбец 12-я сверху	в табл. 7.4	в табл. 7.5
680	Формула (11.9)	О — «О F	ус	1'Da f.l—a}i Hs== Ч 	'
580	Левый столбец 7-я и 6-я	/А, то при равномерно рас-	fr, при равномерно распре-
682	снизу Левый столбец 1-я снизу	яределенкой нагрузке вме- сто м2.	деленной нагрузке, то вме- сто Т2М.
СПРАВОЧНИК ПРОЕКТИРОВЩИКА
ПРОМЫШЛЕННЫХ, ЖИЛЫХ И ОБЩЕСТВЕННЫХ
ЗДАНИИ И СООРУЖЕНИИ
РАСЧЕТНО-ТЕОРЕТИЧЕСКИЙ
под редакцией Л. Л. Уманского
Издание второе переработанное
и дополненное
в двух книгах
Книга 2
® в ®
Стройиздат
Москва, К-31, Кузнецкий мост, д. $
Редакторы издательства И. С. Бородина и Э, М. Осипова
Технический редактор Т. М. Кан
Корректоры Е. Н. Кудрявцева, М. Ф, Казакова
Сдано в набор 7/1—1972 г. Подписано к печати 23/XI— 1972 г’
Т-18190. Бумага № [«’Формат 84x108/щ—13 бум. л. 43,68 усл. печ. л”
(уч.-изд. 52.47 л.). Тираж 50.000 экз. Изд. № X—593. Зак. № 26
Цена 3 р. 18 к.
Владимирская типография Союзполиграфпрома
при Государственном комитете Совета Министров СССР
по делам издательств, полиграфии и книжной торговли
Гор, Владимир, ул. Победы, д. 18-6,
О 4Т F Ч Л г к и
	111	М'.^О^г-’ЛВУ	Дад^ло бить
1ЯШЛ	: 1>г :р-'?фг, 5->г с; река г-.ч.^у	91в1^ШШ^^^ЯвЯЯЯ1 ШЯШЯЩШШЯЯ1ЯШ1	1ИИ^ШИМ|М|И||МИИ|В 1вв1ИИ^ИИ111ЯЯИИ1
	г?ггз:? <т;-:бедо	y?v^z-y^ л' К	П:.:-чи'1!-!: /"ОГлугп^и'е ,!'^-;'.?,;'i'':ct-:J’:.-: гр’" <иь-'Стар’--чН(С’' <Пг1С, 17.75, 0) И ДВуСлОЗПНЯСЙ (уГ!'\ 17-76,6)	{’iiiyi;-iri:'AinQt\	J7.76, £•) 1як7«л?''/п-;л Пригпгнл i’.7y;j,vw->
	Ф‘ла <J7,SKI5?	i\;	HLu :	ь~ь
||||||	EIp3B£j<? еГ&Я&^'г5 В-'Г' <.":;jy	И1Ив«ЯИв1Я» ШШШЯШЯШШШШЛ	11ЯШя^Я^^^ЯШ1Я1Л
	®-.-г <;.р 77)	МИ1И1ИМД^^^^ЖММ	ШЯШЯШй№№ШШШШШ№ЯВ№ЯШЯШ
			9ШвЯЯЯЯ^Ш1НвЛ1Ш1КЛ
	Г»р<70Ь1ь		
us	^ОйЬЗЙ ОТ^СЗД, £"S Й е.ш:-зу		
iiiijii	Левый гтагбгч «-в скезу