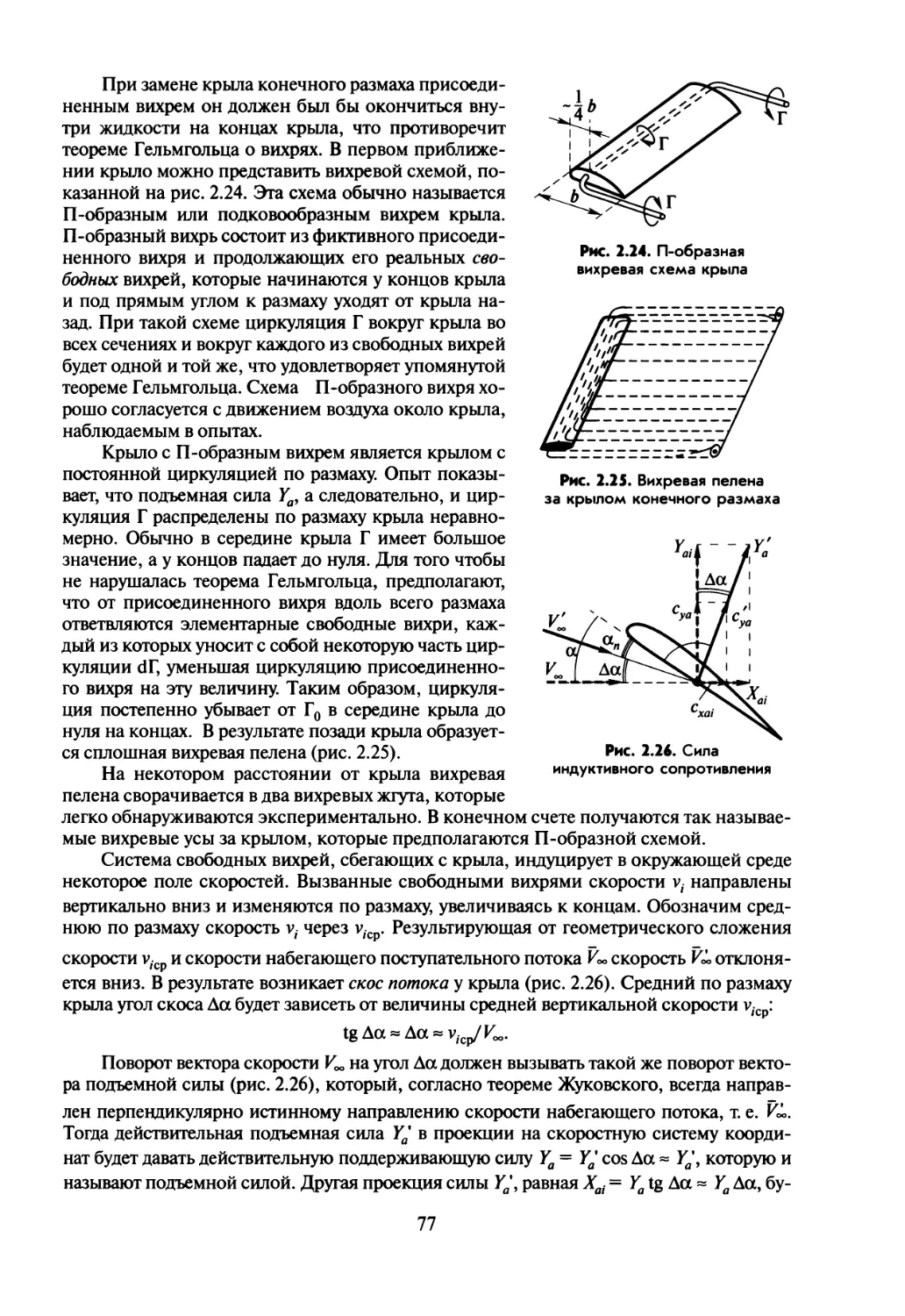
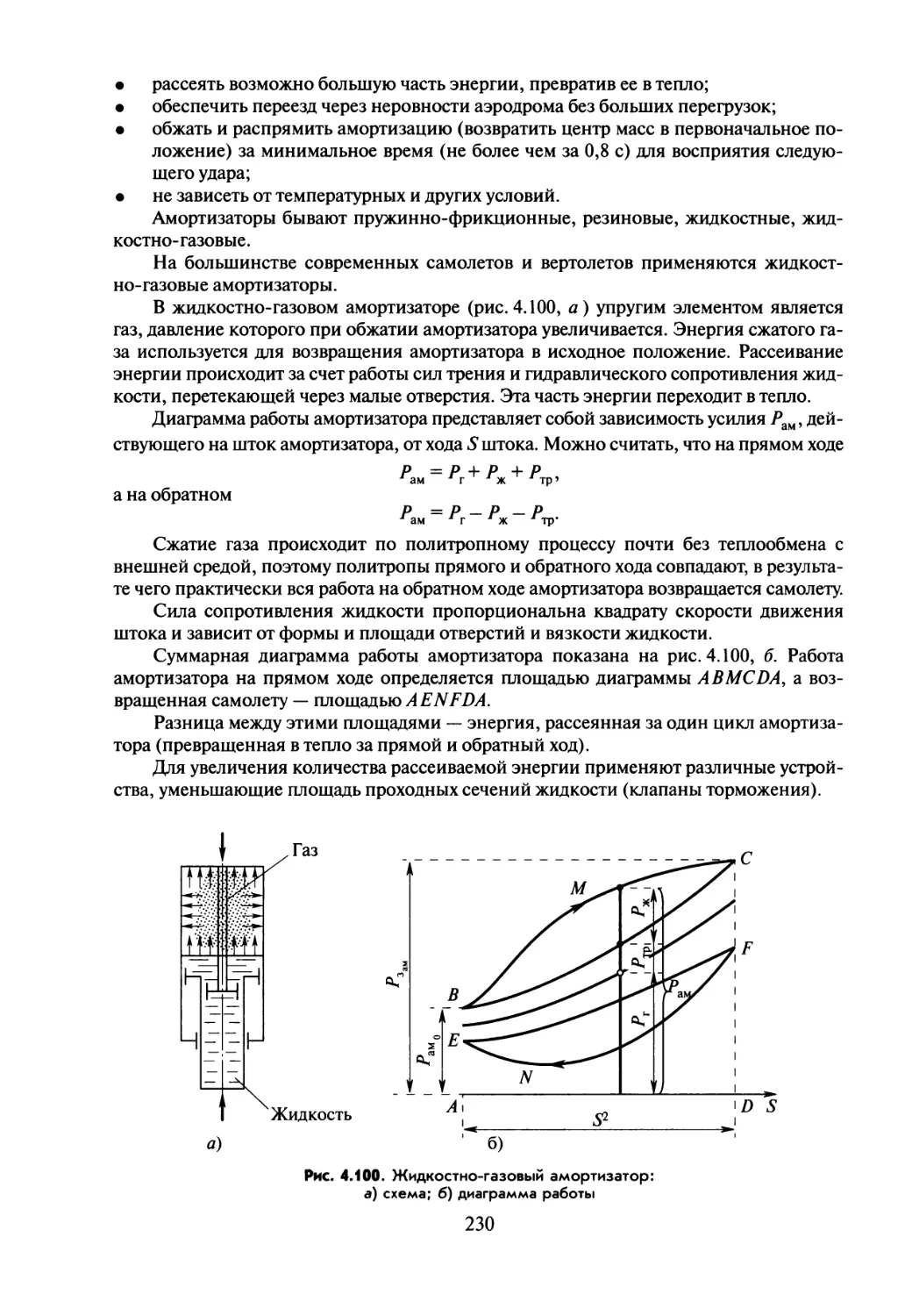
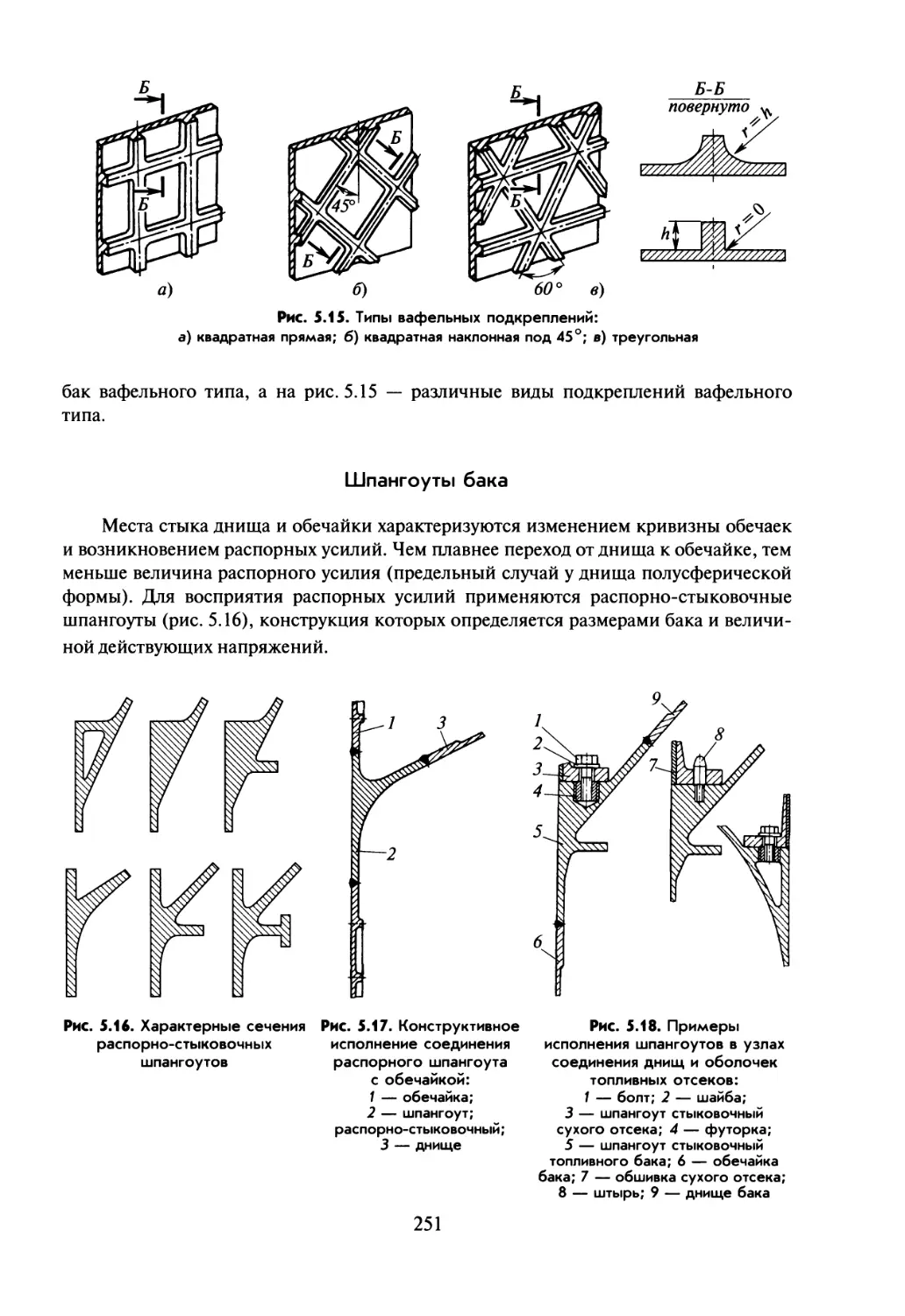
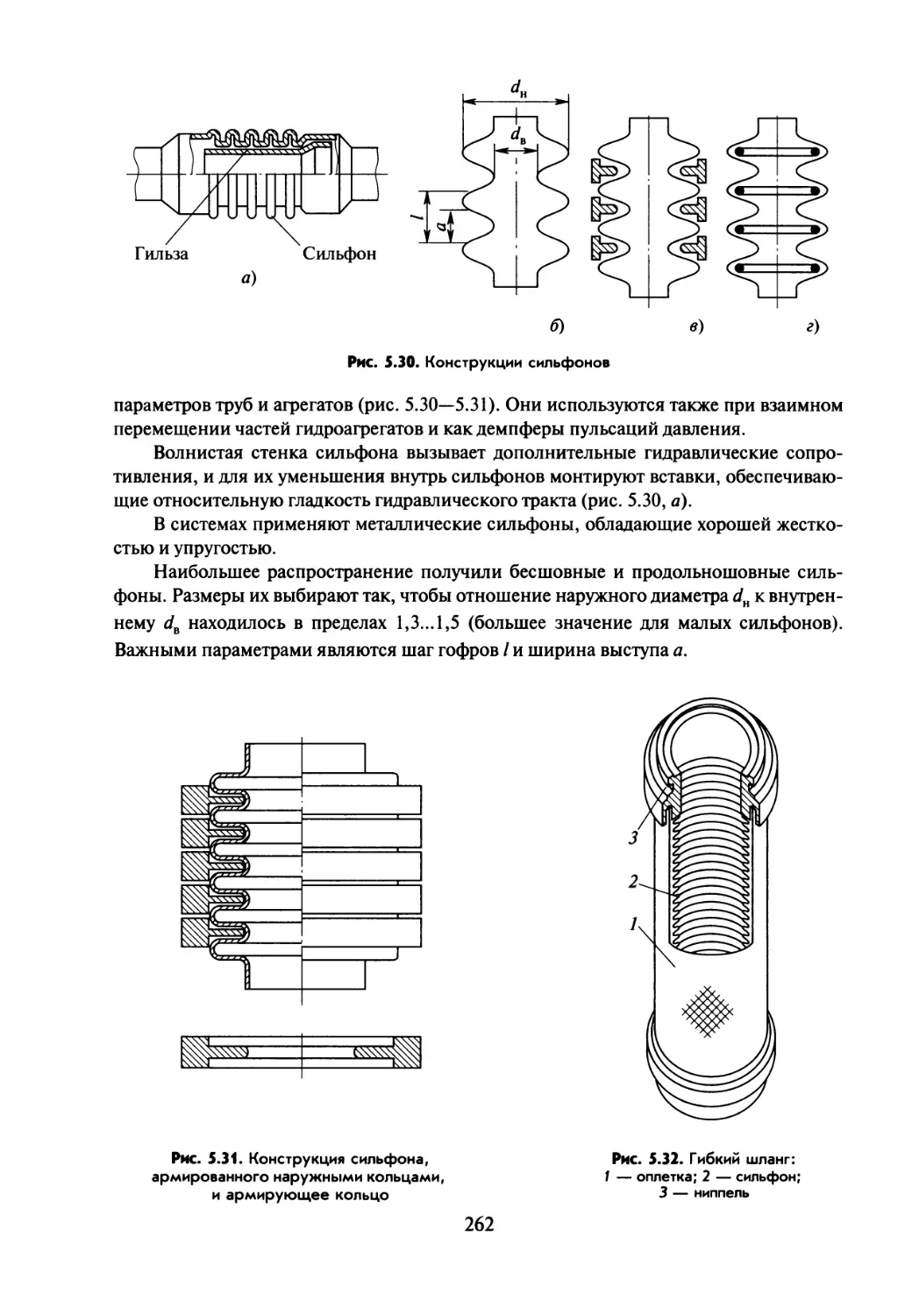
Текст
ПРОЕКТИРОВАНИЕ, КОНСТРУКЦИЯ
И ПРОИЗВОДСТВО ЛЕТАТЕЛЬНЫХ АППАРАТОВ
ТЕОРЕТИЧЕСКИЕ
ОСНОВЫ
АВИА-
И РАКЕТОСТРОЕНИЯ
ПРОЕКТИРОВАНИЕ, КОНСТРУКЦИЯ
И ПРОИЗВОДСТВО ЛЕТАТЕЛЬНЫХ АППАРАТОВ
ТЕОРЕТИЧЕСКИЕ
ОСНОВЫ
АВИА-
И РАКЕТОСТРОЕНИЯ
В КОНСПЕКТАХ ЛЕКЦИЙ
Допущено
Министерством образования Российской Федерации
в качестве учебного пособия
для студентов высших учебных заведений,
обучающихся по специальности «Ракетостроение»
направления подготовки дипломированных специалистов
«Ракетостроение и космонавтика»
и специальности «Самолето- и вертолетостроение»
направления подготовки дипломированных специалистов
«Авиастроение »
МОСКВА *2005
УДК 629.7
ББК 39.5
ТЗЗ
Серия «Проектирование, конструкция и производство летательных аппаратов»
Авторы:
А. С. Чумадин, В. И. Ершов, В. А. Барвинок, В. И. Богданович, В. В. Васильев,
А. Е. Волхонский, И. Н. Егоров, Ю. Л. Иванов, Н. Ю. Каратаева, А. И. Киселев,
В. Н. Кобелев, Л. Н. Лысенко, Б. Н. Марьин, А. П. Петров, В. Е Попов, Г. А. Резниченко,
М. Ю. Русин, А. В. Цырков, Ю. А. Цуриков, В. Г. Шахов, В. И. Якунин
Рецензенты:
д-р техн, наук, проф. В. А. Тарасов; кафедра «Летательные аппараты» Самарского
государственного аэрокосмического университета имени академика С. П. Королева
Теоретические основы авиа- и ракетостроения (в конспектах лекций): учеб.
ТЗЗ пособие для вузов / А. С. Чумадин, В. И. Ершов, В. А. Барвинок и др. — М.:
Дрофа, 2005. — 784 с.: ил. — (Проектирование, конструкция и производство
летательных аппаратов).
ISBN 5-7107-8537-7
Пособие является первым из серии «Проектирование, конструкция и производство
летательных аппаратов».
Излагаются современные представления в теоретических дисциплинах: гидро-
газоаэродинамике, ракетной баллистике, динамике полета, строительной механике, проек-
тировании и конструировании летательных аппаратов. Отдельные лекции посвящены те-
ории изготовления деталей из композиционных материалов и методом пластического
деформирования, теории надежности, методологии научного эксперимента, способам опи-
сания аэродинамических поверхностей, системам автоматизированного проектирования,
а также теории автоматического регулирования.
Для студентов аэрокосмических вузов, обучающихся по специальностям «Ракето-
строение» и «Самолето- и вертолетостроение».
УДК 629.7
ББК 39.5
Учебное издание
А. С. Чумадин, В. И. Ершов, В. А. Барвинок, В. И. Богданович,
В. В. Васильев, А. Е. Волхонский, И. Н. Егоров, Ю. Л. Иванов,
Н. Ю. Каратаева, А. И. Киселев, В. Н. Кобелев, Л. Н. Лысенко,
Б. Н. Марьин, А. П. Петров, В. Г. Попов, Г. А. Резниченко, М. Ю. Русин,
А. В. Цырков, Ю. А. Цуриков, В. Г. Шахов, В. И. Якунин
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ АВИА- И РАКЕТОСТРОЕНИЯ
(В КОНСПЕКТАХ ЛЕКЦИЙ)
Учебное пособие для вузов
Редактор Б. В. Панкратов. Художественное оформление А.Л.Кашеков
Технический редактор В. Ф. Козлова. Корректоры Г. И. Мосякина, Н. С. Соболева
Компьютерная верстка А. В. Егоров, А. В. Маркин
Подписано в печать 15.03.05. Формат 70x100 Vi6- Бумага офсетная. Гарнитура «Ньютон».
Печать офсетная. Усл. печ. л. 63,21. Тираж 1000 экз. Заказ № 666
ООО «Дрофа». 127018, Москва, Сущевский вал, 49.
Отпечатано в полном соответствии
с качеством предоставленных диапозитивов
в ОАО «Можайский полиграфический комбинат».
143200, г. Можайск, ул. Мира, 93.
© Коллектив авторов, 2005
© ОАО«КнААПО», 2005
ISBN 5-7107-8537-7 © Оформление. «Дрофа», 2005
ОГЛАВЛЕНИЕ1
Предисловие ........................................ 4
ГЛАВА 1. Введение в ракетно-космическую технику
(Киселев А. И., Кобелев В. Н.)...........................6
ГЛАВА 2. Гидрогазоаэродинамика летательных аппаратов
(Шахов В. Г.)...........................................48
ГЛАВА 3. Основы проектной баллистики ракет-носителей
и космических аппаратов (Лысенко Л. Н.)................107
ГЛАВА 4. Динамика полета и основы устройства самолета
(Волхонский А. Е., Резниченко Г. А., Иванов Ю. Л.).....163
ГЛАВА 5. Основы устройства ракет-носителей (Кобелев В. Н.).234
ГЛАВА 6. Реактивные двигатели летательных аппаратов (Попов В. Г.). 284
ГЛАВА 7. Элементы строительной механики
летательных аппаратов (Волхонский А. Е.)...............342
ГЛАВА 8. Основы теории автоматического регулирования
(Цуриков Ю. А.)........................................393
ГЛАВА 9. Обеспечение надежности летательных аппаратов
в процессе их производства
(Барвинок В. А., Богданович В. И.).....................435
ГЛАВА 10. Методы оценки конструкторско-технологических
решений (Егоров И. Н.).................................478
ГЛАВА 11. Методология научного эксперимента в производстве
аэрокосмической техники (Ершов В. И., Петров А. П.)....523
ГЛАВА 12. Основы теории изготовления элементов конструкций
пластическим деформированием (Чумадин А. С.)...........576
ГЛАВА 13. Проектирование конструкций летательных аппаратов
из композиционных материалов (Васильев В. В.)..........625
ГЛАВА 14. Способы задания, описания и увязки
аэродинамических поверхностей (Якунин В. И., Каратаева Н. Ю.)670
ГЛАВА 15. Системы автоматизированного проектирования в авиа-
и ракетостроении (Цырков А. В., Марьин Б. Н., Русин М. Ю.) ... 716
гВ конце каждой главы имеется более подробное содержание.
3
ПРЕДИСЛОВИЕ
XX век стал свидетелем бурного развития авиационной и ракетно-космической
техники во многих странах мира и, в первую очередь, в России, Соединенных Штатах
Америки, Германии, Франции, Великобритании, Японии и Китае. Еще ряд стран
создают или потенциально способны создавать летательные аппараты, однако только
указанные страны способны это делать самостоятельно и независимо друг от друга.
И связано это не столько с ограниченными материальными, трудовыми, энергетиче-
скими, финансовыми и другими ресурсами конкретного государства, сколько, в це-
лом, с развитием науки, техники и наукоемких технологий.
В настоящее время создать (спроектировать, сконструировать и изготовить) лета-
тельный аппарат, который был бы конкурентоспособным на мировом рынке авиаци-
онных и ракетно-космических услуг, очень сложная задача, решение которой требует
участия в работе больших коллективов высококвалифицированных специалистов,
обладающих современными знаниями и опытом в различных областях науки
и техники: гидрогазоаэродинамике, динамике полета, строительной механике, мате-
риалах, композиционных конструкциях, защитных покрытиях, технологии производ-
ства, проектировании заводов и цехов, эксплуатации, менеджменте, маркетинге и т. д.
Кроме того, эта работа требует согласованного взаимодействия и прогрессивного ди-
намического развития всех предприятий-участников проекта: КБ, НИИ, заводов (са-
молетостроительных, двигателестроительных, приборных, ремонтных и т. д.) и других
предприятий и организаций.
В связи с тем что от начала проектирования до момента серийного производства
летательного аппарата проходит обычно несколько лет, необходимо учитывать, что за
время создания летательного аппарата возможно существенное изменение экономи-
ческих, политических, демографических, экологических и иных условий и обсто-
ятельств, которые могут привести к изменению задач, решения которых возлагались
на новый аппарат. Это накладывает еще одно условие на его создание: требование
к возможной модернизации изделия или заранее предполагаемой многофункци-
ональности. Более того, следует всегда предусматривать не самые благоприятные ва-
рианты развития за это время событий внутри страны-производителя, связанные, на-
пример, с кризисом той или иной отрасли.
Таким образом, ясно, что создание нового летательного аппарата — задача со
многими неизвестными, однако доподлинно известно, что без современных знаний
в областях проектирования, конструирования и производства летательных аппаратов
достичь каких-либо успехов в этом деле изначально не представляется возможным.
В России, как в одной из ведущих авиационных и ракетно-космических держав
мира, к настоящему времени опубликовано много капитальных трудов в областях
авиа- и ракетостроения. Отметим лишь некоторые широко известные учебные изда-
ния. Это труды Н. Я. Фабриканта (Аэродинамика), В. И. Феодосьева и Г. Б. Синярева
(Введение в ракетную технику), М. Н. Шульженко (Конструкция самолетов),
М. И. Шевелюка (Теоретические основы проектирования ЖРД), Ю. П. Григорьева
(Строительная механика авиационных конструкций), Н. И. Безухова (Основы теории
упругости, пластичности и ползучести), М. Н. Горбунова (Основы технологии произ-
водства самолетов) и многие-многие другие.
Однако непрерывное совершенствование конструкции летательных аппаратов и
технологии их производства требуют постоянного обновления и учебных материалов.
Настоящее пособие открывает новую серию учебной литературы — конспекты
лекций в областях проектирования, конструкции и производства летательных аппара-
4
тов. Оно написано большой группой преподавателей и ученых известных аэрокосми-
ческих университетов и предприятий страны, среди которых:
• Московский государственный авиационный институт (технический универси-
тет) им. С. Орджоникидзе;
• Московский государственный технический университет им. Н. Э. Баумана;
• «МАТИ» — Российский государственный технологический университет им.
К. Э. Циолковского;
• Самарский государственный аэрокосмический университет им. С. П. Королева;
• Государственный космический научно-производственный центр им. М. В. Хру-
ничева;
• Комсомольское-на-Амуре авиационное производственное объединение
им. Ю. А. Гагарина.
Авторы предполагают издание нескольких подобных пособий, каждое из кото-
рых, охватывая определенный круг дисциплин, носит вполне законченный и само-
стоятельный характер, но вместе с тем объединенных одним объектом изучения — ле-
тательным аппаратом.
Данное пособие написано в виде конспектов лекций по теоретическим дисцип-
линам для студентов аэрокосмических университетов, обучающихся по направлени-
ям подготовки «Авиа- и ракетостроение», «Авиастроение» и «Ракетостроение и кос-
монавтика» (большей частью по специальности «Ракетостроение»). Название курсов
и их содержание авторы стремились привести в соответствие с образовательными
стандартами.
Цель настоящего пособия — дать студенту целостное представление о науке со-
здания летательного аппарата, показать неразрывность связей всех этапов его созда-
ния (проектирования, конструирования и производства), уяснить сущность этих эта-
пов и закономерности их развития.
Рукопись данного пособия готовилась с 2000 года. Авторы благодарны коллекти-
ву сотрудников кафедры «Технология производства летательных аппаратов» МАТИ
им. К. Э. Циолковского за помощь в оформлении рукописи.
Идея написания такого пособия, содержащего различные курсы, считалась авто-
рами (профессиональными преподавателями, много лет читающими эти курсы) инте-
ресной и вполне достижимой. Итог этой работы — в Ваших руках.
Все замечания и пожелания, связанные с настоящим изданием, авторы примут
с благодарностью.
Коллектив авторов
ГЛАВА 1___________________________
Введение
в ракетно-космическую технику
1.1. ЭТАПЫ РАЗВИТИЯ РАКЕТ И РАКЕТНОЙ ТЕХНИКИ
История развития ракет восходит к глубокой древности. Появление ракет нераз-
рывно связано с изобретением пороха, продукты сгорания которого создают реактив-
ную силу, способную сообщить ракете достаточно высокую скорость. В литературе
указывается, что рецепт изготовления пороха был известен в Китае, Индии, арабских
странах, но где порох появился впервые, до настоящего времени неизвестно. Считает-
ся, что в Китае ракеты («огненные стрелы») применялись еще в X—XII веках (рис. 1.1).
Использование ракет в качестве оружия всегда обусловливалось относительно
высокими энергетическими возможностями реактивных устройств, что делало раке-
ты эффективными при боевом применении. Однако постоянное соперничество дру-
гих видов метания снарядов, как правило, приводило на многих этапах создания ра-
кет к отказу от использования последних. В основном причиной отказа была низкая
точность попадания в цель ракетами по сравнению с конкурирующими системами.
Это связано с тем, что в неракетных системах сообщение требуемой скорости снаряду,
пуле и т. д. производится на коротком участке движения снаряда по направляющей,
которую можно достаточно точно навести на цель.
В результате этого сориентировать вектор скорости бросания снаряда, величина
которого формируется при движении снаряда в стволе, можно более или менее точно,
и на него относительно мало влияют внешние условия полета снаряда. Однако эти же
условия требуют сообщения снаряду больших ускорений, а следовательно, и больших
нагрузок, вызываемых реакциями, действующими на метательное устройство. Это за-
ставляет изготавливать неракетную метательную систему значительно более тяжелой
по сравнению с массой снаряда (в сотни раз).
В ракетной системе сообщение скорости снаряду происходит в основном вне
пусковой установки, на сравнительно длинном участке траектории полета. Это при-
водит к тому, что ускорения снаряда невелики, поэтому невелики и нагрузки на систе-
му метания. Вес ракетной метательной системы становится сравнимым с весом раке-
ты и может отличаться всего в несколько раз.
Широкое распространение «огненные стрелы» получили в Индии. Европейцы
(англичане) впервые столкнулись с «огненными стрелами» в период колонизации
Индии. Изучением их занялся военный инженер полковник Вильям Конгрев. Он вы-
вез ракеты в Англию, усовершенствовал их и добился принятия ракет на вооружение
английской армии. Ракеты достаточно широко и успешно использовались в боевых
действиях английской армии. Так, в 1807 году во время войны с Наполеоном англий-
ский флот при осаде Копенгагена практически полностью уничтожил город с по-
мощью ракет. Появление ракет на вооружении Англии заставило заняться ими и в
других странах (рис. 1.2, 1.3).
В России ракеты описываются в «Уставе» Анисима Михайлова, написанном им
в 1607—1621 гг. При Петре I ракеты широко применялись в русской армии. В начале
6
Рис. 1.1. «Огненная
стрела» (Китай):
1 — оболочка; 2 — порох;
3 — стрела; 4 — хвост
a)
Рис. 1.2. Ракеты начала XIX в.:
а) ракеты конструкции Конгрева 1807 г.;
б) шведская ракета 1827 г.
80-х годов XVII века в Москве было учреждено «Ракетное заведение», которое затем
было переведено в Санкт-Петербург. В начале XVIII века в нем была создана сигналь-
ная ракета, которая состояла на вооружении русской армии больше полутора веков.
Одним из первых создателей боевых ракет для русской армии был генерал Алек-
сандр Дмитриевич Засядко (1779—1837). Им были созданы удачные рикошетные
и зажигательные ракеты, которые использовались в ракетных ротах и батареях рус-
ской армии.
В 1840-х годах русский ученый генерал К. И. Константинов разработал научные
основы расчета и проектирования пороховых ракет, а также предложил стенды для их
испытаний (рис. 1.4). Используя его методики, ученые создали ракеты с дальностью
стрельбы до 4—5 км, которые стали эффективным оружием русской армии.
Однако развитие во второй половине XIX века нарезной артиллерии, позволив-
шей получить большую дальность стрельбы и более высокую точность и меньшее рас-
сеивание попадания, вытеснило ракеты. Как уже отмечалось, воздействие внешних
нагрузок (аэродинамических, вызванных неточностью изготовления снаряда, мета-
тельной установки и др.) на снаряд-ракету при полете на участке разгона под действи-
ем реактивной силы приводит к большим угловым отклонениям вектора скорости
снаряда от требуемого значения, а следовательно, и к отклонениям параметров дви-
жения снаряда по траектории. Эти отклонения значительно превышали аналогичные
отклонения артиллерийских орудий, разработанных во второй половине XIX века.
Точность стрельбы ракетами была много ниже, чем точность попадания снарядов при
стрельбе из этих орудий. Это явилось причиной отказа от использования ракет в каче-
стве снарядов для поражения целей.
В ходе развития методов вооруженной борьбы в период бурного развития науки и
техники в конце XIX — начале XX веков наметился переход к позиционным войнам,
ведение которых требовало огромного напряжения всего экономического и мораль-
ного потенциала стран-противников и расходования больших людских ресурсов, ор-
ганизации управления хозяйством этих стран, маневра силами и средствами.
7
Рис. 1.3. Боевые ракеты середины XIX века:
а) русская ракета 1849 г.; б) прусская ракета 1850 г.; в) французская ракета 1857 г.;
г) русская ракета 1859—1863 гг.
8
Рис. 1.4. Ракетный баллистический маятник конструкции К. И. Константинова
В ходе таких войн постоянно возрастали требования к возможности поражения
объектов противника на значительном удалении от переднего края вооруженной
борьбы сражающихся армий. К таким объектам относились центры управления, узлы
коммуникаций всех типов, важнейшие центры энергоснабжения, производства про-
мышленной продукции, скопления войск, боевой техники, основные склады различ-
ных запасов. Для нанесения морального ущерба населению страны и для сокращения
его трудовых ресурсов считалось возможным нанесение ударов по крупным населен-
ным пунктам противника.
Одной из первых попыток создания средств доставки боевого снаряда в глубокий
тыл противника (по понятиям того времени) было создание в Германии в ходе Пер-
вой мировой войны сверхдальнобойного орудия, предназначенного для обстрела це-
лей, расположенных на удалении от орудия на 200—250 км.
Уникальный опыт использования этого орудия показал, что эффективность та-
кой метательной системы крайне низка. Для доставки к цели снаряда весом 7 кг по-
требовалось создать орудие весом 350 т, обладающее малой скорострельностью,
имеющее очень низкую живучесть в связи с крайне высокой нагрузкой на ствол при
выстреле.
Кроме того, круговое отклонение снаряда от точки прицеливания, равное 2 км,
было столь велико, что реально мог быть осуществлен только обстрел площадных це-
лей (например, крупного города). Это показало, что при подобных параметрах рассе-
ивания повышение эффективности до приемлемого уровня может быть достигнуто
только за счет резкого увеличения (в сотни раз) массы боевого заряда. То есть, ис-
пользуя ствольные системы для доставки такого заряда к цели, добиться успеха
практически было невозможно.
Развитие авиации в первые два десятилетия XX века позволяло предположить,
что использование самолетов решит поставленную задачу. Уже в конце Первой миро-
вой войны во всех крупных воюющих странах были созданы бомбардировщики, спо-
собные доставлять до тонны и больше бомбовой нагрузки на дальность 300 — 350 км
(Fridrichshafen G-IV, Gotha G-V в Германии, Handley Page Н-12, Handley Page H-15 в
9
Англии, Илья Муромец в России, Martin МВ в США). Правда, в период Первой ми-
ровой войны практически не было осуществлено ни одного авиационного налета на
глубокие тыловые объекты противников, кроме нескольких бомбовых ударов, совер-
шенных немецкими дирижаблями. Но накопленный опыт применения авиации для
атаки наземных войск противника на переднем крае и ближних войсковых тылах,
тенденции развития авиации (повышение дальности полета, скорости, грузоподъем-
ности, развитие вооружения самолета) позволили создать теории авиационных войн,
основоположники которых доказывали, что в таких войнах практически только сила-
ми авиации можно подавить сопротивление противника, нанести непоправимый
ущерб экономике противника и деморализовать население. Но авторы этих теорий не
учли боевые способности развивающихся средств противовоздушной обороны (ПВО),
построенных на применении современной истребительной авиации, зенитной артил-
лерии, средств раннего обнаружения атакующих самолетов противника, средств связи
и управления. Развитие ПВО позволяло срывать маневры противника даже ограничен-
ными силами, обеспечивая местное противодействие в оборонительных целях.
Понимание этого привело к тому, что в странах, имеющих развитую научно-тех-
ническую базу (США, СССР, Германия), возникла идея создания боевых летательных
аппаратов-роботов, сочетающих возможности самолетов в достижении удаленных це-
лей, с повышением надежности выполнения задачи при сравнимых затратах матери-
альных средств на создание и производство этих аппаратов — либо за счет массового
их применения в относительно дешевом варианте, либо за счет повышения их неуяз-
вимости при полете по таким траекториям и с такой скоростью, что делало их недося-
гаемыми для средств ПВО того времени. Наибольших успехов в реализации этой идеи
добились немецкие ученые и инженеры. В значительной степени это объяснялось тем,
что в европейских странах — победительницах в Первой мировой войне, а также в
США и СССР большое внимание было уделено развитию оправдавшей себя военной
авиации. А в Германии Версальский мирный договор запрещал иметь и разрабатывать
такую авиацию, и силы ученых были направлены на создание нетрадиционных
средств нападения, инструмента подавления тыловых целей, на который не распрост-
ранялись ограничения мирного договора. Таким инструментом оказались беспилот-
ный крылатый самолет-снаряд V-l (FZG-76) и баллистическая ракета V-2 (А4).
В Германии, которая в значительной степени сохранила научный и технический
потенциал, а в середине 30-х годов получила экономические возможности создания
новых систем вооружения, удалось создать значительно более мощный и более эф-
фективный, чем в других странах, беспилотный баллистический аппарат, организо-
вать его массовое производство, а также производство агрегатов наземного оборудо-
вания, произвести испытания всего боевого ракетного комплекса, найти, создать и
опробовать организационные и эксплуатационные принципы применения.
Создание беспилотных летательных аппаратов типа самолетов-снарядов V-1
и управляемых баллистических ракет V-2 и использование опыта их эксплуатации
и боевого применения резко активизировало работы над аналогичными системами
вооруженной борьбы в различных странах мира, особенно в СССР и США.
Это было связано с тем, что именно постановка на борт баллистической ракеты
системы управления позволила повысить точность стрельбы ракеты по малоразмер-
ным целям и сделать ее конкурентоспособной по эффективности любой метательной
системе.
В Советском Союзе в марте 1946 года на первой послевоенной сессии Верховного
Совета СССР в числе других первостепенных задач развития страны называлась зада-
ча обеспечения работ по развитию реактивной техники. Постановлением ЦК КПСС
и Совета Министров СССР принимается решение о создании новых и развитии су-
10
шествующих научно-исследовательских, опытно-конструкторских и испытательных
организаций, деятельность которых должна быть направлена на создание ракет раз-
личных классов и назначения, в первую очередь баллистических ракет дальнего дей-
ствия, наземного оборудования, обеспечивающего их подготовку, запуск, управление
полетом и измерения параметров полета.
В начале 50-х годов Советский Союз вышел на передовые рубежи по разработке и
применению мощных ракет. Это позволило СССР в 1957 году сделать первый шаг в
практическом освоении космоса — запустить первый искусственный спутник Земли
(ИСЗ), а затем в 1961 году — и первого космонавта.
При дальнейшем развитии ракетной техники ее создателями решались две за-
дачи:
• совершенствование ракет как средства вооруженной борьбы, повышение их не-
уязвимости от воздействия противника и увеличение боевого могущества ракет.
Решение этой задачи всегда связывалось со стремлением уменьшить габариты
ракеты при сохранении или даже увеличении мощности боевого заряда, его эф-
фективности. Это позволяло бы, в свою очередь, либо увеличить защитные свой-
ства шахтных пусковых установок, увеличение размеров которых не допускалось
международными соглашениями, либо создать приемлемых размеров подвиж-
ные ракетные комплексы разных типов. Как правило, ракеты, удовлетворяющие
этим требованиям, создаются твердотопливными;
• увеличение возможностей ракет как инструмента для освоения ближнего и даль-
него космоса. А на этом пути постоянно наблюдались тенденции к увеличению
размеров ракет, так как задачи, которые ставились и ставятся в данной области,
требуют обычно запуска более тяжелых объектов.
На первом этапе этого развития почти все задачи освоения космоса решались пу-
тем использования в качестве средства выведения космических объектов боевых ра-
кет и их ступеней. В дальнейшем для решения задач освоения космоса были созданы
специальные носители космических средств.
Ракеты среднего и тяжелого классов, которые использовались для этой цели, ос-
нащаются в основном жидкостным ракетным двигателем (ЖРД). И в настоящее вре-
мя только очень небольшая часть задач по освоению космоса может решаться путем
использования ступеней современных боевых ракет (ракеты двойных технологий). То
есть все в большей мере прослеживается определенная дифференциация боевых ракет
и ракет-носителей космических объектов.
1.2. ТЕОРИЯ ТЕЛ ПЕРЕМЕННОЙ МАССЫ —
ФУНДАМЕНТ КОСМОНАВТИКИ. РАЗВИТИЕ КОСМОНАВТИКИ
И ПРАКТИЧЕСКОЙ РАКЕТНОЙ ТЕХНИКИ
В основе создания теории и практики использования ракет лежат основные по-
ложения механики тел переменной массы. Механика тел переменной массы — наука
XX столетия. Современная ракетная техника ставит новые и новые задачи для этого
сравнительно недавно возникшего раздела теоретической механики.
Ракеты разных типов, реактивные снаряды, торпеды освоены сейчас промыш-
ленностью почти всех стран мира. Все ракеты — это тела, масса которых существенно
изменяется во время движения. Вообще случаи движения тел, масса которых изменя-
ется с течением времени, можно видеть во многих явлениях природы. Например, мас-
са падающего метеорита, движущегося в атмосфере, убывает вследствие того, что час-
тицы метеорита отрываются вследствие сопротивления воздуха или сгорают.
11
Основной закон динамики точки переменной массы был сформулирован профес-
сором Петербургского политехнического института И. В. Мещерским в 1897 году. По-
казано, что имеется два фактора, отличающих уравнения движения точки переменной
массы от уравнений Ньютона: переменность массы и гипотеза отделения частиц, опре-
деляющих добавочную или реактивную силу, создающую движение точки.
Закон движения точки переменной массы гласит: «Для любого момента времени
произведение массы излучающего центра на его ускорение равно геометрической
сумме равнодействующей приложенных к нему внешних сил F и силы реактивной R».
d(m' V)/dt=F+R.
Полученное И. В. Мещерским основное уравнение движения точки переменной
массы дало возможность установить количественные закономерности для различных
задач. Одной из существенных гипотез, лежащих в методе Мещерского, является ги-
потеза близкодействия (контактного воздействия тела и отбрасываемых частиц). До-
пускается, что в момент отделения частицы от тела происходит явление, аналогичное
удару, частица за очень малый промежуток времени получает относительную скорость
И2, и дальнейшее взаимодействие частицы и основного тела прекращается.
Важный вклад в механику тел переменной массы внес русский ученый
К. Э. Циолковский. В 1903 году он опубликовал работу «Исследование мировых про-
странств реактивными приборами», в которой обстоятельно исследовал ряд интерес-
ных случаев прямолинейного движения тел переменной массы (ракет). Простейшая
задача, решенная в исследовании К. Э. Циолковским, касается самого принципа ре-
активного движения. Изучая движение точки в среде без внешних сил, Циолковский
показал, что при достаточно большой скорости отбрасывания частиц и величине от-
ношения начальной массы точки к конечной массе можно получить весьма большие
(космические) скорости.
В механике тел переменной массы К. Э. Циолковскому принадлежит идея изуче-
ния таких движений точки переменной массы, когда на некоторых интервалах време-
ни масса точки изменяется непрерывно, а в некоторые моменты времени — скачком.
Это позволило построить теорию многоступенчатых ракет.
Космонавтика как наука, а затем и как практическая отрасль, сформировалась
в середине XX века. Но этому предшествовала увлекательная история рождения и раз-
вития идеи полета в космос, начало которой положила фантазия, и только затем по-
явились первые теоретические работы и эксперименты. Так, первоначально в мечтах
человека полет в космические просторы осуществлялся с помощью сказочных средств
или сил природы (смерчей, ураганов). Ближе к XX веку для этих целей в описаниях
фантастов уже присутствовали технические средства — воздушные шары, сверхмощ-
ные пушки и, наконец, ракетные двигатели и собственно ракеты. Не одно поколение
молодых романтиков выросло на произведениях Ж. Верна, Г. Уэллса, А. Толстого,
А. Казанцева, основой которых было описание космических путешествий.
Все изложенное фантастами будоражило умы ученых. Так, К. Э. Циолковский
говорил: «Сначала неизбежно идут мысль, фантазия, сказка, а за ними шествует точ-
ный расчет».
Публикации в начале XX века теоретических работ пионеров космонавтики
(рис. 1.5) К. Э. Циолковского, Ф. А. Цандера, Ю. В. Кондратюка, Р. X. Годдарта,
Г. Гансвиндта, Р. Эно Пельтри, Г. Оберта, В. Гомана и других в какой-то степени орга-
низовали полет фантазии, но в то же время вызвали к жизни новые направления
в науке — появились попытки определить, что может дать космонавтика обществу
и как она на него повлияет.
12
Н. И. Кибальчич
1853—1881
К. Э. Циолковский
1857—1935
Ф. А. Цандер
1887—1933
Ю. В. Кондратюк
1897—1941
Н. И. Тихомиров
1859—1930
И. Т. Клейменов
1899—1938
Г. Э. Лангемак
1898—1938
В. П. Глушко
1908—1989
С.П. Королев
1907—1966
Рис. 1.5. Пионеры отечественной космонавтики
13
Одним из пионеров ракетно-космической техники является Роберт Эно Пельтри
(Einaut Pelterie) — французский ученый, инженер и изобретатель.
В космонавтику он пришел после увлечения авиационной техникой. Он был од-
ним из первых, кто обратил внимание на возможность использования в космической
технике атомной энергии.
В 1930 году Р. Эно Пельтри опубликовал в Париже первый том капитального тру-
да «Астронавтика». Второй том вышел в 1935 году. В этих работах суммировано все,
что имеет отношение к космическим полетам.
В 1912—1913 годах Роберт Годдард (Goddard) в США разрабатывал теорию дви-
жения ракеты. Годдард вывел дифференциальное уравнение движения ракеты и раз-
работал приближенный метод его решения, определил минимальную стартовую мас-
су для подъема одного фунта полезного груза на разные высоты, получил значение
КПД ракеты. Им была показана возможность запуска многоступенчатой ракеты и оп-
ределены выгоды ее применения. На рис 1.6 приведена схема двухступенчатой ракеты
Годдарда. С 1915 года занимался стендовыми экспериментами с ракетами на твердом
топливе. В 1920 году в Вашингтоне была издана фундаментальная работа Годдарда
«Метод достижения предельных высот». Эта работа относится к числу классических в
истории ракетно-космической техники.
В 1921 году Годдард начал проведение экспериментальных исследований с ЖРД,
используя в качестве окислителя жидкий кислород, а в качестве горючего — углеводо-
роды. Первый запуск ЖРД на стенде состоялся в марте 1922 года. Впервые успешный
полет ракеты с ЖРД, созданной Годдардом, произошел 16 марта 1926 года (рис. 1.7),
ракета массой 4,2 кг достигла высоты 12,5 м и пролетела 56 м.
Рис. 1.6. Схема двухступенчатой ракеты
(патент Годдарда 1914 г.):
1 — первая ступень; 2 — вторая ступень
Рис. 1.7. Ракета
Р. X. Годдарда
(1926 г.)
14
Надо сказать, что идеи соединить космическое и земное направление человече-
ской деятельности принадлежит основателю теоретической космонавтики
К. Э. Циолковскому. Когда ученый говорил: «Планета есть колыбель разума, но нель-
зя вечно жить в колыбели», он не выдвигал альтернативы — либо Земля, либо космос.
Циолковский никогда не считал выход в космос следствием какой-то безысходности
жизни на Земле. Напротив, он говорил о рациональном преобразовании природы на-
шей планеты силой разума. Люди, утверждал ученый, «изменят поверхность Земли, ее
океаны, атмосферу, растения и самих себя. Будут управлять климатом и будут распо-
ряжаться в пределах Солнечной системы, как и на самой Земле, которая еще неопре-
деленно долгое время будет оставаться жилищем для человечества».
В области теоретической разработки вопросов космонавтики и межпланетных пу-
тешествий работал талантливый исследователь Ю. В. Кондратюк, который независи-
мо от К. Э. Циолковского в своих работах «Тем, кто будет читать, чтобы строить»
(1919 г.) и «Завоевание межпланетных пространств» (1929 г.) получил основные урав-
нения движения ракеты. В ряде положений, рассмотренных в его работах, были до-
полнены основные положения, изложенные в работах К. Э. Циолковского. Например,
Кондратюк предложил при полетах на Луну выводить космическую систему на орбиту
ИСЗ, а затем взлетно-посадочный аппарат направлять к Луне. Показана энергетиче-
ская эффективность такого выведения полезной нагрузки, направляемой к Луне.
Другим крупным представителем отечественной школы космонавтики был
Ф. А. Цандер. В опубликованной в 1932 году книге «Проблемы полета при помощи
реактивных аппаратов» собраны материалы по конструкциям ракет, теории полета ра-
кет, предложения по использованию в качестве топлив для ракетных двигателей неко-
торых металлов и сплавов.
В 1921 году по инициативе и под руководством Н. И. Тихомирова в составе Воен-
но-исследовательского комитета при Реввоенсовете РСФСР была создана Газодина-
мическая лаборатория (ГДЛ), занимавшаяся разработкой реактивных снарядов на
баллистических порохах. На основе этих разработок был созданы, успешно испытаны
и приняты на вооружение РККА установки залпового запуска реактивных снарядов,
сыгравшие немалую роль в боях на Халхин-Голе и в Великой Отечественной войне.
В мае 1929 года в ГДЛ по инициативе В. П. Глушко был создан отдел, в котором
в 1930—31 годах были разработаны жидкостные реактивные двигатели ОРМ-1 и ОРМ-2
(опытные реактивные моторы).
В качестве компонентов топлива в двигателях использовалась четырехокись азо-
та (окислитель) и толуол или смесь бензина с толуолом (горючее). Двигатели развива-
ли тягу до 20 кг. На основе результатов испытаний в 1931—32 годах создана и испыта-
на серия ЖРД вплоть до ОРМ-52 с тягой 250—300 кг.
В 1931 году в Москве и Ленинграде при Осовиахиме были созданы группы по
изучению реактивного движения (МосГИРД и Ленинград), которые на обществен-
ных началах объединяли энтузиастов ракетостроения.
В МосГИРДе работали Ф. А. Цандер, С. П. Королев, Ю. А. Победоносцев,
М. К. Тихонравов и др.
В МосГИРДе под руководством С. П. Королева была создана по проекту
М. К. Тихонравова первая ракета ГИРД-09 с двигателем тягой 25—33 кг, работавшим
на гибридном топливе — желеобразном бензине и газообразном кислороде. Ракета
была испытана в августе 1933 года. В ноябре того же года под руководством
С. П. Королева была создана ракета ГИРД-Х, работающая на жидком топливе —
спирте и жидком кислороде. Двигатель ракеты развивал тягу до 65 кг. Ракета создава-
лась по проекту Ф. А. Цандера.
15
В 1933 году на базе ГДЛ и МосГИРДа был создан в системе Наркомата обороны
Реактивный научно-исследовательский институт РККА (РНИИ РККА), который че-
рез несколько месяцев был передан в промышленность. В институте в 1934—38 годах
был создан ряд ЖРД (от ОРМ-53 до ОРМ-102), причем ОРМ-65 (созданный в
1936 году) развивал тягу до 175 кг и был наиболее совершенным двигателем того вре-
мени.
В 1939 году по инициативе В. П. Глушко и под его руководством было создано
опытное конструкторское бюро по жидкостным ракетным двигателям (ОКБ-ГДЛ),
где в сороковых годах было разработано семейство авиационных ЖРД, послуживших
прототипами при разработке мощных ракетных двигателей.
В СССР сразу после Второй мировой войны практические работы по космиче-
ским программам связаны с именами С. П. Королева и М. К. Тихонравова. В начале
1945 года М. К. Тихонравов организовал группу специалистов РНИИ по разработке
проекта пилотируемого высотного ракетного аппарата (кабины с двумя космонавта-
ми) для исследования верхних слоев атмосферы. Проект решено было создавать на
базе одноступенчатой жидкостной ракеты, рассчитанной для вертикального полета на
высоту до 200 км (проект ВР-190). Проект предусматривал решение следующих задач:
• исследование условий невесомости при кратковременном полете человека в гер-
метичной кабине;
• изучение движения центра масс кабины и ее движения около центра масс после
отделения от ракеты-носителя;
• получение данных о верхних слоях атмосферы;
• проверка работоспособности систем (разделения, спуска, стабилизации, призем-
ления и др.), входящих в конструкцию высотной кабины.
В проекте ВР-190 впервые были предложены решения, нашедшие применение
в современных космических аппаратах (КА):
• парашютная система спуска, тормозной ракетный двигатель мягкой посадки,
система разделения с применением пироболтов;
• электроконтакгная штанга для упредительного зажигания двигателя мягкой по-
садки, бескатапультная герметичная кабина с системой обеспечения жизнеде-
ятельности экипажа;
• система стабилизации кабины за пределами плотных слоев атмосферы
с применением сопел малой тяги.
В целом проект ВР-190 представлял собой комплекс новых технических решений
и концепций, подтвержденных ходом развития отечественной и зарубежной ракет-
но-космической техники. В 1946 году материалы проекта ВР-190 были доложены Ти-
хонравовым И. В. Сталину. С 1947 года Тихонравов со своей группой работает над
идеей ракетного полета и в конце сороковых — начале пятидесятых годов показывает
возможность получения первой космической скорости и запуска ИСЗ при помощи
разрабатывающейся в СССР ракетной базы. В 1950—53 годах усилия сотрудников
группы М. К. Тихонравова были направлены на изучение проблемы создания состав-
ных ракет и ИСЗ.
В докладе Правительству в 1954 году о возможности разработки и запуска ИСЗ
С. П. Королев писал: «По вашему указанию представляю докладную записку тов.
Тихонравова М. К. «Об искусственном спутнике Земли»». В отчете о научной де-
ятельности за 1954 год С. П. Королев отмечал: «Мы полагали бы возможным произ-
вести эскизную разработку проекта самого ИСЗ с учетом ведущихся работ (особенно
заслуживают внимания работы М. К. Тихонравова)».
16
Развернулись работы по подготовке запуска
первого ИСЗ ПС-1. Был создан первый Совет
главных конструкторов во главе с С. П. Короле-
вым, который в дальнейшем и осуществлял руко-
водство космической программой СССР, ставшего
лидером в освоении космоса. Созданное под руко-
водством С. П. Королева ОКБ-1-ЦКБЭМ-НПО
«Энергия» стало с начала 1950-х годов центром
космической науки и промышленности в СССР.
Космонавтика уникальна тем, что многое, пред-
сказанное сначала фантастами, а затем учеными,
свершилось воистину с космической скоростью.
Всего 40 с небольшим лет прошло со дня запуска
первого искусственного спутника Земли, 4 октяб-
ря 1957 года, а история космонавтики уже содер-
жит серии замечательных достижений, получен-
ных первоначально СССР и США, а затем и дру-
гими космическими державами.
Уже многие тысячи спутников летают на
орбитах вокруг Земли, аппараты достигли Лу-
ны, Венеры, Марса; научная аппаратура посы-
лалась к Юпитеру, Меркурию, Сатурну для по-
лучения знаний об этих удаленных планетах
Солнечной системы.
С момента запуска первого космонавта
Земли Ю.А. Гагарина на космическом корабле
(КК) «Восток» (рис. 1.8.), после запусков других
КК, долговременных орбитальных станций
«Салют» и «Мир», СССР стал на долгое время
ведущей страной мира по пилотируемой космо-
навтике. Крупномасштабные космические сис-
темы используются для решения широкого
спектра задач (в т. ч. социально-экономических
и научных), идет интеграция космических от-
раслей различных стран.
Первые мощные ЖРД (созданные под руко-
водством В. П. Глушко), реализация новых науч-
ных идей и схем, практически исключивших по-
тери на привод турбонасосного агрегата (ТНА),
выдвинули российское двигателестроение на пе-
редовые рубежи космической техники. Началось
развитие термо- и гидродинамики, теории про-
чности, металлургии материалов, химии топлив,
измерительной техники, вакуумной и плазменной
технологий.
В других странах (в первую очередь в Герма-
нии) с 20-х годов XX века велись практические ра-
боты по созданию ЖРД и разрабатывались проек-
ты баллистических ракет. В работах приняли учас-
тие крупные немецкие ученые и инженеры:
Г. Оберт, Р. Небель, В. Ридель, К. Ридель. Герман
Блок
III ступени
Рис. 1.8. Ракета-носитель «Восток»:
1,6 — головной обтекатель; 2 —
КА «Луна»; 7 — КА «Восток»; 3, 9 —
кислородный бак; 4, 10 —керосиновый
бак; 5 — двигатель РД-0105; 8 —
двигатель РД-0109; 11 — двигатель
РД-108; 12 — двигатель РД-107
17
Оберт работал над созданием ракет. Еще в 1917 г. он создал проект боевой ракеты на жид-
ком топливе (спирт и жидкий кислород), которая должна нести боевой заряд на дальность
в несколько сот километров. В 1923 году Оберт написал диссертацию «Ракета в межпла-
нетном пространстве». Дальнейшее развитие идеи Г. Оберта получили в книге «Пути осу-
ществления космического полета» (1929 г.), в которой рассмотрен, в частности, вопрос о
возможности использования при межпланетных перелетах энергии солнечного излучения.
В 1957 году вышла книга Оберта «Люди в космосе», где он снова возвращается
к использованию энергии излучения Солнца с помощью развертываемых в космосе
зеркал.
Обертом разработаны несколько проектов космических ракет с ЖРД, где предла-
гаются в качестве горючего спирт, углеводороды, жидкий водород, а в качестве
окислителя — жидкий кислород.
Р. Небель работал над проектом ракеты, запускающейся по наземным целям
с самолета.
В. Ридель проводил экспериментальные исследования ракетных двигателей.
В 1927 году в Бреслау было создано общество межпланетных сообщений, члены кото-
рого создали и испытали в Руссельчейме ракетную тележку.
В конце 20-х годов для проведения экспериментальных работ, направленных на
создание ракет с ЖРД, при отделе баллистики и боеприпасов управления вооружения
Рейхсвера создана группа по исследованию жидкостных ракетных двигателей под руко-
водством В. Дорнбергера. В 1932 году в Кюнельсдорфе недалеко от Берлина в специаль-
но организованной экспериментальной лаборатории началась разработка ЖРД для
баллистических ракет.
В этой лаборатории ведущим конструктором становится Вернер фон Браун. В 1933
году группой инженеров под руководством Дорнбергера и Брауна была сконструирова-
на баллистическая ракета с ЖРД А-1 со стартовым весом 150 кг, длиной 1,4 м, диа-
метром 0,3 м. Двигатель развивал тягу 295 кг. Хотя конструкция оказалась неудачной, но
ее усовершенствованный вариант А-2, созданный на базе А-1, в декабре 1934 года был
успешно запущен с острова Боркум (Северное море). Ракета достигла высоты 2,2 км.
В 1936 году при полной поддержке командования Рейхсвера группа Дорбергера —
Брауна приступила к разработке баллистической ракеты с расчетной дальностью 275 км
с весом головной части в 1 т. Тогда же было принято решение о строительстве на остро-
ве Узедом в Балтийском море научно-исследовательского ракетного центра Пенемюн-
де, состоящего из двух частей: Пенемюнде-Вест для испытания новых видов оружия
ВВС и Пенемюнде-Ост, где проводились работы над ракетой для сухопутных войск.
После неудачных пусков ракеты А-3 начались работы над ракетой А-4 с ЖРД,
имевшей следующие тактико-технические характеристики: стартовый вес 12 т, длина
14 м, диаметр корпуса 1,6 м, размах стабилизаторов 3,5 м, тяга двигателей на Земле
25 т, дальность полета около 300 км. Круговое отклонение ракеты должно быть в пре-
делах 0,002—0,003 км. Головная часть имела заряд взрывчатого вещества, равный 1 т.
Первый экспериментальный пуск ракеты А-4 состоялся 13 июня 1942 года и
окончился неудачей, ракета упала через 1,5 минуты после старта. 3 октября 1942 года
ракета пролетела 190 км, достигнув высоты 96 км, и отклонилась от расчетного места
падения на 4 км.
В период с сентября 1944 года по март 1945 года командование немецких вооружен-
ных сил направило в боевые ракетные подразделения около 5,8 тыс. ракет А-4 (V-2). По-
чти 1,5 тыс. ракет не достигло пусковых установок. Около 4,3 тыс. ракет было запущено в
сторону Англии. Из них только 15% достигли цели. Такой низкий процент успешных пу-
сков объясняется конструктивными недостатками V-2 («Фау-2»). Однако был получен
опыт применения ракетного оружия большой дальности, который был в дальнейшем ис-
пользован в СССР и США.
18
1.3. ОБРАЗОВАНИЕ РЫНКА КОСМИЧЕСКИХ УСЛУГ
И РАЗВИТИЕ РАКЕТНО-КОСМИЧЕСКОЙ ТЕХНИКИ
НА СОВРЕМЕННОМ ЭТАПЕ
Если в первый период бурного развития ракетной техники (в первую очередь во-
енной) решение задач в этой области осуществлялось любой ценой и для решения
каждой новой задачи разрабатывалась новая, обычно более совершенная ракета, то
уже в конце 1960-х годов встал вопрос об экономической эффективности ракетной
техники. Это было связано с ростом ее эффективности и в гражданских областях че-
ловеческой деятельности.
Но часто собственных ресурсов у отдельных даже крупных государств на эти цели
не хватало, поэтому начали создаваться интернациональные космические объедине-
ния по реализации крупных космических проектов, например Европейское космиче-
ское агентство (ЕКА) и ряд других.
С конца 1970-х годов рынок космических услуг представляет собой уже устойчи-
во и интенсивно развивающийся сектор мировой экономической системы. Это обус-
ловлено возрастанием потребностей в услугах, которые предоставляются на коммер-
ческой основе с использованием ракетно-космических систем: телекоммуникации,
продукты и услуги дистанционного зондирования поверхности Земли, геодезические
и навигационные услуги, выведение в космос летательных аппаратов и т. д. Кроме то-
го, политические изменения привели к ослаблению государственного регулирования
и к развитию частной инициативы в сфере космической деятельности. В результате
создания перспективных технологий и разработки средств выведения и космичес-
ких аппаратов открылись новые возможности в освоении космоса на коммерческой
основе.
Анализ состояния и прогноз развития космического рынка стал наряду с проект-
но-конструкторской и промышленно-производственной деятельностью неотъемле-
мой частью научно-практической работы ракетно-космической структуры любого
достаточно развитого государства.
Способность заблаговременно выявить возникающие здесь тенденции, понять
новые формирующиеся потребности рынка космических услуг и перевести их в конк-
ретные технические требования к перспективным образцам ракетно-космической
техники является необходимым условием для успешной деятельности предприятий,
предлагающих свои услуги в различных сферах космического рынка.
Развитие мирового космического рынка в значительной степени зависело от зна-
чительной государственной поддержки и целенаправленного финансирования со сто-
роны государственных организаций деятельности, направленной на практическое ос-
воение и использование космического пространства, осуществляемое в рамках госу-
дарственных космических программ.
В настоящее время собственные космические программы имеют свыше пятидеся-
ти стран мира, однако уровень их финансирования значительно различается. Реально
прогресс космической техники и технологии определяется ведущими космическими
державами: Россией, США, Японией, Францией, Германией, Италией, Китаем, Вели-
кобританией, Индией и Канадой. Основные разработки ракетно-космической техники
(РКТ) иностранных государств представлены на рис. 1.9—1.17.
Государственное финансирование космических программ направлено на разра-
ботку перспективных проектов по созданию новых образцов РКТ
Затраты на эксплуатацию и разработку новых космических транспортных сис-
тем занимают третью позицию после перспективных разработок и фундаменталь-
ных исследований. Возрастают относительные и абсолютные затраты на дистанци-
19
IV
Рис. 1.9. Программа «Меркурий»:
1 — кабина экипажа; 2 — бак со спиртом; 3 — кислородный бак;
4 — двигатель (347 кН); 5 — система спасения; 6 — твердотопливная установка;
7 — парашют; 8 — герметичная кабина. I—VII — этапы полета
онное зондирование Земли. Для стран со скромным космическим бюджетом ха-
рактерно сосредоточение финансов на решении практических вопросов, в первую
очередь, в сфере телекоммуникаций, дистанционного зондирования Земли и нави-
гации.
Затраты на освоение телекоммуникационных технологий значительны в бюдже-
тах всех стран, имеющих национальные космические программы. Однако наиболее
значительны расходы на эти цели в Японии и Китае.
В последнее время резко возрос объем ассигнований на экономический монито-
ринг и дистанционное зондирование Земли из космоса. Это направление космиче-
ской деятельности особенно характерно для стран Западной Европы и Канады. Фи-
нансирование работ по освоению технологии производства материалов и препаратов
на орбите проводят преимущественно США и Япония.
В области развития космических транспортных систем достаточно сильны пози-
ции европейских стран, где расходы на эти цели значительно подкрепляются государ-
ственным финансированием и можно ожидать дальнейшего усиления конкуренции с
их стороны в сфере предоставления транспортных услуг.
Страны Европейского космического агентства сосредоточили усилия в основном
на развитии транспортной системы «Ариан», на создании технической основы для
системы глобального экологического мониторинга и космических систем связи. Раз-
20
Рис. 1.10. Программа
исследований Луны
«Сатурн-5» — «Аполлон»:
1 — система спасения;
2 — КА «Аполлон»;
3 — водородный бак;
4 — кислородный бак;
5 — двигатель (900 кН);
6 — водородный бак;
7, 8 — кислородный бак;
9 — керосиновый бак;
10, 11 — маршевые
двигатели 1-й и 2-й ступеней
Рис. 1.11. Орбитальный самолет
«Спейс Шаттл»:
1 — маршевые двигатели;
2 — двигатели маневрирования на орбите;
3 — манипулятор;
4, 7, 8 — сопла маршевых двигателей;
5, 6 — трубопроводы подачи водорода
и кислорода соответственно;
9 — сопла двигателя маневрирования;
10 — горючее; 11 — гелиевые баллоны;
12 — окислитель
ворачивается программа разработки Европейской Системы космической навигации, в
том числе для неземных видов транспорта, что позволит ЕКА резко укрепить свои по-
зиции на перспективном направлении навигационных услуг.
В настоящее время в структуре мирового космического рынка можно выделить
следующие сегменты:
• производство ракет-носителей (РН>и космических аппаратов (КА);
• запуски КА на коммерческой основе;
• космические телекоммуникационные системы и услуги;
21
Рис. 1.12. Ракеты-носители «Атлас» различных модификаций (I—XVIII) и «Атлас-Центавр»:
1 — КА «Пионер-10»; 2 — водородный бак; 3 — кислородный бак; 4 — двигатель;
5 — бак с азотной кислотой; 6 — керосиновый бак; 7 — двигатель
22
Второе включение Отделение
Работают
двигатели РБ
двигателей РБ
Отделение
РБ «Центавр»
Сброс
обтекателей
Выключение
двигателей
полезного груза
♦
РБ «Центавр»
уводится с орбиты
Старт PH
«Атлас»
Сброс
бустера
Работает
маршевый ЖРД
РБ «Центавр-ПА»,
2xRL10A-4N
2x185 кН
Pratt&Whitney
PH HAS и IIARS
снабжены ускорителями
Castor-IVA
4x434= 1 736 кН
PH ПА и HAS
снабжены двигателями
RL105NA + 2RL89M
266+ 1 854 кН
Rocketdyne
PH IIARhIIARS
снабжены двигателем РД-180
3 900/4 230 кН
НРО «Энергомаш»
Рис. 1.13. Ракета-носитель «Атлас» HAS—IIARS
23
60 м
Наиме-
нование 401
ПГГПО,т 5
Рис. 1.14. Ракета-носитель «Атлас-5»
• космические навигационные системы и услуги;
• дистанционное зондирование Земли из космоса;
• долговременные орбитальные станции (ДОС) и космический «туризм»;
• использование наземной космической инфраструктуры;
• страхование космических рисков.
Важной областью развития космической техники является создание долговре-
менных орбитальных станций, позволяющих осуществлять комплексное исследова-
ние и освоение околоземного пространства. В этих работах вместе с Россией и США
принимают участие страны Европы через Европейское космическое агентство, Кана-
да и Япония. Некоторые другие страны тоже хотели бы участвовать в этих работах.
Примером такого содружества служит проект создания международной космической
станции (МКС).
Рациональное использование долговременных орбитальных станций возможно
в следующих областях:
• в области физики и астрономии при использовании спектров небесных тел, кос-
мического излучения, характеристик потоков частиц; регистрации микромете-
оритных частиц, спектров солнечных вспышек, излучения звезд, Луны, поверх-
ности атмосферы Земли; изучения распределения газовых компонент верхней
атмосферы Земли, спорадического метеорного вещества, температуры верхней
атмосферы Земли, межзвездного пространства; определения химического соста-
ва ядерного вещества, космических лучей; оценки пробивного действия микро-
метеоритов;
24
Рис. 1.15. Ракета-носитель «Ариан-5»:
1 — головной обтекатель; 2 — полезная нагрузка; 3 — приборный отсек; 4 — 2-я ступень;
5 — 1-я ступень; 6 — ускорители; 7 — ЖРД «Vulcain». I—VII — этапы старта
25
N-I N-II H-I
Масса, т 90 135 140
Длина, м 33 35 40,3
Диаметр, м 2,4 2,4 2,49
ПГ ГПО, кг 130 350 550
H-IIA212
н-п J-I (проект)
260 90 405
50 33,1 53
4 1,8 4
2 200 100 4 000
Рис. 1.16. Ракеты-носители Японии
в области изучения природных ресурсов Земли путем фотографирования поверх-
ности Земли в интересах геологии, геодезии, метеорологии, сельского, рыбного и
лесного хозяйства; спектрографирования ореола Земной поверхности; фотогра-
фирования и спектрометрирования Земли;
в области медико-биологических исследований путем изучения влияния факто-
ров длительного космического полета на организм человека, проведения оценки
условий обитания и функционального состояния человека в условиях полета;
разработки и испытания профилактических средств для снижения влияния на
организм человека факторов длительных космических полетов; путем проведе-
ния исследований различных биологических объектов, особенностей протекания
жизненных процессов при обитании в условиях невесомости у различных орга-
низмов;
в области отработки новых систем и приборов организация испытания приборов
и экспериментальных бортов систем различного назначения; отработка различ-
ных двигательных установок, процессов дозаправки топливом и пополнения рас-
ходуемых материалов, процессов сборки элементов крупногабаритных конструк-
ций, испытания различных вариантов бортовых источников питания;
в области технологических процессов производится отработка базовых техноло-
гий получения перспективных материалов в условиях невесомости; исследование
26
40 м
30 м
20 м
10 м
CZ-1D CZ-2C CZ-3 CZ-2E CZ-3A CZ-3B CZ-3C
Орбита Грузоподъем- НОО НОО гпо НОО ГПО гпо гпо
ность, кг 1000 2 400 1600 9 200 2 600 5 000 3700
Первый полет 1982 1984 1992 1994 1996 1996
Рис. 1.17. Ракеты-носители Китая
механизма массопереноса и скорости роста кристаллов; процесса кристаллизации
в невесомости и влияние микрогравитации на рост кристаллов; организуется про-
цесс полупромышленного получения продукции в интересах микроэлектроники,
лазерной техники, СВЧ-техники и др.;
• в области биологического производства в интересах здравоохранения, сельского
хозяйства, охраны окружающей среды; организация отработки базовых техноло-
гий и создание аппаратуры экспериментального производства; получение опыт-
но-промышленных партий особо ценных биопрепаратов;
• в области военно-прикладного направления организация контроля выполнения
международных обязательств по разоружению;
• в области международного сотрудничества осуществление международных пило-
тируемых полетов, разработка и реализация программы исследований по меж-
правительственным соглашениям;
• в области коммерческой деятельности выполнение программы исследований,
сопутствующих полетам граждан других стран; выполнение рекламных действий;
экспонирование в открытом космосе образцов новых материалов, предназначен-
ных для использования в космической технике и др.
Создание МКС (рис. 1.18), три модуля которой уже функционируют на орбите
несколько лет, было бы невозможно без использования проектного, конструкгорско-
27
Рис. 1.18. Проект международной космической станции
го, технологического, экспериментального и эксплуатационного опыта, полученного
мировым сообществом в результате создания и эксплуатации российских ДОС «Са-
лют» и «Мир».
1.3.1. Основные задачи, решаемые
ракетно-космической техникой
В настоящее время результаты планомерного освоения и использования космоса
в интересах науки, социально-экономического прогресса, повышения обороноспо-
собности используются более чем в 130 странах мира.
В области прикладных космических работ космические аппараты дистанционно-
го зондирования Земли стали основой национальных средств контроля, позволяю-
щих составлять тематические природно-ресурсные карты, оценивать запасы водных
ресурсов, состояние мелиоративных земель, ледовую обстановку, осуществлять эко-
логический мониторинг атмосферы и поверхности Земли.
Эффективно развиваются системы космической связи, телевидения, ретрансля-
ции информации, которые позволяют охватить телевизионными программами всю
территорию земного шара, осуществить международный обмен, магистральную меж-
дународную связь.
Важным направлением является развитие навигационно-геодезических систем,
обеспечивающих привязку координат транспортных подвижных систем и различных
объектов на поверхности Земли. В космосе постоянно находятся несколько десятков
и сотен космических аппаратов, снабжающих навигационной информацией десятки
тысяч наземных потребителей. Например, большинство более крупных морских су-
дов оснащены спутниковой навигационной аппаратурой, что позволяет обеспечить
28
Рис. 1.19. Российские космодромы
определение своего местонахождения с точностью менее 100 м. Кроме того, эти
системы обеспечивают автоматическое определение местонахождения терпящих бед-
ствие судов и самолетов, проводят высокоточные измерения движения земной коры,
в том числе и для прогнозирования землетрясений с помощью космических средств,
эффективно оценивают состояние атмосферы Земли, движение воздушных масс, что
позволяет создавать оперативные и долгосрочные прогнозы погоды.
Результаты научных исследований и практических работ в космосе применяются
во многих отраслях народного хозяйства на Земле. Это и новые конструкционные ма-
териалы, защитные экраны от различных излучений, постоянные магниты на основе
редкоземельных элементов, позволяющие существенно уменьшить размеры прибо-
ров и устройств, повысить ресурс различных электрических машин.
С успехом применяются космические разработки в металлургии, автомобильной,
нефтехимической промышленности.
В настоящее время грузопоток в космосе постоянно растет, что требует создания
более совершенных транспортных космических систем и средств обеспечения, рас-
ширенной сети космодромов и автономных стартовых комплексов морского, воздуш-
ного и наземного базирования.
Начиная с пятидесятых годов XX века такие высокоразвитые страны, как СССР и
США, начали создавать космодромы для научных и практических целей (рис. 1.19).
Первым полигоном для испытания ракет-носителей в СССР стал Капустин Яр.
Его размеры позволяли одновременно проводить пуски баллистических ракет разных
типов в интересах не только Министерства обороны, но и академической науки.
В связи с созданием первой межконтинентальной ракеты Р7 испытательная база
полигона в Капустином Яру оказалась тесной для новой ракеты. Потребовался новый
полигон протяженностью не менее 8000 км для испытаний ракет нового поколения.
В середине 1950-х годов была создана комиссия по выбору места для нового полиго-
на. Им стал космодром «Байконур» в Казахстане (рис. 1.20—1.23). К настоящему вре-
мени отсюда произведено около 2450 пусков ракет, в космос выведено свыше 1380 ап-
паратов различного назначения.
В 1963 году было принято решение о создании космодрома в Архангельской об-
ласти СССР в районе города Плесецк. А в 1967 году на космодроме был проведен пер-
вый пуск ракеты-носителя (рис. 1.24, 1.25).
США с 1950 года также вели интенсивные работы по созданию космодромов для
использования ракет в интересах Министерства обороны и в исследовательских целях
29
Рис. 1.20. Космодром «Байконур».
Стартовый комплекс PH «Протон»
Рис. 1.21. Космодром «Байконур».
На стартовом столе ракета-носитель «Союз»
Рис. 1.22. Космодром «Байконур».
Стартовая площадка
ракеты-носителя «Энергия»
Рис. 1.23. Космодром «Байконур».
Стартовый комплекс PH «Зенит»
Рис. 1.24. Космодром «Плесецк». Стартовый комплекс PH «Космос»
Рис. 1.25. Космодром «Плесецк».
Стартовый комплекс PH «Циклон»
Dryden Flight
Research Center
Edwards AFB, CA
Jet Propulsion
Laboratory
Pasadena, CA
Ames Research
Center
Moffett Field, CA
Lewis Research
Center
Cleveland, OH
Johnson
Space Center
Houston, TX
Stennlis
Space Center
Mississippi
Kennedy
Space Center
Florida
Рис. 1.26. Космические центры США
Goddard Space
Right Center
Greenbelt, MD
NASA
Headquarters
Washington, DC
White Sands Test
Facility
Las Cruces, NM
Wallops Flight
Facility
Wallops Island, VA
Langley Research
Center
Hampton, VA
Marshall Space
Flight Center
Huntsville, AL
Рис. 1.27. Восточный испытательный полигон. Полигон им. Дж. Кеннеди
(рис. 1.26). Созданы Восточный испытательный полигон и Космический центр имени
Дж. Кеннеди (рис. 1.27, 1.28). Они расположены на одной территории, но имеют са-
мостоятельные технологические комплексы для решения задач в интересах ВВС и
НАСА. В штате Калифорния на побережье Тихого океана расположен Западный ис-
пытательный полигон США (рис. 1.29).
Третьей страной, которая создала свою испытательную базу для запуска ракет,
была Франция, которая в 1956 году создала на территории Алжира полигон Хаммагир,
а позднее в рамках ЕКА— полигон Куру (рис. 1.30). Ныне космодромы имеют ряд
стран, такие, как Япония (рис. 1.31), Китай (рис. 1.32), Индия, Израиль, Англия
и другие.
34
Рис. 1.28. Космический центр им. Дж. Кеннеди
Рис. 1.29. Западный
испытательный полигон
Рис. 1.30. Космодром Куру
35
Стартовый комплекс Ешиноби
Стартовый комплекс Осаки
Рис. 1.31. Космические центры Японии
36
КИТАЙСКИЕ
КОСМИЧЕСКИЕ
ЦЕНТРЫ,
КОСМОДРОМЫ
На стартовой позиции PH CZ-3B
Рис. 1.32. Китайские космические центры, космодромы
37
1.3.2. Работы, выполняемые на ракетно-космическом комплексе
при подготовке ракет-носителей к пуску и на этапе пуска
Ракетно-космический комплекс (РКК) представляет собой сложную автомати-
зированную техническую систему, состоящую из функционально связанных между
собой ракет-носителей, полезных нагрузок (космических аппаратов, орбитальных ко-
раблей и т. п.), технических устройств, систем управления и обеспечения, управляе-
мых людьми, предназначенную для выполнения задач, определяемых назначением
полезных нагрузок, которыми комплектуется ракета-носитель РКК.
Исходной характеристикой, определяющей основные параметры PH (размер-
ность ракеты), является масса полезной нагрузки, которую сможет вывести PH на ба-
зовую (опорную) орбиту высотой Якр = 200—500 км.
Полезная нагрузка в зависимости от назначения может включать:
• космические аппараты (КА) или блоки модулей долговременных орбитальных
станций, постоянно размещаемых на орбитах, близких к базовой;
• КА с разгонными блоками, переводимые последними на другие орбиты (в том
числе отлетные, геостационарные, солнечно-синхронные, высокоэллиптические
и т. д.).
Ракеты-носители космических объектов наиболее часто выполняются в виде
многоступенчатых ракет с маршевыми жидкостными ракетными двигателями (ЖРД),
в некоторых случаях снабжаемых стартовыми ускорителями с ракетными двигателя-
ми твердого топлива (РДТТ).
Конструкция современных ракет-носителей имеет высокую степень массовой
эффективности. Высокая массовая эффективность PH, космических объектов в зна-
чительной степени определяется строго ограниченными условиями полета PH, в том
числе регламентируемыми в полете нагрузками на конструкцию PH с полезной на-
грузкой. Вследствие этого в ракетостроении существует принцип, согласно которому
ни при каких условиях наземной эксплуатации ракет-носителей и составных частей
воздействия на них не должны превышать величин полетных нагрузок.
Поэтому схемы конструкций технических устройств и систем обеспечения, вхо-
дящих в состав наземного механического оборудования РКК, должны определяться,
исходя из этого принципа.
В частности, при эксплуатации PH, использующих только жидкостные ступени,
целесообразно применять горизонтальную сборку и транспортировку на стартовую
позицию с последующей установкой ракеты в вертикальное положение установоч-
ным агрегатом.
В случае использования ракет комбинированной конструкции с крупногабарит-
ными стартовыми ускорителями с РДТТ, устанавливаемыми на техническом комп-
лексе, следует использовать вертикальную сборку и транспортировку ракеты на стар-
товую площадку в вертикальном положении.
Процесс подготовки к запуску ракеты, состоящей только из жидкостных ступеней
и полезной нагрузки, включает в отечественном ракетостроении следующие этапы:
• прием и разгрузку составных частей PH и КА на техническом комплексе (ТК);
• проверку правильности функционирования бортовых систем и агрегатов PH изо-
лированно в ходе автономных испытаний, сборку PH и проверку на функциони-
рование систем после сборки при их совместной работе в составе PH на ТК
(комплексные испытания);
• диагностику выявленных отказов в функционировании с последующей заменой
неисправных приборов (агрегатов) и корректировкой по необходимости эксплу-
атационной документации;
38
• заключительные операции с бортовыми системами после завершения полного
объема испытаний на ТК с обеспечением технической готовности полезной на-
грузки к стыковке с PH;
• механическую и электрическую стыковки полезной нагрузки с PH (сборку) и
совместную их проверку на ТК. При этом полезная нагрузка уже может быть за-
правлена компонентами топлива и газами на специальной позиции либо на ТК;
• операции по обеспечению готовности к вывозу PH с полезной нагрузкой на стар-
товый комплекс (перегрузка на транспортный агрегат, при необходимости уста-
новка защиты от воздействия внешней среды, установка и подключение элемен-
тов термостатирования и т. п.);
• транспортировку PH с полезной нагрузкой на стартовый комплекс в горизон-
тальном положении;
• подъем ракеты с полезной нагрузкой в вертикальное положение и установку ее
на стартовое сооружение;
• подведение к ракете устройств, обеспечивающих доступ к зонам обслуживания
ракеты-носителя и полезной нагрузки; устройств, обеспечивающих электриче-
ское и пневматическое соединение ракеты с соответствующими наземными ком-
муникациями; устройств, обеспечивающих экранирование ракеты от действия
ветровой нагрузки; подведение устройств, обеспечивающих экстренную эваку-
ацию обслуживающего персонала и космонавтов при возникновении аварийных
ситуаций;
• отведение по необходимости транспортно-установочного агрегата;
• установку химических источников тока на PH и полезной нагрузке (в некоторых
случаях химические источники тока могут быть установлены на ТК);
• проведение предстартовых испытаний ракеты-носителя и полезной нагрузки;
• проведение операции по подготовке к заправке PH и при необходимости полез-
ной нагрузки компонентами топлива, газами и служебными жидкостями и про-
ведение заправки;
• отстыковку при необходимости заправочных топливных и пневматических ком-
муникаций;
• проведение операций по прицеливанию ракеты (наведение и ввод полетного за-
дания);
• доукомплектование полезной нагрузки, посадка космонавтов в КА (при исполь-
зовании КА с экипажем);
• проведение заключительных операций перед стартом;
• отведение всех наземных технологических устройств, кроме устройств электри-
ческой связи, пневмогидравлической связи (предстартовый наддув, подпитка ра-
кеты легко воспламеняющимся топливом, подача при необходимости газа для
вскрытия ампул пускового горючего, проведение продувок, вентиляции, захола-
живания и т. п.);
• подачу команды на запуск двигателей и старт ракеты;
• подготовку стартового оборудования к последующим пускам.
В течение всего периода после установки ракеты на стартовое сооружение до мо-
мента старта производится автоматизированный контроль состояния параметров
комплекса, обеспечивающих безаварийное обслуживание ракеты. В случае выхода
параметров ракеты, ее систем, систем наземного оборудования за допускаемые значе-
ния и невозможности их приведения в пределы нормальных величин (путем замены,
регулировки элементов систем) производится снятие ракеты-носителя с полезной на-
грузкой со стартового сооружения и вывоз ее на технический комплекс.
39
Для этого проводятся все необходимые технологические операции: производится
высадка экипажа; подстыковываются все электрические и пневматические коммуни-
кации связи борта ракеты с наземным технологическим оборудованием; производит-
ся слив компонентов топлива; подводится установочный агрегат, на который крепит-
ся ракета; отводятся все необходимые агрегаты наземного оборудования, затрудняю-
щие опускание ракеты в горизонтальное положение; ракета опускается и
укладывается на транспортное средство и направляется на технический комплекс.
В настоящее время в отечественной космонавтике реализован принцип подго-
товки к пуску ракеты, при котором на заводе-изготовителе или технической позиции
осуществляется комплектация PH агрегатами, обеспечивающими автоматическую
стыковку всех коммуникаций ракеты с ответными частями наземных коммуникаций
при установке ракеты на стартовое сооружение и автоматическую расстыковку раке-
ты с соответствующими агрегатами в момент старта, либо непосредственно после
взлета ракеты (например, отстрел желоба бортовых коммуникаций через 3—4 секунды
после старта).
Начиная с первых образцов ракетной техники перечисленные операции прово-
дились в большем или меньшем объеме и были в той или иной степени автоматизиро-
ваны.
На общие принципы создания отечественных ракетно-космических комплексов
влияет одно важное обстоятельство: эти комплексы размещаются в удаленных от за-
водов-изготовителей малонаселенных, труднодоступных местностях, связанных
с центрами производства ракет только железной дорогой.
Данное обстоятельство, во-первых, заставляет, как правило, создавать раке-
ты-носители, имеющие стартовую массу более 300—500 т (пакетной схемы), для обес-
печения транспортировки блоков в железнодорожных вагонах, когда максимальный
поперечный размер блока и его длина определяются габаритами железнодорожного
вагона.
Тем самым определяется конфигурация поперечного сечения собранной ракеты,
которое имеет усложненную форму зон обслуживания. Последнее в значительной
степени определяет схемы конструкции транспортно-установочного агрегата и осо-
бенно агрегатов обслуживания.
Во-вторых, несмотря на тот факт, что обычно системы и агрегаты отечественных
ракет или их блоков изготавливаются на разных предприятиях страны, укомплектова-
ние ракет и их полная проверка проводится на головном заводе-изготовителе, после
чего ракета целиком или поблочно транспортируется к местам запуска. Поставка на
РКК дополнительного оборудования, замена агрегатов и приборов является не прави-
лом, а исключением. Это способствует упрощению технологической подготовки ра-
кет к пуску, сокращению сроков подготовки ракеты на РКК и внедрению широкой
автоматизации с использованием достаточно простых алгоритмов управления.
1.3.3. Состав ракетно-космического комплекса
и полигона для испытаний
и штатных запусков ракет-носителей
Для обеспечения выполнения всех вышеперечисленных операций, а также опе-
раций по контролю, управлению полетом, обработке информации о результатах вы-
полнения всех работ, проводимых с ракетой-носителем и полезной нагрузкой на всех
этапах их эксплуатации, полигон (космодром), в состав которого может входить один
или несколько разнотипных ракетных комплексов, имеет следующие основные части
(позиции):
40
• техническую позицию с техническим комплексом ракет-носителей и полезной
нагрузки;
• стартовую позицию со стартовым комплексом;
• комплекс траекторных измерений и управления полетом ракет-носителей на тра-
екториях полета ракеты в автоматическом режиме (стационарного или мобиль-
ного);
• комплекс траекторных телеметрических измерений (и управлений) полетом КА
в космосе (стационарных и мобильных);
• технические системы обеспечения основных технологических комплексов и бы-
товых объектов водой, электричеством, теплом с соответствующими коммуника-
циями;
• хранилища (или заводы) по приему, длительному хранению и выдаче компонен-
тов ракетного топлива для заправки PH и КА;
• жилые городки с требуемыми бытовыми объектами и объектами обеспечения;
• внутренние автомобильные и железные дороги, связанные с основными магист-
ралями; аэродромы с терминалами для приема грузов, их разгрузки, хранения
и транспортировки изделий на основные комплексы;
• системы внутренней и внешней связи;
• системы охраны территории РКК и объектов полигона;
• отчуждаемые охраняемые поля падения ступеней (как правило, первых и вторых)
и частей ракет с подразделениями сбора ступеней для передачи их для последую-
щего анализа результатов пуска. Эти подразделения обеспечиваются авиацион-
ной, автомобильной, подъемной, землеройной, подводной и транспортировоч-
ной техникой поиска ступеней, а также местами складирования, хранения и пе-
редачи ступеней заинтересованным организациям или захоронения;
• подразделения поиска спускаемых с орбиты космических объектов с экипажем
для оказания первой помощи космонавтам и доставки их в центр космодрома.
В случае использования тяжелых спускаемых аэродинамически управляемых ор-
битальных ступеней эти задачи выполняют подразделения обслуживания аэродромов
посадки спускаемых орбитальных ступеней.
Все подразделения, входящие в состав космодрома, размещаются на территори-
ях, имеющих площадь в сотни квадратных километров. Пункты измерительных комп-
лексов, поля падения ступеней могут быть удалены от центра полигона со стартовыми
комплексами на сотни и тысячи километров.
Для обеспечения синхронизации работ всех систем в едином масштабе времени в
состав РКК входит комплекс системы единого времени.
Создание космодромов производится с учетом следующих требований:
• обеспечение необходимого набора трасс запусков PH;
• обеспечение необходимыми районами падения отделяющихся частей;
• удаленность от густонаселенных территорий;
• благоприятные климатические и сейсмологические условия;
• исключение траекторий полета PH над густонаселенными районами и террито-
риями других государств;
• возможность использования существующих транспортных коммуникаций;
• относительная близость к головным предприятиям космической промышлен-
ности.
Место размещения пусковых устройств различного типа (в том числе и подвиж-
ных в момент старта ракеты) определяется с учетом динамики полета КА с момента
окончания активного участка траектории, т. е. с момента начала полета КА как небес-
ного тела.
41
Плоскость, в которой лежит орбитальная траектория полета КА, после выведе-
ния его в космос проходит через точки конца траектории выведения и центра Земли
и наклонена к плоскости экватора на угол наклонения орбиты /, равный широте точ-
ки конца траектории выведения.
Скорость КА на этой траектории складывается из собственно скорости, разви-
ваемой ракетой Кк, и скорости перемещения ракеты относительно поверхности Земли
И3. Последняя максимальна на экваторе и добавляется к Ик, если пуск производится
строго на восток, и вычитается из Ик, если пуск производится строго на запад. При за-
пуске PH из точек, не лежащих в плоскости экватора, к собственной скорости ракеты
добавляется только часть скорости вращения Земли, равная:
ДИ= И3 • cos/K,
где zK — широта точки старта.
Это означает, что при запуске PH с экватора на восток одна и та же ракета облада-
ет способностью вывести большую полезную нагрузку, чем при старте с более высо-
ких широт. Именно поэтому космодромы всех стран стремятся разместить как можно
ближе к экватору. Если такой возможности нет, создаются мобильные стартовые
комплексы (морские, воздушные), способные перемещаться на экватор для запуска
КА на более высокую орбиту или для запуска более тяжелых КА на орбиту одинако-
вой высоты, но запускаемых с высоких широт.
1.4. ПЕРСПЕКТИВЫ РАЗВИТИЯ СРЕДСТВ ВЫВЕДЕНИЯ
Анализ тенденции совершенствования объектов ракетно-космической техники
позволяет выделить два основных направления улучшения конструктивно-экономи-
ческой эффективности ракет:
• постепенное улучшение основных характеристик PH за счет применения новых
конструкционных материалов, повышения качества отдельных узлов, систем
и агрегатов, унификации на уровне узлов, систем, отсеков, агрегатов, ступеней
и т. п.;
• скачкообразное улучшение основных характеристик ракет за счет применения
принципиально новых конструктивно-компоновочных схем, многоразовости
применения как отдельных частей, так и ракеты в целом.
Первое направление реализуется на протяжении всего периода развития ракетной
техники. Каждая новая ракета отличается от ракеты с одинаковой компоновочной схе-
мой более совершенной конструкцией, лучшими удельными характеристиками.
Второе направление реализуется значительно реже, однако оно вносит конкрет-
ные изменения в развитие ракетной техники и открывает новые возможности для
дальнейшей реализации первого направления. Внедрение большинства мероприятий
первого направления в практику создания и совершенствования ракет, как правило,
осуществляется очень быстро, в то же время при реализации идей второго поколения
всегда имеется много противников, которые часто не рискуют отходить от устарев-
ших, но хорошо отработанных и надежных принципов совершенствования ракетной
техники.
Можно считать, что очередными факторами существенного улучшения эффек-
тивности ракет станут следующие:
• более интенсивное использование жидкого, а в дальнейшем и шугаобразного во-
дорода, что приведет к более широкому использованию одноступенчатых ракет;
• использование перелива топлива между параллельно работающими ступенями
ракет, что повысит эффективность ракет, построенных на модульном принципе;
42
использование нового поколения трехкомпонентных двурежимных жидкостных
ракетных двигателей;
использование двигателей с широким диапазоном регулирования тяги для обес-
печения оптимального с точки зрения массы нагружения ракеты при полете на
активном участке траектории;
более интенсивное и хорошо обоснованное с точки зрения надежности и долго-
вечности конструкции внедрение композитных материалов.
На настоящем этапе развития ракетно-космической техники большое значе-
ние придается созданию семейств ракет-носителей на базе универсального ракетно-
го модуля (рис. 1.33) и многоразовых транспортных космических систем (МТКС).
В процессе создания МТКС первого поколения типа «Спейс Шаттл» и «Энергия» —
«Буран» (рис. 1.34) была подтверждена практическая возможность реализации прин-
ципа многоразовости применения элементов конструкции этих систем. Однако энер-
гомассовая и экономическая эффективность таких систем первого поколения уже не
отвечает все возрастающим требованиям перспективных космических программ.
Унифици-
рованные
составные
элементы PH
60 м
Ускоритель
II ступени
9
ЖРД
РД0124А
50 м
40 м
Универ-
сальный
ракетный
модуль
I ступени
(УРМ-1)
20 м
30 м
Юм
Рис. 1.33. Семейство PH «Ангара» на базе универсального ракетного модуля:
1 — головной обтекатель PH «Рокот»; 2 — головной обтекатель PH «Протон»; 3 — разгонный
блок «Бриз-М»; 4 — универсальный ракетный модуль УМР-1; 5 — универсальный ускоритель
2-й ступени; 6 — три УМР-1; 7 — пять УМР-1; 8 — кислородно-водородный разгонный блок;
9 — кислородно-водородная ступень
43
Рис. 1.34. Ракета-носитель «Энергия»
Характеристики блока Ц: стартовая масса блока — 780 т;
масса конструкции блока — 64,3 т; окислитель (жидкий кислород) — 602,3 т;
горючее (жидкий водород) — 100,7 т; тяга двигателей у Земли — 4x147 кН
Проводятся интенсивные работы по созданию многоразовых систем следующего по-
коления, направленные на создание одноступенчатых ракетных или крылатых
МТКС.
В настоящее время в процессе создания нового поколения МТКС исследуются
три направления. Первое направление предусматривает создание многоразовых ра-
кетно-космических систем вертикального взлета и горизонтальной посадки, являю-
щихся развитием МТКС первого поколения. Космические системы данного типа об-
ладают высокими энергетическими характеристиками и обеспечивают выведение на
орбиту полезной нагрузки массой до 50 тонн (рис. 1.35).
Второе направление предусматривает создание авиационно-космических систем
(АКС), использующих в качестве первой ступени дозвуковые самолеты-носители
(ДСН), с которых осуществляется воздушный старт орбитальной ступени. За счет
маневра ДСН в экваториальных широтах АКС способны выводить полезные грузы на
экваториальные орбиты или орбиты с малым наклонением (рис. 1.36).
44
Рис. 1.35. Частично многоразовая ракетно-космическая система
45
Рис. 1.36. Одноступенчатый многоразовый космический ракетоплан
и двухступенчатая АКС с гиперзвуковым самолетом:
1 — кабина экипажа; 2 — топливный бак; 3 — отсек полезной нагрузки;
4 — кислородный бак; 5 — маршевые двигатели
Доставка спутника
на низкую орбиту j, На низкий околоземной
орбите спутник отделяется
Торможение
96 ЖРД, установленных
по периметру,
осуществляют подъем
аппарата
Керосин
«Ротон»
осуществляет
посадку, используя .
подъемную силу 1;
вращающихся лопастей L.
Жидкий
кислород
Грузовой
отсек
Кабина
экипажа
«Ротон»
возвращается
на Землю
Рис. 1.37. Пилотируемый МТКА «Ротон-С9» компании «Ротари Рокет»
ротора
46
Третье направление предусматривает создание одно- или двухступенчатых ракет-
ных или воздушно-космических систем. На рис. 1.37 приведен многоразовый
транспортный космический аппарат (МТКА) и схема его полета.
Каждое из этих направлений требует решения сложных научно-технических,
экономических и экологических проблем, что обусловливает необходимость поэтап-
ного создания соответствующих типов многоразовых космических систем.
Крупные космические программы, в том числе и по созданию МКС новых поко-
лений, требуют привлечения огромных материальных и интеллектуальных ресурсов.
Решение задач в рамках таких программ для одной, даже высокоразвитой страны, ста-
новится затруднительным. Стратегия развития космической техники должна форми-
роваться при международном сотрудничестве различных стран, имеющих достаточ-
ный научно-технический задел по проектированию, производству и применению
объектов ракетно-космической и авиационной техники.
ЛИТЕРАТУРА
1. Феодосъев В. И., Синярев Г. Б. Введение в ракетную технику. — М.: Оборонгиз,
1961. С. 506.
2. Киселев А. И., Медведев А. А., Меньшиков В. А. Космонавтика на рубеже тысячеле-
тий. Итоги и перспективы. — М.: Машиностроение. 2001. С. 665.
3. Космодемьянский А. А., Таре С. М. Курс теоретической механики. 2-е изд., пере-
раб. и доп. Ч-Б. — М.: Изд-во. ВВИАим. Н. Е. Жуковского, 1958.
4. Уманский С. П. Ракеты-носители. Космодромы. — М.: Рестарт+, 2001. С. 216.
5. Введение в аэрокосмическую технику: Учеб, пособие / В. Н. Кобелев,
А. Г. Милованов, А. Е. Волхонский; Под ред. проф., д. т. н. В. Н. Кобелева;
МГАТУ. - М., 1994. С. 264.
СОДЕРЖАНИЕ ГЛАВЫ 1
1.1. Этапы развития ракет и ракетной техники.......................6
1.2. Теория тел переменной массы — фундамент космонавтики.
Развитие космонавтики и практической ракетной техники.................11
1.3. Образование рынка космических услуг
и развитие ракетно-космической техники на современном этапе...........19
1.3.1. Основные задачи, решаемые
ракетно-космической техникой..................................28
1.3.2. Работы, выполняемые на ракетно-космическом комплексе
при подготовке ракет-носителей к пуску и на этапе пуска.......38
1.3.3. Состав ракетно-космического комплекса
и полигона для испытаний и штатных запусков ракет-носителей...40
1.4. Перспективы развития средств выведения.......................42
Литература............................................................47
ГЛАВА 2____________________
Г идрогазоаэродинамика
летательных аппаратов
Гидрогазодинамика, как и всякая наука, возникла и развивается в соответствии
с потребностями практики. Отвечая запросам древних кораблестроителей, Архимед
(287—212 гг. до н. э.) сформулировал законы плавания и устойчивости плавающих
тел. Строительство каналов, плотин, шлюзов, фонтанов, дальнейшее развитие судо-
строения и мореплавания в XVII—XVIII вв. служило серьезным стимулом для разви-
тия гидромеханики. Именно в это время появились фундаментальные работы членов
Петербургской академии наук Д. Бернулли (1700—1782) и Л. Эйлера (1707—1783).
Бернулли ввел термин «гидродинамика», и его книга, вышедшая в свет в 1738 г., так
и называлась. Эйлер вывел общие уравнения движения невязкой жидкости, которы-
ми мы пользуемся и в настоящее время.
Зарождение и развитие авиации в конце XIX и начале XX в. обусловили расшире-
ние работ по аэродинамике летательных аппаратов. И здесь, прежде всего, следует
упомянуть профессора Н. Е. Жуковского (1847—1921). Формулы и профили Жуков-
ского и теперь играют большую роль в аэродинамике.
В связи с практическими проблемами повышения скорости полета самолетов,
а затем и новых типов летательных аппаратов (ЛА) — ракет различного назначения,
в середине XX столетия наступил период быстрого развития газовой динамики. При
этом основополагающую роль в теории сыграла опубликованная в 1903 г. работа
С. А. Чаплыгина (1869—1942) о газовых струях.
Не имея достаточного места для подробного изложения истории развития меха-
ники жидкости и газа, ограничимся лишь перечислением фамилий отечественных
и зарубежных исследователей, внесших существенный вклад. Это, кроме упомянутых
выше, И. Ньютон, Ж.-Б. Лагранж, Г. Гельмгольц, Г. Кирхгоф, И. С. Громека,
В. Кутта, Ф. В. Ланчестер, Л. Прандтль, Т. Карман, А. Буземан, Л. Крокко, М. А. Лав-
рентьев, М. В. Келдыш, Л. И. Седов, Н. Е. Кочин, С. А. Христианович, Л. Г. Лойцян-
ский, А. А. Дородницын, Г. И. Петров и многие другие.
Все материальные тела, в соответствии с молекулярно-кинетической теорией,
имеют дискретное строение, состоящее из отдельных частиц (молекул, атомов и т. д.).
Изучение движения всех этих частиц представляет колоссальные трудности даже
с использованием современных суперЭВМ. Однако в малых, по сравнению со всей
исследуемой областью, объемах содержится очень большое число таких частиц. Это
позволяет рассматривать некоторые осредненные свойства материальных сред как
непрерывные функции пространственных координат и времени, что составляет суть
гипотезы сплошности и позволяет исследовать движение таких сред средствами мате-
матического анализа, опирающегося на понятие непрерывных функций.
Раздел теоретической механики, занимающийся изучением движения сплошных
сред, называют механикой сплошных сред, а часть ее, относящаяся к жидким и газооб-
разным средам, — механикой жидкости и газа. Изучение прикладных задач, связан-
ных с движением жидкостей, составляет предмет гидродинамики, движение воздуха
изучает аэродинамика, а движение различных газов — газовая динамика.
48
Силовое взаимодействие жидкостей и газов, в том числе воздуха, рассматривается
в разделе механики жидкости и газа, который носит название гидрогазоаэродинамика.
При решении задач гидрогазоаэродинамики, так же как и задач теоретической
механики, используют точные и приближенные математические приемы интегриро-
вания основных дифференциальных уравнений, выражающих законы сохранения
при движении жидкостей и газов. Значительная сложность явлений при этих движе-
ниях вынуждает широко использовать экспериментальные методы исследования.
Обобщение результатов этих исследований приводит к эмпирическим, а иногда и по-
луэмпирическим теориям. При этом теория учит, как ставить эксперимент, как наи-
более точно проводить измерения и, что особенно важно, как обобщать результаты
отдельных экспериментов на целые классы явлений и устанавливать управляющие
ими общие количественные закономерности.
2.1. СВЕДЕНИЯ О СВОЙСТВАХ ЖИДКОСТЕЙ И ГАЗОВ
Основной механической характеристикой жидкости или газа является их плот-
ность. Плотностью р называется масса жидкости или газа, заключенная в единице
объема. В случае однородной жидкости или газа массой М в объеме W их плотность
определяется формулой
р = Л//ИС (2.1)
Удельным или объемным весом указывают вес единицы объема жидкости или газа
у=б/РК (2.2)
где G — вес жидкости или газа в объеме ИЛ
Связь между удельным весом у и плотностью р с учетом очевидного равенства
<7 = #Л/имеет вид
p = G/(g4/)=y/g. (2.3)
Здесь и далее g — ускорение свободного падения тел.
Если жидкости или газы неоднородны, то формулы (2.1) и (2.2) определяют лишь
средние значения удельного веса или плотности в данном объеме. Для определения ло-
кального значения у и р в рассматриваемой точке, занятой жидкостью или газом, сле-
дует рассматривать малый объем АРК, масса и вес которого АЛ/ и А(7 соответственно, и
находить пределы соответствующих отношений, когда объем стягивается в точку, т. е.
Polini о(АЛ//АИ/)иу=дКт ^(Аб/АИО, (2.4)
тогда как связь между ними остается прежней (2.3).
Вязкость представляет собой свойство жидкостей или газов сопротивляться
сдвигу или скольжению их слоев. Это свойство проявляется в том, что в жидкостях
или газах при определенных условиях возникают касательные напряжения. Вязкость
жидкостей — свойство, противоположное текучести: более вязкие жидкости (глице-
рин, смазочные масла и др.) являются менее текучими и наоборот.
Согласно гипотезе, высказанной впервые И. Ньютоном в 1686 г., касательное на-
пряжение в жидкости зависит от рода жидкости и характера течения и при слоистом
течении изменяется прямо пропорционально так называемому поперечному градиен-
ту скорости. В случае течения вдоль плоской безграничной стенки касательное напря-
жение т вычисляется по формуле
т = р((1и/ф0, (2.5)
где ц — динамический коэффициент вязкости жидкости или газа; и — скорость жидкос-
ти или газа вдоль плоской безграничной стенки; у — пространственная координата,
направленная нормально к плоской безграничной стенке.
В случае произвольного течения соотношение (2.5) усложняется.
49
Наряду с коэффициентом вязкости ц применяют еще так называемый кинемати-
ческий коэффициент вязкости v, равный v = ц/р.
Вязкость жидкостей уменьшается с ростом температуры, тогда как вязкость га-
зов, наоборот, с повышением температуры возрастает. Объясняется это различием
природы вязкости в жидкостях и газах. В газах вязкость обусловлена главным образом
беспорядочным тепловым движением молекул, интенсивность которого увеличивает-
ся с температурой, приводя к возрастанию вязкости. В жидкостях вязкость вызывает-
ся силами молекулярного взаимодействия, которые с увеличением температуры
уменьшаются, вызывая падение вязкости.
Из других общих для газов и жидкостей свойств отметим их сжимаемость и тем-
пературное расширение. Сжимаемость или свойство тел изменять свой объем под
действием давления наиболее ярко выражено у газов. Для них это свойство проявля-
ется в том, что под действием сравнительно небольших давлений происходит замет-
ное изменение плотности. В жидкостях при достаточно больших давлениях, имею-
щих место в различных устройствах, плотность настолько незначительно изменяется,
что ее можно считать постоянной. Поэтому в большинстве случаев жидкости счита-
ются несжимаемыми.
Температурное расширение представляет собой свойство изменения объема при
изменении температуры. В жидкостях это свойство проявляется слабо, за исключени-
ем случаев, когда она занимает весь объем сосуда, который подвергается нагреву или
охлаждению. Газы имеют значительно большее температурное расширение, но его су-
щественное влияние также проявляется в определенных условиях, например, в так
называемых свободно конвективных течениях.
Жидкости и газы отличаются друг от друга тем, что газы стремятся занять весь
предоставляемый им объем, тогда как жидкости могут легко менять форму объема,
величина которого остается практически неизменной. В связи с этим жидкости обла-
дают рядом свойств, не присущих газам. Так, в отличие от газов, в которых, по опре-
делению, давления могут существовать лишь как сжимающие напряжения, внутри
жидкостей сопротивление растяжению, в соответствии с молекулярной теорией, мо-
жет быть весьма значительным. Однако при опытах с тщательно очищенной и дегази-
рованной водой в ней были получены значительно более низкие кратковременные
напряжения растяжения, а технически чистые жидкости, содержащие взвешенные
твердые частицы и мельчайшие пузырьки газов, не выдерживают даже незначитель-
ных напряжений растяжения. Поэтому считают, что напряжения растяжения в жид-
костях невозможны, и в гидрогазоаэродинамике рассматривают только сжимающие
напряжения.
На поверхности жидкости действуют силы поверхностного натяжения, стремя-
щиеся придать объему жидкости сферическую форму и вызывающие некоторое до-
полнительное давление в жидкости. Это давление заметно сказывается лишь при ма-
лых размерах или когда другие силы малы или отсутствуют. Так, в трубках малого диа-
метра это дополнительное давление вызывает подъем (или опускание) жидкости
относительно нормального уровня, называемый капиллярностью. Это обстоятельство
требует учета, например в жидкостных манометрах. В условиях значительного пони-
жения силы тяжести или в невесомости поверхностное натяжение совместно со сте-
пенью смачиваемости жидкостью твердых поверхностей определяет форму объема,
занятого жидкостью, что имеет первостепенное значение для работы различных уст-
ройств на борту искусственных спутников. В зависимости от характеристик растека-
ния жидкость считается смачивающей или несмачивающей. Смачивающая жидкость
в отличие от несмачивающей растекается по поверхности. Степень смачиваемости
жидкостью твердых поверхностей характеризует так называемый краевой угол — угол
50
между касательными к поверхности жидкости и контактирующей с ней поверхностью
твердого тела. Для смачивающей жидкости краевой угол меньше 90°. При значении
краевого угла больше 90° жидкость не растекается.
Наконец, испаряемость свойственна всем жидкостям. Одним из показателей, ха-
рактеризующих испаряемость жидкости, является температура ее кипения при нор-
мальном атмосферном давлении. Чем выше температура кипения, тем меньше испа-
ряемость жидкости. Более полной характеристикой испаряемости следует считать
давление (упругость) насыщенных паров, зависящее от температуры. Чем больше дав-
ление насыщенных паров при данной температуре, тем больше испаряемость жид-
кости.
В некоторых случаях при движении жидкости происходят явления, связанные с
изменением агрегатного состояния жидкости, т. е. с превращением ее в пар, а также с
выделением из жидкости растворенных в ней газов. Примером таких явлений может
служить кавитация.
2.2. ОСНОВНЫЕ СВЕДЕНИЯ
ИЗ КИНЕМАТИКИ ЖИДКОСТИ И ГАЗА
Для задания положения и движения жидкости или газа существуют два способа,
известные еще Л. Эйлеру.
Первый, широко используемый Лагранжем и связанный с его именем, заключа-
ется в задании текущих значений координат частиц жидкости или газа как функций
времени Z, т. е. совпадает с применяемой в кинематике системой материальных точек.
Другой способ, являющийся основным в исследованиях Л. Эйлера по гидродина-
мике и по этой причине названный его именем, значительно шире распространен-
ный, чем метод Лагранжа, заключается в задании поля исследуемых характеристик
течения. Так, поле скоростей вектора скорости F с проекциями к, v и w в декартовой
системе координат (х, у, г) можно описать как
и = и (х, у, z, t),v = v (х, у, z, t),w = w (х, у, z, t), (2.6)
или И = И(х, у, г, 0-
С математической точки зрения описанные методы задания движения жидкости
или газа эквивалентны; всегда можно от одного метода задания движения перейти к
другому. В дальнейшем будет удобнее пользоваться методом Эйлера и задавать движе-
ние в форме (2.6).
Поле скоростей является однородным, если векторы скорости во всех точках поля
одинаковы. Поле скоростей называют стационарным, если оно не меняется с течени-
ем времени (ЭИ/дГ= 0), в противном случае — нестационарным.
Для более наглядного представления полей физических величин используют
специальные приемы. Скалярное поле разбивается поверхностями уровня скаляр-
ной функции. Примерами являются изотермы — поверхности одинаковой темпера-
туры.
В векторных полях рассматривают так называемые векторные линии. В гидро-
газоаэродинамике при рассмотрении векторного поля скоростей такими линиями
являются линии тока (рис. 2.1), т. е. линии, в каждой точке которых в фиксирован-
ный момент времени вектор скорости жидкости или газа направлен по касательной
к ним. Условие параллельности вектора скорости F в данной точке и дифференциала
51
dr = (dx, dy dz) (рис. 2.1) радиуса-вектора ? этой точки приводит к следующим диффе-
ренциальным уравнениям для линий тока:
dx dy dz
------Л - “7 Л = “7-------л , Г = const. (2.7)
и(х, У, Z, t) v(x, у, z, t) w(x, у, Z,t)
Так как в соотношениях (2.7) время входит как параметр, эти соотношения мож-
но рассматривать как систему двух обыкновенных дифференциальных уравнений
(третье — следствие остальных).
Через каждую точку поля скоростей в данный момент времени можно, вообще
говоря, провести линию тока и притом только одну. Существуют, однако, и такие —
их называют особыми — точки поля скоростей, через которые проходят две или бес-
численное множество линий тока. В этих точках скорость либо равна нулю и их назы-
вают критическими точками, либо принимает бесконечно большие значения.
От линий тока cлeдveт отличать траектории движения частиц жидкости или газа,
определяемые как геомегрическое место точек последовательных положений отдель-
ных частиц в пространстве в следующие друг за другом моменты времени.
Их дифференциальные уравнения известны из курса теоретической механики, и им
можно придать вид
-Г^-й = = *• (2.8)
w(x,y, z, 0 V(x,y, z, t) w(x,y,z,t)
Здесь, в отличие от соотношений (2.7) для линий тока, время t будет таким же не-
зависимым переменным, какх, у, z.
Если поле скоростей стационарно, то время t не будет входить в проекции ско-
ростей, исчезнет оно и из уравнений (2.8), которые совпадут с (2.7). Отсюда следует,
что в стационарных полях скоростей траектории и линии тока в любой момент време-
ни совпадают.
Проводя в данный момент времени через точки замкнутого контура С (рис. 2.2) ли-
нии тока, получим поверхность тока, заключающую внутри себя часть жидкости, назы-
ваемую трубкой тока. В любой точке поверхности тока вектор скорости Р направлен по
касательной к линии тока, поэтому жидкость или газ не проникает сквозь поверхность
тока. На этом основании можно заключить, что любая непроницаемая поверхность,
помещенная в движущуюся жидкость, совпадает с одной из поверхностей тока.
В кинематике абсолютно твердого тела, представляющего простейший пример
сплошной среды, имеет место теорема Эйлера о разложении вектора скорости V любой
точки тела произвольных размеров на составляющую Ио поступательного движения вмес-
те с произвольно выбранным полюсом О и вращательную составляющую с вектором угло-
вой скорости Й. Аналогичная по содержанию теорема, учитывающая возможные дефор-
мации среды и по этой причине ограниченная применением к бесконечно малому объему,
справедлива для любой сплошной среды, в частности для жидкости или газа. Это так на-
зываемая первая теорема Гельмгольца: скорости точек элементарного объема сплошной
среды складываются из скоростей квазитвердого и деформационного движений.
При решении обратной задачи теоретической механики, когда по заданному по-
лю вектора скорости V устанавливается выражение вектора угловой скорости враще-
ния тела Й, приходят к новому векторному полю вектора, именуемому ротором, или
вихрем вектора скорости и обозначаемому символом rot К. В декартовой системе ко-
ординат проекции этого вектора имеют вид
(£-£) ™
52
в
**
r//dr + r
Рис. 2.1. К определению
линии тока
Рис. 2.2. Трубка тока
dr
Рис. 2.3. К определению
циркуляции скорости
С
А
Если для простоты бесконечно малый объем сплошной среды в некоторый мо-
мент времени выбрать в виде параллелепипеда, то его деформационное движение
можно представить в виде суммы, вызывающей растяжение или сжатие сторон этого
объема и скашивание первоначально прямых углов сторон параллелепипеда.
Движение жидкости или газа, сопровождаемое вращением отдельных элементар-
ных объемов, при котором Й = (1/2) rot 0, называют вихревым, а сам вращающийся
объем (иногда его угловую скорость) — вихрем. Если движение элементарных объемов
среды сводится только к поступательному и деформационному, то такое движение
именуют безвихревым.
Векторному полю вектора Й = (l/2)rot V или Й = rot V соответствуют свои вектор-
ные линии, называемые вихревыми линиями, которые аналогично линиям тока явля-
ются линиями, в каждой точке которых в выбранный момент времени касательная
совпадает по направлению с вектором Й или Й.
Подобно поверхности тока строится вихревая поверхность, а ограниченную ею
часть жидкости, участвующую во вращении, называют вихревой трубкой. В соответст-
вии со второй теоремой Гельмгольца поток вектора Й или Й сквозь любое поперечное
сечение вихревой трубки одинаков в данный момент времени вдоль всей трубки.
Из второй теоремы Гельмгольца следует, что вихревые трубки не могут заканчи-
ваться внутри жидкости или газа, так как при этом Й или Й должны были бы стано-
виться бесконечными. Отсюда вихревые трубки могут иметь вид замкнутых колец,
либо начинаться и оканчиваться на поверхностях раздела твердой поверхности и жид-
кости или жидкости и газообразной среды, либо один из концов вихревой трубки мо-
жет уходить в бесконечность.
Для нахождения вектора вихря Й или Й при экспериментальных исследованиях
приходится прибегать к численному дифференцированию измеренных компонент век-
тора скорости в соответствии с формулами (2.9), что приводит к большим ошибкам.
Теорема Стокса позволяет заменить интенсивность вихревой трубки, вычисляемой как
поток вектора Й или Й сквозь любое поперечное сечение вихревой трубки, равной ей
циркуляцией скорости по контуру, расположенному на поверхности вихревой трубки и
один раз ее опоясывающему. Циркуляция вектора скорости V по произвольному конту-
ру С (рис. 2.3) определяется криволинейным интегралом вдоль контура С:
в
rAB=^'dr.
А
53
В случае замкнутого (В—> Л), самого себя не пересекающего контура С, циркуляция
обозначается символом
rc=p«dr.
С
Направление обхода контура С выбирается таким, чтобы ограниченная контуром по-
верхность оставалась при обходе слева.
Вихревая трубка, заключающая внутри себя завихренные части жидкости, может
быть окружена жидкостью, частицы которой не вращаются вокруг своих осей, а дви-
жутся поступательно по замкнутым, в том числе круговым траекториям. В этом случае
для определения интенсивности вихревой трубки достаточно вычислить циркуляцию
скорости по любому контуру, один раз охватывающему трубку.
По измеренной циркуляции по замкнутому контуру в поле скоростей можно су-
дить не о наличии или отсутствии внутри его вихревых трубок, а лишь о суммарной их
интенсивности. Равенство нулю циркуляции скорости по замкнутому контуру не по-
зволяет сделать заключение об отсутствии вихревых трубок, так как внутри этого кон-
тура могут быть вихревые трубки с различными направлениями вращения, которым
соответствуют разные по знаку интенсивности.
23- УРАВНЕНИЕ НЕРАЗРЫВНОСТИ
В ньютоновской механике масса жидкого, т. е. состоящего во все время движения
из одних и тех же частиц, объема сохраняет постоянную величину. Это положение на-
зывают законом сохранения массы.
Масса элементарного объема жидкости или газа непосредственно следует из оп-
ределения плотности среды (2.4)
ДЛ/=рДРИ (2.10)
а масса М выделенного в среде конечного объема W находится интегрированием вы-
ражения (2.10)
М = J pdH<
W
В соответствии с законом сохранения массы ДЛ/ = рД№= const. Отсюда, диффе-
ренцируя это соотношение по времени Г, имеем
£ (ДМ) = £ (рДЖ) = % Д1Г+ р * (ДИО = 0. (2.11)
Деля выражение (2.11) на Д РИи переходя к пределу при ДИ^—> 0, получаем
Второй член в уравнении (2.12) носит название скорости относительного объемно-
го расширения среды в данной точке и обозначается 0, т. е.
в- lim (2.13)
ДИ^— о Л Jv dr
Вычисление скорости относительного объемного расширения среды по формуле
(2.13) приводит к так называемой скалярной пространственной производной вектор-
ной функции вектора скорости F, обозначаемой как div И. Эта производная носит на-
звание дивергенции. В декартовой системе координат величина этой производной оп-
ределяется формулой
.. ди . dv . dw
div V = з- + -г- + .
дх оу dz
54
(Введенная ранее величина rot И является векторной пространственной производной
той же векторной функции.) С учетом сказанного уравнение (2.12) принимает вид
dp/dr + р div И = 0. (2.14)
С точки зрения Эйлера, наряду с заданием вектора скорости V в виде (2.6), анало-
гичное задание имеет место и для других параметров жидкости или газа. Поэтому
плотность р является функцией времени t и пространственных координат х, у, z : р =
= р(х, У, z,1). В свою очередь, при движении жидкой частицы плотностью р происхо-
дит изменение ее пространственного положения, что необходимо учитывать при диф-
ференцировании по переменной t. В соответствии с формулой дифференцирования
сложной функции, используя кинематические соотношения (2.8), имеем
dp _ Эр
d7
Эр
Яс
+ w
Эр
Я'
(2.15)
Величина, стоящая в левой части соотношения (2.15), т. е. dp/d/, носит название пол-
ной производной плотности по времени. Так как она характеризует изменение во времени
плотности частицы жидкости или газа, то ее называют еще материальной или субстанци-
ональной производной. Частная производная Эр/dr характеризует изменение плотности в
единицу времени в данной точке пространства х, у z и называется местной или локальной
производной плотности. Последние три слагаемые в формуле (2.15) описывают изменение
плотности, зависящее от движения частицы, и называются конвективной производной.
Введем еще одну пространственную производную — векторную пространственную
производную скалярной функции, — называемую вектором-градиентом, или кратко гра-
диентом. На примере плотности в декартовой системе координат проекции этого векто-
ра есть
(grad р)х = др/дх, (grad = др/ду, (grad р)г = dp/dz. (2.16)
Использование формулы скалярного произведения двух векторов три последних
слагаемых в (2.15), т. е. конвективную производную, позволяет записать в форме
и^Я + + * gradp-
Эх оу oz г
Тогда уравнение неразрывности (2.14) принимает вид
Эр/Эг + (И • grad р + р div И) = 0.
Вспоминая формулу дифференцирования произведения двух функций, уравне-
ние неразрывности можно представить как
Эр/Э/+ div (рИ) = 0. (2.17)
Уравнение (2.17) представляет собой другой вид уравнения неразрывности (2.14),
в котором отсутствует полная производная плотности по времени.
Если поле плотности стационарно (Эр/Э/= 0), уравнение неразрывности примет вид
div(pK) = 0, (2.18)
или в проекциях скорости в декартовых координатах
Э(рм)/Эх + d(pv)/3y + 3(pw)/3z = 0.
Наконец, в случае постоянной плотности (однородная несжимаемая среда) полу-
чим уравнение несжимаемости жидкости
divP = 0 (2.19)
или
Эи , Эр , Эи> _ п
зг F зг °-
55
2.4. ОСНОВЫ ДИНАМИКИ ЖИДКОСТИ И ГАЗА
В динамике жидкости и газа рассматривают два вида действующих на частицы
среды сил: объемные (иногда их еще называют массовыми) и поверхностные. Под объ-
емными силами понимают силы, действующие на элементы объема, например: силы
веса, тяготения, инерции, электростатического притяжения или отталкивания, силы
действия магнитного и электрического поля на частицы среды. К поверхностным от-
носят силы, которые действуют на элементы поверхности, ограничивающей объем,
например, силы давления или силы внутреннего трения (вязкости) в среде. В качестве
поверхности, ограничивающей объем среды, могут выступать любые поверхности, в
том числе и мысленно проведенные внутри объема, занятого жидкостью или газом.
В гидрогазоаэродинамике имеют дело не с самими силами, а с их плотностями.
Плотность распределения объемных сил f в данной точке среды равна пределу отноше-
ния вектора ДГ сил, приложенных к точкам малого объема ДИ^, заключающего в себе
данную точку, к массе ДЛ/= р ДИ^ когда объем ДРИстремится к нулю, сохраняя внутри
себя рассматриваемую точку, т. е.
/= lim д//ДЛ/= lim д//(рД[Г).
ДЛ/—о ди^—о г
Так как по закону Ньютона сила равна произведению массы тела на его ускоре-
ние, то в случае силы тяжести f = g, где g — вектор ускорения свободного падения.
Аналогично, поверхностные силы задаются вектором напряжения
р = lim //Д5,
AS—О
где ДЛ — главный вектор сил, приложенных со стороны среды к выделенной в ней
малой площадке Д5. Напряжения, как это следует из последнего соотношения, изме-
ряют в Н/м2.
Отметим, что вектор /* является однозначной векторной функцией точек про-
странства и времени, т. е. образует векторное поле, тогда как вектор / принимает
в каждой точке пространства бесчисленное множество значений в зависимости от
ориентации площадки, к которой приложено напряжение, и, таким образом, вектор-
ного поля не образует.
Отличая лицевую и тыльную стороны площадки Д5, включающей рассматривае-
мую точку М жидкости или газа, проведем к лицевой стороне единичный вектор нор-
мали г? (рис. 2.4). Тогда вектор напряжения поверхностных сил, действующих на ли-
цевую сторону площадки, будем обозначать как р*я, индекс п у вектора напряжения
указывает на то, что поверхностные силы приложены к лицевой стороне площадки
с ортом нормали г?. Наоборот, к тыльной стороне площадки, согласно закону дейст-
вия и противодействия, будут приложены поверхностные силы, вектор напряжения
которых есть —рп.
Вырежем в движущейся среде элементарный тетраэдр МАВС с вершиной в дан-
ной точке М, с основанием в форме треугольника АВС, образованного пересечением
наклонной плоскости с тремя координатными плоскостями, и боковыми гранями,
расположенными в координатных плоскостях (рис. 2.5). Обозначим площадь тре-
угольника АВС через d5n, а площади треугольников ВМС, АМС и АМВ, представляю-
щих собой проекции треугольника АВС на координатные плоскости, соответственно
d5x, d5r d5r причем индексы х, у, z при этих площадках, так же как и при напряжени-
56
Рис. 2.4. К определению
вектора напряжений
Рис. 2.5. К определению
свойств вектора напряжений
ях рх, ру, pz, приложенных к этим площадкам, обозначают оси, перпендикулярные
площадкам.
Записывая уравнение движения центра инерции системы жидких частиц, запол-
няющих рассматриваемый бесконечно малый тетраэдр, пренебрегая величинами
третьего порядка малости и оставляя лишь малые второго порядка малости, будем иметь
Рп ASn = рх dSx + Fy dSy + dSr (2.20)
Так как
d5x = d5„ cos (Я, x) = nx d5n, d5y = d5n cos (n, y) = ny d5n, d5z = d5„ cos (Я, z) = nz d5„,
где nx, ny, nz обозначают косинусы углов единичной нормали И с осями координат,
после сокращения обеих частей уравнения (2.20) на dSn получим выражение
Рп = пхРх + ПуРу + nzPv (2-21)
или в проекциях на оси декартовых координат,
Рпх = пхРхх + nyPyx + nzPzx’
Рпу ^хРху + ПуРуу + Hj>zy' (2.22)
Pnz = nxPxz +nyPyz +nzPzz-
Вспоминая определение напряжений рх, ру, pz, отметим, что при принятых
обозначениях первый подстрочный индекс при напряжениях рхх, ... обозначает
ось, перпендикулярно к которой ориентирована элементарная площадка, второй —
ось, на которую спроектировано это напряжение. Например, pxz обозначает проекцию
на ось z напряжения, приложенного к площадке, перпендикулярной к оси х.
Величины с одинаковыми индексамир^,р^р^, представляющие проекции век-
торов напряжений рх, ру, pz на нормали к соответствующим площадкам, называют
нормальными напряжениями, а проекции р^, р^ pxz, ... на оси, лежащие в плоскости
площадок, — касательными напряжениями.
Из соотношений (2.22) следует, что напряженное состояние в рассматриваемой
точке пространства, занятого средой, описывается совокупностью девяти величин
Рхх’ Рух’ Pzx
Рху Рур Рф
Pxz’Pyz’Pzz
57
(2.23)
Рис. 2.6. К выводу
уравнения количества
движения жидкого объема
Эти соотношения обладают определенными свойствами,
что позволило связать их с тензором напряжений Р, компо-
ненты которого определяются таблицей
Рхх’ Рхр Pxz
Pyx'* Рур Pyz
Pzx’PzyPzz
(2.24)
В большинстве жидкостей и газов отсутствуют объем-
ные и поверхностные пары сил. Если записать уравнение ра-
венства нулю главного момента приложенных сил к тетраэд-
ру МАВС, взятому в таких средах, то можно показать, что
Рху Рух’ Pxz Pzx’ Pyz Р& (2.25)
Равенства (2.25) выражают теорему о взаимности касательных напряжений и ус-
танавливают факт, что компоненты тензора напряжений не зависят от порядка индек-
сов, а это означает симметричность тензора напряжений.
Таким образом, из девяти компонент тензора напряжений различными являются
только шесть и можно менять порядок индексов при компонентах тензора напряже-
ний, т. е. для таких сред таблицы (2.23) и (2.24) выражают компоненты одного и того
же тензора.
Выделим в жидкости произвольный конечный жидкий объем W(рис. 2.6). Тогда
в соответствии с теоремой об изменении количества движения приходим к уравнению
динамики жидкости или газа или просто к уравнению движения в напряжениях:
dK
Pd7
эл . э/$ . э#
Эх ду dz *
(2.26)
Для записи этих уравнений в декартовой системе координат используем формулу
вычисления полной производной скалярной функции (2.15). В данном случае в фор-
мулу (2.15) вместо плотности р необходимо подставить проекции вектора скорости V.
В результате из (2.26) следуют
(ди , ди , ди , Э«Л_ z. .^Рхх . друх , дрzx
Р(э7 + м^ +v^ +^ГрЛ + ^+<+^’
(dv , dv , dv dv\ , _>дрху др др
p(di + ud-x +vTy +wd-zFpfy+ IF + -ЭГ’
(dw , dw , dw dw\ , .^p . ^Pyz . <*PZZ
р(э7 + мЭх +va? + # + 17’
гдеfxJ fz — проекции вектора плотности распределения объемных сил f.
При движении газа с большими скоростями происходит обмен энергией между
его частицами, поэтому полная система уравнений динамики газа должна включать
уравнение энергии, являющееся выражением закона сохранения энергии. В соответ-
ствии с этим законом изменение полной энергии рассматриваемой частицы за время
dr равно сумме работы приложенных к ней внешних сил и подведенной теплоты.
Полная энергия частицы d£ складывается из кинетической энергии ее поступа-
тельного движения и внутренней энергии
dE= (y+tfj dM = (y+tf) Р<НК
где U — плотность внутренней энергии или удельная внутренняя энергия среды в рас-
сматриваемой точке.
58
Уравнение энергии в дифференциальной форме записывается как
Р£ + £/) = pf • И + div (РИ) + pt,, (2.27)
где q — удельное количество тепла, подведенное к частице извне.
Дифференциальные уравнения неразрывности (2.17), количества движения
(2.26) и энергии (2.27) выполняются для любых движений жидкостей или газов, не об-
ладающих объемными и поверхностными парами сил. Однако различные жидкости и
газы при одних и тех же внешних условиях ведут себя по-разному. Добавление соот-
ветствующих граничных условий недостаточно, так как число уравнений меньше чис-
ла входящих в них неизвестных, т. е. система незамкнута. Построение замкнутой сис-
темы уравнений связано с установлением дополнительных соотношений между пара-
метрами данной среды.
2.5. СЖИМАЕМЫЕ И НЕСЖИМАЕМЫЕ ТЕЧЕНИЯ
Идеальной жидкостью или идеальным газом называют такую среду, в которой век-
тор напряжения рп на любой площадке с нормалью Ft ортогонален площадке, т. е. рп
параллелен Ft. В таких жидкостях или газах обращаются в нуль все касательные на-
пряжения
Рху ~ Рух ~ Pxz ~ Pzx ~ Pyz ~ Pzy ~ О’
а выражения нормальных напряжений имеют вид
Р„ = Рп*’ Рх = Рх Ру = РуТ’ Рг = Pjc- (2.28)
Используя вышеперечисленные соотношения и равенства (2.22), найдем
Рхх~ Руу~ Pzz~ Рп’ (2.29)
т. е. нормальные напряжения в идеальных жидкостях и газах не зависят от ориентации
поверхности. В случае неподвижных жидкостей или газов, обладающих вязкостью,
также не будут возникать касательные напряжения, и для них будут справедливы со-
отношения (2.29), которые выражают закон Паскаля.
Общее значение нормальных напряжений в данной точке среды, взятое со зна-
ком минус, называют давлением в этой точке и обозначают буквой р, так что
Pxx=Pyy=Pzz=Pn = -P- (2.30)
Выбранный в (2.30) знак минус обеспечивает положительность давления р, т. к.
считается невозможным возникновение в жидкостях или газах растягивающих напря-
жений (см. п. 2.1).
Дальнейшим упрощением модели жидкости или газа служит предположение об
их несжимаемости. В несжимаемой жидкости плотность р есть некоторая постоян-
ная, которая считается известной. Уравнение неразрывности (2.17) переходит в урав-
нение несжимаемости (2.19). Учитывая (2.28), (2.30) и вспоминая определение векто-
ра-градиента (2.16), можно записать
_ др др др А
+ Ъ Ъ ~~Txl -yzk~~gTadp-
После этого уравнение движения невязкой жидкости или газа — уравнение Эйлера
принимает вид
=/-^gradp, (2.31)
59
или в декартовой системе координат
ди . ди . ди . ди г 1 Эр з?=£-p3v
dv 37 dv + “3i . dv + v3y . dv _ r 1 dp P ’ (2.32)
dw 37 dx . dw +v^ .div - 1 dp + w3i =Л-рЭ7-
В системе из четырех уравнений (уравнение несжимаемости (2.19) и уравнения
Эйлера (2.32)) неизвестными являются четыре величины: и, v, w, р, зависящая каждая
от аргументов х, у, z, t. Величины fx,fyfz являются заданными функциями тех же аргу-
ментов. Таким образом, задача исследования течения несжимаемых жидкостей или
газов является замкнутой.
В случае движения сжимаемых жидкостей или газов плотность р является пятой
неизвестной функцией, и вместо уравнения несжимаемости (2.19) необходимо ис-
пользовать уравнение неразрывности (2.17). Для исследования движения сжимаемой
среды в общем случае оказывается необходимым учет нового фактора — обмена энер-
гией как между частицами среды, так и между ними и внешней средой. Поэтому необ-
ходимо привлечение уравнения энергии (2.27).
В дальнейшем ограничимся случаем совершенных газов, в которых давление р,
плотность р и температура Т связаны уравнением Клапейрона
р = рЯ7; (2.33)
где R — некоторое постоянное число, называемое газовой постоянной, различное для
разных газов.
Для совершенных газов, определяя температуру как характеристику средней
энергии, приходящейся на одну степень свободы в хаотическом тепловом движении,
удельную внутреннюю энергию U можно представить в виде
U = cvT 4- const. (2.34)
Значение постоянной в равенстве (2.34) несущественно, так как нас интересует
изменение удельной внутренней энергии, а не сама ее величина. Поэтому в дальней-
шем эту постоянную будем опускать.
Коэффициент пропорциональности cv, входящий в (2.34), имеет простой физи-
ческий смысл — он представляет собой количество тепла, которое необходимо под-
вести к единице массы среды, чтобы при постоянном объеме поднять ее температуру
на один градус. Поэтому cv называется теплоемкостью при постоянном объеме или изо-
хорной теплоемкостью. Количество тепла, которое необходимо подвести к единице
массы среды, чтобы при постоянном давлении поднять температуру на один градус,
называется теплоемкостью при постоянном давлении или изобарной теплоемкостью и
обозначается через ср. Для совершенного газа теплоемкости при постоянном давле-
нии и объеме и газовая постоянная связаны формулой
c„-cv = R. (2.35)
Теплоемкости при постоянном давлении и объеме определяют так называемый
показатель адиабаты k = cp/cv, с помощью которого можно связать давление и плот-
ность для двух состояний в адиабатическом процессе, при котором отсутствует тепло-
обмен с внешней средой.
В общем случае, когда можно установить некоторую связь между плотностью и
давлением, имеет место термодинамический процесс, называемый баротропным. Для
60
него вместо давления р можно ввести в рассмотрение однозначно связанную с ним
функцию давления
(2.36)
Когда массовые силы обладают потенциалом Ф, т. е. вектор плотности массовых
сил f определяется как f = —grad Ф, то уравнение Эйлера (2.31) для стационарного
течения имеет своим интегралом так называемый интеграл Бернулли
у2
-у + р' + Ф = const. (2.37)
Это равенство выполняется как вдоль линий тока, так и вдоль вихревых линий.
Численные значения постоянных в (2.37) на каждой линии тока или вихревой линии
различны. Это же равенство (2.37) имеет место и для частного случая безвихревого
движения, когда Й = (1/2) rot F = 0, и тогда численное значение постоянной одинако-
во для всех точек области течения.
Когда тепло извне к частице не подводится (q = 0) и можно пренебречь влиянием
сил тяжести (/* = 0), в стационарных течениях идеального совершенного газа уравне-
ние энергии (2.27) вдоль любой линии тока имеет интеграл
у2
i 4- -у = const, (2.38)
где i = срТ — удельная энтальпия, или, кратко, энтальпия газа, а постоянная в (2.38)
может принимать различные значения на разных линиях тока.
2.6. ПОТЕНЦИАЛЬНЫЕ ТЕЧЕНИЯ
(2.39)
Рассмотрим один частный, но весьма важный случай движения жидкости или га-
за, которое происходит без вращения частиц. Так как в этом случае Й = rot V = 0, то из
соотношений (2.9) получается, что
dw _ dv ди _ dw dv _ ди
Эу 3z’ 3z Эх ’ Эх Эу ‘
Простой подстановкой можно проверить, что последним равенствам можно
удовлетворить, если существует такая скалярная функция <р = <р (х, у, z,t), с помощью
которой компоненты вектора скорости И выражаются как
Эф Эф Эф
и= з2-, v= V-, w= V-.
дх ду dz
Вспоминая определение вектора-градиента скалярной функции (2.16), равенства
(2.39) записываются в виде, применимом для любой системы координат, V = grad <р. От-
сюда понятно, почему введенная выше функция ср носит название потенциала скоростей.
Так как условие Й = 0 означает отсутствие вихрей в рассматриваемом течении, то
изложенное выше позволяет заключить, что безвихревое течение является потенци-
альным. Верно и обратное — потенциальное течение будет безвихревым.
В данном разделе ограничимся случаем несжимаемых потенциальных течений.
Подставляя в уравнение несжимаемости (2.19) вместо компонент скорости их выра-
жения через потенциал скоростей, получим
^Ф + дЧ + дЧ=0.
Эх2 ду2 д?2
61
Таким образом, потенциал скоростей в случае несжимаемых жидкостей или га-
зов удовлетворяет уравнению Лапласа.
Любой потенциальный поток идеальной несжимаемой среды можно представить
как результат наложения друг на друга более простых потенциальных течений. При
наложении потенциальных потоков скорость результирующего потока является век-
торной суммой скоростей составляющих потоков. Описанный выше метод получения
сложных потенциальных течений носит название метода наложения потенциальных
потоков.
Рассмотрим простейшие плоские потенциальные течения несжимаемой среды.
Уравнение несжимаемости (2.19) для плоских несжимаемых, не обязательно потен-
циальных, течений принимает вид
= 0. (2.40)
дх ду v
Простой подстановкой можно убедиться, что этому уравнению тождественно
удовлетворяет некоторая функция \|/ = у (х, у), если
„ = = (2.41)
ду ’ Эх v
Вспоминая дифференциальные уравнения линий тока (2.7), которые в случае
плоских течений сводятся к одному, записанному в форме
иду — vdx = 0,
и подставляя в него соотношения (2.41), получаем
^dx+^dy = 0. (2.42)
Эх ду л
Так как полный дифференциал функции у есть
d\|/ = fpdx + ^dy,
Y Эх ду ”
то условие (2.42) означает равенство нулю d\|/ вдоль линии тока, или постоянство
функции v вдоль линии тока, поэтому эту функцию называют функцией тока.
Два первых равенства (2.39) в плоских потенциальных течениях выпадают из рас-
смотрения. После подстановки в последнее из этих равенств вместо компонент ско-
рости их выражения через функцию тока (2.41) получаем
-ч2
э у э у _п
Эх2 Эу2 U’
т. е. в плоских потенциальных течениях несжимаемых жидкостей или газов функция
тока, так же как и потенциал скоростей, удовлетворяет уравнению Лапласа.
Соотношения (2.39) и (2.41) позволяют установить следующую связь между про-
изводными потенциала скоростей и функций тока:
Эф _ Эу Эф _ Эу
Эх Эу ’ Эу Эх’
которая является условием ортогональности линий тока \|/ = const и линий посто-
янных значений потенциала скоростей — эквипотенциален ф = const в каждой точке
потенциального течения несжимаемой среды и условием существования аналитиче-
ской функции w(^) одной комплексной переменной z = x + iy, определяемой соотноше-
нием
w(z) = <p(x,y) + /у(х,^).
62
Здесь и далее в этом параграфе w, z, i имеют особый смысл, а именно: w(^) —
комплексный потенциал, z — комплексная переменная, i = — мнимая единица.
Рассмотрим производную dw/dz комплексного потенциала по комплексному ар-
гументу
dw Э«р Эу = Эу .Эф = ,2 ....
где использованы (2.39) и (2.41).
Каждому комплексному числу можно сопоставить в плоскости вектор с проек-
циями, соответственно равными действительной и мнимой частям этого комплекс-
ного числа. Далее в этом параграфе буквой Ибудем обозначать комплексную скорость
V= и + iv, а для величины скорости используем обычное обозначение модуля скорос-
ти |И| = Ju2 + v2. Тогда сопряженная скорость К*, определяемая как
V* = u-iv, (2.44)
из равенства (2.43) оказывается равной производной от комплексного потенциала по
комплексной координате
Если 0 — угол между Vи осью Ох, то
V = и 4- iv = |К| (cos 0 4- i sin 0) = |И| е'0,
V* = и — iv = \V\ (cos 0 — isin 0) = |И| e_/0.
Отделяя в произвольной функции комплексной переменной w(^) действитель-
ную Re и мнимую Im части, получим потенциал скоростей ф (х, у) и функцию тока
V (х, у) некоторого плоского потенциального течения
ф (х, у) = Rew (г), \|/ (х, у) = Imw(^). (2.46)
Приравнивая функцию ф(х, у) к различным постоянным ф(х, у) = С, получим се-
мейство эквипотенциалей, а семейство линий тока определяет равенство у(х, у) = С.
Приведем несколько примеров простейших плоских потоков идеальной несжи-
маемой жидкости. По известным выражениям комплексного потенциала таких тече-
ний в соответствии с (2.46) определяются потенциалы скоростей и функции тока, а по
(2.44) и (2.45) — распределение скорости.
Однородный поток с вектором скорости (мто, уто,) направленный к оси Ох под
углом 0^ (рис. 2.7), характеризуется соотношениями:
* * -/О
Hz) = K»z, - iv„ = | Kje ~= | KJ (cos - i sin ),
Ф = их 4- vv, w = -voox4-w y, V= И = w 4- iv.
Очень часто удобно направление оси Ох выбирать совпадающим с направлением
скорости однородного потока (0ТО = 0). В этом случае
Hz) = Uxz, К~=К°° = и„, <р = итех, V = и„у, К= их. (2.47)
Течение, вызванное источником или стоком, находящимся в начале координат
(рис. 2.8) и обладающим секундным объемным расходом Q, имеет комплексный по-
тенциал, описываемый логарифмической функцией комплексной переменной с дей-
ствительным множителем:
Hz)= glnz, Ф=^1пг, v=ge, r=^,|H=g. (2.48)
63
Рис. 2.7. Линии тока и эквипотенциали Рис. 2.8. Линии тока и эквипотенциали для течения,
однородного потока вызванного источником (а) или стоком (б)
В этих соотношениях Q — действительная величина, положительная в случае ис-
точника и отрицательная в случае стока; г, е — полярные координаты (z = ге‘£).
Если в формуле для комплексного потенциала перед логарифмом стоит мнимый
множитель, то он описывает течение, образованное вихрем, расположенным в начале
координат (рис. 2.9), для которого
wW=2^ln^’ <Р = £е’ V = -^lnr, |И|=1!1, (2.49)
где Г — действительная величина, равная циркуляции скорости по любому контуру,
охватываемому один раз начало координат. Когда Г > 0, жидкость движется по кон-
центрическим окружностям в направлении против движения часовой стрелки
(рис. 2.9), при Г < 0 движение жидкости происходит по часовой стрелке.
Метод наложения потенциальных потоков позволяет получать новые потоки.
Так, складывая потоки источника и стока одинаковой мощности (2.48), размещенных
по оси Ох симметрично относительно начала координат О в точках с абсциссами ±h ,
при предельном переходе (А —> О, |Q| —, Q* 2h стремится к конечной величине т)
получаем
w(z) = lirn ОПП. ^z + h)-4n(z-h) = т dlnz = т
v ' a—o.iqi—оф 2л 2h 2л dz 2nz
Q • 2h—
откуда следует:
m= mx =mx w= тУ = тУ И= m IH= |m| Г25П
Ф 2л(х2+?) V 2л(?+?) 2Fr’ V ^-(2-5l)
Конечная величина m называется моментом диполя; значение т > 0 соответствует
расположению стока с положительной стороны оси Ох , т < 0 — противоположному
случаю. Картина линий тока и эквипотенциалей для течения, вызванного диполем
в начале координат, приводится на рис. 2.10.
Бесциркуляционное обтекание круглого цилиндра радиуса а потоком вдоль оси Ох
(рис. 2.11) можно получить наложением однородного потока (2.47) на поток диполя
(2.50) и (2.51) при т = 2ла2моо. Тогда
2ла2и„ 1 / а1 ч
wfe) = и„ z + 2д - = [z + - J. (2.52)
Нулевая линия тока (у = 0) для этого течения представляется двумя кривыми.
Одна из них окружность х2 + у2 = а2 радиуса а с центром в начале координат; другая —
ось Ох (у = 0).
64
Рис. 2.9. Линии тока и эквипотенциали
для течения, образованного вихрем
Рис. 2.10. Линии тока и эквипотенциали
для течения, вызванного диполем
Скорость К* в произвольной точке потока (2.52) равна
Отсюда распределение скоростей по контуру окружности z - определяет-
ся формулой |К| = 2i/oo|sin£|, где е— полярный угол между радиусом окружности
и осью Ох.
В точках Л (е = я) и В (е = 0) скорости равны нулю. Эти точки, как уже отмечалось
в п. 2.2, называются критическими точками потока. При направлении движения, ука-
занном на рис. 2.11, точка А называется передней критической точкой, точка В — за-
дней. В точках С и Л миделевого сечения цилиндра (е = ±л/2) скорость на поверхно-
сти цилиндра принимает максимальное значение, равное |Итах| = 2иж, т. е. равна удво-
енной скорости набегающего потока.
Распределение давления в потоке и, в частности, по контуру цилиндра может
быть представлено в форме коэффициента давления
(2.53)
_ Р~Р-
Ср 1/2р«Г
Рис. 2.11. Линии тока при бесциркуляционном обтекании цилиндра
65
Через рж обозначено давление в набегающем потоке. Применяя теорему Бернул-
ли в форме (2.37), где отброшен член с потенциалом массовых сил как несуществен-
ный в задачах гидрогазоаэродинамики, и при вычислении функции давления (2.36)
учтено постоянство плотности для несжимаемых жидкостей и газов, и определяя
константу как 4- (1/2)р и^, найдем в рассматриваемом случае
с = 1 — = 1-4 sin2 е.
Woo
Полученное распределение давления по контуру окружности, как это прямо сле-
дует из симметрии обтекания по отношению к осям Ох и Оу, результирующей силы не
дает, что составляет суть парадокса Даламбера.
Циркуляционное обтекание круглого цилиндра получается наложением вихря
с циркуляцией Г (2.49) на бесциркуляционное обтекание круглого цилиндра (2.52).
Комплексный потенциал составного движения будет
Нг) = + ^.1пг,
что при Г > 0 соответствует направлению циркуляционного движения по часовой
стрелке.
Определим сопряженную скорость
откуда для точек на контуре окружности
|H=«j2sine+^|. (2.54)
В зависимости от величины циркуляции возможны три типа обтекания.
а) Циркуляция мала: Г < 4памоо. В этом случае на контуре окружности существу-
ют две критические точки, в которых И= 0. Их положения из соотношения (2.54) оп-
ределяются значениями полярного угла, при котором
sin£* = —х——. (2.55)
2паи00 v 7
Положение критических точек показано на рис. 2.12, а. При уменьшении Г до
нуля критические точки будут перемещаться, стремясь занять положение на пересе-
чении окружности с осью Ох, как это и должно быть при Г = 0.
б) Промежуточный случай: Г = 4twmoo. Положение критических точек на контуре ци-
линдра, определяемое равенством (2.55), удовлетворяет условию sin £♦ = -1, откуда следу-
ет, что критические точки совпадают и находятся на оси Оу, где £♦ = —тс/2 (рис. 2.12, б).
в) Циркуляция велика: Г > 4ламоо. В этом случае в выражении (2.55) окажется
sin £♦ < — 1, что невозможно. Это означает отсутствие критических точек на контуре
цилиндра. Критическая точка А будет лежать вне круга на отрицательной стороне
мнимой оси, а критическая точка В — на той же оси, но внутри круга (рис. 2.12, в).
Найдем коэффициент давления на контуре цилиндра. Из (2.53) и (2.54) будет
/ г \2
с = 1 — [ 2sine + 5- I. (2.56)
р V 2каиоо ) ' '
При циркуляционном течении в соответствии с формулой (2.56) симметрия распре-
деления давления по окружности нарушается относительно оси Ох при сохранении сим-
66
Рис. 2.12. Схема линий тока при циркуляционном обтекании цилиндра
метрии относительно оси Оу. В связи с этим главный вектор сил давления жидкости на
поверхность цилиндра R будет отличен от нуля и направлен вдоль оси Оу. Над цилинд-
ром скорость больше, а давление, согласно уравнению Бернулли, меньше; под цилинд-
ром, наоборот, скорость меньше, а давление больше. Это приводит к тому, что главный
вектор сил давления R будет направлен по оси Оу в положительную сторону (вверх).
Тогда проекция R на ось Оу, вычисляемая как
2л
= —$pnyds = -a J р sin е de,
о
где ds = flde — элемент дуги контура окружности, после подстановки в выражение Ya
значения р по уравнению Бернулли и с учетом (2.56) оказывается равной
zn 2
J f2"“sine + 2й) sinede = Pu«, Г.
(2.57)
Как и в случае бесциркуляционного обтекания цилиндра, при циркуляционном
обтекании сопротивления нет, но возникает поперечная сила. Ее называют подъем-
ной силой. Выражение (2.57) для Ya является частным случаем общей теоремы
Н. Е. Жуковского о подъемной силе: в плоскопараллельном безвихревом потоке идеаль-
ной несжимаемой жидкости на произвольный контур действует сила, равная произ-
ведению плотности жидкости на величину скорости набегающего потока и величину
наложенной циркуляции. Направление этой силы (рис. 2.12) определяется поворотом
на 90° вектора скорости набегающего потока в сторону, противоположную цирку-
ляции. Н. Е. Жуковский своей теоремой впервые установил вихревую природу подъем-
ной силы. Для определения этой силы Жуковский заменяет обтекаемый плоский кон-
тур некоторым воображаемым жидким контуром, ограниченным замкнутой линией
тока, внутри которого находятся вихри. Такие вихри он назвал присоединенными.
Идея присоединенного вихря и дополнительное допущение, позволяющее опре-
делять интенсивность присоединенных вихрей, составляют основу теории профиля и
крыла (см. далее).
2.7. ВЯЗКИЕ ТЕЧЕНИЯ И ПОГРАНИЧНЫЙ СЛОЙ
Все реальные жидкости обладают определенной вязкостью, которая проявляется
при деформации в виде внутреннего трения. Как отмечалось в п. 2.2, деформацион-
ное движение можно представить в виде суммы, вызывающей растяжение или сжатие
объема среды и скашивание первоначально прямых углов между линиями, состоящи-
67
ми во время движения из одних и тех же частиц среды. Уравнение изотермического
движения вязкой несжимаемой жидкости в векторной форме имеет вид
Tfr = / “ | gradp + у. Др, (2.58)
где символ Др — лапласиан V — обозначает вектор с проекциями Дм, Ду, Aw, a v* = ц/р
называется кинематическим коэффициентом вязкости (использование не общеприня-
того обозначения кинематического коэффициента вязкости со звездочкой в нижнем
индексе связано с очень похожим очертанием греческой буквы «ню» с проекцией ско-
рости v).
Уравнение (2.58), называемое уравнением Навъе-Стокса, отличается от уравнения
Эйлера (2.31) наличием члена у* ДИ. При решении задач гидрогазоаэродинамики в ка-
честве исходных данных выступает значение скорости набегающего потока И^ и ее
направление, а также некоторый размер обтекаемого тела £, который принимают за
характерный. Тогда из соображений размерностей для рассматриваемой жидкости с
известной величиной кинематического коэффициента вязкости у* может быть обра-
зован безразмерный комплекс, например И^А/у*, который носит название числа Рей-
нольдса Re, т. е.
Re=HoeL/K. (2.59)
Число Рейнольдса характеризует отношение инерционных и вязких сил и играет
большую роль при изучении движений вязких жидкостей и газов. От числа Рейнольд-
са зависит, в частности, коэффициент сопротивления различных тел, обтекаемых по-
током вязкой жидкости или газа.
Наблюдения показывают, что для вязкой жидкости возможны две существенно раз-
ные формы движения. Одна из них носит название ламинарной, а другая — турбулентной.
Ламинарный режим характерен для малых скоростей течения, турбулентный — для срав-
нительно больших.
Условия, которые управляют переходом течения из одной формы в другую, впер-
вые были экспериментально установлены О. Рейнольдсом. Их можно охарактеризо-
вать критическим числом Рейнольдса Rer для подсчета которого используется формула
(2.59), а характерные значения скорости и линейного размера выбираются исходя из
решаемой задачи.
При ламинарном режиме течения каждая частица потока жидкости или газа дви-
жется вдоль плавно изменяющейся траектории, определяемой в основном геометрией
стенок, ограничивающих поток. Именно для ламинарного режима течения примени-
мы уравнения изотермического движения вязкой несжимаемой жидкости (2.58).
Турбулентный режим течения характеризуется тем, что мгновенные значения
скорости и давления испытывают случайные пульсации во времени. Наличием пуль-
саций скорости в турбулентном потоке обусловлены дополнительные нормальные
и касательные напряжения. Механизм турбулентного течения очень сложен и еще
полностью не изучен. Поэтому расчетные методы турбулентных течений в большей
или меньшей мере используют эмпирическую информацию, полученную в экспери-
ментальных исследованиях.
Так как коэффициент кинематической вязкости воздуха мал, то типичные значе-
ния числа Рейнольдса очень большие, порядка 106...108 и выше. В этих условиях вяз-
кость существенно влияет на течение только в тонком слое, прилегающем к поверх-
ности обтекаемого тела, называемом пограничным слоем, и в следе (рис. 2.13). Вне этих
68
Рис. 2.13. Обтекание тела вязким газом или жидкостью
областей влияние вязкости практически не проявляется. Понятие пограничного слоя
ввел Л. Прандтль.
Характерной особенностью течения жидкости или газа в пограничном слое, воз-
никающем при обтекании тел, является быстрое возрастание касательной к поверх-
ности составляющей скорости от нуля («прилипание» частиц среды к поверхности) до
значения этой скорости при обтекании рассматриваемого тела невязкой жидкостью
или газом. Расстояние, измеренное по нормали от поверхности тела до точки,
в которой местная касательная составляющая скорости отличается на малую величи-
ну (обычно равную 1%) от скорости при обтекании этого тела невязкой жидкостью
или газом, называют толщиной пограничного слоя и обозначают 8.
Давление по толщине пограничного слоя практически не меняется и равно дав-
лению на его внешней границе, что является следствием малости толщины погранич-
ного слоя по сравнению с радиусом кривизны обтекаемых поверхностей. Обычно
пренебрегается взаимным влиянием пограничного слоя и невязкого течения, тогда
давление внутри пограничного слоя равно давлению на обтекаемой поверхности при
ее обтекании невязкой средой.
Перечисленные особенности пограничного слоя позволяют существенно упрос-
тить полные уравнения движения вязких сред — уравнения Навье-Стокса. Так, в слу-
чае плоского стационарного течения несжимаемой жидкости или газа, когда парамет-
ры потока зависят от двух переменных, например х и у, вместо (2.58) будем иметь:
ди , ди tAU . д2U п,лч
uTx+vTy=Ub+v^^ (2-60)
которое должно быть дополнено уравнением несжимаемости (2.40). В уравнении
(2.60) введено обозначение Uдля касательной к поверхности составляющей скорости
при ее обтекании невязкой жидкостью или газом.
Течение в пограничном слое может быть как ламинарным, так и турбулентным.
Вспоминая формулу Ньютона для касательного напряжения (2.5), уравнение движе-
ния в пограничном слое (2.60) можно переписать в виде
°б,>
которое одинаково применимо как для ламинарного, так и для турбулентного режима
течения в пограничном слое. Различие заключается в дополнительной связи между
касательным напряжением т и скоростью и внутри пограничного слоя.
Хотя система дифференциальных уравнений с частными производными, описы-
вающая движение жидкости в пограничном слое, значительно проще уравнений
Навье-Стокса, ее интегрирование требует применение численных методов. Т. Карман
69
еще больше упростил задачу. Для формулировки расчетных уравнений он применил
так называемый метод контрольного объема. В дальнейшем его уравнение, называе-
мое интегральным соотношением пограничного слоя, было получено формальными пре-
образованиями системы уравнений (2.61) и (2.40). Один из возможных видов этого
соотношения можно записать как
^_+11£(2 + Я)8"=Д, (2.62)
dx U dx v 7 р у29 v 7
в котором т0 — касательное напряжение на обтекаемой поверхности, 8** — толщина
потери импульса, Н= 8*/8** — формпараметр профиля скорости, 8* — толщина вытес-
нения. Условные толщины 8* и 8** вычисляются по формулам
5 5
8’ = Ц1 ~v)dy и 8”=Ш1 -vft- <2-63)
о о
Строго говоря, условной толщиной является толщина пограничного слоя 8 (см.
определение выше). Так как вне пограничного слоя подынтегральные выражения в
(2.63) равны нулю, то толщины 8* и 8** не зависят от условия определения 8.
Так как скорость течения внутри пограничного слоя меньше, чем при невяз-
ком движении, то и расход жидкости или газа через сечение пограничного слоя мень-
ше, чем при обтекании тела невязкой средой. Мерой уменьшения расхода служит
толщина вытеснения 8*. Толщина вытеснения определяет также расстояние по
нормали к поверхности тела, на которое вследствие влияния вязкости смещают-
ся линии тока, соответствующие обтеканию этого тела потоком невязкой жидкости
или газа.
Толщина потери импульса 8** характеризует изменение количества движения
движущейся среды, протекающей через рассматриваемое сечение пограничного слоя,
вследствие действия сил трения.
Интегральное соотношение (2.62) является обыкновенным дифференциальным
уравнением первого порядка, интегрирование которого представляет простую задачу.
Однако оно содержит три неизвестные величины (8**, И, т0), и для его интегрирова-
ния необходимы дополнительные связи между этими неизвестными (скорость невяз-
кого течения Uв теории пограничного слоя считается заданной).
Наиболее просто задача интегрирования уравнения (2.62) решается для случая
продольного обтекания плоской пластины, когда U = = const. Интегрирование
(2.62) для такой задачи выполняется до конца аналитически, и толщина пограничного
слоя изменяется вдоль пластины по закону
8/x = 5,O(Koox/v0“1/2 (2.64)
для ламинарного пограничного слоя и
8/x = O,37(Koox/v0-1/5 (2.65)
для турбулентного пограничного слоя.
В выражениях (2.64) и (2.65) координата х измеряется вдоль поверхности пласти-
ны от ее передней кромки. Вспоминая определение числа Рейнольдса (2.59), комп-
лекс, входящий в формулы для толщины пограничного слоя 8, может быть назван
местным числом Рейнольдса Rex = V^x/v*. Для ламинарного режима приближенная
формула (2.64) практически совпадает с точной формулой, полученной Блазиусом
при точном интегрировании системы дифференциальных уравнений с частными про-
изводными (2.60) и (2.40). Поэтому ее можно использовать во всем диапазоне чисел
70
Рейнольдса ламинарного режима. Применимость формулы (2.65) в силу приближен-
ности дополнительной информации, используемой при ее получении, ограничивает-
ся условием Rex <5 • 106.
Зная зависимость напряжения трения на поверхности пластины т0 = т0 (х), мож-
но вычислить силу одностороннего сопротивления трения пластины длиной b и ши-
риной / по формуле
ь
F=i\xq{x)6x.
о
В гидрогазоаэродинамике вместо сил рассматривают их коэффициенты, которые
являются безразмерными величинами, независящими от размеров тела и скорости
потока. Если коэффициент сопротивления трения плоской пластины определить как
то для ламинарного пограничного слоя
cF= 1,328/Re1/2, (2.66)
а для турбулентного
cF=0,074/Re1/5. (2.67)
В этих формулах число Рейнольдса вычисляется по длине пластины: Re = VJj/v.
Формула (2.67) справедлива при Re < 5 • 106. Более универсальна эмпирическая
формула Прандтля-Шлихтинга
cF=0,455/(lg Re)2’58, (2.68)
которую можно использовать при 2,5 * 105 < Re < 5 • 108.
В общем случае при турбулентном режиме течения в пограничном слое на вели-
чину cF существенное влияние оказывает шероховатость обтекаемой поверхности.
Когда высота бугорков шероховатости значительно меньше так называемого вязкого
подслоя, коэффициент сопротивления трения шероховатой пластины рассчитывается
по формулам (2.67) или (2.68). В вязком подслое молекулярные процессы обмена пре-
обладают над турбулентными. Его образование является следствием демпфирующего
влияния стенки. Течение в вязком подслое похоже на течение при ламинарном режи-
ме, поэтому его ранее называли ламинарным подслоем. Толщина вязкого подслоя
очень мала, она составляет величину порядка одного процента толщины погранично-
го слоя.
Обычно пограничный слой бывает смешанным. На передней части тела погранич-
ный слой ламинарный, а далее он может стать турбулентным. Переход от ламинарно-
го к развитому турбулентному течению происходит в переходной области. Обычно
протяженность этой области невелика. Поэтому полагают, что переход ламинарного
течения в турбулентное происходит скачкообразно в некотором сечении, продольная
координата которого xt такова, что местное число Рейнольдса Rex становится равным
критическому Re, = V^/v*. Если значение Re, известно, то относительную координа-
ту точки перехода находят по формуле
xt = xt/b = Re, /Re.
Величина Re, для пластины зависит от многих факторов. Здесь этот вопрос не
рассматривается.
71
Рис. 2.14. Зависимость удвоенного коэффициента сопротивления трения
плоской пластины для несжимаемого газа или жидкости
Зная положение точки перехода хп с помощью формул (2.66), (2.67) или (2.68)
можно рассчитать суммарный коэффициент сопротивления трения плоской пласти-
ны при смешанном пограничном слое в несжимаемом потоке. На рис. 2.14 приведены
результаты таких расчетов для ряда значений хг
Пограничный слой не всегда прилегает к обтекаемой поверхности на всем ее про-
тяжении. Он может отойти от поверхности, не доходя до кормовой части тела. Такие те-
чения называют отрывными (рис. 2.15). При обтекании криволинейной поверхности
давление вначале убывает (до сечения АА\ рис. 2.15). Вниз по течению за сечением АА'
давление возрастает. Частицы пограничного слоя, перемещаясь от этого сечения вниз
по течению, затрачивают энергию для преодоления возрастания давления. Это приво-
дит к уменьшению кинетической энергии, а следовательно, и скорости частицы. Части-
цы, движущиеся вблизи стенки, имеют меньшую кинетическую энергию, быстрее ее
израсходуют и затормозятся (сечение 55’). Ниже этого сечения возрастание давления
вызовет у поверхности обратное движение жидкости или газа, навстречу основному по-
току. В результате основной поток отделится от поверхности, произойдет отрыв потока.
Точка 5 на обтекаемой поверхности называется точкой отрыва пограничного слоя.
iA'
Давление нарастает
Рис. 2.15. Отрыв пограничного слоя от обтекаемой поверхности
72
2.8. АЭРОДИНАМИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПРОФИЛЕЙ
И КРЫЛЬЕВ КОНЕЧНОГО РАЗМАХА В НЕСЖИМАЕМОМ ПОТОКЕ
Профилем крыла называют сечение крыла плоскостью, параллельной плоскости
симметрии крыла, летательного аппарата или плоскости, принятой за базовую. Чаще
всего под хордой профиля понимают отрезок прямой, соединяющий наиболее удален-
ные точки контура профиля (рис. 2.16), и обозначают Ь. Переднюю точку хорды про-
филя называют передней кромкой, а заднюю точку — задней кромкой.
Толщина профиля с определяется как максимальное расстояние между точками
профиля на верхней и нижней сторонах, измеренное по перпендикуляру к его хорде.
Относительной толщиной профиля с называется отношение с = с/b. Положение мак-
симальной толщины на профиле определяется ее абсциссой хс, измеренной от перед-
ней кромки вдоль хорды. Относительная координата максимальной толщины профиля
выражается в долях хорды хс = хс/Ь.
Для определения кривизны или вогнутости профиля проводят среднюю линию
профиля, для чего на хорде выбирается произвольное число точек, через которые
проводят перпендикуляры к хорде. Середины отрезков этих перпендикуляров, огра-
ниченных верхней и нижней сторонами профиля, определяют его среднюю линию.
Максимальное расстояние средней линии от хорды, т. е. стрелка ее прогиба/, опреде-
ляет кривизну профиля. Отношение / =f/b называется относительной кривизной или
вогнутостью профиля. Положение стрелки f определяется абсциссой максимальной
кривизны xf или ее относительной величиной xf= xf/b.
Все относительные геометрические характеристики профиля с, хс, J, лу часто вы-
ражаются в процентах хорды.
Толщина профиля крыльев колеблется от 2 до 20%. Кривизна у профилей обыч-
но не превышает 1...2 и редко 3...4%; кривизна симметричных профилей равна нулю.
Формы крыльев в плане, оказывающие значительное влияние на их аэродинами-
ческие свойства, очень разнообразны. На рис. 2.17 представлены некоторые из них.
Основными геометрическими характеристиками крыла являются его размах /,
площадь в плане S, корневая bQ и концевая Ьк хорды и стреловидность х (рис. 2.18).
Стреловидность крыла обычно определяется углами стреловидности передней кром-
ки крыла Хо> задней кромки Xi и линии фокусов Х1/4» условно проводимой через кон-
цы четвертей хорд крыла, откладываемых от передней кромки. Для прямой стрело-
видности (рис. 2.17, в) угол стреловидности принимается положительным, для обрат-
ной (рис. 2.17, г) — отрицательным. Стреловидность у некоторых крыльев может
изменяться по размаху (крылья с переменной стреловидностью).
Относительное удлинение, или, короче, удлинение крыла X произвольной формы
в плане определяется по формуле X = l2/S; в случае прямоугольного крыла X = 1/Ь. От-
Рис. 2.16. Геометрические параметры профиля
73
Рис. 2.17. Формы
крыльев в плане
ношение корневой хорды крыла bQ к концевой Ьк называется относительным сужени-
ем, или, короче, сужением т|, т. е. Т| = bQ/bK.
Аэродинамическими характеристиками профиля называются аэродинамические
характеристики элемента крыла бесконечного размаха. В общем случае вектор пол-
ной аэродинамической силы Ra, действующей на профиль, можно разложить на две
составляющие (рис. 2.19). В скоростной системе координат это сила сопротивления Ха,
действующая вдоль оси х, направленной параллельно скорости набегающего потока,
и подъемная сила Ya, действующая вдоль оси у, которая перпендикулярна скорости
набегающего потока. По аналогии с введенным выше коэффициентом сопротивле-
ния трения коэффициент сопротивления сха и коэффициент подъемной силы суа опреде-
ляются как
'ха 1 2 И Суа 1 2
(2.69)
В этих формулах в качестве характерной площади S для подсчета коэффициентов
сха и суа используется площадь части крыла бесконечного размаха единичной длины,
т. е. S= b • 1.
Угол, образованный направлением скорости набегающего потока и хордой про-
филя, называют углом атаки а. На рис. 2.19 он положителен. Точку приложения пол-
ной аэродинамической силы Ra условно принимают в точке пересечения ее с хордой
(точка D на рис. 2.19). Эта точка носит название центр давления. Его координата xd,
измеренная вдоль хорды профиля, определяет относительную координату центра дав-
ления xd = xd/b.
Аэродинамические свойства профиля оцениваются его аэродинамическим каче-
ством, или, кратко, качеством К. Аэродинамическим качеством профиля называется
отношение подъемной силы к силе лобового сопротивления К= Ya/Xa, или, исполь-
зуя соотношения (2.69), отношение аэродинамических коэффициентов К = суа/сха.
Эта величина представляет собой тангенс угла наклона полной аэродинамической си-
лы Ra к направлению скорости набегающего потока (см. рис. 2.19).
Момент полной аэродинамической силы относительно передней кромки крыла
Mza называется продольным моментом или аэродинамическим моментом тангажа. Мо-
мент Mza считается положительным, если он стремится повернуть крыло в сторо-
ну увеличения угла атаки а, и отрицательным — в обратную сторону. Положитель-
ный момент называется кадрирующим, а отрицательный — пикирующим. Коэффициент
74
Рис. 2.20. График зависимости
коэффициента подъемной силы
от угла атаки
Рис. 2.19. Составляющие аэродинамической
силы крыла и центр давления
момента тангажа в общем случае связан с действующим моментом тангажа соотно-
шением
(2.70)
= Mza
mza 1 ? ’
где L — условное плечо момента (для профиля это хорда Ь).
Как уже упоминалось ранее, согласно теореме Н. Е. Жуковского, подъемную си-
лу, действующую на профиль, можно рассматривать как силу, действующую на вихрь
или систему вихрей, находящихся в потоке жидкости или газа. Это обстоятельство ле-
жит в основе теоретических методов определения подъемной силы и продольного мо-
мента, действующих на тонкий профиль, установленный под малым углом атаки к
скорости набегающего потока.
При установившемся поступательном движении коэффициент подъемной силы
профиля определяется соотношением
= (2.7D
где с^а = dc^/da = 2л — производная коэффициента подъемной силы по углу атаки; —
угол атаки, при котором суа = 0.
Угол а0 зависит от формы средней линии и практически не зависит от толщины
профиля. Если профиль симметричный, то = 0.
На рис. 2.20 штриховой линией показана теоретическая зависимость суа от а, за-
даваемая соотношением (2.90), сплошной линией — типичная экспериментальная за-
висимость. Абсолютная величина а0 и наклон кривой суа (а), измеренные в аэродина-
мической трубе, оказываются меньше, чем это предсказывается теорией, и составля-
ют примерно 85...90% теоретических данных. Различие между приведенными
величинами объясняется влиянием сил вязкости. С ростом угла атаки эксперимен-
тальные значения суа возрастают почти точно по линейному закону. При значениях а,
превышающих 8... 15°, эта зависимость отклоняется от линейной и после достижения
своего максимального значения суа начинает убывать. Угол, при котором суа достигает
максимального значения (максимальный коэффициент подъемной силы суатю), называ-
ется критическим углом атаки акр.
75
Рис. 2.21. Зависимость
коэффициента
продольного
момента профиля
от коэффициента
подъемной силы
Рис. 2.22. К определению
фокуса профиля
(2.73)
Рис. 2.23. Зависимость
коэффициента Т|с
от относительной
толщины профиля
и положения
точки перехода
При углах атаки, приближающихся к а^, профиль
перестает плавно обтекаться, так как возникающие
большие градиенты давления на верхней стороне вызы-
вают отрыв пограничного слоя (рис. 2.15).
Коэффициент продольного момента профиля cmz
принято представлять в виде зависимости от суа. В ре-
зультате получается график, который в диапазоне
линейной зависимости суа от а чрезвычайно близок
к прямой, следующей из теории (рис. 2.21). Теория
профиля для этой прямой дает уравнение
Cmz ~ CmzO тсуа> (2.72)
где коэффициент продольного момента при нулевой
подъемной силе cmz0 = —л/, а коэффициент т = -0,25.
В действительности cmz0 получается по абсолютной ве-
личине значительно меньше из-за влияния вязкости,
не учитываемой в теории.
Относительная координата центра давления с уче-
том соотношения (2.72) может быть найдена по формуле
V — Cfnz — ™ CmzQ
Xd с т С
''уа уа
Ддя симметричного профиля cmz0 = 0, тогда из
(2.73) следует постоянство положения центра давления
на хорде. Если cmz0 * 0, то центр давления перемещается
вдоль хорды с изменением суа и при суа = 0 он уходит в
бесконечность. На хорде профиля можно найти такую
точку, относительно которой продольный момент на ли-
нейном участке его зависимости от подъемной силы ра-
вен одной и той же величине. Эта точка называется фо-
кусом профиля. Для того чтобы точка F (рис. 2.22) была
фокусом, необходимо, чтобы
xF=—m. (2.74)
Возвращаясь к формуле (2.73), видим, что для
симметричного профиля (cmz0 = 0) центр давления и
фокус совпадают.
При безотрывном обтекании профиля идеальным
несжимаемым потоком коэффициент его лобового со-
противления равен нулю. В реальной вязкой среде воз-
никают сопротивление трения и вызванное вязкостью
сопротивление давления. В первом приближении сопро-
тивление трения равно сопротивлению двустороннего
трения плоской пластины длиной, равной хорде профи-
ля Ь. Минимальное сопротивление профиля будет при
так называемом безударном обтекании. В этом случае
коэффициент сопротивления профиля, обозначаемый
как c^q, можно рассчитать по приближенной формуле
сх»о = 2сЯс, (2.75)
где коэффициент одностороннего трения плоской пластинки cF можно определить по
соотношениям (2.66)...(2.68) или по графику рис. 2.14. Коэффициент Т|с зависит от от-
носительной толщины профиля с и положения точки перехода xt (рис. 2.23).
76
При замене крыла конечного размаха присоеди-
ненным вихрем он должен был бы окончиться вну-
три жидкости на концах крыла, что противоречит
теореме Гельмгольца о вихрях. В первом приближе-
нии крыло можно представить вихревой схемой, по-
казанной на рис. 2.24. Эта схема обычно называется
П-образным или подковообразным вихрем крыла.
П-образный вихрь состоит из фиктивного присоеди-
ненного вихря и продолжающих его реальных сво-
бодных вихрей, которые начинаются у концов крыла
и под прямым углом к размаху уходят от крыла на-
зад. При такой схеме циркуляция Г вокруг крыла во
всех сечениях и вокруг каждого из свободных вихрей
будет одной и той же, что удовлетворяет упомянутой
теореме Гельмгольца. Схема П-образного вихря хо-
рошо согласуется с движением воздуха около крыла,
наблюдаемым в опытах.
Крыло с П-образным вихрем является крылом с
постоянной циркуляцией по размаху. Опыт показы-
вает, что подъемная сила Ya, а следовательно, и цир-
куляция Г распределены по размаху крыла неравно-
мерно. Обычно в середине крыла Г имеет большое
значение, а у концов падает до нуля. Для того чтобы
не нарушалась теорема Гельмгольца, предполагают,
что от присоединенного вихря вдоль всего размаха
ответвляются элементарные свободные вихри, каж-
дый из которых уносит с собой некоторую часть цир-
куляции 6Г, уменьшая циркуляцию присоединенно-
го вихря на эту величину. Таким образом, циркуля-
ция постепенно убывает от Го в середине крыла до
нуля на концах. В результате позади крыла образует-
ся сплошная вихревая пелена (рис. 2.25).
На некотором расстоянии от крыла вихревая
Рис. 2.24. П-образная
вихревая схема крыла
Рис. 2.25. Вихревая пелена
за крылом конечного размаха
индуктивного сопротивления
пелена сворачивается в два вихревых жгута, которые
легко обнаруживаются экспериментально. В конечном счете получаются так называе-
мые вихревые усы за крылом, которые предполагаются П-образной схемой.
Система свободных вихрей, сбегающих с крыла, индуцирует в окружающей среде
некоторое поле скоростей. Вызванные свободными вихрями скорости направлены
вертикально вниз и изменяются по размаху, увеличиваясь к концам. Обозначим сред-
нюю по размаху скорость v. через v/cp. Результирующая от геометрического сложения
скорости v/cp и скорости набегающего поступательного потока Й» скорость Й« отклоня-
ется вниз. В результате возникает скос потока у крыла (рис. 2.26). Средний по размаху
крыла угол скоса Да будет зависеть от величины средней вертикальной скорости vzcp:
tgAa = Aa = v,.cp/K..
Поворот вектора скорости на угол Да должен вызывать такой же поворот векто-
ра подъемной силы (рис. 2.26), который, согласно теореме Жуковского, всегда направ-
лен перпендикулярно истинному направлению скорости набегающего потока, т. е. Й«.
Тогда действительная подъемная сила У/ в проекции на скоростную систему коорди-
нат будет давать действительную поддерживающую силу Ya = Ya' cos Да « Ya\ которую и
называют подъемной силой. Другая проекция силы Ya\ равная Xai = Ya tg Да ~ Ya Да, бу-
77
Рис. 2.27. Влияние удлинения
прямоугольных крыльев
на зависимость коэффициента
подъемной силы от угла атаки
дет направлена по потоку (в сторону, об-
ратную движению крыла). Она называется
индуктивным сопротивлением.
Таким образом, оказывается, что у
крыла конечного размаха, работающего в
идеальной среде, т. е. при отсутствии тре-
ния и отрыва потока, все-таки появляется
сопротивление особого рода благодаря
скосу потока из-за влияния концов крыла.
Формулы для нахождения среднего по раз-
маху значения угла скоса потока Да и ко-
эффициента индуктивного сопротивления
могут быть представлены в виде
&а=суа/(пк) (2.76)
и
cxai=c2ya/(nX). (2.77)
Формула (2.77) является вполне пра-
вильной только для крыльев с эллипти-
ческим распределением циркуляции по
размаху крыла, у которых скос потока
постоянен вдоль размаха и определяется
формулой (2.76). Для всех других крыль-
ев величины Да и cxai несколько больше, чем для крыльев с эллиптическим распреде-
лением циркуляции по размаху крыла. Однако эти отличия невелики.
При малых углах атаки коэффициент подъемной силы крыла конечного размаха
суа изменяется по линейному закону, как и для профиля (см. формулу (2.71)), если
вместо геометрического угла атаки а использовать аэродинамический угол атаки а0 =
= а - Да. Тогда получаем
Cjokp а а0>-
1+-^
Л Л,
(2.78)
Из формулы (2.78) производная суа кр по геометрическому углу атаки а находится как
а
а ____ Суа
Суа кр ~оГ ’
1+-4?
ЯЛ
откуда видно, что с уменьшением относительного удлинения крыла X угол наклона
кривой коэффициента подъемной силы крыла в функции угла атаки а убывает
(рис. 2.27). При этом эксперимент показывает уменьшение суа тах и увеличение акр
с уменьшением X. В случае крыльев малого удлинения (X < 3) кривые суа(а) теряют
свой линейный характер при малых углах атаки и приобретают характерную для них
5-образность. Такой характер кривых объясняется тем, что торцевое перетекание по-
тока с нижней поверхности крыла, где давление повышенное, на верхнюю, где образу-
ется разрежение, приводит к срыву потока, особенно заметному при острых боковых
кромках (рис. 2.28). Этот срыв создает вихревое разрежение, увеличивающее подъем-
ную силу. Подъемная сила крыла малого удлинения при а ~ 10° и выше создается в
меньшей степени за счет циркуляции, связанной со сходом вихревой пелены с задней
кромки, и в большей степени за счет срыва и вихревого обтекания боковых кромок.
78
Рис. 2.28. Перетекание воздуха через боковые
стороны и образование вихревых жгутов
у треугольного крыла малого удлинения
первого рода
Лобовое сопротивление крыла конечного размаха складывается из профильного и
вихревого сопротивлений. При безударном обтекании профильное сопротивление
крыла минимально, и его коэффициент можно найти с помощью формулы (2.75) по
значениям средней хорды и средней толщины крыла. Для коэффициента вихревого или
индуктивного сопротивления используется выражение (2.77). Таким образом, коэффи-
циент сопротивления крыла конечного размаха описывается следующей зависимостью:
сха = СхаО + Cxai = Cxrt + <уа /(лА). (2.79)
График зависимости между коэффициентами подъемной силы и сопротивления
называют полярой первого рода (рис. 2.29). В дальнейшем будем называть ее просто по-
лярой. Обычно на поляре проставляют углы атаки. В линейном диапазоне зависимости
суа от а экспериментальные результаты подтверждают теоретическую формулу, расчет
по которой на рис. 2.29 показан штриховой линией. Коэффициент пропорциональнос-
ти перед cja в формуле (2.79), т. е. 1/(яХ), называют коэффициентом отвала поляры.
2.9. ИЗОЭНТРОПИЧЕСКИЕ ТЕЧЕНИЯ
В случае движения совершенных сжимаемых жидкостей или газов давление р,
плотность р и температура Т связаны уравнением Клапейрона (2.33), внутренняя
энергия Uопределяется по формуле (2.34), теплоемкости при постоянном давлении и
объеме и газовая постоянная удовлетворяют соотношению (2.35). В общем случае не-
обратимых термодинамических процессов, имеющих место при движении газов, рас-
сматривается еще одна термодинамическая характеристика — энтропия, удельная ве-
личина s которой для совершенных газов связана с давлением и плотностью как
s = cv In (р/рк) + const. (2.80)
Так как обычно интерес представляет изменение 5, значение постоянной не су-
щественно.
Процессы, при которых энтропия не меняется, называются изоэнтропическими.
Из (2.80) следует, что при изоэнтропическом процессе в совершенном газе
р/р* = const. (2.81)
Это уравнение называется уравнением изоэнтропы.
Уравнение состояния (2.33) и уравнение изоэнтропы (2.81) позволяют записать
для изоэнтропических процессов в совершенном газе
к 1
р/Т к -1 = const, р/ Т к -1 = const. (2.82)
79
Малые возмущения давления в газе распространяются, не вызывая изменения
энтропии, как упругие волны сжатия — разрежения со скоростью звука
а= Jdp/dp. (2.83)
Видно, что а зависит от закона изменения плотности при изменении давления.
Следовательно, скорость звука может служить характеристикой сжимаемости газа
(чем выше скорость звука в среде, тем меньше ее сжимаемость).
Для изоэнтропических процессов в совершенном газе из (2.81) и (2.83) получаем
а = Jkp/p = JkRT.
Рассмотрим установившееся течение невесомого идеального совершенного газа,
полагая отсутствие теплообмена между его частицами. Такое течение является изо-
энтропическим. Тогда уравнение энергии имеет своим интегралом выражение (2.40).
Учитывая очевидные соотношения
<2-84)
имеем
V2 к о У2 к V2 а2 V2
i + -у = const, j- + -у = const, -j—[RT4- -у = const, £—у 4- -у = const. (2.85)
Термодинамические параметры изоэнтропически заторможенного потока назы-
ваются параметрами торможения и отмечаются как /0, р0, р0, То, а0. Давление тормо-
жения р0 называют также/юлным давлением.
Определяя постоянные в (2.85) из условий изоэнтропически заторможенного по-
тока (И= 0), получаем следующие соотношения:
..Г2 . к р , V2 к Ро к D^.V2 к Dr, а2 .V2 а20
2 °’£-1р 2 £-1р0’£-1 2 к-1 °’ к -1 2 к-I v '
Из соотношений (2.86) видно, что с ростом скорости потока V происходит
уменьшение термодинамических параметров. Полагая в этих соотношениях i = р/р =
= Т= а = 0, находим максимально возможное значение скорости потока Итах
- Ж". - ». <2-8’>
Используя эти формулы, из (2.86) получаем уравнения
. । У _ Ивах к р .У ______ Нпах к туг t У ____ Ивах Л .У _______ Ивах
/ + Ыр Т ГЛ
Разделив обе части первого соотношения (2.88) на И^/2 и учитывая, что по
формуле (2.87) /0 = И^/2, получим выражение
///0=1-(К/Итах)2. (2.89)
Из формул (2.84) следует, что Z/Zo = T/TQ = а//а^. Поэтому
Г/Го = а'/ат- = 1 - (У/У^?. (2.90)
Теперь зависимости давления и плотности от скорости с учетом (2.82) примут
следующий вид:
к 1
р/Ро=[1-(К'Итах)2]ГЛ, р/Ро = [1-(И/Итах)2]ГЛ. (2.91)
80
Зависимости термодинамических параметров от
скорости, построенные по формулам (2.89)...(2.91),
показаны на рис. 2.30.
Разделив обе части четвертого соотношения
(2.88) на а1/(к — 1), получим равенство
-г = 1 + Ц-1 М2, (2.92)
а 2
где М = V/a — число Маха, наряду с числом Рей-
нольдса являющееся основным критерием подобия.
Число Маха, так же как и скорость звука, является ме-
рой сжимаемости движущегося газа. В несжимаемом
потоке скорость звука принимает бесконечно боль-
шое значение, поэтому для него М = 0. При М < 1
течение называют дозвуковым, при М > 1 — сверхзву-
ковым. Течение газа со скоростями, близкими к ско-
Р Р Т
АьРо’ То
Рис. 2.30. Зависимости
термодинамических
параметров от скорости
роста звука, называют трансзвуковым или околозвуковым. Если М = 1, течение называют
звуковым.
Соотношение (2.92) позволяет последовательно получить формулы
? = (1+Ц^м7 1; 7=0+ЛмТ'- (2-93)
При увеличении местной скорости потока от нуля до Итах местная скорость звука
убывает от а0 до нуля. Следовательно, при некоторой скорости потока должны выпол-
няться условия: V = а, М = 1. Сечение, в котором местная скорость потока равна
местной скорости звука, называют критическим. Все газодинамические параметры
в этом сечении называют критическими и отмечают нижним индексом *. Полагая в
соотношениях (2.92) и (2.93) М = 1, получаем формулы, связывающие критические
параметры и параметры торможения:
2 k 1
- Г* - Z* - 2 Р* - ( 2 Р* - ( 2 /О О/П
в2 То i0 к+1’ р0 (л+1) ’ р0 U+1J • (294)
Для струйки с малым поперечным сечением F, в котором все параметры газа
предполагаются постоянными, уравнение неразрывности можно записать в виде
уравнения постоянства массового расхода р VF = const. После его логарифмирования,
последующего дифференцирования, исключения плотности с помощью уравнения
Бернулли (2.37), представленного в виде VdV = —dp/p, и некоторых преобразований
следует равенство
^=(М2-1)^.
Это уравнение устанавливает связь между относительным изменением площади
сечения струйки dF/F, скорости dK/Ии числом М.
В дозвуковом потоке М < 1 и, следовательно, М2 — 1 < 0. Приращения площади
dF и скорости d V имеют противоположные знаки. Это означает, что при расширении
струйки (dF> 0) скорость уменьшается (dV< 0), а при сужении (dF< 0) — увеличива-
ется (dV> 0).
Когда поток сверхзвуковой (М > 1, М2 — 1 > 0), знаки приращений площади dFn
скорости d Vодинаковы. Следовательно, при расширении струйки скорость увеличи-
вается, а при сужении — уменьшается.
Из сказанного следует, что для непрерывного увеличения скорости от дозвуковой
до сверхзвуковой площадь проходного сечения струйки должна сначала уменьшаться,
81
Рис. 2.31. Изменение скорости
и давления в сопле Лаваля
для Р,ь.« с Р„ (0. Р.ых > рн (2)
и в режиме трубки Вентури (3)
а затем увеличиваться. Эти закономерности ре-
ализованы в сопле Лаваля (рис. 2.31). Для его нор-
мальной работы (расчетный режим) необходимы
следующие условия: самое узкое сечение сопла
Лаваля АА должно быть критическим (скорость
потока и скорость звука равны); давление на вы-
ходе из сопла рвых, определяемое формой сопла и
параметрами торможения газа на его входе, рав-
няется наружному давлению рн. При />вых > рн ре-
ализуется режим недорасширения. Течение вну-
три сопла на этом режиме не отличается от рас-
четного, но за выходным сечением струя
продолжает расширяться. Условие рвых < рн соот-
ветствует режиму перерасширения. При этом на
сверхзвуковом (расширяющемся) участке сопла
образуется скачок уплотнения, при переходе че-
рез который течение становится дозвуковым.
Торможение сверхзвукового потока сопро-
вождается появлением скачков уплотнения и рос-
том энтропии (см. следующий раздел). Поэтому
параметры газа, наблюдаемые при физическом
торможении сверхзвукового потока, нельзя считать
его параметрами торможения. Но всегда можно
осуществить изоэнтропический разгон газа из со-
стояния покоя до заданной сверхзвуковой скорос-
ти. Параметры этого неподвижного газа и считают
параметрами торможения сверхзвукового потока.
Другим примером изоэнтропического течения
служит случай обтекания выпуклого угла сверхзву-
ковым потоком. Рассмотрим однородный сверх-
звуковой поток идеального газа, обтекающего вы-
Рис. 2.32. Обтекание выпуклого
угла сверхзвуковым потоком
пуклый угол, образованный плоскими стенками АО и ОВ (рис. 2.32). Расчеты показыва-
ют, что поворот потока происходит плавно в пределах области между линиями слабых
возмущений ОС и OD. Такое течение называют течением Прандтля-Майера. Оно хоро-
шо изучено. Имеются формулы, таблицы и графики, позволяющие легко определять
значения газодинамических переменных во всей области течения. Угол 9, при повороте
на который звуковой поток (М = 1) разгоняется до скорости Итах, называют максималь-
ным углом поворота потока 0тах. Для воздуха (к = 1,4) 0тах = 130,4°.
2.10. ТЕОРИЯ СКАЧКОВ УПЛОТНЕНИЯ
При движении тел со сверхзвуковой скоростью перед ними возникает ударная
волна (рис. 2.33, а). Перед ударной волной газ не возмущен. Область между волной и
телом является областью сильно возмущенного движения. Здесь давление, плотность
и температура намного больше, чем в невозмущенном газе.
В обращенном движении, когда невозмущенный поток набегает на неподвижное
тело (рис. 2.33, б), ударную волну называют скачком уплотнения. При пересечении
скачка уплотнения давление, плотность и температура потока скачкообразно возрас-
тают, а скорость и число Маха скачкообразно уменьшаются, причем скорость может
изменить направление.
82
Угол между вектором скорости невозмущенного потока и плоскостью, касатель-
ной к скачку (не превышающий я/2), называют местным углом наклона скачка и обо-
значают Р (рис. 2.33, б). Угол между векторами скорости до и после скачка обознача-
ют 9 и называют местным углом поворота потока.
При обтекании тел с затупленной головной частью всегда возникают отсоединен-
ные скачки уплотнения (рис. 2.33, б). На тонком заостренном теле (например, в фор-
ме клина) может образовываться присоединенный скачок (рис. 2.34).
В дальнейшем ограничимся рассмотрением плоских скачков уплотнения, имею-
щих вид бесконечной плоскости. Для них углы 0 и р остаются постоянными вдоль
скачка.
Скачок называют прямым, если он перпендикулярен скорости потока, т. е. 0 = я/2.
В этом случае направление течения за скачком не изменяется (р = 0). В случае 9 < я/2
имеем косой скачок уплотнения.
Так как при возникновении скачков уплотнения нарушается предположение о не-
прерывности функций, описывающих изменение газодинамических параметров, нель-
зя применять уравнения неразрывности, движения и энергии, выведенные выше. Для
таких течений можно использовать так называемый метод контрольного объема.
Выделим контрольный объем A BCD EGA (рис. 2.35), боковые грани которо-
го ограничены линиями тока, а торцы AG и CD параллельны плоскости скачка. Так
как все газодинамические параметры до скачка, отмеченные нижним индексом 1,
и после скачка с нижним индексом 2 постоянны, закон сохранения массы принима-
ет вид
РЛ1 Р2^л2’
(2.95)
Рис 2.33. Движение тела со сверхзвуковой
скоростью (а) и обтекание тела
сверхзвуковым потоком (б)
Рис. 2.34. Присоединенный
скачок уплотнения
Рис. 2.35. Контрольный объем
для вывода основных соотношений
на скачке уплотнения
83
и, соответственно, проекции уравнения движения, выражающего закон изменения
количества движения, и уравнение энергии запишутся как
Р,+Р1^,2=Р2 + Р2^22> (2-96)
Р1^1 = Р2^2^ (2-97)
И2 У2
h + ^=h+^- (2-98)
В последнем соотношении
Из уравнений (2.95) и (2.97) следует важное равенство
И(| = И,2=И„ (2.99)
которое означает, что касательная составляющая скорости при переходе через скачок
не изменяется.
Уравнение энергии (2.98) позволяет сделать заключение о постоянстве во всей
области течения энтальпии торможения и связанных с ней соотношениями (2.84)
других термодинамических параметров или их комбинаций
zoi = z02= z0’ Г01 = Т02 = Tq, а01 = а02 = а0, Poi/Poi = Рог /Рог- (2.100)
Так как параметры торможения однозначно связаны с критическими параметра-
ми формулами (2.94), то при переходе через скачок уплотнения сохраняют свои зна-
чения /*, Т*, а*.
Учитывая равенство (2.99) и связи (2.94), уравнение энергии можно записать в
следующих эквивалентных формах
• + = • + ^ к р' - к Р2 ^уп22 _к+\а2 У2
1' 2 Z2“r2’A:-lp12 к - 1 р2 2 Ы 2 2 ’
(2.101)
£ DT । DT ।
Уп\ _ *2 Уп\
2 к-\ 2 ’
Исключая из уравнения неразрывности (2.95), первого уравнения движения
(2.96) и второй формы уравнения энергии (2.101) давления и плотности до и после
скачка и учитывая равенство (2.99), приходим к основному соотношению для плоских
скачков
Ия1Кя2 = а?-^ГД (2.102)
В случае прямого скачка уплотнения И, = 0, VnX = Vx, Vnl = И2 и вместо соотноше-
ния (2.102) имеем
VxV2 = al. (2.103)
Так как Vx > а*, то из последнего равенства следует, что И2 < а*, т. е. за прямым
скачком уплотнения скорость всегда дозвуковая. Причем чем больше скорость перед
скачком, тем меньше скорость за ним. Подставляя в (2.103) Vx = Kmax, получим пре-
дельную минимальную скорость за скачком
В случае воздуха, когда к = 1,4, из полученной формулы находим, что Kmin2
= 0,41а*.
84
Из сравнения формул (2.102) и (2.103) видно, что на косом скачке уплотнения
нормальная составляющая скорости уменьшается в большей мере, чем на прямом.
Однако поток за косым скачком уплотнения при малых 0 может остаться сверхзвуко-
вым вследствие большого значения касательной составляющей скорости, не изме-
няющейся при переходе через скачок.
Соотношения давлений, плотностей и температур до и после скачка находятся из
уравнений (2.95), (2.96), (2.99), (2.101) и (2.33):
Р_1 = Щ2 sjn2 R _ ______I
рх к + 1 Mi Sin Р к + 1
Р2 = Г 2 + *-Г1 -I
Pi 1(Л + l)M|Sin2P * + 1J ’
(2.104)
II
Т\
Р2Р1 _ ( 2к ..2 . 2а к-1) Г 2 , *-Г]
Р1Р2 U+1 1 Р *+1J ЦЛ + l)Mjsin2p * + lJ’
Из этих формул следует, что с увеличением Mj sin 0 давление и температура за
скачком растут неограниченно. Плотность также увеличивается, но не беспредельно.
При Mj sin 0—> 00 из (2.104) получаем
Р2 А-Н
Pi
Для воздуха р2/р! —* 6, если принять, что £=1,4.
Неизменность касательной и уменьшение нормальной составляющей скорости
при переходе через скачок уплотнения приводят в общем случае к скачкообразному из-
менению не только величины, но и направления скорости. Из рис. 2.33, б следует, что
tg (₽ - о) = тД2 tg р.
"1
Учитывая соотношения (2.102), (2.94), (2.92) и очевидные геометрические соот-
ношения (см. рис. 2.33, б), получаем выражение
tg (Р - 0) = + гтт> Р-
-г 1 Mj sin20 Л -г
На рис. 2.36 приведен график этой зависимости. Штриховая линия здесь прове-
дена через точки, соответствующие максимальным значениям 9, при которых скачок
остается присоединенным и плоским.
Из рисунка видно, что при заданном числе Маха каждому углу 9 < 9max (Mj) соот-
ветствуют два значения угла 0. Дополнительные исследования показывают, что чаще
всего реализуются слабые скачки уплотнения, которым соответствуют меньшие зна-
чения 0.
Штрихпунктирная линия на этом рисунке соединяет точки кривой, для которой
М2 = 1. Если 0 оказывается в области, расположенной выше этой линии, то за скач-
ком течение будет дозвуковым, если ниже — сверхзвуковым.
На основании (2.199) при переходе через скачок остается неизменным отноше-
ние Ро/Ро- Однако полное давление р0 и плотность изоэнтропически заторможенного
потока р0 за скачком будут меньше, чем до скачка. Это связано с необратимым пере-
ходом на скачке части кинетической энергии потока в теплоту.
85
Рис. 2.36. Зависимость угла поворота
потока от угла наклона скачка
при различных числах Маха
Рис. 2.37. Зависимость коэффициента
изменения полного давления
от параметра Mtsin(3
Потери полного давления на скачке характеризуют коэффициентом изменения
полного давления
ъ=Ро2/Ры- (2.105)
По определению полные давления — давления изоэнтропически заторможенных по-
токов. Поэтому из формул (2.93), (2.103) и (2.105) выражение для о преобразуется к виду
о =
к
Г 2* 2 . 2r к~ П1 ~к ( 2к 1
U+1 1sin Р fc+J U+lM?sin2P
к —
к + \)
к
На рис. 2.37 приведен график изменения о с ростом Mj sin р. С увеличением
Mj sin р растет интенсивность скачка, увеличиваются потери кинетической энергии,
приводящие к уменьшению давления торможения за скачком и снижению о.
Необратимые потери давления торможения за скачком вызывают увеличение
энтропии в этой области течения. Использование формул (2.80), (2.100) и определе-
ния а позволяет получить формулу
Ду = s2 - 5, = ev In gglj] = -cv In <j.
Так как при Mj sin p > 1 коэффициент изменения полного давления а < 1, и из
последней формулы следует, что As > 0, т. е. течения со скачками уплотнения — неизо-
энтропические течения.
2.11. ПОТЕНЦИАЛЬНЫЕ ТЕЧЕНИЯ
ИДЕАЛЬНОГО СЖИМАЕМОГО ГАЗА
Распространение возмущений давления от непрерывно действующего непо-
движного точечного источника слабых возмущений, расположенного в точке О, в по-
коящемся газе (V= М = 0) происходит во всех направлениях с одинаковой скоростью
а, образуя систему концентрических волн с центром в точке О (рис. 2.38).
В дозвуковом потоке (0<М< 1, 0 < V < а) волны возмущения давления, сохраняя
сферическую форму, сносятся вниз по потоку со скоростью Vи занимают последователь-
но положения, показанные на рис. 2.39. Здесь возмущения распространяются во все сто-
роны, в том числе навстречу потоку, и с течением времени они охватывают весь поток.
В звуковом потоке (М = 1, V= а) скорость сноса волн возмущения давления рав-
на скорости увеличения их радиуса (V= а), и волны возмущений образуют семейство
сфер, касающихся нормальной к направлению потока плоскости АА, проходящей че-
86
рез точку О (рис. 2.40). В этом случае возмущения распространяются только в облас-
ти, лежащей вниз по потоку от указанной плоскости.
В сверхзвуковом потоке (М > 1, V > а) волны возмущений за время t сносятся
вниз по потоку на расстояния, превышающие их радиус, соответствующий этому мо-
менту времени. Возмущения в этом случае распространяются в ограниченной облас-
ти, огибающей всю последовательность волн возмущений. Эта огибающая имеет вид
конуса с углом при вершине ц (рис. 2.41). Из данного рисунка следует, что угол ц удов-
летворяет условию
sinp = ar/(P7) = a/K= 1/М.
Тогда
tgjx= 1/л/м 2 — 1. (2.106)
Рассматриваемую поверхность называют конусом возмущений или конусом Маха,
линии пересечения с плоскостями, проходящими через ось конуса, — линиями Маха,
угол ц между линией Маха и вектором скорости невозмущенного потока — углом Маха.
Из рис. 2.41 видно, что Vn = Ksin ц = а, следует, что нормальная к конусу
возмущений скорость набегающего потока Vn будет равна скорости звука а.
Для стационарного течения невесомого баротропного газа, когда р = р(р), урав-
нение неразрывности (2.18) и уравнение движения (2.31) с помощью соотношения
(2.73) сводятся к виду
(и2-а2)^- +(v2-a2)^ + (w2-fl2)^ +
v ’ ox v ’ dy v 7 dz
+ uv
fdu . . (dv
fe + + v"U
(2.107)
Рис. 2.38. Распространение слабых
возмущений в неподвижном газе
Рис. 2.40. Распространение слабых
возмущений в звуковом потоке
возмущений в дозвуковом потоке
Рис. 2.41. Распространение слабых
возмущений в сверхзвуковом потоке
87
Величина а1 выражается через составляющие скорости с помощью четвертой
формы уравнения энергии (2.88). Уравнение (2.107) справедливо как для безвихрево-
го, так и вихревого движений.
В случае безвихревого движения необходимо присоединить еще условие отсутст-
вия вихря. Это условие эквивалентно тому, что существует потенциал скоростей ф =
= ф(х, у, z), с помощью которого компоненты вектора скорости И выражаются соотно-
шениями (2.39). Тогда уравнение (2.107) принимает следующую форму:
2 2 2 2 2 2
(и2-а2)^ +(v2-fl2)^ + (и>2-я2)^-у 4-2fwv^-X + 1=0. (2.108)
дх2 Эу2 dz V dxdy dydz azox ) v 7
Величина а2 снова исключается с помощью уравнения энергии. В соответствии
с (2.39) составляющие скорости выражаются через частные производные потенциала
скоростей ф. Таким образом, уравнение (2.108)— нелинейное дифференциальное
уравнение относительно функции ф. Однако в него старшие производные искомой
функции входят линейно, поэтому его называют квазилинейным дифференциальным
уравнением второго порядка с частными производными. В общем случае для решения
такого уравнения требуется использование численных методов.
Во многих аэрогазодинамических задачах большой интерес представляет опреде-
ление возмущений, налагаемых на известное движение газа. В качестве такого движе-
ния чаще всего выбирается установившееся движение с постоянной скоростью иж.
Выберем систему координат, в которой эта скорость направлена параллельно оси х.
Плотность, давление и температура при этом исходном движении также имеют посто-
янные значения и обозначаются соответственно через , рж и Тж. Соответствующая
скорость звука равна ах, а число Маха — = ujаж.
Поле скоростей исходного течения определяется равенствами и = woo,v = 0,w = 0,
которому отвечает потенциал скоростей ф^ = ижх.
Если в этот однородный поток помещается некоторое твердое тело, например,
крыло, оно вызывает возмущения исходного течения и изменяет поле его скоростей.
Поле скоростей в присутствии тела можно представить как
и = иж +u',v= v,w = w'. (2.109)
Величины и, v' и w называют скоростями возмущения, а определяемое ими
течение — возмущенным течением.
Если вносимое в поток тело имеет малую относительную толщину и установлено
в нем под малым углом атаки, то почти во всей области течения выполняется предпо-
ложение
и v w
и ’ и ’ и
•*оо а
(2.110)
Сделаем дополнительное предположение о том, что возмущенное течение без-
вихревое, так что существует потенциал возмущенного течения ф’, определяемый ра-
венствами
(2.1Н)
, Эф' , Эф' , Эф'
Подставляя в уравнение (2.108) равенства (2.109) и (2.111), учитывая предполо-
жение (2.110) и пренебрегая членами, содержащими квадраты и произведения ско-
ростей возмущения, считая их малыми по сравнению с членами, содержащими пер-
вые степени, представим его в виде линейного уравнения
(1_м2А + ^ + ^-'=о.
Эх э/ э?
(2.112)
88
Более точный анализ показывает, что
уравнением (2.112) нельзя пользоваться при
трансзвуковых течениях, когда —> 1.
Так как основное дифференциальное
уравнение потенциального движения сжи-
маемого газа подверглось линеаризации, то
уравнение Бернулли, эквивалентное в этом
случае уравнению энергии, также может быть
упрощено. Существует несколько способов
его линеаризации, которые приводят к одной
и той же формуле р = рж — ижи. Тогда ко-
эффициент давления для линеаризованных
сжимаемых течений в соответствии с форму-
лой (2.53) можно записать как
cp = -2(u'/uj. (2.113)
В качестве примера сверхзвукового по-
тенциального течения рассмотрим обтекание
тупых углов (рис. 2.42). Считая угол поворота
потока во внешнюю сторону 0 > 0 (рис. 2.42, а),
б)
Рис. 2.42. К определению
изменения давления при отклонении
сверхзвукового потока на малые углы
а во внутреннюю 0 < 0 (рис. 2.42, б) малым, можно использовать линеаризованное
уравнение (2.112). Веер волн разрежения в течении Прандтля—Майера (рис 2.42, а)
становится очень узким, и можно принять, что он совпадает с линией Маха набегаю-
щего потока. В течении сжатия (рис. 2.42, б) из-за малости угла поворота потока 0
скачок уплотнения вырождается в слабую волну сжатия, наклоненную под углом Ма-
ха к направлению движения невозмущенного потока.
Так как течение плоское, то его характеристики не зависят от координаты z и
w = 0. В этом случае > 1 и уравнение (2.112) будет гиперболического типа, поэто-
му его решение можно находить в виде
где >2 = У +х tg ц, a tg ц определяется в (2.106) для Мто.
Функция /2(^) описывает распространение возмущений влево, т. е. навстречу
набегающему потоку, что физически невозможно. Поэтому ее исключают из рассмот-
рения. Тогда составляющие возмущенных скоростей определяют как
и = Эф’/Эх = - /1 tg р, v’ = Эф’/Эу = /.
Точка над функциейозначает дифференцирование по переменной Исклю-
чая из двух последних равенств /, имеем
и=— v’tgp. (2.114)
Геометрические соображения, используя рис. 2.42, позволяют записать
tg0 = 0 =---(2.115)
В этом соотношении первый знак относится к течению разрежения (рис. 2.42, а),
второй — к течению сжатия (рис. 2.42, б).
Исключение из (2.114) и (2.115) составляющей возмущенной скорости v приво-
дит к равенству
«' = “„etg ц,
89
подставляя которое в выражение для коэффициента давления в линеаризованной за-
даче (2.113) получаем формулу
ср = -20 tg ц = -20/7м 2-1. (2.116)
В соответствии с физикой явления в течениях с расширением (0 > 0) давление
понижается и ср < 0, в течениях со сжатием (0 < 0) происходит возрастание давления и
ср > 0, что согласуется с формулой (2.116).
2.12. АЭРОДИНАМИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПРОФИЛЕЙ
И КРЫЛЬЕВ КОНЕЧНОГО РАЗМАХА В ДОЗВУКОВОМ
И СВЕРХЗВУКОВОМ ПОТОКАХ
Рассмотрим для простоты обтекание симметричного профиля, расположенного
под нулевым углом атаки к скорости невозмущенного сжимаемого дозвукового потока
невязкого газа. В этом случае нулевая линия тока перед и за профилем будет прямоли-
нейной, совпадающей с осьюх, вдоль которой направлена скорость их набегающего по-
тока (их < аж, < 1, см. рис. 2.43). Такое течение можно считать изоэнтропическим.
Перед профилем поток замедляется до нулевой скорости на передней кромке. За-
тем она возрастает вдоль поверхности профиля до максимальной скорости, большей
скорости набегающего потока. После этого при безотрывном обтекании скорость
снова убывает до нуля на задней кромке. В следе за профилем происходит рост ско-
рости до ее значения в набегающем потоке. На рис. 2.43 такое изменение скорости
показано сплошной линией. Так как в кормовой части профиля может возникать от-
рыв потока, то в области около задней кромки скорость снижается не до нуля (см.
штриховую линию на рис. 2.43).
В соответствии с изоэнтропическими соотношениями (см. п. 2.9) при убывании
скорости потока местная скорость звука возрастает и наоборот. Максимальное значе-
ние скорости звука будет в точках торможения потока. Наименьшее значение скорости
звука достигается на поверхности профиля в точке максимума скорости (см. рис. 2.43).
При некоторых значениях числа Маха набегающего потока будет выполняться ус-
ловие wmax < В этом случае во всей области потока течение будет дозвуковым.
Если скорость набегающего потока возрастет до и'ж, то произойдут количествен-
ные изменения распределения местной скорости потока и местной скорости звука,
показанные на рис. 2.43 штрихпунктирной линией. При этом может оказаться, что
w max = а min- Число Маха невозмущенного дозвукового потока, при котором где-либо
на поверхности обтекаемого тела впервые местная скорость потока становится равной
скорости звука, называется критическим числом Маха и обозначается через М*.
Величина М* зависит от формы профиля и его относительной толщины с, рас-
стояния максимальной толщины от передней кромки профиля хс и угла атаки. Для
крыла конечного размаха критическое число Маха М* зависит еще от угла стреловид-
ности и удлинения крыла.
Так как местная скорость потока впервые станет равной скорости звука в той же
точке на поверхности, в которой она имеет при заданной скорости набегающего пото-
ка максимальную величину, то в этой точке давление будет минимальным. Тогда ми-
нимальному значению давления соответствует минимум коэффициента давления
cpmin. Минимальное давление будет меньше давления в набегающем потоке, поэтому
минимальное значение коэффициента давления ср min < 0.
90
С. А. Христианович установил связь
между М* и минимальным коэффициен-
том давления на поверхности обтекаемого
тела в условиях несжимаемого потока
Ср min нсж (Рис- 2.44).
В зависимости от величины числа Ма-
ха набегающего потока различают: дозву-
ковые течения (Мм < М*); трансзвуковые
течения (М* < Моо< 1,2); сверхзвуковые
течения (1,2 < < 5); гиперзвуковые
течения (Мм > 5).
Когда тонкий профиль установлен
под малым углом атаки к скорости набе-
гающего потока, можно использовать ме-
тод малых возмущений, описанный в пре-
дыдущем пункте. Потенциал скоростей
возмущенного течения для дозвукового
или сверхзвукового режима удовлетворя-
ет уравнению (см. (2.112))
=0. (2.117)
Эх ду
Рис. 2.43. К определению
критического числа Маха
с
pmin нсж
-2,0-
-1,5 -
-1,0
—0,5-
0---------1---1----1---1----►
0,4 0,5 0,6 0,7 0,8 М»
Рис. 2.44. Зависимость критического числа
Маха от минимального коэффициента
давления в несжимаемом потоке
В дозвуковом потоке (Мм < М* < 1)
уравнение (2.117) можно привести к урав-
нению Лапласа, производя замену пере-
менных. Известно, что уравнению Лапласа
удовлетворяет потенциал скорости потока несжимаемой жидкости (см. п. 2.6). Пользуясь
уравнением Лапласа, можно найти потенциал скоростей потока несжимаемой жидкости,
обтекающей некоторый новый контур. Этот новый контур будет иметь ту же хорду Ь, что
и исходный профиль. Все его поперечные координаты, следовательно, и толщина воз-
растут в 1/J1-M~ раз, так что максимальная толщина нового профиля с , будет связана с
максимальной толщиной исходного профиля с соотношением cl = c/^l—М^. В таком
же соотношении увеличивается и угол атаки а1? т. е. а) = а/ а/1-М^ .
Такие преобразования приводят к тому, что подъемная сила для профиля в сжи-
маемом газе и подъемная сила для утолщенного профиля, установленного под увели-
ченным углом атаки в несжимаемой жидкости, одинаковы.
Если один и тот же профиль располагается при равных углах атаки в сжимаемом
газе и несжимаемой жидкости, то между коэффициентами сил и моментов этих про-
филей существуют следующие связи:
__ Суа нсж ОС _________ Суа нсж __ нсж
(2.1 IS)
Первое и последнее соотношения в (2.118) позволяют заключить, что фокус про-
филя в дозвуковом потоке не зависит от М^, т. е. xF = хГнсж, так как увеличение подъ-
емной силы и продольного момента происходит в одинаковой мере.
91
В этом диапазоне чисел Маха с ростом сопротивление трения профиля убыва-
ет, а сопротивление давления возрастает. Для профилей средней толщины эти тенден-
ции примерно одинаковые, и их коэффициент сопротивления в дозвуковом потоке ос-
тается приблизительно постоянным. В случае тонких профилей возрастание сопротив-
ления давления происходит медленнее уменьшения сопротивления трения, что
приводит к незначительному уменьшению их коэффициентов сопротивления. При об-
текании толстых профилей коэффициент сопротивления слабо возрастает, так как со-
противление давления увеличивается быстрее, чем снижается сопротивление трения.
В трансзвуковом диапазоне чисел Маха (М* < < 1,2) возникают зоны местных
сверхзвуковых скоростей, которые замыкаются местными скачками уплотнения. При
этом наличие необратимых потерь в скачках уплотнения вызывает дополнительное со-
противление, называемое волновым сопротивлением. Коэффициент лобового сопротив-
ления сха начинает резко возрастать, увеличиваясь в несколько (иногда в 15...20) раз.
Зона местных сверхзвуковых скоростей при а > 0 вначале образуется на верхней по-
верхности профиля. Это приводит к повышению давления за замыкающим ее скачком
уплотнения, что вызывает уменьшение коэффициента подъемной силы по сравнению с
зависимостью (2.118). С ростом интенсивность скачка увеличивается, увеличивают-
ся и вызванные им потери подъемной силы, что приводит к снижению суа или с^а. Затем
появляется местная сверхзвуковая зона снизу. Повышение давления за замыкающим ее
скачком вначале замедляет уменьшение подъемной силы, а затем приводит к ее росту.
Фокус крыла в трансзвуковом диапазоне чисел начинает резко перемещаться
вдоль хорды профиля. Обычно сначала он передвигается вперед, а затем назад. Опи-
санные выше изменения аэродинамических характеристик профиля вместе с вызы-
вающими их причинами принято называть волновым кризисом.
В сверхзвуковом потоке > 1 и уравнение для потенциала возмущенных ско-
ростей (2.117) становится гиперболическим в противоположность дозвуковому режи-
му, когда оно являлось эллиптическим. Это приводит к тому, что картины течения
около всякого тела, в том числе около профиля, в дозвуковом и сверхзвуковом пото-
ках оказываются различными.
Если в сверхзвуковой поток поместить тонкую пластину (? = 0), поставив ее под
некоторым малым углом атаки, то картина ее обтекания будет такой, как она пред-
ставлена на рис. 2.45. Волна сжатия (слабый скачок уплотнения) появится снизу, где
линии тока образуют углы, меньшие 180°. Сверху, где происходит поворот потока око-
ло угла, большего 180°, возникнет веер волн разрежения. Вдоль самой пластины, как
сверху, так и снизу, поток остается параллельным, давления и скорости постоянны
вплоть до задней кромки, где поворот потока происходит в обратном порядке.
Так как на передней кромке пластины сверху поток поворачивается на угол 0В =
= а, а снизу — на угол 0Н = —а, то по формуле (2.116) коэффициенты давления на
верхней и нижней поверхностях пластины равны соответственно
Срв = -2а/- 1, cpH = 2а/- 1.
Результирующая аэродинамическая сила давления будет перпендикулярна пласти-
не или ее хорде. Такая сила называется нормальной силой и обозначается через Y. Коэф-
фициент этой нормальной силы су равняется площади фигуры, образованной графиком
распределения коэффициента давления на профиле единичной хорды. Для плоской
пластины соответствующий подсчет можно произвести непосредственно; в результате
имеем
Cy=4a/jMj-l. (2.119)
92
Рис. 2.45. Картина обтекания плоской
пластины под малым углом атаки
в сверхзвуковом потоке
Рис. 2.46. Картина обтекания ромба
под нулевым углом атаки
в сверхзвуковом потоке
С учетом малости угла атаки коэффициент подъемной силы суа = су cos а = су и
тогда, используя формулу (2.119), запишем
суа = 4а/- 1, с“ = 4/Jm* - 1. (2.120)
Проекция нормальной силы пластины на направление скорости набегающего
потока имеет название волнового индуктивного сопротивления, а его коэффициент оп-
ределяется как
с^в1 = суыпа~суи.
Тогда с учетом (2.119) получим
^/=4a2/jMj - 1. (2.121)
Если из выражений для суа и схав1 исключить угол а, то получается следующая
формула:
2
с . = —______С
xaei 4 ya ’
что означает, как и для индуктивного сопротивления крыла конечного размаха в не-
сжимаемом течении, квадратичную связь между индуктивной составляющей волно-
вого сопротивления профиля в сверхзвуковом потоке и подъемной силой.
Так как давление распределено по длине пластины равномерно, то точка прило-
жения результирующей сил давления, а следовательно, и фокус находятся в средней
точке хорды, т. е.
Xf=1/2. (2.122)
Анализ обтекания тонкого профиля (? Ф 0) приводит к тем же формулам (2.119)—
(2.122), независимо от его формы и величины ?.
По формуле (2.121) для a = 0 следует равенство нулю коэффициента волнового
индуктивного сопротивления. Однако, если ? Ф 0, перед профилем при a = 0 будут об-
разовываться слабые скачки уплотнения (рис. 2.46), что приведет к волновому сопро-
тивлению, которое называют волновым нулевым сопротивлением XaeQ.
Для ромба при a = 0 качественная картина обтекания представлена на рис. 2.46.
Вдоль каждой стороны ромба скорость и давление не меняются. Углы поворота пото-
ка относительно направления невозмущенного потока на передней части профиля
как сверху, так и снизу будут одинаковыми и равными 0, = —а. На кормовой его части
эти углы равны 02 = а. В результате простых подсчетов с использованием формулы
(2.116) и малости угла а приходим к следующему выражению для коэффициента вол-
нового нулевого сопротивления ромбовидного профиля в сверхзвуковом потоке:
^ = ^77м--1- (2.123)
93
Если профиль имеет форму, отличную от ромба, то линейная теория приводит к
формуле
cxae0 = ^K/jMi - 1,
(2.124)
где К — коэффициент формы профиля. Наименьшее значение К = 1 имеет место для
ромбовидного профиля, когда (2.124) переходит в (2.123). Для всех остальных профи-
лей К > 1.
Волновое сопротивление Хав состоит из суммы волнового индуктивного и волно-
вого нулевого сопротивлений, поэтому его коэффициент сопротивления с учетом
(2.121) и (2.123) выражается как
= схав0 + Cxaei = 4(KS2 + а2)/7мГП.
На рис. 2.47 приведена качественная зависимость основных аэродинамических
характеристик профиля в дозвуковом, трансзвуковом и сверхзвуковом диапазонах
скоростей полета.
При переходе от профиля к крылу конечного размаха в основном изменяются две
характеристики крыла: с^а и cxaj.
Для стреловидного крыла с углом стреловидности по передней кромке %0 в ос-
новном изменяется составляющая скорости потока по нормали к передней кромке
крыла, что приводит к уменьшению его подъемной силы. Если сравнивать стреловид-
ное и прямое крылья при одинаковых углах атаки и одинаковых формах профилей
в сечениях, параллельных скорости набегающего потока, то их основные аэродина-
мические характеристики в несжимаемом потоке будут связаны между собой соотно-
шениями
СУаХ ~~ СУа прям Хо’ Суах~ Суа прям Хо» Сха^ ~ Сха прям’ Cmzx ~ ^тгпрям %q- (2.125)
Поскольку cmz и суа изменяются одинаково и пропорционально cos %, то фокус
стреловидного крыла сдвигается назад от носка корневой хорды на величину, равную
X tg х/4 хорды.
При определении дозвуковых характеристик стреловидных крыльев конечного
размаха дополнительно следует учесть, что сжимаемость воздуха влияет на них только
через поток, нормальный к передней кромке крыла, число Маха которого равно
cos %. Тогда из соотношений (2.78), (2.118) и (2.125) можно записать
При % = 0 и = 0 эта формула переходит в формулу (2.78), справедливую для
прямого крыла и несжимаемого потока.
Поделив обе части равенства (2.126) на X и выполнив преобразования, имеем
Суа кр
са
уа нсж
(2.127)
са
уа нсж
Коэффициент индуктивного сопротивления для всех крыльев конечного размаха
в дозвуковом сжимаемом потоке может быть с достаточной точностью выражен той
же формулой (2.77), что и в несжимаемом потоке.
94
Рис. 2.47. Качественная зависимость
основных аэродинамических
характеристик профиля во всем
диапазоне изменения чисел Маха
Обтекание крыла сверхзвуковым потоком сопровождается образованием около
него систем слабых скачков уплотнения и волн разрежения, которые создают качест-
венно иную, чем на дозвуковых скоростях, картину распределения давления.
На рис. 2.48 показана часть передне-боковой кромки крыла произвольной фор-
мы в плане. Каждая точка кромки является источником возмущений, распространяю-
щихся внутри конических волн, следы которых на плоскости рисунка показаны
штриховыми линиями.
Часть кромки BD встречает невозмущенный поток, другая его часть АВ встреча-
ется с потоком, предварительно прошедшим через волны, возникающие в точках
кромки, расположенных выше по течению. Скорости, давления и другие параметры
газа в этой части потока начнут изменяться еще до того, как частицы газа подойдут
к кромке АВ, подобно тому, как это происходит при дозвуковом обтекании.
Из рис. 2.48 видно, что на кромке АВ касательная к кромке крыла образует с на-
правлением скорости их слишком острый угол у < LV Поэтому составляющая скорос-
ти, нормальная к кромке,
1 floo
V„= «« sin у < и sin и = w = и — = а.
fl оо | оо ”оо оо °° U ОО "
т. е. нормальная составляющая меньше скорости звука в невозмущенном потоке Vn < аж.
Такие кромки принято называть дозвуковыми. Наоборот, участок BD, как видно из того же
рисунка, встречает поток под углами у > поэтому во
всех точках этого участка кромки Vn > Такие участ-
ки кромки называют сверхзвуковыми.
Простейшей формой крыла конечного размаха
является форма тонкой прямоугольной пластины
(рис. 2.49). Передняя кромка такого крыла будет сверх-
звуковой, а боковые — дозвуковыми. Возмущения от
боковых кромок будут распространяться внутри кону-
сов Маха с вершинами в угловых точках крыла а и ах.
Это приведет, как и в дозвуковом потоке, к выравнива-
нию давлений и перетеканию воздуха с нижней по-
верхности на верхнюю, что вызвано повышением дав-
ления снизу и разрежением сверху крыла.
/
а ____12L_?i
Рис. 2.49. Концевые
конусы возмущения
на прямоугольном крыле
95
Перетекание вдвое уменьшает подъемную силу на концах крыла по сравнению с
той, которую они имели, если бы данное крыло являлось частью крыла бесконечного
размаха. Коэффициент подъемной силы прямоугольного крыла находится по формуле
( _ 1 tgp«\
Суокр S'*!/ )'
(2.128)
Заменяя в (2.128) tg его выражением через по соотношению (2.106) и ис-
пользуя формулу (2.119) для коэффициента подъемной силы профиля в сверхзвуко-
вом потоке, получаем
(2.129)
Величину Х^М^ — 1 называют эффективным удлинением крыла в сверхзвуковом
потоке. Аналогично величинах У1 — , входящая в (2.127), может быть названа эф-
фективным удлинением крыла в дозвуковом потоке.
Коэффициент волнового индуктивного сопротивления для пластинчатого кры-
ла, как и для профиля, находится по формуле
С .= Г CL— Га
ха в/ уа кр**' суа кр^ •
Аэродинамические характеристики треугольного пластинчатого крыла сильно
зависят от того, будет крыло обтекаться в режиме с дозвуковыми или сверхзвуковыми
передне-боковыми кромками (рис. 2.50). Если ввести отношение
tg7_ 1 _
Л — 7---7----7------7---- — Л—V7--- , (2. 1 3U)
tg Poo tg Хо tgpTO tgXo XtgXo
то треугольное крыло будет обтекаться в режиме с дозвуковыми передне-боковыми
кромками, когда п > 1. В случае сверхзвуковых передне-боковых кромок треугольного
крыла п < 1.
Анализируя приведенные выше соотношения для с^а кр , можно сделать вывод,
что эта аэродинамическая характеристика крыла зависит от числа М^, формы крыла
в плане, характеризуемой для трапециевидных крыльев удлинением X, сужением Т| и
углом стреловидности Таким образом, Суа кр = /(М^, X, т|, %). Из формул линейной
теории (2.127), (2.129) и (2.130) последнее соотношение можно преобразовать к виду
а
^=F(MM~-1|AtgX,n). (2.131)
Результаты обработки экспериментальных данных показали, что в качестве ха-
рактерного угла стреловидности в (2.131) следует брать угол стреловидности по ли-
нии, проходящей через середины хорд, т. е. Хо,5-
В этом случае влияние относительного суже-
ния крыла Т| на кр менее значительно.
В трансзвуковой области отношение Суа кр /X
существенно зависит от параметра X .
На рис. 2.51 в качестве примера приводит-
ся график зависимости Суа кр для т| = «>. Из
этого рисунка видно, что стреловидное крыло
О О
Рис. 2.50. Треугольное крыло
с дозвуковыми и сверхзвуковыми
кромками
96
Дозвуковые кромки
Сверхзвуковые кромки
Рис. 2.51. График изменения несущих свойств крыла во всем диапазоне изменения чисел Маха
не имеет провала несущих свойств в трансзвуковой области, характерной для профи-
ля и нестреловидного крыла большого удлинения (см. рис. 2.47).
Коэффициент волнового нулевого сопротивления схаъОкр крыла с произвольным
симметричным профилем можно рассчитать по формуле
^хавОкр — (Сха вОкр^ромбП + ф(^— DL
где (сха вокр)ромб “ коэффициент волнового нулевого сопротивления крыла с ромбиче-
ским профилем (см. рис. 2.52), зависящий от параметров т|, X tg и XV^, причем угол %с
отсчитывается от линии максимальных толщин крыла с данным профилем, а не с
ромбовидным; К — коэффициент формы профиля (см. формулу 2.124); вспомогатель-
ная функция <р зависит от разности (ХдД/J—1 - X tg хс) и показана на рис. 2.53.
Рис. 2.52. Зависимость коэффициента
волнового сопротивления крыльев
с ромбическим профилем от геометрических
параметров и числа Маха
1 - Xtgxc
Рис. 2.53. Зависимость коэффициента,
учитывающего характер линии максимальных
толщин крыла, от геометрических
параметров и числа Маха
97
При дозвуковой и звуковой линии максимальных толщин — X tg х 0)
значение ф принимают равным нулю. Когда — X tg хс) —> °°, функция
ф—> 1.
2.13. ИНТЕРФЕРЕНЦИЯ ЧАСТЕЙ ЛЕТАТЕЛЬНЫХ АППАРАТОВ
Аэродинамические характеристики летательного аппарата не являются простой
суммой аэродинамических характеристик его изолированных частей. В результате
взаимного влияния расположенных близко друг к другу в потоке воздуха тел картина
обтекания каждого из этих тел изменяется. В одних случаях это взаимовлияние, или
интерференция, может быть благоприятным, и тогда говорят о положительной интер-
ференции, или неблагоприятным, когда интерференцию считают отрицательной.
Увеличение сопротивления крыла на дозвуковых скоростях обусловлено наличи-
ем сопряжений крыла с корпусом летательного аппарата, с гондолами двигателей
и происходит главным образом из-за влияния частей летательного аппарата, соеди-
няющихся с крылом. Рост индуктивного сопротивления крыла учитывается введени-
ем эффективного удлинения крыла Х^ вместо геометрического удлинения X в форму-
лу (2.77). Эффективное удлинение определяется по формуле Х^ = Х(1 + SQ/S), где
50 — площадь крыла, занятая корпусом, мотогондолами и другими частями летатель-
ного аппарата, размещенными на крыле.
Кроме того, вследствие сопряжения крыла с корпусом и другими частями возрас-
тает профильное сопротивление крыла. Это обусловлено тем, что в месте стыка крыла
с фюзеляжем вблизи задней кромки крыла образуется диффузорный участок, где воз-
никает отрыв пограничного слоя. При расчете профильного сопротивления его уве-
личение вследствие интерференции обычно определяется по формуле
Сха 0 кр “ Сха 0 изжр Р ~ ^инт*у I >
где сха 0 и — коэффициент сопротивления изолированного крыла; £инт — коэффи-
циент интерференции.
Чем большая часть крыла занята корпусом и другими частями, тем меньшая по-
верхность крыла обтекается потоком и, следовательно, полный коэффициент сопро-
тивления уменьшается. Отрицательные явления, связанные с взаимным влиянием
крыла и корпуса, учитываются коэффициентом интерференции, который меньше
единицы. Чем меньше коэффициент интерференции, тем больше коэффициент со-
противления крыла Для летательного аппарата схемы низкоплана £инт =
= 0,25...0,6, для среднеплана £инт = 0,85 и для высокоплана £инт = 1. Аналогично учи-
тывается влияние корпуса на горизонтальное и вертикальное оперение.
При определении аэродинамических характеристик как горизонтального, так и вер-
тикального оперения необходимо учитывать уменьшение скорости за крылом, располо-
женным выше по потоку от оперения. Скоростной напор у горизонтального оперения,
осредненный вдоль его размаха, может уменьшиться на 20 и более процентов. С умень-
шением удлинения горизонтального оперения торможение потока увеличивается. Кроме
того, при полете летательного аппарата скос потока, имеющий место за крылом, достига-
ет горизонтального оперения и существенно изменяет его действительный угол атаки.
Угол скоса потока в области горизонтального оперения увеличивается с ростом
угла атаки или коэффициента подъемной силы крыла и с уменьшением удлинения
98
крыла и уменьшается с увеличением расстояния от крыла до горизонтального опере-
ния. На угол скоса у горизонтального оперения оказывает влияние расположение го-
ризонтального оперения по высоте относительно крыла. С ростом расстояния до
плоскости расположения крыла угол скоса потока уменьшается.
При аэродинамическом расчете дозвуковых летательных аппаратов обычно при-
нимают, что подъемная сила системы крыло—корпус равна подъемной силе условных
изолированных крыльев, образованных продолжением передней и задней кромок
консолей до плоскости симметрии. Такое предположение хорошо подтверждается
опытом при небольших значениях отношения диаметра корпуса D к размаху крыла
(D = D/1) и при малых числах Маха полета.
У современных сверхзвуковых летательных аппаратов отношение D/1 доходит до
0,3...0,5. В этом случае замена системы крыло—корпус изолированными крыльями
может привести к значительным ошибкам в определении подъемной силы.
Рассмотрим комбинацию крыло—корпус, установленную в потоке под углом
атаки а (рис. 2.54). Для простоты предположим, что на корпусе в форме бесконечно
длинного кругового цилиндра крыло закреплено по схеме среднеплана. Разложим на-
бегающий на комбинацию со скоростью Уж невозмущенный поток на две составляю-
щие: направленную вдоль оси корпуса со скоростью Ухоо = Уж cos а и нормально к ней
со скоростью Ууж = Ко sin а. При обтекании корпуса этим поперечным потоком его
скорость v увеличивается по сравнению с Ууоо.
Полагая скорости Ууоо малыми, из теории потенциального обтекания цилиндра
поперечным потоком со скоростью Ууоо = У» sin а для местных скоростей обтекания
вдоль оси OZ в плоскости OXZ можно получить (см. п. 2.6)
v = ИД! + r$/z2) sin а,
где г0 — радиус цилиндра, z — координата рассматриваемой точки на оси OZ.
Из последнего соотношения видно, что в точках на поверхности цилиндра, т. е.
при z = rQ, поперечные скорости обтекания в два раза больше, чем Ууоо, а вдали от ци-
линдра стремятся к этой величине. Увеличение поперечной скорости обтекания v
вблизи цилиндрического корпуса вызывает увеличение местных углов атаки. Вслед-
ствие этого возрастает и подъемная сила сечений, причем тем больше, чем ближе се-
чение крыла к поверхности корпуса. Наибольший прирост подъемной силы за счет
интерференции реализуется в схеме среднеплана.
В свою очередь, крыло оказывает влияние на обтекание корпуса. При положи-
тельном угле атаки повышенное давление с нижней поверхности крыла передается на
Рис. 2.54. Схема обтеканий комбинации крыло — фюзеляж
99
без учета правила площадей (1) и с учетом этого правила (2)
Рис. 2.56. Эффект применения правила площадей
нижнюю поверхность корпуса, а пониженное давление с верхней поверхности
крыла — на верхнюю поверхность корпуса. В результате на корпусе образуется допол-
нительная подъемная сила, вызванная влиянием крыла. На дозвуковых скоростях этот
прирост реализуется на всем корпусе, так как возмущения распространяются во все
стороны. На сверхзвуковых скоростях возмущения распространяются только вниз по
потоку, поэтому подъемная сила на корпусе увеличивается только в области, ограни-
ченной конусами Маха, выходящими из начала бортовой хорды каждой консоли, и,
следовательно, зависит от числа Маха набегающего потока.
При трансзвуковых и сверхзвуковых режимах полета минимальное волновое со-
противление летательного аппарата обеспечивается при выполнении так называемого
правила площадей. По этому правилу, следующему из линейной теории сверхзвуковых
течений, волновое нулевое сопротивление всего летательного аппарата определяется
в основном распределением площадей его поперечных сечений вдоль продольной
оси. Для того чтобы сопротивление летательного аппарата было наименьшим, эпюра
площадей поперечных сечений летательного аппарата вдоль его продольной оси
должна быть возможно более плавной (рис. 2.55).
Внезапное увеличение объема тела, например, в месте неплавного сопряжения
крыла с корпусом, необходимо компенсировать уменьшением объема других элемен-
тов компоновки. Поэтому применение правила площадей приводит к характерному
«поджатию» корпуса в зоне сопряжения крыла и корпуса (см. рис. 2.55, б).
Эксперименты показывают, что при скорости полета, соответствующей числу
Мю = 0,95... 1,05, «поджатие» корпуса снижает увеличение сопротивления на 60...80%
(рис. 2.56). При дальнейшем увеличении скорости полета эффект от применения пра-
вила площадей уменьшается и при Мю = 1,7...2,0 он исчезает.
100
2.14. СВЕРХЗВУКОВОЙ ПОГРАНИЧНЫЙ СЛОЙ
И АЭРОДИНАМИЧЕСКИЙ НАГРЕВ
При движении летательного аппарата в атмосфере частицы газа, примыкающие к
стенке, увлекаются стенкой или, что одно и то же, при обтекании аппарата из-за тре-
ния тормозятся у стенки. Процесс торможения сопровождается выделением тепла и
диссипацией кинетической энергии потока. Если скорость полета достаточно велика,
то вблизи стенки образуется слой газа с высокой температурой, нагревающей поверх-
ность аппарата.
Температура газа может достигнуть значений, близких к значениям температуры
торможения:
Т0=Т„(1 + ^М.2). (2.132)
Здесь Тж — температура набегающего потока газа.
Уже при числах Мю > 2,5 температура в простеночном слое газа может достиг-
нуть 575 К, что связано с переходом от обычно применяемых в авиационных конст-
рукциях дюралюминиевых сплавов к более теплостойким материалам. При Мю > 5
стальные конструкции должны защищаться специальными покрытиями, а при Мю >10
не всегда удается создать необходимую конструкцию. Наконец, при еще более высо-
ких скоростях полета температура газа у стенки и тепловые потоки становятся такими
большими, что приходится допускать унос вещества самой поверхности в силу плав-
ления, сублимации и др.
Высокие температуры, возникающие в пограничном слое и передающиеся дви-
жущемуся телу, оказывают обратное влияние на пограничный слой, изменяя его тол-
щину 8 и напряжение трения т0 на стенке. Поэтому невозможно правильно рассчи-
тать эти величины без учета нагрева. И наоборот, невозможно точно рассчитать на-
грев, не имея данных о структуре и характеристиках пограничного слоя.
Поскольку при больших скоростях температура в пограничном слое изменяется
существенно, то оказывается переменной и плотность газа. Вследствие того, что дав-
ление по сечению пограничного слоя примерно постоянно, плотность в пограничном
слое изменяется обратно пропорционально температуре. При этих условиях по сече-
нию пограничного слоя оказываются переменными вязкость ц(Г) и теплопровод-
ность Х(Г). С увеличением температуры ц и X возрастают.
Из-за нарушения адиабатичности движения в пограничном слое, вызываемого
вязкостью газа, его температура около стенки будет несколько ниже, чем это следует
из формулы (2.132). Если обтекаемая поверхность будет теплоизолирована, то теплота
не сможет отводиться от поверхности тела или излучаться ею в окружающее про-
странство и ее температура достигнет так называемой равновесной температуры или
температуры адиабатического восстановления. Величина этой температуры восста-
новления Тг зависит от числа Маха Мю (в общем случае от числа Маха на границе пог-
раничного слоя) и от рассеяния кинетической энергии течения в пограничном слое
вследствие трения и теплообмена:
+гЦ-1м_2), (2.133)
где г = (Tr — Te)/(TQ — Те) — коэффициент восстановления, представляющий собой от-
ношение прироста температуры при адиабатическом торможении в пограничном
слое (Тг — Те) и в идеальном внешнем и невязком потоке (Го — Те), здесь Те — темпе-
ратура на внешней границе пограничного слоя.
Величина г зависит от числа Прандтля Рг = ргр/Х.
101
Число Прандтля представляет собой отношение количества тепла, выделяемого
за счет работы сил молекулярного трения, к количеству тепла, уносимого молекулами
при непрерывном перемещении. Для воздуха число Рг изменяется от 0,75 при очень
низких температурах до 0,65 при высоких. Ввиду того что оно изменяется очень мало,
его считают постоянной величиной, равной осредненному его значению 0,72.
Коэффициент восстановления температуры в ламинарном пограничном слое
приближенно можно определить как г « ТРг, а в турбулентном как г ~ 2/Рг. Для возду-
ха в ламинарном и турбулентном пограничных слоях принимаются г = 0,85 и г = 0,90
соответственно. Подставляя эти значения в (2.133) и полагая для воздуха к = 1,4, полу-
чаем ддя ламинарного пограничного слоя Тг = 7^(1 -I- 0,17М£) и ддя турбулентного
Тг = 7^(1 -I- 0,18М£). Из этих формул следует, что поверхность, обтекаемая турбулент-
ным пограничным слоем, будет нагреваться сильнее, чем обтекаемая ламинарным слоем.
Формула (2.132) дает максимальную величину повышения температуры плоской
стенки при больших скоростях полета и кладется в основу расчета аэродинамического
нагрева различных сверхзвуковых летательных аппаратов. По этой формуле темпера-
тура поверхности тела или, точнее говоря, температура газа у стенки очень быстро (по
квадратичной параболе) растет с возрастанием числа Маха полета Мм.
Распределение температуры в пограничном слое существенно изменится при на-
личии подвода или отвода тепла. При охлаждении стенки максимальная температура
в пограничном слое меньше температуры восстановления. Поскольку у стенки темпе-
ратура снижается вследствие отвода теплоты внутрь тела, то в этом случае температура
газа имеет максимальное значение внутри пограничного слоя.
При нагревании стенки до температуры, превышающей температуру восстанов-
ления (Tw > Тг), появляется тепловой поток от стенки к пограничному слою. Это вы-
зывает увеличение температуры внутри пограничного слоя.
В общем случае толщина температурного пограничного слоя, т. е. слоя, где про-
исходит основное изменение температуры, не совпадает с толщиной динамического
пограничного слоя, определяемого как область изменения скорости.
При больших скоростях характеристики пограничного слоя, т. е. формы профи-
лей скорости, напряжения трения, толщина слоя и т. д., находятся под сильным влия-
нием сжимаемости. Так как давление в одном и том же поперечном сечении погра-
ничного слоя одно и то же, то из уравнения состояния следует, что плотности и темпе-
ратуры в любом поперечном сечении связаны зависимостью р/ре = TJT, где ре —
плотность газа на внешней границе слоя. Отсюда следует, что при больших числах М
вследствие нагрева газа у стенки плотность pw сильно уменьшается по сравнению с
плотностью на внешней границе.
Как уже отмечалось, коэффициент вязкости воздуха ц увеличивается с ростом
температуры. Поэтому в тонком пограничном слое на поверхности тела, движущегося
с большими скоростями, имеется сильное возрастание кинематической вязкости
жидкости v* = ц/р в направлении от внешней границы к стенке. Средняя величина v*
в пограничном слое в несколько раз больше, чем на внешней границе слоя.
Так как толщина пограничного слоя 8 находится в прямой зависимости от кине-
матической вязкости V», то с ростом числа М толщины ламинарного и турбулентного
пограничных слоев сильно возрастают.
Меняется также и форма профилей скорости, которые находятся в тесной связи с
профилями температуры, так как температура увеличивается за счет уменьшения ско-
рости по мере приближения к стенке.
102
Влияние сжимаемости на коэффициент сопротивления трения плоской пластины
при продольном обтекании обычно описывают коэффициентом т|м = cF/(cF)M = 0, где
cF— коэффициент сопротивления пластины при заданном числе Мм, a (cF)M = 0 — ко-
эффициент сопротивления пластины при том же числе Re, но в несжимаемом потоке
(Мю = 0). Тогда для ламинарного пограничного слоя с учетом сжимаемости и теплоот-
дачи можно определить по приближенной формуле
Им = [0,45 + 0,55Tw/Te + 0,09(fc- 1)м27Рг]-°’12.
Эта формула ценна тем, что показывает влияние на трение каждого из трех фак-
торов: Tw/Te, Мю и Рг в отдельности. На рис. 2.57 приведен график (линия 7) этой за-
висимости для теплоизолированной стенки Tw/7^= 1.
Турбулентный пограничный слой также подвержен влиянию числа М и теплоот-
дачи через стенку. Но это влияние имеет свои особенности.
Толщина турбулентного слоя по сравнению с толщиной ламинарного слоя зна-
чительно меньше зависит от вязкости. Поэтому с ростом числа М толщина турбулент-
ного слоя нарастает значительно медленнее, чем ламинарного. Вследствие этого на-
пряжение трения турбулентного слоя будет убывать быстрее по числу М^, чем лами-
нарного. Соответствующая величина коэффициента т|м для турбулентного слоя
представлена кривой 2 на рис. 2.57. Для вычисления коэффициента т]м при турбу-
лентном обтекании используют приближенную формулу
т)м = (1 + 0,1м5-2/3.
Трудности расчета турбулентного пограничного слоя при сжимаемом течении
возрастают по двум причинам. Первая, имеющая место в ламинарном пограничном
слое, является следствием влияния, оказываемого на течение числом набегающе-
го потока и температурой Tw обтекаемой стенки. Вторая причина связана с некоторой
противоречивостью экспериментальных данных, что затрудняет разработки прибли-
женных моделей турбулентности.
Среди многочисленных способов решения задачи о пограничном слое сжимае-
мого потока особенно часто применяют метод так называемой эффективной или опре-
деляющей температуры. Основная идея этого метода состоит в том, что законы сопро-
тивления, полученные для несжимаемого течения, сохраняются и для сжимаемого,
если только для плотности и коэффициента вязкости ввести их значения, соответ-
ствующие подходящим образом выбранной опре-
деляющей температуре Г*. Значение этой температу-
ры Г* обычно лежит между максимальным и мини-
мальным значениями Т внутри пограничного слоя.
Наиболее часто определяющую температуру Т вы-
числяют по формуле Эккерта: Г* = Го + 0,5(7; -7^) +
4-0,22(7;— т;).
Если режим полета летательного аппарата не-
прерывно меняется, то еще одним фактором, суще-
ственно влияющим на характеристики погранично-
го слоя в сжимаемом потоке, является нестационар-
ность, т. е. изменение поля течения и температур во
времени. В этом случае реальные характеристики
могут сильно отличаться от характеристик, вычис-
ленных по формулам данного раздела.
Рис. 2.57. Зависимость
коэффициента влияния
сжимаемости от числа Маха
для ламинарного (/)
и турбулентного (2)
пограничного слоя
103
2.15. АЭРОДИНАМИКА РАЗРЕЖЕННЫХ ГАЗОВ
При движении летательных аппаратов на больших высотах большое значение
приобретает аэродинамика разреженных газов. Основная особенность аэродинамики
разреженных газов заключается в том, что в этом случае нельзя пользоваться гипоте-
зой сплошности (непрерывности) среды. В условиях разреженного газа необходимо
учитывать его молекулярную структуру. При этом газ можно рассматривать как сово-
купность движущихся по всевозможным направлениям молекул, сталкивающихся
постоянно друг с другом и с поверхностью обтекаемого тела.
Молекулярная структура газа может быть охарактеризована длиной свободного про-
бега молекул в промежутке между последовательными столкновениями. Поскольку
скорости хаотического движения отдельных молекул могут изменяться в широких пре-
делах, то длина свободного пробега для различных молекул также различна. Поэтому
обычно рассматривают среднюю длину свободного пробега молекул. Эта длина зави-
сит от числа молекул в единице объема (от плотности среды), скорости хаотического
движения (температуры газа) и от размеров самих молекул. Из кинетической теории
газов среднюю длину свободного пробега молекул можно вычислить по формуле
/= 1,225 Jk v./a. (2.134)
Из (2.134) следует, что средняя длина свободного пробега молекул на высотах по-
рядка 80 км несколько менее 0,5 см, на высотах порядка 120 км она достигает уже не-
скольких метров, а на больших высотах порядка 200 км — сотен метров.
Безразмерное отношение величины / к характерному для данной задачи линей-
ному размеру L (хорда профиля, длина корпуса и т. д.) называется числом Кнудсена
и обозначается Кп. Подставляя сюда / по формуле (2.134), получим
Kn = //Z= 1,255 zAM^/Re. (2.135)
При исследовании пограничного слоя в разреженном газе характерным линей-
ным размером рассматриваемой области является толщина пограничного слоя 8.
Поэтому для характеристики степени разреженности среды в этом случае необходи-
мо использовать число Кнудсена, определяемое как Кп = //8. При достаточно боль-
ших числах Рейнольдса для ламинарного пограничного слоя из соотношения (2.65)
8/£ со 1/7Йё , тогда, снова используя формулу (2.134),
Kn = //8 = (//£)(Z/8)~Moo/TRe. (2.136)
Приочень малых значениях числа Рейнольдса (Re < 100) толщина пограничного
слоя порядка характерного линейного размера тела L. В этом случае
Kn^ML/Re. 2.137)
Из формул (2.135)... (2.137) следует, что степень разрежения среды характеризует-
ся отношениями M^/Re или М^/ТЙё, которые называются параметрами разрежения.
Принято следующее деление газовых течений на основные области.
Если //8 < 0,01 или М^/ТЙё < 0,01 — область обычной аэрогазодинамики.
При 0,01 < //8 < 1 (0,01 < М^/л/Йё < 1) — течение со скольжением.
Для чрезвычайно большой разреженности среды, когда 1/L > 10 (M^/Re > 10), те-
ло находится в свободно-молекулярном потоке.
На рис. 2.58 приведены области течения газа в зависимости от значений чисел
Маха Мю и Рейнольдса Re. Из рисунка видно, что при заданном значении числа
изменение величины числа Re может привести к изменению области потока.
104
В свободно-молекулярном потоке при расчете
обтекания тел можно пренебречь изменением дви-
жения вследствие соударения молекул друг с дру-
гом по сравнению с соответствующим изменением
от соударения с телом. Исследования в области сво-
бодно-молекулярного течения проводятся метода-
ми кинетической теории газов. В свободно-молеку-
лярном потоке частицы газа не взаимодействуют
между собой и пограничного слоя фактически нет.
При течениях со скольжением скорость потока
Рис. 2.58. Границы областей
свободно-молекулярного (/)
и переходного (2) течения,
течения со скольжением (3)
и течения сплошной среды (4)
в зависимости от значений
чисел Маха и Рейнольдса
у стенки не равна нулю, а газ скользит по поверхно-
сти с конечной скоростью. В пограничном слое
скорость потока изменяется от скорости скольже-
ния до скорости на границе пограничного слоя.
При этом температура газа у стенки не равна темпе-
ратуре поверхности тела.
В переходной области от течения со скольжени-
ем до свободно-молекулярного потока происходят чрезвычайно сложные явления. Здесь
одинаково важно как взаимодействие молекул друг с другом, так и соударение молекул с
поверхностью тела, поэтому необходимо учитывать взаимодействие отраженных молекул
с молекулами набегающего потока. В области течения со скольжением уравнения
Навье-Стокса и уравнения пограничного слоя, вообще говоря, не применимы. Эти урав-
нения должны быть дополнены членами, учитывающими влияние разрежения. Кроме
того, граничные условия задачи должны быть записаны с учетом явления скольжения.
В общем случае для определения скорости скольжения и температуры газа у стен-
ки необходимо кроме средней длины свободного пробега молекул знать производную
от температуры вдоль поверхности и коэффициенты аккомодации и отражения.
Наиболее вероятными схемами отражения молекул от поверхности являются
диффузное и зеркальное. При диффузном отражении молекулы газа при столкновении
с телом передают всю кинетическую энергию телу, адсорбируются, т. е. поглощаются
Рис. 2.59. Коэффициент
сопротивления сферы
в свободно-молекулярном
потоке при диффузном (I)
и зеркальном (2) отражении
поверхностью тела на некоторое время, в течение которого происходит уравнивание
температуры газа и стенки, а затем отражаются от поверхности по произвольному на-
правлению со средней скоростью, соответствующей температуре поверхности тела.
При зеркальном отражении угол отражения равен углу падения молекулы. При этом
тангенциальная составляющая скорости остается неизменной, а нормальная состав-
ляющая меняет направление при неизменной величине.
Коэффициент отражения есть отношение числа диффузно отраженных молекул
ко всему числу отраженных молекул. При зеркальном отражении коэффициенты ак-
комодации и отражения равны нулю, а при диффузном — они близки к единице.
Так как в свободно-молекулярном потоке тело не
влияет на набегающий поток, то принимают, что рас-
пределение скоростей молекул в набегающем и отра-
женном потоках подчиняется классическому распреде-
лению Максвелла, а вычисление аэродинамических сил
и теплового потока можно производить отдельно от на-
летающих и отраженных молекул. Понятие скорости
звука для свободного потока молекул теряет смысл, по-
скольку звуковые волны, т. е. распространяющиеся в
среде последовательные волны сжатия и разрежения
малой интенсивности, в сильно разреженном газе не
могут существовать из-за слишком большой длины сво-
бодного пробега молекул. Вместо числа Маха Мм ис-
105
пользуется безразмерный параметр — аналог числа Маха /Vs = , рав-
ный отношению скорости полета к наиболее вероятной скорости молекул Vs отно-
сительно некоторой неподвижной системы координат.
На рис. 2.59 приведены результаты расчета коэффициента сопротивления для
сферы в функции безразмерного параметра . Хотя значения довольно велики, но
из-за малой плотности аэродинамические силы в разреженном газе ничтожно малы и
ими часто пренебрегают, в некоторых случаях (например, при длительном полете ис-
кусственного спутника) даже небольшая сила лобового сопротивления сказывается на
траектории полета и времени существования космического объекта на этой траектории.
ЛИТЕРАТУРА
1. Аэрогидромеханика: Учеб, для студентов высших технических учебных заведе-
ний / Е. Н. Бондарев, В. Т. Дубасов, Ю. А. Рыжов и др. — М.: Машиностроение,
1993. С. 608.
2. Аэродинамика летательных аппаратов: Учеб, для вузов / Г. А. Колесников,
В. К. Марков, А. А. Михайлюк и др. — М.: Машиностроение, 1993. С. 544.
3. Основы прикладной аэрогазодинамики (в 2 кн.). Кн. 1. Аэродинамика крыла
(профиля), корпуса и их комбинаций: Учеб, пособие для техн, вузов /
Н. Ф. Краснов, Е. Э. Боровский, А. И. Хлупнов. — М.: Высш, шк., 1990. С. 336.
4. Основы прикладной аэрогазодинамики (в 2 кн.). Кн. 2. Обтекание тел вязкой
жидкостью. Рулевые устройства: Учеб, пособие для втузов / Н. Ф. Краснов,
В. Н. Кошевой, В. Ф. Захарченко и др. — М.: Высш, шк., 1991. С. 358.
5. Петров К. П. Аэродинамика тел простейших форм. — М.: Факториал, 1998.
С. 432.
6. Петров К. П. Аэродинамика транспортных космических систем. М.: Эдиториал
УРСС, 2000. С. 368.
СОДЕРЖАНИЕ ГЛАВЫ 2
2.1. Сведения о свойствах жидкостей и газов.....................49
2.2. Основные сведения из кинематики жидкости и газа............51
2.3. Уравнение неразрывности....................................54
2.4. Основы динамики жидкости и газа............................56
2.5. Сжимаемые и несжимаемые течения............................59
2.6. Потенциальные течения......................................61
2.7. Вязкие течения и пограничный слой..........................67
2.8. Аэродинамические характеристики профилей
и крыльев конечного размаха в несжимаемом потоке................73
2.9. Изоэнтропические течения...................................79
2.10. Теория скачков уплотнения.................................82
2.11. Потенциальные течения идеального сжимаемого газа..........86
2.12. Аэродинамические характеристики профилей
и крыльев конечного размаха в двузвуковом и сверхзвуковом потоках.90
2.13. Интерференция частей летательных аппаратов................98
2.14. Сверхзвуковой пограничный слой и аэродинамический нагрев.101
2.15. Аэродинамика разреженных газов...........................104
Литература.........................................................106
106
ГЛАВА
Основы проектной
баллистики ракет-носителей
и космических аппаратов
Баллистика представляет собой науку о движении летательных аппаратов (ЛА)
различного назначения, ставящую целью изучение широкого спектра проблем полета
в атмосфере и условиях космического пространства.
В классической постановке основной или «прямой» задачи баллистики предпо-
лагается, что ЛА, которому сообщена некоторая начальная скорость, совершает
в пространстве движение, не ограниченное никакими механическими связями. Сле-
довательно, баллистика имеет дело с наиболее общим видом свободного движения —
движением твердого тела, обладающего шестью степенями свободы. Однако во мно-
гих случаях на это движение накладываются сопутствующие эффекты, обусловлен-
ные факторами взаимодействия аппарата с внешней средой, управляющими воздей-
ствиями, изменением массы ЛА в процессе работы реактивного двигателя, перемеще-
нием центра масс ЛА вдоль корпуса и т. д. В этом случае, строго говоря, движение ЛА
уже не является баллистическим (в смысле движения «свободно брошенного тела»).
Особенно это касается участков управляемого движения ЛА баллистического типа.
Здесь уже при построении математических моделей движения и разработке уп-
равления приходится учитывать не только априорную, но и непосредственно полу-
чаемую в процессе полета информацию о параметрах движения.
В этом смысле применительно к решению задач, связанных с управляемым дви-
жением баллистических ЛА, возможно более корректным было бы применение вме-
сто «баллистики» термина «теория полета». Несмотря на это, учитывая, что за многие
десятилетия термин «баллистика» прочно укоренился в ракетно-космической техни-
ке, ему отдается предпочтение, хотя с содержательной точки зрения различий между
этими понятиями обычно не делается [2, 7].
Перечень вопросов, составляющих содержание баллистики как науки, позволяет
выделить [4] в ней, по крайней мере, два основных направления, первое из которых
называют баллистическим обеспечением полета (в ряде случаев используется [15] менее
строгое название «исполнительная баллистика»), второе — проектной баллистикой.
Баллистическое (более полно «баллистико-навигационное» [7]) обеспечение ста-
вит своей целью выполнение совокупности операций, направленных на непосредст-
венное решение задач полета. К числу таких операций может быть отнесено:
• определение и прогнозирование параметров движения ЛА по результатам нави-
гационных измерений;
• анализ соответствия реализуемых параметров конечной цели полета;
• расчет корректирующих поправок или необходимых управляющих воздействий
для приведения движения ЛА в соответствие с реализуемой программой.
Назначением раздела науки, называемого проектной баллистикой, является получение
исходных данных для проектирования ЛА на основе анализа условий движения без привязки
траекторий к конкретным географическим координатам точки старта или точки выве-
дения полезной нагрузки, выбора наиболее выгодной обобщенной схемы полета и определения
требуемого ресурсного управления, обеспечивающего решение поставленной задачи.
107
В стереотипных курсах баллистики обычно находят взвешенное отражение оба
из указанных направлений [5, 7, 15].
Вместе с тем можно указать немало специальных изданий и учебной литературы,
в которых акцент делается на каком-то одном из направлений.
С определенной долей условности в качестве примера таких изданий могут быть
указаны работы [2, 10, 12, 16].
В ограниченных рамках настоящего издания невозможно даже кратко описать
содержание задач баллистики для всего многообразия существующих типов ЛА.
В связи с этим изложение материала ограничивается рассмотрением основ про-
ектной баллистики для ракет-носителей (PH) и космических аппаратов (КА) различ-
ного назначения, выводимых в космическое пространство, в частности, беспилотных
искусственных спутников Земли (ИСЗ), пилотируемых аппаратов и автоматических
межпланетных станций (АМС).
Учитывая данное обстоятельство, для более углубленного изучения обсуждаемых
вопросов могут быть рекомендованы следующие учебники, учебные пособия и моно-
графии: [2, 7, 11, 16].
Другие источники, использованные при подготовке материалов главы, ссылки на
которые имеются в тексте, также приводятся в списке литературы.
Ставя основной целью изложение с единых методических позиций основ проект-
ной баллистики указанных типов ЛА, автор стремился при написании материала при-
держиваться по возможности схемы, при которой предварительно выявляется физи-
ческая сущность и особенности задачи, вытекающие из ее постановки, затем обсуж-
даются целесообразные пути ее решения.
Важно подчеркнуть, что проектные баллистические расчеты проводятся в несколь-
ко приближений. Сначала определяются проектно-баллистические характеристики для
«идеальной» траектории ЛА с учетом массы полезной нагрузки и целевого назначения
полета. При проведении исследований на этой стадии баллистического проектирования
считается уместным использование специально «затрубленных» упрощенных математи-
ческих моделей, учитывающих лишь определяющие факторы. Дело здесь не столько в
сокращении вычислительных затрат, сколько в стремлении к сохранению понимания
физической сущности задачи, умению находить альтернативные варианты решения,
привитию вкуса к аналитическому осмысливанию расчетных результатов [2].
В процессе последующей разработки ракетного либо ракетно-космического
комплекса баллистические расчеты повторяются с введением в них новых уточнен-
ных данных об аппарате, ограничивающих факторах и условиях, учитываемых при
выборе приемлемого варианта проектно-баллистического решения. Анализ задачи
движения ЛА при этом, конечно, не сводится к расчету какой-то одной траектории —
он трансформируется в проблему комплексного «проектирования траекторий» [2],
что невозможно без широкого использования современных высокопроизводитель-
ных ЭЦВМ, оснащенных эффективным программным обеспечением.
В конечном итоге никогда нельзя забывать, что от того, насколько удачно решена
задача проектной баллистики, зависят важнейшие характеристики ЛА (стартовая мас-
са, тяга двигательной установки, масса полезной нагрузки, выводимой на орбиту, и
т. д.) и целевые задачи полета (дальность и точность доставки полезной нагрузки, эф-
фективность и надежность функционирования ЛА и т. д.).
В методическом отношении задача проектной баллистики обычно рассматрива-
ется раздельно применительно к проблемам активного участка траектории, на кото-
ром движение ЛА осуществляется за счет истечения из соплового блока газовой
струи, образующейся от сгорания топлива, находящегося внутри его корпуса, и пас-
сивного участка, отвечающего условию прекращения действия реактивной силы.
108
Причем, в свою очередь, последний участок, называемый также участком свободного
полета, может представлять собой как участок выведения РН, так и участок спуска
аппарата в атмосфере планеты [6,7, 11].
Свободное движение аппарата вне зоны действия атмосферы, подчиняющееся
теории кеплерова движения (по имени И. Кеплера), принято называть невозмущен-
ным орбитальным движением. Решение задач проектной баллистики на основе указан-
ной теории обычно рассматривается в качестве первого приближения. Последующее
уточнение полученных решений сопряжено с необходимостью учета эффектов не-
центральности гравитационного поля притягивающего тела, либо действия несколь-
ких притягивающих центров [7]. Это бывает особенно важным при решении задач
проектной баллистики межпланетных аппаратов. Учет соответствующего эффекта
позволяет, с одной стороны, исследовать такие схемы, при которых улучшение бал-
листических характеристик достигается за счет использования гравитационных полей
планет, пролетаемых АМС попутно, с другой — использовать методы расчета и опти-
мизации проектно-баллистических характеристик, базирующихся на кусочно-кони-
ческой аппроксимации межпланетных траекторий [16].
3.1. ИСХОДНЫЕ ПРЕДПОСЫЛКИ МАТЕМАТИЧЕСКОГО
МОДЕЛИРОВАНИЯ ДВИЖЕНИЯ ЛА В АТМОСФЕРЕ
3.1.1. Системы координат, характеризующие
положение ЛА в пространстве
Одним из центральных понятий, широко используемых в баллистике вообще и в
проектной баллистике в частности, является понятие траектории движения ЛА.
Под траекторией принято понимать [5] геометрическое место точек последова-
тельного положения центра масс ЛА в функции времени относительно выбранной
системы координат (СК). Системы координат, относительно которых определяется
траектория, в отличие от подвижных СК, связанных с ЛА, называют базовыми.
Уже из сказанного становится очевидной роль, которая отводится выбору той
или иной системы координат при решении рассматриваемых задач.
Краткое описание используемых СК предварим изложением общего принципа
их построения: прежде всего оговаривается тип СК (обычно используются декартовы
правые СК), выбирается основная «отсчетная» плоскость системы и в ней — положе-
ние начала отсчета и направление основной оси. Учитывая, что положение основной
плоскости и ориентация основной оси СК могут меняться со временем, оговаривает-
ся, соответствуют ли они некоторому фиксированному моменту времени или выбира-
ются средними за определенный промежуток времени.
Для решения задач теории полета ЛА, движущихся в поле земного тяготения, ис-
пользуются две большие группы систем координат, различающиеся расположением
начала систем отсчета [2,4, 5]. К первой группе относятся системы координат, связан-
ные с Землей или другими точками пространства, ко второй — системы координат,
связанные с ЛА.
Для исследования абсолютного движения часто применяется инерциальная сис-
тема координат OKXKYKZK. В общем случае под инерциальной системой координат по-
нимают систему, оси которой не изменяют своего направления в пространстве. Поло-
жение ее осей не зависит от суточного вращения Земли (в отличие от систем коорди-
нат, связанных с Землей и вращающихся вместе с ней, используемых при изучении
относительного движения ЛА).
109
Земная система координат О0Х0У070 имеет начало в точке OQ и оси, зафиксирован-
ные по отношению к Земле. Прямоугольная система координат, связанная с Землей,
начало которой совмещено с центром масс Земли, а одна из осей направлена на север
по оси вращения Земли, называется геоцентрической земной системой координат.
Если центр масс Земли выбран за начало сферической системы координат, то ее
называют геоцентрической сферической системой координат.
Системы координат с началом на поверхности Земли называются топоцентриче-
скими.
Нормальной системой координат O0XgYgZg называют систему, начало которой OQ
фиксировано по отношению к Земле, ось OQYg направлена вверх по местной вертикали,
а направление оси OQXg выбирается в соответствии с характером решаемой задачи.
Стартовая система координат OQXCYCZC является разновидностью топоцентрической
прямоугольной системы координат. Начало стартовой системы координат определяется
положением пусковой установки (стартового комплекса) и совпадает с центром масс
ракеты, подготовленной к пуску. При этом координатная ось OQYC направлена верти-
кально вверх, a OQXC и OQZC лежат в плоскости стартового горизонта, причем ось OQXC
указывает направление пуска. Вертикальная плоскость OQXCYC, проходящая через век-
тор начальной скорости, называется плоскостью пуска, а иногда — плоскостью броса-
ния. Положение плоскости пуска относительно Земли определяется азимутом пуска.
Большая группа подвижных систем координат объединена общим признаком —
расположением начала координат в характерной точке движущегося ЛА, обычно в
центре масс. Направления осей подвижно ориентированной системы координат OXHYHZH
неизменны в пространстве (относительно звезд). Оси неподвижной земной системы ко-
ординат OXqYqZq направлены так же, как и соответствующие им оси земной (непо-
движной относительно Земли) системы координат OqXqYqZq. В нормальной системе ко-
ординат OXgYgZg, связанной с ЛА, ось Yg направлена вверх по местной вертикали и, в от-
личие от оси OQYg нормальной земной системы координат, изменяет свое направление
в пространстве в процессе движения ЛА относительно Земли. Оси OYg и OZg нормаль-
ной связанной системы координат параллельны плоскости местного горизонта и на-
правлены удобным образом для решения поставленной задачи.
Оси связанной системы координат OXYZнаправлены следующим образом: продоль-
ная ось ОХ — в плоскости симметрии ЛА или в плоскости, параллельной ей, если нача-
ло координат О помещено вне плоскости симметрии (для осесимметричных аппаратов
ось ОХ направлена по оси симметрии к носовой части ЛА), ось ОУ располагается в плос-
кости симметрии или параллельно ей и направлена к верхней части ЛА. Поперечная ось
OZ направлена вправо перпендикулярно плоскости симметрии. В скоростной (аэродина-
мической) системе координат OXaYaZa скоростная ось ОХа совпадает с вектором воздуш-
ной скорости летательного аппарата (вектором скорости ЛА относительно атмосферы
И, ось подъемной силы OYa лежит в плоскости симметрии ЛА или в параллельной ей
плоскости. Боковая ось OZa дополняет две названные оси до правой СК.
Начало траекторной системы координат OXKyKZK обычно помещено в центре масс
ЛА, ось ОХК направлена по вектору земной скорости ЛА (скорости ЛА относительно
Земли ¥к), ось ОУК направлена вверх от поверхности Земли в вертикальной плоскос-
ти, проходящей через ось ОХ„ ось OZK направлена горизонтально. При безветрии на-
правления вектора скорости, оси ОХа и оси ОХК траекторией системы координат сов-
падают, так как при этом совпадают векторы воздушной и земной скоростей.
ПО
Связь между скоростной и связанной системами координат осуществляется с по-
мощью угла атаки а, угла скольжении 0, пространственного угла атаки ап и аэродина-
мического угла крена фп [5].
Связь между нормальной OXgYgZg и связанной OXYZ системами координат про-
изводится с помощью углов рыскания, тангажа и крена (рис. 3.1).
Угол рыскания у представляет собой угол между осью OXg и проекцией продоль-
ной оси ОХ на горизонтальную плоскость OXgZg. У некоторых ЛА угол рыскания мо-
жет определяться в зависимости от приборной реализации измерений в плоскости,
перпендикулярной плоскости бросания O$XgYg и проходящей через продольную ось
ЛА ОХ. Если угол рыскания, определяемый в указанной наклонной плоскости, обо-
значить через фп, то sin фг1 = sin у cos О. Очевидно, при О = 0 получим фг1 = у.
Угол тангажа О — угол между продольной осью ОХ и горизонтальной плоскостью.
Следует различать угол тангажа по отношению к стартовой горизонтальной плоскос-
ти, т. е. по отношению к нормальной земной системе координат, и местный угол тан-
гажа, измеряемый от плоскости местного горизонта. Это различие целесообразно
учитывать при определении характеристик движения ЛА, предназначенных для поле-
та на большие дальности.
Угол крена у — угол между поперечной осью OZ и осью OZg, смещенной в положе-
ние, соответствующее нулевому углу рыскания.
Связь между нормальной системой координат OXgYgZg и скоростной OXaYaZa осу-
ществляется с помощью так называемых скоростных углов рыскания, тангажа и кре-
на. Скоростной угол рыскания — угол между осью OXg и проекцией скоростной оси
на горизонтальную плоскость OXgZg. Скоростной угол тангажа Ьа — угол между ско-
ростной осью ОХа и горизонтальной плоскостью OXgZg. Скоростной угол крена уа —
угол между боковой осью OZa и осью OZg, смещенной в положение, соответствующее
нулевому скоростному углу рыскания.
Положение траекторной системы координат относительно нормальной опреде-
ляется двумя углами: 0 и 4х, 0 — угол наклона траектории (угол между земной скоростью
ЛА и ее проекцией на горизонтальную плоскость); 4х — угол пути (угол между осью OXg
и проекцией земной скорости ЛА на плоскость OXgZg (путевой скоростью Vg)).
Угловая ориентация одних координатных осей относительно других, принимае-
мых за опорные или базовые, может быть определена с помощью эйлеровых либо
иных углов на основе применения матриц направляющих косинусов [2,5].
3.1.2. Поле тяготения Земли и учет его влияния на движение ЛА
Потенциальной функцией, или потенциалом, называют функцию П(х, у, z), полный
дифференциал которой равен элементарной работе силы, действующей на точку:
ЭП .
dn = Fdr =
^-dx+^-dy +
(3.1)
Проекции на оси координат равнодействующей приложенных к точке сил соот-
ветственно равны
Fx = ЭП/Эх; Fy = дП/ду; Fz = ЭП/Эг (3.2)
Потенциал для точечной единичной массы, находящейся вне Земли на расстоя-
нии / от элементарной массы Земли dM, по закону тяготения Ньютона определяется
выражением
dnT=fdM/l9
111
(3.3)
Рис. 3.1. Схема взаимного
расположения связанной и нормальной
систем координат при первом
повороте относительно оси OYg
Рис. 3.2. Координаты
точечной единичной
массы, находящейся
вне Земли
где f — гравитационная постоянная; / — расстояние между точками с единичной мас-
сой и элементарной массой 6М. Потенциал силы тяготения Земли для точечной еди-
ничной массы получают интегрированием по всей массе Земли:
nr=/JdA///. (3.4)
м
Положения точек с единичной массой вне Земли и элементарной массы Земли
6М определяются (рис. 3.2) сферическими координатами: для точки (тела) с единич-
ной массой — г, (ргц, X; для элементарной массы Земли 6М — р, (р'гц, X'. Потенциал гра-
витационного поля Земли (ГПЗ) в функции сферических координат представляется
следующим образом:
П (г, <pruД) = f J Tt-xdA/ , . (3.5)
Интеграл в выражении (3.5) может быть вычислен только приближенно, так как
неизвестна точно форма Земли, а плотность вещества Земли ц3 существенно изменя-
ется по всему ее объему. Обозначая угол между риг через у, получим
/ = Jr2 + р2 - 2rpcosy. (3.6)
В процессе полета ракеты относительно Земли будут изменяться величины г и у,
а следовательно, и величина /. Очевидно, что потенциал будет изменяться в процессе
движения ракеты относительно Земли в некоторых пределах, и он может быть опреде-
лен приближенно при введении различного рода допущений. Наиболее существен-
ные допущения касаются формы Земли, ее размеров и распределения масс.
За более близкую к реальной форме Земли принимают фигуру, называемую геои-
дом. Геоид — это фигура, ограниченная уровневой поверхностью потенциала силы
тяжести, во всех точках которой значение потенциала одинаково и которая совпадает
с поверхностью океанов, находящихся в невозмущенном состоянии, т. е. при отсутст-
вии приливов, отливов, атмосферных и каких-либо других возмущений. Точное мате-
матическое описание геоида невозможно. При проведении различного рода вычисли-
тельных работ (геодезических, астрономических и баллистических) в качестве после-
довательных приближений к геоиду принимают: сферическую модель Земли — сферу,
сфероидальную модель — сфероид (эллипсоид вращения), трехосный эллипсоид.
112
Ограничимся тремя членами разложения и представим потенциал суммой трех
интегралов
Пг= f- JdA/ +
La/
|JpcoscpdAf + Jp2^cos2(p - jjdAf
м r м v 7
(3.7)
Значение первого интеграла очевидно: jdAf = Мг Остальные интегралы могут
м
быть взяты в конечном виде, если наложить некоторые ограничения на распределе-
ние массы и форму Земли.
Влияние суточного вращения Земли на полет ракет легко проследить, если рас-
смотреть их движение в инерциальной геоцентрической системе координат. В момент
пуска начальная скорость ракеты в относительном движении Vo, а в абсолютном дви-
жении Vfl0 = Vo + Vnep0, где Vnep0 — скорость ракеты, определяемая переносным враща-
тельным движением Земли с угловой скоростью Q и зависящая от географической
широты места расположения стартовой позиции (здесь и далее элементы траектории
центра масс в абсолютном движении будем отмечать индексом «а»).
Очевидно, Vnep0 = Q r0 cos фгц0, где г0 — расстояние стартовой позиции от ус-
ловного центра Земли; фгц0 — геоцентрическая широта расположения стартовой
позиции.
При свободном полете траектория абсолютного движения ракеты в первом при-
ближении, т. е. для сферической Земли с равноконцентрическим распределением
масс, является плоской кривой и ее плоскость занимает неизменное положение в
пространстве. В то же время в результате вращения Земли положение точки падения
либо фиксированной точки (цели) в инерциальном пространстве изменяется. За пол-
ное время полета ракеты цель изменит свое положение на величину
Д£ц = £2Лз'псо8<Ргц> (3-8)
где Д£ц — перемещение цели по долготе; /п — полное время полета; фгц — геоцентри-
ческая широта цели, которая остается неизменной в процессе вращения Земли.
Место старта и место падения ракеты находятся на Земле, наблюдение за поле-
том ракеты осуществляется с пунктов, расположенных на земной поверхности. По-
этому часто расчет траекторий движения ракет проводят в системе координат, связан-
ной с Землей, т. е. в относительном движении.
3.1.3. Атмосфера Земли и ее модели
Атмосферу Земли по химическому составу принято называть азотнокислород-
ной, она содержит -76% азота, -21% кислорода, -3% водяного пара, водорода, угле-
кислого газа и некоторых других газов. Известны различные схемы построения клас-
сификации моделей атмосферы по слоям. По составу воздуха атмосферу подразделя-
ют на гомосферу и гетеросферу. В гомосфере, простирающейся до высот « 95 000 м,
состав воздуха с высотой почти не изменяется.
В гетеросфере азот, кислород и другие газы под воздействием ультрафиолетового
излучения Солнца диссоциируют и находятся в ионизированном состоянии.
Поскольку температура воздуха является основным параметром, определяющим
характеристики состояния атмосферы, наибольший интерес для баллистики пред-
ставляет схема построения моделей атмосферы по характеру распределения темпера-
туры с высотой. В этой схеме атмосферу Земли подразделяют на пять основных слоев,
называемых сферами.
113
Нижний слой — тропосфера, простирается в средних широтах до высот - 11 000 м,
а в экваториальных областях — до высот - 16 000 м. Высота тропосферы зависит от
времени года, увеличиваясь летом и уменьшаясь зимой. В тропосфере содержится
-75% всей массы атмосферы и основная часть водяного пара. Отличительная черта
тропосферы — понижение температуры воздуха с увеличением высоты. Однако зи-
мой и летом после ясных холодных ночей могут наблюдаться температурные инвер-
сии, при которых температура с увеличением высоты сначала возрастает, а затем на-
чинает убывать. В тропосфере имеют место значительные горизонтальные и верти-
кальные течения воздушных масс — ветры. Горизонтальные ветры вызываются
разностью давлений в разных местах земной поверхности, вертикальные — разностью
температур по высоте.
Следующий слой — стратосфера, простирающаяся в средних широтах от-ll ООО
до -50 000 м. Стратосфера до высот -30 000 м характеризуется постоянством темпера-
туры; на большей высоте, по мере приближения к верхней границе стратосферы, тем-
пература возрастает, причем имеют место значительные суточные и межсуточные ко-
лебания температуры. Изменение температурного градиента между тропосферой и
стратосферой происходит в относительно узком слое, называемом тропопаузой. Тол-
щина слоя тропопаузы колеблется от нескольких сотен метров до -2000 м. В относи-
тельно узком слое, охватывающем тропопаузу, наблюдаются мощные перемещения
воздушных масс (так называемые струйные течения) с запада на восток со скоростя-
ми, доходящими до -110 м/с (400 км/ч).
Область струйных течений в атмосфере характеризуется большими скоростными
градиентами в вертикальном и горизонтальном направлениях.
Над стратосферой расположена мезосфера, которая находится в пределах высот
-50 000 до -90 000 м. Она характеризуется понижением температуры до верхней гра-
ницы слоя и повышенной турбулентностью.
Термосфера — это слой атмосферы от -90 000 до -500 000 м, характеризующийся
непрерывным повышением кинетической температуры [5]. В верхней части термосфе-
ры на высотах 400 000... 500 000 м кинетическая температура воздуха достигает
— 1500 °К.
Слой, расположенный от высот 500 000 м до внешней границы атмосферы, т. е.
примерно до 2 000 000...3 000 000м, называется экзосферой. В экзосфере атмосфе-
ра очень разрежена. Обычно говорят о «следах атмосферы». Переходные слои между
названными сферами носят соответственно названия стратопаузы, мезопаузы и термо-
паузы.
Физические параметры атмосферы значительно изменяются в зависимости от
климатических условий, времени года и высоты. Баллистические расчеты проводятся
для нормальных метеоусловий, соответствующих средним статистическим опытным
данным или стандартным атмосферам. Отклонение метеоусловий от их нормальных
значений учитывается отдельно с помощью теории поправок.
Стандартная атмосфера предназначается для использования при расчетах и про-
ектировании ЛА, при обработке результатов геофизических и метеорологических на-
блюдений и приведения результатов испытаний ЛА и их элементов к одинаковым ус-
ловиям. В модели СА-81 (ГОСТ 4401—81) установлены стандартные численные зна-
чения параметров атмосферы в функции геометрической (й) и геопотенциальной (Н)
высот в диапазоне от 2000 до 50 000 м.
По мере накопления данных, характеризующих состояние и динамику измене-
ния состояния атмосферы под действием различных внешних факторов (в частности,
уровня солнечной активности), модели атмосферы подлежат периодическому уточне-
нию (см., например, ГОСТ 25646.115—84 и др.).
114
Формулы, определяющие изменение давления с изменением высоты, основаны
на гипотезе о вертикальном статическом равновесии атмосферы. По этой гипотезе вес
горизонтального слоя воздуха элементарной толщины dh и единичной площади урав-
новешивается элементарной разностью dp давлений, действующих на верхнее и ниж-
нее основания слоя, т. е.
dp = -gpdh. (3.9)
Уравнение состояния для идеального газа
где R — универсальная газовая постоянная; М— молярная масса воздуха.
Для высот до 94 км значение молярной массы остается постоянным отношением
R /М = /Г, где R* — удельная газовая постоянная. Тогда
р = р/Г7? (3.11)
В зависимости от характера изменения температуры модель атмосферы СА-81 по
высоте разбита на ряд слоев; температура в каждом слое аппроксимируется линейной
функцией геопотенциальной высоты
Т=7; + Р(Я-Я*), (3.12)
где Р = dT/dH— градиент температуры по геопотенциальной высоте; TtnHt- темпе-
ратура и геопотенциальная высота нижней границы соответствующего слоя. Для изо-
термических слоев (Р = 0) имеем
In 4 =-^т(Н-Н.) (3.13)
или
р=р.ехр[-^(Я-Я.)], (3.14)
Для слоев с линейно изменяющейся температурой (Р * 0)
ln^ =1п (г.-£(Я-Я.)) (3.15)
ИЛИ
р=р. [1 + £(Я-Я.)] 55 (3.16)
Плотность определяется из уравнения состояния
р=р/{КТ). (3.17)
Удельный вес
Y = pg. (3.18)
Скорость звука
а = №? = 20,046796 JT, (3.19)
N М
где Л° = ср /cv = 1,4 — показатель адиабаты.
Вместо барометрического давления р (в Па) введем давление, измеряемое в мм
рт. ст. и обозначаемое А. Так какр = h = 13,6А, то П = 13,6^4^.
Давление влажного воздуха h может быть определено как сумма парциальных
давлений сухого воздуха h с в и водяного пара е
А = Асв + е. (3.20)
115
Удельный вес влажного воздуха в единице объема (м3) находится по аналогичной
зависимости
П = Псв + Пе. (3.21)
Считая с достаточной для практики точностью, что при одинаковых давлении и
температуре плотность водяного пара равна ~5/8 плотности сухого воздуха, получим
Пе=|13,6^,, (3.22)
и окончательно
п-^АО-м) <зи>
Для учета влажности воздуха в баллистические расчеты вводят [2, 5] «виртуаль-
ную» температуру
<3-24>
и в последующем вместо реального влажного воздуха, характеризующегося парамет-
рами А, П, Т и е, рассматривают условный «сухой воздух», который оказывает такое
же сопротивление движущемуся в нем телу, как и реальный воздух. С учетом т форму-
лы для удельного веса и плотности имеют вид
П=13,бД; (3.25)
R х v
Р-В.6г4-Т. (3.26)
-Я?
Значения давления рассчитывают по формуле h =h0Ne 0 и тогда
У
1 [<fy
h
П=13,6-^е 0 . (3.27)
Если отнести этот удельный вес к нормальному удельному весу воздуха у поверх-
ности Земли, то можно получить безразмерную функцию изменения удельного веса
с высотой. Пусть у поверхности Земли
no.-wfe.
тогда
П г
П _ XON о
Поу Т
Соответственно можно написать и для давления
у
1 (<1У
Д =е » .
nON
Для линейной зависимости т =/(у) получим
1
h ( т
Д =я(у)=[Д) (3.28)
nON \XON /
И
^-=Я(у) = л(у)^. (3.29)
116
3.2. СИЛЫ И МОМЕНТЫ, ДЕЙСТВУЮЩИЕ НА ЛА В ПОЛЕТЕ
3.2.1. Аэродинамические силы и моменты
На ракету при полете в атмосфере действует сопротивление воздуха, называемое
аэродинамическим.
Аэродинамическая сила Ял складывается из сил давления воздуха, направленных
по нормалям к поверхности ЛА, и сил трения воздуха, касательных к ней. Равнодейст-
вующая сила Ra приложена к ЛА в точке, которую называют центром давления. Обыч-
но центр давления не совпадает с центром масс ЛА, и сила ЯА относительно него со-
здает момент М. Силу ЯА, приложенную в центре масс ракеты, называют полной аэро-
динамической силой, а момент М — полным аэродинамическим моментом. Действие
аэродинамической силы приводит к уменьшению скорости полета ракеты. Действие
момента М вызывает вращательное движение ЛА вокруг центра масс. Наука, изучаю-
щая явления, сопровождающие взаимодействие ЛА с набегающим потоком воздуха,
называется аэродинамикой (см. главу 2).
Здесь приведем только сведения, непосредственно связанные с практическим
применением в проектной баллистике формул для расчета аэродинамических сил и
моментов.
Для определения ЯА используют формулу
Ra = ?5СЛ(М, Re, а, 0), (3.30)
где q = рК2/2 — скоростной напор набегающего невозмущенного потока; 5— харак-
терная площадь ЛА; CR — безразмерный аэродинамический коэффициент, зависящий
в основном от формы ЛА, числа Маха М = V/a, числа Рейнольдса Re = Kdp/p, углов
атаки а и скольжения 0.
Если при вычислении RA окажется необходимым учитывать изменение углов а и
0 во времени или угловые скорости ЛА ц относительно /-х осей, т. е. нестационар-
ность обтекания корпуса воздухом, то следует под знак функции CR внести величины
а, 0, coj и время t. Полный аэродинамический момент определяется формулой
M=qSlm, (3.31)
где / — характерная длина ЛА (например, длина ракеты от ее днища до вершины кор-
пуса); т — безразмерный аэродинамический коэффициент, зависящий от формы ра-
кеты, ее положения на траектории, скорости вращательного движения, времени и др.
В проектных расчетах удобнее иметь дело с составляющими сил и моментов, вы-
раженных через их безразмерные коэффициенты:
Х= qScx; Мх = qSlmx\
Y=qScyfMy = qSlmy; (3.32)
Z= qScz; Mz = qSlmz\
где cx, cy, cv mx, my, mz— соответствующие безразмерные коэффициенты сил и мо-
ментов.
В некоторых случаях вектор полного момента аэродинамических сил удобно
представлять в виде суммы
М=МСТ + Ма, (3.33)
где МС1 — стабилизирующий или опрокидывающий момент; Л/д — демпфирующий
момент.
117
Название момента Л/ст определяется характером его реакции на угол атаки а или
скольжения 0. Если момент увеличивает эти углы, он называется опрокидывающим,
если уменьшает — стабилизирующим. Момент демпфирования Л/д действует против
направления вращения ЛА при колебаниях относительно его центра масс. Он стре-
мится затормозить (погасить) колебания ракеты и ее вращение. Отдельно взятый мо-
мент демпфирования может быть представлен выражением
= 9Sl V = qSl I т^‘ I (3 •34)
где |т°'| — соответствующая «вращательная производная» [5], а Ш, = со^/И—
безразмерная угловая скорость ЛА.
В некоторых случаях моменты демпфирования представляют зависящими от
первой степени скорости полета
= qSl |«7'| ГО,- = 5рИ/ 2|тф| ю,.. (3.35)
Здесь тщ называют коэффициентом демпфирования; он равен /ид/ = . При
решении задач пространственного движения коэффициент демпфирования должен
быть определен по всем трем связанным осям (т^ m^Y Коэффициенты и мо-
менты демпфирования ЛА могут быть представлены как суммы соответствующих ко-
эффициентов основных конструктивных узлов ЛА. Например, чтобы найти демпфи-
рующий момент ракеты, выполненной по самолетной компоновочной схеме относи-
тельно оси OZ, нужно определить общий демпфирующий момент как сумму
демпфирующих моментов оперения, крыльев и корпуса. У ракет, не имеющих резко
выступающих поверхностей, т. е. бескрылых и неоперенных, коэффициент демпфи-
рования корпуса будет одинаков по экваториальным осям, а разница в демпфирую-
щих моментах будет определяться различием значений сог и соу.
В процессе невозмущенного сбалансированного полета ракеты происходят плав-
ные изменения углов атаки и скольжения. При этом, как показали многие исследова-
ния, угловые скорости мало влияют на полный вектор аэродинамических сил и его
составляющие. Поэтому аэродинамические коэффициенты для подъемной и боковой
сил часто определяют без учета угловых скоростей, но обязательно учитывают их при
определении аэродинамических коэффициентов моментов. Принято также для упро-
щения считать, что при малых а и 0 подъемная и боковая силы не зависят друг от дру-
га. С учетом отмеченных упрощений имеем
5-=£>0 + с”а; <з.зб>
сг=сг₽р. (3.37)
Для ЛА самолетной схемы при а = 0 су = для осесимметричных ЛА су0 = 0.
При расчете характеристик движения осесимметричных ЛА в первом приближе-
нии можно принять (в скоростных осях)
Ya = 5с“ а; Za = ; (3.38)
Mv Slmfa. ', М = ^-Slm^. (3.39)
Z У a L Уа
118
Для ЛА, близких по аэродинамической форме, графики зависимостей (М)
ла
оказываются также близкими, что позволяет в ряде случаев пользоваться на началь-
ном этапе проектирования аэродинамическими коэффициентами, определенными
для существующих, хорошо себя зарекомендовавших объектов. Так как тождествен-
ное подобие далеко не всегда имеет место, то в расчет вводят коэффициент пропорци-
ональности /, называемый коэффициентом формы:
сХв(И/а)
(3.40)
где сх (V/a) — неизвестный аэродинамический коэффициент для вновь проектируе-
мого объекта;
эт( V/a) — аэродинамический коэффициент известного, аэродинамически по-
хожего на проектируемый объекта-аналога (эталонного).
Если известно сх эт( V/a) какой-либо ракеты, то для ракеты, близкой по аэродина-
мической форме, можно принять
X=^SicXa„{V!d}. (3.41)
Если формы ракет и условия полета нетождественно подобны, то, очевидно, i * 1
и зависит от отношения V/a. Установить точно эту зависимость можно опытным пу-
тем или получив теоретически значение сх эт( V/d) для вновь проектируемого объек-
та, но при этом теряется преимущество введения коэффициента L Поэтому принято
определять значение i приближенно, полагая его постоянным для расчета данной тра-
ектории.
Численное значение i зависит от формы вновь проектируемого объекта и значе-
ний сх эт( V/a) для известных типов объектов, с которыми новый объект сравнивает-
ся. Поэтому всегда необходимо указывать, применительно к какому эталонному зако-
ну сопротивления воздуха сх эт( V/a) определяется коэффициент /. Удобно использо-
вать / в качестве коэффициента согласования расчета по определению дальности
полета с опытом. В этом случае i будет учитывать не только форму ЛА, но и все факто-
ры, не отраженные в данном расчете, например, отличие числовых значений коэффи-
циентов формы от эталонного значения коэффициента, а также различные характе-
ристики колебаний относительно центра масс при различных начальных условиях
движения ЛА.
В уравнение Ха входит массовая плотность р, кг/м3. Если перейти к весовой плот-
ности П, получим
Хв=^П^Сх<эт(К/о).
Умножим и разделим правую часть уравнения на произведение QTI0N • 103. В ре-
зультате будем иметь
х.~Й 1О’г^п?п“,'Ч-"(и/а)- <3-42>
119
В полученной зависимости множитель -q ' 103 = с называется баллистическим
коэффициентом, а член
Г(П=^п^и^эт(К/о) = 4,74 • 1(Нк\эт(И/о),
являющейся функцией сопротивления воздуха, условно называют «законом сопро-
тивления».
После преобразований получим удобную формулу
Xa = mcH(y)F(V). (3.43)
F(V)
При использовании в расчетах уже имеющихся таблиц для F( И) и G( У) = и
при вычислении таблиц для новых типовых функций следует учитывать, что скорость
звука а зависит от температуры воздуха и, следовательно, изменяется с высотой. Как
известно, а = JkgRx, где к — показатель адиабаты.
Если для относительно коротких траекторий (хс < 50 км) принять g = const, ак —
независящим от температуры, то окажется, что скорость звука пропорциональна .
Для того чтобы иметь таблицы функций для F(F) и G(F) с одним входом, надо рас-
считывать их для одной фиксированной скорости звука, сохраняя при этом равенство
Cxa(^) = CXa(^ON) (3-44)
ИЛИ
(V/a) = (Vx/a0N),
где a0N — скорость звука при нормальных условиях, принимаемая постоянной при
вычислении таблиц; — условная табличная скорость.
Очевидно, что
Тогда, используя найденное выражение, имеем
F( V) = 4,74 • 10-4 И2 (А ). (3-45)
XON \aON )
Обозначая
А 2 ( Ут \
ЛГ,>-4,74
получим
F(K)=-Lf(Kt). (ЗЛ6>
Еще раз подчеркнем, что изложенный подход имеет право на существование толь-
ко на самом раннем этапе проектирования, когда еще отсутствует облик будущей раке-
ты, тем более нет представлений об ее основных данных. На этом этапе достаточно
лишь грубо оценить в первом приближении потребную скорость, а следовательно, и за-
пас топлива, которые ракета должна иметь ддя достижения поставленной цели полета.
На более поздних этапах баллистического проектирования уже должны быть ис-
пользованы индивидуальные значения аэродинамических характеристик, например,
получаемых, как правило, расчетным путем для заданной компоновки ЛА, либо экс-
периментально (что является более предпочтительным) на основе продувок моделей
проектируемого ЛА в аэродинамических трубах.
120
3.2.2. Сила тяжести
Вектор силы тяжести можно представить как сумму векторов
F = FT + FU, (3.47)
где FT — вектор силы земного тяготения; Fu — вектор центробежной силы инерции.
В сферических геоцентрических координатах центробежная сила инерции, дейст-
вующая на тело с массой т в направлении, перпендикулярном оси вращения Земли,
Fu=mrQ2cos<pru, (3.48)
где £2 — угловая скорость вращения Земли.
Направление силы тяжести совпадает с направлением отвеса, т. е. с вертикалью
в рассматриваемой точке земной поверхности. Угол между нормалью п к поверхно-
сти и экваториальной плоскостью Земли называется географической широтой (рг в от-
личие от геоцентрической широты (ргц (рис. 3.3).
Географическая долгота отсчитывается от начального меридиана, за который
принят меридиан Гринвича. Связь между геоцентрической и географической широ-
тами устанавливается по приближенной формуле
tg<pru = tg<pr(l-/f), (3.49)
где /j — первый эксцентриситет.
Разность между углами (рг — (ргц может быть найдена также из зависимости
<Pr-<Pru = asin2<Pp
где a = 1/(298,2 ± 0,2) — коэффициент полюсного сжатия Земли.
Наибольшее значение разности (рг — (ргц равно 11,5' при (рг = 45°.
Потенциал силы тяжести также можно представить как сумму потенциалов силы
земного притяжения и центробежной силы инерции, определяемой суточным враще-
нием Земли
П = ПТ+ПЦ. (3.50)
Учитывая, что 6ПЦ = £ц * dru, где гц = г cos (ргц, получим потенциал центробежной
силы инерции, отнесенной к единице массы, в виде
Рис. 3.3. Схема определения
положения местной вертикали
при географической широте фг
и расположения вектора ускорения
свободного падения по осям
косоугольной системы координат
Пц = Q2/*2 cos2 <ргц. (3.51)
Если использовать для Пт формулу в виде разло-
жения потенциала, то
п = - + (3 sin2 <ргц - 1) + 2 Q2r2 cos2 <рга.
(3.52)
Получим формулу для определения ускорения
свободного падения. По свойству потенциала,
найденного для единичной массы,
&=ЭП/Э5, (3.53)
где gs — проекция ускорения свободного паде-
ния на направление 5; ЭП/Э5 — производная от
потенциала силы тяжести, взятая по направле-
нию S.
121
Выберем в качестве направления S нормаль к поверхности сфероида, на которую
вектор ускорения g проецируется полной величиной. Обозначая направление норма-
ли к сфероиду через л°, будем иметь
(3.54)
Имея в виду малую разницу в углах фгц и фг производную по направлению п° за-
меняют производной по направлению г
ЭП =ЭП
71г
(cos плг).
(3.55)
Учитывая противоположность направлений отсчета для лиги малость угла меж-
ду л и г, можно записать
-1 < cos (иЛг) < -0,999995,
где число 0,999995 соответствует наибольшей разности углов фг и фгц, равной 11,5’.
Учитывая малое отличие cos (лЛг) от единицы, получим g = Э П/Э п = — Э П/Э г. Да-
лее, заменив в формуле для gr функции я, их значениями я0 =/Л/ и я2 =/(А — В), где А
и В — моменты инерции Земли относительно главных осей, придем к выражению
g=f-^ +^(A-B)(3sin2<p -1)-Q2rcos2<p . (3.56)
г 2r
Для сферической модели Земли, без учета ее вращения, получим
g =1М/гг = gT.
Зная величину ускорения от силы тяжести, определить значение собственно си-
лы тяжести уже не представляет никаких сложностей.
Действительно,
F=mg, (3.57)
где для активного участка полета
h
т = т0- ffml dt, (3.58)
о
или, учитывая, что для большинства решаемых в проектной баллистике задач секунд-
ный массовый расход |/n| = const,
т = т0 - |/n| t, (3.59)
Для пассивного участка траектории т = тк = const.
3.2.3. Сила тяги
Тягой ракетного двигателя называется равнодействующая реактивной силы и сил
давления окружающей среды, действующих на его внешние поверхности, за исключе-
нием сил внешнего аэродинамического сопротивления. Равнодействующая газо-
и гидродинамических сил, действующих на внутренние поверхности ракетного двига-
теля при истечении из него вещества, называется реактивной силой.
Отдельно измерить реактивную силу не представляется возможным, и ее опреде-
ляют вместе с силами статического давления, действующими в направлении продоль-
ной оси ракеты.
Укрепленная на стенде ракета удерживается от перемещения осевой силой Р’, ко-
торая равна тяге, но направлена противоположно ей Р’ = —Р. На наружную поверх-
ность ракеты действуют силы, определяемые атмосферным давлением р, соответст-
вующим высоте, на которой находится ракета. По величине они равны произведению
122
давления на площадь и направлены перпендикулярно той площадке, на которую дей-
ствуют. Все силы, действующие на боковую поверхность ракеты, уравновешивают друг
друга. Но при работающем двигателе атмосферное давление не действует на выходное
сечение сопла, через которое параллельно оси ракеты ОХ истекают газы со скоростью
И^и, и появляется приложенная к корпусу неуравновешенная сила pSa, направленная
в сторону истечения газов (Sa — площадь выходного сечения сопла). В выходном сече-
нии сопла действует противоположно направленная сила paSa, где ра — давление исте-
кающих из сопла газов в этом сечении (сила сопротивления истечению газов).
Таким образом, применительно к стендовым испытаниям получим формулу для
расчета тяги
+ (3.60)
Заменив в этом уравнении |^| = , найдем выражение для тяги в другой форме:
P^W^ + S^-P). (3.61)
В случае, когда можно принятьр ~ 0,
P=^WmH + Sapa. (3.62)
Если ракета расположена у поверхности Земли на нулевом уровне, то для нор-
мальных метеоусловий (у = 0; р = p0N) ее тяга равна
P=<~^Wam +Sa(pa-p0N). (3.63)
Если условия отличны от нормальных, то при у = 0; Р = Ро. Сравнивая формулы
(3.61) и (3.63), получим
? = Л) + $aPoNО ” P/PoN )•
Так как л (у) =p/p0N, получим окончательно формулу
P=P^Sap0N[\-Tt(y)Y (3.64)
широко используемую при решении задач проектной баллистики.
При проектировании ракет чаще всего используют такую характеристику
реактивного двигателя, как удельная тяга (называемая также удельным импульсом),
под которой понимают тягу двигателя, отнесенную к весовому секундному расходу
топлива. Тогда уравнение (3.63) может быть преобразовано к виду
W V
о *сек
3.2.4. Управляющие силы и моменты
Управление ДА в полете осуществляется системой управления, неотъемлемой
частью которой являются исполнительные органы (органы управления). Исполнитель-
ные органы, или рули, как их часто называют, создают управляющие силы и моменты.
По принципу создания управляющих сил и моментов органы управления принято
разделять на три типа: аэродинамические, газодинамические и смешанные. Аэроди-
намические (воздушные) органы управления работают только в плотных слоях атмос-
феры при взаимодействии с потоком воздуха, обтекающим ДА. Газодинамические ор-
123
ганы управления могут работать и в нижних и в верхних слоях атмосферы (космиче-
ском пространстве), так как они функционируют за счет энергии, выделяющейся при
сгорании топлива.
Многие из управляемых объектов имеют только аэродинамические органы уп-
равления. Некоторые ракеты и, в частности, баллистические ракеты дальнего радиуса
действия и РН космических аппаратов, имеют комбинированные органы управления,
состоящие из различного рода аэродинамических и газодинамических устройств,
Аэродинамические органы управления, используемые на различного типа ЛА, обыч-
но делятся на рулевые поверхности (рули), поворотные крылья и прерыватели воз-
душного потока (интерцепторы).
Принцип действия рулей и поворотных крыльев состоит в том, что они, отклоня-
ясь от своего нейтрального положения и поворачиваясь относительно связанных осей
ЛА, изменяют в процессе полета свои углы атаки, что вызывает изменение угла атаки
(или скольжения) ЛА в целом.
Для учета в уравнениях движения управляющих сил и моментов необходимо выде-
лять составляющие аэродинамических коэффициентов, определяемые поворотом уп-
равляющих органов. Например, для рулей тангажа (высоты) и рыскания (направления)
продольная, нормальная и поперечная управляющие силы соответственно равны
х, - sP «<4 + ^s;s. +
1'r--s'p«£j5.’zp-'sp’c?;6. - <’-6S>
где 5П — характерная площадь рулей; q — скоростной напор; , с?в, — со-
р лр лр yv 4р
ответствующие частные производные; 8Н и 8В — углы отклонения органов управления
(рулей).
Моментные характеристики определяются с учетом угловых скоростей поворота
управляющих органов:
тру= тру8» + '”р^н ; (3.66)
'”рг='”р’8в +'”p?S»;
а моменты управляющих сил по каналам тангажа и рыскания
Mpy = Sq/mpy;Mpz = Sq/mpz. (3.67)
Подавляющее большинство рассматриваемых типов ЛА осуществляют полет ста-
билизированными по крену.
Учитывая, что задача синтеза контура стабилизации относится к этапу динамиче-
ского проектирования ЛА и выходит за рамки задач проектной баллистики, мы не бу-
дем рассматривать здесь вопросы определения характеристик ЛА по каналу крена, ад-
ресовав заинтересованного читателя, например, к работам [3, 4].
3.3. МАТЕМАТИЧЕСКИЕ МОДЕЛИ ДВИЖЕНИЯ ЛА
3.3.1. Уравнения движения ЛА в векторно-матричной форме
и их проекции на оси выбранной СК
Обозначим скорость и ускорение центра масс системы (корпус ракеты—топливо—
газы) в абсолютном движении через Va и аа. Движение корпуса и жестко связанных с
ним частей (т. е. и той точки тела, с которой в данный момент времени совпадает центр
124
масс) относительно неподвижной системы координат будет переносным. Скорость и
ускорение центра масс корпуса в переносном движении обозначим через Ve и ае = dVe/
dt. Скорость и ускорение центра масс системы корпус—топливо—газы относительно
корпуса ракеты обозначим через Vr и аг. Из механики тел переменного состава следует,
что произведение массы тела на переносное ускорение его центра масс равно равно-
действующей всех внешних и реактивных сил, действующих на тело, т. е.
mae = EF + EFp. (3.68)
Скорость и ускорение центра масс ракеты в абсолютном движении соответствен-
но равны
Vfl = Ve +Vr;afl = ae + ar + 2(<oxVr). (3.69)
Из последнего равенства определим ае. Тогда уравнение движения центра масс систе-
мы корпус—топливо—газы, записанное в векторной форме, получим в следующем виде:
dV
/nafl = /n-j^ = EF + EFp +/лаг+2/л(<о х Vr). (3.70)
При выводе уравнений предполагалось, что взаимодействие основного тела с
присоединяющимися или отделяющимися частицами происходит мгновенно. В дей-
ствительности процесс взаимодействия ЛА с подвижными присоединяющимися или
отделяющимися газовыми потоками сложнее. У ракет с двигателями на жидком и
твердом топливе отделяющиеся частицы получают относительную скорость еще в ка-
мере сгорания двигателя до момента выхода частицы за плоскость наружного сечения
сопла, т. е. до потери связи с основной массой ракеты. Кроме того, у ракет на жидком
топливе горючее и окислитель перемещаются в процессе работы двигателя внутри
корпуса ракеты. При взаимодействии движущихся потоков с корпусом, колеблю-
щимся в поперечном направлении, возникает кориолисова сила FKOp. Запишем урав-
нения движения центра масс ракеты с учетом этой силы
таа = EF + EFp + FKOp + /паг + 2/n(m х Vr). (3.71)
Добавим в последнее уравнение слагаемое, учитывающее нестационарность дви-
жения масс внутри корпуса ракеты. Пусть количество движения топлива и газов, пе-
ремещающихся внутри корпуса, в момент времени t равно <?кор, а в момент времени
t + dt равно <?кор + &7вар. Очевидно, за промежуток времени dr изменение количества
движения подвижных масс равно 8^,, и уравнение движения ракеты может быть
представлено в более полной форме:
= EF + EF, + EFKop + mar + 2m(<o х Vr) + (3.72)
Составляющую Sq^/dr принято называть вариационной силой.
Уравнение соответствует так называемому принципу затвердевания, согласно ко-
торому уравнения движения тела переменного состава можно представить в форме
уравнений движения тела постоянного состава, имеющего мгновенно зафиксирован-
ную (затвердевшую) массу.
Только при использовании указанного принципа становится справедливым при-
менение при составлении уравнений движения ракет теорем об изменении количест-
ва движения, кинетического момента и кинетической энергии.
Вариационные силы и моменты отражают нестационарность движения масс вну-
три корпуса ракеты. Однако в большинстве случаев процесс перемещения рабочего
тела внутри ракеты можно принимать за квазистационарный и вариационные силы
не учитывать ввиду малости.
125
Силы Кориолиса, обусловленные движением масс внутри корпуса ракеты и ее
колебаниями, на движение центра масс почти не оказывают влияния. Силы Кориоли-
са, появляющиеся при рассмотрении относительного движения ракеты в связанной с
Землей системе координат, оказывают заметное влияние на ее положение только при
движении со скоростями, превышающими 600...700 м/с.
В инерциальной системе координат уравнение движения центра масс летатель-
ного аппарата записывается в виде
dV„
W-^=EF + EFp, (3.73)
где EF и EFp — векторы суммы внешних и реактивных сил.
Для составления уравнений вращательного движения ракеты относительно осей,
проходящих через центр масс и вращающихся по отношению к ракете с угловой ско-
ростью со*, при вращении самой ракеты с угловой скоростью со надо воспользоваться
известным уравнением
+ [(ш+<о’)хК], (3.74)
где dK /dt — производная от кинетического момента, вычисленная относительно не-
d*K 6К
подвижной системы координат; -jy- = -jy — производная от кинетического момен-
та, вычисленная относительно /-й системы координат OXiY^Zi (локальная производ-
ная).
Если система координат OXiYiZi не перемещается относительно ракеты, то со* = 0 и
dK d*K
dr = +шК = Л/Я’ (3.75)
где MR — результирующий момент системы сил.
Проекции векторного равенства на оси координат, связанные с ЛА, могут
быть представлены через проекции на эти оси вектора момента количества движе-
ния К:
«X
Ку
И
“А.
где А/ — тензор инерции ЛА, выраженный матрицей инерции
Аг Ау А^
~lyx ly ~!yz
Проекции кинетического момента К на оси координат А, УД
Кх. = 1Х,(ох. - /х.у.(Оу - /хл<\;
^у, ^ул ^y^i ^xi ’
^Z,- ~ ~ Iztxt WXt ~ ^Zjy, ®y, ’
(3.76)
(3.77)
где Ix ; Iy ; Iz — моменты инерции ракеты относительно осей Д Yi Д; Ix y IXZj IyjZ —
центробежные моменты инерции, определяемые относительно координатных плос-
костей.
126
При определении осевых и центробежных моментов инерции может быть учтено
перемещение центра масс (начала координат) и вращение осей координат относи-
тельно корпуса:
п п
ix = Z mv(yi + zjv); 1У = X mv(z2iv + x2ivy,
' v=1 ' V= 1
"M* iv~^~y /v)’ ^yjxi ~ (3.78)
v = 1 v = 1
n n
^XjZj ~ ^ZjXj ^V^/V^/V» lyjZj [^У}
V = 1 V = 1
Очевидно, осевые и центробежные моменты инерции в процессе работы двигате-
ля и движения ракеты будут переменными величинами, зависящими от времени.
Уравнения вращательного движения относительно центра масс в скалярной фор-
ме наиболее часто представляют в следующем виде:
4, ®х, + (4, “А-, ~ + аУ, > +
.2 .2
+ 1у^-^) = мХ1 + мрХ1-
.2 .2
1у, <ау. + (/х - IZj) (ох <вг - /Х.Л (<ах. + (йу. ©г ) + 1Х ,г. (<°Х, + <0г,) -
- 1у.г. (®г, - <аУ1 )=Myj + Mpyt; (3.79)
• 2 .2
/г йг. + (1у, - 1Х ) сох <0^ - 1Х ( <ЬХ. - (йу, ©г) - 1УЛ ( (by. + ®х ©г ) + 1х,у. (Пу, - <»х, ) =
Правые части уравнений здесь содержат проекции суммы моментов относитель-
но центра масс всех сил, действующих на ракету, на соответствующие оси координат.
Моменты кориолисовых сил и дополнительный момент, определяемый перемещени-
ем центра масс ракеты относительно корпуса, при решении многих проектных бал-
листических задач ввиду малости не учитываются.
Если подвижные оси координат совместить с главными центральными осями
инерции OXYZ, то матрица Af превратится в диагональную:
L О О
О 1у О
О 0 Iz
а ее элементы Ix, Iy, Iz будут главными центральными моментами инерции. Проекции
уравнений на оси связанной системы координат при этом запишутся в виде
где
(3.80)
(3.81)
127
ЪМХ, ЪМу, ZMz — суммы проекций моментов всех внешних и реактивных сил на оси свя-
занной системы координат; cbx, (by, <bz — составляющие вектора углового ускорения.
Определяя угловые ускорения, запишем динамические уравнения вращательно-
го движения ЛА относительно центра масс в проекциях на оси связанной системы ко-
ординат
(о/
Фу
Л-
ZMz
- Aj
(3.82)
ЕЛ/Х-
где Л7-1 — матрица, обратная Л7. Переходя от матричной формы записи к обычной,
получим уравнения вращательного движения в виде динамических уравнений Эйлера
(3.83)
К динамическим уравнениям, определяющим величину линейной и угловой ско-
ростей ЛА, необходимо добавить кинематические уравнения.
Зададим положение ЛА относительно начала выбранной базовой системы коор-
динат вектором г.
Если рассматривать теперь движение ЛА относительно системы координат, изме-
няющей свою ориентацию при движении ЛА относительно поверхности Земли с угло-
вой скоростью со при вращении самой Земли со скоростью Q, то кинематическое урав-
нение для определения абсолютных параметров движения ЛА записывается в виде
d d*
‘r.= ^r + (Q+<»)xr, (3.84)
d*r
где — локальная производная вектора г относительно вращающейся системы ко-
ординат.
Если принять к рассмотрению случай, при котором движение описывается отно-
сительно связанной с поверхностью Земли системы координат, например географи-
ческой, начало которой совмещено с центром масс ЛА, то
^r = V-®xr, (3.85)
где V — скорость ЛА относительно поверхности Земли, что соответствует системе ска-
лярных уравнений
Гх = +
г = К - <0 гх + тхг (3.86)
Гг = Vl~^xry + ^yrx
Наконец, когда движение рассматривается относительно неподвижной системы
координат, например стартовой, совпадающей с нормальной системой OXgYgZg,
^r = V (3.87)
и система скалярных уравнений принимает вид
dx dyr dx
-т-с = Kcos 0 cos 4х; -£ = Ksin 0; = -Kcos 0 sin 4х. (3.88)
dz dz dz
128
3.3.2. Упрощенная схема составления скалярных
уравнений движения ЛА
Ускорение ракеты при плоском криволинейном движении можно представить
как сумму тангенциального ах и нормального ап ускорений. Эти ускорения направле-
ны по нормальным (естественным) осям системы координат Охп. Тангенциальное уско-
рение у направлено по касательной к траектории. Нормальное ускорение V2/p на-
правлено по нормали к траектории в сторону мгновенного центра кривизны. Кривиз-
на траектории \/р может быть представлена как \/р = |d0/d5|, где d0 — элементарное
изменение угла наклона касательной к траектории; d5 — элементарный отрезок кри-
вой. Здесь/? — радиус кривизны траектории.
Проводя замену и преобразования, получим формулу для модуля нормального
ускорения
<W)
Знак производной d0/d5 зависит от формы траектории: если 0 убывает с возрастани-
ем дуги, то d0/d5 < 0, если наоборот, то d0/d5 > 0. Поскольку для траектории ракет 0 < 0,
то в последующем формулу для нормального ускорения будем записывать в виде
йя=и|^|=-^.
п |dr| d/
Иначе, знак минус есть следствие того, что при рассмотрении движения в правой сис-
теме координат O0XcYc положительному направлению оси п соответствует отрицатель-
ное направление линии отсчета углов 0.
Движение ракеты будем рассматривать в нормальной земной системе координат
O$XgYgZg. При этом для упрощения записи влияние вращения Земли учтем введением
постоянного по величине и направлению ускорения свободного падения, пренебре-
гая кориолисовым ускорением; кривизну Земли учитывать не будем, что для актив-
ных участков ЛА относительно малой протяженности вполне справедливо.
Проще всего записать систему уравнений для определения скорости V поступа-
тельного движения центра масс ракеты относительно Земли в проекциях на оси тра-
екторной системы координат, так как в этой системе Vv = V, Vv = V7 = (Y Тогда
лк У* 4к
уравнения упростятся и будут иметь вид
V =ых/т-, =-LF /пг, Уш = -XFz /т. (3.90)
ZK Лк Ук к
Для определения проекций угловой скорости движения траекторной системы
координат OXKYKZK относительно неподвижной системы OQXgYgZg на оси траекторной
системы координат воспользуемся соотношениями
со„ = 4х sin 0; cov =4' cos 0; cor = 0. (3.91)
к Ук
Подставляя cov и со_ из (3.91) в (3.90), получим систему
Ук 4к
V =
rpcose=----
т
(3.92)
При написании правых частей уравнений будем учитывать составляющие тяги,
силы тяжести, аэродинамических и управляющих сил.
129
В результате получим скалярную систему уравнений, описывающую движение
центра масс ракеты в траекторной системе координат:
Й = - (Рх -ЪХ„ -Xx + Qx );
т v хк Рк к хк
VQ = ^-(P +Y.Y —Y +Q Y, (3.93)
PPcos6 = -l (Л + ZZ +QZ ).
Уравнения вращательного движения ракет обычно записывают в проекциях на
связанные оси. Любая другая не связанная с ракетой система координат перемещает-
ся относительно ракеты, а это приводит к необходимости учитывать при исследова-
нии ее движения переменность моментов инерции даже при т = const, что вносит из-
лишние усложнения. Запишем уравнения вращательного движения в проекциях на
связанные оси координат, предполагая, что они совпадают с главными центральными
осями инерции:
1хсьх + (Iz - Iy) (&y(&z = LMX + ЪМрх;
Iytoy + (/х - Iz) сохсог = ЪМу + ЪМру\ (3.94)
4<ог + (1у - 1Х) сохсоу = ZMz + Щ,
где %МХ9 ЪМу9 ZMz — суммы проекций моментов внешних сил и тяги на связанные
оси координат (без учета управляющих сил); %Мрх9 ЪМру9 ^Mpz — суммы проекций мо-
ментов управляющих сил на связанные оси координат.
Для осесимметричных ракет динамические уравнения вращательного движения
можно принять в упрощенном виде
1хъх=ЪМх + ЪМр;9
Iytoy + (4 - 4) со/ог = ЪМу + ЪМру; (3.95)
4<йг + (4 _ 4) =
При работающем двигателе вследствие изменения масс ракеты из-за расхода топ-
лива моменты инерции будут переменными величинами. Значения 1Х, 1у9 1гддя раке-
ты определяются так же, как и для всякого сложного тела, т. е. вычисляются на основе
изучения чертежей конструкции ракеты при известном законе изменения ее массы в
полете. Работа по расчетному определению моментов инерции и их изменению кро-
потлива и трудоемка, поэтому при приближенных баллистических расчетах их прини-
мают постоянными. При более точных расчетах, связанных с исследованием устойчи-
вости и управляемости, переменчивость моментов инерции необходимо учитывать.
Экспериментальные методы определения моментов инерции сложных тел, дающие
более точные результаты в сравнении с расчетными, достаточно подробно разработа-
ны в механике, и мы их касаться не будем.
Для установления связей между производными О, у, у и угловыми скоростями
сох, соу и сог воспользуемся формулами перехода
сох = V sin О + у; (Dy = у cos О cos у + О sin у;
сог = — v cos О sin у + О cos у. (3.96)
130
Решая эти уравнения совместно, получим
О = соу sin у + сог cos у;
V = cos Y- sin У); (3.97)
у = сох - tg О ((Оу cos у- сог sin у).
При определении аэродинамических сил в процессе решения пространственной
задачи движения ракеты надо знать значения углов а, Р и уа.
Определяя матрицу направляющих косинусов последовательного перехода от
связанной системы координат к скоростной, от скоростной к траекторной, от траек-
торной к земной и приравнивая ее диагональные элементы диагональным элементам
матрицы направляющих косинусов непосредственного перехода от связанной систе-
мы координат к земной, получим следующие соотношения между углами:
sin О = sin 0 cos a cos Р + cos 0 (sin а cos yfl + cos a sin P sin yfl);
sin cos у = sin v cos P cos yfl + cos у (sin P cos 0 + sin yfl sin 0 cos P) —
-cos v sin 0 sin y; (3.98)
cos 0 sin у = sin yfl cos P cos 0 — sin P sin 0.
Если теперь использовать выражения для проекций вектора скорости центра
масс ракеты на оси системы координат O0XgYgZg, то найдем:
dxg/dt = Kcos 0 cos Я*
dyg/dr= Ksin 0; (3.99)
dzg /dt = - Kcos 0 sin T.
Соответственно расстояние от начала координат до центра масс ракеты (наклон-
ная дальность) будет равно
(3.100)
Приведенные уравнения рассмотренных подсистем вместе с уравнением (3.58)
h
т = mQ — J |тй| dr,
о
определяющим изменение массы, будут составлять систему из 17 уравнений (без уче-
та уравнений управления), описывающую пространственное движение ракеты.
3.3.3. Принцип разделения движений
При разделении пространственного движения ракет на продольное и боковое при-
нимают, что в первом приближении продольное движение не зависит от бокового. В со-
ответствии с этим в уравнениях для определения характеристик продольного движения
учитывают только те силы и моменты, которые действуют в плоскости пуска. При опре-
делении же характеристик бокового движения ракеты считать его независимым от про-
дольного нельзя, поэтому в уравнения включаются все силы и моменты, которые в той
или иной степени могут вызывать боковое отклонение движения ракеты.
Другим, весьма существенным упрощением, широко используемым при прове-
дении проектных баллистических расчетов, является допущение о независимости
движений центра масс ЛА и относительно его центра масс.
131
Вообще говоря, данное допущение является достаточно грубым. Его использова-
ние эквивалентно предположению о возможности рассмотрения траекторного движе-
ния ЛА как материальной точки. Подобный подход опять-таки допустим и находит
широкое применение лишь на начальных стадиях баллистического проектирования.
При расчете траекторий для сравнительно небольших дальностей во многих слу-
чаях можно не учитывать кривизну Земли, а ее вращение учитывать приближенно че-
рез ускорение свободного падения, предполагая его постоянным по величине и на-
правлению, т. е. считая гравитационное поле Земли плоскопараллельным.
Расчет параметров движения ракеты на пассивном участке траектории проводит-
ся либо до точки ее пересечения с поверхностью Земли, либо до точки, находящейся
на заданной высоте hB над поверхностью Земли. Для написания упрощенной модели
невозмущенного движения неуправляемого ЛА достаточно воспользоваться двумя
первыми уравнениями исходной системы, а также ее последним уравнением. В ре-
зультате получим в развернутой форме систему уравнений, описывающую продоль-
ное неуправляемое движение ЛА с учетом колебаний его продольной оси относитель-
но центра масс:
dK р5 . Q
dr =-Ч^И-«япе;
d0 _ а р5 v g cosO .
dr СУа 2т а ~ ’
="Г (т“ Г2а + m^pSPV^ ); (3.101)
= -я? ~ ^cos 0; тг? = 0; а = о - о.
dz z dt at
При решении ряда задач можно полагать, что неуправляемый ЛА совершает про-
дольное движение в однородном плоскопараллельном поле притяжения, в неподвиж-
ной атмосфере и с пренебрежимо малыми углами атаки. В этом случае траектория
ЛА— плоская кривая. Система уравнений, описывающая такое движение центра
масс ЛА, при допущении, что cos а « 1, sin а = 0 и Ya = 0, может быть представлена в
следующем виде:
dK Ха . „ d0 g cos0
dr=-m -^sin0; dr =-S^’
= Ksin0; = Kcos0.
at at
Первые два уравнения написаны в скоростной (совпадающей в данном случае
с траекторией) системе координат, т. е. в проекциях на касательную и нормаль к тра-
ектории. Во многих случаях применительно к задачам проектной баллистики оказы-
ваются удобными для решения системы уравнений, записанные в прямоугольной
т> dVx dw v cosO ~
стартовой системе координат. Напомним, что = —Ха—^~ . Тогда, умножив
числитель и знаменатель правой части приведенного уравнения на К, получим
du/dt = —Xau/mV. Значение полной скорости по известной величине и может быть
найдено как V = и + р2, где р = tg 0. Поэтому в качестве второго уравнения рас-
сматриваемой системы возьмем дифференциальное уравнение
dp = d(tgO) = _g
dt dt и'
132
Обозначая для простоты написания Е = Xa/(mV) при т = тк и добавляя кинема-
тические соотношения, получим известную систему уравнений:
dw г dp g dy dx /o
-г- = -Ей; = -- ; ~ = up; -г- = и. (3.103)
dt 9 dt и9 dt п dt v
Е(У)
Если воспользоваться выражением Ха типа (3.43) и ввести функцию G( И) = ,
то первое уравнение системы будет иметь вид
= -cH(y)G{V)u = -Ей, (3.104)
где£=сЯ(у)С7(И).
Для учета изменения скорости звука с высотой воспользуемся соотношением ти-
па (3.46), и тогда du/dt = -cHx(y)G( Vx)u. Соответственно,
E=-cHx(y)G(Vx).
Второе уравнение системы можно заменить дифференциальным уравнением для
определения вертикальной составляющей скорости dl^/dr = dw/dt = — Ха sin 0/m — g.
Вводя составляющую скорости w = Ksin 0, будем иметь систему уравнений:
dw г dw г dy dx
di=~Eu’di w’Tt и- (3105)
Для расчета характеристик движения баллистических ракет на пассивном участ-
ке полета часто более удобно принять за независимую переменную не время, а коор-
динату х. Получим систему уравнений при аргументе х, проведя очевидные преобра-
зования первого и второго уравнений системы (3.103):
du du dt z „ „
d-t = dlTX=(-Eu\u)=-E’
dp = dp dr = _g 1 = _g_
dx dt dx uu u2 ’
Тогда система уравнений при независимой переменной х будет иметь вид
=_£;Ф? =_*;£*=!. (З.Ю6)
dx ’ dx и2 9 dx dx и v '
3.3.4. Уравнения продольного движения
программно-управляемых ЛА на активном участке траектории
Для обеспечения запрограммированного изменения определяющего параметра
исполнительный орган системы управления ЛА должен устанавливаться в положе-
ние, соответствующее отработке разности между измеренным и программным значе-
ниями параметров [4]. Например, при задании программы по углу тангажа, угловой
скорости и углового ускорения тангажного движения уравнение управления для оп-
ределения отклонения руля тангажа будет иметь следующий вид:
80 = Х^ДО + (3.107)
где К^, К1Ъ — коэффициенты усиления контура управления по каналу тангажа.
При рассмотрении движения ЛА с балансировочным углом атаки (аБ), соответ-
ствующим выполнению требования уравновешивания составляющей аэродинамиче-
ского момента в уравнениях типа (3.95) управляющим моментом, угол рассогласова-
133
ния по тангажу может быть приближенно связан с углом поворота управляющего ор-
гана с помощью первого слагаемого уравнения управления (3.107)
8^ = ^-Опр), (3.108)
где — статический коэффициент усиления; Опр — программное значение угла тан-
гажа.
Запишем балансировочную зависимость, предполагая, что ракета имеет только
один управляющий орган (рули тангажа), определяющий ее движение в вертикальной
плоскости.
Тогда
Mz + Mpz = 0. (3.109)
Раскрывая выражения моментов, входящих в равенство (3.109), получим
0,5р И2 Slmzaab + 5/, = 0, (3.110)
5 Э Y
где Yp z = , причем Yp — подъемная сила принятого к рассмотрению органа управ-
ления, 1р — средняя аэродинамическая хорда руля
2 Y^zI Я
«Б = --Ь^=-еД. (3.111)
ру jimz
Знак минус показывает, что при повороте управляющих рулей, расположенных поза-
ди центра масс в хвостовой части ракеты в одну сторону, например, по часовой стрел-
ке, ракета повернется в другую сторону (против часовой стрелки).
Используя (3.108), получим
аБ = -Л(^-^пР) (З.И2)
или, заменяя в (3.112) О = 0 + аБ, найдем
Предположим, что вектор тяги направлен по продольной оси ракеты. Кроме то-
го, включим Хр в полную силу лобового аэродинамического сопротивления Ха, a Yp в
подъемную силу Ya. По малости угла атаки примем
sin а = аБ; cos а = 1; Ya = У“аБ,
где Г« = = с“Б (см.(3.38)).
Тогда согласно (3.93)
mV = Р — Ха — mg sin 0;
тИ0 =(Р+ К“)аБ —mg cos 0. (3.114)
Добавив к полученным дифференциальным уравнениям кинематические урав-
нения для определения текущих координат и программное соотношение для угла тан-
гажа, получим систему уравнений, приближенно описывающую продольное движе-
ние управляемой по каналу тангажа ракеты на активном участке траектории
mV = Р — Ха — mg sin 0;
= е^(Р+ Wnp-tf) cos0
тУ(1 +гМ 8 V ’
0 = 0 + аБ = 0пр(О; (3.115)
yg = Ksin0;
xg = Kcos0.
134
Простейшая система уравнений, приближенно описывающая управляемый полет
центра масс ракеты, может быть получена из (3.115), если считать, что ЛА управляется
идеально и его продольная ось совпадает с вектором скорости (О ~ 0).
Тогда
И = —gsin0;
j^ = Ksin0; (3.116)
0(0
xg = Kcos0.
т mQ — \rtt\t |/^| t
Введя обозначение ll = — =------- = 1 — — t = 1 — , где 71 — фиктивное
m0 m0 7ф ф
время, имеющее физический смысл времени выгорания топлива ракеты при задан-
ном постоянном секундном расходе \rti\ в предположении, что масса топлива равна
начальной массе ракеты, получим очевидное соотношение
d/ = -7^dp, (3.117)
позволяющее осуществить замену независимой переменной в (3.116), задав програм-
му изменения угла тангажа в функции относительной массы ц.
3.4. ВЫВЕДЕНИЕ СПУТНИКА НА ОРБИТУ
3.4.1. Качественный анализ основных участков
траектории выведения
Целью выведения искусственного спутника Земли (ИСЗ) на орбиту является его
доставка ракетой-носителем на заданную высоту с заданной скоростью и в заданном
направлении движения (на орбиту требуемого наклонения).
Реализуемая при этом траектория подразделяется на ряд участков, отличающих-
ся по своей специфике.
Характер этих участков неразрывно связан с выбранной схемой полета, опреде-
ляемой, в свою очередь, типом используемой ракеты-носителя. До настоящего време-
ни, несмотря на наличие и перспективность (с точки зрения отдельных специалистов)
многоразовых транспортных космических систем (МТКС), основным типом PH ос-
таются одноразовые ракетные системы тяжелого («Протон-К», «Протон-М»),
среднего («Союз-СТ») и легкого («Космос-ЗМ», «Рокот», «Старт-1») классов.
Применительно к системам такого типа траекторию выведения принято подраз-
делять на следующие участки: участок старта, работы первой ступени, разделения сту-
пеней, полета последующих ступеней PH и отделения полезной нагрузки.
Старт современной PH осуществляется при ее вертикальном расположении
(0 = 0 = 90°) ввиду относительно невысокой, в большинстве случаев, начальной тяго-
р
вооруженности = 1,2...1,5 , где Рс — стартовая тяга двигателей.
После 10... 15 с вертикального полета, в результате которого PH, как правило, не
успевает достичь сверхзвукового режима движения, происходит относительно крат-
ковременное изменение угла атаки, вследствие чего траектория PH отклоняется от
вертикального направления.
135
Управление с ненулевым углом атаки (порядка нескольких градусов) обычно закан-
чивается при значениях чисел Маха, примерно равных 0,8, после чего реализуемая про-
грамма изменения угла тангажа обеспечивает полет с близкими к нулю углами атаки.
Если не учитывать действие возмущений, то искривление траектории на этом
участке достигается исключительно под действием силы притяжения. Поэтому дан-
ный участок называют участком «гравитационного разворота».
На последующих участках траектории выведения, где влиянием скоростного на-
пора оказывается возможным пренебречь (его величина в самых «тяжелых» случаях
не превышает в конце участка работы двигателей первой ступени 1000 кгс/м2), угол
атаки может быть отличным от нуля и принимать значения, вытекающие из условий
энергетической оптимизации траектории.
Участок разделения начинается с момента подачи главной команды на выключе-
ние двигательной установки предыдущей ступени и заканчивается, когда отделив-
шийся ускоритель не в состоянии оказать влияние на полет последующей ступени.
Характер движения PH на участке разделения в основном зависит от компоновки ЛА
и принятого способа разделения. Сам процесс разделения протекает практически
одинаково на всех ступенях.
Принципиально возможно использование двух схем разделения: холодного и го-
рячего.
Холодное разделение (разделение торможением) предполагает запуск двигателя
последующей ступени после достижения безопасного расстояния от отделившегося
ускорителя.
При горячем разделении двигатель последующей ступени запускается еще до мо-
мента разрыва механических связей между разделяющимися частями ЛА.
Для уменьшения возмущающих воздействий и исключения колебательных дви-
жений PH на участке разделения за несколько секунд до начала процесса вводится ре-
жим стабилизации достигнутого значения угла тангажа (участок «выравнивания»).
Уменьшение возмущений от аэродинамических нагрузок достигается путем ограни-
чений скоростного напора на момент проведения разделения.
Процесс выведения заканчивается участком отделения полезной нагрузки при
выполнении следующих конечных условий: Ик* = Ик*, где Ик* = JfM3/(R3 4- у ),
0*к = 0. Здесь М3 — масса Земли; Л, = 6371 км — так называемый «радиус Земли» (радиус
сферы, объем которой равен объему геоида); у* — заданная средняя высота орбиты.
С увеличением высоты орбиты у* возникает необходимость в дополнительном
к гравитационному развороту искривлении траектории выведения с целью обеспече-
ния одного из необходимых условий выхода ИСЗ на заданную орбиту: 0* =0. При
этом, очевидно, будут иметь место возрастающие потери скорости на управление,
а следовательно, и уменьшение массы полезной нагрузки.
Поэтому выведение ИСЗ заданной массы при непрерывной работе двигательной
установки PH (выведение «без дожога» [12]), начиная с некоторой фиксированной
высоты орбиты уп* для конкретного типа PH, оказывается либо нежелательным по
энергетическим соображениям, либо вообще невозможным при у* > упр*.
В этих случаях становится целесообразным применение схемы выведения с про-
межуточным пассивным участком и последующим повторным включением двигате-
ля. Такая схема известна еще и как схема выведения «с дожогом топлива». При этом
схема выведения подразделяется на два этапа. Предварительно производится выведе-
ние полезной нагрузки ракетой-носителем на промежуточный пассивный участок
круговой или эллиптической более низкой орбиты (высотой менее 500 км; обычно
в диапазоне высот 200 км < уп* < 500 км).
136
Затем осуществляется межорбитальный переход с промежуточной орбиты (или
ее ограниченного участка) на заданную «высокую» орбиту.
В принципе для этого может быть использована последняя ступень PH с повтор-
ным запуском ее двигателей. Однако на практике такая ситуация, особенно для комп-
лексов, обладающих ограниченной тяговооруженностыо, маловероятна. Обычно для
этого применяется специальная ступень PH, называемая разгонным блоком (РБ).
РБ находят широкое применение также при решении задач межпланетных поле-
тов, связанных с необходимостью выведения КА в определенную область космиче-
ского пространства в заданное время.
После достижения требуемых терминальных (конечных) условий начинается
участок отделения полезной нагрузки — остающегося на орбите ИСЗ. Для уменьшения
разброса параметров движения в конце активного участка, предшествующего участку
отделения, считается целесообразным [ 15] уменьшать величину тяги либо за счет дрос-
селирования основного двигателя, либо за счет его предшествующего выключения и
завершения активного участка с работающими управляющими двигателями. В резуль-
тате завершение активного участка будет осуществляться на низком уровне тяги, что
приведет к уменьшению случайной составляющей импульса последействия, оказываю-
щего непосредственное воздействие на ошибки выведения ИСЗ на орбиту.
3.4.2. Оптимизация программ выведения
Выбранная траектория выведения должна гарантировать возможно меньшие
энергетические затраты, что является непременным условием экономичности опера-
ции доставки полезной нагрузки на заданную орбиту.
В связи с этим под оптимальной программой выведения на орбиту при заданных
характеристиках PH принято понимать программу, обеспечивающую наибольшую
массу выводимой полезной нагрузки при одновременном удовлетворении вводимых
ограничений на траекторное движение и функционирование систем.
Имея в виду изложенное, оптимизация программ выведения должна быть отне-
сена к оптимальному программированию опорного движения, как задаче количест-
венного и качественного анализа оптимальных в смысле выбранного критерия режи-
мов полета, доказательства существования и единственности решений, а также поис-
ка путей их технического осуществления.
Решение рассматриваемых краевых задач может быть получено с помощью мето-
дов классического вариационного исчисления [3,17].
Аппарат классического вариационного исчисления основывается на представлении
экстремали в виде точки пространства функций. Вариационные свойства этой точки вы-
ражаются уравнениями Эйлера. Для того чтобы найти в каком-либо смысле оптималь-
ную траекторию, приходится решать краевую задачу, подбирая начальные значения мно-
жителей Лагранжа. В большинстве случаев это оказывается весьма сложным процессом,
не соответствующим по трудоемкости требуемой точности получаемого решения.
Более просто соответствующие оценочные результаты могут быть найдены с по-
мощью «принципа максимума», разработанного представителями отечественной
школы советских математиков под руководством Л. С. Понтрягина [14].
Следует иметь в виду, однако, что и на основе «принципа максимума» корректное
решение соответствующей задачи в достаточно полной постановке может быть получено
лишь численно с использованием ЭЦВМ. Другими словами, в этом случае можно рас-
считывать только на получение частных результатов, что не может быть признано на-
илучшим вариантом, особенно для начальных этапов баллистического проектирования.
С другой стороны, надежда на нахождение общего решения может иметь место
только для модельной задачи, предполагающей существенное упрощение ее постанов-
137
ки на основе принятия достаточно грубых, зачастую неадекватных реальным физиче-
ским процессам, допущений.
В результате получаемое решение оказывается весьма далеким от требований
практики. Тем не менее считать, что подобный подход является бесполезным, было
бы принципиально неверным. Дело заключается в том, что оптимальные решения по-
зволяют получить ориентир, к которому следует стремиться при принятии техниче-
ских решений.
Имея в виду отмеченное, покажем в весьма конспективном изложении путь реше-
ния одной из модельных задач выбора оптимальной программы выведения, приоритет
в постановке и решении которой принадлежит Д. Е. Охоцимскому и Т. М. Энееву [13].
Значительно позднее аналогичные задачи рассматривались Д. Лоуденом [9]. За
истекшие десятилетия появилось огромное количество работ, так или иначе связан-
ных с решением обсуждаемых задач, которые тем не менее не дали оснований пере-
смотреть изложенную выше позицию в части оценки практической значимости те-
оретически оптимальных решений.
В рассматриваемой постановке задачи принимаются следующие упрощающие
допущения:
• поле тяготения является плоскопараллельным;
• вращение Земли не учитывается;
• ускорение силы тяжести является постоянным и не зависит от высоты полета;
• сила сопротивления воздушной среды отсутствует.
Уравнения движения РН в плоскости выведения для рассматриваемой постанов-
ки приобретают вид:
В7 = £ cosd; S =£ sinfl-g; J =u; J =w;m = m0- |/й|г,Р=|л| (3.118)
В данной системе в качестве «управлений» выступают параметры, воздействую-
щие на изменение вектора тяги P(t). К таковым относятся ux = cos О; u2 = sin О; и3 =
= тй (/). Тогда в общем виде система (3.118) может быть представлена в форме
•••>хп> ui’ - u3’f);
(i = 1,2, ...,n),
при заданных начальных условиях
xi(ty=xiO’ (i= t2, ..., n)
и ограничениях вида
q>j[ux(t), ..., wr(/)] < 0;
C/ = l,...,m).
Требуется найти такое управление u = [wp u2, u3]T9 которое для системы, описы-
ваемой уравнениями (3.118), гарантировало бы при минимальном расходе топлива
достижение заданных значений высоты и максимальной горизонтальной составляю-
щей скорости (при нулевой вертикальной составляющей).
Область допустимых управлений определяется техническими ограничениями
Чзтт ^3 ^Зтах» (^3min
и очевидным соотношением sin2 О + cos2 0=1,т. е. wf + wj=l.
К данной постановке требуется дополнительная ремарка, касающаяся задания
времени движения на участке выведения. Время Т> /к, где /к — время работы двигателя
может быть фиксированным или свободным. В последнем случае оно получается авто-
138
магически из условия достижения наибольшей горизонтальной скорости в конце этапа
выведения, поскольку выбор оптимального управления не зависит от его задания.
Соответственно в этом случае не накладывается ограничений на горизонтальную
координату конца активного участка, что позволяет исключить из рассмотрения
третье дифференциальное уравнение системы (3.118).
Тогда, обозначив хх = и= Vx; х2= у; х3 = w = Vy\ х4 = т, получим уравнения со-
стояния PH в следующей канонической форме
i/3i/i и3и2
— ^отн-^" ’ *2 —Х3’ *3 — ^отн“^ & -*4 W3’
для которых начальные условия х,(0) = хю (/ = 1,..., 4) известны.
Для нахождения управления, доставляющего экстремум выбранному критерию
качества, необходимо записать гамильтониан, предварительно сформировав вектор-
ную функцию сопряженных фазовых переменных i|/z.
Данная процедура является формализованной [14].
FK ИС- 1/3
Н(х, V, и) = V! —— и{ + + Уз—£7- и2 - Vtf - V4«3
или
Н(х, 1|/, w) = Нх(и) 4- Я2(х, i|f),
- -I
где//,(«) = и3 (Vi«i + Y3«2)-Y4J
представляет собой часть гамильтониана, зависимую от управления.
Система дифференциальных уравнений для сопряженных фазовых переменных
определяется как
Ч(0 = -|^ О’= ь •••>«)•
Следовательно, для рассматриваемой системы переменных состояния имеем:
И^ 1/3
V1 = О, У2 = О, V3 = - V2 , V4 = -J— (V1«1 + V1“2)>
х4
причем для данной системы задано единственное условие в конце участка выведения
= —1, поскольку, помимо выполнения условия х2(Т) = /, необходимо гарантиро-
вать нулевое значение вертикальной составляющей скорости х3( Т) = 0 и обеспечить тре-
бование по фиксированной массе полезной нагрузки, выводимой на орбиту х4(Г) = тк,
В соответствии с принципом максимума для существования оптимального уп-
равления необходимо, чтобы в любой момент времени /е [О, Г] функция Я(х, у, и)
достигала абсолютного экстремума (min для max — оптимального и max для min —
оптимального управления) на множестве допустимых управлений.
Очевидно, что в нашем случае часть гамильтониана Нх(и), зависящая от управле-
ния, будет достигать абсолютного минимума на рассматриваемом множестве при вы-
полнении условий
Vi Жз
М| “ “/ 2_с 2j/i ’ “2 “ ~ 2 , 2JA
(V1 + Уз) (V| + V3)
И
_ 1« max’ еСЛИ #* > О,
“3 ~ I"1 min> если Я* <0,
139
где функция переключения Я* = —— (\gj + Жз)1/2 + ¥<• Таким образом, получим, что
х4
при Я* * 0 циклограмма работы двигателя должна состоять из максимальных либо ми-
нимальных (в пределе нулевых) интервалов тяги. При обращении же на некотором
конечном интервале времени функции переключения в нуль возникает так называе-
мое особое управление, для которого оптимальная величина т (0 на основе принци-
па максимума определена быть не может. Рассмотрение этого случая приводит к необ-
ходимости интегрирования первых трех уравнений сопряженной системы:
Vi = q, v2 = с2> v3 = -q' + q-
С учетом введенного граничного условия ^(Т) = — 1 имеем ct = — 1 и \|/j = — 1.
При определении оптимальной ориентации вектора тяги можно принять, что
а п
и* 2 , поскольку участок вертикального подъема занимает лишь малую часть полного
времени выведения. Тогда, имея в виду выражения управлений и и2, получим
tgd=-2 = c2t-c3. (3.119)
В результате пришли к так называемому «закону линейного тангенса», представляю-
щему собой фундаментальный результат в теории оптимизации программ выведения.
Постоянные сх и с2 в выражении тангенса угла тангажа, являющегося линейной
функцией времени, должны выбираться из условия получения заданной высоты
в конце участка выведения и нулевой вертикальной составляющей скорости.
Определение времени выведения осуществляется на основе решения следующе-
го соотношения:
Я[х(Т),¥(П,и(Т)] = 0.
Детальный анализ возможного поведения функции переключения на отрезке [О,
Т] и определяемые ею режимы работы двигателя PH для рассмотренной модельной
задачи приведены в [15].
3.4.3. Выбор программы изменения угла тангажа
и предъявляемые к ней требования
Практическим средством технического воплощения выбранной оптимальной
программы выведения является реализуемая на борту PH программа изменения угла
тангажа. Действительно, программа угла тангажа служит основным, а чаще всего
единственным фактором, определяющим форму реально обеспечиваемой траектории
выведения существующих PH одноразового типа. Форма же траектории представляет
собой связующее звено между конструкцией PH и решаемой ею задачей.
На программу изменения угла тангажа 0пр (/) влияет большое число факторов,
изменяющихся в зависимости от конкретной решаемой задачи полета.
Однако существуют три достаточно общих группы факторов, оказывающих ре-
шающее воздействие на структуру и вид обсуждаемой программной зависимости.
К ним относятся:
• основные проектно-баллистические параметры, особенности конструкции PH
и ее системы управления;
• цели и задачи, стоящие перед пуском PH;
• ограничения, которым должна удовлетворять выбранная траектория.
140
Прежде всего, ориентируясь на работу [2], сформулируем основные требования и
ограничения, которые следует учитывать при выборе 0пр (/).
1. Вертикальный старт является наиболее рациональным видом пуска РН
одноразового действия, как обеспечивающий не только наилучшие условия предстар-
тового обслуживания, но и минимальные нагрузки на конструкцию заправленной ра-
кеты.
Продолжительность вертикального участка полета определяется главным обра-
зом временем, необходимым для обеспечения эффективной работы органов управле-
ния. В общем случае следует стремиться к сокращению времени вертикального участ-
ка движения.
2. Считается желательным строить программу в предположении о непрерывнос-
ти функций b(t) и О (0 и ограниченности угловых скоростей и ускорений £(/)
и О (0, испытываемых РН в полете, что обусловлено требованиями нормального
функционирования приборов и исполнительных органов системы управления.
3. Определяющим считается гарантия достижения наилучших условий по нагру-
жению конструкции, в частности обеспечению наименьших поперечных перегрузок и
изгибающих моментов. Выполнение соответствующего требования обычно обеспечи-
вается за счет введения ограничений на величину произведения угла атаки а(0 на
рИ2
скоростной напор q = .
В зоне q > 0,5gmax обычно стараются обеспечить a(f) —> 0. Однако это не всегда
возможно из-за действия ветровых возмущений. Особенно опасным считается об-
ласть высот 8... 13 км, в которой обычно достигается gmax, а скорость горизонтального
ветра может составить 70 м/с.
4. Область трансзвуковых скоростей (М = 0,8... 1,2), характеризуемую резким из-
менением аэродинамических коэффициентов, желательно проходить при а = 0.
5. Необходимо предусмотреть ограничения на q и а на участках разделения сту-
пеней из условия обеспечения безударного удаления частей РН друг от друга.
6. Должны быть введены ограничения на параметры движения РН в момент
сброса обтекателя, поскольку многие элементы конструкции полезной нагрузки до-
пускают воздействие q, исчисляемого величиной не более нескольких десятков кило-
грамм (в отдельных случаях нескольких килограмм) на квадратный метр поверхности.
7. Программа должна гарантировать приемлемое качество выведения в широком
диапазоне решаемых РН задач. В частности, она должна обеспечивать допустимость
выведения на орбиту с заданной высотой в точке выведения, но с различным пери-
одом обращения (или высотой апогея) различных масс полезной нагрузки.
Перечисленные ограничения относятся главным образом к условиям формиро-
вания траектории первой ступени РН. Синтез программы для последующих ступеней
должен ориентироваться на решение краевой задачи, поскольку выведение на задан-
ную орбиту предполагает удовлетворение определенных краевых условий в конце тра-
ектории выведения.
Как было показано ранее, решение вариационной задачи на отыскание экстре-
мума функционала, выражающегося в самом общем виде через параметры движения в
конце активного участка, приводит к программе, соответствующей «закону линейно-
го тангенса» (3.119).
Более универсальной считается аппроксимирующая дробно-линейная функция
tgo=^|;. (3.120)
141
На практике «квазиоптимальная» программа выбирается из семейства линейных
программ вида
0(0 = Л) + О/, (3.121)
имеющих два свободных параметра: О" + О77. Их выбор подчиняется удовлетворению
краевых условий. Для трехступенчатой PH аналогично решается задача построения
программы изменения угла тангажа для третьей ступени.
3.4.4. Методы решения проектно-баллистических задач
выведения спутника на орбиту
При решении задач баллистического проектирования PH находит применение
широкий спектр методик, базирующихся как на наиболее универсальных методах
численного интегрирования уравнений движения ЛА, так и различных приближен-
ных аналитических и полуаналитических (графоаналитических) методах. Не имея
возможностей для подробного рассмотрения этих методов, ограничимся здесь их
кратким обзором.
В общем случае уравнения движения ЛА представляют собой системы нелиней-
ных дифференциальных уравнений первого порядка, которые могут быть проинтег-
рированы численно при задании начальных условий.
Применимость численного интегрирования при решении задач определения па-
раметров движения PH на атмосферном участке траектории базируется на воз- мож-
ности вычисления с их помощью значений интеграла от функции, заданной таблич-
но.
Для этой цели используется так называемая интерполирующая функция, которая
под знаком интеграла заменяет действительную функцию, аналитический вид кото-
рой неизвестен. При условии, что такая замена происходит на малом участке кривой,
точность интегрирования может быть достаточно высокой.
Пусть интерполирующей функцией будет функция у = /(х). Тогда приращение
определенного интеграла в пределах от хп до хп + j будет
Д/л = J уйх .
Хп
Самой простой является линейная интерполирующая функция
У-Уп = х-хп
УП + \~УП Хл-Ы-Хл’
где хп + J — хп = hx — интервал изменения аргумента или шаг интегрирования; уп + j - уп =
= &уп — разность между значениями функции, соответствующими данному п и после-
дующему п + 1 значениям аргумента.
Искомую величину функции, соответствующую аргументу х, зададим в виде
х — х„
У = У„+ —Ц—^Уп-
При линейном интерполировании площадь под кривой, изображающей функ-
цию /(х), будет разбита на ряд трапеций. Интегрирование по методу трапеций дает су-
щественную ошибку, и, как правило, он редко применяется при баллистических рас-
четах.
142
Простейшим методом численного интегрирования дифференциальных уравне-
ний является метод Л. Эйлера. Пусть требуется найти решение дифференциального
уравнения первого порядка
Ух'=/(Х,У)
при начальных условиях: х = х0, у = у0. При интегрировании шаг изменения аргумента
hx выбирается так, чтобы в пределах этого шага можно было бы допустить, что функ-
ция /(х, у) сохраняет постоянное значение. Заменяя производную отношением малых
конечных приращений, можно записать
Ух dx Дх ’
Для первого участка интегрирования Дх0 = — х0 = hx, Ду0 = - Уо, и тогда
f<X0,y0)=
В результате преобразования будем иметь
У1=Уо + УМо)’
Повторяя операцию для последующих участков интегрирования, получают по-
следовательные значения функций
У2=У\+Ьх/(х{,у{У,
Уз=У2 + ^х/(х2,у2).
В общем виде формула численного интегрирования дифференциального уравне-
ния первого порядка по методу Л. Эйлера запишется как
Уп+\=Уп + Ьх.КХп’Уп'У
При решении задач баллистики метод Л. Эйлера , так же как и метод трапеций,
может привести к значительным ошибкам. Точность метода повышается с уменьше-
нием шага интегрирования, однако при этом увеличивается общий объем вычисле-
ний и сохраняется накопление ошибок в процессе интегрирования.
Тем не менее, как наиболее простой, метод Л. Эйлера находит применение, как
правило, на стадии решения задач баллистического проектирования, когда использу-
ются достаточно простые математические модели, а точность решения не входит
в противоречие с требуемым уровнем приближения.
Наиболее распространенным методом численного интегрирования, используе-
мым в баллистических расчетах, является метод Рунге-Кутта четвертого порядка и его
различные модификации. В основу метода Рунге-Кутта положено разложение иско-
мой функции y=f(x) около ее известной точки (хп, уп) в степенной ряд по аргументу
(х-х„):
УаУп + ^-хп}у'п + + ... + у™.
Разложение дает возможность получить значение функции у(хп 4- hx) по извест-
ному начальному значению у(хп) и шагу hx. Искомое последующее значение функции
Уя + \=Уп + ^Уп-
Основная расчетная формула для определения Дул имеет вид
&У„ s g (*| + 2*2 + 2к3 +
143
где
Л] = hxf(xn, уп); к2 = hxf(xn +^hx,yn+^ кх);
кз = hxf <Хп + J кх’Уп + J к1У, к4 = hxf(Xn + Лх> Уп + кз )•
Большим достоинством метода является однотипность вычислений для всех точек.
При составлении программы на ЭЦВМ может оказаться более удобной практи-
чески альтернативная по точности следующая формула для вычисления ДуЛ:
Дг„ = 5 (*i + ЗЛ2 + кз +
где
к\ = kxf (*л> Уп ); к2 = hxf + 2 Ах’ Уп + 2 );
к3 = hxf + 2 Их’Уп - 2 + *2 ); *4 = hxf (Хп + Ьх’Уп + 2 к2 + 2 *3 )
Численные методы с использованием ЦВМ позволяют проинтегрировать любую
из приведенных выше систем дифференциальных уравнений с заданной точностью.
Вместе с тем эти методы трудоемки, и их целесообразнее всего использовать для про-
ведения точных баллистических расчетов. На этапах проектирования, особенно на-
чальных, требования к точности баллистических расчетов ниже. Для подобных расче-
тов могут применяться различные аналитические и полуаналитические методы.
Для подтверждения обоснованности этого утверждения приведем весьма впечат-
ляющий пример, заимствованный из [2].
Предположим, что требуется провести исследование зависимости полезной на-
грузки, выводимой на орбиту, от шести проектно-баллистических параметров двух-
ступенчатой PH, например от значений удельных тяг на первой и второй ступенях, тя-
говооруженности на этих же ступенях, соотношения масс ступеней и высоты круго-
вой орбиты. Если даже допустить, что каждый параметр варьируется в пределах пяти
значений (на самом деле число варьируемых значений каждого параметра в ряде задач
исчисляется десятками), то количество вариантов расчета составит 56 = 15 625.
Если учесть, что в каждом случае необходимо решать вариационную или, в край-
нем случае, экстремальную задачу (по массе полезной нагрузки) с заданными краевы-
ми условиями (высота круговой орбиты), то в среднем это потребует расчета 20...30
траекторий.
Следовательно, суммарное решение поставленной задачи сведется к определе-
нию 300...400 тыс. траекторий. Если принять, что для расчета одной траектории затра-
чивается 10 с машинного времени (что является весьма скромным предположением с
учетом необходимости решения вариационных задач), то всего потребуется около
1000 часов машинного времени.
Из этого примера вытекают два важнейших вывода, сформулированных автора-
ми уже цитированной выше работы:
• в проектно-баллистических исследованиях следует ограничивать число варьи-
руемых параметров и проводить их только в предварительно выявленной окрест-
ности разумно выбранных решений;
• на стадии предварительных проектных исследований следует использовать наи-
более простые методы баллистических расчетов, избегая методов интегрирова-
ния уравнений движения и добиваясь сокращения времени счета на два-три по-
рядка. Данные обстоятельства стимулируют использование давно уже созданных
методов приближенных расчетов и их дальнейшее совершенствование.
144
В зависимости от характера принимаемых допущений приближенные, в том чис-
ле аналитические, методы решения задач баллистики можно разделить на четыре ос-
новные группы.
К первой группе следует отнести методы решения систем уравнений, в которых
члены, учитывающие сопротивление среды, опущены. Методы данной группы ис-
пользуются в основном для проведения качественного анализа и находят весьма огра-
ниченное применение.
Ко второй группе отнесем методы, в которых сила сопротивления воздуха учиты-
вается в уравнениях в виде какой-либо аналитической функции, отражающей зависи-
мость между силой сопротивления воздуха и скоростью движения центра масс.
В подобных решениях, как правило, учитываются только одна-две аэродинамические
характеристики, например, только лобовое сопротивление и подъемная сила, связь
между которыми дается в виде специальной функции — поляры ЛА, для которой под-
бирается аналитическое выражение.
К третьей группе отнесем методы, основанные на искусственных преобразованиях
основных дифференциальных уравнений движения, позволяющих разделить перемен-
ные. Однако разделение переменных не всегда приводит к получению решений
в конечном виде, позволяющих иметь численный результат. Во многих случаях оказы-
вается необходимым интегралы представлять в виде таблиц или графиков. Заметим,
что применение этих проектно-баллистических методов предполагает, как правило,
переход при записи уравнений движения и программы 0пр(/) от аргумента t к аргументу
ц на основе соотношения (3.117). Подобные преобразования не всегда бывают доста-
точно строгими и требуют введения согласующих коэффициентов и вспомогательных
таблиц. С примерами такого рода методов можно познакомиться по работам [1,2].
К четвертой группе относятся методы решений, в которых заранее задается вид
функции, определяющей изменение той или иной характеристики движения. Напри-
мер, может быть задан вид зависимости скорости движения центра масс ЛА от време-
ни V(t). Последние методы требуют дополнительного задания закона сопротивления
среды или проведения последовательных приближений при численном вычислении
определенных интегралов, содержащих функции от силы сопротивления воздуха.
Каждый из методов применим для конкретных условий полета, приближающих-
ся к допущениям, принятым при составлении дифференциальных уравнений.
Отдельного обсуждения заслуживают используемые на практике приближенные
методы решения краевых задач, применяемые при синтезе программ изменения угла
тангажа.
К числу таковых, в частности, относится метод, получивший применительно к
двухпараметрической краевой задаче название метода секущей плоскости [2].
Сущность подхода сводится к следующему. Производится расчет трех траекторий
при некоторых, соответствующим образом заданных параметрах программы угла тангажа
[О, О]; [03 + ДО), О]; [О, (О + ДО)].
Расчет ведется до достижения значения граничной скорости, отвечающей усло-
вию выведения ИСЗ на орбиту V*.
Этим программам будут отвечать следующие решения:
[у, 0]; [у + Ду(О), 0 + Д0(О)]; [у + Ду(О), 0 + Д0(О)].
Далее вычисляются приближенные значения производных
Эу _ Ду(О). Э0 _ Д0(О). Эу _ Ду(О) . Э0 _ Д0(О)
Эд Ад ’ Эд Ад ’ эф Ад ’ Эд Ад
145
и определяются потребные приращения ДО и ДО, которые при условии линейной за-
висимости у и 0 от этих параметров ликвидируют имеющиеся невязки по высоте
у и углу 0: у-^=Йдд+^ДО; (3.122) Эй
— ЛА 4- ЛА
- -гд Ди + — Дт>.
Эй
е-ек*
Найденные из (3.122) значения ДО и ДО составляют новую программу, для кото-
рой следует повторить описанный расчетный алгоритм. При этом число итераций бу-
дет зависеть от выбора начального приближения и требуемой точности, которой дол-
жно удовлетворять искомое решение.
При решении проектно-баллистических задач часто параметры движения в кон-
це активного участка сами по себе самостоятельного значения не имеют.
Постановка задачи в этом случае ограничивается поиском решения, обеспечи-
вающим выполнение каких-нибудь более общих условий, например, удовлетворение
требованию выведения на орбиту с заданным периодом обращения максимальной
полезной нагрузки.
При этом на ориентацию эллиптической орбиты в пространстве ограничений,
как правило, не накладывается, но вводится ограничение снизу на высоту орбиты над
поверхностью Земли [2].
Для данной задачи программа также выбирается из семейства двухпараметриче-
ских линейных программ 0пр(/).
При всей своей простоте описываемый алгоритм позволяет получить вполне
приемлемые результаты по точности и сходимости, хотя в отличие от вариационной
процедуры он ограничивается поиском решения в рамках тривиальной задачи нахож-
дения экстремума функции.
тк
Значение относительной конечной массы цк = ~ аппроксимируется некоторой
билинейной функцией параметров программы 0^7 и О77:
цк = afttf + ЬЬП + + d.
(3.123)
Записав условия экстремума цк по варьируемым параметрам
= а + сЬп =0, —г-н = Z> + cOZ7=0,
ЭОП 0
получим
Оопт = _ Е
с ’ опт с
(3.124)
Определение коэффициентов a,b,cnd осуществляется в процессе расчета четы-
рех траекторий с различным сочетанием параметров OJ7 и и подстановки результа-
тов в (3.123).
Расчет каждой траектории должен проводиться до tk, при котором достигается за-
данный период обращения. При этом фиксируется получаемое значение цк.
Условие нарушения ограничения по минимально допустимой высоте контроли-
руется путем одновременного расчета параметров орбит. Далее на основании (3.124)
находятся (Оопт77)7 и (О^/7); в первом приближении. Задавая в окрестности этих най-
денных значений еще несколько их вариаций, процесс поиска повторяют, начиная с
нахождения новых коэффициентов а, Ь, с и Jb уравнении (3.123).
Итерационная процедура завершается, когда уточняемое значение цк будет отли-
чаться от предыдущего значения менее чем на некоторую наперед заданную величину.
146
3.5. ВВЕДЕНИЕ В ТЕОРИЮ ПРОЕКТНО-БАЛЛИСТИЧЕСКОГО
ОБЕСПЕЧЕНИЯ ОКОЛОЗЕМНЫХ
И МЕЖПЛАНЕТНЫХ КОСМИЧЕСКИХ ПОЛЕТОВ
3.5.1. Основы теории невозмущенного орбитального движения
Предварительно ограничимся рассмотрением движения КА в предположении,
что не только определяющим, но и единственным источником силового воздействия,
испытываемого аппаратом, является гравитационное поле Земли. Будем считать, что
гравитационное поле является центральным, т. е. его силовое воздействие подчиняет-
ся ньютоновскому закону притяжения массы КА массой Земли при « М3.
В рамках принятых предположений имеем дело с так называемой классической огра-
ниченной задачей двух тел, исследование и решение которой составляет предмет те-
ории невозмущенного орбитального движения.
В соответствии со вторым законом Ньютона уравнение движения тела с массой т
имеет вид:
.2
mf=m=4=F, (3.125)
At
где f — полное ускорение, г — радиус-вектор, определяющий положение тела с мас-
сой т относительно центра притяжения гравитирующего тела.
Согласно (3.7), для центрального поля тяготения
/Л/3
F = — т grad Пт = — т —у г, (3.126)
где fM3 = ц — гравитационный параметр Земли (не путать с относительной массой,
имеющей то же обозначение).
Тогда
Г + Цг = О. (3.127)
Г
Умножим почленно равенство (3.127) векторно на г:
rx f + Hrxr = rx f =0. (3.128)
Г
Имея в виду, что
X (г X f) = ^ х г + rxf=rxf,
СП v
запишем
£(rxf)=£(rxV) = 0.
Тогда
rxf =rxV = c. (3.129)
Выражение (3.129) отражает зависимость между радиусом-вектором и вектором
скорости тела при его движении в центральном поле. Эту зависимость называют век-
торным интегралом площадей, а вектор с — векторной константой площадей.
Так как вектор с не является нулевым, он ортогонален плоскости, образованной
векторами г и V, а поскольку начало вектора г совпадает с центром притяжения, это
означает, что движение тела будет происходить в фиксированной плоскости, проходя-
щей через центр притяжения, ориентация которой относительно выбранной СК из-
вестна, если известны составляющие вектора с относительно осей координат этой
системы.
147
В полярной СК выражение интеграла площадей принимает вид
с = г2х = const, (3.130)
где х угловая скорость вращения радиуса-вектора относительно выбранной отсчет-
ной базы.
При перемещении в орбитальном движении тела за малый промежуток времени
Д/ радиус-вектор г сместится на малый угол Дх, описав площадь AS
Д5=1г2Дх- (3.131)
Разделив почленно правую и левую части равенства (3.131) на At и переходя к
пределу при At---> 0, получим
.. AS d»£ 1 ? ’ I /э 1
д,™0 Д' ~ di ~ 2Г ~ 2е’ (3.132)
d5 „ о
где производная ду называется секториалыюи скоростью, являющейся постоянной,
согласно (3.132) при движении тела в центральном поле тяготения.
Рассматривая далее совместно интеграл площадей и уравнение движения, запи-
санные в форме
Г =-^r, С = гх f,
Г
после векторного умножения друг на друга соответственно левых и правых частей
этих выражений, найдем
Г хс = -^гх(гх г).
г
Нетрудно показать, что полученное равенство эквивалентно выражению
т,('хс)-Нт,0=°- (3-133)
Из (3.133) следует, что
fxc-n'=f, (3.134)
где f — векторная константа интегрирования, называется вектором Лапласа.
Поскольку векторы f х с и г ортогональны вектору с по определению, с • f = 0,
что означает, что вектор Лапласа лежит в плоскости орбиты.
Для получения следующего интеграла умножим уравнение движения (3.127) ска-
лярно на удвоенное значение вектора f:
2(Г • Г)+ ^(t • г) = 0.
Г
Имея в виду, что 2(Г • f) = (f • f), 2(f • г) = (г * г), a (f • Г) = И2, (г • г) = г2,
получим
1 (и2) 4- н 1 1 (и2) - - 1=о
d/' ' г3 dt' ' dx' ' dx V г)
и, следовательно,
И-^=й. (3.135)
Выражение (3.135) носит название интеграла энергии или интеграла живых сил.
Константа h, называемая константой энергии, является, в отличие от с и f, скаляр-
ной величиной.
148
Из (3.135) вытекает физический смысл полученного интеграла, согласно которо-
му сумма кинетической и потенциальной энергий тела при его движении по орбите
в центральном гравитационном поле остается величиной постоянной.
Поскольку векторное уравнение (3.127) эквивалентно системе шести дифферен-
циальных уравнений первого порядка, ее общий интеграл должен состоять из шести
независимых первых интегралов.
Если провести формальный подсчет полученных нами интегралов, то насчитаем
их семь, соответственно семь постоянных: с(с1? с2, с3); Г(/*!,/2,/з); Однако они не мо-
гут составить решения системы скалярных уравнений движения, эквивалентной век-
торному уравнению (3.127), ибо: а) ни один из них не содержит явно времени; б) име-
ют место два тождественных соотношения
^f^c2f2 + C3f3 = ^ (3.136)
Л2 +Л2 +/з2 = И2 + Л(с? + с2 + с2). (3.137)
Соотношение (3.136) может быть легко получено, если левые части скалярных
выражений интеграла площадей умножить на левые части скалярных выражений ин-
теграла Лапласа. Оно определяет условие перпендикулярности векторов площадей
и Лапласа.
Соотношение (3.137) получается более сложным путем и не имеет такой четкой
физической интерпретации, как (3.136). Отметим, однако, что из него следует одно,
исключительно важное условие, а именно: векторы площадей и Лапласа никогда не мо-
гут быть равны нулю одновременно.
Итак, используя соотношения (3.136) и (3.137), можно выразить любые две из се-
ми постоянных как функции пяти остальных, которые остаются произвольными,
Недостающий шестой независимый первый интеграл может быть найден простой
квадратурой [7].
Исходя из изложенного следует, что общее решение дифференциальных уравне-
ний невозмущенного орбитального движения существует. Вопрос заключается в том,
как их решить практически, т. к. получение решения в общем виде требует оперирова-
ния уравнениями 2-й степени относительно всех шести неизвестных, содержащих ир-
рациональность, представленную радиусом-вектором [7].
Выход может быть найден, если использовать некоторые из ранее выявленных
свойств. Как было показано ранее, траектория невозмущенного движения тела
в центральном гравитационном поле представляет собой плоскую кривую. Чтобы опре-
делить вид и расположение этой кривой, надо иметь уравнение, содержащее координа-
ты тела. Оно может быть найдено из интеграла Лапласа (3.134). Умножив левую и пра-
вую части векторного выражения интеграла Лапласа скалярно на вектор г, получим
(Г- (f хс))-ц^=(г -f). (3.138)
Учтем, что
(Г • (г х с)) = (С • (г X Г)) = (с • с) = с2.
Пусть, далее, х = — угол между векторами г и f.
В космической баллистике при обозначении, совпадающем с ранее введенным
углом тангажа, он называется углом истинной аномалии.
Тогда (3.138) может быть легко приведено к виду
с2 — |LLr= r/cos О,
откуда
= f2 = с2/ц
r n+/cosd '
149
Если теперь обозначить с2/ц = р и//ц = е, окон-
чательно получим
Выражение (3.139) представляет собой уравнение
кривой второго порядка (конического сечения) в поляр-
ных координатах, причем полярная ось кривой, ис-
пользуемая в качестве отсчетной базы, направлена от
фокуса кривой (совпадающего с центром притяже-
ния) к ее ближайшей вершине (рис. 3.4). Значение р
носит название фокального параметра орбиты, е — ее
эксцентриситета.
Если р Ф 0, то при е = 0 коническое сече-
ние представляет собой (рис. 3.5) окружность (кру-
говая орбита), при е = 1 — параболу (параболи-
ческая орбита), при е < 1 — эллипс (эллиптическая
орбита), при е > 1 — гиперболу (гиперболическая
орбита).
При е > 0 ближайшей к фокусу вершине кривой
соответствует угол Ф = 0, т. е. полярная ось будет
совпадать с вектором Лапласа. Прямая, совпадаю-
щая с вектором f, называется линией апсид. Точка
орбиты, лежащая на линии апсид, минимально уда-
ленная от фокуса (центра притяжения), называется
перицентром (перигеем для Земли, перигелием для
Солнца). Точка максимального удаления называется
апоцентром (апогеем, афелием).
Полусумма радиусов перицентра и апоцентра
(гя + га)/2 = а и а = р/( 1 — е2) называется большой по-
луосью эллиптической орбиты, которая связана с ее
эксцентриситетом через межфокусное расстояние d
выражением е = d/a.
Завершим наш краткий экскурс в основы те-
ории кеплерова движения анализом возможных ско-
ростей орбитального движения.
Как следует из рассмотрения выражения ин-
теграла энергии, величина постоянной h зависит
Рис. 3.4. Орбитальная
и полярная системы
координат
Рис. 3.5. Области
возможных траекторий:
А — область гипербол;
Б — область эллипсов,
не пересекающихся
с притягивающим телом;
В — область эллипсов,
пересекающихся
с притягивающимся
телом
от соотношения радиуса и скорости тела в произвольно рассматриваемой точке ор-
биты, которую будем считать начальной или нулевой (кстати отметим, что соответ-
ствующий начальный момент времени /0 называется начальной эпохой или просто
эпохой).
Итак, имеем
г2___ 2Ц
0 г0 '
В случае кругового движения (й = 0) модуль векторной константы площадей с =
= Тцр = г К и поскольку г=р, скорость кругового движения
V = /й.
Ф а/г
(3.140)
150
При г = R = 6371 км круговая скорость, вычисленная у поверхности Земли И7 =
= Ккро=^ =7,91 км/с, называется первой космической скоростью. Под второй косми-
ческой скоростью понимают параболическую скорость
И11=Ипар0=^=И1^» 11,19км/с.
С увеличением радиуса орбиты круговая и параболическая скорости соответ-
ственно уменьшаются по отношению к первой и второй космическим скоростям.
Отметим, что вторая космическая скорость иначе называется скоростью увода
или скоростью освобождения. Она непосредственно связана с понятием сферы дейст-
вия притягивающего центра — планеты.
Рассмотрим движение КА массой т под действием двух тел, например Земли
(Л/3) и Солнца (Л/с). Положим, что исходная система координат, в которой рассматри-
вается движение, связана с центром Земли.
^2
Тогда уравнение движения КА запишется как = а3 + Ф3, где а3 — основное
ускорение, которое имел бы КА только под действием силы притяжения со стороны
Земли, Ф3 — возмущающее ускорение, т. е. дополнительное ускорение, которое полу-
чает КА за счет притяжения Солнца.
При этом
М3 + т
аз f 3 Гм’
Г3а
I Г3С гас )
Отношение Ф3/а3 показывает, какую часть основного ускорения а3 составляет
возмущающее ускорение Ф3.
Аналогичным образом можно получить соответствующие соотношения, когда
центр системы координат совмещен с Солнцем.
Тогда область пространства радиуса Асд, где выполняется условие Ф3/а3 < Фс/ас,
будет называться сферой действия Земли. Радиус сферы действия Земли несколько
меньше 1 млн км.
3.5.2. Элементы баллистического проектирования
при решении задач межпланетного полета
При рассмотрении проблем баллистического проектирования применительно
к задачам межпланетного полета возникает необходимость в расширении представле-
ний о характеристиках орбитального движения, полученных в рамках обсуждения ос-
нов решения «задачи двух тел».
Весьма удобным как при качественных исследованиях, так и при расчетах траек-
торий движения КА является использование понятия гравитационной сферы, в кото-
рой влияние какого-либо притягивающего тела становится основным (среди осталь-
ных притягивающих тел).
Рассмотрение различных видов гравитационных сфер целесообразно [7] осу-
ществить в рамках ограниченной задачи трех тел, причем одним притягивающим те-
151
лом Ро является Солнце, другим Рх — большая планета или Луна, третьим телом Р
с бесконечно малой массой является космический аппарат или спутник.
Обозначим через jQ ускорение, сообщаемое телу Р Солнцем, когда последнее яв-
ляется основным притягивающим телом; через ах — возмущающее ускорение, вызы-
ваемое притяжением тела Рх, через jx — ускорение, сообщаемое телу Р планетой Рх,
когда планета является основным притягивающим телом; я0 — возмущающее ускоре-
ние, вызываемое притяжением Солнца (тела Ро).
В настоящее время выделяется несколько видов гравитационных сфер. Сферой
тяготения планеты Рх обозначается область пространства, в которой справедливо не-
равенство jx > у0, при этом на границе сферы тяготения выполняется равенство jx =JQ.
Приближенное значение радиуса сферы тяготения планеты определяется соотноше-
нием:
где гх есть расстояние планеты Рх от Солнца (Ро), mQ — масса Солнца, тх — масса пла-
неты.
Сферой действия планеты Рх называется область пространства, в которой выпол-
няется неравенство:
Oi/jo > aQ/j\.
Приближенное значение радиуса сферы действия планеты определяется соотно-
шением
R =г l№
Сферой влияния планеты Рх (относительно Солнца Ро) называется сфера, центр
которой совпадает с центром планеты и которая имеет радиус
™Л1/3
гп0)
При расчете траекторий полета КА более выгодным является использование сфе-
ры влияния, чем сферы действия. В этом случае ошибки в параметрах траектории КА
при переходе от одного притягивающего центра к другому становятся наименьшими.
Гравитационной сферой Хилла называется область пространства с центром плане-
ты Рх и с радиусом RH, равным [7] расстоянию от либрационной точки Lx до планеты
Рх. Радиус /^определяется соотношением
н 1 ) 3V3m0 ) 9V3m0 JJ
Гравитационная сфера Хилла определяет ту область пространства, в которой
движения тела Р (космического аппарата, спутника) устойчивы в смысле Хилла, т. е.
тело Р будет вечно спутником планеты.
Численные значения радиусов всех видов гравитационных сфер для больших
планет и Луны приведены в табл. 3.1, причем значения радиусов даны в астрономиче-
ских единицах (а. е.). Для радиусов /?т и /?д приведены два значения (минимальное
и максимальное), так как радиус гх не является постоянной величиной. Для радиусов
Яв и RH взято среднее значение
152
Таблица 3.1
Планета .&Р а. е. Лд, а. е. RB, а. е. е.
min max min max
Меркурий 0,00013 0,00019 0,00060 0,00091 0,00241 0,00148
Венера 0,00112 0,00114 0,00409 0,0415 0,01138 0,00674
Земля 0,00171 0,00177 0,00610 0,00631 0,01672 0,01001
Марс 0,00078 0,00095 0,0035 0,00422 0,01204 0,00724
Юпитер 0,15298 0,16855 0,30665 0,33786 0,58863 0,34697
Сатурн 0,15222 0,17017 0,34428 0,38488 0,72241 0,42881
Уран 0,12091 0,13289 0,32991 0,36261 0,77592 0,46494
Нептун 0,21452 0,21823 0,57551 0,58547 1,29766 0,77035
Плутон 0,04959 0,08214 0,17825 0,29523 0,61885 0,38392
Луна- Земля 0,00027 0,00030 0,00042 0,00047 — 0,00039
Луна- Солнце 0,00019 0,00019 0,00105 0,00108 — 0,00234
Для получения траекторий движения межпланетного КА при проведении прак-
тических проектно-баллистических расчетов осуществляют кусочно-коническую ап-
проксимацию межпланетной траектории на основе методики сфер влияния [8], сущ-
ность которой заключается в следующем. В некоторой окрестности притягивающего
тела (его сфере действия) при расчете траектории движения КА учитывается только
сила притяжения этого тела. Такое допущение позволяет считать траекторию движе-
ния КА в сфере действия невозмущенной и применять для ее определения аналитиче-
скую теорию задачи двух тел. В рамках этой методики все околосолнечное простран-
ство можно назвать сферой действия Солнца, в которой в соответствии с законом все-
мирного тяготения движутся планеты. Так как планеты являются телами,
обладающими конечной массой, то в некоторой окрестности планет их сила притяже-
ния оказывается основной силой, действующей на КА. Значения сферы действия
планет зависят от массы планеты и удаления ее от Солнца.
В итоге каждая планета как бы «вырезает» в сфере действия Солнца некоторую
область, в которой сила ее притяжения является доминирующей. В силу этого все
околосолнечное пространство можно представить в виде сфер действия планет, как
бы «погруженных» в сферу действия Солнца и перемещающихся вместе с планетами
по их орбитам. Тогда траекторию движения КА при перелетах от планеты к планете
можно рассматривать как траекторию, последовательно проходящую через несколько
сфер действия, причем внутри каждой сферы действия траектория определяется на-
чальными условиями на границе этой сферы и притяжением центрального тела.
Сферы действия даже самых массивных планет малы по сравнению со сферой
действия Солнца. В силу этого на большей части межпланетной траектории движение
КА зависит лишь от силы притяжения Солнца, и именно этот участок является опре-
деляющим при расчетах всей траектории перелета. Траекторию движения вблизи пла-
нет выбирают таким образом, чтобы при переходах от одной сферы действия к другой
не нарушалась гладкость траектории.
153
В соответствии с вышесказанным расчеты межпланетных траекторий проводят в
следующей последовательности.
1. Задаются датой старта КА с орбиты Земли и временем прилета КА к планете
назначения. Это позволяет определить положение и скорости планет на их орбитах
для моментов старта и прилета, а также время перелета КА от одной планеты к другой.
2. Считая на первом этапе сферы действия планет бесконечно малыми, определя-
ют параметры межпланетной орбиты в сфере действия Солнца. Для этого используют
параметры межпланетной орбиты в сфере действия Солнца. Здесь применяют хорошо
разработанные методы определения орбит, например метод Ламберта—Эйлера [7].
3. Определив параметры орбиты, вычисляют гелиоцентрические скорости КА
в момент отлета с орбиты планеты старта и в момент прилета к планете назначения.
4. Зная гелиоцентрические скорости КА и планет в моменты старта и встречи,
вычисляют скорость КА относительно планет как разницу соответствующих векто-
ров. Эта скорость «на бесконечности» определяет тот избыток скорости КА относи-
тельно планет на границе их сферы действия, который необходимо иметь для вывода
аппарата на выбранную межпланетную траекторию.
5. По величине вектора скорости «на бесконечности» и его ориентации в про-
странстве определяют траекторию движения КА в сфере действия планет. Знание од-
ного вектора скорости «на бесконечности» недостаточно для определения параметров
планетоцентрической траектории. Поэтому необходимо задавать дополнительные ус-
ловия. При отлете от Земли такими условиями являются параметры стартовой орбиты
ИСЗ (например, наклонение и величина перигея орбиты), при подлете к планете —
параметры пролета у планеты (в зависимости от принятой схемы полета).
6. Зная параметры припланетных траекторий, определяют затраты характеристи-
ческой скорости, необходимые для ее формирования.
Рассмотрим несколько подробнее, каким образом проводится расчет на каждом
из указанных этапов.
1. На этапе проектных исследований вполне достаточно считать орбиты планет
постоянными, заданными шестью кеплеровыми элементами [7]. Кеплеровы элемен-
ты невозмущенного движения образуют три группы:
а) Q i, со — характеризуют положение орбиты в пространстве;
в) р, е — характеризуют форму орбиты;
с) т — характеризует положение тела на орбите в фиксированный момент времени.
Из указанных элементов не получили освещения в предшествующих материалах
элементы первой группы: Q — восходящий узел орбиты, i — наклонение орбиты и
со — угловое расстояние перицентра. Для их определения введем в рассмотрение
(рис. 3.6) понятие «линия узлов», которая представляет собой линию пересечения
плоскости орбиты с плоскостью земного либо небес-
ного экватора. Тогда узлы орбиты — точки пересече-
ния линии узлов с орбитой. Восходящий узел Q — узел
орбиты, который проходит тело, двигаясь из области
отрицательных аппликат в область положительных.
Противоположный узел называется нисходящим.
Угловое расстояние перицентра со представляет
собой угол между положительным направлением
линии узлов и направлением в перицентр, причем
со + О = мв — аргумент широты — угол между ра-
диусом-вектором и направлением из притягиваю-
щего центра в восходящий узел. Наклонение орбиты
i — угол между плоскостью экватора и плоскостью
орбиты.
Рис. 3.6. Кеплеровы элементы
невозмущенного движения
154
Используя эти данные, можно получить вектор положения г и вектор скорости
планеты Упл для любого заданного момента времени t.
Пусть требуется определить траекторию перелета с планеты 1 на планету 2, орби-
ты которых заданы соответствующими элементами. Задаемся временем отлета КА
с орбиты планеты 1 и временем встречи его с планетой 2 — tx и t2 соответственно. Тог-
да время перелета КА определится как разность tn = t2 - tx, и траектория должна про-
ходить через точки пространства, определяемые концами векторов: q — положение
планеты 1 в момент времени tx \ г2 — положение планеты 2 в момент времени t2. Таким
образом, необходимо решить задачу определения элементов орбиты по двум положе-
ниям КА (г1? г2) и времени перелета между этими положениями tn.
Такая задача решается с помощью уже упомянутого выше метода Ламберта—Эй-
лера. С его помощью определяют, прежде всего, такие элементы орбиты перелета, как
большая полуось а и эксцентриситет е.
Далее становится возможным определить скорости отлета КА с планеты старта
и прилета к планете встречи V2 в соответствии с соотношением вида:
v = 4й>
1 r1r2sincp
< Г2-П - COS(p]r,)
(3.141)
(V2 вычисляется аналогично, необходимо поменять лишь местами индексы «1» и «2»),
где г,, г2 — радиусы-векторы положений в момент старта и прилета, ф — угол в плос-
кости перелета между векторами г, и г2. Элементы орбиты перелета определяют обыч-
ным способом по векторам или V2, г2.
Векторы Д¥то1 = Vj - Vlnjl и AV^ = V2 - V2nj] называются гиперболическими из-
бытками (скоростями «на бесконечности») и определяют скорость КА относительно
планеты старта (встречи) в момент выхода (входа) его из сферы действия планеты.
Рассмотрим вопрос определения траектории движения в сфере действия планеты
старта, обеспечивающей «плавный» переход КА на межпланетную траекторию движе-
ния. Такая траектория должна удовлетворять требованию, чтобы после полета в сфере
действия планеты старта на ее границе вектор скорости КА относительно этой плане-
ты совпадал с вектором скорости «на бесконечности».
Рассмотрим планетоцентрическую систему координат, в которой вектор имеет
угловые координаты: 8^ — склонение, — прямое восхождение. Очевидно, что век-
торы и гто коллинеарны, а поэтому через них можно провести бесконечно большое
количество плоскостей орбит с наклонениями 8^ < z0 < 90°. Для определения плос-
кости орбиты отлета необходимо задать значение /0 из указанного диапазона. Старт КА
на траекторию отлета обычно осуществляется с промежуточной орбиты ИСЗ, на кото-
рую он предварительно выводится с наземных полигонов. Параметры орбиты ИСЗ оп-
ределяются трассой выведения и связаны с допустимыми азимутами выведения, рас-
положением станций слежения и рядом других технических ограничений.
Для обеспечения энергетически оптимального старта с орбиты ИСЗ необходимо,
чтобы плоскости орбиты ИСЗ и отлетной гиперболической траектории совпадали,
т. е. чтобы выполнялось равенство: /оисз = /0. При заданных и /0 величина долготы
восходящего узла Q орбиты отлета определяется по формуле:
tg8
sin(a„-Q) = -^. (3.142)
155
Очевидно, что существуют две орбиты с долготами восходящего узла Ц связан-
ные соотношением:
а„ — £12 = л —(a„-Q,).
Остается определить параметры орбиты, обеспечивающие заданную ориентацию
вектора в плоскости орбиты, т. е. элементы орбиты а, е, сп В предположении, что
старт КА на орбиту отлета осуществляется по касательной к опорной орбите ИСЗ,
возможно определить точку схода КА с орбиты ИСЗ и величину потребного разгонно-
го импульса. Определение указанных величин проводится по формулам:
a=p;e=, + ^; <3143>
® ; cosd„ = ;
sinS..
sin и. = . . ;
001 sin/ ’
cos umi = cos (a„ - Q,) cos S„. (3.144)
Таким образом, получены параметры гиперболической траектории отлета, обес-
печивающей заданный вектор при старте с опорной орбиты ИСЗ. Величина по-
требного разгонного импульса старта определится как разность: ДИСТ = Ипг - Икр, где
Ипг — скорость КА в перицентре гиперболы отлета, Икр — скорость КА на опорной
круговой орбите ИСЗ. Величины Ипг и Икр определяются по известным формулам:
где гп — величина перигея опорной орбиты ИСЗ.
При подлете к планете назначения осуществляется перевод с эллиптической ге-
лиоцентрической орбиты на планетоцентрическую гиперболическую орбиту. Пара-
метры гиперболической орбиты определяются так же, как и для предыдущего случая.
Отличие заключается лишь в том, что вектор подл = — VnjI заменяется на проти-
воположный.
3.5.3. Формирование орбит
с использованием гравитационных маневров
В зависимости от конечной цели полета возможны различные маневры КА на ги-
перболической траектории. Наиболее интересными случаями являются:
1. Посадка на поверхность планеты.
2. Пролет над заданным районом планеты.
3. Выход на орбиту искусственного спутника планеты (ИСП) с требуемыми пара-
метрами.
4. Облет планеты с последующим выходом на гелиоцентрическую орбиту, такую,
чтобы обеспечивалось попадание КА в заданный район Солнечной системы.
В первых двух случаях не требуется проведения активных маневров на гипербо-
лической подлетной траектории. Основной задачей здесь является определение век-
тора гп (перигея гиперболы), удовлетворяющего решению поставленной задачи. Для
осуществления посадки на планету необходимо, чтобы обеспечивалось условие: |r J <
< Япл — для планет без атмосферы; |r J < ЯГ1Л + ha — для планет с атмосферой, где ha —
156
Рис. 3.7. Схема облета
планеты назначения:
1 — планета назначения;
2 — траектория облета КА
высота плотных слоев атмосферы. Для планет без атмос-
феры мягкая посадка возможна лишь с применением
реактивной двигательной установки. При наличии ат-
мосферы гашение энергии может быть осуществлено с
помощью пассивного аэродинамического торможения.
Перевод КА на орбиту ИСП с заданными парамет-
рами возможен как с помощью активного торможения,
так и с использованием аэродинамического торможения
в верхних слоях атмосферы.
В первом случае задача решается как обратная зада-
ча разгона КА при выведении его на траекторию ухода от
планеты. Второй случай требует использования специ-
альных методов расчета.
Практически важным является вариант облета пла-
неты с тем, чтобы при дальнейшем полете КА достиг тре-
буемого района космического пространства. Пусть соот-
ветствующая траектория, обеспечивающая перелет КА с
планеты 1 на планету 2, нам известна. Тогда в момент
пролета планеты под действием ее гравитационного поля
вектор скорости КА относительно планеты изменяется
(как по величине, так и по направлению). Угол поворота
вектора скорости КА зависит от величины гк (перицент-
ра пролетной гиперболы) и скорости :
Следует отметить, что модуль вектора скорости после выхода КА из сферы
действия планеты встречи остается постоянным (рис. 3.7).
Рассмотрим возможности использования такого облета для формирования
межпланетных траекторий с заданными свойствами. Пусть для некоторой траектории
перелета от планеты 1 к планете 2 существует траектория возврата от планеты 2 к пла-
нете 1, причем время отлета совпадает с временем прилета к ней. Известно также, что
IV, подл b = I Voo отл Ь- За счет выбора величины гп (при выполнении условия, чтобы пос-
ле облета планеты вектор У^ подл совместился с вектором У^ отл) можно получить тра-
екторию возврата к планете 1 без дополнительных энергетических затрат на ее фор-
мирование (рис. 3.8).
Рис. 3.8. Геометрия изменения межпланетной траектории КА
за счет гравитационного маневра:
1 — точка встречи; 2 — орбита планеты назначения;
3 — траектория перелета; 4 — траектория возврата
157
Реализация опиеанной схемы требует выполнения единственного условия, что-
бы величина гл, обеспечивающая заданный угол поворота вектора подл, была боль-
ше гпл, т. е. чтобы траектория полета КА была физически возможна. Расчет облетной
гиперболической траектории не представляет труда, т. к. плоскость орбиты задается
двумя векторами — подл и отл, а геометрия в плоскости определяется величина-
ми |V. I и гя.
3.5.4. Оптимизация схем полета и выбор возможных дат старта
Для различных схем полета вид и структура критерия оптимизации определяются
количеством активных операций, на проведение которых необходимы запасы топли-
ва на борту КА.
Величина критерия зависит от вида траектории, т. е. от дат пролета планет, дат
старта КА с Земли. Поскольку для методики сфер действия нет конечного аналитиче-
ского решения, описывающего зависимость критерия от временных параметров тра-
ектории, то на практике создаются специальные программные комплексы, с по-
мощью которых рассчитывают критерий для заданной схемы полета, проводится оп-
тимизация траекторий, т. е. выбирают комбинации переменных параметров,
обеспечивающих минимум критерия для заданной схемы полета.
Рассмотрим схемы полета к одной планете без возвращения к Земле. С их ис-
пользованием осуществлены полеты советских и американских КА к Марсу и Венере.
Они позволяют доставлять на планету исследовательские лаборатории, создавать
ИСП, с помощью которых проводятся глобальные исследования планеты. Наиболее
простой из данного типа схем является схема перелета с Земли к планете с посадкой
на ее поверхность.
Одной из главнейших характеристик схемы является величина энергетических
затрат, требуемых на реализацию перелета. Под этим понимают величину скорости,
которую необходимо сообщить КА при формировании траектории перелета, обеспе-
чивающей решение поставленной целевой задачи. Для простейшей схемы эти затраты
связаны с сообщением КА импульса разгона, требуемого для отлета с опорной орбиты
ИСЗ. Как показано в п. 3.5.2, в случае оптимальной схемы старта с орбиты ИСЗ вели-
чина импульса разгона ДИСТ определяется как разность скоростей — скорости Ипг в пе-
рицентре гиперболы отлета от Земли и скорости Икр на круговой орбите ИСЗ. Величи-
на Д Ист зависит от даты старта и времени перелета КА к планете назначения.
На практике выбор энергетически оптимальной траектории осуществляется с
помощью графических зависимостей Кв7л = /(/ст, /пер), называемых полями изоли-
ний. Следует отметить, что значения скорости И^тл однозначно пересчитываются в
значения скорости ДИСТ по соответствующим формулам. На рис. 3.9 приведены поля
изолиний для перелета к Марсу. Расчет полей изолиний проводят по специальным
программам на ЭВМ. Как видно из рис. 3.9, изолиния Ум (сплошная линия) в коор-
динатах /ст, /пер представляет собой замкнутую линию, вдоль которой выполняется ус-
ловие Уж = const. Из анализа кривых следует, что имеется только одна точка на поле
изолиний, где выполняется Уж = min. Эта точка, обозначенная на рис. 3.9 крестиком,
определяет траекторию перелета к планете (/ст, /пер) с минимально возможной скоро-
стью отлета от Земли.
158
Рис. 3.9. Расчетные зависимости для определения параметров межпланетной траектории КА
при старте с орбиты ИСЗ
Поле изолиний Уж = f (tCT, /пер) позволяет получить информацию о диапазоне
возможных дат старта и времен перелета к планете при заданной величине импульса
скорости, который может быть сообщен КА на стартовой орбите ИСЗ разгонной сту-
пенью. Так, например, при Уж = 4,88 км/с возможные диапазоны указанных величин
в 1973 г. составляли: tCT = 02.VIII.73... 15.VIII.73; /пеп = 203...220 сут.
На практике номинальные траектории перелета КА к планете выбирают в неко-
торой окрестности энергетически оптимальной траектории. Это позволяет, с одной
стороны, максимизировать начальную массу КА на траектории перелета, с другой
стороны, получить необходимое время на проведение предстартовой подготовки КА
(в случае отказов бортовых систем — на их устранение).
Однако такой выбор оптимальных траекторий учитывает только энергетические
требования, в то время как существует ряд требований, накладываемых со стороны
средств обеспечения полета. Одним из них является требование наблюдаемости уча-
стка отлета КА с наземных станций слежения. Именно на этом участке проводится
проверка исправности бортовых систем после выведения КА на орбиту ИСЗ, опреде-
ляются параметры фактической траектории перелета и в случае необходимости про-
водится коррекция этой траектории.
Условия наблюдаемости участка отлета КА характеризуются величиной 8^ —
склонением вектора скорости .
Угол возвышения КА над местным горизонтом — угол £ связан со склонением 8^
соотношением
£=2-(ф-8„). (3.146)
Ясно, что при £ < 0 КА с пункта наблюдения не виден. Это произойдет при вы-
полнении условия:
(3.147)
где ф — широта расположения наземного пункта наблюдения.
159
Обычно на поле изолиний скоростей строят также поле изолиний склонений
8^ (на рис. 3.9 поле изолиний 8^ показано пунктирной линией). По значению 8ТО,
соответствующему минимальной скорости Уж (для энергетически оптимальной тра-
ектории), проверяют условия наблюдаемости для наземных пунктов слежения. Если
условие (3.147) выполняется, то рассматриваемая траектория может быть использова-
на для запуска КА. В противном случае необходимо переходить к траектории с боль-
шим значением Уж, что приведет к ухудшению проектных параметров и массовых ха-
рактеристик КА.
Можно также построить изолинии для других критериев (таких, как скорость
входа АМС в атмосферу планеты для посадочного аппарата, широта возможных мест
посадки, границы освещенности поверхности планеты и т. д.), величина которых су-
щественно влияет на проектно-массовые характеристики КА. Представление резуль-
татов расчета с помощью полей изолиний позволяет выбрать номинальные траекто-
рии перелета с учетом всех ограничений. Необходимо отметить, что этот способ пред-
ставления результатов возможен лишь для сравнительно простых схем полета,
у которых число определяющих траекторию перелета переменных невелико. Для бо-
лее сложных схем полета, например, таких, как облет планет с использованием грави-
тационного маневра, графическая интерпретация результатов расчета получается
весьма сложной, что не позволяет определить все необходимые параметры, однознач-
но характеризующие межпланетную траекторию. Для оптимизации таких схем полета
разрабатываются специальные методы, позволяющие получить номинальные траек-
тории с учетом всех заданных ограничений [7].
Отметим, что изменение во времени баллистических параметров различных схем
межпланетных траекторий, а в связи с этим и изменение основных проектно-баллис-
тических параметров межпланетных КА носит циклический характер. Данное обсто-
ятельство обусловлено периодической повторяемостью положения планет в про-
странстве, связанной с различными периодами их обращения по орбитам и различ-
ным наклонением плоскостей их орбит.
Временной интервал повторяемости относительной конфигурации расположе-
ния двух планет может быть представлен в виде синодического периода Тс, выраженно-
го через сидерические Ti (i= 1, 2) периоды обращения планет
TiT2
T2-Ti
(3.148)
причем под сидерическими (звездными) периодами обращения планет принято по-
нимать интервалы времени, через которые повторяются положения этих планет отно-
сительно неподвижных звезд. Важным фактором, определяющим цикличность межп-
ланетных полетов, является период великих противостояний Тв п двух планет. Прибли-
женно он определяется как общее наименьшее кратное сидерических периодов двух
планет и их синодического периода.
При рассмотрении системы из п планет в анализ вводится суммарный период вели-
ких противостояний этих планет, характеризующий период времени, через кото-
рый рассматриваемые планеты займут «исходное положение в пространстве».
Таким образом, приходим к выводу, что цикличность характеристик межпланет-
ных аппаратов будет зависеть, например, от гелиоцентрических дат старта с Земли:
внутри периода великих противостояний они зависят от конкретного синодического
периода — конкретного цикла полетов [16].
160
ЛИТЕРАТУРА
1. Аппазов Р. Ф., Лавров С. С, Мишин В. П. Баллистика управляемых ракет дальнего
действия. М.: Наука, 1966. С. 307.
2. Аппазов Р Ф., Сытин О. Г. Методы проектирования траекторий носителей
и спутников Земли. — М.: Наука, 1987. С. 440.
3. Дмитриевский А. А., Лысенко Л. Н. Прикладные задачи теории оптимального уп-
равления движением беспилотных летательных аппаратов. — М.: Машиностро-
ение, 1978. С. 328.
4. Баллистика и навигация ракет / Дмитриевский А. А., Лысенко Л. Н.,
Иванов Н. М. и др. — М.: Машиностроение, 1985. С. 312.
5. Дмитриевский А. А., Лысенко Л. Н., Богодистов С. С. Внешняя баллистика. 3-е
изд., доп. и перераб. — М.: Машиностроение, 1991. С. 601.
6. Иванов Н. М., Лысенко Л. Н., Мартынов А. И. Методы теории систем в задачах уп-
равления космическим аппаратом. — М.: Машиностроение, 1981. С. 254.
7. Иванов Н. М., Лысенко Л. Н. Баллистика и навигация космических аппаратов: 2-е
изд., перераб. и доп. — М.: Дрофа, 2004. С. 544.
8. Кислик М. Д. Сферы влияния больших планет и Луны // Космические исследова-
ния. 1964. Т 2. № 6. С. 853-858.
9. Лоуден Д. Оптимальные траектории для космической навигации: Пер. с англ. —
М.: Мир, 1966. С. 152.
10. Механика космического полета / Под ред. В. П. Мишина. — М.: Машиностро-
ение, 1989. С. 408.
11. Основы теории полета космических аппаратов / Под. ред. Г. С. Нариманова и
М. К. Тихонравова. — М.: Машиностроение, 1972. С. 607.
12. Основы теории полета и элементы проектирования искусственных спутников
Земли / Под. ред. М. К. Тихонравова. — М.: Машиностроение, 1974. С. 331.
13. ОхоцимскийД. Е., Энеев Т. М. Некоторые вариационные задачи, связанные с за-
пуском искусственного спутника Земли // Успехи физических наук. 1957. Т 63.
Вып. la. С. 5—32.
14. Понтрягин Л. С., Болтянский В. Г., Гамкрелидзе Р В., Мищенко Е. Ф. Математиче-
ская теория оптимальных процессов. 2-е изд. — М.: Наука, 1969. С. 384.
15. Сихарулидзе Ю. Г. Баллистика летательных аппаратов. — М.: Наука, 1982. С. 352.
16. Тарасов Е. В. Космонавтика: (Механика полета и баллистическое проектирова-
ние КЛА). — М.: Машиностроение, 1977. С. 216.
17. ЦлафЛ.Я. Вариационное исчисление и интегральные уравнения; (Справочное
руководство). — М.: Наука, 1970. С. 191.
СОДЕРЖАНИЕ ГЛАВЫ 3
3.1. Исходные предпосылки математического моделирования движения ЛА
в атмосфере.......................................................109
3.1.1. Системы координат, характеризующие положение ЛА
в пространстве................................................109
3.1.2. Поле тяготения Земли и учет его влияния на движение ЛА.111
3.1.3. Атмосфера Земли и ее модели............................113
3.2. Силы и моменты, действующие на ЛА в полете...................117
3.2.1. Аэродинамические силы и моменты........................117
3.2.2. Сила тяжести...........................................121
3.2.3. Сила тяги..............................................122
3.2.4. Управляющие силы и моменты.............................123
161
3.3. Математические модели движения ЛА...........................124
3.3.1. Уравнения движения ЛА в векторно-матричной форме
и их проекции на оси выбранной СК............................124
3.3.2. Упрощенная схема составления скалярных уравнений
движения ЛА..................................................129
3.3.3. Принцип разделения движений...........................131
3.3.4. Уравнения продольного движения программно-управляемых ЛА
на активном участке траектории...............................133
3.4. Выведение спутника на орбиту................................135
3.4.1. Качественный анализ основных участков
траектории выведения.........................................135
3.4.2. Оптимизация программ выведения........................137
3.4.3. Выбор программы изменения угла тангажа
и предъявляемые к ней требования.............................140
3.4.4. Методы решения проектно-баллистических задач
выведения спутника на орбиту..................................142
3.5. Введение в теорию проектно-баллистического обеспечения околоземных
и межпланетных космических полетов................................147
3.5.1. Основы теории невозмущенного орбитального движения.....147
3.5.2. Элементы баллистического проектирования
при решении задач межпланетного полета.......................151
3.5.3. Формирование орбит с использованием
гравитационных маневров......................................156
3.5.4. Оптимизация схем полета и выбор возможных дат старта..158
Литература...........................................................161
ГЛАВА 4_____________________________
Динамика полета
и основы устройства самолета
Динамика полета самолета как наука возникла в начале XX века и развивается па-
раллельно с развитием авиационной техники. Большую роль в ее становлении и раз-
витии сыграли русские ученые — Н. Е. Жуковский и его ближайшие соратники и уче-
ники: С. А. Чаплыгин, Н. П. Ветчинкин, Б. Н. Юрьев и др.
Наша страна имеет все основания гордиться отечественными достижениями
в области самолето- и вертолетостроения. М. В. Ломоносову принадлежит первая в
мире документированная практическая разработка летательного аппарата тяжелее
воздуха — двухосного вертолета. Первый в мире самолет был спроектирован и по-
строен русским изобретателем А. Ф. Можайским в 1882—1886 гг. на 15—20 лет раньше
первых самолетов, построенных в Америке и Западной Европе. Позже появились
самолеты братьев Райт, Фармана и других. В России, начиная с 1910 года, разрабаты-
ваются и испытываются более совершенные конструкции самолетов. Их авто-
ры: Н. В. Ребиков, Я. М. Гаккель, И. И. Сикорский, А. Д. Карпека, И. И. Стеглау,
Д. П. Григорович и др. Позже появляются известные конструкторские бюро
Н. Н. Поликарпова, А. Н. Туполева, С. В. Ильюшина, П. О. Сухого, А. С. Яковлева,
С. А. Лавочкина, В. М. Мясищева, А. И. Микояна и М. И. Гуревича, разрабатываю-
щие как гражданскую, так и военную технику различного назначения. Созданием
вертолетов занимаются конструкторские бюро М. Л. Миля и Н. И. Камова.
Современное воздушное судно представляет собой сложную техническую систе-
му, создание и эксплуатация которой с учетом обеспечения безопасности полетов тре-
бует глубоких знаний в областях динамики полета самолета и его устройства.
Эволюция в развитии весовых и геометрических параметров, повышение требо-
ваний к летно-техническим характеристикам, совершенствование оборудования
и снаряжения приводят к дальнейшему усложнению летательного аппарата и требуют
от разработчиков надежных и точных методов расчета всех летных характеристик са-
молета.
Важно, чтобы еще в процессе проектирования можно было бы предвидеть лет-
ные качества создаваемого аппарата.
Этого можно добиться, опираясь на фундаментальные положения в областях
проектирования и конструирования, на знание типовых конструктивных решений,
на особенности конструктивно-силовых схем летательных аппаратов и условий рабо-
ты элементов конструкции.
4.1. УРАВНЕНИЯ ДВИЖЕНИЯ САМОЛЕТА
В полете на самолет действуют: сила тяжести (7, направленная по вертикали вниз;
подъемная сила Y, лобовое сопротивление X и боковая сила Z, направленные вдоль
соответствующих осей скоростной системы координат; сила тяги двигателей
Р, которая направлена по оси двигателя.
163
Под действием этих сил самолет может осуществлять сложное пространственное
движение, которое в общем случае описывается системой дифференциальных урав-
нений, известных из курсов динамики твердого тела.
Более просто это движение можно представить состоящим из движения центра
тяжести (центра масс) самолета и вращения его вокруг центра масс.
При расчете летных характеристик самолета он рассматривается как материаль-
ная точка, масса которой равна массе самолета.
Для совершения полета по различным траекториям необходимо изменять вели-
чину и направление вектора скорости. Этого можно достигнуть изменением величи-
ны и направления равнодействующей сил, приложенных к самолету. Однако силу ве-
са произвольно изменять нельзя, поэтому управление полетом самолета осуществля-
ется с помощью изменения равнодействующей аэродинамических сил и силы тяги
двигателей. Разложим эту равнодействующую на две силы, направленные по каса-
тельной и нормали к траектории. Тогда касательная сила Nx будет обеспечивать раз-
гон, торможение или равномерное движение самолета, а нормальная сила N служит
для изменения направления полета. Эти силы являются управляющими силами.
Рассмотрим связь сил, приложенных к самолету, и траекторий движения его
центра масс, не рассматривая вопроса о том, как можно изменить эти силы.
Составим уравнения движения центра масс самолета в проекциях на оси прямо-
угольной системы координат. Очевидно, сумма проекций всех внешних сил на ка-
кую-либо ось должна равняться силе инерции, действующей вдоль этой оси. Уравне-
ния движения центра масс имеют следующий вид:
m(-dF +®Л-®Л> = ЕУ’
dK
(4.1)
Здесь Vx, V и Vz — проекции вектора скорости на оси выбранной системы коорди-
нат; шх, Шу, шг— проекции угловой скорости вращения осей выбранной подвижной
системы координат относительно неподвижных (земных) осей на подвижные оси.
Выберем систему координат с началом в центре тяжести самолета; ось Ох напра-
вим по скорости полета; ось Оу *, перпендикулярная оси Ох, лежит в вертикальной
плоскости, и ось Oz * направлена вправо (полускоростная система координат).
Выбранная нами система координат отличается от скоростной (поточной) систе-
мы положением оси Оу: в скоростной системе ось Оу лежит в плоскости симметрии са-
молета. Следовательно, принятая нами система повернута относительно скоростной
системы на некоторый угол крена ус (угол между
осью Оу и вертикальной плоскостью, проходящей
через вектор V).
Положение вектора скорости V в пространстве
относительно некоторой неподвижной (земной)
системы координат Ох^^ определится двумя угла-
ми: углом 0 — между вектором скорости полета и
горизонтальной плоскостью (углом наклона траек-
тории) и углом у — между горизонтальной осью
Охо земной системы координат и проекцией векто-
ра V на горизонтальную плоскость (углом пути или
углом поворота траектории) (рис. 4.1).
Рис. 4.1. Система осей координат
164
Если плоскость симметрии самолета совпадает с вертикальной плоскостью, что
имеет место при совершении большинства маневров, то такая полускоростная систе-
ма координат совпадет со скоростной системой координат.
Проекции вектора скорости в выбранной системе: Ух = К; Vy = 0; Vz = 0, а проек-
ции угловых скоростей вращения осей этой системы координат на нее же:
dw . л dw л d0
“х = d7 sin6; cos0; ^=-37.
Тогда уравнения движения примут следующий вид:
=ЕХ; /иК^ =ЕГ; cos0 = EZ. (4.2)
d/ d/ at ' '
Представляет интерес исследование полета самолета в вертикальной и горизон-
тальной плоскостях. Для случая полета в вертикальной плоскости, совпадающей
с плоскостью симметрии самолета, угол скольжения Р, угол крена ус и производная
dw
dY равны нулю, и уравнения движения принимают вид
= ЕГ. (4.3)
df df
dO
При полете в горизонтальной плоскости = 0 . Тогда
m^=ZX; -m^=ZZ. (4.4)
d/ at v '
Движение самолета в одной плоскости называется плоским.
Движение, при котором в течение какого-то промежутка времени кинематиче-
ские параметры движения (угол атаки, угол скольжения, скорость полета) остаются
неизменными, называется установившимся. К установившемуся движению самолета
относится горизонтальный установившийся полет, установившийся подъем и сниже-
ние (планирование).
К неустановившимся видам движения относится разгон и торможение самолета,
взлет и посадка и все виды маневра.
4.2. ПЕРЕГРУЗКИ, ДЕЙСТВУЮЩИЕ НА САМОЛЕТ
Характер движения самолета зависит от сил, действующих на него.
Отношение равнодействующей всех поверхностных сил /?пов к весу самолета G
называется перегрузкой:
- ^ПОВ / л Е\
п=-д-, (4.5)
где /?пов — равнодействующая всех поверхностных сил, действующих на самолет (вклю-
чая реакции опор, аэродинамические силы и силы тяги двигателей); G — вес самолета.
Величина и направление вектора перегрузки обычно определяются его проек-
циями на оси какой-либо системы координат. Обозначим проекции вектора перегруз-
ки в скоростной системе координат через пх, пу и nz. (Здесь пх — продольная перегруз-
ка; пу — поперечная перегрузка; nz — боковая перегрузка.)
Величина перегрузки п определится геометрическим сложением составляющих
пх, пуи nz:
|«| = + "у+ «Z • (46)
165
Зная проекции внешних сил на соответствующие оси координат и приняв, что
тяга двигателя направлена по вектору скорости, можно записать:
_P—G п* G ’ У ”y=G; Z nz=G- (4.7) (4.8) (4.9)
Здесь Р — сила тяги двигателя; X — сила лобового сопротивления; Y — подъемная
сила; Z — боковая сила.
Перегрузка возникает всегда, когда имеется ускорение в направлении какой-ли-
бо оси. Так, продольная перегрузка пх появляется при разгоне или торможении само-
лета, т. е. при наличии ускорения вдоль траектории; поперечная перегрузка пу всегда
связана с наличием поперечного (центростремительного) ускорения, т. е. с криволи-
нейным полетом.
Для самолетов наибольшее значение имеет поперечная перегрузка п? которая мо-
жет достигать значительной величины.
Поперечная перегрузка пу зависит от параметров траектории, следовательно, для
полета по заданной траектории необходимо создать определенную перегрузку, кото-
рая получила название потребной.
Наибольшая возможная перегрузка, которая может быть получена на данной вы-
соте при максимальном использовании возможностей самолета по созданию подъем-
ной силы, называется располагаемой. Сравнивая потребную и располагаемую пере-
грузки, можно определить возможность полета самолета на данной высоте по задан-
ной траектории. Чем больше высота полета, тем меньшей при заданном числе М
будет располагаемая перегрузка.
Определим наибольшую возможную перегрузку пу, которая может быть получе-
на на данном самолете:
_ max . г _ v
Л v Г' ’ 'О ’
'max О и
где Yq — подъемная сила в горизонтальном полете.
Y0=cy ^5.
Наибольшую подъемную силу Yможно получить при условии выхода на большие
углы атаки на максимальной скорости (например, при выходе из пикирования). Тогда
рИ2
у = г Р max V я
Лпах Су Э “
'max Z
(4.10)
Для современных сверхзвуковых самолетов теоретически возможно получить
Лушах = 40...50, однако величина поперечной перегрузки пилотируемых аппаратов
ограничивается физиологическими возможностями летчика, прочностью самоле-
та, а также условиями надежности работы двигательной установки и оборудова-
ния.
166
4.3. ОПРЕДЕЛЕНИЕ ЛЕТНЫХ ХАРАКТЕРИСТИК.
АЭРОДИНАМИЧЕСКИЙ РАСЧЕТ
4.3.1. Задачи и методы аэродинамического расчета
Задачей аэродинамического расчета является определение основных летных ха-
рактеристик самолета в зависимости от действующих на самолет внешних сил
(рис. 4.2). Значительную часть аэродинамического расчета составляет определение
режимов установившегося полета — установившегося горизонтального полета, уста-
новившегося подъема и снижения самолета.
При расчете летных данных считают, что полет
хФдв происходит без скольжения. Уравнения движения в
У этом случае имеют вид
/ X + Gsin 0 = Pcos (а 4- <р^)
F----1 и <411)
Горизонталь^^-------- + Рsin (а + <рдв) = G cos 0.
В зависимости от того, какая характеристика дви-
гателя <тяга’ мощность или обороты) введена в расчет,
существует несколько методов аэродинамического
Рис. 4.2. Схема сил, расчета: метод тяг, метод мощностей, оборотов и др.
действующих на самолет _ ’ ’
в полете Для расчета летных характеристик самолетов с
турбореактивными двигателями чаще всего приме-
няется аэродинамический расчет по методу тяг, предложенный Н. Е. Жуковским.
Исходными данными для этого расчета служат весовые характеристики самоле-
та, поляры самолета для всех чисел М полета и характеристики двигательной установ-
ки, т. е. зависимости Рдв =/(У, H)nCe=f(V, Н).
Для инженерных расчетов применяется упрощенный метод тяг, в основу которо-
го положены некоторые допущения, не приводящие к значительным ошибкам при
определении летных характеристик.
В этом расчете скорость самолета по траектории принимается равной горизон-
тальной скорости полета (Кпод ~ Кгп), а сила тяги двигателя считается направленной
по вектору скорости, т. е.
Psin (а + фдв)« 0 и Pcos (а 4- <рдв)« Р
Уравнения установившегося прямолинейного полета в вертикальной плоскости
принимают следующий вид:
X+Gsin0 = ^ r=Gcos0. (4.12)
4.3.2. Диапазон скоростей горизонтального полета
При горизонтальном установившемся полете уравнения (4.12) примут вид
Y=G,P=X. (4.13)
В развернутом виде их можно записать так:
c^-S=G,P = cx^-S.
Тяга, потребная для горизонтального полета с данной скоростью,
р = с V
л Сх 2
167
Учитывая, что К= — (аэродинамическое качество), получим
Сх
Рп=%. (4.14)
Потребная для горизонтального полета на данном угле атаки скорость определя-
ется из равенства Y = G:
Задаваясь значениями скорости (чисел М) в требуемом диапазоне, определяют
по соответствующей поляре сх, с и К = — , затем для каждой скорости находят по-
Сх
требную для полета тягу Рп. Такой расчет производится для каждой высоты полета,
и затем строятся зависимости Pn=f(V,H).
На этот же график наносят зависимость располагаемой тяги двигателя от скорос-
ти и высоты Pp~f(V,H) (рис. 4.3). Совместное рассмотрение этих графиков позволяет
определить характерные скорости горизонтального полета (рис. 4.4).
Максимальная скорость полета на данной высоте Ктах определится в точке пере-
сечения графиков Рп = f(V) и Рр =f(V), построенной для режима наибольшей тяги
двигателя (форсажа).
Для осуществления горизонтального полета на какой-либо скорости необходимо
обеспечить выполнение равенств Y = G, Рп = Рр выбором соответствующего режима
(угла атаки) и оборотов двигателя, определяющих тягу Рр.
Минимальная потребная тяга Рп соответствует режиму полета на максималь-
'min
ном качестве Ктах:
р
wmin ^max
Скорость, соответствующая этому режиму, называется наивыгоднейшей. Полет
на скорости, близкой к наивыгоднейшей, будет иметь наибольшую продолжитель-
ность.
Минимальная скорость горизонтального полета может быть определена, если
провести касательную к кривой потребных тяг перпендикулярно оси скоростей.
Рис. 4.3. График зависимости
потребных и располагаемых тяг
от скорости и высоты полета
Рис. 4.4. Режимы полета
на диаграмме потребных
и располагаемых тяг
168
Разность между максимальной скоростью полета и минимальной скоростью на
данной высоте определит диапазон скоростей горизонтального полета. Этот диапазон
будет изменяться по высотам: максимальная скорость Итах, начиная с некоторой высо-
ты, будет понижаться, а минимальная скорость Kmin с подъемом на высоту увеличивает-
ся в соответствии с формулой
V =
min */р5с„ •
1 "max
На некоторой предельной высоте Ятах и скорости Vmax и Hmin становятся равными;
горизонтальный полет на этой высоте возможен лишь на одной скорости.
Обычно бывает невозможно осуществить полет на Итах во всем диапазоне высот,
так как этот полет сопровождается появлением очень больших нагрузок, сильного на-
грева и потери устойчивости и управляемости. Поэтому на величину Ктах накладыва-
ют ограничения, задавая наибольшие допустимые значения скоростного напора <7тах
и наибольшего числа Мпред.
Полученные расчетом значения Kmin также не могут быть реализованы, так как при
полете на су самолет может оказаться неустойчивым и неуправляемым, возникнет
опасность срыва потока и сваливания самолета на крыло. Поэтому вводится ограниче-
ние на уменьшение скорости горизонтального полета до значения ее, равного К_пп
Таким образом, диапазон возможных скоростей горизонтального полета на дан-
ной высоте определится разностью между Ипп₽_ и К__п (рис. 4.5).
1,*л;дтах ди,1!тп
Величиной диапазона скоростей характеризуется степень совершенства самоле-
та. Расширение этого диапазона может быть достигнуто совершенствованием аэроди-
намики самолета, увеличением тяги двигателя, применением механизации крыла.
Эффективным способом расширения диапазона скоростей является применение са-
молета с крылом изменяемой в полете геометрии.
При горизонтальном полете на максимальной скорости располагаемая тяга дви-
гателя, развиваемая им на наибольших оборотах Рп , равна потребной тяге Р„.
"max "
На всех остальных скоростях полета располагаемая тяга больше потребной тяги
для горизонтального полета, т. е. имеется избыток тяги, зависящий от скорости поле-
та. Он может быть использован для подъема самолета, разгона и т. д.
4.3.3. Скороподъемность и потолок самолета
Установившимся подъемом называют равномерное и прямолинейное движение
самолета вверх по наклонной траектории под углом 0 к линии горизонта. Схема сил,
действующих на самолет при подъеме, приведена на рис. 4.6, а.
Согласно принятым допущениям, для установившегося подъема можно написать
Х+ G sin 0 = Рпод; G cos 0. (4.16)
Рассмотрим треугольник скоростей (рис. 4.6,6);
Vy = Ksin 0;
sin 0 — —-q— .
В этом выражении Рпод — тяга, необходимая для совершения подъема. Эта тяга
равна располагаемой тяге двигателя Рр.
169
Рис. 4.5. К определению
диапазона скоростей
Рис. 4.6. Схема сил, действующих
на самолет при подъеме:
а) действующие силы;
б) треугольник скоростей при подъеме
При установившемся подъеме, когда Ипод = И, сила лобового сопротивления X
будет равна потребной тяге при горизонтальном полете Рп.
Тогда можно записать
• гл _ рр ~ рп _ АР
Sln0 G G ’
где АР — избыток тяги на данной скорости полета.
Подставив это выражение в уравнение, определяющее V, получим
КАР
(4.17)
Следовательно, при постоянном весе вертикальная скорость подъема будет зависеть
от произведения КАР. Построив зависимость ИАР=/(И), можно найти скорость полета,
при которой на данной высоте будет достигнуто наибольшее значение V (рис. 4.7).
Эта скорость называется скоростью наиболее быстрого набора высоты, или ре-
жимом максимальной скороподъемности.
Максимальная вертикальная скорость набора высоты Vv зависит от высоты.
У max
С подъемом на высоту Vv уменьшается (рис. 4.8), что связано с уменьшением из-
отах
бытков тяги.
Рис. 4.7. Зависимость Vy^
от высоты и скорости полета
Рис. 4.8. К определению
статического потолка самолета
170
У дозвукового самолета (рис. 4.8, а) наблюдается непрерывное уменьшение
Vv ; у сверхзвукового самолета (рис. 4.8, б) возможны различные режимы набора
У max
высоты, поэтому зависимость Vv —f (И) сверхзвукового самолета может иметь не-
У max
плавный характера. Высота полета, на которой И =0, называется теоретическим
У max
потолком самолета. Теоретический потолок — верхняя граница установившегося го-
ризонтального полета и установившегося подъема. На теоретическом потолке избы-
ток тяги ДР = 0. Время подъема на теоретический потолок бесконечно велико, поэто-
му вводится понятие практического потолка — высоты, на которой максимальная вер-
тикальная скорость равна 0,5 м/сек.
Теоретический и практический потолок являются статическими высотами, т. е.
высотами, достигаемыми при установившемся подъеме самолета.
Современные самолеты обладают большим запасом кинетической энергии, ко-
торую они могут использовать для набора высоты с помощью предварительного раз-
гона вблизи потолка и последующего восходящего маневра.
Такой подъем самолета называется динамическим, а наибольшая высота, полу-
ченная при динамическом подъеме, — динамическим потолком самолета. На динами-
ческом потолке самолет должен иметь скорость, необходимую для сохранения управ-
ляемости.
Прирост высоты при динамическом подъеме может быть оценен по приближен-
ной формуле
И2 - И2
ДЯ= нач2^ кон, (4.18)
где Икон — скорость в конце динамического подъема;
Инач — скорость в начале динамического подъема.
Эта формула предполагает, что ДР = 0.
Для сверхзвуковых самолетов динамический потолок может существенно превы-
шать статический.
Для всех самолетов большой интерес представляет время, которое необходимо
затратить на набор определенной высоты.
Связь между высотой полета и временем ее набора удобно выразить в виде гра-
фика, называемого барограммой подъема (рис. 4.9). Время установившегося подъема
на заданную высоту Я определяется по формуле
н
t=lrdH. (4.19)
о у
Время набора высоты будет наименьшим, если набирать ее с вертикальной ско-
ростью И, . Очевидно, что во время набора высоты режим полета должен изменять-
•'тах
ся. На практике интегрирование ведется графически.
Как видно из графика, время подъема на теоретический потолок стремится
к бесконечности.
4.3.4. Снижение
Установившимся снижением называется прямолинейное и равномерное дви-
жение самолета вниз по наклонной траектории. Угол наклона траектории 0 отрица-
телен.
171
Рис. 4.9. Барограмма
подъема самолета
Рис. 4.10. Схема сил, действующих
на самолет при планировании
Уравнения движения самолета при установившемся снижения имеют вид:
Х= Р + Gsin 0
и (4.20)
Y= Geos 0.
Установившееся снижение при Рдв = 0 называется планированием. Режим пла-
нирования используется при посадке самолета.
При планировании на самолет действуют сила веса и полная аэродинамическая
сила R (рис. 4.10).
Уравнения движения в этом случае
r=Gcos©njl;
X=Gsm0rui.
Скорость планирования может быть определена из равенства сил G= R:
(4.21)
Из рассмотрения сил, действующих при планировании, можно определить угол 0^
«0™-^;-^ (4.22)
Этот угол зависит только от аэродинамического качества самолета.
Самое пологое планирование может быть осуществлено при полете на наивыгод-
нейшем угле атаки, т. е. при наибольшем качестве.
Дальностью планирования L называется путь, пройденный самолетом по горизон-
тали от начала до конца планирования.
Дальность планирования зависит от начальной высоты и угла планирования:
L = —
ПЛ tg © ’
ИЛИ
К. (4.23)
г. G
Современные сверхзвуковые самолеты, имеющие большую нагрузку на крыло т
О
и малое качество, быстро теряют высоту, дальность их планирования мала.
Наибольшую дальность планирования имеют планеры, обладающие высоким
значением качества (40—50) и малой нагрузкой на крыло.
172
4.4. ДАЛЬНОСТЬ И ПРОДОЛЖИТЕЛЬНОСТЬ ПОЛЕТА
Дальностью полета самолета называется расстояние по горизонтали, которое са-
молет может пролететь при израсходовании определенного запаса топлива. Это рас-
стояние складывается из участков набора расчетной высоты, участка крейсерского
полета на дальность и участка снижения (рис. 4.11).
Технической дальностью полета называется горизонтальный путь, проходимый
самолетом до полного выгорания топлива при условии полета в одной и той же верти-
кальной плоскости и в безветрие.
Практическая дальность полета — расстояние по горизонтали, проходимое само-
летом при тех же условиях, но при сохранении аэронавигационного запаса топлива
(7—10% заправки).
Радиус действия — наибольшее расстояние, которое может пролететь самолет
при условии возвращения на аэродром вылета без посадки.
Продолжительностью полета называется время, которое самолет может находить-
ся в воздухе.
Дальность и продолжительность полета зависят от запаса топлива в баках и от
расхода топлива.
Обычно при расчете дальности весь путь, проходимый самолетом, разбивают на 3
участка:
1 — расстояние по горизонтали, проходимое самолетом при наборе расчетной
высоты полета на дальность;
2 — расстояние по горизонтали, которое проходит самолет на основном режиме
полета;
3 — расстояние по горизонтали, проходимое самолетом при снижении.
Основную часть расстояния самолет проходит на втором участке полета. Для
дальних самолетов этот участок составляет 90—95% всего пройденного пути.
Условно считается, что самолет летит на этом участке горизонтально, однако
обычно полет происходит с постепенным набором высоты.
Дальность полета зависит от величины расхода топлива на один километр пу-
ти qK.
Продолжительность полета зависит от расхода топлива за один час полета q4.
Техническая дальность
бт
L=~^> (4.24)
а техническая продолжительность полета
(4.25)
Рис. 4.11. К определению
дальности полета
Здесь Gr — располагаемый запас топ-
*расп
лива.
Для горизонтального участка полета
G^n =Gm- АСнаб - АСпл “ АСизр “ А<7аэр>
где (7Т — полный вес заправляемого топлива;
Д(7наб, Дб^, Д<7изр — топливо, израсходо-
ванное на набор высоты, снижение и работу
двигателей на земле соответственно;
Дб^аэр — аэронавигационный запас топлива.
173
4.4.1. Дальность и продолжительность полета самолета с ТРД
Горизонтальный участок, проходимый самолетом при наборе высоты, определя-
ется по барограмме подъема, а расход топлива может быть оценен по приближенной
формуле
ДЛ-» — ‘0ч
ДСтнаб “go” ’
где tH — время набора самолетом заданной высоты;
q4 — средний часовой расход топлива, определяемый как расход на средней высоте
набора.
Дальность горизонтального участка планирования можно определить, если пре-
небречь тягой двигателей:
(4.26)
И • ДИ
М = (ДН+-^—)К.
(4.27)
Здесь ЛЯ — высота планирования;
ДИ— потеря скорости при планировании.
Для дозвуковых самолетов
Д£ = ДЯ К. (4.28)
Расход топлива при планировании можно определить так же, как и при наборе
высоты, зная часовой расход топлива двигателя, работающего на малых оборотах.
Дальность горизонтального полета
^кон
г _ f
J Як
^нач
Подставив выражение для qK, получим
<?кон
г _ Г ИА^б^топл
L J ~C~e~G~
Снач
(4.29)
(430)
Продолжительность полета
Скон
Г ^^топл
(4.31)
J <1ч
^нач
Здесь (7нач — вес самолета в начале горизонтального полета,
(7КОН — вес самолета в конце полета.
Интегрирование обычно ведется графически. Если принять, что скорость полета,
качество и удельный расход горючего мало изменяются, дальность можно определить
по формуле
/ — э ->^И . ^нач
L = 2,3-~г- log -.
°кон
Учитывая, что <7„пн = (7НЯЧ - (7ТОП_, можно записать
KUn п(1“ 1U1U1
Г_^КУ. 1
Z* 2,3 log
'-'е । '“'топл
^нач
Продолжительность горизонтального полета в часах
т=
7 Й’
174
(4.32)
(4.33)
(4.34)
или
В
п
Рис. 4.12. Режимы наибольшей
и скоростной дальностей
м
Т=2,з£ log------(4.35)
. '-гтопл
°нач
Как следует из формул, наибольшая дальность
горизонтального полета может быть получена при за-
данном располагаемом запасе топлива при максиму-
ме произведения КУ. Скорость полета, при которой
может быть достигнута наибольшая дальность, назы-
вается крейсерской.
Эту скорость можно найти, если построена зави-
симость qK=f (М) и определен минимум этой функции.
Скорости, которые примерно соответствуют ре-
жимам наибольшей дальности и продолжительности
полета, могут быть определены по графику Рп =f(V).
На рис. 4.12 приведена зависимость Рп =
для сверхзвукового самолета и определены скорости,
примерно соответствующие режимам £тах и 7"тах.
Здесь точка касания прямой, проведенной из начала координат к графику Рп =
=/(И), определит скорость полета на наибольшую дальность, а скорость, соответст-
вующая Pmin, определит режим наибольшей продолжительности.
Как известно, кривые потребных тяг сверхзвуковых самолетов имеют перегиб,
прячем касательная, проведенная к этой кривой из начала координат, может близко
подойти к ней также на сверхзвуковом режиме (точки А и В). Оба эти режима — око-
лозвуковой и сверхзвуковой — могут быть реализованы для полета на дальность.
Иногда оказывается более выгодным полет на сверхзвуковой скорости, хотя в этом
случае километровый расход обычно несколько выше.
Как видно из рис. 4.12, режим полета на наибольшую дальность более скорост-
ной, чем режим полета на наибольшую продолжительность.
По мере подъема на высоту уменьшается часовой и километровый расходы топ-
лива, поэтому у самолета с ТРД наивыгоднейшая высота полета близка к его статиче-
скому потолку.
При выгорании топлива уменьшается полетный вес и статический потолок само-
лета увеличивается, поэтому оптимальным профилем полета на дальность обычно
оказывается такой профиль, при котором самолет постепенно набирает высоту. Его
принято называть полетом «по потолкам».
Как видно из вышеприведенных формул, величина дальности и продолжитель-
ности полета зависит от аэродинамического совершенства самолета (его качества),
совершенства двигателя (величины расхода топлива) и выбора режима полета. Кроме
этого, дальность и продолжительность полета сильно зависят от метеорологических
условий: температуры окружающего воздуха, направления ветра и т. д.
Дальность полета можно существенно увеличить дозаправкой самолета топливом
в полете.
4.5. ВЗЛЕТНО-ПОСАДОЧНЫЕ ХАРАКТЕРИСТИКИ
Взлетно-посадочные характеристики самолета определяют возможность его ба-
зирования на аэродромах определенного размера (определенного класса) и, следова-
тельно, возможности его использования.
175
Во всех случаях потребные размеры аэродрома желательно уменьшать.
Взлет и посадка самолета могут быть аэродромными и безаэродромными (верти-
кально-взлетающие самолеты).
Большинство современных самолетов способны совершать только аэродромные
взлет и посадку.
4.5.1. Взлет
Взлетная дистанция состоит из участков разбега по земле, отрыва и воздушного
участка, который складывается из участков выдерживания и набора определенной
высоты над взлетной полосой, определяемой в соответствии с нормами летной год-
ности.
Расстояние по горизонтали, проходимое самолетом от начала разбега до конца
взлета, называется взлетной дистанцией (рис. 4.13).
^взл ^разб + ^выд + ^наб*
Самолеты, обладающие большой тяговооруженностью, после отрыва осуществ-
ляют одновременно разгон и набор высоты.
Скорость отрыва определяется из условия равновесия Y = G в момент отрыва
v =
отр ^Ро5сУс
(4.36)
Если учесть, что в момент отрыва сила тяги не горизонтальна, условие равнове-
сия самолета запишется как
G=Y^+Py,
где Ру — вертикальная составляющая силы тяги;
V = —[1--2
о4> №5су<У G
(4.37)
Наличие вертикальной составляющей тяги уменьшает скорость отрыва. Эту
скорость можно уменьшить и применением механизации при взлете, т. е. увеличени-
ем с .
лотр
Разбег самолета — это движение с ускорением за счет разности сил тяги и суммы
сопротивлений движению: лобового сопротивления и трения колес.
Можно записать:
m^=P-Q-F^ (4.38)
Fip — (G—Y)f, (4.39)
где /— коэффициент трения, зависящий от поверхности аэродрома и давления в
пневматиках. Коэффициент/для бетона равен 0,03—0,04.
Рис. 4.13. К определению взлетной дистанции
176
Тогда ускорение при разбеге
dK = rP-Q-(G-П/1 d/ Jx gL G J’
или Л=Я(; f 2G <4-40)
Проведя некоторые преобразования и проинтегрировав выражение (4.40), можно
определить время разбега
и длину разбега у r отр * g 1 P-Q-f(G-Y) (441) 0 H>rp - £ = (4 42) ^разб 2g J P — Q—f(G—Y)‘ ' ' 0
Если рассматривать разбег как равноускоренное движение и известно среднее
ускорение при разбеге, то длина разбега
V2 <4-43)
Для уменьшения длины разбега применяют форсаж двигателя, стартовые уско-
рители, отклонение струи двигателей вниз или дополнительные двигатели, создаю-
щие вертикальную тягу.
Длина горизонтального участка подъема с разгоном до высоты Н = 10,7 м может
быть определена по формуле
L»«-s,„0cp( 2S + «>’) <4'44>
где 0ср — средний угол подъема самолета;
V — скорость в конце участка набора высоты.
4.5.2. Посадка
Посадочная дистанция состоит из участков планирования, выдерживания и про-
бега по земле. На выходе из планирования летчик выравнивает самолет, а в конце уча-
стка выдерживания самолет парашютирует со скоростью Kmin (рис. 4.14).
Посадочная дистанция
£пос = Ли> + £выр + ^ВЫД + ^пр- (4-45)
Длина зависит от качества К и начальной высоты Я, которую принимают
в соответствии с нормами летной годности.
Рис. 4.14. К определению посадочной дистанции
177
Современные скоростные самолеты, имеющие малое значение качества, обычно
планируют очень круто, что затрудняет выравнивание.
Длина участка выравнивания зависит от скорости в начале участка И^, качества
самолета и техники пилотирования, т. е. создаваемой при выравнивании перегрузки.
Эта длина может быть определена по формуле, которая выводится из условия
Квыр = Ku, = const:
где пу — перегрузка, создаваемая при выравнивании;
— качество самолета на режиме Планирования.
Для уменьшения участка ZBbip следует уменьшать скорость планирования.
Участок выдерживания — горизонтальный полет на малой высоте, в процессе ко-
торого скорость самолета уменьшается от до Ипос (где Ипос — посадочная скорость,
определяемая по формуле)
(4'47)
V U 'ПОС
Длина участка £выд оценивается по приближенной формуле
г (Ипл-и^а: .....
£ВЫЛ=-----------• (4-48)
Последним этапом посадки является пробег самолета по земле, при котором обыч-
но применяются все возможные средства торможения, уменьшающие длину пробега:
тормоза колес, тормозные парашюты, реверс тяги, различные финишеры и т. д.
Эту длину, как и длину разбега, можно оценить по приближенной формуле, если
считать движение самолета на этом этапе равнозамедленным:
И2
1ПРО6 = ^. (4.49)
Здесьу — средняя абсолютная величина ускорения торможения
(4-50)
где 2сум + F — суммарное сопротивление всех тормозящих элементов.
Эффективным средством уменьшения взлетной и посадочной дистанций являет-
ся применение специальных устройств, позволяющих существенно сократить эти
дистанции или осуществить взлет без разбега, а посадку без пробега. Самолеты, осна-
щенные этими устройствами, называются вертикально-взлетающими (СВВП), или с
укороченными дистанциями взлета и посадки (СУВП).
Для современных вертикально-взлетающих самолетов величина тяговооружен-
ности (отношение располагаемой тяги двигателя к взлетной массе) равна 1,2... 1,3.
Создание вертикально-взлетающих самолетов связано с трудностями обеспече-
ния устойчивости и управляемости при очень малых значениях скоростного напора
и на переходных режимах от вертикального взлета к горизонтальному полету. На ре-
жимах взлета и посадки обычные рули не эффективны, и необходимо применять газо-
вые рули, расположенные в струе двигателя, специальные струйные рули (реактивные
насадки) или управляющие двигатели. Кроме того, необходимо обеспечить безопас-
ность экипажа и пассажиров при отказе двигателей на взлете.
178
При компоновке СВВП также возникает ряд трудностей, часть которых на со-
зданных самолетах уже преодолена, однако СВВП являются, безусловно, перспектив-
ными, так как значительно расширяют возможности их эксплуатации.
4.6. МАНЕВРЕННОСТЬ САМОЛЕТА
Маневренностью самолета называется его способность за определенное время из-
менять скорость, направление и высоту полета.
Существует большое количество маневров— разгон и торможение, плоские
и пространственные криволинейные маневры и т. д. Обычно маневренность самоле-
тов оценивают по показателям выполнения маневров: по времени и пути разгона, ра-
диусу и времени выполнения криволинейного маневра и т. д.
Характеристики различных маневров зависят от ускорений, которые могут воз-
никать при их выполнении, а следовательно, и от перегрузок, поэтому наибольшие
возможные перегрузки, которые можно создать при полете на данном самолете, явля-
ются показателем его маневренности. Рассмотрим некоторые характерные маневры
самолета.
4.6.1. Криволинейный полет в вертикальной плоскости
Большинство маневров самолета осуществляется в вертикальной плоскости. При-
мерами таких маневров могут служить: пикирование, горка, петля Нестерова и др.
Все эти маневры имеют общие элементы, содержащие криволинейный полет
в вертикальной плоскости: ввод и вывод из горки, ввод самолета и вывод его из пики-
рования и т. д.
Уравнения движения самолета в вертикальной плоскости имеют вид:
КГ
m-т- = Pcos (а + фпи) - X— <7sin 0;
Q| х 1ДВ' 7
= Psin (а + фпв) + Y- Gcos 0.
QJ х ' ДВ'
(4.51)
Центр
кривизны
Рис. 4.15. Схема сил,
действующих на самолет
при криволинейном полете
в вертикальной плоскости
Силы, действующие на самолет, показаны
на рис. 4.15. Угол а + фдв мал, поэтому можно
принять
cos (а + Фдв) = 1; sin (а + <рдв) = 0.
Тогда
= P—X—Gsin 0;
а/
= К—Geos 0.
Учитывая.
(4.52)
(4.53)
G
что m = - , запишем уравнение
1Р-Х
• - + sin 0 = .
g G
полученное выражение с фор-
(4.52) в виде
dK
d/
Сравнивая
мулой (4.7), можно записать
dKl .
п= -г- - sin0.
х dt g
(4.54)
179
Преобразуем уравнение (4.53):
= У-Geos е,
g dt
или
rd© . _ Y ..
id7+cos®=G- <455>
П d0 V Y А. - <AQ\
Производная = - , а отношение в соответствии с формулой (4.8) является
поперечной перегрузкой пу.
Следовательно,
у2
п= — + cos 0. (4.56)
у gr
К наиболее распространенным маневрам в вертикальной плоскости относятся:
горка (рис. 4.16, а) — маневр, имеющий целью быстрое изменение высоты полета;
пикирование (рис. 4.16, б) — снижение самолета по сильно наклоненной к гори-
зонту траектории (0 = 60—90°).
При 0 = 90° пикирование называется отвесным. Пикирование имеет целью бы-
строе снижение.
Обычно пикирование разбивают на 3 участка: вход в пикирование, прямолиней-
ный участок пикирования, выход из пикирования.
Рассмотрим участок прямолинейного пикирования.
Уравнения движения самолета имеют вид
dK
r=Gcos0;m^ =P+Gsin0-%.
at
При 0 = 90° (отвесное пикирование) уравнения движения примут вид
Г= о-,т^ = P-X+G.
at
С течением времени скорость может достигнуть такой величины, при которой сила
лобового сопротивления уравновесит тягу и составляющую веса. Такая скорость назы-
вается предельной скоростью пикирования. Она может быть уменьшена применением
различных тормозов. Пикирование применяется также для быстрого разгона самолета.
Петля Нестерова — сложный маневр (рис. 4.16, в), имеющий форму петли.
Рис. 4.16. Некоторые виды маневров самолета в вертикальной плоскости
180
Полупетля (рис. 4.16, г) является восходящей фигурой, в конце первой полови-
ны петли летчик переводит самолет в нормальное положение.
Радиус криволинейного маневра (ввода в пикирование и вывода из него, петли,
горки и т. д.) зависит от скорости и перегрузки. Чем больше скорость полета, тем
больше радиус криволинейного маневра.
4.6.2. Разгон и торможение
Для изменения скорости полета применяют разгон самолета или его торможение.
Разгон происходит в том случае, когда суммарная продольная сила, приложенная к са-
молету, направлена вперед, т. е. положительна. Если суммарная продольная сила отри-
цательна, происходит торможение самолета. Интенсивность разгона и торможения ха-
рактеризуется величиной продольного ускорения, определяемого для случая горизон-
тального полета по формуле
dK = Р-Х
„ dt т ’
Cj
где т = - ;
8 dV
% =&г (4.57)
Если траектория наклонена под углом О к горизонту, ускорение -jy определится
по формуле
dK
-jy =gn ±gsin0 = g(/i ±sinO).
4.6.3. Криволинейный полет в горизонтальной плоскости
Криволинейный полет в горизонтальной плоскости называется виражом. Вираж
может быть неустановившимся, если в процессе его выполнения меняются скорость
полета, угол крена, скольжения и т. д., и установившимся, если все параметры движе-
ния остаются неизменными.
Вираж, выполняемый без скольжения, называется правильным.
При правильном вираже силы, действующие на самолет, находятся в равновесии
(рис. 4.17).
Уравнения движения в этом случае имеют вид:
Р = %; Kcos у =6;
Рис. 4.17. Схема сил, действующих
на самолет при правильном вираже
Умпу=^. (4.58)
Потребная перегрузка для виража с задан-
ным креном определится по формуле
<«»>
Эта формула показывает также, какой нуж-
но создать крен для выполнения правильного ви-
ража с заданной перегрузкой.
Радиус виража определится по формуле
'в
Потребная скс
V =
Т вир
Г
gtg у‘
ость виража
I 2G
pc S cos у *
(4.60)
(4.61)
181
4.7. СТРУКТУРНАЯ СХЕМА САМОЛЕТА
Самолеты — летательные аппараты (ЛА) тяжелее воздуха, совершающие полет по
аэродинамическому принципу. Они представляют собой сложные технические уст-
ройства, состоящие из взаимосвязанных по назначению, месту и функционированию
агрегатов, частей и элементов (рис. 4.18).
Основным назначением самолета и вертолета, как и любого ЛА, является транс-
портировка определенного груза на заданное расстояние. Характер целевой нагрузки,
ее вес и расстояние, на которое она должна быть доставлена, определяют параметры
летательного аппарата.
Самолет
Рис. 4.18. Структурная схема самолета
182
Авиационный комплекс
Парк самолетов Вспомогательные средства Подготовительные средства
Рис. 4.19. Укрупненный состав авиационного комплекса
В качестве критерия оценки качества самолета, находящегося в эксплуатации,
служат не только летные характеристики самолета, но и условия его эксплуатации (дли-
на взлетно-посадочных полос (ВПП), длительность и сложность подготовки самолета
к полету и пр.). Поэтому при создании ЛА принято рассматривать не только самолет,
но и весь комплекс средств, обеспечивающий выполнение поставленной задачи.
Авиационный комплекс — совокупность объектов, элементов и устройств, сов-
местная работа которых обеспечивает выполнение самолетом данного типа опреде-
ленного задания в заданных условиях. Укрупненный состав авиационного комплекса
представлен на рис. 4.19.
Парк самолетов— совокупность разных типов самолетов, спроецированных
и построенных для выполнения определенной задачи. Можно провести классифика-
цию самолетов по назначению (по типу решаемых с их помощью задач) (рис. 4.20).
Появление новых народнохозяйственных задач, которые можно решить с по-
мощью самолетов, потребует создания самолета нового, неизвестного пока типа.
Вспомогательные средства (аэродром и совокупность средств управления полетом)
обеспечивают базирование самолета на земле и точную навигацию самолета в полете.
Подготовительные средства (парк машин, механизмов и устройств) обеспечивают
техническое обслуживание самолета на земле, подготовку самолета к полету, конт-
роль технического состояния самолета и всех его систем.
Самолет — главный элемент авиационного комплекса, его параметры и характерис-
тики определяют параметры и характеристики вспомогательных и подготовительных
средств, которые тоже влияют на параметры и характеристики самолета.
САМОЛЕТЫ ЗАДАЧИ, РЕШАЕМЫЕ С ПОМОЩЬЮ САМОЛЕТОВ (классификационный признак)
пассажирские перевозка пассажиров
транспортные транспортировка грузов
учебные обучение летного состава
экспериментальные проведение летных экспериментов
сельскохозяйственные обработка сельскохозяйственных угодий
военные обеспечение обороноспособности страны
спортивные занятия авиационным спортом
санитарные оказание срочной медицинской помощи
геологоразведочные воздушная разведка недр
Рис. 4.20. Классификация самолетов по назначению
183
1
Аэродина-
мическая
схема
самолета
«Бесхвостка»
Нормальная
«Летающее крыло»
«Утка»
С передним
и хвостовым ГО
Конвертируемая
2
Число
и распо-
ложение
Расчалочный
моноплан
т аг । мх»>Ф<1
Расчалочно-сго-
Триплан ечный биплан
3
Форма
угольное
Эллипти-
ческое
полете
Парабо-
лическое
Круглое
косный моноплан| Парасоль
Стоечный
биплан
4
Схема
оперения
Коробчатое
Двухбалочное
5
Схема
Четырехопорное
7
8
9
Стрело- [Трапецие-
видное
видное
Ч=г-\—1
Треу-
гольное
Свободнонесу-
щий биплан |Полутороплан| «Чайка»
Моноплан
Треугольное
с наплывом
Оживальное
Обратной
стреловидности
Разнесенное
Многокилевое [двухкилевое
П- образное
Трехопорное
Со среднераспо-
ложенным ГО
Т- образное
Кольцевое стреловидности
Двухкилевое
сЦПГО
Кресто-
образное
V- образное
Трехопорное
с носовой опорой
Нормальное
Многоопорное
Y- образное
Ъш
опорного
элемента
Колесный
Схема
фюзеляжа
S
Ъш S
двига- и
теля ’’
_____Мускульный
Число
и распо-
ложение
двига-
телей
Лыжный
Колесно-лыжный
Чашечный
Велосипедное
Гусеничный
77ТПТШ
Воздушная подушка Поплавковый
Лодка
Несущий фюзеляж
Нормальная
Двухбалочная
Двухфюзеляжная
И]
а
ТРД/Ф/
РДТТ
ПВРД/ПуВРД/
Поршневой
(дизель)
Гондола
(бесфюзеляжная)
Паровой
ТРДД/Ф/
Комбиниро-
ванный
твд
Звхвосто-
вой части
В носовой
части
В средней
части
В хвостовой
части
В корне
крыла
В средней
части крыла
На концах
крыла
Над
крылом
На пилонах
под крылом
4 под
фюзеляжем
4 на пилонах
под крылом
4 в корне
крыла
Рис. 4.21. Классификация самолетов по различным конструктивным признакам (матрица
альтернативных схемных решений, предложенная проф. Г. И. Житомирским)
4 в хвосто- (Раздельная СУ
вой части
дляСВВП
Проектирование самолета требует умения оценивать свойства самого самолета и
внешней среды, в которой существует и функционирует самолет.
Классификация самолетов по аэродинамической схеме и конструктивным признакам
(см. рис. 4.21) представлена с определенной степенью детализации в виде матрицы кон-
структивно-компоновочных схем отдельных частей и агрегатов самолета, отражающей
все многообразие их форм и схем отдельных частей в процессе развития авиации. Ис-
пользуя последовательно информацию каждого уровня (1...9, см. рис. 4.21), можно по-
лучить (собрать) конструктивно-компоновочную схему почти любого из существовав-
ших и существующих самолетов.
4.8. ОСНОВНЫЕ ЧАСТИ САМОЛЕТА И ИХ НАЗНАЧЕНИЕ
Несмотря на большое разнообразие самолетов, все они, как правило, имеют одни
и те же части и системы.
Любой самолет должен иметь несущую силовую конструкцию, двигательную уста-
новку и запас топлива для нее, органы управления и системы управления полетом, взлет-
но-посадочные устройства (шасси), оборудование (пилотажно-навигационное, конт-
рольно-измерительное, связное и др.), а также источники энергии, питающие агрегаты
оборудования и силовые приводы.
Основой всего самолета, воспринимающей действующие на него силы, является
планер, в который входят крыло, фюзеляж и оперение. Основные части самолета пока-
заны на рис 4.22.
Крыло служит для создания подъемной силы и обеспечения поперечной устойчи-
вости.
Фюзеляж (корпус) является базой, к которой крепятся крыло и оперение. Фюзе-
ляж служит для размещения экипажа, оборудования и перевозимых грузов.
Оперение представляет собой несущие
Рис. 4.22. Основные
конструктивные части самолета:
/ — обтекатель радиолокатора;
2 — фонарь кабины пилотов;
3 — фюзеляж; 4 — крыло;
5 — двигательная установка;
6 — киль; 7 — руль направления;
8 — триммер руля направления;
9 — триммер руля высоты;
10 — руль высоты; 11 — стабилизатор;
12 — закрылки; 13 — интерцептор;
14 — элероны; 15 — предкрылки;
16 — шасси
поверхности, предназначенные для обеспе-
чения устойчивости и управляемости.
Большинство самолетов имеет горизон-
тальное оперение (ГО), предназначенное для
обеспечения продольной устойчивости и уп-
равляемости, и вертикальное оперение (ВО),
обеспечивающее путевую устойчивость и уп-
равляемость.
Горизонтальное оперение дозвукового са-
молета состоит из неподвижной или ограни-
ченно подвижной (стабилизатора) и под-
вижной части (руля высоты). На сверхзвуко-
вых самолетах обычно применяется
цельноповоротное горизонтальное оперение.
Вертикальное оперение состоит из не-
подвижного киля и подвижного руля на-
правления.
Шасси — система опор самолета, пред-
назначенная для взлета, посадки и движе-
ния самолета по аэродрому. Сухопутные са-
молеты обычно имеют колесное шасси.
Двигательная установка создает силу
тяги, необходимую для движения самолета.
185
Она состоит из двигателя, движителя (винта у ТВД и поршневых двигателей), преобра-
зующего мощность двигателя в силу тяги, топливной и масляной систем, системы защи-
ты двигателя и контроля за его работой.
В настоящее время на самолетах в основном применяются воздушно-реактивные
двигатели, однако эксплуатируются самолеты и с поршневыми, турбовинтовыми и ра-
кетными двигателями.
Система управления полетом самолета — комплекс устройств и механизмов, при
помощи которых летчик управляет движением самолета, воздействуя на соответст-
вующие органы управления.
Для осуществления управления в кабине летчика имеются командные рычаги —
ручка (штурвал) и педали.
Кроме системы управления полетом, на самолете имеется целый ряд систем уп-
равления различными агрегатами’, двигателем, уборкой и выпуском шасси и др.
Оборудование самолета. Для осуществления полета по заданной программе, вы-
полнения поставленной задачи самолет должен иметь разнообразное оборудование:
пилотажно-навигационное, электро- и радиооборудование, системы жизнеобеспече-
ния, энергетическое оборудование, противообледенительное, пожарозащитное и спе-
циальное.
4.8.1. Крыло
Крыло служит для создания подъемной силы, обеспечивает поперечную устой-
чивость. К крылу крепятся органы поперечного управления (элероны); устройства, на-
зываемые механизацией крыла, часто — шасси и двигатели, а также внешние подвески.
Форма в плане и профиль крыла в значительной степени определяют летные ка-
чества самолета (рис. 4.23, 4.24). Геометрия крыла определяется назначением самоле-
та и тактико-техническими требованиями к нему. Самыми распространенными явля-
ются прямые трапециевидные, стреловидные и треугольные крылья.
На крыло действуют аэродинамические силы, массовые силы конструкции кры-
ла, агрегатов и грузов, размещенных в крыле.
Рис. 4.23. Некоторые формы
(серии) профилей крыла:
а) несимметричный плосковыпуклый;
б) несимметричный двояковогнутый;
в) симметричный двояковыпуклый;
г) ромбовидный; д) клиновидный
Рис. 4.24. Различные формы крыла в плане:
а) прямоугольное; б) эллиптическое;
в) трапециевидное; г) стреловидное;
д) треугольное; е) ромбовидное;
ж) комбинированной формы
(треугольное с наплывом)
186
Воздушная (аэродинамическая) нагрузка приложена непосредственно к обшив-
ке в виде сил разрежения и давления и распределена по поверхности крыла. Мас-
совые силы конструкции распределены по всему объему крыла. Массовые силы от
агрегатов и грузов — сосредоточенные силы, приложенные к крылу в узлах крепления
агрегатов.
Элементы конструкции крыла.
Работа крыла под нагрузкой
Крыло самолета и вертолета представляет собой тонкостенную контурную балку,
имеющую металлическую обшивку, продольный набор — лонжероны и стрингеры
и поперечный набор — нервюры.
В плоскости хорд крыло имеет большую жесткость, поэтому нагрузками крыла от
продольных сил обычно пренебрегают. Воздушная нагрузка, приложенная к обшивке
в виде сил разрежения и давления, передается через связи (заклепки, сварку)
в основном на нервюры, которые собирают распределенную нагрузку с участков об-
шивки и стрингеров (рис. 4.25, а). Нервюра работает под этой вертикальной нагруз-
кой в своей плоскости, как тонкостенная балка — диафрагма, опертая на стенки
(рис. 4.25, б).
Нагрузка, действующая на нервюру, стремится ее переместить в направлении
действующей силы. Перемещению нервюры препятствуют ее связи со стенками,
в которых возникают реакции &QX и AQ2. Стенки являются упругими опорами, поэто-
му сила Рнерв распределяется по ним пропорционально их изгибным жесткостям
(£J)j и (£J)2. Равнодействующая этих сил AQ будет приложена в центре жесткости.
Под действием момента Рнерв • с, где с — расстояние от центра давления до центра
жесткости, нервюра стремится повернуться, повороту нервюры препятствуют связи
ее с обшивкой и стенками, образующие замкнутый контур. В этом контуре возникает
поток касательных усилий q, уравновешивающий момент поворота.
Силы AQ, и AQ2 суммируются по размаху крыла, обусловливая его срез и изгиб.
Уравновешиваются эти силы на фюзеляже. Потоки касательных сил также суммиру-
ются по размаху, вызывая кручение крыла, и уравновешиваются в конечном итоге
также на фюзеляже.
Рис. 4.25. Передача нагрузок по крылу:
а) нагружение отсека крыла; б) нагружение нервюры;
I — стрингер; 2 — нервюра; 3 — обшивка
187
Рис. 4.26. Напряжения в сечении крыла:
а) от действия изгибающего момента М;
б) от действия поперечной силы Q
и крутящего момента Мк
Рис. 4.27. Работа
элементов лонжерона
В сечениях крыла возникают касательные напряжения в обшивке и стенках от
действия перерезывающей силы и крутящего момента и осевые усилия (нормальные
напряжения) в поясах лонжеронов, стрингерах и обшивке (рис. 4.26).
Лонжероны, продольные стенки и стрингеры
Лонжерон является основным силовым элементом крыла. В конструкциях крыль-
ев современных летательных аппаратов обычно применяют лонжероны балочного ти-
па, которые представляют собой двухпоясные балки, пояса которых работают на сжа-
тие и растяжение от изгиба, а стенки воспринимают сдвиг от поперечной силы и сов-
местно с обшивкой образуют замкнутый контур от крутящего момента (рис. 4.27).
Пояса балочных лонжеронов выполняются из специальных прессованных или
катаных профилей различного сечения (рис. 4.28). Из условия равнопрочности пло-
щади сечения поясов уменьшаются к концу крыла. Материал пояса выбирается в со-
ответствии с нагружением крыла; для слабо нагруженных крыльев пояса изготавлива-
ют из алюминиевых сплавов, для сильно нагруженных крыльев — из высокопрочной
стали; если крыло работает в условиях нагрева, пояса делают из титана или специаль-
ной стали, форма сечения пояса должна обеспечивать наибольший момент инерции
Jz при заданной строительной высоте крыла.
Рис. 4.28. Типовые сечения поясов лонжеронов
188
Стенки лонжеронов выполняют из разнообразных листовых материалов. Для
увеличения критических напряжений потери устойчивости стенки ее подкрепляют
профилями, на стенке делают штамповку ребер жесткости (зиговку), отверстия облег-
чения отбортовывают или окантовывают.
Ферменный лонжерон представляет собой плоскую ферму, пояса которой соеди-
нены между собой стойками и подкосами, выполненными из труб или профилей
(рис. 4.29). Детали лонжерона могут соединяться при помощи заклепок или сварки.
Такие лонжероны выгодны в весовом отношении при большой строительной высоте
(для современных тонких крыльев практически не применяются).
Продольные стенки в конструктивном отношении аналогичны лонжеронам кры-
ла со слабыми поясами, что ограничивает восприятие ими изгибающего момента.
Продольные стенки воспринимают перерезывающую силу и крутящий момент.
Стрингеры являются элементами продольного набора. Они подкрепляют обшив-
ку и передают воздушную нагрузку на нервюры. Кроме того, стрингеры совместно
с обшивкой участвуют в восприятии изгибающего момента.
Стрингеры изготавливают из прессованных, катаных или гнутых профилей
(рис. 4.30). Форма поперечного сечения и длина стрингера (расстояние между сосед-
ними нервюрами) выбираются из условия получения высоких критических напряже-
ний при общей и местной потере устойчивости.
Обшивка обеспечивает необходимую форму поверхности крыла, воспринимает
местную воздушную нагрузку, работает на растяжение (сжатие) и сдвиг от общих де-
формаций изгиба и кручения крыла. Обшивка в современном крыле является одним
из основных элементов, обеспечивающих прочность и жесткость.
Обшивка штампуется или выколачивается из листов дюраля, титана или стали,
соединяемых между собой заклепочными, сварными или клеевыми швами. Толщина
ее колеблется в пределах 0,8—10 мм. В крыльях современных самолетов, помимо лис-
товой обшивки, широко применяют монолитные панели (рис. 4.31), изготавливаемые
из толстых листов с последующей обработкой механическим или химическим фрезе-
рованием, и многослойную обшивку с различными заполнителями (рис. 4.32).
Обшивка слоистой конструкции состоит из двух внешних металлических листов,
связанных между собой легким заполнителем, чаще всего сотовым. Соты выполняют
из металлической фольги, текстолита или стеклопластика. Наибольшее распростра-
нение получили алюминиевые соты толщиной 8 = 0,03...0,1 мм. Заполнители соеди-
няются с внешними слоями склеиванием или пайкой. Заполнители обеспечивают
совместную работу внешних несущих слоев и увеличивают жесткость обшивки. Под-
крепление несущих слоев осуществляется по всей их площади, что существенно улуч-
шает качество поверхности крыла. Трехслойная обшивка имеет высокие критические
напряжения сжатия и сдвига и малый вес. Кроме сот и других легких заполнителей
в таких конструкциях применяют гофр.
Нервюры крыла по своему назначению и конструкции разделяются на нормальные
и усиленные, по конструктивно-силовой схеме — на балочные, рамные и ферменные.
Нормальные нервюры служат для сохранения заданной формы крыла, передают
аэродинамическую нагрузку на лонжероны и обшивку, участвуют в общей работе
крыла, подкрепляя обшивку и стрингеры. Усиленные нервюры устанавливают в мес-
тах приложения к конструкции больших сосредоточенных нагрузок, в местах перело-
ма осей элементов продольного набора, вырезов и т. п. Они выполняют те же функ-
ции, что и нормальные нервюры, и, кроме того, воспринимают и передают сосредото-
ченную нагрузку на стенки и обшивку в виде потоков касательных усилий.
Нормальные нервюры балочного типа выполняются в виде сплошных стенок из
листового материала (рис. 4.33). Их пояса образуются отбортовками стенок или спе-
189
1
Рис. 4.29. Ферменный лонжерон:
1,2 — пояса; 3 — раскос
Рис. 4.30. Типовые сечения стрингеров:
а) гнутые профили; б) прессованные или катаные профили;
в) форма стрингера для придания жесткости задней кромке крыла
Рис. 4.31. Монолитные
панели обшивки
Рис. 4.32. Трехслойная обшивка
с различными заполнителями
Рис. 4.33. Типовые нормальные нервюры
Рис. 4.34. Рамная нервюра
циальными профилями. В стенках делают отверстия облегчения, а для повышения
критических напряжений устанавливают специальные стойки или делают зиговку.
Рамные нервюры состоят из двух половин, не связанных стенкой друг с другом
(рис. 4.34). Они менее выгодны в весовом отношении, однако применение рамных не-
рвюр облегчает сборку крыла и позволяет лучше использовать его внутренние объемы.
Ферменные нервюры по конструкции аналогичны ферменному лонжерону.
В современных крыльях применяются редко.
Усиленные нервюры выполняются по тем же конструктивным схемам, что и нор-
мальные, однако их силовые части сильно развиты и напоминают по конструкции
лонжерон крыла. Пояса нервюр нагружаются аналогично поясам лонжерона осевыми
усилиями сжатия и растяжения, а стенки — сдвигом. Разрушающие напряжения по-
ясов и стенок нервюр определяются по тем же формулам, что и лонжеронов.
Конструктивно-силовые схемы крыльев
В зависимости от степени участия обшивки (панелей крыла) и поясов лонжеро-
нов в работе крыла на изгиб крылья делят на лонжеронные и моноблочные (кессон-
ные) (рис. 4.35). К лонжеронным (рис. 4.35, а) относят крылья, у которых изгибаю-
щий момент воспринимается мощными поясами лонжеронов, а сравнительно слабые
стрингеры подкрепляют тонкую обшивку.
Моноблочным крылом (рис. 4.35, б) называется крыло, у которого изгибающий
момент воспринимается верхней и нижней панелями, состоящими из толстой обшив-
ки, подкрепленной развитыми стрингерами и сравнительно слабыми поясами лонже-
ронов, несущая способность которых обычно такая же, как и стрингеров.
191
Лонжеронные крылья. В зависимости от количества лонжеронов крылья подраз-
деляются на одно-, двух- и многолонжеронные. Лонжероны стремятся расположить
так, чтобы лучше использовать строительную высоту профиля. В однолонжеронном
крыле лонжерон размещают в месте наибольшей строительной высоты, что увеличи-
вает момент инерции и уменьшает вес поясов лонжерона. Для создания замкнутого
контура, воспринимающего кручение, на 60—70% хорды устанавливается продольная
стенка. Иногда для крепления носка крыла впереди лонжерона ставится передняя
стенка (рис. 4.36,4.37).
Расстояние между стрингерами выбирают из условия допустимых прогибов об-
шивки от действия воздушной нагрузки, а шаг между нервюрами — из условия обес-
печения о0601- гтп = аместн-п Этот шаг обычно колеблется в пределах 200—300 мм.
up. vip. KjJ. vip
Рис. 4.36. Конструкция однолонжеронного прямого крыла с передней и задней стенками:
1 — лонжерон; 2 — передняя стенка; 3 — задняя стенка;
4 — стрингеры; 5 — нервюры; 6 — обшивка; 7 — стыковые узлы
192
Рис. 4.37. Конструкция многолонжеронных крыльев:
а) трехлонжеронное крыло умеренной стреловидности;
б, в) многолонжеронные стреловидные крылья с силовыми нервюрами
В двухлонжеронном крыле передний лонжерон обычно располагают на 20—30%,
задний — на 60—70% хорды. Лонжеронная конструкция крыла позволяет делать
в крыле значительные вырезы без нарушения прочности основных элементов,
Моноблочные крылья. Характерной особенностью моноблочного крыла является
утолщение обшивки и равномерное распределение материала по периметру сечения.
Такое крыло имеет повышенную по сравнению с лонжеронным жесткость, меньшие
деформации обшивки от воздушной нагрузки, а хорошо подкрепленная обшивка (па-
нель) полностью воспринимает изгибающий момент. Панели моноблочного крыла
могут быть сборно-клепаной конструкции, монолитными или трехслойными.
Если основой силовой схемы моноблочного крыла является кессон — централь-
ный контур, составленный верхней и нижней панелями и двумя стенками, то такое
крыло часто называют кессонным (рис. 4.38).
Рис. 4.38. Конструкция кессонного крыла со стыковыми узлами
крепления отъемной части крыла (ОЧК) между собой и к центроплану:
/ — панели крыла; 2 — усиленные кронштейны; 3 — концевой обтекатель; 4 — нормальные
нервюры; 5 — носовая часть крыла; 6 — концевая часть крыла; 7, 8 — лонжероны кессона крыла
193
узел
элементы
«вилка — ухо»
Рис. 4.39. Конструкция и нагружение узлов крепления лонжеронных крыльев:
а, б, в, д) соединение моментными узлами; г) проушины; е) шарнирный узел
Стенки кессона расположены обычно так же, как у двухлонжеронного крыла.
Они воспринимают поперечную силу Q и крутящий момент Мк.
Стыковые соединения крыльев. Крылья современных самолетов обычно имеют
эксплуатационные разъемы, упрощающие их сборку, транспортировку и эксплуата-
цию. Конструкция разъема, а также количество и размещение узлов определяются
конструктивно-силовой схемой крыла (рис. 4.39).
У лонжеронных крыльев основные стыковые узлы устанавливаются на лонжеро-
нах (рис. 4.40). Обычно такие узлы изготавливаются вместе с лонжероном и представ-
ляют собой монолитную конструкцию. Минимальное количество узлов в стыке опре-
деляется из условия неподвижности стыка и равняется трем. В связи с тем что связь
отъемной части и центральной (центроплана) осуществляется при помощи отдельных
узлов на лонжероне и стенке, такой стык называют точечным.
Рис. 4.40. Стыковой узел на лонжероне крыла и варианты нагружения
и уравновешивания усиленных шпангоутов от нагрузок крыла:
а, в) крепление отъемной части крыла (ОЧК); б) центральная часть крыла
в виде балки (лонжерона), проходящей через фюзеляж
194
Центроплан
Рис. 4.41. Конструкция стыкового соединения центроплана с ОЧК
Отсеки моноблочных крыльев соединяются при помощи контурного стыка
(рис. 4.41). При контурном стыке силовая связь осуществляется по всем продольным
элементам панели.
Стыковые узлы бывают моментными, передающими изгибающий момент в виде
пары сил, и шарнирными. Примером моментных узлов могут служить узлы на поясах
лонжерона. Шарнирные узлы устанавливаются на стенках, они передают только силу.
Детали узлов являются сильно нагруженными элементами конструкции, изготавли-
ваются из высокопрочных материалов и обычно имеют дополнительный запас прочности.
Конструкция стреловидных и треугольных крыльев
Стреловидные крылья, как и прямые, по конструктивно-силовой схеме могут
быть лонжеронными и моноблочными. Нервюры в стреловидных крыльях могут раз-
Рис. 4.42. Нагрузки стыка
стреловидного крыла
мещаться по потоку или перпендикулярно оси
лонжерона. При двухлонжеронном стреловид-
ном крыле задний лонжерон, как более корот-
кий, имеет большую изгибную жесткость и по-
этому работает с большими напряжениями.
Конструктивно-силовые элементы стреловид-
ного крыла и выполняемые ими функции анало-
гичны элементам и функциям прямого крыла.
Особенности конструкции стреловидных крыль-
ев проявляются только в их корневой части.
Продольные силовые элементы стреловид-
ных крыльев в корневой части у фюзеляжа имеют
перелом, что существенно изменяет и усложняет
передачу и уравновешивание изгибающего мо-
мента. В точках перелома 1 и 2 (рис. 4.42) осевые
усилия от изгиба раскладываются на две состав-
ляющие: и S2. Усилие 5, уравновешивается
в плоскости симметрии, а усилие S2, параллельное
борту фюзеляжа, нагружает крыло дополнитель-
ным моментом в плоскости бортовой нервюры.
195
Рис. 4.44. Схемы треугольных крыльев:
а и б) с параллельными лонжеронами;
а) с веерообразным расположением лонжеронов;
г) с внутренним подкосом
Для восприятия дополнительных нагрузок, связанных с наличием стреловиднос-
ти, корневая часть стреловидного крыла должна иметь конструкцию, отличную от
конструкции прямого крыла.
В зависимости от конструктивно-силовой схемы корневой части различают стре-
ловидные крылья с переломом осей элементов продольного силового набора у борта
фюзеляжа (рис. 4.43, а) с переломом осей элементов продольного силового набора в
плоскости симметрии самолета (рис. 4.43, б) и с внутренним подкосом (рис. 4.43, в).
Крыло с переломом продольных элементов у борта фюзеляжа имеет мощную борто-
вую нервюру, воспринимающую часть изгибающего момента и связанную с лонжеронами
поясами и стенкой. Необходимость установки такой нервюры исключает возможность
реализовать вырез в корневой части крыла, что затрудняет уборку шасси в крыло.
Схема крыла с переломом продольных элементов в плоскости симметрии широ-
кого практического применения не нашла, так как в этом случае необходимо устано-
вить центральную нервюру, воспринимающую составляющую изгибающего момента
в плоскости симметрии, что связано с компоновочными трудностями.
В стреловидных крыльях с внутренним подкосом лонжерон получает вторую
опору, в результате чего уменьшается изгибающий момент в корневой части крыла.
Крыло такой схемы удобно при размещении шасси, которое крепится одновременно
к подкосу и лонжерону, а объем между ними используется для размещения опоры
шасси в убранном положении.
Треугольные крылья могут иметь расположение силовых элементов, аналогичное
их расположению в прямом или стреловидном крыле (рис. 4.44). Наибольшее рас-
пространение получили многолонжеронные крылья с параллельным расположением
Рис. 4.43. Схемы стреловидных крыльев
196
Рис. 4.45. Схема крыла
изменяемой геометрии
лонжеронов или с подкосной балкой. Многоточечное креп-
ление треугольного крыла обеспечивает более равномерное
распределение нагрузки по стыковым узлам и жесткость за-
делки.
Крыло изменяемой стреловидности в полете нашло
применение на современных многорежимных самолетах,
поскольку позволяет улучшить их технические и тактиче-
ские характеристики.
Изменение стреловидности (геометрии) крыла осу-
ществляется за счет поворота консоли относительно цент-
рального шарнира (рис. 4.45), расположенного на непо-
движном центроплане. Угол стреловидности обычно изме-
няется в широких пределах: от 12 до 75°.
Нагрузки с консоли на центроплан передаются в ос-
новном через узел поворота (шарнир) и силовой рычаг при-
вода. При расчете эти нагрузки определяют для различных
положений крыла и различных режимов полета.
Крылья обратной стреловидности могут иметь такие же
конструктивно-силовые схемы, как и крылья прямой стре-
ловидности. Однако в отличие от силовых схем крыльев
прямой стреловидности, за исключением однолонжеронного крыла, более нагружен-
ными в корневой части, будут передний лонжерон и панель вблизи него. Скоростные
самолеты с крылом обратной стреловидности могут иметь более высокие маневрен-
ные характеристики на больших углах атаки и иметь более высокий уровень безопас-
ности полетов. Применение такого крыла может обеспечить устойчивость и эффек-
тивное поперечное управление до углов атаки порядка 80°.
Малая скорость захода на посадку может быть достигнута без применения слож-
ных средств механизации. Посадочная скорость также может быть уменьшена на
20...25%. Это делает перспективным применение крыла обратной стреловидности на
самолетах короткого взлета и посадки (рис. 4.46).
Рис. 4.46. Компоновочная схема самолета С-37-1:
1 — штанга ПВД (приемника воздушного давления); 2 — откидывающийся носовой конус;
3 — оптико-электронная обзорно-прицельная система; 4 — приборная доска; 5 — топливные баки;
6 — встроенная пушка; 7 — пусковая установка барабанного типа с ракетами средней дальности
класса «воздух—воздух»; 8 — створки перепуска воздуха; 9 — отклоняемый носок крыла;
10 — гидроусилитель рулевого привода; 11 — антенна системы связи; 12 — РЛС обзора задней полу-
сферы; 13 — контейнер тормозного парашюта; 14 — сотовая конструкция; 15 — сопла двигателей
с гидравлическими приводами; 16 — флаперон; 17 — несущая конструкция с панелями из композици-
онных материалов; углепластик и титановые сплавы; 18 — места крепления наружных подвесок;
19 — элерон; 20 — основная стойка шасси; 21 — переднее горизонтальное оперение; 22 — воздухо-
заборник; 23 — отсеки радиоэлектронного оборудования; 24 — импульсно-допплеровская РЛС
197
4.8.2. Оперение и элероны
Аэродинамические поверхности, образующие оперение самолета, являются его
органами устойчивости и управляемости. Горизонтальное оперение в основном обес-
печивает продольную балансировку, устойчивость и управляемость, вертикальное —
путевую. Иногда горизонтальное оперение используют как орган поперечного управ-
ления.
Вертикальное оперение обычно состоит из неподвижной части — киля и руля на-
правления, горизонтальное — из стабилизатора и руля высоты (рис. 4.47). Сверхзву-
ковые самолеты имеют цельноповоротное горизонтальное, а иногда и вертикальное
оперение.
Компоновка на самолете и параметры оперения должны обеспечивать его эф-
фективность на всех режимах полета. При размещении оперения на самолете необхо-
димо, чтобы оно не затенялось крылом и фюзеляжем и чтобы скосы потока в зоне
оперения были минимальными.
По своим внешним формам горизонтальное и вертикальное оперение подобно
крылу. Профили оперения чаще всего (вертикального оперения всегда) симметричны.
Элероны, представляющие собой отклоняющиеся хвостовые части профиля
крыла, обеспечивают поперечное управление самолетом и располагаются в конце
размаха крыла для увеличения плеча до продольной оси самолета. Эффективность
элеронов заметно снижается на больших скоростях вследствие деформаций крыла,
а на больших углах атаки из-за срыва потока с крыла. Для обеспечения поперечного
управления на всех режимах применяют внешние и внутренние элероны в сочетании
с интерцепторами.
В полете на оперение действуют аэродинамические и массовые силы. Основны-
ми аэродинамическими нагрузками оперения являются уравновешивающая, манев-
ренная и нагрузки при полете в неспокойном воздухе.
Конструкция оперения. Стабилизаторы и кили по своей силовой схеме и конст-
рукции подобны крыльям. Они могут быть лонжеронными или моноблочными. Эле-
менты конструкции, их работа и способы соединения такие же, как у крыльев. На
многих современных самолетах стабилизатор в полете управляем. Для этого устанав-
ливается привод и механизм перестановки стабилизатора.
Рули и элероны представляют собой балки на упругих опорах; количество опор
обычно выбирается из условия обеспечения жесткости руля. Чаще всего рули имеют
Вертикальное Руль направления
Рис. 4.47. Оперение самолета
Рис. 4.48. Конструкция элерона:
1 — лонжерон; 2 — нервюра;
3 — заполнитель; 4 — обшивка;
5 — законцовка
198
Рис. 4.49. Схема внутреннего аэродинамического компенсатора элерона:
а) схема устройства компенсатора; б) принцип действия компенсатора; 1 — гибкая перегородка;
2 — залонжеронное пространство; 3 — компенсатор; 4 — щели; 5 — лонжерон
Рис. 4.50. Конструктивно-силовые схемы цельноповоротного горизонтального оперения:
а) балка жестко связана с оперением; б) балка защемлена в фюзеляже
однолонжеронную конструкцию, иногда с применением легкого пористого или сото-
вого заполнителя (рис. 4.48). Работа элементов элерона и руля подобна работе эле-
ментов однолонжеронного крыла.
Элероны и рули обычно имеют аэродинамическую компенсацию для уменьше-
ния шарнирных моментов и нагрузок на привод управления. Наибольшее распрост-
ранение получила осевая и внутренняя компенсация (рис. 4.49).
Для повышения критической скорости автоколебаний применяется весо-
вая балансировка — противофлаттерный груз, который крепится впереди оси вра-
щения.
Цельноповоротное оперение имеет некоторые конструктивные особенности
и может выполняться по двум основным схемам: с балкой — осью крепления опере-
ния, принадлежащей самому оперению и установленной в подшипниках на фюзеля-
же (рис. 4.50, а), и несущей балкой — осью, принадлежащей фюзеляжу и неподвижно
закрепленной на силовых шпангоутах (рис. 4.50, б), В первом случае тяга управления
крепится непосредственно к кронштейну на балке, во втором — к корневой нервюре
оперения, а поворот оперения осуществляется в подшипниках, установленных в си-
ловых нервюрах.
Обычно балки имеют круговое замкнутое сечение, что обеспечивает удобство их
крепления в подшипниках и меньший вес. Способ передачи усилий с оперения на
балку зависит от схемы крепления оперения.
199
4.8.3. Фюзеляж
Фюзеляж служит для размещения экипажа, пассажиров, оборудования, топлива,
шасси и грузов, определяемых назначением самолета или вертолета. Часто в фюзеля-
же размещаются двигатели (рис. 4.51).
В силовом отношении фюзеляж представляет собой базу, к которой крепятся
крыло, оперение и шасси.
Внешние формы фюзеляжа определяются назначением самолета (или вертоле-
та), его схемой, диапазоном чисел М полета и другими факторами. Формы, размеры и
поверхность фюзеляжа должны обеспечивать при заданной емкости минимальное со-
противление самолета, минимальный нагрев конструкции, а также удобство
эксплуатации — хороший обзор, удобное размещение экипажа и пассажиров, воз-
можность быстрой загрузки и выгрузки.
Основными внешними нагрузками фюзеляжа являются силы, передающиеся с
крыла, оперения, несущего винта, двигателей и шасси; массовые силы от грузов и аг-
регатов, размещенных в фюзеляже, и от конструкции самого фюзеляжа; аэродинами-
ческие силы разрежения и давления, распределенные по поверхности, а также силы
избыточного давления в кабине и в специальных отсеках. От внешних сил фюзеляж
работает как балка на изгиб в двух плоскостях и на кручение. Опорами фюзеляжа слу-
жат узлы крепления крыла.
Конструктивно-силовые схемы балочных фюзеляжей
Ферменные конструкции фюзеляжей представляют собой пространственную фер-
му, состоящую из четырех плоских ферм (рис. 4.52). Ферма состоит из четырех по-
ясов, соединенных между собой стойками, распорками, раскосами (жесткий элемент)
или расчалками (гибкий элемент). Элементы конструкции фермы под действием
внутренних сил работают на растяжение или сжатие. Для придания обтекаемой фор-
мы ферму покрывают обшивкой и делают специальные надстройки (гаргроты).
Балочные конструкции фюзеляжей представляют собой тонкостенную балку, все
элементы которой участвуют в восприятии нагрузок. В зависимости от участия об-
шивки в работе фюзеляжа на изгиб и ее подкрепления различают балочно-лонжерон-
ный, балочно-стрингерный и балочно-обшивочный фюзеляжи (рис. 4.53).
Рис. 4.51. Общий вид
и конструкция фюзеляжа
3 4
Рис. 4.52. Конструкция
ферменного фюзеляжа:
1 — пояс; 2 — стойка; 3 — раскос;
4 — расчалки; 5 — профилированный
шпангоут; 6 — стрингер
200
4
Рис. 4.53. Конструкция балочного фюзеляжа:
1 — лонжерон; 2 — стрингер; 3 — шпангоут; 4 — обшивка
Рис. 4.54. Лонжеронный фюзеляж и его поперечное сечение
Рис. 4.55. Стрингерный фюзеляж и его поперечное сечение
Балочно-лонжеронные фюзеляжи (рис. 4.54) состоят из лонжеронов (усиленных
стрингеров), стрингеров, шпангоутов и обшивки. Такая конструкция применяется
при наличии больших вырезов (фонаря летчика, отсеков шасси и т. п.), поскольку
в месте выреза необходимо для сохранения требуемой прочности и жесткости конст-
рукции фюзеляжа на изгиб усилить продольные элементы, окантовывающие вырез.
Балочно-стрингерные фюзеляжи (рис. 4.55) состоят из стрингеров, шпангоутов
и обшивки. Стрингерный набор равномерно распределяется по контуру фюзеляжа,
так как изгибающий момент может действовать в различных плоскостях. Такая кон-
струкция применяется при отсутствии больших вырезов.
201
Рис. 4.56. Отсек
бесстрингерного фюзеляжа
Рис. 4.57. Конструкция
бимса
Балочно-обшивочные фюзеляжи (рис. 4.56) состоят из обшивки и шпангоутов.
Обшивка из листового материала хорошо воспринимает растягивающие нагрузки
и плохо — сжимающие, поскольку при сжатии она теряет устойчивость при малых
значениях нормальных критических напряжений от изгиба. Обшивочная конструк-
ция фюзеляжа с обшивкой из листового материала применяется на участках с малыми
значениями изгибающего момента. Обшивки из панелей с сотовым или другим за-
полнителем хорошо работают на растяжение и сжатие, и благодаря этому обшивоч-
ную конструкцию можно применять при любой величине изгибающего момента. При
такой конструкции существенно снижается масса.
Рассмотренные конструктивно-силовые схемы балочных фюзеляжей в чистом
виде по всей длине фюзеляжа встречаются редко, поскольку на фюзеляж действуют
значительные по величине и направлению силы и моменты, а по условиям эксплуата-
ции в конструкции необходимо предусматривать вырезы для фонаря кабины летчика,
люков, дверей, окон и т. п. По этой причине конструкция по длине фюзеляжа часто
выполняется из сочетания двух, а иногда и всех трех типов балочных фюзеляжей, что
вызвано стремлением получить конструкцию минимальной массы.
В продольный набор балочного фюзеляжа входят стрингеры и балки местного
усиления (бимсы). Бимсы обычно выполняются в виде мощных прессованных про-
филей или тонкостенных замкнутых балок (рис. 4.57), подкрепляющих вырезы. У гра-
ниц выреза балки не заканчиваются, а продолжаются в невырезанной части фюзеля-
жа на длину, которая зависит от относительных размеров выреза, жесткостей шпан-
гоутов, обшивки и стрингеров на участке фюзеляжа в районе выреза.
От действия изгибающего момента в обшивке и стрингерах возникают нормаль-
ные напряжения, а от действия поперечной силы и крутящего момента — касатель-
ные напряжения в обшивке.
Обшивка в фюзеляже выполняет те же функции, что и в крыле. Она выполняется
из листовых материалов или изготавливается в виде монолитных либо слоистых кон-
струкций.
Листы обшивки соединяются заклепочными, сварными или клеевыми швами.
Стрингеры фюзеляжа по своей форме подобны стрингерам крыла. Наибольшее при-
менение имеют стрингеры уголкового, Z-образного и Т-образного сечения (рис. 4.58).
Рис. 4.58. Сечения сложных лонжеронов и стрингеров фюзеляжа
202
Рис. 4.59.
На сильно загруженных участках фюзеля-
жа стремятся ставить стрингеры с двойными
полками и неразрезные, что повышает несу-
щую способность обшивки и улучшает условия
ее работы (рис. 4.59).
Шпангоуты по назначению бывают нор-
мальные, служащие для подкрепления обшив-
ки, стрингеров и придания формы фюзеляжу, и
усиленные (силовые) шпангоуты, устанавли-
ваемые в местах приложения к конструкции
больших сосредоточенных сил (воспринимают
поперечные сосредоточенные нагрузки от оперения, двигателей и т. д. и передают эти
силы на обшивку в виде потока касательных усилий).
Шпангоуты, как правило, выполняются в виде кольцевых рам, работающих на
изгиб. Нормальные шпангоуты могут либо непосредственно соединяться с обшивкой,
либо через стрингеры. Для прохода стрингеров в шпангоутах выполняют вырезы.
По конструкции шпангоуты бывают стеночные и рамные. Нормальный рамный
шпангоут состоит из нескольких частей (1), соединенных друг с другом накладками (2).
Типовые сечения нормальных шпангоутов показаны на рис. 4.60.
Силовые шпангоуты разнообразны по конструкции (см. рис. 4.61—4.63). Они
обычно выполняются в виде замкнутых мощных плоских рам — клепаных или моно-
литных, обладающих высокой жесткостью при изгибе в своей плоскости. При необ-
ходимости силовые шпангоуты имеют глухие стенки, подкрепленные профилями. Та-
кова конструкция, в частности, гермошпангоутов, отделяющих герметичные отсеки
фюзеляжа.
Рис. 4.60. Нормальный шпангоут и типовые сечения рамных шпангоутов
203
А-А
Рис. 4.61. Усиленный рамный шпангоут
Рис. 4.62. Цельноштампованный
усиленный рамный шпангоут
Рис. 4.63. Шпангоут, выполняющий
роль перегородки
Герметические кабины и отсеки
Современные самолеты совершают полеты на больших высотах в разреженных
слоях атмосферы, где давление и температура воздуха, а также парциальное давление
кислорода и его весовое содержание в единице объема не обеспечивают нормальных
условий для жизнедеятельности человека.
Условия жизнедеятельности экипажа и пассажиров, а также надежность работы
специального оборудования при полете на больших высотах достигаются путем со-
здания герметических кабин и отсеков, в которых поддерживается необходимое со-
держание кислорода, повышенное по сравнению с окружающей атмосферой давле-
ние воздуха, а также необходимые температура и влажность.
Типы герметических кабин. В зависимости от способа создания необходимого
парциального давления кислорода и очистки воздуха от вредных примесей различают
вентиляционные и регенерационные кабины.
Вентиляционные кабины наиболее широко применяются на современных самоле-
тах. Они представляют собой герметические отсеки фюзеляжа, в которые непрерывно
подается атмосферный воздух, забираемый чаще всего от компрессора двигателя. Коли-
чество воздуха, подаваемого в кабину, и необходимое давление обеспечиваются соответ-
ствующим оборудованием кабины — клапанами, регуляторами и пр. Отработанный
воздух стравливается в атмосферу. Для поддержания необходимого температурного ре-
жима воздух подогревается или охлаждается в специальных устройствах и фильтруется.
На рис. 4.64, а приведена принципиальная схема вентиляционной кабины, а на
рис. 4.64, б — один из возможных законов изменения давления в такой кабине.
Вентиляционные герметические кабины могут использоваться до высот 25—
30 км. При малом избыточном давлении в кабине на высотах более 12—15 км исполь-
зуют дополнительное индивидуальное питание кислородом (маску).
Регенерационные кабины полностью изолированы от внешней среды. Питание
кабины осуществляется от воздушных и кислородных баллонов, а продукты дыхания
удаляются с помощью специальных поглотителей в регенерационной установке, цир-
куляция через которую происходит при помощи вентилятора или эжектора. Регенера-
ционные кабины обладают неограниченной высотностью, однако имеют относитель-
но большой вес, повышенную пожароопасность и зависимость продолжительности
полета от бортового запаса кислорода.
Герметизация и теплозвукоизоляция кабины. Сохранение созданного режима в каби-
нах и отсеках требует тщательной их герметизации. Герметизации подлежат заклепочные
швы соединения элементов каркаса и обшивки, выводы трубопроводов, электропровод-
ки, тяг системы управления, а также люки, входные двери, фонари и остекление. Для
Рис. 4.64. Вентиляционная кабина и давление в ней
(MCA — международная стандартная атмосфера)
205
Атмосфера
Атмосфера
Рис. 4.65. Герметизация люков и дверей при помощи ножевого уплотнения:
1 — стенка кабины; 2 — уплотнительная прокладка; 3 — окантовка люка; 4 — стенка люка; 5 —
рамка люка с ножом; 6 — прокладка из мягкой резины; 7 — прокладка из пластинчатой резины
Рис. 4.66. Герметизация люков или двери при помощи резиновой трубки:
1 — стенка кабины; 2 — уплотнительная прокладка; 3 — окантовка люка;
4 — стенка люка; 5 — рамка люка с ножом; 6 — резиновая трубка
герметизации всех швов соединения покрывают слоем герметика или устанавливают
пленки-прокладки. Окна, двери и люки герметизируются резиновыми прокладками или
надувными резиновыми шлангами, а остекление фонаря — при помощи замазки-герме-
тика (рис. 4.65,4.66).
Теплозвукоизоляция защищает кабины и отсеки от шума двигателя и других ис-
точников, а также снижает количество тепла, поступающего в кабину из погранично-
го слоя. Толщина теплозвукоизоляции выбирается из условия поглощения тепла и
обеспечения уровня шума не выше 90—100 дБ.
Теплозвукоизоляция состоит из нескольких слоев звуко- и теплоизолирующего
материала (асбеста, стекловаты, пеностекла) и внутренней декоративной обшивки.
4.8.4. Расположение двигателей на самолете
При размещении двигателей обычно руководствуются требованиями аэродина-
мики и удобства эксплуатации. Установка двигателя должна создавать минимальное
дополнительное лобовое сопротивление, а тяга — как можно меньше влиять на устой-
Рис. 4.67. Типовые схемы расположения двигателей:
а — ж) сверхзвуковые самолеты; з — м) дозвуковые транспортные самолеты
206
чивость и управляемость самолета. Кроме того, должен быть обеспечен хороший под-
ход к двигателям для их технического обслуживания, монтажа и демонтажа, а также
предусмотрена пожарная безопасность.
На рис. 4.67 приведены возможные схемы расположения двигателей на самолетах.
Крепление двигателей
Крепление двигателя к самолету должно обеспечить передачу всех нагрузок, дей-
ствующих на двигатель и на элементы конструкции. Величина этих нагрузок зависит
от типа двигателя, его расположения и маневренных характеристик самолета.
В общем случае на двигатель действуют массовые силы, сила тяги, реактивный
момент и аэродинамическая нагрузка. Величины нагрузок определяются в соответст-
вии с расчетными случаями «Норм прочности».
Массовая сила R? определяется по формуле
^Р = ^ДУлЭтах/’
где (7ду включает в себя вес двигателя 6дв, моторамы, капота и гондол.
Для самолетов с ТВД (7ДУ = (1,9...2,2)(7ДВ; для самолетов с ТРД (7ДУ =
= (1,2...1,6)(7ДВ.
Для расчета элементов крепления тяга двигателя Р принимается наибольшей.
Реактивный крутящий момент от винта
Мп = 716,2-кгс * м,
р ’ п ’
где N — развиваемая двигателем мощность (на валу винта) в л. с.;
п — число оборотов винта в минуту.
Аэродинамическая нагрузка приложена к обтекаемым элементам установки — ка-
потам и гондолам. Она невелика; учитывают ее обычно при расчете местной прочнос-
ти капотов и гондол.
Как правило, крепление двигателей осуществляется с помощью пространствен-
ных стержневых систем, силовые схемы которых определяются типом двигателя
и размещением его на самолете.
Узлы крепления двигателя чаще всего устанавливают в двух плоскостях, перпен-
дикулярных к его продольной оси.
Крепление имеет основные и вспомогательные узлы. Основные узлы, восприни-
мающие нагрузки, располагают как можно ближе к центру тяжести двигателя, а до-
полнительные, обеспечивающие регулировку положения двигателя, — на некотором
расстоянии от его центра масс.
Конструкция крепления двигателя должна обеспечивать свободу тепловых де-
формаций корпуса двигателя.
Для удобства монтажа в основных опорных узлах подвески реактивных двигате-
лей ставят амортизаторы (пружины или резиновые шайбы) для ограничения переда-
ваемых на конструкцию летательного аппарата колебаний.
Поршневые и турбовинтовые двигатели крепятся к крылу или фюзеляжу самоле-
та с помощью пространственных ферм (рис. 4.68).
Для обеспечения геометрической неизменяемости конструкции крепления необ-
ходимо иметь не менее шести стержней, направления которых не пересекали бы одну
прямую. На рис. 4.69 приведена схема возможного крепления ТРД в фюзеляже. Дви-
гатель закреплен в двух плоскостях с помощью плоских ферм 1—5 и узла Л, смонтиро-
ванного на продольной балке фюзеляжа.
207
Рис. 4.68. Крепление турбовинтового двигателя:
1—6 — узлы крепления двигателя к конструкции самолета
Рис. 4.69. Схема крепления ТРД в фюзеляже
Такое крепление обеспечивает восприятие сил по трем осям, а узлы В выполнены
таким образом, что допускают свободу осевых и радиальных деформаций корпуса
форсажных камер.
Расчет крепления двигателей производят по правилам строительной механики:
усилия в стержнях, работающих на растяжение, сравнивают с разрушающими напря-
жениями растяжения, а сжатые стержни проверяют на потерю устойчивости.
Входные устройства и системы выпуска газов
Воздухозаборники и воздушные каналы
Воздухозаборники и воздушные каналы называют входными устройствами. Их
назначение — подводить воздух к двигателю, обеспечивать устойчивую работу двига-
теля на всех режимах, преобразовывать энергию скоростного напора в энергию давле-
ния воздуха перед компрессором двигателя.
По мере увеличения скорости полета роль воздухозаборника в сжатии воздуха
значительно возрастает. При скоростях, соответствующих числу М = 2,5...3,0, сжатие
воздуха осуществляется почти полностью в воздухозаборнике.
Воздухозаборник и воздушный канал должны обеспечивать наилучшее исполь-
зование скоростного напора, равномерное поле скоростей на входе в компрессор,
устойчивую работу двигателя на всех режимах, возможно меньшее внешнее сопротив-
ление.
По расположению на самолете различают лобовые, боковые и подфюзеляжные
воздухозаборники. Лобовые воздухозаборники размещаются в носовой части фюзеля-
208
жа или гондолы двигателя и имеют круглую (кольцевую) форму. Боковые воздухоза-
борники могут быть полукруглыми, плоскими, клиновидными или совковыми. При
размещении двигателей «пакетом» под фюзеляжем или крылом применяются, как
правило, плоские воздухозаборники.
В зависимости от скорости полета воздухозаборники могут быть дозвуковыми
или сверхзвуковыми. Параметры воздухозаборников выбираются для основного ре-
жима полета.
В дозвуковом воздухозаборнике (рис. 4.70, а; 4.71, а) давление увеличивается за
счет движения воздуха по расширяющемуся каналу. Интенсивность торможения оп-
ределяется степенью изменения площади канала. Дозвуковой воздухозаборник обыч-
но нерегулируемый.
Сверхзвуковые воздухозаборники имеют регулируемые центральный конус или
клин, обеспечивающие эффективную работу воздухозаборника в заданном диапазоне
скоростей (рис. 4.70, б; 4.71, б).
Регулирование такого воздухозаборника производится автоматически различны-
ми способами: осевым перемещением клина или конуса, перемещением подвижных
рамп, изменением диаметра центрального тела, перепуском воздуха через створки.
1 2 3 4 5
Косой скачок Прямой скачок
Рис. 4.70. Схемы воздухозаборников:
а и б) соответственно дозвуковой и сверхзвуковой воздухозаборники;
1 — обечайка, 2 — центральный конус; 3 — клапан перепуска;
4 — клапан впуска; 5 — щель для слива пограничного слоя
а)
Рис. 4.71. Воздухозаборники:
а) дозвуковой боковой нерегулируемый воздухозаборник самолета Су-25,
б) лобовой регулируемый воздухозаборник сверхзвукового самолета Су-17
209
Рис. 4.72. Способы образования скачков уплотнения во входном устройстве:
а, б и в) соответственно воздухозаборники с внешним сжатием,
смешанного сжатия и с внутренним сжатием
Рис. 4.73. Воздухозаборники:
а) боковой регулируемый воздухозаборник самолета МиГ-23;
б) подфюзеляжные регулируемые воздухозаборники самолета Су-30
б)
При полете в воздухозаборнике формируется система скачков уплотнения — ко-
сых и прямых. В зависимости от положения скачков воздухозаборники бывают внеш-
него, внутреннего и смешанного сжатия (рис. 4.72). Требуемую систему скачков мож-
но создать различными способами — профилированием центрального тела или сте-
нок канала (рис. 4.73) и др.
Для обеспечения устойчивой работы воздухозаборника и ограничения пульсаций
потока (помпажа) производят слив и отсос пограничного слоя как с поверхности са-
молета в зоне воздухозаборника, так и с поверхности подвижного клина.
Конструкции воздухозаборников и воздушных подводящих каналов обычно об-
разуются из конструктивных элементов фюзеляжа, крыла или гондолы двигателя.
Элементы входных устройств изготавливают с учетом аэродинамических, тепло-
вых и вибрационных нагрузок.
Для уменьшения потерь энергии в воздушном канале его выполняют без крутых
поворотов, а все стыки герметизируют. Участок воздушного канала перед двигателем
делают прямолинейным.
Система выпуска газов
Система выпуска газов состоит из выхлопной трубы и сопла. Она предназначена
для отвода газового потока и преобразования части теплосодержания газа в кинетиче-
скую энергию его направленного движения. Кроме того, выходные устройства вы-
полняют и другие функции: изменяют направление вектора тяги двигателя, глушат
шум, производимый двигателем.
210
Рис. 4.74. Выхлопные трубы
и сопла двигателей самолета Qy-TJ
Выходное устройство должно удовлет-
ворять следующим требованиям: иметь ми-
нимальные потери в газовом потоке, созда-
вать при реверсе максимальную обратную
тягу, обеспечивать эффективное шумоглуше-
ние.
Тяга двигателя зависит от скорости исте-
чения струи из сопла, т. е. от температуры газа в
камере двигателя, состава газа и перепада дав-
лений между камерой и выходным сечением
сопла.
Для увеличения скорости истечения газов
сопло реактивных двигателей профилируется:
сначала сужается, а затем расширяется. Про-
ходные сечения сопел современных двигателей, как правило, регулируются: выпол-
няются в виде подвижных створок.
Выхлопная труба и сопло изготавливаются из листа жаропрочной стали с ребра-
ми — кольцами жесткости (рис. 4.74). Внутренняя поверхность трубы делается глад-
кой, все стыки герметизируются.
Соединение выхлопной трубы с корпусом двигателя, как правило, выполняется
телескопическим. Узлы крепления трубы с элементами конструкции самолета долж-
ны обеспечивать свободу термических деформаций трубы в продольном и попереч-
ном направлениях. Для уменьшения тепловых потерь труба теплоизолируется, а кон-
струкция планера защищается от нагрева экранами. Кроме того, уменьшению тепло-
вых потерь способствует обдув атмосферным воздухом внешних поверхностей
выходных устройств.
Совместная работа выходного и входного устройств должна обеспечивать необ-
ходимую тягу на всех режимах полета.
Топливные системы
Основное назначение топливных систем состоит в размещении топлива на борту
самолета или вертолета и в обеспечении двигателя топливом. В качестве топлива для
ВРД применяются улучшенные сорта керосина. Основные требования к топливным
системам:
• надежное питание двигателей на всех возможных режимах полета независимо от
атмосферных условий;
• достаточная вместимость топливных баков;
• обеспечение требуемой центровки при выработке топлива и в процессе его рас-
ходования;
• возможность слива топлива в полете;
• удобство технического обслуживания топливных систем;
• живучесть системы и безопасность в пожарном отношении;
• минимальное время заправки.
Топливная система современного самолета состоит из топливных баков, трубо-
проводов, насосов, клапанов, кранов, фильтров, аппаратуры управления и регулиро-
вания.
Подача топлива в двигатели может осуществляться самотеком, вытеснением из
баков газами или воздухом, а также насосами.
211
12 3 4
5
Рис. 4.75. Схема компоновки топливных баков на самолете-истребителе:
I — воздухозаборники; 2 — расходный бак-отсек; 3 — мягкие топливные баки;
4 — двигатель; 5 — выхлопная труба; 6 — жесткий топливный бак;
7 — крыльевые баки-отсеки; 8 — подвесные топливные баки
Топливные баки по конструкции под-
разделяются на мягкие, жесткие и баки-
отсеки.
Мягкие топливные баки изготавли-
ваются склейкой нескольких слоев вул-
канизированной резины и ткани (корда).
Толщина стенок такого бака— 4...6 мм.
Устанавливают их либо в специальные
контейнеры, либо непосредственно в топ-
ливные отсеки конструкции. Отсек, чтобы
не повредить баки, обычно обшивают лис-
тами. Иногда в баки вставляют распорные
обручи. Мягкие баки позволяют хорошо
использовать внутренние объемы самоле-
та, однако срок службы их ограничен из-за
потери герметизации.
Жесткие баки изготавливают обычно
из легких алюминиевых сплавов типа
АМц, допускающих глубокую штамповку.
Применяют их чаще всего в качестве до-
полнительных или подвесных.
Баки-отсеки, представляющие собой
герметизированные отсеки крыла и фюзе-
ляжа, широко используются в топливных
системах самолетов. Герметичные баковые
отсеки позволяют увеличить запас топлива
и уменьшить массу конструкции самолета.
В таких отсеках применяют внутришов-
ную и внутреннюю поверхностную герме-
тизацию с помощью керосиностойких
клеев и мастик (рис. 4.75,4.76).
Для обеспечения бесперебойной
Рис. 4.76. Принципиальная схема
топливной системы пассажирского самолета;
1—3 — крыльевые топливные кессон-баки;
4—6, 10, 11 — трубопроводы подачи топлива;
7 — перекачивающий топливный насос;
8 — расходный отсек;
9 — спаренные подкачивающие насосы;
12 — кран перекрестного питания;
13 — перекрывной (противопожарный) кран;
14 — подкачивающий насос;
15 — датчик расходомера;
16 — топливомасляный радиатор;
17 — фильтр; 18 — насос-регулятор
подачи топлива к двигателю при любых эволюциях в расходных баках предусмотрены
специальные заборные устройства, осуществляющие при отрицательных перегрузках
забор топлива из специального отсека.
212
4.8.5. Системы управления полетом
Система управления полетом — это совокупность устройств, обеспечивающих
полет летательного аппарата по заданной траектории, т. е. обеспечивающих регулиро-
вание действующих на аппарат сил и моментов.
Система управления полетом самолета называется системой основного управле-
ния, в отличие от вспомогательного управления, к которому относится управление
закрылками, переставным стабилизатором, уборкой и выпуском стоек шасси и пр.
Устройства, с помощью которых создаются необходимые для управления силы и
моменты, называются органами управления. К ним относятся рулевые поверхности
(элероны, подвижные поверхности горизонтального и вертикального оперения), ин-
терцепторы и управляющие сопла. На рис. 4.77 показаны органы и проводка управле-
ния дозвукового самолета.
Основные элементы и схемы управления
Требования, предъявляемые к управлению
В зависимости от степени участия летчика в процессе управления полетом само-
лета различают системы непосредственного (прямого или обратимого) управления,
в которых органы управления отклоняются за счет мускульной энергии человека
(рис. 4.78, а), системы полуавтоматического непрямого управления (его часто назы-
вают необратимым управлением), в которых органы управления отклоняются следя-
щими силовыми приводами по сигналам, вводимым летчиком (рис. 4.78, б), и систе-
мы автоматического управления, в которых управляющие импульсы формируются
автоматическими устройствами без участия человека (рис. 4.78, в).
При прямом или полуавтоматическом управлении летчик вводит необходимые
сигналы с помощью командных рычагов, связанных с органами управления проводкой.
При автоматическом управлении пилотирование самолета может осуществлять-
ся без участия летчика или под его контролем. В систему такого управления входят:
программное (задающее) устройство; датчики истинных значений параметров полета;
Рис. 4.77. Органы управления и проводка управления дозвукового самолета:
7 — педали; 2 — штурвальная колонка; 3 — элерон;
4 — проводка управления; 5 — руль направления; 6 — руль высоты
213
Рис. 4.78. Схемы основного управления:
а) принципиальная схема прямого (обратного) управления; б) принципиальная схема непрямого
управления; в) структурная схема управления; 1 — загрузочное устройство; 2 — гидроусилитель
вычислители рассогласования заданных и истинных значений параметров; вычисли-
тель управляющих импульсов; энергетическая система; усилители; связи; исполни-
тельные механизмы; органы управления.
Наряду с общими требованиями (прочность, жесткость, малый вес) системы уп-
равления самолетом должны удовлетворять и ряду специфических требований:
• направления перемещений командных рычагов должны совпадать с направле-
ниями перемещений самолета с минимальным запаздыванием;
• для пилотируемых летательных аппаратов должны быть обеспечены допустимые
потребные усилия на командных рычагах;
214
• углы отклонения рулевых поверхностей должны обеспечивать возможность поле-
та на всех требуемых режимах с регламентированным запасом отклонения рулей;
• должна быть обеспечена независимость действия рулей;
• должны быть обеспечены заданные характеристики управляемости, важнейши-
ми из которых являются:
- максимальные величины перемещений командных рычагов для создания
единичной перегрузки, величины балансировочных усилий на командных
рычагах продольного управления и градиента усилий на единицу перегрузки
р п-
г в’
- градиенты усилий на командных рычагах поперечного управления на еди-
ницу угловой скорости Р™;
- градиенты усилий на педалях на единицу угловой скорости Р®у.
Кроме того, система управления должна иметь устройства, ограничивающие
выход ЛА на опасные режимы, а также систему резервирования и дублирования.
Системы прямого управления
Командные (центральные) посты управления
Командные посты управления устанавливаются в кабине пилота. Они со-
стоят из командных рычагов и элементов их крепления к конструкции аппарата.
Конструкция командных рычагов
На самолете имеется управление тангажом, креном и курсом, осуществляе-
мое с помощью двух типов командных рычагов ручного управления — ручки или
штурвальной колонки и рычагов ножного управления — педалей.
Рис. 4.79. Схемы установки ручки
управления: а, б) различные варианты;
О — ось вращения при управлении рулем
высоты; 1 — труба; 2 — рычаг управления
элеронами; 3 — качалка; 4 — тяга
Рис. 4.80. Штурвальная
колонка
215
Рис. 4.81. Рычажно-параллелограммный
механизм ножного управления
Рис. 4.82. Педали подвесного типа
Для управления продольным движением самолета ручка или штурвальная колон-
ка должны иметь возможность отклоняться в продольной плоскости самолета; при
создании крена ручка отклоняется влево или вправо, а штурвал поворачивается. Для
отклонения руля направления летчик воздействует на педали (ножное управление).
Величина хода командных рычагов должна соответствовать средним величинам пере-
мещений рук и ног летчика, т. е. ходу ручки от нейтрального положения в диапазоне
150...200 мм и повороту штурвала на +90... 180°. Перемещения педалей от их нейтраль-
ного положения составляют 70... 100 мм.
На рис. 4.79 и 4.80 показаны соответственно возможные схемы установки ручки
и штурвала.
На рис. 4.79 видно, что независимость управления рулем высоты и элеронами
обеспечивается креплением тяги 4 к качалке 3, при котором точка А при перемещени-
ях остается на оси ББ. На ручке и штурвале обычно устанавливаются рычаги и разме-
щаются кнопки управления различными агрегатами (тормозами колес, спецподве-
сками, тормозными щитками и т. д.).
Педали ножного управления либо выполняются в виде рычажно-параллелограм-
много механизма (рис. 4.81), либо поворачиваются на оси, расположенной внизу или
наверху (качающиеся педали) (рис. 4.82). Передаваемый сигнал дозируется величи-
ной перемещения педалей или углом их поворота. Педали обычно регулируются по
росту летчика.
Усилия на командных рычагах
Усилия на командных рычагах управления являются обратной связью по управляю-
щему воздействию. При отсутствии этой связи управление становится невозможным.
При прямом управлении обратная связь по управляющему воздействию возника-
ет из-за необходимости преодолевать шарнирный момент, действующий на органы
управления.
Усилия на командных рычагах должны находиться в пределах, определяемых
в зависимости от условий пилотирования. Слишком большие усилия приводят к бы-
строму утомлению, а малые — к ошибкам в пилотировании.
Изменение усилий на командных рычагах лучше ощущается летчиком. Кроме
того, дозирование усилий обеспечивает большую точность управления, нежели дози-
рование перемещений, поэтому характеристики управляемости по усилиям важнее,
чем по перемещениям.
При выполнении маневров по изменению усилий на командных рычагах летчик
дозирует создаваемые перегрузки и ощущает изменение режима полета.
216
Таблица 4.1
Характеристика управляемости Желаемые значения для самолетов
скоростных нескоростных
Оптимальные усилия, потребные для отклоне- ния командных рычагов на режиме 0,8Итах, кгс:
вправо — влево 8...10 10...35
на себя — от себя 15...20 30... 100
на педали 20...30 30.. 100
Величина балансировочного усилия Рв в прямо- линейном полете, кгс -2...10 -20...40
Градиент усилия по перегрузке Рвп, кгс/ед. -2...4 -20...60
Ход ручки (штурвала) для единичного увеличе- ния перегрузки хвп, мм/ед. 12...15 30
В таблице 4.1 приводятся некоторые характеристики управляемости по усилиям.
Уменьшение шарнирного момента руля достигается применением различных ком-
пенсаторов, однако оно также ограничено определенными условиями. В тех случаях,
когда использование аэродинамической компенсации не позволяет получить приемле-
мые значения величины момента, применяют сервокомпенсаторы и серворули.
Рис. 4.83. Элементы жесткой
проводки управления:
1 — тяга; 2 — качалка;
3 — кронштейн
Проводка управления
Механическая проводка управления предназначена для передачи движения от
командных рычагов к рулевым поверхностям. Проводка бывает жесткой, гибкой
и смешанной.
Жесткая проводка состоит из системы последовательно соединенных тяг, направ-
ление которых изменяется посредством качалок. Качалки устанавливаются на эле-
ментах конструкции планера с помощью кронштейнов. Тяги работают на
растяжение — сжатие. Для уменьшения пролетов длинных тяг применяют роликовые
направляющие или опорные качалки.
Тяги изготавливают из дюралевых или стальных труб, качалки и кронштейны —
из легких сплавов. Элементы жесткой проводки пока-
заны на рис. 4.83.
Гибкая проводка включает в себя тросы, направ-
ляющие ролики, тандеры и секторы.
Тросы изготавливаются из многожильной плете-
ной стальной проволоки. Диаметр тросов проводки
управления d = 3...10 мм. Регулирование длины троса
при монтаже и в процессе эксплуатации осуществля-
ют с помощью тандеров. На рис. 4.84 приведены дета-
ли тросовой проводки управления.
Смешанную проводку используют в тех случаях,
когда применение жесткой проводки на отдельных
участках затруднено.
Жесткая проводка по сравнению с гибкой облада-
ет целым рядом преимуществ, поэтому применение ее
217
3
4
2
1
Рис. 4.84. Детали гибкой проводки управления:
7 — трос; 2 — коуш; 3 — тандер; 4 — наконечник
предпочтительнее. Однако гибкая проводка имеет небольшой вес, малые габариты и
легко прокладывается, в связи с чем также применяется как основная и дублирующая.
С ростом действующих на конструкцию самолета нагрузок повышаются линей-
ные деформации крыла, фюзеляжа и оперения, поэтому необходимо принимать спе-
циальные конструктивные меры, которые бы компенсировали эти деформации
и обеспечивали потребные отклонения органов управления. В жесткой проводке для
этой цели применяются компенсационные качалки и механизмы, а в тросовой — ав-
томаты регулирования натяжения тросов.
Основные устройства и механизмы непрямого управления
Системы непрямого управления
С увеличением скоростей полета интенсивно растут шарнирные моменты рулей,
а следовательно, и потребные для управления усилия. Переход от дозвуковых к сверх-
звуковым скоростям полета часто вызывает изменение знака шарнирного момента,
а также углов отклонения рулей, потребных для создания единичной перегрузки, что
исключает возможность дозировать усилия на командных рычагах. Изменения харак-
теристик устойчивости и управляемости самолета при переходе от дозвуковых
к сверхзвуковым скоростям полета требуют принятия специальных мер для обеспече-
ния нормального пилотирования. В систему управления сверхзвуковым самолетом
включается следящий силовой привод, причем нагрузка рулей не передается на ко-
мандные рычаги, а уравновешивается самим приводом (выходное звено привода мо-
жет иметь поступательное или вращательное движение).
Основными элементами приводов с вращательным движением являются гидро-
мотор, редуктор, силовая трансмиссия и преобразователь движения (винтовой меха-
низм), преобразующий вращательное движение валов в поступательное перемещение
штока, соединенного с кронштейном руля.
Силовые приводы с вращательным движением валов имеют при равных переда-
ваемых мощностях существенно большую жесткость проводки и более простую ком-
пенсацию линейных деформаций, однако узлы и детали их сложны, требуют высокой
точности обработки и применения специальной смазки.
Для создания нагрузки на рычагах управления в систему непрямого управления
вводят специальные загрузочные устройства. Кроме того, в систему включают и дру-
гие устройства и механизмы, обеспечивающие заданные характеристики устойчивос-
ти и управляемости ЛА и приемлемые условия работы летчика.
Силовые приводы. На современных самолетах чаще всего применяются гидравли-
ческие силовые приводы, называемые гидроусилителями или бустерами (рис. 4.85).
Гидроусилитель представляет собой следящую гидравлическую систему, состоящую
из исполнительного механизма (силового цилиндра) и распределительного золотни-
ка, регулирующего подачу гидросмеси под большим давлением в соответствующую
полость цилиндра.
218
Рис. 4.85. Схема гидроусилителя:
1 — тяга; 2 — качалка; 3 — распределительный золотник;
4 — канал нагнетания; 5 — канал слива; 6 — корпус; 7 — шток
Потребные для перемещения золотника усилия очень малы, а рабочий ход золот-
ника равен нескольким миллиметрам.
При воздействии на ручку управления перемещается тяга золотника, нужная по-
лость цилиндра соединяется с нагнетающей магистралью, а другая — с линией слива,
и шток (или корпус) исполнительного механизма отклоняет рулевую поверхность.
Эта подвижная часть силового цилиндра имеет обратную связь с золотниковым уст-
ройством, что обеспечивает «отслеживание» движений командных рычагов. При ос-
тановке рычага управления поступление гидросмеси из нагнетающей магистрали пре-
кращается.
На современных самолетах бустеры включаются по необратимой схеме (рис. 4.86).
Загрузочные устройства предназначены для создания усилий на командных ры-
чагах и обеспечения основных показателей управляемости во всем диапазоне скорос-
тей и высот полета.
Наибольшее применение нашли пружинные загрузочные механизмы, кинемати-
чески связанные с устройством изменения передаточных отношений в полете.
Загрузочные механизмы дают возможность летчику дозировать управляющие
движения по усилиям, а кинематическая связь загружателя с механизмом изменения
передаточных отношений обеспечивает единообразие управления в широком диапа-
зоне скоростей и высот полета.
Применяются загружатели с одной и несколькими пружинами. На рис. 4.87 при-
ведена схема однопружинного загружателя и дана характеристика его работы.
К загрузочному устройству обычно присоединяется механизм триммерного эф-
фекта.
Рис. 4.86. Включение бустера по необратимой схеме
219
Рис. 4.87. Однопружинный загрузочный механизм
Механизм триммерного эффекта по желанию летчика снимает усилие, действую-
щее на командный рычаг. Разгрузка командного рычага происходит за счет смещения
корпуса загружателя на величину обжатия пружин.
Механизмы триммерного эффекта, как правило, имеют электрический привод.
Автомат изменения передаточных отношений в полете дает возможность дозиро-
вать управляющие движения, потребные для создания единичной перегрузки на ма-
лых и больших высотах, а также в широком диапазоне скоростей полета современных
самолетов.
Очень малый потребный ход рычагов при полете на небольших высотах с боль-
шой скоростью делает самолет излишне строгим в управлении и повышает опасность
его раскачки.
Автомат изменения передаточных отношений представляет собой качалку с пе-
ременным плечом, изменение которого осуществляется перемещением внутреннего
звена телескопического соединения. Автомат состоит из командного блока и испол-
нительного механизма. Регулировка передаточного отношения осуществляется по
скорости (числу М), высоте Я полета или по скоростному напору.
Устройства эти могут изменять передаточные отношения только к рулевой по-
верхности или одновременно к рулевой поверхности и загрузочному механизму.
На рис. 4.88 приведена принципиальная схема включения механизмов в систему
непрямого (необратимого) управления.
Для уменьшения излишней чувствительности управления в системы управления
могут включаться нелинейные механизмы, которые существенно уменьшают переда-
точное отношение при малых отклонениях командного рычага. Применение нели-
нейных механизмов облегчает управление при переходе от бустерного к ручному пи-
лотированию.
Рис. 4.88. Схема включения основных механизмов в систему непрямого управления:
1 — управляющий блок устройства; 2 — автомат изменения передаточных отношений;
3 — следящий силовой привод; 4 — загружатель; 5 — механизм триммерного эффекта
220
Автоматизация систем управления
Трудности, связанные с пилотированием современного самолета, требуют авто-
матизации управления — частичной или полной, когда практически управление са-
молетом на всех этапах полета будет осуществляться без участия летчика.
Автоматизация позволяет освободить летчика от чрезмерной нагрузки и обеспе-
чить безопасность полета.
К автоматическим устройствам, облегчающим управление сверхзвуковым само-
летом, относятся, например, демпферы тангажа, крена и рыскания, с помощью кото-
рых создаются дополнительные демпфирующие моменты (за счет органов управле-
ния), препятствующие колебаниям самолета. Такие демпферы особенно необходимы
на больших высотах, когда собственное демпфирование самолета существенно
уменьшается.
Автоматы демпфирования состоят из датчика, формирующего управляющий сиг-
нал, пропорциональный угловой скорости вращения самолета, усилителя и исполни-
тельного механизма РАУ, представляющего собой раздвижную тягу винтового типа.
Автоматы балансировки также имеют раздвижную тягу, которая в зоне чисел М,
соответствующих неустойчивости самолета, отклоняет рулевые поверхности на углы,
потребные для балансировки, независимо от отклонения командного рычага. Закон
управления раздвижной тягой должен быть функцией скорости и высоты полета.
В систему автоматизированного управления включаются также устройства для
искусственного увеличения устойчивости по перегрузке или по скорости в тех случа-
ях, когда она мала. Автомат устойчивости обеспечивает отклонение рулевой поверх-
ности для создания восстанавливающих моментов. Исполнительный механизм этого
автомата также представляет собой раздвижную тягу, работающую от сигнала соответ-
ствующего датчика.
Включение в систему управления устройств, предотвращающих превышение за-
данных перегрузок в полете, и устройств, не позволяющих выйти на закритические
углы атаки, существенно увеличивает безопасность полета.
Автоматизация управления современных самолетов может обеспечить как пол-
ностью автоматическое управление, при котором все этапы полета будут осуществ-
ляться без участия летчика, так и комплексное управление, которое при наличии ав-
томатических систем позволит летчику осуществить ручное пилотирование на любом
этапе полета. В последнем случае система автоматизированного управления дополня-
ется автопилотом.
В целях повышения надежности и уменьшения массы все автоматические уст-
ройства объединяются в единую систему автоматического управления (САУ), схема
которой разрабатывается для каждого самолета индивидуально.
Надежность систем управления обеспечивается многократным резервировани-
ем, дублированием и непрерывным контролем.
4.8.6. Взлетно-посадочные устройства
Для осуществления взлета, посадки и маневрирования по аэродрому самолеты
снабжаются взлетно-посадочными устройствами, характеристики которых в значи-
тельной степени определяют эффективность и возможность использования этих ЛА.
К взлетно-посадочным устройствам относятся приспособления, улучшающие
взлетно-посадочные характеристики (уменьшающие скорости взлета и посадки, дли-
ну разбега и пробега, взлетной и посадочной дистанций), и система опор (шасси),
обеспечивающая движение самолета или вертолета по земле и снабженная для этого
221
колесами или лыжами. Гидросамолеты для посадки на воду снабжены поплавками
или имеют специальный фюзеляж-лодку.
Для уменьшения времени и пути разбега летательного аппарата при взлете и про-
бега при посадке необходимо уменьшить минимальную скорость управляемого поле-
та Kmin и увеличить абсолютное значение среднего тангенциального ускорения. Для
уменьшения взлетной и посадочной скорости все современные самолеты снабжены
устройствами, увеличивающими несущую способность крылатого аппарата (механи-
зация крыла), или устройствами, обеспечивающими создание вертикальной состав-
ляющей тяги двигателя.
Изменение ускорения при взлете и посадке осуществляется применением форса-
жа и реверса тяги двигателей, тормозных парашютов, тормозов колес, всевозможных
финишеров и стартовых ускорителей.
Механизация крыла
Аэродинамические средства механизации
Для увеличения значения CyS крыло современного самолета механизируется по
задней и передней кромкам.
Основными устройствами механизации задней кромки являются: простые и вы-
движные щитки, простые и щелевые закрылки, выдвижные закрылки, выдвижные
многощелевые закрылки.
Передняя кромка крыла оснащается предкрылками, щитками Крюгера и откло-
няемым носком самого крыла. На рис. 4.89 показаны различные варианты механиза-
ции.
Все вышеперечисленные устройства принято называть аэродинамическими сред-
ствами механизации.
Рис. 4.89. Различные варианты
механизации крыла:
а) простой щиток; б) простой закрылок;
в) выдвижной щелевой закрылок;
г) многощелевой выдвижной закрылок;
д) предкрылок; е) комбинация
предкрылка и закрылка
Рис. 4.90. Зависимость Су = Ца) профиля
с различными видами механизации:
1) трехщелевой закрылок с предкрылком;
2) двухщелевой закрылок; 3) выдвижной
закрылок; 4) простой щиток; 5) щиток
с предкрылком; 6) исходный профиль
222
Увеличение Су^ крыла достигается за счет изменения профиля (увеличения его
кривизны) и воздействия на пограничный слой струи воздуха, проходящей через щель
между крылом и закрылком.
Наибольший прирост создают выдвижные многощелевые закрылки. На сов-
ременных самолетах чаще всего применяют комбинацию нескольких видов механиза-
ции, например многощелевые закрылки и предкрылки. Такая комбинация обеспечи-
вает получение при посадке СУтах = 2,5...2,8. На рис. 4.90 показан характер зависимос-
тей Су = /(а) профиля крыла с различными видами механизации, а на рис. 4.91 —
схема механизации крыла современного самолета.
Приращение максимального коэффициента подъемной силы профиля крыла
ДСУт х для различных устройств механизации составляет: для щелевых закрылков —
0,8... 1,0; для выдвижных однощелевых закрылков— 1,4... 1,5; для предкрылка —
0,7...0,8; для выдвижных однощелевых закрылков и предкрылка 1,7... 1,9.
Конструкция элементов механизации
По своей конструкции элементы механизации представляют собой тонкостенные
балки с продольным и поперечным силовым набором и обшивкой. Элементы силового
набора средств механизации выполняют те же функции, что и аналогичные элементы
крыла. Такая конструкция способна воспринимать изгибающий и крутящий моменты
и перерезывающую силу. Опорами для устройств механизации служат узлы их подве-
ски к крылу. Выдвижные закрылки перемещаются на роликовых каретках по направ-
ляющим рельсам (рис. 4.92). На стреловидных крыльях для обеспечения выдвижения
закрылка по потоку чаще применяется навеска с кареткой, установленной на закрылке
с помощью шкворня. Выдвижной закрылок можно навешивать и на выносных
кронштейнах. На рис. 4.93 показан схематично простой закрылок.
В выпущенном положении закрылки нагружаются воздушной нагрузкой, вели-
чина которой задается «Нормами прочности». Рассчитываются они по правилам
строительной механики как балки на соответствующем числе опор.
Энергетические средства механизации
Если в пограничный слой крыла внести дополнительную энергию от струи газа,
то можно существенно уменьшить срыв потока с крыла (за счет управления погра-
ничным слоем) и увеличить циркуляцию.
Рис. 4.91. Схема современного
механизированного крыла:
I — закрылки; 2 — предкрылки;
3 — интерцепторы
Рис. 4.92. Система
выдвижения закрылка
223
Рис. 4.93. Схема
простого закрылка
Рис. 4.94. Схемы сдува
пограничного слоя:
а) с крыла; б) с закрылка
Активное воздействие на пограничный слой осуществляется с помощью уст-
ройств управления пограничным слоем (УПС), которые часто называют струйной ме-
ханизацией. С помощью УПС можно отсасывать и сдувать пограничный слой с по-
верхности крыла или отклоненного закрылка. На рис. 4.94 приведены схемы сдува
с крыла и закрылка, а на рис. 4.95 — зависимости ДСу от и 83.
Воздух обычно отбирается от компрессора ТРД и с большой скоростью выдувает-
ся через щель на верхнюю поверхность крыла или отклоненного закрылка.
Величина прироста коэффициента Су зависит от коэффициента импульса струи Сц:
_ тсек
И ^обсл’
где тсек — секундный массовый расход воздуха в системе; Vj — скорость выходящей
струи; — скоростной напор невозмущенного потока; 5обсл — площадь крыла, об-
служиваемая УПС.
При значениях Сц > 1 прирост Су получается в основном за счет увеличения цир-
куляции. При этом можно отказаться от механического закрылка и перейти на реак-
тивный (струйный) закрылок. В этом случае в результате реакции струи создается до-
полнительная подъемная сила.
Устройства для изменения ускорений самолета при взлете и посадке
Длина разбега и пробега самолета зависит не только от взлетной Ивзл и посадоч-
ной Ипос скоростей, но и от среднего ускорения (замедления) при разбеге и пробеге jx:
V2 V2
j ~ г вал . j ~ г пос
Ьразб ~ 2/~ ’ Ьпроб ~ 2/Z ‘
лср. разб. лср. проб.
Увеличение ускорения при разбеге осуществляется с помощью форсажа двигате-
ля и стартовых ускорителей, сбрасываемых после взлета самолета.
224
Рис. 4.96. Схема работы реверсивного устройства ТРД:
а) прямая тяга; б) обратная тяга
Для интенсивного торможения после посадки применяются тормозные колеса,
тормозные парашюты, тормозные щитки на крыле и фюзеляже, а также устройства
реверсирования тяги двигателей.
Использование интерцепторов на пробеге позволяет уменьшить подъемную силу
крыла, а следовательно, увеличить эффективность тормозов колес.
Реверс тяги широко используется на современных самолетах. Схема работы ре-
версивного устройства ТРД приведена на рис. 4.96. С помощью такого устройства
можно получить обратную тягу, примерно равную 40% прямой, что позволяет умень-
шить длину пробега на 25...80%.
Устройства для создания вертикальной
составляющей тяги силовой установки
Для резкого сокращения взлетной и посадочной дистанций наиболее эффектив-
ным средством является создание вертикальной составляющей тяги силовой установки.
Самолеты, на которых используются устройства такого типа, называются само-
летами укороченного или вертикального взлета и посадки (СУВП и СВВП). При на-
личии вертикальной составляющей тяги Рв
= 2GO(1-PB)
*min J Vn Г
N dpoSmax
где Рв = ^. При Рв« 1 становятся возможными взлет и посадка с небольшими разбе-
гом и пробегом.
Для осуществления вертикального взлета и посадки необходимо иметь тягу, до-
статочную для подъема заданной взлетной массы самолета и создания потребного ус-
корения на взлете.
СВВП могут иметь единую силовую установку для взлета и горизонтального по-
лета или раздельную с маршевыми и подъемными двигателями.
Самолеты с комбинированной силовой установкой для создания вертикальной
тяги используют как струю маршевых двигателей, так и специальные подъемные дви-
гатели.
На рис. 4.97 показаны различные самолеты вертикального взлета и посадки.
Самолеты вертикального взлета и посадки имеют существенные преимущества
перед вертолетами вследствие большей скорости и дальности полета, однако требуют
225
4
в)
Рис. 4.97. Вертикально взлетающие самолеты:
а) «Си-Харриер»; б) Як-38; в) конвертоплан V-22
оснащения их специальными управляющими системами, так как аэродинамические
поверхности при отсутствии поступательного движения на взлете и посадке не обес-
печивают управления.
Шасси
Шасси — это система опор самолета и вертолета, обеспечивающая возможность
их многоразового применения и базирования на аэродромах, т. е. позволяющая осу-
ществлять маневрирование, взлет и посадку.
По типу опор шасси сухопутных самолетов бывают колесными, лыжными и гусе-
ничными. На гидросамолетах применяются лодки и поплавки.
Каждая опора шасси включает следующие элементы: собственно опоры — колеса
или лыжи, стойку — несущий элемент, соединяющий опоры с конструкцией самоле-
та; амортизатор; механизм уборки и выпуска шасси; фиксаторы убранного и выпу-
щенного положения шасси; систему сигнализации.
226
Часто элементы опоры выполняют несколько функций (например, амортизатор
совмещается со стойкой, механизм уборки и выпуска является частью силовой конст-
рукции и т. д.).
Шасси наряду с общими требованиями, предъявляемыми к авиационным конст-
рукциям, должно удовлетворять и специфическим, а именно:
• обеспечивать устойчивость и управляемость движения самолета по грунту;
• обеспечивать возможность эксплуатации самолета на аэродромах заданного
класса, т. е. обеспечивать проходимость самолета;
• обеспечивать мягкую посадку, поглощение и рассеивание энергии удара самолета
о грунт при посадке и движении по аэродрому;
• поглощать и рассеивать большую часть кинетической энергии поступательного
движения самолета при пробеге.
Схемы шасси
Схему шасси определяют количество опор и расположение их относительно
центра масс самолета.
В настоящее время применяются четыре основные схемы шасси (рис. 4.98):
1) трехопорное шасси с передней опорой;
2) трехопорное шасси с задней опорой;
3) двухопорное (или велосипедное) шасси;
4) многоопорная схема шасси.
Рис. 4.98. Схемы шасси:
а) трехопорная с передней опорой; б) трехопорная с задней опорой;
в) велосипедная; г) многоопорная
227
Рис. 4.99. Параметры трехопорного шасси с передней опорой
Наибольшее распространение на современных самолетах получило трехопорное
шасси с передней опорой (рис. 4.98, а). Такое шасси обеспечивает безопасность при
скоростной посадке и исключает возможность капотирования, т. е. опрокидывания
самолета при торможении на пробеге. Самолет с носовой опорой шасси обладает ус-
тойчивостью пути, а его горизонтальное положение на земле обеспечивает экипажу
лучший обзор из кабины.
Недостатком схемы является большая нагрузка на переднюю опору и возмож-
ность возникновения на ней самовозбуждающихся колебаний типа «шимми».
Основные параметры шасси (рис. 4.99): b — база шасси, В — колея, е — вынос
главных опор; у — угол выноса главных опор, ф — посадочный угол.
Параметры шасси определяются из условия устойчивого движения самолета, за-
данного распределения нагрузки между опорами Лпер = (0,1 ...0,15)(70 и предотвраще-
ния опрокидывания самолета на хвост.
Велосипедная схема (рис. 4.98, в) имеет две основные опоры и две подкрыльевые
стойки, предохраняющие самолет от опрокидывания на крыло.
Параметры шасси велосипедной схемы определяются теми же условиями, что
и для трехопорной схемы, однако для транспортных самолетов вынос задней опоры
относительно центра масс составляет е = (0,40...0,45)д вследствие необходимости раз-
мещения вблизи центра масс отсека со спецоборудованием или топливом.
Поскольку в этом случае на переднюю опору приходится большая нагрузка, что
затрудняет отрыв ее при взлете, в конструкцию велосипедного шасси включаются
устройства, удлиняющие при взлете переднюю опору (механизмы «вздыбливания»)
или укорачивающие заднюю опору (механизмы «приседания»).
Велосипедная схема применяется в тех случаях, когда размещение опор на крыле
затруднено или невозможно (например, у тяжелых самолетов с высокорасположен-
ным крылом).
Для легких самолетов выбор велосипедной схемы связан со стремлением умень-
шить вес шасси.
Трехопорная схема с задней опорой (рис. 4.98, б) в настоящее время применяет-
ся редко из-за присущих ей недостатков, главным из которых является небезопасная
посадка скоростных самолетов.
На вертолетах, как правило, применяется трехопорное шасси с передней опорой,
параметры которого выбираются аналогично параметрам подобной схемы самолетно-
го шасси.
Колеса и лыжи
Тип и характеристики колес выбираются из условия эксплуатации самолета на
аэродроме заданного класса.
Проходимость самолета, т. е. обеспечение его движения без нарушения прочнос-
ти покрытия взлетной полосы, зависит в основном от удельного давления колеса или
228
лыжи на грунт. Удельное давление колеса на грунт примерно равно его внутреннему
давлению, поэтому выбор давления в пневматике колеса, а также выбор количества
и расположения колес на опоре в значительной степени определяют проходимость
самолета по ВПП заданной прочности.
Основными элементами конструкции колеса являются барабан, пневматик
и тормозное устройство. Барабан выполняется обычно литьем из магниевого или
алюминиевого сплава. Пневматик состоит из покрышки и камеры, а в бескамерном
пневматике — только из покрышки. Силовой каркас покрышки образуется слоями
корда, выполненного из высокопрочных нитей.
В зависимости от типа пневматика и давления в нем колеса делятся на полубал-
лонные с PQ « 5 атм., арочные с Ро « 6...7 атм. и высокого давления с Ро « 15... 17 атм.
(здесь PQ — давление зарядки). Авиационные колеса стандартизованы и подбираются
по таблицам, в которых приведены геометрические данные, стояночные и предель-
ные нагрузки на колесо и поглощаемая пневматиком работа при его обжатии.
Все колеса главных опор — тормозные. В авиационных колесах применяются
тормоза фрикционного типа — камерные и дисковые. В камерном тормозе тормозной
момент создается за счет сил трения тормозных колодок и тормозной рубашки, воз-
никающих при прижатии колодок к рубашке в результате подачи сжатого воздуха в
камеры тормоза.
В дисковом тормозе тормозной момент создается за счет сил трения, возникаю-
щих между дисками — биметаллическими и металлокерамическими.
Использование в качестве опор лыж существенно повышает проходимость само-
лета по грунту небольшой прочности. Удельное давление лыжи на грунт составляет
1...3 кгс/см2.
Лыжи для грунта изготавливают из металла, полоз лыжи в целях уменьшения из-
носа выполняют из специальных сталей и делают съемным, что увеличивает срок
службы лыжи. Для обеспечения требуемого положения лыжи ее снабжают стабилизи-
рующим амортизатором.
Находит также применение и колесно-лыжное шасси, позволяющее производить
пробег по прочному грунту на колесах, а по мягкому, влажному — на лыжах или одно-
временно на колесах и лыжах.
Амортизация шасси
Амортизация шасси предназначена для поглощения энергии удара при посадке
самолета или вертолета, а также при переезде неровностей ВПП.
В момент касания земли самолет имеет значительную вертикальную скорость V?
зависящую от посадочной скорости Ипос и массы самолета А/пос. Быстрое гашение вер-
тикальной скорости от значения ее в момент посадки до нуля вызывает появление
больших ускорений и ударных нагрузок, действующих на конструкцию шасси и пла-
нера самолета.
Для поглощения кинетической энергии самолета шасси снабжаются амортизи-
рующими устройствами — пневматиками колес и специальными амортизаторами.
Одна часть кинетической энергии превращается в потенциальную энергию деформа-
ции амортизации, а другая — в тепловую энергию, которая рассеивается.
Пневматики колес воспринимают часть энергии удара и аккумулируют ее. Амор-
тизаторы не только воспринимают, но и рассеивают энергию, благодаря чему колеба-
ния самолета и вертолета при посадке затухают.
К амортизации шасси предъявляются следующие требования:
• поглотить полную энергию удара с минимальной перегрузкой и плавно нарас-
тающими нагрузками на опоры шасси:
229
• рассеять возможно большую часть энергии, превратив ее в тепло;
• обеспечить переезд через неровности аэродрома без больших перегрузок;
• обжать и распрямить амортизацию (возвратить центр масс в первоначальное по-
ложение) за минимальное время (не более чем за 0,8 с) для восприятия следую-
щего удара;
• не зависеть от температурных и других условий.
Амортизаторы бывают пружинно-фрикционные, резиновые, жидкостные, жид-
костно- газовые.
На большинстве современных самолетов и вертолетов применяются жидкост-
но-газовые амортизаторы.
В жидкостно-газовом амортизаторе (рис.4.100, а) упругим элементом является
газ, давление которого при обжатии амортизатора увеличивается. Энергия сжатого га-
за используется для возвращения амортизатора в исходное положение. Рассеивание
энергии происходит за счет работы сил трения и гидравлического сопротивления жид-
кости, перетекающей через малые отверстия. Эта часть энергии переходит в тепло.
Диаграмма работы амортизатора представляет собой зависимость усилия Рам, дей-
ствующего на шток амортизатора, от хода S штока. Можно считать, что на прямом ходе
р =р + р + р
J ам J г J ж J тр ’
а на обратном
Р = Р - Р - Р
л ам л г л ж л тр*
Сжатие газа происходит по политропному процессу почти без теплообмена с
внешней средой, поэтому политропы прямого и обратного хода совпадают, в результа-
те чего практически вся работа на обратном ходе амортизатора возвращается самолету.
Сила сопротивления жидкости пропорциональна квадрату скорости движения
штока и зависит от формы и площади отверстий и вязкости жидкости.
Суммарная диаграмма работы амортизатора показана на рис. 4.100, б. Работа
амортизатора на прямом ходе определяется площадью диаграммы ABMCDA, а воз-
вращенная самолету — площадью АЕ NFDA.
Разница между этими площадями — энергия, рассеянная за один цикл амортиза-
тора (превращенная в тепло за прямой и обратный ход).
Для увеличения количества рассеиваемой энергии применяют различные устрой-
ства, уменьшающие площадь проходных сечений жидкости (клапаны торможения).
Рис. 4.100. Жидкостно-газовый амортизатор:
а) схема; б) диаграмма работы
230
Рис. 4.101. Способы соединения колеса со штоком амортизатора:
а) телескопическая стойка;
б—г) рычажные стойки:
1 — двухзвенник; 2 — рычаг; 3 — кардан
Способы соединения колеса с амортизатором
и расположение амортизатора в конструкции шасси
Условия работы амортизатора в значительной степени зависят от его расположе-
ния и способа соединения штока амортизатора с осью колеса.
В зависимости от расположения и крепления амортизатора различают:
• шасси с непосредственным креплением колес к амортизатору (телескопическая
стойка);
• шасси с рычажной подвеской колеса с выносным амортизатором;
• шасси с рычажной и полурычажной подвеской колеса и внутренним амортиза-
тором.
В телескопической стойке (рис. 4.101, а) колеса закреплены непосредственно на
штоке амортизатора. Такая стойка амортизирует лишь осевые нагрузки, лобовые си-
лы вызывают изгиб стойки. Для передачи крутящего момента шток связывается с ци-
линдром с помощью двухзвенника (шлиц-шарнира). Для улучшения работы аморти-
затора колесо выносят вперед, а стойку устанавливают наклонно.
В стойках с рычажной и полурычажной подвеской (рис 4.101, б—г) нагруз-
ки в плоскости колеса вызывают поворот рычага относительно шарнира и обжа-
тие амортизатора. Наилучшие условия работы обеспечиваются при выносном
амортизаторе (рис. 4.101, б) В этом случае амортизатор нагружен только осевыми
силами.
Шасси с рычажной подвеской колес амортизирует лобовые нагрузки, возникаю-
щие при посадке и рулежке, и позволяет осуществить компоновку опоры на крыле
любой формы, поэтому в шасси современных самолетов чаще всего применяют имен-
но такую подвеску колес.
При непосредственном креплении колеса к рычажной подвеске колесо крепится
к штоку либо консольно, либо с помощью вилки и полувилки.
На тяжелых самолетах, где на каждой опоре устанавливается несколько колес,
применяют спаренное крепление колес или крепление их на тележке.
231
Конструктивно-силовые схемы стоек
Конструктивно-силовая схема и размеры шасси определяются назначением
и компоновкой самолета, способом уборки опоры, размещением амортизатора и ус-
ловиями удовлетворения требований к шасси.
Все действующие на стойку шасси силы могут быть сведены к вертикальной, ло-
бовой и боковой. Эти силы, приложенные к колесу, передаются на конструкцию пла-
нера самолета или вертолета через стойку.
Стойки могут иметь ферменную, балочную или балочную с подкосами конструк-
цию (рис. 4.102).
Ферменная конструкция представляет собой стержневую систему, элементы ко-
торой работают на сжатие и растяжение. Большие габариты такой стойки затрудняют
ее уборку, поэтому она применяется лишь на нескоростных самолетах и вертолетах с
неубирающимся шасси.
На современных самолетах применяются стойки балочной и балочно-подкосной
схем.
Балочная конструкция стойки представляет собой консольную балку, жестко за-
деланную в верхнем конце. Такая балка нагружается в верхней части большим изги-
бающим моментом, вследствие чего вес ее сравнительно велик. В целях разгрузки
стойку подкрепляют подкосами, за счет которых существенно уменьшается корневой
изгибающий момент. Подкосы чаше всего являются элементами механизма уборки и
выпуска шасси; для фиксации они снабжаются гидравлическими и механическими
замками.
При трехопорной схеме шасси передняя опора выполняется со свободно-ориен-
тирующимися колесами, что позволяет самолету маневрировать по аэродрому.
Наличие большого количества степеней свободы передней стойки может привес-
ти к возникновению самовозбуждающихся колебаний передних колес.
Для борьбы с этим явлением (получившим название «шимми») в конструкции
передних опор предусмотрено специальное устройство — «демпфер шимми». Это уст-
ройство часто используется для управления разворотом передних колес в тех случаях,
когда они управляемы.
Расчет шасси на прочность производят для всех заданных случаев нагружения,
при этом строят эпюры сил и моментов в плоскостях действия сил и определяют дей-
ствующие напряжения, которые затем сравнивают с допускаемыми.
Рис. 4.102. Конструктивно-силовые схемы стоек шасси:
а) ферменная КСС шасси самолета Ан-2; б) балочная с подкосом КСС шасси;
в) основная (балочная) стойка шасси самолета МиГ-25
232
ЛИТЕРАТУРА
1. Егер С. М., Матвеенко А. М., Шаталов И. А. Основы авиационной техники:
Учебник / Под ред. И. А. Шаталова. — Изд. третье, испр. и доп. — М.:
Машиностроение, 2003. С. 72.
2. Житомирский Г. И. Конструкция самолетов: Учебник для студентов
авиационных специальностей вузов. — М.: Машиностроение, 1995. С. 416.
3. Конструкция самолетов: Учебник для вузов / О. А. Гребеньков, В. П. Гоголин,
А. И. Осокин, В. Ф. Снегирев, В. Г. Шатаев; Под ред. проф. О. А. Гребенькова. —
Казань: Изд-во Казан, гос. техн, ун-та, 1999. С. 320.
4. Шульженко М. Н. Конструкция самолетов. — М.: Машиностроение, 1971. С. 416.
5. СклянскийФ. И. Управление сверхзвукового самолета. — М.: Машиностроение,
1964. С. 388.
6. Нечаев Ю. Н, Входные устройства сверхзвуковых самолетов. — М.: Воениздат,
1963. С. 143.
7. Авиастроение: Экспресс-информация ВИНИТИ.
8. Техническая информация / ЦАГИ, ОНТИ, Мемориальный музей им.
Н. Е. Жуковского.
9. Остославский И. В. Аэродинамика самолета. — М.: Оборонгиз, 1957. С. 500.
10. Авиация: Энциклопедия. — М.: Изд-во «Большая Российская энциклопедия»;
ЦАГИ, 1994. С. 736.
СОДЕРЖАНИЕ ГЛАВЫ 4
4.1. Уравнения движения самолета.................................163
4.2. Перегрузки, действующие на самолет..........................165
4.3. Определение летных характеристик. Аэродинамический расчет...167
4.3.1. Задачи и методы аэродинамического расчета.............167
4.3.2. Диапазон скоростей горизонтального полета.............167
4.3.3. Скороподъемность и потолок самолета...................169
4.3.4. Снижение..............................................171
4.4. Дальность и продолжительность полета........................173
4.4.1. Дальность и продолжительность полета самолета с ТРД...174
4.5. Взлетно-посадочные характеристики...........................175
4.5.1. Взлет.................................................176
4.5.2. Посадка...............................................177
4.6. Маневренность самолета......................................179
4.6.1. Криволинейный полет в вертикальной плоскости..........179
4.6.2. Разгон и торможение...................................181
4.6.3. Криволинейный полет в горизонтальной плоскости........181
4.7. Структурная схема самолета..................................182
4.8. Основные части самолета и их назначение.....................185
4.8.1. Крыло.................................................186
4.8.2. Оперение и элероны....................................198
4.8.3. Фюзеляж...............................................200
4.8.4. Расположение двигателей на самолете...................206
4.8.5. Системы управления полетом............................213
4.8.6. Взлетно-посадочные устройства.........................221
Литература ..........................................................233
233
ГЛАВА 5_________________
Основы устройства
ракет-носителей
В настоящее время известно большое количество образцов ракетной техники.
Некоторые из них имеют между собой много общего по конструкции, двигательным
установкам, энергетическим системам, назначению и т. д. Это дает возможность клас-
сифицировать ракеты, разделяя их на группы по отдельным признакам, что, в свою
очередь, существенно облегчает процесс их изучения.
Классифицировать ракеты можно по различным признакам:
• по многократности применения;
• по компоновочным схемам;
• по конструкции отсеков;
• по весу и габариту;
• по источнику энергии;
• по агрегатному состоянию топлив;
• по способу подачи топлива;
• по типу старта;
• по назначению;
• по применению.
Для грамотного проектирования и конструирования ракет-носителей (РН) и дру-
гих подобных летательных аппаратов необходимо использовать отработанные типы уз-
лов и систем современных ракет. Описанию таких узлов и систем посвящена эта глава.
В ней приняты следующие сокращения:
Бак «Г» — бак горючего;
Бак «О» — бак окислителя;
ВРД — воздушно-реактивный двигатель;
ГБ — головной блок;
ГО — головной обтекатель;
ГЧ — головная часть;
ДПК — дренажно-предохранительный клапан;
ДУ — двигательная установка;
ЖРД — жидкостный ракетный двигатель;
ИСЗ — искусственный спутник Земли;
КА — космический аппарат;
КГЧ — космическая головная часть;
КЗМ — кабель-заправочная мачта;
КМ — композиционный материал;
КРТ — компоненты ракетного топлива;
ЛА — летательный аппарат;
ПГ — полезный груз;
ПГС — пневмогидравлическая система;
ПН — полезная нагрузка;
РБ — разгонный блок;
РБл — ракетный блок (часть ступени РН, включающая корпус, ДУ, элементы СУ,
систему разделения и пр.);
234
РД — ракетный двигатель;
РКН — ракета космического назначения;
РН — ракета-носитель;
РТ — ракетное топливо;
САПС — система аварийного покидания и спасения;
СК — стартовый комплекс;
СКУ — системы контроля уровня;
СОБ — синхронное опорожнение баков;
СП — стартовая позиция;
СРС — система разделения ступеней;
СТ — система телеизмерений;
СУ — система управления.
5.1. ХАРАКТЕРИСТИКА РЕАКТИВНОГО ПРИНЦИПА ДВИЖЕНИЯ
И ОСОБЕННОСТИ РАКЕТНОГО ПОЛЕТА
Реактивный принцип движения — движение под воздействием силы отдачи, т. е.
реакции потока частиц, отбрасываемых от летательного аппарата.
Всякий способ передвижения основан на силах отдачи, т. е. на отбросе какой-то
массы в обратном направлении (лодка и пароход отбрасывают массу воды; винтовой
двигатель самолета отбрасывает массу воздуха; человек отбрасывает назад землю и т. д.).
Но такое движение не принято называть реактивным, потому что оно возникает в ре-
зультате реакции непрямого действия. При этом типе движения между двигателем (источ-
ником и преобразователем энергии) и отбрасываемой массой имеется промежуточный
механизм — движитель. (У лодки двигатель — гребец, движитель — весла; у парохода —
движитель — гребной винт; у самолета — воздушный винт; у человека — ноги).
У реактивного принципа характерным является отсутствие движителя и возни-
кающая реакция поэтому называется реакцией прямого действия.
Для осуществления реактивного движения необходимы следующие компоненты:
• источник энергии;
• рабочее тело (вещество, масса которого отбрасывается в направлении, обратном
движению).
Масса воды, отбрасываемая гребным винтом парохода, несет в себе функции ра-
бочего тела, но называть ее так не принято. Это пассивная масса окружающей среды,
и к пароходу она не относится.
Масса воздуха, попадающая в камеру ВРД через воздухозаборник, также
пассивна, но содержит кислород, используемый для сжигания горючего, а продукты
сгорания и не участвующий в реакции горения азот истекают через сопло с высокой
скоростью, вследствие чего и создается реактивная сила. Эту отбрасываемую массу
называют рабочим телом, т. к. ее состояние в результате предварительного сжатия и
последующего нагрева изменилось (это уже не пассивная внешняя масса, а масса,
участвующая в рабочем процессе двигателя). Работа ВРД связана с наличием атмос-
феры. Без кислорода нельзя обеспечить горения и энергию, а без массы воздуха не
было бы рабочего тела, т. е. в вакууме ВРД работать не может.
Двигатели, энергия и рабочее тело которых черпаются только из запасов, находя-
щихся на борту ЛА, называются ракетными, а Л А — ракетами. То есть понятие «ракет-
ный» включается в более общее — «реактивный».
При большом разнообразии ракетных двигательных систем, основанных на исполь-
зовании различных видов энергии, они решают одну задачу — выбрасывание из ракеты
некоторой массы, запас которой (так называемое рабочее тело) находится внутри ЛА. На
выбрасываемую массу со стороны ракеты действует некоторая сила, и согласно одному
235
из основных законов механики — закону равенства действия и противодействия — такая
же сила, но противоположно направленная, действует со стороны выбрасываемой массы
на ракету. Эта сила, приводящая ракету в движение, называется силой тяги.
При исследовании движения ЛА с работающим двигателем мы имеем дело с тре-
мя группами сил.
1. Реактивные силы. Они возникают в результате реакции истекающей среды. Это
силы внутреннего взаимодействия между различными частями одной механической
системы.
2. Массовые силы. Подчинены закону всемирного тяготения. Они складываются
из элементарных сил, приложенных к каждой материальной частице ЛА, и являются
внешними силами.
3. Поверхностные силы. Это аэродинамические силы, приложенные к каждой
элементарной площадке поверхности корпуса ЛА. К ним относятся также силы, дей-
ствующие на органы управления, расположенные в зоне действия истекающих газов
(силы на газоструйных рулях). Включаются в число внешних поверхностных сил
и реакции опор.
Результатом действия всех сил на ракету является ускорение, которое она получает.
Результирующее ускорение складывается из ускорений, сообщаемых каждой силой в
Fi
отдельности: ар = Е у (М— масса ракеты в некоторый момент времени).
Ракета является телом переменной массы. Такие тела с размерами, несоизмеримо
малыми по сравнению с проходимыми ими путем под действием всех сил, рассматри-
вают как точки переменной массы.
5.2. ЗАДАЧИ К. Э. ЦИОЛКОВСКОГО
Первая задача Циолковского
Рассмотрим движение ракеты в безвоздушном пространстве при отсутствии гра-
витационного поля. Движение в этом случае будет происходить только под действием
реактивной силы.
Какую скорость V приобретет ракета к моменту, когда начальная масса MQ умень-
шится до конечного значения Мк (до полной выработки топлива)? Это — первая зада-
ча Циолковского.
Запишем уравнение Мещерского:
lxdr dA/
Mdi =rttWe = -Si^-
Здесь we — эффективная скорость истечения, равная удельному импульсу тяги
(тяги РД, отнесенной к секундному массовому расходу топлива).
После разделения переменных получим:
Так как we = const, после интегрирования получим:
к= IT = -w*1п м+ с-
Значение С получим из начальных условий: при t = 0 скорость К= Ио = 0 и масса
M=MQ.
Тогда: Ио = -we In MQ + С = 0.
Откуда: С = —In A/o.
236
Подставив С в выражение для И окончательно получим:
V= —we In М + we In MQ = — we In = —we In p, (5.1)
где M— текущая масса ракеты;
M
ц = — относительная текущая масса ракеты.
Это формула Циолковского для определения идеальной скорости одноступенча-
той ракеты, которая характеризует энергетические характеристики собственно ра-
кеты.
По мере выработки топлива масса М и соответственно ц уменьшаются, а ско-
рость V — возрастает.
В частности, при значении ц = ^ = 0,368 скорость Иракеты всегда равна эффек-
тивной скорости истечения (рис. 5.1).
Когда топливо будет полностью выработано, а двигатель выключен, скорость V
достигнет своего наибольшего конечного VK значения:
Ик = -wKln цк = we In z,
(5.2)
Мк
ГДе;Нк=^о
— относительная конечная масса;
Мк, MQ — конечная и начальная масса ракеты соответственно;
М0 we
z= тг = е — число Циолковского.
Другая форма записи конечной скорости:
Л/о 1
^О^уп. Цк ~ S0^у.п. In Z ~ Д/о _ Д/~ £о^у.п. ^П । ,
где Мт — масса топлива;
g0 — ускорение свободного падения;
Руп — удельная тяга в пустоте (тяга РД, отнесенная к секундному весовому
расходу топлива);
_ Мт
— относительная масса топлива.
Рассмотрим, от каких параметров зависит путь 5К, пройденный ракетой в идеаль-
ных условиях за время /к.
Очевидно: 5К = - J we In pdz.
о
При rh = const текущая масса Мракеты линейно зависит от времени:
М= Мо — rht.
Поэтому:ц=1-Д;ф = -Д<1Л
Тогда после замены переменных:
Нк
Sk = W'W Л" МФ,
1
237
или после интегрирования:
Л/о
SK = We~^ (1 +Нк1пНк-Нк)-
-г D . Мо Mogo we Go
Так как лп = rhw„, то — = —— — = -5-
п е’ rh itiwe g0 Яп
Поэтому:
\ = 7 we2v0[l-gK(l-lngK)],
60
(5.3)
(5.4)
Go
где v0 = „--стартовая нагрузка на тя!у.
Величину, обратную v0, называют тяговооруженностью т|0:
_ 1 _
По ”0 Go •
Выясним, какое влияние оказывает тяговооруженность на время t работы двига-
теля. Выше отмечалось, что при линейном законе изменения массы ЛА
th Мп
М=М0-rht и ц = 1 - ^/,откуда/= -^(1 -ц)= —(1 — |л).
Яп
Учитывая, что т|0 = —, получаем:
SqMq
Wn Руп
^У0
Из последних двух выражений следует, что для ракет с одинаковыми скоростями
истечения we равным значениям ц может соответствовать разное время работы двига-
теля: чем больше начальная тяговооруженность т|о, тем меньше время.
На рис. 5.2 дана зависимость V = f(t) для we = const и различных значений на-
чальной тяговооруженности Г|о. Равные значения скорости, очевидно, имеют место
при равных ц.
К м/с
Рис. 5.1. Изменение скорости V в
зависимости от Ц для различных w(
= const
ц=0,2
_Ц = 0,4
|1 =0,6
~Ц=0,8
0 100 200 300 400 Г, с
Рис. 5.2. Зависимость скорости V от времени t
полета для различных значений
начальной тяговооруженносги Г|о
_ц=0,1
к
238
Увеличения конечной идеальной скорости ракеты можно достичь либо увеличе-
нием эффективной скорости истечения продуктов сгорания, либо уменьшением
относительной конечной массы цк (увеличением числа z Циолковского). Закон же
расхода топлива, равно как и абсолютные значения начальной и конечной масс, не
оказывают влияния на приобретенную скорость.
Путь, проходимый ракетой, зависит не только от we и цк, но и обратно пропорци-
онален тяговооруженности т|0, т. е. стартовому ускорению. Этот факт объясняется
тем, что с увеличением Г|о уменьшается время t работы двигателя, а следовательно,
снижаются гравитационные потери скорости. В итоге это приводит к увеличению ко-
нечной скорости ракеты, движущейся в поле тяготения планеты, а следовательно,
растет и проходимый ею путь.
Формула Циолковского для многоступенчатой ракеты
Основная задача ракеты — сообщить заданному полезному грузу определенную
скорость. В зависимости от полезного груза и необходимой скорости назначается и запас
топлива. Чем больше масса полезного груза Л/пг и конечная скорость Ик, тем больший за-
пас топлива Мт должен находиться на борту, а следовательно, тем большим оказывается
стартовый вес ракеты Л/о, тем больше необходима тяга двигателя R, что приводит к уве-
личению веса двигательной установки и веса всей конструкции ракеты в целом Л/констр:
|Л/пги ]МТ^> ]R—+ Жонстр.
Реальный предел для существующих конструкций на сегодня цк = 0,12, а макси-
мально достижимое для химических ракетных двигателей значение we = 4400 м/с
(топливо — «водород — кислород»). Тогда:
Ик = -4400 In 0,12 = 9300 м/с.
Можно показать, что для выведения полезного груза на низкую круговую орбиту
Земли необходима характеристическая скорость Их = 9400 м/с (необходимая фактиче-
ская скорость Ифакт = 7800 м/с). Разность между ними — ДИ= 1600 м/с — это суммар-
ные потери скорости, обусловленные совокупностью потерь скорости из-за отличий
реальных условий полета от идеальных.
Приведенные количественные опенки свидетельствуют, что достижение первой
космической скорости для создания ИСЗ Земли находится на пределе реальных воз-
можностей одноступенчатых ракет с двигателем на химическом топливе. Такая одно-
ступенчатая ракета уже создана в Японии — в 1986 г. с ее помощью был осуществлен
запуск ИСЗ массой ~ 800 кг на круговую орбиту Земли. Добиться этого удалось за счет
широкого применения в конструкции неметаллических и композиционных материа-
лов, что обеспечило снижение цк ниже вышеуказанного предела. Однако вывод боль-
ших полезных грузов с помощью одноступенчатых ракет в ближайшем будущем не
представляется возможным.
Основной недостаток одноступенчатой ракеты заключается в том, что конечная
скорость сообщается не только полезному грузу, но и всей конструкции в целом. При
увеличении веса конструкции это ложится дополнительным бременем на энергетику од-
ноступенчатой ракеты, что накладывает ограничения на величину достижимой скорости.
Одна из плодотворных идей К. Э. Циолковского относится к созданию многосту-
пенчатых ракет, способных за счет избавления от ненужной (балластной) массы, ос-
вободившихся от топлива баков и других элементов конструкции, значительно повы-
сить скорость по сравнению с простой одноступенчатой ракетой.
239
На рис. 5.3 приведена схема трехступенчатой раке-
ты с так называемым поперечным делением (схема
«Тандем»).
Под ступенью многоступенчатой ракеты понимает-
ся одноступенчатая ракета, состоящая из ракетного
блока (РБл) и условного полезного груза в виде остав-
шейся (верхней) части ракеты. То есть последующая /-я
ступень является полезным грузом предыдущей (/ — 1)-й
ступени.
Вывод полезного груза с помощью многоступенча-
той ракеты осуществляют следующим образом.
На старте работает наиболее мощный двигатель
первой ступени, способный поднять ракету со старто-
вого устройства и сообщить ей определенную скорость.
После того, как будет израсходовано топливо в баках
первой ступени, она отбрасывается, а дальнейшее уве-
Рис. 5.3. Схема
трехступенчатой ракеты
личение скорости достигается за счет работы двигателей следующей ступени и т. д.
Теоретически процесс деления можно вести до бесконечности. Однако на практике
выбор числа ступеней следует рассматривать как предмет поиска оптимального кон-
структивного варианта. Увеличение числа ступеней при заданной массе Мпг полезно-
го груза ведет к уменьшению стартовой массы Мо ракеты, но при переходе от и-й сту-
пени к (и + 1)-й выигрыш с числом п уменьшается, ухудшаются весовые характерис-
тики отдельных ракетных блоков, увеличиваются экономические затраты и
снижается надежность (табл. 5.1).
Таким образом, в отличие от одноступенчатой, в многоступенчатой ракете одновре-
менно с полезным грузом заданную конечную скорость приобретает масса конструкции
не всей ракеты, а только последней ступени. Массы же ракетных блоков предыдущих сту-
пеней получают меньшие скорости, что приводит к экономии энергетических затрат.
Введем следующие обозначения:
И/, Н/к “ соответственно текущее и конечное значения относительной массы /-й
ступени;
wei — скорость истечения при полете /-й ступени;
V\, — соответственно текущее значение скорости и конечное значение, при-
обретенное Z-й ступенью.
Тогда:
= -wei In Ц,.; = -wei In ц,к.
После того, как выработается топливо 1-й ступени:
^K = -we/lnH/K>
А/о - Мт,
где ц/к = —ду-----относительная конечная масса 1-й ступени;
Мт/ — масса топлива в баках 1-й ступени.
Таблица 5.1
Зависимость стартовой массы ракеты от количества ступеней
Количество ступеней (л) 2 3 4 5 6
Стартовая масса Af0, т 848 185 140 124 116
240
Скорость полета 2-й ступени складывается из конечной скорости 1-й ступени и те-
кущей скорости, приобретенной 2-й ступенью: Vn = — weI In ц/к — weII In p/z. После выра-
ботки топлива 2-й ступени:
К//к = ~wel In Ц/к - И'е// >П Ц//к,
A/nZZ — 4ZZ
где ц//к = ---у---- — относительная конечная масса 2-й ступени;
Л/о// — стартовая масса 2-й ступени;
Мт11 — масса топлива в баках 2-й ступени.
Таким образом, каждая последующая ступень дает приращение скорости. В итоге
конечная скорость многоступенчатой ракеты определится как сумма скоростей, при-
обретенных всеми п ступенями:
п п п
= Z Кк, = - Z wei1п Ик, = X wei1п Z, • (5.5)
/=1 ,=1 ,=1
Если weI = we2 =... = wen = we, то:
= i - 1П Ик, = ~We 1П П UK, = We In П Zi. (5.6)
z=l /=! /=1
5.3. ОБЩИЕ СВЕДЕНИЯ ОБ УСТРОЙСТВЕ PH
Летательный аппарат (ракета-носитель) — сложная иерархическая техническая
система, состоящая из большого количества элементов, состав и наиболее существен-
ные взаимосвязи которых раскрываются ее структурной схемой (рис. 5.4).
РАКЕТА-НОСИТЕЛЬ
> корпус РБл
> маршевые ДУ
> приборы и кабели СУ
> приборы и кабели СТ
> элементы СРС
система
стабилизации
система
наведения
полезный
груз S
головной .
обтекатель
САПС <
система
энергообеспечения
элементы связи
> с технологическим
оборудованием
Рис. 5.4. Структурная схема РН
241
В проектных расчетах используется деление ЛА на ступени и ракетные блоки
(РБл). Совокупность РБл многоступенчатой ракеты является собственно ракетной
частью, обеспечивающей в конце активного участка траектории транспортируемому
полезному грузу требуемые кинематические параметры движения. В ракетах косми-
ческого назначения (РКН), предназначенных для выведения полезных грузов на ор-
биту ИСЗ, ракетную часть принято называть ракетой-носителем (PH).
Второй уровень иерархии (наиболее высокий) составляют ступени многоступен-
чатой PH.
Ступень — часть составной ракеты, обеспечивающая ее полет на определенном
отрезке активного участка и состоящая из:
• РБл с запасами топлива;
• ДУ;
• элементов СУ;
• полезного груза ступени.
Полезный груз ступени может служить последующей ступенью многоступенча-
той ракеты после отделения опорожнившихся РБл.
Третий уровень иерархии составляют:
• ракетные блоки (РБл) ступеней;
• головной блок (ГБ);
• системы управления (СУ);
• системы телеизмерений (СГ);
• системы разделения ступеней (СРС);
• дополнительные устройства, необходимые для функционирования ступеней PH
в целом.
Размещение на 3-м уровне СУ, СГ и СРС определяет их функциональную связь
со ступенями PH, т. к. они существуют в законченном виде только в составе полно-
стью собранной PH, хотя их отдельные элементы входят составной частью в автоном-
ные РБл.
На 3-м уровне структурной схемы размещены и элементы связи PH с технологи-
ческим оборудованием наземного комплекса, а также элементы системы наведения
(переходные конструкции типа рам, кабель-заправочная мачта (КЗМ), прицельные
призмы ит. д.).
Эти элементы являются вспомогательными и после старта PH остаются на стар-
товой позиции. Функционально они обслуживают всю PH в целом в период подго-
товки и проведения пуска.
Ракетный блок (РБл) — автономная часть составной ракеты, состоящая из отсе-
ков корпуса (топливный отсек с запасами топлива, хвостовой и переходный отсеки),
маршевых ДУ, аппаратуры, агрегатов и бортовой кабельной сети СУ и СГ, элементов
СРС и отброса пассивных масс конструкции, а также элементов конструкции, служа-
щих для связи борта PH с технологическим оборудованием наземного и испытатель-
ного комплексов.
Космическая головная часть (КГЧ), Головной блок (ГБ) PH является автономной
структурной единицей, состав которой меняется в зависимость от решаемой задачи и
практически не влияет на комплектацию РБл.
ГЧ включает:
• полезный груз (ПГ);
• головной обтекатель (ГО);
• систему аварийного покидания и спасения (САПС) — для пилотируемых косми-
ческих кораблей;
• может иметь РБ.
242
Головной обтекатель, образуя обтекаемую поверхность передней части PH при ее
полете в атмосфере, защищает конструкцию ПГ от силового и теплового воздействия
набегающего потока воздуха, а также служит для размещения (монтажа) на его внут-
ренней поверхности ряда систем (или их элементов), участвующих в подготовке к пу-
ску, но не функционирующих в полете.
ГО позволяет облегчить конструкцию ПГ и является пассивным элементом, на-
добность в котором отпадает после выхода PH из плотных слоев атмосферы (после
этого он сбрасывается).
5.3.1. Конструктивно-силовые схемы корпуса ступени
Основой конструкции ступени, воспринимающей и передающей (перераспреде-
ляющей) все виды нагрузок: статических, динамических, сосредоточенных и распре-
деленных, является корпус.
Масса корпуса, зависящая прежде всего от эксплуатационных нагрузок, может
составлять 70—80% массы конструкции PH (без топлива).
Для обеспечения высокого конструктивного совершенства PH конструкция кор-
пуса должна иметь минимальную массу. Это обусловливает работу корпуса в области
напряжений, предельно допустимых для применяемых материалов с учетом аэроди-
намического нагрева, снижающего их механическую прочность. Корпус, объединяя
все системы PH в единое целое, одновременно определяет и условия их работы, т. е.
действующие на них нагрузки, температуру, вибрации, параметры среды в отсеках
и др. Корпус можно считать составным элементом каждой из систем PH.
Из-за необходимости расстыковки при эксплуатации, функционировании, тех-
нологичности изготовления, сборки и возможности транспортировки обычными ви-
дами транспорта крупногабаритные ракетно-космические изделия проектируются и
изготавливаются разделяемыми на отдельные отсеки.
Членятся и корпусные конструкции. Каждый отсек корпуса имеет поверхности
стыка со смежными отсеками.
Стыки снабжаются конструктивными узлами для сборки и соединения отсеков
друг с другом, для уплотнения (герметизации) стыков, а также при функциональной
необходимости — узлами для разделения отсеков или отброса смежного отсека, агре-
гата. Конструкцию корпуса отдельного РБл условно делят на отсеки по функциональ-
ному (выполняемая отсеком роль) или конструктивно-технологическому (тип его кон-
струкции) признакам.
Корпус ступени включает (рис. 5.5):
1) передний отсек — предназначен для стыковки с последующим РБл и служит
для размещения приборов СУ и СГ при «холодном» разделении ступеней и для обес-
печения выхода струй газов при запуске ДУ последующей ступени при «горячем» раз-
делении;
2) топливный отсек состоит из баков окислителя и горючего и служит для разме-
щения топлива на борту;
3) межбаковый отсек — объединяет баки окислителя и горючего в топливный от-
сек, а также служит для размещения в его объеме приборов СУ и СГ. Конструктивно
топливный отсек может быть выполнен и без межбакового отсека с одним общим для
обоих баков днищем;
4) хвостовой отсек — образует хвостовую часть РБл и предназначен для размеще-
ния двигателей и агрегатов ДУ. Корпус хвостового отсека РБл и последующих ступе-
ней обычно сбрасываемый и выполняет роль переходного отсека;
243
Рис. 5.5. Структура корпуса РБл
5) донная защита (теплозащитный экран) — предназначена для защиты располо-
женных в хвостовом отсеке конструкций и агрегатов от теплового и газодинамическо-
го воздействия струй работающих РД;
6) отражательное устройство — предназначено для защиты расположенного ни-
же бака от силового и теплового воздействия струй ДУ последующей ступени в про-
цессе ее запуска при горячем разделении ступеней;
7) силовая рама крепления двигателей — служит для передачи и рассредоточения
силы тяги двигателей на корпус хвостового отсека или заднюю юбку;
8) силовые кольца (силовые шпангоуты) — предназначены для передачи сосре-
доточенных нагрузок от ненесущих (подвесных) топливных баков к внешнему сило-
вому корпусу;
9) узлы связи с комплексом наземного оборудования (связь типа «борт-
земля») — обеспечивают связь с агрегатами и системами стартового комплекса в про-
цессе подготовки и проведения пуска.
Требования, предъявляемые к конструкции корпуса, должны обеспечивать:
• минимальную массу при необходимых прочности и жесткости;
• эксплуатацию PH во всем диапазоне заданных внешних условий;
• простоту изготовления и минимальную стоимость.
Элементы конструкции ракеты покажем на примере одноступенчатой ракеты
с ЖРД (см. рис. 5.6).
244
Рис. 5.6. Компоновочная
схема баллистической
двухступенчатой
ракеты УР-100:
1,2 — двигатели 1-й ступени;
3 — тормозной двигатель (4 шт.);
4 — блок разъемов магистралей
пневмогидравлической системы
(ПГС) 1-й ступени; 5 — продольные
демпфирующие перегородки;
6 — магистраль наддува бака
окислителя 1-й ступени;
7 — бак горючего 1-й ступени;
8 , 11, 21, 29 — датчики системы
опорожнения баков (СОБ);
9 , 18 — тоннельные трубы;
10 — бак окислителя 1-й ступени;
12 — двигатель 2-й ступени;
13 — бугель (4 шт.); 14 — рама
для крепления двигателя
2-й ступени; 15 — блок разъемов
магистралей ПГС 2-й ступени;
16 — камера сгорания (4 шт.)
рулевого двигателя 2-й ступени;
17 — электрическая рулевая
машина (4 шт.); 19 — магистраль
наддува бака окислителя 2-й ступени;
20 — бак окислителя 2-й ступени;
22 — головная часть;
23 — приборы системы управления;
24, 27, 30, 33 — коллекторы
магистралей наддува баков;
25 — поперечная демпфирующая
перегородка; 26 — продольные
демпфирующие перегородки;
28 — бак горючего 2-й ступени;
31 — защитный экран двигательной
установки 2-й ступени; 32 — гаргрот;
34 — расходная магистраль
окислителя; 35 — расходная
магистраль горючего;
36 — стартовая опора (4 шт.);
37 — защитный экран двигательной
установки 1-й ступени
245
5.3.2. Баки
Назначение баков и требования, предъявляемые к ним
Баки предназначаются для размещения компонентов ракетного топлива (КРТ),
а баллоны — для газа (воздуха). Топливо необходимо для работы двигательной уста-
новки. Газ (в том числе и сжиженный) используется для создания необходимого дав-
ления в баках при вытеснительной подаче топлива, а при подаче топлива турбонасос-
ным агрегатом — для создания такого давления в баках, которое обеспечивает беска-
витационную работу насосов. Кроме того, газ используется как рабочее тело
в системе органов устойчивости и управляемости, разделении ступеней и головной
части ракеты.
Топливный отсек (отсеки) является наиболее крупногабаритным агрегатом раке-
ты, часто до 70—80% длины ракеты (или ступени многоступенчатой ракеты). При
конструировании ракет большое внимание должно уделяться выбору формы баков
горючего и окислителя, а также расположению их относительно других частей раке-
ты, т. к. при заданном количестве топлива форма баков и их взаимное расположение
будут в значительной степени определять размеры ракеты в целом, ее баллистические
и массовые характеристики.
На современных ракетах применяются две разновидности баков: несущие и нене-
сущие. Несущие баки представляют собой часть силовой конструкции ракеты, поэто-
му они участвуют в восприятии внешних нагрузок, действующих на ракету. Если же
баки расположены внутри корпуса и воспринимают лишь нагрузки от избыточного
давления газа (воздуха), их называют ненесущими. Такие баки используются только
для размещения рабочего тела.
Конструкции топливных баков выбираются исходя из конкретных условий ком-
поновки ракеты и должны отвечать следующим основным условиям:
• топливные баки, поскольку они занимают самый большой объем ракеты,
должны выбираться такой формы, чтобы обеспечить хорошие аэродинамические
и баллистические характеристики ракеты;
• конструкция баков и их относительное расположение должны быть такими, что-
бы перемещения центра масс ракеты в полете были малыми и лежали в допусти-
мых пределах;
• при заданном количестве топлива баки должны иметь возможно меньшую массу,
что достигается использованием прочных и легких материалов, имеющих высо-
кие значения характеристик о/p (удельная прочность материала) и Е/р (удельная
жесткость), выбором рационального типа конструкции с относительно неболь-
шими запасами прочности, обеспечивающими, однако, работу баков без оста-
точных пластических деформаций под действием внешних и внутренних сил во
всех случаях полета и эксплуатации;
• свободные объемы баков и гарантийные запасы топлива должны быть обосно-
ваны;
• баки должны быть простыми по конструкции и технологичными в изготовлении;
• конструкция баков должна обеспечить быструю и простую заправку топливом,
требуемую точность заправки, удобный слив топлив и, если необходимо, должна
обеспечить повторный запуск двигателя;
• топливные баки должны иметь устройства, обеспечивающие надежный забор
топлива и минимальный остаток недозабора;
• баки должны быть устойчивыми против коррозии (это необходимо в случае дли-
тельного хранения ракеты в заправленном состоянии и при применении агрес-
сивных компонентов топлива).
246
Конструкция топливных баков состоит из собственно баков, куда входят обечай-
ки, днища, шпангоуты, стрингеры, узлы крепления, которые образуют силовую схе-
му, и арматуры, состоящей из заборных устройств, датчиков уровня жидкости, трубо-
проводов, тоннельных труб, заливных и сливных горловин, лючков, дренажных от-
верстий, различных клапанов и т. д. Арматура предназначена для заправки (слива)
топлива и подачи топлива в двигатель.
Схемы баков
Для обеспечения приемлемой аэродинамической формы ракеты широко приме-
няются баки цилиндрической формы. Принципиальные конструктивные схемы ба-
ков показаны на рис. 5.7.
Конструкция топливных баков схемы «а» (рис. 5.7, а ) применима для любых компо-
нентов топлива, включая и низкокипящие. В этом случае легко осуществить теплоизоля-
цию днищ, а при использовании самовоспламеняющихся топлив легче обеспечить без-
опасность при эксплуатации. Топливные баки просты в производстве и эксплуатации.
Межбаковое пространство может быть использовано для размещения приборов.
Топливные баки, выполненные по схеме «б» — «бак в баке» (рис. 5.7, 0, — более
сложны в производстве, чем баки первой схемы, но длина топливного отсека и его
масса в этом варианте значительно меньше, чем у отсека, выполненного по схеме «а».
Схема «в» — «бак в баке» (рис. 5.7, в ) — выгодна в весовом отношении для корот-
ких баков высокого давления. Схема «г» — «бак за баком» (рис. 5.7, г ) — имеет сфери-
ческий бак горючего и цилиндрический — окислителя, принципиально не отличается
от баков схемы «б».
Чтобы уменьшить длину ракеты и полнее использовать объемы, в некоторых
случаях на последней ступени ракеты применяются торовые баки (рис. 5.7, д ).
Для баков высокого давления, где размещается рабочее тело (азот, гелий, воздух и
т. д.), и в случае использования низкокипящих топлив целесообразно применять сфери-
ческие баки, поскольку они, при одинаковой емкости с цилиндрическими, имеют мень-
шую поверхность, и следовательно, вес теплоизоляции будет меньшим. Кроме того, при
одинаковом давлении наддува масса такого бака будет меньше, чем цилиндрического.
Днища баков выполняются в виде элементов сферических поверхностей. Такая
форма днища выгодна в весовом отношении. Для обеспечения бескавитационной по-
дачи топлива в баках создается избыточное давление, что сказывается на работе кон-
струкции. За счет наддува в стенках бака создаются растягивающие усилия, которые
частично или полностью уравновешивают сжимающие усилия от внешней нагрузки.
Рис. 5.7. Конструктивные схемы топливных баков
247
Кроме того, наддув повышает критические напряжения сжатия (потери устойчи-
вости) обшивки. При некотором значении избыточного давления необходимость в
шпангоутах для подкрепления обшивки отпадает. Такие отсеки могут выполняться в
виде тонкостенной цилиндрической оболочки.
Конструкционные материалы для изготовления элементов топливных баков вы-
бираются с учетом их стойкости по отношению к химическому воздействию горючего
и окислителя. Материал баков должен обладать высокой удельной прочностью в ши-
роком диапазоне температур. Несущие баки для азотной кислоты, перекиси водоро-
да, керосина и жидкого кислорода обычно изготовляют из легированной стали. Несу-
щие баки также изготовляют и из алюминиевых сплавов, допускающих сварку. Баки
для жидкого фтора, окиси и нитрата фтора могут выполняться из никелевых и медных
сплавов. Возможно использовать клепаные конструкция из материалов типа Д16Т,
которые при одинаковом удельном весе имеют лучшие механические характеристи-
ки, чем, допустим, хорошо свариваемый алюминиевый сплав АМгб.
Топливные отсеки в полете нагружаются, как часть силовой схемы корпуса, сжи-
мающими нагрузками, поперечными силами, изгибающим и крутящим моментами. Кро-
ме того, они нагружаются внутренним избыточным давлением и гидростатическим
давлением столба жидкости.
Конструкция баков
Топливные баки состоят из обечаек и днищ. Обечайки топливных баков выпол-
няются в виде тонкостенных гладких или подкрепленных оболочек. Типы обечаек,
применяемых в топливных баках современных ракет, показаны на рис. 5.8.
Каждый бак может иметь собственные верхнее и нижнее днища (рис. 5.9).
Часто днища двух соседних баков выполняются общими или совмещенными. Та-
кая конструкция днищ дает определенный выигрыш в массе и длине топливного отсе-
ка, однако требует значительно более тщательного изготовления, т. к. возникает опас-
ность соединения компонентов ракетного топлива (КРТ), находящихся в баках, при
проникновении их через микродефекты в сварных швах. Это особенно опасно при
размещении в баках пар самовоспламеняющихся компонентов.
Рис. 5.8. Виды обечаек
цилиндрических топливных баков:
а) подкрепленная легкими шпангоутами;
б) панельная обечайка;
в) вафельная обечайка
Рис. 5.9. Схема топливного отсека, состоящего
из баков с раздельными днищами:
1 — бак окислителя; 2 — днище бака окислителя;
3 — межбаковый отсек; 4 — бак горючего;
5 — днище бака горючего
248
Гладкие баки
При некотором значении избыточного давления необходимость в продольном
и поперечном наборе для подкрепления обечайки отпадает. Такие баки могут выпол-
няться в виде тонкостенной цилиндрической оболочки. Конструкция гладкого бака
показана на рис. 5.10.
Если размеры и нагрузки, действующие на бак, не позволяют выполнить бак
гладкой конструкции, используют баки каркасного типа.
Бак с продольным набором
Как правило, баки основных PH являются несущими, т. е. передающими нагруз-
ки от двигателя к вышележащим частям PH. Поэтому такие баки могут подвергаться
действию интенсивных сжимающих нагрузок, вследствие чего может произойти по-
теря устойчивости оболочек баков. Для предупреждения потери устойчивости баки
подкрепляются. Подкрепление оболочек может осуществляться с помощью продоль-
ных тонкостенных элементов (стрингеров), поперечных кольцевых элементов (шпан-
гоутов), соединяемых с обечайками сваркой, либо оболочки баков могут иметь ва-
фельную конструкцию.
На рис. 5.11 показана конструкция бака с продольным набором, на рис. 5.12 —
бак со шпангоутами, на рис. 5.13— бак каркасного типа, на рис. 5.14 —
Рис. 5.11. Бак с продольным набором:
7 — верхнее днище; 2 — опорный шпангоут;
3 — панель обечайки; 4 — нижнее днище;
5 — тоннельная труба
Рис. 5.10. Конструкция бака
без подкрепляющих элементов:
1 — верхнее днище; 2 — опорный шпангоут;
3 — обшивка; 4 — распорный шпангоут;
5 — обечайка
249
Место А
Место Б
Место В
Рис. 5.12. Бак со шпангоутами:
/ — опорный шпангоут; 2 — обшивка; 3 — верхнее днище; 4 — распорный шпангоут;
5 — обечайка; 6 — шпангоут; 7 — промежуточный шпангоут; 8 — перегородка бака;
9 — шпангоут; 10 — нижнее днище; 11 — фланец
Рис. 5.13. Бак каркасного типа:
1 — верхнее днище; 2 — обечайка; 3 — шпангоут; 4 — стрингер; 5 — нижнее днище;
6 — ребро панели; 7 — уголок (вариант а) шпангоут крепится к обечайке, а стрингеры
крепятся только к шпангоуту; вариант б) шпангоут крепится уголками к продольному ребру)
Рис. 5.14. Бак вафельного типа:
1 — опорный шпангоут;
2 — обшивка;
3 — верхнее днище;
4 — обечайка вафельного типа;
5 — нижнее днище;
6 — тоннельная труба
Б-Б
jQ|^zyi
уггггггг/^г/г^л
Рис. 5.15. Типы вафельных подкреплений:
а) квадратная прямая; б) квадратная наклонная под 45°; в) треугольная
бак вафельного типа, а на рис. 5.15 — различные виды подкреплений вафельного
типа.
Шпангоуты бака
Места стыка днища и обечайки характеризуются изменением кривизны обечаек
и возникновением распорных усилий. Чем плавнее переход от днища к обечайке, тем
меньше величина распорного усилия (предельный случай у днища полусферической
формы). Для восприятия распорных усилий применяются распорно-стыковочные
шпангоуты (рис. 5.16), конструкция которых определяется размерами бака и величи-
ной действующих напряжений.
Рис. 5.16. Характерные сечения
распорно-стыковочных
шпангоутов
Рис. 5.17. Конструктивное
исполнение соединения
распорного шпангоута
с обечайкой:
1 — обечайка;
2 — шпангоут;
распорно-стыковочный;
3 — днище
Рис. 5.18. Примеры
исполнения шпангоутов в узлах
соединения днищ и оболочек
топливных отсеков:
1 — болт; 2 — шайба;
3 — шпангоут стыковочный
сухого отсека; 4 — футорка;
5 — шпангоут стыковочный
топливного бака; 6 — обечайка
бака; 7 — обшивка сухого отсека;
8 — штырь; 9 — днище бака
251
В местах концентрации напряжений (резком изменении кривизны обечайки или
жесткости элементов конструкции) нежелательно использовать сварные соединения.
Поэтому, если шпангоуты не предусмотрены, днища желательно изготавливать вместе
с цилиндрической частью высотой более 30 мм.
Аналогичные требования предъявляются к элементам шпангоутов, стыкуемым с
обечайкой и днищами.
Части шпангоута и обечайки, примыкающие друг к другу, под сварку должны иметь
участки одинаковой толщины протяженностью 20...25 мм с обеих сторон сварного шва.
При соединении днища и обечайки или этих элементов со шпангоутами желательно,
чтобы их срединные поверхности являлись одна продолжением другой (рис. 5.17).
Конструктивное оформление типового соединения распорного шпангоута с обе-
чайками представлено на рис. 5.18.
В некоторых случаях для сохранения формы обечаек при изгибе внутри баков
могут устанавливаться легкие шпангоуты. Иногда эти шпангоуты могут использо-
ваться как элементы гашения колебаний жидкости.
Схемы других соединений топливных и сухих отсеков показаны на рис. 5.19.
Рис. 5.19. Схемы соединения топливных и сухих отсеков:
а) внутреннее соединение с помощью шпилек: 1 — обечайка бака; 2 — днище бака; 3 — силовой
стыковочный шпангоут бака; 4 — стыковочный шпангоут сухого отсека; 5 — обечайка сухого
отсека; 6 — соединительная шпилька с гайкой;
б) внутреннее соединение с помощью болтов: 1 — обечайка бака; 2 — днище бака; 3 — силовой
шпангоут бака; 4 — стыковочный шпангоут бака; 5 — стыковочный шпангоут сухого отсека; 6 —
обечайка сухого отсека; 7 — стыковочные болты с гайками;
в) внешнее соединение с помощью утопленных шпилек: 1 — обечайка бака; 2 — днище бака; 3 —
силовой стыковочный шпангоут; 4 — стыковочный шпангоут сухого отсека; 5 — обечайка сухого
отсека; 6 — стрингер сухого отсека; 7 — заклепочное соединение стрингера и обечайки сухого
отсека; 8 — «карман» для установки стыковочных шпилек; 9 — соединительные шпильки с гайками;
г) внешнее соединение с помощью болтов: 1 — обечайка бака; 2 — днище бака; 3 — стыковочный
силовой шпангоут бака; 4 — стыковочный шпангоут сухого отсека; 5 — обечайка сухого отсека;
6 — наружный стрингер сухого отсека; 7 — соединительный болт с гайкой;
д) сварное соединение бака с сухим отсеком: 1 — обечайка бака; 2 — днище бака; 3 — силовой
стыковочный шпангоут бака; 4 — обечайка сухого отсека; 5 — стыковочный шпангоут сухого отсека
252
5.4. СИСТЕМЫ НАДДУВА ТОПЛИВНЫХ БАКОВ
В ракетах с насосной подачей топлива применяются в основном центробежные
насосы. Для обеспечения их бескавитационной работы необходимо, чтобы давление
жидкости при входе в насос было всегда выше давления упругости паров этой жид-
кости. Это превышение должно быть тем больше, чем больше расход компонента топ-
лива и число оборотов насоса.
Для обеспечения работы центробежных насосов особенно при высоких давлени-
ях в камере двигателя (свыше 100—200 и более кг/см2) необходимо на входе в насос
иметь достаточно высокое давление в расходуемом компоненте (несколько атмос-
фер). Для этого баки наддуваются газом.
Системы наддува топливных баков — составные части ПГС ракет с ЖРД.
К этим системам предъявляются следующие основные требования:
• безотказность действия и обеспечение заданного режима наддува;
• малая масса и небольшие габариты элементов системы;
• удобство и безопасность эксплуатации.
Давление жидкости на входе в насос Рвх складывается из давления столба жидкости
Рст и давления газа наддува над свободной поверхностью жидкости Рб.
Для обеспечения нормальной работы двигателя применяются следующие виды
наддува баков:
• предстартовый наддув баков первой ступени, обеспечивающий запуск двигателей
этой ступени;
Рис. 5.20. Типовые конструкции распылителей газонаддува:
а) при наддуве горячим газом с защитой от действия газа как стенки бака, так
и поверхности жидкости: 1 — коллектор; 2 — полукольцевой экран защиты стенки бака;
3 — стенка бака; 4 — форсуночные отверстия; 5 — элемент крепления экрана на стенке бака;
6 — основание крепления коллектора; 7 — трубопровод подачи газа;
б) при наддуве горячим газом с направляющими экранами: 1 — форсунка; 2 — направляющий экран;
в) при наддуве холодным газом: 1 — форсунки; 2 — коллектор наддува
253
• бортовой наддув, обеспечивающий работу двигателей на номинальном режиме;
• гарантийный наддув или поднаддув баков второй и последующих ступеней,
обеспечивающих запуск их двигателей.
В современных ракетах используются следующие системы бортового наддува топ-
ливных баков:
• системы наддува, использующие продукты сгорания основных компонентов топ-
лива;
• газобаллонные системы наддува (воздухом, азотом или гелием);
• испарительные системы наддува.
Выбор системы наддува определяется:
• конструктивной схемой ракеты;
• физико-химическими свойствами компонентов топлива;
• требованием обеспечения минимальной массы конструкции.
Конструкция распылителей газа наддува показана на рис. 5.20.
В настоящее время решена задача организации наддува баков путем впрыска не-
посредственно в бак окислителя некоторого количества горючего, а в бак горючего —
окислителя. Происходящая реакция в баках обеспечивает выработку газа наддува
прямо в баке. Такая схема значительно упрощает систему наддува, хотя может приме-
няться только при использовании самовоспламеняющихся КРТ
Предохранительные устройства для сброса избыточного давления
При наддуве баков давление в баке может превысить допустимое. Во избежание
разрушения оболочки бака имеется предохранительный клапан. Обычно клапан уста-
навливается в верхней части бака, так, чтобы при заправленном баке дренаж происхо-
дил из газовой подушки, всегда имеющейся над зеркалом жидкости. В некоторых слу-
чаях при совмещенном днище в нижнем баке невозможно установить дренажный
клапан в верхней части бака. Тогда сброс давления происходит через трубу, соединяю-
щую газовую подушку с дренажным клапаном.
Предохранительные клапаны, как правило, размещаются в диаметрально проти-
воположных зонах баков (особенно в баках для самовоспламеняющихся компонен-
тов), что следует учесть при размещении площадок обслуживания.
Предохранительный клапан открывается и закрывается автоматически при до-
стижении давления в баке, равного давлению настройки. При снижении давления
после выхода части газов из бака клапан закрывается.
В процессе наземной эксплуатации возникает необходимость соединения полос-
ти бака с атмосферой или другой внешней емкостью при выполнении некоторых тех-
нологических операций. Например, при заправке, захолаживании или вентиляции
бака необходимо сбрасывать газ, заполняющий бак, по мере наполнения бака захола-
живающим или вентилирующим газом или компонентом топлива. Аналогично при
сливе компонента в случае несостоявшегося старта необходимо обеспечить заполне-
ние освобождающегося от компонента объема бака газом (воздухом или другим спе-
циальным газом) во избежание образования в баке пониженного по сравнению с ат-
мосферным давления и потери устойчивости оболочки бака. Для исключения необхо-
димости установки специального, управляемого по командам от технологической
системы управления клапана эту функцию передают предохранительному клапану.
Для этого в последнем устанавливают специальное устройство, открывающее и за-
крывающее клапан по командам технологической системы управления. Такой клапан
называется дренажно-предохранительным (ДПК).
Схема установки ДПК на корпусе топливного бака показана на рис. 5.21.
254
4
5
Рис. 5.21. Схема установки ДПК:
а) на верхнем днище бака: 1 — ДПК; 2 — стенка верхнего днища; 3 — горловина трубопровода
ДПК; 4 — трубопровод ДПК; 5 — фланец крепления ДПК; 6 — трубопровод управляющего газа;
б) на обечайке бака с помощью разъемного соединения: 1 — ДПК; 2 — обечайка бака;
3 — основание ДПК; 4 — фланец ДПК; 5 — трубопровод управляющего газа;
в) на обечайке бака с помощью сварки: 1 — ДПК; 2 — обечайка бака;
3 — трубопровод управляющего газа;
г) на нижнем днище заднего бака топливного отсека с совмещенным днищем: 1 — ДПК;
2 — трубопровод сброса газа наддува из верхней полости бака; 3 — нижнее днище топливного
отсека; 4 — обечайка заднего бака топливного отсека; 5 — совмещенное днище;
6 — горловина трубопровода ДПК; 7 — трубопровод управляющего газа
255
5.5. АРМАТУРА ТОПЛИВНЫХ БАКОВ
Помимо систем наддува и сброса избыточного давления баки должны быть осна-
щены следующими дополнительными системами и устройствами:
• устройствами для забора топлива;
• системой для предохранения бака от потери устойчивости (складывания бака)
из-за разрежения давления внутри бака при колебаниях температуры окружаю-
щей среды (система «дыхания»). Конструкции баков допускают разрежение не
более 0,01 ...0,02 МПа;
• люком для монтажа систем внутри бака и ремонта;
• тоннельной трубой для прохода трубопровода подачи второго компонента;
• иногда дополнительно устанавливаются специальные устройства (демпферы)
для ограничения подвижности топлива в баках, которые служат для устранения
динамической неустойчивости ракет на активном участке полета.
Демпферами могут быть радиальные перегородки в баках, перфорированные ди-
афрагмы, сетки, которые эффективны при малых частотах, близких к частотам перво-
го тона колебаний поверхности жидкости.
5.5.1. Заборные устройства баков
Заборные устройства — важный элемент топливных баков и систем подачи ком-
понентов топлива к двигателю, обеспечивающих максимальную выработку компо-
нента топлива из бака без нарушения сплошности потока. Уменьшение неиспользо-
ванных остатков топлива в баках, входящих в конечную массу ракеты, является суще-
ственным совершенствованием топливных систем ракеты.
К заборным устройствам предъявляются следующие требования:
• обеспечение минимальных остатков незабора;
• минимальное гидравлическое сопротивление;
• устойчивость при максимальных механических нагрузках;
• простота в изготовлении и монтаже в баке;
• минимальная масса конструкции.
На выбор типа заборного устройства определяющее влияние оказывает геомет-
рия нижних днищ топливных баков (рис. 5.22).
Рис. 5.22. Разновидности принципиальных схем заборных и внутрибаковых устройств:
а) центральный отбор без тарели; б) центральный отбор с та ре лью; в) смещенный отбор топлива
с воронкогасителем над сливным отверстием; г) сильфонное заборное устройство;
д) заборное устройство топливного бака с коническим днищем; е) кольцевое заборное устройство
тороидального бака: ж) кольцевое заборное устройство топливного бака с утопленным двигате-
лем; з) кольцевое заборное устройство в цилиндрическом баке с вогнутым днищем, имеющее
многоточечный отбор топлива;
1 — стенка бака; 2 — днище; 3 — сливной трубопровод: 4 — тарель; 5 — тоннельная труба;
6 — воронкогаситель; 7 — сифонное заборное устройство с гидрозатвором; 8 — желоб
кольцевого заборного устройства
256
Рис. 5.23. Заборные устройства топливных баков:
а) периферийные устройства тарельчатого типа с противозакручивающими лопастями:
1 — днище бака; 2 — противозакручивающие лопасти; 3 — труба датчика СОБ; 4 — тарель;
б) устройство сифонного типа с противозакручивающими успокоительными лопастями:
I — заборный сифонный трубопровод; 2 — противозакручивающие лопасти; 3 — днище бака;
в) тарельчатое центральное заборное устройство с пластинами-гасителями продольных
и поперечных колебаний уровня жидкости: 7 — пластина гасителя продольных колебаний;
2 — пластина гасителя поперечных колебаний; 3 — днище бака; 4 — тарель;
5 — трубопровод расходный; 6 — датчик остатков топлива
На PH часто применяются заборные устройства в виде сливных отверстий в ниж-
них днищах баков с различными воронкогасящими устройствами и противопроваль-
ными тарелями, а также сифонные заборные устройства (рис. 5.23).
Применение боковых заборных устройств приводит к существенному росту ос-
татков незабора. В этом случае целесообразно применение сифонных заборных уст-
ройств, которые дают возможность организовать забор топлива из центра днища при
наличии бокового сливного отверстия из бака (рис. 5.23, б). Гидравлические остатки
незабора для сифонных заборных устройств такие же, как и для заборных устройств
с тарелями при одинаковой геометрии входного участка. Применение сифонного за-
борного устройства позволяет организовать центральный забор при наличии в баке
тоннельной трубы, ось которой совпадает с осью бака. Его целесообразно применять
для питания нескольких двигателей, т. к. обеспечивается равномерное течение на вхо-
де в заборное устройство.
На торовых баках применяются желобковые заборные устройства, представляю-
щие собой кольцевые желобы переменного сечения. Над желобом устанавливается
перфорированная диафрагма, закон распределения отверстий в которой обеспечивает
равномерное опускание уровня в топливном баке.
В процессе истечения компонента из бака через расходный трубопровод на входе
в последний возможно возникновение воронки в ос-
тавшемся компоненте топлива, ось которой совпада-
ет с осью заборного отверстия (провал уровня топли-
ва в баке) (рис. 5.24).
При достижении нижней частью воронки вход-
ного отверстия трубопровода в трубопровод начина-
ет поступать двухфазная смесь жидкости и газа
наддува, что может привести к срыву подачи ком-
понента.
Если не принять меры по снижению высоты об-
разования воронки (hKp), в баке остается значитель-
ное количество компонента в виде остатков незабора,
существенно снижающее коэффициент заполнения
ракеты топливом.
Рис. 5.24. Провал уровня
топлива в баке
257
Рис. 5.25. Принципиальные схемы конструкций воронкогасителей:
а, б, в) радиальные ребра, установленные над тарелью;
г, д) тарель неправильной формы; е) радиальные ребра;
1 — концентрическое ребро; 2 — радиальное ребро;
3 — днище бака; 4 — тарель воронкогасителя; 5 — слив
Для снижения высоты начала образования воронки на входе в расходный трубо-
провод устанавливают специальные воронкогасители (рис. 5.25), которые позволяют
уменьшить остатки незабора до (0,5—0,8)% исходного объема жидкости.
5.5.2. Система синхронного опорожнения баков
Ракеты всегда заправляются КРТ до срабатывания датчиков заправки, фиксиро-
ванно установленных в баках. Таким образом, заправка производится по объему. Одна-
ко весовая доза заправки получается различной в зависимости от температуры компо-
нента (часто она зависит от температуры окружающей среды на стартовой позиции).
Лишь температура криогенных КРТ практически не меняется при изменении темпера-
туры окружающей среды. Следовательно, в разное время года весовое соотношение
компонентов в баках одной и той же ступени PH К = Сок/(7гор будет разным. Однако в
двигателе весовое соотношение компонентов должно оставаться одинаковым. Это обес-
печивается геометрическими размерами трубопроводов и других трактов двигателя. По-
этому заправка компонентов без системы синхронного опорожнения баков (СОБ)
должна быть такова, чтобы обеспечить гарантированное значение параметра К для лю-
бого времени года. Отсюда следует, что необходимо иметь гарантированный избыток
компонентов, являющихся пассивной массой и уменьшающих значение ступени.
Для снижения или, возможно, исключения этих избытков следует изменять по не-
обходимости К в небольших пределах. Это можно сделать, если определить фактическое
К в начальный момент работы системы и производить управление его значением в тече-
ние всего времени работы двигателя для того, чтобы в конечный момент его работы все
258
топливо в баках было израсходовано (кроме топлива, незабор которого связан с другими
причинами).
В момент окончания заправки определяется истинное значение К при данной
температуре и производится расчет необходимых текущих значений К, обеспечиваю-
щих достижение значения, необходимого в конце работы. Программа управления
расходом заводится в счетно-решающий прибор (СРП) системы СОБ (обычно зада-
ются дискретные значения К, т. к. измерение истинных текущих значений К произво-
дится дискретно). Измерение К производится датчиками СОБ, установленными в
каждом баке ступени. Сигналы от датчиков СОБ поступают в СРП, где вычисляется
разность заданных и текущих значений К. При наличии сигнала рассогласования вы-
рабатывается команда, пропорциональная этой величине. Команда подается на дрос-
сель СОБ, представляющий управляемую заслонку, установленную в одном из рас-
ходных трубопроводов. Заслонка изменяет сечение трубопровода и тем самым управ-
ляет опорожнением бака по заданной программе расхода компонента топлива.
СОБ снижает потребные гарантийные запасы компонентов топлива, что дает
возможность увеличить полезную нагрузку или дальность полета ракеты.
Уровни, а следовательно, и объемы компонентов в баках контролируются диск-
ретными датчиками уровней. При прохождении зеркалом топлива контрольной точ-
ки датчиков вырабатываются сигналы уровней окислителя и горючего.
Во время полета ракеты свободная поверхность топлива в баке колеблется. Коле-
бания уровня топлива вызываются пульсацией перегрузок, боковыми перегрузками,
упругими колебаниями ракеты, колебаниями ракеты относительно продольной и по-
перечной осей и другими факторами.
Вследствие этого положение уровня жидкости в месте установки чувствительно-
го элемента датчика может не совпадать со средним значением уровня топлива в баке.
Для замера осредненного уровня чувствительные элементы датчика устанавливаются
в специальном устройстве (рис. 5.26).
При заправке контроль за объемным количеством топлива, поступающего в бак,
осуществляется сигнализатором наполнения. Они бывают разного принципа дей-
ствия. Наибольшее распространение получил сигнализатор с поплавковым дискрет-
ным индуктивным датчиком (рис. 5.27).
5.5.3. Трубопроводы, тоннельные трубы
По трубопроводам компоненты топлива подаются к ЖРД.
Тоннельные трубы служат:
• для надежной изоляции одного компонента топлива от другого;
• повышения надежности ракеты при хранении в заправленном состоянии и в ус-
ловиях полета.
Расходные трубопроводы из верхних баков могут проходить к двигательной уста-
новке по наружной поверхности нижнего бака (ракета «Ариан», HI, «Ангара» и др.),
или внутри объема нижнего бака. В последнем случае, как правило, расходный трубо-
провод монтируется внутри специальной коаксиально установленной тоннельной
трубы. Необходимость этого объясняется следующими причинами. Во-первых, если
используются самовоспламеняющиеся компоненты, то в случае даже микроскопиче-
ских течей компонента через поры может начаться взрывная реакция и произойти
разрушение ракеты. Во-вторых, при использовании КРТ, имеющих разную темпера-
туру замерзания, при отсутствии тоннельной трубы возможно замерзание либо само-
го компонента, либо воды, растворенной в компоненте. Кристаллы замерзшего веще-
ства, поступая в двигатель, могут забить форсунки и сорвать процесс горения.
259
Рис. 5.26. Система одновременного опорожнения баков:
1,3 — труба; 2 — отверстия-демпферы; 4 — герморазъем; 5 — силовые растяжки
Рис. 5.27. Система
контроля уровня
топлива в баке
Рис. 5.28. Типы тоннельных труб:
а) с элементами усиления, выполненными точением;
б) с элементами усиления, выполненными в виде зигов:
1 — толщина ребра; 2 — толщина стенки;
3 — шаг элементов усиления; 4 — радиус элементов усиления
Рис. 5.29. Размещение арматуры в баках:
а) 1 — нижнее днище бака окислителя; 2 — фланец; 3 — сильфон; 4 — трубопровод;
5 — верхнее днище бака горючего; 6 — тоннельная труба
б) / — трубопровод окислителя; 2 — сильфон окислителя; 3 — фланец; 4 — нижнее днище бака
горючего; 5 — нижняя перегородка баков; 6 — верхняя перегородка баков; 7 — обечайка бака
окислителя; 8 — промежуточный шпангоут; 9 — фланец; 10 — трубопровод окислителя;
11 — тоннельная труба; 12 — обечайка бака горючего; 13 — шпангоут; 14 — фланец;
15 — сильфон; 16 — трубопровод горючего
Тоннельная труба подвержена действию избыточного внешнего давления, рав-
ного давлению наддува в нижнем баке, а также давления столба жидкости (с учетом
перегрузки). Во избежание потери устойчивости стенок тоннельной трубы последняя
подкрепляется поперечными кольцевыми элементами (зигами или шпангоутами).
Схемы конструкции тоннельной трубы, варианты расположения отдельных элемен-
тов бака и арматуры показаны на рис. 5.28, 5.29.
Сечения трубопроводов определяются гидравлическим расчетом в зависимости
от состава и секундного расхода топлива.
Для удаления просочившихся компонентов в полость между трубопроводом и
тоннельной трубой может проводиться принудительная вентиляция полости (особен-
но в случае длительного хранения ракеты в заправленном состоянии).
5.5.4. Сильфоны и гибкие трубопроводы
Сильфоны — тонкостенные устройства с концентрическими волнообразными
складками-гофрами, устанавливаемые в трубопроводах для компенсации неточнос-
тей изготовления и сборки, а также температурных изменений геометрических
261
б)
в) г)
Рис. 5.30. Конструкции сильфонов
параметров труб и агрегатов (рис. 5.30—5.31). Они используются также при взаимном
перемещении частей гидроагрегатов и как демпферы пульсаций давления.
Волнистая стенка сильфона вызывает дополнительные гидравлические сопро-
тивления, и для их уменьшения внутрь сильфонов монтируют вставки, обеспечиваю-
щие относительную гладкость гидравлического тракта (рис. 5.30, а).
В системах применяют металлические сильфоны, обладающие хорошей жестко-
стью и упругостью.
Наибольшее распространение получили бесшовные и продольношовные силь-
фоны. Размеры их выбирают так, чтобы отношение наружного диаметра dH к внутрен-
нему db находилось в пределах 1,3...1,5 (большее значение для малых сильфонов).
Важными параметрами являются шаг гофров / и ширина выступа а.
Рис. 5.31. Конструкция сильфона,
армированного наружными кольцами,
и армирующее кольцо
Рис. 5.32. Гибкий шланг:
1 — оплетка; 2 — сильфон;
3 — ниппель
262
Сильфоны отечественного производства выполняют так, чтобы соблюдались от-
ношения (рис. 5.30, бу.
£ < 0,085; < 0,035; при d„ < 40 мм;
“н “н н
£ < 0,056; < 0,022; при 40 < dH < 100 мм.
Для работы при высоких давлениях применяют многослойные сильфоны, со-
стоящие из набора концентрических тонкостенных оболочек, либо сильфоны, арми-
рованные наружными или внутренними кольцами (рис. 5.30, в, г—5.31).
В пневмогидравлических системах применяются гибкие трубопроводы (шланги).
Они устанавливаются для соединения расходных неподвижных магистралей с двига-
телем, когда управление ракетой в полете осуществляется его качанием.
Такие трубопроводы применяются также в местах значительных взаимных пере-
мещений частей корпуса и трубопроводов из-за тепловых расширений.
Наибольшее распространение получили гибкие металлические трубопроводы
с тонкостенной гофрированной оболочкой, конфигурация гофров которой зависит от
способа изготовления и назначения трубопровода. Снаружи выполняется проволочная
оплетка, которая может быть силовой или экранирующей. Силовая проволочная оплет-
ка предохраняет гофрированную оболочку от разрушения и обеспечивает работоспо-
собность трубопровода в поле переменных осевых и радиальных нагрузок (рис. 5.32).
5.5.5. Соединения трубопроводов
Соединения трубопроводов делятся на три группы:
• неразъемные соединения;
• разъемные соединения;
• быстроразъемные соединения.
При этом все группы объединены единым требованием обеспечения герметич-
ности и прочности трубопроводов, входящих в систему.
К неразъемным относятся соединения трубопроводов, выполняемые сваркой
или пайкой, как правило, по торцам соединяемых участков трубопроводов.
Такие соединения применяют в случаях, когда не требуется индивидуальная под-
гонка участков трубопровода и их замена.
К числу наиболее распространенных разъемных соединений относятся фланце-
вые (см. рис. 5.33, а), которые могут выполняться как с приварными, так и со свобод-
ными фланцами.
Фланцевые соединения применяются при отсутствии угловых смещений соеди-
няемых трубопроводов.
Если в процессе монтажа оси соединяемых трубопроводов будут расположены
под некоторым углом друг к другу, то в этом случае используют разъемные соедине-
ния, в которых сопряжение производится между конусной и сферической поверхно-
стями или между сферическими и другими профилированными поверхностями
(рис. 5.33, б).
К быстроразъемным относится класс соединений, предназначенных для разъе-
динения или соединения трубопроводов ракеты и наземного оборудования или тру-
бопроводов отдельных ступеней многоступенчатой ракеты. Они являются самоконт-
рящимися и могут быть отнесены к одной из двух групп:
• соединения с вторичным фиксатором;
• соединения без вторичного фиксатора.
263
а)
6)
Рис. 5.33. Разъемные
соединения трубопроводов
б)
Рис. 5.34. Быстроразъемные
соединения трубопроводов
Первая группа (рис. 5.34, а) используется при стыковке трубопроводов ракеты
и наземного оборудования и характеризуется тем, что для разъединения или соедине-
ния трубопроводов необходимо предварительно приложить осевое или радиальное уси-
лие к вторичному фиксатору, сдвинуть его в сторону, а затем развести трубопроводы.
Вторая группа (рис. 5.34, б) соединений позволяет расстыковать или состыко-
вать трубопроводы только выполнением одной операции — приложением осевого
усилия к трубопроводам.
Такие соединения применяются при стыковке (расстыковке) трубопроводов от-
дельных ступеней многоступенчатой ракеты.
Иногда разъемные соединения выполняют с клапанными механизмами, герме-
тизирующими концы магистралей после расстыковки.
5.5.6. Устройства для гашения колебаний топлива в баках
Корпус ракеты испытывает продольные и поперечные колебания в широком
диапазоне частот от воздействия внешних сил и возмущений (работа пульсирующего
двигателя, порывы ветра, работа автоматов стабилизации и т. п.).
Колебания воздействуют на массу жидкости, находящуюся в баках, что приводит
к значительному смещению центра масс. Это отрицательно сказывается на работе ор-
ганов устойчивости и управляемости, а при совпадении частот свободных колебаний
жидкости с частотой собственных колебаний корпуса может привести к резонансу и
разрушению РН.
Для уменьшения колебаний зеркала жидкости в баках предусматривают:
• устройства гашения колебаний жидкости;
• перфорированные перегородки (демпфирующие устройства);
• конусы и продольные перегородки.
264
5
Рис. 5.35. Гасители поперечных
gj колебаний жидкости:
1 — пластина гасителя колебаний;
2 — обечайка бака;
3, 4 — стержни крепления пластины;
5 — опоры крепления стержней
Рис. 5.37. Компоновочная схема гаргрота:
1 — труба; 2 — крышка; 3 — кронштейн;
4 — обечайка; 5 — кронштейн; 6 — кабель
Рис. 5.36. Крепление элементов арматуры внутри бака
Перфорированные поперечные перегородки и
конусы уменьшают амплитуду колебаний топлива и
устанавливаются в передней части бака верхней сту-
пени и в нижней части первой ступени. Они эффек-
тивны при определенном уровне топлива.
Гасители поперечных колебаний выполняют
в виде тонких продольных пластин (6—8 шт.), ус-
тановленных равномерно по окружности вдоль всей
длины бака или на части длины. Ширина пластин
составляет ~ 0,5 радиуса бака. Для повышения жест-
кости пластин последние имеют продольные зиги
(рис. 5.35).
Гасители продольных колебаний выполняют в
виде плоских перфорированных пластин, установ-
ленных перпендикулярно продольной оси ракеты в
передней части бака. Продольные перегородки повы-
шают запас статической устойчивости ракеты по углу
крена. Эффективность их ниже, чем у поперечных, но
они гасят колебания жидкости во все время работы
двигателя.
Отметим, что демпфирующие устройства увели-
чивают пассивную массу ракеты.
Рис. 5.38. Крепление труб
снаружи (а) и внутри (б) бака:
1 — труба; 2 — хомут;
3 — ложемент;
4 — кронштейн;
5 — панель
5.5.7. Крепление элементов арматуры
Для крепления элементов арматуры внутри и снаружи предусматривают установ-
ку кронштейнов, привариваемых к корпусу бака.
Кронштейны используются для монтажа элементов арматуры с помощью болто-
вых и винтовых соединений.
На рис. 5.36 показан вариант крепления внутри бака демпфирующих перегоро-
док и датчика СОБ.
Компоновка элементов электрических и пневмогидравлических связей снаружи
баков под гаргротом показана на рис. 5.37, 5.38.
Во всех соединениях должны быть предусмотрены меры по их контровке. При-
меняют пружинные и отгибные шайбы, самоконтрящиеся гайки, контровочную про-
волоку.
5.5.8. Люки, штуцера, фланцы баков
Для выполнения сборочных и монтажных работ у баков больших диаметров на
одном из днищ делают люк-лаз, который закрывается крышкой. Необходимо, чтобы
люк располагался на части днища, имеющей меньшую кривизну для более равномер-
ного нагружения горловины и крышки.
Диаметр люка-лаза выбирается из технологических соображений (обычно
400...500 мм).
Люк-лаз (обычно самый большой вырез в оболочке днища) требует компенсации
в толщине материала (в утолщении по сечению шпангоута люка). Отметим, что кон-
центрация напряжений возрастает с увеличением диаметра отверстия. Конструкции
люков-лазов показаны на рис. 5.39.
266
Рис. 5.39. Варианты конструктивного исполнения люка-лаза и крышки:
1 — люк-лаз; 2 — крышка
Рис. 5.41. Конструкция фланцев:
1 — фланец; 2 — горловина; 3 — днище
Рис. 5.40. Конструктивное
исполнение ввода труб в бак:
а) ввертный; б) вварной
Окантовка люка (усиление) может быть реализована в виде шпангоута или в виде
приварных накладок (их применение нежелательно, т. к. сама сварка требует допол-
нительного усиления).
Необходимость усиления вырезов относится и другим вводам в бак элементов
пневмогидросистем и выводу расходных магистралей (рис. 5.40).
Отверстия под фланцы и штуцера не следует располагать в одном сечении (чтобы
не нарушать требуемую прочность бака), а на определенном удалении друг от друга и
в шахматном порядке.
Фланцы изготовляют обычно точением и приваривают к отбортовке отверстий
бака.
Форма фланца и размеры определяются агрегатом, который на нем устанавлива-
ется.
Фланцы могут иметь резьбовые или гладкие отверстия под шпильки и болты
(рис. 5.41).
Если диаметр штуцера меньше 15 мм, то его вваривают в отверстие на баке. При
больших диаметрах штуцеров их делают из трубы соответствующего диаметра и при-
варивают к отбортовке отверстия.
5.6. КОНСТРУКТИВНО-СИЛОВЫЕ СХЕМЫ
СУХИХ ОТСЕКОВ КОРПУСА PH
Все небаковые отсеки ракеты называются сухими. К ним относятся двигательные
отсеки ракет с ЖРД, межбаковые отсеки, обтекатели, переходники, корпус ракеты с
подвесными баками и т. д.
Конструкция и форма сухих отсеков зависит от назначения и общей компоновки
ракеты. Наибольшее распространение имеют цилиндрические и конические отсеки,
выполненные в виде оболочек, подкрепленных силовым набором.
Главным фактором, определяющим конструктивно-силовую схему корпуса отсе-
ка, является величина и характер действующей нагрузки (растяжение, сжатие, внеш-
нее давление и т. д.), а также его специальные свойства (сбрасываемость отсека и др.).
По конструктивному признаку сухие отсеки РБл подразделяют на:
• бесстрингерные (гладкие) — выполняются в виде неподкрепленной оболочки,
усиленной только по местам стыковки со смежными конструкциями;
• каркасные — выполняются в виде оболочки, подкрепленной силовым набором
(каркасом);
• отсеки вафельной конструкции — выполняются в виде оболочки с часторасполо-
женными подкрепляющими ребрами, выполненными заодно со стенкой;
• отсеки гофрированной и сотовой конструкции — выполняются из многослойных
оболочек с заполнителем;
• ферменные — выполняются в виде фермы, т. е. каркаса, лишенного оболочки.
Тот или иной тип корпусной конструкции выбирается из соображений миниму-
ма ее массы при удовлетворении известных эксплуатационных требований.
5.6.1. Бесстрингерные (гладкие) отсеки
На рис. 5.42 показана бескаркасная конструкция переходного отсека, состоящая
из обшивки и двух стыковочных шпангоутов. Гладкий отсек выполняется в виде не-
подкрепленной гладкой оболочки 4 (иногда с лючками), имеющей по торцам стыко-
вочные шпангоуты 3 и 5, предназначенные для соединения с соседними отсеками
(рис. 5.42). В общем случае нагружения в сечениях отсеков корпуса действуют про-
268
дольные (нормальные) силы N, изгибающие моменты Л/изг поперечные силы Q, кру-
тящий момент Л/кр. Герметичные отсеки нагружены еще и внутренним давлением.
Оболочка в гладком отсеке воспринимает все эти виды нагрузки.
Отметим, что при осевом сжатии критические напряжения, вызывающие потерю
устойчивости гладкой оболочки, очень малы: окр ~ (0,1...0,2)вг где ат — предел теку-
чести материала.
5.6.2. Каркасные отсеки
Основными силовыми элементами каркасного отсека являются (рис. 5.43): об-
шивка 7, продольные силовые элементы — стрингеры 4, поперечные кольцевые
элементы — стыковочные 2 и промежуточные шпангоуты 3.
В каркасных отсеках обшивка работает на
растяжение (сжатие и изгиб) совместно со стрин-
герами. Конструкция отсека, в которой растяже-
ние (сжатие и изгиб) воспринимаются мощными
продольными силовыми элементами — лонжеро-
нами, — называется лонжеронной.
В этих конструкциях при осевом сжатии и из-
гибе удается достигнуть более высокого уровня
критических напряжений (окр == (0,5...0,7)ат), чем
в гладких отсеках.
Обшивка образует форму отсека, ограничивает
его внутренний объем, защищая его от воздействия
факторов окружающей среды. Как самостоятель-
ный силовой элемент обшивка работает на растя-
жение, в частности, от внутреннего давления.
Относительный вклад обшивки в работу кон-
струкции корпуса определяется:
• толщиной обшивки;
• частотой силового набора;
• характером соединения между обшивкой и
элементами набора.
Каркасные отсеки изготавливаются клепаны-
ми, что позволяет использовать более высоко-
прочные материалы. Это обеспечивает уменьше-
ние массы конструкции РБл.
Стрингеры — продольные элементы, под-
крепляющие обшивку, — воспринимают совмест-
но с обшивкой осевые нагрузки и изгибающие
моменты, действующие на отсек. Стрингеры че-
рез обшивку воспринимают и распределенные по-
перечные нагрузки, например, от внешнего аэро-
динамического давления — при этом шпангоуты
служат опорами для стрингеров.
Лонжероны — мощные продольные элементы
силового набора, воспринимающие сосредото-
ченные продольные и изгибающие нагрузки боль-
шой интенсивности (от узлов крепления двигате-
лей, смежных отсеков и агрегатов).
Рис. 5.42. Конструкция гладкого
(переходного) отсека:
/ — лючок; 2 — верхний шпангоут;
3 — направляющий штырь;
4 — обшивка; 5 — нижний шпангоут;
6 — отверстие под стыковой болт;
7 — болты; 8 — анкерная гайка
Рис. 5.43. Конструкция
каркасного отсека:
1 — обшивка; 2 — стыковочный
шпангоут; 3 — промежуточный
шпангоут; 4 — стрингер
269
1 2 3 4 5 6
a)
10 11 12
в)
Рис. 5.44 Типовые сечения элементов силового набора:
а) стрингеры; б) лонжероны; в) шпангоуты
7—5 открытые профили, 6 — закрытый профиль, 7 — лонжерон с усиленной верхней полкой, 8 —
лонжерон с верхней полкой, усиленной композиционным материалом, 9 — сборный лонжерон, 10—12 —
промежуточные шпангоуты, 13, 14 — усиленные шпангоуты (сборные), 15 — торцевой шпангоут
Общие требования к лонжеронам аналогичны требованиям к стрингерам.
Но есть и отличия: поскольку лонжерон работает в основном автономно на сосредо-
точенную нагрузку, связь его с обшивкой не имеет такого значения, как для стринге-
ра, но для повышения работоспособности обшивки целесообразно максимально ис-
пользовать опору на лонжерон.
Шпангоуты — по назначению подразделяются на:
• торцевые (стыковочные) — подкрепляют край
отсека корпуса и обеспечивают его надежное
соединение со смежными конструкциями;
• промежуточные — подкрепляют обшивку на
участке между торцевыми шпангоутами и
обеспечивают сохранение формы попереч-
ного сечения отсека. Позволяют повысить
общие критические напряжения потери ус-
тойчивости за счет уменьшения длины уча-
стка между опорами.
Типовые сечения элементов силового набо-
ра, изготавливаемых обычно прессованием, лис-
товой штамповкой или механической обработ-
кой, представлены на рис. 5.44.
В зависимости от включения тех или иных
элементов силового набора различают следую-
щие типы корпусных конструкций:
Монокок — корпус, у которого основным си-
ловым элементом является обшивка (глад-
кие отсеки или каркасные, когда обшивка
подкреплена набором из часто расположен-
ных стрингеров малого сечения). Монококо-
вые корпуса применяются тогда, когда про-
дольные нагрузки невелики и могут быть
восприняты обшивкой относительно не-
большой толщины. Конструкции корпусов
с обшивкой, подкрепленной только шпан-
гоутами, называют еще бесстрингерными.
Стрингерная — конструкция корпуса, со-
стоящая из тонкой обшивки, подкреплен-
ной стрингерами и шпангоутами.
Рис. 5.45. Конструкция
переходника со стрингерами.
1 — верхний шпангоут;
2 — направляющий штырь;
3 — фитинг; 4 — стрингер;
5 — обшивка; 6 — нижний шпангоут;
7 — отверстие под разрывной болт
270
Рис. 5.46. Конструкция приборного отсека каркасного типа:
1 — верхний опорный шпангоут; 2 — стрингер; 3 — промежуточный шпангоут;
4 — усиленный стрингер; 5 — обшивка; 6 — нижний опорный шпангоут
• Лонжеронная (балочная) — конструкция корпуса, в которой сжимающие и изги-
бающие нагрузки воспринимаются лонжеронами, а обшивка воспринимает
прежде всего напряжение сдвига и местные нагрузки.
Некоторые типовые конструкции приведены на рис. 5.45—5.46.
Так как тонкая обшивка плохо воспринимает и передает сосредоточенные силы,
то обычно в отсеках по узлам крепления ставят стрингеры или фитинги, которые по-
степенно включают обшивку в работу. Приближенно можно считать, что обшивка пол-
ностью включается в работу на длине, равной расстоянию между стыковыми болтами.
5.6.3. Отсеки вафельной конструкции
К ним можно отнести монолитные секции (панели) (рис. 5.47), применяющиеся
с целью:
• уменьшения количества соединений;
• улучшения совместности восприятия нагрузок обшивкой и подкрепляющим на-
бором и, следовательно, уменьшения массы конструкции в сильнонагруженных
корпусах.
В монолитных секциях обшивка и подкрепляющие ее ребра жесткости представ-
ляют единое целое. Чаще всего изготавливаются из толстых плит методами химическо-
го фрезерования, электрохимической обработки или механической обработки. Характер-
ным недостатком для этих процессов является низкий коэффициент использования
материала.
Рис. 5.47. Монолитные панели:
а, б, в) полученные фрезерованием; г) штампованная панель; д) литая панель
271
Ребра на секциях располагают обычно либо продольно (вдоль образующей по-
верхности одинарной кривизны), либо в виде системы перекрещивающихся
утолщений — секций вафельного типа. Вафельные секции могут использоваться для
изготовления оболочек как одинарной, так и двойной кривизны.
Применение монолитных секций в конструкциях баков и других емкостей, помимо
уменьшения массы, обеспечивает большую надежность сохранения герметичности.
Монолитные секции применимы в основном в сильнонагруженных корпусных
конструкциях, т. к. при малых величинах погонных усилий, действующих в оболочке,
оказывается технологически невозможным выполнить столь малые толщины стенок
и ребер, чтобы использование монолитных ребристых или вафельных секций было
рациональным-по массе.
5.6.4. Отсеки гофрированной и сотовой конструкций
Гофрированные обшивки обладают высокой эффективностью по массовым ха-
рактеристикам в конструкциях, работающих на сжатие и изгиб, так как гофрирован-
ный лист имеет значительно больший момент инерции относительно средней линии
обшивки (центра масс сечения), чем негофрированный той же толщины.
В то же время масса его увеличивается в сравнении с негофрированным незначи-
тельно. Гофрированные обшивки технологичнее, чем монолитные, и обеспечивают
лучшее использование металла, т. к. изготавливаются из тонкостенного листа путем
его гибки. Недостатком гофрированных обшивок является плохая работа на сдвиг
в направлении, перпендикулярном гофрам, а также сложность их соединения с тор-
цевыми шпангоутами.
Гофрированные листы (рис. 5.48—5.49) применяются в качестве продольного под-
крепления гладкой обшивки и в качестве заполнителя в трехслойных панелях и секциях.
в) г) д)
Рис. 5.48. Применение гофрированного листа в конструкции корпуса:
а) соединение гофрированной оболочки и торцевого шпангоута; б) продольное
и поперечное соединение гофрированных листов в обшивке; в) соединение гофрированной
обечайки (играет роль и продольного силового набора) с различными шпангоутами;
г) панели корпуса, изготовленные из гладких и гофрированных листов; д) сборный
лонжерон с гофрированной стенкой
272
Рис. 5.49. Нижний
переходник ракеты:
1 — гофрированная обшивка;
2 — шпангоут
Многослойные (чаще трехслойные) обшивки с
заполнителем эффективны в корпусных конструк-
циях, работающих на внешнее давление, сжатие, а
также при повышенных требованиях к жесткости об-
шивки (сохранению формы под нагрузкой). Стенка
многослойной оболочки имеет жесткость на изгиб в
продольном направлении, в несколько десятков раз
превышающую жесткость эквивалентной по массе
однослойной гладкой оболочки. Обеспечивается это
тем, что тонкие несущие слои из высокопрочного
материала, разделенные более толстым слоем запол-
нителя, в качестве которого обычно используются
материалы или конструктивные элементы низкой
плотности, образуют конструктивную схему, имею-
щую момент инерции сечения значительно боль-
ший, чем однослойная обшивка такой же массы.
Широко применяются различные конструкции
стенок многослойных оболочек (рис. 5.50).
В качестве заполнителя применяются легкие
материалы и конструкции (пенопласт, легкие пласт-
массы, гофры, соты и ребра из стекло- и углепласти-
ков, из алюминиевой, титановой и стальной фольги).
Толщины трехслойных обшивок, определяемые тол-
щиной заполнителя, выбираются в зависимости от вида заполнителя и конкретных
конструктивно-силовых требований и могут составлять от нескольких до нескольких
десятков мм.
Для соединения заполнителя с обшивкой применяются в зависимости от исполь-
зуемых материалов и формы заполнителя сварка, пайка, клепка или клеевое соединение.
Для отсеков гофрированной и сотовой конструкций значение критических на-
пряжений при осевом сжатии доводится до акр «(0,7...0,8)аг
5.6.5. Ферменные отсеки
Ферменные конструкции используют:
• в межблочных переходниках при «горячем» разделении ступеней;
• в силовых рамах крепления двигателей;
• в качестве термомостов баков, заправляемых низкокипящими (криогенными)
компонентами топлива.
Стержни ферменных отсеков соединяют два торцевых шпангоута. При этом каж-
дая пара стержней и участок шпангоута образуют неизменяемый треугольник. Фер-
менные отсеки изготавливают сварными. Не уступая каркасным в восприятии осевых
сил и изгибающих моментов, они хуже работают на нагрузки сдвига (перерезываю-
Рис. 5.50. Конструкции стенок многослойных оболочек:
а) трехслойная с гофром; б) трехслойная с сотовым заполнителем; в) трехслойная
с теплозащитным и теплоизоляционным слоями; г) двухслойная с теплозащитным слоем
273
Вид A
Рис. 5.51. Примеры конструкций ферменных отсеков:
а) 12-стержневая ферма; б) 24-стержневая ферма
с промежуточным поясом для отсеков большого удлинения
щую силу и крутящий момент). Усилия с ферменной конструкции передаются в точ-
ках, а не по контуру, что требует местного усиления конструкции стыкуемой части. На
стержни ферм, используемых в качестве межблочных переходников при «горячем»
разделении ступеней, действует нагрузка, обусловленная давлением струй двигателей
при их работе до завершения процесса разделения ступеней.
Для поддержания температуры стержней не выше допустимой по условиям про-
чности на стержни наносят теплозащитное покрытие. Для облегчения ферм применя-
ют биметаллическое соединение стержней и узлов, при котором стержни изготавли-
вают из высокопрочного конструкционного материала (сталь, титановый сплав),
а узел их стыковки — из более легкого алюминиевого сплава.
В конструкции ферм — термомостов, используемых для подвески ненесущих
криогенных емкостей, для изготовления стержней применяют материалы с низкой
теплопроводностью (стеклопластики, титановые сплавы).
При конструировании ферм стремятся обеспечить их статическую определи-
мость, так как статически неопределимая конструкция обычно оказывается тяжелее
из-за трудности точного учета распределения внешних нагрузок между отдельными
элементами. Оси нескольких стержней в узлах должны сходиться в одной точке.
Основное внимание уделяется соединению стержней между собой. Задача состо-
ит в том, чтобы по возможности уменьшить передачу на стержень изгибающих мо-
ментов, т. е. приблизить характер его нагружения к силовой схеме фермы, в которой
соединения стержней считаются шарнирными. Примеры конструкций ферменных
отсеков приведены на рис. 5.51—5.52.
Рис. 5.52. Переходный отсек в виде рамы:
1 — кольцо; 2 — башмак под штырь; 3 — штырь; 4 — стержень;
5 — башмак под пироболт (замок); 6 — нижний башмак (под пироболт или замок)
274
Симметрично расположенные стержни должны иметь одинаковую жесткость. Рабо-
тоспособность стержней фермы существенно ухудшается при наличии начальной непря-
молинейности, конструктивных изломов и изгибов. Все это необходимо учитывать как
при конструировании, так и при предъявлении требований к деталям и полуфабрикатам.
5.7. СИСТЕМЫ РАЗДЕЛЕНИЯ СТУПЕНЕЙ И ОТДЕЛЕНИЯ
ГОЛОВНОЙ ЧАСТИ
К системам разделения ступеней и отделения головной части предъявляются сле-
дующие требования:
• обеспечение надежного и безопасного разделения без соударения с последующей
ступенью или ГЧ отработавшей ступени;
• минимальное возмущение параметров движения последующей ступени и осо-
бенно ГЧ;
• быстрота процесса отделения для сокращения потерь скорости;
• простота последовательности выполняемых операций при разделении;
• минимально возможное увеличение массы конструкции за счет введения эле-
ментов систем разделения (отделения).
Разделение ступеней и отделения ГЧ является сложной задачей, обеспечиваю-
щей надежность вывода полезной нагрузки в космос. Это объясняется тем, что при
разделении (отделении) на разделяемые части ракеты действуют не только силы, ко-
торые можно довольно точно определить (сила тяжести, тяга двигателей разделяемых
ступеней), но и параметры, имеющие вероятностный характер. К этим параметрам
относятся импульсы последействия и характеристики набора тяги двигателя при за-
пуске, аэродинамические силы, действующие на разделяемые части PH, особенно на
последние ступени при отделении ГЧ, или на предыдущие ступени при движении
в аэродинамической тени предыдущей ступени и при выходе из нее.
При разделении ступеней следует учитывать то, что максимальное значение силы
тяги маршевого двигателя предыдущей ступени в момент его выключения в несколь-
ко раз больше, чем максимальное значение силы тяги маршевого двигателя после-
дующей ступени (в 8—10 раз), а масса предыдущей ступени, практически не имеющей
топлива, сравнима или меньше массы ракеты после разделения. Поэтому дополни-
тельная скорость, сообщаемая предыдущей ступени, может быть достаточной для то-
го, чтобы эта ступень догнала ракету после разделения.
Любая система разделения (отделения) включает устройства силовой связи раз-
деляющихся частей и собственно устройства разделения (отделения).
Устройства силовой связи (крепления) обеспечивают механическую связь отделяе-
мых элементов конструкции до подачи команды на отделение и обеспечивают разрыв
этих связей в момент подачи этой команды.
Устройства разделения (отделения) сообщают от-
Рис. 5.53. Пироболт:
1 — фланец;
2 — пиропатрон;
3 — корпус
носительное перемещение отделяемым частям конст-
рукции (для обеспечения отведения их на безопасное
расстояние с точки зрения возможности соударений с
конструкцией, продолжающей полет по заданной
траектории).
Элементы силовой связи могут быть выполнены
в виде пироболтов, пиро- или пневмозамков и эле-
ментов оболочечных конструкций с пиротехнически-
ми устройствами кумулятивного действия.
Простейшим устройством силовой связи является
пироболт (рис. 5.53). При подаче напряжения на дето-
275
натор болта происходит подрыв заряда взрывчатого вещества и корпус болта разрушает-
ся по ослабленному сечению, разрывая связь между разделяющимися частями ракеты.
Разрывные болты просты и надежны в работе. Однако при разрушении их образуются
осколки. Для защиты агрегатов отделяемых частей от действия этих осколков устанавли-
ваются специальные экраны значительной массы. Кроме того, при подрыве пироболтов в
шпангоутах возникают локальные перегрузки, величина которых в течение короткого
времени может достигать 2000—3000 единиц. Поэтому разрывные болты устанавливают-
ся только в точках отделения, где нагрузка на болт не превышает 20 тс. В более нагружен-
ных точках (с нагрузкой до 100 тс) устанавливаются пиро- или пневмозамки.
В зависимости от требуемых характеристик разделения, места установки и на-
правления действия сил, возникающих при отделении ГЧ и других отделяемых час-
тей, используются следующие системы отделения:
• расталкивающие;
• тормозящие;
• комбинированные.
Расталкивающие системы отделения создают силы, действующие на все разде-
ляемые системой элементы в противоположных направлениях. Они сообщают неко-
торый импульс каждому из разделяемых элементов и придают этим элементам неко-
торую добавочную скорость.
Использование расталкивающих систем отделения целесообразно для сброса эле-
ментов конструкции ракеты, значительно меньших по массе, чем масса ракеты. При
этом к параметрам движения отбрасываемых элементов высоких требований по точ-
ности не предъявляется (например, сброс стартовых ускорителей ракеты «Ариан-4»).
Тормозящие системы отделения сообщают импульс только тем элементам конст-
рукции, которые уже не участвуют в полете по заданной траектории. Эти системы не
вносят возмущения в движение частей конструкции, продолжающих полет по задан-
ной траектории.
Комбинированные системы отделения применяются в тех случаях, когда необхо-
димо отделяемым частям конструкции придать движение по некоторой траектории,
отличающейся от прямой. При этом могут использоваться элементы отделения рас-
талкивающего и тормозящего типа, обеспечивающие комбинированное воздействие
как по времени, так и по направлению.
В качестве расталкивающего устройства отделения применяются пневмо- или
пиротолкатели, источником энергии которых является аккумулированный в балло-
нах газ или газ, полученный от сжигания порохового заряда, и также пружинные тол-
катели.
Торможение отделяемых частей конструкции производится:
• тормозными ракетными двигателями;
• аэродинамическими силами, образуемыми за счет увеличения лобового сопро-
тивления отделяемой части ракеты.
Тормозные ракетные двигатели могут быть твердотопливными, жидкостными
или газовыми. В последнем случае используется газ, запасенный в специально уста-
новленных на борту ракеты баллонах, или газ, имеющийся в других емкостях, напри-
мер, газ наддува топливных баков.
Для разделения ступеней используются две основные схемы разделения ступе-
ней: холодная и горячая. Часто используется комбинированная схема, использующая
элементы этих двух основных схем.
При «холодном» разделении недопустимо воздействие газов запускаемого мар-
шевого двигателя последующей ступени на конструкцию предыдущей ступени.
При «горячем» разделении такое воздействие допустимо, однако для этого на
элементах конструкции предыдущей ступени устанавливаются дополнительные теп-
лозащитные экраны.
276
При «холодном» разделении или разделении торможением отработавшей ступе-
ни основной двигатель последующей ступени запускается после того, как расстояние
между разделяющимися частями ракеты будет так велико, что газы реактивной струи
запускаемого двигателя последующей ступени не смогут разрушить конструкцию от-
деляемой предыдущей ступени.
«Горячее» или огневое разделение происходит путем запуска основного двигате-
ля последующей ступени еще до разрыва или в момент разрыва механической связи
между разделяющимися ступенями. При этом разделение происходит частично за
счет того, что предыдущая ступень тормозится вследствие газодинамического воздей-
ствия газов, истекающих из сопла двигателя последующей ступени.
Для защиты верхнего днища предыдущей ступени на нем устанавливается тепло-
защитный экран, одновременно поворачивающий газовый поток перпендикулярно
к направлению полета.
После прекращения работы ДУ предыдущей ступени и выхода двигателя после-
дующей ступени на режим ракета продолжает полет, а отделенная ступень выходит на
траекторию падения на Землю.
Разделение происходит за короткое время, поэтому при огневом разделении по-
тери скорости, связанные с разделением, малы. Платой за использование этой прос-
той схемы разделения является некоторое увеличение массы конструкции ракеты,
связанное с установкой стержневого отсека и газового отражателя.
«Холодное» разделение чаще применяется на ракетах, имеющих на последующих
ступенях специальные управляющие двигатели (третья ступень PH «Протон», вторая
ступень PH «Рокот»). Управляющие двигатели последующей ступени могут быть
включены до выключения двигателей предыдущей ступени, что обеспечивает непре-
рывное управление ракетой в процессе разделения.
Одновременно с подачей команды на выключение маршевого ЖРД включается
рулевой двигатель последующей ступени, который создает рулевые силы для управле-
ния полетом ракеты. По мере спада тяги маршевого двигателя предыдущей ступени в
некоторый момент подается команда на нарушение механической связи между ступе-
нями и включение тормозного двигателя предыдущей ступени. Команда подается так,
чтобы максимально возможное значение импульса последействия выключаемого
двигателя предыдущей ступени было меньше импульса, создаваемого тормозным
двигателем. Последующая ступень под действием силы тяги своего рулевого двигате-
ля и относительной скорости, создаваемой разностью импульсов тормозного двигате-
ля и импульса последействия выключаемого двигателя предыдущей ступени, отходит
от предыдущей ступени на некоторое безопасное расстояние, после чего включается
маршевый двигатель этой ступени. Разделение закончено, ракета продолжает полет,
предыдущая ступень летит как свободно падающее тело.
Если на предыдущей ступени имеются рулевые двигатели, разделение происхо-
дит так же, но команды на разрыв связей и запуск тормозных двигателей предыдущей
ступени подаются при спаде тяги рулевого двигателя предыдущей ступени.
5.8. КОНСТРУКЦИЯ ЭЛЕМЕНТОВ СПЕЦИАЛЬНОГО НАЗНАЧЕНИЯ
5.8.1. Теплозащитные днища (донная защита)
Теплозащитные днища (донную защиту), экраны, а также отражательные уст-
ройства применяют для защиты конструкции РБл при старте, в полете и при разделе-
нии ступеней от силового воздействия и воздействия лучистых и конвективных теп-
ловых потоков струй работающих РД.
277
Теплозащитные днища и экраны устанавливают по нижнему торцу РБл. В про-
цессе старта РН они воспринимают ударно-волновые и импульсные нагрузки, обус-
ловленные взаимодействием струй РД с элементами стартового сооружения, а также
возвратные тепловые потоки, а на траектории выведения — лучистые и конвективные
тепловые потоки от струй работающих РД. Типовой пакет теплозащиты, применяе-
мый в РН, состоит из двух слоев:
• наружного, допускающего воздействие высокой температуры в течение заданно-
го времени;
• внутреннего, имеющего низкий коэффициент теплопроводности.
Толщину наружного слоя выбирают с учетом обеспечения на контактной поверх-
ности с внутренним слоем температуры, гарантирующей его работоспособность
в течение всего времени полета РН, а толщину внутреннего слоя — из условия выдер-
живания заданной температуры на силовой конструкции.
Теплозащитное покрытие соединяют с силовой конструкцией с помощью клея
и дополнительного механического крепления специальными болтами, имеющими
тепловую защиту головок. Швы между панелями теплозащитного покрытия заклады-
вают специальными термостойкими герметиками и элементами, отличающимися вы-
сокой эрозионной стойкостью. Толщину покрытия делают переменной в соответст-
вии с законом распределения теплового потока по поверхности и изменением его по
времени.
В некоторых случаях конструкция донной защиты может выполняться трехслой-
ной. Наружный слой экрана теплозащиты делают из материала с высокой отража-
тельной способностью, например, полированной нержавеющей стали.
Топливные баки для жидкого водорода для снижения потерь на испарение при
нахождении ракеты на ПУ и в полете покрывают теплоизоляцией. Даже при этом по-
тери на испарение на стартовой позиции и в полете достигают 6% в час. Теплоизоля-
ция наносится с наружной стороны бака.
5.8.2. Теплозащитные экраны
Теплозащитные экраны устанавливают в открытых хвостовых отсеках на уровне
плоскости крепления РД к корпусу РН для предохранения от нагрева вышерасполо-
женных конструкций. Применяют термостойкий материал с высокой отражательной
способностью (например, полированные титановые сплавы). Индивидуальная защи-
та элементов двигателя выполняется в виде кожухов или обмоткой термостойкой
тканью (лентой).
5.8.3. Отражательные устройства
Отражательные устройства устанавливают по верхнему торцу РБл. Они предназ-
начены для защиты его конструкции (баков, находящихся под давлением) от разру-
шения взрывного характера в процессе «горячего» разделения ступеней РН, собран-
ных по схеме «тандем», и при разделении ступеней воспринимают силовое и тепловое
воздействия струй двигателей последующей ступени. Если время действия тепловых
потоков на теплозащитные днища -100—500 с, то на отражательные устройства —
-Юс. Однако при этом тепловой поток воздействует на них в условиях эрозии тепло-
защитного материала, обусловленной действием скоростного напора струи РД.
Форма отражательных устройств определяется компоновкой межблочного пере-
ходного отсека и зависит:
• от количества и расположения РД последующей ступени;
• местоположения донной защиты относительно среза сопел РД и т. д.
278
Нагрузки, действующие на отражательное устройство, являются производными
от энергии струй РД и определяются формой поверхности и линейными размерами
отражательного устройства. В настоящее время среднеинтегральное давление на по-
верхность отражательного устройства достигает 0,2—0,3 МПа, а непосредственно под
струей РД — до 1 МПа.
Наиболее распространенными формами отражательных устройств являются:
• сферический сегмент;
• коническая поверхность со скруглением при вершине (угол полураствора а =
= 45-60°).
По конструктивно-силовой схеме различают отражательные устройства несущего
и разгруженного типа.
В первом случае их конструкцию рассчитывают на восприятие всех действующих
нагрузок и тепловых потоков и выполняют в виде самостоятельного клепаного или
сварного корпуса.
Во втором случае учитывают давление в газовой подушке бака как силовой фак-
тор, разгружающий конструкцию отражательного устройства, в силовую схему кото-
рого включено верхнее днище топливного отсека.
Конструкция несущего отражателя состоит из обшивки, подкрепленной ради-
альным и кольцевым наборами, и опорного торцевого шпангоута. С внешней сторо-
ны наносят тепловую защиту из материала с низкой теплопроводностью и высокой
эрозионной стойкостью (например, прессованный асботекстолит).
Разгруженное отражательное устройство состоит из обшивки с тепловой защитой
и наполнителя, обеспечивающего контакт с днищем топливного отсека. Наполнитель
должен обладать достаточной прочностью на сжатие и быть легко обрабатываемым.
Этим требованиям хорошо отвечают пенопласты.
5.8.4. Узлы связи с комплексом наземного оборудования
Узлы связи PH с комплексом наземного оборудования обеспечивают:
• транспортирование PH;
• установку на стартовое сооружение;
• связь с агрегатами и системами стартового комплекса в процессе подготовки
и проведения пуска.
Окончательно собранная и испытанная PH перекладывается с монтажно-стыко-
вочных тележек или со стенда общей сборки на транспортно-установочный агрегат,
с помощью которого доставляется на стартовую позицию (СП) и устанавливается на
стартовое сооружение.
К установленной PH стыкуют средства комплекса наземного оборудования, сов-
местно с бортовыми системами и устройствами обеспечивающие заправку баков ком-
понентами топлива, зарядку баллонов сжатыми газами, электропитание в период
предстартовой подготовки, подключение технологических систем, в том числе: сис-
тем обогрева, предпусковой продувки, вентиляции и др.
В период собственно старта PH связь между нею и комплексом наземного обору-
дования осуществляется до отделения ее торца от плоскости стартового сооружения,
которое фиксируется после прохождения -100 мм от начала подъема.
Можно выделить ряд общих для различных PH узлов связи, которые обеспечива-
ют ее взаимодействие с комплексом наземного оборудования:
• транспортировочные опоры, узлы крепления траверс (балок) для кантования
и перекладывания блоков и собранной PH;
• узлы силового крепления к стартовому сооружению;
279
• узлы силовой связи с агрегатами обслуживания;
• заправочные соединения компонентов топлива;
• платы электрических и пневматических разъемов;
• узлы связи, расстыковка которых происходит после отделения PH от стартового
стола.
5.8.5. Транспортировочные опоры
Наиболее распространено горизонтальное транспортирование РБл или собранной
PH (исключение составляет вертикальное транспортирование PH «Сатурн-V»). РБл
или собранную PH укладывают на ложементы транспортного агрегата на специальные
опоры корпуса PH. Положение опор выбирают из условия минимальных нагрузок, дей-
ствующих на корпус PH при транспортировании и обеспечения более равномерного
распределения реакции между опорами. Чаще всего опоры располагают вблизи стыков
отсеков РБл или по их торцам. Для разгрузки основных опор иногда применяют так на-
зываемую тарированную опору, обеспечивающую приложение к PH в месте ее установ-
ки вполне определенной силы, уменьшающей реакции на основные опоры. Конструк-
ция узлов, используемых в качестве опор, должна предусматривать минимальное уве-
личение массы шпангоута в месте его постановки. Одна из возможных конструкций
подобного узла приведена на рис. 5.54, а, где опора имеет вид накладного фитинга, а
нагрузка параллельна касательной к контуру шпангоута. При этом для уменьшения из-
гибающего момента, действующего на шпангоут, вылет h должен быть минимальным.
В качестве опоры может быть использован шпангоут корпуса. В этом случае опора
транспортного устройства имеет вид ложемента с углом охвата -120°. Опоры в виде на-
кладных фитингов могут быть съемными — их снимают после установки PH на стартовое
сооружение. Это улучшает массовые характеристики PH, но усложняет ее эксплуатацию.
В большинстве случаев узлы, предназначенные для транспортирования, исполь-
зуют и в качестве технологических опор для крепления съемного технологического
оборудования (например, балок). Использование технологической балки, опираю-
щейся на фитинги, закрепленные на блоке, позволяет обеспечить удобство работ
и минимальные нагрузки на корпус при перекладывании РБл, собираемого вертикаль-
но, на стыковочную тележку для последующей горизонтальной сборки (рис. 5.54, б).
5.8.6. Узлы силового крепления PH к стартовому сооружению
Для удержания PH на стартовом сооружении при действии ветровых нагрузок
в период подготовки к пуску предусмотрено ее крепление с помощью специальных
замков. Эти замки размещают в плоскости, по которой в процессе старта происходит
расстыковка PH со стартовым сооружением или со специальным узлом крепления,
остающимся на стартовом сооружении, но входящим в состав PH. Подобный узел
крепления может быть выполнен в виде переходной рамы прямоугольного или трапе-
циевидного сечения (рис. 5.55).
Во внутреннем объеме переходной рамы располагают трубопроводы, арматуру,
различные соединения связей «борт—земля», а также замки силовой связи с PH. Ко-
личество замков зависит от нагрузки, действующей в стыке, и допустимого усилия на
один замок. Обычно замки не воспринимают перерезывающую силу, поэтому на сты-
ке PH с переходной рамой устанавливают шпильки, выполняющие роль направляю-
щих в момент старта. Замки силового крепления могут открываться как заранее, так и
в процессе старта. В первом случае старт называется свободным, во втором — стес-
ненным (заневоленным). Стесненный старт уменьшает динамические нагрузки в мо-
280
Вид A
б)
Рис. 5.54. Конструкция опоры (а)
и схема перекладки блока с помощью
технологических балок (б):
1 — передний узел; 2 — корпус;
3 — балка; 4 — задний узел
Рис. 5.55. Схема крепления РН на стартовом
сооружении с помощью переходной рамы:
1 — корпус РН; 2 — переходная рама;
3 — пусковое устройство; 4 — плоскость
разделения при старте РН; 5 — замок
Рис. 5.56. Схема узла системы
управляемого освобождения
РН «Сатурн-V» и пускового устройства:
1 — деформирующийся стержень;
2 — основание матрицы; 3 — корпус РН;
4 — серьга; 5 — болты крепления; 6 — щеки
матрицы; 7 — кронштейн; 8 — опорная тумба
Рис. 5.57. Схема конструкции
разрывной платы электроразъемов:
1 — нижняя плата; 2 — верхняя плата;
3 — разъемы; 4 — крышка; 5 — замок
мент старта и обеспечивает более быстрое прохождение участка начального движе-
ния. При стесненном старте силовые узлы крепления имеют специальные
устройства— механические демпферы, усилие сопротивления движению которых
уменьшается по мере подъема РН. Схема такого устройства, применяемая на РН «Са-
турн-V», показана на рис. 5.56.
281
5.8.7. Узлы силовой связи с агрегатами обслуживания
Предназначены для исключения соударения PH с агрегатами обслуживания при
нахождении PH на стартовом сооружении. Эти соударения возможны из-за различий
конструкционных материалов и жесткостных характеристик конструкций PH и агре-
гатов обслуживания, из-за их перемещения относительно друг друга под действием
ветровых нагрузок и т. п.
Исключение соударений обеспечивается двумя путями:
1) установкой на площадках агрегата обслуживания следящего привода в виде
катков (роликов) на PH, по которым скользят контактирующие узлы площадки;
2) установкой зажимного устройства на агрегате обслуживания и Т-образного
кронштейна (кнехта) на PH.
5.8.8. Заправочные соединения компонентов топлива
Заправочные соединения предназначены для заправки баков PH компонентами
топлива и их слива (при необходимости). Заправочные соединения различают по типу
стыковки (ручная или автоматическая) и по моменту расстыковки (до старта или в
момент старта). Стыковка и расстыковка заправочных устройств регистрируется спе-
циальными датчиками. Заправочные соединения для зарядки систем PH сжатыми га-
зами в большинстве случаев располагают на ее торце.
5.8.9. Платы электрических и пневматических разъемов
Платы электрических и пневматических разъемов служат для:
• связи бортовых электрических систем с наземными;
• снабжения их электрической энергией от наземных источников вплоть до мо-
мента старта и переключения питания на бортовые источники.
По конструкции (рис. 5.57) плата состоит из верхней и нижней половин, которые
соединяются между собой замковым механизмом, обеспечивающим надежную сты-
ковку при значительных вибрациях и расстыковку при движении PH или кабель-за-
правочной мачты (КЗМ).
После расстыковки разъемы закрываются защитными крышками. Платы на PH
размещают как на торце, так и на боковой поверхности (при наличии КЗМ).
ЛИТЕРАТУРА
1. Основы конструирования ракет-носителей космических аппаратов: Учеб, для
студентов вузов / Б. В. Грабин, О. И. Давыдов, В. И. Жихарев и др.; Под ред.
В. П. Мишина, В. К. Карраска. — М.: Машиностроение, 1991. С. 416.
2. Кобелев В. И., Милованов А. Г. Ракеты-носители. Учеб, пособие: МАТИ. — М., 1993.
С. 184.
3. Паничкин Н. И., Слепушкин Ю. В. и др. Конструкция и проектирование космиче-
ских летательных аппаратов. — М.: Машиностроение, 1986. С. 344.
4. Пенцак И. Н. Теория полета и конструкция баллистических ракет. — М.: Маши-
ностроение, 1974. С. 344.
5. Ракеты-носители / Под ред. проф. С. О. Осипова. — М.: Воениздат, 1981. С. 315.
6. Синюков А. М., Морозов Н. И. Конструкция управляемых баллистических ракет. —
М.: Воениздат, 1969. С. 444.
282
СОДЕРЖАНИЕ ГЛАВЫ 5
5.1. Характеристика реактивного принципа движения
и особенности ракетного полета...................................235
5.2. Задачи К. Э. Циолковского...................................236
5.3. Общие сведения об устройстве PH.............................241
5.3.1. Конструктивно-силовые схемы корпуса ступени...........243
5.3.2. Баки..................................................246
5.4. Системы наддува топливных баков.............................253
5.5. Арматура топливных баков....................................256
5.5.1. Заборные устройства баков.............................256
5.5.2. Система синхронного опорожнения баков.................258
5.5.3. Трубопроводы, тоннельные трубы........................259
5.5.4. Сильфоны и гибкие трубопроводы........................261
5.5.5. Соединения трубопроводов..............................263
5.5.6. Устройства для гашения колебаний топлива в баках......264
5.5.7. Крепление элементов арматуры..........................266
5.5.8. Люки, штуцера, фланцы баков...........................266
5.6. Конструктивно-силовые схемы сухих отсеков корпуса PH........268
5.6.1. Бесстрингерные (гладкие) отсеки.......................268
5.6.2. Каркасные отсеки......................................269
5.6.3. Отсеки вафельной конструкции..........................271
5.6.4. Отсеки гофрированной и сотовой конструкций............272
5.6.5. Ферменные отсеки......................................273
5.7. Системы разделения ступеней и отделения головной части......277
5.8. Конструкция элементов специального назначения...............277
5.8.1. Теплозащитные днища (донная защита)...................277
5.8.2. Теплозащитные экраны..................................278
5.8.3. Отражательные устройства..............................278
5.8.4. Узлы связи с комплексом наземного оборудования........279
5.8.5. Транспортировочные опоры..............................280
5.8.6. Узлы силового крепления PH к стартовому сооружению.....280
5.8.7. Узлы силовой связи с агрегатами обслуживания..........282
5.8.8. Заправочные соединения компонентов топлива............282
5.8.9. Платы электрических и пневматических разъемов.........282
Литература ...........................................................282
ГЛАВА 6________________________________
Реактивные двигатели летательных
аппаратов
Двигатель является основной частью силовой установки летательного аппарата.
От конструктивного и технологического совершенства двигателя зависят и характе-
ристики летательного аппарата, и качество решаемых с его помощью задач в авиации
и космонавтике.
Реактивный двигатель создает тягу для перемещения аппарата в пространстве пу-
тем преобразования энергии собственного или внешнего источника в кинетическую
энергию отбрасываемой струи вещества. Для работы реактивного двигателя можно
использовать как вещество, размещенное на борту летательного аппарата, так и окру-
жающую среду, в которой движется аппарат.
Для создания реактивной силы необходимы:
• вещество, которое в виде реактивной струи выбрасывается из двигателя;
• источник первичной энергии, которая преобразуется в кинетическую энергию
реактивной струи;
• двигатель , то есть устройство, обеспечивающее преобразование энергии.
Источником первичной энергии реактивных двигателей в основном является хи-
мическая энергия топлива, которая при сгорании последнего в камере двигателя пре-
образуется в термическую энергию, сообщаемую обычно газообразному рабочему те-
лу, формирующему реактивную струю. В результате осуществления термодинамиче-
ских процессов в двигателе термическая энергия преобразуется в кинетическую
энергию реактивной струи. Такие двигатели называются химическими термическими
реактивными двигателями.
Рабочим телом или его составной частью могут быть:
• газообразная или жидкая окружающая среда, например, атмосфера Земли или
других планет, вода морей, рек, океанов;
• вещество, размещаемое в специальных емкостях (баках) аппарата или непосред-
ственно в камере двигателя;
• смесь вещества окружающей среды (например, воздуха) и жидкого или твердого
топлива, подаваемого в камеру из бака или размещенного непосредственно в ка-
мере двигателя.
Реактивные двигатели, используемые в настоящее время, представляют собой
широкий класс двигателей самого различного назначения. Область их применения
постоянно расширяется. Подавляющее большинство реактивных двигателей исполь-
зуют на летательных аппаратах различных типов.
В наименьшей степени зависят от окружающей среды реактивные двигатели, у
которых рабочее тело и источник первичной энергии размещены на самом летатель-
ном аппарате. Они широко используются в ракетах, поэтому такие реактивные двига-
тели получили название ракетных двигателей (РД).
284
Для полетов самолетов в пределах атмосферы (тропосферы и стратосферы) Зем-
ли широко используются реактивные двигатели, использующие в качестве рабочего
тела продукты сгорания топлива (например, углеводородного) в кислороде атмосфер-
ного воздуха. Такие двигатели называются воздушно-реактивными (ВРД).
6.1. РАКЕТНЫЕ ДВИГАТЕЛИ
6.1.1. Параметры и характеристики ракетных двигателей
Тяга ракетного двигателя (Р) — это равнодействующая сил давления на его поверх-
ность. При работе двигателя в пустоте его тяга может быть определена из выражения
Рп= ThWa+paFa, (6.1)
где rh — секундный расход топлива; Wa — скорость истечения газа на срезе сопла; ра ,
Fa — соответственно давление газа на срезе сопла и его площадь; Рп — тяга в пустоте.
При наличии давления окружающей среды для расчета формулы тяги использу-
ется выражение
Ph=rhWa + Fa(pa-ph), (6.2)
где ph — давление окружающей среды; Ph — тяга при наличии давления окружающей
среды.
Удельный импульс (/уд)
4д=^=5 = Ж’ (6.3)
где I— импульс двигателя; т — масса израсходованного за время т рабочего тела.
Удельный импульс является основным параметром, характеризующим совер-
шенство конструкции и эффективность преобразования в нем энергии. Величина
удельного импульса не зависит от тяги, создаваемой двигателем. Для химических ра-
кетных двигателей (ХРД) величина удельного импульса лежит в диапазоне 2000—
4000 нс/кг.
Суммарный импульс (/z) двигательной установки можно определить по следую-
щим зависимостям:
4=^,4=/мт, (6.4)
т
где Рср — средняя тяга двигателя; Ат — интервал времени работы двигателя.
Величину импульса последействия (/пд) стараются уменьшить, т. к. это обеспечи-
вает точность доставки полезного груза к цели.
Удельный расход топлива (Суд)
Суд=?=Т!-- <6-5)
Для химических ракетных двигателей величина удельного расхода топлива суще-
ственно выше, чем для воздушно-реактивных двигателей (ВРД). Поэтому время рабо-
ты ВРД существенно больше, чем ХРД.
Удельная мощность реактивной струи уд)
N._ ih W* FK
^стр.уд р- ~ 2 • /й • |КЭ ” Т ’
где Ncrp — мощность реактивной струи; — эффективная скорость истечения реак-
тивной струи.
285
Удельная масса двигательной установки (у)
М
где М — масса ДУ без учета топлива; Р — тяга ДУ
(6.7)
Дополнительные параметры, характеризующие
работу ракетного двигателя
1) Тип рабочего тела — выбирается в зависимости от области применения.
2) Время работы двигателя.
Если двигатель обладает системой многократного включения, то задается коли-
чество включений и интервал времени между ними.
3) Отклонение величины тяги от ее номинального значения Рном.
4) Значения давлений в камере Рк и на срезе сопла Ра.
5) Величина суммарного импульса /х.
6) Величина импульса последействия /пд.
Для оценки качества работы ракетных двигателей используются энергетические
коэффициенты полезного действия (кпд) т| и импульсные коэффициенты потерь ф.
7) Энергетические кпд Т| учитывают совершенство процесса преобразования теп-
лоты в работу, а импульсные коэффициенты потерь ф — потери энергии в элементах
камеры ракетного двигателя.
8) Суммарный коэффициент полезного действия (т|ц):
Я ’
7 7 раб
где £ц — работа, совершаемая ракетным двигателем за цикл; Яраб — теплота, выделяе-
мая двигателем за цикл.
Пц = Пр -Пс Пх = Пр с ' % (6.9)
где Т|р — энергетический кпд импульса давления Р, р = (PKF*)/rit; Т|с — энергетический
кпд в канале сопла; Т|р с — энергетический кпд процесса расширения; Т|т — термиче-
ский кпд.
9) Импульсный коэффициент потерь в камере сгорания (фк):
_ рд _ Лс,д * ^*»д
Фк /йд • рк,„ • f. „
где Рк — давление в камере двигателя; Л — площадь критического сечения сопла.
Индексы «и» и «д» соответствуют идеальным и действительным значениям пара-
метра.
Принято считать, что /йи = /йд; F* и = Л д, тогда:
Фк р
1 к. и
(6.8)
(6.10)
(6.Н)
(6.12)
10) Импульсный коэффициент потерь в канале сопла:
Фс=т^ =0,92^-0,99,
*Р,И
где Кр — коэффициент тяги. Нижний предел изменения величины (рс соответствует
ДУ с малыми тягами, а верхний — с большими тягами.
286
11) Импульсный коэффициент потерь удельного импульса:
_ Лд,д — РД ’ Ли _ * Лс,и * Лс,д _
фуд /уд,и *ДЛ ЛлЛЛл *р>и-Рк,И Фс Фк’
(6.13)
где / , / — действительный и идеальный удельный импульс.
Характеристики ракетного двигателя
Дроссельная характеристика
Зависимость тяги и удельного импульса двигателя от массового секундного рас-
хода топлива при постоянной высоте полета и неизменном соотношении компонен-
тов топлива называется дроссельной характеристикой ракетного двигателя.
В действительности при работе ракетного двигателя изменение массового се-
кундного расхода топлива rh сопровождается изменением параметров потока по трак-
ту двигателя (И^, Ра, Тк ). Однако, т. к. изменение rit на стабилизированном участке
полета незначительно, то принимают:
р
jr = const и = const. (6.14)
Дроссельные характеристики представляют собой семейство прямых с угловым
коэффициентом Л, зависящим от скорости на срезе сопла,
Высотная характеристика
Высотная характеристика — зависимость тяги и удельного импульса от высоты
полета при постоянном значении массового секундного расхода и неизменном соот-
ношении компонентов топлива.
6.1.2. Жидкостные ракетные двигатели (ЖРД)
Различают следующие типы ЖРД:
1 — ЖРД с вытеснительной системой подачи компонентов (ВСПК) топлива;
2 — ЖРД с турбонасосной системой подачи компонентов (ТНСПК) топлива,
среди которых можно выделить:
• ЖРД с газогенератором, работающим на автономном топливе;
• ЖРД с газогенератором, работающим на основных компонентах топлива;
• ЖРД без газогенератора с газификацией охладителя в зарубашечном пространст-
ве;
• ЖРД с двумя газогенераторами.
В зависимости от агрегатного состояния компонентов («Ж» — жидкость или «Г» —
газ), поступающих в камеру сгорания, все конструктивные схемы жидкостных ракет-
ных двигательных установок (ЖРДУ) можно условно классифицировать на «Ж — Ж»,
«Ж — Г» или «Г — Г». Необходимо отметить, что газификация компонента способству-
ет улучшению энергетических показателей ЖРДУ.
В ЖРД с ВСПК рабочее тело (инертный газ) из газового аккумулятора давления
через редукторы направляется в баки окислителя и горючего. Далее окислитель по-
ступает в смесительную головку камеры, а горючее в тракт охлаждения, образованный
двойными стенками камеры ЖРД.
Основным преимуществом данной схемы является конструктивная простота из-
за отсутствия турбонасосного агрегата (ТНА). Однако для ЖРД, работающих по ука-
287
занной схеме, характерны сравнительно невысокие значения тяги и удельного им-
пульса, что определило ее применение в качестве двигателей ориентации. Кроме того,
в связи с нагруженностью баков для компонентов с избыточным давлением они вы-
полняются толстостенными, что приводит к существенному ухудшению массовых ха-
рактеристик ЖРДУ в целом.
В конструктивной схеме ЖРДУ с ТНА, в качестве рабочего тела для приведения
во вращение турбины ТНА используется перекись водорода Н2О2, поступающая в па-
рогазогенератор и разлагающаяся в нем под действием катализатора перманганата ка-
лия KMgO4 с образованием высокотемпературного (600—800 К) парогаза. Турбина
обеспечивает вращение насосов окислителя и горючего, то есть подачу компонентов
топлива в камеру двигателя. Генераторный газ из турбины выводится через патрубок
и сопло за пределы двигателя. В некоторых ЖРД, работающих по указанной схеме, ге-
нераторный газ использовался для создания управляющих усилий для ориентации ЛА
в пространстве и для создания дополнительной тяги путем его введения в расширяю-
щуюся часть сопла.
Более эффективное использование генераторного газа в ЖРД достигается путем
его подачи в смесительную головку камеры через специальный газовод.
Если одним из компонентов топлива является жидкий водород, то его предвари-
тельно пропускают через систему последовательно расположенных насосов (это обес-
печивает снижение вероятности взрыва при резком повышении давления такого ком-
понента топлива) и затем подают в тракт охлаждения камеры, где происходит его га-
зификация, и в турбину ТНА, после чего через газовод в камеру двигателя.
В некоторых ЖРДУ оба компонента поступают в головку камеры в газообразном
состоянии. При этом один из газогенераторов относится к окислительному типу,
другой — к восстановительному.
Общие сведения о жидкостных ракетных топливах
Успешное освоение космического пространства осуществляется в основном
с помощью жидкостных ракетных двигательных установок. Жидкие ракетные топли-
ва (ЖРТ), по сравнению с твердыми (ТРТ) обеспечивают лучшие энергетические ха-
рактеристики, возможность многократного включения и выключения двигателя,
а также оперативное изменение тяги при полете ЛА. Перспективное в принципе ис-
пользование ядерных ракетных двигателей сдерживается в настоящее время их массо-
выми характеристиками, а также сложностями, связанными с обеспечением радиаци-
онной безопасности и отводом тепла от активной зоны после выключения двигателя,
вследствие остаточного тепловыделения радиоизотопов — продуктов цепной реакции
деления. Несомненно, что ЖРТ останутся основным энергетическим источником для
ракетных двигателей различного назначения на ближайшие десятилетия.
В ракетных двигателях на химическом топливе выделение энергии происходит за
счет следующих химических реакций:
а) реакции окисления-восстановления (окисления), когда энергия выделяется
при реакции между окислительными и горючими элементами; топливо состоит
в этом случае по крайней мере из двух веществ — окислителя и горючего;
б) реакции разложения, когда тепло выделяется в процессе разложения сложного
вещества на более простые; топливо в этом случае может состоять только из одного
вещества;
в) реакции рекомбинации (соединения), когда тепло выделяется при соединении
одноименных атомов или радикалов в молекулы.
288
Окислитель и горючее в общем случае являются сложными соединениями, в со-
став которых могут входить как окислительные, так и горючие элементы, а также
нейтральные.
Горючим является такое вещество, которое независимо от того, содержатся в нем
окислительные элементы или нет, для полного окисления своих горючих элементов
требует окислителя извне. Так, например, этиловый спирт С2Н5ОН, кроме горючих
элементов (С и Н), содержит в себе и окислительный элемент — кислород, но его со-
вершенно недостаточно для полного окисления горючих элементов спирта; поэтому
этиловый спирт является горючим.
Окислителем является вещество, в котором хотя и могут быть горючие элементы, но
окисляющих элементов в нем имеется значительный избыток, так что при полном окис-
лении его собственных горючих элементов остается свободное количество окислитель-
ных элементов, которые могут быть использованы для окисления какого-либо другого
горючего. Например, азотная кислота HNO3 или перекись водорода Н2О2 содержат в се-
бе горючий элемент — водород, однако окислительный элемент (кислород) в них имеет-
ся в таком количестве, что при полном окислении водорода азотной кислоты или пере-
киси водорода в них остается избыток кислорода, который можно использовать для
окисления какого-либо горючего; поэтому HNO3 и Н2О2 являются окислителями.
К горючим элементам относятся углерод С, водород Н, бор В, алюминий А1, литий
Li и другие. Окислительными элементами являются фтор F, кислород О, хлор С1. Фтор и
кислород значительно превосходят по эффективности другие окислительные элементы.
Доли окислителя и горючего в топливе определяются величиной, называемой со-
отношением компонентов. Теоретическим (стехиометрическим) соотношением ком-
понентов % называется такое минимальное количество окислителя, которое необхо-
димо для полного окисления 1 кг горючего. Иначе говоря, теоретическое соотноше-
ние компонентов— это такое отношение расходов окислителя и горючего, при
котором окислитель полностью окисляет горючее, не оставаясь при этом в избытке.
Действительным соотношением компонентов Хо называется действительное от-
ношение расходов окислителя и горючего, подаваемых в камеру, которое может отли-
чаться от теоретического. Обычно х < Хо-
Отношение а = х/Хо называется коэффициентом избытка окислителя. Коэффи-
циент избытка окислителя, при котором получается максимальная величина удельно-
го импульса, называется оптимальным.
На рис. 6.1 представлена классификация жидкостных ракетных топлив, а в таб-
лице 6.1 — их основные параметры и области применения.
Рис. 6.1. Классификация ЖРТ
289
Таблица 6.1
Тип топлива Характер воспламе- нения а р, кг/м3 т 1 гор’ к ^УД’ Нс/кг Область применения
Н2О2 Катализа- тор — 1440 1250 1900 Рабочее тело для турби- ны
n2h4 (гидразин) Катализа- тор — 1000 1475 2200 Рабочее тело для турби- ны или вспомогатель- ного ЖРД
n2h4 + + N2H2(CH3)2 (несимметрич- ный диметил- гидразин) Самовос- пламене- ние 3,05 1180 3415 2770 Маршевые двигатели PH типа «Протон»
02>ж + + керосин Нет само- воспламе- нения 2,7 1020 3690 2930 Маршевые двигатели PH «Союз» и 1-й ступе- ни «Энергия»
HNO3 + N2H4 + + N2H2(CH3)2 Самовос- пламене- ние 3,0 1270 3165 2680 Маршевые двигатели ракет и малых PH
F2, ж + Н2, ж + + Li (LiH) (гидрид лития) Самовос- пламене- ние 15,0 670 4760 3970 Опытные образцы сверхмощных PH
О2, ж + Н2>ж Нет само- воспламе- нения 6,0 350 3420 3790 Маршевые двигатели верхних ступеней PH
Топлива ракетных двигателей могут быть разделены на следующие виды: жидкие
топлива раздельной подачи (многокомпонентные) и жидкие унитарные (однокомпо-
нентные) топлива.
В случае жидкого топлива раздельной подачи выделение энергии происходит
в результате реакции окисления — восстановления. Процесс окисления условно мо-
жет быть представлен как обмен электронами на внешней электронной оболочке ато-
мов, участвующих в этом процессе. При этом атомы горючих элементов отдают свои
электроны, а атомы окислительных элементов приобретают их.
Унитарным (однокомпонентным) топливом может быть такое индивидуальное
вещество или такая заранее приготовленная смесь веществ, которые при определен-
ных условиях выделяют тепло в результате химических реакций разложения или
окисления; в последнем случае все необходимые для окисления элементы находятся в
самом унитарном топливе. Несомненным преимуществом унитарных жидких топлив
перед жидкими топливами раздельной подачи является большая простота конструк-
ции двигателей, использующих эти топлива, так как при этом требуется лишь одна
линия системы подачи.
Однако жидкие унитарные топлива не нашли широкого применения в ЖРД
и используются главным образом для вспомогательных целей.
290
Жидкие топлива раздельной подачи находят самое широкое применение, так как
они обеспечивают двигателю достаточно высокие удельные параметры при сравни-
тельно приемлемых эксплуатационных свойствах.
Многокомпонентные гетерогенные топлива включают в себя высокоэнергетиче-
ские пары типа О2 + Be, О3 + Be, F2 + Li и водород в качестве разбавителя. Металл
в порошкообразном состоянии может находиться в горючем, и смесь при необходи-
мости может быть подана в камеру центробежным насосом. Обычно в состав гетеро-
генных топлив включается полимерное горючее-связка, предотвращающее вынос из
камеры несгоревшего порошкообразного горючего.
Топлива, имеющие температуру кипения при Рн = 101 325 Па более 293 К, назы-
ваются высококипящими, а менее 120 К — низкокипящими (криогенными). К по-
следним относятся О2 ж, Н2 ж, F2 ж, и они заправляются в ракету, как правило, непо-
средственно перед пуском.
Топлива раздельной подачи могут быть самовоспламеняющимися и несамовоспла-
меняющимися. К первым относятся такие топлива, воспламенение которых начинает-
ся самопроизвольно при контакте окислителя и горючего в условиях, имеющихся
в камере при запуске, без какого-либо дополнительного вмешательства. Несамовосп-
ламеняющиеся топлива для первичного воспламенения (при запуске двигателя) тре-
буют средства зажигания.
Наибольшее распространение получили двухкомпонентные самовоспламеняю-
щиеся и несамовоспламеняющиеся топлива.
Требования, предъявляемые к ЖРТ
Основные требования, предъявляемые к ЖРТ и идущие от особенностей ЖРДУ
и ЛА, можно разбить на четыре группы:
1. Энергетические требования.
2. Эксплуатационные требования для обеспечения надежной работы двигателя.
3. Требования при эксплуатации топлив вне двигателя.
4. Экономические требования.
Энергетические требования
• высокая теплопроизводительность;
• высокая температура продуктов сгорания;
• низкая молекулярная масса продуктов сгорания;
• высокая плотность топлива.
Если под энергетической эффективностью ЖРТ понимать совместное влияние
удельного импульса тяги и плотности топлива на конечную скорость ступени ЛА, то
для обеспечения высокой эффективности необходимо в общем случае учитывать все
четыре требования.
Наиболее эффективные ракетные топлива должны обладать высокой теплопро-
изводительностью химической реакции; малой молекулярной массой продуктов сго-
рания и высокой плотностью компонентов.
Для получения высокотеплопроизводительных топлив в качестве окислителей
выгодно использовать фтор, кислород или соединения с большим содержанием реак-
ционноспособных F2 и О2. В качестве горючих выступают элементы первых трех пе-
риодов и, в первую очередь, водород, углерод и обогащенные водородом соединения
углерода и азота.
291
Наиболее высокоэнергетическим ЖРТ является фторводородное топливо, теоре-
тический удельный импульс в пустоте которого составляет 4880 Н • с/кг.
Высоким удельным импульсом обладает кислородно-водородное топливо, проч-
но вошедшее в ракетно-космическую технику.
Продукты сгорания кислородно-водородного топлива нетоксичны, а сами ком-
поненты коррозионно не активны, что создает благоприятные эксплуатационные ус-
ловия. К сожалению, кислород и водород при криогенных и обычных температурах не
обеспечивают самовоспламенения, поэтому для процесса горения необходима систе-
ма зажигания.
Эксплуатационные требования для обеспечения надежной работы двигателя
Жидкостной ракетный двигатель является высокотеплонапряженным преобразо-
вателем тепловой энергии топлива в кинетическую энергию струи, и для его работы не-
обходимо обеспечить надежное охлаждение камеры. Охлаждение огневой стенки каме-
ры обычно осуществляют компонентами топлив. Охлаждающая способность компо-
нента в значительной степени определяется комплексом его теплофизических свойств.
Топливо или его компонент, являющийся охлаждающей жидкостью, должны об-
ладать:
1. Высокой удельной теплоемкостью, при этом единицей веса жидкости погло-
щается наибольшее количество тепла.
2. Высокой теплопроводностью. Такая жидкость способна пропускать и распре-
делять по объему большие тепловые потоки.
3. Значительной скрытой теплотой парообразования. При более высокой скры-
той теплоте парообразования охлаждающая жидкость закипит при более высокой
температуре и будет способна отнять от стенок большее количество тепла.
4. Наиболее высокой температурой кипения, что обеспечивает большую надеж-
ность охлаждения без вскипания жидкости в охлаждающем тракте.
5. Высокой химической стойкостью против разложения при высокой температу-
ре в охлаждающем тракте двигателя, что обеспечивает надежность охлаждения двига-
теля жидкостью с одинаковыми, принятыми в расчете, физическими свойствами.
6. Наименьшей возможной вязкостью, так как при высокой вязкости резко рас-
тут гидравлические сопротивления, увеличивается давление насосов, что ведет к уве-
личению веса турбонасосного агрегата (ТНА).
7. Наименьшим коэффициентом поверхностного натяжения, что способствует
лучшему растеканию по поверхности охлаждающей жидкости и исключает возмож-
ность образования паровых пузырей, вызывающих местные перегревы и точечные
прогары стенок камеры.
8. Высокой скоростью сгорания.
9. Малым периодом задержки воспламенения.
Требования при эксплуатации топлив вне двигателя
Эксплуатационные требования определяются свойствами топлив. Ими же опре-
деляются и эксплуатационные затраты, связанные с заправкой, хранением и контро-
лем. Выбор конструкционных материалов зависит как от коррозионной активности
компонентов топлива, так и от температуры их застывания. Длительное хранение ЛА
в заправленном состоянии требует высокой стабильности компонентов топлива. От-
работка ЖРДУ на нетоксичных, пожаро- и взрывобезопасных топливах значительно
упрощается вследствие снижения требований по герметичности, значительного уде-
шевления стендовой базы, транспортных расходов. Значение эксплуатационных тре-
292
бований возрастает для пилотируемых ЛА, а также для аппаратов многократного ис-
пользования и длительного хранения. Наконец, экологические проблемы требуют до-
полнительного и подробного анализа воздействия компонентов топлива и их
продуктов сгорания на окружающую среду. Поэтому в данном случае желательно ис-
пользовать нетоксичные, пожаробезопасные, взрывобезопасные, коррозионно-неак-
тивные, стабильные при длительном хранении, имеющие низкую температуру засты-
вания жидкие ракетные топлива.
Экономические требования
При массовом использовании ЛА с ЖРДУ, в том числе с ЖРДУ многократного
использования, возрастает роль экономического фактора. Производство новых высо-
коэффективных ракетных топлив невозможно без подготовки и развития сырьевой
и производственной базы. При этом стоимость производимых компонентов должна
быть достаточно низкой.
Выполнить все требования, предъявляемые к ЖРТ и сформулированные в на-
стоящем разделе, практически невозможно. Более того, одна группа требований часто
противоречит другой. Поэтому выбор компонентов топлива должен определяться в
основном теми задачами, которые выполняет ЛА.
Перспективные ЖРТ
Вслед за освоением и широким применением одного из наиболее эффективных
топлив — кислородно-водородного — стали осваивать топлива с применением наибо-
лее активного окислителя — жидкого фтора и его соединений. Применение этих
окислителей для двигателей нижних ступеней ракет сдерживается высокой токсично-
стью фтора и его продуктов сгорания. Поэтому возможной областью использования
фторных топлив являются верхние ступени ракет и космические аппараты, для кото-
рых исключительно важны высокие энергетические характеристики. Для межпланет-
ных космических аппаратов ведется разработка многофункциональных двигателей на
фторгидразиновом топливе. При малых уровнях тяг (для коррекции траектории поле-
та) используется режим работы двигателя на однокомпонентном гидразиновом топ-
ливе. Для обеспечения высоких уровней тяг (торможение космического аппарата,
увеличение скорости полета и т. д.) используется режим работы на двухкомпонентном
топливе (впрыск фтора в поток продуктов разложения гидразина). Дальнейшей перс-
пективой по применению более эффективных топлив может явиться освоение и вне-
дрение металлосодержащих топлив. Для двигательных установок боевых ракет имеет-
ся существенное ограничение круга возможных топлив — они должны допускать дли-
тельное хранение ракет в заправленном состоянии. При этом необходимо сочетать
высокий удельный импульс и большую плотность топлива. Работы по созданию и ос-
воению металлосодержащих топлив, типичным среди которых является гелирован-
ный гидразин с алюминиевым порошком в качестве горючего и высококонцентриро-
ванная перекись водорода или четырехокись азота в качестве окислителя, могут при-
вести к существенному улучшению энергетических и массовых характеристик
двигательных установок на высококипящих топливах.
Низкая плотность и низкая температура кипения жидкого водорода затрудняют
его использование в ракетах для продолжительных космических полетов. В связи с
этим перспективным представляется применение шугообразного водорода. Содержа-
ние твердого водорода в двухфазной смеси может составлять около 50%. Основные
преимущества шугообразного водорода перед обычным — повышенная плотность
и увеличенная хладоемкость, а следовательно, увеличение времени хранения.
293
Большое внимание уделяется улучшению свойств высококипящих углеводород-
ных горючих. Разрабатываются углеводородные горючие нефтяного происхождения и
синтетические с улучшенными физико-химическими свойствами, повышенной плот-
ностью и т. п. В США создано углеводородное горючее RJ-5, имеющее плотность, су-
щественно более высокую, чем керосин.
Гелеобразные топлива исследуют в связи с решением задач создания хранимой
однородной суспензии металлов в компонентах топлива, увеличения срока хранения
криогенных компонентов топлив в условиях невесомости, улучшения эксплуатаци-
онных характеристик топлив (гелирование способствует быстрому затуханию колеба-
ний в баке) и т. д. Создание новых гелеобразных топлив и комбинирование современ-
ных окислителей с гелеобразными горючими позволит существенно уменьшить раз-
меры крупных ракет-носителей.
Псевдожидкое топливо (или его компонент) состоит из порошкообразных ве-
ществ, которые можно флюидизировать газом по методу кипящего слоя и подавать
в камеру сгорания ракетного двигателя аналогично жидкому компоненту. При про-
хождении с некоторой скоростью потока газа, т. е. оживающего агента, через слой сы-
пучего, зернистого вещества частицы этого вещества начинают интенсивно переме-
щаться относительно друг друга, напоминая при этом кипящую жидкость и приобре-
тая некоторые ее свойства. Переход неподвижного слоя в кипящий происходит при
такой скорости газа, когда гидродинамическое давление потока уравновешивает си-
лы, действующие на частицу: инерционные, силы тяжести и др.
В качестве псевдоожижаемого окислителя рассматриваются порошкообразные
перхлорат аммония, нитрат аммония, гексанитроэтан и др., а в качестве горючего —
алюминий, бор, полиэтилен, гидриды алюминия, бериллия, циркония и др. Сжижаю-
щим агентом может быть нейтральный газообразный азот, а также активные сжижаю-
щие газы, например, для окислителя — кислород, а для горючего — водород.
В настоящее время работы в области псевдожидких и гелеобразных топлив нахо-
дятся в стадии экспериментальных исследований и стендовых испытаний опытных
образцов.
6.1.3. Особенности конструкции
жидкостных ракетных двигателей
Основные технологические узлы камеры
Камера ЖРД — важнейший агрегат ЖРД, работающий в весьма трудных услови-
ях. Сгорание топлива происходит в малом объеме при высоких значениях температу-
ры и давления. С целью повышения скорости сгорания поступающие жидкие компо-
ненты должны быть очень мелко распылены и равномерно перемешаны. Распыление
осуществляется форсуночной головкой (ФГ), от хорошей работы которой зависит эф-
фективность работы камеры ЖРД. Смешивание газообразных компонентов осу-
ществляется смесительной головкой.
Внутренние стенки камеры сгорания омываются газами, температура которых
значительно превышает температуру плавления материала стенки. Поэтому стенки
должны интенсивно охлаждаться. Кроме того, стенки камеры ЖРД испытывают вы-
сокое давление газов. Так как вес камеры сгорания должен быть минимальным, ее
выполняют из высокопрочных тонколистовых материалов.
Камера ЖРД, рис. 6.2, состоит из следующих основных технологических узлов:
форсуночной или смесительной головки (СГ); камеры сгорания или средней части;
охлаждаемой сопловой части; неохлаждаемой сопловой части — насадка.
294
Рис. 6.2. Разбивка камеры ЖРД
на технологические узлы:
1 — форсуночная (смесительная)
головка; 2 — камера сгорания;
3 — охлаждаемая сопловая часть;
4 — насадка
2 1 8 7 Б
Рис. 6.4. Конструкция
средней части камеры ЖРД:
1 и 2 — внутренняя и внешняя
стенки камеры ЖРД соответственно;
3 — цапфа; 4 — коллектор;
5 — патрубок с фланцем
Рис. 6.3. Схема форсуночной головки:
А — полость окислителя; Б — полость горючего;
1 — огневое днище; 2 — среднее днище;
3 — верхнее днище; 4 — шаровая опора;
5 — патрубок; 6 — коллектор; 7 — форсунка
горючего; 8 — форсунка окислителя
Эти узлы камеры ЖРД соединяются сваркой или с помощью болтов. Средняя
часть и сопловая охлаждаемая часть часто выполняются как одно целое.
Форсуночная головка схематически изображена на рис. 6.3. Количество форсу-
нок определяется размером камеры ЖРД и требованиями к распылению компонентов.
Некоторые камеры ЖРД вместо центральной шаровой опоры 4 имеют специаль-
ные цапфы, приваренные к рубашке средней части камеры примерно в центре тяжес-
ти (например, камеры ЖРД «Гамма» для ракеты «Блек Найт»).
Узел камеры сгорания и охлаждаемая часть сопла схематически изображены на
рис. 6.4. Стенка 1 соприкасается с газами при высокой температуре и должна интен-
сивно охлаждаться. С этой целью по каналам межрубашечного пространства протека-
ет охлаждающая жидкость — один из компонентов топлива, чаще всего горючее.
Каналы для жидкости могут быть образованы несколькими способами:
• установкой гофрированных проставок между рубашкой и стенкой (рис. 6.4, а);
• соединением пайкой П-образных профилей с последующей проточкой по по-
верхности прилегания рубашки (рис. 6.4, б);
• соединением пайкой профилированных трубок (рис. 6.4, в);
• фрезерованием, травлением или выдавливанием продольных каналов в стенке
(рис. 6.4, г).
Наибольшее распространение в практике фирм США, Англии и Франции полу-
чил метод изготовления стенок из профилированных стальных или алюминиевых
трубок (см. рис. 6.4, в), хотя применяется и метод, указанный на рис. 6.4, б.
Рубашка 2 изготовляется из высокопрочных материалов — стали, титана. Она
может быть выполнена сплошной по всему контуру стенки или в виде отдельных ко-
лец, что определяется расчетом на прочность камеры ЖРД при условии минимально-
го веса конструкции. В некоторых конструкциях рубашка изготовляется намоткой
стальной ленты или проволоки с последующей пайкой. Применяются также рубашки
из стекловолокна, пропитанного пластмассой.
Цапфы 3 воспринимают силу тяги камеры и привариваются к усиленной части
рубашки камеры ЖРД. Чтобы избежать больших деформаций гибких трубопроводов
при поворотах качающихся камер, горючее и окислитель можно подводить через осе-
вые сверления в цапфах.
Коллектор 4 служит для равномерного распределения охлаждающей жидкости по
каналам стенки камеры. Он выполняется из листового металла и приваривается или
припаивается к рубашке. Жидкость подводится через один, два или более патрубков с
приваренными фланцами 5 для соединения с трубопроводами, идущими от TH А.
Неохлаждаемая часть сопла испытывает сравнительно небольшое внутреннее
давление и изготовляется из тонколистового материала (стали, титана). Для защиты
от высокой температуры применяются различные покрытия, наносимые электро-
осаждением, плазменным распылением, диффузионным и другими способами.
Требования, предъявляемые к камерам ЖРД
Камера ЖРД любого типа и конструкции должна удовлетворять определенным
требованиям, обусловленным особенностями ее работы и эксплуатации.
Основными особенностями камеры ЖРД, отличающими ее от камер сгорания
других тепловых двигателей, являются:
1) высокая теплонапряженность ее рабочего объема, что предъявляет особые тре-
бования к конструкции камеры сгорания;
2) большие давления и температуры газов в ней (около 2—8 МПа и 2800—
3600 К), что предъявляет особые требования к материалам и системе охлаждения;
296
3) малое время, отводимое для сгорания в ней топлива (не больше 0,005 сек.), что
требует очень хорошего распыла компонентов топлива при подаче в камеру сгорания
для более полного их сгорания;
4) большие секундные расходы компонентов топлива, в силу чего требуется на-
дежное зажигание его при запуске двигателя;
5) резкое ухудшение экономичности работы камеры двигателя и условий ее ох-
лаждения при изменении режима работы относительно расчетного;
6) жесткое ограничение по весу вследствие специфики использования ЖРД на
летательных аппаратах, что требует применения для изготовления камеры легких и
прочных материалов при условии их работы с весьма малыми запасами прочности.
Главной задачей при проектировании и конструировании камеры двигателя яв-
ляется обеспечение возможно большего удельного импульса при минимальном весе
и максимальной надежности конструкции. В ряде случаев, когда это компенсируется
соответствующим уменьшением веса, вполне допустимо некоторое снижение удель-
ного импульса. Хотя такое мероприятие дает косвенный эффект и связано иногда со
значительным изменением конструкции двигателя, но тем не менее им не следует
пренебрегать.
Конструктивные и эксплуатационные особенности ЖРД во многом зависят от
вида применяемых компонентов топлива.
При проектировании камеры двигателя необходимо стремиться обеспечить:
1) надежное воспламенение топлива при запуске в любых атмосферных условиях;
2) устойчивое горение топлива (без пульсаций давления) в диапазоне установ-
ленных режимов работы двигателя;
3) малые потери энергии топлива при сгорании в минимальном объеме и задан-
ном режиме работы двигателя;
4) надежность охлаждения (если двигатель охлаждаемый) и работы в пределах ус-
тановленных режимов и ресурса;
5) небольшой перепад давления жидкости в охлаждающем тракте;
6) простоту конструкции камеры, минимальные удельный вес и стоимость.
Камеры ЖРД существующих двигателей, созданные на основании эксперимен-
тальных исследований, большинству этих требований в значительной мере удовлет-
воряют.
Выбор материала для камеры ЖРД
Материал камеры двигателя должен быть прочным, легким и обладать хорошими
пластическими свойствами. Для материала внутренней оболочки желательно сочета-
ние высокой теплопроводности и удовлетворительных прочностных свойств при вы-
соких температурах, однако, как правило, жаропрочные сплавы имеют плохую тепло-
проводность. Для внешней оболочки теплопроводность большого значения не имеет,
и поэтому здесь главным требованием к материалу является его высокая прочность и
возможно меньшая плотность. В некоторых случаях, при высокотеплопроводных
скреплениях, температура наружной оболочки может достигать 300—400 °C, и тогда
материал должен обладать достаточно хорошей жаропрочностью.
Кроме того, в зависимости от типа конструкции и применяемых компонентов,
материал должен удовлетворять условиям свариваемости, кислотостойкости и не яв-
ляться катализатором.
Основные рекомендации по выбору конструкционных материалов при произ-
водстве камер ЖРД представлены ниже:
297
1. Сталь 12Х18Н10Т применяется для внутренних оболочек цилиндрической
и сужающейся части камер при температуре газа менее 3000 К, а также для внутрен-
ней оболочки расширяющихся частей сопел.
2. Сталь 12Х18Н9Т в настоящее время не рекомендуется для внутренних оболо-
чек камер из-за склонности к межкристаллической коррозии.
3. Сталь 1Х21Н5Т целесообразно применять для выполнения силовых колец ка-
мер, т. к. она не требует термообработки после сварки.
Кроме того, сталь 1Х21Н5Т хорошо сваривается с бронзой и поэтому может ис-
пользоваться в качестве промежуточного кольца при сварке внутренних оболочек из
стали 12Х18Н10Т и бронзы типа БрХ-08. Сталь 1Х21Н5Т рекомендуется также для из-
готовления наружных оболочек расширяющихся частей сопел. Эта сталь при темпе-
ратуре пайки обладает высокой пластичностью, что обеспечивает хороший контакт со
связями и высокое качество пайки узлов сложной формы.
4. Сталь Х16Н4БА используется для изготовления наружной оболочки цилинд-
рической и сужающейся частей камеры двигателя, т. к. при температуре более 500 К
она обладает высокими механическими характеристиками.
5. Титановые сплавы применяются для изготовления наружной и внутренней
оболочек расширяющейся части сопел, работающих в восстановительной среде. Для
окислительной среды титановые сплавы применять не рекомендуется, т. к. они могут
возгораться из-за растрескивания окисной пленки.
6. Медные сплавы используются для изготовления внутреннего днища и внут-
ренних оболочек цилиндрической части камеры и суживающейся части сопла в дви-
гателях с высоким давлением в камере (более 10 МПа).
Конструктивные особенности выполнения
систем охлаждения камер сгорания
Камеры сгорания в основном выполняются двухстенными. В отдельных случаях
находят применение одностенные и трехстенные конструкции. Возможны и комби-
нированные конструкции, когда отдельные части камеры при принятой в целом двух-
стенной конструкции могут иметь одну или три стенки. Все эти различия в основном
определяются принятой схемой охлаждения или тепловой защиты стенок.
Простейшими являются одностенные камеры; они могут быть неохлаждаемыми
и охлаждаемыми. При малой продолжительности работы двигателя и невысоком теп-
ловом режиме иногда применяются одностенные камеры с емкостным охлаждением.
Значительно большую длительность работы обеспечивает нанесение на стенку
теплоизолирующих покрытий из тугоплавких материалов или материалов с малой
теплопроводимостью. Тогда стенка сохраняет относительно низкую температуру и ее
несущая способность практически не понижается к концу работы двигателя. Приме-
нение теплоизолирующих (керамических) покрытий, наносимых непосредственно на
стенку, в некоторых случаях, например при кратковременной работе двигателя с не-
высокой температурой в камере сгорания, может дать экономию в весе по сравнению
с системой наружного охлаждения до 20—30%.
Находят применение также конструкции камер сгорания с теплоизолирующим
покрытием, образующимся в процессе работы двигателя, рис. 6.5. Если одностенная
камера выполняется из стекловолокна, пропитанного фенольными или эпоксидными
смолами, то теплоизолирующее покрытие наносить не обязательно. При нагреве свя-
зующие вещества стеклопластика, выгорая, обугливаются, образуя на обращенной к
камере сгорания поверхности стенки покрытие, плохо проводящее тепло и обеспечи-
вающее сохранность механических свойств материала в невыгоревших слоях.
298
6
Рис. 6.5. Камера с вихревой головкой,
выгорающей вставкой и неохлаждаемым насадком сопла:
1 — грибовидный распылитель окислителя; 2 — форсунки горючего; 3 — коллектор горючего;
4 — выгорающая вставка; 5 — стенка камеры; 6 — сопловая приставка
В некоторых конструкциях камера образована из стекловолокна с ненаправлен-
ным расположением волокон. Толстостенный корпус камеры сгорания жестко соеди-
нен с металлическим фланцем, с помощью которого корпус камеры винтами крепит-
ся к головке. Уплотнение достигается с помощью пазового стыка. Лучшими механи-
ческими свойствами под действием газовой нагрузки обладает корпус камеры
сгорания, выполненный из стеклопластиковой узкой ленты с направленным распо-
ложением волокон, которая в процессе намотки укладывается ребром к оси камеры.
Стенки камеры могут защищаться от нагрева как в конструкции камеры с вихре-
вой головкой и выгорающей вставкой, изготовленной из силиконовой ткани, пропи-
танной фенольными смолами. Вставка с зазором входит внутрь алюминиевого корпу-
са камеры сгорания со стороны расширяющейся части сопла. Кольцевой зазор между
вставкой и корпусом заливается изоляционным материалом. К сопловому фланцу
корпуса на болтах крепится неохлаждаемая сопловая приставка с ребрами жесткости
на наружной поверхности.
Охлаждаемые одностенные камеры могут быть с внутренними каналами и без ка-
налов. В первом случае камера сгорания и сопло выполняются толстостенными
с внутренними сверлеными и относительно редко расположенными каналами. Для
облегчения камера может изготавливаться из алюминиевого сплава. Недостатком та-
кой конструкции является трудность выполнения каналов внутри стенки на сужаю-
щейся и расширяющейся части сопла. При этом требуется либо большая толщина
стенки для возможности сверления наклонного относительно оси камеры длинного
канала, либо изготовление сопла из отдельных коротких отсеков.
Наиболее просто осуществляется охлаждение одностенной камеры сгорания при
размещении ее непосредственно в баке одного компонента топлива (рис. 6.6).
Такая конструкция применима, если двигатель имеет сравнительно малую тягу,
а диаметральные размеры летательного аппарата позволяют разместить бак вокруг ка-
меры ЖРД. Стенка камеры сгорания может быть практически разгружена от действия
сил давления газов, когда применяется баллонная подача топлива.
299
Двухстенные конструкции применя-
ются в тех случаях, когда камеры имеют
регенеративное охлаждение. Они отлича-
ются типами связей между стенками и
формами каналов для наружного охлажде-
ния. Двухстенные камеры могут быть сов-
сем без силовых связей между стенками на
участке между головкой и соплом, с редко
расположенными и часто расположенны-
ми связями.
Рис. 6.6. ЖРД с камерой сгорания,
размещенной внутри топливного бака:
1 — стенка сопла; 2 — бак горючего;
3 — кожух; 4 — внутренняя стенка камеры
сгорания; 5 — наружный корпус бака
Двухстенные камеры без промежу-
точных связей могут выполняться при ма-
лых диаметрах камеры сгорания, а также
при низких давлениях в камере и темпера-
туре внутренней стенки порядка 250—
400 °C. При таких температурных услови-
ях внутренняя стенка толщиной 2—5 мм обладает достаточной жесткостью и способ-
на без потери устойчивости выдержать нагрузку от сил давления охлаждающей жид-
кости и газов. Наружная стенка, имеющая еще более благоприятные температур-
ные условия, также способна воспринять нагрузку от сил давления охлаждающей
жидкости.
Внутренняя и наружная стенки в таких конструкциях связываются между со-
бой через головку и вблизи обреза сопла, а иногда дополнительно у конца камеры сго-
рания.
Применение конструкции без связи между стенками возможно для камер сгора-
ния двигателей с небольшой тягой или рулевых и вспомогательных двигателей при
давлении в камере 1,5—2,0 МПа. Развитие ЖРД, сопровождающееся увеличением
диаметра камер, температуры горения и давления, вынудило перейти к конструкции
сначала с редко расположенными, а затем и с часто расположенными связями.
Редко расположенные связи выполняются в виде жестких колец, связывающих
стенки, что способствует уменьшению деформации. Кроме того, вблизи колец внут-
ренняя и наружная стенки работают совместно, что повышает общую несущую спо-
собность камеры. На участках между связями для разгрузки от температурных напря-
жений, которые возникают от разности продольных температурных деформаций сте-
нок, размещаются кольцевые компенсаторы, которые служат одновременно
дополнительными ребрами жесткости.
Такого типа конструкции применимы при толщине стенок порядка 5 мм и более,
сравнительно низкой температуре стенок и давлениях в камере порядка 2,5—3,0 МПа.
В весовом отношении конструкции с редко расположенными связями невыгодны.
Наиболее легкими и надежными являются конструкции с часто расположенными
связями, находящимися столь близко друг от друга, что действие избыточного давле-
ния охлаждающей жидкости не вызывает сколько-нибудь заметных местных проги-
бов стенки и работоспособность камеры определяется только несущей способностью
под действием сил давления газов и осевой силы. Стенки связываются между собой
сваркой или пайкой.
При сварном соединении на наружной стенке выполняются точечные или
сплошные выштамповки. Точечные выштамповки могут быть круглыми или оваль-
ными с большой осью, направленной вдоль образующей камеры. Точечная сварка
производится в местах выштамповок. Однако выштамповки при большой толщине
стенок загромождают тракт охлаждающей жидкости и не позволяют расположить свя-
зи достаточно часто.
300
Рис. 6.7. Трубчатая камера двигателя:
1 — карданная подвеска; 2 — подвод жидкого О2; 3 — штуцер для замера давления; 4 — фланец;
5 — головка; 6 — входной коллектор керосина; 7 — уплотнительное кольцо; 8 — пирозапальник;
9 — кабель; 10 — камера сгорания; 11 — место крепления рычага для управления вектором тяги;
12 — критическое сечение; 13 — бандажные кольца; 14 — сливной штуцер, 15 — спрямляющая
решетка; 16 — крышка головки; 17 — подвод пускового горючего, 18 — фланец; 19 — вход
горючего; 20 — трубки; 21 — силовое кольцо в критическом сечении; 22 — фланец для крепления
экрана; 23 — выходное сечение сопла; 24 — коллектор горючего; 25 — корпус головки; 26 —
подвод кислорода; 27 — подвод пускового горючего; 28 — подвод горючего
Сплошные выштамповки под роликовую сварку могут располагаться в зависи-
мости от принятого способа циркуляции охлаждающей жидкости — вдоль образую-
щей камеры сгорания и сопла или по винтовой линии, как в конструкции камеры
ЖРД с соединением стенок сваркой по винтовым выштамповкам. При многозаход-
ной винтовой связи увеличивается длина контактной поверхности стенок, по сравне-
нию с продольными связями, что способствует увеличению жесткости камеры и про-
чности связей.
Повышение давления газов приводит к необходимости значительно уменьшить
расстояние между связями, что возможно в паяных конструкциях. Для пайки исполь-
зуются твердые припои. Припои наносятся предварительно на спаиваемые поверхно-
сти. Пайка производится в печи. Твердые припои имеют температуру плавления до
1500 °C. При рабочей температуре в месте соединения 500 °C допустимые напряже-
ния в паяном шве составляют до 8 кг/мм2 (80 МПа), а при температуре 700 °C — около
1 кг/мм2 (10 МПа).
Паяные конструкции выполняются с ребрами и трубчатого типа. Простейшей
является конструкция с припайкой ребер, выполненных зацело с одной из стенок по
301
преимуществу с внутренней, к другой стенке. Ребра на внутренней стенке получают
механической обработкой. Они могут иметь переменный шаг по сечениям камеры
и сопла и располагаются вдоль образующей или по винтовой линии.
Трубчатые камеры выполняются из отдельных тонкостенных трубок, уложенных
вдоль образующей камеры сгорания и сопла, а иногда по винтовой линии. Трубки
имеют прямоугольное, овальное и U-образное сечение. На нецилиндрической части
камеры сгорания и сопла площадь поперечного сечения трубок переменна. Трубки
спаиваются по боковым прилегающим поверхностям. Для обеспечения надлежащей
прочности паяных швов используются усиливающие элементы. Такими элементами
могут быть наружные кожухи, бандажи или сплошная обмотка.
На рис. 6.7 показана трубчатая камера двигателя RZ-2, работающего на топливе
жидкий кислород — керосин. Тяга двигателя на земле 62 т (~ 620 кН), удельная тяга
24 • 102 Н • сек/кг; отношение FK/F* = 1,8, т. е. камера сгорания скоростная; степень
уширения сопла равна 8; давление в камере сгорания 3,8 МПа.
Охлаждение производится в «два хода». Охладитель по трубке проходит в сопло-
вой коллектор 24 и возвращается обратно по соседней трубке, после чего поступает
в форсуночное днище головки 5.
Жидкий кислород поступает в головку через угловой патрубок 2. Из головки кис-
лород и керосин поступают в камеру сгорания, где смесь воспламеняется от пиротех-
нического запальника 8, который в свою очередь поджигается электрической искрой.
Оболочка камеры выполнена из 312 спаянных никелевых трубок. Для повыше-
ния прочности набор трубок стягивается бандажными кольцами 13, которые на участ-
ке камеры сгорания образуют сплошную обечайку. Керосин, охлаждающий стенки
камеры, подается во входной коллектор 6 и через отверстия 19 поступает в трубки.
6.1.4. Ракетные двигатели твердого топлива
Компоновочная схема РДТТ
Ракетным двигателем на твердом топливе (РДТТ) называется двигатель прямой
реакции, в котором химическая энергия твердого топлива преобразуется сначала
в тепловую, а затем в кинетическую энергию продуктов сгорания, отбрасываемых
с высокой скоростью в окружающее пространство.
В РДТТ твердое топливо является одновременно источником получения энергии
и рабочего тела — продуктов сгорания.
Ракетный двигатель на твердом топливе (рис. 6.8) состоит из следующих основ-
ных частей: обечайки 7 с теплозащитным покрытием, соплового днища 9 с теплоза-
щитным покрытием, переднего днища 4 с теплозащитным покрытием, заряда твердо-
Рис. 6.8. Компоновочная схема РДТТ
302
го топлива 6 с бронировкой 5, деталей крепления заряда в двигателе 8, воспламени-
тельного устройства 3, поворотного сопла 12 с заглушкой 11, соплового вкладыша 13,
привода поворота сопла 10, реверсивных сопел с заглушками 1 и датчиков давления 2.
Заряд может состоять из одной или нескольких шашек твердого топлива. Частично
наружная поверхность заряда может быть бронирована, когда необходимо часть по-
верхности заряда предохранить от горения, с целью получения заданного закона из-
менения поверхности горения. Сопло с вкладышем и исполнительным органом уп-
равления тягой обычно называют сопловым блоком.
Воспламенительное устройство может входить непосредственно в конструкцию
РДТТ или быть обособленным. В простейшем случае воспламенительное устройство
состоит из навески дымного ружейного пороха (ДРП), иногда в сочетании с навеской
крупнозернистого дымного пороха (КЗДП) или пиротехнического состава, заключен-
ной в оболочку из тонкой материи. Навеска воспламенителя поджигается с помощью
электрозапала или пиросвечи с пиропатроном. Воспламенительное устройство дол-
жно обеспечить воспламенение всей площади горящей поверхности основного заряда.
Система исполнительных органов управления тягой служит для изменения
в процессе работы двигателя тяги по величине и направлению для обеспечения полета
ракеты по заданной траектории.
Для обеспечения точности попадания ракеты в цель она должна выйти в задан-
ную точку пространства и при этом иметь вполне определенные скорость и направле-
ние. В этот момент двигатель должен быть отключен или реверсирован.
Система крепления и фиксирования заряда зависит от назначения РДТТ. Иногда
в двигателях с небольшим временем работы заряд опирают на так называемую диаф-
рагму или колосниковую решетку, расположенную у соплового днища. Заряды, горя-
щие с поверхности канала, закрепляют в камере так, чтобы исключить возможность
их случайных перемещений и разрушения.
Узлы крепления двигателя к ракете зависят от ее типа. В многоступенчатой раке-
те двигатели отдельных ступеней скрепляются друг с другом. Двигатель первой ступе-
ни имеет устройство для закрепления на стартовом столе. Двигатель последней ступе-
ни скрепляется с приборным отсеком или головной частью ракеты.
РДТТ обладают следующими основными достоинствами:
1. Простота конструкции и технологии изготовления. Горение топлива в РДТТ
происходит в камере, где размещается весь заряд, без поступления каких-либо допол-
нительных веществ. Продукты сгорания топлива, омывая поверхность горения заря-
да, истекают через сопловой аппарат в окружающую среду. Поэтому, кроме систем за-
пуска и управления полетом, в РДТТ практически нет никаких трущихся и вращаю-
щихся элементов.
2. Простота конструкции РДТТ предопределяет крайнюю простоту их эксплуата-
ции. Смонтированный на летательном аппарате РДТТ лишь периодически должен
подвергаться профилактическому осмотру. Прост и запуск: после «прозванивания»
электрической системы воспламенительного устройства включается источник тока,
который, накаливая мостик пиропатрона, обеспечивает срабатывание воспламени-
тельного устройства.
3. Постоянная готовность к действию. Благодаря возможности длительного хра-
нения в снаряженном состоянии РДТТ может находиться на стартовой позиции неог-
раниченное время независимо от времени года и атмосферных условий. Требования,
предъявляемые к твердым ракетным топливам, обусловливают возможность длитель-
ного их хранения в определенном интервале температур. Конструкционные металли-
ческие и неметаллические детали РДТТ покрываются антикоррозионными покры-
тиями и красятся влагоустойчивыми красками. Дымные пороха, применяемые в
303
воспламенительном устройстве, гигроскопичны. Для устранения возможности на-
копления влаги в них обеспечивается герметичность корпуса воспламенителя.
Все эти мероприятия обеспечивают готовность РДТТ к запуску без проведения
каких-либо специальных подготовительных работ.
4. Надежность и безотказность. Надежность действия какой-либо установки рав-
на произведению надежностей отдельных агрегатов, из которых она состоит. Следова-
тельно, чем из большего количества отдельных агрегатов, надежность которых всегда
меньше единицы, состоит установка, тем меньше надежность всей установки. Так как
РДТТ сравнительно прост по своей конструкции, то и надежность его работы велика.
5. Малые объемы камеры для хранения топлива, обусловленные высокими зна-
чениями его плотности (1550—1850 кг/м3).
К недостаткам РДТТ можно отнести следующие его особенности:
1. Более низкие энергетические характеристики твердых ракетных топлив по
сравнению с другими ракетными топливами, и, соответственно, более низкий удель-
ный импульс РДТТ;
2. Сложность управления процессом горения твердого ракетного топлива (ТРТ);
3. Трудность осуществления многократного запуска РДТТ;
4. Значительное влияние начальной температуры заряда на скорость горения
ТРТ, что определяет необходимость его термостатирования;
5. Более низкая, по сравнению с ЖРД, продолжительность работы.
Особенности рабочего процесса РДТТ
Если физические условия во всех точках горящей поверхности одинаковы и топ-
ливо однородно, то горение происходит равномерно, параллельными слоями.
Начальное воспламенение твердого топлива вызывается тепловым импульсом
обычно с помощью специального воспламенителя. При прогреве определенного слоя
у поверхности и при температуре поверхности выше некоторого критического значе-
ния, первоначально достигаемой с помощью воспламенителя, начинаются самоуско-
ряющиеся химические превращения топлива. Эти превращения являются экзотерми-
ческими и приводят к разогреву продуктов реакций. Между продуктами сгорания и не
прореагировавшим топливом возникает теплообмен, обеспечивающий дальнейшее
протекание процесса без участия воспламенителя.
Собственно горение представляет собой процесс распространения реакции от по-
верхностных слоев в глубь заряда. Разложение и газификация твердых топлив протека-
ют в общем случае с различными скоростями и зависят от природы компонентов. Реак-
ции между газифицированными горючим и окислителем могут определяться процес-
сом диффузии и смешения или кинетикой химических реакций, или тем и другим в
зависимости от давления, температуры, размеров зерен окислителя и других факторов.
При наличии алюминия представляет интерес процесс сгорания частиц металла. Ис-
следования показывают, что на поверхности горящего топлива частицы алюминия пла-
вятся и сливаются в более крупные. Специфической стадией горения топлив является
процесс разложения и газификации твердой фазы. Этот процесс существенно зависит
от интенсивности теплопередачи к поверхности твердого топлива. Все факторы, увели-
чивающие теплопередачу, ускоряют разложение и газификацию поверхностного слоя.
Ускорение процессов в поверхностном слое и в газовой фазе означает увеличе-
ние линейной скорости горения твердого топлива. Скорость горения зависит от при-
роды топлива, давления, при котором осуществляется горение, температуры топлива,
скорости движения газа вдоль поверхности горения и других факторов, воздействую-
щих на скорость реакций в конденсированной или газовой фазе.
304
При горении твердого ракетного топлива в РДТТ происходят следующие процессы:
• преобразование в камере двигателя химической энергии топлива в энтальпию га-
зового потока;
• преобразование в канале сопла энтальпии газового потока в кинетическую энер-
гию истекающей струи;
• сложный теплообмен (теплопроводность, конвекция и тепловое излучение) меж-
ду продуктами сгорания топлива, стенками корпуса и соплового блока РДТТ
При малых значениях давления и температуры в камере (Р* и Тк*) скорость газо-
образования мало зависит от притока тепла из зоны горения, а с дальнейшим умень-
шением Р* зона пламени настолько отдаляется от поверхности твердого топлива, что
внешний приток тепла становится практически ничтожным, и при некотором давле-
нии сгорание прекращается, так как одной экзотермической реакции разложения
оказывается недостаточно для самоподдержания процесса.
При высоком давлении зона пламени приближается к поверхности горения
и приток тепла на поверхность топлива возрастает. В этом случае, особенно при высо-
ких Гк*, скорость горения топлива возрастает, так как растет скорость разложения
и газообразования топлива. Таким образом, при высоких Р* скорость горения опреде-
ляется в большей мере величиной Т*, т. е. теплоподводом из зоны горения к поверх-
ности топлива. При низких давлениях в камере фронт пламени дальше отстоит от по-
верхности твердого топлива, поэтому скорость горения меньше зависит от Г*.
Излучение тепла из зоны пламени оказывает влияние на скорость разложения
топлива. Однако это влияние должно быть правильно использовано, иначе возможно
вредное избирательное воздействие лучистой энергии на отдельные компоненты топ-
лива. В результате могут образоваться трещины, приводящие к увеличению поверхно-
сти горения, к увеличению давления в камере и к разрушению заряда. Для устранения
этого явления в твердое топливо добавляют непрозрачные для лучистой энергии ве-
щества (например, газовую сажу).
Скорость горения твердых топлив
Основной характеристикой процесса горения является его скорость. Различают
линейную и массовую скорости горения.
Линейная скорость горения ТРТ, называемая обычно просто скоростью
горения, — это перемещения очага разложения заряда ТРТ по нормали к поверхности
горения в единицу времени, см/с; мм/с , т. е.:
w = de/dT, (6.15)
где е — сгоревшая за время т толщина свода заряда ТРТ.
Поверхность горения — это поверхность, на которой наблюдается разложение ТРТ.
Массовая скорость (ит) горения представляет собой массу топлива, сгорающего с
единицы поверхности горения за одну секунду, г/(см2 с)
«т=РАЖ (616)
где рт — плотность топлива в г/см3. Таким образом,
ит = ирг (6.17)
На скорость горения твердого топлива влияют многие факторы:
• физико-химические характеристики твердого топлива (природа топлива);
• давление Рк в камере сгорания двигателя;
• начальная температура Гт заряда твердого топлива;
305
• скорость w потока продуктов сгорания, движущихся вдоль поверхности горения
заряда;
• деформация е заряда твердого топлива;
• скорость изменения давления dPK/dx продуктов сгорания в камере двигателя.
Давление, при котором протекает процесс горения, является важнейшим фак-
тором, воздействующим на скорость горения твердого топлива. Для большинст-
ва топлив наблюдается рост скорости горения при повышении давления. Объясня-
ется это ростом плотности тока и соответствующей интенсификацией теплоотдачи
к поверхности топлива. Скорость реакций, протекающих в конденсированной фа-
зе, при этом увеличивается. Одновременно увеличение концентрации газообраз-
ных реагирующих веществ приводит к росту скорости экзотермических реакций
в газовой фазе. Высокотемпературная зона пламени приближается к поверхности
твердого топлива.
С увеличением давления в камере скорость горения твердого топлива возрастает.
Эта зависимость может быть аппроксимирована единым аналитическим выражени-
ем. Однако роль гетерогенных и гомогенных реакций в комплексе явлений горения
различна при различных давлениях. В связи с этим нельзя ожидать одного и того же
закона изменения скорости горения в широком диапазоне давления. Обработка ре-
зультатов опытов дает различные зависимости в разных интервалах давления. Эти за-
висимости обычно имеют вид
и = aPKv (Рк меньше 120 • 105 Па), (6.18)
и = А + ВРК (Рк больше 120 Ю5 Па), (6.19)
где а, А, B,v — коэффициенты.
При сравнительно невысоких давлениях зависимость и = /1(Рк) криволинейная
и хорошо описывается формулой
ЦРк) = и}Рк\ (6.20)
где Mj — начальная скорость горения твердого топлива, которую называют степенным
законом скорости горения в функции от давления. Этот закон может быть использо-
ван при давлениях примерно до 120 Ю5 Па.
Вторым важным фактором, влияющим на скорость горения ТРТ, является его на-
чальная температура. Влияние начальной температуры топлива на скорость горения
объясняется зависимостью скорости гомогенных и особенно гетерогенных химиче-
ских реакций от температуры. Влияние начальной температуры на скорость горения
учитывается с помощью безразмерной функции:
= Uj^ 1ит№ (6.21)
которая представляет собой отношение скорости горения топлива при действитель-
ной температуре заряда — ит к скорости горения при температуре топлива, приня-
той за нормальную — uTN. Функцию/2(Л) обычно называют температурной функцией
скорости горения ТРТ. Чем выше начальная температура топлива, тем больше его ско-
рость горения.
По сравнению со скоростью горения топлива скорость распространения тепла
сравнительно мала, поэтому за время горения заряд не успевает прогреваться, т. е.
температура в основной его толще практически не изменяется. Таким образом, зави-
симость скорости горения от начальной температуры заряда сохраняется в течение
всего времени горения, а функция/2(Тт) Для закона скорости горения может рассмат-
риваться как постоянная величина.
306
Температурная функция скорости горения обычно представляется соотношением:
Л<Л)=е_(7*_Гд). (6.22)
где 0 — термохимическая характеристика природы твердого топлива; Тт — температу-
ра заряда топлива; TN — температура заряда, принятая за нормативную.
Изменение начальной температуры топлива оказывает влияние на скорость горе-
ния топлива; поэтому при заданной конструкции РДТТ и при неизменном критиче-
ском сечении сопла изменяются давление в камере, тяга двигателя и период его рабо-
ты. Большим начальным температурам соответствуют и большие значения тяги
и давления в камере, но, соответственно, меньшая продолжительность работы двига-
теля. Существенная зависимость давления, тяги и времени работы РДТТ от началь-
ной температуры заряда является недостатком ТРТ.
Закон горения ТРТ
Под законом скорости горения твердого топлива понимают функциональную за-
висимость скорости горения от перечисленных выше факторов:
и =f(Ni9PK, Тт, w, е, dPK/dx), (6.23)
где Ni — физико-химические характеристики твердого топлива.
Факторы, влияющие на скорость горения, принимаются независимыми друг от
друга. При таком подходе выражение для закона скорости горения примет вид:
« =/1(Л)/2( rT)/3(w)/4(e)/5(dPK/dT). (6.24)
Рассмотрим основные факторы, влияющие на скорость горения.
Для перехода от функционального вида подставим в вышеприведенное соотно-
шение вместо/1(РК),Л(ГТ) и/з^) их выражения.
В результате будем иметь:
ц = ц1рке_(7^_ т^П+АпХм'-*„)]• (6.25)
Величина/2( Тт) сохраняется постоянной в течение всего времени горения, поэто-
му обозначим;
«1т = «1Л(Л) = «10 _ (_ ^) •
При этом выражение для закона скорости горения примет вид:
u = u^[l+Kw(w-wn)], (6.26)
где Kw — коэффициент эрозии заряда; уц wn — действительная и пороговая скорость
продуктов.
Если учесть, что для большинства случаев работы РДТТ эрозионный «взмыв»
давления недопустим, т. e./3(w) = 1,0, то предыдущее соотношение запишется как:
« = (6.27)
где w1T — начальная скорость горения топлива при заданной температуре.
Это выражение закона скорости горения ТРТ является наиболее употребительным.
Геометрический закон горения позволяет определять характер изменения по-
верхности горения заряда при работе двигателя и в совокупности с законом скорости
горения устанавливать закономерности, характеризующие процесс поступления про-
дуктов сгорания твердого топлива в камеру РДТТ.
307
Основные положения геометрического закона горения:
• масса твердого топлива в заряде однородна по химической природе и физиче-
ским свойствам, все шашки заряда строго одинаковы по размерам;
• параметры рабочего процесса (прежде всего давление и температура) одинаковы
в данный момент времени во всех точках поверхности горения заряда;
• воспламенение горящей поверхности всех шашек заряда происходит мгновенно
и одновременно.
При выполнении перечисленных условий горение заряда ТРТ идет с одинаковой
линейной скоростью во всех направлениях, т. е. твердое топливо горит параллельны-
ми слоями.
Теплозащитные покрытия в РДТТ
В процессе работы РДТТ его основные узлы и элементы конструкции испытыва-
ют значительные тепловые нагрузки. Действительно, в камере сгорания большинства
использующихся на практике РДТТ реализуются следующие условия:
• уровни давления в камере РДТТ — 1...20 МПа;
• температура продуктов сгорания — 2000...3800 К;
• скорости продуктов сгорания — до 2500 м/с;
• массовые концентрации конденсированных частиц — до 40%;
• время работы РДТТ до 100 с;
• значения тепловых потоков, поступающих в элементы конструкции, — 20...
...200 МВт/м2.
Отсутствие тепловой защиты элементов конструкций двигательной установки
может привести к ее разрушению одним из следующих способов:
• разогрев конструкций до недопустимых температур, при которых не обеспечива-
ются ее механические характеристики, что приводит к разрушению узлов, эле-
ментов и РДТТ в целом;
• прогорание стенок РДТТ без общего разрушения двигателя приводит к нерасчет-
ным значениям модуля тяги РДТТ и к изменению его направления;
• оплавление или деструктивное разрушение материалов элементов конструкции
двигателя, что приводит к исключению из рабочего процесса функций, выпол-
няемых этими элементами, и, как следствие, к нерасчетному варианту функци-
онирования РДТТ в целом.
Несмотря на то что теплонапряженность рабочих процессов в камере РДТТ вели-
ка, для ряда непродолжительно работающих двигателей прогрев элементов их конст-
рукций может быть не катастрофическим, что допускает отсутствие в РДТТ теплоза-
щитных материалов. Из-за различия уровней тепловых потоков по длине камеры
РДТТ наличие теплозащитных материалов может оказаться необходимым лишь в от-
дельных областях. Так, для большинства РДТТ внутрикамерное пространство и со-
пловой блок по уровням реализующихся тепловых потоков могут быть разделены на
следующие основные области:
• застойные зоны — скорости продуктов сгорания не превосходят 25...50 м/с;
• зона переднего днища — скорости продуктов сгорания не превосходят 25...70 м/с;
• цилиндрические участки камеры РДТТ — скорости продуктов сгорания соответ-
ствуют уровням 50...200 м/с;
• зона входа в дозвуковую часть соплового блока — скорости продуктов сгорания
равны 100...350 м/с;
• зона критического сечения сопла — уровни скоростей составляют 1000...2500 м/с.
308
Таким образом, можно определить задачи, решаемые при проектировании теп-
лозащитных покрытий:
• установление уровней тепловых потоков и времени их воздействия на элементы
конструкции РДТТ;
• определение необходимости применения теплозащитных покрытий;
• выбор материалов для тепловой защиты элементов конструкций, если имеется
необходимость в их использовании;
• определение толщины теплозащитных материалов на элементах конструкций
двигательной установки.
Учитывая необходимость в обеспечении высоких показателей качества РДТТ
в целом (например, по коэффициентам массового совершенства), к материалам, ис-
пользование которых допускается в качестве теплозащитных, предъявляются следую-
щие требования:
• низкая плотность;
• высокая теплоемкость;
• низкие тепло- и температуропроводность;
• механические характеристики по прочности и жесткости теплозащитных мате-
риалов должны быть близки к характеристикам сопряженных деталей;
• химическая стойкость теплозащитного материала;
• стойкость к термической и термоокислительной деструкции;
• высокие технологические свойства;
• низкая стоимость теплозащитного материала и технологии работы с ним.
Под внутренней теплозащитой корпусов и днищ подразумевают теплозащитное
покрытие (ТЗП) и защитнокрепящий слой (ЗКС).
Назначение ТЗП — защита несущих обечаек конструкции от воздействия высо-
котемпературного газового потока. Назначение ЗКС — обеспечение прочного скреп-
ления твердотопливного заряда с обечайкой корпуса и защита твердого топлива от
внешних тепловых потоков (аэродинамического нагрева).
К ЗКС предъявляются следующие требования: низкая плотность; прочностные
и жесткостные характеристики должны быть близки к характеристикам заряда; ста-
бильность свойств во времени; надежная адгезия к поверхности несущей обечайки и к
поверхности заряда; достаточная негигроскопичность ЗКС.
Все применяемые теплозащитные материалы (ТЗМ) можно разделить на две
большие группы — пассивные и активные. К пассивным материалам относятся мате-
риалы, которые весь рабочий период сохраняют неизменной свою первоначальную
геометрическую форму. Эти материалы сочетают высокую теплоемкость, большую
температуру разрушения (емкостные ТЗМ) и относительно низкую температуро-
и теплопроводность (теплоизоляционные ТЗМ). Теплозащитный эффект от приме-
нения материалов этой группы состоит в реализации аккумулирующего и теплоизо-
ляционного эффектов при условии выдерживания высоких значений температур, со-
ответствующих разрушению материала. В эту группу можно отнести тугоплавкие ма-
териалы, графиты, окислы ряда металлов, бориды, нитриды, карбиды и цирконаты
ряда металлов. Некоторые из этих материалов представлены в таблице 6.2.
К активным покрытиям следует отнести материалы, работа которых сопровожда-
ется их разрушением. Различают три группы активных покрытий:
• с внутренним уносом массы разрушающегося компонента (испаряющиеся ТЗМ);
• с внешним уносом массы (коксующиеся ТЗМ);
• с комбинированным уносом (композиционные теплозащитные покрытия, в ко-
торых в отдельные периоды их работы может наблюдаться и тот и другой меха-
низмы разрушения — сгорающие ТЗМ).
309
Таблица 6.2
Характеристики некоторых пассивных материалов
Название материала Плотность, кг/м3 Гдоп,*
Молибден 10240 2320
Тантал 16610 2350
Вольфрам:
Топливо без алюминия 19380 1970
Топливо с алюминием 19380 2370
Графиты:
Поликристаллические 1600...2000 —
Силицированные 1900...2000 —
Пиролитические 2200 3500
Окиси металлов — 3073
Бориды металлов — 3200...3300
Карбиды металлов — 4100...4430
Нитриды металлов — 3OOO..36OO
Цирконаты металлов — 2900...3100
Активные теплозащитные материалы с внутренним уносом массы представляют
собой тугоплавкий пористый материал, пропитанный (заполненный) хладагентом, —
металлами (например, медью), минералами или органическими соединениями с вы-
сокой теплотой плавления и испарения. В качестве пористой основы в таких материа-
лах могут использоваться металлы: вольфрам, молибден и т. п. Теплозащитный эф-
фект активных покрытий с внутренним уносом массы состоит в следующем:
• на разложение наполнителя, размещенного в порах тугоплавкого каркаса, затра-
чивается значительная часть поступающего в конструкцию тепла;
• за счет вдува в пограничный слой продуктов разложения наполнителя снижается
величина теплового потока в конструкцию узла, поступающего от продуктов сго-
рания топлива или навески воспламенителя.
Активные теплозащитные покрытия с внешним уносом массы представляют со-
бой сублимирующие покрытия, состоящие из минерального наполнителя (например,
минеральные соли типа Mg3N2, Si3N4, AIN, NH4F, NH4C1, A1F3, ZnO, CdO и т. д.) и ор-
ганической связки (например, фенольные, эпоксидные, кремнийорганические смо-
лы). Теплозащитный эффект этих покрытий основан на явлениях, характерных для
материалов с внутренним уносом массы. Однако, помимо рассмотренных явлений,
присутствует и дополнительное — унос разогретого до температуры разрушения теп-
лозащитного материала, обеспечивающий удаление от поверхности ТЗМ дополни-
тельного источника тепла.
Активные теплозащитные покрытия с комбинированным уносом массы пред-
ставляют собой твердотопливную композицию, в которой элементов, являющихся
горючим, гораздо больше, чем относящихся к группе окислителей; их можно рассмат-
ривать как композиционные материалы, содержащие уносящийся (разлагающийся)
310
наполнитель, заполняющий пространство внутри каркаса, образованного связующим
материалом. Унос такого теплозащитного материала происходит по двухступенчатой
периодической схеме:
• в первоначальный момент разрушение теплозащитного материала происходит
аналогично ТЗМ с внутренним уносом массы — разлагается поверхностно распо-
ложенный наполнитель;
• по мере разрушения наполнителя все большая часть каркаса из связующего ком-
понента обнажается, что при дальнейшем воздействии теплового потока приво-
дит к разрушению обнаженного (без наполнителя) слоя каркаса; поведение ТЗМ
в данном случае может быть сравнено с уносом аблирующего материала.
Указанный тип ТЗМ получил широкое распространение в качестве бронировки
зарядов твердого ракетного топлива.
Твердые ракетные топлива
Комплекс требований к твердому топливу чаще всего определяется необходимо-
стью создания ракеты с высокой надежностью; минимальными размерами и габари-
тами; минимальной стартовой массой при заданных величинах массы полезного груза
и дальности полета.
Обеспечение высокой энергетической эффективности двигательной установки
является важнейшим требованием к топливу, которое при большой плотности должно
обеспечивать получение высокого удельного импульса.
Камера сгорания РДТТ нагружена высоким давлением. В ней размещается весь
запас топлива, поэтому его плотность оказывает существенное влияние на показатели
двигателя и ракеты в целом. При постоянной массе топлива повышение его плотнос-
ти приводит к уменьшению объема камеры сгорания и ее массы. Плотность освоен-
ных ТРТ составляет 1,4... 1,9 г/см3.
Стремление к повышению удельного импульса определяет основные направле-
ния разработок новых твердых топлив. При этом важным ограничивающим условием
является необходимость одновременного получения достаточно высоких баллистиче-
ских, механических, технологических и других свойств ТРТ.
Важнейшей характеристикой ТРТ, определяющей характер внутри камерных
процессов, является скорость горения. При номинальном давлении она должна быть
достаточной для достижения необходимых характеристик двигательной установки.
Например, в некоторых случаях от РДТТ может требоваться большая тяга в течение
короткого времени при очень высоких перегрузках. Последнее обстоятельство не по-
зволяет по соображениям прочности применить многошашечный заряд с развитой
поверхностью горения. Приемлемым решением является применение скрепленного
с корпусом заряда, но в этом случае повышенная скорость горения должна обеспечи-
вать необходимое газообразование при ограниченной поверхности горения. Иногда
необходима относительно малая скорость горения для достижения длительного вре-
мени работы. Для выполнения сложной программы полета в одном двигателе воз-
можно размещение зарядов ТРТ с разной скоростью горения, например, в двигателях
со ступенчатым изменением тяги: для короткого старта с большой тягой и длительно-
го полета с пониженной тягой.
Топливо должно обеспечивать устойчивое и равномерное горение в условиях
требуемых давлений в камере сгорания, в том числе и сравнительно невысоких.
Весьма важной характеристикой является величина разброса скорости горения
для одного состава или одной партии топлива, т. е. хорошая воспроизводимость ха-
рактеристик топлива.
311
Физико-механические свойства топлива должны обеспечивать возможность со-
здания заряда необходимой конфигурации и сохранение зарядом заданной формы
и плотности в процессе хранения, воспламенения и горения. Топлива, используемые
для скрепленных с корпусом двигателя зарядов, должны быть достаточно эластичны-
ми, чтобы не происходило разрушения заряда под действием термических напряже-
ний или при деформации их вместе с корпусом под действием давления и полетных
перегрузок. Значение коэффициента теплопроводности ТРТ равно 0,2...0,3 Вт/(мК),
т. е. примерно в 100 раз меньше, чем у стали. Поэтому ТРТ могут хорошо предохра-
нять стенки камеры двигателя от воздействия высокотемпературных продуктов сгора-
ния. Но это же обстоятельство приводит к тому, что при изменении температуры ок-
ружающей среды в зарядах ТРТ возникают термические напряжения, которые могут
вызвать их растрескивание.
Для зарядов, скрепленных со стенками камеры сгорания, к термическим напря-
жениям добавляются и механические, вызванные давлением, разностью коэффици-
ентов линейного расширения ТРТ и корпуса. Опасные термические и механические
напряжения в зарядах ТРТ возникают в результате теплового и механического удара
при воспламенении, особенно если начальная температура заряда мала. Кроме того, в
заряде возникают напряжения от воздействия перегрузок.
Уровень требований к физико-механическим свойствам ТРТ зависит от матери-
ала корпуса. Чем менее жестким является корпус, тем выше требования к допусти-
мым деформациям ТРТ. В качестве основных физических характеристик ТРТ обычно
рассматривают предел прочности (напряжение растяжения ТРТ), относительное уд-
линение и модуль упругости топлива. Эти характеристики в значительной мере зави-
сят от состава топлива, особенностей технологии изготовления и температуры заряда.
При разработке состава топлива учитывается необходимость достаточно высокой
эластичности заряда при низких температурах и повышенной прочности в условиях
максимальных температур, что является одним из условий работоспособности двига-
тельной установки в заданном температурном диапазоне.
Большое значение имеют экономические характеристики: желательно, чтобы
компоненты топлива были не дефицитными и не дорогими. Одним из требований
к ТРТ является минимальная зависимость скорости его горения от давления и на-
чальной температуры заряда во всем диапазоне эксплуатационных значений. Техно-
логия изготовления должна быть не сложной и не дорогостоящей, допускающей при
необходимости серийное производство зарядов.
Особое значение придается стабильности физико-механических, баллистиче-
ских и энергетических показателей ТРТ в условиях хранения и эксплуатации. Ста-
бильность характеристик топлива определяет его гарантийный срок хранения. В од-
них случаях основным лимитирующим фактором является химическое разложение
топлива и реакции взаимодействия между его компонентами, в других — физические
процессы, проявляющиеся в пластических деформациях, образовании трещин в заря-
де, процессах диффузии. Часто химические и физические изменения происходят од-
новременно, что приводит к старению топлива. По зарубежным данным, заряды оста-
ются пригодными для эксплуатации в течение 15—20 лет.
В зависимости от физико-механических свойств и требуемых внутрибаллистиче-
ских характеристик для ТРТ устанавливают допустимые пределы изменения темпера-
туры при хранении снаряженных двигателей. В некоторых случаях эти пределы могут
быть настолько узкими, что ракеты можно хранить только в специальных условиях,
принимая необходимые меры предосторожности при транспортировке зарядов.
312
К числу других требований следует отнести исключение опасности детонации
и взрыва, иногда — требование бездымного выхлопа и малой токсичности продуктов
сгорания.
По химическому составу и структуре твердые ракетные топлива подразделяют на
коллоидные (двухосновные), смесевые и модифицированные двухосновные.
Коллоидные топлива представляют собой твердые растворы органических ве-
ществ, молекулы которых содержат горючие и окислительные химические элементы.
Иногда эти топлива называют также балл петитными, двухосновными или гомоген-
ными. Одной из основ этих топлив является нитроцеллюлоза с различным содер-
жанием азота, получаемая при различных условиях нитрации целлюлозы. Степень
нитрации определяет соотношение горючих и окислительных элементов и коэф-
фициент избытка окислителя (кислорода) в нитроцеллюлозе. На практике приме-
няют нитроцеллюлозу с содержанием азота не менее 11%, так как при меньшем
его содержании энергетические характеристики ТРТ оказываются неудовлетвори-
тельными.
Вторая основа гомогенных топлив — вещества типа нитроглицерина C3H5(ONO2)3,
называемые растворителями. Они образуют с нитроцеллюлозой коллоидные системы.
Энергетические характеристики ТРТ улучшаются с увеличением содержания в них нит-
роглицерина.
Однако предельное содержание нитроглицерина, которое может быть введено
в топливо, не превышает 45%, так как при большем содержании нитроглицерина про-
изводство топлив становится весьма опасным, резко снижаются физико-химические
свойства двойных систем: они становятся студнеподобными, текучими.
Наиболее часто в качестве коллоидного ТРТ используется твердый раствор, в ко-
тором содержится 50—75% нитроцеллюлозы и 25—43% нитроглицерина.
С целью повышения химической стойкости в период хранения в топливо вводят
стабилизаторы. В качестве стабилизаторов в современных двухосновных ТРТ приме-
няют этилцентралит и дифениламин. Срок хранения зарядов ТРТ, в состав которых
входят стабилизаторы, достигает 15—20 лет.
Двухосновные топлива обладают такими преимуществами, как бездымность про-
дуктов сгорания, хорошими механическими свойствами и малым нижним пределом
давления (минимальное значение давления в камере, при котором начинается разло-
жение ТРТ). Однако эти топлива имеют и недостатки, в частности, более низкий
удельный импульс по сравнению с другими типами ТРТ; ограниченный диапазон ско-
ростей горения; пожаро- и взрывоопасность при изготовлении топливного заряда
(продавливание через фильеры определенного диаметра с помощью экструдера); не-
достаточная эластичность, исключающая возможность скрепления заряда со стенка-
ми корпуса.
Из-за этих недостатков заряды коллоидных топлив применяют в основном
в РДТТ небольших тяг.
Смесевые топлива представляют собой механические смеси окислителя, горюче-
го и специальных добавок. Для большинства современных смесевых топлив характер-
но использование трех основных компонентов: кристаллического окислителя, поли-
мерного горючего связующего и металлической добавки.
Окислитель — основной энергонесущий компонент ТРТ, определяющий удель-
ный импульс и скорость горения. К окислителям предъявляют ряд требований. Они
должны быть совместимыми по химическим и физическим свойствам со связующим.
Содержать возможно большее количество кислорода; по возможности не образовы-
вать при сгорании твердых частиц и коррозионно-активных газов, а также быть при-
емлемыми по экономическим показателям.
313
Большинство современных смесевых ТРТ (в США более 80%) разработано на ос-
нове окислителя перхлората аммония NH4C1O4 (ПА). Температура разложения его
невысока, а газообразные продукты разложения имеют малую молекулярную массу.
Для топлив на основе ПА и обычных полимерных связующих характерна слабая зави-
симость скорости горения от давления и начальной температуры и сравнительно вы-
сокие энергетические характеристики. Скорость горения серийных топлив на основе
ПА находится обычно в пределах от 4 до 20 мм/с.
Из нитратов в производстве смесевых ТРТ наибольшее распространение получил
нитрат аммония NH4NO3 (селитра). Топливо на основе этого окислителя эффективно
для применения в тех случаях, когда необходимо иметь небольшую скорость горения
и умеренные температуры продуктов сгорания. К недостаткам топлива на основе ни-
трата аммония следует отнести невысокое значение удельного импульса (не более
2000 Нс/кг), малую плотность, гигроскопичность и повышенную температурную чув-
ствительность. Отмечается также изменение размеров кристаллов нитрата аммония
при полиморфных превращениях, что приводит к нестабильности физико-механиче-
ских свойств топлив на его основе.
В качестве связующего может быть использовано множество веществ органиче-
ского происхождения. Используют тяжелые нефтепродукты (асфальты, битумы).
Применяются современные полимеры, такие, как полиэфирные, фенольные эпок-
сидные смолы, пластмассы, каучуки и др.
Применение каучуков в качестве связующего началось с полисульфидного
каучука (тиокол). Однако топливо на основе полисульфидного каучука имеет низкие
энергетические характеристики и неудовлетворительные механические свойства.
Снижение удельного импульса вызвано большим содержанием серы (до 40%).
Лучшими, по сравнению с топливами на основе полисульфидного каучука, ха-
рактеристиками обладают топлива, в которых в качестве связующего применен поли-
уретановый каучук. Эти топлива сохраняют эластичность до -50 °C и имеют удель-
ный импульс 2440 Нс/кг и более.
Относительное содержание окислителя и горючего в смесевых топливах можно
менять в довольно широких пределах. Однако максимальные значения удельного им-
пульса и температуры горения получаются при содержании горючего (связующего) до
15%. Содержание же твердого окислителя и других добавок обычно не превышает
85%, так как при большем количестве ухудшаются физико-механические свойства
топлива в процессе изготовления и эксплуатации.
Практически все современные смесевые топлива содержат металлы в виде мел-
кодисперсных порошков. Введение металла позволяет значительно поднять удельный
импульс, увеличить плотность, повысить стабильность и скорость горения ТРТ. Для
современных смесевых топлив, по зарубежным данным, типичным является содержа-
ние 10...20% алюминия.
Для улучшения физико-механических свойств, внутрибаллистических характе-
ристик и эксплуатационных качеств в смесевые топлива вводят различные добавки.
Пластификаторы и стабилизаторы вводятся в смесевые топлива с теми же целями, что
и в двухосновные.
К числу преимуществ смесевых ТРТ перед коллоидными топливами относятся:
• больший удельный импульс;
• весьма малый нижний предел давления;
• более широкий допустимый интервал начальных температур заряда;
• большая плотность топлива;
• большая термическая стабильность и более продолжительный допустимый срок
хранения;
• простота изготовления топливного заряда и РДТТ в целом.
314
Основные направления совершенствования РДТТ
Эффективность РДТТ в большей степени зависит от типа твердого топлива, по-
этому особое внимание уделяется созданию высокоэнергетических твердых топлив.
Уменьшение массы конструкции РДТТ достигается уменьшением давления Рк,
при использовании скрепленных зарядов с внутренним горением, совершенствова-
нием конструкции, а также применением материалов с высокой удельной прочно-
стью: титановых и алюминиевых сплавов, стеклопластиков.
Регулирование тяги РДТТ может осуществляться следующими способами:
• изменением площади критического сечения путем перемещения центрального
тела вдоль оси сопла или путем подачи рабочего тела в критическое сечение через
кольцевую щель или пояс отверстий;
• вводом химически активной жидкости (F2, OF2, C1F3, N2O4 и др.), самовоспламе-
няющейся с твердым топливом. Меняя расход жидкости, можно изменять тягу
двигателя в отношении от 20 : 1 до 50 : 1;
• изменением скорости горения ТРТ путем изменения его температуры или обдува
поверхности горения дополнительным газом;
• увеличением площади горения заряда каким-либо принудительным способом,
например, путем разрушения бронирующего покрытие заряда химически актив-
ным жидким компонентом;
• использованием компенсирующих зарядов.
Для увеличения времени работы РДТТ при использовании высокоэнергетиче-
ских ТРТ применяется внутреннее охлаждение, причем охладителем может служить
жидкость или газ.
Для многократного включения и выключения РДТТ необходима система много-
кратного воспламенения заряда и его гашения. Для многократного воспламенения
топливного заряда можно использовать химическую систему зажигания, а для много-
кратного гашения — подачу специального рабочего тела (жидкости, газа или субли-
мирующего порошка) на поверхность горения заряда.
6.2. ВОЗДУШНО-РЕАКТИВНЫЕ ДВИГАТЕЛИ
6.2.1. Основные типы воздушно-реактивных двигателей (ВРД)
Прогресс авиации во многом определяется прогрессом двигателестроения. Об этом
красноречиво говорит вся история развития авиации с самого начала и до наших дней.
До конца Второй мировой войны основными авиационными двигателями явля-
лись поршневые двигатели. Начиная с 1945 г. военная авиация, а спустя 10 лет
и гражданская авиация постепенно перешли на газотурбинные двигатели (ГТД), ко-
торые являются основными двигателями современной авиации.
В настоящее время используются несколько типов этих двигателей: турбореак-
тивные (ТРД), турбовинтовые (ТВД), двухконтурные (ТРДД).
Рассмотрим вкратце схему, принцип работы и область применения каждого из
указанных двигателей.
Турбореактивные двигатели
ТРД (рис. 6.9) состоит из пяти основных частей: входного устройства 7, комп-
рессора 2, камеры сгорания 5, газовой турбины 4 и выходного устройства (выходного
сопла) 5.
315
Рис. 6.9. Принципиальная схема ТРД:
1 — входное устройство; 2 — компрессор; 3 — камера сгорания;
4 — газовая турбина; 5 — выходное устройство
При полете самолета на двигатель набегает воздушный поток. Во входном уст-
ройстве этот поток тормозится, и скоростной напор преобразуется в давление. Из
входного устройства воздух поступает в компрессор, где осуществляется дальнейшее
повышение давления.
Далее поджатый воздух направляется в камеру сгорания, где нагревается при
сжигании топлива. Процесс подвода тепла в камеру в отличие от поршневых двигате-
лей происходит при почти постоянном давлении.
Из камеры сгорания поджатый и подогретый газовый поток направляется в тур-
бину. Расширяясь в турбине, газы совершают работу, которую передают компрессору
и вспомогательным агрегатам, обслуживающим двигатель и самолет. При выходе из
турбины давление газа значительно превышает атмосферное. Дальнейшее расшире-
ние газов до атмосферного давления происходит в выходном сопле. В результате ско-
рость истечения газов из сопла получается намного больше, чем скорость полета И
Разность количества движения секундных масс, вытекающих из двигателя газов ,
и входящего воздуха G3V9 согласно формуле Б. С. Стечкина, равна силе тяги двигателя,
/? = Grec-GBK
где (7Г, GB — соответственно расход газа и воздуха; сс, V— скорость истечения газов
и полетная скорость.
Турбореактивные двигатели получили широкое применение в летательных аппа-
ратах, развивающих большие дозвуковые и сверхзвуковые скорости полета, где они
наиболее эффективны.
При форсировании ТРД путем дополнительного сжигания топлива в специаль-
ной форсажной камере, расположенной между турбиной и выходным устройством,
он становится эффективным и на больших сверхзвуковых скоростях полета (до чисел
М полета 3.. .3,5).
Турбовинтовые двигатели
На малых и средних скоростях полета (до 750—800 км/ч) ТРД значительно усту-
пает турбовинтовым двигателям и по экономичности, и по своим взлетно-посадоч-
ным характеристикам. Этим объясняется применение ТВД для указанного диапазона
скоростей полета. ТВД состоит из тех же основных элементов, что и ТРД, но, помимо
того, снабжен воздушным винтом, вал которого соединен с валом турбокомпрессора
через редуктор (рис. 6.10).
Необходимость применения редуктора вызвана тем, что оптимальная частота
вращения турбокомпрессора значительно больше оптимальной частоты вращения
воздушного винта.
316
Рис. 6.10. Принципиальная схема ТВД:
1 — воздушный винт; 2 — редуктор; 3 — компрессор;
4 — камера сгорания; 5 — турбина; 6 — выходное сопло
Рис. 6.11. Принципиальная схема ТВаД:
1 — компрессор; 2 — камера сгорания; 3 — турбина компрессора;
4 — турбина винта; 5 — выходное сопло
В отличие от ТРД, в ТВД расширение газов полностью (до атмосферного давле-
ния) или почти полностью осуществляется в турбине. Вследствие этого мощность
турбины ТВД при прочих равных условиях больше мощности ТРД. Избыточная мощ-
ность турбины ТВД (сверх потребной мощности для компрессора и агрегатов) переда-
ется на воздушный винт.
Тяга ТВД создается в основном воздушным винтом (85—90%) и только частично
реакцией струи. Большинство ТВД, применяемых в настоящее время, выполняются
по одновальной схеме. В частности, по этой схеме выполнены ТВД «НК-12»,
«АИ-20», «Дарт», «Аллисон» и др. Одновальные ТВД отличаются относительной про-
стотой конструкции и регулирования, а также малой массой.
На практике получили применение и двухвальные двигатели, у которых комп-
рессор и винт приводятся во вращение от разных турбин. Двигатели, выполненные по
такой схеме (называемые также турбовальными — ТВаД), устанавливаются, как пра-
вило, на вертолетах и в отдельных случаях на самолетах (рис. 6.11).
Двухконтурные двигатели
За последние годы широкое применение в гражданской авиации получили двух-
контурные двигатели. Они, по существу, являются основными двигателями современ-
ной авиации. ТРДД состоит из двух контуров: внутреннего (первый контур) и наруж-
ного, расположенного вокруг внутреннего (второй контур).
По аналогии с ТВД здесь «избыточная» мощность турбины передается вентиля-
тору (компрессору) второго контура (рис. 6.12).
Рабочие процессы во внутреннем контуре ТРДД аналогичны процессам ТРД
и ТВД. А во втором контуре сжатый воздух расширяется в выходном сопле этого кон-
317
Рис. 6.12. Принципиальная схема ТРДД:
1 — вентилятор; 2 — компрессор высокого давления, 3 — турбина высокого давления;
4 — турбина низкого давления; 5 — выходное устройство первого контура;
6 — выходное устройство второго контура
тура и развивает тягу. Таким образом, тяга ТРДД образуется и во внутреннем, и в на-
ружном контурах.
В ТРДД средняя скорость истечения смеси (воздуха и газов) из выходных сопел
контуров при прочих равных условиях примерно в 1,5 раза меньше, чем у ТРД. Вслед-
ствие этого экономичность ТРДД на земле, по сравнению с ТРД, выше (на 40...50%), а
уровень шума меньше (на 12... 15 дБ).
Лучшая экономичность двухконтурных двигателей по сравнению с ТРД сохраня-
ется и на значительно больших скоростях полета (до М = 1,2...1,3). ТРДД могут быть
эффективными и для больших сверхзвуковых скоростей полета. Такую возможность
открыло сжигание топлива в двух контурах.
6.2.2. Входные устройства воздушно-реактивных двигателей
Входные устройства (ВУ) ГТД предназначены для забора воздуха из окружающей
атмосферы, подвода его к двигателю и осуществления процесса сжатия за счет ис-
пользования кинетической энергии набегающего воздушного потока. Они состоят из
ряда элементов. Обычно ими являются воздухозаборник, каналы подачи воздуха к
двигателю, створки перепуска и подпитки, устройства слива пограничного слоя, за-
щитные устройства от попадания посторонних предметов.
Основными требованиями, предъявляемыми к входным устройствам (ВУ), явля-
ются: малые внутренние и внешние потери в процессе сжатия и подвода воздуха
к двигателю; устойчивость процесса течения воздуха при всех условиях полета и ре-
жимах работы двигателя; приемлемый (допустимый для двигателя) уровень неравно-
мерности и нестационарности потока на выходе.
Размещение воздухозаборника на ЛА должно производиться с учетом совмести-
мости с применяемой системой оружия и максимальной защищенности двигателя от
попадания посторонних предметов и выхлопных газов от собственных двигателей при
включении устройств реверса и отклонения вектора тяги. Важным требованием явля-
ется обеспечение мер для снижения радиолокационной заметности. К числу эксплу-
атационных требований относится надежность работы всех систем и простота обслу-
живания.
318
Основные параметры входных устройств ВРД
К числу основных параметров ВУ относятся следующие.
1. Коэффициент восстановления полного давления (овх), оценивающий внутрен-
ние потери. При сжатии воздуха во входном устройстве и его подводе к двигателю:
пвх=^, (6.29)
где Рв, Р* — давление воздуха на входе в двигатель и перед двигателем.
Значение овх с ростом числа М полета очень интенсивно возрастает. Значение овх
зависит от числа М набегающего потока и способа организации процесса сжатия воз-
духа в ВУ. При дозвуковых скоростях полета сжатие воздуха от скоростного напора
сопровождается лишь небольшими потерями на трение и вихреобразование. При
сверхзвуковых скоростях полета возникают потери в скачках уплотнения. Эти потери
и оказывают основное влияние на реально достижимые значения овх при М > 1,0. На-
ибольшее снижение степеней повышения давления явх по сравнению с идеальным
квх.ид получается при сжатии воздуха в прямом скачке уплотнения. Организация сжа-
тия сверхзвукового потока в системе скачков уплотнения позволяет при М > 1,5 су-
щественно повысить лвх.
На стадии проектирования при подборе силовой установки (СУ) к летательному
аппарату (ЛА) пока еще конкретного ВУ не имеется, величину овх определяют по так
называемой стандартной зависимости овх = овх(М), которая отражает достигнутую
степень совершенства воздухозаборников данного типа.
Увеличение лвх за счет повышения овх сопровождается увеличением давления
воздуха во всех сечениях двигателя. Это вызывает пропорциональный овх рост расхода
воздуха и повышение перепада давлений в реактивном сопле. В результате увеличива-
ется тяга (мощность) и уменьшается удельный расход топлива двигателя. В среднем
увеличение овх на 1% вызывает повышение тяги на 1,5...2% и снижение удельного
расхода топлива суд на 0,3...0,5%.
Отсюда вытекает основное требование к входным устройствам — получение макси-
мально возможных значений коэффициента овх в целях повышения лвх. Это достигается
снижением уровня внутренних потерь при сжатии воздуха во входном устройстве.
2. Коэффициент расхода ф служит для определения расхода воздуха, пропускае-
мого ВУ, или, как иногда говорят, для оценки производительности ВУ. Он определя-
ется как отношение действительного расхода воздуха через ВУ к максимально воз-
можному:
где FBX — площадь входа ВУ, a FH — площадь струи тока, втекающей в ВУ, в невозму-
щенном потоке; рн — плотность воздуха, FBX — площадь входа в ВУ.
3. Коэффициент внешнего сопротивления сх вх служит для оценки внешнего со-
противления ВУ. Он определяется выражением схвх = X^JqFM, где q — скоростной на-
пор невозмущенного потока; FM — площадь миделя входного устройства; — сум-
марное внешнее сопротивление ВУ.
4. Коэффициент запаса устойчивости сверхзвуковых ВУ АКувх служит для оценки
удаления рассматриваемого режима работы ВУ от границы устойчивой работы (помпажа).
319
5. Неравномерность и нестационарность потока за ВУ оценивается по степени
неравномерности потока и относительной амплитуде пульсаций полных давлений.
Эти параметры нормируются из условия обеспечения устойчивой работы двигателя.
Применяемые ВУ отличаются большим разнообразием типов и конструктивных
форм. Их подразделяют на дозвуковые, трансзвуковые и сверхзвуковые в соответст-
вии со значениями максимальных скоростей полета самолетов, на которых они при-
меняются. Диапазоны скоростей полета самолета и требования к его маневренным
свойствам, наряду с применяемым типом двигателя, оказывают наибольшее влияние
на облик ВУ.
Дозвуковые военно-транспортные самолеты и самолеты гражданской авиации
являются маломаневренными и преимущественно однорежимными. Числа М крей-
серского полета у них не превышают 0,8...0,9. В СУ этих самолетов сжатие воздуха
осуществляется в основном компрессором, а повышение давления от скоростного на-
пора невелико. Этим обусловлена относительная простота конструктивного выпол-
нения и регулирования дозвуковых ВУ
Трансзвуковые самолеты, имеющие большие дозвуковые (крейсерские) и относи-
тельно небольшие сверхзвуковые (максимальные) скорости полета (М < 1,6...1,7), явля-
ются, как правило, высокоманевренными. Повышение давления от скоростного напора
в таких ВУ является более значительным, но определяющими становятся требования
обеспечения многорежимности и маневренности. ВУ этих самолетов также обычно вы-
полняются нерегулируемыми. Сжатие воздуха при сверхзвуковых скоростях полета у
них осуществляется, как правило, в прямом скачке уплотнения, расположенном перед
плоскостью входа.
Сверхзвуковые самолеты, у которых максимальные скорости полета соответству-
ют М = 2,0...3,0, имеют сверхзвуковые ВУ. Они отличаются большим разнообразием
типов и схем и классифицируются по расположению скачков уплотнения относи-
тельно плоскости входа воздухозаборника (внешнего, смешанного и внутреннего
сжатия); по форме входных сечений (плоские, осесимметричные), по компоновке
входных устройств на ЛА (лобовые, подкрыльевые, подфюзеляжные, боковые).
У дозвуковых самолетов двигатель может размещаться внутри фюзеляжа или в
отдельной гондоле. Фюзеляжные компоновки более характерны для самолетов с ТРД
и ТРДД с малыми степенями двухконтурности, когда вследствие высоких удельных
тяг двигатель имеет небольшие лобовые размеры. Отличительной особенностью та-
кой компоновки является лобовое расположение заборника воздуха и наличие между
ним и входом в компрессор длинного соединительного канала.
Дозвуковые ВУ
Обечайка воздухозаборника выполняется с профилированными относительно
толстыми плавно обтекаемыми входными кромками. Площадь на входе в обечайку Fm
выбирается такой, чтобы в расчетных условиях полета она была больше площади
струи втекающего воздуха FH. При этом практически все сжатие воздуха от скоростно-
го напора осуществляется перед плоскостью входа.
Такое внешнее сжатие, вследствие отсутствия ограничивающих поток стенок,
осуществляется практически без потерь на трение о стенки и обеспечивает малые ско-
рости воздуха на входе во внутренний канал, за счет чего снижаются внутренние поте-
ри и обеспечивается безотрывное течение воздуха в канале и выравнивание поля ско-
ростей. Непосредственно перед входом в двигатель канал выполняется конфузорным
для выравнивания поля скоростей на входе в компрессор. Получение малого внешне-
го сопротивления рассматриваемого ВУ обеспечивается надлежащим профилирова-
нием внешней и внутренней поверхностей обечайки. Струя воздуха, втекающая в воз-
320
р
возмущенный
поток
Рис. 6.13. Дозвуковое ВУ в фюзеляжной компоновке:
1 — обечайка; 2 — соединительный канал; 3 — конфузорный участок вне воздухозаборника
духозаборник, при внешнем сжатии имеет на участке между сечениями Н—Н и Вх—
Вх расширяющуюся форму (рис. 6.13). Это вызывает возмущение внешнего потока
(отклонение струек тока, обтекающих обечайку, от осевого направления) и служит ис-
точником внешнего сопротивления, которое называют дополнительным сопротивле-
нием. Значение этого сопротивления равно сумме проекций на направление полета
сил избыточного давления, действующих на жидкую линию тока а—к. На внешней
поверхности обечайки происходит ускорение потока. Задача профилирования — не
допускать срыва потока с этой поверхности или образования вблизи нее сверхзвуко-
вых зон и скачков уплотнения, способствующих увеличению внешнего сопротивле-
ния обечайки. При безотрывном обтекании обечайки с докритическими скоростями
ускорение потока на ее внешней поверхности создает разрежение. Возникает аэроди-
намическая сила Р, осевая составляющая которой является подсасывающей силой.
Она частично компенсирует дополнительное сопротивление.
Сверхзвуковые ВУ
Если скорость полета ЛА с дозвуковым ВУ превышает указанные расчетные зна-
чения, характеристики ВУ резко ухудшаются. На внешней поверхности обечайки об-
разуется течение с местными сверхзвуковыми скоростями, что приводит к резкому
росту коэффициента лобового сопротивления сх вх. При М > 1,0 перед плоскостью
входа появляется головная волна. Вследствие этого повышается избыточное давление
как на поверхности обечайки, так и на внешней поверхности втекающей в двигатель
струи за головной волной. Вместо подсасывающей силы на обечайке возникает внеш-
нее сопротивление. Оно суммируется с дополнительным сопротивлением. Коэффи-
циент сх вх интенсивно увеличивается, но потери полного давления при умеренных
сверхзвуковых скоростях (М < 1,4...1,6) в самой головной волне относительно неве-
лики, и коэффициент овх снижается не очень значительно.
Для улучшения характеристик дозвукового ВУ на сверхзвуковых скоростях поле-
та применяют обечайки с меньшей относительной толщиной и заостряют переднюю
кромку.
Воздухозаборники с острыми передними кромками имеют худшие характеристи-
ки на взлете, а также на углах атаки и скольжения (из-за срыва потока и снижения ве-
личины подсасывающей силы).
321
У дозвуковых самолетов с ТРДД, имеющими высокие степени двухконтурности,
двигатели располагаются в отдельных гондолах, которые устанавливаются на пилонах
несколько впереди и ниже крыла. Крейсерские числа М полета таких самолетов со-
ставляют 0,75...0,85. Двигатели этих самолетов отличаются большими расходами воз-
духа и в связи с этим имеют значительные лобовые размеры, что обусловлено их ма-
лыми удельными тягами. При стартовой тяге 200...250 кН расход воздуха у этих двига-
телей достигает 650...800 кг/с. Уменьшение массы воздухозаборников при их очень
большом диаметре (до 2,0...2,5 м) достигается сокращением относительной длины ВУ,
которая на выполненных конструкциях составляет 0,6...0,9 от диаметра входа
в двигатель.
К другим конструктивным особенностям рассматриваемых ВУ, помимо того что
они выполняются очень короткими, следует отнести их несимметричность — наличие
некоторого скоса плоскости входа — для обеспечения эффективной работы на углах
атаки, а также возможность применения окон подпитки, открывающихся на взлете и
при малых скоростях полета, когда предварительное внешнее сжатие поступающего в
двигатель потока воздуха отсутствует или мало и подача воздуха только через входное
отверстие не обеспечивает потребности двигателя.
Малая длина ВУ требует более тщательного его профилирования. Оно выполня-
ется на основе применения численных методов решения уравнений газовой динами-
ки с учетом сжимаемости, вязкости и пространственного характера течения газового
потока.
Внешние обводы и форма внутреннего канала оптимизируются из условия полу-
чения максимальной тяги при заданной степени равномерности потока на входе в
двигатель.
Для трансзвуковых самолетов ВУ также выполняются нерегулируемыми, и они
отличаются конструктивной простотой. Основное требование, которому должны
удовлетворять ВУ маневренных самолетов, — хорошая совместимость с двигателем
в широком диапазоне изменения углов атаки а и скольжения р, поскольку даже при
кратковременном полете при больших аир возможно возникновение значительной
неравномерности потока на входе в двигатель и потеря его газодинамической устой-
чивости.
Углы атаки при дозвуковых скоростях полета (М < 0,8) могут у них изменяться в
диапазоне 0...+300, а углы скольжения — в диапазоне ± 15°. При сверхзвуковых ско-
ростях полета (М = 1,5...1,7) диапазоны изменения аир сокращаются до значений:
а = -4...+15°; Р = ± 4°. Этим требованиям лобовые ВУ не удовлетворяют. Предпочти-
тельно применение подфюзеляжных, подкрыловых или боковых ВУ.
На сверхзвуковых самолетах нашли применение многоскачковые сверхзвуковые
ВУ внешнего сжатия. Они рассчитываются на определенное число М полета (Мя).
Схема такого ВУ с указанием характерных геометрических параметров представ-
лена на рис. 6.14. Здесь FBX — площадь входа; Fr — площадь горла; Р,, Р2, Р3... — углы
наклона отдельных ступеней поверхности сжатия. При обтекании сверхзвуковым по-
током поверхности сжатия, выполненной в виде ступенчатого клина, образуется сис-
тема косых скачков уплотнения, которая замыкается прямым скачком (головной вол-
ной). Схема ВУ с головной волной на входе имеет дозвуковое втекание потока во
внутренний канал и является наиболее распространенной. Обычно осуществляют не-
которую расфокусировку косых скачков, чтобы головная волна не разрушала их в не-
посредственной близости перед обечайкой. Течение во внутреннем канале на расчет-
ном режиме является дозвуковым. В указанной схеме на расчетном режиме ф < 1,0, и
поэтому коэффициент сх вх имеет более высокое значение, чем у ВУ со сверхзвуковым
втеканием (смешанного сжатия). Но расфокусировка косых скачков способствует по-
322
Рис. 6.14. Схема течения в лобовом ВУ внешнего сжатия
при наличии головной волны (а); расчетная схема течения (6)
вышению запаса устойчивости ВУ. В расчетах с достаточной степенью точности ре-
альную схему течения заменяют упрощенной, в которой система косых скачков уп-
лотнения замыкается прямым скачком, расположенным непосредственно у передней
кромки обечайки. Это приводит к некоторому снижению овх.
Форму внутреннего канала и площадь горла выбирают таким образом, чтобы за-
медлить нарастание пограничного слоя и уменьшить размеры зоны отрыва. Для этого
канал делают вначале конфузорным, а затем, после завершения поворота потока, —
диффузорным. Максимальную скорость дозвуковой поток имеет в минимальном се-
чении канала — горле. Наиболее выгодным с точки зрения уменьшения зоны отрыва
потока является выбор скорости в горле, близкой к скорости звука. Если скорость по-
тока в горле равна скорости звука, то горло называют оптимальным.
Для уменьшения вредного влияния вязкости принимают ряд специальных мер.
К ним относятся: отсос пограничного слоя через перфорацию на поверхности тормо-
жения; слив пограничного слоя через щель в области горла; установка в канале за гор-
лом турбулизаторов в виде небольших лопаток, соизмеримых по высоте с толщиной
пограничного слоя. Таким образом, предотвращается развитие зон отрыва погранич-
ного слоя от стенок и происходит выравнивание полей скоростей и уменьшение пуль-
саций потока перед двигателем.
6.2.3. Компрессоры воздушно-реактивных двигателей
Основные типы компрессоров
В авиационных газотурбинных двигателях широкое применение получили не-
сколько типов компрессоров: осевые, в которых движение потока в среднем происхо-
дит параллельно оси; центробежные, в которых поток разворачивается и движется в
радиальном направлении; осецентробежные, состоящие из комбинации осевого и
323
Рис. 6.15. Принципиальная
схема многоступенчатого
осевого компрессора
Рис. 6.17. Принципиальная
схема осецентробежного
компрессора
Рис. 6.16. Принципиальная
схема центробежного
компрессора
Рис. 6.18. Принципиальная
схема диагонального
компрессора
центробежного; диагональные, в которых движение потока в среднем происходит по
диагонали (рис. 6.15—6.18).
Назначение всех типов компрессоров одно — компрессор предназначен для пе-
ремещения определенного количества газа (воздуха) из области низкого в область вы-
сокого давления.
Поэтому основными техническими характеристиками компрессора являются:
степень повышения давления я (отношение давления воздуха за компрессором к дав-
лению перед компрессором), производительность — секундный расход воздуха, отне-
сенный к площади входа в компрессор, и коэффициент полезного действия.
В компрессорах современных ГТД я доходит до 25...30 и более. Такие высокие
степени повышения давления применяют для улучшения экономичности двигателя.
Дело в том, что в ГТД около 70% тепла, введенного с топливом в двигатель, теря-
ется с уходящими газами. Эти потери обусловлены вторым законом термодинамики
(в двигатель засасывается холодный воздух, а выходит горячий).
При увеличении степени повышения давления в компрессоре соответственно
увеличивается и степень понижения давления на тракте расширения газа в двигателе
(во сколько раз воздух сжимается — во столько же раз газы расширяются). А чем боль-
ше степень понижения давления, тем ниже (при заданной температуре газа перед тур-
биной) температура уходящих газов и, следовательно, тем меньше потери тепла
с уходящими газами.
Иначе говоря, с увеличением степени повышения давления воздуха степень по-
лезного использования введенного в двигатель тепла увеличивается.
Из всех перечисленных компрессоров требованиям скоростной авиации наилуч-
шим образом удовлетворяют осевые компрессоры, у которых при заданном расходе
воздуха габариты и вес значительно меньше, а КПД намного выше, чем у других
компрессоров.
324
Этим объясняется их наибольшее применение в двигателях современной авиации.
Центробежные и диагональные компрессоры, также достаточно простые и ком-
пактные, получили широкое применение во вспомогательных силовых установках
(ВСУ): в приводах энергоузлов самолетов, в холодильных агрегатах, в турбостартерах
для запуска основных двигателей и т. д.
Осецентробежные компрессоры чаще применяются в двигателях вертолетов
средних мощностей.
Осевые компрессоры, как правило, выполняют многоступенчатыми. Ступенью
осевого компрессора называется совокупность одного ряда рабочих (вращающихся)
лопаток и одного ряда направляющих (неподвижных) лопаток. Количество ступеней
доходит до 15...17 и обычно не бывает меньше 5...6.
Применение большого количества ступеней связано с тем, что степень повыше-
ния давления каждой ступени п в среднем не превышает 1,3...1,4, а потребная
величина л значительно больше.
Таким образом, процесс сжатия воздуха в многоступенчатом компрессоре состо-
ит из ряда последовательно протекающих процессов сжатия в отдельных ступенях.
Поэтому для уяснения принципа действия компрессора достаточно рассмотреть ра-
боту одной ступени.
Схема и принцип работы ступени осевого компрессора
Как было отмечено выше, ступень осевого компрессора (рис. 6.19) состоит из
вращающегося рабочего колеса (РК) и неподвижного направляющего аппарата (НА).
Рассечем ступень компрессора цилиндрической поверхностью а—Ь, ось которой сов-
падает с осью вращения колеса, а затем развернем это цилиндрическое сечение на
плоскость. В большинстве случаев (особенно для средних и последних ступеней) по-
верхность а—b приближенно можно рассматривать как поверхность тока, хотя в об-
щем случае поверхность тока представляет собой поверхность вращения с криволи-
нейной образующей. На рис. 6.19 и 6.20 приняты следующие обозначения: сечение
1—1 на входе в рабочее колесо; сечение 2—2 на выходе из рабочего колеса (на входе
в направляющий аппарат); сечение 3—3 на выходе из направляющего аппарата.
Чтобы уяснить принцип работы ступени компрессора, рассмотрим течение воз-
духа через решетки, образованные лопатками РК и НА.
Разберем случай, когда воздух перед рабочим колесом в своем абсолютном дви-
жении имеет осевое направление. Пусть РК вращается с окружной скоростью и. Для
нахождения вектора скорости w, относительно рабочих лопаток используем извест-
ное правило теоретической механики, что абсолютная скорость сх равна сумме пере-
носной (окружной) скорости и и относительной скорости Wj, т. е.
cx=u + wx. (6.31)
Треугольник, образованный из векторов сх, и, называется треугольником ско-
ростей на входе в РК.
Во избежание срыва потока передние кромки рабочих лопаток необходимо ори-
ентировать по направлению вектора относительной скорости >₽Р Что же касается за-
дних кромок, то их нужно направить так, чтобы поперечное сечение на выходе из ка-
нала, образованного между соседними лопатками, было больше, чем сечение на входе
f Это объясняется следующим: для сжатия воздуха на валу колеса ступени затрачива-
ется работа, чтобы увеличить давление воздуха, а это можно реализовать, если канал
между двумя лопатками (для дозвукового потока) сделать расширяющимся. При этом
325
относительная скорость на выходе из канала будет
меньше, чем на входе. Иначе говоря, каналы между
соседними лопатками должны быть диффузорными.
Очевидно, что чем больше степень диффузорности
канала, тем больше степень повышения давления в
рабочих лопатках.
Однако увеличение степени диффузорности свя-
зано с увеличением кривизны профилей лопаток и со-
ответственно с увеличением степени поворота потока,
поэтому чрезмерное увеличение диффузорности ка-
нала может привести к срыву потока со «спинок» ра-
бочих лопаток. На практике максимальная степень
диффузорности и максимальная степень поворота по-
тока выбираются из условия отсутствия срыва.
Скорость воздуха за рабочим колесом определит-
ся как векторная сумма относительной и окружной
скорости, т. е.
С2 = w2 + и- (6.32)
Задача НА заключается в том, чтобы направлять
поток (в абсолютном движении) до первоначального
или другого заданного направления. Для выполнения
этой функции задние кромки направляющих лопаток
необходимо направить так, чтобы скорость на выходе
из аппарата была параллельна или почти параллельна
скорости. Передние кромки во избежание срыва пото-
ка необходимо ориентировать по направлению ско-
рости с2. При таком выполнении НА поперечное сече-
Рис. 6.19. Схема ступени
осевого компрессора
ние на выходе будет больше, чем на входе (диффузорный канал).
Таким образом, течение воздуха через решетку лопаток РК и НА можно рассмат-
ривать как течение через систему вращающихся и неподвижных диффузорных кана-
лов с уменьшением относительной скорости в рабочих лопатках и абсолютной в на-
правляющем аппарате.
Примерный характер изменения параметров потока вдоль оси ступени показан
на рис. 6.19.
Рис. 6.20. Сечение лопаток рабочего колеса (РК) и направляющего аппарата (НА)
326
Температура потока воздуха вследствие сжатия воздуха растет и в рабочем, и в на-
правляющем аппаратах. Температура и давление заторможенного потока в рабочих
лопатках из-за подвода внешней работы растут. В НА температура заторможенного
потока сохраняется постоянной, а давление из-за гидравлических потерь несколько
падает.
Основные параметры ступени осевого компрессора
Ступень компрессора прежде всего характеризуется своими геометрическими
параметрами (размерами): наружным диаметром Z)H, диаметром втулки £>вт
(рис. 6.21). Эти основные размеры определяют и средний диаметр колеса, под кото-
рым понимают либо среднеарифметический диаметр:
либо среднегеометрический, окружность которого делит площадь сечения на равные
части (рис. 6.21).
Среднегеометрический диаметр получается из соотношения:
-Z>2p) = 5(Z)2p-^), (6.34)
„ /dk2 +
откуда Z>cp = j----•
Важное значение для оценки лобовых габаритов имеет относительный диаметр
втулки 3, под которым понимают отношение диаметра втулки к диаметру колеса:
л2
F1 = 5(Z)2-^)=^(l-32). (6.35)
2=^. (6.36)
Уменьшать d ниже 0,3...0,35 нет смысла, так как уже при этих значениях d около
90% общей площади компрессора FK используется полезно.
Кроме того, при дальнейшем уменьшении диаметра втулки невозможно будет
помещать лопатки на диске.
Поэтому относительный диаметр втулки первых сту-
пеней выбирают в пределах 2 = 0,35...0,6, а последних
ступеней (где плотность воздуха достаточно большая и
нет «дефицита» в площадях) d = 0,8...0,9.
Другим важным параметром ступени является осевая
составляющая абсолютной скорости с. Выбор осевой ско-
рости существенно влияет на секундный расход воздуха
через выбранную полезную площадь .
Для первых ступеней компрессора принимаются с =
= 180...220 м/с, так как с от ступени к ступени постепенно
уменьшают, то для последних ступеней принимают с =
= 100... 110 м/с.
Следующим важным параметром ступени осевого
компрессора является окружная скорость рабочих лопа-
ток и. Очевидно, что чем больше и, тем больше работа,
передаваемая воздуху, прошедшему через ступень, и тем
больше напорность ступени.
Рис. 6.21. Геометрические
параметры ступени колеса
327
На практике ее величина ограничивается прочностью лопаток и диска рабочего
колеса компрессора (или турбины), а также из газодинамических соображений.
В современных компрессорах окружная скорость на наружном диаметре меняет-
ся в пределах 300—500 м/с.
Кроме так называемых размерных параметров, большое значение в теории комп-
рессоров играют безразмерные параметры, перечисленные ниже.
1. Степень повышения давления п. В первых ступенях п = 1,3... 1,4, а в последних
1,15...1,2. Это объясняется тем, что даже при одной и той же передаваемой воздуху ра-
боте температура от ступени к ступени растет и тем самым степень повышения давле-
ния уменьшается (горячий воздух сжимается труднее холодного).
2. КПД ступени лст лежит в пределах 0,86—0,90.
3. Коэффициент расхода ступени са. Коэффициентом расхода называется отно-
шение осевой скорости к окружной скорости колеса:
'г'г (6.37)
ин
Название объясняется тем, что осевая скорость определяет объемный расход воз-
духа через единицу площади входа в рабочее колесо.
Для первых ступеней с ~ 0,5...0,7, а для последних 0,25...0,4.
4. Коэффициент затраченного напора ступени Hz. Этот коэффициент часто назы-
вается и коэффициентом затраченной работы; под ним понимают отношение затрачен-
ной на валу и переданной 1 кг воздуха работы к квадрату окружной скорости колеса.
Коэффициент передаваемой энергии характеризует степень использования ок-
ружной скорости и меняется в пределах от 0,25 до 0,3—0,35.
5. Коэффициент адиабатического напора Яад. Под коэффициентом адиабатиче-
ского напора понимают отношение адиабатической работы ступени в параметрах за-
торможенного потока к квадрату окружной скорости.
Кроме коэффициентов Яад, в теории осевых компрессоров используют так назы-
ваемый коэффициент ц нагрузки ступени, под которым понимают отношение работы
ступени к квадрату средней окружной скорости. Коэффициент нагрузки обычно ме-
няют в пределах 0,25...0,7.
6. Степень реактивности р.
Степенью реактивности ступени называется отношение адиабатической работы
рабочего колеса к адиабатической работе ступени.
Степень реактивности показывает, как распределяется общая адиабатическая ра-
бота ступени между рабочим колесом и направляющим аппаратом. Если принять
среднее значение ц = 0,5, то р = 0,75, т. е. при осевом входе воздуха в колесо 75% ади-
абатической работы падает на колесо и только 25% — на направляющий аппарат.
Таким образом, в этом случае сжатие воздуха происходит в основном в колесе.
Многоступенчатые осевые компрессоры
На рис. 6.22 показана схема многоступенчатого осевого компрессора и обозначе-
ны характерные сечения.
Основными величинами, характеризующими работу компрессора, являются:
а) степень повышения давления воздуха:
< = (или <=£). (6.38)
328
которая представляет собой отношение полного (статического) давления на выходе
из компрессора рк к полному (статическому) давлению на входе в компрессор рв (* —
параметры заторможенного потока газа).
б) удельная производительность GF\
Gf= , (6.39)
г D
где
л/),? р‘
Fl=-r;G,=^.F^
V В
FB=^(1 -^в)-
(6.40)
(6.41)
в) адиабатический КПД компрессора, характеризующий гидравлическое совер-
шенство компрессора, и представляет собой отношение адиабатического подогрева
воздуха в компрессоре к действительному подогреву:
(илиЯ>^), (6.42)
1 К 1 В К
где Т\ L — температура заторможенного потока воздуха и работа компрессора.
Связь основных параметров многоступенчатого компрессора
с параметрами ступеней
Рассмотрим четырехступенчатый компрессор. Для отдельных ступеней можно
написать
яст1 “ р ’ ястп “ 7^ ’ ястш ” > Kcriv ~ т5- • (6.43)
Р\ Рп Рп\ Р\у
Перемножая левые и правые части приведенных соотношений, получим:
Пст1 ЯсгПЯст11 IKctIV = ~ПК- (6.44)
В общем виде:
<= П<(> <6-45)
i = 1
где z — число ступеней компрессора.
Рис. 6.22. Схема многоступенчатого компрессора:
в — сечение на входе в компрессор; к — сечение на выходе из компрессора;
/, //, III, ... z — сечения на входе в рабочие колеса соответствующих ступеней
329
Таким образом, степень повышения давления многоступенчатого компрессора
равна произведению степеней повышения давления отдельных ступеней.
Работа, затраченная на вращение компрессора, равна сумме работ затраченных
на вращение отдельных ступеней:
Z
Ьн= ЕЬСТ/. (6.46)
/ = 1
Это связано с тем, что в реальных ступенях имеются гидравлические сопротивле-
ния, на преодоление которых затрачивается работа. Поэтому действительный процесс
сжатия идет круче, чем адиабатический, и температура за ступенью оказывается выше
при одинаковой степени повышения давления.
При создании компрессора стремятся к уменьшению его массы и размеров,
к увеличению КПД. Эти задачи решаются рациональным выбором скоростей потока по
тракту компрессора, геометрических форм и размеров его проточной части. Очевидно,
что поперечные размеры компрессора будут тем меньше, чем больше осевая скорость
потока. Они уменьшаются также с уменьшением относительного диаметра втулки.
Длина компрессора определяется числом ступеней, необходимых для получения задан-
ной величины я. Чем больше работа каждой ступени, тем меньше требуется ступеней.
В современных компрессорах в первой ступени d выбирают не меньше 0,3, а ве-
личина осевой скорости са = 180...220 м/с. В последней ступени принимают са =
= 100...НО м/с.
Обычно на первых двух-трех ступенях са уменьшают несколько меньше, чем на
последующих ступенях. Это вызвано, прежде всего, необходимостью плавного изме-
нения меридионального профиля проточной части. Длина компрессора определяется
выбором закона изменения скорости.
На рис. 6.23 показаны различные схемы многоступенчатого осевого компрессо-
ра. При схеме а внешний диаметр Лк остается неизменным, а втулочный Dm возрас-
тает. Может оказаться, что при указанном законе изменения упомянутых параметров
по ступеням в компрессоре с большим я величины d в последних ступенях недопус-
тимо велики. Поэтому иногда находят применение компрессоры, выполненные
по схеме рис. 6.23, б. В этой схеме втулочный диаметр остается неизменным,
а наружный — уменьшается. Соответственно получаются малыми £ст, что приво-
дит к большой длине компрессора. Для исключения этого недостатка может оказать-
ся целесообразным использование схемы рис. 6.23, в, в которой средний диаметр
приближенно остается постоянным, или комбинированной схемы компрессора
рис. 6.23, г, когда передняя часть компрессора выполнена по схеме рис. 6.23, а, а за-
дняя часть — по схеме рис. 6.23, б. Возможно применение и других форм проточной
части компрессора.
При выбранных форме проточной части, профиле осевых скоростей и извест-
ной суммарной работе производят распределение этой работы по отдельным сту-
пеням.
Рис. 6.23. Различные схемы многоступенчатого осевого компрессора
330
Работа ступени определяется из условия предельно допустимой аэродинамиче-
ской нагруженности, характеризуемой величиной коэффициента теоретического на-
пора.
В настоящее время для обеспечения эффективной и устойчивой работы при
лк > 10 создаются двухкаскадные и трехкаскадные компрессоры.
Двухкаскадный компрессор состоит из компрессора низкого давления (КНД)
и компрессора высокого давления (КВД). Каждый из компрессоров приводится во
вращение от своей турбины. Однако их совместная работа обусловлена равенством
расходов воздуха и зависимостью условий работы КВД от параметров потока за КНД.
В свою очередь, режим работы КНД в значительной мере определяется режимом ра-
боты КВД.
Работа и лк компрессора распределяется между каскадами с учетом возможнос-
тей распределения работы между соответствующими турбинами и особенностей рабо-
ты компрессора в условиях эксплуатации, при этом особое внимание уделяется обес-
печению его устойчивой работы. Обычно примерно 40% работы подводится к КНД и
60% — к КВД. Это распределение корректируется с учетом целесообразного распре-
деления работы между турбинами.
6.2.4. Основные камеры сгорания ВРД
Требования к камерам сгорания
и организации рабочего процесса
1. Высокие значения коэффициента полноты сгорания топлива на рабочих режи-
мах т| > 0,99.
2. Обеспечение надежного запуска двигателя в заданном диапазоне высот и ско-
ростей полета.
3. Достаточно широкий диапазон устойчивой работы (без погасания пламени
и без вибраций) при изменении значений коэффициента избытка воздуха.
4. Допустимый уровень потерь полного давления (ог = 0,92...0,96).
5. Заданное распределение средних температур по радиусу выходного сечения
(заданная эпюра температур) и допустимый уровень окружной неравномерности тем-
ператур. Допустимый уровень температуры стенок.
Рис. 6.24. Схема основной камеры сгорания:
1 — диффузор; 2 — форсунка; 3 — фронтовое устройство;
4 — кольцевые каналы; 5 — жаровая труба; 6,7 — отверстия
для подвода вторичного и смесительного воздуха соответственно
331
Рис. 6.25. Фронтовое устройство
с форсункой (!) и двумя
завихрителями воздуха (2)
6. Низкая (ниже порога видимости) концентра-
ция сажистых частиц (дыма) в продуктах сгорания.
7. Низкое содержание вредных веществ (СО,
CH, NO) в выхлопных газах.
Перечисленные требования предопределяют
сложность рабочего процесса в камерах сгорания.
Значение коэффициента избытка воздуха на ра-
бочих режимах в основной камере сгорания составля-
ет а = 2,5...5. Однородные смеси такого состава явля-
ются негорючими. В основных камерах сгорания
подвод воздуха распределен по длине, а топливо вво-
дится в головной части жаровой трубы через форсун-
ки. Благодаря этому в первой половине жаровой тру-
бы смесь является значительно богаче (а = 1,2...1,8),
чем в целом по камере, что обеспечивает интенсив-
ное протекание здесь процесса горения.
Фронтовое устройство камеры сгорания пред-
назначено для обеспечения стабилизации процесса
горения и подготовки горючей смеси. По конструктивному выполнению фронтовые
устройства весьма разнообразны. Наибольшее распространение в настоящее время
получили завихрительные фронтовые устройства, содержащие один или несколько
лопаточных завихрителей.
Область жаровой трубы от фронтового устройства до первого пояса основных от-
верстий называется первичной зоной. В пределах первичной зоны из-за малого подво-
да воздуха смесь является богатой (а = 0,4...0,7). Вследствие высокой температуры газа
(1500... 1800 К) в начале первичной зоны капли топлива быстро нагреваются и испаря-
ются. В первичной зоне непосредственно за фронтовым устройством располагается
циркуляционная зона, в которой осуществляется стабилизация процесса горения.
Расход воздуха, подводимого в первичную зону, недостаточен для полного сгора-
ния топлива, и значение коэффициента полноты сгорания топлива здесь в лучшем
случае может приближаться к значению коэффициента избытка воздуха (0,4...0,7). По-
этому сгорание топлива продолжается ниже по потоку (вторичная зона) по мере под-
вода вторичного воздуха. Процесс сгорания заканчивается в том сечении, где средний
коэффициент избытка воздуха составляет 1,5...1,7. Часть жаровой трубы от форсунки
до этого сечения называется зоной горения. Далее расположена зона смешения, где
горение практически отсутствует. Благодаря подводу воздуха здесь происходит сниже-
ние температуры газа до значений, определяемых суммарным коэффициентом избыт-
ка воздуха. От организации подвода воздуха в зоне смешения в значительной степени
зависит обеспечение требуемого поля температур газа в выходном сечении.
Потери полного давления в основных камерах сгорания
Течение газа по тракту камеры сгорания сопровождается потерями полного давле-
ния, которые характеризуются значениями коэффициента гидравлических потерь £кс и
коэффициента восстановления полного давления окс. Обычно разделяют потери пол-
ного давления в диффузоре камеры и в ее жаровой трубе.
Широкое распространение получили диффузоры с внезапным расширением.
В них торможение потока сначала осуществляется в диффузорном патрубке, имею-
щем степень расширения 1,5...1,8, а затем следует резкое расширение канала. Такие
диффузоры характеризуются стабильным течением и умеренной величиной потерь
полного давления: во входном патрубке 0,04...0,06; в диффузоре в целом 0,2...0,3.
332
Потери полного давления в жаровой трубе достаточно точно могут быть определе-
ны в результате гидравлического расчета камеры сгорания. Наряду с этим получили
распространение приближенные формулы, основанные на рассмотрении упрощенной
схемы работы камеры. Предполагается, что воздух подводится только через один пояс
отверстий, площадь сечения жаровой трубы постоянна, поля параметров потока
в каждом сечении равномерны, газ несжимаем, осевая составляющая скорости воздуха
в отверстиях равна скорости потока в кольцевых каналах, относительный расход топли-
ва пренебрежимо мал. Применив к течению в такой камере уравнения газовой динами-
ки, можно получить следующее выражение для определения потерь полного давления:
Ркк’ - Рг = РАп/2 + Рк(Скк - Сжх)2/2 + РкС2жх(вкс - 1). (6.47)
Здесь соп — нормальная составляющая скорости воздуха в отверстиях; сжх — ско-
рость газа в жаровой трубе при отсутствии подогрева; скк — скорость воздуха в кольце-
вых каналах; Р*к, Р* — давление на выходе из компрессора и в камере сгорания; 0КС —
степень подогрева газа в камере. Соотношение хорошо иллюстрирует структуру по-
терь полного давления в жаровой трубе. Сумма первых двух слагаемых характеризует
потери на смешение. Как видно, они состоят из потерь скоростного напора, соответ-
ствующего нормальной составляющей скорости в отверстиях соп, и потерь на удар при
перетекании воздуха из кольцевого канала в жаровую трубу (аналогичны потерям при
внезапном расширении). Третье слагаемое характеризует потери полного давления,
вызванные подводом тепла к движущемуся газу, — тепловые потери. Разделив обе
части уравнения на величину скоростного напора потока при входе в диффузор каме-
ры сгорания и заменив (из уравнения расхода) отношение скоростей отношением со-
ответствующих площадей, получим выражение для коэффициента гидравлических
потерь в жаровой трубе через конструктивные параметры камеры сгорания:
^=^M)2 + (FK/FKK-FK/Fx^ + (eKC- 1)(Гк/^)2. (6.48)
Здесь FK — площадь сечения на входе в камеру; FKK и £ж — площади сечений коль-
цевых каналов и жаровой трубы, соответственно; FQ — суммарная площадь отверстий
в стенках жаровой трубы (коэффициент расхода воздуха через отверстие 0,7...0,8); ц —
коэффициент вязкости воздуха. Наибольшую долю (70...80%) составляют потери, оп-
ределяемые скоростным напором. Эти потери тем больше, чем меньше значение pF0.
Потери на «удар», как правило, достаточно малы (3...5%). Тепловые потери состав-
ляют 10...20%. Для практического использования в формулу вводятся эмпирические по-
правочные коэффициенты. Например, может быть использована следующая формула:
^ж= l,2(FK/pF0)2 + О,5(0КС — 1)(ГК/£Ж)2. (6.49)
Коэффициент гидравлического сопротивления камеры сгорания представляет
собой сумму этих коэффициентов для диффузора и жаровой трубы.
6.2.5. Газовая турбина ВРД
Газовая турбина представляет собою лопаточную машину, в которой потенциаль-
ная энергия сжатого и подогретого газа преобразуется в механическую работу на валу
турбины с помощью вращающегося ротора, снабженного лопатками. Это преобразо-
вание обратно тому, которое имеет место в компрессоре, и с этой точки зрения турби-
на как гидравлическая машина представляет собой обращенный компрессор,
и наоборот. Газовая турбина обладает рядом ценных качеств, основными из которых
являются: высокая экономичность, возможность получения большой мощности, ма-
лые габариты и масса, удобство эксплуатации.
333
Эти качества газовой турбины обусловили ее широкое применение в двигателях
летательных аппаратов для привода компрессора, вентилятора, воздушного винта и
вспомогательных агрегатов.
Схема и принцип действия ступени газовой турбины
На рис. 6.26 показана конструктивная схема трехступенчатой осевой газовой тур-
бины. Она состоит из вращающегося ротора Л и неподвижного статора Б. Газотурбин-
ные двигатели гражданской авиации имеют обычно 3...5 ступеней и более.
Процесс расширения газа в многоступенчатой турбине состоит из ряда последо-
вательно протекающих процессов расширения его в отдельных ступенях. Поэтому для
уяснения принципа действия турбины рассмотрим работу одной ступени.
На рис. 6.27 схематически показана ступень газовой турбины. Она состоит из со-
плового аппарата и рабочего колеса. Рассечем ее цилиндрической поверхностью а—б,
ось которой совпадает с осью вращения ротора, а затем развернем это цилиндриче-
ское сечение на плоскость. На рис. 6.28 показаны полученные таким образом сечения
неподвижного ряда лопаток соплового аппарата и движущихся относительно него со
скоростью и лопаток рабочего колеса. Поверхность а—б приближенно можно рас-
сматривать как поверхность тока, хотя в общем случае поверхность тока представляет
собой поверхность вращения с криволинейной образующей.
Состояние газа на входе в сопловой аппарат турбины характеризуется давлением
и температурой. Лопатки соплового аппарата образуют криволинейные каналы, су-
жающиеся от сечения 0— 0 к сечению 1—1. Течение газа на этом участке сопровожда-
ется падением давления и температуры и соответствующим увеличением скорости.
Направление потока на выходе из соплового аппарата в основном определяется на-
Рис. 6.26. Принципиальная схема
трехступенчатой турбины
с\
Рис. 6.27. Схема ступени
газовой турбины
334
Рис. 6.28. Сечение лопаток соплового аппарата и рабочего колеса
на произвольном радиусе по высоте канала:
О—0 — сечение на входе в сопловой аппарат;
1—1 — сечение на выходе из соплового аппарата;
2—2 — сечение на выходе из рабочего колеса
правлением выходных кромок лопаток и составляет с плоскостью вращения колеса
некоторый угол. Таким образом, в сопловом аппарате часть потенциальной энергии
газа преобразуется в кинетическую. Одновременно в результате поворота потока
обеспечивается его закрутка у входа в рабочее колесо.
Относительная скорость на входе в рабочее колесо определяется из треугольника
скоростей, как разность векторов сх и и. Величина и направление относительной ско-
рости w, при заданных значениях скорости истечения газа из соплового аппарата q
и угла выхода cq зависят от окружной скорости и. Чем меньше и, тем больше и
меньше и наоборот, от величины угла в свою очередь, зависит форма рабочих
лопаток, так как для предотвращения срыва потока в колесе входные кромки рабочих
лопаток должны быть ориентированы по направлению, относительной скорости vv,.
Лопатки рабочего колеса обычно также образуют сужающиеся каналы. Поэтому газ
продолжает в них расширяться от давления рх до давления р2. При этом относительная
скорость движения газа увеличивается от Wj на входе до w2 на выходе, а температура
газа падает от Тх др Т2. Таким образом, течение газа через сопловой аппарат и лопатки
рабочего колеса может рассматриваться как течение через систему неподвижных и
вращающихся сопел с увеличением абсолютной скорости в сопловом аппарате и от-
носительной в рабочем колесе, а также уменьшением давления и температуры в обоих
элементах.
При обтекании газом лопаток соплового аппарата и рабочего колеса вследствие
поворота потока на вогнутой поверхности лопаток (корытце) образуется повышенное
давление, а на выпуклой (спинке) — пониженное.
Треугольники скоростей, построенные для сечений 7—7 и 2—2, обычно совме-
щают на одном рисунке и называют треугольниками скоростей элементарной ступе-
ни турбины. Заметим, что осевая скорость газа со в колесе может изменяться в зависи-
мости от высоты лопаток и отношения плотностей на входе и на выходе. Она обычно
увеличивается, но может оставаться постоянной или даже уменьшаться.
Так как газ в турбине расширяется и его плотность уменьшается, то в общем слу-
чае высота лопаток от ступени к ступени и в пределах ступени увеличивается.
335
Основные параметры ступени турбины
Ступень турбины прежде всего характеризуется своей геометрией. Основными
геометрическими размерами рабочего колеса (рис. 6.29) являются:
DT — наружный диаметр (по концам лопаток);
Z)BT — внутренний диаметр (по основанию лопаток);
Dcp — средний диаметр
Отношение и DT принято называть относительным диаметром
г-^. (6.51)
Кроме того, в теории турбин широко пользуются понятием относительной дли-
ны лопаток h /Dcp, под которой понимают отношение длины лопаток h к среднему
диаметру Яср. Очевидно, что d и h/Dcp между собой связаны однозначно. Относитель-
ная длина лопаток первой ступени турбины ТРД, ввиду достаточно большой плотнос-
ти газа перед турбиной, не очень велика и в среднем равна 1/6... 1/12 (d = 0,70...0,85).
Относительная длина лопаток последней ступени турбины, ввиду падения плот-
ности газа при его расширении, существенно больше и в среднем составляет 1/5... 1/4
и более (3 = 0,65...0,6).
Другими параметрами турбины являются скорость сл газа, на входе в сопловой
аппарат первой ступени и осевая скорость сад на выходе из рабочих лопаток последней
ступени, определяющая длину лопаток этой ступени. Значение сад колеблется
в пределах от 150 до 200 м/с, а значение са = 200...350 м/с и более.
Помимо абсолютных значений параметров в теории турбин очень важное значе-
ние имеют относительные параметры ступени. К ним относятся:
1. Отношение давления перед и за ступенью называемое степенью расшире-
ния газа или степенью понижения давления. Часто этот параметр называют перепа-
дом давления ступени. Среднее значение ят = 1,7...2,2 (определяет величину адиаба-
тической работы ступени).
2. Степень реактивности ступени. Под степенью реактивности понимают отно-
шение располагаемого теплоперепада (Як) в колесе к располагаемому тепл ©перепаду
(Я) в ступени
Як
Р=^к. (6.52)
Степень реактивности показывает, как
распределяется общий адиабатический тепло-
перепад между сопловым аппаратом и рабочим
колесом.
Как показывает опыт, гидравлические по-
тери в сопловом аппарате невелики, и с точно-
стью до одного процента можно принять:
Я=ЯС + ЯН. (6.53)
откуда Яс = (1 - р)Я — располагаемый
теплоперепад в сопловом аппарате.
Для авиационных турбин на среднем ради-
усе р = 0,3. Это означает, что 60...70% распола-
Рис. 6.29. Основные геометрические
размеры рабочего колеса:
в — радиальный зазор;
А — осевой зазор;
Y — угол уширения;
Sc, SK — ширина лопаток сопла и колеса
336
гаемой энергии вырабатывается на лопатках соплового аппарата, а 30...40% на лопат-
ках рабочего колеса.
3. Параметры u/с, и и/с^. Форма рабочих лопаток при заданной абсолютной ско-
рости газа с зависит от окружной скорости и. Наиболее полно это положение можно
характеризовать для любого изменения иис отношением и/с.
4. Коэффициент нагрузки ступени турбины.
LT
(6.54)
и
где Лт — работа турбины.
Коэффициент нагрузки характеризует нагруженность ступени турбины при за-
данной окружной скорости. Он также является функцией двух безразмерных пара-
метров, рассмотренных выше. Для турбин ТРД на среднем радиусе изменяется в пре-
делах 1,2...1,8.
Сравнительно небольшой диапазон употребляемых значений коэффициента на-
грузки позволяет пользоваться этой величиной как конструктивным параметром, оп-
ределяющим величину необходимой окружной скорости турбины.
Многоступенчатые турбины
Многоступенчатые турбины применяют в тех случаях, когда располагаемая энер-
гия велика и ее нельзя преобразовать в одной ступени с высоким коэффициентом по-
лезного действия (КПД).
Применение многоступенчатой турбины позволяет при допустимом значении и
(с точки зрения прочности) работать вблизи оптимального отношения и/сад и тем са-
мым повысить КПД.
Применение многоступенчатой газовой турбины требует (особенно при высокой
начальной температуре газа) интенсивного охлаждения лопаток, что связано с допол-
нительной затратой работы.
Многоступенчатые турбины в настоящее время получили широкое применение
в авиации. В ТРД число ступеней доходит до трех, а в ТРДД и ТВД до 5...7.
Чем больше адиабатический КПД отдельных ступеней, тем больше и общий ади-
абатический КПД многоступенчатой турбины.
С ростом адиабатического КПД отдельных ступеней уменьшается разница между
адиабатическим КПД отдельных ступеней и многоступенчатой турбины в целом (для
идеальной турбины адиабатический КПД отдельных ступеней и всей турбины равен
единице) и, наоборот, чем меньше адиабатический КПД отдельных ступеней, тем
больше эта разница.
Для современных многоступенчатых турбин без учета охлаждения т]ад =
= 0,92...0,94, Т|т = 0,9.. .0,93.
Увеличение потерь на первых ступенях многоступенчатой турбины меньше влия-
ет на уменьшение общего КПД, чем такое же увеличение в последующих ступенях
(напомним, что в многоступенчатом компрессоре — наоборот).
Одним из основных вопросов теории многоступенчатых турбин является распре-
деление общей эффективной работы или общего адиабатического теплоперепада
между отдельными ступенями. В связи с этим необходимо уточнить, что можно счи-
тать допустимым теплоперепадом для одной ступени и из каких соображений следует
исходить при выборе числа ступеней турбины, если общий теплоперепад известен.
337
Величина теплоперепада в ступени определяется перепадом давлений и начальной
температурой газа. Последняя обычно является заданной, так что определение допусти-
мого теплоперепада в ступени сводится к определению допустимого перепада давления.
Наиболее употребительны следующие схемы меридионального профиля:
1) средний диаметр всех ступеней остается постоянным;
2) средний диаметр увеличивается за счет увеличения внешнего диаметра,
а внутренний диаметр остается постоянным.
Величина и является некоторой функцией (1//сад) многоступенчатой турбины.
В теории многоступенчатых турбин пользуются также соотношением
Ц=Д, (6.55)
Zi/,
величина которого меняется в пределах 1,5...1,8.
Окончательное распределение теплоперепада между отдельными ступенями ус-
танавливается в результате детального газодинамического расчета каждой ступени
6.2.6. Выходные устройства ВРД
Общая характеристика выходных устройств
Выходные устройства силовых установок с ВРД предназначены для преобразова-
ния тепловой и потенциальной энергии газов в кинетическую энергию вытекающей
струи с учетом структуры потока на входе, компоновки двигателя на летательном ап-
парате и назначения последнего. В выходном устройстве в результате падения давле-
ния скорость рабочего тела увеличивается. В зависимости от скорости в выходном се-
чении выходные устройства делятся на до- и сверхзвуковые.
В настоящее время выходное устройство — это сложный элемент силовой уста-
новки, существенно отличающийся от простых сопел первых реактивных силовых ус-
тановок. Конструкция выходного устройства может содержать элементы управления
площадью среза сопла, устройства для реверса или девиации тяги, системы управле-
ния вектором тяги и др.
Основные параметры выходных устройств
Величина расчетного отношения давлений на сопле определяется соотношением:
Лс.расч=Рф//’с> (6.56)
где — давление торможения во входном сечении сопла; рс — статическое давление
в выходном сечении сопла.
Для сужающегося сопла значение расчетной скорости в выходном сечении при-
нимается равным скорости звука, в соответствии с этим величина относительной
плотности тока X с = 1,85 (для к = 1,33). Для сверхзвуковых сопел значение расчет-
ной скорости в выходном сечении больше скорости звука и для идеального сопла од-
нозначно определяется отношением площади (FKp) критического сечения к выходной
площади Fc сопла
с.расч) = Л<р /Fc =f& с.расч’ *). (6.57)
Для таких выходных устройств значение Хсрасч > 1,85 и может определяться по
соотношению:
Л с.расч =1/л(Хсрасч). (6.58)
338
Значение тс, при котором на срезе сужающегося сопла достигается скорость, рав-
ная скорости звука, называется расчетным (для сужающегося сопла это отношение
равно критическому).
к
п с.кр = П с.расч = f~Г • (6.59)
Работа выходного устройства в системе двигателя определяется значением распола-
гаемого отношения давлений:
яс.р=Рф/Рн- (6.60)
Особенности функционирования выходных устройств
Режим работы выходного устройства определяется соотношением располагаемо-
го и расчетного отношений давлений, откуда имеем расчетный режим работы выход-
ного устройства.
Дозвуковое (сужающееся) сопло может работать в двух режимах, с полным рас-
ширением и недорасширением. В режиме с полным расширением давление газа на
срезе равно давлению в окружающей среде рс = рн, а скорость меньше скорости звука.
В режиме с недорасширением (лс > п ч) давление на срезе больше давления в окру-
жающей среде рс > рн, а скорость истечения равна скорости звука.
Наиболее характерным сверхзвуковым выходным устройством является сопло
Лаваля. Для сверхзвукового выходного устройства такого типа возможны три режима
работы: с перерасширением, расчетный режим и режим с недорасширением.
Режимы течения с дозвуковой или смешанной скоростью в выходном сечении
встречаются в некоторых специальных случаях работы силовых установок. Величина
тяги (Рс) у любого выходного устройства в расчетном режиме определяется выраже-
нием:
^с = ^срасч. (6.61)
Величина тяги сопла в нерасчетных режимах (для всех тс) определяется выраже-
нием:
Л = <?гС с.расч + Fc(Pc-Ph)’ <6.62)
где Fc — площадь выходного сечения сопла; рс, рн — давление воздуха на срезе сопла и
перед двигателем.
Н = Сг/Сил-
"ЧУ <6«>
где Rr — газовая постоянная; к — показатель адиабаты; Т$, рф — температура и давле-
ние газа перед соплом.
Тяговую эффективность выходных устройств можно оценивать коэффициентом
скорости
Фс “ ^сд/^хар'
и относительным импульсом Jc.
Значение действительной скорости на срезе выходного устройства сс может быть
определено различными путями: рассчитано для случая течения идеальной жидкости
с последующим внесением поправок; вычислено по измеренному полю скоростей;
определено по измеренной тяге или по распределению давления по стенкам. Значе-
ния скорости в выходном сечении, полученные различными способами, отличаются
339
друг от друга; наиболее достоверные значения скорости дают испытания с измерени-
ем тяги:
Фс “ ^сд/^ с.расч ~~ с.расч (6.64)
Ф с ~ Сы/С с.ид ~ ^сд/^ с.ид-
Поскольку наиболее достоверные данные получаются по измерениям тяги, то
можно оценивать эффективность выходных устройств, относя измеренную тягу Рс к
идеальной Рад. Отношение действительной тяги к идеальной носит название коэффи-
циента тяги по внутренним параметрам:
~Рс = Рт/Рс.т- (6.65)
Р =Gc
с.ид rv с.ид»
Рсд = САд + Fqpq =faca)Fcpc* =PcFc/r(kcJ. (6.66)
Внешний поток взаимодействует со струей рабочего тела, вытекающей из выход-
ного устройства, в результате чего тяга, определенная по внутренним параметрам, уже
не равна силе, движущей летательный аппарат. В таком случае движущей силой будет
эффективная тяга силовой установки. Как уже отмечалось, учесть характер взаимо-
действия струи рабочего тела и внешнего потока можно, используя коэффициент
внешнего сопротивления (схкор):
^кор=2Лкор/(рнКТтИ), (6.67)
где сопротивление кормовой части %кор состоит из сопротивления давления Хр и со-
противления трения Хф. Обе эти составляющие должны быть определены с учетом
взаимодействия струи рабочего тела с наружным потоком. Fmid — площадь миделя
двигателя.
Эффективная тяга сопла определяется из соотношения
Лэф^сд-Люр- (6.68)
Рационально для оценки тяговой эффективности выходного устройства исполь-
зовать измеренную тягу, которую характеризует коэффициент эффективной тяги
(?сэф), равный отношению измеренной эффективной тяги к идеальной:
^сэф = Л:эф с.ид = (Лщ “ Люр С.ид- (6.69)
Величина Рсэф определяется с учетом взаимодействия струи рабочего тела
с внешним потоком по результатам модельных исследований или по натурным ис-
пытаниям.
ЛИТЕРАТУРА
1. Алемасов В. Е., ДрегалинА. Ф., Тишин А. П. и др. Теория ракетных двигателей /
Под ред. акад. Глушко В.П., 3-е изд. — М.: Машиностроение, 1980. С. 553.
2. ГОСТ 17655—72. Двигатели ракетные жидкостные. Термины и определения,
1981. С. 47.
3. Васильев А. П., Кудрявцев В. М., Головное Л. Г. и др. Основы теории и расчета ЖРД. —
М.: Высшая школа, 1975. С. 656.
4. Попов В. Г., Ярославцев Н. Л. Жидкостные ракетные двигатели: Учеб, пособие. —
М.: МАТИ, 2001. С. 170.
5. Фахрутдинов И. X., Котельников А. В. Конструкция и проектирование ракетных
двигателей твердого топлива, учебник. — М.: Машиностроение, 1987. С. 325.
340
6. Дюнзе М. Ф., Жимолохин В. Г. Ракетные двигатели твердого топлива для космиче-
ских систем. — М.: Машиностроение, 1982. С. 159.
7. Попов В. Г., Ярославцев Н. Л. Ракетные двигатели твердого топлива: Учеб, посо-
бие. - М.: МАТИ, 2001, С. 188.
8. Акимов В. М., Бакулев В. И., Мирзоян С. А. и др. / Под ред. Шляхтенко С. М. Те-
ория и расчет воздушно-реактивных двигателей: Учебник. — М.: Машиностро-
ение, 1987. С. 567.
9. Казанджан П. К, Кузнецов А. В., Рыбко П. Г. Теория авиационных двигателей:
Учебник. — М.: Машиностроение, 1983. С. 160.
10. Нечаев Ю. Н. Законы управления и характеристики авиационных силовых уста-
новок: Учебник. — М.: Машиностроение, 1995. С. 395.
11. Попов В. Г. Практикум по курсу «Теория и расчет ВРД». Учеб, пособие. — М.:
МАТИ, 2002. С. 116.
СОДЕРЖАНИЕ ГЛАВЫ 6
6.1. Ракетные двигатели.........................................285
6.1.1. Параметры и характеристики ракетных двигателей.......285
6.1.2. Жидкостные ракетные двигатели (ЖРД)..................287
6.1.3. Особенности конструкции жидкостных ракетных двигателей.294
6.1.4. Ракетные двигатели твердого топлива..................302
6.2. Воздушно-реактивные двигатели..............................315
6.2.1. Основные типы воздушно-реактивных двигателей (ВРД).....315
6.2.2. Входные устройства воздушно-реактивных двигателей....318
6.2.3. Компрессоры воздушно-реактивных двигателей...........323
6.2.4. Основные камеры сгорания ВРД.........................331
6.2.5. Газовая турбина ВРД..................................333
6.2.6. Выходные устройства ВРД..............................339
Литература..........................................................340
ГЛАВА 7
Элементы строительной механики
летательных аппаратов
Современные летательные аппараты (ЛА), воспринимающие нагрузки, дейст-
вующие на них в процессе эксплуатации, без повреждений и недопустимых измене-
ний формы должны при этом обладать минимальной массой конструкции. Требова-
ние достижения минимальной массы находится в противоречии с требованиями запа-
са прочности и жесткости. Успешное разрешение этого противоречия определяется
степенью полноты и достоверности информации, которой располагает разработчик
относительно взаимосвязи между геометрическими параметрами конструкции, свой-
ствами материала и допустимым уровнем ее нагружения. Эта взаимосвязь формирует-
ся в процессе расчета на прочность летательного аппарата и его элементов, который
предусматривает определение расчетных нагрузок, выбор расчетных схем и моделей,
адекватно описывающих реальные элементы конструкции; анализ напряженно-де-
формированного состояния, устойчивости и динамического поведения отдельных
моделей и их совокупности; переход от расчетных моделей к реальным объектам и
оценку их работоспособности.
Наличие широкого класса расчетных схем, моделирующих работу элементов
конструкции ракеты, методов, необходимых для решения вопросов о напряженном
и деформированном состоянии, устойчивости и динамическом поведении моделей,
определило появление строительной механики как науки о принципах и методах оп-
ределения напряженно-деформированного состояния типовых расчетных моделей,
анализа их устойчивости и динамического поведения.
Целью преподавания данной дисциплины является научить студентов использо-
вать принципы и методы определения напряженно-деформированного состояния ти-
повых расчетных моделей, проводить тщательный анализ работы их элементов, бази-
руясь на современных методах расчета, успешно применять методики, основанные на
использовании ЭВМ; подойти к решению проблем проектирования и расчета ЛА на
прочность; существенно уточнить расчетные модели, приблизив их к реальной конст-
рукции и из различных вариантов обоснованно выбрать наиболее целесообразный.
7.1. СТЕРЖНЕВЫЕ КОНСТРУКЦИИ И РАСЧЕТ ИХ НА ПРОЧНОСТЬ
7.1.1. Стержневые системы в ракетных конструкциях
Стержень — тело, поперечные размеры которого (л, Ь) малы по сравнению с дли-
ной /. Среди стержней особое место занимают тонкостенные. У них толщина h мала
по сравнению с другими размерами поперечного сечения.
Одиночные стержни могут использоваться как вспомогательные силовые эле-
менты корпусов ЛА. Стержневые системы, рамы и фермы, используются для крепле-
ния двигателей, приборов и т. п. (рис. 7.1).
342
Рис. 7.1. Пространственные и плоские стержневые системы: фермы и рамы
В строительной механике стержневых систем обычно рассматривают только та-
кие системы, перемещения и деформации которых являются линейными однородны-
ми функциями внешних сил. Для них справедлив принцип независимости действия
сил, и перемещение от нескольких сил есть сумма:
= S/l^l + $2*2 + ••• + 8/Л>
где 8Л — перемещения под действием силы Fk = 1.
Геометрически неизменяемой будем называть такую стержневую систему, в кото-
рой невозможны относительные перемещения частей без деформации.
В зависимости от связей между стержнями и мест приложения внешних сил
стержневые системы делятся на фермы и рамы. Фермой называется геометрически
неизменяемая стержневая система, в которой стержни между собой соединяются
шарнирно и работают преимущественно на растяжение и сжатие. Внешние силы при-
кладываются только в узлах (рис. 7.1, в).
Геометрически неизменяемая стержневая система, в которой элементы соединены
между собой жестко и работают преимущественно на изгиб или кручение (сдвиг), назы-
ваются рамами. Силы к рамам могут прикладываться в любом сечении (рис. 7.1, г, д).
Различают плоские и пространственные рамы и фермы. Плоской будем называть
такую раму, у которой оси всех элементов расположены в одной плоскости. В этой же
плоскости лежат и внешние силы (рис. 7.1, б).
В пространственных системах (рис. 7.1, а, е) оси элементов лежат в разных плос-
костях. Если нагрузки, действующие на плоскую раму, направлены перпендикулярно
к плоскости рамы, такую раму называют плоскопространственной (см. рис. 7.1, д).
В ракетной технике используются преимущественно рамы. Задача расчета стержне-
вых систем при заданной геометрической схеме, внешних силах (нагрузках) состоит
в подборе сечений всех элементов с целью обеспечения достаточной надежности при
минимальных затратах материалов и стоимости. Основное содержание этой задачи
заключается в определении внутренних силовых факторов и перемещений системы.
Расчет стержневых систем основан на применении начала возможных перемеще-
ний. Для упругих систем принцип возможных перемещений можно сформулировать
так: сумма работ внешних и внутренних сил на любом возможном малом перемеще-
нии равна нулю, если система находится в равновесии под действием приложенных к
343
ней внешних сил. Таким образом, в упругих системах к активным силам относятся и
внутренние силы.
За возможные перемещения принимают упругие перемещения, вызываемые лю-
быми видами нагрузки, т. е. наряду с заданным нагружением вводится некоторое
фиктивное нагружение при условии, что смещения малы, граничные условия соот-
ветствуют действительным, и выполняется условие совместности деформаций
(сплошности) конструкции.
Можно считать, что в упругих системах вся работа внутренних и внешних сил за-
трачивается только на деформацию. При таком допущении суммарная работа внеш-
них и внутренних сил на возможных перемещениях линейно деформируемой систе-
мы зависит только от исходного и конечного состояний. Для неупругих тел это допу-
щение неправомерно, так как при пластических деформациях часть работы
превращается в тепловую и другие виды энергии.
Для удобства анализа работы упругой системы пользуются понятиями «обобщен-
ная сила» и «обобщенное перемещение». Под обобщенной силой понимают любое
силовое воздействие на систему: пары сил, распределенную нагрузку, группу сосредо-
точенных сил и т. п. Перемещение, на котором обобщенная сила производит работу,
называют обобщенным перемещением. Каждой обобщенной силе соответствует оп-
ределенный тип обобщенного перемещения; сосредоточенной силе — линейное пе-
ремещение; моменту — угловое перемещение; распределенной нагрузке — площадь
эпюры перемещений на участке приложения нагрузки. Далее для сокращения записи
слово «обобщенная» опускаем.
7.1.2. Работа внешних и внутренних сил
Работа внешних сил
Под действием нагрузки упругие тела (системы) деформируются. Нагрузка может
прикладываться с различными скоростями. В этом разделе изучается только статиче-
ское действие сил. Внешние силы от начала и до конца нагружения уравновешивают-
ся внутренними силами. Так как деформации тела растут постепенно, согласно зако-
ну Гука, так же постепенно возрастает и воспринимаемая упругим телом внешняя на-
грузка, так как в силу третьего закона Ньютона силы существуют только в паре.
Пусть на упругую систему действует система внеш-
них сил Fj, Г2,... Fn (рис. 7.2).
Каждая из сил будет вызывать перемещение точек
системы. Для некоторой точки в направлении i эти пе-
ремещения будут следующие:
&iF\ = 8/1Л
Рис. 7.2. Действие
на упругую систему
внешних сил
&iF2 ~ 8,2^2
&iFn
где 8ik — удельное перемещение этой точки в направлении /—/, вызванное силой Fk = 1
(первый индекс указывает направление; второй — причину перемещения). В соот-
ветствии с принципом независимости действия сил полное перемещение в этом на-
правлении будет равно сумме перемещений, вызванных отдельными силами:
или
\f~~ &iF\ + + +
&iF = 8/1^1 + 5/2^2 + +
344
Перемещение системы в направлении действия всех заданных сил можно запи-
сать так:
Д1г= 51 + 512^*2+ 51з^з + ••• + 31л£л;
.................................................... (7.1)
\f= 8я1^1 + ад + ад + - + 5ЛЛЛ>-
Закон, выраженный (7.1), характеризует свойства материала и свойства системы.
Использовав свойства однородной линейной функции, его можно записать так:
+ 812 + 813 + ••• + 81л у?
А2£= F2 ^811^7 + 822 + З23 jr + ... + 82л
(7.2)
ДЯГ= Fn [8Л1 у + 8л2 у + 8л3 У + ... + 8ЛД
\ 1 п л п 1 п J
На основании принципа независимости действия сил можно считать все силы при-
ложенными одновременно и нарастающими пропорционально, так что отношения сил
Г2 Fn
-г ... т— постоянны. Тогда суммы в скобках тоже постоянны, поскольку oik характе-
"1 "л - 1
ризуют только жесткость самой системы. Формулы можно переписать в другом виде:
A|f =
A2f=^F2; (7.3)
ДлГ= В F.
Пг П П
Таким образом, перемещения системы в направлении некоторой силы линейно
зависят от этой силы. Уравнения (7.3) графически представлены на рис. 7.3.
Действительной работой внешней силы называют работу, совершаемую силой на
перемещениях, вызванных всеми силами. Она равна площади под прямой:
т. е.
4 = 2 ^iF'
Работа всех сил системы
1 п
Л=~2 LW- (7.4)
Суммарная действительная работа внешних сил равна полусумме произведений
конечного значения каждой силы на конечное значение суммарного перемещения по
направлению действия силы. Как видно из (7.2) и (7.4), работа есть квадратичная
функция сил, т. е. работа, не пропорциональная силе. Она не равна сумме работ, кото-
рые могли быть произведены каждой силой в отдельности, кроме случаев, при кото-
рых перемещение в направлении одной силы, вызванное другой силой, равно нулю.
Для определения возможной работы кроме заданного состояния системы будем
рассматривать еще и некоторое возможное состояние. Возможной работой заданных
внешних сил будем называть их работу на возможных перемещениях, а возможными пе-
ремещениями полагать перемещения, вызванные некоторой фиктивной системой сил.
Эти перемещения не существуют в действительности и не имеют физического смысла.
Представим их таким образом. Допустим, что к балке (рис. 7.4) приложены силы
F, и F2. Под их действием балка прогнется и останется в состоянии равновесия. Пред-
положим, что затем к балке приложены силы F3 и F4, вызывающие в сечениях, где при-
345
Рис. 7.3. Зависимость
перемещений системы от силы
Рис. 7.4. Действие
сил на балку
ложены внешние силы и F2, возможные перемещения Wj и w2. Тогда эти силы совер-
шают возможную работу:
Л12 = FjW, + F2w2.
Работа внутренних сил
Во всех деформируемых силовых элементах конструкций возникают внутренние
силы. Пусть в сечениях А—А и В—В стержня, отстоящих друг от друга на величину ds,
действуют нормальная сила N, поперечная сила Q и изгибающий момент М. Для эле-
мента, выделенного этими сечениями, они будут внешними силами (рис. 7.5). Действи-
тельная работа их может быть определена как сумма работ статически приложенных
сил. Работа каждой из этих сил на перемещениях, вызванных другой силой, равна нулю.
Перемещение от действия нормальной силы равно удлинению элемента:
AdS=
L * А
Работа силы на этом перемещении
^="2 ' fer • (7’5)
Работу внешних сил принято считать отрицательной, так как внутренние силы
всегда направлены против перемещений от внешних сил. Для всего стержня
(7-6)
S
Под действием изгибающего момента крайние сечения элемента повернутся на
1 Mv Mv
угол d<p (рис. 7.6). Так как d<p = — и - = , то d<p = • ds.
Рис. 7.5. Выделенный элемент
Рис. 7.6. Деформация элемента
под действием изгибающего момента
346
Работа изгиба
(7-7)
S у
От действия поперечных сил концевые сечения элемента сдвигаются относи-
тельно друг друга на величину Д = yds, называемую абсолютным сдвигом. При равно-
Ч. Q
мерном распределении касательных напряжений, т. е. при т = , абсолютный сдвиг
Д = ds, где G — модуль сдвига; А — площадь сечения.
О • А
Работа поперечной силы на этом перемещении
Ий*- <’’>
S
На самом деле распределение касательных напряжений зависит от формы сече-
ния, влияние неравномерности учитывается путем введения в (7.8) коэффициента
формы поперечного сечения т|. Тогда
= (7.9)
S
Для прямоугольного сечения т| = 1,2; для круглого сечения т| = 1,2; для двутавро-
вого профиля т| = , где Ас — площадь сечения стенки. Во всех случаях интегрирова-
ние ведется в пределах длины участка с одинаковой нагрузкой и одинаковой жестко-
стью сечений.
Полная работа внутренних сил находится как сумма работ на всех участках. Сум-
марная работа, взятая с обратным знаком, называется потенциальной энергией U
и выражает запас работы, который можно получить при разгрузке упругого тела. Для
плоской стержневой системы
1 г " v2 п п2 п М2
P-J <7.10)
i=15 / = 15 /=15 y
В случае пространственной системы при произвольном нагружении в сечениях
возможны все шесть внутренних сил. Тогда потенциальная энергия
1 _ п жГ2 п Л)2 п П2 п М2
и= И i r\yiehds+
/=15 / = 15 /=15 /=15 y
Правая часть (7.11) есть однородный алгебраический многочлен второй степени от-
носительно внешних сил. Такие многочлены называют квадратичными формами, по-
этому говорят, что потенциальная энергия может быть представлена в виде квадратич-
ной формы от внешних сил. За независимые переменные принимали внешние силы. Ес-
ли принять за независимые переменные суммарные перемещения Д/Я соответствующие
этим силам, потенциальную энергию можно представить как функцию перемещений.
Потенциальная энергия (7.11) может быть получена из обобщенного закона Гу-
ка, если представить полную удельную потенциальную энергию в напряжениях со-
347
гласно выражению U= Iai + а2+ аз “ 2ц (0^2 + а2аз+ аза1)1» и из формул для на-
пряжений растяжения, сдвига, кручения и изгиба.
Возможной работой внутренних сил будем называть работу внутренних сил од-
ного состояния на перемещениях другого состояния.
Пусть имеются два состояния: рик (рис. 7.7). Определим возможную работу рас-
Nk • ds
тягивающей силы № на перемещениях состояния к, равных Ads = Е д .
Получим: Арк = - ds.
s
Для остальных внутренних сил можно получить аналогичные зависимости. Тогда
возможная работа внутренних сил для пространственной системы может быть пред-
ставлена в таком виде:
/=ls /=1 s /=1 s
п tMp • Мк
у J ту lvly
i=\S E J>'
(7.12)
При вычислении работы внутренних сил линейно упругой системы (если в нее не
входят стержни с большой кривизной) справедлив принцип независимости действия
сил, так как работа каждой из сил N, Qz и Му на перемещениях, вызываемых другими
силами, равна нулю.
7.1.3. Теоремы об упругих системах
Теорема о взаимности работ
Теорема 1. Работа сил первого состояния на перемещениях, вызванных силами
второго состояния, равна работе сил второго состояния на перемещениях, вызванных
силами первого состояния.
Доказательство. Пусть даны два различных состояния (рис. 7.8) некоторой ли-
нейно деформируемой системы, отвечающие двум различным нагрузкам, и в обоих
ds + Ads
Рис. 7.7. Два состояния
деформируемого тела
при растяжении
Рис. 7.8. Два состояния
линейно деформируемой
системы
348
случаях система уравновешена. Пусть вначале приложена сила Fx. Обозначим ее рабо-
ту Аи. После окончания этого процесса нагружения прикладывается сила F2, совер-
шающая работу А22. Сила F2 не только сама совершает работу и смещает точку прило-
жения силы Fj, вторично вовлекая последнюю в работу. Обозначим эту работу Л12.
Суммарная работа А=Ап + А22 -I- Л12.
Рассмотрим полную работу при приложении сил в другом порядке: сначала дей-
ствует сила F2, затем Fx. Эта работа равна:
А = А22 + Ахj + Л21.
Работа внешних сил системы, находящейся в равновесии, равна потенциальной
энергии, которая зависит лишь от начального и конечного состояний. Так как исход-
ные и конечные состояния в обоих случаях одинаковы, то
Ахх А22 АХ2 “ А22 + ^2р
откуда
Л12=Л21. (7.13)
Эта теорема известна под названием теоремы Бетти, доказавшего ее в общем ви-
де. Для случая стержня при растяжении теорема впервые доказана Максвеллом.
Теорема о взаимности перемещений
Теорема о взаимности перемещений вытекает из теоремы о взаимности работ.
Теорема 2. Перемещение точки приложения первой силы по ее направлению от
действия второй силы равно перемещению точки приложения второй силы по ее на-
правлению под действием первой силы.
Доказательство. Рассмотрим два состояния упругой системы. В первом состоянии
система нагружена единичной силой F х = 1, направленной по линии 1—1, во втором
состоянии система нагружена силой F2 = 1, направленной по линии 2—2 (рис. 7.9).
Рис. 7.9. Два состояния
упругой системы
Пусть под действием силы Fx точка переместилась в
положение В\ Проекцию ее перемещения на направ-
ление силы обозначим 821. Первый индекс указывает
направление перемещения; второй индекс — причину,
ее вызвавшую. Под действием силы F2 точка А пере-
местится в положение А'. Обозначим 812 проекцию ее
перемещения на направление силы Fx.
На основании теоремы о взаимности работы
F1812 = ^2^21-
Так как Fx = F2, то
512 = 521. (7.14)
Эта теорема носит название теоремы Максвелла.
В некоторых случаях ее выгодно применять непосред-
ственно для определения перемещений.
Аналогично из теоремы о взаимности работ выво-
дится теорема о взаимности реакций. Реакция, возни-
кающая в связи 1, когда связь 2 переместится на еди-
ницу в своем направлении, равна реакции в связи 2
349
при перемещении связи 1 на единицу. В этом случае определяется возможная работа
от сил реакций одной из опор на единичном перемещении второй опоры. Теорема
справедлива для реакции любого вида (силы и момента).
7.1.4. Перемещения в стержневых системах
от внешних сил. Формулы Мора
Перемещения точек стержневой системы определяются как для оценки ее жест-
кости, так и для расчета статически неопределенных систем.
Рассмотрим некоторую стержневую систему (рис. 7.10). Определим перемещение
произвольной точки системы в произвольном направлении при действии заданной
системы сил. Обозначим его. Это действительное состояние системы 1 называют ос-
новным. Рассмотрим также возможное, т. е. воображаемое, состояние 2 этой же сис-
темы, в котором на систему действует только единичная фиктивная сила, приложен-
ная в искомой точке по направлению i—i, и в котором требуется найти перемещение.
В случае определения угла поворота прикладывается сосредоточенный момент.
Обозначим внутренние усилия в состоянии 7: N, Му, Mz, Мк, Qy, Qv в состоянии
2: N,MyMvMk, Qyi Qz.
Для состояния 2 за возможные перемещения примем перемещения под действи-
ем сил состояния 7. Примем направление силы F = 1 за положительное. Ее работа на
возможном перемещении Дл (здесь «1» есть индекс сил основного состояния).
Индекс «2» при А означает, что это работа внешних сил второго состояния; ин-
декс «1» означает, что эта работа выполняется на перемещениях, вызванных внешни-
ми силами первого состояния.
Согласно теореме о взаимности работ при F = 1
^12 = ^21 = 1
где Л12 — возможная работа заданных внешних сил (состояния 7) на перемещени-
ях, вызванных фиктивной (единичной) силой F = 1. Но на основании принципа воз-
можных перемещений для упругой системы возможная работа внешних сил Л12 равна
возможной работе внутренних сил, взятой с обратным знаком. Последняя определя-
ется (7.12).
Рис. 7.10. Действительное (основное)
и возможное (воображаемое) состояния стержневой системы
350
Таким образом, из теоремы о взаимности работ и принципа возможных переме-
щений следует
A/f= —А1.
Подставив значение работы внутренних сил по (7.12), получим искомое переме-
щение:
a v + v « + v « + v гЧ^я + v Г^я +
Л = X I --Яс 4- X т» I ’-Яс 4- X n I -Яс 4- X J Ц5 + у J £ j QS +
о у /=,о z
о
"1 о
~ 1 о
о
(7.15)
Эта формула известна как формула Мора, входящие в нее интегралы называют
интегралами Мора.
Формулу (7.15) можно применять и для криволинейных стержней, если радиус
кривизны значительно превышает высоту сечения (R > 5Я). В таких системах можно
пренебречь изгибом от действия продольных сил и линейной деформацией за счет из-
гибающих моментов. Во многих конкретных случаях расчета выражение (7.15) может
упрощаться. При расчете ферм, например, учитываются лишь нормальные силы N,
Я; при расчете рам пренебрегаем их нормальными и поперечными силами, если не
малы жесткость на растяжение и сдвиг, и т. п.
Перемещение точки приложения силы по направлению этой силы можно найти
также из теоремы Кастилиано: перемещение некоторой точки по направлению действия
заданной силы равно частной производной от потенциальной энергии по этой силе:
|^=0. (7.16)
Доказательство ее аналогично доказательству теоремы о взаимности работ.
Подынтегральные функции в формуле (7.14) есть функции внутренних усилий
М и Q. Интегралы Мора при известных функциях этих усилий могут быть вычислены
аналитически для участков стержней с одинаковыми законами изменения внутрен-
них усилий и жесткости; полученные значения суммируются.
Перемещения точек системы определяют по формуле Мора в такой последова-
тельности:
1) вычисляют внутренние силы N, М, Q от заданных нагрузок;
2) прикладывают единичную силу по направлению искомого перемещения; при
необходимости определения взаимных перемещений отдельных точек (сечений) нуж-
но приложить единичные силы, направленные в разные стороны (точка А на рис. 7.11);
3) рассчитывают внутренние силы N, М, Q возможного состояния;
4) найденные значения сил подставляют в формулу (7.14) и вычисляют интегра-
лы Мора.
Рис. 7.11. Действия единичных сил
на стержневую систему
Перемещения в статически неопределимых
системах находят после вычисления внутренних си-
ловых факторов методом сил. Единичные силы
прикладывают не к заданной, а к основной системе,
которая всегда статически определима. Если одна
из сил в (7.16) — линейная функция s, для определе-
ния интеграла Мора в этом случае необходимо ум-
ножить площадь криволинейной эпюры на распо-
ложенную под ее центром тяжести ординату прямо-
линейной эпюры по способу Верещагина. Знак
351
перемещения зависит от знаков эпюр сил. При одинаковых знаках эпюр перемеще-
ние направлено по единичной силе. Эпюра единичных сил для прямолинейного
стержня постоянного сечения всегда прямолинейна. Если эпюра имеет вид ломаной
или жесткость стержня переменная, то при вычислении интегралов Мора ее разбива-
ют на участки с одинаковым законом изменения внутреннего силового фактора или с
постоянной жесткостью. Полученные значения интегралов суммируют.
7.1.5. Метод сил
Статическая неопределимость
Теоремы об упругих системах составляют основу методов расчета статически не-
определимых систем. Наиболее широкое распространение получил метод сил.
В строительной механике применяется также метод перемещений.
Балки, рамы и фермы подразделяются на статически определимые и статичес-
ки неопределимые. Статически определимыми называются такие системы, у кото-
рых реакции опор могут быть определены из уравнений равновесия системы как
жесткого тела, а внутренние усилия — из уравнения равновесия мысленно отсечен-
ной части. Статически неопределимыми будем называть такие системы, у которых ре-
акции опор и внутренние силовые факторы не могут быть найдены из уравнений рав-
новесия.
Разность между числом неизвестных — реакций связей, внутренних усилий —
и числом уравнений статического равновесия, которые могут быть составлены
для системы, называют степенью статической неопределимости. Число связей, обес-
печивающих кинематическую неизменяемость системы, называется необходи-
мым. Связи, наложенные сверх необходимых, называются дополнительными или
«лишними».
Связи делятся на внутренние и внешние. Внешние связи обеспечиваются опо-
рами.
Если системы состоят из одного стержня (балки), то для обеспечения ее кинема-
тической неизменяемости в плоскости нужно наложить три связи. По стержневой
схеме необходимые для этого опоры изображены на рис. 7.12, а. Теперь система со-
стоит из четырех стержней, соединенных пятью шарнирами, из которых один двой-
ной. Для них в плоскости можно составить двенадцать уравнений равновесия, шар-
ниры накладывают столько же связей. Цилиндрический шарнир в плоской раме на-
кладывает две связи. Введение двойного или многократного шарнира эквивалентно
к = п - 1 шарнирам, где п — число соединяемых звеньев. В пространственных рамах
могут устанавливаться сферические шарниры, накладывающие по три связи.
Поставим в середине пролета балки еще одну подвижную опору (рис. 7.12, в).
Теперь для системы можно составить пятнадцать уравнений, а шарниры накладывают
шестнадцать связей. Одна связь оказывается «лишней». Жесткая заделка или жесткое
соединение стержней в плоской системе накладывает на систему три связи. Если на
свободный конец жестко заделанной консольной балки установить подвижную шар-
нирную опору, одна связь окажется «лишней» (см. рис. 7.12, б). Таким образом, число
«лишних» связей равно разности между числом наложенных связей и числом уравне-
ний равновесия для свободных стержней.
Из этих примеров нетрудно установить формулу для определения общего числа
«лишних» связей плоских систем:
Я=2Р1 + ЗР2-Зи,
352
(7.17)
стержня (балки)
неопределимая система
определимая система
а для пространственных систем формулу
Н= 5Р} + 6Р2 + ЗР3 - 6л, (7.18)
где Я — число «лишних» связей (степень статической неопределимости);
Р} — число простых шарниров;
Р2 — число жестких заделок или жестких соединений стержней;
Р3 — число сферических шарниров;
п — число стержней.
Различают внутреннюю и внешнюю статическую неопределимость. Под внеш-
ней статической неопределимостью понимают разность между числом внешних свя-
зей и числом уравнений равновесия всей системы как твердого тела. Для плоской ра-
мы внешняя статическая неопределимость
Я^с-3,
где с — число внешних связей.
Рама, изображенная на рис. 7.13, имеет 8 внешних связей, для нее Н= 3. Внут-
ренняя статическая неопределимость равна числу внутренних связей.
Рассмотрим раму, состоящую из пяти стержней (рис. 7.14). Пусть точки Л и Б не
соединены. Тогда лишних внутренних связей нет. Система статически определима.
По формуле (7.17) Я= 2 • 6 + 3* 3 - 3*7 = 0.
Методом сечений можно определить деформации всех стержней. Соединим точ-
ки Я и В шарниром, который позволит только взаимный поворот стержней, т. е. нало-
жит две связи. Система станет дважды статически неопределима. Если шарнир затем
заменить жестким соединением, степень статической неопределимости увеличится
на единицу и будет равна трем (рис. 7.15, а, б).
Из этих рассуждений можно установить, что замкнутый контур при жестком со-
единении стержней между собой трижды статически неопределим. Таким образом,
внутренняя статическая неопределимость
Я2 = ЗЯ-Рр
где Р} — число внутренних шарниров; N — число замкнутых контуров.
Общая статическая неопределимость
Я=Я1 + Я2.
Выбор основной системы метода сил
При расчете методом сил заданная статически неопределимая система освобож-
дается от лишних внешних и внутренних связей. Действие связей заменяется силами
и моментами, которые и оказываются неизвестными.
353
fl) б)
Рис. 7.15. Система с шарниром (а)
и жестким (б) соединением
Рис. 7.16. Заданная
расчетная система
Система, освобожденная от «лишних» связей, называется основной системой.
Оставшиеся связи должны обеспечить кинематическую неизменяемость системы.
Рассмотрим конкретный пример (рис. 7.16).
Степень статической неопределимости
Я= 3*8 —3*6 = 6.
Заданной системе соответствует несколько основных систем. Наиболее удобны-
ми для расчета являются статически определимые основные системы, однако расчет
возможен и при статически неопределимой основной системе, и при основной систе-
ме вида кинематической цепи, но метод сил в двух последних случаях неприменим.
Для нашего примера неудобны основные системы, изображенные на рис. 7.17, а
и 7.17, б, так как в первом случае подвижна правая стойка, а во втором случае замкну-
тый контур является мгновенным механизмом. Допустимы схемы с одним разрезом
замкнутого контура и удалением одной из опор (рис. 7.17, в), с тремя шарнирами в
замкнутом контуре и одной подвижной опорой (рис. 7.17, г). После приведения за-
Рис. 7.17. Основные системы, используемые для расчета заданной системы
354
данной системы к статически определимой вместо устраненных связей вводят неиз-
вестные: моменты — там, где запрещены повороты; силы — если запрещены линей-
ные перемещения. Неизвестные силовые факторы будем обозначать хк\ наибольшее
значение номера неизвестной силы равно степени статической неопределенности.
За основную примем систему, изображенную на рис. 7.17, д. В случае симметрич-
ной нагрузки удобна система, изображенная на рис. 7.17, е. Уравнение для определе-
ния неизвестных усилий в симметричной системе проще.
Канонические уравнения метода сил
Составим уравнения для определения неизвестных силовых факторов хк в раме,
изображенной на рис. 7.17, д. Смещение точек системы обозначим буквой
с индексами — A/(Xi Fу Первый индекс i указывает направление перемещений;
второй индекс — силы, вызвавшие перемещения (х( ... х6, F).
В точке А удалена жесткая опора, поэтому все три смещения точки Л, линейные и
угловые от заданных и неизвестных сил должны быть равны нулю:
дкх! ...х6, F) = °;
A2(jc, ...x6,F) = ()’
А3(х, ...x6,F) = 0-
Первые индексы указывают направление перемещений. Второй индекс у перемеще-
ний указывает, что полное смещение зависит от всех шести неизвестных сил .q ... х6 и за-
данной силы Е Аналогичное условие должно выполняться и в точке В. Вследствие прин-
ципа независимости действия сил каждое из перемещений можно записать в виде суммы:
Y = + А/г + ...+ A,F. (7.19)
/(Х| ... г ) /Х| IX2 1г v '
Так как перемещение пропорционально силе, можно записать его в таком виде:
\k=bik'xk- (7.20)
Коэффициенты 8/А. есть перемещения по направлению i силы под действием еди-
ничной силы. Под индексом /’будем понимать всю систему заданных сил.
В местах, где мысленно удалены связи, в заданной с учетом принятых обозначе-
ний раме (см. рис. 7.17, а) перемещений нет. Они должны быть равны нулю и в основ-
ной системе (см. рис. 7.17, д, е):
1 A1(x|...x6,F)-°; А2(х, ...x6,F)-Q’ A3(x,...x6,F)-°; | А4(х, ...х6, F) ~ 0’ А5(х, ...x6,F)~ A6(JC] ...х6, F) ~ 0- Учтя (7.19) и (7.21), получим (7.21) в таком виде; (7.21) (7.22)
< 8,1%, + 812х2 + 813х3 + 814х4 + 815х5 + 816х6 + A1F 0; 821х, + 822х2 + 823х3 + 824х4 + 825х5 + 826х6 + A2F= 0;
$61*1 + $62Х2 + $63*3 + $64*4 + $65*5 + $66*6 + A6F = 0.
Эти уравнения можно получить и энергетическим методом в виде
Линейные уравнения (7.22) называются каноническими уравнениями мето-
да сил, число их равно числу лишних связей. Такие уравнения могут быть составле-
355
ны для любой плоской или пространственной рамы. В краткой форме их можно запи-
сать так:
Ькхк + a,f= °-
В этой записи использовано правило суммирования по «немым» индексам. «Не-
мым» индексом называется индекс, встречающийся в произведении дважды (к —
в нашем случае). Наличие «немого» индекса и означает, что по нему берется сумма, знак
которой для сокращения опускается. «Свободный» индекс i означает, что имеется не од-
но, а Я уравнений (/ = 1, 2, 3,..., Я), т. е. число уравнений равно числу лишних связей.
В случае симметричной системы число уравнений можно уменьшить правиль-
ным выбором основной системы. Кроме того, уравнения упростятся, так как, соглас-
но теореме о взаимности перемещений,
^ik =
При выводе уравнений причина возникновения перемещений ничем не обуслов-
лена, поэтому уравнения справедливы при действии любой системы сил.
При малом числе лишних неизвестных Хк систему канонических уравнений мож-
но решить вручную, пользуясь алгоритмом Гаусса, определяющим последователь-
ность исключения неизвестных.
При большом числе уравнений используются машинные методы. Наибольшее
распространение в настоящее время получил матричный метод. В матричной форме
система имеет следующий вид:
AX=-A/f (7.23)
Матрица единичных перемещений (матрица податливости) симметрична и квад-
ратична:
Г»,, 812 8,3.. •5|я
82| 822 З23..
А = 83i 832 833.. •53л
3„2 V -8ЛЛ
(7.24)
При статическом нагружении она вычисляется просто. Вследствие симметрии от-
носительно главной диагонали определитель такой матрицы det А > 0. Следовательно,
решение канонических уравнений не может быть неопределенным или равным беско-
нечности, если все 8Л определены и конечны и одновременно не равны нулю. Эти усло-
вия обеспечиваются геометрически неизменяемой основной системой.
Матрица-столбец лишних неизвестных:
*2
Х =
(7.25)
п
матрица-столбец свободных членов (грузовых перемещений):
ч/
Д2Г
(7.26)
AfT-
Так как det А * 0, существует матрица А-1; решение (7.23) записывается так:
Х=—А”1 ’ A/f
356
Единичные перемещения 8ik вычисляют по формуле Мора, в интегралы Мора под-
ставляют единичные силовые факторы Мк Их эпюры строят для основной системы.
При вычислении перемещения от заданных сил подынтегральные функции интегралов
Мора — произведения внутренних сил от заданной нагрузки и от единичных сил. Грузо-
вые и единичные перемещения могут вычисляться матричным методом. После решения
системы (7.22) строят эпюры найденных усилий хк и складывают с грузовой эпюрой. Сум-
ма их есть эпюра силовых факторов заданной системы. Таким образом, метод сил состоит
в одновременном преобразовании сооружения и действующей на него системы сил.
Вместо расчета сложной системы с простой известной нагрузкой решают задачу
расчета простой системы при сложной, частью неизвестной нагрузке с помощью сис-
темы линейных уравнений, содержащей все неизвестные.
7.1.6. Метод перемещений
Некоторые задачи расчета на прочность статически неопределимых стержневых
систем проще решаются методом перемещений. Так же, как и в методе сил, использу-
ется основная система.
При расчете по методу сил наиболее удобна статически определимая основная
система, не содержащая простых и мгновенных механизмов. Неизвестными становят-
ся силы, приложенные взамен удаленных связей.
Самая простая основная система метода перемещений представляет собой сово-
купность однопролетных балок с жестко защемленными или шарнирно опертыми
концами. При ее выборе вводятся дополнительные связи, запрещающие поворот
и линейное смещение узлов соединения стержней.
Для сравнения основных систем метода сил и метода перемещения рассмотрим
статически неопределимую раму (рис. 7.18).
Рама состоит из двух стержней, жестко связанных между собой и с неподвижной
опорой, степень статической неопределимости ее по формуле (7.17)
Н= 3 -3-2- 3 = 3.
Наиболее простой основной системой метода сил является система с одной уда-
ленной опорой (рис. 7.19, а).
Для определения неизвестных сил хк составляются три канонические уравнения
(7.22).
Узел В рамы (см. рис. 7.19, б) при изгибе ригеля и стойки рамы может поворачи-
ваться в плоскости; смещению вверх и вниз, вправо и влево препятствуют стержни АВ
Рис. 7.18. Статически
неопределимая рама
Рис. 7.19. Основная система
для расчета рамы
357
и ВС, поэтому выбор основной системы метода перемещений однозначен — нужно
запретить поворот узла В.
Этот поворот устраняется введением дополнительной связи, запрещающей толь-
ко вращение узла В. На рис. 7.19, б эта связь показана условно в виде балочки.
Введение новой связи вызовет появление реакции, не имеющей места в заданной
системе. Обозначим ее RF, индекс Fуказывает причину появления реакции — прило-
женные к раме внешние силы. Так как в заданной системе реакций от запрета поворо-
та узла В нет, то сумма реакций в узле, вызванных самим защемлением узла и задан-
ными внешними силами вследствие запрета поворота, должна быть равна нулю.
В этом смысл канонических уравнений метода перемещений. За неизвестные прини-
маются запрещенные перемещения Zk. Так как само Z неизвестно, реакцию от него
представляют в виде произведения rikZk, где rik — реакция в направлении /, вызванная
запретом смещения на единицу. Единичная реакция rik играет роль, аналогичную ро-
ли единичных перемещений Ь1к в методе сил.
Итак, для рамы, изображенной на рис. 7.18, в которой запрещен поворот только
одного узла, можно записать для определения величины этого поворота одно канони-
ческое уравнение метода перемещения:
1 \Z^ И- R\F= 0. (7.28)
Расчет рамы методом перемещений требует решения только одного канониче-
ского уравнения вместо трех в методе сил. Всегда ли метод перемещения предпочти-
тельнее метода сил?
Ответим на этот вопрос на примере другой трижды статически неопределимой
рамы (рис. 7.20). В ней возможны повороты узлов В и С и их смещение по горизонта-
ли, т. е. в основной системе метода перемещений три дополнительных связи, показан-
ные на том же рис. 7.20. Для определения трех перемещений придется, как и в методе
сил, составлять три канонических уравнения.
Заметим, что rik = rki в силу теоремы о взаимности реакций.
Как же найти число необходимых дополнительных связей? В методе силы число
неизвестных точно определялось по формуле (7.17).
Число свободных узлов, а равно их поворотов, определить просто. Иногда не яс-
но число возможных поступательных движений этих узлов. Для их определения вво-
дят взамен жестких узлов, в том числе и опорных, простые шарниры (рис. 7.21), нала-
гающие в плоскости две связи, если подвижность системы как разность между
числом степеней свободы всех стержней до их соединения и числом наложенных свя-
зей W\ = 3H— 2Р2 > 0. У этой рамы = 1, и нужно ввести одну подвижную шарнир-
ную опору, как показано на рис. 7.21.
Рис. 7.20. Трижды статически
неопределимая рама
Рис. 7.21. Расчетная схема
с простыми шарнирами
358
Определение свободных членов и коэффициентов
канонических уравнений метода перемещений
Основные системы метода перемещений представляют собой совокупность ста-
тически неопределимых балок, поэтому реакции от заданных внешних сил можно
найти методом сил. Возможны три варианта таких балок (рис. 7.22).
Для типичных случаев нагружения их опорные реакции можно найти и в спра-
вочниках, и в учебниках.
Если пренебрегать при расчетах рам нормальными силами в сечениях, то для са-
мой сложной схемы (рис. 7.22, а) степень статической неопределимости можно счи-
Рис. 7.23. Вычисление опорных реакций
для простой балки
тать равной двум.
Покажем последовательность вычис-
ления опорных реакций для самой простой
балки (рис. 7,22, в), нагруженной равно-
мерно распределенной силой. Степень ста-
тической неопределимости ее Я = 1; основ-
ную систему примем в виде, показанном на
рис. 7.23.
Каноническое уравнение
содержит только одну неизвестную. Коэф-
фициент уравнения 8И и свободный член
а
Д1Г найдем по формуле Мора: 8И = jy \М\ х
о
х М jdx; A1F= ' M{dx
1 о
способом Верещагина:
11 2 1 3
= j а ’ 5 Q ' а2 = g q * a3,
, 3
Л1 = 4л.
Так как
1 1 2 > 2
co2 = 2 fl ’ fl = J a ’ "2 = J a'>
to8h = зЁ1а3'
Неизвестная реакция шарнирной опо-
A1F 3
рых/=^ =13^-
Реакции левой опоры равны попереч-
ной силе и изгибающему моменту на ней
(рис. 7.23, г), т. е.
QA=^qa;MA=^qa2.
359
Для других схем опорные реакции можно найти в литературе.
Коэффициенты канонических уравнений rikZk + RiF = 0, представляющие собою
реакции от единичных перемещений опор, можно найти из уравнения изгиба балки
.2
Е1—^=М, (7.29)
dx2
„ dM dQ crd4w
так как Q = , q = , то = 9-
Мы ищем силы, возникающие от единичного поворота опоры, поэтому примем
q = 0, и тогда уравнение получит вид:
^-0.
dx4
Его общее решение — прогибы балки
w = Схх* + С2х2 + С3х + С4, (7.30)
первую производную от него — угол поворота
= ЗС1х2 + 2С2х + С3 (7.31)
можно рассматривать как единичное перемещение, от которого потом с помощью
уравнения изгиба (7.29) можно перейти к единичным реакциям rik.
Постоянные С, в (7.31) находятся из граничных условий. При описании обоих
концов балки (рис. 7.23, а) х = 0 и х = а, примем
w = wo;d7=(Po; (7.32)
dw
W = W^=(P‘-
Подставим (7.30) и (7.31) в граничные условия (7.32) и найдем постоянные реше-
ния. Они будут
Q = W0» ^3 = Фо»
С1 = А (Фо - Фо) - A (W1 - wo); С2 = " (2фо + Фо) + A (wo - wo)’ (7.33)
а а а а
Для отыскания опорных моментов по уравнению (7.29) найдем вторую производ-
ную от (7.30), для опорных сил — третью производную:
= 6С.х + 2С,;
dx2 1 2
Изгибающий момент на опоре: Му = Е1(6Схх + 2С2).
Поперечная сила: Q = Е • I • 6 • Сх.
Если повернуть левую опору балки (х = 0) на угол ф0 и положить ф0 = w0 = wa = 0,
„ 1 „ 2
получим Сх = ; С2 = — - .
4£/
Момент на левой опоре MQ = —— ф0.
360
Если ф0 = 1, имеем единичный момент rik = —— ; на другой опоре (х = а) момент
Ma = EI(6C{a-2C2)=^<pQ.
Задавая поочередно все четыре граничных условия (7.32), можно получить
все опорные моменты опирания балки. Другие значения можно найти в литера-
туре.
Канонические уравнения метода перемещений.
Изгибающие моменты в сечениях рам
Канонические уравнения метода перемещений (7.28) можно записать в матрич-
ной форме
А^ + И = 0 (7.34)
Матрица коэффициентов
(7.35)
называется матрицей жесткости системы, она симметрична относительно главной
диагонали. Матрицы — столбцы неизвестных перемещений и реакций
(7.36)
Единичные реакции rik, возникающие за счет поворота узлов, и узловые реакции
от внешних сил берут из справочных таблиц либо вычисляют, как показано в п. 7.6.1.
Решение в матричном виде
Z = Ar1 R (7.37)
ищется так же, как и в методе сил.
Изгибающие моменты в сечениях балки находятся по формуле
M=MF+rik * Zk. (7.38)
Для облегчения построения эпюры изгибающих моментов строят единичные
эпюры (Zn = 1) от единичных реактивных моментов rik и эпюры моментов от заданных
сил и реакций RiF.
После решения канонических уравнений единичные эпюры перестраиваются
перемножением ординат на опорах на найденные по (7.37) неизвестные Zk и склады-
ваются с грузовыми эпюрами.
Легко увидеть, что при наличии подобных таблиц rik и RiF при одинаковом числе
канонических уравнений на расчет методом перемещений времени затратится мень-
ше. Выигрыш во времени увеличивается, если число канонических уравнений оказы-
вается меньше, чем при расчете методом сил.
Как и в методе сил, возможно упрощение задачи за счет использования симмет-
рии системы.
361
7.1.7. Порядок расчета статически неопределимых систем
Расчет статически неопределимых систем осуществляется в такой последова-
тельности:
1) выбор основной системы;
2) замена действий отброшенных связей неизвестными усилиями;
3) составление единичных эпюр и эпюр от заданной нагрузки;
4) составление канонических уравнений;
5) вычисление коэффициентов уравнений и свободных членов;
6) решение канонических уравнений;
7) построение суммарных эпюр моментов и других силовых факторов.
7.1.8. Расчет на прочность силовых шпангоутов
Силовыми шпангоутами называют кольцевые (овальные и тому подобные) рамы,
устанавливаемые в местах приложения сосредоточенных или распределенных нагру-
зок большой интенсивности. Внешние нагрузки уравновешиваются потоком каса-
тельных усилий со стороны обшивки. Величину этого потока определяют вид и место
приложения нагрузки. Все многообразие нагрузок можно свести к сумме двух нагру-
зок, радиальных сил и моментов (рис. 7.24).
Из условия равновесия шпангоута величины касательных усилий соответственно
равны:
F . т z_
(7.39)
F ГХ
где — погонная сила; qF— ее проекция на касательную к контуру. Эпюры этих ка-
сательных усилий изображены на рис. 7.25.
Будем пренебрегать влиянием кривизны на деформации вследствие малости вы-
соты сечения по сравнению с радиусом, изменением круговой формы при нагруже-
нии и поддерживающим влиянием обшивки, т. е. положим £/0 « Е1Ш, жесткость
шпангоута будем считать постоянной. Влияние продольных и поперечных сил на ве-
личину сдвига не учитываем.
Задачу можно решить различными методами, воспользуемся методом сил.
Рассмотрим случай нагружения сосредоточенной силой. Система в силу симмет-
рии дважды статически неопределима. Основную систему выберем в виде, изобра-
женном на рис. 7.26. Составим каноническое уравнение:
8]!*! + 812*2 + &\F~ 0; (7.40)
821^1 + 822^2 + ^2F 0*
Рис. 7.25. Эпюры касательных усилий,
действующих на силовой шпангоут
Рис. 7.24. Нагружение
силового шпангоута
362
Определим изгибающий момент от касательных усилий. Для этой цели удобен
следующий прием.
Для вычисления изгибающих моментов в сечении шпангоута введем подвижную
систему координат. В некотором сечении А—А (рис. 7.27), расположенном под углом
Ф к линии действия силы F, которая проходит через разрез, изгибающий момент ра-
вен сумме моментов реактивных касательных сил qF, приложенных левее сечения.
Координаты произвольной точки В окружности относительно осей, совпадающих
с направлением радиуса и касательной в точке А, очевидно, будут следующие:
z = Я[1 - cos (ф - а)]; (7.41)
у = Л sin (ф — а),
где а — текущее значение угла. Тогда
F
9f=^sina. (7.41)
Элементарная сила dqF в точке В создает момент относительно произвольного се-
чения А—А
6Mq = -qFR2 [ 1 - cos (ф - a)] da, (7.42)
так как dMq = -dq • z; dq = ^F/?da.
Подставив в (7.42) значение qFi получим
FR
dMq = —— [sin a — sin a • cos (ф - a)] da.
Тогда
Ф
FR г
Mq = J (sin a - sin a • cos a - sin2 a * sin ф) da.
о
Единичные моменты (рис. 7.28) равны:
Мх = 1; М2 = Х2Т?(1 - со8ф) = Я(1 — cos ф).
Перемещения от изгиба определим по формуле Мора для одной половины шпан-
гоута.
Единичные перемещения:
я
8I, = -^jA7?Ad<p=^;
О
я я 2
512 = Ji f ^1 Д> Л(1Ф = J(1 - cos Ф) d<P ; (7.43)
О о
я я
822= ^J^2/?d(p= ^J(l-COS<p)2/M<p=
О о
Перемещения от силы qF (грузовые):
я я
Ai«=S7/4A/iAd<P = _^-f(1_cos<p~2 9sin9)W = -£fj; (7.44)
о о
я з я з
= J (1 — COS ф) (1 - COS ф - j ф Sin ф)^ф = - g .
О о
363
Рис. 7.26. Основная
система для расчета
силового шпангоута
Рис. 7.27. Система
координат, введенная
для расчета шпангоута
Рис. 7.28. Эпюры
единичных моментов
Подставив найденные перемещения (7.43) и (7.44) в канонические уравнения
(7.40), после сокращения на 4 имеем:
£
nRXl + nR2X2- ^FR2 = 0;
я R2Xx + j nR?X2 -\fR2 = 0.
Разделив второе уравнение на R и вычтя его из первого, найдем
X = —
2
Умножив первое уравнение на R и вычтя из него второе, получим
у = FR
” 4Н ’
В любом сечении шпангоута изгибающий момент
M=Mq+MiXl + M2X2.
После подстановки значений моментов и приведения подобных членов имеем:
FR 1
М=- 2^ (1 - j cos ф - ф sin ф). (7.45)
Аналогично можно найти нормальную силу:
F 3
N = 2л (Ф^ПФ“ J СО8Ф)-
„ . 6М
Поперечную силу можно наити как
F 1
Q = 2^ (j sin ф + ф cos ф).
Распределение усилий по сечениям может быть показано эпюрой, построенной
по полученным зависимостям для М, N, Q. Оно имеет вид, изображенный на рис. 7.29.
При нагружении парой сил с моментом т аналогичное решение дает следующее:
М= (sin Ф — 2<р);
АГ т * Л Ю / 1 ч
№__81пф;е=_(сО!5(р__).
364
Рис. 7.29. Распределение усилий
по сечениям силового шпангоута
180 Z 240
Рис. 7.30. Двутавровое
сечение шпангоута
Для других случаев нагружения подобные данные можно найти в справочниках.
Там же приводятся зависимости для расчета шпангоутов на прочность с учетом под-
держивающего влияния обшивки. При более сложных видах нагружения можно,
пользуясь законом независимости действия сил, разложить действующие усилия на
ряд сил, для которых известно распределение М, N, Q, и результаты сложить.
После вычисления внутренних силовых факторов М, N и Q подбирают сечение
шпангоутов. Форму сечения выбирают из условия минимума веса; наиболее эффек-
тивным по весу является шпангоут двутаврового сечения (рис. 7.30). Нередко форму
сечения выбирают по конструктивным соображениям.
Стенки шпангоутов обычно выполняют тонкими, поэтому пренебрегают нормаль-
ными напряжениями в их сечениях и считают, что они работают только на сдвиг. Толщину
стенок (высота определяется потребным моментом сопротивления сечения изгибу) вы-
числяют приближенно, полагая напряжение равномерно распределенным по сечению:
После этого их проверяют на устойчивость от сдвига.
Площади сечения полок шпангоута подбирают по нормальным напряжениям
определенным без учета кривизны оси. Расчетные силы определяют умножением уси-
лий в опасном сечении шпангоута на коэффициент безопасности/; условие прочнос-
ти выражают неравенством о < ов. Сжатые полки проверяют на устойчивость.
7.1.9. Расчет неразрезанных балок
Неразрезанной балкой называется балка, имеющая несколько пролетов и проходя-
щая через все опоры, не прерываясь шарнирами или разрезами. В качестве основной
системы для нее удобно применять балку с врезанными над опорами шарнирами. Систе-
ма представляет собой совокупность шарнирно опертых балок. Лишними неизвестными
для нее будут моменты, запрещающие взаимный поворот соседних пролетов (рис. 7.31).
Канонические уравнения при такой основной системе упрощаются, так как еди-
ничные моменты прикладывают к двум соседним пролетам. В п-м уравнении отлич-
ными от нуля оказываются только коэффициенты 8„ п _ j и 8„ п + ,.
365
При одинаковой жесткости пролетов EI имеем единичные перемещения:
5„,я 1 = Лт,8 = tU (4 + 4+1), 8Л n+i = тг? ,
и7 п — 1 kj?]7 пп 'П n^i'7 п, п + 1 ’
грузовые перемещения:
ДиГ Е1^АЧ„ + Л"+'/л + 1
где Ап и Ап +1 — площади грузовых эпюр п и п + 1 пролетов (см. рис. 7.31).
Обозначим Апап = Sn, Ап + j bn + j = Sn + Р Тогда канонические уравнения примут
следующий вид:
хя_,/я + 2ля(/я + /я+1)+ая+1/я+1 = -6^ + ^2.
Такие уравнения составляют для каждой пары пролетов (число пар пролетов рав-
но числу промежуточных опор) и называют уравнениями трех моментов.
Для двух соседних пролетов (левого и правого) можно обозначить
4» ~ +1 ~
соответственноХп_ , = МЛ ; Хп = Л/ср;Хп+1 = Мп.
В этих обозначениях обычно и записывается уравнение трех моментов:
М„1Л + 2Л/ср (7л + /п) + Мп 1П = -б(£ + £).
Решение системы уравнений дает моменты на опорах. Дальнейший расчет балки
выполняют так же, как и д ля рам.
7.2. НАПРЯЖЕНИЯ И ДЕФОРМАЦИИ В ОБОЛОЧКАХ,
СИММЕТРИЧНЫХ ОТНОСИТЕЛЬНО ОСИ
Оболочкой называют тело, ограниченное двумя криволинейными замкнутыми
поверхностями, расстояние между которыми (толщина оболочки h) мало по сравне-
нию с другими характерными размерами, например, с радиусами кривизны
(рис. 7.32). В корпусах баллистических ракет применяются только оболочки враще-
Рис. 7.31. Схема расчета
неразрезанной балки
Рис. 7.32. Типы оболочек, применяемых
в корпусах ракет-носителей
366
Рис. 7.33. Виды трехслойных оболочек, применяемых в авиа- и ракетостроении
ния (цилиндрические, конические, сферические, торовые). Их срединную поверх-
ность, равноудаленную от внешних поверхностей, можно представить полученной
вращением плоской кривой.
Основные силовые элементы корпуса ракеты, оболочки можно разделить на три
класса:
• гладкие;
• подкрепленные силовым набором (вафельные);
• трехслойные (рис. 7.33).
Гладкие и подкрепленные оболочки могут быть металлическими или композит-
ными. Композитные оболочки получают намоткой на оправку высокопрочных нитей
(стеклянных, органических или углеродных) или тканей из них. При намотке или пе-
ред нею нити и ткани пропитываются компаундами, состоящими из синтетических
смол, отвердителей и пластификаторов.
Трехслойные оболочки состоят из двух высокопрочных тонких несущих слоев,
металлических или композитных, и относительно толстого легкого малопрочного
заполнителя — пенопласта, стеклопластиковых или металлических сот.
Подкрепленные оболочки состоят из продольного (стрингеров) и поперечного
(шпангоутов) силовых наборов — тонкостенных стержней, скрепленных с тонкой ме-
таллической обшивкой. Силовой набор и обшивка могут быть получены намоткой
высокопрочных нитей.
Различают тонкие и толстые оболочки. Тонкими оболочками обычно считают
такие, отношение минимального радиуса кривизны которых к толщине R/h > 30.
7.2.1. Краткие сведения о геометрии оболочек
Наиболее распространены оболочки постоянной толщины. Геометрия таких
оболочек полностью определяется формой срединной поверхности, под которой по-
нимается поверхность, равноотстоящая от наружной и внутренней поверхностей,
а также толщиной и граничными контурами.
В большинстве случаев оболочки симметричны относительно оси, их срединная
поверхность представляет собой поверхность вращения — поверхность, образован-
ную вращением плоской кривой вокруг оси, лежащей в ее плоскости (рис. 7.34).
След пересечения оболочки с плоскостью, содержащей ось вращения, называет-
ся меридианом, он совпадает с образующей.
367
Линии на поверхности, перпендику-
лярные меридиану, называются паралле-
лями и являются окружностями. Эти ли-
нии можно получить, рассекая оболочку
конусом, образующая которого совпадает
с нормалью в каждой точке поверхности
оболочки вращения, а вершина лежит на
оси оболочки. Любую точку срединной
поверхности можно задать как пересече-
ние некоторого меридиана с некоторой
параллелью. Радиус кривизны меридиана
в данной точке называется первым глав-
ным радиусом и обозначается R{) а радиус
кривизны параллели R2 — вторым глав-
ным радиусом кривизны; на рис. 7.35 они
соответствуют отрезкам 0}Ми О2М. Точки
Ох и О2 — центры главных кривизн обо-
лочки в точке N, лежат на пересечении
нормалей к поверхности в точке М и в бес-
конечно близких к ней точках мериди-
ана и TV2 параллели. Точка О2 лежит на оси
вращения. Величины, обратные радиусам
главных кривизн, называются главными
кривизнами поверхности в данной точке.
Одна из них максимальна. Другая мини-
мальна. Величины кривизн всех других ли-
ний на поверхности, проходящих через
точку, лежат между ними. Кроме радиусов
7?! и R2, удобно использовать радиус ок-
Рис. 7.35. Элемент, выделяемый
на поверхности оболочки
ружности, образованной пересечением
поверхности оболочки плоскостью, перпендикулярной оси вращения (рис. 7.35). Со-
гласно известной в дифференциальной геометрии теореме Менье,
р = R2 • sin ф. (7.46)
Меридианы и параллели, пересечение которых определяет положение точки на
поверхности оболочки, принимаются за криволинейные координаты. Их положение
можно задать различным образом: например, меридиан определять углом ф, а
параллель — углом 0 или координатой £ (рис. 7.34 и 7.35).
7.2.2. Перемещения оболочки
Оси координат £, £, т| связаны с оболочкой, поэтому положение произвольной
точки в этой системе координат может изменяться только при деформировании. Обо-
значим через w, v, w проекции вектора полного перемещения точки срединной по-
верхности на направление меридиана, параллели и нормали к поверхности, а проек-
ции вектора перемещения произвольной точки, находящейся на расстоянии Zot сре-
динной поверхности, — через uv
Вследствие деформации оболочки точки М и N (рис. 7.36) переместятся и займут
новое положение. Для тонкой оболочки можно ввести следующие допущения (гипо-
тезы Кирхгофа—Лява): нормаль к срединной поверхности, проведенная до деформа-
368
Рис. 7.36. Схема
деформации тонкой оболочки
Рис. 7.37. Схема определения
перемещения точки оболочки по параллели
ции, остается нормалью в данной точке деформированной поверхности; материал
оболочки в направлении нормали несжимаем. Гипотезы вносят погрешность порядка
h/R по сравнении с единицей.
Основываясь на принятых допущениях, установим связь между перемещениями uz,
vz, wz и перемещениями соответствующей точки срединной поверхности u, v, w (точки N).
В силу принятых допущений отрезок NM остается прямым, не изменит длины и займет
новое положение N'M', оставаясь перпендикулярным к срединной поверхности.
Представим перемещения произвольной точки в направлении осей суммами пе-
ремещения соответствующей точки срединной поверхности вдоль меридиана, вдоль
параллели и по нормали. Тогда перемещение произвольной точки с координатой
вдоль меридиана будет
u=uz + u'z + u\. (7А7)
Пусть w # О, a v = w = 0. Тогда из рис. 7.37 легко установить, что
(7.48)
Перемещение точки по параллели (плоской кривой) не вызывает перемещения в
меридиональном направлении, т. е. u"z = 0. Смещение точки срединной поверхности
по нормали (w # 0, и = v = 0) вызывает в произвольной точке М дополнительное сме-
щение из-за поворота нормали в меридиональном направлении:
величина его легко находится из рис. 7.37.
Смещение vz в направлении параллели устанавливается аналогично:
vz = ^ + v’’z + v’V (7.50)
Первое слагаемое v'z = 0, так как угол между параллелью и меридианом равен 90°.
Второе слагаемое находится так же, как и и z.
<™>
Определяя у*”г, нужно учесть, что dSr = pd0 (см. рис. 7.34). Из-за поворота норма-
ли в кольцевом направлении перемещение произвольной точки вдоль параллели бу-
дет отличаться от перемещения соответствующей точки срединной поверхности на
величину
Л—fas- <7'52)
369
Вследствие несжимаемости оболочки по толщине смещение всех точек по нор-
мали одинаково:
= (7.53)
После подстановки соответствующих слагаемых (7.47 и 7.50) станут такими:
7.2.3. Деформации в оболочках
Деформация элементарного параллелепипеда, выделенного в окрестности про-
извольной точки, при перемещениях, малых по сравнению с толщиной оболочки, мо-
жет быть разложена на следующие составляющие три линейные — в меридиональном
е1г кольцевом по нормали е3г; три угловые, как изменение величины углов между
меридианом и параллелью, между нормалью и параллелью и между меридианом и
нормалью соответственно у12г у13г у23г
При принятых допущениях три компонента деформации
Езг = Т1зг = Ъг = 0-
Радиусы кривизны поверхности в точке М обозначим так:
^2z ~ ^2 +
p, = p + z.
При определении линейных деформаций воспользуемся приемом поочередных
перемещений и представим
e2z = e,2z + e\ + e’\.
Пусть точка М перемещается вдоль меридиана, т. е. положим и'z * 0, vz = w = 0.
Рассмотрим бесконечно малый отрезок меридиана, выделенный в окрестности точки
(рис. 7.38).
Перемещения uz его концов М и N отличаются на величину, соответствующую
ди
изменению координаты 5, и равную Uz + d<P Л z —*; Рис. 7.38. Малый отрезок меридиана, выделенный в окрестности точки Л|ё<р. По определению, деформация v 1 ^.ае Г^</рТ 7с Лм —n I V \ ИГ У9О°-Ф \ \f V 1 УМ ' а) б) Рис. 7.39. Схема определения перемещения кольцевой компоненты деформации
370
в точке есть относительное изменение длины бесконечно малого линейного эле-
мента:
Эм
diVi + м-+-я—ч—м_—dSi
lz z Я1гЭф z _ ^uz
Перемещение по кольцу не вызывает изменения длины d515 поэтому е”1г = 0. По-
лагая w * 0 и uz = Vz = 0, от смещения отрезка MNno нормали (рис. 7.39, м)а получим
р”’ = 2L
k Л1г-
Таким образом, меридиональная деформация
Е = Э“г + —
k л,/
(7.55)
Для определения кольцевой компоненты деформации рассмотрим бесконечно
малый отрезок недеформированной параллели d52z = PzdO. При перемещении вдоль
меридиана uz * 0, w = vz = 0 его длина изменится и станет равной (рис. 7.39,6).
Деформация в кольцевом направлении из-за перемещения точки вдоль мериди-
ана будет
_ dS"^ - dS^
* dS2z
На рис. 7.39, а видно приращение радиуса pz на величину dpz = uz cos ф, отсюда
Относительное удлинение параллели из-за перемещения vz при uz = w = 0 нахо-
дится так же, как е’1г
е * р^Эё’
а от перемещения по нормали определяется подобно е”'1г
= w
* R2z'
Сложив полученные значения, имеем
и dv w
e^-'coscp+^ + jj-. (7.56)
Сдвиг не зависит от перемещения точки по нормали. Выделим в окрестности
точки бесконечно малый элемент. Будем смещать его поочередно вдоль меридиана и в
кольцевом направлении, соответственно деформацию сдвига представим суммой
Y12z = Y + Y'-
При перемещении по параллели vz * 0, uz = w = 0, как видно из рис. 7.40.
При смещении элемента оболочки вдоль меридиана (yz = w = 0, см. рис. 7.41) угол
между d5j и d52 изменится из-за разницы в величине перемещений точек М и ЛГ, вы-
Э?_
званной приращением координаты z. Эта разница равна jy d5P Кроме того, переме-
371
Рис. 7.40. Перемещение точки
оболочки по параллели
Рис. 7.41. Смещение элемента
оболочки вдоль меридиана
щение точек Ми М' будет зависеть от длины радиуса рг При повороте радиусов рг и
pz + dpz на равный угол ДО точка М пройдет по параллели путь vz = pzdO, а точка М —
путь v*z = (pz + dpz)dO. При этом произойдет жесткий поворот всего элемента относи-
тельно точки М. Чтобы учесть жесткий поворот, следует из перемещения точки М'
вычесть И*, а не Vz.
dv
,_Vz~ ~ ”г
У' ‘
„ ♦ ( dp.\ dp. , dv. v.
Так как v = v J 1 + — , a = cos ф, то у = -5—5-----cos ф.
* 4 pj’ d5k pz
Подставив значения Y и Y’, имеем
dll dv V
7127=^3+ o4------------ costp. (7.57)
,12г ргЭ0 Л1гЭ<р рг v ’
Уравнения (7.55—7.57) называют геометрическими уравнениями оболочек.
В дальнейшем полезно преобразовать их, связав деформацию в произвольной точке
с деформацией соответствующей точки срединной поверхности. Кроме того, у тон-
кой оболочки можно считать:
= R2z = R2, Pz = P- (7.58)
Погрешность от этого упрощения меньше погрешности, вносимой принятыми ги-
потезами. После подстановки (7.55) и (7.58) геометрические уравнения станут такими:
__ 1 (du , \ , d Г 1 / dlvYl
£|<“ Я| Ьф + W) + Z А,Э<р ” Эф)) ’
м . w . dv . Г 1 ( ЗиЛ , d ( v dw VI z-
е2г = - cos ф + + z|^(« - ]со$ф + “ ^ЭёJJ J <7’59)
_ 1 (du у dv Г d (u dw A costp/ v dw A d ( v dw Yi
7|ь “ p (ao-v cos<₽) л,Эф Чрэо1я, ~ я^ф)- p и?2-рЭ0) ~ рэе)]'
Здесь и далее индексы 1 и 2 у деформаций и напряжений указывают главные на-
правления срединной поверхности.
372
Выделим из (7.59) деформации в точках срединной поверхности (z = 0):
1 z Эи>
е' Л| ~ Эф
e2=K"C0S<₽ + ^)+V (760)
1 Эм , Эу v
Ь=рЭё+А^-р^Ч>
и параметры изменения кривизны срединной поверхности:
_ _ Э Mf dw Л-|.
05• л1Эф[Л|(" ЭфЦ’
„ _ 1 f сМ . Э ( V dw \
052 рАД"_ЭфJcos<p+ рэо(/?2 рэе} (761)
_ = 1 Г Э г 1 Л Эи> An dw \ Э /у dw
“ 2 Lpao[яД““ЭфJJ р(я2“рэеJcosф я^ф^Яз “рэеЦ
Параметры Oj и со2 характеризуют изменение кривизны нормальных мериди-
ональных и кольцевых сечений; параметр со12 — кручение срединной поверхности.
Теперь (7.59) можно представить в следующем виде:
Ej^Ej+zGJi;
£2г=Е2+ги2; (7.62)
Y|2z = 712 + 2zGJ12.
При осесимметричном нагружении оболочки вращения кольцевые перемещения
vz = 0, uz и w не зависят от координаты 0.
Деформации срединной поверхности будут
_ 1 (&и , А
ei /?1(d<p + wJ;
е2 = (и ctg <р + w); (7.63)
Т12 = °’
В последнем уравнении учтено (7.60).
Параметры изменения кривизны срединной поверхности:
_ d rj_f dw Vi
“ ” Я,(1ф [я1“-<1ф II’
И2 = (и dg Ф + к); (7.64)
И12 = 0.
7.2.4. Напряжения и усилия в оболочке
Допущение о несжимаемости оболочки по толщине означает, что напряженное со-
стояние следует считать плоским. Закон Гука для плоского напряженного состояния
изотропной оболочки при отсутствии температурных деформаций записывается так:
oiz=77^2(£k+M£2z);
о2г = (£^ + М£и); (7.65)
Tl2z = ^Y12z-
373
Согласно (7.62) деформации по толщине
меняются линейно. Если подставить (7.62) в
(7.65), можно разделить напряжение по любому
направлению на напряжение в срединной по-
верхности и изгибное напряжение. Вместо на-
пряжений в некоторых случаях удобнее пользо-
ваться статически эквивалентными им погонны-
ми силами и моментами.
Выделим бесконечно малый элемент обо-
лочки (рис. 7.42).
Напряжение на каждой его грани можно
свести к равнодействующим усилиям. Так как
напряжения меняются по толщине оболочки,
они эквивалентны силе и моменту, приложен-
ным к границам срединной поверхности выде-
ленного элемента. Если, например, напряжения
Рис. 7.42. Схема бесконечно
малого элемента оболочки
перенести на серединную поверхность, то их статическими эквивалентами будут нор-
мальная сила где — погонная нормальная сила, и момент M}dS2, где М{ —
погонное значение изгибающею момента; d52 — длина элемента срединной поверх-
ности. Длина дуги, проходящей через заданную точку:
d52z = de2(l + ^).
Очевидно,
h/2
^d52= J ok(l + ^)d52dz.
—h/2 2
Как и ранее, положим R2z = R2. Нет смысла удерживать малые члены в подынтег-
ральной функции, т. е. вычислять интеграл с точностью, большей точности, обуслов-
ленной принятыми допущениями, поэтому будем полагать силу, приходящуюся на
единицу длины:
h/2 h/2
f 7? г
Ni= J aiA=---------2 J (ei + (7.66)
-h/2 ” -h/2
Так как деформации срединной поверхности ер е2 и параметры изменения кри-
визны и ю2 не зависят от z, интегрирование выполняется просто, но без упроще-
ний, конечная формула для Nx была бы сложной.
Из (7.66) получим погонную меридиональную силу (силу, приходящуюся на еди-
\ с г» Е' h
ницу длины), обозначив В =------2,
1 -ц
N} = B(^ + p£2). (7.67)
Аналогично найдем:
погонную кольцевую силу
N2 = В(г2 + pej); (7.68)
погонные сдвигающие усилия
h/2
^\2=^2\= I T12z^ = ^(l -Н)Т12»
-h/2
374
погонный изгибающий момент в меридиональном направлении
h/2
мх = I ак ’ + цю2); (7.69)
-h/2
погонный кольцевой изгибающий момент
h/2
М2 = J • zdz = Z>(u)2“,"HWi); (7.70)
-h/2
погонные крутящие моменты
h/2
мп = м2\ = f т12г • pdz = Z)(l-p)io12. (7.71)
-h/2
Индексы усилий и напряжений указывают их направление.
Равенства Т12 = Т21 и Л/12 = Л/21 — не только следствие закона парности касатель-
ных напряжений; они становятся возможными, если при интегрировании пренебре-
гать z/Rx и z/R2, как указывалось ранее. Поперечные силы Qx и Q2 определить из гео-
метрических уравнений нельзя, так как при принятых гипотезах
Y13z = Y23z = О*
Поперечные силы определяются из уравнений равновесия элемента оболочки.
В формулах (7.68—7.71) введены следующие обозначения:
Eh3
D =--------5---жесткость на изгиб;
12(1-Ц2)
П Eh
В =-----X — жесткость на растяжение;
1 -н
Е и ц — модуль упругости и коэффициент Пуассона.
В общем случае внутренние силы в сечениях оболочки приводятся к пяти парам
статических эквивалентов: двум нормальным силам, двум изгибающим моментам,
двум поперечным силам, двум касательным силам и двум крутящим моментам, по-
следние две в тонких оболочках в силу закона парности касательных напряжений счи-
таются равными между собой.
Уравнения, связывающие внутренние силы с деформациями или кривизнами,
называются уравнениями состояния (соотношениями упругости).
7.2.5. Безмоментная теория оболочек
Если у тонкой оболочки нет резких изменений кривизны и жесткости, нагрузка
по ее поверхности меняется плавно, перемещения по нормали на краях не стеснены,
то внутренние силы в ее сечениях можно считать равномерно распределенными по
толщине оболочки.
Статическими эквивалентами таких сил, приведенных к срединной поверхности,
будут нормальные (Nx и N2) и касательные (Г12, Г21) силы, а поперечные силы, изги-
бающие и крутящие моменты можно считать равными нулю. Теорию оболочек, по-
строенную на этом предположении, называют безмоментной теорией, а сами
оболочки — безмоментными оболочками.
Резкое изменение кривизны возможно в местах сопряжения различных средин-
ных поверхностей, например, цилиндрической или конической со сферической и то-
375
ровой и т. п. Резкое изменение жесткости происходит в месте подкрепления силовым
набором или у ребер, изготовленных за одно целое с тонкой оболочкой. Плавность
изменения распределенной нагрузки оценивается степенью изменяемости ее функ-
ции q(xy) и отсутствием сосредоточенных сил. Нагрузками с малой степенью изменя-
емости называют нагрузки, заданные такими функциями, которые несущественно
вырастают при дифференцировании (порядки производной и функции одинаковы).
Условия безмоментного состояния в оболочках ракетных конструкций чаще вы-
полняются не для всей оболочки, а для ее части, удаленной от области, которая содер-
жит особенности, нарушающие безмоментные состояния. Трудно, например, закре-
пить края так, чтобы крепление не препятствовало перемещению по нормали.
Если всюду можно пренебречь напряжениями от моментов, безмоментная те-
ория дает приближенную расчетную модель, степень приближения которой тем боль-
ше, чем тоньше оболочка. Для тех частей оболочки, где моментные напряжения быст-
ро затухают, напряженное состояние разделяют на безмоментное и краевой эффект.
Зоны краевого эффекта существуют в областях резкого изменения кривизны или
жесткости. У конических оболочек они примыкают к вершине конуса, у торовых —
вблизи плоскости симметрии, перпендикулярной оси вращения оболочки. Зона крае-
вого эффекта имеет малую протяженность, поэтому проектная толщина оболочки оп-
ределяется по безмоментной теории.
Безмоментное напряженное состояние может вызываться как нагрузками, при-
ложенными симметрично относительно оси оболочки (собственный вес, давление га-
за на внутреннюю поверхность, аэродинамические нагрузки при симметричном обте-
кании и т. п.), так и асимметрично (ветровые нагрузки, аэродинамические силы при
углах атаки, не равных нулю, поражающие факторы оружия, давление жидкости
и др.). При симметричном нагружении в сечениях будут только нормальные силы,
при несимметричном появляются еще и касательные силы Г12 и Г21.
Уравнения равновесия безмоментной оболочки
при осесимметричном нагружении
Усилия и напряжения в сечениях оболочки определяются из уравнения равнове-
сия. Уравнения равновесия могут быть получены различными способами. Здесь мы
воспользуемся условиями равновесия бесконечно малого элемента оболочки.
Выделим мысленно из оболочки (рис. 7.43, а) двумя меридиональными и двумя
кольцевыми нормальными сечениями бесконечно малый элемент (рис. 7.43, б). При-
ложенную к нему осесимметричную нагрузку интенсивностью q разложим на две со-
ставляющие: нормальную qn и меридиональную q^ (кольцевая составляющая q$ = 0).
По граням элемента приложим нормальные усилия, погонные значения которых рав-
Рис. 7.43. Схема усилий, действующих на выделенный элемент оболочки
376
ны и N2, остальные усилия при безмоментном напряженном состоянии симмет-
рично нагруженной оболочки равны нулю.
Так как элемент находится в равновесии, то сумма проекций сил на ось z (на нор-
маль) равна нулю: EZK = 0. Остальные уравнения равновесия элемента удовлетворя-
ются тождественно. Учтя малость углов dtp и d0, из рис. 7.43 легко установить, что это
уравнение может быть записано так:
q„dSxdS2 - N^dff - NtdS2dq> - d(NtdS2) = 0.
Отбросим последний член, имеющий более высокий порядок малости, и разде-
лим все члены на d5j, d52. Из рис. 7.43, б видно, что
о d
de=de4=T!7-
Получим уравнение
известное как уравнение Лапласа. В уравнении (7.72) два неизвестных. Второе урав-
нение легко найти из условия равновесия части оболочки, отсеченной по нормали
к срединной поверхности (рис. 7.44).
Здесь и далее за положительное направление распределения по поверхности сил
принято такое, как на рис. 7.44, при ином направлении знаки усилий меняются на об-
ратные. Составив уравнение равновесия в проекциях сил на ось £, получим
—2nrN{ cos р — 2л J sin ф d5j + 2л J <?лр cos ф d5j = 0.
5i 5!
Так как d^ cos ф = dp, то, заменив переменную и сократив на 2л, имеем
yv> = ^/(^-^tg<’>)pdp’
о
(7.73)
где г — радиус сечения плоскостью, перпендикулярной оси, в котором определяется
усилие.
Если оболочка имеет круговой срез у вершины, нижний предел интегрирования
будет г0 — радиус сечения среза.
Рис. 7.44. Схема усилий,
действующих на часть оболочки,
отсеченной по нормали
к срединной поверхности
Уравнения (7.72) и (7.73) можно записать в на-
пряжениях.
N2
Так как Gj = , о2 = -у ,то
При равномерном распределении давления по
поверхности (<?ф = 0) определение меридиональных
усилий заметно упрощается:
N ~ дг -к ~ qr •
1 2cosР ’ 1 2Acos|J ’
^2 = ^;о2=?- Р-75)
377
Усилия и напряжения в оболочках
от внутреннего давления и осевых сил
Рассмотрим напряжения и деформации в цилиндрическом баке с полусфериче-
скими днищами при нагружении внутренним давлением.
В цилиндрической оболочке (рис. 7.45) =©©, R2 = г, в полусферических обо-
лочках R{ = R2 = R = г. Из (7.72) и (7.74) при постоянном q получим кольцевые усилия
и напряжения:
N2 = qr,G2=%. (7.76)
Из (7.75) имеем меридиональные усилия и выражения:
= = (7.77)
Кольцевые напряжения вдвое больше меридиональных, поэтому разрушение ци-
линдрических оболочек от внутреннего давления происходит с образованием трещин
вдоль образующих. Деформации определяем из обобщенного закона Гука:
ei = ^(°1-на2);
е2= e(°2-h<*i)-
Подставив (7.76) в (7.77), получим:
е,-^(0,5-и);
e2-g(l-0,5g). (7.78)
В сферических оболочках (днищах) усилия и напряжения такие:
М = N2 = 1 qR', G, = О2 = 1 qr. (7.79)
Деформации
£|=е2=2^ d-H). (7.80)
При сравнении деформации цилиндрической и полусферической оболочек видим,
что выполняется условие совместности деформаций частей бака в месте соединения их
между собой, хотя напряжения одинаковы. Это несоответствие является недостатком
безмоментной теории, не учитывающей изгибающие моменты и поперечные силы, ко-
торые возникают в местах изменения кривизны оболочки. Вследствие разной жесткос-
ти цилиндрической и сферической оболочек условие неразрывности выполняется
только путем изгиба частей сосуда в области, примыкающей к сечению стыка.
Таким образом, в зоне, прилегающей к месту со-
единения оболочек, должны действовать изгибаю-
щие моменты и поперечные силы. Напряжения в
этой зоне, если радиус днища больше радиуса ци-
линдрической оболочки, могут достигать больших
значений, быстро затухая по мере удаления от стыка.
Если сосуд изготовлен из малопластичного матери-
ала (таковы многие сплавы с высокой удельной проч-
ностью и стеклопластики), принимаются меры для
их снижения.
Рис. 7.45. Схема
действующих напряжений
в цилиндрической
оболочке
378
Внутреннее давление может создаваться жидкостью и газом. Тогда
q = q^Q„ (7.81)
где qn — давление газа (наддува); qv — гидростатическое давление.
Гидростатическое давление действует по нормали к поверхности оболочки, вели-
чина его зависит от высоты столба жидкости над данным сечением оболочки и не за-
висит от формы сосуда:
где у — удельный вес жидкости; Н— высота столба жидкости.
Для определения напряжения от внутреннего давления в формулы (7.76), (7.77),
(7.79) нужно подставить (7.81).
7.3. МОМЕНТНАЯ ТЕОРИЯ ОБОЛОЧЕК
ПРИ ОСЕСИММЕТРИЧНОМ НАГРУЖЕНИИ
7.3.1. Основные понятия
Безмоментное состояние элементов, выполненных в виде оболочек, не всег-
да возможно и условия совместности деформаций выполняются только за счет из-
гиба части или всей области. Из-за малости толщины оболочек незначительные
по величине изгибающие моменты могут быть эквивалентами больших напряже-
ний. При расчетах на прочность в зонах, где нарушено безмоментное состояние,
нужно знать напряжения, чтобы принять меры, необходимые для обеспечения на-
дежности конструкций. Напряженное состояние в этих зонах в некоторых случаях
нагружения удобно расчленять на основное напряженное состояние и краевой
эффект:
Р=РО + РК, (7.82)
где Р — совокупность всех внутренних сил;
Ро — совокупность внутренних сил безмоментного напряженного состояния;
Рк — совокупность внутренних сил и моментов краевого эффекта.
Основное (безмоментное) напряженное состояние и краевой эффект определяют
раздельно из разных уравнений равновесия (движения) оболочки.
Краевым эффектом называют напряженное состояние, при котором напряжения
быстро убывают по мере удаления от линий искажения до величины напряжений, оп-
ределяемых безмоментной теорией. Линии искажения — это линии, на которых нару-
шаются условия безмоментного состояния. Ими могут быть шарнирно опертые или
заделанные края, линии скачкообразного изменения кривизны и жесткости, линии,
где изменяется интенсивность поверхностной нагрузки.
Расчленение напряженного состояния недопустимо в следующих случаях:
• если радиусы кривизны этих линий велики (асимптотические линии);
• если срединная поверхность оболочки особая (конусная с вершиной или малым
радиусом, плоская или близкая к плоскости, касающаяся плоскости вдоль зам-
кнутой кривой, например, торовая, длинный цилиндр);
• если показатель изменяемости внешних поверхностных сил выше некоторого
значения.
379
Показатель изменяемости можно ввести следующим образом. Аппроксимиро-
вать (задать приближенно) внешние силы суммой функций вида
Тогда
Хф. = Хф. (х, у)ек^у\
ЭФ,-
дх.
кФ*
где к =
величина для тонких оболочек большая;
/(х, у) — функция со средней изменяемостью, при дифференцировании возрастает
меньше, чем напряжения.
Пусть Д- ~ 10“3; t = 0,3. Тогда при дифференцировании Ф возрастает на поря-
док, так же возрастают и показатели основного напряженного состояния, т. е. оно не
может считаться безмоментным. Для такой оболочки показатель изменяемости дол-
жен быть меньше 0,3. При больших показателях изменяемости и особых срединных
поверхностях расчленение напряженного состояния неправомерно, решение уравне-
ний равновесия будет неограниченно возрастать.
В случае асимптотических линий искажения возможно расчленение напряженно-
го состояния на основное и обобщенный краевой эффект. Здесь такой способ расчле-
нения не рассматривается. В оболочках ракетных конструкций расчленение напря-
женного состояния на основное безмоментное и краевой эффект выгодно, когда ли-
ниями искажения являются края, а нагрузка симметрична относительно оси оболочки.
7.3.2. Уравнения равновесия оболочек вращения
при осесимметричном нагружении
Если в окрестности некоторой точки оболочки вращения, нагруженной симмет-
рично относительно оси, выделить нормальными сечениями (сечения линейчатой по-
верхностью, составленной из нормалей к срединной поверхности) бесконечно малый
элемент, то внутренние силы в сечениях оболочки будут для него внешними (рис. 7.46).
Из шести уравнений равновесия элемента три Ху, = 0; ZMxi = 0; ZMzi = 0 удовлет-
воряются тождественно, так как из условия симметрии в меридиональных сечениях
напряжения приводятся к нормальным силам N2 и моментам М2, одинаковым на обе-
их сторонах.
(AT, + dArI)(p+dp)d£
Рис. 7.46. Схема внутренних сил в сечениях оболочки вращения
при ее осесимметричном нагружении
380
Составим оставшиеся уравнения, пренебрегая разницей кривизны поверхности в
бесконечно близких точках и учитывая малость углов dtp и d0. Получим:
(N{ + dNJ (р + dp) d0 - Nx pdG - (Q, + d^) (p + dp) d0 +
+ Q, pde - 2N2 + qx d5, d52 = 0;
qn d5, d52 - + d/V,) (p + dp) d0 pdO + Q, pdO -
- (Qi + d0j) (p + dp) d6 - 2N2 Rt dtp dO = 0;
(А/, + dA/,) (p + dp) dO - AfjpdO - 2M2 R{ dtp+
dS.
+ (Oi + dO,) (P + dp) /?,dtpde - qn dS} dS2 -y1 = 0.
Здесь ~ sin S (см. рис. 7.46).
А|йф z
Разделим на dS^dS^ ~ AjdcppdO. Отбросим малые высших порядков и получим
систему уравнений:
^тР)-^^-е,р+9Лр=о;
N N и
+е,рЯ1-0.
В уравнениях (7.83) пять неизвестных усилий: две нормальные силы Nx и N2, попе-
речная сила Q, два момента М{ и М2, Уравнения можно преобразовать, например, иск-
лючить из них Q. Для этого Q из третьего уравнения подставим в два других. В оставших-
ся уравнениях нормальные силы Nx и N2, изгибающие моменты Мх и М2 можно заменить
деформациями через уравнения состояния (7.67—7.70). Затем, использовав геометриче-
ские уравнения (7.63), (7.64), получить два уравнения относительно перемещений и и ж
7.3.3. Уравнения краевого эффекта оболочек
при осесимметричном нагружении
Топливные отсеки ракет, емкости топливозаправщиков обычно состоят из ци-
линдрических и сферических оболочек, соединенных друг с другом. Одним из расчет-
ных случаев для них является нагружение внутренним давлением. При сравнении
(7.68) и (7.80) видно, что при раздельном их нагружении деформации сферической
оболочки меньше цилиндрической.
При нагружении внутренним давлением сферической и цилиндрической оболочек,
соединенных по краю, сферическая оболочка препятствует свободному расширению ци-
линдрической. Последняя, в свою очередь, стремится увлечь за собой край сферической
оболочки (днища). Совместная их деформация возможна лишь при изгибе краев. В крае-
вых зонах оболочки будут растягиваться и изгибаться. Мысленно разделив оболочки, мы
должны приложить к их краям равномерно распределенные силы и моменты (рис. 7.47).
Эти силы и моменты для оболочек внешние. Их действие вызовет внутренние си-
лы, статическими эквивалентами которых будут нормальные силы TVj и N2, изгибаю-
щие моменты Мх и М2. Для их определения можно преобразовать уравнения (7.83).
381
Рассмотрим способ преобразования, предложен-
ный Е. Мейснером. Введем новые функции: угол по-
ворота касательной к меридиану
Выразим через них нормальные усилия и мо-
менты в сечениях оболочки. Часть оболочки уравно-
вешена, поэтому сумма проекций сил на ось 'LZi = О,
т. е. 2лр0 cos ф - 2лр^ sin ф = 0, откуда
= -Qctg ф = Ctg ф.
Рис. 7.47. Усилия, действующие
в краевых зонах оболочки
(7.85)
Подставив Nx во второе уравнение (7.83), получим
U * . N2 1 d (U \_n
A1A2Ctg<<’+ Л2 рЯ, d<p U Р) °'
Так как р = R2 sin ф, то после дифференцирования и приведения подобных чле-
нов имеем
Изгибающие моменты (7.69) и (7.70) можно выразить через угол поворота V, уч-
тя (7.64):
м'=+ *4С‘8Ф); М1=С‘8Ф + ) • (7-87)
Уравнение (7.83) представим предварительно в таком виде:
(7.88)
(MxR2 sin ф) - cos ф + QRxR2 sin ф = 0.
В (7.88) использованы зависимости р = R2 sin ф, = Rx cos ф.
Подставим в (7.88) моменты (7.87) и поперечную силу (7.84), приведем подобные
члены и получим такое уравнение второго порядка:
, rdA). R2 , 1 dK 1 ( . Л! t 2 ).z_ u
Из первого и второго уравнений (7.83) нельзя получить уравнение второго поряд-
ка. Уравнение типа (7.89) можно составить из условия совместности деформаций,
комбинируя геометрические (7.63) и физические уравнения:
= (ЛГ1-ц^);е2=^5 (ЛГ2-ц^).
Из геометрических уравнений следует
n n d«
£1Л1 - е2Л2 = - И Ctg Ф-
Из физических уравнений эта же разность
ЕД - 1*1 W - № - R2 - ЦЛГ,)],
т. е.
- и ctg Ф = ± [Я( (Nt - ilN2) - R2 (N2 - ЦЛГ2)]. (7.90)
382
Если (7.90) умножить на ctg ф и вычесть из него производную
d(£2^2) du и . dw 1 d rn/Xr >Г X n /АГ кт хл
= ^Ctg<P"^ ^=^d4i ~ Ri(Ni ~ ^')L
ТО
Eh (“ - й)=ctg <₽ - ^2> - r2 (n2 - Н^)1 - IR2(N2 - HAG)]. (7.91)
Левая часть (7.91) есть
После подстановки в правую часть (7.85) и (7.87), приведения подобных членов
получим второе уравнение:
к2 d2U . rd л2 , -I dU
r} d<p2 Ldq>W A, ctg<jA|d<p
+ (h-
V®1’)
%rav-
(7.92)
Таким образом, для определения внутренних усилий в оболочке, нагруженной
силами и моментами по краю нужно решить уравнения (7.89) и (7.92). Их решения со-
держат функции вида
е^Ф • ДХ) и е-А:ф * /(х),
где f(x) — ограниченная знакопеременная функция; к — постоянная, имеющая поря-
док jR/h .
Поэтому функции U и И быстро возрастают при дифференцировании. Если коэффи-
циенты при первых производных
dU dK
dtp В 9 * * * 13 dtp
и функциях U, V имеют порядок единиц, урав-
нения (7.89) и (7.92) можно упростить и свести к одному уравнению четвертого порядка.
7.3.4. Цилиндрический бак со сферическими днищами
под равномерным внутренним давлением
В общем сечении соединенных цилиндрической и сферической оболочек при на-
гружении внутренним давлением возникает неуравновешенная сила Рр, равномерно рас-
пределенная по краю (ввиду симметрии оболочек и нагрузки (рис. 7.48, а) — радиальная
составляющая реактивного усилия, приложенного к цилиндрической оболочке со сто-
роны сферической. Меридиональная составляющая этой реакции уравновешивается
нормальным усилием в концевом сечении цилиндрической оболочки 7Vlu. Тонкие обо-
лочки слабо сопротивляются изгибу распорной силой Рр, напряжения краевого в раз
больше безмоментных, поэтому между оболочками устанавливается силовой шпангоут.
Рассмотрим бак, состоящий из цилиндрической оболочки и двух сферических
днищ, соединенных на шпангоуте прямоугольного сечения, показанный на рис. 7.48,
б расчлененным. Положим длину цилиндрической части такой, что позволительно
пренебрегать взаимным влиянием ее краев, а угол ф0 > 30°. Будем считать, что сре-
динные поверхности частей бака на общих краях совпадают.
Обозначим:
£ш, /ш, Аш — модуль упругости, момент инерции и площадь сечения шпангоута;
h{,h2 — толщина оболочек — сферической и цилиндрической;
Д — смещения в плоскости, перпендикулярной к оси бака;
13 3 — угол поворота сечения шпангоута.
383
Рис. 7.48. Схема сил, действующих
в общем сечении соединенных
цилиндрической и сферической оболочек
Рис. 7.49. Деформация
шпангоута постоянной
жесткости
Индексы у смещений 1, 2, 3 относятся к сферической, цилиндрической оболоч-
кам и шпангоуту соответственно.
Рассечем мысленно бак (рис. 7.48) и приложим неизвестные усилия Ни М. Под
действием внутреннего давления более податливая цилиндрическая оболочка изгиба-
ется, краевое сечение ее поворачивается вместе со шпангоутом, вовлекая в движение
краевую зону сферической оболочки. Обе оболочки растягиваются в главных
направлениях — кольцевом и меридиональном, вблизи краев изгибаются, а шпангоут
постоянной жесткости сжимается и вывертывается (выкручивается) из своей плос-
кости (рис. 7.49).
Одни точки сечения удаляются от центра (эта часть шпангоута удлиняется), дру-
гие приближаются (шпангоут сжимается), в этих точках возникают нормальные на-
пряжения. Относительное удлинение осевой линии шпангоута при осесимметричной
. w Аз
деформации ее = - = — •
Смещение точек шпангоута в плоскости, перпендикулярной к оси бака, вслед-
ствие выкручивания Д3 (у) = уФ3.
Этому смещению, согласно закону Гука, соответствует напряжение
0=1 ЕуЪ3.
(7.93)
Перемещения точек сечения шпангоута за счет выкручивания аналогичны пере-
мещениям при изгибе, поэтому напряжение можно представить как напряжение ста-
тически эквивалентного изгиба
V
а=7-г У. (7.94)
Jz
Вектор момента Mz лежит в плоскости шпангоута и направлен к центру кривизны
(рис. 7.50).
Из условия равновесия бесконечно малого элемента шпангоута длиной rdO име-
ем M,d6 = mrdO.
Приравнивая значения напряжений (7.93) и (7.94):
2
384
Рис. 7.50. Нагружение шпангоута из плоскости
получаем угол поворота сечения шпангоута
д3=
тг2
(7.95)
необходимый для решения задачи определения внутренних усилий в кольцевом и ме-
ридиональном сечении бака. Выкручивающий момент
т = М{11-М[с,
где М}с и Л/1ц — изгибающие моменты в концевых сечениях сферической и цилиндри-
ческой оболочек. Формула (7.95) пригодна и для вычисления углов поворота тонко-
стенного шпангоута замкнутого профиля, контур которого обычно принимается не-
изменным.
Внутренние усилия N2, Мх, М2 определяются по краевым силам Н и М. По-
следние можно находить двумя способами: методом сил или решением уравнений
совместности деформаций. Из условий совместности деформаций перемещения об-
щих точек обеих оболочек и шпангоута в радиальной плоскости должны быть одина-
ковы, одинаковыми должны быть углы поворота их общих сечений и кольцевые де-
формации:
Д1 = Д3 - а$3;
Д2 = Д+я^3; (7.96)
е/ = егц,
где а — половина ширины шпангоута (см. рис. 7.66); и V2 — углы поворота норма-
лей к срединным поверхностям сферической и цилиндрической оболочек.
Перемещения Д* находятся как суммы перемещений безмоментного состояния и
краевого эффекта. Для сферической оболочки Aj = Д^ + &хнм. Смещение при безмо-
ментном состоянии есть приращение радиуса р = г сечения плоскостью, перпендику-
лярной к оси бака, от внутреннего давления: Д^ = ДА sin ф0.
При осесимметричной деформации ^ев=^)
получим ДА = £2R.
В безмоментном состоянии кольцевая деформация сферической оболочки (см.
формулу 7.80)
поэтому
Al,= ^(l-H)sin<p0. (7.97)
385
Так как Nx « N2, то кольцевую деформацию сферической оболочки можно при-
нять такой:
е
е2 Ehx'
где TV2 — нормальная сила. Подставив С и у на краю (у = 0), получим
Я2 = ^(^Я,япф0-^).
Перемещение концевого сечения сферической оболочки от Ну и МХс
А1ям= sin <р0( J2H (sin Фо - ). (7.98)
Перемещение центра сечения шпангоута Д3 = е2 • г.
Н3г
Деформация в центре сечения шпангоута е2 = •
Погонная сила Н3 равна сумме распорной силы и краевых сил оболочек (см.
рис. 7.48, б):
Н3 = qr cos ф0 + Нх + Я2.
Перемещение центра сечения шпангоута
дз= Щ^(29Лсо5<ро + Я' + Я2)- (7.99)
Угол поворота сечения шпангоута
^=^(Л/1и-Л/|с). (7.100)
Первое уравнение (7.96) составляется из (7.97), (7.98), (7.99) и (7.100). Перемеще-
ние края цилиндрической оболочки также есть сумма Д2 = Д2(? + &2нм-
Безмоментная часть перемещения с учетом (7.78) равна:
Д2?=^(1-0,5И). (7.101)
Перемещение в зоне краевого эффекта определяется так, как и соответствующее
перемещение сферической оболочки. Поскольку Nx = 0, то
е
е2 £Л2 ’
где N2 — нормальная кольцевая сила на краю:
Я2 = 2гр(Я2 + 2Л/1цр).
Следовательно, радиальное смещение цилиндрической оболочки от краевых сил
НиМ
^нм=^-2т + ^1а). (7.102)
Второе уравнение (7.96) складывается из (7.101), (7.102), (7.95) и (7.100). Угол по-
ворота нормалей к срединной поверхности сферической оболочки находится как:
386
м л r~ 2M$k
После подстановки Q = Ce-^ sin (ky + у); у = ; C = 41HQ sin <p0-
имеем
2k2 2M\rk
^ = H = S;(^sin<p0-^
(7.103)
.. - « d4y .
Угол поворота нормали к цилиндрическом оболочке есть решение уравнения —? +
dx
А М. HQ HQ
+ 4B4w = 0. После подстановки в него постоянных С, = ; С4 =---? на краю
J DP 2Z)p 2Z>p2
(х = 0) угол поворота будет
Л/1и Н2
^2=И2=-^ +^~.
W 2РР
Нетрудно увидеть, что после подстановки нужных перемещений уравнения (7.96)
станут громоздкими. Решать их приходится численно. Чтобы удобнее было состав-
лять программу для ЭВМ, представим их в следующем виде:
4- С12Я2 + Qз^\с+ СХ4МХц = С15;
4- С22//2 4- С23Л/1с 4- С24Л/|Ц = С25;
4- С32Я2 4- С33МХс 4- С34Л/1Ц = 0;
4- С42Н2 + С4^МХс 4- = 0.
Коэффициенты Ctj зависят от давления в баке, размеров оболочек и шпангоута
и будут такими:
(7.104)
синх
C2XHX
C3iHx
C4iHx
(7.105)
Сн ^flsin<p0--S-;C12 -J-;
С13 = -(^ *2sin Фо+ ; С14 = -^
C>5=Mi"£(1"g)Sin<Po];
z 1 ->Qx 2
2
Т = Г .
*"*" V2*1 ш п2 J 1z
с25 = ЯГ2 [^(1 - 0,5ц) - cos <р0] ;
2 RP-
Cjl Ей. Sin Фо’ С32 Ёр5 ’ С” Eh\R ’Сз4 ’
r _ 2к . г = 2гР . r 2j2k2 г _ 2г2^
41 Ehx sin<Po>L42 ел2’4з Ей.Л’С« Eh2 '
По найденным при решении (7.105) краевым силам определяются внутренние
силы краевого эффекта, к ним добавляются усилия 7V, и N2 от внутреннего давления.
Находятся суммарные усилия ATj и N2 от внутреннего давления (основное, безмомент-
ное состояние) и усилия краевого эффекта Ni9 N2i Мх, М2.
Расчет на прочность ведется по максимальным напряжениям. В краевой зоне
они представляют собой сумму напряжений безмоментного состояния и краевого эф-
фекта.
387
Меридиональное напряжение, например, можно
записать в таком виде:
th — —
----5[е, + he2 + z((O| + ц®2)].
1 -и
Затем подставить значения деформаций и кривизн
из уравнений состояния, а также zmax = +^h. Тогда
_Nt 6Mt
°lmax- ТГ -~ГГ-
п h
Аналогично получаем
Ы2 6М2
^2тах — . 2 ’
" h
Рис. 7.51. Сечение силового
шпангоута сложной формы
(7.106)
(7.107)
Нормальные силы и N2 здесь — суммы сил безмоментного состояния и крае-
вого эффекта; изгибающие моменты Мх и М2 — внутренние силы краевого эффекта.
Силовые шпангоуты баков имеют тонкостенные сечения сложной формы
(рис. 7.51). Нормальные напряжения в них определяются по формуле
Му Mz H3z
о = ± —z± Ту~ I-’
где Му = m * г • sin а и Mz = m г • cos а — изгибающие моменты; у и z — главные оси
инерции; Н3 — погонное значение силы, действующей на шпангоут.
7.4. КРАТКИЕ СВЕДЕНИЯ О ВАРИАЦИОННОМ МЕТОДЕ
И ЕГО ПРИМЕНЕНИИ
Вариационное исчисление — раздел математики, главной задачей которого явля-
ется отыскание экстремальных значений функционалов. Функционал есть сложная
функция, независимыми переменными в ней служат другие, более простые функции.
Обычно функционал представляется определенным интегралом от сложной функ-
ции, например,
Необходимое условие экстремума функционала — обращение в нуль его первой
вариации (дифференциала)
87=0.
Символ 8 в вариационном исчислении требует тех же действий, что и символ d
в дифференциальном исчислении. Операции варьирования и дифференцирования
могут меняться местами.
Задача отыскания минимума функционала (точнее, его стационарного значения)
заключается в составлении дифференциальных уравнений, которым должна удовлет-
ворять подынтегральная функция, и в решении этих уравнений. По форме эта задача
совпадает с задачей об отыскании экстремумов функций, в которой находятся значе-
ния независимых переменных (координат точек, соответствующих экстремуму). По
существу своему задачи различны, так как экстремальные значения функционала оп-
ределяются не координатами точек, а функциями, получаемыми из решения диффе-
388
ренциальных уравнений равновесия (движения). Решение этих уравнений отыскива-
ется не в малой окрестности точки, а в некоторой фиксированной области. Функции,
обеспечивающие экстремум функционала, должны удовлетворять граничным усло-
виям этой области.
В задачах строительной механики функционалом является определенный интег-
рал от полной энергии системы, взятый по ее объему. Преобразование этого интегра-
ла позволяет получить дифференциальные уравнения и естественные граничные ус-
ловия. Чтобы ознакомиться с методом вывода уравнений, получим дифференциаль-
ное уравнение изгиба балки постоянной жесткости на шарнирных опорах,
нагруженной силой q, которая равномерно распределена по всей длине.
Потенциальная энергия может быть записана в напряжениях (погонных силах)
или в перемещениях, соответственно и уравнение изгиба получится в перемещениях
или в силах. Получим уравнение изгиба в перемещениях.
Полная энергия
3=U-Aq9
где
U= El JI |d2x — потенциальная энергия изгиба балки;
0\dx )
/
Aq = J qwdx — работа внешних сил.
о
Пусть перемещения уравновешенной балки получили бесконечно малые прира-
щения 8ш Согласно принципу возможных перемещений работа внешних и внутренних
сил должна быть равна нулю, иными словами, полная энергия балки стационарна:
1 (2 У
8Э = 8/[|£71^4 |-^dx = 0. (7.108)
Символы вариации и производной можно менять местами; следовательно,
d2w^ _ d f-dwA
d? J"d^ldd^J"
j2
p(M.
dx
Тогда (7.108) можно представить в следующем виде:
83=
о
Если первое слагаемое дважды проинтегрировать по частям, в подынтегральной
функции останутся только вариации 8w:
Z 2 ’ 1
_ A z Л... х
d2w_dw 1 rd3wcdw, d2w~dw|Z d3w ~ I7, rd4w~ ,
—78-3- - I—T 8-5- dx =—78-3------T8w + —jSwdx.
dx dx J dx3 dx dx dxl dx I J dx4
0 0 0
d2w dw
d?
dx =
0
Теперь (7.108) будет
/
о 0
о
I4 j2 , 1 I ,3 . I
I w K, . dwjdw d w o.
-4-q 8wdx+—jSgj -—j8w .
lx -I dx I dx I
о 0
(7.109)
389
В силу произвольности вариаций 8^ и би; а также независимости слагаемых
друг от друга, каждое из них должно быть равным нулю:
,4
^—4 -9=0;
dx
^S^|'=0; (7.110)
о
.3 . /
= 0.
dx3 I
о
Первое уравнение (7.110) есть дифференциальное уравнение изгиба балки, на-
груженной силой q. Два других уравнения выражают возможные условия на краях
балки: из второго уравнения следует, что может быть равным нулю изгибающий мо-
мент или угол поворота сечения; из третьего уравнения — поперечная сила или пере-
мещение конца. Функционал Э для пластин и оболочек определяется всеми функция-
ми перемещений и их производными. Уравнения и граничные условия для них полу-
чают так же, как и для балки.
Такой путь решения задач расчета упругих систем состоит в выводе дифференци-
альных уравнений и их решении. В сложных случаях нагружения необходимые преоб-
разования громоздки, а уравнения решаются приближенно, часто в рядах. В этих слу-
чаях дифференциальные уравнения сводят к алгебраическим. Искомые функции пе-
ремещений подбирают так, чтобы они удовлетворяли граничным условиям и
приближенно отражали характер перемещений, хотя последнее требование и не обя-
зательно. Их амплитуды находят из условий минимума функционала.
В строительной механике широкое распространение получили методы прямого
решения вариационной задачи — Ритца, Тимошенко и Бубнова—Галеркина. Рас-
смотрим сущность метода Ритца применительно к той же балке.
Пусть изогнутая ось балки представлена рядом
(7.111)
где / — амплитуды составляющих прогиба; T|z — функция, удовлетворяющая геомет-
рическим граничным условиям задачи или подходящей кривой.
Подставим (7.111) и (7.108). Вариация энергии уравновешенной балки представ-
ляется как сумма вариаций:
5Э= £^5/.
Вследствие независимости вариации равенство нулю возможно, если каждый
из множителей при них равен нулю:
^ = 0,/=1,2,3,...,и. (7.112)
Так как энергия есть квадратичная функция прогиба, то (7.112) есть система
п линейных алгебраических уравнений. Их решение дает амплитуды составляю-
щих прогиба (7.111). По прогибу определяют изгибающий момент, затем напря-
жения.
390
Метод Бубнова—Галеркина применяется для решения дифференциальных
уравнений. Решение задается в виде (7.111). После подстановки решения уравне-
ние умножают на (7.111) и интегрируют. Для балки сумму интегралов приравнивают
к нулю:
/ 4
^/f£/^-9W.dx = 0. (7.113)
dx 7
Легко видеть, что каждое из слагаемых (7.113) вытекает из (7.109), так как внеин-
тегральные члены после подстановки (7.111) и умножения на него станут нулями, ме-
тод Бубнова—Галеркина в сущности есть вариационный метод.
Так как вариации §/• независимы и произвольны, вместо (7.113) имеем п уравне-
ний следующего вида:
/ л
J(£/^-^)qzdx = O, (7.114)
0v dx 7
которые после подстановки (7.111) становятся алгебраическими. Оба метода и подоб-
ные им называют прямыми методами вариационного исчисления, так как они сразу
приводят к алгебраическим уравнениям.
ЛИТЕРАТУРА
1. Строительная механика летательных аппаратов: Учебник для авиационных спе-
циальностей вузов / И. Ф. Образцов, Л. А. Булычев, В. В. Васильев и др.; Под
ред. И. Ф. Образцова. — М.: Машиностроение, 1986. С. 536.
2. БалабухЛ. И., Алфутов Н. А., Усюкин В. И. Строительная механика ракет: Учеб-
ник для машиностроительных спец, вузов. — М.: Высш, шк., 1984. С. 391.
3. Образцов И. Ф., Савельев Л. М., Хазанов X. С. Метод конечных элементов в
задачах строительной механики летательных аппаратов: Учеб, пособие для
студентов авиац. спец, вузов. — М.: Высшая школа, 1985. С. 390.
4. Григорьев Ю. П. Строительная механика авиационных конструкций. — М.:
Изд. ВВИА им. проф. Н. Е. Жуковского, 1966. С. 352.
5. КанС.Н. Строительная механика оболочек.— М.: Машиностроение, 1966.
С. 508.
6. КанС.Н., ПановкоЯ.Г. Элементы строительнойк механики тонкостенных
конструкций. — М.: Оборонгиз, 1952. С. 163.
СОДЕРЖАНИЕ ГЛАВЫ 7
7.1. Стержневые конструкции и расчет их на прочность.............342
7.1.1. Стержневые системы в ракетных конструкциях............342
7.1.2. Работа внешних и внутренних сил.......................344
7.1.3. Теоремы об упругих системах...........................348
7.1.4. Перемещения в стержневых системах от внешних сил.
Формулы Мора.................................................350
7.1.5. Метод сил.............................................352
7.1.6. Метод перемещений.....................................357
7.1.7. Порядок расчета статически неопределимых систем.......362
7.1.8. Расчет на прочность силовых шпангоутов................362
7.1.9. Расчет неразрезанных балок............................365
391
7.2. Напряжения и деформации в оболочках,
симметричных относительно оси.................................366
7.2.1. Краткие сведения о геометрии оболочек..............367
7.2.2. Перемещения оболочки...............................369
7.2.3. Деформации в оболочках.............................370
7.2.4. Напряжения и усилия в оболочке.....................374
7.2.5. Безмоментная теория оболочек.......................375
7.3. Моментная теория оболочек при осесимметричном нагружении..379
7.3.1. Основные понятия...................................379
7.3.2. Уравнения равновесия оболочек вращения
при осесимметричном нагружении............................380
7.3.3. Уравнения краевого эффекта оболочек
при осесимметричном нагружении............................381
7.3.4. Цилиндрический бак со сферическими днищами
под равномерным внутренним давлением......................383
7.4. Краткие сведения о вариационном методе и его применении..388
Литература........................................................391
ГЛАВА 8_____________________________
Основы теории автоматического
регулирования
8.1. ОБЩИЕ СВЕДЕНИЯ О СИСТЕМАХ РЕГУЛИРОВАНИЯ
Автоматическим регулированием называется процесс поддержания или изме-
нения по заданным условиям какой-либо величины в машинах, аппаратах или
иных технических устройствах, осуществляемый без непосредственного участия
человека, с помощью специально для этой цели присоединяемых приборов —
автоматических регуляторов.
Установленный режим машины или иного технического устройства обычно
нарушается внешними воздействиями. Их называют возмущениями. Какова бы
ни была природа этих возмущений, их вредное действие на процесс должно быть
скомпенсировано соответствующим управляющим воздействием регулятора. Так,
например, постоянство оборотов, развиваемых любым двигателем, нарушается
изменением внешней нагрузки и должно поддерживаться за счет воздействия на
органы, дозирующие подвод пара, топлива и т. д.; постоянство температуры в
помещении нарушается при изменении условий теплообмена и должно компен-
сироваться изменением интенсивности обогрева помещения; курс самолета на-
рушается порывами ветра, воздушными ямами и другими изменениями условий
полета и должен сохраняться воздействиями на рули и т. д.
Для поддержания постоянства какой-либо величины можно было бы замерять
возмущения и воздействовать на машину в зависимости от этих замеров. Такой путь
стабилизации процесса — его называют автоматической компенсацией — иногда при-
меняется, но этот путь непрактичен в тех случаях, когда источники возмущений могут
быть самыми разнообразными для одной и той же машины. Далеко не всегда можно
предусмотреть все возможные источники возмущений, притом часто они находятся
внутри самой машины (например, изменение условий смазки, теплового режима
и т. д.). Во многих же случаях управление процессом только путем автоматической
компенсации вообще невозможно.
Значительно чаще для поддержания постоянства какой-либо величины вмес-
то замера самых разнообразных возмущений ограничиваются замером величины,
которую необходимо регулировать, и воздействуют на машину в зависимости от
отклонения этой величины от заданного значения. При такой системе управле-
ния можно обойтись одним измерителем при наличии любого числа самых раз-
нообразных возмущений. Разумеется, замеряемая величина не может при этом
поддерживаться абсолютно точно, так как только при отклонении величины от
требуемого значения и формируется управляющее воздействие на машину. Прин-
ципиальная схема системы регулирования, построенной на этом принципе, показана
на рис. 8.1.
Машина, аппарат или иное устройство, к которому присоединяется регулятор
для осуществления процесса автоматического регулирования, называется регулируе-
мым объектом, а часть регулируемого объекта, на которую воздействует регулятор, —
393
Регулируемая величина
Рис. 8.1. Принципиальная схема системы регулирования
регулирующим органом объекта. Величина, подлежащая регулированию, называется
регулируемой величиной, или регулируемым параметром.
Чтобы осуществить воздействие на регулирующий орган, регулятор должен со-
держать измерительное устройство, измеряющее отклонение регулируемого парамет-
ра от заданного значения, — его называют чувствительным элементом регулятора, — и
устройство, с помощью которого это заданное значение регулируемой величины мо-
жет быть установлено, — задающее устройство.
В том случае, когда чувствительный элемент регулятора развивает при от-
клонении регулируемого параметра от заданного значения усилие и энергию,
достаточные для перемещения регулирующего органа с требуемой скоростью,
чувствительный элемент непосредственно соединяют с регулирующим органом.
В этом случае регулятор называют регулятором прямого действия. Благодаря иск-
лючительной простоте конструкции регуляторы прямого действия до сих пор
очень широко распространены, но область применения их ограничена объекта-
ми, требующими небольших усилий для перемещения регулирующих органов.
Во всех остальных случаях чувствительный элемент регулятора используется
лишь в качестве командного прибора: сигнал с чувствительного элемента управ-
ляет каким-либо усилителем (гидравлическим, пневматическим, электронным,
электромашинным и т. д.), в котором за счет подвода энергии извне развивается
усилие и мощность, достаточные для перемещения регулирующего органа.
Регулятор, включающий такого рода усилитель, называется регулятором не-
прямого действия.
Устройство регулятора непрямого действия, непосредственно связанное с
регулирующим органом и приводящее его в движение, называется исполнитель-
ным устройством регулятора. Исполнительными устройствами служат различ-
ные электрические моторы, гидравлические и пневматические приводы и т. д.
Выше уже указывалось, что ни один регулятор не может точно выдержать заданное
значение регулируемой величины, так как по самому принципу действия регулятор
вступает в работу только после того, как процесс нарушился под действием того или
иного возмущения. Изменение регулируемого параметра во времени, происходящее в
результате какого-либо возмущения и вызванного этим возмущением действия регуля-
тора, называется процессом регулирования. При проектировании регулятора приходится
удовлетворять жестким техническим требованиям на протекание процесса регулирова-
ния. Регулятор же обладает обычно склонностью к раскачиванию процесса, наруше-
нию его устойчивости, которую преодолевают в процессе проектирования и наладки
регулятора. Для обеспечения устойчивости регулирования и для облегчения условий,
394
удовлетворяющих высоким требованиям, предъявляемым техническими заданиями к
процессу регулирования, регулятор усложняют введением различных устройств, специ-
ально предназначенных для этой цели. Такими устройствами служат различные внут-
ренние обратные связи, воздействия по производным, по интегралу, форсировки, ис-
кусственно вводимые запаздывания или разрывы цепи воздействия и т. д. Все устройст-
ва подобного рода носят названия стабилизирующих или контролирующих устройств.
Если режим объекта нарушен изменением нагрузки на регулируемый объект и если
далее во времени она сохраняет постоянное значение (остаточная нагрузка), то регуля-
тор может вернуть регулируемый параметр к требуемому значению независимо от вели-
чины возмущения либо может установить новое значение параметра, мало (на величину
статической ошибки) отличающееся от старого, но зависящее от величины остаточного
возмущения. В первом случае регулятор называется астатическим, во втором — стати-
ческим по отношению к этому возмущению. Зависимость поддерживаемого регулято-
ром значения регулируемого параметра от остаточной нагрузки на регулируемый объект
называется статической характеристикой системы регулирования. В ряде случаев необ-
ходимо астатическое регулирование, но часто можно довольствоваться статическим ре-
гулированием с малой статической ошибкой. Статические регуляторы, как правило,
оказываются более устойчивыми, и высокое качество регулирования в них обеспечива-
ется с помощью более простых, а следовательно, и более дешевых стабилизирующих
средств. Иногда статическое регулирование необходимо для правильной работы объек-
та, например, при регулировании нескольких машин, работающих параллельно.
Все изложенное выше непосредственно относится к регуляторам, устанавливае-
мым для регулирования какой-либо одной величины. В промышленной практике
часто приходится в одном и том же объекте регулировать несколько величин. Если ве-
личины не связаны друг с другом через объект, т. е. если отклонение каждого регули-
рующего органа вызывает отклонение только одной регулируемой величины и не вы-
зывает отклонения остальных регулируемых величин, то каждая из них регулируется
своим регулятором. Регуляторы, установленные на одном и том же объекте, действу-
ют в этом случае независимо друг от друга.
Часто приходится регулировать объекты, в которых регулируемые величины
взаимосвязаны. Отклонение одного регулирующего органа в таких объектах вызывает
отклонение нескольких регулируемых величин. Если на такой объект установить не-
сколько независимых регуляторов, то срабатывание одного из регуляторов вызовет
отклонение остальных регулируемых величин, а в результате — срабатывание осталь-
ных регуляторов. В таких условиях регуляторы могут мешать друг другу.
Так, например, при регулировании паровой турбины с промежуточным отбором
пара на теплофикационные цели устанавливается как регулятор угловой скорости ро-
тора, так и регуляторы давления пара в промежуточных камерах. Изменение давления
в одной из камер вызывает изменение давления в остальных камерах и изменение уг-
ловой скорости ротора. Наоборот, изменение нагрузки, приложенной к ротору, меня-
ет не только его угловую скорость, но и давление пара.
В подобных случаях часто оказывается целесообразным связывать отдельные ре-
гуляторы между собой в единую систему регулирования. В такой связанной системе
исполнительное устройство каждого регулятора управляет не одним, а несколькими
или всеми регулирующими органами.
Подобные системы называются связанными. В связанных системах процесс регу-
лирования какой-либо одной величины не может быть рассмотрен независимо от ос-
тальных величин и система в целом должна рассматриваться как единый связанный
комплекс. В ряде случаев связи между отдельными регуляторами могут быть подобра-
ны так, чтобы отклонение одной из регулируемых величин не вызывало отклонения
395
Рис. 8.2. Принципиальные схемы трех видов систем регулирования:
а) одноконтурная; б, в) многоконтурные
остальных, несмотря на взаимосвязи регулируемых величин через объект. Они ком-
пенсируются внешними связями, осуществленными между регуляторами. Такие сис-
темы называются автономными.
На рис. 8.2 показаны принципиальные схемы трех видов систем регулирования.
8.2. КЛАССИФИКАЦИЯ АВТОМАТИЧЕСКИХ СИСТЕМ
Каждая автоматическая система состоит из целого ряда блоков или звеньев, раз-
лично соединенных между собой (см. рис. 8.2). Каждое отдельно взятое звено имеет
вход и выход в соответствии со стрелками на рис. 8.3, обозначающими воздействие
или передачу информации с одного звена на другое. В общем случае звено может
иметь несколько входов и выходов, но сейчас это несущественно. Входная величина
Xj и выходная х2 могут иметь любую физическую природу (ток, напряжение, переме-
щение, температура, освещенность и т. п.).
В процессе работы автоматической системы величины Xj и х2 изменяются во вре-
мени. Динамика процесса преобразования сигнала в данном звене описывается неко-
торым уравнением (или экспериментально снятой характеристикой), связывающим
выходную переменную х2 с входной переменной хР Совокупность уравнений и харак-
теристик всех звеньев описывает динамику процессов управления или регулирования
во всей системе в целом. Существуют различные характеристики звеньев: статиче-
ские, переходные, частотные и др. Далее все они будут изучены.
396
Рис. 8.4. Примеры непрерывных
статических характеристик звеньев
Рис. 8.3. а) отдельное
звено; б) статическая
характеристика звена
Основными признаками деления автоматических систем на большие классы по
характеру внутренних динамических процессов являются следующие:
1) непрерывность или дискретность (прерывистость) динамических процессов во
времени;
2) линейность или нелинейность уравнений, описывающих динамику процессов
регулирования.
По первому признаку автоматические системы делятся на системы непрерывного
действия, системы дискретного действия (импульсные и цифровые) и системы релей-
ного действия.
По второму признаку каждый из указанных классов (кроме релейного) делится
на системы линейные и нелинейные. Системы же релейного действия относятся цели-
ком к категории нелинейных систем.
Дадим определение каждого класса автоматических систем, а затем рассмотрим
их примеры.
Системой непрерывного действия называется такая система, в каждом из звеньев
которой непрерывному изменению входной величины во времени соответствует не-
прерывное изменение выходной величины. При этом закон изменения выходной ве-
личины во времени может быть произвольным, в зависимости от формы изменения
входной величины и от вида уравнения динамики (или характеристики) звена.
Чтобы автоматическая система в целом была непрерывной, необходимо, прежде
всего, чтобы статические характеристики всех звеньев системы были непрерывными.
Примеры непрерывных статических характеристик показаны на рис. 8.4.
Системой дискретного действия называется такая система, в которой хотя бы
водном звене при непрерывном изменении входной величины выходная величина
изменяется не непрерывно, а имеет вид отдельных импульсов, появляющихся через
некоторые промежутки времени (рис. 8.5). Звено, преобразующее непрерывный вход-
ной сигнал в последовательность импульсов, называется импульсным. Если после-
дующее звено системы тоже дискретное, то для него не только выходная, но и входная
величина будет дискретной (импульсной).
К дискретным автоматическим системам относятся системы импульсного регу-
лирования (т. е. системы с импульсным звеном), а также системы с цифровыми вы-
числительными устройствами. Эти последние дают результат вычисления на выходе
дискретно, через определенные промежутки времени, в виде чисел для отдельных
дискретных числовых значений входной величины.
397
Рис. 8.5. Характеристика
дискретного (импульсного) звена
Рис. 8.6. Статические
характеристики релейного звена
Системой релейного действия называется такая система, в которой хотя бы в од-
ном звене при непрерывном изменении входной величины выходная величина в не-
которых точках процесса, зависящих от значения входной величины, изменяется
скачком. Такое звено называется релейным звеном. Статическая характеристика ре-
лейного звена имеет точки разрыва, как показано в разных вариантах на рис. 8.6.
Обратимся теперь ко второму признаку классификации автоматических систем.
Линейной системой называется такая система, динамика всех звеньев которой
вполне описывается линейными уравнениями (алгебраическими и дифференциаль-
ными или разностными). Для этого необходимо, прежде всего, чтобы статические
характеристики всех звеньев системы были линейными, т. е. имели вид прямой
линии.
Если динамика всех звеньев системы описывается обыкновенными линейными
дифференциальными (и линейными алгебраическими) уравнениями с постоянными
коэффициентами, то систему называют обыкновенной линейной системой.
Если в уравнении динамики какого-либо звена линейной системы имеется хотя
бы один или несколько переменных во времени коэффициентов, то получается линей-
ная система с переменными параметрами. Если какое-либо звено описывается линей-
ным уравнением в частных производных (например, имеют место волновые процессы
в трубопроводе или электрической линии), то система будет линейной системой с рас-
пределенными параметрами.
В отличие от этого обыкновенная линейная система является системой с сосре-
доточенными параметрами. Если динамика какого-либо звена системы описывается
линейным уравнением с запаздывающим аргументом (т. е. звено обладает чисто вре-
менным запаздыванием или временной задержкой т передачи сигнала (рис. 8.7.)), то
система называется линейной системой с запаздыванием. Динамика линейных импульс-
ных систем описывается линейными разностными уравнениями. Все эти системы
объединяются общим названием особые линейные системы, в отличие от обыкновен-
ной линейной системы, указанной выше.
Заметим, что хотя классификация систем и производится по уравнениям дина-
мики звеньев, в дальнейшем будет применяться исследование динамических процес-
сов не только с помощью аппарата уравнений, но также и с помощью эквивалентного
ему частотного аппарата, в большинстве случаев более удобного для практических
приложений.
Нелинейной системой называется такая система, в которой хотя бы в одном звене
нарушается линейность статической характеристики или же имеет место любое дру-
398
Рис. 8.7. Характеристика звена
с временным запаздыванием
Рис. 8.8. Нелинейная
система регулирования
гое нарушение линейности уравнений динамики звена (произведение переменных
или их производных, корень, квадрат или более высокая степень переменной, любая
другая нелинейная связь переменных и их производных).
Следовательно, к нелинейным системам относятся, в частности, все системы,
в звеньях которых имеются статические характеристики любого из многих видов, по-
казанных на рис. 8.4. К ним же относятся и все системы релейного действия (рис. 8.6).
Нелинейными могут быть, разумеется, также и системы с переменными парамет-
рами, с распределенными параметрами, с запаздыванием, импульсные и цифровые
системы, если в них где-либо нарушается линейность уравнений динамики
(в цифровых системах это связано, в частности, с квантованием сигнала по уровню).
При исследовании, расчете и синтезе автоматических систем нужно иметь в виду,
что наиболее полно разработаны теория и различные прикладные методы для обыкно-
венных линейных систем. Поэтому в интересах простоты расчета всегда желательно
(там, где это допустимо) сводить задачу к такой форме, чтобы максимально использо-
вать методы исследования обыкновенных линейных систем. Обычно уравнения дина-
мики всех звеньев системы стараются привести к обыкновенным линейным, и только
для некоторых звеньев, где это недопустимо или где специально вводится особое ли-
нейное или нелинейное звено, учитываются эти особые их свойства. Тогда при нали-
чии одного такого звена система при расчете разбивается на два блока (рис. 8.8), в од-
ном из которых объединяется весь комплекс обыкновенных линейных звеньев.
Однако это вовсе не значит, что при проектировании новых автоматических сис-
тем нужно стремиться к обыкновенным линейным системам. Наоборот, уже из при-
веденных выше определений совершенно очевидно, что обыкновенные линейные
системы обладают ограниченными возможностями. Введение особых линейных и не-
линейных звеньев может придать системе лучшие качества. Особенно богатыми воз-
можностями обладают системы со специально вводимыми нелинейностями и диск-
ретные системы, в том числе с цифровыми вычислительными устройствами, а также
самонастраивающиеся, экстремальные, самоорганизующиеся системы.
8.3. ПРИМЕРЫ НЕПРЕРЫВНЫХ АВТОМАТИЧЕСКИХ СИСТЕМ
Один из первых в истории техники автоматических регуляторов был изобретен
И. И. Ползуновым в 1765 г. Это был автоматический регулятор уровня воды в котле
его паровой машины (рис. 8.9).
Здесь полностью осуществлен общий принцип действия любого автоматического ре-
гулятора прямого действия. Измерительное устройство (поплавок 7), измеряющее регули-
руемую величину (высоту уровня воды в котле 2), непосредственно перемещает регули-
рующий орган (клапан питания котла водой 5). Котел является регулируемым объектом.
399
Изменение величины отбора пара из котла в
паровую машину является основным возмущаю-
щим воздействием 4 на регулируемый объект. Ес-
ли отбор пара увеличится, испарение воды уско-
рится, уровень воды (регулируемая величина)
начнет уменьшаться. Тогда поплавок, опускаясь,
будет шире открывать регулирующий клапан,
усилится приток питающей воды 5, и уровень ее
будет автоматически восстанавливаться. Кроме
изменения отбора пара, возмущающее воздейст-
вие на объект будет проявляться также и в изме-
нении условий теплового режима работы котла
(интенсивность топки, температура питающей
Рис. 8.9. Регулятор уровня воды в котле
воды и окружающего пространства). Регулятор во всех случаях будет действовать так,
чтобы ликвидировать нежелательное отклонение уровня воды, по каким бы причинам
оно ни возникало.
Следующим в истории техники автоматическим регулятором, получившим ши-
рокое распространение, был центробежный регулятор скорости вращения вала паро-
вой машины, изобретенный Уаттом в 1784 г. (рис. 8.10). Этот регулятор имеет другую
конструкцию и другую природу регулируемой величины (угловая скорость со), но со-
вершенно тот же общий принцип действия регулятора прямого действия. Измери-
тельное устройство регулятора (центробежный механизм) реагирует на изменение ре-
гулируемой величины со. Так, если угловая скорость вала со увеличивается, шары
центробежного механизма расходятся, муфта поднимается и перемещает непосредст-
венно регулирующий орган (например, заслонку в трубе питания машины паром).
Это изменяет приток энергии в машину, чем автоматически уничтожается нежела-
тельное отклонение угловой скорости со.
Основным возмущающим воздействием на регулируемый объект здесь является
изменение нагрузки на валу паровой машины. Кроме этого, может иметь место и дру-
гое возмущающее воздействие в виде нарушения нормальных параметров пара в трубе
питания машины. Регулятор гасит влияние любого воздействия (в определенных пре-
делах), стремясь все время ликвидировать отклонение, по какой бы причине оно ни
возникало.
После изобретения этих первых автоматических регуляторов, чисто механиче-
ских, в течение XIX—XX вв. в связи с потребностями промышленности, транспорта и
энергетики появляется много различных конструкций регуляторов, сначала механи-
машины
паром
Рис. 8.10. Регулятор скорости вращения вала паровой машины
400
ческих, а затем и электрических. Дальнейшее развитие автоматики идет все больше и
больше по пути электрификации систем автоматического регулирования, в том числе
и для механических, тепловых и химических объектов.
8.4. ТИПЫ ЧАСТОТНЫХ ХАРАКТЕРИСТИК
Частотные методы исследования и расчета систем автоматического управления,
получившие наиболее широкое распространение, основаны на использовании так на-
зываемых частотных характеристик.
Основными типами частотных характеристик являются следующие.
Для разомкнутых систем:
1) амплитудно-частотная характеристика А(<о);
2) фазочастотная характеристика <р(<х>);
3) амплитудно-фазовая характеристика ИХ/ш);
4) логарифмические амплитудная и фазовая частотные характеристики.
Характеристики Л(<о) и ф(со) строятся в вещественной, a W(j&) — в комплексной
плоскости в функции частоты <о. Логарифмические характеристики строятся в лога-
рифмическом масштабе частоты.
Для замкнутых систем:
1) вещественная частотная характеристика Р(<о);
2) мнимая частотная характеристика Q(<o);
3) амплитудно-частотная характеристика;
4) фазочастотная характеристика.
Амплитудно-фазовая характеристика разомкнутой системы представляет собой
годограф вектора функции ИИС/со), построенный в комплексной плоскости. Комп-
лексная частотная функция ИХ/со), получаемая из передаточной функции разомкну-
той системы заменой р наущ может быть представлена в виде
ИХ/ш) = £/(со) + j И(ш) = Л(со)е>ф<4 (8.1)
При этом
Л(со) = 7t/2(co) + И(<о) и <р((0) = arctg (8.2)
8.5. ДИНАМИЧЕСКИЕ ЗВЕНЬЯ И ИХ ХАРАКТЕРИСТИКИ
Как уже было сказано, для расчета различных систем автоматического регулиро-
вания они обычно разбиваются на динамические звенья. Под динамическим звеном
понимают устройство любого физического вида и конструктивного оформления, но
описываемое определенным дифференциальным уравнением.
В соответствии с этим классификация звеньев производится именно по виду
дифференциального уравнения. Одним и тем же уравнением могут описываться весь-
ма разнообразные устройства (механические, гидравлические, электрические и т. д.).
Для теории автоматического регулирования это будет один и тот же тип звена. Конк-
ретные же элементы автоматических систем, их теория, конструкция и расчеты изла-
гаются в соответствующих учебниках и руководствах.
Обозначим входную величину звена через а выходную через х2 (рис. 8.11). Воз-
мущение, действующее на звено, в соответствии с изложенным выше обозначим f(t).
1 ф((0) находится в квадранте, определяемом знаками t/(a>) и И(а>).
401
Рис. 8.11. Динамическое
звено
Рис. 8.12. Позиционное (а), интегрирующее (б),
дифференцирующее (в) звенья
Статическая характеристика любого звена может быть изображена прямой лини-
ей (рис. 8.12), так как пока будут рассматриваться линейные или, точнее, линеаризо-
ванные системы.
В звеньях позиционного, или статического, типа линейной зависимостью х2 = кхх
связаны выходная и входная величины в установившемся режиме (рис. 8.12, а). Ко-
эффициент пропорциональности к между выходной и входной величинами представ-
ляет собой коэффициент передачи звена.
dx2
В звеньях интегрирующего типа линейной зависимостью = кхх связаны про-
изводная выходной величины и входная величина в установившемся режиме
(рис. 8.12, б). В этом случае для установившегося режима будет справедливым равен-
ство х2 = к\Xj dr, откуда и произошло название этого типа звеньев. Коэффициент про-
порциональности к в этом случае также является коэффициентом передачи звена. Ес-
ли входная и выходная величины звена имеют одинаковую размерность, то коэффи-
циенту передачи соответствует размерность [с-1 ].
dxj
В звеньях дифференцирующего типа линейной зависимостью х2 = к-^ связаны в
установившемся режиме выходная величина и производная входной (рис. 8.12, в), от-
куда и произошло название этого типа звеньев. Коэффициент пропорциональности к
является коэффициентом передачи звена. Если входная и выходная величины имеют
одинаковую размерность, то коэффициенту передачи соответствует размерность [с].
Классификация звеньев, как уже отмечалось, производится по виду дифферен-
циального уравнения или, что то же, по виду передаточной функции звена. Предпо-
ложим, что звено, изображенное на рис. 8.11, описывается дифференциальным урав-
нением, представленным в стандартной форме:
_ d2x9 dx? dx,
^2 + +x2= k\x\ + +kj(t). (8.3)
При нулевых начальных условиях, т. е. в том случае, если для t < 0 входная и вы-
ходная величины, а также их производные тождественно равны нулю, и при отсутст-
вии внешнего возмущения (/*(/)) = 0 может быть найдена передаточная функция звена
как отношение изображений по Лапласу (или Карсону) выходной и входной величин:
\ = Х^ = к'+к^ = fcj(l 4-Т’зр)
W Хх(р) \ + Тхр + т$Р2 1 + Г1Р + Т22р2 ’
(8.4)
к2
где кх — коэффициент передачи звена, Т3 = т-постоянная времени.
к\
402
При известной передаточной функции выходная величина (точнее, ее изображе-
ние по Лапласу или по Карсону) может находиться из выражения Х2(р) = lV(p)X}(p).
Аналогичным образом может быть найдена передаточная функция звена по воз-
мущению, если положить при нулевых начальных условиях входное воздействие рав-
ным нулю (*! = 0). Тогда искомая передаточная функция будет равна отношению изо-
бражений выходной величины и внешнего возмущения:
= 7^ = 1 + 7> + Т}р2 • (8-4,
В дальнейшем изложении для характеристики звена будет использоваться в ос-
новном передаточная функция, так как именно она дает связь между входной и вы-
Типовые звенья
Таблица 8.1
№ п/п Тип звена Передаточная функция
1 Позиционные Безынерционное W(p) = k
2 Апериодическое 1 -го порядка Х + Тр*™
3 Апериодическое 2-го порядка W(j>} \ + Т\р+ Т}р1 (1 + Т3р)( 1 + 7» г, ^4= у (Тргтр
4 Колебательное к, к W{p} X + Тхр + Т^р1 2С 1 чр ч1 Тх < 2Т2
5 Консервативное к к 1+72V =р> <72
6 Интегрирующие Идеальное интегрирующее W(p)=-p
7 Интегрирующее с замедлением w{p) р(Х+Тр)
8 Изодромное +кх = к(1+рТр} ,т=к-^
9 Дифференцирующие Идеальное дифференцирующее W(p) = kp
10 Дифференцирующее с замедлением it'rp
403
ходной величинами, что необходимо знать при использовании того или иного звена в
автоматической системе.
В соответствии с этим в табл. 8.1 приведены передаточные функции десяти раз-
новидностей так называемых типовых динамических звеньев. Под типовым звеном
понимается такое звено, которое описывается дифференциальным уравнением не
выше второго порядка. Характеристики типовых звеньев рассматриваются более под-
робно ниже.
8.6. ВРЕМЕННЫЕ ХАРАКТЕРИСТИКИ
Динамические свойства звена могут быть определены по его переходной функции
и функции веса.
Переходная функция, или переходная характеристика h(t), представляет собой пе-
реходный процесс на выходе звена, возникающий при подаче на его вход скачкооб-
разного воздействия при величине скачка, равной единице (рис. 8.13). Такое входное
воздействие называется единичной ступенчатой функцией и обозначается Xj = 1(0, что
соответствует х1 = О при t < 0 и Xj = 1 при t > 0. Предполагается, что единица имеет ту
же размерность, что и физическая величина на входе звена.
Если входное воздействие представляет собой нееди-
ничную ступенчатую функцию х1 = N\(t), выходная вели-
чина будет равна х2 = Nh(f).
Ступенчатая функция представляет собой распрост-
раненный вид входного воздействия в автоматических
системах. К такому виду сводятся мгновенное изменение
нагрузки электрического генератора, мгновенное возрас-
тание нагрузки на валу двигателя, мгновенный поворот
входного валика следящей системы и т. п.
Умножение какой-либо функции времени х(0 на еди-
ничную ступенчатую функцию 1(0 означает, что функция
времени x(f) будет существовать только при t > 0, при t < 0
она обращается в нуль.
Это иллюстрируется рис. 8.14.
Функция веса w(t) представляет собой реакцию звена
на единичную импульсную функцию, поданную на его вход
(рис. 8.15). Единичная импульсная функция, или дель-
та-функция, представляет собой производную от единич-
ной ступенчатой функции: 8(0 = 1'(Г).
Дельта-функция тождественно равна нулю повсюду,
кроме точки t = 0, где она стремится к бесконечности. Ос-
новное свойство дельта-функции заключается в том, что
J5(r)dr=l, (8.5)
— оо
т. е. она имеет единичную площадь. Дельта-функция мо-
жет быть представлена как предел некоторого выражения,
например:
8(/)= limoe-°4(0. (8.6)
Q —>°о
Рис. 8.13. Переходный
процесс h(t) на выходе
звена при действии
ступенчатой функции f(t)
Рис. 8.14. Результат
умножения функции x(t)
на единичную ступенчатую
функцию 1(f)
404
Рис. 8.15. Функция веса w(t)
как реакция звена на единичную
импульсную функцию 8(f)
t
Рис. 8.16. Входное
воздействие звена в виде
импульса с площадью Л/е = 1
Нетрудно установить связь между переходной функцией и функцией веса. Рас-
смотрим входное воздействие звена в виде конечного по высоте и ширине импульса
с площадью jVe = 1, прикладываемого при t = 0 (рис. 8.16). Такой импульс может быть
заменен двумя ступенчатыми функциями ЛГ* 1(0 и 7V* 1(/ — е), прикладываемыми ко
входу звена со сдвигом во времени е. Тогда выходная величина звена будет равна
x2(t) = N[h(f) - h(t - г)]. (8.7)
Будем теперь увеличивать высоту импульса N, одновременно уменьшая его ши-
рину е, но так, чтобы все время площадь импульса равнялась единице, т. е. № = 1.
Помножив и поделив правую часть равенства (8.7) на е и перейдя к пределу, получим
функцию веса
(8.8)
е—>°° е а*
Таким образом, функция веса может быть получена дифференцированием по
времени переходной функции.
В случае, если на вход звена поступает неединичная импульсная функция
Xj = 66(0, на выходе звена получится х2 = Gw(t).
Импульсная функция также представляет собой распространенный вид входного
воздействия в автоматических системах.
К такому виду можно свести, например, кратковременный удар нагрузки на валу
двигателя, кратковременный ток короткого замыкания генератора, отключаемый
плавкими предохранителями, и т. п. В действительности реальные импульсные воз-
действия на автоматическую систему всегда будут конечными по величине и продол-
жительности. Однако в случае, если их продолжительность весьма мала по сравнению
с временем переходного процесса звена или автоматической системы, то с большой
степенью точности реальный импульс может быть заменен дельта-функцией с неко-
торым масштабирующим коэффициентом, что позволяет оценить переходный про-
цесс по виду функции веса.
405
Функция веса звена связана с его передаточной функцией преобразованием Лап-
ласа, а именно: передаточная функция есть изображение функции веса и связана
с ней интегральным преобразованием
1Г(р) = J w(t)e~p'dt. (8.9)
— оо
В свою очередь переходная функция звена связана с его передаточной функцией
преобразованием Карсона, т. е. имеет место интегральное преобразование
^(р)=р f/i(t)e p'dt. (8.10)
Для входного воздействия произвольного типа, прикладываемого в момент t = 0,
переходный процесс на выходе звена при нулевых начальных условиях может быть
определен на основании интеграла Дюамеля — Карсона по переходной функции:
t
x2(t) = x,(0)h(t) +Jx, (т)й(г-т) dx (8.11)
о
или по функции веса:
t
Х2(О = Х!(0)й(г) +/х] (т)й(г — т) dx, (8.12)
о
где т — вспомогательное время интегрирования, изменяющееся в пределах от нуля до
рассматриваемого текущего момента времени t.
8.7. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ЛИНЕЙНОГО
ЭЛЕМЕНТА И ЛИНЕЙНОЙ МОДЕЛИ СИСТЕМЫ
Передаточная функция системы является исходной для последующих расчетов
в тех случаях, когда свойства всех элементов системы заданы уравнениями движения.
Часто процессы, происходящие в отдельных элементах (например, в объектах ре-
гулирования), изучены слабо, и вывод исходных уравнений для таких элементов за-
труднен.
В таких случаях в основу расчета кладут не уравнения движения, а так называе-
мые частотные характеристики системы. Особенность частотных характеристик со-
стоит в том, что их можно не только построить по линеаризованным уравнениям от-
дельных элементов, но и найти экспериментально для тех элементов, уравнения кото-
рых неизвестны. Необходимо лишь следить за тем, чтобы элементы, у которых
частотные характеристики определяются экспериментально, были линейными или
близки к таковым. Метод экспериментального определения частотных характерис-
тик, описываемый ниже, позволяет попутно установить, линеен рассматриваемый
элемент системы или нет.
Рассмотрим частотные характеристики линейного элемента. Подадим на вход
элемента внешнее гармоническое воздействие Хвх = A sin со/. Устройство, создающее
это гармоническое воздействие, выполним так, чтобы оно позволяло в широких пре-
делах изменять частоту со и амплитуду Л подаваемого воздействия.
Пусть сначала со имеет какое-либо фиксированное значение <ot, а А предельно
мало. В результате этого возмущения входной координаты возникнут вынужденные
колебательные движения выходной координаты. Зафиксируем их с помощью како-
го-либо прибора, записывающего колебания (осциллографа, вибрографа и т. д.).
406
Рис. 8.17. Амплитудно-фазовая
характеристика линейного элемента
Если элемент линейный, то выходная
координата совершает колебания по закону
Л>ЫХ = -МП (®1'+ <Р1)-
Начертим в декартовых координатах
w, v вектор, начало которого совпадает с
началом координат, модуль (длина векто-
х Л
ра) равен rt = , а аргумент (угол между
положительным направлением оси абс-
цисс и вектором) равен углу cpj с обратным
знаком (обычно cpj отрицательно). У кон-
ца вектора сделаем отметку сор
Изменим теперь частоту со колебаний,
подводимых на вход системы, не меняя их
амплитуды и фазы. Пусть со = со2. Тогда и на
выходе установятся колебания частоты со2
Лых = 52sin (<О2/ + ф2).
Построим на рис. 8.17 вектор с модулем г2 =
, аргументом ср2 и отметкой со2.
В2
Аналогично повторив эксперимент при новом значении со = со3, построим на этом же
рис. 8.17 вектор с отметкой со3 и т. д. для разных значений соотсо = Одосо=оо (практи-
чески до достаточно больших со) и соединим плавной линией концы этих векторов.
Построенная таким образом кривая является амплитудно-фазовой характеристи-
кой линейного элемента.
Чтобы определить по амплитудно-фазовой характеристике линейного элемента
амплитуду и фазу колебаний выходной координаты, зная амплитуду А и частоту
со = со* колебаний входной координаты, надо найти на амплитудно-фазовой характе-
ристике точку, имеющую отметку со = со*. Пусть вектор, проведенный из начала коор-
динат в эту точку, имеет длину г и аргумент ср. Тогда амплитуда колебаний %вых равна
В = - , а фаза равна ср (рис. 8.17).
Часто амплитудно-фазовые характеристики строят иначе: длину каждого вектора
А _ В
принимают равной не , а, наоборот, , а аргумент — равным не —ср, а +ср.
Чтобы различать эти два способа построения характеристик, условимся называть
характеристики, у которых г = , амплитудно-фазовыми характеристиками 1-го ро-
да, а у которых г = — характеристиками 2-го рода1.
На рис. 8.18 показаны примеры амплитудно-фазовых характеристик 1-го и 2-го
рода для различных типовых звеньев.
Связь амплитудно-фазовых характеристик 1-го и 2-го рода устанавливается век-
торным равенством:
Г1-Г2=1,
1 В литературе часто амплитудно-фазовые характеристики 1 -го рода называют обратны-
ми или инверсными, а 2-го рода — обыкновенными или простыми. Эти термины, на наш
взгляд, неудачны, так как использование амплитудно-фазовых характеристик 1-го рода часто
значительно удобнее и проще, чем 2-го рода.
407
Наименование звена Оператор звена Амплитудно-фазовые характеристики 1-го рода Амплитудно-фазовые характеристики 2-го рода.
Одноемкостное Тр + \ Vi 8 .|з со = 0 v, СО = оо^ со = 0
и
Колебательное Т$р2 + Т\р + 1 V1 СО = оо ^со = 0 Vi СО = оо со = 0
и и
Астатическое р Vi оо = СО — Vi С0 = оо г
со = 0 и |О и 4 и 3
Консервативное Ttf+X Vi г Q Чн II II 3 3^^ Vi со = у-, СО = тр —►
со"=оо и СО = оо Г'2<о2 > 1 ' со=°(Г" T'W < 1
Неустойчивое Тр-1 8 V‘ III з Vi (0 = 0 СО = оо
и -i^^ и
где Tj и r2 — векторы, проведенные из начала координат к точкам с одинаковым со на
амплитудно-фазовых характеристиках 1-го и 2-го рода. Векторы перемножают при
этом по обычным правилам, т. е. модули их перемножаются, а аргументы складыва-
ются.
Кривая зависимости (или ) от со называется амплитудной характеристикой
элемента, а кривая зависимости —ср (или +ср) от со — его фазовой характеристикой.
Обозначим через и и v проекции вектора амплитудно-фазовой характеристики на
оси абсцисс и ординат (рис. 8.19).
Кривые зависимости и и v от со называются соответственно действительной
и мнимой характеристиками элемента.
Причина, обусловившая эти наименования, будет выяснена в следующем пункте.
Термин «частотные характеристики» охватывает характеристики всех перечис-
ленных пяти типов: амплитудно-фазовую, амплитудную, фазовую, действительную
и мнимую.
408
Рис. 8.19. Действительная (и)
и мнимая (v) характеристики
элемента в зависимости
от частоты со
У линейного элемента амплитуда В пропорци-
ональна А и поэтому построение амплитудно-фазовой
характеристики не зависит от А. Таким образом, эле-
мент линеен, если при подводе ко входу элемента гармо-
нического колебания на выходе устанавливается также
гармоническое колебание той же частоты с амплиту-
дой, пропорциональной амплитуде входных колебаний.
Если элемент не является линейным, то форма
колебаний выходной координаты отлична от сину-
соидальной и ординаты ее не пропорциональны А.
Колебания выходной координаты в этом случае
можно представить рядом Фурье и после этого по-
рознь для каждой гармоники построить амплитуд-
но-фазовые характеристики. Но при этом придется
строить отдельную кривую для каждого значения А.
Если элемент нелинеен, но линеаризуем, то выходные колебания зависят также
от расположения среднего (равновесного) значения входной координаты на нелиней-
ной статической характеристике элемента.
Чтобы в этом случае правильно снять экспериментально амплитудно-фазовую
характеристику элемента, надо подвести к входной координате синусоидальные коле-
бания малой амплитуды. Эти колебания должны происходить относительно того зна-
чения входной координаты, которое устанавливается на рассматриваемом режиме.
Это значение находится статическим расчетом и принималось ранее при выводе урав-
нений за нуль отсчета. Для каждого рассматриваемого режима должна быть снята
своя амплитудно-фазовая характеристика. При этом для каждого режима надо прово-
дить серию опытов, постепенно увеличивая амплитуду подводимых колебаний до тех
пор, пока изменение амплитуды подводимых колебаний не вызовет изменения проте-
кания снимаемой амплитудно-фазовой характеристики. Таким образом, для каждого
режима определится своя амплитудно-фазовая характеристика и выяснится область
применения линейного анализа.
Опыт показывает, что снятие таких серий частотных характеристик для линеари-
зуемых элементов удается осуществить далеко не всегда и экспериментальное опреде-
ление частотных характеристик широко используется главным образом применитель-
но к линейным элементам.
Рассмотрим теперь определение амплитудно-фазовой характеристики линейной
модели по уравнению движения. В тех случаях, когда для некоторых элементов систе-
мы выведены уравнения движения, а свойства некоторых линейных элементов систе-
мы заданы экспериментально полученными частотными характеристиками, необхо-
димо для первых элементов по уравнениям движения построить частотные характе-
ристики1, с тем чтобы по частотным характеристикам всех элементов построить
частотную характеристику системы и принять ее в качестве исходного материала для
дальнейших расчетов.
Воспользуемся тождеством Эйлера
е/со/ = cos + j sjn
Если заменить возмущение, подаваемое на вход элемента при снятии частотной
характеристики
Хвх = A sin со/,
1 Обратная задача, связанная с определением уравнений движения по частотным
характеристикам, значительно более сложна, и в расчетной практике к ней по возможности не
прибегают.
409
комплексной функцией
А^х = Яе/шГ, (8.13)
то истинное возмущение явится лишь мнимой частью (8.13).
Подставив это значение в уравнение элемента, вычислим вынужденные дви-
жения выходной координаты, найдя частный интеграл этого уравнения.
В силу принципа суперпозиции его мнимая часть и определит вынужденные дви-
жения выходной координаты разомкнутой системы, вызванные внешним возмущением
Хвх = A sin со/.
Пусть в самом общем виде уравнение элемента имеет вид
(РХвых dmXBX dm“lX
+- + «Лых = *о-^ + - + Мвх- (8-14)
Будем искать частный интеграл уравнения (8.14) в форме
Хвых = Ве'^+ф) = Ве/шГе/(Р.
Заметим, что
dX
= Ве^(/й))е^,
= Ве'<₽(/со)2е'<",
6пХ
Подставляя эти значения в уравнение (8.14), найдем:
[а0(/й))л + а1(/<о)Л_ 1 + ... + ал]Ве/шГе/(Р = [£0(/(o)m + Z>1(/(o)m _ 1 + ... + bm]Aei(Ot (8.15)
или
d(zco) • = k(i(o)Ael°*.
Отсюда
^e-'<P=^^. (8.16)
В к(цп) v '
Отделяя в равенстве (8.16) действительную и мнимую части, запишем его так:
у(со)
- е_/Ф = «(со) + zv(co) = 7[«(<о)]2 + [v(co)]2 е/аГС g“(tn).
D
Следовательно,
5 = V[«(®)]2 + [v«o)]2 (8.17)
И
<p=-arctgSS- (818)
Таким образом, при внешнем возмущении
ЛВх = Ле'“'.
Вынужденные движения выходной координаты равны
X = А Д*0' - arctgSD]
7[н(со)]2 + [ v(®)]2
410
или
А_ы = . ]cos [со/-arctg ^^"1 + isin [co/ —arctg 1 L (8.19)
7["«D)]2 + [V«D)]2 I L *"(*»J L 5 "(CO) J J
Реальное внешнее возмущение имеет вид
Хвх = A sin со/ = ImAe™*.
Поэтому и колебания на выходе определяются мнимой частью (8.19), т. е.
V А . Г < v(co)l
Ar„v = z ------------------ sin со/ - arctg .
7[w(<o)]2 + [ v(<x>)]2 L "(co) J
Длина вектора, направленного из начала координат к точке амплитудно-фазовой
характеристики 1-го рода, имеющей отметку со, определяется формулой (8.17), а аргу-
мент вектора — формулой (8.18).
Формула (8.17) определяет амплитудную, а (8.18) — фазовую характеристику.
Выражения для м(со) и v(co) определяют действительную и мнимую характерис-
тики.
Зная уравнения движения, т. е. d(p) и к(р), легко по этим формулам построить
точку амплитудно-фазовой характеристики для любого со.
8.8. ПОСТРОЕНИЕ ЧАСТОТНЫХ ХАРАКТЕРИСТИК
РАЗОМКНУТЫХ СИСТЕМ
Задача. Построить амплитудно-частотные, фазочастотные и амплитудно-фазо-
вые характеристики апериодического звена направленного действия с передаточным
коэффициентом к = 1 и постоянной времени Т= 2,5 с и Т= 0,5 с.
Решение. Передаточная функция апериодического звена имеет вид
Заменяя р на усо, получим выражения для амплитудно-частотной и фазочастот-
ной характеристик:
Л(ш) = . 1 ;
л/1 + со27’2
ср(со) = arg [ Ж(/со)] = -arctg со Т.
Таблица 8.2
Т=2,5с Т=0,5с
(0 Л(о>) ф((О) (0 Л(<о) ф((0)
0,5 0,622 —51°6' 1 0,895 —26°36'
1 0,372 —68°24' 2 0,708 -46°
1,5 0,258 —75°6' 3 0,554 -56° 18'
2 0,195 —78°48' 5 0,372 —68°12'
2,5 0,158 -81° 7 0,279 -74°
3 0,127 —82°6' 10 0,196 —78°42'
20 0,02 —86°30' 50 0,04 —87°48'
411
Рис. 8.20. Частотные характеристики апериодического звена:
а) амплитудные, б) фазовые, в) амплитудно-фазовые
Подставив числовые значения Т, вычислим Л (со) и ср(со).
Результаты вычислений представлены в таблице 8.2, по которой построены кри-
вые Л((о) и ф(<о) (рис. 8.20, а, б).
Амплитудно-фазовая характеристика апериодического звена (рис. 8.20, в) пред-
ставляет собой расположенную в четвертом квадранте полуокружность с диаметром,
равным отрезку к, и координатами центра на вещественной оси (к/2; 0).
8.9. ПОНЯТИЕ ОБ УСТОЙЧИВОСТИ ЛИНЕЙНЫХ СИСТЕМ
Движение любой механической системы, например машины, гироскопического
устройства, самолета, снаряда, зависит от действующих сил и начальных условий, от
положений и скоростей точек системы в момент начала движения. Зная действующие
силы и начальные условия, можно теоретически рассчитать, как будет двигаться сис-
тема; это движение называется невозмущенным. Но поскольку все измерения произ-
водятся с той или иной степенью точности, то на практике истинные значения на-
чальных условий обычно несколько отличаются от расчетных. Кроме того, механиче-
ская система может во время движения подвергнуться незначительным случайным
воздействиям, не учтенным при расчете, что тоже эквивалентно изменению началь-
ных условий. Возникающие по разным причинам отклонения начальных условий от
их расчетных значений называются начальными возмущениями, а движение, которое
система совершает при наличии этих возмущений, — возмущенным движением.
Если при достаточно малых начальных возмущениях какой-нибудь из характе-
ристик движения во все последующее время мало отличается от своего значения в не-
возмущенном движении, то движение системы по отношению к этой характеристике
называется устойчивым. Если же при сколь угодно малых, но не равных нулю началь-
ных возмущениях данная характеристика со временем будет все более и более отли-
чаться от своего значения в невозмущенном движении, то движение системы по отно-
412
шению к этой характеристике называется неустойчивым. Эти определения соответст-
вуют определению устойчивости по А. М. Ляпунову. Условия, при которых движение
механической системы является устойчивым, называются критериями устойчивости.
Рассмотрим дифференциальное уравнение движения линеаризованной систе-
мы автоматического регулирования, записанное для регулируемой величины y(t) при
наличии управляющего воздействия g(t) и при равенстве нулю возмущающих воздей-
ствий:
+ а[рп~1 + ап_ {р + an)y(t) = + bm)g(t). (8.20)
Коэффициенты aQ, ..., ап и bQ, ..., bm представляют собой постоянные величины,
d
а оператор р = .
Дифференциальное уравнение движения системы регулирования можно запи-
сать и для возмущающего воздействия. В этом случае левая часть (8.20) останется без
изменения, а правая часть будет иметь иной вид. В общем виде дифференциальное
уравнение, определяющее изменение регулируемой величины, может быть записано
так, что в правой его части будет находиться некоторая функция времени/(/).
Характер переходных процессов в системе определяется видом левой части диф-
ференциального уравнения (8.20). Поэтому для определения качественной картины
переходных процессов является практически безразличным, записать ли исходное
дифференциальное уравнение для управляющего или возмущающего воздействия.
Уравнение (8.20) может с равным успехом быть записано для ошибки регулиро-
вания x(t). При этом левая часть уравнения (8.20) полностью сохраняет свой вид.
Процесс регулирования определяется решением дифференциального уравнения
как сумма двух решений — частного решения неоднородного уравнения (8.20) с пра-
вой частью и общего решения уравнения (8.20) без правой части, т. е. с правой частью,
равной нулю:
У® = Участий + З'общСО- (8-21)
В случае участн(0 = const это будет установившееся значение. Первое слагаемое
(8.21) называют также вынужденным решением а второе слагаемое — переходной
составляющей уп(/). Тогда формула (8.21) может быть записана в виде
У(0=Ув(0+Уп('). (8.22)
Система будет называться устойчивой, если с течением времени при t > оо пе-
реходная составляющая будет стремиться к нулю: уп(/) > 0. Найдем эту составляю-
щую из (8.21). Для этой цели необходимо решить дифференциальное уравнение без
правой части
+ • + вя-1^ +а^ = °. (8.23)
Общее решение ищется в виде
Уп(0=УобЩ(') = Се*'. (8.24)
Дифференцируя выражение (8.24) п раз и подставляя в (8.23), получаем после со-
кращения на общий множитель Се5'
а08" + ах&~1 + ... + ап_ j8 + ап = 0. (8.25)
Полученное алгебраическое уравнение называется характеристическим. Корни
его 8j,..., 8„ будут определять характер переходного процесса в системе. Нетрудно за-
метить, что по своему виду левая часть (8.25) полностью совпадает с левой частью
413
(8.20). Поэтому характеристическое уравнение получается приравниванием левой
части (8.20) нулю:
aoP" + «|P"_|+ ол_1Р + оя = 0. (8.26)
Однако здесь буква р = 8 означает уже не символ дифференцирования, а некото-
рое комплексное число, которое является решением (корнем) характеристического
уравнения.
Так как в решении характеристического уравнения содержится п корней, то пе-
реходная составляющая может быть записана в виде
yn(t) = С^'1 + С2еР2' + ... + Спер"', (8.27)
где Pj, ..., рп — корни характеристического уравнения (8.20), С\, ..., Сп — постоянные
интегрирования, определяемые из начальных условий.
Корни характеристического уравнения определяются только видом левой части
уравнения (8.20). Постоянные интегрирования определяются также и видом правой
его части. Поэтому быстрота затухания и форма переходного процесса определяются
как левой, так и правой частями исходного дифференциального уравнения. Однако
поскольку в понятие устойчивости системы входит только факт наличия или отсутст-
вия затухания переходного процесса (независимо от быстроты затухания и формы пе-
реходного процесса), то устойчивость линейной системы не зависит от вида правой
части дифференциального уравнения (8.20) и определяется только характеристиче-
ским уравнением (8.26).
Чтобы определить, устойчива система или нет, нет необходимости решать харак-
теристическое уравнение и определять его корни. Выясним, какие свойства корней
необходимы и достаточны для того, чтобы система была устойчивой.
Корни могут быть вещественными, комплексными и чисто мнимыми. Рассмот-
рим эти случаи.
Вещественный корень. Пусть один из корней, например является ве-
щественным.
Если он отрицательный (^ = — cq), то слагаемое, определяемое этим корнем в
(8.27), будет представлять собой экспоненту С^е-011*. Очевидно, что при / —> оо этот
член будет затухать.
При рх = ч-оц получится не затухающий, а расходящийся процесс (рис. 8.21).
Комплексные корни. Комплексные корни
бывают попарно сопряженными. При отрицательной
вещественной части два корня, например рх и р2, будут
иметь видр{ 2 = -а ±Ур. В этом случае слагаемые, оп-
ределяемые этими корнями в уравнении (8.27), могут
быть представлены в виде
С1е-(а + C2e-<a -Я)' = Ле“" sin (pz 4- у),
где А и v — новые постоянные интегрирования.
Видно, что в этом случае получаются затухающие
колебания, причем мнимая часть корня р представляет
собой круговую частоту затухающих колебаний, а a —
показатель затухания, определяющий затухание оги-
бающей к кривой переходного процесса (рис. 8.22, а).
При положительной вещественной части рх 2 =
= +а ±ур колебания будут не затухающими, а расходя-
щимися (рис. 8.22, б).
Рис. 8.21. Затухающий
и расходящийся процессы
при отрицательном
и положительном
вещественных корнях
характеристического
уравнения
414
Чисто мнимые корни. В этом случае рх = +/р ир2 = —УР- Слагаемое, опре-
деляемое этими корнями в (8.27), будет представлять собой незатухающие колебания,
т. е. колебания с постоянной амплитудой:
Qe^3' + С2е = A sin (pz + у).
Такой процесс изображен на рис. 8.22, в.
Следовательно, для затухания переходного процесса необходимо, чтобы вещест-
венные части корней были отрицательными. Это относится как к вещественным, так
и к комплексным корням.
Если хотя бы один корень характеристического уравнения будет иметь положи-
тельную вещественную часть, то переходный процесс в целом будет расходиться, т. е.
система окажется неустойчивой. Корни характеристического уравнения можно пред-
ставить в виде точек на комплексной плоскости величиныр (рис. 8.23).
Для устойчивости линейной системы необходимо и достаточно, чтобы все корни
лежали слева от мнимой оси плоскости корней. Если хотя бы один корень окажется
справа от мнимой оси, то система будет неустойчивой.
Таким образом, мнимая ось представляет собой граничную линию в плоскости
корней, за которую не должны переходить корни характеристического уравнения.
Вся левая полуплоскость представляет собой при этом область устойчивости.
Превращение устойчивой системы в неустойчивую произойдет в том случае, если
хотя бы один вещественный или пара комплексных корней перейдет из левой полу-
плоскости в правую. Границей перехода будет так называемая граница устойчивости
системы. Система будет находиться на границе устойчивости при наличии:
1) нулевого корня;
2) пары чисто мнимых корней;
3) бесконечного корня.
Во всех трех случаях предполагается, что все остальные корни имеют отрицатель-
ные вещественные части.
В первом случае вещественный корень попадает на границу устойчивости (ось
мнимых) в начале координат, т. е. выполняется условие рк = 0. Это означает, что в ха-
Рис. 8.22. Затухающий (а) и расходящийся (б) процессы
и колебания с постоянной амплитудой (в) при различных
значениях вещественной части корней
415
Рис. 8.23. Корни характеристического
уравнения на комплексной плоскости
для устойчивой системы
рактеристическом уравнении (8.26) будет отсутствовать свободный член ап = 0. Диф-
ференциальное уравнение (8.20) в этом случае может быть записано в виде
(РоР"~1 + aiPn~2 + - + ап-= (ЬоРт + ... + bm)g(t)
и система будет устойчивой не относительно регулируемой величины у, а относитель-
но ее скорости изменения ру. Величина же отклонения регулируемой величины может
принимать произвольные значения. Такую систему называют нейтрально устойчивой,
имея в виду ее безразличие к значению самой регулируемой величины.
На границе устойчивости второго типа, которая называется колебательной грани-
цей устойчивости, два корня попадают на ось мнимых. Система в этом случае будет
иметь незатухающие гармонические колебания с постоянной амплитудой (рис. 8.22, в).
Наконец, вещественный корень может попасть из левой полуплоскости в пра-
вую, проходя через бесконечность. В этом случае соответствующее слагаемое в
выражении (8.27) обращается в нуль, что соответствует понижению порядка диффе-
ренциального уравнения на единицу. Это будет при а0 = 0. Граница устойчивости
третьего типа встречается сравнительно редко, и в дальнейшем будут рассматриваться
практически только первый и второй типы границы устойчивости.
Как было сказано выше, ни одна реальная система автоматического регулирова-
ния не является строго линейной. Линейные характеристики звеньев и линейные
дифференциальные уравнения получаются путем линеаризации реальных характе-
ристик и уравнений. При разложении в ряд Тейлора удерживались линейные члены
и отбрасывались члены высших порядков, которые для малых отклонений считались
пренебрежимо малыми.
Обоснование законности такой линеаризации содержится в теоремах Ляпунова:
1. Если характеристическое уравнение линеаризованной системы имеет все кор-
ни с отрицательными вещественными частями, то реальная система будет также ус-
тойчивой, т. е. малые нелинейные члены не могут в этом случае нарушить устойчи-
вость системы.
2. Если характеристическое уравнение линеаризованной системы имеет хотя бы
один корень неустойчивый, то реальная система будет также неустойчивой, т. е. ма-
лые нелинейные члены не могут сделать ее устойчивой.
3. При наличии нулевых и чисто мнимых корней поведение реальной системы не
всегда даже качественно определяется ее линеаризованными уравнениями. При этом
даже малые нелинейные члены могут коренным образом изменить вид переходного
процесса, сделав систему устойчивой или неустойчивой.
К сильно выраженным нелинейностям на больших участках, в том числе и к не-
линейностям релейного типа, эти теоремы, вообще говоря, неприменимы. Для иссле-
дования устойчивости нелинейных систем общего вида имеются другие теоремы Ля-
пунова.
Далеко не всегда бывает удобно вычислять корни характеристического уравне-
ния. Поэтому желательно иметь такие критерии, с помощью которых можно было бы
судить об устойчивости системы непосредственно по коэффициентам характеристи-
ческого уравнения, без вычисления корней. Эти критерии называются критериями ус-
тойчивости.
Покажем, что необходимым (но не достаточным) условием устойчивости систе-
мы является положительность всех коэффициентов характеристического уравнения.
Это значит, что при положительности всех коэффициентов система может быть ус-
тойчивой, но не исключена возможность неустойчивости системы. Если же не все ко-
эффициенты характеристического уравнения положительны, то система наверняка
неустойчива и никаких дополнительных исследований устойчивости не требуется.
416
Заметим, что вместо того, чтобы быть положительными, все коэффициенты ха-
рактеристического уравнения могут быть отрицательными. Умножая все члены ха-
рактеристического уравнения на минус единицу, можно сделать все коэффициенты
положительными, т. е. в этом случае выполнить указанное выше требование.
Для доказательства сформулированного необходимого условия устойчивости бу-
дем вначале предполагать, что все корни вещественные. Представим левую часть ха-
рактеристического уравнения (8.26) в виде произведения
аоО>-Р1)О’-Р2)-О’-Р„) = О, (8.28)
где ..., рп — корни характеристического уравнения. При этом будем считать, что
aQ > 0. Это всегда можно выполнить умножением уравнения на минус единицу.
В устойчивой системе все корни должны быть отрицательными, т. е. = — cq,
р2 = —и т. д. При этом (8.28) приобретает вид
aQ(p + «1)(р + ^...(р + а„) = 0. (8.29)
Если теперь раскрыть скобки и вернуться к уравнению вида (8.26), то все ко-
эффициенты уравнения получатся положительными, так как, перемножая и скла-
дывая положительные величины cq > 0, а2 > 0 и т. д., нельзя получить отрицательных
величин.
При наличии в решении характеристического уравнения комплексных кор-
ней с отрицательной вещественной частью, например рх 2 = -а ± ур, результат не
изменится, так как множители в уравнении, соответствующие этим корням, будут
иметь вид
(р + а -Ур)(р + а 4-ур) = (р 4- а)2 4- р2.
Очевидно, что появление такого множителя не может изменить вывод о положи-
тельности всех коэффициентов характеристического уравнения.
Имея в виду рассмотренное необходимое условие устойчивости, далее будем
всегда предполагать, что все коэффициенты характеристического уравнения положи-
тельны.
Необходимое условие устойчивости становится достаточным только для уравне-
ний первого и второго порядков. В этом случае система будет устойчивой при поло-
жительности всех коэффициентов характеристического уравнения, в чем нетрудно
убедиться прямым нахождением корней уравнения.
8.10. КРИТЕРИЙ УСТОЙЧИВОСТИ ГУРВИЦА
Задача отыскания критерия устойчивости для систем, описываемых дифферен-
циальными уравнениями любого порядка, была сформулирована Максвеллом в
1868 году. Эта задача была впервые решена в алгебраической форме Раусом
в 1873 году для уравнений четвертой и пятой степени и в 1877 году — полностью.
Поскольку критерий Рауса дан в форме алгоритма, определяющего последова-
тельность математических операций, необходимых для решения задачи, использова-
ние его в практике является неудобным. Поэтому большее распространение получил
алгебраический критерий устойчивости, сформулированный в 1895 году математиком
А. Гурвицем. Этот критерий был найден Гурвицем по просьбе словацкого профессора
Стодолы, занимавшегося исследованием процесса регулирования турбин.
Ниже критерий Гурвица приводится без доказательства.
417
Для характеристического уравнения (8.26) составим квадратную матрицу (табли-
цу) коэффициентов, содержащую п строк и п столбцов:
а\ I а3 «5 ... 0 0
а0 а2 а4 ... 0 0
0 ах а3 ... 0 0
0 «о ... 0 0 (8.30)
0 0 0 ... а„_1 0
0 0 0 ••• ап-2 ап
Эта таблица составляется следующим образом.
По диагонали от левого верхнего до правого нижнего углов выписываются все
коэффициенты по порядку от а ] до ап. Каждая строка дополняется коэффициентами с
возрастающими индексами слева направо так, чтобы чередовались строки с нечетны-
ми и четными индексами. В случае отсутствия данного коэффициента, а также если
индекс его меньше нуля или больше л, на месте его пишется нуль.
Критерий устойчивости сводится к тому, что при aQ > 0 должны быть больше нуля
все п определителей Гурвица, получаемых из квадратной матрицы коэффициентов.
Определители Гурвица составляются по следующему правилу (см. (8.30)):
Д^арО, (8.31)
Аз“
а\ а3 а5
а0 а2 а4
0^1 а3
(8.33)
Последний определитель включает в себя всю матрицу. Но так как в последнем
столбце матрицы все элементы, кроме нижнего, равны нулю, то последний определи-
тель Гурвица выражается через предпоследний следующим образом:
А„ = *А-1>0- (834)
Однако в устойчивой системе предпоследний определитель тоже должен быть
положительным. Поэтому условие положительности последнего определителя сво-
дится к условию ап > 0, т. е. к положительности свободного члена характеристическо-
го уравнения.
Условия нахождения системы на границе устойчивости можно получить, при-
равнивая нулю последний определитель: Дл = 0, при положительности всех остальных
определителей. Как следует из (8.34), это условие распадается на два условия: ап = 0
и Дл _ j = 0. Первое условие соответствует границе устойчивости первого типа (апери-
одическая граница устойчивости) и второе — границе устойчивости второго типа (ко-
лебательная граница устойчивости).
Раскрывая определители, фигурирующие в общей формулировке критерия
устойчивости Гурвица, можно получить в виде частных случаев критерии устойчи-
вости для системы первого, второго, третьего, четвертого и более высоких по-
рядков.
418
Уравнение первого порядка
а^р 4- ах = 0.
Для этого уравнения критерий Гурвица дает
а0>0,
Aj = а, > 0,
т. е. коэффициенты характеристического уравнения должны быть положительными.
Уравнение второго порядка
а^р2 4- ар + а2 = 0.
Для этого уравнения критерий Гурвица требует
aQ > 0,
Aj = а} >0.
Последний определитель, как отмечалось выше, сводится к условию положи-
тельности последнего коэффициента: а2 > 0.
Таким образом, и для уравнения второго порядка необходимым и достаточным
условием устойчивости является положительность всех коэффициентов характерис-
тического уравнения.
Уравнение третьего порядка
а^р3 4- ар2 4- ар 4- а3 = 0.
Для этого уравнения получаем условия
о0>0,
Aj = ах > 0,
А2 -
а\ аз
а0 а2
=ар2 ~ апаз > 0-
Третий (последний) определитель А3 дает условие а3 > 0. Условие А2 > 0 при
а0 > 0, ах > 0 и а3 > 0 может выполняться только при а2 > 0.
Следовательно, для уравнения третьего порядка уже недостаточно положитель-
ности всех коэффициентов характеристического уравнения, Требуется еще выполне-
ние определенного соотношения между коэффициентами: аха2 > аоа3.
Уравнение четвертого порядка
ар4 4- ар3 4- ар2 4- ар 4- а4 = 0.
На основании критерия Гурвица можно получить, что для уравнения четвертого
порядка, кроме положительности всех коэффициентов, требуется выполнение условия
о3(О1^2 — аоаз) — a4 > 0.
Уравнение пятого порядка
ар5 4- ар4 4- ар3 4- ар2 4- ар 4- а5 = 0.
Для уравнения пятого порядка, кроме положительности всех коэффициентов,
должны выполняться еще два условия:
- <№3 > 0,
(<7^2 - а0аз)<аЗа4 - а2°5> - (а1а4 “ а0аз)2 > °-
419
Как видно, уже для уравнения пятой степени условия устойчивости по критерию
Гурвица получаются достаточно громоздкими. Поэтому использование этого крите-
рия практически ограничивается уравнениями четвертого порядка.
Существенным недостатком критерия Гурвица является также то, что для урав-
нений высоких порядков в лучшем случае можно получить ответ о том, устойчива или
неустойчива система автоматического регулирования. При этом в случае неустойчи-
вой системы критерий не дает ответа на то, каким образом надо изменить параметры
системы, чтобы сделать ее устойчивой. Это обстоятельство привело к поискам других
критериев, которые были бы более удобными в инженерной практике.
Для иллюстрации применения критерия Гурвица рассмотрим пример на оп-
ределение устойчивости дистанционной следящей системы.
Принципиальная и структурная схемы изображены на рис. 8.24. В качестве чувст-
вительного элемента использованы два сельсина (СД и СП), включенные по трансфор-
маторной схеме. Передаточная функция сельсинов равна коэффициенту передачи схемы
где 0 = 0j — 02 “ ошибка, равная разности углов поворота командной и исполни-
тельной осей.
Передаточная функция усилителя:
к7
^ = 77;= Г+Ь’
где к2 — коэффициент усиления и Гу — постоянная времени усилителя.
Передаточная функция двигателя (Д):
где к3 — коэффициент передачи двигателя по скорости, Гм — электромеха-
ническая постоянная времени двигателя совместно с оконечным каскадом уси-
лителя.
Передаточная функция редуктора (Р) равна его коэффициенту передачи, опреде-
ляемому передаточным отношением:
02
W= = *4.
Так как цепь регулирования состоит из включенных последовательно звен-
ьев, то передаточная функция разомкнутой цепи будет равна произведению пере-
даточных функций отдельных звеньев:
Г(р)=^(р)^2(р)^3(р)^4(р) = Рв+Гур)(1+Гмр),
Рис. 8.24. Принципиальная и структурная схемы дистанционной следящей системы
420
где К = кхк2кук^ [ 1/с] — общий коэффициент усиления разомкнутой цепи.
Характеристическое уравнение:
1 + HV) = 0.
После подстановки W(p) получаем
TyTMp^(Ty+TM)p^p + K=Q.
В данном случае характеристическое уравнение имеет третий порядок. Видно,
что условие положительности всех коэффициентов выполняется всегда, если выпол-
нено условие К > 0, что будет при правильном согласовании направления вращения
двигателя со знаком рассогласования.
Дополнительное условие аха2 > яоя3, накладываемое на коэффициенты характе-
ристического уравнения, сводится при подстановке значений коэффициентов
(я0 = ГуГм, ах = Ту + Тм, а2 = 1 и а3 = К) к неравенству
’ + *
' м
которое и является условием устойчивости рассматриваемой системы.
Из этого неравенства, в частности, можно заметить, что увеличение каждой по-
стоянной времени сказывается отрицательно на устойчивости системы, так как при
этом снижается предельное значение общего коэффициента усиления К, при котором
система еще остается устойчивой.
8.11. ПОСТРОЕНИЕ ОБЛАСТЕЙ УСТОЙЧИВОСТИ, D-Р АЗБИЕНИЕ
При расчете и проектировании системы автоматического регулирования иног-
да бывает необходимым исследовать влияние ее различных параметров на устой-
чивость. Для решения этой задачи служит построение областей устойчивости, т. е.
определение таких областей значений параметров, при которых система оказывается
устойчивой.
Различают построение областей устойчивости в плоскости одного парамет-
ра и в плоскости двух параметров. Ниже будет рассматриваться только построе-
ние областей устойчивости в плоскости двух параметров. Для построения таких
областей на плоскости двух параметров Ли В необходимо нанести линии, соответст-
вующие границе устойчивости. Тогда область, ограниченная этими линиями, будет
представлять собой область устойчивости. Для того чтобы окончательно убедиться
в этом, необходимо для любой точки, лежащей внутри полученной области, по ка-
кому-либо критерию проверить устойчивость. Если устойчивость для этой точки
будет иметь место, то она будет выполняться и для всех других точек, лежащих в этой
области.
Для построения границ области устойчивости используются все три признака су-
ществующих типов границы устойчивости. Для границы устойчивости первого типа
это будет равенство ап = 0. Для границы устойчивости третьего типа — равенство aQ = 0.
Для получения условия, соответствующего границе устойчивости второго типа
(колебательной), можно использовать различные критерии устойчивости.
Для систем, описываемых уравнением не выше четвертого порядка, может при-
меняться критерий Гурвица. В этом случае колебательной границе устойчивости со-
ответствует равенство нулю предпоследнего определителя Гурвица: Дл _ j = 0.
Для уравнений любого порядка удобно использовать критерий Михайлова. Ко-
лебательной границе устойчивости в этом случае соответствует равенство нулю харак-
421
теристического комплекса: D(/co) = 0, т. е. прохождение кривой Михайлова через на-
чало координат.
Предположим, что два рассматриваемых параметра системы регулирования Ли В
входят линейно в характеристический комплекс. Тогда для границы устойчивости ко-
лебательного типа уравнение Dfjcn, А, В) = 0 распадается на два уравнения:
Х(со, А, В) = О
У(со,Я, В) = 0
Два последних выражения представляют собой параметрические уравнения гра-
ницы устойчивости при соблюдении дополнительного условия отрицательности ве-
щественных частей всех остальных корней, кроме чисто мнимых. Полная же совокуп-
ность всех кривых на плоскости параметров, разбивающая всю плоскость на области с
определенным распределением корней, называется D-разбиением плоскости парамет-
ров. Обычно практическое значение имеет лишь часть кривых D-разбиения, соответ-
ствующая границе устойчивости.
Для упрощения выделения границ области устойчивости из всего комплекса
кривых D-разбиения на плоскости двух параметров вводится штриховка этих кривых,
производимая по правилу, которое будет приведено без доказательства. Перемещаясь
вдоль кривой в сторону увеличения щ надо штриховать ее с левой стороны, если будет
положительным определитель, составленный из частных производных
ЭХ
51
эг
51
ЭХ
55
эг
55
(8.35)
Если же определитель отрицателен, то кривую надо штриховать справа. При со-
блюдении этого правила штриховка будет направлена внутрь области устойчивости.
В качестве иллюстрации рассмотрим следящую систему, схема которой изобра-
жена на рис. 8.24. Для этой системы было получено характеристическое уравнение
ryrMP3 + (ry+rjp2+p + * = o.
Предположим, что электромеханическая постоянная времени двигателя Тм являет-
ся заданной величиной и требуется построить область устойчивости в плоскости двух
параметров: общего коэффициента усиления К и постоянной времени усилителя Ту
Характеристический комплекс
Ж/®) = Х+>- 0)2(7; + Тм) -№ТУТЫ.
Уравнения, определяющие границу устойчивости,
Х= К-о)2(Гу + Тм) = О,
У=0)-©зГу7’м = о.
Решая их совместно относительно параметров К и Ту, получим
К=^+ Т„&.
1 м
Задаваясь затем различными значениями со в пределах от нуля до бесконечности,
по этим формулам можно вычислить значения искомых параметров и составить
таблицу 8.3, одинаковую для положительных и отрицательных частот.
По полученным данным строим кривую D-разбиения (рис. 8.25).
422
Таблица 8.3
со к т У
0 оо 1 Т л м оо оо 0
Кривая имеет гиперболический вид с асимптотами К = при со = 0 и Ту = О
при со—> оо.
Для нанесения штриховки найдем знак определителя (8.35). Необходимые для
этого частные производные будут
ЭХ . ЭХ 2
ЭЛ =1’Л>=-°)2’
эг _п эг _
ЭХ ~ °’ ТГу “ т»-
Определитель получается равным
1
О
-со3Гм.
Для отрицательных частот, т. е. при изменении частоты в пределах от -оо до О,
полученный определитель будет положительным. Поэтому при движении по полу-
ченной кривой снизу вверх (от -оо до 0) необходимо штриховать область, лежащую
слева от кривой.
Рис. 8.25. Область устойчивости
следящей системы в плоскости линейных
параметров К и Ту
Для положительных частот, т. е. при изменении частоты в пределах от 0 до +°о,
полученный определитель будет отрицательным. Поэтому при движении по получен-
ной кривой сверху вниз (от 0 до +°о) необходимо штриховать область, лежащую спра-
ва от кривой. Снизу полученной кривой получится двойная штриховка.
Область устойчивости практически уже
сформировалась. Так как параметры К и Ту
должны быть положительными, область ус-
тойчивости будет ограничиваться полученной
кривой и положительными направлениями
осей К и Ту
Это можно показать и на основе использо-
вания двух оставшихся условий устойчивости.
Граница устойчивости первого типа будет по-
лучена, если приравнять нулю свободный член,
ап = 0, что дает условие К = 0. Это условие вы-
полняется на оси ординат. Граница устойчи-
вости третьего типа получается при aQ = 0, что
дает условие Ту = 0. Это условие выполняется
на оси абсцисс.
423
Таким образом, область устойчивости в плоскости параметров К и Ту получена
окончательно. Для любых значений К и Ту можно сразу ответить, устойчива или неус-
тойчива система, смотря по тому, попадает или не попадает точка, определяемая эти-
ми значениями параметров, в область устойчивости.
8.12. КРИТЕРИЙ УСТОЙЧИВОСТИ НАЙКВИСТА
Введем понятие передаточной функции разомкнутой системы. Эта функция мо-
жет быть представлена в виде
R(p) = Ь^рт + bipm~l + ... + bm
Q(P) CQpn + с{рп+cn
(8.36)
причем степень числителя не может быть выше степени знаменателя, m < п. При под-
становке р =jay получается частотная передаточная функция разомкнутой системы
= Л((0)еМ<0) = U(ai) +уК(со).
(8.37)
Частотная передаточная функция разомкнутой системы представляет собой комп-
лексное число. На основании рассмотренных ранее частотных характеристик смысл ее
можно объяснить следующим образом (рис. 8.26). Представим себе систему регулирова-
ния в разомкнутом состоянии в виде некоторого звена с передаточной функцией И^(р).
Если на вход этого звена подавать сигнал ошибки в виде гармонических колеба-
ний х = Xmax sin со/ с амплитудой A"max и частотой со, то в установившемся режиме на
выходе регулируемая величина будет изменяться также по гармоническому закону
.у = ^rnax sin № + V) с амплитудой Ктах, той же частотой со и фазовым сдвигом у. Мо-
дуль частотной передаточной функции представляет собой отношение амплитуд вы-
ходной и входной величин:
Л«о) = ^,
лтах
а аргумент — сдвиг фаз у.
Если изменять частоту входного воздейст-
вия от —оо до +оо и откладывать на комплексной
плоскости точки, соответствующие получаю-
щимся комплексным числам, то геометрическое
место этих точек образует амплитудно-фазовую
характеристику разомкнутой системы (рис. 8.27).
Ветвь этой характеристики, соответствующая
отрицательным частотам, является зеркальным
отражением ветви, соответствующей положитель-
ным частотам, относительно вещественной оси.
На амплитудно-фазовой характеристике для
удобства могут отмечаться точки, соответствую-
щие определенным частотам, например со15 со2, юз
и т. д. Вдоль кривой иногда рисуют стрелки, ко-
торые показывают направление возрастания час-
тоты со (рис. 8.27).
В реальных системах всегда удовлетворяется
условие т < п. Поэтому при частоте, стремящей-
ся к бесконечности, модуль частотной переда-
точной функции стремится к нулю и точка с час-
тотой со —> ±оо попадает в начало координат.
Рис. 8.26. Система регулирования
в разомкнутом состоянии
Рис. 8.27. Амплитудно-фазовая
частотная характеристика (АФЧХ)
разомкнутой системы
с передаточной функцией W(p)
424
Сформулируем достаточные и необходимые требования к амплитудно-фазовой
характеристике разомкнутой системы, при выполнении которых система автоматиче-
ского регулирования в замкнутом состоянии будет устойчивой.
Ограничим вначале задачу и будем рассматривать только такие передаточные
функции (8.36), которые соответствуют статическим системам. Это значит, что знаме-
натель (8.36) не будет иметь в качестве множителя операторр. Кроме того, будем пока
рассматривать только устойчивые в разомкнутом состоянии системы. Это значит, что
полюсы выражения (8.36), т. е. корни уравнения
с^р” + с\р'1~х + ... +ся_1р + ся = 0 (8.38)
лежат в левой полуплоскости.
Введем в рассмотрение вспомогательную функцию
= 1 + W(p) = Q(P}Q{p^(p} = , (8.39)
где числитель
Dtp) = аоР" + °\Р" “1 + ••• + а„ - |Р + ап (8 40)
представляет собой характеристический полином системы. Сделаем подстановку
р =До и найдем комплекс
РИ(/со) =
£(/ш)
О(/со) •
(8.41)
Будем теперь изменять частоту от -оо до +оо и изобразим получившуюся ампли-
тудно-фазовую характеристику И^О’со) на комплексной плоскости (рис. 8.28, а).
Рассмотрим результирующий угол поворота вектора И^О’со) при изменении час-
тоты от -оо до +оо. Этот угол представляет собой изменение аргумента (8.41), кото-
рый по правилу деления комплексных чисел равен разности аргументов числителя Vi
и знаменателя у2:
V = Vi-V2-
Числитель (8.41) представляет собой характеристический комплекс. Если все
корни характеристического уравнения лежат в левой полуплоскости, то при измене-
нии частоты от -оо до +оо аргумент ^(До) изменится на величину Vi = ил, где п —
степень характеристического полинома. При построении кривой Михайлова резуль-
тирующий угол поворота был равен yj = л , но там частота изменялась от 0 до +°°.
Знаменатель (8.41) представляет собой комплекс той же степени м, причем по
предположению все корни (8.38) лежат в левой полуплоскости. Поэтому результи-
рующий угол поворота вектора Q(Jay) при изменении частоты от —оо до +°° будет ра-
вен \|/2 = пп.
Отсюда следует, что в рассматриваемом случае результирующий угол поворота
вектора W\ (До) будет равен нулю: V = V] — у2. '^то означает, что для устойчивой в зам-
кнутом состоянии системы годограф вектора ^(До) не должен охватывать начало ко-
ординат (рис. 8.28, а).
Частотная передаточная функция И^ХДо) отличается от вспомогательной функ-
ции IFjt/co) на единицу. Поэтому можно строить амплитудно-фазовую характеристику
разомкнутой системы по выражению (8.37), что проще. Но в этом случае амплитуд-
но-фазовая характеристика не должна охватывать точку с координатами (—1,0). Это
является достаточным и необходимым условием того, чтобы система была устойчи-
вой в замкнутом состоянии (рис. 8.28, d).
425
Рис. 8.28. Амплитудно-фазовая
характеристика W^co)
на комплексной плоскости
Рис. 8.29. Поведение АФЧХ для устойчивой
(а, б), нейтральной (граница устойчивости) (в)
и неустойчивой (г) систем
При определении устойчивости достаточно построить амплитудно-фазовую ха-
рактеристику только для положительных частот, так как ее ветвь, соответствующая
отрицательным частотам, может быть легко получена зеркальным отображением от-
носительно вещественной оси.
На рис. 8.29, а изображен случай так называемой абсолютно устойчивой системы.
Этот термин означает, что система остается устойчивой при любом уменьшении ко-
эффициента усиления разомкнутой цепи. Напомним, что передаточная функция разо-
мкнутой статической системы может быть представлена в виде
“ 1+С._,р + ... + С,Р-
Нетрудно видеть, что уменьшение общего коэффициента усиления К приводит
к уменьшению модуля (8.37), а это в случае, изображенном на рис. 8.29, а, не может
привести к охвату годографом точки (—1, jO).
На рис. 8.29, б изображен случай так называемой условно устойчивой системы.
Здесь система будет устойчивой при значении общего коэффициента усиления, лежа-
щем в некоторых пределах. Как увеличение, так и уменьшение общего коэффициента
усиления К может привести к охвату годографом точки (— 1, jO), что будет соответство-
вать неустойчивости системы в замкнутом состоянии.
На рис. 8.29, в изображен случай, когда система находится на границе устойчи-
вости. Граница устойчивости будет колебательного типа. Это вытекает из того, что
при некоторой частоте, при которой годограф пересекает точку (—1, jO), имеет место
равенство И^до) = -1 -I- jO, что может быть записано в виде
1 + РИ(» = 0.
Последнее выражение представляет собой характеристическое уравнение, кото-
рое обращается в нуль при подстановке р — /со. Таким образом, чисто мнимый корень
является решением характеристического уравнения.
426
Рис. 8.30. Движение
на плоскости корней
при изменении частоты
ОТ -ОО до 4-00
вдоль мнимой оси
На рис. 8.29, г изображен случай неустойчивой системы.
Обратимся теперь к передаточной функции разомкнутой сис-
темы, соответствующей астатизму первого порядка. В этом
случае передаточная функция может быть изображена в виде
W XI +Сл_2^ + ... + С^-‘)*
Будем предполагать, что все корни знаменателя переда-
точной функции (кроме нулевого корня р = 0) лежат в левой
полуплоскости, т. е. в разомкнутом состоянии система явля-
ется нейтрально устойчивой.
Амплитудно-фазовая характеристика разомкнутой сис-
темы будет иметь разрыв непрерывности в точке со = 0.
В этой точке модуль Л(0) —> оо5 а фаза делает скачок на 180°.
Для получения определенности в ходе амплитудно-фазовой
характеристики необходимо отнести нулевой корень знаменателя передаточной
функции W(p) либо к левой, либо к правой полуплоскости корней (рис. 8.24). Первое
является более удобным, так как при этом все корни знаменателя W(p) будут располо-
жены в левой полуплоскости.
Для выполнения сказанного поступают следующим образом. При изменении
частоты от —оо до 4-оо происходит движение на плоскости корней вдоль оси мнимых
снизу вверх (рис. 8.30). В начале координат расположен нулевой корень. Обойдем
этот корень по полуокружности бесконечно малого радиуса так, чтобы корень остался
слева. При движении по этой полуокружности против часовой стрелки независимая
переменная р меняется по закону
р = ре^Ф,
где р —> 0 представляет собой радиус полуокружности, а ф — аргумент, меняющийся
от до 4-5 . При этом передаточная функция И^(р) может быть представлена в виде
1У(р) = j = e-J* =
где R —> оо, а аргумент (—ф) меняется в пределах от 4- 5 до - 5 .
Таким образом, во время движения по полуокружности бесконечно малого радиуса
передаточная функция может быть представлена в виде вектора бесконечно большой
длины, поворачивающегося на комплексной плоскости по часовой стрелке на угол, рав-
ныи л I от 2 до — 2 I, что соответствует полуокружности бесконечно большого радиуса.
На рис. 8.31 изображена амплитудно-фазовая характеристика абсолютно устой-
чивой системы с астатизмом первого порядка. Характеристика начинается в начале
координат при со —> —оо и затем уходит в бесконечность при со —> 0 (верхняя ветвь).
Далее характеристика дополняется полуокружностью бесконечно большого радиуса
так, чтобы вектор И^усо) повернулся по часовой стрелке на угол я.
Нижняя ветвь характеристики соответствует изменению частоты от 0 до 4-оо.
Видно, что характеристика не охватывает точку (— 1, jO) и система в замкнутом со-
стоянии будет устойчивой.
Амплитудно-фазовые характеристики для условно устойчивой системы, для слу-
чая колебательной границы устойчивости и случая неустойчивой системы будут похо-
жими на изображенные на рис. 8.29, б, в, г кривые, за тем исключением, что при со —> О
427
Рис. 8.31. АФЧХ
абсолютно устойчивой
системы с астатизмом
первого порядка
Рис. 8.32. АФЧХ абсолютно устойчивой
системы при наличии астатизма второго
порядка
характеристика будет уходить в бесконечность в соответствии с нижней ветвью характе-
ристики, изображенной на рис. 8.31.
Аналогичными рассуждениями можно показать, что для системы с астатизмом
второго порядка, имеющей передаточную функцию вида
tfP(l + Вт }р + ... +
при обходе двойного нулевого корня в начале координат (см. рис. 8.30) передаточная
функция разомкнутой системы может быть представлена вектором бесконечно боль-
шой длины, поворачивающимся по часовой стрелке на угол 2л.
На рис. 8.32 изображена амплитудно-фазовая характеристика абсолютно устой-
чивой системы при наличии астатизма второго порядка. Так же, как и ранее, здесь
можно получить условную устойчивость, колебательную границу устойчивости, если
характеристика пройдет через точку (—1, jO), и неустойчивость, если характеристика
будет охватывать точку (— 1, jO).
Обобщая проведенные рассуждения, получаем, что для определения устойчивос-
ти системы с астатизмом любого порядка достаточно построить только одну ветвь
амплитудно-фазовой характеристики, соответствующую положительным частотам,
которая должна быть дополнена окружностью бесконечно большого радиуса. При
этом для устойчивой в замкнутом состоянии системы эта ветвь вместе с частью ок-
ружности, заключенной между положительной полуосью вещественных и амплитуд-
но-фазовой характеристикой, соответствующей положительным частотам, не должна
охватывать точку (— 1, jO) в соответствии с рис. 8.33.
Из рис. 8.33 следует, что абсолютная устойчивость может быть получена при сте-
пени астатизма г < 2. При большей степени астатизма может быть получена только ус-
ловная устойчивость.
Обратимся теперь к более общему случаю, когда знаменатель передаточной
функции разомкнутой системы с любой степенью астатизма содержит корни, лежа-
щие в правой полуплоскости. Это соответствует неустойчивой в разомкнутом состоя-
нии системе.
428
Рис. 8.33. АФЧХ устойчивой системы
Появление неустойчивости разомкнутой системы может вызываться двумя при-
чинами. Во-первых, это может быть следствием наличия неустойчивых звеньев.
Во-вторых, это может быть следствием потери устойчивости звеньев, охваченных по-
ложительными или отрицательными обратными связями.
Наличие неустойчивости системы в разомкнутом состоянии не означает, что сис-
тема будет неустойчивой в замкнутом состоянии. Она может быть как устойчивой, так
и неустойчивой. Однако формулировка критерия устойчивости Найквиста при этом
несколько меняется. Пусть знаменатель передаточной функция разомкнутой системы
(8.36) содержит / корней в правой полуплоскости ил-/ корней — в левой. Тогда при
изменении частоты от —оо до +оо для устойчивой в замкнутом состоянии системы ре-
зультирующий угол поворота вектора JF(/co) относительно точки (-1, jO) должен со-
ставить
V = Vi ~ Жг= пк ~ К*2 “ Ол - /я] = / • 2п.
8.13. ОЦЕНКА КАЧЕСТВА РЕГУЛИРОВАНИЯ.
ОБЩИЕ СООБРАЖЕНИЯ
Качество работы любой системы регулирования в конечном счете определяется
величиной ошибки, равной разности между требуемым и действительным значения-
ми регулируемой величины: x(t) = g(t) — y(t). В системах стабилизации при g(t) = О
ошибка x(t) =
Знание мгновенного значения ошибки в течение всего времени работы регули-
руемого объекта позволяет наиболее полно судить о свойствах системы регулирова-
ния. Однако в действительности, вследствие случайности управляющего и возмущаю-
щего воздействий, такой подход не может быть реализован. Поэтому приходится оце-
нивать качество системы регулирования по некоторым ее свойствам, проявляющимся
при различных типовых воздействиях. Для определения качественных показателей
системы регулирования в этом случае используются так называемые критерии ка-
чества.
429
В настоящее время разработано большое число различных критериев качества
систем регулирования. Все их можно разбить на четыре группы.
К первой группе относятся критерии, в той или иной степени использующие для
оценки качества величину ошибки в различных типовых режимах. Эту группу назо-
вем критериями точности систем регулирования.
Ко второй группе относятся критерии, определяющие величину запаса устойчи-
вости, т. е. критерии, устанавливающие, насколько далеко от границы устойчивости
находится система регулирования.
Почти всегда опасной для системы является колебательная граница устойчивос-
ти. Это определяется тем, что стремление повысить общий коэффициент усиления
в системе, как правило, приводит к приближению системы именно к колебательной
границе устойчивости и затем — к возникновению незатухающих автоколебаний.
Третья группа критериев качества определяет так называемое быстродействие
систем регулирования. Под быстродействием понимается быстрота реагирования
системы регулирования на появление управляющих и возмущающих воздействий.
Наиболее просто быстродействие может оцениваться по времени затухания переход-
ного процесса системы.
К четвертой группе критериев качества относятся комплексные критерии, даю-
щие оценку некоторых обобщенных свойств, которые могут учитывать точность, за-
пас устойчивости и быстродействие. Обычно это делается при помощи рассмотрения
некоторых интегральных свойств кривой переходного процесса.
При рассмотрении понятий запаса устойчивости и быстродействия можно исхо-
дить из двух существующих в настоящее время точек зрения.
Во-первых, можно основываться на характере протекания процессов во времени
и использовать для формирования критериев качества переходную или весовую
функцию, расположение полюсов и нулей передаточной функции замкнутой системы
и т. п.
Во-вторых, можно основываться на некоторых частотных свойствах рассматри-
ваемой системы, характеризующих ее поведение в установившемся режиме при дей-
ствии на входе гармонического сигнала. К ним относятся полоса пропускания, отно-
сительная высота резонансного пика и др.
Оба эти подхода имеют в настоящее время большое распространение и использу-
ются параллельно. И тот и другой подход требует изучения условий эксплуатации по-
строенных систем автоматического регулирования, так как только на основании та-
кого изучения можно правильно сформулировать количественные оценки, которые
могут быть использованы в практике проектирования и расчета новых систем.
Связь между временными и частотными свойствами системы автоматического
регулирования имеет сложный характер и может быть определена в общем виде толь-
ко в простейших случаях, например для систем, описываемых дифференциальным
уравнением второго порядка.
Однако отсутствие зависимостей, связывающих в общей форме свойства систе-
мы во временном и частотном представлениях, не может служить препятствием для
развития и независимого использования критериев качества того или иного направ-
ления. Кроме того, в настоящее время получены приближенные зависимости, позво-
ляющие производить некоторое сопоставление временных и частотных свойств сис-
тем регулирования на базе рассмотрения вещественных частотных характеристик.
Использование того или иного подхода при формулировании критериев качества
определяется в настоящее время удобствами его применения в системах конкретного
вида, а также в известной мере сложившимися в данной области традициями.
430
8.14. ОПРЕДЕЛЕНИЕ ЗАПАСА УСТОЙЧИВОСТИ
И БЫСТРОДЕЙСТВИЯ ПО ПЕРЕХОДНОЙ ХАРАКТЕРИСТИКЕ
Оценить запас устойчивости и быстродействия можно по виду кривой переход-
ного процесса в системе автоматического регулирования при некотором типовом
входном воздействии, которым может быть как управляющее, так и возмущающее
воздействие. В качестве типового входного воздействия берется обычно единичный
скачок. В этом случае кривая переходного процесса для регулируемой величины бу-
дет представлять собой переходную характеристику системы (рис. 8.34). Она может
строиться для регулируемой величины y(t) или для ошибки х(/).
Склонность системы к колебаниям, а следовательно, и запас устойчивости могут
быть охарактеризованы максимальным значением регулируемой величины утах или
так называемым перерегулированием
v — v(°°)
а% =Лтах . 100%, (8.42)
У(°°)
где у(°°) * 0 представляет собой установившееся значение регулируемой величины
после завершения переходного процесса.
Допустимое значение перерегулирования для той или иной системы автоматиче-
ского регулирования может быть установлено на основании опыта эксплуатации по-
добных систем. В большинстве случаев считается, что запас устойчивости является
достаточным, если величина перерегулирования не превышает 10-5-30%.
Однако в некоторых случаях требуется, чтобы переходный процесс протекал во-
обще без перерегулирования, т. е. был монотонным; в ряде других случаев может до-
пускаться перерегулирование 50-5-70%.
Быстродействие системы может определяться по длительности переходного про-
цесса /п. Она определяется как время, протекающее от момента приложения на вход еди-
ничного скачка до момента, после которого имеет место неравенство |у(/) —у(°°)1 < Д, где
Д — заданная малая постоянная величина, представляющая собой обычно допусти-
мую ошибку. Величина у(°°) в частном случае может равняться нулю.
Допустимое значение времени переходного процесса определяется на основа-
нии опыта эксплуатации систем регулирования. В следящих системах за единичный
скачок принимается мгновенное изменение управляющего воздействия g(t) = 1(f).
В этом случае под величиной Д обычно понимают некоторую долю входного воздей-
ствия — как правило, от 1 до 5% величины скачка на входе.
Иногда дополнительно к величине перерегулирования а% (или к величине у^)
задается допустимое число колебаний, которое может наблюдаться в течение времени
переходного процесса. Это число составляет обычно 1 -5-2. В некоторых системах коле-
бания могут вообще не допускаться, а иногда может допускаться до 3-5-4 колебаний.
Графически требования к запасу устойчивости и быстродействию сводятся к то-
му, чтобы отклонение регулируемой величины не выходило при единичном входном
воздействии из некоторой области (см. рис. 8.35). Эта область называется областью
допустимых отклонений регулируемой величины в переходном процессе.
В следящих системах удобно применять сформулированные требования качества
к ошибке системы x(t) = g(t) — y(t). В этом случае можно рассматривать область допус-
тимых значений ошибки и при более сложных входных воздействиях, например при
мгновенном приложении на входе постоянной скорости.
Дальнейшее развитие критериев качества, использующих переходную характе-
ристику, приводит к введению дополнительных оценок качества (кроме введенных
выше /п, утах и а%). К ним относятся следующие оценки.
431
Рис. 8.34. Переходный процесс
системы при типовом входном
воздействии
Рис. 8.35. Область допустимых
отклонений регулируемой величины
в переходном процессе
1. Время запаздывания /3, равное отрезку времени, заключенному между момен-i
том приложения входного скачкообразного сигнала и моментом времени, при кото-
ром осредненная выходная величина становится равной половине ее установившего-
ся значения. Примененный здесь термин «осредненная» означает, что в случаях, когда
на передний фронт выходного сигнала накладываются высокочастотные колебания
(это может иметь место в системах высокого порядка), величина t3 определяется по
сглаженной кривой, аппроксимирую-
щей реальную переходную характерис-
тику системы.
2. Время нарастания /н, равное от-
резку времени, заключенному между
точкой пересечения оси времени с каса-
тельной, проведенной к осредненной
кривой переходной характеристики в
точке t = /3, и координатой t точки пере-
сечения указанной касательной с гори-
зонтальной прямой, соответствующей
установившемуся значению регулируе-
мой величины. Максимальное время на-
растания /™ах ограничивается требуе-
мым быстродействием. Минимальное
время нарастания ограничивается
допустимыми в системе ускорениями и
колебательными режимами.
Уточненная диаграмма качества пере-
ходного процесса изображена на рис. 8.36.
Рис. 8.36. Уточненная диаграмма
качества переходного процесса
8.15. ИНТЕГРАЛЬНЫЕ ОЦЕНКИ
Интегральные оценки имеют целью дать общую оценку быстроты затухания
и величины отклонения регулируемой величины в совокупности, без определения то-
го и другого в отдельности.
432
Простейшей интегральной оценкой может служить величина
/(=Jx(r)dr, (8.43)
О
где x(t) — отклонение регулируемой величины от нового установившегося значения,
которое она будет иметь после завершения переходного процесса.
В устойчивой системе х—> 0 при t—> оо и этот интеграл имеет конечную величи-
ну. Геометрически это будет площадь под кривой переходного процесса, построенно-
го для отклонения (рис. 8.37, а).
Площадь будет тем меньше, чем быстрее затухает переходный процесс и чем
меньше величина отклонения. Поэтому параметры системы рекомендуется выбирать
таким образом, чтобы добиваться минимума этой интегральной оценки.
Для вычисления интеграла (8.43) нет необходимости в нахождении х(/), так как
его можно легко вычислить, используя изображение Лапласа или Хевисайда — Кар-
сона. Действительно, изображение Лапласа определяется выражением
Х(р) = Jx(r)e-"dr.
О
Тогда интеграл (8.43) можно найти посредством предельного переходар —> 0:
]х (Г) dr = lim JX dr = lim X(p). (8.44)
о '’—° о ₽_>0
Неудобством интегральной оценки вида (8.43) является то, что она годится толь-
ко для монотонных процессов, когда не меняется знак отклонения х. Если же имеет
место колебательный процесс (рис. 8.37, б), то при вычислении интеграла (8.43) пло-
щади будут складываться алгебраически и минимум этого интеграла может соответст-
вовать колебаниям с малым затуханием или вообще без затухания. Так как форма
переходного процесса при расчете систем регулирования может быть неизвестна, то
применять интегральную оценку вида (8.43) оказывается практически нецелесообраз-
оо
ным. Поэтому предлагалась другая интегральная оценка: j [х| d/, т. е. сумма абсолют-
о
ных величин всех площадей под кривой переходного процесса. Но оказалось, что вы-
числение ее по коэффициентам уравнения затруднительно.
В свете вышесказанного целесообразно перейти к квадратичной интегральной
оценке, называемой иногда «квадратичной площадью регулирования»:
/= Jx2df (х—> 0 при t—> оо), (8.45)
о
Рис. 8.37. Площадь под кривой переходного процесса, как интегральный критерий качества,
при монотонном (а) и колебательном (б) процессе затухания
433
которая не зависит от знаков отклонений,
а значит, и от формы переходного процес-
са (монотонной или колебательной).
Величина /(8.47) будет тем меньше, чем
меньше сумма заштрихованных на рис. 8.38
площадей (взятых для квадратов ординат),
т. е. чем лучше переходный процесс прибли-
жается к идеальному скачку регулируемой
величины вслед за скачком управляющего
или возмущающего воздействия.
Рис. 8.38. Сумма заштрихованных площадей
(взятых для квадратов координат)
как характеристика качества
переходного процесса
ЛИТЕРАТУРА
1. Бессекерский В. А., Пальтов И. П., Фабрикант Е. А., Федорове. М., Чинаев П. И.
Сборник задач по теории автоматического регулирования. — М.: Физматгиз,
1963. С. 408.
2. Айзерман М. А. Лекции по теории автоматического регулирования. — М.: Физ-
матгиз, 1958. С. 520.
3. Васильев Д. В., Чуич В. Г. Расчет систем автоматического управления. — М.:
Машгиз, 1959. С. 390.
4. Бессекерский В. А., Попов Е. Г. Теория систем автоматического регулирования. — М.:
Наука, 1966. С. 992.
5. Нелинейные нестационарные системы / Под ред. Ю. И. Топчеева. — М.: Маши-
ностроение, 1986. С. 333.
Содержание главы 8
8.1. Общие сведения о системах регулирования.......................393
8.2. Классификация автоматических систем...........................396
8.3. Примеры непрерывных автоматических систем.....................399
8.4. Типы частотных характеристик..................................401
8.5. Динамические звенья и их характеристики.......................401
8.6. Временные характеристики......................................404
8.7. Частотные характеристики линейного элемента
и линейной модели системы..............................................406
8.8. Построение частотных характеристик
разомкнутых систем.....................................................411
8.9. Понятие об устойчивости линейных систем.......................412
8.10. Критерий устойчивости Гурвица................................417
8.11. Построение областей устойчивости, D-разбиение................421
8.12. Критерий устойчивости Найквиста..............................424
8.13. Оценка качества регулирования. Общие соображения.............429
8.14. Определение запаса устойчивости и быстродействия
по переходной характеристике...........................................431
8.15. Интегральные оценки..........................................432
Литература.............................................................434
434
ГЛАВА 9_________________________
Обеспечение надежности
летательных аппаратов
в процессе их производства
Одним из основных показателей, характеризующих качество современных изде-
лий, является надежность. В настоящее время в связи со своей многоплановостью
и важностью наука о надежности определилась как самостоятельная отрасль знаний.
Она изучает закономерности изменения показателей качества изделий (технических
устройств) и на основании этого разрабатывает методы, обеспечивающие с наимень-
шими затратами времени и средств необходимую продолжительность и безотказность
их работы. Основными разделами науки о надежности являются: теория физико-хи-
мического старения, статистическая теория надежности, методы конструирования
и расчетов на надежность, технологические методы обеспечения надежности, эконо-
мика надежности изделий.
Целью настоящей главы является ознакомление с современным состоянием
и основными понятиями прикладной научной дисциплины о надежности изделия и
ее роли в обеспечении качества летательных аппаратов на стадии их производства.
При этом в отличие от существующего методического материала по этому вопро-
су в данной главе с единых позиций рассматриваются надежность изделий, надеж-
ность технологических систем и влияние технологии на формирование показателей
надежности.
9.1. НАДЕЖНОСТЬ КАК ПРИКЛАДНАЯ НАУЧНАЯ ДИСЦИПЛИНА
И ЕЕ ЗАДАЧИ ПО ОБЕСПЕЧЕНИЮ КАЧЕСТВА
ЛЕТАТЕЛЬНЫХ АППАРАТОВ
Основной характеристикой любого технического изделия (самолета, космиче-
ского аппарата, ракеты-носителя и т. д.) является его эффективность [1, 2]. Под эф-
фективностью понимают свойство изделия соответствовать своему назначению. Эф-
фективность определяется качеством изделия и условиями его эксплуатации. Качест-
во изделия определяется не всеми его свойствами, а только той совокупностью его
свойств, которые обусловливают пригодность изделия для удовлетворения опреде-
ленных потребностей в соответствии с его назначением. В зависимости от вида изде-
лия и его назначения совокупность его свойств, определяющих качество изделия, мо-
жет существенно изменяться. Однако абсолютно для всех изделий в эту совокупность
свойств входит такое свойство изделия, как надежность.
Надежностью называется свойство изделия выполнять заданные функции, сохра-
няя во времени значения установленных эксплуатационных показателей в заданных
пределах, соответствующих заданным режимам и условиям использования, техниче-
ского обслуживания, ремонта, хранения и транспортировки (ГОСТ 27.002—83).
Надежность является комплексным свойством, состоящим из следующей сово-
купности свойств: безотказность, долговечность, сохраняемость и ремонтопригод-
435
ность. В зависимости от вида изделия каждая из этих составляющих имеет различную
относительную значимость.
Хотя надежность является только одним из свойств качества, тем не менее имен-
но она в абсолютном большинстве случаев определяет эффективность (в том числе
экономическую и тактико-техническую) и безопасность использования изделия. Так,
из-за недостаточной надежности изделий стоимость затрат на их ремонт и техниче-
ское обслуживание может в несколько раз превышать стоимость нового изделия. Су-
щественное недоиспользование потенциальных возможностей изделий имеет место
при завышении требований к их безотказности, так как в этом случае изделия снима-
ются с эксплуатации при меньших сроках службы. Существуют и такие последствия
ненадежности изделий, которые нельзя оценить никакими экономическими и техни-
ческими показателями — гибель людей и экологические катастрофы. Проблема на-
дежности изделий в настоящее время общепризнана, и на обеспечение надежности
новых изделий вкладываются суммы, достигающие 80...90% всех затрат по техниче-
скому проекту [1, 3, 4].
9.1.1. Вероятностная природа показателей надежности
При испытаниях любой партии деталей, изготовленных из материала одной
плавки по одной технологии, всегда наблюдается разброс значений в измеренных ха-
рактеристиках. Так, коэффициент вариации предела прочности специальных образ-
цов из сталей достигает 0,07, коэффициент вариации предела выносливости таких же
образцов достигает 0,15, а коэффициент вариации интенсивности изнашивания мо-
жет достигать 0,2. Значения же коэффициентов вариации этих же параметров для де-
талей изделия могут быть существенно больше [1, 5, 6]. Поэтому при проведении рас-
чета специального образца или детали изделия на предельные характеристики по ка-
кому-либо параметру возникает вопрос: какое значение предела прочности (предела
усталости, интенсивности изнашивания и т. д.) необходимо подставить в расчет? Если
мы подставляем наименьшее возможное, то это заведомо приводит к снижению эф-
фективности изделия. Подстановка же максимального значения будет приводить к
слишком частому возникновению поломок. Реальное же значение рассматриваемой
характеристики для выбранной детали неизвестно. Его можно получить только после
ее испытания, но при этом деталь уже будет непригодна для эксплуатации в составе
изделия.
Правильный ответ на такой вопрос может быть сформулирован только в вероят-
ностном аспекте — подставляя выбранное значение параметра в расчет, необходимо
указать или рассчитать вероятность возникновения отказа для этого значения пара-
метра.
Аналогичная ситуация возникает при испытании самих изделий — отказы оди-
наково изготовленных изделий и испытываемых в одинаковых условиях также возни-
кают через различные промежутки времени. В этом случае также возникает вопрос:
какой ресурс назначить для этого изделия? Ответ на этот вопрос совпадает с ответом
в предыдущем случае. Таким образом, анализ надежности изделия должен проводить-
ся с учетом вероятностной природы обеспечения требуемого уровня характеристик
материалов, изготовленных из них деталей и изделия в целом. При этом необходимо
иметь в виду, что реально эксплуатируемое изделие (ракета, самолет и т. д.) находится
под воздействием внешних нагрузок, значения которых также имеют разброс. Не ме-
нее важное влияние на параметры надежности и их дисперсию оказывают внутренние
физико-химические процессы, протекающие при работе самого изделия [1,4, 7].
436
9.1.2. Основные задачи прикладной
научной дисциплины о надежности изделия
Важнейшая роль надежности в обеспечении эффективности изделий, а также ее
методологические особенности привели к выделению надежности в самостоятельную
прикладную научную дисциплину. Наука о надежности изучает закономерности из-
менения показателей качества изделий и на основании этого разрабатывает методы
анализа и обеспечения показателей надежности при проектировании, изготовлении,
испытании и эксплуатации изделий [1,4].
В связи со спецификой различных видов технических изделий в науке о надежности
есть самостоятельные направления, определяемые видом изделия. В этих направлениях
много общего, но есть и отличия, связанные в основном с технологическими и конст-
руктивными методами обеспечения надежности конкретных видов изделий [1, 2, 7, 8].
Перед наукой о надежности стоят следующие основные задачи:
1) установление источников информации об изменении показателей надежности;
2) разработка методов диагностики изменения показателей качества;
3) исследование физико-химических закономерностей, приводящих к измене-
нию показателей качества;
4) разработка математических методов расчета, прогнозирования и подтвержде-
ния значений показателей качества по результатам испытаний;
5) разработка технических рекомендаций, конструктивных и технологических
методов и организационных мероприятий, обеспечивающих достижение заданного
уровня надежности изделий.
Как любая наука, надежность в своем развитии и становлении прошла сложный
диалектический путь. На начальном этапе надежность развивалась по двум самостоя-
тельным направлениям. Первое направление возникло в технологии машиностро-
ения на основе изучения физико-химической природы изменения свойств материа-
лов (усталости, старения, износа, деградации, коррозии и т. д.) при внешних (эксплу-
атационных и технологических) воздействиях. Это направление в настоящее время
получило название «Физика отказов» [1,3, 7].
Второе направление возникло в радиотехнике на основе разработки математиче-
ских методов оценки показателей надежности сложных систем со статистической об-
работкой эксплуатационной информации методами теории вероятностей. Это на-
правление заложило основы второго раздела науки о надежности математической те-
ории надежности [9].
Математическая теория надежности разрабатывает математические модели на-
дежности технических систем и прогнозирует поведение таких систем методами те-
ории вероятностей и математической статистики. Физика отказов разрабатывает фи-
зические и математические модели изменения свойств материалов в результате внеш-
них воздействий. Результаты этих двух разделов служат исходными данными для
проектирования и расчета изделий на надежность, а также для разработки технологий
производства изделий с нужным уровнем надежности и качества.
9.2. ЭТАПЫ ФОРМИРОВАНИЯ
НАДЕЖНОСТИ ЛЕТАТЕЛЬНЫХ АППАРАТОВ
Действующими стандартами регламентирован единый порядок разработки, про-
изводства и эксплуатации создаваемых изделий, который состоит из трех основных
стадий: разработка изделия, серийное производство, эксплуатация изделия.
437
Особенность решения вопросов по надежности при создании изделий заключа-
ется в том, что эти вопросы должны решаться на каждой из перечисленных стадий,
так как изменить уровень надежности изготовленного изделия нельзя, как, например,
изменить его товарный вид. Только после эксплуатации или специальных испытаний
можно определить уровень его надежности, а затем, если это необходимо, внести кор-
рективы в конструкторскую, производственную или эксплуатационную документа-
цию и изготовить новое изделие с более высоким уровнем надежности. В общем слу-
чае только в результате определенного цикла таких итераций можно гарантировать
определенный уровень надежности изготавливаемого изделия. Естественно, такой
итерационный путь длителен и требует больших материальных ресурсов. В связи с
этим при создании новых изделий закладываются специальные мероприятия для ус-
корения и удешевления процесса отработки изделия на надежность, которые оформ-
ляются в виде комплексных программ [1,7, 8].
Необходимость решения вопросов по надежности на каждой из трех стадий часто
подчеркивается в так называемой формуле надежности изделия — надежность закла-
дывается на этапе проектирования (разработки), обеспечивается на этапе производ-
ства и реализуется на этапе эксплуатации изделия [2, 3].
Рассмотрим кратко основные особенности этих трех этапов с точки зрения на-
дежности.
После получения задания на разработку изделия производится сбор и изучение
данных по диапазонам нагрузки и внешних воздействий на разных стадиях эксплуата-
ции изделий. Изучают фактически достигнутый уровень надежности в эксплуатации
изделия и его узлов, выбранных прототипами. Особый интерес для надежности пред-
ставляют изделия, снятые с эксплуатации из-за отказов или полной выработки ресур-
са. На основании этой информации уточняют требования к отдельным элементам из-
делия и производят подбор материалов с учетом их прочностных характеристик, об-
рабатываемости, производственных возможностей и стоимости. После этого
разрабатывается комплексная программа достижения нужного уровня надежности
изделия с конкретизацией выполняемых работ по отдельным узлам и изделию в це-
лом на каждой стадии его создания.
При проектировании и конструировании закладывается надежность изделия.
Она зависит от конструкции изделия и его узлов, применяемых материалов и техно-
логий, методов защиты от внешних воздействий, систем смазки, приспособленности
к ремонту и обслуживанию и так далее. Любой узел и агрегат можно сконструировать
бесконечным числом способов, рассчитав надежность конструкции по статическим
нагрузкам. Однако в настоящее время существует не много расчетов, позволяющих
прогнозировать поведение конструкции в реальных условиях эксплуатации с учетом
динамики и статистического характера внешних воздействий. Поэтому проектирова-
ние строится на основании использования конструкций, которые были в изделиях,
прошедших эксплуатацию. Обычно при создании новых типов изделий используется
до 50% и более агрегатов и узлов, выполненных по ранее разработанным схемам и ап-
робированных в серийной эксплуатации. Это, с одной стороны, ускоряет и удешевля-
ет процесс запуска в серию изделия, но, с другой стороны, замедляет качественное
развитие техники. Для вновь же проектируемых узлов и агрегатов проводится комп-
лекс опережающих мероприятий по их изготовлению и испытанию на моделирующих
установках, стендах и в специальных летающих лабораториях. Опережающие мероп-
риятия планируются таким образом, чтобы на сборку опытного образца поступали уз-
лы и агрегаты с известными показателями надежности.
При производстве изделия должна быть обеспечена надежность, заложенная при
ее проектировании, т. е. технология изготовления определяет, насколько могут быть
438
реализованы потенциальные возможности конструкции. Известно, что до 80% отказов
в работе изделий возникает по вине заводов-изготовителей. На данном этапе надеж-
ность зависит от технологий изготовления и сборки деталей, методов контроля, воз-
можностей управления технологическими процессами, соответствия оборудования и
технологической дисциплины серийного завода параметрам опытно-эксперименталь-
ного завода, а также от других показателей. Пока летательные аппараты подвергались
эксплуатационным нагрузкам небольшого уровня, делались из среднепрочных мате-
риалов, имели большие коэффициенты безопасности и небольшие ресурсы, статиче-
ские расчеты и существующие технологии обеспечивали требуемую надежность изде-
лий. Однако, переход на высокопрочные материалы для обеспечения более высокой
эффективности изделия показал, что такие материалы значительно более чувствитель-
ны к внешним воздействиям как при эксплуатации, так и при изготовлении [1,3].
В этих условиях выяснилось, что конструкторско-технологические аспекты
очень сильно влияют на надежность изделий. В очень небольшой степени это тради-
ционно учитывается в чертежах, например, по требованиям шероховатости поверхно-
стей и покрытиям, а также ссылками на соответствующие технологические инструк-
ции по изготовлению. Однако этого совершенно недостаточно, так как два изделия,
изготовленные на разных заводах по одинаковым чертежам, будут иметь совершенно
разные показатели надежности. В связи с этим во всех высокоразвитых странах мира
достаточно давно пришли к пониманию того, что практически все основные элемен-
ты «know how» новых изделий связаны с технологией их изготовления. Как отмечает-
ся в работах [1, 3], ссылки в чертежах на технологические инструкции «отражают в ос-
новном печальный опыт конструкторов и конструкторских подразделений», но в ма-
лой степени обеспечивают такую регламентацию технологии, при которой
гарантирован определенный уровень надежности изделия. Обеспечение гарантиро-
ванного уровня надежности изделия, особенно в условиях серийного производства,
является сложной технической задачей, решаемой в течение достаточно длительного
периода запуска изделия в производство с помощью специальных программ или по-
литики обеспечения качества.
Важнейшей особенностью и отличием показателей надежности от других показа-
телей качества является то, что их уровень выявляется только при эксплуатации, при-
чем их значения нельзя измерить с помощью прибора на готовом изделии и указать,
сколько времени осталось до наступления отказа. Надо отметить, что по некоторым
частным направлениям диагностики (спектры акустической эмиссии, наличие час-
тиц износа в смазках и т. д.) намечается прогресс в оперативной диагностике изделий
по текущему состоянию.
Приведенная общая схема отработки изделия на надежность конкретизируется
в зависимости от вида летательного аппарата (ЛА) и опыта, накопленного в подразде-
лении, обеспечивающем его выпуск. Вместе с тем, общая схема отработки изделия на
надежность обязательно включает следующие этапы: задание уровня показателей
надежности; анализ проекта на надежность; обеспечение заложенного уровня надеж-
ности в процессе изготовления; испытания на надежность; контроль и подтверждение
уровня надежности.
9.3. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ
И ПОНЯТИЯ ТЕОРИИ НАДЕЖНОСТИ
Летательный аппарат, как и любое техническое изделие, характеризуется опреде-
ленным набором свойств. Для количественной оценки определенного свойства вво-
дится понятие показатель. Например, показатели качества, показатели надежности,
439
показатели точности функционирования, показатели экономичности и так далее. По-
казатель характеризует в количественном виде степень свойств, присущих конкрет-
ному изделию. При рассмотрении показателя следует различать: его наименование;
его формулировку, содержащую указание о способе экспериментального или расчет-
ного определения его численного значения; размерность показателя; его численное
значение, которое может изменяться в зависимости от условий измерения, условий
эксплуатации или стадии разработки изделия.
Показатели могут быть единичными или комплексными, и они оговариваются
в нормативных документах на изделие. При этом также оговаривается допустимая ве-
личина отклонения этих параметров от установленных значений, уровень внешних на-
грузок при измерении параметра и необходимость проведения измерений при обяза-
тельном соблюдении методов и сроков технического обслуживания и ремонта изделия.
Свойство изделия сохранять во времени в установленных пределах значения па-
раметров, оговоренных в нормативно-технической документации, характеризует тех-
ническое состояние изделия. Различают следующие пять основных видов технического
состояния изделий: исправное, работоспособное, неисправное, неработоспособное,
предельное (рис. 9.1).
В исправном состоянии изделие соответствует всем требованиям норматив-
но-технической и конструкторской документации. Если же изделие не соответствует
хотя бы одному требованию этой документации, то его состояние неисправное. В не-
исправное состояние изделие переходит вследствие возникновения дефекта. Однако
в неисправном состоянии изделие может быть работоспособным и неработоспособ-
ным. Работоспособное состояние накладывает меньше ограничений на изделие, чем
исправное состояние, и требует, чтобы только те значения параметров, которые ха-
рактеризуют способность изделия выполнять заданные функции, соответствовали до-
кументации на изделие. При этом в документации должно оговариваться, какие пара-
метры обеспечивают работоспособное состояние.
Дефект, приводящий к переходу изделия из исправного состояния в неисправное,
но работоспособное, получил название повреждения. В неработоспособном состоя-
нии хотя бы один параметр изделия, характеризующий его способность выполнять за-
данные функции, не соответствует требованиям документации. Дефект, приводящий к
Рис. 9.1. Виды состояния изделия
440
переходу изделия из исправного или работоспособного неисправного состояния в не-
работоспособное состояние, получил название отказа. Таким образом, повреждение
изделия сохраняет его способность выполнять заданные функции, а отказ — нет.
Предельное состояние — это такое состояние изделия, при котором его эксплу-
атация должна быть прекращена в соответствии с требованиями документации.
Обычно переход в предельное состояние изделия задается после выработки им ресур-
са или срока службы. То есть переход в предельное состояние определяется нецелесо-
образностью или недопустимостью дальнейшего применения изделия по его назначе-
нию. Для изделия в предельном состоянии ставится вопрос либо о целесообразности
проведения его ремонта, для перевода изделия в исправное или работоспособное со-
стояние, либо о его списании.
Переход изделия из неработоспособного (непредельного) состояния в работо-
способное осуществляется с помощью операций восстановления или ремонта
(ГОСТ 27.002—83). К операциям восстановления в основном относят операции иден-
тификации отказа (определение его места и характера), замены, регулирования
и контроля технического состояния и работоспособности изделия в целом. При ре-
монте же происходит восстановление ресурса изделия в целом. В основном термин
«ремонт» применяется при восстановлении работоспособности изделия из предель-
ного состояния.
В зависимости от вида дефекта изделия подразделяют на восстанавливаемые
и невосстанавливаемые. Восстанавливаемые изделия — это те, для которых в рас-
сматриваемой ситуации (вид дефекта) восстановление работоспособности предус-
мотрено нормативно-технической и конструкторской документацией. Таким обра-
зом, восстанавливаемое изделие может при определенных видах дефектов не подле-
жать восстановлению.
В зависимости оттого, предусмотрено ли документацией проведение ремонта из-
делия в предельном состоянии, все изделия подразделяют на ремонтируемые или пе-
ремонтируемые. Причиной списания ремонтируемого изделия из предельного со-
стояния или восстанавливаемого изделия из неработоспособного состояния может
быть: невозможность обеспечения нужного уровня эффективности или надежности
после восстановления или ремонта; неоправданно большие затраты на восстановле-
ние или ремонт; моральное старение изделия.
В настоящее время значительная часть авиационных изделий эксплуатируется по
фактическому состоянию. При этом в процессе планового технического обслуживания
проводится дефектация и восстановление исправного состояния без отправки изделия
в специализированные ремонтные предприятия. Для применения этого прогрессивно-
го метода необходимо оснащать изделия эффективными средствами контроля и диаг-
ностики работоспособности основных частей, отказы которых влияют на безопасность
полетов, а также обеспечивать контролепригодность, доступность, взаимозаменя-
емость и идентичность функциональных характеристик отдельных узлов и агрегатов.
9.3.1. Виды отказов технических изделий
В нормативно-технической документации на изделие указываются признаки,
позволяющие установить факт нарушения его работоспособности. Эти признаки по
своей сути являются критериями отказа технического изделия.
Отказы технических изделий происходят внезапно и могут быть детерминиро-
ванными или случайными. Детерминированные отказы возникают из-за грубых оши-
бок на этапах разработки, изготовления или эксплуатации изделий. Случайные отка-
зы возникают из-за неблагоприятного сочетания множества различных факторов.
441
При классификации отказов необходимо различать классификацию, проведен-
ную для строгого применения математического аппарата теории надежности, и клас-
сификацию, проведенную для применения ее в инженерном анализе.
Случайные отказы с позиций применения законов теории вероятностей подраз-
деляются на постепенные и внезапные, совместные и несовместные, зависимые и не-
зависимые. Внезапные отказы характеризуются скачкообразным изменением некото-
рого параметра изделия, и для них считается, что факт возникновения отказа не свя-
зан со временем функционирования изделия. Постепенные отказы связаны с общим
временем функционирования изделия и происходят при постепенном изменении не-
которого его параметра. Однако постепенное изменение параметра в конечном счете
может также приводить к скачкообразному изменению свойств технического изде-
лия. Такая ситуация, например, наблюдается при износе узла трения, накоплении ус-
талостных или коррозионных повреждений и так далее.
С точки зрения инженерного анализа выявления причин возникновения отказа
принята следующая классификация:
1) по месту проявления отказа (в полете или на земле);
2) по его последствиям (летное происшествие, невыполнение полетного задания
или без последствий);
3) по причинам возникновения (конструкционный, производственный, эксплу-
атационный из-за внешних или случайных причин, эксплуатационный из-за ошибок
наземного технического персонала, эксплуатационный из-за ошибок летного состава);
4) по способу устранения (восстановление на месте эксплуатации, восстановле-
ние в ремонтных организациях, списание).
В зависимости от периода эксплуатации изделия выделяют отказы, возникаю-
щие в начальный период (приработочные отказы), в период нормального функци-
онирования и в период естественного старения материалов конструкции.
Кроме того, отказы подразделяют на отказы функционирования, при которых
выполнение изделием своих функций прекращается, и параметрические отказы, при
которых значения некоторых параметров изделия достигли оговоренных допусков, но
само изделие еще могло бы выполнять свои функции. Отказы функционирования мо-
гут быть внезапными или постепенными, но обязательно приводят к прекращению
выполнения своих функций изделием. Этим определяется особая опасность отказов
функционирования. В параметрических отказах такой внезапной остановки работы
изделия нет. В связи с этим важной задачей науки о надежности является разработка
диагностических методов, позволяющих перевести отказы функционирования в па-
раметрические. Например, постоянный контроль содержания металла (частиц изно-
са) в смазке узла трения позволяет прогнозировать износ узла трения и исключить его
заклинивание или другой отказ функционирования. Также весьма перспективными
являются методы акустической эмиссии для определения накопления микроповреж-
дений конструкции.
9.3.2. Функция распределения вероятности отказов
и ее числовые характеристики
При многократных наблюдениях за случайными событиями выявляется, что они
подчиняются определенным закономерностям. Эти закономерности описываются за-
конами теории вероятностей. Случайная величина может быть непрерывной (время,
длина и т. д.) или принимать дискретные значения (число отказов). Из-за невозмож-
ности заранее указать, какое конкретное значение примет случайная величина, для ее
характеристики вводится понятие вероятности.
442
Вероятность — это численная мера объективно существующей возможности по-
явления (или непоявления) изучаемого события А, которая обычно обозначается че-
рез Р(Л).
Классический способ определения вероятности основан на рассмотрении равно-
возможных событий, являющихся исходами данного испытания. В случае, когда та-
кие испытания независимы, а события несовместны и образуют полную группу, веро-
ятность события определяется как отношение числа случаев, благоприятных появле-
нию данного события, к общему числу испытаний при неограниченном возрастании
числа испытаний. При проведении конечного числа испытаний эта вероятность оце-
нивается с помощью эмпирической (или статистической) оценки, которая получила
название частота или частость случайного события. Частость равна отношению числа
испытаний, в которых появилось данное событие, к общему числу испытаний. Вели-
чина частости сама является случайной величиной (в отличие от вероятности), так
как в различных сериях испытаний ее величина будет изменяться случайным обра-
зом, группируясь около своей вероятности. Из определения вероятности следует, что
О < Р(Л) < 1. Событие, вероятность которого Р(Л) = 1, называется достоверным, а со-
бытие, вероятность которого Р(Л) = 0, называется невозможным.
Если случайная величина может принимать конечное (более двух) или бесконеч-
ное число значений, то для ее характеристики необходимо использовать функцию рас-
пределения вероятности (ФРВ) случайной величины.
По определению ФРВ некоторой случайной величины X, имеющей множество
реализаций [ан, лв], называется вероятность того, что случайная величина Xпринима-
ет на этом множестве значения меньшие, чем значение некоторой детерминирован-
ной величины х, т. е. Р(х) = Р(Х < х).
Все множество реализаций случайной величины X называется генеральной сово-
купностью, верхняя ав и нижняя ан границы которого могут принимать различные
значения. Например, пусть какое-нибудь изделие начинает работать в момент време-
ни t = 0, а в некоторый момент времени t=T возникает случайное событие — отказ
изделия. Тогда множество реализаций этих событий количественно характеризуется
множеством значений, которое может принимать случайная величина Т. Это множе-
ство (генеральная совокупность) имеет границы ан = 0, ав = +оо. в теории надежности
величина Тполучила название наработки до отказа, а ФРВ — функции распределения
отказов или просто функции отказов:
F(t) = P(T<t). (9.1)
Статистической оценкой вероятности наступления отказа в интервале от t = 0 до
1 = к At будет величина:
(9-2)
i = 1
где Рк = Ank/N — частота или статистическая оценка вероятности наступления отказа
на некотором к-м интервале t е [(к — 1) Д/, к Д/]; Апк — число изделий, отказавших на
к-м интервале; N— полное число изделий, поставленных на испытание и отказавших
в результате этих испытаний.
Очевидно, что Р(0) = 0 и F(oo) = 1, а сама функция F(t) является монотонной не-
убывающей функцией в области своей реализации.
В практических расчетах на надежность с помощью специальной процедуры ста-
раются всегда перейти от кусочно-непрерывной, ступенчатой функции F к оценки
распределения отказов к непрерывной функции отказов, которую также называют те-
оретической функцией распределения отказов. Это связано с тем, что, несмотря на
443
большое разнообразие технических изделий, а следовательно, бесконечное множест-
во экспериментальных распределений, все они сводятся к небольшому числу теорети-
ческих распределений (см. п. 9.4.1).
Дифференциальной характеристикой функции распределения отказов является
плотность функции распределения и интенсивность распределения отказов:
ЛО = dF/dt, Х(о =/(Г)/[1 - ЛО], (9.3)
а их статистической оценкой являются величины:
Л(0 = и X* = Уди,)]. (9.4)
/ = 1
Интенсивность распределения отказов Х(/) определяется как условная плотность
распределения отказов невосстанавливаемого изделия для рассматриваемого момента
времени при условии, что до этого момента отказ не наступил. Следовательно, интен-
сивность отказов является дифференциальной характеристикой, учитывающей толь-
ко возможность возникновения отказа в рассматриваемый момент времени, без учета
предыстории функционирования изделия.
Закон распределения всегда представляет собой некоторую функцию, указание
которой полностью описывает случайную величину с вероятностной точки зрения.
Однако во многих практических вопросах нет надобности в таком полном описании,
а достаточно бывает указать только некоторые отдельные численные параметры, ха-
рактеризующие существенные черты распределения. Основными числовыми харак-
теристиками ФРВ являются: математическое ожидание, дисперсия, коэффициент ва-
риации и квантиль.
Математическое ожидание непрерывной случайной величины (9.1) определяется
одним из следующих соотношений:
M[t]=m,= °jt-f(t)dt = Jrd£ (9.5)
О о
Дисперсия непрерывной случайной величины характеризует ее рассеивание во-
круг математического ожидания и определяется следующими выражениями:
ОД = d, = J (t - т,Ш dt = J (t - m? dE (9.6)
О о
В практических расчетах часто вместо дисперсии используют стандартное откло-
нение имеющее ту же размерность, что и случайная величина. Стандартное откло-
нение равно = Jdt. Рассеивание случайной величины вокруг ее математического
ожидания в относительных единицах (долях математического ожидания) характери-
зуется коэффициентом вариации: vt =
Квантиль порядка а случайной величины, имеющей ФРВ F(t), это такое значе-
ние случайной величины, при котором функция распределения этой величины при-
нимает значение, равное а, т. е. квантиль ta является корнем уравнения:
F(U = a. (9.7)
Квантиль порядка а = 0,5 называется медианой распределения, так как делит
площадь под графиком функции плотности распределения пополам, модой случай-
ной величины является такое значение квантиля, которое соответствует максималь-
ной величине плотности распределения.
444
9.3.3. Безотказность, долговечность, сохраняемость
и ремонтопригодность. Единичные и комплексные
показатели надежности
Надежность изделия является сложным свойством, которое в зависимости от на-
значения изделия и условий его применения состоит из сочетания свойств: безотказ-
ности, долговечности, ремонтопригодности и сохраняемости.
Безотказность — это свойство изделия непрерывно сохранять работоспособное
состояние в течение некоторой наработки. Безотказность должна быть присуща изде-
лию в любом из режимов его существования (в период работы, хранения и транспор-
тировки), хотя часто безотказность рассматривается только применительно к режиму
эксплуатации.
Долговечность — это свойство изделия сохранять работоспособное состояние до
наступления предельного состояния при установленной системе технического обслу-
живания и ремонта.
Ремонтопригодность — это свойство изделия, заключающееся в его приспособ-
ленности к предупреждению и обнаружению причин возникновения дефектов и под-
держанию и восстановлению работоспособного состояния путем проведения техни-
ческого обслуживания и ремонта. Свойство ремонтопригодности характеризует изде-
лие не только при проведении ремонтов в предельном состоянии, но и характеризует
его приспособленность для профилактических мероприятий и восстановления после
возникновения дефекта.
Сохраняемость — это свойство изделия сохранять значения показателей безот-
казности, долговечности и ремонтопригодности в течение его хранения и транспор-
тировки, а также после них. Сохраняемость характеризует свойство изделия проти-
востоять отрицательным условиям хранения и транспортировки и представляется
в виде двух составляющих: одна из них проявляется во время хранения и транспорти-
ровки, а другая — во время применения объекта после его хранения и транспортиров-
ки. Эта вторая составляющая имеет особенно существенное значение, так как хране-
ние или транспортировка могут повлиять на составляющие надежности изделия.
Каждое из перечисленных свойств надежности характеризуется набором показа-
телей. Безотказность характеризуется следующими показателями: вероятностью без-
отказной работы, средней наработкой до отказа, гамма-процентной наработкой до
отказа, интенсивностью отказов, средней наработкой на отказ, параметром потока
отказов. Вероятность безотказной работы Рн — это вероятность того, что в пределах
заданной наработки отказ изделия не возникает. Используя (9.1) и тот факт, что отказ
и безотказная работа образуют полную группу несовместных событий, получаем:
= 1 - ЛО = 1 - Р(Т< 0 = Р(Т> t). (9.8)
Вероятность безотказной работы выражается через плотность распределения на
основе соотношения:
t оо
ЛХО = 1 - J АО d' = J/(0 dr, Р/ДО) = 1, Рн(оо) = 0. (9.9)
0 t
Важной особенностью вероятности безотказной работы является то, что указание
ее величины без указания пределов наработки не имеет смысла. Как видно из рисун-
ка 9.2, у одного и того же изделия вероятность безотказной работы Р^Т^ = у, рассмат-
риваемая в период наработки [0, Ту], во много раз больше вероятности безотказной ра-
боты Р^Ту) = ур рассматриваемой за период наработки [0, Гу] при Гу) > Тг
445
Рис. 9.2 Вероятность безотказной
работы изделия в зависимости
от времени его эксплуатации
Для режимов хранения и транспортировки мо-
гут также использоваться термины «вероятность
безотказного хранения» или «вероятность безотказ-
ной транспортировки».
Средняя наработка до отказа — это математиче-
ское ожидание наработки изделия до отказа, т. е. (9.5).
Показатель «средняя наработка до отказа» может при-
меняться не только в период эксплуатации изделия,
но и в период его хранения и транспортировки.
Гамма-процентная наработка до отказа — это
наработка, в течение которой отказ изделия не воз-
никает с вероятностью у, выраженной в процентах,
т. е. гамма-процентная наработ-ка — это квантиль функции распределения (9.7) веро-
ятности безотказной работы, определяемый как корень одного из уравнений:
/>я(7’г) = 'Уили J/(')<!' = У-
Л
Величины гамма-процентной наработки для значений у и представлены на
рисунке 9.2.
Интенсивность отказов — это условная плотность вероятности возникновения
отказа невосстанавливаемого изделия, определяемая для рассматриваемого момента
времени при условии, что до этого момента отказ не возник. Используя выражения
(9.3) и (9.9), получаем:
(9.10)
(9.И)
1 d/\
Средняя наработка на отказ — это отношение наработки восстанавливаемого из-
делия к математическому ожиданию числа его отказов в течение этой наработки.
Средняя наработка на отказ и параметр потока отказов используются в качестве пока-
зателя безотказности восстанавливаемого изделия, например технологического обо-
рудования или обрабатывающего инструмента. Эксплуатация таких изделий может
быть описана следующим образом. В начальный момент времени изделие начинает
работу и работает до отказа, после отказа происходит его восстановление и изделие
вновь работает до отказа. Моменты отказов на оси суммарной наработки или на оси
непрерывного времени образуют поток отказов. В качестве характеристики потока
отказов используют ведущую функцию Q(/) данного потока — математическое ожи-
дание числа отказов за время /, т. е.: Q(/) = Л/[г(/)], где М— символ математического
ожидания; r(t) — число отказов за время t. Поэтому средняя наработка на отказ Гср бу-
дет определяться из соотношения
Tcp(t) = = t/M[r(t)]. (9.12)
Поток отказов также характеризуют параметром потока отказов со(/) — отноше-
нием среднего числа отказов восстанавливаемого изделия за произвольно малую его
наработку к значению этой наработки, т. е.: со(/) = dQ(/)/d/.
Долговечность изделия характеризуется следующими показателями: ресурсом
(средним, гамма-процентным, назначенным, техническим); сроком службы (сред-
ним, гамма-процентным, назначенным).
Ресурс, или технический ресурс, — это время работы изделия от начала его экс-
плуатации или ее возобновления после ремонта до перехода в предельное состояние.
Срок службы же определяется календарной наработкой до перехода в предельное со-
стояние.
446
Для перемонтируемых изделий ресурс совпадает с продолжительностью пребы-
вания в работоспособном состоянии в режиме применения по назначению, если пе-
реход в предельное состояние обусловлен только возникновением отказа. Поскольку
средний или капитальный ремонт позволяет частично или полностью восстановить
ресурс, отсчет времени работы, образующей ресурс, возобновляют по окончании та-
кого ремонта, различая в связи с этим доремонтный, межремонтный, послеремонт-
ный и полный (до списания) ресурсы. Аналогичным образом выделяют виды срока
службы.
Средний ресурс и средний срок службы — это математическое ожидание ресурса
или срока службы соответственно.
Гамма-процентный ресурс (гамма-процентный срок службы) — это время (ка-
лендарная продолжительность) от начала эксплуатации, в течение которой он не до-
стигнет предельного состояния с заданной вероятностью у, выраженной в процентах.
Величина гамма-процентного ресурса в случае аналитического задания вероятности
безотказной работы определяется из соотношения (9.10) или графически (рис. 9.2).
Из этого следует, что увеличение вероятности безотказной работы изделия без его со-
вершенствования возможно только за счет уменьшения величины гамма-процентно-
го ресурса.
Назначенный ресурс (срок службы) определяется суммарной наработкой (кален-
дарной продолжительностью эксплуатации) изделия, при достижении которой его
применение по назначению должно быть прекращено. Цель установления назначен-
ного ресурса или назначенного срока службы — обеспечение принудительного забла-
говременного прекращения применения изделия по назначению, исходя из требова-
ний безопасности или экономического анализа.
Для объектов, подлежащих длительному хранению, может быть установлен на-
значенный срок хранения, по истечении которого дальнейшее хранение недопустимо.
При достижении изделием назначенного ресурса или срока службы, в зависи-
мости от его назначения, особенности эксплуатации, технического состояния и дру-
гих факторов, изделие может быть: списано; направлено на средний или капитальный
ремонт; передано для применения не по назначению или принято решение
о продолжении эксплуатации.
Ремонтопригодность изделия характеризуется следующими показателями: веро-
ятностью восстановления работоспособного состояния; средним временем восста-
новления работоспособного состояния; средней трудоемкостью восстановления ра-
ботоспособного состояния.
Вероятность восстановления работоспособного состояния — это вероятность то-
го, что время восстановления работоспособного состояния изделия не превысит за-
данного времени.
Среднее время (средняя трудоемкость) восстановления работоспособного
состояния — это математическое ожидание времени (трудоемкости) восстановления
работоспособного состояния.
Время восстановления отсчитывают либо непрерывно, либо из него по опреде-
ленным правилам исключают интервалы времени, не обусловленные непосредствен-
но выполнением восстановительных работ. В связи с этим различают общее время
и оперативное время восстановления работоспособности изделия.
Сохраняемость характеризуется средним и гамма-процентным сроком сохраня-
емости.
Средний срок сохраняемости определяется как математическое ожидание срока
сохраняемости, а гамма-процентный срок сохраняемости — как срок сохраняемости,
достигаемый изделием с заданной вероятностью у, выраженной в процентах.
447
Необходимо отметить, что показатели безотказности и долговечности определя-
лись на основе функции распределения отказов (или функции надежности), в то же
время для ремонтопригодности необходимо знание функции распределения вероят-
ности времени восстановления, а для сохраняемости — функции распределения
вероятности срока сохраняемости. Причем различают сохраняемость изделия до вво-
да в эксплуатацию и сохраняемость изделия в период эксплуатации (при перерывах в
работе). Во втором случае срок сохраняемости входит составной частью в срок служ-
бы. Кроме того, для срока сохраняемости до ввода изделия в эксплуатацию выделяют
срок сохраняемости в законсервированном виде, срок сохраняемости при монтаже и
срок сохраняемости на более сложном законсервированном объекте.
К комплексным показателям надежности относят: коэффициент готовности; ко-
эффициент оперативной готовности; коэффициент технического использования; ко-
эффициент планируемого применения; коэффициент сохранения эффективности.
9.4. МАТЕМАТИЧЕСКИЕ МОДЕЛИ ОТКАЗОВ
ТЕХНИЧЕСКИХ СИСТЕМ
Прогнозировать потерю работоспособности любого изделия можно только тогда,
когда создана математическая модель процесса потери работоспособности [1, 2, 9].
Применительно к задачам теории надежности изделий такая математическая модель
[1, 2, 10] представляет собой совокупность аналитических, графических и табличных
зависимостей выходных параметров от входных, управляющих и возмущающих
(внешних воздействий) параметров, а также параметров состояния изделия (рис. 9.3).
Причем в отличие от физико-химических, технологических или конструктивных мо-
делей [10] математические модели теории надежности [1,2] обладают повышенной
сложностью, так как включают в себя все перечисленные модели (рис. 9.3).
Математическое моделирование, по сути, решает две задачи:
1) получение формализованного описания функционирования изделия;
2) исследование изделия при помощи вычислительного эксперимента над мате-
матической моделью.
Решение сформулированных статистических моделей (рис. 9.3) в общем случае
представляет значительные математические трудности. Это связано со следующими
обстоятельствами.
Летательный аппарат состоит примерно из 103... 106 деталей. Количество отдель-
ных параметров, определяющих качество конкретной детали и ее положение в изде-
лии (размеры, допуски, характеристики материала и т. д.), равно примерно 102. Таким
образом, ЛА в целом характеризуется 105... 108 параметрами. Несоответствие хотя бы
одного из них номинальным значениям может привести к отказу всего изделия. Кро-
ме того, каждый из этих параметров является случайной величиной, которая че-
рез функциональные зависимости зависит от большого числа других случайных пара-
метров.
Поэтому в теории надежности разработаны специальные подходы, позволяющие
упростить решение поставленных задач. Первое упрощение связано с введением по-
нятия «элемент», под которым понимают любую систему, не подлежащую разбиению
на более простые элементы в рамках данного исследования. В зависимости от постав-
ленной задачи элементом может быть агрегат, отсек, панель, узел, любая деталь
и места их соединения или сопряжения, любое из сечений детали или конструк-
ции, а также само изделие. Статистическое изучение этого элемента позволяет по-
строить функцию распределения вероятности для рассматриваемого параметра
448
Входные параметры
начальные значения параметров
функционирования
Управляемые параметры
нерегулируемые регулируемые
конструктивные особенности режимы функционирования
Рис. 9.3 Структурная схема математической модели потери работоспособности изделия
(обычно это параметры, определяющие отказ или точность функционирования).
С помощью этого распределения можно найти все показатели надежности элемента.
В связи с тем, что ЛА состоит из большого числа описанных элементов, их анализ
проводится с помощью приближенного метода, получившего название метода струк-
турных схем.
Два описанных вида упрощений (элемент и структурная схема из элементов) по-
зволяют решать основные задачи прикладной теории надежности.
9.4.1. Основные распределения теории надежности
Причина возникновения внезапных отказов не связана с изменением состояния
изделия и временем его предыдущей работы, а зависит от неблагоприятного сочета-
ния множества факторов. При возникновении внезапных отказов величина интен-
сивности отказов X (показатель безотказности) практически не зависит от времени.
Возникновение постепенных отказов определяется процессом постепенного накоп-
ления повреждений в изделии.
449
Рис. 9.4. Зависимость
интенсивности отказа изделия
от времени его эксплуатации
На практике установлено, что изменение интен-
сивности отказов в течение всего жизненного цикла из-
делия можно представить в виде обобщенной зависи-
мости (рис. 9.4). На этой зависимости можно выделить
три различных участка. На первом участке, называемом
периодом приработки, интенсивность отказов в зависи-
мости от времени эксплуатации уменьшается. В этот
период выявляются и устраняются внезапные отказы,
вызванные явными ошибками производства (непра-
вильная регулировка, неточная сборка и т.д.); отказы,
связанные с отклонениями фактических условий рабо-
ты и нагрузок от предполагаемых при выполнении про-
ектных работ, а также отказы, связанные с приработкой различных узлов и сопряжений.
Период приработки обычно включают в продолжительность обкаточных или прирабо-
точных испытаний.
На втором участке интенсивность отказов для технического изделия остается
примерно постоянной. Этот период получил название периода нормальной эксплу-
атации. В этот период постепенные отказы еще не проявляются, а могут возникать
только внезапные отказы.
Третий период получил название периода естественного старения материалов.
В этот период кроме внезапных отказов начинают возникать постепенные отказы,
вызванные накоплением износных, коррозионных, усталостных, деструкционных
и других повреждений. Вероятность возникновения отказа изделия с течением вре-
мени возрастает, поэтому эксплуатация изделия становится небезопасной или нерен-
табельной и должна быть прекращена. Изделие направляется в ремонт или списыва-
ется.
Установим зависимость от времени вероятности безотказной работы, используя
в качестве основного параметра интенсивность отказов. С этой целью используем со-
отношение (9.11) для интенсивности отказов, из которого получим дифференциаль-
ное уравнение и, проведя интегрирование в пределах от 0 до t с учетом того факта, что
Р//0) = 1, будем иметь:
t
ЛХ0 = ехр(-/Х(0<1/). (9.13)
О
Соотношение (9.13) получило название основного уравнения теории надеж-
ности.
Для периода нормальной эксплуатации X = const. Подставляя это значение
в (9.13), получим экспоненциальный закон теории надежности:
Ря=е~Ч (9.14)
Распределение (9.14) является однопараметрическим, так как зависит от одного
параметра X, который выражается через математическое ожидание и дисперсию на
основе следующих соотношений: mt = 1/X, dt = 1/Х2.
В связи с простотой аналитического выражения экспоненциальное распределе-
ние нашло очень широкое применение в теории надежности. Его применяют:
1) для всех систем в период нормального функционирования при возникновении
только внезапных отказов;
2) для всех систем при рассмотрении небольших отрезков времени, на которых
можно считать X ~ const;
3) сложных систем, состоящих из большого числа элементов.
450
В тех случаях, когда у изделия возникают постепенные отказы, параметр X можно
аппроксимировать некоторой степенной функцией времени и получить распределе-
ние вероятности для описания математических моделей возникновения постепенных
отказов. Основные виды таких распределений, используемых в теории надежности,
представлены в табл. 9.1. В таблице использованы общепринятые обозначения: Ф(х) =
1 X X2 ОО
= -= Je 2 dx — интеграл ошибок; Г(х) = Je-'/x-1d/ — гамма-функция,
о о
Нормальное распределение Гаусса (табл. 9.1) возникает всегда, когда случайная
величинах является суммой большого числа независимых (или слабо зависимых) слу-
чайных величин, подчиненных каким угодно законам распределения. Нормальным
распределением описываются: наработки до отказа восстанавливаемых и невосста-
навливаемых изделий; погрешности технологических операций и результатов измере-
ний; отказы, возникающие из-за износа, и так далее. В случае применения нормаль-
ного распределения для описания наработки до отказа необходимо учесть, что об-
ласть значений наработки совпадает с (0, оо).
Широкое применение нормального распределения в практике основано на том,
что распределение суммы независимых случайных величин у = Ех, при нормальном
законе распределения слагаемых также является нормальным с математическим ожи-
данием и дисперсией, определяемыми соотношениями:
ту = 1Лх, > ау = L°x,. • (9.14)
/ Z
Таким свойством, которое называется свойством устойчивости распределения,
обладает также только распределение Пуассона. Кроме того, при малых коэффициен-
тах вариации нормальное распределение хорошо аппроксимирует биноминальное,
Пуассоново и логарифмическое нормальные распределения. Логарифмическое нор-
мальное распределение (табл. 9.1) используют для описания наработки до отказа де-
талей по усталости. Распределение Вейбулла (табл. 9.1) обладает большой универ-
сальностью, так как путем варьирования параметров /0 (параметр масштаба) и т (па-
раметр формы) переходит в другие виды распределений. Его используют для
описания надежности изделий по приработочным отказам и усталостным разрушени-
ям. Распределение %2 (табл. 9.1) в основном используется для оценки границ довери-
тельных интервалов и проверки правдоподобия гипотез. Распределение Стьюдента
(табл. 9.1) применяют для оценки границ доверительных интервалов при конечном
числе измерений.
Обычно с помощью приведенных распределений решают две основные задачи:
1) определение вероятности безотказной работы в течение заданной наработки г;
2) определение средней наработки до отказа, обеспечивающей вероятность без-
отказной работы не менее у (гамма-процентный ресурс).
Первая задача решается на основе следующего алгоритма.
По заданному значению t, виду и параметрам распределения вычисляется аргу-
мент U(f) соответствующего распределения.
По табл. 9.1 выбирают соответствующее распределение и вычисляют ве-
роятность безотказной работы P^U^)) =1 — F(U(t)).
Вторая задача является обратной для первой и решается на основе следующего
алгоритма.
По заданному виду распределения и заданной вероятности безотказной работы
у находят квантиль распределения Uy(f) (обычно по таблицам распределения вероят-
ности) у = = 1 - F(Uy(t)).
451
Основные непрерывные распределения теории надежности
Таблица 9.1
№ Название распределения Область значений Плотность распределения Функция распределения вероятности Математиче- ское ожидание Дисперсия
1 2 3 4 5 6 7
1) Равномерное 1 b —а х - а b — а а +Ъ (/> - а)2 12
2) Нормальное (Гаусса) (—оо, оо) 1 (х ~g)2 1 е 2о2 a Jin а о2
452 Логарифмическое нормальное (0, °о) (inr-o)2 1 е 2<у2 о 72л 0.5 + ф('п'а °) о 4г e2a + <j2(e°2- 1)
4) Вейбулла (0, ^/т-1е 'о Ч) J” 1-е '° 2 М1+т)"Г2(1+т]1 L \ mJ \ /J
5) Экспоненциальное (0, оо) Хе-Х/ 1 - е ~Kt 1 X 1
6) %2-распределение (0, °о) 2’г© X2 J /(Х2) dx 0 V 2v
7) Стьюдента (—оо, оо) J^rg) ’ X 2 J/(x)dx 0 0 -I7 1 > 104
Таблица 9.2
Основные дискретные распределения теории надежности
№ Название рас- пределения Область значений Функция распределения вероятностей Матема- тическое ожидание Дисперсия
1) Биномиальное 0, 1,2,... 9п P„(m)= Qp'V-'” пр npq
2) Пуассона 0, 1,2,... т ml X X
3) Геометриче- ское 0, 1,2,... Рт=РЯ'п~{ 1/р q/p1
По полученному значению Uy(t) находят t = f(Uy), которое и является значением
Ty = t— гамма-процентным ресурсом.
Как уже отмечалось, при проведении испытаний на надежность используется
выборка из генеральной совокупности. При этом достоверность результата зависит от
объема выборки и, кроме того, важным практическим вопросом является вопрос о
количестве изделий, которое необходимо поставить на испытание. В этих случаях в
теории надежности используются дискретные распределения. Основными из них яв-
ляются биномиальное, геометрическое и Пуассона. Свойства этих распределений
и их числовые характеристики приведены в табл. 9.2, где С™ = п\/[т\(п — /и)!].
9.4.2. Моделирование сложных технических систем
прямым аналитическим методом
В предыдущем разделе при построении функций распределения вероятности не-
которого параметра элемента мы не учитывали, что этот параметр может быть функ-
цией большого числа аргументов распределенных с некоторыми плотностями ве-
роятности /(г,). Необходимость решения задач такого типа в теории надежности воз-
никает всегда, когда надо ответить на следующие вопросы: из-за каких причин
получена недостаточная надежность элемента или изделия и каким образом можно
повысить показатели надежности.
Сформулируем задачу моделирования следующим образом. Выходной параметр
х некоторого технического элемента является случайной величиной, зависящей через
функциональную зависимость* = <p(Zj, ..., гл) от случайных аргументов Из ре-
зультатов исследований известны плотности распределения /(Zi). ./(z„). Требуется
найти плотность распределения/(*).
Необходимо отметить, что в замкнутом аналитическом виде решение такой зада-
чи может быть получено только в некоторых частных случаях [1,4, 5, 9]. Причем даже
в случае простых функциональных зависимостей между выходными и входными па-
раметрами законы распределения входных параметров претерпевают изменение на
выходе системы. Законы распределения, которые при определенных функциональ-
ных преобразованиях не претерпевают изменений, носят название устойчивых. Мож-
но показать, что только при композиции случайных величин х = + ... + zn устойчи-
выми будут законы нормального распределения, Пуассона и биномиальный.
453
9.4.3. Моделирование сложных технических
систем методом структурных схем
Сущность метода структурных схем заключается в том, что рассматриваемое из-
делие или система представляется в виде расчетной схемы, состоящей из отдельных
элементов, которые в результате последовательного или параллельного их соедине-
ния образуют соответствующую структурную схему. Разбивка сложного изделия на
отдельные элементы может быть произведена сколь угодно большим числом спосо-
бов. Однако при этом необходимо соблюдать следующие принципы.
1. Каждый элемент должен выполнять вполне определенные функции и форми-
ровать определенный выходной параметр.
2. Каждый элемент должен иметь вполне определенные характеристики надеж-
ности.
3. Все элементы изделия могут иметь только по одному отказу.
4. Изделие представляется в виде единой структурной схемы, состоящей из сум-
мы последовательных и параллельных соединений. События, изображенные в виде
элементов и звеньев структурной схемы, должны быть независимыми.
5. В структурной схеме не должно быть событий, среди которых одно событие яв-
ляется отрицанием другого. Одно и то же событие должно представляться в виде од-
ного звена.
Основой структурных схем являются условные виды последовательных и парал-
лельных соединений звеньев, выражающих событие безотказности действия отдель-
ных элементов системы. Эти виды соединений не всегда совпадают с монтажными
названиями соединений.
Последовательным соединением элементов с точки зрения надежности называ-
ется такое соединение, при котором для безотказной работы системы требуется безот-
казная работа всех элементов. Последовательное соединение графически представле-
но на рис. 9.5, а.
Обозначим через Yt случайное событие, заключающееся в безотказности работы
/-го элемента. Тогда событие Ус, заключающееся в безотказности работы всей систе-
мы, наступит тогда и только тогда, когда насту-
пят события К|, У2, Ту. Используя независи-
мость событий и то, что событие Yc представ-
лено в виде произведения исходных событий,
получим для вероятности безотказной работы со-
отношение
N N
= П^^)илиРяс= T[PHi, (9.15)
z = 1 i = 1
где Ру( Yc) = Рн с, Pj^i Y) = Рн j.
Параллельным соединением элементов с
точки зрения надежности называется такое со-
единение, при котором для безотказной работы
системы требуется безотказная работа хотя бы
одного элемента. Параллельное соединение гра-
фически представлено на рис. 9.5, б.
Для установления связи между вероятностью
безотказной работы системы и вероятностью без-
отказной работы элемента обозначим через
случайное событие, заключающееся в отказе /-го
Рис. 9.5. Виды соединения
элементов по надежности:
а) последовательное соединение;
б) параллельное соединение;
в) смешанное соединение
454
элемента. Тогда для наступления отказа всей системы Qc необходимо, чтобы отказали
все элементы или наступило событие, равное произведению событий Ql9 Q2, ..., QN.
Используя независимость событий и теорему умножения вероятностей, получим
для вероятности наступления отказа и вероятности безотказной работы системы со-
отношения:
N N N
FC=P(QC) = П ЛО,) = П Г» рн,с= 1 - П (1 - (916)
/ = 1 Z = 1 Z = 1
С помощью последовательного и параллельного соединения элементов можно
смоделировать структурную схему для любой технической системы. Например, систе-
му выпуска шасси некоторых самолетов можно представить в виде рис. 9.5, в, где
элемент 1 моделирует основную гидросистему, элементы 2 и 3 моделируют основную
и аварийную системы выпуска шасси, а элемент 4 моделирует шасси. Обозначая веро-
ятности безотказной работы каждого элемента через P^i), получим вероятность без-
отказной работы Рн с для этой системы в виде:
Ллс = ЛХ W4)[l - (1 - ЛХ2))(1 - Р^З))].
Рассмотрим расчетные формулы для вероятности безотказной работы и средней
наработки до отказа сложной системы, состоящей из N элементов, в период нормаль-
ного ее функционирования.
Учитывая, что в период нормального функционирования вероятность безотказ-
ной работы z-ro элемента подчиняется экспоненциальному закону Рнj = exp (—X/),
получим для последовательного соединения:
N N
Рн,с= ПЛ/.,= ПеА' (9.17)
Z = 1 Z = 1
__t_
В случае Xj = = ... = = X будем иметь Рн с = е тцс 9 где mt с = mt/N, X = \/mt.
Из этих соотношений видно, что последовательное соединение элементов по
надежности очень сильно снижает как вероятность безотказной работы системы, так
и среднюю наработку до отказа. Например, система из 10 последовательных элемен-
тов в 10 раз уменьшит величину средней наработки до отказа, а вероятность безотказ-
ной работы системы за наработку t = mt уменьшится почти в 103 раз.
Для случая параллельного соединения N элементов с одинаковой интенсивно-
стью отказов X получим: 4
N N
Рн,с= 1 - П (1 - PH,i) = 1 - П (1 - еА') = 1 - (1 - е~х-')у. (9.18)
Z = 1 Z = 1
Из этого соотношения видно, что система параллельно соединенных элементов
с экспоненциальными законами надежности не подчиняется экспоненциальному за-
кону.
Средняя наработка до отказа такой системы определяется выражением:
N
= L^-1. (9.19)
к — 1
Из соотношений (9.18) и (9.19) видно, что параллельное соединение элементов
по надежности увеличивает вероятность безотказной работы системы и среднюю на-
работку до отказа. Видно, что применение в системе параллельных элементов по на-
дежности позволяет очень сильно повысить вероятность безотказной работы систе-
455
мы, однако средняя наработка до отказа с увеличением числа элементов возрастает
существенно медленнее. Использование параллельного подключения элементов по
надежности является одним из способов повышения показателей надежности слож-
ных изделий резервированием.
9.5. ПОВЫШЕНИЕ НАДЕЖНОСТИ ЛЕТАТЕЛЬНЫХ
АППАРАТОВ РЕЗЕРВИРОВАНИЕМ
Как было отмечено в предыдущем разделе, любое техническое изделие с позиций
надежности может быть разбито на элементы, соединенные последовательно, парал-
лельно или смешанно. Например, топливный бак ракеты имеет сварные швы, соеди-
няющие обечайку с верхним и нижним днищем. С позиций надежности топливный
бак может быть представлен как последовательное соединение элементов, описываю-
щих безотказную работу обечайки, верхнего и нижнего днища, всех сварных швов на
баке, так как с отказом любого из этих элементов отказывает весь отсек. С другой сто-
роны, хвостовой отсек состоит из обшивки и большого числа стрингеров. Стрингеры
как элементы, обеспечивающие надежность отсека, можно считать соединенными
параллельно, так как с разрушением одного стрингера нагрузка, действующая на от-
сек, с помощью торцевых шпангоутов перераспределяется на неотказавшие стринге-
ры, и весь отсек не теряет работоспособность. Однако отказавший стрингер не явля-
ется лишним, потому что без него надежность отсека уменьшается. Если при сжатии
отсека допускается образование волны (частичная потеря устойчивости), то стринге-
ры и обшивку можно считать соединенными параллельно. Если же образование вол-
ны недопустимо, то соединение — последовательное.
Конструктивные элементы могут быть зависимыми и независимыми. Примером
зависимых элементов является пример со стрингерами, когда надо учитывать измене-
ние надежности отсека при отказе одного из стрингеров. Если с определенным допу-
ском такое изменение надежности можно не учитывать, тогда стрингеры можно счи-
тать независимыми элементами.
Как было отмечено при выводе соотношений (9.18) и (9.19), существует эффектив-
ный способ повышения надежности изделий за счет параллельного включения эквива-
лентных элементов. Такой способ связан с резервированием. Сущность резервирова-
ния заключается в том, что в системах предусматриваются избыточные (резервные) аг-
регаты, детали, узлы, блоки, вступающие в работу при появлении неисправностей
основных рабочих элементов. В летательных аппаратах имеется много примеров резер-
вирования. Например, в самолетах предусматривается установка двух подкачивающих
насосов в топливных системах, двух заборников топлива из баков, резервное питание
тормозной системы, аварийный выпуск шасси, щитков и закрылков, аварийное управ-
ление стабилизатором и так далее. Примерами резервирования являются также стати-
чески неопределимые силовые элементы конструкций планера, ракеты или космиче-
ского корабля. Большое количество резервных элементов, агрегатов и блоков имеется в
бортовом радио- и радиотехническом оборудовании летательного аппарата.
Основной характеристикой резервирования является его кратность s, т. е. отно-
шение числа резервных элементов изделия пр к числу резервируемых ими основных
элементов л0, выраженное несокращаемой дробью s = пр/п^ = (п - nQ)/nQ, где п — об-
щее число элементов в системе. Резервирование с з = 1/1 называется дублированием.
Существует два метода резервирования — общее резервирование (резервируется
вся система) и резервирование системы по элементам. Сравним эти два метода с по-
зиций повышения вероятности безотказной работы всей системы. Считая (для про-
456
стоты анализа), что вероятность безотказной работы Рн всех элементов одинакова, и,
используя выражения (9.18), получим для системы с общим и поэлементным резерви-
рованием соотношения:
Ри,о = 1 - (1 - Ркн У, Рн, э = [1 - (1 - РнП-
Перейдя в этих соотношениях к вероятности отказа F = 1 — Рн и воспользовав-
шись тем, что (1 - F)r « 1 - rF(npn F« 1), получим для вероятности отказа при об-
щем Fc 0 и поэлементном Рс э резервировании следующие выражения:
FC o = 1 ~ ?н,о~ nkF> ^с, э = 1 — ?н, э ~ kFn- (9.20)
Полученные соотношения (9.20) показывают, что поэлементное резервирование
дает выигрыш в увеличении вероятности безотказной работы. Например, при
F= 0, 1 и п = 3 получим Fc 3/Fc 0 = Fn~x/n~3* 104, т. е. вероятность отказа снижается
в 3 • 104 раза.
Однако надо учитывать, что при поэлементном резервировании возникает суще-
ственно большее число дополнительных элементов, обеспечивающих включение
каждого элемента в систему. Эти элементы подключения являются элементами систе-
мы по надежности, обладающими вероятностью безотказной работы Рн* 1, которую
необходимо учитывать при расчете и которая, естественно, снизит полученный выиг-
рыш. Отметим также, что при поэлементном резервировании количество резервных
элементов для каждого из основных может быть выбрано неодинаковым.
Резервные элементы могут быть включены на все время эксплуатации в режиме
основного элемента (нагруженный резерв), могут включаться после выхода из строя
основных элементов (ненагруженный резерв) или могут быть включены постоянно, но
в менее нагруженном режиме, чем основной элемент (облегченный резерв). Особен-
ность резервирования систем летательных аппаратов, например, гидравлических сис-
тем, систем управления стабилизатором и т. д. состоит в том, что в них, как правило,
применяются системы и агрегаты с нагруженным резервом. Это объясняется условия-
ми работы и тяжелыми последствиями, к которым ведет выход из строя этих систем.
Системы с ненагруженным резервом не всегда обеспечивают условия непрерывной ра-
боты (на включение резервной системы требуется определенное время) и в процессе
работы изделия возникает задержка. Поэтому в большинстве случаев ненагруженный
резерв применяется как аварийный, обычно действующий кратковременно.
В жизненно важных системах летательных аппаратов, отказ которых угрожает
безопасности полетов, резервированию уделяют особое внимание. Целесообразно
структуру управления резервных систем в этих случаях строить по методу «пересили-
вания» или «подавления» отказавшего агрегата. Этот метод более надежен по сравне-
нию с методом использования специальных систем для определения отказа элемента,
его отключения и включения резервного. Кроме того, например, при отказе основной
и резервной систем управления стабилизатором их система управления обеспечивает
перестановку стабилизатора в посадочное положение.
При общем резервировании с постоянно включенным резервом все системы ра-
ботают на одну нагрузку. При отказе какой-либо одной системы нагрузка перераспре-
деляется на оставшиеся системы. Это понижает вероятность безотказной работы не
только потому, что уменьшается кратность резервирования, но также из-за увеличе-
ния нагрузки на каждую оставшуюся систему.
Анализ характеристик надежности при общем резервировании с постоянно
включенным резервом показывает (см. (9.18) и (9.19)), что вероятность безотказной
работы резервированной системы всегда больше вероятности безотказной работы не-
457
резервированной и она растет с ростом кратности резервирования. Средняя наработ-
ка до отказа при этом растет существенно медленнее. Вероятность безотказной рабо-
ты при поэлементном резервировании при прочих равных условиях всегда выше ве-
роятности безотказной работы системы с общим резервированием. Причем это
отличие возрастает в случае уменьшения интенсивности отказов (9.20) (точнее, в слу-
чае уменьшения X/). Следовательно, резервировать целесообразно мелкие узлы и де-
тали сложной системы.
Резервирование позволяет из малонадежных элементов изготовить достаточно
надежную систему. Однако при этом может существенно увеличиться масса, габариты
и стоимость изделия. Поэтому на практике решается задача оптимального
проектирования — обеспечение нужного уровня надежности резервированием (часто
поиск максимума вероятности безотказной работы) при ограничениях на массу, габа-
риты, стоимость и так далее.
Роль влияния кратности резервирования на вероятность безотказной работы хо-
рошо демонстрирует соотношение (9.19). Так, например, из трех одинаковых элемен-
тов с малым значением Рн = 0,9 в течение некоторой наработки можно изготовить вы-
соконадежную систему с Рн = 0,999, повысив среднюю наработку на отказ в 1,83 раза.
9.6. ОБОСНОВАНИЕ ВЫБОРА ПОКАЗАТЕЛЕЙ
НАДЕЖНОСТИ ТЕХНИЧЕСКИХ ИЗДЕЛИЙ
Выбор вида показателей надежности зависит от общего назначения изделия
и ответственности выполняемых им функций.
Основным показателем безотказности любого технического изделия является ве-
роятность безотказной работы Рн. Однако по мере эксплуатации изделия Рн убывает.
Поэтому вероятность безотказной работы связана с основным параметром долговеч-
ности — гамма-процентным ресурсом функциональной зависимостью Р^Ту) = у.
Следовательно, задаваясь допустимыми изменениями Рн в процессе эксплуата-
ции, можно назначить Тг при достижении которого изделие попадает в предельное
состояние. После капитального ремонта и восстановления Рн для изделия может быть
назначено новое значение Ту г При последующей эксплуатации величина Рн опять
начинает снижаться и так далее. Обычно при каждом последующем ремонте число за-
мененных узлов увеличивается Nx< N2< N3< .... Эксплуатация изделия с ремонтами
продолжается до тех пор, пока восстановление уровня надежности станет или невоз-
можным, или невыгодным.
Таким образом, возможны два варианта выбора показателей надежности.
Первый вариант. При высоких требованиях к надежности изделия задаются до-
пустимые значения у, и по этому значению определяют гамма-процентный ресурс.
Второй вариант. При обычных требованиях к надежности, когда отказ изделия не
приводит к катастрофическим последствиям и большим экономическим потерям, за-
даются величиной Тг и по этому значению рассчитывают Рн. Исходя из полученного
значения назначают сроки плановых ремонтов и технического обслуживания таким
образом, чтобы величина Рн в межремонтный период лежала в приемлемых пределах.
Однако и в первом, и во втором вариантах существуют предельные случаи, когда
параметр безотказности Рн перестает быть наглядным.
Первый случай характерен для тех отказов, которые легко устранимы и не приво-
дят к каким-либо значительным последствиям. Например, замена режущего инстру-
мента при работе на станке, необходимость поправлять в транспортном лотке закли-
458
нившие детали и так далее. В этом случае характеристикой безотказности является
параметр потока отказов.
Другой крайний случай возникает при оценке высоконадежных изделий, когда
значение P^t) близко к единице. В этих случаях расчет производится по коэффици-
ентам безопасности или коэффициентам запаса надежности. В теории надежности
такой расчет обычно проводится как расчет вероятности безотказной работы изделия
по заданному параметру.
В связи с особой важностью этого вопроса рассмотрим его более подробно. На-
пример, при расчетах на прочность, жесткость, износостойкость, теплостойкость, ус-
талость, точность изготовления и т. д. проводится сопоставление по некоторым кри-
териям расчетных параметров с их предельными значениями.
Считают, что работоспособность по данному критерию обеспечена, если расчет-
ный параметр критерия х меньше (или больше) заданного предельного значения хп.
Учитывая требования надежности, в такой расчет вводят коэффициент безопасности
л, принимая расчетное условие в виде:
х < хп/п (или х > хп/п). (9.21)
В этом случае х и хп считают детерминированными величинами, хотя в действи-
тельности эти параметры являются статистическими и имеют определенное рассеива-
ние. Для учета такого рассеивания расчет ведется по наиболее неблагоприятным зна-
чениям. Поэтому, хотя надежность и завышается по одному из критериев в ущерб дру-
гим, истинное значение показателя надежности неизвестно. Теория надежности
позволяет корректно ответить на все возникающие в этой ситуации вопросы.
Пусть задан некоторый параметр х, являющийся случайной величиной с плотно-
стью распределенияfx(x), и односторонний допуску на этот параметр, также являю-
щийся случайной величиной с плотностью распределения /,(хл). Требуется опреде-
лить вероятность выполнения задания по параметру х, т. е. вероятность того, что слу-
чайная величина L = х - хп > 0.
В этом случае вероятность выполнения задания определяется соотношением:
P^L > 0) = J fL(l) dl,fL(I) = J fx (x)fn(x - /) dx = J fn (x„ - l)fx(xn) dx„, (9.22)
Q —oo —oo
где, как обычно, детерминированная переменная / описывает область реализации
случайной величины L.
Пусть параметры х и хп имеют нормальные законы распределения с числовыми
характеристиками тх, ох и тп9 <зп. Используя устойчивость нормального закона к ли-
нейному преобразованию, получим:
(9.23)
где т1 = тх — тп; о/ = oj + UP— квантиль нормального распределения.
Введя коэффициент запаса надежности т = mjmn и коэффициент вариации
vx = <зх/тх и vn = <зп/тп, представим выражения для квантиля в виде:
л/ =__ ”
р v«)2 + ”2 ‘
(9.24)
459
Из соотношений (9.24) и (9.23) видно, что вероятность выполнения задания по
параметру зависит как от величины коэффициента запаса надежности, так и от коэф-
фициентов вариации параметра х и его предельного значения хп.
Например, пусть х — несущая способность детали, распределенная по нормаль-
ному закону с параметрами тх = 3 кН и ох = 0,7 кН, ахл — действующая нагрузка, рас-
пределенная также по нормальному закону с параметрами тп = 2 кН и ол = 0,5 кН.
Коэффициент запаса надежности будет mjmn = 1,5 и, казалось бы, можно утверждать,
что от этой нагрузки деталь не разрушится. Однако расчет дает: Up = — 1,16; Ф(-1,16) =
= —0,38 и PH(L < 0) = 0,88. Следовательно, получается, что хотя коэффициент запаса
надежности выбран 1,5, тем не менее из каждых 100 деталей следует ожидать разруше-
ние в 12 случаях.
Такое низкое значение вероятности безотказной работы по параметру (вероят-
ности выполнения задания) определяется наличием дисперсии (точнее, величинами
коэффициентов вариации) в распределениях как параметра, так и допуска на него.
Видно, что даже в случае одинаковых коэффициентов запаса надежности можно по-
лучить различные вероятности выполнения задания в зависимости от рассеивания
(дисперсии) случайной величины.
Величина дисперсии oz зависит от дисперсий <зх и ол. Если величина хп, как в рас-
смотренном примере, характеризует внешнюю нагрузку на некоторую деталь, то
ол определяется стабильностью и диапазоном изменения внешних нагрузок на все из-
делие, стабильностью работы агрегатов изделия (скорости вращения, диапазонов
вибраций, диапазонов температур и т. д.) и качеством сборки изделия (разброс натя-
гов, вибрации и т. д.).
В этом же примере несущая способность детали х дает дисперсию ох, которая за-
висит от стабильности и однородности технологического процесса получения мате-
риала заготовки, стабильности качества и геометрии детали, стабильности обеспече-
ния качества при сборке изделия.
Математические ожидания в этом же примере соответствуют тх — прочностным
возможностям материалов после изготовления детали (предел текучести, предел про-
чности, предел выносливости и т. д. данного сечения детали), тп — средним значени-
ем нагрузок на деталь в данном сечении.
Таким образом, простейший анализ вероятности выполнения задания по неко-
торому параметру позволяет включить в анализ обеспечения надежности изделия ко-
личественный учет производственных факторов не только через средние значения па-
раметров качества, но и стабильности производства. Причем за счет повышения ста-
бильности производства возникают возможности не менее эффективного влияния на
надежность изделия, чем за счет повышения средних значений свойств деталей.
Для анализа и понимания вопроса о роли влияния коэффициента запаса надеж-
ности и коэффициентов вариации на вероятность выполнения задания рассмотрим
несколько предельных случаев. В основу анализа положим выражение квантиля (9.24)
и учтем, что с ростом \U^ величина PH(L > 0) растет.
Пусть vn » nvx, т. е. коэффициент вариации параметра изделия существенно
меньше коэффициента вариации внешней нагрузки. Тогда соотношение (9.24) при-
нимает вид:
|С/Р| = (л-l)/v„. (9.25)
Из выражения (9.25) видно, что надежность изделия можно повысить либо уве-
личением п, либо уменьшением vn (не зависит от ох). Но увеличение п требует либо
создания новых материалов с большим тх, либо усовершенствования конструкции,
460
либо увеличения массы изделия. В то же время, например, отстройка изделия по резо-
нансным частотам от внешних воздействий, повышение качества сборки и повыше-
ние стабильности работы агрегатов изделия могут существенно увеличить вероят-
ность безотказной работы.
Если же уровень технологии такой, что vn « nvx9 соотношение (9.24) принима-
ет вид:
\UP\~ (п — l)/nvx. (9.26)
Из соотношения (9.26) видно, что увеличение п больше, чем 1,5...2 раза слабо
влияет на надежность, делая конструкцию неэффективной; в то же время, уменьше-
ние vx требует только повышения стабильности технологического производства. По-
этому повышение надежности изделия через производство существенно эффектив-
нее, чем увеличение п. Рациональным является совершенствование технологии до
уровня, когда vn ~ nvx9 и только затем осуществляется поиск возможностей повыше-
ния п.
Для анализа выпуска дефектной продукции некоторым производством (техноло-
гической системой, см. пп. 9.8, 9.9) соотношению (9.26) можно придать следующий
вид: |t/p| ~ А/)/отс, где М) — установленный допуск на величину анализируемого пока-
зателя качества изделия; отс — суммарное стандартное отклонение технологической
системы. Легко рассчитать, что только в результате статистической природы форми-
рования показателя качества вероятность выхода дефектной продукции составит
2,3%; 0,14%; 0,006% и 0,0006% в случаях, когда в пределах допуска М) укладывается
2отг (±2отг), Зотг (±3отг), 4отг (±4отг) и 5отг (±5отг) соответственно. Следовательно,
для обеспечения высокой надежности изделий, которая не всегда может быть выявле-
на оперативным контролем на выходе технологической системы, необходима высо-
кая стабильность технологической системы производства. Причем бытующая уверен-
ность в высокой стабильности производства, обеспечивающего стандартное отклоне-
ние отс ~ АР/З, не вполне оправдана из-за вероятности выхода дефектной продукции
в 0,14%. В частности, именно этими соображениями определяются тенденции произ-
водств Японии и США, направленные на достижение отс ~ AD/(5—6).
Таким образом, хотя основным параметром безотказности при PH(t) —> 1 по об-
щепринятой терминологии является коэффициент запаса надежности, в расчетах не-
оправданно забывается роль коэффициентов вариации, снижение которых может
быть эффективным направлением повышения надежности изделий.
9.7. ОРГАНИЗАЦИЯ ИСПЫТАНИЙ И КОНТРОЛЯ.
ОЦЕНКА ПОКАЗАТЕЛЕЙ НАДЕЖНОСТИ
ПО РЕЗУЛЬТАТАМ ИСПЫТАНИЙ
Под экспериментальной оценкой надежности понимают определение и конт-
роль показателей надежности по результатам испытаний или наблюдений в процессе
эксплуатации.
В общем комплексе мероприятий по обеспечению надежности эксперименталь-
ные оценки играют важную роль, так как позволяют оценить достигнутые значения
показателей надежности и обосновать необходимые мероприятия по повышению
этих показателей. Результаты экспериментальной оценки показателей надежности
типовых узлов и элементов служат исходными данными при априорных оценках на-
дежности вновь разрабатываемых изделий.
461
Испытания — это экспериментальное определение характеристик изделий, про-
водимое по специально разработанному плану. Испытания могут быть специальными
или совмещенными. В совмещенных испытаниях определение или контроль показа-
телей совмещается с экспериментальными исследованиями других параметров изде-
лий. В специальных испытаниях обычно заранее планируется их объем, а условия ис-
пытаний устанавливаются исходя из требований конкретного показателя надежнос-
ти. Такие испытания, как правило, организуются для изделий, выпускаемых
в достаточно большом количестве, либо для особо ответственных изделий. Часто про-
водить специальные испытания для сложных изделий и систем не представляется воз-
можным, так как объем выпуска обычно ограничен единицами экземпляров,
а процесс изготовления, отладки, проверки функционирования и доводки занимает
слишком много времени. Показатели надежности таких изделий оценивают в основ-
ном по результатам либо совмещенных испытаний, либо наблюдений на этапе экс-
плуатации.
Экспериментальная оценка показателей надежности требует значительного вре-
мени, большого числа образцов, необходимости испытания до разрушения и больших
материальных затрат.
В связи с этим разрабатываются специальные методы ускорения испытаний.
Ускоренными испытаниями называют любые испытания, при которых используются
те или иные методы сокращения объема испытаний. Объем испытаний сокращают
путем:
форсирования режимов испытания (форсированные испытания);
оценки надежности по малому числу отказов или вообще по отсутствию отказов;
сокращения числа испытываемых образцов за счет увеличения длительности ис-
пытаний.
Экспериментальные оценки надежности преследуют одну из следующих целей:
определение фактического значения показателей надежности; контроль соответствия
изготовленного изделия требованиям по надежности, заложенным в технических ус-
ловиях на изделие. В связи с этим в испытаниях на надежность выделяют определи-
тельную и контрольную процедуры. Эти процедуры имеют существенные отличия.
При планировании определительной процедуры принципиально невозможно
однозначно указать необходимый объем испытаний, так как точность оценок показа-
телей надежности при заданной достоверности зависит не только от объема испыта-
ний, но в большей степени от объема получаемой информации. Исходя из требуемых
точности и достоверности оценок, в результате планирования определительной про-
цедуры получают не объем испытаний, а минимально необходимое число информа-
тивных реализаций.
Требуемый объем испытаний (число изделий, число опытов, продолжительность
испытаний) зависит от фактической надежности изделия, которая до испытания не-
известна. Поэтому при планировании объем испытаний определяется ориентировоч-
но и в процессе испытаний корректируется.
Планирование контрольной процедуры опирается на требуемое значение пока-
зателя надежности, записанное в ТУ по результатам определительных испытаний.
В результате планирования определяются необходимый минимальный объем испыта-
ний и оценочный норматив, по которому принимается решение о соответствии или
несоответствии изделия заданным требованиям. Поэтому в контрольной процедуре
корректность планирования непосредственно определяет достоверность принятого
решения о принятии или браковке изделия или всей партии.
462
9.7.1. Характер статистической информации
при испытаниях. Стратегии испытаний
Результаты испытаний, очищенные предварительной обработкой, подлежат ста-
тистической обработке, т. е. оценке параметров функций распределения случайных
величин, определяющих искомые показатели надежности.
При экспериментальной оценке показателей надежности многие задачи незави-
симо от конкретного содержания имеют одинаковый алгоритм решения, а все много-
образие оцениваемых показателей сводится к показателям двух типов:
показатели типа наработки — средняя или гамма-процентная (наработка до от-
каза, между отказами, до предельного состояния; срок сохраняемости; время восста-
новления и т. д.);
показатели типа вероятности (безотказной работы, исправного состояния в про-
извольный момент, восстановления за заданное время и т. д.).
При определении показателей типа наработки непосредственно наблюдение осу-
ществляется в случайные интервалы времени.
При определении показателей типа вероятности непосредственно наблюдаемы-
ми величинами являются числа событий в испытаниях — число отказов, число вос-
становлений и т. д.
В зависимости от априорных сведений о функции распределения все многообра-
зие практических задач сводится, по существу, к двум вариантам.
1. Вид функции распределения наблюдаемой величины известен априори. Задача
статистической обработки — получение оценок числовых характеристик функции
распределения и показателей надежности с учетом вида функции распределения и ха-
рактера имеющегося статистического материала.
2. Вид функции распределения наблюдаемой случайной величины не известен
или известен лишь предположительно. В этом случае на основании анализа процес-
сов, приводящих к отказам, опыта эксплуатации аналогичных изделий и предвари-
тельного анализа полученной при испытаниях информации (например, по виду гис-
тограммы) принимается некоторая гипотеза о виде функции распределения. Задача
обработки — проверить, не противоречат ли экспериментальные данные принятой
гипотезе, и далее повторить вариант № 1.
Естественно, вариант № 2 является наиболее трудоемким.
Особым является случай, когда оценка параметров распределения не производится,
а требуется лишь оценить непосредственно значение функции распределения в некото-
рой фиксированной точке, т. е. оценить показатель типа вероятности (вероятность отка-
за для фиксированной наработки, вероятность восстановления за фиксированное время
и т. д.). Задача такого типа в математической статистике носит название непараметриче-
ской. Этот случай является наиболее простым с точки зрения организации и трудоем-
кости испытаний. В этом случае испытания каждого изделия проводятся в течение фик-
сированной наработки. Статистической обработке подлежат только два числа — общее
число испытаний и число успешных испытаний. Естественно, что получаемая в этом
случае оценка несет минимум информации (значение распределения в точке фиксиро-
ванной наработки) и не подлежит экстраполированию на другие значения наработки.
Все виды испытаний проводятся в соответствии со стратегией испытания, кото-
рая должна содержать информацию о следующих факторах:
число изделий, подвергаемых испытаниям;
порядок контроля функционирования;
порядок восстановления изделия;
порядок поступления изделия на испытания;
критерии окончания испытаний.
463
Для нахождения законов распределения случайных величин необходимо обла-
дать достаточно большим статистическим материалом, т. е. провести большой объем
испытаний. На практике всегда приходится иметь дело с ограниченным статистиче-
ским материалом. Такого ограниченного материала явно недостаточно, чтобы найти
заранее неизвестный закон распределения, но этот материал может быть использован
для оценки важнейших численных характеристик распределения — математического
ожидания, дисперсии и так далее. На практике нередко бывает, что вид закона рас-
пределения известен заранее, а требуется найти только параметры распределения
и надежности. В некоторых задачах закон распределения может быть вообще несу-
ществен, а требуется найти только числовые характеристики.
Оценки параметров распределения могут быть точечными и интервальными. Для
нахождения точечных оценок используются аналитические методы: метод макси-
мального правдоподобия, метод моментов, метод квантилей и др. Кроме того, ис-
пользуются графические методы с использованием вероятностных бумаг и номог-
рамм. Особенности применения этих методов к различным планам испытаний приве-
дены в пособиях по теории вероятностей и надежности.
Любая точечная оценка обладает существенным недостатком в том смысле, что
она сама представляет лишь частное значение случайной величины. Мы не имеем
представления о степени доверия к этой оценке (степени ее точности).
Поэтому кроме точечной оценки желательно знать интервал оценок, который
с достаточно высокой вероятностью накрывает оцениваемый параметр. Очевидно,
что абсолютно достоверными интервалами для наработки Т будет интервал [0, оо],
а для вероятности отказа или вероятности безотказной работы — [0, 1].
Указание других границ сопряжено с риском совершить ошибку. Вероятности
ошибок £j и е2 называют уровнями значимости оценок: — вероятность того, что
найденный интервал не накроет параметр своим левым концом, а £2 — своим правым
концом.
В качестве меры достоверности оценки (доверительной вероятности) принима-
ется величина у* = 1 - q - £2, показывающая, с какой вероятностью можно утверж-
дать, что доверительный интервал покрывает истинное значение параметра:
у* = Р(ГН < Г< Гв), (9.27)
где Гн и Тв — нижняя и верхняя границы доверительного интервала соответственно.
Обычно £j и £2 выбирают одинаковыми, поэтому у* = 1 — 2е и, следовательно,
каждая из доверительных границ выбирается с уровнем значимости £ = (1 - у*)/2 или
с односторонней доверительной вероятностью у = 1 — £.
Если известен вид функции распределения, то границы доверительного интерва-
ла вычисляются через соответствующие квантили.
Цель контрольной процедуры, в отличие от ранее рассмотренной определитель-
ной процедуры, — установление соответствия изделия заданным требованиям по на-
дежности. Результатом контроля является решение о приеме или браковке изделия
или всей партии изделий.
На языке математической статистики задача контроля показателя надежности
формулируется как задача проверки гипотезы о значениях показателя надежности.
Пусть в технической документации на изделие указано требуемое значение показате-
ля надежности RT (в данном случае R может обозначать либо показатель типа наработ-
ки Т, либо показатель типа вероятности безотказной работы Рн)9 тогда при разработке
контрольной процедуры стремятся обеспечить приемку изделий с уровнем надежнос-
ти R > RT и браковку с уровнем надежности R< Rr
464
В процессе разработки изделий контроль надежности проводят как минимум
один раз на приемочных испытаниях, часто используя статистику других испытаний.
При серийном производстве контроль надежности обычно предусматривают в соста-
ве периодических испытаний. Контроль надежности высоконадежных мелкосерий-
ных изделий целесообразно вводить в состав типовых испытаний, проводимых при
изменении конструкции, технологии или комплектующих. Контроль надежности
больших сложных изделий с широким применением резервирования может быть
включен в состав приемо-сдаточных испытаний.
9.8. Технологическое обеспечение
НАДЕЖНОСТИ ЛЕТАТЕЛЬНЫХ АППАРАТОВ
Технология изготовления, сборки и контроля изделия должна с максимальной
производительностью и наименьшими затратами обеспечить качество продукции,
в том числе и ее надежность, заложенную в технической документации на изделие. Од-
нако связь параметров технологического процесса с показателями надежности изделия
сложна, неоднозначна, проявляется через длительный промежуток времени вне сферы
деятельности предприятия и, кроме того, многие требования по надежности вступают
в противоречие с такими основными требованиями к технологическому процессу, как
его производительность и экономичность. Вместе с тем организация производства
данного изделия, применяемые технологические процессы и методы контроля и испы-
таний оказывают самое решающее влияние на показатели надежности изделия.
Зависимость показателей надежности изделия от параметров технологического
процесса можно представить в виде структурной схемы (рис. 9.6).
Рис. 9.6. Структурная схема связи параметров технологического процесса
с показателями надежности изделия
465
В результате выполнения технологического процесса изготовления деталей и их
последующей сборки в изделии обеспечиваются и контролируются на производстве
выходные параметры продукции, заложенные в конструкторской документации
(ТУ на параметры изделия), — точность, качество поверхностного слоя, механиче-
ские свойства и другие.
Однако знание этих выходных параметров не позволяет сделать заключение
о показателях надежности изделия, так как показатели надежности будут определяться
отказами по таким эксплуатационным свойствам изделия (рис. 9.6), как выносливость,
износостойкость, теплостойкость и др. Установление же взаимосвязи между эксплуата-
ционными показателями изделия и параметрами качества изготовляемых деталей и
сборочных единиц само по себе является сложной, неоднозначной и многовариантной
задачей. Более того, на производстве не всегда имеется четкое представление о том кру-
ге вопросов, которые должна решать технология с целью обеспечения заданной надеж-
ности изделия. В связи с этим часто наблюдается ситуация, когда после доводки изде-
лия на производстве очень сложно ввести даже самые эффективные изменения в техно-
логию, так как это потребует проведения длительного и дорогостоящего комплекса
испытаний изделия на надежность. Такая же ситуация наблюдается, когда выявляются
отклонения технологического регламента. В этом случае проще забраковать часть про-
дукции, так как практически невозможно предсказать, каким образом установленное
отклонение в технологическом регламенте повлияет на надежность изделия.
Таким образом, в результате функционирования технологической системы изго-
тавливается изделие с некоторым набором показателей качества {х,}, соответствую-
щих ТУ на изделие. В процессе эксплуатации изделия этот набор показателей качест-
ва {*,} и набор факторов внешних воздействий на изделие^} определят набор эксплу-
атационных показателей изделия {Эу}, т. е. эксплуатационные показатели изделия
должны определяться некоторой функциональной зависимостью вида:
Э^Ф^Х!,...,^,^,...,/;), (9.28)
при условии, что в ТУ на изделие правильно выбраны и регламентированы все пока-
затели качества изделия, влияющие на его эксплуатационные свойства.
В свою очередь набор показателей {ЭД, набор допусков на эксплуатационные по-
казатели и набор факторов внешних воздействий должны определять через некото-
рую функциональную зависимость показатели надежности изделия.
Показатели качества изделия обладают определенными допусками и имеют рас-
сеивание, т. е. являются случайными величинами с соответствующими законами рас-
пределения (часто с нормальным законом распределения). Внешние факторы также
являются случайными величинами, поэтому соотношение (9.28) приводит к тому, что
все Эу являются случайными величинами. Если воспользоваться результатами реше-
ния задачи об обеспечении работоспособности изделия по некоторому эксплуатаци-
онному параметру, то получим, что работоспособность изделия по этому эксплуата-
ционному параметру будет определяться величиной квантиля (9.24), а вариации
внешней нагрузки и эксплуатационного показателя можно представить в виде:
(9.29)
Из соотношения (9.29) и проведенного ранее анализа соотношения (9.24) следу-
ет, что вероятность безотказной работы изделия по эксплуатационным показателям
зависит от коэффициента запаса надежности, вариации внешней нагрузки и вари-
ации показателей качества изделия. Поэтому надежность изделия технологическими
466
методами можно повысить увеличением средних значений показателя качества (его
математического ожидания) при сохранении уровня его дисперсии в процессе изго-
товления, либо уменьшением дисперсии показателей качества при его неизменном
среднем значении. Увеличение среднего значения показателя качества определяется в
основном использованием новых высокоэффективных материалов в конструкции и
новых прогрессивных технологий при изготовлении деталей и сборке изделия.
Уменьшение же дисперсии может быть достигнуто ужесточением технологического
регламента и допусков на продукцию. Выбор первого либо второго направления
в каждом конкретном случае определяется технико-экономической целесообразно-
стью. Однако второе направление (снижение дисперсии показателей качества) явля-
ется в определенных условиях существенно более эффективным, чем первое, что бы-
ло показано ранее при анализе соотношения (9.24).
Повышение качества продукции за счет снижения дисперсии показателей в про-
цессе производства является одним из важнейших элементов технологической рево-
люции, прошедшей во всех ведущих странах мира.
9.8.1. Производственные причины снижения
надежности летательных аппаратов
В настоящее время принято классифицировать отказы, связанные с технологией
изготовления изделия, в соответствии со схемой [1,3], представленной на рис. 9.7.
Первая группа причин связана с недостаточной обоснованностью технических
условий на параметры изделия и его составляющие, на параметры технологических
процессов, а также на методы испытания изделия и его составляющих на надежность.
Технические условия на изделие и его составляющие должны отражать основные
требования к надежности изделия. Но при выполнении технологических операций по
изготовлению деталей и их последующей сборке измеряются не показатели надеж-
ности изделия, которые практически и невозможно измерить (определить) на том или
ином этапе технологического процесса. Поэтому в конструкторской документации
(в чертежах) задаются параметры, «удобные» для измерения и которые должны были
бы однозначно обеспечить требуемый уровень надежности изделия. Однако парамет-
ры конструкции, указанной в чертежах по точности изготовления, по шероховатости,
твердости и т. д., оказывается, еще не определяют однозначно показатели надежное -
Рис. 9.7. Классификация отказов, связанных с технологией изготовления изделия
467
ти. Даже более жесткая регламентация технологии со ссылками на соответствующие
технологические инструкции, ОСГы и ГОСТы часто также не обеспечивает одинако-
вые показатели надежности изделий, изготовленных на разных предприятиях. Поэто-
му чем выше требования к надежности изделия, тем большее число параметров дол-
жно быть оговорено техническими условиями и тем достовернее должны быть опре-
делены основные взаимосвязи между эксплуатационными и технологическими
параметрами (9.28). Практически же такие вопросы решаются в процессах доводки
изделий на стадии серийного производства специалистами КБ. В результате такой до-
водки происходит жесткая регламентация не только технологического процесса, но и
всей конструкторско-технологической документации, всей технологической системы
конкретного производства, обеспечивающей необходимый уровень надежности изде-
лий. При этом очень важную роль играют заданные технические условия на испыта-
ния. Сложность разработки методов и средств испытаний изделий на надежность
привели к тому, что испытания стали самостоятельной областью в проблеме надеж-
ности.
Таким образом, обоснованность технических условий для обеспечения заданно-
го уровня надежности изделий связана не только с техническими условиями на изде-
лие, на технологический процесс и на испытания, но и с жесткой регламентацией
всей технологической системы (в том числе и технологического процесса) изготовле-
ния и испытания изделий.
Следующая группа, приводящая к отказам по вине технологии, связана с оста-
точными и побочными явлениями технологических процессов.
При выполнении любой технологической операции материалы деталей подвер-
гаются очень значительным силовым, тепловым, химическим и другим воздействиям.
Уровень этих воздействий во много раз превышает уровень воздействий при эксплу-
атации изделий и создает объективные условия для возникновения в изделиях таких
нежелательных воздействий, как изменение свойств и структуры материалов, образо-
вание пор, раковин, микро- и макротрещин. Особенно высоко такое воздействие на
приповерхностный слой материала детали. В общем случае к технологическим дефек-
там относят любые несоответствия продукции требованиям, установленным норма-
тивно-технической документацией. Поэтому к дефектам относят как отклонения
свойств и состояний материалов (трещины, раковины, включения, структурные из-
менения, выход параметра качества за пределы допуска и т. д.), так и нарушения за-
данной точности формы и размеров. Обычно дефекты формы и размеров рассматри-
вают отдельно как погрешности обработки, а к дефектам относят все остальные нару-
шения установленных требований к материалу и приповерхностным слоям.
Образование дефектов в изделии зависит от применяемого технологического ме-
тода (способа изготовления), средств технологического оснащения, режимов обра-
ботки, систем автоматизации процесса и других характеристик. Для каждой техноло-
гической операции имеются, как правило, типичные виды дефектов, связанные как
с нарушением хода процесса, так и с неблагоприятным сочетанием различных факто-
ров при его выполнении.
Например, при отливке деталей из-за неравномерного остывания, окисления,
попадания в материал различных включений и газа могут появляться дефекты в виде
трещин, раковин, пор, ликвации и неоднородности структуры. Кроме того, возника-
ют остаточные напряжения, которые могут приводить к снижению эксплуатацион-
ных показателей деталей, а также к их короблению как при последующей обработке,
так и в процессе эксплуатации. Аналогичные дефекты возникают при сварке, терми-
ческой и химико-термической обработке, при нанесении покрытий.
468
Особое влияние на работоспособность изделий оказывают механическая и элек-
трохимическая обработки, которые придают деталям окончательную форму и свойст-
ва рабочим поверхностям деталей. В результате такой обработки поверхность матери-
ала и приповерхностные слои переходят в особое состояние с комплексом свойств,
существенно отличающихся от свойств материала в объеме детали.
Часто различные варианты технологии, приводящие к одинаковым, с точки зре-
ния регламентированного качества параметра, результатам, при более глубоком изу-
чении обнаруживают разные склонности к образованию дефектов. Так, шлифование,
полирование и алмазное выглаживание позволяют получить одинаковую величину
шероховатости поверхности, однако шлифованная поверхность имеет большее число
рисок глубиной до 1 мкм, полированная — существенно меньшее число рисок с глу-
биной до 0,05 мкм, а выглаженная — практически не имеет рисок. Это приводит к су-
щественному отличию в таких эксплуатационных свойствах, как выносливость, изно-
состойкость и коррозионная стойкость.
У никелевых и титановых сплавов после электрохимической полировки сущест-
венно снижается предел выносливости по сравнению с деталями после механической
обработки с теми же параметрами шероховатости поверхности. Более того, на
10... 15% снижается предел прочности на растяжение и изгиб, в то же время предел
прочности на сжатие и кручение практически не изменяется. Снятие же припуска
после электрохимической обработки механическим методом (от 0,15 до 0,3 мм) вос-
станавливает величины этих параметров. У ряда алюминиевых сплавов механическая
и электрохимическая обработки незначительно изменяют значения пределов вынос-
ливости и прочности.
В пределах одного технологического метода на возможность возникновения де-
фектов основное влияние оказывают обычно выбранные средства технологического
оснащения и режимы обработки. Например, широко известно, что в зависимости от
режимов резания и геометрии режущего инструмента предел выносливости обраба-
тываемого материала может измениться более чем в два раза при практически одной и
той же шероховатости поверхности. Еще более сильное влияние оказывает изменение
режимов шлифования, особенно высокопрочных материалов.
Часто считают, что возникновение дефектов в процессе обработки является след-
ствием нарушения технологической дисциплины, наличия оборудования с низкими
техническими характеристиками, нарушения ритмичности работы предприятия, пло-
хой организации труда и так далее. Такой взгляд является поверхностным, так как
фиксирует лишь грубые нарушения в ходе технологического процесса. Надо отме-
тить, что, по существующим данным, 85% технологических дефектов связано
с недостатками в технологии, в основном из-за неправильного обоснования техноло-
гических систем, а только 15% являются следствием нарушения технологической дис-
циплины.
В действительности физико-химические воздействия, которые сопровождают
любой технологический процесс, порождают в материале изделия отклонения от
первоначального состояния и изменение свойств материала. Выход этих отклоне-
ний (они существуют всегда) за установленные пределы и приводит к возникнове-
нию дефектов. Поэтому технологический процесс при одних требованиях к изделию
будет бездефектным и дефектным — при повышенных нормативах на выходные па-
раметры.
Хотя основную роль в формировании показателей качества выпускаемых изде-
лий часто играют финишные операции технологического процесса, однако многие
свойства изделия передаются с промежуточных операций на последующие. Явление
переноса свойств изделия от предыдущих операций к последующим получило назва-
469
ние технологического наследования, а сохранение этих свойств — технологической
наследственностью [1, 2, 3]. Носителем информации о наследственности являются
материал детали и ее геометрическая форма. Физико-химическая природа технологи-
ческой наследственности особенно хорошо видна при анализе формулы суммирова-
ния парциальных повреждений. В соответствии с этим соотношением разрушение
материала наступает при выполнении условия:
* дл
<9'30’
где Д/у — промежуток времени нахождения материала детали при растягивающих на-
пряжениях oz и температуре 7}; t(oz, 7}) — долговечность материала детали при тех же
напряжениях и температуре. В соотношении (9.30) каждое слагаемое A/z/t(oz, 7}) ха-
рактеризует долю потерянной долговечности (ресурса) при данном нагружении дета-
ли в течение Arz.
Часть слагаемых в выражении (9.30) можно отнести к технологическим операци-
ям, а часть — к эксплуатации. Видно, что в результате определенных технологических
операций происходит частичная потеря долговечности всей детали из-за потери ее
долговечности по определенным сечениям, в которых действуют растягивающие на-
пряжения (кинетическая теория прочности).
После ряда технологических операций, особенно термических или упрочняю-
щих, удается восстанавливать первоначальную долговечность всей детали или ее наи-
более опасных сечений, к которым, в частности, относятся и приповерхностные слои.
Полученные на отдельных операциях дефекты (в том числе микротрещины) могут
либо развиваться, либо «залечиваться» на последующих операциях. Поэтому технологи-
ческая наследственность может играть как положительную, так и отрицательную роль в
зависимости от того, какие свойства сохраняются и передаются готовому изделию.
Технологическая наследственность в большинстве случаев оказывает все-таки
отрицательное влияние на показатели качества и является побочным явлением при
обработке деталей и их сборке. Поэтому технологический маршрут необходимо стро-
ить таким образом, чтобы исключить передачу дефекта или погрешности обработки
с операции на операцию, сделать операции как бы независимыми в технологическом
отношении. Считается, что наиболее благоприятным будет такой технологический
процесс, где на начальных операциях происходит практически полная ликвидация
отрицательных свойств и эти свойства не наследуются на финишных операциях.
Следующая группа причин, приводящая к недопустимым производственным от-
казам изделий, связана с недостаточной надежностью технологической системы изго-
товления изделия. Как было отмечено при анализе первой группы причин, в результа-
те доводки (на стадии опытного или серийного производства) возникает необходи-
мость в жесткой регламентации технологической системы производства изделия.
Однако в процессе эксплуатации технологической системы ее свойства изменяются
и, более того, она сама, как любое техническое изделие, подвержена отказам. Следо-
вательно, технологическая система должна характеризоваться таким важным свойст-
вом, как надежность, т. е. свойством сохранять во времени способность обеспечивать
изготовление продукции в заданном объеме, с заданной производительностью и за-
данными параметрами качества. Чем выше заданная надежность изделия, тем выше
должна быть надежность технологической системы.
Важной задачей обоснования и создания технологических систем производства
ЛА является выявление наименее надежных элементов технологических систем (даю-
щих наибольшие дисперсии показателей качества) и их совершенствование, а также
сокращение числа элементов в системе, в том числе и за счет их кооперации.
470
Рис. 9.8. Схема мероприятий повышения надежности технологических систем
за счет обоснованности и полноты технических условий на показатели качества деталей,
сборочных единиц и изделий
На рис. 9.8 представлена типовая схема повышения надежности технологической
системы за счет создания обоснованных и полных технических условий на показатели
качества деталей, сборочных единиц и изделия в целом. В связи с таким сильным влия-
нием надежности технологической системы на надежность изделия в последнее деся-
тилетие активно развиваются методы формализованного описания технологических
процессов с точки зрения науки о надежности технологических систем. При этом тех-
нология изготовления изделия представляется в виде технологической системы, кото-
рая должна обеспечить определенную вероятность выполнения задания по параметрам
качества, параметрам производительности и параметрам затраченных ресурсов (п. 9.6).
9.9. ОСНОВНЫЕ НАПРАВЛЕНИЯ ПОВЫШЕНИЯ
НАДЕЖНОСТИ ЛЕТАТЕЛЬНЫХ АППАРАТОВ
СОВЕРШЕНСТВОВАНИЕМ ТЕХНОЛОГИЧЕСКИХ СИСТЕМ
ИХ ПРОИЗВОДСТВА, ИСПЫТАНИЯ И КОНТРОЛЯ
Изделия аэрокосмической техники характеризуются непрерывным ростом не
только летно-технических и экономических показателей, но и в значительной мере
ростом их показателей надежности. Обеспечение высокой надежности летательных
471
аппаратов осуществляется на этапе их производства и невозможно без высокой на-
дежности технологических систем.
До определенного этапа развития аэрокосмической техники основным методом
получения изделий высокого качества было постоянное обнаружение и исправление
возникших дефектов. При такой организации производства считалось, что получение
некоторого процента дефектных деталей в серийном производстве является неотъем-
лемым свойством технологического процесса.
Однако качество изделия создается не в процессе контроля или испытаний, а в про-
цессе производства. Поэтому основой должен быть анализ объективных и субъективных
причин дефекта с тем, чтобы субъективные причины исключить, а отрицательное влия-
ние объективных факторов научиться измерять количественно и ограничивать до нуж-
ных пределов. В этом заключается суть систем бездефектного изготовления продукции.
В настоящее время российская аэрокосмическая промышленность все более ак-
тивно выходит на международный рынок. В связи с этим возникает необходимость не
только обеспечения показателей качества продаваемой продукции, но и создание уве-
ренности у потребителя в том, что поставщик способен обеспечить стабильность это-
го качества в соответствии с контрактом. Гарантией стабильности качества продук-
ции является наличие на производстве сертифицированной независимым междуна-
Рис. 9.9. Система технологического обеспечения надежности ЛА
472
родным органом системы качества продукции. Одной из составляющих системы
качества является комплексная система технологического обеспечения надежности
летательных аппаратов. В зависимости от вида изделия, традиций КБ-разработчика
изделия и конкретного завода-изготовителя системы технологического обеспечения
надежности и качества имеют некоторые отличия. Однако их общую сущность можно
представить в виде следующей системы (рис. 9.9).
Технологическое обеспечение качества и надежности ЛА начинается с этапа конст-
рукторско-технологического анализа изделия (подсистема «Проектирование. Конструк-
торско-технологический анализ»), отрабатывается в результате доводки изделия (под-
система «Доводка»), реализуется на этапе производства (подсистема «Производство») и
совершенствуется по результатам эксплуатации изделия (подсистема «Эксплуатация»).
Некоторые элементы этих подсистем изображены на рис. 9.10 и рис. 9.11. Основ-
ными этапами работ в подсистеме «Проектирование. Конструкторско-технологиче-
ский анализ» является проведение опережающих исследований, разработка мероп-
риятий по подготовке опытного и серийного производства и создание опытного об-
Подсистема «Доводка»
Рис. 9.10. Элементы подсистем "Проектирование" и "Доводка1
473
Рис. 9.11. Элементы подсистемы "Производство"
разца изделия (рис. 9.10). На этапе опережающих исследований проводится
конструкторско-технологическая оптимизация элементов конструкции, узлов и агре-
гатов на надежность, разрабатываются технологические процессы обработки мате-
риалов и сборки изделия.
Особенно важным на данном этапе является выяснение влияния выбранных тех-
нологических процессов на надежность элементов изделия, особенно в случае ис-
пользования новых материалов и новых технологий. Как уже отмечалось, свойства
материалов для элементов конструкции нельзя рассматривать изолированно, без уче-
та влияния на эти свойства условий и режимов обработки и сборки, а также после-
дующих условий их эксплуатации.
Известно, что воздействие конструктивных концентраторов напряжений в дета-
лях в виде галтелей, в резьбовых и сварных соединениях, воздействие повышенных
температур и коррозионных сред приводят к тому, что допускаемые эксплуатацион-
ные напряжения в реальных деталях не превышают 10...70% предела усталости стан-
дартных образцов из этих материалов по ГОСТу. Кроме этого, существует дисперсия
механических свойств поставляемых материалов, дисперсия режимов обработки
и точности настройки. Отсюда появляется дисперсия параметров качества деталей.
Очень часто эта дисперсия наиболее явно проявляется в свойствах поверхностного
слоя, который наиболее сильно влияет на основные эксплуатационные показатели
474
изделия. Например, изменение условий обработки изменяет дисперсию этих свойств
в 3...4 раза и уменьшает математическое ожидание параметров качества, а следова-
тельно, уменьшает вероятность безотказной работы детали и изделия в целом (п. 9.6).
В связи с этим важным направлением уменьшения дисперсии из-за технологических
факторов является использование адаптивного управления технологическими про-
цессами и введение специальных операций модифицирования поверхностного слоя.
В настоящее время поверхностное упрочнение и упрочняющие покрытия явля-
ются одной из обязательных финишных операций при изготовлении ответственных
деталей. В случае обеспечения стабильности во времени и по всей площади детали об-
работка поверхностным пластическим деформированием обеспечивает повышение
надежности технологических систем как за счет увеличения номинальных значений
параметра качества, так и снижения его дисперсии. По сравнению с другими методами
обработки она в 2...4 раза уменьшает величину доверительного интервала на сжимаю-
щие остаточные напряжения в приповерхностном слое (при доверительной вероят-
ности 0,95) и до 40% увеличивает однородность других свойств поверхностного слоя.
Одним из основных направлений является также повышение технологичности
конструкций, особенно для проведения сборочно-монтажных работ.
Конечной целью всех этих мероприятий является разработка наиболее полных
и обоснованных ТУ на параметры качества изделия, на параметры технологических
систем и методы испытания и контроля (рис. 9.7, 9.8).
Одним из наиболее важных и эффективных средств обеспечения объективности
перечисленных мероприятий являются испытания, которые проводятся на всех эта-
пах жизненного цикла изделия со сбором информации для уточнения поведения ма-
териалов и конструкций в реальных условиях эксплуатации.
Испытания образцов и изделий подразделяют на лабораторные (стендовые),
проводимые на месте изготовления изделия, и летные испытания, проводимые на ле-
тательном аппарате.
Лабораторные испытания опытных образцов, деталей, узлов, отсеков и пр. дают
первичную информацию о их работе при воздействии на них различных факторов.
Однако при лабораторных (стендовых) испытаниях нельзя учесть всего разнообразия
факторов, имеющих место при эксплуатации опытных образцов на летательных аппа-
ратах различных классов. Для одного и того же агрегата характер нагрузок, уровни,
последовательность и цикличность их действия могут изменяться в зависимости от
типа летательного аппарата. Поэтому, как показывает опыт, характеристики надеж-
ности, полученные при лабораторных испытаниях, значительно отличаются как по
уровню, так и по характеру отказов. В связи с этим кроме лабораторных испытаний
проводится большой объем летных испытаний, в том числе и испытания материалов
узлов в условиях экспонирования в открытом космическом пространстве.
Таким образом, при технологической подготовке производства и выпуске опыт-
ного образца должны быть решены вопросы выбора оптимальных технологических
процессов, режимов технологических операций и методов и мест контроля, а также
выбора оптимального состава технологической системы по надежности.
В случае серийного производства летательного аппарата работы по созданию из-
делия не ограничиваются выполнением проектных работ, постройкой опытных об-
разцов, проведением лабораторных и летных испытаний. Продолжением процесса
проектирования с учетом требований серийного производства и эксплуатации явля-
ется конструкторско-технологическая доводка. Необходимость этапа доводки вызы-
вается спецификой опытного производства и его отличием от серийного.
В процессе опытного производства в первую очередь решаются вопросы обеспече-
ния необходимых тактико-технических данных летательного аппарата. К моменту
475
окончания летных испытаний вносится достаточно большое число конструктивных
изменений в изделие. Необходимость этих изменений становится обычно ясна только
к концу испытаний и анализа полученных данных. Поэтому в процессе запуска изде-
лия в серийное производство производится конструктивно-технологическая доводка.
Особую важность доводка изделия на стадии серийного производства приобрета-
ет в связи с тем, что оборудование серийного и опытно-экспериментального заводов
или технологической базы ОКБ имеют различие как по номенклатуре, так и степени
износа, отличается также квалификация технического персонала этих коллективов.
Процесс конструктивно-технологической доводки и подготовки серийного про-
изводства максимально используется для повышения показателей надежности изде-
лия и корректировки директивных технологических процессов (рис. 9.10).
Повышение надежности изделия на этом этапе достигается в результате значи-
тельного улучшения его производственной, эксплуатационной, а для ремонтируемых
изделий и ремонтной технологичности, продолжения и расширения объема начатых
ранее ресурсных испытаний, уточнения технических условий и программ испытания
готовых изделий. В этот период решаются многие вопросы рационального размеще-
ния оборудования, коммуникаций и увязки с элементами конструкции аппарата. Па-
раллельно с плазовыми работами ведется разработка технологии монтажных работ.
При этом необходимо обращать внимание на выбор баз, относительно которых долж-
ны фиксироваться агрегаты силовой установки, систем управления, топливной и гид-
росистем, связанные трубопроводами.
Окончательную отработку сложных пространственных систем целесообразно
проводить на макете летательного аппарата. Это позволяет изыскать еще более прос-
тые решения компоновки агрегатов, монтажа элементов коммуникаций, сократить
число соединений и повысить эксплуатационные качества изделий. По мере отработ-
ки монтажей должны быть изготовлены эталоны всех элементов систем. Эти детали в
дальнейшем используются при изготовлении всей заготовительной, монтажной
и контрольной оснастки.
На стадии серийного производства технологическая надежность летательного
аппарата обеспечивается стабильностью технологического процесса, надежностью
технологических систем и введением новых технологических процессов, позволяю-
щих снижать дисперсию и повышать номинальные значения показателей качества
продукции (рис. 9.11).
Обеспечение надежности технологических систем реализуется за счет выявления
технологических дефектов и обоснованной корректировки технологических систем.
Стабильность технологических систем обеспечивается их адаптивным управлением
и адаптивной настройкой средств технологического оснащения, использованием
средств автоматизации и гибких автоматизированных производств, применением
систем автоматизированного проектирования, а также использованием активного
и автоматизированного контроля.
ЛИТЕРАТУРА
1. Сборочные, монтажные и испытательные процессы в производстве летательных
аппаратов: Учебник для студентов высших технических учебных заведений/
В. А. Барвинок, В. И. Богданович, П. А. Бордаков и др.; Под ред. проф. В. А. Бар-
винка. — М.: Машиностроение, 1996. С. 576.
2. Кузнецов А. А. Надежность конструкции баллистических ракет. — М.: Машино-
строение, 1978. С. 256.
3. Вигдорчик С. А. Технологические основы проектирования и конструирования са-
молетов: Конспект лекций. Ч. II. — М.: МАИ, ротапринт, 1976. С. 96.
476
4. ПрониковА. С. Надежность машин. — М.: Машиностроение, 1978. С. 92.
5. Решетов Д. Н., Иванов А. С., Фадеев Ф. 3. Надежность машин.— М.: Высшая
школа, 1988. С. 37.
6. Кузнецов А. А., Зотов А. А., Комягин В. А. Надежность механических частей конст-
рукции летательных аппаратов. — М.: Машиностроение, 1979. С. 144.
7. Соломонов П. А. Надежность планера самолета. — М.: Машиностроение, 1974.
С. 320.
8. Золотов А. А., Титов М. И. Обеспечение надежности транспортных аппаратов
космических систем. — М.: Машиностроение, 1988. С. 216.
9. Надежность технических систем: Справочник / Ю. К. Беляев, В. А. Богатырев,
В. В. Болотин и др.; Под ред. И. А. Ушакова. — М.: Радио и связь, 1985. С. 608.
10. Богданович В. И., Барвинок В. А. Системный анализ технологических методов об-
работки в производстве летательных аппаратов: Учеб, пособие. — Куйбышев:
КуАИ, 1989. С. 68.
СОДЕРЖАНИЕ ГЛАВЫ 9
9.1. Надежность как прикладная научная дисциплина и ее задачи
по обеспечению качества летательных аппаратов......................435
9.1.1. Вероятностная природа показателей надежности ...........436
9.1.2. Основные задачи прикладной научной дисциплины
о надежности изделия ..........................................437
9.2. Этапы формирования надежности летательных аппаратов...........437
9.3. Основные определения и понятия теории надежности..............439
9.3.1. Виды отказов технических изделий........................441
9.3.2. Функция распределения вероятности отказов
и ее числовые характеристики ..................................442
9.3.3. Безотказность, долговечность, сохраняемость
и ремонтопригодность. Единичные и комплексные показатели
надежности.....................................................445
9.4. Математические модели отказов технических систем..............448
9.4.1. Основные распределения теории надежности................449
9.4.2. Моделирование сложных технических систем прямым
аналитическим методом .........................................453
9.4.3. Моделирование сложных технических систем методом
структурных схем ..............................................454
9.5. Повышение надежности летательных аппаратов резервированием....456
9.6. Обоснование выбора показателей надежности технических изделий.458
9.7. Организация испытаний и контроля. Оценка показателей надежности
по результатам испытаний...........................................461
9.7.1. Характер статистической информации при испытаниях.
Стратегии испытаний............................................463
9.8. Технологическое обеспечение надежности летательных аппаратов..465
9.8.1. Производственные причины снижения надежности
летательных аппаратов..........................................467
9.9. Основные направления повышения надежности летательных аппаратов
совершенствованием технологических систем их производства, испытания
и контроля........................................................471
Литература ...........................................................476
477
ГЛАВА 10_________________________________________________
Методы оценки
конструкторско-технологических
решений
В связи с бурным развитием авиационной техники и технологий, в особенности
высоких, наукоемких, получивших такое название из-за большой стоимости их разра-
боток на начальном этапе жизненного цикла — научно-исследовательских и опыт-
но-конструкторских работ (НИОКР), в настоящее время весьма актуальной задачей
является обоснование и выбор наиболее приоритетных направлений создания и ис-
пользования (коммерциализации) технологий. Решение этой задачи требует разра-
ботки соответствующего научно-методического обеспечения и, в частности, форми-
рования системы критериев, позволяющей производить всестороннюю (многокрите-
риальную) и достаточно полную оценку конструкторско-технологических решений
или технологий (в широком смысле этого слова).
10.1. ОСОБЕННОСТИ ЭТАПА НИОКР
Зарождение конструкции и технологии происходит на стадии научно-исследова-
тельских работ (НИР), когда в результате теоретических и (или) экспериментальных
исследований выдвинутая идея (концепция) о разработке нового образца продукции
получает достаточно весомое подтверждение, чтобы перейти к следующей фазе — со-
зданию полноразмерного опытного экземпляра, образца «в металле» и последующей
проверке (испытаниям) его на соответствие заданным в техническом задании (ТЗ)
требованиям (стадия опытно-конструкторских работ (ОКР)).
На стадии ОКР происходит развитие конструкции и технологии, а по результа-
там испытаний образца принимается решение о внедрении и дальнейшем промыш-
ленном применении технологии (серийное производство). Как испытания, так и экс-
плуатация образцов являются своеобразной обратной связью, позволяющей совер-
шенствовать создаваемую (применяемую) технологию с учетом мнения потребителей.
Процесс улучшения характеристик образцов за счет модификации технологии на ос-
нове дополнительных нововведений со временем имеет тенденцию к насыщению, а
затем неизбежно наступает момент спада, старения и снятия с производства продук-
ции и замены устаревшей технологии.
Следовательно, технология как бы «отслеживает» все этапы и стадии выпускаемого
на ее основе продукта. При этом решающая роль в правильном выборе технологии при-
надлежит именно стадиям НИР и ОКР, где наряду с прямой задачей — созданием конк-
ретного образца продукции — закладываются перспективность технологии и ее потен-
циальные возможности существенно сжимать предпродажную стадию и уменьшать из-
держки и, стало быть, себестоимость продукции при сохранении достигнутого уровня
качества. Именно поэтому оценка и отбор технологий создания перспективных образ-
цов продукции должны быть особенно тщательными на этих стадиях разработки.
Что касается этапов изготовления и эксплуатации образцов продукции, то здесь
методы оценки технологий также необходимы как в плане их возможного совершен-
ствования и развития, так и своевременного определения момента прекращения про-
478
изводства и замены устаревших технологий на новые. В этом смысле можно говорить
о мониторинге применяемых технологий.
Таким образом, жизненный цикл любого продукта, по существу, включает две фазы.
В первой (дорыночной) происходит оценка, выбор (отсев) идей и выполняется весь необ-
ходимый круг научно-исследовательских и опытно-конструкторских работ (НИОКР).
В конце этой фазы затраты на реализацию идей лавинообразно растут, а сама новация
приобретает все более зримые формы, воплощаясь в патенте, прототипе, модели и т. д.
Вторая (рыночная) фаза характеризуется быстрым ростом объемов производства,
продаж и прибылей до определенного уровня «зрелости» нового продукта, после чего
начинается его старение, рост конкуренции со стороны продуктов-аналогов, сниже-
ние объемов продаж и в итоге снятие с производства и замена новым продуктом.
Технологии, будучи неразрывно связанными с получаемыми на их основе про-
дуктами, не только в значительной мере «копируют» жизненный цикл последних, но
и являются в современных условиях движущей силой конкуренции, занимая в миро-
вой торговле больший удельный вес, чем продажа готовой продукции.
Очевидно, оценить эффективность и состояние уже используемых технологий
можно как по показателям качества и спроса, относящимся к выпускаемой на их ос-
нове продукции, так и по аналогичным показателям, характеризующим сами техно-
логические процессы. Ситуация с выбором показателей усложняется по мере продви-
жения от готовой технологии к ранним этапам ее создания, несмотря на то, что общее
число показателей в этом процессе, казалось бы, должно уменьшаться.
На последних стадиях проектирования технического объекта (технический и ра-
бочий проекты) и постановки его на производство уже имеются количественные дан-
ные об основных технико-экономических показателях объекта, полученные в резуль-
тате испытаний опытных образцов. Соответствующие показатели для перспективных
и экспериментальных образцов-аналогов, поступление которых на мировой рынок
должно быть спрогнозировано на период выпуска продукции по разработанной тех-
нологии в этот период, как правило, не известны.
Еще более сложная ситуация с выбором показателей оценки эффективности тех-
нологий возникает на этапах, предшествующих этапу технического проектирования
объекта (этапы технического предложения или эскизного проектирования), по ре-
зультатам которых планируется выполнение ОКР.
Эта ситуация характеризуется тем, что объект разработки существует лишь как
идеальный образ создаваемого объекта и полностью отсутствуют данные о его техни-
ко-экономических показателях, за исключением тех, которые указаны в ТЗ в виде
прогнозных показателей, ожидаемых на момент завершения разработки. В этой ситу-
ации разработчик располагает набором отобранных технических решений (собствен-
ной разработки или заимствованных из источников информации), которые он пред-
полагает использовать в разрабатываемом объекте, и в лучшем случае — эскизными
проработками вариантов воплощения этих технических решений в объекте.
Неопределенность информации, достигающая на данных этапах оценки техно-
логий наибольшего значения, требует и наиболее тщательного обоснования и выбора
оценочных показателей, так как именно на этих этапах закладывается техническое
совершенство будущего объекта — основа его конкурентоспособности.
10.2. ОЦЕНКА ИЗОБРЕТЕНИЙ
На ранних этапах исследований и разработок, по существу, формируются и опре-
деляются те технические решения, которые должны быть заложены в объект разработ-
ки, чтобы обеспечить на дату завершения этапов его высокий технологический уро-
вень. Как показывает опыт, это достигается путем выбора наиболее эффективных тех-
479
нологических решений из числа известных или разработанных в процессе проведения
исследований, находящихся, как правило, на уровне открытий или изобретений, в
связи с чем оценка технологий на данных этапах их жизненного цикла тесно увязана с
проблемой оценки значимости предлагаемых технических решений (изобретений).
По этой причине показатели и критерии, используемые при оценке важности
и значимости изобретений, представляют несомненный практический интерес и для це-
лей рассматриваемой проблемы. Понимание необходимости совершенствования системы
оценки научно-технического и технико-экономического уровней завершенных исследо-
ваний и разработок, включая выбор показателей, критериев анализа и оценки изобрете-
ний, позволяющих уже на стадии подачи заявок выявлять наиболее крупные (приоритет-
ные) из них, имеющих важное народнохозяйственное значение, в общем, существовало и
декларировалось всегда. Так, в совместном документе 1974 года «Порядок оценки науч-
но-технической деятельности научно-исследовательских, проектно-конструкторских и
проектно-технологических организаций» ГКНТ и Госкомизобретений СССР определили
систему показателей, первым из которых является научно-технический уровень завер-
шенных исследований и разработок, характеризуемый, в свою очередь, новизной и перс-
пективностью разработок, их патентной защищенностью. Очевидно, что актуальность
этих главных показателей полностью сохраняется и в настоящее время.
При укрупненной классификации показателей оценки изобретений можно вы-
делить в качестве основных показатели научно-технической, экономической и соци-
альной значимости, которые, в свою очередь, могут быть охарактеризованы соответ-
ственно показателями научно-технического уровня, масштаба продаж (внедрения),
важности, величины экономического эффекта, затрат времени на внедрение изобре-
тения, стоимости отдельных этапов жизненного цикла изобретения, социальных тре-
бований (стандартов), степени удовлетворения потребностей населения и т. п.
Существующие в настоящее время критерии, по которым в России и других стра-
нах мира новое техническое решение официально признается изобретением, различ-
ны. В России, как известно, это мировая новизна, существенность отличий, положи-
тельный эффект предлагаемого в качестве изобретения технического решения по
сравнению с известными на дату приоритета решениями.
Законы других стран основным показателем патентоспособности также считают но-
визну. Кроме того, используются понятия: промышленная применимость изобретения,
изобретательский уровень, прогрессивность технического решения. К числу признаков
патентоспособности в США, Великобритании, Канаде и некоторых других странах анг-
лийской патентной системы отнесена полезность изобретения вместо промышленной
применимости. Понятие «полезность изобретения» в Великобритании подразумевает до-
стижение на практике технического эффекта от использования запатентованного техни-
ческого решения, а в США — работоспособность технического объекта.
В отечественной литературе многими авторами неоднократно рассматривались воп-
росы, связанные с разработкой критериев и методов оценки значимости изобретений.
Ниже рассмотрены наиболее детально разработанные критерии и методы оценки
изобретений и, как показали исследования, чаще других используемые в практике
оценки значимости изобретений и в научно-техническом прогнозировании.
Установлено, что наибольшее влияние на характеристику значимости изобрете-
ния оказывают следующие факторы:
новизна;
научная значимость;
сложность;
масштабность;
готовность к практической реализации изобретения.
480
Наиболее важно, чтобы в ранжированной последовательности были определены
подфакторы, формирующие основные пять факторов.
Для осуществления практической оценки значимости изобретения предлагается
матрица, в которой каждому изобретению соответствует набор координат, опреде-
ляющий его положение в л-мерном пространстве. В результате каждое изобретение,
подвергаемое оценке, может быть формализовано (закодировано) в виде набора (со-
вокупности) цифр, соответствующих числу факторов, формирующих интегральный
критерий.
Для оценки значимости изобретений предлагается использовать шесть критериев:
степень фундаментальности изобретений (пионерность);
многоаспекгность;
территориальную широту применения (страны мира);
актуальность;
экономичность;
применимость в различных отраслях техники.
Перед проведением конкретного анализа изобретений по указанным критериям
метод оценки предполагает построение логического классификатора понятий в виде
дерева (основание — корень которого составляет тема), позволяющего охватить около
9000 простых понятий.
Из описаний изобретений выбираются понятия и каждому из них присваивается
индекс в ступенчатой (логической) системе индексации. Первая цифра индекса обо-
значает класс понятия, к которому относится изобретение (ствол), вторая — подкласс
(сук) и т. д. Содержание каждого описания изобретения предлагается кодировать по
6—12 признакам классификатора понятий.
Изобретение оценивается по приведенным выше шести критериям таким обра-
зом, что, если, например, в кодовую ведомость включен индекс, соответствующий че-
рез рубрику стволу или суку, то изобретение может быть отнесено к пионерному и т. д.
Рассмотренные выше критерии и методика могут успешно использоваться для
выявления важных изобретений, правда, при несколько увеличенной трудоемкости
подготовительной работы, связанной с построением логических классификаторов
понятий по темам, к которым относятся предполагаемые для внедрения изобретения.
В то же время необходимо отметить отсутствие оценки изобретений по критерию
«время внедрения», характеризующему возможности реализации изобретения в ми-
нимальные сроки, что соответствует жестким требованиям по сокращению длитель-
ности цикла «исследование — производство» в современных рыночных условиях.
Не менее перспективным является метод оценки изобретений по л-балльной
системе с окончательной группировкой оценок в два критерия: коэффициент инже-
нерно-технической значимости и показатель рентабельности изобретения.
При оценке изобретений по этому методу конкретные значения коэффициентов
q и 0, представляющие соответственно сумму фактических и максимально возмож-
ных оценок изобретения и своим отношением определяющие коэффициент инже-
нерно-технической значимости (полноты) изобретения Т, предлагается определять по
единой для каждой отрасли техники общей (генеральной) матрице.
Основу применения этого метода составляет процедура сопоставления коэффи-
циента инженерно-технической значимости изобретения с определенными, пред-
ставленными в таблице, интервальными (нормативными) их значениями (1,0—0,75;
0,75—0,50; 0,50—0,30; 0,30—0,20), находящимися во взаимно однозначном соответст-
вии с категорией «перспективность изобретения» (соответственно очень перспектив-
ное, перспективное, малоперспективное, неперспективное).
481
Показатель рентабельности в данном методе определяется отношением стоимос-
ти производимых в настоящее время конструкций машин, технологических процес-
сов, включая накладные расходы и амортизационные отчисления, к стоимости про-
изводимых в будущем конструкций машин, технологических процессов, включая на-
кладные расходы и амортизационные отчисления, на базе внедряемого изобретения.
Необходимо отметить, что это понятие показателя рентабельности не соответст-
вует используемому в экономике показателю общей рентабельности, определяемому,
как известно, отношением балансовой прибыли к среднегодовой стоимости основ-
ных производственных фондов и нормируемых оборотных средств, т. е. отношением
абсолютного размера прибыли к использованным ресурсам.
Сравнительный анализ рассмотренных критериев и методов оценки важности
и значимости изобретений показывает, что имеются общие закономерности их разра-
ботки. Так, общее число критериев оценки колеблется от 2 до 6. В это число входят
как главные критерии оценки значимости изобретения: научная значимость; степень
фундаментальности изобретения (пионерность) и многоаспектность; инженерно-тех-
ническая значимость.
Указанное единство методического подхода в назначении главного критерия
оценки изобретений научно обосновывает использование всех рассмотренных крите-
риев и методов при оценке возможностей продажи и «внедрения» высокоэффектив-
ных изобретений в государственном масштабе. В силу имеющихся различий в назна-
чении других критериев оценки изобретений эффективность и сфера применения
каждого из предложенных методов различаются между собой.
103. ОТБОР ПРОЕКТОВ НИОКР
Рассмотрим теперь показатели, непосредственно используемые при отборе про-
ектов НИОКР. Среди этих показателей важное место занимает соотношение
«издержки — прибыль».
Проект, который обеспечивает максимальную чистую денежную прибыль орга-
низации, выбирают для дальнейшего финансирования и разработки. Время, в тече-
ние которого идут издержки, меняется от проекта к проекту так же, как и период, ког-
да ожидается прибыль.
Расчеты чистой сегодняшней (дисконтированной) стоимости основываются на
понятий изменения стоимости денег во времени, которое исходит из того, что буду-
щие издержки менее обременительны, чем издержки в настоящем. Аналогично при-
были, полученные в будущем, менее привлекательны, чем полученные в настоящем.
Большинство людей ценит деньги, исходя из альтернативного использования, по ко-
торому их можно увеличить. Согласно этому, в большинстве случаев временная сто-
имость денег, примененная для оценки исследовательских проектов, равняется при-
близительно норме процента, который может быть заработан от аналогичных инвес-
тиций, включая ту же степень риска.
Наряду с рассмотренным показателем используется и целый ряд других факто-
ров, число которых может быть шесть-восемь, а иногда достигает и нескольких десят-
ков. Для первичного отбора проектов НИОКР предлагается так называемый потен-
циал нововведения, который определяется как сумма семи факторов, имеющих зара-
нее определенный удельный вес (в баллах):
• известность проекта внутри научной организации — 30;
• научная и техническая компетентность сотрудников — 20;
• наличие защитника проекта среди руководства — 15;
• возможности сбыта на рынке — 15;
482
• технические и научные возможности организации — 10;
• давление конкуренции — 5;
• время, необходимое для осуществления проекта, — 5.
Каждый фактор оценивается управляющим НИОКР исходя из личного опыта.
Для прохождения на первичном этапе отбора проект должен набрать по меньшей ме-
ре 70 баллов.
При отборе проектов НИОКР в одной из крупных научно-исследовательских ла-
бораторий ВВС США используются, например, следующие критерии отбора:
• соотношение «издержки — прибыль». Этот критерий включает в себя издержки,
необходимые для завершения проекта, и выгоды, которые должны быть получе-
ны ВВС в результате осуществления проекта;
• технические достоинства. Критерий сводится к тому, в какой степени научный
проект обеспечивает новые или лучшие технические возможности для ВВС;
• доступность ресурсов. Критерий включает в себя доступность кадров, оборудова-
ния и других ресурсов, необходимых для завершения проекта;
• вероятность успеха. Этот критерий оценивает вероятность того, что предложен-
ный проект достигнет технического успеха в заданное время и при ограниченных
ресурсах;
• необходимое время для завершения исследовательского проекта. При прочих
равных условиях короткие проекты предпочтительнее долгосрочных. Особо дол-
госрочные проекты почти не имеют шансов на то, чтобы их отобрали;
• потребности ВВС. Этот критерий показывает, насколько остро в ВВС существует
потребность в результатах проекта.
Таким образом, проанализированный перечень показателей и критериев всесто-
ронне характеризует предлагаемые технические решения (изобретения) и может быть
использован в качестве основы при выборе и формировании показателей и критериев
оценки эффективности технологий на ранних этапах их создания (НИОКР).
10.4. ПОКАЗАТЕЛИ ТЕХНИЧЕСКИХ СИСТЕМ
Изучение работ отечественных и зарубежных ученых, посвященных методам
анализа и определения оптимальных параметров машин, показывает, что они опира-
ются на системный подход, методы оценки эффективности, функционально-стоимо-
стный анализ и методы прогнозирования. Наиболее эффективны среди них методы
экспертных оценок и статистические методы корреляции и регрессии, а применение
информационных технологий облегчает анализ и переработку значительных масси-
вов информации.
Эволюционный характер развития техники можно представить в виде некоторо-
го ступенчатого процесса. Появление принципа действия, основанного на использо-
вании новых данных фундаментальных исследований, дает толчок к созданию нового
класса технических систем (ТС), имеющих существенный (скачкообразный) прирост
технической и экономической эффективности. Затем следует период совершенство-
вания этих ТС и разработка машин, отличающихся новыми конструкторско-техноло-
гическими решениями с использованием новых материалов, технологий. Объектив-
ный процесс развития ТС приводит к исчерпыванию возможностей дальнейшего уве-
личения эффективности на базе данного принципа действия, но продолжается
процесс экстенсивного развития и создания параметрических рядов, т. е. характери-
зуемый незначительным приростом параметров на базе существующих конструктор-
ско-технологических решений.
483
Таким образом, процесс развития ТС можно разделить на три качественно отли-
чающихся направления.
1. Создание нового класса ТС, использующих новый принцип действия. Появле-
ние новых поколений машин со значительным приростом эффективности.
2. Создание новых видов ТС с использованием данного принципа, отличающих-
ся конструкторско-технологическими решениями (разработка машин со средним
приростом эффективности).
3. Разработка ТС, отличающихся незначительным изменением конструкции
и параметров, например параметрических рядов (создание ТС с малым приростом
эффективности).
Наиболее распространено третье направление развития ТС как следствие расши-
ряющегося (в смысле масштабов проектирования, производства и использования)
развития ТС от первой к третьей группе. Меньшим объемом характеризуется созда-
ние ТС второй группы. И лишь, как правило, открытие и использование новых фун-
даментальных явлений и законов приводит к изменениям первой группы.
В создании новой техники участвуют две стороны — изготовитель и потребитель,
заказчик. Интересы этих двух сторон при разработке ТС должны учитываться и нахо-
диться в определенном соотношении, а возможности изготовителя выступают в роли
ограничений, которые можно снимать или ослаблять, совершенствуя существующие
и внедряя новые производственные технологии.
Совокупность качественных и стоимостных характеристик изделия, обеспечи-
вающая удовлетворение конкретной потребности покупателя, определяют его конку-
рентоспособность. Конкурентоспособным является тот товар, комплекс потребитель-
ских и стоимостных свойств которого обеспечивает ему коммерческий успех. Прак-
тика определения конкурентоспособности товара основывается на сравнительном
анализе его совокупных характеристик с товарами — конкурентами по степени удов-
летворения конкретных потребностей и по цене потребления.
Точно так же посредством показателей, характеризующих технический уровень,
качество и стоимость изготовления и эксплуатации, совершенство конструкции
машины можно оценить только в сравнении с технико-экономическими показателя-
ми (ТЭП) лучших отечественных и зарубежных образцов техники аналогичного на-
значения.
Определение оптимальных значений ТЭП проектируемого изделия требует изу-
чения информации о результатах работы подобных машин в эксплуатации. Необхо-
дим также прогноз условий эксплуатации, надежности и технически достижимого
уровня экологических, эргономических и эстетических показателей.
Исходя из изложенного, для получения оптимальных ТЭП необходимы следую-
щие методики: оценки уровня качества заменяемого (базового) изделия; анализа ТЭП
базового изделия с позиций соответствия мировому техническому уровню и требова-
ниям потребителя; выбора направлений совершенствования или разработки нового
изделия; оптимизации ТЭП нового изделия.
Необходимо отметить, что к показателям относятся и такие свойства машин, как
цвет, форма и т. п., которые могут быть выражены, например, числом баллов при экс-
пертной оценке. В дальнейшем под системой ТЭП будем подразумевать совокупность
размерных и безразмерных количественных показателей, подчиняющихся опреде-
ленным принципам и правилам формирования.
Разумеется, состав ТЭП будет зависеть от отрасли производства (самолетострое-
ние, двигателестроение, станкостроение и т. д.), объекта проектирования (самолет,
двигатель, станок с ЧПУ); вида разработки и соответственно ТС (принципиально но-
484
вое изделие, модернизация существующего и т. д.); комплексности проектируемого
объекта (система машин, отдельная машина, агрегат, блок, сборочная единица).
Обобщая изложенное выше, приходим к выводу, что основой систематизации со-
вокупности показателей должна быть иерархия. Совокупность показателей, входящих
в иерархию, определяется целью проводимого исследования. На ее вершине находит-
ся показатель, характеризующий потребительскую стоимость, создаваемую техноло-
гическим процессом. На нижних уровнях иерархии расположены единичные показа-
тели, как правило, имеющие размерность. Они могут быть непосредственно измере-
ны или наблюдаемы на практике.
Для построения иерархической структуры ТЭП машин можно использовать при-
знаки построения классификационных схем, приведенные ниже:
1) достаточная полнота охвата;
2) единство классификационного признака на каждом уровне членения;
3) непересекаемость разделов иерархической структуры;
4) открытость структуры (возможность дополнения другими показателями).
Добавим к этим признакам требование ограниченного объема ТЭП, так как
слишком большое их число затрудняет работу проектировщиков в процессе поиска
оптимальных решений.
10.5. ОБОБЩЕННЫЕ КРИТЕРИИ И ПОДКРИТЕРИИ
На стадии НИОКР, когда собственно и происходит зарождение и становление
технологии, по существу, отбираются концепции, идеи и технические решения, кото-
рые должны быть положены в основу разрабатываемого образца продукции, сущест-
вующего на данной стадии в виде идеального образа будущего объекта, чтобы обеспе-
чить к концу разработки его высокое техническое совершенство. Как правило, чтобы
достичь такого качества продукции, в первую очередь, должны использоваться прин-
ципиально новые технические решения, основанные на последних достижениях фун-
даментальной науки и прикладных поисковых исследований и находящиеся на уров-
не открытий или изобретений.
Таким образом, основу первого и, возможно, главного критерия отбора техноло-
гий на стадии НИОКР должен составлять критерий научно-технической значимости.
В соответствии с принципом системного анализа альтернатив при разработке и созда-
нии продукции в рыночных условиях в состав этого критерия необходимо включить
также показатели, отражающие такие аспекты предлагаемой к разработке технологии,
как преимущества по сравнению с известными технологиями-аналогами (отечествен-
ными и зарубежными), применимость во многих отраслях промышленности, перс-
пективность и вероятность технического успеха.
Итак, в качестве наиболее важного при отборе технологий, разрабатываемых
в рамках «Программы», предлагается использовать критерий научно-технической зна-
чимости, включающий, в свою очередь, показатели (подкритерии):
• новизны;
• степени фундаментальности;
• преимуществ по сравнению с известными технологиями-аналогами;
• патентоспособности;
• применимости во многих отраслях промышленности;
• перспективности;
• вероятности технического успеха.
485
Структура этих подкритериев, на наш взгляд, наиболее полно (всесторонне) от-
ражает существо критерия научно-технической значимости, при этом наибольшее
предпочтение в соответствии с существующими в мире подходами к оценке изобрете-
ний или открытий отдано новизне предлагаемого технического решения. В свою оче-
редь, новизна как бы «вытекает» из результатов новых фундаментальных или поиско-
вых исследований, которые либо не использовались еще для создания новых техноло-
гий, либо применялись лишь частично.
Степень фундаментальности, второй по значимости подкритерий в рассматри-
ваемой структуре, призван подтвердить происхождение (фундамент) новизны.
Той же цели, что второй подкритерий, служат два следующих (третий и четвер-
тый) подкритерия — преимуществ предлагаемого технического решения по сравне-
нию с уже известными, воплощенными в «работающих» технологиях-аналогах, и его
патентоспособность.
Важно, что новое техническое решение основано на результатах фундаменталь-
ных НИР, но не менее важно и то, какие конкретные преимущества оно имеет перед
известными технологиями-аналогами (третий приоритет), и раз оно действительно
новое, то, значит, и патентоспособно (четвертый приоритет).
Аналогично, немаловажную роль играют многопрофильность использования
предлагаемого решения (применимость в различных отраслях промышленности)
и его перспективность в плане развития новых наукоемких и сверхнаукоемких техно-
логических направлений, в связи с чем соответствующим подкритериям установлены
два последующих (пятое и шестое) места по приоритетности.
Наконец, последнее (седьмое) место по важности в структуре критерия науч-
но-технической значимости занимает подкритерий «вероятность технического успе-
ха». Его наличие здесь позволяет произвести предварительную оценку вероятности
успешного исхода технологического проекта НИОКР, основываясь лишь на содержа-
тельной информации, заключенной в первых шести подкритериях, а затем уточнить
ее с использованием всех данных о проекте.
Разумеется, предпринятая попытка обоснования структуры и приоритетности
подкритериев главного критерия оценки проектов на стадии НИОКР не претендует
на какую-либо «незыблемость». И самую структуру, и приоритеты под критериев сле-
дует рассматривать в качестве первого приближения, которое может быть уточнено и
дополнено в результате обоснованного анализа высококвалифицированных (компе-
тентных) экспертов в данной предметной области.
Согласованность же мнений экспертов можно оценить, воспользовавшись новой
методикой, которая учитывает уровень компетентности экспертов. Это же замечание в
равной мере относится и ко всем остальным критериям и подкритериям, используе-
мым для оценок технологических проектов на различных стадиях их жизненного цикла.
Очевидно, что одного (даже главного) критерия оценки проектов НИОКР еще
недостаточно, чтобы сделать заключение о перспективности того или иного проекта
из представленных на конкурс. Необходимо привлечь и другие и уже потому не менее
важные обобщенные критерии, характеризующие рассматриваемые проекты с дру-
гих, помимо научно-технической, сторон.
Если обобщить данные по критериям (показателям, факторам), которые обычно
на практике используются для отбора проектов НИОКР, то можно заметить, что од-
ним из наиболее приоритетных является критерий «издержки — прибыль». Именно
этот экономический критерий и предлагается использовать в качестве второго по
приоритетности при оценках технологических проектов на стадии НИОКР.
Что касается самих показателей экономической эффективности технологий, рас-
смотренных ранее, то на стадии НИОКР, когда имеется еще достаточно большая сте-
486
пень неопределенности исходной информации, достаточно ограничиться оценками
всего двух показателей: срока окупаемости инвестиций и простой нормы чистоты
прибыли.
Эти оценки необходимо произвести для возможных случаев реализации продук-
ции, изготовленной с применением рассматриваемой технологии, на внешнем
и внутреннем рынках.
Из двух рассматриваемых показателей (подкритериев) предпочтение отдано
«сроку окупаемости инвестиций» ввиду того, что в первую очередь важно, чтобы сред-
ства, потраченные на реализацию проекта, по крайней мере, были возвращены
в более или менее обозримой перспективе (чем быстрее, тем лучше). А еще лучше, ес-
ли бы инвестиции вернулись с прибавленной стоимостью (вторая очередь), измеряе-
мой отношением чистой прибыли к инвестиционным затратам за определенный про-
межуток времени после начала реализации технологического проекта.
Жизнеспособность любой технологии проверяется после выведения произведен-
ной на ее основе продукции на рынок, к потребителю, которые и дают окончательное
заключение об эффективности технологий. Этот момент является очень важным (ре-
шающим) в жизненном цикле технологий, и поэтому уже на стадии НИОКР необходи-
мо уделить этому — третьему по приоритетности — «рыночному критерию» пристальное
внимание и спрогнозировать некоторые характеризующие рынок показатели. В число
этих показателей на стадии НИОКР можно включить, например, такие, как:
• наличие спроса на продукцию и возможные потребители;
• размер потенциального рынка;
• возможности сбыта продукции.
Среди этих трех подкритериев приоритет имеет «наличие спроса на продукцию и
возможные потребители», так как это обстоятельство имеет важнейшую (решающую)
роль в плане успешной реализации проекта и должно подтверждаться изучением
рынка (маркетинговыми исследованиями) и определением наиболее вероятных по-
требителей. Далее важно оценить размер потенциального рынка (второе место), а так-
же реальные возможности сбыта продукции (третий приоритет).
Экологичность и безопасность технологических процессов и произведенной при
помощи их продукции в настоящее время приобретают исключительно важное значе-
ние, причем имеет место тенденция по ужесточению соответствующих требований
в международных стандартах. При оценке технологий уже на стадии НИОКР эти фак-
торы должны быть представлены в виде четвертого обобщенного критерия «экологич-
ности и безопасности», включающего в свой состав показатели:
• возможное вредное воздействие техпроцесса и продукции на человека и окру-
жающую среду;
• степень безопасности работ;
• затраты, необходимые на обеспечение экологичности и безопасности техпроцес-
са и продукции.
В данной группе подкритериев, представленной в порядке уменьшения их значи-
мости, факту присутствия (отсутствия) вредного воздействия техпроцесса и продук-
ции на человека и окружающую среду придается первостепенное внимание. При от-
сутствии вредного воздействия следующим важным моментом, на который, как пред-
ставляется, необходимо обратить пристальное внимание, является вопрос о том, в
какой мере безопасны работы по изготовлению и эксплуатации продукции. Наконец,
в случае наличия хотя бы одного (или тем более двух) из перечисленных факторов
важно знать затраты средств, которые могут потребоваться для их уменьшения или
нейтрализации (третий приоритет).
487
Заключительной фазой оценки технологий на стадии НИОКР должен стать ана-
лиз реализуемости проекта разработки конкретной технологии. Соответствующий
критерий при этом может включать следующие подкритерии:
• доступность всех видов ресурсов (финансовых, производственных, трудовых,
сырья, материалов, энергоносителей), необходимых для реализации техпроцесса;
• готовность к практической реализации;
• научные и технические возможности организации (предприятия, фирмы) выпол-
нить проект.
Очевидно, что доступность всех видов ресурсов является главным (решающим)
условием реализации того или иного технологического проекта, в силу чего данный
подкритерий поставлен на первое место. Большое значение, несомненно, имеют так-
же имеющийся у предприятия (фирмы) производственно-технологический задел
(второй приоритет) и научные и технические возможности выполнить проект своими
силами или в кооперации с исполнителями-партнерами (третий приоритет).
Результаты изложенного подхода к выбору обобщенных критериев оценки тех-
нологий на стадии НИОКР сведены в итоговую таблицу 10.1.
Таким образом, на стадии НИОКР оценку технологических проектов предлага-
ется осуществлять при помощи пяти обобщенных критериев и 18 подкритериев, про-
нумерованных в порядке последовательного уменьшения их значимости.
Таблица 10.1
Критерии и показатели оценки технологий на стадии НИОКР
Критерии Показатели
1. Научно-техническая значимость, Кнтз 1.1. Новизна 1.2. Степень фундаментальности 1.3. Преимущества по сравнению с аналогами 1.4. Патентоспособность 1.5. Применимость во многих отраслях (системах оружия) 1.6. Перспективность 1.7. Вероятность технического успеха
2. Экономическая эффективность, Кээ 2.1. Срок окупаемости инвестиций 2.2. Простая норма чистой прибыли
3. Рыночный, Кр 3.1. Наличие спроса на продукцию и по- требители 3.2. Размер потенциального рынка 3.3. Возможности сбыта продукции
4. Экологичность и безопасность, Кэб 4.1. Возможное вредное воздействие тех- процесса и продукции 4.2. Степень безопасности работ 4.3. Затраты на обеспечение экологичнос- ти и безопасности
5. Реализуемость проекта, КрП 5.1. Доступность всех видов ресурсов 5.2. Готовность к практической реализа- ции 5.3. Научные и технические возможности организации выполнить проект
488
10.6. РАЗРАБОТКА МЕТОДИКИ СРАВНИТЕЛЬНОЙ ЭКСПЕРТНОЙ
ОЦЕНКИ ТЕХНОЛОГИЧЕСКИХ ПРОЕКТОВ
10.6.1. Применение экспертно-аналитических методов
для оценки и отбора перспективных технологий
В связи с отсутствием удовлетворительных количественных методов оценки тех-
нологий, в которых объективное всегда превалирует над субъективным, на практике
преимущественное развитие получили различные экспертные методы анализа. Экс-
пертные оценки обычно получают путем статистической обработки результатов опро-
са группы или нескольких групп экспертов. Существуют различные методики опроса,
смысл которых в большинстве случаев сводится к следующему:
• составляется таблица экспертного опроса, которую должны заполнить эксперты,
и пояснения к ней, указывающие, как следует заполнять таблицу и какие при
этом учитывать факторы;
• выбирается состав экспертов из числа специалистов, имеющих большой опыт
разработки и (или) использования аналогичных или близких по характеру техно-
логий. При этом важно обеспечить независимость высказываний экспертов;
• опрашиваемые эксперты заполняют таблицу опроса, например, проставляют
оценки в баллах по стобалльной шкале каждой предложенной для оценки техно-
логии;
• производится статистическая обработка данных опроса, имеющая целью:
а) определить средние статистические значения оценок, например, средние бал-
лы, присваиваемые каждой оцениваемой технологии;
б) определить степень надежности полученных оценок.
При этом о надежности оценок судят по таким статистическим характеристикам,
которые описывают разброс оценок отдельных экспертов и групп экспертов или, что
эквивалентно, степень согласованности (совпадения) оценок.
Пусть эксперты 1,2, ..., N должны дать оценки технологиям Р2,..., Pz,...,
Рт. Тогда разброс оценок, даваемых N экспертами технологии Pz (продукции 5Z весо-
вому коэффициенту с, и т. п.) характеризуется величиной вариации'.
vi= > (10.1)
где jllz и о? — среднее значение и дисперсия оценки, данной технологии Pz (усредне-
ние производится по Nрешениям экспертов).
Степень согласованности оценок, даваемых по совокупности всех оцениваемых
технологий, характеризуют так называемым коэффициентом конкордации (согласия) W
и соответствующим уровнем значимости а. Здесь 0< W < 1, а а есть вероятность того,
что согласованность мнений (оценок), характеризуемая данным коэффициентом
конкордации W, есть случайное совпадение. Чем больше Wи чем меньше а, тем более
согласованными (надежными) являются оценки. Обычно согласованность считают
удовлетворительной, если W> 0,5; а < 0,01, и хорошей, если 0,7; а < 0,01.
Степень согласованности решений двух групп (I и II) экспертов характеризуется
коэффициентом ранговой корреляции р (0 < р < 1) — чем ближе р к единице, тем более
согласованы решения. Обычно согласованность считается удовлетворительной при
р > 0,85...0,9 и хорошей при р > 0,95.
Для вычисления значений W, а и р приходится предварительно находить ранги
Rx,..., Ri9..., Rm соответствующих технологий ..., Pz,..., Рт.
489
В математической статистике ранжированием называется присвоение элементам
а, Ь, с, d некоторого множества порядковых номеров 1, 2, 3, 4, ... в зависимости
от убывания (возрастания) какого-либо количественного или качественного призна-
ка; при этом присваиваемый элементу порядковый номер называется рангом этого
элемента.
Если ранжирование элементов некоторого множества не может быть произведе-
но непосредственно по количественному признаку, то это ранжирование может быть
произведено по качественному признаку («лучше» — «хуже») или оно может быть
произведено в два этапа. На первом этапе каждому элементу экспертом дается оценка
в баллах, например, по стобалльной шкале — чем «лучше» оцениваемый элемент, тем
выше его оценка в баллах. На втором этапе происходит ранжирование элементов по
степени убывания присвоенных баллов — первый ранг присваивается элементу, полу-
чившему наивысший балл, второй ранг — элементу, имеющему следующий по вели-
чине балл, и т. д.
Если несколько сравниваемых элементов имеют одинаковый количественный
(или качественный) признак, используемый для ранжирования, то им присваивается
одинаковый ранг, равный среднему арифметическому.
Среди групповых методов экспертизы, разновидностей которых существует мно-
жество, следует выделить метод Дельфи, который непосредственно использовался
при определении национальных технологических приоритетов в Японии, Германии,
Великобритании, США и России.
В России этот метод использовался также при оценках технологий на более низких
уровнях иерархии (ведомство, предприятие). Так, на основе обобщающего экспертного
анализа технических проблем с учетом «среза мнений» конструкторов, исследователей,
технологов, представителей заказывающих и эксплуатирующих организаций обоснова-
ны перспективные научно-технические направления и разработаны рекомендации по
внедрению новых технологий и материалов, обеспечивающих опережающее создание
новых поколений специальных транспортных средств, снижение их шума на 10...20 дБ.
Всего к опросу было привлечено 112 специалистов. Такой подход к экспертизе техниче-
ских проблем практикуется американскими и японскими специалистами.
Широкомасштабные экспертные оценки критических технологий федерального
уровня были выполнены в 1998 году Центром исследований и статистики науки Мин-
науки России и РАН. В процессе экспертизы с использованием взаимосвязанной
трехуровневой иерархической структуры технологий (7 приоритетных направлений
науки и техники, 70 критических технологий федерального уровня и 258 детализиро-
ванных технологий, входящих составной частью в число указанных 70 и являвшихся
непосредственными объектами экспертизы), опрашивалось около 1500 экспертов, в
числе которых были ученые и ведущие специалисты из академического сектора нау-
ки, государственных научных центров, ведущих отраслевых НИИ, КБ и промышлен-
ных предприятий, эксперты Российского фонда фундаментальных исследований,
Российского фонда технологического развития и др.
Система основных показателей (критериев), по которым оценивались эти
258 технологий, включала:
1) актуальность (значимость, полезность) каждой технологии со следующих то-
чек зрения:
а) экономический прогресс (повышение эффективности экономики, создание
продукции и услуг, конкурентоспособных на внешнем рынке);
б) социальное развитие (повышение уровня и качества жизни населения);
в) обеспечение обороноспособности страны;
г) улучшение экологической обстановки;
490
2) практическую значимость конечных результатов реализации технологий со сле-
дующих точек зрения:
а) возможности выхода на мировой рынок и развития внутреннего рынка;
б) целесообразность использования других (подобных или замещающих) техно-
логий или переориентации на импорт готовой продукции.
Для проведения экспертизы была разработана единая форма анкеты для всех се-
ми приоритетных направлений науки и техники. При расчете оценок по всем исполь-
зуемым показателям в расчетную базу по каждой технологии включались лишь ответы
экспертов, причисливших себя по компетенции к одному из трех уровней: работаю в
данной области; работаю в смежной области; имею общие представления. По ряду
показателей рассчитывались балльные оценки (по пятибалльной шкале), по другим
показателям в качестве оценок вычислялись доли экспертов, выбравших соответст-
вующий вариант ответа. По каждому показателю рассчитывался рейтинг по рангово-
му критерию. Технологии были ранжированы по каждому из показателей, для набора
основных показателей был рассчитан интегральный рейтинг. Для каждой из 70 крити-
ческих технологий федерального уровня произведены экспертные оценки основных
анализируемых показателей и рейтинги по этим показателям.
В целом, несмотря на масштабность работы, большие затраты на ее проведение
и определенные положительные результаты (определены 2 критические технологии
федерального уровня, превышающие лучшие зарубежные аналоги, 17 технологий, ко-
торые соответствуют мировому уровню, и установлены 15 лучших технологий по ин-
тегральному рейтингу), итоги экспертизы оказались в значительной мере противоре-
чивыми. В частности, исследование показало низкую корреляцию между уровнем
отечественных разработок отдельных технологий и их актуальностью и практической
значимостью. Например, эксперты, отметившие высокую актуальность критической
технологии «Информационно-коммуникационные системы» (высшие рейтинги по
актуальности с точки зрения экономического прогресса, социального развития
и обороноспособности), отводят ей место в третьем-четвертом десятке по перспекти-
вам выхода на мировой рынок и соотношению с лучшими зарубежными аналогами.
А всего лишь по шести из 70 критических технологий более 40% экспертов отметили
потенциальные возможности выхода России на мировой рынок. В перечень 15 луч-
ших из 258 технологий по интегральному рейтингу вошло шесть технологий из на-
правления «Топливо и энергетика», четыре из «Информационных технологий
и электроники» и лишь по одному из остальных пяти направлений (производственные
технологии; новые материалы и химические продукты; технологии живых систем;
транспорт; экология и рациональное природопользование).
Отмеченные результаты обусловливают дилемму: что поддерживать государству
в первую очередь — те технологические области, где Россия является мировым лиде-
ром, или технологии, в которых имеет место отставание от зарубежных аналогов, но
которые жизненно необходимы для отечественной экономики. Решение дилеммы да-
леко не очевидно и требует серьезного экономического анализа.
Существо метода Дельфи в его современном варианте заключается в том, что для
лучшего использования объединенного мнения групп, вопросники направляются
участникам-экспертам в несколько этапов. На каждом новом этапе экспертам переда-
ется информация, полученная по итогам проведения предыдущего этапа. Результатом
таких повторяющихся экспертных опросов является согласованное мнение участни-
ков-экспертов по существу проблемы. На каждом новом этапе опроса в качестве «ин-
формации для размышления» участникам предоставляются не только вопросы, кото-
рые ставились на предыдущем этапе, но и сведения о степени согласия между участ-
никами-экспертами. В результате проведения нескольких этапов опроса среди его
491
участников достигается высокая степень согласованности, появляется конвергенция
оценок.
Одно из преимуществ метода Дельфи состоит в анонимности участвующих, что
позволяет изменять мнение без «потери лица». К достоинствам следует также отнести
наличие обратной связи от этапа к этапу и положительный эффект коллегиальности.
В чем находит свое выражение обратная связь — уже отмечалось. Механизм обеспече-
ния анонимности также довольно прост: участникам-экспертам передаются опрос-
ные листы, которые затем «обобщаются» без требования их персонификации. Эф-
фект коллегиальности достигается ввиду вынесения последующих ответов с учетом
мнения коллег-экспертов.
Обычно проводится 2—4 этапа опроса, поскольку, как показала практика, этого
достаточно для «стабилизации» оценок экспертов, после чего проведение новых эта-
пов опроса не имеет смысла.
Как правило, большинство корректировок оценок вносится между первым
и вторым кругами. Лишь в немногих исследованиях точность оценки была улучшена
после второго круга. В тех случаях, когда применялся третий и даже четвертый круг,
часто бывало, что «пресловутые аутсайдеры» уже не участвовали в процессе, а другие
изменяли своему мнению только для того, чтобы положить конец продолжающимся
опросам. Поскольку большое количество кругов связано с существенными затратами,
можно сделать вывод, что оптимальное число кругов — два.
Критический анализ опыта использования метода Дельфи и соответствующей
литературы по данному вопросу свидетельствует о том, что при оценке перспектив-
ности его применения необходимо исключить крайние оценки: либо слишком хоро-
шие, либо слишком плохие.
Важное значение при оценке технологий по методу Дельфи имеет правильно ор-
ганизованный подбор экспертов.
Необходимо выделить отдельные подходы и принципы в подборе экспертов, ко-
торыми требуется руководствоваться, в частности, при решении задачи отбора крити-
ческих технологий:
• должно быть обеспечено представительство исследователей и разработчиков;
специалистов, занимающихся внедрением технологий, их распространением;
потребителей;
• эксперты должны обладать достаточно широкой специализацией, так как межот-
раслевой характер технологий является важнейшей отличительной чертой с точ-
ки зрения их критичности;
• важно, чтобы эксперты хорошо представляли себе состояние соответствующих
исследований и разработок, перспективы внедрения и распространения техноло-
гий не только в России, но и за рубежом;
• существенное значение имеет способность участников экспертной оценки про-
гнозировать временной срок практической реализации тех или иных технологий;
• должна быть обеспечена возможность привлечения к участию в экспертизе до-
статочно большого количества участников.
Очевидно, что выполнение перечисленных требований к экспертам в полной ме-
ре не всегда возможно. Кроме того, использование экспертов всегда накладывает на
результат отпечаток субъективизма, не говоря о довольно значительных затратах
средств, которых требует проведение экспертизы с участием большого количества
экспертов. Разработка экономичных количественных методов оценки технологий яв-
ляется актуальной задачей, а их использование должно существенно повысить объек-
тивность в принятии решений по технологическим приоритетам и формированию
эффективной технологической политики.
492
10.6.2. Подход к анализу экспертных оценок
на основе теории важности критериев
Экспертно-аналитические методы получили в последние годы существенное раз-
витие на основе принципиально нового подхода к анализу экспертных оценок при
помощи теории важности критериев.
Как отмечалось, при решении практических задач обработки экспертных оценок
возникает сложность с обоснованным выбором метода их анализа. Для каждого вида
экспертных оценок существует, как правило, несколько методов их агрегирования, но
научно обоснованных рекомендаций по выбору одного метода из многих имеющихся
нет. Каждый из методов имеет свои достоинства и недостатки, в силу чего пользова-
тель выбирает «лучший», исходя из личного вкуса и опыта, с учетом наличия подходя-
щих компьютерных программ. Но разные методы очень часто приводят к несовпа-
дающим результатам, а в итоге оказываются разными и рекомендации. Преодолеть
данное противоречие позволяет вновь разработанный для решения задач принятия
решений при многих критериях рассматриваемый ниже подход.
Основу подхода составляет допущение не о полном, а лишь о частичном, поэтапно
пополняемом агрегировании значений экспертных оценок, при этом вначале использу-
ются более простые и потому весьма надежные решающие правила и лишь затем, при
необходимости, привлекаются правила более сложные, но менее надежные. Что осо-
бенно важно, в рамках этого подхода возможно корректное использование как качест-
венных, так и количественных оценок компетентности экспертов, поскольку очевидно,
что далеко не все эксперты «равнокомпетентны» или «равнонекомпетентны», хотя этот
фактор, как правило, не учитывается при решении практических задач экспертизы.
Приведем основные результаты этого подхода применительно к одному из наи-
более распространенных видов экспертных оценок — ранжировкам. Как отмечалось,
полной ранжировкой называется ряд объектов, упорядоченный по убыванию пред-
почтительности. Если в ранжировке имеются равноценные объекты, то она называет-
ся нестрогой, а при отсутствии таковых — строгой. Рангом объекта называется его но-
мер в строгой ранжировке или среднее арифметическое мест его и всех равноценных
ему объектов в нестрогой ранжировке. Например, если эксперт, сравнивая четыре
объекта, указал, что наиболее предпочтителен объект О3, далее идут одинаковые по
предпочтительности объекты О2 и О4, а наименее предпочтителен объект Ои то тем
самым он построил нестрогую ранжировку (О3, О2—О4, 00. Ранг объекта О3 равен 1,
каждый из объектов О2 и О4 имеет ранг (2 + 3)/2 = 2,5, а ранг объекта Oj равен 4. По-
нятно, что вектор рангов (4; 2,5; 1; 2,5) восстанавливает исходную ранжировку.
Пусть т экспертов ранжировали п объектов. Полученные значения экспертных
оценок сведем в матрицу:
Хц...Х1Л,
хт1...хти, (10-2)
ml тп’ у 7
в которой первая строка представляет вектор объектов в ранжировке первого экспер-
та, вторая — второго и т. д. В общем, х/7 — ранг объекта Оу в ранжировке эксперта Э;.
Порядок анализа экспертных оценок на первом этапе включает определение со-
гласованности суждений экспертов. Для оценок согласованности вычисляется вы-
бранный критерий согласия, например, статистика Фридмана Л2:
12 п т
= ^Г+Т) х ( W - 3/«(« + 1). (10.3)
j = 1 J = 1
493
При этом в качестве нулевой выдвигается гипотеза, согласно которой каждый
эксперт указывает оценки случайным образом: появление любой из п\ возможных
ранжировок равновероятно. Следовательно, на этом этапе проблемы учета компе-
тентности экспертов не возникает: все они по нулевой гипотезе «равнонекомпетент-
ны». Если для самого высокого уровня значимости а = 0,01 вычисленное по (10.3)
значение Х2абл > %0201 , где %0202 берется из соответствующей таблицы работы [4], то
нулевая гипотеза отвергается, после чего находится значение коэффициента конкор-
дации Кендэла
^=^н2абл/[/п(«-1)]. (10.4)
Если полученное значение Wдостаточно близко к своему возможному максиму-
му (единице), то согласованность экспертной группы принимается достаточной,
и можно приступать к агрегированию исходных ранжировок в одну обобщенную
(групповую), не требуя, однако, чтобы она сразу была полной, т. е. допуская непол-
ную упорядоченность объектов.
Частичные ранжировки удобно представлять при помощи бинарных отношений
нестрогого предпочтения R, строгого предпочтения Р и безразличия Г.
Оу R Ок означает, что объект Оу не менее предпочтителен, чем объект Ок (и потому
в частичной ранжировке Оу стоит не дальше, чем Ол);
Оу Р Ок означает, что объект Оу предпочтительнее объекта Ок (и потому в частич-
ной ранжировке Оу стоит перед Ол);
Оу / Ок означает, что объекты Оу и Ок одинаковы по предпочтительности (в час-
тичной ранжировке стоят вместе, и ранги у них одинаковы).
Каждый объект характеризуется вектором рангов х' = (х1у, ..., хшу), выставленным
ему экспертами. Этот вектор представлен в матрице (10.2) у-м столбцом. Самое прос-
тое и надежное решающее правило вводит отношение Парето RQ:
OjRQOk<—>Xij<xik,i= 1,...,/и, (10.5)
при этом, если все равенства нестрогие, то в (10.5) выполняются как равенства,
Оу /° Ок, а если среди них хотя бы одно строгое, то Оу Р° Ок. Смысл отношения (10.5)
прост: если объект Оу в ранжировке каждого эксперта стоит не далее объекта Ок, то та-
кое же взаимное расположение должно сохраниться для этих объектов и в обобщен-
ной ранжировке. Если, по мнению всех экспертов, они одинаковы по предпочтитель-
ности, то так же должно быть в обобщенной ранжировке. А если хотя бы один эксперт
предпочитает объект Оу объекту Ок, то в обобщенной ранжировке первый из них дол-
жен стоять раньше второго.
В качестве следующего шага частичного упорядочивания объектов можно использо-
вать качественную информацию о компетентности экспертов, выраженную ранжиров-
кой, в которой эксперты расположены по убыванию их компетентности, и представляе-
мую вектором рангов
г=(Г],...,гт). (10.6)
Пусть далее у = (j^,..., уд) — числовой вектор. Обозначим через = (у(1),..., у(^),
гдеу(1) < у(2) < y{q}, перестановку векторау по неубыванию. Например, если у = (2, 7, 3,
0, 2), то = (0, 2, 2, 3, 7) и у(|) = 0; у(2) = у(3) = 2; у(4) = 3 иу(5) = 7.
Введем вектор G= представляющий собой перенумерованные в поряд-
ке возрастания все возможные значения х/? в матрице (10.2). В частности, если все экс-
перты указали только строгие ранжировки, то G = (1,..., п).
494
Для каждого / = 1,h введем в рассмотрение векторы т*7 = (r/z,..., ), где
г/7
ri XiJ<gb
М Ху>8„
(Ю.7)
ъМ— произвольное число, которое больше наибольшего из чисел х- в матрице (10.2).
Этим числом, очевидно, может быть М = п + 1.
Решающее правило, задающее отношение Rr на основе качественной информа-
ции о компетентности экспертов, представленной ранжировкой (10.6), таково:
OjRr<\ <—> r(!} < r^,i= 1,т, 1= 1,А,
(10.8)
причем, если все нестрогие неравенства выполняются как равенства, то О;1г Ок, а ес-
ли хотя бы одно из них строгое, то Оу Pr Ок. В частном случае, когда все эксперты рав-
нокомпетентны: г{ = ... = rm = (т + 1 )/2, решающее правило (10.8) для соответствую-
щего отношения, которое обозначим RE, можно представить в виде:
О, А£О*4—* x(<v сх«)’/= Ь•••>т- (Ю.9)
Дальнейшее частичное упорядочивание объектов может быть произведено на ос-
нове количественной информации о компетентности экспертов, представленной ко-
эффициентами компетентности Xz-, образующими вектор
Х = (ХР...,ХШ), (10.10)
где Е Xz = 1.
Очевидно, количественная информация о компетентности экспертов должна до-
полнять качественную информацию о них, что требует выполнения условий
Г; < /у -> X; > Ху, Г; = fj -> X,- = Ху.
В этом случае для каждого объекта Оу (для /=1,...,Л—1) подсчитываются суммы
Д'7 коэффициентов Х/5 соответствующие i таким, что xzy < gt (если таких компонент xzy
нет, то AtV7 = 0), а само решающее правило записывается так:
ОуЯХОЛ<—>Л'7>Л*',/= 1,...,Л- 1. (10.11)
При решении практических задач частичной ранжировки, соответствующей Кк
или даже Rr, может оказаться достаточно. В противном случае придется провести пол-
ное агрегирование — построить полную ранжировку всех объектов, например с по-
мощью отношения Rs, определяемого сравнением взвешенных сумм рангов
т
*' = ЪЧу (10.12)
/• = 1
следующим образом:
О,- Rs Ok <—> s' < sz < s* (10.13)
В такой обобщенной ранжировке будут упорядочены все объекты. И в результате
будет известно, какие пары объектов оказались упорядоченными на основании
какие — на основании Rr или же Rk и, наконец, какие пары оказались упорядоченны-
ми только после полного агрегирования, надежность которого, естественно, меньше
всех предыдущих частичных агрегирований.
495
10.6.3. Решение многокритериальных задач
оптимизации при помощи метода анализа иерархий
Анализ показывает, что набор показателей и критериев, необходимых для всесто-
роннего анализа технических проектов, достаточно большой. В принципе все задачи
техники и экономики многокритериальны по своей сути, так как при выборе наилуч-
ших вариантов приходится учитывать множество требований, предъявляемых к со-
здаваемым объектам (системам), и среди них многие противоречат друг другу. Попыт-
ки неоправданными упрощениями свести многокритериальную проблему к решению
математической задачи оптимизации одной функции (одного критерия) не всегда
обоснованы. Возникновение многокритериального подхода обычно связывают с име-
нем итальянского экономиста и социолога В. Парето (1848—1923), применившего его
при исследовании рыночного обмена товаров. В дальнейшем, в связи с практически-
ми потребностями принятия решений по многим критериям, методы многокритери-
альной оптимизации были существенно развиты.
В наиболее законченном виде в теории многокритериальной оптимизации пред-
ложен многокритериальный подход к проектированию машин и технологического
оборудования на основе метода исследования пространства параметров.
Однако в классической форме многокритериальный подход может быть приме-
ним во всех случаях, когда известны все определяющие техническую систему или тех-
нологический процесс параметры, функциональные выражения, связывающие между
собой эти параметры, зависимости локальных критериев качества от параметров,
а также заданы параметрические, функциональные и критериальные ограничения. Во
всех таких случаях решение оптимизационных задач обеспечивается с наибольшей
полнотой и строгостью, так как выполняется с использованием наборов только коли-
чественных параметров и критериев. Показатели, которые в совокупности необходи-
мо использовать для экспертной оценки и отбора технологических проектов, носят
как количественный, так и качественный характер. В связи с этим при решении по-
добных задач, как правило, требуется применение других, неклассических методов
многокритериального анализа.
Среди них получил известность и распространение метод анализа иерархий, раз-
витый американским ученым Т. Саати. Суть этого метода, который на практике приме-
нялся в решении целого ряда важных практических задач (нахождение приоритета ре-
сурсов для развивающейся страны, оценки меры влияния стран в мире, анализа конф-
ликтов, энергетических, транспортных проблем и т. п.), кратко излагается ниже с
учетом его применения для оценки и выбора приоритетных технологических проектов.
На рис. 10.1 приведена трехуровневая иерархия структуры системы для случая
оценки и выбора проектов при помощи четырех обобщенных критериев.
Целью (верхний уровень иерархии) является выбор (или ранжирование) при по-
мощи четырех обобщающих критериев Кр ..., К4 (второй уровень) наилучшего из трех
альтернативных (или разных) проектов Пt, П2 и П3 (нижний уровень иерархии).
Рассмотрим (общий случай) множество элементов С}...Сп некоторого уровня
иерархии и попытаемся определить веса Vn их влияния на некоторый элемент сле-
дующего, более высокого уровня. Составим для этого матрицу парных сравнений А =
= [aj, в которой через а- обозначено число, соответствующее значимости элемента Ct
по сравнению с Су . Элементы = VJVj определим по следующим правилам:
1) если ау = а, то а# = 1/а, где а * 0;
2) если результаты сравнения таковы, что С, имеет одинаковую с Cj относитель-
ную важность, то = 1 и ар. = 1; в частности, аи = 1 для всех /.
496
Цель
Критерии
Ki
Выбор приоритетных
технологических
проектов
к4.
Научно-
техническая
значимость
Экономическая
эффективность
Реализуемость
проекта
Конкуренто-
способность
продукции
Альтернативы
П,
Рис. 10.1. Структурная схема оценки и выбора технологических проектов
При выполнении условий 1) и 2) матрица А называется обратносимметричной.
Если наши оценки безошибочны при всех сравнениях, то aik = atj ajk для всех z, у, к
и матрица Л является согласованной.
Легко показать, что для проведения парных сравнений п объектов при условии,
что каждый объект представлен в данных по крайней мере один раз, требуется (п - 1)
суждений. Из них можно вывести все остальные суждения, используя правило: ес-
ли объект Л, в 3 раза превосходит объект А{ и в 6 раз превосходит Л3, то Л1 = ЗЛ2 и
Л] = 6Л3. Тогда Л2 = 2Л3 и Л3 = 1/2Л2. Если же численное значение суждения в позиции
(2, 3) матрицы Л отличается от 2, то матрица Л будет несогласованной, что часто
и случается на практике. Если диагональ матрицы Л состоит из единиц и Л — согласо-
ванная матрица, то при малых изменениях в а у наибольшее собственное значение
матрицы Хтах остается близким к л, а остальные собственные значения — близкими
к нулю.
Как показано в работе [8], для нахождения вектора приоритетов (среди Си ..., Сп)
нужно найти вектор V, который удовлетворяет уравнению
^V = XmaxV. (10.14)
Так как малые изменения а-, вызывают малое изменение Хтя¥, то отклонение по-
IJ Шал*'
след него от п можно принять в качестве меры согласованности и ввести соответст-
вующий индекс согласованности (ИС)
ИС = (Хтах-«)/(«-1). (10.15)
Для оценок степени важности сравниваемых элементов может быть предложена
шкала от 1 до 9, отражающая соотношения между сравниваемыми элементами
(табл. 10.2).
Обоснование этой шкалы по степени важности включает несколько пунктов,
из которых остановим внимание только на одном. Способность человека произво-
дить качественные разграничения хорошо представлена пятью определениями: рав-
ный, слабый, сильный, очень сильный и абсолютный. Можно принять компромис-
497
Таблица 10.2
Оценка степени важности
Степень важности Значимость Предпочтение
1 Одинаковая значимость Два действия вносят одинаковый вклад в достижение цели
3 Некоторое преобладание значи- мости одного действия перед другим (слабая значимость) Опыт и суждение дают легкое предпочтение одному действию перед другим
5 Существенная или сильная зна- чимость Опыт и суждение дают легкое предпочтение одному действию перед другим
7 Очень сильная или очевидная значимость Предпочтение одного действия перед другим очень сильно. Его превосходство практически явно
9 Абсолютная значимость Свидетельство в пользу предпоч- тения одного действия другому в высшей степени убедительно
2, 4, 6, 8 Промежуточные значения меж- ду соседними значениями шка- лы Ситуация, когда необходимо компромиссное решение
Обратные вели- чины приведен- ных выше чисел Если действию / при сравнении с действием j приписывается одно из приведенных выше чисел, то действию j при сравнении с i приписывается обратное значе- ние Обоснованное предположение
Рациональные значения Отношения, возникающие в за- данной шкале Если постулировать согласован- ность, то для получения матри- цы требуется п числовых значе- ний
сные определения между соседними определениями, когда нужна большая точность.
В целом требуется девять значений, и они могут быть хорошо согласованы, что под-
тверждается практикой.
Индекс согласованности, сгенерированный случайным образом по шкале от 1 до
9 обратносимметричной матрицы с соответствующими обратными величинами эле-
ментов, назовем случайным индексом (СИ).
В национальной лаборатории Ок-Ридж (США) была произведена генерация
средних СИ для матриц порядка от 1 до 15 на базе 100 случайных выборок. Как
и ожидалось, СИ увеличивались с увеличением порядка матрицы. Так как величина
выборки была невелика (100), наблюдались статистические флуктуации в индексе
при переходе от матрицы одного порядка к другому. Вычисления были повторены
в шкале Уортона для величины случайной выборки 500 с порядком матриц до 11 х 11,
а далее использовались предыдущие результаты для п = 12, 13, 14, 15. Ниже представ-
лены порядок матрицы (первая строка) и средние СИ (вторая строка), определенные,
как описано выше (табл. 10.3).
498
Таблица 10.3
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
0,00 0,00 0,58 0,90 1,12 1,24 1,32 1,41 1,45 1,49 1,51 1,48 1,56 1,57 1,59
Отношение ИС к среднему СИ для матрицы того же порядка называется отноше-
нием согласованности (ОС). Значение ОС, меньшее или равное 0,1, считают прием-
лемым для оценок.
Точное вычисление вектора приоритетов среди элементов С1?..., Сп можно полу-
чить, решая задачу о собственных значениях на ЭВМ. При отсутствии ЭВМ можно
получить оценки этого вектора следующими четырьмя способами, которые приведе-
ны ниже в порядке увеличения точности оценок.
1. Суммировать элементы каждой строки и нормализовать их делением каждой
суммы на сумму всех элементов; сумма полученных результатов будет равна единице.
Первый элемент результирующего вектора будет приоритетом первого объекта,
второй — второго объекта и т. д.
2. Суммировать элементы каждого столбца и определить обратные величины
этих сумм. Нормализовать их так, чтобы их сумма равнялась единице, разделив каж-
дую обратную величину на сумму всех обратных величин.
3. Разделить элементы каждого столбца на сумму элементов этого столбца
(т. е. нормализовать столбец), затем сложить элементы каждой полученной строки
и разделить эту сумму на число элементов строки (усреднение по нормализованным
столбцам).
4. Перемножить п элементов каждой строки и извлечь из произведения корень
и-й степени. Нормализовать полученные числа.
Применительно к оценке технологических проектов (рис. 10.1) элементы Cz соот-
ветствуют критериям Kh ..., Кя. Вычисление относительного ранга каждого проекта
по каждому критерию производится так же, как было проиллюстрировано для эле-
ментов Cz.
Для получения общей оценки каждого проекта необходимо умножить вес оценки
этого проекта по некоторому критерию на вес этого критерия, а затем сложить значе-
ния, полученные для каждого проекта по всем критериям. В результате вычислим об-
щие оценки проектов Пр П2 и П3 из соотношений:
ОП| = £7| Kq “I" #2^2 + Л3К3 “I" АдКд,
ОП2 = Z?|K| + />2^2 + *3К3 + ^4^4» (10.16)
ОП3 = С|К| + с2К2 + с3К3 + с4К4.
Естественным образом изложенный подход обобщается на большее число техно-
логических проектов и уровней в иерархии.
В частности, для случая i = 1, ..., п критериев и v = 1, ..., Pz подкритериев можно
получить следующее выражение для оценки ди-го технологического проекта Пш:
л Р,
оПи= X (1017)
/ = 1 V = 1
где Liv — веса подкритериев критерия z; emv — оценка (собственный вектор) т-го про-
екта по v-му подкритерию.
499
Таким образом, метод анализа иерархий (МАИ) удовлетворяет следующим четы-
рем требованиям к научному обоснованию способов принятий решений и выбора
приоритетов.
1. В МАИ способы получения информации от эксперта соответствуют данным
психологических исследований о возможностях человека переработать информацию.
Действительно, аксиома гомогенности и принцип иерархической декомпозиции при-
водят в соответствие проблему получения оценок с психометрическими возможнос-
тями человека.
2. В МАИ имеется возможность проверки экспертной информации на непроти-
воречивость посредством индекса и отношения согласованности как для отдельных
матриц, так и для всей иерархии.
3. Любые соотношения между вариантами решений в МАИ объяснимы на основе
информации, полученной от экспертов (четвертая аксиома МАИ). Так анализ при-
оритетов элементов решения по нисходящим уровням иерархии позволяет понять,
как получено то или иное значение вариантов решения.
4. Математическая правомочность решающего правила в МАИ прозрачна и бази-
руется на методе собственного значения и принципа иерархической композиции,
имеющих четкое математическое обоснование.
Следовательно, МАИ удовлетворяет четырем основным критериям, обеспечи-
вающим всестороннюю научную обоснованность принятия решений в задачах при-
кладного характера с качественными показателями.
10.6.4. Рациональная процедура
многокритериальной экспертной оценки
технологических проектов
В принципе каждый из подходов, рассмотренных выше, может быть независимо
использован для экспертных оценок и отбора приоритетных технологических проек-
тов. Однако применение экспертно-аналитического метода Дельфи сопряжено
с привлечением большого числа экспертов, необходимостью проведения нескольких
туров экспертизы, громоздкостью обработки полученной информации и значительны-
ми финансовыми затратами. При этом не исключается существенное влияние субъек-
тивизма, что зачастую приводит к противоречивым результатам, как это имело место
при анализе 258 критических технологий федерального уровня (см. п. 10.6.1). Методи-
ки опросов при этом подходе, как правило, не включают оценок значимости (весомос-
ти) критериев и под критериев экспертами, а устанавливаются разработчиками мето-
дик обработки анкет экспертизы, что усиливает субъективность окончательных ре-
зультатов. Одним из существенных недостатков проведенной с использованием
данного подхода широкомасштабной экспертизы 258 критических технологий феде-
рального уровня, на наш взгляд, является невыполнение одного из принципиальных
требований к составу участников опросов, изложенных выше.
А именно — при проведении экспертизы должно быть обеспечено представи-
тельство исследователей и разработчиков, специалистов, занимающихся внедрением
технологий, их коммерциализацией и распространением, потребителей продукции.
Отсутствие в должной мере выделенных специалистов и потребителей, хорошо знаю-
щих рынок предлагаемой к разработке продукции и его конъюнктуру (развитие), не
позволило сделать правильные (квалифицированные) оценки перспектив выхода
российских товаров и технологий на мировые рынки наукоемкой продукции, что
и обусловило, в конечном итоге, те противоречивые результаты, о которых говори-
лось выше.
500
Новый подход к анализу экспертных оценок, основанный на теории важности
критериев, позволяет существенно повысить эффективность экспертизы за счет рез-
кого снижения числа участников опроса и проведения его в индивидуальном порядке
с каждым экспертом. Можно было бы ограничиться всего четырьмя экспертами —
представителями разработчиков технологий (лучше которых технологию не знает ни-
кто), производителей продукции с использованием предлагаемой технологии (вла-
деющих технологическим процессом и хорошо знающих продукцию), специалистов
по маркетингу, занимающихся коммерциализацией и распространением технологий
и продукции (хорошо знающих рынок данной продукции) и потребителей данной
продукции (знающих плюсы и минусы используемой продукции). Однако ожидать
хорошей согласованности ранжирования заданного списка технологий по всем кри-
териям вряд ли следует, так как каждый из экспертов является специалистом в своей
(узкой) области, которой и отдаст приоритетность по сравнению с другими. Отсюда
следует, что лучшим вариантом набора экспертов был бы выбор из числа независимых
высококомпетентных специалистов, обладающих познаниями во всех указанных об-
ластях или, по крайней мере, имеющих точную информацию в отдельных областях от
«узких» специалистов, что не всегда может быть реализовано на практике (но именно
к этому случаю необходимо стремиться). По сути, основные достоинства подхода,
включая учет уровня компетентности экспертов (и качественного, и количественно-
го), являются лучшими в плане корректного сведения мнений (ранжировок) отдель-
ных экспертов к единому (групповому) результату, и по этой причине могут стать не-
заменимым элементом всех экспертно-аналитических методов в их заключительной
стадии.
Основная идея многокритериального экспертного метода анализа иерархий, за-
ключающаяся в попарном сравнении анализируемых объектов (технологий, проек-
тов, критериев и подкритериев), выгодно отличает его от метода Дельфи (в котором
объекты рассматриваются не парами, а как бы все «одновременно»). МАИ лучше со-
гласуется с возможностями человека перерабатывать информацию, имеет достаточно
обоснованную качественно-количественную шкалу сравнения значимости объектов
и, что следует особенно подчеркнуть, сводит решение задачи определения вектора
приоритетов объектов к известной математической задаче нахождения собственных
значений матрицы парных сравнений (см. п. 10.6.3). В этом методе также требуется
производить оценку согласованности суждений экспертов при помощи специального
коэффициента, называемого отношением согласованности. Применение МАИ тре-
бует установления приоритетности (весов) критериев и подкритериев и оценок весо-
мости каждого из рассматриваемых технологических проектов по каждому критерию
(подкритерию) при их попарном сравнении. В случае достижения необходимой со-
гласованности суждений экспертов по всем отмеченным приоритетам окончательная
оценка проектов и их ранжирование легко осуществляются при помощи полученных
в п. 10.6.3 соотношений типа (10.17). Однако именно достижение полной согласован-
ности суждений экспертов относительно весомости критериев, подкритериев и про-
ектов по причинам, свойственным всем экспертным методам и отмеченным выше
при рассмотрении метода Дельфи может стать «ахиллесовой пятой» данного метода
и потребовать проведения многочисленных туров экспертизы и обработки больших
объемов информации, а значит, и больших затрат, что может нивелировать казалось
бы вполне очевидные преимущества МАИ перед методом Дельфи.
В связи с изложенным для эффективного решения проблемы многокритериаль-
ной экспертной оценки технологических проектов представляется привлекательной
идея построить некий симбиоз из рассмотренных методов, используя их сильные сто-
роны и «опуская» основные недостатки. Прежде всего, в силу очевидных преиму-
501
ществ примем в качестве основного метод анализа иерархий, как в наибольшей степе-
ни формализованный для решения задач многокритериальной экспертной оценки
технологических проектов. В соответствии с полученными в п. 10.6.3 соотношениями
(10.17) оценка эффективности предлагаемых технологических проектов включает две
составные части: определение (установление) весов всех критериев и подкритериев
и оценку вектора приоритетов каждого проекта по каждому из критериев (подкрите-
риев).
В настоящее время нет строгих правил обоснования приоритетности обобщен-
ных критериев и соответствующих подкритериев. Более того, при решении конкрет-
ных задач эта приоритетность может меняться в зависимости от того, какие аспекты
(технологические, экономические или экологические) будут иметь первостепенное
значение для инвесторов. Поэтому определение весов не может быть выполнено ина-
че, как на основании информации, представляемой либо лицом, принимающим ре-
шение (Л ПР), либо экспертами, которым Л ПР доверяет. Если привлекаются экспер-
ты, то, очевидно, при установлении весов обобщенных критериев должны использо-
ваться высококомпетентные независимые специалисты, занимающиеся внедрением
технологий, их коммерциализацией и распространением и владеющие в силу этого
наиболее полной информацией в данной предметной области. Это должно быть не
более 3—4 указанных специалистов, которые должны установить места обобщенным
критериям, при этом, очевидно, следует ожидать как строгие, так и нестрогие ранжи-
ровки. Далее по методу, описанному в п. 10.6.2, индивидуальные ранжировки экспер-
тов могут быть сведены к единому (групповому) результату при наличии требуемой
согласованности суждений экспертов с учетом их компетентности.
Распределение же полученных весов обобщенных критериев по подкритериям
целесообразно поручить группам экспертов, специализирующихся в соответствую-
щих (узких) областях: разработчикам технологий и изготовителям продукции, эконо-
мистам, специалистам по маркетингу, экологам и специалистам по охране труда и, на-
конец, лицу, формирующему решение (ЛФР) в части готовности организации-заяви-
теля НИОКР выполнить проект. Хотя в принципе ЛФР, специализируясь на анализе и
оценке проектов и располагая всей необходимой точной информацией о продукции
(технологии), экономических, рыночных и экологических показателях технологиче-
ских проектов, может самостоятельно производить распределение представленных
Л ПР или экспертами весов критериев по соответствующим подкритериям, варьируя
их при необходимости внутри каждой группы.
Итак, решение первой части задачи оценивания технологических проектов, свя-
занной с установлением весов небольшого числа (4—6) критериев и такого же относи-
тельно небольшого числа (от 4 до 7) подкритериев, предлагается осуществлять при
помощи модификации экспертно-аналитического метода Дельфи с применением
в его заключительной стадии нового подхода к сведению индивидуальных суждений
экспертов к единому (групповому) мнению при наличии требуемой согласованности
суждений экспертов и с учетом уровня их компетентности.
Что касается второй части этой задачи, включающей оценку технологических
проектов путем сравнения по каждому обобщенному критерию (подкритериям) и ис-
пользование метода анализа иерархий для вычисления соответствующих векторов
приоритетов, то ее решение предлагается поручить полностью ЛФР на основании
точной количественной и качественной информации об анализируемых проектах, ко-
торая должна содержаться в специальной информационной карте. При этом сравне-
ние количественных показателей не вызывает каких-либо затруднений (основной
упор здесь делается на точности, с которой получены те или иные показатели). При
сравнении же идентичных качественных показателей, оценку которых можно произ-
502
водить при помощи балльной шкалы, Л ФР необходимо снабдить разработанной для
этих целей инструкцией. В качестве такой инструкции можно использовать, напри-
мер, следующую таблицу, в которой приведены данные по двум критериям науч-
но-технической значимости Кнтз и экономической эффективности Кээ, весам их под-
критериев и пяти (по аналогии со шкалой, принятой в МАИ) возможным значениям
показателей технологических проектов по каждому из подкритериев в десятибалль-
ной шкале.
Как видно из табл. 10.4, для целей формализации всего вычислительного процес-
са оценки технологических проектов удобно и все количественные данные сводить к
указанным значениям десятибалльной шкалы.
Очевидно, пользуясь точными данными о технологических проектах, содержа-
щихся в табл. 10.3 и 10.4, ЛФР тем самым имеет возможность строить все матрицы
парных сравнений таким образом, что они будут полностью согласованными обрат-
носимметричными матрицами, у которых главное собственное значение равно числу
сравниваемых объектов, а отношение согласованности по (10.5) тождественно равно
нулю. Следовательно, при решении второй части задачи с помощью МАИ проблемы
оценок согласованности суждений экспертов вообще не возникает (эта согласован-
ность достигается при решении первой части задачи) в силу того, что решение этой
части выполняется не экспертами, а ЛФР, использующим точную информацию о
сравниваемых технологических проектах, представленную разработчиками продук-
ции (технологии).
В целом же предлагаемый подход, построенный на идее вполне определенного
сочетания сильных сторон известных экспертно-аналитических методов и который,
на наш взгляд, должен существенно повысить эффективность многокритериальной
экспертной оценки и отбора перспективных технологических проектов, включает
следующие этапы процедуры их анализа.
1. Лицом, принимающим решение (или ЛФР), формируются группы экспертов
для установления весов всех обобщенных критериев и подкритериев, при этом работа
с каждым экспертом ведется оперативно в индивидуальном порядке.
2. Полученные от экспертов ранжировки важности обобщенных критериев обра-
батываются ЛФР и при наличии необходимой согласованности сводятся к единому
групповому суждению, при этом Л ПР (ЛФР) устанавливает уровни (качественные ли-
бо количественные) компетентности экспертов. Достижение требуемой согласован-
ности суждений экспертов может потребовать двух-трех итераций.
3. Эксперты-специалисты в узких областях распределяют установленные ранее
веса обобщенных критериев по подкритериям, а обработка полученной от них ин-
формации производится точно так же, как это делалось на предыдущем этапе проце-
дуры (этап 2).
4. ЛФР на основании количественной и качественной информации, содержа-
щейся в информкарте, производит оценку каждого из выбранных для ранжирования
технологических проектов по каждому подкритерию, проставляя соответствующие
баллы из пяти возможных значений десятибалльной шкалы (10, 8, 5, 2, 0).
5. Данные, полученные на этапе 4, используются при формировании матриц по-
парных сравнений анализируемых технологических проектов по каждому из подкри-
териев (число матриц равно числу всех подкритериев), которые позволяют вычислить
векторы приоритетов сравниваемых проектов по каждому подкритерию.
6. С учетом установленных на этапах 2 и 3 весов критериев и подкритериев и вы-
численных на этапе 5 значений векторов приоритетов проектов по каждому подкри-
терию при помощи соотношений (10.16) производится окончательная оценка всех
рассматриваемых технологических проектов и их ранжирование.
503
Таблица 10.4
Соответствие баллов характеристикам показателей
Обобщенный критерий Показатель Балл Характеристика показателей
К-НТЗ 1.1. Новизна Вес 8 Б],1 max = 80 10 Аналогичные технические ре- шения отсутствуют или неиз- вестны
8 Принципиально новое решение в сравнении с известными аналога- ми, позволяющее существенно улучшить технологию
5 Техническое решение дает полез- ную модификацию известных ре- шений (незначительно улучшает технологию)
2 Техническое решение не дает улучшений технологий
0 Решение может ухудшить извест- ную технологию
1.2. Степень фунда- ментальности Вес 7 Б 1.2 max — 70 10 Технология решения основана на новейших результатах фундамен- тальных исследований
8 Использованы ранее известные фундаментальные данные, кото- рые не применялись
5 Решение основано на известных и применявшихся результатах фундаментальных исследований
2 Решение основано на данных по- исковых исследований
0 Решение основано на давно из- вестных фактах
1.3. Преимущества по сравнению с аналогами Вес 5 Б 1.3 max = 50 10 Решение имеет существенные ка- чественные и количественные преимущества перед известными
5 Преимущества незначительные
2 Нет преимуществ
0 Решение уступает известным по некоторым показателям
504
Продолжение таблицы 10.4
Обобщенный критерий Показатель Балл Характеристика показателей
IZ 1Хнтз 1.4. Патентоспособ- ность Вес 4 ^1.4 max = 40 10 Патент получен (имеется)
8 Получено положительное реше- ние, патент оформляется
5 Подана заявка
2 Заявка не подана, идет поиск ана- логов
0 Вопрос о патентовании не рас- сматривался
1.5. Применяемость во многих от- раслях Вес 3 ^1.5 max = 30 10 Более чем в трех отраслях
8 Не меньше трех
5 В одной-двух отраслях
2 Узкое применение в одной отрас- ли (стабильное)
0 Применяется эпизодически
1.6. Перспектив- ность Вес 2 Б 1.6 max = 20 10 Открывает новое направление в технике
8 Может быть основой существен- ной модернизации многих видов техники
5 Позволяет улучшить характерис- тики техники данной отрасли
2 Решение полезно, но эффектив- ность применения не очевидна
0 Перспективность сомнительна
1.7. Вероятность технического успеха Вес 1 Б 1.7 max = Ю 10 0,8
8 0,6
5 0,4
2 0,2
0 0,1
Б1 max = 300
505
Окончание таблицы 10.4
Обобщенный критерий Показатель Балл Характеристика показателей
Кээ 3.1. Срок окупаемое- ти инвестиций Вес 9 &3 1 max = 90 10 До 1 года
8 Менее 2-х лет
5 3 года
2 До 5 лет
0 Свыше 5 лет
3.2. Простая норма чистой прибыли Вес 6 ^3 2 max = ^0 10 30%
8 20%
5 15%
2 8%
0 Менее 7%
Б3тах=150
7. С целью определения чувствительности оценок к изменению соотношений
приоритетов критериев и подкритериев, в том числе отличных от установленных экс-
пертами, МАИ применяется несколько раз для различных рекомендуемых Л ПР или
ЛФР распределений приоритетности, чтобы Л ПР имел перед собой общую возмож-
ную картину для принятия окончательного решения о первоочередности финансиро-
вания предлагаемых технологических проектов.
10.7. АЛГОРИТМ ОЦЕНКИ
ПРЕДВАРИТЕЛЬНОГО ОТБОРА И РАНЖИРОВАНИЯ
ТЕХНОЛОГИЧЕСКИХ ПРОЕКТОВ НА СТАДИИ НИОКР
10.7.1. Определение приоритетности
и весовых коэффициентов критериев и подкритериев
1.1. В соответствии с обоснованием, приведенным выше, все критерии и подкри-
терии (табл. 10.1) запишем в порядке уменьшения их значимости. Принимая этот ва-
риант в качестве базового (варианта по умолчанию) для оценки, предварительного от-
бора и ранжирования технологических проектов, найдем значения весовых коэффи-
циентов критериев и под критериев по формуле:
ку= /[«•«(«+1)/2], (10.18)
i = 1
принимая в ней т = 1 (все эксперты согласны с исходными ранжировками критериев
и подкритериев, указанными в таблице).
1.2. Вычисляем весовые коэффициенты Ку пяти обобщенных критериев Кнтз,
Кк> кэб и КрП
Ку= JT'y/[n(n 4- 1)/2], (10.19)
506
где j = 1, 2, п; п = 5 — число критериев; X'j; = п + 1 — Xf, Xj = 1, 2, 3, 5 — ранги
критериев.
1.3. Находим, пользуясь (10.19), весовые коэффициенты семи (п = 7) подкрите-
риев первого (Кнтз) критерия, которые обозначим через К1у. (/ = 1,2,..., 7).
1.4. Точно таким же образом определим весовые коэффициенты К2у (/=1,2) двух
подкритериев второго (Кээ) критерия и К3у, К4у и К5у (во всех случаях j = 1, 2, 3) трех
подкритериев соответственное третьего (Кк), четвертого (Кэб) и пятого (Кр) обобщен-
ных критериев.
В общей сложности получаем 18 весовых коэффициентов подкритериев и 5 весо-
вых коэффициентов критериев, при этом в соответствии с (10.18)
5 7 2 3 3 3
'£КУ=1; E*v=i; L4= 2 К4У = (10.20)
j = 1 7 = 1 7=1 7 = 1 7 = 1 7 = 1
10.7.2. Предварительный отбор проектов
2.1. Обозначим оценки р-го технологического проекта, имеющего уникальный
шифр в базе данных, по каждому подкритерию, произведенные в соответствии
с п. 10.5 итаблицей 10.1, через а£у, v = 1,..., 5 (число критериев), а/принимает значе-
ния, указанные в соотношениях (10.20). Оценки а£у представляют собой дискретные
величины: 10, 8, 5, 2, 0.
2.2. Зная оценки каждого проекта по каждому подкритерию а£у и значения весо-
вых коэффициентов каждого подкритерия К1у,..., К5у, можно вычислить:
2.2.1. Общие оценки р-го проекта по каждому из 5 критериев
Bf = • а^ + К12 • а^2 + ... + К17 • af7,
В2 = К-21 * а51 + ^22 * а§2 ’ (10.21)
в? K5i • а^ + К52 • а^2 + К53 • af3.
2.2.2. Итоговую оценку р-го проекта по всем пяти обобщенным критериям
О£ = Kj • Bf + К2 • в^ + ... + К5 • в£ . (10.22)
2.2.3. Суммарный балл, набранный проектом:
БРЕ = 100-Og. (10.23)
2.3. Полученные значения Б£ можно использовать для предварительного отбора
(отсева) проектов в соответствии с формулой
БРЕ >670, (10.24)
что составляет 2/3 от максимально возможного суммарного балла (1000).
507
10.7.3. Ранжирование технологических проектов
3.1. Проекты, удовлетворяющие условию (10.24), для выбранного базового вари-
анта распределения весов критериев и подкритериев могут быть непосредственно
проранжированы, исходя из итоговой оценки по соотношению (10.22).
3.2. Для других возможных (и более реалистичных) сочетаний весовых коэффи-
циентов критериев и подкритериев, включая их равномерные распределения, незна-
чительные отличия и равенство отдельных составляющих, смену приоритетности од-
них над другими, ранжирование технологических проектов после их предварительно-
го отбора будем осуществлять, основываясь на решающем правиле метода анализа
иерархий [2].
В связи с этим ЛФР, выступающему в роли единственного эксперта, необходимо
прежде всего сформировать шесть матриц парных сравнений.
3.2.1. Матрица парных сравнений для обобщенных критериев, табл. 10.5.
В этой матрице, которая формируется как согласованная обратносимметричная
матрица, по главной диагонали стоят единицы (равноважность каждого критерия
с самим собой), а числа д^ (z,y = 1,..., 5), где i — номер строки, ау — номер столбца, по-
казывают соотношение важности критериев, расположенных на z-й строке и в у-м
столбце. В общем случае п элементов для формирования такой матрицы необходимо
задать (п — 1) независимых значений (чисел) д^. Для случая п = 5 обобщенных критери-
ев необходимо задать всего четыре числа, в качестве которых выберем д12, д 13, д14 и д15.
Остальные необходимые для формирования матрицы числа находим из соотно-
шений:
Д23 5?2’Д24 ЯП’Д25 ^’Дз4 ЯП’Дз5 ЯП,Д45 д]? ( 2)
Чтобы вычислить нормализованные компоненты собственного вектора приори-
тетов Kj,..., К5, введем обозначение:
К1 = (Д12-Д|3«Д14-Д15)1/5. (10.26)
Тогда
57 __ К1 . Т7 _ К] . Т7 _ К] . — _ К-1
К2 — -- , К3 — - , К4 — - , К5----
Д12 Д13 Д14 5 Д15
и к( + к2 +... + к5 = к, fi + -L + -L +... + ± \
\ Д12 Д13 Д15 /
Таблица 10.5
Критерии К-НТЗ Кээ Кк Кэб Крп Собствен- ный век- тор
Кн„ 1 Д12 Д|з Д14 Д15 К.
Кээ 1/Д12 1 Д23 Д24 Д25 к2
Кк 1/Д.з 1/д23 1 Д34 Д35 К3
Кэб 1/Д14 1/Д24 1/Д34 1 д45 к4
Крп 1/Д15 1/Д25 1/д35 1 К5
508
Это позволит определить компоненты К1?..., К5:
К| =
д12 Д13 д15
д12 д13 д15
К. к, к.
К, = — ; К4 = — ; К, = —
3 д13 4 д14 5 д15
(10.27)
5
Очевидно, У = 1.
v = 1
Таким образом, задание четырех чисел д12,д13,д15ид15 позволяет не только пол-
ностью сформировать матрицу парных сравнений, но и при помощи соотношений
(10.27) вычислить нормализованный собственный вектор приоритетов обобщенных
критериев.
3.2.2. Матрица парных сравнений для подкритериев критерия Кнтз. В этом случае
число сравниваемых элементов п = 7, а следовательно, чтобы построить матрицу, не-
обходимо задать шесть независимых величин д12, д13,..., д17. Соответствующий собст-
венный вектор будет иметь 7 нормализованных составляющих К1у (/=1,2,..., 7), кото-
рые вычислим из соотношений, аналогичных (10.27):
Д12 Д13 Д17
K13=^;K13=^;Kv=^(/‘ = 4’-’7)- (10-28)
3.2.3. Находим нормализованные компоненты собственных векторов приорите-
тов для подкритериев:
второго критерия Кээ (п = 2)
1 К21
2'" 1 + 1/д12’К22"^’
(10.29)
третьего, четвертого и пятого критериев (Кк, К.^, КрП), имеющих одинаковое чис-
ло (п = 3) подкритериев
1 Кз1 К31
К31 =------J----г , К32 = , К33 = . (10.30)
1 + _ + _ Д12 Д13
Д12 Д13
Выражения для К41 (К51), К42 (К52) и К43 (К53) будут иметь точно такой же вид, как
(10.30), но необходимо подчеркнуть, что числа д^для каждой из шести матриц парных
сравнений будут в общем случае различаться между собой (будут зависеть от важности
сравниваемых критериев и подкритериев).
3.3. Представим в таблице 10.6 некоторые возможные варианты распределения
соотношений важности критериев и под критериев (чисел д1у), введя ограничение
Ду<3,0.
509
Таблица 10.6
Возможные соотношения важности критериев и подкритериев
Критерии (подкритерии) Вариант Д12 Д13 Д14 Д15 д1б Д17
1. Критерии K„T3,КрП 1 1,5 2,0 2,5 3,0
2 1,1 1,4 1,7 2,0
3 1,0 1,0 1,0 1,0
2. Подкритерии Кнтз 1 1,5 1,8 2,1 2,4 2,7 3,0
2 1,0 1,2 1,4 1,6 1,8 2,0
3 1,0 1,0 1,0 1,0 1,0 1,0
3. Подкритерии Кээ 1 2,0
2 0,5
2 3
4. Подкритерии Кр 1 2,0 3,0
2 1,2 2,0
3 1,0 1,0
5. Подкритерии Кэб 1 1,5 3,0
2 1,0 2,0
3 1,0 1,0
6. Подкритерии КрП 1 1,5 3,0
2 1,2 2,0
3 1,0 1,0
3.4. Проведем ранжирование технологических проектов, прошедших предвари-
тельный отбор по условию (10.24), для девяти вариантов распределений весов крите-
риев и подкритериев, указанных в табл. 10.5.
3.4.1. Вариант № 1 (вариант 1 для всех критериев и подкритериев табл. 10.6).
1) Вычисляем весовые коэффициенты критериев по формулам (10.25) и соответ-
ствующих подкритериев по формулам (10.26)—(10.30), подставляя в них соответст-
вующие числа д1у из строк, отвечающих варианту 1 для всех критериев и подкритериев
табл. 10.6.
2) Для каждого из отобранных к ранжированию проектов находим общие оценки
вР — вР по формулам (10.21) и итоговую оценку Og по формуле (10.22).
3) Проекту, получившему максимальную оценку Og , присваиваем ранг № 1, сле-
дующему за ним по величине Og — ранг № 2 ит. д.
3.4.2. Вариант № 2 (вариант 2 для критериев и вариант 1 для всех подкритериев
табл. 10.6).
1) Вычисляем весовые коэффициенты критериев по формулам (10.27) при значе-
ниях д1у, взятых из строки варианта 2 для критериев в табл. 10.6.
510
2) Находим итоговые оценки проектов Og по формуле (10.22), используя значе-
ния общих оценок вР — в£, полученные для варианта № 1 (п. 3.4.1).
3) Ранжируем технологические проекты в порядке убывания их итоговых оце-
нок Og.
3.4.3. Вариант № 3 (вариант 3 для критериев и вариант 1 для всех подкритериев
табл. 10.6).
1) Вычисляем весовые коэффициенты критериев по формулам (10.27) при значе-
ниях д1у, взятых из строки варианта 3 для критериев в табл. 10.6.
2) Находим итоговые оценки проектов Og по формуле (10.22), используя значе-
ния общих оценок вР — вР, полученные для варианта № 1 (п. 4.4.1).
3) Ранжируем технологические проекты в порядке убывания их итоговых оце-
нок Og.
3.4.4. Вариант № 4 (вариант 1 для критериев и вариант 2 для всех подкритериев
табл. 10.6).
1) Вычисляем весовые коэффициенты подкритериев по формулам (10.28)—
(10.30) при значениях д, взятых из строк, отвечающих варианту 2 для всех подкрите-
риев табл. 10.6.
2) Находим общие оценки каждого проекта по каждому критерию вР— вР по
формулам (10.21) и итоговые оценки проектов Og по формуле (10.22), используя зна-
чения весовых коэффициентов критериев, полученные для варианта № 1 (п. 3.4.1).
3) Ранжируем технологические проекты в порядке убывания их итоговых оце-
нок Og.
3.4.5. Вариант № 5 (вариант 2 для всех критериев и подкритериев табл. 10.6).
1) Находим итоговые оценки проектов Og по формуле (10.22), используя значе-
ния весовых коэффициентов критериев, полученные для варианта №2 (п. 3.4.2),
и значения общих оценок вР — вР, полученные для варианта № 4 (п. 3.4.4).
2) Ранжируем технологические проекты в порядке убывания их итоговых оце-
нок Og.
3.4.6. Вариант № 6 (вариант 3 для критериев и вариант 2 для всех подкритериев
табл. 10.6).
1) Находим итоговые оценки проектов Og по формуле (10.22), используя значе-
ния весовых коэффициентов критериев, полученные для варианта №3 (п. 3.4.3),
и значения общих оценок вР — вР, полученные для варианта № 4 (п. 3.4.4).
2) Ранжируем технологические проекты в порядке убывания их итоговых оце-
нок Og.
3.4.7. Вариант № 7 (вариант 1 для критериев и вариант 3 для всех подкритериев
табл. 10.6).
1) Вычисляем весовые коэффициенты подкритериев по формулам (10.28)—
(10.30) при значениях д1у, взятых их строк, отвечающих варианту 3 для всех подкрите-
риев табл. 10.6.
511
2) Находим общие оценки каждого проекта по каждому критерию вР— в£ по
формулам (10.21) и итоговые оценки проектов Og по формуле (10.22), используя зна-
чения весовых коэффициентов критериев, полученные для варианта № 1 (п. 3.4.1).
3) Ранжируем технологические проекты в порядке убывания их итоговых оце-
нок Og.
3.4.8. Вариант № 8 (вариант 2 для критериев и вариант 3 для всех подкритериев
табл. 10.6).
1) Находим итоговые оценки проектов Og по формуле (10.22), используя значе-
ния весовых коэффициентов критериев, полученные для варианта № 2 (п. 3.4.2),
и значения общих оценок вР — в£, полученные для варианта № 7 (п. 3.4.7).
2) Ранжируем технологические проекты в порядке убывания их итоговых оце-
нок Og.
3.4.9. Вариант № 9 (вариант 3 для всех критериев и подкритериев табл. 10.6).
1) Находим итоговые оценки проектов Og по формуле (10.22), используя значе-
ния весовых коэффициентов критериев, полученные для варианта № 3 (п. 3.4.3),
и значения общих оценок вР — вР , полученные для варианта № 7 (п. 3.4.7).
2) Ранжируем технологические проекты в порядке убывания их итоговых оце-
нок Og.
3.5. Просмотр и печать результатов ранжирования технологических проектов на
этапе их анализа лицом, формирующим решение.
3.5.1. ЛФР должно иметь возможность просмотреть и при необходимости распе-
чатать результаты предварительного отбора проектов по условию (10.24) в виде, пред-
ставленном в табл. 10.7.
Таблица 10.7
Результаты предварительного отбора проектов
Шифр проекта Ранг Суммарный балл оЕ Баллы по критериям
К™ (0,33) Кээ (0,27) (0,20) Кэб (0,13) Крп (0,07)
1
2
3
•
т
т + 1
т 4- 2
512
Таблица 10.8
Результаты ранжирования проектов после предварительного отбора
Шифр проекта ~ Ранг Отношение для вариантов распределения критериев '“и и подкритериев по табл. 10.6
1 2 3
1 2 3 1 2 3 1 2 3
1 8,5 3 5Л 2 7,2 2 7,3
...
Таблица 10.7 разделена двойной линией на две части. В верхней части перечисля-
ются проекты, которые набрали 670 или более баллов, в нижней — проекты, набрав-
шие менее этого числа баллов. В скобках под обозначениями критериев указаны их
весовые коэффициенты, вычисленные на основании соотношения (10.19).
3.5.2. Результаты ранжирования технологических проектов по девяти вариантам
распределения весов критериев и подкритериев, указанным в табл. 10.6, целесообраз-
но представить в итоговой табл. 10.8.
В строке таблицы 10.8, разделенной на три части, цифры 1, 2 и 3 обозначают ва-
рианты распределения весов критериев по таблице 10.6, а в следующей строке, разде-
ленной на девять частей, эти цифры указывают варианты распределения весов под-
критериев по таблице 10.6. В целях анализа полученных данных ЛФР (ЛПР) должно
иметь перед собой одновременно обе таблицы: табл. 10.8 и табл. 10.6.
4. Обработка значений экспертных оценок приоритетности критериев и подкри-
териев.
После получения от шести групп экспертов, сформированных для оценок значи-
мости одной группы критериев и пяти групп подкритериев, таблиц ранжирования
критериев и подкритериев и таблиц их парного сравнения можно приступать к обра-
ботке представленной информации.
4.1. Обработка экспертных оценок приоритетности обобщенных критериев.
4.1.1. ЛФР, используя полученные от экспертов первой группы (их минимальное
число т = 3) таблицы с ранжировками критериев Кнтз, К^, Кр, Кэб и КрП (п = 5), запол-
няет таблицу 10.9.
Таблица 10.9
Эксперты Критерии
Кшэ «ээ Кр Кэб Крп
э, (X,) *11 ^12 *13 *14 ^15
э2(М x2i *22 *23 х24 ^25
Э3(Хз) *31 ^32 *33 *34 ^35
513
В этой таблице \ — уровни компетентности экспертов, Ху — ранги (числа 1, 2, 3,
4, 5), назначенные у-му критерию z-м экспертом). Табл. 10.9 составлена для случая
трех экспертов, но должна иметь возможность «размещения» в ней 6—7 экспертов
(это замечание касается и всех дальнейших таблиц с оценками экспертов).
4.1.2. Вычисляем статистику Фридмана, пользуясь формулой
12 " ( т f
%набл = „„(„+!) < S + *>’ <10’31)
Здесь л = 5, а/и = 3 — 7 (конкретное значение т ЛФР берет из табл. 10.9). Форму-
ла (10.31) используется в случае, если все эксперты указали строгие ранжировки
(в каждой из строк нет одинаковых чисел). В противном случае (среди Ху хотя бы
в одной строке имеются одинаковые ранги) Х^йбл находят по формуле
z \2
" [ ” т(п + 1)
I " хи 2
*н2абл = ---------------> (Ю-32)
1 1 т
У2тп(п + ^-^^Т‘
i =/
где 7} = -^ ^ki^ki “О, hi ~ число первой, второй и т. д. связей в ранжировке z-ro
к
эксперта.
Принимаем «среднее» значение уровня значимости а = 0,05. Тогда табличное
значение Х£ при л = 5и/и = 3-*-6составляет8,3 +9.
Если вычисленное значение Х^л6л > 8,5, то нулевая гипотеза о «равнонекомпе-
тентности» экспертов отвергается, и ЛФР переходит к п. 4.1.3. В противном случае не-
обходимо провести второй тур экспертизы по определению приоритетности критери-
ев, а ЛФР переходит к п. 4.2.
4.1.3. Определяем степень согласованности суждений экспертов, которая харак-
теризуется коэффициентом конкордации
^=%2абл /[«(« -DL (Ю.зз)
п = 5, а т берется из табл. 10.5.
Если 0,7 > 0,5, согласованность считается удовлетворительной, при IK > 0,7 —
хорошей, и ЛФР переходит к п. 4.1.4. При W< 0,5 необходимо проведение второго тура
экспертизы, а ЛФР переходит к п. 4.2.
4.1.4. При удовлетворительной или хорошей согласованности суждений экспер-
тов относительно приоритетности критериев переходим к построению обобщенной
(групповой) ранжировки критериев по правилу:
т
Z^;;=i-5, (Ю.34)
/•=i
где \ — весовые коэффициенты (см. табл. 10.9), характеризующие уровень компе-
тентности экспертов (Е \ = 1), входящих в первую группу (ранжирование критериев).
После вычисления пяти значений Sj наименьшему из них и соответствующему
критерию присваивается ранг 1 и т. д.
4.2. Обработка экспертных оценок приоритетности подкритериев критерия Кнтз.
514
Таблица 10.10
Эксперты Подкритерии критерия Кнтз
Пц П12 П13 п14 П15 п|6 П.7
Э1 (М ^11 *17
Э2(1г)
Э3(М *31 *37
4.2.1. В этом случае ЛФР заполняет табл. 10.10, используя данные второй группы
экспертов.
В таблице 10.10 П1у — подкритерии первого критерия, XtJ — ранги (1—7), назна-
ченные у-му подкритерию z-м экспертом, т = 3—6, п = 7.
4.2.2. Вычисляется статистика Фридмана Х^абя по формуле (10.31) или (10.32)
в зависимости от того, отсутствуют или присутствуют в табл. 10.6 связанные (одина-
ковые) ранги.
Если > 9,5, то можно переходить к следующему пункту 4.2.3. В противном
случае необходимо проведение второго тура экспертизы, а ЛФР переходит к п. 4.3.
4.2.3. Определяем коэффициент конкордации W по формуле (10.33) при п = 7
(т берется из табл. 10.11). При 0,5 можно приступить к сведению мнений экспер-
тов к единому групповому результату путем вычисления Sj (j = 1...7) по формуле
(10.34) с учетом того, что ранжирование подкритериев П1у осуществляла вторая груп-
па экспертов, которые будут иметь «свои» уровни компетентности (величины \ для
этой группы в общем случае будут отличаться от соответствующих значений для экс-
пертов первой группы, но всегда Е \ = 1). При W< 0,5 ЛФР переходит к п. 4.3.
4.2.4. После вычисления семи значений Sj ранжируем их, присваивая ранг 1 на-
именьшему из Sj и соответствующему подкритерию и т. д.
4.3. Обработка экспертных оценок приоритетности подкритериев критерия К^.
4.3.1. ЛФР заполняет табл. 10.11 экспертной информацией по ранжированию
подкритериев экономической эффективности проектов, полученной от третьей груп-
пы экспертов-экономистов. В этом случае п = 2, а т > 8, П2у (J = 1,2) — подкритерии
второго (Кээ) критерия.
4.3.2. Вычисляется статистика Фридмана Х^абл по формуле (10.31) или (10.32)
в зависимости от того, отсутствуют или присутствуют в табл. 10.11 связанные (одина-
ковые) ранги.
Таблица 10.11
Эксперты Подкритерии Кээ
П21 П22
Э, (X!) *11 *12
э2(М *21 *22
...
э8(М *31 *32
515
4.3.3. Затем вычисляют:
•^набл 2^“абл — О^набл! ’
г ____ (^ ~ ^)^набл
НЯбЛ - «(«-О-^абл ’
Ja[(n - 1), (т - 1)(л - 1)] = | {£2 [л - 1] + (л - 1)£а[(л - 1), (т - 1)(л - 1)]}. (10.35)
Здесь £2 _ распределение «хи-квадрат», при п = 2 и a = 0,05 Е£ = 3,84; Fa —
распределение Фишера, при и = 2и/и = 8£а = 5,59.
Если /набл > Ja [1, (т — 1)], то принимают гипотезу о согласованности суждений
экспертов и переходят к п. 4.3.4. В противном случае необходимо проведение второго
тура экспертизы, а ЛФР переходит к п. 4.4.
4.3.4. Вычисляют коэффициент конкордации W по формуле (10.33) и при
W> 0,5 можно переходить к следующему пункту.
В противном случае необходимо вновь повторить экспертизу важности рассмат-
риваемых подкритериев, а ЛФР переходит к п. 4.4.
4.3.5. Строим окончательную (групповую) ранжировку по правилу (10.34).
4.4. Обработка экспертных оценок приоритетности подкритериев критерия Кр.
4.4.1. ЛФР заносит в табл. 10.12 результаты ранжирования трех (п = 3, т = 3—6)
подкритериев критерия конкурентоспособности продукции, полученные им от экс-
пертов четвертой группы (специалистов по маркетингу).
4.4.2. Вычисляется статистика Фридмана Х^абл по формуле (10.31) или (10.32)
в зависимости от того, отсутствуют или присутствуют в табл. 10.12 связанные (одина-
ковые) ранги.
Если 2f2a6jl > 63, то можно переходить к следующему пункту 4.4.3. В противном
случае необходимо проведение второго тура экспертизы, а ЛФР переходит к п. 4.5.
4.4.3. Вычисляют коэффициент конкордации по формуле (10.33) и при 0,5
переходят к следующему п. 4.4.4. При 1У< 0,5 требуется проведение второго тура экс-
пертизы, а ЛФР переходит к п. 4.5.
4.4.4. При помощи правила (10.34) сводим суждения экспертов к обобщенной
групповой ранжировке подкритериев критерия Кр.
4.5. Обработка экспертных оценок приоритетности под критериев критерия Кэб.
4.5.1. ЛФР заносит в табл. 10.13 результаты ранжирования трех (п = 3, т = 3—6)
подкритериев критерия экологичности и безопасности технологического процесса
и продукции, полученные им от экспертов пятой группы, являющихся специалиста-
ми в данной предметной области.
Таблица 10.12
Эксперты Подкритерии Кр
П31 П33
э, <Х.) ^11 *12 *13
э2(М *21 *22 *23
Э3(Хэ) *31 *32 *33
516
Таблица 10.13
Эксперты Подкритерии
П41 П42 П43
Э, (X,) ^11 *12 *13
э2(М Х21 *22 *23
Э3(Хз) *31 *32 *33
4.5.2. Вычисляется статистика Фридмана Л^абл по формуле (10.31) или (10.32)
в зависимости от того, отсутствуют или присутствуют в табл. 10.9 связанные (одина-
ковые) ранги.
Если Х„абл > 6,3, то можно переходить к следующему пункту 4.5.3. В противном
случае необходимо проведение второго тура экспертизы, а ЛФР переходит к п. 4.6.
4.5.3. Вычисляют коэффициент конкордации по формуле (10.33) и при 0,5
переходят к следующему п. 4.5.4. При W< 0,5 требуется проведение второго тура экс-
пертизы, а ЛФР переходит к п. 4.6.
4.5.4. При помощи правила (10.34) сводим суждения экспертов к обобщенной
групповой ранжировке подкритериев критерия К^.
4.6. Обработка экспертных оценок приоритетности подкритериев критерия КрП.
4.6.1. ЛФР заносит в табл. 10.14 результаты ранжирования трех (п = 3, т = 3—6)
подкритериев критерия реализуемости проекта, полученные им от экспертов послед-
ней (шестой) группы.
4.6.2. Вычисляется статистика Фридмана Х^а6л по формуле (10.31) или (10.32)
в зависимости от того, отсутствуют или присутствуют в табл. 10.14 связанные (одина-
ковые) ранги.
Если Х„абл > 6,3, то можно переходить к следующему пункту 4.6.3. В противном
случае необходимо проведение второго тура экспертизы, а ЛФР переходит к п. 4.7.
4.6.3. Вычисляют коэффициент конкордации по формуле (10.33) и при W> 0,5
переходят к следующему п. 4.6.4. При W < 0,5 требуется проведение второго тура экс-
пертизы, а ЛФР переходит к п. 4.7.
4.6.4. При помощи правила (10.34) сводим суждения экспертов к обобщенной
групповой ранжировке подкритериев критерия КрП.
4.7. Просмотр результатов обработки экспертных оценок приоритетности крите-
риев и подкритериев.
Т абл ица 10.14
Эксперты Подкритерии КрП
П51 П52 П5з
э, (X,) *11 *12 *13
32(Xj) *21 *22 *23
Э3(Хз) *3. *32 *33
517
Таблица 10.15
Обобщенные (групповые) ранжировки критериев и подкритериев
Критерии Кнтз К,э Кк Кэб Крп
Ранги 1 2 3 5 4
Подкритерии Кнтз Пи Пп П|3 Пн П.5 П16 П17
Ранги 1 2 4 3 5 6 7
Подкритерии КзЭ n2i П22
Ранги 2 1
Подкритерии Ккк П31 ^32 П3з
Ранги 1 2 3
Подкритерии К^ П4| П42 п43
Ранги 1 2 3
Подкритерии КрП П5, П52 П5з
Ранги 1 2 3
ЛФР должен иметь возможность просмотреть и при необходимости распечатать
результаты обработки экспертных оценок приоритетности критериев и подкритери-
ев, которые целесообразно свести в одну общую (итоговую) табл. 10.15.
Табл. 10.15 показана для случая, когда суждения соответствующих групп экспер-
тов относительно приоритетности всех критериев и подкритериев являются согласо-
ванными. В противном случае отдельные строки табл. 10.15 с названием «Ранги» мо-
гут оказаться незаполненными. Для соответствующих критериев или под критериев
следует провести дополнительные туры экспертизы и вновь повторить описанную
выше процедуру обработки.
5. Обработка значений экспертных оценок сравнительной важности критериев
и подкритериев.
5.1. Обобщенные критерии.
5.1.1. ЛФР, используя полученные от экспертов первой группы таблицы парных
сравнений критериев Кнта, К^, Кр, и КрП, заполняет табл. 10.16.
В этой таблице числа д1у — соотношение важности первого критерия (Кнтз) со
вторым (Кэз), третьим (Кр), четвертым (К^) и пятым (КрП) критериями соответствен-
но (/ = 2, 3, 4, 5), Yik — значение числа д1у, назначенное z-м экспертом (/ = 1, 2, ..., /и,
Таблица 10.16
Эксперты Отношение важности критериев
Д12 Д13 ДМ Д.5
э, (М К„ К.2 К.з К.4
э2(М У22 ^23 К24
...
э6(М К61 Кб2 К6з Кб4
518
Таблица 10.17
Эксперты Отношение важности подкритериев Кнтз
Д12 Ав Д14 Д15 Дм Дп
Э, (X,) Гц ^12 Г.з
э2(М ^21 ^26
...
э4(^) г61 ?66
5.1.2. Для каждого столбца (к = 1—4) табл. 10.16 вычисляют:
среднее арифметическое значение чисел д1у
1 т
(ю.зба)
среднеквадратическое отклонение
г 1 т _ „П1/2
2] ; (ю.36 6)
коэффициент вариации
К =. (10.36 b)
rk
5.2. Подкритерии критерия К^.
5.2.1. После определения коэффициентов вариации для табл. 10.16 ЛФР перехо-
дит к табл. 10.17, которую заполняет, используя экспертные оценки сравнительной
важности подкритериев критерия научно-технической важности Кнтз, полученные им
от экспертов второй группы.
5.2.2. Для каждого столбца табл. 10.13 (к = 1—6) вычисляют Yk, Sk и Kv по форму-
лам (10.36 а)—(10.36 в), после чего ЛФР переходит к табл. 10.18.
5.3. Подкритерии критерия К^.
5.3.1. Табл. 10.18 ЛФР заполняет, используя оценки сравнительной важности
подкритериев критерия экономической эффективности К^, полученные им от экс-
пертов третьей группы.
5.3.2. Для единственного столбца табл. 10.18 (к = 1) вычисляют Yk, Sk и Kv по
формулам (10.36 а)—(10.36 в), после чего ЛФР переходит к табл. 10.19.
Таблица 10.18
Эксперты Отношения важности подкритериев
Д12
э, Гц
э2 ^21
...
Э8 ^81
519
Таблица 10.19
Эксперты Отношения важности подкритериев Кр
Д12 Ди
Э. Гц Г.2
Э2 *21 *22
...
Эб *6. *62
5.4. Подкритерии критерия Кр.
5.4.1. Табл. 10.19 ЛФР заполняет, используя оценки сравнительной важности
подкритериев критерия конкурентоспособности продукции Кр, полученные им от
экспертов четвертой группы.
5.4.2. Для каждого столбца табл. 10.19 (к = 2) вычисляют Yk, Sk и Kv по формулам
(10.36 а)—(10.36 в), после чего ЛФР переходит к табл. 10.20.
5.5. Подкритерии критерия К^.
5.5.1. Табл. 10.20 ЛФР заполняет, используя оценки сравнительной важности
подкритериев критерия экологичности и безопасности техпроцесса и продукции К^,
полученные им от экспертов пятой группы.
5.5.2. Для каждого столбца табл. 10.20 (к = 2) вычисляют Yk, Sk и Kv по формулам
(10.36 а)—(10.36 в), после чего ЛФР переходит к табл. 10.21.
5.6. Подкритерии критерия КрП.
5.6.1. Табл. 10.21 ЛФР заполняет, используя оценки сравнительной важности
подкритериев критерия реализуемости проекта КрП, полученные им от экспертов по-
следней, шестой группы.
5.6.2. Для каждого столбца табл. 10.21 (к = 2) вычисляют Yk, Sk и Kv по формулам
(10.36 а)—(10.36 в).
5.7. Просмотр результатов обработки экспертных оценок сравнительной важнос-
ти критериев и подкритериев.
ЛФР (после завершения п. 5.6.2.) должно иметь возможность просмотреть и при
необходимости распечатать результаты обработки экспертных оценок сравнительной
Таблица 10.20
Эксперты Отношения важности подкритериев К^
Д12 Д1з
Э, Гц *12
Э2 *21 У22
...
Э6 *61 ^62
520
Т абл ица 10.21
Эксперты Отношения важности подкритериев КрП
Д12 Д1з
Э1 ?! Г12
Э2 г2, У22
...
Э6 Гб. ?б2
важности критериев и подкритериев, которые целесообразно свести в одну общую
(итоговую) табл. 10.22.
В табл. 10.22, помимо рассчитанных средних арифметических значений Yk для
всех критериев и подкритериев, указаны также соответствующие им величины коэф-
фициентов вариации Kv Анализируя табл. 10.22, ЛФР отмечает все значения Kv > 0,3.
Для всех таких значений Kv необходимо проведение вторых туров экспертизы в соот-
ветствующих группах экспертов.
После получения результатов вторых туров экспертизы ЛФР должно иметь воз-
можность, указав номера (названия) групп критериев и подкритериев и номера необ-
ходимых столбцов в этих группах (для которых Kv > 0,3 по результатам первого тура),
провести повторно для них вычисления Yk и Kv с помещением полученных значений
в табл. 10.22 до тех пор, пока в табл. 10.22 не останется ни одного Kv > 0,3. Процесс мо-
жет потребовать нескольких итераций (и соответственно туров экспертизы).
5.8. Ранжирование технологических проектов.
5.8.1. После получения согласованных значений экспертных оценок приоритетнос-
ти и сравнительной важности критериев и подкритериев вычисляются весовые коэффи-
циенты критериев и подкритериев с использованием соотношений (10.27)—(10.30).
5.8.2. Затем с использованием формулы (10.22) для каждого’из выбранных для
ранжирования проектов определяют их итоговую оценку.
Таблица 10.22
Отноше- ния важ- ности д1у Критерии Подкри- терии Кнт, Подкри- терии К^ Подкри- терии Кр Подкри- терии Подкри- терии КрП
?* «V Yk Yk Yk Yk
Д12 ?! ?i ?i ?! к. ?! ?!
Д13 ?2 ?2 «2 ?2 «2 ?2 «2 ?2 «2
Д14 ?3 ?3 ?з
Д15 ?4
Д16
Д17 ?6 К6
521
ЛИТЕРАТУРА
1. Конов Ю. П, Мазнев С. Ф. Ускорение использования изобретений. — М.: Маши-
ностроение, 1989. С. 152.
2. Петушков В. В., Чернышев В. И. Методы и критерии оценки разработок, содержа-
щих изобретения. — М.: Машиностроение, 1979. С. 73.
3. Давыдов М. Г., Лисичкин В. А. Этюды о прогностике. — М.: Знание, 1977. С. 96.
4. Гмошинский В. Г. Инженерное прогнозирование. — М.: Энергоиздат, 1982. С. 180.
5. Постников В. И., Мымрин Ю. И. Эффективность исследований и разработок
в машиностроении. — М., 1980. С. 199.
6. Николаев И. А. Приоритетные направления науки и технологии. Выбор и ре-
ализация. — М.: Машиностроение, 1995. С. 164.
7. Соболь И. М., Статников Р. Б. Выбор оптимальных параметров в задачах со мно-
гими критериями. — М.: Наука, 1981. С. 110.
8. Саати Т. Принятие решений. Метод анализа иерархий. Пер. с англ. — М.: Радио
и связь, 1993. С. 314.
СОДЕРЖАНИЕ ГЛАВЫ 10
10.1 . Особенности этапа НИОКР...................................478
10.2 . Оценка изобретений........................................479
10.3 . Отбор проектов НИОКР......................................482
10.4 . Показатели технических систем.............................483
10.5 . Обобщенные критерии и подкритерии.........................485
10.6 . Разработка методики сравнительной экспертной оценки
технологических проектов.........................................489
10.6.1 . Применение экспертно-аналитических методов для оценки
и отбора перспективных технологий.............................489
10.6.2 . Подход к анализу экспертных оценок
на основе теории важности критериев...........................493
10.6.3 . Решение многокритериальных задач оптимизации
при помощи метода анализа иерархий............................496
10.6.4 . Рациональная процедура многокритериальной
экспертной оценки технологических проектов....................500
10.7 . Алгоритм оценки предварительного отбора
и ранжирования технологических проектов на стадии НИОКР..........506
10.7.1 . Определение приоритетности и весовых коэффициентов критериев
и подкритериев...............................................506
10.7.2 . Предварительный отбор проектов......................507
10.7.3 . Ранжирование технологических проектов...............508
Литература...........................................................522
ГЛАВА 1 1___________________________________________________________
Методология научного
эксперимента
в производстве
аэрокосмической техники
Особенностями экспериментальных исследований в авиа- и ракетостроении яв-
ляется их большой объем и структурное разнообразие. Эксперименты охватывают все
этапы жизненного цикла изделия от проектирования до утилизации. Несмотря на
это, они носят комплексный характер, что связано со сложностью объекта исследова-
ния и повышенными требованиями к качеству деталей, узлов, отсеков, агрегатов
и систем летательного аппарата. Многообразие исследований по конечным целям
можно разделить на три стратегических направления:
1) повышение тактико-технических характеристик объекта исследования (ско-
рость, дальность, высота полета, тяга, масса, удельный расход топлива и т. п.);
2) повышение надежности или ее составляющих (работоспособность, ремонто-
пригодность, безотказность, долговечность, наработка на отказ, интенсивность отка-
зов, ресурс, сохраняемость и др.) определенных узлов, агрегатов или изделий в целом
различными конструкторскими и технологическими методами;
3) повышение экономической эффективности производства ЛА (себестоимость,
трудоемкость, материал о- и энергоемкость и т. д.).
Предметом рассмотрения данной главы являются методические вопросы подго-
товки и проведения экспериментальных исследований в области авиастроения, кото-
рые встречаются при разработке новых конструкций и технологий изготовления и ис-
пытаний изделий авиационной техники, при проектировании и применении нового
технологического оборудования, новых методов обработки и др.
Основные рассматриваемые задачи:
— ознакомление с основными этапами проведения исследований;
— изучение методов обработки и представления результатов экспериментов.
11.1. ОПРЕДЕЛЕНИЯ И ТЕРМИНЫ
Оборудование для эксперимента делится на три части: измерительные приборы,
испытательная аппаратура и образец для эксперимента.
Измерительные приборы воспринимают, считают, измеряют, наблюдают, а затем
записывают, хранят, корректируют и показывают все параметры, которые они долж-
ны «видеть».
Испытательная аппаратура — все, что воздействует на испытываемый объект.
Образец для испытаний — объект, подвергаемый испытаниям, который при не-
обходимости можно заменить другим. Не во всех экспериментах имеется образец для
испытаний, например, при испытании нового метода производства с использованием
станков, материалов, привлечением рабочих и т. п.
План эксперимента определяет набор инструкций по проведению эксперимента,
которые указывают последовательность работы, характер и величину переменных
и дают указания о проведении повторных экспериментов.
523
Последовательность проведения эксперимента означает порядок, в котором вно-
сятся изменения в работу испытательной аппаратуры.
Репликация означает повторение экспериментов — возвращение к первоначаль-
ным условиям. Проведение нескольких повторных опытов при одних и тех же услови-
ях не является репликацией.
Переменная может быть независимой или зависимой.
Независимая переменная может быть изменена независимо от других величин.
Зависимая переменная изменяется при изменении одной или большего числа не-
зависимых величин.
Если некоторая физическая величина изменяется случайным образом и ее нельзя
контролировать, то это внешняя переменная.
Коэффициент полезного действия, температура обмотки и входной ток — при-
меры зависимых переменных.
В контролируемом эксперименте влияние внешних переменных исключено,
а независимые переменные можно изменять в соответствии с принятым планом.
Проведение контролируемого эксперимента — основной принцип научного исследо-
вания. На рис. 11.1 показана схема типичного эксперимента.
Измерения осуществляют с помощью приборов. Для каждой измеряемой вели-
чины имеется «наилучшее» или «наиболее вероятное» значение. «Наилучшее» значе-
ние можно улучшить еще более, используя более дорогие приборы, повторные отсче-
ты и привлекая более квалифицированный персонал.
В зависимости от стандартов точности, принятых для данного эксперимента, ре-
зультаты измерений могут быть точными или неточными (иметь систематическую
и случайную ошибки).
Ошибка выражается некоторым числом и определяется как разность между ка-
либрованным значением или известным отсчетом и отсчетом, снятым с прибора. Та-
ким образом, ошибку можно определить только зная точное значение измеряемой ве-
личины. Так как точное значение может быть неизвестно, то используют понятие
«неопределенности» (неточности) значения.
Неопределенность представляет собой оценку ошибки, т. е. ошибку, если бы ее
можно было измерить путем калибровки.
Вопросы Результаты эксперимента
Рис. 11.1. Упрощенная схема типичного эксперимента
524
Если нельзя провести калибровку, то трудно разделить систематическую и слу-
чайную погрешности, и мы производим оценку их комбинации.
Данные — все символические продукты эксперимента (фотоснимки, магнитная
запись, показания счетчиков и т. п.). Необработанные данные сняты непосредственно
с приборов. Обработанные данные — та же информация после выполнения над ней
некоторых действий, например математической обработки.
11.2. ЭКСПЕРИМЕНТ КАК ПРЕДМЕТ ИССЛЕДОВАНИЯ
Общей чертой, объединяющей исследователей, является эксперимент. Методы
проведения экспериментов имеют много общего: исследователи стараются контроли-
ровать свой эксперимент или исключить влияние внешних переменных; стремятся
уменьшить число переменных для уменьшения сроков и стоимости; всех интересует
точность измерительных приборов и точность полученных данных. Каким бы прос-
тым ни был эксперимент, вначале составляется план его проведения. Требуется обна-
ружить ошибки и погрешности, неполадки в самом широком смысле. Нужно прове-
рить приемлемость полученных результатов. В конце следует анализировать получен-
ные результаты и дать их интерпретацию, поскольку без этого этапа весь процесс не
имеет смысла.
Инженерный эксперимент обычно связывают с исследованиями механических,
гидродинамических, электрических, тепловых и других процессов, происходящих
в механизмах, машинах и приборах. Мы не будем делать различий между промыш-
ленными, лабораторными, поисковыми или другого типа экспериментами. Будем
рассматривать только общие черты, присущие всем экспериментам.
Эксперименты и экспериментаторы могут отличаться друг от друга, но планиро-
вание, проведение и анализ данных осуществляются в одинаковой последовательнос-
ти. Многие эксперименты являются дорогостоящими и на первый взгляд очень слож-
ными. Однако каким бы сложным ни был эксперимент, его результаты мало отлича-
ются от отчетов по лабораторным работам. Например, при запуске исследовательской
ракеты составляется несколько отчетов: о работе двигателей, о работе элементов сис-
темы управления, о траектории полета, о регистрации космического излучения, о по-
ведении экипажа и др.
Любой эксперимент, каким бы сложным он ни казался, заканчивается представ-
лением результатов, формулировкой выводов и выдачей рекомендаций. Результаты
представляются в виде таблиц, графиков, аналитических или эмпирических зависи-
мостей, в словесной форме.
Таким образом, сложные испытания ракет или ядерных реакторов в действитель-
ности представляют собой большое число отдельных экспериментов, выполняемых с
помощью дорогостоящего испытательного оборудования. Более того, хотя
и возможно представить себе исключительно сложный эксперимент, результаты ко-
торого удастся постигнуть после многочасового напряженного изучения, сомнитель-
но, что такой эксперимент имеет большую ценность. Можно знать о существовании
множества сложных взаимосвязей между данными, однако, если эти связи не будут
представлены в виде графиков, уравнений или словесных описаний, понятных колле-
гам, будет просто потеряно время. Большинство инженерных экспериментов ведет к
определенному действию — принятию решения, признанию неудачи или к продолже-
нию испытаний. Эти действия возможны лишь только тогда, когда мы показываем
другим то, что сами сделали.
525
При проведении экспериментов часто не задаются вопросом, почему именно
этот прибор или установка используются в эксперименте в данном месте. И вместо
вопроса:
«Почему здесь стоит термопара?» (разумеется, для измерения температуры)
следовало бы задать вопрос:
«Почему установлена железоконстантановая термопара, припаянная к трубе, об-
мотанная асбестовой лентой и присоединенная к регистрирующему устройству, рабо-
тающему в диапазоне от 0 до 500 °C и точностью ±3%?»
Маловероятно сразу получить ответ на эти вопросы.
Если мы не думаем о точности и погрешности измерений, влиянии переменных,
не составляем план эксперимента и не думаем о представлении результатов, вполне ве-
роятно, что эксперимент не принесет никакой пользы. Вероятность случайно натолк-
нуться на удачный план ничтожно мала: известно не так много открытий, подобных
случайному открытию пенициллина благодаря немытым бутылкам. Настоящий иссле-
дователь тщательно готовит эксперимент, всесторонне обдумывая все возможности.
11.3. СОВОКУПНОСТЬ СЛУЧАЙНЫХ ПОГРЕШНОСТЕЙ.
ЗАКОН НОРМАЛЬНОГО РАСПРЕДЕЛЕНИЯ
Обозначим случайные погрешности N отдельных измерений через:
8j = х1-х, 82=х2-х;..., 8n = xm-x,
где X; — результат отдельного измерения (/ = 1, 2,..., TV), х — истинное значение изме-
ряемой величины (обычно неизвестно).
Просуммируем случайные погрешности:
N N
Z8,= Yxi~N’x-
i = 1 i = 1
Введем xcp — среднее значение результата N измерений по формуле
Yxi = N'xcp’
/• = 1
тогда
/ = 1
ХСР"Х=Т-
Погрешность среднего (т. е. отклонение среднего от истинного значения) равна
средней погрешности измерений. При N—> оо (хср — х) —> 0, т. е. среднее значение
совпадает с истинным.
Остаточные погрешности:
Д*1 = *1 - *ср, Дх2 = х2 - хср,bxN = xN - хср.
Просуммируем остаточные погрешности. Учитывая, что У xz = 7V-xcp, получим:
z= 1
X Дх,.= X х, —А^х^ = 0.
i = 1 i = 1
Эти формулы служат для проверки правильности вычисления хср.
526
Закон нормального распределения (рис. 11.2).
V ДР dP г+5
Предел „1™,^ - = у называют плотностью вероятности, где Р = J ^У^~~
вероятность.
Для нормального распределения
1 -Д 1
у = Уо.е-^^ = __.е 2c.yo=__t
где т| — модуль точности, а — среднеквадратическая погрешность.
Основные аксиомы при выводе закона Гаусса.
1. Аксиома случайности: число отрицательных погрешностей равно числу поло-
жительных.
2. Аксиома распределения: малые погрешности возникают чаще, чем большие.
Площадь под кривой равна вероятности Р
P = J е-’’2'82 ск= -УО;
В нормированном виде Р = 1; у0 = -у= . Тогда у = -у= • е -Г|2 5\
a/я а/я
Вероятность нахождения ошибки в диапазоне от —8 до +8:
Ps=fn.e-n2S2d8=4j+5e-n252d8.
6 -5TS a/я -5
Заменим переменную на (т|8). Тогда
.+т]8 , ,
Л(8=1 -е-я2 82 d(n3).
-П8
Показатель точности определяется экспериментально через среднеквадратиче-
1 тт
скую погрешность о = . Для этого вычисляем дисперсию
л/2т|
N N
а2 = Z 82 ’ TV ’ X 82 = 82 • п\ + 82 • Л2 + - + 8У •
z = 1 z = 1
где ni — число ошибок 8Z.
На рис. 11.3 показаны два распределения с различными среднеквадратическими
погрешностями.
Рис. 11.2. Нормальное
распределение погрешностей
8
Рис. 11.3. Кривые рапределений
с большой и малой
среднеквадратическими
погрешностями
527
Если рассматривать генеральную совокупность, то вероятность появления 8Z
П 2 2
в интервале A8Z равна у= х A8Z. Тогда
N „ 1
У 8?= [82 -e-n2 *2d8 = .
' 3 Jn J2r\
Если количество измерений N—> оо (или вероятность появления всех погрешнос-
тей равна 1), то о = и вероятная ошибка Ф = ” = 0,477 • • а = 0,6746 • а.
В интервале ±Т|Ф находится 50% все погрешностей измерений.
Оценка точности с помощью среднеквадратической погрешности.
Чтобы вычислить среднеквадратическую погрешность в случае выборки, вычтем
из равенства 8Z = xz — х равенство Axz = xz — хср. Получим: 8Z — Axz = хср — х — отклоне-
ние среднего значения от истинного.
W N
Z 8/ X 5,.
Z = 1 Z = 1
Поскольку хср - х = —Jy - , то 8,- - Ах,- = -у- = 8ср, т. е. 8,- = Ах,- + 8ср.
Возведем обе части в квадрат:
8? = (Ах,)2 + 2 Ах,8ср + 82р .
Просуммируем обе части по i от 1 до N:
N N N
£ (Ч)2 + 28сР X Ч + N‘ 8сР •
Z = 1 Z = 1 Z = 1
У Axz = 0 на основании аксиомы случайности. Поэтому
Z = 1
При N-----> оо
Тогда
N N Z=1
Z82= Z(5,)2+^r
или
Так как
(У-1) X 8? =NY (Ax,.)2.
i=l i=1
N N
Z 8? L (Ax,.)2
° W-l ’
528
то среднеквадратическая погрешность:
X (д*,)2
/• = 1
— формула Бесселя.
«Наилучший» результат выборки и обоснование
метода наименьших квадратов.
Так как точное значение измеряемой величины
практически никогда не известно, встает вопрос о
«наилучшем» или наиболее вероятном значении ее
величины. Если сделано несколько измерений, ре-
зультаты которых существенно отличаются друг от
Рис. 11.4. К определению
«наилучшего» значения выборки
друга, то можно предположить, что имеет место
большая случайная ошибка. Встает вопрос о наилучшей оценке отсчета.
Рассмотрим выборку из п отсчетов, содержащую значения хр х2, •••> хп- Допустим,
что эти отсчеты представляют собой выборку из нормально распределенной беско-
нечной совокупности. Погрешности отдельных измерений равны Axj = х{ - хс,
Дх2 = х2 — хс и т. д. Каждая из погрешностей находится в малом интервале dx, как по-
казано на рис. 11.4.
Вероятность ее появления равна площади небольшого прямоугольника у • dx. Или
ДР) = -у= dx • е
-Т]2(хс -Xj)2
Аналогичные выражения могут быть получены для вероятностей появления по-
грешностей Дх2, Дх3 и т. д. Какова вероятность появления именно этой, а не другой
выборки? Вероятность появления всей выборки, состоящей из п отсчетов, равна про-
изведению вероятностей (пример: бросание монеты). Следовательно, вероятность по-
явления последовательности, состоящей из п отсчетов, равна
Р
dx"e’i2 [(хс - х,)2 + (хс - х2)2 + ...(хс - х„)2]
Рассмотрим одно из фундаментальных допущений математической статистики и
теории вероятностей. Допустим, что отсчеты хь х2,..., хп в совокупности отклоняются
от «истинного» отсчета хс таким образом, что суммарная вероятность появления этих
отклонений максимальна. Прямое следствие этого допущения применительно к на-
шему случаю выражается следующим образом:
(Xj - хс)2 - (х2 - хс)2 - (х3 - хс)2 - ... - (х„ - хс)2-> min,
т. е. сумма квадратов отклонений от наилучшего или точного отсчета должна быть ми-
нимальной. Этот важный результат лежит в основе известного метода наименьших
квадратов.
Неизвестное наилучшее значение хс должно быть таким, чтобы вероятность
Р была бы максимальной, т. е.
dP/dxc = -(т|/7л)" • dx" • 2т|2 • [(хс - х^] + [(хс - х2)] + ...
+ [(хс - х„)] ехр (-п2 • ((хс - х,)2 + (хс - х2)2 + (хс - х3)2...)).
Xj + х2 + х3 + ...
Производная равна нулю только в одном случае: хс =-----------------
529
Распределение
среднего
Средне-
квадратическая
ошибка \
среднего _j
Средне-
квадратическая
\ / ошибка
•'ср
Ошибка среднего
(Ошибка результата)
"и Измеряемая
величина х
Рис. 11.5. Погрешности измерений и погрешности среднего
Проверка второй производной показывает, что хс есть максимум функции.
Использование среднего арифметического не ограничивается только нормаль-
ным распределением, однако только в случае нормального распределения среднее яв-
ляется наилучшей оценкой точного или истинного значения.
В случае несимметричного распределения среднее не всегда будет наилучшей
оценкой.
Среднеквадратическая ошибка среднего (рис. 11.5) равна оср = ~^= для генераль-
а/ /V
нои совокупности, ИЛИ О = -у=== для выборки.
£8/
Погрешность среднего 8ср = .
Распределение ошибок, отличающееся от нормального.
Рассмотрим гипотетическое распределение ошибок, полученное при 50 замерах
длины трубы в см, скорректированное под нормальное распределение (рис. 11.6).
Для нормального распределения сумма квадратов этих 50 отклонений
Е Дх2 = 6(0)2 + 10(0,2)2 + 10(0,4)2 + 8(0,6)2 + 6(0,8)2 + 4(1,0)2 +
+ 2(1,2)2 + 2(1,4)2 + 2(2,0)2 = 26,52.
Рис. 11.6. Гистограммы для 50 ошибок, распределенных по нормальному закону
и равномерному закону. Вероятная ошибка для каждого распределения
составляет примерно 0,5 см
530
£ДЛ?
Среднеквадратическое отклонение о = J _ =0,737.
Вероятная ошибка Ф = 0,6745о = 0,495, т. е. в диапазоне ±0,5 находится половина
(25) всех измерений.
Рассмотрим равномерное распределение (распределении рулетки), подобранное
таким образом, чтобы вероятная ошибка составляла ±0,5 см.
Вычислим снова сумму квадратов отклонений:
£Дх,2 = 10(0,1)2 + 10(0,3)2 + 10(0,5)2 + 10(0,7)2 + 10(0,9)2 = 16,5.
Среднеквадратическое отклонение равно 0,58 см (для нормального распределе-
ния — 0,737). Вероятная ошибка Ф = 0,392 (вместо 0,495 для нормального закона).
Очевидно, что очень немногие распределения будут так отличаться от нормального,
как равномерное. Но даже в этом случае вероятная ошибка отличается только при-
мерно на 20%. Поэтому можно пользоваться оценками точности для любого распре-
деления как для нормального, если ошибка в 20% несущественна.
11.4. ОШИБКА И НЕОПРЕДЕЛЕННОСТЬ
ЭКСПЕРИМЕНТА В ЦЕЛОМ
Анализ ошибок отдельных измерений позволяет выявить ошибки измерительной
системы, включающей чувствительный элемент, индикаторную часть и наблюдателя.
Чаще используется эксперимент, когда производятся измерения несколькими прибо-
рами нескольких величин, а затем с помощью математической обработки получают
окончательный результат.
Может быть, что относительно точные измерения, выполненные на отдельных
приборах, после обработки с помощью математических операций дадут неприемле-
мые данные, и наоборот.
К числу наиболее часто используемых функций относятся произведение и част-
ное. Типичными примерами являются вычисление числа Рейнольдса (произведение
скорости, длины и плотности, деленное на вязкость), числа Маха (отношение скорос-
ти объекта к скорости звука) и т. п.
Рассмотрим линейную функцию результата от произведения:
R = kXY,
где к — нормирующий множитель.
Допустим, что для величин X и Y известны средне квадратические ошибки ох,
В данном измерении случайные ошибки X и Y составляют AXj и ДУ,. Для конкретной
пары измерений формула принимает вид:
R + Д^ = к(Х + ДХ1)(У+ ДУ0 = k(XY+ Д^ Д^ + XД^ + YAX}).
Членом второго порядка малости ДХ, ДУ, можно пренебречь. Тогда &R} = к(ДХ{ +
+ ДГ,).
N
У ^XlYl = 0, так как любое произведение может быть с равной вероятностью по-
/= 1
ложительным и отрицательным, и для большой выборки сумма таких произведений
стремится к нулю. Поэтому
N N
о2 = k2(Y2 У &X2/N+X2 у ДУ^/А),
/ = 1 i = 1
531
или, разделив на (ХУ)2-
a2/R2 = k2(a2/X2+ tf/Y2).
Аналогичные формулы справедливы для случая, когда R = kX/Y. При R = kXY/Z
используется выражение
<52IR2 = /X2 + а2 /У2 + ayZ2e
Отметим, что отношение о/Л есть отношение среднеквадратического отклоне-
ния к его точному отсчету и, следовательно, является показателем точности, выражае-
мым в процентах (после умножения на 100). Данный анализ справедлив не только при
использовании среднеквадратического отклонения и нормального распределения, но
и для произвольного интервала отклонений со (например, для 50, 68 или 95%). Важно
только, чтобы все сох, со^, сог содержали один и тот же процент генеральной совокуп-
ности.
ЛГ
Если распределение является асимметричным, то У, 1ХХ1ЬХ1 в пределе не будет
i = I
стремиться к нулю. Второе ограничение: случайные ошибки со, должны быть незави-
симыми. Например, коэффициент преломления призмы К = [sin (А + 5)/2]/sin (А/2)
является функцией двух углов. Так как величины двух синусов не являются независи-
мыми, полученные формулы использовать нельзя, а для определения ошибки резуль-
тата следует использовать более общее выражение, справедливое при наличии триго-
нометрических, логарифмических и др. функций.
Пример.
Через трубу в единицу времени протекает определенное количество воды. Темпе-
ратура воды измеряется с помощью термопары, а затем из таблиц свойств воды нахо-
дят вязкость и плотность. На основе показаний приборов получены следующие зна-
чения вероятных ошибок при максимальном и минимальном расходах воды
(табл. 11.1).
Требуется найти вероятную ошибку Ф в определении числа Рейнольдса при мак-
симальном и минимальном расходах (Re = KZ)p/p).
Решение.
Для минимального расхода
ФКе = л/(Ю2 + 0,08 + 0,332)/1002 = (1/100) • 10,005763 = 10%.
Таблица 11.1
Величина Минимальный расход Максималь- ный расход Ошибка при минимальном расходе,% Ошибка при максимальном расходе,%
Скорость И м/с 0,30 6,0 10 0,50
Диаметр трубы D, мм 10 10 0 0
Плотность р, г/мм3 IO-3 ю-3 0,08 0,08
Вязкость ц, г/мм • с 0,01116 0,001116 0,33 0,33
532
В случае максимального расхода
ФКе = 725/1000000 + 0,64/1000000 + 10,9/1000000 = 0,00605 или 0,61%.
После вычисления ошибок получаются следующие результаты (рис. 11.7): при
малом расходе в половине случаев вычисленные числа Рейнольдса имеют ошибку,
превышающую 10%, при больших значениях расхода ее величина уменьшается до
0,61%. Поэтому целесообразно стремиться повысить точность измерения скорости
при малых расходах, так как все остальные ошибки перекрываются вероятной ошиб-
кой, равной 10%.
Скорость можно вычислить, разделив массу воды М на промежуток времени
Т, площадь сечения л/)2/4 и плотность р. Тогда Re = 4Л//7тс7)ц. Возможно, что в этом
случае результат будет более точным.
В математической статистике полоса разброса называется доверительным интер-
валом. При этом мы знаем, с какой вероятностью данный отсчет будет находиться
в пределах или за пределами этой области.
Показатель точности для произвольной функции.
Рассмотрим общий случай, когда результат является функцией двух измеряемых
величин Хи У:
R + АЛ = f(X+ AX; Y+ АГ).
Если эта функция непрерывна и имеет производные, что наблюдается практиче-
ски всегда при использовании экспериментальных зависимостей, то ее можно разло-
жить в ряд Тейлора. Ограничимся двумя первыми членами:
R + AR =/(Х; Г) + [(dR/dX)(AX/l!) + (dR/dY)(АГ/1!)],
или АА = (dR/dX) ДХ+ (dR/dY) АК
ЕАТ?2 = [(д/?/дХ)2 • Е АХ2] + [(дЯ/дY)2 • Е АГ2], (Е АХ- АГ= 0).
Поэтому интервал неопределенности со2 = [(д/?/дХ)2 • со2] + [(д/?/дГ)2 • со2]. Таким
путем можно найти любой другой показатель точности.
Планирование эксперимента с точки зрения анализа ошибок.
На примере проиллюстрируем применение анализа ошибок для планирования
эксперимента.
На рисунке 11.8 показано устройство, состоящее из трубы, по которой подается
воздух с неизвестной концентрацией паров воды С и гигроскопического вещества, ко-
торое постепенно поглощает водяной пар из воздуха, проходящего по трубе, в соот-
ветствии с уравнением
АС = кС exp (-/>/А0),
Рис. 11.7. Доверительный интервал
при определении числа Рейнольдса
Поток газа
О Гигроско-
пическое
вещество
Рис. 11.8. Схема измерения
влажности газа
533
Таблица 11.2
Д0 3/Д0 ехр (3/Д0) ДС= (1 • 20)/ехр (3/Д0)
1 3 20 1
3 1 2,6 7,65
30 0,1 1,15 17,4
300 0,01 1,01 20
где ДС — вес воды в поглотителе через Д0 сек; к — известная постоянная (в данном
случае она равна единице), имеющая размерность 1/л; b — постоянная, зависящая от
геометрии и химического состава поглотителя (3 сек).
Необходимо определить концентрацию С путем измерения ДС и време-
ни Д0.
Вероятная ошибка измерения времени оказалась равной 0,2 сек; а для ДС вероят-
ная ошибка Ф = 2 г (погрешность взвешивания).
Отсчеты должны производиться как можно чаще. Ожидается, что концентрация
С составит ~ 20 г/л.
Вопросы:
1. Какой должна быть последовательность работы?
2. Какова вероятная ошибка для С ?
3. До каких пор можно увеличивать точность и частоту этих измерений?
Решение.
Исходная формула для определения концентрации С имеет вид:
кС = ДС ехр (Ь/Д&).
Покажем, что вероятная ошибка для С находится из уравнения
к\Фс/СУ = (Фдс/ДС)2 + (6/Д0)2(Фд0/Д0)2.
Для С = 20 г/л с помощью исходной формулы построим таблицу 11.2 для ДС и Д0
при указанных значениях постоянных b и к.
Теперь эти значения Д0 и ДС можно подставить в формулу для вероятной ошиб-
Рис. 11.9. Использование графика
для вычисления неопределенности
ки результата. При Д0 = 1 сек и ДС = 1 (первая
строка таблицы):
(Фс/С) = 7(2/1 )2 + (3/1)2*(0,2/1)2 = 2,09 или 209%.
При Д0 = 3 сек и ДС = 7,65 г, (Фс/С) = [0,0675 +
+ 0,00445]-0,5 = 26,8%.
При ДО = 30 сек и ДС = 17,4 г, (Фс/С) = [0,1152 +
+ 0] -0,5 11,5%.
При Д0 = 300 сек и ДС = 20 г, (Фс/С) = 10%, т. е.
неопределенность является минимально возможной.
Следовательно, при заданном наборе вероят-
ных ошибок и постоянных наилучшие результаты
получим при выполнении измерений через 20—
30 с. При меньших интервалах неопределенность
будет чрезмерно большой. При больших интерва-
лах вероятная ошибка уменьшается незначитель-
но. При таком рабочем плане вероятная ошибка
для С довольно большая и составляет 10—15%.
534
Т абл ица 11.3
X Y
85 100 ПО
10 400 500 700
15 250 270 300
23 180 200 210
Очевидно, что уменьшение неопределенности в измерении времени приведет к не-
большому повышению скорости и точности эксперимента. Таким образом, необхо-
димо стремиться к более точному измерению приращения веса гигроскопического
вещества.
Следовательно, изучение ошибки результата позволяет предсказать ошибки для
системы в целом, помогает приобрести комплект приборов, точность которых удов-
летворяет требованиям, предъявляемым к эксперименту в целом, дает возможность
обнаружить «слабые» места в выполняемых экспериментах и помогает выбрать пра-
вильный план проведения эксперимента.
Нахождение неопределенности результата с помощью графиков и диаграмм.
Если функциональная связь между результатом R и величинами X, Y неизвестна,
то неопределенность можно найти с помощью соотношений, представленных в виде
графиков, шкал, диаграмм, номограмм или таблиц (рис. 11.9). При использовании та-
ких графических или табличных данных обычно необходимо применять метод конеч-
ных разностей.
Например, если используется прибор, отсчет которого, согласно оценке, имеет
неопределенность сох, для получения неопределенности результата следует воспользо-
ваться графиком на рис. 11.9:
g)r= (dR/dX)(»x.
Величину производной можно оценить как отношение ДЯ к ДУ.
При использовании табличных данных действия аналогичны. Допустим, что
R =f(X, Y) и получены результаты, представленные в табл. 11.3:
Оценим величины производных при X = 15 и Y= 270.
dR/dX = (200 - 500)/(23 - 10) = -23; dR/dY= (300 - 250)/( 110 - 85) = 3,33.
Если неопределенности У и Кравны соответственно 2 и 10, то неопределенность
R равна ©2 = (22). (-23)2 + (102)(3,33)2 = 3225 и соА = 56,8 или 21% (табл. 11.3).
11.5. ЭЛЕМЕНТЫ ТЕОРИИ ПОДОБИЯ И РАЗМЕРНОСТЕЙ
Принципиальное содержание методов подобия и размерностей заключается
в том, что они позволяют объединить физические величины, имеющие размерность
(первоначальные переменные), в безразмерные комплексы. Последние и являются
теми переменными (параметрами), изменяющимися вместе с физической обстанов-
кой, в которых рассматривают задачу, в соответствии со спецификой исследуемого
процесса. В связи с этим в основе методов подобия и размерностей лежит один и тот
же принцип — замещение обычных переменных обобщенными (комплексными). По-
этому эти методы объединяют в один метод обобщенных переменных.
535
Вследствие сложности технологических процессов целесообразно определить сис-
тему параметров на основе факторов, определенных экспериментально или мысленно.
Ценность теории подобия и размерностей заключается в том, что они позволя-
ют распространить данные единичного опыта на группу подобных процессов и полу-
чать обширные теоретико-экспериментальные зависимости в виде критериальных
уравнений. То есть теория подобия и размерностей является научной основой моде-
лирования.
Подобие физических явлений.
Для получения количественных зависимостей при изучении физических явлений
используются методы теоретической и экспериментальной физики.
При выводе дифференциальных уравнений теоретической физики используют
самые общие законы природы, которые являются результатом чрезвычайно широкого
обобщения опытных данных. Поэтому полученные дифференциальные уравнения
представляют собой наиболее общую связь между существенными для явления вели-
чинами и характеризуют свойства, присущие всем явлениям данного класса. В диф-
ференциальном уравнении нет никаких сведений о конкретных значениях отдельных
величин, характерных для какого-либо единичного явления.
Таким образом, любое дифференциальное уравнение или система уравнений яв-
ляется математической моделью целого класса явлений.
Под классом явлений понимается такая совокупность явлений, которая характе-
ризуется одинаковым механизмом процессов и одинаковой физической природой.
Чтобы из множества возможных решений получить одно частное, надо знать все
характерные особенности данного явления, выделяющего его из всего класса одно-
родных явлений. Эти дополнительные условия, которые вместе с дифференциальны-
ми уравнениями однозначно определяют единичное явление, называются условиями
однозначности.
Они состоят из следующих условий:
1) геометрических, характеризующих форму и размеры тела или системы;
2) физических (свойств), которыми обладают тела, составляющие данную систему;
3) граничных, которые характеризуют взаимодействие системы с окружающей
средой;
4) временных, характеризующих состояние системы в начальный момент време-
ни по всему объему системы.
Дифференциальные уравнения и условия однозначности определяют конкрет-
ное единичное явление. В большинстве случаев из-за сложности совместное их реше-
ние невозможно.
Недостатком экспериментальных методов является невозможность распростра-
нения результатов, полученных в данном опыте, на другие явления, отличающиеся от
изученного.
Недостаток теоретических методов— трудности решения дифференциальных
уравнений совместно с условиями однозначности, характеризующими данное явление.
Положительные стороны теоретических и экспериментальных методов объеди-
няет теория подобия.
Теория подобия позволяет сделать из анализа дифференциальных уравнений
и условий однозначности ряд выводов, не прибегая к интегрированию, и тем самым да-
ет теоретическую базу для постановки опытов и обработки экспериментальных данных.
Кроме класса и единичного явления введем понятие группы явлений.
Группой явлений называют совокупность физических процессов, описываемых
одной и той же системой дифференциальных уравнений и подобными условиями од-
нозначности.
536
В теории подобия группу явлений выделяют путем умножения каждой величины,
входящей в условие однозначности, на постоянные численные множители, называе-
мые множителями преобразования или константами подобия. Так, если в двух рас-
сматриваемых процессах размеры в направлении оси X равны Хн (натура) и %м (мо-
дель), и аналогично по осям Yи Z, то
XM/XH=YM/YH=ZM/ZH = a,
где а — критерий подобия.
Такие системы будут геометрически подобными. Для разных параметров процес-
сов коэффициенты подобия различны.
Два явления называют физически подобными, если для них можно установить
соответственные точки пространства и соответственные моменты времени так, чтобы
в этих точках пространства и моменты времени все физические параметры, характер-
ные для данных явлений, были пропорциональны (см. рис. 11.10):
^Н1 Дм1 = ^Н2^М2 = ••• = °-
Теория подобия не может распространить результаты изучения единичного явле-
ния на весь класс явлений, так как внутри одного класса бывают явления, мало похо-
жие или сильно отличающиеся друг от друга.
Например, рассмотрим теплопередачу при сварке двух металлических листов и в
цилиндрической заготовке, обрабатываемой точением. Здесь процессы распростра-
нения тепла значительно различаются из-за резкого различия условий однозначнос-
ти. Нельзя перенести результаты изучения процесса сварки на процесс точения заго-
товки, хотя эти явления и относятся к одному классу: описываются одним и тем же
дифференциальным уравнением теплопроводности и характеризуются одним и тем
же физическим механизмом распределения тепла в твердых металлических телах. По-
этому в теории подобия рассматривается группа явлений, которая значительно уже
класса и объединяет только сходные (подобные) явления.
Группа выделяется из класса с помощью следующих приемов:
— из всего класса выделяется единичное явление путем численного задания ве-
личин, входящих в условия однозначности;
— создается группа явлений, подобных выделенному единичному явлению, пу-
тем умножения всех величин, входящих в условия однозначности выделенного явле-
ния на некоторые постоянные множители — множители преобразования, имеющие
постоянные значения для каждой однородной величины одного и того же явления, но
разные значения для всех подобных явлений.
Например, рассмотрим получение группы подобных заготовок цилиндрической
формы. Пусть задан весь класс цилиндров, разнообразных по длине L и диаметру D
(рис. 11.11). Длина и диаметр — параметры явления (заготовки). В данном случае они
являются условиями однозначности (материал и др. свойства для всех цилиндров
одинаковые).
ТН1 Тн2
Тнз
Рис. 11.10. Подобие натуры и модели
Рис. 11.11. Класс (а) и группа (б) цилиндров
537
Выделяем из всего класса заготовок конкретную заготовку с размерами Lx и Dx.
Для создания группы подобных заготовок умножаем параметры этой заготовки на по-
стоянные для всех параметров одинакового физического смысла множители, отли-
чающиеся для каждого нового подобного явления. Отметим, что L и D являются ли-
нейными однородными величинами и поэтому они должны умножаться на один и тот
же множитель преобразования.
Например, для второй заготовки L2 = a2Lx; D2 = a2Dx. Для третьей заготовки
L3 = a3Lx\ D3 = a3Dx и т. д. Поэтому Lx/Dx = L2/D2 = ... = Ln/Dn = a = idem.
Другая группа цилиндров будет иметь другой множитель преобразования.
Критерии подобия.
В качестве примера рассмотрим две подобные системы теплопередачи.
Пусть имеется тепловой поток Q через стенку толщиной 8 с коэффициентом теп-
лопроводности X [ккал/(м • час • градус)]:
Q = KTx-T2)F/b,
где F— площадь поверхности стенки, Тх и Т2 — температуры на одной и второй по-
верхностях.
Для первой системы Qx = X/Tj — Ту^/бр
Для второй системы Q2 = \2(ТХ — T2)2F2/82.
Константы подобия:
aQ = Qi/Qv» ак = ^2/^1» ат= ^Т2/А; aF — F2/Fx, = 82/8^
Выразим величины для второй системы через константы подобия:
a0>Q\ = a^\aTATxaFFx/a$x.
Так как aF= aj , то
Ql = a\ala^\^\ ^\/^\aQ'
Сравнив полученное выражение с формулой для первой системы, видим, что
0^5/00= L (11.1)
Это выражение называется индикатором подобия. Следовательно, константы
подобия не могут быть произвольными.
Заменим выражения констант на отношения:
= 1,
т. е.
Х2 AT2F2/(82Q2) = X! \TXFX/^XQX) = idem. (11.2)
Эти безразмерные комбинации называются критериями подобия. У подобных
процессов эти критерии должны быть одинаковыми в сходственных точках:
XA777(8Q) = idem.
Если имеется отношение двух каких-либо однородных физических величин, то
оно называется критерием параметрического типа или симплексом. Однородные
величины — это физические величины, имеющие одинаковое физическое содержа-
ние и размерность.
Любая комбинация критериев подобия является также критерием подобия.
Для характеристики подобия можно использовать и константы подобия, и крите-
рии подобия. Константы подобия сохраняют постоянное значение во всех сходствен-
ных точках рассматриваемых систем. Критерии подобия сохраняют постоянное зна-
чение в сходственных точках систем, но в различных точках одной и той же системы
могут иметь разное значение.
Основными являются следующие три теоремы.
538
Теорема 1.
У подобных систем критерии подобия численно одинаковые. Иначе говоря, не-
обходимым условием подобия двух систем является равенство соответствующих кри-
териев подобия, составленных из параметров систем и процессов.
Теорема указывает на то, что при выполнении опыта необходимо и достаточно
измерять лишь те величины, которые входят в критерии подобия.
Теорема 2 (так называемая л-теорема).
Интеграл дифференциального уравнения или системы уравнений может быть
представлен как функция критериев подобия дифференциального уравнения. То есть
операция интегрирования не изменяет вида критериев подобия. Результат любого
эксперимента можно представить в виде функциональной зависимости критериев по-
добия /(Kj, л2, л3, ..., ял) = 0. Уравнения такого типа называют уравнениями подобия.
Теорема 3.
Два явления подобны, если они описываются одной и той же системой диффе-
ренциальных уравнений и имеют подобные условия однозначности.
Три метода составления критериев подобия.
1. Метод деления друг на друга двух однородных величин, которые выявляются из
анализа задачи. Например, отношение D/L для цилиндрических заготовок или отноше-
ние температур 1\/Т2. Возможно и нахождение отношения величин, выраженных через
основные единицы размерностей, например Ух/Уг (размерность скорости [Z71-1]).
2. Переход от исходного уравнения к безразмерным комбинациям — критериям
подобия.
Сравнивая выражение (11.1) для индикатора подобия и (11.2) для критерия подо-
бия, видим, что они построены идентично. Поэтому для получения критерия подобия
достаточно заменить константы подобия на соответствующие физические величины
(параметры).
В свою очередь, индикатор подобия (11.1) построен таким же образом, что и ис-
ходное уравнение, записанное в безразмерной форме: 1 = \(ТХ - Г2)//(8£>). Поэтому
для получения критериев подобия нужно просто записать исходное уравнение в без-
размерном виде, опустить все индексы, знаки дифференцирования, суммирования,
убрать все константы (для них константы подобия равны 1). При этом:
d(avy}/d^ = д(У)/д(Х)ау/ах,
д2(ауУ)/д(ахХ)2 = д[д(ауУ)/д(ахХ)]/д(ахХ) = (а2/(а2)(д2У/дХ2).
Пример.
Уравнения Навье—Стокса (закон количества движения, или импульса)
p(dcox/dr + (пхд(пх/дХ + со/сох/дГ+ cozda>x/dZ= pgx - дР/дХ +
+ n(d2cox/dX2 + d2(ox/dY2 + d2nx/dZ2),
где gx — проекция ускорения на ось X, Р — давление; ш — компоненты скорости;
т| — вязкость; X, Y, Z— координаты.
Тогда:
ра>/77 рсо2//-> pg, P/l, V(to/l2.
Разделим правую и левую части на рсо2//. Получаем следующие критерии:
Но = (ьТ/1— критерий гомохронности (одновременности). Характеризует ско-
рость изменения поля скоростей движущейся жидкости во времени. Показывает,
в какой момент в натуре и в модели будет подобная обстановка.
РУ = co2/(g/) — критерий Фруда — отношение сил инерции к силам тяжести.
539
Eu = P/(pco2) = ДР/(рсо2) — критерий Эйлера. Отношение сил гидродинамическо-
го давления к силе инерции.
Re = р со//т| = coZ/v — число Рейнольдса. Отношение сил инерции к силам вязкого
трения.
Таким образом, мы установили, что существует зависимость между критериями
подобия вида Но =/(Ег, Eu, Re).
3. Метод анализа размерностей на основе применения л-теоремы.
Теорема Букингема утверждает (первая часть): если какое-либо уравнение одно-
родно относительно размерностей, то его можно преобразовать к соотношению, со-
держащему набор безразмерных комбинаций величин.
Однородным относительно размерностей является уравнение, форма которого
не зависит от выбора основных единиц. Безразмерные комбинации представляют со-
бой произведения или отношения величин, составленных таким образом, что в каж-
дой комбинации размерности сокращаются. Можно не знать всех переменных, вли-
яющих на эксперимент, но следует помнить, что эти переменные и связывающие их
безразмерное уравнение объективно существуют.
Для нахождения безразмерных комбинаций используют так называемый рэлеев-
ский метод или поэтапный метод Ипсена исключения размерностей.
Метод Рэлея основан на решении системы уравнений размерностей. Например,
предположим, что какой-либо процесс описывается функцией вида
Р= <p(La, Db, Р, рУ, ре, gO,
где L, D,e — имеют размерность длины (см. таблицу размерностей 11.4); V — размер-
ность скорости; ц — размерность вязкости; р — размерность плотности; g — размер-
ность ускорения; Р — размерность давления.
Подставив вместо символов их размерности из таблицы и составив уравнения
размерностей, получим три уравнения для определения соответствующих степеней
трех основных величин — массы М, длины L и времени 0:
для М: 1 = J + е;
для L: -1=а +b + c-d-le+f+g',
для 0: 0 = —с — d — 2g.
Формулы размерностей технических величин (М — масса, L — длина, 0 — время)
Таблица 11.4
Величина Размерность Величина Размерность
Длина L Момент количества движения ML2®-'
Объем L~3 Сила ML®~2
Кривизна L~' Работа и энергия ML2®r2
Скорость L0-1 Мощность ML2®-3
Ускорение LQ3 Вязкость ML~'Q~'
Угловая скорость Кинематическая вязкость L2®'
Плотность ML3 Поверхностное натяжение M®~2
Количество движения ML&-' Давление ML-'®~2
540
Решив совместно эти уравнения и подставив значения степеней в исходное урав-
нение, объединим соответствующие символы с одинаковыми степенями. В результате
получаем следующее уравнение из безразмерных комбинаций:
Ф[(£/ЛГ, (KDp/pH, (e/Z))/, (Dg/V^} = Р/(рИ.
Таким образом, количество переменных с семи уменьшено до четырех.
я-теорема (вторая часть теоремы Букингема).
Если существует соотношение между п физическими величинами, для описа-
ния которых используется к основных единиц, то существует также соотношение
между (п — к) безразмерными комбинациями, составленными из этих физических ве-
личин.
Безразмерные комбинации подбираются таким образом, чтобы каждая перемен-
ная появилась хотя бы один раз. Включение излишних переменных обнаруживается
из анализа полученных экспериментальных данных.
Поэтапный метод Ипсена заключается в последовательном исключении размер-
ностей путем произвольного составления безразмерных комбинаций.
11.6. ОПРЕДЕЛЕНИЕ ИНТЕРВАЛОВ МЕЖДУ
ЭКСПЕРИМЕНТАЛЬНЫМИ ТОЧКАМИ
Лишь для немногих экспериментов можно правильно оценить объем экспери-
ментальной работы. При слишком малом объеме экспериментальных данных может
оказаться невозможным найти закон или функцию, исследователь может получить
низкую точность постоянных величин или не заметить какой-либо эффект.
С другой стороны, при слишком большом объеме полученных данных экспери-
мент длится долго, обработка данных затягивается, затрудняется представление мате-
риала. В некоторых случаях чрезмерное количество экспериментов препятствует об-
наружению важных эффектов. Например, при определении напряжений при растя-
жении одного образца для низкоуглеродистых сталей можно обнаружить некоторое
уменьшение напряжений в конце упругого участка. При испытании нескольких об-
разцов, для каждого из которых зона уменьшения несколько смещена вдоль оси на-
пряжений или деформаций (рис. 11.12), если не делать различия между разными
образцами, этот спад может полностью исчезнуть. Построение графика для несколь-
ких образцов целесообразно, когда нужно определить усредненные данные. Для изу-
чения общего поведения стали (при одноосном растяжении)
целесообразно проводить испытания на одном образце.
Последовательность экспериментов.
План экспериментов получается компактным и эффек-
тивным, если заранее устанавливаются интервалы между
значениями переменных.
Кривая, отображающая искомую зависимость, содер-
жит бесконечно большое число точек, из которых необходи-
мо выбрать некоторое практически приемлемое число точек.
Критерии выбора интервалов между точками:
— относительная точность данных на различных участ-
ках области исследуемых значений: чем ниже точность, тем
большее количество точек должно быть на этом участке.
— характер экспериментальной функции, который
обычно заранее известен, например, из предварительных
экспериментов или ранее выполненных исследований.
Деформация
Рис. 11.12. Иллюстрация
исчезновения тонкого
эффекта при большом
числе экспериментов
541
Рис. 11.13. При одинаковом
интервале ДХ количество
значений функции в области
больших величин недостаточно
Рис. 11.14. График
зависимости с одинаковыми
интервалами вдоль кривой
Рис. 11.15. График
с равными приращениями
функции
Если точность измерений неизвестна или одинакова на различных участках, то
чаще всего назначают равномерную разбивку между значениями аргумента или
функции (рис. 11.13 и 11.15).
Лучшей является разбивка кривой на участки равной длины (рис. 11.14).
Длина участка кривой определяется зависимостью
Д5 ~ {1 + (d T/dX)2}0’5 • ДХ.
Если интервал между двумя заданными точками, начиная отХ,, берется равным
AXj, то следующий интервал ДХ2 находится из условия = Д52:
Если ожидается, что функция будет простой, то с помощью тех или иных алгеб-
раических преобразований ее можно привести к линейному виду (используя, напри-
мер, логарифмические или полулогарифмические шкалы и т. п.).
11.7. ПЛАН ЭКСПЕРИМЕНТОВ
Кроме изучаемых факторов на результаты эксперимента могут оказывать неуп-
равляемое влияние так называемые внешние переменные, которые могут быть непре-
рывными (например, атмосферное давление, влажность, работоспособность операто-
ра и др.) или дискретными (например, различные группы оборудования, людей, пар-
тии материалов и др.).
Так как часто невозможно исключить влияние внешних переменных или вычис-
лить поправку на их воздействие, минимизация их эффекта обеспечивается путем ис-
пользования рандомизированных (от англ, random — случайный) планов.
Пример нерандомизированного плана приведен в таблице 11.5.
Здесь 1, 2, 3,4 — уровни изучаемого фактора.
Такой план является несовершенным, так как не учитывает влияния последова-
тельности изменения условий эксперимента.
Более совершенный план можно получить, если уровни фактора изменять не в
определенной последовательности, а, например, по жребию (табл. 11.6).
Это более совершенный план, но имеет недостатки, так как уровни фактора 1 и 4
выпали в основном в последние два столбца таблицы.
Полностью рандомизированный план имеет вид, показанный в табл. 11.7.
542
Этот план также удовлетворяет условию, чтобы данный уровень фактора не повто-
рялся приданной величине переменной У2. Такой план называют «латинским квадратом».
При трех внешних переменных: Yj(A, В, С, D), Y2(A, Б, В, Г) и Y3(W, X, Y, Z) ис-
пользуют греко-латинские квадраты (табл. 11.8).
Таблица 11.5
Внешняя переменная Внешняя переменная Y2
А Б В г
А 1 2 3 4
В 1 2 3 4
С 1 2 3 4
D 1 2 3 4
Таблица 11.6
Внешняя переменная У, Внешняя переменная У2
А Б В Г
А 4 2 1 3
В 2 3 1 4
С 3 2 1 4
D 1 3 4 2
Таблица 11.7
Внешняя переменная Yl Внешняя переменная У2
А Б В Г
А 1 2 3 4
В 3 4 1 2
С 2 1 4 3
D 4 3 2 1
Таблица 11.8
Внешняя переменная Yl Внешняя переменная У2
А Б В Г
А ПГ 2Х 3Z 4У
В зх 4W 1У 2Z
С 2Y 1С 4Х 3W
D 4Z ЗУ 21Г IX
543
Таблица 11.9
Вид пластика Завод 1 (камера 1) Завод 2 (камера 2)
Л Т3 Т5 Т2 Л Т6
Рз А В с А в С
Рз В с А В с А
Рз С А В С А В
Т абл ица 11.10
Вид пластика Завод 1 (камера 1) Завод 2 (камера 2)
т, Тз Т5 Тз Л То
Рз А С В В А С
Рз А с в в А с
Рз А с в в А с
Известны также греко-латинские кубы.
В том случае, если фактор имеет большее количество значений, чем другие пере-
менные, для многих экспериментов квадрат является не самым удобным планом.
Часто для обычных инженерных экспериментов достаточно построить несколько гре-
ко-латинских квадратов типа 3x3, которые будут не полностью рандомизированны-
ми, но вполне удовлетворительными.
Например, при скоростях резания 1,2,3, 4, 5, 6 рабочими А, В, С на станках X, К
Z можно построить два квадрата 3x3.
Здесь шесть скоростей будут распределены равномерно между первым и вторым
блоками, стремясь обеспечить как можно большее перекрытие. Этот план не является
таким же рандомизированным, как один квадрат с 36 ячейками, составленными для
шести рабочих, шести станков и шести рабочих дней, но, по-видимому, вполне удов-
летворителен.
Пример.
Требуется проверить работу радиоприемников при шести различных темпе-
ратурах (Гр Г2, Г3, Г4, Г5, Г6) и определить потерю чувствительности через каж-
дые 100, 200 и 300 часов (А, В, С) (каждый приемник испытывается только один
раз). Печатные платы приемников выполнены из разных пластиков Р2, Л и
изготовлены на двух различных заводах. Имеется всего две термокамеры. Внеш-
ней переменной является влажность воздуха, и ее невозможно контролировать.
Хотя этот факторный план (табл. 11.9) имеет почти минимальный объем, для его
проведения потребуется 900 часов, так как в каждую из двух термокамер можно по-
местить на 100 часов только один приемник. Возможно, было бы лучше распределить
периоды времени менее случайным образом, чтобы быстрее завершить эксперимент.
Тогда план не будет представлять собой два латинских квадрата.
Теперь в каждой камере будет по три приемника, и весь эксперимент займет
300 часов (табл. 11.10).
544
11.8. МНОГОФАКТОРНЫЕ ЭКСПЕРИМЕНТЫ:
КЛАССИЧЕСКИЕ ПЛАНЫ
Во многих экспериментах варьируется два или большее число переменных
факторов. Такие эксперименты называют двух-, трехфакторными и т. д. Воз-
можными планами эксперимента являются классический и факторный.
Если нужно найти функцию R =f(X, У), то основной классический план состоит в
том, что все независимые переменные, за исключением одной, полагают постоянны-
ми, а эта переменная изменяется во всем интервале значений (выбор интервалов между
значениями переменной производится по одному из рассмотренных правил). Если
между независимыми переменными существует простое математическое соотношение,
то можно определить зависимость R от изменяемой переменной, например X. Затем все
переменные, кроме следующей (например, У), полагают постоянными, а изменяя К
находят зависимость R от У По существу, классический многофакторный эксперимент
представляет собой просто последовательность однофакторных экспериментов.
Этот ограниченный классический подход позволяет найти такие простые
зависимость R от Хи Y, как, например,
R = AYn + BXm,
R = A(Yn)(Xm),
R = AY(BCX) ит. д.
План двухфакторного эксперимента, в котором каждый фактор берется на
пяти уровнях, схематически представлен в следующем виде (табл. 11.11):
Таблица 11.11
Уровни перемен- ной X Уровни переменной У
1 2 3 4 5
1 ♦
2 ♦
3 ♦ ♦ ♦ ♦ ♦
4 *
5 *
Таблица 11.12
Уровни переменной X Уровни переменной У
1 2 3 4 5
1 * * * * *
2 * * ♦
3 ♦ ♦ ♦ ♦ ♦
4 * ♦ ♦
5 * ♦ ♦ ♦ *
545
Здесь символом * помечены условия проводимых экспериментов.
В более сложных случаях (например, R = АХ sin (BY/Х)) маловероятно, что с
помощью такого ограниченного плана, когда обе переменные берутся на одном
уровне, удастся определить эти зависимости. Возможно, будет необходимо рас-
смотреть несколько уровней переменных Хи Y(см. табл. 11.12).
Наконец, возможно, потребуется заполнить весь квадрат и провести все
25 экспериментов.
Классический план не обязательно должен быть сбалансированным, т. е.
можно выбрать 10 уровней для одной переменной и 5 для другой, если считается,
что зависимость R от первой переменной более важная, чем от второй.
11.9. МНОГОФАКТОРНЫЕ ЭКСПЕРИМЕНТЫ:
ФАКТОРНЫЕ ПЛАНЫ
Факторные планы применяют только в случаях рабочих формул двух типов: сум-
мы функций любой сложности от независимых переменных R =f{(X) + f2(Y) 4-/3(Z)
или произведение отдельных функций независимых переменных
(11.3)
Функция (11.3) является частным случаем суммы, так как путем логарифмирова-
ния ее можно преобразовать к выражению суммы:
log R = log/^X) + log/2(K) + log/3(Z).
Выражение (11.3) является весьма общим соотношением в научных исследова-
ниях.
Примеры:
R = k(Xa)(Yb)(Zc), R = k(Xa)(Yb)(ecZ), R = (k/X)(AY) sin BZ.
К данному классу не относятся, например, R = АХа + (Yb)(Zc) и множество дру-
гих.
Если функция относится к классу (11.3), то рассмотрим сбалансированный экс-
перимент, в котором все переменные варьируются на трех уровнях (табл. 11.13):
Допустим, нам известно, что (11.3) является соотношением, описывающим
влияние переменных X, Y, Z на R.
Запишем три логарифмических выражения для строки, содержащей Х}\
log Ra = log/ (%,) + log/2( К,) + log/3(Z3);
log Rb = log/, (X,) + log/2( K.) + log/3(Z,);
log Rc = log/GT,) + log/2( Г3) + log/3(Z2).
Суммируем эти три уравнения:
X log Rx = 3 log/u,) + log [Г2(Г,)/2(Г2У2(Г3)] + log [r3(Z3y3(Z2V3(Z,)].
Таблица 11.13
is У3
*3 N N
*2 N kj N
Z, z} N Z2
546
Повторим эту процедуру для второй строки, содержащей Х2, и для верхней строки:
Zlog Rx2 = з log/i^) + log [f2(Ytf2(Y2)f2(Y3)] + log [f3(Z3)/3(Z2)/3(Z,)];
Xlog RX) = 3 log/,(Z3) + log [f2(ВД Y2)f2( Г3)] + log [/'3(Z3)/3(Z2)/3(ZI)].
Полученные выражения можно записать в виде
log/iCx,) = X|og Rx} ln -const;
log/, (Х2) = X log Rx2 /я - const; (11.4)
log/^Zj) = £log RXi /я - const.
Здесь n — равно числу уровней (в данном случае 3).
Следовательно, если логарифмы усредняются по какому-либо уровню перемен-
ной, например X, то влияние остальных переменных (в данном случае К остается
неизменным при переходе от одного уровня X к другому, т. е. все изменения усреднен-
ного логарифма определяются только влиянием переменной X.
Если добавить еще одну переменную то получается греко-латинский квадрат и это
же правило следует применить для нахождения влияния переменной Wна результат R.
Если до начала эксперимента известно, что рабочая формула имеет вид суммы
функций независимых переменных, то влияние переменных X, Y, Z находится усред-
нением соответствующих значений R, а не log R. Если вид функций неизвестен, то
следует проводить классический эксперимент.
Формулы (11.3) можно преобразовать к виду:
Rx = £,/,(%);
Ry= k2f2(Y)'9
&z =
Здесь Rx, RY, Rz~ антилогарифмы ZlogAxj/л, Zlog Ryjn, ZlogT^/л. Учи-
тывая, что R =/\(X)f2(Y)f3(Z)9 можно записать:
R = RxRyR7K, где K=(k.k2kX~\
Л I Z. 1 v I Z u'
Пример.
Зависимость расхода топлива двигателя внутреннего сгорания от скорости, на-
грузки, температуры воды в системе охлаждения предположительно описыва-
ется функцией типа (11.3). Выбираем квадрат 4x4, имеющий следующую структуру:
Таблица 11.14
Число оборотов в минуту п 1400 1600 1800 2000
Нагрузка на динамометр Р, кгс Температура Т, °C
87,5 43 57 71 93
66,0 93 43 57 71
44,0 71 93 43 57
22,0 57 71 93 43
Вначале следует убедиться, что все 16 режимов приемлемы. Например, если
в верхней строке будет такая последовательность температур: 93, 71, 57, 43, то та-
547
кой план невозможен, так как система не в состоянии поддерживать минимальную
температуру 43 градуса при максимальной нагрузке и максимальном числе оборотов.
В результате эксперимента получены результаты (табл. 11.15) по расходу горюче-
го R, л/час.
Таблица 11.15
21,2 24,5 28 29
14 16 19 22
8 11 14 16
6 8 8 11
Вычислим логарифмы, найдем их суммы по отдельным параметрам, найдем
среднее значение логарифма, найдем антилогарифм. Соответствующие данные пред-
ставлены в табл. 11.16.
Аналогичные показатели для фактора температуры представлены в табл. 11.17.
По полученным данным можно построить графики зависимостей расхода топли-
ва от нагрузки, скорости и температуры и аппроксимировать полученные зависимос-
ти (см. рис. 11.16—11.18).
Таблица 11.16
Число оборотов в минуту п 1400 1600 1800 2000 При нагрузке
Нагрузка на динамометр/^ кгс Сумма Среднее Антило- гарифм
87,5 > 1,326 1,392 1,447 1,4622 5,625 1,406 25,5
66,0 —> 1,146 1,204 1,279 1,342 4,971 1,243 17,5
44,0 > 0,903 1,041 1,146 1,204 4,295 1,072 11,9
22,0 > 0,778 0,903 0,903 1,079 3,664 0,916 8,2
Сумма 4,154 4,532 4,775 5,088
Среднее 1,038 1,135 1,194 1,272
Антилогарифм 11,9 13,6 15,6 18,7
При скорости 1400 1600 1800 2000
Таблица 11.17
Т=43 1,326 1,204 1,146 1,079 4,756 1,189 15,5
Т= 57 0,778 1,392 1,279 1,204 4,050 1,163 14,5
Г=71 0,903 0,903 1,447 1,342 4,596 1,149 14,1
Т=93 1,446 1,041 0,903 1,462 4,553 1,138 13,8
Сумма Среднее Антило- гарифм
548
- Логарифмический ряд
у= 11,727 In (х)-29,773
Рис. 11.16. Зависимость
осредненного расхода
от нагрузки
— Степенной ряд
у = 0,0014х! >2489
Рис. 11.17 Зависимость
осредненного расхода
от скорости
• Ряд 3
— Экспоненциальный ряд
у= \6972Se~Q^22x
Рис. 11.18. Зависимость
осредненного расхода
от температуры
Эти кривые нельзя использовать для определения, например, КПД, так как они яв-
ляются усредненными по одному из параметров и не учитывают влияния других парамет-
ров. Вычислим коэффициент К, используя верхнюю строку и второй столбец (Р = 87,5,
п = 1600, Т= 57, R = 24,5) (Рр= 25,5, Rn = 13,6, RT= 14,5). В результате получим:
К = R/(RpRnRT) = 24,5/(25,5 • 13,6 • 14,5) = 0,00488.
Для вычисления К можно использовать все 16 значений. С максимальной ошиб-
кой 11% Кс = 0,00485.
ср
Теперь можно определить расход и для практически невозможных режимов, на-
пример, при п = 2000, Т= 43, Р = 87,5.
R = 0,00485 • 25,5 • 15,5 • 18,7 = 35,6 л/ч.
Достоинства факторного планирования заключаются в повышении точности.
В классическом сбалансированном эксперименте с варьированием трех факторов на
трех уровнях можно получить три кривые при семи экспериментах вместо 9 при фак-
торном планировании. Однако при вычислении с использованием факторного пла-
нирования используются результаты всех девяти экспериментов, т. е. каждая экспери-
ментальная точка фактически представляет собой средний результат трех отдельных
измерений. Следовательно, точность будет в Уз выше, чем в классическом плане.
По классическому плану 4x4 необходимо выполнить 10 экспериментов. По фак-
торному плану— 16экспериментов. Однако для достижения той же точности по
классическому плану нужно было бы продублировать каждый эксперимент 4 раза,
т. е. выполнить 40 измерений вместо 16.
В результате получим зависимость:
R = 1,727 In Р- 29,773)(0,0014п1’2489)(16)728е-0’00227).
11.10. ФАКТОРНОЕ ПЛАНИРОВАНИЕ
ПРИ ПОИСКЕ ОПТИМАЛЬНЫХ УСЛОВИЙ
Различают задачи интерполяционные (направленные на описание зависимости
между некоторыми величинами в определенной области) и оптимизационные или
экстремальные.
Эксперимент, который ставится для решения задач оптимизации, то есть для по-
иска экстремума некоторой функции, называют экстремальным. Пример экстремаль-
549
Рис. 11.19. Представление
объекта исследования
в виде «черного ящика»
ного эксперимента: определить содержание углеро-
да в стали для обеспечения максимальной ударной
вязкости. Пример интерполяционного эксперимен-
та: найти зависимости между ударной вязкостью и
содержанием углерода в стали.
Объект исследования удобно представить в ви-
де «черного ящика» (рис. 11.19).
Математическую модель, связывающую параметр
процесса (параметр оптимизации в данном случае)
с факторами в виде j; =f(x}, х2, ..., хп) называют функцией отклика.
Каждый фактор может принимать несколько значений (уровней). Фиксирован-
ный набор уровней всех факторов определяет состояние «черного ящика» (одновре-
менно и условия эксперимента). Каждому состоянию «черного ящика» соответствует
определенное значение функции отклика, но не наоборот. Число возможных состоя-
ний ящика при одинаковом числе уровней к всех факторов р равно кр. Для системы
с пятью факторами, каждый из которых может изменяться на пяти уровнях, число со-
стояний равно 3125.
Требования к объекту исследования:
— эксперимент должен быть воспроизводимым, т. е. обеспечена возможность его
повторения или выполнения в произвольной последовательности;
— эксперимент должен быть активным, т. е. обеспечивать возможности выбора
уровней факторов в каждом опыте.
Планирование экстремального эксперимента — это метод выбора количества
и условий проведения опытов, минимально необходимых для отыскания оптималь-
ных параметров.
Параметр оптимизации — это признак, по которому мы хотим оптимизиро-
вать процесс. Движение к оптимуму возможно, если выбран один-единственный
параметр оптимизации (частный или обобщенный). Параметр оптимизации может
быть техническим (долговечность, надежность, КПД и т. п.), технологическим (на-
пример, максимальная степень формоизменения), экономическим (себестоимость,
рентабельность и др.) либо иным (психологическим, эстетическим, статистическим
и др.).
Требования к параметру оптимизации:
— простой количественный характер, т. е. задание одним числом или рангом
(ранг — субъективная количественная оценка параметра оптимизации);
— измеряемость при любом состоянии объекта исследования;
— однозначность: любому набору значений факторов должно соответствовать
одно с точностью до ошибки эксперимента значение параметра оптимизации (обрат-
ное неверно);
— желательна простота, наличие физического смысла и легкая вычисляемость;
— эффективность в статистическом смысле, т. е. определяемость с наибольшей
точностью (если точность недостаточна, то приходится увеличивать число опытов).
Возможно планирование экстремального эксперимента для оптимизации одного
параметра при ограничениях, накладываемых другими важными параметрами. Воз-
можна оптимизация обобщенного параметра оптимизации, представляющего собой
некоторую функцию от частных параметров. Известно много способов построения
обобщенного параметра оптимизации.
Если параметры принимают только два значения (например, 0 — брак, 1 — год-
ное изделие), то обобщенный параметр может быть представлен в виде произведения
Л ~У\У1'"Уп- Это весьма условный и грубый параметр.
550
Если известны желаемые или оптимальные значения параметров, то можно оце-
нить меру близости к оптимуму в безразмерном виде (yz — yopt) /уДля того чтобы
снивелировать знаки, можно возвести это выражение в квадрат:
где — вес данного частного параметра, изменяющийся от 0 до 1.
Каждый фактор имеет область определения (рис. 11.20), которая может быть не-
прерывной или дискретной. Для факторов, имеющих непрерывную область определе-
ния, всегда выбирают некоторые дискретные значения.
Факторы могут быть количественными (измеряемыми, взвешиваемыми, выде-
ляемыми и т. п.) и качественными (виды марок материалов, разные технологические
пробы, исполнители и др.). Иногда граница между количественными и качественны-
ми факторами весьма условна.
Требования к факторам при планировании эксперимента:
— фактор должен быть управляемым. Например, влажность окружающего возду-
ха мы произвольно изменять не можем; поэтому влажность нельзя включать в число
факторов;
— точность замера факторов должна быть возможно более высокой;
— факторы должны непосредственно воздействовать на объект, так как трудно
управлять фактором, который является функцией других факторов. Но в планирова-
нии могут участвовать сложные факторы, такие, как, например, логарифмы, отноше-
ния, безразмерные комбинации и др.;
— факторы должны быть совместимыми;
— факторы должны быть независимыми друг от друга, т. е. должна отсутствовать
корреляция факторов.
Выбрать математическую модель — значит выбрать вид функции и записать ее
уравнение.
Требования к поверхности отклика (рис. 11.21):
— непрерывность поверхности;
— гладкость;
— наличие единственного оптимума;
— способность предсказывать направления дальнейших опытов;
— функция должна быть аналитической, т. е. должна раскладываться в степенной
ряд.
Типичные полиномы для случая двух факторов:
— полином нулевой степени у = £0;
— полином первой степени у = Ьо 4- b + b^x2,
— полином второй степени у = bQ + bxxx + Ь^2 + Ьх2ххх2 + Ъххх^ + Ь22х%\
— неполный полином второй степени у = Ьо 4- Ьххх + Ь^х2 + Ьх2ххх2.
х2 Область
/определения
/ факторов
Поверхность
удовлетворяет
требованиям
Поверхность
не удовлетворяет
требованиям
Рис. 11.20. Область определения факторов
Рис. 11.21. Виды поверхностей отклика
551
Поиск оптимума
по методу
Гауса—Зейделя
Движение
по градиенту
Рис. 11.22. Поверхность отклика и способы поиска экстремума
Наибольшую известность получили два метода поиска экстремума: метод Гауса—
Зейделя и метод Бокса—Уилсона «движения по градиенту» (рис. 11.22).
Схема исследования отклика двух факторов.
Областью определения двух факторов х2 является часть плоскости xfix2; эта
область называется двухфакторным пространством, а соответствующий
эксперимент— двухфакторным экспериментом. По аналогии могут быть одно-
и многофакторные пространства и эксперименты.
Рассмотрим принцип исследования отклика двух факторов у = f(x{, х2)
(рис. 11.23). Сначала эксперимент ставится в области со1 с центром Ох и определяются
значения отклика У) у12, у13, у14 в угловых точках области первого эксперимента C0j —
точки 1,1; 1,2; 1,3; 1,4. Затем, если необходимо, осуществляется переход в область со2 и
определяются значения отклика у21, у22, у23, у24 и т. д. Все области со1? со2... принадле-
жат области определения факторов Q которая называется областью исследования.
В каждой области z-ro эксперимента со, проводятся четыре опыта (по числу вер-
шин области со,) и каждый фактор (х1? х2) принимает только два значения, или 0 и 1,
или -1 и +1. Эти значения называются уровнями факторов.
Рис. 11.23. Графическая интерпретация двухфакторного эксперимента
552
Рассмотрим область со одного двухфакторного эксперимента.
По оси ординат отложены значения отклика в отдельных точках 1,1; 1,2; 1,3 и 1,4.
В данном случае два уровня факторов отмечены индексами «н» и «в». Сочетания двух
факторов на двух уровнях дают N = 22 = 4 набора, или 4 опыта. При каждом наборе
факторов (в каждом опыте) измеряется отклик в результате получаются четыре
точки уц, ^12, у13, у14, которые образуют некоторую поверхность отклика (xh х2). Ес-
ли на двух уровнях варьируется к факторов, то число всех наборов W= 2к. Число набо-
ров определяет число опытов — измерений отклика в данном эксперименте.
При проведении трехфакторного эксперимента область со представляет собой па-
раллелепипед или куб, число вершин которого равно числу опытов (W= 23 = 8), и в
случае ^-факторного эксперимента — гиперкуб с N=2k вершинами, в каждой из ко-
торых должен быть поставлен опыт и измерено значение отклика.
Таким образом, число опытов в одном эксперименте равно числу различных на-
боров факторов. Число экспериментов в области исследования Q зависит от задач ис-
следования и от соотношения между размерами области одного эксперимента со и об-
ласти Q. Иногда используются не все N = 2к наборов факторов, а факторы могут
варьироваться не на двух, а на трех уровнях.
Выбор факторов.
При планировании эксперимента необходимо выбрать факторы и определить:
1) влияние их на выходную величину у;
2) какими из них можно задаваться по желанию экспериментатора и какие неуп-
равляемы или случайны;
3) точность аппаратуры, с помощью которой задаются значения варьируемых
факторов и измеряются значения выхода у;
4) являются ли факторы независимыми или зависимыми величинами.
Выбранные факторы должны быть доступны измерению с точностью, на порядок
большей, чем измерение выходной величины. Они должны быть совместными, неза-
висимыми величинами (при взаимной зависимости факторов их следует объединить
в один обобщенный). Необходимо выбрать для каждого эксперимента интервал
варьирования факторов I, которым называется половина разности между большим
(верхним) и меньшим (нижним) значениями фактора (х1н, х1в, х2н, *2в)- Значение фак-
тора в центре области эксперимента со (точка О}) называется его основным уровнем
и отмечается подстрочным индексом «О» (х10, х20,...).
Для удобства записи плана эксперимента и обработки экспериментальных данных
обычно пользуются кодированными значениями факторов, которые обозначаются ма-
лыми буквами .... Кодированные Ху и физические ^ переменные связаны между со-
бой следующим отношением:
_Л-Л-о
х,. .
Кодирование факторов равносильно переносу начала координат в точку основ-
ного уровня факторов (центральная точка эксперимента 00 и изменению масштаба
(рис. 11.24). Все кодированные факторы — безразмерные и нормированные величи-
ны. В процессе эксперимента они могут принимать значения -1, 0, +1.
Выбор модели (уравнение модели).
В методе планирования эксперимента — это неформализованный этап, который
основывается обычно на интуитивных соображениях с учетом предыдущего опыта
экспериментатора, а количественное определение коэффициентов выбранных урав-
нений модели — на результатах эксперимента. Поэтому правильный выбор модели
должен подтверждаться экспериментально.
553
Модель определяется переменными х{ и постоянными параметрами pf. и в общем
случае имеет вид:
у = Y(x},x2, ...,хк, Рр Р2,.... Р*).
В планировании эксперимента чаще всего применяются модели линейные отно-
сительно переменных х, и параметров 0,:
У = Ро + Р1*1 + ••• + Рл-
Однако модели могут быть и нелинейного вида.
Построение планов полного факторного эксперимента. Полным факторным
экспериментом называется такой эксперимент, в котором реализуются все возмож-
ные комбинации (наборы) уровней факторов. Если к факторов варьируется на двух
уровнях, то число всех возможных наборов N2 — 2к. Если к факторов варьируется на
трех уровнях, то N3 = 3* В полном факторном эксперименте число опытов равно чис-
лу различных наборов, т. е. различных точек факторного пространства. С увеличени-
ем числа факторов к быстро растет число опытов.
Используя полученные данные, представляем план эксперимента в виде табли-
цы-матрицы (табл. 11.18):
Т абл ица 11.18
№ опыта Уровни переменных Отклики
*1 х2 Л1 Уи2 Уц)
1 -1 -1 ^11 Уп Ум
2 +1 -1 ^21 У12 Уу
3 -1 +1 А’З! У32 Уу
4 +1 +1 Хн У42 Уч
Матрица содержит четыре (22) строки и два основных столбца переменных
%! и х2. В остальных столбцах записываются измерения отклика у в отдельных точках
факторного пространства.
План эксперимента задается графами 2 и 3. Первая строка соответствует точке 1 с
координатами (—1, —1). В первой строке матрицы записаны эти значения координат
Xj, х2 и результаты измерения отклика в точке 1. В каждой точке может проводиться
несколько опытов пи, которые называют параллельными. Для проведения экспери-
мента значения факторов разделяются на уровни, задаваемые соответствующими
строками. После этого измеряются значения отклика. Если проводится одна серия
опытов, то заполняется одна графа (4 графа таблицы). При низкой точности измере-
ний отклика или при действии случайных факторов повторяется и записывается еще
одна серия результатов (5 графа таблицы). Для повышения точности серии измерений
могут повторяться несколько раз (параллельные опыты).
Полный факторный эксперимент (ПФЭ) 23.
Трехфакторный эксперимент.
Для построения плана полного факторного эксперимента 23 необходимо соста-
вить все возможные комбинации из трех факторов (табл. 11.19), когда каждый варьи-
руется на двух уровнях (±1) (рис. 11.25).
554
Рис. 11.24. Область эксперимента для факторов: Рис. 11.25. Модель ПФЭ 23
а) физических; б) кодированных
Начало кодированных координат помещается в центре куба, вершины которого
соответствуют отдельным опытам (различным наборам факторов при двух уровнях
варьирования ±1). Совокупность наборов дает матрицу планирования полного фактор-
ного эксперимента 23, в которой выделена матрица 22, а отдельные уровни факторов
обозначены символами + и —. Отсюда следует правило получения матрицы 23, в кото-
рой матрица 22 повторяется дважды: первый раз при х3 = -1, второй — при х3 = +1, что
соответствует нижней и верхней граням куба.
При проведении опытов в данной последовательности неучитываемые медленно
меняющиеся величины могут исказить результаты. Поэтому при нестабильных усло-
виях эксперимента последовательность опытов должна быть случайной (рандоми-
зированной).
Определение коэффициентов модели.
Введя фиктивную переменную х0 = +1, уравнение простейшей двухфакторной
линейной модели удобно записывать в виде
У = Ро*о + Р1*1 +
где Pz — коэффициенты моделей (/ = 0, 1, 2).
Таблица 11.19
№ опыта Уровни переменных
*1 *2 *3
1 - - -
2 + - —
3 — + -
4 + + -
5 — - +
6 + — +
7 — + +
8 + + +
555
Таблица 11.20
№ опыта Уровни переменных Отклику
*0 *1 х2
1 + — - J'l
2 + + - У1
3 + - + Уз
4 + + 4- У4
С учетом значений фиктивной переменной матрица планирования эксперимента
22 имеет вид, как на табл. 11.20.
По аналогии фиктивную переменную можно внести в любой план эксперимента.
Уравнение модели содержит неизвестные коэффициенты pf.. Если эти коэффициенты
определяются по статистическим данным, то получаются не точные их значения,
а статистические оценки.
Из-за случайности величину получают не точное уравнение модели, а его оценку:
у = boXQ + ZjjXj + b^x2 — модель или уравнение регрессии (Ь, — статистические
оценки). Функция y(xi, ..., хп) называется поверхностью (п < 2) или гиперповерхно-
стью регрессии (п > 2).
Для отыскания оценок применяется метод наименьших квадратов, а сама про-
цедура отыскания называется регрессионным анализом:
лг
УuXiи
и = 1
N
где / = 0, 1, 2,..., п.
Оценки коэффициентов регрессии определяются следующим образом:
При проведении пи параллельных опытов в данной строке в формулу подставля-
ются средние значения отклика:
- = 1 V
Уи Пи^\УиГ
Для учета нелинейности типа произведения факторов (эффект взаимодействия
факторов) уравнение регрессии запишем в виде:
У и = Vo + Ь\Х\ + V2 + Ь\1*\Х2-
Эффект взаимодействия означает, что влияние одного фактора на выходную ве-
личину у зависит от того, какое значение принимают другие факторы. Коэффициент
взаимодействия вычисляется по той же формуле, что оценки коэффициентов регрес-
сии. Справедливость такого утверждения обеспечивается образованием графы произ-
ведения взаимодействия факторов хр х2, удовлетворяющего условиям ортогональнос-
ти, нормировки и симметрии. Произведение факторов обозначим вспомогательной
переменной х3 = ххх2, которая в модели фактически не содержится. Обозначая коэф-
фициент взаимодействия Ьх2 = Ь3, получаем уравнение
У и = Ь0Х0 + 61Х1 + ЬЛ + Ь3ХУ
556
Дробный факторный эксперимент (ДФЭ).
ДФЭ отличается от ПФЭ тем, что позволяет существенно сократить количество
опытов. В теории планирования эксперимента имеются методы построения частей
планов ПФЭ, которые называют дробными. ДФЭ составляет часть ПФЭ 2к. Если про-
водится половина ПФЭ (вместо Nk = 2к используется половина наборов: 1/2Л^ =
= 2к~ *), то эксперимент называется полурепликой ПФЭ; если используется 1/4Л* =
= 2к ~2 наборов, то эксперимент называется четвертью реплики ПФЭ 2к и т. д. Дробные
реплики уменьшают число необходимых опытов— наборов различных сочетаний
факторов, — в частности, число опытов можно сделать равным числу факторов. План,
в котором число опытов равно числу коэффициентов регрессии bi9 называется насы-
щенным. Дробные реплики удобны для построения линейных моделей большого чис-
ла факторов (при этом априори должно быть известно, что эффекты взаимодействия
проявляются слабо), а также для исследования многофакторного пространства в пер-
вом приближении, когда поверхность отклика мало отличается от гиперплоскости.
11.11. ОБРАБОТКА И ОЦЕНКА
ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ
В результате многофакторного эксперимента получают значения отклика yuj в Nточ-
ках факторного пространства. Для повышения точности экспериментальных данных от-
клик в ряде случаев измеряется в /-Й строке и ставятся параллельные опыты (табл. 11.21).
Из-за погрешностей измерения и влияния неконтролируемых возмущающих
факторов отдельные значения yuj, которые являются независимыми случайными ве-
личинами, называются выборкой из гипотетической совокупности.
Обработка экспериментальных данных в теории планирования эксперимента
в значительной мере формализована. Обработка данных делится на два этапа, содер-
жащих часть операций условного перехода, допускающих переход к последующему
этапу при определенных условиях. Если условия не выполняются, то вычисления
прекращаются и делаются необходимые изменения в планировании эксперимента.
Характер изменений и направление дальнейших действий определяет сам экспери-
ментатор.
Рассмотрим этапы и возможности вариантов неформализованных решений.
Для исключения явно аномальных грубых погрешностей, которые могут значи-
тельно исказить результаты в отдельных строках матрицы, проводится проверка од-
нородности значений yuj. Для этого используют критерий Стьюдента:
Su ’
где у* — наименьшее или наибольшее значение отклика в /-й строке, которое полага-
ется ошибочным; уи — среднее значение отклика в z-й строке, вычисленное без учета
у *; Su — дисперсия.
п -1
£ yuJ „
; — 1 и
где пи = п — 1 — число опытов без учета одного, в котором yuj = у*.
557
Т абл ица 11.21
y»j Уи
J
1 2... N
1 ^11 ^21 - У\П У1
2 У21 У22 - У2п У2
N Ум У N2 - yNn Уп
Оценка среднеквадратического отклонения:
I 1 и
su=jsl= X(yUj - уи) >
Ч и ;=1
где Su — оценка среднеквадратического отклонения; S* — оценка дисперсии в /-й
точке без учета сомнительного фактора у*.
Величина t имеет следующее количество степеней свободы: f=nu— 1. По числу
степеней свободы и заданному уровню значимости а из таблицы распределения
Стьюдента находят табличное значение критерия (Гт).
Уровень значимости принимают обычно а = 0,05. Если расчетное значение кри-
терия /р окажется больше табличного /р > /т, то с надежностью вывода Р = 0,95 можно
утверждать, что у* — грубая погрешность, которая должна быть исключена из даль-
нейшей обработки. При /р < /т результат у* согласуется с данными z-й строки и остав-
ляется для дальнейшей обработки. Используют также r-критерий и критерий Шовене.
Пример.
При исследовании коррозии сделано четыре параллельных опыта и получены ре-
зультаты: 3,580, 2,710, 2,370 и 2,761 мг/см2 • час. Результат первого опыта сомнителен.
Исключим первый опыт из расчетов. По остальным результатам найдем среднеквад-
ратическую ошибку:
_ 2,370 + 2,710 + 2,761 -
У = —-------j----:— =2,613;
с _ /(—0,243)2 + 0,0972 + 0,1482 _
а/ 3 U’2L
п . У-У 3,580- 2,613 . ,
Производим проверку по критерию Стьюдента: t = ---- = 4,6.
При числе степеней свободы/= 2 и уровне значимости 0,05 t = 4,303. Поэтому
первый результат неверен.
Пример.
Пусть имеется п повторных наблюдений у1? у2, •••, Уп- Считаем, что /-е наблюдение
несовместимо с остальными. Подставляем среднее у и ошибку Su\
/=1 ' о £(У/-У)2
У ~ ’ S“ ~ ч
558
и найдем относительное отклонение /-го параметра:
У,-у
Если полученное значение для данного уровня значимости и числа степеней
свободы/= п — 2 (одна степень определяет сомнительный результат, вторая — для вы-
числения среднего) не превышает табличного значения, то можно применять гипоте-
зу об однородности выбора.
Получим значения: 12,15; 10,85; 16,00. Оценим последний результат, у = 13,0,
5* = 6,172, Sy = 2,46, rmax = 16,00 — 13,0 = Табличное значение при а = 0,05 и f = 1
равно 1,412. Поэтому наблюдение 16,00 можно признать грубым. Разница между /-
критерием и критерием rf состоит в том, что в первом случае несовместимый резуль-
тат не используется в расчетах.
При планировании эксперимента желательно, чтобы число опытов во всех стро-
ках было одинаковым, т. е. пи = п = const. Среднее значение отклика в отдельных точ-
ках факторного пространства рассчитывается после проверки измерений. Во всех
точках плана рассчитывается среднее значение отклика и заносится в последнюю гра-
фу. Среди всех средних значений отклика находятся экстремальные значения, и если
разность между ними незначительна, то считается, что эксперимент содержит мало
информации об объекте исследования. Значимость разности средних значений от-
клика также проверяется по критерию Стьюдента.
Расчетное значение критерия определяется по формуле
. _ ”^wmax ‘3^wmin
р П i' ’
5V1 2 — + —
N^max wmin
где Sy — оценка дисперсии воспроизводимости; nmax и nmin — число опытов соответ-
ственно в строках максимального и минимального откликов.
Табличное значение критерия определяют по условию, когда а = 0,05 и по числу
степеней свободы f = nmax + nmin. Если tp < среднее значение отклика отличается ста-
тистически незначимо. В этом случае экспериментальные данные нельзя признать
удовлетворительными и необходимо поставить такой эксперимент, в котором значе-
ние отклика в отдельных точках отличалось бы более существенно. Этот результат мо-
жет быть достигнут изменением масштаба переменных интервала варьирования
и применением планов 2-го порядка или перенесением области эксперимента в дру-
гое место области исследования Q.
Оценки построчных дисперсий рассчитываются по формуле
1 Пи
l(yv-yu)2,
“ ; = i
гдеи= 1,2,..., N— число всех точек плана, равное числу строк; пи— 1 =/— число па-
раллельных опытов без одного.
559
Однородность дисперсий при одинаковых количествах опытов в каждой строке про-
веряется по критерию Кохрена (7р:
и = 1
Величина этого критерия связана с числами степеней свободы /тах = п - 1 и
Л = ^о.
По уровню знчимости а = 0,05 и числу степеней свободы находят табличные значе-
ния критерия Кохрена (табл. 11.22). Если выполняется неравенство (7р < то прини-
мается гипотеза об однородности дисперсий, в обратном случае принимается неформа-
лизованное решение, чтобы добиться выполнения этого условия. Одним из возможных
путей является переход к другому виду функции отклика. В тех случаях, когда число
опытов в различных строках плана различно, применяется критерий Бартлета.
/ N N ч
в=\/с ig5/. ,
V и = 1 и = \ 7
N
I/.
и = I
= —-------средняя дисперсия, рассчитанная по формуле (11.1); 52 — построч-
У Yfu
ная дисперсия.
Бартлет показал, что величина В приближенно подчиняется х2-распределению
с (N — 1) степенями свободы, где N— число оцениваемых дисперсий. Если В меньше
Таблица 11.22
Значения критерия Кохрена GT
fl Степени свободы j\=n—\
1 2 3 4 5 6 7 8
2 0,999 0,975 0,939 0,906 0,877 0,853 0,833 0,816
3 0,967 0,871 0,798 0,746 0,707 0,677 0,653 0,633
4 0,907 0,768 0,684 0,629 0,590 0,500 0,637 0,518
5 0,841 0,684 0,598 0,544 0,507 0,478 0,456 0,439
6 0,781 0,616 0,532 0,480 0,445 0,418 0,398 0,382
7 0,727 0,561 0,480 0,431 0,397 0,373 0,354 0,338
8 0,680 0,516 0,438 0,391 0,360 0,336 0,319 0,304
9 0,639 0,478 0,403 0,358 0,329 0,307 0,290 0,277
10 0,602 0,445 0,373 0,331 0,303 0,282 0,267 0,254
12 0,541 0,392 0,326 0,288 0,262 0,244 0,230 0,219
15 0,471 0,336 0,276 0,242 0,220 0,203 0,191 0,182
20 0,389 0,271 0,221 0,192 0,174 0,160 0,150 0,142
560
Таблица 11.23
Значения %2 при 5%-м уровне значимости (уровне риска)
Число степеней свободы Значения х2 Число степеней свободы Значения х2 Число степеней свободы Значения х2
1 3,84 5 11,07 10 18,31
2 5,99 6 12,59 12 21
3 7,82 8 15,51 13 22,4
4 9,49 9 16,92 15 25
табличного х2 ДЛЯ данного числа степеней свободы и принятого уровня значимости,
то дисперсии однородны, и наоборот.
Рассмотрим применение критерия Бартлета для проверки однородности диспер-
сий. Допустим, что матрица планирования предусматривала проведение четырех
опытов. Первый опыт повторен пять раз, второй — шесть, третий и четвертый — по
четыре раза. При этом дисперсия первого опыта равна 3,5; второго — 4,22; третьего —
5,88; четвертого — 11,36. Проверим гипотезу об однородности дисперсий.
Дисперсия параметра оптимизации
w
52 = —------- = (3,5 • 4 + 4,22 • 5 + 5,88 • 3 + 11,86 • 3)/15 = 5,79;
у W
с = о,4343[1 + 1/3 - (4 — 1)( 1/4+ 1/5+ 1/3- 1/15)] = 0,485.
Определяем В = 1/0,485(151g 5,79 - 41g 3,5 - 51g 4,22 - 31g 5,88 - 31g 11,36] = 1,37.
Табличное значение x2 для трех степеней свободы (N— 1 = 3) и 5%-го уровня зна-
чимости равно 7,82 (табл. 11.23). Поэтому гипотеза однородности дисперсий прини-
мается. Однородность построчных дисперсий свидетельствует о том, что в статисти-
ческих данных нет статистических ошибок и измерения в любых точках плана имеют
примерно одну и ту же точность.
Дисперсией воспроизводимости 52 или дисперсией опытов называется величи-
на, определяемая соотношением:
N пи
Z £ (л,-л,)2
^2 =
i(nu-\)N
При пи = п = const она имеет вид:
N
L s*fu
s,2 =
N
где N(n - 1) =f — число степеней свободы.
561
Дисперсия воспроизводимости вычисляется по данным о построчных дисперси-
ях. В этом случае это выражение принимает вид:
где—Jn ~ числа степеней свободы дисперсий соответственно 5^ , Sj,Sjf.
Если число параллельных опытов п во всех точках плана одно и то же/ =/2 = ...
=fN = п — 1. Тогда формула принимает вид:
1 N
•ч-i
и = 1
Из этой формулы следует, что дисперсия воспроизводимости есть среднее ариф-
метическое построчных дисперсий. Дисперсия воспроизводимости характеризует
точность эксперимента. Дисперсия воспроизводимости может быть вычислена толь-
ко при пи > 1.
Если в каждой строке ставится только один опыт, дисперсия не может быть
вычислена. Ее величина оценивается косвенно — по известным метрологическим ха-
рактеристикам измерительных приборов.
По результатам эксперимента рассчитывают коэффициенты регрессии:
N
где У х} — число независимых опытов (строк).
. и
и = 1
После расчета коэффициентов проверяют гипотезу об их статистической зна-
чимости. Отметим, что процедура проверки статистических гипотез формально пре-
дусматривает сравнение некоторого критерия, рассчитываемого по эксперименталь-
ным данным, с его табличным значением при выбранном уровне значимости (или до-
верительной вероятности = 1 — а).
Для проверки гипотез о статистической значимости коэффициентов регрессии
прежде всего рассчитывают дисперсию оценок коэффициентов:
С2 8У
= -jj — средняя дисперсия всего эксперимента, если отсутствуют параллель-
ные опыты (дублирование).
Если имеются параллельные опыты, то
с2 = __L_
52
где п = const — число дублей при равномерном дублировании (-^ = Sj — дисперсия
среднего).
Из формул видно, что дисперсии всех коэффициентов равны друг другу, так как
они зависят только от ошибки опыта и числа опытов для этого и проверяют однород-
ность дисперсий опытов, так как если все опыты выполнены с одинаковой точно-
562
стью, то и коэффициенты регрессии вычисляются с одинаковой погрешностью. Те-
перь можно построить доверительный интервал AZ>z = ±t* Sb , где t— табличное зна-
чение критерия Стьюдента при числе степеней свободы, которыми определялась
Sb — средняя дисперсия всех опытов, и выбранном уровне значимости, a Sb — сред-
неквадратическая ошибка коэффициента регрессии: Sb = + Js] .
Коэффициент значим, если его абсолютная величина больше доверительного
интервала. Доверительный интервал задается верхней и нижней границами bi + Л/г;
b-^b.
Если расчетное значение критерия окажется меньше табличного, то следует при-
нять гипотезу о возможном равенстве коэффициента нулю, а соответствующий член
из уравнения регрессии исключить. В этом случае считаем, что фактор xz существенно
не влияет на отклику. Но перед принятием решения об исключении члена bpci необхо-
димо выяснить причину малости коэффициента bt. После проверки значимости ко-
эффициентов bt уравнение регрессии принимает вид:
у = Ьц 4- ZjjXj 4- Ь^Х2 4" ... 4" £12Х|Х2 + 3х!хз + •••
Последний шаг — это проверка адекватности модели по имеющимся статистиче-
ским данным (последняя графа в табл. 11.24). Под дисперсией адекватности S^ понима-
ется характеристика разброса средних значений измеренных уи относительно поверхно-
сти отклика, предсказанной уравнением регрессии:
w
Z (у и -Уи>
с 2 = и= 1_____
ад (jv-i)-tf’
где N - 1 — число степеней свободы дисперсии адекватности; К— число значимых
коэффициентов в уравнении регрессии; уи — среднее значение отклика; уи — значе-
ние отклика в м-й точке плана, вычисленное по уравнению регрессии.
Адекватность определяется по критерию Фишера:
р =
р sj
и сравнивается со значением критерия FT, которое определяется из табл. 11.25 по за-
данному уровню значимости (обычно а = 0,05) и двум числам степеней свободы /ад =
— п— 1 wfy = N(n- 1).
Условием адекватности является выполнение неравенства: Fp < Fr
При Fp > Fr модель не адекватна. В последнем случае для получения адекватной
модели необходимы следующие действия: уменьшить интервалы варьирования /z =
Таблица 11.24
№ опыта Уровни переменных Отклики:
х0 *1 Х2 х3 У Уи
1 2 3 4
563
Таблица 11.25
Значения критерия Фишера FT
Число степеней свободы для знаменателя Значения FT при Р= 0,95 в зависимости от числа степеней свободы для числителя
2 4 6 8
2 19,00 19,25 19,33 19,37
4 6,94 6,39 6,16 6,04
6 5,14 5,53 4,28 4,15
8 4,46 3,84 3,58 3,44
24 3,92 2,80 2,53 2,38
всех или нескольких факторов; увеличить число параллельных опытов; ввести новые,
ранее неучтенные факторы; учесть взаимодействия более высокого порядка; изме-
нить функцию отклика.
Анализом адекватности модели заканчивается исследование объекта.
Таким образом, определяется последовательность расчетов при статистической
обработке результатов эксперимента:
1. Определение дисперсии параметра оптимизации:
т
Е (л - у)2
/ = 1
S2 = —т _ 1--------эксперименты в центре плана;
п
Ё (у, - у)2
i = 1
S2 = —п~- }--------построчная дисперсия;
N
Z sifu
и = 1
S2 = —=Г7------дисперсия эксперимента (параметра оптимизации).
и
N N
fu Е SI X 52
При равномерном дублировании 52 = “ ' = ' .
*’ J и 14
2. Проверка однородности дисперсии:
при равномерном дублировании критерий Кохрена
S2
G = ПрИyj = Л _ j = ДГ;
и = 1
при неравномерном дублировании критерий Бартлера
N N
В= (l/c)[lg52 • ХЛ- Z /ulg^2]-
564
3. Определение коэффициентов регрессии:
N
ЪхгУи
bi= —------•
1 N
и
и = 1
4. Проверка статистической значимости коэффициентов регрессии:
S2
= -ft — дисперсия коэффициентов регрессии;
Д/\- = ± Jsl •t=±Sb *t — доверительный интервал.
5. Проверка адекватности модели:
с2 -у')2
=----”-------дисперсия адекватности;
f=N-(k + 1),
где к — число коэффициентов регрессии.
Если/= 0, то проверку осуществляют в нулевой точке:
т
Е -у)2
s2 - И!_______
ад т -1 ’
S2
F= — критерий Фишера.
Пример.
Применение метода Бокса—Уилсона для нахождения оптимальных параметров
режущего инструмента.
Метод позволяет резко сократить число опытов, получить количественные оцен-
ки влияния отдельных факторов и их взаимодействие на изучаемый параметр, устано-
вить оптимальные значения параметра процесса или оптимальные значения парамет-
ров инструмента.
Рассмотрим влияние заднего угла а, переднего угла у, главного угла в плане ф,
вспомогательного угла в плане и радиуса при вершине г (рис. 11.26) на стойкость
токарного резца и определим значения этих геометрических параметров, обеспечи-
вающих максимальную стойкость при обработке аустенитной стали в заданном режи-
ме. На основании определенной информации были выбраны основные уровни и ин-
тервалы варьирования факторов (табл. 11.26).
Приняв в качестве параметра оптимизации стойкость резца и обозначив ее через
у, используем для «крутого восхождения» линейную модель: y = bQ + blxi + b^x2 +
+ Ь*х4 + />5X5.
Рис. 11.26. Параметры резца
565
Таблица 11.26
Уровни и интервалы варьирования
Факторы Кодовое обозначе- ние Интервал варьирова- ния Уровни факторов
верхний 4-1 основной 0 нижний —1
у — передний угол *1 2 -3 -5 —7
а — задний угол х2 2 14 12 10
cpj — вспомога- тельный угол в плане х3 4 20 16 12
(р — главный угол в плане х4 10 45 35 25
г — радиус при вершине *5 0,5 1,5 1,0 0,5
На первом этапе в качестве плана эксперимента принимаем 1/4 реплики (25-2)
от полнофакторного эксперимента 25. Реплика задана генерирующими соотношения-
ми х4 = х, • х2; х5 = Xj • х2 • х3 (табл. 11.27).
При исследовании пяти факторов нужно выполнить 25 = 32 опыта. При исполь-
зовании 1/2 реплики — 16 опытов, при 1/4 реплики — 8 опытов. В выбранном вариан-
те генерирующих соотношений умножим обе части равенств на х4 и х5 соответствен-
но: 1 = Xj • х2 • х4 и 1 = xj • х2 • х3 • х5 — это определяющие контраста. Обобщающий оп-
ределяющий контраст: 1 = хх • х2 • х4 = Xj • х2 • х3 • х5 = х3 • х4 • х5.
Мы можем определить 8 коэффициентов (см. табл. 11.27).
Но вместо модели
у = bQ + bx - Xj + b2 -х2 -I- Ь3 -х3 -I- ЬХ2 *х, -х2 + b23*x2*x3 -I- Z^’Xj -х3 4- ЬХ23 *хх -х2-х3
будем использовать модель
у = bQ 4- Ьх • хх 4- Ь2 • х2 4- Ь3 • х3 4- Ь4 • х4 4- Ь5 • х5,
так как мы можем определить 8 коэффициентов.
Таблица 11.27
Полный факторный эксперимент 23
Номер опыта ^0 *1 х2 *3 х4 хгх3 х2-х3 *5
1 4- 4- 4- — 4- — - -
2 4- — 4- - - 4- - 4-
3 4- 4- - - - - 4- 4-
4 4- - — - 4- 4- 4- -
5 4- 4- 4- 4- 4- 4- 4- 4-
6 4- — 4- 4- - - 4- -
7 4- 4- — 4- — — - -
8 4- - — 4- 4- 4- - 4-
566
Полный факторный эксперимент 23
Таблица 11.28
Номер опыта *1 х2 х3 х4 Х5 *0 У=т, мин
1 — - — 4- — 4- 34,7
2 4- - — - 4- 4- 29,8
3 — 4- — - 4- 4- 42,5
4 4- 4- — 4- — 4- 39,2
5 - — 4- 4- 4- 4- 35,5
6 4- - 4- - - 4- 16,7
7 - 4- 4- — — 4- 31,0
8 4- 4- 4- 4- 4- 4- 39,6
Получаем матрицу планирования и результатов опытов (см. табл. 11.28):
Значения коэффициентов найдем по формуле
N
2^ Уи ' Xui
где xui — кодированное значение /-го фактора в и-м опыте; уи — значение параметра
оптимизации в данном опыте.
8 8
^Уи 2*1, л
Например, J = 33,625; Ь} = -----------5--- = -2,3, Ь7 = 4,45, Ь, = 2,925,
и о 1 о L J
b4 = 3,625, b5 = 3,225. Дисперсию параметра оптимизации определяют по результатам
четырех опытов в центре плана, т. е. при = х2 = х3 = х4 = х5 = 0 (табл. 11.29).
q 153
Дисперсия коэффициентов регрессии: Sfi = =0,019.
Таблица 11.29
Расчет дисперсии параметра оптимизации
Номер опыта в центре Уи У Уи- У (уи - У )2
1 33,1 4 %Уи и = 1 _ 4 =1^-4 =33,6 4 ’ -0,5 0,25 L (Уи -у)2 и = 1 _ («0-1) = ^ =0,153
2 33,5 -0,1 0,01
3 34,0 0,4 0,16
4 33,8 0,2 0,04
4 Е уи= и = 1 = 134,4 X (Уи -У)2 = и = 1 = 0,46
567
Таблица 11.30
Таблица для расчета
№ опыта Уи Ур Уи-Ур <Уи~Ур? N Ъ<уи- УрУ и = 1
1 34,7 34,8 -0,1 0,01 0,68
2 29,8 29,4 0,4 0,16 0,68
3 42,5 42,9 -0,4 0,16 0,68
4 39,2 39,1 0,1 0,01 0,68
5 35,5 35,4 0,1 0,01 0,68
6 16,7 17,1 -0,4 0,16 0,68
7 31,0 30,6 0,4 0,16 0,68
8 39,6 39,7 -0,1 0,01 0,68
Доверительный интервал коэффициентов при числе степеней свободы, равном 3
(проведено 4 опыта, определено 1 среднее значение); число степеней свободы опреде-
ляется для опытов, по которым определялась дисперсия параметра оптимизации
(/=3,18 при а = 0,05) AZ>z- = ± Sb • t = ±3,18 • 70,0191 = ±0,44. Так как абсолютные зна-
чения коэффициентов регрессии больше доверительного интервала, они все значи-
мы. Тогда уравнение регрессии с кодированными переменными имеет вид:
у = 33,625 - 2,3 -Xj + 4,45 -х2 - 2,925 -х3 + 3,625 -х4 + 3,225 -х5.
Проверка гипотезы адекватности полученной модели (табл. 11.30).
N
£ (Уи ~У,)2
Найдем дисперсию неадекватности: 5^ = ----------у-----, где уи — эксперимен-
тальное значение параметра оптимизации в и-м опыте; ур — расчетное значение па-
раметра в том же опыте; f — число степеней свободы/= N— (к + 1).
N
X (Уи -уР)2
Дисперсия неадекватности: Sln = -q—zg-r-iv = 0,34.
**** о —(J ' 1)
Ранее вычисленная дисперсия параметра оптимизации: S'* = 0,153.
Проверку гипотезы адекватности модели произведем с использованием Fкрите-
рия Фишера: F = -=у = 2,22.
Для числителя Д = 2, для знаменателя/2 = 3. = 9,55, так как FTa6 > Fp, то мо-
дель адекватна.
«Крутое восхождение» начинаем из центра плана, т. е. из точки с координатами
= х2 = х3 = х4 = х5 = 0, что соответствует у = -5°, а = 12°, cpj = 16°, ф = 35°, г = 1 мм.
Шаг движения по графику для радиуса г принимаем А5 = 0,3. Для остальных фак-
bi •е/
торов шаг движения вычисляется по формуле: А,. = А5т---, где А5 — принятый шаг
05 • е5
погрешности 5-го фактора; ez, е5 — интервалы варьирования /-го и пятого факторов.
568
Таблица 11.31
Шаг движения по градиенту для остальных факторов
Y а <Р1 Ф т Т, мин
основной уровень -5 12 16 35 1 —
коэффициент -2,3 4,45 -2,925 3,625 3,225 —
интервал варьирования ez 2 2 4 10 0,5 —
-4,6 8,9 -11,7 36,25 1,6125 —
шаг движения по градиенту -0,86 1,66 -2,18 6,74 0,3 —
округленный шаг -1 2 —2 7 о,з —
опыт 9 (мысленный) -6 14 14 42 1,3 —
опыт 10 (реализованный) —7 16 12 49 1,6 45,0
опыт 11 (реализованный) -8 18 10 56 1,9 52,9
опыт 12 (реализованный) -9 20 8 63 2,2 50,3
Например, для первого фактора у шаг движения по градиенту: Л) = Д5 • —- =
“5 ' е5
(—2 3) • 2
= 0,3 • з 22$ Q 5 = —0,86, или округленно ~ -1.
Из 8-ми новых опытов реализовано только три на основе анализа модели
(табл. 11.31).
Если полученное значение Т = 52,9 неудовлетворительно, то следует провести
все 8 опытов и снова двигаться по градиенту. При решении данной задачи оптималь-
ной оказывается следующая геометрия резца: у = -8°, а = 18°, cpj = 10°, ф = 56°, г = 1,9.
При проведении эксперимента число степеней свободы /2 для дисперсии адекват-
ности равно числу различных опытов (числу строк), результаты которых используются
для получения коэффициентов регрессии минус число определяемых коэффициентов.
Параллельные опыты (несколько опытов в строке) дают одну степень свободы.
Опыты в центре плана не используются для определения коэффициентов регрессии, а
используются для другой цели — проверки адекватности (для этого используются
только значимые коэффициенты).
Если все опыты использованы для расчета коэффициентов, то дисперсию адек-
, £(У -у)2
ватности по формуле S* =----7----достоверно определить нельзя, а следует прово-
дить эксперименты в центре плана. В этом случае
Е (Уо -У)2
_ ' = 1
гдеу0 — расчетное значение на нулевом уровне; у — экспериментальное значение; п —
число экспериментов на нулевом уровне.
Если число определенных коэффициентов равно числу строк, то это значит, что
N
справедливо У (уи — у)2—> min (из условия «наименьших квадратов», по которому
/ = 1
определялись коэффициенты).
569
11.12. ПОДБОР ЭМПИРИЧЕСКИХ ФОРМУЛ
ПО ВИДУ ЭКСПЕРИМЕНТАЛЬНЫХ ГРАФИКОВ
Приведенные на рис. 11.27 графики могут быть описаны зависимостями вида:
а)у = я0 + + ^гХ2; ж)у = аелх;
б) у = ках ; з) у = яхелх;
bx+c9 ’
в) у = 1/х; и) у = охе-"*;
ч ч 1
г)у = ахл; к)у =—----------5;
а0 +а2х2
д) у = х In х; л) у = aQ + а}х + а?х2 + ауХ3.
ч 1пх
е)у= —;
Использование гармонического анализа для подбора эмпирических формул.
Если функция у -f(x) при монотонном изменении аргумента х такова, что
У =/(%) =/(х + Т) =/(х + 2Т) = ... =/(х + пТ),
где Т= const — период функции, п — любое целое положительное или отрицательное
число (рис. 11.28), то такую функцию называют периодической.
Периодические кривые могут иметь сложный вид, но всегда можно найти такую
точку пересечения с осью абсцисс, начиная с которой все ординаты кривой в точнос-
ти повторяются.
Периодические кривые получаются, в частности, в результате сложения ординат
нескольких гармонических колебаний.
Обратная задача, т. е. разложение исходной периодической функции на состав-
ляющие колебания, является более сложной. В общем случае, если число составляю-
Рис. 11.27. Примеры экспериментальных графиков
570
щих колебаний и их параметры нам не извест-
ны, эта задача не может быть решена. Поэтому
вводятся определенные ограничивающие
предположения, что составляющие колебания
образуют ряд синусоидальных колебаний, из
которых одно — основное имеет наибольший
период, равный периоду функции f(x). Что ка-
сается остальных колебаний, мы предполага-
ем, что их периоды по отношению к периоду
основного колебания постепенно уменьшают-
ся, следуя тому же закону, по которому происходит уменьшение последовательных
членов так называемого гармонического ряда: 1 + 1/2 + 1/3 + 1/4 + ...
То есть мы предполагаем, что периоды всех остальных составляющих колебаний
пропорциональны периоду функцииДх), причем коэффициенты пропорциональности —
последовательные члены ряда натуральных чисел. Таким образом, обозначая периоды со-
ставляющих колебаний через Тс соответствующими индексами, можно написать:
TQ = 21\ = ЗТ2 = 4Т3 = ...
Здесь TQ — период основного колебания, равный периоду функцииДх).
Ряды колебаний, удовлетворяющие этому условию, называются гармоническими
рядами колебаний. Наибольший период или наименьшая частота в таких рядах обра-
зует их основной период, или основную частоту.
Мы накладываем условия только на периоды гармонических колебаний, что же
касается их амплитуд и начальных фаз, то здесь никаких ограничений не вводим. За-
дачи этого рода составляют содержание раздела прикладной математики, который на-
зывается гармоническим анализом.
Теорема Фурье.
Некоторые классы функций, в том числе и функции периодические, при опреде-
ленных условиях допускают разложение в виде бесконечного гармонического ряда,
т. е. ряда, в котором независимая переменная входит под знаком тригонометрической
функции, а именно под знаком синуса или косинуса.
Так как число членов ряда бесконечно велико, то при вычислении у по данным
значениям х число членов ряда ограничивается, используется только несколько пер-
вых членов. Таким образом, при вычислениях мы заменяем функцию Дх) некоторой
приближенной функцией ф(х), так же как и при интерполировании, поэтому гармо-
нический анализ называют иногда тригонометрическим интерполированием. При
анализе периодических функций накладывают ограничение: период функции полага-
ют равным 2л (рис. 11.28). Поэтому всегда удобно заменить переменную на угловую:
х = 360°(z - Zo)/(^! - Zo), если Zq = 0, то z = xzj/360
и рассматривать интерполяционные функции вида sin (пх) и cos (пх).
11.13. ПРОЕКТИРОВАНИЕ ИЗМЕРИТЕЛЬНЫХ СИСТЕМ
Термин «граница раздела» (interface) обычно обозначает физическую поверх-
ность раздела двух сред (например, воздух — вода). В области измерительной техники
и обработки данных этот термин приобрел более широкое значение. В вычислитель-
ной технике границей раздела между человеком и машиной называют устройства, с
помощью которых инженер кодирует информацию для вычислительной машины и
вводит ее непосредственно в машину. Кроме того, обычно считают, что граница раз-
дела вычислительной машины включает выходное устройство, посредством которого
машина «общается» с человеком.
571
. давления
а)
Рис. 11.29. а) Схема измерительного устройства без границы раздела;
б) Схема манометра Бурдона;
в) Увеличение числа границ раздела при измерении давления
При проектировании измерительных систем проблема «границы раздела» возника-
ет в тех случаях, когда определенный объем информации, получаемый при проведении
эксперимента, должен существенно менять свой энергетический характер или форму.
В некоторых случаях граница раздела отсутствует. Например, при измерении дав-
ления с помощью наклонной трубки (рис. 11.29, а).
При использовании манометра Бурдона жидкость давит на полую изогнутую
пружину. Здесь имеется граница раздела между жидкостью и механическим устрой-
ством.
Еще один уровень сложности появляется при использовании упругой мембраны,
на которую наклеен тензодатчик (рис. 11.29, в). Имеется несколько границ раздела:
между жидкостью и мембраной, между механической мембраной и электрической
цепью считывания. Можно считать, что и электрическая часть прибора имеет не-
сколько границ раздела: между тензодатчиком и мостовой схемой, между мостовой
схемой и усилителем и т. д. Практическое правило, общее для всех измерительных
приборов: чем меньше границ раздела, тем выше точность измерений. Однако могут
быть и исключения. Например, U-образный манометр не может реагировать на быст-
рые изменения давления (пульсации).
Манометр Бурдона также не пригоден — из-за вибраций стрелки. Но это только
потому, что эти два прибора (в отличие от тензодатчика) не предназначены для изме-
рения неустановившегося давления.
Импеданс и нагрузка.
Наличие границ раздела ведет к появлению импеданса. В электротехни-
ке импеданс — кажущееся сопротивление прибора при разомкнутых контактах. Бо-
лее широко, импеданс — величина нагрузки или энергии, которую надо затратить
(приложить), чтобы передать сигнал через границу раздела (от одного устройства
к другому).
Если сигнал передается плохо, то мы говорим о большом рассогласовании импе-
дансов двух сред. Тонкая мембрана хорошо передает колебания жидкости, поэтому
граница раздела обладает более высокой передающей способностью.
Максимальная передача энергии имеет место, когда выходной импеданс изме-
ряемой системы равен входному импедансу измерительного прибора.
Такая максимальная передача энергии не всегда желательна. Например, при из-
мерении напряжения в электрической сети импеданс вольтметра (т. е. его сопротив-
ление) должен быть много больше импеданса измеряемой нагрузки. Кроме того, что
при равенстве импедансов вольтметр может выйти из строя, это может привести и к
572
Контролирующий
спай „
Гальванометр
с большим
сопротивлением Rf
Охлаждаемый
эталонный
спай
Рис. 11.30. Схемы устройства для измерения температуры
выходу из строя измеряемой системы (по существу, в этом случае мы закоротили бы
измеряемую систему цепью вольтметра).
В экспериментах, не связанных с измерением электрических величин, часто не-
обходима максимальная передача энергии. Большие ошибки вследствие нагрузки, со-
здаваемой измерительным прибором, — частая проблема.
Например, если сопротивление (импеданс) гальванометра будет большим, то по-
казания термопары или другого устройства для измерения небольшого напряжения
будут неточными. Поэтому более рациональными являются схемы измерения темпе-
ратуры с помощью устройств, чувствительных к изменению напряжения (рис. 11.30).
Рассмотрим три схемы измерения неизвестного напряжения (рис. 11.31).
Принцип действия тензодатчиков, реохорд как датчиков перемещений и многих
других устройств для измерения, например, температуры основан на изменении их
электрического сопротивления.
В первой схеме (рис. 11.31, а) прибор включен последовательно с сопротивлени-
ем, он не только создает нежелательную токовую нагрузку на резистор, чувствитель-
ный к такой нагрузке, но имеет нелинейную характеристику:
I=V0/(R+Rm).
Во второй схеме (рис. 11.31, б), сопротивление вольтметра много больше R. Из-
меряемое напряжение линейно связано с величиной измеряемого сопротивления:
Иг= Ио(Л/Яо).
Рис. 11.31. Схемы измерения напряжения
573
Более удобна мостовая схема (рис. 11.31, в). Если
резисторы R2— постоянны, то подбором перемен-
ного сопротивления R3 можно добиться, чтобы ток,
проходящий через гальванометр, был бы равным нулю.
При этом условии:
R = R}R3/R2.
Изменяя величину Я3, можно определить величи-
ну R. Кроме того, мостовую схему можно разбаланси-
ровать и, используя соотношение между током дисба-
ланса и изменением R, определить изменение R3 (об-
ратная задача).
Мостовые схемы предназначены главным обра-
зом для того, чтобы свести к минимуму или вообще
исключить электрическую нагрузку на испытываемую
схему. На практике встречаются самые разные виды
нагрузок. Нагрузка, связанная с массовым расходом,
имеет место тогда, когда для работы измерительного прибора необходимо отбирать
очень большое количество жидкости или газа. Тепловая нагрузка наблюдается в слу-
чаях, когда прибор для измерения температуры имеет довольно большие размеры и
происходит утечка тепловой энергии из испытываемого устройства.
В идеальном случае датчик должен иметь небольшие размеры, нулевую массу, не
поглощать энергии и давать достаточно мощные и точные сигналы, способные при-
вести в действие измерительный прибор.
Динамические характеристики.
Если измерительный прибор не может следить за быстрыми изменениями пара-
метра, то на границе раздела между измерительным прибором и объектом измерений
имеется рассогласование импедансов (рис. 11.32). Сильное рассогласование импедан-
сов может существовать, даже если на более низких частотах согласование импедан-
сов достаточно для передачи сигнала. Причинами неудовлетворительных динамиче-
ских характеристик измерительных приборов могут быть:
— инерционность датчика или считывающего устройства;
— большая теплоемкость или теплопроводность термопары;
— наличие трения;
— значительное время восстановления или запаздывания (например, остывания
термопары).
Важно иметь в виду, что при исследовании требуется хорошо знать динамиче-
скую характеристику прибора и обращаться при необходимости к соответствующим
специалистам.
ЛИТЕРАТУРА
1. Адлер Ю. IL, Маркова Е. В., Грановский Ю. В. Планирование эксперимента при
поиске оптимальных условий. — М.: Наука, 1976. С. 280.
2. ШенкХ. Теория инженерного эксперимента. — М.: Мир, 1972. С. 384.
3. Седов Л. И. Методы подобия и размерностей в механике. — М.: Наука, 1965. С. 386.
4. Чистяков В. В. Методы подобия и размерностей в литейной гидравлике. — М:
Машиностроение. 1990. С. 224.
5. Ершов В, И., Патраков Н. Н., Курицына В. В. Методология научных
экспериментальных исследований в производстве аэрокосмической техники:
Учебное пособие. — М.: «МАТИ»—РГТУ им. К.Э.Циолковского, 2003. С. 196.
574
СОДЕРЖАНИЕ ГЛАВЫ 11
11.1. Определения и термины.....................................523
11.2. Эксперимент как предмет исследования......................525
11.3. Совокупность случайных погрешностей.
Закон нормального распределения.................................526
11.4. Ошибка и неопределенность эксперимента в целом............531
11.5. Элементы теории подобия и размерностей....................535
11.6. Определение интервалов между экспериментальными точками...541
11.7. План экспериментов........................................542
11.8. Многофакторные эксперименты: классические планы...........545
11.9. Многофакторные эксперименты: факторные планы..............546
11.10. Факторное планирование при поиске оптимальных условий....549
11.11. Обработка и оценка экспериментальных данных..............557
11.12. Подбор эмпирических формул по виду экспериментальных
графиков........................................................570
11.13. Проектирование измерительных систем......................571
Литература .........................................................574
575
ГЛАВА 12________________________________________________________
Основы теории изготовления
элементов конструкций
пластическим деформированием
Летательный аппарат состоит из десятков тысяч различных металлических деталей
(первичных элементов конструкции), большую часть которых получают методами
пластического деформирования: объемной и листовой штамповкой. Теория изготовле-
ния элементов конструкций пластическим деформированием (или теория обработки
металлов давлением) — наука о методах расчета напряженно-деформированного со-
стояния заготовки, получаемой детали и технологических параметров обработки. Она
базируется на теории пластичности, которая развивается в двух направлениях:
— физика процесса пластической деформации (здесь процесс исследуется на
микроуровне);
— механика процесса пластической деформации (процесс деформирования ис-
следуется на макроуровне).
Основы этой теории созданы трудами нескольких поколений ученых [1—17].
Первыми работами (в конце 1860-х годов), положившими начало научной теории
пластичности, можно считать работы французского ученого Г. Треска. Основополож-
ником теории обработки металлов давлением в России считают Д. К. Чернова
(в 1867 г. он опубликовал статью «О выделке стальных осей для подвижного состава
железных дорог», где высказал предположения о рациональности подходов к ряду
процессов обработки давлением).
Дальнейшее развитие теории связано с работами Б. Сен-Венана, М. Леви,
М. Губера, Р. Мизеса, Г. Генки, А. Надаи, Р. Хилла, В. Прагера и других зарубежных
ученых.
Отечественные ученые внесли огромный вклад в науку о пластических деформаци-
ях. В областях физики, физико-химии и механики пластической деформации капиталь-
ные исследования проводились В. Д. Кузнецовым, Н. С. Курнаковым, Н. Н. Давиден-
ковым, А. А. Бочваром, С. И. Губкиным, С. А. Христиановичем, В. В. Соколовским,
Л. М. Качановым, А. А. Ильюшиным, Е. П. Унксовым, Г. А. Смирновым-Аляевым,
А. Д. Томленовым, Л. А. Шофманом, И. А. Норицыным, И. Я. Тарновским, М. В. Сто-
рожевым, Е. А. Поповым, Н. Н. Малининым, А. Д. Матвеевым, М. Н. Горбуновым,
Г. Д. Делем, В. И. Ершовым и многими другими.
Целью данной главы является изучение методов теоретического анализа процес-
сов пластического деформирования, необходимых для расчета основных технологи-
ческих параметров (деформирующего усилия, скорости обработки, температуры на-
грева, предельных деформаций и др.), обеспечивающих получение детали заданного
качества.
В связи с тем, что в конструкции летательного аппарата преобладают тонкостен-
ные детали, полученные из традиционных металлических полуфабрикатов (листов,
труб и профилей), в данной главе рассматриваются большей частью вопросы, связан-
ные с листовой штамповкой.
576
12.1. ПОНЯТИЕ О ПЛАСТИЧЕСКОЙ ДЕФОРМАЦИИ
12.1.1. Деформации
Приложение внешних сил к твердому телу вызывает изменения расстояния меж-
ду отдельными материальными точками тела, т. е. тело изменяет свою форму
и размеры.
Для количественной оценки величины этого формоизменения вводят понятие
деформации.
Деформации бывают упругими и пластическими.
Если деформация исчезает после прекращения действия внешних сил и тело
полностью восстанавливает свою исходную форму и размеры, то такая деформация
называется упругой. Если восстановление формы и размеров происходит не полно-
стью, то такую остаточную деформацию называют пластической.
Способность тела пластически деформироваться без разрушения называют плас-
тичностью.
Различают деформации линейные (рис. 12.1) и угловые (рис. 12.2). Эти деформа-
ции могут относиться как ко всему телу, так и к элементу тела. Линейные деформации
характеризуют изменение расстояния между какими-либо двумя точками тела. Угло-
вые деформации характеризуют изменение угла между какими-либо двумя линиями.
Указанные деформации (в первую очередь линейные) можно разделить на абсо-
лютные деформации, относительные и логарифмические.
Абсолютная деформация выражает абсолютное изменение какого-либо размера.
Относительная деформация характеризует относительное изменение этих же ве-
личин, как отношение абсолютного изменения какого-либо размера к первоначаль-
ному значению этого размера.
Логарифмическая деформация — разновидность относительной. Она равна нату-
ральному логарифму отношения получаемого размера к первоначальному размеру.
Для расчета линейных деформаций (см. рис. 12.1) имеем следующие выражения:
А/ = / — /0 — абсолютная линейная деформация на участке А—В\ (12.1)
/ — /0 А /
£отн = ~г~ = 1--относительная линейная деформация на участке А—В; (12.2)
елог = In логарифмическая линейная деформация на участке А—В. (12.3)
Логарифмическая мера деформации более предпочтительна в расчетах, чем отно-
сительная мера деформации, так как она обладает свойством аддитивности (целое
Рис. 12.1. К определению линейных
деформаций: а) до деформирования;
б) после деформирования
Рис. 12.2. К определению угловых
деформаций: а) до деформирования;
б) после деформирования
577
равно сумме составляющих). Например (рис. 12.3), если образец длиной /0 поэтапно
удлинять в два раза, то на каждом этапе логарифмическая деформация составит вели-
чину 0,69, а относительная — 1,0. Если теперь рассматривать конечное (суммарное)
формоизменение, то получим, что логарифмическая деформация будет равна 1,38
(и равна сумме деформаций на каждом этапе, т. е. 0,69 + 0,69 = 1,38), а
относительная — равна здесь 3,0 (и не равна сумме деформаций по этапам, так как
1,0+ 1,0 = 2,0).
Между логарифмической елог и относительной еотн деформациями существует связь:
елог = 1п (^) = 1П (^7~) = 1П +Е°тн)’ (12’4)
При малых деформациях (до 10%) отличия между логарифмической и относи-
тельной мерами незначительны (менее 5%).
Относительные деформации используется обычно в теории упругости и в проч-
ностных расчетах, где величины деформаций не превышают нескольких долей про-
цента; логарифмические деформации — в теории пластичности и обработки металлов
давлением, где деформации достигают десятки и сотни процентов.
Поэтому здесь под линейной деформацией будем иметь в виду ее логарифмиче-
скую меру, если деформации большие. Если деформации невелики (менее 10%), мера
линейной деформации может быть и относительной, и логарифмической.
Угловая мера деформации (см. рис. 12.2) рассчитывается выражением
у=Оо- а, (12.5)
где у — угловая деформация или угол сдвига (в радианах).
Между линейной и угловой деформациями существует связь.
При малых деформациях линейное удлинение материала в каком-либо направле-
нии в окрестностях рассматриваемой точки определяется зависимостью
е = V* + ^уау + е A2 + + lyfiyflz+ Х^А> (12-6)
где ех, ег Ег — малые линейные деформации в прямоугольной и произвольной относи-
тельно заготовки системе координат X, Y, Z; ах, a? az — косинусы угла между рассмат-
риваемым направлением и осями координат; у^ у у^ — малые сдвиговые деформа-
ции в соответствующих плоскостях.
При больших деформациях взамен уравнения (12.6) используются более слож-
ные зависимости.
12.1.2. Скорость деформации
и скорость деформирования
Изменение относительной или логарифмической деформации в единицу време-
ни называют скоростью деформации и обозначают обычно Ё.
е = -зг’илие = ~аг- (12-7)
Введение понятия скорости деформации связано с необходимостью учета вре-
менного фактора в процессах пластического деформирования, влияющего главным
образом на механические свойства деформируемого материала, а также для учета
инерционных сил при высокоскоростных методах штамповки.
578
2 этап
Суммарное формоизменение
елог=1,38
еотн = 3,0
Рис. 12.3. К свойству аддитивности
логарифмической деформации
Рис. 12.4. К понятиям о скорости деформации Е
и скорости деформирования уд
Между скоростью деформации материала Ё и скоростью деформирования образ-
ца гд имеется следующая связь:
dlnfr)
Vo 7 _ 1 dl = у'д
dt 7 * dr 7 •
(12.8)
В соответствии с (12.8) скорость деформации Ё обратно пропорциональна длине
образца /.
На рис. 12.4 показано одноосное растяжение образца с постоянной уд скоростью
деформирования (скоростью движения исполнительных органов испытательной ма-
шины). Отметим, что скорость деформации здесь Ё по ходу процесса, в соответствии с
выражением (12.8), будет переменной (будет уменьшаться). В некоторых операциях
штамповки или при механических испытаниях, когда требуется обеспечить постоян-
ство скорости деформации Ё = const по времени, управление производят скоростью
деформирования уд или внешней нагрузкой.
12.1.3. Условие постоянства объема
при пластическом деформировании
Экспериментально установлено, что при пластическом деформировании объем
тела меняется незначительно (изменение объема связано только с упругими деформа-
циями). Поэтому, приравняв друг к другу объемы те-
ла до и после деформирования (рис. 12.5), получим:
xyz ,
x0y0z0 = xyzmm —— = 1.
лоУо<-о
Логарифмируя обе части последнего равенст-
ва, получим:
In- + In— + In- = О,
*0 Уо Zo
или, возвращаясь к обозначениям логарифмических
деформаций,
ех + гу + Ег = 0. (12.9)
Полученное выражение (12.9) — есть условие
постоянства объема при пластическом деформирова-
нии, записанное в логарифмических деформациях.
Рис. 12.5. К условию постоянства
объема при пластическом
деформировании:
а) до деформирования;
б) после деформирования
579
В скоростях деформаций получим:
ex+e,+ ez = 0. (12.10)
В главных деформациях условие постоянства объема имеет вид, аналогичный (12.9):
Ei +е2 + е3 = 0. (12.11)
Отметим, что деформации называются главными, когда выбрана такая система
координат, где по соответствующим направлениям (координатам) возможны только
линейные деформации, а угловые (сдвиговые) — отсутствуют.
12.2. ФИЗИКА ПЛАСТИЧЕСКОЙ ДЕФОРМАЦИИ.
ХОЛОДНАЯ ПЛАСТИЧЕСКАЯ ДЕФОРМАЦИЯ
МОНОКРИСТАЛЛА И ПОЛИКРИСТАЛЛА
Пластическая деформация монокристалла может происходить в основном двумя
путями: скольжением и двойникованием.
Скольжение — параллельное смещение тонких слоев монокристалла относи-
тельно друг друга (характерно для металлов).
Экспериментально установлено, что полосы скольжения отстоят одна от другой
в среднем на расстоянии ~ 1 мкм (расстояние между соседними атомными плоскостя-
ми составляет ~ 10-4 мкм).
Характер деформации монокристалла путем скольжения имеет вид, изображен-
ный на рис. 12.6.
Скольжение обычно происходит по определенным кристаллографическим плос-
костям, которые называют плоскостями скольжения (это плоскости с наибольшей
плотностью размещения атомов).
Двойникование — смещение атомов, расположенных в плоскостях, параллель-
ных некоторой плоскости, которая называется плоскостью двойникования
(рис. 12.7).
12.2.1. Дислокации
Экспериментально установлено, что расчетные значения касательных напряже-
ний при пластическом деформировании превышают фактические на 3—4 порядка.
Эту разницу объясняют тем, что процесс скольжения осуществляется не одновре-
менным смещением всех атомов в одной кристаллографической плоскости относитель-
но друг друга, а их последовательным смещением. Это возможно, если есть дефек-
Плоскость
деформация
отсутствует
Рис. 12.6. Схема скольжения
при пластическом деформировании
180°-2а
Рис. 12.7. Схема двойникования
при пластическом деформировании
580
т _
Направление
движения
дислокации
и пластического
сдвига
Рис. 12.8. Схема краевой дислокации.
Смещение центра дислокации
из положения «а» в положение «Ь»
ты в кристаллической решетке — так называе-
мые дислокации, вызывающие нарушения пра-
вильного расположения атомов.
Различают краевую (рис. 12.8) и винтовую
(рис. 12.9) дислокации.
Реальные металлы и сплавы — поликрис-
таллы. Они состоят из большого числа моно-
кристаллов, хаотично ориентированных в твер-
дом теле (рис. 12.10).
Общее формоизменение поликристалли-
ческого тела складывается из пластических де-
формаций зерен (монокристаллов) и их отно-
сительного смещения. Поэтому различают вну-
трикристаллическую и межкристаллическую
деформации.
В первую очередь, пластическая деформация возникает в зернах с наиболее бла-
гоприятной ориентировкой плоскостей скольжения (при одноосном растяжении и
сжатии наиболее благоприятную для начала пластической деформации ориентиров-
ку имеют зерна, у которых плоскости скольжения расположены под углом 45° к на-
правлению действия внешней силы, где развиваются максимальные касательные
напряжения).
Затем в пластическое состояние переходит большинство зерен металла. Дальнейшее
формоизменение приводит к тому, что зерна получают вытянутую форму в направлении
течения материала. Одновременно с этим происходит поворот кристаллографических
осей отдельных зерен со стремлением совмещения отдельных плоскостей скольжения и
образованием сквозных плоскостей скольжения, пронизывающих все тело.
Это приводит к тому, что при значительной деформации возникает преимущест-
венная ориентировка кристаллографических осей зерен поликристалла, называемая
текстурой деформации. В конечном итоге это приводит к анизотропии свойств поли-
кристаллического тела.
При межкристаллической деформации (из-за поворота кристаллов) возникают
повреждения по границам зерен, ведущие к образованию микротрещин, а затем
и макротрещин, что может приводить к разрушению деформируемого тела.
Разная ориентировка плоскостей скольжения в зернах поликристалла и, соответ-
ственно, разная величина упругой деформации, приводит при разгрузке к возникно-
вению остаточных напряжений II рода.
Рис. 12.10. Схематический вид
поликристаллического тела
Произвольно
ориентированные
плоскости
скольжения
581
Отметим, что остаточные напряжения I рода образуют силы, уравновеши-
вающиеся между отдельными частями заготовки, остаточные напряжения II рода —
между отдельными зернами, III рода — между отдельными группами атомов (дисло-
кациями).
12.3. МЕХАНИКА ПЛАСТИЧЕСКОЙ ДЕФОРМАЦИИ
12.3.1. Кривые упрочнения
Холодная пластическая деформация металлов и сплавов существенным образом
изменяет их физико-механические свойства. Происходит повышение прочностных
свойств: предела упругости, предела пропорциональности, предела текучести, вре-
менного сопротивления (предела прочности), твердости. Снижаются показатели
пластичности: относительное удлинение, относительное сужение, ударная вязкость
и т. д. Эти изменения свойств, связанные с деформационным упрочнением матери-
ала, называют наклепом.
Другими словами, если в конструкциях, которые работают в области упругих де-
формаций, показатели прочностных и пластических свойств конструкционных мате-
риалов в большинстве случаев считаются постоянными, то в процессах пластического
деформирования эти же показатели переменны и зависят от многих факторов: от ве-
личины пластической деформации, от скорости деформации, температуры нагрева,
«истории» деформирования и схемы напряженного состояния заготовки. Все это
и составляет главную особенность определения и последующего учета в расчетах ре-
альных механических характеристик материала, подвергнутого пластическому дефор-
мированию.
Прочностные и пластические свойства металлов и сплавов определяют по ре-
зультатам различных механических испытаний специально подготовленных образ-
цов. Наиболее часто используется испытание образца материала на одноосное растя-
жение до его разрушения (ГОСТ 1497—84).
Первичная (машинная) диаграмма растяжения образца имеет вид, приведенный
на рис. 12.11.
Для определения стандартных показателей прочности и пластичности машин-
ную диаграмму (рис. 12.11) перестраивают в координатах условные напряжения
Оусл — относительная деформация еотн (рис. 12.12).
Здесь ов — временное сопротивление или предел прочности, от — предел теку-
чести, о02 — условный предел текучести (при деформации 0,2%), 810, 35, 32 5 — относи-
Рис. 12.11. Первичная (машинная) диаграмма растяжения образца
582
Рис. 12.12. Диаграмма растяжения образца в координатах оусл — еотн
тельное удлинение образца на базовой длине я0, величина которой нормируется в за-
висимости от площади поперечного сечения образца.
Расчет последних показателей осуществляют по известной формуле 8 =
а0 ~а
=-----• 100% после совмещения частей разрушенного образца (рис. 12.12).
flo
Этих показателей механических характеристик материала еще недостаточно для
полного описания поведения материала при пластическом деформировании.
Для получения механических характеристик материала в процессе пластической
деформации первичную диаграмму (рис. 12.11) строят в координатах напряжение те-
кучести — интенсивность деформаций е,.
Напряжение текучести о5 — это напряжение, с которым материал сопротивляет-
Р
ся пластическому деформированию: = р. Интенсивность деформаций рассчиты-
вается выражением £f = ln(p J В результате получают кривую упрочнения материала
в виде диаграммы, изображенной на рис. 12.13.
На кривой упрочнения можно отложить полученные ранее прочностные харак-
теристики испытуемого образца: ав, ат, а0 2, однако они уже не будут являться посто-
янными величинами в процессе пластического деформирования. Так, если нагрузить
образец до точки В (кривая О В), а затем разгрузить до точки С (прямая ВС), а затем
Рис. 12.13. Кривая упрочнения материала
и распределение деформаций по длине деформированного образца
583
снова нагрузить до точки В, то предел текучести ат сместится в точку В, предел про-
чности ов будет лежать выше точки В.
Из рис. 12.13 видно, что распределение деформаций по длине образца неравно-
мерное. Уменьшая базовую длину л0, дополнительно определяют равномерное 8равн
и сосредоточенное 8соср относительные удлинения соответственно за пределами и в
зоне разрушения образца.
Отметим, что приведенные здесь количественные показатели пластических
свойств материала из-за неравномерного распределения деформации и различной ве-
личины базовых длин подчиняются неравенству 8равн < 810 < 85 < 82 5 < 5соср.
Кривые упрочнения строятся при конкретных температурно-скоростных усло-
виях испытания образцов.
Экспериментально установлено, что в условиях «простого» (монотонного) нагру-
жения, когда внешние силы возрастают пропорционально общему параметру, кривые
упрочнения, полученные при различных схемах испытаний образцов из одного матери-
ала, практически совпадают. Тогда говорят о «единой кривой упрочнения» (рис. 12.14).
Различаются только моменты разрушения образцов (предельные деформации).
Реальность существования «единой» кривой упрочнения материала при различ-
ных схемах нагружения образцов (схемах напряженно-деформированного состояния)
упрощает основы классической теории пластичности.
12.3.2. Аппроксимация кривых упрочнения
Так как механические свойства деформируемых металлов и сплавов определяют
в результате экспериментальных исследований, то для удобства их дальнейшего ис-
пользования в теоретических и практических расчетах, полученные опытным путем
данные заменяют (аппроксимируют) аналитическими выражениями.
Обычно кривые упрочнения материала при холодной пластической деформации
аппроксимируют линейной или степенными функциями различных видов (рис. 12.15):
о5 = oTO + nef — линейная аппроксимация; (12.12)
= Ае” — степенная аппроксимация; (12.13)
п5= п0 + Л1е"1 — степенная аппроксимация; (12.14)
о5 = Л2(ЕуСл + С/)”2 — степенная аппроксимация. (12.15)
Интенсивность деформации, е,
Рис. 12.14. «Единая» кривая упрочнения
Рис. 12.15. Кривая упрочнения алюминиевого
сплава Д16Т и ее аппроксимация
аналитическими функциями
584
Здесь gto — экстраполированный предел текучести; П — модуль упрочнения;
А, п9 а0, еусл, Al9 А2, nl9 п2 — экспериментальные константы.
Параметр п в выражении (12.13) часто называют показателем деформационного
упрочнения материала.
12.3.3. Влияние температуры
и скорости деформации на процесс деформирования
Влияние температуры нагрева. При нагревании деформируемого металла в пос-
леднем возникают разупрочняющие процессы (возврат и рекристаллизация). Таким
образом, при повышенных температурах в процессах деформирования идут как уп-
рочняющие, так и разупрочняющие процессы. В зависимости от времени деформиро-
вания (скорости деформации) будет преобладать тот или иной процесс.
На основе многочисленных экспериментов установлено, что с нагревом прочно-
стные свойства металлов, как правило, снижаются, а пластические свойства увеличи-
ваются. Эти экспериментальные данные могут быть аппроксимированы экспоненци-
альными зависимостями Н. С. Курнакова:
а, = аоеу(/~/о) (здесь у СО), (12.16)
e, = eoeY'<'“'°) (здесь/>0). (12.17)
В выражениях (12.16) и (12.17) ор е,— показатели прочностных и пластических
свойств материала при температуре /; п0, е0 — показатели прочностных и пластиче-
ских свойств материала при температуре /0; у, у' — температурные (эксперименталь-
ные) коэффициенты.
При формоизменении с нагревом возможности штамповки значительно увели-
чиваются в широком диапазоне скоростей деформаций. Например, если для алюми-
ниевого сплава АМгбМ при t = 20 °C относительное удлинение 35 « 25%, то при t =
= 400 °C 35~ 100%.
Влияние скорости деформации. Обычно механические свойства металлов опреде-
ляют на испытательных машинах при малых скоростях деформирования уд (не более
10 мм/с), при этом скорость деформации лежит в пределах ё = 10~3 + 10-4 с"1.
Обработка давлением на прессах осуществляется со скоростями уд = 10-*-500 мм/с,
ё = 10-2+ 1,0 с-1.
Деформирование при указанных малых скоростях называют статическим.
При обработке на молоте взаимодействие уже носит динамический характер
(уд = 5 + 10 м/с). Еще большие скорости возникают при штамповке взрывом, магнито-
импульсной и элекгрогидравлической обработках, где уд = 20+30 м/с и более.
В первом приближении можно сказать, что при увеличении скорости деформа-
ции ё прочностные характеристики металлов и сплавов возрастают, а пластические
снижаются.
Особенно большое влияние скорости деформации происходит при горячем де-
формировании металлов и сплавов.
Экспериментальные зависимости напряжения текучести от скорости деформа-
ции аппроксимируют выражениями типа:
о5 = ^, (12.18)
gs = °so + £1п—, (12.19)
£/0
585
где К,к,т — коэффициенты, определяемые экспериментально; — напряжение те-
кучести (течения) при условной скорости деформации ёю.
Параметр т в выражении (12.18) называется показателем скоростного упрочне-
ния материала.
Отметим, что с точки зрения размерностей наиболее предпочтительным является
аппроксимация по выражению (12.19).
Для одновременного учета и деформационного, и скоростного упрочнения иногда
используют аппроксимацию типа:
(12.20)
Если не брать во внимание «историю» деформирования образца, то наиболее
полно результаты экспериментальных исследований могут быть представлены в виде
кривой упрочнения, зависящей от трех переменных: интенсивности деформации ef,
интенсивности скорости деформации и температуры испытаний t.
С целью учета совместного влияния температурно-скоростных факторов на со-
противление материалов пластическому деформированию используют методы рег-
рессионного анализа, метод термомеханических коэффициентов, а также различные
эмпирические формулы.
Уравнение регрессии имеет вид:
= + + ^2*2 + + ^\х2 + ^5*2*3 + ^6*3*1 + ^1^3, (12.21)
где о50 — сопротивление деформированию в базисной точке; хх — деформация;
х2 — скорость деформации; х3 — температура нагрева; ки к2, к3, к4, к5, кв, к7 — коэффи-
циенты регрессии.
С использованием метода термомеханических характеристик расчетные значе-
ния сопротивления деформированию определяют выражением:
(12.22)
где 0£О — сопротивление деформации при базисных условиях, ки к2, к3 — термомеха-
нические коэффициенты, соответственно учитывающие влияние деформации, ско-
рости деформации и температуры нагрева (обычно приводятся в виде трех кривых).
Сверхпластичность. Явление сверхпластичности можно рассматривать как ано-
малию в поведении материала при пластическом деформировании. Сверхпластич-
ность характеризуется резким (на один-два порядка) увеличением относительного уд-
линения образца при значительном (на один-два порядка) уменьшении сопротивле-
ния деформированию.
Экспериментально установлено, что сверхпластичность проявляется в узком
диапазоне температурно-скоростных условий (рис. 12.16). При этом скорость дефор-
мации не должна отличаться от оптимальной скорости (определяемой эксперимен-
Таблица 12.1
Характеристики промышленных сплавов в состоянии сверхпластичности
Марка материала т = const в формуле (12.18) о5, кг/мм2 8, % t °C ‘ОПТ > v ё, , с-' опт’
АМгб 0,38 2,2 280 400 2 х IO-3
ВТ6 0,8 2,5 1250 900 1,8хЮ-3
ВТ9 0,8 1,5 2840 900 IO"3
586
Рис. 12.16. Интерпретация узкого
диапазона температурно-скоростных
условий штамповки
Рис. 12.17. Кривая скоростного
упрочнения материала
тально) более чем на 3%, а температура штамповки — более чем на 5% от оптималь-
ной температуры.
do5
В области Ez величина —- имеет максимальное значение (рис. 12.17).
de,
При сверхпластическом деформировании зависимость о5 =/(ё,) часто аппрокси-
мируют выражением (12.18), причем в общем случае показатель скоростного упроч-
нения не является константой.
В табл. 12.1 приведены некоторые механические характеристики промышленных
сплавов в состоянии сверхпластичности.
12.4. ТЕОРИЯ НАПРЯЖЕНИЙ
12.4.1. Общие понятия
Тело, подверженное действию сил, находится в напряженном состоянии.
Внешние силы, действующие на тело, могут быть поверхностными и объемными.
К поверхностным силам относятся силы, действующие на поверхность тела.
К объемным силам относятся силы, действующие на все материальные точки те-
ла пропорционально их массам (это сила тяжести, силы инерции и др.). В данной гла-
ве действие объемных сил не рассматривается.
При изучении напряженного состояния принимаем, что тело однородно, изо-
тропно и непрерывно (т. е. здесь не принимается во внимание дискретная, атомисти-
ческая структура материала).
Под действием внешних сил в теле возникают внутренние усилия.
Предел отношения внутреннего усилия АР, действующего на какую-либо эле-
ментарную площадку, к площади этой площадки Ар при неограниченном уменьше-
нии последней, называется напряжением S:
с г
S= lim — .
дг-»оАг
(12.23)
Каждая точка в напряженном теле находится в напряженном состоянии и в лю-
бой плоскости, проведенной через данную точку, на нее будет действовать напряже-
ние определенной величины и направления.
Отметим, что напряжения реально (физически) не существуют, это математиче-
ское понятие.
587
Полное напряжение S по «правилу параллелепипеда» всегда можно разложить на
три: одно нормальное а и два касательных Tj и т2 (рис. 12.18).
В равной мере полное напряжение всегда можно разложить на три по направле-
ниям осей координат.
12.4.2. Напряжения в координатных площадках
Проведем через точку Л, находящуюся в деформируемом теле, три плоскости, па-
раллельные осям координат: х, у, z. Построим параллелепипед, ребра которого беско-
нечно малы. На видимых и невидимых гранях параллелепипеда в общем случае дейст-
вуют нормальные и касательные напряжения (рис. 12.19). Напряжения на каждой паре
параллельных граней параллелепипеда разнятся на бесконечно малую величину.
Нормальные напряжения ах, считаются положительными, если они вызы-
вают растяжение материала, и отрицательными — если сжатие. Их обозначение (ин-
дексы) указывают направление действия в соответствии с обозначением координат-
ных осей.
Касательные напряжения тух, xyV т^, т^, xxz положительны, если их направ-
ление совпадает с положительным направлением осей координат, при условии, что
направление положительного (растягивающего) нормального напряжения на той же
площадке совпадает с положительным направлением координатной оси (или, если
сжимающее нормальное напряжение направлено по отрицательному направлению
координатной оси). Первый индекс в обозначении касательного напряжения указы-
вает направление действия и совпадает с соответствующим направлением координат-
ной оси, второй — называется адресом и указывает площадку действия касательного
напряжения. Обозначение адреса совпадает с индексом нормального напряжения на
этой площадке.
Напряжения в точке А по трем координатным площадкам можно записать в фор-
ме матрицы:
°х Хху Xxz ~~ направление х,
Gy xyz — направление у
xzy ~~ направление z.
Т 1 т
адрес адрес адрес
х у z
Рис. 12.18. Правило разложения
полного напряжения на составляющие
Рис. 12.19. Обозначение компонентов
напряжений в окрестностях точки А
588
Эту матрицу можно переписать иначе (учитывая закон парности касательных на-
пряжений: тхг = = -с^,):
( ^ху Txz 1
J • 0^ xyz I — симметричная матрица. (12.25)
г • |
Написанную выше симметричную матрицу (12.25) называют тензором напря-
жений.
Отметим, что название тензора было введено в науку именно для обозначения
всех компонентов (три нормальных и три касательных напряжения) напряженного
состояния в точке деформируемого тела.
Таким образом, напряженное состояние в точке можно описать шестью пере-
менными. Покажем, что в этом случае напряженное состояние в точке вполне опре-
делено.
12.4.3. Напряжения на наклонной площадке
Проведем наклонную плоскость через три вершины параллелепипеда на
рис. 12.19, как изображено на рис. 12.20. Определим напряжения на полученной пло-
щадке, если напряженное состояние в точке известно (т. е. задан тензор напряжений).
Из сопротивления материалов известно, что нормальное напряжение в наклон-
ной площадке ол определяется выражением:
= ^хах + °уау + °zal + ^хуахау + + 2 Wx- (12’26>
Здесь ах, ау, az — косинусы углов ах, ау и az между нормалью к наклонной пло-
щадке и соответствующими осями координат (направляющие косинусы).
Касательные напряжения в наклонной площадке определяются по правилу па-
раллелограмма:
(12.27)
где S — полное напряжение в площадке.
Уравнения равновесия по соответст-
вующим направлениям (по рис. 12.20) запи-
шем в виде:
— Gx • “Ь • ау + Xxz • Gz,
Sy = xyx-ax + ay-ay + xyz-az, (12.28)
~ ^zx * ax + • ay + ®Z • az’
Полное напряжение S получается из вы-
ражения
S2 = S2 + S2 + S2. (12.29)
Таким образом, если задан тензор напря-
жений (шесть напряжений), действующих в
точке А по трем взаимно перпендикулярным
площадкам, то можно определить напряже-
ния на любой наклонной площадке, проведен-
ной через эту точку, т. е. напряженное состоя-
ние в точке вполне определено шестью пере-
менными.
Рис. 12.20. Обозначение
напряжений в наклонной площадке
589
Из аналитической геометрии известно, что уравнение (12.26) представляет собой
поверхность второго порядка. Кроме того, всегда через точку Л можно провести такие
три взаимно перпендикулярные плоскости, в которых касательные напряжения
туи, ти7 обратятся в нуль, а останутся только нормальные оу, о7.
Лу У4, Ж У 4,
Тогда эти напряжения (обозначаемые о2, аз)’ направления их действия и сами
площадки называют главными.
Отметим, что главные напряжения о2, о3 единственны для конкретного на-
пряженного состояния.
12.4.4. Геометрическая интерпретация
тензора напряжений
Так как напряженное состояние в точке выражается уравнением типа (12.26), то
это значит, что напряженное состояние есть величина тензорная и в отличие от ска-
лярной (число) и векторной (число и направление) определяется шестью переменны-
ми. Тензор напряжений имеет вид матрицы (12.25) и обозначается Гст.
(12.30)
Пусть три перпендикулярные площадки главные. Тогда из системы (12.28) имеем
51
^2 " ^2’
*У3 О3 " tZj.
(12.31)
После преобразований получим:
Уравнение (12.32) есть уравнение трехосного эллипсоида, полуоси которого
представляют собой главные напряжения о2, о3 в данной точке, а координаты то-
чек поверхности — проекции полного напряжения 5 на координатные оси для раз-
личных наклонных площадок (рис. 12.21).
Этот эллипсоид называют эллипсоидом напряжения (эллипсоид Ламе), он как
бы геометрически отражает тензор напряжений.
Если два из трех главных напряжений равны между собой, то этот эллипсоид
превращается в эллипсоид вращения, а если = о2 = о3 — то в шар.
В последнем случае материальная точка находится в условиях всестороннего рас-
тяжения или сжатия (в условиях гидростатического давления). Этот тензор напряже-
ния (шаровой тензор) имеет вид:
т°=\ 0
о
(12.33)
где аср = (О| + о2 + о3)/3.
590
Рис. 12.21. Геометрическая
интерпретация напряженного
Рис. 12.22. К выводу
инвариантных характеристик
напряженного состояния
состояния в точке
Если одно из напряжений равно нулю, то эллипсоид превращается в эллипс. Ес-
ли два напряжения равны нулю — то в прямую линию.
12.4.5. Инвариантные характеристики
напряженного состояния
Анализировать (или сравнивать) напряженное состояние в различных точках де-
формируемого тела по шести компонентам тензора напряжений практически не
представляется возможным. Выясним теперь, можно ли определить некие инвари-
антные (независимые от систем координат) характеристики напряженного состояния
в точке.
Пусть в какой-то наклонной площадке действует только нормальное напряжение
о (рис. 12.22). Определим величину главных напряжений и положение главных плос-
костей по тензору напряжений, данному в произвольных координатных осях.
Из системы (12.28) имеем:
" оау = ту<дх + оЛ + т>,А,
. = да + да +
После преобразований получим:
(ох-о)ах + т^ + тхА = 0,
Хухах + = °,
да + да + (ог-о)аг = 0.
Решение (12.35) через определитель имеет вид:
(12.34)
(12.35)
•О'
(оу - о)
(12.36)
(о. - а)
Раскрывая определитель и проведя преобразования, получим:
а3 - о2(ох + оу + ог) + ода + да + да - т2у - т2г - т2х) -
- (°да + 2VA - охт2г - да2х - crfy) = 0. (12.37)
Уравнение (12.37) имеет три действительные корня о2 и
При выводе уравнения (12.37) оси координат были выбраны произвольно, глав-
ные же напряжения оь о2, °з ПРИ данном напряженном состоянии имеют, как извест-
но, единственные значения. Из этого следует, что коэффициенты уравнения (12.37)
591
(заключенные в скобки) также имеют единственные значения. Они не зависят от то-
го, как были выбраны оси координат, т. е. они инвариантны к преобразованию коор-
динат. А так как эти коэффициенты составлены из компонент тензора напряжений,
то они являются и его инвариантами при преобразовании координат.
Первый инвариант тензора напряжений — линейный:
/1(Та) = ох + су + ог = const. (12.38)
Второй — квадратичный:
/2(ТО) = ахау + - х^у - = const. (12.39)
Третий — кубический:
7з( га) = + 2- °х^г - °у^ - <Vxy = const- (12-4°)
Если ох, оу cz — главные напряжения, то имеем:
Jx(Ta) = Oj 4- о2 4- о3 = const;
J2(Tg) = 0^2 + + аза1 = consti (12.41)
J3(TO) = о1о2аз = const-
Пользуясь инвариантами, можно однозначно сказать, одно напряженное состоя-
ние определяют два тензора при разных системах координат или нет.
Отметим, что инвариантные характеристики напряженного состояния, записан-
ные в виде выражений (12.38)—(12.40), не исчерпывают всех возможных комбинаций
из компонентов напряжений, которые также были бы инвариантны к ортогонально-
му преобразованию координат, однако приведенные следует рассматривать как базис-
ные (основные) характеристики. Компоненты же напряжений, связанные с осями ко-
ординат, следует рассматривать как вспомогательные характеристики напряженного
состояния.
12.4.6. Главные касательные напряжения
Касательные напряжения в наклонных площадках (если тензор дан в главных на-
пряжениях) определяются уравнением:
т2 = af 4- 4- oj а} - (о^? 4- о2а2 + азаз )2- (12.42)
Из (12.42) можно получить максимальную величину касательного напряжения
ттах и величины направляющих косинусов ах, а2, а3. Получим:
ах = а2 = а3 = -!= (угол равен 45°).
л/2
(12.43)
На рис. 12.23 изображены площадки, где действуют ттах. Их обозначают т12, т23,
т31. Индексы в обозначении ттах показывают, какие главные нормальные напряжения
вызывают данное максимальное касательное напряжение.
Величины максимальных касательных напряжений рассчитываются выраже-
ниями:
т12 = ±2(°1 — Т23 = ±2 <ст2 — Т31 = ±| (03-01). (12.44)
Эти касательные напряжения называют также главными касательными напряже-
ниями.
Отметим, что главные касательные напряжения являются инвариантными харак-
теристиками, так как о2, °з ~ инварианты.
592
Рис. 12.23. Площадки действия максимальных касательных напряжений
В общем случае на площадках, где действуют максимальные касательные напря-
жения, действуют и нормальные напряжения, которые рассчитываются соответст-
вующими выражениями:
°12 = 2 (°1 + °2>> °23 = 2 (°2+ °з)> °31 = 2 (°3 + °1)- (12.45)
Важным выводом здесь является то, что из выражений (12.44) видно, что при уве-
личении или уменьшении главных нормальных напряжений на одну и ту же величину
значение ттах не изменяется. Это дает возможность не только математически, но и
физически представить тензор напряжений в виде суммы двух тензоров, так как экс-
периментально установлено, что гидростатическое давление не оказывает влияние на
момент перехода материала из упругого состояния в пластическое.
Таким образом, можно выделить те компоненты напряженного состояния, ко-
торые связаны с изменением объема тела, и те, которые связаны с изменением
формы.
12.4.7. Вывод обобщенных характеристик
напряженного состояния
Представим приведенный выше тензор напряжений (12.30) в виде двух состав-
ляющих (рис. 12.24):
+ (12.46)
где Т® — шаровой тензор напряжений (12.33) — характеризует объемную (только уп-
ругую) деформацию, Da — девиатор (отклонение) напряжений — характеризует изме-
нение формы (упругую и пластическую деформации).
Из (12.46) определим компоненты девиатора напряжений Z)CT:
[ <\ 1 [С ~ Л ^ух ^yz Г ~ 1 0 К м 1° | (°Х ~ ^Ср) ^ху = 1 V (<\-<*ср) 1 Xzx xzy ср 0 0 1 °ср » = ° °ср] С L (12.47) <аг-°ср)|
593
Рис. 12.24. Составляющие тензора напряжений
Нетрудно установить, что девиатор напряжений (12.47) имеет три инвариантные
характеристики:
Л(ПО) = (<\ - °ср) + (ау - °ср) + - °ср) = const = °; (12-48)
/2(Д»> = 5 - °Р2 + (°у - °г)2 + (°г “ °х)2 + 6(тху + Zyz + t2J] = const; (12.49)
J3(D„) = ...= const. (12.50)
Введем с помощью второго инварианта девиатора напряжений две обобщенные
инвариантные характеристики напряженного состояния, связанные с изменением
формы: интенсивность напряжений о, и интенсивность касательных напряжений tz.
oz = J3 • J2(Dg) — интенсивность напряжений; (12.51)
т/= 7*^2<Л?) ~ интенсивность касательных напряжений. (12.52)
Подставим (12.49) в (12.51) и в (12.52), получим:
О,- = 7(°х -°у)2 + <°у ~cz)2 + (°z -°х)2 + 6(тх>. + Zyz + т«) > (12.53)
Т,- = 7(°х -°у)2 + (°У -°г)2 + (°z -°х)2 + 6(тху + + т«) • (12-54)
Отметим, что введение дополнительных инвариантных характеристик девиатора
деформаций в виде (12.51)—(12.54) сделано с целью удобства их использования. Так,
например, при одноосном растяжении образца напряжение вдоль его оси Oj = oz. Для
других схем напряженного состояния эти обобщенные инвариантные характеристики
всегда лежат в пределах:
oz=(l-l/l,155)(omax-omin); (12.55)
т, = (1+1,155)ттах. (12.56)
В выражении (12.55) omax, omin — соответственно максимальное и минимальное
главное нормальное напряжения.
12.4.8. Условия пластичности
Энергетическое условие пластичности (условие пластичности Губера—Мизеса)
формулируется следующим образом.
Любая элементарная частица металлического тела переходит из упругого состоя-
ния в пластическое, когда интенсивность напряжений достигает величины, равной
напряжению текучести при одноосном пластическом напряженном состоянии (при
соответствующих температурно-скоростных условиях деформирования и интенсив-
ности деформации).
Математическая запись этого условия имеет вид
oz = о5.
594
(12.57)
Иначе можно сказать так: при пластическом деформировании интенсивность на-
пряжений oz в любой точке деформируемого тела и при любой схеме нагружения всег-
да равна напряжению текучести gs материала этого тела, определяемого по резуль-
татам механических испытаний образцов на одноосное растяжение в идентичных ус-
ловиях.
Отметим, что в настоящее время энергетическое условие пластичности считается
точным условием пластичности.
Условие (12.57) с учетом (12.53) может быть переписано в виде
= т -°у)2 + (°у -°г)2 + -°х)2 + 6(^ + 'yz + ТхР • (12-58)
В главных напряжениях (12.58) имеет вид
Оу = 7(°1 ~°2)2 + (°2 - Оз)2 + (°3 -°1)2 • (12-59)
Геометрическая интерпретация условия пластичности (12.59) приведена на
рис. 12.25. Это цилиндрическая поверхность неограниченной длины, равнонаклонен-
/2
ная к осям Ср о2 и о3 с радиусом г = JjGs-
Если напряжения о2 и а3’ действующие на элемент тела, таковы, что их ре-
зультирующая находится внутри указанного цилиндра, то этот элемент находится
в упругом состоянии; если напряжения Qj, о2 и о3, действующие на элемент тела, та-
ковы, что их результирующая находится на поверхности цилиндра, то этот элемент
находится в пластическом состоянии. Точки, лежащие вне поверхности цилиндра, не
имеют физического смысла.
Отметим, что если материал упрочняется, то о5 увеличивается по ходу процесса
деформирования и, соответственно, радиус цилиндра увеличивается.
Приближенное условие пластичности (условие
пластичности Треска—Сен-Венана) формулирует-
ся следующим образом: при пластическом дефор-
мировании напряжение текучести равно разности
крайних главных нормальных напряжений, отло-
женных на числовой оси (рис. 12.26).
Математическая запись этого условия имеет
вид
= (°тах ~ °min)- (12-60)
Условие (12.60)— это условие пластичности
по гипотезе максимальных (главных) касательных
напряжений.
Максимальная разница между двумя условия-
ми пластичности (12.59) и (12.60) возникает при
плоском деформированном состоянии и составля-
ет около 15%.
Рис. 12.25. Геометрическая
интерпретация
энергетического условия
пластичности
Условия пластичности для плоского напряжен-
ного состояния. Для плоского напряженного со-
стояния принимают Gy = xxy = xzy = 0. Тогда условие
(12.58) перепишется в виде
—о <-------А-----
--1---1---1----и-
о3----о2 о-----ai
Ое= Jo2 -о о 4- О2 + зт2
Л/ X X Z Z Ха
(12.61)
Рис. 12.26. К записи приближенного
условия пластичности
595
Рис. 12.27. Геометрическая интерпретация
условия пластичности до плоского напряжения состояния
В главных напряжениях (12.61) имеет вид
= -а1 • °з + °з • (12.62)
Геометрическая интерпретация энергетического условия пластичности для пло-
ского напряженного состояния в главных напряжениях (12.62) приведена на
рис. 12.27.
Приближенные условия пластичности для плоского напряженного состояния оп-
ределяются из выражения (12.60). Графически (рис. 12.27) — это вписанный в эллипс
шестиугольник. Отметим, что в шести точках приближенные условия совпадают
с точным (энергетическим) условием.
Аналитическая запись приближенного условия пластичности может быть пред-
ставлена в виде 6 уравнений прямых линий:
±о5 = О] - о3 (при < 0),
±о5 = Oj (при о^з > 0 и |Oj| > |о3|), (12.63)
±о5 = о3 (при 0^3 > 0 и |оj| < |о3|).
Для уменьшения разницы между приближенным и энергетическим условиями
пластичности выражения (12.63) записывают в форме:
±Ро5 = Oj - о3 (при о^з < 0),
±Ро5= Oj (при о^з > 0 и loj > |о3|), (12.64)
±Ро5 = о3 (при о^з > 0 и loj < |о3|),
где Р = 1,01,155 — коэффициент Лодэ, учитывающий влияние среднего по величи-
не главного нормального напряжения.
12.4.9. Уравнения равновесия
В деформируемом теле каждая материальная частица находится в равновесии,
в то время как напряжения непрерывно изменяются от одной точки тела к другой, яв-
ляясь непрерывными функциями координат.
596
Рис. 12.28. К выводу уравнений равновесия
Из условия равенства сил, действующих на материальную частицу в каком-либо
направлении, составляются уравнения равновесия для этой типовой частицы.
Уравнение равновесия для объемного напряженного состояния в прямоугольной систе-
ме координат. Рассмотрим равновесие элементарного параллелепипеда в окрестностях
точки Л (см. рис. 12.19) в произвольной прямоугольной системе координат (рис. 12.28).
Как уже отмечалось ранее, напряжения на видимых и невидимых гранях паралле-
лепипеда близки, но не равны друг другу. Они отличаются на бесконечно малую вели-
чину приращения функции (напряжения) при бесконечно малом приращении аргу-
мента (координаты). Тогда, если размеры параллелепипеда равны dx, dy, dz, то прира-
щения соответствующих напряжений составят величины, приведенные на рис. 12.28.
Усилия, действующие по граням параллелепипеда, определяются умножением
соответствующих напряжений на площади соответствующих площадок.
Взяв суммы проекций всех сил, действующих по осям координат, приравняем
эти силы к нулю. После простых преобразований получим:
+ -ду + = 0 (по направлению х),
Этух
< -д^- 4- -ду 4- -д^- = 0 (по направлению у),
Этгх Этгу
-д^- 4- = 0 (по направлению z).
(12.65)
Приведенные три дифференциальных уравнения равновесия содержат шесть не
известных и составлены из компонент тензора напряжений.
От уравнений, записанных в одной
системе координат, всегда можно перейти
к другой системе координат, так как всегда
можно установить связь между координа-
тами точки в одной и другой системах, од-
нако удобнее пользоваться уравнениями
равновесия, составленными непосредст-
венно в новой системе координат.
Уравнения равновесия для осесиммет-
ричного напряженного состояния в цилиндри-
ческой системе координат. Пользуясь прави-
лами составления уравнений равновесия,
597
описанными выше, можно получить два уравнения равновесия для осесимметрично-
го напряженного состояния в цилиндрической системе координат (рис. 12.29).
Для этой задачи компоненты напряжений в силу осевой симметрии очага дефор-
мации не зависят от координаты 0 и, следовательно, все производные по этой коорди-
нате равны нулю. Кроме того, для большинства задач из-за симметрии внешней на-
грузки касательные напряжения: xQz = = т0р = тр0 = 0.
Окончательно получим:
(12.66)
Из уравнений (12.66) видно, что напряженное состояние в объемных осесиммет-
ричных задачах зависит от двух координат.
Уравнения равновесия для осесимметричных задач листовой штамповки. Эти уравнения
получают аналогичным образом, однако при их выводе используются дополнительные
допущения. Рассматривается равновесие элемента с переменной толщиной стенки, рав-
ной толщине тонкостенной осесимметричной оболочки (рис. 12.30); действие изгибаю-
щих моментов не учитывается; нормальные к поверхности оболочки напряжения счита-
ются неизменными по толщине, малыми по сравнению с двумя другими нормальными
напряжениями и положительными; схема напряженного состояния считается плоской;
касательные напряжения на контактных поверхностях от действия сил контактного тре-
ния приводятся к срединной поверхности и считаются нормальными напряжениями.
Напряженное состояние зависит здесь от одной координаты (текущего радиуса р).
В результате путем проекции сил на касательную и нормаль к поверхности рас-
сматриваемого элемента оболочки получим два уравнения равновесия:
n , pdS ,аеч_п
Р ~7~ + & Л 1 + ) “ <^А-:- ( d- + d“ ) ~ 0,
тХ Sdp' 0 sinav/?m RQ ’
. ^0
К V
(12.67)
В уравнениях (12.67) все напряжения главные: о0, — окружные и мериди-
ональные напряжения; — напряжение по нормали к поверхности; 7?0, Rm — окруж-
ной и меридиональный радиусы оболочки; S— толщина стенки оболочки; ц — коэф-
фициент трения; a — угол между касательной к элементу оболочки и ее осью симмет-
рии; р — текущий радиус (координата).
Рис. 12.30. К выводу уравнений равновесия для осесимметричных задач листовой штамповки
598
Представленные уравнения (12.67) учитывают переменную толщину оболочки,
силы контактного трения, возможное изменение меридионального радиуса и распре-
деление окружных и меридиональных напряжений.
Известны также уравнения равновесия и для ряда других схем деформирования
в операциях объемной и листовой штамповки.
Отметим, что уравнения равновесия не обязательно должны записываться
в дифференциальной форме, однако в последнем случае они носят более универсаль-
ный характер.
12.5. ТЕОРИЯ ДЕФОРМАЦИЙ. МАЛЫЕ ДЕФОРМАЦИИ
Деформация любого элементарного объема тела всегда может быть разложена на
простые составляющие. Так, в случае элементарного параллелепипеда можно говорить о
шести составляющих: о трех линейных деформациях (ребер) и трех угловых (сдвигах в
плоскостях). Положительными линейными деформациями считают удлинения, отрица-
тельными — укорочения. Положительному сдвигу соответствует уменьшение угла между
положительными направлениями осей, отрицательному — увеличение тех же углов.
Обозначение компонентов деформаций приведено на рис. 12.31.
При малых (по сравнению с единицей) углах сдвига объем тела в окрестности
рассматриваемой точки считается неизменным. Объем тела меняется лишь линейны-
ми деформациями.
Таким образом, деформированное состояние в точке может быть описано
шестью переменными: тремя линейными деформациями ех, и тремя угловыми
Уху Yxr lyv причем у^ = у^, ухг = у^, ул = у^
Тензор деформаций имеет вид
Рис. 12.31. Компоненты линейных и угловых деформаций в элементарном объеме
599
Тензор деформаций обладает теми же свойствами, что и тензор напряжений. Он
полностью определяет деформированное состояние в точке, имеет такие же инвари-
анты, как и тензор напряжений, его также можно разложить на шаровой тензор и де-
виатор деформаций.
Заметим, что можно доказать, что между теорией напряжений и теорией дефор-
маций имеется полная аналогия. Так, в окрестностях рассматриваемой точки всегда
могут быть определены такие три взаимно перпендикулярные площадки, где сдвиги
Yxr Yxr YyZ отсутствуют, а возникают только линейные деформации ех, ег, которые
называют главными, как и площадки их действия, и обозначают е2, Ез- Здесь же мо-
гут быть определены площадки, которые расположены под углом 45° к двум главным,
где возникают наибольшие (главные) сдвиги у12, у23, Тзг Главные сдвиги связаны с
главными линейными деформациями зависимостями
Т12 = е! - %’’ Ъ = е2 - ез; Т31 = ез - ei- U2.69)
12.5.1. Компоненты перемещений
и деформаций в элементарном объеме
Если тело деформируется, то каждая его точка смещается от своего первоначаль-
ного положения. Рассмотрим эти перемещения в плоскости хОу.
Пусть исходные координаты точки а будут х, у, z (рис. 12.32). Выделим элемен-
тарный прямоугольник в окрестностях этой точки с размерами dx, dy.
В последующий момент времени точка а сместится в точку а'.
Рассмотрим относительную линейную деформацию ребра ab в направлении ко-
ординаты х. Перемещение точки а равно их. Перемещение точки b равно иЬх. Если рас-
сматривать перемещение их, как функцию по координате х, получим:
Ubx = Ux +
(12.70)
Тогда относительная линейная деформация ребра ab по оси х составит:
Ubx ~“х = Ъих
dx 7)х *
(12.71)
Аналогичным образом можно показать, что по направлениям других осей линей-
ные деформации равны:
ди.
(12.72)
Рис. 12.32. К определению
малых перемещений и деформаций
Определим угловые деформации, т. е.
величину уменьшения прямого угла, рав-
нуюс^ + с^.
Так как изменения углов бесконечно
малые, то tg а = а ; tg а = а .
лу Л/ ул
Определим Получим:
Uby~uy
ахи tg ахи и 4- dx -U
“Ьх х
^УА
~3xdx~uy
^х
ит + -к— dx + dx —и
(12.73)
600
Окончательно I учитывая, что
« 1 имеем:
(12.74)
Аналогично можно получить, что
диг
(12-75)
И, наконец, определим угловую деформацию (относительный сдвиг):
диг
Уху = аху + аух = -57 + -ду • (12.76)
С использованием круговой подстановки индексов можно записать выражения
для угловых деформаций и в других плоскостях.
В итоге имеем следующие 6 дифференциальных зависимостей, связываю-
щих малые перемещения и малые деформации, которые называют уравнениями
Коши:
дих ди duz
^=‘37’e>'='37’ez=’5F’
диу дих
. Ъу= -37 + -37’
_Эиу <12-77>
ди дих
Ь=-Э7 +‘Э7-
К
Подчеркнем, что уравнения (12.77) связывают между собой малые деформации
и малые перемещения, когда малы по сравнению с единицей компоненты тензора де-
формаций, а углами поворота элементов, их квадратами и произведениями можно
пренебречь. Если деформации (или перемещения) большие, их связь типа (12.77) зна-
чительно усложняется.
12.5.2. Вывод обобщенных характеристик
деформированного состояния
По аналогии с теорией напряженного состояния представим тензор деформаций,
состоящим из двух тензоров
Te=Te° + De, (12.78)
где Ге° — шаровой тензор деформаций, De — девиатор деформаций.
Шаровой тензор деформаций имеет вид
Еср о о
7? = |0 еср 0 [, где еср = £jt + ^+£;. (12.79)
О 0 еср .
601
Вычитая шаровой тензор деформаций из тензора деформаций, получим девиатор
деформаций в виде
Ех-Еср 1 2 Yxy 1 2 ^xz
Тух Zy ~ £ср 1 2^ > (12.80)
1 1
— еср
Компоненты шарового тензора деформаций Т® учитывают изменение объема,
компоненты Ле — изменение формы.
Девиатор деформаций Ле имеет три инварианта (отметим, что при разви-
тых пластических деформациях из условия постоянства объема (12.9) следует, что
% = 0):
= (ех - еср) + (еу - Еср) + (ez - Еср) = const = 0, (12.81)
Ji(De) = g К£х - 92 + (еу - е/ + (£г - ех)2 + 2 (У2у + Y2z + Yxz)] = const> (12.82)
J3(Z>E) = ... = const. (12.83)
По аналогии с интенсивностью напряжений введем понятие интенсивности де-
формаций и интенсивности деформаций сдвига %.
2
£,.= -т=7^2(^е) — интенсивность деформаций,
л/ 3
(12.84)
%•= 2л//2(^е) — интенсивность деформаций сдвига. (12.85)
Величины ef и yf считаются всегда положительными.
Подставим (12.82) в (12.84) и (12.85), получим формулы для расчета интенсив-
ности деформаций и интенсивности деформаций сдвига:
£/ = Т ~£У)2 + ~Ег)2 + (£г ~£*)2 + + rfz + > (12-86)
X = Л J(£x -Еу)2 + (Еу -М2 + (£z -£х)2 + ^Хху + Yyz + Ухг) • (12-87)
В главных осях выражение (12.86) перепишется в виде
е,- = 7(£i -е2)2 + (е2 -е3)2 + (е3 -<М2 • (12.88)
Обобщенные инвариантные характеристики £z и у сконструированы таким образом
(см. выражения (12.84) и (12.85)), что при одноосном растяжении £z = £и при чистом
сдвиге yf = утах, причем для любой схемы деформированного состояния эти характерис-
тики лежат в пределах:
е/ = (1+ 1,155)|е|тах, (12.89)
у, = (1^1,155)Мтах, (12.90)
где |е|тах и Ытах — наибольшие по абсолютной величине главная линейная деформа-
ция и главный сдвиг.
602
12.5.3. Скорости перемещений и скорости деформаций
Обозначим скорость перемещения через й, тогда компоненты скоростей переме-
щений можно выразить частными производными функции перемещения по времени:
дих ди duz
Компоненты скоростей деформации, соответственно, будут равны
(12.91)
_ Эйх _ Эех
. _ дйу _ дгу . _ дйх дйу _ духу
е^-'Э7-'Э7; +‘ЭГ --ЭТ;ит-д- (12’92)
_ 3“z —
Для скоростей деформаций сохраняется полная аналогия приведенных выше вы-
ражений и свойств так же, как и для самих деформаций с проставлением над каждым
компонентом деформации точки, что обозначает дифференцирование по времени.
Например, условие постоянства объема запишется в виде
ex+e,+ ez = 0. (12.93)
Выражение для расчета интенсивности скорости деформации:
ё,- = 7(ё| -ё2)2 + (^2 -ё3)2 + (ё3 -ё,)2 и т. д. (12.94)
12.5.4. Условие неразрывности
(совместности) деформаций
Компоненты деформации в уравнениях (12.77) определяются тремя компонента-
ми перемещений, следовательно, они не могут быть произвольными. Между ними
должны существовать определенные зависимости.
Приведем два выражения из уравнений (12.77):
дих ди.
(12.95)
(12.96)
Продифференцируем первое равенство в (12.95) дважды по z, а второе — дважды
по х, сложим почленно и после преобразований получим
Э2ех Э2е Э2у
dz2 Эх2 dxdz '
Выражение (12.96) — это условие неразрывности (совместности) деформаций, из
которого следует, что при двух заданных деформациях третья получит вполне опреде-
ленное значение.
Для осесимметричного напряженно-деформированного состояния условием
совместности линейных деформаций является выражение
Эее _ — Ее
Зр р
При осесимметричном деформировании тонкостенных оболочек условие сов-
местности линейных деформаций записывается в виде
de0 = 1 -Jexp(ee)/exp(e/7J)
dp р
где А = sin (a0)/sin (a) — отношение синусов угла между касательной к элементу обо-
лочки и ее осью симметрии до и после деформирования.
603
(12.97)
(12.98)
12.6. ФИЗИЧЕСКИЕ УРАВНЕНИЯ ТЕОРИИ ПЛАСТИЧНОСТИ
12.6.1. Механическая схема деформации
При обработке металлов давлением в общем случае различают три схемы деформи-
рованного состояния (рис. 12.33) и девять схем напряженного состояния (рис. 12.34), ко-
торые совместно характеризуют напряженно-деформированное состояние в точке.
Но не все схемы деформированного и напряженного состояний сочетаются друг
с другом. Любая из двухосных и трехосных схем напряженного состояния может соче-
таться с любой из трех схем деформированного состояния. То есть конкретному на-
пряженно-деформированному состоянию в точке соответствует одна из схем дефор-
мированного состояния и одна из схем напряженного состояния. В итоге имеем 21
возможных сочетания или схем напряженно-деформированного состояния. Схемы
одноосного напряженного состояния сочетаются только с соответствующими схема-
ми деформированного состояния. Таким образом, в общем случае имеем: 21 + 2 = 23
схемы напряженно-деформированного состояния, которые могут быть реализованы в
процессах пластического деформирования.
12.6.2. Связь между напряжениями и деформациями
Основная предпосылка (гипотеза) теории пластичности (если деформирование осу-
ществляется в условиях «простого» нагружения) формулируется следующим образом.
При сложном напряженном состоянии связь между интенсивностью напряжений
о, и интенсивностью деформаций ez принимается такой же, как связь между напряжени-
ем и деформацией при механических испытаниях образцов на одноосное растяжение.
Математическая запись этого условия при активном нагружении (когда интенсив-
ность напряжений о, постоянно возрастает) имеет вид:
0/ = ^ (12.99)
где Е' — модуль пластичности, определяемый из диаграммы механических испыта-
ний образца (см., например, рис. 12.13).
Одноосное напряженное состояние:
Сдвиг
(плоская деформация)
Рис. 12.33. Схемы
Двухосное (плоское) напряженное состояние:
Трехосное (объемное) напряженное состояние:
Рис. 12.34. Схемы
напряженного состояния
деформированного состояния
604
Модуль пластичности Е' отличается от модуля
упругости Е тем, что Е' является переменной величи-
ной (рис. 12.35).
Например, если после механических испытаний
образца связь между напряжениями и деформациями
может быть аппроксимирована функцией типа (12.13):
о5 = Ле?, то модуль пластичности Е' равен Ле? ~ L
Из условия (12.99) можно получить уравнения
связи между напряжениями и деформациями в раз-
личных формах записи:
еГ
и
6“
Кривая упрочнения
E;
Рис. 12.35. К понятию
о модуле упругости Е
(модуле Юнга)
и модуле пластичности Е1
tga = Е- const
az tgaz = F * const
О2 ——Oj 2 • Q
Е2 —е3 е3 —^1 3 ‘ £
£| = з-[ст1_2(ст2 + аз)];
е2=5-[е2-2<стз + °1)];
ез=5’[Оз-2(о2 + о1)];
2о(
СТ1 -стср_
_ 2о<
°2 “ °ср ~ Зё^ е2’
2a,
°з - °ср - ез-
(12.100)
(12.101)
(12.102)
Уравнения (12.101) и (12.102) действительны и в том случае, если главные напря-
жения и деформации заменить напряжениями и деформациями в произвольной сис-
теме координат х, у9 z, но тогда необходимо добавить еще три уравнения, связываю-
щие касательные напряжения и сдвиги:
Тху 3с,- Xyz 3ez 3ez (12.103)
Физический смысл условий (12.102) и (12.103) можно истолковать так: для каж-
дой точки деформируемого тела компоненты напряжений (по различным площад-
кам) являются линейными функциями соответствующих компонентов деформаций.
Для осесимметричных задач листовой штамповки уравнения связи между напря-
жениями и деформациями значительно упрощаются:
или
ае = +
^0
5 = 1+<У<*е
бе -2 + °m/°e '
(12.104)
(12.105)
Отметим, что в скоростях деформаций уравнения связи между напряжениями
и скоростями деформаций записываются аналогичным образом, например:
Q] —О2 _ а2 —a3 _ а3 — а1
£1 -Ё2 £2 -Ез Ёз -£1
(12.106)
605
или
= % [°' - 2 (°2 + <ъ>];
ё2= 5- [°2 - 2 <стз+ ст1)] > (12-107)
ё/ г 1 / । J
ез = Ч |°3 " 2 (°2 + СТ1)] •
При разгрузке тела, когда интенсивность напряжений о, начинает убывать,
А. А. Ильюшиным доказана следующая теорема: перемещения точки тела в некоторый
момент разгрузки отличаются от их значений на момент начала разгрузки на величины
упругих перемещений, которые бы возникли в теле, если бы к недеформированному
телу были приложены внешние силы, равные разностям внешних сил, действующих на
тело в указанные моменты. То же относится к деформациям и напряжениям.
12.6.3. Контактное трение
при пластическом деформировании
Подавляющее число операций обработки металлов давлением осуществляется
в условиях соприкосновения обрабатываемого металла с деформирующим инстру-
ментом. При этом частицы металла скользят по поверхности инструмента, в результа-
те чего возникают силы контактного трения, затрудняющие это скольжение.
Трение при обработке металлов давлением, за исключением отдельных опера-
ций, когда оно играет активную роль, является вредным фактором.
1. Оно ведет к возникновению неоднородности деформации и увеличивает эту
неоднородность.
2. Изменяет схему напряженного состояния материала в зонах контакта.
3. Увеличивает деформирующее усилие, работу и мощность в системе инстру-
мент-заготовка.
4. Снижает стойкость инструмента.
5. Требует применения (нанесения и удаления) смазок.
Трение при пластическом деформировании отличается от «непластического»
трения в «машинных парах», главным образом тем, что площадь контакта здесь при-
ближается к фактической площади соприкасаемых поверхностей.
В расчетах процессов штамповки используют два различных закона контактного
трения в зависимости от величины нормального контактного давления и температур-
ных условий деформирования.
В условиях «холодной» штамповки при небольших контактных давлениях, когда
нормальные контактные напряжения много меньше напряжения текучести матери-
ала (ол « <т5), используется закон Амонтона—Кулона:
тк = ро„, (12.108)
где тк — касательные напряжения от действия сил контактного трения, ц — коэффи-
циент трения.
При больших контактных давлениях в условиях «горячей» штамповки, когда
нормальные контактные напряжения соизмеримы с напряжениями текучести мате-
риала, используется закон Зибеля:
тк = ц5ро5, (12.109)
где — фактор трения, Р = 1,155 — коэффициент Лодэ, as — напряжение текучести.
606
В выражениях (12.108) и (12.109) наибольшее значение касательного напряжения
рОу
тк не должно превышать его максимальной величины, равной —. Из этого следует,
чтоц5< 0,5.
12.7. МЕТОДЫ РЕШЕНИЯ ЗАДАЧ
ПЛАСТИЧЕСКОГО ДЕФОРМИРОВАНИЯ
12.7.1. Общие положения
Для решения задач пластического деформирования математическую модель
в общем случае можно представить совокупностью трех уравнений равновесия
(12.65), шести уравнений Коши (12.77), шести физических уравнений (12.102),
(12.103), двух выражений для расчета интенсивностей напряжений и деформаций
(12.53), (12.86) и экспериментальных зависимостей типа (12.13). В эти 18 уравнений
входит 18 неизвестных.
Решением задачи пластического деформирования, следовательно, является такое
решение, которое для каждой точки деформируемого тела будет удовлетворять 18 ука-
занным выше уравнениям, а также учитывать условия на границе тела.
Для частных задач (плоское напряженное состояние, плоское деформированное
состояние и др.) количество исходных уравнений может быть сокращено, однако
с практической точки зрения прямое аналитическое решение указанных уравнений
почти всегда невозможно из-за большого числа этих уравнений в частных производ-
ных и нелинейности самих уравнений.
Непреодолимые трудности в реализации точного решения задач пластического
деформирования исторически привели к тому, что исследователи ограничивались оп-
ределенным кругом решаемых задач, вводя упрощающие предпосылки. Вследствие
этого возникли и достигли определенного этапа в своем развитии различные методы
решения задач. Все они с математической точки зрения (если речь не идет о простей-
шей схематизации сложного процесса) относятся к приближенным методам, но сле-
дует отличать методы, предполагающие совместное решение всей исходной системы
уравнений, и методы, где изначально предполагается использование только части
этих уравнений. С практической точки зрения первые можно было бы назвать точны-
ми, а вторые — приближенными.
К основным методам, которые нашли наибольшее применение, можно отнести
инженерный метод, метод баланса работ и его варианты, метод линий скольжения,
методы численного решения исходной системы уравнений.
Термины и определения.
1. Очаг деформации — часть заготовки, где развиваются пластические дефор-
мации.
2. Зона передачи усилия — часть заготовки, служащая для передачи деформирую-
щего усилия в очаг деформации и находящаяся в упругом состоянии.
3. Стационарный очаг деформации — очаг деформации, размеры которого не из-
меняются по ходу процесса (по времени).
4. Нестационарный очаг деформации — очаг деформации, размеры которого из-
меняются (увеличиваются или уменьшаются) по ходу процесса (по времени).
5. Установившееся течение — процесс деформирования со стационарным харак-
тером напряженно-деформированного состояния заготовки в очаге деформации, при
котором поля напряжений и деформаций не зависят от времени.
607
6. Монотонный процесс деформации (или простое нагружение) — процесс де-
формации, в котором для каждого элемента заготовки реализуется условие постоян-
ства соотношения главных деформаций (или напряжений) по ходу процесса.
7. Осесимметричный процесс деформирования — процесс деформирования, осу-
ществляемый в условиях осевой симметрии очага деформации, при котором напря-
женно-деформированное состояние в общем случае зависит от двух переменных: ко-
ординаты (радиуса) и времени.
12.7.2. Инженерный метод решения задач
Инженерный метод решения задач нашел большое распространение для реше-
ния самых разнообразных задач пластического деформирования. Это один из первых
теоретических методов расчета напряженно-деформированного состояния, который
получил свое развитие в начале 1900-х годов в работах немецкого ученого Т. Кармана.
Применительно к операциям листовой штамповки этот метод наиболее полно изло-
жен в работах Е. А. Попова, М. Н. Горбунова и др.
Для решения осесимметричных задач листовой штамповки имеем следующую
систему исходных уравнений (табл. 12.2).
Таблица 12.2
Основные исходные уравнения для осесимметричных задач листовой штамповки
Неизвестные Исходные уравнения
Уравнения равновесия: 1 dQfn Л । pdS А ИР (®т . ае А п 1- р-з— + aJ 1 + т-i- п“ + п- = 0 н rfp 5dp J 0 sina Re) ~ . ^0 ~S ~ R~m Rq
3. Условие пластичности: = a,
<5m 2sm + £0 4. Уравнение связи напряжений и деформаций: — = ~—т— ое z£e-i- ет
5. Условие постоянства объема: £да + £0 + £л = 0
ez 6. Уравнение состояния материала: о5 = Ле? (или о5 = ото + Пе/9 или иная аппроксимация)
7. Выражение для расчета интенсивности деформаций: е, = Т л/(£0 -£m)2 + <ет -е»)2 + -£е)2
8. Выражение для расчета интенсивности напряжений: <*,= -°mae + °0
9. Выражение для расчета окружных деформаций: е0 = 1п[ — ]
10. Выражение для расчета деформации по толщине: £л = In J
608
В итоге имеем 10 уравнений и 10 неизвестных, при этом считаем известными:
текущий радиус р; геометрические параметры заготовки So, р0, ос0; форму получае-
мой детали (которая определяется жестким инструментом) Rm, RQ, а; свойства мате-
риала: Л, л; коэффициент трения ц.
Концепция инженерного метода состоит в том, что поле напряжений в заготовке
должно удовлетворять уравнению равновесия, условию пластичности и граничным
условиям. При этом кинематические условия (деформации) не учитываются или учи-
тываются приближенно.
Решение состоит из двух этапов. На первом рассчитываются приближенные поля
напряжений путем совместного решения только двух уравнений из десяти: первого
уравнения равновесия (12.67) и условия пластичности (12.62) (заметим, что и они
обычно предварительно упрощаются). На втором определяются приближенные поля
деформаций по рассчитанным полям напряжений с использованием уравнения связи
между напряжениями и деформациями (12.105).
Метод позволяет рассчитать напряженно-деформированное состояние заготовки
в аналитической форме.
Приведенное решение можно уточнить, повторив расчет с учетом рассчитанных
полей деформаций, однако это, как правило, не делается из-за чрезмерного усложне-
ния расчетных зависимостей.
Из-за того, что в инженерном методе решения не учитываются полностью кине-
матические условия задачи, считается, что он дает заниженную оценку мощности
в системе инструмент—заготовка.
Важно отметить то обстоятельство, что этот метод применим для расчета моно-
тонных или приближенно монотонных процессов с явно выраженными граничными
условиями. Если процесс немонотонный, то при больших (конечных) деформациях
не существует однозначной связи между напряжениями и деформациями в виде при-
веденных выше выражений (12.105) и др.
Для расчета немонотонного процесса деформирования его следует разбивать на
небольшие (по времени) расчетные этапы, где на каждом этапе можно было бы счи-
тать процесс монотонным или приближенно моно-
тонным. Таким же образом можно учитывать неста-
ционарные факторы, сопутствующие процессу де-
формирования.
Пример.
Расчет напряженно-деформированного состояния
и деформирующего усилия Р при раздаче концевого
участка трубы (рис. 12.36).
Основные допущения:
— напряженное состояние плоское, ~ 0;
— контактное трение не учитывается (ц = 0);
— процесс считаем монотонным или прибли-
женно монотонным.
Уравнение равновесия (12.67) без учета сил тре-
ния и изменения толщины стенки 5 будет иметь вид:
do_
Р^+о'п-°е = 0- <12Л1°)
Приближенное условие пластичности (12.63)
запишется в виде
(12.111)
Рис. 12.36. Схема раздачи
цилиндрической трубы
с постоянной толщиной стенки
на коническом пуансоне
609
Совместное решение уравнений (12.110) и (12.111) имеет вид: p-j^- = Раз-
деляя переменные и интегрируя при граничных условиях на кромке заготовки, по-
лучим:
&т р
J dom = J o5dp/p. (12.112)
0 ^max
Окончательно имеем распределение меридиональных напряжений в виде выра-
жения
Gm=GfPlnLP-Y (12.113)
V'max /
где = const — средняя величина напряжения текучести (как средняя подынтег-
ральная величина).
Распределение окружных напряжений получим совместным решением (12.111)
и (12.113). Имеем:
°0= °5Р(1-|п^) (12.114)
Таким образом, поля напряжений определены.
Из уравнения связи напряжений и деформаций (12.105) имеем:
(12.115)
Из уравнения (12.115) получим распределение толщины стенки по текущему ра-
диусу:
+ °е
или
I -2lnS?
Р
--------D-
. х Э 4- In ПШ
Необходимое для деформирования усилие Р определится выражением (без учета
изгиба заготовки):
Р= 2яЯ05'0|о“ах|, (12.118)
гдео^ = о§Р 1п^).
V max /
Аналогичным образом решены многие осесимметричные задачи листовой штам-
повки: вытяжка цилиндрических стаканчиков из листовой заготовки, гибка широкого
листа, обжим труб, отбортовка листовых заготовок и ряд других.
12.7.3. Метод баланса работ
Метод баланса работ, как и другие энергетические методы, основан на законе
сохранения энергии. Он использовался для решения различных задач пластического
деформирования многими исследователями: Э. Зибелем (1930), И. Л. Перлиным
(1958) и др.
610
Исходным положением метода баланса работ является следующее: при пластиче-
ском деформировании работа внешних сил на соответствующих им перемещениях
равна работе внутренних сил (или работе деформации):
Ан=А> (12.119)
где Лвн — работа внешних сил, Лд — работа деформации.
С учетом работы сил трения выражение (12.119) может быть уточнено:
^„=4 + ^. (12.120)
Работа внешних (поверхностных) сил, в общем случае, определяется выраже-
нием:
Ан = И + Ч + ZuJ dF> (12.121)
F
где X,Y,Z— проекции сил, действующих на площадку 6F поверхности тела по соот-
ветствующим осям координат х, у, z', их, и? uz — соответствующие им перемещения
в направлении этих осей.
Работа деформации равна:
Лд = ШаЛ<1К=ШО5е,.<1К (12.122)
V V
где d V— элементарный объем.
Работа сил трения определяется выражением:
Ар J J \WK
Fk
(12.123)
где тк — касательные напряжения от действия сил контактного трения, мк — переме-
щение на контактной поверхности.
Метод баланса работ, таким образом, дает, по крайней мере, еще одно условие
(уравнение) в систему исходных уравнений (табл. 12.2) с одним или несколькими не-
известными.
Отметим, что если в приведенных выше уравнениях (12.119)—(12.123) дефор-
мации и перемещения заменить на скорости деформаций и скорости перемещений,
то вместо работ А получим соответствующие мощнос-
ти W.
Пример.
Расчет деформирующего усилия Р при осадке прут-
ка (рис. 12.37).
Пусть высота заготовки h уменьшится на весьма
малую величину ДА, тогда работа внешней силы Р со-
ставит по выражению (12.121) величину
Ан = ^« (12.124)
Работа деформации (внутренних сил) в соответст-
вии с выражением (12.122) будет равна:
A = as JJJe,p dpdOdz.
V
Рис. 12.37. Схема осадки
(12.125) прутка между шероховатыми
плитами штампа
611
Работа сил трения (на двух торцах заготовки, контактирующих с плитами штам-
па) определится выражением (12.123):
d
2п2
A„ = 2tk JJi/ppdpdO. (12.126)
О о
В уравнениях (12.125), (12.126) неизвестны интенсивность деформации £z и пере-
мещения на контактных поверхностях мр.
Допустим, что интенсивность деформаций £z в каждой точке тела одинакова, т. е.
заготовка остается цилиндрической, тогда
е, = -ег=^. (12.127)
Для определения ир воспользуемся условием постоянства объема (12.9) и уравне-
ниями Коши (12.77). Имеем: £р + £е + £г = 0. Подставим в это условие деформации,
определяемые по (12.77) и (12.127). Получим:
ТГ£+--^=0- (12.128)
Эр р h v 7
Решение (12.128) имеет вид:
«Р=2^р. (12.129)
Т _ Э“р _ 1 АЛ _ “р _ 1 АЙ
Тогдаер- 2 т,ее- - - 2 -у-
Работа деформации будет равна:
d
52лА
А = о4гШрФ<10^=^Чал. (12.130)
ООО
Работа сил контактного трения составит:
d
2л 2
. ~ г г 1 ДА , ,Л лё2 ДА • d /i/ч
Ap = 2\J J 2TPPdPde=TMT’ (12.131)
о о
Подставим (12.130) и (12.131) в (12.120). Окончательно получим:
',= т(°. + з’4) <12132>
Из последнего выражения видно влияние сил контактного трения (и геометриче-
ских размеров заготовки) на величину деформирующего усилия.
Дальнейшим развитием метода баланса работ можно считать использование экс-
тремальных принципов для решения задач пластического деформирования, в том
числе таких энергетических принципов, как возможных перемещений, возможных
изменений напряжений, возможных изменений деформированного состояния.
Использование указанных принципов требует, обычно, применение вариацион-
ных методов расчета, разработанных в трудах Г. Генки, Р. Хилла, И. Я. Тарновского,
В. JI. Колмогорова, В. И. Ершова и др.
612
12.7.4. Метод линий скольжения
Основоположником метода считается немецкий ученый Л. Прандтль. Его разви-
тие связано с работами Г. Генки, Р. Хилла, А. А. Ильюшина, В. В. Соколовского и др.
Метод применим к анализу плоского деформированного состояния.
Суть метода заключается в построении сетки (поля) линий скольжения и в ис-
пользовании их свойств.
Пусть известна траектория действия главных касательных напряжений в плос-
кости xz тела, находящегося в плоском деформированном состоянии, в точке ах
(рис. 12.38). Получим два направления действия. Перейдем от точки ах к точке а2
и т. д. При неограниченном увеличении числа точек а получим семейства кривых а и
Р, определяющие собой траектории действия главных касательных напряжений или
линии скольжения (рис. 12.39).
Касательные к линиям скольжения совпадают с направлениями главных каса-
тельных напряжений и пересекают оси х, z под какими-то углами сц со' (рис. 12.40).
По сетке линий скольжения можно построить сетку траекторий главных напря-
жений. Эти линии пересекают линии скольжения под углом .
Из рис. 12.40 видно, что
= tg со (для линии а),
Х (12.134)
= —ctg со' (для ЛИНИИ Р).
Уравнения (12.133)— дифференциальные уравнения линий скольжения, где
, я
СО = ф + л •
* 4
При плоском деформированном состоянии компоненты напряжений могут быть
записаны в зависимости функции угла ср в виде
>=ос +t3i cos 2ф,
/т I J1 1
(12.134)
Txz= T3i 8*п 2<p,
где аср = (<\ + ог)/2; т31 = к = as = 0,575Оу
— пластическая постоянная.
линий скольжения
Рис. 12.39. Семейства
линий скольжения
613
Рис. 12.40. Касательные
к линиям скольжения
Рис. 12.41. Переход
к криволинейным координатам
Заменим < р на со. Имеем: > = ± к sin 2со, (12.135) txz = —к cos 2со.
Эти выра> Подстави] Кения тождественно удовлетворяют условию пластичности, и напряжения из уравнений (12.135) в уравнение равновесия: ЭтХ7 * 4- =0, Z (12.136) « + г = о. дх dz
Получим: 4- 2к fcos 2со^ 4- sin 2со^ 1 = 0, 1 ) (12.137) - 2к (cos 2со|^ - sin 2со|^ = 0.
Перейдем ной сетки при] Здесь к криволинейной системе координат аир, где в качестве координат- мем сетку линий скольжения (рис. 12.41). dx = da; dz = dp; = X ; Л = X ; S ” (12.138 Л dco d(O co = 0, однако * 0, * 0.
Получим: (ocp + 2tao) = 0; (ocp -2tao) = 0. (12.139)
Последни Интегрир e выражения действительны для любой точки, уя (первое по а, второе по р), получим: а) осп4-2£со = с1, б)аср-2^ = С'
Заменим (где!!=0)’ в (а) произвольную постоянную q на произвольную функцию от Р а в (б) — с2 на функцию от а (где = 0 j.
614
Имеем:
Gcp + 2Ахо = 2Лтг|(Р) (по линии а),
аср - 2£со = 2^(а) (по линии Р). (12.141)
Уравнения (12.141) носят название интегралов Г. Генки.
Произвольные функции 2Лт|(р) и 2А:£(а) имеют постоянные значения при пере-
мещении вдоль линии скольжения и изменяются при переходе от одной линии сколь-
жения к другой. Если бы поля линий скольжения были известны, то интегралы
Г. Генки (12.141) представляли бы общее решение задачи плоского деформированно-
го состояния.
Пусть в какой-то точке М данной линии скольжения напряжение оср = пср м и
со = со^, а в другой точке N на той же линии пср = пср N и со = coN, тогда, подставив это
в первое уравнение (12.141), получим:
аСРМ+2Л®М=2ШВ₽))|’ = (12.142)
°ср N Z/UKP/ j
второе уравнение (12.141) дает:
Ocpw-^w^cpjv-2^- (12.143)
Объединяя эти уравнения, получим:
OcpW-CTcpN=±2^(“4/-“^- (12.144)
Из уравнения (12.144) следует, что изменение среднего напряжения пср при движе-
нии вдоль линии скольжения пропорционально углу поворота линии скольжения со.
Таким образом, если известно поле линий скольжения и пср в узловой точке, то
можно установить пср по всему полю. Далее можно определить ох, rxz по всему по-
лю, используя (12.135).
Свойства линий скольжения.
1. Линии скольжения непрерывны.
2. Линии скольжения образуют два семейства.
3. Семейства линий скольжения взаимно ортогональны.
4. Линии скольжения пересекают траектории главных напряжений под углом .
5. Изменение среднего нормального напряжения при движении вдоль линий
скольжения пропорционально углу ее поворота.
6. Угол между касательными к двум линиям скольжения одного семейства в точках
пересечения их линиями другого семейства остается постоянным (первая теория Генки).
7. Радиусы кривизны линий скольжения изменяются на величину расстояний,
пройденных по линиям скольжения другого семейства (вторая теория Генки).
8. Углы наклона линий скольжения при выходе на контур (поверхность) зависят
от величины касательного напряжения на контуре:
— если трение отсутствует (тк = 0), то ©j 2 = ±45°;
— если трение максимально (тк = к), то = 0, со2 = 90°.
Решение задач методом линий скольжения заключается в построении сетки (по-
лей) линий скольжения, пользуясь их свойствами. Для построения полей линий
скольжения можно применять аналитическое интегрирование уравнений для пло-
ской деформации или строить линии скольжения графическими методами. Затем из
граничных условий (обычно на контуре) определяются средние нормальные напря-
жения и их распределение по всему полю. В расчетах используются уравнения, опи-
сывающие траектории линий скольжения и условия пластичности.
615
Отметим, что решение какой-либо задачи, полученное методом линий скольже-
ния, не является единственным, возможны другие решения, справедливые для задан-
ных граничных условий. Это требует определенного опыта и интуиции исследовате-
ля, как, впрочем, и при использовании любого другого метода решения.
Пример.
Расчет напряженно-деформированного состояния при вытяжке листовой заготовки
(рис. 12.42).
При вытяжке цилиндрических стаканчиков из листовой заготовки очаг
деформации — фланец заготовки, который затягивается в полость матрицы и из него
получается стенка стаканчика. Стенка получаемого стаканчика находится в упругом
состоянии и является зоной передачи деформирующего усилия.
Фланец листовой заготовки деформируется в условиях, близких к плоской дефор-
мации (в условиях сдвига), его толщина незначительно увеличивается к периферии.
Таким образом, легко установить траектории действия главных нормальных на-
пряжений: в меридиональном направлении (по радиусу р) действуют растягивающие
меридиональные напряжения аш, по окружностям — окружные сжимающие напря-
жения ое. Пользуясь свойством линий скольжения, можно легко установить их траек-
тории. Они будут пересекать траектории действия главных нормальных напряжений
под углом 45°.
Из теории кривых известно, что такие кривые, которые пересекают все лучи, выхо-
дящие из одной точки под одним и тем же углом у, — есть логарифмическая спираль.
Уравнение логарифмической спирали имеет вид:
р = г ехр (0 ctgy). (12.145)
В нашем случае у = 45°, 0 = Gab = cofld.
Тогда из (12.145) получим: = cofl - cnb = In (R/r).
На основании уравнения (12.144) можно записать:
OcPa-OcPi = 2*-ln(A/r).' (12.146)
Определим среднее напряжение в точке b с использованием граничного условия:
<зтЬ = 0 и приближенного условия пластичности: = —2к. Имеем:
оср4 = «^ + а№)/2 = -Л. (12.147)
Рис. 12.42. Фланец заготовки при вытяжке
616
Определим среднее напряжение в точке а из (12.146), получим:
осро = 2£-1п(Я/г)--£. (12.148)
С другой стороны, среднее напряжение в точке а по определению равно:
+ (12.149)
Совместное решение (12.148) и (12.149) с условием пластичности <5та — = 2к
приводится к виду:
= 2к [In (R/r) - 1]. (12.150)
При этом меридиональные напряжения в точке а равны
ста = 2к In (R/r) = 1,155<j5 In (R/r). (12.151)
Решение этой же задачи инженерным методом дало бы ответ:
cma=cf\n(R/r). (12.152)
Отметим, что близкие к выражениям (12.151) и (12.152) решения можно полу-
чить, решая эту же задачу методом баланса работ.
12.7.5. Методы численного решения
исходной системы уравнений
Если рассмотренные выше методы решения задач пластического деформирова-
ния являются, в общем случае, приближенными, так как изначально оперируют не
всей системой исходных уравнений, то методы численного решения всей системы ис-
ходных уравнений можно считать точными. Математическая неточность последних
может быть вызвана только особенностями самих численных методов, однако эта
ошибка численного расчета может быть сведена к сколь угодно малой величине.
К этим методам может быть отнесено несколько известных методов расчета: ме-
тод конечных элементов, некоторые вариационные методы и ряд других.
Здесь подробно рассматривается метод численного решения осесимметричных
задач, связанных с деформированием тонкостенных заготовок.
Концепция численного метода решения осесимметричных задач состоит в том,
что вначале осуществляется совместное решение всей системы исходных уравнений
с получением общего дифференциального уравнения, которое может быть решено
относительно получаемой детали (прямая задача), относительно заготовки или режи-
мов ведения процесса (обратные задачи). Графическая интерпретация решения пря-
мой и обратных задач дана на рис. 12.43—12.45.
Рис. 12.43. Геометрическая интерпретация прямой задачи: расчет получаемой детали
617
Рис. 12.44. Геометрическая интерпретация первой обратной задачи:
расчет режимов ведения процесса
Метод позволяет получать точные решения по расчету напряженно-деформиро-
ванного состояния детали (или заготовки) произвольной формы в условиях сложного
температурного, силового или скоростного воздействий на заготовку.
Прямая задача листовой штамповки. Решение исходной системы уравнений без
учета уравнения 6 (см. табл. 12.2) относительно распределения толщины стенки полу-
чаемой детали имеет вид:
где
2Е , F рр (Ст <*е А
d5 = -^Р^-Sp + Ъ -ВРОе(20е ~<>т) + + лв J
dp р С
С= Зе» •
5(ее -е„)2 ’
P = 2o0-om + E(2om-oe);
г~ —Е0 ,
,
ев —
/3 з dp з d5c\
(р6” pc£”dp s/edpj
(Ее ~ел)2
— I — I
°е _ ±Л/Е2 + 1 —Е’ °т " + 1 -Е'
Рис. 12.45. Геометрическая интерпретация второй обратной задачи: расчет заготовки
618
Уравнение (12.153) справедливо для любой схемы плоского напряженного со-
Л « dPc d5c
стояния при * 0. В этом уравнении величины определяются из усло-
вия равенства элементарных объемов заготовки и детали в очаге деформации
(см. рис. 12.43):
dpc = Sp sinac d5c_ dpc d5c
dp 5cpc since ’ dp dp dpc ’
(12.154)
d-Se
здесь величина определяется геометрией заготовки.
Отметим, что в уравнениях (12.153) и (12.154) и далее по тексту переменные
с нижним индексом «с» относятся к предыдущей форме детали.
В уравнении (12.153) величина напряжения текучести материала должна быть за-
дана как исходная или определяться известной из эксперимента зависимостью. Если
упрочнение материала аппроксимируется степенной функцией типа (12.13), то после
doj.
определения производной подставим ее выражение в (12.153). После преобразо-
ваний окончательно получим расчетное дифференциальное уравнение для решения
прямой задачи:
4Е F
dp “
ИР
sinaUm
p C . 4£ п /2ея + евч
-pP<W2°e -с») + 3pP®H«e? Д—5— J
—, (12.155)
me os = A ef; г-, = + eee„ + eg;
1 1 dpr 1 dV.
L = (2eft + £„)(- - - -p) - -t-c (2e_ + efl).
\ pc dp* 1 * * * * * 7 В Sc dp v n
Из (12.155) следует, что толщина стенки S получаемой детали полностью оп-
ределяется геометрическими параметрами об
олочки-заготовки: Sc, рс, ас; механическими свойствами материала: а5; формой
получаемой детали: Rm, R$, а; условиями контактного трения: ц; и текущим радиусом
оболочки-детали р.
Таким образом, по выражению (12.155) можно рассчитать напряженно-дефор-
мированное состояние заготовок, форма которых в любой момент времени определя-
ется геометрией жесткого инструмента.
В общем случае уравнение (12.155) можно решить, используя численные методы
интегрирования. Наиболее простым и удобным из них является метод Эйлера, соглас-
но которому уравнение (12.155) решают в последовательности
~ Рг) dPl’
$2 = ^1 Pl) dP2’
Sn = Sn-i V(^_i,P„_i)dpn, (12.156)
где S(— толщина стенки /-го элемента оболочки; рг— начальные (граничные)
условия — соответственно толщина стенки и радиус граничного элемента; dpz — шаг
интегрирования.
По рассчитанному распределению толщины стенки получаемой детали одновре-
менно определяются деформации ея, ее, еш и напряжения ое, ош, оя.
619
Граничные условия 5Г и рг задают в той части заготовки, где из условия формоиз-
менения известна величина меридиональных напряжений <зт[:
1 Ф зм
5’г = 5с^У±274-зл/2, (12.157)
где М = emr/es— относительная величина меридиональных напряжений на гранич-
ном элементе.
Если граничные условия не известны, то их можно определить последовательно,
приближая первоначально заданные условия к фактическим, при которых обычно вы-
полняется ряд дополнительных условий: равенство объемов материала заготовки и детали
в очаге деформации; заданное перемещение материала заготовки в очаге деформации и
другие условия, имеющие место в каждом конкретном процессе листовой штамповки.
Уравнение (12.155) в последовательности (12.156) можно решить двумя различ-
ными способами в зависимости от величины промежутка времени Дт. Если Дт соот-
ветствует полному времени формоизменения заготовки, то, решая уравнение
(12.155), определяют толщину стенки получаемой детали, деформации и напряжения.
Это решение соответствует деформационной теории пластичности. Оно не учитывает
нестационарность и немонотонность процесса формоизменения и осуществляется
при некоторых осредненных (независимых от времени) режимах процесса.
Если промежуток времени Дт достаточно мал (для того, чтобы считать процесс
деформирования заготовки на этом участке монотонным и стационарным), то, решая
уравнение (12.155), определяют напряженно-деформированное состояние промежу-
точной детали, которая является заготовкой для расчета последующей формы, и т. д.
Это решение будет соответствовать теории течения, так как логарифмические дефор-
мации при этом расчете станут по существу скоростями деформации. Здесь уравнение
(12.155) решают в последовательности (12.156) несколько раз в зависимости от степе-
ни дробления процесса формоизменения на этапы.
Графическая интерпретация этих двух способов решения приведена на
рис. 12.46. Первый способ можно использовать при моделировании приближенно мо-
Рис. 12.46. Графическая интерпретация способов расчета:
а) по методу конечного формоизменения
(по деформационной теории); б) по теории течения
620
нотонных процессов, второй— предназначен для моделирования немонотонных
процессов с нестационарным воздействием на заготовку.
Обратные задачи листовой штамповки. Для решения первой обратной задачи, свя-
занной с расчетом режимов ведения процесса, должны быть известны геометрические
параметры заготовки и получаемой детали, т. е. 5С = 5с(рс) и 5 = 5(рс), где 5С, S — со-
ответственно толщина стенки заготовки и получаемой детали; рс, р — соответствую-
щие текущие радиусы.
Решим уравнение (12.153) относительно искомого параметра — распределения
напряжения текучести, получим:
doe -d^04-Z)P0®<20® + °® -Р°еВрае(2ов + Яе)
dp=—---------------------------2Ё----------------------<Ш58>
р-ро
Решение математической модели (12.158) осуществляется в общем случае чис-
ленно. По рассчитанному распределению о5 = о$(р) определяется требуемый закон
нагрева материала t = /(р), скорость деформации £ = Ё.(р) или закон предварительно-
го упрочнения материала заготовки.
Для решения второй обратной задачи уравнение (12.155) должно быть решено отно-
сительно геометрических параметров заготовки: 5С при заданных режимах ведения про-
цесса: о5= о5(р) и геометрических параметрах получаемой детали: S= 5(р). Имеем:
2Е dSr р С и J
6SC Dр°5dp dpLO/”5 pP°e(2°e + °e
dp poe_ 3Eft
/33 dPA .
... + _______, '"'°"- 4 (12.159)
pOg 3Eg
-р-(2ое
Пример решения прямой задачи (12.155) по деформационной теории применительно
к процессу формовки листовой заготовки с постоянной толщиной стенки 5С = const при-
веден на рис. 12.47. Расчеты (12.155) применительно к раздаче труб даны на рис. 12.48.
Рис. 12.47. Расчет распределения толщины стенки получаемой детали при формовке
листовой заготовки давлением жидкости или газа (h/rm = 0,7; п = 0,5):
1 — формовка с неподвижным фланцем заготовки;
2 — формовка с утяжкой фланца Ы/гт = 5,5%
621
Рис. 12.48. Расчет распределения толщины стенки получаемой детали при раздаче труб:
1 — раздача в стационарном очаге деформации (расчет по теории течения);
2 — раздача в нестационарном очаге (расчет по деформационной теории);
3 — раздача средней части трубы (расчет по деформационной теории)
Требуемое распределение толщины стенки заготовки по ее длине dSc/dHc полу-
чим с использованием выражения:
;пт = тг5 sin “• (12.160)
dHc dp 5р
Пример расчета требуемого распределения толщины стенки заготовки (обратная задача)
при получении равнотолщинной конической детали (с отношением диаметров 1:2) пу-
тем раздачи концевого участка трубчатой заготовки на коническом пуансоне с зональ-
ным нагревом материала приведен на рис. 12.49. В расчетах принято уравнение состоя-
ния материала в соответствии с зависимостями (12.12) и (12.16). Расчет был осуществлен
по методу конечного формоизменения без учета промежуточных форм заготовки.
Численные решения прямых и обратных осесимметричных задач листовой штам-
повки дают возможность существенно расширить области поиска оптимальных усло-
вий ведения процесса пластического деформирования, что повышает качество разра-
ботки технологического процесса и, соответственно, качество получаемой детали.
Как показывают исследования [18, 19] погрешность в расчете толщины стенки
получаемой детали по приведенным дифференциальным уравнениям (12.155),
Рис. 12.49. Требуемое распределение толщины стенки трубной заготовки при получении
равнотолщинной конической детали
(П/0,0 = 3,3; у = -0,007; t^/t^ = 0,5)
622
(12.158) и (12.159) не превышает обычно 5%. Погрешность в расчете напряжений до-
стигает 15—25% и определяется главным образом приближенными эксперименталь-
ными зависимостями напряжения текучести материала о5 =/(е, е, ...).
* * *
В данной главе изложены основные положения теории обработки металлов дав-
лением, связанные с расчетами напряженно-деформированного состояния и техно-
логических параметров в процессах изготовления элементов конструкций летатель-
ных аппаратов методами пластического деформирования.
Фундаментальные основы этой теории были заложены к середине 1940-х годов и
в последующие годы исследования были связаны с совершенствованием методов рас-
чета напряженно-деформированного состояния. И в наше время эти методы непре-
рывно обновляются, а круг решаемых задач постоянно расширяется. При этом увели-
чивается число расчетно определяемых параметров, все больше учитывается влияние
дополнительных технологических факторов на характеристики готового изделия и др.
Использование в расчетах ЭВМ позволяет численно решать всю систему исход-
ных уравнений, т. е. определять перемещения, деформации, напряжения, деформи-
рующие усилия, оценивать влияние сил контактного трения, дополнительного сило-
вого нагружения заготовки, нагрева материала и целого ряда других факторов, т. е. по
существу моделировать процесс изготовления детали в широком смысле.
На основе численных решений созданы и другие расчетные методы: метод ко-
нечных элементов, численные методы расчета предельных деформаций и некоторые
другие, рассмотрение которых выходит за рамки данного курса. Их изучению будут
посвящены отдельные главы следующего тома.
ЛИТЕРАТУРА
1. Ильюшин А. А. Пластичность. — М.; Л.: ГИТТЛ, 1948. С. 376.
2. Безухов Н. И. Основы теории упругости, пластичности и ползучести. — М.:
Высш, шк., 1961. С. 538.
3. Соколовский В. В. Теория пластичности. — М.: Высш, шк., 1969. С. 608.
4. Сторожев М. В., Попов Е. А. Теория обработки металлов давлением. — М.: Ма-
шиностроение, 1977. С. 423.
5. Попов Е. А. Основы теории листовой штамповки. — М.: Машиностроение, 1977.
С. 278.
6. Горбунов М. Н. Технология заготовительно-штамповочных работ в производстве
самолетов. — М.: Машиностроение, 1981. С. 224.
7. Колмогоров В. Л. Механика обработки металлов давлением. — М.: Металлургия,
1986. С. 688.
8. Малинин Н. Н. Прикладная теория пластичности и ползучести. — М.: Машино-
строение, 1975. С. 278.
9. Томленое А. Д. Механика процессов обработки металлов давлением. — М.:
ГНТИМЛ, 1963. С. 236.
10. Теория пластических деформаций металлов/Под ред. Унксова Е. П.,
Овчинникова А. Г. — М.: Машиностроение, 1983. С. 598.
11. Хилл Р. Математическая теория пластичности. — М.: ГИТТЛ, 1956. С. 407.
12. Теория обработки металлов давлением/Тарновский И. Я., ПоздеевА. А.,
Ганаго О. А. и др. — М.: Металлургиздат, 1963. С. 672.
13. Томсен Э., Янг Ч., Кобояши III. Механика пластической деформации при обработ-
ке металлов. — М.: Машиностроение, 1969. С. 504.
14. Смирнов-Аляев Г. А. Сопротивление материалов пластическому деформирова-
нию. — Л.: Машиностроение, 1978. С. 368.
15. Дель Г. Д. Технологическая механика. — М.: Машиностроение, 1978. С. 174.
623
16. Бэкофен В. Процессы деформации. — М.: Металлургия, 1977. С. 288.
17. Hosford W. Е, Caddell R. М. Metal forming: mechanics and metallurgy. Printice-Hall,
Inc., 1983. P. 330.
18. Ершов В. И., Чумадин А. С. Математическое моделирование процессов осесим-
метричного деформирования листовой штамповки: Учеб, пособие. — М.:
МФТИ, 1988. С. 47.
19. Листовая штамповка. Расчет технологических параметров: Справочник / Под
ред. Ершова В. И., Чумадина А. С. — М.: МАИ, 1999. С. 516 с.
СОДЕРЖАНИЕ ГЛАВЫ 12
12.1. Понятие о пластической деформации..........................577
12.1.1. Деформации...........................................577
12.1.2. Скорость деформации и скорость деформирования........578
12.1.3. Условие постоянства объема при пластическом
деформировании ..............................................579
12.2. Физика пластической деформации. Холодная пластическая
деформация монокристалла и поликристалла.........................580
12.2.1. Дислокации...........................................580
12.3. Механика пластической деформации...........................582
12.3.1. Кривые упрочнения....................................582
12.3.2. Аппроксимация кривых упрочнения......................584
12.3.3. Влияние температуры и скорости деформации
на процесс деформирования....................................585
12.4. Теория напряжений..........................................587
12.4.1. Общие понятия........................................587
12.4.2. Напряжения в координатных площадках..................588
12.4.3. Напряжения на наклонной площадке.....................589
12.4.4. Геометрическая интерпретация тензора напряжений......590
12.4.5. Инвариантные характеристики напряженного состояния...591
12.4.6. Главные касательные напряжения.......................592
12.4.7. Вывод обобщенных характеристик напряженного состояния.593
12.4.8. Условия пластичности.................................594
12.4.9. Уравнения равновесия.................................596
12.5. Теория деформаций. Малые деформации........................599
12.5.1. Компоненты перемещений и деформаций
в элементарном объеме........................................600
12.5.2. Вывод обобщенных характеристик
деформированного состояния...................................601
12.5.3. Скорости перемещений и скорости деформаций...........603
12.5.4. Условие неразрывности (совместности) деформаций......603
12.6. Физические уравнения теории пластичности...................604
12.6.1. Механическая схема деформации........................604
12.6.2. Связь между напряжениями и деформациями..............604
12.6.3. Контактное трение при пластическом деформировании....606
12.7. Методы решения задач пластического деформирования..........607
12.7.1. Общие положения......................................607
12.7.2. Инженерный метод решения задач.......................608
12.7.3. Метод баланса работ..................................610
12.7.4. Метод линий скольжения...............................613
12.7.5. Методы численного решения исходной системы уравнений.617
Литература...........................................................623
624
ГЛАВА 13___________________________
Проектирование конструкций
летательных аппаратов
из композиционных материалов
В последние десятилетия в авиационной и ракетной технике все шире применя-
ются композиционные материалы (композиты), состоящие из армирующих элемен-
тов и соединяющего их связующего материала, называемого матрицей. В качестве ар-
мирующих элементов используются тонкие (диаметром порядка 10 мкм) стеклянные,
углеродные, керамические или органические волокна, из которых формируются ни-
ти, жгуты и ткани. В качестве материалов матриц применяются полимерные смолы
(эпоксидные, фенольные, полиэфирные и другие), а также металлические сплавы на
основе алюминия. Наиболее широкое распространение в авиа- и ракетостроении по-
лучили полимерные композиты, в которых используются углеродные и органические
волокна и эпоксидные матрицы. Эти материалы обладают высокими показателями
прочности и жесткости, которые обеспечиваются соответствующими характеристи-
ками волокон, низкой плотностью и хорошей технологичностью. Традиционные для
полимерных композитов технологические процессы, которые описаны в учебниках
[1, 2], включают: укладку пропитанных армирующих элементов на технологическую
поверхность, форма которой соответствует форме будущего изделия; термообработку,
в процессе которой связующее полимеризуется (отверждается), образуя жесткую мат-
рицу, связывающую волокна; отделение композитной детали от технологической по-
верхности; механическую обработку и финишные операции. Использование для опе-
рации укладки армирующих элементов многокоординатных выкладочных машин и
намоточных станков с программным управлением позволяет реализовать автоматизи-
рованное промышленное производство композитных конструкций, обладающих вы-
сокой степенью весового совершенства, стабильностью свойств и надежностью.
Основная особенность проектирования композитной конструкции связана с тем,
что материал, из которого она выполняется, не существует отдельно от конструкции и
создается в процессе ее изготовления. При этом механические свойства композита,
зависящие от направления, в котором укладываются армирующие элементы, могут
изменяться в довольно широких пределах. Таким образом, процесс проектирования
композитной конструкции включает определение как традиционных проектных па-
раметров (например, толщины обшивки, площади сечения стрингера и т. д.), так и
структурных параметров материала (например, углов, которые волокна составляют с
направлениями нагружения, числа слоев и т. д.).
В рационально спроектированной композитной конструкции нагрузка в основ-
ном воспринимается волокнами, удельная прочность (отношение предела прочности
к плотности) которых значительно превышает соответствующую характеристику тра-
диционных металлических сплавов и определяет потенциально высокую весовую эф-
фективность композитных конструкций по отношению к металлическим. Первым
примером такой конструкции стал корпус ракетного двигателя твердого топлива вто-
рой ступени баллистической ракеты «Поларис А2» [3], изготовленный из стеклоплас-
625
тика и запущенный в производство в 1960 году. Современные композитные корпуса,
которыми оснащены все стратегические твердотопливные ракеты, обладают пример-
но вдвое большей весовой эффективностью, чем металлические аналоги, а массовая
доля композитов в конструкции таких ракет превышает 80%. Помимо высокой удель-
ной прочности композиты характеризуются высокой демпфирующей способностью и
вязкостью разрушения, которые определяют хорошую сопротивляемость этих мате-
риалов циклическим и вибрационным нагрузкам. В связи с этим использование этих
материалов для изготовления лопасти несущего винта вертолета позволяет увеличить
ресурс лопасти в несколько раз, а массовая доля композитов в конструкции вертолета
достигает 50%. В несколько меньшем объеме композиты используются в настоящее
время в конструкции планера самолета — их массовая доля составляет порядка 20% в
военных, 10% в транспортных и 5% в пассажирских самолетах, что связано не столько
со свойствами композитов, сколько с недостаточным для широкого внедрения этих
материалов опытом эксплуатации композитных конструкций. В рекордных самолетах
массовая доля композитов, как правило, очень высока. Например, планер самолета
«Вояджер», совершившего в 1987 году беспосадочный полет вокруг земного шара,
был полностью изготовлен из углепластика. На рис. 13.1 показан фюзеляж легкого са-
молета, изготовленный из стеклопластика методом намотки.
Ниже обсуждаются особенности проектирования композитных элементов конст-
рукций аэрокосмической техники. Основное внимание уделяется конструкциям, для
которых эффективность использования композитов является в настоящее время об-
щепризнанной. Вывод расчетных соотношений, а также вопросы, относящиеся к ма-
териаловедению и технологии, освещенные в литературе [1, 2, 4, 5, 6], для сокраще-
ния изложения опускаются.
Рис. 13.1. Фюзеляж легкого самолета, изготовленный из стеклопластика методом намотки
626
13.1. КОНСТРУКЦИОННЫЕ СВОЙСТВА композитов
Типовые элементарные структуры композиционных материалов показаны на
рис. 13.2. Наиболее распространенной и наиболее полно отражающей особенности
материала является однонаправленная структура (а), образованная из параллельных
волокон, соединенных матрицей. Структура (6) состоит из слоев ткани, обеспечиваю-
щих армирование материала сразу в двух ортогональных направлениях. Структуры (в)
и (г) близки к изотропным, хаотическое армирование которых неориентированными
непрерывными или короткими волокнами приводит к тому, что свойства получаемого
материала не зависят от направления нагружения. Естественно, что прочность и
жесткость таких материалов значительно ниже соответствующих характеристик мате-
риалов с ориентированным армированием (рис. 13.2, а и б), нагружаемых вдоль воло-
кон. И наконец, структура (д) образуется специальными технологическими методами
и армирована в трех ортогональных направлениях. Элементарные структуры, пока-
занные на рис. 13.1, могут быть использованы как непосредственно, так и в качестве
слоев материалов с более сложной структурой.
Как уже отмечалось, высокие механические свойства волокон наиболее полно ре-
ализуются в однонаправленных композитах (рис. 13.2, а), которые используются
обычно для формирования слоистых материалов с различными углами армирования
отдельных слоев. Типовая слоистая структура (рис. 13.3) включает слои, армированные
под углами 0°, 90° и ±45° по отношению к сторонам слоистой панели. Механические и
теплофизические свойства слоя обычно задаются в координатах 1, 2, 3 (рис. 13.4) та-
композиционных материалов:
а) однонаправленный
композит; б) композит,
армированный тканью;
в) хаотически армированный
композит; г) композит,
армированный короткими
волокнами; д) трехмерно
армированный композит;
Рис. 13.3. Типовая слоистая
структура композита, состоящего
из однонаправленных слоев
Рис. 13.4. Система координат
и напряженное состояние
однонаправленного слоя
627
ких, что ось 1 направлена вдоль волокон, ось 2 — поперек волокон в плоскости слоя, а
ось 3 — нормально к плоскости слоя. В условиях плоского напряженного состояния
(рис. 13.4) закон Гука в осях 1, 2, 3 имеет следующий вид:
_ а1 а2 _ а2 а1
£| “ -V12£2, е2 - £2 “v21^>
Y12 = (^lv12 = ^2v21)>
(13.1)
где Ej и е2 — деформации слоя вдоль и поперек волокон; у12 — деформация сдвига;
Е — модуль упругости в соответствующем направлении; (712 — модуль сдвига; v — ко-
эффициент Пуассона.
Существуют следующие приближенные зависимости, позволяющие выра-
зить упругие постоянные, входящие в уравнение (13.1), через упругие постоянные
волокон (£в, (7В, vB), матрицы (£м, (7М, vM) и относительное объемное содержание во-
локон v [2]
Е\ = EBv + Ем( 1 - v), v21 = vBv + vM( 1 - v),
l—V.l-V.vjj 1 _ V . 1 - V
£2 Eb ’ g;2 Gb ~G^ •
Эти зависимости могут быть использованы лишь для качественного анализа зависи-
мости свойств композитного материала от свойств его компонентов. Так как Еъ» Ем
и GB » GM, можно заключить, что модуль Е{ определяется свойствами волокон, а мо-
дули Е2 и 612 — свойствами матрицы. Типовые свойства однонаправленных компози-
тов на основе стеклянных, углеродных, органических и борных волокон, а также
эпоксидной матрицы приведены в таблице 13.1 (индексы 1 и 2 соответствуют направ-
лениям, показанным на рис. 13.4).
Приведенные в таблице значения являются ориентировочными. Фактические
свойства композита зависят от технологии изготовления конструкции и определяют-
ся экспериментально методами, описанными в работах [5, 7].
Процесс разрушения композитных материалов имеет достаточно сложный и
многоступенчатый характер. Как следует из табл. 13.1, пределы прочности <J2 и t12, со-
ответствующие нагружению материала поперек волокон и сдвигу, значительно мень-
ше пределов прочности при нагружении вдоль волокон (с^). Вследствие этого на пер-
вом этапе разрушения материала в нем образуются трещины в матрице между волок-
нами и происходит нарушение монолитности материала. Соответствующая нагрузка
определяется из следующего условия прочности:
Здесь g2 и т12 — действующие напряжения в слое, a <J2 и t12 — соответствующие преде-
лы прочности (см. табл. 13.1). Как уже отмечалось, в рационально спроектированных
конструкциях внешняя нагрузка воспринимается в основном волокнами, и наруше-
ние монолитности материала не приводит к разрушению конструкции, которая мо-
жет работать до разрушения волокон. Соответствующая предельная нагрузка может
быть найдена с помощью следующих условий прочности:
Gj < (при а1 > 0),
lajCGf (при Gj < 0). (13.3)
Первое условие соответствует растяжению волокон, а второе — сжатию.
628
Т абл ица 13.1
Механические и теплофизические свойства однонаправленных композитов
Свойства однонаправленных композитов Материал
стекло- пластик угле- пластик органо- пластик боро- пластик
Модуль упругости, ГПа Ех — вдоль волокон Е2 — поперек волокон 60 13 130 и 95 5,1 210 19
Модуль сдвига (712, ГПа 3,4 5,5 1,8 4,8
Коэффициент Пуассона, v21 0,3 0,27 0,34 0,21
Предел прочности при растяжении, МПа — вдоль волокон в* — поперек волокон 1800 40 2000 50 2500 30 1300 70
Предел прочности при сжатии, МПа Of — вдоль волокон Of — поперек волокон 650 90 1200 170 300 130 2000 300
Предел прочности при сдвиге Т12, МПа 50 70 30 80
Плотность р, кг/м3 2100 1550 1320 2100
Коэффициент теплопроводности, Вт/м • К Xq — ВДОЛЬ волокон Х2 — поперек волокон 0,6 0,4 1 0,6 0,17 0,1 0,5 0,3
Коэффициент линейного расширения, 1/°С*106 oq — вдоль волокон 02 — поперек волокон 7,4 22,4 -о,з 34 -3,6 60 4,1 19,2
Таким образом, имеется два условия прочности — (13.2) для матрицы и (13.3) для
волокон.
Если руководствоваться условием (13.2), то уровень допускаемых напряжений
оказывается настолько низким, что композитные материалы теряют свои преимуще-
ства по отношению к металлам. Эти преимущества полностью проявляются, если ис-
пользовать условие прочности в форме (13.3), однако при этом допускаются микро-
трещины в матрице при эксплуатационных нагрузках. При проектировании конст-
рукций одноразового использования условие прочности обычно принимается в
форме (13.3), допускающей нарушение монолитности материала. Однако для конст-
рукций, эксплуатирующихся многократно и в течение длительного времени, появле-
ние трещин в материале недопустимо. Этим, в частности, объясняется то обстоятель-
ство, что объем применения композитов в планере пассажирского самолета значи-
629
тельно меньше, чем в ракете. Из композитов изготавливаются в настоящее время
только слабо нагруженные элементы планера пассажирского самолета. Рациональ-
ный подход к проектированию авиационных композитных конструкций предполага-
ет задание такой величины коэффициента безопасности (т. е. отношения разрушаю-
щей нагрузки к эксплуатационной), чтобы были выполнены оба условия прочности.
При этом неравенство (13.2) выполняется при эксплуатационной нагрузке, а неравен-
ство (13.3) переходит в равенство при разрушающей нагрузке.
Выше были рассмотрены основные свойства однонаправленных композитов.
Характеристики материалов, армированных тканями (рис. 13.2,6), зависят от соот-
ношения числа взаимно ортогональных нитей, образующих ткань и обычно ниже
характеристик слоистых композитов, образованных из взаимно ортогональных од-
нонаправленных слоев аналогичных материалов. В связи с этим тканые компози-
ты используются главным образом из технологических соображений, в частности,
при изготовлении крупногабаритных элементов конструкций методом выкладки
заранее раскроенных заготовок. Механические свойства таких материалов описаны
в работах [5, 6].
Хаотически армированные материалы (рис. 13.2, в и г), свойства которых приве-
дены в справочнике [8], используются главным образом в несиловых деталях, полу-
чаемых методами литья и прессования.
Трехмерно армированные композиты (рис. 13.2, д), а также композиты, армиро-
ванные более чем в трех направлениях, составляют специальный класс материалов на
основе углеродных волокон и карбонизованной матрицы. Структура и свойства этих
материалов, применяемых в элементах летательных аппаратов, работающих при вы-
соких температурах, описаны в работах [5, 9, 10].
Таким образом, композиционные материалы могут обладать различной микро-
структурой и, соответственно, характеризоваться широким диапазоном свойств, за-
висящих от вида армирующих элементов и направлений армирования. В конструкци-
ях эти материалы используются, как правило, в виде слоистых пакетов, состоящих из
различным образом ориентированных слоев однонаправленных композитов, тканых
композитов, а также их комбинаций, включающих при необходимости слои из метал-
лов, термопластов, резины и т. д. Для определения механических характеристик таких
материалов рассмотрим слоистую панель, нагруженную в своей плоскости нормаль-
ными силами Nx и Ny и сдвигающими силами N (рис. 13.5), которые считаются равно-
мерно распределенными по соответствующим краям панели (размерность N — Н/м).
Панель состоит из к слоев, причем каждый слой является ортотропным, т. е. имеет две
оси симметрии 1 и 2 такие, что растяжение вдоль этих осей не вызывает изменения
прямого угла между ними, а связь между напряжениями и деформациями определяет-
ся равенствами (13.1). Главная ось ортотропии слоя 1 составляет некоторый угол ф с
осьюх, характеризующей координатную систему х, у, к которой отнесена панель. Вы-
делим из панели некоторый слой и запишем соотношения, связывающие напряжения
и деформации в осях ортотропии 1, 2 и в осях панели х, у (рис. 13.6) [4]:
ах = ахс2 + a^s2 - 2т12су,
/ ау = + а2с2 + 2т12су,
Ъсу = (<*1 - о2)“ + ^12<с2 -j2); <13-4)
£, = e/r2 + е/2 + y^cs,
J е2 = SyS2 + ЕУС2 - y^cs,
Уи = 2(еу - EX)CS + у^с2 - s2). (13.5)
630
Рис. 13.5. Слоистая панель,
нагруженная в своей плоскости
Рис. 13.6. Напряжения, действующие
в слое в координатах 1, 2, 3 и х, у, z.
Здесь для сокращения записи обозначено:
с = cos ф, s = sin ф. (13.6)
Если теперь выразить в равенствах (13.4) напряжения о2, Ti2 чеРез деформа-
ции £j, е2, у12 с помощью закона Гука для слоя (13.1) и заменить е2, у12 через ех, у^
используя соотношения (13.5), получим
— ЛцЕх + Л12Еу + ^1зУхИ>
< ву= А2Х£Х + А22£у + ^2зУху
Ъ = Лз>ех + Л32£, + Лззу^ (13.7)
где
Л11 = £1с4 + £/ + 2£12А2,
Л12 = Л21 = Ёхух2 4- (£\ 4- Ё2 - 2£12)А2,
Л13 = Л31 = [Ёхс2 - Ё^2 - ЕХ2(с2 - 52)]С5,
Л22 = Ех^ 4- Е2с* 4" 2£12А2,
Л23 = Л32 = [£XS2 — Ё2С2 4- £12(С2 — 52)]С5,
А33 = (Ёх + Ё2 — ЁхуХ2)с252 + G12(c2-s2)2 (13.8)
и
^1, 2= 1 _ J;22v21 ’ ^*12= Ё 1v 12+ ^12-
Равенства (13.7) связывают напряжения с деформациями слоя в системе координат х,
у (рис. 13.6), а входящие в них величины А (13.8) являются коэффициентами жесткос-
ти слоя. Как следует из соотношений (13.7), в осяхх, у слой является анизотропным,
так как нормальные напряжения ох и <зу вызывают не только относительные удлине-
ния слоя ех и ег но и деформацию сдвига уху
Для слоистой панели, показанной на рис. 13.5, имеем
к к к
(13.9)
/=1 /=1 /=1
Здесь hi — толщина слоя с номером i (i = 1, 2, 3, ..., к), а напряжения определяются
равенствами (13.7), в которых угол ф и упругие постоянные зависят от номера слоя
i (ф = ф. и т. д.). Будем считать, что слои панели деформируются совместно без взаим-
ного проскальзывания. При этом деформации ех, гу и у для всех слоев одинаковы,
631
что обеспечивается за счет межслоевых касательных напряжений т13, т23 или txv xyz,
показанных на рис. 13.6. Тогда, подставляя соотношения (13.7) в равенства (13.9), по-
лучим:
*Х = + ^12еу +
Ny = В21£х+ В22^у + В2зУху>
Nxy = Д31Ех + В32*у + ВззЧху* О3- Ю)
где
к
в=в = УЖ (13.11)
тп пт тп / v 7
/ = 1
и тп = 11, 12, 13, 22, 23, 33. Величины В являются коэффициентами жесткости слоис-
того композита при его растяжении или сжатии в направлении осей х и у и сдвиге в
плоскости слоев.
Равенства (13.10) добавляются в качестве соотношений упругости к остальным
уравнениям (уравнениям равновесия и геометрическим соотношениям), описываю-
щим напряженно-деформированное состояние конструкции. В результате решения
этой системы уравнений определяются деформации слоистого композита ех, и уху
Эти деформации подставляются в равенства (13.5) для каждого слоя и находятся де-
формации Ер е2 и У12 в осях ортотропии слоя. Затем с помощью соотношений (13.1)
определяются напряжения в слое ор о2 и т12. Прочность слоя оценивается с помощью
условий прочности (13.2) и (13.3). Как уже отмечалось, неравенство (13.2) позволяет
определить нагрузку, при которой нарушается монолитность композита, т. е. появля-
ются микротрещины в матрице. Если по условиям проектирования эти трещины яв-
ляются допустимыми, то расчет конструкции продолжается. При этом в коэффици-
ентах жесткости А (13.8) для слоев, у которых имеет место нарушение неравенства
(13.2) принимается Е2 = 0, (712 = 0, v12 = 0, а прочность таких слоев оценивается с по-
мощью критерия (13.3), определяющего нагрузку, при которой разрушаются волокна
слоя. Более подробно процедура анализа несущей способности слоистого композита
описана в работах [11, 12]. Одной из возможных форм разрушения слоистого компо-
зита является расслоение, вызываемое межслоевыми касательными напряжениями
т13, т23 или xxz, xyz (рис. 13.6). Эти напряжения находятся из уравнений равновесия для
слоя, в котором действуют уже найденные напряжения ор о2, т12 или напряжения ох,
оу и тху, определяемые с помощью равенств (13.4). Для оценки межслоевой прочности
используется условие
Т<тс, (13.12)
где
т = 7^13 + '23 = -М + tfz -
межслоевое касательное напряжение, а Тс — предел прочности слоистого материала
при межслоевом сдвиге.
Наиболее распространенной структурой слоистого композита является симмет-
рично армированная структура, в которой слою с углом +ф соответствует такой же
слой с углом —ф (рис. 13.7). Для таких слоев коэффициенты Л13 и Л23, определяемые
равенством (13.8), имеют разный знак и взаимно уничтожаются в суммах (13.11).
В результате соотношения (13.10) упрощаются и принимают вид
*Х = 1£х + ^12er *у = ^21ех + ^22ег
Л^ = ^зГхг (ШЗ)
632
Рис. 13.7. Симметрично армированная пара слоев
Отсюда следует, что симметрично армированный слоистый композит является орто-
тропным. Вводя осредненные по толщине панели h (рис. 13.5) напряжения ох = Nx/h\
<зу = Ny/h\ = N^/h и разрешая равенства (13.13) относительно деформаций, по-
лучим
р=^_м^ р = -V —
* ех ФЕ/ у Еу ^Е/
(13.14)
Сюда входят средние упругие постоянные слоистого композита, которые имеют вид
= ^’ ^=йДзз- 03.15)
Аналогичным образом могут быть записаны средние коэффициенты теплопровод-
ности в направлении осей х и у
/=1
1 *
Ч=й + азлб)
/=1
и коэффициенты линейного расширения
(^11-^22), “ £ (^22 “ VxjAl)- (13.17)
у
Здесь Ей v определяются равенствами (13.15) и
1 — —
*11= й £ [^(“i0 + + £^((4° +
i=i
ь22 = J Z [^(10(а(10 + v<0a<0)s2 + E(0(a(0 + v^)cj]h, (13.18)
/=1
Для однонаправленных композитов коэффициенты теплопроводности слоя и
соответствующие коэффициенты линейного расширения cq, a2, входящие в равенст-
ва (13.16) и (13.18), представлены таблице 13.1.
Рассмотрим изгиб и кручение слоистой панели и приложим дополнительно к си-
лам, действующим в плоскости панели (рис. 13.5), изгибающие моменты Мх, Му и
633
крутящие моменты (рис. 13.8). Тогда соотношения упругости (13.10) обобщаются
следующим образом [4]:
Nx = ^11£х + ^12еу + + Q 1Кх + ^12KJ + ^13Кху’
Ny = ^21£х + ^22гу + ^23^ху + ^21Кх + ^22Ку +
^ху ~ ^31£х + ^32ej + ^ЗзТху + ^314: + ^32Ку + ^ЗЗ1^
Мх = СцЕх + ^12ej + ^1зУху + Л1К, + ^12^ + Аз1^
Му = ^21ех + ^22гу + ^2зУху + ^214: + ^22Ку + ^23Клу
^ху = ^31ех + ^32еу + СнУху + ^З!1^ + ^32*^ + ^33Кху (13.19)
Входящие сюда коэффициенты жесткости Втп называются мембранными жесткостя-
ми слоистого материала и определяются равенствами (13.11).
При определении изгибных коэффициентов жесткости Dmn принципиальную
роль играет так называемая базовая поверхность слоистой стенки (она иногда называ-
ется также поверхностью приведения или начальной поверхностью), относительно
которой задаются моменты (рис. 13.8). Рассмотрим слоистую стенку (рис. 13.9) и вве-
дем базовую поверхность z = 0, расположив ее на некотором расстоянии е от нижней
поверхности. Тогда изгибные жесткости принимают вид:
Dm = Dnm = 1тп “ Кп + ^Втп, (13.20)
где
Imn = i У А<0 (t3 -t3 ,) = i У A^htt1 + LL x + fi .)
mn 3 mnx i / — 1' 3 mn t 1 ~~ * / — 1'
Z=1 /=1
1 1
Jmn=2^A^-^=2^A^+^- (13-21)
/=1 Z=1
В равенствах (13.21) коэффициенты A^n (mn = 11, 12, 13, 22, 23, 33) определяются со-
отношениями (13.8) для слоя с номером /, a — координата этого слоя, равная рас-
стоянию от нижней поверхности стенки до верхней поверхности слоя.
Соотношения (13.19) связывают силы и моменты, действующие в панели, с обоб-
щенными деформациями ее базовой поверхности (рис. 13.10). Деформации ех, гу и
называются мембранными деформациями и они соответствуют растяжению, сжатию
и деформации сдвига базовой поверхности, а деформации кх, ку и соответствуют
изгибу и кручению базовой поверхности. Деформации ех, еу в любой точке слоис-
Рис. 13.9. Структура
слоистой стенки
Рис. 13.8. Силы и моменты,
действующие на элемент
слоистой панели
634
того материала, имеющей координату z, отсчитывае-
мую от базовой поверхности, можно выразить через
обобщенные деформации этой поверхности, т. е.
+ zk*, еу — €у + zKy, — Yxy +
Как следует из равенств (13.19), поведение слоисто-
го материала под нагрузкой носит в общем случае
довольно сложный характер. Растягивающие силы,
например Nx, вызывают деформации кх, ку и кху, т. е.
искривление и закручивание панели. Соответст-
вующие коэффициенты жесткости Стп называются
смешанными и выражаются следующим образом:
С =А (13.22)
тп тп тп х 7
Здесь Jmn определяется вторым равенством (13.21).
Как следует из соотношений (13.20) и (13.22),
изгибные и смешанные коэффициенты жесткости
слоистой стенки зависят от расположения базовой
поверхности, которые определяются координатой е
(рис. 13.9). Рассмотрим возможное упрощение об-
щих соотношений (13.19) за счет соответствующего
выбора координаты е. Естественным и традицион-
ным является задание координаты е, обеспечиваю-
щее разделение плоского и изгибного состояний па-
нели, что имеет место если все смешанные коэффи-
циенты жесткости обращаются в нуль. Полагая в
равенстве (13.22) Стп = 0, получим:
е = еп„=^. (13.23)
Следует иметь в виду, что при тп= 11, 12, 13, 22, 23,
33 имеется шесть уравнений (13.23) для одной неиз-
вестной е. Таким образом, в общем случае единой
базовой поверхности, обеспечивающей выполнение
условий Стп = 0 для всех комбинаций тп, не сущест-
вует. Равенство (13.23) показывает, что соответст-
Рис. 13.10. Деформации базовой
поверхности панели
вующим выбором координаты е можно обратить в нуль только один смешанный ко-
эффициент.
Важным частным случаем является симметричная структура слоистой стенки,
показанная на рис. 13.11. В такой стенке базовая поверхность совпадает со срединной
поверхностью, разделяющей толщину стенки пополам, а каждому слою с координа-
той Zi соответствует такой же слой, расположенный по другую сторону от срединной
поверхности и имеющий координату —г,. Для симметричной стенки коэффициенты
жесткости, входящие в соотношения (13.19), имеют вид:
к/2
Втп = 2^4М:, С=0,
тп тп р тп ’
/=1
? к/2
от„ = J z + + С,)- (13.24)
/=1
В этом случае Zq = 0, а суммы распространяются только на те слои, которые лежат
по одну сторону от срединной поверхности стенки. Если число слоев является не-
635
четным, то срединный слой условно разделяется поверхностью z = 0 на два одинако-
вых слоя.
В задачах проектирования соотношения (13.19) часто упрощаются путем вве-
дения приведенных изгибных жесткостей слоистой стенки. Для определения при-
веденных изгибных жесткостей Drmn в равенствах (13.20) и (13.22) подставляются зна-
чения етп, найденные из формулы (13.23) при соответствующих комбинациях тп.
Тогда
1>гтп = 1тп-^^ сгтп=^ (13.25)
тп тп н ’ /ил у '
тп
В результате соотношения (13.19) разделяются на две независимые группы. Первая
группа соотношений для Nx, Ny и N совпадает с равенствами (13.10), а вторая прини-
мает вид:
jK* +
Му = &2\*х + ^22^ +
^ху = ^314: + ^32^ + ^ЗЗ^ху (13.26)
Следует подчеркнуть, что равенства (13.25) и (13.26) в общем случае являются при-
ближенными — базовая поверхность должна быть единой для слоистой стенки и ее
координата е в строгом смысле не зависит от комбинации тп, что предполагается при
выводе соотношений (13.25).
13.2. БАЛОЧНЫЕ И СТЕРЖНЕВЫЕ ЭЛЕМЕНТЫ
Композиты широко применяются для изготовления балочных и стержневых эле-
ментов авиационных конструкций, а высокомодульные композиты на основе угле-
родных и борных волокон используются для усиления металлических профилей.
Рассмотрим балку, ширина сечения которой b и модуль упругости материала
Ех = Е зависят от координаты у (рис. 13.12). Система уравнений, описывающих осевое
растяжение балки и ее изгиб поперечными нагрузками pnq, имеет вид [4]
7V' = 0, M' = Q, Q'-p = Q, P=pbx-qbK,
N=Bu', M=DQ', 0 = -v', (13.27)
где штрих означает производную по х; и — осевое перемещение; v — прогиб балки;
0 — угол поворота сечения.
Входящие в уравнения (13.27) величины В и D определяют жесткость балки при
растяжении и изгибе и выражаются следующим образом:
h
В = \ bEdy, D = I—eJ, (13.28)
о
где
Л h
I=f ЬЕу2 dy J = J ЬЕу dy. (13.29)
о о
Параметр е является координатой нейтральной оси балки и определяется формулой,
аналогичной равенству (13.23), т. е.
e=g. (13.30)
636
Рис. 13.12. Характер нагружения
и геометрические параметры балки
Рис. 13.13. Сечение
слоистой балки
Для слоистой балки, сечение которой показано на рис. 13.13, имеем
к
/=1
1
/=з Z
/=1
1 к
2 Z (13.31)
/=1
Общее решение уравнений (13.27), определяющее зависимости осевой силы N, попе-
речной силы Q, изгибающего момента М, осевого перемещения и, угла поворота сече-
ния 0 и прогиба v от координаты х имеет вид
М*) = ^о>
Q(x) = Q0-Qp,
М(х) = Mq — Q^c —Мр,
No
u(x) = u0- -jX,
0(x) = e0 + ^x + ^x2 - ep,
V(x) = vo - 0qX - ^x2 - + vp.
Здесь величины с нижним индексом «О» являются значениями соответствующих
функций при х = 0. Они определяются из традиционных для балок граничных усло-
вий, согласно которым на концахх = 0 и х = L (рис. 13.12) должны быть заданы: и или
N, v или 0 и 0 или М. Функции с нижним индексом «р» зависят от нагрузки и опреде-
ляются следующим образом:
= 4 = /Q>dx’ 0/>=fj4dx’ vp = fepdx-
0 0 0 0
Если на балку действуют сосредоточенные силы, то эти интегралы вычисляются по
участкам. Нормальные и межслоевые касательные напряжения находятся по форму-
лам [4]
ax = £[J + £(y-e)], (13.32)
Хху = _^] Eb(y-e)dy. (13.33)
о
637
В качестве примера рассмотрим двутавровый профиль, усиленный сверху одно-
направленным композиционным материалом (рис. 13.14). Примем b = 0,5Л, 8 = 0,05й,
модуль упругости алюминия 70 ГПа и модуль упругости композита на основе волокон
бора и алюминиевой матрицы — 230 ГПа. Тогда в равенствах (13.31) следует принять
к = 4; tQ = 0, tx = 0,05Л, t2 = t3 = 0,95Л, t4 = h;bx = b3 = b4 = 0,5Л, b2 = 0,05Л; Ex = E2 =
= E3 = 70 ГПа, E4 = 230 ГПа.
В результате получим В = 12,85Л2,1 = 8,41 Л4, J = 9,29Л3. Подстановка в формулу
(13.30) дает е = 0,7\h.
При h = 0,1м из равенств (13.29) получим В = 12,85 • 10-2 ГПа* м2, D =
= 1,69* 104 ГПа*м4.
Для сравнения приведем характеристики аналогичного профиля без накладки:
е = 0,5Л, В = 7,1 • IO"2 ГПа • м2, D = 1,16 • 10"4 ГПа • м4.
Таким образом, композитная накладка увеличивает осевую жесткость балки на
81%, а изгибную жесткость — на 46%. При этом масса балки увеличивается на 27%. За-
метим, что увеличение толщины накладки ограничивается максимальными нормальны-
ми напряжениями ох (13.32), действующими в накладке, и межслоевыми касательными
напряжениями (13.33), действующими на границе раздела металла и композита.
Эффективность усиления рассмотренной выше балки композиционным мате-
риалом можно увеличить, если ввести две одинаковые накладки на верхней и на ниж-
ней полках так, чтобы сечение оставалось симметрично относительно средней линии
балки. Для того чтобы показать, что балка с симметричным сечением обладает боль-
шей изгибной жесткостью, чем балка с несимметричным расположением слоев, вве-
дем координату у0 = у — Л/2, отсчитываемую от средней линии у = h/2. Тогда равенст-
ва (13.28), (13.29) и (13.30) дают
/> = /0-:5> (1334)
где
h/2 h/2 h/2
/0= j ^dy0, JQ = j Z>£yodyo, B = J Z>Edy0.
-h/2 -h/2 -h/2
Если функция Ду0) = Ь(уц)Е(уц) является симметричной (т. е. четной), то 70 = 0 и, со-
гласно равенству (13.34), D принимает максимальное значение.
В качестве примера рассмотрим балку, сечение которой показано на рис. 13.15.
Средняя часть балки изготовлена из алюминиевого сплава, а накладки толщиной аЛ
выполнены из боропластика, свойства которого приведены в таблице 13.1. Используя
равенства (13.34), получим
s=^=1+2a(^-1)’
D=£- = 1 + 2af^ - 11(4a2-6a + 3).
Масса единицы длины балки может быть записана следующим образом
В этих равенствах £к, рк и Ем, рм — модули упругости и плотности композита и металла;
*м ~~ — 12 W РмМ
соответствующие характеристики металлической балки без накладок.
638
Рис. 13.14. Двутавровый профиль,
усиленный композитной накладкой
Рис. 13.15. Сечение
композитной балки
Зависимости В, D и g от параметра а показаны на рис. 13.16, из которого следует,
что симметрично расположенные композитные накладки из боропластика значитель-
но увеличивают жесткость балки из алюминиевого сплава и снижают ее массу.
Композиты на основе углеродных и борных волокон, обладающие высокой жестко-
стью, используются в виде жгутов, усиливающих стандартные металлические профили
(рис. 13.17). Стрингеры такого типа показаны на рис. 13.18. Для стержней, усиленных в
отдельных точках композитом, равенства (13.31) обобщаются следующим образом:
п
/=1
п
;=i
п
j=i
Здесь В, /, /определяются равенствами (13.31), п — число жгутов; и — модуль уп-
ругости и площадь сечения жгута с номером j (j= 1,2, 3,..., п); tj — координата, пока-
занная на рис. 13.17.
Стержневой элемент, сжатый осевой силой Т (рис. 13.19), может потерять устой-
чивость. Величина критической нагрузки, при которой стержень теряет устойчивость,
определяется равенством
Рис. 13.16. Зависимости приведенных
характеристик балки от относительной
толщины композитных накладок
Рис. 13.17. Тавровый
профиль, усиленный
композитным жгутом
639
Рис. 13.18. Алюминиевые
стрингеры, усиленные композитом
Рис. 13.19. Формы потери
устойчивости сжатых стержней
Здесь D — изгибная жесткость, вычисляемая по второй формуле (13.28); с — коэффи-
циент, зависящий от условий закрепления стержня. Для шарнирно опертого стержня
(рис. 13.19, а) с = 1, для консольного (6) с = 0,25 и для защемленного (в) с = 4.
13.3. ТОНКОСТЕННЫЕ БАЛОЧНЫЕ
И СТЕРЖНЕВЫЕ ЭЛЕМЕНТЫ
Наиболее перспективно применение композитов в тонкостенных стержнях
(рис. 13.20), которые изготавливаются намоткой или выкладкой однонаправленной
или тканой ленты под различными углами к оси и используются в качестве элементов
ферменных конструкций, подкосов, лонжеронов, винтов самолетов и вертолетов,
приводных валов и т. д. Модель тонкостенного стержня широко используется при
расчете и проектировании крыльев большого удлинения, корпусов ракет и других
конструкций, у которых размеры поперечных сечений значительно меньше длины.
Расчет тонкостенных стержней с замкнутым контуром поперечного сечения осу-
ществляется на основе гипотез балочной теории, согласно которым принимается, что
поперечное сечение не деформируется в своей плоскости. При нагружении в стенке
стержня возникают осевые нормальные усилия nz(z, s) и касательные усилия n&(z, s)
(рис. 13.21), которые сводятся к осевой силе Pz(z), поперечным силам Qx(z) и Qy(z), из-
гибающим моментам Mx(z), My(z) и крутящему моменту Mz(z) (рис. 13.22). Силы и мо-
менты, действующие в сечении z = const стержня, определяются традиционными для
тонкостенных стержней методами [13] и считаются известными функциями осевой
координаты z-
Рис. 13.20. Элементы тонкостенных
композитных стержней
Рис. 13.21. Нормальные и касательные
усилия, действующие в стенке стержня
640
Для ортотропных стержней соотношения упругости (13.13) записываются для
усилий, показанных на рис. 13.21, и имеют вид
пг = ЛиЕг, па = В33у^. (13.36)
Здесь коэффициенты жесткости В определяются равенствами (13.11) и (13.8), в кото-
рых ф угол между основным направлением армирования слоя и осью z (рис. 13.22).
Осевые усилия определяются следующим образом [4]
«<=*>.[5 (13-37)
Здесь
Мх = Mx-yoPv Му = My-XoPz
— изгибающие моменты, приведенные к центральным осям
х = х-Хо-кх(у-у0), y = y-yQ-kx(x-x0)
с центром в точке с координатами
Х0 = $у/^0 = $х/ В’
выражающимися через осевую жесткость стержня В и обобщенные статические мо-
менты сечения 5Г и т. е.
Л
B=jBnds, Sx=j Bnyds, Sy=jB"Xds. (13.38)
Величины D® и D® являются изгибными жесткостями стержня и имеют вид
D°x = Dx-ylB, D* = Dy-xlB, D% = Dxy-xoyoB,
Dx = jBt^ds, Dy = jBitx2ds, Dxy = jBtlxyds (13.39)
Интегралы вычисляются вдоль контура сечения, начиная от некоторой начальной
точки Oj (рис. 13.22).
Касательные усилия определяются равенством
М
Па=ело)++ d • (1 з.4О)
641
Здесь Q — поперечные силы; Mz — крутящий момент (рис. 13.22) и
Fx(5) = -^[J/5)-^ fjords],
= fJx(s)rds],
^=jfrds. (13.41)
Величина г является длиной перпендикуляра, опущенного из начала координат на ка-
сательную к контуру (рис. 13.21). Функции S(s) имеют вид
5х(5) = j Впу ds, 5/s) = j Btixds. (13.42)
О о
Осевая деформация стержня задается по теории тонкостенных стержней в форме
5) = w'(z) + 0'U)y(-s) + 0'UM-s), (13.43)
где штрих означает производную по z- В соотношении (13.43) w является осевым пере-
мещением сечения стержня, а 0Х и 0у — углами поворота сечения вокруг осей х и у.
Имеем [4]:
w=wo+ j I 1 Mxdz-k№, J му^
О иу' о V У xJ о
Ох = 02 + Ж - W 0, = у + та I (Му - dz. (13.44)
х О У ь
Здесь w0 и 0° — значения соответствующих функций при z = 0, которые определяются
условиями закрепления концов стержня. Прогиб оси стержня в направлении х и у
(рис. 13.22) может быть найден из следующих соотношений
и = «о + J (Гх - Qy) V = v0 + j (Г, - 0Х) dz. (13.45)
О о
Здесь и0 и v0 — начальные значения, определяемые из граничных условий; 0Х и 0у зада-
ются в соответствии с равенствами (13.44); Гх, Гу — деформации сдвига в плоскостях
xz и yz (рис. 13.22), которые определяются из следующей системы уравнений:
ГХ = CxQx + CxyQy + CXZMZ>
Гу = CyxQx + CyQy + суМ>
^ = ^x + c^Qy + CtMv (13.46)
где 0' = d0/dz и
c=if2— с =с =$FF —
х J х B33f *у w J *y B33 ’
____г pi ds __ ____ 1 f r< ds
Cy ~ J F у B^} > cxz~czx~ 2A J F*B^>
1 f ds 1 г „ ds
Cz “ 4Л5 j ’ cyz ~ czy ~ 2A * Fy ’
Входящие сюда функции Ги величина Л определяются равенствами (13.41). Последнее
уравнение (13.46) позволяет найти угол закручивания сечения z = const стержня, т. е.
0 = 00 + J (^Ох + ^Qy + сА) dr (13.47)
Здесь 0О = 0 (z = 0). °
642
Конструкции типа крыла и корпуса летательного аппарата, как правило, под-
крепляются стингерами. В этом случае коэффициенты жесткости В, S и D в равенст-
вах (13.38) и (13.39) заменяются следующими
A-=*n+ X
;=1
т
Syr = Sy+
J=t
т
Dyr=Dy + X
sxr=sx+ Z ДВЛ,
7=1
т
АВ/,
J=i
т
DXyr=DXy+ X
У=1
Первые члены в этих равенствах соответствуют обшивке и определяются соотноше-
ниями (13.38) и (13.39), ДБу = EjFj — произведение модуля упругости на площадь сече-
ния стрингера с номером j и с координатами и уу. Напряжения в стрингерах опреде-
ляются формулой, аналогичной равенству (13.37), т. е.
гР_ / М
МУ-Х\
D° XJ Jj ‘
vr /J
(13.48)
При вычислении касательных усилий с помощью равенства (13.40) функции 5($)
обобщаются следующим образом:
ЗД = ^(5)+ 5 Д2?Л
7=1
ms
Syr(s) = Sy(s) + X Д^ху.
у=1
Здесь S(s) соответствуют обшивке и определяются равенствами (13.42), а через ms обо-
значено число стрингеров, расположенных на интервале от s = 0 до текущего значения s.
В качестве примера приведем распределение напряжений по контуру сечения
трехслойной круговой цилиндрической оболочки, показанного на рис. 13.23, а. Обо-
лочка, подробно рассмотренная в работе [5, с. 342], имеет трехслойную стенку с за-
полнителем из пенопласта и несущими слоями из углепластика, армированными под
углами ±45° и 90° по отношению к оси. Между несущими слоями трехслойной стенки
располагаются 12 стрингеров прямоугольного сечения, изготовленные из однонап-
равленного боропластика. Заметим, что обсуждаемая конструкция является характер-
ным примером рациональной конструкции из композитов, каждый элемент которой
воспринимает в основном одну из внешних нагрузок. Действительно, стрингеры
воспринимают в основном осевую силу Pz и изгибающие моменты Мх и Му
(рис. 13.22). Проектная площадь сечения стрингера может быть найдена, если подста-
вить максимальное напряжение, вычисленное по формуле (13.48), в условие прочнос-
ти (13.3). Слои обшивки с углами армирования ±45° воспринимают в основном попе-
речные силы Qx и Qy и крутящий момент Mz (рис. 13.22). Толщины этих слоев можно
определить, используя равенство (13.40) и соотношения, приведенные в разделе 13.1.
И наконец, кольцевые слои обшивки обеспечивают жесткость контура сечения и
воспринимают внутреннее давление (если оно имеется). Необходимо также подчерк-
нуть, что обсуждаемая конструкция является не только сравнительно простой и на-
дежной, но и очень технологичной. Для ее изготовления на цилиндрическую оправку
сначала наматывается внутренний слой трехслойной обшивки, затем на него уклады-
ваются блоки пенопласта и заранее изготовленные методом прессования стрингеры,
643
a)
Рис. 13.23. Сечение композитной цилиндрической оболочки (а)
и распределение относительных нормальных напряжений (б)
и потока касательных напряжений (в) по контуру сечения
и наконец, наматывается наружный слой обшивки. Изготовление завершается от-
верждением связующего и съемом оболочки с оправки. Распределение относитель-
ных нормальных напряжений в стрингерах (ог) и в обшивке (й5), а также потока каса-
тельных напряжений (п&) в сечении оболочки, нагруженном силой Qy и моментом Мх
(рис. 13.22), показано на рис. 13.23, бив. Ввиду того, что модуль упругости материала
стрингера больше, чем модуль упругости обшивки, напряжения (5Г значительно пре-
восходят напряжения <?5 и являются максимальными при р = 0. В местах установки
стрингеров поток касательных напряжений в обшивке изменяется скачкообразно и
достигает максимальной величины при Р = 90°.
Другим примером композитной конструкции, которая проектируется на основе
принципа раздельного восприятия нагрузки ее элементами, является лонжерон ло-
пасти несущего винта вертолета, сечение которого показано на рис. 13.20 (снизу).
Лонжерон должен воспринимать большую осевую силу, образующуюся при вращении
винта, и обладать высокой жесткостью при кручении. Первое условие обеспечивает-
ся, если направить волокна композита по размаху лопасти, т. е. вдоль оси z, а второе —
если ввести еще два слоя однонаправленного композита, армированные под углами
±45° к оси z- Таким образом, можно предположить, что материал лонжерона состо-
ит из двух слоев, причем первый слой с ф = 0 обеспечивает прочность при растяже-
нии, а второй с ф = ±45° — жесткость при кручении. Толщины слоев приближен-
но находятся из равенства (13.37) в сочетании с соответствующим условием прочнос-
ти и из третьего уравнения (13.46), в котором задается крутильная податливость
стержня cz.
Заметим, что композитные структуры, которые определяются двумя неизвестны-
ми параметрами (например, двумя толщинами слоев при заданных углах или толщи-
ной и углом армирования) достаточно просто оптимизируются графическим мето-
дом. Для этого на плоскости параметров строятся линии, соответствующие заданным
ограничениям и определяющие границу области допустимых значений этих парамет-
644
ров. Затем на плоскость наносятся линии уровня целевой функции (например, массы
конструкции) и определяются оптимальные параметры, находящиеся в области до-
пустимых значений и обеспечивающие минимальное значение целевой функции.
При трех неизвестных параметрах такая оптимизация может быть реализована в трех-
мерном пространстве. Пример проектирования сжатой композитной стойки обсуж-
даемым методом приведен в работе [6, с. 105].
Принципиально новые возможности проектирования тонкостенных авиацион-
ных конструкций открываются при использовании анизотропных композиционных
материалов. Применительно к тонкостенным стержням анизотропия композицион-
ного материала порождает связанность осевой деформации, угла закручивания и про-
гиба стержня, что позволяет создавать так называемые адаптивные конструкции,
обеспечивающие управление кинематикой системы при заданных силовых воздейст-
виях. Характерным примером такой системы является композитное крыло с передней
стреловидностью экспериментальных самолетов Х-29 и Су-47. При изгибе такое кры-
ло закручивается, подавляя возможную дивергенцию. Еще одним примером может
служить анизотропная лопасть винта, которая при изменении числа оборотов винта
автоматически изменяет свой угол атаки.
Для анизотропного тонкостенного стержня соотношения упругости (13.36) обоб-
щаются следующим образом
nz = fil lez + ВнЪ’ пи = Brfz + ВУ&Г
Соотношение (13.40), определяющее касательное усилие, остается без измене-
ния, а равенство (13.37) для нормального усилия усложняется и принимает вид
nz = Bz^ + в,к[мх^ + ] + Qx<t»x(S) + ФО),
где
фх(5) = eFx(s) --gj eFx(s) ds - B^ [ f eFx(s)(y -y0)ds+ eFx(s)(x - x0) ds] ,
в — —
Ф/s) = eFy(s) - -J f eFy(s) ds-B^^j eFy(s)(y -y0) ds + f eFy(s)(x-x0) ds] ,
в — —
ф0) = е- -gj eds-5^|]^f e(y-j>0)d$+ f e(x - x0) ds]
И
а остальные обозначения даны в пояснениях к равенствам (13.37) и (13.40). При от-
сутствии анизотропии е = 0 и записанное соотношение вырождается в равенство
(13.37) для ортотропного стержня.
Соотношения упругости типа равенств (13.46) связывают для анизотропного
стержня все кинематические и силовые факторы, т. е. [14]:
(13.49)
645
Коэффициенты стп = спт симметричной матрицы податливости имеют вид
С11 рО’ С22 С33 В + ро(Уо“^уХоУо)»
С44 = f [Ф&) - 2еРх(з)Фх(з) + cF2(s)] ds,
с55 = f (Ф^) - 2еРу(з)Фу(з) + cf2(s)] ds,
С66 = 4^2 f уг 1ф2(х) - 2еФ(5) + с]
к кк к л _
с12 = -д£> ci3 = po-Vo+ cI4 = -^feFx(s)yds,
ci5 = -^f eF/s)yds, ei6 = -2jDjf еУ<^
c23 = -^xo+T%y<» c* = ~i^ eF№ds’
c25 = -^f eFy{s)xds, c26 = -j^j ex ds,
c34 = - i f ^(s) + f eFx(s)y & + f eFx(s)x
C35= - 5 f eFy(s)y ds + f eFy(s)x ds+^j eFy(s)y ds,
1 Г kVc\ е кХл f
C36 = ~2AB ie & + 2ADS * + ЪШ}
C45 = f 5; [Фх(«)Ф/5) - eFx(s)O/s) - eFx(s)Fy(s) + cFx(s)F/s)] ds,
c46 = 21 f 5; 1ф( W) - еф(з)рх(з) - еФ/s) + cFx(s)] ds,
c56 = f [Ф(*)Ф/5> - еФ&Ру<1) ~ еФу(з) + cF/s)] ds
и с = ]/В33.
Уравнения (13.49) содержат 21 независимый коэффициент податливости. Из них
15 внедиагональных членов описывают различные типы связанности деформаций.
Часть из этих коэффициентов можно обратить в нуль соответствующим расположе-
нием координатных осей. Например, для главных центральных координатных осей
х0 = у0 = 0, кх = ку = 0, с12 = 0, с13 = 0 и исчезает связанность между растяжением и из-
гибом оси стержня. Однако коэффициенты с индексами 4, 5, 6 описывают связан-
ность деформаций, вызванную анизотропией стержня, т. е.
— поворот сечения вокруг осей хи у, связанный с поперечной силой (с14, с24, с15, с25);
— поворот сечения вокруг осей хи у связанный с крутящим моментом (с16, с26);
— осевое смещение сечения, связанное с поперечной силой (с34, с35);
— осевое смещение сечения, связанное с крутящим моментом (с36);
— поперечный сдвиг, связанный с крутящим моментом (с46, с56);
— поперечный сдвиг, связанный с силой, действующей в ортогональной плос-
кости (с45);
646
— поворот сечения вокруг оси z, вызванный осевой силой (с63) и изгибающими
моментами (с61, с62).
Для иллюстрации приведенных соотношений рассмотрим два консольных
стержня прямоугольного сечения, изготовленных из углепластика и эксперименталь-
но исследованных в работе [15].
Первый стержень имел следующие размеры (рис. 13.24, а):
£ = 762 мм, а = 24,2 мм, />=13,6 мм, А = 0,76 мм
и был изготовлен выкладкой однонаправленного углепластика под углом ф = 15° к об-
разующей. Более наглядно структура материала элементов стержня может быть пока-
зана на развертке его поверхности, представленной на рис. 13.24, б.
Введенные ранее коэффициенты жесткости стенки одинаковы для полок и сте-
нок стержня и имеют следующие значения: = 96,7 МН/м, Я13 = 22,7 МН/м,
В33 = 10,3 МН/ м. Соотношения упругости для рассматриваемого стержня следуют из
системы (13.49) и имеют вид
в; = спМх, Гх = с41Л/х, w' = CJ3PZ + с36л/г,
Оу= с25^4> Гу = с550у, 0 = c63Pz + c66Mz, (13.50)
где
1 = 1
сп сзз
С41 = - eFx(s) ds, с25 = -1 f eFy(s)y ds,
c55 = f [«$*) - 2eFy(s)<by(s) + cf2(s)] ds,
С36 — С63 2AB f e ds,
c66 = 4J! f уг 1ф2(5> - 2еф<0 + C1
Как следует из системы (13.50), стержень с рассматриваемой структурой компози-
ционного материала обладает связанностью деформаций при осевом нагружении и
кручении. Зависимость угла закручивания стержня, нагруженного осевой силой
Pz = 4,45 Н, от безразмерной осевой координаты z = z/L показана на рис. 13.25 сплош-
ной линией. Точки соответствуют результатам эксперимента [15].
Рис. 13.24. Геометрические параметры (а)
и развертка поверхности (б)
композитного стержня
в, rad
0,00025
0,0002 -
0,00015-
0,0001
0,00005-
0,4
0,8 z
Рис. 13.25. Зависимость угла
закручивания от осевой
координаты для стержня,
нагруженного осевой силой
647
Таблица 13.2
Коэффициенты жесткости панелей анизотропного стержня
Коэффициент жесткости, МН/м Верхняя полка Нижняя полка Стенки
Вп 96,7 96,7 96,7
взз 10,3 10,3 10,3
В13 22,7 -22,7 0
Второй экспериментальный стержень (рис. 13.26) имел аналогичные размеры, но
более сложную структуру материала — его верхняя полка была армирована под углом
15°, нижняя — под углом -15°, а стенки — под углами ±15° так, что они являлись ор-
тотропными. Развертка поверхности такого стержня показана на рис. 13.26, б. Коэф-
фициенты жесткости панелей рассматриваемого стержня представлены в таблице 13.2.
Система уравнений (13.49) принимает вид
вх = С1 \Мх + С\6Н’ Гх = С43ЛГ + С4&х’
®у ~ ^21^у> Гу ~ C55Qy,
< = СЗЗЛ + С34<?х, Q, = C614 + C66^> О3’51)
где
сп_ д" > с1б —c6i 2ADX eyds'
с22=1)у> сзз=5> c34 = c43 = -sf eFx(s)te,
С44 = f 1Ф&) - 2eFx(5) + СВД] ds;
с55 = f 5; - 2е£х(5)Ф/5) + c£2(s)] ds;
С66 = 4^5 f 1ф2<5) - 2еФ0) + с] ds.
Как следует из уравнений (13.51), в рассматриваемом стержне имеет место связь меж-
ду изгибом и кручением. Для стержня, изгибаемого силой Qy = 4,45 Н, зависимость
угла закручивания от осевой координаты показана на рис. 13.27 сплошной линией.
Точки, как и ранее, соответствуют результатам эксперимента [15].
Рис. 13.26. Геометрические параметры (а)
и развертка поверхности (б) композитного стержня
648
Рис. 13.27. Зависимость угла закручивания
от осевой координаты для стержня,
нагруженного поперечной силой
Рис. 13.28. Композитный
стержень
Таким образом, изменяя структурные параметры композита, можно управлять
эффектами связанности деформации и создавать адаптивные элементы конструкций
с достаточно сложным характером поведения под нагрузкой.
В заключении этого раздела рассмотрим круглые тонкостенные стержни, яв-
ляющиеся перспективными элементами для ферменных конструкций космических
платформ и телескопов. Типовой элемент такой конструкции показан на рис. 13.28.
Для круглого тонкостенного стержня с радиусом сечения R уравнения (13.49) прини-
мают вид:
®х с\\^х + сиОх’
Гх ~ С41^х + с440х»
0J, с22^у + C25Q>
Гу = С52^у + C5sQy
0' = с63Рг + с6бМг
(13.52)
Если свойства материала стержня не изменяются по контуру его сечения, коэффици-
енты податливости стп записываются следующим образом:
С11 С22 С'4 ~C2S ~^BZ’ С<м С« 05/
л _ 1 _ с
CM~2nRBz’ сзб ~2лЛ2В/ Сб6 2п№Вг
(13.53)
Как следует из равенств (13.52), рассматриваемый стержень обладает связанно-
стью деформаций при осевом нагружении и кручении, т. е. при растяжении осевой
силой Pz в стержне появляется не только осевая деформация = и>', но и угол закру-
чивания 0. Для ортотропного стержня е = 0 и коэффициенты (13.53) значительно уп-
рощаются, т. е.
С" С22 с<м С55 05^’ сзз 205^’ С« 2яЛЗВ33 ’
С14 = С25 ~ С36 = 0- (13.54)
Круглые стержни для космических конструкций изготавливаются, как правило, из
однонаправленного углепластика, укладываемого так, что волокна составляют срав-
нительно небольшие ±ф углы с осью стержня. Снаружи наматывается тонкий кольце-
вой слой, который уплотняет спиральные слои, обеспечивает жесткость контура сече-
ния и предотвращает расслоение материала.
649
Зависимости модуля упругости и модуля сдвига однонаправленного углепласти-
ка от угла +<р показаны на рис. 13.29 пунктирными линиями, а аналогичные зависи-
мости для пары слоев, армированных под углами ±<р (рис. 13.7), показаны сплошны-
ми линиями, построенными по формулам (13.15). Точки соответствуют эксперимен-
тальным результатам [16]. Заметим, что слой, армированный в одном направлении и
растягиваемый под углом +<р к этому направлению, является анизотропным и при
растяжении в нем появляется деформация сдвига. В слое, растягиваемом под углом
—<р, также появляется деформация сдвига, которая компенсирует соответствующую
деформацию первого слоя, если эти слои связаны и образуют симметричную структу-
ру с углами ±ф (рис. 13.7). В результате такая структура оказывается ортотропной и
обладающей жесткостями, большими чем жесткости материала такой же толщины,
но армированного в одном направлении. Как следует из рис. 13.29, модуль упругости
£х(±ф) является максимальным при ф = 0. Однако по технологическим соображениям
этот угол обычно отличается от нулевого и составляет (5—15)°. Расчетная толщина
стержня определяется по напряжениям, найденным с помощью процедуры, описан-
ной в разделе 13.1, и критериев прочности (13.2) или (13.3). Сжатые стержни проверя-
ются на устойчивость. При этом критическая сила определяется по формуле (13.35), а
изгибная жесткость D = 1/сп — по соответствующей формуле (13.54).
Важным для проектирования космических конструкций свойством композитов
является возможность создавать так называемые термостабильные конструкции, об-
ладающие нулевым коэффициентом линейного температурного расширения (КЛТР).
Как следует из таблицы 13.1, однонаправленные углепластики и органопластики об-
ладают отрицательным КЛТР в направлении волокон. Зависимость КЛТР однонап-
равленного углепластика от угла армирования показана на рис. 13.30 пунктирной ли-
нией. Аналогичная зависимость для материала, симметрично армированного под уг-
Рис. 13.29. Зависимости упругих
постоянных однонаправленного (—)
и симметрично армированного (-)
углепластика от угла армирования
Рис. 13.30. Зависимость КЛТР
однонаправленного (1) и симметрично
армированного (2) углепластика
от угла армирования
650
лами ±<р, построенная с помощью равенств (13.17), показана сплошной линией.
Точки соответствуют экспериментальным результатам [17].
Для того чтобы спроектировать термостабильный стержень с помощью графи-
ков, представленных на рис. 13.29 и 13.30, предположим, что ось х направлена по оси
стержня. Тогда, как следует из рис. 13.30, ах = 0, если <р = 0 или <р = 41,4°. Однако стер-
жень с <р = 0 не может быть изготовлен методом намотки, а стержень с ф = ±41,4° об-
ладает сравнительно низким модулем упругости Ех (рис. 13.29). Допустим, что стер-
жень состоит из двух слоев с толщинами hx и h2 и углами ±ф! и ±ф2. По условиям жест-
кости и технологичности примем ф! = 10°. Тогда, как следует из рис. 13.29 и 13.30,
Е*1) = 118 ГПа и а*? = —0,8 • 10~6 1/°С. Коэффициент линейного расширения стенки
из двух слоев определяется следующим образом:
Полагая ах = 0, получим:
аРЕО)*, + аРЕрл2
E<»hx+EVh2
h2 _ арЕр
h\ ~ -ар£р ’
(13.55)
Пусть ф2 = 45°. Тогда согласно рис. 13.29 и 13.30 имеем Е^ = 24 ГПа, аР = 3,2 • 10-61/°С
и равенство (13.55) дает h2 = 1,23/ij. Стержень с таким соотношением толщины слоев
не изменяет своей длины при нагревании и охлаждении, а конструкция, собранная из
таких стержней, является термостабильной.
13.4. ПАНЕЛИ ИЗ КОМПОЗИЦИОННЫХ МАТЕРИАЛОВ
Плоские панели, образованные из совокупности ориентированных различным
образом композитных слоев, обладают высокой удельной прочностью и жесткостью и
используются в качестве элементов обшивок летательных аппаратов различного на-
значения.
Рассмотрим основной расчетный случай нагружения такой панели нормальными
и касательными усилиями, действующими в ее плоскости (рис. 13.5). Средние дефор-
мации ех, у^ находятся из уравнений (13.10), а деформации e'j, ez2, у*12 и напряжения
а2’ т12 во всех слоях — по формулам (13.5) и из равенств (13.1). Далее с помощью
одного из критериев прочности, изложенных в разделе 13.1, можно определить уси-
лия Nx, Ny, при которых происходит нарушение монолитности и разрушение во-
локон композиционного материала.
Рассмотрим типовые схемы армирования композитных панелей. Если панель
растянута или сжата в направлениях осей х и у (рис. 13.5) так, что N = 0, наиболее
простой и естественной является структура, состоящая из слоев с углами армирова-
ния 0° и 90° (рис. 13.31). Коэффициенты жесткости этих слоев (13.8) принимают вид
Л0 — А90 — р АО = Л 90 = р V Л 90 = АО = р
71И ^22 П1’ ^12 ^12 r'lv12’ 7111 л22 ^2»
л0 — л 90 — /7 АО = АО = л 90 — Л 90 — П
Л33 7133 СГ12, /113 л23 Л13 л23 и,
а коэффициенты жесткости панели (13.11) определяются следующим образом:
= Exh0 + Е2А90, Б12 = (Ао + A9o)E|V|2,
Б12 = E2h§ + Exh^, В33 = (Ао + Л9о)6\2.
651
Рис. 13.32. Элемент панели
с углами армирования ± 45°
Рис. 13.31. Элемент панели
с углами армирования 0° и 90°
Здесь й0 и йэд — толщины слоев с углами 0° и 90°. Средние модули упругости панели
находятся по формулам (13.15). Если панель нагружена только касательными усилия-
ми N (рис. 13.5), т. е. Nx = Ny = 0, наиболее простой является структура с углами ар-
мирования ±45° (рис. 13.32). Тогда согласно равенствам (13.8)
=^=i<Ei + Е2 + 2^|2), = Е^п + | (Г, + Е2 - 2Е|2),
A^^(E + E2-2E{v{2), Л«=Л«=0
и коэффициенты жесткости панели (11) Втп = ЯШЛЛ45 (тп = 11, 12, 22, 33).
В общем случае напряженного состояния, когда отличны от нуля все три усилия
Nx, Ny и N (рис. 13.5), панель часто набирается из слоев с углами армирования 0°, 90°
и ±45°. Коэффициенты жесткости такой панели определяются следующим образом:
Вт = AQmnh. + A^Jign + Л45 A45, (13.56)
тп тп и тп w тп 4j ’ х 7
а средние модули упругости панели находятся по формулам (13.15). Если принять, что
толщины слоев с углами 0°, 90°, +45° и —45° одинаковы, т. е.
, h h
по П90 4’Л45 2 ’
где h — общая толщина панели, то равенства (13.56) принимают вид:
= ^22= § [3(^1 ^2) + 2(£jV12 + 2Gl2)],
Bl2 = ^El + E2 + 2(3Elvl2-2Gl2)],
В33 = ^[Et + E2-2(Elvl2-2Gl2)].
Если подставить эти выражения в формулы (13.15) для упругих постоянных, получим
Ех=Еу=Е’ Vxy = V>>x = V> Gxy = G = 2(l+v) ’ (1357)
где г, (Е\ + Е2 + 2£’jVj2)(£'i + Е2 + 2£'jV12 + 4G12) 3(Е, + Е2) + 2(£,v12 + 2G12) + Ег + 2(3£,v12 - 2G,2) 3(£, + £2) + 2(£,v12 + 2GI2) ‘ (13’58)
Как следует из равенств (13.57), рассматриваемая структура является квазиизотроп-
ной и обладает двумя упругими постоянными Е и v. Такая структура не является
единственной — слоистый композит является квазиизотропным при плоском напря-
женном состоянии (рис. 13.5), если он состоит из трех и более слоев (к > 3), все слои
изготовлены из одного материала, имеют одинаковую толщину и углы армирования
<pz=(/-l)J (/= 1, 2, 3,Л > 3).
(13.59)
652
При к = 3 равенство (13.59) определяет следующую структуру материала: (0°, 60°,
-60°); при к = 4 имеем случай, рассмотренный выше, т. е. (0°, 45°, —45°, 90°); при к =
= 5 (0°, 36°, -36°, 72°, —72°); при к = 6 (0°, 30°, -30°, 60°, -60°, 90°) и т. д. Все квази-
изотропные структуры имеют упругие постоянные, определяемые равенствами
(13.58). Такие структуры используются для замены металлических панелей на компо-
зитные. Сравнительные характеристики традиционных и квазиизотропных компози-
ционных материалов представлены в таблице 13.3.
Т абл ица 13.3
Характеристики традиционных
и композитных конструкционных материалов
Материал Плот- ность р, кг/м3 Модуль уп- ругости £, ГПа Коэффици- ент Пуассо- на, V Удельный мо- дуль £/р, ГПа • м3/кг
Алюминиевый сплав 2700 71 0,3 0,0263
Титан 4500 142 0,3 0,0315
Сталь 7850 200 0,3 0,0255
Стеклопластик
— квазиизотропный 2100 27 0,34 0,0129
— армированный по траекториям главных напряжений 2100 36,9 0,053 0,0176
Углепластик
— квазиизотропный 1550 54,8 0,31 0,0353
— армированный по траекториям главных напряжений 1550 75,9 0,039 0,049
Органопластик
— квазиизотропный 1320 34,8 0,33 0,0264
— армированный по траекториям главных напряжений 1320 50,3 0,035 0,0381
Боропластик
— квазиизотропный 2100 80,3 0,33 0,0382
— армированный по траекториям главных напряжений 2100 114,8 0,035 0,0547
653
Наиболее широкое применение в конструкциях летательных аппаратов получили
в настоящее время углепластики, удельный модуль которых, а следовательно, и рас-
четная весовая эффективность, превышает соответствующую характеристику алюми-
ниевого сплава на 34,2%. Реальный выигрыш в массе, получаемый в результате заме-
ны алюминиевого сплава на углепластик в рамках традиционной силовой схемы пла-
нера самолета, обычно не превышает 25%.
Структура панели, состоящей из к слоев, определяется заданием 2к параметров:
к значений углов армирования <pz и к значений толщин слоев Az (рис. 13.5), причем в
общем случае материал слоев может быть различным. Естественно попытаться распо-
рядиться структурными параметрами панели так, чтобы она оказалась в некотором
смысле оптимальной, например, чтобы масса ее была минимальной.
Рассмотрим сначала такую задачу для одного армированного слоя с толщиной h
и углом (р. Напряжения, действующие в слое, определяются равенствами (13.4). Для
одного слоя имеем
где h — толщина слоя. Выражая из равенств (13.4) напряжения Gj, о2 и т12’ получим
Gj = (Nx cos2 ф + Ny sin2 ф 4- sin 2ф),
a2= Jj Sin2 Ф + Ny cos2 Ф + ^xy s^n 2ф),
Ti2 = й - Nx) sin ф cos ф 4- cos 2ф]. (13.59)
Применим условие прочности (13.3). Полагая о, = Gj, найдем расчетную толщину
h=________________<*i_____________
Nx cos2 ф + Ny sin2 ф 4- N sin2 2ф ’
Записывая условие минимума Л, т. е. ёй/ёф = 0, найдем
2NXV
Если угол ф удовлетворяет этому условию, то последнее соотношение (13.59) дает
т12 = 0. Отсюда следует, что условие (13.60) определяет армирование слоя вдоль траек-
торий главных напряжений. Как известно, главные нормальные напряжения облада-
ют экстремальными свойствами, т. е. включают наибольшее и наименьшее значения
нормального напряжения в данной точке тела. Условие (13.60) определяет совпадение
направления армирования с направлением главного и, как можно показать, наиболь-
шего напряжения оР Напряжение о2 при этом является минимальным. Минималь-
ной оказывается и толщина слоя h. Заметим, что так как период функции tg 2ф равен
тг, условие (13.60) определяет два угла ф, отличающиеся на л/2. В связи с этим введем
двухслойную структуру с углами
Ф1 = 2 arctg , Ф2 = <р1 + 2. (13.61)
В такой панели волокна в каждом из двух слоев направлены по траекториям макси-
мальных главных напряжений. Преобразуя соотношения упругости (13.10) с по-
мощью равенств (13.61), получим [2, 11]
= £ой(ех + voex), Ny = Eoh(ey + voex), Nxy = G(fq39> (13.62)
654
где
г _ Ео г -
0 ,_v^ 2(1+v0)’
£0 = 2(£,£+ £2) [ЯД1 + VI2> + £2(1 + V2l)][^d - V12) + £2(1 - v21)J, (13.63)
£,v)2 + £2v2i
v0 £, + £2
Равенства (13.62) по форме совпадают с законом Гука для изотропного матери-
ала, а £0 характеризует модуль упругости такого условно изотропного материала, об-
разованного из двух слоев композита, ортогонально армированных вдоль траекторий
главных напряжений. Значения £0 и v0 для типовых композитов приведены в
таблице 13.3.
Сравнивая £0 с £, определяемым первым равенством (13.58), можно заключить,
что £0 > £. При этом следует иметь в виду, что квазиизотропная структура с упругими
постоянными в форме (13.58) существует при любых комбинациях усилий Nx, N? Nxy,
а двухслойная структура, армированная по траекториям главных напряжений с упру-
гими постоянными в форме (13.63), существует только при вполне определенных уси-
лиях, которые определяют углы армирования слоев (13.61).
Рассмотрим многослойные панели, армированные по траекториям главных на-
пряжений. Используя соотношения (13.1) и (13.5), запишем выражение для касатель-
ных напряжений, действующих в слое с номером i
Т<12 = G<12^ey “ £х) Sin 2(₽' + Уху COS 2<Р/] •
Отсюда следует, что = 0, если гу = ех = е и = 0. Тогда равенства (13.10) дают
Nx = (-#11 + ^12)е» *у = (-#21 + #22^’ *ху = (#31 + #32)е-
Отсюда можно найти деформацию
и записать следующие два условия, которые связывают действующие усилия и струк-
турные параметры композита
(£п + £12)^-(£21 + £22Ил = 0,
(£31 + £32)(^ + Ny) - (Би + 2£12 + В22)^ = 0.
Если все слои изготовлены из одного материала, эти условия имеют вид:
к
У sin2 (pz — Ny cos2 ф, + n(Nx cos2 фу - Ny sin2 ф,)] = 0,
/=1
к
X Az[m(^ + Ny) sin ф, cos ф, - (1 + и)Лу = 0, (13.65)
/=1
где
_£2(l+v21) _ £j-£2
П £,(1+v12)’ т £,(1+v12)-
Напряжения в слоях определяются соотношениями (1), (5) и (64), т. е.
= °(2O = °2=”viT У Т<12 = 0- <13-66>
1 1 Л(1 + л)’ 2 2 й(1 + П) ’12 ' ’
655
Расчетная толщина панели
к
h=Yhi
/=1
может быть найдена с помощью условий прочности (13.2), (13.3). Как следует из ра-
венств (13.66), напряжения не зависят от номера слоя, т. е. рассматриваемая структура
является равнонапряженной. Она существует, если выполняются условия
п <____< 1 Nxy < 1 ~п (13 67)
1+л^ЛГх + ЛГ,^1+л’ V + V 2(1 + п) •
У х ‘'у
Наибольшее применение равнонапряженные структуры получили при проекти-
ровании конструкций типа баллонов давления и трубопроводов, для которых усилия
Nx и N являются растягивающими, a = 0. Для таких условий нагружения ограни-
чения (13.67), как правило, выполняются, второе равенство (13.65) требует, чтобы схе-
ма армирования была симметричной, а первое определяет возможные сочетания
структурных параметров композита. Поскольку имеется 2к таких параметров (к зна-
чений и <pz), равнонапряженная структура является неединственной, однако все воз-
можные варианты имеют одинаковую суммарную толщину h. Рассмотрим, например,
цилиндрический трубопровод радиуса R, нагруженный внутренним давлением р. На-
правляя ось* вдоль оси трубопровода и считая, что концы его закрыты, получим [4]
Nx = pR/2, Ny=pR, Nxy = 0. Тогда первое условие (13.65) принимает вид
к
X Л,[3(л - 1) cos2 (pz + 1 - 2п\ = 0. (13.68)
/=1
Пусть трубопровод образован симметричной намоткой под углами ±ф. Тогда к = 1 и
условие (13.68) позволяет найти оптимальное значение угла, т. е.
2 2п — 1
cos <Р=30ПП)-
Если трубопровод состоит из осевого (hx = Ао, ф! = 0°) и кольцевого (й2 = й90, <р2 = 90°)
слоев, то к = 2 и условие (13.68) дает оптимальное соотношение толщины слоев
= 1 - 2п
2 — п *
Сжатые панели могут терять устойчивость по форме, показанной на рис. 13.33.
Критическое значение усилия Тх определяется в результате минимизации следующе-
го выражения [4]
тх = [АЛ2.+ (*>12 + 21>зз)Ч^ + (13.69)
по параметрам = тъ/а и = пъ/Ь, где т = 1, 2, 3,... и п = 1, 2, 3,... являются числа-
ми полуволн искривленной поверхности панели, показанной пунктирными линиями
на рис. 13.33 (для этой панели т = 2 и п = 1). Приближенная минимизация правой
части равенства (13.69) дает
rjp = (JD^2 + Р|2 + 2Л22). (13.70)
О
Коэффициенты жесткости Dmn, входящие в формулы (13.69) и (13.70), определяются
равенствами (13.24) для панелей с симметричным расположением слоев по толщине и
равенствами (13.25) в общем случае.
656
Рис. 13.33. Форма
потери устойчивости
сжатой панели
Рис. 13.34. Трехслойная панель
с несущими слоями из углепластика
с сотовым заполнителем
Для тонких панелей величина критической нагрузки оказывается, как правило,
довольно низкой. Для повышения критической нагрузки металлические панели
обычно подкрепляются стрингерами. Применительно к композиционным материа-
лам более технологичными представляются трехслойные панели, состоящие из тон-
ких композитных слоев и легкого заполнителя из пенопласта, а также из полимерных
или алюминиевых сот (рис. 13.34). Для проектирования панели толщина, найденная
из условия прочности, разделяется на две составляющие, соответствующие несущим
слоям, а расстояние между несущими слоями, т. е. толщина заполнителя Ло, определя-
ется из условия устойчивости трехслойной панели. Равенство (13.69), определяющее
критическую нагрузку, обобщается для трехслойной панели следующим образом [4]:
Z) Dmn 1
^х~ V V ’
+ D„mX2 + 2Z)X2X2 + -г? + - Л2Х2Х2)
тп т пт п т п К К v тп пт п'
где
Dmn = + D33Vn, Dnm = D^i + D33Mn, D = Dn + D33,
Kx=G^h., K2 = G^h0.
Здесь GQXZ и GQyz — модули сдвига заполнителя в плоскостях xz и yz (рис. 13.6).
13.5. КОМПОЗИТНЫЕ БАЛЛОНЫ ДАВЛЕНИЯ
Применение композиционных материалов в конструкциях летательных аппара-
тов, в частности широко распространенная замена алюминиевых сплавов на угле-
пластики, позволяет снизить массу конструкции на величину порядка 20—30%.
Однако существуют уникальные примеры применения композитов, в которых
сочетание высоких механических свойств этих материалов и возможностей специфи-
ческих для них технологических процессов порождает качественно новые конструк-
ции, обладающие исключительно высокой степенью весового совершенства. К таким
конструкциям относятся тонкостенные оболочки вращения, нагруженные внутрен-
ним давлением, которые являются типичной расчетной моделью для баллонов давле-
ния, корпусов ракетных двигателей твердого топлива, баков и резервуаров различного
назначения. Композитные конструкции этого типа изготавливаются методом непре-
рывной намотки, согласно которому на вращающуюся оправку укладываются спи-
ральные ленты из волокон, пропитанных связующим, образующие цилиндрическую
часть баллона и днища, а затем цилиндрическая часть усиливается лентами, наматы-
ваемыми в кольцевом направлении. Намотка кольцевого слоя на предварительно уло-
женные симметричные спиральные слои показана на рис. 13.35. После завершения
657
Рис. 13.35. Намотка композитного баллона давления
намотки производится отверждение связующего и удаление оправки. Технология на-
мотки описана в работах [1, 2, 3, 5].
Рассмотрим оболочку вращения, армированную волокнами под углами ±<р к об-
разующей и нагруженную равномерным внутренним давлением р и осевыми силами
Т> равномерно распределенными по параллелям с радиусом г0 (рис. 13.36). Мериди-
ональное и кольцевое усилия, действующие в оболочке, выражаются через заданные
нагрузки и уравнение образующей z(r) следующим образом [2,4, 5, 11]:
Na = -О[1 + ^)2]1/2, ЛГр = Д [1 + (z')2]1/2 {рг- [ (13-71)
где
Q=Tr. + p^-rl), z'=%,
Q — осевая сила, действующая в сечении г = const. Для того чтобы спроектировать обо-
лочку, т. е. найти оптимальную форму ее меридиана, воспользуемся условием прочнос-
ти в форме (13.3), т. е. будем считать, что несущая способность оболочки определяется
прочностью волокон, и игнорировать возможное появление трещин в матрице, обсуж-
давшееся в разделе 13.1. Тогда в равенствах (13.4) следует принять с2 = 0 и т12 = 0.
Предполагая, что оболочка состоит из двух симметрично армированных слоев с угла-
ми ±<р(г), и используя формулы (13.9), получим
Na = d{h cos2 <р, Wp = d{h sin2 <p, (13.72)
где h(r) — толщина оболочки. Равенства (13.72) дают следующее условие
5 =tg2q>, (13.73)
J’a
которое отражает тот факт, что усилия Na и TVp воспринимаются только волокнами
композита. Подставляя усилия (13.71) в уравнение (13.73), получим
7= Г22 ?гг -tg2<P- (13.74)
z 1-^4- __
г2 р Г
658
Рис. 13.36. Армированная
оболочка вращения
Рис. 13.37. Схема расположения фланца
в вершине композитной оболочки
Изменение угла <р(г) можно задать различным образом, однако наибольшее рас-
пространение получила геодезическая намотка, при которой волокна совпадают с гео-
дезическими линиями поверхности. Это связано с тем, что гибкое волокно, укладывае-
мое под натяжением на абсолютно гладкую поверхность, стремится принять форму
геодезической линии. Поведение геодезической линии на поверхности вращения оп-
ределяется формулой Клеро
rsin(p = r0. (13.75)
Отсюда следует, что угол <р при уменьшении г возрастает и достигает значения 90° при
г = г0, т. е. волокно, уложенное по геодезической линии, касается полюсного отверс-
тия радиуса г0 (рис. 13.35, 13.36). Приг=Яимеем
r0 = R sin <рл.
(13.76)
Таким образом, чем больше угол фл на экваторе днища, тем больше радиус полюсно-
го отверстия. Замкнутая в вершине оболочка получается только при <р = 0, т. е. при
армировании вдоль меридианов. Исключая <р из уравнения (13.74) с помощью форму-
лы (13.75), запишем следующее уравнение, определяющее оптимальную форму мери-
диана
rz
Г[1 +(z)2]
2>о
1+^4-
1 г2 pRr2
(13.77)
Здесь введены безразмерные координаты г = r/R,
z = z/Rhz' = dz/dr.
Как следует из равенств (13.75) и (13.76), при гео-
дезической намотке с углом <р > 0 в вершине оболочки
образуется отверстие с радиусом г0. В баллонах давле-
ния это отверстие должно быть закрыто. Для этого пе-
ред намоткой на оправку устанавливается металличе-
ский фланец, показанный на рис. 13.37 и 13.38, к ко-
торому крепится крышка, закрывающая полюсное
отверстие. Если полюсное отверстие закрыто, то об-
разующую оболочки можно разделить на два участка,
соответствующих R>r>bnb>r>rQ (рис. 13.37).
При R > г > b конструкция работает как
оболочка, нагруженная равномерным внутренним
Рис. 13.38. Композитный
баллон давления
с металлическим фланцем
659
давлениемр при закрытом полюсном отверстии. При этом ^2лг0 = т. е. q = О,5рго,
и уравнение (13.77) принимает вид
Отсюда после некоторых преобразований и интегрирования получим
7(1 - Г2)(г2 - rj)(r2 - г2) ’
где
При выводе уравнения (13.79) было учтено условие параллельности касательной
к контуру оси вращения при r= R (рис. 13.36) (z' — °° при г -> 1). Образующая z(f)
на первом участке (R > г > Ь) может быть получена в результате численного интегри-
рования равенства (13.79). Отметим, что результат может быть выражен и через табу-
лированные эллиптические интегралы:
Z = F(k, 0) + Е(к, 0), (13.80)
71 “ г2
где _____
0 = arcsin к—- , к = ,
Ч1 _ ч N1 _ г2
в
F(k, 0) = J . — эллиптический интеграл I рода,
0 71 - &2sin2 0
0
Е(к, 0) = J 71 - A^sin2 0 d0 — эллиптический интеграл II рода,
о
При > г > г0 оболочка соприкасается с фланцем и нагружена давлением рх, ко-
торое в силу малой ширины полки фланца считается постоянным. Из условия равно-
весия фланца имеем (рис. 13.37)
Р\К(Ь2 - rl) =pnb2,
т. е.
_ _ pb2 _ pb2 .....
b2-rl b2-r%’ (1181)
где Ъ = b/R.
Отверстие радиуса г0 свободно, т. е. Т= 0. Таким образом, уравнение (13.77) при-
нимает вид
rz{ = 2г2 - rl
Z\ [1 + (Zi )2] г2-fl 9
b>r>r0.
(13.82)
Интегрируя уравнение (13.82) с учетом условия плавного сопряжения участков, т. е.
z'(b) = z\(b), получаем
г _ 'J'2 -
1 7(':3 - + г2) ’
(13.83)
где
= И *2 - г%
3>4 »|4 +*4(1 - 2 •
660
На участке b > г > rQ образующая оболочки может быть построена численным ин-
тегрированием уравнения (13.83). Как и ранее, результат может быть записан через
эллиптические интегралы:
Z,=—^L=F(k,Q) + JF^74E(k,Q) + C, (13.84)
+ r4
где
a lr2 ~
0 = arccos /—-— .
ч "4
Постоянная С определяется из условия непрерывности участков z(b) = Z[(b).
Таким образом, образующая днища может быть построена по формулам (13.79),
(13.83) или (13.80), (13.84). Радиус фланца b (рис. 13.37) может быть выбран из конст-
руктивных соображений, причем давление определяемое формулой (13.81), не
должно превышать предела прочности материала на сжатие поперек волокон. Анали-
зируя правую часть уравнения (13.78), можно заключить, что она, а следовательно, и
z" обращаются в нуль при г = г0Л/й5 = 1,225г0. При этом значении г кривизна обра-
зующей, определяемой уравнением (13.79), изменяет свой знак. Для того чтобы дни-
ще оставалось всюду выпуклым (т. е. чтобы выполнялось условие ?" < 0 при ?' < 0),
необходимо принять b > 1,225г0.
Образующие оболочек при различных значениях радиуса г0 и Ъ = 1,225г0 показа-
ны на рис. 13.39 и представлены в таблице 13.4.
Толщина оболочки Л(г) увеличивается к полюсному отверстию, так как одно и то
же число лент, проходящих через все сечения оболочки, располагается вдоль парал-
лелей с уменьшающимся радиусом г (рис. 13.37). Предположим, что через сечение
г = const оболочки проходит т лент с углами ±<р(г). Обозначая ширину ленты через с,
а ее толщину — через 5, можно записать площадь сечения оболочки следующим обра-
зом: F= тпсб/cos ф. С другой стороны, F= 2itrh(r). Отсюда следует, что
г/ \ _
v 7 2nrcos ф ’
На экваторе оболочки, т. е. при r= R, имеем:
д _ тсб
R 2nRcos фЛ ’
Таким образом,
R cos ф₽
h(r) = hR----(13.85)
v 7 Arcos ф(г) v 7
Заметим, что при г = г0, т. е. на краю полюсного отверстия, равенство (13.75) дает ф =
= 90°, и толщина Л(г), определяемая формулой (13.85), обращается в бесконечность.
Это связано с тем, что при выводе формулы (13.85) предполагалось, что все волокна в
ленте имеют один и тот же угол ф и, следовательно, касаются параллели г = г0. Однако
в действительности параллели г0 касается только крайнее волокно ленты. Поэтому ра-
венство (13.85) справедливо только при г > г0 + с, т. е. при удалении от края полюсного
отверстия на расстояние, превышающее ширину ленты. При г0 + с > г > г0 толщину
оболочки можно приближенно считать постоянной и равной значению, следующему
из равенства (13.85) при г = г0 4- с (рис. 13.37).
661
Образующие композитных оболочек
Таблица 13.4
V = 0 ?о = 0,05 го = 0,10 го = О,15 г0 = 0,20 г0 = 0,25 го = 0,30
г Z Г Z Г Z Г Z Г Z Г Z Г Z
1,00000 0,00000 1,00000 0,00000 1,00000 0,00000 1,00000 0,00000 1,00000 0,00000 1,00000 0,00000 1,00000 0,00000
0,99691 0,05545 0,99706 0,05417 0,99909 0,03015 0,99738 0,05138 0,99908 0,03056 0,99774 0,04826 0,99909 0,03090
0,98768 0,11038 0,98826 0,10786 0,99637 0,06030 0,98955 0,10235 0,99633 0,06112 0,99099 0,09619 0,99636 0,06180
0,97236 0,16430 0,97366 0,16060 0,99180 0,09045 0,97655 0,15252 0,99171 0,09169 0,97977 0,14346 0,99178 0,09270
0,95105 0,21670 0,95334 0,21193 0,98535 0,12060 0,95845 0,20150 0,98519 0,12225 0,96416 0,18976 0,98531 0,12360
0,92387 0,26710 0,92741 0,26139 0,97695 0,15076 0,93536 0,24889 0,97670 0,15281 0,94425 0,23476 0,87689 0,15450
0,89100 0,31503 0,89605 0,30855 0,96652 0,18090 0,90741 0,29432 0,96615 0,18337 0,92016 0,27818 0,96645 0,18540
0,85264 0,36006 0,85943 0,35301 0,95394 0,21105 0,87477 0,33746 0,95343 0,21394 0,89202 0,31971 0,95388 0,21630
0,80901 0,40180 0,81776 0,39438 0,93907 0,24120 0,83763 0,37797 0,93841 0,24450 0,86001 0,35910 0,93904 0,24720
0,76040 0,43988 0,77131 0,43233 0,92172 0,27172 0,79621 0,41556 0,92089 0,27506 0,82434 0,39610 0,92176 0,27810
0,70710 0,47401 0,72035 0,46656 0,90166 0,30150 0,75077 0,44997 0,90064 0,30562 0,78525 0,43048 0,90182 0,30900
0,64944 0,50394 0,66518 0,49685 0,87856 0,33165 0,70160 0,48099 0,87733 0,33619 0,74300 0,46208 0,87894 0,33990
0,58778 0,52954 0,60614 0,52304 0,85210 0,36180 0,64902 0,50846 0,85056 0,36675 0,69791 0,49073 0,85275 0,37080
0,52249 0,55073 0,54360 0,54504 0,82144 0,39195 0,59342 0,53227 0,81977 0,39731 0,65035 0,51635 0,82276 0,40170
0,45399 0,56759 0,47795 0,56289 0,78603 0,42210 0,53522 0,55242 0,78415 0,42788 0,60078 0,53889 0,78829 0,43260
0,38268 0,58030 0,40963 0,57672 0,74460 0,45255 0,47496 0,56895 0,74257 0,45844 0,54971 0,55835 0,74839 0,46350
0,30901 0,58921 0,33911 0,58682 0,69526 0,48240 0,41330 0,58204 0,69320 0,48900 0,49783 0,57482 0,70163 0,49440
0,23344 0,59482 0,26699 0,59359 0,63472 0,51255 0,35117 0,59194 0,63299 0,51956 0,44603 0,58846 0,64580 0,52530
0,15643 0,59779 0,19413 0,59759 0,55631 0,54270 0,29003 0,59904 0,55591 0,55012 0,39552 0,59950 0,57708 0,55620
0,07845 0,59890 0,12247 0,59951 0,44175 0,57285 0,23248 0,60382 0,44696 0,58069 0,34806 0,60824 0,48831 0,58710
0,00000 0,59907 0,06123 0,60015 0,12230 0,60300 0,18371 0,60687 0,24391 0,61125 0,30618 0,61509 0,36790 0,61800
0,06123 0,60015 0,11477 0,60317 0,18073 0,60704 0,22907 0,61256 0,30132 0,61584 0,34500 0,62256
0,06023 0,60016 0,10856 0,60327 0,17508 0,60733 0,21683 0,61335 0,29205 0,61713 0,32608 0,62530
0,05833 0,60017 0,10389 0,60333 0,16988 0,60755 0,20765 0,61375 0,28345 0,61816 0,31186 0,62670
0,05579 0,60018 0,10099 0,60334 0,16303 0,60780 0,20194 0,61390 0,27203 0,61928 0,30301 0,62722
0,05000 0,60020 0,10000 0,60335 0,15000 0,60805 0,20000 0,61392 0,25000 0,62048 0,30000 0,62729
Окончание таблицы 13.4
го = 0,35 *0 = 0,40 г0 = 0,45 ^0 = 0,50 Л) = 0,55 го = 0,60 г0 = 0,65
г Z Г Z Г Z Г Z Г Z Г Z г Z
1,00000 0,00000 1,00000 0,00000 1,00000 0,00000 1,00000 0,00000 1,00000 0,00000 1,00000 0,00000 1,00000 0,00000
0,99813 0,04479 0,99913 0,03094 0,99853 0,04096 0,99923 0,03045 0,99894 0,03674 0,99939 0,02924 0,99934 0,03206
0,99253 0,08933 0,99653 0,06187 0,99414 0,08174 0,99690 0,06900 0,99577 0,07337 0,99754 0,05847 0,99739 0,06405
0,98324 0,13335 0,99216 0,09281 0,98685 0,12215 0,99302 0,09135 0,99051 0,10975 0,99446 0,08772 0,99415 0,09591
0,97031 0,17662 0,98600 0,12375 0,97671 0,16201 0,98754 0,12180 0,98320 0,14577 0,99013 0,11695 0,98965 0,12757
0,95382 0,21889 0,97800 0,15468 0,96378 0,20144 0,98044 0,15225 0,97387 0,18131 0,98454 0,14619 0,98390 0,15897
0,93387 0,25992 0,96809 0,18562 0,94814 0,23937 0,97170 0,18270 0,96260 0,21626 0,97766 0,17543 0,97696 0,19005
0,91058 0,29949 0,95618 0,21656 0,92990 0,27654 0,96120 0,21325 0,94946 0,25051 0,96949 0,20466 0,96886 0,22074
0,84411 0,33739 0,94217 0,24750 0,90917 0,31250 0,94892 0,24360 0,93452 0,28396 0,95999 0,23390 0,95967 0,25100
0,85464 0,37343 0,92591 0,27844 0,88611 0,34710 0,93477 0,27405 0,91792 0,31652 0,94914 0,26314 0,94943 0,28076
0,82237 0,40743 0,90724 0,30375 0,86087 0,38022 0,91863 0,30450 0,89975 0,34810 0,93689 0,29237 0,93824 0,30998
0,78754 0,43926 0,88594 0,34031 0,83367 0,41174 0,90040 0,33495 0,88017 0,37862 0,92322 0,32161 0,92616 0,33862
0,75044 0,46877 0,86173 0,37125 0,80471 0,44157 0,87992 0,36540 0,85933 0,40802 0,90809 0,35085 0,91330 0,36663
0,71139 0,49589 0,83427 0,40219 0,77427 0,46963 0,85702 0,39585 0,83740 0,43624 0,89147 0,38009 0,89975 0,39399
0,67079 0,52056 0,80311 0,43312 0,74263 0,49588 0,83150 0,42630 0,81460 0,46324 0,87333 0,40325 0,88562 0,42066
0,62908 0,54277 0,76764 0,46406 0,71015 0,52028 0,80313 0,45675 0,79114 0,48899 0,85365 0,43856 0,87103 0,44662
0,58683 0,56254 0,72708 0,49500 0,67720 0,54283 0,77166 0,48720 0,76727 0,51348 0,83246 0,46780 0,85611 0,47186
0,54471 0,57994 0,68038 0,52594 0,64426 0,56357 0,73685 0,51765 0,74326 0,53671 0,80979 0,49704 0,84100 0,49637
0,50357 0,59512 0,62612 0,55687 0,61185 0,58255 0,69854 0,54810 0,71942 0,55869 0,78578 0,52627 0,82586 0,52016
0,46445 0,60825 0,56274 0,58781 0,58057 0,59986 0,65686 0,57855 0,69608 0,57947 0,76066 0,55555 0,81083 0,54322
0,42866 0,61956 0,49030 0,61875 0,55113 0,61562 0,61266 0,60900 0,63760 0,59909 0,73487 0,58475 0,79608 0,56557
0,42211 0,62154 0,45984 0,62954 0,54325 0,61697 0,57465 0,63061 0,66503 0,60623 0,68936 0,62477 0,78798 0,57707
0,40984 0,62497 0,43467 0,63591 0,52775 0,62677 0,54326 0,64281 0,64758 0,61896 0,65178 0,64552 0,77029 0,59804
0,39760 0,62775 0,41577 0,63912 0,51284 0,63260 0,54167 0,64884 0,63010 0,62962 0,62354 0,65539 0,75118 0,61608
0,38160 0,63080 0,40400 0,64029 0,49226 0,63910 0,50499 0,65102 0,59713 0,64483 0,60597 0,65888 0,71199 0,64275
0,35000 0,63412 0,40000 0,64046 0,45000 0,64635 0,50000 0,65133 0,55000 0,65572 0,60000 0,65937 0,65000 0,66274
Рис. 13.39. Образующие
композитных оболочек
при различных размерах
полюсного отверстия
Рис. 13.40. Зависимости коэффициента весовой
эффективности оболочки |1 и относительного
внутреннего объема V от относительного
радиуса полюсного отверстия г0.
Подставляя усилия (13.71) и толщину (13.85) в соотношения (13.72), можно най-
ти напряжение, действующее в композите вдоль волокон. Окончательный результат,
справедливый для обоих участков образующей z£r) (13.80) и zx(r) (13.84), имеет вид:
а - pR
1 2ЙЛСО82фя‘
(13.86)
Отсюда следует, что ст! не зависит от г, т. е. спроектированная оболочка является рав-
нонапряженной.
Масса оболочки М и ее внутренний объем Ксвязаны следующим соотношением:
где ц — коэффициент весовой эффективности; р — плотность материала; с?! — напря-
жение, связанное с действующим давлением равенством (13.86). Зависимости коэф-
фициента ц и относительного объема V = V/R? от г0 для рассматриваемых оболочек
показаны на рис. 13.40. Расчетная толщина hR определяется с помощью равенства
(13.86) и критерия прочности (13.3).
Образующие, показанные на рис. 13.39, и приведенные выше соотношения могут
быть использованы для проектирования баллонов давления с формой, близкой к эл-
липсоиду вращения (рис. 13.41) или для проектирования днищ цилиндрических бал-
лонов (рис. 13.35, 13.38).
Для цилиндрической части баллона г = r0 = R, Т — pR/2 и соотношения типа
(13.71) имеют вид:
^а=Т’ N?=PR- (1387)
Если считать, что цилиндрическая часть баллона состоит из симметричных слоев с уг-
лами ±фЛ, то равенство (13.73) дает
tg2 фЛ = 2, фЛ = 54,7356°.
При таком угле армирования уравнение (13.78) определяет образующую цилиндриче-
ской оболочки, т. е. намотка оболочки с днищами невозможна. Для существования
цилиндрического баллона с днищами необходимо, чтобы фЛ < 54,7356°. В этом случае
для того, чтобы волокна воспринимали усилия (13.87), необходимо усиление спи-
664
Рис. 13.41. Композитный баллон
давления с формой, близкой
к эллипсоиду вращения
Рис. 13.42. Намотка
сетчатого композитного
отсека
рального слоя с углами ±фА кольцевым слоем (ф = 90°). Тогда равенства (13.72) при-
нимают вид
Na = ccxhR cos2 фл, Wp = acxhR sin2 фА + о*Лк. (13.88)
Здесь индексы «с» и «R» относятся к спиральному слою, а индекс «к» — к кольцевому
слою. Предполагая, что оптимальный баллон является равнонапряженным, примем
ai = aii = а1’где а1 определяется равенствами (13.86). Тогда соотношения (13.88) дают
hK = hR(3 cos2 фл - 1). (13.89)
Это условие, обеспечивающее равнонапряженность материала баллона, является частным
случаем условия (13.68) и следует из него при к = 2, ф] = фА, hx = hRi ф2 = 90°, h2 = hK,n = 0.
Для проектирования композитного баллона давления с днищами, изготавливаемо-
го методом непрерывной намотки (рис. 13.35), необходимо задать расчетное давление р,
предел прочности композита при растяжении вдоль волокон радиус цилиндриче-
ской части баллона R и радиус полюсного отверстия г0. В процессе проектирования по
заданной величине г0 = Гц/R находится с помощью уравнений (13.79), (13.84) или
таблицы 13.4 образующая днищ баллона, при р = р и Gj = определяется с помощью
формулы (13.86) толщина днища на экваторе, равная толщине спирального слоя на ци-
линдрической части баллона hR, и по формуле (13.89) находится толщина кольцевого
слоя Ак. Композитные баллоны из стеклопластика и органопластика имеют весовую эф-
фективность, которая в два и более раза превосходит соответствующую характеристику
традиционных стальных и титановых баллонов. Более подробное изложение вопросов
проектирования композитных баллонов давления и корпусов ракетных двигателей
твердого топлива, изготовленных методом намотки, можно найти в работах [2,5,11,18].
13.6. СЕТЧАТЫЕ КОМПОЗИТНЫЕ КОНСТРУКЦИИ
Еще одним примером конструкции, для которой рациональное сочетание сило-
вой схемы, высоких механических характеристик однонаправленных композитов и
возможностей метода непрерывной намотки позволяет получать качественные новые
конструктивные элементы, обладающие высокой степенью весового совершенства,
являются сетчатые отсеки летательных аппаратов, состоящие из системы ребер, обра-
зованных из однонаправленного углепластика. Типовой процесс изготовления сетча-
665
Рис. 13.43. Сетчатый
композитный отсек
Рис. 13.44. Проектные
параметры сетчатой конструкции
той конструкции, более подробно описанный в работе [19], заключается в следую-
щем. На поверхность оправки укладываются эластичные матрицы, изготовленные из
резины и имеющие пазы, в которые укладываются в процессе намотки пропитанные
связующим углеродные жгуты, образующие систему симметричных спиральных и
кольцевых ребер (рис. 13.42). После заполнения пазов наматывается кольцевая или
близкая к кольцевой обшивка (рис. 13.42). Затем осуществляется отверждение свя-
зующего, удаление оправки и удаление эластичных матриц, которые вытягиваются во
внутреннюю полость оболочки. Изготовленный сетчатый отсек показан на рис. 13.43.
Сетчатая конструкция в форме цилиндрической оболочки определяется следую-
щими проектными параметрами (рис. 13.44):
— высотой ребер А;
— углами, которые спиральные ребра составляют с осью оболочки, (р;
— толщинами спиральных и кольцевых ребер 8С и 8К;
— расстояниями между ребрами (по нормали к осям) ас и як;
— толщиной обшивки Ао.
Сетчатые композитные конструкции находят в настоящее время применение в
качестве отсеков космических носителей, воспринимающих сжимающие и изгибаю-
щие нагрузки. Проектирование осуществляется по условию минимума массы сетча-
той оболочки на действие эквивалентной осевой силы
р= р + Ш
где Ро — осевая сила; М— изгибающий момент; R — радиус отсека. В качестве ограни-
чений используются условие прочности спиральных ребер при сжатии (13.3), условие
устойчивости сетчатой оболочки при сжатии силой Р и условие местной устойчивости
элементов спиральных ребер между точками пересечения ребер. Для построения ана-
литического решения, определяющего оптимальные значения проектных парамет-
ров, вводятся следующие предположения:
1. Несущая способность обшивки не учитывается, т. е. предполагается, что на-
грузка воспринимается только ребрами сетчатой структуры. Толщина обшивки Ао за-
дается по условиям, обеспечивающим необходимые аэродинамические, тепло- или
звукоизоляционные характеристики отсека.
2. Предполагается, что при осевом сжатии сетчатая оболочка теряет устойчивость
по осесимметричной форме.
666
3. Для обеспечения максимальной величины критической нагрузки, вызываю-
щей местную форму потери устойчивости спиральных ребер, кольцевые ребра распо-
лагаются так, что разделяют расстояние между точками пересечения спиральных ре-
бер пополам (рис. 13.44).
В зависимости от величины предела прочности материала спиральных ребер при
сжатии (5С существуют два класса оптимальных сетчатых конструкций [20]:
1. При9с< а0, где
/Р2О \1/5
оптимальные параметры имеют вид:
6R2
РЕС JЕсрс
5с = 1 gj
ас nsin 2ф ц Ес
tg2 ф =
8к = pKs*n ф /зй;
ак npccos3 <р а/ Ес
(13.90)
В записанных выше соотношениях Е — модуль упругости и р — плотность материала,
а индексы «с» и «к» относятся к спиральным и кольцевым ребрам. Сетчатые конст-
рукции, параметры которых определяются равенствами (13.90), являются равнопроч-
ными, расчетная сила Р вызывает одновременно разрушение ребер, а также местную
и общую потери устойчивости.
2. При ос > о0 имеем
/Р4/?^1710
Л = °,971-^4) > <р = 26,565°,
(13.91)
В конструкции, определяемой этими соотношениями, расчетная сила Р вызывает об-
щую и местную формы потери устойчивости, а ограничение по прочности спираль-
ных ребер выполняется с некоторым запасом па = где
а<: 4 л ЯЛ 6С cos2 ф
— напряжения, действующие в спиральных ребрах и вызванные расчетной силой Р
Запас па может быть использован для компенсации концентрации напряжений в спи-
ральных ребрах в окрестности люков и торцевых шпангоутов отсека (рис. 13.43).
Реальные сетчатые конструкции из углепластика, т. е. отсеки, имеющие вырезы,
торцевые шпангоуты и обшивку, обеспечивают экономию массы порядка 50% по
сравнению с прототипами из алюминиевых сплавов и порядка 20% по сравнению с
композитными трехслойными отсеками.
Оценивая в целом уровень и перспективы применения композиционных мате-
риалов в конструкциях аэрокосмической техники, следует заметить, что основным
достоинством этих материалов является их низкая плотность в сочетании с высокими
прочностью и жесткостью. Однако последнее свойство композитов проявляется толь-
ко при нагружении в направлении волокон. Поэтому основной задачей проектирова-
ния композитной конструкции является проектирование самого материала, структура
которого должна быть выбрана так, чтобы направления равнодействующих напряже-
667
ний, действующих в армированных слоях, совпадали с направлениями волокон в этих
слоях. При нарушении этого условия композиты утрачивают свои преимущества по
отношению к металлам.
Как отмечалось в разделе 13.1, в композитах с полимерной матрицей разрушение
матрицы происходит, как правило, раньше разрушения волокон. Для правильно
спроектированного материала разрушение матрицы не приводит к разрушению кон-
струкции, так как нагрузка воспринимается в основном волокнами. Однако возника-
ет вопрос о допустимости появления микротрещин в материале при эксплуатацион-
ной нагрузке. Для конструкций одноразового использования такая допустимость яв-
ляется в настоящее время общепризнанной. На таком допущении основан, в
частности, метод проектирования композитных корпусов ракетных двигателей твер-
дого топлива, изложенный в разделе 13.5. Однако для авиационных конструкций по-
явление трещин, вызывающих непредсказуемые последствия при циклической и дли-
тельной эксплуатации, естественно, недопустимо. Для предотвращения нарушения
монолитности композитов при эксплуатационных нагрузках соответственно понижа-
ется уровень допускаемых напряжений и снижается весовой эффект от применения
композитов. По этой причине эффективность и объем использования композитов в
авиационной технике значительно ниже, чем в ракетной.
Существенными недостатками полимерных композитов, связанными с особен-
ностями полимерной матрицы, являются сравнительно низкая теплостойкость ма-
териала, которая сохраняется до температур, не превышающих 120 °C, и низкая
твердость, вызывающая низкое сопротивление материала при механическом повреж-
дении и эрозии. Большой проблемой является влагопоглощение полимерных компо-
зитов, которое увеличивает плотность и снижает прочность материала. Перечислен-
ные недостатки вызывают необходимость защиты поверхности композитной конст-
рукции и периодического контроля целостности защитного покрытия.
Тем не менее, объем применения композитов в аэрокосмической технике интен-
сивно возрастает. Следует отметить, что современные композиты являются только
первыми и не вполне совершенными представителями материалов нового класса.
В отличие от универсальных материалов, таких, как металлические сплавы, свойства
которых не зависят от назначения конструкции, для которой они используются, ком-
позиты являются специализированными материалами, ориентированными на конк-
ретную конструкцию. Поэтому в принципе они более эффективны для конструкции,
чем универсальные материалы. В некоторой степени композиты являются аналогами
природных материалов, свойства и структура которых совершенствовались в течение
длительной эволюции. В настоящее время нет оснований утверждать, что композиты
могут заменить металлы как конструкционные материалы. Однако очевидно, что
объем применения композитов по мере совершенствования их свойств будет нарас-
тать, особенно в аэрокосмической технике, развитие которой связано с увеличением
весовой эффективности конструкций.
ЛИТЕРАТУРА
1. Буланов И. М., Воробей В. В. Технология ракетных и аэрокосмических конструкций
из композиционных материалов. — М.: Изд. МГТУ им. Н. Э. Баумана, 1998. С. 514.
2. Васильев В. В., Добряков А. А., Дудченко А. А. и др. Основы проектирования и изго-
товления конструкций летательных аппаратов из композиционных материалов. —
М.: МАИ, 1985. С. 218.
3. РосатоД. В., Грове К. С. Намотка стеклонитью: Пер. с англ. — М.: Машиностро-
ение, 1969. С. 310.
668
4. Васильев В. В. Механика конструкций из композиционных материалов. — М.:
Машиностроение, 1988. С. 270.
5. Композиционные материалы: Справочник / Под ред. Васильева В. В., Тарно-
польского Ю. М. — М.: Машиностроение, 1990. С. 510.
6. Бунаков В. Л., Головкин Г. С, Машинская Г. П. и др. Армированные пластики. — М.:
Изд. МАИ, 1997. С. 404.
7. Тарнопольский Ю. М., Кинцис Т. Я. Методы статических испытаний армирован-
ных пластиков. — М.: Химия, 1981. С. 272.
8. Назаров Г. И., Сушкин В. В., Дмитриевская Л. В. Конструкционные пластмассы:
Справочник. — М.: Машиностроение, 1973. С. 191.
9. Тарнопольский Ю. М., Жигун И. Г., Поляков В. А. Пространственно-армированные
композиционные материалы: Справочник. — М.: Машиностроение, 1987. С. 224.
10. Воробей В. В., Морозов Е. В., Татарников О. В. Расчет термонапряженных конст-
рукций из композиционных материалов. — М.: Машиностроение, 1992. С. 235.
11. Образцов И. Ф., Васильев В. В., Бунаков В. А. Оптимальное армирование оболочек
вращения из композиционных материалов. — М.: Машиностроение, 1977. С. 144.
12. Алфутов Н. А.; Зиновьев П. А., Попов Б. Г. Расчет многослойных пластин и оболо-
чек из композиционных материалов. — М.: Машиностроение, 1984. С. 264.
13. Образцов И. Ф., Булычев Л. А., Васильев В. В. и др. Строительная механика лета-
тельных аппаратов. — М.: Машиностроение, 1986. С. 536.
14. Johnson Е. R., Vasiliev V. К, Vasiliev D. V. Anisotropic Thin-Walled Beams with Closed
Cross-Sectional Contours//AIAA Journal, Vol. 39. 2001. № 12. P. 2389—2393.
15. Chandra R., Stemple A. D., Chopra I. Thin-Walled Composite Beams under Bending,
Torsional, and Extensional Loads // Journal of Aircraft, 1990. Vol. 27. № 7. P. 619—626.
16. Lagace P. A. Nonlinear Stress-Strain Behavior of Graphite / Epoxy Laminates // AIAA
Journal, 1995. Vol. 23. № 10. P. 1583-1589.
17. Barnes J. A., Simms I. J., Farrow G. J., Jackson D., Wostenholm G., Yates B. Thermal Ex-
pansion Behavior of Thermoplastic Composite Composite Materials// Proc. Am. Soc.
for Composite Materials, Fourth Tech. Conf., Blacksburg, Virginia, Technomic Publ,
1989. P. 717-725.
18. Лавров Л. H., Болотов А. А., Гапаненко В. И. и др. Конструкции ракетных двигате-
лей на твердом топливе. — М.: Машиностроение, 1993. С. 216.
19. Барынин В. А., Бунаков В. А., Васильев В. В., Разин А. Ф. Аэрокосмические сетча-
тые конструкции из композиционных материалов // Полет, 1998. № 1. С. 40—43.
20. Бунаков В. А. Оптимальное проектирование сетчатых композитных цилиндриче-
ских оболочек // Механика конструкций из композиционных материалов. — М.:
Машиностроение, 1992. С. 101—125.
Содержание главы 13
13.1. Конструкционные свойства композитов....................627
13.2. Балочные и стержневые элементы.........................636
13.3. Тонкостенные балочные и стержневые элементы............640
13.4. Панели из композиционных материалов....................651
13.5. Композитные баллоны давления...........................657
13.6. Сетчатые композитные конструкции.......................665
Литература ......................................................668
ГЛАВА 14______________________
Способы задания, описания
и увязки аэродинамических
поверхностей
Основной целевой функцией летательного аппарата является выполнение возло-
женных на него задач, которые реализуются в том числе в устойчивом и управляемом
полете в атмосфере Земли на всех режимах полета. Эта задача решается за счет двига-
тельной установки, создающей необходимую тягу, и планера, при обтекании которого
воздушными потоками возникают аэродинамические силы.
Архитектура планера, его внешние формы, взаимное расположение отдельных
частей определяются из условия обеспечения заданных летно-технических характе-
ристик: скорости, высоты и дальности полета, длины разбега при взлете и посадке,
устойчивости и маневренности и так далее. В каждом конкретном случае определен-
ному набору требований отвечают оптимальные геометрические формы планера: фю-
зеляжа, крыла, горизонтального и вертикального оперения, которые носят название
агрегатов. Эволюция их форм в зависимости от назначения ЛА представлена на
рис. 14.1.
Проектирование начинается с формирования обводов. Обводом называется мно-
жество линий и точек, принадлежащих поверхности. Обводы определяют форму лета-
тельного аппарата, внешние очертания корпуса ракеты, планера самолета и отдель-
ных его частей. Выбранные при проектировании формы оцениваются с точки зрения
аэродинамики и корректируются по результатам продувок моделей в аэродинамиче-
ских трубах.
Окончательная увязка формы поверхностей производится с помощью точ-
ных графических построений или аналитически заданных кривых. Сформирован-
ная поверхность оформляется в виде теоретического чертежа (в масштабе 1 : 10
или 1 :20), на котором указывается необходимая и достаточная информация о гео-
метрии внешних форм агрегатов и взаимном положении основных конструктив-
ных элементов. В приложениях к теоретическим чертежам оговариваются методики
и рекомендации по математическому обеспечению построений линейчатых поверх-
ностей и поверхностей двойной кривизны, построению и расчету контуров нормаль-
ных и наклонных сечений, а также по определению значений величин малок и многое
другое.
Очевидно, что производственная точность исполнения теоретических обводов
оказывает определяющее влияние на аэродинамические характеристики и качество
летательного аппарата, поэтому допустимые общие и локальные отклонения жестко
регламентируются техническими условиями. Устанавливаемые допустимые отклоне-
ния от теоретических контуров особо важны при выборе технических методов и
средств, обеспечивающих максимальное соответствие реальных аэродинамических
обводов и геометрических форм теоретическим. Технические условия закладываются
в основу разработки технологии и фактически определяют весь технологический
670
a)
Рис. 14.1. Эволюция внешних форм самолета*: а) самолет Airco D.H.2 (1915 г.);
б) истребитель-перехватчик МиГ-1 (1941 г.); в) истребитель-бомардировщик Су-7БМ (1958 г.);
г) бомардировщик Avro 698 Vulcan В.2 (1960 г.); д) стратегический бомардировщик Mirage IV
(1961 г.); е) штурмовик Saab-37 Viggen (1971 г.); ж) истребитель-перехватчик МиГ-25 (1970 г.);
з) пассажирский самолет Boeing-767 (1981 г.).
* Полная энциклопедия мировой авиации. — Корпорация «Федорову 1997.
671
комплекс от изготовления элементарных деталей и сборки отдельных узлов и агрега-
тов до общей сборки летательного аппарата.
Увязка внешних обводов планера, получение плавных, близких к теоретичес-
ким контуров всех агрегатов, правильное их взаимное расположение является весь-
ма сложной и трудоемкой технической задачей. Успех и эффективность решения
этой задачи зависят от того, каким образом заданы контуры сечений и поверхности
агрегатов, а также каким образом осуществляется перенесение заданных теорети-
ческих форм и размеров на технологическую оснастку и элементы конструкции
планера.
14.1. СПОСОБЫ ЗАДАНИЯ И ПОСТРОЕНИЯ
ВНЕШНИХ ОБВОДОВ ПЛАНЕРА
Достаточно долго в силу определенной специфики летательных аппаратов (слож-
ность форм, большие габариты, малая жесткость) наиболее приемлемым способом
задания поверхностей было создание моделей, обеспечивающих графическое постро-
ение и увязку отдельных сечений в натуральную величину на «безразмерных черте-
жах» — плазах.
С развитием и внедрением вычислительной техники, технологического оборудо-
вания с числовым программным управлением более актуальной стала разработка ма-
тематических моделей, позволяющих однозначным образом определить параметры
поверхности в любой ее точке.
Применяемые в настоящее время способы задания аэродинамических поверхно-
стей можно разделить на каркасные и кинематические (рис. 14.2).
Каркасным называется способ задания поверхности совокупностью лежащих на
ней линий. Однозначное определение точки поверхности возможно лишь на линии
каркаса. Каркасные способы основаны на приемах построений, применяемых в на-
чертательной геометрии, а также на задании и аппроксимации плоских обводов мето-
дами аналитической геометрии, вычислительной математики и др.
При кинематическом способе поверхность задается движением линии (постоян-
ной или переменной формы) в пространстве по определенному закону.
Как при каркасных, так и при кинематических способах задания поверхностей
последние определяются формой и взаимным расположением некоторого числа ли-
Графический способ
батоксов и горизонталей
Аналитический способ
аппроксимации поверхностей
Задание поверхностей
дискретно заданными сечениями
Способ кривых
второго порядка
Способ трансцендент-
ных уравнений
Способ степенных
уравнения и др.
Рис. 14.2. Основные способы задания поверхностей в авиа- и ракетостроении
672
Базовая ватерлиния 89,0
FS Для верхней части кривой Для нижней части кривой
45,8 7,9 7,9
46,0 7,0 8,9
47,0 6,18 9,5
48,0 5,7 9,7
49,0 5,23 9,85
50,0 4,8 9,9
51,0 4,4 10,0
52,0 4,2 10,0
53,0 4,0 10,0
54,0 3,9 10,0
55,0 3,79 10,0
56,0 3,7 10,0
57,0 3,67 10,0
58,0 3,66 10,0
59,0 3,65 10,0
60,0 3,65 10,0
Рис. 14.3. Задание аэродинамических поверхностей графическим способом
(точечным базисом и дискретным каркасом): а) построение профиля
по таблице координат; б) система координат и плоскостей планера самолета
(1 — плоскость симметрии; 2 — строительная горизонталь;
3 — плоскость нулевой дистанции); в) плоскости батоксов (1, 2),
горизонталей (3, 4) и шпангоутов (5)
ний (контуров). На практике применяют три способа задания контуров: графический,
табличный и аналитический.
Точечное задание контура в основном применялось при задании исходных про-
филей линейчатых поверхностей крыла, оперения и других поверхностей. Необходи-
мое для воспроизведения контура с достаточной степенью точности количество точек
определяется различными расчетными интерполяционными способами, причем в ка-
честве опорных используются исходные точки профиля. Координаты точек записы-
ваются в специальные таблицы (рис. 14.3, а).
Графическое задание контура применяется при использовании классическо-
го плазового способа батоксов и горизонталей. Форма каждого контура сечения
поверхности определяется последовательным процессом увязки и достижения
плавности обводов поверхности путем многократных графических построений
(рис. 14.4).
Графическая информация на плазе о форме и размерах поверхности служит эта-
лоном — основным источником информации о поверхности, которая затем перено-
673
а)
Батоксы
Рис. 14.4. Задание и вычерчивание аэродинамических поверхностей графическим
способом (точечным базисом и дискретным каркасом):
а) задание поверхности методом батоксов и горизонталей; б) вычерчивание кривой
по точкам на плазе (1 — плаз; 2 — рейка; 3 — крица); в) расчерчивание
теоретического контура большого транспортного самолета на плазе
сится на заготовительную и сборочную технологическую оснастку и элементы конст-
рукции посредством системы шаблонов и эталонов.
Несоответствие между длительными сроками формирования теоретической по-
верхности самолета, низкой точностью вычерчивания контуров и изготовления шаб-
лонно-эталонной оснастки, большим объемом работ, с одной стороны, и необходи-
мостью сокращения сроков подготовки производства, с другой, потребовало корен-
ной модернизации классического плазово-шаблонно-эталонного метода.
674
Работы российских ученых и конструкторов А. Н. Туполева, Н. Н. Рыжова,
В. А. Андреева, Н. И. Шарохина, И. И. Котова, В. А. Осипова и многих других в об-
ласти математического моделирования поверхностей создали предпосылки для вне-
дрения аналитических методов задания обводов.*
При аналитическом задании графическая линия теоретического контура, опре-
деляемая конечным числом точек, с помощью математических методов заменяется
совокупностью аналитических зависимостей, т. е. подвергается кусочной аппрокси-
мации. В точках стыка смежных аналитических кривых добиваются соблюдения усло-
вий первого или, лучше, второго порядка гладкости.
При аналитическом задании контуров применяются кривые второго порядка,
степенные и тригонометрические функции, полиномы различных степеней, транс-
цендентные уравнения и другие. В последнее время наибольшее распространение по-
лучили сплайн-функции (spline) и их разновидности.
Для задания поверхностей сложной формы широко применяется метод кривых
второго порядка. Уравнение кривой второго порядка в общем виде представляется
зависимостью ах2 + 2Ьху + су2 + 2dx + 2еу +1=0. Известно, что для определения кри-
вой второго порядка необходимо и достаточно пяти геометрических условий — пяти
точек кривой, пяти касательных или любой комбинации точек и касательных, если их
общее число равно пяти. В число условий может также входить радиус кривизны, за-
данный в определенной точке, и другие геометрические параметры.
В инженерной практике кривая второго порядка задается в большинстве случа-
ев двумя касательными в начальной и конечной точках и дополняется инженер-
ED
ным дискриминантом/= (рис. 14.5, а). Сложный контур, имеющий точки пере-
dU
гиба и прямые участки, задается несколькими кривыми второго порядка (рис. 14.5, б),
причем точки перегиба и конечные точки прямых являются граничными точка-
ми стыкующихся участков контура. Порядок гладкости обвода определяется мак-
симальным порядком непрерывной производной на кривой и на стыке образующих
ее дуг.
Иногда применяют метод сопряженных дуг эллипсов (рис. 14.5, в). В этом случае
полагают, что дуга эллипса, ограниченная концами двух сопряженных полудиамет-
ров, имеет постоянный дискриминант/= J2 - 1, а радиус кривизны в любой точке i
I2 .
эллипса определяется зависимостью pz = т-, где / — величина сопряженного полуди-
ко
аметра; Ло — расстояние по перпендикуляру между / и касательной в точке L
Для задания внешних обводов агрегатов, которые могут быть образованы из сты-
кующихся цилиндрических или циклических поверхностей, применяют метод сопря-
женных дуг окружностей (рис. 14.5, г). Задание заключается в определении величин
радиусов сопрягаемых дуг окружностей и определении координат их центров.
Для задания контуров сечений агрегатов часто используют степенные зависимос-
ти у = [4х(1 — х)]"1. Сущность способа заключается в подборе такого значения показа-
теля степени т, при котором задающая кривая соответствовала бы конструируемой в
пределах установленного допуска. Контур задается (рис. 14.6, а) двумя уравнениями,
одно из которых описывает часть контура от начала до миделя, другое — часть конту-
ра от миделя до конечной точки. Исходными данными при подборе показателя степе-
ни уравнения контура являются координаты точки миделя (Л/) и координаты некото-
рой промежуточной точки (К).
675
Рис. 14.5. Способы задания контуров:
а) задание кривой второго порядка, б) задание сложного контура кривыми второго
порядка, в) задание контура сопряженными дугами эллипсов, г) задание контура
сопряженными дугами окружностей
Рис. 14.6. Задание контуров степенными (а) и трансцендентными (б) функциями
В ряде случаев наиболее адекватным является задание контуров трансцендент-
ными уравнениями (рис. 14.6, б), при этом кривые задающего контура представляют-
ся в параметрическом виде, например:
х = cos а, у = у0 sin1! а + Ь.
В практике применяют и другие способы задания контуров, например способы
линейной и линейно-круговой аппроксимации и интерполяции, задание контуров
полиномами и тому подобное. Достаточно часто применяют комбинированное зада-
ние контуров. Например, контуры шпангоутов могут задаваться кривыми второго по-
676
рядка в сочетании с круговой аппроксимацией, продольные сечения — степенными
функциями, а поперечные — окружностями и кривыми второго порядка.
Опираясь на аналитические способы задания контуров, принадлежащих аэроди-
намическим поверхностям, выбирается тот или иной способ построения этих поверх-
ностей.
Линейчатые поверхности, в частности поверхности крыла, вполне определяются,
если заданы контуры исходных профилей у = /Дх) и у угол стреловидности а,
абсолютные величины хорд корневого и концевого сечений bh Ьи, угол геометриче-
ской крутки со, проекция расстояния между исходными параллельными профилями
(рис. 14.7, а) или при непараллельных плоскостях исходных профилей — расстоянием
от точки концевого профиля на задней кромке до плоскости корневого профиля.
В этом случае задаются углы наклона плоскости концевого профиля относительно
плоскости корневого профиля. Перечисленные величины назначаются и уточняются
на стадии проектирования.
Задание криволинейных поверхностей является более сложной задачей. При
каркасном задании широко применяется аналитический способ аппроксимации по-
верхности. Сущность способа заключается в задании дискретного каркаса продоль-
ными лучевыми сечениями поверхности. Опорными точками для нахождения анали-
тических зависимостей для линий каркаса служат точки пересечения продольных лу-
чевых плоскостей с контурами исходных поперечных формообразующих сечений
первичного каркаса (рис. 14.7, б).
В настоящее время в качестве основного рассматривается кинематический спо-
соб задания поверхностей. Кинематические поверхности образуются непрерывным
движением линий. Линия, движение которой создает поверхность, называется обра-
зующей. Линия, задающая траекторию движения образующей, называется направ-
ляющей. В общем случае образующая и направляющая являются кривыми различных
порядков, причем образующая по мере перемещения может деформироваться по оп-
ределенному закону (рис. 14.8, а). Линейчатые поверхности (рис. 14.8, б, в, г) являют-
ся частными случаями. Первоначальные сведения о криволинейной поверхнос-
ти, подлежащей математическому заданию, берут из эскиза общего вида летательного
аппарата. Совокупность этих данных позволяет составить первичный каркас поверх-
Параболы
Рис. 14.7. Способы задания поверхностей:
а) задание линейчатых поверхностей; б) задание криволинейных поверхностей;
677
ности агрегата, в который включаются мидельное сечение агрегата, сечение агрегата
плоскостью симметрии, очерк агрегата в плановой проекции, ряд характерных сече-
ний и точек поверхности, обусловленных особенностями компоновки агрегата, а так-
же включаются влияющие на форму поверхности дополнительные геометрические
условия. Поверхности сложных форм могут рассматриваться как ряд отдельно взятых
простых поверхностей (фюзеляж, воздухозаборники, гондолы двигателей и т. п.).
Разработка и внедрение в практику проектно-конструкторских работ рассмот-
ренных аналитических методов задания поверхностей позволило перейти от графиче-
ских моделей, заданных на плазе, к математическим моделям поверхностей, что и со-
здало предпосылки для перехода к так называемому расчетно-плазовому методу про-
изводства. При расчетно-плазовом методе основные теоретические обводы и
поверхности задаются математически, а некоторые построения выполняются на пла-
зах вручную. Оснащение производства технологическим оборудованием с числовым
программным управлением позволило не только значительно сократить необходи-
мый комплект плазово-шаблонно-эталонной оснастки, но и коренным образом из-
менить технологию ее изготовления без потери точности.
Дальнейшее развитие математических методов описания сложных поверхнос- тей в
пространстве, учет множества граничных условий, разработка и внедрение современ-
ных информационных технологий, в частности систем геометрического моделирования
различного уровня, информационно-измерительных систем, предопределяет использо-
вание математических и электронных моделей в качестве единственного источника ин-
формации как для элементов конструкции, так и технологической оснастки.
Рис. 14.8. Кинематические способы задания поверхностей
а) кинематическая поверхность двойной кривизны (1,2 — направляющие,
3 — образующая, 4 — кривая изменения инженерного дискриминанта вдоль оси х),
б) кинематическая цилиндрическая поверхность, в) кинематическая коническая
поверхность, г) кинематическая линейчатая поверхность
678
14.2. ОПИСАНИЕ КРИВЫХ В ПАРАМЕТРИЧЕСКОМ ВИДЕ
Параметрический метод имеет определенные преимущества среди различных
методов описания кривых в неявном виде. Основными преимуществами являются:
1. Более простое вычисление координат точек по изменяющимся значениям па-
раметров кривой. Заметим, что для кривой, заданной в неявном виде, при вычисле-
нии текущих координат точек приходится решать каждый раз нелинейное уравнение.
2. Упрощение расчета при обработке информации при воспроизведении кривых
на графическом дисплее и оборудовании с программным управлением (графопостро-
ителе, станках с ЧПУ).
3. Простота осуществления операций «преобразования» объекта: сдвиг, враще-
ние, масштабирование, симметрия за счет использования операций преобразования
векторов, непосредственно задающих исходную кривую.
4. Широкая распространенность описаний гладких обводов в различных методах
(кривые второго порядка, Фергюсона, Безье, Кунса и др.) и системах автоматизиро-
ванного проектирования (AFT, UNISURF и др.).
Рассмотрим основные положения параметрического метода.
Пусть точка М движется в трехмерном пространстве относительно системы коорди-
нат Oxyz и занимает положения М1, М2, ..., М‘ в различные моменты времени t2,
(рис. 14.9). Текущее положение точки М1 зададим радиусом-вектором ?. Таким образом,
значение радиуса-вектора г является функцией от времени Г. r=r(t).
В координатной форме аналогичное представление кривой будет
x = x(t); y = y(t); z = z(t).
Вид представленной кривой как траектории движения точки М в зависимости от
времени t в действительности может зависеть от любого параметра и. Например, опреде-
лять положение точки на рассматриваемой пространственной кривой может длина участ-
ка кривой (пройденный путь) между точками или какой-то другой параметр, т. е. г = г(и).
14.2.1. Параметрические кривые 3-го порядка
в форме Фергюсона
Кривая на отрезке [a, Z>] описывается кубическим уравнением вида:
г = г(и) = aQ + а}и + а2и2 + я3м3, (0 < и < 1).
Пусть даны параметры начальной А и конечной В точек кривой, а также значения
производных гА и гв в этих точках (рис. 14.10). Так как кубическое уравнение является
четырехпараметрическим, то четырех исходных данных достаточно, чтобы опреде-
лить коэффициенты я0, а{, а2, а3
а0 = г(0);
dr(O) ,/ЛЧ
а, + 1аг + За3 = =г(1);
а0 + + а2 + а3 = г(1).
Во второе и третье уравнения подставим значения известных величин из первых
двух уравнений:
2а2 + Зя3 = г(1) — г(0);
а2 + а3 = г(1)-г(0)-г(0).
679
Рис. 14.9 Рис. 14.10 Рис. 14.11
Из решения этой системы уравнений получим значение а2:
а2 = 3[г(1) — г(0)] — 2г(0) — г(1).
Далее получим параметр а3:
a3 = 2[r(0)-r(l)]+r(0) + r(l).
Подставляя их в исходное уравнение, получим известное уравнение Фергю-
сона:
г = г(и) = г(0) + г(0)и + 3r( 1 )w2 - 3r(0)u2 - 2r(0)u2 - r(l)w2 + 2r(0)u3 + r(0)w3 + r(l)w3 =
= r(0)(l - 3u2 + 2u3) + r(l)(3u2 - 2u3) + r(0)(u - 2u2 + u3) + r(l)(-2u2 + u3).
Это уравнение можно записать в матричном виде г = И* С* 5, т. е.
10 0 0 ’г(0)’
г(и) = [ 1 и и2 и3] 0 0 10 -3 3 -2 -1 г(1) W)
2-211 г(1)
14.2.2. Параметрические кривые в форме Безье
Безье остроумно перегруппировал члены параметрического уравнения Фергюсо-
на и получил более наглядное представление этого уравнения. Уравнение Безье по-
зволяет образовать кривую требуемой из конструктивных соображений формы.
Здесь кривая задается не соприкасающимся с кривой треугольником, а соприка-
сающейся в граничных точках ломаной — четырехугольником (рис. 14.11).
Перегруппировка членов заключается в следующем:
г(0) = г0;
г(1) = г3;
г(0) = 3(rj - г0);
г(1) = 3(г3-г2).
Кривая в форме Безье, оставаясь четырехпараметрической, проходит через точки
г0 и г3 и имеет касательные, идущие соответственно от г0 к rj и от г2 к г3.
Прямые р0Рр P\Pi и Р2Р3 образуют обычно незамкнутую ломаную, которая назы-
вается характеристической ломаной заданной кривой. Подставим перегруппировку,
предложенную Безье, в формулу Фергюсона:
г = r(u) = г0(1 - Зи2 -I- 2u3) И- г3(Зи2 - 2и3) + 3(fj - r0)(u - 2и2 -I- и3) -I- З(г3 - r2)(-u2 + и3).
Упростив это уравнение, получим:
г = г(и) = г0(1 - и)3 + Tj3u(l - и)2 + r23u2(l - и) + г3и3.
680
Матричная запись кривой третьего порядка по Безье будет:
о
о
3
г(и) = [1 и и2 и3]
1
-3
3
-1
О
3
-6
о
о
о
1
го
Г2
гз
Для плоских кривых вогнутость кривой всегда обращена к хорде рор3, если точки
рх и р2 лежат на сегментах р^с и хр3.
Управление формой кривой осуществляется изменением длин отрезков р$рх и
р2р3. При их одновременном увеличении кривая получает большую кривизну. Если
увеличивать длину только одного отрезка, то кривая будет ближе к этому отрезку, яв-
ляющемуся касательной к кривой в граничной точке. Если pQpx > PqX, р2р3 > хр3, то
кривая может образовать петлю.
Формы кривой при различных значениях длин и расположениях характеристиче-
ской ломаной представлены на рис. 14.12.
Форрест предложил, чтобы длины отрезков popj и р2р3 никогда не превышали
длины хорды рор3, тогда любые петли, появляющиеся на кривой, будут лежать вне ин-
тервала, ограниченного характеристической ломаной.
Зависимость формы кривой от ее характеристической ломаной называется свой-
ством выпуклости кривой.
Другой вид записи кубической кривой Безье:
г = г0 + Зи(1 - и)2(г, - г0) + Зи2(1 - и)(г2 - г0) + и3(г3 - г0),
или
Г = г0 + а(г, - г0) + Р(г2 + г0) + у(г3 - г0),
гдеа = 3и(1 — и)2, р = 3и2(1—и), у=и3.
Параметрическое представление кривой второго порядка
В последние годы получил распространение способ задания обводов с использо-
ванием метода одного, двух и трех отношений.
Пусть дан соприкасающийся треугольник р$рхр2 и величина отношения X =
= и: (1 — и) (рис. 14.13). Рассмотрим графоаналитический алгоритм построения точки
С и составления уравнения кривой при использовании метода одного отношения:
1. Сторону popj делим в отношении X и обозначаем точку Л: rA = (1 — u)r0 -I- игх.
681
2. Сторону р{р2 делим в отношении X и фиксируем точку В: rB = (1 — и)гх + иг2.
3. Сторону АВ делим в том же самом отношении X и получаем точку С, лежащую
на параметрической кривой гс = (1 — и)гл + игв.
Подставляем значения гл и гв в это уравнение, получаем уравнение кривой второ-
го порядка в параметрическом виде:
rc = (1 — u)2r0 + 2w(l — и)г{ + и2г2.
Точка С определена параметром и. Меняя параметр и, получаем множество точек
кривой второго порядка.
Безье обобщил этот метод нахождения точки на кривой и его аналитический ана-
лог на кривые более высокого порядка, используя полиномы Бернштейна.
14.2.3. Полиномиальная кривая в форме Бернштейна—Безье
Полином Бернштейна имеет вид
п I /ь-х
= - к)\к\ ЧУ ° ~Х^П~к-
С увеличением степени полинома увеличивается непрерывность большего коли-
чества производных, т. е. увеличивается гладкость обвода.
Безье сделал обобщение на векторозначные функции полиномов Бернштейна и
предложил форму записи полиномиальной кривой в более общем виде:
п 1
Г = Г(и) = L «'( 1 - И)" -
где г0, ..., гп — радиус-вектор п + 1 вершинРъ,рир2, —,Рп некоторой обобщенной ха-
рактеристической ломаной.
Форма записи кубической кривой Безье является частным случаем этой обоб-
щенной записи. Рассмотрим примеры.
Пример 1. Пусть п = 3. Вычислим каждое слагаемое полинома Бернштейна-
Безье, получим:
3’ п
при/ = 0: w0(l-W)3ro;
при i = 1: 1 — и)2г^
при i = 2: 3u2( 1 — 1/)!г2;
при i = 3: 3u3( 1 - u)°r3.
Просуммировав члены, получим обычную кубическую параметрическую кривую Безье:
г = г(и) = г0(1 - и)3 + ^31/(1 - и)2 4- r23u2( 1 - и) + r3u3.
Пример 2. Пусть п = 1, тогда имеем:
при/ = 0: ту^и°(1 -м)‘г0;
при i = 1: 1/!(1 — //)%.
Просуммировав, получим известное из школьного курса уравнение прямой:
r=(l -u)rQ + ur}.
Пример 3. Пусть п = 2, тогда имеем:
2’
при/ = 0: 2тщи°(1-и)2г0;
при/= 1: 2u1(l —
при i = 2: и2( 1 — u)°r2.
682
Просуммировав, получим уравнение кривой второго порядка:
г= г0(1 — и)2 + r}2u( 1 — и) + г2и2.
Необходимо заметить, что с увеличением степени полиномов ослабевает нагляд-
ная связь между формой кривой и соответствующей характеристической ломаной.
Это усложняет процесс конструирования кривой требуемой формы.
14.2.4. Рациональные параметрические кривые
Рациональная функция обычно задается как отношение двух многочленов. Ра-
циональные функции обладают рядом преимуществ:
— свойством оставаться рациональными при преобразовании сдвига и растяже-
ния независимой переменной;
— они позволяют описывать прямые линии, а также кривые, имеющие бесконеч-
ные значения ординат при конечных значениях абсцисс;
— их легко и быстро рассчитать на ЭВМ.
Уравнение рациональной кривой запишется:
п
. X
>voro + *’|Г|И + w2r2u2 + ... + w„r„u" , = 1
f = ___________________________________ = _.
4 - W,U + WjU2 + ... + w„un "
2, WjU1
/ = !
Используя параметризацию Безье, запишем уравнение рациональной парамет-
рической кубической кривой:
Woro(l — W)3 + SWjfj и( 1 — и)2 + w2r2u2(\ — и) + w3r3u3
Г W0(l - и)3 + Зи>! и( 1 - и)2 + w2w2(1 - и) + w3u3
Используя формулу Бернштейна—Безье, можно записать уравнение рациональ-
ной параметрической кривой любой степени:
п ।
5П я! .
W/7----г-т-ттМЧ! - и)л-'г.
,=0 '(" -')!'!
'•(«) = —-----;------------------•
п\
X W,7--ТГчИ'(1 - и)п~1
i=0 ‘(n-i)lil 7
Здесь 2 iy n ~ и>)п ' образуют базис Бернштейна для множества всех поли-
номов степени п.
Например, уравнение рациональной квадратичной кривой будет
woro(l — и)2 + \ — и) + w2r2u2
Г w0(l - и)2 + W]2w(l - и) + w2u2
Представление кривой в рациональном параметрическом виде обладает ря-
дом обобщающих свойств, например у квадратичной кривой могут быть точки пе-
региба.
14.2.5. Описание кривых универсальной степенной функцией
Метод Безье позволяет проектанту конструировать кривую желаемой формы. Еще
большими конструктивными возможностями обладает универсальная степенная функ-
ция (УСФ).
683
Универсальная степенная функция имеет вид
__ г 2х(1-0,5х) -р
У U -/+ 2/х(1 - 0,5x)J ’
где х = (О < х < 1); у = (О < у < 1); /ит - числовые коэффициенты.
I У max
УСФ описывает достаточно большой класс кривых и является обобщением мно-
гих частных методик, традиционно применяемых в самолетостроении.
При/= 0 имеем уравнение степенной функции у = [2х(1 - 0,5х)]т, аналогичное
уравнению Н. И. Шарохина: у = [4х( 1 — х)]т; при/= 0 и т = 0,5 имеем уравнение ок-
ружности; при/= 0 и т = 1 — уравнение параболы: у = 2х — х2; при/= 1 и т = 0 —
уравнение прямой у = 1; при т = 0,5 — уравнение, известное под названием МСК:
Универсальная степенная функция позволяет строить кривые с одной, двумя,
тремя и более точками перегиба. Причем этот процесс конструктивно управляем.
Универсальную степенную функцию можно подвергнуть преобразованиям де-
формации и сдвига и получить кривые, полезные в авиа- и судостроении.
14.2.6. Формирование обводов на основе теории полюсов
Полиномы Бернштейна—Безье удобно применять при диалоговом режиме рабо-
ты, так как характеристические точки кривой высвечиваются на экране дисплея и их
положение может целенаправленно изменяться проектировщиком. Локальная моди-
фикация участка обвода осуществляется посредством увеличения кусочности обвода
и повышением степени интерполяционной функции.
Большими обобщающими возможностями обладает интерполяционная тео-
рия полюсов, предложенная французским математиком П. Кастельжо. Здесь ло-
кальное управление формой обвода осуществляется с помощью управляющих то-
чек — полюсов.
Рассмотрим способы задания и алгоритмы конструирования одномерных обво-
дов на базе теории полюсов.
Введем основные понятия: стек, полюс и примитивный ряд. На их основе полу-
чим полярную форму представления кривой.
Пусть кривая порядка п задана векторно-параметрическим уравнением
п
p(t) = X
1=0
где t — параметр кривой; 2, — векторный коэффициент; p(t) — радиус-вектор точки на
кривой с параметром t (на рис. 14.14 значение t = 0,4) и
/ - л!
Сп /!(« — /)!’
Стек кривой представляет собой неубывающую последовательность t2,t^ ..., ti9
составленную из некоторых значений параметра t.
Полюсом кривой называется точка, определяемая радиусом-вектором
п
Рк=ъ
i=0
684
где к — порядковый номер полюса; — симметрический полином, который вычис-
ляется следующим образом:
$2к = *к + \*к + 2 + *к + Л + 3 + ••• + h + n- \*к + п>
^(пк = *к + \*к + 2*к + 3—*к + п>
4+1> 4 + 2» 4 + з> ••••> *к + п~ последовательность значений параметра /, взятых из стека,
называется индексом полюса рк. Последовательность полюсов, индексы которых взя-
ты из стека со сдвигом на один шаг вправо, называют примитивным рядом полюсов.
Для вычисления новых полюсов и координат точек на кривой используется рекур-
рентное соотношение:
где Д — радиус-вектор полюса, включенного в примитивный ряд полюсов между по-
люсами pti и ptJ в результате включения параметра в стек между параметрами Г, и tj.
Таким образом, кривая и-го порядка задается множеством из п + 1 полюсов при-
митивного ряда. Такой способ задания кривой определяет полярную форму ее пред-
ставления (рис. 14.15).
Для задания обвода в полярной форме необходимо составить стек с кратностью
повторения/(1 fn): ..., t2, t2, t2,..., t2, t3,..., tm, где значению параметрасоот-
ветствует некоторая интерполяционная точка г,.
При этом порядок гладкости с сшивки составной кривой вычисляется по форму-
ле с = п —f
Отсюда видно, что составные кривые, заданные в полярной форме, сохраняют
порядок гладкости сшивки дуг кривых при произвольном перемещении полюсов
(рис. 14.16). Такое важное свойство позволяет производить локальное управление
геометрической формой обвода без полного его пересчета.
685
Теорию полюсов удобно применять для задания треугольных и четырехуголь-
ных ячеек поверхности при обеспечении высокого порядка стыковки ячеек по-
верхности.
14.2.7. Суперпозиционное моделирование обводов
на основе универсальной степенной функции
Задачу оперативного управления формой обвода можно решить с помощью су-
перпозиционного моделирования. Под суперпозицией функции понимают операцию
взятия функции от функции. Формулы 5-отображения:
для прямого отображения:
у] = ф(л);
для обратного отображения:
Здесь <pOz) — старшая функция суперпозиции, которая осуществляет указанное ото-
бражение.
При управлении формой обводов и поверхностей с помощью суперпозиционно-
го моделирования будем использовать следующую теорему. Для того чтобы вогнутая
функция и =f(x) на отрезке [а, £] отобразилась в выпуклую функцию, необходимо и
достаточно, чтобы максимальный прогиб кривой на заданном отрезке не превышал
максимального прогиба в направлении оси и кривой у = ср(и) на этом же отрезке.
Рассмотрим возможности суперпозиционного моделирования при управлении
формой обводов, заданных универсальной степенной функцией
_ _ г 2/7(1 - 0,577) "р
У ~ [1 -/+ 2Z«(1 — 0,5«)J ’
и _ у
где и = 7; у = -У— .
1 У max
После преобразований получим:
-о.
| _ fy\!m
Отсюда
W12
у"т(А -Г)
1 -fyx,m
или
"12
yl/m(l
1 -fyV” /
Прогиб кривой на участке АВ в направлении оси и определим как разность орди-
нат кривой и прямой АВ, соединяющей границы рассматриваемого участка.
Уравнение прямой АВ\
и = к(у-ув) + ив,
, "л - “в
где к =------.
Уа-Ув
Прогиб 8 определим как разность между значениями мпр и икр:
1 У1//я(1 ~/)П
1 -fy'"» JJ
5 мпр мкр
686
Рис. 14.17. Суперпозиционное моделирование обвода носовой части фюзеляжа
Найдем экстремум этой функции, приравняв ее производную нулю, т. е.
7(1 l)ly(l>-l)
8' = к ± /-, ... ......-...... = 0.
71 \
Данное уравнение можно решить численными методами. Точка экстремума дан-
ного уравнения характеризует максимальный прогиб кривой на рассматриваемом
участке.
Многократное суперпозиционное моделирование позволяет управлять формой
проектируемых обводов с большим числовым значением стрелки прогиба. В результа-
те имеем обобщенный метод конкурирующих обводов.
На рисунке 14.17 даны примеры суперпозиционного моделирования обвода но-
совой части фюзеляжа.
Суперпозиционное моделирование поверхностей надстроек
Математическое представление поверхности должно соответствовать конкрет-
ным геометрическим и функциональным требованиям, предъявляемым к проекти-
руемой поверхности.
Рассмотрим процесс суперпозиционного моделирования каркаса поверхности
при проектировании специального обтекателя носовой части фюзеляжа.
Ранее был рассмотрен процесс суперпозиционного моделирования обводов с
применением универсальной степенной функции. Применим многократное суперпо-
зиционное моделирование для задания выпуклых надстроек.
Алгоритм формирования нулевого батокса надстройки:
1. Выделяем на исходном контуре фюзеляжа зону О А (х0, w0; хА, иА) существования
надстройки. Уравнение нулевого исходного батокса фюзеляжа:
У =f(x).
2. Определяем меру выпуклости надстройки и выбираем параметры mnf модели-
рующей функции.
Уравнение моделирующей функции:
/ = ф(м).
При трехразовом 5-отображении будем иметь уравнение
у = <р(ф(ф(Лх)))).
687
В поперечных сечениях поверхности надстройки будут кривые, заданные уни-
версальной степенной функцией.
Для получения поверхности надстройки с еще большей выпуклостью можно
применить п-кратное 5-отображение:
у = фМф-ХфСф^*)))-)))-
Совмещение преобразований исходной функции
для решения задач проектирования поверхностей
Управление формой каркаса поверхности с помощью суперпозиционного моде-
лирования можно совместить с введением весовых функций и получить одно сложное
преобразование. В этом случае геометрические возможности совмещенного метода
управления формой обводов и поверхностей возрастут.
Уравнение моделирующей кривой:
п
у = <р(ф(ф...ф(ф( ЛСФ,•(*)))•••))),
/ = 1
где/(х), pz(x), ф(и) — универсальные степенные функции. Заметим, что в общем виде
обводы могут задаваться и любыми другими функциями.
143. ОПИСАНИЕ ПОВЕРХНОСТЕЙ
Исходная информация о технической поверхности может быть представлена:
1. Точечным базисом. Аппроксимация (интерполяция) точечно-представленной
поверхности осуществляется на основе выбранной базовой кривой в виде декартова
тензорного произведения.
2. Линейным каркасом, т. е. каркасом линий одного семейства (люфтинг-пред-
ставление поверхности). Каждая линия каркаса аппроксимируется одним и тем же
параметрическим уравнением. Линии каркаса поверхности имеют в этом случае раз-
личные фиксированные значения одного и того же параметра.
3. Сетчатым каркасом (трансфинитное представление). Здесь используется ин-
терполяция посредством семейства параметрических кривых. Этот метод применяет-
ся для описания широкого класса поверхностей и обеспечивает хорошую точность
представления поверхности и гибкость в управлении формой поверхности.
Решение задачи формирования поверхности высокого порядка гладкости сво-
дится к решению общей задачи интерполирования: найти функцию F(u, v), непре-
рывно дифференцируемую требуемое число раз на заданной области и обеспечиваю-
щую заданный порядок касания рассматриваемого участка с соседним.
Простейший алгоритм построения поверхности по исходному точечному базису
заключается в обобщении метода Лагранжа для нахождения единственного полино-
ма, который будет интерполировать все заданные точки:
р я
z(x,y)= X
i=0j=0
При достаточно больших р и q на построенной таким образом поверхности появ-
ляются нежелательные осцилляции. Поэтому практически на исходной поверхности
выделяют отдельные ячейки с малым количеством точек на этом участке поверхности
и для описания каждой ячейки используют полиномы низкой степени. Далее из этих
ячеек синтезируют гладкую составную поверхность.
Для описания ячеек поверхности используют бикубические сплайны, методы
Инаба, Кунса и других.
688
14.3.1. Описание поверхности в параметрическом виде
Пусть исходная кривая /0, заданная в параметрическом виде уравнением г = r(u),
перемещается в трехмерном пространстве в направлении v и одновременно подверга-
ется деформации. Тогда кривые /у, являющиеся последовательными положениями дви-
жущейся деформированной исходной /0 кривой, образуют поверхность (рис. 14.18).
Каждая точка М этой поверхности характеризуется значением параметра и, для
данной точки на исходной рассматриваемой кривой /0 и параметром vy, характеризую-
щим путь, который проходит эта точка в v-м направлении. Здесь и и v — криволиней-
ные координаты точки М. Уравнение поверхности будет г = г (и, v).
Координаты точек поверхности определяются функциями:
х = х(и, v); у = у(и9 v); z = z(u9 v).
При таком параметрическом способе задания поверхности можно достаточно
просто выделить на ней необходимые линии каркаса. Например, если параметры и
или v будут зафиксированы, то имеем один переменный параметр, например г = r(u0, v)
или г = r(u, vfl). Эти уравнения описывают кривые, лежащие на поверхности. Такие
кривые называются параметрическими кривыми. Их характер зависит от способа вы-
бора параметров.
Эти кривые могут быть траекториями режущего инструмента при обработке по-
верхности на оборудовании с программным управлением или линиями каркаса по-
верхности при решении различных позиционных, метрических и конструктивных за-
дач, а также при вычерчивании поверхности на графопостроителе.
14.3.2. Описание поверхности в форме Фергюсона
Пусть кривая /0, представленная в форме Фергюсона уравнением
г = г(и) = я0 + а}и + а2и2 + а3и3,
непрерывно перемещается в трехмерном пространстве в направлении v и изменяет
свою форму в процессе этого движения. В результате получим поверхность r(w, v),
представленную на рисунке 14.19 своим дискретным каркасом /2,
Для вывода уравнения поверхности можно обобщать способ задания кривой пу-
тем установления зависимости коэффициентов я0, ах, а2, а3 от второго параметра v.
Используя параметрическую запись кубической кривой Фергюсона, запишем:
а, = аю + anv + aav2 + aj3v3 (i = 1,2, 3).
689
Тогда уравнение поверхности будет
г = r(u, V) = %) + а01v + д02у2 + аозу3 + а\ои +
+ aniiv + fl12wv2 + fl13wv3 + ... + fl23i/2v3 + лзз^3у3-
Более краткая запись уравнения:
3 3
r=r(u, v)= Y Е aijuivJ'
/=0j=0
В матричном виде можно записать r(u, v) = U*A*V или в развернутом виде:
r(w, v) = [1 и и2 w3]
Лоо Л01 а02 аоз 1
Л10 а11 а12 а\з V
Л20 а21 а22 а23 V2
Л30 а31 а32 азз V3
Из этого уравнения видно, что поверхность определяется шестнадцатью векторны-
ми коэффициентами. При фиксированном значении параметра и = w, = const можно оп-
ределить на кривых /0, /р /2,... векторы касательных ги в точках поверхности в направле-
нии и и rv в направлении v, а также значения смешанных производных ruv = d2r/dw dv.
Значение смешанной производной ruv характеризует скорость изменения значе-
ния ги с изменением параметра v или rv — с изменением и и называется вектором кру-
чения.
14.3.3. Уравнение поверхности в форме Безье
Методика описания поверхности Безье аналогична методике описания поверх-
ности Фергюсона, однако она более наглядна в конструктивном отношении. Здесь
мы перемещаем в направлении v характеристическую ломаную — наглядный аналог
исходной кривой.
Пусть кривая /0, представленная по Безье характеристической ломаной, движется
в направлении v. Каждая точка (вершина) характеристической ломаной проходит оп-
ределенный путь, и в фиксированные моменты времени эти ломаные задают каркас
поверхности /,, /2, /3,....
Матричная запись поверхности Безье будет r(u, v) = U*A*V, где
U=[\и и2 и3];
А = М* R* Мт,гд&
10 0 0
-3 3 0 0
3-630
-1 3-3 1
roo г01 г02 гоз
г10 Г11 г12 г13
г20 Г21 г22 г23
г30 Г31 г32 г33
Управление формой поверхности происходит за счет изменения четырех вер-
шин, расположенных во внутренней зоне поверхности. Самой поверхности прина-
690
длежат только граничные вершины г00, г03, г30, г33. Уравнение бикубической поверхно-
сти в форме Бернштейна—Безье запишется в виде:
3 3
г=г(и, V) = Ё Ё ги\3 - /)!/!(3 -»!;! и'(1" - v)3“y’
где Гу — вершины характеристического многогранника.
Уравнение полиномиальной поверхности в форме Бернштейна—Безье:
r=r(u, v) = У У г/7-----ъ'гг—лгч wz(l - u)n-‘vj(\ -
J(n ~ -у)!у!
14.3.4. Описание составных поверхностей
При задании каркаса поверхности или точечного базиса на прямоугольной об-
ласти значительно упрощается процесс составления уравнения поверхности. К тому
же любую сложную техническую поверхность всегда можно разбить на отдельные
прямоугольные или квадратные ячейки, заданные граничными кривыми или четырь-
мя точками. В этом случае уравнение, описывающее каждую ячейку поверхности,
имеет минимальный порядок и позволяет легко управлять формой поверхности.
Получается однородный, удобный для ЭВМ алгоритм описания каждой ячейки
поверхности, и его легко обобщить на описание сложной составной поверхности,
синтезированной из однородных ячеек.
Покажем на различных примерах алгоритмы формирования из простых ячеек со-
ставной сложной поверхности непрерывной и гладкой.
Бикубические поверхности в форме Фергюсона
Запишем уравнение бикубической поверхности в форме Фергюсона:
3 3
r(u, v) = У У a^vJ = Ф(«) • А • Ф(г), где
/=оу=о
Ф(«) = [а0(м) a^w) Р0(м) Pt(w)] = [1 — Зм2 + 2м3 Зм2 — 2и3 и — 2и2 + и3 —и2 + w3] =
= [1 и и2 и3]
10 0 0
0 0 10
-3 3-2-1
2-211
Аналогично:
Ф(и) =
a0(v) 1 — 3v2 + 2v3
a^v) 3v2 — 2v3
PoO) v — 2v2 + v3
PiO) —v2 + v3
10-32
0 0 3 -2
0 1-21
0 0-1 1
V2
V3
= CTV
Таким образом, развернутое уравнение поверхности в матричном виде будет
r(w, v) = UCACTV.
Для непрерывности поверхности и ее градиента на общей границе двух ячеек (1 и 2)
необходимо соблюсти условия:
r(1)(l, v) = r(2)(0, v);
r(1)(l, 0) = г(2)(0, 0); г<1>(1, 1) = г<2)(0, 1);
/•<|)(1,0) = г<Ж 0);г<»(1, l) = r<2)(0,1);
v) = г<2»(и, v) или UCA^CTV= UCA^CTK
691
Поверхности Безье
Обобщенное уравнение поверхности в форме Безье запишется:
г(и, V) = £ rtJg^(u)^9\v),
i=0j=0
где g№ и gW — базисные функции Бернштейна степени pwq соответственно.
Такая поверхность задается характеристическим многогранником с (р + 1)(^ + 1)
вершинами. Однако получить требуемую форму поверхности и управлять ее формой в
процессе проектирования сложно.
В инженерной практике сложную поверхность разбивают на ячейки. Для их за-
дания часто используют бикубические уравнения поверхности в форме Безье, когда
р = 3 nq = 3:
3 3
г(ц, v) = X Z rijSitu)gj(v), 0 < и, v < 1,
/=0у=0
где
&(') = fc!(3-Jt!) - /)3 к = °’ b 2’1
Многогранник с 16 вершинами дает конструктору возможность изменением од-
ного или более векторов характеристического многогранника целенаправленно уп-
равлять изменением формы каждой ячейки поверхности и в результате получать со-
ставную поверхность требуемой формы.
Такое единообразное задание каждой ячейки поверхности дает более однород-
ный алгоритм формирования составной поверхности. При этом легче вносить ло-
кальные изменения формы поверхности.
Запишем уравнение поверхности Безье в матричной форме:
r(w, v) = G(u)BGT(y),
где В = [г^] — матрица 4x4 вершин многогранника;
<?(«) = ISbC") £i(«) &(«) &(“)] = [(1 - «)3 Зи(1 - и)2 Зи2(1 - и) и3] =
= [1 и и2 W3]
1 О О
-3 3 0
3-6 3
-1 3 -3
о
о
о
1
= и-м.
Аналогично G(v) = MW, где V= [1 v v2 v3].
Используя эти выражения, запишем
r(u, v) = UMBMW
Гладкость составной поверхности
обеспечивается гладкостью стыковки меж-
ду собой смежных ячеек поверхности
(рис. 14.20).
Рассмотрим алгоритм гладкой сты-
ковки по линии ВС двух смежных ячеек
поверхности. Уравнения бикубической по-
верхности Безье для ячеек 1 и 2 соответ-
ственно будут:
r^(u, v) = UMB^MW,
r&\u, v) = UMB&MW
уравнения ячеек поверхности в виде
692
Условием непрерывности этой поверхности по границе ВС будет r(1)(l, v) = r(2)(0, v)
при v е [0, 1] или в матричном виде [1111] [ 1 000]MBWbflV
После упрощений получим уравнение
[10001^0 = [ЮОО]#2),
которое сведется к уравнению = rffi, i = 0, 1,2, 3, т. е. по линии ВС должна быть об-
щая характеристическая ломаная.
Для обеспечения гладкости первого порядка составной поверхности необходимо,
чтобы касательная плоскость по линии ВС к ячейкам поверхности 1 и 2 совпадали.
Тогда и направление нормали к составной поверхности по линии стыковки ячеек бу-
дет изменяться непрерывно при выполнении условия:
Ни2>(0, v)r<2)(0, v) = k(v)r^\ 1, v)rt')(l, v).
Заметим, что r<2)(0, v) = /^(l, v) и тогда r<2)(0, v) = v).
Это означает, что на линиях v = const составной поверхности направление гради-
ента будет непрерывно. Матричная форма записи будет:
[0 1 0 0]Л/В<2)Л/7’И= X(v)[0 1 2 3]M»^MTV.
После сокращений тождественных членов в левой и правой части уравнения по-
лучим:
= /=о, 1,2,з.
Эти четыре уравнения означают, что сходящиеся на границе ребра характеристиче-
ских многогранников смежных ячеек должны быть коллинеарны.
14.3.5. Описание поверхности методом Кунса
Пусть на прямоугольной области задан сетчатый каркас поверхности. Сетка кри-
вых разбивает поверхность на совокупность ячеек, каждая из которых ограничена па-
раметрически представленной парой w-кривых и парой v-кривых (рис. 14.21, а).
Параметрически заданная ячейка поверхностей r(«, v) имеет 0 < и, v < 1 и пред-
ставляет внутреннюю часть поверхности, ограниченную четырьмя исходными гра-
ничными кривыми: г(и, 0), r( 1, v), г(и, 1), r(0, v).
Форрест предложил наглядную трактовку алгоритма составления уравнения по-
верхности Кунса, которая заключается в следующем: для вывода уравнения ячейки
поверхности вначале решается более простая задача: по двум граничным кривым r(0, v)
и r(l, v) строится линейчатая поверхность, т. е. применяется интерполяция в «-на-
правлении (рис. 14.21, б): rx(u, v) = (1 — и) т(0, v) + «т(1, v).
и =0
Уравнение линейчатой поверхности в направлении v по другим граничным кри-
вым г(и, 0) и r(u, 1) (рис. 14.21, в) запишется так: r2(u, v) = (1 — v)r(u, 0) + vr(w, 1), или
в матричном виде:
r2(u, V) = [(1 - v) V]
r(w, 0)
г(и, 1)
Сумма выражений rx{u, v) + r2(u, v) для двух линейчатых поверхностей дает но-
вую поверхность, у которой граничные кривые будут являться суммой гранич-
ной кривой и прямолинейного отрезка. Например, при и = 0 вместо r(0, v) имеем
r(0, v) + [(1 - v)r(0,0) + vr(0, 1)].
Для восстановления первоначальных, исходных граничных кривых необходимо
из уравнения r{(u, v) + r2(u, v) вычесть некоторую линейчатую поверхность r3(«, v),
границами которой служат эти прямолинейные отрезки. Тогда результирующая по-
верхность определится следующим образом:
r(u, v) = r{(u, v) + r2(u, v) — r3(w, v).
Уравнение поверхности r3(w, v) определяется по известным граничным кривым и = 0
и v = 1 соответственно:
[(1 - v)r(0, 0) + vr(0, 1)] и [(1 - v)r(l, 0) + vr(l, 1)].
Последующая линейная интерполяция в v-м направлении дает уравнение искомой
поверхности r3(«, v):
r3(w, v) = (1 - w)(l - v)r(0, 0) + w(l - v)r(l, 0) + (1 - w)vr(0, 1) + wvr(l, 1).
Это поверхность гиперболического параболоида.
Уравнение результирующей поверхности г = гх + г2 — г3 (рис. 14.21, г) удобно
представить в матричном виде:
r(u, v) = [(!-«)«]
г(«, 0)
г(и, 1)
+ [r(u, 0)г(и, 1)]
v J |r( 1,0) г(1,1)
1 - V
V
При подстановке значений и = 0, w = 1, v = 0, v = 1 в уравнение поверхности Кун-
са получаются четыре исходные граничные кривые рассматриваемой части поверхно-
сти. Вспомогательные функции и, (1 - и), v и (1 — г) называются «функциями сшива-
ния». В современной трактовке метода Кунса предлагается линейные «функции сши-
вания» заменить функциями более высокой степени.
Сделаем следующую замену: (1 — и) и и обозначим через a0(w) и а{(и) и соответ-
ственно (1 - v) и v обозначим через a0(v) и a^v), тогда «функции сшивания» могут
быть любыми непрерывными и монотонными, обычно полиномиальными, для кото-
рых выполняется условие a0 + cq = 1.
В этом случае уравнение поверхности Кунса запишется в виде:
r(u, V) = [а0(и)а,(и)]
r(0, v)
_r(!, v)
+ [г(и, 0)r(u, 1)]
ao(v)
a,(v)
- [а0(м)«](«)]
r(0,0) r(0, 1)
r(1,0) r(l, 1)
a0(v)
a^v)
Таким образом, по заданному сетчатому каркасу или точечному базису можно из
ячеек, описанных методом Кунса, сконструировать составную поверхность. Такая по-
694
верхность будет непрерывна и иметь нулевой порядок гладкости. Для увеличения по-
рядка гладкости необходимо в рассмотренном выше алгоритме при определении линей-
чатых поверхностей r}(u, v) и r2(u, v) заменить линейную интерполяцию на обобщенную
интерполяцию Эрмита. Это позволит обеспечить более гладкую стыковку смежных гра-
ничных кривых и при соответственно выбранном более высоком порядке «функций
сшивания» обеспечит высокий порядок гладкости всей составной поверхности.
14.3.6. Поверхности в рационально-параметрическом
представлении
Свойства поверхности определяются свойствами линий, образующих эту поверх-
ность. Поэтому обобщающие свойства рациональных параметрических кривых опре-
деляют обобщающие геометрические свойства поверхностей, представленных в раци-
онально-параметрическом виде.
Рассмотрим алгоритм формирования рациональной бикубической поверхности,
построенной посредством тензорного (декартова) произведения исходных раци-
ональных кривых с использованием «функций сшивания», которые также представим
в рациональном виде.
Уравнение рациональной кубической кривой в форме Бернштейна—Безье будет
3 3» 3
Z wlrlSlW,
r(u).'-° |3~|)-------------. ц,
W'(3 - z)!Z! 1 “ w)3”' Y
/=0 <=o
где#/^) — базисные функции Бернштейна.
Обозначим знаменатель через w(w), тогда
з
r(u) = w-\u) Y W/(w)-
/=0
Используя декартово произведение, запишем уравнение бикубической поверх-
ности в рационально-параметрическом представлении:
3 3
r(u) = w-\u)w~i(v) % % WjWjrjjg^ujgjiy).
i=0у=0
Запишем это уравнение в матричном виде:
r(u) = ^{u^-^UMDRDMTV.
Здесь U= [1 и и2 и3]; D = diag(w0, w1? w2, w3); R = [r^] — матрица 4x4 вершин характе-
ристического многогранника;
1 0 0 0 1
м= -3 3 0 0 , v= V
3 -6 3 0 V2
-1 3 -3 1 v3_
Сравнивая это бикубическое рациональное уравнение поверхности с обычным
бикубическим уравнением поверхности в форме Безье
r(u)=UMRATV,
695
можно видеть обобщающий вид уравнения рационально-параметрически представ-
ленной поверхности.
Аналогично можно составить уравнение любой степени в рационально-парамет-
рическом виде.
14.4. МЕТОДЫ ОПИСАНИЯ СПЛОШНЫХ ТЕЛ
СЛОЖНОЙ ПЕРЕМЕННОЙ ФОРМЫ
Решение большинства инженерных геометрических задач автоматизированного
конструирования значительно упрощается, если формирование геометрических мо-
делей проектируемых объектов производится методами объемного моделирования,
широко применяемого в современных промышленных системах автоматизированно-
го проектирования.
Существуют три основных типа математических моделей геометрических объек-
тов, применяемых в САПР: каркасные (рис. 14.22, а), полигональные (рис. 14.22, б) и
объемные (рис. 14.22, в).
Конструктивными элементами каркасной модели являются ребро и точка. С по-
мощью этой модели можно описать только ограниченный класс технических объек-
тов, у которых аппроксимирующими поверхностями являются плоскости. Каркасные
модели используются в основном для представления геометрических объектов на
плоскости, например в виде проекций. Однако в общем случае получаемые изображе-
ния являются неоднозначными. С помощью таких моделей невозможно автоматизи-
ровать процессы удаления невидимых линий и получения сечений.
Полигональные модели позволяют описывать сложные криволинейные грани
технических объектов. При построении таких моделей предполагается, что объект ог-
раничен контурами, которые являются результатом пересечения или касания поверх-
ностей. Вершины объекта могут быть заданы пересечением трех поверхностей или
множеством точек, удовлетворяющих геометрическим требованиям, в соответствии с
которыми определяется контур.
При формировании полигональной модели должны быть учтены следующие по-
ложения:
1) любую поверхность можно аппроксимировать многогранником, каждая грань
которого является простейшим плоским многоугольником;
2) наряду с плоскими многоугольниками можно использовать квадрики и криво-
линейные поверхности, допускающие возможность проведения сложных расчетов и
работу с моделью в интерактивном режиме.
Объемные модели позволяют представлять сложные технические объекты с
большой степенью точности. Конструктивными элементами объемной модели явля-
ются точка, контурный элемент и поверхность. При синтезе объемной модели конст-
руктивные элементы образуют узлы сетевой структуры. Например, узел есть точка пе-
ресечения трех контурных элементов, контурный элемент всегда принадлежит двум
поверхностям, поверхности всегда принадлежат объемам. С помощью объемной мо-
б)
Рис. 14.22
696
Рис. 14.23. Модель мастер-
геометрии отсека фюзеляжа
Рис. 14.24. Модель
поверхности самолета
дели в любой момент времени можно разделить точки на внутренние и внешние по
отношению к реальному объекту.
Методы объемного моделирования, реализуемые с помощью современных сис-
тем геометрического моделирования, являются основой полного электронного опре-
деления изделия. Компьютерная модель самолета включает в себя модель мастер-гео-
метрии, модель распределения объемов и модель полного определения. На рис. 14.23
показана модель мастер-геометрии отсека фюзеляжа, а на рис. 14.24 — твердотельная
модель самолета.
14-5- МЕТОДЫ УВЯЗКИ ФОРМ И РАЗМЕРОВ ИЗДЕЛИЙ
Главными с точки зрения обеспечения взаимозаменяемости сборочных единиц
увязываемыми геометрическими элементами являются поверхности, контуры, от-
верстия деталей, узлов, агрегатов изделия или специальной оснастки, выбранные в
качестве технологических сборочных баз при узловой и агрегатной сборке.
Состав технологических сборочных баз определяется в зависимости от принято-
го, удовлетворяющего требованиям точности метода сборки. Различают внешние и
внутренние сборочные базы. Внешние создаются с помощью взаимоувязанных «базо-
вых» элементов сборочных приспособлений, на которых выполняются базовые по-
верхности, контура или отверстия. Носителями внутренних сборочных баз являются
сопрягаемые детали узлов, отсеков и агрегатов изделия.
Методы сборки с базированием по сопрягаемым поверхностям и по отверстиям
существенно различаются по содержанию и составу необходимой увязочной и сбо-
рочной оснастки.
Наиболее сложными и трудоемкими с точки зрения увязки являются детали, из-
готавливаемые механической обработкой и пластическим деформированием с по-
мощью обводообразующей и контрольной оснастки — штампов, формблоков, гибоч-
ных и обтяжных пуансонов, контрольных приспособлений. К ним относятся
(табл. 14.1):
— плоские детали из листа типа стенок, диафрагм, шпангоутов и нервюр с борта-
ми, вырезами и элементами жесткости, для изготовления которых используют штам-
повку резиной или инструментальные штампы;
— пространственные детали сложной конфигурации типа обшивок, окантовок,
люков, обтекателей, изготавливаемые из листового материала штамповкой, вытяж-
кой, обтяжкой со значительными деформациями;
697
— криволинейные детали из профилей и труб постоянного и переменного сече-
ния, изготавливаемые гибкой-прокаткой или обтяжкой в штампах;
— детали из профилей и плит, изготавливаемые механической или иной обработ-
кой, связанной с удалением металла заготовки.
Таблица 14.1
Типовые детали летательных аппаратов и способы их изготовления
Схема процесса
Г ибка-прокатка
Ударная штамповка Штамповка резиной
Штамповка в инструментальных штампах
698
К увязываемым типовым сборочным единицам относятся:
— плоские каркасные узлы типа шпангоутов, нервюр, лонжеронов, полов, пере-
городок;
— пространственные узлы типа дверей, крышек люков, створок;
— панели одинарной, двойной и знакопеременной кривизны;
— секции и отсеки агрегатов.
Тщательной пространственной увязке подлежат элементы сборочной оснастки —
носители технологических баз, необходимых для установки деталей и узлов, — ру-
бильники, ложементы, стапельные плиты, фиксаторы и т. п.
Методы увязки, технические средства их реализации во многом определяются
способами задания геометрии поверхностей изделия и отдельных его составляющих.
Составляющими метода увязки геометрических параметров поверхностей, за-
данных тем или иным способом, являются: первоисточник увязки, средства увязки и
содержание процесса увязки.
В авиа- и ракетостроении в качестве первоисточников увязки используют черте-
жи, математические модели — электронные макеты, плоские и объемные безразмер-
ные носители информации в натуральную величину — плазы и эталоны.
Использование чертежей в качестве первоисточника в отрасли ограничено в свя-
зи с ограниченностью номенклатуры жестких деталей простых геометрических форм,
увязываемых по стандартной системе допусков и посадок.
Применение в проектно-конструкторских работах систем геометрического моде-
лирования позволяет описывать изделие и отдельные его элементы с помощью элек-
тронных макетов, но реализация этого способа требует широкого внедрения техноло-
гического обрабатывающего и контрольно-измерительного оборудования с програм-
мным управлением. Большая часть увязок, по-прежнему, осуществляется по плазам и
эталонам.
Средства увязки делятся на универсальные и специальные. К универсальным от-
носятся инструментальные и оптические приборы и устройства, координатные стен-
ды, а также оборудование для механической обработки.
Специальные плоские и объемные средства увязки создаются только для одного
конкретного летательного аппарата и включают в себя комплекты шаблонов, маке-
тов, контрмакетов деталей, сборочных единиц, разъемов, слепки и контрслепки по-
верхностей деталей.
Содержание процесса увязки определяется принятым в производстве принципом
увязки форм и размеров. Увязка на основе принципа независимого образования разме-
ров и форм изделия не содержит общих этапов переноса размеров. Образование сопря-
женных размеров на деталях или узлах осуществляется независимо друг от друга, увели-
чивая поле погрешности увязки этих размеров. Уменьшить рассогласование сопрягае-
мых размеров можно только за счет повышения точности исполнения каждого из них.
Менее точными являются этапы, связанные с заданием и построением поверхно-
стей изделий больших габаритов, сложных форм и малой жесткости. Независимый
перенос геометрии на технологическую заготовительную и сборочную оснастку при-
водит к значительным погрешностям увязки форм и размеров.
Зависимая или связанная увязка предусматривает наличие общих для двух сопря-
гаемых размеров этапов их переноса. Если поле погрешности каждого размера вклю-
чает погрешности общих и индивидуальных этапов, то поле погрешности увязки фор-
мируется только индивидуальными этапами. Чтобы обеспечить высокую точность
увязки размеров, необходимо все этапы, имеющие большие погрешности в каждой из
индивидуальных ветвей, перенести в общие для обоих размеров этапы. В этом случае
погрешность увязки будет меньше погрешности каждого из размеров.
699
Последовательность этапов переноса геометрических параметров от первоисточ-
ника увязки на средства оснастки и далее на объекты увязки называется схемой увязки
оснастки.
Схемы увязки оснастки весьма разнообразны и по содержанию, и по оформле-
нию. Тем не менее, все они включают четыре группы однородных элементов, распо-
ложенных последовательно: первоисточник увязки, средства увязки, средства оснаст-
ки, объекты увязки. Это позволяет, выделив типовые объекты увязки, установив ти-
повые способы изготовления и сборки и типовой состав технологического
оснащения, создать типовые схемы увязки (модули) отдельных геометрических пара-
метров при определенных методах их увязки. Общая схема увязки заготовительной и
сборочной оснастки на изделие, агрегаты или отсеки может быть составлена из от-
дельных типовых модулей.
Состав технологической, а следовательно, и увязочной оснастки, определяется
технологией изготовления деталей и сборки узлов, панелей, агрегатов, а также уста-
новленной в данном конкретном случае степенью взаимозаменяемости.
Традиционно авиаракетостроение базируется на плазово-шаблонно-эталонном
методе обеспечения взаимозаменяемости.
Сущность этих методов заключается в том, что теоретические чертежи летательно-
го аппарата заменяются плазовыми разбивками в натуральную величину, а рабочие чер-
тежи деталей и технологической оснастки — шаблонами и эталонами. Исходными дан-
ными для плазовых разбивок являются теоретические чертежи летательного аппарата.
Теоретический плаз (ТП) (плаз совмещенных сечений) служит для увязки внеш-
них обводов летательного аппарата по отдельным сечениям относительно его конст-
руктивных осей. Расчерчивается в двух или трех проекциях на плоской металличе-
ской поверхности.
Конструктивный плаз (КП) служит для геометрической и конструктивной увязки
всех входящих в сборочную единицу деталей. На конструктивном плазе расчерчива-
ются или копируются фотоконтактным способом конструктивные оси и обводы от-
дельного сечения, в котором осуществляется конструктивная увязка деталей. Конст-
руктивный плаз, на который наносятся технологические базы (риски, отверстия
и т. п.) называется технологическим. По нему изготавливают рабочие шаблоны. Для
изготовления конструктивных плазов применяется прозрачный листовой пластик
винироз.
Шаблоны являются жесткими носителями формы и размеров деталей и сбороч-
ных единиц летательных аппаратов. Шаблоны подразделяются на основные (техноло-
гические) и производственные (рабочие).
Оптимальная номенклатура и количество шаблонов, устанавливаемых на детали,
зависит от технологических процессов их изготовления и от характера и оснащеннос-
ти производства.
Традиционно условно плоские детали типа нервюр изготавливают штамповкой
резиной на формблоках. Раскрой заготовки, сверление инструментальных, шпилеч-
ных, сборочных направляющих отверстий выполняют по шаблонам развертки деталей
(ШРД). Формблоки изготавливают по шаблонам внутреннего контура (ШВК). Взаим-
ную увязку шаблонов ШРД и ШВК осуществляют по шаблону контурному (ШК).
Для изготовления листовых деталей сложной формы необходима объемная фор-
мообразующая оснастка типа обтяжных пуансонов, штампов, оправок и т. п. В этом
случае заготовку вырезают по шаблону заготовки (ШЗ), обрезку припуска по контуру
и сверление отверстий выполняют по шаблону обрезки (ШОК). Технологическая ос-
настка выполняется по шаблонам контура сечения (ШКС).
700
Гибка профильных деталей осуществляется на различных профилегибочных
станках по оправкам или в штампах. Контуры оправок и штампов обрабатываются по
шаблонам гибки (ШГ).
Большую группу составляют шаблоны, необходимые для увязки и монтажа сбо-
рочных приспособлений, — шаблоны приспособлений (ШП) и шаблоны монтаж-
но-фиксирующие (ШМФ).
Взаимная увязка шаблонов ШК, ШВК, ШРД, ШКС и ШОК для плоских и про-
фильных деталей, относящихся к каждому данному сечению агрегата, обеспечивается
их изготовлением по одному исходному КП или ШКК. Взаимная увязка ШКС, пред-
назначенных для изготовления объемной технологической оснастки и стапельной ос-
настки, производится по теоретическим и конструктивным плазам, ШКК — по обус-
ловленному ряду сечений.
Используются также ШР — шаблоны разные.
Взаимная увязка всего комплекта плазово-шаблонной оснастки осуществляется
по базовым отверстиям (БО), которые переносятся на шаблоны с помощью плаз-кон-
дукторов.
Для разметки шаблонов чаще всего применяется фотоконтактный метод. Допол-
нительная символьная информация организационно-технологического плана набива-
ется на лицевую сторону шаблона. Одним из основных недостатков плазово-шаблон-
ного метода является низкая точность увязки отдельных сечений в пространстве. Для
всего комплекта оснастки, изготавливаемой по шаблонам нескольких сечений агрега-
та, необходимы дополнительные технические средства, обеспечивающие координа-
цию шаблонов. Применяют пространственные координатные стенды, специальные
прецизионные оптические приборы, оптико-телевизионные и лазерные установки.
В ряде случаев целесообразно изготовление «корзин» шаблонов контура сечения
и монтажных эталонов, по которым изготавливают объемную технологическую осна-
стку и монтируют сборочные приспособления. Монтажные эталоны (МЭ) позволяют
выполнить увязку аэродинамических обводов агрегатов по отдельным сечениям и их
стыковых узлов. По существу, монтажный эталон объединяет шаблоны контуров се-
чения и калибры стыков и разъемов. Шаблоны и калибры устанавливаются в про-
странстве лишь один раз и погрешности их установки определяют точность монтаж-
ного эталона. В дальнейшем МЭ входит в связанную схему переноса размеров общим
этапом и не влияет на точность взаимной увязки сборочных приспособлений.
Типовые схемы увязки оснастки по плазово-шаблонно-эталонному методу, при-
меняемые в авиа- и ракетостроении, приведены на рис. 14.25—14.28.
Главным недостатком увязки по отдельным сечениям является необходимость
интерполировать промежуточные сечения при переносе их на формообразующую ос-
настку — болванки, пуансоны, оправки и т. п., что приводит к значительным относи-
тельным погрешностям. Эталонирование поверхностей позволило частично устра-
нить этот недостаток и перейти к методам объемной увязки оснастки.
Носителями форм и размеров при объемной увязке являются базовый эталон
(БЭ) и объемный плаз (ОП) (рис. 14.29).
Базовый эталон — жесткая конструкция, имеющая стабильные обводы по внут-
ренней поверхности обшивки и обеспечивающая необходимую точность в пределах
погрешностей плазового источника. Объемный плаз включает в себя контрэталон ба-
зового эталона с установленными в нем элементами планера и систем бортового обо-
рудования. Рабочая поверхность контрэталона образована точным копированием ме-
тодом слепка обводов и точным переносом всей информации с базового эталона —
теоретических и конструктивных осей, стыков листов обшивки, втулок, сборочных и
других конструктивных и технологических отверстий. Элементы конструкции уста-
навливают на соответствующие места контрэталона, базируя по сборочным отверсти-
701
Рис. 14.25. Принципиальная схема увязки технологической
и сборочной оснастки плазово-шаблонным методом
Рис. 14.26. Типовая схема увязки оснастки по плазово-шаблонному методу
702
1. Шпангоут № 1
2. Шпангоут № 2
3. Шпангоут № 3
4. Обшивка
5. Стрингер
6. Стрингер стыковой
7. Кроштейн
Рис. 14.27. Схема увязки оснастки при изготовлении приборного отсека
ям и конструктивным осям. При этом проверяются и увязываются обводы сложных
деталей, сопряжения поверхностей, обрезы, подсечки и сопрягаемые элементы кон-
струкции. Выявленные на образцах погрешности устраняются, и уточненная инфор-
мация переносится на плазовые источники и весь комплект технологической оснаст-
ки для изготовления деталей.
Объемный плаз позволяет провести увязку деталей каркаса, не связанных с обво-
дами, и деталей, изготавливаемых по чертежам без шаблонов. Для этого весь каркас-
ный набор последовательно монтируется на ранее установленные обводообразующие
детали. При этом выявляются и устраняются погрешности увязки и исполнения сбо-
рочных отверстий, сопряжения плоскостей, обрезы и т. п. Корректируется плазо-
во-шаблонная и технологическая оснастка.
703
Рис. 14.28. Принципиальная схема увязки технологической оснастки
по эталонно-шаблонному методу
Кроме этого, метод объемной увязки позволяет провести отработку размещения
блоков оборудования, прокладки коммуникаций бортовых систем, размещения узлов
крепления с учетом требуемых зазоров, монтажных напряжений, эксплуатационных
подходов и т. п. Отработанные в объемном плазе монтажи эталонируются и служат
источником информации для изготовления и контроля оснастки и деталей. По ре-
зультатам отработки изменения вносятся и в серийные чертежи систем изделия.
Изготовление и увязка оснастки по объемному плазу осуществляется в несколько
этапов. Сначала известными плазово-шаблонно-эталонными методами производят
предварительную увязку формблоков, обтяжных пуансонов, контрольных плазов для
изготовления деталей каркаса планера, по которым из материалов, указанных в черте-
жах, изготавливают образцовые детали. Сборочные отверстия увязываются по шабло-
нам. Затем по базовому эталону осуществляется увязка оснастки для изготовления об-
разцовых обшивок. Базовые и сборочные отверстия переносятся на обшивки с по-
мощью шаблонов ШОК. Увязка обшивок по обрезам, осям конструктивных
элементов и строительным осям осуществляется непосредственно на базовом этало-
не. На образцовые обшивки наносится полная информация о строительной оси, осях
704
Рис. 14.29. Метод объемной увязки:
а) базовый эталон отсека фюзеляжа и воздухозаборников (1 — лекала по конструктивным
элементам агрегата, 2 — рабочая поверхность, 3 — втулки под болты крепления отсеков
базового эталона, 4 — каркас, 5 — стыковой узел, 6 — репер-стойки); б) объемный плаз
отсека фюзеляжа; в) схема заливки объемного плаза (1 — базовый эталон, 2 — эпоксидная
композиция); г) образцовая обшивка (1 — оси шпангоутов, 2 — оси стрингеров, 3 — базовые
отверстия, 4 — сборочные отверстия); д) отработка деталей каркаса, не связанных
с обводами; е) отработка каркасов по макетам элементов бортовых систем
продольных и поперечных конструктивных элементов, базовых и сборочных отверс-
тиях. Схема обеспечения взаимозаменяемости методом объемной увязки приведена
на рис. 14.30.
Метод объемной увязки позволяет повысить степень взаимозаменяемости дета-
лей планера и бортовых систем, тем самым снизив объем подгоночных работ на этапе
сборки.
Высокая степень взаимозаменяемости дает возможность использовать в качестве
технологических сборочных баз, взаимоувязанных на сопрягаемых деталях, конструк-
тивных и технологических отверстий — сборочных, базовых, координатно-фиксирую-
щих, и производить сборку в упрощенных сборочных приспособлениях (рис. 14.31).
Технология переноса отверстий, используемых в дальнейшем в качестве устано-
вочных и сборочных баз, определяется принятой схемой обеспечения взаимозаменя-
емости. На рис. 14.32 приведены типовые случаи увязки положения отверстий.
Если при конструкторско-технологической отработке размерных связей деталей
и узлов изделия в чертежах предусматриваются сборочные или координатно-фикси-
рующие отверстия, координаты которых сведены в таблицы, увязка оснастки не-
сколько упрощается.
Общим недостатком методов увязки по жестким носителям форм и размеров яв-
ляется высокая трудоемкость и длительность изготовления, увязки и тиражирования
комплекта плазов, шаблонов, эталонов, макетов, объемных плазов и т. д.
705
Условные обозначения технологических цепей: I — создание источников средств увязки — 1,2; II — из-
готовление сборочных стапелей — 1, 2 и т. д.; III — увязка и изготовление обшивок — 1, 2 и т. д.; IV —
увязка и изготовление деталей каркаса в обводке — 1,2 и т. д.; V — увязка и изготовление деталей набора
каркаса (не обводи.) — 1, 2 и т. д.; VI — увязка и изготовление деталей оборудования — 1, 2 и т. д.; VII —
увязка и изготовление элементов систем (трубопровод, жгуты — 1,2 и т. д.).
Рис. 14.30. Принципиальная схема метода объемной увязки
деталей планера и системы оборудования изделий
Рис. 14.31. Сборка узлов и отсеков планера по взаимоувязанным отверстиям:
а) сборка панели по сборочным отверстиям СО; б) сборка отсека
по базовым отверстиям БО в ранее собранных панелях
706
Варианты процесса
I« Оснастка для образования СО,
Т НО в стойке и профиле обвода
б)
в)
г)
Рис. 14.32. Образование сборочных отверстий в обшивках и деталях каркаса, входящих
на обвод агрегата: а) перенос сборочных и направляющих отверстий с конструктивного плаза;
б) увязка СО и КФО при сборке панелей; в) увязка сборочных отверстий
по ранее изготовленному объемному плазу; г) увязка сборочных отверстий параллельно
с изготовлением объемного плаза
709
а) б)
Чертежи контрольно-увязочной оснастки
Чертежи рабочей оснастки
Рис. 14.33. Схема увязки оснастки с применением координатных стендов:
а) инструментальный стенд, б) плаз-кондуктор, в) схема увязки оснастки;
в)
710
Внедрение в практику проектно-конструкторских работ координатных методов
увязки сечений агрегатов в системе базовых осей изделия, оснащение производства
плаз — кондукторами и инструментальными стендами (рис. 14.33, я, б) в значитель-
ной мере упростили процессы увязки шаблонно-эталонной и сборочной оснастки.
Схема увязки оснастки с использованием координатных стендов приведена на
рис. 14.33, в.
Развитие и внедрение в отрасли современных средств вычислительной техники,
совершенствование методологии плоского и объемного математического и геометри-
ческого моделирования изделий, появление компьютерных систем геометрического
моделирования высокого уровня, позволяющих представлять конструкцию в виде
трех- и двумерных моделей с точностью 1...3 мкм, оснащение производства высоко-
точным обрабатывающим оборудованием с ЧПУ и информационно-измерительными
системами позволяет кардинально изменить систему технологической подготовки
производства.
В настоящее время методологически и технически отрасль еще не готова перейти
к комплексной автоматизации процессов технической подготовки производства, по-
этому широкое распространение получил переходный метод геометрической увязки и
формообразования — расчетно-плазовый метод (РПМ).
Основными принципами РПМ являются следующие:
— более полное образмеривание конструктивных чертежей, исключающее воз-
можности неоднозначного их прочтения исполнителями;
— создание единых носителей геометрической информации коллективного
пользования;
— применение в производстве согласованной схемы параллельно-последова-
тельного формообразования всех элементов обводообразующей оснастки и деталей
для каждого агрегата в отдельности;
— максимальное использование ЭВМ, чертежных автоматов, станков с ЧПУ для
изготовления основной номенклатуры плазово-шаблонной оснастки, влияющей на
точность воспроизведения форм и размеров и сокращающей количество переходов от
чертежа до готовой детали.
Единым носителем геометрической информации являются: математическая модель
агрегата, содержащая весь объем необходимых и достаточных данных о теоретической по-
верхности агрегата; информационная модель пространственного или плоского конструк-
тивного узла; графическая модель плоского конструктивного узла, представленная в виде
плаза. Использование единых моделей резко сокращает количество неувязок и рассогла-
сований форм и размеров деталей и узлов на ранних стадиях подготовки производства.
Применение РПМ предусматривает группирование деталей агрегата по способам
и средствам образования, согласования и переноса форм и размеров — расчетного
(группа А) и плазового (группа Б) и организацию технологических процессов по по-
следовательно-параллельной схеме формообразования (рис. 14.34). Особенно эффек-
тивен РПМ для производств, связанных с большим количеством сложной обводооб-
разующей оснастки.
Сочетание расчетно-плазового метода с современными оптическими и лазерны-
ми системами позволяют значительно сократить затраты на изготовление и увязку
эталонной и сборочной оснастки (рис. 14.35).
В отрасли широко внедряются «бесплазовые» методы увязки на базе трехмерных
электронных макетов (ЭМ). Электронный макет представляет собой электронное
описание конструкции и является носителем геометрических параметров деталей из-
делия, определяет их привязку к базовым осям и плоскостям, взаимное расположение
711
Рис. 14.34. Принципиальная схема расчетно-плазового метода увязки
в сборочной единице. При этом точность увязки по электронному макету значитель-
но выше, чем по жестким носителям форм и размеров.
Полный переход на бесплазовые методы увязки в настоящее время сдерживается
целым рядом объективных (недостаточная техническая и кадровая оснащенность
производства) и субъективных (традиционность) факторов. Поэтому осуществляется
поэтапное освоение и внедрение этого метода.
Одним из внедренных вариантов является метод электронных плазов. В этом
случае сохраняются основные принципы системы плазовой подготовки производ-
ства, но плазовые разбивки, расчерчивание шаблонов выполняется не ручным
способом, а с помощью плоских систем компьютерного проектирования по пра-
вилам, характерным для ручного проектирования. Изготовление или, в крайнем
случае, прочерчивание шаблонов, существующих в виде отдельных файлов, произ-
водится на фрезерных или лазерных станках с числовым программным управлени-
ем. Контроль изготовления осуществляется по тем же файлам на контрольно-из-
мерительных машинах. На рис. 14.36 показан выполненный в Mechanical Desktop
электронный макет средней части нервюры (рис. 14.36, а), комплект шабло-
нов (рис. 14.36, б), формблок (рис. 14.36, в) и твердотельная геометрическая модель
детали.
Вопросы комплексной автоматизации конструкторско-технологической отра-
ботки изделий на базе современных информационных технологий весьма сложны и
специфичны и будут рассмотрены в других главах. В качестве примера на рис. 14.37
приведена принципиальная схема увязки оснастки на базе электронного макета.
712
a)
Рис. 14.35. Применение лазерных систем при увязке оснастки расчетно-плазовым методом:
а) схема увязки оснастки; б) разметка объемной оснастки;
в) монтаж сборочных приспособлений
713
Рис. 14.36. Увязка средней части нервюры на основе электронного плаза:
а) электронный макет детали; б) комплект шаблонов; в) формблок; г) деталь
Рис. 14.37. Принципиальная схема увязки оснастки по электронному макету
для изготовления многослойных клееных панелей
714
ЛИТЕРАТУРА
1. Алгоритмы и программы решения геометрических задач на ЭВМ / Под ред.
В. И. Якунина. - М.: МАИ, 1982. С. 69.
2. Феоктистов С. И., Макарова Е. А., Меркулов В. И. и др. Автоматизация технологи-
ческой подготовки производства летательных аппаратов / Под общ. ред. Макаро-
вой Е. А. - М.: Изд-во «ЭКОМ», 2001. С. 288.
3. Братухин А. Г., Давыдов Ю. В., Елисеев Ю. С. и др. CALS в авиастроении. — М.:
Изд-во МАИ, 2000. С. 304.
4. Гард ан И., ЛюкаМ. Машинная графика и автоматизация конструирования. —
М.: Мир, 1987. С. 272.
5. ГОСТ 23501.201—85 Системы автоматизированного проектирования. Комплек-
сы средств. Общие технические требования. — М.: Изд-во стандартов, 1985.
6. Дубровин Б. А., Новикове. П., Фоменко А. Т. Современная геометрия. — М.: Нау-
ка, 1979. С. 759.
7. Завьялов Ю. С., Леус В. А., Скороспелое В. А. Сплайны в инженерной геометрии. —
М.: Машиностроение, 1985. С. 224.
8. Минаков А. П. К вопросу о равновесии идеально гибкой нити на шероховатой по-
верхности. Ученые записки МГУ. Вып. 154. — М.: Изд-во МГУ, 1951. С. 420.
9. Рашевский П. К. Курс дифференциальной геометрии. — М.: Гостехиздат, 1956.
С. 420.
10. Соколов В. П., Цырков А. В. Информационные технологии проектирования слож-
ных технических объектов. В сб. Информационные технологии. Вып. 3. — М.:
Машиностроение, 1997. С. 9—15.
11. Фокс А., Пратт М. Вычислительная геометрия. Применение в проектировании и
производстве / Пер. с англ. — М.: Мир, 1982. С. 304.
Содержание главы 14
14.1. Способы задания и построения внешних обводов планера.......672
14.2. Описание кривых в параметрическом виде.....................679
14.2.1. Параметрические кривые 3-го порядка в форме Фергюсона.679
14.2.2. Параметрические кривые в форме Безье.................680
14.2.3. Полиномиальная кривая в форме Бернштейна—Безье.......682
14.2.4. Рациональные параметрические кривые..................683
14.2.5. Описание кривых универсальной степенной функцией......683
14.2.6. Формирование обводов на основе теории полюсов........684
14.2.7. Суперпозиционное моделирование обводов на основе
универсальной степенной функции..............................686
14.3. Описание поверхностей......................................688
14.3.1. Описание поверхности в параметрическом виде..........689
14.3.2. Описание поверхности в форме Фергюсона...............689
14.3.3. Уравнение поверхности в форме Безье..................690
14.3.4. Описание составных поверхностей......................691
14.3.5. Описание поверхности методом Кунса...................693
14.3.6. Поверхности в рационально-параметрическом представлении ... 695
14.4. Методы описания сплошных тел сложной переменной формы.......696
14.5. Методы увязки форм и размеров изделий......................697
Литература ..........................................................715
715
ГЛАВА 15
Системы автоматизированного
проектирования в авиа-
и ракетостроении
15.1. ФУНКЦИОНАЛЬНАЯ МОДЕЛЬ
Если под проектированием понимать любой процесс преобразования информа-
ции [1], то данному определению будет соответствовать весьма широкий круг де-
ятельности человека, затрагивающий все стадии процесса создания продукции. По-
нятие жизненного цикла является одним из центральных, используемых в методоло-
гии управления качеством продукции. Пока нет единой классификации этапов
жизненного цикла технической системы. Неоднозначность выделения этапов, стадий
или фаз жизненного цикла обусловлена многообразием самих систем, множественно-
стью их целевого назначения, способов их производства и т. п. Тем не менее логика и
содержание основных процессов периодов создания и полезной жизни во всех случа-
ях являются общими. Концептуальная схема жизненного цикла изделия, которой мы
будем придерживаться, приведена на рис. 15.1.
Концепции жизненного цикла продукции и ее системному представлению по-
священо много работ. Остановимся только на тех аспектах, которые помогают сфор-
мировать платформу методологии функционального моделирования.
Инструментальной основой концептуальных исследований среди прочих являет-
ся принцип функциональной декомпозиции, формализованный на языке теории от-
ношений как функциональное отношение над входным Xи выходным Yмножествами
(входами х и выходами у) или как функциональная система, в дальнейшем просто
«функция».
Рис. 15.1. Концептуальная схема жизненного цикла изделия
716
Поэтому на этапе «Проектирование» (рис. 15.1) задача проектирования может
быть структурирована в виде теоретико-множественной модели Р.
1. Выбор функциональных элементов А:
1.1 — поиск функциональных элементов Л,
1.2 — определение свойств функциональных элементов Fj
2. Формирование частичных функций:
2.1 — определение управляющей функции И
V={Ai,...,Am},
2.2 — определение качественной функции Q
Q={Fi,...,Fp\.
3. Формирование общих функций:
3.1 — определение системной функции S
S={V,Q},
3.2 — представление системной функции D
D={Ak9S}.
Таким образом, задача проектирования функциональной системы может быть
представлена в виде кортежа
P=D={Ak, 5} = <Ц, FJ9 К 0>,( 15.1)
где все обозначения введены выше.
В процессе конструирования (рис. 15.1) отыскиваются функциональные реше-
ния, представляемые и документируемые в виде некоторой функциональной структу-
ры, способствующей применению компьютерных технологий в промышленном про-
изводстве и позволяющей понять пути повышения эффективности производства. Эти
документы (служащие для изготовления изделий) составляются таким образом, чтобы
все поставленные перед изделием функциональные требования были выполнены: в
этом смысле процесс конструирования предполагает получение не только всех необ-
ходимых чертежей изделия, но и разработку технологических процессов его изготов-
ления, т. е. целесообразным является объединение конструирования и технологиче-
ской подготовки производства (рис. 15.1) в единый процесс конструкторско-техноло-
гической подготовки производства, что выдвигает определенные требования к
системе интегрированного изготовления конструкторской и технологической доку-
ментации (рис. 15.2).
Можно определить, что целью конструирования являются разработка и форми-
рование функций изделия путем переработки геометрической, технологической и ор-
ганизационной информации; подготовка производства обеспечивает технологиче-
скую реализацию превращения исходной заготовки в изделие. Поэтому конструиро-
вание можно интерпретировать как геометрическую обработку информации,
обеспечивающую выполнение функциональных требований к изделию, а подготовку
производства — как геометрическую обработку информации, обеспечивающую вы-
полнение технических и технологических требований к системе.
Сложность и многоплановость задач, возникающих на разных стадиях жизнен-
ного цикла изделия, приводит к необходимости разработки эффективных методов ис-
следования (рис. 15.1). Моделирование как метод исследования включает в себя два
основных этапа: построение модели и использование ее для исследования свойств и
717
Рис. 15.2. Требования к системе интегрированного изготовления конструкторской
и технологической документации [2]
поведения объекта. Математическая модель включает математическое описание свя-
зей между основными переменными и ограничения, накладываемые на область их из-
менения. Математические модели должны быть предельно простыми, иметь стан-
дартную форму и обеспечивать достаточную точность.
Этим общим требованиям полностью отвечает рассматриваемая концепция
функционального моделирования, базирующаяся на принципах:
— функциональной декомпозиции;
— ограничения сложности;
— контекста (т. е. системности).
Функциональное моделирование близко примыкает к известной методологии
SADT, результатом применения которой является модель, состоящая из диаграмм,
фрагментов текста и глоссария, имеющих ссылки друг на друга.
Функциональная модель объединяет формализованные функции объекта и пото-
ки данных, связывающие функциональные зависимости.
Функциональная модель организуется по многоуровневому принципу, отражаю-
щему иерархию функциональных требований, когда каждому функциональному тре-
бованию ставится в соответствие технологическая операция, выполняется агрегиро-
вание этих операций в группы и указываются логические компоненты (функциональ-
ные модули), необходимые для реализации этих групп. Функциональная модель
(ФМ) представляется в виде упорядоченного набора функциональных модулей (ком-
понент)
(15.2)
ФМ = <ФЬ ..., Фк>.
718
Каждый функциональный модуль Ф, в свою очередь характеризуется набором
технологических операций Фу. Функциональные модули связаны между собой пото-
ками данных, связь системы с внешним миром также осуществляется через потоки
данных (рис. 15.3).
Разработка функциональной модели осуществляется в следующей последова-
тельности:
1) приводится перечень функциональных модулей (каждый модуль определяет
конкретную группу операций);
2) для каждого функционального модуля Ф, указываются в определенной после-
довательности все определяющие его операции Фу, описывается входная и выходная
информация;
3) если имеют место особые случаи, не укладывающиеся в предложенную схему,
или необходим специальный комментарий к агрегированию технологических опера-
ций в группы, следует указать это отдельным пунктом для дальнейшего учета при раз-
работке алгоритма реализации функциональной модели.
Указанные особые случаи могут включать в себя параллельные процессы, кото-
рые могут взаимодействовать, или группы функций, включающие одни и те же типы
вычислительных (технологических) операций.
Далее выполняются структуризация информационных потоков данных и алго-
ритм реализации функциональной модели.
При структуризации информационного потока необходимо выделить обобщен-
ные входные и выходные данные с точки зрения их содержания и назначения: доку-
менты, нормативно-справочную информацию, бухгалтерскую информацию, отчеты,
файлы и базы данных. Также необходимо провести классификацию информационно-
го потока с точки зрения входных, выходных потоков данных функциональной моде-
ли — связи с внешним миром и связи между модулями.
При необходимости может быть приведена диаграмма потока данных функциональ-
ной модели в графическом виде. На диаграмме отображаются функциональные модули в
виде прямоугольников и потоки данных в виде связывающих их дуг. Также должны быть
показаны внешние входные и выходные данные (пример — раздел 15.9, рис. 15.22).
Технологические операции, агрегированные по группам
—► — внешние потоки данных
—— потоки данных между функциональными модулями
‘ ~ ** — взаимосвязи между функциональными модулями и группами операций
Рис. 15.3. Структура функциональной модели
719
В описании алгоритма реализации функциональной модели приводится после-
довательность действий для реализации автоматизируемого процесса. При этом на
каждом шаге необходимо кратко указать суть технологической операции, роли испол-
нителей и соответствующую автоматизированную систему.
Для каждого функционального модуля Ф,, входящего в структуру модели
(рис. 15.3), разработаны следующие описания:
— входная информация;
— выходная информация;
— роли исполнителей, права доступа;
— алгоритм реализации функционального модуля.
При описании входной информации указываются все входные данные функци-
онального модуля с точки зрения их содержания и назначения: документы, норматив-
но-справочная информация, базы данных, записи, поля данных, сообщения, таблицы.
Состав и содержание выходной информации описываются по тем же правилам,
что и входной.
Под участниками понимаются все исполнители, реализующие данную функцию
(функциональный модуль): подразделения и персонал предприятия, внешние орга-
низационные структуры и пр.
Необходимо привести перечень ролей пользователей, которые будут использо-
вать функциональный модуль.
Описание алгоритма реализации функционального модуля состоит из текстового
описания предварительных условий, правил и последовательности выполнения действий.
В предварительных условиях описываются необходимые условия, без которых
нельзя приступить к выполнению технологических операций, определяющих рас-
сматриваемый функциональный модуль.
Последовательность действий в алгоритме реализации функционального модуля
упорядочивается в рамках основного и альтернативного сценариев.
События основного сценария отражают штатную последовательность технологи-
ческих операций; события альтернативного сценария отражают нештатные ситуации,
возникающие при выполнении той или иной технологической операции. В альтерна-
тивном сценарии должны быть указаны изменяемые шаги основного сценария и но-
вая последовательность действий в связи с нештатной ситуацией.
В описании событий сценариев при необходимости должны быть приведены
расчетные формулы.
Таким образом, построение функциональной модели позволяет определить:
1. Модель Р задачи проектирования (15.1), отражающую представление системной
функции D как композиции функциональных элементов их свойств функции
управления V и функции качества Q.
На этапе конструирования конструкция изделия как функциональная система
составляется из отдельных функциональных элементов — подконструкций — по оп-
ределенным правилам, т. е. в качестве референтной модели при декомпозиции реали-
зуется концепция подконструкций. Синтез конструкции с заданными свойствами
осуществляется с применением математического аппарата функционального модели-
рования, о котором речь пойдет ниже.
Функциональная система Л (15.1) (проектируемое изделие) на этапе конструк-
торского проектирования моделирует набор конструкторских решений и формирует
исходные данные для последующего технологического проектирования.
На этапе технологической подготовки производства алгоритмизация решения
сложных технологических задач основана, в первую очередь, на разработке математи-
ческих моделей, описывающих структуру (состав элементов), функцию и свойства
720
объекта как технической системы, т. е. на этапе технологического проектирования
модель (15.1) «заполняется» технологическими данными.
Функциональная модель Р (15.1) позволяет выполнить формализацию на теорети-
ко-множественном уровне процессов: проектирования, организации и управления
производством и формированием данных о материальных и информационных потоках
производства; изготовления изделия путем выполнения операций над материальными
объектами на основе информации, созданной на предыдущих этапах жизненного цик-
ла; оценки качества изделия на основе сравнения требуемых и реальных характеристик.
2. Конструкцию функциональной модели (15.2), для определения которой необхо-
димо выполнить следующее:
— выделить функциональные модули;
— определить входные и выходные значения;
— построить диаграммы потоков данных (ДПД), показывающие функциональ-
ные зависимости;
— сформулировать при необходимости критерии оптимизации;
— уточнить набор технологических операций в объектной модели.
Определение входных и выходных значений реализует принцип контекста в
функциональном моделировании. Эти значения являются параметрами событий
между системой и ее окружением и фиксируют границы моделируемой функции.
ДПД обычно строится по уровням, функциональные модули отображаются в ви-
де прямоугольников; на ДПД каждого уровня удобно показать элементы данных бо-
лее высоких уровней, чтобы показать данные, обрабатываемые каждой функцией.
Ограничения — это функциональные зависимости между объектами, не сводя-
щиеся к непосредственным зависимостям между выходами и входами. Ограничения,
которым должны удовлетворять входные значения функции, называются ее предус-
ловиями, а ограничения, которым должны удовлетворять выходные значения функ-
ции, — ее постусловиями.
15.2. СРЕДСТВА АВТОМАТИЗАЦИИ ПРОЕКТНЫХ РАБОТ
Автоматизированным называется такое проектирование, при котором все или
часть проектных решений получается при взаимодействии человека и средств автома-
тизации. В качестве основных средств автоматизации проектных работ применяют
средства вычислительной техники, являющиеся техническим обеспечением систем
автоматизированного проектирования. В общем случае употребление термина «авто-
матизированное» означает применение в процессе выполнения работ средств вычис-
лительной и организационной техники.
Свойства вычислительной техники, накладываясь на реальные процессы проек-
тирования, приводят к неизбежному их усложнению и удорожанию. Но вместе с тем
применение средств вычислительной техники:
— уменьшает количество ошибок (в силу объективности представления результа-
тов, повышения их точности и т. д.);
— ускоряет процессы обмена данными при выполнении совместных работ, моди-
фикацию объектов, обеспечивая возможность повторной обработки больших объ-
емов информации при внесении небольших исходных изменений.
Система автоматизированного проектирования (САПР) — организационно-тех-
нический комплекс, состоящий из взаимосвязанных и взаимодействующих компо-
нентов для автоматизированного проектирования объектов и их составных частей на
основе применения математических моделей, автоматизированных проектных про-
цедур и средств вычислительной техники.
721
Целью создания САПР является совершенствование конструкторско-технологи-
ческой (технической) подготовки производства (ТПП) на базе математических мето-
дов, оптимизация процессов проектирования и управления с применением современ-
ных средств вычислительной и организационной техники.
Каждую из установленных форм организации ТПП допускается реализовывать
множеством структурных вариантов, зависящих от специфики конкретного пред-
приятия и степени охвата задач ТПП средствами механизации и автоматизации.
Основные особенности технического проектирования, влияющие на анализ ав-
томатизированных систем технической подготовки производства, следующие:
1) в процессе проектирования формируется информационная модель нового или
модернизируемого объекта;
2) процедуры проектирования обеспечивают поэтапное преобразование исходного
описания объекта в конечном пространстве образов (символов) предметной области;
3) процедуры преобразования для сложных объектов являются трудноформали-
зуемыми;
4) процесс проектирования не только формирует внутреннюю структуру, но и ус-
танавливает (разрешает) внешние связи, так как любой проектируемый объект являет-
ся частью включающей его системы;
5) в связи с тем, что при техническом проектировании сложных объектов на раз-
личных стадиях и этапах привлекаются новые коллективы специалистов, должны
быть обеспечены передача информации и согласование проектных решений,
6) для обеспечения качественных показателей и эффективности изделий процесс
проектирования должен обеспечивать итерационность принятия решений, а сами
проектные решения должны быть многовариантными.
Задачи систем автоматизированного проектирования покрывают широкий круг
вопросов информационного сопровождения продукции, связанных с организацией
различных инженерных расчетов, геометрического и графического моделирования,
формирования управляющих программ для оборудования.
На сегодняшний день особенно остро для предприятий обозначены три направления
в выборе стратегии информационного сопровождения сложных технических объектов.
1. Определение правильного и разумного применения многочисленных програм-
мно-технических решений, причем решений дорогостоящих, которые позволяют ав-
томатизировать и упростить работу персонала по конкретным направлениям своей
деятельности при сопровождении изделия на всех этапах его жизненного цикла. На
каждой стадии можно выделить целые комплексы средств информационной и
компьютерной поддержки, научные и прикладные направления.
2. Не менее важная, но менее проработанная задача — это задача информацион-
ной интеграции и преемственности информации между различными стадиями жиз-
ненного цикла сложных технических объектов. Интегрирующая информационная
среда, благодаря коллективному использованию данных и согласованному решению
отдельных задач, должна обеспечить создание изделий в установленные сроки и с ми-
нимальными затратами.
3. Учет, сохранение и активная работа с интеллектуальной собственностью, кото-
рую можно определить как совокупность сложившихся технологических традиций,
инженерного опыта, особенностей индивидуальных стратегий проектирования, яв-
ляющихся основой для принятия решений (с использованием расчетно-аналитиче-
ских методов, с учетом многокритериального подхода, фактора времени, вероятности
достижения коммерческих результатов, технического и экономического рисков, со-
циальных и экологических последствий использования интеллектуальной собствен-
ности и т. д.).
722
Анализ процессов проектирования, технологической подготовки и производства
изделий на различных стадиях их жизненного цикла позволяет сделать вывод о том,
что, несмотря на признанное отставание от мирового уровня отечественных средств
механизации и автоматизации производственных процессов, все-таки первичным и
гораздо большим сдерживающим фактором является слабая оснащенность интеллек-
туального труда и слабая подготовка проектировщиков к работе в новых условиях
современных информационных технологий. Комплексное решение всех задач, свя-
занных с проектированием, производством и эксплуатацией изделий, необходимо
осуществлять в рамках постоянно совершенствуемых интегрированных автоматизи-
рованных систем, использующих единые методы и средства для решения всех задач
конструирования и технологической подготовки производства на основе применения
современных информационных технологий. Эти технологии позволяют связать в еди-
ную систему все службы предприятия, участвующие в проектировании и создании
нового изделия, технологической подготовке его производства, а также поставке и его
сервисной поддержке. Основными компонентами таких интегрированных систем яв-
ляются:
— система автоматизированного проектирования изделий (CAD — Computer
Aided Design);
— система автоматизации технологической подготовки производства (САМ —
Computer Aided Manufacturing);
— инструментальный комплекс программных средств инженерного анализа
(САЕ — Computer Aided Engineering);
— инструментальные средства технологии автоматизированного параллельного
проектирования (СЕ — Concurrent Engineering);
— система управления проектными и инженерными данными (PDM — Product
Data Management).
Целесообразно проводить координацию работ и создавать систему корпоратив-
ного управления данными на основе базовых программных комплексов, создаваемых
единым разработчиком. В настоящее время наиболее распространенными в России
являются программные продукты трех фирм: EDS (Unigraphics, IMAN), IBM (CATIA,
CNEXT), Computervision (CADDS 5, Optegra).
Новые информационные технологии предоставляют возможность радикального
изменения процессов проектирования, производства и эксплуатации. Учет структуры
проектируемого объекта и методов проектирования и производства приводит к воз-
никновению методов объектно-ориентированного проектирования. На существую-
щем уровне становления информационных технологий пока еще окончательно не
сложились представления и понятия этой специфической технологической области.
Существующие и наиболее часто применяемые в этой области понятия большей
частью заимствованы из смежных областей: вычислительной техники, программиро-
вания, системного анализа. Для целостного и взаимосвязанного подхода к информа-
ционным технологиям должны быть проведены классификации объектов, процессов
и инструментальных систем, применяемых в новой области, называемой информаци-
онными технологиями, и разработана специфическая нормативная база. Специфика
объектов и процессов существенно различается для стадий проектирования, техноло-
гической подготовки производства, организации и управления производством, экс-
плуатации.
Эффективная взаимосвязь этапов обеспечивается в технологической среде CALS
(Continuous Acquisition and Life cycle Support — непрерывная информационная под-
держка жизненного цикла продукции). CALS-технологии — это информационное со-
провождение всех этапов жизненного цикла изделий в форме, позволяющей конструк-
723
тору общаться с эксплуатационщиком, учесть его мнение, используя электронную сис-
тему, единый язык, единую базу данных и т. п. Для производства сложных технических
изделий это прежде всего проблема обеспечения технологичности, которая была всег-
да одной из главных проблем организации эффективного производства. CALS-техно-
логии предоставляют отработанный инструмент для решения этой проблемы.
Новые методы организации процессов проектирования в CAD/CAM-системах в
настоящее время известны под обобщенным названием САМЕ, обозначающим па-
раллельные технологические среды для создания изделий. В специальном издании
GartnerGroup, основная в США аналитическая группа по исследованию рынка, регу-
лярно представляет отчеты со стратегическим анализом основных поставщиков
CAD/CAM-систем, реализующих средства САМЕ. Аналитики приводят ряд продук-
тов фирм, занимающих лидирующие позиции в области разработки и поставки CAD/
САМ-систем:
UNIGRAPHICS - EDS-Unigraphics (EDS),
CATIA V4, V5 — Dassault Systemes (Dassault) и IBM,
Pro/ENGINEER — Parametric Technology Corporation (PTC),
AutoCAD Designer — Autodesk,
Master Series — Structural Dynamics Research Corporation (SDRC),
Clipper, SunSPARC — Intergraph,
Precision Engineering SolidDesigner — Hewlett-Packard (HP).
CAME, по заключению аналитиков, представляет основополагающую проект-
но-конструкторскую философию объединения проектирования и производства в ин-
тегрированный процесс создания изделия на основе расширенного производства
(комплексного автоматизированного производства), которую должны принять и ус-
воить производители, чтобы выжить и остаться конкурентоспособными.
Параллельные технологические среды комплексных предприятий предполагают
включение всех участников в проектно-технологический процесс: специалистов по
конструкторской разработке, по подготовке производства, по вопросам качества, по-
купки, продажи, маркетинга; поставщиков и заказчиков. Участники такого коллекти-
ва, работая параллельно в составе тесно взаимодействующей многодисциплинарной
(многопрофильной) проектной команды, смогут значительно улучшить результаты
процесса создания изделия, особенно на ранних его этапах.
В большинстве зарубежных CAD/CAM-систем, реализующих новую проектно-
конструкторскую философию параллельных технологических сред для создания ма-
шиностроительных изделий, и в отечественных системах комплексного автоматизиро-
ванного производства (КАП), а также в САПР технологического назначения и в
АСГПП основные задачи технологического проектирования так или иначе базируют-
ся на вариантном проектировании технологических процессов различных видов работ.
По своим возможностям (составу функций и размерности обрабатываемой моде-
ли) системы подразделяются на:
— тяжелые (большие) — такие, как UNIGRAPHICS, CATIA, Pro/ENGINEER;
— средние — Cimatron, SolidWORKS, Solid Edge;
— легкие — AutoCAD, T-flex, «Компас».
Состав направлений анализа процессов и систем проектирования сложных тех-
нических объектов с учетом их взаимосвязи приведен на рис. 15.4. Основными взаи-
мосвязанными аспектами анализа процессов проектирования и технической подго-
товки производства с целью определения перспектив применения и развития систем
автоматизированного проектирования являются функциональный, структурный и
инструментальный.
724
Рис. 15.4. Схема направлений анализа систем проектирования
Функциональный аспект анализа процессов и систем проектирования с целью
выявления перспективных направлений создания и развития методов и средств авто-
матизации технологического проектирования определяет стадии жизненного цикла
объектов проектирования, схемы информационных и материальных потоков техно-
логического проектирования и реализации объектов, функциональные взаимосвязи
пространств моделирования и задач технологической подготовки производства.
Структурный анализ систем автоматизированного проектирования дает возмож-
ность определить перспективы развития объектно-ориентированных подсистем,
средств обеспечения и компонентов.
Постоянное усложнение средств автоматизации интеллектуального труда, а так-
же расширение их потенциальных возможностей привело к необходимости примене-
ния инструментальных средств не только разработки систем автоматизированного
проектирования и их подсистем, но и отдельных средств обеспечения и даже их ком-
понентов.
Для каждой стадии жизненного цикла изделия характерны два слоя: информаци-
онный и материальный. В информационном слое создаются описания изделий и про-
цессов различного назначения. Он характеризуется преобладанием интеллектуально-
го труда. В материальном слое по описаниям, представленным в различной форме,
выполняется материализация изделий и процессов.
Структура производственной системы реализации изделия на различных стадиях
жизненного цикла показана на рис. 15.5.
Анализ предметной области для установления закономерностей функциониро-
вания, существующих в технологических системах с непрерывными процессами, сло-
жен, что характерно для дискретных производственных систем. В дискретной техно-
логической системе варианты технологических процессов изготовления сложного
объекта можно представить множеством путей от исходного к конечному заданному
состоянию. Если это пространство состояний возможно формировать формально, ис-
пользуя правила вывода, то можно построить имитационную модель. Модель упро-
щенно можно рассматривать как цепочку из элементов, в которых задано начальное и
конечное состояния. Каждый из элементов модели в зависимости от составов преды-
дущих и последующих элементов меняет значение своих показателей, что является
основой для постановки оптимизационной задачи имитационного моделирования
дискретного технологического процесса сборочных работ.
725
Слои
Организационный Проектирование и организация производства и эксплуатации изделия
Информационный Научные исследования и конструирование Технологическое проектирование Оценка технологичности, эффектив- ности производства и эффективности и эксплуатации изделия
Материальный Визуализация результатов проектирования изделия Изготовление те оснаи ихнологического зения Эксплуатация, техническое обслуживание и ремонт изделия
Модельный (имитационный) Имитационное математическое моделирование изделия, его производства и эксплуатации
Проектирование изделия Т ехнол огическая подготовка Изготовление Эксплуатация изделия
Производство изделия
СТАДИИ
[~~----------7----
Проектные работы
технической под-
готовки производ-
ства
— область разработки и применения методов моделирования
Рис. 15.5. Структура проектных и производственных работ реализации изделия
Основным законом проектирования и организации функционирования производ-
ственной системы, включающей изделия, элементы технологической системы и техно-
логические процессы, является закон контроля за соблюдением локальных и глобаль-
ных технологических ограничений и технико-экономических условий. Цели различных
производственных программ в конкретный момент времени могут не совпадать и могут
возникать объективные противоречия между универсальностью и специализацией тех-
нологического оборудования, подготовкой производства и производством, изготовле-
нием деталей и сборкой. Разрешение этих противоречий — основная задача проектиро-
вания, организации и управления ТПП. Локальные ограничения определяют требова-
ния к качеству изделий, оборудования и инструмента, производительности при
выполнении операций. К глобальным относятся ограничения использования (избы-
точности) ресурсов во всей технологической системе в целом и ограничения взаимо-
действия отдельных функциональных подсистем технологической системы.
Структурный аспект анализа распространяется на определение состава подсис-
тем, средств обеспечения и компонентов систем автоматизации технологической
подготовки производства. Структура САПР независимо от функционального назна-
чения разделяется на три уровня и включает:
— объектно-ориентированные (функциональные) и объектно-независимые (ин-
вариантные) подсистемы;
— математическое, лингвистическое, информационное, программное, техниче-
ское, методическое и организационное обеспечения;
— компоненты всех видов обеспечений.
Назначение средств обеспечения САПР определяет состав и содержание компо-
нентов средств обеспечения.
Различают следующие виды обеспечений.
1. Математическое — методы, математические модели и алгоритмы автоматизи-
рованного проектирования.
2. Лингвистическое — совокупность языков, используемых в САПР для представ-
ления информации о проектируемых объектах, процессах и средствах проектирования.
3. Информационное — документы, содержащие описание изделий, производст-
венной системы, их элементов (предметной области), а также файлы и блоки данных
на машинных носителях с записями этих документов.
4. Программное — совокупность программ, представленных в заданной форме,
вместе с необходимой программной документацией.
5. Техническое — совокупность аппаратных средств, включающая устройства
вычислительной и организационной техники, средства передачи данных, измери-
тельные и другие устройства, используемые в САПР.
6. Методическое — документы, в которых отражены состав, правила выбора и
эксплуатации средств автоматизированного проектирования.
7. Организационное — положения, инструкции, приказы, штатные расписания,
квалификационные требования и другие документы, регламентирующие организаци-
онную структуру проектной организации.
Для разработки основных средств обеспечения необходимо создавать и приме-
нять современные инструментальные средства.
Состав инструментальных средств автоматизации технической подготовки про-
изводства зависит от функционального назначения и структуры подсистем САПР.
В зависимости от функций системы технической подготовки производства уста-
навливается следующий состав объектно-ориентированных подсистем специального
назначения: обеспечение технологичности конструкции изделия; проектирование
технологических процессов; проектирование средств технологического оснащения;
управление ТПП; изготовление средств технологического оснащения.
727
Математическое обеспечение подсистемы проектирования технологических
процессов может быть построено на основе типовых математических моделей.
Для эффективного решения задач конструкторско-технологического проектиро-
вания при технической подготовке производства, а также для создания методов и
средств автоматизации проектирования необходимы встроенные в производственную
систему подсистемы САПР, реализуемые на основе применения инструментальных
систем моделирования.
В связи с этим необходимы разработка и исследование инструментальных систем
компилирующего типа, ориентированных на создание основных средств обеспечения
САПР конструкторского и технологического назначения, функционирующих на ос-
нове имитационного моделирования таких разнородных объектов, как изделие, тех-
нологическая система и технологический процесс изготовления изделия средствами
технологической системы. При разработке проблемно-ориентированных инструмен-
тальных систем должны быть соблюдены основополагающие принципы построения и
применения САПР и обеспечено такое перспективное направление создания и разви-
тия инструментальных систем, как функциональное разделение на объектно-незави-
симое (инвариантное) ядро системы, объединяющее математическое и программное
обеспечение, и проблемно-ориентированное проектирование, основанное на имита-
ционном моделировании разнородных объектов предметной области.
15.3. ИНВАРИАНТНАЯ ИНФОРМАЦИОННАЯ МОДЕЛЬ
ОБЪЕКТА ПРОЕКТИРОВАНИЯ
Рассматриваемая область моделирования дает возможность строить математиче-
ские модели объектов. Имея теоретико-множественную модель (15.1), нужно опреде-
литься с математическим аппаратом, обеспечивающим адекватный переход от абст-
рактной модели и позволяющим выполнить описание функциональной модели
(15.2). В настоящее время математические методы моделирования получили широкое
развитие и имеется обширная литература по этим вопросам [3—7 и др.].
Функциональное моделирование не требует разработки каких-либо специальных
математических методов, поскольку в его основе лежит представление объекта как
функциональной системы, состоящей из совокупности элементов, функционально
выступающих как единое целое и обладающих структурой, функциями и свойствами
(15.1). Из известного набора математических методов следует лишь выбрать те, кото-
рые обладают свойством универсальности и пригодны для моделирования одинако-
выми средствами самых разнородных по своей природе объектов: конструкции изде-
лия или средств технологического оснащения производства, технологического процес-
са или процесса проектирования, организационно-экономических процессов и т. д.
Следует учитывать, что выбор адекватного математического аппарата для постро-
ения математической модели зависит не только от характера (функции) самого объек-
та, но и от поставленной задачи. Поэтому при моделировании реального объекта мо-
жет потребоваться не одна, а несколько математических моделей, описывающих его
свойства, в зависимости от решаемых при проектировании или исследовании задач.
Нахождение компромисса между простотой модели и необходимостью учета мно-
гочисленных характеристик сложной системы является не простой задачей, решение
которой ищется в иерархическом описании. Система задается семейством моделей,
каждая из которых описывает поведение системы с точки зрения различных методоло-
гических уровней анализа. Для каждого уровня существует ряд характерных особен-
ностей и переменных, законов и принципов, с помощью которых и описывается пове-
дение системы. При этом необходимо обеспечить связность и совместимость частных
математических моделей, отражающих разнородные свойства и стороны объекта.
728
Используемый в функциональном моделировании аппарат формализации опи-
рается на структурные свойства систем и является аппаратом структурно-параметри-
ческого моделирования [3, 4]. Исходными данными для построения моделей являют-
ся данные об элементах самого объекта моделирования, данные о свойствах и данные
об отношениях между элементами и свойствами.
В структурно-параметрическом моделировании составы этих данных представ-
ляются в виде множества элементов самого объекта А, множества Ф контуров и мно-
жества R отношений между элементами, элементами и контурами, контурами [5, 6].
Понятие контура является экспликацией таких понятий, как свойство, признак, ха-
рактеристика, параметр и т. п. При функциональном моделировании понятие контура
может быть использовано для описания свойств функциональных элементов Ф, в
(15.1), компонент функции качества Q, общих функций системы (контуров, опреде-
ляющих функциональное назначением элемента); контуры могут описывать все кон-
структивно-технологические свойства изделия, специфические особенности произ-
водства (технологические контуры), элементы организационной структуры.
Таким образом, концепция структурно-параметрической модели
5(Л) = {А, С, R}, (15.3)
где А — отображение элементов объекта; Ф — отображение контуров (признаков,
свойств элементов объекта); R — отображение отношений между элементами, эле-
ментами и свойствами, свойствами, является адекватной задачам функционального
моделирования.
Элементы реальной системы, будучи материальными объектами, обладают разно-
родными, органически связанными друг с другом свойствами. Эти связи различаются по
их роли в назначении и функционировании объекта, по природе, по уровню абстрагиро-
вания при математическом моделировании и т. д. Основными связями являются струк-
турные и причинно-следственные, характеризующие взаимосвязь объектов при абстра-
гировании от природы действующих факторов, а с учетом этих факторов — функци-
ональные, вещественные, энергетические, пространственные и информационные связи.
Структурные связи обусловлены отношениями принадлежности объектов, их
элементов и свойств к определенным множествам, отношениями иерархической под-
чиненности, а также отношениями инцидентности, смежности и порядка.
Причинно-следственные связи отражают последовательности изменения со-
стояний объекта или его свойств с учетом состояния других, не обязательно смежных
с ним объектов.
Описание состава, свойств и поведения объекта моделирования может быть вы-
полнено на трех основных уровнях:
— на уровне структурных свойств и отношений;
— на уровне логических свойств и отношений;
— на уровне количественных свойств и отношений.
На каждом из этих основных уровней возможны описания объектов с различной
степенью полноты и обобщения, соответствующие различным уровням абстрагирова-
ния структурных, логических или количественных свойств и отношений.
При переходе от одного к другому уровню абстрагирования в описании свойств
объектов указываются количественные, логические или структурные условия перехо-
да одних свойств в другие.
Изложенные концептуальные принципы структурно-параметрического модели-
рования реализованы в соответствующих моделях и алгоритмах их обработки при
решении широкого круга задач в машиностроении. Модели машиностроительных
объектов нельзя сводить лишь к конструкторским (графическим, геометрическим)
характеристикам. Модели могут описывать технологические и экономические про-
729
цессы и позволять находить численные значения их характеристик. Модели такого
типа значительно шире чисто конструкторских структурных моделей.
Информационная модель должна развиваться и совершенствоваться в соответствии
с нуждами всех работающих с ней пользователей: проектировщиков, конструкторов, тех-
нологов, экономистов, технических руководителей. Информационные объекты форми-
руют единую технологическую среду, которая служит для всех пользователей источником
информации, выбираемой в соответствии с профессиональными интересами и преобра-
зуемой в форму, пригодную для решения их задач. Возможность работы с такими инфор-
мационными объектами — основное требование к организации конструкторско-техно-
логической базы данных. Под термином «модель» будем понимать информационно на-
сыщенное описание объектов и процессов, определяющее как структуру, так и поведение
моделируемой системы. Если модель используется в конструкторском проектировании,
в нее должны входить геометрические данные, обрабатывая которые прикладная про-
грамма может построить графическое изображение. В виде графических изображений
могут быть представлены: структурные схемы процессов (схема сборки), топологические
карты микросхем, чертежи механических деталей, строительные чертежи.
Математическое обеспечение объединяет методы моделирования, математиче-
ские модели и алгоритмы их обработки. Математическая структура 5, или просто
структура, представляет собой базисные множества М, элементы которых состоят в
некоторых отношениях R, описываемых свойствами, и обозначается
5 = {Мх, М2,..., Мп, Я,, R2,..., Rm}. (15.4)
Примем, что состав базисных множеств информационных моделей определяется
следующим набором
М={А,Ф} = {А, 7, Л}, (15.5)
где А = {л,, ..., ап} — множество элементов моделируемого объекта; F = {/j, ...,/„} —
множество свойств (контуров) [3] элементов на логическом уровне представления;
N = {лр ..., nt} — множество свойств элементов на количественном уровне представле-
ния — параметры элементов. Здесь Ф = F и N.
Исследования задач конструкторско-технологической подготовки производства
позволили определить:
— состав атрибутов, определяющих элементы базисных множеств;
— отношения между элементами множеств;
— процедуры, формирующие значения свойств и параметров.
В результате исследований был определен состав инвариантной структурно-па-
раметрической модели (СПМ) объекта проектирования [3]
5(Л) = {А, 7, N, R, р}, (15.6)
где р — процедуры, формирующие значения свойств и параметров.
В практике выполнения проектных работ существует необходимость варьирова-
ния полнотой определения моделей объектов в силу, во-первых, различий в составе
информации для решения разных задач, во-вторых, различий в самих объектах и их
составных частей, и в-третьих, в силу первоначальной неопределенности многих ха-
рактеристик объекта на начальной стадии процесса проектирования, предполагаю-
щей последующее наращивание полноты определения модели объекта. Этому требо-
ванию удовлетворяет СПМ, инструментальные средства которой позволяют вести на-
ращивание описания модели объекта «в глубину» по следующим шагам:
А — формирование макета объекта;
Б — построение системы параметризации;
В — определение условий работы с вариантами структурных решений;
и «в ширину» — по мере детализации определения функциональных, конструк-
тивных и технологических особенностей объекта.
730
А. Макет объекта
представляет собой совокупность информации, позволяющей воспроизвести
внешний облик объекта и идентифицировать иерархически связанные компоненты
объекта, определяющие его функциональные (конструктивные) особенности. Для
этого необходимо обобщить информацию о содержании базисных множеств, струк-
турных взаимосвязей между элементами модели и элементах, формирующих графи-
ческий образ объекта.
Базисные множества, модели.
Определим некоторые особенности элементов базисных множеств.
Элемент множества А
а^А (15.7)
представляется теоретико-множественной величиной; может входить или не входить
в анализируемые структуры; существует при любых значениях свойств и параметров.
Элемент множества F
f^F (15.8)
представляется логической величиной (двузначная логика); принимает значение из
конечного ряда методом указания состояния (есть v нет; истина v ложь; 1 v 0); может
характеризоваться одним или несколькими параметрами; имеет зависимый характер —
его значение может быть определено только при сопоставлении с элементом, т. е. дол-
жно быть определено отношение принадлежности
RaJ=l(a,Fa), (15.9)
где 1 — таблица отношений, Fa — подмножество F (Fa с Fa).
Элемент множества N
N^N (15.10)
является характеристикой элемента или свойства, имеющей количественное или
лингвистическое значение, которое определяется из бесконечного ряда значений.
Среди параметров выделяется множество параметров объекта 7V и множества пара-
метров Na составных частей объекта, т. е. должно быть определено отношение прина-
длежности
Ran=T(a,Na). (15.11)
Взаимосвязи между элементами модели.
Точно описать все информационные элементы недостаточно — необходимо
определить все связывающие их отношения. Под отношением понимается четко оп-
ределенная связь между информационными элементами. Таким образом, информа-
ционные объекты связаны друг с другом отношениями. Например, отношения связы-
вают сборочный чертеж и спецификацию, поскольку известно, что каждому сбороч-
ному чертежу соответствует спецификация, причем она может быть представлена в
виде документа в формате текстового процессора. Аналогично перечень комплектую-
щих элементов связан отношениями со списком поставщиков, поскольку каждый та-
кой элемент закупается у какого-либо поставщика.
При создании системы моделирования возникает проблема разработки простых и
естественных средств создания и модификации моделей отдельных элементов и их сбо-
рок. Эффективность подобной системы во многом зависит от того, насколько удачны
структура данных, способ описания элементов данных и методы работы с данными.
Важным элементом работы с информационной моделью является возможность
выделения функционально завершенных фрагментов (модуляризация среды). С по-
мощью модуляризации можно добиться снижения сложности не только конструктор-
ских, но и прочих, например, технологических объектов. Для этого требуется четкое
определение структуры моделируемых объектов (т. е. должна быть выполнена декомпо-
зиция структуры изделия на сборочные узлы, а для тех, в свою очередь, — на сборочные
731
ABC
Элемент модели
А Идентификатор элемента в модели «Метка»
В Тип описывае- мого элемента С, У — сборка, узел Д — деталь К — конструктив 0 — примитив Ф — фиктивный эле- мент «ТИП»
С Т опологический признак «+» — объединение «-» — вычисление «♦» — пересечение «ТЕЛО»
D Признак формы Используется для идентификации модели «КОД»
а) Идентификация элемента (объекта)
Элемент модели
а Область определения струк- турно-параметрического модуля А
b Отношения подчиненности в иерархии
с Пространственная взаимо- связь элементов
d Связь элементов «по умол- чанию» Ra
б) Отношения иерархической подчиненности
732
a a
в) Параметризация элементов модели
Рис. 15.6. Формы представления результатов анализа
узлы более низкого уровня и детали). При реализации структур низкого уровня инфор-
мационные объекты высокого уровня становятся более информационно прочными.
Вместе с тем, для того чтобы работать со структурами низкого уровня, проекти-
ровщик должен оперировать моделью:
— структурируемой в соответствии с устройством изделий;
— воспроизводящей иерархию уровней абстракции;
— позволяющей взаимодействовать с библиотеками моделей стандартных дета-
лей и сборочных узлов, описаний технологически однородных групп изделий.
Связи, отражающие конструктивную либо функциональную иерархию объекта,
определяются отношением
R\ = GX(A, С,), (15.12)
где Gj — граф вида «дерево», С\ — множество ребер, отражающих связи между элемен-
тами А (рис. 15.6, б).
Пространственные взаимосвязи элементов задаются отношением
Ri = G2(A,G2), (15.13)
где G2 — ориентированный граф без циклов, С2 — множество дуг. Граф G2 является взве-
шенным. Такой объект может быть задан через указание пар элементов и относительных
перемещений и поворотов их координатных систем в пространстве (см. рис. 15.6, б). На
схемах пары элементов соединяются сплошными дугами. Пунктирными дугами обозна-
чены связи, формируемые в модели автоматически и отражающие правило, согласно ко-
торому система координат объекта совпадает с системой координат первого включенно-
го в объект элемента. Для реализации этого правила создана процедура pj^.
733
В конструкторском и технологическом проектировании предложенная модель
пространственных взаимосвязей позволяет решать задачи размерного анализа, возни-
кающие при проектировании изделий и технологических процессов.
Визуализация элементов модели.
Для того чтобы система моделирования позволяла строить изображения некоторого
объекта, в его описание должны входить геометрические (графические) примитивы,
идентификаторы которых соотнесены с описаниями базовых элементов форм (БЭФ)
подсистемы визуализации (ри), и часть их собственных параметров с параметрами БЭФ.
В системе визуализации поддерживаются следующие модели базовых элементов формы:
— правильные тела;
— кинематические элементы;
— элементы произвольной топологии;
— сплайновые элементы.
Модели низшего уровня, созданные для представления базовых элементов фор-
мы, помещаются в специальную библиотеку.
Все выполняемые с примитивами действия задаются с помощью проблемно-
ориентированного языка, операторы которого позволяют пользователю переносить,
вращать и масштабировать примитивы, создавая объемные тела с помощью операций
объединения, пересечения и вычитания БЭФ.
Значения собственных (персональных) параметров Na каждого элемента конкре-
тизируют содержание признака формы, либо определяют дополнительные, напри-
мер, функциональные характеристики элемента. Кроме того, каждому элементу мо-
дели ставится в соответствие координатная система и параметры, определяющие ее
положение в глобальной системе координат Nu (унитарные параметры)
Nu = (x,y,z,Mc)9 (15.14)
где х, у, z — положение центра системы координат элемента, Мс — матрица направ-
ляющих косинусов, определяющая ориентацию координатной системы.
Б. Система параметризации
Параметры, характеризующие структурные элементы и объект проектирования в
целом, увеличивают размерность предметной области. Параметрическое моделирование
является наиболее отработанным методом, аккумулирующим способы вычислительной
математики. Основными функциями параметрического моделирования являются: опре-
деление значений параметров; оптимизация значений параметров. Параметры могут
быть непрерывными и дискретными, независимыми и связанными между собой.
СПМ позволяет строить гибкую систему параметризации объекта, способную
управлять не только проектированием внешнего облика объекта, но и воспроизво-
дить его кинематические возможности. Система параметризации объекта в СПМ
включает совокупность параметров и конструкций над ними, позволяющих управ-
лять значением собственных параметров объекта и параметров положения его эле-
ментов. Ниже приведены пять таких конструкций.
1. Древовидная структура взаимосвязей параметров элементов различных уров-
ней, представленная отношениями, определяющими иерархическую подчиненность
параметров:
4 = (15.15)
где G3 — несвязанный граф, объединяющий некоторое количество связанных струк-
тур вида «дерево», корнями которых могут быть параметры, принадлежащие элемен-
там различных уровней иерархии; С3 — множество дуг.
2. Правила распространения значений между параметрами элементов, реализуе-
мые процедурой р)у.
734
3. Отношения R2N между параметрами элемента и процедура р^, реализующая об-
работку аналитических и таблично заданных зависимостей.
4. Внешние процедуры, обрабатывающие сложные алгоритмические зависимос-
ти между параметрами, и механизм их реализации в структурно-параметрической мо-
дели р^.
5. Атрибуты описания взаимного положения элементов объекта в пространстве
R'AN=T(C2,QU), (15.16)
где 0й = (Л, Y, Z, UX, UY, UZ) — операторы элементарных перемещений координатных
систем в пространстве; а также процедура расчета положения элементов в простран-
стве р^.
Выделение общих проектных процедур в самостоятельные модули способствует
организации компонентов баз знаний в предметных областях.
Невозможно создать универсальное вычислительное средство, которое нашло бы
широкое распространение. Либо оно будет слишком громоздким, либо найдутся спе-
циалисты, «сросшиеся» с другими системами расчетов, либо расчетная задача уже
удачно реализована и нет возможности (ресурсов) повторить ее реализацию.
Для обеспечения возможности адаптации алгоритмов (программ), обитающих
вне технологической среды структурно-параметрической модели, предусмотрена воз-
можность организации вызова (обращения) ко внешним процедурам. Под внешней
процедурой будем понимать выполняемый модуль (программу), реализованный и
функционирующий под управлением операционной системы ЭВМ. Для организации
информационного обмена предлагается аппарат «таблиц обмена».
В. Структурное моделирование
является наиболее сложной областью для формализации. В большинстве систем
автоматизированного проектирования и систем искусственного интеллекта основные
функции структурного моделирования выполняет человек. Выполнение этих функций
может осуществляться как в процессе проектирования, так и при описании предмет-
ной области. При автоматизированном проектировании объекта вначале формируется
порождающая среда, в которой будет осуществляться синтез этого объекта. Порож-
дающая среда включает данные о предметной области, к которой относится объект, о
существующих и разрабатываемых структурах объекта, известные или прогнозируемые
отношения и связи между элементами и свойствами объекта и внешней среды. Вклю-
чение в модель вариантов структур позволяет менять состав элементов в решении в за-
висимости от изменения внешних воздействий. Такими воздействиями могут быть:
— наследование свойств от элементов вышестоящих уровней;
— изменение значений параметров;
— диалоговая корректировка структуры пользователем.
Одна модель 5(Л) порождающей среды содержит в себе данные о множестве проек-
тируемых объектов
Ak(i) = {л,, а2,...» ап},к= \ ,т,АкаА.
Построение такой модели основано на свойствах эквивалентности элементов ai9
Це А, входящих в различные объекты (решения). Проектное решение получается как
некоторое условное сечение объекта, реализованного в информационной среде. Состав
элементов, входящих в решение, определяется в модуле с помощью аппарата типовых
математических моделей структурного проектирования [7]. Все возможные варианты
решений должны быть заложены в модель. Условия, по которым происходит принятие
решения, задаются разработчиком модели, а вычисляются при обработке модели.
При разработке модели необходимо:
— выделить набор контуров F, т. е. набор структурных свойств (признаков), кото-
рые будут управлять процессом принятия решения;
735
— определить принадлежность контуров элементам (15.9);
— установить отношения, определяющие механизм наследования свойств от эле-
ментов вышестоящих уровней
R'f = G4(F9C4)9 (15.17)
где G4 — несвязанный граф, объединяющий некоторое количество связанных струк-
тур вида «дерево», корнями которых могут быть контуры; С4 — множество дуг.
Контуры могут объединяться в группы, образуя отношения вида
R2F = W (15.18)
где 7; — подмножество контуров, образующее группу. В каждой группе одновременно
может быть реализован лишь один контур. В качестве условия существования контура
могут быть заданы дополнительно ограничения на нахождение значения параметра в
некотором интервале
Rnf= T(f9 п9 ВО, НО), (15.19)
где ВО, НО — верхнее и нижнее предельные отклонения.
Модели порождающей среды классифицируются в зависимости от способа задания:
— отношений смежности и порядка между элементами модели 5(Л);
— отношений смежности и порядка элементов проектируемого объекта Л*;
— состава и количества элементов в различных вариантах Ак.
Если отношение смежности между R3A элементами модели 5(Л) задано в виде гра-
фа, то модель будет связной
Я = (75(Л,С5), (15.20)
а если граф G5(A9 С5) не задан, то модель будет несвязной.
В зависимости от наличия отношений смежности и порядка между элементами
проектного решения Ак, все модели порождающей среды разделяются на сочетатель-
ные и упорядочивающие. Сочетательные модели 59(Л) применяются в тех случаях,
когда определяется только состав элементов проектируемого объекта, а упорядочи-
вающие модели 5/Л) — когда определяются и состав, и структурные отношения меж-
ду элементами проектируемого объекта.
В табличной модели каждому заданному набору контуров F(Ak) соответствует
единственный вариант проектируемого объекта Ак. Поэтому табличные модели ис-
пользуются для поиска стандартных или готовых проектных решений. Модели осталь-
ных классов используются для получения унифицированных и индивидуальных про-
ектных решений при наличии их вариантов и необходимости оптимизации решения.
Структура элементов RA сетевой модели описывается ориентированным графом,
не имеющим ориентированных циклов. В сетевой модели может содержаться не-
сколько вариантов проектируемого объекта Ак9 но во всех вариантах Ак сохраняется
неизменным отношение порядка между входящими элементами.
В перестановочных моделях отношение порядка между элементами проектного
решения Ак задается либо графом, содержащим ориентированные циклы, либо с по-
мощью наборов отношений вида:
R3AB=T(akf В(ак))9
R^=T(ak,^(ak)),
где В(ак) — подмножество элементов, при наличии которых возможно существование
ак на данном месте в упорядоченном множестве Л; №(ак) — подмножество элементов,
при наличии которых существование ак на данном месте невозможно.
Все варианты Ак, проектируемые по перестановочной модели, различаются по-
рядком между входящими в них элементами.
736
По табличной модели проектное решение ищется в виде единственного элемента
(строки) или в виде упорядоченного набора элементов (строк).
По сетевой и перестановочной моделям проектное решение ищется в виде упо-
рядоченного набора элементов (путь, цепь в графе), замкнутого цикла (в графе с цик-
лами) и подграфа (набор вершин со связывающими их ребрами). При наличии вари-
антов модели обеспечивают поиск вариантов проектных решений.
По сочетательной модели проектное решение ищется либо в виде неупорядочен-
ного набора с заданным числом элементов (сочетание), либо в виде неупорядоченно-
го набора с незаданным числом элементов (выборка).
В заключение отметим, что бинарные отношения в структурных моделях описы-
ваются в виде булевых матриц.
Отношения {с/у}, отражающие взаимосвязь элементов А = {а19 ...9 ап}9 могут быть
представлены
а2 ... а С11 с12 ••• с\п а1
У = [ЛхЛ] = с\2 с22 - с2п а2 (15.21)
_Сп\ сп2 Спп_ ап
где czy = 1, если взаимосвязь элементов az и существует, и с у = 0 — в противном слу-
чае. В записи [А х А] первый символ соответствует множеству строк, а второй символ —
множеству столбцов булевой матрицы {с у}. Каждая z-я строка (столбец) матрицы рас-
сматривается как представление бинарного отношения /?(az) между я, и элементами
(ап, ай9..., а^п_ J)), для которых элементы строки (столбца) матрицы равны единице.
Аналогично описываются бинарные отношения между контурами объекта А:
[£(Л) х £(Л)], между контурами элемента az — [F(flz)] х F(az)].
Матрица состава свойств математической модели состоит из строк, соответствующих
отношениям вида (1.3). Бинарные отношения RAF описываются в виде булевых матриц
Л -
С11 с12 ••• с1т а1
||С^| = [А х F(A)] = с12 с22 — с2т а2 (15.22)
_сп1 сп2 "• спт_ ап
где Су = 1, если Fj входит в состав F(ai) контуров элемента.
Разработка структурных математических моделей осуществляется в следующей
последовательности:
— определение состава элементов объекта моделирования;
— установление отношений между элементами объекта моделирования;
— группирование элементов и отношений;
— выбор класса типовых математических моделей;
— разработка математических моделей;
и полностью отвечает организационным признакам построения функциональной мо-
дели.
Аппарат структурно-параметрического моделирования может быть использован
для конструкторско-технологического анализа изделий. Формы представления ре-
зультатов анализа приведены на рис. 15.6.
Система моделирования должна оперировать конечным набором базовых эле-
ментов (примитивов). Был определен минимальный состав атрибутов, определяющих
примитив системы моделирования. В него вошли следующие группы признаков:
737
1) идентификатор элемента;
2) система координат элемента и параметры, определяющие ее положение в гло-
бальной системе;
3) собственные параметры элемента.
Для идентификации примитива (а в дальнейшем и любого другого элемента мо-
дели) необходимо задать (рис. 15.6, а):
«КОД» — признак формы (уникальный топологический признак) элемента,
«ИМЯ» — признак функционального назначения,
«ТИП»— признак уровня абстрагирования элемента (например, сборочная еди-
ница, деталь, конструктивный элемент, примитив).
Как расширение множества функциональных признаков может быть задан атри-
бут «ТЕЛО» — признак заполненности объема материалом (аналог вида теорети-
ко-множественной операции). Например, элемент формы «КОД=цилиндр» может
имитировать наружную цилиндрическую поверхность при «ТЕЛО = +», либо — от-
верстие при «ТЕЛО = —».
Таким образом, базовый элемент информационной модели может быть опреде-
лен как
А = (КОД, ИМЯ, ТИП, ТЕЛО). (15.23)
Структура объекта проектирования, определяемая составом и взаимосвязями эле-
ментов, в своей основе многомерна. В основу построения структурно-параметрической
модели положен принцип модульности. Каждый модуль представляет собой функци-
онально завершенную СПМ (рис. 15.6, б). Модуль может создаваться и отлаживаться
отдельно. Модуль, объединяющий несколько примитивов, называется конструктив-
ным элементом (КЭ) или конструктивом и помещается в библиотеку пользователя.
Моделируемый объект может быть представлен различными наборами конструктивов и
примитивов. Многовариантность существенно осложняет сравнение конструктивов и
требует решения задач топологических преобразований, оптимизации представления
конструктивов, а также разработки схемы классификации конструктивов.
Состав элементов объекта определяется декомпозицией внешнего облика на
фрагменты, которые проектировщик может соотнести с базовыми элементами систе-
мы, либо с формами, ранее определенными в среде (конструктивами, деталями, узла-
ми). Этот процесс слабо поддается формализации.
Подводя итоги обзору элементов математического описания сложных техниче-
ских систем с помощью аппарата структурно-параметрического моделирования, сле-
дует отметить адекватность этого аппарата задачам функционального моделирования.
Напомним, что под свойствами Ф(Л) в функциональном моделировании понимается
функция, признак, характеристика изделия.
Сказанное и объясняет дальнейшее использование структурно-параметрических
моделей при формализации процесса конструирования изделий и моделировании
технологической подготовки производства изделий строительной техники.
Таким образом, структурно-параметрическая модель является объединением 17
информационных структур
5(Л) = (Л, л м Nu, яуз ^2,3, ^2, Д1.2, Rfn)9 (15.24)
построенных на трех базовых множествах: А = {яр ..., ап} — множестве элементов мо-
делируемого объекта; F= {/j, — множестве контуров (свойств) элементов; мно-
жествах собственных — N= {л,,..., и унитарных — Nu = (х, у, z, Мс) параметров эле-
ментов; R — отношениях, определенных на множествах элементов, их свойствах и па-
раметрическом множестве.
В таблице 15.1 показано, каким образом информация об объекте ТПП может
быть распределена (представлена) в СПМ.
738
Т абл ица 15.1
СПМ объекта ТПП
Структурная модель Количественная модель Лингвистическая информация Геометрическая информация
1 А Множество элементов моделируемого объекта • •
2 F Множество контуров элементов • •
3 N Множество параметров (собственных) элементов • •
4 Nu Унитарные параметры элементов •
5 Функциональная иерархия объекта • •
6 К Пространственные взаимосвязи элементов • •
7 Функциональная сопряженность элементов • •
8 Иерархическая подчиненность параметров •
9 Аналитические и таблично заданные зависимости • •
10 Внешние процедуры •
11 Группы контуров • •
12 Иерархическая подчиненность контуров •
13 R\f Отношение принадлежности контуров элементам •
14 R2AF Матрица свойств элементов структурной модели • •
15 Ran Отношение принадлежности параметров элементам •
16 Ran Атрибуты описания взаимного положения элементов • •
17 Rfn Условия существования контуров •
739
15.4. ПРОЦЕДУРЫ ОБРАБОТКИ ИНВАРИАНТНОЙ
ИНФОРМАЦИОННОЙ МОДЕЛИ
Анализ информационных объектов технологической среды, генерируемой ста-
диями жизненного цикла изделия, позволил сформировать инвариантное ядро систе-
мы конструкторско-технологического проектирования, объединяющее 17 информа-
ционных структур и шесть групп процедур, реализующих их обработку (рис. 15.7,15.8).
Полный набор процедур определен в результате анализа процессов обработки модели,
условий решения проектных задач, уровня технических и общесистемных програм-
_______I
Формирование
модели
Трансляция Компоновка структурно- параметрических баз Интерактивное редактирова- ние Автоматическая коррекция структуры Комплексирование СПБ
pi Ра pi Р/М n Ра
Определение состояний контуров Распространение значений контуров Обработка типовых мате- матических моделей Распространение результатов проектирования Оптимизация проектных решений
Psf Pf р$ PSA Popt
3
________L________
П араметрические
расчеты
I ~
Г еометрические
расчеты
Управление
процессом
обработки
Расчет значений параметров Внешние процедуры Распространение значений параметров Определение состояния Параметрическая идентифи- кация
Аналитические зависимости Выбор из таблиц Округление и нормализация
Pn Pn Pn Pn Pn
Расчет «жестких» связей Размерный анализ Расчет «нежестких» связей
P/1/V 2 Pan рА
Интерактивное задание значений Модели исходных данных Настройка алгоритма обработки модели
FN Ри Ри Ри
Рис. 15.7. Процедуры обработки СПМ
740
мных средств. В целом можно выделить
две группы процедур: обработка структур-
но-параметрических моделей (рис. 15.7)
и анализ результатов обработки СПМ
(рис. 15.8).
Значительная часть представленных
процедур реализована в комплексе инст-
рументальных средств создания САПР
конструкторско-технологического назна-
чения МОСКИТ (Моделирование Объ-
емных Структур Конструкций и Техно-
логий) [10, 11, 12, 13], структурная схема
которого изображена на рис. 15.9. Его ос-
нову составляют программно-методиче-
ские комплексы (ПМК):
— структурно-параметрического мо-
делирования (ПМК СПМ);
— обслуживания баз данных конст-
рукторско-технологического назначения;
— обработки геометрической инфор-
мации.
Наиболее существенны отличия ПМК
СПМ, по сравнению с аналогичными средствами, в алгоритмах параметрического моде-
лирования. Рассмотрим одну из основных процедур обработки инвариантной информа-
ционной модели — процедуру параметрических расчетов. Алгоритм параметрических
расчетов обрабатывает структуры RXN, R2N и включает процедуры р^, pjy, р^, р^.
Разработка моделей сложных технических систем (СТС) и особенно требование
постепенного наращивания возможностей, закладываемых в модели, приводит к рас-
пределению технических знаний и связанных с ними вычислений в различных фраг-
ментах модели СТС. Возникает необходимость согласования локальных решений. Ре-
шение задачи может быть обеспечено созданием процедуры (р^), обслуживающей от-
ношения взаимосвязи параметров RXN таким образом, что распространение значений
(информационный поток) будет направлено не только от корней структуры RXN, но и в
противоположном направлении. Для того чтобы обеспечить двустороннюю направ-
ленность информационных потоков, необходимо установить некоторые условия (ос-
новные правила).
1. Значение параметра должно определяться один раз. Необходимо ввести «неоп-
ределенное» состояние параметра и процедуру его оценки р^.
2. Процесс должен быть построен по итерационной схеме. На каждой итерации
должны быть организованы подпроцессы передачи информации от корней структуры
к конечным элементам и в противоположном направлении.
3. Процесс завершается, если на очередном шаге не удалось определить либо рас-
пространить ни одного значения параметра.
При построении алгоритма приняты следующие условия.
Способы определения значений параметров. Значения параметров могут быть опре-
делены:
— как внешние (исходные величины);
— передачей от элементов верхнего уровня;
— расчетом по формулам, состоящим из арифметических выражений, в состав
которых входят тригонометрические функции, алгебраические функции, специал fa-
Процедуры анализа
результатов обработки
ce
X
5
0
о
&
о
3
0
О
&
о
&
X
X
§
5
&
е
X
X
3
н
X
X
X
£
о
3
0
О
о
эХ
о
х
S
0
PSF
PsN
Pnn
Pint
s
3
3
§
i
X
i
Q
X
X
Л
Л
ю
о
0
0
3
О
а
X
и
О
5
5
О
2
о
X
0
5
з
X
X
о
а
<8
3
PQ
§
5
а
а
5
X
а
S
Ри
PVD
Popt
Рис. 15.8. Процедуры анализа
результатов обработки СПМ
741
BAZ
Программно-методический комплекс
обслуживания баз данных
§
X
г
SPM
Транслятор
S
&
INT
Структурные
§ Параметриче-
х ские
£ Геометриче-
ские
я
S
§
X
X
i
2
2
О
о
X
X
Ввод, контроль KWD
параметров
KNP
STR
Средства
выбора (поиска)
элемента
в БД «GIN»
PAR
CEO
INT
иници-
ирование
интер-
фейса
OGI
Средства
разгрузки
БД
х
I
а Интерфейс
WGD
WXY
WPR
GTS
я s ----------------*—
& Редактор БД «GIN»
*8 §
Z о
Я о
Редактор SPB
GAB
расчет га-
баритов
объекта
RIS
визуализа-
ция
объекта
(каркасная
модель)
S S Интерпретатор
§ входного
х 5
О &
языка
GIN
«Call» интерфейс
SYS
Средства общесистемной
поддержки разработок
ACAD
.scr
.dxf
^Call».
.gin
OKN
Система оконно-
го интерфейса
Средства прото-
колирования
диалога
?«Call>x
Система интерфейса SPM
Интерфейс
в граничное
моделирование
“ Интерфейс
AML
Плоское граничное моделирование SEC
Объемное граничное моделирование PSD
.gin
Идент. Назначение
.spm .isd .spb .mcb .int .see .gin .me .scr .dxf > .ami — структурно-параметрическая модель — модель исходных данных — структурно-параметрическая база данных — база данных чертежа — протокол работы системы INT — модель примитивов — графическая база данных — графическая информация на входном языке системы OGI — формат системы AutoCAD — формат системы AutoCAD — формат системы IDEF
Рис. 15.9. Структура ПМК обработки СПМ
ные функции (округление значений, выбор значений из таблиц, обращение ко внеш-
ним процедурам);
— передачей от элементов нижнего уровня.
Приоритеты способов определения значений параметров. Указания оператора
(пользователя, а не разработчика) предпочтительнее. Установлены следующие при-
оритеты:
— внешние (исходные значения);
— константы;
— передача «сверху вниз»;
— расчет по формулам;
— передача «снизу вверх».
Правила (алгоритм) параметрического проектирования.
Значение параметра определяется один раз (существует неопределенное состоя-
ние параметра).
Обработка модели осуществляется в соответствии с порядком ее построения:
— обход конструктивной (функциональной) структуры «сверху вниз» и «слева
направо»;
— расчет формул в последовательности их задания.
Расчет производится по итерационной схеме:
1) ввод исходных значений;
2) обработка элемента: расчет по формулам, передача значений параметров
«вниз»;
3) повторение пункта 2 для всех элементов структуры;
4) передача значений параметров «вверх»;
5) повторение шага итерации (п. 2, 3, 4), если было определено значение хотя бы
одного параметра.
Алгоритм параметрических расчетов реализован в процедуре «PAR» ПМК СПМ
(рис. 15.9).
15.5. ЛОГИЧЕСКОЕ МОДЕЛИРОВАНИЕ
При проектировании объекта Ai по модели порождающей среды 5(Л) исходными
данными об At служит требуемый состав контуров F(A) этого объекта; результатом
проектирования является структура At, элементы которой реализуют контуры F(A^).
Поэтому Ai может быть спроектирован по модели 5(Л) только в том случае, если F(A)
является подмножеством контуров ДЛ) модели [62].
Процесс проектирования представляется как последовательность проектных
операторов т*, воздействующих на модель проектируемого объекта А{ и осуществляю-
щих преобразование модели из предшествующего (Л,)л_ j в последующее (Л,)* состоя-
ние. Содержание этих преобразований зависит от уровня моделирования. На струк-
турном уровне осуществляются преобразования состава элементов объекта, его кон-
туров и бинарных отношений между элементами и контурами:
— исключение из Af элемента а-,
— добавление в А{ элемента ау;
— замена в А( элемента ау на az;
— исключение из F(Aj) контура Ff,
— добавление в F(Aj) контура
— замена в ДЛ,) контура Fj на Fz и т. д.
743
При проектировании объекта по структурной модели 5(Л) проектным воздей-
ствием тк является воздействие на (Л,)* _ j элемента ак модели
F(A')k = К(Р(А)к_{, F(ak>). (15.25)
Для математического представления отношения (15.25) используются две формы
представления связей между контурами проектируемого объекта и модели порождаю-
щей среды — дизъюнктивная и конъюнктивная.
При дизъюнктивной форме связи контуров объекта Л,- и структурной модели 5(Л)
принимаются следующие значения контуров проектируемого объекта:
1) состав контуров, которым должен обладать проектируемый объект в соответ-
ствии с заданием на проектирование, обозначается ДЛ,.); истинностное значение кон-
туров, входящих в ДЛ,), принимается равным единице;
2) исходное состояние контуров объекта Л z обозначается ДЛД,. В исходном и всех
последующих состояниях истинностные значения контуров принимаются: если кон-
тур Fj реализован, то = 1, а если не реализован, то Ff = 0.
Матрица контуров структурной модели в этом случае называется дизъюнктивной.
Истинностные значения контура Fj оператора, воздействующего на объект про-
ектирования, принимаются: F^a^ = 1, если контур F^Afr будет реализован под воздей-
ствием данного оператора, и F^a^ = 0 — в противном случае, т. е.
г/ х _ [1, если включение ак в Л,- приводит к реализации Ш), z t
г* Дяр — -s (15.26)
[0 — в противном случае.
Состав контуров Л,- после включения ак определяется по формуле
F(A)k = F{A)k_^F{ak). (15.27)
Возможность участия элемента ак в реализации проектируемого объекта, харак-
теризуется следующими группами контуров:
1) контуры, которые могут быть реализованы элементом ак
Р(А)1к = Р(А)к_} л F(ak), (15.28)
где “(Л,)*.! — результат инверсии вектора Р(А{)к_
2) контуры, которые не могут быть реализованы элементом ак
F(Ai^ = F(Ai)k_^F(ak)9 (15.29)
где ~(ак) — результат инверсии вектора F(aky
3) контуры, которые уже реализованы, но могли бы быть реализованы элементом ак
= (15.30)
4) контуры, которые уже реализованы, но не могли бы быть реализованы элемен-
том ак
= (15.31)
Состав контуров, реализуемых элементами данной модели порождающей среды,
равен (на логическом уровне)
Г(Л,)= С F(ak). (15.32)
к = 1
Модель порождающей среды с составом элементов достаточна для проектирова-
ния при условии
Л(Л,.) = Г(Л) л ЛА)- (15.33)
744
При конъюнктивной форме связи и в исходном, и в конечном состоянии объекта
проектирования истинностные значения логической величины контура F^A), подле-
жащего реализации, принимаются равными единице — Fj(Aj) = 1.
Истинностные значения контура элемента ак, включаемого в At, принима-
ются равными
w=
1 — если элемент ак участвует в реализации F^A)
либо не влияет на его реализацию,
О — в противном случае.
(15.34)
Матрица контуров структурной модели в этом случае называется конъюнк-
тивной.
Возможность участия элемента ак в реализации контуров проектируемого объек-
та Л, характеризуется следующими группами контуров:
1) контуры, которые могут быть реализованы с участием ак
F(A^k = F{A^F(ak\ (15.35)
где F(A) — вектор состава контуров, подлежащих реализации в проектируемом объекте;
2) контуры, подлежащие реализации, в реализации которых не может участвовать ак
F{A^ = F{A^F{ak)\ (15.36)
3) контуры, не подлежащие реализации, в реализации которых мог бы участво-
вать элемент ак
F{A^ = F{A^F{akY (15.37)
4) контуры, не подлежащие реализации, в реализации которых не может участво-
вать элемент ак
F(AW = F(A^F(ak). (15.38)
Вопрос о действительной реализации контуров Fj^A^ объекта решается при конъ-
юнктивной форме связи путем анализа состава элементов, которые должны участво-
вать в реализации Fj(A).
Если
= (aj{, afl,aJm),
ТО
tyAi) = Fk(aj{) a tyaj а ... а FfaJ. (15.39)
Контур Fj(A^ будет реализован при условии
т
£Д)=ЛДай)=1. (15.40)
к = 1
Состав элементов (15.39), реализующих контур FjtAj), задается заранее, так как он
не может быть выявлен на основании формул (15.35)—(15.38).
Состав контуров, которые могут быть реализованы совокупностью А{ элементов,
равен
п т
*F(ak). (15.41)
j = 1 к = 1 J J
Дизъюнктивная форма связи контуров объекта проектирования и модели порож-
дающей среды применима только в тех случаях, когда любой контур объекта реализу-
ется единственным элементом. Если для реализации контура необходимо несколько
элементов, то дизъюнктивная форма неприемлема. В этих случаях применяется конъ-
юнктивная форма связи.
745
15.6. СТРУКТУРНОЕ МОДЕЛИРОВАНИЕ
Структурное моделирование является наиболее сложной областью для формали-
зации [5, 6]. В большинстве систем автоматизированного проектирования и систем
искусственного интеллекта основные функции структурного моделирования выпол-
няет человек. Выполнение этих функций может осуществляться как в процессе про-
ектирования, так и при описании предметной области. При автоматизированном
проектировании объекта вначале формируется порождающая среда, в которой будет
осуществляться синтез этого объекта. Порождающая среда включает данные о пред-
метной области, к которой относится объект, о существующих и разрабатываемых
структурах объекта, известные или прогнозируемые отношения и связи между эле-
ментами и свойствами объекта и внешней среды. Все возможные варианты решений
должны быть заложены в модель. Условия, по которым происходит принятие реше-
ния, задаются разработчиком модели, а вычисляются при обработке модели. Включе-
ние в модель вариантов структур позволяет менять состав элементов в решении, в за-
висимости от изменения внешних воздействий. Такими воздействиями могут быть:
— исходное (начальное) определение свойств проектируемого объекта;
— наследование свойств от элементов вышестоящих уровней;
— изменение значений параметров;
— диалоговая корректировка структуры пользователем.
Одна модель 5(Л) порождающей среды содержит в себе данные о множестве про-
ектируемых объектов
Aik = а2к’ •••> апкУ’к = (15.42)
Построение такой модели основано на свойствах эквивалентности элементов ai9
dj е Л, входящих в различные объекты. Проектное решение получается как некоторое
условное сечение объекта (порождающей среды), реализованного в информационной
среде. Состав элементов, входящих в решение, может определяться с помощью аппа-
рата типовых математических моделей структурного проектирования [7].
В зависимости от наличия отношений смежности и порядка между элементами
проектного решения Ак все модели порождающей среды разделяются на сочетатель-
ные и упорядочивающие. Сочетательные модели ^(Л) применяются в тех случаях,
когда определяется только состав элементов проектируемого объекта, а упорядочи-
вающие модели S/Л) — когда определяются и состав, и структурные отношения меж-
ду элементами проектируемого объекта.
В работах [5, 6] определены три класса сочетательных и 12 классов упорядочи-
вающих моделей. Среди упорядочивающих моделей выделены табличные, сетевые и
перестановочные. Для упорядочивающих моделей в проектном решении определяет-
ся как состав, так и порядок следования элементов. При отсутствии вариантов реше-
ний применяются табличные математические модели. Модели остальных классов ис-
пользуются для получения унифицированных и индивидуальных проектных решений
при наличии их вариантов и необходимости оптимизации решения. При наличии ва-
риантов структур проектного решения используются сетевые и перестановочные мо-
дели. При этом сетевые модели применяются тогда, когда возможны варианты только
по составу элементов.
Матрицы состава свойств математических моделей (15.22) могут иметь дизъюнк-
тивный, конъюнктивный и комбинированный характер. Соответственно, основной
проектной процедурой могут быть дизъюнкция, конъюнкция или одновременное соче-
тание дизъюнкции и конъюнкции. Значение определяется по (15.26) либо (15.34).
746
Полученное проектное решение должно содержать тот набор свойств, который
задан во входных данных (модель изделия), — тогда имеет место эквивалентность
свойств
F(A^F(Aik). (15.43)
Однако проектное решение может содержать и избыточный набор свойств. Тогда имеет
место включение исходного набора свойств в состав свойств проектного решения
F(A^F(Aik). (15.44)
1 5.6.1. Табличные модели
В табличной модели каждому заданному набору контуров F(Ak) соответствует
единственный вариант проектируемого объекта Ак. Поэтому табличные модели ис-
пользуются для поиска стандартных или готовых проектных решений. По табличной
модели проектное решение ищется в виде единственного элемента (строки) или в ви-
де упорядоченного набора элементов (строк).
Табличная модель моделируемой системы состоит из матрицы состава свойств
элементов, строки которой полностью упорядочены.
На рис. 15.10 представлен пример табличной математической модели проектиро-
вания технологических процессов. Модель изделия (рис. 15.10, а) дана в виде вектора
£(Л) = {/^,/6}. Модель технологической системы (рис. 15.10, б) задана в виде матрицы
[А х f], где А = {flj, ..., а7} — технологические операции, F= {Д, ...,/7} — признаки
свойств.
Единственное решение, получаемое по модели (рис. 15.10, в), содержит упорядо-
ченный набор строк — Ак = {ди д3, а6}.
1 5.6.2. Сетевые модели
В сетевой модели может содержаться несколько вариантов проектируемого объ-
екта Ак, но во всех вариантах Ак сохраняется неизменным отношение порядка между
входящими элементами.
Сетевая модель состоит из матрицы состава свойств, строки которой частично
упорядочены. Граф взаимосвязи элементов сетевой модели может быть ориентиро-
ванным или неориентированным, с циклами или без циклов. На рис. 15.11 представ-
лена сетевая математическая модель проектирования технологических процессов, в
которой можно получать варианты составов технологических операций при неизмен-
ном их порядке. Проектное решение представляется в виде упорядоченного набора
строк (путь в графе).
Для заданного входного набора свойств получено два варианта решений, содер-
жащих упорядоченные наборы строк: Акх = {flj, д3, а6} и АкХ = {д1? д3, а7}.
15.7. ПРОЦЕДУРЫ СИНТЕЗА
ИНФОРМАЦИОННЫХ ОБЪЕКТОВ
Целью применения процедур синтеза информационных объектов является полу-
чение описания объекта произвольной сложности.
Разработанная инвариантная структурно-параметрическая модель с объект-
но-ориентированными процедурами анализа и синтеза структуры, параметрического
проектирования, расчета геометрии позволяет представить образ объекта в информа-
ционной среде, используя соответствующие методы синтеза с применением конечно-
747
б) модель технологической системы
б) модель технологической системы
в) первый вариант решения
Рис. 15.11. Сетевая
математическая модель
Лк2
Рис. 15.10. Табличная
математическая модель
го набора процедур над структурно-параметрическими базами. В результате взаимо-
действия инвариантного ядра с процедурами синтеза информационных объектов
формируется система объекта и порождающая система.
1. «Трансляция» — процесс образования структурно-параметрической базы
(СПБ) на основании интерпретации внешнего представления посредством пакетной
или диалоговой обработки (рис. 15.12). Выполнение процедуры позволяет перевести
структурно-параметрическую модель из внешнего языкового представления в ма-
шинно-ориентированное, информационно упорядоченное представление структур-
но-параметрической базы.
2. «Объединение» — образование новой модели между обособленными СПБ
(рис. 15.13).
Процедуры «Трансляция» и «Объединение» реализуют процессы начального
построения информационной среды, позволяют строить относительно простые
по структуре конструкции информационных объектов.
3. «Сечение» — образование новой модели на основании выделения элементов в
обособленной СПБ (рис. 15.14). Процедура организует «новую точку входа» в сущест-
748
Рис. 15.12. Процедура «Трансляция»
Рис. 15.13. Процедура «Объединение»
Рис. 15.14. Процедура
«Сечение»
Рис. 15.15. Процедура
«Управляемая декомпозиция»
вующую СПБ, объединяет (комплексирует) для обработки изначально не связанные
элементы объекта. При использовании вновь включенного элемента и построенных
отношений как нового корня (точки входа) СПБ можно изменить первоначально ус-
тановленный порядок обработки модели.
В случае использования нового образования в модели для анализа результатов
обработки его можно интерпретировать, например, как модель замыкающего звена
размерной цепи.
4. «Управляемая декомпозиция» — разделение обособленной СПБ с образовани-
ем новой модели, выполняющей функции согласования (рис. 15.15). Это процедура,
позволяющая построить распределенную информационную среду. Выделение моде-
лей, выполняющих функции согласования, приводит к необходимости создания спе-
циальных процедур обработки. Если «согласующие модели» построить на основе
СПМ (а это возможно), то единственным отличием специальных процедур будет ор-
ганизация доступа к структурно-параметрическим базам в распределенных вычисли-
тельных сетях. Для сохранения адресов размещения моделей в распределенной среде
используется атрибут «КОД» (15.23) описания элемента объекта. При этом поле хра-
нения значения данного атрибута увеличивается до необходимого размера.
Процедуры, реализующие процесс обработки структурно-параметрической мо-
дели в распределенной информационной среде, получили название глобальных
(стратегических) процедур обработки.
5. «Замещение» — преобразование структуры с согласованием внутренних связей
в модели (рис. 15.16). Процедура «Замещение» является одной из множества возмож-
ных сервисных процедур аппарата построения и развития мультиплексной информа-
ционной среды. Ее выделению среди других способствовала реализация в процедуре
идей связанного метода обеспечения взаимозаменяемости: некоторая структурно-па-
раметрическая модель может быть представлена как носитель формы, размеров и ме-
тодов построения (модификации), т. е. стать своеобразным эталонным объектом. Та-
кой эталонный объект может переноситься в различные «ветви» одной СПБ либо в
различные СПБ, согласуя между ними параметрические характеристики объектов.
749
Рис. 15.16. Процедура «Замещение»
6. «Проектирование» — акт комплексных преобразований объектов (рис. 15.17).
Это процедура, реализующая решение типовой задачи конструкторско-технологиче-
ского проектирования, предполагающей генерацию вариантов проектных решений.
Повторение естественной структуры моделируемых объектов при их описании при-
водит к использованию иерархической структуры данных. Базовые элементы, опреде-
ляющие индивидуализацию информационных потоков, собираются (как правило) в
конечных элементах такого описания. Естественная логика описания процесса про-
ектирования, структура информационно-алгоритмической среды требуют «навески»
на эти элементы изделия А сначала элементов порождающей среды Р, а затем и допус-
тимых вариантов решений Т.
Несложный расчет показывает, что при весьма скромных характеристиках исход-
ного объекта (К= 50 — количество точек воздействия), порождающей среды (L = 100 —
количество элементов в модели порождающей среды) и технических решений (М = 5 —
количество элементов в решении, N= 6 — количество вариантов решений) число эле-
ментов в описании такого проекта будет весьма внушительным
Q=KxLxN= 50x100x6 = 30 000.
Применение процедуры «Проектирование» позволяет сократить количество ин-
формационных объектов в описании задачи за счет установления неявных связей
между элементами
(Задача^- <70 «ОУ* \ ' " " Л о - СГОг \ Изделие ' - Технологическое ' ' _ решение (процесс) А / у / \£ \ / Производная система
Рис. 15.17. Процедура «Проектирование:
750
L+KxMxN= 100 + 50x5x6= 1600.
Несмотря на это, установление явных отношений между элементами А — Р — Т
удобно и целесообразно при решении задач анализа производственной системы либо
отработки изделий на технологичность.
Реализация процедуры «Проектирование» сводится к организации взаимодейст-
вия четырех групп структурно-параметрических моделей, различающихся по содер-
жанию (рис. 15.17).
СПМ «Задача» координирует обработку и взаимодействие:
А — модели исходного объекта,
Р — моделей порождающих систем,
Т — модели технического решения.
Модель технического решения определяет информацию, сохраняемую как ре-
зультат процесса проектирования: состав элементов и параметров, структуру взаи-
мосвязей элементов решения. Одним из элементов процесса управления технологи-
ческим проектированием в этой схеме является постановка задачи выбора варианта
проектного решения на множестве элементов как задачи целочисленного программи-
рования.
В общем случае процесс проектирования может быть представлен совместным
преобразованием следующих информационных объектов: модели исходного объекта
5(Л) и модели порождающей среды S(P) с получением в результате преобразований
модели проектного решения S( Т)
Ь(Р)\А^Т. (15.45)
Для различных методов решения задач проектирования состав информационных
объектов может различаться. Минимально необходимыми являются следующие:
— при ручном проектировании — S(T);
— при автоматизированном проектировании — S(P) и 5(7);
— при автоматическом проектировании — 5(Л), S(P) и S(T).
Модель исходного объекта (МИО) А рассматривается как взаимосвязанная сово-
купность a j,..., ап конструктивных элементов изделия и элементов, наделенных спе-
цифическими признаками (свойствами/ и параметрами лу), отвечающими за управле-
ние процессом принятия решений и называемыми при конструкторском проектиро-
вании элементарными проектными воздействиями (ЭПВ), а при технологическом —
элементарно обрабатываемыми поверхностями (ЭОП) для механической обработки
или «детале-операциями» (ДО) для сборки
А = {а^...,ап}. (15.46)
Порождающая среда Р рассматривается в качестве структуры, содержащей весь
спектр конструкторских (конструктивные решения, детали, узлы, агрегаты) либо тех-
нологических элементов (операции, переходы, оборудование, приспособления, инст-
румент и др.), входящих в состав изделий и технологических процессов их изготовле-
ния. При этом совокупность элементов, являющаяся порождающей средой производ-
ственной системы, составляет упорядоченное множество
P=(pi9p29...9 pN), (15.47)
а возможные варианты получаемых технических решений, сохраняемые в модели тех-
нического решения (МТР), образуют множество
7=ЦД,/ = 1,...,л; J= 1,...Д. (15.48)
Для описания 5(Л), S(P) и S(T) при решении задач проектирования использован
аппарат структурно-параметрического моделирования.
751
Математическая модель задачи конструкторско-технологического проектирова-
ния представляется в виде совокупности
S={A,P, (15.49)
где О — процедуры управления структурно-параметрическим моделированием при
проектировании.
Состав модели ИС, необходимый для решения задач, возникающих на различных
стадиях жизненного цикла изделия (ЖЦИ), в том числе и производственных, должен
различаться при сохранении целостности модели. Таким образом, в модели изделия
целесообразно предусмотреть выделение нескольких информационных слоев:
— конструкторского (геометрическая информация);
— технологического (технологические параметры изделий, результаты решения
задач технологического проектирования);
— функционального;
— организационно-экономического и пр.
Практически все решения, получаемые в процессе конструкторско-технологиче-
ского проектирования, привязываются к элементам создаваемого изделия. Наиболее
естественным способом представления модели изделия является структура, воспро-
изводящая конструктивную иерархию объекта. Поэтому в основу модели информа-
ционной среды производственных стадий жизненного цикла положена именно эта
структура. Анализ задач конструкторско-технологической подготовки производства
позволил определить состав основных информационных объектов: изделие, конст-
рукторская документация, технологическая система, технологическая документация.
Интеграция совокупности указанных моделей в единую информационную среду под-
систем КПП и ТПП реализуется средствами структурно-параметрических моделей,
обзор которых выполнен выше.
Каждому элементу модели изделия ставится в соответствие один или несколько
элементов информационной модели, называемый «задачей проектирования».
Элемент информационной среды «задача проектирования» объединяет (опреде-
ляет) все компоненты информационной среды, участвующие в типовом процессе
проектирования для элемента конструкции изделия и определенной (конкретной) за-
дачи конструкторско-технологической подготовки производства. Элементами ин-
формационной модели «задача проектирования» являются: модель процедуры (руч-
ное проектирование, автоматизированное либо автоматическое), модель исходного
объекта, одна или несколько моделей порождающей среды, модель технического ре-
шения, модель элементарного решения.
Модель элементарного решения (МЭР) содержит указание на типы элементов
(«О», «и», «п», «о» — при решении задач технологического проектирования) и состав
параметров, обработанных и включаемых в решение в ходе элементарного акта про-
цесса проектирования. Ссылки на элементы, вошедшие в решение, и значения пара-
метров сохраняются в модели технического решения.
Рассмотрим подробнее схему информационного взаимодействия подсистем
КПП и ТПП и охарактеризуем «роли» информационных моделей.
Модель исходного объекта содержит минимально необходимую выборку инфор-
мации об изделии для выполнения технологического проектирования. Например, для
операций заготовительно-штамповочного производства такая информация включает:
— вид заготовки (качественная характеристика геометрии);
— материал;
— геометрические характеристики.
Качественная характеристика геометрии оформляется, помимо задания логиче-
ского признака, в виде модели, воспроизводящей геометрический образ обрабатывае-
752
мой заготовки. Геометрическая модель заготовки используется для формирования
операционных эскизов и технологической анимации.
Модель порождающей среды (МПС) организует процесс технологического про-
ектирования на основании информации, содержащейся в МИО.
Модель технологического процесса (МТП) сохраняет в виде ссылок на МИО и
МПС варианты допустимых технологических решений. МТП содержит информацию,
необходимую для формирования технологического документа.
15.8. МОДЕЛЬ ПРОЦЕССА ПРОЕКТИРОВАНИЯ
Модель процесса проектирования (МПП) устанавливает состав, значения атри-
бутов и последовательность выполнения операций проектирования. Существуют два
основных способа общения с системой проектирования: интерактивный и пакетный.
В основе обоих способов лежит последовательное выполнение команд исполняющей
системы. Несмотря на стремительное развитие средств интерактивного взаимодейст-
вия проектировщика и системы, «пакетная» обработка данных не потеряла своей
актуальности, особенно при выполнении многократно повторяющихся элементов об-
работки данных. Своеобразным «пакетом заданий на обработку» может стать запи-
санная последовательность действий проектировщика. Механизмы диалогового ин-
терфейса исполняющей системы можно организовать таким образом, чтобы обеспе-
чить: с одной стороны, возможность записи (фиксации) команд проектировщика; а с
другой, возможность автоматической обработки протоколов команд. Тогда протокол
команд можно рассматривать как модель процесса проектирования. В общем случае,
МПП определяет методику построения автоматизированных процедур и системы ин-
формационного сопровождения в целом.
Элементами модели процесса проектирования являются: операции (команды)
исполняющих систем, структурные переменные, диагностические переменные.
Механизмами, обеспечивающими реализацию модели процесса проектирова-
ния, являются: обработка протокола решения задачи, структурная параметризация,
логический контроль процесса.
Информационная модель процесса проектирования может быть представлена
композицией шести структур
П(С)={С, (7е, 5, Z, GL, р}, (15.50)
где С = {Cj,..., — множество команд исполняющей системы; (7е — цепочка команд
исполняющей системы (протокол процесса); S= {sb ..., sk} — множество структурных
переменных; L = {/1?..., 1т] — множество диагностических переменных; GL — последо-
вательность логических меток исполняющей системы (протокол анализа); р — сово-
купность процедур, поддерживающих механизмы модели.
Автоматическое (параллельное основному процессу) формирование МПП при
выполнении проектных действий реализует функцию самообучения системы.
Повторная отработка МПП с фиксацией определенных операций относительно
структурных переменных объекта позволяет автоматизировать организацию итера-
ций при проектировании с целью уточнения решений.
Особенно эффективно применение данного метода решения задач при оформле-
нии конструкторско-технологической документации. Этот процесс требует выполнения
большого количества рутинных операций. Эффект от применения МПП достигается
при применении как типовых фрагментов оформления, настраиваемых с помощью
структурных переменных, так и при повторении процесса оформления в целом в случае
внесения изменений в модель исходного объекта (при повторном проектировании).
753
Элементы модели формирования чертежа (протокола) — директивы — содержат
значения атрибутов, определяющих условия выполнения процедур (команд) испол-
няющей подсистемы графического моделирования. Большая часть значений может
быть выражена в виде элементарной символьной цепочки:
«Элемент=технологическая модель>торец>поверхность до обработки;».
На рис. 15.18 приведен фрагмент записанной последовательности команд проек-
тировщика по формированию операционного эскиза.
Формирование эскиза предполагает выполнение трех действий:
1) выделение информационно значимых объектов;
2) формирование размерных элементов;
3) импортирование эскиза во внешний формат данных.
Выделение информационно значимых объектов можно осуществить двумя спо-
собами.
А. Выполнить извлечение элементов визуального сопровождения, соответствую-
щих текущему фрагменту технологического процесса. Дополнить полученное изобра-
жение графическими образами общих элементов (изделие, оснастка), извлекаемыми
из МТР, либо других структурно-параметрических баз.
База=Ър146-97; инициир.=; Формат=; обработкам
Пр-циям обработкам
Эл-ты=;
выбор элемента=а4;
элемент=технологическая модель>наружная цилиндрическая 4;
выбор=а41;элемент=а4>до обработки;
выбор=а42;элемент=а4>после обработки;
- 1: ;
Видм
Разм элм
Размерные линиим Линейный=гас1; вертикальный=;
Первая=”Н:Ц (а41) ”; верхняям —>$=;
Вторая="Н:Ц (а41) "; нижняям -»1=;
Смещение от первой точки размера=-40; посерединем
Текст=$!!;
Размерм Линейный=зЫг; горм
Первая="Н:Б (а41) ”; леваям -»$=;
Вторая="Н:Б (а41) ”; праваям ->$=;
Смещ=-5 0; посередине=; умолчанию=;
Размерм ЛинейныйМ; вертм
Первая=”Н:Б (а41) "; нижняям = ;
Вторая=”Н:Б (а42) ”; нижняям —>5=;
Смещ=-20; правым=4; Текст=”П:глубина(а4)”;
* =.
- 4: ;
- 1: ;
Рис. 15.18. Модель формирования операционного эскиза
754
Рис. 15.19. Выделение информационно значимых объектов
* «ж' Ямдаьад вмм»
" _ -Гл ч ч ч s в с
НсГЛ < их
755
Рис. 15.21. Фрагмент изображения,
переданный через формат «emf»
Б. Выбрать все элементы технологического
процесса. Удалить изображение фрагментов ТП,
предшествующих текущему.
На рис. 15.19 показано, как из комплексного
представления решения получен эскиз, соответст-
вующий элементу процесса «я061», для формиро-
вания которого были удалены элементы «яОН»,
«а021», «лОЗ!». Существенным элементом процес-
са выделения является управление типом линий,
их толщиной и цветом.
Формирование размерных элементов выпол-
няется интерактивной процедурой «Размерные
элементы» (рис. 15.20). Процедура, помимо образа
размерных элементов, фиксирует действия пользо-
вателя в модели процесса и позволяет в дальней-
шем автоматически воспроизвести построенные
элементы. Таким образом, при формировании раз-
мерных элементов можно воспользоваться ранее
построенным фрагментом отображения размерных
цепочек, соответствующих реализуемым техноло-
гическим базам.
Импортирование эскиза во внешний формат данных необходимо для формиро-
вания конструкторско-технологического документа, представляемого в принятом на
предприятии программном комплексе (ПК). Наиболее распространенным является
ПК MS \\brd. В качестве форматов обмена выбраны «emf» и «dxf». На рис. 15.21 пока-
зан фрагмент изображения, переданный через формат обмена.
Методическое и программное обеспечение проектирующих систем, построенное
с применением элементов МПП, обеспечивает логический контроль процесса реше-
ния задач.
Применение МПП увеличивает эффективность создаваемых компонентов авто-
матизированной системы выполнения проектных работ за счет повышения открытос-
ти разработки (системы).
15.9. ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ ТЕХНИЧЕСКОЙ
ПОДГОТОВКИ ПРОИЗВОДСТВА
15.9.1. Проектирование типового
машиностроительного изделия
Одним из самых популярных примеров анализа в процессе подготовки инжене-
ров-механиков является редуктор. Назначение редуктора — понижение угловой ско-
рости и соответственно повышение вращающего момента ведомого вала по сравне-
нию с ведущим.
Редуктор состоит из корпуса (литого чугунного или сварного стального) в кото-
ром помещают элементы передачи — зубчатые колеса, валы, подшипники и т. д. В от-
дельных случаях в корпусе редуктора размещают также устройства для смазывания за-
цеплений и подшипников (например, внутри корпуса редуктора может быть помещен
шестеренчатый масляный насос) или устройства для охлаждения (например, змеевик
756
Рис. 15.22. ДПД задачи «Проектирование редуктора»
Р Nd Nu Nup Kbd HB1 HB2 V M
Передаточное
отношение 1,5 — 8
Передаточное
отношение 8 — 35
>едукто]
__Изменение угла
передачи движения
ред2с
ред2ц
r3 |C|
ред2к
r4 |C|
ред1ц
rl • • •
г2 • • •
гЗ • • • •
г4 • • •
г5 • • •
ред1к
korpus
Косозубое
зацепление
stupen
Шевронное
зацепление
ss| 0 I
cilindr
kk| О I
cilindr
Рис. 15.23. Структурная схема модели «редуктор»
с охлаждающей водой в корпусе червячного редуктора). Редуктор проектируют либо
для привода определенной машины, либо по заданной нагрузке (моменту на выход-
ном валу) и передаточному числу без указания конкретного назначения. Второй слу-
чай характерен для специализированных заводов, на которых организовано серийное
производство редукторов.
Редукторы классифицируют по следующим основным признакам: типу передачи
(зубчатые, червячные или зубчато-червячные); числу ступеней (одноступенчатые,
двухступенчатые и т. д.); типу зубчатых колес (цилиндрические, конические, кониче-
758
+ОБ"ЕКТ;
ИМЯ=СТУПЕНЬ; KOfl=STUPEN; ТИП=С;
+ЭЛЕМЕНТЫ;
ЭЛЕМЕНТ=Ь; ИМЯ=база; ТИП=Ф;
ЭЛЕМЕНТ=з; ИМЯ=точка привязки шестерни; ТИП=Ф;
ЭЛЕМЕНТ=зз; ИМЯ=Шестерня; KOfl=cilindr; fl=ds; B=bs;
ЭЛЕМЕНТ=к; ИМЯ=точка привязки колеса; ТИП=Ф;
ЭЛЕМЕНТ=кк; ИМЯ=Колесо; KOfl=cilindr; fl=dk; B=bk;
4-ПОЛОЖЕНИЕ;
CBH3b=b-s; UY=90;
CBH3b=s-ss; X=-bs2;
CBH3b=s-k; Z=Aw;
СВЯЗЬ=к-кк; X=-bk2;
4-ПАРАМЕТРЫ;
U (4-передаточное отношение) =;
Ur( расчитанное передаточное отношение)=;
Т(4-крутящий момент)=;
s (4-допускаемое напряжение) =;
и(4-угловая скорость) =;
Р (4-мощность) =;
Aw( межосевое расстояние)=; aw=;
ds( диаметр шестерни)=; bs( ширина шестерни)=; bs2=;
dk( диаметр колеса)=; bk( ширина колеса)=; Ьк2=;
М( модуль зуба)=; т=;
z_s( число зубьев шестерни)=;
z_k( число зубьев колеса)=; z=;
к_Ьы(коэф. ширины зубчатого венца) =1.1; bw(ширина зубчатого венца) =;
bl=; dl=; dwl=;
kl = ; k2=1.0;
k_ha=;
k_hb=; c_h=0.11; g_h=1.32;
k_hv=; de=0.006; g0=5.6; V=;
u='cc';uu=;
4-ФОРМУЛЫ;
kl= 780/ s**(2/3) ;
dl=kl*k2* ( 1.4*T* (l/k_bw4-0.15) )**(l/3); k_ha= 1;
k_hb= 14- c_h*k_bw* *g_h;
V=dl*w/2000;
k_hv= 14-de*gO*k_bw*V**2*dl**1.5/(144*P*k_ha*k_hb)*SQRT( (U4-D/U) ; dwl=kl*k2* ( T*
k_ha*k_hb*k_hv*(U4-l) / (k_bw*U) )**(l/3);
bl= k_bw*dwl;
bk=OKR(0,bl); bk2 =bk/2;
bs=bk4-5; bs2=bs/2;
aw= 0.5*dwl* (LJ4-1) ; m=0.02*aw;
M=TABL('MDLZ', 'M ', m, ' ', 0, ’M ’);
z= 2*aw/M;
z_s=OKR(0, z/(U4-l) );
z_k=OKR (0 , z) - z_s;
ds= M*z_s 4- 2*M;
dk= M*z_k 2*M;
Aw= M* (z_s4-z_k) /2;
Ur= z_k / z_s;
uu= EXT( ' 'stup', ' ’, u);
Рис. 15.24. Модель «Элемент STUPEN*
ско-цилиндрические и т. д.); относительному расположению валов редуктора в про-
странстве (горизонтальные, вертикальные); особенностям кинематической схемы
(развернутая, соосная, с раздвоенной ступенью и т. д.). При решении задачи проекти-
рования редуктора принята стратегия, заключающаяся в реализации двух основных
этапов: компоновочный расчет и конструкторский расчет. Диаграмма потоков дан-
ных этой задачи представлена на рис. 15.22.
Компоновочный расчет. По заданным основным характеристикам (Р— мощность, Nd
— обороты двигателя, Nu — обороты на выходном валу) выполняется выбор общей схемы
редуктора (рис. 15.23). Для этого в модели, по рассчитанному значению передаточного от-
759
А111.1лм].ии!1Я1.шшлшнийиаядет^-- ,|0д
файл Элементы Вид Размергые anew. Формат Проъ. ол О программе...
Проекция
вращение
СХ оу 02
I Мин вращение jlO *tJ
Свойства Изображение |
Фч €< g 0
vnmivi«iv/ii л inn опшшш
I .llllllllllir »«
лшншвю и ши ^iiinimw
а)
б)
760
ал _ iu ill_—hi asixi
Файл Вид Читать прог • ,
П 3 & й*
МсГА I ItT^X
в)
Рис. 15.25. Модель «Редуктор»:
а) анализ компоновочного решения; б) отображение промежуточных результатов
обработки; в) формирование конструкторской документации
ношения и конструктивным характеристикам (изменение угла передачи движения; вид
зацепления: косозубое, шевронное) определяется область возможных решений, из кото-
рой, при наличии альтернативных вариантов, проектировщик выбирает решение.
Далее производятся проектировочные расчеты. Они распределены между унифи-
цированными элементами модели объекта. Так, модель STUPEN (рис. 15.24) выполняет
расчет зубчатого цилиндрического прямозубого зацепления и используется для расчета
всех ступеней данного вида. Входными данными для расчета являются: U — передаточ-
ное отношение ступени, Т — крутящий момент, со — угловая скорость, Р — передавае-
мая мощность, S — характеристика материала. Поток выходных данных разделяется.
Часть информации поступает для оперативной обработки в модель вышестоящего эле-
мента «ред2ц» (рис. 15.23). Полностью результаты расчета сохраняются в таблице «stup»
(рис. 15.22), откуда и поступают на второй этап решения задачи. Аналогично организо-
вано построение модели «ию/».
Управление моделью редуктора, с целью оптимизации решения, производится
по двум параметрам: kbd — коэффициенту ширины колес и НВ — твердости матери-
ала. Проектировщик получает упрощенное изображение результатов обработки, ко-
личественную информацию (рис. 15.25, а) и принимает решение либо о корректиров-
ке данных, либо о переходе ко второму этапу.
Конструкторский расчет. Результаты первого этапа сохраняются в таблицах «red»,
«stup», «wal». Они поступают на обработку либо в комплексные модели редукторов,
либо в модели отдельных деталей. Структурно-параметрические модели, используе-
761
мне на втором этапе, обеспечивают конструкторскую проработку решений и выпол-
нение проверочных расчетов. Результаты обработки представляются в виде завершен-
ных конструкторских документов на отдельные детали и сборочные узлы
(рис. 15.25, б). Если в процессе конструкторской проработки проекта выясняется не-
возможность реализации выбранной схемы либо необходимость коррекции компоно-
вочных решений, выполняется возврат на первый этап решения задачи.
В основу предложенной схемы решения задачи заложены идеи распараллелива-
ния работ при выполнении:
— проектных и конструкторских работ;
— конструкторских проработок узлов и отдельных элементов проекта.
Приведенная схема организации проектно-конструкторских работ может быть
использована для реализации типовой САПР узлов и деталей машиностроительного
назначения.
Инструментальные средства моделирования позволяют проводить параметриче-
ский анализ моделей с целью выявления рациональных сочетаний конструктивных
характеристик создаваемых объектов. Например, для элемента «Редуктор» можно оп-
ределить влияние на габариты и вес параметров, управляющих распределением пере-
даточного отношения между ступенями (рис. 15.26).
15.9.2. Проектирование технологических процессов
Для автоматизированного решения задачи проектирования технологических
процессов необходимо разработать модель технологической системы (порождающей
среды) и определить правила построения модели изделия (исходного объекта).
В процессе разработки модели технологической системы необходимо решить две
задачи: определить схему формирования структурного решения и построить модель
количественных расчетов.
762
Построение схемы формирования структурного решения
Структурное решение может приниматься в рамках одного структурного фраг-
мента информационной модели (модуля), как это показано на рис. 15.17, либо про-
цесс принятия решения может быть разделен на локальные задачи выбора: состава
операций, оборудования, состава инструмента, приспособлений и т. п. В любом слу-
чае должна быть выполнена декомпозиция технологической системы на элементы, в
которых можно локализовать принятие элементарных (частных) структурных реше-
ний, либо выполнение технико-экономических расчетов. Каждый модуль представ-
ляет собой функционально завершенную СПМ. Модуль может создаваться и отлажи-
ваться отдельно.
Разработка структурных моделей осуществляется в следующей последователь-
ности:
— определение состава элементов объекта моделирования;
— определение состава свойств объекта;
— выбор класса типовой математической модели;
— установление отношений между элементами модели.
Состав элементов модели технологической системы определяется в зависимости от:
— вида технологического процесса;
— степени детализации получаемых решений.
Состав элементов модели технологической системы механической обработки
приведен на рис. 15.27, б. Модель «mechob2» может быть использована для проектиро-
вания маршрутно-операционных технологических процессов для производственного
участка, оснащенного четырьмя видами станков: фрезерным, сверлильным, токар-
ным и шлифовальным.
В модели выделены четыре группы элементов:
— операции (технологические воздействия);
— оборудование;
— инструмент;
— приспособления.
Состав элементов технологической системы определяется декомпозицией функ-
ционального облика на фрагменты, которые разработчик может соотнести с базовы-
ми элементами системы, либо с формами ранее определенными в среде моделирова-
ния (моделями операций, оборудования, инструмента, приспособлений).
В случае, если элементы каждой из групп определяются одинаковыми наборами
характеристик (состав структурных составляющих и параметров), то для их представ-
ления могут быть использованы модели типовых элементов. Для группы приспособ-
лений модель типового элемента и пример их описания приведены на рис. 15.28.
Если какой-либо элемент модели обладает уникальным набором характеристик,
то для его представления необходимо разработать уникальную структурно-парамет-
рическую модель, отличительным признаком которой будет уникальное значение ат-
рибута «КОД».
Состав свойств (контуров) модели технологической системы определяется исхо-
дя из функциональных возможностей элементов оснащения. Контуры объединяются
в группы. Выделено пять групп (рис. 15.27, а):
— вид поверхности (fl—fl2);
— точность обработки (f5q—fl4q);
— шероховатость поверхности (f320—f3a);
— две группы характерных размеров (flD—f3D) и (flL, f2L).
763
2(
3(
l):fl
2) :f2
3):f3
4) :f4
5) : f 5
6) :f6
7) s f 7
8) :f8
9) :f9
5(
6(
7(
8(
9(______
10(10):flO
11(11):fll
12(12):f12
13(13):f5q
14(14):f6q
15(15):f7q
16(16):f8q
17(17):f9q
18(18):fl0q
19(19):fllq
20(20):fl2q
21(21):fl3q
22(22):fl4q
23(23):f320
24(24):f80z
25(25):f60z
26(26):f40z
27(27):f20z
28(28):f25a
29(29):fl2a
30(30):f6a
31(31):f3a
32(32):flD
33(33):f2D
34(34):f3D
35(35):flL
36(36):f2L
ww= 1 gr= 1:
ww= 2 gr= 1:
ww= 3 gr= 1:
ww= 4 gr« 1:
ww= 5 gr= 1:
ww= 6 gr* 1:
ww= 7 gr« 1:
ww= 8 gr= 1:
ww= 9 gr= 1:
ww=10 gr= 1:
ww=ll gr*= 1:
ww=12 gr= 1:
ww=13 gr» 2:
ww=14 gr» 2:
ww=15 gr= 2:
ww=16 gr= 2:
ww=17 gr= 2:
ww=18 gr= 2:
ww=19 gr= 2:
ww=20 gr= 2:
ww=21 gr= 2:
ww=22 gr= 2:
ww=23 gr~ 3:
ww=24 gr= 3:
ww=25 gr= 3:
ww=26 gr= 3:
ww=27 gr« 3:
ww=28 gr= 3:
ww=29 gr= 3:
ww=30 gr= 3:
ww=31 gr= 3:
ww=32 gr*= 4:
ww=33 grx 4:
ww=34 gr= 4:
ww=35 gr= 5:
ww=36 gr= 5:
К 2):Б
2( 3):o02
3( 4):o03
4( 5):o04
5( 6):o05
6( 7):o06
7( 8):o07
8( 9):o08
9(10):o09
ТОРЕЦ
|НАРУЖНАЯ ЦИЛИНДРИЧЕСКАЯ
I|НАРУЖНАЯ ФАСОННАЯ
I||ВНУТРЕННЯЯ ЦИЛИНДРИЧЕСКАЯ
Illi ВНУТРЕННЯЯ ФАСОННАЯ
I I I | I КАНАВКА НАРУЖНАЯ
I I I I I I КАНАВКА ВНУТРЕННЯЯ
I I I I I I|ОТВЕРСТИЕ
I I I I I I I I РЕЗЬБА НАРУЖНАЯ
I I I I I I|| |РЕЗЬБА ВНУТРЕННЯЯ
I I I I I I I I I(ПЛОСКОСТЬ
I I I I | I I | I I|СЛОЖНЫЙ КОНТУР
I I I I I I I I I I I I 5 КВАЛИТЕТ
I I I I I I I I I I I I I 6 КВАЛИТЕТ
I I I I I I I I I I I I I I 7 КВАЛИТЕТ
I I I I | | I I I | I I I I I 8 КВАЛИТЕТ
I I I I I I I I I I I I I I I I 9 КВАЛИТЕТ
I I I I I I I I I I I I I I | I 110 КВАЛИТЕТ
I I I I I I I I I I I | I I | | I 111 КВАЛИТЕТ
I I I I I I I I I I I I I I I I I I 112 КВАЛИТЕТ
I I I I I I I I I I I I I I I I I I I 113 КВАЛИТЕТ
I I I I I I I I I I I I I I I I I I I I 114 КВАЛИТЕТ
I I I I I I I I I I I I I I I I I I I I I(ШЕРОХОВАТОСТЬ Rz 80 - 320
I I I I I I I I I I I I I I I I I I I I I I |ШЕРОХОВАТОСТЬ Rz 60 - 80
I I I I I I I I I I I I I I I I I I I I I I I(ШЕРОХОВАТОСТЬ Rz 40 - 60
I I I I I I I I I I I I I I I I I I I I I I I I(ШЕРОХОВАТОСТЬ Rz 20 - 40
I I I I I I I I I I I I I I I I I I I I I I I I I(ШЕРОХОВАТОСТЬ Rz 10 - 20
I I I I I I I I I I I I I I I ( I I I I I I I I I I(ШЕРОХОВАТОСТЬ Ra 1.25 - 2.5
I I I I I I I I I I I I I I I I I I I I I I I I I I I (ШЕРОХОВАТОСТЬ Ra 0.63 - 1.25
I I I I I I I I I I I I I I I I I I I I I I I I I I I I(ШЕРОХОВАТОСТЬ Ra 0.32 - 0.63
I I I I I I I I I I I I I I I I I I I I I I I I I I I I I(ШЕРОХОВАТОСТЬ Ra 0.16 - 0.32
I I I I I I I I I I I I I I I I I I I I I I I I I I I I I I (ДИАМЕТР 1
I I I I I I I I I I I I I I I I I I I I I I I I I I I I I I I I ДИАМЕТР 2
I I ( I I I I I I I I I I I I I I I I I I I I I I I I I I I I I I ДИАМЕТР 3
I I I I I I I I I I I I I I I I I I I I I I I I I I I I I I I I I I ДЛИНА 1
I I I I I I I I I I I I I I I I I I I I I I I I I I I I I I I I I I I ДЛИНА 2
: 111111111111111111111111111111111111
: 100000000000000000011001100000011111
: 100000000000000001100000011000011111
: 011000000000000000011001100000011111
: 011000000000000001100000011000011111
: 000110000000000000011001100000011111
: 000110000000000001100000011000011111
: 000001100000000001111001111000011110
: 000000001100011111111001011111111010
код
_ 2
3 tochpt
4 tochpt
5 toch
6 toch
7 toch
8 toch
В 9 tochpd
10 narrezb
5 11 toch
о 12 sverl
§ 13 sverl 1
14 zenk
15 razv
16 frez
17 frez
18 shlif
19 shlif
исходный оператор
"ПОДРЕЗАТЬ ТОРЕЦ (черновой проход)
ПОДРЕЗАТЬ ТОРЕЦ (ЧИСЛОВОЙ ПРОХОД)
ТОЧИТЬ ПОВЕРХНОСТЬ (черновой)
ТОЧИТЬ ПОВЕРХНОСТЬ (ЧИСТОВОЙ)
РАСТОЧИТЬ ПОВЕРХНОСТЬ (черновой)
РАСТОЧИТЬ ПОВЕРХНОСТЬ (^ИСТОВОЙ)
ПРОРЕЗАТЬ.КАНАВКУ
НАРЕЗАТЬ РЕЗЬБУ
ТОЧИТЬ ПОВЕРХНОСТЬ (тонкое точение)
ЦЕНТРОВАТЬ ОТВЕРСТИЕ
СВЕРЛИТЬ ОТВЕРСТИЕ
ЗЕНКЕРОВАТЬ ОТВЕРСТИЕ
РАЗВЕРТЫВАТЬ ОТВЕРСТИЕ
ФРЕЗЕРОВАТЬ ПОВЕРХНОСТЬ(черновой)
ФРЕЗЕРОВАТЬ ПОВЕРХНОСТЬ(чистовой)
ШЛИФОВАТЬ (черновой проход)
ШЛИФОВАТЬ чистовой проход
' booooooooooooooooosssssiiiiiiiiiiiiiiiiippppp
100000000111111111222222222333333333344444444
123456789012345678012346789012345678901245678
b OllfflllllllllllllllOOOOOOOOOOOOOOOOOOOOOOOOOOO
оО2 000000000000000000000001000000000000000000000
оОЗ OOOOOOOOOOObOGOOOOOOOOOlOOOQOOOOOOOOOOOOOOOOO
О04 OOOOOOOOOOOOOOOOOOOOOOOOffllOOOOOOOQOOOOOOOOOOO
о05 00000000000000000000000011000000000000000QOOO
606 000000000000000000000008001100000000000000000
О07 000000000000000000000000081100000000000000000
О08. 0000.00000000000000000000008010000000000000000
о09 ооооооооооооооорооооооооооооошооооооооооооо
О10 OOOOOOQOOOOOOOOOOOOOOOOOllOOOOOOOOOOOOOOOOOOO
он ооооообоооооооооооооооооооооооооюооооооооооо
012 обоооооооооооооооооооооооооооооооюоооооооооо
013 000000000000000000800000000000000010000000000
014 000000000000000000000000000000000001000000000
015 000000000000008000100000000000000000000000000
016 000000000000000008100000000000000000000000000
017 000000000000000000000000000000000000001000000
: 1- . 000. С I _'i J 000000 JPOOOOOOOOOOOOOOOOOOOOOIOOOOO
'о 20 frchpu ФРЕЗЕРНЫЙ С ЧПУ 6520ФЗ
«2 21 svrchpu СВЕРЛИЛЬНЫЙ С ЧПУ ВМ12-500
£2 22 tokchpu ТОКАРНЫЙ С ЧПУ MDW-10/20
о 2 23 rezbultгРЕЗЬБОНАРЕЗНОЙ "УЛЬТРОМАТ"
’g 24 shlifzu ШЛИФОВАЛЬНЫЙ ЗУ142
s20 000000000000000000000000000000000000110000000
s21 000000000000000000000000000000000000000001000
S22 ooooooooooooooooooooooooooooooooooooooooffloooo
s23 000000000000000000000000000000000000000000001
s24 000000080000000000000000000000000000000000010
25 rezpdr РЕЗЕЦ ПОДРЕЗНОЙ T5K10
26 rezpro РЕЗЕЦ ПРОХОДНОЙ ВКЗ
27 rezpro РЕЗЕЦ ПРОХОДНОЙ Р6М5
28 rezrastlPE3E4 РАСТОЧНОЙ ВКЗ
29 rezrast2PE3E4 РАСТОЧНОЙ Р6М5
.в 30 rezkan РЕЗЕЦ КАНАВОЧНЫЙ ВК8
£ 31 rezrezb РЕЗЬБОВОЙ РЕЗЕЦ Т15К6
з 32 metchik МЕТЧИК Р6М5
£ 33 plashka ПЛАШКА Р6М5
в* 34 sverentгЦЕНТРОВОЧНОЕ СВЕРЛО Р6М5
£ 35 sver1с СВЕРЛО Р6М5
S 36 zenker ЗЕНКЕР Р6М5
37 razvert РАЗВЁРТКА Р6М5
38 frzcil ФРЕЗА ЦИЛИНДРИЧЕСКАЯ Р6М5
39 frzkonc КОНЦЕВАЯ ФРЕЗА Р6М5
40 зЬ11£кг1ШЛИфОВАЛЬНЫЙ КРУГ 24А40СТ1АК5
41 shlifкг2ШЛИФОВАЛЬНЫЙ КРУГ 24А10ПВМ1К12
126 00000000000000000.0001000000000000000000000000
i27 ooooooooooooooooooooffioooooooooooooooooooooooo
128 оооОоооооооооооооооотоооооооооооооооооооооооо
129 O0OOOOOOQOOOOOOOOQOO1OOOOOOOOOOOOOOOOOOOOOOOO
i30 000000000000000000001000000000000000000000000
131 обоообоообооооооооооюооооооооооооооооооооооо
132 OOOOOOOOOOOOOOOOOOOOOIOGOOOOOOOOOOOOOOOOOOOOO
133 000008000000000000000100000000000000000000000
i34 OOOOOOOOQOQOQOOOOOOOOIOOOOOOOOOOOOOOOOOOOOOOO
135 0000'00000000000000010000000000000000000000000
136 000000000080000000010000000000000000000000000
137 ooooooooooooooooOooiooooooooooooooooooooooooo
138 000008000000000000010000000000000000000000000
i39 OOOOOOOOOOOOOOOOOOOOOOOOOOOOOCOOOOOOOOOOOOlOO
140 000000000000000000000000000000000008000000100
i4i ooooooOoooooooooooooooioooooooooooooooooooooo
142 000000000008000000000010000000000000000000000
I 5 42 patr3kl ПАТРОН ТРЕХКУЛАЧКОВЫЙ
Sa 43 kondukt КОНДУКТОР
og 44 prfrez ПРИСПОСОБЛЕНИЕ ДЛЯ ФРЕЗЕРОВАНИЯ
Sc 45 prshlif ПРИСПОСОБЛЕНИЕ ДЛЯ ШЛИФОВАНИЯ
eg 46 prrezb ПРИСПОСОБЛ. ДЛЯ НАРЕЗКИ РЕЗЬБЫ
р44 000000000000000000000000000000000000000000000
р45 000000000000000000000000000000000000000000000
р46 000000000000000000000000000000000000000000000
р47 000000000000000000000000000000000000000000000
р48 000000000000000000000000000000000000000000000
S
б) в)
Рис. 15.27. Модель «mechob2»:
а) контуры и фрагмент матрицы свойств структурной модели;
б) элементы; в) матрица взаимосвязей элементов
764
+ОБ”ЕКТ;
КОД=рг±вр; ТИП=п; ИМЯ=приспособление;
+ПАРАМЕТРЫ;
Т( период эксплуатации)=;
TW( время снятия-установки)=;
ST( стоимость)=;
ЭЛЕМЕНТ=р44; КОД=рг1вр; ИМЯ=Патрон трехкулачковый;
Т=15000; TW=22; ST=4500;
ЭЛЕМЕНТ=р45; КОД=рг1вр; ИМЯ=Кондуктор;
Т=12000; TW=16; ST=4750;
ЭЛЕМЕНТ=р46; КОД=рг1вр; ИМЯ=Приспособление для фрезерования;
Т=1400; TW=12; ST=3650;
ЭЛЕМЕНТ=р47; КОД=рг1вр; ИМЯ=Приспособление для шлифования;
Т=1200; TW=14; ST=2000;
ЭЛЕМЕНТ=р48; КОД=рг1яр; ИМЯ=Приспособление для нарезки резьбы;
Т=10000; TW=10; ST=370;
Рис. 15.28. Описание приспособлений:
а) типовой элемент «prisp»; б) описание группы приспособлений
Значение контура в ходе процесса проектирования может быть установлено сле-
дующим образом:
— задано в технологической модели изделия при описании элементарно-обраба-
тываемой поверхности;
— вычислено на основании условий существования контура.
Во втором случае должны быть заданы условия существования контура в виде
ограничений (15.19) на нахождение значения параметра в некотором интервале.
Для контуров «диаметр заготовки» условия могут быть записаны следующим об-
разом:
"... ПО(ДИАМЕТР 1)=(ДИАМЕТР, 0,20);
12О(ДИАМЕТР 2)=(ДИАМЕТР, 20, 200);
□□(ДИАМЕТР 3)=(ДИАМЕТР, 200, 400);...”.
В этом примере значение параметра «ДИАМЕТР», находящееся в интервале от 20
(включая нижнюю границу) до 200, приводит к установлению истинностного значе-
ния контура «f2D». Одновременно в группе может иметь такое значение (быть реали-
зованным) только один контур.
Выбор класса типовой математической модели (модели порождающей сре-
ды) производится на основании классификационных признаков, определяющих
(п. 15.6):
— отношения смежности и порядка между элементами модели порождающей
среды;
— отношения смежности и порядка элементов проектируемого объекта;
— состав и количество элементов в различных вариантах проектируемого объекта.
Анализ показывает, что для описания большинства моделей технологических
систем достаточно табличной (п. 15.6.1) и сетевой (п. 15.6.2) конъюнктивных моделей
структурного проектирования.
Для представления модели «mechob2» использована сетевая конъюнктивная мо-
дель.
Все типовые модели структурного проектирования характеризуются наличием
матрицы состава свойств. Заполнение конъюнктивной матрицы осуществляется на
основании условий (15.34). Фрагмент бинарной матрицы, описывающей отношения
R2AFi приведен на рис. 15.27, а.
765
В сетевой модели должны быть определены отношения R3A, описывающие взаи-
мосвязи между элементами технологической системы, одновременно участвующими
в выполнении технологического процесса. Такие взаимосвязи могут быть представле-
ны в виде цепочек взаимосвязанных элементов (путей в графе)
“... ЦЕПЬ=Ь—р04;... IJEnb=o04-i27-s22;... ЦЕПЬ=822-р44;...”,
которые для унификации алгоритмов обработки типовых моделей представляются
также в виде бинарных матриц (15.22). На рис. 15.27, б в матрице взаимосвязей эле-
ментов показаны выделенными элементами приведенные выше цепочки, участвую-
щие в процессе токарной черновой обработки (о04) на оборудовании (s22) резцом
(i27) при помощи приспособления (р44).
Построение модели количественных расчетов
При построении модели количественных расчетов в структурированной модели
порождающей среды анализу подлежат вопросы:
— распределения вычислений между элементами среды;
— согласования локальных решений (значений параметров).
Для различных элементов объекта эти задачи являются во многом противоречи-
выми и решаются обычно посредством объединения вычислительных процедур в
один модуль, решающий как задачу расчета, так и согласования решений (рассчитан-
ных значений параметров).
Для модели технологической системы целесообразно распределить количествен-
ную информацию в структурных элементах с соответствующим семантическим на-
полнением. Например, как это показано на рис. 15.29:
а) модуль «mechob» содержит информацию по решению в целом:
— исходную информацию, описывающую изделие в целом — KMD, WES, RAZR,
Npr и одну из элементарно-обрабатываемых поверхностей — D, R, В, L, t, Пр, s;
- технико-экономические характеристики — tO, Тшт, Трвсп, Тпз, STin, STos,
STob, TR, ZT, ZTin, ZTos, ZTob, SB;
— режимы обработки — t, Пр, s, i, n;
— параметры, используемые для согласования решений, — KMI, Tin, Tos, Tob,
Cv, m, vl, xl, yl, Ср, x2, y2, r, nl, si;
— расчетные зависимости для «интегральных» характеристик — Тшт, Трвсп, Тпз,
ZT, ZTin, ZTos, ZTob, SB и вычисления значений параметров «по умолчанию» — R, i,
D, В, L, t, Пр, s, KMD, WES, RAZR, Npr;
б) в модуле «toch» организован расчет режимов обработки;
в) модуль «tokchpu» содержит:
— технико-экономические характеристики оборудования — STob, Tob, TWin;
— расчетные зависимости для «нормализации» характеристик режимов обработ-
ки — п, s;
г) модуль «rezpro» содержит:
— значения стоимости (STin) и стойкости (Т) инструмента;
— значения характеристик геометрии и материала инструмента, используемые
для расчета режимов обработки, — KMI, ш, у 1, xl, Ср, х2, у2, г;
д) в модуле «patr3kl» содержатся технико-экономические характеристики при-
способления — Tos, TWos, Stos.
При построении системы параметризации необходимо, помимо расчетных зави-
симостей R2N, задать условия взаимосвязи параметров R'N. Для группы приспособле-
ний (рис. 15.28) необходимо осуществить передачу значений параметров Т (период
766
элемент= 1(1), код= Mechob2, имя=Модель технологической системы
параметры(48, 1) формулы(25, 1) связи(69, 1)
-1(1): t=1.5
-2(2): Пр=3
-3(3): D=58
- 4( 4): d=5
-5(5): В=50
-6(6): L=40
- 8( 8): KMD=80
- 9( 9) : WES=0.2
-10(10): RAZR=4
-11(11): Npr=100
-7(7): R=D/2
-13(13): i=np/t
-12(12): Tin=1.5*T
-14(14): t0=lp*i/(s*n)
-15(15): Тшт=1.14* tO
-16(16): Трвсп= Tin/50
-17(17): Тпз= tO*.75
-18(18): КолШт=Ырг
-19(19): TR=Tuit
-20(20): ZTin=STin*TR/Tin
-21(21): ZTos=STos*TR/(Tos*60)
-22 (22): ZTob=STob*TR/(Tob*60)
-23(23): ZT=ZTob+ZTin+ZTos
-24 (24): a=16/60
-25(25): SB=a*TR+ZT/Npr
I 1 I 2|_________________3___________
стр.модель(1)
a)
1)
2)
3)
4)
5)
6)
7)
8)
9)
- К
- 2(
- 3(
- 4(
- 5(
- 6(
- 7(
- 8(
- 9( .
-12(12): 0
0:
0:
0:
0:
0:
0:
0:
0:
0:
58.00000
29.00000
5.00000
50.00000
40.00000
80.00000
0.20000
4.00000
100.00000
2.62106
D
R
d
В
KMD
WES
RAZR
Npr .
tO [Ц]
[Ц]
[Ц]
[..Диаметр обработки]
[Ц]
[...Диаметр обработки малый]
[...Ширина обрабатываемой поверхности]
[...Длина обработки]
[...КОД ГРУППЫ МАТЕРИАЛА ДЕТАЛИ]
[...ВЕС]
[...РАЗРЯД РАБОТ]
[...Программа выпуса]
-13(13): 0: 2.98800 = Тшт
-14(14): 0: 1.50000 = Трвсп
-15(15): 0: 1.96579 = Тпз
-26(26): 0: 115.00000 = STin
-27 (27): 0: 4500.0000 = STos
-28(28): 0: 15000.000 = Tos
-29(29): 0: 635000.00 = STob
-30(30): 0: 11000.000 = Tob
-21(21): 0: 7.47137 = Znp
-22(22): 0: 0.87152 = Бед
-33(33): 0: 4.58161 = ZTin
-34(34): 0: 0.01494 = ZTos
-35(35): 0: 2.87482 = ZTob
-36(36): 0: 2.98800 = TR
-37(37): 0: 7.47137 = ZT
-17(17): 0: 1.50000 = t
-18(18): 0: 3.00000 = Пр
-19(19): 0: 0.12000 = s
-20(20): 0: 2.00000 = i
-25(25): 0: 254.35031 = n
-23(23): 0: 50.00000 = T
-24(24): 0: 40.00000 = Ip
-31(31): 0: 0.70000 = KM I
-32 (32) : 0: 75.00000 = Tin
-38(38): 0: 0.87152 = SB
-39(39): 0: 0.28000 = m
-41(41): 0: 0.12000 = xl
-42(42): 0: 0.50000 = yi
-43(43): 0: 50.00000 = Cp
-44(44): 0: 1.00000 = x2
-45(45): 0: 1.00000 = У2
-46(46): 0: 0.00000 =
-47 (47) : 0: 254.35031 = nl
-48(48) : 0: 0.12000 = si
-50(50) : 0: 0.26667 = a
4 |5|б| 7 | 8 1
[Ц]
[Ц]
[Ц]
[Ц]
[Ц]
[... Затраты приведенные]
[... Себестоимость единичная]
[Ц]
[Ц]
[Ц]
[Ц]
[Ц]
[...Глубина резания]
[...Припуск на обработку]
[Ц Подача]
[Ц Количество рабочих ходов]
[Ц]
[Ц]
[Ц]
[Ц]
[Ц]
[Ц]
[Ц]
[Ц]
[Ц]
[Ц]
[Ц]
[Ц]
[Ц]
[Ц]
[Ц]
[ц]
9
767
б)
элемент= 6( 3), код=ЪосЬ , имя=ТОЧИТЬ ПОВЕРХНОСТЬ (чистовой проход)
параметры(27, 128) формулы(9, 53) связи(3, 75) стр.модель(3)
- 53( 1): ks=1.0
- 54 ( 2): sl=ks*sp
- 55( 3): Cv=0.9*KMD*KMI
- 56 ( 4): vl=Cv/(T**m*s**yl*t**xl)
- 57( 5): nl=1000*vl/(3.1415*D)
- 58( 6): v=3.1415*D*n/1000
- 59( 7): Pz=10*Cp*t**x2*s**y2*v**r
- 60( 8): N=Pz*v/(1020*60)
-6К
131 ( 2):31:
132( 3):18:
133 ( 4) : 0:
134( 5):23:
135 ( 6):39:
136( 7):17:
137 ( 8) : 41:
138 ( 9) :19:
139(10):42:
140(11): 1:
142(13):43:
143(14):44:
144(15):45:
145(16): 0:
146(17): 0:
147(18): 0:
148(19):47:
149(20):25:
150 (21) : 0:
151(22): 0:
152(23):46:
153 (24) : 0:
154(25):48:
155(26):24:
156(27): 5:
9): lp=L
0.70000
3.00000
50.40000
50.00000
0.28000
1.50000
0.12000
0.12000
0.50000
58.00000
50.00000
1.00000
1.00000
0.12000
1.00000
46.34441
254.35031
254.35031
46.34441
90.00000
0.00000
0.06815
0.12000
40.00000
40.00000
[Ц]
[Ц]
[Ц]
[Ц]
[Ц]
[Ц]
[Ц]
[Ц]
[Ц]
[Ц]
[Ц]
[Ц]
[Ц]
[Ц]
[Ц]
[Ц]
[Ц]
[Ц]
[Ц]
[Ц]
[Ц]
[Ц]
[Ц]
[Ц]
элемент=22( 5), код=ЪоксЬри , имя=ТОКАРНЫЙ С ЧПУ MDW-10/20
параметры(11, 494) формулы(4, 183) связи(0, 0) стр.модель(0)
- 185( 1): s= OKR(0,si);
- 186( 2): n= OKR(0,nl);
- 187( 3): to=tm/0.9
- 188( 4): TWob=5+G*l.03
e)
- 496( 1):25: 254.35031 = n [Ц]
- 497( 2):47: 254.35031 = nl [Ц]
- 498( 3) :19: 0.12000 - s [Ц]
- 499( 4):48: 0.12000 = si [Ц]
- 500( 5) :12: 2.62106 = tm [Ц]
- 501 ( 6) : 0: 1.00000 = G [Ц]
- 502( 7): 0: 6.03000 = TWob [Ц]
- 503 ( 8)tl3: 2.98800 = to [Ц]
- 504( 9):29: 450000.00 = STob [Ц стоимость]
- 505(10) :30: 14000.000 = Tob [... период эксплуатации]
- 506(11): 0: 0.60000 = Twin [... время смены инструмента]
элемент=26( 4), код=гвхрго , имя=РЕЗЕЦ ПРОХОДНОЙ ВКЗ
параметры(10, 529) формулы(0, 0) связи(2, 88) стр.модель(0)
— 531 ( 1) :31: 1.00000 = KMI [Ц]
- 532 ( 2):39: 0.28000 = m [Ц]
- 533( 3):42: 0.50000 = у1 [Ц]
ч -534( 4):41: 0.12000 = xl [Ц]
г) -535( 5):43: 40.00000 = Ср [Ц]
- 536 ( 6):44: 1.00000 = х2 [Ц]
- 537( 7):45: 0.75000 = у2 [Ц]
- 538( 8):46: 0.00000 = г [Ц]
- 539( 9) :23: 55.00000 = Т [... стойкость]
- 540(10) :26: 120.00000 = STin [... стоимость]
элемент=42( 6), код=раЪгЗк1 , имя=ПАТРОН ТРЕХКУЛАЧКОВЫЙ
параметры(3, 764) формулы(0, 0) связи(0, 0) стр.модель(0)
— 766( 1) :28: 15000.000 = Т [... период эксплуатации]
- 767 ( 2): 0: 22.00000 = TW [... время снятия-установки]
- 768( 3) :27: 4500.0000 = ST [... стоимость]
Рис. 15.29. Фрагменты количественной модели
а) элемент *Mechob2* — технологическая система:
1 — абсолютный номер выражения (формулы); 2 — номер выражения элемента;
3 — выражение; 4 — абсолютный номер параметра; 5 — номер параметра элемента;
6 — номер связанного параметра; 7 — значение параметра; 8 — идентификатор параметра
9 — комментарии параметров
б) элемент «toch» — операция; в) элемент «tokchpu* — оборудование;
г) элемент «rezpro» — инструмент; д) элемент *patr3kl* — приспособление
768
эксплуатации) и ST (стоимость) в модель головного элемента. Установление взаимо-
связей можно осуществить указанием на пары параметров
“... T=Tos; ST=STos;...”.
Тогда фрагмент описания группы приспособлений в модели «mechob2» будет выгля-
деть так, как это показано на рис. 15.30.
В модели «mechob2» выполняется расчет технико-экономических характеристик
процесса и режимов обработки. При состоянии модели по завершению структурного
моделирования, соответствующему рис. 15.29 (включены в решение элементы 1,6, 22,
26, 42) автоматически реализуется алгоритм расчета (рис. 15.31), соответствующий
правилам обеспечения двусторонней направленности информационных потоков (см.
п. 15.4).
1. Выполняется доопределение значений параметров (расчет значений «по
умолчанию»). При полностью определенных исходных данных — это параметры
Я и/.
2. Из выбранных на основании структурного моделирования элементов извле-
каются значения и передаются параметрам головной модели для последующей обра-
ботки:
— оборудование — STob, Tob, TWuv,
— инструмент — STin, Т, TWin, STin, T, KMI, m, yl, xl, Cp, x2, y2, r;
— приспособления — Tos, STos.
3. В модуле «Операция» рассчитывается предварительное значение подачи при
обработке si.
4. В модуле «Оборудование» нормализуется значение подачи s.
5. В модуле «Операция» рассчитывается предварительное значение числа оборо-
тов шпинделя станка nl.
6. В модуле «Оборудование» нормализуется значение числа оборотов шпинделя
станка п.
7. В модуле «Операция» рассчитываются еще не определенные значения пара-
метров и передаются в головной модуль.
8. В головном модуле «Модель технологической системы» рассчитываются зна-
чения «интегральных» характеристик решения — Тшт, Трвсп, Тпз, ZT, ZTin, ZTos,
ZTob, SB.
Включение в модель объектов, имитирующих геометрию средств оснащения и
обрабатываемых поверхностей, позволяет получать элементы визуального сопровож-
дения решений (рис. 15.31).
ЭЛЕМЕНТ=р44; КОД=рг1яр; ИМЯ=Патрон трехкулачковый;
Т=15000, T=Tos; ; TW=22; ST=4500; ST=STos;
ЭЛЕМЕНТ=р45; КОД=рг±яр; ИМЯ=Кондуктор;
Т=12000, ; TW=16; ST=4750;
T=Tos; ST=STos;
ЭЛЕМЕНТ=р46; КОД=рг1вр; ИМЯ=Приспособление для фрезерования;
Т=1400; TW=12; ST=3650;
T=Tos; ST=STos;
ЭЛЕМЕНТ=р47; КОД=рг±вр; ИМЯ=Приспособление для шлифования;
Т=1200; TW=14; ST=2000;
T=Tos; ST=STos;
ЭЛЕМЕНТ=р48; КОД=рг1вр; ИМЯ=Приспособление для нарезки резьбы;
7=10000, ; TW=10; ST=370;
T=Tos; ST=STos;
Рис. 15.30. Описание приспособлений
769
вид элемента технологической системы
код поля технологического документа количественная информация
тип элемента СПМ параметры и зависимости шаги алго ритма
информационные А В О О технологические воздействия код=ЪосЬ ТОЧИТЬ ПОВЕРХНОСТЬ (чистовой про- ход) ks=1.0 31-ks*sp Cv=0.9*KMD*KMI vl«Cv/’ (Т* *®*S * *yl*t* *xl) nl=1000*vl/(3.1415*D) v=." . 1415*D*n/1000 Pz=10*Cp*t**x2*s**y2*v**r N=Pz*v/(1020*60) lp=L 3 5 7
О О дополнительные условия код=1пвЪгик
О О технологические инструкции KO£=instruk *
Г О инструкции по ТБ Kon=instruk
материальные д О оборудование Kon=tokchpu ТОКАРНЫЙ С ЧПУ MDW-10/20 S= OKR(0,sl); n= OKR(0,nl); to=tm/0.9 TWob=5+G*l.03 2 4 б
код=вЫ1£НЫ ВНУТР. ШЛИФОВАЛЬНЫЙ j + Л + -C k„i~0 l<Jt2 * dt € M p Fi^Cpzs^^D,;klk2k3 tostm/0.9
т и инструмент Kon=rezpro РЕЗЕЦ ПРОХОДНОЙ ВКЗ KMI=1; m=0.28; yl=0.5; xl=0.12; Cp=40; x2=1.0; y2=0.75; r=0; T=55; STin=120;
п приспособления код=раЪгЗк! ПАТРОН ТРЕХКУЛАЧКОВЫЙ Tos=15000; TWos=22; STos=4500;
общие информаци-
онные элементы
код=тесЬоЬ2
дополнительные информационные
код^гег!
элементы визуаль-
ного сопровождения
решений
код=пагс!1
t==1.5; D=58; d=5; В=50;
L=40
KMD=80; WES=0.2; RAZR=4; Npr=100
R=D/2; i«np/t___________
Tin»1.5*T
tO=lp*i/(s*n)
Тшт=1.14* tO
Тпз= tO*.75
КолШт=Ырг
TR=Tuit
ZTin=STin*TR/Tin
ZTos=STos*TR/(Tos*60)
ZTob=STob*TR/(Tob* 6 0)
ZT=ZTob+ZTin+ZTos
a=TABL(*TARF’, 'razr',RAZR,'
’,0, ’TRF')
SB*a*TR+ZT/Npr
8
Рис. 15.31. Классификационная схема элементов технологической системы
Способы построения технологической модели изделия
Для получения технологического решения по обработке поверхности необходи-
мо задать:
— свойства поверхности, конкретизирующие условия выполнения технологиче-
ской операции;
— параметры поверхности.
Решение, получаемое по модели технологической системы, включает подмноже-
ство элементов модели, выделяемое процедурами структурно-параметрического мо-
делирования на основе заданной информации, и рассчитанные значения техни-
ко-экономических показателей. Такое решение можно определить как элементарное
технологическое решение, а совокупность информации для его получения — как эле-
ментарно обрабатываемую поверхность (ЭОП). Состав обрабатываемых поверхно-
стей, выделенных для технологического процесса, фиксируется в виде технологиче-
ской модели изделия (ТМИ). ТМИ является объектом, фиксирующим точки прило-
жения и факторы (свойства, параметры) проектных воздействий к моделируемому
изделию. ТМИ или ее фрагмент могут быть повторно (автоматически) применены для
получения проектного решения.
Описание технологической модели изделия может быть выполнено с помощью
языка структурно-параметрической модели либо специальными программными
средствами.
Технологическая модель изделия, используемая для решения задачи проектиро-
вания технологического процесса, включает следующую информацию (рис. 15.32):
а) описание общих свойств, к которым относятся:
+ОБНЕКТ•
ИМЯ=Крышка насоса НП72/012; КОД-kryshka; ТИП=А;
+ПАРАМЕТРЫ;
КМЭ(КОД ГРУППЫ МАТЕРИАЛА ДЕТАЛИ)=80;
RAZR(+PA3PHfl РАБОТ)-4;
Npr(Программа выпуска)=50;
Разработал(Т:)-Иванов П.С.; Проверил(Т:+) =Петров С.И.; Н.контроль(Т:)-Сидоров И.П.;
Шифр(Т:)=981612264; МассаДетали=0.250; Код(Т:)=04; ЕдВеса(Т:)=кг;
а) общие свойства
+ЭЛЕМЕНТЫ;
ЭЛЕМЕНТА; ИМЯ-БАЗА; ТИП-Ф;
ЭЛЕМЕНТ=а011; КОД-EOPotwgl; ИМЯ-поверхность 1.1; D=25.6; L=66.5; JT-13; Rz-80;
ЭЛЕМЕНТ-аО21; KOfl-EOPtrc2; ИМЯ-поверхность 2.1; D=62; d-25.6; Пр=4; t-2; JT-12; Rz=40;
ЭЛЕМЕНТ=аО31; КОД=ЕОРЪгс2; ИМЯ-поверхность 3.1; D-140; d-62; Пр=4; t-2.5; JT-12; Rz-40;
ЭЛЕМЕНТ-аО61; КОД-EOPnrcil; ИМЯ-поверхность 6.1; D-58; L-40.5; Пр-2; t-2; JT-12; Rz-40;
ЭЛЕМЕНТ-а041; КОД-EOPwncil; ИМЯ-поверхность 4.2; D-45; L-32.5; Пр-9.7; t-2.5; JT-11; Rz-20;
ЭЛЕМЕНТ-аО51; КОД-EOPwnci1; ИМЯ-поверхность 5.1; D-48.5; L-17.5; Пр-1.75; t-2.3; JT-12; Rz-40;
ЭЛЕМЕНТ=аО52; КОД-EOPwncil; ИМЯ-поверхность 5.2; D-50.5; L-17.5; Пр-l.O; t-0.5; JT-11; Rz-20;
ЭЛЕМЕНТ-аО22; KOfl=EOPtrc2; ИМЯ-поверхность 2.2; D-58; d-50.5; Пр=2.5; t=1.25; JT-13; Rz-80;
ЭЛЕМЕНТ-аО32; KOfl-EOPtrc2; ИМЯ-поверхность 3.2; D-140; d-58; Пр-2; t-1; JT-11; Rz-20;
ЭЛЕМЕНТ=аО62; КОД-EOPnrcil; ИМЯ-поверхность 6.2; D=56; L-40; Пр-l; t=0.5; JT-11; Rz-20;
ЭЛЕМЕНТ-аО12; КОД-EOPwncil; ИМЯ-поверхность 1.2; D-30; L-30; Пр-2.2; t-1.1; JT-13; Rz-80;
б) описание элементов
+ПОЛОЖЕНИЕ;
СВЯЗЬ=Ь-а011; Х=60; Х=2.5; Х=4;
СВЯЗЬ=Ь-а012;
СВЯЗЬ=Ь-аО22; Х=60;
СВЯЗЬ=аО22-аО21; Х=2.5;
СВЯЗЬ=аО22-аО62; Х=-40;
СВЯЗЬ=аО62-аО61; Х=2;
СВЯЗЬ=аО22-аО52; Х=-15;
СВЯЗЬ=аО52-аО51;
СВЯЗЬ=Ь-аО32; Х=20;
СВЯЗЬ=аО32-аО31; Х=2;
СВЯЗЬ=Ь-а041; Х=30;
в) описание геометрии
Рис. 15.32. Описание технологической модели изделия
772
— “КОД=” — уникальный топологический признак объекта, значение которого
используется дл формирования имен файлов с содержательной информацией об объ-
екте;
— “ИМЯ=” — наименование объекта;
— “ТИП=А” — признак, подтверждающий принадлежность объекта к классу
«Технологические модели изделий»;
— параметры — количественная и текстовая информация, используемая в расче-
тах и для оформления технологической документации;
+ОБ"ЕКТ•
ИМЯ=КРЫШКА_НАСОСА_НП72_012; КОД-kryshka; ТИП=А;
+ЭЛЕМЕНТЫ;
ЭЛЕМЕНТ=Ь; ИМЯ=БАЗА; ТИП=Ф;
ЭЛЕМЕНТ=с1; КОД=Крышка; ИМЯ=Конструктивная модель; .
hH=H; D=Dzag; d=d; D1=D; H=h; h=hfl; d2=dd2; x2=xh2; d3=dd3; x4=xh3; 3)
ЭЛЕМЕНТ=аб11; KOfl=EOPotwgl; ИМЯ=поверхность 1.1; D=D11; L=L11; JT=li; Rz=80;
ЭЛЕМЕНТ=аО21; КОД=ЕОРЪгс2; ИМЯ=поверхность 2.1; D=D21; d=d21; Пр=Рг21; t=t21; JT=12; Rz=40;
ЭЛЕМЕНТ=аО31; КОД=ЕОРЪгс2; ИМЯ=поверхность 3.1; D=D31; d=d31; Пр=Рг31; t=t31; JT=12; Rz=40;
ЭЛЕМЕНТ»аО61; КОД-EOPnrcil; ИМЯ=поверхность 6.1; D=D61; L=L61; Пр=Рг61; t-t61; JT=12; Rz=40;
ЭЛЕМЕНТ=аО41; KOfl=EOPwncil; ИМЯ=поверхность 4.2; D=D41; L=L41; Пр=Рг41; t=t41; JT=11; Rz=20;
ЭЛЕМЕНТ=аО51; KOfl=EOPwncil; ИМЯ=поверхность 5.1; D=D51; L=L51; Пр=Рг51; t=t51; JT=12; Rz=40;
ЭЛЕМЕНТ=аО52; КОД=ЕОРшпс11; ИМЯ=поверхность 5.2; D=D52; L=L52; Пр=Рг52; t=t52; JT=11; Rz=20;
ЭЛЕМЕНТ=аО22; KOfl=EOPtrc2; ИМЯ=поверхность 2.2; D=D22; d=d22; Пр=Рг22; t=t22; JT=13; Rz=80;
ЭЛЕМЕНТ=аО32; KOfl=EOPtrc2; ИМЯ=поверхность 3.2; D=D32; d=d32; Пр=Рг32; t=t32; JT=11; Rz=20;
ЭЛЕМЕНТ=аО62; КОД=ЕОРпгсд.1; ИМЯ=поверхность 6.2; D=D62; L=L62; Пр=Рг62; t=t62; JT=11; Rz=20;
ЭЛЕМЕНТ=аО12; KOfl=EOPwncil; ИМЯ=поверхность 1.2; D=D12; L=L12; Пр=Рг12; t»tl2; JT=13; Rz=80;
4-ПОЛОЖЕНИЕ;
СВЯЗЬ=Ь-а011; X=H; X=Pr22; X=Pr21;
СВЯЗЬ=Ь-аО12;
СВЯЗЬ=Ь-аО22; Х=Н;
СВЯЗЬ=аО22-аО21; Х=Рг22;
СВЯЗЬ=аО22-аО62; X=-L62;
СВЯЗЬ=аО62-аО61; Х=Рг32;
СВЯЗЬ=аО22-аО52; X=-h3; !UY=180;
СВЯЗЬ=аО52-аО51;
СВЯЗЬ=Ь-аО32; X=hfl;
СВЯЗЬ=аО32-аО31; Х=Рг32;
СВЯЗЬ=Ь-аО41; X=xh2;
CBH3b=b-d;
4-ПАРАМЕТРЫ;
КМО(КОД ГРУППЫ МАТЕРИАЛА ДЕТАЛИ)=80;
RAZR (4-РАЗРЯД РАБОТ)-4;
Npr(Программа выпуска)=50;
Разработал (Т:) «Иванов П.С.; Проверил (Т: 4-) =Петров С. И.; Н.контроль(Т:)«Сидоров И.П.;
Шифр(Т:)=981612264; МассаДетали=0.250; Код(Т;)=04; ЕдВеса(Т:)=кг;________________________________
ДЛИНА (4-ДЛИНА ДЕТАЛИ) - ;
ДИАМЕТР (4-ДИАМЕТР ДЕТАЛИ)»;
Н=; Dzag=;
d=; D=; h=; hfl=;
dd2=; h2=; xh2=; dd3=; h3=; xh3=;
Dll=; Lll=;
D21=; d21=; Pr21=4; t21=2;
D31=; d31=; Pr31=4; t31=2.5;
D61=; L61=; Pr61=2; t61=2;
D41=; L41=; Pr41=; t41=2.5;
D51=; L51=; Pr51=; t51=2.3;
D12=; L12=; Prl2=2.2; tl2=l.l;
D22=; d22=; Pr22=2.5; t22=1.25;
D32=; d32=; Pr32=2; t32=l;
D62=; L62=; Pr62=l; t62=0.5;
D52=; L52=; Pr52=l; t52=0.5; в)
4-ФОРМУЛЫ;
h2=H-xh2; h3=H-xh3;
Dll=D12-2*Prl2; L11=H4-Pr224-Pr21 ;
D21=D614-2*Pr61; d21=Dll;
D31=Dzag; d31=D21;
D61=D624-2*Pr62; L61=L624-Pr22-Pr32 ;
D41=dd2; L41=h24-Pr22; Pr41= (D41-D11)/2 ;
D51=D52-2*Pr52; L51=h34-Pr22; Pr51= (D51-D41)/2;
D12=d; L12=xh2;
D22=D624-2*Pr62; d22=D52;
D32=Dzag; d32=D22;
D62=D; L62=h;
D52=dd3; L52=h34-Pr22;
Рис. 15.33. Параметризованная ТМИ
773
б) описания элементов (ЭОП), выделенных при конструкторско-технологиче-
ском анализе изделия, включающие:
— “ЭЛЕМЕНТ=” — идентификатор элемента, уникальный в пределах модели;
— ”КОД=” — указание на соответствие выделенной поверхности элементу клас-
сификатора ЭОП модели производственной системы;
— ”ИМЯ=” — обозначение поверхности;
— количественные характеристики ЭОП (параметры элемента);
в) описание геометрии — используется при необходимости геометрической ин-
терпретации как технологической модели изделия, так и результатов проектирования
в целом.
Технологическая модель изделия может быть настроена на изменение структуры
и количественных характеристик конструкторской модели изделия.
Если в технологическую модель изделия включить ссылку на модель исходно-
го объекта (рис. 15.33, а), то это обеспечит доступ к параметрам детали (hH=, D=,
d=, ...), значения которых передаются параметрам ТМИ (=Я, =Dzag, =d, ...). Блок
параметризации (рис. 15.33, в) добавляет в ТМИ дополнительные параметры и за-
висимости, по которым могут быть определены их значения. Операторы элемен-
тарных перемещений также должны быть увязаны со значениями параметров
(рис. 15.33, б).
В таком исполнении технологической модели изделия (рис. 15.34) исходная ин-
формация (значения параметров) поступает из элемента «Конструктивная модель». За-
б) вариант 1
а) варианты параметрических решений по изделию
в) вариант 2
Рис. 15.34. Изменение характеристик параметризованной ТМИ
774
тем преобразованная (дополненная) в расчетном блоке модели она передается осталь-
ным элементам ТМИ, что приводит к изменениям настроек собственных параметров и
параметров положения моделей ЭОП. На рис. 15.34 показаны примеры такого согласо-
ванного преобразования конструкторской и технологической моделей изделия.
! ••••* Слесарно-сборочные работы
♦ОБЪЕКТ;
ИМЯ-Установка деталей из швеллерной стали при сборке металлоконструкций (карта 8);
КОД=к8; ТИП-Р;
fsl(no одному торцу)-;! 1;
fs2(no двум торцам)-;
fs3(e трех, четырех местах по стенке - замыкающий швеллер)-;
fs4(no всей длине швеллера)-;
ГРУППА(Схема)=Г51 ,fs2,fs3,fc4;
frl(no месту)-;
fr2(no разметке)-;! 1;
ГРУППА(Разметка) =frl,fr2;
6п1(вручную)=(0,Д5); !1(Q„25);
Гш2(краном)= (Q.25,);
ГРУППА(Механизация)=Гт1 /m2;
fuO(отсутствуют)-;! I;
ful (сопряжения по двум торцам в жестком контуре)-;
{^(контролируемые отверстия, вырезы, требующие точной координации и выверки)-;
Л13(гнутые детали - с подрезкой торцов газом)-;
Л14(фигурная обработка сопрягаемых торцов)-;
ГРУППА(Дополнительные условия)=(и0,(и1 ,fu2,fu3,fti4;
МОДЕЛЬ-ТАМК;
♦ЭЛЕМЕНТЫ;
ЭЛЕМЕНТ-b; ТИП-Ф; ИМЯ-база для эскиза;
ЭЛЕМЕНТ-rl; КОД-shwel; ИМЯ-Устанавливаемая деталь; N-N; L-L; V-V;
ЭЛЕМЕНТ=г2; КОД-shwel; ИМЯ-Элемент схемы 1; N-N; L-1000; CBOflCTBA-fsl,fs2;
ЭЛЕМЕНТ-гЗ; КОД-shwel; ИМЯ-Элемент схемы 2; N-N; L-1000; CBOftCTBA=fs2;
ЭЛЕМЕНТ-Г4; КОД-shwel; ИМЯ-Элемент схемы 3; N-N; L-1000; СВОЙСТВАМ;
ЭЛЕМЕНТ-ol; КОД-Ор; ИМЯ-Взять деталь(узел); СВОЙСТВА-finl;
ЭЛЕМЕНТ-о 1а; КОД-Ор; ИМЯ-Застропить деталь(узел); СВОЙСТВА=йп2;
ЭЛЕМЕНТ=о2; КОД-Ор; ИМЯ-Перемсстать деталь(узел) к месту установки, провести внешний осмотр;
ЭЛЕМЕНТ-оЗ; КОД-Ор; ИМЯ-Разметить место установки детали на сборочном узле; СВОЙСТВА=1т2;
ЭЛЕМЕНТ=о4; КОД-Ор; ИМЯ—Установить деталь по резметке, выверить и подогнать места сопряжений,
выдержав размеры по чертежу и техническим условиям; СВОЙСТВА-й2;
ЭЛЕМЕНТ=о5; КОД-Ор; ИМЯ-Прихватитъ деталь электросваркой;
ЭЛЕМЕНТ-об; КОД-Ор; ИМЯ-Отстропить деталь(узел); СВОЙСТВA=fm2;
ЭЛЕМЕНТ-pl; КОД=рЗ;СВОЙСТВA=fsi,fri; pl=0.286;р2=0.48;рЗ=0.51; pl=kT; p2=pL;p3=pN;
ЭЛЕМЕНТ-plr; КОД=рЗ; СВОЙСТВ A=fel,fr2; pl=0.343; р2=0.48; p3=O.5l; pl=kT; p2=pL; p3=pN;
ЭЛЕМЕНТ=р2; КОД=рЗ; СВОЙСТВA-fc2,frl; pl-0.509; р2-0.54; рЗ=0.42; pl=kT; p2=pL; p3=pN;
ЭЛЕМЕНТ=р2г, КОД=рЗ; CBOftCTBA=fs2,fr2; pl=0.610; р2=0.54; рЗ=0.42; pl=kT; p2=pL; p3=pN;
ЭЛЕМЕНТ=рЗ; КОД=рЗ; CBOftCTBA=fs3,fr 1; pl=0.684; р2=0.54; p3=0.39; pl=kT; p2=pL; p3=pN;
ЭЛЕМЕНТ-рЗг; КОД=рЗ; СВОЙСТВA-fs3,fr2; pi-0.820; р2=0.54; p3-0.39; pl-kT; p2=pL; p3-pN;
ЭЛЕМЕНТ=р4; КОД=рЗ; CBOftCTBA-fs4,frl; pl=0.822; р2=0.43; рЗ=0.42; pl-kT; p2=pL; p3=pN;
ЭЛЕМЕНТ=р4г; КОД=рЗ; СВОЙСТВ A=fs4,fr2; р1 =0.986; р2=0.43; рЗ=0.42; р 1 =kT; p2=pL; p3=pN;
ЭЛЕМЕНТ-plu; КОД=рЗ; СВОЙСТВА-ful; pl=1.4; р!=К;
ЭЛЕМЕНТ=р2и; КОД-рЗ; СВОЙСТВАМи2; pl=1.2; pl-K;
ЭЛЕМЕНТ-рЗи; КОД-рЗ; СВОЙСТВАНиЗ; pl-1.5; р!=К;
ЭЛЕМЕНТ=р4и; КОД-рЗ; CBOftCTBA=fu4; pl=1.2; р!=К;
♦ПАРАМЕТРЫ;
N (Аномер швеллера)-;
Ц+длина детали)-;
0( вес детали, кг)=;
V( объем детали, м**3)=;
Т( трудоемкость операции)-;
kT=; pL=; pN=; К=;
♦ФОРМУЛЫ;
N-14; L-10000;
Q=7800*V;
К-1;
Т= К* kT* (L/1000)**pL* N**pN;
♦ПОЛОЖЕНИЕ;
СВЯЗЬ=Ь-г1; UX-30; UY--30;
СВЯЗЬ=г1-г2; UY-90;
СВЯЗЬ=г2-гЗ; Y-L; UY-180; Х=-1000;
СВЯЗЬ=г1-г4; UY-180; Х--1000;
Рис. 15.35. Модель элемента технологической системы слесарно-сборочных работ
775
Рис. 15.36. Представление результатов обработки модели «к8»:
а) схема 1: по одному торцу, без разметки
6) схема 4: по всей длине швеллеров, с разметкой
Рис. 15.37. Формирование технологических решений
Модели технологических систем, для построения которых используется аппарат
структурно-параметрического моделирования, могут реализовывать различные мето-
дики расчета технико-экономических показателей. Например, модель «Mechob2» ре-
ализует методику расчета трудоемкости операций обработки резанием на основании
аналитического расчета режимов обработки [8].
776
Рис. 15.38. Фрагменты технологической документации
В модели «к8» (рис. 15.35) реализована методика определения трудоемкости сле-
сарно-сборочных работ, изложенная в отраслевых материалах «Единые нормы и рас-
ценки» [9]. В [9] расчет рекомендуется производить на основании таблиц замера дли-
тельности выполнения (хронометража) технологических операций либо приводимых
там же аппроксимирующих эти таблицы зависимостей. Процедуры анализа СПМ по-
зволяют получить наглядное представление (рис. 15.36, а, б) о характере зависимостей
для модели «к8» (карта №8, [9]).
Обработка структурно-параметрических моделей с целью получения техноло-
гических решений осуществляется программой «PrTech» (рис. 15.37). Исходной ин-
формацией для работы программы является структурно-параметрическая модель
«Задача технологического проектирования» (15.45), определяющая совместную об-
работку: технологической модели изделия; моделей одной или нескольких технологи-
ческих систем; модели технологического решения. Программа обеспечивает вывод
модели технологического решения в форме карт технологического процесса
(рис. 15.38).
15.9.3. Проектирование элементов штамповой оснастки
Для большой группы объектов технологического оснащения конструктивные
элементы объединяются в две группы. В состав первой входят силовые, каркасообра-
зующие элементы, воспринимающие нагрузки, подводящие энергопотоки. Опреде-
лим их как группу каркасных элементов. Элементы второй группы образуют рабочую
зону, основная задача которой — обеспечить необходимые геометрические характе-
ристики изделия.
Система параметризации для элементов первой группы должна строиться исходя
из соображений максимальной унификации и типизации как отдельных используе-
мых элементов, так и целых конструктивных решений.
Система параметризации элементов рабочей зоны должна настраиваться на
восприятие, передачу и преобразование информации об изделии. Эти процессы мож-
777
но организовать, установив соответствующие связи (отношения) между элементами
рабочей зоны. Однако с увеличением количества таких связей модель становится
сложной, ее трудно модифицировать даже разработчику.
Модель рабочей зоны можно упростить, если в ее состав ввести обособленный
элемент, воспроизводящий геометрию изделия. Необходимо сделать этот элемент
чувствительным к «технологическим модификациям», т. е. изменениям, необходи-
мым для реализации технологических воздействий, например образованию зазора
между режущими кромками инструмента. Тогда его можно будет внедрить во все объ-
екты рабочей зоны.
Рассмотрим построение подобной модели на примере вырубного штампа совме-
щенного действия (рис. 15.39). Конструкция верхнего и нижнего блоков, плит и ко-
лонн является унифицированной. На выбор типоразмера каркасных элементов влия-
в) формирование эскиза
Рис. 15.39. Модель штампа
778
ют габариты изделия и величина рабочего усилия. Изделие представлено совокупно-
стью двух СПМ: «NARKON» — наружного и «WNUKON» — внутреннего контуров
вырубаемой (формируемой) детали. Их одновременное в пуансономатрице
(рис. 15.40, а) либо поочередное в матрице и в пуансоне использование позволяет
сформировать модели элементов рабочей зоны.
Применение процедуры «Замещение» относительно элементов «NARKON» и
«WNUKON» обеспечивает простую и быструю модификацию структурно-параметри-
ческой модели штампа и вместе с ней всех проектных решений.
а) пуансон
б) узел выталкивателя
D t ’
stamp, spbj
0 ШТАМП
® БЛОК
ф НИЖНИЙ ПАКЕТ
0 ВЕРХНИЙ ПАКЕТ
to ПРОКЛАДКА 1
ф ПРОКЛАДКА 2
Й ПУАНСОНОДЕРЖАТЕЛЬ
Й ПУАНСОН
база
Ф РАБОЧАЯ ПОВ
ФЛАНЕЦ
ПРОТОЧКА
ПОСАДОЧНАЯ ПОВ.
Irr ПРОКЛАДКА 3
Ь МАТРИЦА
; I диск
Г РАБОЧИЙ КОНТУР
Ь С КРЕПЛЕНИЯ 1
СКРЕПЛЕНИЯ 2
t О.КРЕПЛЕНИЯ 3
' О.КРЕПЛЕНИЯ 4
ГНЕЗД01
ГНЕЗДО 2
ГНЕЗДО 3
; ГНЕЗДО 4
ф УЗЕЛ ВЫТАЛКИВАТЕЛЯ
ffiХВОСТОВИК
to БОЛЬШОЙ БОЛТ 1
ф БОЛЬШОЙ БОЛТ 2
ф БОЛЬШОЙ БОЛТ 3
Ф БОЛЬШОЙ БОЛТ 4
д=дшт;в=дашт; *»<w;Bi-«;fli=4;
звешятм; xofisvm; имя*ша*п
д=дагг. в=даш; > «•*♦; др*;
вд-му. жмямипятг
д-дшг в-дщш *•«; вхнеддо;
аисшда*; жда>впи«4
д-дшт; в=дашт; ►ми, bi-«; Д1«е;
здвмг нт*}-. лд№орлвжр>
ДЧП в пв нзмкдо;
ход=фп;
Param | Formul| Arc | Contour j Efe
ЕДЛУ 208500000
to ДУ 68.000000
0 ДЛВТ 31,500000
ЕЭ ДШТ КШЮ000
0 ДЛШТ 45,000000
ЩТТР 12.000000
to ДТ 16,000000
В ДЛТ 120,000000
а РОШТ 29.000000
ВДФ .....44000000
Файл Элементы
ф'Йрак Л
Ф1
to 2 I
«з '
Й-4
to 5 I
to-6 _
to-7
to 8 |
® 9
to io
Ф и
to 12
to 13
Вид Размерные элементы Формат Протокол О программе...
Свойства Изображение}
30
View 3d |
Скмр
10:26
^ВПусх}] (J) А ЙЙ > S ggVisua»spb| 5gSPM Jj^Showvb
в) анализ решения
Рис. 15.40. Элементы рабочей зоны
779
15.9.4. Моделирование элементов сборочной оснастки
Разработка моделей сборочных приспособлений, позволяющих автоматизиро-
вать процесс принятия решений по составу элементов структуры, а также по измене-
нию геометрии собираемого изделия является интересной задачей, требующей при-
менения аппарата, способного сочетать выполнение процедур структурного и пара-
метрического моделирования.
Модель объекта «Балка» (рис. 15.41) позволяет осуществлять синтез структуры
решения, в зависимости от значений функциональных характеристик изделия, опре-
деляющих: уровень воспринимаемых нагрузок, наличие стыковых узлов.
Для объекта необходимо выделить набор структурных свойств (контуров), которые
будут управлять процессом расчета решения. Контуры объединяются в группы.
В каждой группе в данный момент времени может быть реализован лишь один контур.
Контуры описываются в блоке «4-ОБЪЕКТ». В модели сборочной единицы «balka» вы-
делено три группы контуров (рис. 15.42, а). Первая группа включает три контура, вторая
и третья — по два. Условия выбора решения для контуров первой группы (i/7, i/2, иЗ) пос-
тавлены в зависимость от значения параметра «UN» (уровень нагрузки). Например, если
параметр UN в результате расчетов окажется лежащим в пределах от 0 до 5, истинным
окажется состояние контура и1 (слабо нагруженная конструкция); если от 5 до 50, то ис-
тинным окажется состояние контура и2 (средне нагруженная конструкция); если от 50 и
выше — иЗ (сильно нагруженная конструкция). Условие выбора решения для контуров
второй группы (пннт, пнда) зависит от значения параметра «критПпН». Выбор решения
для контуров третьей группы принимается пользователем при обработке модели.
Задание условий включения элемента в проектное решение производится установ-
кой соответствия свойств и элементов с помощью директивы «СВОЙСТВА» в блоке
«4-ЭЛЕМЕНТЫ». Например, элементы балки а21 и а22 будут включены в решение, ес-
ли необходима реализация контура иЗ, и их включение не зависит от состояния конту-
ров других групп. Те элементы, которые не содержат в своем описании директивы
«СВОЙСТВА», входят в решение при любом состоянии управляющих воздействий.
Вся информация об объекте разделена на отдельные фрагменты (модули) и раз-
мещена в различных файлах. Рис. 15.42, а — это описание сборочной единицы в це-
лом (файл «balka.spm»), рис. 15.42, б содержит описание элемента «полка» (файл «pol-
ka—m.spm»). Иерархическая подчиненность (15.12) элементов изделия задается отно-
шением «ОБЪЕКТ — ЭЛЕМЕНТЫ». При описании состава элементов модели
задаются: признак формы элемента — код элемента («КОД=Ьа1ка;»); функциональное
назначение («ИМЯ=балка»); тип элемента («ТИП=С;»); признак заполненности объ-
ема материалом («ТЕЛО=4-;»); значения собственных параметров (параметров фор-
мы) каждого элемента («1=1000; bl=B 1;...»).
Рис. 15.41. Объект «Балка»
780
+ОБ"ЕКТ; К0Д=Ьа1ка; ИМЯ=Балка; ТИП=С;
ul(UN,,5)=слабо нагруженная конструкция;
u2(UN,5,50)=средне нагруженная конструкция;
u3(UN,50,)=сильно нагруженная конструкция;
пннт(критПпН,,50)=поперечный набор отсутствует;
пнда(критПпН,50,)=поперечный набор необходим;
стнт=узлы стыка отсутствуют;
стда=узлы стыка имеются;
ГРУППА=и1,u2,иЗ; ГРУППА=пннт,пнда; ГРУППА=стнт,стда;
4-ЭЛЕМЕНТЫ;
ЭЛЕМЕНТ=а1; К0Д=зГепка; ИМЯ=стенка; 1=L; Ы=В1; Ь2=В2; t=t;
ЭЛЕМЕНТ=а21; КОД=ро1ка-Ь; ИМЯ=полка большая!;1=L; СВОЙСТВА=иЗ;
ЭЛЕМЕНТ=а22; КОД=ро1ка-Ь; ИМЯ=полка большая2;1=L; СВОЙСТВА=иЗ;
ЭЛЕМЕНТ=а23; КОД=ро!ка-ш; ИМЯ=полка малая!; 1=L; СВОЙСТВА=и2,u3,стда;
ЭЛЕМЕНТ=а24; КОД=ро!ка-т; ИМЯ=полка малая2; 1=L; СВОЙСТВА=и2,иЗ,стда;
ЭЛЕМЕНТ=аЗ; КОД=рорпаЬог; ИМЯ=поперечный набор; В1=В1;В2=В2;L=L;
СВОЙСТВА=пнда;
ЭЛЕМЕНТ=а41; КОД=иЬо; ИМЯ=узел стыка верхний; СВОЙСТВА=стда;
ЭЛЕМЕНТ=а42; K0fl=uho; ИМЯ=узел стыка нижний; СВОЙСТВА=стда;
4-ПОЛОЖЕНИЕ;
СВЯЗЬ=а1-а21; Y=t; Z=-B1_2; UY=-alfa;
СВЯЗЬ=а1-а22; Y=t; Z=B1_2; UY=alfa; UY=180;X=-L;
СВЯЗЬ=а1-а23; Z=-B1_2; UY=-alfa;
СВЯЗЬ=а!-а24; Z=B1_2; UY=alfa; UY=180;X=-L;
СВЯЗЬ=а1-а41; Y=-6; Z=-76.9;Z=-p; UY=-alfa; X=-15;
СВЯЗЬ=а1-а42; Y=-6; Z= 76.9;Z=p; UY=alfa; X=-15;
СВЯЗЬ=а1-аЗ; Y=4;
4-ПАРАМЕТРЫ; UN (4-уровень нагрузки) =60;
L(4-длина балки) =1000; t (4-толщина стенки) =4;
В! (4-ширина балки в корне)=200; В2 (4-ширина балки)=150;
критПпН( критерий поперечного набора)=;
alfa( )=; В1_2=; р=;
4-ФОРМУЛЫ;
критПпН=С/((В1+В2)/2);
alfa=ATAN(0.5*(В1-В2)/L); В1 2=В1/2; р=(В1-200)/2 ;
а) модель «Ьа1ка»
+ОБ”ЕКТ;
КОД=ро!ка-т; ИМЯ=полка малая; ТИП=Д;
4-ЭЛЕМЕНТЫ;
ЭЛЕМЕНТ=з; KOfl=plast20; ИМЯ=полка; В=1; КГР=9;
Yl = 0; Y2=0; Y3=-4; Y4=-6; Y5=-6; Y6=-8; Y7=-23; Y8=-25; Y9=-25;
Z!=0; Z2=40; Z3=40; Z4=38; Z5=8; Z6=6; Z7=6; Z8=4; Z9=0;
ЭЛЕМЕНТ=с; ИМЯ=центр; ТИП=Ф;
4-ПОЛОЖЕНИЕ;
СВЯЗЬ=з-с; Х=1_2;
4-ПАРАМЕТРЫ; !( длина) =; 1_2=;
В! (4-ширина балки в корне) =; В2 (4-ширина балки) =;
df (4-дистанция фитинга) =; L(4-длина балки) =;
4-ФОРМУЛЫ;
1=В2+(В1-В2)*(1-df/L);
1=1000; 1 2=1/2;
б) модель «polka—т»
Рис. 15.42. Модель объекта «Балка»
781
Ориентированный граф, описывающий пространственное положение элементов
(15.13), задается через указание пар элементов и относительных перемещений и пово-
ротов их координатных систем в пространстве (15.16). Например, конструкция
”СВЯЗЬ=я7—о27; Y=t;Z=-BY2; UY=-alfa" -
указывает на то, что координатная система элемента а21 перемещена относительно
элемента al вдоль оси «У» на величину /, в отрицательном направлении оси «Z» на ве-
личину В12 и затем повернута в отрицательном направлении оси « У» на величину alfa,
содержащую значение величины угла поворота в градусах. При обработке моделей
выполняется правило, согласно которому система координат объекта совпадает с сис-
темой координат первого включенного в объект элемента.
Модель сборочного переналаживаемого приспособления (рис. 15.43) включает
элементы, обеспечивающие имитацию каркаса (karkas), ложементов приспособления
(styk, urfiks) и способа монтажа приспособления (linejka).
Модуль «sborka» (рис. 15.44, а) обеспечивает согласование параметров положения
ложементов приспособления (prisp) с опорными точками изделия (balka). Элементы мо-
дулей «linejka» (рис. 15.43, б), «montav—fi> (рис. 15.44, б) реализуют модель метода увязки
средств технологического оснащения, позволяющую «параметризировать» этот процесс.
Использование показанного подхода позволяет распараллелить процессы описа-
ния изделий и сборочных приспособлений. Геометрическая интерпретация результа-
тов параллельного проектирования приведена на рис. 15.45.
4-ОБЪЕКТ;
К0Д=рг1зр; ИМЯ=Приспособление сборочное переналаживаемое; ТИП=С;
4-ЭЛЕМЕНТЫ;
ЭЛЕМЕНТ=р1; К0Д=кагказ; ИМЯ=каркас;
ЭЛЕМЕНТ=р21; KOfl=linejka; ИМЯ=линейка 1; 1=0; Ь1=350;
ЭЛЕМЕНТ=р22; КОД=зЁук; ИМЯ=стыковой узел;
ЭЛЕМЕНТ=р31; К0Д=игГ1кз; ИМЯ=узел фиксаторов 1; 1=350;
ЭЛЕМЕНТ=р32; КОД-uzfiks; ИМЯ=узел фиксаторов 2; 1=350;
ЭЛЕМЕНТ=рЗЗ; KOfl=uzfiks; ИМЯ=узел фиксаторов 3; 1=300;
4-ПОЛОЖЕНИЕ;
СВЯЗЬ=р1>р1-р21; Х=135;
СВЯЗЬ=р21-р22; Х=7.5; Y=149;
СВЯЗЬ=р21-р31; Х=150;
СВЯЗЬ=рЗ1-р32; Х=4 00;
СВЯЗЬ=р32-рЗЗ; Х=400;
а) головной модуль «balka»
4-ОБЪЕКТ;
KOfl=linejka; ИМЯ=линейка; ТИП=С;
4-ЭЛЕМЕНТЫ;
ЭЛЕМЕНТ=Г; ИМЯ-БАЗА; ТИП=Ф;
ЭЛЕМЕНТ=р1; КОД=рага1; ИМЯ=линейка; 01=450;02=70;03=15;
ЭЛЕМЕНТ=р21;КОД=кгзИЪ; ИМЯ=кронштейн линейки левый; l=100;b=150;h=35;
ЭЛЕМЕНТ=р22;KOfl=krsht; ИМЯ=кронштейн линейки правый;1=100;Ь=150;Н=35;
ЭЛЕМЕНТ-f21;ИМЯ=база левого фиксатора; ТИП=Ф;
ЭЛЕМЕНТ=£22;ИМЯ=база правого фиксатора; ТИП=Ф;
4-ПОЛОЖЕНИЕ;
CBH3b=f-p21; Z—Ы2;
СВЯЗЬ—f-p22; Z=bl2;
CBH3b=f-pl; Y=15; Y=35; UY=90; X—225;
СВЯЗЬ-pl-f21; X=225;X=12;UZ=90;X=35;X=15;
СВЯЗЬ-f21-f22; Y=l;UX=180;
4-ПАРАМЕТРЫ; 1( )=; 12=; bl ( )=; bl2 = ;
4-ФОРМУЛЫ; 12=1/2; b!2=bl/2;
б) модуль «linejka»
Рис. 15.43. Модель сборочного приспособления
782
4-ОБЪЕКТ; KOfl=sborka; +ЭЛЕМЕНТЫ; ИМЯ=Сборка; ТИП=С;
ЭЛЕМЕНТ=а1; К0Д=Ьа1ка;
ЭЛЕМЕНТ=р1; KOfl=prisp;
ЭЛЕМЕНТ=р21; KOfl=montav-f; dist=80;
ЭЛЕМЕНТ=р22; KOfl=montav-f; dist=480;
ЭЛЕМЕНТ=р23; KOfl=montav-f; dist=880;
ЭЛЕМЕНТ=р24; KOfl=montav-f; dist=120;
ЭЛЕМЕНТ=р25; КОД=montav-f; dist = 52 0;
ЭЛЕМЕНТ=р26; +ПОЛОЖЕНИЕ; KOfl=montav-f; dist=920;
СВЯЗЬ=р1- al; X=200; Y=155;
СВЯЗЬ=р21 >f-al>a23;
СВЯЗЬ=р21 >fl-pl>p31>p31>f1;
СВЯЗЬ=р22 >f-al>a23;
СВЯЗЬ=р22 >fl-pl>p32>p31>fl;
СВЯЗЬ=р23 >f-al>a23;
CBH3b=p23>fl-pl>p33>p31>fl;
CBH3b=p26>f-al>a24; CBH3b=p26>fl-pl>p31>p32>fl; CBH3b=p25>f-al>a24; CBH3b=p25>fl-pl>p32>p32>f1; CBH3b=p24>f-al>a24; СВЯЗЬ=р24 > f1-pl>p3 3 >p3 2 >f1;
а) головной модуль «sborka»
4-ОБЪЕКТ;
KOfl=montav-f; ИМЯ=ШМФ фиксаторов; ТИП=К;
4- ЭЛЕМЕНТЫ;
ЭЛЕМЕНТ=:£; ИМЯ=БАЗА; ТИП=Ф;
ЭЛЕМЕНТ=£1; ИМЯ=БАЗА; ТИП=Ф;
4-ПОЛОЖЕНИЕ;
CBH3b=f-fl; X=dist; Y=-6; UY=-90;
4-ПАРАМЕТРЫ; dist (4-дистанция фиксатора) =;
б) модуль «montav—f»
Рис. 15.44. Модель увязки средств технологического оснащения
Рис. 15.45. Приспособление для сборки балки
783
ЛИТЕРАТУРА
1. Винер Н. Кибернетика или управление и связь в животном и машине: Пер. с англ.
2-е изд. — М.: Сов. Радио, 1968. С. 326.
2. Шпур Г., Ф.-Л. Краузе. Автоматизированное проектирование в машиностроении:
Пер. с нем. Г. Д. Волковой и др. / Под ред. Ю. М. Соломенцева, В. П. Диденко. —
М.: Машиностроение, 1988. С. 648.
3. Павлов В. В. Математическое обеспечение САПР в производстве летательных ап-
паратов. — М.: МФТИ, 1978. С. 68.
4. Павлов В. В. Структурное моделирование производственных систем. — М.: Мос-
станкин, 1987. С. 80.
5. САП Р Типовые математические модели объектов проектирования в машиностро-
ении. Руководящий нормативный документ. РД 50—464—84. — М.: Изд-во Стан-
дартов, 1985. С. 201.
6. Цырков А. В. Методология проектирования в мультиплексной информационной
среде: Монография. — М.: ВИМИ, 1998. С. 281.
7. Цырков А. В. Особенности создания технологической среды параллельного про-
ектирования объектов производства. — Техника. Экономика. Сер. Автоматиза-
ция проектирования / Всероссийский научно-исследовательский институт ме-
жотраслевой информации. Вып. 3—4. — 1995. С. 19—30.
8. Прогрессивные режущие инструменты и режимы резания металлов: Справочник /
Баранчиков В. И., Жаринов А. В., Юдина Н. Д. и др.; Под общ. ред. Баранчико-
ва В. И. — М.: Машиностроение, 1990. С. 400.
9. Общемашиностроительные нормативы времени на слесарно-сборочные работы
при сборке металлоконструкций под сварку. Научно-исследовательский инсти-
тут труда Государственного комитета СССР по труду и социальным вопросам. —
М: НИИ труда, 1982. С. 128.
Содержание главы 15
15.1. Функциональная модель.....................................716
15.2. Средства автоматизации проектных работ....................721
15.3. Инвариантная информационная модель объекта проектирования.728
15.4. Процедуры обработки инвариантной информационной модели....740
15.5. Логическое моделирование..................................743
15.6. Структурное моделирование.................................746
15.6.1. Табличные модели....................................747
* 15.6.2. Сетевые модели......................................747
15.7. Процедуры синтеза информационных объектов.................747
15.8. Модель процесса проектирования............................753
15.9. Примеры решения задач технической подготовки производства.756
15.9.1. Проектирование типового машиностроительного изделия.756
15.9.2. Проектирование технологических процессов............762
15.9.3. Проектирование элементов штамповой оснастки.........777
15.9.4. Моделирование элементов сборочной оснастки..........780
Литература..........................................................784