Текст
НПО «ПРОФЕССИОНАЛ», Санкт-Петербург
ютовцев, Е.Б. Маховенко
_ J еоретическая
криптография
СОДЕРЖАНИЕ
ВВЕДЕНИЕ................................3
ГЛАВА 1. МНОЖЕСТВА, АЛГОРИТМЫ,
СЛУЧАЙНЫЕ ОТОБРАЖЕНИЯ...................6
1.1. Сведения из теории множеств.......6
1.2. Сведения из теории алгоритмов.....8
1.2.1. Алгоритм и исчисление.......8
1.2.2. Сложность алгоритма........10
1.3. Нестандартные вычислительные модели... 12
1.3.1. Молекулярный компьютер.....13
1.3.2. Квантовый компьютер........14
1.4. Случайные последовательности
и случайные отображения..........16
1.4.1. Понятие случайности........16
1.4.2. Свойства случайного отображения... 17
Упражнения к главе 1...................20
Литература к главе 1...................20
ГЛАВА 2. ГРУППЫ........................22
2.1. Понятие группы...................22
2.2. Подгруппы........................23
2.3. Гомоморфизмы и изоморфизмы.......26
2.4. Действие группы на множестве.....28
2.5. Группа подстановок...............28
2.6. Вложимость коммутативной полугруппы
в группу..........................31
2.7. Прямые произведения групп........31
2.8. Категории........................32
Упражнения к главе 2...................33
Литература к главе 2...................33
ГЛАВА 3. КОММУТАТИВНЫЕ КОЛЬЦА..........34
3.1. Понятие кольца...................34
3.2. Гомоморфизмы колец...............36
3.3. Частные..........................36
3.4. Предварительные сведения о полиномах... 37
3.5. Идеалы и классы вычетов..........38
3.6. Делимость идеалов................41
3.7. Евклидовы кольца и кольца главных
идеалов...........................42
3.8. Разложение на множители..........43
3.9. Кольцо эндоморфизмов модуля.
Модули над кольцами...............45
3.10. Свойства полиномов...............46
3.11. Производная и кратные корни......46
3.12. Симметрические функции...........47
3.13. Разложение на множители полиномов
от нескольких переменных..........48
3.14. Полукольца и решетк! i...........50
3.15. Кольцо полиномов Жегалкина.......51
3.15.1. Полиномы Жегалкина........51
3.15.2. Разложение на множители
в кольце Gn.......................53
3.15.3. Симметрические функции
кольца G„.........................54
3.15.4. Кольцо дифференциальных
операторов кольца G„..............54
3.15.5. Эндоморфизмы кольца G„.......55
Упражнения к главе 3......................56
Литература к главе 3......................57
ГЛАВА 4. ПОЛЯ.............................58
4.1. Общие сведения о полях. Простые поля.58
4.2. Расширения полей.....................59
4.2.1. Простые расширения............60
4.2.2. Конечные расширения...........62
4.2.3. Целые элементы поля...........64
4.3. Конечные поля........................65
4.3.1. Строение конечных полей.......65
4.3.2. Автоморфизмы конечных полей...67
4.3.3. Норма и след в конечных полях.69
4.4. Элементы теории Галуа................70
4.5. Поля деления круга...................72
4.6. Дискретное преобразование Фурье......73
4.7. Нормирования.........................74
4.8. Пополнения поля Q ир-адические числа ...75
Упражнения к главе 4....................77
Литература к главе 4....................78
ГЛАВА 5. СВЕДЕНИЯ ИЗ ТЕОРИИ ЧИСЕЛ.. .79
5.1. Однозначное разложение на множители
в кольце Z...........................79
5.2. Некоторые числовые функции...........79
5.3. Кольцо Z/hZ..........................81
5.4. Квадратичные и кубические вычеты.
Квадратичный закон взаимности........83
5.5. Суммы Гаусса и Якоби.................87
5.6. Квадратичные числа и квадратичные
формы................................89
5.6.1. Кольцо целых . *
квадратичных чисел................89
5.6.2. Идеалы квадратичных порядков..91
5.6.3. Квадратич ные формы...........93
5.7. Алгебраические числа.................95
Упражнения к главе 5....................98
Литература к главе 5....................98
ГЛАВА 6. ЭЛЕМЕНТЫ АЛГЕБРАИЧЕСКОЙ
ГЕОМЕТРИИ. ЭЛЛИПТИЧЕСКИЕ КРИВЫЕ ...99
6.1. Аффинные алгебраические многообразия ...99
6.2. Проективная плоскость
и проективное пространство.............100
475
6.3. Сложение точек на конике............102
6.4. Кубические кривые. Закон сложения...102
6.5. Особые и неособые кубики............105
6.6. Касательные и точки перегиба
алгебраической кривой...............106
6.7. Нормальные формы
эллиптической кривой................107
6.8. Группа неособых точек кубики........108
6.9. Невозможность рациональной
параметризации эллиптической кривой.109
6.10. Параметризация эллиптической кривой
с помощью эллиптических функций.....110
6.10.1. Эллиптические функции........НО
6.10.2. Функция Вейерштрасса........112
6.10.3. Параметризация эллиптической
кривой над полем С..................113
6.11. Дискриминант иу-инвариант...........115
6.12. Закон сложения точек
эллиптической кривой................115
6.13. Эллиптические кривые
над числовыми полями................117
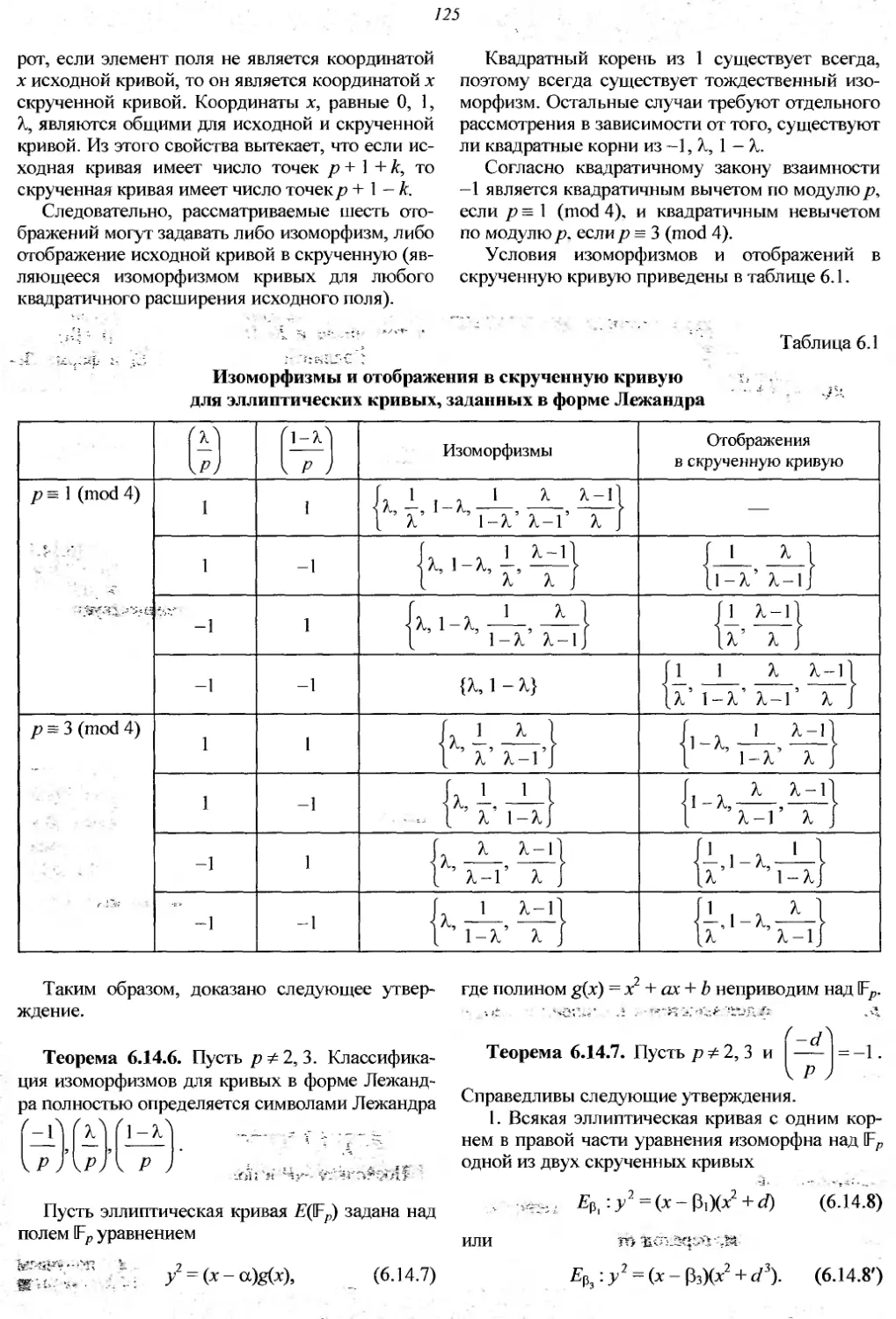
6.14. Изоморфизмы и эндоморфизмы
эллипти ческих кривых...............119
6.14.1. Изоморфизмы над полями
характеристики, отличной от 2 и 3 .. 119
6.14.2. Изоморфизмы над полями
характеристики 3....................120
6.14.3. Изоморфизмы надполями
характеристики 2....................121
6.14.4. Бирациональный изоморфизм
кривых..............................121
6.14.5. Эндоморфизмы эллиптических
кривых..............................123
6.14.6. Изоморфизмы эллиптических
кривых над алгебраически
незамкнутым полем...................124
6.15. Отображения алгебраических кривых...128
6.15.1. Регулярные функции и
отображения.........................128
6.15.2. Рациональные функции и
рациональные отображения............130
6.15.3. Проективные кривые..........131
6.15.4. Изогении эллиптических
кривых..............................132
6.15.5. Полиномы Жегалкина как
функции на поверхности
единичного куба.....................133
6.16. Дивизоры на алгебраических кривых...134
6.16.1. Локальное кольцо точки и
нормирование........................134
6.16.2. Дивизоры....................135
6.16.3. Спаривание Вейля............137
6.17. Эллиптические кривые
над конечными полями................139
6.18. Гиперэллиптические кривые...........141
6.18.1. Функции на кривых
6.18.2. Якобиан
Упражнения к главе 6......................148
Литература к главе 6......................149
ГЛАВА 7. ВЫЧИСЛИТЕЛЬНЫЕ АЛГОРИТМЫ
АЛГЕБРЫ И ТЕОРИИ ЧИСЕЛ.....................151
7.1. Алгоритмы умножения...................151
7.1.1. Алгоритм умножения
Карацубы-Офмана....................151
7.1.2. Умножение в классах вычетов..151
7.1.3. Умножение с помощью быстрого
преобразования Фурье...............153
7.1.4. Модульное умножение. Метод
Монтгомери.........................155
7.1.5. Деление.......................157
7.2. Алгоритмы обращения и вычисления
наибольшего общего делителя..........158
7.3. Минимизация базиса решетки............160
7.4. Разложение над конечным полем
полиномов от одной переменной........161
7.5. Извлечение квадратных и кубических
корней в конечном поле...............161
7.5.1. Извлечение квадратного корня
в случае q = 3 (mod 4)..........162
7.5.2. Извлечение квадратного корня
в случае q s 5 (mod 8),
q = 9 (mod 16)..................162
7.5.3. Извлечение квадратного корня
в общем случае для нечетного q.163
7.5.4. Извлечение квадратного корня
в случае четного q.................163
7.5.5. Решение квадратного уравнения.163
7.5.6. Извлечение кубического корня
в конечном поле....................164
7.6. Вычисление символа Якоби..............165
7.7. Проверка чисел и полиномов
на простоту..........................165
7.8. Разложение чисел в мнимом
квадратичном порядке 166
7.9. Приведение числа по модулю решетки....169
7.10. Умножение точки
эллиптической кривой на число........171
7.11. Вычисление функции Вейля.............172
7.12. Сложение элементов якобиана
гиперэллиптической кривой............173
7.13. Арифметика группы классов мнимых
квадратичных порядков................174
Упражнения к главе 7.......................175
Литература к главе 7.......................176
ГЛАВА 8. КРИПТОГРАФИЯ И ЗАЩИТА
ИНФОРМАЦИИ.................................177
8.1. Основные понятия защиты информации.... 178
8.2. Исчисление атак.....................181
8.2.1. Упорядоченность моделей
нарушителя и безопасных систем ... 181
8.2.2. Множества возможностей
нарушителя.....................182
8.2.3. Тривиальная модель нарушителя.... 184
8.2.4. Нетривиальная модель
нарушителя............................186
8.2.5. Место криптографии
в защите информации...................188
476
8.3. Основные понятия и определения
криптографической защиты данных...........189
8.3.1. Криптографические примитивы..189
8.3.2. Хэш-функция....................190
8.3.3. Шифр...........................191
8.3.4. Понятие стойкости
криптографических алгоритмов..191
8.4. Шифрование............................192
8.4.1. Симметричное и несимметричное
шифрование.........................193
8.4.2. Способы шифрования.............194
8.5. Аутентификация........................195
8.5.1. Опознавание....................197
8.5.2. Контроль целостности и
подлинности данных.................198
8.6. Управление ключами....................198
8.7. Задачи, положенные в основу
безопасности криптографических
алгоритмов............................199
Упражнения к главе 8......................201
Литература к главе 8......................202
ГЛАВА 9. СИСТЕМА RSA И ЗАДАЧА
РАЗЛОЖЕНИЯ..................................203
9.1. Безопасность системы RSA и задача
разложения на множители.............203
9.2. Детерминированные методы разложения.. 204
9.2.1. Метод пробного деления............204
9.2.2. Метод «giant step — baby step».205
9.2.3. Метод Ферма....................205
9.2.4. Метод диофантовой
аппроксимации...................206
9.3. Вероятностные методы разложения.......207
9.3.1. p-метод Полларда
(метод «Монте-Карло»)...........207
9.3.2. Метод непрерывных дробей.......207
9.3.3. Метод квадратичного решета.....209
9.3.4. (р-1)-метод....................210
9.3.5. Разложение на эллиптической
кривой..........................210
9.3.6. Разложение на квантовом
компьютере......................212
9.4. Атаки на систему RSA, не требующие
разложения............................213
9.4.1. Случай малого секретного
показателя......................213
9.4.2. Случаи специальных открытых
показателей........................214
9.4.3. Атаки на основе эндоморфизмов.... 215
Упражнения к главе 9........................216
Литература к главе 9........................217
ГЛАВА 10. ДИСКРЕТНОЕ
ЛОГАРИФМИРОВАНИЕ В КОНЕЧНОМ ПОЛЕ
И СМЕЖНЫЕ ЗАДАЧИ......................218
10.1. Метод базы разложения...........218
10.2. Логарифмирование в простом поле
методом решета числового поля.........222
10.2.1. Подготовительные
теоретико-числовые результаты....222
10.2.2. Метод решета числового поля.223
10.3. Логарифмирование в расширенном поле.227
10.4. Группа классов мнимого квадратичного
порядка.................................228
10.5. Логарифмирование в группе
функций Лукаша..........................229
10.6. Связь между задачами Диффи-Хеллмана
и дискретного логарифмирования..........229
Упражнения к главе 10....................230
Литература к главе 10....................231
ГЛАВА 11. ЗАДАЧА ДИСКРЕТНОГО
ЛОГАРИФМИРОВАНИЯ f
НА ЭЛЛИПТИЧЕСКОЙ КРИВОЙ.................233
11.1. Универсальные методы
логарифмирования.......................233
11.1.1. Метод Гельфонда...........233
11.1.2. Методы встречи посередине и
«giant step — baby step».........234
11.1.3. Метод Полларда............235
11.1.4. Метод встречи
на случайном дереве..............235
11.1.5. Сравнение сложности
логарифмирования на эллиптической
кривой и в конечном поле..........238
11.1.6. Логарифмирование с помощью
квантового компьютера.............239
11.2. Влияние комплексного умножения на
сложность логарифмирования..............240
11.3. Логарифмирование с использованием
функции Вейля...........................241
11.4. Другие задачи, связанные
с логарифмированием.....................243
11.5. Время жизни параметров криптосистемы,
основанной на дискретном
логарифмировании.......................246
11.5.1. Мультипликативная группа поля ....247
11.5.2. Группа точек
эллиптической кривой.......247
11.6. Логарифмирование в якобиане
гиперэллиптической кривой..............248
11.7. Требования к эллиптической кривой.249
Упражнения к главе 11...................250
Литература к главе 11...................251
ГЛАВА 12. ШИФРОВАНИЕ С ОТКРЫТЫМ
КЛЮЧОМ..................................252
12.1. Шифрование с открытым ключом
для группы вычислимого порядка..........252
12.1.1. Бесключевое шифрование
Месси-Омуры.................253
12.1.2. Протокол Эль-Гамаля шифрования
с открытым ключом.................254
12.2. Шифрование с открытым ключом
для группы трудновычислимого порядка...255
12.2.1. Протокол шифрования Рабина.256
12.2.2. Вероятностное шифрование..256
12.3. Ранцевые алгоритмы шифрования с
открытым ключом........................258
477
12.4. Генераторы псевдослучайной
последовательности..................260
Упражнения к главе 12.....................261
Литература к главе 12.....................262
ГЛАВА 13. ЦИФРОВАЯ ПОДПИСЬ................263
13.1. Под пись на группе трудновычислимо го
порядка.............................263
13.1.1. Схема подписи RSA...........264
13.1.2. Схема подписи Рабина........264
13.1.3. Схема подписи Фиата-Шамира..265
13.2. Подпись на группе вычислимого
порядка.............................265
13.2.1. Схема подписи Эль-Гамаля....265
13.2.2. Схема подписи Шнорра........267
13.2.3. ГОСТ Р 34.10-94 и DSS.......268
13.3. Сравнительный анализ представленных
схем подписи........................269
13.4. Скрытый канал.......................270
13.5. Другие схемы подписи................271
13.5.1. Схема «неоспоримой» подписи.271
13.5.2. Схема подписи «вслепую».
Электронные платежи...........273
13.5.3. Схема подписи с восстановлением
сообщения..........................274
13.5.4. Инкрементальная подпись.....274
Упражнения к главе 13.....................275
Литература к главе 13.....................276
ГЛАВА 14. ДРУГИЕ
КРИПТОГРАФИЧЕСКИЕ
ПРОТОКОЛЫ.................................278
14.1. Схемы предъявления битов............278
14.2. Диалоговые доказательства
с нулевым разглашением....................279
14.2.1. Доказательство знания
изоморфизма графов..................279
14.2.2. Доказательство знания разложения
составного числа....................280
14.2.3. Доказательство знания
дискретного логарифма...............281
14.2.4. Доказательство правильности
выбора составного числа.............281
14.3. Бездиалоговые доказательства
с нулевым разглашением....................283
14.4. Передача информации
со стиранием.............................285
14.5. Разделение секрета..................287
14.6. Протоколы управления ключами........288
14.6.1. Установление ключа на основе
симметричных методов...............289
14.6.2. Доставка ключа..............290
14.7. Временная метка.....................291
14.7.1. Централизованная реализация
временной метки....................291
14.7.2. Децентрализованная реализация
временной метки....................292
Упражнения к главе 14.....................293
Литература к главе 14.....................293
ГЛАВА 15. КРИПТОСИСТЕМЫ
НА ЭЛЛИПТИЧЕСКИХ
И ГИПЕРЭЛЛИПТИЧЕСКИХ КРИВЫХ.............294
15.1. Расчет числа точек эллиптической
кривой в общем случае...................294
15.1.1. Предварительные сведения...295
15.1.2. Полиномы деления...........296
15.1.3. Алгоритм Чуфа..............297
15.2. Расчет числа точек эллиптической
кривой над расширенным полем............299
15.3. Расчет числа точек эллиптических кривых
cj = 0, 1728 над простыми полями.........301
15.3.1. Криваяу2 = х3 +7?..........301
15.3.2. Кривая у2 = х3 + Ах...........303
15.4. Эллиптические кривые с комплексным
умножением..............................305
15.4.1. Генерация эллиптических кривых
с комплексным умножением..........306
15.4.2. Влияние комплексного умножения
на скорость вычислений............308
15.5. Эллиптические кривые над расширенными
полями специальных характеристик...311
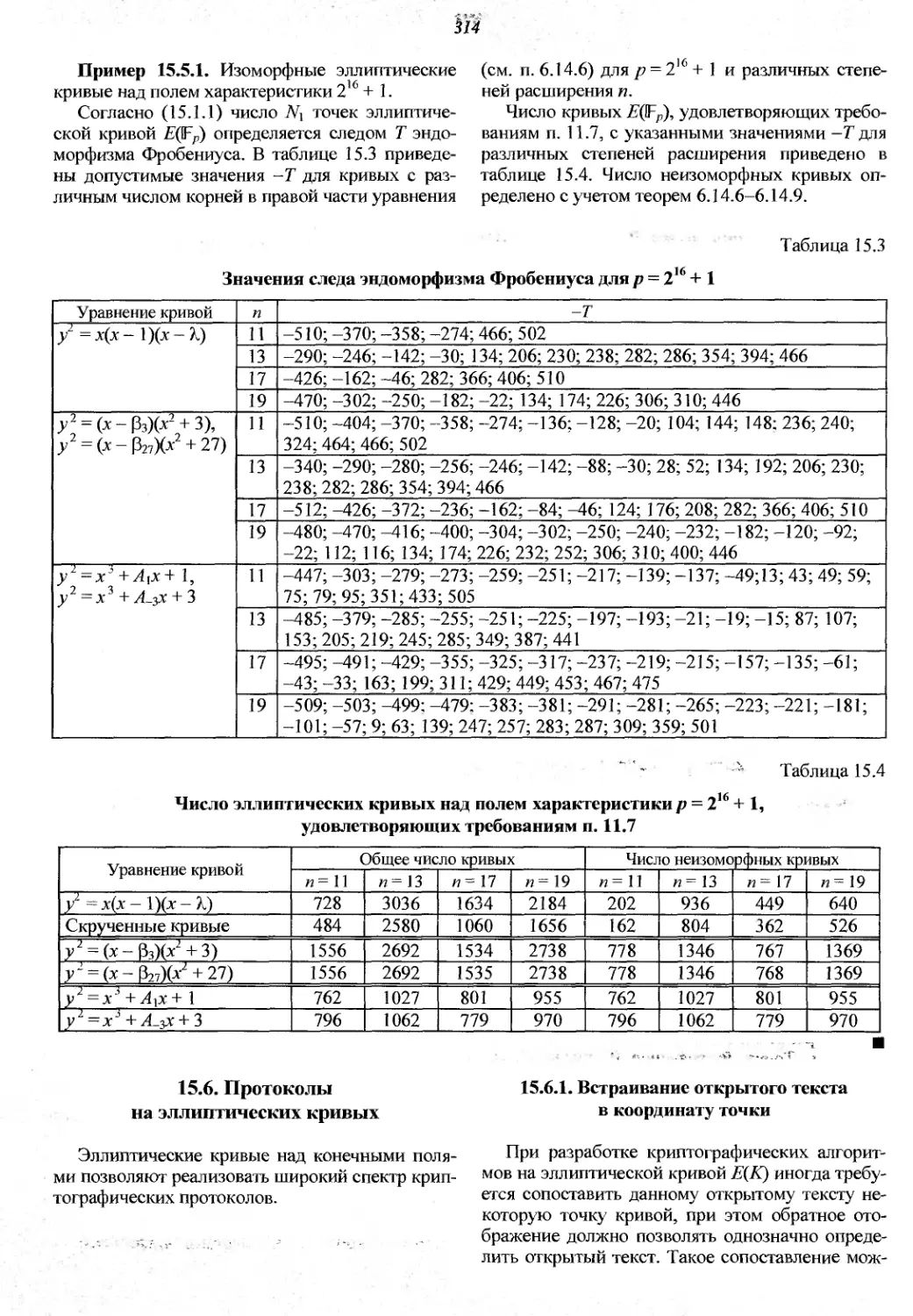
15.6. Протоколы на эллиптических кривых....314
15.6.1. Встраивание открытого текста
в координату точки................314
15.6.2. Аналог криптосистемы RSA...315
15.6.3. Установление сеансового ключа.316
15.6.4. Шифрование.................317
15.6.5. Цифровая подпись...........318
15.6.6. Опознавание, канал со стиранием
и доказательства с нулевым
разглашением......................321
15.6.7. Вычислимая в одну сторону
функция, свободная от коллизий.....324
15.6.8. Генераторы псевдослучайной
последовательности.................325
15.6.9. Протоколы для электронных
платежей...........................326
15.7. Криптосистемы на гиперэллиптических
кривых...................................329
15.8. Криптосистемы на изогениях
эллиптических кривых.....................331
15.8.1. Задача вычисления изогении и
квантовый компьютер...............331
15.8.2. Криптографические протоколы
на изогенных кривых...............332
Упражнения к главе 15...................334
Литература к главе 15...................335
ГЛАВА 16. ОБЩИЕ СВЕДЕНИЯ
ОБ ИТЕРИРОВАННЫХ
КРИПТОАЛГОРИТМАХ......................336
16.1. Основные понятия классической
криптографии...........................336
16.2. Некоторые положения
теории секретности Шеннона.............336
16.2.1. Объем текстов, однозначно
определяющих ключ...........339
16.2.2. Теория аутентификации Симмонса.... 340
16.3. Булевы функции и булевы формулы..340
478
16.4. Аффинно эквивалентные
булевы функции и подстановки.......342
16.5. Задача вскрытия ключа
и математические задачи............344
16.5.1. Задача вскрытия ключа
и NP-полные задачи.................345
16.5.2. Задача о выполнимости......345
16.6. Требования к шифрам................347
16.7. Шифры замены и перестановки........350
16.7.1. Моноалфавнтная замена......350
16.7.2. Полиалфавитная замена......351
16.8. Операторы, используемые
при построении блочных шифров.......353
16.9. Описание итерированных шифров
в терминах булевых функций.........356
Упражнения к главе 16.....................357
Литература к главе 16....................358
ГЛАВА 17. АЛГЕБРАИЧЕСКИЕ МЕТОДЫ
КРИПТОАНАЛИЗА............................359
17.1. Метод обобщения и редукции. Метод
гомоморфизмов............................359
17.2. Замкнутые и чистые шифры...........360
17.2.1. Вскрытие ключей замкнутых
и чистых шифров....................360
17.2.2. Проверка шифра на замкнутость
и чистоту..........................361
17.3. Решеточный криптоанализ............362
17.3.1. Решеточно продолженные булевы
функции и решеточные полиномы ..362
17.3.2. Метод криптоанализа........365
17.4. Метод арифметического продолжения
булевых функций..........................369
17.5. Анализ шифров с малым
порядком нелинейности....................375
17.6. Криптоанализ на основе рационального
продолжения полиномов Жегалкина..........377
17.6.1. Теоретические основы.......377
17.6.2. Метод криптоанализа........379
17.7. Криптоанализ на основе 2-адического
продолжения полиномов Жегалкина..........383
17.7.1. Теоретические основы.......383
17.7.2. Метод криптоанализа........384
17.8. Максимизация числа совпавших
разрядов промежуточных текстов...........385
17.9. Анализ с использованием сжимающих
гомоморфизмов............................386
17.10. Поиск коллизий хэш-функции........388
17.11. Компромисс время/память...........389
17.12. Сочетание перебора и вычисления ключа... 390
17.13. Отбраковка классов ключей.........391
17.14. Задачи, к которым сводится задача
вскрытия ключа...........................392
17.15. Вскрытие ключа
на квантовом компьютере..................393
Упражнения к главе 17....................394
Литература к главе 17....................395
ГЛАВА 18. СТАТИСТИЧЕСКИЕ МЕТОДЫ
КРИПТОАНАЛИЗА...........................396
18.1. Некоторые определения.............396
18.2. Дифференциальный криптоанализ.....397
18.2.1. Конечные разности.........397
18.2.2. Метод криптоанализа.......398
18.2.3. Анализ с помощью усеченных
дифференциалов....................405
18.2.4. Анализ с помощью дифференциалов
высших порядков...................406
18.2.5. Атака «бумеранг»..........406
18.3. Криптоанализ на основе списка ключей и
связанных ключей.......................407
18.4. Линейный криптоанализ.............408
18.5. Анализ степенных
шифров методом сдвига..................416
18.6. Генерация экстремальных
подстановок для шифров.................418
18.6.1. Экстремальные подстановки.418
18.6.2. Булевы функции для
экстремальных подстановок....419
18.6.3. Примеры экстремальных
подстановок.......................420
Упражнения к главе 18...................422
Литература к главе 18...................423
ГЛАВА 19. ПРИМЕНЕНИЕ ИТЕРИРОВАННЫХ
ШИФРОВ И ХЭШ-ФУНКЦИЙ....................425
19.1. Режимы шифрования.................425
19.1.1. Режим । ,ростой замены....425
19.1.2. Режим гаммирования........425
19.1.3. Режим гаммирования
с обратной связью.................426
19.1.4. Режим сцепления блоков.
Выработка имитовставки.......426
19.2. Некоторые вопросы
применения шифров.................427
19.3. DES...............................429
19.4. FEAL..............................431
19.5. IDEA..............................432
19.6. ГОСТ 28147-89.....................433
19.6.1. Стойкость шифра ГОСТ 28147-89....435
19.6.2. Стойкость шифра ГОСТ 28147-89
при наличии у нарушителя
лабораторных возможностей.....435
19.7. RC5...............................436
19.8. Blowfish..........................438
19.9. SAFER.............................439
19.10. RUISDAEL (AES)...................440
19.11. MD5..............................441
19.12. ГОСТ P 34.11-94 ................ 442
Упражнения к главе 19...................444
Литература к главе 19...................445
ОТВЕТЫ И УКАЗАНИЯ
К УПРАЖНЕНИЯМ...........................447
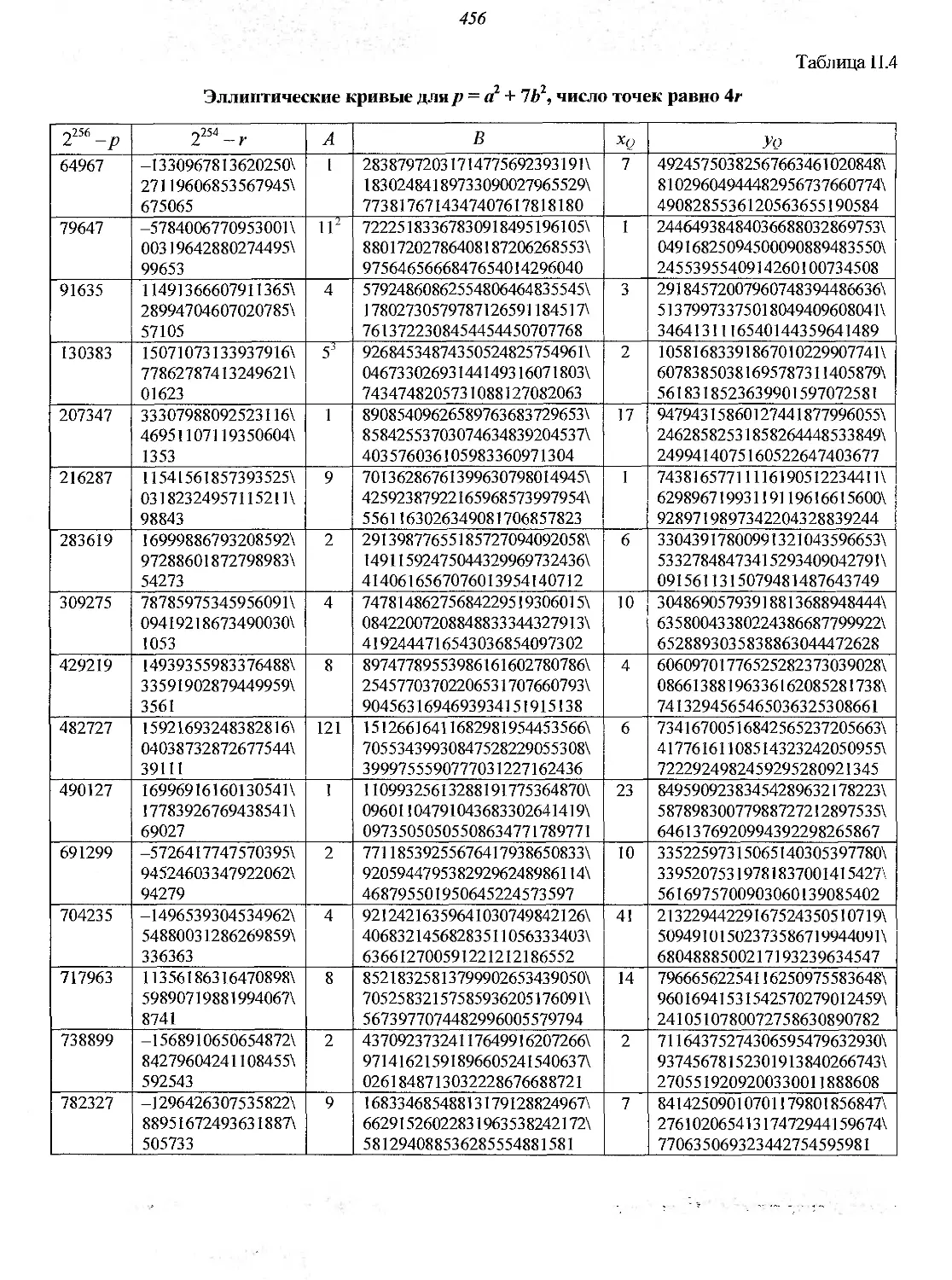
ПРИЛОЖЕНИЕ. ЭЛЛИПТИЧЕСКИЕ КРИВЫЕ
ДЛЯ СТАНДАРТА ПОДПИСИ ГОСТ P34JG-2001 .452
УКАЗАТЕЛЬ...............................464
ВВЕДЕНИЕ
В последние годы в России и за рубежом поя-
вилось множество изданий по криптографии.
Большинство книг носит прикладной характер и
ориентировано на применение готовых крипто-
графических алгоритмов. Вопросам безопасности
криптографических алгоритмов и теоретическим
основам криптографии в этих книгах уделяется
недостаточное внимание. В настоящем издании
предпринята попытка восполнить этот пробел.
Как и другим наукам из области информаци-
онного противоборства, криптографии присущи
два направления: защита и нападение. Первое на-
правление представлено собственно криптогра-
фией, второе — криптоанализом. За рубежом эти
направления объединяют термином «криптоло-
гия». Авторы придерживаются мнения, что разде-
ление криптографии на две различных дисципли-
ны неправильно. Это разделение служит «обосно-
ванием» появления множества слабых криптогра-
фических алгоритмов— ведь анализом их безо-
пасности занимается другая наука. Такая позиция
разработчиков криптоалгоритмов представляется
безответственной. Представьте себе инженера-
строителя, который заявляет: «Я спроектировал
мост, но простоит ли он десять лет, я не знаю, так
как не умею рассчитывать прочность мостов».'
Интеграция России в международное сообще-
ство ведет к росту популярности зарубежных
криптографических алгоритмов. Если разработ-
чик информационной системы не хочет пола-
гаться на мнение экспертов, он должен составить
собственное мнение о безопасности тех или
иных криптосистем. Для этого он должен отве-
тить себе на вопросы: каков уровень стойкости
данной криптосистемы и каким он ожидается в
будущем; чем именно обеспечивается стойкость
и чем обусловлена уязвимость криптосистемы по
отношению к данному методу анализа, и каким
образом криптосистему можно усилить. Данная
книга ориентирована именно на такого читателя.
Криптография — это в основном анализ крип-
тографических алгоритмов (а отнюдь не их про-
граммно-аппаратная реализация, которую часто
-1 Некоторым оправданием для разработчиков яв-
ляется то, что методы криптоанализа часто не публи-
куются, так как по сути являются информационным
оружием.
называют криптографией дилетанты). Криптогра-
фические алгоритмы — нематериальные объекты,
слабо связанные с окружающим физическим ми-
ром, а методы их анализа и вовсе относятся к «ми-
ру идей». Поэтому в криптоанализе часто исполь-
зуются разделы математики, не имеющие прямого
отношения к описанию физической реальности и
относящиеся к области алгебры, теории чисел и
алгебраической геометрии. Поскольку в россий-
ских технических вузах этим дисциплинам тради-
ционно уделяется явно недостаточное внимание,
главы 1-6 содержат необходимые результаты из
этих областей математики (множества и алгорит-
мы, группы, кольца, поля, алгебраические числа,
эллиптические кривые). В главе 7 рассматриваются
вычислительные методы алгебры и теории чисел,
которые могуг быть использованы при разработке
и анализе криптографических алгоритмов.
Быстрое развитие криптографии приводит к
расширению ее предметной области и росту чис-
ла методов исследования. Принято различать
криптографию с открытым ключом (несиммет-
ричную) и криптографию с секретным ключом
(симметричную). По-видимому, такое разделе-
ние обусловлено не тем, является ключ откры-
тым или секретным, а типом математической
задачи, положенной в основу безопасности соот-
ветствующих криптоалгоритмов, и, следователь-
но, методами решения этой задачи.
Для криптографии с открытым ключом харак-
терны «нерукотворные» задачи, сформулированные
для хорошо исследованных алгебраических струк-
тур (групп, колец, категорий). Вряд ли кто-либо
сможет утверждать, что задача разложения нату-
рального числа на множители создана (не сформу-
лирована, а именно создана) человеком, поскольку
натуральные числа «существуют» независимо от
человека. То же можно сказать и о задаче дискрет-
ного логарифмирования в циклической группе. Ме-
тоды анализа таких задач используют алгебраиче-
скую теорию соответствующих структур.
Главы 9-15 посвящены вопросам криптогра-
фии с открытым ключом. Безопасность соответст-
вующих криптографических алгоритмов основана
на сложности решения массовых математических
задач, число которых быстро растет. Системати-
зация этих задач по степени их общности, начиная
с унифицированных задач (определение структу-
4
ры и порядка конечной группы, вычисление дис-
кретного логарифма в циклической группе вы-
числимого порядка, вычисление категорного
морфизма) позволяет упорядочить методы их ре-
шения. Поэтому сначала подробно рассматрива-
ются методы решения этих задач (универсальные,
применимые к любым математическим структу-
рам, и специальные, применимые к конкретным
алгебраическим структурам), в том числе на кван-
товом компьютере, а затем — собственно крипто-
графические алгоритмы и протоколы, построен-
ные на указанных задачах. Рассматриваются спо-
собы противодействия квантовому компьютеру.
Большое внимание уделено вопросам проекти-
рования криптосистем на эллиптических кривых:
выбору кривой, разработке быстрых вычислитель-
ных алгоритмов, анализу и прогнозированию стой-
кости, построению криптографических протоколов.
Методы решения математических задач и
проектирования криптосистем поясняются мно-
гочисленными примерами, позволяющими луч-
ше уяснить теоретический материал.
В главах 16-19 рассматриваются вопросы ана-
лиза и проектирования итерированных шифров.
Симметричные шифры и хэш-функции имеют
конкретных авторов, а задача, положенная в осно-
ву безопасности, каждый раз уникальна. Про ал-
гебраические свойства таких криптоалгоритмов
обычно ничего определенного сказать нельзя, по-
этому их анализ часто представляет собой «набор
трюков» и относится скорее к области искусства,
чем науки. Это обстоятельство открывает возмож-
ности для изобретения новых методов и приемов
криптоанализа. По-видимому, некоторые симмет-
ричные шифры можно считать стойкими лишь по-
стольку, поскольку не найдены способы их взлома.
Обычно симметричные шифры и хэш-
функции строятся на основе циклической компо-
зиции отображений, описываемых несложными
наборами булевых функций. Такие криптоалго-
ритмы будем называть итерированными. Сюда
относятся шифры и хэш-функции DES, FEAL,
IDEA, ГОСТ 28147-89, Blowfish, RIJNDAEL,
ГОСТ Р 34.11-94, MD5 и т. п.
Итерированные криптоалгоритмы, исполь-
зующиеся в компьютерных системах, а также
методы их анализа можно охарактеризовать сро-
ком их жизни:
Методы крипто- анализа Крипто- алгоритмы Компьютер- ные системы
Число Единицы- десятки Десятки- сотни Сотни- тысячи
Время жизни Практически не ограни- чено Десятки лет Несколько лет
Поэтому изучение конкретных компьютер-
ных систем или используемых в них шифров не-
избежно носит оттенок «сиюминутности». Дей-
ствительно глубокие фундаментальные знания в
области криптографии дает изучение методов
криптоанализа.
Вряд ли возможно в одной книге разобрать
все известные варианты атак на криптоалгорит-
мы. Задача осложняется тем, что атаки постоян-
но совершенствуются, а оценки стойкости шиф-
ров снижаются. Кроме того, авторы далеки от
мысли, что в открытой печати публикуются все
разработанные методы криптоанализа. Поэтому
перечень методов, рассмотренных в книге, ко-
нечно, не полон, и заинтересованный читатель
может испытать себя в разработке новых мето-
дов (взлом шифров — решение увлекательных
головоломок). Для уяснения механизмов крип-
тоанализа большинство указанных методов со-
провождается примерами.
Данная книга обобщает криптографическую
серию издательства «Мир и Семья» (Ростов-
цев А.Г. Алгебраические основы криптографии.
СПб., 2000; Ростовцев А.Г.. Маховенко Е.Б. Вве-
дение в криптографию с открытым ключом.
СПб., 2001; Ростовцев А.Г., Маховенко Е.Б. Вве-
дение в теорию итерированных шифров. СПб.,
2003). Это издание включает в себя материалы
курсов лекций, читаемых авторами в Санкт-
Петербургском государственном политехниче-
ском университете на кафедре «Информацион-
ная безопасность компьютерных систем» по
дисциплинам «Теоретико-числовые методы в
криптографии», «Основы алгебры и теории чи-
сел», «Элементы алгебраической геометрии»,
«Криптографические методы защиты информа-
ции», «Теория итерированных шифров».
Книга содержит 19 глав. Главы 1-6, 8, 10—12,
14, 16, 18 написаны А.Г. Ростовцевым, главы 7,
9, 13, 15, 17, 19 написаны совместно А.Г. Рос-
товцевым и Е.Б. Маховенко.
В конце глав приведены упражнения, позво-
ляющие закрепить теоретические сведения. Не-
которые упражнения предполагают использова-
ние стандартных математических пакетов
(Maple, Mathematica). Упражнения, помеченные
символом *, носят исследовательский характер.
Для более глубокого изучения материала заинте-
ресованный читатель может обратиться к источ-
никам, указанным в списке литературы.
В приложении приведены параметры крипто-
систем на эллиптических кривых для реализации
электронной цифровой подписи по стандарту
ГОСТ Р 34.10-2001.
ОБОЗНАЧЕНИЯ
(а) — циклическая группа, образованная эле-
ментом а;
(а) — главный идеал, образованный элемен-
том а;
|а) — состояние квантового бита, квантового
регистра;
а+-Ь — присвоение переменной а значения Ь;
21, 23, С, ... — идеалы;
а, Ь, с, ... — векторы;
А\В — разность множеств А и В;
А® В—прямая сумма колец или модулей А и В;
а © b — сумма по модулю 2;
а | b — а делит b (Ь делится на а);
А] =Аг — изоморфизм алгебраических струк-
тур (групп, полугрупп, колец, полей и т. п.);
А2(К) — аффинная плоскость над полем К,
— — символ Лежандра (Якоби);
\р)
f °
— биномиальный коэффициент;
аН— левый смежный класс по подгруппе Н;
С — множество (поле) комплексных чисел;
chai'(A') — характеристика поля К;
С1(С/>) — группа классов идеалов квадратич-
ного порядка Od',
Div(Q — группа дивизоров на алгебраиче-
ской кривой С;
div(/) — дивизор функции/на алгебраической
кривой;
Е/К — эллиптическая кривая, заданная урав-
нением с коэффициентами из поля А;
Е(К) — эллиптическая кривая, рассматривае-
мая над полем К;
End(A/) — кольцо эндоморфизмов модуля М;
Ер, Е9 — конечные поля из р или из q=pn
элементов, где р — простое число;
g(%, \j) — сумма Гаусса для мультипликатив-
ного характера % и аддитивного характера \j;
Gal(ZzK) — группа Галуа расширения L/Кл,
G„ = F2[xj, ..., x„]/(xt(l © хД ..., х„(1 © х„)) —
кольцо полиномов Жегалкина;
G/H — факторгруппа группы G по нормаль-
ной подгруппе Н;
На — правый смежный класс по подгруппе Н;
j(E) — /инвариант эллиптической кривой Е;
J(C) — якобиан алгебраической кривой С;
J(%, X) — сумма Якоби для характеров %, X;
К, К — поле и его алгебраическое замыкание;
А]х], Афх|, ...,х„] — кольца полиномов над
полем К\
А)С] — аффинное координатное кольцо ал-
гебраической кривой С над полем К,
К(С) — поле рациональных функций алгеб-
раической кривой С над полем К;
К(х), К(х,у) — поля рациональных функций
над полем К,
L/K — расширение L поля К,
(L-.K) — степень расширения L над К,
L,,(c; v) = O(exp(c(ln ri)'(In In л)1-’’)) — субэкс-
поненциальная функция сложности;
#М— мощность множества М;
ЯЛ — максимальный идеал;
SRp — максимальный идеал локального коль-
ца ОР;
N(j(x, у) = 0) — число решений уравнения
/(х, у) = 0 над конечным полем;
Od — квадратичный порядок дискриминанта D;
Ор — локальное кольцо точки Р алгебраиче-
ского множества, состоящее из функций, регу-
лярных в точке Р;
Р’(А), Р2(А) — проективная прямая, проек-
тивная плоскость над полем К,
ф — простой идеал;
Q — поле рациональных чисел;
Qp — поле />-адических чисел;
Q[ol] — числовое поле, полученное присоеди-
нением к полю Q алгебраического числа а;
IR — поле вещественных чисел;
R — множество обратимых элементов кольца А;
А-21 — кольцо классов вычетов кольца R по
идеалу 21;
rem(/7) — удаление решеточно продолженной
булевой функции Н;
val(/7) — значение 2-адического нормирова-
ния целевой функции Н;
SL2(Z) — модулярная группа;
Тг(х) — след элемента х;
|_xj — целая часть положительного числа х
(наибольшее целое число, не превосходящее х);
Z — кольцо целых рациональных чисел;
Zp — кольцо целых />адических чисел;
А — дискриминант эллиптической кривой;
% — характер абелевой группы;
g <. ф = £(ф(*)) — композиция отображений g и ф
для координатных колец.
Глава 1. МНОЖЕСТВА, АЛГОРИТМЫ, СЛУЧАЙНЫЕ ОТОБРАЖЕНИЯ
1.1. Сведения из теории множеств
Множество А — совокупность объектов
а е А (элементов множества), обладающих неко-
торым общим свойством. Элементами множества
могут быть другие множества, однако говорить о
множестве всех множеств нельзя [2].
Множество, состоящее из элементов а,, обо-
значается {а,}. Пустое множество 0 не содержит
ни одного элемента. Равные множества состоят из
одних и тех же элементов. Если каждый элемент
множества А является элементом множества В, то
А называется подмножеством множества В, обо-
значается А с В. Если при этом А Ф В, то говорят,
что А является собственным подмножеством
множества В, обозначается А с В. Если А с В и
А □ В, то А = В. Множество всех подмножеств
данного множества А обозначается Р(А). Если
А = {а, Ь,с}, то Р(А) = {{0},{а}, {Ь}, {с}, {а,Ь},
{а, с}, {Ь, с}, {а, Ь, с}}.
На множествах определены бинарные опера-
ции, сопоставляющие каждой паре элементов
множества элемент этого же множества. Множе-
ство А замкнуто относительно бинарной опера-
ции *, если а * Ъ е А для всех а,Ь е А. Бинарная
операция * называется:
- коммутативной, если а* b = Ъ * а для всех а,
Ъ е А;
- ассоциативной, если а * (Ь * с) - {а * Ь) * с
для всех а, Ъ, с е Л;1
- дистрибутивной (относительно операции •),
если а * (Ь • с) = (а * Ь) • (а * с) для всех а, Ь,
с g А.
Объединением множеств А и В называется
множество Ли В, состоящее из тех элементов,
которые являются элементами Л или В. Пересе-
чением множеств Л и В называется множество
Ас. И, состоящее из элементов, которые являют-
ся элементами Л и В. Бинарные операции объе-
динения и пересечения коммутативны и ассоциа-
тивны, каждая из них дистрибутивна одна отно-
сительно другой.
Разность множеств А\В определяется как
множество элементов Л, не являющихся элемен-
1 Ассоциативность означает, что в выражении
аг * а2 * ... * ап скобки можно расставлять произволь-
но, при этом значение выражения не изменится.
тами В. Симметрическая разность определяется
как Л - В = (А \ В) о (В \ А). Нетрудно видеть, что
А-В = В-А. Если все рассматриваемые множе-
ства Л], Л2,... являются подмножествами неко-
торого универсального множества U, то можно
определить дополнение множества Л, как раз-
ность и\А(.
Декартовым произведением множеств А\, ...,А„
называется множество В = Л] х ... хЛ„, состоящее
из упорядоченных наборов {(сц,..., а,,)}, где а, е Л,.
Декартово произведение Ах ... х А называется
декартовой степенью и обозначается Л".
Если каждому элементу а множества Л по ка-
кому-либо правилу сопоставляется единствен-
ный объект <р(а), то это сопоставление называет-
ся функцией на Л. Если все объекты q>(a) принад-
лежат некоторому множеству В, то сопоставле-
ние а —> <р(а) называется отображением А в В и
обозначается q>: Л —> В. Элемент q>(a) называется
образом элемента а, элемент а называется про-
образом элемента q>(a). Для данного прообраза
образ единственный, но для данного образа про-
образ в общем случае единственным не является.
Совокупность всех прообразов элемента <р(а) на-
зывается полным прообразом. Совокупность всех
прообразов отображения называется областью
определения отображения, совокупность всех
образов — областью значений.
Ограничением отображения q>: Л —> В на мно-
жество СсЛ называется такое отображение цт,
заданное на С, что (р(х) = ц/(х) для всех х е С.
Продолжением отображения ср: Л -> В на множе-
ство С zd Л называется такое отображение \/, за-
данное на С, что <р(х) = i|j(x) для всех х е Л (при
этом области значений <р иду могут различаться).
Пример 1.1.1. Ограничение и продолжение
отображений.
1. Пусть М — множество целых чисел,
Л с М— множество положительных простых
чисел и q>: М—> М— отображение, ставящее в
соответствие каждому целому числу количество
его положительных делителей, отличных от еди-
ницы. Например, <р(2)= 1, (р(4) = 2, ср(6) = 3. То-
гда ограничением (р на Л будет отображение
<р(Л) = 1, так как каждое простое число имеет
единственный неединичный положительный де-
литель.
7
2. Пусть М — множество положительных
простых чисел, А — множество положительных
целых чисел и ф: 7И—> А — отображение, ставя-
щее в соответствие каждому элементу из М чис-
ло 1. Продолжения отображения ф на А опреде-
лены неоднозначно. Например:
- Ф(Л)=1;
- ср(о) равно числу положительных простых
делителей числа а;
- ф(а) = 1, если а простое, ф(а) = 0, если а со-
ставное.
Отображение А -> В называется инъектив-
ным, если из а * b следует ф(о) ф(Л)- Отобра-
жение А В называется сюръективным, или
отображением А на В, если каждый элемент из
В имеет хотя бы один прообраз из А. Инъектив-
ное и сюръективное отображение называется би-
ективным. Для биективного отображения ф су-
ществует обратное отображение ф"1 такое, что
если ф(а) = Ь, то ф'(Л) = а.
Если f А -> В и g-. В —> С — отображения, то
их композиция (или произведение) gf отображает
Ав Си определяется как g(/(x)) для всех х е А.
Композицию отображений удобно иллюстри-
ровать диаграммами. Диаграмма
называется коммутативной, если h = gf. Анало-
гично, диаграмма
называется коммутативной, если gf= FG [6].
Теорема 1.1.1. Композиция отображений
множества в себя ассоциативна.
Доказательство. Областью определения и
областью значений таких отображений является
данное множество А, поэтому композиция ото-
бражений определена корректно. Пусть fg,h —
отображения множества А в себя и а е А. Тогда
(fg)h(a) = (/g)(M«)) =/g(M«)));
Xg/z)(a) =Xg/?(a)) =/g(/?(a))).
Бинарным отношением на множестве А явля-
ется любое подмножество R множества А х А.
Бинарные отношения могут обладать сле-
дующими свойствами:
1) симметричность', если aRb, то bRa',
2) антисимметричность', если aRb и bRa, то
а = Ь',
3) рефлексивность'. aRa;
4) транзитивность', если aRb и bRc, то aRc.
Симметричное, рефлексивное и транзитивное
отношение R называется эквивалентностью.
Пример 1.1.2. Эквивалентность.
1. Равенство целых чисел.
2. Подобие треугольников.
3. Бинарное отношение, определенное на
множестве плоских многоугольников (углы в
180° не допускаются), при котором эквивалент-
ными являются многоугольники с одинаковым
числом углов.
Теорема 1.1.2. Бинарное отношение являет-
ся эквивалентностью тогда и только тогда, ко-
гда оно разбивает множество, на котором оно
определено, на попарно непересекающиеся
классы.
Доказательство. Пусть отношение является
эквивалентностью. Объединим все элементы,
эквивалентные данному элементу а, в один класс
Kq. Элементы в этом классе попарно эквивалент-
ны в силу транзитивности: если а ~ b и а ~ с, то
b ~с. Кроме того, все элементы, эквивалентные
какому-либо элементу класса, принадлежат это-
му же классу, что также следует из свойства
транзитивности. Таким образом, каждый класс
задается любым своим элементом: если а ~ Ь, то
Ка = Kh. Если построить сначала класс элементов,
эквивалентных а, а затем класс элементов, экви-
валентных Ъ, то эти два класса будут совпадать
при а ~ b и не будут пересекаться в противном
случае. Действительно, если предположить, что а
и b неэквивалентны и элемент с принадлежит
обоим классам Ка и Kh, то а ~ с и с ~ b, то есть
а~ b — противоречие. Таким образом, эквива-
лентность разбивает множество на попарно не-
пересекающиеся классы.
Обратно, если задано разбиение множества на
попарно непересекающиеся классы, то можно
определить отношение: а ~ Ь, если а и b лежат в
одном классе. Это отношение симметрично,
рефлексивно, транзитивно, то есть является эк-
вивалентностью.
Антисимметричное, рефлексивное и транзи-
тивное бинарное отношение называется отно-
шением (частичного) порядка >. Если а > b и
а ф Ь, то говорят, что а строго больше Ь, и запи-
8
сывают а> b. Двойственное отношение порядка:
если а > Ь, то b < а.
Указанное отношение в общем случае приме-
нимо не ко всем элементам множества. Если это
отношение применимо ко всем элементам, то
множество называется линейно упорядоченным.
Пример 1.1.3. Упорядоченные множества.
1. Множество (Z, <) целых чисел, упорядо-
ченных отношением «меньше или равно» (ли-
нейное упорядочение).
2. Множество (Р(М), с) всех подмножеств
множества М, упорядоченных отношением тео-
ретико-множественного включения (частичное
упорядочение).
3. Множество положительных целых чисел
(Z>o, |), в котором «х|у» означает, что х делит у
(частичное упорядочение).
Мощностью множества называется число его
элементов. Мощность множества Л/обозначается
#М. Для множества подмножеств имеет место
равенство #Р(М) = 2Ш. Например, #0 = 0, но
Р(0) непусто и #Р(0) = 1. Справедливо неравен-
ство #Р(М) > #М.
Два множестваMhNравномощны, если суще-
ствует биективное отображение M-c^N. Конеч-
ные множества равномощны, если они состоят из
одинакового числа элементов. Конечное множе-
ство не может быть равномощно собственному
подмножеству. Для бесконечных множеств это
неверно. Например, множество Z целых чисел
равномощно собственному подмножеству 2Z чет-
ных чисел (отображение Z -> 2Z задается умно-
жением на 2). Множества, равномощные нату-
ральному ряду, называются счетными.
Мы придерживаемся так называемой «наив-
ной» теории множеств. Она характеризуется на-
личием парадоксов. Различают логические и се-
мантические парадоксы.
Логические парадоксы связаны непосредственно
с аксиоматикой и определениями теории множеств.
Парадокс Кантора. Существует ли множест-
во всех множеств? С одной стороны, это не за-
прещено. С другой стороны, если оно существу-
ет, то оно является элементом самого себя, то
есть его мощность строго меньше самой себя,
так как #Р(М)>#М. Это рассуждение можно
считать доказательством того, что множества
всех множеств не существует.
Парадокс Рассела. Пусть для множества М
выполняется свойство D тогда и только тогда,
когда М у М. Пусть Т— множество элементов
М, для которых выполняется свойство D. Какое
свойство выполняется для Т: Т е Т или Т у Т?
Если предположить, что Т g Т. то Т g Т, а если
предположить, что Т g Т, то Т g Т. В обоих слу-
чаях получаем противоречие. Можно сказать,
что свойство D не определяет никакого множе-
ства. Но это значит, что не каждое точно описан-
ное свойство определяет множество.
Семантические парадоксы, в отличие от ло-
гических, включают в себя понятия «истина»,
«ложь», «определяет».
Парадокс лжеца. Некто говорит: «Я лгу». Ес-
ли он лжец, то он сказал правду. Если он солгал,
то он не является лжецом.
Парадокс Ришара. В русском языке существу-
ет конечное число букв. Следовательно, сущест-
вует конечное число фраз, содержащих не более
150 букв. Поэтому с помощью таких фраз можно
охарактеризовать лишь конечное множество на-
туральных чисел. Конечное множество натураль-
ных чисел содержит наименьший элемент
(см. также и 3.14). Рассмотрим фразу «А:— наи-
меньшее из натуральных чисел, которые нельзя
охарактеризовать никакой фразой русского языка,
содержащей не более 150 букв». Она характери-
зует число к и содержит менее 150 букв. Можно
сказать, что эта фраза не определяет никакого на-
турального числа, но тогда возникает вопрос, по
каким критериям можно определить, какие фразы
определяют числа, а какие нет.
Прилагательное, обладающее свойством, ко-
торое оно обозначает, назовем автологическим.
Примеры автологических прилагательных:
«трехсложный», «русский». Прилагательное, не
обладающее свойством, которое оно обозначает,
назовем гетерологическим. Примеры гетерологи-
ческих прилагательных: «односложный», «крас-
ный», «горячий», «французский». Очевидно, что
прилагательное не может одновременно обла-
дать и не обладать свойством, которое оно обо-
значает. Попробуем определить тип прилагатель-
ного «гетерологическое». Если предположить,
что оно не обладает свойством, которое обозна-
чает, то оно гетерологическое, то есть обладает
этим свойством. Если предположить, что оно
обладает свойством, которое обозначает, то оно
является автологическим, то есть не обладает
свойством, которое обозначает.
Парадоксы встречаются при попытке приме-
нить некоторое суждение к самому себе.
1.2. Сведения из теории алгоритмов
1.2.1. Алгоритм и исчисление
Под алгоритмом будем понимать корректно
определенный дискретный вычислительный
процесс, перерабатывающий входные данные в
выходной результат за конечное число шагов.
Понятие алгоритма тесно связано с вычисли-
тельной моделью, описывающей процесс пере-
работки. Существуют различные вычислитель-
ные модели, отражающие уровень развития тех-
ники, например, машина Тьюринга или специа-
лизированный конечный автомат.
Будем различать детерминированные и веро-
ятностные алгоритмы. Детерминированный ал-
горитм всегда действует по одной и той же схеме
и гарантированно решает поставленную задачу
(или не дает никакого ответа). Вероятностный
алгоритм использует генератор случайных чисел
и дает не гарантированно точный ответ [17].
Пример 1.2.1. Алгоритмы.
1. Детерминированным является алгоритм де-
ления дробей: "
„ а с ad
Если оса ф 0, то —: — = —, иначе ответа нет.
b d be
2. Вероятностным является следующий алго-
ритм, отвечающий на вопрос: «Является ли чис-
ло р простым?»:
1) сгенерировать случайное число а, где
2 < а <р - 2;
2) проверить равенство ар4 = 1 (mod р). Если
оно выполняется, то число р, вероятно, простое.
Если оно не выполняется, то число р составное.2
Для гарантированного ответа на вопрос, явля-
ется ли число р длины 100 десятичных знаков
простым, необходимо перебрать все числа а от 2
до р — 2. Однако, если нас устраивает ответ
«Число р простое с вероятностью 0,9999», то
достаточны всего три успешных итерации 1, 2
алгоритма.
Вероятностные алгоритмы в общем случае не
менее эффективны, чем детерминированные (ес-
ли генератор случайных чисел всегда дает набор
одних и тех же чисел, возможно, зависящих от
входных данных, то вероятностный алгоритм
становится детерминированным).
В современной логике наряду с понятием ал-
горитма существует столь же фундаментальное
понятие исчисления (дедуктивной системы) [9].
Исчисление — способ задания множества пу-
тем указания исходных элементов и правил вы-
вода новых элементов из исходных или уже по-
строенных. Исчисление отражает и обобщает
интуитивное представление об индуктивном по-
рождении множества [8]. Примерами исчислений
являются игры с четкими правилами (шахматы,
преферанс и др.). Некоторые виды исчислений
используются для задания алгебраических струк-
тур (например, теория колец строится из исход-
ной системы аксиом), описания формальных
грамматик и задания множеств, распознаваемых
конечными автоматами [8].
2 Этот алгоритм реализует псевдопростой тест Ферма
По сути дела, исчисление есть список «раз-
решительных правил», называемых также поро-
ждающими правилами. В отличие от алгоритма
эти правила не предписывают, а разрешают пе-
реходить от одних конструктивных объектов к
другим.
Подобно тому как алгоритм задает алгоритми-
ческий (или вычислительный) процесс, исчисле-
ние задает исчислительный (или порождающий)
процесс. Этот процесс разбивается на отдельные
шаги, каждый из которых состоит в получении
нового объекта из уже полученных к началу этого
шага объектов путем применения произвольного
разрешительного правила. Объекты, к которым
применяется правило, называются его посылками.
При этом одно и то же правило, примененное к
одной и той же посылке, может давать различные
результаты, так как может применяться по-
разному. Например, правило хода пешки в шах-
матах может применяться к каждой пешке.
Объекты, получающиеся в ходе работы ис-
числения, называются допустимыми. Допусти-
мый объект определяется по индукции: если объ-
ект b получается из допустимых объектов
<71,..., а„ с помощью разрешительного правила,
то он является допустимым. Начало индукции
определяется нульпосылочными правилами: если
объект h удовлетворяет такому правилу (получа-
ется «из ничего»), то он допустим. В шахматах
нульпосылочным является правило, задающее
начальное расположение фигур.
Всякое исчисление работает с элементами не-
которого множества, называемого рабочей сре-
дой исчисления. Все состояния исчислительного
процесса лежат в этом множестве. Работа исчис-
ления состоит в образовании новых допустимых
элементов (или допустимых состояний) рабочей
среды. Исчислительный процесс можно описать
деревом, корень которого — нульпосылочное
состояние, каждая вершина соответствует допус-
тимому состоянию, ребра— получению нового
допустимого состояния с помощью разреши-
тельных правил. Путь от корня до данной вер-
шины называется выводом для данного допусти-
мого состояния.
Исчисление можно рассматривать как инстру-
мент не только образования множества допусти-
мых состояний, но и преобразования начального
состояния, являющегося входом исчисления. Это
приводит к понятию исчисления со входом.
Пример 1.2.2. Исчисления.
1. Шахматная игра, заданная фиксированной
начальной позицией, правилами ходов и целью
игры.
2. Игра в преферанс, заданная случайной на-
чальной позицией, правилами ходов и целью игры.
10
3. Дифференциальное исчисление (как и мно-
гие другие разделы математики) строится дедук-
тивно из системы аксиом.
Алгоритмы и исчисления жестко связаны [9].
Для каждого исчисления, порождающего пару
(х, у), существует алгоритм, для которого х явля-
ется входом, а у — выходом.
1.2.2. Сложность алгоритма
Как правило, если задача имеет решение, то
она может быть решена различными алгоритма-
ми. При этом возникает вопрос сравнения алго-
ритмов. Одной из основных характеристик каче-
ства алгоритма является его сложность. Для оп-
ределения сложности алгоритма свяжем с каж-
дой конкретной задачей некоторое число, назы-
ваемое ее размером, которое выражало бы меру
количества входных данных. Например, для за-
дачи умножения чисел размером может быть
длина наибольшего из сомножителей, для задачи
умножения квадратных матриц— число строк
матрицы.
Время (число элементарных операций вычис-
лительной модели), затрачиваемое алгоритмом
как функция размера задачи, называется времен-
ной сложностью (или просто сложностью) этого
алгоритма. Значение этой сложности при неог-
раниченном увеличении размера задачи называ-
ется асимптотической временной сложностью.
Сложности вероятностных алгоритмов можно
сравнивать, если вероятности получения пра-
вильного результата одинаковы.
Иногда алгоритм требует хранения некоторых
данных, полученных в ходе его работы. Объем
памяти, требуемый для работы алгоритма при
решении задачи данного размера, называется ем-
костной сложностью данного алгоритма. Соот-
ветствующим образом определяется и его асимп-
тотическая емкостная сложность.
Обычно на практике при оценке сложности ал-
горитмов пользуются именно асимптотической
сложностью, которую определяют с помощью О-
символики. Если алгоритм решает задачу за время
не более сп, где с остается ненулевой ограничен-
ной величиной при увеличении числа п, то гово-
рят, что асимптотическая временная сложность
алгоритма равна (fin). Соответственно, произ-
вольная константа может быть записана как 0(1).
Для функций/и g одной переменной можно запи-
сать fin) = O(g(n)), если существует константа с
такая, что при неограниченном увеличении числа
п выполняется неравенство fin) < cgfii).
Алгоритмы можно разбить на два класса: ал-
горитмы, сложность S которых оценивается в О-
символике некоторым полиномом от п или, бо-
лее общо, S = n)'r'1 {полиномиальная сложность),
и алгоритмы, сложность которых невозможно
оценить полиномом. Алгоритмы полиномиаль-
ной сложности называют также эффективными.
Такое разбиение алгоритмов позволяет ис-
пользовать их композицию. Если алгоритм А
имеет полиномиальную сложность на данной
вычислительной модели и алгоритм В содержит
полиномиальное число шагов, на которых вы-
полняется алгоритм А, то итоговая сложность
алгоритма ВА является полиномиальной.
Типичный алгоритм, сложность которого не
является полиномиальной, — перебор ключей
шифра при известных открытых и зашифрован-
ных текстах. В классе алгоритмов, сложность
которых не является полиномиальной, будем
различать два подкласса: алгоритмы с экспонен-
циальной сложностью S = e(i("'1 (или экспоненци-
альные) и алгоритмы с субэкспоненииалъной
сложностью ео<-"^ <S< п°т (или субэкспоненци-
альные). К первому подклассу относится алго-
ритм «giant step — baby step» (см. п. 11.1.2) со
сложностью S' = 0(п4^~) = O(e2ln2+'n"), где п —
длина входа алгоритма в битах; ко второму под-
классу — алгоритм разложения составного числа
длины п бит на множители (см. п. 9.3) со слож-
ностью s = eO(^}.
Будем называть функцию у =fix\,..., х„) вы-
числимой, если существует алгоритм полиноми-
альной сложности, ее вычисляющий. Если (наи-
лучший известный) такой алгоритм имеет слож-
ность выше полиномиальной, то функцию будем
называть трудновычислимой.
Для широкого класса вычислительных моделей
оказывается справедливой полиномиальная эквива-
лентность-. если алгоритм решает задачу за поли-
номиальное время на модели А, то существует ал-
горитм, который решает эту же задачу за полино-
миальное время на модели В. и обратно. Это от-
ношение разбивает множество вычислительных
моделей на классы эквивалентности. В рамках
такого класса можно не различать вычислитель-
ные модели, оперирующие с битами (умножитель
битов), и модели, оперирующие со словами фикси-
рованной длины и имеющие встроенные специали-
зированные вычислители (умножитель слов).
Однако радикальная смена вычислительной
модели может приводить к изменению понятия
вычислимости. Например, квантовый компьютер
(см. п. 1.3.2), обладая экспоненциально большим
объемом виртуальной памяти, позволяет с поли-
номиальной сложностью решать задачу разло-
жения составных чисел, тогда как для традици-
онной вычислительной модели такие алгоритмы
не известны.
11
Как правило, на практике требуется, чтобы
алгоритм решал не частную задачу (например,
разложить на множители число 2128 + 1), а широ-
кий класс частных задач (например, разложить
на множители число длины п бит или разложить
на множители число вида 2" + с для малого цело-
го числа с). Это требование вытекает из естест-
венного желания разработчика алгоритмов при
минимуме затрат получить наиболее общий ре-
зультат. Такой класс частных задач будем назы-
вать массовой задачей или просто задачей.
Будем говорить, что алгоритм А решает зада-
чу Г, если он решает каждую частную задачу из
класса Т, то есть является в этом смысле универ-
сальным. Под сложностью массовой задачи Т
будем понимать минимальную по всем универ-
сальным алгоритмам А сложность решения алго-
ритмом А наиболее трудной частной задачи из
класса Т.
Алгоритмические проблемы удобно исследо-
вать на классе задач выбора, допускающих ответ
«да» или «нет» на поставленный вопрос. Для то-
го чтобы оставаться в конструктивных рамках,
потребуем, чтобы предъявленный результат до-
пускал эффективную проверку. Вычислительное
устройство, решающее задачу выбора, должно
предъявлять сертификат, позволяющий прове-
рить правильность ответа и собственную досто-
верность с полиномиальной сложностью. Серти-
фикат должен выдаваться хотя бы для одного из
ответов «да» или «нет». Указанные ограничения
на практике не являются существенными [9].
Пример 1.2.3. Задачи выбора.
1. Задача решения квадратного уравнения.
Дано квадратное уравнение с целыми коэффици-
ентами длины п. Имеет ли оно вещественные
корни? Сертификатом для любого из ответов
«да» или «нет» является дискриминант полино-
ма. Соответствие дискриминанта уравнению лег-
ко проверить. Неотрицательный дискриминант
определяет существование вещественных кор-
ней.
2. Задача о корнях полинома. Дан полином
fix) степени п с целыми коэффициентами огра-
ниченной длины. Имеет ли он целые корни?
Сертификатом для любого из ответов «да» или
«нет» являются п корней полинома. Правиль-
ность представленного сертификата можно про-
верить, поделив fix) поочередно на полиномы
вида х - xh где {х,} — множество корней. Слож-
ность проверки правильности сертификата явля-
ется полиномиальной от п и от длины коэффици-
ентов полинома.
3. Задача о составном числе. Дано натуральное
число п. Является ли оно составным? Сертифика-
том для ответа «да» является делитель числа п.
4. Задача о простом числе. Дано натуральное
число п. Является ли оно простым? Сертифика-
том для ответа «нет» является делитель числа п?
5. Задача об изоморфизме графов. Даны два
графа с п вершинами. Можно ли перенумеровать
вершины первого графа так, чтобы получить
второй граф? Сертификатом для ответа «да» яв-
ляется перестановка вершин первого графа. Граф
можно задать квадратной матрицей размера п с
элементами из множества {0, 1}. Элемент ау = 1
означает, что существует ребро, связывающее
вершину г с вершиной j; нулевой элемент означа-
ет, что такого ребра не существует.
6. Задача о выполнимости булевой формулы.
Дана вычислимая булева формула от п перемен-
ных в виде совокупности наборов булевых фор-
мул, подставляемых друг в друга. Принимает ли
она значение «истина»? Сертификатом для отве-
та «да» является набор переменных, при котором
булева формула принимает значение «истина».
7. Задача коммивояжера. Дана карта, содержа-
щая п городов и расстояния между ними. Сущест-
вует ли замкнутый путь длины менее т через все
города? Сертификатом для ответа «да» является
требуемый маршрут. Карта может быть представ-
лена квадратной матрицей (ау), в которой номера
столбцов и строк соответствуют городам, а эле-
менты ау — расстоянию между городами i и j. й
Будем называть массовую задачу выбора ре-
шаемой, если существует решающий ее эффек-
тивный алгоритм. Если асимптотическая слож-
ность (наилучшего известного) такого алгоритма
выше полиномиальной, то задачу будем назы-
вать трудиорешаемой.
Не для каждой массовой задачи выбора может
существовать универсальный алгоритм.
Пример 1.2.4. Задачи выбора, для которых не
существует универсального алгоритма.
1. Разрешимость диофантова уравнения. Дан
полином от нескольких переменных с целыми
коэффициентами. Требуется указать универсаль-
ный алгоритм, который распознавал бы, имеет ли
этот полином целые корни.
2. Представимость матриц с целыми коэффици-
ентами. Назовем квадратную матрицу М предста-
вимой через матрицы М\,...,М,„ если имеет место
равенство M = , где г, е {1, 2, ..., и}. Тре-
буется указать алгоритм, который для каждой
матрицы М распознавал бы, представима ли М
через Mi,
3 Сертификат определен неоднозначно. В данном
случае сертификатом для ответа «нет» также может быть
число а, 1 < а < п, такое, что а"' ф 1 (mod и), см. п. 4.3.1.
3. Эквивалентность слов в свободной полу-
группе4 (или в алфавите с определяющими соот-
ношениями). Из букв пятибуквенного алфавита
а, Ь, с, d, е образуются слова (цепочки конечной
длины). Для любых слов А, В задана ассоциатив-
ная операция композиции АВ, заключающаяся в
записывании слова В непосредственно за словом
А, при этом А(ВС) = (АВ)С. Имеют место опреде-
ляющие соотношения ас = са, ad = da, be = cb,
bd = db, eca = ce, edb = de, cca = ссае. Требуется
построить алгоритм, который распознавал бы
эквивалентность слов.
Отметим, что отсутствие универсального ал-
горитма, решающего каждую частную задачу
данного класса, не означает, что не существует
алгоритма, решающего данную частную задачу
или даже некоторый подкласс частных задач.
Анализ сложности перечисленных в примере
1.2.3 задач выбора показывает, что задачу 1 мож-
но решить с полиномиальной сложностью. Для
этого нужно вычислить знак дискриминанта
квадратного уравнения. Задача 2 также допуска-
ет полиномиальный алгоритм, основанный на
том факте, что свободный член полинома равен
произведению всех корней. Тогда можно пере-
брать все целые делители и свободного члена (их
число ограничено) и проверить делимость поли-
нома на х - и. Что касается остальных задач, то
возможность решения их с полиномиальной
сложностью неочевидна (например, для задачи 4
требуется точный ответ, а не ответ типа «число п
простое с вероятностью 99 %»).
В множестве задач выбора можно выделить
несколько классов. Одним из них является класс
Р задач, для которых известен детерминирован-
ный алгоритм полиномиальной сложности (для
этих задач наличие сертификата излишне).
По определению задачи выбора ответ может
быть проверен с помощью сертификата детерми-
нированным алгоритмом полиномиальной слож-
ности. Если вычислительная модель обращается к
некоему оракулу, который может угадывать пра-
вильный сертификат, то проверить правильность
ответа можно с полиномиальной сложностью.
Класс задач, обозначаемый NP, обладает тем
свойством, что правильность ответа «да» может
быть проверена с полиномиальной сложностью,
хотя ответ и сертификат могут вырабатываться с
помощью недетерминированной вычислитель-
ной модели. Примером задач из класса NP слу-
жат задачи 1-3, 5-7 из примера 1.2.3.
Класс задач, обозначаемый co-NP, обладает
тем свойством, что правильность ответа «нет»
может быть проверена с полиномиальной слож-
4 Определение свободной полугруппы см. в гл. 2.
ностью. Примером задачи из класса co-NP слу-
жит задача 4 из примера 1.2.3.
Пересечение классов NP и co-NP непусто:
Р cz NP n co-NP. Совпадают ли классы Р и NP, Р
и NP n co-NP, неизвестно.
По аналогии с полиномиальной эквивалент-
ностью вычислительных моделей (для данного
класса алгоритмов) можно ввести понятие поли-
номиальной сводимости задач. Говорят, что за-
дача А полиномиально сводится (или просто сво-
дится) к задаче В, если существует алгоритм по-
линомиальной сложности, сводящий каждую
частную задачу из класса А к частной задаче из
класса В. Это означает, что массовая задача А
является не более сложной (с точностью до алго-
ритма полиномиальной сложности), чем массо-
вая задача В, причем решение с полиномиальной
сложностью задачи В означает и решение задачи
А. Отношение полиномиальной сводимости реф-
лексивно, антисимметрично и транзитивно, то
есть является отношением частичного порядка.
Если же при этом и задача В полиномиально
сводится к задаче А, то эти задачи полиномиаль-
но эквивалентны, решение любой из них означа-
ет решение другой.
С помощью отношения полиномиальной сво-
димости в классе NP была выявлена «самая
сложная» задача, к которой сводятся все осталь-
ные задачи из NP, — задача о выполнимости бу-
левой формулы (теорема Кука [1]). Кроме того,
было установлено, что эта задача не единствен-
ная, существует класс задач, полиномиально эк-
вивалентных задаче о выполнимости. В настоя-
щее время известно несколько сотен таких задач.
Этот класс задач называется NP-иолиыл/ (или
NPC), сюда относятся задачи 6, 7 из примера
1.2.3. Для некоторых задач из класса NP, напри-
мер, для задачи об изоморфизме графов и задачи
о составном числе, NP-полнота не доказана.
Класс NP-сложных задач состоит из тех за-
дач, к которым сводятся задачи из класса NP-
полных. Типичными NP-сложными задачами
являются экстремальные задачи, аналогичные
NP-полным, например, следующая переформу-
лировка задачи коммивояжера. Дана карта, со-
держащая п городов и расстояния между ними.
Какова минимальная длина замкнутого маршру-
та через все города?
1.3. Нестандартные
вычислительные модели
Традиционно для решения математических (в
том числе криптоаналитических) задач исполь-
зуются компьютеры, реализованные в виде элек-
тронных устройств, универсальных (программи-
руемых) или специализированных, сконструиро-
ментарная спираль ДНК может быть присоеди-
нен или удален.
Каждый фрагмент цепочки представляет со-
бой один двоичный разряд строки, который мо-
жет быть взаимно однозначно сопоставлен буле-
вой переменной или промежуточной булевой
функции. Если фрагмент цепочки снабжен сти-
кером, то значение соответствующего разряда
строки равно 1, если не снабжен, то 0.
Молекулярный компьютер может выполнять
следующие базовые операции:
1) объединение двух множеств строк в одно
множество;
2) разделение множества строк на два таких
подмножества, что в одно подмножество по-
падают те строки, в которых значение бита
на данной позиции равно 0, а в другое под-
множество— строки, в которых значение
бита на этой же позиции равно 1;
3) установка данного двоичного разряда строки
в состояние 1;
4) установка данного двоичного разряда строки
в состояние 0.
Эти операции, а также считывание результата
выполняются с использованием физических и
химических механизмов. Например, объедине-
ние двух множеств строк реализуется выливани-
ем их содержимого, переведенного в состояние
раствора, в общий сосуд. Разделение множества
строк можно выполнять с помощью нагрева или
электрофореза (пропускания постоянного тока
через раствор). Установка бита на данной пози-
ции строки в состояние 1 выполняется добавле-
нием в раствор соответствующих стикеров.
Лишние стикеры удаляются фильтрацией. Дли-
тельность вычислений на молекулярном компь-
ютере оценивается в сотни часов [14].
На сегодняшний день задача вскрытия ключа
шифра на молекулярном компьютере решается
перебором.5 6 Основное преимущество молеку-
лярного компьютера— высокая параллельность
и малая энергоемкость вычислений — реализу-
ется одновременным проведением вычислений с
большим множеством строк.
Сложность задачи по отношению к молеку-
лярному компьютеру оценивается требуемым
объемом раствора (один литр раствора содержит
примерно 103° молекул ДНК). Например, для
вскрытия ключа длиной 256 бит требуется по-
рядка 1040 литров раствора.
13
ванных для решения конкретной задачи. Такие
компьютеры могут различаться разрядностью,
объемом памяти, тактовой частотой, конфигура-
цией. Все эти компьютеры как вычислительные
модели полиномиально эквивалентны (предпола-
гается, что объем памяти достаточен для реали-
зации данного вычислительного алгоритма). Это
означает, что если задача может быть решена за
п шагов на одной вычислительной модели, то она
может быть решена за шагов на другой вы-
числительной модели. Поэтому множества вы-
числимых (с полиномиальной сложностью) фун-
кций для этих моделей совпадают. Мерами
сложности задач для таких компьютеров наряду
со сложностью алгоритма могут быть и физиче-
ские параметры: энергия, необходимая для реше-
ния задачи, физический объем компьютера и др.
Несколько лет назад были предложены каче-
ственно новые вычислительные модели — моле-
кулярный компьютер и квантовый компьютер,
которые могут изменить представление о вычис-
лимых функциях и для которых ограничения по
рассеиваемой энергии не столь значительны.
1.3.1. Молекулярный компьютер
Молекулярный компьютер [10, 13] основан на
использовании химических свойств молекул
ДНК. Каждая молекула ДНК представляет собой
двойную спираль, состоящую из комплементар-
ных половин? Информация в ДНК представлена
в алфавите из четырех букв А, С, Т, G. В двой-
ной спирали блок А спирали соединяется с бло-
ком Т комплементарной спирали, блок С соеди-
няется с блоком G. Цепочке ATTGTC спирали
соответствует цепочка TAACAG комплементар-
ной спирали. При нагревании двойные спирали
ДНК распадаются на одиночные и при наличии
соответствующих комплементарных фрагментов
могут быть достроены до двойных.
В молекулярном компьютере информация
представляется строками. Каждая строка состоит
из цепочки неперекрывающихся попарно раз-
личных фрагментов, представленных символами
в алфавите {А, Т, С, G} молекул ДНК (одиноч-
ная спираль) с возможно присоединенными ком-
плементарными спиралями — стикерами (от
англ, sticker— наклейка) для некоторых фраг-
ментов [18]. В соответствии с законом компле-
ментарности, код стикера однозначно определя-
ется кодом фрагмента. Для каждого фрагмента
цепочки соответствующий стикер как компле-
5 В живой природе дублирование молекул происхо-
дит путем превращения двойной спирали в две одиноч-
ных и достраивания одиночных спиралей до двойных.
6 По-видимому, в ближайшее время можно ожи-
дать появления вычислительных алгоритмов для мо-
лекулярных компьютеров.
14
1.3.2. Квантовый компьютер
Другой «экзотический» вычислитель — гипо-
тетический квантовый компьютер,7 позволяю-
щий с полиномиальной сложностью решать за-
дачи разложения составного числа и логарифми-
рования в произвольных группах вычислимого
порядка [7, 12, 19]. Например, задача разложения
на множители числа длины L бит может быть
решена со сложностью O(Z2). Однако несмотря
на то, что алгоритмы для квантового компьютера
существуют, проблема создания его работающей
модели далека от решения. Квантовый компью-
тер, как и молекулярный, удобен для решения
лишь немногих задач.
Информация в квантовом компьютере пред-
ставлена квантовыми битами— кубитами (от
англ, qubit = quantum bit). Бит информации пред-
ставлен квантовой частицей, которая может на-
ходиться в двух состояниях. Состояние частицы
может характеризоваться ее спином («спин
вверх» или «спин вниз»), поляризацией (для
квантов света— горизонтальная или вертикаль-
ная) и т. п.
Квантовая частица, находящаяся в двух воз-
можных ортогональных состояниях 0 или 1, ха-
рактеризуется вектором этих состояний (волно-
вой функцией): Т = ос|0) + Р| 1), где ос, Р— ком-
плексные амплитуды. Нормализацией амплитуд
можно получить равенство |ос|2 + |Р|2 = 1. Тогда
значения |сс|2 и |Р|2 можно интерпретировать как
вероятность нахождения частицы в состоянии О
или 1. Случай а = Р = 1/V2 соответствует одина-
ковой вероятности состояний 0 и 1.
В отличие от обычного бита, представляюще-
го 0 или 1, кубит может находиться в суперпози-
ции этих состояний. Однако при измерении ку-
бита его состояние фиксируется.
Одним из фундаментальных ограничений на
традиционные компьютеры является энергетиче-
ская необратимость переключения логического
элемента из одного состояния в другое: при пе-
реключении энергия необратимо рассеивается.
Поэтому для создания мощного компьютера тре-
буется мощный источник питания, а также вен-
тилятор для охлаждения.
Квантовый компьютер позволяет реализовать
переключение из одного состояния в другое без
рассеивания энергии. Для этого необходимо,
чтобы реализуемые отображения для всевозмож-
ных состояний квантовой системы, состоящей из
п кубитов, задавали биекцию на множестве из 2"
7 Квантовый компьютер и популярная в послед-
ние годы квантовая криптография (включая кванто-
вые шифраторы) — разные вещи.
элементов (состояний системы). Это условие яв-
ляется необходимым для реализации такого ото-
бражения на квантовом компьютере.
Например, одновходовая логическая функция
НЕ: 0 <-> 1 реализует подстановку на множестве
{0,1} или, для кубитов, [Л)->||Л). Логическая
функция © суммы по модулю 2 (операнды запи-
саны парой) может быть представлена в виде би-
ективного отображения пар битов (00) —> (00),
(01) -> (01), (10) (11), (11) (10). Здесь сумма
по модулю 2 задается вторым разрядом выход-
ной пары. Соответствующее отображение для
кубитов имеет вид \А) |В) -> \А) \А Ф В). Влияние
«лишнего» выходного кубита в дальнейшем мо-
жет быть устранено.
Логическая функция установки бита в 0 необ-
ратима, поэтому введем второй бит для получе-
ния обратимости: (00)->(00), (01) —>(10),
(10) -> (01), (11) —> (11). Здесь аргумент функции
представлен первым (левым) разрядом входа,
значение — первым разрядом выхода. Для уста-
новки бита в 0 второй разряд входа должен быть
нулевым. Получаем отображение для кубитов ви-
да И) |0> -> |0> \А).
Логическая двухвходовая функция И (л) не
может быть реализована обратимым отображе-
нием пары битов, однако ее можно реализовать
для тройки битов [15, 16]:
Вход Выход
0 0 0 0 0 0
0 0 1 0 0 1
0 1 0 0 1 0
0 1 1 0 1 1
1 0 0 1 0 0
1 0 1 1 0 1
1 1 0 1 1 1
1 1 1 1 1 0
Здесь операнды представлены первым и вто-
рым разрядами входа (при этом третий разряд
должен быть нулевым), а результат— третьим
разрядом выхода. Соответствующее отображение
для кубитов имеет вид |Л) [В) |0) -> \А) |Z) \А л В).
Аналогично можно реализовать и другие ло-
гические функции, а следовательно— произ-
вольный вычислительный процесс по аналогии с
обычным компьютером. При этом операции «ус-
тановки в 0», «стирания» и т. п. должны зада-
ваться обратимыми отображениями множеств за
счет введения дополнительных кубитов.
Одна из основных операций, реализуемых
квантовым компьютером, — когерентная супер-
позиция. Эта операция для одиночного кубита
описывается следующим образом:
15
Например,
(| 0) + j 1)) — кубит
переводится из нулевого состояния в равноверо-
ятные состояния.
Квантовым регистром называется совокупность
кубитов в одной квантово-механической системе.
Предположим, что квантовый регистр, со-
стоящий из « кубитов, находится в нулевом со-
п
стоянии: ]~[ 10), . Операция когерентной супер-
,=1
позиции И —примененная ко всем кубитам
регистра, переводит регистр из нулевого состоя-
ния в суперпозицию всех 2" возможных состоя-
ний с равной вероятностью любого состояния от
(00...0) до (11...1):8
п п 2"-1
ПI0), -> 2 ';/2 П(| 0), +11>, )= 2-/2 £| а>.
(=1 /=1 о=0
Эту операцию можно рассматривать как экспо-
ненциальное увеличение объема памяти кванто-
вого регистра: с п до 2".
Квантово-механическая система описывается
вектором состояний в гильбертовом пространст-
ве (оно аналогично линейному векторному про-
странству над полем С комплексных чисел за
исключением того, что векторы могут иметь
комплексную длину). Для квантового регистра
из п кубитов гильбертово пространство имеет
размерность N — 2". Всевозможные N состояний
регистра задают ортогональный базис гильбер-
това пространства, при измерении состояние ре-
гистра фиксируется. Вектор состояний квантово-
го регистра имеет вид а = (с/|,.... aN). Здесь а, —
амплитуда (волновой функции) в состоянии z.
Вероятность того, что при измерении регистр
окажется в состоянии г, равна
KI2
где |с|2 — норма комплексного числа: если
с = а + Ы, то |с|2 = а2 + Ь2.
8 Такая операция называется также преобразова-
нием Уолша—Адамара.
Если перейти к нормализованным значениям
к
I2 то вероятность состояния i равна
./=1
|«,|2. По теореме Шредингера [10], если квантово-
механическая система нормализована в некото-
рый момент времени, то она нормализована в
любой момент времени.
Поскольку состояние «-разрядного квантово-
го регистра описывается вектором из Л' = 2'; со-
стояний и все состояния обратимы, то любое
преобразование информации, реализуемое реги-
стром, можно описать квадратной невырожден-
ной матрицей размера N. Невырожденная матри-
ца соответствует преобразованию информации в
квантовом регистре тогда и только тогда, когда
она унитарна (обратима, сохраняет нормализо-
ванность вектора состояний; транспонированная
матрица комплексных дополнений равна обрат-
ной матрице).
Предположим, что на квантовом компьютере
с помощью логических операций реализовано
вычисление функции F произвольного аргумента
a: F: | я) 10) —> | я) | F(a)), в левом регистре на-
ходится аргумент, а в правом — значение функ-
ции F. Тогда с помощью когерентной суперпо-
зиции за один шаг можно получить значение
функции для всех 2" аргументов:
2”-1 г”-!
F: Х|о')|0)^Х|о')|Но')}.
1=0 1=о
Здесь начальное состояние левого регистра мо-
жет быть получено из нулевого состояния.
Чтобы «измерить» значение функции F для
определенного значения аргумента, эту опера-
цию нужно повторить 6)(2';) раз, каждый раз «из-
меряя» состояние правого регистра. Очевидно,
что в этом случае квантовый компьютер не имеет
преимуществ по сравнению с традиционным —
временная сложность вычислений оценивается
экспонентой от п. Однако, если нас интересует
период функции F. то его можно быстро найти с
использованием квантового дискретного преоб-
разования Фурье (см. также п. 4.6). Это преобра-
зование может быть легко реализовано с исполь-
зованием типовых логических функций. Поэтому
одной из особенностей квантового компьютера
является то, что он эффективно вычисляет скры-
тые периоды функций.
Если квантовый компьютер дает решение за-
дачи, то оно должно быть наблюдаемым. Это зна-
чит, что при измерении состояния квантового ре-
гистра результат измерения с большой вероятно-
стью должен соответствовать решению задачи.
16
1.4. Случайные последовательности
и случайные отображения
1.4.1. Понятие случайности
Рассмотрим бесконечные двоичные после-
довательности (вместо двоичного алфавита
иожно рассмотреть любой конечный алфавит).
<акую последовательность можно считать слу-
зайной? Является ли случайной последова-
гельность, образованная начальными цифрами
зисла л? Традиционная теория вероятностей не
дает ответа на этот вопрос: она описывает
звойства совокупности таких последовательно-
стей. Если в теории вероятностей утверждается
зечто про свойство случайной последователь-
зости, то это означает, что свойство выполня-
ется для подавляющего большинства последо-
зательностей [11].
Существуют частотный, сложностный и ко-
шчественный подходы к понятию случайности
зесконечной последовательности [9].
Частотный подход Мизеса основан на том,
по в случайной последовательности должна на-
шюдаться устойчивость частот. Например, в
случайной двоичной последовательности симво-
зы 0 и 1 должны встречаться независимо и с
завными вероятностями не только в основной
тоследовательности, но и в любой ее подпосле-
ювательности, выделенной в соответствии с не-
которым правилом, не зависящим от последова-
тельности.9 Иными словами, этот подход означа-
ет, что в случайной последовательности отсутст-
зуют какие-либо закономерности.
При таком подходе определение случайности
зависит от правила выбора указанной подпосле-
щвательности из исходной последовательности.
Различные правила выбора давали Мизес, Черч,
Холмогоров, Лэвленд, соответственно получа-
шсь различные определения случайности. Одно
аз правил выбора, использующихся на практике,
заключается в отбрасывании некоторых членов
тоследовательности, причем вопрос об оставле-
нии или отбрасывании решается алгоритмически
2 помощью вычислимой функции. Согласно это-
му определению последовательность, содержа-
щая в начальном отрезке тысячу идущих подряд
нулей, считается случайной, что противоречит
интуиции.
Согласно сложностному подходу Колмого-
рова случайная последовательность должна
иметь сложное строение, которое не может быть
описано с использованием короткого текста.
9 Это требование включает в себя и одинаковые
застоты для пар символов, троек символов и др.
Под (колмогоровской) энтропией объекта
понимается наименьший объем его описания.10
Шенноновская энтропия определяется как
Hs = 1оВА ’
I
где {Pt} — совокупность вероятностей рассмат-
риваемой полной схемы событий. Использование
шенноновской энтропии в описании информаци-
онных процессов (в частности, при анализе безо-
пасности) неявно предполагает, что наилучшим
алгоритмом предсказания очередного символа
последовательности является его угадывание.
Это предположение с очевидностью противоре-
чит практике, если последовательность порожда-
ется детерминированным алгоритмом.
Конечный отрезок бесконечной случайной
последовательности не допускает простого опи-
сания. Сложность такого описания близка к дли-
не последовательности. Бесконечная последова-
тельность называется случайной по Колмогоров)’,
если колмогоровская энтропия ее начальных от-
резков быстро возрастает с увеличением длины
этих отрезков. Количество информации, содер-
жащейся в конечной последовательности, равно
ее Колмогоровской энтропии.
Поскольку двоичные знаки числа л допуска-
ют простое описание и могут быть легко найде-
ны (несколько тысяч бит числа л можно найти за
несколько секунд), эту последовательность нель-
зя считать случайной по Колмогорову.
Количественный подход Мартин-Лёфа осно-
ван на том, что случайных последовательностей
много, а неслучайных— мало. Неслучайными
считаются те последовательности, в которых на-
блюдается закономерность, то есть любое прове-
ряемое свойство последовательностей, присущее
лишь узкому их классу. Последовательность
случайна, если она выдерживает тесты, выяв-
ляющие такие закономерности. Однако если по-
требовать, чтобы последовательность выдержи-
вала любой тест, то окажется, что случайных по-
следовательностей вообще не существует. По-
этому принято ограничиваться теми тестами, для
которых доля удовлетворяющих им последова-
тельностей стремится к нулю при неограничен-
ном увеличении длины последовательности.
Между указанными определениями случайно-
сти имеются следующие соотношения. Последова-
тельность случайна по Колмогорову тогда и толь-
ко тогда, когда она случайна по Мартин-Лёфу.
Определения случайности на основе частотного
10 Понятие оптимального способа описания не-
конструктивно и поэтому допускает произвол. Однако
на практике для алгоритмических (криптографиче-
ских) генераторов (псевдослучайной последователь-
ности это описание известно.
It7:
подхода с использованием различных правил вы-
бора являются более широкими. Множество по-
следовательностей, случайных согласно частот-
ному подходу, строго включает последовательно-
сти, случайные по Колмогорову и Мартин-Лёфу.
Пример 1.4.1. Энтропия.
Предположим, что шифр ГОСТ 28147-89
(см. п. 19.6) вырабатывает гамму — последова-
тельность, полученную рекуррентно повторным
зашифрованием шифртекста, длина гаммы равна
268 бит. Гамма статистически похожа на случай-
ную последовательность в том смысле, что ус-
пешно выдерживает наиболее употребительные
статистические тесты. Тогда шенноновская эн-
тропия гаммы равна 268 бит, тогда как колмого-
ровская энтропия (т.е. количество информации)
равна шенноновской энтропии ключа и состав-
ляет 256 = 28 бит.
Разработчики криптографических систем час-
то необоснованно используют шенноновский
подход к описанию алгоритмов защиты инфор-
мации. Это иногда приводит к досадным ошиб-
кам. Типовая ошибка— использование крипто-
графически слабых генераторов псевдослучай-
ной последовательности, вырабатывающих по-
следовательность, которая обладает хорошими
статистическими свойствами, но не является
случайной по Колмогорову. На самом деле сле-
дует использовать алгоритмический подход и
определение случайности по Колмогорову (или,
что то же самое, по Мартин-Лёфу).
Пример 1.4.2. Неслучайные по Колмогорову
последовательности с хорошими статистически-
ми свойствами.
1. Линейный конгруэнтный генератор, выра-
батывающий последовательность т;+| = ах, + Ъ
(mod тэт),11 где а, т е Z и НОД(а, тэт) = 1. Длина
последовательности равна т. Сложность пред-
сказания х,т] по известному х, минимальна.12
2. Генератор так называемой М-последова-
тельности, используемой в технике связи, обла-
дает очень хорошей автокорреляционной харак-
теристикой и просто реализуется, однако неслу-
чаен по Колмогорову. Генератор описывается
линейным сравнением13 х,+| = lxt (mod (2, Д/))),
где идеал (2, Д/)) задается вычетами по модулю 2
и по модулю неразложимого полинома fit) тако-
го, что всевозможные степени элемента t порож-
11 Подробнее о сравнениях см. п. 3.5.
12 Использование квадратичного или иного кон-
груэнтного генератора с несложным уравнением, как
правило, не позволяет получить последовательность,
случайную по Колмогорову.
13 См. подробнее пп. 3.5,4.3.
дают все множество ненулевых вычетов по мо-
дулю fit). Такой генератор легко реализуется ап-
паратно на сдвиговых регистрах. Например, при
fit) = fi + t + 1 = 0 получаем 1 = t + fi. Генератор
реализуется на четырехразрядном сдвиговом ре-
гистре, где выход четвертого разряда складыва-
ется по модулю 2 с выходом первого разряда и
поступает на вход первого разряда. Сложность
вычисления очередного бита последовательно-
сти — линейная от длины регистра.
1.4.2. Свойства случайного отображения
Случайные отображения широко используют-
ся при анализе криптографических алгоритмов
«в среднем».
Рассмотрим случайное отображение f конеч-
ного множества М в себя. В общем случае это
отображение не является обратимым. Его можно
задать в виде направленного графа, вершинами
которого являются элементы множества М, а
стрелки (ребра) показывают, в какой элемент из
М переходит данный элемент. Если j =fii) для i,
j е M. то на графе это соответствует стрелке, вы-
ходящей из вершины i и входящей в вершину j.
Поскольку к любому элементу i конечного мно-
жества М отображение можно применять неог-
раниченное число раз, то траектория, начинаю-
щаяся с вершины I, должна зациклиться. Поэто-
му соответствующий направленный граф должен
иметь вид леса (совокупности деревьев), ребра
которого направлены от листьев к корням, а кор-
ни соединены в циклы. Так как отображение
применимо к каждому элементу множества М, то
из каждой вершины графа стрелка выходит, од-
нако не в каждую вершину стрелка входит.
Долю листьев графа случайного отображения
(то есть элементов множества М, не являющихся
образом ни одного элемента при действии ото-
бражения f) можно определить через вероятность
того, что данная вершина является листом. Чис-
ло всевозможных отображений, переводящих
элементы множества М в элементы М за исклю-
чением данного элемента, равно числу #М-
буквенных слов в (#М- 1)-буквенном алфавите.
Действительно, отображение можно задать таб-
лицей из двух строк длины #М, в которой верх-
няя строка соответствует имени прообраза, а
нижняя — имени образа, причем информацию об
отображении несет только нижняя строка. Ниж-
няя строка содержит #М символов в (#М- 1)-
буквенном алфавите. Поэтому число таких ото-
бражений равно (#М-])#м. Поскольку число
всевозможных отображений равно #М, вероят-
ность выбираемого наугад отображения, при ко-
тором ни один элемент не переходит в данный
элемент, равна •. тч tixs&xxgi я «. ц > п?
18
(#М)Ш
где е — основание натурального логарифма.
Если множество М велико, то оказывается,
что почти все отображения М имеют оди-
наковые статистические свойства [3, 5]. В част-
ности, для графа случайного отображения:
— почти все вершины лежат на одном дереве;
- длина цикла равна средней высоте дерева, то
есть среднему числу ребер, соединяющих
данную вершину с корнем. Эта длина равна
О(у/¥М)-,
- структура леса при обращении стрелок опи-
сывается ветвящимся процессом (процессом
размножения и гибели), порожденным час-
тицами, которые соответствуют корням де-
ревьев. Каждая частица живет ровно один
такт. На следующем такте она дает случай-
ное число потомков, распределенное по за-
кону Пуассона с параметром к = 1, и при
этом погибает. Распределение Пуассона в
этом случае имеет вид [5]: Р(к) = 1/(еИ).
Рекуррентное применение отображения f к
данному элементу а множества М дает последо-
вательность a, fia), fifict}) =f2(a), f3(a), .... Она
соответствует последовательности вершин с на-
чальной вершиной а, если двигаться по стрел-
кам. Начиная с некоторого элемента с номером
т, последовательность начнет повторяться. Это
соответствует входу в цикл графа. Обозначим
длину цикла через I.
Оценим длину цикла и расстояние до него для
заданного начального элемента а. Полагаем, что
элемент а под действием f с равной вероятно-
стью переходит в любой элемент множества М.
Вероятность того, что I = 1, т = 0, для данного
элемента равна \/#М, то есть элемент должен
переходить в себя. Вероятность того, что I = 1,
т = 1 (или того, что I = 2, т = 0), равна вероятно-
сти того, что данный элемент не переходит в се-
бя, а его образ переходит в себя (или в исходный
элемент), то есть равна (1 -1/#М)(1/#М). Веро-
ятность того, что длина пути до входа в цикл
равна т, а длина цикла равна I, можно найти с
помощью выражения
РСт, I) = —-—
#М
т + 1-\
#М
Математическое ожидание длины цикла оп-
ределяется равенством 1^= ^l-P(m, I), где
суммирование ведется по всем длинам циклов I
от 1 до т и по всем т от 0 до #М. Приближенное
значение для средней длины цикла равно
/ср = у]п #М/8 [4]. Таким же выражением оцени-
вается и длина пути до входа в цикл:
тср = #М/%.
Случайное дерево обладает сжимающим
свойством (один образ может иметь несколько
прообразов), которое используется при исследо-
вании криптографических алгоритмов. Оценим
параметры этого сжатия.
Определим понятие глубины на дереве. Все
листья имеют глубину 0; вершина, не являющая-
ся листом, имеет глубину d, если максимальное
расстояние от нее до какого-нибудь листа равно
d. Глубина задает отношение порядка на верши-
нах дерева (и на вершинах графа случайного
отображения, не лежащих в цикле). Если А, В —
вершины дерева, то А>В при d(A) > d(B). Поня-
тие глубины иллюстрируется рисунком 1.1 (глу-
бина отсчитывается дискретно сверху вниз, ли-
стья имеют глубину 0).
Будем рассматривать деревья, в которых чис-
ло вершин #М велико.
Определим ширину p(d) графа как долю вер-
шин, имеющих заданную глубину. Зададим оди-
наково распределенные случайные величины
xk(t), к= 1,2, .... 1 = 0, 1,..., для которых вероят-
ность определяется выражением
Р(хА.(0 = г) = р,. =1/(ег!).
Рассмотрим ветвящийся процесс ц(/) с дис-
кретным временем t = 0, 1, ...; состояние систе-
мы определяется числом р(/) частиц, сущест-
вующих в системе в момент времени /:14
ц(/ + 1) = x,(f) + х2(/) + ... +
причем p(Z + 1) = 0, если ц(/) = 0. Пусть процесс
начинается с ц(0) = 1 частиц.
Рис. 1.1. Глубина на случайном дереве
14 Частицы считаются неразличимыми.
19
Вероятности рг можно задать с помощью про-
изводящей функции— формального (без учета
сходимости) степенного ряда
G(Z) = ^PrZr •
г>0
Формальная переменная z маркирует вероят-
ности.
Определим производящую функцию для ве-
роятностей вырождения процесса к поколению t
Ft(z) = M^,t = Q,l,...,
где Л/— математическое ожидание. Имеет место
равенство для производящих функций [3, 5]
Fl+}(z) = Ft(F(z)) = ... =F(F(z)),F0(z) = zF
Для вырождения процесса к поколению 1+1
справедливо равенство
F,(z°) = F(F,4(z°)) =
= F(F(Fz_2(z0))) =... =F(F(...F(z0)...)).
Обозначим P(i) вероятность вырождения про-
цесса к поколению I. По определению произво-
дящей функции получаем:
P(O) = F(z°) = po=l/e.
Это событие соответствует гибели частицы без
потомства, а при обращении стрелок графа — то-
му, что данная вершина является листом. Полу-
пенная вероятность совпадает с вероятностью
писта, найденной выше. Для вырождения процес-
са к поколению 2 (то есть в поколении 0 или 1)
пли, что то же самое, для того, чтобы глубина
вершины была не более 1, имеем вероятность
Р(1) = F/(z0)) = (1/е)е'А' = ехр(-1 + ехр(-1)).
Аналогично, вероятность вырождения к поко-
пению 3 (вероятность того, что глубина вершины
пе превышает 2) равна
Р(2) = F(F(F(z0))) = ехр(-1 + ехр(-1 + ехр(-1))).
Индуктивный переход очевиден. Вероятность
юго, что глубина вершины не превышает d, опи-
сывается башней из d экспонент:
P(d) = ехр(-1 + ехр(-1 + ... + ехр(-1)...)).
Последовательность ехр(-1), ехр(-1 +ехр(-1)),
схр(-1 +ехр(-1 +ехр(-1))),... стремится к еди-
нице снизу. Действительно, если предположить,
что некоторый элемент последовательности пре-
вышает 1, то тогда и предыдущий элемент по-
следовательности превышает 1. Продолжая этот
переход, получаем, что первый элемент последо-
вательности должен превышать 1. Поскольку в
действительности он меньше 1, то и все элементы
последовательности меньше 1.
Для рассматриваемых вероятностей при боль-
ших d имеет место рекуррентное соотношение
P(d) = ехр(-1 + P(d- 1)).
Раскладывая его в ряд, видим, что
P(d) = P(d -1) + 7 + —- 7 +...,
где Q(d) = 1 - P(d), причем P(d)> P(d- 1). Сле-
довательно, последовательность P(d) при нату-
ральных d монотонно стремится к некоторому
пределу. Этот предел единственный и равен 1.
Будем искать оценку для P(d) в виде степенного
ряда
P(d) = tz0 + a}/d + a2/d2 +... .
Поскольку с ростом d вероятность P(d) стре-
мится к единице, ясно, что Oq = 1. Раскладывая
экспоненту в ряд, получаем для больших глубин
асимптотическую оценку
Q(d) = O(l/d), P(d) = l-O(l/d).
Точнее, Q(d)^2/d при больших значениях d.
Ширина графа определяется выражением
p(d) = P(d) - P(d -1) = 0(1/d2).
Точнее, p(d)~2/d2 при больших значениях J.
При #М / —> сд и t/4#М 0 процесс ц(/) не
вырождается с вероятностью, стремящейся к
единице [5]. Вырождение процесса происходит в
моменты /, имеющие порядок 4#М. Следова-
тельно, и высота случайного дерева, содержаще-
го #Мвершин, асимптотически равна О(4#М).
Сжимающие свойства случайного отображе-
ния положены в основу алгоритма Полларда
(см. п. 9.3.1).
Теорема 1.4.1. Пусть/— отображение конеч-
ного множества М в себя. Для любого х е М су-
ществует натуральное число и такое, что
/V) =/2"(х), где/(х)
Доказательство. Очевидно, что равенство
/"(х) =/2”(х) при п > 0 возможно только в цикле.
Пусть у е М— лежащий в цикле корень дерева,
на котором расположен элемент х. Тогда для не-
которого натурального к будет выполняться ра-
венство у =j(x), при этом значение f2k(x) будет
лежать в том же цикле. Определим расстояние г
между значениями f2k(x) и j (х) как число шагов,
которые необходимо сделать из вершины /2fc(x),
чтобы попасть в вершину fk(x). Если из вершины
/2"(х) делать два шага, а из вершины fk(x) — один
шаг, то расстояние будет сокращаться на 1. Таким
образом, после г одиночных шагов в цикле полу-
чим равенство/^(х) =/2(А+7)(х)- Отсюда п = к + г.
Следствие 1.4.2. В обозначениях теоремы
1.4.1 имеет место равенство п-О(у[#М).
Упражнения к главе 1
1. Пусть а, b — целые числа и г2 = -1. Опреде-
лим отображение <р: (а + bi) —> а, которое
может быть рассмотрено как отображение
множества комплексных чисел в себя. Явля-
ется ли это отображение инъективным, сюръ-
ктивным, биективным?
2. Постройте продолжение отображения <р из
предыдущей задачи на множество пар ра-
циональных чисел, ограничение на множест-
во пар чисел от 0 до 9.
3. Покажите, что для любых множеств А, В, С
выполняется равенство
Сс\(А-В) = (Сс\А) — (Сг\В).
4. Оцените сложность умножения в столбик
двух и-битных чисел на вычислительной мо-
дели, использующей сложение и умножение
й-битных слов?
5. Оцените сложность алгоритма сложения двух п-
битных чисел в операциях сложения двух битов.
6. Найдите асимптотическую сложность в би-
товых операциях деления (без остатка) числа
длины 2и бит на число длины и бит на вы-
числительной модели, использующей сложе-
ние и умножение битов.
7. Найдите асимптотическую сложность деле-
ния (без остатка) числа длины 2и бит на чис-
ло длины и бит на вычислительной модели,
использующей сложение и умножение слов
длины Ъ бит.
8. Найдите асимптотическую сложность вычис-
ления остатка от деления числа длины 2и бит
на число длины п бит на вычислительной мо-
дели, использующей сложение и умножение
слов длины Ъ бит.
9. Найдите сложность вычисления наибольшего
общего делителя двух натуральных чисел ал-
горитмом Евклида на вычислительной моде-
ли, использующей сложение и умножение
слов длины Ъ бит.
10. Найдите сложность решения системы линей-
ных уравнений методом гауссова исключе-
ния в предположении, что элементарной опе-
рацией является сложение и умножение эле-
ментов матрицы.
11. Определите экспериментально высоту дерева
и длину цикла графа «случайного» отобра-
жения видаДх) = 2х + х (mod р), где р ~ 103 —
простое число.
12. Проверьте экспериментально поведение по-
следовательности, описываемой башней из
экспонент, при малых и больших глубинах.
13. Опровергните закон исключения третьего:
«каждое высказывание или истинно или ло-
жно».
Литература к главе 1
1. Ахо А., Хопкрофт Дж., Ульман Дж. Построение и
анализ вычислительных алгоритмов. М.: Мир,
1979.
2. Ван дер Варден Б.Л. Алгебра. М.: Наука, 1979.
3. Гульден Я., Джексон Д. Перечислительная ком-
бинаторика. М.: Наука, 1990.
4. Кнут Д. Искусство программирования для ЭВМ. В
3-х т. Т. 1: Основные алгоритмы. М.: Мир, 1976.
Т. 2: Получисленные алгоритмы. М.: Мир, 1977.
5. Колчин В.Ф. Случайные отображения. М.: Наука,
1984.
6. Ленг С. Алгебра. М.: Мир, 1968.
7. Манин Ю.И. Классическое вычисление, кванто-
вое вычисление и факторизация Шора // Кванто-
вый компьютер и квантовые вычисления. Ижевск:
Ижевская республиканская типография, 1999.
Т. 2. С. 248-286.
8. Математический энциклопедический словарь. М.:
Сов. энциклопедия, 1988.
9. Успенский В.А., Семенов А.Л. Теория алгорит-
мов: основные открытия и приложения. М.: Нау-
ка, 1987.
10. Фейнман Р. Моделирование физики на компью-
терах И Квантовый компьютер и квантовые вы-
числения. Ижевск: Ижевская республиканская
типография, 1999. Т. 2. С. 96-124.
11. Феллер В. Введение в теорию вероятностей и ее
приложения. В 2-х т. Т. 1. М.: Мир, 1984.
12. Шор П. Полиномиальные по времени алгоритмы
разложения числа на простые множители и нахо-
ждения дискретного логарифма для квантового
компьютера И Квантовый компьютер и квантовые
вычисления. Ижевск: Ижевская республиканская
типография, 1999. Т. 2. С. 200-247.
13. Adleman L.M. Molecular computation of solutions to
combinatorial problems // Science. 1994. Vol. 266.
P. 1021-1024.
14. Braich R., Johnson C., Rothemund P., et. al. Solution
of satisfiability problem on a gel-based DNA com-
puter // DNA computing 6-th international workshop.
Leiden, Netherlands. June, 2000. P. 31-42.
15. Chuang L., Laflamme R., Shor P.W., Zurek W.H.
Quantum computers, factoring and decoherence. Tech-
nical Report LA-UR-95-241 // http://www.if ufrgs.
br/~jgallas /QUBITS/CURSO/fatoracao9503007. pdf.
16. Hughes R.J. Quantum computation. Technical Re-
port LA-UR-98-288 // Feynman and Computation,
A.J.G. Hey (ed.), Perseus, Reading, 1999 // http:
//p23.lanl.gov/Quantum/papers/feynman.pdf.
17. Menezes A., van Oorschot P., Vanstone S. Handbook
of Applied Cryptography. CRC Press, 1997.
18. Roweis S., Winfree E., Burgoyne R., et. al. A sticker
based model for DNA computation // Proceedings of
the second annual meeting on DNA based computers.
Princeton university. June, 1996. P. 1-27.
19. Shor P.W. Algorithms for quantum computation:
discrete logarithms and factoring // Proceedings of
the IEEE 35-th ann. Symposium. On Foundation of
Computer Science, 1994. P. 124-134.
лава 2. ГРУППЫ
Аппарат теории групп является основопола-
ающим в криптографии.
2.1. Понятие группы
(Мультипликативной) группой называется
множество G 0, на котором задана бинарная
юсоциативная операция, обычно называемая ум-
ножением, если выполняются следующие усло-
5ИЯ.
L Замкнутость по умножению: для любых а,
b е G выполняется ab е G.
’. В множестве G существует единичный элемент
е такой, что еа - ае = а для любого а е G.
!. Для любого а е G существует обратный эле-
мент a 4 е G такой, что а ~'а = аа = е.
Группа G называется абелевой, или коммута-
пивной, если операция умножения коммутативна.
В определении группы операция (умножение)
ie конкретизируется. Групповой операцией мо-
кет служить и сложение, например, сложение це-
1ых чисел. Если операция называется сложением,
о группа является аддитивной. В этом случае
:диничный элемент называется нулем, а вместо
)братного элемента с/1 используется противопо-
южный элемент -а. Аддитивная абелева группа
газывается модулем. В аддитивной группе вместо
i + (-b) для краткости пишут а-b, а в мульти-
,-1 а
тликативнои группе вместо ab пишут —.
Называть операцию сложением или умноже-
шем — дело вкуса. Операцию обычно называют
:ложением, если на элементах группы задана
хругая операция или отображение, которое опре-
хеляется как умножение.
Умножение одного и того же элемента на себя
записывают в виде степени: а а = а2, сГа = сГ+п,
yf)~i = а~т, (сТ)" = dnn. Очевидно, что здесь т,
1 — целые числа.
Группы обладают следующими свойствами.
I) Уравнения ах = Ь и уа = Ъ в группе G всегда
имеют единственные решения, а именно
х~а~1Ъ и у = Ъа'\ Поэтому условия 2, 3
можно заменить условием однозначной раз-
решимости уравнений ах = Ъ, уа = Ъ. Для до-
казательства достаточно подставить эти ре-
шения в уравнения:
а(а~1Ь) = (aa^)b = eb = Ь,
(ba~l)a = Ь(сГ]а) = be = b.
Предположим, что есть два решения х, и х2
уравнения ах = Ъ. Умножив равенства ах}= b
и ах2 = Ь слева на а~1, получим а'ахА = alb,
а'ах2 = a~xb, отсюда X| = a~}b — x2.
2) Однозначность деления. Если ax = ay, то x=y,
если xa=ya, то x=y. Для доказательства умно-
жим равенство ах - ау слева на аЛ, равенство
ха = уа справа на а~'. Получим аЛах = аЛау,
следовательно, ех = еу, х=у. Во втором слу-
чае получим хаа = уаа -1, хе = уе, х = у.
3) В группе существует единственный единич-
ный элемент. Доказательство следует из
единственности решения уравнения ах = а.
4) Каждый элемент группы имеет единствен-
ный обратный элемент. Доказательство сле-
дует из единственности решения уравнения
ах — е.
5) Обращение произведения: (ab)~} = b~}a\ Для
доказательства достаточно умножить обе
части равенства справа или слева на (ab).
Множество, замкнутое по отношению к ассо-
циативной операции умножения, называется по-
лугруппой. Если это множество обладает единич-
ным элементом, то оно называется моноидом.
Единичный элемент е в моноиде единственный,
так как из предположения о существовании дру-
гого единичного элемента е' вытекает равенство
е = ее' = е'. Если умножение коммутативно, то
полугруппа называется коммутативной.
Если рассматриваемое множество замкнуто
по отношению к операции умножения и каждое
из уравнений ах = Ь, ха = Ь имеет единственное
решение при любых а, Ь, то это множество назы-
вается квазигруппой.
Элементы, для которых выполняется равенст-
во а2 = а, называются идемпотентными.
Пример 2.1.1. Полугруппы.
1. Натуральные числа по сложению образуют
полугруппу без нулевого элемента и по умноже-
нию образуют моноид.
23
2. Отображения множества в себя образуют по-
лугруппу, в которой умножение определяется как
композиция отображений (ассоциативность ум-
ножения отображений доказана в теореме 1.1.1).
3. Подмножества некоторого множества с
операцией объединения образуют коммутатив-
ную полугруппу, любой элемент является идем-
потентным.
4. Подмножества некоторого множества с
операцией пересечения образуют коммутатив-
ную полугруппу, любой элемент является идем-
потентным.
Пример 2.1.2. Группы по умножению (муль-
типликативные группы).
1. Множество Q* ненулевых рациональных
чисел.
2. Множество комплексных корней и-й степе-
ни из 1.
3. Множество подстановок (обратимых ото-
бражений конечного множества в себя, см.
п. 2.5). Если S', Т— подстановки, то их произве-
дение TS определяется как 7(S(x)) для некоторого
х. Единичным элементом группы подстановок
является единичная, или тождественная, подста-
новка, обеспечивающая S(x) = х.
4. Множество невырожденных (обратимых)
квадратных матриц одного и того же размера.
5. Множество вращений плоскости относи-
тельно начала координат.
6. Группа кватернионов, состоящая из восьми
элементов ±1, ±z, +j, +k с законом умножения
i2 =j2 = 7г = -1, ij = -ji = к, jk = -kj = i, ki = -ik =j,
H) • i = 4 (-1) j = -j, (-1) k = -k, (-1)2 = 1.
Операция умножения подстановок и операция
умножения матриц в общем случае не коммута-
тивны, следовательно, некоммутативными ока-
зываются и соответствующие группы.
Элементы а, Ъ группы, для которых выполня-
ется равенство ab = Ъа, называются перестано-
вочными. Совокупность элементов, перестано-
вочных с любым элементом группы, называется
ее центром. Центр любой группы содержит еди-
ничный элемент.
Группа называется конечной, если число ее
элементов является натуральным числом, в про-
тивном случае группа бесконечна. Число элемен-
тов конечной группы называется ее порядком.
2.2. Подгруппы
Подмножество Н группы G называется под-
группой, если из а, b е Н следует ab е Н и а~\
о е Н. Тогда е = аа' е Н.1 Подгруппами любой
1 Операции умножения в G и Н совпадают.
группы являются сама группа и единичный эле-
мент.
Пример 2.2.1. Подгруппы.
1. Группа Z+ целых чисел по сложению со-
держит подгруппу 2Z четных чисел и подгруппу
«Z чисел, кратных натуральному числу п.
2. Группа Q* ненулевых рациональных чисел
по умножению содержит подгруппу {1,-1} и
подгруппу рациональных чисел, представляю-
щих собой положительные и отрицательные це-
лые степени двойки.
3. Группа невырожденных квадратных матриц
содержит в качестве подгруппы группу невыро-
жденных верхних (нижних) треугольных матриц,
в которой единичным элементом является еди-
ничная матрица.
4. Если F и Н— подгруппы группы G, то
Fr\H— подгруппа группы G. Действительно,
из е 6 F, е е Н следует е е F С\Н', из а е F,
а' е Н следует а е Er Н и а 1 е F <~\ Н-, из а, Ъ е
еГ и а, Ъ е Н следует ab е F n Н.
5. Центр группы G является ее подгруппой.
Действительно, если а, Ъ принадлежат центру
группы, то для всех элементов х группы G имеет
место равенство ах = ха. Умножая слева и справа
это равенство на а~\ получим
а^аха^ = а~}хаа~\
С учетом равенства а'а = аа} = е получим
ха' = а'х, то есть центр вместе с каждым эле-
ментом содержит и обратный элемент. Умножим
равенство ах = ха на Ь. Получим Ъах = Ьха. В си-
лу перестановочности элементов а, b и х имеем
abx = xab, то есть центр вместе с элементами а, Ъ
содержит их произведение.
Группа, образованная положительными и от-
рицательными степенями одного элемента а, на-
зывается циклической и обозначается (tz):
(tz) ={..., а”, ..., а\ а° = е, а, ..., сГ, ...}.
Элемент а называется образующей цикличе-
ской группы (tz). Если в циклической группе нет
одинаковых элементов, то она называется сво-
бодной. Примером свободной циклической груп-
пы может служить группа Z целых чисел отно-
сительно сложения; образующей является число
1 (или-1).
Циклическая группа является конечной, если
среди ее элементов есть равные. Если </ = «'" при
к > т, то = е, так что в этом случае некоторая
степень с натуральным показателем образующей
группы равна е. Наименьший натуральный пока-
затель, обладающий этим свойством, называется
порядком элемента а. Если порядок элемента а
равен п, то среди элементов е, а,..., о"-1 нет рав-
24
ных (в противном случае выполнялось бы d = d'
при к > т, тогда d~m = е — противоречие). Вся-
кий же элемент вида d” равен одному из е,
а, ..., d~\ именно d, где г— остаток от деления
т на п. Таким образом, порядок циклической
группы, образованной элементом порядка п, то-
же равен п.
Для любого элемента b циклической группы
порядка п имеет место равенство № = е. Если по-
рядок циклической группы (а) является простым,
го (а) не имеет подгрупп, отличных от {е} и (а),
в противном случае циклическая группа имеет
подгруппы. Например, если п = 12, то группа
имеет подгруппы порядков 2, 3, 4, 6, образован-
ные соответственно элементами a6, a, a3, d.
Циклическая группа всегда абелева. Это не-
посредственно следует из коммутативности сло-
ения для целочисленных показателей:
d'a^ d1- = cdh = aV.
Если a — образующая конечной циклической
группы G порядка п, то каждому элементу b е G
можно взаимно однозначно сопоставить его
(скалярный) индекс или дискретный лога-
рифм — целое число т, 0 < т < п - 1, такое, что
Ь = сГ.
Пусть а— некоторый элемент группы G. То-
гда элементами группы G будут также ..., а\ а~\
а0 = е, a, d, d,... . Если G содержит еще один
элемент Ь, не являющийся степенью элемента а,
го элементами группы G являются и всевозмож-
ные произведения ab, ba, cdbba, baaldab и во-
обще произвольные конечные произведения вида
a^b'^a'^b'4..., где и, е Z. Среди этих произведе-
ний могут быть равные. Такие произведения об-
разуют подгруппу II группы G. Если группа II
бесконечна, то она называется свободной груп-
пой, образованной элементами а и Ь, а сами эле-
менты а и b называются образующими группы Н.
В общем случае группа может содержать не-
сколько и даже бесконечно много элементов (об-
разующих), ни один из которых не представим в
виде произведения других элементов. Например,
образующими группы Q рациональных чисел по
умножению являются все простые числа.
Аналогично определяется свободная полу-
группа.
Если бесконечная группа не имеет элементов
конечного порядка, то ее называют группой без
кручения. В противном случае группа имеет кру-
чение. Элементы конечного порядка в такой
группе составляют группу кручения. Например,
бесконечная группа Q содержит группу круче-
ния {1,-1}. Бесконечная группа Z с операцией
сложения является группой без кручения.
Если множество образующих группы конеч-
но, то говорят, что группа конечно порождена. В
конечно порожденной свободной абелевой груп-
пе для заданного множества образующих
<71, ...,<?„ каждый элемент b с точностью до эле-
мента t из группы кручения характеризуется
(векторным) индексом i = (ц, ...,/„) таким, что
b = to}1 ...а'".
Множество образующих можно рассматривать
как множество букв из некоторого алфавита S,
при этом если а — буква, то а'1 — тоже буква. Из
букв можно составлять слова, в том числе одно-
буквенные и пустое слово, не содержащее ни од-
ной буквы. В словах допускается сокращение, при
котором подряд стоящие буквы аа3 или а'1 а вы-
черкиваются. Определим операцию умножения
слов как конкатенацию, то есть приписывание к
первому слову второго слова. Символ конкатена-
ции не представлен ни одной буквой. Например,
(abbc) (c~lbca) - abbbca. Эквивалентность слов
определим как их совпадение с учетом указанного
сокращения. Такое умножение определено на всех
словах и обладает ассоциативностью. Единичным
элементом является пустое слово; каждое слово
имеет обратное, записанное «задом наперед» и
состоящее из обратных букв. Например, обрат-
ным к слову abcd^c будет слово dadldaV По-
этому слова с операцией конкатенации и указан-
ным сокращением образуют свободную группу.
Подмножество S' букв из алфавита 5 такое, что
элементом S' является только одна из букв а или
а\ называется системой образующих группы.
Пример 2.2.2. Система образующих группы
SL2(Z).
Рассмотрим множество квадратных матриц
размера 2 с элементами из Z. Произведение таких
матриц обладает свойством ассоциативности и да-
ет матрицу с элементами из Z. Чтобы обратная
матрица имела элементы из Z, ее определитель
должен быть равен ±1. Такие матрицы образуют
(общую линейную) группу GL2(Z). Эта группа со-
держи!' подгруппу SL2(Z) матриц с определителем
1, называемую модулярной группой3 Систему об-
разующих группы SL2(Z) составляют матрицы
причем S2 =
-1 О
О -1
и
. Доказательство этого утверждения см.
в работе [6].
Множество аН (соответственно, На), где И—
подгруппа группы G и а — некоторый элемент из
G, называется левым смежным классом (соответ-
2 SL2(Z) называется также специальной линейной
группой.
35
ственно, правым смежным классом) группы G по
подгруппе Н. Смежные классы иногда называют
классами смежности. Между элементами группы Н
и элементами правого смежного класса На имеется
естественное взаимно однозначное соответствие
z—>za = u, и-^иа~1-г.
Если подгруппа Н конечна, то число элемен-
тов в каждом правом смежном классе равно по-
рядку группы Н. В абелевой группе левый и пра-
вый смежные классы совпадают.
Теорема 2.2.1. Два правых смежных класса
группы G по подгруппе Н либо совпадают, либо
не имеют общих элементов.
Доказательство. Достаточно установить, что
если два правых смежных класса имеют общий
элемент, то они совпадают. Пусть х е На и
х е НЬ. Рассмотрим смежный класс Нх. Так как
х е На, то х = za при некотором z е Н и
Нх = Hza cz На. Но а = z х, так что На = Hz~xx с Нх.
Следовательно, На = Нх. Аналогично, НЬ = Нх,
так что На = НЬ. - • : < •
Теорема 2.2.2. Группа является объединением
попарно непересекающихся правых смежных
классов по подгруппе.
Доказательство непосредственно следует из
теоремы 2.2.1, ибо любой элемент а группы принад-
лежит некоторому смежному классу, именно На, а
различные классы не имеют общих элементов.
Таким образом, каждый правый смежный
класс может быть представлен единственным
элементом. Указанное в теореме 2.2.2 разбиение
группы называется разложением группы по под-
группе. Число (правых) смежных классов группы
G по подгруппе Н называется (правым) индексом
подгруппы Н. Для левых смежных классов имеют
место аналогичные утверждения. Число смеж-
ных классов обозначается (G: Н). Тогда порядок
конечной группы равен (G : {е}).
Теорема 2.2.3. Пусть G — конечная группа и
GzoH2эF, где Н, F — подгруппы группы G. То-
гда (G : Г) = (G ://)(//: Г).
Доказательство. Запишем G,H в виде объ-
единений непересекающихся смежных классов:
G = o(g,//), H=<j(hjF). Умножив второе равен-
ство на gh получим giH= ufah'F) — объедине-
ние попарно непересекающихся множеств, то
есть G - '^)(glhjF).
Пример 2.2.3. Смежные классы.
Пусть G = Z (группа по сложению), Н=1Ж,
то есть //={...,-14, -7, 0, 7, 14,...}. Тогда
смежные классы по Н: {...,-6, 1, 8, 15,...},
{...,-5, 2, 9, 16,...}, {...,-А, 3, 10, 17,...},
{...,-3, 4, 11, 18,...}, {...,-2, 5, 12, 19,...},
{..., -1, 6, 13, 20, ...}, {..., -7, 0, 7, 14,...}.
Смежные классы можно задать числами 1, 2,
3, 4, 5, 6, 0 (наименьшими неотрицательными
представителями).
Элемент b е G называется сопряженным с
элементом а, если существует элемент h е G та-
кой, что b = h^ah. Сопряженность является экви-
валентностью, так как это отношение рефлек-
сивно (а = е 'ае), симметрично (из b = h~'ah сле-
дует а = (А1)'/?//') и транзитивно (из b = h1 ah и
с = g~Abg следует с = (hg)~'a(hg)).
Подгруппа N группы G называется нормальной,
если она вместе с каждым элементом содержит все,
с ним сопряженные. Эквивалентное определение
нормальной подгруппы: A’=g4Ag для любого
g g G (то есть gN=Ng, элементы нормальной под-
группы перестановочны со всеми элементами
группы). Правые и левые классы по нормальной
подгруппе совпадают. Каждая группа содержит
нормальную подгруппу, например, саму себя или
подгруппу, состоящую из единичного элемента.
Центр группы является ее нормальной подгруппой.
В абелевой группе любая подгруппа нормаль-
на, однако обратное неверно: если любая под-
группа группы G нормальна, то G не обязательно
абелева.
Любая подгруппа Н группы G индекса 2 явля-
ется нормальной. Действительно, существует
элемент g е G\Hтакой, что G = H\J gH. Поэто-
му gH является дополнением Н в G. Но точно так
же G = H<J Hg и Hg является дополнением Н в
G. Поэтому Hg = gH. . .
Теорема 2.2.4. Смежные классы группы G по
нормальной подгруппе //образуют подгруппу в G.
Доказательство. Рассмотрим произведение
смежных классов (аН)(ЬН) = аНЬН= аЪНН= аЪН,
то есть произведение смежных классов является
смежным классом и соответствует произведению
их представителей. Представители являются эле-
ментами группы G, поэтому их произведение ас-
социативно. Единичным элементом подгруппы,
образованной смежными классами, является сама
нормальная подгруппа Н. Обратным к классу аН
является класс а~п.
Группа, образованная смежными классами
группы G по нормальной подгруппе Н, называ-
ется факторгруппой G по Ни обозначается G/H.
Так, смежные классы аддитивной группы Z це-
лых чисел по подгруппе тЖ целых чисел, крат-
ных т, составляют факторгруппу Z7/wZ. Эта
факторгруппа порядка т является циклической с
образующей 1.
26
2.3. Гомоморфизмы и изоморфизмы
Пусть G и G' — группы с операциями • и *
соответственно. Отображение ф: G —> G' называ-
ется гомоморфизмом, если ф(<т • Ъ) = ф(<т) * <р(Ь)
для любых a,b g G. Часто операции в группах G
и G' полагают очевидными и гомоморфизм оп-
ределяют как <p(ab) = ф(<т)ф(/?).
Понятие гомоморфизма можно определить и
для полугрупп: это отображение ф полугрупп
5 -> Т такое, что фО’Ф’г) = фОДфОД для любых лу
,s’2 е S. Поскольку каждая группа является также
полугруппой, то можно определить гомоморфное
отображение полугруппы в группу и обратно, го-
моморфное отображение группы в полугруппу.3
Пример 2.3.1. Гомоморфизмы.
1. Гомоморфизм мультипликативной группы
(R>o) положительных вещественных чисел в ад-
дитивную группу R+ вещественных чисел можно
задать следующим образом:
log: (R>o)* -> R+,
logxy = logx + logy, x, у e R>0.
2. Гомоморфизм аддитивной группы R+ веще-
ственных чисел в мультипликативную группу
([R >о) положительных вещественных чисел
exp: R+ —> (R>o)*,
ехр(х + у) = ехр(х) - ехр(у), х, у е R+.
3. Для каждого элемента а е G отображение
а -> аг‘, где и е Z, есть гомоморфизм группы G в
себя.
Биективный гомоморфизм ф: G -> G' называ-
ется изоморфизмом групп G и G', группы G и G'
называются изоморфными-, обозначается G = G'.
Гомоморфизм ф: G —> G называется эндомор-
физмом. Эндоморфизмы допускают умножение
как композицию отображений группы, при этом
если ф и ц/ — эндоморфизмы, то фф — эндомор-
физм.4 Эндоморфизмы группы образуют моноид
End(G) по умножению, единичным элементом
которого является тождественное отображение.
3 Например, существует гомоморфизм полугруппы
2 целых чисел по умножению в мультипликативную
группу вычетов по модулю простого или составного
числа п, при котором умножению целых чисел в 2 со-
ответствует умножение их образов — вычетов по мо-
дулю п. Этот гомоморфизм положен в основу методов
дискретного логарифмирования и разложения, исполь-
зуемых в криптографии с открытым ключом при ана-
лизе стойкости криптографических алгоритмов.
4 По определению фф(а) = <р(ф(а)).
Изоморфизм ф: G -> G называется автомор-
физмом. Произведение автоморфизмов является
автоморфизмом. Автоморфизмы группы образу-
ют группу автоморфизмов, обозначаемую
Aut(G). Единичным элементом этой группы яв-
ляется тождественное отображение. Отображе-
ния а —> а и а —> а ' являются автоморфизмами
циклической группы.
Множество элементов группы G, которое при
гомоморфизме ф: G -> G' переходит в единичный
элемент, называется ядром гомоморфизма ф и
обозначается Кег(ф). Как любое отображение, го-
моморфизм имеет образ (который может не сов-
падать с G'). Образ гомоморфизма обозначается
1пг(ф). Инъективный гомоморфизм ф: G -> G', ко-
торый устанавливает изоморфизм между груп-
пой G и ее образом в G’, называют вложением.5
Например, группа рациональных чисел может
быть вложена в группу вещественньгх чисел.
Лемма 2.3.1. Гомоморфный образ группы яв-
ляется группой.
Доказательство. Пусть G' — гомоморфный
образ группы G. Пусть a, b, с е G и а', Ь', с' — их
гомоморфные образы. На множестве G' по опре-
делению гомоморфизма задано умножение. Из
(аЪ)с = а(Ьс) следует (а'Ь')с' = а'(Ь'с') — ассоциа-
тивность умножения в G'. Из ае = а следует
а'е' = а', то есть в G' существует единичный эле-
мент е'. Из существования для каждого а е G
такого Ь, что Ъа - е, следует существование Ъ'
такого, что b'd = е', то есть каждый элемент в G'
имеет обратный.
Лемма 2.3.2. Ядро гомоморфизма ф: G —> G'
является нормальной подгруппой группы G.
Доказательство. Сначала покажем, что яд-
ро гомоморфизма является подгруппой. Пусть а,
b е Кег(ф). Тогда ф(<т/?) = ф(а)ф(&) - е'е' = е', то
есть ядро замкнуто по умножению. По определе-
нию гомоморфизма ф(а ') = ф(а) 1 = (е')1 = е', то
есть если а е Кег(ф), то и а-1 е Кег(ф). Тогда
е = аа1 е Кег(ф). Поэтому ядро гомоморфизма
является подгруппой группы G.
Для левого смежного класса <Жег(ф) имеем
ф(аКег(ф)) = а'е' = а'. Пусть ф(/?) = а'. Определим
гомоморфный образ элемента х из уравнения
ф(<хД = Ь. Тогда а'х' = d, х' = е', следовательно,
а' е <?Кег(ф). Значит, класс, соответствующий
элементу а', является левым смежным классом
<Жег(ф).
Таким же образом можно показать, что класс,
соответствующий элементу d, является правым
5 Предполагается, что операции умножения в G и
G' совпадают.
смежным классом Кег(ф)а. Получаем аКег(ф) =
= Кег(ф)<7. Следовательно, Кег(ф)— нормальная
подгруппа.
Построим гомоморфный образ G' группы G с
заданным ядром гомоморфизма Н.
Теорема 2.3.3 (о гомоморфизмах групп).
Гомоморфный образ G' группы G изоморфен
факторгруппе группы G по ядру этого гомомор-
физма. Обратно, каждая нормальная подгруппа
Н определяет гомоморфизм, для которого она
является ядром.
Доказательство. Первая часть утверждения
доказана в лемме 2.3.2, вторая часть доказана в
теореме 2.2.3, так как равенство {аН^ЪН) = аЪН
определяет гомоморфизм групп G и G/Н, при
этом Н является ядром гомоморфизма. Следова-
тельно, имеет место изоморфизм G' = GIH.
Теорема о гомоморфизмах групп устанавлива-
ет существование единственного изоморфизма ф'
такого, что диаграмма рисунка 2.1 коммутативна.
Рис. 2.1. Коммутативная диаграмма
гомоморфизмов групп
<Р'
G/H
Гомоморфизмы групп иногда изображают в
виде следующих диаграмм. Пусть
Gj —2—>G2—>G3
— последовательность из двух гомоморфизмов.
Будем говорить, что эта последовательность
точная, если 1т(ф) = Кег(щ). Например, после-
довательность
H—^G—^G/II
является точной, если Н— нормальная подгруп-
па группы G, ф — вложение, щ — гомоморфизм
с ядром II. Более длинная последовательность
гомоморфизмов называется точной, если она
точна в каждой паре последовательных гомо-
морфизмов. Например, точность последователь-
ности
е--->11 —^->G —^G/H------>е
означает, что ф инъективно, щ сюръективно и
1т(ф) = Кег(щ). Здесь Кег(ф) = {е}, если группы
II, G мультипликативные (в случае аддитивных
групп пишут 0 вместо е) и Н= Кег(щ).
Пример 2.3.2. Изоморфизмы.
1. Пусть G— циклическая группа порядка
п = тк. Пусть II— ее подгруппа, порожденная
элементом </, где а— образующая группы G.
Ясно, что порядок элемента г/ равен т и порож-
денная им группа состоит из элементов е, d1,
сГк, ..., Представителями смежных классов
G по Н могут служить а, а, ..., d~}. Умножение
смежных классов сводится к сложению показа-
телей по модулю к, ибо порождает Н. Таким
образом, здесь факторгруппа изоморфна цикли-
ческой группе порядка к.
2. Целые числа 1, 2, ...,р - 1 с операцией умно-
жения по модулю простого числа р образуют цик-
лическую группу (см. теорему 4.3.6). Для р=11
множество образующих: {2, 6, 7, 8}. Для образую-
щей 2 группа содержит десять элементов: {1, 2, 4,
8, 5, 10, 9, 7, 3, 6} — это степени двойки от 0 до 9.
Следовательно, автоморфизм полностью опреде-
ляется образом образующей. Поэтому группа ав-
томорфизмов содержит четыре элемента: ф(2) = 21
(тождественное отображение), ф(8) = 23, ф(7) = 27,
ф(6) = 29. Видно, что автоморфизмы группы со-
ответствуют возведению образующей в степень,
взаимно простую с порядком группы.
3. Если G— циклическая группа порядка п и
G = II, то группа II тоже циклическая того же
порядка. Действительно, группа G имеет обра-
зующую а и все элементы группы G являются
степенями элемента а. Тогда изоморфный образ
элемента а в группе Н является образующей
циклической группы II порядка п. Следователь-
но, порядок группы Н кратен п. Но изомор-
физм— взаимно однозначное отображение, ка-
ждый элемент группы Н имеет единственный
прообраз в группе G. Следовательно, группа
II— циклическая порядка п.
Каждой паре элементов g, h группы G можно
поставить в соответствие их коммутатор
[g, h\ =ghgxh~\ при этом [g, Л] е G переставляет
элементы g и h: [g, h]hg = gh. Если элементы g, h
перестановочны, то [g, Л] = е. Интуитивно ясно,
что чем больше в группе коммутаторов, тем силь-
нее она отличается от абелевой. Множество всех
коммутаторов группы G образует подгруппу
[G, G] группы G, называемую коммутантом
группы G, где [g, g] = е — единичный элемент и
[g, й]1 = [h, g], Поскольку <т' [G, G]a = a~la[G, G] =
= [G, G], то коммутант — нормальная подгруппа.
Факторгруппа G/[G, G] является абелевой.
Характером конечной абелевой группы G на-
зывается гомоморфизм % группы G в группу С
ненулевых комплексных чисел. Для х, у е G вы-
полняется равенство х(х)х(у) = %(ху), %(е) = 1.
При этом 'Х(<т)'Х(<т ') = 1. Любое комплексное
число может быть записано в виде ге"1’, а по-
скольку z2 = -l и F1e'Q1r2eH|>2 = х'|Г2е''<,>1+<(,?1, то лю-
бому значению характера соответствует г = 1, то
есть значения характера являются комплексными
корнями из 1.
Если Xi и %2 — характеры группы G, то мож-
но определить произведение характеров Х1Хг(«)
как Xi(a)X2(«)- Произведение характеров являет-
ся характером группы G. Определим характер
X-1 равенством Х-1(а) = х(а), где черта означает
комплексное сопряжение, и единичный харак-
тер в, где г(а) = 1 для всех a е G (произведение
сопряженных комплексных чисел с единичным
модулем равно единице). Таким образом, харак-
теры абелевой группы G образуют абелеву
группу.
Теорема 2.3.4. Пусть G — циклическая груп-
па порядка п и а— ее образующая. Тогда каж-
дый характер группы G может быть представлен
в виде % = у1: (.а>") = е11Ш”к1’', 0 < т < п - 1, для не-
которого к, ®<к<п-\, Хо = е, группа характе-
ров изоморфна группе G.
Доказательство. Пусть х — характер груп-
пы G. Тогда х"(«) = Х(°") = х(^) = Г то есть все
характеры циклической группы порядка п явля-
ются корнями степени п из 1. Поэтому
Х(а) = Ха («) = <?2от/:/" для некоторого к, 0 < к < п-1.
Тогда г^к(ат}-е111<кп1^. Таким образом, все ха-
рактеры группы G различны и образуют группу
корней степени и из 1. Эта группа циклична с
образующей Xi и- следовательно, изоморфна
группе G.
2.4. Действие группы на множестве
Пусть М — некоторое конечное множество из
п элементов, G — группа. В общем случае мно-
жество М и группа G имеют различную природу.
Например, М— множество из десяти цифр, а
G — множество всевозможных перестановок
этих цифр. Под действием группы G на множе-
стве М понимают отображение G х М—> М та-
кое, что если х е G, т е М, то хт е М, где через хт
обозначен образ пары (х, т). Множество М назы-
вают G-множеством. Имеет место равенство:
(ху)т — х(ут), ет = т
для любых х, у е G, т е М; е — единичный эле-
мент группы G. Каждый элемент х группы G ин-
дуцирует взаимно однозначное отображение Тх
(перестановку элементов) множества М:
Тх(т) = хт
для т е М. Элемент е индуцирует тождественное
отображение.
Отображение т -> Тх(т) является гомомор-
физмом группы G в группу подстановок множе-
ства М.
Пример 2.4.1. Действие группы на себе.
В качестве множества М может использовать-
ся сама группа G. Для всякого элемента у е G
определим отображение оу: G -> G формулой
сд(х) = у~'ху. Это действие группы G на себе на-
зывают сопряжением, или трансформировани-
ем. Каждое отображение о3, является автомор-
физмом группы G, то есть для всех z, х е G име-
ет место Oj,(xz) = о?(х)Оу(г), и обладает обратным,
что достигается заменой у на у-1. Таким образом,
отображение у-><зу есть гомоморфизм группы G
в ее группу автоморфизмов. Ядро этого гомо-
морфизма состоит из таких элементов у, для ко-
торых выполняется равенство у~Аху = х для всех
х е G, то есть из всех у, перестановочных со все-
ми элементами группы. Другими словами, ядро
гомоморфизма группы совпадает с центром этой
группы.
Аналогично определяется действие полугруппы
5’ на множестве М. В общем случае полугруппа 5
представляет собой набор отображений (не обяза-
тельно обратимых) множества М в себя. Множест-
во всех отображений множества из п элементов в
себя допускает ассоциативное умножение (см. тео-
рему 1.1.1) и поэтому образует полугруппу. Пере-
нумеруем элементы этого множества от 0 до п - 1.
Отображения можно задавать таблично. Каждое
отображение f полностью определяется набором
образов /(0), ...,fin— 1). Если числа от 0 до п- 1
считать буквами в некотором алфавите, то сущест-
вует взаимно однозначное соответствие между
множеством отображений и множеством слов из п-
буквенного алфавита. Число таких слов равно пп.
2.5. Группа подстановок
Подстановка — это взаимно однозначное
отображение конечного множества в себя. При
соответствующей нумерации (или упорядоче-
нии) элементов конечного множества М, на ко-
тором определена подстановка, ее можно свести
к подстановке на некотором конечном подмно-
жестве натуральных чисел. Любая подстановка
является элементом некоторой группы, задаю-
щей взаимно однозначное отображение этого
множества в себя.6
6 Иногда говорят не о подстановках, а о переста-
новках элементов множества М.
Совокупность всех подстановок, действую-
щих на М, определяет симметрическую группу
Sn, п = #М. Действительно, в силу обратимости
для каждой подстановки существует обратная
подстановка. Единичным элементом группы яв-
ляется тождественная подстановка. Произведе-
ние подстановок определяется как последова-
тельное выполнение этих подстановок. Если
множество М состоит из п элементов, то симмет-
рическая группа имеет порядок п\. Если некото-
рое множество подстановок образует группу, то
она является подгруппой симметрической груп-
пы. Заметим, что симметрическая группа неком-
мутативна.
Пусть задана подстановка на множестве нату-
ральных чисел 1, 2,..., и. Подстановки можно
представлять различным образом: в виде табли-
цы, в виде функции (для небольшого класса под-
становок аналитическое представление может
быть сравнительно простым), в виде произведе-
ния циклов.
Обычно подстановка представляется в виде
таблицы из двух строк: первая содержит числа 1,
2, ...,п в естественном порядке, а вторая— об-
разы соответствующих элементов первой строки.
Например, для п = 9
1 2 3 4 5 6 7 8 9
5 3 8 9 7 6 1 4 2
Вообще говоря, первая строка не несет ника-
кой информации, поэтому она может быть опу-
щена. Нижняя строка содержит некоторую пере-
становку чисел 1, 2, ..., п.
Рассмотрим результаты многократного при-
менения подстановки к множеству чисел, на ко-
тором она определена. Поскольку это множество
конечно, то для числа а и подстановки 5 после-
довательность a, S(a), S(S(a)) = S\a), >S'?(<7), ...
дает цикл, образованный элементом а. Очевидно,
что такой же цикл дают любые числа, лежащие в
цикле, образованном числом а. Выбрав число Ъ,
не принадлежащее этому циклу, можно постро-
ить другой цикл, образованный числом Ь. Про-
должая эту процедуру до тех пор, пока не будут
перечислены все числа 1, 2, ..., п, получим пред-
ставление подстановки в виде совокупности не-
пересекающихся циклов.
В рассмотренном примере имеются следую-
щие циклы: (6), (1, 5, 7), (2, 3, 8, 4, 9). Длины
циклов, образованных числами 6, 1, 2, равны,
соответственно, 1, 3, 5. Если в общем случае
подстановка разбивается на циклы длины
...,гр то подстановка, полученная возведени-
/
ем исходной подстановки в степень рТг (и да-
же в степень НОК(гр ..., г,)), дает тождествен-
ную подстановку. Таким образом, подстановку
можно задавать набором циклов.
Степени подстановки образуют циклическую
подгруппу симметрической группы. Действи-
тельно, произведение подстановок является под-
становкой, операция умножения ассоциативна;
подгруппа степеней подстановки 5 содержит тож-
дественную подстановку; подстановка 5-1 непо-
средственно предшествует тождественной под-
становке в последовательности подстановок
{S,S2,S\...}. Коммутативность подгруппы следу-
ет из коммутативности сложения для показателей:
5'57 = 575' = 5,+/.
Транспозицией называется подстановка, со-
храняющая неподвижными все элементы, кроме
двух, которые меняются местами.
Каждая подстановка может быть представле-
на (различными способами) как произведение
конечного числа транспозиций. Например, если
транспозицию, переставляющую местами эле-
менты i и у, обозначить (z,J), то подстановку с
цикловым строением (6), (1,5,7), (2, 3, 8, 4, 9)
можно получить из тождественной подстановки
последовательным применением следующих
транспозиций (очередность слева направо):
(1. 7), (7, 5), (2, 9), (9, 4), (4, 8), (8, 3).
Отсюда вытекает алгоритм представления
подстановки, заданной совокупностью циклов, в
виде произведения транспозиций. Достаточно
построить представление для одного цикла
(ц, ...,ц). Этот цикл состоит из транспозиций
(ц, ik), (ik, ..., (z3, z2).
Разбиение подстановки .S’ на циклы индуциру-
ет эквивалентность. Два элемента а и b множест-
ва, на котором действует подстановка, эквива-
лентны, если существует натуральный показа-
тель j такой, что S'(a) = Ъ. Это отношение сим-
метрично (если а переводится в Ь, то Ъ некоторой
степенью подстановки 5 переводится в а), реф-
лексивно (а переводится в а тождественной под-
становкой), транзитивно (если а переводится в Ъ,
Ъ переводится в с, то а переводится в с). Поэтому
каждый элемент множества {1, 2, ..., п} входит в
один и только в один цикл. Таким образом, по-
следовательность циклов в записи подстановки
можно произвольно менять — это все равно бу-
дет та же подстановка.
Последовательность длин циклов подстановки
задает ее цикловый тип. Наиболее часто встре-
чающийся тип подстановки из п элементов имеет
один цикл длины п - 1 и один цикл длины 1.
Пусть подстановка представлена в виде про-
изведения t циклов длины г,. Составим сумму
(г| - 1) + (z-2 - 1) + ... + (г, - 1), равную n — t. Значе-
за
ние суммы называется декрементом подстановки
S'. Если декремент четный, то подстановка называ-
ется четной, в противном случае подстановка на-
зывается нечетной. Любая транспозиция, приме-
ненная к подстановке, меняет ее четность. Поэто-
му транспозиция является нечетной подстанов-
кой. Число четных подстановок равно числу не-
четных подстановок той же степени. Произведе-
ние четных подстановок является четной подста-
новкой. Четные подстановки образуют нормаль-
ную подгруппу группы подстановок, называемую
знакопеременной группой. Знакопеременная группа
является коммутантом симметрической группы.
Рассмотрим один цикл подстановки, содер-
жащий некоторое подмножество элементов
множества М= {1, 2, ...,п}. Этот цикл содер-
жится не только в рассматриваемой подстановке,
но и в других подстановках, определенных на
том же множестве. Свяжем с данным циклом
подстановку, определенную на М, которая все
элементы множества М, не входящие в данный
цикл, оставляет неподвижными. Тогда любая
подстановка, разложенная на циклы, может быть
представлена в виде произведения подстановок,
связанных с этими циклами.
Обобщением понятия цикла является орбита.
Пусть G — группа подстановок, действующих на
множестве М. Тогда G является подгруппой
симметрической группы. Определим орбиту О
элемента теМ относительно группы подста-
новок G как подмножество О clM такое, что лю-
бая подстановка из G не выводит элемент т за
пределы О, и при этом для любого элемента
о g О существует подстановка из G, переводя-
щая т в о. Иначе говоря, 0 = G(m). Тогда суще-
ствует подстановка из G, которая переводит о в
т. Для любых двух элементов i, j g О существу-
ет подстановка из G, которая переводит i в j. Ес-
ли G состоит из степеней единственной подста-
новки, то орбита элемента т е М совпадает с
циклом элемента т.
Так же, как и циклы, две орбиты одной и той
же группы или не пересекаются, или совпадают.
Достаточно показать, что если две орбиты G{mx) и
Gimi) одной и той же группы имеют общий эле-
мент т, то они совпадают. Пусть /и = х(/щ) для
некоторой подстановки х е G. Следовательно,
G(m) = Gx(mi) = G{m\). Аналогично можно пока-
зать, что G(m) = G(w2)- Поэтому G{ni\) = G{mi).
Всякая группа подстановок имеет орбиты.
Орбитой симметрической группы является все
множество М.
Пример 2.5.1. Орбита.
Пусть на множестве М= {1, 2, 3, 4, 5, 6, 7, 8}
действует группа подстановок G, образованная
двумя подстановками: S) = (1, 2, 3, 4, 7, 8, 5, 6) и
S”2 = (8, 7, 4, 3, 6, 5, 2. 1). Цикловое строение под-
становок имеет вид: (1), (2), (3), (4), (5, 7), (6, 8)
для S', и (1, 8), (2, 7), (3, 4), (5, 6) для S’2. Орбита
элемента 3 относительно группы G равна {3, 4},
орбита элемента 1 равна {1, 8, 6, 5, 7, 2}. Эле-
мент 1 переводится в 8 подстановкой S'2, в 6 под-
становкой S2S1S2, в 2 подстановкой S'2S'1S'2S'iS'2.
Пусть М= {х\, ...,хп}. Определим стабили-
затор элемента тсМ как множество подстано-
вок, сохраняющих элемент т неподвижным.
Стабилизатор данного элемента является под-
группой группы подстановок. В симметрической
группе S„ стабилизатор изоморфен группе Sn-i.
Смежные классы группы S„ по стабилизатору
элемента Х| состоят из всех подстановок, перево-
дящих X] в элементы xh пробегающие все множе-
ство М.
Если группа G действует на себе посредством
сопряжений, то стабилизатор называется нор-
мализатором элемента х g G. В этом случае
число орбит конечной группы G определяется по
формуле
#O = £(G:GJ,
/еС
где С— множество представителей различных
классов сопряженных элементов; Gx — нормали-
затор элемента х; (G.GX)— число левых смеж-
ных классов G по Gx.
Подстановка, не имеющая неподвижных эле-
ментов, называется беспорядком.
Число беспорядков может быть найдено по
формуле включения-исключения [5]. Пусть даны
N предметов, которые могут обладать к задан-
ными свойствами Pi, ...,Pk. Обозначим N. , для
Г" г
1 < г < к число предметов, обладающих свойст-
вами Р,, ...,Pir (и, возможно, другими). Тогда
число предметов, не обладающих ни одним из
свойств Ptj, ..., Р(, равно
Nо=А-У Nf+Y Nn - yNn, +...+ (-l)kNi t .
0 z_i < z_i '1'2 Z—< '1'2'3 v ' ч -1к
Согласно этой формуле число беспорядков
среди подстановок из п элементов равно
и!| 1- — + — . + (-1)"
< 1! 2!
где е — основание натурального логарифма.
Группа подстановок G некоторого множества
М называется транзитивной над М, если некото-
рый элемент а из М может быть переведен с по-
мощью подстановок из этой группы во все эле-
менты М.
31
Если группа G не является транзитивной над
М (интранзитивная группа), то множество М
распадается на области транзитивности, то есть
такие области, которые под действием подстано-
вок из G переводятся сами в себя. В основу этого
разбиения положено следующее отношение.
Элементы a, b g М входят в одну область тран-
зитивности, если существует подстановка из G,
которая переводит аъЪ. Это отношение рефлек-
сивно (под действием единичной подстановки,
входящей в группу G, а переходит в а), симмет-
рично (если а под действием подстановки пере-
ходит в Ь, то Ъ под действием обратной подста-
новки переходит в а), транзитивно (если а под
действием подстановки Л'| переходит в с и с под
действием подстановки Л'2 переходит в Ъ, то а
под действием подстановки переходит в Ъ).
Следовательно, этим условием М разбивается на
классы эквивалентности, которые называют сис-
темами интранзитивности.
Пусть G — группа подстановок множества М.
Группа G дважды транзитивна, если для любых
двух пар (a, b), (с, d), где a, b, с, d е М, а Ф Ь,
c^ d, найдется подстановка h g G такая, что
Л(<т) = с, h(b) = d. Ясно, что дважды транзитивная
группа транзитивна.
Пример 2.5.2. Транзитивность.
1. Пример 2.5.1 иллюстрирует разбиение на
системы интранзитивности, совпадающее с раз-
биением на орбиты.
2. Симметрическая группа любой степени
транзитивна и дважды транзитивна. Знакопере-
менная группа любой степени также транзитив-
на, а для степени 4 и более — дважды транзи-
тивна [2, 3].
2.6. Вложимость коммутативной
полугруппы в группу
Иногда в прикладных задачах возникает во-
прос о возможности гомоморфного вложения
полугруппы 5 в группу G так, чтобы умножению
элементов в полугруппе соответствовало умно-
жение элементов в группе.
Если полугруппа 5 не содержит единичный
элемент, то пополним ее единичным элементом е
так, чтобы еа = ае = а для всех a g S. Поэтому
можно рассматривать задачу о вложении моноида
в группу. В случае коммутативного моноида М
необходимым и достаточным условием такой
вложимости является закон сокращения: каждое из
равенств ас = Ьс пса- cb влечет за собой а = Ъ [4].
Теорема 2.6.1. Пусть М— коммутативный
моноид. Тогда существует коммутативная груп-
па К(М), называемая группой Гротендика, и го-
моморфизм моноидов у: М—> К(М).
Доказательство. Пусть F(M)— свободная
абелева группа, порожденная моноидом М. Обо-
значим через [х] образующую группы F(M), со-
ответствующую элементу х g М. Пусть В —
нормальная подгруппа, порожденная всеми эле-
ментами вида [ху] |х]' [у]-1, где х, у е М. Поло-
жим К(М) - F{M)/B. Определим отображение
у: М^> К(М) как композицию вложения М в
F(M), задаваемого соответствием х -> [х], и ото-
бражения F(M) F(M)/B. Тогда у— требуемый
гомоморфизм.
Теорема 2.6.2. Если в коммутативном моно-
иде М выполняется закон сокращения (из ас = Ьс
следует а = Ъ и из са = cb следует а = Ь), то ото-
бражение у: Л/—> К(М) инъективно.
Доказательство. Рассмотрим пары (х, у),
где х, у g М, и определим эквивалентность
(х, у) ~ (х', у'), если ху' = х'у. Это отношение
рефлексивно и симметрично. Если выполняют-
ся законы сокращения, то это отношение тран-
зитивно. Умножение пар определим покомпо-
нентно. Тогда классы эквивалентности пар об-
разуют группу с единичным элементом (1, 1),
представляющим класс (х, х). Эта группа сов-
падает с группой Гротендика К(М). Обратным
элементом к паре (х, у) является (у, х). Имеет
место гомоморфизм, переводящий х е М в
класс пары (1, х). Из закона сокращения следу-
ет, что этот гомоморфизм инъективен. Таким
образом, построен инъективный гомоморфизм
коммутативного моноида М в коммутативную
группу К(М).
Следовательно, коммутативный моноид мо-
жет быть вложен в группу, если в нем действует
закон сокращения согласно теореме 2.6.2.
2.7. Прямые произведения групп
Группа G называется прямым произведением
групп А и В (обозначается G = А х В), если вы-
полнены следующие условия.
1. А и В — нормальные подгруппы в G.
2. G = AB.
3. Аг В- {е}.
Эти требования равносильны тому, что каж-
дый элемент группы А перестановочен с каждым
элементом группы В, каждый элемент g группы
G является произведением g = ab элементов
a G А и b G В, и элементы а, Ъ однозначно опре-
деляются элементом g.
По индукции можно определить прямое про-
изведение нескольких групп. В случае аддитив-
32
ных групп аналогом прямого произведения (для
конечного числа слагаемых) является прямая
сумма, обозначаемая символом ©. Тогда
G = А © В, если А и В — нормальные подгруппы
в G, G-A + В иА В= {0}.
Теорема 2.7.1 (основная теорема об абеле-
вых группах). Любая конечная абелева группа
может быть представлена в виде прямого произ-
ведения циклических групп, порядки которых
являются степенями простых чисел.7
Доказательство см. в работе [1].
Если. G = Gi х ... х Gr имеет порядок
п = И1...иг, где п,=р*', то каждый характер
группы G имеет вид
2itin\kx 2nimrkr
Хт1, ^-...-а^ = е^... е
для некоторых w, = 0, 1, ...,п- 1, и группа ха-
рактеров конечной абелевой группы G изоморф-
на G. Доказательство этого утверждения анало-
гично доказательству теоремы 2.3.4.
2.8. Категории
Категорией С назовем класс (множество, ко-
торое не может быть элементом другого класса)
ОЬ(С) объектов, на котором определен класс
отображений Мог(Л, В), называемых морфизма-
ми Ав В, причем выполняются следующие свой-
ства:
- для каждой пары объектов (А, В) существует
морфизм и: А В',
— для каждой тройки объектов (А, В, С) задано
произведение (композиция) морфизмов
Mor(Z?, С) х Мог(Л, В) -> Мог(Л, С).
При этом произведение морфизмов удовле-
творяет аксиомам:
- два множества Мог(Л, В) и Мог(Л', В’) не пе-
ресекаются за исключением случая, когда
А = А’, В = В’. В этом случае множества мор-
физмов совпадают;
— для каждого объекта А существует единич-
ный морфизм 1А = Мог(Л, А) такой, что для
каждого и е Мог(Л, В) и для каждого
v е Мог(Д А) выполняется и\л - и, 1 Av = v;
- закон композиции ассоциативен, то есть для
и е Мог(Д В), v е Мог(Д С), w е Mor(C, D)
выполняется w(vz/) = (wv)u для любых объек-
тов А, В, С, D.
Морфизм w. А —> В называется изоморфиз-
мом, если существует морфизм v: В —> А такой,
что им является единичным морфизмом в
Мог(Д В) и ми является единичным морфизмом в
Мог(Л, А).
Морфизмы объекта А в себя называются эн-
доморфизмами объекта А и обозначаются
Епс1(Л). Из определения категории следует, что
композиция эндоморфизмов является эндомор-
физмом, то есть эндоморфизмы Епб(Л) образуют
моноид.
Эндоморфизмы объекта А, являющиеся изо-
морфизмами, будем называть автоморфизмами.
Легко видеть, что автоморфизмы объекта А обра-
зуют группу, так как для них определена ассо-
циативная операция композиции, существует
единичный автоморфизм, и каждый автомор-
физм имеет обратный.
В теории категорий объект характеризуется
не как множество (то есть из каких элементов
он состоит), а своими связями с другими объек-
тами.
Функтор — отображение категорий, согласо-
ванное со структурой категории. Если С\ и С2 —
категории, то функтор Р. Cj —> С2 состоит из
отображения объектов А, В е ОЬ(С]) в объекты
Т(А), Т(В) е ОЬ(С2) и отображения морфизмов
щ: А —> В в морфизмы г/2 = Дщ): Т(А) —> Р(В).
При этом выполняются условия:
- Д1д)=1 7(л) для всех Л е ОЬ(С]);
- для двух морфизмов и\ А —> В и v: В —> С из
Mor(Ci) выполняется условие
Т(уи) = Р(у) Т(и).
Пример 2.8.1. Категории.
1. Категория групп. Объектами являются
группы, а морфизмами — гомоморфизмы групп.
2. Категория множеств. Объектами являются
множества, а морфизмами— отображения мно-
жеств.
3. Категория моноидов. Объектами являются
моноиды, а морфизмами— гомоморфизмы мо-
ноидов.
4. В криптографии важную роль играет циф-
ровая подпись для сообщения (см. гл. 13). Под-
пись и сообщение связаны с помощью провероч-
ного соотношения. Пары (сообщение, подпись)
можно рассматривать как объекты категории, а
отображения таких пар— как морфизмы (см.
п. 13.2).
7 Эта теорема положена в основу метода дискрет-
ного логарифмирования А.О. Гельфонда в цикличе-
ской группе (см. п. 11.1.1).
Упражнения к главе 2
1. Какие из перечисленных систем образуют
группу, полугруппу, квазигруппу:
- множество натуральных чисел по сложению;
- множество вещественных чисел по ум-
ножению;
- множество наборов булевых функций с
операцией композиции (подстановки на-
боров в другой набор вместо переменных);
, „ ах + Ь
- множество функции у =------ с вещест-
cx + d
венными коэффициентами с операцией
композиции;
- подмножество группы подстановок мно-
жества М, сохраняющее неподвижным
данный элемент a g М\
- подмножество группы подстановок мно-
жества М, переводящих элемент а е М в
другой элемент ЬеМ;
- множество целых чисел с операцией
а*Ь = аЬ',
- множество целых чисел с операцией
а*Ъ = \а - Ь\',
- множество вещественных чисел с опера-
цией a*b = 1 - ab;
— множество вещественных чисел с опера-
цией a*b = а + b- аЪ2
2. Опишите все нормальные подгруппы адди-
тивной группы Z целых чисел.
3. Опишите все эндоморфизмы аддитивной
группы Z целых чисел.
4. Что собой представляет факторгруппа Q/Z?
Покажите, что в этой группе каждый элемент
имеет конечный порядок.
5. Почему отображение а -> а~} в общем случае
не является автоморфизмом группы?
6. Найдите все нормальные подгруппы группы
всех подстановок из трех элементов.
7. Покажите, что любая подгруппа циклической
группы будет циклической и, следовательно,
нормальной.
8. Что собой представляет свободная подгруппа
мультипликативной группы рациональных
чисел, образованная числами -1, 2, 3?
9. Найдите множество образующих мультипли-
кативной группы ненулевых рациональных
чисел.
10. Пусть G— циклическая группа порядка 15 с
образующей а. Что собой представляет фак-
торгруппа Gl(pc")2
11. Пусть GL„([R) — группа невырожденных (об-
ратимых) квадратных матриц размера п с
вещественными коэффициентами. Покажите,
что множество матриц SL„([R) с GL„(IR) с оп-
ределителем 1 образует нормальную под-
группу группы GL„(IR).
12. Установите изоморфизм между мультипли-
кативной группой чисел {1,-1} и аддитив-
ной группой {0, 1} с операцией сложения по
модулю 2.
13. Найдите знакопеременную подгруппу груп-
пы подстановок из четырех элементов.
14. Покажите, что доля беспорядков среди все-
возможных подстановок асимптотически
равна 1/е.
15. Покажите, что порядок группы делится на
порядок подгруппы.
16. Изоморфны ли аддитивная группа Q рацио-
нальных чисел и мультипликативная группа
положительных рациональных чисел?
17. Покажите, что в любой группе ее подгруппа
индекса 2 является нормальной.
18. Покажите, что группа простого порядка все-
гда циклическая и, следовательно, абелева.
19. Покажите, что если произведение двух левых
смежных классов группы G по подгруппе Н
является левым смежным классом, то подгруп-
па Н является нормальной подгруппой в G.
20. Множество {истина, ложь} с операцией И
образует коммутативный моноид. Можно ли
вложить этот моноид в группу?
21. Подстановки А, В имеют следующее цикло-
вое строение: А = (1,5), (2, 7, 3, 9), (4,8,6),
В = (1,4, 8), (2, 3, 7, 9), (5, 6). Найдите орби-
ты элементов 1 и 2 в свободной группе G,
образованной подстановками А, В.
22. Покажите, что если абелева группа содержит
р элементов порядка р, где р — простое чис-
ло, то она не циклическая.
23. Группа G действует на себе посредством со-
пряжения. Орбита элемента х е G совпадает
с х. Покажите, что х принадлежит центру
группы.
Литература к главе 2
1. Ван дер Варден Б.Л. Алгебра. М.: Наука, 1979.
2. Каргополов М.И., Мерзляков Ю.И. Основы тео-
рии групп. М.: Наука, 1982.
3. Курош А.Г. Теория групп. М.: Наука, 1967.
4. Ленг С. Алгебра. М.: Мир, 1968.
5. Тараканов В.Е. Комбинаторные задачи и (0,1)-
матрицы. М.: Наука, 1985.
6. Milne J.S. Group theory (Lecture notes) //
http://www.jmilne.org/math/.
Глава 3. КОММУТАТИВНЫЕ КОЛЬЦА
Теория колец позволяет обращаться с различ-
ными на первый взгляд множествами, такими как
целые числа, полиномы, рациональные функции,
ряды, отображения групп, с использованием оди-
наковых правил. Аппарат теории коммутативных
колец широко применяется при разработке и ис-
следовании криптографических алгоритмов.
3.1. Понятие кольца
Кольцом называется непустое множество R,
на котором определены две операции — «сложе-
ние» и «умножение»,— сопоставляющие каж-
дым двум элементам а и b их сумму а + b е R и
произведение ab е R. Предполагается, что опера-
ции удовлетворяют следующим условиям.
1. Все элементы по сложению образуют модуль
с нулевым элементом 0.
2. Умножение дистрибутивно относительно
сложения (слева и справа): (а + b)c = ас + Ьс,
с(а + b) = ca + cb.
Из однозначной разрешимости уравнения
а + х = b следует, что дистрибутивность выпол-
няется и относительно вычитания.
Умножение на 0 дает 0:
а • 0 = а(а - «) = аа-аа = 0',
0 • а = (а- а)а = аа- аа = 0.
В определении кольца на операцию умноже-
ния не накладывается никаких ограничений,
кроме дистрибутивности. Однако часто возника-
ет необходимость рассматривать кольца, в кото-
рых умножение удовлетворяет тем или иным ес-
тественным дополнительным требованиям. Наи-
более часто встречаются:
3. Ассоциативность умножения: (ab)c = а(Ьс).
4. Коммутативность умножения: ab = Ьа.
5. Существование единичного элемента е тако-
го, что ае = еа = а для любого элемента а
(при этом элемент е может отличаться от
числа I).1
1 Если кольцо не содержит единичного элемента,
такой элемент можно формально присоединить к
кольцу, дополнив этим кольцо суммами вида ае. По-
этому обычно считают, что кольцо уже содержит
единичный элемент.
Если в кольце выполняется условие 3, то го-
ворят, что кольцо ассоциативно-, если выполня-
ется условие 4, то говорят, что кольцо коммута-
тивно-, если выполняется условие 5, то говорят с
кольце с единичным элементом. Если в кольце
выполнены требования 3-5, то элементы кольца
образуют коммутативный моноид по умноже-
нию.
На основе закона ассоциативности сложения
и умножения можно определить суммы и произ-
ведения элементов кольца:
п
^aj =а, +а2 + ...+а„,
/=1
п
J~]a, =а1а2...а,„
г=1
причем слагаемые, а в коммутативных кольцах и
сомножители, можно переставлять произволь-
ным образом.
Индукцией по п получаем равенства
(щ + ... + а„)Ь = + ... + a„b,
а(1ц + ... + bm) ~= аК + ... + abm,
(й] + . . . + Я,;)(/>! + ... + Ь,„) =
= aifej + ... + а]Ь„, + ... + a„bj +... + anbm.
Пример 3.1.1. Кольца.
1. Кольцо Z целых чисел (ассоциативное,
коммутативное, с единичным элементом).
2. Кольцо mZ целых чисел, кратных т (ассо-
циативное, коммутативное, без единичного эле-
мента при т > 1).
3. Кольцо булевых формул с операциями
сложения по модулю 2 («сложение») и конъюнк-
ции («умножение») (ассоциативное, коммута-
тивное, с единичным элементом).
4. Кольцо формальных (без учета сходимости^
степенных рядов (ассоциативное, коммутатив-
ное, с единичным элементом).
5. Кольцо квадратных матриц с целыми эле-
ментами с обычными операциями сложения г
умножения матриц (ассоциативное, некоммута-
тивное, с единичным элементом).
6. Кольцо квадратных матриц с рациональ-
ными элементами с обычной операцией сложе-
ния матриц и операцией Йорданова умножения
35
А-В- — (АВ + ВА), где в скобках— обычное
2
умножение матриц (неассоциативное, коммута-
тивное, с единичным элементом).
7. Кольцо подмножеств некоторого множества
с операциями симметрической разности («сложе-
ние») и пересечения («умножение») (ассоциатив-
ное, коммутативное, с единичным элементом).
8. Пусть 1, i,j, к — элементы группы кватер-
нионов (см. пример 2.1.2, п. 6), рассматриваемые
как базисные векторы пространства векторов с
рациональными коэффициентами. Тогда {а + Ы +
+ cj + dk} — кольцо кватернионов с операцией
умножения (о + bi + cj + dk)(A + Bi + Cj + Dk) =
= (aA -bB-cC- dD) + (aB + bA + cD- dC)i + (aC +
+ cA + dB - bD)j + (aD + dA + hC- cB)k (ассоциа-
тивное, некоммутативное, с единичным элемен-
том 1 1 0/ t О/ । Ок). ..
Далее будем рассматривать только ассоциа-
тивные кольца с единичным элементом.
Коммутативное кольцо называется целост-
ным, если из равенства ab = 0 следует, что хотя
бы один из сомножителей а или b равен нулю.
Если же ab - 0 при а Ф О, b Ф 0, то элементы а и b
называются делителями нуля. Примером целост-
ного кольца является кольцо Z целых чисел.
Пример 3.1.2. Кольца с делителями нуля.
1. Целые числа с операциями сложения и ум-
ножения по модулю 35 образуют кольцо. Для
а = 10, b = 21 имеем ab = 210 = 0 (mod 35).
2. Кольцо булевых функций с операциями сло-
жения по модулю 2 и умножения (конъюнкции).
Любая булева функция/при возведении в квадрат
равна сама себе, /2 =/ поэтому /~ + /=//+ 1) = 0,
то есть каждый отличный от константы элемент
этого кольца является делителем нуля.
3. Кольцо R, элементами которого являются
пары целых чисел. Операции сложения и умноже-
ния: (a, b) + (с, d) = (а + с, b + d), (a,h)(c,d) = (ac,hd).
Здесь снаружи скобок символы сложения и ум-
ножения означают операции в кольце R, а внутри
скобок— сложение и умножение в кольце Z.
Поскольку покоординатные операции удовле-
творяют условиям 1, 2, то и операции в R удов-
летворяют им. Нулем здесь служит пара (0, 0).
Делителями нуля являются пары вида (а, 0) и
(0, Ь), поскольку (а, 0)(0, Ь) = (0, 0).
Сокращение равенств ах = ау, ха = уа на эле-
мент а в общем случае возможно лишь тогда,
когда а не является делителем нуля. Например, в
кольце Z735Z справедливо равенство 5 • 2 = 5 • 9,
но 2 Ф 9.
Для некоторых элементов коммутативного
кольца R могут существовать обратные элементы
такие, что выполняется равенство аа~] = а~'а = е.
Элементы а е R, для которых в R существуют об-
ратные элементы, образуют группу по умноже-
нию. Действительно, если аа~1 = е, hb> = е, то
(ab)~l = Ь~Аа~] — элемент кольца R. Такие элемен-
ты называют обратимыми, а указанную груп-
пу — группой обратимых элементов кольца.2
Если произвольный элемент а кольца склады-
вать сам с собой, то после нескольких сложений
может получиться нулевой элемент. В этом слу-
чае циклическая группа по сложению, образо-
ванная элементом а, является конечной. Наи-
меньшее положительное целое число п, для ко-
торого выполняется равенство па = 0 при любом
ненулевом а, называется характеристикой коль-
ца. Если это равенство не выполняется ни при
каких положительных п, то говорят, что кольцо
имеет характеристику 0. Если характеристика
кольца является составным числом, то кольцо не
может быть целостным. '
На основе закона ассоциативности можно
ввести степени и кратные, при этом {-п)а = -па\
а а - а ) = а ; (ab) =ab ,
па = а + а + ... + а', та + па = (т + п)а~.
_ п(та) = пта, п(а + b) = na + nb~, •
‘ ' n(ab) = {na)b = a(nb)
(здесь т, п — целые числа и в общем случае мо-
гут не быть элементами кольца).
Если в коммутативном кольце с единичным
элементом е ф 0 разрешимо уравнение ах = b
при а Ф 0, то кольцо называется полем. В поле
все ненулевые элементы образуют абелеву
группу по умножению. Действительно, сущест-
вование единичного элемента е по умножению
следует из разрешимости уравнения ах = а, су-
ществование обратного элемента а} следует из
разрешимости уравнения ах = е. Поле является
целостным кольцом: умножая равенство ab = 0
при а ф 0 на а-1 получаем b = 0. Уравнение
ах = b разрешимо однозначно, так как, предпо-
ложив существование двух решений, имеем
ах = ах' и, умножая последнее равенство на а-1,
получаем х = х'.
2 Группу обратимых элементов иногда называ-
ют группой единиц, а сами обратимые элементы —
единицами. В этом случае единица кольца и еди-
ничный элемент — разные понятия. Например,
комплексные числа с целыми коэффициентами об-
разуют кольцо, в котором обратимые элементы со-
ставляют множество {1, -1, /, -i}, однако единич-
ный элемент — число 1.
36
3.2. Гомоморфизмы колец
На кольца естественным образом распростра-
няются понятия гомоморфизма и изоморфизма.
Отображение ср: R -> R' называется гомоморфиз-
мом колец R и R', если выполняются равенства
ср(а + Ь) = ср(а) + <р(Л), ср(аЬ) = <р(а)(р(Ь)
для любых a, b е R. Биективный гомоморфизм
колец называется изоморфизмом колец.
Теорема 3.2.1. Гомоморфный образ кольца яв-
ляется кольцом. Гомоморфный образ коммутатив-
ного кольца является коммутативным кольцом.
Доказательство [3]. Пусть А— кольцо, R’ —
множество, на котором определены две операции,
и ср: R -> R' — гомоморфизм. Покажем, что в R'
выполняются аксиомы кольца. Пусть а', Ь', с' —
образы элементов a, b, се R. Из равенства
(а + Ь) + с = а + (Ь + с) следует (а' + Ь') + с '=
= d + (/У + с'). Так же доказываются ассоциатив-
ность умножения и коммутативность сложения.
Из равенства а + 0 = а следует d + 0' = d, то есть
в R' существует нулевой элемент О', совпадающий
с ср(О). Так же доказывается существование в R'
противоположного элемента -а', совпадающего с
ср(-а). Покажем, что выполняется дистрибутив-
ность. Поскольку a{b + c) = ab + ас, то по опреде-
лению гомоморфизма получаем
(р(а(Л + с)) = а\Ь' + с'), ср(аЬ + ас) = db’ + de',
поэтому а\Ь' + с') = db’ + de'. Кроме того,
ср(-а) = ср(О - а) = ср(О) - ср(а) = -ср(п). Из ab = Ьа
следует db' = b'd.
Такими же рассуждениями можно показать,
что ср(е) = е', ср(а-1) = ср(а)-1 (если кольцо является
полем).
В случае изоморфизма А -» R' все алгебраиче-
ские свойства кольца R переносятся на кольцо R'.
Поэтому изоморфный образ целостного кольца
является целостным кольцом. При гомоморфиз-
ме это неверно, — например, отображение
Z -> Z735Z является гомоморфизмом, но Z735Z
содержит делители нуля. Изоморфный образ по-
ля является полем.
Пример 3.2.1. Изоморфизм колец.
Кольцо кватернионов (см. пример 3.1.1, п. 8)
изоморфно кольцу квадратных матриц размера 2.
Пусть V-T — мнимая единица. Тогда изомор-
физм колец задается отображением базисных
векторов:
Кольца можно рассматривать как объекты ка-
тегории, а гомоморфизмы колец— как морфиз-
мы этой категории.
3.3. Частные
Предположим, что каждый элемент коммута-
тивного кольца R является одновременно эле-
ментом поля К, а сумма и произведение двух
любых элементов кольца R в поле К совпадают с
суммой и произведением этих элементов в коль-
це R. Тогда говорят, что кольцо R (эндоморфно)
вложено в поле К. Например, кольцо Z является
подмножеством поля С комплексных чисел, при
этом сумма и произведение чисел в Z совпадают
с суммой и произведением чисел в С.
Если коммутативное кольцо R вложено в не-
которое поле К, Rci К, то внутри поля К из эле-
ментов кольца R можно строить частные'.
— = аЬГ]=Ь'а, если b * 0. Выполняются сле-
b
дующие правила:
.. а с , ,
1) — = — тогда и только тогда, когда ad = Ьс и
b d
bd *0 (для проверки достаточно умножить
обе части первого равенства на bd);
„.а с ad + bc , , п
2) —+ —=-------, bd* 0:
b d bd
_. ас ас j , ~
3) =—, bd* 0.
bd bd
Частные составляют целостное кольцо (так
как поле К не содержит делителей нуля). Кроме
того, каждый ненулевой элемент — имеет об-
b
.. b
ратный —. Поэтому частные составляют поле,
а
которое называется полем частных коммутатив-
ного кольца R. Если кольцо R целостное, то ча-
а
стные — можно строить для всех b 0.
В общем случае для построения поля частных
коммутативного кольца R не обязательно нахо-
дить поле К.
Теорема 3.3.1. Каждое целостное кольцо R
можно вложить в некоторое поле К.
Доказательство [3]. Очевидно, что если R
состоит из одного нуля, то это возможно. Рас-
смотрим случай, когда R содержит ненулевой
элемент. Паре элементов (а, Ь) кольца R сопоста-
37
вим дробь —. Определим эквивалентность на
b
парах (a, b) ~ (с, d) в соответствии с указанным
выше правилом 1. Очевидно, что это отношение
симметрично и рефлексивно. Кроме того, оно
транзитивно, так как если (a, b) ~ (с, d),
(c,d)~(g,f), то ad=bc, cf=dg, следовательно,
adf= bcf= bdg. Сократим на d ф 0 крайние эле-
менты двойного равенства и получим af= bg, то
есть (a, b) ~ (g,f). Это отношение разбивает
множество пар (а, Ь) на классы эквивалентности,
о ~
которые обозначим —. Определим сложение и
b
___а с
умножение дробей — и — в соответствии с пра-
b d
_ _ а с ad + be
вилами 2, 3: —+ —=-------
b d bd
а с ас
b d bd
Опе-
рации определены корректно, так как если b + О
. - , . _ ad + bc ас
и d + 0, то bd 0 и выражения ------ и —
bd bd
имеют смысл. При переходе от (а, Ь) к эквива-
лентной паре (а', Ь') получаем ab' = а'Ь. Тогда:
adb' = a'db-, •
adb' + beb' = a'db + b’cb;
(ad + bc)b'd = (a'd + b'c)bd.
~ ad + bc a'd + b'c
Следовательно, ---------=---------, то есть
bd bd
сложение каждой из эквивалентных пар с одной
и той же дробью дает одинаковые суммы. Ана-
логично можно показать, что умножение каждой
из эквивалентных пар на одну и ту же дробь дает
одинаковый результат. Нетрудно проверить, что
введенные операции ассоциативны, коммутатив-
ны и дистрибутивны. Кроме того, полученное
поле частных содержит само кольцо R, если ото-
ждествить элемент а е R с дробью —, b 0.
Ъ
Эти дроби складываются и умножаются так же,
как элементы кольца R. Следовательно, постро-
енное поле К содержит кольцо R, и операции
сложения и умножения в К соответствуют сло-
жению и умножению в А.
Эта конструкция может быть перенесена и на
коммутативное кольцо R с делителями нуля. В
этом случае знаменателем дроби может быть
любой элемент кольца, не являющийся делите-
лем нуля. Построенное таким образом множест-
во частных образует кольцо, содержащее исход-
ное кольцо R, и называется кольцом частных.
В общем случае в качестве возможных знаме-
нателей можно использовать не все элементы, не
являющиеся делителями нуля, а лишь некоторое
мультипликативное подмножество S кольца R
такое, что ху & S для всех х, у е S. Построение
частных в этом случае приводит к кольцу част-
ных R по 5.
Пример 3.3.1. Кольца и поля частных.
1. Полем частных для кольца Z является поле
Q рациональных чисел.
2. Кольцом частных кольца Z по мультипли-
кативному подмножеству, образованному степе-
нями двойки {1, 2, 2',...}, является кольцо ра-
циональных чисел, у которых в знаменателе сто-
ит степень двойки.
3. Кольцо частных кольца Z735Z совпадает с
Z/35Z.
3.4. Предварительные сведения
о полиномах
Пусть R — целостное кольцо. С помощью но-
вого элемента х & R построим выражение вида
/(х) = ^а,х' , в котором а, е R и сумма содер-
/>0
жит конечное число слагаемых. Такие выраже-
ния называются полиномами над кольцом R, сим-
вол х называется переменной, элементы а, — ко-
эффициентами. Степенью deg(/) полинома/на-
зывается наибольшее число z, для которого а, ф 0.
Полиномы можно складывать и умножать, при
этом символ х считается перестановочным со
всеми элементами кольца. Сложение и умноже-
ние выполняется по формулам
^а,х'+ ^6,х'= ^с,х', с^а^Ьр,
1>0 />0 />0
£О,х'-£б(.х;=£с,.х', с, = ^a,bk.
/>0 1>о t>0 j+k=t
Теорема 3.4.1. Полиномы образуют кольцо.
Доказательство. Выполнение требований
по сложению очевидно, так как сложение коэф-
фициентов выполняется в кольце R. Нулем коль-
ца полиномов является полином с нулевыми ко-
эффициентами. Дистрибутивность следует из
равенства
^а,(ЬЛ. + ск) = ^а,Ьк + YaJck - ,т
j+k=i j+k-i j+k~i
Ассоциативность умножения следует из ра-
венства для коэффициентов
X ак = YakblC.- “
' J+k=i \1+т=1 у k+l+m=i
38
Кольцо полиномов над R обозначается А[х].
Полиномы степени 0 являются элементами коль-
ца R, поэтому кольцо полиномов содержит R.
Переход от R к А[х] называется присоединением
переменной х к кольцу R. К кольцу 7?[л'|] можно
присоединить новую переменную х2 й R\x 1 ], при
этом в силу перестановочности х! и х2 получится
кольцо /?[х|][х2] = /?[хь х2]. Таким образом можно
получить кольцо /?[xb ...,х„] полиномов от не-
скольких переменных, элементы которого имеют
вид ^хф.-х'" . В случае полинома от не-
скольких переменных различают степень по пе-
ременной х„ при этом коэффициенты при х, в
различных степенях являются полиномами от
остальных переменных. Степенью полинома от
п переменных называют наибольшую сумму по-
казателей /] + ...+ i„.
Вместо переменной х в полином /(х) е /?[х]
можно подставлять произвольный элемент
а е R (и даже произвольный элемент а некото-
рого кольца R' R), перестановочный со всеми
элементами из R, при этом Да) называется зна-
чением полинома fix) для аргумента а. Если
fid) — значение полинома Дх), g(a) — значение
полинома g(x) и fix) + g(x) = r(x), fix)g(x) = .s(x),
то fid) + g(a) = r(d), fid)g(d) = s(d). Поэтому
сопоставление переменной x произвольного
элемента а е R задает гомоморфизм колец
А[х] R.
Теорема 3.4.2. Если кольцо R— целостное,
то кольцо 7?[х] тоже целостное, и
deg(/g) = deg(/) + deg(g)
для любых Дх), g(x) е /?[х].
Доказательство. Пусть /(х) = ^а,х' ,
/>0
g(x) = ]Гб,х', deg(/) = т, deg(g) = п. Тогда стар-
ее
шим коэффициентом полинома fix)fix) будет
атЬ„ ф 0, так как а,„ О, Ь„ ф 0 и кольцо R целостное.
Поэтому fix)g(x) ф 0, a deg(/g) = deg(/) + deg(g).
Следствие 3.4.3. Если кольцо R целостное, то
кольцо 7?[х|,...,х„] тоже целостное.
Доказательство выполняется индукцией по
числу переменных.
Пусть R— кольцо и пусть /(х) = ]Га,х' ,
;>0
g{x) = ^_bixl, deg(/) = m, deg(g) = n, т>п, а,,
i>0
bi<E R и bn = e. Тогда, если g(x) умножить на
атХт~" и вычесть полученный полином из f(x), то
старший коэффициент полученного полинома
будет равен 0. Из результата опять можно вы-
честь кратное g(x) и т. д. Повторяя эту процедуру
несколько раз, получим остаток со степенью
меньшей, чем deg(g). Значит, можно записать
равенство f~gh + r, где deg(r) < deg(g). Такая
процедура называется делением (с остатком).
3.5. Идеалы и классы вычетов
Пусть R— некоторое кольцо. Собственное
подмножество S’ a R будет подкольцом кольца R,
если оно замкнуто по сложению и умножению и
вместе с каждым элементом содержит противопо-
ложный (считается, что правила сложения и ум-
ножения в R и в S’ одинаковые). Ассоциативность
сложения и умножения и дистрибутивность для S
выполняются автоматически, так как S a R.
Пример 3.5.1. Подкольца.
Поле Q рациональных чисел является коль-
цом и содержит в себе следующие подкольца:
- кольцо Z целых чисел;
- кольцо nZg
- кольцо, состоящее из одного нуля;
тр
- кольцо рациональных чисел вида —, где п
п
не делится нар.
Подмножество 21 с R, 21 0, называется пра-
вым идеалом, если:
1) 21 является подгруппой аддитивной группы R
(то есть для любых а, Ь е 21 выполняется
а + b е 21);
2) для любых х е R и а е 21 выполняется
ах е 21, то есть 21х с 21.
Аналогично определяется левый идеал. Если
идеал является одновременно правым и левым,
то его называют двусторонним идеалом или про-
сто идеалом. В коммутативных кольцах все
идеалы двусторонние.
Идеал, в отличие от подкольца, замкнут отно-
сительно умножения на элементы кольца, то есть
идеал является подкольцом, но обратное невер-
но. Например, для кольца А[х] кольцо R будет
подкольцом, но не идеалом.
Пример 3.5.2. Идеалы.
1. Нулевой идеал (то есть состоящий из одного
нуля).
2. Единичный идеал (то есть содержащий все
кольцо R).
3. Идеал кольца полиномов, состоящий из по-
линомов, имеющих общий корень (см. п. 3.11).
4. Идеал (а), порожденный элементом а. то
есть состоящий из всевозможных выражений вида
га. гпе г е R. Такой идеал называется главным.
39
5. Идеал (щ,..., аг), порожденный элементами
Oi, ...,аг. Такой идеал состоит из сумм вида
^jF,a, , где г, е R. Элементы аь ...,аг образуют
базис идеала?
Любой идеал 21 как нормальная подгруппа
аддитивной группы кольца R определяет разбие-
ние кольца R на смежные классы, или классы
вычетов по идеалу 21: f + 21, где г е R. Для клас-
сов вычетов можно задать умножение:
(г + 2l)(.s + 21) = rs + 2L Умножение определено
корректно. Действительно, зададим эти классы
вычетов другими элементами п + 21 и + 21, где
Fi = г + а, «1 = s + b и а, b е 21. Тогда
(i\ + 2l)(.S| + 21) = (f + а + 2l)(,s' + b + 21). Посколь-
ку а + 21 = b + 21 = 21, то F| лу + 21 = rs + 21.
Два элемента а, b называются сравнимыми по
идеалу 21 (или по модулю 21), если а - b е 21.
Этому соответствует запись a = b (mod 21) или,
короче, а = Ь (21), называемая сравнением. Если
21 = (с) — главный идеал, то пишут а = Ь
(mod (с)) или a = b (mod с).
Над сравнениями можно выполнять операции.
Очевидно, что сравнение a = h (mod 21) остается
в силе, если к обеим его частям прибавить один и
тот же элемент или если обе части умножить на
один и тот же элемент. Если a = b (mod 21), то
а + с = b + с (mod 21), ас = be (mod 21) и ca = cb
(mod 21). Если а = b (mod 21) и а' = b' (mod 21), то
а + d = b + d = b + b' (mod 21), то есть сравнения
можно почленно складывать и, следовательно,
умножать на целое число. Кроме того, сравнения
можно почленно перемножать: ad s bd = bb'
(mod 21). Таким образом, co сравнениями можно
оперировать как с равенствами, за исключением
того, что сокращать в кольцах на делитель нуля,
вообще говоря, нельзя.
Теорема 3.5.1. Ядро гомоморфизма R-+R'
(не обязательно коммутативных) колец является
идеалом в R, а полные прообразы элементов из R
являются классами вычетов по этому идеалу.
Доказательство. Пусть ср: 7? —>/?'— гомо-
морфизм. Покажем, что 21 = Кег(ср) является дву-
сторонним идеалом. Если а, b е 21, то есть
ф(«) = <р(Ь) = 0' е R’, то -Ь е 21 и, следовательно,
a- b е 2L Значит, 21 — модуль. Кроме того, если
г е R, а е 21, то ср(га) = ср(г)ср(а) = О', ср(йг) =
= ср(а)ср(г) = О'. Поэтому 21 — идеал. Теперь по-
кажем, что полные прообразы элементов из R'
являются классами вычетов по этому идеалу. Ес-
ли <р(г) = г', то <р(а + г) = 0' + г' = г'. Если
3 Базис идеала и число элементов базиса опреде-
лены неоднозначно. Если {аь ..., а,} — базис идеала
21 и b е 21, то {щ, ...,аг,Ь} — тоже базис идеала 21.
ср(г) = <p(.s) = f' для s е R, то ср(г - .s) = О', то есть
F-5S2L
Таким образом, каждому гомоморфизму соот-
ветствует идеал, являющийся его ядром. Гомо-
морфный образ кольца R по идеалу 21 называется
кольцом классов вычетов R по 21, или фактор-
кольцом, и обозначается R№.
Рассмотрим обратную задачу. Построим
кольцо R', являющееся гомоморфным образом
кольца R по идеалу 2L
Теорема 3.5.2 (о гомоморфизмах колец).
Гомоморфный образ кольца изоморфен кольцу
классов вычетов по ядру гомоморфизма.
Доказательство. В качестве элементов
кольца R возьмем классы вычетов кольца 7?/2Г
Отображение, при котором каждому элементу а
соответствует образ а', корректно определено и
является гомоморфизмом колец. Между элемен-
тами кольца R’ и классами вычетов из R/%L суще-
ствует биекция. Класс Ка соответствует элементу
d е R', класс Kh — элементу b' е R', сумма и
произведение классов переходят в Ка+ь и Kah, то
есть им соответствуют а' + Ь' и а'Ь'. Поэтому
(а + Ь)’ = а' + b(ab)' =а'Ь'. Таким образом,
имеет место изоморфизм колец R’ = R/QI.
Теорема 3.5.2 устанавливает точность после-
довательности гомоморфизмов колец [5]
s .. . 0 -> 21 ->/? ->/< 21 -> 0.
Пример 3.5.3. Кольца классов вычетов.
1. Для кольца Z и идеала «Z кольцом классов
вычетов является Z7hZ.
2. Для кольца Q[x] полиномов с рациональ-
ными коэффициентами и главного идеала,
образованного полиномом J(x), кольцом классов
вычетов является Q[x]/(/(x)).
На множестве идеалов коммутативного коль-
ца можно определить бинарные операции сло-
жения, умножения и пересечения.
Пусть 21 и SB — идеалы коммутативного
кольца R. Определим сумму идеалов 21 + SB как
подмножество кольца R, образованное суммами
вида а + Ь, где а е 21, b е SB.
Сложение идеалов коммутативно: 21 + SB =
= SB + 21 и ассоциативно: для любых трех идеалов
21, SB, С имеет место равенство (21 + SB) + € =
= 21 + (SB + С) = 21 + SB + С. Каждый идеал идемпо-
тентен по сложению: 21 + 21 = 21. Нулем для опе-
рации сложения идеалов является нулевой идеал
(0). Поэтому идеалы образуют коммутативный
моноид по сложению (для ненулевого идеала 21 не
существует идеала SB такого, что 21 + SB = (0)).
40
Теорема 3.5.3. Пусть 21 и SB — идеалы ком-
мутативного кольца R. Справедливы следующие
утверждения.
1. 21 + SB—идеал.
2. 21 + 03 — наименьший идеал, содержащий 21
и SB.
3. Если 21 = (аь ..., аг), SB = (Z>i, ...,bs), то
2X + SB = (аь bb ...,bs).
Доказательство [4]. 1. Пусть a, d g 21 и Ь,
b' g SB. Тогда (а + b) + (d + b') = (а + a') + (b +
+ Ь') g 21 + 03. Если г — любой элемент кольца R,
то r{a + b) = га + rb, где га е 21, rb g 03. Поэтому
сумма идеалов является идеалом кольца R.
2. Пусть идеал С содержит идеалы 2Х и 03. То-
гда € содержит суммы а + Л, где а е 21, b е 03, то
есть € э 21 + 03, поэтому наименьший такой иде-
ал € совпадает с 21 + 03.
3. Идеал (аь ..., ar, Ьь ..., bs) содержит идеалы
21 и 03. В соответствии с п. 2 получаем
21 + 03 с (аь ..., а,., Ьь bs). По определению
суммы идеалов 21 + 03 з (ш, ..., ar, bh..., bs), по-
этому 21 + 03 = («ь /д, ...,/д).4
Пересечение идеалов коммутативного кольца
(как множеств) является идеалом.5 Действитель-
но, если 21 и 03 — идеалы кольца R, то 21 п 03
непусто и содержит по крайней мере 0. Если сь
с2 g 21 п SB, то С], с2 g 2Х и с}, С2 е SB, поэтому
С] + с2 е 21 и Ci + с2 е SB, то есть щ + с2 g 2Х п SB.
Поскольку для г е R и с g 21 п 03 справедливо
гс е 21, re g SB, то тс g 21 n SB.
Пусть 21 и 03 — идеалы коммутативного
кольца R. Идеал 2XSB, порожденный всеми произ-
ведениями а,Ь;, где а, g 21 и b, g SB, состоит из
сумм вида ^afii и называется произведением
идеалов.6 Произведение идеалов коммутативно и
ассоциативно: 2lO3 = SB2l, 2X(SBC) = (2XSB)<£. Еди-
ничным элементом для операции умножения
идеалов является само кольцо R. Поэтому идеа-
лы коммутативного кольца образуют коммута-
тивный моноид по умножению.
Теорема 3.5.4. Если 21 = (аь ..., ar), SB =
= (Ьь ..., bs), то 2XSB = (aiZ>i, ad>2,..., arbs).
4 Сумму идеалов 2t + SB обозначают также (21, SB)
и называют их наибольшим общим делителем.
5 Пересечение идеалов называют также их наи-
меньшим общим кратным.
6 Отметим, что 2XSB не состоит из попарных про-
изведений элементов, входящих в 21, SB (эти произве-
дения не образуют идеал), а порождается, этими про-
изведениями.
Доказательство. По определению произве-
дения идеалов 2XSB о (с/Д). Кроме того, для лю-
бого h g 2XSB существует представление h =fg,
где /е 21, g е SB. Однако f = g = ’
где r„ s, е R. Поэтому h = fg = ^t a,bt .
Имеет место включение 2XSB £ 21 n SB, по-
скольку элементы идеала 2XSB имеют вид ab, где
а g 21, b g SB. Но ab g 2Х и ab g SB. Поэтому
ab g 2Х n SB.
Пример 3.5.4. Произведение и пересечение
идеалов.
В кольце Ж[х] идеалы 2Х = SB = (х, 3) представ-
ляют собой множество полиномов, свободный
член которых делится на 3. Тогда
21п 23 = 2l = SB = (x, 3), a 2XSB = (х2, Зх, 9) и
21 n SB строго больше, чем 2XSB: 2х + 3 g 21 n SB,
но 2х + 3 ё 2XSB.
Теорема 3.5.5. Для идеалов коммутативного
кольца R выполняется дистрибутивность:
21(58 + С) = 2XSB + 2ХС.
Доказательство. Идеал 2l(SB + С) порожда-
ется элементами вида а(Ь + с), где a g 21, b g SB,
с g С Но для элементов кольца R выполняется
a(b + с) = ab + ас g 21SB + 2ХС. Поэтому 2l(SB + С) cz
cz 21SB + 2ХС. Однако идеал 2XSB + 2ХС порождается
элементами ab + ac, для которых справедливо
равенство ab + ас = a(b + с) g 2l(SB + С), то есть
21(93 + С) о 2XSB + 2XGZ, поэтому 2t(SB + С) =
= 2XSB + 2XC.
Иногда классы вычетов коммутативного
кольца R по идеалам 2Х1з..., 2Х„ определяют коль-
цо R.
Теорема 3.5.6 (китайская теорема об остат-
ках). Пусть R — коммутативное кольцо и
2Х[, ...,2l(i— идеалы кольца R такие, что
2Х, + 2Х; = R для всех i ф j. Тогда для любого набо-
ра элементов хь ...,х„, где х, g 7?/2Х„ существует
элемент х g R такой, что х = х, (mod 21() для всех
1 <i<n.
Доказательство. Докажем теорему по ин-
дукции. Для п = 2 существуют элементы идеалов
О] g 2Х1з а2 g 2Х2 такие, что ai + а2 = е. Тогда тре-
буемое представление для элемента х g R:
X = Х2П] + Х]«2.
Предположим, что теорема доказана для п - 1
идеалов со свойством 2Х, + 2Х, = 7? для всех i^ j.
Следовательно, существуют пары элементов
a, g 21] и bt g 2Х„ i > 2, такие, что а, + Ь, = е. Про-
41
п
изведение сумм [ (а, + Ь,) = е. Кроме того, по
1=2
определению идеала это произведение является
элементом идеала 21] +Р[21 . Следовательно,
/=2
этот идеал совпадает с кольцом R:
п
21] + [21] = R. В силу справедливости теоре-
i=2
мы при п = 2, можно найти элемент yi е R такой,
что yi = е (mod 21]) и у1 = 0 (mod]""[2li). Но тогда
1=2
точно так же найдутся элементы у, е R такие, что
у, = е (mod 21/) и у, s 0 (mod 21,). В этом случае
п
требуемый элемент х е R имеет вид х = л(у( .
/=1
Китайская теорема об остатках часто исполь-
зуется в криптографии и вычислительной техни-
ке. Примеры ее использования:
- быстрое умножение больших чисел (см.
п. 7.1.2);
- нахождение индекса элемента конечной цик-
лической группы алгоритмом Гельфонда
(см. п. 11.1.1) за счет представления ее в виде
прямого произведения групп в соответствии
с теоремой 2.7.1;
- вычисление дискретного логарифма в группе
методом базы разложения (см. п. 10.1).
Кольцо R, в котором существует единствен-
ный элемент х для каждого набора х, е Д/21„ на-
зывается прямой суммой колец 7?/21, и обознача-
ется R= R3.{y ®...®/?2l„.
3.6. Делимость идеалов
Для элементов коммутативного кольца можно
ввести понятие делимости на идеал. Пусть 21 —
идеал кольца R. Если а е 21, то говорят, что а
делится на идеал 21. Если все элементы идеала 21
принадлежат идеалу 2V, то говорят, что 21 делит-
ся на 2V, или что 2V делит 21, и обозначают 2V121.
Например, идеал (а, Ь) делится на идеал (а, Ь, с).
Пусть 21 = (Ь), 2V = (Ь'). Тогда запись (Ь) = 0
(mod (/>')) означает, что b = rb’, где г е R, и дели-
мость главных идеалов соответствует делимости
элементов.7
7 Определение делимости для идеалов дает неко-
торые преимущества по сравнению с определением
делимости для элементов. Одним из преимуществ
Ненулевой необратимый элемент р целостно-
го кольца называется простым, если из p\ab
следуетр | а или р | Ь. Простым идеалом кольца R
называется такой идеал ф, кольцо классов выче-
тов Д/ф которого является целостным. Если а',
Ь' е 7?/ф, то из условия а'Ь' = 0 следует, что
d = 0 или Ъ' = 0. Другими словами, из ab = 0
(mod ф) следует а = 0 (mod ф) или b = 0 (mod ф),
то есть произведение двух элементов делится на
идеал ф тогда и только тогда, когда на ф делится
один из сомножителей. '
Пример 3.6.1. Простые идеалы.
1. Единичный идеал, содержащий все кольцо R.
2. Для кольца Z простым идеалом является
идеал (р), образованный простым числом р.
3. Нулевой идеал является простым только
для целостного кольца. Например, в кольце
Z735Z имеет место равенство 10-21 =0
(mod 35), но 10 и 21— ненулевые элементы
кольца.
Идеал ЯЛ коммутативного кольца R называет-
ся максимальным,8 если он не содержится ни в
каком другом идеале, кроме самого кольца R.
Теорема 3.6.1. Каждый отличный от еди-
ничного максимальный идеал ЯЛ коммута-
тивного кольца R является простым, и кольцо
классов вычетов RI201 является полем. Обрат-
но, если R/ЯП — поле, то ЯЛ — максимальный
идеал.
Доказательство. Для доказательства того,
что RI^IR является полем, достаточно показать,
что в кольце классов вычетов RffiR разрешимо
уравнение а'х' = Ь’ при а' О'. Это равносильно
разрешимости сравнения ах = b (mod ЭЛ) при
а £ ЯЛ. Идеал ЯЛ и элемент а порождают совме-
стно идеал (ЯЛ, а). Поскольку а <£ 9R, то идеал ЯЛ
является делителем идеала (ЯЛ, а) и ЯЛ (ЯЛ, а).
Так как ЯЛ— максимальный идеал, то
(ЯЛ, а) = R. Из последнего равенства следует, что
произвольный элемент b кольца R можно пред-
ставить в виде b = т + аг, где т е ЯЛ, г е R. Го-
моморфизм из кольца R в кольцо А/ЯЛ переводит
это равенство в равенство Ь' = dr', которое дает
решение уравнения а'х' = Ь’. Таким образом,
является то, что в разложении можно не учитывать
обратимые элементы. Действительно, пусть кольцо
R — целостное, 21 — идеал этого кольца и а — обра-
тимый элемент. Тогда вместе с каждым элементом а
идеал 21 содержит и еа. Если идеал содержит элемент
е, то он содержит и элемент е = ее-1, то есть совпадает
с кольцом R.
R Максимальный идеал называют также идеалом,
не имеющим делителей.
7
сольдо А/9Л— поле и, следовательно, не имеет
делителей нуля. Поэтому идеал является про-
стым.
Докажем обратное утверждение. Если А/9Л —
юле и 21 — собственный делитель идеала 9Л, то
для а е 21, а <£ 9Л, сравнение ax = b (mod 9Л) од-
юзначно разрешимо при любом b (это следует
13 однозначной разрешимости уравнения а'х' = Ь'
з рассматриваемом поле). Следовательно, ах = Ь
mod 21), отсюда 0 = b (mod 21) для произвольного
? е R. Значит, 21 = R.
Таким образом, любой максимальный идеал
шляется простым. Обратное, однако, неверно.
Запример, в кольце Q[x,y, z\ идеалы (х) и (х,у)
шляются простыми, при этом идеал (х, у) являет-
ся собственным делителем идеала (х). Действи-
гельно, для колец классов вычетов справедливы
равенства Q[x,y, z]/(x) = Q[y, z], Q[x,y, z]/(x,y) =
= Q[z], Поскольку Q — поле, то эти кольца клас-
сов вычетов являются целостными согласно тео-
эеме 3.4.2. Следовательно, идеалы (х), (х,у) яв-
1яются простыми.
Если 9Л — максимальный идеал коммутатив-
юго кольца R, то для любого идеала 21 произве-
дение идеалов 21 и 9Л равно их пересечению.
3.7. Евклидовы кольца
и кольца главных идеалов
Понятие евклидова кольца, связанное с алго-
ритмом Евклида, удобно пояснить на примерах,
’ассмотрим сначала кольцо целых чисел.
Лемма 3.7.1. В кольце Z каждый идеал явля-
ется главным.
Доказательство. Пусть 21— произвольный
адеал кольца Z. Если 21— нулевой идеал, то
М = (0) — главный идеал. Если в 21 есть ненуле-
зое число с, то -с е 21. Одно из этих чисел поло-
кительное. Пусть а — наименьшее положитель-
зое число идеала 2L Тогда для произвольного
тела b е 21 имеет место равенство b = qa + г, где
- — остаток от деления b на а. Так как 0 < г < а и
7— наименьшее положительное число идеала,
го г = 0. Следовательно, b = qa, то есть все числа из
адеала 21 кратны а, 21 = (а) и идеал 21 — главный.
Лемма 3.7.2. Если К— поле, то в кольце ТДх]
толиномов от одной переменной каждый идеал
главный.
Доказательство. Если 21— нулевой идеал,
то 21 = (0) и утверждение теоремы верно. Пусть
21 — произвольный ненулевой идеал. Поскольку
степень полинома — целое неотрицательное
число, то в идеале 21 существует полином а наи-
меньшей степени. Поскольку в ТДх] существует
алгоритм деления, то для b е 21 справедлива
представление b = qa + r, где 0 < deg(r) < deg(a)
Поэтому deg(r) = 0. Но если г ф 0, то г е 21 явля-
ется элементом поля К. Поскольку каждый эле-
мент идеала 21 делится на некоторый полином, тс
г не может быть ненулевой константой. Следова-
тельно, г = 0. Тогда b = qa, то есть 21 = (а), идею
21 — главный.
Целостное кольцо, в котором каждый идею
является главным, называется кольцом главны:
идеалов. Таким образом, Z и ТЦх] являются коль-
цами главных идеалов.
Любое поле является кольцом главных идеа-
лов, так как если 21 — произвольный ненулевог
идеал поля, то вместе с любым элементом а ог
содержит и а~{а = е, то есть 21 = (е) — единствен-
ный ненулевой идеал.
Эти рассуждения можно обобщить следую-
щим образом. Пусть R— целостное кольцо г
существует функция g: R которая каждо-
му ненулевому элементу а е R сопоставляет не-
отрицательное целое число g(a) со следующимг
свойствами:
1) для а Ф 0, b Ф 0 справедливо g{ab) > g(a);
2) для любых двух элементов a, b е R, где а Ф 0
существует представление b = qa + г, в кото-
ром г = 0 или g(r) < g(a).
Для кольца Z целых чисел g(a) = |а|, для коль-
ца А)х] полиномов g(a) = deg(a).
Кольцо с такими свойствами называют евкли-
довым кольцом, или евклидовой областью
Обобщением лемм 3.7.1, 3.7.2 является следую-
щая теорема.
Теорема 3.7.3. В любом евклидовом кольце
каждый идеал является главным. ;
Применяя эту теорему к единичному идеалу
совпадающему с евклидовым кольцом R, получа-
ем, что все элементы кольца R являются кратны-
ми некоторого элемента а е R. В частности, caiv
элемент а представляется в виде а = ае, где
е е R. Для b = qa получаем qa = qae, откудг
b = be, то есть евклидово кольцо обязательно со-
держит единичный элемент е.
В кольце главных идеалов R два любых нену-
левых элемента а, b порождают идеал (а, Ь) виде
{га + sb}, который тоже является главным и
следовательно, порожден некоторым элементов
d, то есть d= га + sb, а = gd, b = hd для некотс
рых g, h е R. Значит, d является наибольшие
общим делителем элементов а, b и (d) = (а, b
Таким образом, в кольце главных идеалов кал
дые два элемента имеют наибольший общий д<
литель.
43
Пример 3.7.1. Евклидовы кольца.
1. Кольцо Z[f], где i = — мнимая едини-
ца. Присоединив к кольцу Z элемент i, получим
множество, состоящее из чисел вида а = а + bi,
где а, Ь е Z, и представляющее собой кольцо це-
лых гауссовых чисел. Это кольцо является под-
множеством поля комплексных чисел и поэтому
целостно. Определим функцию
g(a) = (а + Ы)(а - Ы) = а2 + b2 е Z>0.
Функция g обладает свойством мультиплика-
тивности: g(ap) = g(a)g(P) для любого р е Z[i],
что легко проверить прямым вычислением. При
_ . „ а
Р 0 можно наити частное — = s + ti, где s, t —
Р
рациональные числа. Пусть тип — ближайшие
I I 1 I I 1
целые к s и t такие, что |5-ти|<—,р-и|< —, и
пусть у = т + ni е Zp], Тогда
z ч2 z ч2 1 1 1
= (s-m) + (t-ri) + - = -
Число 8 = а - Ру является элементом кольца
Zp]. Тогда либо 8 = 0, либо g(8) < g(P), так как
,х, о {а zR\ а g(P)
g(8) = g Р’ — -У = g(P)g — -У р—— •
I IP J) <Р J 2
2. Кольцо Z[co], где
ком-
плексный кубический корень из 1, удовлетво-
ряющий уравнению со2 + со + 1 = 0. Присоединим
к кольцу Z элемент со; полученное множество
состоит из чисел вида а = а + Ьсо (поскольку
вместо со2 можно подставить -1 - со), где а,
е Z, и представляет собой кольцо. Это кольцо
целостно как подмножество поля комплексных
чисел. Определим функцию
g(a) = (а + Ьоз)(а + бсо2) = а2 + b2 - ab е Z>0.
Функция g обладает свойством мультиплика-
тивности: g(ap) = g(a)g(p) для любого р е Z[co].
(х а[3
При р Ф 0 можно найти частное —=—= = s + to,
Р РР
где s, t — рациональные числа. Пусть тип —
ближайшие целые к s и t такие, что
1
“,|f — и пусть у = т + поз е Z[co],
Тогда
I ОС ।
gl — - У 1 = (« - ni)2 + (t - и)2 - (s - mfit - п) <
--1--Ь — — —-.
4 4 4 4
Число 8 = а - ру является элементом кольца
Z[co]. Тогда либо 8 = 0, либо g(8) < g(P), так как
g(8) = gfp-f-^-y]] = g(P)gf^-.
I 1р )) Ip J 4
Кольцо полиномов К[х,у] от двух перемен-
ных (а также кольца полиномов от большего
числа переменных) над полем К не является евк-
лидовым. Например, для fix, у) = х4 +у3 + 1,
g(x, у) = ху + х + у не существует остатка г от де-
ления f на g со степенью меньшей, чем deg(g).
Это кольцо также не является и кольцом главных
идеалов. Например, идеал (х, у) не главный.
В евклидовом кольце наибольший общий де-
литель двух элементов а, b (вычисляемый алго-
ритмом Евклида) образует главный идеал, совпа-
дающий с идеалом (а, Ъ), образованным этими
элементами. Поэтому иногда вместо НОД(а, Ь)
пишут (а, Ь).
3.8. Разложение на множители
Согласно основной теореме арифметики в
кольце Z существует однозначное разложение на
простые множители. Однако такая однознач-
ность имеет место не во всех целостных кольцах.
Пример 3.8.1. Отсутствие однозначного раз-
ложения на множители.
Рассмотрим кольцо Z[V-^5]sZ[x]/(x2+5)
чисел вида с целыми коэффициентами
а, Ь. Здесь число 6 может быть разложено суще-
ственно разными способами:
6 = 2- 3и6 = (1 + ур5)(1 -ур5). мз
Покажем, что полученные сомножители 2, 3,
1 + у/-5, 1 - у/-5 далее не раскладываются. Дей-
ствительно, если предположить, что
2 = (a + byp5)(c + d>p5) с целыми a, b, с, d, то
легко видеть, что делители числа 2 должны быть
сопряженными. Значит, 2 = (а+Ьу]-5)(а-
= <? + 5Ь2 с целыми а и Ь, что невозможно. Оче-
видно, аналогичное предположение о разложимо-
сти числа 3 тоже ведет к противоречию. С другой
44.
стороны, если предположить, что существует раз-
1 + у[-5 = (a + b4-5)(c + d4~5)
ложение
с целы-
ми а, Ь, то должно существовать и разложение
1 -4-5 - (а-ъ4-5)(с-d4-5) Перемножив эти
числа, получаем
(1 + - лр5) = (о2 + 5/>2 )(с2 + 5с/2 ) = 6 .
Поскольку с?2 + 512 ^2, а2 + 5Ь2 Ф 3, то остает-
ся а2 + 5b2 = 1. с2 + 5с/2 = 6, откуда а = ±1, 6 = 0,
с = ±1, с/=±1, то есть числа \ + 4~5, 1-4-5
тоже на множители не раскладываются.
Любой элемент а целостного кольца может
быть представлен как произведение самого себя
на произвольный обратимый элемент b кольца и
обратного к нему элемента 6-1: а = (ab)b~A. Такие
разложения называются тривиальными. Эле-
мент, допускающий только тривиальное разло-
жение, называется неразложимым. Простой эле-
мент всегда неразложим, но неразложимый эле-
мент может не быть простым. В примере 3.8.1 в
выполняется (1 + 4-5) | (2 • 3), но
(1 + V^5)|2 и (1 + V^5)[ 3, то есть элемент
1 + 4- 5 неразложимый, но не простой.
Элементы а и с = ab, для обратимого Ь, назы-
вают ассоциированными. Каждый из них являет-
ся делителем другого. Поэтому (а) щ (с), (с) щ (а)
и, значит, (а) = (с), то есть ассоциированные эле-
менты порождают один и тот же идеал. Отноше-
ние ассоциированности является эквивалентно-
стью и разбивает множество элементов кольца на
классы. Таким образом, класс неразложимых ас-
социированных элементов можно представить
одним неразложимым элементом.
Если элемент b является делителем элемента
а, но b не ассоциирован с а (то есть а = Ъс и с не
является обратимым), то Ъ называется собствен-
ным делителем элемента а. В этом случае а не
является делителем b и идеал (6) является собст-
венным делителем идеала (а). (В противном слу-
чае выполнялось бы равенство b = ad, то есть
а = acd и е- cd, и элемент с был бы обратимым.)
Поэтому неразложимый элемент можно опреде-
лить как ненулевой элемент, не имеющий необ-
ратимых собственных делителей.
Лемма 3.8.1. Пусть а е R — ненулевой эле-
мент целостного кольца и идеал (а) — простой.
Тогда а — неразложимый элемент.
Доказательство. Если а = Ьс, то один из со-
множителей, например, Ь, лежит в (а). Тогда
можно написать b = ad, где d' е R. Следовательно,
а = acdncd= е, то есть с — обратимый элемент.
Говорят, что элемент а целостного кольца R
обладает однозначным разложением на про-
стые множители, если имеет место равенство
а = upi.. .рп где и — обратимый элемент кольца,
р, — неразложимые элементы, и для двух таких
разложений а = ир\...рг и а = u'qA...qs имеет ме-
сто г = а и pt: = ирр, где и, — обратимые элементы,
U = U]...USU'.
Целостное кольцо называется факториаль-
ным, если всякий его элемент имеет однозначное
разложение на простые множители. В фактори-
альном кольце неразложимые элементы являют-
ся простыми. л»,';., ч Гё*
Теорема 3.8.2. Всякое кольцо главных идеа-
лов обладает однозначным разложением на про-
стые множители. В факториальном кольце не-
разложимые элементы являются простыми.
Доказательство. Сначала докажем, что ка-
ждый ненулевой элемент имеет однозначное
разложение на простые множители. Обозначим
через S множество главных идеалов кольца R,
образующие которых не имеют разложения на
простые множители. Предположим, что S 0, и
покажем, что это ведет к противоречию. Рас-
смотрим произвольную цепочку возрастающих
главных идеалов (<?]) с ... с (<?„) с ... из S. Мы
утверждаем, что она не может быть бесконечной.
Действительно, сумма идеалов такой цепочки
является идеалом в А и, следовательно, главным
идеалом, который обозначим через (а). Обра-
зующая а этого идеала должна лежать в некото-
ром элементе цепочки, скажем, в (с?,,). Имеем
(с/„) £ (4) С (<7»)- Значит, цепочка обрывается на
(с?„). Следовательно, любой идеал, содержащий
(<?„) и отличный от (с/„), имеет образующую, до-
пускающую разложение на простые множители.
Элемент ап не может быть простым, так как
иначе он имел бы тривиальное разложение на
простые множители. Значит, существует пред-
ставление а,, - Ъс, где (6) Ф (а„), (с) ф (д„), а потому
бис обладают разложением на простые множи-
тели. Но произведение этих множителей дает раз-
ложение на простые множители для ап. Следова-
тельно, множество S может быть только пустым.
Предположим, что а е R имеет два разложения
a = upi...pr = u'q\...qs на простые множители. Так
как pi делит произведение в правой части равенст-
ва, то р] делит один из элементов q,. После перену-
мерации (в силу коммутативности) можно считать,
что это q\. Тогда найдется обратимый элемент щ
такой, что qx = пру. Сокращая на р\, получаем
ирг-.-Pr-du\qi...qs. Доказательство однозначно-
сти разложения завершается по индукции.
Однозначное разложение на простые множители
имеет место и в евклидовых кольцах, так как они яв-
ляются кольцами главных идеалов по теореме 3.7.3.
45
Для коммутативных колец справедливы сле-
дующие включения: {коммутативные кольца} о
д> {целостные кольца} zd {факториальные коль-
ца} о {кольца главных идеалов} {евклидовы
кольца}.
Теорема 3.8.3. В произвольном кольце глав-
ных идеалов неразложимый необратимый эле-
мент р порождает максимальный идеал, то есть
кольцо классов вычетов по этому идеалу являет-
ся полем.
Доказательство. Если элемент р неразло-
жим, то у него нет собственных делителей. По-
скольку по условию каждый идеал является
главным, то у идеала (р) тоже нет собственных
делителей, кроме единичного идеала. Следова-
тельно, идеал (р) максимален. По теореме 3.6.1
кольцо классов вычетов по идеалу (р) является
полем.
3.9. Кольцо эндоморфизмов модуля.
Модули над кольцами
Пусть М— модуль. Отображение <р модуля М
в себя по определению является эндоморфизмом,
если <р(п + Ъ) = <р(п) + <р(6) для всех а,Ъ^М. Оп-
ределим произведение эндоморфизмов ср и ц/ как
композицию отображений. Тогда для т е М вы-
полняется ((pip)(///) = (p(ip(/;?)).
Поскольку областью определения и областью
значения эндоморфизмов являются элементы мо-
дуля М, то можно определить сумму эндомор-
физмов как сумму их образов, при этом сложение
образов выполняется в соответствии с групповой
операцией модуля. Если а, Ь, т — элементы мо-
дуля М, (р, ip — эндоморфизмы и (p(zzz) = а,
vp(m) = Ъ, то ((р + ip)(m) = (p(zzz) + ip(w) = а + b.
Теорема 3.9.1. Эндоморфизмы модуля обра-
зуют кольцо.
Доказательство. Сумма эндоморфизмов яв-
ляется эндоморфизмом: ((р + ip)(r/ + b) = ((р + ip)(o) +
+((р + ip)(6) = (р(п) + ip(n) + (р(Ь) + \р(Ь) = (р(п + Ь) +
+ ip(<? + b). В силу свойств модуля сложение эн-
доморфизмов коммутативно и ассоциативно.
Отображение о всех элементов модуля в нулевой
элемент модуля является нулевым эндомор-
физмом:
((р + о)(а) = (р(п) + о(п) = (р(п) + 0Л/ = (р(<а).
Кроме того, для каждого эндоморфизма <р су-
ществует противоположный эндоморфизм —<р та-
кой, что -<р(п) = (р(-а). Следовательно, эндомор-
физмы образуют модуль по сложению. Дистрибу-
тивность умножения эндоморфизмов относитель-
но сложения следует из того, что для любого эн-
доморфизма (р выполняется (р(<? + Ь) = (р(<?) + (р(6).
Тогда (%(ф + vp))(n) = х((р(п)) + X(V(«)) или
Х(<р + ip) = Х<Р + XV- Наконец, существует единич-
ный эндоморфизм в, отображающий каждый эле-
мент модуля в себя, при этом £<р = (ре = (р для лю-
бого (р.
Кольцо эндоморфизмов модуля не обязательно
целостное или даже коммутативное. Например,
аддитивная группа кольца Z[z] является модулем.
Пусть (р: (<з + Ы) —> <7, ip: (а + bi) -> Ы. Легко убе-
диться, что это эндоморфизмы модуля (но не
кольца!) Z[z]. Тогда (pip = ip(p = o— нулевой эн-
доморфизм, при этом ни один из сомножителей не
является нулевым эндоморфизмом. В модуле
квадратных матриц размера 2 над полем операция
умножения на матрицу является эндоморфизмом.
Однако произведение матриц некоммутативно.
Модуль, имеющий простой порядок р, являет-
ся циклическим с образующей а. Следовательно,
каждый элемент такого модуля можно предста-
вить в виде па, 0 < п <р - 1. Тогда эндоморфизм
полностью определяется образом образующей.
Образующая может иметь р образов, следова-
тельно, кольцо эндоморфизмов состоит из р эле-
ментов. Если (р(п) = та, vp(a) = па, то (<р + ip)(n) —
= (т + п)а, ((р\р)(й) = тпа, при этом сложение и
умножение выполняются по модулю р. Таким
образом, кольцо эндоморфизмов модуля порядка
р изоморфно кольцу TLIpTL.
Эндоморфизмы конечных групп часто ис-
пользуются в криптографии как для анализа
безопасности алгоритмов, так и для ускорения
вычислений. Примером может служить ком-
плексное умножение на эллиптических кривых
(см. пп. 6.14.5, 7.10).
Пусть R— коммутативное кольцо, М— мо-
дуль, для которого определено умножение на
элементы кольца R, и при этом выполняются
свойства (а + b)m = ат + bm, (ab)m = a(bni) для
любых a,b е Rvt т е М.
Такая конструкция называется модулем над
кольцом R.9
Пример 3.9.1. Модули над кольцами.
1. Модулем над кольцом является векторное
пространство над произвольным полем К, при
этом в качестве кольца R используется поле К.
1. Аддитивная группа кольца Z[z] может быть
рассмотрена как двумерный модуль над 7L
3. Аддитивная группа кольца /фт] может быть
рассмотрена как модуль над R.
4. Любое коммутативное кольцо может быть
рассмотрено как одномерный модуль над собой [7].
9 Модуль над R называют также /^-модулем.
46
5. Для любого модуля существует эндомор-
физм: а —> па = а + а + ... + а (и раз, п е Z). По-
этому любой модуль является модулем над Z.
Любой идеал кольца R является его подмоду-
лем, если рассматривать R как модуль над собой.
Разные идеалы могут быть изоморфны как моду-
ли над R. Идеал 21 целостного кольца R как мо-
дуль изоморфен кольцу R тогда и только тогда,
когда он главный. Действительно, если 21 - (а) и
г е R, то г —> га — нужный изоморфизм. Обрат-
но, пусть ср: R -> 21 — изоморфизм модулей, е —
единичный элемент кольца R и <р(е) = а. Тогда
ф(г) = <р(7де) = 7'<р(е) = га, то есть 21 = (а). Поэтому
число неизоморфных как модули идеалов цело-
стного кольца является мерой его отклонения от
кольца главных идеалов [7].
3.10. Свойства полиномов
Если R — целостное кольцо, то присоединени-
ем переменной х получаем коммутативное кольцо
полиномов А[х]. Такое присоединение можно вы-
полнять несколько раз, в результате чего получа-
ется кольцо Я[хь ...,х„]. В этом случае говорят,
что полином fix\, ...,xfi е А[хь ...,х„] определен
над кольцом R. Согласно теореме 3.4.2 кольцо
А[хь ...,х„] — целостное. Если К~~ поле частных
кольца R, то поле частных кольца А[хь ..., х„] обо-
значается через К{х\, ...,х„). Элементы поля
К(Х], ...,х„) называются рациональными функция-
ми. Всякая рациональная функция может быть
f
записана в виде —, где fig A[xi, ..., х„] и g Ф 0.
g
Если для некоторого набора (Ъ\, ..., Ь„), где
b, е R, знаменатель gt/л, Ь„) отличен от нуля,
f
то говорят, что рациональная функция — опре-
g
делена в (Ъ\, ..., hfi. Подставив вместо перемен-
ных х, элементы Ь„ можно получить значение
функции в поле К.
Полином из /?[Х1,...,х„] от нескольких пере-
менных можно рассматривать как полином от од-
ной переменной х„ над кольцом А[хь ...,x„_i], то
есть как элемент кольца А[хь ..., x„-i][x„].10 В этом
случае его коэффициенты являются полиномами.
Например, для полинома х2у3 + 2х2у + Зу3 коэффи-
циент при х2 равен у3 + 2у, коэффициент при у
равен х2 + 3.
10 Действительно, имеет место изоморфизм
Z?[xj, ...,х„] —> 7?[xi, ...,x„-i][x„], задаваемый подста-
новкой.
Пусть К— поле. Тогда А^х] является кольцом
главных идеалов, то есть каждый идеал порож-
ден единственным элементом. Аналогичное ут-
верждение справедливо и для колец от несколь-
ких переменных над полем К.
Теорема 3.10.1. В кольце А^Х], ...,х„] каждый
идеал конечно порожден.
Доказательство см. в работе [3].
Полином называется однородным}1 если все
его слагаемые имеют одинаковую степень. Про-
изведение однородных полиномов является од-
нородным полиномом.
Теорема 3.10.2. Полином fix], ...,хп) степени
d является однородным тогда и только тогда, ко-
гда для любого и имеет место равенство
fiuX], ..., их,,) = udfix\, ..., х„).
Доказательство. Поскольку каждый одно-
член ах}' х}' однородного полинома f имеет
степень d, то а(их})“' ...(их,, )“" = aud xfi ...xfi’.
Вынося общий множитель и, получаем, что для
каждого однородного полинома выполняется
равенство fiuxy. их,,) = udfix\, х„). Необхо-
димость доказана.
Докажем достаточность. Для любого одно-
члена степени d выполняется равенство
д(мх1)а’...(ш,„)“и = au°l+ '+“,’х|“1...х“’’. Поскольку
оно справедливо для любого и, то из гомомор-
физма, получаемого подстановкой элементов
кольца вместо переменных х, и и, следует, что
для каждого слагаемого выполняется равенство
«] + ...+ а„ = d. Следовательно, все слагаемые
имеют одинаковую степень d, то есть полином
является однородным.
Отметим, что символ и в формулировке тео-
ремы можно рассматривать как новую независи-
мую переменную. В случае полиномов от не-
скольких переменных можно определить опера-
цию подстановки полинома вместо независимой
переменной.
3.11. Производная и кратные корни
Пусть R — коммутативное кольцо и
/(х) е А[х] — произвольный полином. Присоеди-
ним к коммутативному кольцу А[х] новую пере-
менную h и построим полином fix + h) е А[х, А].
Разложим этот полином по степеням А:
fix + А) =Дх) + hfi(x) + А2/2(х) + ... .
11 Однородный полином также называют формой.
47
Найдем вычет по модулю й2:
fix + h) =fix) + hfi(x) (mod /?2).
Коэффициент f(x) при h называется произ-
водной полинома/х) и обозначается/'(х). Оче-
видно, что значение f'(x) можно получить, если
найти разность fix + h) -fix), разделить ее на Л и
положить h = 0. Поэтому в поле вещественных
чисел это определение производной совпадает с
определением производной в дифференциальном
исчислении.
Такое чисто алгебраическое определение про-
изводной применимо к кольцам, в которых нель-
зя определить производную традиционными ме-
тодами, например, к кольцам полиномов над ко-
нечными полями, кольцам полиномов над коль-
цом циркулянтных матриц, кольцам классов вы-
четов и т. п.
Теорема 3.11.1. Пусть fix), fix') — произволь-
ные полиномы из коммутативного кольца. Имеют
место равенства (f+ g)’ =f + fi. (fg)' =f'g +ffi.
Доказательство. По определению произ-
водной
fix + h) +fix + h) =
=fix) + hf’(x) + g(x) + hfi(x) (mod /?2),
то есть производная суммы равна сумме произ-
водных.
Аналогично,
fix + h)fix + h) = (fix) + hf(x))(fix) + hg '(x)) =
=fix)fix) + (f'(x)fix) +fix)g'(x))h (mod /?2).И
Утверждение теоремы по индукции обобща-
ется на произвольное число слагаемых и сомно-
жителей. Имеет место равенство (ах?)' = сих”-1 и,
следовательно,
Если кольцо R является полем, то для про-
изводной рациональной функции также спра-
ведлива формула дифференциального исчисле-
ния:
^/'(x)g(x)-/(x)g'(jc)
<g(x)J g2(x)
Кроме того, выполняются формулы для част-
ных производных полиномов от нескольких пе-
ременных, а также для производной сложной
функции: если F(x\, ..., х„) и/(xj, ...,х„) — поли-
номы из /ф.Х|, ...,х„] и Ft= cF/cfi , то
/=1
где F',/' — полные производные.
Пусть R— целостное кольцо с единичным
элементом. Элемент а е R называется корнем
полинома fix) е А[х], если/б?) = 0. В этом случае
полином fix) делится на х - а. Действительно,
поскольку /?[х] — евклидово кольцо, то деление
fix) на х - а дает равенство fix) = q(x)(x - а) + г,
где г — константа. Подстановка в это равенство
х = а дает г = 0, то есть fix) = q(x)(x - а). По ин-
дукции получаем, что если ...,£%— различ-
ные корни полинома fix), то fix) делится на про-
изведение (х - а\)...(х - ak).
Отсюда следует, что полином степени п над
целостным кольцом имеет не более п корней.
Однако, если кольцо имеет делители нуля, то
число корней может быть больше п. Например, в
кольце Z/35Z квадратное уравнение х2 = 1 имеет
четыре корня: 1, 6, 29, 34.
Если /(х) делится на (х - а)к, но не делится на
(х - а)к+\ то а называется корнем кратности к
полинома/х).
Корень кратности к полинома fix) над целост-
ным кольцом характеристики, отличной от к, яв-
ляется корнем кратности к - 1 производной f'(x).
Действительно, из равенства fix) = (х - affix),
где g(x) не делится на х - а, следует, что f'(x) =
= к(х - df^fix) + (х - dffi(x). Очевидно, что сум-
ма в правой части делится на (х - а)к~х. При пере-
ходе к сравнению по модулю (х - af второе сла-
гаемое обращается в нуль, а первое слагаемое
отлично от нуля. Таким образом, сумма не де-
лится на (х - af.
Следовательно, корень кратности 1 (или про-
стой корень) не является корнем производной.
Эти рассуждения остаются верными и при за-
мене линейного полинома х - а, соответствую-
щего корню а, на произвольный полином.
Назовем полином (от одной переменной)
fix) е А[х] свободным от квадратов, если он не
делится на квадрат полинома, отличного от кон-
станты. Полином/х) над целостным кольцом R
свободен от квадратов, если НОД(/(х),/'(х)) е R.
3.12. Симметрические функции
Пусть R— целостное кольцо. Полином из
кольца /фхн ...,х„] называется симметрическим
полиномом12 от переменных хц ...,х„, если он
переходит в себя при любой перестановке этих
переменных.
12 Симметрический полином называют также сим-
метрической функцией.
48
С помощью новой переменной z построим по-
лином fiz)=z(z-xl)...(z-x„). Разложим его по
степеням z: fiz) -z1 — Giz"1 + ... + (—I )"g„. Тогда
Oi = Xi + x2 + ... + x„,
G2 ~ + X|X3 + ... + X„_1X„,
G3 = ХЦХ2Х3 + X]XlX4 + ... + X„^X„^X„,
Очевидно, что это симметрические функции.
Функции о, называются элементарными сим-
метрическими функциями.
Если в некоторый полином <р(оь ..., о„) вместо
переменных о, подставить элементарные симмет-
рические фуНКЦИИ ОТ X], ...,х„, то этот полином
будет симметрической функцией отхь ...,х„. При
этом слагаемое вида со^.-.о^ окажется одно-
родным полиномом степени ц, + 2ц2 + ... + от
х„ так как каждая элементарная симметрическая
функция с, является однородным полиномом сте-
пени z. Сумму pi + 2р2 + ... + «Ц„ назовем весом
слагаемого от)1' ...о^’. Весом полинома <р(оi,..., g„)
назовем наибольший вес его слагаемых. Оказы-
вается, любой симметрический полином может
быть выражен как полином от элементарных
симметрических функций.
Теорема 3.12.1. Симметрический полином
над целостным кольцом может быть единствен-
ным образом представлен в виде полинома от
элементарных симметрических функций.
Доказательство. Упорядочим словарно задан-
ный симметрический полином от х,- так, чтобы
слагаемое х^'.-.х"" предшествовало слагаемому
хр‘...х^", если первая ненулевая разность а,~Р,
положительна. Поскольку этот полином симмет-
рический, то в него вместе со слагаемым
axf' ...xfi входят и все слагаемые, показатели ко-
торых являются некоторой перестановкой показа-
телей а,. Первое (в словарном упорядочении) сла-
гаемое обозначим а^Ху'...x“”, для этого слагае-
мого «!>...>«„. Такую же сумму дает произведе-
ние элементарных симметрических функций
zzgJ11 а2 g2 2-аз... g^" . Вычтем это произведение из
данного полинома, упорядочим разность словарно,
найдем старшее слагаемое и повторим процедуру.
Поскольку степень разности не превышает сте-
пени первоначального симметрического поли-
нома, а число его слагаемых конечно, то на неко-
тором шаге алгоритм остановится.
Докажем единственность. Если <р1(у],...,%)^
^фгОь —,Уп), то и ффоь ...,0,0^92(01, ...,о„).
Пусть (р = (pi - (р2, тогда достаточно показать, что
из <р(у], * 0 следует <p(oi,..., о„) Ф 0. Каж-
дое слагаемое в <р(уь ••,»/) * 0 можно записать в
cxj —ct-2 g.2— ct3 ccR
виде вУ\ Уг — Уп . Среди всех наборов
показателей (си,..., а„), соответствующих коэф-
фициенту а ф 0, существует первый в словарном
упорядочении. Заменим у, на g„ тогда получится
первое в словарном смысле слагаемое полинома
а1 СС„ гх
(p(oi,.... g„): axi т2 ~ — х„ . Это слагаемое
нельзя ни с чем сократить, следовательно,
(p(Gi, ..., о„)^0.
Следствие 3.12.2. Каждая симметрическая
функция корней полинома выражается через ко-
эффициенты этого полинома.
Доказательство. Если Xz)=(z-xi)...(z-x„)=
= z + a\z + — + ат то а\ ~ —Gj, <72 = g2,_,
а„ = (-1 )”g„. Остается применить теорему 3.12.1.
Важной симметрической функцией является
произведение квадратов разностей корней поли-
номаДх) = х” + gix'7-1 + ... + а„ е А[х]
П = П(х,-ху)2.
i>J
Выражение для D как полинома от коэффици-
ентов а\ = -G1, <?2 = g2, ..., а„ = (-1)”g„ называется
дискриминантом полинома fix). Если кольцо R
целостное, то нулевой дискриминант означает,
что хотя бы один из сомножителей в выражении
для D равен нулю, то есть fix) имеет хотя бы
один кратный корень.
Симметрические функции можно представ-
лять и с помощью другого базиса. Обозначим
Т1 = Е Х< ’ Т2 = £ Х> = Ё Х” •
1=1 1=1 1=1
Здесь Ti = G], т2 = О]2 - 2о2, т3 = Gi3 - 3gig2 +
+ Зо3 и т. д. Если полином рассматривается над
полем характеристики 0 или р (при п < р), то
функции т, алгебраически независимы (см. п. 4.2),
и можно выражать целую симметрическую функ-
цию через т;.
3.13. Разложение на множители
полиномов от нескольких переменных
Кольцо полиномов /Дх|, ..., х„] над целостным
кольцом R целостно. Следуя работе [3], покажем,
что аналогичное утверждение имеет место и для
факториальных колец.
49
Пусть R — целостное кольцо и
п
f(x) = У^а,х' — произвольный полином из А[х].
i=0
Наибольший общий делитель а коэффициентов
ао, ...,а„ называется содержанием полинома/(х).
Тогда/х) = afix), где g(x) — полином с содержа-
нием 1, причем a, g(x) определены однозначно с
точностью до обратимых элементов.
Если f— полином от нескольких переменных,
то различают содержание относительно различ-
ных переменных.
Пример 3.13.1. Содержание.
Полином ху2 +у2 + ху-у + х3 + 1 из кольца
Z[x,y] = Z[x][y] имеет содержание х + 1 по пере-
менной у, так как имеет место равенство
(х + 1)у2 + (х + 1)(х - 1)у + (х + 1)(х2-х + J).
Лемма 3.13.1. Произведение двух полиномов
с содержанием 1 вновь является полиномом с
содержанием 1.
Доказательство. Пусть fix) = ao +а\х+...,
g(x) = bo + b\X + ... — полиномы с содержанием 1.
Предположим обратное: содержание полинома
fix)g(x) равно с и является необратимым элемен-
том кольца R. Если р— произвольный простой
делитель элемента с, то р должен делить все ко-
эффициенты полинома/(х/4х). По условию не все
коэффициенты fix) и g(x) делятся на р. Пусть г и
s — максимальные степени х, для которых а, и bs
не делятся на р. Коэффициент при xns полинома
fix)fix) равен arbs + ar_i bs+i + bK-\ + a,-2bs+2 +
+ a^b.^ + .... В этой сумме все слагаемые, кроме
первого, делятся на р, так как один из сомножите-
лей делится на р. Поскольку коэффициент при xns
по предположению делится на р, то arbs тоже
должно делиться на р. Получили противоречие.
Следовательно, содержание полинома fix)g(x)
равно 1. Я
Пусть К— поле частных кольца R. Тогда ка-
ждый полином из К[х] однозначно раскладыва-
ется на простые множители. Чтобы перейти от
разложения в К[х] к разложению в А[х], предста-
F(x)
вим каждый полином fix) е К[х] в виде -----------,
b
где F(x) е 7?[х] и b е R — произведение знамена-
телей коэффициентов полинома fix). Полином
F(x) представим как произведение его содержа-
ния а на полином g(x) с содержанием 1, то есть
F(x) = a fix), и f(x)=—g(x). Имеет место сле-
b
дующая лемма.
Лемма 3.13.2. В равенстве /(х)= —g(x) по-
b
лином g(x) с содержанием 1 определяется одно-
значно с точностью до обратимых в R элементов.
Обратно, полином/х) определяется полиномом
fix) однозначно с точностью до обратимых в
К[х] элементов. Произведению Д(х)/2(х) биектив-
но соответствует произведение gi(x)g2(x) поли-
номов с содержанием 1. Если полиномах) не-
разложим в К[х], то полином g(x) неразложим в
/хДх], и обратно.
Доказательство. Пусть даны два разных
представления полинома/х):
а с
f(x)=-g(x)=—h(x).
b а
Тогда adfix) = cbh(x). Содержание в левой
части равно ad, содержание в правой части равно
Ьс. Следовательно, ad = ebc, где в — обратимый
элемент кольца R. Подставим это равенство в
предыдущее и сократим на ch. Получим
sg(x) = h(x). Значит, полиномы g и h отличаются
обратимым в R множителем.
Таким же образом для произведения полино-
мов / (х) = у g, (х), /2 (х) = 4 g2 (х) получаем
b d
/i(x)/2(x) = -^|g](x)g2(x). Согласно лемме
bd
3.13.1 произведение gi(x)g2(x) опять является по-
линомом с содержанием 1. Следовательно, про-
изведению fifififix) соответствует произведение
gi(x)g2(x).
Если полином fix) неприводим, то и g(x) будет
неприводимым, поскольку любое разложение
вида fix) = gi(x)g2(x) приводит к разложению
/(x)=yg(x)=yg1(x)g2(x). Обратное утвер-
b b
ждение доказывается аналогично.
Теорема 3.13.3. Если R— факториальное
кольцо, то и А[х] — факториальное кольцо.
Доказательство. Целостность кольца 1?[х]
была доказана в теореме 3.4.2. Рассмотрим раз-
ложение на множители произвольного полинома
из А[х]. Неприводимый полином обязательно
является константой в R или неприводимым по-
линомом с содержанием 1, так как любой другой
полином разложим в произведение своего со-
держания и полинома с содержанием 1. Следова-
тельно, для разложения fix) нужно сначала раз-
ложить его в произведение содержания и поли-
нома с содержанием 1, а потом каждый из со-
множителей раскладывать на простые множите-
ли. По условию теоремы содержание однозначно
50
раскладывается на простые множители с точно-
стью до обратимых элементов, полиномы с со-
держанием 1 также однозначно раскладываются
согласно лемме 3.13.2.
Следствие 3.13.4. Если R— факториальное
кольцо, К— его поле частных и полином fix)
неразложим в К[х], то/(х) неразложим и в А[х].
3.14. Полукольца и решетки
Полукольцом S будем называть структуру с дву-
мя операциями— сложением и умножением, — в
которой выполняются следующие свойства [1]:
1) все элементы по сложению образуют комму-
тативный моноид с нулем 0;
2) все элементы идемпотентны относительно
операций сложения и умножения: а + а = а,
а - а = а для всех а е S;
1) все ненулевые элементы образуют коммута-
тивный моноид по умножению с единичным
элементом 1, причем 0 является аннулято-
ром: 0 • а ~ а • 0 = 0 для всех а е S;
I) умножение дистрибутивно относительно
сложения: a(b + c) = ab + ас.
Примерами полукольца являются: множество
тодмножеств некоторого множества с операция-
ми объединения и пересечения подмножеств;
множество высказываний, принимающих истин-
юе или ложное значение, с операциями ИЛИ, И.
Теория решеток имеет дело со свойствами от-
ношения порядка, заданного на некотором (час-
тично) упорядоченном множестве.
Очевидно, что всякое подмножество упорядо-
ченного множества является упорядоченным
ножеством с тем же отношением порядка.
Легко показать, что всякое упорядоченное
ножество М содержит не более одного элемента
7, удовлетворяющего неравенству а < х для всех
лементов х из М. Действительно, если а и Ъ —
два таких элемента, то имеет место а < Ъ, Ь<а,
откуда а = Ъ. Такой элемент, если он существует,
называется наименьшим элементом (нулем) и
обозначается символом 0; двойственный к нему
элемент упорядоченного множества, если он су-
ществует, называется наибольшим элементом
(единицей) и обозначается символом 1. Таким
образом, если такие элементы существуют, то
для всех х е М имеет место двойное неравенство
0<х<1. Ясно, что если X] < ... <х„ <хь то
X] = ... - Х„.
Пример 3.14.1. Упорядоченные множества.
1. Для упорядоченного множества (Р(М), с)
элементом 0 будет пустое множество, а элемен-
том 1 — само множество М.
2. Для упорядоченного множества (Z>0, |)
элементом 0 будет число 1.
Элемент а упорядоченного множества М на-
зывается минимальным, если неравенство х < а
невозможно ни для какого х е М. Элемент а упо-
рядоченного множества М называется макси-
мальным, если неравенство х > а невозможно ни
для какого х е М.
Наименьший элемент обязательно будет ми-
нимальным, но обратное неверно. Различие меж-
ду минимальным и наименьшим элементами
можно пояснить на следующем примере. В упо-
рядоченном множестве (Р*(М), с:) непустых под-
множеств множества М наименьшего элемента
нет, а минимальными являются все одноэлемент-
ные подмножества. Если упорядоченное множе-
ство имеет наименьший (наибольший) элемент,
то он будет единственным минимальным (мак-
симальным) элементом.
Теорема 3.14.1. Каждое непустое конечное
множество имеет минимальный и максимальный
элементы.
Доказательство [6]. Пусть множество М
состоит из элементов хь ..., х„. Положим пц <— Xj
и для k> 1 положим Шк<г- Хк, если xJ.<m(t_], и
пц <— в противном случае. Тогда т„ — ми-
нимальный элемент. Аналогично доказывается
существование максимальных элементов.
Элементы а и b упорядоченного множества
(М, <) называются сравнимыми, если а<Ъ или
b < а. В противном случае элементы несравнимы.
Линейно упорядоченные подмножества упоря-
доченного множества называются цепями. В це-
пи понятие наименьшего и минимального эле-
ментов совпадают.
Элемент а е А называется верхней гранью не-
пустого подмножества X упорядоченного множе-
ства (А, <), если выполняется неравенство х < а
для всех х е X. Двойственно вводится понятие
нижней грани. Ясно, что подмножество может
иметь много верхних и много нижних граней, а
может не иметь ни одной. Наименьшая верхняя
грань подмножества X называется точной верх-
ней гранью и обозначается sup АС Из свойства
антисимметричности отношения порядка следу-
ет, что если точная верхняя грань существует, то
она единственна.
Двойственно вводится понятие точной ниж-
ней грани inf А". Если точная нижняя грань суще-
ствует, то она единственна.
Решеткой называется упорядоченное множе-
ство L, в котором любые два элемента х, у имеют
точную нижнюю грань, или «пересечение», обо-
значаемое х л у, и точную верхнюю грань, или
51
«объединение», обозначаемое х v у. Решетками
являются множества (Z>0, | ), (Z>0, <), (К>(|, <),
(ЛЖ)-
Решетка L называется полной, если любое ее
подмножество X имеет в L точные верхнюю и
нижнюю грани. Ясно, что любая непустая полная
решетка содержит наибольший элемент 1 и наи-
меньший элемент 0 (для этого надо положить
X=L). Любая конечная решетка является пол-
ной. Любое линейно упорядоченное множество
является решеткой. Действительно, для пары
сравнимых элементов упорядоченного множест-
ва точной нижней гранью будет меньший из этих
элементов, а точной верхней гранью — больший.
Пусть (L, <) — некоторая решетка. Сопоставляя
каждой паре элементов х, у е L их точную ниж-
нюю грань, определим на множестве L бинарную
операцию (х,у)~>х л у. Аналогично определим
бинарную операцию (х, у) -> х v у. Эти операции:
- идемпотентны: х лх= х vх = х;
- коммутативны: х лу= у лх, х v у = уv х;
- ассоциативны: х л (у л z) = (х лу) л z, х v (у v z) =
= (х V у) V Z.
Кроме того, имеют место законы поглощения:
XA(yVz)=XV(yAz)=X.
Гомоморфизмом решеток L и М называется
отображение ц/: L -> М такое, что для любых а,
b g L выполняются условия \Да v b) = ху(а) v \y(b)
и лЬ) = Х|/(г/) а <у(6). Биективный гомомор-
физм решеток называется изоморфизмом.
Решетка L называется дистрибутивной, если
для любых элементов a, b, с е L выполняются
равенства:
a a (b v с) = (a a 6) v (а л с);
a v (Ъ л с) = {a v b) л (a v с).
Каждое из этих равенств влечет другое. Лю-
бая цепь является дистрибутивной решеткой.
Имеет место следующая теорема [2].
Теорема 3.14.2. Если в дистрибутивной ре-
шетке L для любого с g Z имеют место равенства
cvx = evyHCAx = CAy, где х, у е L, то х = у.
Доказательство. Из закона поглощения
следует, что х = х л (с vx). Из первого условия
теоремы имеем х = х л (с v х) = х л (с v у). В силу
дистрибутивности решетки, раскрывая скобки,
получаем х = (х л с) v (х л у). Заменяя хлс на
у л с, получаем х = (у л с) v (х л у). В силу дист-
рибутивности X = у А (с V х) = у л (с V у) = у.
Аксиоматика дистрибутивной решетки с ну-
лем и аксиоматика полукольца совпадают, по-
этому такую решетку можно рассматривать как
полукольцо с двумя бинарными операциями:
сложением v и умножением л.
Пусть L — решетка с нулем и единицей. До-
полнением к элементу х е L называется элемент
у е L такой, что хлу=0, xvy=7. Если каждый
элемент решетки L имеет дополнение, то гово-
рят, что L является решеткой с дополнениями. Не
все решетки имеют дополнения. Например, в це-
пи элементы, отличные от 0 и 1, не имеют допол-
нений.
Пример 3.14.2. Булевы функции как решетки.
Булевой функцией п переменных будем назы-
вать отображение {true, false}" -> {true, false}.
Если сопоставить true о 1 и false -о 0, то булева
функция задается отображением F2„ —> F2.13
Множество булевых функций п переменных,
заданных в базисе И (а), ИЛИ (v), НЕ ( ), обра-
зуют дистрибутивную решетку, в которой каж-
дый элемент обладает единственным дополнени-
ем. Дополнением к булевой функции /будет ее
инверсия f . При этом / = 0 тогда и только
тогда, когда/= 1. Кроме того, это множество яв-
ляется полукольцом, в котором операция ИЛИ
является сложением, а И — умножением.
3.15. Кольцо полиномов Жегалкина
3.15.1. Полиномы Жегалкина
Кольцом G„ полиномов Жегалкина называется
кольцо классов вычетов
Р2[ХЬ ..., Х„]/(Х1(1 ©X]), ...,х„(1 ®х„)).
Элементы кольца G„ называются полиномами
Жегалкина.
Кольцо G„, в отличие от обычного кольца по-
линомов над F2, конечно. Степень полинома Же-
галкина по каждой переменной не превосходит
1. Поэтому можно записать:
G„ - ап © У а.х. © У а/.х.х,- ©... © д, „х,... х„ >,
Г1 V £_ 4 I I £_ 4 J I J L...rf 1 П 7
где все 2" коэффициентов а„ а,,, ..., а]...„ лежат в
поле F2. В G„ выполняется равенство х/ = х„ и,
следовательно, х,'” = х, для т > 1. Нетрудно заме-
тить, что мощность множества G„ равна 22, как и
мощность множества булевых функций п пере-
менных. \ . 1
13 См. также п. 16.3.
52
Каждый полином Жегалкина задает некото-
рую булеву функцию, если сопоставить true <-> 1,
false О 0. Если бы два полинома Жегалкина
представляли одну и ту же булеву функцию, то
их сумма (XOR-разность) представляла бы нуле-
вую константу. Однако сумма двух различных
полиномов отлична от нуля. Поэтому каждая бу-
лева функция может быть представлена в виде
полинома Жегалкина единственным образом.
Полиномы/и f® 1 задают инверсные функции.
Булеву функцию...,х„) можно задать как
двоичным вектором из 2" значений, так и двоич-
ным вектором из 2" коэффициентов полинома
Жегалкина. Переход от табличного задания бу-
левой функции fixi, ...,хп) к заданию полиномом
Жегалкина выполняется следующим образом.
Очевидно, что а$ = ДО), где 0 — вектор, состоя-
щий из одних нулей. Коэффициенты а„ 1 < i < п,
можно найти так: a, =J(0) ®fy), где i — вектор,
z-я координата которого равна 1, а остальные ко-
ординаты нулевые. Сложение выполняется по
модулю 2. Аналогично получаем
^=/0)©Xi)©Ai)©/ij),
где ij — вектор, z-я и j-я координаты которого
равны 1, а остальные координаты нулевые. Далее
находим
^=X0)©Xi)©AD©/k)©
©/ij)©Xik)@Xjk)©Xijk),
где ijk—вектор, <-я,/-я и к-я координаты которого
равны 1, а остальные координаты нулевые, и т. д.
Данная процедура задает алгоритм представления
булевой функции полиномом Жегалкина.
Перевод вектора значений в вектор коэффи-
циентов можно задать умножением на квадрат-
ную матрицу Д, размера 2" над F2- Перенумеруем
наборы аргументов числами от 0 до 2” - 1, где
вектору 0 соответствует число 0, вектору i —
число 2' и т. д. Аналогично перенумеруем коэф-
фициенты полинома Жегалкина. Тогда матрица
Ln будет нижней треугольной, в которой главная
диагональ, первый столбец и последняя строка
состоят из единиц.
Запишем результирующее преобразование в
виде а = Z„f, где а — 2”-мерный вектор коэффи-
циентов полинома Жегалкина, f— 2''-мерный
вектор значений булевой функции.
Матрицы L„ имеют регулярную блочную
структуру:
'1 0 0 О'
'\0А 1100
J 1 / 2 ~ 1010
Jill,
%
o'
% O'
<^2 Д 2
и т. д. Рекуррентное построение матрицы Еп опре-
деляет способ быстрого вычисления коэффици-
ентов полинома Жегалкина для таблично задан-
ной булевой функции (по аналогии с быстрым
преобразованием Фурье, см. пп. 4.6, 7.1.3).
Обозначим через Е, единичную матрицу с 2'
строками. Поскольку Д2 = Е}, и из Z24 = Ek_}
следует l3k-Ek, то по индукции получаем:
Z2 = Еп и Z”1 = L„ Поэтому если булева функ-
ция f (как вектор) обладает списком коэффици-
ентов а, то булева функция а (как вектор) обла-
дает списком коэффициентов f.
Пример 3.15.1. Представление булевой функ-
ции полиномом Жегалкина.
Пусть булева функция четырех переменных
на наборах (0, 0, 0, 0), (0, 0, 0, 1), ..., (1, 1, 1, 1)
принимает соответственно значения (1, 0, 0, 0, 1,
1, 0, 0, 1, 1, 1, 1, 0, 1, 0, 0). Вычисляем над F2
произведение а = Z4f:
'100000000000
110000000000
101000000000
111100000000
100010000000
11001 1000000
101010100000
111111110000
100000001 000
110000001 100
101000001010
111100001111
100010001000
110011001100
101010101010
J 1 1 1 1 I 1 1 1 1 1 1
0 0 0 О'
0 0 0 0
0 0 0 0
0 0 0 0
0 0 0 0
0 0 0 0
0 0 0 0
0 0 0 0
0 0 0 0
0 0 0 0
0 0 0 0
0 0 0 0
10 0 0
110 0
10 10
1 1 1 д
'Г
о
о
о
1
1
о
о
1
1
1
1
о
1
о
<0,
= (111 1 010 1 011110 0 0).
Эта строка задает следующие коэффициенты
полинома Жегалкина: а$, а4, <7з, г/34, <?2, <724, <72з,
^234, й14, Й]3, <7134, <?12, <7124, Ф23, Й1234-
Соответствующий полином Жегалкина равен
1 © Х4 © Хз © Х3Х4 © Х2Х4 ©
© Х2Хз%4 © Х1Х4 © Х]Хз © Х1Х3Х4 © Х1Х2-
В терминах кольца G„ удобно описывать
свойства шифров. Рассмотрим алгебраические
свойства этого кольца.
53
Теорема 3.15.1. В кольце G„ каждый элемент
идемпотентен, каждый непостоянный элемент
является делителем нуля.
Доказательство. Каждый элемент кольца
G„ взаимно однозначно соответствует булевой
функции п переменных. Полиномы f и /Ф 1 за-
дают инверсные булевы функции, поэтому
/(/ ©1) = О,/2 ©/= 0 и/2 =/
В общем случае сокращение в Gn недопустимо.
Например,а(а®b) = a(\©b.
Теорема 3.15.2. Кольцо G„ содержит единст-
венный обратимый элемент — константу 1.
Доказательство. Будем искать представле-
ние 1 =fg. Умножив это равенство на / получим
f=fg', умножив его на g, получим g =fg. Отсюда
следует/= g. Тогда 1 =fg =f\ 1 =fg = g1-, значит,
в силу идемпотентности, f= 1 и g = 1. Других
делителей единицы нет.
Поскольку каждый непостоянный полином из
G„ является делителем нуля, кольцо частных
кольца G,, совпадает с G„, а поле частных кольца
G„ оказывается тривиальным и совпадает с !/•
3.15.2. Разложение на множители в кольце Gn
Согласно теореме 3.15.2 элемент 1 является
неразложимым в G„. Посмотрим, существуют ли
в G„ другие неразложимые элементы. В силу
идемпотентности выполняется равенство f-fn'
для любого f и натурального т. Такое разложе-
ние наряду с разложением f= 1 -/назовем три-
виальным. Назовем неразложимым полином, об-
ладающий только тривиальными разложениями.
Некоторые полиномы, кажущиеся неразло-
жимыми, можно нетривиальным образом разло-
жить на множители. Например, в Gj
х - (ху © у © 1 )(ху © л © у);
у = (ху © х © 1 )(ху © л Ф у);
х Ф у = (х © у)(ху © 1);
х © у © 1 = (ху © у © 1 )(ху © х © 1);
х © 1 = (ху © 1 )(ху © х © 1)
и т. д. Однако в &2 (и в G„) есть элементы, кото-
рые невозможно разложить на множители. На-
пример, в G2 не раскладываются на множители в
точности четыре полинома:
ху©х® у; ху Ф 1; ху Ф х Ф 1; ху©у@].
Полином Жегалкина/однозначно определен
набором своих нулей S(f). В силу изоморфизма
мультипликативных моноидов кольца G„ и мно-
жества булевых функций для / g g G„ выполня-
ется равенство S(fg) = S(f) о S(g).
Лемма 3.15.3. Неразложимыми в кольце G„
являются те и только те полиномы, которые на
множестве из 2" аргументов принимают единст-
венное нулевое значение.
Доказательство. Если элемент f^G„ мож-
но представить в виде произведения двух раз-
личных элементов: /= gh, то /= 1 тогда и только
тогда, когда g= 1 и h = 1. Следовательно, если /
принимает единственное нулевое значение, то на
всех остальных наборах gvih принимают значение
1. Тогда либо g=f причем h- 1 или h-f, либо
g= 1 и h =f. Обратно, если полином / неразложим,
то есть его как строку из 2" символов {0.1} нельзя
представить в виде поразрядной конъюнкции двух
различных строк, из которых хотя бы одна отлична
от строки / то строка /должна содержать единст-
венный нулевой символ. Действительно, в случае
двух (и более) нулевых символов на наборах х и х'
строку / можно представить как поразрядную
конъюнкцию двух строк, из которых одна имеет
единственный нуль на наборе х, а другая — един-
ственный нуль на наборе х'.
Следствие 3.15.4. В Gf, существует в точности
2" неразложимых полиномов, принимающих зна-
чение 0 в точности на одном из 2" наборов аргу-
ментов (0,0,..., 0), (0,0,..., 1),..., (1, 1,..., 1).
Доказательство. По лемме 3.15.3 эти поли-
номы являются неразложимыми. Других неразло-
жимых полиномов не существует, так как в G„ су-
ществует лишь 2" различных, наборов аргументов.
Набору (0, 0, ..., 0) соответствует полином
1 Ф Х]Х2.. .х„, набору (1,0,..., 0) — полином
1 Ф (1 Фxi)x2...Xn, набору (1, 1, 0,..., 0)— поли-
ном 1 Ф (1 ФХ])(1 ©Х2)хз...хт ..., набору (1,1,
..., 1)- ПОЛИНОМ 1 ф (1 ф Х1)(1 ф х2)...(1 Ф х„).
Все неразложимые полиномы имеют степень п.
Произведение всех неразложимых полиномов
равно 0. .....
Теорема 3.15.5. Каждый полином из G„ облада-
ет однозначным разложением на неразложимые
множители. Число неразложимых делителей поли-
нома равно числу нулей в его табличном задании.
Доказательство. Пусть полином f G,, от-
личен от константы. Тогда существуют наборы
аргументов, на которых он принимает различные
значения. Перечислим наборы, на которых /= 0.
Каждому такому набору можно взаимно одно-
значно сопоставить неразложимый полином
Pi е G„, на котором р, = 0. Произведение указан-
ных неразложимых полиномов будет принимать
значение 0 тогда и только тогда, когда /= 0, то
54
есть f - ]J[ р, . В соответствии с указанным по-
строением разложение единственно. Число не-
разложимых делителей полинома f равно числу
наборов, на которых f- 0. Поскольку рассматри-
ваются только нетривиальные разложения, то
каждый делитель полинома f входит в произве-
дение только в первой степени.
Таким образом, кольцо G,, обладает однознач-
ным разложением на неразложимые множители,
хотя и не является целостным. Поскольку в коль-
це G„ все непостоянные элементы являются де-
лителями нуля, то для степеней выполняется не-
равенство
deg(f) <^deg(p,).
Неразложимые элементы кольца G„ перестают
быть таковыми в кольце G„+i-
Пример 3.15.2. Разложение на простые мно-
жители полинома Х| © Л'2 в кольце G^.
Составим таблицу истинности для полинома
Ф х2. Этот полином принимает значение 0 на
следующих наборах (хь х2, х3, х4): (0,0,0,0),
(0,0,0,1), (0,0,1,0), (0,0,1,1), (1,1,0,0), (1,1,0,1),
(1,1, 1,0), (1,1,1, 1). Составим таблицу соответ-
ствия неразложимых полиномов и указанных
наборов переменных:
Набор переменных Неразложимый полином
(0, 0, 0, 0) 1 Ф Х1Х2ХзХ4
(0, 0, 0, 1) 1 ©Х1Х2Хз(1 Фх4)
(0, о, 1, 0) 1 Ф Х1Х2(1 Ф Хз)х4
(0, 0, 1,1) 1 Ф Х1Х2( 1 Ф Хз)(1 Ф х4)
(1,1,0,0) 1 ф (1 ф Х1)(1 Ф Х2)ХзХ4
(1,1,0,1) 1 Ф (1 Ф Х1)(1 ф х2)хз(1 Ф х4)
(1,1,1,0) 1 Ф (1 Ф Х!)(1 Ф х2)(1 Ф х3)х4
(1,1,1,1) 1 Ф (1 Ф X] )(1 Ф Х2)(1 Ф Хз)( 1 Ф х4)
Перемножая все элементы второго столбца таб-
лицы, получаем разложение полинома xt Ф х2.
Каждый идеал кольца G„ является главным.
Действительно, каждый полином из некоторого
идеала 21 = можно задать таблично
списком наборов переменных, на которых этот
полином принимает значение 0. Пересечение
всех таких списков даст список нулей, который
соответствует некоторому полиному f е 21, при
этом f = Л..Х. Тогда, очевидно. 21 = (У).
3.15.3. Симметрические функции кольца G„
Пусть ст„^ е G„ — элементарная симметриче-
ская функция степени к от переменных Х|, ...,х„.
По основной теореме о симметрических функци-
ях [3] сумма и произведение элементарных сим-
метрических функций д в Gh являются симмет-
рическими функциями. Следовательно, симмет-
рические функции образуют подкольцо кольца
G„. Это подкольцо содержит делители нуля, на-
пример, (о„;1 Ф = 0.
Теорема 3.15.6. Каждую симметрическую
функцию единственным образом можно пред-
ставить в виде суммы элементарных симметри-
ческих функций.
Доказательство. Пусть симметрическая
функция f имеет степень т. Тогда в f будут вхо-
дить всевозможные произведения т переменных,
(
число которых равно . Но элементарная
симметрическая функция содержит те же
всевозможные произведения т переменных.
Следовательно, сумма f Ф стИ1,„ будет являться
симметрическим полиномом степени меньше т.
Повторяя эту процедуру несколько раз, получим
полином нулевой степени.
Все элементарные симметрические функции
можно получить из меньшего числа элементар-
ных симметрических функций, а именно из мно-
жества {о ( ,} для 0 < i < log2«. В частности,
,.£2' Паи,2- •
Например, для п = 8 получаем = °8,з5
08,1^8,4 = °8,5; ^8,2^8,4 “ ^8,6? ^8,1^8,2^8,4 = °8,7- КрО-
ме того, о ^„0 ^ = 0 для всех i^2n. Доказательство
этих утверждений следует из того, что число оди-
наковых слагаемых в симметрическом полиноме
после раскрытия скобок оказывается четным.
3.15.4. Кольцо дифференциальных
операторов кольца G„
В кольце G„ можно определить дифференци-
рование. Операцию дифференцирования (диф-
ференциальный оператор} полинома f по пере-
менной х, будем обозначать D,. Как обычно, про-
изводной полинома по переменной х, назовем ко-
эффициент при к, в случае замены х, на х, Ф Л,.
Этот коэффициент, очевидно, равен коэффици-
енту при х,: если /= x,fo Ф /, где /0, /| не зависят от
х„ то £>,(/) = fn.
53
Значение производной вычисляется как
ад=л,.=о®л,.=ь
Из определения производной вытекают сле-
дующие свойства:
1. Д(1) = Д(0) = 0.
2. W©g) = D,(/)®D,(g).
3. Dfaifo Ф/i) =/>, где/ не зависит от х,-.
Для произведения элементов кольца G„ фор-
мула дифференцирования с учетом идемпотент-
ности выглядит следующим образом. Если
/= Xjfo ©fi, g=x,g0 Ф gi, где/, gj не зависят от xh
Tofg = x(f0g0 ®fgi ®fgo) Ф/igi- В этом случае
Wg) =/ogo ®/ogi Ф/igo =М,=о ФД=1-
Аналогично для трех сомножителей получаем:
Dtfgty =fogoh0 ®fogofii ®fogih0 ©fogfi ®
®fgJk ®f\goh\ ®fgfo =fgh\*ro ®fgh\Xj=i.
Индукционный переход очевиден.
Запись Dj(f) можно рассматривать как умноже-
ние полинома f на D,. Произведение дифференци-
альных операторов D,Dj означает дифференциро-
вание по ху, а затем по х„ при этом Z>/>7 = £>/),.
Вторая производная в G„ по любой переменной
равна нулю. Можно определить сумму дифферен-
циальных операторов (D, Ф Dff) - D,(f) Ф Dff).
Определим множество дифференциальных опе-
раторов как множество полиномов от Di, с
указанными операциями сложения и умножения.
Множество дифференциальных операторов яв-
ляется подкольцом кольца эндоморфизмов адди-
тивной группы кольца G„. Для двух полиномов F
и G от Di, и двух полиномов f g & G„
справедливо равенство
(F Ф G)(f® g) = F(f)® F(g) ® Gif ® Gig).
Поэтому свойства кольца дифференциальных
операторов можно доказывать только для одно-
членов вида J~[x7 •
j
Дифференциальные операторы образуют ком-
мутативное кольцо характеристики 2, единич-
ным элементом которого является тождествен-
ное отображение Е, нулевым— оператор, ото-
бражающий любой полином в 0, каждый опера-
тор противоположен сам себе. Два элемента
кольца дифференциальных операторов будем
считать равными, если их образы равны для лю-
бого прообраза.
Кольцо дифференциальных операторов над G,
изоморфно кольцу Г2[Д,..., £>„]/(Д2,..., £>2) для
формальных переменных Д, .... Д. Каждый эле-
мент кольца дифференциальных операторов, от-
личный от 0 и Е, является делителем нуля.
Замену переменной х, в полиноме f е G,, на
инверсное значение можно описать в терминах
кольца дифференциальных операторов:
/Д,..., х,_], х„х,+у,..., х„)- Д/Д,..., х„) =
= (Д+Е)/Д,...,х„).
3.15.5. Эндоморфизмы кольца G„
Эндоморфизмы модуля G„ с операциями сло-
жения (<р + <;/)(/) = <р(/) Ф \\tif) и умножения
(ффХД= ф(ф(/)) образуют кольцо End(G„), вклю-
чающее в себя кольцо дифференциальных опера-
торов.
Кольцо End(G„) совпадает с множеством
квадратных матриц размера 2" над 1Д. Если таб-
лично заданные булевы функции fug предста-
вить в виде 2"-мерных векторов f и g, то для опе-
рации умножения на матрицу L будет выпол-
няться условие L(f Ф g) = Lf Ф Eg.
Эндоморфизм <р модуля G,, является эндо-
морфизмом кольца G„, если ф(/ Ф g) = <р(/) Ф> <p(g)
и <p(fg) = ф(/)(!)(х)- Для эндоморфизмов кольца и
любых/ g е G„ справедливы равенства:
1) (фф)(/© g) = ф(чЧ/)) © ф(ф&));
2) (фф)(&) = ф(ф(/))ф(Ш));
3) ф(0) = ф(/Ф/) = ф(/)Фф(/) = 0;
4) ф(Д = фО ’/)= ф(1)ф(/)» отсюда ср(1) = 1, если
ср — ненулевой эндоморфизм (существует
многочлен f такой, что <р(/) Ф 0);
5) <р(1 ®f) = <р(1) Ф <?(/) = 1 Ф <р(/), то есть эн-
доморфные образы инверсных функций для
ненулевого эндоморфизма инверсны.
По теореме о гомоморфизмах колец каждый
эндоморфизм кольца G„ характеризуется идеа-
лом, который является ядром этого эндомор-
физма — множеством элементов, отображаю-
щихся в 0.
Обратимые эндоморфизмы являются авто-
морфизмами кольца G,„ их ядро состоит из нуля.
Автоморфизмом является, в частности, единич-
ное отображение, а также произвольная переста-
новка переменных ..., х„.
По теореме 3.15.6 каждый полином из G„ яв-
ляется произведением неразложимых полино-
мов, принимающих единственное нулевое значе-
ние на наборе из 2" аргументов.
Лемма 3.15.7. Любой автоморфизм <р кольца
G, переводит неразложимый полином в нераз-
ложимый полином. ... ...
56
Доказательство. Перестановка S 2" нераз-
ложимых полиномов является автоморфизмом
кольца G„. Для неразложимых полиномов р, Ф pj
имеем S(p,pj) = S(p,)S(pj), S(pt + р}) = S(pi)S(pj). По
индукции в силу однозначности разложения по-
лучаем S(fg) = S(f)S(g).
Предположим противное: <p(p) = gh, где р —
неразложимый полином. Тогда, применяя обрат-
ный автоморфизм <р', получаем: ср-1 (gh) =
= <р 1 (g)(!)Поскольку при автоморфизме у
любого элемента кольца G„ есть ровно один
прообраз, то cp 'tg)^! и ф1 (А) 1. Следовательно,
<fl(<fp))^p—противоречие.
Каждый полином f е G„ полностью определя-
ется 2"-мерным вектором f значений над F2. Оп-
ределим операции л поразрядной конъюнкции и
Ф поразрядного сложения векторов. Тогда про-
изведению полиномов fg будет соответствовать
вектор f л g. Сумме полиномов /Ф g будет соот-
ветствовать вектор f Ф g.
Теорема 3.15.8. Множество автоморфизмов
кольца G, совпадает с множеством перестановок
2" неразложимых полиномов.
Доказательство. Такая перестановка обра-
тима и сохраняет вес булевой функции (число
единичных значений функции на всем множестве
наборов аргументов), заданной полиномом Же-
галкина. Взаимно обратные перестановки задают
взаимно обратные отображения. Поскольку пере-
становка ф неразложимых полиномов fug задает-
ся квадратной невырожденной над F2 матрицей L
размера 2", то равенство L(f Ф g) = Lf Ф Zg экви-
валентно равенству <p(f Ф g) = ф(/) Ф (p(g), где ф —
эндоморфизм, соответствующий матрице L. Кро-
ме того, g>(fg) = <p(/)cp(g). Поэтому перестановка
неразложимых полиномов является автоморфиз-
мом кольца G„.
Предположим, что существует автоморфизм
кольца G„, который нельзя задать матрицей пере-
становки (квадратной невырожденной матрицей
размера 2", в которой каждая строка и каждый
столбец содержат по одному единичному эле-
менту, а остальные элементы — нулевые). Тогда
в матрице, задающей эндоморфизм модулей,
должна существовать строка по крайней мере с
двумя единичными элементами (если хотя бы в
одной строке нет единичных элементов, то мат-
рица вырожденная). Поскольку позиции каждой
строки матрицы взаимно однозначно соответст-
вует неразложимый полином, должен существо-
вать автоморфизм кольца G„, переводящий не-
разложимый полином в произведение не менее
двух неразложимых полиномов, что противоре-
чит лемме 3.15.7.
Таким образом, существует 2"! автоморфиз-
мов кольца G,,.
Рассуждая так же, как и при доказательстве
теоремы 3.15.8, получаем, что эндоморфизмы
кольца G„ задаются произвольными матрицами
L, поскольку равенство Z(f л g) = (Zf) л (Zg) вы-
полняется для любых векторов f, g.
При исследовании безопасности криптогра-
фических алгоритмов часто используются гомо-
морфизмы колец G„ -> F2, при которых перемен-
ные хь ...,хп заменяются элементами поля F?.
Поскольку поле F? содержится в кольце G„ в ви-
де полиномов нулевой степени, эти гомомор-
физмы могут быть очевидным образом дострое-
ны до эндоморфизмов кольца G„.
Упражнения к главе 3
5.
1. Образуют ли кольцо булевы функции п пе-
ременных с операциями ИЛИ (сложение), И
(умножение)?
2. Покажите, что конечные множества с опера-
циями симметрической разности (сложение) и
объединения (умножение) образуют коммута-
тивное кольцо. Является ли оно целостным?
3. Покажите, что числа а + Ьу/15, где а, Ь,
D е 7L, образуют кольцо. Является ли это
кольцо целостным?
4. Кольцо Z[z] евклидово, следовательно, в нем
работает алгоритм Евклида. Найдите
НОД(13, 3 + 2z), НОД(3 + 4z, 2z + 1) в кольце
ОД-
Постройте ненулевой гомоморфизм из коль-
ца Z[x] в кольцо Z. Что является ядром этого
гомоморфизма? Будет ли это отображение
гомоморфизмом в случае х = i, где i2 = -1 ?
6. Пусть R — кольцо с единичным элементом
1. Что означает сравнение a = b (mod (0)),
а = Ъ (mod(l))? Что собой представляет го-
моморфный образ кольца по нулевому идеа-
лу?
7. Пусть R — коммутативное кольцо. Будет ли
кольцом множество идеалов кольца R с опе-
рациями сложения и умножения идеалов?
8. Почему выполняется равенство К[х][у] =
= £[X,J]?
9. Что собой представляют сумма, произведе-
ние и пересечение идеалов (10) и (15) кольца
Z; идеалов (3) и (5) кольца Z?
10. Что собой представляет идеал (х1 2, ху) кольца
Q[x, у]; идеал (х2 + у2, 3) кольца Q[x, у]?
11. Найдите кратный делитель полинома х8 - х7 +
+ 2х6 + х5 - х4 + Зх3 + 1 е Z[x].
12. Найдите производную полинома х7 + х4 + х2 +
+ х + 1 е (Z72Z)[x] и наибольший общий де-
литель его с производной.
13. Какие из полиномов: х2 + 6, х2 - 2х, х3 + х + 1,
9, х - 1 лежат в идеале (х, 3) кольца Z[x]?
14. Является ли простым идеал (0) кольца Z[x];
кольца (Z/35Z)[xJ?
15. Постройте ненулевой гомоморфизм из коль-
ца G„ в кольцо G„-\. Что является ядром этого
гомоморфизма?
16. Пусть К— некоторое поле. Покажите, что в
кольце K[x,y,z] идеал (х) делится на идеал
(х,у).
17. Постройте кольца частных для следующих
колец:
- кольцо Z целых чисел;
- кольцо nZL для целого и;
- кольцо, состоящее из рациональных чи-
сел, знаменатель которых не делится на
заданное число п;
- кольцо TLInZL классов вычетов для целого и;
- кольцо С[х, у\/(у - х3 - 1) классов выче-
тов, где полином у2 - х3 - 1 неразложим
(над полем С в общем случае расклады-
ваются на линейные множители полино-
мы только от одной переменной, но не от
двух).
При каких условиях эти кольца частных бу-
дут полями?
18. Исследуйте алгебраические свойства «коль-
цеподобной» структуры, образованной идеа-
лами целостного кольца с операциями сло-
жения и умножения идеалов.
19. Покажите, что дискриминант полинома над
полем равен нулю тогда и только тогда, ко-
гда этот полином имеет неединичный общий
делитель со своей производной.
20. Чему равно содержание полинома fix,y)~
= х3 + Зх2 + Зх + 1 + ху2 + у2 в кольце Z[x, у]
относительно переменной х? Относительно
переменной у?
21. Существуют ли в поле простые элементы?
22. Разложите на неразложимые множители по-
лином ху + XZ + yz В G3.
23. Опишите все автоморфизмы кольца G2.
Литература к главе 3
1. Ахо А., Хопкрофт Дж., Ульман Дж. Построение и
анализ вычислительных алгоритмов. М.: Мир,
1979.
2. Биркгоф Г. Теория решеток. М.: Мир, 1984.
3. Ван дер Варден Б.Л. Алгебра. М.: Наука, 1979.
4. Кокс Д., Литтл Дж., О'Ши Д. Идеалы, многообра-
зия, алгоритмы. М.: Мир, 2000.
5. Ленг С. Алгебра. М.: Мир, 1968.
6. Салий В.Н. Решетки с единственными дополне-
ниями. М.: Наука, 1984.
7. Шафаревич И.Р. Основные понятия алгебры.
Ижевск: Редакция журнала «Регулярная и хаоти-
ческая динамика», Ижевская республиканская ти-
пография, 1999.
Глава 4. ПОЛЯ
4.1. Общие сведения о полях.
Простые поля
Напомним, что полем называется целостное
кольцо с единичным элементом е Ф 0, в кото-
ром каждый ненулевой элемент имеет обрат-
ный. В поле все ненулевые элементы образуют
абелеву группу по умножению, называемую
мультипликативной группой поля. Типичный
способ построения поля из целостного коль-
ца— присоединение частных или нахождение
кольца классов вычетов по максимальному
идеалу.
Поле К не содержит идеалов, отличных от ну-
левого и единичного (совпадающего с К). Дейст-
вительно, пусть 21— ненулевой идеал поля К.
Тогда существует обратимый в К элемент а е 21.
По определению идеала е = аа] е. 21, и, следова-
тельно, любой элемент поля К лежит в 21.
Пример 4.1.1. Поля.
1. Множество Q рациональных чисел является
полем частных кольца Z целых чисел. Мультип-
ликативная группа Q поля Q состоит из ненуле-
вых рациональных чисел. Множество четных
чисел образует кольцо 2Z, поле частных которо-
го в результате сокращения числителя и знаме-
нателя на 2 тоже совпадает с полем Q. Анало-
гично, множество рациональных чисел является
полем частных любого кольца вида п%. для цело-
го п.
2. Для произвольного поля К полем частных
кольца полиномов Х[х] от одной переменной х
является поле рациональных функций К(х). Поле
. г - \
Кух) состоит из дробей вида ----, где аух),
Ъ(х)
Ь(х) — полиномы с коэффициентами из поля К и
й(х) отличен от нуля. Мультипликативная группа
поля К(х) состоит из дробей с ненулевым знаме-
нателем.
3. Кольцо Z[i] = Z + Zi содержит Z, поэтому
его поле частных К должно содержать всевоз-
можные рациональные числа Q, а также мнимую
единицу i как дробь |. Покажем, что
К — Q(i) = Q + Qi. Действительно, частное
a + bi _ac + bd + (be -ad)i _ac + bd be-ad .
c + di c2+d2 c2+d2 c2+d2
имеет вид g + hi, где g, h — рациональные числа.
Обратно, любое число вида g + hi с рациональ-
ными g, h может быть представлено как частное
r t
элементов кольца Z[i]. Пусть g = —, h = —, где г,
S и
s, t, и Тогда можно записать
.. ru st . ru + sti
g + hi =--1--i--------,
su su su
где числитель и знаменатель являются элемента-
ми кольца Z[i].
Все гомоморфизмы полей инъективны (на-
пример, гомоморфное вложение поля Q в поле
IR) или биективны (в противном случае в поле
существовал бы собственный ненулевой идеал,
что невозможно).
Если К— произвольное поле и его подмно-
жество к тоже является полем, то к называется
подполем поля К. Поскольку любое поле содер-
жит не менее двух элементов (0 и е), каждый из
которых единственный, то пересечение двух
подполей поля К является полем. Очевидно, что
пересечение любого числа подполей поля К
вновь является полем.
Простым называется поле, не содержащее
собственных подполей.
Теорема 4.1.1. Каждое поле содержит одно и
только одно простое подполе.
Доказательство. Пересечение всех подпо-
лей поля К является подполем, не имеющим соб-
ственных подполей. Предположим, что сущест-
вуют два различных простых подполя. В этом
случае пересечение этих подполей было бы соб-
ственным подполем в каждом из них. Следова-
тельно, эти подполя— не простые. Противоре-
чие доказывает теорему.
Теорема 4.1.2. Простое поле изоморфно
кольцу ZTpZ, где — простое число, или полю Q
рациональных чисел.
Доказательство. Пусть К— простое под-
поле поля L. Поле К содержит нуль 0 и единицу е
59
и, следовательно, кратные единичного элемента
пе = е + е + ... + е. Сложение и умножение этих
п раз
кратных осуществляется по правилу пе + те =
= (и + т)е, (пе)(те) - = пте1 - пте. Следователь-
но, целочисленные кратные пе образуют комму-
тативное кольцо Р. Отображение п -> пе задает
гомоморфизм кольца Z на кольцо Р. По теореме
о гомоморфизмах колец Р = Z76, где & — идеал,
состоящий из тех целых чисел п, которые лежат
в ядре гомоморфизма, то есть дают равенство
пе = 0.
Кольцо Р целостное, так как поле К — цело-
стное кольцо. Поэтому и Z76 тоже целостное.
Кроме того, идеал 6 не может быть единичным,
так как иначе выполнялось бы 1 - е = 0. Следова-
тельно, существуют только две возможности:
1.6 = (р), где р — простое число. В этом случае
р является наименьшим положительным числом,
для которого ре = 0. Ядро гомоморфизма содержит
целые числа, кратные р,— это идеал (р) или, в
другой записи, рЖ. Поэтому Р = 2Z./(p) = ~ZJp7L явля-
ется полем. В этом случае простое поле изоморфно
полю Z/pZ.
Простейшее простое поле состоит из двух
элементов, 0 и 1. Таблица сложения и умножения
имеет вид:
0 + 0 = 0, 0 + 1 = 1, 1 + 0 = 1, 1 + 1 = 0,
0 0 = 0,0- 1 =0, 1 0 = 0, 1 • 1 = 1.
2. © = (0). Тогда гомоморфизм Z -> Р являет-
ся изоморфизмом. Кратные пе все попарно раз-
личны: если пе = 0, то п = 0. В этом случае коль-
цо Р не является полем, так как Z не является
полем. Простое поле К должно содержать не
только элементы из Р, но и их частные. В этом
случае целостные кольца Р и Z имеют изоморф-
ные поля частных. Поэтому простое поле К изо-
морфно полю Q рациональных чисел. В
Таким образом, строение содержащегося в L
простого поля К с точностью до изоморфизма
определяется заданием простого числа р или
числа 0, которые порождают идеал 6, состоящий
из целых чисел п со свойством пе = 0. Число п
называется характеристикой поля L и обознача-
ется char(Z). При этом char(Z) = char(K).
Числовые поля IR, С (см. п. 5.7) и поля функций,
содержащие поле Q, имеют характеристику 0.
Теорема 4.1.3. Пусть а, b Ф 0 — произвольные
элементы поля L и р- char(Z). Тогда из равенст-
ва та = па, где т и п— целые числа, следует,
что т = п (mod р), и наоборот. Кроме того, если
па = nb и р | п, то а = Ь.
Доказательство. Поскольку a^Q, то суще-
ствует а~\ Умножим обе части равенства та = па
на а'. Получим те = пе или, по определению
характеристики поля, т = п (mod р). Обратно,
если т = п (mod р), то (т - п)а = 0, та = па. Если
па = nb, то п(а -Ь) = 0. Тогда а-Ь-0, а = Ь.
Теорема 4.1.4. В полях характеристики р
имеют место равенства
(а + ЪУ = ар + Ь”, (а - Ь)р = ар - Ьр.
Доказательство. По формуле бинома Нью-
тона имеем
{а + Ь)р - ар
Р
abp~'+bp.
Здесь все коэффициенты, кроме первого и по-
следнего, делятся на р, так как числитель у них
делится на р. Поскольку р — характеристика по-
ля, то в рассматриваемом поле все эти слагаемые
равны нулю, то есть (а + Ъ)р = ар + Ър.
Аналогично рассуждаем и в случае разности.
Положим с = а + Ь. Тогда а = с - Ъ, ср = (с - Ь)р + Ьр,
(с-Ъ)р = ср-Ър.
Если р — нечетное число, то число слагаемых
в формуле бинома Ньютона четное и коэффици-
ент при Ьр равен -1. Если р = 2, то коэффициент
при Ьр равен 1. Отсюда заключаем, что в поле
характеристики 2 выполняется равенство -1 = 1.
4.2. Расширения полей
Пусть К— подполе поля L. Тогда L называет-
ся расширением поля К. Расширение L поля К
будем обозначать L/К. Рассмотрим строение
расширения L.
Пусть L— расширение поля К, S— произ-
вольное множество элементов из L. Существует
поле, содержащее в себе (как в множестве) поле К
и множество S (таким полем является, например,
L). Пересечение всех полей, содержащих К и .S’,
является полем, причем наименьшим из полей,
содержащих в себе К и S, и обозначается K(S).
Говорят, что K(S) получается присоединением
множества S к полю К. Имеет место включение
K^K(S)^L.
Полю K(S) принадлежат все элементы из К,
все элементы из S, а также все элементы, полу-
ченные при сложении, вычитании, умножении и
делении этих элементов, то есть K(S) состоит из
У«,«,
всех рациональных комбинаций ——, где
: -- X"
60
bj e К, st, tj e S. (Отсюда следует, что множество
S можно выбирать различными способами.) Эти
рациональные комбинации могут быть записаны
как рациональные функции, то есть как отноше-
ния полиномов, где переменные— элементы
множества S, а коэффициенты полиномов —
элементы поля К.
Например, если AZ = Q— поле рациональных
чисел, a L — поле рациональных функций от
хь ...,х„ с коэффициентами из Q, то в качестве
множества S, содержащего только степени пере-
менной X], можно выбрать {xj}, {хь Х]2},
{xi, X]2, Xi3}, .... Все эти множества определяют
одно и то же поле Q(xj).
Если множество S можно выбрать так, что оно
является конечным, то пишут S= {щ, ...,и„}. В
этом случае расширение K(S) обычно обознача-
ют через К(и\, ...,u,i) и говорят, что элементы
W], ..., и,, присоединены к полю К. Отметим, что
если присоединяемые элементы записаны в
круглых скобках, — К(гц, ..., w„), — то имеется в
виду множество рациональных комбинаций, то
есть элементы щ,..., w„ присоединяются к полю,
и полученная конструкция также является полем.
Если присоединяемые элементы записаны в
квадратных скобках, — Ди,, ..., w„], — то имеет-
ся в виду множество целых рациональных ком-
бинаций (полиномов), то есть элементы и\, ...,ип
присоединяются к кольцу.
Элементы w, можно присоединять поочеред-
но. Поскольку элементы и, лежат в поле L и, сле-
довательно, перестановочны с любыми элемен-
тами из L, имеет место равенство К(и,)(ц) =
= ДиДи,) = K(uj, Uj). По индукции это равенство
продолжается на любое число присоединяемых
элементов. Таким образом, для любого поля
можно построить расширение.
Расширение, полученное присоединением од-
ного элемента, называется простым.
4.2.1. Простые расширения
Пусть К— поле и KcL. Пусть t е L\K—
произвольный элемент поля L, не являющийся
элементом поля К. Рассмотрим простое расши-
рение K(f) поля К.
Поле K(t) содержит кольцо R полиномов от пе-
ременной t с коэффициентами из Д R - L
а, е К. Сравним R с кольцом Дх] полиномов от
одной переменной х. Отметим, что здесь х — фор-
мальная переменная, не имеющая отношения к
полю Kit), at — элемент этого поля. Отображение
fix)ft), то есть ^а;х' , является го-
моморфизмом колец. При этом сумма элементов
кольца Дх] отображается в сумму элементов
кольца R, произведение элементов кольца Дх]
отображается в произведение элементов кольца R,
так как и в кольце R, и в кольце Дх] присоеди-
ненный элемент перестановочен со всеми элемен-
тами поля К. По теореме о гомоморфизмах колец
имеет место изоморфизм R = Дх]/ф, где %) — не-
который идеал.
Уточним структуру идеала ф. Рассуждаем
так же, как в случае простых полей. Гомомор-
физм будет существовать при ф = (0), тогда
R = Дх]. Элементы кольца R получаются заме-
ной переменной х на переменную t, при этом
из ft) = 0 следует fx) = 0. Здесь кольцо R не
является полем, однако оно может быть вло-
жено в свое поле частных. Поэтому поле К(1),
являющееся полем частных кольца R = ДО, и
есть требуемое расширение поля К. Очевидно,
что K(f) в этом случае изоморфно полю рацио-
нальных функций от одной переменной х с ко-
эффициентами из поля К. Здесь элемент t на-
зывается трансцендентным над К, а поле K(t)
называется простым трансцендентным рас-
ширением.
Однако возможна и более общая конструк-
ция, когда некоторые ненулевые полиномы при
подстановке t вместо х обратятся в нуль. Не-
трудно видеть, что здесь также будет иметь ме-
сто изоморфизм колец R = Дх]/ф. Поэтому
можно сказать, что идеал ф состоит из тех по-
линомов fx), для которых t является корнем, то
есть ДО = 0.
Поскольку кольцо R является подмножеством
поля L с теми же операциями, оно не содержит
делителей нуля. В силу последнего изоморфизма
кольцо классов вычетов Дх]/ф тоже не имеет
делителей нуля. Следовательно, идеал ф явля-
ется простым. Поскольку R содержит ненуле-
вые элементы, то идеал ф отличен от R, то есть
не является единичным (в противном случае
все элементы отображались бы в нуль). По-
скольку в кольце Дх] все идеалы главные и
ф ф (0), ф Ф R, единственно возможный слу-
чай: ф = (р(х)), где р(х) — неприводимый над К
полином такой, что p(t) = 0. Полином р(х) обла-
дает наименьшей степенью среди всех полино-
мов, для которых I является корнем, так как ина-
че существовал бы полином с корнем I, не яв-
ляющийся элементом идеала (р(х)). При этом
идеал (р(х)) является максимальным. Следова-
тельно, имеет место изоморфизм R = Дх]/(р(х)).
По теореме 3.6.1 кольцо классов вычетов по мак-
симальному идеалу является полем. Следова-
тельно, ДО = R = Дх]/(р(х)).
Элемент t удовлетворяет уравнению p(f) = 0.
Это уравнение называется уравнением, опреде-
ляющим поле K(t). Элемент I называется алгеб-
раическим над К, а поле K(t) — простым алгеб-
раическим расширением.
Таким образом, любой элемент поля K(t) в
этом случае является полиномом. С такими по-
линомами можно обращаться как с классами вы-
четов по модулю р(х), то есть степень каждого из
них меньше степени полинома р(х). Для некото-
рого полинома fit) е. X[Z] равенство fit) = 0 экви-
валентно сравнению /Д) = 0 (mod p(t)).
Для построенных алгебраических и трансцен-
дентных расширений можно строить новые рас-
ширения; при этом характеристика поля не меня-
ется.
Пример 4.2.1. Расширения полей.
1. Если К= к(х)— поле рациональных функ-
ций, то трансцендентное расширение К(у) = к(х, у)
будет полем рациональных функций от двух пе-
ременных над к.
2. Пусть К= IR. Трансцендентным расширением
этого поля будет поле IR(x) рациональных функ-
/(х)
ции, то есть всевозможных частных--, где по-
g(x)
линомы fi g имеют вещественные коэффициенты
и g(x)^o. Для построения алгебраического рас-
ширения присоединим к полю IR корень неприво-
димого над IR квадратного полинома х2 + 1. Этот
корень обычно обозначается через i и удовлетво-
ряет уравнению /2 = -1. Тогда элементы расши-
ренного поля представляют собой комплексные
числа а + Ы, то есть полиномы от i с веществен-
ными коэффициентами. Присоединение к полю
IR корня любого неприводимого полинома дает
одно и то же поле С.
3. Пусть К= {0, 1}. Здесь, очевидно, транс-
цендентное расширение представляет собой поле
рациональных функций с коэффициентами из К.
Построим алгебраическое расширение K(f) сте-
пени 4. Выберем неприводимый полином вида
р(х) = х4 + х + 1. Обозначим корень этого поли-
нома через t. Тогда K(f) = K[l\/(p(t)). Циклическая
группа, образованная элементом t, имеет вид:
{z, z2, z3, z4 = z+l, t2 + t, z3 + z2, Z4 + Z3 = Z3+Z+1,
Г +12 +1 = t2 + 1, z3 +1, ? +12 = t2 + t + 1, Z3 + t2 + t,
z4 + z3 +12 = t3 + t2 + t+ 1, z4 + z3 + t2 + t = t3 +12 + 1,
Z4 + Z3 + Z = Z3+1, Z4 + Z= 1}. Здесь все степени
элемента Z представлены классами вычетов по
модулю p(f). В частности, Z1 = Z3 + 1. Действи-
тельно, произведение Z(Z3 + 1) дает единицу по
модулю p(t).
4. Пусть К = Z[i]/(7) — поле классов вычетов
(7 является простым элементом в кольце £[i]).
Поле К состоит из сумм вида а + Ы и включает в
себя поле 2/(7) в качестве простого подполя, то
есть характеристика поля К равна 7. Очевидно,
что 0 < а, Ъ < 6. Тогда поле К состоит из 49 эле-
ментов. Это поле является алгебраическим рас-
ширением поля ZfiJ) и определяется уравнением
г + 1 = 0.
Q(z)
является простым
5. Пусть Q — основное поле, z— переменная,
поле рациональных функций. Поле Q(z)
алгебраическим расширением
г3
поля
Действительно, положим
-----= w . Тогда z - wz - w - 0. Корни этого
уравнения не являются рациональными функ-
циями с коэффициентами из Q. Поле Q(z) полу-
чается присоединением корней этого уравнения
к полю Q(m’).
6. Пусть К = С(х) — поле рациональных
функций. Простым квадратичным расширением
поля К является, например, поле, образованное
присоединением элемента у — квадратного
корня из полинома нечетной степени (несмотря
на то, что в поле С каждый полином от одной
переменной раскладывается на линейные мно-
жители. не существует рациональной функции
из С(х), квадрат которой является полиномом
нечетной степени). Однако присоединяемый
элемент не может быть корнем из х, так как в
этом случае х = fi и все элементы такого поля
были бы рациональными функциями от у, то
есть такое поле было бы изоморфно полю К.
Точно так же нельзя присоединять и корень из
линейной функции от х. Следовательно, про-
стейшее квадратичное расширение поля К по-
лучается присоединением квадратного корня из
кубического полинома, не имеющего кратных
корней, например элемента у такого, что
у2 = (х - а)(х - Ь)(х - с). Последнее уравнение
задает так называемую кубическую кривую)
Элементы полученного расширения представ-
ляют собой функции вида а(х) + Ъ(х)у, где а(х),
Ь(х) & К, и называются функциями на кубиче-
ской кривой. В общем случае квадратичное
расширение получается присоединением эле-
мента у такого, что у2 +fix) = 0. Здесь дискри-
минант -4/(х) имеет нечетную степень и не име-
ет кратных корней.
Степень неприводимого над К полинома р(х) с
корнем Z называется степенью элемента t. Если
степень элемента Z равна 1, то Z является элемен-
том поля К, то есть по существу расширения нет.
Назовем два расширения L и L' поля К изо-
морфными (над К), если существует изоморфизм
1 Подробнее об этом см. гл. 6.
62
L = L', оставляющий неподвижными элементы
поля К.
Поскольку простые трансцендентные расшире-
ния поля К изоморфны полю рациональных функ-
ций и этот изоморфизм сохраняет константы (эле-
менты поля К), то такие расширения изоморфны.
Простые алгебраические и трансцендентные
расширения можно строить и не прибегая к
включающему K(f) полю L. При этом трансцен-
дентное расширение изоморфно полю рацио-
нальных функций, а алгебраическое— кольцу
классов вычетов Х[х]/(р(х)). Следовательно, ал-
гебраическое расширение однозначно определя-
ется полиномом р(х).
Поле L называется алгебраически замкнутым,
если каждый полином из £[х] раскладывается на
линейные множители. Алгебраически замкнутое
поле не допускает дальнейших алгебраических
расширений. Поэтому можно говорить о макси-
мальном алгебраическом расширении данного
поля. Примером алгебраически замкнутого поля
является поле С комплексных чисел.
Каждое поле К обладает единственным с точ-
ностью до изоморфизма алгебраически замкну-
тым алгебраическим расширением [2]. Такое од-
нозначно определенное алгебраическое расши-
рение называется алгебраическим замыканием
поля К. Поле С, однако, не является алгебраиче-
ским замыканием поля Q, поскольку содержит
неалгебраические над Q числа, например, число
л, которое не служит корнем ни одного алгеб-
раического уравнения с рациональными коэффи-
циентами.
Пусть L — расширение поля К. Элемент v е L
называется алгебраически зависимым от щ, ...,
ип, если он является корнем полинома
..., u,fi +ainfiu\, —, + ... +
+ a0(wb и„) = О,
где ..., w„)— полиномы из К\щ,и„\, не
все равные нулю. Элементы щ, ..., w„ е L назы-
ваются алгебраически независимыми, если ни
один из них не является алгебраически зависи-
мым от остальных.
Например, если квадратичное расширение
поля С(х) рациональных функций получается
присоединением корня полинома у2 +fix) = 0, где
f— полином нечетной степени, не меньшей 3, то
элементы расширенного поля будут иметь вид
а(х) + Ъ(х)у, где fix), Ь(х) е С(х). В этом случае
переменные х и у алгебраически зависимы. Если
трансцендентное расширение поля С(х) строится
присоединением новой переменной у, то пере-
менные х и у в поле С(л", у) алгебраически неза-
висимы.
Имеет место следующая теорема.
Теорема 4.2.1. Пусть L — расширение поля
К. Элементы щ, ..., и„ е L алгебраически незави-
симы тогда и только тогда, когда из равенства
Ж,..., и„) = 0,
где Дщ, ..., w„) е Х[щ, ..., и„], следует равенство
нулю всех коэффициентов полинома f
Доказательство см. в работе [4].
Подмножество S поля L назовем алгебраиче-
ски независимым, если ни один из его элементов
не зависит алгебраически от остальных.
На алгебраически независимых подмножест-
вах поля L можно ввести отношение порядка по
возрастающему включению. Эти подмножества
оказываются индуктивно упорядоченными, и
среди них существуют максимальные. Наиболь-
шая мощность подмножества среди мощностей
всех таких множеств называется степенью
трансцендентности поля L над К.
Пример 4.2.2. Степень трансцендентности.
1. L = К(х). Элемент х алгебраически незави-
сим от элементов поля К. Степень трансцендент-
ности поля L над К равна 1.
2. Если L = K(x), М= К(х,у), то степень
трансцендентности М над L равна 1, а степень
трансцендентности М над К равна 2.
3. Если L = К(х), М= К(х, y)/(fix, у)), где поли-
ном fix, у) неприводим над алгебраическим за-
мыканием поля К, то степень трансцендентности
М над L равна 0, а степень трансцендентности М
над К равна 1.
4.2.2. Конечные расширения
Поле L называется конечным расширением
поля К, если L является конечномерным вектор-
ным пространством над К. При этом все элемен-
ты из L являются линейными комбинациями ко-
нечного множества элементов щ, ...,и„ с коэф-
фициентами из К. Число элементов базиса век-
торного пространства называется степенью рас-
ширения L над К и обозначается (L-.K)'1
Например, если к полю К присоединяется ко-
рень t полинома р(х), deg(p) = n, то элементы
1° = е, t, t\ ..., t"~l образуют базис поля L над К и
(L.K) = п.
Теорема 4.2.2. Если поле К конечно над к и
поле L конечно над К, то L конечно над к и
(К.к) = (L-.KfiK-.k).
2 Иногда в литературе степень расширения обо-
значается L/K. а 5 ,-я.
63
Доказательство. Пусть {щ. ...,и„} — базис
L над К и {vi,vm} — базис К над к. Тогда ка-
ждый элемент из L можно представить в виде
<T|Wi + ... + a„w„, где а, & К, и каждый элемент из
К можно представить в виде b\Vi +... + b,„vm, где
bj е. к. Подстановка второго выражения в первое
показывает, что каждый элемент поля L линейно
зависит от пт элементов w;v7. Следовательно,
число (L\k) конечно. Элементы w,y, линейно неза-
висимы над к, так как w, линейно независимы над
/Сиу, линейно независимы над к. Следовательно,
(L.k) = (L:K)(K:k).
Следствие 4.2.3. Если поле К конечно над к и
(К.к) = и. поле L конечно над к и (L:k) = пт, то L
конечно над К и (L.K) = т.
Элемент w е L называется алгебраическим над
К, если он удовлетворяет алгебраическому уравне-
нию/w) = 0 с коэффициентами из К. Расширение L
поля К называется алгебраическим над К, если каж-
дый элемент поля L является алгебраическим над К.
Теорема 4.2.4. Каждое конечное расширение L
поля К получается присоединением к К конечного
числа алгебраических над К элементов. Каждое
расширение, полученное присоединением конеч-
ного числа алгебраических элементов, конечно.
Доказательство. Пусть поле L является ко-
нечным расширением поля К, и степень расши-
рения равна п. Пусть w е L\K. Тогда среди сте-
пеней м,и = е, м, ..., w” не более п линейно неза-
висимых. Значит, должно выполняться равенство
«о + <7|И’ + ... + a„w" - 0 при а, е К, то есть каж-
дый элемент поля L алгебраичен над К. Обратно,
пусть м— алгебраический элемент степени г.
Тогда элементы е, и, линейно независи-
мы и образуют базис, то есть расширение явля-
ется конечным. Применение нескольких после-
довательных алгебраических расширений по
теореме 4.2.2 дает конечное расширение.
Таким образом, каждое конечное расширение
является конечным алгебраическим расширением.
Если при алгебраическом расширении к ис-
ходному полю К присоединяются все корни урав-
нения^) = 0, то полученное поле называется по-
лем разложения полинома fix). В этом поле поли-
номах) раскладывается на линейные множители.
Для каждого полинома fix) е А]х] существует
поле разложения, которое строится следующим
образом. Сначала присоединим к К какой-либо
корень Z] неприводимого делителя fi(x) полинома
fix). При этом полином f(x) будет иметь вид
(х - t\)mffix), т > L Затем присоединим к полу-
ченному расширению К(р) корень t2 неприводи-
мого полинома ffix) и т. д. Ясно, что процесс за-
кончится после конечного числа шагов.
Пример 4.2.3. Поле разложения.
Пусть /= х3 + ах2 + Ьх + с е. Q[x] — неприво-
димый над Q полином и «ь а2, а3— его ком-
плексные корни. Тогда поле разложения имеет
вид Q[ab а2, а3] = Q[ab а2] (по теореме Виета
aj + a? + a3 = -a е Q). Степень расширения
(Q[«i]:Q) = 3 и (Q[al,a2]:Q[a1])= 1 или 2. По-
этому (Q[ab a2]:Q) = 3 или 6.3
Построим поле разложения К присоединени-
ем всех корней неприводимого над Q полинома
/=х3 + 2. Положим a, = V~2\ После линейной
над К замены переменной х <- zV-2 полином f
примет вид —2(z3 — 1). Этот полином после деле-
ния на -2 раскладывается на простые множители
над С.-
z3-l=(z-l)(z2+z + l) =
= (z-l) z —
Следовательно, полином fix) над С расклады-
вается на линейные множители:
Присоединение к полю Q элемента aj = V~2
не влечет за собой присоединение элемента
a 2 = V- 2 1-+ . Поэтому для получения поля
разложения к исходному полю Q необходимо
присоединить два элемента: V- 2 и у[-3 , то есть
К = Q[V-2, V~3 ] Степень расширения (K:Q) = 6.И
Теорема 4.2.5. Пусть К— поле и полином
fix) е /С[х] неприводим над К. Тогда существует
поле L разложения полинома fix) и
(Z:X)<deg(/)!.
Доказательство. Пусть а!— корень поли-
нома fix) в поле L. Тогда в кольце £[х] полином
fix) делится на х - aj. Положим Д (х) = - .
х - aj
Тогда deg(/j) = deg(/) - 1. Вычленяем все корни
/1(х), лежащие в поле Kfa,], находим корень
a2 £ /Да,] и повторяем процедуру. Поскольку на
каждой итерации степень полинома уменьшается
Из формул Кардано для корней кубического
уравнения следует, что (Q[ab a2]:Q) = 3 тогда и толь-
ко тогда, когда дискриминант полинома f является
квадратом в Q. .
64
по крайней мере на 1, то после конечного числа
шагов будут присоединены все корни полинома
/, при этом (L:K) < deg(/)!.
Следствие 4.2.6. Для любого (не обязательно
неприводимого) полинома fix) е Аф] существует
поле разложения L, и (L:K) < deg(/)!.
Очередность присоединения корней полинома
для получения поля разложения несущественна,
так как в поле разложения все элементы переста-
новочны. Пусть полином fix) е Аф] обладает
корнями «.j, ос„. Тогда поле A[oti,ос„] и по-
ле разложения полинома / изоморфны над К.А
Поэтому поле разложения полинома полностью
определяется этим полиномом.
Расширение L поля К называется нормальным
над К, если оно алгебраично над К и каждый не-
приводимый в Аф] полином, обладающий хотя
бы одним корнем в L, раскладывается в Аф] на
линейные множители. Расширение L поля К, по-
лученное присоединением всех корней одного,
нескольких или бесконечного числа полиномов
из Аф], является нормальным.
Каждое алгебраическое расширение может
быть вложено в некоторое нормальное расшире-
ние, например, в алгебраически замкнутое поле.
Среди всех нормальных расширений, содержа-
щих данное поле, существует наименьшее.
Пример 4.2.4. Нормальные расширения.
1. Построим нормальное квадратичное расши-
рение поля К с характеристикой, отличной от 2,
присоединением корня неприводимого квадратно-
го полинома fix) е Аф]. Корни полинома fix) ли-
нейно зависимы, поэтому присоединение одного
корня означает присоединение и второго корня.
Следовательно, любое квадратичное расширение
поля К является нормальным. Отсюда следует, что
поле L = , где D,&K (мулыпи-
квадратичное расширение), нормально над К.
2. Поле разложения является нормальным
расширением.
3. Алгебраическое замыкание поля Q, полу-
ченное присоединением всех корней всех непри-
водимых полиномов, является нормальным рас-
ширением поля Q.
4. Пусть К — произвольное поле. Присоеди-
ним к полю К все корни полинома хп - е. Они об-
разуют циклическую группу порядка п, изоморф-
ную группе корней степени п из 1 в поле С. По-
этому группа корней степени п из е в рассматри-
ваемом расширении поля К тоже циклична и име-
ет порядок п. Следовательно, все корни полинома
4 Доказательство этого утверждения см. в работе [4].
хп -е в рассматриваемом расширении являются
степенями одного корня. Для получения нормаль-
ного расширения достаточно присоединить к по-
лю К образующую группы корней степени п из е,
то есть некоторый корень уравнения У - е.
Теорема 4.2.7. Нормальное расширение не за-
висит от очередности присоединения корней не-
приводимых полиномов.
Доказательство см. в работе [2].
Поскольку поле разложения нормально, все
поля разложения данного полинома совпадают.
4.2.3. Целые элементы поля
Обобщим понятие целого числа на произ-
вольные поля. Пусть R— целостное подкольцо
кольца Т и элемент t е Т удовлетворяет уравне-
й-1
нию вида th = 0, где г, е R. Такой эле-
1=0
мент называется целым над R. Суммы и произве-
дения целых над R элементов являются целыми
над А.4 5 Поэтому целые над R элементы кольца Т
образуют кольцо.
Пусть теперь R — целостное кольцо, К — его
поле частных, L — расширение степени п поля К
н S— множество элементов поля L, являющихся
целыми над R. Тогда А является кольцом, содер-
жащим R. Например, А = Z, К = Q, L = Q(z),
A = Z[z],
Теорема 4.2.8. Любой элемент I поля L можно
представить в виде I = —, где 5 e .S', г е А.
г
Доказательство. Элемент I поля L удовле-
творяет алгебраическому уравнению с коэффи-
циентами из К:
Г + а^Г1 + ... +zzo = O. (4.2.1)
Поскольку L — поле частных кольца А, то а,
являются дробями с числителем и знаменателем
из А. Умножим все эти дроби на произведение
всех знаменателей, тогда левая часть уравнения
= 0. (4.2.1) превратится в полином с коэффи-
циентами из А: ЪПГ + bn_\V'~x + ... + bo = 0. Ум-
ножив это уравнение на А,,"-1, получим
(Ь„1)" + b^bJT1 + ... + bob,;-1 = 0.
5 Иногда целый над А элемент кольца Т определя-
ется как такой элемент, все степени которого линейно
выражаются через конечное множество элементов Т.
Эти определения эквивалентны, если кольцо Т явля-
ется конечным над А.
65
Следовательно, b„l является целым элементом
над R. Положив г = bm s = bnl, получим заключе-
ние теоремы.
R-порядком поля L называется всякое коль-
цо в L, которое содержит R и является конеч-
ным модулем над R. Кольцо S всех целых эле-
ментов поля L называется максимальным по-
рядком поля L.6
Например, если R = Z, К = Q, L = Q(z), S' = Z[z],
то порядками в поле L будут кольца Ж[п1], где
п > 1 — целое число. Порядками поля функций
Q(x) над Z будут кольца Z[x], Zfx2], Zjfix)], где
fix) — произвольный полином из Ж[х].
Целостное кольцо R называется целозамкну-
тым, если каждый элемент поля частных кольца
R, являющийся целым над R, лежит в R. Напри-
мер, для Q кольцо Z целозамкнуто, для Q[z]
кольцо Z[z] целозамкнуто. Целозамкнутым явля-
ется любое факториальное кольцо.
4.3. Конечные поля
4.3.1. Строение конечных полей
Поле К называется конечным, или полем Га-
луа, если оно состоит из конечного числа эле-
ментов. Примером конечного поля является про-
стое поле, состоящее из р элементов, то есть по-
ле классов вычетов по модулю р. Поле из q эле-
ментов обозначается F9.7
Поскольку поле F9 конечно, его характеристика
не может быть нулевой. Следовательно, характе-
ристика поля F9 равна некоторому простому числу
р. Таким образом, поле F9 является конечным рас-
ширением некоторого простого поля Fp, то есть
конечномерным векторным пространством над Fp.
Пусть размерность этого пространства равна п. То-
гда каждый элемент поля F9 может быть единст-
венным образом представлен в виде линейной
комбинации щг/i + ... + <7„w,„ где <7, е F,, и q =р”.
Алгебраическое расширение поля Fp получа-
ется присоединением корня неприводимого над
Fp полинома fix). Выясним, могут ли у этого по-
линома быть кратные корни.
Теорема 4.3.1. Неприводимый полином
fix) е Fp[x] имеет кратные корни, если он являет-
ся полиномом от хр. В этом случае в поле разло-
жения каждый корень имеет кратность р.
6 Максимальный порядок называют также глав-
ным порядком.
7 Иногда поле из q элементов обозначается также
GF(<7).
Доказательство. Полином fix) обладает
кратными корнями лишь тогда, когда/и/' имеют
в Fp[x] общий делитель, отличный от обратимого
элемента в поле Fp. Но fix) неприводим, поэтому
он может иметь нетривиальный наибольший об-
щий делитель с производной (совпадающий с fix))
И
лишь при /' = 0. Если f(x) = ^a,x', то
г=0
п
f'(.x) = ^jiaix'~i-0 и z<7; = 0 (mod/у). Отсюда
i=i
следует, что полином f имеет ненулевые коэффи-
циенты <7, лишь при степенях х, кратных р, то есть
fix) = g(s), где s = xp. Полином g может опять
представлять собой полином от sp, тогда эта опе-
рация повторяется. Предположим, что g(.s) не яв-
ляется полиномом от sp. Если его разложить на
множители в некотором расширении поля Fp, то
он будет иметь только простые корни. Пусть t —
корень полинома g, тогда элемент и такой, что
ир = t, будет корнем кратностир полиномаf.
Пусть К — поле характеристики р. Если t —
корень неприводимого над К полинома, обла-
дающего только простыми корнями, то говорят,
что расширение Л'|/] сепарабельно, в противном
случае — несепарабелъно. Несепарабельным
может быть только расширение расширенного
поля, то есть коэффициенты неприводимого по-
линома fix) из теоремы 4.3.1 должны лежать в
расширении поля К (если коэффициенты fix) ле-
жат в К, то fix) = g(xp) = (g(x)p). Например, пусть
К = F,,(y) — поле рациональных функций. Тогда
расширение L\K, заданное полиномом f -у = f -
- (y!pf = (t — y'p'f будет несепарабельным.В даль-
нейшем будем рассматривать сепарабельные рас-
ширения. Все конечные поля сепарабельны [4].
Пример 4.3.1. Конечное поле матриц.
Рассмотрим поле квадратных матриц размера
3 над полем F2; в нем единичным элементом яв-
ляется единичная матрица Е. Такое поле состоит
из следующих элементов:
Д 0 0" "0 1 ол <0 о Г
- ООО ,д = 0 0 1 ,А2 = 10 1,
.0 0 0, .1 0 1, J 1 р
о Г Д 1 Р '1 1 0"
А3- 11 1 ,А4 = 1 1 0 ,А5 = 0 11,
J1 °, 1 0 0
го 1 Г ') 0 О'
А6 = 1 0 0 ,А7 = 0 1 0 -
.0 1 0, <° 0 р
66
Нетрудно заметить, что выполняются равен-
ства А1 + Е = А3, А2 +А + Е = Л4, А + Е = А5,
А2 + А = А6, Е = А'. Сумма любых элементов это-
го поля дает снова элемент поля, причем все
элементы поля представляют собой линейные
комбинации матриц £, А, Л1. Матрица Ао являет-
ся нулевым элементом поля. Из курса линейной
алгебры известно, что для матриц выполняются
аксиомы дистрибутивности. Группа ненулевых
элементов по умножению является циклической
и, следовательно, коммутативной; в кольце мат-
риц нет делителей нуля. Каждая из матриц В = А'
удовлетворяет уравнению В3 + В2 + £ = Ао. Мат-
ричный полином В3 + В2 + Е является неприво-
димым над кольцом квадратных матриц размера
3 над полем F2. Полученное поле изоморфно по-
лю классов вычетов F2[x]/(x3 + х2 + 1). Изомор-
физм задается заменой символа х на матрицу А.
Теорема 4.3.2. Каждый элемент х конечного
поля F9 удовлетворяет равенству х1 - х — 0.
Доказательство. Мультипликативная груп-
па поля F9 состоит из q - 1 элементов (имеет по-
рядок q - 1). Поэтому каждый ненулевой эле-
мент поля F9 удовлетворяет равенству x'rl = 1,
где 1 — единичный элемент поля. Умножим ра-
венство хч-l = 1 на х. Получим равенство хч = х,
справедливое для всех элементов поля F9, вклю-
чая нуль, то есть каждый элемент поля F9 являет-
ся корнем полинома xq-x. Иначе говоря, для
всех элементов х е F? выполняется равенство
х9-х = 0.
В случае простого поля получаем малую тео-
рему Ферма, согласно которой для числа а, вза-
имно простого с р, имеет место сравнение
ар~} = 1 (mod р).
Теорема 4.3.3. Имеет место равенство
xq -х- ГТ/*-0)’ где произведение берется по
всем элементам поля F9.
Доказательство [1]. Рассмотрим правую и
левую части равенства как полиномы из F/х]. По-
скольку каждый элемент поля F9 является корнем
полинома xq - х и число сомножителей в правой
части равно q, получаем утверждение теоремы.
Поле F9 состоит из всех корней полинома хд - х,
которые присоединяются к простому полю F,,.
Теорема 4.3.4. Для каждой степени простого
числа рп = q существует единственное (с точно-
стью до изоморфизма) конечное поле F9.
Доказательство. В случае п = 1 это очевид-
но. Пусть п > 1. Построим такое расширение по-
ля Fp, в котором полином xq - х полностью рас-
кладывается на линейные множители. В полу-
ченном поле разложения рассмотрим множество
корней полинома xq — х. Это множество корней
тоже является полем, так как если хч = х и у' = у,
то (х ± y)q = xq ± yq, (xy)q = xqyq и (х/yf =xqIyq
при ненулевом у. Полином xq - х имеет в F9
только простые корни. Действительно, его про-
изводная равна qxq4-l = -l, поскольку q = 0
(mod/?), то есть производная не имеет корней в
рассматриваемом поле. Следовательно, поле F9
является полем из q элементов.
Теорема 4.3.5. Если полином /х) степени d
делит полином xq -х, то он имеет ровно d раз-
личных корней в поле F<;.
Доказательство [1]. Рассмотрим полиномы
/х) и xq -х как элементы кольца F/х]. В этом
кольце справедлива теорема 3.8.2. Поскольку fix)
делит xq - х, то множество корней полинома fix)
является подмножеством корней полинома х‘ - х.
Но xq - х раскладывается над F9 на различные
линейные множители, поэтому и/раскладывает-
ся на линейные множители и среди этих множи-
телей нет двух одинаковых.
Таким образом, поле F9 является нормальным
расширением поля Fp.
Покажем, что мультипликативная группа ко-
нечного поля всегда циклична.
Теорема 4.3.6. Мультипликативная группа F(/*
конечного поля F4 циклична.
Доказательство [1]. Пусть х— произволь-
ный ненулевой элемент поля F?. Поскольку xq~} = 1,
то степени элементах образуют подгруппу в группе
F9, порядок этой подгруппы является делителем
числа q - 1. Разложим число q - 1 на простые мно-
п п
жители: q -1 = = ГГ г, > причем все г, вза-
,=1 <=1
имно просты. В группе F(/ существует не более
(q-\)lp, элементов х, для которых х(9-1^й =1,
так как полином х(ч~^1р‘ -1 имеет (q -1)/pt кор-
ней. Следовательно, в F9* существует элемент а„
для которого а-'! У^г‘ ф 1. Тогда элемент
Ъ, = a^q~x^'' имеет порядок г,. Все г, степеней эле-
мента Ь, являются различными, так как единст-
венным простым делителем числа г, является /?,,
и bq!p' = й/«“1У'''><л7д) Произведение С =
/=1
элементов взаимно простых порядков г, имеет
67
порядок q - 1, то есть является образующей
группы F? .
Следствие 4.3.7. Число образующих группы
F9 равно числу чисел, меньших q - 1 и взаимно
простых с q - 1.
Доказательство. Пусть а— образующая
группы F9 . Рассмотрим группу, образованную
элементом b = as. Эта группа совпадет с группой
F9 , если существует показатель t такой, что
Ъ‘ = а, то есть as‘ = a или st= 1 (mod(^-l)).
Элемент s обратим в Ж/(д - 1)Z тогда и только
тогда, когда он взаимно прост с q - 1.
4.3.2. Автоморфизмы конечных полей
Опишем автоморфизмы поля F9, q=pn. Рас-
смотрим отображение о: х —> хр. Тогда о — эн-
доморфизм поля F9 с ядром 0, так как
(ab)p = арЪр, (а + bf = ар + Ьр. Следовательно,
каждый образ эндоморфизма имеет единствен-
ный прообраз. Поскольку поле F9 конечно, то
отображение о взаимно однозначно. Таким обра-
зом, о является автоморфизмом.
Простое поле Fp не имеет автоморфизмов, от-
личных от тождественного. Действительно, поле
из р элементов изоморфно полю TZJpTL Группа Z
циклична, поэтому аддитивная группа поля Fp
тоже циклична с образующей 1. Каждый авто-
морфизм сохраняет неподвижными нулевой и
единичный элементы, а значит и все элементы
поля Fp. Поскольку поле F9 содержит простое
поле Fp, то все автоморфизмы поля F9 сохраняют
неподвижными элементы из поля Fr.
Автоморфизмы можно умножать с помощью
композиции отображений. Произведение двух
автоморфизмов является эндоморфизмом, так
как оно сохраняет операции сложения и умно-
жения. С другой стороны, произведение двух
автоморфизмов как биективных отображений
является биективным отображением и, следо-
вательно, автоморфизмом. Единичное отобра-
жение, сохраняющее неподвижными все эле-
менты поля F9, является единичным автомор-
физмом. Кроме того, каждый автоморфизм как
обратимое отображение имеет обратный авто-
морфизм.
Рассмотрим множество автоморфизмов, со-
стоящее из степеней автоморфизма о. Здесь
с(х) = хр, о2(х) = (хр)р = ХР ИТ. д.
Теорема 4.3.8. Автоморфизмы {о, о2, о3, ...}
образуют циклическую группу порядка п.
Доказательство. Поскольку автоморфизмы
действуют на конечном поле F9, их можно рас-
сматривать как подстановки. Степени подста-
новки образуют циклическую группу, поэтому
автоморфизмы {су, о2, о3, ...} образуют цикли-
ческую группу. Но d\x) = xp =х для всех
х g F9. Следовательно, порядок группы авто-
морфизмов является делителем числа п. Пред-
положим, что существует положительный пока-
затель d такой, что и(х)=х. Тогда уравнение
хр -х = 0 имеет корень при любом х. Но это
уравнение имеет не более pd корней. Значит,
d = n. Поскольку для любого х из поля F9 вы-
полняется равенство и"(х) = хр =х, то о" явля-
ется единичным отображением (единичным
элементом группы).
Покажем, что других автоморфизмов поля F9
нет. Из теоремы 4.3.8 следует, что существует
не менее п автоморфизмов поля F(/, q=pn. Поле
F9 получено присоединением к простому полю
корня неприводимого полинома степени п. Ав-
томорфизм достигается заменой одного корня
на другой. Однако число корней полинома сте-
пени п не более п, поэтому и число автомор-
физмов не более п. Следовательно, других ав-
томорфизмов нет. Таким образом, все автомор-
физмы поля F9 являются степенями автомор-
физма о: х —>хр.
Теорема 4.3.9. Если п = rs, то поле L из р"
элементов содержит поле К из р' элементов. В
этом случае существуют автоморфизмы поля L,
оставляющие неподвижными элементы поля К.
Эти автоморфизмы образуют циклическую
подгруппу группы автоморфизмов с образую-
щей о'.
Доказательство. Поля L и К являются ко-
нечными расширениями поля F,„ (A’zF,,) | (£:F,,).
Тогда по следствию 4.2.3 поле L является конеч-
ным расширением поля К. Поскольку число п
составное, то в циклической группе (о) автомор-
физмов, оставляющих неподвижными элементы
поля Fp, существует подгруппа, образованная
автоморфизмами с/. Поскольку группа (о) ко-
нечна и циклична, то ее подгруппа тоже циклич-
на. При этом группа (с/) имеет порядок s. Любой
элемент х поля К удовлетворяет равенству хр = х.
Следовательно, автоморфизм с£ оставляет не-
подвижными элементы поля К.
Поскольку числа г, s в формулировке теоремы
4.3.9 не обязаны быть простыми, то для конечно-
го поля существуют автоморфизмы, оставляю-
щие неподвижными элементы любого его под-
поля. Если степень расширения конечного поля
К над подполем к равна s, то порядок группы ав-
томорфизмов, оставляющих неподвижными эле-
менты из к, равен s.
Таким образом, поле L можно рассматривать
как алгебраическое расширение конечного поля
К, не обязательно простого.
Теорема 4.3.10. Если fix) — неприводимый
над F,, полином степени d, то полином хр - х де-
лится наДх) тогда и только тогда, когда d\ п. п
Доказательство. Корни полинома хр -х
являются простыми и образуют поле L. Предпо-
ложим, что хр -х делится наДх). В этом случае
множество корней полинома fix) является под-
множеством корней полинома хр -х, то есть
элементами поля L. Тогда поле L содержит поле
разложения полинома^)- Следовательно, d\n.
Обратно, если п = md, то поле L является расши-
рением степени т поля К, состоящего из р эле-
ментов. Поскольку все поля из одинакового чис-
ла элементов изоморфны, то поле К изоморфно
полю разложения полинома fix). Значит, поле L
содержит все корни полинома fix), то есть хр -х
делится наДх).
Следовательно, произведение всех неприво-
димых полиномов из Fp[x] степени, делящей п,
равно хр - х. Здесь учитываются и линейные не-
приводимые полиномы.
Теорема 4.3.10 позволяет оценить число непри-
водимых полиномов из Fz,|x] степени п. Поскольку
кольцо F,,[x] факториальное и все ненулевые эле-
менты поля F,, являются обратимыми в кольце
Fp[x], то неразложимые элементы этого кольца
можно рассматривать с точностью до обратимых
элементов. Достаточно рассмотреть только непри-
водимые полиномы с единичным старшим коэф-
фициентом. Умножение такого полинома на про-
извольный обратимый элемент кольца даст ассо-
циированный с ним неприводимый полином.
Если число п простое, то хр -х делится толь-
ко на линейные полиномы и на неприводимые
полиномы степени п. В этом случае в любом
расширении поля F,, степени менее п ни один из
неприводимых полиномов степени п не раскла-
дывается на множители, но в расширении степе-
ни п каждый такой полином раскладывается на
линейные множители. Корни различных поли-
номов попарно различны, так как в противном
случае не все коэффициенты полиномов были бы
элементами поля Fp. Корни полинома хр - х об-
разуют поле из рп элементов. Это поле содержит
простое поле, элементы которого соответствуют
неприводимым линейным полиномам. Осталь-
ные элементы соответствуют корням неприво-
димых полиномов степени и, каждый полином
имеет п корней. Следовательно, число приведен-
ных (с единичным старшим коэффициентом) не-
приводимых полиномов степени п для простого
п равно (//' - р)/п.
Для составного показателя п полином х!' -х де-
лится на все линейные полиномы, а также на все
неприводимые полиномы, степень которых делит-
ся на п. Поэтому формула для числа приведенных
неприводимых полиномов степени п несколько
усложняется. Например, для п = qr, где q, г — раз-
личные простые числа, число неприводимых по-
линомов степени п равно (р" - pq - рг + р)/п .
Формула для числа неприводимых полиномов
степени п в общем случае определяется теоремой
5.2.6.
Пример 4.3.2. Число неприводимых полино-
мов над конечным полем.
1. Для р = 2 число неприводимых полиномов
степени п = 5 равно (25 — 2)/5 - 6. Это полиномы
х5 + х~ + 1, х5 + Х’ + 1, Х$ + № + X2 + X + 1, х5 + х4 +
+ X2 + X + 1, X5 + X4 + X3 + X + 1, х5 + х4 + х3 + х2 + 1.
2. Для р = 2 и п = 6 число неприводимых поли-
номов равно (26 -23 -22 + 2)/б -9. Это полино-
мы х6 + х+1, х6 + х3 + 1, х6+х5+1, х6 + х4 + х2 +
+ X + 1, X6 + X5 + X2 + X + 1, X6 + X4 + X3 + X + 1,
X6 + X5 + X3 + X + 1, X6 + X5 + X4 + X + 1, хб + х5 + х4 +
+ х2+1.
Конечное расширение конечного поля задается
неприводимым полиномом. Если полином степе-
ни п раскладывается на множители в Fp[x], то хотя
бы один из них имеет степень не более и/2. Сле-
довательно, полином fix) неприводим в Fp[x], если
НОД(/-х,/х)) е Fp для всех к < п - 1.
Изложенное очевидным образом переносится
на случай кольца F9[x], если q=p. При этом
символ р заменяется на q. Например, для поля
F4= ПР2[/]/(/2 +1+ 1) число приведенных неприво-
димых полиномов степени 3 в F4[x] равно
(43-4)/з = 20. Это неприводимые полиномы
х3+х+1, х3 + х2+1. х3 + х2+х+1, а также 17
других полиномов, в частности х3 +1,
х3 + х + t + 1, х3 + tx + t + 1. Здесь x — перемен-
ная, a t — элемент поля F4.
Все конечные поля из q=pn элементов изо-
морфны как векторные пространства над Fp оди-
наковой размерности п [5]. Переход от одного
поля к другому осуществляется заменой базиса.
Поэтому вид неприводимого полинома, задаю-
щего поле классов вычетов, непринципиален.
Алгебраическое расширение L степени п ко-
нечного поля К является «-мерным векторным
пространством над К. Пусть поле L получено
присоединением корня t неприводимого над К
полинома f Тогда L = K[t\/(fit)).
69
Естественным базисом L над К является набор
различных степеней t. Однако в вычислительном
плане часто удобнее задавать базис L над К не в
виде степеней элемента t, а в виде нормального
базиса, представляющего собой п значений авто-
морфизмов поля L для некоторого элемента
g е L , например, g = t, для которого все значения
автоморфизмов различны: {g, c(g),«/'“’(g)}.
4.3.3. Норма и след в конечных полях
Пусть L — расширение степени п конечного
поля К = F,,. Покажем, что существует гомомор-
физм аддитивных групп Z —> К и гомоморфизм
мультипликативных групп L К .
Определим след элемента х е L в поле К как
сумму
Тг(х) = о°(х) + с(т) + ... + =
к-1
= X + хр + ... + хр .
Теорема 4.3.11. След Тг является гомомор-
физмом аддитивных групп Z, —> К.
Доказательство [1]. Доказательство прове-
дем в четыре этапа. Сначала покажем, что след
произвольного элемента х е L лежит в К. За-
тем — что выполняется равенство Тг(х + у) =
= Тг(т) + Тг(у) и что для а е К справедливо
Тг(лт) = аТг(х). На последнем этапе покажем, что
след отображает поле L на все поле К.
1. Возведем след Тг(х) в степень р. Получим
(Tr(x))' = (х + хр + ... + хр"~Х}р =
2 п
= хр + хр + ... + хр .
Для каждого элемента х е L выполняется ра-
венство хр' = х. Поэтому (Тг(х)У’ = Тг(х). Но поле
К= F,, состоит в точности из тех элементов х, для
которых выполняется равенство хр = х. Следова-
тельно, Тг(х) е К.
2. В поле характеристики р выполняется ра-
„А k к
венство (х+уу ~хр +ур для 0<к<п- 1. Под-
ставляя эти равенства в выражение для следа
Тг(х + у), получаем Тг(х) + Тг(у).
13. Элементы поля К удовлетворяют равенству
ар = а для 0 < к < п - 1. Поэтому
Тг(ш?) = У^ар хр = а'У'хр = пТг(х).
<=0 /=0
4. Полином х + хр + ... + х1' имеет не более
р"-1 корней в поле К. Поле L содержит р" > р,]
элементов. Следовательно, существует элемент
х е L такой, что Тг(х) = с Ф 0, с е К. Тогда для
Ъ е К получаем Тг(йс-1х) = йс-1Тг(х) = Ьс~Ас = Ь.
Если b пробегает все поле К, то след Tr(bc х)
тоже пробегает все поле К.
Таким образом, это отображение является го-
моморфизмом групп.
Определим норму элемента х g L в поле К как
произведение
N(x) = о°(х) • о(х) • ... • <Т' '(х) =
= х хр ... х^ .
Теорема 4.3.12. Норма N является гомомор-
физмом мультипликативных групп L —> К .
Доказательство [1]. Доказательство, как и
в теореме 4.3.11, проведем в четыре этапа. Снача-
ла покажем, что норма произвольного элемента
х g L лежит в К. Затем — что выполняется равен-
ство N(xy) = N(x)N(y) и что для а е К справедливо
N(ax) = a”N(x). На последнем этапе покажем, что
норма отображает группу L на группу К*.
1. Возведем норму N(x) в степень р. Получим
(N(x))p = (х хр ... -хр''У =
= ХР Хр1 • • х^
Для каждого элемента х g L выполняется ра-
венство хр =х. Поэтому (N(xjf = N(x). Но поле
К = F,, состоит в точности из тех элементов х, для
которых выполняется равенство хр = х. Следова-
тельно, N(x) е К, причем Л'(0) = 0 и N(x) е К для
х Ф 0.
2. Для произведения выполняется равенство
(ху^ = хруР для 0<А<//-1. Подставляя эти
равенства в выражение для нормы N(xy), получа-
ем N(x)N(y). Следовательно, норма является го-
моморфизмом группы L в некоторое подмноже-
ство группы К.
3. Элементы поля К удовлетворяют равенству
ар = а для 0 < к < п - 1. Поэтому
N(ax)-ax-apxp-ар хр ...ар хр =
= ах ахр • ... ахр = a"N(x).
4. Рассмотрим ядро гомоморфизма, индуци-
рованного нормой. Для элементов ядра имеем
1 = X + хр + хрг +... + хр"1 =
_ х^р+рг+-+р"’ _ x(p'’-i)/(p-i) >
В соответствии с теоремой 4.3.5 уравнение
x(p-i)/(p-i) _ j ИМеет (р'! -1)/(р -1) корней в
поле L, то есть ядро гомоморфизма имеет поря-
док (р" —!)/(/? — 1). Тогда по теореме 2.3.3 фак-
торгруппа L* по ядру гомоморфизма имеет поря-
70
док р - 1. Следовательно, эта факторгруппа сов-
падает с группой К.
Пусть L/K— простое алгебраическое расши-
рение и t е L. Тогда существует неприводимый
над К полином fix) = х" + att-}Xn~x + ... + ао с кор-
нем t е L: fit) - 0. Выразим норму и след элемен-
та t через коэффициенты этого полинома. В ка-
честве базиса поля L выберем степени элемента
t: е, t, t1, Если базисные векторы умно-
жить на t, то получим набор t, t1,Тогда
элементы второго набора можно выразить через
элементы первого набора (базиса): t = t, ? = Z2,..
Z"-1 = z"-1, z" = -о,,-/''1 - ... - a\t- ао- Этому пре-
образованию соответствует матрица
( 0 1
ч °о а1
0 ... О'
1 ... о
0 ... 1
-а2 ... -ап_х>
Сумма диагональных элементов матрицы
равна -<7и-ь поэтому след элемента Z равен
Tr(Z) = и совпадает со следом матрицы Т.
Найдем определитель матрицы Т. Для этого
циклически сдвинем вниз на одну позицию все
строки матрицы Т. Это преобразование соответ-
ствует умножению определителя на (-1То-
гда определитель матрицы будет равен N(t) =
= (—1)" (-йо) = (-1)"<7о- След и норма являются
инвариантами матрицы Г и не зависят от выбора
базиса L над К.
В поле L полином fix) раскладывается на ли-
нейные множители:
fix) = (х - Zj)(x - Z2).. .(х - Z„).
Тогда можно выразить след и норму следую-
щим образом:
Tr(Z) = -о„_1 = Z, + Z2 + ... +t„,
7V(Z) = (—1)”йо = Z]Z2...Z„.
След и норма элемента Z g L являются сим-
метрическими функциями от всех п значений
автоморфизма L над К для аргумента Z и прини-
мают значения в поле К. Поэтому все п корней
полинома fix) имеют одинаковую норму и след.
Покажем, что все симметрические функции от
указанных аргументов тоже принимают значения
в поле К. Действительно, любая симметрическая
функция может быть выражена в виде элементар-
ных симметрических функций. Каждая элементар-
ная симметрическая функция может быть выраже-
на в виде полинома от следов Tr(Z), Tr(Z2),..., Tr(Z")
элементов Z', как показано в п. 3.12. Все элемен-
ты Z' лежат в поле L, а их следы — в поле К. По-
этому и значения полинома от следов этих эле-
ментов лежат в поле К.
Пример 4.3.3. Норма и след в конечном поле.
1. Пусть L = F)6 = F2[Z]/(Z4 + z + 1), К = F2. Най-
дем норму и след элемента Z3 + z из поля L в поле
К. Норма будет равна (Z3 + /)|]2,4+8 =
= (Z3 + Z)15 = 1, так как для любого ненулевого
элемента у g FJ6 справедливо у15 = 1. След этого
же элемента равен (Z3 + Z)1 + (Z3 + Z)2 + (Z3 + Z)4 +
+ (Z3 + Z)8 = (Z3 + Z2) + (Z3 + Z2 + Z + 1) + (Z3 + Z+ 1) +
+ (z3 + 1) = 1.
2. Пусть L = F5[Z]/(Z3 + 2z + 4), K’ = F5. Норма
элемента 3z2 + 4z + 3 равна (3Z2 + 4z + 3)1+5+25 = 3.
След этого же элемента равен (3Z“ + 4Z + 3) +
+ (4Z2 + 3Z+ 1) + (3Z2 + 3z + 3) = 2.
4.4. Элементы теории Галуа
Автоморфизм конечного расширения конеч-
ного поля, сохраняющий неподвижными элемен-
ты исходного поля, достигается заменой одного
корня неприводимого полинома на другой:
Z —> f. Это справедливо и для бесконечных по-
лей. Например, поле С обладает двумя очевид-
ными автоморфизмами над IR: тождественное
отображение и комплексное сопряжение.
Пусть L/K— нормальное расширение. Ав-
томорфизмы расширения L/К, оставляющие
неподвижными элементы из К, образуют груп-
пу, называемую группой Галуа Gal(£/K), по-
скольку произведение автоморфизмов является
автоморфизмом и ассоциативность умножения
следует из теоремы 1.1.1; каждый автоморфизм
имеет обратный; тождественное отображение
является единичным автоморфизмом. При этом
под группой Галуа алгебраического расширения
L/К понимают группу Галуа минимального
нормального расширения, содержащего данное
расширение £.8
Расширение L/К называется абелевым, если
его группа Галуа абелева; циклическим, если его
группа Галуа циклическая [6].
Под группой полинома понимают группу Га-
луа поля разложения этого полинома.
Пусть fix) е. К[х] — неприводимый над К по-
лином, — его корни в некотором
расширении поля К и L — поле разложения этого
полинома, являющееся нормальным расширени-
ем. Тогда L = K[oci,..., ос„].
Автоморфизмы такого расширения L/К зада-
ются заменой одного корня полинома Дх) на дру-
8 Конечное нормальное сепарабельное расшире-
ние называют также расширением Галуа. - •
71
гой. Корни {<Х|, ...,ос„} алгебраически зависимы
над К, поэтому достаточно рассмотреть не все
перестановки корней, а отображения (произ-
вольного) данного корня а. Таким образом, су-
ществует п автоморфизмов L над К [6].
Пример 4.4.1. Группа Галуа.
1. Пусть fix) е Дх] — неприводимый над К
полином и char(K) 2. Квадратичное расшире-
ние L поля К, полученное присоединением корня
полиномаДх), нормально, так как каждый корень
линейно зависит от другого. Поэтому существует
группа Gal(£/K), состоящая из двух автоморфиз-
мов: тождественного и замены одного корня на
другой. Пусть дискриминант полинома fix) равен
D. Второй автоморфизм переводит элемент
а + bjD &L в элемент а - Ь-Jd . Эта группа
циклична. Соответственно расширение L/К явля-
ется циклическим.
2. Рассмотрим мультиквадратичное расшире-
ние L поля К характеристики 0, полученное по-
следовательным присоединением корней не-
скольких неприводимых квадратных полиномов
с дискриминантами D],D„. Такое расширение
нормально (см. пример 4.2.4, п. 1), а автомор-
физм, отличный от тождественного, заменяет
элемент поля на сопряженный. Пусть автомор-
физмы ср, и <р7 осуществляют соответственно за-
мену элементов на -.JZT" . То-
гда ср2 = (р7 = 1. Автоморфизм <р,ср7 переводит эле-
менты + д/Д и Jd^Dj в -
и соответственно; автоморфизм ср/р,
переводит элементы -JlT + JD- и JD- в
этому ср,ср7 = ф7<р,. Это равенство выполняется для
всех /, /, поэтому группа Галуа мультиквадра-
тичного расширения абелева и изоморфна пря-
мому произведению циклических групп порядка
2, а само мультиквадратичное расширение явля-
ется абелевым.
Понятие нормы и следа для конечных полей
можно перенести и на конечные расширения
бесконечных полей. Пусть L — конечное расши-
рение поля К, и Д,..., е„] — базис расширения
L/К. Если р g L, то Ре, = ауе , где о,7 е К. То-
гда след Тг(р)— это сумма диагональных эле-
ментов матрицы (<7у), норма А(р)— определи-
тель матрицы (ау). След является гомоморфиз-
мом аддитивных групп полей, а норма— гомо-
морфизмом мультипликативных групп.
Обобщим на произвольные поля теорему о
существовании кратных корней неприводимого
полинома над конечным полем (теорема 4.3.1).
Теорема 4.4.1. Пусть К— поле,/(х) е Дх] —
неприводимый над К полином. Следующие ут-
верждения эквивалентны.
1. fix) имеет кратные корни в поле разложения.
2. llOJfifix),f{x))eK.
3. Поле К имеет характеристику р ф 0 и
ХД е ДД].
4. Кратность всех корней fix) делится на р.
Доказательство [6]. 1 =>2. Пусть а— ко-
рень кратности т > 1 полинома fix) и
f(x) = (х- a)"'g(x). Тогда
f(x) = т(х - a)”’ g(x) + (х - a)n‘g(x) =
= (х - a)'”~'(mg(x) + (х - a)g'(x)),
отсюда НОД(Дх),/'(х)) g К.
2 => 3. Поскольку fix), f’(x) е Дх], то и
1ЮД(/(х),/'(х)) е Дх] (это следует из алгоритма
Евклида). Но deg(/') < deg(/) и fix) не имеет дели-
телей в Дх], поэтому /'(х) = 0. Это возможно
только тогда, когда характеристика поля К равна
р и fix) является полиномом от хр.
3 => 4. В поле характеристики р справедливо
равенство (х + а)р = хр + ар(см. теорему 4.1.4).
Пусть fix) = fix’’) и g(x) = (хр - ос,)"'' в поле
разложения. Тогда
Ях)=П(^=П^-р()р"”’
где pf = ос,.
4 => 1 — очевидно.
Связь между расширениями полей и их группа-
ми Галуа устанавливается следующей теоремой.
Теорема 4.4.2 (основная теорема теории
Галуа). Пусть М— нормальное конечное рас-
ширение поля К и L— промежуточное поле,
K<^L<^M. Между промежуточными полями L и
подгруппами Н группы G = Gal(AfZK) существует
биекция. При этом
1) если ДсД то подгруппа Д, соответст-
вующая Li, содержит подгруппу Д, соответ-
ствующую Lf,
2) порядок подгруппы Н в G равен (M'.L), ин-
декс HaG равен (L:K).
3) Н— нормальная подгруппа в G тогда и толь-
ко тогда, когда L — нормальное расширение
поля К.
Доказательство см. в работе [2].
72
Пусть К— поле и £ = /Да]— его конечное
расширение. Тогда а называется примитивным
элементом поля L (над К). К каждое конечное
сепарабельное расширение L/К обладает прими-
тивным элементом (это означает, что присоеди-
нение корней нескольких различных неприводи-
мых полиномов эквивалентно присоединению
корня одного неприводимого полинома).
Теорема 4.4.3 (о примитивном элементе).
Пусть L = a,J — алгебраическое расши-
рение поля К и минимальные полиномы для эле-
ментов ос, не имеют кратных корней. Тогда суще-
ствует такой элемент р е L, что L = £С[р].
Доказательство см. в работе [6].
Пример 4.4.2. Примитивный элемент.
1. Пусть £C = Q[V2, л/З] . Рассмотрим группу
Галуа Gal(Q[V2, д/З] / Q). Положим c(V2) = --^2 ,
т(л/3) = —J3 . Тогда
o(72+V3) = -V2+V3;
т(72+л/3) = 72-л/3;
(от)(л/2 + 73 ) = (то)(Т2 + VI) = -V2 - л/з.
Группа автоморфизмов порождается авто-
морфизмами о, т, поэтому К = Q[V2 + д/з ].
Пусть a = V2 + д/з — примитивный элемент по-
ля К. Поле К является полем разложения поли-
нома
(х - а)(х - <т(а)Хх - т(а)Хх - сгс(а))=х4 - 1 Ох2 + 1.
2. Пусть К =Q[V-T, V2, д/З]. Это поле имеет
23 = 8 автоморфизмов. Группа автоморфизмов
порождается тремя автоморфизмами о, т (см. п. 1
данного примера) и V-1 —> —У-Т. Примитивный
элемент имеет вид V-1 + у[2 + д/з . Поле К явля-
ется полем разложения полинома
| | (х + Cj yj— 1 + <?2 + 63 л/З) —
= xs - 16х6 + 88? + 192х2 + 144,
где произведение берется по всем различным
наборам коэффициентов е, из {1, -1}.
4.5. Поля деления круга
Рассмотрим уравнение х" = е над произволь-
ным полем К, где п — натуральное число. Корни
этого уравнения называются корнями степени п
из единицы.
Корни степени п из е образуют абелеву груп-
пу по умножению, так как из d' = е и Ьп = е сле-
дует (abf = d'b" = е и (о-1)" = (?) 1 = е. Если К—
поле комплексных чисел, то эта группа циклична
и порождается образующей (примитивным кор-
нем степени п из е), которая может быть записа-
на как 0 = ехр(2га/и). Очевидно, что вместо О
можно использовать Qk, где НОД(£, п) = 1. Тогда
х" - е = (х - е)(х - 0)(х - 02).. .(х - 0"-1).
Если поле К имеет характеристику р. то за-
пишем п =pmh, где h не делится на р. Тогда для
корня степени п из е
(0Л -е/' = ehd’ _е==е" _е;
поскольку (а + Ь)р -ар + Ър. Следовательно, все
корни степени п из е являются и корнями степе-
ни h из е.
Поле, получающееся присоединением к К
всех корней полинома х1’ - е, называется полем
деления круга над К, или полем корней степени
h из е (если К имеет характеристику 0, то пола-
гаем п = h).9 В этом поле полином fix) =xh - е
раскладывается на линейные множители, так
как /'(х) = /zx/,_1 имеет корень лишь при х = О,
поскольку h Ф 0, то есть fix) и f\x) взаимно
просты.
Пусть 0Ь ..., 0Л — образующие группы корней
степени h из е. Полином Ф/,(х) = (х - 0,).. .(х - 0Л.)
называется полиномом деления круга. Очевидно,
что ФЛ(х) делит х1’ - е. Если h — простое число,
то число образующих равно h - 1 и х1’ - е =
= (х - е)(Л' + хЛ“2 + ... + х + е), поэтому
Ф/,(х) = Л1 + хЛ2 + ... + х + е.
Поле деления круга совпадает с полем разло-
жения полинома Ф/,(х). Полином деления круга
имеет целые коэффициенты и не зависит от ха-
рактеристики поля [2].
Связь между цикличностью группы Галуа ко-
нечного нормального расширения и полиномом
деления круга установлена в следующей теоре-
ме.
Теорема 4.5.1. Пусть поле К содержит при-
митивный корень степени п из е. Тогда группа
полинома х" - а, где а е К, циклична и ее поря-
док делит п. Обратно, если группа Gal(£/K) цик-
лична и имеет порядок и, то L — поле разложе-
ния полинома х" - а.
Доказательство см. в работе [5].
9 Поле деления круга называется также циклото-
мическим полем.
73
4.6. Дискретное преобразование Фурье
Пусть К — поле и АДх] — кольцо полиномов.
По определению полином задается своими ко-
эффициентами; если fix) g Афт] имеет степень
п - 1, то число коэффициентов равно п.
Для сложения полиномов достаточно сложить
их коэффициенты при одинаковых степенях х.
Оказывается, что можно и умножать полиномы
путем «покоординатного» умножения.10 Для это-
го нужно перейти от задания полинома множест-
вом коэффициентов к заданию его множеством
значений.
/7-1
Пусть f(x) - арс’ е ЛГ[х]. Г омоморфизм
1=0
колец ЛДх] —> К определяется следующим обра-
зом: для полинома fix) вычисляется значение fix',)
подстановкой вместо х некоторого элемента
X, е К. Покажем, что множество значений поли-
нома fix) для п аргументов полностью определя-
ет полином степени п.
Теорема 4.6.1. Полином fix) е /фс] степени
п - 1 полностью определяется своими значения-
ми fixo), ...,fix„fi), где элементы х( е К попарно
различны.
Доказательство. Предположим, что в поле
К существуют п различных элементов хь,*n-i-
Для каждого полинома fix) можно вычислить
значение fix,), то есть каждому полиному соот-
ветствует единственный набор значений
{fix0), ..., .Дх,;-])}. Покажем, что не существует
двух различных полиномов, дающих одинаковые
наборы {fixo), fix„-i)}. Для этого рассмотрим
отображение {Дх0), ..., fix,^)} -> /фс], задавае-
мое формулой
П(—;)
gW = ^f(x,)^----------. (4.6.1)
/=0
7=0,7*'
Теорема 4.6.1 справедлива и при
deg(/) < п - 1. Пусть/х), g(x) е К[х],
/(х) = ]Гй,х', g(x) = £*,x',
i=0 (=0
причем старшие коэффициенты могут быть ну-
левыми. Пусть существуют наборы значений по-
линомов /ng для 2й-1 значений аргументов
{xq, ..., х2и-2}. В силу гомоморфизма колец /фк] и
К имеют место равенства
fix,) + g(x,) = (f+ gfiXi),fix,)g(x,) = (fg)(x). (4.6.2)
Поэтому умножение полиномов, заданных
наборами значений, выполняется «покоординат-
ным» умножением значений.
Если полиномы, заданные набором коэффи-
циентов и набором значений, рассматривать как
векторы, то из (4.6.1) следует, что переход от од-
ного способа задания к другому является линей-
ным преобразованием над К, то есть описывается
некоторой невырожденной матрицей Q. Очевид-
но, что вид матрицы определяется набором пе-
ременных {х,}.
Удобный для практики вид этой матрицы по-
лучается, если в качестве набора {хД использо-
вать множество корней степени п из е в поле К. В
этом случае поле К должно быть алгебраическим
расширением поля Q или, для простой характе-
ристики р, должно выполняться сравнение р = 1
(mod 2"). Например, если К- Fj7, то для п = 4, 8,
16 значения корня степени п из 1 равны соответ-
ственно 4, 2, 3.
Отображение, определяемое матрицей Q, век-
тора коэффициентов полинома степени не выше
п - 1 в вектор значений называется дискретным
преобразованием Фурье.
Пусть со — образующая группы порядка п в
группе К. Тогда матрицы Q и Q-1 имеют вид
Так как К — поле, знаменатель каждого сла-
гаемого отличен от нуля. Полином g(x) имеет
степень не более п -1, поэтому полином
r(x) =fix) ~ g(x) имеет степень не более п-1. Не-
трудно видеть, что г(х) имеет п различных кор-
ней. Такое может быть лишь в том случае, если
полином г(х) нулевой. Следовательно, полином
степени п - 1 однозначно определяется набором
значений {Дх0), ... ,/x„-i)} и fix) = g(x).
10 Непосредственное умножение полиномов «в
столбик» имеет квадратичную от п сложность.
Если п = 2*, то произведения у = Qx и х = Q ’у
удобно вычисляются; преобразование вектора
14
умножением его на матрицу Q в этом случае на-
зывается быстрым преобразованием Фурье (см.
п. 7.1.3).
п-\
Имеют место равенства ^(й!/ =0 для любого
/=0
0 <j < п. Например, при j = 1: о” - е = 0, и
со" - е = (со - е)(со"-1 + ... + о + е), поэтому со”-1 +
+ ... + со + е = 0.
Если элемент со7 образует группу порядка г,
то г является делителем п. Тогда со7' - е =
= (со7 - е)(со7(г“п + ... + со7 + е), откуда следует
со7(г-1) + ... + со7 + е = 0.
Любая элементарная симметрическая функ-
ция, кроме нормы, может быть представлена в
/1—1
виде полинома от ^со'7 , где 0 < / < и, с нулевым
/=0
свободным членом и, следовательно, равна ну-
лю. Это обстоятельство положено в основу вы-
числения преобразования Фурье.
Теорема 4.6.2. Дискретное преобразование
Фурье является гомоморфизмом колец
К\х\-уК[х\1(/ -е).
Доказательство. То, что дискретное преоб-
разование Фурье задает гомоморфизм из Аф'] в
некоторое кольцо R, следует из формулы (4.6.2).
В общем случае степень полинома, задаваемого
набором значений, может быть больше п. По-
скольку значение преобразования Фурье как век-
тор всегда имеет размер и, то R является кольцом
Аф]/21 классов вычетов по некоторому идеалу 21.
Каждый идеал в кольце Кф] — главный, поэтому
нахождение идеала 21 сводится к нахождению
полинома степени и, имеющего нулевое значе-
ние преобразования Фурье. Подставляя в хп - е
вместо х значения корней степени п из е, получа-
ем нули. Следовательно, 21 = (У - е).
4.7. Нормирования
Поле называется упорядоченным, если:
1) для его элементов выполняется ровно одно из
соотношений а = 0, а > 0, -а > 0;
2) из условия а > 0 и Ъ > 0 следует а + b > 0 и
ab > 0.
Этих требований достаточно, чтобы охарак-
теризовать поле в целом. Например, если
а - Ь> 0, то а > Ь. Элемент а отрицательный,
если -а > 0.
Абсолютной величиной |п| элемента а из упо-
рядоченного поля назовем неотрицательный из
элементов а, -а. Тогда \ab\ = |a||Z>|,
|а + Ь\ < |п| + |6|. Кроме того, а2 = (-а)2 = |а|2 > 0,
причем равенство возможно лишь при а = 0, то
есть сумма квадратов элементов упорядоченного
поля всегда неотрицательна. Единичный элемент
е2 = е всегда положителен. Для единичного эле-
мента получаем п е = п • е = е + е + ... + е> 0
для любого п. Поэтому упорядоченное поле все-
гда имеет нулевую характеристику.
Простейшим случаем упорядоченного поля
является поле Q рациональных чисел.
Поле К называется нормированным, если для
каждого элемента а е К определено значение
функции ср(а), называемой нормированием
(valuation), со свойствами:11
1) (р(а) — элемент некоторого упорядоченного
поля; . .
2) ф(а) > 0 для а Ф 0, ср(О) = 0;
3) ср(ай) = <р(а)<р(Ь);
4) ср(п + Ь) < ср(п) + (р(Ь).
Из свойств 2, 3 получаем, что ср(е) = е,
ср(-е) = е, ср(а) = ср(-п). Из свойства 4 следует, что
ср(п - Ь) < ср(п) + ср(6). Каждое поле обладает
тривиальным нормированием'. ср(а) = е для а * 0
и ср(О) = 0. В дальнейшем не будем рассматри-
вать это нормирование. Если K = Q, то можно
положить ср(а) = |а|.
Существуют и другие виды нормирования.
Если р— простое число, то каждое рациональ-
ное ненулевое а можно представить в виде
а - (t[ s)pn для целого п, где s, I не делятся на р.
Положим срДа) =р~п. При этом выполняются
свойства 1-4. Такое нормирование называется р-
адическим нормированием поля Q.
Например, ср2(3) = 2°, ср2(Ю) = 2Ч, ср2(16) = 2“4,
Любое нормирование поля Q эквивалентно
абсолютному нормированию или некоторому р~
адическому нормированию [3].
Обобщим эту конструкцию. Пусть R— про-
извольное целостное кольцо, К — его поле част-
ных, ф — произвольный простой идеал кольца R
такой, что:
1) все степени ф, ф2, ... попарно различны и их
пересечение равно нулю;
2) если элемент а делится в точности на ф"', а
элемент Ъ делится в точности на ф", то эле-
мент ab делится в точности на ф'"4".
Эти свойства выполняются, например, для
поля Пуф) рациональных функций, являющегося
полем частных кольца главных идеалов EF/7[a'].
11 Значение нормирования, а иногда и функцию
нормирования, называют нормой.
75
Простым идеалом кольца является любой глав-
ный идеал, образованный неприводимым поли-
номом. ^-одическое нормирование поля К зада-
ется максимальной степенью идеала ф, на кото-
рую делится данный элемент поля (степени ф, на
которые делится числитель, берутся со знаком
«+», а степени, на которые делится знамена-
тель— со знаком «-»). В качестве значения
нормирования используется максимальная сте-
пень идеала ф, на которую делится числитель
(знаменатель).
Например, для поля Q(x) нормирование по
идеалу (х) дает:
(pw(x2 + 2х) = (х)’,
Нормирование ср поля К называется неархи-
медовым, если ср(а + b) < шах(<р(а), <р(Л>)), в про-
тивном случае нормирование называется архи-
медовым. Примером архимедова нормирования
поля служит абсолютная величина, 72-адическое
нормирование поля Q неархимедово.
Неархимедово нормирование обладает свой-
ством: если ср(х) > (р0!), то ср(х + у) = ср(х). Дейст-
вительно, если предположить обратное, то един-
ственно возможный случай: ср(х + у) < ср(х). Тогда
х = (х +у) - у и <р(х +у) < ср(х), ср(-у) = ср(у) < ср(х).
Это противоречит определению неархимедова
нормирования: ср(х) < тах(ср(х + у), ср(-у)).
Часто используют показательное неархиме-
дово нормирование, когда вместо нормирования
ср(а) = р'(а} рассматривают показатель v(a). Тогда:
1) г(а) — вещественное число;
2) v(0) = co;
3) v(ab) = v(a) + v(b);
4) v(a + b')> min(v(a), v(b)).
Среди нормирований различают дискретные
и недискретные. Дискретные нормирования ха-
рактеризуются тем, что для каждого из них су-
ществует наименьшее положительное v(a) такое,
что все остальные v(a) кратны ему. Недискрет-
ные нормирования характеризуются тем, что их
значения могут быть сколь угодно близки к ну-
лю. Нормирование абсолютной величиной не-
дискретно, jo-адическое нормирование дискрет-
но.
Теорема 4.7.1. В показательно нормирован-
ном поле К все элементы а со свойством v(a) > О
образуют кольцо. Совокупность элементов, для
которых нормирование положительно, является
простым идеалом 3 этого кольца.
Доказательство. Из v(a) > 0, v(b) > 0 следует
v(a + b)> 0, v(a - b) > 0 и v(ab) = v(a) + v(b) > 0.
Поскольку в поле К выполняются свойства ассо-
циативности, коммутативности и дистрибутивно-
сти, то элементы с неотрицательным нормирова-
нием образуют кольцо.
Из v(a) > 0, г(й) > 0 получаем
v(a + b)> min(v(a), v(b)) > 0,
v(a -b)> min(v(a), v(b)) > 0.
Если c— произвольный элемент этого коль-
ца, v(c) 0, то v(ac) = г(а) + г(с) > г(а) > 0. По-
этому элементы с положительным нормировани-
ем образуют идеал 3. Наконец, из ab = 0 (3) или,
что то же самое, из v(ab) = v(a) + v(b) > 0 следует,
что хотя бы один из элементов а или b имеет по-
ложительное нормирование, то есть а е 3 или
b <е 3 (а = 0 (3) или b s 0 (3)). Поэтому идеал 3
простой.
Кольцо А элементов поля К, обладающих не-
отрицательным дискретным нормированием, на-
зывается кольцом дискретного нормирования.
Элементы кольца А называются целыми (относи-
тельно нормирования). Говорят, что а делится на
b (относительно нормирования г), если а/Ь —
целый элемент, то есть v(a) > v(Z>). Элементы
кольца А с нулевым значением нормирования
являются обратимыми элементами кольца нор-
мирования. Поскольку все элементы множества
А \ 3 обратимы, то идеал 3 не имеет делителей в
кольце А. Поэтому он является максимальным.
Следовательно, кольцо классов вычетов АП яв-
ляется полем, это поле называют полем классов
вычетов нормирования.
4.8. Пополнения поля Q
и р-адические числа
Последовательность {а,} элементов нормиро-
ванного поля называется фундаментальной, если
для каждого положительного s из поля значений
нормирования ср существует натуральное п — п(г)
такое, что ср(ар-a9)<s для любых р>п, q>n.
Определим сумму и произведение фундаменталь-
ных последовательностей: с, = а, + b,, ф = афц. То-
гда последовательности {с,} и {d,} тоже будут
фундаментальными. Введенные операции сложе-
ния и умножения удовлетворяют аксиомам коль-
ца, поэтому фундаментальные последовательно-
сти образуют коммутативное кольцо.
Поле К называется полным относительно
нормирования ср, если оно удовлетворяет крите-
рию Коши: каждая фундаментальная последова-
тельность элементов поля К имеет предел в К.
Определим нуль-последовательность как
фундаментальную последовательность со свой-
76
ством «сходимости к нулю», то есть для любого
s > 0 существует натуральное п такое, что |а,| < 8
при z > п. Нуль-последовательности образуют
идеал 21 в кольце R фундаментальных последова-
тельностей. Следовательно, можно образовать
кольцо классов вычетов L = А/21. Это кольцо яв-
ляется нормированным полем [2]. Действитель-
но, если элемент a g L определяется фундамен-
тальной последовательностью {а,} над полем К с
нормированием ср, то по определению нормиро-
вания |ср(с/,) - cp(a7)| < <р(а, - о,), то есть {<р(а,)} —
тоже фундаментальная последовательность, об-
ладающая некоторым пределом в поле вещест-
венных чисел. Положим ср(а) = %. Все фундамен-
тальные последовательности с одним и тем же
пределом S, определяют одно и то же значение
ср(а). Нетрудно проверить, что функция ср в поле
L удовлетворяет всем четырем требованиям,
предъявляемым к нормированию.
В случае неархимедова нормирования доста-
точно потребовать, чтобы ср(а,+1 - а,) < 8 для
i > zz(s). Действительно, \ар - aq\ — это сумма
\р - q\ слагаемых вида а,+1 - а„ и если все они име-
ют значение, меньшее 8, то и значение суммы
тоже меньше 8, так как
<р(с/,+1 - а,) < тах(ср(а,+1), ср(а,)).
Таким образом, в поле, полном относительно
неархимедова нормирования, любая последова-
тельность {а,} имеет предел, если только разно-
сти а,+1 - а, стремятся к нулю, то есть если
lim ап - 0.
Этот критерий можно переформулировать.
Для сходимости бесконечного ряда ах + а2 + • -
необходимо и достаточно, чтобы lim ап - 0. В
И->00
случае архимедова нормирования это не так, на-
пример, гармонический ряд 1 + ’/2 + '/з + ... рас-
ходится.
Если поле Q рациональных чисел нормиро-
вать относительно абсолютной величины (архи-
медово нормирование), то в результате пополне-
ния получим поле IR вещественных чисел.
Если использовать р-адическое нормирование,
то в результате пополнения получим поля Q2, Q3,
Q5, Q7, Qu,... р-адических чисел, равноправные с
полем IR. Элементы поля Qr могут быть представ-
лены в более удобной форме, чем фундаменталь-
ная последовательность. Поле Qr как пополнение
поля Q имеет нулевую характеристику.
Рассмотрим для неотрицательных целых чисел
I - 1,2,... модуль Mi, состоящий из рациональных
чисел, числитель которых делится на р, а знаме-
натель не делится на р. Для таких чисел нормиро-
вание удовлетворяет неравенству ср(п) < Д. Назо-
вем два числа сравнимыми по модулю р, если их
разность принадлежит модулю Mt. Если {г,} —
некоторая р-адическая фундаментальная последо-
вательность рациональных чисел, то для каждого
У, начиная с некоторого п = u(f), имеем
cp(zy “ Гк) < Р 3 при z > n(j), к > n(j), то есть г, = гк
(mod/?7). Таким образом, все числа г„ начиная с
некоторого лежат в однозначно опреде-
ленном классе вычетов /?, по модулю МР Поэтому
фундаментальная последовательность {г,} опре-
деляет некоторую последовательность классов
вычетов 7?о z) A] Z) Т?2 Z)..., вложенных друг в дру-
га указанным способом. При этом если {г} —
нуль-последовательность, то R}— нулевой класс
вычетов. Сумме фундаментальных последова-
тельностей соответствует сумма классов вычетов.
В частности, прибавление к фундаментальной
последовательности нуль-последовательности не
изменит последовательности классов вычетов.
Каждому /?-адическому числу взаимно одно-
значно соответствует некоторая последователь-
ность классов вычетов. Поэтому /?-адическое
число можно представить с помощью последова-
тельности классов вычетов. Кроме того, р-
адическое число а можно представить в виде
бесконечной суммы, положив rG = s0, гг - г0 =
= sxp,rj+] - I-J = SjpJ,.... Тогда Z)+1 = ,s0 + s^p +
+ ... + SjpJ. Получаем
a - lim Vs,p' = Vs,p' .
^”/=0 ,=o
При этом Si— обычные целые числа. Такие
числа а называют целыми р-адическими числами.
Множество целых /?-адических чисел является
целостным кольцом, которое обозначается Жр.
Дробное р-адическое число имеет вид
а = а_1Гр~т + б/_,н|р-'"" + ... + а0 + сцр + а-р2 + ...
и содержит слагаемые с отрицательными степе-
нями р. Поэтому каждое дробное р-адическое
число можно превратить в целое р-адическое
число умножением на некоторую степень р.
Сложение и умножение р-адических чисел
выполняется аналогично сложению и умноже-
нию рациональных чисел в р-ичной системе
счисления, только рациональные числа записы-
ваются, начиная со старших разрядов, а р-
адические числа — начиная с младших разрядов.
Пример 4.8.1. Арифметика кольца Жр.
1. Найдем в Z2 элемент 5-1. Запишем
5 = 2° + 22. 2-адическое число 1 имеет вид
00
1 = 1 + ^2 0 • 2Z . Представим искомый элемент в
1=1
00
виде х = ai • Тогда 5х = х + 22х = 1. Коэффи-
-=0 .. . - V-
77
циенты неизвестного найдем последовательными
сравнениями по модулям 2, 4, 8 и т. д. Сравнение
по модулю 2 дает х0 = 1. Сравнение по модулю 4
дает 2x1 = 0 (mod 4), откуда х, = 0. Сравнение по
модулю 8 дает 4х2 + 4х0 = 0, откуда х2 = 1 и т. д.
Таким образом, в Z2 имеет место равенство
5Ч=^22'.
/=о
оо
2. Найдем сумму х = ^р' в Жр. Имеем для
/=о
разности />-адических чисел х—рх=]. Отсюда
х - —-—. В частности, число -1 = —-— в ZS
1-р 1-2
ОО
имеет вид -1 = ^2' .
1=0
3. Решим квадратное уравнение х2 = 11 в Z7.
Корень из 11 будем находить последовательным
решением сравнений для степеней числа 7.
Пусть х = х0 + 7xi + 72х2 + ... . Имеем х2 = 4
(mod 7). Тогда х0 = 2 или х0 = 5. Выберем значе-
ние х0 = 2. Находим Х] решением сравнения
4 + 28xi = 11 (mod 72). Отсюда 28xi = 7 (mod 72),
X] = 2. Находим х2 решением сравнения
(2 + 14 + 7х,)2 = 11 (mod 73), откуда 4 • 72х2 = 2 72
(mod 73), х2 = 4 и т. д. Второе значение корня из
11 будет задаваться последовательностью коэф-
фициентов, противоположных по модулю 7 ко-
эффициентам первой последовательности.
Упражнения к главе 4
1. Что собой представляет простое поле с нуле-
вой характеристикой?
2. Существует ли эндоморфизм поля в его соб-
ственное подполе?
3. Покажите, что поле не имеет идеалов, отлич-
ных от нулевого и единичного.
4. Покажите, что алгебраическое замыкание поля
Q не совпадает с полем С комплексных чисел.
5. Постройте квадратичные расширения: а) по-
ля F3; б) поля Q; в) поля С(х) рациональных
функций.
6. В поле F2|7]/(£4 +1+ 1) найдите корни поли-
нома У(0 = + ? + 1 и корни других неприво-
димых полиномов степени 4: g(/) = / 4 +13 + 1,
h(j) = +13 +12 +1 + \. Выразите корни по-
линомов g, h через корни полинома f как век-
торы над F2.
7. Почему квадратичное расширение поля явля-
ется нормальным? Приведите примеры нор-
мальных расширений, получающихся при-
соединением одного корня полинома, отлич-
ного от х7' - е.
8. Пусть Fr — простое поле и Fr(x) — его про-
стое трансцендентное расширение. Тогда ка-
ждому элементу поля Fp(x) можно поставить во
взаимно однозначное соответствие рациональ-
ное число заменой переменной х на число р~.
Y,aix' Ца'Р‘
^bjPJ
Изоморфны ли поля Q и Fr(x)?
9. Как найти число приведенных неприводимых
полиномов степени п в кольце Fp[x] для про-
стого и составного и?
10. Найдите кратные корни полинома fix') = х7 +
+ х5+х4-х3-х2-х+1 е F3[x] в его поле
разложения путем вычисления НОД(/(х),/'(х)).
11. Найдите все неприводимые полиномы вида
х2 + а, х3 + b в кольце F]9[x].
12. Какие ненулевые полиномы в F/;[x] имеют
нулевую производную? Какие ненулевые ра-
циональные функции в Fp(x) имеют нулевую
производную?
13. Пусть Z[z], z2 = -l— кольцо целых гауссо-
вых чисел. Покажите, что идеал (2 + z) в этом
кольце является максимальным, то есть
2Е[/]/(2 + z) является полем. Покажите, что
полученное поле изоморфно полю F5.
14. Покажите, что для р > 2 в кольце Fp[x] суще-
ствует неприводимый полином вида х2 + а.
15. Исследуйте действие отображений ср и ср2, где
ср:х~>х2, на элементы поля F2[Z]/(Z4 + Г+ 1).
Найдите порядок циклической группы, обра-
зованной отображением ср.
16. Пусть F9, q=p,— расширение степени п
простого поля F/;, где z? — простое число.
След и норма для F9 по определению явля-
ются элементарными симметрическими
функциями от п переменных и отображают
F9 в Fr. Являются ли остальные элементар-
ные симметрические функции отображения-
ми F9 в Fr?
7. Покажите, что над полем F?, </ = 2", уравне-
ние х2 + а = 0, где a g F9 , всегда имеет един-
ственное решение. Найдите это решение.
8. Пусть F9, q = 2", — конечное поле. При каких
условиях квадратное уравнение х2 + х + а = О,
где а е F9 , имеет корни в F9?
9. Пусть К — поле. Покажите, что если для по-
линома f из К[х] выполняется условие
НОД(//') е К, то/свободен от квадратов.
!0. Покажите, что алгебраически замкнутое поле
не может быть конечным.
!1. Пусть К— поле и К(х)— поле рациональ-
ных функций. Пусть / е К(х) и /' — произ-
водная функции / Покажите, что /' g К(х) и
что отображение /'// является гомомор-
физмом мультипликативной группы поля
К(х) в аддитивную группу этого поля.
22. Покажите, что элементы кольца дискретного
нормирования, нормирование которых боль-
ше 1, образуют идеал.
23. Найдите произведение целых 5-адических
чисел 2 + 2- 5+ 2-52 + 2-53+...иЗ + 3- 5 +
+ 3 52 + 3 • 53 + ... .
24. Что собой представляет факторгруппа Z/Z?
Является ли она циклической?
25. Пусть F9 = Fp[x]/(/(x)) — расширение степени
п поля Fj, и t— корень полинома/х). Пока-
жите, что элементы Г °, t, t2, образуют
базис F9 над Fp.
Литература к главе 4
Айерлэнд К., Роузен М. Классическое введение в
современную теорию чисел. М.: Мир, 1987.
Ван дер Варден Б.Л. Алгебра. М.: Наука, 1979.
Коблиц Н. р-адические числа, р-адический анализ
и дзета-функции. М.: Мир, 1982.
4. Ленг С. Алгебра. М.: Мир, 1968.
5. Лидл Р., Нидеррайтер X. Конечные поля. М.:
Мир, 1988.
6. Milne J. Fields and Galois theory (Lecture notes) //
http://www.jmilne.org/math/.
Глава 5. СВЕДЕНИЯ ИЗ ТЕОРИИ ЧИСЕЛ
Теоретико-числовые задачи являются хоро-
шим фундаментом для построения криптографи-
ческих алгоритмов. Это обусловлено достаточ-
ной изученностью указанных задач и удобством
их программного воплощения.
5.1. Однозначное разложение
на множители в кольце Z
Множество Z является евклидовым кольцом
и, следовательно, обладает однозначным разло-
жением на простые множители. Поскольку коль-
цо Z содержит два обратимых элемента (1 и -1),
разложение на простые множители производится
с точностью до обратимого элемента кольца, то
есть до знака простого числа.
Простых чисел бесконечно много. Доказа-
тельство этого факта дал еще Евклид. Действи-
тельно, если предположить обратное, то сущест-
вует наибольшее простое число. Тогда, если к
произведению всех положительных простых чи-
сел прибавить единицу, получим число, превы-
шающее наибольшее простое число, которое не
будет делиться ни на одно из простых чисел.
Противоречие доказывает неправильность пред-
положения.1
Для большого натурального числа п количе-
ство простых чисел, меньших и, обозначим через
л(и). Имеет место асимптотическое равенство
{теорема П.Л. Чебышева)'.
л(и) ® .
In и
На практике представляют интерес простые
числа вида 2"' — 1 и 2Z + 1, так как в кольцах вы-
четов по модулю этих чисел удобно выполнять
арифметические операции. Если число т состав-
ное, т = rs, то
2rs - 1 = (2Г - 1 )(2rs~r + 2rs~2r + ... + 1),
поэтому 2т - I может быть простым только то-
гда, когда г = 1, то есть число т простое. Числа
1 Аналогично доказывается, что для произвольно-
го поля К существует бесконечно много неприводи-
мых полиномов в кольце К[х]. В этом случае упоря-
дочивание полиномов проводится по их степеням.
вида 2"' - 1 для простого т называются числами
Мерсенна.
Если существует разложение I = rs, где г —
нечетное, то число 2" + 1 может быть представ-
лено в виде
2rs + 1 = (2s + 1)(2"“* - 2n'~2s + ... + 1),
поэтому числа вида 21 + 1 могут быть простыми,
если I не имеет нечетных делителей, то есть яв-
2*
ляется степенью двойки. Числа вида 2 +1 назы-
ваются числами Ферма. На сегодняшний день
известны следующие простые числа Ферма: 3, 5,
17, 257, 65537.
Теория чисел изобилует нерешенными про-
блемами, которые на первый взгляд выглядят
несложными.2 * * Например:
- конечно или бесконечно множество простых
чисел вида 2" -1 (числа Мерсенна) или
22 + 1 (числа Ферма);
- можно ли каждое четное число представить в
виде суммы двух простых чисел (гипотеза
Гольдбаха);
- конечно ли множество простых чисел вида
и2 + 1.
5.2. Некоторые числовые функции
Число n е Z называется свободным от квад-
ратов, если оно не делится на квадрат никакого
простого числа.
Теорема 5.2.1. Любое число и е Z может
быть записано в виде n = ab2, где a, b е 7L и а
свободно от квадратов.
Доказательство. Пусть n = J~[pf‘ — раз-
ложение числа п на простые множители. Каждый
показатель d, можно записать в виде d, = 2b, + r„
где г, = 0 или 1 в зависимости от того, четно или
нечетно число d,. Положим а - р?‘', b = р^ .
Тогда n = ab2 — требуемое разложение.
2 Знаменитая великая теорема Ферма была дока-
зана в 1990-х годах с использованием аппарата эллип-
тических кривых.
80
На множестве Z>0 положительных целых чи-
сел существует ряд естественно определенных
функций.
Определим функцию Мебиуса ц(и), п g Z>0.
Положим р.(1) = 1, ц(и) = 0, если и не свободно от
квадратов, и p(pi.../ty) = (-!)*, где /?,— различ-
ные простые числа.
Теорема 5.2.2. При п>\ имеем ^ц(</) = 0,
d\n
где сумма берется по всем делителям d числа п,
включая 1 и и.
i
Доказательство. Если n = ]~[pf' , то вклад
/=1
в сумму показателей dh превышающих единицу,
нулевой. Следовательно, имеем равенство
где сумма берется по всем наборам (еь ..., 8/),
8, g {0, 1}. Тогда
(г\ 11} 11}
2>(О = 1- + - +... + (-!)'=(1-1)'=0.И
d\n V7
Определим умножение Дирихле для двух ком-
плекснозначных функций f и g, определенных на
множестве Z>0: (J-g)(n) = £ f(dt)g(d2). Здесь
d}d2=n
сумма берется по всем парам положительных
целых чисел d\, d2. дающих в произведении и.
Умножение Дирихле коммутативно, так как ум-
ножение комплексных чисел коммутативно, и
если одно из слагаемых имеет вид fiddgfcdi), то
существует и слагаемое видаДс/2)я(</)- Сложение
таких пар слагаемых, очевидно, коммутативно.
Кроме того, умножение Дирихле ассоциатив-
но, так как выполняется равенство
(/•(g/z))(«) = ((/g)A)(«) =
=
- dydyd-^n
Функции с умножением Дирихле образуют
коммутативный моноид. Единичным элементом
является функция Е со свойством £(1) = 1 и
Е(п) = 0 для всех целых п > L
Рассмотрим функцию I вида I(n) = 1 для всех
п 6 Z>0. Для любой функции f имеет место ра-
венство (/ /)(и) = (/ • /)(и) = f(d). Тогда
d\n
функция / является обратной к функции Мебиуса
относительно умножения Дирихле. Действи-
тельно,
(ц • Z)(l) = ц(1)/(1) = L
(ц-/)(и) = ]Гц(</) = 0, н>1.
d\n
Теорема 5.23 (теорема обращения Мебиу-
са). Пусть F(n) - ^f(d). Тогда
d\n
fW = ^P(d)F(n/d).
d\n
Доказательство. Можно записать F=f l.
Тогда F • ц = (/• Z) • ц =/(/• ц) =/ Е =f
Поэтому
/(и) = (Е-ц)(и) = ^ц(</)Е’(и/</).
d\n
Определим функцию Эйлера <р(и), где п g Z>0,
как количество положительных целых чисел,
меньших п и взаимно простых с и, включая еди-
ницу (при этом по определению <р(1) = 1). На-
пример, ср(2) = 1, ср(5) = 4, ср(6) = 2, ср(12) = 4. Ес-
ли р — простое число, то ср(р) = р - 1.
Теорема 5.2.4. Выполняется равенство
^<р(б/) = и.
<7|и
Доказательство. Рассмотрим п рациональ-
ных чисел вида 1/и,2/и,...,н/п и сократим каж-
дую из дробей на наибольший общий делитель
числителя и знаменателя. Множество знаменате-
лей будет представлять собой все множество по-
ложительных делителей числа п. включая 1 и п.
Если d\ п, то в точности <р(</) чисел рассматривае-
мого множества после сокращения будут иметь d
в качестве знаменателя. Поэтому значение суммы
]Гср(</) совпадает с числом элементов рассмат-
d\n
риваемого множества, то есть ср(с/) = п.
I
Теорема 5.2.5. Если п = ]~J /?“ , то
'=•
' ( И
ф(«)=«П 1— •
ilk Pi J T-UTW
Доказательство. Поскольку ^<р(б/) = и, то
d\n
из теоремы обращения Мебиуса следует, что
</|и « / Pi i>j PiP
< Pi А Рэ 7 I Pi J
81
Для больших чисел п имеет место асимптоти-
Z ч п
ческое равенство ср(и) ~---. ..
In In и ’ '
Функция Мебиуса позволяет определить так-
же точное число неприводимых над F/3 приве-
денных полиномов степени и.
Теорема 5.2.6. Число N„ неприводимых в
FJx] полиномов степени п равно
.........................................
Доказательство. Обозначим через СДх) не-
приводимый над Fp полином степени d из РДх].
Покажем, что для полинома хр — х выполняется
равенство:
= (5-21)
d\n
Действительно, поскольку Z'
(х^ - х)' = рх''~]- 1 = -1 (mod р) 4
и НОД(х/; - х, (хр - х)') = 1, то полином хр - х не
имеет кратных корней в алгебраическом замыка-
нии поля Fp и, следовательно, свободен от квад-
ратов в Fp[x], По теореме 4.3.10 неприводимый
полином fix) степени d делит хр - х тогда и толь-
ко тогда, когда d\n. Следовательно, полином
хр — х представляет собой произведение непри-
водимых полиномов, степени которых делят п.
Тогда, приравнивая степени обеих частей равен-
ства (5.2.1), имеем рп - ^dNd . Применяя тео-
б/|л?
рему обращения Мебиуса к последнему равенст-
ву, получаем заключение теоремы.
Теорема 5.2.6 показывает различие между коль-
цами Z и Fp[xJ. Если для первого кольца точная
формула для числа простых элементов, меньших
заданного, неизвестна (возможно, в явном виде ее
и не существует), то для второго такая формула
есть. Другое отличие характеризуется сложностью
разложения. Если наилучший известный алгоритм
разложения чисел обладает субэкспоненциальной
сложностью, то полиномы раскладываются с по-
линомиальной сложностью (см. гл. 7,9).
Числовая функция f называется мультипли-
кативной, если для чисел а, b таких, что
НОД(а, Z>) = 1, выполняется условие fiab) =
=fia)fib). Поэтому мультипликативная функция
полностью определяется своими значениями на
степенях простых чисел. Если функция fin)
мультипликативна, то функция g(«) = ]F/(<7)
d\n
также мультипликативна.
Из китайской теоремы об остатках следует,
что для взаимно простых чисел р\, ...,pk имеет
место изоморфизм колец TJriZL = TLIpfiL © ... ©
© Д_1рйД. Отсюда вытекает, что функция Эйлера
является мультипликативной. Мультипликатив-
ной является также функция ц(и).
- 5.3. Кольцо 'ZJnZ- ’
Уточним некоторые положения теории срав-
нений (см. п. 3.5) применительно к целым числам.
Аппарат теории сравнений часто использует-
ся при изучении вопросов, относящихся ко всему
множеству целых чисел, в частности при реше-
нии диофантовых уравнений. Диофантовым на-
зывается уравнение вида/(х|, . ..,х„) = (), где f—
полином над Z, с целочисленными решениями.
Из теоремы о гомоморфизмах колец следует, что
если диофантово уравнение имеет решение в Z,
то оно имеет решение в как сравнение по
произвольному модулю п. И наоборот, если
сравнение не имеет решения хотя бы по одному
модулю, то соответствующее диофантово урав-
нение неразрешимо.
Пример 5.3.1. Диофантовы уравнения.
1. Уравнение х + ах + b = 0 при нечетных а, b
не имеет целочисленных решений. Для доказа-
тельства достаточно рассмотреть соответствую-
щее сравнение по модулю 2. Если х s 0 (mod 2),
то х1 + ах s 0 (mod 2), х2 + ах + b s 1 (mod 2). Ес-
ли х = I (mod 2), то х2 + ах = 0 (mod 2),
х2 + ах + b = 1 (mod 2).
2. Уравнение х3 - 7у3 + 4 = 0 не имеет цело-
численных решений. Для доказательства рас-
смотрим соответствующее сравнение по модулю
7. То, что сравнение х’ + 4 = 0 (mod 7) не имеет
решений, легко можно проверить перебором.
3. Уравнение у2 = х3 + 11х + 8 не имеет реше-
ний в целых числах. Это утверждение следует из
рассмотрения соответствующего сравнения по
модулю 3. Получаем у2 = х3 + 2х + 2 (mod 3).
Правая часть всегда принимает значение 2, а ле-
вая — значения 0 или 1.
Китайская теорема об остатках устанавливает
гомоморфизм кольца Z и колец классов вычетов
Дт^. для взаимно простых т,. Следовательно,
произведению и сумме чисел соответствуют
произведение и сумма вычетов по модулям пр.
Для восстановления числа х по его вычетам
можно использовать следующее утверждение
(целочисленный аналог интерполяционной фор-
мулы Лагранжа).
82
Теорема 5.3.1 (китайская теорема об остат-
ках для кольца Z). Пусть числа т\, вза-
имно простые, х = х, (mod w,), М=т\...тк,
М, = М/т,, N, = М,~' (mod mt). Тогда
к
х = xiM, Nj (mod N).
i=l
Доказательство. Идеал, образованный лю-
бой парой чисел (т„ пу) в кольце Z равен Z. то
есть применима китайская теорема об остатках
(см. теорему 5.3.5). Кольцо Z/A7Z изоморфно
прямой сумме колец:
7LIMZL = © ... ©
Поэтому достаточно показать, что значение х
из заключения теоремы удовлетворяет сравне-
нию х = х, (mod т,). Так как ММ = 1 (mod т,), то
сравнение х = х, (mod m2) выполняется.
Поскольку в Z имеет место однозначное раз-
ложение на множители, то изучение сравнений
по произвольному модулю сводится к изучению
сравнений по модулям степеней простых чисел
~ZL!p~HL в соответствии с китайской теоремой об
остатках.
Любой элемент х g IFp удовлетворяет сравне-
нию хр - х = 0 (modр). Следовательно, имеет ме-
сто равенство хр-х = х(х- l)(x-2)...(x-z? + 1).
После сокращения на х получим хр~ - 1 =
= (х- 1)(х-2)...(х-/? + 1) (mod/?). Полагая х = 0
(mod/?), получаем теорему Вильсона'. (р - 1)! = -1
(mod р).
Образующую мультипликативной группы
кольца 2EJn%_ иногда называют примитивным
корнем по модулю п.
Посмотрим, для каких п группа (Z7«Z) цик-
лическая. Согласно теореме 4.3.6 и следствию
4.3.7 группа IFp прир Ф 2 циклическая, число об-
разующих равно ср(р - 1).
Теорема 5.3.2. Если р — простое число, рф2,
то группа (Z7/?AZ)* циклическая.
Доказательство см. в работе [1].
Для случая /? = 2 ситуация иная. Группа
(Z78Z) состоит из четырех элементов: 1, 3,
5, 7. Каждый из них в квадрате дает единицу:
I2 = З2 = 52 = 72 = 1 (mod 8). Следовательно,
группа (Z/8Z) не является циклической. То
же имеет место и для степеней двойки, боль-
ших 3.
Теорема 5.3.3. Группы (Z72Z)* и (Z74Z)* цик-
лические. Группа (Z72AZ) при к>3 является
прямым произведением двух циклических групп,
одна из которых имеет порядок 2, а другая —
порядок 2к~2.
Доказательство см. в работе [1].
Теорема 5.3.4. Группа (Z7«Z)* является цик-
лической тогда и только тогда, когда п = 2, 4, ра,
2ра для нечетного простого р.
Доказательство см. в работе [1].
Например, (Z/15Z)*= {1, 2, 4, 7, 8, 11, 13, 14}.
Ни один из этих элементов не образует группу
порядка 8.
Рассмотрим вопрос о разрешимости сравнения
х" = a (mod /?), где а Ф 0 (mod /?), для простого р.
Теорема 5.3.5. Пусть р — простое число. Ес-
ли НОД(и, р - 1) = 1, то сравнение х" = a (mod /?),
где а Ф 0 (mod /?), разрешимо при любом а. Если
НОД(и, р - 1) = d > 1, то это сравнение разреши-
мо при = 1 (mod/?).
Доказательство. Если НОД(и,р- 1)= 1, то
п обратимо по модулю р - 1, отображение х -> х"
взаимно однозначно и является автоморфизмом
группы F/3. Следовательно, сравнение разреши-
мо всегда. Пусть НОД(и,/? - 1) = d> 1. Мультип-
ликативная группа Fp циклична с образующей g.
Тогда x = g" (mod/?), a = gv (mod/?). Рассматри-
ваемое сравнение имеет вид gmi = gv (mod р). По-
этому для показателей выполняется сравнение
nu = v (mod (р - 1)). Последнее сравнение разре-
шимо тогда и только тогда, когда d\ и.
В соответствии с китайской теоремой об ос-
татках теорема 5.3.5 остается справедливой при
замене р на число т такое, что группа обратимых
элементов по модулю т циклична, при этом сле-
дует заменить р - 1 на ср(?и).
Если сравнение х" = a (mod in) разрешимо, то
говорят, что а является вычетом степени п по
модулю т. В противном случае а является невы-
четом степени п по модулю т.
Вопросы разрешимости сравнений хп = а
(mod/? ) и х" = a (mod/?), где а Ф 0 (mod/?),/?> 3,
тесно связаны.
Теорема 5.3.6. Сравнение xri = а (mod/?), где
а ф 0 (mod/?), р > 3, ПОД(и, р) = 1, разрешимо
тогда и только тогда, когда сравнение х" = а
(mod рк) разрешимо при всех к.
Доказательство. Если п = 1, то утверждение
очевидно. Предположим, что п > 1. Пусть сравне-
ние х" = a (mod /?е) разрешимо и х0 — его решение.
Тогда Х| = х0 + Ъре — тоже решение этого сравне-
ния, при этом X]" = Хд + пЪрех^~А (mod /?е+') . Най-
дем коэффициент Ь, при котором выполняется
'83
сравнение х" s a (mod /?е+1). В этом случае
пхд=(а-з§)1 ре (modр), где (а-х„)/ре —
целое число. Это сравнение разрешимо единст-
венным образом. Следовательно, сравнение хп = а
(modр} разрешимо при всех к> е. При е = 1 оно
разрешимо при всех к.
Обратно, пусть сравнение у" = a (mod рк) раз-
решимо и у = хо + рх\ + ...+ р '’x^i — его реше-
ние. Тогда хо будет решением этого сравнения по
модулю/?.
5.4. Квадратичные и кубические вычеты.
Квадратичный закон взаимности
Если сравнение х2 = a (mod т), где
НОД(<т, т) = 1, разрешимо, то а называется квад-
ратичным вычетом по модулю т, в противном
случае а называется квадратичным невычетом
по модулю т. Если сравнение х3 г a (mod ш), где
НОД(<7, т) = 1, разрешимо, то а называется куби-
ческим вычетом по модулю т, в противном слу-
чае а называется кубическим невычетом по мо-
дулю т.
Пример 5.4.1. Квадратичные вычеты и невы-
четы.
При т = 7 для х = 1, 2, 3, 4, 5, 6 получаем
х2Л, 4, 2, 2, 4, 1 (mod 7) их’ = 1. 1, 6, 1, 6, 6
(mod 7) соответственно. Поэтому 1,2,4 являются
квадратичными вычетами, а 3, 5, 6 — квадратич-
ными невычетами по модулю 7. Числа 1, 6 явля-
ются кубическими вычетами, а 2, 3, 4, 5 — куби-
ческими невычетами по модулю 7.
В соответствии с результатами предыдущего
параграфа вопрос о разрешимости сравнения
x2s<r (mod и?) по модулю произвольного нату-
рального т сводится к вопросу о разрешимости
этого сравнения по модулям простых делителей
числа т. Если р > 2 — простое число и
а(р~^!2 = 1 (mod р), то факторгруппа Тр7(<т) имеет
четный порядок и сравнение разрешимо, причем
существуют два решения.
Аналогичное утверждение справедливо и для
кубических вычетов. Сравнение х3 s a (mod р)
имеет единственное решение для любого а е F,,,
если НОД(/? - 1, 3) = 1, то есть еслир = 2 (mod 3).
Если же р = 1 (mod 3), то НОД(/? - 1, 3) = 3. Сле-
довательно, кубическое сравнение разрешимо,
если = 1 (mod р) (при этом существуют
три разных решения) или если а = 0. В остальных
случаях оно неразрешимо.
Обратный вопрос — для каких т разрешимо
сравнение х2 = а (mod т) — является более
сложным. Покажем, как свести данную задачу в
кольце классов вычетов по модулю т к задачам в
кольцах классов вычетов по простым нечетным
модулям р. Пусть т = 2е р? Достаточно рас-
/
смотреть случай НОД(а, т) - 1. Тогда по китай-
ской теореме об остатках сравнение х2 = а
(mod и?) разрешимо тогда и только тогда, когда
разрешимы сравнения
х2 = a (mod 2е), х2 = a (modpet’). .
Из теорем 5.3.4, 5.3.5 следует, что сравнения
х2 = a (mod /?е') разрешимы тогда и только то-
гда, когда разрешимы сравнения х2 = a (mod /?,).
Поскольку единственным квадратичным выче-
том как по модулю 4, так и по модулю 8 являет-
ся 1, сравнение х2 = a (mod 2е) разрешимо тогда
и только тогда, когда а = 1 (mod 4) при е = 2 и
а = 1 (mod 8) при е>3. Таким образом, доста-
точно рассмотреть разрешимость сравнения
х~ = a (mod р) для простых нечетных р. При
этом порядок группы (Е/; всегда четный, и во-
прос о разрешимости квадратичного сравнения
нетривиален.
Определим символ Лежандра — для числа
\PJ
А « ’ -<, . у -. v, х: ... . ?
f а I 1
а по простому нечетному модулю р: — = 1,
\Р)
если а является квадратичным вычетом по моду-
I
лю р, — = -1, если ° является квадратичным
\Р)
невычетом по модулю р, и — = 0, если а = 0
\Р)
(mod/?). Таким образом, для чисел а, взаимно
простых с /?, символ Лежандра является квадра-
тичным характером.
Теорема 5.4.1. Символ Лежандра обладает
следующими свойствами:
1)
2)
3)
Р
а + кР _ I а
< Р
ab2
а
V Р ) \Р)
НОД(Ь,/?)=1;
(а
для всех к 6 Z;
для всех b таких, что
1
= а г (mod р). В частности,
VPJ
I —- | = 1, если р = 1 (mod 4), и
\Р )
если р = 3 (mod 4);
= 1;
= -1,
р
84
4)
ab
a
b
5)
VP )
( 2^
Vp)Vp)
А
Теорема 5.4.1 показывает, что вычисление
а
символа Лежандра
VP)
сводится к вычислению
VP)
при изменении а от 1 до р - 1 символ
Лежандра принимает значения 1 и -1
одинаково часто.
Доказательство [1]. Свойство 1 следует из
определения символа Лежандра. Свойство 2 сле-
дует из свойства 4. Свойство 3 следует из теоре-
мы 5.3.5. Свойство 4 следует из утверждения 3.
Получаем цепочку равенств в поле Fy.
'ab\ ( кА
— ={ао) 2
6)
символов Лежандра — для простых делителей
VP)
q числа а.
Теорема 5.4.2 (квадратичный закон взаим-
ности). Для нечетных простых /?, q выполняется
q
Р~1 Г"1
= а2 b2 =
а
b
Р_
Q)VP)
Доказательство см. в работах [1, 4].
равенство
Vp) Vp)Vp)
Докажем свойство 5. Пусть ^ = е2га/8 — ком-
плексный корень степени 8 из 1 (квадратный ко-
рень из г). Тогда
Обобщением символа Лежандра для произ-
т
= PI р, является символ Яко-
вольного модуля и
2
(а\ ™ \ а
би — = П — , где р, — нечетные простые (не
2 2
и (2, + £,-1)2 = 2. Положим т = Оба ком-
плексных числа £, и т являются корнями полино-
мов с целыми рациональными коэффициентами,
то есть целыми алгебраическими числами. Ком-
мутативное кольцо А = Z[S,] содержит кольцо Z.
Поэтому можно рассматривать кольцо классов
вычетов А!(р). Это кольцо имеет характеристику
р, в нем (£ + У У = У + (У У = У + У’ (modр).
Имеем
обязательно различные) числа. Положим
( а । ,
Теорема 5.4.3. Символ Якоби обладает сле-
дующими свойствами. Для нечетного и
1)
а
т
= (т2) 2 = 2 2
2
= — (mod/?)
2)
п
п
для всех к 6 Z;
и
х=х
2
— (mod/?) = ^p+£, '’(mod/?).
3)
ab
а
п
НОД(Д п) = 1;
f-1
п
для всех b таких, что
= (-1)2 ;
Поскольку У = 1, то для /? = ±1 (mod 8) спра-
ведливо У + У = 2, + У, и для р = ±3 (mod 8)
справедливо У + = У + У = -(£, + У’), так
как У = -у1. Отсюда хр = т, если р = ±1 (mod 8),
( 2^1
-т, если р = ±3 (mod 8). Поэтому — = 1,
Ы
и ХР =
если р = ±\ (mod 8), и
2
= -1, если ps±3
4)
5)
ab
а
b
п
2
п
И
„2.
и
(mod 8). Объединение
(1
р -
8
\Р)
Свойство 6 следует
^(P-D/2
решений.
VP)
этих условий дает
из того, что сравнение
s 1 (mod р) имеет в точности (р -1)/2
o'
~Ь
жительных а и Ь.
Доказательство [1]. Свойства 1, 2 и 4 сле-
дуют из определений символов Лежандра и Якоби.
Для доказательства свойства 3 отметим, что для
нечетных p\,pi выполняется сравнение
6)
-] = (-!)
<7 I
(о-1)(6-1)
4 для нечетных поло-
-1 = +^_J_(mod 2) . (5.4.1)
2
85
Действительно, (р\ - 1)0’2 - 1) = 0 (mod 4), по-
этому pqp -1^(р]-1) + (р2-1) (mod 4). Поде-
лив обе части последнего сравнения на 2, полу-
чим выражение (5.4.1). По индукции получаем
eV
(mod 2).
Тогда
Р\-Рт-У п-1
= (-1) 2 =(-1) 2 .
Для доказательства свойства 5 отметим, что
для нечетныхpy,pi выполняется сравнение
Р'Рг 1 —U^2_l(mod2). (5.4.2)
8 8 8
Действительно, р2 -1 и -1 делятся на 4,
(р2 - 1)(р2 -1) = 0 (mod 16), поэтому р2р2 -1 =
= (р2 -1) + (Р2 -1) (mod 16). Поделив обе части
на 8, получим сравнение (5.4.2). По индукции
получаем
(mod 2).
Тогда
п2 — 1
eV
,=1 О
2
п
Ру-Гт~1 и2-1
= (-1) 8 =(-1) 8
Докажем свойство 6. Если а = р\...рк, Ь =
= q\...qi, то с учетом свойства 4, определения
символа Якоби и квадратичного закона взаимно-
сти имеем
v v 1
£YALf_iw 2 2
bka)
Сумму в
показателе степени достаточно вычислить по
модулю 2. Получаем
гу/И qj-\_a-\y
1=1 j=l
=VVmcd2)-
4/”1
Символ Якоби в вычислительном плане явля-
ется более удобным, чем символ Лежандра. Дей-
ствительно, для вычисления символа Лежандра
нужно знать, что число р простое, а выяснить это
достаточно сложно. Поэтому на практике символ
Якоби используется для вычисления символа
Лежандра. Например,
42)_(НИ)_(_7_)__(5)__/7)_ Г2)
101) I. 47) 1.47) 1.7) IjJ” 1.5)
Кроме того, символ Якоби используется для
распознавания простоты числа в вероятностном
алгоритме Соловэя-Штрассена (см. п. 7.9).
Если п состоит из нескольких различных не-
четных простых сомножителей, то количество
квадратичных вычетов и невычетов по модулю п
различно. По китайской теореме об остатках а
является квадратичным вычетом по модулю п,
если а— квадратичный вычет по каждому про-
стому делителю числа п. Если же а является
квадратичным невычетом хотя бы по одному из
простых делителей числа п, то а — квадратичный
невычет по модулю п. Таким образом, квадратич-
ных вычетов по модулю п не больше, чем квадра-
тичных невычетов по модулю п. Поэтому равен-
ство — = 1 не означает, что а является квадра-
)
тичным вычетом по модулю и. Если а является
квадратичным невычетом по модулям двух раз-
личных простых делителей, то символ Якоби по
модулю их произведения равен 1. Например, для
( 3 )
л = 35 = 5 -7 выполняется равенство 1 — 1 =
= | — | — | = (-1)(-1) = 1 • Однако, если | — | = —1,
15 Д 7 ) I и J
то а является квадратичным вычетом не для всех
простых делителей п и по китайской теореме об
остатках является квадратичным невычетом по
модулю п.
Пример 5.4.2. Применение квадратичного за-
кона взаимности.
1. Найдем все нечетные простые числа, для
которых число 5 является квадратичным выче-
том. Согласно квадратичному закону взаимности
V (р\
— = — . Поэтому для р = ±1 (mod 10) число 5
V) 15)
является квадратичным вычетом по модулю р.
2. Найдем все нечетные простые числа, для ко-
торых число 7 является квадратичным вычетом.
Согласно квадратичному закону взаимности
86
''Г
если р = 1
(mod 4), и
'т_
если р = 3 (mod 4). Квадратичные вычеты по моду-
( 7^1
лю 7 — это 1,2,4. Получаем — =1 в следующих
VPJ
( р] \
случаях: I -у 1 = 1 и p=l (mod4); I — 1 = -1 и
р = -\ (mod 4); то есть если р е {±1, ±3, ±9}
(mod 28).
Из квадратичного закона взаимности вытекает
ряд интересных свойств, касающихся разложе-
ния простых чисел на множители в расширениях
кольца Z.
Теорема 5.4.4. Пусть i = V-T. Простое ра-
циональное число р = 1 (mod 4) раскладывается
на простые множители в 2ВД.
Доказательство. Согласно квадратичному за-
кону взаимности -1 является квадратичным вы-
четом по модулю простого числа р = 1 (mod 4).
Следовательно, существуют х, к е Z такие, что
х2 + 1 = кр. Левая часть равенства раскладывается
на простые множители в евклидовом кольце 2[г]
единственным образом: (х + г)(х - г) = кр. Если
бы число р являлось простым элементом кольца
2[г], то один из сомножителей х + г или х - i де-
лился бы на р как полином от г. Поскольку это не
так, то число р раскладывается на множители в
2|7]:/> = ар.
Определим норму числа а + Ы как N(a + bi) =
= (а + Ы)(а - Ы) = а2 + Ь2. Справедливо равенст-
во А!(сф) = 7V(a)7V(P). Комплексные делители
числа р являются простыми элементами кольца
2ф], поскольку из разложения р = ар следует
разложение в целых числах: р2 = А!(а)Л(Р). Сле-
довательно, возможны два случая: Л(с/.)=1,
А!(Р) =р2 или 7V(a) =7V(P) =р. В первом случае а
является обратимым элементом кольца 2ф] и
число р ассоциировано с Р, то есть р — простой
элемент этого кольца. Во втором случае элемен-
ты а и Р кольца 2[г] являются простыми и со-
пряженными.
Доказательство. Имеют место равенства
7^3 = 2со +1, -7^3 = 2со2 +1. Согласно квадра-
тичному закону взаимности -3 является квадра-
тичным вычетом по модулю простого числа р = 1
(mod 6). Следовательно, существуют х, к g Z
такие, что х2 + 3 = кр. Левая часть равенства рас-
кладывается на простые множители в евклидо-
вом кольце Z[co] единственным образом:
(х + 1 + 2со)(х + 1 + 2со2) = кр.
Предположим, что число р является простым
элементом кольца Z[co], Тогда один из сомножи-
телей х + 1 + 2со или х + 1 + 2со2 должен делиться
на р как полином от со. Поскольку это не так, то
числор раскладывается на множители в Z.
Определим норму числа а + Ьа> как N(a + Ьсо) =
= (а + Ьса)(а + bca~) = a2 -ab + Ъ2. Справедливо
равенство Л(аР) = AXajAXP). Комплексные дели-
тели числа р являются простыми элементами
кольца Z[co], поскольку из разложения р = оф
2
следует разложение в целых числах: р =
= 7V(a)7V(P). Следовательно, возможны два слу-
чая: 7V(oc) = 1, А'(р)=/?2 или N(a) =МР) =Р- В
первом случае а является обратимым элементом
кольца Z[co] и числор ассоциировано с Р, то есть
р— простой элемент этого кольца. Во втором
случае элементы аир кольца Z[co] являются
простыми и сопряженными.
Следствие 5.4.7. Простое число р = 1 (mod 6)
представимо в видер = а2 - аЪ + Ъ2, где a.b e Z.
Для доказательства достаточно раскрыть
скобки в представлении р = (а + &со)(<7 + Ь&2).
Следствие 5.4.8. Простое число р = 1 (mod 6)
представимо в видер = с2 + 3d2, где c,d e Z.
Доказательство. В следствии 5.4.7 пред-
ставление неоднозначно:
р = a2 — ab + Ь2 =
= (а - b)2 -(а- Ь\-Ь) + (-Ь)2 =
= (Ь - а)2 ~(Ь - а)(-а) + (-а)2.
Следствие 5.4.5. Простое число р = 1 (mod 4)
представимо в виде суммы квадратов двух нату-
ральных чисел.
При этом числа а и b не могут быть оба чет-
ными, так как р — нечетное число. Поэтому су-
ществует представление р = (а + Ыл)(а + bd2),
при котором а = 1 (mod 2), b = 0 (mod 2). Тогда с
-1 + лРз
учетом равенства со =-------получаем - .• -
,г- —1 + -V —э
Теорема 5.4.6. Пусть со = VI =---------.
Простое рациональное число р = 1 (mod 6) рас-
кладывается на простые множители в Z[co].
где c = a-bj2,d -Ъ/2. Поскольку для
р = (а - Ь)2 - (а - b)(-b) + (-Ь)2 получаем те же
87
значения с2 и d2, то представление простого чис-
ла/? = с2 + 3</ единственно.
Имеют место также кубический и биквадра-
тичный законы взаимности [1].
5.5. Суммы Гаусса и Якоби
Поле включает в себя мультипликативную и
аддитивную группы. Для каждой из этих групп
можно определить характеры.
Мультипликативный характер конечного по-
ля F,, представляет собой гомоморфизм % из
группы F/; в группу С*: %(п)%(Ь) = %(<тА). Значе-
ниями характера являются корни степени р - 1
из 1, то есть числа вида е2™п!С-д, причем если
g — образующая группы FP и а = g", то, полагая
X(g) = е2га^/’“1), получаем %(<т) = . Со-
гласно теореме 2.3.4 группа характеров изо-
морфна группе F,,. Единичным элементом груп-
пы характеров является характер %0: Хо(<Д= 1 Для
всех а е F,,.
Примером характера для поля Fp является
символ Лежандра. Теорема 5.4.1 показывает, что
отображение, задаваемое символом Лежандра,
представляет собой гомоморфизм группы Fp в
подгруппу квадратных корней из 1 группы С .
Доопределим значение характера для нуля.
Если % Ф Хо, то х(0) = 0, и Хо(О) = 1.
Обозначим через 7V(x" = а) число решений
сравнения х" = a (mod /?) (без учета кратности).
Если НОД(и, р- 1)=1, то это сравнение всегда
имеет единственное решение. Если НОД(и, р - 1) =
= d> 1, то это сравнение имеет d решений или ни
одного решения в зависимости от того, является
ли а вычетом степени d. На практике достаточно
рассмотреть случай, когда п\ (р - 1).
Теорема 5.5.1. N(xn = а) = ^х(а), гДе сумма
берется по тем характерам, порядок которых де-
лит п.
Доказательство. В поле Fp существует п
корней степени п из 1. В силу изоморфизма
группы характеров и группы Fp существует ров-
но п характеров, порядок которых делит п, вклю-
чая единичный характер Хо-
Для <т = 0 сумма всех характеров, кроме еди-
ничного, равна нулю. Поскольку Хо(О)=1, то
сумма характеров равна 1, что соответствует од-
ному решению.
Если для а ф 0 сравнение имеет решение, то
существует элемент Ъ такой, что b" = a (mod /?).
Тогда х(а) = хЮ = Х(&)” = Хо(&) = 1 •
Если для <7^0 сравнение не имеет решений,
то существует характер ц такой, что ц(<т) Ф 1.
Действительно, характеры порядка п образуют
циклическую подгруппу с образующей
М - > гДе Xi = — образующая цик-
лической группы характеров. Если бы для всех j
выполнялось равенство р7(<7) = 1, то из изомор-
физма группы Fp и группы характеров следова-
ло бы, что существует элемент g е F/; такой, что
g" = <7 (mod р). Пусть сумма характеров порядка п
/7-1 1'1
равна S'. Тогда S = ]Tp7(<7) = ]Tp7(<7) = p(a)S.
J=0 J=L
Отсюда S'= 0. *
Таким образом, N(x2 - а) = 14-
Все изложенное справедливо и для мультип-
ликативных характеров расширенного конечного
поля из q = рп элементов. При этом р просто за-
меняется на q.
Аддитивный характер поля Fp представляет
собой гомоморфизм аддитивной группы этого
поля в группу комплексных корней степени р из
1. Аддитивный характер имеет вид
V<V) = v„, (а) = е2л"”й//’ = 1|/о (/„). Аддитивные
характеры образуют группу, изоморфную F/n с
единичным элементом \|/0(<з) = 1 для всех <7 е F;„
включая 0. Отметим, что \j7m (а) - \|/т (-а) .
Характеры <|т0 и Хо совпадают, хоть и являют-
ся элементами различных групп.
Суммой Гаусса поля F/; называется выражение
g(x,v)= ZjWvW-
(5.5.1)
Для комплексного числа g(x, v) = Re(g) + hn(g)i
положим | g(x, V)| = VRe(g)2 +bn(g)2 •
Теорема 5.5.2. Сумма Гаусса обладает сле-
дующими свойствами.
1- g(Xo,Vo)=A
2. Если х * Хо, то g(x, Vo) = 0. -
3. Если v * Vo, то g(xo, V) = 0-
4. Еслих^Хо, V* Vo, то |g(x,V)l=-/p •
Доказательство. Если х = Хо, V = Vo, то ка-
ждое слагаемое в правой части равенства (5.5.1)
равно 1, а их сумма g(xo, Vo) равна р.
Если v = Vo, Х^Хо, то сумма Гаусса пред-
ставляет собой сумму мультипликативных ха-
рактеров и поэтому равна нулю (см. доказатель-
ство теоремы 5.5.1).
88
Если Х = Хо, V^Vo, то сумма Гаусса пред-
ставляет собой сумму аддитивных характеров и
также равна нулю.
Если % Ф %о, V Vo и Vi — образующая цик-
лической группы аддитивных характеров, то для
а е (Ер
Х(« )g(X> Vo) = Х(«) Е XWV а (*) =
«Fp
= Ex(«*)Vi(«*) = g(X>Vi)-
Отсюда следует, что для ненулевых а все зна-
чения |g(x,Va)l равны, так как |%(<т)| = 1. Кроме
того,
< g(X, Va) = x(«“’)g(x, Vl)
и
g(x, Vo) = x(«“' )g(x, V!) = X(a)g(X, Vl) •
Перемножим эти две суммы:
g(x, vo )g(x, Vo) = x(«)x(a-1 )g(x, V] )g(X, Vi) =
= |g(X,Vi)|2-
Суммируя g(x,Vo)g(X,V«) по всем ненуле-
вым <т, получаем (p - l)|g(%, Vi)|2-
С другой стороны,
g(x, v a )g(x, vo)=E E x(*)x(y)vo(*)vfl(y)=
x у
= E E xO)x(y M (* - у)-
x у
В последнем выражении аргументы аддитив-
ного характера <|/я пробегают все множество зна-
чений от 0 до р - 1, при этом каждое значение
встречается одинаковое число раз. Тогда
]Tvfl(0 = 0, если а Ф 0, и a(t) = р, если
t t
<7 = 0. Суммируя по ненулевым <7, получаем
X g(x, Vo )g(X, Vfl )=E E х(*)х(у)8(ч У>Р =
a x у
= E x(*)x(*)p=p(p - о,
где 5(x, y) = 1, если x=у, и 5(x, у) = 0 в противном
случае. Получаем (р - 1)Ш у/ = (р -1 )|g(x, у])|2 =
=/?(/?-1)и\g(x,y)\ = Jp •
Пусть % и ?. — мультипликативные характеры
поля (Fp. Суммой Якоби называется выражение
ЛхЛ)= Ex(fl)^).
а+Л=1
Теорема 5.5.3. Справедливы следующие ра-
венства.
1- ЛХо, Хо)=А
2- ЛХо, Х)=ЛХ,Хо) = О.
з. Лх,х’') = -х(-1)-
4. Если XX' * Хо, то Т(х,х') = .
g(XX>Vi)
Доказательство. Утверждение 1 следует из
определения единичного характера Хо- Утвер-
ждение 2 доказывается аналогично утверждению
2 теоремы 5.5.2.
Для доказательства утверждения 3 заметим,
что
Лх,х ’)= Ех^/^^Ех^Л1-0))^ Е^(с)’
<7+6=1 Л *0 с^-1
где с - a/Q - а). Поскольку сумма характеров по
всем с равна нулю, то .7(х, X ') = ~Х(_Ь-
Для доказательства утверждения 4 рассмот-
рим произведение
g(X, Vi )g(x', Vi )= Е 2-W Vi (*) E X'(y)Vi (y) =
= E x(*)x'(y)V] (* + У) = E E x(*)x'(y)Vi (0-
x,y t x+y=t
Если t = 0, to
ExWx'(y) = Ex(a')x'(-t)=x(-i)ExxV)=0,
x+y=0 x x
так как xx' * Xo-
Если t ф 0, to
Ех(-т)х'(у)= Ex(/w)x'0’’) =
x+y=Z u+v=\
= E^w^'^=хх'(ОЛьх')-
M+V=l
Таким образом, ’ ' "
g(x, Vi )g(x', Vi)=E хх'ОУ(x, x')vi (0=
= 4x, x')g(xx', Vl)-
Если подставить значения для норм гауссо-
вых сумм из теоремы 5.5.2 в выражение для
суммы Якоби, то получим | J(x,x') I= -\[р
Через суммы Якоби выражается число реше-
ний алгебраического уравнения от двух перемен-
ных над конечным полем. Обозначим через
N(x* Уу1- 1) число решений уравнения
х2 + у2 = 1 (5.5.2)
в поле (Ер. Можно записать
7V(x2 + у2 = 1) = ЕМл'2 = a)N(y2 = b),
а+Ь=\
89
где сумма берется по всем парам a, b g (Fp таким,
2 1^1
что а + b = 1. Поскольку N(x = а) = 1 + — , то
\Р)
N(x2+y2 = 1) =
'—1 ~
<ркР;
Две первые суммы равны нулю, поэтому чис-
ло решений уравнения (5.5.2) определяется сум-
мой Якоби ддя квадратичных характеров
Mx2 + /=D=p+yf“Y-'|.
a+b=\\PKPJ
Применяя утверждение 3 теоремы 5.5.3, полу-
чаем У — 1 — | = -f—Уравнение (5.5.2)
а+ьЛРЛР) \Р J
имеет р + 1 решений, если р = 3 (mod 4), и р - 1
решений, если р = 1 (mod 4).
Аналогично,
А(х3 * *+у3=1) =
= Е (Хо (°) + Х(«) + X2 (°))(Хо (^) + Х(&) + X2 (*)),
а+Ь=1
где — кубический характер. В соответствии с
теоремой 5.5.3 получаем:
£Хо(°)Х(6) = О,
1»х2(*) = Хх(а)х’’(^)=-Х(-О-
а+Ь-А а+Ь=]
Тогда
А(х3+у3 = 1) =
=р - х(-1) - х2(-1)+-Лх, х)+Лх2, х2)-
Поскольку —1 = (—I)3, то ^(-1) = %3(-1) = 1 и
%2(-1)=1. Уравнение л3+у = 1 имеет р-2 +
+ 2Re(./(%, %)) решений.
В общем случае сумма Якоби может быть
распространена на произведение нескольких ха-
рактеров. Обозначим
ЛХ1,—х„)= ЕхДО-хЖ),
Z]+...+Zn=l
Л(Х],-,х„)= ЕхДМ-хЖ)-
Zj +...+z„=0
Выразим число решений уравнения с разде-
ленными переменными над конечным полем че-
рез сумму Якоби.
Теорема 5.5.4. Число N решений уравнения
п
~Ь в поле Fp выражается формулами:
м
N=рп^ + £х]«’ )-х„«' )Л (Xi,-,х„)
для b = 0; - -.
N=pn~i+2L(X] -ХП)(Ж)-Х„«’ ШХп-, Х„)
для b Ф 0, где суммы берутся по всем и-наборам
характеров Хь •••, X» таким, что х/' = Хо > X, * Хо и
Хп--Х„ = Хо-
Доказательство см. в работе [1].
5.6. Квадратичные числа
и квадратичные формы
5.6.1. Кольцо целых квадратичных чисел
Пусть /C = Q[TZ>] — квадратичное расшире-
ние поля Q, то есть D не является квадратом це-
лого числа. Если записать D = m2D', где D' сво-
бодно от квадратов, то Q[Vd] = Q[-/57] . Эле-
менты поля К называются квадратичными чис-
лами дискриминанта D.
Если D > 0, то К называется вещественным
квадратичным полем', если D < 0, то К называет-
ся мнимым квадратичным полем. Соответствен-
но определяются вещественные и мнимые коль-
ца целых квадратичных чисел. Свободное от
квадратов число D называется дискриминантом
квадратичного поля.3 Далее под целым элемен-
том квадратичного поля будем понимать целое
над Z квадратичное число.
Будем рассматривать кольца целых (над Z)
квадратичных чисел дискриминанта D с еди-
ничным элементом. В таком кольце дискрими-
нант может быть не свободен от квадратов [7],
например, кольцо, образованное числами вида
а + 6-7-4 = а + 26-Т-Т.
По определению элемент кольца целых квад-
ратичных чисел — это корень полинома
х2 + Ах + В, ... (5.6.1)
где А, В е Z и Л2 - 4В = D = m2D'. Корни поли-
нома (5.6.1) имеют вид
3 Если знак дискриминанта непринципиален, то
поле К называют квадратичным, а его элементы —
квадратичными числами. - =.
90
-А + у1а2-4В
2
(5.6.2)
Из (5.6.2) следует, что целые квадратичные
числа могут иметь вид
a+bjD
а =------
(5.6.3)
где а, b 6 Z. Если числа а и b оба четные, то
дробь (5.6.3) можно сократить на 2. Числа
а + by[D образуют кольцо. Выясним, для каких
значений D в знаменателе (5.6.3) стоит 2 (счита-
ем, что хотя бы одно из чисел а или b нечетное).
Поскольку А не может быть четным, то
m2D' = 1 (mod 4). Если в (5.6.3) двойка в знаме-
нателе не сокращается, то есть число т нечетное,
то т2 = 1 (mod 4) и О' = D = 1 (mod 4).
Сравнивая коэффициенты в (5.6.1) и (5.6.3) с
учетом (5.6.2), получаем: а = -А, ———— = В.
Тогда коэффициент а должен быть нечетным (в
противном случае, чтобы В было целым, коэф-
фициент Ъ тоже должен быть четным, то есть
дробь (5.6.3) может быть сокращена). Тогда, что-
бы В было целым, коэффициент b тоже должен
быть нечетным. Нетрудно убедиться, что пронз-
ал- Ьл/15
ведение квадратичных чисел а =---------- и
a'+b'Jl) , ,
р =--------, где все коэффициенты а, Ь, а,
Ь' — нечетные числа, равно:
_ ad + bb'D + (ab' + a'byjD
“₽=----------------------
Найдем для числителя вычеты по модулю 4:
ad + bb'D = 2 (mod 4), ab' + a'b = 2 (mod 4),
то есть числитель и знаменатель можно сокра-
тить на 2. Если числа а, b (или а', Ь’) оба четные,
то, очевидно, произведение ар можно записать в
виде (5.6.3). Таким образом, доказана следующая
теорема.
Теорема 5.6.1. Целые квадратичные числа
дискриминанта D имеют вид а + b-J~D при про-
а + Ь4Т>
извольном дискриминанте и ------- при 0=1
(mod 4) и а = b = 1 (mod 2).
Замена D <— 40 позволяет все целые квадра-
тичные числа записать со знаменателем 2. При
этом О = 1 (mod 4) или 0 = 0 (mod 4).
Кольцо целых над Z квадратичных чисел дис-
криминанта О называется квадратичным поряд-
ком и обозначается OD. Одно и то же квадратич-
ное поле содержит различные квадратичные по-
рядки, упорядоченные по включению. Например,
квадратичными порядками поля Q[V2] являют-
ся кольца Z[V2]=>Z[V18]oZ[V72].
Пусть О = mid, где т > 1 и О' свободно от
квадратов. Кольцо Оц называется максимальным
порядком поля К - QpZo7], а коэффициент т —
кондуктором квадратичного порядка.
Аддитивная группа квадратичного порядка
OD дискриминанта D = m2D' является двумерным
модулем над Z. Пусть t,„, — элемент, присоеди-
няемый к Z для получения квадратичного по-
рядка, при этом = J15 при D Ф 1 (mod 4) и
ПРИ = 1 (mod 4). Тогда базис мо-
дуля имеет вид [1, то есть OD = Z + Z£,,„.
Очевидно, что при D = n2D' выполняется
включение 0/,-^Оп. Например, если П' = -1,
D = -4, то 2 + Зл/-Т е О1У, но 2 + З-УчГ g OD.
Имеет место изоморфизм колец ОаЮп = Т.1т1..
Поскольку квадратичный порядок О» содержит-
ся в поле К, он является целостным кольцом.
Пример 5.6.1. Квадратичные поля, их целые
элементы и базисы.
Квадратичное поле Целый элемент Базис
QhR| Х+у4~5
Qh/^2] х + у4~2 [1,7^2]
QhRl i+V^i х +у 2 L 2 J
Qh/б] + у4б [i,V6]
Элементы поля Q[-/D] имеют вид Q + 415 Q .
Для квадратичного числа a = a + h415 сущест-
вует сопряженное число а = а-bJU. Опреде-
лим норму квадратичного числа. N(a) = aa.
Норма квадратичного числа является рациональ-
ным числом вида а2 - Db2, норма целого квадра-
тичного числа является целым числом, при этом
М«Р) = Ма)МР)- ____,
Например, норма целого квадратичного числа
,1 + jD 2 7 1~ Г) ,2
а + Ь—-—равная + ab +—-—Ь .
Норма квадратичного числа позволяет задать
на некоторых квадратичных порядках структуру
евклидова кольца. Квадратичный порядок OD
является евклидовым, если для любых элементов
а, Р 6 OD существует элемент у е Он такой, что
Ja
TV--у
1.
(5.6.4)
В случае D < 0 евклидовыми являются кольца
целых элементов при D е {-1, -2, -3. -7, -11}.
Доказательство этого факта можно провести
геометрически. Зададим на комплексной плоско-
сти точечную решетку, состоящую из тех точек
плоскости, которые являются элементами коль-
ца. Каждая точка имеет несколько ближайших к
ней точек. Свяжем с точкой (0, 0) ее зону как
множество точек комплексной плоскости, кото-
рые расположены к ней ближе, чем к другим
точкам решетки. Неравенство (5.6.4) означает,
что зона точки (0, 0) должна лежать строго внут-
ри единичного круга. С ростом абсолютной ве-
личины дискриминанта зона точки (0, 0) растет.
В случае D > 0 евклидовыми являются кольца
целых элементов при D 6 {2, 3, 5, 6, 7, 11, 13, 17,
21,29,33,37,41,57, 73}.
Группы обратимых элементов мнимых и веще-
ственных квадратичных порядков различаются/
Теорема 5.6.2. Группа обратимых элементов
мнимого квадратичного порядка содержит четы-
ре элемента при D = -l, шесть элементов при
D = -3 и два элемента при остальных значениях
дискриминанта.
Доказательство. Элемент мнимого квадра-
тичного порядка является обратимым тогда и толь-
ко тогда, когда его норма является обратимым эле-
ментом в Z, то есть равна I.4 5 Иными словами, об-
ратимые элементы являются комплексными кор-
нями из 1. В случае D = -l целые квадратичные
числа имеют вид a + bj-l, их норма задается
симметрической функцией а2 + Ь2. Единичную
норму имеют только наборы а = ±1, 6 = 0 и а = 0,
Ь = ±1, соответствующие числам ±1 и ± 7-Л .
В случае D = -3 целое квадратичное число
, 1 + 7^3 „
имеет вид а + Ь-------. Его норма
4 Обратимые элементы квадратичных порядков
называют также единицами (не путать с числом 1).
5 Норма элемента мнимого квадратичного поряд-
ка неотрицательна.
a2 + аЪ + Ъ2 является симметрической функцией.
Единичную норму имеют в точности корни сте-
i + 7-з
пени 6 из 1: {±1, ±со, ±со }, где со =---.
Для остальных значений дискриминанта D
норма не является симметрической функцией.
Условию a2 + Db2 = 1 или а2 + ab + -——Ь2 = 1
4
удовлетворяют лишь а = ±1, Ь = 0.
Вещественные квадратичные порядки имеют
бесконечные группы обратимых элементов, об-
ладающих нормой ±1. Если в— обратимый эле-
мент, то е" — тоже обратимый элемент для про-
извольного и 6 Z. Нахождение группы обрати-
мых элементов связано с решением в целых чис-
лах уравнения Пелля х2 - Dy2 = +1.
Пример 5.6.2. Обратимые элементы.
1. Для D = 2 обратимым является элемент
1 + у/2 с нормой -1, а также все степени этого
числа и сопряженного с ним. Обратным к обра-
тимому элементу является сопряженный эле-
мент, умноженный на его норму.
2. Для D - 12 обратимым является элемент
7 + 2712 с нормой 1, а также все степени этого
числа и сопряженного с ним. Обратным к обрати-
мому элементу является сопряженный элемент.
Группа обратимых элементов вещественного
квадратичного порядка циклическая. Образую-
щая группы обратимых элементов называется
фундаментальной единицей. Например, фунда-
ментальной единицей кольца Z[V2] является
число 1 + 72 с нормой -1.
5.6.2. Идеалы квадратичных порядков
В общем случае идеал квадратичного порядка
может быть порожден несколькими элементами,
например в кольце Z [7-5] существует идеал
(3, 1 + 7-5), образованный двумя простыми эле-
ментами кольца (см. пример 3.8.1).
Теорема 5.6.3. Множество 2l = aZ + Z(6 +
+Т^)/2, где a, b е Z и (4а) | (b2 - D), является
идеалом в Ос. Любой идеал квадратичного по-
рядка OD может быть задан в указанном виде.
Доказательство. Сначала докажем, что эле-
менты 21 образуют' аддитивную группу в Ос.
Действительно,
92
(ас + А(Ь + \П5)/2) + (ае + f(b + \П5)/2) =
= а(с + ё) + (d + f)(b + y[D)/2.
Теперь покажем, что произведение элемента
Оо на элемент 21 лежит в 21. Пусть D = 1 (mod 4),
а = (с + dy[D)/2 е Od, где c = d (mod 2), р =
=(ат + n(b + Jd)/2) g 21иу = ар = (А + bJd)/2 ,
где А = атс + bnc/2 + ndD/2 g Z и В = amd +
+ bnd/2 + нс/2 6 Z. Тогда можно записать
у = аА' + B(b + VT))/2. Покажем, что А'-(А-
-ЬВ)12а g Z, рассмотрев сравнение по модулю
4а: А-ЬВ = bnc + ndD - b2nd - bnc = = (D- b2)nd
(mod 4a). Поскольку b2 = D (mod 4a), to
A -Bb = 0 (mod 4a). Аналогично рассматривает-
ся и случай D = 0 (mod 4).
Осталось показать, что любой идеал может
быть представлен в виде суммы идеалов:
21 = aZ + Z (b + \П5)/2 . Пусть D = 1 (mod 4). Ад-
дитивная подгруппа кольца O/j как двумерного
Z-модуля порождается элементами вида
(а, (Ь + Ь')/2), где a, b, b' g Z. Покажем, что если
эта подгруппа совпадает с идеалом 21, то b' = 1.
Потребуем выполнения условия оф g 21, если
а 6 OD и Р g 21. Положим а = (с + Ja/D)/2 , р =
=am + n(b + b'-Jo )/2. Тогда у - осР = (А + B-Jd )/2,
где А = атс+ bnc/2 + nb'dD/2 viB = amd+ bnd/2 +
+ nb'c/2. Запишем у = аА' + B'(Z> + Z>VD)/2. Ус-
ловие B'gZ выполняется, если Ь' = ±1 (без на-
рушения общности можно положить b' = 1). То-
гда любой идеал может быть представлен в виде
2l = aZ + Z(A + VZ))/2.
Теорема 5.6.4. Каждый идеал кольца целых
квадратичных чисел может быть единственным
образом представлен в виде произведения про-
стых идеалов.
Доказательство см. в работе [6].
Пример 5.6.3. Разложение на простые идеалы.
Неоднозначность разложения на простые
множители в кольцах числовых полей пропадает
при переходе к идеалам. Так, возвращаясь к
примеру 3.8.1, получаем однозначность разложе-
ния идеала (2) на простые идеалы в Z[V- 5 ]:
(2) = (2, \ + 4^5)(2, (-4^5).
Действительно,
(2, 1 + лРГ)(2, 1-5^5) =
= (4, 2 + 2л/-У, 2-2л/-У, 6).
Но (4, 6) = (2), и (2, 2а) - (2) для любого
а е OD. Поэтому
(4, 2 + 27^5, 2-27^5, 6) = (2).
Аналогично получаем другие разложения на
простые идеалы:
(3) = (3, 1 + дГ5)(3, I-a/^5),
(i+V^)=(2, \+4^)(з, \+4^),
(1 - V-5) = (2, 1-зр5)(3, l-V3^).
Кроме того, нетрудно убедиться, что каждый
из четырех указанных простых идеалов при воз-
ведении в квадрат дает главный идеал. Напри-
мер, (2, 1 + V-5)2 = (2). Действительно,
(2, 1 + 7=Т)2 =(4, 2 + 27^5, -4 + 2>/^5).
Все элементы, порождающие этот идеал, де-
лятся на 2. Разность двух последних элементов,
образующих идеал, дает 6, и (4, 6) = (2).
Подмножество рациональных чисел, знаме-
натель которых не делится на заданное простое
число р, образует кольцо R сд Z. Идеалы кольца
R имеют вид (pR, p2R, ...}. Поэтому для любого
главного идеала (р) кольца Z существует кольцо
21^, состоящее из рациональных чисел, знамена-
тель которых не делится на р (такие кольца на-
зываются дробными идеалами). Тогда /Г1 G 21р,
р 6 (р), и 1 6 (р)21р. Поэтому можно сказать, что
идеал 21р является обратным к идеалу (р).
Аналогичная ситуация справедлива и для
квадратичных полей: 21' называется дробным
идеалом квадратичного порядка О», если суще-
ствует такое J g Z, что J21' = О».
Теорема 5.6.5. Дробные идеалы квадратично-
го порядка OD образуют группу относительно
операции умножения идеалов. Единичным эле-
ментом группы является кольцо
Доказательство см. в работе [6].
Таким образом, в кольце целых квадратичных
чисел разложение на простые идеалы однозначно
с точностью до обратимых элементов (в случае
D > 0 желательно учитывать влияние бесконеч-
ной группы обратимых элементов).
Нормой А(21) идеала 21 квадратичного поряд-
ка О/, является порядок факторгруппы Од/21.
Норма идеала задает гомоморфизм из муль-
типликативной полугруппы идеалов в мультип-
ликативную полугруппу Z*: 7V(2123) = 7V(2l)7V(®).
Поэтому из равенства идеалов 21 = 23С следует
равенство норм А(21) = А'(23)АЛ(С). В частности,
идеал с простой нормой является простым.
Норма идеала 21 поля К может быть определена
с использованием группы Галуа: 7V(2t) = 21 <з(21),
где автоморфизм а заменяет уЦ5 на - VZ).
Простое рациональное число р при перехо-
де от Z к квадратичному порядку может оста-
93
ваться простым, раскладываться на простые
множители или разветвляться. Соответственно,
главный идеал (р) является простым, расклады-
вается на множители, если (р) = фф, где ф, ф —
сопряженные простые идеалы, и разветвляется,
если (р) = ф2. Пусть D — дискриминант квадра-
тичного порядка. Если выполняется равенство
или
то простое
число р, соответственно, остается простым, рас-
кладывается на сопряженные множители или
разветвляется.
Например, в кольце Z[a/-2] идеал (5) остает-
ся простым, при этом
= -1. Идеал (3) рас-
кладывается на множители:
3 = (1+#2)(1-#2),
при этом
Идеал (2) разветвляется:
2 = -(V-2)(V-2), при этом
Назовем два дробных идеала 21 и 23 квадра-
тичного порядка О,, эквивалентными (21 ~ 23),
если существуют ненулевые элементы ос, р е OD
такие, что oc2i = р23. Поскольку (а) = aOD, все
ненулевые главные идеалы эквивалентны:
а(Р) = Р(а) [3].
Это отношение разбивает все множество
идеалов на классы эквивалентности. Число клас-
сов эквивалентности называется числом классов
поля К (или кольца OD). Поля К при D = -1, -2,
-3, -7, -11, -19, -43, -67, -163 имеют число
классов, равное 1, а каждый элемент в макси-
мальных порядках OD имеет однозначное разло-
жение на простые множители.
Число классов мнимого квадратичного поряд-
ка Ои может быть вычислено со сложностью
O(D(logZ))2) [8].
Кольцо главных идеалов обладает числом
классов 1. Действительно, если 21 = (а), 23 = (р),
сс
то, положив у = —, получаем 21 ~ 23. Число клас-
сов показывает, насколько данный идеал отстоит
от главного идеала. Если h — число классов поля
К, то для каждого идеала 21 идеал 2(А является
главным [6].
Класс, содержащий идеал 21, будем обозна-
чать А.
Классы идеалов можно умножать. Определим
произведение классов идеалов С ЛВ как класс,
содержащий идеал С = 2(23. Умножение классов
идеалов квадратичных порядков коммутативно и
ассоциативно: АВ = ВА, А(ВС) = (АВ)С. Единич-
ным классом является класс, содержащий главный
идеал. Пусть идеал 21 соответствует классу А и
2(23 — главный идеал. Тогда класс В, содержащий
идеал 23, является обратным к классу А. Таким об-
разом, классы идеалов квадратичного порядка OD
образуют абелеву группу классов 0(0/?), и эта
группа конечна, поскольку каждый класс А содер-
жит идеал с нормой, меньшей чем Z) |, где D —
дискриминант квадратичного порядка [6].
Классы идеалов группы С1((ф>) представлены
идеалами, определенными с точностью до главно-
го идеала. Поскольку идеалы 21 и (а)21 лежат в
одном классе, естественно задать класс идеалом с
минимальной абсолютной величиной нормы (та-
кой идеал всегда существует, поскольку в под-
множестве натуральных чисел существует наи-
меньшее). Назовем идеал класса приведенным,
если абсолютная величина его нормы минимальна.
Заметим, что произведение приведенных
идеалов не обязательно дает приведенный идеал,
поэтому после умножения идеалов необходимо
выполнить операцию приведения (см. п. 7.13).
В криптографии представляет интерес раз-
ложение простых чисел на множители в мни-
мых квадратичных порядках. Простое число р
может раскладываться в мнимом квадратичном
порядке только на сопряженные множители.
Если D ф 1 (mod 4), то р = о2 - Db7. Такое раз-
ложение можно найти с полиномиальной слож-
ностью (см. п. 7.8). Если D = 1 (mod 4), то раз-
ложение имеет вид
р- а + Ъ
и
Ap-(2a + b + b4D)(2a + b- b4D)-c7 -Dd2,
где d=b, c = 2a + b. Поэтому число 4р можно
представить в виде указанной разности (суммы
для отрицательного дискриминанта). .. ,5, . -
5.6.3. Квадратичные формы
Связь идеалов и квадратичных форм над Z
следует из выражения для нормы идеалов. Если
21 = (ос, Р) = (ах + ру) для х, у е Z, то
Л’(2() = (ах + Ру)(ах + ру) = ах2 + Ьху + су1,
где а, b,c (Z. . , . /
94
Пусть fix, у) = б/т2 + bxy + су2 = (а, Ь, с) — квад-
ратичная форма над 2 с дискриминантом
D = Ь2 - Лас [2]. Тогда D = 0 (mod 4) при четном
Ъ и D = 1 (mod 4) при нечетном 6: b = D (mod 2).
Любое число О е Z указанного вида является
дискриминантом квадратичной формы вида
(1 ту, АЛУ О(упоАЛ)-В\
11, Z)(mod4), -------I.
Квадратичная форма положительно опреде-
лена, если а > 0 и D < 0. Будем рассматривать
положительно определенные квадратичные фор-
мы. Кондуктор квадратичной формы дискрими-
нанта D — такое наибольшее натуральное число
т, что существует квадратичная форма с дис-
криминантом D/m2 .
С квадратичной формой f можно связать сим-
метрическую матрицу Мf =
' а Ь/2У
<ь/2 с ,
с опреде-
лителем -D/4.
Рассмотрим
М|| М12
/21 М22?
произведение
матрицы
е SL2(Z) на вектор (х, у):
Например, для дискриминанта -3 существует
единственная приведенная форма (\1, 1, 1); для
дискриминанта -4 — единственная приведенная
форма (1,0, 1). Однако для больших по абсолют-
ной величине дискриминантов приведенная фор-
ма не единственна. Для D = -15 существуют две
приведенные формы (1, 1,4), (2, 1,2). Для
Z) = —71 существует семь приведенных форм:
(1,1,18), (2, ±1,9), (3,±1,6), (4, ±3,5). Число
классов положительно определенных квадратич-
ных форм дискриминанта D совпадает с числом
классов идеалов мнимого квадратичного порядка
дискриминанта D и асимптотически равно
о(/о[) [6].
Каждый класс эквивалентных квадратичных
форм содержит единственную приведенную
квадратичную форму.
Если положительно определенная форма
f = (а, Ь, с) нормальна и а < , то f является
приведенной [6].
Для нормализации квадратичной формы
f = (а, Ь, с) нужно выполнить следующие дейст-
вия:
U (х, у) = (и]}х + w12y, u-i pc + ?22?y).
- вычислить л <—
a-b
2а
С/ =
Тогда можно определить функцию fiU (х, у)).
Положим (fU)(x, у) = det U -fiU • (х, у)).
Назовем квадратичные формы f и g эквива-
лентными, если существует матрица U е SL2(Z)
с единичным определителем такая, что f=gU.
Нетрудно заметить, что дискриминанты эквива-
лентных квадратичных форм совпадают. Ука-
занная эквивалентность разбивает множество
квадратичных форм на классы.
Группа
SL2(Z) порождается парой матриц
(см. пример 2.2.2). Тогда
<1 fix
S* = E, Т" = , fS = (c,-b,a),
\ V 1
fT" = (a,b + 2ап, an2 + bn + с).
Форма (а, b, с) называется нормальной, если
-а<Ь<а. Нормальная форма называется приве-
денной, если а < с и b > 0 при а = с. Приведенная
форма/называется главной, если
_ (. , b2-D]
f= ЪЬ, —-—
I 4 J
(поскольку b2 = D (mod 4), третий коэффициент
формы является целым). Других приведенных
форм с коэффициентом а = 1 не существует.
— положить f <—(a,b + 2sa, as1 + hs + с).
Если /= (а, Ь, с) нормальна и не приведена, то
нормализация квадратичной формы (с, -Ь, а),
полученной применением отображения Т, даст
приведенную форму:
1. Выполнить (/<— нормализация (/)).
2. Пока /= (а', V, с') не приведена, выполнять:
(f <- нормализация (с', -Ь', а')).
Пример 5.6.4. Приведение квадратичной
формы.
Пусть/=(10, 101,256) — квадратичная фор-
ма дискриминанта —39. Выполняем нормализа-
10-101
цию: s — ——— =-5;/=(10, 1, 1). Эта форма
не приведена. Выполняем нормализацию формы
1 + 1
2
(1,-1, Ю):
= 1, /-(1, 1, Ю)— приве-
денная форма.
По теореме 5.6.3 идеал квадратичного порядка
может быть представлен как двумерный Z-
модуль, одна из координат которого веществен-
ная, поэтому любой (целый) идеал О» может быть
представлен двумя образующими (а, р), а дроб-
95
ный идеал OD — произведением целого идеала на
рациональное число. Если аир взаимно просты в
Od, то идеалу 21 = (ос, р) может быть взаимно од-
нозначно сопоставлена квадратичная форма. Дей-
ствительно, норма идеала задается квадратичной
формой: 7/(21) = 2121 = Ах2 + Бху + Су2, где х, у
пробегают все множество 2. Поскольку 2112121,
то А, В, С = 0 (mod Л?(2()). Тогда можно опреде-
лить квадратичную форму
А В С
kA(2l)’A(2l)’A(2l)/ .
(а,Ь,с) =
На множестве квадратичных форм одного и
того же дискриминанта определена коммутатив-
ная операция композиции fi, ~ffi, которой соот-
ветствует операция умножения идеалов.
Пусть квадратичной форме f = аук2 + Ьху +
+ а^суу2 соответствует идеал 2li = (сц, X), форме
г 2 - 2
j2 ~ а2х + Ьху + fliCoy соответствует идеал
Z - . Л Ъ + -/о
212 = («2, к), где Л. = —-—. Тогда идеалу
Щ Г 21з = 2l|2l;; ~ (О[О2, X) . !•: !
соответствует форма
/з = алаух2 + Ьху + суу2.
По аналогии с приведением квадратичных
форм можно выполнять приведение идеалов в
группе классов мнимого квадратичного поряд-
ка. Для этого нужно соотнести идеал
( ь ГпУ
524—(a,b) = q aZ+%. 4
мнимого квадра-
2
тичного порядка дискриминанта D, где q е Q, с
положительно определенной квадратичной фор-
мой (а, Ь, с) этого же дискриминанта, операцию
композиции квадратичных форм с операцией ум-
ножения идеалов, а операцию приведения квадра-
тичных форм — с операцией приведения идеалов.
Квадратичные формы позволяют лучше уяс-
нить структуру групп классов мнимых квадра-
тичных порядков. Пусть 21 = аЖ + 2 и
а е 21, а = ах + у + Свяжем с идеалом 21
2
квадратичную форму fix, у) = ах2 + Ьху + су2, где
Ь2-D т
с =------. 1огда норма элемента а равна
4а
N(a) = аа = af (х, у).
Пусть 21 = q aZ. +Z^+ &
дробный
2
идеал, о, е Z и е Q. Тогда его норма равна
7V(2l) = q2a. Соответствующий целый идеал имеет
q = 1, и его норма равна а. Поэтому идеал мни-
мого квадратичного порядка с коэффициентом
а = 1 является обратимым целым идеалом, то
есть единичным элементом группы классов.
Простой идеал ф е О» мнимого квадратич-
bn+jD
ного порядка имеет вид ф = pAL + 2 —-— -, где
р — простое число такое, что
Ф -1 и
\.Р )
bp = 4d (mod 4р) ,0<bp<p.
5.7. Алгебраические числа
Обобщим понятие целого квадратичного чис-
ла. Назовем целым алгебраическим числом ко-
рень некоторого приведенного полинома
fix) = х" + а„_ук'’~} + ... + ао из кольца 2[х].
Пример 5.7.1. Целые алгебраические числа.
Все числа из Ж являются целыми алгебраиче-
/ г 1 + -\/— 3 кг гг
скими. Числа V-1, ----------, V2+V3 — это
2
корни полиномов х2 + 1, х2 — х + 1, х4 - 10х2 + 1
соответственно и поэтому являются целыми ал-
к 1
гебраическими, но числа —, ----- таковыми не
2 2
являются. _,
Если допустить, что коэффициент при х" по-
линома fix) может быть произвольным ненуле-
вым целым числом, то корень такого полинома
называется алгебраическим числом. Поделив fix)
на старший коэффициент, получаем, что алгеб-
раические числа являются корнями полиномов
из Q[x], Поэтому каждое рациональное число
является алгебраическим.
Алгебраическое расширение К поля Q назы-
вается числовым полем (или полем алгебраиче-
ских чисел). Кольцо Ок целых элементов число-
вого поля называется кольцом целых алгебраиче-
ских чисел.
Согласно теореме о примитивном элементе,
каждое числовое поле имеет вид Q[a], где a —
корень неприводимого полинома Дх) е Z[x].
Кольцо 2[х] обладает однозначным разложе-
нием на множители. ЕслиДх) е Z[x] — полином
96
с корнем а, то ос является корнем хотя бы одного
из неприводимых делителей полинома Дх).
Теорема 5.7.1. Алгебраическое число ос явля-
ется корнем единственного приведенного непри-
водимого полинома Дх) е Q[x]. Если ос является
корнем другого полинома g(x) е Q[x], то
7A)|g(A
Доказательство. Предположим, что суще-
ствует полином g(x) e Q[x] с корнем а и Дх) не
делит g(x). Кольцо Q[x] евклидово, поэтому
НОД(Дх), g(x)) = 1 и существуют полиномы Дх),
b(x) е Q[x] такие, что Дх)/(х) + /?(x)g(x) = 1. Под-
становка в последнее равенство ос вместо х дает
противоречие. Следовательно,Дх)^(х).
Полином Дх) из теоремы 5.7.1 определен од-
нозначно числом ос и называется минимальным
полиномом числа а. Если deg(/) = и, то ос — ал-
гебраическое число степени п. Полином Дх) яв-
ляется минимальным для всех своих п корней.6
Пусть К— расширение степени п поля Q и
Оо,..., ос,,-! — базис К над Q.
Норма Аг(ос) элемента а представляет собой
гомоморфизм К -> Q , сохраняющий непод-
вижными элементы поля Q , и вычисляется как
определитель матрицы (а,]) (см. п. 4.3.3). След
Тг(ос) элемента ос представляет собой гомомор-
физм аддитивных групп К -> Q, сохраняющий
неподвижными элементы из Q, и вычисляется
как сумма диагональных элементов матрицы
(д).
Пусть о0, ..., <j„-i — автоморфизмы числового
поля К, сохраняющие неподвижными элементы
из Q. Образ элемента а е К под действием изо-
морфизма о, обозначим через ос(,). Элементы ocw
называют сопряженными с ос. Тогда
Ма) = Па(,\ Тг(ос) = £осА
7=0
Минимальный полином Дх) е Q[x] числа ос
раскладывается на линейные множители в нор-
мальном расширении поля Q:
/А)~ПА «<и).
1=0
Тогда коэффициент при х" 1 равен -Тг(ос), сво-
бодный член равен (-l)'W(oc).
6 Примитивный элемент поля определен неодно-
значно, например, Q[cc, р] = Q[cc, ар]. Разным прими-
тивным элементам соответствуют разные минималь-
ные полиномы.
Пример 5.7.2. Норма и минимальный поли-
ном алгебраического числа.
1. Сопряженными с целым алгебраическим
числом ос = а + by[D^ + c-JD2 являются числа
Произведение четырех сопряженных чисел рав-
но Дос) = а4 + Ь4 + с - 2aWi - 2а2с2А - 2b2c2D}D2.
Соответствующее числовое поле получается при-
соединением одного элемента £, = T^i + ТА .
Минимальный полином числа £, равен
д(х)=(х+Та + Та х*+Та - Та) х
х (х - Та+Та х* - Та - Та )=
=х4 - 2(а + А А2+(А - А )2
2. Норма мультиквадратичного числа
п
а = а0 + a,равна произведению сопря-
'=i
женных чисел:
/ н __________Л
Л'(а) = П "o+ZTaTA |5
1=1 J
где произведение берется по всем 2" наборам
(у), ...,/„). Полагая Д, = 1, можно получить вы-
ражение для нормы в виде элементарных сим-
метрических функций от a2Dh Например, для
и = 3 получаем:
3 3 3
N(a) = «о +Х a*D< ~ 4ао Е а< D>+ 6"o X a'D' ~
1=1 1=1 , ,, 1=1
3
- 4п2£п6А3 + 4«о X Ч ajD,Dj +
1=1 1>J
+4а2^а>2А2А-4«о Х^А2^ААА-
i*/ i*j*k
Нетрудно заметить, что если над мультиквад-
ратичным полем К норма числа ос е К равна
№(ос), то над квадратичным расширением L поля
К норма этого числа будет равна Лу.(ос) = АД ос)2.
Пусть £, = Та” + ••• + Та и = ФИ- Мини-
мальный полином для примитивного элемента,
задающего мультиквадратичное расширение К,
Л и _______Л
равен /(х) = х + X А Та” I ’ где пРоизве-
J,e{-1,l}\ '=! J
дение берется по всем 2" наборам (у), ...,/„). По-
этому степень мультиквадратичного расширения
равна 2”.
Пусть (AT:Q) = 2 и Ок — кольцо целых элемен-
тов поля К. Если а е К, то существует число
97
a &7L такое, что аа. е Ок. Действительно, суще-
ствует полином + ... + h[, с рациональны-
ми коэффициентами, для которого а является
корнем. Умножив этот полином на наименьшее
общее кратное знаменателей коэффициентов Ь„
получим полином с целыми коэффициентами.
Поэтому можно считать, что Ь,— целые числа.
Умножим этот полином на Тогда
(^аГ1 + Ъп-2(Ъп^аГг + + Ь0(Ь„^Г2 = 0 и
bn-ia — целое алгебраическое число.
Для базиса а0, нй | g А" определим дис-
криминант Д(осо, ocK-i) как определитель мат-
рицы (Тг(ос,ос7)).
Норма и след целого алгебраического числа
лежат в 2. Поэтому все а, являются целыми ал-
гебраическими числами и Д(ос0, ..., е 2.
Базис поля К над Q, как и в случае квадратич-
ных чисел, может быть выбран неоднозначно.
Целые элементы поля К образуют «-мерную ре-
шетку. Любой набор линейно независимых век-
торов, проведенных из начала координат в точки
решетки, образует базис, при этом каждый век-
тор содержит лишь две точки решетки, включая
начало координат. Определим .минимальный ба-
зис ос0, ..., ос,,-!, для которого абсолютная величи-
на дискриминанта Д(а0, ..., оСи-О минимальна.
Теорема 5.7.2. Пусть К— поле алгебраиче-
ских чисел с минимальным базисом осо, ..., ос,,-,.
Каждый идеал 21 кольца целых алгебраических
чисел поля К может быть представлен в виде
21 = 2ос0 + ... + .
Теорема 5.7.3. Каждый ненулевой идеал
кольца целых алгебраических чисел может быть
однозначно представлен в виде произведения
простых идеалов.
Доказательство теорем 5.7.2, 5.7.3 см. в ра-
ботах [1,5].
Группа обратимых элементов кольца Ок в
общем случае свободная, не циклическая, но ко-
нечно порожденная. Число образующих (ранг)
группы обратимых элементов определяется сле-
дующей теоремой.
Теорема 5.7.4. Пусть полином, задающий
расширение A7Q, имеет г вещественных и 2s
комплексных корней. Тогда ранг группы обра-
тимых элементов кольца Ок равен г + s - 1.
Доказательство см. в работе [8].
Например, если K = Q[oc] и ос задается мини-
мальным полиномом, который имеет три веще-
ственных корня, то ранг группы обратимых эле-
ментов равен 2. Если минимальный полином
имеет один вещественный и два комплексных
корня, то ранг группы равен 1. Если расширение
A7Q задается п последовательными мнимыми
квадратичными расширениями присоединением
элементов A)j,..., -J- Dn , то степень непри-
водимого полинома равна 2", все корни ком-
плексные и ранг группы обратимых элементов
равен 2'7-1 - 1.
Кольца целых алгебраических чисел обычно
не обладают однозначным разложением на про-
стые множители. Например, в кольце целых эле-
ментов поля Q[VZ1+ 7^2] справедливы равен-
ства 2 = (1 + V-T)(l - V-T) = -(-7- 2)2. Однако
однозначность разложения появляется при пере-
ходе к идеалам: любой идеал однозначно предста-
вим в виде произведения простых идеалов (следо-
вательно, главный идеал, образованный данным
алгебраическим числом, однозначно представим в
виде произведения простых идеалов).
Понятие нормы идеала, введенное для квадра-
тичных полей, переносится и на числовые поля.
Пусть К— числовое поле, обладающее коль-
цом целых Ок, Id(O/c) — множество идеалов
кольца Ок, L — алгебраическое расширение поля
К, обладающее кольцом целых OL, Id(O/_) —
множество идеалов кольца OL, и А(сс)— норма
элемента ос е А в К. Тогда норма задает гомо-
морфизм мультипликативных групп идеалов
Id(O/) и И(ОД при этом диаграмма гомомор-
физмов на рисунке 5.1 коммутативна [8].
А* ------------► ld(OA)
N N
К -------------> Id(O^)
Рис. 5.1. Коммутативная диаграмма
гомоморфизмов групп идеалов
Диаграмма рисунка 5.1 утверждает равенство
А?(2(23) = ЛГ(2()АГ(23). Здесь О/, отображается на
все кольцо Ок- При этом достаточно определить
норму только для простых идеалов.
Если числовое поле К нормально над Q, то
норма идеала 21 может быть вычислена с исполь-
зованием группы Галуа Gal(A7Q) [8]:
АД21) = П^)-
ccGal(7</Q)
Норма главного идеала (ос) равна |7V(cc)|.
Приведем без доказательств ряд результатов,
доказанных в работе [8].
Теорема 5.7.5. Каждый простой идеал кольца
Ок максимален.
Теорема 5.7.6. Число классов h числового по-
ля К конечно, для любого идеала 21 кольца Ок
идеал 21а является главным.
Теорема 5.7.7. Пусть L — расширение число-
вого поля К, (L-.K) = т. Тогда
1. Если р — простой идеал в Ок, то N(yOL) = р'".
2. Если ф — простой идеал в OL и р = ф п Ок,
™nW)Ol= ПаСР)-
cy6Gal(7./ К)
Целые квадратичные и алгебраические числа
используются при анализе криптографических
алгоритмов с открытым ключом, основанных на
задачах разложения, нахождения индекса в
мультипликативной группе конечного поля, на-
хождения индекса в группе классов мнимого
квадратичного поля.
Упражнения к главе 5
1. Покажите, что мультипликативная функция
полностью определяется своими значениями
на степенях простых чисел.
2. Восстановите по китайской теореме об ос-
татках число, сравнимое с 1 по модулю 5, с 2
по модулю 6 и с 3 по модулю 7.
3. Покажите, что уравнение х3 + Зу3 +13=0
неразрешимо в целых числах.
4. Найдите корни уравнения 1 + х2 + х4 + х6 +
+ х8 + х’° = 0 в поле 1Ез ।.
5. Символ Лежандра является квадратичным
характером группы Fr. Пусть и — нечетное
составное число. Является ли символ Якоби
квадратичным характером группы (Z/nZ) ?
6. Покажите, что кольцо Z[V-2] — евклидово,
и найдите его обратимые элементы.
7. Разложите число 17 на множители в кольце
^[7^2] и покажите, что эти множители про-
стые.
8. Для каких простых р числа -3, 6, 21 будут
квадратичными вычетами?
9. Покажите, что V2 + V5 — целое алгебраиче-
ское число, и найдите группу Галуа для чи-
слового поля, полученного присоединением
этого числа к полю Q.
10. *При каких условиях простое число раскла-
дывается на простые множители в мнимом
квадратичном кольце с числом классов 1?
Является ли условие = 1 необходимым и
\Р)
достаточным для разложения простого числа
р в евклидовом квадратичном кольце дис-
криминанта £)?
11. Покажите, что имеет место изоморфизм ад-
дитивных групп OiJOmiD = Z/zwZ.
12. Является ли Om2D идеалом в Ок?
13. Какова наименьшая натуральная степень, в
которой идеал (7, 1 + 27) является глав-
ным в кольце z[V-2'7]?
14. Что собой представляет кольцо целых эле-
ментов поля разложения полинома х3 + 2?
Выберите какой-нибудь неглавный идеал
этого кольца. В какой степени этот идеал
станет главным?
15. Покажите, что в зависимости от вычета дис-
криминанта D по модулю 4 норма целого
квадратичного числа равна а - Db2 или
a2 +ab + b20-D)/4.
Литература к главе 5
1. Айерлэнд К., Роузен М. Классическое введение в
современную теорию чисел. М.: Мир, 1987.
2. Боревич З.И., Шафаревич И.Р. Теория чисел. М.:
Наука, 1985.
3. Ван дер Варден Б.Л. Алгебра. М.: Наука, 1979.
4. Виноградов И.М. Основы теории чисел. М.: Нау-
ка, 1981.
5. Кэртис Ч., Райнер И. Теория представлений конеч-
ных групп и ассоциативных алгебр. М.: Наука, 1969.
6. Bachmann J. Algorithms for binary quadratic forms
// www.cdc.informatik.todarmstadt.de/~buchmann/
AlgorithmsForQuadraticForms.ps.
7. Cohn H. A Second Course in Number Theory.
J. Wiley & Sons, Inc., 1962.
8. Milne J.S. Algebraic number theory (Lecture notes) //
www.math.lsa.umich.edu/~milne/.
Глава 6. ЭЛЕМЕНТЫ АЛГЕБРАИЧЕСКОЙ ГЕОМЕТРИИ.
ЭЛЛИПТИЧЕСКИЕ КРИВЫЕ
Алгебраическая геометрия изучает геометри-
ческие объекты, задаваемые алгебраическими
уравнениями с коэффициентами из некоторого
поля, и тесно связана с алгеброй, теорией чисел,
топологией. Идеи и методы алгебраической гео-
метрии и теории алгебраических кривых оказа-
лись плодотворными не только в прикладном
плане (криптография), но и при решении фунда-
ментальных проблем математики. Например, в
1995 г. с использованием теории эллиптических
кривых была доказана великая теорема Ферма'.
не существует целых чисел X, Y, Z таких, что при
и > 3 выполняется равенство X” + Y" = Z".
Эллиптические кривые — один из самых
перспективных инструментов для построения
криптографических алгоритмов. Кроме того,
аппарат теории эллиптических кривых оказыва-
ется полезным и при анализе криптографиче-
ский алгоритмов, основанных на задачах разло-
жения и дискретного логарифмирования в ко-
нечном поле.
6.1. Аффинные алгебраические
многообразия
Пусть К— поле. Аффинным п-мерным про-
странством Х\К) над К назовем множество то-
чек {Р = (х!, ...,х„)} е К”; значения хь ...,х„ на-
зываются аффинными координатами.
Аффинное алгебраическое множество 1 V—
это подмножество аффинного пространства, на
котором обращаются в нуль полиномы
/ь ...,fke /фц, ...,х„]:
F= {Р е К' | (А (Р) = 0, ..., Л(Р) = 0)}.
Если из этих полиномов построить идеал
3 = (/}, ....fk), то множество нулей полиномов f,
совпадет с множеством нулей всех элементов
идеала 3. Поэтому алгебраическое многообразие
V= V(J) можно охарактеризовать идеалом 3. При
этом К(3) = Е(3") для п е Z>0.
Согласно теореме 3.10.1 каждый идеал кольца
К[Х|, ...,х„] конечно порожден (то есть определя-
1 Алгебраическое многообразие иногда называют
алгебраическим множеством.
ется конечным числом полиномов/ь По-
этому каждый идеал определяет некоторое ал-
гебраическое многообразие [7, 8].
В случае п = 2 аффинное пространство назы-
вается аффинной плоскостью, а алгебраическое
многообразие, идеал которого образован оди-
ночным полиномом, — (плоской) алгебраиче-
ской кривой} Степень полинома, задающего кри-
вую, называется степенью кривой.
Пример 6.1.1. Алгебраические многообразия
и их идеалы.
1. Все аффинное пространство А"(К) совпада-
ет с множеством нулей нулевого идеала (0).
2. Полином ах + Ъу + с, где а * 0 или b Ф 0, за-
дает прямую на аффинной плоскости.
3. Точка (Х\, ...,ХГ) аффинного пространства
задается набором п линейно независимых линей-
ных уравнений.
4. Пустое множество является алгебраическим
многообразием, заданным полиномом Ох + 1.
Для алгебраического многообразия V как
множества общих корней нескольких полино-
мов из Тфсь ..., х„] можно определить идеал
3(F). Этот идеал состоит из всех полиномов
кольца Х[х], ...,х„], обращающихся в нуль в ка-
ждой точке многообразия V. Множество поли-
номов из 3(F) действительно является идеалом,
так как если f и g — полиномы, обращающиеся в
0 на F, то полиномы f± g тоже обращаются в 0
на F. Кроме того, для h е .... х„] полиномfh
всюду равен 0 на V.
Соответствие {алгебраические многообра-
зия} <-> {идеалы кольца К\х\, ...,х„]} не является
биекцией: F(3(F)) = V, но 3(К(3)) Ф 3. Это можно
объяснить тем, что идеалы 3 и З2 определяют
одно и то же алгебраическое многообразие, но
различны между собой.
Пусть алгебраические многообразия V\ и
задаются идеалами 3] и Зг соответственно. Тогда
объединение Vi о F2 задается идеалом 3]32, а
пересечение К о К2 — идеалом 3i + Зг- Поэтому
2 Поскольку алгебраическая кривая — множество
нулей полинома fix, у), говорят, что она задана урав-
нением /= 0.
100
можно ограничиться рассмотрением многообра-
зий, заданных простыми идеалами. Такие много-
образия называются неприводимыми. Неприво-
димая алгебраическая кривая задается неприво-
димым (над алгебраическим замыканием К по-
ля К) полиномом из кольца К\х, у].
Рассмотрим примеры алгебраических кривых.
Пример 6.1.2. Алгебраические кривые.
1. Алгебраическая кривая, заданная полино-
мом
Л*, у) = (ху + 1 )(х2 + у2 + 1).
Полином fix, у) раскладывается на множите-
ли, поэтому алгебраическая кривая является объ-
единением кривых ду + 1 = О и х2 + у2 + 1 = 0.
Вместо этой кривой можно рассмотреть две бо-
лее простых алгебраических кривых, задаваемых
неразложимыми делителями левой части уравне-
ния. Таким образом, изучение алгебраической
кривой сводится к изучению ее подмножеств,
задаваемых нулями неприводимых полиномов.
2. Алгебраическая кривая, заданная полино-
мом
fix,y) = x2-xy + y2.
Полином fix, у) неприводим над Q, и кривая
состоит из одной точки (0, 0). Однако при пере-
ходе к полю Q[V-3] полином fix, у) раскладыва-
ется на множители:
Поэтому данная алгебраическая кривая над
алгебраически замкнутым полем является объе-
динением двух прямых.
3. «Непохожие» полиномы х2+у2 + 1 и
х4 + 2у4 + 3 определяют над IR одно и то же пус-
тое многообразие. Однако при переходе к алгеб-
раически замкнутому полю С такая неоднознач-
ность исчезает.
Приведенные примеры показывают, что ино-
гда целесообразно рассматривать алгебраические
многообразия над алгебраически замкнутым по-
лем.
Алгебраическую кривую С, заданную уравне-
нием с коэффициентами из поля К, будем обо-
значать С/К, алгебраическую кривую, точки ко-
торой лежат в К2, будем обозначать С(К).
Даже если уравнение fix, у) - 0, задающее
кривую С, имеет коэффициенты из простого по-
ля к, множество решений этого уравнения (и,
соответственно, множество точек кривой) может
рассматриваться над расширением поля к, на-
пример, над его алгебраическим замыканием.
6.2. Проективная плоскость
и проективное пространство
Аффинная прямая А1 (А) над полем К пред-
ставляет собой поле К.
Проективной прямой Р'(А) над полем К назо-
вем множество пар {(X, Y) е К2 \ (0, 0)} с эквива-
лентностью (X, Y) ~ (аХ, а¥), если а е К*. Если
IV 0, то каждая точка (X, Y) е Р1 (К) эквивалент-
на точке (х. 1) аффинной прямой. Но на проек-
тивной прямой есть точка вида (X, 0), не соответ-
ствующая никакой аффинной точке. Эта точка
Рх называется бесконечно удаленной. Поэтому
Р'(А) = А’(А)и {АД.
Проективной плоскостью Р2(А) над полем К
назовем множество троек {(X, Y,Z) е А3 \ (0,0, 0)}
с эквивалентностью (X. Y,Z)~ (аХ, aY, aZ), если
а е К. Здесь X, Y, Z—проективные координаты.
Свяжем аффинную плоскость с проективной.
X Y
Полагая х = —, у = — для Z Ф 0, получаем биек-
цию между множеством точек (х,у) аффинной
плоскости и подмножеством точек (х, у, 1) про-
ективной плоскости. Однако на проективной
плоскости есть точки с нулевой Z-координатой,
которые не соответствуют никаким точкам аф-
финной плоскости.
Прямые на проективной плоскости задаются
линейными однородными полиномами
аХ +bY+ cZ. Проективная прямая, заданная
уравнением Z = 0, называется бесконечно удален-
ной. Точки этой прямой называются бесконечно
удаленными. Поэтому Р2(А) = А2(А') о Р'(А), где
«добавка» Р'(А') соответствует бесконечно уда-
ленной проективной прямой.
Все три проективные координаты равноправ-
ны. Поэтому в качестве аффинной плоскости,
содержащейся в проективной плоскости, можно
X Y
рассматривать плоскости с координатами —
при Аф 0, при Р*0, приХф 0.
По аналогии с проективной плоскостью можно
определить «-мерное проективное пространство
Р”(А) как множество точек {(АД...,Х„+1) е
е A'+I \ {0,0,..., 0)} с эквивалентностью (АГЬ ...,
X„+i) ~ (aXi, ..., aX„fi) для любого а е К*.
При этом Р"(А) = АГ'(К) о Р"-1(А), где «добав-
ка» Р,,-1(А) соответствует бесконечно удаленно-
101
му проективному подпространству размерности
и -1, заданному условием Аю = 0.
На проективной плоскости любые прямые пе-
ресекаются. Достаточно рассмотреть в аффинной
плоскости две параллельные прямые ах + by +
+ с = 0 и ах + by + d = 0. При переходе к проек-
тивным координатам получим систему уравне-
ний аХ +bY+ cZ = 0 и аХ + bY+ dZ=0. Решение
этой системы дает Z = 0, то есть точка пересече-
ния прямых лежит на бесконечно удаленной пря-
мой. Тогда аХ+ bY=Q. Поскольку а = Ь = 0 не-
возможно, предположим, что b Ф 0. Последнее
уравнение при Х= 0 дает У= 0. Точка (0, 0, 0) не
лежит в проективной плоскости, поэтому можно
считать Х^ 0. Получаем искомую точку пересе-
чения вида (1, - а/Ь, 0) .
Класс эквивалентности (X. Y, Z) при Z Ф 0
имеет единственного представителя вида (х, у, 1);
при Y* 0 — (х, 1, z); при XФ 0 — (1, у, z).
Аффинной алгебраической кривой соответст-
вует алгебраическая кривая на проективной плос-
кости. Если аффинная алгебраическая кривая
задана полиномом степени п вида '^,ai)x'yJ >
0<i+j<n
то соответствующая проективная кривая задает-
ся однородным полиномом степени и вида
^a^X’Y1 Z"~''~j . Например, аффинной кривой,
0<Z4- )<И
заданной полиномом х2 + ху+у3 + 1, соответству-
ет проективная кривая, заданная полиномом
x2z+xyz+y3 + z3.
Аффинное преобразование координат над по-
лем К имеет вид Д х) = Lx + b, где х = (х, у) е К,
L — обратимая матрица над К, b — вектор сдвига.
Проективное преобразование координат
плоскости Р2(К) — это линейное преобразование
вида ДХ) = Л/Х, где X = (X, Y, Z), М— обрати-
мая матрица размера 3x3 над К. Это преобразо-
вание на аффинной плоскости действует как аф-
финное преобразование координат, в чем не-
трудно убедиться, положив Z = 1.
Поскольку множество обратимых матриц об-
разует группу, проективное преобразование ко-
ординат задает на множестве проективных ал-
гебраических кривых симметричное, рефлексив-
ное и транзитивное бинарное отношение. При
этом множество проективных кривых разбивает-
ся на классы эквивалентности.
Пример 6.2.1. Проективные кривые второго
порядка.
(Аффинной) коникой в А2 называется алгеб-
раическая кривая, заданная квадратным уравне-
нием
q(x, у) = ах2 + Ьху + су2 + dx + еу +f= 0.
Множество невырожденных кривых вто|
порядка в аффинной плоскости над (R предо
лены эллипсом о2х2 + А2у2 = 1, гипербо.
а~х2 - Л2у2 = 1 и параболой у = тх2. Все эти
кривые эквивалентны относительно проектив!
замены переменных. С помощью аффинной
мены переменных можно получить а = Ь =
т = 4. Тогда проективные уравнения для эллг
са. гиперболы, параболы соответственно прим
вид А2 + Y2 = Z2, А - У2 = Z2, У2 = 4XZ. Переход
эллипса к гиперболе и обратно задается замене
переменных Z <-> X. Переход от эллипса к параб,
ле задается заменой переменных (X, Y,Z)~
—» (X- Z, Y,X+ Z). При этом уравнени
А2 + У2 - Z? примет вид У2 = 4AZ. Таким образох
в проективной плоскости P2(IR) эллипс, гипербс
ла и парабола эквивалентны относительно обра
тимого преобразования координат. . Л I
Пример 6.2.2. Пифагоровы тройки.
Согласно теореме Пифагора в прямоугольном
треугольнике с катетами А, У и гипотенузой Z
имеет место равенство
A2 + y2 = Z2 ; (6.2.1)
или /
А2 + У2 - Z2 = 0.
Уравнение (6.2.1) задает алгебраическую кри-
вую. В некоторых случаях стороны могут выра-
жаться целыми числами, например, (3, 4, 5) или
(5, 12, 13). Как же найти все целочисленные ре-
шения уравнения (6.2.1)? Для этого можно пе-
рейти к плоской кривой над Q, поделив обе части
А У
этого уравнения на Z и положив х =—,у = —.
Тогда уравнение (6.2.1) примет вид
х2+у2=1. (6.2.2)
Уравнение (6.2.2) задает окружность, и наша
задача сводится к поиску рациональных точек на
окружности. Параметризуем окружность (6.2.2)
(то есть от двух переменных перейдем к одной):
2/* /2-1 X - ....
' " * = ,У=-т J=—— •
А Г2+1 /2+1 1-у
Отсюда получаем все решения уравнения
(6.2.1):
«ин;. А= 21т, У = /2 - in, Z = I2 + т2
для произвольных I, т е Z. Если (А, У, Z) — реше-
ние, то (аХ aY, aZ) — тоже решение. Поэтому дос-
таточно рассмотреть I, т такие, что НОД(/, т) = 1 .
Многообразия в проективном пространстве
задаются однородными полиномами. Пусть сте-
пень полинома из идеала, задающего аффинное
многообразие, равна т. Переход от аффинного
многообразия к проективному выполняется за-
меной одночленов V а, , х,' ...х‘1" одночленами
V yd,. yni-dl-...-d„
6.3. Сложение точек на конике
На окружности существует естественный за-
кон сложения, имеющий простую геометриче-
скую интерпретацию. Пусть Е — фиксированная
точка окружности над (R, А и В — произвольные
точки. Проведем через точку Е прямую, парал-
лельную прямой АВ. Она пересечет окружность в
точке С, которая является суммой точек А + В
(рис. 6.1).
Рис. 6.1. Сложение точек на окружности
Таким же способом можно определить закон
сложения на эллипсе, параболе или гиперболе:
достаточно, чтобы прямая пересекала конику в
двух точках. При совпадении точек А и В секу-
щая АВ становится касательной.3
Теорема 6.3.1. Указанный закон сложения
превращает множество точек коники, заданной
над полем (R, в абелеву группу.
Доказательство. Поскольку все невырож-
денные коники эквивалентны относительно про-
ективного преобразования переменных, доста-
точно рассмотреть эллипс. Любые две точки
можно складывать. Очевидно, что сложение
коммутативно (прямые АВ и ВА совпадают). Ну-
лем является сама точка Е. Для нахождения эле-
3 В общем случае касательная определяется над
пополнением L поля К с помощью понятия сходимо-
сти. Однако в полном поле L уравнение касательной в
точке с координатами из К совпадает с уравнением
касательной, определенным с помощью алгебраиче-
ской производной. Это совпадение обусловлено тем,
что уравнение кривой алгебраично и алгебраическое
определение производной в поле К совпадает с анали-
тическим.
мента -А нужно провести через точку А прямую,
параллельную касательной в точке Е. Покажем,
что сложение ассоциативно. Рассмотрим на ко-
нике три точки А, В, С, и пусть А + В = Р,
В + С = Q (рис. 6.2).
Рис. 6.2. Сложение точек на конике
Равенство А + (В + С) = (А + В} + С эквива-
лентно утверждению: «Если А, В, С, Е, Р, Q —
точки коники и АВ\\ЕР, BC\\EQ, то АОЦСР».
Это частный случай теоремы Паскаля [5].
Если слагаемые совпадают, то секущая стано-
вится касательной.
Все эти рассуждения справедливы в любом
поле К, в том числе и в конечном поле.
Пересечение алгебраической кривой С(К) с
прямой, заданной уравнением ах + by + с = О,
можно описать алгебраически. Выразим из урав-
нения прямой одну переменную через другую и
подставим в уравнение кубики. Получим урав-
нение от одной переменной. Корни этого урав-
нения дают точки пересечения кривой С(К) с
прямой. Кратность корня называется кратно-
стью пересечения. В общем случае для описания
точек пересечения удобно рассматривать алгеб-
раически замкнутое поле.
6.4. Кубические кривые. Закон сложения
Назовем (плоской аффинной) кубической кри-
вой (кубикой) над полем К алгебраическую кри-
вую С(К), заданную полиномом ^iaix'yJ, где
м
а,& К и наибольшее значение i + j равно 3. Соот-
ветствующая проективная кубика С(К) задается
4 Согласно теореме Паскаля, если в проективную
конику вписан произвольный шестиугольник и про-
тивоположные стороны продолжены до пересечения,
то точки пересечения противоположных сторон лежат
на одной прямой.
103
полиномом '^jaiX'YJ Z3~'~J . На любой кубике
тоже существует естественный закон сложения.
Зафиксируем произвольную точку Е кривой.
Для сложения точек А и В проведем прямую АВ,
она пересечет С(К) в некоторой точке Р. Точку
пересечения прямой РЕ с кубикой будем назы-
вать суммой точек А и В (рис. 6.3).
Рис. 6.3. Сложение точек на кубике
Обычно в качестве точки Е выбирают беско-
нечно удаленную точку Р№. Существование та-
кой точки следует из того, что, положив в проек-
тивном уравнении кубической кривой Z = 0, по-
лучим непустое множество решений для коорди-
нат X, Y, которое соответствует точкам пересече-
ния кубики с бесконечно удаленной прямой (в
противном случае бесконечно удаленной можно
назвать прямую Х= 0 или Y= 0).
В определении сложения использовано сле-
дующее свойство кубики: если прямая пересе-
кает С(К) в двух точках, то она пересекает ее
еще ровно в одной точке. Действительно, из
уравнения прямой ах + by + с = 0 можно выра-
зить х через у и подставить результат в уравне-
ние кубики. Получим уравнение от одной пере-
менной с коэффициентами из К. По условию, у
него есть два корня в К, значит, должен быть и
третий корень в К. Если рассматривать проек-
тивную кривую, то степень уравнения после
подстановки равна 3.
Возможно ли, чтобы кубика и прямая, участ-
вующие в геометрическом законе сложения, име-
ли менее трех точек пересечения на аффинной
плоскости? Поскольку прямая проходит через две
точки кубики, то единственно возможный слу-
чай — две точки пересечения. Например, кубика
у2 = х3 + х + 1 пересекается с прямой х = 0 в двух
точках: (0, 1) и (0, -1). Подставив уравнение пря-
мой х = 0 в уравнение кубики, получим у2 = 1.
Степень этого уравнения равна 2, то есть третьей
точки пересечения нет. Однако при переходе к
проективной кривой Y2Z = Х3 + XZ2 + Z3 и про-
ективной прямой X = 0 получаем для точек пере-
сечения уравнение Y2Z = Z3, которое имеет три
решения: два соответствуют случаю Z = 1, а
третье имеет вид Z = 0 и соответствует беско-
нечно удаленной точке (0, 1, 0).
Покажем, что точки кубики с операцией сло-
жения образуют абелеву группу. Коммутатив-
ность операции сложения очевидна. Легко мож-
но показать, что Е — нулевой элемент. Докажем
ассоциативность введенной операции. Равенство
А + (В + С) = (А + С) + В эквивалентно тому, что
точки пересечения прямых, соединяющих точки
А + В и С, А + С и В, лежат на кубической кри-
вой. Обозначим pi=AC, р2 = Е(А+В), р3 =
= В(А + С), = АВ, q2 = Е(А + С), q3 = С(А + В),
где pi — прямая, проходящая через точки Л и С,
р2 — прямая, проходящая через точки Е и А + В,
и т. д. Будем считать, что все точки пересечения
этих прямых попарно различны. Тогда ассоциа-
тивность операции сложения вытекает из сле-
дующей теоремы [4].
Теорема 6.4.1. Пусть Ау — точка пересечения
прямых р, и 7„ 1 <z,j<3, причем точки AtJ по-
парно различны. Про все точки А,,, кроме А33,
известно, что они лежат на кубике. Тогда точка
Лзз тоже лежит на этой кубике.
Доказательство. Пусть р,{х,у) = 0 и
qj(x,y) = 0— уравнения прямых р, и qr Тогда
уравнение р\р2рз = 0 задает тройку прямыхр}, р2,
рз, уравнение q\q2q3 = 0 задает тройку прямых q\,
q2, 7з-
Кубика ар^рзрз + bq\q2q3 = 0 проходит через
все точки Л/,. Покажем, что в таком виде можно
представить уравнение любой кубики, проходя-
щей через восемь из девяти точек Л,;. Выберем в
качестве осей координат прямые р\ и qx, то есть
выполним замену переменных х <— рАх, у),
у<— qi(x,y). Пусть рассматриваемая кубика зада-
ется уравнением Р(х,у) = 0. Функции Р(0,у) и
УРг(0, у)рз(0, у) обращаются в нуль в трех точках
Лц3 Л2Ь Лзь лежащих на оси Оу. Кроме того, эти
функции— полиномы степени не более 3. Сле-
довательно,
Р(0, у) = аур2(0, у)рз(0, у).
Аналогично можно показать, что Р(х, 0) =
= bxqAx, 0)7з(х, 0). - ’ д «»,
Рассмотрим полином
у)=Р(х, у) - аур2(0, у)р3(0, у) - bxq2(x, O)q3(x, 0).
Ясно, что
(Х°, у) = Р(0, у) - аур2(0, у)рз(0, у) = 0.
Равенство ао(у) + а\(у)х + а2(у)х2 + ... = 0 при
х = 0 выполняется тогда и только тогда, когда
о0(у) = 0, следовательно, полином (Х-Т, у) делится
на х. Аналогично можно показать, что полином
104
Q(x,y) делится на у, то есть Q(x, у) = xyQ}(x, у).
Степень полинома Q(x,y) не более 3, следова-
тельно, Qi(x,y)— линейная функция или кон-
станта. В точках А-п, А2з, А33 обращаются в нуль
функции P,pzPi и q2q3, то есть в них обращается в
нуль и функция Q. Поскольку в этих точках
ху^О, то в них обращается в нуль и линейная
функция Q\. Точки Ап, Л2з, ^зг не лежат на одной
прямой, а для ненулевой линейной функции f
уравнение/х, У)= 0 определяет прямую. Следова-
тельно, (91 = 0, то есть Р(х, у) = ар\ртрз + hq^q^q-i. В
частности, точка А33 лежит на кубике Р(х, у) = О
(рис. 6.4).
Теорему 6.4.1 можно применять и в тех слу-
чаях, когда некоторые точки А„ совпадают.
Для кривых степени п >3 теорему 6.4.1 мож-
но обобщить.
Теорема 6.4.2. Пусть Ау — точки пересечения
прямых р, и qy, 1 < i,j < п, причем точки Ау по-
парно различны. Про все точки Ау, для которых
i + j < п + 3, известно, что они лежат на кривой
степени п. Тогда и остальные точки тоже лежат
на этой кривой.
Доказательство см. в работе [4].
В общем случае точки пересечения могут
быть кратными. Например, две коники над полем
IR могут пересекаться в четырех, трех, двух или
одной точке (рис. 6.5). Этот результат можно
обобщить и на случай произвольных кривых и
произвольных полей.
Рис. 6.5. Пересечение коник
Теорема 6.4.3. Пусть F(X, Y)— ненулевая
форма степени d от двух переменных. Тогда F
имеет на проективной прямой Г*1 (ТС) не более d
нулей. В случае алгебраически замкнутого поля
она имеет ровно d нулей (при условии, что корни
подсчитываются с учетом их кратности).
Доказательство. Пусть
F(X, Y) = adXd + a^xXd~'Y \ ... + a(!Yd.
C F связан неоднородный полином от одной
переменной
fix) = ajx d + а^х^1 + ... + Oq,
полученный делением F(X, Y) на Yd ф 0, где
X п
х = —. Ясно, что для всех а е К справедливы
следующие равносильные утверждения:
У(а) = 0 <2> (х - а) [Дх)
(X- aY) | F(X, Y) о F(a, 1) = 0.
Значит, нули полинома/соответствуют нулям
полинома F на Р'СК), отличным от точки (1,0)
(то есть точки на проективной прямой). Нали-
чие у F нуля на бесконечности (F(l, 0) = 0) озна-
чает, что ad = 0, то есть deg(/) < d. Кратность нуля
полинома F в точке (a, 1) на Р!(К) равна кратно-
сти нуля полинома f в соответствующей точке
a е К, то есть равна J-deg(/). Таким образом,
кратность нуля полинома F в точке (a, 1)— это
наибольшая степень выражения X- о.У, на кото-
рую делится F, а в точке (1,0)— наибольшая
степень Y, на которую делится F.
Пусть т,л— кратность нуля полинома F в
точке (1,0). Кольцо К[х] целостное, то есть по-
лином f степени d - тх имеет не более d - пи-
нулей и ровно d - тх нулей в случае алгебраиче-
ски замкнутого поля.
Обобщением теоремы 6.4.3 является теорема
Безу, согласно которой общее число точек пере-
сечения проективных кривых С и D степени
deg(C) = т, deg(D) = п над алгебраически замк-
нутым полем равно тп, если точки пересечения
подсчитываются с соответствующей кратностью
(с учетом бесконечно удаленных точек) [5].
Таким образом, геометрический закон сложе-
ния точек на неприводимой кубической кривой
задает структуру абелевой группы. Нулем груп-
пы является точка Е, а точка -Р (третья точка
пересечения прямой РЕ и кубики) является про-
тивоположной к точке Р. В случае алгебраически
замкнутого поля эта группа бесконечна.
105
6.5. Особые и неособые кубики
Рассмотрим примеры пересечения кубики с
прямой. ......
Пример 6.5.1. Пересечения кубики с прямой.
1. Покажем, что кривая у2=х3+Ах + Б пересе-
кает бесконечно удаленную прямую Z = 0 в одной
точке, причем кратность пересечения равна 3. Пе-
реходим к проективной форме кривой. Подставляя
в уравнение кривой K2Z = Х3 + AXZ2 + BZ3 значе-
ние Z = 0, получаем X3 = 0. Последнее уравнение
имеет тройной корень X- 0. По определению про-
ективной кривой Y^ 0, так как точка (0, 0, 0) не
лежит на проективной плоскости, поэтому коор-
динаты точки пересечения кривой с бесконечно
удаленной прямой можно записать как (0,1,0).
Поскольку эта точка лежит на бесконечно удален-
ной прямой, она является бесконечно удаленной.
2. Покажем, что кривая у2 =х3+х2 (рис. 6.6) пе-
ресекает произвольную прямую, проходящую че-
рез точку (0,0), в этой точке с кратностью 2 или 3.
Рис. 6.6. Кривая у2 = х° + х2
Переходим к проективной форме кубики.
Уравнение кривой имеет вид Y2Z = X3+X2Z'.
уравнение прямой, проходящей через точку (0, 0):
у = ах; соответствующее проективное уравнение:
Y= аХ. Подставляя уравнение прямой в уравнение
кубики, получаем Х2(Х + Z - <rZ) = 0, то есть име-
ем двойное (тройное при а = ±1) пересечение в
проективной точке (0,0, 1). Отсюда следует, что
Р +(0,0) = (0,0). з
3. Покажем, что кубика у2 = х3 (рис. 6.7) пере-
секает произвольную прямую, проходящую через
точку (0,0), в этой точке с кратностью 2 или 3.
Рассуждая аналогично, получаем для пересе-
чения прямой и кубики уравнение aX2Z = X3.
Пересечение двойное (тройное при а = 0). Сле-
довательно, также имеет место равенство
Р + (0, 0) = (0, 0).
Из рассмотренных примеров видно, что в
двух последних случаях точка (0, 0) ведет себя
по-особому, а именно является аналогом понятия
«бесконечность» для натуральных чисел.
Точка Р кривой, заданной уравнением
f(X, Y, Z) = 0, называется неособой, если в этой
точке хотя бы одна частная производная ,
дХ
df df
—, — отлична от нуля, в противном случае
dY dZ
точка называется особой. Кривая, которая не со-
держит особых точек, называется неособой.5 В
противном случае кривая называется особой.6
Покажем, что если алгебраическая кривая не
является неприводимой, то она содержит особую
точку. Пусть кривая задана нулями полинома F,
где F(X, Y, Z) = f(X, Y, Z)g(X, Y,Z)nfg — одно-
родные полиномы. В соответствии с теоремой
Безу кривые /= 0 и g = 0, рассматриваемые над
алгебраически замкнутым полем, пересекаются.
Согласно правилам дифференцирования
dF dg df
— - f—^ + g^—. Аналогичные равенства име-
дХ дХ дХ
ют место и для частных производных по Y, Z.
Рассмотрим производную полинома F по X в
точке пересечения кривых /= 0 и g = 0. В этой
dF .
точке -------= 0. Аналогично получаем
dX
dF' dF' r
---------- 0, -= 0 . 1 аким образом, кривая, не яв-
dY--------dZ
ляющаяся неприводимой, всегда особая.
Пример 6.5.2. Особые точки.
1. Кривая у2 = х3 + х2 содержит особую точку
(0, 0), так как в этой точке
dF „ 2 „ dF „ л
= Зх2 + 2х = 0, = 2у - 0.
dx-----------------dy ..
Точка (0, 0) называется точкой самопересече-
ния, или узлом.
5 Неособая кривая называется также гладкой, не-
вырожденной, несингулярной.
6 Особая кривая называется также вырожденной,
сингулярной. Однако супервырожденная (суперсин-
гулярная) кривая не является особой.
106
2. Кривая ,)’2 = х3 содержит особую точку
(О, 0), так как в этой точке
8F . 2 . 8F
— -Зх = 0, ----= 2у = 0.
8х ду
Точка (0, 0) называется острием, или точкой
возврата.
3. Покажем, что бесконечно удаленная точка
(0, 1, 0) является особой для кривой у = (х- а)у
х(х - Ь)(х - с). Для этого перейдем к проективной
форме: YZ2 = (X- aZ)(X- bZ)(X- cZ) и поделим
обе части этого уравнения на Y Ф 0. Пусть
X Z
х — —, z = —, тогда проективной точке (X, Y, Z)
будет соответствовать аффинная точка (х, l,z).
Получим уравнение
F(x, z) = z2 - (х - az)(x - bz)(x -cz) = 0.
Нетрудно видеть, что при х = 0, z = 0 обе про-
изводные обращаются в нуль. Значит, кривая яв-
ляется особой.
Понятие особой точки не зависит от способа
описания кривой, то есть от способа задания ко-
ординат, в чем легко убедиться, подставив
х = аи + bv, у = си + dv в уравнение кривой.
Покажем, что кубика у2 = (х - лг)(х - 6)(х - с),
где числа а, Ь, с различны, является неособой.
Действительно, для аффинного уравнения частная
производная по у равна нулю только при у = 0, то
есть этому условию может удовлетворять одна из
точек (а, 0), (Ь, 0), (с, 0). Очевидно, что частная
производная по х в этих точках отлична от нуля.
Например, при х = а производная равна
(а - Ь)(а - с) 7- 0, так как одновременно a7b.
а 7 с. Легко проверить, что бесконечно удаленная
точка (0,1,0) на проективной кривой K2Z =
= (X- aZ)(X~ bZ/X- cZ) тоже не является особой.
6.6. Касательные и точки перегиба
алгебраической кривой
Касательная к проективной кривой С(К) в
точке Р задается уравнением
dF 8F 8F
—(Р)Х + —(Р)У+—(P)Z = о,
8Х 8Y 8Z ’
где частные производные вычисляются в точке
Р. Это уравнение первой степени, следовательно,
оно задает прямую. Теперь ясна связь между
особой точкой и касательной: в особой точке ка-
сательная не определена.
Касательная к кривой в неособой точке зада-
ется однозначно уравнением кривой и не зависит
от аффинного (или проективного) преобразова-
ния координат. Пусть х = (Х\,Х2,Х3),
и = (И,, L72, L73), где Xt = 'XjaijUJ , afJ е К. Пусть
F(x) — уравнение кривой, тогда эта же кривая ь
координатах U\, U2, U3 имеет вил
GfUi, Ui, L’3) = F(X|(u),X2(u),A3(u)). Найдем част-
ные производные, задающие касательную к этой
кривой в произвольной точке:
8G ^8F 8Х, v-
----= /---------~ - 7 F.a,. .
8U, Y 8Xi 8UJ V J
Поскольку преобразование координат обра-
тимо, то матрица А = (а^) невырождена. Следо-
r 8G
вательно, набор ----- нулевой тогда и толькс
л 8F с
тогда, когда набор -------- нулевой. Если
8Х:
, {8F 8F 8F\ {8G 8G 8G~\
8X2 8X3J [dU^ 8U2 8U3)
векторы-строки, x и u — векторы-столбцы, тс
х = Ли, g = £4. Поэтому gu = (fA)(X\) = fx. Зна-
чит, уравнения gu = 0 и fx = 0 определяют одну г
ту же прямую.
Пусть точка Р = (ХР, YP, ZP) принадлежит ку-
бической кривой F = 0, то есть F(P) = 0, и пусть
R = (Хк, Yr, Zr) — произвольная точка проектив-
ной плоскости. Точки проективной прямой Ph
имеют вид аР + bR. Здесь точки рассматривают-
ся как векторы над полем К, сложение точек оз-
начает покоординатное сложение векторов (иль
сложение точек на проективной плоскости, от-
личное от сложения точек на кривой), умноже-
ние точки на элемент а е К означает скалярное
умножение вектора:
аР + bR= (аХР + bXR, aYP + bYR, aZP + bZR).
Точки прямой PR, отличные от R, имеют вил
Р + tR. Рассмотрим точки пересечения этой пря-
мой и кривой F = 0 как функции от I. В нашек
случае F — полином степени 3, поэтому
F(P + tR) = F(P) + at + btl + ct3 = Q(t).
Здесь t = 0 соответствует точке P; кроме того
F(P) = 0 по условию, тогда
а = F^P)X+ Fy(P)Y+ F^P)Z,
где Fx, Fy, Fz — производные по X, Y, Z соответ
ственно,
ь = |(Лх (П^2 + Fxy (P)XY + Fxz {P)XZ +
+ FYY {P)Y2 + Fyz (P)YZ + Fzz (P)Z2),
107
где Fxx— вторая частная производная по X,
Fxy— вторая частная производная по X, Y и т. д.
Полином (Д/) имеет в нуле кратный корень при
а = 0, то есть точка Р неособая.
В неособой точке Р кривой F = 0 определена
касательная. Если кратность пересечения кривой
с касательной равна 3, то Р называется точкой
перегиба. В этом случае b = 0 (и, конечно, а = О,
так как прямая PR является касательной).
Неособая проективная кубика С(К) всегда
имеет хотя бы одну точку перегиба [4].
Кубика над алгебраически замкнутым полем
имеет девять точек перегиба. Прямая, проходя-
щая через две точки перегиба кубики, проходит
и через третью [4].
6.7. Нормальные формы
эллиптической кривой
Назовем эллиптической кривой неособую ку-
бическую кривую.
Рассмотрим наиболее употребительные (нор-
мальные) формы уравнения эллиптической кри-
вой, получаемые линейной заменой проективных
переменных. Большинство из них являются част-
ными случаями обобщенной формы Вейерштрас-
са, содержащей единственную бесконечно уда-
ленную точку, которая является точкой перегиба,
а бесконечно удаленная прямая является каса-
тельной в этой точке. Существование нормальных
форм обосновывается следующей теоремой.
Теорема 6.7.1. Справедливы следующие ут-
верждения.
1. Уравнение кубики над произвольным по-
лем может быть сведено к обобщенной форме
Вейерштрасса
у2 + арсу + щу = х3 + ар:2 + арс + а6. (6.7.1)
2. Если характеристика поля отлична от 2, то
уравнение (6.7.1) может быть преобразовано к
виду
у2 = х3 + Ьрс2 + Ьух + bf>, (6.7.2)
а над алгебраически замкнутым полем — к виду
Е[а, Ь]
у2 = х3 + ах2 + Ьх (6.7.3)
или к форме Лежандра
у2 = х(х - 1 )(х - Z). (6.7.4)
3. Если характеристика поля отлична от 3, то
уравнение (6.7.1) может быть преобразовано к
виду
у2 + арсу + ауу = х3 + аух + а^, (6.7.5)
а над алгебраически замкнутым полем — к нор-
мальной форме Дойринга
у2 + аху + у = х3. (6.7.6)
4. Если характеристика поля отлична от 2 и 3,
то уравнение (6.7.1) может быть преобразовано к
виду ; ‘ V
у2 =х3+Лх + В. (6.7.7)
Доказательство. Условию того, что кубика
неособая, в уравнениях (6.7.3), (6.7.4^, (6.7.6),
(6.7.7) соответствуют неравенства а~ -АЪф 0;
Е £ {0, 1}; а3 Ф 27; 4Л3 + 27В2 Ф 0.
Для доказательства утверждения 1 рассмот-
рим проективную кубику
E(X,T,Z) = '^aiJX'YJz3~,~J= 0 (6.7.8)
,+7<з
над полем С. У нее есть точка перегиба. Линей-
ной заменой переменной Z <— аХ + bY + cZ мож-
но обеспечить координаты этой точки равными
(0, 1,0), причем касательная в этой точке будет
задаваться уравнением Z = 0. Это значит, что пере-
сечение кубики F = 0 с бесконечно удаленной
прямой Z = 0 имеет кратность 3, то есть полином
(X Y, Z)|z=0 = азоУ3 + б/21Х2У + о|2ХТ2 + г/03У3 име-
ет корень Х=0 кратности 3. Следовательно,
= г/|2 - «оз ~ 0, но озо Ф 0, так как иначе рас-
сматриваемая кривая целиком содержала бы
прямую Z = 0 (уравнение делилось бы на Z и ку-
бика не являлась бы неприводимой кривой). Ка-
сательная в точке(0, 1,0)задается уравнением
ЕД0, 1, 0)Х + ЕД0, 1, 0)У + ЕД0, 1, 0)Z = 0.
Для найденного ограничения на о3(Х3 имеем
ЕД0, 1,0) = ЕД0, 1, 0) = 0. Но при этом
Ег(0, 1,0)^ 0, так как в противном случае точка
(0, 1, 0) была бы особой. Однородный полином
ЕДХ Y, Z) степени 2 в точке (0, 1, 0) принимает
значение «ог- Можно считать, что оог = 1 • Тогда в
аффинных координатах уравнение (6.7.8) запи-
шется в виде
у2 + а^рсу + а<пу + Рз(х) = 0,
где Р3(х)— полином степени 3. Сделав подхо-
дящую замену переменной х, можно получить
коэффициент при х3, равный -1. Тогда уравнение
(6.7.8) примет вид (6.7.1).
Это уравнение неособой кубической кривой
справедливо для поля любой характеристики.
Первое утверждение доказано.
Несложные выкладки показывают, что замена
переменных вида х <— и2х + г, у <— и у + sux +t
сохраняет вид уравнения (6.7.1) при и е X* и г, s,
teK.
108
Если характеристика поля отлична от 2, то
возможно деление на 2. Тогда заменой перемен-
ных у <— у-a^x/'l-ay/'l в левой части уравне-
ния (6.7.1) можно выделить полный квадрат.
Уравнение примет вид (6.7.2), где
г. 1 2 L 1 , 1 2
®2“fl'2+~°i > о4 =о4+уО'|о,3, ^б~аъ+—а3.
Если поле является алгебраически замкнутым,
то правую часть в (6.7.2) можно разложить на
линейные множители: (х - С|)(х - е2)(х - е3). За-
меной переменной х<— х-е^ получаем (6.7.3).
Правую часть в (6.7.3) тоже можно разложить на
множители: х(х - d2)(x - d3). Заменой перемен-
ных х <— d2x, у <— y-Jdl получим уравнение вида
(6.7.4). Утверждение 2 доказано.
Если характеристика поля отлична от 3, то
возможно деление на 3. Заменив в (6.7.2) х на
х~Ь2/3, получим нулевой коэффициент при х2.
Тогда, если характеристика поля отлична от 2 и
3, уравнение примет вид (6.7.7). Утверждение 4
доказано.
В общем случае, если характеристика поля
отлична от 3, то в уравнении (6.7.1) аналогично
можно обеспечить нулевой коэффициент при х2 и
привести его к виду (6.7.5). Этим доказана пер-
вая часть утверждения 3.
Покажем, что если характеристика алгебраи-
чески замкнутого поля отлична от 3, то кривая
может быть представлена в форме Дойринга
(6.7.6). По аналогии с доказательством утвер-
ждения 2 приводим (6.7.5) к видуу~ + срсу + с3у =
= х3 + с2х2 + С4Х, причем точка (0, 0) лежит на
кривой. Эта точка по условию неособая, то есть в
ней существует касательная, задаваемая уравне-
нием (2у + С]Х + сз)У = Зх2 + 2с2х + с4 - с^у. Точка
(0, 0) имеет порядок, отличный от 2, если каса-
тельная в ней имеет конечный угловой коэффи-
циент, то есть с4 = 0. Точка (0, 0) является точкой
перегиба тогда и только тогда, когда с2 = 0 и
с3 Ф 0. Выполнив нормализацию с3 = 1 подходя-
щей заменой переменной у, получим нормаль-
ную форму Дойринга (6.7.6), определенную для
кривой над алгебраически замкнутым полем с
характеристикой, отличной от 3.
Для кубики над алгебраически замкнутым по-
лем, характеристика которого отлична от 3, су-
ществует нормальная форма Гессе [4, 13, 21]:
X3 + Y3 + Z3 = 3pXYZ.
(6.7.9)
Кривая, заданная таким уравнением, неосо-
бая, если ц ф 0 и ц3 Ф 1 (при ц = 0 кривая над ал-
гебраически замкнутым полем не является не-
приводимой и представляет собой объединение
трех прямых). Если перейти к аффинной форме
X Y
этого уравнения с координатами х =—, И
затем сделать замену переменных т<— у3,
3 3 /
и <-ху, то с учетом равенства х = -и /V полу-
чим уравнение в форме Вейерштрасса (Дойрин-
га):7 т2 + Зцыт + г = и3.
Уравнение (6.7.9) удобно описывает точки
перегиба неособой кубики, которые имеют вид
(0, 1, -1), (1, 0, 1), (-1, 1, 0), (0, о, 1), (со, 0, -со2),
(-1, со2, 0), (0, -со2, 1), (со2, 0, -со), (-1, со, 0), где со
удовлетворяет уравнению со2 + со + 1 = 0.
Теорема 6.7.2. Все девять точек перегиба не-
особой проективной кубики над алгебраически
замкнутым полем характеристики, отличной от 2
и 3, различны.
Доказательство см. в работе [4]. , Е;.
6.8. Группа неособых точек кубики
Эллиптическая кривая над алгебраически
замкнутым полем с характеристикой, отличной
от 2, может быть задана уравнением
у2 = х(х - о)(х - h),
где корни правой части уравнения попарно раз-
личны. Если правая часть уравнения имеет крат-
ный корень, то кубика является особой (в том
числе над полем характеристики 2).
Любая прямая у = кх пересекает кубику в осо-
бой точке с кратностью не менее 2. Поэтому, ес-
ли соединить особую точку кубики с любой дру-
гой ее точкой, то третья точка пересечения полу-
ченной прямой с кубикой будет этой же самой
особой точкой. Таким образом, сложение особой
точки с любой другой точкой всегда дает один и
тот же результат. Поэтому особая точка не может
быть рассмотрена как элемент абелевой группы
точек кубики.
Однако для неособых точек кубики можно
определить геометрический закон сложения, как
для эллиптических кривых.
Теорема 6.8.1. Если в уравнении кривой
у~ ~ 0» полином Q(x) над полем К имеет корень
кратности 2, то существует вычислимый в обе
стороны изоморфизм между группой неособых
точек кривой и мультипликативной группой по-
7 Обратный переход к форме Гессе (с учетом про-
ективного уравнения кривой) тоже задается полино-
миальными уравнениями, поэтому указанная замена
переменных корректна.
ля К. Если полином Q(x) над полем К имеет ко-
рень кратности 3, то существует вычислимый в
обе стороны изоморфизм между группой неосо-
бых точек кривой и аддитивной группой поля К.
Доказательство. Докажем сначала второе
утверждение для кривой у2=х3. Эта кривая до-
пускает параметризацию (Г2, Г3). В качестве ну-
ля будем использовать бесконечно удаленную
точку. Точки пересечения этой кривой с прямой
ах + by + с = 0 определяются соотношением
ci3 + at + b = 0. Если прямая не проходит через
особую точку, то с^О. Получаем кубическое
уравнение от t с нулевым коэффициентом при Z2.
Сумма корней такого уравнения по теореме Вие-
та равна нулю. Для бесконечно удаленной точки
О значение параметра t() равно нулю. Пусть точ-
кам А и В соответствуют значения параметра tA,
tB. Прямая АВ пересекает кубику в точке R. Тогда
tA + 1в + Ir = 0. Прямая OR пересекает кубику в
точке А + В, значит, to + tR + tA+B = 0. Следова-
тельно, tA+B = tR = tA + tB. Особой точке соответ-
ствует t = co. Вычислимость прямого и обратного
изоморфизмов очевидна.
Кривая у2 = X3 + х2 также допускает рацио-
нальную параметризацию (Z2 - 1, ? -t). Прямая
ах + by + с = 0 пересекает эту кривую в точках,
для которых значения параметра I удовлетворя-
ют соотношению а(/ - 1) + Z>(? -t) + с = 0. Если
b # 0, то после деления обеих частей этого соот-
ношения на b получим кубическое уравнение для
1 с коэффициентом 1 при ? и коэффициентом -1
при t. Корни такого уравнения удовлетворяют
соотношению Z]Z2 + ^3+ 6А =_1- Если сделать
1+Z
замену переменной s <— -—, то последнее усло-
вие будет эквивалентно равенству = Е Вы-
берем в качестве нуля на кривой точку (0, 1, 0),
которой соответствуют значения t = 0 и s = 1.
Для нахождения суммы точек А и В рассмотрим
точку R, в которой прямая АВ пересекает кри-
вую. Так как sAsBsR = 1 и srSqSa+b = 1, то
sA+B = sAsB. Особой точке соответствует не одно,
а два значения параметра I, а именно t = ±1 (л = 0
или оо). Вычисление изоморфизма требует вы-
полнения фиксированного числа арифметиче-
ских операций в поле К, то есть имеет полино-
миальную сложность.
При рассуждении мы не фиксировали поле К
и не использовали специфических свойств поля
комплексных или вещественных чисел. Поэтому
данная теорема верна для кубики над любым по-
лем, конечным или бесконечным.
В основу безопасности многих криптографи-
ческих алгоритмов положена задача дискретного
логарифмирования: в простом поле F,, для дан-
ных образующей а и элемента b найти число х
такое, что ct' = b (mod р).8 Для изоморфных обра-
зов эта задача формулируется так. Пусть ф—
изоморфизм из группы в группу неособых
точек кубики. Для образующей точки А = ф(о) и
точки В = ф(6) кубической кривой с точкой са-
мопересечения над полем найти число х такое,
что В = хА.
Следствие 6.8.2. Задача логарифмирования на
кубической кривой над конечным полем не ме-
нее сложная, чем задача дискретного логариф-
мирования в том же поле.9
Доказательство. Если сложность задачи
дискретного логарифмирования в F,, меньше,
чем сложность задач логарифмирования на всех
неособых кубиках, то можно перейти к особой
кубике с точкой самопересечения.
6.9. Невозможность рациональной
параметризации эллиптической кривой
Согласно примеру 6.2.1 невырожденная кони-
ка может быть сведена к уравнению и = г2 и па-
раметризована (и, г) = (Z2, t). Очевидным образом
параметризуется и прямая у = ах + Ь, любая точ-
ка которой может быть выражена в виде (х, у) =
= (/, at + b). Заметим, что в обоих случаях пара-
метризация имеет вид полиномов. Особые куби-
ки также допускают параметризацию. Однако
эллиптическая кривая не может быть параметри-
зована с помощью рациональных функций.
Теорема 6.9.1. Пусть эллиптическая кривая
Е(К) задана в форме Лежандра уравнением
(6.7.4) над алгебраически замкнутым полем К,
характеристика которого отлична от 2. Не суще-
ствует полиномов Р], Pi, Q\, Qi таких, что функ-
ции y(t) = Py{t}lP2(t),x(t) = QA{t)lQ2{t) отличны
от константы и удовлетворяют эллиптической
кривой над полем К .
Доказательство [4]. Случай, когда y(t) и x(t)
являются элементами поля К ,_неинтересен — это
константы. Пусть y(t), x(t) <£ К . Тогда, подстав-
ляя полиномы Р, Q в уравнение кривой, получим
3L_ Q Q Q -^2
Pi Qi Qi Qi ' ..................
8 Эта задача положена в основу стандартов циф-
ровой подписи РФ и США (см. пи. 13.2.3, 15.6.5).
9 Здесь имеется в виду сложность «самой сложной
частной задачи» данного класса.
110
Можно считать, что полиномы Р\ и Р2 взаим-
но просты, Q\ и Qx взаимно просты. Так как
p^qI-PxQAQa- 02X0i~W,
то полином Д2, взаимно простой с Д2, делится
на Qi, и полином Ql, взаимно простой с Qi,
Q\ ~ Оъ Q\ - 'PQi, делится на Д2. Следовательно,
полиномы Д2 и Ql различаются на константу (в
поле все ненулевые элементы обратимы). Сокра-
тим на эти полиномы и домножим Ру на квадрат-
ный корень из константы. Получим равенство
^2= &(&-axei-w (6.9.1)
Кроме того, полином Q2 — квадрат некоторого
полинома, следовательно, и Qx — квадрат некоторо-
го полинома. Полиномы в правой части равенства
(6.9.1) попарно взаимно просты, поэтому каждый из
них— полный квадрат. Значит, четыре полинома
01, 02, 01 ~ 02, 01 - ^02, попарно различных и вза-
имно простых, являются полными квадратами (по-
парное различие следует из того, что Z. Ф 0,1).
Покажем, что такое невозможно. Рассмотрим
линейную комбинацию вида aQ\ + Z>g2, где
a.h^K , и предположим, что существуют четыре
полинома, квадраты которых попарно различны и
представимы в виде указанной комбинации. Два из
этих квадратов обозначим А2 и . Так как А2 и
А2 взаимно просты, то два оставшихся квадрата
можно представить как Rl=axRx-bxRl и
Т?4 = a2Rx - b2Rf . Поскольку А| и А2 взаимно про-
сты, то и д/оД?! ± -yfb^Rx тоже взаимно просты
(отметим, что это линейная комбинация с коэф-
фициентами из К). Но их произведение является
полным квадратом (А32 и R] ). Значит, каждый из
JaJR-x ± ^R2 тоже является полным квадратом.
Такие же рассуждения можно провести и для А3,
R4, выразив через них Ai и А2. Получим, что R] и
Rx тоже являются полными квадратами. Таким
образом, в линейной комбинации cRx + dRx оказа-
лось четыре полных квадрата, но степень R, в два
раза меньше, чем степень Q,. Такое рассуждение
можно проводить неограниченно долго, однако
степень полиномов Q, конечна, следовательно, на
некотором шаге получим, что А, не может являть-
ся квадратом. Противоречие доказывает теорему.
Аналогичное утверждение имеет место и для
эллиптических кривых, заданных над полем ха-
рактеристики 2.
Таким образом, рациональная (то есть с ис-
пользованием алгебраических функций) пара-
метризация для эллиптической кривой невоз-
можна. Однако существует параметризация с
использованием неалгебраических аналитиче-
ских (так называемых эллиптических) функций.
6.10. Параметризация эллиптической
кривой с помощью эллиптических
функций
6.10.1. Эллиптические функции
Функция /над С называется двоякопериодиче-
ской, если существуют комплексные числа од и
со2 такие, что со/о^ g 1R , и для любых т, п е Z
имеет место равенство f(z + тсд + исо2) =fiz). Бу-
дем считать, что поворот от од к со2 происходит
по часовой стрелке.
Назовем решеткой L свободный Z-модуль
ранга 2: L = ZcO] + Zco2.
Двоякопериодическая функция, все особые
точки которой являются полюсами, называется
эллиптической. В окрестности полюса а эллип-
тическая функция/допускает разложение
flz) = cQ(z - d)r + с, (z - a)r+x + ...,
где co 0, г е Z.
В силу периодичности эллиптическая функ-
ция полностью определяется своими значениями
в области {<дод + о2со2 | 0<<д, о2<1}, которая
называется фундаментальным параллелограм-
мом решетки П = С/Z (рис. 6.8). Противополож-
ные стороны параллелограмма П в силу перио-
дичности по (01 и со2 отождествляются («склеи-
ваются»), поэтому он эквивалентен тору.
Сложение комплексных чисел можно выпол-
нять по модулю решетки L. При этом комплекс-
ная плоскость разбивается параллельными пря-
мыми на параллелограммы. Комплексные числа
складываются как векторы комплексной плоско-
сти; затем все параллелограммы отождествляют-
ся. Образом суммы по модулю решетки является
точка параллелограмма, соответствующая ука-
занной сумме векторов.
Рис. 6.8. Фундаментальный параллелограмм
Ill
Теорема 6.10.1. Эллиптическая функция, не
имеющая полюсов, постоянна.
Доказательство. Предположим, что эллип-
тическая функция /z) не имеет полюсов. Функ-
ция ]/(z)| непрерывна на С и поэтому ограничена
на С/Z и — в силу двоякой периодичности — на
всей комплексной плоскости С. По теореме Лиу-
вилля всюду ограниченная функция постоянна.
Все особые точки эллиптической функции яв-
ляются изолированными. Поэтому фундамен-
тальный параллелограмм содержит лишь конеч-
ное число особых точек. Следовательно, его
можно сдвинуть на комплексной плоскости так,
что на его сторонах не будет особых точек. Бу-
дем считать, что на сторонах фундаментального
параллелограмма нет особых точек.
Пусть fiz) — эллиптическая функция, П — ее
фундаментальный параллелограмм с вершинами
а, а + (01, а + со?, ос + <щ + со2 и 5П — его грани-
ца. Тогда ^"/(z)Jz = 0. Действительно, в силу
5П
периодичности функции f интегралы по проти-
воположным сторонам параллелограмма унич-
тожаются.
Из этого утверждения можно получить ин-
формацию о пулях и полюсах эллиптической
функции. Напомним, что вычетом res (g) в точ-
ке z = а аналитической функции g(z) называется
коэффициент при (z - а) в ее разложении в ряд
Лорана.
Теорема 6.10.2. Справедливы следующие ут-
верждения.
1. Сумма вычетов точек эллиптической функ-
ции, расположенных внутри фундаментального
параллелограмма, равна 0.
2. Пусть о, — нули и полюсы эллиптической
функции, расположенные внутри фундаменталь-
ного параллелограмма, г,— их порядки (поло-
жительные для нулей, отрицательные для полю-
сов). Тогда = 0 и '^rlai -т<лх + исо2 , где т,
п — целые числа.
Доказательство [4]. Если функция j\z) =
= C({z - a)r + ci(z- a)’^ + ... не имеет на границе
<ЭП особых точек, то
X res(/) = <^f(z)dz = 0.
Заметим, что если f— эллиптическая функ-
ция, то /' и — тоже эллиптические функции.
Кроме того,
—(z) = r(z - а)-1 + eq + a2(z - а) +...,
а значит, вычет функции —- в точке а равен г.
Поэтому ^/, = 0.
Докажем равенство =т(лх +исо2. По-
f'tz}
ложим g(z) = z ——. Тогда g(z) = ar(z - а)л +...,
/(^)
а значит, вычет функции g(z) в точке а равен аг.
Теперь вычислим интеграл <jg(z)dz . Получаем
5П
для противоположных сторон параллелограмма:
“71 zf'(z)dz _ а+у2 zf\z)dz =
/(z) J /(z)
а к / а+со2 J v 7
_ а+?1 zf'(z)dz “+r’ (z + со 2)f\z)dz _
~ J /(z) j 7v) “
“Т f'(Z}dZ I ч|“+и1
j /(xF=““21n/(z)l“ •
Поскольку Да) = Да + соД, то при изменении z
от а до а + coi логарифм может измениться лишь
на lidd. В результате получаем, что одна пара
сторон дает вклад исо?, а другая — mcot, где
т. п е Z. Поэтому г, а, = 0 (mod L).
Согласно теореме 6.10.1 непостоянная эллип-
тическая функция имеет хотя бы один полюс в
фундаментальном параллелограмме. Число по-
люсов эллиптической функции, лежащих внутри
фундаментального параллелограмма, с учетом их
кратности называется порядком эллиптической
функции. Минимальный возможный порядок ра-
2 10
Для эллиптической функции сумма порядков
пулей, лежащих внутри фундаментального па-
раллелограмма, равна сумме порядков полюсов,
то есть порядку функции. Поскольку при замене
f(z) на /z) - с полюсы сохраняются, то эллипти-
ческая функция порядка г имеет г нулей и при-
нимает любое значение ровно г раз.
Сумма, разность и произведение двух эллип-
тических функций с одинаковыми периодами
снова дают эллиптическую функцию с такими
же периодами. Кроме того, функция, обратная к
эллиптической, также является эллиптической.
Поэтому множество эллиптических функций с
одинаковыми периодами является полем.
10 Так как сумма вычетов в особых точках внутри
параллелограмма равна 0, то функция не может там
иметь единственный полюс кратности 1.
112
6.10.2. Функция Вейерштрасса
Поскольку эллиптическая функция имеет бес-
конечное число нулей на комплексной плоскости
С, она не может быть алгебраической. Для любой
решетки L эллиптической будет функция
1 ( \ 1 >
= —+ X ------------, (6-10.1)
Z ое£\{0} \\Z ®) ® 2
где суммирование ведется по всем ненулевым
элементам о решетки L.
Покажем, что все особые точки функции
(6.10.1) являются полюсами. На любом компакт-
ном множестве,11 не содержащем точек решетки,
этот ряд сходится равномерно и абсолютно, так как
При больших значениях |со| модуль правой
части равенства (6.10.2) ограничен величиной
С|со“3|. Ряд Х|со| 3 сходится:
сое/_Л{0}
СО со
£|юГ3=£ Xl/7C°1 +т®2 Г3 ’
<dg£\{0) к-1 тах(|/л|,|и|)=А: к-1
где h — наименьшая из высот фундаментального
параллелограмма. Таким образом, функция p(z)
имеет полюсы в точках решетки. Она называется
функцией Вейерштрасса.
Покажем, что функция Вейерштрасса перио-
дична. Рассмотрим для этого ее производную
p'(z) = -2^(z-®)^3.
сое/.
Очевидно, что сдвиг в сумме на любое число
периодов по направлениям од и со2 не меняет
значения производной, то есть она двоякоперио-
дическая с периодами со j и со2. Поэтому функции
p(z) и p(z + со,) могут отличаться лишь на кон-
станту с. Подставив значение z = -со,/2 в равен-
ство p(z) = p(z + со,) + с, получим
р(ч72)=р(-®,72)+с-
Но функция p(z) по определению четная. По-
этому с = 0, то есть функция Вейерштрасса имеет
два периода: СО] и со2-
Кратность полюсов функции p(z) равна 2.
Других особых точек у нее нет. При смещении
11 Компактным называется множество, любая
бесконечная последовательность точек которого со-
держит подпоследовательность, сходящуюся к неко-
торой точке этого множества.
фундаментального параллелограмма внутри него
будет расположена только одна точка решетки.
Поэтому сумма полюсов функции р сравнима с
нулем по модулю решетки. Согласно теореме
6.10.2 функция р имеет в фундаментальном па-
раллелограмме два нуля: и и т, причем и + т = 0
(modZ). Для любой комплексной константы с
полюсы функции р (z) - с совпадают с полюса-
ми функции p(z). Поэтому внутри фундамен-
тального параллелограмма есть ровно две точки и
и у, для которых р(н) = р(т) = с, причем и + у s 0
(mod L). Если при некотором с будет выполнять-
ся сравнение и = -и (mod Z), то точки и и -и в
фундаментальном параллелограмме будут сов-
падать, то есть функция р принимает соответст-
вующее значение двукратно. В этих точках сли-
ваются два нуля функции р (z) - с, поэтому про-
изводная р '(z) обращается в 0. В фундаменталь-
ном параллелограмме можно выбрать ровно че-
тыре точки таких, что и = -и (mod Z), а именно
0, (Oj/2, <в2/2, (cOj +со2)/2 . Первая из них— по-
люс функции р, остальные — нули функции р'.
Итак, значения
^1 -р(со,/2),е2 =p((G)t +со2)/2),е3 = р(со2/2)
двукратны для функции р, и других двукратных
значений нет. В этих точках, то есть при
z COj/2, (cOj +со2)/2, <в2/2 (modZ), производная
p'(z) равна 0.
Функция Вейерштрасса позволяет описать,
как устроены все эллиптические функции.
Теорема 6.10.3. Пусть f(z)— произвольная
эллиптическая функция и р (z) — функция Вей-
ерштрасса с теми же периодами. Тогда сущест-
вуют рациональные функции 7?i, Т?2 такие, что
/=А|(р) + А2(р)р'.
Доказательство см. в работе [4].
Таким образом, множество эллиптических
функций с данным периодом может быть полу-
чено алгебраически из двух «элементарных» эл-
липтических функций — функции Вейерштрасса
и ее производной.
Рассмотрим четную эллиптическую функцию
p'(z)2. Она имеет двукратные нули при
z = С0|/2,со2/2,(со, +со2)/2 и шестикратный по-
люс в точке решетки. Следовательно,
р '(z)2 = с( р (z) - р X р {z) - е2)( р (z) - е3).
Поскольку р (z) = z“2 + ..., р'(z) = -2z“3 + ...,
то с = 4. . ., ,......,
из
Если раскрыть скобки и приравнять соответ-
ствующие коэффициенты в ряде Лорана, то по-
лучим уравнение:
Р '(г)2 = 4 р3(z) -g2@(z) - g3, (6.10.3)
где
g2 = -4(^2 + + e2e3),
£3=4^263.
Легко проверить, что
g23-27g32 =16(q -e2)2(ej -e3)2(e2 -e3)2.
Поскольку все числа e, попарно различны, то
gl-27g2 ф0.
Для любой пары чисел g2 и g3 существует ре-
шетка такая, что g2, g3 выражаются формулами
(6.10.4).
6.10.3. Параметризация
эллиптической кривой над полем С
Дифференциальное уравнение для функции
p(z) похоже на уравнение эллиптической кри-
вой в форме Вейерштрасса. Поэтому кубику
у2 = 4х3 - g2x - g3, соответствующую уравнению
(6.10.3), можно параметризовать с помощью
функции Вейерштрасса, положив p(z),
у = £>'(z). Переходя к проективным координатам
в Р2(С), получим отображение проективной пря-
мой Р’(С) в эллиптическую кривую
K2Z = 4Х3 - g2XZ2 - g3Z3, где z -> (p(z), p'(z), 1)
при z ф 0 и z -> (0, 1,0) при z = 0. Очевидно, что
это отображение аналитично всюду за исключе-
нием точек решетки. Поделив координаты на
р '(z), получим отображение
p'(z)’ ’ ^'(z),
которое аналитично и в окрестности точки ре-
шетки. Кроме того, оно взаимно однозначно ото-
бражает тор С/L в эллиптическую кривую Y2Z =
= 4Х3 - g2XZ2 - g3Z3 на проективной плоскости
Р2(С). Действительно, на бесконечно удаленной
прямой Z= 0 лежит лишь точка (0, 1, 0) кубики.
В нее отображаются точки решетки, которым
соответствует одна точка на фундаментальном
параллелограмме. Для остальных точек можно
рассмотреть аффинную кривую у2 = 4х3 - g2x - g3
и отображение z-»(p(z), p'(z))- Уравнение
p(z) = с может иметь одно или два решения. Два
решения возможны, если с Ф 0, то есть когда
р '(z) ф 0. Решения в этом случае имеют вид +z.
Их образы при отображении не совпадают, так
как ненулевые числа р '(z) и р '(-z) = - @ '(z) от-
личаются знаком.
Сложение точек плоскости для аргументов
(как комплексных чисел) эллиптической функ-
ции можно заменить сложением точек тора (как
комплексных чисел по модулю решетки). Это
сложение индуцирует сложение точек кубики
(геометрическое сложение с помощью касатель-
ных и секущих), когда в качестве нуля использу-
ется бесконечно удаленная точка (0, 1, 0).
Действительно, пусть Рх, Р2 — точки кубики,
которые соответствуют точкам zb z2 решетки, то
есть Р, = (p(z,), p'(z,)). Проведем через них пря-
мую у = ах + Ъ, которая соответствует уравнению
р '(z) - а fp (z) - Ъ = 0 на комплексной плоскости.
Эллиптическая функция /= р '(z) - a @ (z) - b
имеет полюс кратности 3 в точке z = 0, других
полюсов в фундаментальном параллелограмме у
нее нет. Следовательно, порядок этой функции
равен 3, то есть она имеет в фундаментальном
параллелограмме ровно три нуля. Это знакомые
нам zi и z2, а также еще один нуль z3. Поскольку
сумма полюсов эллиптической функции равна 0
и, следовательно, сумма нулей равна 0, то
Z] + z2 + z3 = 0 (mod L),
то есть
z3 = -Z! - z2 (mod L).
Итак, третьей точкой пересечения прямой
Р|Р2 с кубикой будет точка
А' = ( Р (-Z1 - г2), р '(-Z] - z2)) =
= ( р (zj + z2), - р '(zi + z2)).
Таким образом, точка Р3, соответствующая
сумме точек Р] и Р2, симметрична точке Р3 от-
носительно оси Ох (рис. 6.9).
Рис. 6.9. Сложение точек эллиптической кривой
В окрестности бесконечно удаленной точки
Р№ справедливо неравенство Y Ф 0, поэтому мож-
но задать закон сложения в аффинных координа-
тах —(рис. 6.10).
114
Рис. 6.10. Сложение точек эллиптической
кривой в окрестности точки Рх
Параметризация эллиптической кривой эл-
липтическими функциями (6.10.3) позволяет ус-
тановить связь между сложением элементов в
С/£ и сложением точек кривой.
На аддитивной группе комплексных чисел
можно задать эндоморфизм, определяемый ум-
ножением на комплексную константу. Этот эн-
доморфизм индуцирует гомоморфизм решеток.
При этом диаграмма гомоморфизмов на рисунке
6.11 является коммутативной. Здесь а — умно-
жение на комплексное число а, к — комплекс-
но-аналитический гомоморфизм решеток [13], а
вертикальные стрелки задают редукцию по мо-
дулю решетки. Каждому эндоморфизму а соот-
ветствует некоторый гомоморфизм к и наобо-
рот. Два комплексных тора С/L и С/М изоморф-
ны тогда и только тогда, когда L = аМ для
а е С*.
* к ♦
C/L -----------> С/М
Рис. 6.11. Коммутативная диаграмма
гомоморфизмов решеток
Изоморфизм комплексных торов индуцирует'
изоморфизм соответствующих эллиптических
кривых. Необходимое и достаточное условие
изоморфизма торов (и, следовательно, эллипти-
ческих кривых у2 = 4х3 - g-pc - g3 и у'2 = 4х'3 -
- g/x' - g/) задается равенством [13]:
g2 _ g'2
g32~21gl gf-Zlg?’
где J— функция периодов соь со2. На практике
вместо J используется функция
1728g3
gl-^gl ’
(6.10.5)
Решетка периодов эллиптических функций
допускает преобразование путем обратимой над
Z замены переменных со/<—czcoi + йсо2, со2'<—
<—ССО] + с/®2, при которой поворот' ОТ СО]' к <в2'
выполняется по часовой стрелке. Такая замена
эквивалентна умножению вектора периодов на
матрицу из SL2(Z). Можно получить со2' = 1,
co'j/coj = т и рассматривать j =/(т) как функцию
одной комплексной переменной т.
Функция у(т) может' быть разложена в ряд Фу-
рье, если положить q = e ^ [11]. Логарифмиче-
ская производная равенства
дает
COSTtT 1 1 1
—------+ Х ---------+------ (6-10.6)
Sin TtT Т „=1 \Х~П X + nJ
С учетом
е1т+е~'т . e,JtT _е-'т
COS TtT =---------, silTTtT =--------, получим
2 2z
costtt q + \ . 2та ,
Tt----= to-------= Ttz ч---= to + / q .
sinTtT q-\ q-\
(6.10.7)
Соотношения (6.10.6), (6.10.7) позволяют вы-
разить g2, g3 как функции переменной q:
1 f 00
g2=(2Tt)4— 1 + 2402>2(л)У' , (6.10.8)
И=1 J
I ( 00
g3=(2Tt)6— 1-504^ a3(«)g”
/2 \ «=1 )
(6.10.8')
где <зк(ri) = ^dk (сумма берется по всем дели-
d\n
телям d числа п, включая 1 и п).
Подстановка (6.10.8), (6.10.8') в (6.10.5) дает
ряд с целыми коэффициентами:
j(q) = — + 744 +196844g +...
q
Функция j(q) позволяет определить симмет-
рические модулярные полиномы, используемые
при вычислении изогенных эллиптических кри-
вых (см. п. 6.15.4).
115
6.11. Дискриминант и /-инвариант
Рассмотрим кубику в обобщенной форме
Вейерштрасса (6.7.1) и свяжем с этой кривой на-
боры новых коэффициентов b„ i = 2, 4, 6, 8, и с,,
j = 4, 6, которые получаются при выделении
полного квадрата от у и полного куба от х. После
замены переменных
уравнение кривой примет вид
у2 = 4х3 + Ь2х2 + 2Ьрс + Ье„ (6.11.1)
где
й2 = а2 + 4а2, Z>4 = а}а3 + 2<т4, Ъ6 = а\ + 4о6.
Определим
Z>8 = а2а6 - а}а3а4 + 4о2о6 + о2о| -о4,
причем 4Z>g = b2b6 - Z>4 . Положим
с4 -bl -24Z>4, с6 -bl +36Z>2fe4 ~216Z>6.
В этом случае уравнение (6.11.1) примет вид
у2 = х3 - 22сус - 54с6. (6.11.2)
Определим дискриминант кубики
д = -bib* - Ml - 22bj + %/Д =
Дискриминант кубики с точностью до кон-
станты совпадает с дискриминантом кубического
полинома в правой части уравнения, задающего
кубику, то есть по значению дискриминанта
можно определить, является ли кубика особой.
Теорема 6.11.1. Кубика, заданная в форме
Вейерштрасса над полем, характеристика кото-
рого отлична от 2, является особой тогда и толь-
ко тогда, когда ее дискриминант равен нулю.
Доказательство. Перейдем к проективной
форме кривой:
fiX, Y, Z) = Y2Z + aX-YZ + o3EZ2 -
- X3 - a2X2Z - atXZ2 - abZ3 = 0.
Производная полинома fiX, Y, Z) no Z в точке
(0, 1, 0) равна 1, то есть точка Р№— неособая.
Предположим, что на кривой существует особая
точка (х0, уо). С помощью замены переменных
х<— х + х0, у<— у + уо, сохраняющей значение
дискриминанта, можно изменить уравнение ку-
бики так, что эта точка будет иметь координаты
(0. 0). Тогда
а6= /(0,0,1) = 0,
а4 =—(0,0,1) = 0, а3 = -^(0,0,1) = 0.
4 дХ 3 SY ’
Получаем уравнение кубики
fix, у) = у2 + аусу - х3 - <т2х2 = 0.
Тогда с4 = (о2 + 4а2 )2 и Д = 0.
Докажем обратное утверждение. Пусть Д = 0.
Выделяя полный квадрат от у, получаем
у2 = Q(x); при этом полином Q(x) имеет кратные
корни. Выше было показано, что такая кубика
является особой.
Теорема 6.11.1 оказывается справедливой и
для поля характеристики 2.
В случае ненулевого дискриминанта опреде-
с з
лен j-инварианпг. Для уравнения (6.11.2)
Д
выполняется равенство 123 Д = с4 - cj. Поэтому
/ = 123
Нетрудно показать, что единственно возмож-
ная замена переменных, сохраняющая вид урав-
нения^ (6.11.2),— это преобразование х<— и2х,
у <- иу, с4 <— w4с4, с6 <— ис6. Если кривая задана
уравнением (6.7.7), то
Д =-16(4Л3+27Т?2), у = 123—------Т.
4А3+21В2
Если кривая задана в форме Лежандра, Дой-
ринга или уравнением (6.7.3), то ее /инвариант
соответственно равен
= э8 (Z2~Z + 1>3 • = «3(«3~24)3
7 Х2(Х-1)2 ’ 7 а3-27
. 8 (а2-ЗЬ)3 X
7 Ь2(а2-4Ь)
6.12. Закон сложения точек
эллиптической кривой
Сложению точек фундаментального паралле-
лограмма соответствует геометрический закон
сложения точек эллиптической кривой в форме
Вейерштрасса, который может быть проиллюст-
рирован с помощью метода касательных и секу-
116
щих. В качестве нуля будем использовать беско-
нечно удаленную точку Рт. Секущая, проходя-
щая через бесконечно удаленную точку и дан-
ную точку кривой (6.7.1), является вертикальной
прямой.
Пусть уравнение прямой (касательной или се-
кущей) имеет вид у = Ах + V. Для секущей, про-
ходящей через различные точки 7>i = (xJ,yi) и
Р2 = (х2, Уг), получаем
У = .У^ . (6.12.1)
Если Aj = х2, то секущая является вертикаль-
ной прямой. По определению вертикальные пря-
мые пересекаются между собой и с эллиптиче-
ской кривой в бесконечно удаленной точке.
Если Р] = 7*2, то прямая представляет собой
касательную. Для нахождения углового коэффи-
циента найдем полный дифференциал от поли-
нома fix, у), задающего кривую в форме Вейер-
штрасса. Получим
. df , df ,
df (х, у) = —dx ч——dy.
дх ду
Угловой коэффициент касательной равен
7 = —. Имеем f'dx - -fdy, — = . Поэто-
dx х jy dx f'
J У
му угловой коэффициент касательной и свобод-
ный член равны, соответственно,
A = v = у, - Ах., (6.12.2)
4уу}+а}х+а3
где F(x) — кубический полином в правой части
уравнения Вейерштрасса (6.7.1).
Подставив уравнение прямой в уравнение ку-
бической кривой, получим кубическое уравнение
относительно х
(Ах + v)2 + <71Х(Ах + v) + <73(Ах + v) =
= х3 + фх2 + лрс + а6
или
х3 + (ф - А2 - Аа()х2 + ... = 0.
Это уравнение имеет три корня, соответст-
вующих х-координатам трех точек пересечения
кривой и прямой. Две координаты нам известны.
Нужно найти третью. По теореме Виета сумма
трех корней равна коэффициенту при х2, взятому
с обратным знаком. Получаем
х3 = А2 + А«1 - ф - Xi - х2.
В случае х, =х2 формула не меняется. Коор-
динату уз находим из уравнения прямой.
Таким образом, для обобщенной формы Вей-
ерштрасса (6.7.1) закон сложения имеет сле-
дующий вид.
1. Бесконечно удаленная точка Рх = (0, 1, 0) яв-
ляется нулем группы.
2. Противоположной к точке Р = (х0, ус) являет-
ся точка -Р = (х0, —у0 - OiXo - аз).
3. Сложение точек Р} + Р2 = Р3, где Р, = (х„у,),
задается следующими формулами. Если
7*2 = -7*1, то Р3 = Рк. В противном случае
х3 = А2 + щ А - а2 - X! - х2,
уз = -(А + а{)хз - v - «з,
где
у = Уг~У\ v = J^2~T2^i
х2 - xt х2 - X]
при Р\ Р2,
_ 3Xj2 + Т-аух^ + <?4 - alyi <
2у]-t-^X]+а3
v = -Х13+о4х1+2<тб-о3У1
2 У] +«|X] +а3
При Р] = Р2.
Если кривая задана уравнением
у2=х3+Ях + Р, то в формулах сложения у-
координату можно вычислять по формуле
Уз = А(Х] -Х3)-У!
г, г, . Зх.2 + А
и в случае Р\=Р2 положить А = —5---.
2у]
Рассмотрим умножение на 2 точки эллипти-
ческой кривой у2-fix), заданной над полем К с
характеристикой, отличной от 2 (К— не обяза-
тельно поле рациональных чисел). При таком
отображении каждой точке кривой ставится в
соответствие удвоенная точка. Это отображение
является эндоморфизмом кривой как абелевой
группы. Ядро эндоморфизма (множество точек
порядка 2) состоит из точки Р«, и точек вида
(х, 0), то есть для этих точек х является корнем
полинома fix). Поскольку эллиптическая кривая
является кубикой, то fix) может иметь не более
трех корней. Следовательно, ядро эндоморфизма
состоит не более чем из четырех точек, а над ал-
гебраически замкнутым полем — ровно из четы-
рех точек.
По теореме о гомоморфизмах групп ядро го-
моморфизма абелевых групп является абелевой
группой, причем, как следует из закона сложе-
ния, группа точек порядка 2 состоит из четырех
элементов и не является циклической. Если Дх) =
117
= (х - t?)(x - fe)(x - с), то из точки (а, 0) нельзя
получить точку (Ь, 0) путем сложений самой с
собой. При этом (о, 0) + (Ь, 0) = -(с, 0) = (с, 0), то
есть группа точек порядка 2 порождается одной
из пар точек {(а, 0), (Ь. 0)}, {(а, 0), (с, 0)} или
{(Ь, 0), (с, 0)}. Таким образом, группа кручения
порядка 2 (ядро указанного эндоморфизма) изо-
морфна прямой сумме групп Z72Z © Z72Z.
Точки перегиба (и только они) являются точ-
ками порядка 3. Как было показано выше, все
точки порядка 3 попарно различны и над алгеб-
раически замкнутым полем их ровно девять. Ум-
ножение точки на 3 является эндоморфизмом
группы точек кривой над алгебраически замкну-
тым полем. Ядро этого эндоморфизма совпадает
с множеством точек перегиба и изоморфно пря-
мой сумме аддитивных групп Z73Z © Z73Z.
Таким же образом рассматривается умноже-
ние точки на произвольное целое число п. Мож-
но показать, что если целое число п взаимно про-
сто с характеристикой поля К, то умножение на п
является эндоморфизмом, ядро которого в случае
алгебраически замкнутого поля состоит из п то-
чек порядка п и изоморфно прямой сумме адди-
тивных групп © Uifl..
6.13. Эллиптические кривые
над числовыми полями
В криптографии и теории чисел кривые часто
рассматриваются над полем Q рациональных чи-
сел или над числовым полем. Кривая над полем
может иметь конечное или бесконечное число
точек.
Для данной аффинной точки Р кривой над Q
можно образовать циклическую группу вида Р,
2Р, ЗР,.... Эта группа также может быть конеч-
на или бесконечна. Если циклическая группа
бесконечна, то она полностью определяется об-
разующей Р и индексом (логарифмом) элемента
группы, при этом сама образующая определена с
точностью до знака (группы, образованные точ-
ками Р и -Р, совпадают). Такая группа изоморф-
на группе Z целых чисел. Однако точка Р может
быть кратным некоторой точки. Среди множест-
ва всех точек Q, таких, что Р = niiQj, существует
точка Qj с максимальной абсолютной величиной
индекса т}. Тогда циклическая группа, образо-
ванная точкой Р, является подгруппой индекса т}
группы, образованной точкой Qj. Эта группа яв-
ляется наибольшей из циклических групп, со-
держащих точку Р, и изоморфна группе Z целых
чисел.
Пример 6.13.1. Группы конечного и бесконеч-
ного порядка на эллиптических кривых над Q.
1. Эллиптическая кривая £(Q), заданная урав-
нением у2+у-ху = х3. Точка Р = (1, 1) лежит на
кривой. Тогда 2Р = (0,0), ЗР = (-1, -1), 4Р = (0, -1),
5Р = (1, -1), 6Р = Рт. Значит, точка (1,1) образу-
ет циклическую группу порядка 6.
2. Эллиптическая кривая £(Q), заданная урав-
нением у2 = х3 + 17. Циклическая группа, образо-
ванная точкой Pi = (-2,3), имеет вид:
(19 522^
2Pi = (8, -23), ЗР = —,---,.. Эта точка по-
1 1.25 125 у
рождает группу бесконечного порядка с рацио-
нальными координатами. На кривой существует
точка Р2 = (2, 5), тоже образующая группу беско-
нечного порядка. Оказывается, любая точка дан-
ной эллиптической кривой может быть представ-
лена в виде тР\ + пР2. Например, (4, 9) = Pi - Р2.
Группа точек кривой P(Q) изоморфна прямой
сумме групп Z © Z.
Точки, имеющие конечный порядок на эллип-
тической кривой Е(К), заданной над бесконеч-
ным полем К, называются точками кручения.
Эти точки образуют группу кручения Tors£(K).
Группа кручения эллиптической кривой уст-
роена просто.
Теорема 6.13.1 (теорема Мазура). Группа
кручения эллиптической кривой, заданной над
полем Q, изоморфна одной из следующих групп:
- 'EJnifl. для т < 10 или для т = 12,
- Z/2Z © Z72///Z для w < 4. -
Доказательство см. в работе [16].
Группу Tors£(Q) кривой (6.7.2) легко вычис-
лить, так как координаты точек кручения (х,у)
являются целочисленными и у | Д.
Как и любая конечно порожденная абелева
группа, группа точек эллиптической кривой Е(К)
над числовым полем К допускает разложение
Е{К) = Zrank(/;(A'!) © Tors Е(К), . t
где rank(£(K)) — ранг кривой (число образующих
циклических групп бесконечного порядка).
Возникает вопрос: чему равен ранг кривой?
Конечен он или бесконечен? Ответ на этот во-
прос неочевиден. Например, особая кубика с
двойным корнем, изоморфная мультипликатив-
ной группе Q , имеет бесконечное число обра-
зующих (в Q множество образующих совпадает
с множеством простых чисел).
118
Теорема 6.13.2 (теорема Морделла—Вейля).
Эллиптическая кривая над числовым полем ко-
нечно порождена.
Доказательство см. в работах [13, 21].
Эту теорему сначала доказал Морделл для
поля Q рациональных чисел, а затем Вейль рас-
пространил ее на конечные расширения поля Q,
то есть на числовые поля.
Обычно эллиптическая кривая E(Q) имеет ма-
лый ранг (0, 1, 2 или 3). Ранг равен нулю, если
кривая содержит лишь конечное число рацио-
нальных точек. Например, все точки эллиптиче-
ской кривой E(Q), заданной уравнением
у2 = х3 + 1, образую!' циклические группы конеч-
ного порядка. Вопрос о том, существует ли эл-
липтическая кривая «самого большого» ранга, на
сегодняшний день открыт.
Ранг кривой Е(К) над числовым полем К мо-
жет быть вычислен, если справедлива гипотеза
Берча и Свиннертона-Дайера (см. п. 6.17).
Для числового поля K = Q[y/D] на эллипти-
ческой кривой Е(К)-. у1 = х3 + Ах + В, где А,
В g Z, можно определить группу, порожденную
точками вида (x,yjD), гдех, у е Q.
Непосредственно из закона сложения следует,
что удвоение или сложение таких точек дает
точку указанного вида. Точка (x,y>jD) лежит на
эллиптической кривой Е(К) тогда и только тогда,
когда точка (х,у) лежит на эллиптической кри-
вой £/j(Q): Dy2 = х3 + Ах + В.
Определим группу Ё(К), порожденную точ-
ками с рациональными х-координатами. Посколь-
ку группа Ё(К) порождена точками кривых E(Q)
и E/XQ), и эти кривые не имеют общих точек, кро-
ме Рю, можно записать Ё(К) = E(Q) © E/XQ),
rank( Ё(К)) = rank(E(Q)) + rank(En(Q)).
Аналогично для поля К = С)[-7Д\-\/Д/1 мож-
но определить группу Ё(К), порожденную точ-
ками с рациональными х-координатами (группа,
порожденная такими точками, не совпадает с
множеством этих точек). Имеет место изомор-
физм групп
Ё(Е) = E(Q) © EDi (Q) © Е„г (Q) © ЕД|йг (Q).
Точно так же для поля К = JIT]
имеет место изоморфизм групп
E(E) = E(Q)®^E[1d(Q).
Поскольку Ё(К) является нормальной под-
группой группы Е(К), определим факторгруппу
Е(К)/Е(К), которую будем использовать при
вычислении ранга.
Теорема 6.13.3. Пусть G — конечно порож-
денная абелева группа без кручения и Н — ее
подгруппа. Ранги групп G и Н равны тогда и
только тогда, когда порядок любого элемента в
факторгруппе G/Н конечен.
Доказательство. Пусть ранги групп G и Н
равны, g = (gi, ..., g„), h = (/?ь ...,/?„) — множест-
ва образующих для G и Н. Тогда существует та-
кая матрица М е SL„(Z), что h = A/g. Матрица М
над Z может быть приведена к диагональной
форме М= (mh), где т„ Ф 0, т,, = 0 для z ф j. Пусть
т — наименьшее общее кратное чисел тп. Лю-
бой элемент c}gt + ... + c„g„ е G, с, е Z, после
умножения на т будет принадлежать группе Н.
Обратно, пусть порядок любого элемента в
факторгруппе GIH конечен и g = (gb ..., g„),
h = ..., hi) — множества образующих для G и
Н. Предположим, что п > I. Тогда существует
такая вырожденная над Z матрица М, что
h = A/g. Матрица М над Z может быть приведена
к диагональной форме М= (тп), где zw„ Ф О,
mt] = 0 для z Ф j. Тогда порядок элемента в
факторгруппе G/Н не может быть конечен. Про-
тиворечие доказывав!' теорему.
Каждая точка группы Е(К)! Ё(К) имеет ко-
нечный порядок [22]. Поэтому ранги групп Е(К)
и Ё(К) равны и могут быть вычислены как сум-
ма рангов эллиптических кривых над Q.
Если последовательно умножать какую-либо
точку Р кривой E(Q) с небольшими целыми ко-
ординатами на целые числа к = 2, 3, ..., то длина
координат точек кР будет возрастать с ростом к.
Например, на эллиптической кривой у = х3 + 3
существует точка Р = (1,2). Тогда
<23 зр-[ 1873 130870Л
L 64’ 64/ ”11521’ 59319 J
Длина знаменателя х-координаты точки
ЮР— 32 десятичных знака. Возрастание длины
числителя и знаменателя с ростом к подчиняется
некоторым закономерностям.
Определим (логарифмическую) высоту hx
точки Р эллиптической кривой как функцию
hg. E(Q) -> R,
ЙХ(Р) =
log(max(/1, | q |), если P Ф P„,
О, еслиР = Рю,
где p и q—числитель и знаменатель несократимой
дроби, представляющей х-координату точки Р.
Приведем без доказательства ряд результатов
(доказательства можно найти в работе [21]).
119
Пусть К— алгебраическое расширение поля Q.
Из теоремы Морделла-Вейля следует, что Е(К)
содержит лишь конечное число точек, высота
которых меньше некот орого заданного числа.
Если Р и Q— точки бесконечного порядка на эл-
липтической кривой Е{К), то имеет место равенство
hx(P + 0 + htf ~Q) = U^P} + 2ЛХ(0 + 0(1),
то есть функция высоты ведет себя почти как
квадратичная форма.
Определим для точек кривой Е(К) канониче-
скую высоту h: Е(К) IR как
7 4w
Точки кручения и бесконечно удаленная точ-
ка имеют нулевую каноническую высоту. Для
всех остальных точек каноническая высот а явля-
ется ненулевым вещественным числом. Функция
канонической высоты обладает свойствами
h(P + 0 + КР - 0 = 2Й(Р) + 2Й(0 ;
h(mP) = m2h(P) (6.13.1)
и является положительно определенной квадра-
тичной формой.
Пусть Р — точка бесконечного порядка и О —
точка кручения. Обозначим Р,=Р + Ю, тогда из фор-
мулы (6.13.1) следует, что /?(/}_,) +Л0+1 ) = 2/?(7*).
Каноническая высот а каждой точки представляет
собой среднее арифметическое высот' предыду-
щей и последующей точек. Последовательность
{Р,} циклическая, поэтому h(P + 0 = /г(Р).
Имеет место гомоморфизм абелевых групп
E(Q) -> Е(Е/;), полученный редукцией по модулю
р [21]. Аналогичный гомоморфизм существует и
для кривой Е(К), если поле К получено присое-
динением корней неприводимого над Q полино-
ма fit) такого, что fit) раскладывается на линей-
ные множители в поле Fp.
6.14. Изоморфизмы и эндоморфизмы
эллиптических кривых
Пусть Е(К) и Е'(К)— эллиптические кривые,
заданные уравнениями (6.7.1) с аффинными коор-
динатами (х, у) и (х', У) соответственно. Определим
изоморфизм эллиптических кривых Ен Е' как ото-
бражение, индуцируемое допустимой заменой пе-
ременных х7 <— и~х + г, у <— и’у + su2x +t (см.
п. 6.2) и сохраняющее значение /-инварианта.1
12 Иногда изоморфизм эллиптических кривых оп-
ределяют как взаимно обратные отображения, зада-
ваемые полиномами из £'[£] (соответственно из £]£'],
см. и. 6.15.1). Эти определения совпадают.
Пусть изоморфизм из Е в Е' задается отобра-
жениями х' = <pi(x, у), у = \/|(х, у), а изоморфизм из
Е в Е— отображениями х = ф2(х',у'), у = ij/2(x',y').
Тогда равенства
X = ф2(ф 1 (х, у), чл(х, у)), у = y2(<Pi(x, У), Vifc J'));
Л7 = Ф1(ф2« У), ^,УУ),У = V'i(cp2(x',y), <И2«У))
всюду определены на эллиптических кривых Е и
Е'.
Теорема 6.14.1. Эллиптические кривые изо-
морфны над алгебраически замкнутым полем
тогда и только тогда, когда они имеют одинако-
вые /-инварианты.
Доказательство см. в работе [13].
Понятие изоморфизма эллиптических кри-
вых и изоморфизма абелевых групп точек этих
кривых не совпадают. Например, изоморфизм
групп точек кривых над конечными полями не
означает изоморфизм кривых. Однако, если
кривые изоморфны, то они, очевидно, изоморф-
ны как группы.
6.14.1. Изоморфизмы над полями
характеристики, отличной от 2 и 3
Пусть эллиптические кривые Е и Е' заданы
над полем К уравнениями у2 = х‘ + Ах + В и
у'2 = х'3 +Л'х' + В' соответственно и таковы, что
j(E) =j(E'), и пусть ср: Е -> Е' — изоморфизм.
Тогда допустимая замена переменных, сохра-
няющая /-инвариант, и соответствующая замена
коэффициентов уравнения имеют вид
(х', У) = <р(х, у) = (и2х, и у), А' = и А, В' = и В,
где и е К*. Заметим, что здесь 123 = 2б33 Ф 0, так
как характеристика поля отлична от 2 и 3. Рас-
смотрим зри возможных случая.
1. j Ф 0, 0123. Это эквивалентно условию
АВ Ф 0. Кривые Е и Е' изоморфны над К тогда и
АВ 2 тл г г- п
только тогда, когда - и . Изоморфизм Е = Е
имеет место над любым расширением поля К,
АВ' с
содержащим квадратный корень из . Если
уравнения кривых совпадают, то есть Е = Е', то
изоморфизм становится автоморфизмом и груп-
па автоморфизмов содержит всего два элемента:
{1,-1}. (Для Р е Е(К) справедливо <р(Р) = Р или
ср(Р) = -Р.) Эти автоморфизмы представляют со-
бой группу квадратных корней из 1.
2. /= 123 или, что то же самое, В = 0. Типич-
ный пример такой кривой: у2 = х3 - х. Кривые Е и
120
Е изоморфны над К тогда и только тогда, когда
~ = и4. Изоморфизм Е = Е имеет место над
любым расширением поля К, содержащим ко-
рень четвертой степени из —. Если Е = Е, то
группа автоморфизмов состоит из четырех эле-
ментов: {l,-],z, -i}, где z2 = -1, представляю-
щих собой группу корней степени 4 из 1. Изомор-
физмы имеют вид <р(Е) = Р, <р(Е) = -Р, q(P) = iP,
<p(P) = -iP.
3. j = 0 или, что то же самое, А = 0. Типичный
пример такой кривой: у2 = х3 + 1. Изоморфизм
Е = Е имеет место тогда и только тогда, когда
В'
— -и6. Поэтому кривые Е и Е изоморфны над
расширением поля К, содержащим корень шес-
В’
той степени из —. Если Е = Е, то группа авто-
морфизмов совпадает с группой корней степени
6 из 1: {1,-1, со, -со, со2, -со2}, где 1 + со + со2 = 0.
Изоморфизмы имеют вид ср(Е) = Р, ср(Р) = -Р,
ср(Р) = соЕ, <р(Р) = -соР, ср(Р) = со2Р, ср(Р) = -со2Р.
В каких же случаях данный элемент j е К
является /-инвариантом некоторой эллиптиче-
ской кривой? Если АВ Ф 0 и поле К алгебраиче-
ски замкнуто, то можно подобрать такую заме-
ну переменных, чтобы уравнение кривой при-
няло вид
у2 = 4х3 - сх - с.
Тогда j =
1728с3
с3-27с2
1728с 27/
-----и с =-----±.
с-27 у-1728
Поэтому /-инвариант эллиптической кривой
вида
у2=4х3
27/ х 27/
/ — 1728 / — 1728
равен параметру / в этом уравнении.
6.14.2. Изоморфизмы над
полями характеристики 3
Пусть К— поле характеристики 3, то есть
За = 0 для любого a g К. Согласно теореме 6.7.1
в этом случае уравнение эллиптической кривой
может быть преобразовано к виду
у2 = g(x) = х3 + а2х2 + аус + с?б- (6.14.2)
Используя выкладки п. 6.7 и учитывая равен-
ство 3 = 0, получим
А — с?2с/д а2а6 а4.
Кубическая кривая является неособой, если
кубический полином g(x) в (6.14.2) и его произ-
водная не имеют общих нулей. Поскольку А и
дискриминант полинома g(x) совпадаю!' с точно-
стью до константы, то кривая неособая тогда и
только тогда, когда А Ф 0.
/-инвариант задается выражением
J 2 2 3 3 ’
(72#4 ^2^6 ^4
Рассмотрим изоморфизмы между неособыми
кривыми с одинаковыми /-инвариантами. Пусть
Е задана уравнением (6.14.2) и Е — уравнением
У2 = х'3 + ф'х'2 + <74'х' + Об', (6.14.2')
при этом /(Е) =j(E) и ср: Е -» Е — изоморфизм.
Возможны два случая: j Ф 0 и/ = 0 = 1728.
1 . j ф 0 или, что то же самое, «2 * 0- Выделяя
полный куб в уравнениях (6.14.2) и (6.14.2'), по-
лучаем о4 = о4' = 0. Тогда, так как /(Е) =j(E),
аci'j
справедливо - = и выполняются равенства
«6 «6
(х', У) = ср(х, у) = (и2х, и3у), а2 = иа->, = иа(>,
где и g К*. Изоморфизм Е = Е' над К имеет ме-
сто, если — = и (условие для выполняет-
€?2
ся автоматически). Поэтому кривые Е и Е' изо-
морфны над любым расширением поля К, со-
держащим квадратный корень из —. Если
а2
Е = Е, то группа автоморфизмов содержит два
элемента: {1,-1} и совпадает с группой квадрат-
ных корней из 1.
2 ./ = 0= 1728 или, что то же самое, <т2 = 0. То-
гда А = «4- Изоморфизм задается условиями
(х', у) = ф(х, у) = (их + г, и у),
, _ 4 г 6 4 3
«4 — w «4, Об ~и — и га$ — г ,
где и 6 К*. Значит, изоморфизм имеет место,
^4 4 6 / 3 । 4 г| j~
если — = и и и а^- а6 = г + и raf,. 1 юэтому Е
«4
и Е' изоморфны над любым расширением поля
„ «4
К, в котором — является четвертой степенью и
«4
где существует решение кубического уравнения
121
от г. Это условие выполняется всегда, когда
степень расширения кратна 12 и расширение
сепарабельно.
Если Е = Е', то группа автоморфизмов имеет
вид так называемого полупрямого произведения
групп /УяЩЕ) - (Z73Z) х (Z/4Z), где циклическая
группа порядка 4 действует на группе порядка 3
(так как г зависит от и).
Если j отлично от 0 и 1728, то для алгебраиче-
ски замкнутого поля К можно задать кривую в
обобщенной форме Вейерштрасса так, что дан-
ный элемент j g К будет ее /-инвариантом. Урав-
нение кривой может иметь вид у2 = х + х2 + <т6
или у2 + ху = х3 + а6. В обоих случаях /-инвариант
равен - я/1.
6.14.3. Изоморфизмы
над полями характеристики 2
Пусть К — поле характеристики 2 и эллипти-
ческая кривая задана уравнением
у2 + арсу + а3у = х3 + а2х2 + apt + <т6.
Используя преобразования уравнения Вейер-
штрасса из п. 6.7 с учетом равенства 2 = 0, полу-
чим j - О)12/д. В частности, а3 = 0 тогда и только
тогда, когда / = 0 = 1728.
Рассмотрим, когда кубика над К является не-
особой при нулевом и ненулевом /-инварианте.
1 ./ Ф 0 или, что то же самое, щ Ф 0. Тогда по-
сле замены переменных х <— х + с левая часть
уравнения кривой примет вид у2 + щху + (щс + о3)у.
Поскольку щ 0, можно считать а\с + а3 = 0.
Линейной заменой переменных можно получить
= 1 и <т4 = 0, тогда
у2 + ху = х3 + аух2 + <г6.
В этом случае Д = а6 = \/j . Частные произ-
водные /'/=у + х2 и f'y-x равны нулю тогда и
только тогда, когда точка х = у = 0 лежит на кри-
вой, то есть Д = <76 = 0. Поэтому кривая является
неособой тогда и только тогда, когда дискрими-
нант отличен от нуля.
2 . / = 0 или, что то же самое, щ = 0. Выделяя
полный куб, получим нормальную форму кривой
у2 + а3у = х3 + арх + а(..
Тогда Д = а3. Частные производные f'x =
= х2 + «4, f'y ~ а3 равны нулю в точке (х, у), если
а3 = 0 и а4 = х2. Отсюда следует, что кривая явля-
ется неособой тогда и только тогда, когда а3 Ф 0,
то есть Д Ф 0.
Рассмотрим изоморфизмы кривых с одинако-
выми /-инвариантами. Пусть Е и Е' — кривые с
одинаковыми /-инвариантами и ср — изоморфизм
между ними.
1. j Ф 0 или, что то же самое, at 0. Рассмат-
ривая соответствующее уравнение кривой в нор-
мальной форме, получим
(х', у') = <р(х, у) = (х, у + ХХ),
ф' = «2 + S2 + S, Об = Об, ’’
где s g К. Изоморфизм Е = Е' имеет место тогда
и только тогда, когда разность а2 - а2 имеет вид
л2 + s. Поэтому кривые Е и Е' изоморфны над
любым расширением поля К, в котором разре-
шимо квадратное уравнение относительно л:
s2 + s = а2 - а2. Если Е = Е', то Aut(E) = {1, -1}.
Это значит, что автоморфизмом является ото-
бражение (х, у) -> (х, у) или (х, у) -> (х, х + у), то
есть cp(/J) = Р или ф(Р) = -Р.
2. / = 0 или, что то же самое, щ = 0. Использу-
ем нормальную форму для этого типа кривой.
Получаем условие изоморфизма между двумя
кривыми Е и Е' :
(х', у') = <р(х, у) = (и2х + S2, и у + su2x + t)
и для коэффициентов
, 3 ,4 з 4
а3 —иа3, а^ = и а$ + и sa3 + s ,
Об - и Об + + u(s3 + f)a3 +12,
где .v, t g К. Изоморфизм E = E’ имеет место то-
гда и только тогда, когда
, «3 3 -гр
а) — =и', где и g К ;
«з
б) уравнение четвертой степени от s:
х4 + usa3 + i/4«4 + «4' = 0
имеет решение в К',
в) квадратное уравнение от t:
t2 + ua3t + (иаб + us2a$ + w3s3a3 + <т6') ~ 0
имеет решение в К.
Кривые изоморфны над любым расширением
поля К, в котором выполняются условия а)-в).
При Е = Е' группа автоморфизмов кривой над
полем К состоит из 24 элементов.
6.14.4. Бирациональный изоморфизм кривых
Пусть кривые Ci и С2 (не обязательно кубиче-
ские) над полем К задаются неприводимыми по-
линомами /1(х, у) и f2(u, v) соответственно. Ра-
122
циональным отображением кривой С] в кривую
С2 называется пара рациональных функций
g(x,y), h(x,y), определенных на кривой С] (то
есть на множестве пар (х, у), на которых
Д(х,у) = 0), такая, что f7(g(x, у), Л(х,у)) = 0 (см.
подробнее п. 6.15.2).
Кривые Ci и С2 называются бирационалъно
изоморфными над К, если существуют рацио-
нальные над К отображения С) -> С2 и С2 -> Сь
обратные друг другу. Эти отображения называ-
ются бирациональным изоморфизмом. Они опре-
делены во всех точках кривых, кроме конечного
их числа (поскольку знаменатель отображения
является полиномом, он может обращаться в О
только на конечном числе точек кривой).
Все рассмотренные выше замены перемен-
ных для кубических кривых являются поли-
номиальными (регулярными) отображениями
и, следовательно, бирацио нальными изомор-
физмами. Таким образом, если две эллиптиче-
ские кривые изоморфны, то они и бирацио-
нально изоморфны, обратное, однако, невер-
но. Множество кривых, бирационально изо-
морфных эллиптической кривой Е, строго
больше множества эллиптических кривых,
изоморфных Е.
Пример 6.14.1. Бирациональные изомор-
физмы.
1. Особая кубика С): у2 = х3 + х2 бирациональ-
но изоморфна конике С2: т2 = и. Действительно,
замена переменных в виде рациональных функ-
ций т<— —, w <— х + 1 задает отображение из
х
СД(0,0) в С2. Обратная замена переменных
х <— и - 1, у <- v(u - 1) задает отображение из С2
в QX0,0). Отображения С) -> С2 -> С, и С2 -> С] ->
-> С2 являются тождественными.
2. Коника С: ху = х + 1 бирационально изо-
морфна прямой L: и = т. Действительно, замена
переменных в виде рациональных функций
и <— ху, г <— х + 1 задает отображение С -» L. Об-
, и
ратная замена переменных х <— г - 1, у <--
т -1
задает отображение Z\(l, 1) -» С.
3. Особая кубическая кривая, заданная над
полем К уравнением в форме Вейерштрасса, би-
рационально изоморфна проективной прямой
Р'(А'). Действительно, параметризация (х(Д,у(0)
особой кубики всюду, кроме особой точки, явля-
ется рациональным отображением проективной
прямой в кубику. Поскольку параметр I является
рациональной функцией от х и у, то отображение
кубики в прямую тоже рационально (см. также
п. 6.15.2).
Теорема 6.14.2. Пусть К— поле характери-
стики, отличной от 2 и 3. Кривая четвертой сте-
пени у2 = ах4 + Ьх3 + сх2 + dx + е бирационально
изоморфна кривой т2 = и + Аи + В над К .
Доказательство. Если « = 0, то утвержде-
ние очевидно. Рассмотрим случай а Ф 0. Заменой
переменных х<— ха~^2,у <—уа^2 получаем урав-
нение со старшим коэффициентом а = 1. Заменив
х на х - bl4, получаем уравнение у2 = х4 - бсх2 +
+ 8<7х + е (с другими с, d, е). Бирациональный
изоморфизм задается парой функций
v-d
х =,
и —с
v-d
и—с
-2и-с.
Обратное отображение задается парой рацио-
нальных функций
Покажем, что рассматриваемое отображение
переводит кривую степени 4 в кубическую кри-
вую. Действительно, подставим х2 - 2и - с вме-
сто у в уравнение кривой
х4 — 2(2и + с)х2 + (2и + с)2=х4 — бсх2 + 8dx + е,
значит,
2 2 С2 — С
(u-c)x -\-2dx — (u+cuA-----—) = 0.
Тогда, решая квадратное уравнение относи-
тельно х, находим
х(и - с) = -d ±
л2, з
Cl -г и ' С U Ч--------------.
4
Отсюда получаем требуемое уравнение куби-
ческой кривой. Аналогично можно показать, что
обратное отображение переводит кубическую
кривую в кривую степени 4.
Композиция двух рациональных отображений
определена не всегда, поскольку рациональное
отображение является лишь частично опреде-
ленным отображением. Если ср: С) -> С2 и
у: С2 -» С3, то областью определения отображе-
ния ср является множество точек кривой С(, на
которых знаменатели функций, задающих ср, от-
личны от нуля, областью определения отображе-
ния у — множество точек кривой С2, на которых
знаменатели функций, задающих у, отличны от
нуля. При этом отображение vp<p может иметь
пустую область определения. , , ... .
123
6.14.5. Эндоморфизмы эллиптических кривых
Эллиптическую кривую можно рассматривать
не только как алгебраическую кривую с авто-
морфизмами (см. пп. 6.14.2-6.14.4), но и как ад-
дитивную абелеву группу (модуль) с автомор-
физмами и эндоморфизмами, присущими моду-
лю. Эндоморфизмы модуля образуют кольцо
End(£) (см. гл. 3). Оно имеет характеристику О,
если кривая рассматривается над алгебраически
замкнутым полем. Выясним структуру этого
кольца.
На эллиптической кривой Е(К) можно опреде-
лить отображение ср2: Р —> 2Р и вообще отобра-
жение ср„: Р ~^>пР для произвольного целого п.
Тогда уфР) + срД0 = пР+nQ=и(Р+Q) = ц,(Р+Q),
то есть ср„ является эндоморфизмом кривой (как
модуля). Поскольку кривую мы не фиксировали,
то кольцо эндоморфизмов эллиптической кривой
Е(К) всегда содержит подкольцо Z.
Если кольцо эндоморфизмов эллиптической
кривой Е(К) удовлетворяет строгому включе-
нию End(£) z) Z, то говорят, что кривая обладает
комплексным умножением. Комплексное умно-
жение является важным инструментом, позво-
ляющим повысить скорость криптографических
алгоритмов без заметного снижения стойкости.
Рассмотрим некоторые частные случаи ком-
плексного умножения.
1. Важным примером эндоморфизма в случае
поля ненулевой характеристики р является эндо-
морфизм Фробениуса ср, сопоставляющий каж-
дой точке (х,у) эллиптической кривой Е/К, где
К— поле из q=pn элементов, точку (хч,уч).
Пусть кривая Е/К задана уравнением в форме
Вейерштрасса
у2 + арсу + ару = х + а2х2 + арс + а6, (6.14.3)
где а, е Ки (х,у)е Е/К). Тогда точка /хд,у1) то-
же будет принадлежать этой кривой. Действи-
тельно, если возвести обе части уравнения
(6.14.3) в степень q, то получим
(у9)2 + аух^!+«зУ = У)3 + «2W + асУ + а£.
Поскольку at е К, то ад -at, и точка /хд, уд)
лежит на кривой Е/К. При этом точки с коорди-
натами из поля К остаются неподвижными. Ото-
бражение Фробениуса является эндоморфизмом
эллиптической кривой Е/К) и, следовательно,
эндоморфизмом кривой Е/L) для любого алгеб-
раического расширения L поля К. Поскольку
точки кривой Е/К) неподвижны, отображение
Фробениуса для кривой Е/К) не может соответ-
ствовать умножению точки ни на какое целое
число. Следовательно, рассмотренная кривая об-
ладает комплексным умножением. Эндоморфизм
Фробениуса образует по умножению цикличе-
скую группу порядка п для кривой Е/Е),
/Е:К) = п. Эта группа действует на Е/L) так же,
как группа Галуа, разбивая множество точек на
циклы вида /Р, ср(Р), ф“(С), ..., ф"~'(Р)). При со-
ставном п циклы могут распадаться на кратные
подциклы неединичной длины.
2. Эллиптическая кривая Е/К, заданная урав-
нением у2 = х3 + В, с нулевым у-инвариантом об-
ладает эндоморфизмом вида ср: (х, у) -> (сох, -у),
-1 + лУз п з ,
где со =--------. Поскольку со = 1, то
ср(х, у) е £(Е) для /L:K) = 3. Нетрудно заметить,
что это отображение для Е/К) удовлетворяет
характеристическому уравнению ср6 = 1. Поэтому
эндоморфизм ср не соответствует умножению
точки ни на какое целое число, однако соответ-
ствует умножению точки на комплексное число,
равное примитивному корню степени 6 из 1, то
с 1 + л/—3 v ,
есть на с, --------. Кольцо эндоморфизмов
этой кривой над алгебраически замкнутым полем
изоморфно кольцу Z[SJ. Если поле L конечно, то
в нем существует элемент £,. Отметим, что хотя
выражения для £, и со похожи, эти элементы су-
щественно различны: первый — элемент кольца
эндоморфизмов, второй — элемент поля L.
3. Эллиптическая кривая Е/К, заданная урав-
нением у2 = х3 - Ах, с у-инвариантом у = 1728 об-
ладает эндоморфизмом вида ср: (х, у) —> (-х, iy),
где z =уГа, ср(х, у) е Е/Е) для (£:£) = 2. Не-
трудно заметить, что это отображение для ал-
гебраического замыкания поля К удовлетворяет
характеристическому уравнению ср4 = 1. Поэто-
му эндоморфизм ср не соответствует умноже-
нию точки ни на какое целое число. Так как
ср4=1, то отображение соответствует умноже-
нию точки на комплексное число, равное при-
митивному корню степени 4 из 1, то есть на
i = V=4. Кольцо эндоморфизмов этой кривой
над алгебраически замкнутым полем изоморфно
кольцу Z[i], Если поле L конечно, то в нем су-
ществует элемент г. Здесь также i и i имеют раз-
личную природу: z — элемент поля L, a t — эле-
мент кольца эндоморфизмов.
Приведем без доказательства ряд свойств
кольца эндоморфизмов эллиптических кривых
над алгебраически замкнутым полем.
Теорема 6.14.3. Кольцо эндоморфизмов эл-
липтической кривой над полем С является цело-
стным кольцом характеристики 0.
Доказательство см. в работе [13].
124
Теорема 6.14.4. Кольцо эндоморфизмов эл-
липтической кривой над полем С представляет
собой одно из трех колец:
- кольцо Z;
- квадратичный порядок поля Q(VZd);
- алгебру кватернионов.
Кольцо End(/i) коммутативно тогда и только
тогда, когда имеет место случай 1 или 2.
Доказательство см. в работе [21].
Теорема 6.14.5. Эндоморфизм Фробениуса ср
удовлетворяет характеристическому уравнению
ср2 - Tr(cp) + q = 0, где Tr(cp) = q + 1 - N— след
эндоморфизма ср, N — число точек кривой £(F6/).
Доказательство см. в работе [13].
Эллиптическая кривая не может иметь два
комплексных умножения на элементы различных
мнимых квадратичных полей. Однако может су-
ществовать комплексное умножение на элемен-
ты различных квадратичных порядков одного и
того же мнимого квадратичного поля. Например,
эллиптическая кривая с j = 0 над расширенным
конечным полем может иметь эндоморфизм
Фробениуса и комплексное умножение на
6.14.6. Изоморфизмы эллиптических кривых
над алгебраически незамкнутым полем
Будем классифицировать эллиптические кри-
вые по числу корней правой части уравнения
у2 =fix) в поле Fr. Полином fix) может иметь три
корня, один корень или не иметь корней в поле F/;.
Если для эллиптической кривой, заданной в
форме Лежандра (6.7.4), выполняется X е F/;, то
кубическая часть уравнения кривой имеет три
различных корня в F/;.
Рассмотрим изоморфизмы эллиптических
кривых, заданных в форме Лежандра. Над алгеб-
раически замкнутым полем эта кривая имеет
шесть изоморфизмов [13] при замене параметра
X на параметр ц вида
X Х-1
це]Х,—,1-Х, ,
I X 1-Х Х-1 X
(6.14.4)
Эти изоморфизмы получаются путем замены
переменных вида у <- и у, х <- и2х + г. Подстав-
ляя новые переменные в (6.7.4), получим преоб-
разованное уравнение вида
2 ( vY V-1Y V-X^ z.. .
у — х ч—г- |1 хч -— | хЧ--—-z— |. (6.14.5)
у и Д и" Д и J
Приравняем правые части выражения (6.14.5)
и уравнения
у2=х(х- 1)(х-ц). (6.14.6)
Для этого пронумеруем сомножители в пра-
вых частях уравнений (6.14.5) и (6.14.6) слева
направо. Равенство полиномов от х будет обес-
печено в шести случаях, описываемых переста-
новками сомножителей: (1,2,3), (1,3,2),
(2, 1, 3), (2, 3, 1), (3, 1,2), (3, 2, 1). Например, по-
следняя запись означает, что первый сомножи-
тель правой части уравнения (6.14.5) равен
третьему сомножителю в правой части уравне-
ния (6.14.6), второй сомножитель в (6.14.5) равен
второму сомножителю в (6.14.6), третий сомно-
житель в (6.14.5) равен первому сомножителю в
(6.14.6).
Рассмотрим действие указанных перестановок
в случае алгебраически незамкнутого поля.
Перестановка (1,2,3). Приравнивая соответ-
ствующие сомножители в (6.14.5) и (6.14.6),
получаем т = 0. Тогда г/2=1, и = Л = +\,
ц = X. Это тождественный изоморфизм.
Перестановка (1,3,2). Приравнивая первые
сомножители в (6.14.5) и (6.14.6), получаем
v = 0. Приравнивая третий сомножитель в
(6.14.5) и второй сомножитель в (6.14.6), по-
-X 2 г
лучаем —= откуда и ="к, и-уХ . При-
и
равнивая оставшиеся сомножители, получаем
v-1 1 1
Y X X
1.
2.
3. Перестановка (2, 1, 3). Приравнивая сомножи-
тели, соответствующие этой перестановке в
(6.14.5) и (6.14.6), получаем w2 = -v, v=l,
и = 1 ? ~ Ц = 1 — А.
и
4. Для (2, 3, 1): v = X, и = -J-К, ц = ——
X
5. Для (3, 1, 2): v = 1, и-д/Х-1, ц = —-—.
1 — X
6. Для (3,2, 1): у = Х, и = д/1-Х, ц- .
X —1
Рассмотренные случаи задают изоморфные
кривые тогда и только тогда, когда существуют
квадратные корни в поле Fr соответственно из 1,
X, -1, -X, Х-1, 1 - X. Если какого-либо из кор-
ней не существует, то соответствующее отобра-
жение определяет скрученную кривую, которая
характеризуется следующим свойством: если
элемент поля F/;, отличный от 0, 1, X, является
координатой х исходной кривой, то он не являет-
ся координатой х скрученной кривой, и наобо-
125
рот, если элемент поля не является координатой
х исходной кривой, то он является координатой х
скрученной кривой. Координаты х, равные 0, 1,
X, являются общими для исходной и скрученной
кривой. Из этого свойства вытекает, что если ис-
ходная кривая имеет число точек р + 1 + к, то
скрученная кривая имеет число точек р + 1 - к.
Следовательно, рассматриваемые шесть ото-
бражений могут задавать либо изоморфизм, либо
отображение исходной кривой в скрученную (яв-
ляющееся изоморфизмом кривых для любого
квадратичного расширения исходного поля).
Квадратный корень из 1 существует всегда,
поэтому всегда существует тождественный изо-
морфизм. Остальные случаи требуют отдельного
рассмотрения в зависимости от того, существуют
ли квадратные корни из -1, к, 1 - X.
Согласно квадратичному закону взаимности
-1 является квадратичным вычетом по модулю
если р = 1 (mod 4), и квадратичным невычетом
по модулюр. еслир = 3 (mod 4).
Условия изоморфизмов и отображений в
скрученную кривую приведены в таблице 6.1.
Изоморфизмы и отображения в скрученную кривую
для эллиптических кривых, заданных в форме Лежандра
Таблица 6.1
г Л (1-4 1 с J Изоморфизмы Отображения в скрученную кривую
р = 1 (mod 4) 1 1 L 1 , . 1 к X-ll [1 1-Х Х-Г X J —
у 1 -1 дч 1 >> гн- 1 —д 1_1 Х_1 [1-Х’ X-1J
-1 1 (х,1 -к, —, —] [ 1 -Z. 2C-1J J1 [X’ X J
-1 -1 {X, 1 - X} И J X Х-1] [х’ i-х’ х-Т х j
р s 3 (mod 4) 1 1 1*. - -М [ к к-} J кл, -к 7Д1 [ 1-Х X J
1 -1 |х, | ... [ к' 1-XJ к^,1к [ х-Г х J
-1 1 [ Х-1 к J (-,1 - X,—Д1 [х 1-XJ
-1 -1 [. 1 х-1] 1 1-Х к J С.-хЧ [х X-1J
где полином g(x) = х2 + ах + b неприводим над Fr.
Таким образом, доказано следующее утвер-
ждение.
Теорема 6.14.6. Пусть р Ф 2, 3. Классифика-
ция изоморфизмов для кривых в форме Лежанд-
ра полностью определяется символами Лежандра
ГгГИлИ! .^ ? у' -
р J ...
Пусть эллиптическая кривая E(Fp) задана над
полем Fp уравнением
Теорема 6.14.7. Пусть р Ф 2, 3 и
Справедливы следующие утверждения.
1. Всякая эллиптическая кривая с одним кор-
нем в правой части уравнения изоморфна над Fp
одной из двух скрученных кривых
, • Ep.V^x-pjX^ + J) (6.14.8)
или
у = (х - a)g(x),
(6.14.7)
Ерз:у2 = (х-Рз)(х2 + А
(6.14.8')
126
2. /-инвариант эллиптической кривой Ер есть
26(3<з" —р2)3
d'^+d'Y
где d' = d при р = рь d' = d~ при р = р3.
3. Для каждого р существуют в точности две
изоморфные над F/; эллиптические кривые с j-
инвариантом /(Ер), за исключением случая
/(Ер) =1728 (единственная кривая).
Доказательство. Полином g(x) = х2 + ах + b
неприводим над Fp, однако над квадратичным
расширением этого поля он раскладывается на
линейные множители:
. . f <7 + V«2 -4/) Y a--Ja2 -4b
g(x) = хч-----------хч------------- .
ных, которая определена во всех точках исход-
ной кривой. Обратная замена переменных зада-
ется всюду определенными на (6.14.8) или на
(6.14.8') функциями. Преобразование кривых
(6.14.7)-о-(6.14.8) или (6.14.7)-о-(6.14.8') всюду
определено и взаимно однозначно, то есть явля-
ется изоморфизмом кривых. Утверждение 1 до-
казано.
Утверждение 2 доказывается непосредствен-
ным вычислением.
Докажем утверждение 3. Согласно работе
[13], над полем Fp всякая эллиптическая кривая,
в том числе и Ер (где р = Pi или р = р3), изо-
морфна эллиптической кривой Ех в форме Ле-
жандра. Замена переменных
(l^Pd^ у,
Замена переменных х <- х - — приводит
уравнение (6.14.7) к виду
у2=(х-^±^)(х2 + Е>), (6]49)
где d' =d при р = pb d' = d3 при р = р3, приводит
Ер к Ех с
(6.14.10)
а2 - 4Ь
где -£> =---------квадратичный невычет по
4
Значит, над полем Fp существует ровно
модулю р.
Очевидно, что D/d является квадратичным
вычетом по модулю р, следовательно, D/d мо-
жет являться либо вычетом, либо невычетом 4-й
степени по модулю р.
Если D/d — вычет 4-й степени по модулю р,
шесть изоморфных кривых для Ех (а значит, и
для Ер). Покажем, что кривые вида (6.14.8) (и
(6.14.8')) допускают изоморфизм вида
Р<->у = -Р, и других изоморфизмов в поле F,,
нет. Действительно, для каждого значения ц из
(6.14.4) с учетом (6.14.10) получаем ц = X, тогда
то замена переменных x4-(JDld)2x,
у <— (JDjdy у в уравнении (6.14.9) даст кривую
вида (6.14.8) с
откуда у = р.
Аналогично,
Р1=(яЧ-2а) ———
V а - 4Ь
для ц = 1 - X: у = -Р;
Если D/d — невычет 4-й степени по модулю
р, то D/d21 будет вычетом 4-й степени по моду-
лю р, и обратно. Следовательно, кривые (6.14.8)
и (6.14.8') являются скрученными. Замена пере-
3 1 3 з
менных x<—(Dfd )2х, y<-{Djd )4 у в уравне-
нии (6.14.9) даст кривую вида (6.14.8') с
для
для
для
для
р3 = (а + 2а)
-d3
а2 -4Ь
Таким образом, переход от кривой (6.14.7) к
кривой (6.14.8) или (6.14.8') осуществляется с
помощью обратимой линейной замены перемен-
= _-4б/'р-(р2-Зй")У^7-
p2+J'
, '1 . V_4J'P-(P2-3J')V^.
М 1-Х ‘ 7 p2+J'
X _-4J'p+(p2 -3<hP7
Ц-Х-Г7~ р2ч-б/'
Х-1. _4<7'рч-(р2 -3<h/^T
X ’7~ В2ч-<7'
Поскольку -d' в поле F/; является квадратич-
ным невычетом, то, очевидно, в этом поле воз-
можны только случаи у е {р, -Р}.
При р = -р = 0, то есть для кривой вида
у2 = х(х2 + d'), из утверждения 2 получаем
/(Ер) = 1728.
127
Пусть эллиптическая кривая E(FP) задана над
полем уравнением
у2 = х3 + ах + Ь, (6.14.11)
где полином х3 + ах + Ъ неприводим над Fp.
Теорема 6.14.8. Пусть р Ф 2, 3 и
Справедливы следующие утверждения.
1. Всякая эллиптическая кривая с неразложи-
мой правой частью уравнения изоморфна над F/;
одной из двух скрученных кривых
ЕА^.у2=х3 +Ахх + 1 (6.14.12)
или
EAj у2 = х3 + Ajx - d. (6.14.12')
2. у-инвариант эллиптической кривой ЕА есть
28-(ЗЛ)3
4Л3 + 21В2
где В = 1 при А = Ах, В = -d при А = Ad.
3. Для каждого А над полем Fr существует
единственная эллиптическая кривая ЕА с j-
инвариантом j(EA}, если р = 2 (mod 3), и три изо-
морфных кривых с у-инвариантом j(EA), если
р=\ (mod 3).
Доказательство. Если Ь-— квадратичный
вычет по модулю р, то замена переменных
1 1
хe-biх,у4-Ь1 у в уравнении (6.14.11) даст
_2
кривую вида (6.14.12) с Ах=аЬ 3 (очевидно, что
b ф 0, поскольку полином в правой части непри-
водим).
Если b —- квадратичный невычет по модулю
р, то замена переменных х <— х,
у<— (b/( d)^y в уравнении (6.14.11) даст кри-
вую вида (6.14.12') с Ad ~a(b/(~d)) 3. Утвер-
ждение 1 доказано.
Утверждение 2 доказывается непосредствен-
ным вычислением.
Докажем утверждение 3. Необходимым усло-
вием изоморфизма кривых является равенство их
у'-инвариантов, то есть, если кривые ЕА'.
у2=х+Ахх + Вх и Еа^. у2 = х3+А2х + В2 изо-
морфны, то j(EA) =j(E,<Ay Итак, пусть изоморф-
ны две кривые вида (6.14.12) или (6.14.12'), то
есть Вх = В2 ~ В, где В = 1 или В = -d. Тогда из
равенствау-инвариантов следует, что И3 = , то
есть А2 =Дл/1 .
Если р = 2 (mod3), то в поле Fp справедливо
у/} =1, то есть А? = АХ. Если р = 1 (mod 3), то в
поле F,, существует три корня третьей степени из
. 2 -l + T^I
единицы: 1, со, со , где со =--.
2
Замена переменной х <— сох в уравнении
у = х3 + Ах + В дает у2 = х3 + Асах + В, а замена
переменной х <— со2х дает у2 = х3 + Лсо2х + В. Сле-
довательно, эти три кривые изоморфны.
Теоремы 6.14.6-6.14.8 остаются справедли-
выми и для эллиптических кривых Е/К, где
К = F^,, при этом F/; меняется на К, символы Ле-
жандра — на квадратичные характеры поля К, а
р — нар".
Теорема 6.14.9. Кривые, принадлежащие объ-
единению множеств эллиптических кривых из
теорем 6.14.6-6.14.8, остаются попарно неизо-
морфными и при переходе к расширенному полю
простой степени расширения больше 3.
Доказательство. Поскольку степень рас-
ширения нечетна, кубический полином остается
неприводимым в расширенном поле. Поэтому не
существует замены переменных, переводящей
кривую с одним корнем над простым полем в
кривую с тремя корнями и обратно. Следова-
тельно, эти кривые неизоморфны над расширен-
ным полем, даже если они имеют одинаковое
число точек и изоморфны как абелевы группы.
Поскольку степень расширения не кратна 3,
кубический полином остается неприводимым и
над расширенным полем. Следовательно, кри-
вые, неизоморфные над простым полем (случай
трех корней и случай неразложимой правой час-
ти), остаются неизоморфными и над расширен-
ным полем. При этом в любом расширенном по-
ле неприводимый полином или остается непри-
водимым, или раскладывается на линейные мно-
жители, то есть изоморфизм кривой с одним
корнем и кривой с неразложимой правой частью
возможен только тогда, когда степень расшире-
ния кратна 6, что в нашем случае исключено.
Значит, рассмотренные эллиптические кривые
действительно попарно неизоморфны над рас-
ширенными полями простых степеней расшире-
ния более 3. -Л
На основании теорем 6.14.6-6.14.9 получаем,
что число неизоморфных (как алгебраические
кривые, но не как абелевы группы) эллиптиче-
ских кривых Е(К) = EbFp, где К = F^„, асимптоти-
чески равно 6>(р/(1п р)) и не зависит от числа п.
Аналогичные рассуждения справедливы и для
эллиптической кривой Е(К) = Е/К-, число неизо-
128
морфных эллиптических кривых Е/К асимптоти-
чески равно О(рп /(In/?)).
6.15. Отображения
алгебраических кривых
В данном разделе изучается связь между
множеством точек алгебраической кривой и по-
лем рациональных функций на этой кривой. Со-
поставление точек алгебраических кривых и ра-
циональных функций может быть полезным при
анализе криптографических алгоритмов с откры-
тым ключом.
6.15.1. Регулярные функции и отображения
Пусть С(К) — неприводимая аффинная алгеб-
раическая кривая, заданная идеалом 3(C). Функ-
цией на кривой С назовем отображение точек
кривой (то есть пар (х,у) g С(К)) в поле К.
Функция f. С(К) —> К называется регулярной, ес-
ли она индуцирована некоторым полиномом
F(x, у) g К\х, у], то есть еслиДР) = F(P) в каждой
точке Р g С(К). Множество всех регулярных
функций образует кольцо R, совпадающее с
кольцом ЕДС]. Действительно, имеет место го-
моморфизм колец К\х, у] -> R с ядром 3(C), при
этом в соответствии с теоремой 3.5.2 имеет ме-
сто равенство R - А.'[С] =
fiC/K)
Рассмотрим некоторые свойства координатного
кольца ДЕ] = {а(х) + b(x)y | а(х), b(x) g К[х]} эл-
липтической кривой Е: у2=Дх)-В Кольцо ДЕ]
является целостным, поскольку Дх, у] — цело-
стное кольцо, а его идеал (у2 -fix)) — простой.
Норма элемента а + by кольца ДЕ] равна
N(a + by) = а - b2f g Дх], при этом норма произ-
ведения равна произведению норм. Функции
а + by и a —by являются сопряженными. Имеет
место равенство (а + Ьу)(с + dy) = {а + by)(c + dy)
(чертой обозначен сопряженный элемент).
Арифметика кольца ДЕ] аналогична арифметике
кольца целых квадратичных чисел, вместо -Jd
используется y = Jf .
Единственными обратимыми элементами
кольца ДЕ] являются элементы группы К*. Дейст-
вительно, из равенства (а + /у)(с + dy) — 1 и муль-
типликативности нормы следует а2 - b2f g А*. Но
13 Предполагается, что char(E) Ф 2 и старший ко-
эффициент полиномаДх) единичный.
deg(A'(a + by)) = 2deg(a), если deg(a) > deg(6) + 2;
deg(A'(a + by)) = 2deg(Z>) + 3, если deg(a) < deg(A) + 1.
Поэтому b = 0 и a g К . Группы обратимых эле-
ментов колец ЕДЕ] и ЕДх] совпадают. В этом про-
является аналогия кольца ЕДЕ] с мнимым квадра-
тичным кольцом.
Теорема 6.15.1. Кольцо ДЕ] евклидово.
Доказательство. Покажем, что функция
g: а + by -> deg(A'(a + by)) = deg(<?2 - b2f) задает на
ДД структуру евклидова кольца (см. п. 3.7).
Пусть а + by, с + dy е ДД, и fia + by) > g(c + dy).
Запишем
a + by = (c + dy)(e + hy) + (r + sy),
при этом g(a + by) = g(c + dy) + g(e + hy). Доста-
точно показать, что можно выбрать полиномы
е(х), h(x) так, что g(r + sy) < g(c + dy). Для этого
покажем, что на каждом шаге деления
g(r + sy) < g(a + by), тогда, продолжая деление,
можно получить g(r + sy) < g(c + dy). Обозначим
ас, b0, с0, d0, е0, ho — старшие коэффициенты по-
линомов а, Ь, с, d, е, h соответственно.
Предположим, что оба значения g(<7 + by) и
g(c + dy) четные. Тогда g(a + by) = 2deg(a),
g(c + dy) = 2deg(c) и значение g(e + hy) должно
быть четным, то есть g(e + hy) = 2deg(e). Поло-
жим e0 = aficG и deg(e) = deg(a) - deg(c). Тогда
g(r + sy) < g(a + by). Для перехода к следующей
итерации алгоритма деления полагаем а + by <-
<— a + by - (с + c/y)coxdeg(e\
Предположим, что значение g(a + by) четное,
а значение g(c + <7y) нечетное. Тогда значение
g(e + hy) должно быть нечетным, то есть
g(a + by) = 2deg(o), g(c + dy) = 2deg(J) + 3 и
g(e + hy) = 2deg(E) + 3. Из равенства g(« + /y) =
= g((c+ dy)(e + hy)) следует ao = JoEol, где 1 —
старший коэффициент вДх). Поэтому h0 =a0/d0
и deg(A) = deg(a)-deg(<7)-3. Получаем g(r + sy)<
< g(a + by). Для перехода к следующей итерации
алгоритма деления полагаем а + by <— а + by -
-(c + dy)Eoxdeg(h)y.
Предположим, что значение g(a + by) нечетное,
а значение fic + dy) четное. Тогда значение
g(e + hy) должно быть нечетным, то есть
fia + by) = 2deg(6) + 3, g(c + dy) = 2deg(c) и g(e + hy) =
= 2deg(E) + 3. Из равенства g(a + by) = g((c + dyfi
fie + hy)) следует bo = coho- Поэтому Ao = a0/J0 и
deg(h) = deg(a)-deg(d)-3. Получаем g(r + sy)<
< fia + by). Для перехода к следующей итерации
алгоритма деления полагаем а + by <-а + by-
- (с + dyfiiox^^y.
Предположим, что оба значения g(a + by) и
g(c + dy) нечетные. Тогда g(e + hy) должно быть
четным, то есть g(a + by) = 2deg(A) + 3, g(c + dy) =
129
= 2deg(c/) + 3 и g(e + hy) = 2deg(e). Из равенства
g(n + by) = g((c + ф)(е + hy)) следует bG = doeo. По-
этому и deg(e) = deg(Z>) - deg(J). Полу-
чаем gO + .sy) < g(a + by). Для перехода к следую-
щей итерации алгоритма деления полагаем
а + by <- а + by - (с + dy)e&ie^h\
Доказательство остается справедливым для
произвольной нечетной степени deg(/) >5.
Поэтому кольцо К\Е\ обладает однозначным
разложением на простые множители, и каждый
идеал в является главным.
Таким же образом можно определить коорди-
натное кольцо для алгебраического многообра-
зия Е, заданного простым идеалом r3(VIK):
K.[V} =
К[Х],...,хД
3(V/K)
Пусть алгебраические кривые С\(К), С2(А) за-
даны полиномами f(x,y), fyu, г) соответственно.
Регулярным отображением14 алгебраических
кривых С, -> С2 назовем пару регулярных функ-
ций w = F](x,y), v = Fi(x,y) таких, что если
Д(х,у) = 0, то /2(Т|(х, у), Fi(x,y)) = 0. Композиция
регулярных отображений также является регу-
лярным отображением.
Пусть ф: Ci —> — регулярное отображение
кривых. Тогда каждой функции g: С2 —> F соот-
ветствует функция h: С, —> К такая, что Л(С|) =
= gt^>(Ci)). Если функция g регулярна, то функ-
ция h тоже регулярна.
Определим отображение ф*: F[Ci] —> F[CJ
для координатных колец следующим образом:
Ф* = g “ Ф = £<Ф(С1)) Для всех g е АГ[С2].
Теорема 6.15.2. Регулярное отображение ф ал-
гебраических кривых С, -> Сг индуцирует гомо-
морфизм ф* координатных колец К[С2 ] —> KfC j ].
Доказательство. Ясно, что композиция по-
линомов представляет собой полином, поэтому
g«ф при g g К[С2 ] является регулярным отобра-
жением Cj —> К, следовательно, g ° ф е F[C, ].
При ЭТОМ (g о ф)(соп.81) = const. Тогда для суммы и
произведения получаем
((gi + g2)°ФХЛ = (gi + ЯгХФС?)) =
= ^(ф(Р)) + ₽2(ф(Р)) = gl»ф(Р) + gi о ф(Р),
((gig2)»ФХП = (gig2X<m) =
14 Регулярное отображение называется также
морфизмом.
= gi (Ф(П)Я2(Ф(П) = (gl « Ф(Р))^2 ° Ф(П),
где g|, g2 g К[С2], Р е С], то есть координатные
кольца гомоморфны.
Аналогичное утверждение справедливо для
произвольных аффинных алгебраических много-
образий. Имеет место и обратное утверждение:
всякий гомоморфизм аффинных координатных
колец ф:АГ[Г2]-> АГ[Р|] алгебраических много-
образий V] и имеет вид ф = ф*, где ф — неко-
торое регулярное отображение из F в К2. Дока-
зательство аналогично.
Пусть С/К— алгебраическая кривая и
Р = (х/>,у/>)— точка на этой кривой. Рассмотрим
регулярные функции F(x, у) на кривой С, обра-
щающиеся в нуль в точке Р, то есть F(xP, ур) = 0.
Сумма любых двух таких функций обращается в
нуль в точке Р. Произведение такой функции на
любой полином из К[х, у] обращается в нуль в
точке Р. Поэтому совокупность всех таких функ-
ций образует идеал Шр в кольце АГ[С].
ХВД -
Имеет место изоморфизм колец ——> К ,
который вычисляется как значение функции из
__ /кгл",'1
АфС] в точке Р. Поэтому----- является полем,
ЭЛ р
а идеал т,> максимален по теореме 3.6.1. Обрат-
но, любой максимальный идеал ЭЛ с А'[С] соот-
ветствует некоторой точке Р е С [9].
Пример 6.15.1. Регулярные отображения.
1. Пусть Е: у2 = х3 + 1 — эллиптическая кри-
вая. Отображение ф(х, у) = (х2, ху) этой кривой в
другую кривую является регулярным.
2. Пусть С— алгебраическая кривая над по-
лем By,. Отображение Фробениуса (х, у) (хр, у)
является регулярным отображением кривой С в
себя.
3. Отображение аффинной прямой .у = t в вы-
рожденную кубику у2 = х3 + х2, задаваемое пара-
метризацией (? - Z, t2 - 1), является регулярным.
Однако обратное отображение, задаваемое
функцией t = —, регулярным не является.
х
Регулярное отображение алгебраических
кривых ф: С, -> Ci называется изоморфизмом,
если существует регулярное обратное отобра-
жение ф: С2^> С\, при этом фф — единичное
отображение на С2, а фф — единичное отобра-
жение на С]. Алгебраические кривые Q и С2
130
называются в этом случае изоморфными)5 Яс-
но, что если ф — изоморфизм алгебраических
кривых, то ф* — изоморфизм соответствующих
аффинных координатных колец. Справедливо и
обратное утверждение. Поэтому аффинные ко-
ординатные кольца изоморфны тогда и только
тогда, когда изоморфны соответствующие ал-
гебраические кривые.
Алгебраической группой называется алгебраи-
ческое многообразие G, которое одновременно
является группой, причем выполнены следую-
щие условия: отображения ср: G —> G, cp(g) = g-1 и
y:GxG->G, vp(gi,g2)=gtg2 Для любых g, gb
g2 e G являются регулярными отображениями.
Таким образом, эллиптическая кривая является
алгебраической группой.
6.15.2. Рациональные функции и
рациональные отображения
Пусть аффинная алгебраическая кривая С не-
приводима, то есть задана простым идеалом
3(C). Тогда координатное кольцо АфС] является
целостным, и для него можно построить поле
частных К (С ), называемое полем рациональных
(функций на алгебраической кривой С. По определе-
нию поля частных любую рациональную функцию
можно представить в виде —, где /, geK[C],
g
f F
g Ф 0 на С. Функции — и — равны, если
g G
jG-Fg<= 3(C). Аналогично определяется поле К(С).
Это определение автоматически переносится
и на неприводимые алгебраические многообра-
зия в и-мерном аффинном пространстве. Размер-
ность неприводимого алгебраического многооб-
разия V определяется Kaj< степень трансцендент-
ности поля K(V) над К. Алгебраические кри-
вые имеют размерность 1.
Пример 6.15.2. Рациональные функции на
кривой.
Поле К(С) рациональных функций на кривой
С: у2 =fix), где/-— полином нечетной степени не
меньше 3, является квадратичным расширением
поля К(х) рациональных функций одной пере-
менной за счет присоединения корня неприво-
димого над К(х) полинома у2-fix). Поскольку
этот полином неприводим даже над алгебраиче-
ски замкнутым полем К, то поле К(С) является
15 Нетрудно убедиться, что это определение изо-
морфизма является обобщением изоморфизма эллип-
тических кривых из п. 6.14.
квадратичным расширением поля К(х) для любо-
го подполя К поля К . Регулярные функции на
кривой С (К) имеют вид а(х, у) - а(х) + Ь(х)у,
где а(х), b(x) g Афх]. Это обусловлено тем, что
каждый член полинома из К[х,у] можно запи-
сать в виде y2kyeg(x), где е е {0, 1}, и заменить у2
па/х). Аналогично можно показать, что элемент
поля А?(С) имеет вид А(х) + В(х)у, где А(х),
В(х) е К(х). Действительно, рациональная функ-
ция может быть записана в виде отношения ре-
гулярных функций. Тогда
а + by _ (а + by)(с - dy) _
c + dy c2-d2f
= ac-bdf + (bc-ad)y _A + B
c2-d\f У'
Для функции а(х, у) = а(х) + Ь(х)у е К(С)
можно определить норму умножением на сопря-
женную функцию: N(a) = себе = а2 - b2 f е К(х),
при этом Л'(а|3) = А(а)А(Р). Для а е А/С] имеем
Л'(а) е АГ[х]. Из мультипликативности нормы и
нечетности степени полинома fix) следует, что
группа обратимых элементов кольца Л[С] совпа-
дает с К.
Рациональная функция / gK(C) называется
регулярной в точке Р g С, если существует пред-
g(P)
ставление f(P) ----такое, что Ь(Р) Ф 0. В этом
А(Р)
g(P) -
случае элемент ---- поля К называется значе-
КР)
нием функции /в точке Р.
Сумма и произведение функций из К(С), ре-
гулярных в точке Р, регулярны в Р. Совокуп-
ность всех функций из К(С), регулярных в точке
Р, называется локальным кольцом точки Р е С и
обозначается Ор.
Рациональные функции F(x, у) е Ор, обра-
щающиеся в нуль в точке Р, образуют идеал Шц>.
Гомоморфизм колец ——>К задается вычис-
лением значения функции из Ор в точке Р. По-
этому идеал Шс/. максимален по теореме 3.6.1.
Очевидно, что все элементы ОфЗЯр являются об-
ратимыми.
Если точка Р неособая, то идеал ШС является
главным. Он порожден элементом из ,
который определен с точностью до обратимого
элемента кольца Ор [21].
Например, на эллиптической кривой
у2 = х3 + ах2 + Ьх для Р = (0, 0) функции
131
x2 + 2 + y(x +1) x+y(x + l)
------— ,-— --- лежат в OP, при
x + 3----------------x + 3
этом первая функция является обратимым эле-
ментом кольца ОР, а вторая функция лежит в 3Jlp.
Теорема 6.15.3. Если рациональная функция
определена во всех точках алгебраической кри-
вой С(К), то она регулярна.
Доказательство см. в работе [9].
Пусть Сь С2 — алгебраические кривые. Ото-
бражение ф: С, —> С2 называется рациональным,
если оно задается набором рациональных функ-
ций/ g е К(С{) таких, что если знаменатели этих
функций отличны от нуля, то/ g е С2.
Пусть ф: С| —> С2 — рациональное отображе-
ние алгебраических кривых. Тогда каждой функ-
ции g: С2 —> К соответствует функция К
такая, что Л(С]) = £(ф(С1)). Если функция g рацио-
нальна, то функция h тоже рациональна. Опреде-
лим отображение ф*: К(С2) -> К(С}) полей функ-
ций следующим образом: ф* =g° ф = g^(Ci)) для
всех g е К(С2) . Рациональное отображение
ф: С] —> С2, для которого обратное отображение
vp: С2 -> С\ тоже рационально и фф = 1Г уф = 1С
является бирациональным изоморфизмом.
Теорема 6.15.4. Алгебраические многообра-
зия бирационально изоморфны тогда и только
тогда, когда изоморфны их поля функций. Л>1
Доказательство см. в работе [9].
Отображение ф* индуцирует и отображение
полей функций К(С2) К(С{). В этом случае
поле К(С\) является конечным расширением
поля К(С2) (см. работу [12]). Степень расшире-
ния (А?(С():ф*А?(С2)) называется степенью
отображения ф. Постоянное отображение
ф: С(К) К по определению имеет степень 0.
Отображение Фробениуса (х,у) (хг,ур) имеет
степень р [13]. Рациональное отображение [Z],
заключающееся в умножении точки на число I,
имеет степень /2. _ ,л.,,т. ...
6.15.3. Проективные кривые
Пусть Р2(Х) — проективная плоскость. С уче-
том того, что
(X, У, Z) ~ (ХХДК, XZ) (6.15.1)
для X е К , точка (X, У, Z) может лежать в Р2(К),
даже если ее координаты не лежат в поле К.
Проективная алгебраическая кривая С задается
нулями полиномов из однородного идеала 3(C).
Проективная алгебраическая кривая С неприво-
дима тогда и только тогда, когда ее однородный
идеал 3(C) над алгебраически замкнутым полем
является простым.
Однородный полином / из К[Х, У, Z] не явля-
ется функцией из С(К) в К, так как из условия
(6.15.1) при любом ненулевом X е К следует, что
значение полинома/должно быть одинаково для
всех X. Однако нулевое значение полинома в
точке проективной плоскости определено пра-
вильно, так как из /X, У, Z) = О, где deg(/) = d, и
/XX, ХУ, XZ) = XJ/X У, Z) следует/ХХ, ХУ, XZ) = 0.
Рациональной функцией на проективной кри-
вой С называется частично определенное отобра-
жение /: С -> К, заданное соотношением
g(P) —
f(P) = 77X7 где & h е К^Х--У’ Z1 ~ однород-
ен)
ные полиномы одной и той же степени d, h g 3(C)
g(P)
и P e С. В случае h(P) Ф 0 частное коррект-
но определено, так как для ненулевого X
g(Xy,Xy,XZ) _ Xrfg(Z,y,Z) _ g(X,y,Z)
A(Xy,Xy,XZ) XJX(Z,y,Z) h(X,Y,Z)
Кроме того, — и — определяют одну и ту
h Д
же функцию на С тогда и только тогда, когда
h\g - hg\ е 3(C), так что множество рациональ-
ных функций является полем
K(C) = U
[А
g,heK[X,Y,Z],h£3(C)
с учетом эквивалентности (6.15.2).
Пусть С— неприводимая проективная алгеб-
раическая кривая. По аналогии с аффинной кри-
вой рассмотрим локальное кольцо ОР точки
Р е С, состоящее из всех рациональных функ-
ций / е K(X,Y,Z) , регулярных в точке Р. Един-
ственным максимальным идеалом кольца ОР яв-
ляется идеал = {/е ОР | /Р) = 0], состоящий
из всех необратимых элементов кольца ОР.
'* При изучении некоторых свойств кривой С
иногда достаточно исследовать С в окрестности
произвольной точки Р. Например, проективная
эллиптическая кривая в форме Вейерштрасса
y2Z = X- + AXZ1 + BZ-
является объединением двух аффинных кривых •
£0: у2 = х3 + Ах + В, '
и
Е} : г, = xj5 + Axtz2 + Bzy
132
(где Ео получена в окрестности любой конечной
точки (Z = 1), а Е] — в окрестности бесконечно
удаленной точки (Y = 1)), склеенных при помо-
щи изоморфизма
Е0\(у = 0) -> ЕД^ = 0),
Здесь
X Y X Z
х = —, у-—,х1 -—,
Z Z Y
6.15.4. Изогении эллиптических кривых
Пусть Е](Е) и Е2(Е) — эллиптические кривые.
Рациональное отображение ср: Е\(К) —> Ei(K) та-
кое, что <р(Роо) = Роо, назовем изогенией, а кривые
Ei и Е2 — изогенными. Изогению, переводящую
все точки кривой в бесконечно удаленную точку,
назовем нулевой.
Изогении эллиптических кривых индуциру-
ются гомоморфизмом решеток (D/Zj и C/Z2 (см.
рис. 6.11). Например, решетка Z|=Za>i + Za>2
, Г ИС01
гомоморфна решетке Z2 = + Z., где т =- и
со2
п > 1. При п = 1 решетки изоморфны.
Ядром изогенны Е} —> Е2 называется множест-
во точек кривой Е], отображающихся в е Е2.
Изогения ср: Е\(К) Е-^К) как рациональное
отображение индуцирует отображение полей
функций на кривых. Степень расширения
(Е(Е|):ср*Е(Е2)) называется степенью изогении.
Для изогении ср: Е}(К) —> ЕХК) существует
дуальная изогения ф: Е2(К) - > Е^К) такая, что
ФФ = [/], гДе [Л — умножение точки кривой Е, на
число I. Аналогично фф = [/] — умножение точ-
ки кривой Е2 на I, причем I — степень изогении.
Дуальные изогении имеют одинаковые степени.
В случае алгебраически замкнутого поля опе-
рация умножения точки на число I задает эндо-
морфизм эллиптической кривой с ядром из I2
точек. Поскольку изогения соответствует «квад-
ратному корню» из операции умножения на I,
ядро изогении состоит из I точек порядка Z, обра-
зующих циклическую группу (одной из них яв-
ляется точка Роо).
Между эллиптическими кривыми Е](К) и
Ег(К) с у-инвариантами у] и у2 соответственно
изогения степени I существует тогда и только
тогда, когда выполняется равенство над К'.
= 0, где Ф/(п, v) g Z\u, г] — /-й симмет-
рический модулярный полином [11]. Число сла-
гаемых в Ф/ равно О(12), степень Ф[ по каждой
переменной равна I + 1. Размер коэффициентов
модулярного полинома быстро растет с ростом I.
Модулярные полиномы для изогений степеней 2,
3 и 5 имеют вид [17]:
Ф2(г/, т) = и + v3 - iZv2 + 1488z/v(z/ + v) -
- 162000(г/2 + v2) + 40773375i/v +
+ 8748 • 10б(г/ + v) - 157464 • 109;
Ф3(гг, v) = г/4 + v4 - их + 2232г?v2(u + v) -
- 1069956от(г? + v2) + 36864000(г/3 + v3) +
+ 2587918086г/2 v2 + 8900222976000г/т(гг + v) +
+ 452984832 106(г/2 + v2) - 770845966336 • 106wv +
+ 1855425871872- 1О9(гг + v).
Ф5 (и, v) = и + v5 — г/4г4 + 3720г/4т,4(гг + v) -
- 4550940г/3 v3(z/2 + v2) + 1665999364600гЛ3 +
+ 2028551 200zz2v2(zz3 + v3) +
+ 107878928185336800гЛ3(гг + v) -
- 246683410950г/т(гг4 + v4) +
+ 383083609779811215375гА>2(и2 + v2) -
- 441206965512914835246100г? v3 -
- 246683410950гл<гг4 + v4) + 1963211489280(г? + v5) +
+ 128541798906828816384000гл-(г? + v3) +
+ 26898488858380731577417728000гЛ2(гг + v) +
+ 1284733132841424456253440(гг4 + v4) -
- 192457934618928299655108231168000г«(г? +
+ v2) + 5110941777552418083110765199360000гЛ? +
+ 280244777828439527804321565297868800(г/3 + v3) +
+ 36554736583949629295706472332656640000wx
x {и + v) +
+ 6692500042627997708487149415015068467200 x
x (u2 + v2) -
- 264073457076620596259715790247978782949376//V +
+ 53274330803424425450420160273356509151232000 x
x (u 1- v) +
+ 141359947154721358697753474691071362751004672000.
Уравнение Ф^и,]) = 0 для нечетного I имеет в
поле F/; один корень или / + 1 корней при
п г
1 — 1 = 0, имеет два корня при 1 — 1 = 1 и не име-
( D\
ет корней при I — I = -1, где D — дискриминант
характеристического уравнения эндоморфизма
Фробениуса л2 - Тп +р = 0, л(х, у) = (хр, ур),
Т=р+ 1 -#E(FP) [15]. Из симметричности поли-
нома Ф/(п, v) следует, что для каждой изогении
существует дуальная. Для простых I модулярные
полиномы удовлетворяют сравнению:
Ф/(и, v) = (и1 - v)(y' - й) (mod /).
Модулярный полином неприводим над Q.
Ф/(г/.у) может быть определен по методике работ
[3, 11] с помощью функции j(q) (см. п. 6.10.3).
133
Пример 6.15.3. Изогении степеней 2 и 3.
Пусть кривые Е\ и Е2 заданы уравнениями
Е}-.у~ = х> + ах2 + Ьх,
Е2: V2 = и3 - 2аи2 + (а2 - 4Ь)и.
Тогда можно построить изогении степени 2
<p:£’i -> Е2,
Изогения задается формулами
v =
(y-ygMj
(х-х0)2
(х-х^)2
Кривая £2(£) задается коэффициентами
Я, —Я — 5 /£?о, В} = В — 2~У (so + x()t()).
QeR QeR
Непосредственные вычисления показывают,
что фф соответствует удвоению точки на кривой
Е2, а фф — удвоению точки на кривой Е}. Точки
(О, 0) и Рх лежат в ядре изогении. Заменой пере-
менной х <- х - кривую Е] можно привести к
виду у2 = xJ + Ах + В.
Пусть £i(£): у1 = х3+Ах + В, Е2(К): г2 = и3 +
+ Atu+ В} и (xR,yK) е Е}(К) — аффинная точка
порядка 3 (точка перегиба). Изогения степени 3
задается выражениями
_ х2 (2хд - х) + х(2 А + 5xJ;) + 4В + 2Ахп - 2х^ _
(х-х/()2
_ х2 (Зх;; - х) - х(2А + 9х2) - 8£ - 6 Ах,, - х3,
(х фУ ’
At = -9А - 30л-/Л Bl = -22 В - 70х/ - 42ЯхЛ.
Ядро изогении содержит точки порядка 3:
(xR,yR), (xR, -yR), Pw, а также другие точки пере-
гиба.
Изогении составных степеней могут быть
найдены как композиция изогений соответст-
вующих простых степеней. Изогения простых
степеней 1 > 5 для эллиптических кривых над
полями характеристики Ф 2, 3 может быть вы-
числена следующим образом [15].
Пусть £i(£): у2 = х3 + Ях + В; Е2(К): г2 = и +
+ A}U + Bi и (xR, yR) е £i(£)— аффинная точка
порядка I. Ядро изогении степени I содержит
аффинные точки порядка / из множества
R u -R аффинных точек, причем R n -R = 0.
Таким образом, множество R состоит из
(Z—1)/2 точек.
Для Q е R положим gQ* = 3xq + Я; gQy = -tyo,
SQ = ^XQ + 4Яхр + 4В; 1q - 6xq + 4А.
Изогения степени 7, отображающая кривую в
себя, соответствует комплексному умножению
на элемент мнимого квадратичного порядка с
нормой 7, при этом модулярный полином Ф^и,]}
имеет корень j.
6.15.5. Полиномы Жегалкина как функции
на поверхности единичного куба
Кольцо полиномов Жегалкина F2[xi, ...,х„]/21,
где 21 = (Х](1 © Xi), ..., х„(1 © х„)), можно рас-
сматривать как алгебро-геометрическую струк-
туру — кольцо функций на некотором алгебраи-
ческом многообразии.
Множество нулей полинома f = x,{x, © I)
соответствует паре параллельных плоскостей
х, = 0 и х, = 1 в «-мерном аффинном простран-
стве над Т2. Множество нулей идеала 21 пред-
ставляет собой совокупность плоскостей, огра-
ничивающих поверхность «-мерного единич-
ного куба.
Перейдем от аффинных координат к проек-
тивным. Выберем проективные координаты так,
чтобы все полиномы были однородными. Для
этого положим x,Z, — Xt. Тогда при Z, ф 0 выпол-
X, п
няется равенство х, =—-. При таком переходе
единичный аффинный куб отображается в еди-
ничный проективный куб.
Z
Определим z, = ~ при Xt Ф 0 и потребуем,
чтобы выполнялось условие z,(z, © 1) = 0. Тогда
идеал 21 наряду с полиномами Х^Х, © Z,) будет
содержать полиномы ZyX, Ф Z,). В этом случае
полином х,- ... х на поверхности аф-
финного куба перейдет в однородный полином
Еа, , X, ...Х: Z, ...Z, степени п на по-
верхности проективного куба, где индексы
ji, ...,jn-k являются дополнением к исходному
134
множеству индексов {ц, ...,4} в множестве
{1,2, ...,«}. Отметим, что переход от аффинного
пространства к проективному приводит к удвое-
нию числа переменных, тогда как согласно клас-
сической алгебраической геометрии число пере-
менных увеличивается на 1. Проективный поли-
ном, соответствующий полиному f е G,„ имеет
степень, не меньшую чем число непостоянных
слагаемых и не большую чем и. Например, поли-
ному Xi © 1 соответствует проективный полином
Xi © Zb полиному л'| © л'2х-, — проективный по-
лином X]Z2Z3 © X?XiZ}.
Обратный переход от проективного полинома
к аффинному осуществляется делением на
YJ Z, . Все координаты проективного полино-
ма равноправны, поэтому его можно делить на
любой одночлен вида yj^X,Z/ ; а так как на О
I,/е{1,...,/?}
делить нельзя, соответствующая аффинная
функция оказывается частично определенной.
Таким образом, одному и тому же проективному
полиному могут соответствовать разные (частично
определенные) аффинные полиномы. Назовем та-
кие аффинные полиномы проективно эквива-
лентными. Аналогично можно определить про-
ективную эквивалентность для наборов булевых
функций одних и тех же переменных. Проектив-
но эквивалентные подстановки имеют одинако-
вые проективные уравнения (с точностью до пе-
реименования переменных).
В исходной аффинной области проективного
куба выполняется условие Z] = ... = Z„ = 1. Одна-
ко в проективном кубе все 2и координат равно-
правны и допускается Z, = 0.
Переход от однородного полинома
F(Xy, ...,Х„, Zi, ..., Z,7) степени d на поверхности
проективного куба к соответствующему полино-
му fa на поверхности аффинного куба путем де-
ления на одночлен G степени d задается (частич-
но определенной) рациональной функцией
F
fG = —. В этом случае знаменатель
G может
принимать значение 0 в некоторых вершинах
рассматриваемого куба. На этих вершинах функ-
ция fG не определена.
6.16. Дивизоры на алгебраических кривых
Использование дивизоров позволяет устано-
вить связь между функциями на алгебраических
кривых и точками этих кривых. Дивизоры явля-
ются важным инструментом при исследовании
безопасности криптографических алгоритмов на
эллиптических и гиперэллиптических кривых, а
также при разработке таких алгоритмов.
6.16.1. Локальное кольцо точки и нормирование
Пусть Ор — локальное кольцо неособой кри-
вой С в точке Р и Wip— максимальный идеал
кольца ОР.
Лемма 6.16.1. Справедливо соотношение
со
Пж>=(0).
/7=1
Доказательство см. в работе [6].
Теорема 6.16.2. Пусть Р— точка кривой С.
Справедливы следующие утверждения.
1. Каждый идеал 21 кольца Ор, отличный от
нулевого и единичного, является некоторой сте-
пенью идеала (Dip.
2. (Dip— единственный ненулевой простой
идеал в кольце ОР.
3. Ор — кольцо главных идеалов.
Доказательство. Так как 21^ С/., то 21 с
Из леммы 6.16.1 следует существование целого
и > 1 такого, что 21 с. ЯЛ", и 21 . Значит,
найдется элемент а е 21 cz ЯЛ", такой, что
а & ЯЛ",+1. Идеал — главный, то есть
ЯЛР = Юр для некоторого I, и, значит, а = fu,
где и обратим в ОР. Тогда /' = ан-1 е 21 и
ЯЛ", cz 21. Отсюда 21 = ЯЛ",.
Так как всякий нетривиальный идеал кольца
Ор является степенью ЯЛр, то ЯЛР — единствен-
ный простой идеал.
Поскольку идеал ЯЛр— главный и любой
идеал 21 кольца Ор имеет вид 21 = ЯЛ",, то ОР —
кольцо главных идеалов.
Введем дискретное ^нормирование поля ра-
циональных функций К (С) на кривой С/К (см.
п. 4.7). Положим для любой функции g, регуляр-
ной в точке Р,
vp(g) = тах(и g Z: g е ЯЛ",).
Для рациональной функции f е.К(С) имеет
место представление j = — . Положим г>(/) =
h
= v>(g) - vP(h). Нетрудно убедиться, что введен-
ная функция Vp:K(C)~является дискрет-
ным нормированием. '
135
Если f е ЯЛр, то говорят, что функция f имеет
нуль в точке Р; если g SDiP, то говорят, что
функция f имеет полюс в точке Р. Значение нор-
мирования vp(f) задает порядок нуля функции f в
точке Р, значение гР(/“') задает порядок полюса
функции f е. Ор в точке Р.
Кольцо Ор является кольцом нормирования, а
— идеалом нормирования. Униформизукпцим
параметром нормирования называется функция из
К (С), имеющая в точке Р нуль кратности 1.
Пример 6.16.1. Нормирование поля рацио-
нальных функций.
Рассмотрим эллиптическую кривую Y2Z =
+ XZ2 + 2Z3 над полем Q. Эта кривая содер-
жит точку Р = (1,2,1). Кольцо нормирования
состоит из функций, не имеющих полюсов в точ-
ке Р. Идеал (Dip состоит из функций, имеющих
нуль в точке Р. Обратимый элемент кольца —
это функция, не имеющая нулей и полюсов в
точке Р. Униформизующий параметр нормиро-
вания имеет в точке Р нуль кратности 1 и являет-
ся образующей для идеала 9Лр. Это может быть
любой полином, задающий кривую, которая
имеет пересечение над полем Q с эллиптической
кривой в точке Р с кратностью 1, например, по-
лином, задающий прямую, проходящую через
точки (1,2,1) и (1, -2, 1), то есть полином X- Z.
Это может быть также функция, имеющая в точ-
ке (1,2, 1) нуль кратности ж и полюс кратности
5 — 1. Например, касательная в точке Р задается
полиномом, который имеет в этой точке нуль
кратности 2. Полином, задающий касательную,
Y — X — Z
имеет вид: Y-X-Z. Тогда функция ---------
X — Z
имеет в точке (1, 2, 1) нуль кратности 2 и полюс
кратности 1, то есть ее нормирование равно I.
Аффинная функция у2 + х~ - 5 на кривой, имею-
щая нуль в точке (1,2), может быть представлена
в виде х3 + х + х - 3 с учетом замены у2 на
х3 + х + 2. Последний полином делится на х - 1,
но не делится на (х - 1 )2, следовательно, функция
имеет нуль кратности 1. Пример обратимой
, (х2+1)у + х5 „
функции: -----X.----. Значение этой функции
ху + х + 3
в точке (1, 2) равно .
6.16.2. Дивизоры
Перейдем от рассмотрения функции в одной
точке кривой к рассмотрению ее на всей кривой.
Рациональную функцию F(x) одной перемен-
ной из поля К(х) можно с точностью до кон-
станты задать списком нулей и полюсов с учетом
их кратностей. Поскольку числитель и знамена-
тель функции F(x) являются полиномами из
К[х], они раскладываются на конечное число
линейных множителей. Чтобы различать нули и
полюсы функции F, будем их учитывать с раз-
ными знаками: нули со знаком «плюс», а полю-
сы— со знаком «минус». Точно так же рацио-
нальную функцию на алгебраической кривой
С(К) можно с точностью до константы задать
конечным списком ее нулей и полюсов с учетом
кратностей. _
Дивизором на алгебраической кривой С(К) на-
зовем формальную сумму (без указания конкретной
арифметики) точек кривой с кратностями П/>
D = (6.16.1)
РеС(Х) . . .. .
в которой все пр, за исключением конечного чис-
ла, равны нулю. Сумма берется по конечному
числу точек, поскольку мы рассматриваем ра-
циональные функции на кривой, а числа пР свя-
заны с нормированием функции в точке Р. Мно-
жество дивизоров образует абелеву группу с за-
коном сложения ; х . , - .. 1
]Ги7)(Р)+ ^тДР) = ^(Пр+тГ)(Р),
РеС(К) РеС(К) РеСуК)
которая называется группой дивизоров алгебраи-
ческой кривой С(К) и обозначается Div(C(K)).
Конечное множество точек Р в (6.16.1), для ко-
торых пр Ф 0, называется носителем дивизора.
Дивизор для кривой С(К) определяется по
формуле (6.16.1) с заменой К на К.
Степенью deg(D) дивизора D=^np(P) на-
РеС
зывается целочисленная сумма его коэффициен-
тов: deg(D) = пр . Имеем deg(D|) + deg(Z)2) =
РеС
= deg(Z)1 + D2) для любых Z>]5 D2 g Div(C), то
есть отображение deg: Div(C) -> Z является го-
моморфизмом. Ядром гомоморфизма deg являет-
ся группа Div°(C) дивизоров степени нуль.
Дивизор D вида (6.16.1) назовем положи-
тельным (D > 0), если все его коэффициенты пР
неотрицательны. Это понятие позволяет частич-
но упорядочить множество дивизоров. Будем
считать, что D| > Z)2 тогда и только тогда, когда
D] — D2 — 0.
Пусть /, g&K(C) и D- ^пр(Р)— фик-
РеС(Х)
сированный дивизор на кривой С(К). Будем
говорить, что функции f g сравнимы по модулю
136
D (записывается f=g (mod 0), если vX/”- S) - nr
для всех точек кривой.
Ненулевая рациональная функция f заданная
на алгебраической кривой С(К), может иметь
лишь конечное число нулей и полюсов. Можно
определить дивизор функции
<W)= X_vT(/)(^)eDiv(C(O
РеС(К)
Тогда произведению функций на кривой бу-
дет соответствовать сумма их дивизоров, то есть
существует гомоморфизм абелевых групп
РГ(С)* —> Div(C(/Q).
Дивизор на кривой, равный дивизору некото-
рой рациональной функции, называется главным
дивизором. Назовем два дивизора А и О2 линей-
но эквивалентными, если D\ - D2 является глав-
ным дивизором.
Теорема 6.16.3. Главные дивизоры алгебраи-
ческой кривой С(К) образуют подгруппу
Pr(C(/Q) группы Div(C(К)). Имеет место изо-
морфизм групп К(С)*!К* ^Рг(С(АД).
Доказательство. Для разности дивизоров
получаем
div(/) - div(g) = vP (//g\P) = div(//g).
PeC(K)
Значит, Pr(C(/Q) — подгруппа группы диви-
зоров. Рассмотрим отображение
ф:ДС)’->Рг(С(Л),
сопоставляющее функции f ее дивизор div(/). Так
как di\(/g) = div(/) + div(g), то ф — гомоморфизм.
Его ядро
Кег(ф) = {f е 7C(C)*|div(/) = 0 }= {f е К* }.
Поэтому К(С)/К* —>Pr(C(/Q)— изомор-
физм по теореме 2.3.3.
Теорема 6.16.4. Дивизор D-^np(P) явля-
рер
ется дивизором некоторой функции на эллипти-
ческой кривой Е тогда и только тогда, когда од-
новременно выполняются равенства У'пр = О
(сумма целых чисел) и ^пРР = Р№ (сумма точек
эллиптической кривой).
Доказательство см. в работе [21].
Следствие 6.16.5. Главные дивизоры неосо-
бой алгебраической кривой образуют группу,
которая является нормальной подгруппой диви-
зоров степени 0.
Доказательство. Операция умножения
функций на кривой индуцирует сложение их ди-
визоров. Нулем является функция, не имеющая
полюсов на кривой, то есть ненулевая константа.
Поскольку дивизор каждой функции имеет степень
0, то группа главных дивизоров является подгруп-
пой дивизоров степени 0. Группа дивизоров и
группа дивизоров степени 0 абелевы, поэтому лю-
бая подгруппа группы дивизоров или группы ди-
визоров степени 0 является нормальной.
На практике дивизоры на алгебраической
кривой удобно рассматривать «с точностью до
главного дивизора», по аналогии с группой клас-
сов числового поля. Из утверждения 6.16.5 сле-
дует существование факторгруппы
J(C) = Div°(C(P))/Pr(C(0).
Эта факторгруппа называется якобианом кри-
вой. Якобиан является аддитивной абелевой
группой.
Теорема 6.16.6. Якобиан эллиптической кри-
вой Е(К) состоит из дивизоров вида (Р) - (A).
Доказательство. Предположим, что в диви-
зор якобиана входят две (не обязательно различ-
ные) точки Р и Q-. D = (Р) + (0 - 2(РЮ). Тогда су-
ществует функция f е 7Д£), описывающая пря-
мую, проходящую через Р и Q. Эта прямая пере-
секает кривую в третьей точке R. Тогда div(/) =
= (Р) + (0 + (Р) - 3(РЮ). Поскольку якобиан Р(Е)
определен с точностью до главного дивизора, вы-
полняется равенство D = D- div(/) (mod Р(£)), то
есть D = -(Р) + (Роэ). Кроме того, существует
главный дивизор div(g) = (Р) + (-Р) - 2(РХ) функ-
ции g, которая задает вертикальную прямую, про-
ходящую через точки Р и -Р. Поскольку D =
= D- div(g) (mod J(£)), получаем D = (-R) - (P„_).
Рассуждение по индукции распространяется
на произвольное число точек дивизора.
Отсюда следует, что якобиан эллиптической
кривой изоморфен группе точек кривой (см. так-
же п. 6.18.2), однако для кривых больших степе-
ней порядок якобиана больше, чем число точек.
Пример 6.16.2. Рациональные функции и их
дивизоры.
1. На эллиптической кривой Y2Z = X3 +
+ AXZ2+ BZ\ заданной над полем С комплекс-
ных чисел, функция, определяющая прямую, ко-
торая проходит через три аффинные точки кри-
вой, имеет нули в этих точках и полюс кратности
3 в бесконечно удаленной точке. Эта функция
137
, Y-XX-vZ „
имеет вид j =----—-----. Действительно, при
Z = 0 знаменатель обращается в нуль. Для того
чтобы определить кратность полюса, рассмотрим
окрестность бесконечно удаленной точки, где
У 0. Тогда можно поделить X и Z на Y. Обозна-
X Z
чим и =—, w = —. Функция f примет вид
_ 1-Eu-vw rr
j ----------. Нетрудно видеть, что поведение
w
функции f вблизи нулевого w определяется пер-
вым слагаемым —. Поскольку эллиптическая
w
кривая имеет пересечение с бесконечно удален-
ной прямой Z = 0 кратности 3, то соответствую-
щий полюс при w = 0 тоже имеет кратность 3.
Следовательно, дивизор функции /, нули которой
задают прямую, проходящую через точки Р\, Р3,
Р3, равен
div(/) = (Pi) + (Л) + (Р3) - 3(7Д).
Уравнение прямой может быть найдено с ис-
пользованием формул сложения на эллиптиче-
ской кривой.
2. Функция, определяющая секущую, которая
проходит через точки Р и -Р, имеет нули в этих
точках и полюс кратности 2 в точке Рт. Эта
, X-aZ
функция имеет вид j = ———, где а — коор-
дината X точек Р и -Р. В окрестности точки Р№
г и-aw
получаем j =-----. Как и в предыдущем слу-
w
чае, знаменатель функции f имеет на бесконеч-
ности нуль кратности 3. Однако в точке w = 0
числитель тоже имеет нуль. Оценим его крат-
ность. Подставим и = aw в уравнение кривой
w = и3 + Auw1 + Bw3. Получим кубическое урав-
нение от w. Нетрудно видеть, что поскольку ко-
эффициент при w отличен от нуля, то корень
w = 0 имеет кратность 1. Следовательно, функ-
ция f имеет в точке Р«, полюс кратности 3-1 = 2.
Поэтому div(/) = (Р) + (-Р) - 2(Роо).
Пустьf — функция на кривой С и D — диви-
зор на этой же кривой, причем носители дивизо-
ров div(/) и D не пересекаются. Определим зна-
чение функции f на дивизоре D как
f{D)=пжг -
Теорема 6.16.7 (закон взаимности Вейля).
Пусть С (К) — неособая кривая и /, g е К/С) —
рациональные функции такие, что носители их
дивизоров не пересекаются. Тогда
/div(g)) = g(div(/)).
Доказательство см. в работе [21].
Если фгСДАД—>С2(АД — рациональное ото-
бражение неособых кривых СДАГ) и С2/К), то
отображение §*:К/С2)* ->К/С})* задает ото-
бражение непостоянных рациональных функций.
Каждая рациональная функция с точностью до
константы определяется своим дивизором, по-
этому можно считать, что отображение ф* задает
отображение групп дивизоров:
ф*: Div(C2 /К)) -> Div(C, (АД) .
Теорема 6.16.8. Пусть ф: С] (АД —> С2 (АД—
рациональное отображение неособых кривых
Q(К) и C2/K),D— дивизор на кривой С2/К),
f— рациональная функция на кривой С2/К). То-
гда deg^*D) = deg^)deg(D), ф *(d i v(/)) = бй(ф*/).
Доказательство см. в работе [21].
6.16.3. Спаривание Вейля
Пусть К — конечное поле характеристики р и
Е/К— эллиптическая кривая. Предположим, что
на кривой Е/К существует точка простого поряд-
ка т > 2 и НО Д/р, т) = 1.
Рассмотрим эту эллиптическую кривую над
алгебраически замкнутым полем. Тогда каждая
точка кривой Е/К) является одновременно точ-
кой кривой Е/К), так как поле К содержит в
себе поле К. Точки кривых Е/К) и Е/К) образу-
ют абелевы группы с одним и тем же законом
сложения. Следовательно, £(АД_ является нор-
мальной подгруппой группы Е/К), и существу-
ет гомоморфизм из Е/К) в Е/К). Таким образом,
существуют точки кривой Е/К), имеющие поря-
док т. Эти точки образуют подгруппу Е[т] груп-
пы кручения. Число точек кручения порядка т
кривой Е/К) равно л?2. Все точки порядка т ле-
жат в некотором конечном расширении L поля К
Пусть Т— точка кривой Е/L), имеющая поря-
док т, то есть точка кручения порядка т. Тогда
по теореме 6.16.4 существует функция fT<=L/E)
на кривой Е/Е) с дивизором
div(/y) = т/Т) - т/Рх).
Пусть Т\ — точка кривой Е/L) такая, что
тТ\ = Т (при необходимости можно перейти к
расширению поля L). Пусть отображение [т]
138
кривой Е(Е) на себя задается умножением точки
Р е E(L) на число т:
[ли](Р) = тР.
Тогда можно составить композицию функции
fr и отображения [ли]:
(До[ш])(Р)=/7([™](Р)).
Эта функция имеет нули кратности т в тех
точках, которые после умножения на т дадут Т.
Такие точки имеют вид Ту + Д, где R, — любая из
тг точек порядка т. Функция fT ° [т] имеет по-
люсы кратности т в точках Д, которые после
умножения на т дадут Рт. Поэтому
div(4- [От]) = т (Т\ + R)-т £ (7?).
ReE[m] RcE[m]
Определим функцию gT g L(E) с дивизором
div(g7 )= X + R) - (Rf).
Функция gj существует, так как ее дивизор
имеет степень 0 и соответствующая сумма точек
на кривой равна (7, + R - R) = т2Тх - Р°,.
ReE[m]
Функции fr ° [/и] и gf имеют один и тот же
дивизор, поэтому с точностью до константы из L
имеем fT ° [т] = gm.
Пусть S g Е[т] — еще одна точка кручения
кривой Е(Е) (допускается и S = Т). Тогда для лю-
бой точки X g Е(Е) имеет место равенство
gfx+ST =f{\m\(X) + [ллл](5)) =
=/W) = gW'
Следовательно,
/ \m
g-AX + S)
I gTW J
Определим спаривание Вейля
e„. E\m\ © E[m\ -> {p„J,
где p,„ — корень степени ли из 1 в поле L, полагая
gT(X)
Здесь X— любая точка кривой Е(Е) такая, что
оба значения g(X) и g(X + S) определены и нену-
левые. Подчеркнем, что хотя g определена с точ-
ностью до ненулевой константы из L (известен
лишь ее дивизор), спаривание Вейля не зависит
от этой константы, так как она сокращается при
делении.
Спаривание Вейля эквивалентно можно опре-
делить с помощью значений функций на дивизо-
рах. Пусть Ds = (S)-(Pf), Dr=(T+R)-(R) —
дивизоры степени 0. Тогда найдутся функции fs,
gr с коэффициентами из L такие, что
div(/$) = m(S) - ли(7Д),
div(g7) = т(Т + 7?) - m(R).
Тогда
„ Щ) fs<T + R)gr(E)
Л } gT(Ds) fs(R)gr(S) ’
поскольку дивизоры функций fs, gr имеют непе-
ресекающиеся носители. Все вычисления прово-
дятся в поле L.
Теорема 6.16.9. Спаривание Вейля обладает
следующими свойствами:
1) билинейность: e„,{Sy + S2,T) = ein(Sy, T)e,fA T),
e,„(S, Ту + T2) = e,„(S, Ty)eltl(S, T2f
2) знакопеременность: e„,(S, T) = em(T, S)~l;
3) если о— элемент группы Галуа Gal(Z/7Q, то
en,(S,T)° = en,(S\ry,
4) существуют точки S, Т такие, что e,fS, Т) —
примитивный корень степени ллл из 1.
Доказательство см. в работе [21].
Из свойства 1 спаривания Вейля следует, что
это отображение при фиксированной точке Т яв-
ляется изоморфизмом группы кручения Е\т\ на
подгруппу порядка т мультипликативной группы
L . Кроме того, точки кривой Е(К), имеющие по-
рядок ли, являются точками кручения порядка т
кривой Е(Е). Тогда, если на эллиптической кривой
Е(К) выполняется равенство Р = IQ, то в группе L
выполняется равенство ет(Р, Т) = e„,(Q, Т)1. Точку
Т нужно выбирать так, чтобы значения спарива-
ния Вейля пробегали в L всю подгруппу порядка
ли. Имеем последовательность гомоморфизмов:
Е(К) E[m](L) -> L*.
Первое отображение означает переход от кри-
вой Е(К) к кривой E(L) над расширенным полем,
где число #L - 1 делится на ли. Второе отображе-
ние есть спаривание Вейля.
Подобрать точку Т порядка ли можно сле-
дующим образом.
1. Выбрать произвольную точку кривой Е(Е).
Например, для произвольного элемента
х g L\K извлечь квадратный корень у из
xi + Ах + В.
2. Найти число точек NL кривой E(L) по извест-
ному числу точек NK кривой Е(К) (подробнее
см. п. 6.17).
3. Найти Njfm = r. Вычислить г (х,у) и про-
верить, что результат отличен от Рж. Если это
условие выполнено, то положить Т <— (х, у).
139
Способ вычисления спаривания Вейля (под-
робнее см. п. 7.14), предложенный И.А. Семаевым,
основан на следующих рассуждениях.
В поле ЦЕ) определена и существует функция
Вейля h,„ с дивизором
div(/zm) = m(S) - (mS) - (т - 1 )(Ал) =
= /77(5) (АС ) О« - 1 )(^) =
= m(S) - т(Рсо) = div(^)
(нетрудно проверить, что сумма степеней диви-
зора и сумма точек с учетом кратности дают
нуль и точку Рт соответственно). Поэтому с точ-
ностью до константы из К имеем h,„ =fs.
По теореме 6.16.4 для произвольного нату-
рального к существует функция £, с дивизором
div(/^) = Ц8) - (kS) - (к - 1 )(£Д,
поскольку этот дивизор имеет степень 0 и сумма
точек дивизора на эллиптической кривой дает
точку Рт. Пусть к = и + v. Тогда
hk = gtl,vhuhv, (6.16.2)
h2.+^hlg2,2„
где
divfe,.,,) = ЦкЯ) + (uS) + (yS) - (£»).
Функция существует, так как ее дивизор
имеет степень 0 и сумма точек на эллиптической
кривой дает точку Рх. Покажем справедливость
равенства (6.16.2). Действительно,
div(^) = Ц8) - (kS) -(к- 1)(РЮ) =
= н(£) - (uS) - (и - 1 )(Р„) + v(5) - (v£) -
- (v - 1 ХР») - (kS) + (uS) + (v£) - (РЦ =
= div(/?„) + div(/?v) + div(guv).
Рекурсивное применение этой процедуры
сводит вычисление функции Вейля к вычисле-
нию линейных функций на кривой.
Таким образом, если #£(Fp) =р - 1, то группа
точек эллиптической кривой изоморфна группе
Fp , а если #£(Fp) =р + 1, то группа точек эллип-
тической кривой может быть вложена в группу
, так как (p + l)|#F^2 • Указанное вложение
вычислимо с полиномиальной сложностью.
Все изложенное справедливо и для эллипти-
ческой кривой £(F9), q =рт.
Теорема 6.16.10. Пусть #£(FP) = A Если
НОД(/?, N) = 1, то существует конечное расшире-
ние L поля Fp такое, что группа £(FP) вложима в
группуL .
Доказательство. Пусть (Z:Fp) = h. Тогда
#L =//' - 1. Вложение £(Fp) —> L существует,
если Аделитр" - 1, то естьр" = ] (mod А). В соот-
ветствии с китайской теоремой об остатках (тео-
рема 3.5.3) достаточно показать, что сравнение
р" = 1 (mod г) выполняется для степени простого
делителя г числа N. Поскольку р является обра-
тимым элементом кольца ШгАЦ указанное срав-
нение справедливо при п = <р(/) = r~\r - 1).
Если #£(Fp)=p, то группу точек кривой не-
возможно вложить в мультипликативную группу
поля ни при каком расширении. Однако в этом
случае, как показано в работе [19], существует
вычислимый с кубической от log/? сложностью
изоморфизм #£(FP) -> Fp. Этот изоморфизм су-
ществует для произвольной подгруппы порядка р
эллиптической кривой над конечным полем ха-
рактеристики р и представляет собой вычисле-
ние логарифмической производной функции
Вейля. В гл. 3 было показано, что если К(х) —
поле рациональных функций, то отображение
f'(x)
------> К для всех f е К(х) задает гомомор-
f(x)
физм групп К(х) —> К. Аналогичное утвержде-
ние имеет место и для функции Вейля на эллип-
тической кривой (см. также п. 11.3).
Алгоритм вычисления логарифмической про-
изводной функции Вейля приведен в п. 7.14.
Функция Вейля используется при анализе
криптографических алгоритмов с открытым
ключом, а также при разработке криптографиче-
ских алгоритмов на эллиптических и гиперэл-
липтических кривых.
6.17. Эллиптические кривые
над конечными полями
Пусть Ff/ — поле из q = р" элементов и
£(F9) — эллиптическая кривая, заданная уравне-
нием у2 = х3 + Ах + В. Число точек на кривой
£(F(;) конечно. Действительно, если предполо-
жить, что любой элемент поля может быть коор-
динатой х и при этом у Ф 0 ни для одной из точек,
то с учетом бесконечно удаленной точки получа-
ем \q + 1 - А] < q. Более точно число точек А на
эллиптической кривой определяется теоремой
Хассе. ..
Теорема 6.17.1 (теорема Хассе). Для кривой
£(F(;) выполняется неравенство
| q +1 - А | < 2-Jq.
Доказательство см. в работах [13, 21].
140
Таким образом, число точек эллиптической
кривой £(Ег;) близко к q.
Пусть число точек эллиптической кривой
£(Ег;): у2 = х3 + Ах + В равно N. Тогда число точек
эллиптической кривой £j(!F9): dy2 = x3+Ax + B,
где d не является квадратом в поле F9, равно
Ni = 2q + 2 - N. Действительно, значение
х3 + Ах + В может быть нулем, квадратом или
произведением квадрата на элемент d. Каждое
значение х, для которого х3 + Ах + В Ф 0, является
координатой двух точек (х, у) и (х, -у) только
одной из кривых. Значение х, соответствующее
у = 0, является координатой единственной точки
обеих кривых. Поэтому каждое значение х соот-
ветствует ровно двум точкам на объединении
кривых Е и Е\. С учетом бесконечно удаленных
точек получаемN+N}=2q + 2.
Кривые Е и £i являются скрученными. Скру-
ченные кривые изоморфны над квадратичным
расширением поля F9, так как квадратичное рас-
ширение эквивалентно присоединению квадрат-
ного корня из квадратичного невычета.
Если £(F/?) имеет число точек р + 1, то у скру-
ченной кривой столько же точек. В этом случае
эллиптическая кривая £(Fp) называется супервы-
рожденной. Группа точек супервырожденной
кривой с помощью спаривания Вейля может
быть вложена в группу F\ .
На алгебраической кривой C7F9, q=р”\ дейст-
вует отображение Фробениуса <р: (х, у) —> (xq,yq) с
характеристическим уравнением (см. теорему
6.14.5)
<р2 — <рТг(<р)deg(<p) = 0. (6.17.1)
Поскольку отображение <р является комплекс-
ным умножением, для точки Р g £(F,;) выполня-
ется равенство <р(Е) = QP, где целое квадратичное
число 0 является корнем уравнения (6.17.1) в
мнимом квадратичном поле Q(-v-D). Здесь
D = 4q- Тг(<р)2.
Квадратное уравнение (6.17.1) имеет два со-
пряженных комплексных корня: 0 и 0. Тогда
Тг(<р) = 0 + 0, где
|0|=|е|=^
0+0=2+1 -#£(F?).
Пусть г = #£(ЕД. Тогда в группе точек £(Ег;)
существует -v-£>(modr).16
16 В криптографии используются эллиптические
кривые, имеющие большой простой порядок группы.
Поэтому на практике число г является простым, при-
чем число точек кривой не делится на г2.
По аналогии с дзета-функцией Римана можно
определить дзета-функцию неособой алгебраи-
ческой кривой
00 ГГП \
Z(C/F9,T) = exp L
где #C(F^,)— число точек на кривой C/F9, рас-
сматриваемой над полем F^,. Если функция
Z(C! IFq, Т) известна, то для любого п можно най-
ти#^,):
#C(F „) = —!---— lnZ(C7F ,Т)
1 (и-1)!б/Г V q
. (6.17.2)
г=о
Теорема 6.17.2. Дзета-функция Z(C7F9, Т) не-
особой алгебраической кривой рода g (см.
п. 6.15) обладает следующими свойствами:
1) ЦС№Ч, Т) G Q(7);
2) Z(C /F а,Т) =---------- где полином
4 ' (1 — T)(l—qT)
Р(Т) степени 2g раскладывается на множите-
2g
ли над полем С: Р(Т) = J~[(l - сс,Т).
/.I
Доказательство см. в работах [2, 6, 21].
Для эллиптической кривой £/F(; имеет место
равенство
Z(£/F ,£) = X~aT + qT- . (6.17.3)
4 (1 —T)(l—дТ)
Коэффициент а в формуле (6.17.3) является
следом эндоморфизма Фробениуса: а = Тг(<р).
Определим функцию
1 — 4- 1-2л
^/F (,s) = Z(£7F = •
9 (1-q )(l~q *"')
Числитель в формуле (6.17.3) можно предста-
вить в виде (1 -а<7-4)(1 -a.q~s), где
|а| = |а| = 77-
Теорема Хассе эквивалентна гипотезе Римана
для эллиптических кривых', все нули функции
Cjj/f (л) лежат на прямой Re(.s) = 0,5.
Из уравнения (6.17.2) следует, что если
#Е(^ q) = q + ]~ci-u,
то
#£(F ) = ?"+1-а"-а". (6.17.4)
Формула (6.17.4) позволяет найти число точек
эллиптической кривой над произвольным конеч-
ным расширением поля Ff/, если известно значе-
ние ttEQFg).
Пример 6.17.1. Число точек кривой.
1. Эллиптическая кривая Е/ЪД у2 + ху = х + 1
содержит точки (0, 1), (1,0), (1, 1), Р«, то есть
#Е/^2= 4, Тг(<р) = -1. Характеристическое урав-
нение имеет вид <р2 + <р + 2 = 0, его корни равны
-1 ± -7-7 _ г
--------. Тогда отображение Фробениуса
(х, у) —> (х2, у2) на кривой E(F2) соответствует
умножению точки (х, у) на одно из чисел
-1 + лр7 -1-V=7 „
-------- или ----------. Число точек кривой
над F2 можно представить в виде
В соответствии с (6.17.4) число точек этой
кривой над полем из 211 элементов равно
= 2116.
2. Эллиптическая кривая Е/ Т4: у2 + ху = х? + t
содержит четыре точки: (0, 1), (0, t + 1), (t, 0), Рх.
Тогда Тг(<р) = 1. Характеристическое уравнение
имеет вид <р2 - <р + 4 = 0, его корни равны
1 ± -7-15 _ _
--------. Тогда отображение Фробениуса
(х, у) —> (х4, у4) на кривой E(F 4 ) соответствует
умножению точки (х, у) на одно из чисел
i+V-15 i-T^Ts тг
--------или----------. Число точек кривой над
F4 можно представить в виде
В соответствии с (6.17.4) число точек этой
кривой над полем из 47 элементов равно
Дзета-функция Z(E/ Fp, Т) эллиптической кри-
вой Е/Е„ несет информацию о числе точек над
всеми конечными расширениями поля Fp. Обоб-
щением дзета-функции эллиптической кривой
является L-функция Хассе-Вейля, которая несет
информацию о числе точек над всеми конечны-
ми полями.
Определим Z-функцию комплексной пере-
менной s
£<ад=П;---------5—
pfAl-Op/’ +Р
где произведение берется по всем простым чис-
лам, не делящим дискриминант кривой Е.
Согласно гипотезе Берча и Свиннертона-
Дайера ранг кривой E(Q) равен кратности нуля
s = l функции L(E, s). Если эта гипотеза верна, то
можно найти ранг эллиптической кривой не
только над полем Q, но и над числовым полем К,
немного изменив формулу для 1-функции.
Для нахождения числа точек эллиптической
кривой над конечным полем в общем случае
используется алгоритм Шэнкса с экспоненци-
альной сложностью или алгоритм Чуфа с поли-
номиальной сложностью (см. п. 15.1, а также
работу [18]).
Теорема 6.17.3 (теорема Чуфа). Число точек
#E(Fy) может быть найдено детерминированным
алгоритмом с полиномиальной сложностью.
Доказательство см. в работе [18].
6.18. Гиперэллиптические кривые
6.18.1. Функции на кривых
Гиперэллиптической кривой С над полем К на-
зывается аффинная кривая, задаваемая уравнением
у2 + h(x)y =Ях) (6.18.1)
и не имеющая особых точек на аффинной плос-
кости над К, где h, f— полиномы с коэффици-
ентами из К, deg(/) = 2g + 1, deg(/?) < g.
Натуральное число g называется родом кри-
вой. Эллиптическую кривую можно рассматри-
вать как гиперэллиптическую кривую рода 1.
Теорема 6.18.1. Если характеристика поля
равна 2, то h ф 0. Если характеристика поля от-
лична от 2, то с помощью обратимой аффинной
замены переменных можно задать гиперэллип-
тическую кривую уравнением
у2=/х), (6.18. Г]
Доказательство [23]. Пусть характеристика
поля равна 2 и h = 0. Положим Е'(х, у) = у2 -Дх).
Тогда F'y = 0. Пусть х0 — корень полинома F'x.
Тогда существует уо такое, что (х0,у0)еС(Х).
142
при этом обе частных производных обращаются в
О в точке (xq, j'o)- Д;1я того чтобы кривая не имела
особых аффинных точек, необходимо й # 0.
Пусть характеристика поля отлична от 2. То-
гда определено деление на 2. С помощью обра-
z ( у-Ых)^
тимой замены переменных (х, у) -> I х, -— -I
можно получить уравнение вида
где полином в правой части имеет степень
2g + 1. Поэтому уравнение кривой можно запи-
сать в виде (6.18. Г).
Для того чтобы кривая (6.18. Г) не имела осо-
бых точек в аффинной плоскости, необходимо,
чтобы полином / не имел кратных корней, то есть
чтобы его дискриминант был отличен от нуля.
Действительно, приравняв к нулю частные произ-
водные, получаем 2уо =f(xo) = 0. Для того чтобы
точка (а'о, j'o) лежала на кривой, необходимо, что-
бы fixo) — 0. Поскольку полином Дх) не имеет
кратных корней, множества корней fix) и f(x) над
К не пересекаются и (x,.,y,.)gC(K). Если же
полином fix) имеет кратный корень, то он будет
и корнем производной, тогда (х0,у0)еС(К) —
особая точка.
Над полем комплексных чисел гиперэллипти-
ческая кривая изоморфна замкнутой поверхности
без краев (у которой есть наружная и внутренняя
стороны) с g «отверстиями» аналогично тому, как
тор является замкнутой поверхностью без краев с
одним «отверстием».
Гиперэллиптическая кривая во многом анало-
гична эллиптической кривой. Пересечение соот-
ветствующей проективной гиперэллиптической
кривой с бесконечно удаленной прямой Z = 0 за-
дается условием Х=0. Таким образом, гипер-
эллиптическая кривая имеет единственную веско-
нечно удаленную точку Рт = (0,1, 0). Если g> 1,
то точка Ра является особой.
Если род g гиперэллиптической кривой отли-
чен от 1 (то есть deg(/) >5), то бесконечно уда-
ленная точка всегда является особой. Однако это
не накладывает ограничений на использование
такой кривой, поскольку на практике можно рас-
сматривать только аффинную часть кривой.
В общем случае прямая пересекается с гипер-
эллиптической кривой над алгебраически замкну-
тым полем более чем в трех точках. Например,
прямая у = 0 пересекается с кривой (6.18.Г) в
2g +1 точках (это следует из того, что правая
часть уравнения кривой имеет 2g + 1 корень над
К ). Поэтому арифметика на гиперэллиптической
кривой задается с помощью функций на кривой.
Аффинное координатное кольцо 7ДС] кривой
(6.18.1) задается как кольцо классов вычетов
К[х, у]/(у2 + h(x)y -.fix)). Поскольку полином
у2 + h(x)y -.fix) неприводим, кольцо Л’[6 ] целост-
ное, а также евклидово (см. теорему 6.15.1). По-
лем частных кольца Х[С] является поле рагшо-
налъных функций К(С).
Любой полином q(x,y) е К [С] можно запи-
сать в виде
q(x, у) = а(х) - Ь(х)у, (6.18.2)
где а,ЬеХ[х], поскольку на кривой С полином
у~ рекурсивно заменяется полиномом f-hy.
Для каждой функции вида (6.18.2) определим
сопряженную функцию вида
(х, у) = а(х) + b(x\y + h(x)).
Норма функции из поля функций равна
N(q) = X(q) = qqe К(х). Для (6.18.2) имеем
N(q) = а1 + abb - b2f е Х[х], норма является квад-
ратичной формой с коэффициентами h,f& Х[х].
Степень дискриминанта квадратичной формы
равна 2g + 1. Поскольку deg(JV(^)) > 0 при q £ К,
то квадратичная форма положительно определена.
Как и для квадратичных чисел, норма муль-
типликативна:
N(rs) = rs-rs = rrss = N(r)N(s).
Рациональная функция из К(С) также имеет
вид (6.18.2), но здесь а,Ь^К{х). Справедливы
равенства qy <у2 = qxq2 и 1/ q ~ Х/q.
Определим степень полинома q(x, у) = а(х) -
- Ь(х)у е К[С]: . ,
deg(<?) = max(2deg(n), 2g + 1 + 2deg(/?)).
Поэтому deg(<?) = deg(<?) = deg(A'(<7)). Непо-
средственной проверкой можно показать, что
deg(#i#2) = deg(<?i) + deg(^2), поэтому отображе-
ние deg является гомоморфизмом моноидов
Х[С] —> Z. Обратимыми элементами кольца Х[С]
являются ненулевые элементы из К.
Любая функция из поля функций с точностью
до константы задается списком нулей и полюсов,
то есть дивизором.
Функция q(x, у) е К(С) определена в аффинной
точке (хр, уР) е С(Х), если ее знаменатель отличен
от 0. Значение функции вычисляется как q(xP, уР).
Определим значение функции
q2(x,y)
в точке Рт. Если deg(<?]) < deg(#2), то q имеет нуль
в Рт. Если deg(^i) > deg(</2), то q имеет полюс в
143
Рт. Если deg(gi) = deg(g2), то q(PP) равно отно-
шению старших коэффициентов (по отношению
к функции deg) числителя и знаменателя.
Определим для точки Р = (хР, уР) е С(К) един-
ственную «противоположную» точку
P’ = (xP,-yP-h(xP)\ (6.18.3)
при этом по определению Р^ = Рт. Другие точки,
удовлетворяющие условию Р = Р', характеризу-
ются равенством уР = -уР - h(xp) или 2уР + h(xP) = 0.
Для любой точки Р справедливо равенство
(Р')' = Р.
Легко проверить, что с учетом (6.18.2) и
(6.18.3) для Р е С(К) справедливо равенство
д(Р)=д(Р')-
Лемма 6.18.2. Пусть Р е С(К), q = а{х) - Ь(х)у е
g К(С), q(P) = 0 и а, b не обращаются в нуль од-
новременно в точке Р. Тогда условия д(Р) = 0 и
Р = Р' эквивалентны.
Доказательство [23]. Если уР = -уР - Ыхр),
то Р = Р', и из д(Р) = 0 следует q(P') = q(P) = 0 .
Предположим, что Р ф Р' и а(хР) - Ь(хР)ур = 0,
а(хР) + b(xP)(h(xP) + уР) = 0. Вычитая первое урав-
нение из второго, получаем b(xp)(2yP + h(xP)) = 0,
отсюда Ъ(хр) = 0. Тогда и а(хР) = 0, что противо-
речит условию.
Теорема 6.18.3. Пусть q(x, у) е К(С), Р е
е С(К) — аффинная точка такая, что 2уР + h(xP) # 0
и q(xP,yP) = 0. Тогда существует представление
q(x, У) = (х - хР)тг(х, у) и г(хР, уР) <t {0, оо}.
Доказательство [23]. Запишем функцию q в
qq N(q) a2+abh-b2f
виде д - _ =-----------— . Здесь чис-
q q a — b(h + у)
литель как полином из Х[х] делится на х-хР.
Выделим максимальную степень полинома
х - хР, на которую делится числитель:
a2+abh-b2f _ (х-Хр)тд, _ v „
a-b(h + y)
при этом функция г(х,у) не имеет ни нулей, ни
полюсов в точке Р.
Теорема 6.18.4. Пусть Р е С'(К) — аффинная
точка такая, что Р = Р'. Тогда существует пред-
ставление функции х - Хр = (у - уР)2г(х, у), где
функция г е К(С) не имеет ни нулей, ни полюсов
в точке Р.
Доказательство [23]. Поскольку Р = Р', то
2jy + h(xp) = 0. Точка Р неособая, поэтому
h\xP)yP -f(xP) ф 0. Кроме того, fixp)=yP -
- h(xp)yP = yP - (2уР)уР = -ур. Отсюда
(У - УрУ =У2- ЪУр + Ур =.fix) ~ Кх)у ~ 2ууР + уР2.
Поэтому
(6.18.3)
г(х,у) х-х,, J х-х,, )
Заметим, что правая часть этого равенства яв-
ляется полиномом. Обозначим л(х) = (у - ур)2.
Тогда s(xP) = 0, но s'(x) =f'(x) - h'(x)yp, поэтому
s'(xp) Ф 0, то есть .s'(x) делится на х - хР, но не де-
лится на (% - хР)2. Поэтому правая часть равенст-
ва (6.18.3) отлична от 0 в точке Р.
Определим порядок нуля \:p(q) функции q{x,y) =
= а(х) - Ь(х)у е К(С) в точке Р следующим обра-
зом [23].
1. Пусть Р — аффинная точка и (х - хр)' — наи-
большая степень двучлена, на которую делят-
ся полиномы а(х) и Ь(х). Положим q(x,y) =
= (х - хР)’\а^х) - bt(x)y). Если at(xP) - bt(xP)yp #
# 0, то 5 = 0. Если Oj(xP) - bi(xp)yP = 0, то s —
наибольшая степень полинома х - хР, на ко-
торую делится N(a1 - by). Если Р = Р', то
гДд) = 2г + а; если Р ф Р', то гДд) = г + л.
2. Пусть Р = Рт. Тогда 4>(д) =-max(2deg(a),
2g + 1 + 2deg(Z>)).
Нулевая функция имеет бесконечно большой
порядок нуля.
Нетрудно убедиться, что тДд) является дис-
кретным нормированием. Как обычно, нормиро-
вание рациональной функции зададим как раз-
ность нормирований числителя и знаменателя
этой функции.
В качестве униформизующего параметра
нормирования тР гиперэллиптической кривой
обычно используется функция х - хр с дивизором
(7’)-|(7’') 2/’„.
6.18.2. Якобиан
Дивизор на гиперэллиптической кривой С(К)
представляет собой формальную сумму конечно-
го числа слагаемых D = ш,(Д). ±,?,
P.'CU) .
Теорема 6.18.5. Число нулей полинома q е А'[С]
равно числу полюсов с учетом кратности.
Доказательство. Пусть q = a-by, deg(g) = n.
Разложим норму на линейные множители над К :
Л (7) - П(л"
144
Поскольку поле алгебраически замкнуто, для
каждого Xj существует у, такой, что (А'„у,) е
е С(К). Тогда q имеет единственный полюс в
точке Рт и нули в аффинных точках (х,,у,). По
определению нормирования кратность полюса
равна п.
Поскольку рациональная функция из К(С)
является отношением двух полиномов, число ее
нулей равно числу полюсов с учетом кратности.
Следовательно, дивизор функции имеет нулевую
степень.
Норма функции является константой тогда и
только тогда, когда сама функция является кон-
стантой. Поэтому единственные функции, не
имеющие нулей и полюсов, — это ненулевые
константы. Дивизор таких функций имеет пустой
носитель и является нулем в группе дивизоров.
Если д'], 92 — рациональные функции, то
div(9i92) = div(9i) + div(92). Отображение div мож-
но рассматривать как гомоморфизм из мультип-
ликативной группы поля функций в конечномер-
ный Z-модуль (носитель дивизора).
Функции на кривой образуют группу по ум-
ножению, поэтому и их гомоморфные образы —
дивизоры функций — образуют группу главных
дивизоров и имеют степень 0. Следовательно, оп-
ределен и существует якобиан J(C) гиперэллип-
тической кривой С — факторгруппа дивизоров
степени 0 по подгруппе главных дивизоров.
Элементы якобиана определены с точностью до
главного дивизора, так же как классы идеалов
квадратичных порядков определены с точностью
до главного идеала. Поэтому группа классов
квадратичного порядка аналогична якобиану ги-
перэллиптической кривой.
Теорема 6.18.6. Каждый дивизор D е J(C)
может быть представлен в виде
гп
= С6’18’4)
1=1
где точки Р, не обязательно различны, причем в
носитель дивизора входит не более чем одна из
точек Р, Р'.
Доказательство. Допустим, что в дивизор
якобиана входят точки Р и Р'. Тогда этот дивизор
не изменится, если мы прибавим к нему или вы-
чтем из него главный дивизор (Р) + (Р') - 2(Р,ду
Выполняя эту процедуру несколько раз, полу-
чим, что хотя бы одна из точек Р или Р' в диви-
зоре сократится. Таким образом, можно утвер-
ждать, что в дивизор не входят одновременно
точки Р и Р'. Поскольку равенство Р = Р' выпол-
няется только при у = 0, точка (х, 0) может поя-
виться в дивизоре якобиана лишь один раз. Если
какая-то точка Р входит в дивизор с отрицатель-
ным показателем —пР, то, прибавляя к этому ди-
визору главный дивизор и(Р) + п(Р’) - 2п(Рк)..
заменим -п^Р) на п^Р') с положительным пока-
зателем.
Дивизоры вида (6.18.4) со свойствами, ука-
занными в теореме 6.18.6, будем называть полу-
приведенными.
Пусть ;
д =]>^p)-Q>?p)(pj,
^2=E«p(^)-(Xw/’)(^)
— полуприведенные дивизоры. Определим наи-
больший общий делитель дивизоров :
НОД( Д, Д>) = Е min(/w?, пр Х^)-
-(Emin(»6> А>))(Д )•
Лемма 6.18.7. Пусть Р = (хР, уР) е С(К) и
9 е К(С) — функция, регулярная в точке Р. Для
любого к > 0 существуют такие однозначно оп-
ределенные элементы с0, ср е К и функция
гк е К(С), регулярная в точке Р, что
А
я=Е с>(х ~ у + - хр У+1 •
1=0
Доказательство [23]. Элемент с0 = q(P) оп-
ределен однозначно, Р является нулем функции
9 - с0. Поскольку х — хр — униформизующий па-
раметр нормирования, можно записать q - с0 =
= (х - Хр)гь где функция щ определена однознач-
но. Поскольку 9 регулярна в точке Р, то и щ ре-
гулярна в Р. Далее действуем по индукции.
Лемма 6.18.8. Пусть Р = (хР, уР) — аффинная
точка такая, что Р Ф Р'. Тогда существует единст-
венная последовательность полиномов Ьр(х) для
к > 1 таких, что
- deg(^) < к,
- Ьк(хР)=уР;
- Ьк(х)2 + h(x)bk(x) =/Д) (mod Д - хР)к).
Доказательство [23]. Положим по лемме
6.18.7
А-1
Т = X <4 О -*/>)' + Д - Хр У гк-х
z=0
145
A—1
Определим i\(x) = Xе, (*--*/>)' . Тогда с0=ур
1=о
и Ьк =уР. Из уравнения у2 + hy =f для k > 1 полу-
чаем сравнение у2 + hy=f (mod (% - хР)к).
Наибольший общий делитель дивизоров име-
ет степень 0. Покажем, как полуприведенный
(неглавный) дивизор D можно представить в ви-
де наибольшего общего делителя двух главных
дивизоров, заданных полиномами из Х[С].
Теорема 6.18.9. Пусть
£=Xw^)-(XwM) -
полуприведенный дивизор и Р, = (х,, у,). Пусть
<а(х) = (а ~ х,.)"7' и Ь(х) — такой однозначно оп-
ределенный по лемме 6.18.8 полином, что
- deg(Z>) < deg(o);
- b(Xi) = у, для всех т, > 0;
- а делит Ь2 + bh -f.
Тогда D = HOfl(div(o(x)), div(/?(x) -у)).
Доказательство [23]. Пусть So и Si — мно-
жества тех аффинных точек из носителя дивизо-
ра, для которых соответственно Р = Р' и РфР'.
Пусть S2 = {F I Р е Si(D)}. Пусть носитель диви-
зора содержит т аффинных точек. Тогда
^Х^+Х"^)-^,)-
Докажем, что полином Ь(х) определен одно-
значно. Согласно лемме 6.18.8 для каждой точки
Р, е Sj существует единственный полином Ь,(х)
такой, что
- deg(Z>,) < т;,
- Ь,(х,)=у,;
- (х-х,Г\bi(x)2 + b,(x)h(x)~f(x).
Если Р, е So, то существует единственная кон-
станта bi — у, такая, что
- deg(Z>,)<l;
- bi(x,) =уг,
- (х - х,) I bt (x)2 + b, (x)h(x) - /(x).
По китайской теореме об остатках существует
единственный полином такой, что для всех i вы-
полняется сравнение
b(x) = b,(x) (mod(x - х,)"'-),
и для него выполняются все три условия теоре-
мы.
Докажем, что D является наибольшим общим
делителем главных дивизоров (о(х)) и (Ь(х) -у).
div(o-)= X 2(^)+ X т-(р,) +
/}е£0
+Х тхр^-то(рл
div(Z>-y) = X *АР,) + X S(p,) +
+ X тАр,)~ть(рЛ
Здесь Si > т» так как
(x-x,.)"'- \N(b-y) = b2 +bh-f.
Третье слагаемое в div(6 - у) можно не учиты-
вать, так как его носитель не пересекается с но-
сителем дивизора div(o'). Поэтому для Р е С(К)
полином х - х, делит b2 + bh -f.
Оценим коэффициенты /, для div(6 - у). Имеем
(х - х,) | Ъ2 + bh —f.
Найдем кратность корня N(b - у) в точке Р, е
So, вычислив производную b2 + bh -f в точке Р, с
учетом равенства й(х,) = у,.
2/>(х,)//(х,) + i>'(x,)/z(x,) + й(х,)/?'(х,) -/(х,) =
= й'(х,)(2у, + Zz(xz)) + /г'(х,)у, -/(х,).
Поскольку Pt = Р’ в So, то 2у, + й(х,) = 0, и
производная равна //(х,)у, -/(х,) # 0. Поэтому, х,
является корнем функции N(b - у) с кратностью
1, то есть /, = 1. Следовательно,
1IO/[(div(<7(x)), div(/?(x) -у)) =
= Х^+Ет^)-о=д
P^S0 P,eSt
На практике вместо 11ОД(61\(<7), div(6 - у))
часто используют сокращенную запись div(<7, b).
Нулевой дивизор можно записать как div(l, 0).
Поэтому каждый приведенный дивизор можно
записать как div(a, b).
Из доказательства теоремы 6.18.9 вытекает
следующее утверждение.
Следствие 6.18.10. Если а(х), b(x) е Х[х],
deg(6) < deg(<a) и a\(b2 + bh -f), то div(<7, b) — по-
луприведенный дивизор.
Представление элемента якобиана в виде по-
луприведенного дивизора в общем случае неод-
нозначно, так как прибавление к нему (вычита-
ние из него) дивизора произвольного полинома
меняет вид полуприведенного дивизора, но не
изменяет соответствующий элемент якобиана.
Покажем, как можно однозначно задать элемент
якобиана. -----
146
Полуприведенный дивизор (6.18.4) называет-
ся приведенным, если m<g, где g — род кривой.
Определим норму дивизора D = '£mj(Pi) как
| D |= | Ш/1. Среди дивизоров, эквивалентных
Р,*Р„
данному элементу якобиана, есть дивизор с ми-
нимальной нормой. Представление элемента
якобиана приведенным дивизором означает ми-
нимизацию его нормы.
Теорема 6.18.11. Каждый элемент якобиана
может быть однозначно представлен приведен-
ным дивизором.
Эта теорема будет доказана ниже.
Если рациональная функция f е К(С) не имеет
полюсов среди аффинных точек С (К), то/е К[С],
то есть функция является полиномом.
Сложение двух приведенных дивизоров
Д = div(ob 6]) и Д = div(a2, b2), представленных
полиномами, выполняется в два этапа: сначала
вычисляется полуприведенный дивизор, соответ-
ствующий сумме дивизоров, затем выполняется
его приведение. Пусть D = div(a, b) = Д + Д. Для
вычисления div(<73, bi) необходимо выполнить
следующие действия.
1. Расширенным алгоритмом Евклида най-
ди di = НОД(сц, а2) в АД] и линейное
представление di = еуа\ + е2а2.
2. Расширенным алгоритмом Евклида найди
d = НОД(Д 1у + Ь2 + й) в АД] и линейное
представление d = cxd\ + c2(bi + Ъ2 + й).
3. Положить sj = Ci6i, s2 - с2е2, s2 = с2, так что
d ~ AiGi + s2a2 + хз(й>! + Ь2 + й).
4. Положить
а. а,
Л — 1 L
d2 ’
, s,a,b2 + s2a2b. + s3(btb2 + f), , .
d
Теорема 6.18.12. Дивизор div(<7, й) является
полуприведенным и D = Д + Д.
Доказательство [23]. Поскольку d\d], то а
е АД]. Покажем, что b е К[х]. Имеем
_ sxa}b2 + s2a2bA + s3(bAb2 + f) _
~ d ~
_ b-Ad-s^ -s3(bx +b2 + h))+s2a2bl + s3(bxb2 + f)
- d ’
= b f (fii ~b2)-s3fe2 + b2h- f)
2 d
Поскольку d i a2 и a21 (b2 + b2h - /), to 6 g АД].
Представим полином b(x) в виде
, s.a.b2 +s?a,b. + s3(b.b2 + /') ,
Ь=-1-±Л---2_2J---1 2. J ’ +sa, где 5 e щ
d
Тогда
b _ = Д& + s2a2bi + лз (bjb2 + f)-dy +
У d
sxaxb2 + s2a2bx + s3(bxb2 + f)-dy
+ sa~
d
s2a2y + s3 Д + b2 + h)y
________
Поэтому
b _ = дА-у)+уШ~у) +
d
+ (6.18.5)
d
Покажем, что a | (й2 + bh - f). Действительно,
й2 + bh - f равно произведению левой части
(6.18.5) на сопряженную функцию. Из а\ | Ъ\ +
+ й]й -/= (Й1 - y)(bi + й + у) и б721 Ь22 + й2й -/=
= (Ь2 - у)(Ь2 + й + у), следует, что ауь делит каж-
дое из слагаемых S\O\(b2 - у), s2a2(b\ - у), s2(b\ -
-y)(b2 - у). По следствию 6.18.10 div(o, й) — по-
луприведенный дивизор.
Покажем, что Д = Д + Д и точка Р лежит в
носителе дивизора Di или Д.
Пусть Р # Р', vP(Di) = т2, Vp'(D\) = 0, 1>(Д) -
= т2, гр(Д) = 0 и т}, т2 > 0. Тогда 17Д1) = пц,
vp(bi - у) > тл, vl-(a2) = т2, vp(b2 - у) > т2. Если
л/i = 0 или т2 = 0, то гР(б/|) = vP(d) = 0. Поэтому
гДт?) = т2 + т2. Если > 0 и т2 > 0, то из усло-
вия (й] + b2 + li)(,xp) = 2jy + й(л>) Ф 0, получаем
г/Д) = 0 и Г/Д) = + т2. Согласно (6.18.5) име-
ем гР(й - у) > min(?wi + т2, т\ + т2, т\ + т2) - тх +
+ т2. Поэтому гДД) = т2 + т2.
Пусть Р Ф Р', ViiPi) = mi, Vp(D2) = т^ и mi > т2 > 0.
Тогда Г/Д) = mi, vr(a2) = т2, Vpfdi) = т2, г,<й] -
- у) > mi, viib2 - у) = 0 и vp(b2 - у) > т2. Поэтому
Г/>(й2 + й + у) > т2 и 1>(й| + й2 + й) > т2. Отсюда
следует, что vp(d) = т2 и v/Д) = пц - т2. Из
(6.18.5) получаем, что гДй - у) > mi - т2. Поэто-
му гДД = mi ~ т2.
Пусть Р = Р'. Возможны два случая: точку Р
содержат оба дивизора Di и Д или только один из
них. Пусть гДД) = Г/>(Д) = 1. Тогда Vp(ai) =
= 17Д2) = 'лДА) = 2. Поскольку (bi + й2 + h)(xP) =
= 2jy + h(xP) = 0, то Vp(bi + й2 + й) > 2 и 1-7Д) = 2,
Г/>(а) - 0. Поэтому V/>(D) = 0.
Пусть vp(D1) = 1, гр(Д) = 0. Тогда 17Д1) = 2,
V/Дг) = v/ДО = Vp(d) = 0, Ур(а) = 2. Поскольку
147
iyf/д - у) = 1, то из (6.18.5) получаем \y(b - у) > 1.
Однако случай i>(/? - у) > 1 невозможен. Дейст-
вительно, из предположения \у(Ь - у) > 1 следует
V/<52«2 + $з(Ь2 -уУ) > 1 и vP(s2a2 + у(/>1 + Ь2 + й)) > 1,
что ведет к противоречию. Поэтому vP(D) = 1.
Приведение полуприведенного дивизора
div(o, Ь) —> divfc/, b') выполняется следующим
образом.
, п , f + bh-b2 ,, . .
1. Положить а ----------, b = -п - b
а
(mod а').
2. Если deg(o') > g, положить а <— d, b <— Ь'
и перейти на шаг 1.
Для удобства можно представить d полино-
мом с единичным старшим коэффициентом, ум-
ножив его на соответствующую константу, при
этом нули и полюсы полинома d не изменятся.
Докажем теорему 6.18.11 с помощью данного
алгоритма. Доказательство выполним в три этапа.
Сначала докажем, что deg(o) < g, затем что диви-
зор div(<7, b') полуприведенный, и что div(o', b')
и div(<7, b) представляют один и тот же элемент
якобиана.
Если deg/o) = тп, deg/й) = и, где т >пи т >g +
+ 1, то deg/c/) = max(2g + 1, 2и) - т. Если т > g +
+ 1, то max(2g + 1, 2п) < 2(т - 1) и degdy/) < т - 2.
Если т = g + 1, то max(2g + 1, 2и) = 2g + 1 и
degdZZ) = g. Поэтому degA(rZ) < g.
Поскольку/- bh - b2 = ad, то
f+(b' + h)h - (b' + h)2 = 0 (mod d),
f-b'h- b'2 = 0 (mod d).
По следствию 6.18.10 дивизор div(a, b) — по-
луприведенный.
Разобьем носитель дивизора S на непересе-
кающиеся подмножества аффинных точек So =
= {Р\Р = Р'}, Si = {Р|Р # Р'} и S2 = {Р': Р е 5J.
Тогда по теореме 6.18.9 имеем
D=X^+Xm^-^pJ-
Pi<=S0 PfeSi
Тогда
div(o) = £ 2(Д) + т,{Pl)+^mi{Pl,)-ma(Рк),
TJeSb PtsSi PfCSi
div(£ ~ т) = X (Д) + X +
P,eS0 PfsSi
+ Ys^~mb^-
№3
Здесь 53 = 5 \ {50 о 5] о 52}, n, > m,, s, > 1, и
Si = 1 для P = P'. Из равенства b2 + bh-f= N(b - v)
следует, что
div(62 + M-/)= £2(Д)+ Хи,.(Д) +
P,eS0 PfeS\ •-
+ 2>,m+ X x Ъ(Р^-т(Рк).
P,sSt P,eS3 l‘,eS:t
Поэтому div(a') = div(/?2 + bh -f) - div(o') =
= X'^)+X^')+X^)+
P,eS}' P^S^ PfeS3
+ ^т~тАРЛ
p.^
где /, = n, - m, и 5/ = {P, e Sj : n,> m,}. Можно
записать b' = -h - b + sd, где л g К[х]. Для точек
Pt= (-V, yi) е 5/ и 53 справедливо равенство
Р(х,) = -/?(%,) - b(x,) + s(Xi)a'(xl) = -h(Xi) - yt.
Тогда рассуждая как при доказательстве тео-
ремы 6.18.9,получаем
div(6--y)= X °^)+ X X °w+
P^S}' P,eS}' />е53
+Х wx^')+ X z,(Pi)~mh-(pj,
Pi е^з Pt e54
где г, > w, > s,; w, = 1, если P, = P'-, 5i = 5\ {5Z u 5з}.
Поэтому
div(a',b')= t,P'+ s,Pi'-m\Px)'~
7,g5i'
~-X^'-X 5, Д' + m \PK )-D- div(b - y).
P^S,' P,eS3
Здесь - — символ эквивалентности дивизоров
в якобиане.
Алгоритмы вычислений в якобиане гиперэл-
липтической кривой приведены в п. 7.15.
Обозначим через J\m\ якобиан порядка т ги-
перэллиптической кривой С(К), где поле К ко-
нечно. На кривой С(К) можно определить спари-
вание Вейля е„„ устанавливающее вложение яко-
биана J[m] в мультипликативную группу расши-
рения L поля К, порядок которой делит порядок
якобиана.
Можно записать J[m] = Div°[m]/Pr(C(Z)), где
Div°[m] — группа дивизоров степени 0 таких, что
для любого D е Div°[m] дивизор mD является
главным. Пусть {ц,„} — группа корней степени т из
1 в L . Если D], D2 е Div°[m] — дивизоры с непере-
секающимися носителями, Д,Д е Т(С) — функ-
148
ции с дивизорами div(/o ) = mD\, div(/o2) = mD2, то
можно определить функцию
wm: Div°[m] © Div°[/w] -> {ц,,,},
fD1W
С помощью функции му, определяется спари-
вание Вейля
ет: J[m\ © J[m] -> {ц,„}
следующим образом. Пусть А, В е J\m\ и носи-
тели дивизоров D], D2 е Div°[mJ не пересекают-
ся, при этом D] е A, D2 е В. Тогда
ет(А, В) = w,„(Di, D2).
Спаривание Вейля на гиперэллиптических
кривых является важным инструментом при ана-
лизе криптографических алгоритмов с открытым
ключом.
Упражнения к главе 6
1. Касательные в двух различных точках Р и Q
эллиптической кривой, заданной в форме
Вейерштрасса, пересекаются в некоторой
точке эллиптической кривой. Покажите, что
точка Р -Q имеет нулевую у-координату.
2. В точке перегиба эллиптической кривой про-
ведена касательная. В какой еще точке она
пересекает кривую?
3. Покажите, что точки кручения эллиптиче-
ской кривой образуют группу.
4. Приведите примеры изогений на эллиптиче-
ской кривой. Что такое нулевая изогения?
5. Эллиптическая кривая над конечным полем
задана уравнением у2 = (х - а)(х - Ь)(х - с). Яв-
ляется ли группа точек кривой циклической?
6. Является ли редукция поля комплексных чи-
сел по модулю решетки с периодами (щ, со2
гомоморфизмом колец?
7. Поясните, чем отличаются изоморфизм и би-
рациональный изоморфизм кривых. Приве-
дите примеры.
8. Каким образом из фундаментального парал-
лелограмма получается тор и обратно? Чему
на торе соответствуют вершины фундамен-
тального параллелограмма? Существует ли
на торе образ бесконечно удаленной точки?
9. Установите взаимно однозначное соответст-
вие между точками коники над IR и точками
прямой над R методом проектирования точки
на прямую. Будет ли это отображение бира-
циональным изоморфизмом, изоморфизмом,
морфизмом?
10. Установите соответствие между вырожден-
ной кубикой у2 =х3 +х2 и прямой путем па-
раметризации. Является ли это соответствие
взаимно однозначным отображением, мор-
физмом, бирациональным изоморфизмом,
изоморфизмом алгебраических кривых, изо-
морфизмом групп?
11. Покажите, что эллиптические функции с
одинаковым фундаментальным параллело-
граммом образуют поле.
12. Является ли кривая у2 = х3 + ах2 + Ьх + с над
алгебраически замкнутым полем характери-
стики 2 эллиптической?
13. Является ли кривая у2 = х3 + b над алгебраи-
чески замкнутым полем характеристики 3
эллиптической?
14. Является ли особая кубическая кривая
у2 = х3 + А'2 неприводимой?
15. Может ли характеристическое уравнение эн-
доморфизма Фробениуса иметь нулевой ко-
рень?
16. Покажите, что идеал нормирования поля
К(Е) рациональных функций на кривой Е со-
держит все необратимые элементы кольца
нормирования и является главным.
17. Для кривой E(Q): у2 = х3- 1 приведите пример
функции, являющейся обратимым элементом
кольца нормирования в точке (1, 0), и функции,
являющейся необратимым элементом этого
кольца нормирования. Найдите униформи-
зующий параметр нормирования в этой точке.
18. Пусть Е(Ку. у2 =х3 -х — эллиптическая кри-
вая. Найдите ошибку в следующих рассуж-
дениях по вычислению значения нормирова-
ния функции f = — в точке (0, 0): «Если f
У
имеет значение нормирования k, то /2 имеет
значение нормирования 2А. Получаем
2 _ хг _ х2 _ х
у2 х3 -х х2 -1
149
Функция/1 2 при х = 0 имеет нуль кратности 1.
Значит, / имеет в точке (0, 0) нуль дробной
кратности 1/2».
[9. Найдите значение нормирования функции
х2 -х
f = ----— на кривой E(Q): у = х3 4 5 - х в точ-
2у
ках Р = (0, 0) и Q = (1, 0).
10. Покажите, что нормирование поля функций
на эллиптической кривой Е(К) в точке Р яв-
ляется гомоморфизмом из (А7(7£)) в Z. Най-
дите образ униформизующего параметра
нормирования.
11. Пусть/= х2 + у — функция на эллиптической
кривой у2 = х3 + 4.x2 - 4х. Найдите число ну-
лей и дивизор этой функции над алгебраиче-
ски замкнутым полем.
12. Дивизоры функций на кривой имеют степень
0 и образуют подгруппу в группе дивизоров.
Образуют ли подгруппу дивизоры функций,
имеющих нуль в данной точке Р кривой?
13. Является ли аффинное координатное кольцо
гиперэллиптической кривой факториальным?
14. Пусть Е — эллиптическая кривая вида у2 =
3
= х -х над полем характеристики, отличной
от 2 и 3. Найдите представление дивизора
функции ху как дивизора на кривой.
15. На эллиптической кривой, заданной уравне-
нием (6.7.7) над полем характеристики, от-
личной от 2 и 3, существует функция /с ди-
визором div(/) = -2(Р) + 2(P„j. Что можно
сказать о координатах точки Р?
26. Может ли эллиптическая кривая над полем
характеристики, отличной от 2 и 3, иметь
функцию/с дивизором div(/) = 3(E) - 3(Рт)2
27. Рациональные функции на эллиптической
кривой образуют поле. Что собой представ-
ляют дивизоры функций, являющихся нулем
и единицей в этом поле?
28. Является ли кольцо аффинных координат
эллиптической кривой целостным? Может ли
кольцо аффинных координат алгебраическо-
го многообразия иметь делители нуля? При-
ведите пример.
29. Пусть Е/К—эллиптическая кривая. Покажи-
те, что при переходе к алгебраическому за-
мыканию поля К любая функция из кольца
Х[£] с точностью до константы представля-
ется в виде дроби, числитель и знаменатель
которой являются произведениями полино-
мов, задающих прямые, проходящие через
точки кривой Е(К).
30. Пусть Е/Г5: у2=х3 + Зх— эллиптическая
кривая и f— функция с дивизором div(/) =
= ((0, 0)) + ((1, 2)) - ((2, 2)) - ((4, 1)). Найдите
/(4,4)//(2,3).
31. Пусть Е(К} — эллиптическая кривая над ал-
гебраически замкнутым полем. Кольцо поли-
номов от двух переменных Аф.х'.у] содержит
неприводимые полиномы. Однако функции на
кривой из кольца аффинных координат, яв-
ляющиеся элементами кольца Е[Е], раскла-
дываются на линейные множители. Почему?
32. Покажите, что эндоморфизм Фробениуса на
эллиптической кривой над конечным полем
коммутирует с любым эндоморфизмом.
33. Почему комплексное умножение позволяет
ускорить умножение точки на число?
34. Пусть Qp —алгебраическое замыкание поля д-
адических чисел. Можно ли в поле Q/? ввести
аналог функции Вейерштрасса и с его помощью
параметризовать эллиптическую кривую?
Литература к главе 6
1. Ван дер Варден Б.Л. Алгебра. М.: Наука, 1979.
2. Коблиц Н. Введение в эллиптические кривые и
модулярные формы. М.: Мир, 1988.
3. Ленг С. Эллиптические функции / Пер. с англ.
С.А. Степанова. Новокузнецкий физико-матема-
тический институт, 2000.
4. Прасолов В.В., Соловьев Ю.П. Эллиптические
кривые и алгебраические уравнения. М.: Изд-во
«Факториал», 1997.
5. Рид М. Алгебраическая геометрия для всех. М.:
Мир, 1991.
6. Степанов С.А. Арифметика алгебраических кри-
вых. М.: Наука, 1991.
7. Хартсхорн Р. Алгебраическая геометрия. М.:
Мир, 1981.
8. Ходж В., Пидо Д. Методы алгебраической гео-
метрии. М.: ИЛ, 1955.
9. Шафаревич И.Р. Основы алгебраической геомет-
рии. М.: Наука, 1988.
10. Cantor D. Computing in the jacobian of a hyperellip-
tic curve // Mathematics of Computation. 1987.
Vol. 48. P. 95-101.
11. Dolgachev Г. Lectures on Modular Forms //
www.math.lsa.umich.edu/~idolga/lecturenotes.html.
12. Fulton W. Algebraic curves. New York: Benjamin. 1969.
13. HusemollerD. Elliptic curves. Springer-Verlag, 1987.
14. Koblitz N. Hyperelliptic cryptosystems // Journal of
Cryptology. 1989. Vol. l.P. 139-150.
15. Lercier R., Morain F. Algorithms for computing
isogenies between elliptic curves // Computational
perspectives on number theory. AMS/1P Studies on
Advanced Mathematics. Vol. 7.
16. Mazur B. Rational points on modular curves. Lecture
Notes in Mathematics. Springer-Verlag, 1976. Vol. 601.
17. Schoof R. Counting points on elliptic curves over
finite fields // Journal de Theorie des Nombres de
Bordeaux. 1995. Vol. 7. P. 215-254.
18. Schoof R. Elliptic curves over finite fields and the
computation of square roots mod p 11 Mathematics of
Computation. 1985. Vol. 44. P. 483-494.
19. Semaev LA. Evaluation of discrete logarithms in a
group of /> tors ion points of an elliptic curve in char-
acteristic p II Mathematics of Computation. 1998.
Vol. 67. P. 353-356.
20. Shanks D. Class number, a theory of factorization,
and genera // Proceedings of Symposia in Pure
Mathematics. 1969. Vol. XX. New York: Number
Theory Institute. American Mathematical Society,
1969. P. 415-440.
21. Silverman J.H. The arithmetic of elliptic curves.
Springer-Verlag, 1986.
22. Semaev LA. Elliptic curve points over the maximal
multiquadratic extension of rational numbers //
www.wis.kuleuven.ac.be/algebra/artikels/semaev.htm.
23. Menezes A.J., Wu Y.-FL, Zuccerato R.J. An elementary
introduction to hyperelliptic curves // Technical report
CORR 96-19, university of Waterloo, Canada, 1996.
http://www.securitytechnet.com/crypto/algoriflim/ecc.htmL
Глава 7. ВЫЧИСЛИТЕЛЬНЫЕ АЛГОРИТМЫ
АЛГЕБРЫ И ТЕОРИИ ЧИСЕЛ
В этой главе приведены некоторые алгорит-
мы, часто используемые в криптографии. Алго-
ритмы линейной алгебры (решение системы ли-
нейных уравнений, вычисление ранга матрицы,
нахождение линейно зависимых строк матрицы,
умножение и обращение матриц) остались за
пределами данной книги.
7.1. Алгоритмы умножения
Алгоритмы умножения целых чисел и поли-
номов обладают большим сходством, поскольку
представление числа U е 2Z в позиционной сис-
теме счисления с основанием Ъ в виде
л-1
U = , где и, g TEJlyZL, аналогично представ-
,=о
л-1
лению полинома 67(х) = из кольца
/=0
(Z/ftZ)[x]. Однако отображение х <-> b не являет-
ся изоморфизмом колец (Z7Z?Z)[x] и Z, посколь-
ку при сложении чисел возникает перенос в сле-
дующий разряд, а при сложении полиномов пе-
ренос отсутствует.
Умножение чисел и полиномов с помощью
микропроцессора требует выполнения сложения
и умножения слов. Длительность операции сло-
жения и умножения слов зависит от типа про-
цессора. При этом длительность сложения не
превышает длительности умножения.
7.1.1. Алгоритм умножения
Карацубы-Офмана
Пусть U(x) и V(x) — полиномы степени не бо-
лее 2т - 1 из кольца ТДх]. Для умножения этих
полиномов представим их в виде
Цх) = Щх)хт + U0(x), V(x) = Г1(х)х'п + F0(x),
где deg(t/i), deg(t/0), deg(Fi), deg(K0) < m - 1.
Тогда имеет место равенство
UV= U^' + (Щ + t/oXFi + Vo) -
~ UjV - Uovo)x” + uovo.
Здесь вместо четырех умножений (как при
умножении «в столбик») полиномов степени
т - 1 требуется только три. Операция умноже-
ния полинома на х” выполняется сдвигом масси-
ва коэффициентов и имеет линейную сложность.
Асимптотическая сложность алгоритма при
умножении полиномов степени п равна
<?(3Llog2 "+,J) = О(т№23><9(«’’58).
Этот алгоритм эффективен, если операция
умножения слов выполняется медленнее, чем
операция сложения.
Умножение целых чисел происходит анало-
гично: вместо переменной х нужно подставить
2Л, где Ъ — разрядность процессора, а при сло-
жении чисел учитывать переносы.
7.1.2. Умножение в классах вычетов
Алгоритм умножения в классах вычетов,
предложенный А. Шенхаге [10], основан на ис-
пользовании китайской теоремы об остатках
(теорема 3.5.6). В силу изоморфизма колец клас-
сов вычетов
7LIMZL = ZVrnoZ © ... © Z/»4„iZ;,
где М= т0...тк-\, знаком «®» обозначена прямая
сумма колец, каждое число из единствен-
ным образом можно представить в виде набора
элементов классов вычетов по модулям т>. При
этом сумме и произведению чисел соответству-
ют суммы и произведения по модулям т,. Для
умножения двух больших чисел длины не более
(log2A/)/2 можно действовать по следующей
схеме.
1. Перейти к представлению сомножителей в
классах вычетов по модулям т,.
2. Вычислить произведения сомножителей по
модулям т,.
3. Восстановить произведение по китайской
теореме об остатках.
Пусть максимальный размер входа алгоритма
равен п. Тогда произведение будет иметь длину
не более 2п. Найдем к взаимно простых (но не
обязательно простых) чисел то, ...,mk-i таких,
что их произведение
A--I
/=0
имеет длину больше 2п. Для умножения двух
чисел U и V по модулю числа N можно выбрать
М> (N- ])2, поскольку каждый из сомножите-
лей меньше N. Представим U и V в системе клас-
сов вычетов по модулям то, ..., тк^у.
Л=*/2
V/2-1
+ n
V=V2 7 '-o
A--1
(mod M),
где
Mb = m0...m,_iml+i...mk/2_},
M2j^mk/2...mJ-imj+i...mk_i.
</г/2-1
W= yM.,N,w,
/ J If I I
U = iij (mod те,), V = v, (mod m,), 1 <i<k.
Таблица чисел mt фиксирована, поэтому мож-
но заранее вычислить вспомогательные величи-
ны
М, = тот} ...т^т^ ...тк_А (mod m,),
Nj = М~г (modmi).
На практике удобно выбирать число к так, что-
бы оно было степенью двойки. Нахождение выче-
тов по модулям т, можно ускорить следующим
образом: сначала вычислить произведения тот\,
т2тз, пцпц, т^т^,после этого — произведения
топцт^пц, пцпцтвп^, т^т^т\оШ\\, ..., затем
то-..т-i, mg...mi5, ... и т. д. и, наконец, найти с по-
мощью «деления пополам» вычеты по соответст-
вующим модулям. Пусть известен вычет х по мо-
дулю mom^m-i. Тогда представление х по моду-
лям тот\ и т2тз будет иметь вид:
х = Л'о| (mod тот{), х = х2з (mod т2тз).
Находим вычеты по модулям то, ..., ту.
хо 1 = хо (mod то), Xoi = *1 (mod гщ),
х2з = х2 (mod т2), *23 = Х3 (mod m3).
Для перехода от представления в классах вы-
четов к обычному надо воспользоваться китай-
ской теоремой об остатках:
к-1
w = UV = ^щ,М,Л(тобМ), (7.1.1)
i=0
где w, = W (mod mt).
Процедуру вычисления W можно ускорить,
поскольку слагаемые WjMNi для разных i имеют
много общих делителей. Например, пусть к = 2'.
Тогда все WiMNj, где 0 < i < к - 1, имеют общий
делитель вида mQmx...mki-1_i, если i>k/2, и
mki2mki2+\—mk-\ > если i<k/2. Поэтому запишем
(7.1.1) в виде
Данное разбиение дает возможность приме-
нить тот же метод, что и при нахождении остат-
ков по модулю mt.
Найдем произведения подряд идущих двух,
четырех, восьми и т. д. модулей: тот\, т2тз, ...,
тк-2тк-\, т0т1т2т3, , тк_^к_зтк-2тк_х,.... Обо-
/+2'|
значим через х^ = PJ777, произведение 2' под-
ряд идущих модулей, начиная с т,. Найдем це-
лые числа
Для ускорения вычисления у^ можно восполь-
зоваться рекуррентной формулой:
У,о = N,Wi,
Уу = -1
Тогда yOl = W.
Пример 7.1.1. Умножение в классах вычетов.
Найдем произведение чисел 67=31, Г=57.
Пусть (т0, т\, т2, ту) = (5, 6, 7, 11), М = 2310.
Вычисляем Ху, Ny.
х00 ~ 5, Хю — 6, %20 ~ 7, Хзо — 11,
Xoi = 30, х21 = 77, х02 = 2310,
N0 = 3,Ni = 1,7V2 = 1,M= 1.
Находим векторы U= (1,1,3,9), V= (2,3,1,2).
Тогда W = (2, 3, 3, 7). Отсюда
Уоо = WoNo = 6, у10 = = 3,
У20 = = 3, узо = W3N3 = 7,
Уот =yoo*io +Т10Х00 = 515 У21 =у2оХзо + УзоМо = 82,
У02 =Уо1*21 + УиХо] — 6387.
153
Поэтому W=yo2 (mod M), W= 1767. Вычисле-
ние Уд можно проводить по модулю М.
Асимптотическая сложность рассмотренно-
го алгоритма равна iogA). Практически
данный метод умножения эффективнее, чем
умножение «в столбик», лишь тогда, когда
длина сомножителей превышает разрядность
процессора в десятки раз. Наибольший вклад в
сложность дают процедуры перевода сомно-
жителей в классы вычетов и восстановление
произведения. Если выполняется подряд не-
сколько умножений небольших сомножителей
без восстановления промежуточных произве-
дений, то необходимо принять меры, исклю-
чающие «переполнение», при котором произ-
ведение превышает модуль М.
Поскольку китайская теорема об остатках
справедлива для произвольных коммутативных
колец, то этот метод умножения очевидным об-
разом переносится и на кольца полиномов над
целостным кольцом, например, на кольца Ер|7].
Необходимо лишь, чтобы сумма (w,) + (my) двух
любых различных идеалов совпадала с кольцом.
Идеи, положенные в основу данного метода,
могут использоваться в других областях инфор-
мационной техники, например, при разработке
корректирующих кодов. Китайская теорема об
остатках устанавливает требуемый изоморфизм
колец, а приведенный выше способ обеспечивает
быстрое вычисление прямого и обратного изо-
морфизма.
7.1.3. Умножение с помощью
быстрого преобразования Фурье
Этот метод умножения, предложенный Шен-
хаге и Штрассеном, основан на использовании
гомоморфизма целостных колец /?[х] и R и теоре-
мы об интерполяции полиномов из /?[х] (см. тео-
рему 4.6.1). Имеет место вычислимый в обе сто-
роны изоморфизм 7?[x]/(/(x)) s К'. В качестве fix)
используются полиномы х ± 1, сомножители
задаются значениями в корнях степени п из +1 в
кольце частных кольца R, п является степенью
двойки, кольцо R имеет вид TLImT., где
т = 2к + 1. В этом случае прямой и обратный
изоморфизмы вычисляются как быстрое преоб-
разование Фурье.
Пусть ср — отображение, задающее интерполя-
цию полинома в корнях степени п из 1. Вследствие
указанного изоморфизма имеет место равенство
fiah) = ср(<2)ср(й), поэтому ab = <p-1(<p(cz)cp(£>)). Ал-
горитм умножения предусматривает представле-
ние чисел как полиномов, вычисление быстрого
преобразования Фурье (БПФ) для сомножителей,
их покомпонентное умножение и вычисление об-
ратного БПФ (см. п. 4.6).
Определим положительно обернутую свертку
и отрицательно обернутую свертку «-мерных
векторов а, Ь. Положительно обернутая сверт-
ка — это /7-мерный вектор d такой, что
/ иЧ
а,=ХаЛ-2+Ха2Ь^-J
j=0 j=i+l
Отрицательно обернутая свертка — это 77-
мерный вектор е такой, что Кг?;г ,
I /1-1
7=0 7=7+1
Обычная свертка — это вектор с = (с0,..., c2llfi)
коэффициентов произведения в А[х] двух поли-
номов степени 77 - 1; отрицательно обернутая
свертка— вектор е коэффициентов произведе-
ния тех же полиномов в 7?[х]/(х" + 1), при этом
е, = с, - с„+/; положительно обернутая свертка —
вектор d коэффициентов произведения тех же
полиномов в jR[x]/(x'' - 1), при этом d, = с, + с„+|.
Длина обернутой свертки равна длине вход-
ного вектора, то есть длине сомножителя. Ум-
ножение 77-разрядных двоичных чисел по моду-
лю 2" выполняется за счет отбрасывания стар-
ших разрядов, начиная с 2". Произведение по
модулю 2" + 1 задается отрицательно обернутой
сверткой, то есть разряды старшей половины
произведения вычитаются из разрядов младшей
половины произведения. Произведение по моду-
лю 2" -1 задается положительно обернутой
сверткой, то есть разряды старшей половины
произведения складываются с разрядами млад-
шей половины произведения.
Для того чтобы покомпонентное произве-
дение векторов было положительно обернутой
сверткой d, необходимо выполнить операции
d = Q4((Qa)*(Qb)), где Q — матрица преобразо-
вания Фурье, * — операция покомпонентного
умножения векторов. При вычислении отрица-
тельно обернутой свертки е операнды умножа-
ются на матрицу Т, а произведение — на обрат-
ную матрицу 'Р“1: е = 4J-lQ-l((Q4Ja)*(Q4Jb)).
Матрица Т является диагональной, ее элементы
тр,, равны где цт2 = со. Умножение вектора на
матрицу Т равносильно умножению z-й коорди-
наты вектора на ц/ [1].
В случае БПФ положим п = 2к, со— прими-
тивный корень степени п из 1. Имеют место ра-
венства -со' = со"-'. Способ вычисления прямого и
обратного БПФ аналогичен методу Шенхаге (см.
п. 7.1.2) и определяется разложением двучленов.
Например, для 77 = 8:
ха - со0 = (х - co°)(x4 - со4);
154
х4 - co0 = (х2 - (1)°Хх2 - со4);
х4 - <в4 = (х2 - со2)(х2 - со6);
х2 - со0 = (х - со°)(х - со4);
х2 - со4 = (х - <о2)(х - со6);
х2 - со2 = (х - <о)(х - со5);
х2 — со6 = (х — <о3)(х — со7).
Разложение двучлена х8 - со0 можно описать
деревом высоты 3, где х8 - со0 является корнем,
а линейные двучлены— листьями (рис. 7.1).
Из каждой вершины, не являющейся листом,
выходят две стрелки, соответствующие разло-
жению на два сомножителя. Аналогично, для
п = 2к дерево с корнем х" - со0 имеет высоту к и
п листьев.
Рис. 7.1. Разложение двучлена для п = 8
Покажем, как можно использовать БПФ для
умножения больших чисел. Пусть а, b — п-
разрядные двоичные числа от 0 до 2" - 1, кото-
рые нужно перемножить по модулю 22" + 1.
Пусть п = 2Л, каждое число состоит из d блоков
длины I - n/d бит.
Идея быстрого умножения целых чисел за-
ключается в следующем. Сначала для каждого
сомножителя выполняется БПФ так, чтобы Фу-
рье-образы имели двойную длину (это делается
для того, чтобы не было переполнения). Затем
Фурье-образы покоординатно перемножаются по
модулю 22/ + 1 (обычно удобно выбирать число
21 равным разрядности процессора), и после это-
го выполняется обратное БПФ, то есть вычисля-
ется отрицательно обернутая свертка. При этом
необходимо принять меры, исключающие влия-
ние переносов, возникающих при целочислен-
ном сложении d слагаемых (умножение целых
чисел отличается от умножения полиномов тем,
что появляются переносы). Для исключения пе-
реноса Шенхаге и Штрассен предложили ис-
пользовать «разреженные» слагаемые, содержа-
щие достаточное число нулей в старших разря-
дах. При этом, естественно, длина каждого сла-
гаемого возрастает в несколько раз.
Для БПФ по модулю 22/ + 1 положим <в рав-
ным примитивному корню степени d из 1 в коль-
це вычетов 2/(22/ + 1)2. Тогда у будет квадрат-
ным корнем из о, то есть примитивным корнем
степени 2d из 1 в том же кольце.
Алгоритм 7.1.1. Вычисление быстрого пре-
образования Фурье по модулю 22Z +1 [1].
Вход. Вектор а = (а0, или, что то же
самое, ао + а\х + ... + ad-ixd~\ где d = 2"'.
Выход. Вектор Ь = (й0, , bd~\), b = Qa.
Метод.
На этапе предвычислений найти элемент <в —
примитивный корень степени d из 1 в кольце вы-
четов 2/(22' + 1)2.
d-1
1. Положить ГОю(х)<—^ОуХ7 .
7=0
2. Положить s <- т - 1.
3. Если 5 < 0, то перейти на шаг 8.
4. Положить t <- 0.
5. Если t > 2!п - 1, то перейти на шаг 7, иначе
выполнить следующие действия.
2S+1-1
5.1. Представить г,в виде У<з,-х7 .
7=0
5.2. Представить //2Л в виде <?0 + 2в\ + ... +
I л
“Ь 2 .
5.3. Положить е <- е,,,^ + 2<?,„_2 + ... + 2"'“'ео.
5.4. Положить
2 s-1
+ аеа , )(mod22/ + l)x7.
7=0 J+
5.5. Положить
..........................tS T '
* - ЧА ' *%-& “S. •©“
2* -1
r/+2s +&e+d/2aj^ Xmod22/ + O*'-
7=0
6. Положить 1 <— I + 2s+1 и вернуться на шаг 5.
7. Положить 5 <— 5 - 1 и перейти на шаг 3.
8. Для t = 0, 1, ..., d - 1 выполнить следующие
действия.
8.1. Представить t в виде во + 2в1 + ...+
+ 2
8.2. Положить е <- <?,„_| + 2е„,_2 + ... + 2"'~|е0-
8.3. Положить Ье <- г,.о.
9. Результат: Ь = (й0, ..., (>d_i). ’
Пример 7.1.2. Быстрое преобразование Фурье.
Пусть 22/ + 1 = 65537. Пусть d = 23, то есть
т = 3. Вычислим БПФ вектора а = (0, 1,2, 3, 4, 5,
6, 7).
На этапе предвычислений находим со = 16 —
примитивный корень степени 8 из 1 в кольце
2/655372. .
155
Полагаем
гслз(л‘) = х + 2х2 + Зх3 + 4х4 + 5х5 + 6хб + 7х7.
Все вычисления проводим в кольце
2/65537Z.
Для 5 = 2 находим: t = 0, z/24 = О/22 = 0, е = О,
"02(х) = (0 + 4) + (1 + 5)х + (2 + 6)х2 + (3 + 7)х3 =
= 4 + 6х + 8Х2 + 1 Ох3,
^(х) = (0 + 4о4) + (1 + 5®4)х + (2 + 6о4)х2 + (3 +
+ 7<в4)х3 = 65533 + 65533х + 65533х2 + 65533х3.
Для 5 = 1 находим:
f = 0, t/2s = 0/21 = 0,е = 0,
‘'o,i(x) = (4 + 8) + (6 + 10)х = 12 + 16х,
”2д(х) = (4 + 8<в4) + (6 + 10(В4)х = 65533 + 65533х;
f = 4, f/2^4/21 = 2,е = 2,
4i(x) = (65533 + 65533®2) + (65533 + 65533<в2)х =
= 64509 + 64509х,
r6;i(x) = (65533 + 65533®6) + (65533 + бЗЗЗЗо^х =
= 1020+ 1020х.
Для 5 = 0 находим:
Г = 0, 1/2'=0/2° =0, е = 0,
го,о(х)= 12 + 16 = 28,
г1,о(х)= 12 + 16<в4 = 65533;
1 = 2, z/2s=2/2°=2,e = 2,
г2>0(х) = 65533 + 65533g)2 = 64509,
гз,о(х) = 65533 + 65533O)6 = 1020;
t = 4, t/2s =4/2° =4,e=l,
r4,o(x) = 64509 + 64509g) = 48061,
r5j0(x) = 64509 + 64509g)5 = 15420;
1 = 6, //2' = б/2° = 6, <? = 3,
r6,o(x) =1020+ 1020G)3 = 50109,
r7,o(x) = 1020 + 1020g)7= 17468.
Выполняя шаг 8, получаем bo = ro,o, = г1>0,
bl = /'2,0, Ь(> — r3fl, Ь\ = Г40, 65 = r5fl, Ьз = Г6.0, Ь-/ = Гу fl.
Результат: b = (28, 48061, 64509, 50109, 65533,
15420,1020,17468,65533).
Произведение чисел а и b (заданных в систе-
ме счисления с основанием 2Z в виде векторов
длины d, п = 2к-Id) вычисляется следующим
алгоритмом. Параметрами алгоритма являются
числа I, d, причем d = 2к^, если к четно, и
d = 2(к~^2, если к нечетно.
Алгоритм 7.1.2. Умножение целых чисел с по-
мощью БПФ (алгоритм Шенхаге-Штрассена) [1 ].
Л-1 Д-1
Вход. Сомножители а = а, 2Л, 6 = ^6,2Z'.
1=0 (=0
Выход. Произведение с -ab.
Метод.
На этапе предвычислений найти элементы гр, ®.
1. Для каждого сомножителя умножить его z-ю
координату на затем выполнить быстрое
преобразование Фурье в кольце Z/(22Z + 1)Z.
2. Вычислить покомпонентное произведение
векторов преобразования Фурье, полученных
на шаге 1.
3. Выполнить обратное преобразование Фурье
в кольце Z/(22'+ 1)Z для вектора произведе-
ний, полученных на шаге 2.
4. Умножить каждую i-ю координату вектора,
полученного на шаге 3, на в кольце
Z/(22Z+1)Z.
5. Вычислить произведение ab в кольце £/2dZL
следующим образом.
5.1. Найти числа
а’ tf,'2(31og2 d\ b’ <-£ 6'2(310g2 d)i,
1=0 1=0
где a,' = a, (mod d) и b' = b, (mod d) для
0<i<d- 1.
5.2. Вычислить произведение
2Д-1 2Д-1
с <- a'b' = ^c}2^d\ c', = f/W-j’
i=0 j=0
например, методом Карацубы-Офмана
(и. 7.1.1).
5.3. Вычислить координаты вектора произ-
ведения ah в кольце 2/2^2 по формуле
с'-с^+, (mod d) для 0 < i < d- 1.
6. Каждую из координат с, произведения восста-
новить по китайской теореме об остатках для
колец классов вычетов Z7(22z + 1)Z, Z72dZ.
7. Вычислить точное значение произведения
Л- I
с - с, 2Ь по модулю 22" + 1.
<=0
Таким образом, этот метод умножения осно-
ван на том же принципе, что и умножение в
классах вычетов, — на гомоморфизме колец.
7.1.4. Модульное умножение.
Метод Монтгомери
Модульное умножение — наиболее часто
встречающаяся операция при построении алгорит-
мов криптографии с открытым ключом. Обычно
приходится выполнять умножение целых рацио-
нальных чисел по простому или составному мо-
дулю или умножение полиномов по модулю не-
приводимого полинома. Модульное умножение
чисел мнимого квадратичного порядка можно
выполнять с использованием алгоритма 7.13.1.
Если выполнять модульное умножение непо-
средственно, сначала перемножая целые числа (по-
156
линомы), а потом вычисляя остаток от деления, то
сложность алгоритма будет определяться процеду-
рой нахождения остатка. Рассмотрим методы мо-
дульного умножения, не требующие деления.
Наиболее просто выполняется умножение по
модулю чисел Мерсенна р = 2' - 1 /у1я простого г
или по модулю чисел Ферма р = 22 + 1. Для ум-
ножения двух чисел по модулю числа р = 2" ± 1
нужно вычислить целочисленное произведение
сомножителей и представить его в виде 2пА + В,
где В — младшие п бит произведения. Произве-
дение по модулю р будет равно В + J(mod р).
Обобщением этого метода является умноже-
ние по модулю чисел р = 2" ± с для малого с. В
этом случае, если ab = 2’А + В, где В < 2", то
ab = В + cJ(mod р). При необходимости приме-
няется рекурсия.
П. Монтгомери предложил метод модульного
умножения, не требующий выполнения опера-
ции деления [8]. Для вычисления произведения
чисел А и В по модулю нечетного числа N, где А,
В, N— большие числа, выберем число R, равное
степени числа 2 и превышающее N. Определим
N-вычет числа А по модулю N как AR (mod N) и
произведение Монтгомери по модулю N как
МР(А, В, N, R) = ABR~X (mod N).
В основу вычисления произведения Монтго-
мери положено преобразование Монтгомери
А -> ARa (mod N), базирующееся на следующей
теореме.
Теорема 7.1.1. Пусть N и R— взаимно про-
стые положительные целые числа, N' = -NA
(mod R). Тогда для всех чисел Т и М= TN'
(mod R) справедливы следующие утверждения.
, тт T + MN
1. Число---------целое.
R
о TD-i / л дп Т + MN Т + MN
2. TR (mod N) =------ или---------N.
R R
Доказательство см. в работе [8].
Пусть процессор оперирует со словами длины
m бит.
Алгоритм 7.1.3. Вычисление преобразования
Монтгомери для многоразрядного числа Т.
Вход. T=(Z2„_1,...,Z0), b = 2m, R = bn, N =
= (A„_i, ..., Ao), N<R, N'=-NA (mod 6) (A' —
одиночное слово).
Выход. TR -1 (mod A).
Метод.
1. Положить U<-T.U= (um-\, wo).
2. Для z = 0, 1,..., n - 1 выполнить следую-
щие действия.
2.1. г, <- iijN' (mod b).
2.2. U<^U+viNb'.
3. U^-UfR.
4. Если U> N, to U<- U-N.
5. Результат: U.
Для вычисления произведения Монтгомери
достаточно перемножить операнды как целые
числа и затем выполнить преобразование Монт-
гомери. Для перевода числа в А-вычет нужно
вычислить МР(А, R2 (mod A), A, R). Для обратно-
го преобразования А-вычета в число нужно вы-
числить произведение MP(AR (mod TV), 1, A, R).
Алгоритм 7.1.4. Модульное умножение
больших чисел методом Монтгомери [7].
Вход. AR (mod А) = (а„_ь ..., а0), BR (mod А) =
= (&,_!, ..., b0), N,b = 2"', R = b", N' = -A“'(mod b).
Выход. С = ABR (mod N).
Метод.
1. Положить С <- 0 (С = (с„^, ..., с0)).
2. Для 1 = 0, 1, 1 выполнить следую-
щие действия.
2.1. zz, <— (с0 + a,bo) N (mod b).
2 2 С < С + а' (BR (m°d+ U,N
2.3. Если C> А, то С <- C- N.
3. Результат: C. .
Имеют место равенства:
MP(AR (mod A), BR (mod A), A, R) = ABR (mod A),
AR + BR = (A + B)R (mod A).
Таким образом, множество А-вычетов с опера-
циями умножения по Монтгомери и сложения
является кольцом. Нетрудно видеть, что это коль-
цо изоморфно кольцу классов вычетов по модулю
А, изоморфизм задается умножением на R, обрат-
ный изоморфизм задается умножением на RA:
MP(AR (mod A), R~'R (mod A), A, R) =
= AR~lR (mod A) = A (mod N).
Пример 7.1.3. Умножение чисел методом
Монтгомери.
Исходные данные: А =64553, А = 30000,
В = 45678, R = 65536 = 216, Ъ = 16 = 24.
Вычисляем вспомогательные параметры:
А = 7, R2 = 62547 (mod А).
Результаты вычислений алгоритмом 7.1.4 све-
дем в таблицу:
1 и, (mod 16) с
МР(А, R2 (mod A), A, R)
0 0 0
1 15 7693
2 4 36165
3 6 53832
157
Продолжение таблицы
i u, (mod 16) Q
Результат: AR = 53832 (mod N)
МР(В,В" (mod N),N,R)
0 6 14383
1 7 52596
2 6 35313
3 14 37139
Результат: BR = 37139 (mod N)
MP(AR (mod N), BR (mod N), N, R)
0 8 50846
1 6 36670
2 12 55349
3 4 49773
Результат: ABR = 49773 (mod N)
MP(1, ABR (mod N), N, R)
0 11 47491
1 5 23141
2 3 13550
3 2 8916
Результат: AB = 8916 (mod A)
В арифметике Монтгомери можно выполнять
не только умножение, но также сложение и воз-
ведение в степень. При этом нет необходимости
переводить промежуточные результаты из N-
вычетов в обычное представление.
Асимптотическая сложность алгоритма ум-
ножения Монтгомери такая же, как и у алго-
ритма, выполняющего сначала умножение опе-
рандов «в столбик», а затем деление с остат-
ком. Поэтому необходима более точная оценка
сложности. На практике часто требуется не
одиночное умножение, а цепочка умножений и
сложений. В этом случае можно исключить
преобразование произведения из А-вычета в
обычную форму и преобразование операндов в
Л'-вычеты. Тогда сложность умножения алго-
ритмом Монтгомери составляет 2п(п + 1)
обычных умножений слов.
Алгоритм Монтгомери был предложен для ум-
ножения в кольце классов вычетов Z/AZ. Однако
вместо кольца целых чисел Z можно использо-
вать и произвольное евклидово кольцо. Напри-
мер, если требуется вычислить произведение по-
линомов в кольце /c|x]/A(x)A[x], то выбирают
вспомогательный полином R(x) удобного вида,
например, R(x) = xn+i, deg(7?) > deg(A), находят
расширенным алгоритмом Евклида полиномы
R~\x), N'(x) такие, что R(x)R~Xx) - N(x)N'(x) = 1.
Затем проводят такие же вычисления, как и в
алгоритме 7.1.3. Отличие заключается в том, что
на последнем шаге после деления на R(x) всегда
получается deg(D’) < deg(A), поэтому операция
вычитания N(x) не требуется.
Если арифметика Монтгомери используется
для сложения точек эллиптической кривой и вы-
числения ведутся в проективной форме с тремя
координатами AT?, YR, ZR (см. п. 7.10), то для пе-
рехода к аффинной форме нет необходимости
сначала переходить от арифметики Монтгомери к
XR
нормальному виду, так как при делении х =--
ZR
происходит автоматическое сокращение на R.
7.1.5. Деление
Деление в кольце R может использоваться и
как составная часть операции модульного умно-
ения, и самостоятельно, например, в задачах,
связанных с корректирующим кодированием.
Практический интерес представляет деление в
кольце Z целых чисел, в кольце Z[a] целых алгеб-
раических чисел и в кольце полиномов Х[х]. Обыч-
но деление выполняется на простой элемент q со-
ответствующего целостного кольца R, так что Rl(q)
является полем. Если R = Х[х], то q задает конечное
расширение поля К. Если К конечно, то в качестве
элемента q может использоваться любой неприво-
димый полином той же степени.
Наиболее просто в ЕДх] выполняется деление на
полином х + а. Однако такой полином неприводим
только если -а является в невычетом степени п,
то есть если НОД(/?,р — I)?* 1. Таких полиномов
сравнительно мало, а в случае р = 2 их не сущест-
вует. В этом случае можно использовать состав-
ной полином j? + а, большой простой делитель
которого является искомым полиномом.
Например, над F2 выполняется равенство
У + 1 = (х + 1 )(У’-1 + ... + х + 1), при этом для
половины простых чисел п полином г/(х) =
= У”1 + ... + х + 1 является неприводимым. Это
имеет место для п е {131, 139, 149, 163, 173, 179,
181, 197, 211, 227, 269, 293, 317, 347, 349, 373,
379, 389, 419, 421, 443, 461, 467, 491, 509}. По-
этому элемент поля F2„„, можно задать элемен-
том кольца F2[x]/(x" - 1). Если старший разряд
элемента кольца будет иметь степень п - 1, нуж-
но вычесть из него q(x).
Алгоритм 7.1.5. Целочисленное деление с ос-
татком.
Вход. Делимое N и делитель р = 2'" - а. д /
Выход. A (mod р).
Метод.
1. Представить число N в системе счисления с
основанием d = 2'": N = Nq + N\d+ ... + N^lk.
2. Если к = 0, то при No >р положить No <-
<- No ~р. Результат: No. .
158
3. Положить i <- к - 1, L <- N^.
4. Положить M<r- La + Nt.
5. Пока M> d, выполнять: Мо<— М (mod d'y
Мх <-(M-M0)ld, М<- Mo + aMt.
6. Если z = 0, то при M>p положить
M <- M- p. Результат: M.
7. Положить z— 1, L<-M и перейти на
шаг 4.
Деление в А]х] выполняется аналогично.
Пример 7.1.4. Целочисленное деление с ос-
татком.
Пусть р = 232 - 209.
Для наглядности используем шестнадцати-
ричную систему счисления. Найдем остаток от
деления числа
1234567890abcdeffedcba0987654321
на р (р = ffffff2f, а = d 1).
Берем два старших 32-разрядных слова. На-
ходим Л/ = 12345678 + dl • 90abcdef = f6d6665e7;
М= 6d667226.
Берем следующее 32-разрядное слово. Нахо-
дим М= fedcba09 + dl • 6d667226 = 5a4f7feb0f;
M— 4f803489.
Берем следующее 32-разрядное слово. Нахо-
дим М= 87654321 + dl • 4а803489 = 416fl026fa;
M=6fl05c0b.
Результат: 6Н05с0Ь.
В общем случае деление М/N больших чи-
сел с остатком можно выполнять по следующей
схеме. Предположим, что процессор может вы-
полнять деление слов. Пусть разрядность слова
равна d. На каждой итерации из делимого М бе-
рем три старших слова т, а из делителя N— два
старших слова п. Находим разность b длин де-
лимого и делителя (в словах). Выполняем деле-
ние с остатком т на п. При этом находим одно
слово частного х (приближенное). Затем вычис-
ляем М <— М— 2xN и проверяем неравенства
Л/>0; M-2hdN <§. Если первое (второе) нера-
венство не выполняется, заменяем х на х - 1 (со-
ответственно на х + 1). Затем повторяем проце-
дуру до получения х = 0. Остаток равен М.
Аналогично можно выполнять деление с ос-
татком в произвольном евклидовом кольце.
7. 2. Алгоритмы обращения и вычисления
наибольшего общего делителя
Вычисление наибольшего общего делителя и
обращение элемента целостного кольца — тесно
связанные задачи, которые часто используются
при разработке криптографических алгоритмов.
Наибольший общий делитель в евклидовом
кольце может быть найден алгоритмом Евклида.
В случае кольца Z алгоритм Евклида имеет
сложность <9(??2), если размер задачи составляет
п бит и вычислительная модель содержит умно-
житель слов. Если наибольший общий делитель
двух элементов х и у равен 1, то представление
ах + by = 1 дает обратные элементы: а =. х-1
(mod у), b=y~{ (modx), используемые при деле-
нии в конечном поле. Это представление выра-
батывается расширенным алгоритмом Евклида.
Алгоритм 7.2.1. Алгоритм Евклида для коль-
ца Z.
Вход, х, у, 0 <у < х.
Выход. НОД(х, у).
Метод.
1. Пока у Ф 0, выполнять г <- х (mod у), х <- у,
У г.
2. Результат: х.
Алгоритм 7.2.2. Расширенный алгоритм Евк-
лида для кольца Z.
Вход, х,у, 0 <у < х.
Выход, d = НОД(х, у); целые числа а, b такие,
что ах + by = d.
Метод.
1. ПОЛОЖИТЬ <22 <- 1, <2] <- 0, &2 0, б] <- 1.
2. Покау Ф 0, выполнять следующие действия.
г <- X - qy,
а й2~ qa\,
3.
4.
b <^bz- qb\.
1.2. Х<-у, у<— Г, <22 <-<2Ь <21 <— а, Ь2<-Ь],
/у^Ь.
Положить d <— х, а <— <22, b <- 62.
Результат: d, а, Ь.
Существует более быстрая версия алгоритма
Евклида для вычисления наибольшего общего
делителя целых чисел и обращения.
Алгоритм 7.2.3. Бинарный алгоритм Евклида
для кольца Z. ( _
Вход, х, у, 0 < у < х. ’ ’
Выход, d - НОД(х, у).
Метод.
1. Положить g <- 1.
2. Пока х и у оба четные, выполнять х<-х/2,
у <- у/2, g <— 2g до получения хотя бы од-
ного нечетного значения х или у.
3. Пока х ф 0, выполнять следующие действия.
3.1. Пока х четное, выполнять х <- х/2.
3.2. Покау четное, выполнять у <- у/2.
1х — у|
3.3. Положить t <- -----.
2
159
3.4. Если х > у, то х <- 1, иначе у <- г.
4. Положить d <— gy. Результат: d.
Сложность этого алгоритма равна О(п2), если
длина операндов составляет п бит.
Этот алгоритм (если не выполнять шаг 3.4)
можно использовать и для деления с остатком.
В бинарном виде можно реализовать и рас-
ширенный алгоритм Евклида.
Алгоритм 7.2.4. Расширенный бинарный ал-
горитм Евклида для кольца Z.
Вход, х, у, 0 <у < х.
Выход, d = НОД(х, у); целые числа а, b такие,
что ах + by = d.
Метод.
1. Положить g <- 1.
2. Пока х и у оба четные, выполнять х<- х/2,
у <- у/2, g <- 2g до получения хотя бы од-
ного нечетного значения х или у.
3. Положить и <— х, г <- у, А <- 1, В <— О, С <- О,
D <- 1.
4. Пока и четное, выполнять следующие дейст-
вия.
4 .L Положить г/<—г//2.
4 .2. При А = В = 0 (mod 2) положить А <- Э/2,
В <— В/2 . В противном случае положить
А <- (А + у)/2, В <- (В - х)/2.
5. Пока г’ четное, выполнять следующие дейст-
вия.
5 .L Положить v <—v/2 .
5 .2. При С=D = 0 (mod 2) положить С <-С/2,
D <- D/2. В противном случае положить
С <-(С+ y)/2,D<~(D-x)/2.
6. Если и > г, то и <— и - г, А <- А - С,
В <- В - D. Иначе v<-v-u, С<- С-А,
D<-D-В.
7. При и = 0 положить d <— gv, а<- С, b <— D.
Иначе вернуться на шаг 4.
8. Результат: d, а, Ь.
Сложность этого алгоритма равна О(??2), если
длина операндов составляет п бит.
Пример 7.2.1. Расширенный бинарный алго-
ритм Евклида для Z.
Пусть х= 123, у= 100. Последовательность
шагов алгоритма 7.2.4 представлена следующей
таблицей.
№ шага и V А в С D
3 123 100 1 0 0 1
5 50 50 -61
5 25 75 -92
6 98 -74 92
4 49 -37 46
6 24 -112 138
4 12 -56 69
4 6 22 -27
4 3 61 -75
6 22 14 -17
5 11 57 -70
6 8 -4 5
5 4 48 -59
5 2 74 -91
5 1 87 -107
6 2 1 -26 32
4 1 1 -13 16
6 0 1 -100 123 87 -107
Получив и = 0, на шаге 7 полагаем d= 1,
<2 = С = 87, Ь = В =-107.
Алгоритм 7.2.5. Расширенный бинарный ал-
горитм Евклида для Ег|7].
Вход. х(0, у(0, 0 < deg(y) < deg(x).
Выход. d(t) = НОД(х(/), ХО); полиномы а(1),
b(f) такие, что X0X0 + X0X0 = ХО-
Метод.
1. Положить g(t) <- 1.
2. Пока ХО - 0 (mod f) и ХО - 0 (mod /), выпол-
нять х(0 <- x(t)/1, y(t) <- y(t)/l, g(t) <- tg(f)
до получения ненулевого свободного члена в
ХО или ХО-
s. Положить u(t) <—x(J), v(t)<-y(t), A(f)<-\,
B(Z) <-0, С(Д <-0, £>(0 <- 1.
4. Пока u(f) = 0 (mod /), выполнять следующие
действия.
4.1. Положить u(t) <— u(t)11.
4.2. При A(f) = B(f) = 0 (mod t) положить
A(t) <- А(1)/1,В(1) <- B(t)lt. В против-
ном случае положить
Л(0<-(Д0+Х0)/х :
В(0<-(В(0+Х0)Л-
5. Пока v(f) = 0 (mod f), выполнять следующие
действия.
5.1. Положить -
5.2. При С(0 = D(l) = 0 (mod /) положить
C(t) <- D(t) <— В противном
случае положить
С(0<-(С(0+Х0)/Е . . . -
D(t)<-{D(l}+x(ty)ll. ' •"* ‘
160
6. Если deg(z7) > deg(v), то ы(Г) <— u(f) + v(7),
A{f)<r-A(t) + C(t\ B(t) <- B(l) + D(t). В про-
тивном случае v(Z) <- v(7) + u(t), C(t) <- C(Z) +
+ A(f), D(t) <-D(t) + B(t).
7. Если u(t) = 0, то положить d(f) <- gttjvif),
a(f) <- C(t), b(f) <- D(t). В противном случае
вернуться на шаг 4,
8. Результат: d(f), a(t), b(t).
7.3. Минимизация базиса решетки
Алгоритм LLL (Ленстры-Ленстры-Ловаша)
служит для минимизации базиса решетки и ис-
пользуется при исследовании безопасности ран-
цевых криптоалгоритмов, а также является инст-
рументом для разложения составных чисел (см.
п. 9.2), вычисления дискретных логарифмов в
конечном поле и на эллиптической кривой (при
поднятии точек).
Здесь под решеткой понимается модуль над
кольцом Z, состоящий из целочисленных линей-
ных комбинаций базисных векторов с координа-
тами из поля К. Если В = (Ьь ..., Ь„) — множест-
во линейно независимых m-мерных векторов над
полем К, то решетка — множество вида
L = Zbi + ... + Zb„. Отметим, что базис В решет-
ки в общем случае не совпадает с базисом век-
торного пространства.
Пусть A=IR и х = (хь ...,х„,), У = (У1, ...,у,„) —
элементы решетки L. Определим скалярное про-
т
изведение векторов х и у: (x,y) = y^xfyz и норму
/=1
Jvn
Уде2 .
(=1
Решетка может иметь много базисов. Алго-
ритм LLL дает базис, состоящий из векторов с
минимальной нормой.
Определим по индукции для базиса В набор
из п векторов Ь* и набор из п2 вещественных
чисел Цу следующим образом:
Ы
/•-1
b- = b, - £ K/b’ для 1 < i < п.
7=1
Наибольшую норму имеет вектор bj = Ь,. Ба-
зис (bi, ..., b„) решетки называется минимальным
по Ловашу, если |р( J < 0,5 для 1 < i <j < п и
||b;||2>(0,75-p2i_1)||b;_1||2 для 1 </<77.
Алгоритм 7.3.1. Алгоритм LLL минимизации
базиса решетки [7].
Вход. Базис (Ьь ..., Ь„) решетки в IR'", т > п.
Выход. Минимальный по Ловашу базис ре-
шетки.
Метод.
1. ь;<-ь1,2?1<-||ь;||2.
2. Для z = 2, 3, ...,п выполнить следующие дей-
ствия.
2.1. b*<-b*.
2.2. Для j = 1, 2. ..., z - 1 вычислить
2.3. В, <-||b’||2.
3. Положить к <- 2.
4. При IjLPt^-il> °’5 положить рА>1 <- RED(piy1).
5. При Вк <(0,75-р7. к^}Вк_х выполнить сле-
дующие действия.
5.1. Положить р <- руы, В <— Вк+ \кВк.!,
> Р^к-1 р > ^к-\^к р , р
JD JD
5.2. Поменять местами Ьц иЬц.
5.3. При к>2 поменять местами р*э, и р*_у
дляj = 1, 2,..., к-2.
5.4. Положить t <— pZ7t, р,л <- р,л_1 - р/,
Р/Л-1 <-1 + Рл>1 р,л для i = к + 1,
к+ 2, ..., 77.
5.5. Положить к <— тах(2, к - 1) и вернуться
на шаг 4.
При Вл>(0,75-р^_,)5лч для 7 = к -2,
к-3, ..., 1 положить ру <— RED(py) для та-
ких ру, что |pfc,/| > 0,5, и положить к <- к + 1.
6. Если к < 77, то вернуться на шаг 4, иначе ре-
зультат: (Ьь ...,b„). S
Процедура редукции RED(py).
RED1. Если ру > 0, то положить г <-1_0,5 + pyj,
иначе г <-------1_0,5 - pyj.
RED2. Положить Ьд < Ь/ — rb/.
RED3. Для j = 1,2,..., I - 1 положить
RED4. Положить < pkj - г. '
Сложность алгоритма 7.3.1 равна О(/74) ариф-
метических операций над вещественными чис-
лами.
Пример 7.3.1. Минимизация базиса решетки
алгоритмом LLL.
161
Пусть п - 3 и базис решетки задан векторами
bj = (1, 0, 1,2), Ь2 = (1,-1, 2, 0), Ь3 = (-1,2, 0. 1).
Полагаем Ь, = (1, 0, 1, 2), В3 - 6.
Выполняем шаг 2. Для i = 2: b2 = (1, -1,2, 0),
Ц2,г='Д b2 = (1/2,-1,3/2,-1), ^2 = 9//2- Для г’=3:
(-1,2, 0,1), Цз.1 = 1/б, Ь>(-76,2,-76,73),
Цз,2 = —'!% Ь3=(-7/9, 1!/9, 1, %), В3 = 28/9.
Поскольку В2 > (0,75 - ц| j )Bj, полагаем к = 3
и переходим на шаг 4.
Выполняем RED(p32): г = -1, Ь3 = (0, 1, 2, 1),
— 21 . 2 /
РЗЛ ~ '3, Цз,2 — Л)-
Теперь В3 < (0,75 - ц| 2)В2. Вычисляем
Р = Рз,2 = 2/9, В = 10/3, Цз>2 = 3/]0, В3 = 21/5, В2 = 10/3.
Полагаем Ь2 = (0, 1, 2, 1), b3 = (1,-1, 2, 0),
Цз,1 = 72, ц2j = 2/3, к = 2 и возвращаемся на шаг 4.
Выполняем RED(p21): г = 1, Ь2 = (-1, 1, 1, -1),
Р2,1 =-'/3.
Так как В2 < (0,75 - ц2 ।) Д, полагаем
Р = Р2.1 = _1Л, В = 4, p2j = -’/2, В2 = 5, В\ = 4.
Меняем местами bi и b2: b2 = (1, 0, 1,2),
bi = (-1.1,1,-1).
Вычисляем I = р3>2 = 3/10, р3>2= Лъ Цзз = 0, по-
лагаем к = 2 и возвращаемся на шаг 4.
Выполняется неравенство В2 > (0,75 - р| JBj,
поэтому полагаем к = 3 и возвращаемся на шаг 4.
Выполняем RED(p32): г = 1, Ь3 = (0, -1, 1, 2),
Рз,1 = /з, Цз,2 =-'/5.
Выполняется неравенство В3 > (0,75 - ц| 2)В2,
поэтому полагаем к = 4 и получаем результат:
bj=(-l, 1, 1,-1), b2 = (1,0, 1,2),
Ь3 = (0,-1, 1,-2).
7.4. Разложение над конечным полем
полиномов от одной переменной
Разложение на множители полиномов над ко-
нечным полем требуется при решении задачи
дискретного логарифмирования в расширенном
поле (к которой сводится задача логарифмиро-
вания на эллиптической кривой). Кроме того,
этот алгоритм может использоваться при выборе
неприводимого полинома, задающего расширен-
ное поле.
Пусть у(х) 6 F£/[x], q ~рп- Полином fx) не сво-
боден от квадратов тогда и только тогда, когда
наибольший общий делитель полинома/(х) и его
производной f'(x) отличен от константы (от эле-
мента поля ОРД. Мы рассмотрим алгоритм, кото-
рый раскладывает полиномы, свободные от
квадратов. Для разложения полинома fx), не
свободного от квадратов, нужно найти его про-
изводную fix) и алгоритмом Евклида вычислить
g(x) = НОД(/(х),/'(%))• Полином f(x)/g(x) будет
свободен от квадратов.
Все ненулевые коэффициенты полинома об-
ратимы как элементы группы ИД. Поэтому дос-
таточно рассмотреть полиномы с единичным
старшим коэффициентом.
Отличный от константы полином над полем
характеристики р имеет нулевую производную
лишь тогда, когда он содержит ненулевые коэф-
фициенты только при степенях х, кратных р. По-
этому fx) =fo(xp) = (fix)/. Этот алгоритм зада-
ется рекурсивной процедурой SquareFree(/(x)).
Алгоритм 7.4.1. Разложение полинома над
конечным полем [7].
Вход, fx) е FJx], q -р, свободный от квад-
ратов.
Выход. Делитель F = SquareFree(/(x)) полино-
ма fx).
Метод.
1. Положить i <— 1, F <— 1, вычислить/^).
2. Если f(x) = 0, то положить /(%)<—/(xfp и
F <— (SquareFree(/(x))y'. Иначе выполнить
следующие действия.
2.1. Вычислить g(x) <— НОД(/(л'), /'(л')) и по-
ложить h(x) <— f(x)]g(x) .
2.2. При h(x) g. выполнить следующие
действия.
2.2.1. Вычислить gi(x) <— НОД(/г(х),^(х))
и h}ix)<^f(x)/g}(x).
2.2.2. Положить F <— F • Лфх)', i <— i + 1,
Ых) g\(x), g(x) <- g(x)/gj(x).
2.3. При g(x) g ИД положить g(x) <- g(x)^1’
nFF• (SquareFree(g(x)))/’.
3. Результат: F.
Сложность алгоритма 7.4.1 — О(и3) арифме-
тических операций в поле F9.
7.5. Извлечение квадратных
и кубических корней в конечном поле
Алгоритмы решения квадратных и кубиче-
ских уравнений над конечным полем использу-
ются при разработке криптосистем на алгебраи-
ческих кривых.
162
Пусть Fg— поле из q=pn элементов. Если
порядок мультипликативной группы поля
четный, то квадратное уравнение х2 = а в поле
при а Ф 0 имеет либо два корня, отличаю-
щихся знаком, либо ни одного, в зависимости
от того, является элемент а квадратичным вы-
четом или невычетом. При а = 0 уравнение име-
ет двойной нулевой корень, так как поле не
имеет делителей нуля. Если порядок мультип-
ликативной группы Ед нечетный (то есть ха-
рактеристика поля равна 2), то квадратное
уравнение х2 = а в поле Ед при а Ф 0 всегда име-
ет один корень.
7.5.1. Извлечение квадратного
корня в случае q = 3 (mod 4)
По свойству элементов поля выполняются
равенства aq = a, di+} = а2. Показатель q + 1 де-
лится на 4, следовательно, имеет место равен-
ство а(ч+г>^ = V14а . Поскольку корни степени
4 из 1 в поле Ед равны ±1, то алгоритм вычисля-
ет корень с точностью до знака, причем если
одно значение удовлетворяет исходному урав-
нению, то и второе значение тоже является ре-
шением.
Алгоритм 7.5.1. Извлечение квадратного
корня в поле из q = 3 (mod 4) элементов.
Вход. Элемент а е Е9; характеристика поля Fg
и полином, задающий это поле, q = 3 (mod 4).
Выход. Квадратный корень х из а в поле Fg.
Метод.
1. Вычислить х <— «(?+1^4.
2. Если х2 = а, то результат: х, иначе результат:
решений нет.
Сложность алгоритма 7.5.1 при использова-
нии умножения «в столбик» равна O((log^)3).
Пример 7.5.1. Извлечение корня в случае
q = 3 (mod 4).
1. Для простого поля: q =р = 19, а - 11. Тогда
х=115 = 7. Проверка показывает, что решение
правильное.
2. Для расширенного поля: р = 3, q = 27, поле
задано полиномом ? + It + 1, а = 2? +1 + 1. На-
ходим х = (2? + / + 1 )7 = /2 +1. Проверка показы-
вает, что решение правильное.
7.5.2. Извлечение квадратного корня
в случае q = 5 (mod 8), q = 9 (mod 16)
По свойству элементов поля выполняются ра-
венства а4 = a, aqi2 = а4. Поскольку в случае q = 5
(mod 8) показатель q + 3 делится на 8, имеет ме-
сто равенство а(?+3)/8 = VlVa . Множество кор-
ней степени 8 из 1 состоит из четырех элементов:
+i и ±1, где i2 = -l. Это множество совпадает с
множеством корней степени 4 из 1. Для нахож-
дения нужного значения корня степени 4 из 1
следует найти порядок по модулю 4 элемента а в
поле Fg: при '^4 = 1 корень из а имеет поря-
док, сравнимый с 2 по модулю 4, требуемое зна-
чение корня степени 4 из 1 равно ±1. При
а(«-1)/4 КОрень из а имеет порядок, сравни-
мый с ±1 по модулю 4, требуемое значение кор-
ня степени 4 из 1 равно +i. В соответствии с
квадратичным законом взаимности для простого
поля элемент 2 является квадратичным невыче-
том в поле Fg, поэтому i = 2(9“1)yf4. Вместо эле-
мента 2 можно использовать любой квадратич-
ный невычет, тогда алгоритм будет работать и в
расширенном поле.
Алгоритм 7.5.2. Извлечение квадратного
корня в поле из q = 5 (mod 8) элементов.
Вход. Элемент а е Fg, характеристика поля Fg
и полином, задающий это поле, q = 5 (mod 8).
Выход. Квадратный корень х из а в поле Fg.
Метод.
1. Вычислить Ъ <— <я(9+3)/8.
2. Вычислить с <— <7(9-1^4. При |с| Ф 1 результат:
решений нет. При с = 1 положить х <- ±h;
3. Вычислить i <— 2(Ч~'У4 и положить х <— ±Ы.
4. Результат: х.
Аналогично для q = 9 (mod 16) получаем
х - а<-9+7У'6 и т. д. Здесь нужно подобрать
квадратичный невычет, найти с его помощью
примитивный корень степени 8 из 1, а затем
уточнить степень этого корня. Таким же образом
можно строить алгоритм извлечения корня в
произвольном поле из q = 1 (mod 4) элементов.
Сложность алгоритма 7.5.2 при использова-
нии умножения «в столбик» равна O((log#)3).
Пример 7.5.2. Извлечение квадратного корня
в случае q = 5 (mod 8) и q = 9 (mod 16).
1. Простое поле: q =р = 37 = 5 (mod 8), а = 21.
Находим Л = 215^4 (mod/?), i = 29 г 31 (mod/?),
х = ±13 (mod /?), х2 = 21 (mod /?).
163
2. Простое поле: ^=j> = 41=9 (mod 16),
а = 37. Находим b = З73 = 18 (modр). Подбираем
квадратичный невычет j = 3, примитивный ко-
рень степени 8 из 1 равен 38, 37(9“1)/8 = j (modр),
х = ±18 (mod р), х = 37 (mod р).
3. Расширенное поле: р=11, #=112 = 9
(mod 16), — задано неприводимым полиномом
z2 + 1 с корнем /; a = 9t+\Q. Вычисляем корень
степени 8 из 1: г = 4/+ 7. Проверка показывает,
что г4 = 10. Вычисляем х — л[а :
х = (4Г + 7)(2/+5)8 = 2/ + 5.
Проверка: (2t + 5)2 = 9^+10.
7.5.3. Извлечение квадратного корня
в общем случае для нечетного q
Этот алгоритм основан на построении квадра-
тичного расширения исходного поля выбором
неприводимого над полинома/степени 2 и на
вычислениях в расширенном поле [7].
Алгоритм 7.5.3. Извлечение квадратного
корня в поле из q = 1 (mod 2) элементов.
Вход. Элемент а е Ff/; характеристика поля F9
и полином, задающий это поле.
Выход. Квадратный корень х из а в поле Ff/.
Метод.
1. Подбором найти элемент Ъ такой, что Ь2 - 4а
является квадратичным невычетом в поле F,r
2. Положить /у) <— у2 - by + а в кольце Ff/ [у].
3. Вычислить х <— ±/'+^2 (mod /(у)).
4. Результат: х.
Сложность алгоритма 7.5.3 при использова-
нии умножения «в столбик» равна O((log/)3).
Пример 7.5.3. Извлечение квадратного корня
в случае q = 1 (mod 2).
1. Простое поле: ^=/> = 41, а = 32. Выбираем
6 = 4,/у) =У - 4у + 32, х = /у21 = ±14 (mod /у)).
2. Расширенное поле: F317]/(/4 +1 + 2), а = 2? +
+ 2^ + t+2. Выбираем b = t, fiy)=y-ty + 2t'1 ±2? +
+1 + 2. Находим х = ±у41 = +(2i + 2t) (mod/у)).
7.5.4. Извлечение квадратного
корня в случае четного q
Решением квадратного уравнения х2 = а являет-
ся х = aq!2. Сложность алгоритма при использо-
вании умножения «в столбик» равна O((log/)3).
7.5.5. Решение квадратного уравнения
Решение квадратного уравнения
х2 + ах + b = 0
в случае поля нечетной характеристики выпол-
няется по обычным формулам. Решение сущест-
вует, если дискриминант а2 - 4b является квад-
ратичным вычетом в поле F?.
В случае F9 = F2|/]/(/(r)) деление на 2, требуемое
обычными формулами, невозможно. Квадратное
уравнение в поле из 2" элементов может иметь либо
два корня, либо ни одного. Непосредственная под-
становка показывает, что если а— корень квад-
ратного уравнения, то а + а тоже будет его корнем.
При а = 0 решение уравнения х2 + b = (х + 4b)2 = 0
сводится к извлечению квадратного корня из b (а
и Ь, вообще говоря, полиномы от f), уравнение
имеет двойной корень. При а Ф 0 замена перемен-
ных х <— ах приводит к случаю а = 1. Поэтому
достаточно рассмотреть уравнение
х2 + х + й = 0. (7.5.1)
Гомоморфизм по сложению из поля F „ в поле
F2 задается следом. Пусть а — корень уравнения
(7.5.1). Тогда о!2 + а + b = 0. Гомоморфный образ
последнего равенства в поле F2 задается услови-
ем Тг(ос2) + Тг(ос) + Тг(Л) = 0. Для любого а е F2„
следы элементов а и а2 равны:
п э2 7/1-I
Тг(а) = а + а + а + ... + а ,
Тг(а2) = а2 + а22 + ... + а2"' + а2" = Тг(а).
Поскольку Тг(а) е F2, то Тг(а2) + Тг(а) = 0.
Поэтому решение уравнения (7.5.1) существует
тогда и только тогда, когда Тг(Л) = 0.
Если X] и х2 — корни уравнений х2 + х + Ъ\ = 0
и х2 + х + Ь2 = 0 соответственно, то х( + х2 — ко-
рень уравнения х + х + (Ьг + Ь2) = 0. Действи-
тельно,
х2 + X] + Ь\ + х22 + х2 + Ь2 =
= (*I + х2)2 + (Xi + х2) + (&I + Ь2) = 0.
Подставим в (7.5.1) вместо переменной х все
ненулевые степени t,i, ..., fи обозначим через
b„ i= 1, 2,..., п - 1, векторы коэффициентов по-
лученных полиномов b£t). Векторы Ь, линейно
независимы, так как в противном случае сущест-
вовали бы два различных полинома от t с нуле-
выми свободными членами— корни уравнения
(7.5.1), — что невозможно. Векторы Ь, образуют
базис множества векторов с нулевым следом.
Поэтому возможный способ решения уравнения
(7.5.1) заключается в поиске указанных п - 1 ли-
нейно независимых векторов Ь, и представлении
164
вектора b коэффициентов полинома b(t) в этом
базисе. Такое разложение существует и единст-
венно, так как Тг(Ь) = 0. Тогда, если
ь-Дь,,
то решение уравнения (7.5.1) есть
* = •
Алгоритм 7.5.4. Решение квадратного урав-
нения над q = 2".
Вход. Полином fit), задающий поле F9, и ко-
эффициент Ъ уравнения (7.5.1).
Выход. Корни уравнения (7.5.1).
Метод.
1. Вычислить Т <— Тг(/>). Если Т- 1, то резуль-
тат: решений нет.
(«-1)/2 2]
2. При п = 1 (mod 2) положить х0 <- Ь2 и
перейти на шаг 4.
3. При п s 0 (mod 2) выполнить следующие дей-
ствия.
3.1. Выбрать у g F2 такое, что Tr(y) = 1.
3.2. Доя/ = 1,2,...,пвычислить
к=1
п 1-1
3.3. Положить х0 2 .
7=1
4. Результат: {х0, х0 + 1}.
Пример 7.5.4. Решение квадратного уравне-
ния в поле характеристики 2.
1. Пусть п = 4, х + х +1 = 0 (mod Z4 +1 + 1).
Находим след свободного члена f. Tr(Z) = / +
+ Z2 + Z4 +1& = t + t2 + (t + 1) + (f + 1) = 0. Решение
существует. Выбираем у = Z3, тогда у2 = Z3 + Z2,
у4 = Z3 + Z2 +1 + 1, y8 = Z3 + Z. Вычисляем 6] = Z,
62 = Z2, 63 = t + 1, 64 = Z2 + 1. Получаем x0 = ? +
+1 + 1. Решения: t3 +1, t3 +1 + 1.
Проверка: x(J2 + x0 + / = 0 (mod Z4 + Z + 1).
2. Пустьh = 5,x2+x + Z = 0 (mod Z5 + Z2 + 1).
Находим след элемента Z: Tr(Z) = 0. Решение
существует. Вычисляем
х0 = Z2 = Z + Z4 + Z16 = Z3 +1.
Решения: Z3, Z3 + 1.
Сложность алгоритма 7.5.4 равна О(и4), так
как вычисляются О(п) экспонент со сложностью
О(и3).
7.5.6. Извлечение кубического корня
в конечном поле
Решение уравнения х3 = a (mod р), где число
р— простое, будем рассматривать для случаев
р = 2 (mod 3) и /2 = 1 (mod 3).
При р = 2 (mod 3) решение существует и един-
ственно для любого a, x = ±a(/’+l)Z6(mod р), так
как порядок группы не делится на 3. Знак реше-
ния уточняется проверкой. Действительно,
</+1 = ст (mod р). Поскольку р + 1 четное и де-
лится на 3, то р + 1 делится на 6. Тогда
а(т+1)/б = ^2/6 ^moj
Из а^6 s (mod р) получаем требуемую
формулу.
При р = 1 (mod 3) решение существует, если а
является кубическим вычетом по модулю р, и не
существует, если а является кубическим невыче-
том по модулю р. Если х0 — кубический корень
из а, то сохо, оА'о — тоже кубические корни из а,
где 0) =—~(mod р) е Fp. Извлечение квад-
ратного корня из -3 может быть выполнено ал-
горитмом 7.5.3.
Поскольку при нечетном р выполняется р = 1
(mod 6), возможны следующие сравнения: р = {1,
7, 13} (mod 18). Тогда xp~p+2sx (mod/?) и
р2 -р + 2 = 0 (mod 3).
Для р = 1 (mod 18) справедливо соотношение
хр+2 = х3 = a<p+2)Z3(mod р), тогда х=а(р+2^9 (mod р).
Аналогично, для р=13 (mod 18) получаем
x = ai'2p+l^9(modp). Такие же рассуждения мож-
но провести и в случае р = 1 (mod 18).
Алгоритм 7.5.5. Извлечение кубического
корня в поле изр = {7, 13} (mod 18) элементов.
Вход. Элемент а е Fp.
Выход. Кубический корень х из а в поле Fp.
Метод.
1. Подбором найти элемент с такой, что
с(р-1)/з ] (mo(j ру положить со <— с(р'1)/3
(mod р) или найти со =—~ (m°d р) из-
влечением квадратного корня из -3 алгорит-
мом 7.5.3.
2. При р = 1 (mod 18): x<-n(p+2)Z9-{1, со, со2}
(mod р). В противном случае положить
х <— <я(2р+1)/9 • {1, со, со2} (modр).
3. Результат: х.
165
Алгоритм 7.5.6. Извлечение кубического
корня в поле изр = {19, 37} (mod 54) элементов.
Вход. Элемент а е F,,.
Выход. Кубический корень х из а в поле Fp.
Метод. •
1. Подбором найти элемент с такой, что с^'1^9 Ф 1
(modр), положить 6 <— с^"1^9 (mod р).
2. При р= 19 (mod 54): у<—<7(/,+8)yf27(mod/?). В
противном случае у <— a(2/’+7^27(mod р).
3. Найти х0 вида у • {1, 6, О2} такой, что х03 s а
(mod р).
4. Положить х <— хо • {1, О3, О6} (mod/?).
5. Результат: х. •>/:•...
Алгоритм 7.5.7. Извлечение кубического
корня в поле кзр = 1 (mod 3) элементов.
Вход. Элемент а е Fp.
Выход. Кубический корень х из а в поле Fp.
Метод.
1. Подбором найти элемент с такой, что
с(р-1)/з у, । (тос|р), положить о <— с‘р~1*3 (mod/?)
-1+лГз, , ч
или наити (0 =--------(mod/?) извлечением
квадратного корня из -3 алгоритмом 7.5.3.
2. Подбором найти элемент Ъ е F;, такой, что
полином fly) = у + by - а неприводим над Fp.
3. Положить
х<-_v<f,2+p+1)/3 .{15 (.), о2} (mod/(у)).
4. Результат: х.
Пример 7.5.5. Извлечение кубического корня.
Пусть р = 73, а = 52. Находим со = 8. Подбо-
ром находим b = 1, тогда fly) = у3 + у - 52. Вы-
числяем х = {28. 5, 40} (mod 73).
7.6. Вычисление символа Якоби
Символ Якоби необходимо вычислять при
проверке числа на простоту тестом Соловэя—
Штрассена (алгоритм 7.7.2).
Символ Лежандра — для простого р можно
\Р)
вычислять возведением а в степень (/?-!)/2.
Однако в общем случае порядок группы обрати-
мых элементов кольца TJrifl. для составного п
неизвестен. В основу вычисления символа Якоби
положен квадратичный закон взаимности (тео-
рема 5.4.2). -; •
Алгоритм 7.6.1. Вычисление символа Якоби.
Вход. Целое число п > 3, целое число а,
0 <а <п.
Выход. Символ Якоби v___
\п) -
Метод. '' ''
1. Положить g <— 1.
2. При а = 0 результат: 0. .
3. При а - 1 результат: g.
4. Представить а в виде а = 2Э/|, где су — не-
четное.
5. Если е -— четное, то s <— 1. В противном случае,
если п = ±1 (mod 8), то s <— 1, иначе 5 <—1.
6. При щ = 1 результат: g s.
7. Если п = 3 (mod 4) и щ = 3 (mod 4), то s <—s.
8. Положить а <— п (mod щ), п <— щ, g <— g • s и
вернуться на шаг 2.
Сложность алгоритма 7.6.1 равна O((log п)2).
Пример 7.6.1. Вычисление символа Якоби.
< 541 А
Вычислим символ Якоби ---- .
U829J
Полагаем g=l. ’
Первая итерация. Находим представление
числа а: 541 = 2° • 541, су = 541. Число е = 0 чет-
ное, поэтому s=l. Полагаем а = 1829
(mod 541) = 206, п = 541, g = 1 • 1 = 1.
Вторая итерация. Находим представление
числа а: 206 = 21 • 103, щ = 103. Число е = 1 не-
четное и и s 5 (mod 8), поэтому s = -1. Полагаем
а = 541 (mod 103) = 26, п = 103, g= 1 (-1) = -1.
j Третья итерация. Находим представление
числа а'. 26 = 2 • 13, щ = 13. Число е= I нечет-
ное и п = -\ (mod 8), поэтому s = 1. Полагаем
а = 103 (mod 13) = 12, п = 13, g = (-1) 1 = -1.
Четвертая итерация. Находим представление
числа а: 12 = 2“- 3, а\ = 3. Число е = 2 четное,
поэтому s=l. Полагаем а = 13 (mod 3) = 1, п = 3,
g = (-l)-l=-l-
ГТ 1 Г 54П 1
Поскольку а = 1, результат: I - I = -1.
7.7. Проверка чисел
и полиномов на простоту
Для проверки целого рационального числа на
простоту обычно используются вероятностные
алгоритмы. Это обусловлено тем, что детерми-
нированные тесты значительно менее «прозрач-
ны» и более сложны, а разницы между понятием
доказуемо простого числа и числа, предположи-
тельно являющегося простым с вероятностью
ошибки 1О”100, практически нет.
166
Ниже приводятся наиболее известные алго-
ритмы.
Алгоритм 7.7.1. Тест Миллера-Рабина.
Вход. Тестируемое нечетное число р, число
повторов к.
Выход. Результат теста.
Метод.
1. Представить число р - 1 в виде р - 1 = 2"’s,
где s — нечетное.
2. Положить i <— 0.
3. При I > к результат: число р вероятно простое.
4. Выбрать случайное основание а,
1 <а<р-\, НОД(а, р) = 1.
5. Вычислить b as (modр). При Ъ=\ вер-
нуться на шаг 3. При Ъ=р-1 положить
i <— i + 1 и вернуться на шаг 3. ;
6. Для /= 1,2, 1 вычислить с<— as2
(mod/)). Если для некоторого I имеет место
с =р - 1, то положить i <— i + 1 и вернуться на
шаг 3. Иначе результат: число р составное.
Примечания.
1. Можно доказать, что для вероятности ошиб-
ки 2“2к достаточно к циклов. Однако сущест-
вуют теоретико-числовые оценки того, что
для чисел длины 100 десятичных знаков ве-
роятность ошибки для одного цикла не пре-
вышает 10“7 [6]. С ростом длины числа р ве-
роятность ошибки снижается.
2. Если основания а на шаге 4 выбирать по
фиксированному списку, то можно найти та-
кое составное число р, которое успешно
пройдет тест.
3. Проверка взаимной простоты чисел а и р
нужна для строгости алгоритма, в противном
случае для составного р на шаге 5 или 6 мо-
жет получиться 0 (mod р).
Сложность алгоритма 7.7.1 при использова-
нии умножения «в столбик» равна O((log/))3).
1.
2.
Алгоритм 7.7.2. Тест Соловэя-Штрассена.
Вход. Тестируемое нечетное число р, число
повторов к.
Выход. Результат теста.
Метод.
Положить i <— 0.
При 1>к результат: число р вероятно про-
стое.
Выбрать случайное основание
1 < а <р - 1, НОД(а,Д) = 1.
3.
а,
4.
Вычислить символ Якоби Ь<- — алгорит-
\PJ
мом 7.6.1 и положить с <— (mod р). Ес-
ли Ь = с, то положить i <— i + 1 и вернуться на
шаг 2. Иначе результат: число р составное.
Сложность алгоритма 7.7.2 при использовании
умножения «в столбик» равна O((log/))3). Для числа
повторов к вероятность ошибки равна 2~к.
Мощным тестом на простоту числа р является
проверка соответствия числа точек эллиптиче-
ской кривой над кольцом вычетов по модулю р
расчетному значению (см. п. 15.4). Для проверки
полиномов над конечным полем на простоту
можно использовать алгоритм разложения 7.4.1.
Для доказательства простоты полинома /}/) про-
стой степени п достаточно проверить, что сво-
бодный член полинома /}/) ненулевой и что вы-
полняются условия:
/^’-^l (mod/(/)), )
НОД(/7’4 -1 (mod /(/)), /(/)) е F р.
Тест основан на следующей теореме.
Теорема 7.7.1. Если ft) е ГД/] — полином
простой степени п с ненулевым свободным чле-
ном, причем выполняются условия (7.7.1), то/}/)
является неразложимым элементом кольца Fp[/].
Доказательство. Предположим, что/}/) яв-
ляется составным. Тогда он делится на некото-
рый неприводимый полином g(/) степени т < п.
Кольцо классов вычетов FP[/]/(g(/)) является по-
лем, и это поле содержится в кольце Fp[/]/(/(/)).
Элемент / является обратимым элементом кольца
Рр[/]/(Я0), так как/}/) и / взаимно просты. По-
У-' 1
этому для выполнения равенства / = 1
(mod /}/)) необходимо, чтобы число р” - 1 дели-
лось на порядок рт - 1 мультипликативной груп-
пы поля Fp[f]/(g(0)- Это возможно лишь тогда,
когда п делится на т. В случае простого п полу-
чаем, что единственно возможный случай —
т= 1. Тогда tp4 = 1 (modg(/)) и НОД)/7'4 - 1
(mod /}/)), /}/)) отличен от константы, что проти-
воречит условию теоремы.
Очевидно, что вместо / для доказательства
неприводимости можно использовать любой по-
лином a(t), взаимно простой с ft).
Тест, доказывающий неприводимость поли-
нома ft) составной степени и, заключается в сле-
дующем. Сначала, вычислив НОД(/(/),/'(/)), про-
веряем, что полином ft) свободен от квадратов, а
затем подбираем полином «(/), взаимно простой
с ft) и такой, что выполняются условия
a(ff ' = 1 (mod/}/)), „ч.-
167
НОД(б< 1 - 1 (тоаЛОХЛО) е Fp
для всех делителей d числа и.
7.8. Разложение чисел в мнимом
квадратичном порядке
Этот вариант расширенного алгоритма Евк-
лида, предложенный Поллардом и Шнорром
[9], может использоваться при разработке и
анализе криптосистем с открытым ключом, в
частности, при генерации эллиптической кривой
(см. гл. 15).
Пусть р — нечетное простое число, р -D.
Если базис квадратичного порядка равен
[1,тГ0], то есть D = 1 (mod 4), то разложение
имеет вид р = с2 + Db2. Если базис равен
, то есть D = 3 (mod 4), то разложе-
2 , D + 1 ,2 т
ние имеет вид р = с +cd +------------d . Тогда
4
4/7 = (2с + d)2 + Dd2 = а + Db2.
полнялось условие
Теорема 7.8.1. Для того чтобы искомое раз-
ложение существовало, необходимо, чтобы вы-
---- = 1. Если такое разло-
. Р 7
жение существует, то оно единственно.
Доказательство. Пустьр~а + Db2. Тогдаb
обратимо по модулю р (иначе число р не было
бы простым). Имеем ст + Db2 = 0 (mod р),
(ab1)2 = -D (mod р), поэтому —D является квад-
ратичным вычетом по модулю р. Аналогично
рассматривается случай 4р = сг + Db2.
Определим норму А(л) для л eZ[7-Z>] как
Л'(л) = ля е Z . Для любых л, р е вы-
полняется равенство А(л)Л'(р) = А(лр). Предполо-
жим, что существует два различных разложения:
р = лл = рр , тоща N(p) =р2 = лр = лр = лр = л р .
Пусть Tt = a + b-y/-D, p~c + dyJ--D. Тогда все
числа a, b, с, d отличны от нуля. Подставляя эти
выражения в предыдущие пять равенств для N(p),
из условия вещественности нормы получаем
ad= 0 и Ьс = 0. В силу целостности кольца Z по-
лучаем противоречие, то есть предположение не-
верно.
Необходимое условие теоремы 7.8.1 не явля-
u f~5>l 1
ется достаточным. Например, = но раз-
ложение 28 = а + 5b2 невозможно.
Алгоритм разложения числар в Z[V-Z>] вы-
полняется в два этапа по аналогии с расширен-
ным алгоритмом Евклида. На первом этапе на-
ходим целочисленное представление
pm} -Uq + D = (-yJ-D (mod р))2 + D • 12
извлечением квадратного корня из -D по модулю
р, затем такое же представление для т\ и т. д., по-
ка не получим тк = 1. Тогда тк_х = ик_х + D 12. На
втором этапе, используя равенства
(,sf 2 + Dt}2)(s22 + Di?2) = S2 + DI2,
S = sis2 ± Didi, T = S]/2 + s2h ,
справедливые для любых s2, t\, t2, находим
представление
mk-2 = ак-2 + -ЗДе-2’ mk-3 ~ ak-3 + -ЗДс-3
и т. д., пока не будет найдено такое представле-
ние для т0 = р.
Алгоритм 7.8.1. Разложение простого числа в
zhTz)].
Вход. Простое число р, D > 0.
Выход. Числа а, b такие, что р = а + Db2.
Метод.
1. Вычислить символ Лежандра -—
• - \ Р )
Если
он равен -1, то результат: решений нет.
2. Вычислить и <— V-Z)(mod р) одним из алго-
ритмов 7.5.1-7.5.4 в зависимости от вида
числа р.
3. Положить i <— 0, г/, <— и, т, <— р.
4. Вычислить . А А'.
и + D
т1+1 <---------
mi
и,+} <— min{w, (mod m,+i), m,+1 - w, (mod m,+i)}.
5. Если ml+\ = 1, то перейти на шаг 6 (в этом
случае обеспечивается /и, = и2 + I2 • Z)), иначе
положить i <— i + 1 и перейти на шаг 4. е я
6. Положить а, <— и„ b, <— 1.
168
7. Если i = 0, то положить а <— at, b <- Ь, и пе-
рейти на шаг 9. Иначе положить
ai-l
+ ul_}al +Dbj
а, + Db,
— a, ± tij_Abl
a2 + Db2
Знаки подбираются так, чтобы деление было
целочисленным.
8. Положить i <- i’ - 1 и вернуться на шаг 7.
9. Результат: а, Ъ.
Сложность алгоритма 7.8.1 равна O((log/>)3).
Если число р не имеет искомого разложения,
nj на шаге 4 алгоритм зацикливается и значение
mi+i недостижимо. Такая ситуация возможна, ес-
2 D +1 п
ли Os3 (mod4) и р = с -cd +----------d — нор-
ма простого делителя числа р в квадратичном
порядке Z
В этом случае существует
разложение для числа 4/> = а2 + Db2, где а и b не-
четны, и это значение может быть вычислено
алгоритмом 7.8.1. Тогда на шаге 4 получается
тм = 4. Соответственно на шаге 5 необходимо
контролировать условие от,, । = 4. После этого
можно переходить к шагам 6-9. При этом на ша-
и2 + jD
ге 6 имеем mj = ----. Формулы на шаге 7 со-
храняются, но в качестве знаменателя нужно ис-
пользовать значение т,.
В основу алгоритма 7.8.1 положено деление в
использующее мультипликативное
свойство нормы: если число р = сг + Db2 делит
число н<2 + D = тр, то, переходя к Z[V-E>], по-
лучим, что целое квадратичное число а + b^-D
должно делить целое квадратичное число
w0 + y/-D . При этом (по крайней мере для евк-
лидова кольца) должно существовать частное —
целое квадратичное число, норма которого равна
т}. Следовательно, должен существовать эле-
мент ц = -J-D (mod ). Легко заметить, что
щ — ±wo (mod т}). Далее процедура рекурсивно
повторяется для i + 1.
Алгоритм 7.8.1 использует функцию, которая
делает кольцо евклидовым (см. п. 3.7), а именно
норму N: Z[V- D] —> Z>0 такую, что
Д(ар)>Л(а) и для любых двух элементов
а,ре2[ТЙЙ], где а Ф 0, существует представ-
ление р = уа + р, в котором р = 0 или
Л'(р) < А'(а). Поэтому если квадратичный
док не является евклидовым, алгоритм 7.8.
жет не дать результата.
Существуют квадратичные порядки, не
ляющиеся евклидовыми, в которых алго£
7.8.1 дает результат. Например, в код
д-йй] нечетное простое число р раскладь
ется на множители тогда и только тогда, ко
р = 1 (mod 4) (см. п. 5.4). При этомр ~ сг + Ь2,
а, Ъ имеют различную четность. Не умаляя об
ности, можно считать, что Ъ четное. Полож
b = 2с. Тогда р = а2 + 4с2, что соответствует р<
ложению числа р в квадратичном поряд.
не являющемся евклидовым (после,
нее следует из неоднозначности разложени
2-2 = -(й^4)2).
Пример 7.8.1. Разложение числа в Z[-7-£)].
Г-ТЙ
1. Пусть р = 43, D = 2. Поскольку —— = 1,
\ Р J
решение может существовать. Вычисляем
и = -7-2 (mod43) = 16(mod43) алгоритмом 7.5.1:
162-1-2 = 43 - 6, то есть /и, = 6, щ = ±2. Далее:
т2 = 1, »Ц = 22 + 2, /»о(22 + 2 • I2) = 162+ 2 • I2.
Отсюда
-16-2 + 2-1 с , -2-16 „
а------------= -5, Ь=--------= -3.
6 6
Таким образом, 43 = (-5)2 + 2 • (-3)2.
Г-тЙ
2. Пусть р = 127, D = 7. Поскольку - = 1,
I Р J
решение может существовать. Вычисляем
и = -7-7(mod 127) — 45 (mod 127). Тогда = 127,
«о ~ 45. Находим 452 + 7 = 127 • 16, то есть = 16,
щ — 3, т2 = 1. Далее гщ = З2 + 7, то(32 + 7 • I2) -
— 452 + 7 I2. Отсюда
-45-3 + 7-1
-3-45
16
= -8, Ъ =
Таким образом, 127 = (-8)2 + 7 • З2.
3. Пусть/> = 31, £)= 11. Поскольку - =1,
I Р J
решение может существовать. Вычисляем
us -7-11 (mod31)s!2(mod31). Тогда /н0 = 31,
w0= 12. Находим 122 + 11 = 31 - 5, то есть пц - 5,
«1 = 2. На следующей итерации получаем т2 = 3,
и2 = 1, после чего процесс зацикливается с пе-
риодом 2, где и, = 1, а т, принимает поочередно
значения 3 и 4. Искомое представление для р не
существует (однако для числа 4/? получаем
4/?= 124 = 52 + 1 1 -З2).
Искомое разложение для числа 4/> можно по-
лучить, если заметить, что для т2 - 3 справедли-
во равенство 4?и2 = I2 + 11 • I2, что соответствует
t 1 + УЛТ
2
1 + V-11
2
в
разложению т2 =
кольце целых квадратичных чисел. Выполняем
шаги 6-9 алгоритма для учетверенных чисел mt.
Имеем а2 = 1, Ь2 = 1. Для того чтобы на шаге 7
получались целые числа, в качестве знаменателя
формул для a,, bj используем Тогда
-2-1 + 11 . , -1-2-1 .
«1 =—-— = 3, й,=-----= -1,
то есть
ние числа к по модулю решетки L, то есть нахо-
ждение комплексного числа к (mod L).
В силу равенства р - лл существует значение
тВ (mod р) и, следовательно, значение
rn^-D (modр) такое, что л = 0 (mod р). Вычет
по модулю л произвольного элемента а решетки
не изменится, если к нему прибавить число,
кратное л, то есть а = а - рл (mod л), где р —
элемент решетки. Алгоритм основан на пооче-
редном выборе р, кратного 1 или тВ, обеспечи-
вающего минимум нормы комплексного числа
а - рл. Направления 1 и тВ чередуются до тех
пор, пока не получится нулевая длина шага в
обоих направлениях, что соответствует мини-
мальной норме числа а = х + тВу.
Для вещественного направления размер шага
п определяется условием А(ос - mt) -> min, отсю-
да
4/и,=32+ 11 -(-I)2;
12-3-11-1 с , -3-12-1 .
а,, =---------= 5, Ьп =----------= — j .
° 5 5
Результат: 4р = 52 + 11 • (-3)2.
п =
ax + bym2D
Р
(7.9.1)
1.9. Приведение числа по модулю решетки
если D = 1 или 2 (mod 4), или
„ 1 + m2D, .
;*/: =• 2<2x4-----by + bx + ay
^Tp
п =
(7.9. Г)
Этот алгоритм может использоваться при раз-
работке криптосистем на эллиптических кривых
с комплексным умножением [3].
Пусть Z[mO] — мнимый квадратичный поря-
док и р > 3 — простое нечетное число, которое
раскладывается на простые множители в Z[mO]:
если D= 1 или 2 (mod 4); 6 = - - — —, если
D = 3 (mod 4); 0 < D < р и D свободно от квадра-
тов. Норма А(а) = асс квадратичного целого
числа а = х + тВу равна Л'(сх) = х + m2Dy2, если
B = -J-D , и N(a) = х2 + у2 +*У, если
. Алгоритм обеспечивает миними-
2
зацию нормы (и, следовательно, абсолютной ве-
личины составляющих) произвольного к е IF,,.
Будем рассматривать целые алгебраические
числа а = х + тВу как двумерную решетку L с
базисом [1,т6], элементами которой являются
целочисленные точки (х, у). Процедуру миними-
зации нормы можно рассматривать как приведе-
если D = 3 (mod 4).
Выражение в квадратных скобках означает
ближайшее целое. Для комплексного направле-
ния размер шага п определяется услови-
ем Д(о. - и/иОл) —> min, отсюда
п =
qy-bx
Р
(7.9.2)
если D = 1 или 2 (mod 4), или, с учетом равенства
е’=-1±£+в, —
4
п =
ах + bx - ^-^-^-(2bx - 2ау - by)
____________4__________________
•• ••/ - - - • 4р
(7.9.2')
если D = 3 (mod 4).
Алгоритм 7.9.1. Приведение числа по моду-
лю решетки.
Вход. k,p,D, л = а + bm^- D .
Выход, к е с + mBd (mod тс). :
Метод. "-..-.v .•
170
1. Положить х <— к, у <— 0, а <— х + тву.
2. Вычислить оптимальную длину шага п, в
вещественном направлении по формулам
(7.9.1), (7.9.Г) и норму числа ai = a-«in;
вычислить оптимальную длину шага п2 в
комплексном направлении по формулам
(7.9.2), (7.9.2') и норму числа а2 = « ~ п2т0т1.
3. При «j = «2 = 0 результат: с = х, d = y. В про-
тивном случае: если A(cq) < N(cl2), то a <- аь
иначе — ос <- ос2 и вернуться на шаг 2.
Примечания.
1. Оптимальные направления чередуются, по-
этому оптимальное направление можно оп-
ределять только на первой итерации.
2. Знаки коэффициентов а, Ь, участвующих в раз-
ложении числа р, определяются так, чтобы вы-
полнялось сравнение а + Ьт4~ D = 0 (mod р)
для некоторого значения квадратного корня
из -D по модулю р.
3. Целочисленное деление с остатком можно
выполнять согласно п. 7.1.5.
Пример 7.9.1. Приведение числа по модулю
решетки.
1. Пустьр = 43, т = 1, 6 = -7-2 = 16(mod43),
л = -5 + 3-7-2 = 0 (mod43), к = 15.
На первой итерации находим щ = -2,
2V(cc -/ЦП) = 97, п2 = -1, N(a- п2 2л) = 131,
лучшее направление — вещественное, ос=5+6дГ2.
На второй итерации лучшее направление — мни-
мое, п2 = -1, jV(oc - п2 -7-2 л) = 6, a = -1 + -7-2.
На третьей итерации = п2 = 0. Результат:
к = -1 + -7-2 (mod л).
2. Пустьр = 1\,т = \,D=1, тогда
др7 = 63 (mod 71), 6 = 1+-^ 7 = 32 (mod 71),
л = 7+ 20 = 0 (mod 71), £=23.
На первой итерации находим «1=3,
N(v. - /дл) = 64, п2 = 0, N(a - п2&п) = 529, лучшее
направление — вещественное, ос = 2 - 60.
На второй итерации лучшее направление —
мнимое, п2 = -1, N(p. - «20тс) = 16, a = -2 + 30.
На третьей итерации щ = п2 = 0. Результат:
к = -2 + 30 (mod л).
Сложность алгоритма 7.9.1 равна O((logj>)3).
точки решетки к эллипсу х2 + Dy2 =р при D = 1
« . . . 2 1 + ТП D 2
или 2 (mod 4) или х +ху+--------—у -р при
D = 3 (mod 4) до попадания внутрь эллипса. Ал-
горитм останавливается, если одновременно вы-
полняются неравенства
<ax + bym2D <—, -~<ay-bx< —
2 2 2 2
при D = 1 или 2 (mod 4) или
-р < (2а + Ь)х +
1 + m2D
. 2
У<Р,
b + a
-р <(a + b)x-+ (2bx -2ау- by) < р
при D = 3 (mod 4). Таким образом, область оста-
нова представляет собой параллелограмм с цен-
тром в начале координат, целиком расположен-
ный внутри эллипса.
Теорема 7.9.1. Алгоритм 7.9.1 при р> 3 зада-
ет биекцию между Fp и целыми точками парал-
лелограмма.
Доказательство. Отображение поля Fp в
целые точки, лежащие внутри параллелограмма,
инъективно, так как л = а + 60 = 0 (mod р) и на
каждом шаге алгоритма значение a (mod р) со-
храняется. Точки решетки и параллелограмма
можно складывать как комплексные числа, ну-
левая точка является нулем, каждая точка имеет
единственную противоположную точку. Поэто-
му точки решетки образуют абелеву группу, а
точки внутри параллелограмма— ее нормаль-
ную подгруппу. Отображение точек параллело-
грамма в поле Fp путем нахождения вычета по
модулю р для данного 0 является гомоморфиз-
мом аддитивных групп. Для доказательства того,
что отображение является биекцией, достаточно
показать, что число целых точек в параллело-
грамме отлично от 1 и меньше, чем 2р.
Рассмотрим случай, когда D = 1 или 2
(mod 4). С учетом того, что целые точки решетки
расположены вдоль координатной оси у с шагом
m4~D, можно ввести нормированные координа-
ты у' = my4~D и Ь' = тЬ4Й. Такое нормирова-
ние соответствует случаю D = 1, при этом эллипс
представляет собой окружность, а параллело-
грамм— квадрат. Вершины квадрата располо-
жены в точках
Геометрически алгоритм 7.9.1 представляет
собой процесс последовательных приближений
171
(a-b' a+b'\ (a + b' a-b'у
(2’2/t 2 ’ 2 J’
(-a-b' а-Ь'Л (-a+b' -a-b'\
I 2 ’.2 J ’ I 2 ’ 2 J ‘
Сторона квадрата равна ^a2 +b2 =y[p. C
учетом поворота квадрата относительно центра
число целых точек внутри квадрата лежит в диа-
пазоне р ± 2-yfp . Случай D = 3 (mod 4) рассмат-
ривается аналогично. Таким образом, алгоритм
7.9.1 задает биекцию между множеством цело-
численных точек квадрата и множеством чисел
{0,1,...,/?-!}.
Аналогичными рассуждениями можно пока-
зать, что алгоритм 7.9.1 задает изоморфизм по-
лей = Z[6]/(n).
7.10. Умножение точки
эллиптической кривой на число
Сложение точек эллиптической кривой по-
зволяет определить умножение точки на целое
число. Умножение точки Р эллиптической кри-
вой на показатель I выполняется методом сложе-
ний и удвоений. Показатель представляется в
п~1
виде Z = ^Z,2', где Z, е {-1, 0, 1}. Затем после-
<=о
довательно вычисляются точки 2'+1Р удвоением
точки 2'Р (z = 0, 1, ...,и-2) и складываются те
из них, для которых коэффициент I, отличен от
нуля с учетом знака. Если порядок группы, обра-
зованной точкой Р, равен г, то вычисляется пока-
затель Г = г -1. Умножать точку можно на лю-
бой из показателей I или Г.
Более удобным является второй способ ум-
ножения: начиная со старших разрядов показа-
теля вычисляется текущая точка Р„ где P„_j = Р,
и для перехода к предыдущему разряду выпол-
няется рекурсия:
Р;_! = 2Р, + 7,-jP.
Для уменьшения числа ненулевых коэффици-
ентов в представлении I проводится процедура
минимизации. При этом сначала используются
двоичные коэффициенты Z, е {0, 1}. Затем, начиная
с младших разрядов, цепочки вида 0,1,1,..., 1 заме-
к
няются на цепочки вида 1,0,0,..., 0, -1. В резуль-
к-\
тате минимизации доля ненулевых разрядов в
представлении числа I уменьшается в среднем с
% до ’А.
Критерием выбора показателя I или I' является
число ненулевых разрядов с учетом минимизации.
Для умножения точки на число можно вос-
пользоваться системой счисления с основанием
d, равным степени двойки (на практике 8 или
16). В случае d= 16 показатель Z разбивается на
тетрады Z = lo + 16Z, + ... + 1Вычисляются
точки 2Р, ЗР, 15Р, затем, начиная со старших
тетрад, выполняется рекурсия Р,_] = 16Р; + 1,-iP.
Если базу данных вида {Z,P} находить на этапе
предвычислений, то число сложений точек со-
кращается примерно в четыре раза по сравнению
с числом удвоений.
Для сложения точек можно использовать аф-
финный или проективный вариант арифметики.
Аффинная арифметика требует модульного об-
ращения бинарным алгоритмом Евклида для ка-
ждой операции сложения точек. Проективная
арифметика требует большего числа умножений
и сложений, но обращение выполняется лишь
однажды, при переходе к аффинному виду после
завершения умножения точки на число.
Для кривой Y2Z = X3 + AXZ2 + BZ3 формулы
удвоения в проективных координатах имеют
вид:
ее 2Y]ZA(3X(+AZ()2 - в^У/УД (mod/?),
Уз = 4YJ2Z1(3X1(3XI2 + AZ2) - 2Y}2Zt) -
- (ЗА}2 + ZZ/)3 (mod/?),
Z3 = 8y]3Z13(mod/?). . ;s
Формулы сложения в проективных координа-
тах для этой же кривой имеют вид:
Х3 ее (X2Z, - AlZ2)(Z1Z2(y2Zl - yz2)2 -
- (X2Zj + A1Z2)(A2Zi -A,Z2)2) (mod/?),
Уз (X2Zj - AlZ2)2(y2Z1(A2Zl + 2A}Z2) -
- Y,ZAXxZ3 + 2X2Zj)) - ZIZ2(y2Z1 - У^)3 (mod/?),
Z3 ее Z,Z2 (X2Z, -XZ2)3 (mod/?).
Если характеристика поля отлична от 3 и эл-
липтическая кривая задана в форме Гессе
X3 + У3 + Z3 = 3pXYZ,
то формулы сложения точек Р\ + Р2 = Р3,
Р, = (Xj, Yh Z,) приобретают симметричный вид:
Х3 = X^-Yi3) (modр),
y3 = Z1(y13-X13)(mod/?),
Z3 = y1(X]3-Z13)(mod/?)
172
При Pl = Р2 И
Х3 = YiZiX2 2 - Y2Z2X2 (modр\
Уз = Xi YiZ2 - X2Y2Z2 (modp),
Z3 = XiZi Y2 - X2Z2Yi (modp)
при Pi Ф P2.
Единичный элемент группы имеет проективные
координаты (0, 1,-1). Таким образом, задание эл-
липтической кривой в форме Гессе позволяет уско-
рить удвоение точек по сравнению с традиционной
арифметикой в форме Вейерштрасса.
Чтобы ускорить умножение точки Р на число,
можно использовать комплексное умножение на
элемент mQ мнимого квадратичного порядка
Z[mQ]. Для этого нужно минимизировать пока-
затель / с помощью алгоритма 7.9.1 и предста-
вить его в виде I = 10 + kmQ, затем уменьшить
число ненулевых цифр в троичном представле-
нии показателей Zo и Ц, вычислить точки lGP и 1}Р,
используя общую базу из точек вида 2'Р, и найти
точки mQ • ltP, lGP + mQ ltP.
Комплексное умножение имеет наиболее про-
стой вид в случаях, рассмотренных в п. 6.11.5.
Кроме того, для кривых у2 = х3 - 4/х2 + 2t2x при
р = 1 (mod 8) или р = 3 (mod 8) существует ком-
плексное умножение на V-2 , задаваемое ото-
бражением
<р(х,у) =
-^-(modp),
< 2*
у(х2 -2t2)
24^2х2
Л
(mod р)
7
Для этих кривых нет необходимости представ-
лять показатель в двоичной системе счисления, по-
скольку можно воспользоваться равенствами
l0 = /о,о + 2/о,1 + • • • + 2к ’/ол-ь
Л = ^i,o + 2Zij + ... + 2Л'-1/]>],
Z-Zo + Zj4-2 -l00 + V~2Z]j0 + (V-2)2^o,i +
+(4~2)3+—+(-v-2)2/‘ +—+(yJ-2)2k llik_} ,
где 2k бит — длина порядка группы. Последняя
запись соответствует представлению числа I в
системе счисления с основанием 4-2 . Умноже-
ние точки на 4-2 выполняется быстрее удвое-
ния, поэтому указанная система счисления по-
зволяет ускорить умножение точки на число.
Аналогичный подход может быть использован и
в том случае, если существует комплексное ум-
ножение на элемент мнимого квадратичного по-
рядка Z[mQ] для т > 1.
Можно изначально представлять показатель I
в виде квадратичного числа Z = Z0 + Zi6. Чтобы
исключить нежелательную для криптографии
зависимость от показателя / длительности умно-
жения точки на число,1 можно изначально пред-
ставлять 10 и /] в троичном виде с запретом появ-
ления двух ненулевых символов подряд (при
этом число ненулевых символов должно быть
постоянным). Число показателей длины т с к
ненулевыми символами, обладающих таким
свойством, равно 2
. Это число мак-
симально при к-т/3 и близко по порядку ве-
личины к 2"' с точностью до О(т). Таким обра-
зом, использование троичного представления
показателя в виде пары коэффициентов, в кото-
рых доля ненулевых коэффициентов равна ’/3, не
дает заметного снижения энтропии множества
возможных показателей.
Если эллиптическая кривая рассматривается
над алгебраическим замыканием поля ненулевой
характеристики, то на ней может существовать
более одного варианта коммутирующих между
собой комплексных умножений. Это позволяет
дополнительно ускорить вычисления за счет
комбинирования двух способов комплексного
умножения как полиномов от двух переменных.
7.11. Вычисление функции Вейля
Вычисление функции Вейля может использо-
ваться при логарифмировании на эллиптической
кривой (см. п. 11.3). Логарифмическая производ-
ная функции Вейля полезна при разработке
криптографических алгоритмов на эллиптиче-
ских кривых специального вида.
Пусть E(FV)— эллиптическая кривая, задан-
ная над полем из q=pr> элементов уравнением
у2 = х3 + Ах + В, и пусть точка Q е E(FV) имеет
простой порядок г > 3. Функция Вейля fo для
точки Q на эллиптической кривой обладает ди-
визором div(/o) = г(0 - г(Рго).
Обозначим через (хт, у,„) координаты точки
mQ, через Х,„.п — угловой коэффициент секущей
(касательной при т = и), проходящей через точ-
ки mQ и nQ эллиптической кривой. Указанный
ниже алгоритм, предложенный И.А. Семаевым,
вычисляет функцию Вейля с точностью до нену-
левой константы.
1 Эта зависимость является потенциально опас-
ной, так как позволяет получить дополнительную ин-
формацию о показателе I путем измерения длительно-
сти вычислений.
173
Алгоритм 7.11.1. Вычисление функции Вейля.
Вход. ДРД Q, Ре ДРД г = #{Q).
Выход. Значение функции Вейля fQ в точке Р.
Метод.
1. Найти представление порядка г группы в
п
двоичном виде: г = rt, где г, = 8,2',
8, е {0, 1},г0= 1-
2. Найти рекуррентно числа s,: s,_] = 2v, + s„ где
i = 1,2, ..., п, sn = 0.
3. Вычислить точки 2Q, 2lQ. ...,2"-1(2,
л-1
(Го + Г|)0, (Го + Г] + Г2)б, ..., .
(=о
4. Вычислить /o(P) = f]g ,-i где
/=о к=о
У-Уио
gu,v ~ ’ gu,-U Х
Х ~ X(u+v)Q
giifi = go,v ~ 1
5. Результат: /(УР)-
Этот же метод может быть использован для
вычисления логарифмической производной
функции Вейля. При этом произведение функ-
ций заменяется на сумму их логарифмических
, Зх2 + А
производных по X, и ух =------.
2у
Алгоритм 7.11.2. Вычисление логарифмиче-
ской производной функции Вейля.
Вход. Е(^р), Q,Pe г = #E(F/;) = р.
Выход. Значение логарифмической производ-
ной функции Вейля fo в точке Р.
Метод.
1. Найти представление порядка г группы в
п
двоичном виде: г = ^г, , где г, = 8,2',
,=0
8, 6 {0, 1},Г0= 1.
2. Найти рекуррентно числа s,: s,-i = 2s, + s„ где
i = 1,2, ..., и, s„ = 0.
3. Вычислить точки 2Q, 2}Q,
и-l
(Го + Г1)б, (Го + И + г2)б, • • , Xr'Q •
i=0
4. Вычислить
L (р)=х - -
)q i=o\gJri^rj k=o\g)2k,A
где
5.
Результат:
Пример 7.11.1. Вычисление логарифмиче-
ской производной функции Вейля.
Исходные данные:
- уравнение эллиптической кривой E(Fp):
у2 = х3 + 5,р = 37;
- число точек г = #E(FP) = 37;
- 0 = (6,31),Р = (22,16).
Разложение р по степеням числа 2:
/> = 37 = 25 + 22 + 1, то есть п = 5, r5 = 1 • 25
(85=1), г4 = 0-24 (84 = 0), г3 = 0-23 (8з = 0),
г2 = 1-22 (82= 1), Г] = 0-2’ (8!=0), Го=1-2°
(8о=1).
Показатели S/,, 0<к<п, в функции fy. s5 = 0,
л4 = 1, S3 = 2, s2 = 4,5] = 9, So = 18.
Функция fQ имеет вид:
/ (v 2 4 9 18
Jо\ ^У1 gy> _/pgp yigp pgp pgp pgy ygy^ 2® *
Логарифмическая производная для точки Q:
у'+ 14
ky + 1.4х-4
У-19 1
^y-Wx + ll х + 6
у'+ 17 1
чу + 17х-14 х-17
+2
+4 -------
- Их+ 12
х-11 J
' У + 1
ky+ х-13
Значение логарифмической производной в
точке Р = (22, 16) равно 9.
7.12. Сложение элементов якобиана
гиперэллиптической кривой
Сложение элементов якобиана выполняется
аналогично композиции квадратичных форм (см.
п. 5.6.3 и работу [5]). При этом получается полу-
приведенный дивизор. Однако поскольку один и
тот же элемент якобиана может быть представ-
лен различными парами полиномов (а, Ъ\ то по-
сле композиции следует выполнить операцию
приведения. Заметим, что в якобиане функции
174
определяются дивизором, то есть с точностью до
константы. Поэтому можно полином а всегда
считать приведенным.
Рассмотрим сложение двух дивизоров, пред-
ставленных парами (аь /д) и (а2, ^2) для гиперэл-
липтической кривой С: у2 + h(x)y =fix).
Композиция
1. Алгоритмом Евклида находим наибольший
общий делитель полиномов из А'[х]
d = НОД(а], а2, b\ + Z>2 + h)
и тройку полиномов hi, h2, h2 таких, что
d = h\ai + h2a2 + 7z3(Z>i + b2 + h).
Вследствие коммутативности операции НОД
можно сначала найти dG = НОД(аь b} + />2), а за-
тем d = НОД(а2, d$).
~ гг а1«2
2. Находим полином а - „ -.
d2
3. Находим полином
b = l¥hb2 + /?з<М +/)(moda)
Если НОД(<7], а2)= 1 (является обратимым
элементом поля К), то можно положить Л3 = О,
поэтому а = а\а2, b = h2a\b2 + h2a2bi (mod а).
Если (a,, bi) = (а2, b2), то есть имеет место уд-
воение элемента якобиана, то можно положить
/?2 = 0 и формула композиции на шаге 3 примет
вид:
, +Лз(Д2+/)
b = 2—------—(mod а).
Приведение
Метод приведения полуприведенного дивизо-
ра D к виду, когда deg(a) < g, заключается в на-
хождении функции с - dy, где с, d— ненулевые
полиномы от х такие, что дивизор D] =
= -((с - dy) - D) является приведенным и поло-
жительным. Для этого необходимо, чтобы
а\(с2 - cbf). Поскольку а\ (b2 -f), то а будет де-
лить (с2 - <f~f), если b будет делителем с и d, то
есть c = db (mod а). Полиномы с, d необходимо
выбрать так, чтобы
deg(c) < (т + g)/2, deg(d) < (т - g -1 )/2.
Тогда deg(Dj) <g, где g— род гиперэллипти-
ческой кривой.
Практически переходим от дивизора (а, Ь) к
эквивалентному дивизору (а', Ь'), где
, f + hb-b2 , ,
а - --------, b =h-b (mode ).
а
Этот шаг при необходимости повторяется не-
сколько раз так, чтобы полученный дивизор был
приведенным (см. алгоритм приведения квадра-
тичных форм, п. 5.6).
Пример 7.12.1. Вычисление в якобиане гипер-
эллиптической кривой.
Рассмотрим гиперэллиптическую кривую
C(F3): у2 = х5 + 1 рода 2. Эта кривая содержит
аффинные точки: (0,1), (0,2), (2,0), причем
(0, 1) = -(0, 2). Эта же кривая над квадратичным
расширением F^X/2 + 1) содержит, кроме ука-
занных трех точек, еше точки: (1, t), (1, 21), (1+ 1,
t + 1), (t + 1, 2t + 2), (2t + 1, t + 2), (2t + 1, 2t + 1).
Получаем Mi = 3 - 3 = 0, M2 = (3 + 6) - 9 = 0 (см.
п.6.15).
Находим коэффициенты дзета-функции: щ =
= а2 = 0, то есть Z(7) = Т4 + 9.
Корни di, ос2, ос3, ос4 дзета-функции равны
±л/б±-7-6
-----------. Порядок якобиана равен произве-
дению (1 - 0С])(1 - СС2)(1 - 0С3)( 1 - 0С4) = Ю.
Составим дивизор как формальную сумму то-
чек: D = ((0, 1)) + ((2, 0)) - 2(РГО) = (х2 + х, х + 1).
Тогда 2D = (х2,1), 3D = (2х2 + 2х + 1, х), 4D =
= (х, 2),..., 8D = (х2,2) = -2D,
9D = (x2 + x,2x + 2) = = -D, 10D = 0.
Поскольку элемент якобиана эллиптической
кривой взаимно однозначно соответствует точке
и представляется в виде пары полиномов
(х-Хр,уР), то указанный вариант арифметики
применим и к эллиптическим кривым.
Для ускорения умножения элемента якобиана
на целое число к можно воспользоваться троич-
ным представлением показателя к с последую-
щей минимизацией числа ненулевых цифр по
аналогии с эллиптическими кривыми.
7.13. Арифметика группы классов
мнимых квадратичных порядков
Вычисления в группе классов С1((9д) мнимого
квадратичного порядка OD выполняются по анало-
гии с композицией квадратичных форм (см.
п. 5.6.3). Идеал 21= (a,b)-q +
со-
2
ответствует квадратичной форме {а, Ь, с), где
с = ---—. Если НОД(а, b, с) = 1, то 2Г1 = (а, -Ь),
4а
при этом q заменяется на q~l.
Приведенный идеал удовлетворяет условиям:
• -а < < а;
• а < D - Ь2;
175
• если а = D - b\ то Ъ > 0.
Для умножения элементов группы классов
необходимо выполнить умножение и приведение
идеалов.
На некоторых шагах используется расширен-
ный алгоритм Евклида над кольцом Z (алгорит-
мы 7.2.2, 7.2.4).
Алгоритм 7.13.1. Умножение приведенных
идеалов мнимого квадратичного порядка [4].
Вход. Приведенные идеалы 21] = (аь Ь}),
21г = (а2, ^г)-
Выход. 213 = (а3, b3) = 21]212.
Метод.
1. Расширенным алгоритмом Евклида найти di,
V], v2 для Я], а2: d} = НОД (аь а2) = Tjaj + v2a2.
2. Положить а3 <— а\а2, b3 <— vct](b3 - b\).
3. При dy ф 1 выполнить следующие действия.
З.Е Расширенным алгоритмом Евклида най-
ти <У2, Wi, w2 для dj, (bi+b2)/2: d2 =
= НОД (Jb (fe, + &г)/2) = + ш2(й] + й2)/2.
3.2 . Положить
п , d h (wyb3 + w2 (D - b1 2 3 )/2)
d2 d2
4. Вычислить b3 <— by + b3 (mod 2a3).
5. Результат: (a3, b3).
Алгоритм 7.13.2. Возведение в квадрат при-
веденного идеала мнимого квадратичного по-
рядка [4].
Вход. Приведенный идеал 21] = (аь Z>i).
Выход. 2l3 = (а3, b3) = 2l2.
Метод.
1. Расширенным алгоритмом Евклида найти d,
v, w для Я], bi. d = НОД (at, b>) = vat + wbj.
on h w(D-b2)
2. Положить a3 <--v, Щ <------—
3 d2 2d
3. Вычислить b3 <— bi + b3 (mod 2a3).
4. Результат: (a3, b3).
Алгоритм 7.13.3. Приведение идеала мнимо-
го квадратичного порядка [4].
Вход. 21 = (a, Z>). - >
Выход. Приведенный идеал 21 = (а, Ь).
Метод.
1. Если b < 0, то положить .$ <—1, в противном
случае положить s <— 1.
2. Положить b <- |Z>|, г <— b (mod 2а).
3. Если а < г, то положить <— а; в противном
случае положить b <— г, s <—s.
. D b2-D
4. Вычислить c<-------.
4a
5. Пока a> с выполнять:
5.E tat- a, a <— c.
5.2.
b
2a
r 4—b (mod 2a).
5.3. c<-ta-q(r + b)/2.
5.4. Если a<r,V) b <^2a -r,c <— с + a- г; в
противном случае b <— r, s <—s.
6. При s<0 положить b <—b.
7. Если b> a, to b <— b - 2a, с <— c - b + а. Если
b < -a, to Z> +2a ис<—c + Z> +a.
8. При a = с и b < 0 положить b <-b.
9. Результат: (a, b).
Пример 7.13.1. Умножение в группе классов
мнимого квадратичного порядка.
Пусть 27 =-167 (число классов равно 11, по-
этому группа классов циклична, ее единичный
элемент представлен идеалом (1, 1), которому
соответствует форма (1,1, 42)). Возведем в квад-
рат идеал (3, 1) согласно алгоритму 7.13.2:
(d, г, и) = (Е 1, -2); а3 = 9, Ь3 = -336 и Ь3 = 7.
Идеалу (9,7) соответствует квадратичная
форма (9, 7,6). Выполним приведение идеала
алгоритмом 7.13.2. Полагаем s=l, b = 2, г = 2.
Так как а > г, полагаем b = 7 и .$ = -1. Вычисляем
с = 6 и находим последовательно: ta = 9, a = 6,
q = 0, г = 7, с = 9, b = 5, с = 8.
Полученному приведенному идеалу (6, 5) со-
ответствует квадратичная форма (6, 5, 8).
Упражнения к главе 7
1. Предложите метод распараллеливания вычис-
лений при умножении больших чисел в пред-
положении, что умножение слов выполняется
значительно медленнее сложения слов.
2. Что собой представляет матрица Q быстрого
преобразования Фурье? Найдите вторую и
четвертую степени матрицы Q.
3. Распространите метод модульного умноже-
ния Монтгомери на полиномы из ЕДх]. По-
кажите, что в этом случае можно исключить
шаг 2.3 алгоритма умножения.
4. *Предложите вариант арифметики Монтгомери
для умножения в конечном поле F,, = Z[oc]/(7t),
где Z[oc] — кольцо целых квадратичных чисел и
л — простой делитель числа р.
5. ^Предложите алгоритмы арифметики (сло-
жения, умножения, обращения и возведения
в квадрат) в расширенном конечном поле ха-
рактеристики 2, если в качестве базиса над F2
использовать элементы I, t2, ... .
6. *Предложите алгоритм целочисленного де-
ления с остатком в мнимом квадратичном
евклидовом кольце.
7. Предложите варианты расширенного алго-
ритма Евклида и расширенного бинарного
алгоритма Евклида для кольца Z[z].
8. Модифицируйте бинарный алгоритм Евкли-
да для вычисления наибольшего общего де-
лителя полиномов из кольца F;,[x].
9. Обобщите алгоритмы извлечения квадратного
корня в поле Fg для q = 5 (mod 8), q = 9 (mod 16)
на случаи q = 17 (mod 32) и q = 33 (mod 64).
10. Предложите алгоритм извлечения кубиче-
ского корня в поле характеристики 3.
11. *Можно ли адаптировать алгоритм LLL к
кольцу целых /?-адических чисел?2
12. Пусть х— кубический характер. Используя
кубический закон взаимности, предложите
метод вычисления кубического характера
для натурального числа п по аналогии с сим-
волом Якоби.
13. Исследуйте аналог псевдопростого теста
Миллера-Рабина для полиномов над конеч-
ным полем.
14. Предложите вариант теста проверки на
простоту для чисел, сравнимых с 5 (mod 6)
по аналогии с тестом Миллера-Рабина (пе-
ред 1 должен появиться кубический корень
из 1).
15. Пусть характеристика р поля Fp раскладыва-
ется на простые множители в кольце целых
алгебраических чисел Z[oc]: р = щ-ж, и
пусть ту (ос) = 0 (mod р). Покажите, что имеет
место изоморфизм полей F;, = Ж[а]/(ту) и что
он вычисляется минимизацией нормы эле-
мента в поле Z[a]/(7tj). Предложите алгоритм
вычисления указанного изоморфизма для
случая к = 3, 4.
16. Покажите, что если р = 1 (mod 3) — простое
число вида р = а2 -ab + b2 и эллиптическая
кривая E(FP) вида у2 = х + В имеет простое
число точек г = 1 (mod 3), то, используя раз-
ложение на простые множители в кольце
, число г можно представить в
виде г = с2-cd + d2. Покажите, что сущест-
2 Эта проблема интересна в связи с дискретным
логарифмированием на эллиптических кривых мето-
дом поднятия.
вует эллиптическая кривая £'(F,) вида
у'2 - х'3 + В', имеющая простое число точек р.
Предложите тест проверки на простоту, ос-
нованный на этих условиях.
17. Кубическая кривая U3 + V3 + CW3 = 0 изо-
морфна эллиптической кривой Y2Z=X3 + BZ3.
Найдите формулы для сложения точек на
первой кривой и сравните по сложности ва-
рианты арифметики на этих кривых.
18. Эллиптическая кривая у2 = х3 + Ах + В при
X=xZ2, Y=yZ3 имеет вид Y2 = X3 + AXZ4 +
+ BZ6. Предложите аналог проективной
арифметики для этой кривой.
19. Предложите способ ускорения умножения
элемента якобиана гиперэллиптической кри-
вой на число за счет представления этого
числа в троичной системе счисления по ана-
логии с эллиптическими кривыми.
20. Пусть С— гиперэллиптическая кривая вида
у2 = х5 + В над полем Fp, р = 1 (mod 10). Как
ускорить умножение элемента якобиана на
целое число за счет использования эндомор-
физма кривой (х, у) —> (6х, -у), где б5 = 1 ?
Литература к главе 7
1. Ахо А., Хопкрофт Дж., Ульман Дж. Построение и
анализ вычислительных алгоритмов. М.: Мир, 1979.
2. Ван дер Варден Б.Л. Алгебра. М.: Наука, 1979.
3. Ростовцев А.Г. Изоморфизм конечных полей для
комплексного умножения // Межрегиональная
конференция «Информационная безопасность ре-
гионов России». Тезисы докладов. Часть 2. СПб.,
1999. С. 117-119.
4. Buchmaim J., Hamdy S. A survey on IQ ciyptogra-
phy//www.cdc.informatik.tu-darmstadt.de/TI/English/
Publications/TR/.
5. Cantor D. Computing in the Jacobian of a hyperellip-
tic curve // Mathematics of Computation. 1987.
Vol. 48. P. 95-101.
6. Kim S.H., Pomerance C. The probability that a ran-
dom probable prune is composite // Mathematics of
Computation. 1989. Vol. 53. №. 188. P. 721-741.
7. Menezes A., van Oorschot P„ Vanstone S. Handbook
of Applied Cryptography. CRC Press, 1997.
8. Montgomery P. Modular multiplication without trial
division // Mathematics of Computation. 1985.
Vol. 44. P. 519-521.
9. Pollard J.M., Schnorr C.P. An efficient solution of the
congruence x2 + ky1 = m (mod ri) // IEEE Transac-
tions on Information Theory. 1987. Vol. IT-33. №. 5.
P. 702-709.
10. Schonhage A. Schnelle Berechnung von Ketten-
bruchentwicklungen // Acta Informatica. 1971. Vol. 1.
P. 139-144.
Глава 8. КРИПТОГРАФИЯ И ЗАЩИТА ИНФОРМАЦИИ >
Защита информации развивается настолько
быстро, что специалисты в различных ее облас-
тях иногда с трудом понимают друг друга, по-
скольку одними и теми же терминами обознача-
ют разные понятия.1 Это заставляет уточнять не-
которые определения. В данной главе сделана по-
пытка ответить на два взаимосвязанных вопроса:
всегда ли верна основная теорема безопасности?2
Что такое криптография и какое место она зани-
мает в защите информации?
Начнем со второго вопроса. В настоящее вре-
мя существует несколько определений крипто-
графии, которые, однако, не в полной мере отра-
жают действительное положение вещей.
Д. Кан [16] называет криптографией искусст-
во хранить информацию в секрете. Однако хра-
нить информацию в секрете можно, запретив или
ограничив доступ к ней (техническими мерами с
помощью соответствующей блокировки или с
помощью первого отдела).
Согласно Н. Коблицу [17] и А. Конхейму [18]
криптография— это искусство и наука сделать
передаваемую информацию доступной только
для данного получателя. Со времен античности
известен следующий способ скрытой передачи
информации. Доверенному рабу брили голову,
писали на ней сообщение, и после отрастания
достаточной щетины отправляли «живое пись-
мо» по адресу. Для прочтения письма нужно бы-
ло снова побрить голову раба.
Г. Симмонс [10] криптографией называет
науку о безопасности связи. Однако многочис-
ленные методы корректирующего кодирования,
обеспечивающие защиту информации от случай-
ных искажений, обычно не имеют отношения к
криптографии.
Б. Шнайер [21] говорит, что криптография за-
нимается решением проблем обеспечения сек-
ретности, подлинности, целостности и защиты от
1 Иногда можно услышать такое суждение: «За-
чем нужна криптография, если ответ на все вопросы
дает „основная теорема безопасности"?».
2 Основная теорема безопасности Белла Лапа-
дулы [14] утверждает, что если информационная сис-
тема начинает работу из безопасного состояния и ка-
ждый переход из состояния в состояние безопасен, то
система безопасна (см. п. 8.2.3).
человеческого мошенничества, не уточняя, ка-
кими методами.
А. Менезес и др. [19] под криптографией по-
нимают изучение математических методов, свя-
занных с такими функциями защиты информа-
ции, как конфиденциальность и целостность
данных. Однако конфиденциальность и целост-
ность часто обеспечиваются разграничением
полномочий пользователей и введением соответ-
ствующих блокировок [5]. Поэтому такое опре-
деление тоже не вполне удовлетворительно.
Криптографию как науку характеризуют пред-
мет, цели и методы исследования. Согласно приве-
денным выше определениям, предметную область
криптографии составляют функции защиты ин-
формации, реализуемые с помощью как общих под-
ходов (методов), так и соответствующих средств.
Эти определения содержат ряд общих положений,
среди которых можно выделить следующие:
- криптография — наука, занимающаяся изу-
чением методов и средств защиты информа-
ции, в частности, методов и средств обеспе-
чения конфиденциальности и аутентичности
данных;
- криптография — раздел прикладной матема-
тики и, следовательно, использует математи-
ческие (в первую очередь алгебраические)
методы исследования.
Если обратиться к многочисленным публи-
кациям в области криптографии, то можно заме-
тить характерные черты методов исследования,
используемых криптографией:
- способы обеспечения и преодоления защит-
ных функций, показывающих, что, от чего и
при каких условиях может быть защищено,
можно описать вероятностными алгоритма-
ми, которые характеризуются сложностью и
вероятностью успеха;
- методы и средства защиты информации, изу-
чаемые криптографией, можно охарактери-
зовать сложностью их преодоления в рамках
некоторой формальной модели (вычисли-
тельной, инженерно-технической, организа-
ционной и т. п.).
Чтобы уточнить определение криптографии и
ее место в теории защиты информации, рассмот-
рим основные понятия этой теории.
( 178
8.1. Основные понятия
защиты информации
Значительная часть материала этого раздела
взята из книги И.Н. Окова [8].
В соответствии с Законом об информации,
информатизации и защите информации инфор-
мационной системой называется организацион-
но упорядоченная совокупность документов
(массивов документов) и информационных тех-
нологий, в том числе с использованием средств
вычислительной техники и связи, реализующих
процессы сбора, обработки, накопления, хране-
ния, поиска и распространения информации.
Информацией являются сведения о лицах,
предметах, фактах, событиях, явлениях и про-
цессах независимо от формы их представления.
Защищаемая информация является собственно-
стью какого-либо субъекта (государства, пред-
приятия, группы лиц или отдельного граждани-
на) и подлежит защите в соответствии с требова-
ниями собственника информации или с требова-
ниями правовых документов.
Защитой информации называется деятель-
ность, направленная на предотвращение утечки
защищаемой информации, несанкционирован-
ных и непреднамеренных воздействий на защи-
щаемую информацию. В стандарте [3] три ос-
новных направления защиты информации опре-
делены следующим образом.
Защитой информации от утечки является дея-
тельность, направленная на предотвращение не-
контролируемого распространения защищаемой
информации в результате ее разглашения, несанк-
ционированного доступа к информации и получе-
ния защищаемой информации разведками. Утечка
информации осуществляется по каналам. Как
правило, множество каналов утечки строго боль-
ше множества штатных каналов передачи инфор-
мации. Доступом к информации называется полу-
чение субъектом возможности ознакомления с
информацией, в том числе с использованием тех-
нических средств. Под несанкционированным
доступом к информации понимается доступ с на-
рушением установленных прав и правил доступа.
Защитой информации от несанкционирован-
ного доступа является деятельность, направлен-
ная на предотвращение получения защищаемой
информации заинтересованным субъектом с на-
рушением установленных правовыми докумен-
тами или собственником (владельцем) информа-
ции прав или правил доступа к защищаемой ин-
формации. При этом заинтересованным субъек-
том, пытающимся получить несанкционирован-
ный доступ к защищаемой информации, могут
быть государство, организация, группа лиц или
отдельные граждане.
Различают защиту от технической и агентур-
ной разведки. Под защитой информации от тех-
нической разведки понимается деятельность, на-
правленная на предотвращение получения защи-
щаемой информации разведкой с помощью тех-
нических средств. Защита информации от аген-
турной разведки ограничивается деятельностью,
направленной на предотвращение получения за-
щищаемой информации агентурной разведкой.
Различают несанкционированное и непредна-
меренное воздействия на информацию [3].
Защитой информации от несанкционированно-
го воздействия является деятельность, направлен-
ная на предотвращение воздействия на защищае-
мую информацию с нарушением установленных
прав и (или) правил. Это воздействие может при-
водить к искажению или уничтожению информа-
ции, блокированию доступа к ней, а также к утра-
те, уничтожению или сбою функционирования но-
сителя информации. Несанкционированное воз-
действие на информацию является целенаправлен-
ным воздействием, которое оказывает нарушитель,
ставящий перед собой цели нарушения работы ин-
формационной системы (например, скрытый пере-
хват управления системой) [8].
Защитой информации от непреднамеренного
воздействия является деятельность, направлен-
ная на предотвращение воздействия на защи-
щаемую информацию в результате ошибок поль-
зователя, сбоя технических или программных
средств информационных систем, природных
явлений или иных не целенаправленных на из-
менение информации мероприятий, приводящих
к искажению, копированию, блокированию дос-
тупа к информации, а также к утрате, уничтоже-
нию или сбою функционирования носителя ин-
формации. Непреднамеренное воздействие носит
случайный характер, однако способно разрушить
информацию или нарушить работоспособность
информационной системы.
Защита информации от утечки предназначена
для сохранения в тайне информации ограничен-
ного доступа. В соответствии с законодательст-
вом России различают секретную информацию,
содержащую государственную тайну, и конфи-
денциальную информацию, содержащую иные
определяемые законом тайны: служебную, ком-
мерческую, профессиональную (включая, в част-
ности, тайну переписки, телефонных, почтовых,
телеграфных отправлений, нотариальную, адво-
катскую, врачебную тайну и др.), персональные
данные [8].
Далее секретность и конфиденциальность ин-
формации различаться не будут, поскольку ме-
тоды и средства их обеспечения весьма схожи.
Секретность или конфиденциальность ин-
формации обеспечиваются ее засекречиванием.
179
Порядок засекречивания информации, состав-
ляющей государственную тайну, определен за-
коном РФ «О государственной тайне». Порядок
засекречивания конфиденциальной информации
устанавливает ее владелец (пользователь).
Защита информации от несанкционированных
и непреднамеренных воздействий предназначена
для обеспечения целостности, подлинности и
доступности.
Под целостностью информации понимают ее
свойство оставаться неизменной при непредна-
меренных или несанкционированных воздейст-
виях или возможность выявлять случаи такого
воздействия со стороны владельца (пользовате-
ля) информации.
Под подлинностью информации понимают ее
свойство оставаться неизменной при несанкцио-
нированных воздействиях или возможность вы-
являть случаи такого воздействия со стороны
владельца (пользователя) информации. Если ин-
формация имеет конкретное физическое вопло-
щение (например, паспорт гражданина или де-
нежная купюра), то установить подлинность
можно с помощью проверки защитных призна-
ков, отсутствия подчисток и т. п.
Для обеспечения подлинности и целостности
информации необходимо снабдить ее некоторым
персональным идентификатором. Согласно ру-
ководящему документу Гостехкомиссии [4]
идентификатор — это уникальный признак
данной информации, на основе которого можно
доказательно установить ее подлинность. Кон-
троль подлинности информации обеспечивается
ее аутентификацией— проверкой соответствия
идентификатора самой информации.
Различают аутентификацию сообщений и ау-
тентификацию корреспондентов (пользователей,
систем, сетей и их элементов).
Под аутентификацией сообщения понимает-
ся установление подлинности сообщения на ос-
нове внутренней структуры самого сообщения
путем проверки соответствия идентификатора
сообщению, установление получателем (верифи-
катором, арбитром) факта, что данное сообщение
было правильно3 сформировано законным от-
правителем (претендентом) и не было изменено
при несанкционированном воздействии на него.
Аутентификация сообщения позволяет соотнести
сообщение с его источником и временем форми-
рования, выявить факты изменения, а также по-
второв и задержек сообщения при передаче по
каналу связи.
3 Примером контроля правильности данных явля-
ется проверка того, что составное число содержит в
точности два различных простых делителя (см.
п. 14.2.4).
Под аутентификацией (или опознаванием)
корреспондента (пользователя) понимается ус-
тановление его подлинности путем проверки со-
ответствия идентификатора, предъявляемого
корреспондентом (пользователем) другому кор-
респонденту (пользователю). Аутентификация
позволяет установить, например, что связь обес-
печивается именно с конкретным корреспонден-
том телекоммуникационной системы или что
доступ к защищаемой информации предоставля-
ется законному пользователю информационной
системы. Примером аутентификации пользова-
теля является проверка удостоверения личности.
Доступность информации -— свойство ин-
формации, обеспечивающее беспрепятственный
доступ к ней для выполнения санкционированных
операций по ознакомлению, модификации, унич-
тожению.
Защита секретности, целостности, подлинности
и доступности информации требует комплексного
использования правовых, организационных, крип-
тографических и технических мер ее защиты.
Целью защиты информации является дости-
жение заранее намеченного результата защиты
информации. Обычно целью защиты информа-
ции является обеспечение ее безопасности. Под
безопасностью информации понимается состоя-
ние ее защищенности, при котором с требуемой
вероятностью обеспечивается защита информа-
ции, информационных ресурсов и информацион-
ных систем от утечки, хищения, утраты, несанк-
ционированного уничтожения, искажения, мо-
дификации (подделки), несанкционированного
копирования, блокирования информации и т. п.
Под эффективностью защиты информации
понимают, в какой степени результаты защиты
информации соответствуют поставленной цели.
Для оценки эффективности используются соот-
ветствующие показатели. Нормы эффективности
защиты информации устанавливаются норма-
тивными документами.
Средством защиты информации является
техническое или программное средство, вещест-
во или материал, предназначенные или исполь-
зуемые для защиты информации.
Защищаемая информация может подвергаться
различным воздействиям со стороны нарушителя
или сил природы. Пути реализации воздействий
на информацию называются угрозами. Среди
угроз можно выделить следующие.
1. Угроза раскрытия информации заключается
в том, что защищаемая информация может
стать известной субъектам, которые не упол-
номочены владеть или пользоваться ею.
2. Угроза целостности информации заключа-
ется в том, что защищаемая информация мо-
жет подвергнуться несанкционированному
180
или непреднамеренному воздействию, при-
водящему к ее искажению или уничтожению.
3. Угроза подлинности информации заключает-
ся в том, что защищаемая информация может
подвергнуться несанкционированному воз-
действию, приводящему к ее искажению
(сюда относится и подмена информации).
4. Угроза доступности информации заключа-
ется в том, что защищаемая информация мо-
жет подвергнуться любому несанкциониро-
ванному или непреднамеренному воздейст-
вию, в результате которого блокируется дос-
туп к информации или происходит сбой
функционирования носителей информации.
С этой угрозой связана угроза отказа в об-
служивании, которая заключается в том, что
на информационную систему может быть
оказано несанкционированное информаци-
онное воздействие, приводящее к нарушению
работоспособности системы.
Например, угроза считывания информации с
дисплея компьютера ведет к нарушению секрет-
ности этой информации. Угроза перегорания
компьютера в результате скачка питающего на-
пряжения ведет к нарушению целостности и дос-
тупности информации, хранимой в памяти ком-
пьютера. Угроза заражения компьютера вируса-
ми ведет к нарушению подлинности и доступно-
сти информации [8].
При построении защищенных информацион-
ных систем наиболее сложно противостоять уг-
розам, исходящим от нарушителя. Под наруши-
телем понимается противоборствующая сторона
(государство, организация или частное лицо),
пытающаяся нарушить безопасность информа-
ции, например, осуществить несанкционирован-
ный доступ или несанкционированное воздейст-
вие. Реализации угрозы, исходящей от наруши-
теля, называются атаками. При разработке атаки
нарушитель преследует некоторые цели, вклю-
чая нарушение секретности, нанесение ущерба
другим корреспондентам или пользователям, по-
лучение незаконного преимущества по сравне-
нию с другими пользователями информационной
системы и т. п. Одна и та же угроза может быть
реализована различными атаками.
Нарушитель может придерживаться пассив-
ной или активной стратегии. В случае пассивной
стратегии нарушитель не проявляет себя путем
вмешательства в информационный обмен между
пользователями или корреспондентами инфор-
мационной системы, в работу информационной
системы, в том числе путем модификации про-
граммного обеспечения или данных. В случае
активной стратегии нарушитель пытается воз-
действовать на процессы обработки, ввода-
вывода, хранения или передачи информации.
При пассивной стратегии нарушитель может
ставить перед собой следующие цели и задачи [10].
1. Получение несанкционированного доступа к
информации, то есть нарушение ее секретно-
сти.
2. Изучение того, кто к какой информации (ис-
точникам, фактам и т. д.) и когда получает
доступ (даже если сама информация остается
скрытой), то есть обобщение данных, полу-
ченных из анализа потока сообщений в кана-
ле связи, на структуру данных, программное
обеспечение и т. д.
При активной стратегии нарушитель может
являться или не являться законным пользовате-
лем информационной системы.
В открытых информационных системах на-
рушитель, как правило, является законным поль-
зователем информационной системы. При этом
он может ставить перед собой следующие цели и
задачи [10].
1. Выдача себя за другого пользователя.
2. Отказ от факта формирования сообщения.
3. Утверждение о том, что данные получены от
некоторого отправителя, хотя на самом деле
они сформированы самим «получателем».
4. Утверждение о том, что получателю (в опре-
деленный момент времени) посылались не-
которые данные, которые на самом деле не
посылались (или посылались в другой мо-
мент времени).
5. Отказ от факта получения сообщения, кото-
рое на самом деле было получено, или лож-
ное утверждение о времени его получения.
6. Расширение своих законных полномочий (на
доступ, формирование, распространение дан-
ных и т. д.).
7. Изменение (без санкции на то) полномочий
других пользователей.
8. Сокрытие факта наличия некоторой инфор-
мации (скрытая передача) в другой информа-
ции (открытая передача). Примером является
скрытый канал в схеме цифровой подписи
(см. п. 13.4).
9. Заявление о сомнительности защитных ка-
честв информационной системы путем рас-
крытия информации, которая по условиям
протокола должна оставаться секретной.
10. Модификация программного обеспечения,
обычно путем незаметного добавления новых
функций.
11. Вынуждение других нарушать протокол пу-
тем введения ложной информации.
181
12. Тайное нарушение протокола, наносящее
ущерб другим пользователям системы. На-
пример, в ходе выполнения протокола Диф-
фи-Хеллмана (см. п. 12.1) один из пользова-
телей, выбрав не случайный, а заранее из-
вестный нарушителю показатель, может сде-
лать ключ легко вычислимым.
13. Подрыв доверия к информационной системе
путем вызова очевидных нарушений и т. д.
Если нарушитель не является законным пользо-
вателем информационной системы, то он может
ставить перед собой следующие цели и задачи [10].
1. Навязывание ложной, в том числе ранее пе-
реданной, модифицированной или переадре-
сованной информации с целью нарушения
работоспособности информационной систе-
мы или изучения ее защитных механизмов.
2. Организация или подтверждение ложных
обменов информацией.
3. Блокирование передаваемой информации и
последующая ее передача с задержкой во
времени.
4. Незаконное пользование ресурсами и услу-
гами информационных систем.
5. Разрушение или блокирование средств защи-
ты информации.
6. Блокирование доступа пользователей к сред-
ствам хранения, передачи или обработки ин-
формации.
7. Попытка помешать передаче сообщений ме-
жду другими пользователями, в частности,
внесение в сообщение скрытых помех с той
целью, чтобы это сообщение при проверке
было отвергнуто.
Большинству целей и задач нарушителя из
приведенного списка можно противостоять с ис-
пользованием достижений криптографии.
8.2. Исчисление атак
8.2.1. Упорядоченность моделей нарушителя
и безопасных систем
Для описания атаки часто используется мо-
дель (действий) нарушителя. Очевидно, что со-
вокупность всевозможных действий нарушителя
(атак) определяется его возможностями, поэто-
му лучше говорить не о модели действий, а о мо-
дели возможностей нарушителя (или просто о
модели нарушителя), которая разрешает (но не
предписывает) нарушителю действовать так или
иначе для достижения своей цели.
Таким образом, модель нарушителя задает
порождающие правила исчисления, а множество
атак является множеством допустимых объектов
этого исчисления. Множество возможностей на-
рушителя в рамках формальной логики является
аналогом системы аксиом некоторой теории, а
совокупность атак — аналогом совокупности ис-
тинных или доказуемо истинных утверждений
этой теории.
Согласно результатам Геделя, Тарского, По-
ста, Шмульяна и ряда других логиков [6, 11, 12],
множества истинных и доказуемо истинных ут-
верждений не совпадают: существуют истинные
утверждения, которые невозможно доказать (а
также опровергнуть, поскольку доказательный
аппарат считается непротиворечивым). Анало-
гично существуют ложные утверждения, для ко-
торых невозможно доказать ложность (а также
истинность, поскольку аппарат доказательства
непротиворечив). При этом каждое утверждение
является либо истинным, либо ложным.
Назовем информационную систему доказуемо
безопасной, если существует доказательство то-
го, что ни одна атака, нарушающая безопасность,
не может быть реализована в рамках данного ис-
числения. Назовем информационную систему
доказуемо уязвимой, если в рамках данного ис-
числения существует вывод для данной атаки,
нарушающей безопасность.
Назовем информационную систему безопас-
ной, если ни одна атака, нарушающая безопас-
ность, не может быть реализована в рамках дан-
ного исчисления. Назовем информационную
систему уязвимой, если в рамках данного исчис-
ления существует атака, нарушающая безопас-
ность.
Отметим, что термины «система», «безопас-
ность» задают интерпретацию соответствующего
исчисления. Замена терминов «система» на «ут-
верждение», «безопасность» на «истинность»
задает изоморфизм интерпретаций. Поэтому ре-
зультаты работ [6, 11, 12] можно интерпретиро-
вать следующим образом: множества безопасных
и доказуемо безопасных систем, а также уязви-
мых и доказуемо уязвимых систем различны.
Иными словами, существуют информационные
системы, которые не являются ни доказуемо
безопасными, ни доказуемо уязвимыми.
Чем меньшими (большими) возможностями
обладает нарушитель, тем легче (труднее) ему
противостоять. В предельном случае, если нару-
шитель не может ничего (множество возможно-
стей пусто), то любая система является безопас-
ной. Другой крайний случай: если нарушитель
обладает экстрасенсорными способностями, то
ни одна система не будет безопасной.
182
Предположим, есть две модели нарушителя,
причем вторая как множество содержит в себе
первую. Тогда можно сказать, что вторая модель
является более сильной, чем первая, или, просто
больше первой, у соответствующего нарушителя
больше возможностей, а множество атак для
второй модели включает в себя множество атак
для первой модели. Таким образом, на множест-
ве моделей нарушителя определена частичная
упорядоченность, заданная упорядоченностью
множеств по включению и индуцирующая упо-
рядоченность множества атак.
Упорядоченность множества моделей нару-
шителя индуцирует также инверсную упорядо-
ченность множества безопасных информацион-
ных систем. Система, безопасная по отношению
к нарушителю, описываемому меньшей моде-
лью, может не быть безопасной по отношению к
нарушителю, описываемому большей моделью.
Таким образом, понятие безопасности информа-
ционной системы подразумевает указание соот-
ветствующей модели нарушителя.
Зададим модель нарушителя (градуирован-
ным) множеством, элементы которого могут со-
провождаться численными значениями, характе-
ризующими возможности нарушителя. Напри-
мер, производительность компьютера нарушите-
ля может варьироваться. Назовем модели нару-
шителя однотипными, если их элементы одина-
ковы с точностью до численных значений. На
однотипных моделях можно установить отноше-
ние порядка, например, упорядочив список воз-
можностей по типам, а затем упорядочив воз-
можности одного и того же типа по их количест-
венным характеристикам.
Теорема 8.2.1. Модели нарушителя образуют
решетку.
Доказательство. Два неградуированных
множества, задающих модель нарушителя, имеют
точную верхнюю грань (объединение этих мно-
жеств) и точную нижнюю грань (пересечение
этих множеств). Для двух однотипных моделей
точной верхней гранью является более сильная
модель, а точной нижней гранью — более слабая.
Композиция этих двух отношений порядка задает
решетку на множестве моделей нарушителя.
Теорема 8.2.2. Для каждой информационной
системы существует (может быть, не единствен-
ная) максимальная модель нарушителя, для ко-
торой система безопасна.
Доказательство. Множество Л моделей на-
рушителя, для которых система безопасна, не-
пусто, так как содержит хотя бы один элемент —
пустое множество возможностей. Для каждой
пары элементов множества А находим точную
верхнюю грань и из найденного множества точ-
ных верхних граней выбираем наибольшие, со-
держащиеся среди элементов множества А. Не-
пустое множество точных верхних граней задает
максимальную модель нарушителя.
На практике защита информации осуществля-
ется подсистемой безопасности. Если безопас-
ность информационной системы может быть
обеспечена, то обычно этого можно достичь с
помощью различных подсистем безопасности.
На множестве подсистем безопасности можно
определить отношение частичного порядка.
Упорядоченность может задаваться стоимостью,
массо-габаритными показателями, номенклату-
рой используемых средств и т. п. Согласно тео-
реме 3.14.1 среди подсистем безопасности, обес-
печивающих защиту по отношению к заданной
модели нарушителя, существует минимальная.
Множество информационных систем можно
разбить на классы так, что к одному классу отно-
сятся информационные системы, для которых
максимальные модели нарушителя совпадают.
При построении и анализе безопасности за-
щищенных информационных систем часто тре-
буется решить три задачи. Во-первых, для задан-
ной модели нарушителя определить, является ли
данная информационная система доказуемо
безопасной, доказуемо уязвимой или неопреде-
ленной (отсутствуют доказательства как безо-
пасности, так и уязвимости). Во-вторых, для за-
данной информационной системы найти макси-
мальную модель нарушителя. В-третьих, для за-
данной модели нарушителя найти минимальную
подсистему безопасности.
8.2.2. Множества возможностей нарушителя
Для того чтобы построить защищенную сис-
тему или хотя бы проверить ее защищенность,
нужно знать, от чего именно осуществляется за-
щита. Поскольку нарушитель в пределах своих
возможностей может действовать произвольно,
действия нарушителя (атаки) следует описывать
в рамках исчисления атак. Совокупность порож-
дающих правил такого исчисления определяется
моделью нарушителя и особенностями информа-
ционной системы. Реализация угрозы с помощью
многоходовой атаки может быть описана как по-
лучение основного состояния в ходе исчисли-
тельного процесса.
На практике эта модель нарушителя опреде-
ляется в нормативных документах и уточняется в
техническом задании на разработку.
С учетом специфики построения информаци-
онной системы и истории защиты информации
183
[2, 5, 16] можно выделить вычислительные, тех-
нические, математические, криптоаналитические
и организационные возможности нарушителя.4
Вычислительные возможностей нарушителя
учитывают тип используемой им вычислительной
модели, ее производительность, объем памяти.
Атаку на информационную систему в рамках за-
данной вычислительной модели можно описать
вероятностным алгоритмом, который характеризу-
ется временной и емкостной сложностью и вероят-
ностью успеха. Поскольку угроза может быть реа-
лизована различными алгоритмами, возникает не-
обходимость их сравнения. Из двух алгоритмов
лучшим является тот, который при одинаковой
вероятности успеха имеет меньшую сложность.
Система является безопасной, если сложность наи-
лучшего известного алгоритма превышает порого-
вую при заданной вероятности реализации угрозы.
Технические возможности нарушителя описы-
вают (общепринятый) инструмент, реализующий
атаку, например, компьютер, используемый для
доступа в систему.
Лабораторные возможности описывают не-
стандартные, уникальные средства, которые по-
зволяют нарушителю получать информацию о
секретных данных, не обращаясь непосредствен-
но к области памяти, где эти данные хранятся.
При любом процессе обработки секретной ин-
формации с помощью материальных средств воз-
никают физические поля (сигналы), которые (по
крайней мере, теоретически) могут быть измере-
ны с помощью лабораторных методов и средств и
дают нарушителю некоторую информацию о за-
щищаемом секрете. Например, информацию, вы-
свечиваемую на дисплее компьютера, можно оп-
ределить с помощью специализированного ра-
диоприемника. Эти сигналы являются слабыми
(иногда значительно меньше уровня шума). Для
выделения их из шума можно использовать то
обстоятельство, что при каждом обращении к
конфиденциальной информации шум различен, а
сигнал — один и тот же. Если конфиденциальная
информация была записана в памяти компьютера
(магнитной, полупроводниковой и т. п.), то стира-
ние этой информации должно исключать возмож-
ность восстановления ее лабораторными метода-
ми, которые в общем случае отличаются от штат-
ных методов считывания информации.
В некоторых случаях нарушитель с лабора-
торными возможностями может активно воздей-
ствовать на аппаратуру защиты информации, из-
меняя ее работу и тем самым снижая ее защит-
ные качества.
4 В общем случае список возможностей наруши-
теля требует уточнения для каждой конкретной ин-
формационной системы.
Математические возможности нарушителя
позволяют разрабатывать новые эффективные
методы и алгоритмы решения массовых матема-
тических задач, положенных в основу безопас-
ности информационной системы, или задач, к
которым сводятся указанные математические
задачи. Например, уже многие годы наблюдается
прогресс в построении быстрых вероятностных
алгоритмов разложения составного числа на
множители, что приводит к необходимости по-
стоянного увеличения длины составного числа в
системе RSA [9].
Криптоаналитические возможности наруши-
теля связаны с математическими и позволяют
разрабатывать алгоритмы взлома данного шифра
с использованием как универсальных, так и при-
менимых только к конкретному шифру методов
криптоанализа. Отличие этих возможностей от
математических заключается в использовании
специальных криптоаналитических методов.
Кроме того, здесь решается не массовая, а част-
ная математическая задача.
Организационные возможности нарушителя
позволяют ему получать дополнительную ин-
формацию, потенциально способную снизить
защитные качества информационной системы.
Эти возможности включают в себя трудно фор-
мализуемый список, например:
- получение открытых текстов, соответствую-
щих имеющимся шифрограммам;
- возможность доступа к шифровальной аппа-
ратуре для тестирования ее с помощью по-
добранных открытых или зашифрованных
текстов;
- захват шифровальной аппаратуры;
- доступ к ключам шифрования, выведенным
из действия;
- возможность подмены существующих про-
грамм;
- вербовка помощников среди обслуживающе-
го персонала и т. п.
Иногда технические и организационные воз-
можности различаются непринципиально. На-
пример, если информационная система пред-
ставляет собой библиотеку с книгами или бу-
мажными документами, то доступ к ним описы-
вается организационными возможностями. Если
документы являются электронными и хранятся в
памяти компьютера, то такой доступ описывает-
ся техническими возможностями.
Указанная классификация возможностей на-
рушителя может быть детализирована на мате-
матическом, техническом, организационном и
других уровнях.
Модель нарушителя на математическом уров-
не допускает детализацию, учитывающую, ка-
184
кую математическую задачу нарушитель может
решить (или предположительно сможет решить в
будущем). Как правило, решить ту или иную ма-
тематическую задачу, положенную в основу
безопасности информационной системы, очень
трудно. Так же непросто прогнозировать, какая
из двух математических задач будет сложнее че-
рез 20 лет. Помочь здесь сможет номенклатур-
ный подход к анализу безопасности.
Предположим, что нарушитель может решить
математическую задачу рА данного размера. То-
гда подсистемы безопасности, для взлома кото-
рых достаточно решить задачу рА (или любую
другую задачу, полиномиально сводимую к за-
даче /?/), оказываются уязвимыми. Можно пред-
положить, что наряду с задачей рА нарушитель
может решить другую задачу рв. Тогда подсис-
темы безопасности, для взлома которых доста-
точно решить любую из задач рА или рв (или лю-
бую другую задачу, полиномиально сводимую к
этим задачам), оказываются уязвимыми.
Продолжение этих рассуждений ведет к сле-
дующему утверждению. Обозначим максималь-
ную модель нарушителя для информационных
систем А и В через 1А и /в соответственно, а мно-
жества математических задач, решение любой из
которых ведет к нарушению безопасности этих
систем, — через РА и Рв соответственно.
Теорема 8.2.3. Если системы А и В таковы,
что РА о Рв, то 1А с /д.5
Доказательство. Множество задач линейно
упорядочено по сложности.6 Поэтому в множест-
ве РА есть задача рА наименьшей сложности. Если
рА е Рв, то 1А = 1В; если рА & Рв, то IA с 1В, так как
нарушитель должен уметь решать задачу рА.
Для уточнения математических и криптоана-
литических возможностей нарушителя составим
список массовых задач, которые он предположи-
тельно может решить.
Определим множество задач, положенных в
основу безопасности информационной системы,
как набор математических задач, решение любой
из которых ведет к нарушению безопасности.
Мощность этого множества задач назовем слож-
ностной неоднородностью.
Теорема 8.2.3 означает, что увеличение слож-
ностной неоднородности (расширение множест-
ва задач, положенных в основу безопасности), не
может повысить безопасность, независимо от
5 Предполагается, что нематематические макси-
мальные возможности нарушителя для систем А и В
одинаковы.
6 Оценка сложности задачи может меняться во
времени.
текущей оценки сложности задачи и от текущей
оценки максимальной модели нарушителя.
Отсюда следует принцип максимальной одно-
родности'. число задач, положенных в основу
безопасности информационной системы, должно
быть минимальным. Это обусловливает целесо-
образность унификации криптографических
примитивов (таких как шифрование, подпись,
хэш-функция, генератор случайных битов и др.,
см. п. 8.3) так, чтобы они основывались на одной
и той же математической задаче, например, на
задаче дискретного логарифмирования на эллип-
тической кривой (см. гл. 11 ).7
Для анализа безопасности информационных
систем математическими методами необходимо
выбрать некоторую систему аксиом. В свете из-
ложенного наиболее естественной системой ак-
сиом, в рамках которой рассматривается безо-
пасность системы, представляется заданное
множество возможностей нарушителя.
Часто нарушитель может предпринимать
комплексные атаки с использованием всех
имеющихся возможностей. Рассмотрим некото-
рые типовые модели нарушителя с учетом их
упорядоченности по включению.
8.2.3. Тривиальная модель нарушителя
Назовем модель нарушителя тривиальной, ес-
ли единственный способ для нарушителя полу-
чить сведения о секретной информации— вы-
полнить ее чтение установленным порядком, а
единственный способ для нарушителя изменить
информацию— выполнить запись установлен-
ным порядком.8
Данная модель может считаться моделью с
техническими возможностями, если система по-
строена с использованием компьютеров, или мо-
делью с организационными возможностями, на-
7 В этом плане представляет интерес возможность
построения криптосистем, безопасность которых ос-
нована на решении не одной (любой), а всех попарно
независимых массовых задач из некоторого списка.
8 Термин «тривиальная» объясняется тем, что сре-
ди непустых моделей нарушителя эта модель, по-
видимому, простейшая. Как показывает многовековая
история защиты информации, если нарушитель дей-
ствительно хочет узнать то, что ему не положено, он
обычно применяет значительно более широкий спектр
действий. Например, для того чтобы прочитать сек-
ретную переписку короля Испании Филиппа II, при-
дворный криптоаналитик короля Франции Генриха
Наваррского Франсуа Виет (известный как один из
родоначальников алгебры), разумеется, не получал
разрешения с печатью испанского короля [16].
185
пример, если система представляет собой обыч-
ную библиотеку. Поэтому безопасность может
быть обеспечена техническими или организаци-
онными мерами— нужно создать необходимые
блокировки, обеспечивающие доступ к инфор-
мации только при наличии соответствующего
разрешения. Способ реализации этих блокировок
(организационный или технический) в систем-
ном плане непринципиален.
Если защищаемая информация упорядочена
по уровню своей секретности, а субъекты систе-
мы (пользователи, аппаратура, программы и
т. п.) — по своим полномочиям, которые соот-
ветствуют грифам информации, то в рамках этой
же модели возможностей получается модель
безопасности Белла-Лападулы.9
Система называется безопасной по чтению
(по записи) в смысле Белла-Лападулы тогда и
только тогда, когда полномочия субъекта по чте-
нию (по записи) соответствуют уровню секрет-
ности информации.
Система называется безопасной в смысле
Белла-Лападулы (БЛП-безопасной) тогда и толь-
ко тогда, когда она безопасна в этом смысле по
чтению и по записи (это определение удобно
считать аксиомой безопасности). Известна ос-
новная теорема безопасности Белла—Лападулъг.
если начальное состояние системы безопасно и
каждый переход из предыдущего состояния в
последующее состояние безопасен, то система
безопасна (всюду имеется в виду БЛП-безопас-
ность).
Тривиальная модель нарушителя в рамках
системы с иерархией субъектов и объектов вза-
имно однозначно соответствует понятию безо-
пасности в смысле Белла-Лападулы. Действи-
тельно, при указанных возможностях нарушите-
ля определения безопасности по чтению и записи
вполне осмысленны и корректны. Обратно, из
определений безопасности по Беллу-Лападуле
следует, что возможности нарушителя ограниче-
ны тривиальной моделью.
Теорема 8.2.4. Все атаки исчисления, порож-
денного моделью безопасности Белла-Лападулы,
описываются на языке логики предикатов перво-
го порядка.
Набросок доказательства. Любая атака
представляется в виде последовательности дей-
ствий пользователей системы и нарушителя. Та-
кая последовательность содержит конечное чис-
ло действий (чтение или запись), каждое из ко-
9 Вместо модели Белла-Лападулы можно рас-
смотреть любую другую мандатную модель управле-
ния доступом.
торых можно описать с использованием пере-
менных (имена субъектов, объектов и их гри-
фов), а также элементов матрицы доступа, опе-
раций чтения и записи, скобок и кванторов су-
ществования и всеобщности. Такая грамматика
определяет язык теории множеств Цермело-
Френкеля [6], который относится к языкам пре-
дикатов первого порядка. Этот язык позволяет
описывать в атаке состояния, полученные на
предыдущих шагах исчисления. Отсюда следует
заключение теоремы.
Назовем информационную систему транзи-
тивной, если для любой цепочки переходов
с?| -> ф ->...-> ап из безопасности каждого от-
дельного перехода следует безопасность резуль-
тирующего перехода at -> а„ (аксиома транзитив-
ности). Аксиома транзитивности эквивалентна
основной теореме безопасности Белла-Лападулы.
Считая определение безопасности Белла-
Лападулы аксиомой БЛП-безопасности, рас-
смотрим взаимную зависимость между аксиома-
ми БЛП-безопасности, транзитивности и триви-
альности модели нарушителя.
Теорема 8.2.5. Справедливы следующие ут-
верждения.
1. Аксиома БЛП-безопасности и аксиома три-
виальности эквивалентны.
2. Любая из аксиом БЛП-безопасности и триви-
альности влечет аксиому транзитивности.
Доказательство. Из аксиомы тривиальности
следует аксиома БЛП-безопасности, так как для
нарушителя единственный способ нарушить кон-
фиденциальность — выполнить операцию чтения,
а единственный способ нарушить подлин-
ность — выполнить операцию записи.
Из аксиомы БЛП-безопасности следует ак-
сиома тривиальности, так как никакие другие
возможности нарушителя, кроме чтения и запи-
си, не предусмотрены. Таким образом, каждая из
аксиом БЛП-безопасности и тривиальности вле-
чет другую.
Из аксиомы БЛП-безопасности согласно ос-
новной теореме безопасности Белла-Лападулы
следует аксиома транзитивности. Аксиомы три-
виальности и БЛП-безопасности эквивалентны,
поэтому аксиома тривиальности также влечет
аксиому транзитивности.
Следствие 8.2.6. Если аксиома транзитивно-
сти неверна, то ни аксиома тривиальности, ни
аксиома БЛП-безопасности не выполняются.
Таким образом, в схеме вывода основной тео-
ремы безопасности из определения БЛП-безопас-
ности посылку и следствие можно менять местами.
186
8.2.4. Нетривиальная модель нарушителя
Иногда чтобы узнать секретную информацию,
нарушителю не надо выполнять операцию чте-
ния — эту информацию можно найти иначе. На-
пример, секретный ключ шифрования или под-
писи обычно можно (по крайней мере, теорети-
чески) вычислить.
Порождающие правила в рамках этого исчис-
ления, помимо перечисленных в п. 8.2.3, предпо-
лагают возможность использования методов ма-
тематики и криптоанализа, направленных на
вскрытие секретной информации (ключа). Для
этой модели система является безопасной, если
сложность вскрытия секретной информации наи-
лучшим (известным) алгоритмом превышает по-
роговую.
Однако методы математики и криптоанализа,
а также вычислительная техника постоянно со-
вершенствуются [1,7]. На практике считается,
что нарушитель является специалистом высшей
квалификации, знает все о системе и средствах
защиты. Это по сути означает, что нарушитель
может обучаться, и множество его возможностей
может со временем расширяться. Рост возмож-
ностей нарушителя приводит к снижению во
времени защитных качеств подсистемы крипто-
графической защиты информации. Это обуслов-
ливает относительность понятия безопасно-
сти-. безопасная сегодня информационная систе-
ма (использующая криптографические средства
защиты) может не быть безопасной завтра. По-
этому необходима периодическая переаттеста-
ция системы на предмет безопасности, то есть
необходимо научное (в первую очередь матема-
тическое и криптоаналитическое) сопровожде-
ние информационной системы в ходе всего срока
ее эксплуатации, тогда как для других техниче-
ских систем требуется не научное, а техническое
сопровождение.
Если разработчик старается обеспечить безо-
пасность системы в течение всего срока эксплуа-
тации, то нарушитель старается эту безопасность
нарушить. Для того чтобы минимизировать
ущерб от возможного взлома подсистемы безо-
пасности в ходе эксплуатации, разработчик дол-
жен обнаружить возможность взлома до того,
как ее обнаружит нарушитель, и принять соот-
ветствующие меры. Между разработчиком и на-
рушителем происходит непрерывное соревнова-
ние в развитии методов нарушения информаци-
онной безопасности (в первую очередь, методов
криптоанализа). Как правило, на начальном эта-
пе разработчик владеет более перспективными
методами анализа данного шифра, чем наруши-
тель. В идеале такое положение должно сохра-
няться в течение всего срока эксплуатации ин-
формационной системы. Таким образом, разра-
ботчик вынужден постоянно разрабатывать но-
вые методы взлома подсистемы безопасности,
чтобы опережать в этом нарушителя.
Покажем, что для этой модели нарушителя
основная теорема безопасности Белла-Лападулы
не выполняется. ,-iS?
Теорема 8.2.7. Существует информационная
система, для которой не выполняется аксиома
транзитивности при наличии у нарушителя ма-
тематических и вычислительных возможностей.
Доказательство. Пусть в информационной
системе используется алгоритм электронной
цифровой подписи по ГОСТ Р 34.10-2001, пре-
дусматривающий использование случайного
числа. Ключ формирования подписи является
охраняемой конфиденциальной информацией.
Алгоритм подписи характеризуется тем, что по-
вторение дважды одного и того же случайного
числа приводит к вскрытию секретного ключа
формирования подписи, причем случай повтора
можно эффективно распознать [9]. В качестве
генератора случайных чисел выберем генератор
Блюма-Блюма-Шуба (см. п. 12.4), формирую-
щий рекуррентную псевдослучайную крипто-
графически стойкую последовательность:
х,+1 = X,2 (mod и). При достаточно длительной
эксплуатации системы последовательность слу-
чайных чисел начнет повторяться, что позволит
нарушителю вскрыть секретный ключ. Парамет-
ры генератора (составное число и) можно вы-
брать так, что сложность предсказания после-
дующего числа при известном предыдущем бу-
дет сколь угодно велика, а период повторения
окажется небольшим. В этом случае каждый пе-
реход системы из предыдущего состояния в по-
следующее, рассматриваемый отдельно, оказы-
вается безопасен, но после определенного числа
таких переходов система не будет безопасной.
Следствие 8.2.8. Если нарушитель обладает
математическими и вычислительными возмож-
ностями, а в системе используются криптогра-
фические алгоритмы, основанные на вычисли-
тельной сложности, то не существует криптоси-
стем, для которых аксиома транзитивности спра-
ведлива.
Доказательство. Практическая стойкость
криптографических методов защиты информа-
ции непрерывно снижается, и при неограниченно
длительной эксплуатации системы стойкость
становится недопустимо низкой [9].
В данной модели множество допустимых
атак является неразрешимым. Действительно,
187
для симметричного шифра (например, DES,
ГОСТ 28147-89, RIJNDAEL) на практике не-
возможно доказать, что не существует алгорит-
ма вскрытия ключа, сложность которого мень-
ше заданного уровня. Это обстоятельство за-
трудняет формализацию процедуры оценки
безопасности системы. Отсутствие транзитив-
ности автоматически ведет к тому, что основная
теорема безопасности Белла-Лападулы не вы-
полняется.
При наличии у нарушителя лабораторных
возможностей безопасность зависит от про-
граммно-аппаратного построения средств защи-
ты информации. Управляющая программа не
может контролировать безопасность— работо-
способность аппаратуры не означает, что стой-
кость к лабораторным методам исследований со
временем не снизилась (и даже что эта стойкость
изначально была достаточной). Для этой модели
основная теорема безопасности Белла-Лападулы
также неверна. Действительно, в процессе пере-
хода системы из состояния в состояние возникают
сигналы, несущие информацию о секрете. Для
приема таких сигналов может использоваться тех-
ника выделения сигналов из шума, позволяющая
принять сигнал и получить информацию о секрете,
если число повторов достаточно велико. При этом
может быть одиночный переход безопасен (сигнал
слабее шума), но несколько таких переходов могут
не являться безопасными. Для любого опасного
сигнала существует некоторое число п такое, что п
и более повторов опасного сигнала позволяют вы-
делить его из шума и вскрыть секретную инфор-
мацию (ключ).
В рамках данной модели персональный ком-
пьютер с произвольной управляющей програм-
мой не может гарантировать безопасность.
На практике подсистема безопасности обычно
использует криптографические средства защиты,
безопасность которых основана на вычислитель-
ной сложности некоторой математической зада-
чи, например, стандарты шифрования и подписи.
Теорема 8.2.9. Пусть в информационной сис-
теме используются криптографические средства,
предусмотренные стандартами шифрования и
подписи.10 В данном наборе высказываний лю-
бое из них влечет два остальных:
1. Справедлива аксиома БЛП-безопасности.
2. Модель нарушителя тривиальна.
3. Справедлива аксиома транзитивности.
Доказательство. Импликация 2 => 1 следу-
ет из того, что в аксиоме безопасности участву-
10 При использовании безусловно стойких крип-
тографических алгоритмов (см. п. 8.3.4) теорема мо-
жет быть неверна. -.о'Ч-'л .. т--
ют только возможности чтения и записи. Импли-
кация 1 => 3 следует из основной теоремы безо-
пасности Белла-Лападулы. Импликация 3 => 2
эквивалентна импликации «не 2 => не 3». Пред-
положим, что возможности нарушителя нетриви-
альны и согласно классификации множество
возможностей содержит математические или ла-
бораторные возможности. Согласно изложенно-
му выше, эта импликация имеет место.
Таким образом, если в информационной сис-
теме используются стандартные криптографиче-
ские средства, то любое из трех высказываний
теоремы 8.2.9 может считаться аксиомой безопас-
ности, а остальные могут считаться теоремами.
Следствие 8.2.10. Если множество возможно-
стей нарушителя нетривиально, а в системе ис-
пользуются стандартные алгоритмы шифрования
и подписи, то аксиома транзитивности не выпол-
няется и основная теорема безопасности Белла-
Лападулы неверна.
Анализ криптографических алгоритмов и
протоколов и особенностей их реализации вы-
полняется на основе сложностного подхода.
Управляет работой информационной системы в
целом (включая криптографические средства)
управляющая программа, безопасность которой
обычно определяется на основе предикатного
подхода. Анализ безопасности компьютерных
систем часто выполняется раздельно для крипто-
графических и некриптографических средств
защиты информации, затем результаты этих двух
направлений анализа объединяются. Во втором
случае анализ безопасности сводится к анализу
безопасности управляющей программы, а крип-
тографические средства защиты рассматривают-
ся как «черный ящик». При этом одним из ос-
новных инструментов анализа безопасности яв-
ляется основная теорема безопасности Белла-
Лападулы. Покажем, что раздельный подход не
может гарантировать безопасность.
Назовем средство криптографической защиты
транзитивно безопасным, если оно удовлетво-
ряет аксиоме транзитивности.
Теорема 8.2.11. Раздельные подходы к анали-
зу безопасности корректны тогда и только тогда,
когда криптографические средства являются
транзитивно безопасными.
Доказательство. Некорректность раздель-
ного подхода обусловлена уязвимостью крипто-
графических средств. Если этой уязвимости нет
(криптографические средства транзитивно безо-
пасны), то раздельный подход не приводит к по-
явлению уязвимостей, то есть корректен. Пред-
188
положим, что раздельный подход является кор-
ректным. Тогда криптографические средства
должны удовлетворять аксиоме транзитивности,
то есть быть транзитивно безопасными.
В действительности если модель нарушителя
нетривиальна, то ни одно средство криптографи-
ческой защиты, использующее стандартные
криптографические алгоритмы, не может быть
транзитивно безопасным. Например, выполнение
определенного числа процедур формирования
электронной цифровой подписи ведет к наруше-
нию секретности ключа и обрушению безопас-
ности системы в целом. То же справедливо и для
шифров (см. п. 19.6).
Раздельный анализ безопасности управляю-
щей программы и криптографических средств в
рамках нетривиальной модели нарушителя при-
водит к тому, что управляющая программа безо-
пасна лишь постольку, поскольку она не может
управлять криптографическими средствами, в
частности, не может вызывать криптографиче-
ские программы и функции. Следовательно, не-
обходимы дополнительные «управляющие про-
граммно-аппаратные средства», которые управ-
ляют совместно упомянутой управляющей про-
граммой и криптографическими средствами, и
возникает задача исследования безопасности
этих средств. Продолжение этой цепочки оче-
видно ведет в тупик.
Возможным выходом из создавшегося поло-
жения является использование криптографиче-
ских средств ограниченной транзитивности: ре-
зультирующий переход щ -> ф безо-
пасен при безопасности всех единичных перехо-
дов тогда и только тогда, когда число шагов п не
превышает порогового значения. Для продления
безопасной эксплуатации необходимо сменить
ключ или параметры криптосистемы.
Это ведет к тому, что основная теорема безо-
пасности Белла-Лападулы справедлива лишь для
ограниченного числа переходов, а само понятие
безопасности оказывается зависимым от успехов
математики.
8.2.5. Место криптографии
в защите информации
Теперь можно уточнить место криптографии
в защите информации. Криптография имеет дело
с нетривиальными моделями нарушителя, пред-
полагающими наличие у него вычислительных,
математических и криптоаналитических воз-
можностей. Практическая реализация крипто-
графических средств защиты информации долж-
на обеспечивать защиту и от нарушителя, обла-
дающего соответствующими лабораторными
возможностями.11 12
Методы криптографии не зависят от вида ин-
формационной системы: неважно, реализована
ли эта система на основе универсальных компь-
ютеров или аппаратно, является ли она системой
связи, управления или базой данных.
Средства защиты информации часто исполь-
зуют физические или криптографические меха-
низмы. Если два варианта защиты решают одну
и ту же задачу, возникает вопрос: какой из них
нарушителю труднее преодолеть? Криптографи-
ческий подход позволяет линейно упорядочить
способы защиты по сложности наилучших из-
вестных алгоритмов взлома в рамках заданной
модели нарушителя. Такое упорядочение позво-
ляет сравнивать варианты защиты и выбирать
наилучший. Физические подходы обычно этого
12
не допускают.
Рассмотрим две ситуации.
1. Пусть безопасная передача конфиденци-
альной информации осуществляется двумя спо-
собами: незащищенная информация передается
по волоконно-оптической линии и информация,
зашифрованная с открытым ключом по схеме
RSA, передается по открытому каналу (см. гл. 9).
Для нарушения конфиденциальности в первом
случае достаточно сделать скрытно отвод от ли-
нии. Эта задача может быть решена необозри-
мым числом вариантов в зависимости от длины и
места прокладки линии, ее охраняемости и мно-
жества других факторов. Поэтому гарантировать
невозможность такого подключения обычно
нельзя. Во втором случае для получения доступа
к информации нарушитель должен разложить на
множители составное число. Сложность разло-
жения не зависит от внешних трудно контроли-
руемых параметров и может быть гарантирована
в рамках заданной вычислительной модели.
2. Пусть имеются два варианта построения
подсистемы опознавания пользователя: по отпе-
чаткам пальцев и по сетчатке глаза. Для какого
из вариантов нарушителю сложнее обмануть
контролирующую аппаратуру? Здесь однознач-
ного ответа также быть не может.
Таким образом, безопасность информационной
системы (в рамках нетривиальной модели нару-
шителя) можно гарантировать, если задача нару-
11 Изучение способов противодействия наруши-
телю, обладающему лабораторными возможностями,
выходит за пределы данной книги.
12 По-видимому, исключением является передача
информации одиночными квантами, где безопасность
основана на квантово-механическом принципе неоп-
ределенности («квантовая криптография»).
189
шения безопасности решается алгоритмом, слож-
ность которого настолько велика, что реализовать
его практически невозможно. Изучением таких
средств защиты и занимается криптография.
Преимуществами криптографических средств
защиты информации по сравнению с другими
являются:
- эквивалентность или сводимость угрозы к
математической задаче, что позволяет дока-
зать безопасность информационной системы
при условии, что указанная задача является
сложной;
- возможность прогнозирования безопасности
информационной системы;
- возможность сравнивания однотипных сред-
ств защиты информации, обеспечивающих
защиту от одних и тех же угроз, и выбора
наилучшего варианта.
8.3. Основные понятия и определения
криптографической защиты данных
Криптография связана с различными облас-
тями математики (алгебра, теория чисел, теория
вероятностей, теория сложности, вычислитель-
ная математика и др.), с теорией связи, а также с
многочисленными техническими дисциплинами,
создающими фундамент для построения аппарату-
ры защиты данных и аппаратуры взлома шифров.
Некоторые разделы науки решают похожие
задачи, например, теория корректирующего ко-
дирования обеспечивает целостность передавае-
мых данных математическими методами. Одно
из основных различий между криптографией и
теорией кодирования заключается в том, что
первая защищает от целенаправленных действий
нарушителя, а вторая— от случайных измене-
ний передаваемых данных.
Существует техника защиты передаваемых
данных, основанная на их сокрытии (стегано-
графия}, например, акростихи или использова-
ние невидимых чернил. В последние годы мето-
ды стеганографии широко используются для за-
щиты от нелегального копирования (то есть для
контроля неповторяемости). Например, если ка-
ждый экземпляр программного продукта поме-
тить индивидуальным номером, спрятанным в
тексте программы, то можно соотнести владель-
ца данного экземпляра программы с владельцем
лицензионного экземпляра, который приобрел
его на законных основаниях. Иногда задачи сте-
ганографии могут решаться с использованием
криптографических средств, например, возможен
скрытый канал передачи зашифрованных данных
в протоколе цифровой подписи (см. п. 13.4).
8.3.1. Криптографические примитивы
Информацию, подлежащую защите, будем пред-
ставлять в виде данных— слов конечной длины в
некотором алфавите, содержащем конечное число
символов. Указанный алфавит может быть русским
алфавитом, дополненным пробелом и знаками
препинания, алфавитом из двух символов {0, 1},
алфавитом из 256 символов, которым кодируется
клавиатура персонального компьютера и т. п. По-
этому данные будем называть также текстом.
Криптографическая защита данных обеспечи-
вает ряд защитных характеристик, таких как кон-
фиденциальность, целостность, подлинность, не-
повторяемость и корректность данных, опознава-
ние субъекта информационной системы и т. д.
Криптографическая защита данных обеспечи-
вается их преобразованием, которое может быть
представлено функцией из множества входов в
множество выходов. Эта функция может быть
как обратимой, так и необратимой. Кроме того,
она может зависеть от изменяемого параметра —
ключа, который обычно бывает секретным. Такая
функция называется криптографическим при-
митивом.
При передаче данных от отправителя к получа-
телю возможны две ситуации: 1) знание ключа од-
ной (любой) стороны позволяет вычислить ключ
другой стороны; 2) знание ключа одной из сторон
не позволяет вычислить ключ другой стороны (со
сложностью, не превышающей порогового уров-
ня). В первом случае говорят, что используется
симметричное преобразование данных (при этом
оно может не быть обратимым). Во втором случае
говорят, что используется несимметричное преоб-
разование данных (хотя оно может быть обрати-
мым). Таким образом, понятие симметричности
означает двунаправленную вычислимость ключа.
По отношению к ключу примитивы можно
разделить на бесключевые, симметричные и не-
симметричные.
К бесключевым примитивам относятся:
- бесключевые хэш-функции для произвольно-
го аргумента;
- бесключевые хэш-функции, свободные от
коллизий (см. п. 15.6.7);
- генераторы псевдослучайной последователь-
ности (см. пп. 12.4, 19.1);
- бесключевые шифры (см. п. 12.1.1).
К симметричным ключевым примитивам от-
носятся:
- симметричные шифры (см. гл. 16, 19);
- ключевые хэш-функции;
- симметричные схемы подписи.
К несимметричным ключевым примитивам
относятся: .... .. ..
190
- шифры с открытым ключом (см. гл. 12);
- несимметричные схемы подписи (см. гл. 13);
- канал передачи информации со стиранием
(см. и. 14.4);
- доказательства с нулевым разглашением
(см. и. 14.2).
Одни и те же криптографические примитивы
позволяют решать разные задачи защиты ин-
формации. Например, шифрование с открытым
ключом может использоваться и для обеспечения
конфиденциальности, и для опознавания.
Изучением математических методов наруше-
ния информационной безопасности, обеспечивае-
мой криптографическими примитивами, занима-
ется раздел криптографии, называемый крипто-
графическим анализом (криптоанализом).
Способность криптографического примитива
противостоять атакам называется стойкостью.
Нарушение информационной безопасности, обес-
печиваемой криптографическим примитивом, бу-
дем называть его вскрытием, или взломом.
Криптографический алгоритм (криптоалго-
ритм)— это алгоритм, реализующий крипто-
графический примитив. Под стойкостью крип-
тоалгоритма понимают стойкость соответст-
вующего криптографического примитива.
Криптографический протокол представляет
собой распределенный криптографический алго-
ритм (то есть алгоритм, выполняемый не менее
чем двумя сторонами), задаваемый последова-
тельностью действий каждой из сторон. Прото-
кол часто использует несколько криптографиче-
ских примитивов. Анализ безопасности протоко-
ла требует как учета безопасности криптографи-
ческих примитивов, так и возможных нарушений
протокола (явных и неявных).
Криптосистема — это совокупность крипто-
графических алгоритмов и протоколов и спосо-
бов их использования, а также алгоритмов
управления ключами, включая выработку, дос-
тавку, ввод в действие, вывод из действия, заме-
ну и уничтожение ключей.
8.3.2. Хэш-функция
Наиболее простым криптографическим при-
митивом является хэш-функция. Хэш-функцией
называется функция, отображающая аргумент
произвольной конечной длины в образ фиксиро-
ванной длины. Вычислимой в одну сторону (one-
way) хэш-функцией называется хэш-функция,
для которой по данному аргументу вычислить
значение функции легко, а по данному значению
функции аргумент найти сложно. В дальнейшем
все хэш-функции будем считать вычислимыми в
одну сторону. Нахождение хотя бы одного зна-
чения аргумента по заданному значению хэш-
функции будем называть ее обращением.
Хэш-функция, зависящая от ключа, называет-
ся ключевой-™ в противном случае хэш-функция
называется бесключевой.
Хэш-функции используются в протоколах ау-
тентификации (опознавания и аутентификации
сообщения). Бесключевые хэш-функции исполь-
зуются также в качестве индикатора корректно-
сти данных, в частности, для проверки того, что
вычисления выполнены в правильном порядке.
Например, пусть выходом алгоритма должна
быть пара текстов А и В, связанных друг с дру-
гом, и пусть имеются два способа вычисления
этих текстов: по правилам — сначала А, потом В;
и с отступлением от правил — сначала В, потом
А. По паре (А, В) невозможно узнать, каким спо-
собом она вычислялась. Превратим эту пару в
тройку (С, А, В), где А = h(C) и h — вычислимая
в одну сторону бесключевая хэш-функция, при-
чем правильной считается тройка, в которой вы-
полняется равенство А = h(C) и существует тре-
буемая связь между А и В. Тогда указанное от-
ступление от правил становится невозможным,
так как хотя из текста В и можно найти текст А,
но по полученному значению А вычислительно
невозможно найти аргумент С.
Коллизией называется пара аргументов М и
М', которым соответствует одно и то же значе-
ние хэш-функции: В(М) = h(M'). Если число та-
ких аргументов равно г, то говорят о коллизии
кратности г.
Допуская вольность речи, будем говорить о
хэш-функции, свободной от коллизий, если эта
функция не имеет коллизий при заданных ограни-
чениях на длину аргумента. Вычислимые в одну
сторону функции, свободные от коллизий, могут
использоваться в схемах предъявления битов (см.
и. 14.1) или, более общо, предъявления связанной
информации, а также в задачах опознавания.
С помощью ключевой хэш-функции может
обеспечиваться имитозащита (частный случай
аутентификации). Говорят, что криптоалгоритм
реализует имитозащиту данных, если он обес-
печивает защиту получателя от навязывания
ложной информации. Имитозащита включает в
себя следующие понятия: •
- контроль целостности данных;
- контроль подлинности данных;
- контроль неповторяемости данных.
13 Ключевая хэш-функция называется также ко-
дом аутентификации сообщения (message authentica-
tion code, MAC).
191
Иногда в понятие имитозащиты включают и
контроль того, что данные предназначены имен-
но тому адресату, который их получил.
Если для имитозащиты используется ключе-
вая хэш-функция, то аргументом хэш-функции
являются защищаемые данные, а значение хэш-
функции передается вместе с данными. Контроль
подлинности и целостности осуществляется пу-
тем срав нения вычисленного и полученного
значений хэш-функции. Если эти значения сов-
падают, то при некоторых условиях можно ут-
верждать, что источником данных является вла-
делец секретного ключа и данные в ходе переда-
чи не были искажены.
8.3.3. Шифр
Шифрование обеспечивает криптографическую
защиту данных от несанкционированного доступа.
Открытый текст (сообщение)— это текст,
подлежащий криптографической защите.
Шифром будем называть обратимое преобра-
зование множества текстов с целью обеспечения
их конфиденциальности, как правило выполняе-
мое с помощью ключа. Устройство (или програм-
му), реализующее шифр, назовем шифратором.
Зашифрованный текст (шифртекст, шифро-
грамма) — это образ открытого текста, получен-
ный в результате действия шифра. Если множе-
ства открытых и зашифрованных текстов совпа-
дают, то шифр называется эндоморфным. Эндо-
морфный шифр реализует подстановку, дейст-
вующую на множестве текстов.
Под шифрованием информации будем пони-
мать процесс перевода открытого текста в зашиф-
рованный (зашифрование) и обратно (расшифро-
вание). Основная цель шифрования — обеспечить
конфиденциальность открытого текста.
Ключом шифрования называется секретный
параметр шифра, обеспечивающий конфиденци-
альность открытого текста при наличии соответ-
ствующего зашифрованного текста.
Дешифрованием (вскрытием ключа) шифра на-
зовем несанкционированное нарушение конфиден-
циальности, достигнутое методами криптоанализа.
Шифрование используется при хранении дан-
ных или при их передаче по незащищенным ка-
налам связи.
8.3.4. Понятие стойкости
криптографических алгоритмов
Стойкость криптоалгоритмов должна быть
достаточной для того, чтобы обеспечить безопас-
ность данных в течение некоторого срока, опре-
деляемого условиями эксплуатации информаци-
онной системы, использующей эти алгоритмы.
Стойкость количественно должна отражать
трудоемкость нарушения информационной безо-
пасности. Наиболее употребительной единицей
измерения стойкости является временная слож-
ность наилучшего известного алгоритма, нару-
шающего безопасность. Однако иногда исполь-
зуются и другие единицы измерения стойкости:
- длительность вычислений по вскрытию клю-
ча (с учетом развития вычислительной моде-
ли нарушителя);
- требуемый объем памяти для вскрытия ключа;
- стоимость вскрытия ключа;
- количество энергии, необходимое для вскры-
тия ключа;
- физический объем вычислительной модели
для вскрытия ключа.
Сложностные характеристики этого алгорит-
ма (число шагов, требуемая память, вероятность
успеха) могут существенно различаться в зави-
симости от вида алгоритма и единиц измерения
его сложности [19]. Кроме того, понятие наи-
лучшего алгоритма, решающего данную задачу,
постоянно меняется.
Часто оказывается, что задача нарушения
безопасности сводится к совокупности других
задач или является эквивалентной некоторым
другим задачам.
Длительность сохранения конфиденциально-
сти зашифрованной информации определяется
совокупностью различных факторов, в том числе:
- производительностью вычислительной моде-
ли, которой может располагать нарушитель;
- объемом памяти вычислительной модели;
- скоростью роста во времени производитель-
ности вычислительной модели нарушителя
при ее совершенствовании;
- сложностью наилучшего известного (вероят-
ностного) алгоритма, решающего задачу на-
рушения конфиденциальности;
- развитием вычислительных методов матема-
тики, которое ведет к появлению новых, бо-
лее эффективных алгоритмов, решающих за-
дачу нарушения конфиденциальности; .
- вероятностью успешного решения задачи
данным алгоритмом;
- возможностью получения дополнительной
информации об используемом ключе, напри-
мер, наличие открытых и соответствующих
зашифрованных текстов, возможность за-
шифрования или расшифрования специаль-
ным образом подобранных текстов и т. п.
Стойкость алгоритма аутентификации данных
или источника данных характеризуется, с одной
стороны, сложностью создания данных наруши-
телем, которые будут восприняты как истинные,
192
с другой стороны, вероятностью навязывания
ложной информации.14
В основу безопасности криптографических
методов защиты данных положены те или иные
математические или физические задачи. Соот-
ветствующие криптографические алгоритмы
можно классифицировать по степени доказуемо-
сти уровня стойкости: безусловно стойкие, дока-
зуемо стойкие и предположительно стойкие [1].
Безусловно стойкие криптоалгоритмы гаран-
тированно не позволяют вскрыть ключ. Приме-
ром такого криптоалгоритма является алгоритм
Вернама. Открытый текст х и ключ к представ-
ляются как «-разрядные векторы над полем (F2-
Шифрование заключается в вычислении пораз-
рядной суммы векторов: у = х Ф к. Ключ пред-
ставляет собой случайный по Колмогорову век-
тор такой, что наилучший способ его вычисле-
ния— перебор. Ключ может быть использован
только один раз. Использование в качестве клю-
ча рекуррентной последовательности, вырабо-
танной с помощью известного детерминирован-
ного алгоритма, недопустимо.
Безопасность доказуемо стойких криптоал-
горитмов определяется сложностью решения
хорошо исследованных многими математиками
и криптографами и общепризнанно сложных
массовых задач, например, задачи разложения
числа на множители или задачи вычисления ин-
декса в конечной группе. При этом следует раз-
личать случаи полиномиальной сводимости за-
дачи нарушения безопасности криптосистемы к
данной хорошо исследованной массовой задаче
и полиномиальной эквивалентности этих задач.
Примером доказуемо стойкого криптоалгорит-
ма, взлом которого эквивалентен вычислению
квадратного корня в кольце классов вычетов по
модулю составного числа, является схема под-
писи Фиата-Шамира (см. п. 13.1.3). Примером
доказуемо стойкого криптоалгоритма, взлом
которого эквивалентен задаче разложения со-
ставного числа на множители, является прото-
кол аутентификации с нулевым разглашением
(см. п. 14.2.2).
Отличительной особенностью доказуемо
стойких криптоалгоритмов является их «жест-
кость», то есть невозможность модификации
(усиления) путем незначительных изменений.
Поэтому падение сложности задачи разложения
приводит к соответствующему снижению стой-
14 Иногда безопасность схемы аутентификации
характеризуют только вероятностью успеха. В этом
случае неявно предполагается, что наилучшим алго-
ритмом для нарушителя является попытка навязыва-
ния случайной шиФпогоаммы.
кости криптографических алгоритмов, основан-
ных на этой задаче.
Изучение доказуемо стойких криптоалгорит-
мов обычно относится к области криптографии с
открытым ключом.
Безопасность предположительно стойких
криптоалгоритмов основана на сложности реше-
ния частной задачи, которая исследовалась в те-
чение небольшого (по историческим меркам)
промежутка времени небольшим числом матема-
тиков или криптографов. Взлом предположи-
тельно стойкого шифра сводится с полиноми-
альной сложностью к задаче о выполнимости
булевой формулы (см. п. 16.5.2).
Предположительно стойкие криптоалгоритмы
обычно допускают модификацию, то есть обла-
дают свойством гибкости. Например, безопас-
ность шифра DES (см. п. 19.3) в значительной
степени определяется тем, что используемые
подстановки хорошо аппроксимируются линей-
ными над полем (F2 булевыми функциями. Ис-
пользование подстановок с большей нелинейно-
стью позволило бы усилить этот шифр. Приме-
ром усиления DES, позволяющим использовать
существующие аппаратные решения, является
шифр DESX (см. п. 19.3).
Предположительно стойкие криптоалгоритмы
изучаются в рамках «классической» криптогра-
фии (см. гл. 16-19).
8.4. Шифрование
Безопасность того или иного криптографическо-
го метода защиты информации иногда описывают,
следуя К. Шеннону [13], на языке теории инфор-
мации. Для того чтобы передать по незащищенно-
му каналу связи данные от отправителя к получа-
телю, используют следующую схему (рис. 8.1).
Рис. 8.1. Схема безопасной передачи данных
193
Отправитель вырабатывает сообщения (от-
крытые тексты); при этом, при необходимости,
для того чтобы одинаковые открытые тексты не
переходили в одинаковые зашифрованные тек-
сты, может использоваться рандомизатор, кото-
рый включает в состав открытых текстов слу-
чайное число. Открытые тексты зашифровыва-
ются в шифраторе с помощью ключа и переда-
ются по незащищенному каналу связи. Наруши-
тель имеет доступ к этому каналу и может пы-
таться на основании зашифрованных текстов и
частично известных открытых текстов опреде-
лить неизвестный ему ключ или осуществить
бесключевое чтение зашифрованных текстов.
Кроме того, нарушитель может сам формировать
тексты и посылать их получателю с целью навя-
зывания ложной информации. На приемной сто-
роне данные расшифровываются с помощью то-
го же ключа (или иного ключа, связанного вы-
числимым способом с ключом отправителя). При
необходимости случайное число, включенное в
состав сообщения рандомизатором, удаляется.
Решающее устройство определяет, является со-
общение подлинным или оно сформировано на-
рушителем. В первом случае сообщение переда-
ется получателю.
Эта схема отражает решение двух задач:
обеспечения конфиденциальности данных и
обеспечения контроля их подлинности и целост-
ности (в этом случае предполагается, что отпра-
витель и получатель доверяют друг другу). Если
отождествить отправителя с получателем, а в
канале связи допустить неограниченно большую
задержку, то схема рисунка 8.1 будет соответст-
вовать хранению зашифрованных данных.
Для того чтобы схема рисунка 8.1 обеспечи-
вала конфиденциальность, необходимо, чтобы
ключи хранились в секрете, при этом возникает
задача безопасной доставки ключей. Доставка
ключей должна осуществляться по защищенному
каналу связи, обеспечивающему не только кон-
фиденциальность ключей, но и защиту их от
подмены. Действительно, однажды навязав свой
ключ и отправителю, и получателю, нарушитель
может узнать все передаваемые данные, зашиф-
рованные на этом ключе, а также навязывать
сколь угодно много ложных сообщений.
Как правило, источник сообщений обладает
избыточностью, и создаваемые сообщения не
являются случайными. Это обстоятельство мо-
жет снизить безопасность шифрования и служит
предпосылкой для частотного криптоанализа
(см. п. 16.7.1). Для снижения избыточности мож-
но использовать кодирование источника сооб-
щений. Обычно требуется, чтобы зашифрован-
ные тексты были статистически неотличимы от
случайных последовательностей.
Безопасность связи в рамках теории информа-
ции можно охарактеризовать с помощью энтро-
пии, которая представляет собой количественную
характеристику сложности преодоления защиты.
Шенноновская энтропия текста из п двоичных
символов определяется следующим образом:
Hs = ^Pi (°) 10ё Pi (°) + Pi С1) 1оё Pi 0)) ’
z—1
где pKJ) — вероятность того, что z-й символ равен j.
Шифр с секретным ключом характеризуется эн-
тропией ключа. Определение шенноновской эн-
тропии через вероятности неявно задает метод
вскрытия ключа, основанный на изучении стати-
стических свойств множества используемых клю-
чей и их последующем переборе. Однако перебор
как метод вскрытия ключа не оправдан, если нару-
шитель знает открытые и соответствующие зашиф-
рованные тексты, что часто имеет место на практи-
ке. Поэтому теоретико-информационные методы
используются для описания криптоалгоритмов и
анализа их безопасности сравнительно редко.
При выборе того или иного способа шифро-
вания перед разработчиком аппаратуры встает
задача сравнения способов шифрования по тем
или иным качествам: стойкости, удобству про-
граммной или аппаратной реализации, размеру
ключа и размеру блока обрабатываемой инфор-
мации, производительности, возможности моди-
фикации способа шифрования, способу доставки
и замены ключей и т. п.
8.4.1. Симметричное
и несимметричное шифрование
Различают ключевые и бесключевые способы
шифрования. При бесключевом шифровании (см.
пп. 12.1.1, 15.6.4) секретный ключ не нужен, но
передача зашифрованных данных требует диалога
между отправителем и получателем. При этом
открытый текст шифруется с помощью случай-
ных ключей, вырабатываемых на время сеанса
отправителем и получателем независимо. Бес-
ключевое шифрование может использоваться, на-
пример, при дуплексной связи по радиоканалу без
помех в реальном масштабе времени. Взаимное
опознавание участников выполняется «по голосу»
или с помощью иных заранее определенных про-
цедур. Однако этот способ шифрования иногда не
позволяет обеспечить имитозащиту и конфиден-
циальность. Действительно, если нарушитель мо-
жет включаться «последовательно» в канал связи
и заменять по своему усмотрению некоторые тек-
сты, то по отношению к законному отправителю
он может вести себя как получатель, а по отноше-
нию к законному получателю — как отправитель
(«атакагроссмейстера»). ....
194
Ключевые шифры подразделяются на симмет-
ричные и несимметричные. Несимметричные шиф-
ры не позволяют вскрыть ключ расшифрования по
известному ключу зашифрования со сложностью
ниже расчетной (однако ключ зашифрования по
известному ключу расшифрования вычисляется
легко). Поэтому ключ зашифрования можно опуб-
ликовать; при этом зашифровать сообщение может
каждый, а расшифровать— только владелец сек-
ретного ключа. Это соответствует способу шифро-
вания с открытым ключом (см. гл. 12 и п. 15.6.4).15
Шенноновская энтропия секретного ключа рас-
шифрования при известном ключе зашифрования
нулевая, а его колмогоровская энтропия равна
сложности вскрытия ключа. Поэтому для описания
несимметричных шифров используется не теорети-
ко-информационный, а сложностный подход.
В случае симметричного шифра понятия за-
шифрования и расшифрования относительны, их
можно менять местами. Для несимметричного
шифра это невозможно.
До недавнего времени использовались исклю-
чительно симметричные способы шифрования.
Это обусловлено их высокой скоростью и воз-
можностью модификации. Однако они имеют и
ряд неудобств.
Рассмотрим в качестве примера сеть связи из
106 абонентов, в которой каждый пользователь
может связаться с каждым так, чтобы никакой
другой пользователь не мог подслушать разго-
вор. Тогда требуется 0,5 101* ключей. Очевидно,
что это практически нереализуемо.
Альтернативный вариант— построить сеть
связи с использованием центров распределения
(сеансовых) ключей. Здесь каждый пользователь
имеет единственный секретный ключ, копия ко-
торого хранится в центре распределения ключей.
Абонент А для связи с абонентом В обращается в
центр С с запросом сеансового ключа. Центр С
генерирует сеансовый ключ, зашифровывает его
на ключах пользователей А и В и посылает шиф-
рограммы сеансового ключа этим пользователям.
Неудобством такого способа построения сети
связи является большой поток служебных сооб-
щений в центре распределения ключей, что может
вызвать очереди. Кроме того, сеть здесь строится
по иерархическому признаку и, следовательно,
может быть выведена из строя отключением цен-
тра или несанкционированным доступом (инфор-
мационным, физическим и т. п.) к нему.
Если в системе возможны повторы, то нару-
шитель может перехватить шифрограммы ключа
для данной пары пользователей и при дальней-
15 Подчеркнем, что термин «открытый текст» оз-
начает данные, требующие защиты, тогда как откры-
тый ключ защиты не требует.
ших сеансах выдавать себя за центр по отноше-
нию к этим пользователям, посылая им перехва-
ченные шифрограммы. При этом увеличивается
объем данных, шифруемых на одном ключе, и
снижается сложность его вскрытия.
Можно построить ключевую сеть и децентра-
лизованно, используя несимметричное шифрова-
ние. В этом случае каждый пользователь знает
свой персональный секретный ключ расшифрова-
ния, а парный к нему открытый ключ зашифрова-
ния известен всем пользователям сети (например,
записан в открытом справочнике, наподобие те-
лефонного). Для того чтобы послать зашифрован-
ное сообщение получателю В, отправитель А на-
ходит в справочнике открытый ключ пользовате-
ля В, зашифровывает на нем свое сообщение и
посылает его получателю. Поскольку шифрование
с открытым ключом выполняется гораздо мед-
леннее, чем с секретным, отправитель может дей-
ствовать так: выработать случайный сеансовый
ключ, зашифровать на нем свое сообщение с ис-
пользованием симметричного криптоалгоритма, а
сам ключ зашифровать по схеме с открытым клю-
чом. После этого обе шифрограммы (сообщения и
сеансового ключа) передаются получателю.
8.4.2. Способы шифрования
В настоящее время обычно используются
блочные шифры. Симметричный блочный шифр
представляет собой функцию, задающую подста-
новку множества число п называется раз-
мером блока. В несимметричных шифрах взаимно
однозначное отображение множества блоков от-
крытого текста в множество блоков зашифрован-
ного текста может не являться подстановкой, при
этом может использоваться не все множество
АНТАА а некоторое его подмножество.
В симметричных шифрах размер блока обыч-
но составляет 64 или 128 бит. При этом длина
ключа может отличаться от длины блока. На-
пример, в DES длина ключа— 56 бит, длина
блока — 64 бита. В российском стандарте шиф-
рования ГОСТ 28147-89 длина ключа — 256 бит,
длина блока — 64 бита (см. гл. 19).
В несимметричных шифрах размер блока
обычно составляет не менее 128 бит. Это разли-
чие обусловлено тем, что симметричные шифры
обычно обладают (предположительно) перебор-
ной сложностью вскрытия ключа,16 а стойкость
несимметричных шифров более низкая.
16 Как правило, стойкость шифра зависит от объ-
ема известных нарушителю открытых и соответст-
вующих зашифрованных текстов и от того, может ли
нарушитель задавать для шифрования специально
подобранные тексты. -
195
Стойкость шифра задается несколькими «ко-
ординатами»— сложностью, требуемым объе-
мом памяти, вероятностью вскрытия ключа, а
также объемом открытых и соответствующих
зашифрованных текстов (для симметричных
шифров). Для заданной вычислительной модели
это позволяет определить время, в течение кото-
рого зашифрованные данные сохраняют конфи-
денциальность.
История криптографии показывает, что задача
вскрытия ключа решается «без правил», то есть
для ее решения могут привлекаться не только
вычислительные, но и другие средства, которы-
ми располагает нарушитель. Иногда нарушителю
могут принести пользу особенности аппаратной
реализации того или иного криптоалгоритма.
Стойкость должна быть достаточной, чтобы
обеспечить требуемый срок сохранения конфи-
денциальности данных даже после вывода ключа
из действия (этот срок может многократно пре-
вышать срок действия ключа).17 Поэтому ключ
шифрования даже после вывода его из действия
во многих случаях представляет интерес для на-
рушителя.
Некоторые методы криптоанализа (используе-
мые в основном для симметричных шифров, см.
гл. 18) накладывают ограничения на объем дан-
ных, зашифрованных на ключе. Поэтому ключи
шифрования должны периодически меняться.
Для однозначного вскрытия ключа на основе
известных открытых текстов необходимо, что-
бы длина открытого текста несколько (пример-
но в 1,368 раза, см. п. 16.2.1) превышала длину
ключа.18
Аналогом шифра является алгоритмический
генератор (псевдо)случайной последовательно-
сти. Действительно, если генератор вырабатыва-
ет случайную по Колмогорову последователь-
ность в алфавите из и символов, то,
складывая по модулю п последовательность с
открытым текстом х\,...,хт, можно получить
надежное зашифрование: jy, На приемной
стороне нужно выработать такую же последова-
тельность Si, и найти открытый текст
Xi=yj-5,(mod и).
Безопасность генераторов псевдослучайной
последовательности основана на сложности пред-
сказания последующих и восстановления предше-
ствующих элементов последовательности, фор-
мируемой генератором. Кроме того, последова-
17 Примером служат не рассекреченные до сих
пор материалы, с которыми в 1941 г. Р. Гесс, третье
лицо в фашистской Германии, летал в Англию.
18 Соответствующие шифртексты считаются из-
вестными. - '
тельность, формируемая генератором, должна
выдерживать статистические тесты (это требова-
ние является более слабым, чем предыдущие).
8.5. Аутентификация
При разработке примитивов аутентификации
предполагается, что нарушитель может навязы-
вать свои данные или изменять данные, переда-
ваемые по каналу связи.
В процессе аутентификации участвуют по
крайней мере две стороны: претендент, доказы-
вающий аутентичность (свою, если решается за-
дача опознавания, или сформированных данных,
если решается задача аутентификации сообще-
ния), и верификатор, проверяющий эту аутентич-
ность (рис. 8.2). В некоторых сложных протоко-
лах число участников может быть больше двух.
Рис. 8.2. Обобщенная схема аутентификации
В ходе аутентификации претендент передает
верификатору служебную информацию р (в слу-
чае аутентификации сообщения претендент пе-
редает еще и сообщение т). Информация р зави-
сит от секретного ключа к претендента, а в слу-
чае диалоговой аутентификации и от запроса v
верификатора. Используя свой ключ к, верифи-
катор проверяет правильность информации р.
Предъявляемая претендентом информация
может характеризоваться конкретным физиче-
ским воплощением, которое трудно подделать.
Например, при оплате покупки наличными кас-
сир проводит аутентификацию — проверяет
подлинность предъявленной купюры, которая
имеет трудноподделываемые физические при-
знаки. Для возможности аутентификации доку-
мента, подготовленного претендентом, отпеча-
танный на бумаге документ может быть подпи-
сан автором, заверен у нотариуса и т. п. В ком-
пьютерных системах данные лишены указанного
трудноподделываемого физического воплоще-
ния. В этом случае аутентификация может быть
выполнена методами криптографии, например,
примитивом цифровой подписи (см. гл. 13).
Цифровая подпись основана на тех же прин-
ципах, что и шифрование с открытым ключом.
Ключ формирования подписи является конфи-
денциальной информацией его владельца, а ключ
проверки подписи опубликовывается. Подписан-
ный текст представляет собой пару сообще-
ние/подпись. Вычислить подпись для данного
сообщения может только владелец ключа фор-
мирования подписи. Проверить правильность
подписи для данного сообщения может любой
пользователь.
Задача аутентификации более многогранна,
чем задача обеспечения секретности. По опреде-
лению верификатор не доверяет претенденту
(иначе проверять нечего), тогда как в задаче
обеспечения конфиденциальности такого недо-
верия нет. Недоверие участников протокола ино-
гда может быть обоюдным. Это, по сути, означа-
ет возможность сговора верификатора с наруши-
телем против претендента.
В ходе проведения сеанса аутентификации
нарушитель может получить некоторую инфор-
мацию о ключе. Пусть Н^к) и Нк(к\ {т,р, v}) —
соответственно колмогоровская энтропия ключа
претендента и колмогоровская энтропия этого же
ключа при наличии информации, передававшей-
ся по каналу связи.
Определим разглашение знаний о ключе:
хи (1Л_НК(к}-НК(к\{т,р,у})
оНК(к)~ ,
нк(к)
если верификатор является доверенной сторо-
ной, и
(1г\ нк(к\к')-нк(к\к'Лт,Р,У})
НК(к\к')
если верификатор не является доверенной сторо-
ной.
Очевидно, что 0 < ЪН^к) < 1. В зависимости
от того, какое из четырех условий:
- 8ЯЦА)=1;
- 8Яа{А) = а < 1;
- 8ЯЦА)«0;
- 6ЯАЯ) = 0
выполняется, говорят о полном, частичном, ми-
нимальном и нулевом разглашении знаний.
Пример 8.5.1. Разглашение знаний.
1. Примером полного разглашения знаний яв-
ляется опознавание по паролю. В этом случае
верификатор и претендент знают конфиденци-
альный пароль. Претендент предъявляет пароль
верификатору, верификатор сравнивает полу-
ченный пароль со своим значением. При совпа-
дении опознавание считается успешным.
2. Примером частичного разглашения знаний
является опознавание по цепочке аргументов
бесключевой хэш-функции Л: х0, = Л(х0),
х2 = /г(х]), ..., х„ = й(хи_]). Здесь верификатор пер-
воначально знает хп. На первом сеансе аутенти-
фикации претендент предъявляет x„_i. Верифика-
тор проверяет равенство х„ = h^x,^). При его вы-
полнении аутентификация считается успешной,
и верификатор заменяет х„ на хп-}. На следующем
сеансе процедура рекурсивно повторяется для х/н2
и т. д., до тех пор, пока претендент не предъявит х0.
3. Примером минимального разглашения зна-
ний является электронная цифровая подпись (см.
гл. 13).
4. Примером нулевого разглашения знаний
является протокол опознавания на основе дока-
зательств с нулевым разглашением (см. гл. 14).
Случаи полного и частичного, а также мини-
мального и нулевого разглашения знаний разли-
чаются непринципиально. При полном разгла-
шении возможна только однократная аутентифи-
кация. В случае нулевого или минимального раз-
глашения возможна многократная аутентифика-
ция (максимальное число сеансов определяется
методами криптографии).
Определим защитные функции аутентифи-
кации, показывающие что, от чего и при каких
условиях может быть защищено, в следующих
координатах'.
- по типу аутентификации: опознавание / ау-
тентификация сообщения;
- по числу сеансов на одном ключе: один / много;
- по типу используемого канала связи: обяза-
тельная двунаправленность (диалоговая ау-
тентификация) / необязательная двунаправ-
ленность (бездиалоговая аутентификация);
- по доверию к верификатору: доверенный /
недоверенный;
- по качеству связи: необходимость надежного
доведения информации / некритичность на-
дежного доведения;
- по наличию службы единого времени: нали-
чие единого времени / необязательность еди-
ного времени;
- по относительному объему передаваемой
служебной информации (отношение объема
передаваемых данных к энтропии Hfkk | к)).
197
В зависимости от особенностей проектируемой
информационной системы можно вводить допол-
нительные координаты, которые будут учитывать,
например, удобство управления ключами.
Служба единого времени необходима для за-
щиты от повторов или задержек информации при
бездиалоговой аутентификации. При этом в со-
став служебной информации вводится время от-
правления документа, а на приемной стороне
проверяется, что разность времени приема и от-
правления гарантированно мала. Надежное дове-
дение информации требуется при однократной
аутентификации: если переданный текст не дой-
дет до получателя, то его может перехватить на-
рушитель с тем, чтобы затем выдать себя за пре-
тендента.
Эти координаты могут накладывать ограни-
чения на смежные алгоритмы работы информа-
ционной системы, не имеющие непосредствен-
ного отношения к аутентификации, в частности,
на алгоритмы управления кодом текущего вре-
мени и алгоритмы передачи данных. Все указан-
ные координаты, кроме последней, являются
двоичными и определяют 64 защитных функции.
Если значение какой-либо из координат некри-
тично, то защитная функция задается неполным
набором координат (например, допускается как
диалоговая, так и бездиалоговая аутентифика-
ция). Таким образом, без учета последней коор-
динаты множество защитных функций является
конечным.
На введенных координатах определим отно-
шение порядка, которое индуцирует упорядо-
ченность защитных функций аутентификации в
части их функциональных возможностей (уни-
версальности):
- аутентификация сообщения о опознавание
(для опознавания в схеме аутентификации на
рисунке 8.2 можно положить сообщение т
фиксированным);
- многократная аутентификация о однократ-
ная аутентификация (если можно выполнять
аутентификацию много раз, то ее можно вы-
полнить и один раз);
- бездиалоговая аутентификация z> диалоговая
аутентификация (при наличии двунаправ-
ленного канала связи можно ограничиться
передачей информации только от претенден-
та к верификатору);
- недоверенный верификатор z> доверенный
верификатор (если аутентификация обеспе-
чивается при недоверенном верификаторе, то
ее можно обеспечить и при доверенном ве-
рификаторе);
- некритичность доведения информации о не-
обходимость доведения (если аутентифика-
ция выполняется при возможных искажениях
сообщения, то она будет выполняться и при
отсутствии искажений);
- необязательность единого времени 2 нали-
чие единого времени (если система единого
времени в информационной системе не обя-
зательна, то ее наличие не повлияет на аутен-
тификацию);
- меньший относительный объем служебной
информации з больший относительный объ-
ем служебной информации (если аппаратура и
каналы связи при прочих равных условиях по-
зволяют обработать и пропустить большой
объем информации, то они могут обработать и
пропустить и меньший объем информации).
Индуцированная частичная упорядоченность
защитных функций позволяет минимизировать
требуемый набор защитных функций.
В отличие от ключа шифрования ключ аутен-
тификации представляет интерес для нарушителя
лишь в течение его срока действия. Например,
после того как ключ проверки подписи выведен
из обращения, секретный ключ формирования
подписи в некоторых случаях может быть опуб-
ликован. Поэтому при прочих равных условиях
стойкость криптосистемы аутентификации мо-
жет быть ниже, чем стойкость криптосистемы
шифрования.
8.5.1. Опознавание
Простейший протокол аутентификации пред-
ставляет собой опознавание по паролю (см. при-
мер 8.5.1). Этот протокол подразумевает, что пре-
тендент доверяет верификатору. Кроме того, если
канал связи не является защищенным и возможна
многократная аутентификация, то протокол не
обеспечивает безопасность, так как нарушитель в
канале связи может скопировать пароль и в даль-
нейшем выдавать себя за претендента.
Если верификатор не является доверенной сто-
роной, то он может выдавать себя за претендента
в протоколах опознавания с другим верификато-
ром или может сам формировать такой протокол
и утверждать, что протокол сформирован с уча-
стием настоящего претендента. Этот протокол
обеспечивает однократную бездиалоговую аутен-
тификацию при условии, что верификатор являет-
ся доверенной стороной, а канал связи обеспечи-
вает надежное доведение информации.
Более сложный протокол представляет собой
опознавание по аргументу хэш-функции. В этом
случае верификатор хранит значение хэш-
функции, а претендент знает соответствующий
аргумент этой хэш-функции. В процессе опозна-
198
вания претендент предъявляет аргумент, верифи-
катор вычисляет значение хэш-функции для этого
аргумента и сравнивает с имеющимся. При совпа-
дении значений аутентификация считается ус-
пешной. Если нужно, чтобы существовал единст-
венный аргумент, позволяющий успешно пройти
аутентификацию, то можно использовать хэш-
функцию, свободную от коллизий (см. п. 15.6.7).
В случае однократного опознавания этот прото-
кол безопасен даже тогда, когда претендент не
доверяет верификатору. Однако при многократ-
ном опознавании нарушитель или верификатор
могут повторно использовать переданную пре-
тендентом информацию.
Если претендент доверяет верификатору, то
для опознавания может использоваться симмет-
ричное шифрование или ключевая хэш-функция.
В этом случае секретный ключ известен претен-
денту и верификатору. Для защиты от повторов
верификатор посылает претенденту случайное
число. Претендент зашифровывает его или вы-
числяет хэш-функцию и возвращает шифртекст
(или значение хэш-функции, зависящей от клю-
ча) верификатору. Верификатор проверяет пра-
вильность шифртекста (значения хэш-функции).
Здесь верификатор может сам сформировать
правильный ответ и поэтому должен быть дове-
ренной стороной.
Если претендент не доверяет верификатору,
то протокол многократного опознавания может
строиться на основе цифровой подписи или
шифрования с открытым ключом. В этом случае
верификатор знает открытый ключ проверки
подписи (зашифрования), а претендент— сек-
ретный ключ формирования подписи (расшиф-
рования). Для опознавания верификатор выраба-
тывает случайное число и посылает претенденту
для подписи (или зашифровывает случайный от-
крытый текст и посылает его для расшифрова-
ния). Претендент подписывает (расшифровыва-
ет) текст и посылает его верификатору. Верифи-
катор проверяет правильность подписи (сравни-
вает полученный расшифрованный текст с исход-
ным открытым текстом).
Если запись протокола аутентификации в спор-
ных ситуациях может предъявляться арбитру, то
необходимо предусмотреть защиту от повторов,
например, вставляя в исходный текст код времени.
В ходе опознавания верификатор получает
один бит шенноновской информации: является
ли служебная информация р (см. рис. 8.2) пра-
вильной, тогда как в ходе аутентификации сооб-
щения верификатор получает еще и само сооб-
щение. Поэтому под опознаванием можно пони-
мать протокол, в ходе которого верификатор по-
лучает один бит шенноновской информации.
При таком определении протоколами опознава-
ния могут являться, например, протоколы про-
верки корректности информации, протокол пра-
вильности выработки составного числа (см. п. 15.6).
8.5.2. Контроль целостности
и подлинности данных
Задачи контроля целостности и подлинности
данных предполагают возможность разбиения
верификатором множества данных на два класса:
удовлетворяющие и не удовлетворяющие прове-
рочному критерию. Для этого в сообщении
должна содержаться проверочная информация.
Если проводится бездиалоговая аутентификация
данных по схеме шифрования с симметричным
ключом, то в текст сообщения должна вводиться
избыточность. Например, при передаче откры-
тых данных отправитель по условиям протокола
вычисляет имитповставку (значение ключевой
хэш-функции) и передает ее вместе с данными.
Получатель вычисляет эту же имитовставку и
проверяет совпадение вычисленного и получен-
ного значений. Если передаются зашифрованные
данные, то можно либо ввести в открытый текст
заранее известные слова, либо вычислить ими-
товставку. Отметим, что введение избыточности
не может усилить защитные свойства в части
обеспечения конфиденциальности сообщения.
Бездиалоговая аутентификация данных, осно-
ванная на использовании несимметричных крип-
тографических алгоритмов, выполняется по схе-
ме рисунка 8.1 с помощью цифровой подписи
(см. гл. 13) или бездиалоговых доказательств с
нулевым разглашением (см. п. 14.3).
Другие задачи аутентификации данных (кон-
троль неповторяемости, отсутствия недопустимо
большой задержки момента приема относитель-
но момента передачи, отсутствия переадресации)
решаются указанными выше способами, при
этом открытый текст должен содержать строку
неповторяющихся данных, допускающих упоря-
дочение (порядковый номер или время отправ-
ки), и адреса отправителя и получателя.
8.6. Управление ключами
Для обеспечения безопасности информации в
информационной системе необходимы ключи.
Кроме того, для практической реализации крип-
тоалгоритмов необходимо выбрать параметры
этих алгоритмов, например, блок подстановок
для симметричного шифра, стартовый вектор
хэш-функции (см. гл. 19) или эллиптическую
кривую (см. гл. 15). ....... .,
199
Если сеть связи достаточно велика, то воз-
никает задача управления ключами, включаю-
щая в себя задачи выработки ключей, их дос-
тавки, распределения, ввода в действие и вы-
вода из действия. Кроме того, поскольку сим-
метричные шифры и ключевые хэш-функции
уязвимы по отношению к статистическим ме-
тодам криптоанализа, которые накладывают
ограничение на объем данных, шифруемых на
одном ключе (см. гл. 18), ключи нужно перио-
дически заменять. ;
В случае несимметричной схемы шифрова-
ния или аутентификации каналы доставки сек-
ретных ключей должны обеспечивать конфи-
денциальность и имитозащиту, а каналы дос-
тавки открытых ключей — только имитозащи-
ту. Подмена открытого ключа при его доставке
предоставит нарушителю полномочия законно-
го владельца соответствующего секретного
ключа. Персональные секретный и открытый
ключи пользователь может создавать сам, но в
выборе общего ключа, от которого в той или
иной степени зависит стойкость криптоалго-
ритма, он не волен. Например, если в основу
безопасности криптосистемы положена задача
дискретного логарифмирования в конечном поле,
то смена персональных ключей при сохранении
параметров криптосистемы практически не по-
зволяет продлить срок безопасной эксплуатации
(см. гл. 10, 11). Соответственно, в сети необхо-
димо обеспечить режим смены общего ключа.
Кроме того, пользователь должен иметь воз-
можность убедиться, что общий открытый ключ
создан правильно.
Задача управления ключами при проектиро-
вании криптосистем является наиболее ответст-
венной. Алгоритмы выработки ключей, достав-
ки, уничтожения (стирания) должны быть согла-
сованы по стойкости с соответствующими алго-
ритмами шифрования и аутентификации. На-
пример, если ключ для шифра ГОСТ 29147-89
устанавливается на основе протокола Диффи-
Хеллмана в мультипликативной группе простого
конечного поля (см. п. 10.2), то размер поля дол-
жен быть несколько тысяч бит, тогда как длина
ключа шифра — 256 бит.
Протоколы управления ключами должны
обеспечивать высокий уровень стойкости в части
конфиденциальности и аутентичности. Кроме
того, если в информационной системе пользова-
тели не доверяют друг другу, то приходится рас-
сматривать случаи, когда один из участников
протокола управления ключами нарушает уста-
новленный порядок действий с целью нанесения
ущерба другим участникам.
В некоторых случаях требуется, чтобы соз-
дание общего секретного ключа было доступно
только коллективу из не менее чем заданного
числа участников протокола, тогда как мень-
шее число участников не смогут создать этот
ключ. Такие протоколы называются протоко-
лами (схемами) разделения секрета (см.
п. 14.5).
8.7. Задачи, положенные в основу
безопасности криптографических
алгоритмов
Задача нарушения безопасности криптогра-
фического алгоритма должна быть достаточно
сложной. В настоящее время для ряда массо-
вых задач выбора доказано, что не существует
универсального алгоритма их решения (см.
п. 1.2).
Эти, а также ряд других задач выбора, для ко-
торых не существует универсального алгоритма,
могут быть положены в основу криптографиче-
ских протоколов, например, опознавания на ос-
нове доказательств с нулевым разглашением (см.
гл. 14).
Обычно в криптографии используются не не-
решаемые, а более удобные труднорешаемые
задачи, такие как задача выбора из класса NP-
полных или из класса NP. Задача вскрытия клю-
ча симметричного шифра (ключевой хэш-
функции), если нарушитель знает несколько от-
крытых и соответствующих зашифрованных тек-
стов, однозначно определяющих ключ, а также
задача обращения хэш-функции сводятся к зада-
че о выполнимости (см. п. 16.5.2).
Криптография с открытым ключом использу-
ет большое число математических задач, их чис-
ло достигает нескольких десятков и постоянно
растет. Это, например, задача разложения со-
ставного числа; задача решения квадратного
уравнения в кольце классов вычетов по модулю
составного числа; задача дискретного логариф-
мирования в конечном поле, на эллиптической и
гиперэллиптической кривой, в группе классов
числового поля; задача вычисления корня из
идеала числового поля и многие другие задачи.
Все это множество задач можно разделить на
следующие четыре класса унифицированных ма-
тематических задач.
1. Задача определения структуры и порядка ко-
нечной группы. К ней сводятся задача разло-
жения составного числа, задача решения
квадратного уравнения в кольце классов вы-
четов по модулю составного числа, задача
извлечения корня из идеала числового поля,
а также задача определения структуры и по-
200
рядка группы классов числового поля.19 На
таких задачах построены криптоалгоритмы
RSA, Фиата-Шамира, а также протокол
Диффи-Хеллмана в группе классов числово-
го поля.
2. Задача дискретного логарифмирования в
циклической группе вычислимого порядка. К
ней сводятся задача вскрытия ключа стан-
дарта цифровой подписи (см. гл. 15), задача
дискретного логарифмирования на эллипти-
ческой кривой или в конечном поле.
3. Задача об укладке ранца. На ней основан
криптоалгоритм Шора-Ривеста (см. п. 12.3).
4. Задача вычисления категорного морфизма. К
этому классу относится задача вычисления
изогении между эллиптическими кривыми,
используемая в алгоритмах аутентификации
(см. п. 15.8.2).
Первые два класса задач могут быть решены с
полиномиальной сложностью на квантовом ком-
пьютере (см. пп. 9.3.6, 11.1.6).
Несмотря на то, что классы унифицированных
задач не являются задачами выбора, они могут
быть сведены с полиномиальной сложностью к
задачам выбора. Например, для второго класса
логарифм можно определить методом деления
пополам после <9(log/') вопросов, допускающих
ответ «да» или «нет», где г— порядок группы.
Первый вопрос: верно ли, что логарифм не
больше, чем г/2 ? Если ответ «да», то следую-
щий вопрос: верно ли. что логарифм не больше,
чем г/22 и т. д.
Параметризация классов унифицированных
задач с помощью различных математических
структур (групп, категорий, суммируемых мно-
жеств) дает массовые основные математические
задачи. Например, параметризация задачи дис-
кретного логарифмирования эллиптическими
кривыми дает задачу логарифмирования на эл-
липтической кривой; параметризация ее мульти-
пликативной группой конечного поля дает зада-
чу логарифмирования в конечном поле и т. п.
При исследовании сложности основных ма-
тематических задач часто используется аппарат
полиномиальной сводимости. Так, иногда оказы-
вается, что исследуемая основная математиче-
ская задача эквивалентна другой задаче или даже
нескольким задачам. Например, задача дискрет-
ного логарифмирования на эллиптической кри-
вой сводится к задаче логарифмирования в неко-
тором расширении исходного поля или в якобиа-
не гиперэллиптической кривой, заданной над
подполем исходного поля (см. гл. 11), а задача
логарифмирования на вырожденной кубической
кривой— к задаче логарифмирования в исход-
ном поле (см. п. 6.8). При этом приходится ис-
следовать сложность всех задач, к которым сво-
дится основная математическая задача.
Кроме задач выбора в криптографии исполь-
зуются задачи распознавания и поиска.
Задача распознавания, как и задача выбора,
допускает ответ «да» или «нет», один из которых
сопровождается сертификатом. Однако слож-
ность проверки сертификата может быть сверх-
полиномиальной.
Пример задачи распознавания: верно ли, что
для любых двух ключей симметричного шифра
последовательное шифрование на этих ключах
эквивалентно шифрованию на третьем ключе?
Сертификат должен содержать «таблицу умно-
жения» подстановок, индуцированных шифром
(см. также п. 17.2). Очевидно, что сложность
проверки правильности этой таблицы превышает
сложность перебора ключей.
Задачи распознавания используются для оп-
ределения применимости неуниверсальных ме-
тодов криптоанализа.
Задача поиска требует нахождения числового
значения некоторой величины. При этом ответ
сопровождается сертификатом, сложность про-
верки которого может быть сверхполиномиаль-
ной.
Пример задачи поиска: найти наиболее веро-
ятный дифференциал шифра и его вероятность
(см. п. 18.2). Задачи поиска используются для
определения стойкости шифра к известным ме-
тодам анализа.
В силу того, что сложность проверки серти-
фиката для задач распознавания и поиска может
превышать полиномиальную, отношение поли-
номиальной сводимости и О-символика здесь
часто оказываются бесполезными. Поэтому при
анализе криптоалгоритмов часто требуется на-
хождение точных числовых оценок сложности
задач распознавания и поиска.
19 Задача вычисления порядка и определения
структуры группы классов числового поля, в том чис-
ле квадратичных полей, в настоящее время недоста-
точно изучена. Известно, что порядок группы классов
для поля дискриминанта D асимптотически равен
д/ID] [20].
201
Упражнения к главе 8
1. Что такое «защита информации»?
2. От какого воздействия (при прочих равных
условиях) легче защититься: непреднамерен-
ного или несанкционированного?
3. Приведите пример нарушения подлинности
информации, при котором сохраняется ее це-
лостность. \
4. Пусть в системе связи действует общий для
всех пользователей ключ шифрования. От-
правитель послал пользователю А зашифро-
ванное сообщение, а нарушитель переадре-
совал это сообщение пользователю В. Будет
ли это нарушением конфиденциальности,
подлинности, целостности?
5. Приведите примеры исчислений.
6. Докажите, что каждый детерминированный
алгоритм является исчислением.
7. Предложите модели нарушителя, отличные
от приведенных в примерах. Выполняется ли
для них основная теорема безопасности?
8. *Попробуйте найти непустую модель нару-
шителя, отличную от тривиальной и обла-
дающую разрешимым множеством атак.
9. Пусть информационная система построена с
использованием процессоров и/или про-
грамм, обладающих недокументированными
возможностями. Предложите механизмы
атак, основанных на активизации этих воз-
можностей. Как можно проверить, что недо-
кументированных возможностей нет?
10. Покажите, что безопасность информацион-
ной системы можно гарантировать (в рамках
определенной модели нарушителя), если ее
подсистема безопасности выполняет все по-
ложенные функции и не выполняет ничего
20
«сверх» этого.
11. Покажите, что если подсистема безопасности
содержит неизвестные недокументированные
функции, то максимальная модель наруши-
теля является «трудновычислимой».
12. *Разрешимость множества атак означает, что
для любой предложенной атаки существует
эффективный алгоритм, распознающий ее
допустимость. Перечислимость множества
атак означает, что существует эффективный
алгоритм, вырабатывающий все допустимые
атаки. Является ли множество допустимых
20 По-видимому, здесь нет четкого разграничения
между подсистемой безопасности и той частью ин-
формационной системы, которая занимается сбором и
обработкой защищаемой информации.
атак в тривиальной модели нарушителя пе-
речислимым? Является ли это множество ко-
нечным?
13. Покажите, что если в схеме симметричного
шифрования нарушитель знает способ шиф-
рования и ключ отправителя или получателя,
то он может расшифровать все зашифрован-
ные на данном ключе тексты. Почему невоз-
можно такое расшифрование в несимметрич-
ном случае, если нарушитель знает зашифро-
ванные тексты и ключ зашифрования?
14. Пусть шифр реализует подстановку, которая
каждую из 26 букв латинского алфавита за-
меняет буквой этого же алфавита. Покажите,
что такие шифры образуют группу по компо-
зиции и, следовательно, композиция произ-
вольного числа таких преобразований не дает
усиления по сравнению с одиночным преоб-
разованием.
15. Инволкщией называется подстановка S, сов-
падающая с 5"1. Покажите, что любая под-
становка множества из п элементов может
быть представлена как композиция конечно-
го числа инволюций для любого п и, следо-
вательно, любой блочный шифратор может
быть реализован как композиция инволюций.
16. Предложите способ построения детермини-
рованного генератора, вырабатывающего
псевдослучайную последовательность с дли-
ной периода более 2", на основе блочного
шифратора с длиной блока п бит, процессора
и запоминающего устройства. Покажите, что
колмогоровская энтропия такой «случайной»
последовательности произвольной длины не
превосходит длины ключа шифратора. Чему
равна шенноновская энтропия этой последо-
вательности?
17. Пусть схема имитозащищенной конфиденци-
альной связи на основе симметричного шиф-
рования реализована согласно рисунку 8.1.
Предложите способ защиты от навязывания
ранее переданной информации.
18. Пусть схема имитозащищенной конфиденци-
альной связи реализована согласно рисунку
8.1 с помощью блочного шифра. Пусть со-
общение состоит из т блоков. Предположим,
что нарушитель знает несколько открытых и
соответствующих зашифрованных блоков и
правила проверки принятого сообщения.
Предложите способы защиты от комплекто-
вания нарушителем формально правильных
сообщений из указанных т блоков. . ..... ?
19. Предложите алгоритм, реализующий поиск
коллизии хэш-функции как вершины с крат-
ностью не менее 2 на случайном дереве, и
оцените его сложность.
20. Предложите способ создания вычислимой в
одну сторону функции на основе задачи о
разрешимости диофантова уравнения над по-
лем Q и способ однократного опознавания с
помощью этой функции.
Литература к главе 8
1. Брикелл Э., Одлижко Э. Криптоанализ: обзор но-
вейших результатов // ТИИЭР. 1988. Т. 76. № 5.
С. 75-94.
2. Введение в криптографию / Под общей редакцией
В.В. Ященко. МЦНМО, ЧеРо. 1998.
3. ГОСТ Р 50992-96. Защита информации. Основные
термины и определения. М.: Госстандарт РФ, 1996.
4. Защита от НСД к информации. Термины и опре-
деления. Руководящий документ. Гостехкомиссия
РФ. М.: Воениздат, 1992.
5. Зегжда Д.П., Ивашко А.М. Как построить защи-
щенную информационную систему / Под ред.
П.Д. Зегжды и В.В. Платонова. СПб.: Мир и Се-
мья, 1997.
6. Манин Ю.И. Доказуемое и недоказуемое (Кибер-
нетика). М.: Сов. Радио, 1979.
7. Месси Дж. Введение в современную криптологию
// ТИИЭР. 1988. Т. 76. № 5. С. 24-42.
8. Оков И.Н. Криптографические системы защиты
информации. СПб.: ВУС, 2001.
9. Ростовцев А.Г., Маховенко Е.Б. Введение в крип-
тографию с открытым ключом. СПб.: Мир и Се-
мья, Интерлайн, 2001.
10. Симмонс Г. Защита информации (малый тематиче-
ский выпуск) // ТИИЭР. 1988. Т. 76. № 5. С. 3-7.
11. Смаллиан Р.М. Принцесса или тигр? М.: Мир, 1985.
12. Успенский В.А., Семенов А.Л. Теория алгорит-
мов: основные открытия и приложения. М.: Нау-
ка, 1987.
1k Шеннон К. Теория связи в секретных систе-
мах / В сб.: К. Шеннон. Работы по теории инфор-
мации и кибернетике. М.: ИЛ, 1963. С. 333-402.
14. Bell D., LaPadula L. Secure Computer Systems:
Mathematical Foundations and Model. Technical Re-
port M74-244. The MITRE Corporation. Bedford,
MA, May 1973.
15. Blum L., Blum M., Shub M. A simple unpredictable
pseudo-random number generator // SIAM Journal on
Computing. 1986. Vol. 15. P. 364-383.
16. Kahn D. The Codebreakers. London: Sphere books
Ltd, 1973.
17. Koblitz N. A Course in Number Theoiy and Cryptog-
raphy. Springer-Verlag, 1987.
18. Konheim A. Cryptography: A Primer. New York:
J. Wiley & Sons, 1981.
19. Menezes A., van Oorschot P., Vanstone S. Handbook
of Applied Cryptography. CRC Press. 1997.
20. Shanks D. Class number, a theoiy of factorization,
and genera // Proceedings of Symposia in Pure
Mathematics. 1969. Vol. XX. New York: Number
Theory Institute. American Mathematical Society,
1969. P. 415-440.
21. Schneier B. Applied Cryptography: Protocols, Algo-
rithms, and Source Code in C, 2nd edition. New York:
J. Wiley & Sons, 1996. [Книга издана также на рус-
ском языке: Шиайер Б. Прикладная криптография.
Протоколы, алгоритмы, исходные тексты на языке
Си. Пер. с англ. М.: Изд-во ТРИУМФ, 2002.]
Г л а в a 9. СИСТЕМА RSA И ЗАДАЧА РАЗЛОЖЕНИЯ
Широко известная криптосистема с открытым
ключом RSA является составной частью многих
стандартов, в том числе ISO 9796, SWIFT, ANSI
X9.3I, французского стандарта ЕТЕВАС 5, авст-
ралийского AS2805.6.5.3 и др. Эта система была
предложена в 1977 г. Р. Ривестом, Э. Шамиром и
Л. Адельманом [16].
9.1. Безопасность системы RSA и задача
разложения на множители
Принцип действия криптосистемы RSA за-
ключается в следующем. Пусть р и q — два раз-
личных больших простых числа и пусть п = pq.
Выбирается число е, 1<е<ф(и)-1, взаимно
простое со значением функции Эйлера
ср(и) = (/2- 1 )(<у — 1), и вычисляется d— мульти-
пликативно обратное к е: d=e~} (modср(и)), то
есть ed = 1 (mod ср(и)). Числа е и d называются
открытым и секретным показателями соответ-
ственно. Открытым ключом является пара (и, е),
секретным ключом — число d. Множители р м q
должны храниться в секрете.
Для зашифрования сообщения т нужно вы-
числить шифртекст с = тс (mod и), для расшиф-
рования— возвести шифртекст в степень d:
m = cd (mod и).
Аналогично реализуется цифровая подпись:
подписью сообщения т является число s = in
(mod и), где d — секретный ключ формирования
подписи.
Определим задачу разложения на множители
числа п (над кольцом Z) как нахождение всех
простых делителей числа п. Аналоги задачи раз-
ложения существуют для любого факториально-
го кольца.
Лемма 9.1.1. Задача разложения числа n^pq
и задача вычисления функции Эйлера ср(и) поли-
номиально эквивалентны.
Доказательство. Если известно разложение
числа п, то значение ср(и) = (р - l)(q - 1) вычис-
лимо с не более чем квадратичной сложностью.
Если известны значения п и ср(и), то делители р и
q числа п являются целочисленными корнями
квадратного уравнения
х2 - (и - ср(и) + 1)х + п = 0.
Сложность решения этого уравнения оцени-
вается кубическим полиномом от logjw.
Теорема 9.1.2. Задача вычисления секретного
показателя d сводится с полиномиальной слож-
ностью к задаче вычисления функции ср(и).
Доказательство. Пусть значение ср(и) из-
вестно. Применяя расширенный бинарный алго-
ритм Евклида к паре (е, ср(и)), получим два целых
числа а, Ъ, удовлетворяющих равенству ае +
+ /хр(и) = 1, причем 0 < а < ср(и), 0 < b < е. Тогда
а = d. Сложность нахождения числа d— квадра-
тичная от log2H.
В общем случае задача дешифрования систе-
мы RSA эквивалентна задаче извлечения корня
степени е в кольце ZVhZL В некоторых случаях
задача извлечения корня может быть выполнена
без разложения (см. п. 9.4).
Если составное число заданной длины имеет
более двух различных простых делителей, то за-
дача разложения облегчается. Это обусловлено
тем, что число различных представлений числа п
в виде произведения двух (не обязательно про-
стых) сомножителей растет экспоненциально с
ростом числа различных простых делителей. Ес-
ли число различных простых делителей состав-
ного числа п равно к, то таких представлений
ровно 2а-1 - 1. Например, в случае четырех про-
стых делителей возможны следующие семь
представлений:
п = a(bcd) = b(acd) = c(a.hd) = d.(abc) =
= (ab)(cd) = (ac)(bd) = (ad){bc).
Задача разложения в этом случае решается
рекурсивно: число п раскладывается на два мно-
жителя и для каждого из них решается задача
разложения. Поскольку размер множителей
меньше, чем размер первоначального числа, то
для них задача разложения является более про-
стой, чем первоначальная.
Сложность задачи разложения по отношению
к ряду методов, в частности, на эллиптических
кривых (см. п. 9.3.5), определяется размером ми-
нимального простого делителя. Чем больше чис-
ло простых делителей, тем меньше размер ми-
нимального из них, а значит, тем проще выпол-
няется разложение. Поэтому сложность разложе-
204
ния составного числа обычно оценивается для
случая, когда это число содержит два различных
простых делителя.
Если в системе RSA у двух пользователей
общее составное число и, но различные откры-
тые еь е2 и секретные d\, d2 ключи, причем ejd\ =
= e2d2 = 1 (mod ф(и)), то каждый пользователь
может найти разложение числа и и тем самым
узнать секретный ключ другого пользователя.
Для этого достаточно найти значение квадратно-
го корня из единицы, отличное от ±1. Если ? = 1
(mod и), t*±l, то ? - I = (t + 1)(?-1) = 0
(mod и), и t + 1, t - 1 имеют нетривиальные об-
щие делители с п. Разложение можно выполнить
по аналогии с псевдопростым тестом Миллера-
Рабина следующим алгоритмом.
Алгоритм 9.1.1. Разложение составного числа
на множители по известным показателям RSA.
Вход. Число и, показатели е, d такие, что
ed = 1 (mod ф(и)).
Выход. Делители рид числа п.
Метод.
1. Положить N<- ed- 1. Представить N в виде
N= 2^s, где 5 — нечетное число.
2. Выбрать случайное а и вычислить b <— а'
(mod //).
2° 21 2° 2
3. Вычислять h =b (mod и), b =(b ) (mod и),
2 1
и = (Ь2) (mod и), ... до получения т такого,
что b = 1 (mod и). Если b s-l(mod«),
то вернуться на шаг 2, иначе положить
_т-1
I <- b (mod ri).
4. Положить р <— НОД(/ + 1, и), q <— НОД(/ - 1, ri).
5. Результат: (р, q).
Сложность задачи разложения быстро падает.
Это обусловлено как развитием вычислительной
техники, так и созданием новых методов разло-
жения. Сложность
£„(с; г) = О(ехр(с(1п и)’(1п In n)lv))
разложения числа п (и, следовательно, стойкость
RSA) падает значительно быстрее, чем стойкость
симметричных криптоалгоритмов. Практически
стойкость RSA падает со скоростью 1,5 десятич-
ных порядка в год. Это выражается в уменьше-
нии коэффициентов с, г. Коэффициент с снизил-
ся с 4 до 1 + о(1) при т = 0,5. Если в 1995 г. безо-
пасным считалось составное число п длины
512 бит, в 2000 г. безопасным считалось число п
длины 1000 бит [14], то в 2003 г. — число и дли-
ны 2000 бит. Таким образом, безопасная длина
характеристики кольца удваивается примерно
через пять лет. Увеличение длины числа п при-
водит к изменению форматов передаваемых тек-
стов, то есть затрагивает смежную аппаратуру.
Это обстоятельство нужно учитывать при разра-
ботке систем защиты информации с использова-
нием задачи разложения.
Создание квантового компьютера позволит
решить задачу разложения с полиномиальной
сложностью [3, 5, 7].
Различают детерминированные и вероятност-
ные методы разложения. На практике их часто
комбинируют, например, методом пробного де-
ления находят делители, меньшие некоторой
границы Ър, затем методом эллиптических кри-
вых находят делители, меньшие некоторой гра-
ницы Ь2>Ъ\, и наконец, методом решета число-
вого поля находят разложение оставшейся части.
Задача разложения нечетного числа п эквива-
лентна некоторым другим задачам, например:
- задаче вычисления всех квадратных корней х,
из заданного числа а (решить квадратное
уравнение х2 = а) в кольце lLlriZL\
- задаче поиска эллиптической кривой над
TLIriZL такой, что разложение для числа точек
этой кривой известно.
Первая из этих задач позволяет найти делите-
ли1 числа п как НОД(х, + х}, п), где х, Ф ±х,. Вторая
задача позволяет найти делители числа п мето-
дом эллиптических кривых.
9.2. Детерминированные
методы разложения
Детерминированные методы позволяют гаран-
тированно найти разложение составного числа.
9.2.1. Метод пробного деления
Это самый очевидный метод разложения, из-
вестный любому школьнику.
Пусть уже установлено, что нечетное число п
составное (это можно сделать, например, с по-
мощью тестов Миллера—Рабина или Соловэя-
Штрассена [14]). Перебираем простые нечетные
числа 3, 5, 7,... и пробуем разделить п на каждое
из них.
Небольшие простые числа можно хранить в
базе данных. Вариант метода пробного деле-
ния— вместо нескольких простых чисел хра-
нить их произведение. Тогда нужно вычислить
алгоритмом Евклида наибольший общий дели-
тель D числа и и этого произведения из базы
1 Число делителей, являющихся степенями про-
стых чисел, равно половине числа корней.
205
данных и поделить п на D, повторяя рекурсивно
эту процедуру до тех пор, пока не получится
D= 1.
«Малость» простых делителей определяется
как функция от размера числа п (или определя-
ется объемом памяти компьютера). Перебрав все
простые числа, меньшие 4п , мы найдем полное
разложение числа п. В наихудшем случае, то
есть когда п представляет собой произведение
двух простых чисел примерно одинакового раз-
мера, для этого потребуется примерно 4п деле-
ний. В общем случае, если делители, получае-
мые на каждом шаге, проверяются на простоту,
то полное разложение числа п методом пробного
деления требует О(р + log и) операций деления,
где р— второй по величине делитель числа п
(см. [14]).
9.2.2. Метод «giant step — baby step»
Метод основан на лемме 9.1.1 и вычисляет
порядок случайного элемента а в группе (Z/wZ) .
Сначала методом пробного деления нужно про-
верить, что п не имеет простых делителей,
меньших иа, где а <0.5. В силу равенства
ф(и) = и -р - q + 1 справедлива оценка
п - па - и1 “ +1 < ф(и) < п - 2-Уи +1.
Алгоритм имеет минимальную сложность при
а = */3.
Алгоритм 9.2.1. Метод «giant step— baby
step».
Вход. Число п = pq, случайный элемент а из
кольца Z/wZ.
Выход. Порядок 5 элемента а в группе
(Z/wZ) .
Метод.
1. Проверить методом пробного деления, что п
не имеет простых делителей, меньших и1 .
2. Найти сГх (mod п) расширенным алгоритмом
Евклида; вычислить т<— |_w^3J.
3. Положить b <- сГ~т~т +1(mod и).
4. Вычислить d<— a" (modи).
5. Построить базу данных: для z = 0, 1,..., т
вычислить bd' (mod п). Пары (bd1,1) отсорти-
ровать по первой «координате».
6. Начиная с j = 0, вычислять a~J (mod и) и срав-
нивать с базой данных. При получении равен-
ства bd' = a~] (modи) положить s<-n-m -
-т2 + 1 +im+ j.
7. Результат: 5. '
Число 5 имеет нетривиальный общий дели-
тель со значением cp(zz). Алгоритм следует повто-
рить несколько раз на тот случай, если а не явля-
ется образующей группы (Z/zzZ) . Алгоритм
9.2.1 с учетом сортировки имеет сложность
О(х^п log и) по времени и по памяти.
9.2.3. Метод Ферма
Дня любого положительного нечетного числа п
существует взаимно однозначное соответствие ме-
жду множеством делителей числа и, больших чем
4п , и множеством пар неотрицательных чисел
{.s, (} таких, что и = № — /2, а именно, если п =pq,
где p>q, то s~{p + q)/2,t = {p-q)/2 (обратно,
если п = s2 -12 = (s + /)(.s -i), тор = 5 +t, q = 5 - f).
Если числа p и q близки друг к другу (что ха-
рактерно для системы RSA), то число t мало, а
значит, 5 немного больше, чем 4п В этом слу-
чае можно найти р и а, последовательно переби-
рая числа 5 = |_VnJ+1, \у/п J+ 2,... до тех пор, пока
не получится s такое, что разность s2 - п является
2
полным квадратом, то есть равна t .
Отметим, что метод работает, если число п не
является полным квадратом.
Пример 9.2.1. Разложение методом Ферма.
Пусть и = 20701. Перебираем последователь-
но значения s.
[_VnJ+l = 143 + 1 = 144. Но 1442 — 20701 =
= 20736-20701 =35.
[_VnJ + 2 = 145. Имеем 1452 - 20701 =21025 -
-20701 =324= 182.
Таким образом, s = 145, t=18. Отсюда
р = 5 + t = 163, q = 5 -1= 127.
Если числа р и q не близки друг к другу, то ме-
тод Ферма потребует слишком большого числа
шагов для подбора .s. В этом случае можно вос-
пользоваться обобщением метода Ферма, а имен-
но, выбрать маленькое число к и последовательно
вычислять Л j+ 1, |_Vbzj+2,..., пока не по-
лучится число л такое, что разность s2 -кп являет-
ся полным квадратом, то есть равна Z2. Отсюда
(л +/)(.s -f) = kn и, значит, числа 5 +1 и п имеют
нетривиальный общий делитель. Метод Ферма
имеет экспоненциальную (от log и) сложность.
Пример 9.2.2. Разложение обобщенным ме-
тодом Ферма.
Пусть и = 39497. . - , - >.. > . •
206
Если попытаться разложить это число преды-
дущим методом, то лишь на 21-м шаге получим
5 = |л/и j + 21 = 198 + 21 = 219, откуда ? = 2192 -
-39497 = 8464, 7 = 92. И далее: « + 7=311,
s-t = 127.
Если же выбрать Л = 3, то уже со второй по-
пытки получим
([V^J+2)2 -кп = ([л/З-39497 J+ 2/ -3 • 39497 =
= 3462-3-39497 = 352.
Находим 5 +1 = 346 + 35 = 381.
НО Д(381,39497)= 127.
Тогда
Еще более эффективный метод получается
при дальнейшем обобщении метода Ферма (схе-
ма Крайчика [12]): если для целого положитель-
ного числа п найти такую пару чисел {у t}, для
которой имеет место сравнение s2st2 (mod и),
где 5 Ф ±7 (mod и), то числа НОД(« + 7, и) и
НОД(л - 7, и) будут делителями числа п.
Действительно, если s2 = t2 (mod и), то число п
делит произведение s2 -12 = (s + 7)(s + 7), но, в
силу того, что л ф +t (mod и), не делит ни один из
сомножителей. Тогда один делитель числа п
(р - НОД(« +1, и)) должен делить нацело число
s + t, а другой делитель (q = n!р) — число s — t.
Пример 9.2.3. Схема Крайчика.
Пусть и = 4321. Находим 1472 = 4 = 22
(mod 4321), тогда НОД(147+ 2, 4321) = 149 и
НОД(147 - 2, 4321) = 29, то есть 4321 = 29 • 149.И
9.2.4. Метод диофантовой аппроксимации
Этот метод разложения, основанный на нахо-
ждении кратчайших векторов решетки, был
предложен К. Шнорром [17].
Назовем число и гладким относительно базы
£)= {р\, ...,р,},2 где р,— малые простые числа,
если и раскладывается на простые множители из
базы D. Если допускаются отрицательные числа
и, то в базу D включают еще ро = -1.
Для получения разности s2 - Т2 = 0 (mod п) ис-
пользуется произведение чисел и и и - vn, где и,
v — взаимно простые гладкие числа. Параметра-
ми метода являются числа а и с>1. Число
7?о = -1 и наименьшие простые числа рь ...,рг,
где pr ~ (In и)“, образуют базу разложения. Веще-
ственные логарифмы чисел р, по произвольному
(например, натуральному) основанию образуют
базис решетки. В ходе работы алгоритма ищутся
2 Число и называют также Е>-гладким.
векторы, близкие к вектору = -
п = (0, 0,..., 0, ис1пи) .
Ч___v —. J
г раз
Алгоритм 9.2.2. Разложение методом дио-
фантовой аппроксимации.
Вход. Число и, числа а и с > 1.
Выход. Нетривиальный делитель q числа п.
Метод.
1. Выбрать базу разложения рх, ...,рг, где
pr = (In и)“.
2. Положить d0 <- п, положить db ..., d,. равны-
ми строкам матрицы
^1п2 0 ... 0 иЧпг'
0 1пЗ ... 0 ис1пЗ
0 0 ... 0 ис1п5 •
ч 0 0 ... Inр,. пс Inр
Векторы d, образуют решетку L.
3. Найти на решетке L не менее г+ 2 нетриви-
альных векторов z,<— У g;Zd , таких, что
7=о
Oij е Z и для w, = J I рр', ’,|1 Р^ абсо-
<7,z>0 я^-сО
лютная величина \и, - г,и| раскладывается на
множители из базы разложения. Найти пред-
ставление
7=0
4. Положить а, <- (а,0, ..., а„), b, <— (bl0, b„)
для a,j, btJ, найденных на предыдущем шаге.
5. Найти непустое множество линейно зависи-
г+2
мых над F2 векторов вида ^с,(а, +Ь,), где
/=1
с, g F2.
6. Положить
г ЕчЧ+*/,)/2
5 <- I I pj1 (modи),
7=0
г+2 .... + , ;• > + . ?
Г Ечо,,-
t <-11 р'р1 (mod и).
7=0
7. При 5 ф ±7 (mod и) положить q <— НОД(« ± 7, и).
8. Результат: q.
Поиск векторов z, можно выполнять с исполь-
зованием алгоритма Ленстры-Ленстры-Ловаша
(111) [И]-
207
Метод диофантовой аппроксимации в на-
стоящее время непрактичен. Его сложность пре-
вышает сложность методов решета (см. пп. 9.3.3,
10.2.2).
9.3. Вероятностные методы разложения
Вероятностные методы используют генератор
случайных чисел и не гарантируют решение зада-
чи разложения. Некоторые приведенные ниже ал-
горитмы разложения имеют субэкспоненциалъную
сложность 5 = Л„(с; г) = О(ехр(с(1п и)' (1п In и)1-')).
Работа таких алгоритмов основана на «просеива-
нии» целозначных функций числа и, имеющих
только гарантированно малые простые делители.
Такие методы относятся к методам решета. Вывод
субэкспоненциальной оценки сложности для ме-
тодов решета см. в п. 10.1.
4. Если 1 < q < п, то результат: q. При q-n ре-
зультат: нет ответа; при q = 1 вернуться на
шаг 2.
Пример 9.3.1. Разложение p-методом Пол-
ларда.
Пусть и = 221. Работа алгоритма для х0 = 2,
fix) = х2 + 1 иллюстрируется следующей таблицей:
Номер итерации а b q = НОД(й - Ь, п)
0 2 2
1 5 26 1
2 26 197 1
3 14 104 1
4 197 145 13
Таким образом, г/=13 является нетривиаль-
ным делителем числа 221 (221 = 13-17).
9.3.1. p-метод Полларда
(метод «Монте-Карло»)
Пусть f: TEJnTL TLlriZL — произвольное ото-
бражение, заданное алгебраической функцией и
обладающее сжимающими свойствами, напри-
мер, fix) = х2 + 1 (mod и). Основная идея метода
состоит в следующем: выбираем случайный эле-
мент хо е Z/wZ и строим последовательность х0,
X], х2, ..., определяемую рекуррентным соотно-
шением
x,+i =fixi) (mod и), i > 0.
Множество TLInZL конечно, поэтому последо-
вательность х, зацикливается. Она состоит из
«хвоста» длины примерно д/то/8 и цикла асимп-
тотически той же длины.
Алгоритм работает так: начиная с i = 1, рекур-
сивно вычисляется (х„х2,) из (х,_ь х2,_2), пока не
будет найдено т такое, что НОД(х,„ - хъ„, п) =
= q^t\. Значение q и будет делителем числа п.
Случай q = n имеет место с пренебрежимо малой
вероятностью.
Алгоритм 9.3.1. Разложение p-методом Пол-
ларда.
Вход. Число и, начальное значение Хо, функ-
ция/ обладающая сжимающими свойствами.
Выход. Нетривиальный делитель q числа п.
Метод.
1. Положить а <- Хо, Ъ <— Хо-
2. Вычислить a <-fid) (mod и), b <—fib) (mod и),
b <^fib) (mod и).
3. Найти q <- НОД(а - Ь, п).
Примечания [14].
1. В предположении, что функция fix) = х2 + 1
(mod#) ведет себя как случайная, алгоритм 9.3.1
требует для нахождения делителя q числа п по-
рядка о(7?) модульных умножений. Следова-
тельно, для нахождения нетривиального делите-
ля числа п требуется О$п) модульных умно-
жений.
2. В случае q~n следует выбрать другой по-
линомах) с целыми коэффициентами. В примере
9.3.1 это может быть, скажем, fix) = х2 + с, где
с Ф 0, -2. (При с = -2 получим неподвижную точ-
ку а = 2, Ь = 2. При с = 0 отображение fix) не бу-
дет обладать сжимающими свойствами — с пер-
вого шага входим в цикл.) г
9.3.2. Метод непрерывных дробей
Непрерывной, или цепной, дробью называется
выражение вида
1 „ . 1 1 1
G1+—L— L A «2 «и J
a2 4------— >
a3+ -.
Элементами a0, a„ (i= 1, 2,...) непрерывной
дроби могут быть вещественные или комплекс-
ные числа, а также функции одной или несколь-
ких переменных. Дроби а0 = —, — (/= 1, 2, ...)
1 G,
называются звеньями непрерывной дроби. Будем
предполагать, что а, 0.
208
Непрерывная дробь, содержащая конечное
число звеньев (например, и, не считая нулевого),
называется конечной и отождествляется с соот-
ветствующей обыкновенной дробью, полученной
в результате выполнения указанных действий.
Непрерывная дробь, имеющая бесконечное чис-
ло звеньев, называется бесконечной.
Отрезок
i = 1, 2,..., п,
непрерывной дроби называют z-й подходящей
дробью. Ч)
Приведем некоторые свойства непрерывных
дробей [2].
1. Закон составления подходящих дробей. Чис-
лители и знаменатели последовательных
р Р_ Р
подходящих дробей - 2 , - ' 1 ,— связаны
е,_2 Qi
рекуррентными соотношениями Р, - а,Р,_\ +
+ Prf, = ciQl} + 0<_2, причем P_j = 1, 0_j = О,
P(! = Qo ~ 1 •
2. Если все элементы непрерывной дроби по-
ложительны, то ее подходящие дроби с чет-
ными номерами образуют монотонно возрас-
тающую последовательность, а подходящие
дроби с нечетными номерами— монотонно
убывающую последовательность. При этом
каждая «четная» подходящая дробь меньше
любой «нечетной». Число, выражаемое не-
прерывной дробью, содержится между двумя
соседними подходящими дробями.
3. Для двух последовательных подходящих
р Р
дробей справедливо соотношение
Л-10, - Ш-1 =±1.
4. Каждое положительное число х можно раз-
ложить в непрерывную дробь с натуральны-
ми элементами, причем это разложение
единственно. Полученная непрерывная дробь
конечна, если число х рациональное, и бес-
конечна, если число х иррациональное.
5. Пусть п— положительное целое число, не
Р
являющееся полным квадратом, и —-----------
Qi
подходящие дроби к числу 4п . Тогда для
абсолютно наименьшего вычета Д2(пюйи)
справедлива оценка [10]
Алгоритм 9.3.2. Разложение методом непре-
рывных дробей.
Вход. Число п.
Выход. Нетривиальный делитель q числа п.
Метод.
1. Положить Р_] <- 1, Ро <— а0 <— |_Vnj,
х0 <-4п-а0.
2. Вычислить P02(modn).
3. Для k= 1, 2, ... выполнить следующие дейст-
вия.
3.1. Положить ак<— [_!/%£_] J, хк<— \jxk^ - ак .
3.2. Положить Рк <— акРк^ + Pfc_2 (mod и).
3.3. Найти абсолютно наименьший вычет
РЛ2(тойи) и разложить его на множи-
тели.
4. Составить базу разложения D = {р0,р\,...,рг},
Рй = -1, из тех простых чисел р„ которые
встречаются в разложении хотя бы в двух
P^(modn) или в четной степени хотя бы в
одном Pfc2(modn) дляР = 0, 1, ... .
5. Для каждого числа P/(modn), являющегося
D-гладким, то есть представимого в виде
произведения степеней чисел р, из базы D:
Г (к)
P;2(modn) = ,
1=0. .
составить вектор (е^\...,е^) .
6. Если можно, найти множество К= {Р|
0<к<г, ©е(4)=0}3 линейно зависимых
над 0~2 векторов е(к\ В противном случае про-
делать шаг 3 еще для одного к, увеличивая по
необходимости базу разложения.
7. Положить
5 <- PJ Рк (mod и); t <- PJ ру2 (mod и),
кеК J=i
W’Y., - ‘
2 кеК
8. Вычислить q <— НОД(л + р и). :
9. При q ф п результат: q. В противном случае
вернуться на шаг 6 и найти другое множест-
во К. Если это невозможно, то проделать шаг
3 еще для одного к, увеличивая по необходи-
мости базу разложения. : ......
|Д2(тойи)| < 2^п.
3 Символом 0 обозначен нулевой вектор.
209
Временная сложность алгоритма 9.3.2 равна
О(ехр(2-71п и In In и)). Объем базы разложения
равен О(ехр(-^ VI п и In In и)).
Пример 9.3.2. Разложение методом непре-
рывных дробей.
Пусть п = 493.
Выполняя шаги 1-3 алгоритма 9.3.2, состав-
ляем таблицу:
к -1 0 1 2
ак 22 4 1
Хк 0,2036 0,9116 0,0970
Рк 1 22 89 111
Рк(тоЛп) -9 33 -4
Разложение -1 • З2 3 • 11 -1 • 22
На шаге 4 составляем базу разложения:
D = {po,pi,pi} = {-1,2,3}.
Числа P02(modw), P22(modn) — D-гладкие.
Тогда е(0) = {1, 0, 2}, е(2) = {1, 2, 0} и К= {0, 2}.
Полагаем л = Р0Р^ (mod и) = 22 • 111 = 470
(mod 493), t = pl' р'у (mod и), где
Значит, t= p\pi = 2-3 = 6 (mod 493).
Наконец, находим q = НОД(.\ + t, и) =
= НОД(476, 493) = 17.
Метод непрерывных дробей был лучшим ал-
горитмом разложения с середины 1970-х до на-
чала 1980-х гг., когда появились методы эллип-
тических кривых, квадратичного решета и реше-
та числового поля [12, 13, 15].
9.3.3. Метод квадратичного решета
Этот метод, как и предыдущий, относится к
методам базы разложения. В ходе вычислений
находятся вспомогательные числа, которые рас-
кладываются на простые множители из базы раз-
ложения.
Алгоритм 9.3.3. Разложение методом квадра-
тичного решета.
Вход. Число п.
Выход. Нетривиальный делитель q числа п.
Метод.
1. Построить базу разложения D = {-1,
/?], ...,рг}, где каждое р„ 1 <i<r,— i-e про-
стое число, для которого и является квадра-
тичным вычетом, то есть выполняется равен-
ство для символов Лежандра
= 1.
Найти г + 2 чисел sk следующим образом.
2.1. Положить к <— 1.
2.2. Положить у<-([VhJ-f- х) -и, где зна-
чения х выбираются в следующем по-
рядке: 0, ±1, ±2, ... .
2.3. Методом пробного деления на элемен-
ты базы D проверить, является ли чис-
ло у D-гладким, то есть
Если это не так, то вернуться на шаг 2.2
и выбрать новое х.
2.4. Положить
sk <- J + х, ет <- (е^,...,е™ ) .
2.5. Положить к <— к+ 1 и вернуться на шаг
2.2.
3. Найти непустое множество Л'={А|
0 < к < г + 1, © е(/;) = 0 } линейно зависимых
кеК
над 11 ? векторов е(А).
4. Положить
5 <— ]~[л, (mod и); t <- [ р’’ (mod и),
ЛеХ у=1
где •
z кеК \
5. Вычислить q <— НОД(« ± /, и).
6. При q Ф п результат: q. В противном случае
вернуться на шаг 3 и найти другое множест-
во К. Если это невозможно, то заменить не-
которые числа
Оптимальное значение объема базы разложе-
m т О(ехр(0,5л/1пи1п1пи))
ния алгоритма 9.3.3 равно v ”.
Время работы — O(exp(71nnln In и)).
Пример 9.3.3. Разложение методом квадра-
тичного решета.
Пусть п = 81089.
Строим базу разложения: D={-l, 2, 5, 7,
17, 19} (числа 3, 11, 13 пропускаем, так как соот-
ветствующие символы Лежандра равны -1).
Таким образом, г = 5.
210
к X У Зк
1 1 23 • 17 285 (0, 3, 0, 0, 1, 0)
2 -1 -1 - 23 - 53 283 (1, 3, 3, 0, 0, 0)
3 3 2s * • 5 287 (0, 8, 1, 0, 0, 0)
4 -3 -1 -24-7- 19 281 (1,4, 0, 1,0, 1)
5 5 27 • 19 289 (0, 7, 0, 0, 0, 1)
6 -8 -1 •173 276 (1,0, 0, 0,3, 0)
7 9 23•5 • 7 • 17 293 (0,3,1,1, 1,0)
Составляем множество К. Например,
Х= {1,2,3,6}.
Полагаем s = (mod ri) = 3728 (mod и).
Вычисляем у] = 7, у2= 2, у3 = ys = 0, у4 = 2.
Тогда t = 27 - 52 • 7° • 172 • 19° = 32821 (mod и).
Отсюда
q = НОД(л + Г, и) = НОД(36549, 81089) = 131 .
Обобщением метода квадратичного решета
является метод решета числового поля (см.
п. 10.2.2) со сложностью4 £„(1,923; 'Д).
9.3.4. (р - 1)-метод
Предположим, что простой делитель р со-
ставного числа п обладает таким свойством, что
число р - 1 является D-гладким.
Пусть L— наименьшее общее кратное всех
степеней I простых чисел z е D таких, что z < п.
Тогда 1 In z < In и, то есть I <
In и
Йт7
. Таким образом,
Число L делится на р - 1 и, следовательно,
для любого а такого, что НОД(а, р) - 1, справед-
лива малая теорема Ферма: а' = 1 (mod р). Сле-
довательно, если Ъ = НОД(^ - 1, и), то Ъ делится
на р. Случай Ъ = п имеет место с пренебрежимо
малой вероятностью.
Алгоритм 9.3.4. Разложение (р - 1 )-методом.
Вход. Число п.
4 Если выполняется сравнение aus + Ь = 0 (mod ri),
где а, Ь, и, s — малые по абсолютной величине числа,
то можно использовать специальное решето числово-
го поля, при этом сложность разложения снижается
на 30% по порядку величины по сравнению с обще-
принятой оценкой для «случайного» правильно вы-
бранного составного числа п. Для доказательства то-
го, что разложение данного числа априори неизвест-
но, часто выбирают число п указанного выше вида,
например, п - 2512 + 1. Этим объясняются успехи «ре-
кордов» разложения. - :
Выход. Нетривиальный делитель р числа и.
Метод.
1. Выбрать базу разложения D.
2. Выбрать случайное целое а, 2<а<п-2, и
вычислить b <- НОД(а, и). Если b > 2, то по-
ложить р <— Ъ и результат: р.
3. Для всех простых чисел z е D выполнить
следующие действия.
3.1. Вычислить 1<- .
Jnz
j
3.2. Положить а <— d (mod ri).
4. Положить b <— 11ОД(<7 - 1, и).
5. При Ь = п результат: нет ответа. В противном
случае положить р <- Ъ и результат: р.
Пример 9.3.4. Разложение (р - 1)-методом.
Пусть п = 23347.
Составляем базу разложения: D= {2, 3}. Вы-
бираем а = 2 и вычисляем НОД(а, ri) =
= НОД(2, 23347)= 1.
Для z-2 имеем: 1= 14, а = 16; для z = 3 име-
ем: 7 = 9, а = 5921.
Находим НОД(а - 1, и) = НОД(5920,23347) =
= 37. Таким образом, 23347 =р • а - 37 • 631.
Заметим, что р - 1 = 36 = 2г З2, a q - 1 =
= 2 • З2 • 5 • 7, то есть р - 1 является D-гладким
числом, a q - 1 — нет.
Временная сложность алгоритма 9.3.4 равна
O(exp(c-\/in п In In п)), емкостная сложность рав-
на O(logn). Для увеличения сложности задачи
разложения по отношению к этому алгоритму
достаточно выбрать числа р, q так, чтобы числа
р - 1 и q - 1 имели большие простые делители.
Обобщением (р - 1 )-метода является метод раз-
ложения на эллиптической кривой.
9.3.5. Разложение на эллиптической кривой
Метод разложения на эллиптической кривой
был предложен X. Ленстрой [13].
В основе метода лежит устанавливаемый ки-
тайской теоремой об остатках изоморфизм групп
£(2/и2) = Е(Рр) © ДЕД (9.3.1)
где и =pq np^q.
Умножение любого элемента группы Е(Ж/пЖ)
на т е Z сохраняет этот изоморфизм:
wzE(Z7nZ) = ш£(Ер) © mE(\F4).
Выражения для углового коэффициента X в
формулах (6.12.1), (6.12.2) сложения и удвоения
точек различаются, и может получиться так, что
211
по модулю р точки различны, а по модулю q
одинаковы. В этом случае использование форму-
лы для сложения точек даст неправильный ре-
зультат, и сумма может не лежать на исходной
кривой.5 Такая ситуация легко распознается вы-
числением значения d= НОД(п, X]), где X] —
знаменатель в формулах (6.12.1), (6.12.2) для уг-
лового коэффициента X, или d = НОД(п, Z), если
точки заданы в проективных координатах
(X Y, Z). Если число d отлично от 1 и п, то оно
является нетривиальным делителем числа п и
задача нахождения делителя числа и решена.
Указанная ситуация означает, что одним из
компонентов разложения точки эллиптической
кривой £(Z/nZ) в прямую сумму является беско-
нечно удаленная точка, которая при дальнейшем
умножении на любое число остается неподвижной.
Пусть £(Z/nZ) — эллиптическая кривая и
Q— точка на этой кривой (нахождение точки
требует вычисления квадратного корня, поэтому
можно сначала выбрать точку, а потом уравне-
ние кривой). Пусть D— база разложения, содер-
жащая простые числа р„ меньшие заданной грани-
цы т. Найдем целочисленное произведение
к = /?“' всех элементов базы D, где
а, =
0,5^
1°ёА.
Эвристически оптимальный размер базы D
_и 1ПП
связан с вероятностью и , где и »----, т — no-
In/??
рядковый номер наибольшего элемента базы D.
Асимптотическая сложность алгоритма равна
<9(ехр((1+о(1))л/1п п In In п)), если наименьший из
простых делителей числа п имеет порядок
(9(7^).
Практически для ускорения вычислений мож-
но использовать эллиптические кривые, которые
при рассмотрении их над числовым полем имеют
большую группу кручения. Это, например, кри-
вая с уравнением
E2Z + (1 - c)XYZ - bYZ2 = X3 - 6X2Z,
для которой точка (0, 0) является точкой круче-
ния максимального порядка. Дискриминант этой
кривой равен (1 - c)4fe3 - 8(1 - c)2b4 - (1 - с)3Ь3 +
+ 36(1 - c)fe4 + 16fe5 - 27fe4. Выбрать точку на та-
5 Иногда это свойство ошибочно трактуют как то,
что точки эллиптической кривой над кольцом Z/nZ не
образуют группу. По китайской теореме об остатках
множество точек кривой £(Z/nZ) изоморфно прямой
сумме групп и, следовательно, является группой.
кой кривой можно без извлечения квадратного
корня [6].
Алгоритм 9.3.5. Разложение на эллиптиче-
ской кривой.
Вход. Число п, размер т базы D.
Выход. Нетривиальный делитель d числа п.
Метод.
1. Выбрать случайную эллиптическую кривую
£(Z/nZ) и точку Q на ней. зтг. <*-
2. Положить i <— 0, Qi <— Q.
3. При /> т вернуться на шаг 1; в противном
случае найти i-e простое число р,.
Положить i<- i + 1, а, =
0,5kip4
log/?,
5. При j > а, перейти на шаг 3. В противном
случае выполнить следующие действия.
5.1. Положить Qit-piQ,. При каждом сло-
жении точек вычислять <7=НОД(п, X)-
При 1 < d < п результат: d.
5.2. Положить j <—j + 1 и вернуться на шаг 5.
6. Если нетривиальный делитель числа и не
найден, то вернуться на шаг 1.
Этот алгоритм не требует создания базы дан-
ных, так как нет необходимости вычислять цели-
ком длинный показатель к, достаточно просто
находить очередной элемент базы разложения D
и умножать на него текущую точку. Поэтому
здесь возможно неограниченное распараллели-
вание с помощью невзаимодействующих компь-
ютеров, каждый из которых работает со своим
семейством эллиптических кривых. Однако раз-
ложение при этом ускоряется незначительно.
Пример 9.3.5. Разложение на эллиптической
кривой.
Найдем делитель числа п = 661643. Выбираем
эллиптическую кривую у2 = х3 - х + 3231 и точку
Q = (87, 2) на ней. Умножаем точку последова-
тельно на 29, З6, 54, 73, 1 12 и т. д., вычисляя наи-
больший общий делитель знаменателя углового
коэффициента и числа п.
Получаем: -.л.
Qi = 29С = (196083, 134895);
& = 36д2 = (470021, 282574);
& = 54д3 = (546729, 237268);
Qi = 73С?5 = (419723, 447921). J
При первом умножении точки Qi на 11 полу-
чаем знаменатель углового коэффициента, рав-
ный 90347. Находим НОД(щ 90347) = 541, то
есть п = 541 • 1223. „ ®
212
Среди составных чисел одинаковой длины
быстрее раскладываются те, которые имеют про-
стой делитель меньшего размера.
Разложение облегчается, если хотя бы одна из
проекций £(FP), ДВ^) обладает гладким числом
точек (то есть если все простые делители числа
точек кривой гарантированно малы). Для неко-
торых (например, супервырожденных) эллипти-
ческих кривых число точек над конечным полем
определяется просто [18]. В частности, если п = 3
(mod 4), то выполняются сравнения р = 3 (mod 4)
или q = 3 (mod 4^ и существует эллиптическая
кривая вида у2 = х3 + Ах (mod п) такая, что одна из
проекций при произвольном ненулевом А имеет
число точек р + 1 или q + 1. Аналогично, если
п = 5 (mod 6), то выполняются сравнения р = 5
(mod 6) или q = 5 (mod 6) и существует эллипти-
ческая кривая вида у2 = х3 + В (mod ri) такая, что
одна из проекций при произвольном ненулевом
В имеет число точек р + 1 или q + 1. Такой метод
разложения называется (р + 1)-методом.
Иногда для противостояния (р- 1)- и (р + 1)-
методам числа р и q выбирают так, чтобы числа
/> + 1 и</ + 1, а также р - 1 и q - 1 имели большие
простые делители. Такие простые числа называ-
ют сильными. Отметим, что в общем случае рас-
сматриваемый метод разложения использует
широкий диапазон эллиптических кривых и ока-
зывается более эффективным, чем (р-1)- и
(р + 1)-методы. Поэтому и выбор сильных про-
стых чисел р, q для системы RSA вряд ли может
привести к ее усилению.
Предположим, что можно выбрать кривую
E{ZJri2Z) и точку Q порядка М на ней, причем
разложение числа М известно и порядки точки Q
на кривых E(fp) и ДО^) не совпадают. Тогда ал-
горитм 9.3.5 имеет полиномиальную сложность,
для этого достаточно заменить к = р^ на М.
Pi&D
Таким образом, задача разложения сводится к
нахождению эллиптической кривой EtfLtriZ.),
число точек которой имеет вычислимое разло-
жение или даже вычислимый нетривиальный
большой делитель. Сложность разложения мо-
жет быть снижена, если выбрать эллиптическую
кривую Е так, чтобы над числовым полем Q|£]
она имела большую группу кручения и чтобы
минимальный полином для числа % имел корень
над ILInTL (согласно теореме Мазура над полем Q
группа кручения имеет порядок менее 20).
9.3.6. Разложение на квантовом компьютере
Составное число может быть разложено на
множители с полиномиальной сложностью на
квантовом компьютере алгоритмом П. Шора
[3, 5]. Задача разложения числа п решается вы-
числением порядка элемента в циклической под-
группе группы (Z/wZ)*. Вид используемой груп-
пы не принципиален, поэтому приведенный ни-
же алгоритм может быть использован для опре-
деления структуры и порядка произвольной ко-
нечной абелевой группы, например, группы
классов числового поля.
Суть квантового метода разложения заключа-
ется в нахождении порядка элемента
а е (Z/«Z), <7^±1, являющегося квадратичным
невычетом по модулю п (для этого достаточно,
чтобы выполнялось равенство
= -1). В этом
случае с помощью обычного компьютера можно
найти разложение числа п.
В основу вычислений положено свойство об-
ратимости каждого отображения (и, следова-
тельно, композиции отображений), реализуемого
квантовым компьютером.
Предположим, что удалось найти показатель г
такой, что d = 1 (mod я). Заметим, что для n=pq и
ср(л7) = (/? — 1)(б/ —I) показатель г должен быть чет-
ным. Пусть 2Л— наибольшая степень двойки, на
которую делится показатель г. Тогда с большой ве-
роятностью одно из целых чисел вида d^2 (mod я)
для i = 1,2,..., к будет иметь нетривиальный общий
делитель с числом п. Неудача возможна лишь в том
случае, когда цепочка сравнений {d = 1 (mod р),
d=l (mod#)}; {d^2 = 1 (mod p), d^2 =1 (mod#)} ;
{d^ = 1 (mod p\ d^ = 1 (mod q)} и т. д. оборвет-
ся по модулю р и по модулю q на одном и том же
шаге. Вероятность такого события равна 2Л'. В
случае неудачи можно провести аналогичную
процедуру для других малых простых делителей
числа г.
Для определения такого показателя г на кван-
товом компьютере выполняются следующие вы-
числения. Для фиксированного элемента
а е (Z/wZ) , фиксированного числа п и перемен-
ной х вычисляется экспонента d (mod ri) методом
возведения в квадрат и умножения. При этом ве-
личины cd (mod ri) являются константами, и нуж-
но реализовать только их модульное умножение с
помощью наборов булевых функций так, чтобы
результирующее отображение было подстановкой
на множестве состояний кубитов.
Для вычисления порядка г элемента а исполь-
зуются два синхронно работающих квантовых
регистра |левый), |правый). Левый регистр со-
держит аргумент х (mod А), где А =2™,
722 < N < 2п. Правый регистр обратимым образом
вычисляет функцию d (mod и). Состояние кван-
тового компьютера описывается парой |х (mod N)\
213
\d (mod n)). Решение задается сравнением а ~ 1
(modw). Вывод решения задается применением
квантового быстрого преобразования Фурье к ле-
вому регистру.
Алгоритм 9.3.6. Разложение числа на кванто-
вом компьютере (алгоритм Шора).
Вход. Число п.
Выход. Нетривиальный делитель числа п.
Метод (первые четыре шага выполняются на
квантовом, остальные — на обычном компьютере).
1. Инициализировать из состояния |0), |0) коге-
। 7V-1
рентную суперпозицию —j= V (| х), 10)).
2. Обратимым образом вычислить
х=0
3. Вычислить преобразование Фурье первого
регистра, отображая состояние |х) в
1 N-1N-1
7V jc=(H=0
Inixt/N ।
4. Измерить состояние регистров |Z), \ак (mod п))
для некоторого к.
5. Вычислить наилучшее приближение из Q
снизу к t/N со знаменателем г', где
rf <п< 4n :
(при этом г' = г с большой вероятностью).
6. Представить г' в виде г’ = 2?sr. Для i = 0, 1,...,
„у
f-\ вычислять ИОД(б/ ±l,w). Результат:
нетривиальный делитель числа п.
Квантовое преобразование Фурье на шаге 3
задается квадратной унитарной матрицей
F = (Fim) размера N, где Flm =e2mlm/N = %z(m) —
/-й характер элемента т. После преобразования
Фурье ненулевыми амплитудами (ненулевыми
вероятностями) будут обладать те и только те
элементы I вектора состояний, для которых чис-
ло I делится на порядок г элемента а (см. п. 5.5,
результаты о сумме характеров).
Пусть состояние второго регистра, измерен-
ное на шаге 4, равно у0- Тогда первый регистр
содержит суперпозицию всех показателей
для которых al=y$ (mod я). Пусть Хо— наи-
меньший натуральный показатель из множества
{я,} и N= Кг. Тогда состояние первого регистра
имеет вид
1 К-1
-/=£|*о +кг).
У К £=0
(9.3.2)
Ненулевыми амплитудами обладают те и
только те элементы, для которых %/(r) = 1. Под-
ставляя эти значения в (9.3.1), получим
К-1
к=0
Г0, если К Ф 0 (mod Z),
К, если К = 0 (mod Z).
В последнее выражение не входит случай-
ный параметр х0. Поэтому измерение состояния
первого регистра всегда даст значение с, крат-
ное N/r. Пусть с = XN/r, где значения с и N
известны. Тогда дробь X/г можно вычислить и
0 < X < г - 1. Если числа X и г взаимно просты,
то можно найти г. Вероятность того, что I и г
будут взаимно просты, равна ср(г)/г, где ср —
функция Эйлера. Поскольку r/cp(r) «In In г (см.
п. 5.2), то после O(loglogw) прогонов вероят-
ность того, что Z и г будут взаимно просты, ста-
новится близкой к 1.
Сложность разложения составного числа
асимптотически равна сложности возведения в
степень и составляет <9((1°ё^)3) элементарных
логических операций. Сложность определения
структуры и порядка конечной абелевой группы
тоже является полиномиальной.
9.4. Атаки на систему RSA,
не требующие разложения
В целях ускорения шифрования в системе
RSA открытый или секретный показатели часто
делают малыми. Поскольку длина характеристи-
ки кольца составляет сотни бит, сокращение
длины показателя первоначально могло выгля-
деть обоснованным. Однако такой способ повы-
шения скорости шифрования часто приводит к
снижению стойкости.
9.4.1. Случай малого секретного показателя
Если секретный показатель d достаточно мал,
то по известным характеристике кольца п и от-
крытому показателю е можно найти d (длину
секретного показателя и число единиц в двоич-
ном представлении можно определить, измерив
длительность шифрования и соотнеся ее с дли-
тельностью модульного умножения). Обозначим
г = log2(6?/V«), тогда задача нахождения показа-
теля d (и, следовательно, задача разложения числа
п) требует перебора 2г + 8 бит. Если d < у[п , то
показатель d можно найти без перебора [19, 20].
214
Открытый и секретный показатели связаны со-
отношением ed = 1 (mod (р - 1 )(q - 1)). Обозна-
чим Н= НОК(р - I, q - 1), G = НОД(р - 1, q - 1).
Тогда существует К е Z такое, что
ed = 1 + КН =l-i-------------
G
откуда
е К(р-\)(д-^ }\ К п р д + } + К
п dGn dn dG п
£(1-5) fc(l-5)
dG ~ dg ’
k 'к
где------это дробь — после сокращения, при
dg dG
этом обычно g = 1 или g = 2. Теперь можно выра-
к е
зить — через 5 и рациональную дробь —, при
dg п
V2 4
этом -у=г<5<-у=г. Далее вычисляются подхо-
dn \п
4
дящие дроби для непрерывной дроби —=. Под-
дп
ходящая дробь со знаменателем, близким к у/п ,
является хорошим приближением к 5. Действуя
таким образом, можно найти секретный показа-
тель d, если его длина достаточно мала.
9.4.2. Случаи специальных
открытых показателей
Каждый пользователь i системы связи с шиф-
рованием по схеме RSA должен иметь свое пер-
сональное число П1=рд,. Для ускорения процес-
са шифрования иногда используются малые от-
крытые показатели <?„ причем они могут быть
одинаковыми, например, 3 или 5. В этом случае,
даже если числа п, различны, можно выполнить
бесключевое дешифрование [4]. Предположим,
что отправитель посылает одно и то же сообще-
ние т трем получателям, открытые ключи кото-
рых равны (и„ е,), причем е, = 3 и т < и,. Обозна-
чим х = т3. Тогда выполняются сравнения с, = т3
(mod и,), х = с, (mod и,) и значение х как целое
число может быть восстановлено по китайской
теореме об остатках по известным с, и взаимно
простым модулям и,. Для нахождения сообщения
т нужно извлечь кубический корень из х в кольце
целых чисел, эта операция имеет полиномиаль-
ную сложность. Очевидно, то же справедливо и в
случае других малых одинаковых открытых пока-
зателей.
Рассмотрим другой простой вариант атаки на
систему RSA на основе «частично известных»
открытых текстов [9]. Если два сообщения ту, т2
не одинаковы, но связаны с помощью аффинного
соотношения с известными параметрами, напри-
мер, т2 = ату + р (mod и), где аир известны, то с
помощью известных шифртекстов с у, с2 можно
восстановить оба сообщения. Например, для е = 3
сообщение ту восстанавливается по формуле
Р(с2 +2а3С! -р3) _
а(с2 -а3с, +2р3)
За3р«7,3 +3а2р2ш,2 +Зар3т, . , .
=----= т\ (mod и).
За3Р/н,2 +3a2p2»?! +ЗаР
Сообщение т2 выражается через ту и коэф-
фициенты а, р.
В случае произвольного показателя е имеют
место соотношения:
nty - с, = 0 (mod и), (a/л; । + Р)с - с2 = 0 (mod и).
Обозначим неизвестное сообщение ту через
переменную z. Тогда, переходя к кольцу поли-
номов (Z/nZ)[z], можно записать:
НОД(/ - сь (az + р)с - с2) = z - ту <= (Z/«Z)[z],
Вычислив этот наибольший общий делитель,
можно определить ту.
Алгоритм 9.4.1. Нахождение двух открытых
текстов по двум шифрограммам и параметрам
аффинного преобразования.
Вход. Составное число и; шифртексты Су, с2;
параметры a, Р; открытый показатель е.
Выход. Открытые тексты ту, т2.
Метод.
1. Вычислить ту как свободный член линейного
полинома z - ту = НОД(/ - Су, (az + Р)е - с2) в
кольце (Z7nZ)[z],
2. Положить т2 <— ату + Р (mod и).
3. Результат: (ту, т2).
Алгоритм 9.4.1 допускает обобщение на слу-
чай, когда т2 задается произвольным полиномом
от ту над27и^: т2 = f(z)\ Тогда
НОД(/ - cy,flz)c -c2) = z- ту
в кольце полиномов (Z7«Z)[z]. Если ту и т2 за-
даются полиномами от т над ^LhiZL'.
^y^fy(z)\^m, т2 = f2(z)\z=m,
и известны шифртексты Су, с2, то
НОД(/|(2)С - Cy,f2(z)e -c2) = z-m
в кольце полиномов (Z7nZ)[z]. ,
215
Пример 9.4.1. Восстановление пары сообще-
ний без разложения числа п.
Пусть п = 81089, cj = 32205, с2 = 38069, е = 17,
а = 1, Р = 1. Вычисляем
НОД((г + 1)17 - 38069, z17 - 32205)
в кольце (Z/hZ)[z], Получаем последователь-
ность вычетов для алгоритма Евклида (для при-
веденных полиномов):
z'6 + 8z15 + 40z14 + 140z13 + 364z12 + 728Z11 +
+ 1144z10 + 1430?+ 1430/+ 1144z7 + 728z6 +
+ 364z5 + 140/ + 40? + 8z2 + z + 9195;
z15 + 40552z14 + 40576z13 + 91z12 + 195zn +
+ 2O594z10 + 47719z9 + 429z8 + 35 lz7 + 40772z6 +
+ 40660z5 + 45z4 + 13z + 3041 lz2 +
+ 36783z +72676;
z2 + 79994z + 24207;
z +68744 = z- 12345,
то есть ni\ = 12345.
Второе сообщение: m2 = m\ + 1 = 12346.
Операция вычисления наибольшего общего
делителя полиномов степени е над кольцом ~ZJnZ_
предусматривает выполнение на каждой итера-
ции следующих действий:
- одну операцию обращения по модулю и;
- О(е) операций умножения чисел по модулю и;
- (9(e) операций сложения чисел по модулю п.
Число итераций равно (9(e).
При использовании умножения «в столбик» и
арифметики Монтгомери (см. п. 7.1.4) сложность
алгоритма 9.4.1 равна <9(e2(logw)2). При исполь-
зовании умножения с помощью быстрого преоб-
разования Фурье сложность алгоритма равна
(9(e2(log w)(log log «)).
Для того чтобы стойкость к методу дешифро-
вания на основе частично известных открытых
текстов была не хуже, чем сложность разложения,
открытый показатель е должен быть достаточно
велик. Минимально возможные значения показа-
теля е для различных размеров задачи разложе-
ния, для которых сложность указанной атаки рав-
на сложности разложения, приведены в табл. 9.1.
Сложность разложения оценивалась по отноше-
нию к методу решета числового поля. Сложность
атаки на основе алгоритма Евклида в (Z/hZ)[z]
оценивалась по отношению к умножению с по-
мощью быстрого преобразования Фурье.
Таблица 9.1
Минимальный размер открытого показателя
emin в системе RSA, при котором атака
по алгоритму 9.4.1 неэффективна
log2H 512 768 1024 2048 4096 8192
^инп 108 Ю10 2-10" 3-1015 1021 IO29
Таким образом, часто используемые откры-
тые показатели вида 216 + 1 не обеспечивают
стойкость к указанному методу анализа.
Еще один вариант атаки на схему шифрова-
ния может быть использован, если порядок эле-
мента е в группе (Z/<p(»)Z) оказывается малым.
В этом случае для нахождения сообщения т по
шифрограмме с = те (mod и) выполняется после-
довательное зашифрование шифрограммы:
С] = с (mod и), с2 =C|(modH) и т. д. — до полу-
чения открытого текста (предполагается, что от-
крытый текст обладает избыточностью, позво-
ляющей его распознать). Отметим, что порядок
элемента е в группе (Z/<p(w)Z) мал лишь в том
случае, если он мал в обеих группах Fp и F9 .
Однако если этот порядок мал хотя бы в одной
из указанных групп, то можно разложить число п
следующим образом. Сначала сгенерировать
случайное п0 е ф-lriZL). Затем для i > 1 вычислять
последовательно а, = а,“Д (mod и) и проверять с
помощью бинарного алгоритма Евклида условие
НОД(а, - а0, п) > 1. Если это условие будет вы-
полнено, то указанный наибольший общий дели-
тель является нетривиальным делителем числа и.
Для исключения этой атаки числа р и выби-
рают так, чтобы порядки групп Fp и F9 имели
большие делители.
В случае малых открытых показателей можно
не только осуществить бесключевое дешифрова-
ние, но и вскрыть ключ d [8]. Для этого доста-
точно знать четверть двоичных разрядов одного
из делителей числа п.
9.4.3. Атаки на основе эндоморфизмов
Схемы шифрования и цифровой подписи RSA
задают эндоморфизмы мультипликативной группы:
(Z/hZ) a Fp х F9 , • -'«к:ч-
а также эндоморфизмы идеалов кольца TLInTL.
Это обстоятельство позволяет создавать специ-
фические атаки на систему RSA.
Предположим, что нарушитель хочет де-
шифровать шифртекст с = те (mod и), причем в
216
системе допустимы методы криптоанализа на
основе открытых и зашифрованных текстов.
Тогда нарушитель вырабатывает произвольный
текст х е (Z/wZ) , вычисляет свою шифро-
грамму с' = ex (mod и) и отдает ее для рас-
шифрования. Полученный открытый текст
имеет вид т' = (с') = cdx (mod п). Умножая его
на г1 (mod и), нарушитель получает т = cd
(mod и).
Схема шифрования с открытым ключом RSA
позволяет получить частичную информацию об
открытом тексте т по известному зашифрован-
ному тексту с и открытому ключу (и, е). По-
скольку открытый показатель е является обрати-
мым элементом в кольце Z/<p(n)Z, то он должен
быть нечетным. Следовательно, выполняется
равенство для символов Якоби:
(т ] (
у п ) \п)
Аналогичное рассуждение справедливо и для
кубических характеров (вычислить кубический
характер можно с использованием кубического
закона взаимности [1]).
Аналогичная атака возможна и на схему циф-
ровой подписи RSA (см. п. 13.1.1). Для защиты
нужно использовать хэш-функцию.
Упражнения к главе 9
1. Какие задачи положены в основу безопасно-
сти системы RSA?
2. Как зависит сложность разложения составно-
го числа заданной длины методом эллипти-
ческих кривых от числа различных простых
делителей числа и?
3. Оцените зависимость числа образующих
группы (Z/nZ) от числа простых делителей
нечетного числа п.
4. Сравните временную и емкостную сложно-
сти методов квадратичного решета и эллип-
тической кривой.
5. Почему метод квадратичного решета облада-
ет меньшей сложностью, чем метод непре-
рывных дробей?
6. Пусть п = 3 (mod 4). Предложите (р + 1)-
метод разложения, аналогичный (р -1)-
методу, основанный на использовании эл-
липтической кривой у = х3 + Ах.
7. Пусть п = 5 (mod 6). Предложите (р + 1 )-
метод разложения, аналогичный (р - 1 )-
методу, основанный на использовании эл-
липтической кривой у2 =х3 + В.
8. Покажите, что (р-1)-метод разложения не
имеет преимуществ по сравнению с методом
эллиптических кривых.
9. Рассмотрим аналог системы RSA, основан-
ный на задаче разложения полиномов в коль-
це Fr[f]: n(f) =p(t)q(t). Предложите метод
взлома такой криптосистемы со сложностью,
полиномиальной от степени полинома n(t).
10. *Положим ф*(и) = ф(ф(...ф(и)...)) (к раз). Из
теории чисел известно, что при к = <9(1п п)
значение ф*(и) вырождается в степень двойки
и имеет порядок О(у[п). Предложите спосо-
бы ускорения вычисления ф(н), если указан-
ное вырождение происходит значительно
быстрее, чем после О(1п«) шагов.
11. Как изменится сложность разложения мето-
дом квадратичного решета при ограничении
объема памяти?
12. *Для метода квадратичного решета оцените
объем базы данных, при котором вероятность
получения непустого множества линейно за-
висимых над F2 строк заметно отличается от
нуля с учетом плотности распределения про-
стых делителей.
13. Сравните сложность разложения на эллипти-
ческой кривой составного числа вида п =p2q,
где р, q— различные простые числа, и со-
ставного числа такой же длины, состоящего
из двух различных простых делителей.
14. Пусть вычислительная модель содержит
т» 1 параллельно работающих процессо-
ров. Сравните временную сложность методов
квадратичного решета и эллиптической кри-
вой.
15. Пусть p = q=\ (mod 6) и #EP(FP) -р\,
= q\ — эллиптические кривые с урав-
нениями вида у2=х3 + В, причем ръ q\—
простые числа. Пусть п = pqu Е(Ж/пЖ) — эл-
липтическая кривая, Е = ЕР (mod/?), Е = ЕЦ
(mod q). Предположим, что (Е,р-\, qt) — «сер-
тификат» того, что число п содержит только
два различных простых делителя и свободно
от квадратов. Покажите, что этот «сертифи-
кат» позволяет найти разложение числа п с
полиномиальной сложностью.
16. Предложите описание эллиптической кривой
Е(К) непрерывной дробью над Х[х].
Литература к главе 9
1. Айерлэнд К., Роузен М. Классическое введение в
современную теорию чисел. М.: Мир, 1987.
2. Демидович Б.П., Марон И.А. Основы вычисли-
тельной математики. М.: Наука, 1970.
3. Манин Ю.И. Классическое вычисление, кванто-
вое вычисление и факторизация Шора И Кванто-
вый компьютер и квантовые вычисления. Ижевск:
Ижевская республиканская типография, 1999.
Т. 2. С. 248-286.
4. Мур Дж.Х. Несостоятельность протоколов крип-
тосистем И ТИИЭР. 1988. Т. 76. № 5. С. 94-104.
5. Шор П. Полиномиальные по времени алгоритмы
разложения числа на простые множители и нахо-
ждения дискретного логарифма для квантового
компьютера И Квантовый компьютер и квантовые
вычисления. Ижевск: Ижевская республиканская
типография, 1999. Т. 2. С. 200-247.
6. Atkin А.О., Morain F. Finding suitable curves for the
elliptic curve method of factorization // Mathematics
of Computation. 1993. Vol. 60. P. 399-405.
7. Chuang I.L., Laflamme R., Shor P.V.. Zurek W.H.
Quantum computers, factoring and decoherence.
Technical Report. LA-UR-95-241, 1995 //
http://www.if.ufrgs.br/~jgallas/QUBITS/CURSO/fato
racao9503007.pdf.
8. Coppersmith D. Small solutions to polynomial equa-
tions and low exponent RSA vulnerabilities // Journal
of Cryptology. 1997. Vol. 10. P. 233-260.
9. Coppersmith D., Franklin M., Patarin J., Reiter M.
Low-exponent RSA with related messages // Ad-
vances in Cryptology — EUROCRYPT ’96. Lecture
Notes in Computer Science. Springer-Verlag, 1996.
Vol. 1070. P. 1-9. '< г ?. -~v
10. Koblitz N. A course in number theory and cryptogra-
phy. Springer-Verlag, 1987.
11. Lenstra A.K., Lenstra H.W., Lovasz L. Factoring
polynomials with rational coefficients // Mathema-
tische Annalen. 1982. Vol. 261. P. 515-534.
12. Lenstra A.K., Lenstra H.W., Manasse M.S., Pollard
J.M. The number field sieve // Proceedings of 22nd
ACM STOC. 1990. P. 564-572.
13. Lenstra H.W. Factoring integers with elliptic curves //
Annals of Mathematics. 1987. Vol. 126. P. 649-673.
14. Menezes A., van Oorschot P., Vanstone S. Handbook
of Applied Cryptography. CRC Press, 1997.
15. Pomerance C. The quadratic sieve factoring algo-
rithm И Advances in Cryptology— Proceedings of
EUROCRYPT 84. Lecture Notes in Computer Sci-
ence. Springer-Verlag, 1985. Vol. 209. P. 169-182.
16. Rivest R.L., Shamir A., Adleman L. A method for
obtaining digital signatures and public-key cryptosys-
tems // Communications of the ACM. 1978. Vol. 21.
№2. P. 120-126.
17. Schnorr C.P. Factoring integers and computing dis-
crete logarithms via Diophantine approximations И
AMS DIMACS series in Discrete Mathematics and
Theoretical Computer Science. 1993. Vol. 13.
P. 171-181.
18. Silverman J. The arithmetic of elliptic curves.
Springer-Verlag, 1986.
19. Verheul E.L., van Tilborg H.C.A. Cryptanalysis of
«less-short» RSA secret exponents // AAECC. 1997.
Vol. 8. P. 425—435.
20. Wiener L.M. Cryptanalysis of short RSA secret ex-
ponents И IEEE Transactions on Information Theory.
1990. Vol. IT-36. P. 553-558.
Глава 10. ДИСКРЕТНОЕ ЛОГАРИФМИРОВАНИЕ
В КОНЕЧНОМ ПОЛЕ И СМЕЖНЫЕ ЗАДАЧИ
Пусть F9 — конечное поле из q=pn элемен-
тов. Задача дискретного логарифмирования в
группе F9 формулируется следующим образом.
Для образующей а подгруппы простого порядка
г группы F9 и экспоненты b найти показатель х
такой, что cf = Ъ. Эта задача может решаться как
универсальными методами логарифмирования
(«giant step— baby step», метод Полларда [14],
см. подробнее гл. 11) в произвольной конечной
циклической группе вычислимого порядка, так и
специальными методами для группы F9.
Универсальные алгоритмы логарифмирова-
ния имеют экспоненциальную сложность
O(Jr log/') (алгоритм «giant step— baby step»),
O(y[rlogr') (алгоритм встречи на случайном де-
реве) или О(4г) (алгоритм Полларда).
Специальные алгоритмы логарифмирования
имеют субэкспоненциальную сложность Z/c; v) =
= <9(exp(c(ln9)’(lnln^)'-1')). Эти алгоритмы основа-
ны на гомоморфном вложении мультипликативной
группы конечного поля в обладающие однознач-
ным разложением на простые множители полу-
группу кольца целых элементов бесконечного поля
характеристики 0 (в случае и = 1) или полугруппу
кольца полиномов Fp[z] (в случае п > 1). Простые
делители случайного целого числа распределены
неравномерно (данный малый делитель встретится
с большей вероятностью, чем данный большой де-
литель). Аналогично, случайный полином из Fp[z] с
большей вероятностью будет иметь данный про-
стой делитель малой степени, чем данный простой
делитель большой степени. Поэтому сначала сле-
дует найти линейные зависимости между лога-
рифмами в подмножестве элементов F9, которые
как целые числа имеют только малые простые де-
лители, а затем с помощью построенной базы дан-
ных решить требуемое показательное уравнение.
Сложность задачи логарифмирования в конеч-
ном поле быстро падает. Это обусловлено как соз-
данием новых методов логарифмирования, так и
развитием вычислительной техники. Скорость па-
дения сложности логарифмирования (и, следова-
тельно, стойкости соответствующих криптосистем)
в поле Fp примерно соответствует скорости паде-
ния стойкости системы RSA. Если экстраполиро-
вать такое же снижение сложности на будущее, то
через 10 лет задача логарифмирования станет в 1015
раз, а через 30 лет — в Ю'раз проще. В настоящее
время безопасным считается уровень сложности
1О2о-ь 1022 операций в год. С учетом того, что про-
изводительность вычислительной техники каждый
год повышается в два раза, для криптосистемы,
рассчитанной на 10 лет эксплуатации, нужно вы-
бирать простое число р длины свыше 2 Кбит, а на
30 лет— около 20 Кбит. Это обстоятельство сле-
дует учитывать при разработке криптосистем, ос-
нованных на логарифмировании в конечном поле.
Создание квантового компьютера позволит
решить задачу логарифмирования в конечном
поле (и на алгебраической кривой) с полиноми-
альной сложностью.
Группа F9* изоморфна группе неособых точек
особой кубической кривой, заданной уравнением
у2 = х3 +Ах2 над Fp причем изоморфизм вычислим
в обе стороны [15,4]. Кроме того, группа F9 изо-
морфна группе точек эллиптической кривой £(F9),
если #EQF4) = q- 1. Поэтому задача дискретного
логарифмирования в F9 является частным случа-
ем задачи логарифмирования на эллиптической
кривой. Сложность задачи дискретного логариф-
мирования в F? не может превышать сложности
вычисления логарифма на эллиптической кривой.
Поэтому для логарифмирования в F9 могут быть
использованы те же методы, что и для логариф-
мирования на эллиптической кривой (см. гл. 11).
Методы логарифмирования в мультиплика-
тивной группе конечного поля могут быть при-
менены и к другим группам, например, к группе
функций Лукаша и к группе классов мнимого
квадратичного поля.
Рассмотрим подробнее субэкспоненциальные
методы логарифмирования.
10.1. Метод базы разложения
Метод базы разложения для вычисления дис-
кретного логарифма в группе Fp основан на вло-
жении этой группы в полугруппу Z кольца це-
лых чисел. По определению гомоморфизма ука-
219
занных полугрупп из равенства АВ = С в кольце
Z вытекает АВ = С (mod р), из равенства Ах = В и
сравнения Ау = В (mod/?) следует х = у (mod/'),
где г— простой порядок группы, образованной
элементом А.
Различные варианты метода базы разложения
были предложены Адельманом, Мерклем и Пол-
лардом (см., например, [12]).
Кольцо Z является кольцом целых элементов
поля Q, при этом группа Q и, следовательно,
полугруппа Z имеют бесконечное множество
образующих, совпадающее с множеством про-
стых чисел. Перенумеруем простые числа 2, 3, 5,
7,..., начиная с 1. Вероятность того, что случайное
число делится на к-е простое число рк, равна р~^ .
Обозначим множество, состоящее из числа pG = -1
и т первых простых чисел р\,. ..,рт, через D.
Алгоритм 10.1.1. Логарифмирование в под-
группе группы F9 методом базы разложения.
Вход. Характеристика поля р, образующая а
подгруппы простого порядка г, экспонента Ъ.
Выход. Показатель х, для которого d = b
(mod /?).
Метод.
1. Выбрать базу разложения D как множество,
состоящее из числа р0 = -1 и т первых простых
чисел pj, где рт = О(ехр(сфп р In In /?)), с « 1.
2. Случайным выбором показателей w, найти
множество из О(т) D-гладких чисел В, <— а'
(mod р) и разложить их на множители путем
вычисления наибольшего общего делителя с
произведениями элементов базы разложения
(при этом D-гладким может быть не В„ а
р - В,, в этом случае в разложении участвует
элемент-1 базы разложения):
i=o •• •••
(здесь в каждом уравнении почти все показа-
тели ау будут нулевыми). -
3. Подбором найти показатель г такой, что чис-
ло b" (mod/?) является D-гладким, и найти
разложение этого числа:
Ь'' = pf’J (mod /?).
, (l
4. Используя показатели ау, Р7, записать систе-
му линейных сравнений:
5. Методом гауссова исключения выразить xv
как линейную комбинацию от ы,:
xvd£d,U'(mod г). Найти логарифм х по
/
формуле х <- г-1 d^ (mod г).
/
6. Результат: х. -
Алгоритм 10.1.1 является вероятностным и
требует объема памяти Lr(c; ’/2), где с » 1. Выбор
на шагах 2 и 3 тех значений г/, и v, для которых
экспонента является D-гладкой, можно рассмат-
ривать как «просеивание» экспонент через «ре-
шето». Поэтому данный метод относится к мето-
дам решета.
Решение большой системы линейных уравне-
ний над полем Fr можно ускорить, если восполь-
зоваться технологиями разреженных матриц [3].
Кроме того, на шаге 2 можно искать числа вида
В, = d'b'1 (mod /?) для целых ы„ г, до получения
системы линейно независимых сравнений, тогда
шаг 3 не нужен. - ;
Пример 10.1.1. Логарифмирование методом
базы разложения.
Пусть // = 993121, а = 4096, £ = 230611.
г = 2069.
Выбираем базу разложения D = {-1, 2, 3, 5, 7,
11, 13, 17, 19, 23, 29, 31,37, 41, 43}.
Находим D-гладкие экспоненты а Ъ". Число
а является D-гладким: а = 212. Построенная база
данных приведена в таблице 10.1 и содержит по-
казатели элементов базы разложения, с которы-
ми они входят в разложение экспонент а Ь'.
Числа -1, 29, 31, 41 из базы разложения не
встречаются ни разу, их можно не учитывать.
Сокращаем число переменных. Для этого вы-
ражаем числа, не встречающиеся в fe101 (послед-
няя строка в таблице), через экспоненты основа-
ния а и числа 3, 5, 13, 17 в поле Fp:
<0 66о~7 *72 206q— 3r-2i ^—1 < rd). 272/^—J с—I1 о-1
2 = а 5 ,1=а 2 5 17 , 19 - а 2 5 13
]77]
и подставляем их в уравнение для а :
я'77’2 = 2123672192 = 2,23672о2722-’5-] В’1 =
= 2,,36а2725-,13-,Л-35-217-' =
= <747828365’313' 17’1 = а478а1323-14365-3 1 3“| 17’1 =
= а6,03"85’313ч * 17'1
или а-863 = З8 53 • 13 17 с учетом того, что по-
рядок группы равен 2069.
.- т т
и, = У ay(modr), xv = у P;(modr).
220
Таблица 10.1
База данных из D-гладких экспонент
а х 2 3 5 7 11 13 17 19 23 29 31 37 41 43
а16 2 5 0 1 0 0 0 1 0 0 0 0 0 0
а-8 1 0 1 1 0 0 0 1 0 0 0 1 0 0
а114 5 0 0 0 0 0 2 0 1 0 0 0 0 0
42 а 3 2 1 0 0 0 0 0 0 0 0 1 0 0
а™ 7 3 1 0 0 0 0 0 0 0 0 1 0 0
а66 4 7 0 0 0 0 0 0 0 0 0 0 0 0
75 а 3 0 0 0 3 0 0 0 0 0 0 0 1 0
999 а 2 0 0 0 0 0 0 0 1 0 0 1 0 0
а220 3 0 4 0 0 0 0 0 0 0 0 0 0 1
о206 3 0 2 2 0 0 1 0 0 0 0 0 0 0
272 а 1 0 1 0 0 1 0 2 0 0 0 0 0 0
а265 6 0 0 1 0 0 0 1 0 0 0 0 0 0
а943 0 6 0 0 0 0 0 0 0 0 0 0 0 0
а315 8 2 0 0 0 0 0 0 0 0 0 0 0 0
а1771 6 3 0 1 0 0 0 1 0 0 0 0 0 0
610' 0 2 3 0 0 1 1 0 0 0 0 0 0 0
Сравнивая это разложение с разложением чис-
ла fe , получаем 36fe10'=а-863. Из разложения
а = 3 получаем b = а , b -а . Для
показателей соответствующее уравнение имеет
вид: 101т = 263 (mod 2069). Отсюда х = 263 • 10Е1 =
= 146 (mod 2069).
Выбор значения т - O(exp(cjln pin In р)),
с»1, является оптимальным. Существование
оптимального размера базы данных следует из
того, что если размер базы данных взять не-
большим, то вероятность D-гладкости случайно-
го числа становится малой и шаги 2 и 3 алгорит-
ма становятся трудоемкими. Если размер базы
данных взять близким к р, то число уравнений
становится велико, а шаги 2 и 5 алгоритма ока-
зываются трудоемкими.
Покажем, что алгоритм 10.1.1 имеет субэкс-
поненциальную сложность. Оценим зависимо-
сти, которые понадобятся в дальнейшем. Во-
первых, в соответствии с формулой Стирлинга
ln(n!)« п In п — п. Во-вторых, для натурального N
и положительного и число наборов из N целых
чисел а,, сумма которых не превышает и, равно
биномиальному коэффициенту
Лu\+N'
I /
Это следует из того, что набору {а,} можно
взаимно однозначно сопоставить набор {[!,} из
чисел 1,2, ...,# +[иJ, где Pi = cxi + 1 и
Phi = Pi + «/и + 1 для i>0. Здесь Р,-! < а, < Р,.
Число наборов {Р,} равно указанному биноми-
альному коэффициенту.
Оценим вероятность того, что случайное чис-
ло, не превышающее р, будет раскладываться на
простые множители, не превышающие у, где
у « р (в алгоритме 10.1.1 у =рт).
Обозначим и = ——. Будем считать, что
In у
и «у (это требование естественно для больших
чисел р). Поскольку число л(у) простых чисел, не
превышающих у, в соответствии с теоремой Че-
бышева равно л(у)«-^-, то и«л(у). Обозна-
чу
чим через А(р, у) множество натуральных чисел,
не превышающих р и представимых в виде про-
изведения простых чисел, не превышающих у.
Поскольку разложение на простые множители
единственное, то существует взаимно однознач-
ное соответствие между числами из А(р, у) и на-
борами из л(у) первых простых чисел, опреде-
ляющими разложение. Число #А(р, у) равно чис-
лу решений неравенства У а, < и.
<=1
221
Поскольку л(у) по порядку величины близко к
у, заменим л(у) на у. Тогда справедливо прибли-
женное равенство: -U- X- :
#А(р,у) ® {число решений ос, = г/}.
/=i
Из второй вспомогательной оценки следует,
что
: „ (и + уЛ • '
#Л(р,у)« • . -ЛЬЖХ
... • V У ) ... . . ..
#А(р,у) ' е
Оценим In------------логарифм вероятности
Р
того, что случайное число, не превышающее р,
будет D-гладким: _......
#А(р,у) (н + у)! .
In---—— »In -----— _ M |П у » . .
Р и-У-
® (и + у) ln(w + у) - и In и - у In у - и In у. = „
Поскольку 1п(н + у) Л In у, то
#А(р,у) ~ . •
In----- - -» -и In и,
р
и можно записать : г‘7 « '
. . р
Это выражение дает оценку вероятности най-
ти с первой попытки случайное D-гладкое число,
не превышающее р.
Теперь можно оценить сложность алгоритма
10.1.1. Наиболее трудоемкие этапы— создание
базы данных и решение системы линейных срав-
нений. Создание базы данных требует тестиро-
вания порядка ип(у) различных В,. Обозначим
т
С = J~[ р, . Проверка D-гладкости каждого В, вы-
ы
полняется нахождением НОД(С, В,), при этом
In С » In В, и In С «у. На каждом шаге при вы-
числении наибольшего общего делителя выпол-
няется вычитание меньшего числа из большего и
циклический сдвиг. Число шагов пропорцио-
нально у, сложность шага пропорциональна Inp.
Тогда сложность первого этапа алгоритма равна
О(ииу1пр). Решение разреженной системы из
О(у) линейных уравнений над F,. с точностью до
константы сводится к умножению матриц [2].
При этом матрица содержит очень мало ненуле-
вых и неединичных коэффициентов в каждой
строке, плотность распределения ненулевых ко-
эффициентов существенно непостоянна. Слож-
ность решения такой системы равна О(у2(1п/?)2).
Итоговая сложность равна
S = О(и“у In/? + у2(1пр)2). (10.1.2)
Оптимальная итоговая сложность алгоритма
10.1.1 достигается, если сложности двух этапов в
(10.1.2) примерно равны. Тогда и1' ~у In/?. Пере-
ходим к логарифмам сложностей:
In р In р . , .
-----In-----«In inp + lny .
: In у In у Oqsx
Отсюда получаем (Iny)2 ~ (ln/?)(ln Inp),
у = О(ехр(Сд/1п pin Inр)), где с = 1 + о(1). Итого-
вая сложность алгоритма 10.1.1 равна
В = £р(2с; ]/2)= О(ехр(2сл/1п pin In р)).
Емкостная сложность алгоритма 10.1.1 равна
O(-Js) = О(ехр(сл/1п р In In р)).
Проведенный анализ учитывает оптимизацию
только временной сложности алгоритма. Однако
вследствие существенно неравномерного рас-
пределения вероятностей того, что случайное
число делится на данное простое /?, из базы D,
может существовать компромисс между времен-
ной и емкостной сложностями. Шаг 2 алгоритма
10.1.1 допускает эффективное распараллелива-
ние. Поэтому практически может быть выгодно
уменьшить объем памяти (размер базы разложе-
ния) в миллионы раз, увеличив при этом число
параллельно работающих процессоров при соз-
дании базы D-гладких чисел В,.
Сложность алгоритма 10.1.1 можно сокра-
тить, если на шаге 2 представлять числа В, в виде
дроби В,
С,
D,
(mod р), где взаимно простые чис-
ла |С,|, |D,| имеют порядок не более O(-Jp). Зна-
чительная часть таких пар |С,|, |D,| дает попарно
различные числа В,. Числа С„ D, могут быть най-
дены расширенным бинарным алгоритмом Евк-
лида со сложностью <9((1пр)2).
Улучшенный вариант шага 2 алгоритма
10.1.1 выглядит так. Выбирается случайный по-
казатель ut, вычисляется В, s a' (mod р), расши-
ренным алгоритмом Евклида вычисляются С, и
D,, малые по абсолютной величине,
В, =— (modp), которые тестируются на D-
гладкость. Показатели, с которыми элементы
базы разложения входят в В„ и показатель и,
записываются в базу данных.
222
Получить С„ Di из В, и р можно так. Расши-
ренным алгоритмом Евклида находим пару чисел
е, f таких, что eBi + fp= 1, где 1 — наибольший
общий делитель чисел Bt и р. При этом на j-м ша-
ге алгоритма выполняется равенство +fjp- gj,
где числа q, кратны НОД (Вь р). Если остановить
этот алгоритм на шаге, когда |ej, |gj имеют поря-
док не более О(у[р), то можно просто положить
Ci gj’ Di €j.
Вероятность того, что оба числа С,, D, будут
D-гладкими, в соответствии с (10.1.1) равна
1пр
In р |п-> _
—— . Оптимальное значение у для улуч-
21nyJ
шейного алгоритма 10.1.1 определяется из ра-
венства
In р
' inp Yn>
<2 In У,
« у In р.
Пример 10.1.2. Представление элемента ко-
нечного поля в виде дроби с малыми числителем
и знаменателем.
Пусть р = 109 + 7, В, = 123456789. Применяем
алгоритм Евклида к р, В,. Получаем q\=p- 8В, =
= 12345695; <?2 = Д - 10# =-161. Обрываем ал-
горитм Евклида и подставляем в последнее
уравнение выражение для q}. Получаем
# = -161 = 81Д-10р. Тогда Де-161-8Г’
(mod р) = -7 • 23 • З-4 (mod /?).
Алгоритм 10.1.1 можно применять и для раз-
ложения чисел на множители. Различие заключа-
ется в том, что при разложении на множители
решается система линейных уравнений над F2, а
в алгоритме 10.1.1 — система линейных уравне-
ний над Fr. Поскольку арифметика в IF, несколь-
ко более сложная, чем в F2, то сложности разло-
жения и логарифмирования с использованием
базы разложения различаются в <9((log г)2) раз, то
есть на полиномиальный множитель. Поэтому
сложности разложения и логарифмирования ме-
тодом базы разложения можно считать асимпто-
тически одинаковыми.
Дальнейшие улучшения метода базы разложе-
ния учитывают неравномерность распределения
вероятностей элементов в матрице, получаемой на
шаге 4 алгоритма 10.1.1 (это позволяет сократить
необходимое число уравнений), и однозначность
разложения на множители в кольце целых алгеб-
раических чисел. Так, использование кольца це-
лых гауссовых чисел позволило снизить времен-
ную сложность дискретного логарифмирования
до уровня D(exp((l + o^lnphdnp)) [12].
Логарифмирование методом базы разложения
допускает предвычисления. Пусть известно толь-
ко простое число р и порядок группы г, а обра-
зующая а и экспонента Ъ неизвестны (считаем,
что р - 1 не делится на г2). Находим произволь-
ную образующую а' группы порядка г, на шаге 2
находим D-гладкие экспоненты для основания а',
составляем базу данных и приводим матрицу
показателей к треугольному виду. Затем, когда
станут известными а и Ъ, на шаге 3 находим пару
D-гладких экспонент для оснований а и Ь, на ша-
гах 4 и 5 вычисляем логарифмы log^a, logyfe, за-
тем вычисляем х = (1о^6)(1о^а)“' (mod/'). По-
скольку найти пару D-гладких экспонент гораздо
легче, чем составить базу данных, а решение
системы линейных уравнений с треугольной
матрицей имеет линейную сложность, то слож-
ность вычислений при составленной базе данных
пропорциональна квадратному корню из слож-
ности предвычислений.
Отсюда следует, что срок действия ключа в
криптосистемах с открытым ключом следует от-
считывать с момента выбора простого поля (см.
п. 11.5).
10.2. Логарифмирование в простом поле
методом решета числового поля
Метод решета числового поля для вычисле-
ния дискретного логарифма был предложен
Д. Гордоном [10] и развит Д. Вебером [18, 19].
Метод использует разложение на простые идеа-
лы в кольцах целых алгебраических чисел.
Прежде чем изложить суть метода, рассмот-
рим подробнее некоторые свойства целых алгеб-
раических чисел.
10.2.1. Подготовительные
теоретико-числовые результаты
Пусть К— числовое поле, то есть конечное
расширение степени п поля Q, и {ось ..., ос,,} —
базис К над Q. Пусть Ок— кольцо целых эле-
ментов поля К, причем Z с Ок- Для произволь-
ного а е К можно записать осос; = ^#,01, , где
j
ay е Q; определитель матрицы (#) является нор-
мой элемента ос. Каждый главный идеал (ос)
можно записать в виде а.Ок.
Для идеалов 21, 93, С кольца Ок имеют место
утверждения:
- если 2193 = 21С, то 93 = С; н
- если 21 с 93, то существует идеал С такой,
что 21 = 93С.
223
Это означает, что в Ок имеет место однознач-
ное разложение на простые идеалы.
Норма идеала (число элементов кольца классов
вычетов С/721) — мультипликативная функция.
Для двух не обязательно различных идеалов 21 и
Я5 имеет место равенство А(21Ж) = А(21)А(Ж).
Следовательно, если фь ...,ф*— простые идеа-
к к
лы и 21 = ПФ,"' = то M2l) = HW,)''' • Здесь в
/=1 /=1
первом равенстве— произведение идеалов, а во
втором — произведение натуральных чисел.
Идеалы кольца ОК образуют коммутативный мо-
ноид по умножению.
/7
Пусть f(X) = X' — приведенный (с
|=о
единичным старшим коэффициентом) неприво-
димый над Q полином с целыми коэффициента-
ми, а — его комплексный корень, К = Q(a) —
числовое поле и ОК — порядок этого поля. Нор-
ма главного идеала (у), образованного целым ал-
гебраическим числом у = с - do. е Ок, вычисля-
ется как А((у)) = 47„с" + a,,~yd’~}d + ... + aod" и сов-
падает с нормой целого алгебраического числа у.
Если 0С|, ...,а„— комплексные корни полинома
fiX), то главные идеалы (с + do.,) являются со-
пряженными. Сопряженные идеалы имеют оди-
наковую норму.
Пусть ф — простой идеал. Тогда в кольце
Ок можно ввести дискретное нормирование v^,
значение нормирования гф(21) для идеала 21
совпадает с максимальной степенью идеала ф,
на которую делится 21. Аналогично, если
а е Ок, то Гф(а) — наибольшая степень идеала
ф, на которую делится целое алгебраическое
число а.
В кольце Ок каждый главный идеал (<у), об-
разованный простым числом q, раскладывается
на множители, разветвляется или является не-
разложимым. В первом случае идеал (q) явля-
ется произведением двух или более простых
идеалов или их степеней, при этом норма идеа-
ла (q) является составным числом. Во втором
случае идеал (q) является степенью простого
идеала, а поле OKKq) является расширением
простого поля.
10.2.2. Метод решета числового поля
Предположим, что в ходе решения задачи
ci = b (mod р) нам удалось найти s и t такие, что
ah' = и'(тоб р) для некоторого w, имеющего по-
рядок г в IF/, причем НОД(г, 0=1. Переходя к
показателям по основанию а, получаем сравне-
ние s + tx = 0 (mod г), отсюда х = -sf* (mod г).
Таким образом, для решения задачи дискретного
логарифмирования нужно записать г-к> степень
элемента w в виде нетривиального произведения
степеней а и Ъ.
Выберем неприводимый над Q полином
/А) = X’ + а„_уХ'~А + ... +т70
из кольца 2|А], целое число тп такое, что/?;;) = 0
(mod/;), и базу разложения D\ = {pif, где р,—
наименьшие простые числа, включая -1. Обо-
значим через а комплексный корень полинома f
Тогда а является целым алгебраическим числом
с минимальным полиномом f Обозначим через К
поле Q(a) и через Ок порядок поля К, содержа-
щий кольцо Z. Каждый идеал из Ок однозначно
раскладывается в произведение простых идеалов.
В общем случае кольцо Ок может быть идеалом
кольца Z[a], На практике в методе решета чи-
слового поля можно использовать как кольцо Ок,
так и все кольцо Z[a],
Если р не делит дискриминант полинома/, то
идеал (/?) раскладывается на множители в Ок,
при этом идеал ф = (р, а - т) является простым
делителем идеала (/?), то есть имеет место изо-
морфизм С//ф = В/, который задается заменой а
на тп.
Выберем базу разложения £>2, состоящую из
первых степеней простых идеалов ф с нормой,
меньшей некоторой границы.
Потребуем выполнения следующих условий:
1) f(m) = 0 (mod р), при этом а = т (mod /;);
2) т = hb, где число h является Dy -гладким;
3) р не делит дискриминант полинома f то есть
идеал (р) не разветвляется в кольце Ор,
4) свободный член а0 полинома f является £>2-
гладким (это означает, что идеал (а0) раскла-
дывается в Ок в произведение простых идеа-
лов из D2);
5) идеал (г) не разветвляется в кольце Ок, то
есть г не делит дискриминант полинома f
Для упрощения рассуждений будем считать,
что идеалы (г,), где г, — простые делители числа
р - 1, не разветвляются в Ок (если г, малы, то не-
выполнение этого требования не означает, что
сложность алгоритма увеличится).
Алгоритм определяет непустое множество 5
пар (с;, di) со свойствами:
- целые числа с, + d^n являются Dy -гладкими
(при этом с, + dyin можно вычислять как вы-
чет по модулю р);
- главные идеалы (с, + dyO.) являются Z>2-
гладкими (то есть норма А(с, + d,o.) как целое
число является П2-гладкой);
- #S>#Dy+#D2 + n. . ...... ... .
224
Методами линейной алгебры для каждой па-
ры (с„ <У) определяется множество показателей е,
такое, что выполняются условия:
- (с; + <АИ)£‘ делится только на а и Ь;
i
- целое алгебраическое число +<i,a)e'
1
является r-й степенью в Z[a] (то есть ф-ади-
ческая норма этого алгебраического числа
делится на г для каждого идеала ф из базы
разложения А)-
Согласно теореме о гомоморфизмах колец
гомоморфизм Ок —> существует тогда и толь-
ко тогда, когда имеет место изоморфизм
Fp = Ок/Cl, где fl — идеал кольца Ок, являющий-
ся ядром указанного гомоморфизма. Поэтому'
отображение ср: Ок —> Fp, ср(а) = т, является го-
моморфизмом колец с ядром fl = (/(а)), где
(Да)) = рОк — главный идеал.
В силу указанного гомоморфизма колец вы-
полняется сравнение
П(С( +dlm)e‘ = П<Р(С +<^,ос)е' =
t / (10.2.1)
= ср(со)' = w' (mod р),
где со е Ок-
Отсюда вытекает, что произведение
]~J(c, +фи)е' является r-й степенью в Fp.
i
Алгоритм включает в себя три этапа:
- просеивание (подбор пар (с„ dt) таких, что
число с, + dtm является Л]-гладким и идеал
(с, + dta) является А-гладким);
- построение нетривиальных r-х степеней в Ок,
- вычисление логарифма х.
Третий этап очевиден. Рассмотрим подробнее
первые два этапа.
При построении базы данных гладкость ос-
татка с, + dtт (mod р), рассматриваемого как це-
лое число, проверяется нахождением наибольше-
го общего делителя этого числа и произведения
элементов pt базы разложения Dx, взятых с крат-
log/?
ностями-----
logp,
Гладкость идеала (с, + <7,а) проверяется вы-
числением нормы алгебраического числа с, + dta
и вычислением наибольшего общего делителя
этой нормы и произведения простых чисел, вхо-
дящих в идеалы из базы А, взятых с соответст-
вующими кратностями.
Если число таких пар (с„ 4) превышает
#А + #А + п, то решение линейных сравнений
по модулю г дает формулу (10.2.1), где левая
часть делится только на а и Ъ. Если а, Ъ -— про-
стые числа, то получается одно сравнение db' = wr
(mod р).
Покажем, как можно свести исходную задачу
логарифмирования к случаю, когда числа а и
b— А-гладкие. Предположим, что разложение
числа р-1 известно, в противном случае нахо-
дим разложение числа (р - 1)/г , например, ме-
тодом эллиптических кривых. В группе F/;* вы-
бираем D] -гладкую образующую, порядок кото-
рой делится на г, и возводим ее в нужную сте-
пень так, чтобы ее порядок был в точности равен
г (при этом значение полученной D}-гладкой об-
разующей d порядка г может превышать р). За-
тем находим две пары линейно независимых над
F,. показателей (wb г,) и (w2, v2) таких, что
Cj = a'b' (mod р) и с2 = a2b'2 (mod р) являются
А-гладкими. Методом решета числового поля
находим логарифмы лу = logyCj (mod г),
х2 = logac2 (mod г). Обозначим и = logiZ-<7 (mod г),
v = loga-b (mod г). Тогда выполняются сравнения
г/i и + Vi v = %] (mod г), и2и + v2v = х2 (mod г). Реше-
ние этой системы относительно неизвестных и, v
позволяет свести исходную задачу к задаче лога-
рифмирования с/ = с2 (mod р), где числа су, с2 —
А-гладкие.
На втором этапе требуется построение г-х
степеней. Пусть главный идеал (г) = гОк раскла-
дывается в произведение простых идеалов в Ок
следующим образом:
(г) = ПФ2- (Ю.2.2)
. . . /=1 ..
Обозначим
* = НОВДф,)_ I}, 1<у</,
где фу — простые идеалы из разложения (10.2.2).
В кольце Ок все идеалы радикальные (то есть
некоторая степень идеала является главным
идеалом) [1]. Поэтому существуют главный иде-
ал (у) е А/ф, и натуральный показатель к такие,
что (у)* = 1 (mod А; /ф) для 1 <j < I.
Определим отображение коммутативных мо-
ноидов [18]:
X: {Ок, •} -> {гОк^Ок, +}, (10.2.3)
у->/-1. .
Поскольку идеал (г) не разветвляется в Ок, то
это отображение является гомоморфизмом.
225
Имеет место следующая теорема [19].
Теорема 10.2.1. Пусть у— элемент кольца Ок
такой, что его норма не делится на г. Пусть U —
группа обратимых элементов кольца Ок. Пусть
U = {т] е [7| т] = 1 (mod г)}. Тогда у является г-й
степенью в Ок, если:
- число классов поля К не делится на г;
- UcU;
- ve(y) ее 0 (mod г) для всех простых идеалов £2
кольца Ок,
- Мт) = о.
Для каждой пары (с„ d^, найденной на этапе
просеивания, находим в соответствии с (10.2.3)
образ отображения Z. по модулю г2, используя
базис из степеней элемента а кольца классов вы-
четов Z[a]/r2Z[a]:
Л-1
л(с, + d)a) = ^hl ^''(mod r2OK),
J=o
где n — степень полинома ДТ). ,
Для построения r-й степени достаточно по-
строить сумму
УЛ.(с, +d,а) = 0(mod г2).
Все образы построенных пар при действии
отображения X делятся на г. Следовательно,
можно каждое , поделить на г и использовать
2
сумму по модулю г вместо суммы по модулю г .
Алгоритм 10.2.1. Логарифмирование мето-
дом решета числового поля.
Вход. Характеристика р, образующая а под-
группы простого порядка г, экспонента Ъ.
Выход. Показатель х, для которого d = b
(mod р).
Метод.
1. Выбрать неприводимый над Q полином
И
f(X) = у , о, еД дискриминант кото-
/=0
рого не делится на р, и целое число т такое,
чтоУ(/и) ее 0 (mod р). Найти целое алгебраиче-
ское число а как корень полинома f поле
К= Q(a) и кольцо Ок целых элементов поля К.
2. Выбрать базу разложения £),, состоящую из
простых целых чисел, не превышающих за-
данного числа N], и базу разложения Z)2, со-
стоящую из простых идеалов кольца Ок,
норма которых не превышает заданного чис-
ла АД включая сопряженные идеалы.
3. Найти D] -гладкую образующую d. Случай-
ным выбором двух линейно независимых над
пар показателей wb vb w2, v2 найти D\-
у, гладкие элементы б <— а]Ь1 (mod/?) и
/2 <— a2h'2 (mod р). Положить а <— d, b <— /ь
4. Найти около #D\ + #Z>2 + п пар небольших
взаимно простых над Z целых чисел (с„ 4)
таких, что целое число с, + dpi (mod р) явля-
ется D\-гладким и идеал (с,+ <7,а) является
П2-гладким.
5. Записать для полученной базы данных ра-
венства:
с, + dt т (mod р)- pt} (с< 'di),
(С,+4а)= '
п, jGD2 .. ._
где — простой идеал с нормой p,j.
6. С использованием методов линейной алгеб-
ры составить множество S' линейно зависи-
мых пар (с„ d,) и множество показателей
е(с„ d,) таких, что выполняются условия:
- число Р[(С'+ =un“b"h де-
(Cj.df )gS
лится только на а и Ъ, причем пь — об-
; - ратимый элемент по модулю г;
, — J~J(c,+J/a)t’(c,’rf,) =((o)p_1 для неко-
(с, ,d, )g5
торого со е Ок, где степень, с которой
каждый простой идеал ф/ входит в это
произведение, кратна г.
7. Вычислить логарифм z <— пап~^ (mod г) для
Оргладких а, Ь.
8. С помощью найденных на шаге 5 соотноше-
ний восстановить логарифм х относительно
первоначальных значений а, Ъ.
9. Результат: х.
База данных, полученная на шаге 4, может
быть представлена парой матриц. Первая матри-
ца состоит из показателей, с которыми элементы
базы разложения D] входят в с, + dpi (mod р).
Вторая матрица состоит из показателей, с кото-
рыми элементы базы разложения £)2 входят в
идеал (с, + <7,а). Для того чтобы можно было вы-
полнить шаг 6, эти матрицы должны содержать
линейно зависимые над IF,, строки.
Все идеалы, входящие во второе произведе-
ние на шаге 6, должны иметь порядок г. Для про-
верки кратности вхождения идеалов в произве-
дение на шаге 6 недостаточно пользоваться
только нормами идеалов, поскольку в произве-
дение могут входить сопряженные идеалы с оди-
наковой нормой.
Для ускорения алгоритма можно воспользо-
ваться представлением элементов с, + dpi (mod р)
в виде дроби с малыми по абсолютной величине
числителем и знаменателем по аналогии с при-
226
мером 10.1.2. Такое представление можно найти
с использованием «незавершенного» расширен-
ного алгоритма Евклида. Д. Вебер указал на воз-
можность использования неприводимого поли-
нома f с целым неединичным старшим коэффи-
циентом [19].
Размеры баз данных Dy и D2 оказываются не-
большими по сравнению с размером базы дан-
ных в методе базы разложения. Сложность алго-
ритма равна Zp(l,923;’/з), где 1,923 в
1996 г. для вычисления логарифма по модулю
простого числа длины 426 бит потребовалось
найти матрицу из 40 000 строк [19].
Для простых чисел вида р = А1 ± В, где А,В-—
малы, сложность метода специального решета
числового поля равна [19]
Zp(l,57; %) = 69(exp(l,57^1n/?(lnln/j)2 ) ,
где 1,57 ~ . Выбор характеристики поля ука-
занного вида можно интерпретировать как заклад-
ку «мины», при этом сначала выбирается удобный
полином для вычисления дискретного логарифма,
а затем — простое число р. Для противодействия
этому стандарт подписи ГОСТ Р 34.10-94 преду-
сматривает специальный порядок генерации ха-
рактеристики поля р, использующий хэш-фун-
кцию в целях исключения неправильной очеред-
ности генерации числар (см. также п. 8.3.2).
Пример 10.2.1. Логарифмирование методом
решета числового поля.
Пусть р = 83, а = 2, Ъ = 5, г = 41. Нужно ре-
шить показательное уравнение d — b.
На шаге 1 выбираем неприводимый над Q по-
лином fiX) = X2 + 2, при этом 7/7 = 9. Полагаем
a = V-2, Ок =Z[V-2], так как p = 9z + 2 =
= (9 + а)(9 - а). Единственные обратимые эле-
менты в Оц — числа ±1.
Выбираем базы разложения: Z>] = {2, 3, 5},
Z>2 = {а, 1 + а, 1 - а}. Нормы идеалов из базы D2
равны, соответственно, 2, 3, 3. В базе Z>2 идеал
(2) разветвляется, а идеал (3) раскладывается на
сопряженные идеалы. Идеал (5) не раскладыва-
ется на множители в Ок, поэтому вхождение
идеала (5) в любой главный идеал кольца Ок оз-
начает, что оба коэффициента с и d алгебраиче-
ского числа с + da делятся на 5, то есть не явля-
ются взаимно простыми.
Находим базу данных из пар (с,, d,) таких, что
число Cj + diin (mod/?) является Dy -гладким, а
главный идеал (с, + d,d) является Е>2-гладким.
Практически для нахождения пары (с„ d,~) рас-
сматриваем алгебраические числа вида
±(1 ±a)kas, где ,s e {0, I}, AeZ, такие, что целые
числа с, + d,m (mod р) являются Dy -гладкими. При
этом сначала раскрываем скобки и производим
упрощение алгебраического числа с учетом вы-
ражения а2 + 2 = 0. Например, -(1 - а)4 = 7 - 4а
(mod (а2 + 2)). Далее, заменяя а на т, получаем
отображение алгебраического числа 7-4а в
7 - 4/77 (mod р), то есть в элемент поля By
7 - 4/77 = -29 = 54 (mod 83) = 2 • З3. База данных
приведена в следующей таблице:
i ci di Ci + d,m (mod p) (<?, + d,a)
1 1 I 2-5 (1 +a)
2 1 -1 3 52 (1 - a)
3 7 -4 2 33 -(1-a)4
4 -4 I 5 -a(l - a)2
5 -5 1 22 (1+a)3
6 2 -5 23 • 5 a(l - a)3
7 -1 11 3-5 -(1+a)5
8 -2 -1 23 • 32 -a(l - a)
Для сокращения объема таблицы два послед-
них столбца представлены в виде произведений
элементов из Dy и Z>2 соответственно.' Преобра-
зуем таблицу, составляя такие линейные комби-
нации строк, чтобы исключить множитель 3 в
столбце с, + <7,/т7, а также удалим лишние строки.
Строку 1 сохраняем. Строку 2 заменяем произ-
ведением (в случае матрицы это будет сумма)
строк (7, 2”'), строку 3 — произведением строк
(3, 2~3), строку 4— произведением строк (6, 4”').
При этом в последнем столбце остаются два па-
раметра: (1+а) и (1-а). Поскольку значения
(с„ <7,) далее не используются, соответствующие
столбцы удаляем. Преобразованная база данных
выглядит так: , , _ . 3 -ч .
i Ci + d/n (mod p) (с, + dyO)
1 2-5 (1 +a)
2 5'1 -(1 + a)5(l - a)-1
3 2 5~6 -(1-a)
4 23 -(1-a)
1 Для получения матрицы нужно перейти от пред-
ставления в виде произведения сомножителей к пред-
ставлению в виде показателей, при этом таблица разо-
бьется на две связанные матрицы (с общими парами
(<?„ Д)). В одной матрице столбцы будут представлять
показатели, с которыми элементы базы Dy входят в
число ct + djm, в другой матрице столбцы будут пред-
ставлять показатели, с которыми элементы базы Z>2
входят в идеал (с, + d,a). ' " ' ’ '
227
В алгоритме нужно получить произведение
идеалов в степени, кратной г. Поскольку 0 кра-
тен г, составляем нетривиальную линейную ком-
бинацию строк матрицы, соответствующей по-
следней таблице, так, чтобы идеалы (1+а) и
(1 - а) в правом столбце имели нулевые показа-
тели. Требуемая линейная комбинация имеет
вид: первая строка с коэффициентом -5, вторая
строка с коэффициентом 1, третья строка с ко-
эффициентом 1. Тогда в среднем столбце полу-
чаем выражение 2-4 • 5”'2. Отсюда 2-4 5”12 s 1
(mod/?). Заменяем 5 на Т, тогда последнее ра-
венство примет вид 2~4’12л = 1 (mod р), 1 + Зх = О
(mod 41), х = 27.
Необходимую линейную комбинацию можно
составить также из двух последних строк.
На практике можно использовать не квадра-
тичное расширение поля Q, а расширение более
высокой степени. Как правило, используются
числовые поля, степень расширения которых над
Q не превышает 5. При этом в базу разложения
£>2 приходится включать сопряженные идеалы.
10.3. Логарифмирование
в расширенном поле
Рассмотренный выше метод решета для лога-
рифмирования в поле fy может быть применен и
для логарифмирования в поле IF(/, где q=pn, с
заменой поля алгебраических чисел на поле ра-
циональных функций IF/0- Это возможно, по-
скольку имеет место изоморфизм полей и
FPH/(/(0), гДе f— неприводимый полином сте-
пени и, задающий поле Fy. Задача логарифмиро-
вания в расширенном поле IFV = Ву,[£|/(ЯО) (для
образующей g(t) подгруппы простого порядка г и
экспоненты h(f) найти показатель х такой, что
выполняется равенство gx = h в поле IF(/) возника-
ет, например, при решении задачи логарифмиро-
вания на эллиптической или гиперэллиптической
кривой с использованием спаривания Вейля.
Задача логарифмирования в расширенном по-
ле малой характеристики р оказывается более
легкой, чем задача логарифмирования в простом
поле близкого размера [9]. Это вызвано тем, что
проверка гладкости полинома из ЕД/] сводится к
разложению его на множители и может быть вы-
полнена с кубической сложностью от степени
полинома (см. п. 7.4).
Оценим влияние этого обстоятельства на
сложность логарифмирования в предположении,
что степень расширения и поля Fy над Fj, доста-
точно велика. Рассуждая так же, как в п. 10.1,
заметим, что выражение (10.1.2) примет вид
Приравнивая сложности создания базы дан-
ных и решения системы линейных уравнений,
получаем uu Inу2. В результате логарифмиро-
вания этого равенства получим условие:
u In w + In In q « 2 Iny. Поскольку u = , то
in у
2 (In у)2 «In q In In q, In у » ^(Inz/lnln ф)/2 . Tогда
сложность логарифмирования в расширенном
поле методом базы разложения описывается
функцией £v(c; 1/2), где можно обеспечить с ~ 1.
Например, в поле характеристики 2 задача лога-
рифмирования методом базы разложения являет-
ся примерно в 1,3 раза по порядку величины бо-
лее легкой, чем задача логарифмирования в про-
стом поле того же размера.
Объем базы данных и базы разложения может
быть сокращен, если полиномы В„ которые ищут-
ся аналогично шагу 2 алгоритма 10.1.1, представ-
С (/)
лять в виде дроби В, (/) = ' (mod f (/)), где
•^(0
степень полиномов С„ £>, не превышает п/2. Это
представление можно получить, используя «неза-
вершенный» расширенный алгоритм Евклида по
аналогии с п. 10.1.
Для ускорения логарифмирования можно ис-
пользовать метод Д. Копперсмита [9] со сложно-
стью £(/(с; ’/з), где с » 1,57 [12].
Рассмотрим этот метод для поля характери-
стики 2 (хотя он может использоваться и для
других полей, если степень расширения доста-
точно велика). Поле Е(/ может быть задано лю-
бым неприводимым полиномомХО степени п. Пе-
реход от одного способа задания поля к другому
осуществляется линейным над IF2 преобразова-
нием (заменой базиса). Как правило, существует
требуемый полином вида ХО= 0’ + Х(0, где
deg(/i) l°g2«.
Выигрыш в скорости достигается за счет того,
что тестируемый на гладкость полином В, степе-
ни п заменяется парой полиномов степени п1'2
каждый.
Положим к = О(^и/(1пи)), h = |_n2~/c +1J. Вы-
берем базу разложения из неприводимых над [F2
полиномов степени не более d « ехр(^и(1пи)2).
Выберем пару взаимно простых полиномов
г/](0, io(0 степени не более h и положим
wj(0 = u\(t)th +г/2(0» w2(0 s wi(02 (modXO)- То-
гда
w2(0 = + w2(Z) (modXO)-
228
Поскольку порядок чисел d и 2* равен /Л3, то
порядок числа h равен й2,/3 , порядок числа
h2k - п равен п‘3. Поэтому степень обоих поли-
номов и’] и и’2 — порядка п^3. Если a(t)x = b(f)
(mod/(/))— показательное уравнение, которое
нужно решить в конечном поле, то выполняется
равенство для логарифмов:
logaw2(0 = 2* logawj(r) (mod (2" - 1)).
Поэтому, если wj и w2 оба имеют простые де-
лители степени не более d, то последнее сравне-
ние позволяет получить линейное сравнение для
логарифмов элементов из базы разложения.
В остальном алгоритм Копперсмита аналоги-
чен алгоритму' 10.1.1. Обобщением этого метода
для поля характеристики, отличной от 2, являет-
ся решето поля функций [5].
10.4. Группа классов мнимого
квадратичного порядка
Группа классов мнимого квадратичного поряд-
ка числового поля К = D) конечна и поэто-
му может быть использована в криптографиче-
ских алгоритмах. Использование группы классов
мнимого, а затем и вещественного квадратичного
поля для ключевого обмена по Диффи-Хеллману
было предложено Бухманом и Вильямсом в рабо-
тах [7,8]. Число классов hx поля К = Q(-V-D)
растет пропорционально О(-^| D |). Например,
максимальное значение дискриминанта с еди-
ничным числом классов hK= 1 равно 163. Классы
задаются приведенными идеалами, для которых
и определяется групповая операция. Она анало-
гична композиции квадратичных форм или эле-
ментов якобиана гиперэллиптической кривой и
содержит две стадии: композицию и приведение
(см. п. 5.6.3).
На сегодняшний день не известны алгорит-
мы полиномиальной сложности, вычисляющие
порядок группы классов. Для решения задачи
дискретного логарифмирования в группе клас-
сов необходимо сначала найти порядок этой
группы (он может быть простым только тогда,
когда дискриминант является простым чис-
лом).
Задача логарифмирования в группе классов
мнимого квадратичного порядка дискриминан-
та D имеет субэкспоненциальную сложность
Л|/_>|(1,06; ’/2), где 1,06[17]. Алгоритм
дискретного логарифмирования в группе клас-
сов основан на гомоморфном вложении группы
классов в мультипликативный моноид целых
идеалов квадратичного порядка (так же как
группа Ер вкладывается в мультипликативный
моноид Z). При этом составляется база разло-
жения, состоящая из простых идеалов (см.
п. 5.6.3) с малой нормой. Разложение идеала
51 = П^ на пРостые идеалы индуцируется
разложением норм: ДГ(2(.) = 1~[ЛДф,) . Алгоритм
логарифмирования в группе классов аналогичен
методу базы разложения, описанному в п. 10.1.
Аналогичным алгоритмом можно найти по-
рядок группы классов. Число классов h(D) мож-
но также найти алгоритмом «giant step — baby
step» (см. п. 9.2.2) с учетом асимптотического
равенства h(D) ~ 0,4616-^1 Z)|.
На первый взгляд, заманчивым представляет-
ся использование немаксимальных квадратичных
порядков с дискриминантом D = p2q, где р, q —
большие простые числа (в частности, подгрупп
простого порядкар группы классов
Однако эта задача сводится к задаче дискретного
логарифмирования в мультипликативной группе
поля из р элементов (если
= 1) или из рг
элементов (если
[11]. Поэтому ис-
пользование мнимых квадратичных порядков с
большим простым кондуктором не имеет пре-
имуществ по сравнению с использованием муль-
типликативной группы конечного поля.
Квантовый компьютер позволяет как найти
порядок группы классов, так и вычислить дис-
кретный логарифм с полиномиальной сложно-
стью.
В последние годы было предложено исполь-
зовать группы классов числовых полей степеней
более 2 (см., например, [13]). Однако для этих
групп, очевидно, также возможны субэкспонен-
циальные методы логарифмирования и вычисле-
ния группы классов, основанные на вложении
группы классов в полугруппу идеалов соответст-
вующего поля. Поскольку умножение идеалов
колец алгебраических чисел коммутативно и эти
кольца обладают однозначным разложением на
простые идеалы, причем произведению идеалов
соответствует произведение их норм, это на-
правление криптографии вряд ли может считать-
ся перспективным.
229
10.5. Логарифмирование
в группе функций Лукаша
Использовать функции Лукаша для крипто-
графии предложили П. Смит и К. Скиннер [16].
Рассмотрим рекуррентную последователь-
ность, порожденную параметрами а и Ь\
t„ = at,,-} - (10.5.1)
где a, b— взаимно простые целые числа. При
а = 1, b = -1 числа t„ — это числа Фибоначчи.
Пусть а и Р— комплексные корни квадрат-
ного уравнения х2 - ах + Ъ = 0. Если d и с2 —
произвольные числа, то для и>2 справедливо
равенство:
o(cia" 1 + dP" ') - Ь(суД2 + с2р'”2) = С1а” + с2р”,
связанное с равенством (10.5.1) следующим об-
разом: t0 = d + d, t] = сух + с2р. Если t, — целые,
то d, d могут быть целыми квадратичными чис-
лами.
Введем в рассмотрение функции Лукаша по-
a”-P" 1
рядка п: ип(а,Ь) =----— для С]=-с,=-------;
a-р а-р
Да, b) = а'1 + Р" для С\= сг = 1. Функции и», v„
являются целыми рациональными функциями
целых переменных а, Ъ и принимают целочис-
ленные значения.
Рассмотрим последовательность, полученную
из (10.5.1) заменой а, Ъ на vk, bk. Корни a', Р' со-
ответствующего квадратного уравнения удовле-
творяют равенствам: a' + Р' = Да, b) = ak + р/!,
а'Р' = аАрА. Тогда композицию функций Лукаша
можно определить по формулам
v„(n(d b), bk) = (a*)” + (p/f)” = v,,k(a, b).
Последнее выражение позволяет вычислять
функции Лукаша составных порядков. Функция
Лукаша произвольного порядка может быть най-
дена по формуле
г„,„ = а'и+” + ри+".
Для ускорения вычислений в работе [16] было
предложено использовать значение b = 1.
Функции Лукаша являются полиномами от
квадратичных целых a, р, в частности г/ = а/с +
+ р/с = ak + a* (modр), поэтому' их можно рас-
сматривать как элементы поля IF,,[а], где
а±уа2-4Ь /1А-ПЧ
а =-----------, (10.Э.2)
то есть для перехода к квадратичному расшире-
нию требуется, чтобы выполнялось условие для
символа Лежандра:
а2 -4Ь
< Р j
= -1. Тогда спра-
ведливы сравнения ар = а, ap+1 = b (mod р).
Функции Лукаша {Да, 1)} образуют цикличе-
скую группу порядка р + 1.
Задача логарифмирования в группе функций
Лукаша формулируется так: для данных обра-
зующей г0(а, 1) и элемента с найти логарифм к
такой, что vk(a, 1)^с (mod/;). Вложением груп-
пы {Да, Ь)} в группу IF\ с помощью (10.5.2)
задача логарифмирования в группе функций Лу-
каша сводится к логарифмированию в группе
субэкспоненциальным алгоритмом [6], на-
пример, методом решета поля функций [5].
10.6. Связь между задачами
Диффи-Хеллмана и дискретного
логарифмирования
Задача Диффи-Хеллмана в циклической груп-
пе G формулируется следующим образом: для
образующей а группы простого порядка г и двух
экспонент d, d с неизвестными показателями х,
у найти экспоненту dy. Эта задача полиномиаль-
но сводится к задаче дискретного логарифмиро-
вания в группе порядка г: для заданных а, b най-
ти показатель х, для которого выполняется ра-
венство ах = Ь. Если по d можно найти х, то по
ау можно найти аху. Проблема обратной своди-
мости задачи дискретного логарифмирования к
задаче Диффи-Хеллмана в общем случае пока не
решена.
Пусть число #IF,, =р-\ имеет большой про-
стой делитель г и разложение числа #F,. = г - 1
известно. Предположим, что решена задача Диф-
фи-Хеллмана, то есть по известным а, ах, ау
можно найти аху. Эта задача эквивалентна нахо-
ждению любого из четырех перечисленных эле-
ментов по трем остальным. Например, положив
d = ax, получаем задачу нахождения сГ по из-
вестным d, du, duv, где и = х-1 (mod г), v = х~]у
(mod г).
Предположим, что число г - 1 имеет только
малые простые делители (максимальный из них
ограничен полиномом от log/;), g— образующая
группы 1Е,- и /г е F,.. Тогда задача вычисления
показателя у такого, что gy = h (mod г), является
легкой и может быть решена алгоритмом Гель-
фонда (см. п. 11.1.1) с полиномиальной от log/?
сложностью.
Покажем, что если в этом случае можно ре-
шить задачу Диффи—Хеллмана, то можно решить
и задачу дискретного логарифмирования. Задачу
230
нахождения образующей g по известному' разло-
жению порядка группы Fr можно решить с по-
линомиальной сложностью с использованием
китайской теоремы об остатках. Вычисление ло-
гарифма на основании решенной задачи Диффи-
Хеллмана выполняется аналогично алгоритму
Гельфонда.
Пусть gi — образующая подгруппы простого
порядка q в группе Fr. Положим ах = Ь, ау - Ъ& ,
а" = Ь 1 . Решая задачу Диффи-Хеллмана, на-
2
ходим с = ayz - ах . Затем полагаем ау - с8<,
</-i - -4
az - с 1 , находим q = ayz =ах и т. д. Выпол-
„ х"
няя такие действия, можно вычислить а для
произвольного п. Придавая числу п значения де-
лителей числа г - 1 и сравнивая с а, находим
наименьшее п такое, что а =а^ при этом х = 1
(mod г). Определяем множество возможных зна-
чений х. Далее, полагая b\ = ci'b' для случайных s,
t и повторяя указанные операции, находим наи-
меньшее натуральное щф п такое, что
(л + /х)”1 = 1 (mod г), и определяем множество
возможных значений х и т. д. Затем восстанавли-
ваем х по аналогии с китайской теоремой об ос-
татках как пересечение указанных множеств.
Таким образом, при указанных выше ограни-
чениях на максимальный простой делитель числа
г - 1 задача дискретного логарифмирования по-
линомиально эквивалентна задаче Диффи-
Хеллмана.
Упражнения к главе 10
1. Покажите, что множество целых чисел с опе-
рацией «умножения» a* b = ab- а-b обра-
зует полугруппу.
2. Установите гомоморфизм полугруппы G из
предыдущего упражнения с мультиплика-
тивной группой простого конечного поля Fp.
Предложите субэкспоненциальный алгоритм
логарифмирования в гомоморфном образе
полутруппы G.
3. Покажите, что в кольце Z[z] идеалы (1 + /) и
(1 - 0 совпадают, а идеалы (1 + 2z) и (1 - 21)
различны.
4. Алгоритм логарифмирования в Fp методом
базы разложения основан на гомоморфизме
* * *
групп Q —> Fp . Поскольку ранг группы Q
бесконечен, а вероятности ненулевых коор-
динат векторного индекса распределены не-
равномерно, используется понятие гладко-
сти. Покажите, что если предположить (аб-
сурдно), что указанные вероятности распре-
делены равномерно, то субэкспоненциаль-
ный алгоритм невозможен.
5. Покажите (также при абсурдном предполо-
жении), что если бы ранг группы Q в преды-
дущей задаче был ограничен полиномом от
log/?, то сложность логарифмирования в Fp
была бы полиномиальной.
6. Алгоритм логарифмирования с помощью
решета числового поля основан на цепочке
гомоморфизмов мультипликативных групп
Q(a) -> Q -> Fp*, где Q[a] — алгебраиче-
ское расширение поля Q. Эти гомоморфизмы
сюръективны (для каждого гомоморфизма
гладкие прообразы имеют гладкие образы).
Найдите ядро каждого гомоморфизма.
7. ^Продолжение). Покажите, что если Q(Z) —
трансцендентное расширение поля Q, то це-
почка гомоморфизмов групп Q(Z) —> Q —> F/;*
сюръективна. Предложите метод логарифми-
рования, аналогичный методу решета число-
вого поля, использующий указанные свойства
гомоморфизмов.
8. *(Продолжение). Рассмотрите цепочку' сюръ-
ективных гомоморфизмов групп Q(a)(0 —>
-> Q(a) —> Q —> Fp*, где Q(a)(Z) — простое
трансцендентное расширение поля Q. Можно
ли понизить порядок v субэкспоненты Lp(c; v)
за счет указанного свойства гомоморфизмов?
Можно ли понизить порядок субэкспоненты,
используя дальнейшие алгебраические рас-
ширения полей?
9. Логарифмирование методом решета числово-
го поля требует субэкспоненциального объе-
ма памяти £р(с; ’/3). Чему равна константа с?
10. Число простых целых чисел, меньших п,
асимптотически равно w/lnw. Число непри-
водимых полиномов степени и в Fp[z] равно
—У\^п1 d]pd , где ц— функция Мебиуса.
п d\„
Как влияет различие плотностей распределе-
ния простых чисел и неприводимых полино-
мов на сложность логарифмирования?
11. Пусть подгруппа группы F/; имеет простой
порядок г. Найдите значение г, при котором
для р ® 21024 метод решета числового поля и
231
метод Полларда имеют одинаковую слож-
ность.
12. Сравните сложность логарифмирования (вре-
менную и емкостную) в группе (Z/pZ) для
простого р и в группе (Z/wZ) обратимых
элементов кольца для составного числа и с
неизвестным разложением.
13. Пусть а— образующая группы Fp и извест-
но разложение числа р - 1. Найдите обра-
зующую подгруппы порядка г, где г | (р - 1).
14. Предложите метод разложения, основанный
на использовании функций Лукаша над коль-
цом Z/nZ по аналогии с методом разложения
на эллиптических кривых.
15. Покажите, что множество решений над Q
уравнения Пелля х - dy2 = 1 образует под-
группу элементов с единичной нормой груп-
пы Q(VcQ , изоморфную аддитивной группе
точек коники над Q с таким же уравнением.
16. Коника C(Q): х2 - dy2 = 1 бирационально изо-
морфна прямой в силу параметризации
s2 d + 1 2s у „
х = ----, у = -^--, 5 = ——. Покажите,
s2d-l s2d-l х-1
что циклической группе, образованной точ-
кой коники, соответствует последователь-
ность подходящих дробей непрерывной дро-
би 1/y/d . Что собой представляет множество
образующих группы C(Q)?
17. (Продолжение). Покажите, что задача лога-
рифмирования в группе функций Лукаша
(или в группе точек супервырожденной эл-
липтической кривой) над эквивалентна за-
даче вычисления индекса подходящей дроби
для непрерывной дроби \/4d в Fp.
18. *Можно ли усилить метод решета числового
поля использованием мультиквадратичных
расширений исходного числового поля? На-
пример, присоединением к полю Q малых по
абсолютной величине дискриминантов, яв-
ляющихся квадратичными вычетами по мо-
дулю р2 Группа Галуа такого поля абелева;
идеал, гладкий в некотором расширении, ос-
тается гладким при остальных расширениях.
19. Как в методе решета числового поля можно
легко учесть влияние обратимых элементов
кольца Ок2
Литература к главе 10
1. Айерлэнд К., Роузен М. Классическое введение в
современную теорию чисел. М.: Мир, 1987.
2. Ахо А., Хопкрофт Дж., Ульман Дж. Построение и
анализ вычислительных алгоритмов. М.: Мир,
1979.
3. Писсаненки С. Технология разреженных матриц.
М.: Мир, 1988.
4. Ростовцев А.Г. Алгебраические основы крипто-
графии. СПб.: Мир и Семья, Интерлайн, 2000.
5. Adleman L. The function field sieve // Algorithmic
Number Theory. Lecture Notes in Computer Science.
Springer-Verlag. 1994. Vol. 877. P. 108-121.
6. Bleichenbacher D., Bosma W., Lenstra A.K. Some
remarks on Lucas-based cryptosystems // Advances
in Cryptology— CRYPTO ’95. Lecture Notes in
Computer Science. Springer-Verlag. 1995. Vol. 963.
P. 386-396.
7. Buchman J., Williams H.C. A key-exchange system
based on imaginary quadratic fields // Journal of
Cryptology. 1988. Vol. 1. P. 107-118.
8. Buchman J., Williams H.C. A key-exchange system
based on real quadratic fields // Advances in Ciyptol-
ogy— CRYPTO ’89. Lecture Notes in Computer
Science. Springer-Verlag. 1990. Vol. 435.
P. 335-343.
9. Coppersmith D. Fast evaluation of logarithms in
fields of characteristic two // IEEE Transactions on
Information Theory. 1984. Vol. IT-30. P. 587-594.
10. Gordon D. Discrete logarithms in GF(p) using the
number field sieve // SIAM Journal on Discrete
Mathematics. 1993. Vol. 6. P. 124-138.
11. Huhnlein D., Takagi T. Reducing logarithms in totally
non-maximal imaginary quadratic orders to logarithms
in finite fields. Technical report TI-99-08//
http://www.informatik.ru-darmstadt.de/ftp/pub/Tl/TR/
TI-99-08.asia-tr.ps.gz.
12. Menezes A., van Oorschot P., Vanstone S. Handbook
of Applied Cryptography. CRC Press, 1997.
13. Meyer A., Neis S., Pfahler T. First implementation of
cryptographic protocols based on algebraic number
fields // Information Security and Privacy 6th Aus-
tralasian Conference, ACISP 2001. Sydney, Austra-
lia. July 2001. Proceedings. Lecture Notes in Com-
puter Science. Springer-Verlag. 2001. Vol. 2119.
P. 84-103.
14. Pollard J. Monte Carlo methods for index computa-
tion (mod/?) // Mathematics of Computation. 1978.
Vol. 32. P. 918-924.
15. Silverman J. The arithmetic of elliptic curves.
Springer-Verlag, 1986. .
16. Smith P., Skinner C. A public-key cryptosystem and
a digital signature system based on the Lucas func-
tion analogue to discrete logarithms // Advances in
Cryptology— ASIACRYPT ’94. Lecture Notes in
Computer Science. Springer-Verlag. 1995. Vol. 917.
P. 357-364.
17. Vollmer U. Asymptotically fast discrete logarithms in
quadratic number fields // Algorithmic Number The-
ory: 4th International Symposium, ANTS-IV. Leiden,
the Netherlands. July 2000. Proceedings. Lecture
Notes in Computer Science. Springer-Verlag. 2000.
Vol. 1838. P. 581-594.
18. Weber D. An implementation of the general number
field sieve to compute discrete logarithms mod/? //
Advances in Cryptology— EUROCRYPT ’95. Lec-
ture Notes in Computer Science. Springer-Verlag.
1995. Vol. 921. P. 95-105.
19. Weber D. Computing discrete logarithms with the
number field sieve // Algorithmic Number Theory:
Second International Symposium, ANTS-II. Talence,
France, May 1996. Proceedings. Lecture Notes in
Computer Science. Springer-Verlag. 1996. Vol.
1122. P. 391-403.
Глава 11. ЗАДАЧА ДИСКРЕТНОГО ЛОГАРИФМИРОВАНИЯ
НА ЭЛЛИПТИЧЕСКОЙ КРИВОЙ
В этой главе рассматривается задача дискрет-
ного логарифмирования в группе точек эллипти-
ческой кривой над конечным полем и в якобиане
гиперэллиптической кривой. Порядок группы
предполагается известным. Это ограничение не
является существенным, так как вычисление по-
рядка группы не относится к трудным задачам.
Эллиптическая кривая Е(Ку. у2-fix) может
быть представлена двояко: геометрически — как
множество точек с групповым законом [1], и ал-
гебраически — в терминах поля функций
К(х)/(у~ -ДХ)) [2, 11]- При анализе стойкости ал-
горитмов на эллиптических кривых используют-
ся оба эти представления.
11.1. Универсальные методы
логарифмирования
В этом параграфе на примере эллиптических
кривых рассматриваются универсальные методы
логарифмирования, справедливые для произ-
вольной группы вычислимого порядка. г
Пусть Е(К)— эллиптическая кривая над ко-
нечным полем К, заданная уравнением Вейер-
штрасса [5, 9]
у2 + ауху + а3у = х3 + аух2 + аух + а(,,
где частные производные по х и по у полинома,
задающего кривую, не обращаются в нуль одно-
временно ни в одной точке кривой даже при пе-
реходе к алгебраически замкнутому полю, и
пусть Q е Е(К) — точка порядка г. Если харак-
теристика поля К отлична от 2 и 3, то уравнение
кривой можно записать в виде
у2 — х3 + Ах + В,
где кубический полином в правой части не имеет
кратных корней над алгебраически замкнутым
полем. Задача дискретного логарифмирования в
группе точек эллиптической кривой формулиру-
ется следующим образом: для данной точки
Р е (Q) найти показатель I такой, что Р = IQ.
Эта задача может решаться универсальными
методами Гельфонда, встречи посередине, «giant
step — baby step», встречи на случайном дереве и
методом Полларда, предложенным первоначаль-
но для логарифмирования в мультипликативной
группе простого поля [15]. В соответствии с ме-
тодом Гельфонда эта задача полиномиально сво-
дится к задаче логарифмирования в подгруппе
максимального простого порядка. Поэтому на
практике число г выбирают простым. Алгоритм
встречи посередине имеет временную сложность
O(Vrlogr) и емкостную сложность О(л[г ). Ал-
горитм встречи на случайном дереве имеет вре-
менную сложность O(-^rlogr) и емкостную
сложность (Хд/r/logr). Алгоритм Полларда
имеет сложность по времени (в операци-
ях сложения точек на кривой) и 0(1) по памяти.
Алгоритмы встречи посередине и встречи на
случайном дереве допускают эффективное рас-
параллеливание, тогда как алгоритм Полларда
распараллеливанию не поддается.
11.1.1. Метод Гельфонда : -л.
Метод А.О. Гельфонда1 базируется на основ-
ной теореме об абелевых группах (теорема 2.7.1),
утверждающей, что конечная абелева группа
раскладывается в прямое произведение цикличе-
ских групп, порядки которых являются степеня-
ми простых чисел. г
Алгоритм 11.1.1. Логарифмирование на эл-
липтической кривой методом Гельфонда.
Вход. Кривая Е(К) над конечным полем К;
образующая точка Q и точка Р е Е(К); разложе-
77
ние порядка группы: # Е(К} = N = р“’ .
/=1 ;
Выход. Логарифм I такой, что P = IQ.
Метод. ’-
1. Для i = 1, 2,..., п выполнить следующие дей-
ствия.
1.1. Положить q <— pt, а <— а,.
1.2. Положить S <r- Pw, k-\ <— 0. . . т
1 В зарубежной литературе этот метод называется
методом Силвера-Полига-Хеллмана. Советские мате-
матики предложили его примерно на 15 лет раньше [4].
234
1.3. Вычислить Q <-Q .
Я
1.4. Для j = О, 1,..., а- 1 выполнить сле-
дующие действия.
1.4.1. Положить S <— S + kj^q^Q,
N
Р'^^Р~^
1.4.2. Вычислить логарифм к> <— logyP'
любым алгоритмом (например,
алгоритмом Полларда).
1.5. Положить I,ко+k\q +... + k^q0-1 (mod q'J).
2. Восстановить логарифм I из I, по китайской
теореме об остатках.
3. Результат: I.
Для обеспечения стойкости к методу Гель-
фонда число N точек на кривой должно быть
простым или иметь большой простой делитель г.
Пусть число г является собственным делите-
лем числа точек эллиптической кривой £|(Fr).
Тогда может существовать эллиптическая кривая
£2(FP), изогенная над Fp кривой £|(FP), причем
изогения переводит подгруппу порядка г кривой
£i(Fp) в подгруппу порядка г кривой £2(Fr), а ду-
альная изогения переводит подгруппу порядка г
кривой £2(FP) в подгруппу порядка г кривой
£i(Fp). В этом случае можно с помощью изоге-
нии перейти от кривой £|(F/;) к вспомогательной
кривой £2(Fp) и искать логарифм на ней.
Пример 11.1.1. Логарифмирование на эллип-
тической кривой методом Гельфонда.
Пусть £(F97): уг = х3 + х + 9, N= 90 = 2 • З2 5,
Q - (34, 16), Р = (69,40). Нужно найти логарифм
I такой, что Р = IQ.
Для Р1=2: Q = 450 = (19,0), £' = 45£ = £а>.
Тогда ко = logo-P' = 2и71 = £о = 2 = О (mod 2).
Для р2 = 3: 2'= 30Q = (72, 49). На шаге 1.4
Р' = ЗОР = (72, 49) и ^O = logo-P'=l для у = 0,
Р' = 10(Р-2) = (72,48) и £ = log^P'= 89 для
J=l. Тогда Z2 = ко + Зк\ = 1 + 3 • 89 = 7 (mod 9).
Для = 5: 2' = 182 = (92,48), Р' = 18Р = (92,49).
Тогда ко = logyP' = 89 и 7з = £) = 89 = 4 (mod 5).
Восстанавливаем логарифм I по китайской
теореме об остатках: I = 34 (mod 90).
11.1.2. Методы встречи посередине
и «giant step — baby step»
Метод встречи посередине предполагает соз-
дание базы данных объема О(4г) из пар вида
(7,2, 0 для случайных lj и сортировку по х-ко-
ординате точки IjQ. Для случайных £ вычисля-
ются точки £Р и сравниваются с базой данных.
Равенство точек £Р = IjQ означает равенство их
показателей в циклической группе, то есть ра-
венство k,l = I,, откуда I = Ijk^ (mod г).
В основу метода встречи посередине положе-
ны следующие рассуждения. Пусть выборка объ-
ема т выбирается с возвращением из генераль-
ной совокупности объема г и т « г. Оценим ве-
роятность того, что в этой выборке не будет двух
одинаковых элементов. Эта вероятность равна
Прологарифмируем это равенство с учетом
того, что ln( 1 - х) « -х при х « 1.
^4 т - i ^4 i т(п: -1) w2
( 2\
т
£ = ехр .
2г
2г ’
(11.1.1)
Поэтому при т - О(4г) можно лолучить
сколь угодно близкую к 1 вероятность совпаде-
ния двух элементов выборки. Это свойств вы-
борки с возвращением называют парадоксом
дней рождения', если предположить, что дни ро-
ждения распределены равновероятно, то вероят-
ность совпадения дней рождения у двух челове,
в группе из 23 человек превышает 0,5.
Сложность метода встречи посередине опре-
деляется этапами создания базы данных и ее сор-
тировки. Сложность создания базы данных равна
<9(ТЙ , сложность сортировки равна O(Vrlogr).
Поэтому итоговая сложность алгоритма равна
(Х4г log г).
Детерминированным вариантом метода
встречи посередине является метод «giant step —
baby step» (см. п. 9.2.2). Здесь сначала вычисля-
ется целое число п, ближайшее к 4г. Затем вы-
числяются точки nQ, 2nQ, ..., n2Q, и полученная
база данных сортируется. После этого вычисля-
ются точки Р, Р - 2, Р - 22, • • - до совпадения с
какой-либо точкой из базы данных. Логарифм
можно представить в виде I =Jn + 7, где
0 < i,j < п. Поэтому встреча произойдет не поз-
же, чем после п шагов, что соответствует равен-
ству jnQ = P-iQ.
Этот метод основан на представлении показа-
теля I как элемента двумерной решетки. Переход
к решеткам большей размерности не позволяет
снизить сложность логарифмирования.
235
11.1.3. Метод Полларда
Метод Полларда (см. п. 9.3.1) требует исполь-
зования «случайного» отображения т, обладаю-
щего сжимающими свойствами и вычислимо-
стью логарифма (логарифм точки т(/?) можно
выразить через / и логарифм точки R). Наиболее
простая ситуация имеет место, когда в качестве
случайного отображения т(/?) используются
«ветвящиеся» отображения вида
(x,y) + Q, если х<р/3,
т(х,у) = Дх,у) + Р, если р/3 < х < 2р/3,
(x,y) + 2Q, если х>2р/3.
В первом случае logyT(7?) = loggA + 1, во вто-
ром случае IogyT(7?) = logo?? +1, в третьем случае
JogyT(/?) = log^J? + 2. Вид отображения и старто-
вой точки не принципиален. Если логарифм про-
образа является элементом кольца Fr[7], то и ло-
гарифм образа является элементом этого кольца.
Алгоритм 11.1.2. Логарифмирование на эл-
липтической кривой методом Полларда.
Вход. Кривая Е(К) над конечным полем К\
образующая точка Q и точка Р е Е(А); простой
порядок г группы (0.
Выход. Логарифм I такой, что Р = IQ.
Метод.
1. Выбрать отображение т, действующее на
Е(К), обладающее сжимающими свойствами
и сохраняющее вычислимость логарифма.
2. Выбрать произвольные показатели a, b, с, d и
положить R <— aQ + ЬР, S<-cQ + dP.
3. Выполнять /? <-т(/?), S' <— t(t(.S')), вычисляя
при этом логарифмы точек R и S в кольце
И>|7], до получения равенства R = ±S.
4. Приравняв логарифмы точек R и ±S, вычис-
лить логарифм 7 решением сравнения над по-
лем F,.. Если решения нет, то вернуться на
шаг 1, иначе результат: I.
Пример 11.1.2. Логарифмирование на эллип-
тической кривой методом Полларда.
Пусть E(F73): у2 = х3 + Зх + 9, г = 83, Q = (31, 6),
Р = (24, 53). Нужно найти логарифм I такой, что
P = lQ.
Выбираем отображение
т(х,у) =
(x,y) + Q, если х нечетное,
(х,у) + Р, если х четное.
В качестве стартовой точки выбираем точку
Q. Строим цепочки отображений т'(0 и т2'(0 до
получения равенства т'(0 = ±т2'(0. Результаты
вычислений приведены в табл. 11.1.
Встреча т'(0 = т2 (0 произошла на шаге 10 (в
таблице обозначено жирным шрифтом). Прирав-
ниваем логарифмы одинаковых точек по модулю
порядка группы: 13 + 8/ = 6 + 5/ (mod 83), откуда
находим логарифм 7 = 53 (mod 83).
Таблица 11.1
Решение задачи дискретного логарифмирования на эллиптической кривой методом Полларда
i 1 2 3 4 5 6 7 8 9 10
(П, 3) (50, 16) (48, 71) (70,22) (40, 53) (9,20) (69, 58) (23, 28) (22, 24) (0,3)
logT(0 2 3 3 + 7 3+27 3 + 37 3 + 47 4 + 47 5 + 47 6 + 47 6 + 57
Ло) (50, 16) (70, 22) (9, 20) (23, 28) (0, 3) (62, 55) (45, 47) (9, 20) (23, 28) (0,3)
logt2'(0 3 3 + 27 3 + 47 5 + 47 6 + 5/ 7 + 67 8 + 77 10 + 77 12 + 7/ 13 + 8/
С учетом того, что длина пути до входа в цикл
и длина цикла асимптотически равны ^(7tr)/8 и
на каждом шаге вычисляется три отображения,
сложность алгоритма Полларда в среднем со-
ставляет 4,57^)78 ® 2,82-х/г операций вычис-
ления отображения т. Обычно вычисление ото-
бражения т заключается в сложении точек.
11.1.4. Метод встречи иа случайном дереве
Метод встречи на случайном дереве аналоги-
чен методу встречи посередине и использует
сжимающие свойства случайного отображения.
Составляется база данных следующим образом.
Для случайных а,, Ь, вычисляется точка вида
R, = a,Q + btP, для которой выполняется к ото-
бражений т и запоминается пара (т*(7?,), log т*(Е,))
или траектория {(/?„ log/?,), (т(/?,), Iogr(/?,)), ...,
(т*(/?,), log ?(/?,))}. Логарифм каждой точки пред-
ставляет собой элемент кольца Fr[7], где I — не-
известный логарифм точки Р по основанию точ-
ки Q. Множество полученных точек и их лога-
рифмов образует базу данных, которая сортиру-
ется по х-координате. При совпадении двух то-
чек в базе данных приравниваются их логариф-
мы, и вычисляется 7 решением сравнения по мо-
236
дулю г. Алгоритм допускает распараллеливание.
Кроме того, вместо точек можно использовать
орбиты автоморфизмов.
Оценим сложность алгоритма при запомина-
нии конечных точек траекторий для к= O(logr).
Это значение выбрано исходя из того, что множи-
тель O(logr) появляется в результате сортировки
базы данных и выполнение O(log/') отображений
не изменит асимптотическую сложность алгорит-
ма. В этом случае встреча возможна на глубинах
не менее O(Jogr). Число точек с такой глубиной
равно (){//log г). Предположим, что после каждо-
го шага вероятность попасть в любую точку с
глубиной не менее O(logr) одинакова (если это не
так, то вероятность встречи после к шагов увели-
чивается, а сложность алгоритма падает). Тогда
достаточно иметь объем базы данных, в соответ-
ствии с (11.1.1) равный т = ()(-Jr/\og г). Алго-
ритм содержит два этапа: построение базы дан-
ных со сложностью О(т log г) и сортировку базы
данных со сложностью О(т iogm). Для итоговой
сложности S алгоритма справедливо неравенство
S < O(yjr\ogr); равенство достигается, если ве-
роятности попадания после к шагов в любую точ-
ку с глубиной не менее О(к) одинаковы.
Можно показать, что если запоминать не ко-
нечные точки траекторий для к шагов, а все тра-
ектории или некоторые их части, то асимптоти-
ческая оценка сложности не улучшается.
Рассмотрим метод встречи на случайном де-
реве подробнее.
Из каждой вершины графа случайного ото-
бражения исходит одна стрелка; в вершину, не
являющуюся листом, входит хотя бы одна стрел-
ка [3]. Выполнение одиночного шага для верши-
ны, лежащей на глубине ведет к вершине с
большей глубиной.
Пусть Nd. — число вершин с глубиной Д. Тогда
Nd^>Nd+i. Положим ANd^=Nd -Nd+i. Тогда из
Aj)+1 вершин, обладающих глубиной стрелки
ведут на глубину d\ + 1, а из АЛЦ вершин, обла-
дающих той же глубиной, стрелки ведут на про-
извольные глубины, превышающие d\ (рис. 11.1;
сплошные стрелки указывают на переход на оче-
редную глубину, пунктирные — на произвольную
глубину, превышающую начальную). Вероят-
ность такой стрелки привести на глубину d2 > d\
пропорциональна числу вершин на глубине d2.
Обозначим P(d) вероятность того, что глубина
вершины не менее J; p(d)— вероятность того,
что глубина вершины равна d. Вероятность
pi(J2|di) за один шаг попасть с глубины d\ на
_ , , p(dx +1) '* 5
глубину d2 > d\ равна ------ при d2 = d\ + 1;
pWi)
р(<4) fi р(<А+1)^ , . , , , ,
— — 1----------- при «2 >«i + l (второе
РД/т!)^ p(d^} )
условие соответствует пунктирным стрелкам на
рисунке 11.1; вероятность P(d\ + 1) в знаменате-
ле учитывает запрет перехода на глубины, мень-
Вероятность перехода на очередную глубину
с учетом частично перекрывающихся условий
для p\(d2 |J|) можно записать следующим обра-
зом:
f 1
PAd,+ 11 = Ж + 1) —тг+Ж)
1Ж) J
Подставляя р{dx)« 2/б/2, P(dx)K2]dx (см.
оценки в п. 1.4.2), получаем
px(dx+ 1 | dx)«2(^+1).
С учетом того, что
p{dx)~p(dx +1) 2 J,+1
p(d,)P(dt +1) dx 2
можно записать
Pi(d2\ dx) =
12(4+1),
P(d2),
если d2 = d, +1,
если d2 > dx +1.
Отсюда следует, что для больших глубин ве-
роятность пропуска очередной глубины при оди-
ночном шаге падает пропорционально квадрату
глубины, а вероятность попасть на глубину d2 в
результате такого пропуска приблизительно рав-
на безусловной вероятности попасть на глубину
237
d2, то есть не зависит от d\. Процесс спуска по
случайному дереву является марковским с мат-
рицей L = (pij) переходных вероятностей
ftGL/)=ft/
'0 2(1) Р(2) р(3)
L = 0 0 2(2) ХЗ)
0 0 0 2(3)
примерно равно log2 М « (log2 г)/2 . Отсюда оп-
тимальное значение
2г
у Рк (di)
P(di)
(11.1.4)
Назовем путем последовательность глубин,
Обозначим pd.di | d\) вероятность перехода с
глубины d\ на глубину d2 за к шагов. Матрица
переходных вероятностей за к шагов равна Lk
[10]. Обозначим pdd) суммарную вероятность
перехода на глубину dsak шагов:
d
Pk(.d)^P^Pk(d\iy
i=0
Пусть М«г— объем выборки, при котором
встреча после к шагов происходит с большой
вероятностью, например, 1/е. Вероятность
встречи зависит от глубины. Встреча не про-
изойдет, если ни на одной глубине в выборке не
окажется двух одинаковых вершин. Если на глу-
бину d попадут Md вершин, то вероятность того,
что среди них не будет двух одинаковых, равна
M2d
2rd)
где rd— общее число вершин дере-
ва с глубиной d. Если на глубины di попадут Md
вершин, то встреча произойдет с вероятностью
d, 2rd,
(11.1.2)
Поскольку Md. = Mpk(dt), rd. = rp(dd, вероят-
ность (11.1.2) можно записать в виде
у1 ft (^)
2г Х^,)
(11.1.3)
Таким образом, задача нахождения оптималь-
ного числа к шагов сводится к минимизации
суммы Мк + M\og2M, при условии, что выраже-
ние (11.1.3) дает 1. Отметим, что минимизация
слагаемого Мк невозможна, так как она требует
поиска максимума монотонно убывающей сум-
1 X Рк (di)
мы —v) ——— . Оптимальное число шагов
к d? РШ
которые встречаются в ходе спуска по дереву.
Вероятность pdd) будем искать как сумму веро-
ятностей путей длины к на глубину <7; число та-
ких путей равно
. Вероятность каждого пути
равна произведению вероятностей соответст-
вующих шагов.
Оценим значение Мъ формуле (11.1.4) снизу,
положив pid^-l/d^ и g(<7,) = 1. Путь длины к
имеет не более к пропусков очередной глубины.
Для вероятности п'(сГ) пути с j пропусками на глу-
бину d имеет место неравенство id(d) <p{d-j)a^d),
где <5,(d) = <з/р(0), ...,p(d-iy)—j-я симметриче-
ская функция. Положим
plidy^Pid-k)^/^- (И.1.5)
7=о
Тогда pk(d)<p*k(d).
Функция <5j(d) стремится к 0 с ростом j и d.
Например, для точных значений вероятностей:
01(64) = 0,603; а,(256) = 0,624; о,(1024) = 0,630;
о2(64) = 0,16; о2(256) = 0,172; о2( 1024) = 0,176;
о3(64) = 0,025; о3(256) = 0,028; о3(1024) = 0,029.
Сумму симметрических функций в (11.1.5) мож-
но оценить сверху числом 2.
Подставим (11.1.5) в сумму в правой части
(11.1.3) с учетом того, что pk(d^ = Q при i<k и
О(Р)
p(d) = Р{к). Получим: ---
d=k * «v
<^^(Pidj-k))2_________4_
fa p(d,) < £к p(d,) * Р(к) ’
Отсюда при к = 0,5 log2r получаем
М >O(-Jr/logr), то есть асимптотическая слож-
ность алгоритма встречи на случайном дереве
равна O^rlogr) и всегда превышает асимпто-
тическую сложность алгоритма Полларда. Одна-
ко алгоритм встречи на случайном дереве допус-
кает распараллеливание.
Аналогичными рассуждениями можно пока-
зать, что при запоминании не конечных вершин
238
после к шагов, а всех к вершин, встречающихся
при спуске, алгоритм Полларда улучшить также
невозможно.
Таким образом, доказана следующая теорема.
Теорема 11.1.1. Алгоритм Полларда невоз-
можно улучшить за счет увеличения объема памяти.
Пример 11.1.3. Логарифмирование методом
встречи на случайном дереве.
Решим ту же задачу, что и в примере 11.1.2, с
помощью того же отображения, используя три
параллельных процессора. Сложность сортиров-
ки базы данных отдельно не учитывается. Запо-
минаем траектории (х-координаты). Для каждой
стартовой точки делаем четыре последователь-
ных отображения. Процесс решения показан в
таблице 11.2.
Получаем равенство х-координат первого
процессора на шаге 0 и третьего процессора на
шаге 4. Поскольку (31, 67) = -(31, 6), приравни-
ваем логарифмы с учетом знака: 37 + 6 = -1
(mod 83), откуда 1=53 (mod 83).
Таблица 11.2
Логарифмирование методом встречи
на случайном дереве
i 0 1 2 3 4
1 -й процессор р, e=(3i,6) (17,3) (50, 16) (48,71) (70, 22)
log(4) । 2 3 7+3 27+3
2-й процессор р, Р = (24, 53) (61,17) (56, 70) (28, 27) (45, 47)
log(4) 1 27 27+ 1 37+ 1 47+ 1
3-й процессор р, 5Q = (63,1) (28, 46) (56, 3) (2, 13) (31,67)
log(4) 5 6 7 + 6 27 + 6 37+6
Сжимающие свойства случайного отображе-
ния наиболее заметны лишь на малых глубинах,
что проявляется в виде увеличения средней глу-
бины до O(logr) после одиночного шага от листа.
Каждый последующий шаг увеличивает глубину
на 0(1). Использование композиции отображений
не усиливает сжимающие свойства, так как после
первого отображения можно попасть в вершину,
которая является листом для второго отображе-
ния. Поэтому композиция отображений ведет себя
как одиночное отображение.
11.1.5. Сравнение сложности
логарифмирования на эллиптической
кривой и в конечном поле
Сравнительный анализ сложности Sec лога-
рифмирования на эллиптической кривой мето-
дом Полларда и сложности логарифмирования в
конечном поле 4 приведен в табл. 11.3 и 11.4
[7]. Значение с= 1,92 соответствует методу ре-
шета числового поля при «правильном» выборе
характеристики поля; с = 1,57 соответствует ме-
тоду Копперсмита для поля характеристики 2.
Кроме того, с учетом тенденции снижения кон-
станты с по опыту предшествующих алгоритмов
логарифмирования, рассмотрен и случай с = 1.
Предполагается, что гкд.
Отметим, что методы Полларда и решета чи-
слового поля сильно разнятся, поэтому их срав-
нение в табл. 11.3, 11.4 носит приблизительный
характер. Кроме того, алгоритм Полларда, в от-
личие от алгоритма решета числового поля,
практически не требует памяти.
Таблица 11.3
Сложность дискретного логарифмирования на эллиптической
кривой и в конечном поле для одного и того же размера задачи
10g2<? 100 200 300 400 500 700 1000
Sec ю16 ю31 ю46 ю61 ю76 ю106 ю151
4(1; 73) ю5 107 10я 10у ю10 ю'1 ю13
4(1,57; 73) 10' 101и 10й ю14 ю16 101* 10"1
4(U92; 73) 10У 10й ю15 ю'7 ю19 10~2 ю26
239
Таблица 11.4
Размер задачи (Кбит) для одинаковой сложности S дискретного
логарифмирования алгоритмом Полларда (строка 2) и субэкспоненциальным
алгоритмом для различных коэффициентов с (строки 3-5)
logioS 10 20 30 40 50 60 70
г 0,066 0,132 0,199 0,266 0,332 0,399 0,465
^(с= 1) 0,5 2,5 6,5 — — — —
q (с =1,57) 0,2 0,9 2,2 4,5 — — —
q (с =1,92) 0,12 0,6 1,4 2,8 4,7 — —
11.1.6. Логарифмирование с помощью
квантового компьютера
Квантовый компьютер позволяет вычислить с
полиномиальной сложностью дискретный лога-
рифм в произвольной циклической группе вы-
числимого порядка алгоритмом Шора. Если по-
рядок (и структура) группы является трудновы-
числимым по отношению к традиционной вы-
числительной модели, то квантовый компьютер
позволит и его вычислить с полиномиальной
сложностью по аналогии с вычислением порядка
элемента в группе (Z/wZ) (см. п. 9.3.6). Соглас-
но результату А.О. Гельфонда задача дискретно-
го логарифмирования в произвольной цикличе-
ской группе сводится к задаче дискретного лога-
рифмирования в подгруппе простого порядка г.
Пусть G — произвольная аддитивная цикли-
ческая группа простого порядка г. Решение зада-
чи дискретного логарифмирования в группе G
(для двух элементов Р, Q е G найти показатель /
такой, что Р = 70 сводится к задаче нахождения
таких двух показателей 12, что liQ + l2P = O,
где О— нулевой элемент группы G. Тогда
/ = (mod г).
Для решения задачи дискретного логарифми-
рования требуются три квантовых регистра.
Первый регистр содержит первый показатель а,
второй регистр — второй показатель Ь, в третьем
регистре обратимым образом вычисляется эле-
мент aQ + ЪР е G.
Алгоритм 11.1.3. Вычисление дискретного
логарифма на квантовом компьютере.
Вход. Элементы Р, Q е. G, порядок группы г.
Выход. Логарифм I такой, что Р = 1Q.
Метод (первые четыре шага выполняются на
квантовом компьютере, последний шаг — на
обычном компьютере).
1. Инициализировать из состояния |0), |0) первых
двух регистров суперпозицию
Г afi
2. Обратимым образом вычислить
Г а,Ь
3. Вычислить преобразование Фурье первого и
второго регистров:
г а=0Ь=0
4. Измерить состояние трех регистров (Ц; 12,
liQ + hP).
5. Вычислить логарифм 1 = -Ц12 1 (mod г). Ре-
зультат: логарифм I.
На втором шаге состояние третьего регистра
описывается всевозможными суммами aQ + ЬР e G,
где а, b пробегают все множество Z/rZ. Если
diQ + biP = d2Q + b2P, то (а2,b2) = (ai, bi)+ Х(!,/),
где X е Z/rZ.
Пусть на четвертом шаге состояние третьего
регистра равно То = dQ + ЬР = c^Q. Тогда
а = С(}-Ы (mod г) и первые два регистра имеют
состояние
4=2(| c0-W(modr)>,|7>». (11.1.6)
Vr ь=о
Элементы матрицы преобразования Фурье —
это характеры порядка г. При этом
Х/1 ,/2 («> Ъ) = е2т(а11 +Ь>2 )/г Равенство %/(h (a, b) = 1
выполняется тогда и только тогда, когда
d/t + bl2 = 0 (mod г). Обозначим %] = е2га^'. Пре-
образование Фурье действует на квантовый ре-
гистр следующим образом:
Vr к=о
и позволяет исключить зависимость результата
от случайных коэффициентов d, b. Действитель-
но, поскольку сумма характеров, входящих в
преобразование Фурье, в остальных случаях ну-
левая, первые два регистра при измерении могут
находиться только в состоянии, соответствую-
240
щем единичным значениям характеров. Поэтому
применение преобразования Фурье к первым
двум регистрам (11.1.6) даст вектор состояний
1 gА(| Z] е _/Z2 (modr)>,| Z2>).
4г i1=Q
Измерение состояния первого и второго реги-
стров даст пару (Zb Z2) = (-ZZ2, /2), где Z2 е —
случайная величина. Тогда I = -Z]Z2-1 (mod г).
Алгоритм 11.1.3 применим для вычисления
дискретного логарифма в произвольной цикли-
ческой группе вычислимого порядка. При этом
необходимо адаптировать квантовый компьютер
для вычислений в соответствующей циклической
группе. Сложность вычисления логарифма на
квантовом компьютере для произвольной адди-
тивно записанной циклической группы равна
O(logr) операций сложения элементов группы.
Для эллиптической кривой E(Fr) и для группы
Ну, сложность вычисления логарифма равна
O((logp)3) логических операций. Для вскрытия
ключа подписи стандарта ECDSS (см. п. 15.6.5)
длина квантовых регистров должна быть около
103 кубитов.
11.2. Влияние комплексного умножения
на сложность логарифмирования
Пусть К — конечное поле из q = рп элементов
и Е/К — эллиптическая кривая, заданная в форме
Вейерштрасса:
у2 + а\ху + еру = х3 + «2х2 + аух + а(„ (11.2.1)
где а, К. Точки (х, у) кривой, как решения
уравнения (11.2.1), могут лежать в алгебраиче-
ском расширении поля К. При переходе^ алгеб-
раически замкнутому полю кривая Е(К) имеет
бесконечное число точек^ Предположим, что эл-
липтическая кривая Е(К} обладает комплекс-
ным умножением, то есть End(E) о Z.
Комплексное умножение позволяет, с одной
стороны, ускорить вычисления на эллиптической
кривой (подробнее см. п. 15.4), с другой сторо-
ны, снизить сложность логарифмирования.
Рассмотрим эллиптическую кривую E(Fr), где
р = 1 (mod 6), заданную неполным уравнением
у2 = х3 + В, при этом j = 0. В поле Fp существует
-1 + 7=3 _
элемент со =----------кубический корень из
единицы. Эта кривая обладает комплексным ум-
ножением ср: (х,у) -> (сох, -у), причем по опреде-
лению ф(Лл) = Рсо- Имеет место равенство
ср3(Р) = -Р, что соответствует характеристиче-
скому уравнению
ср2-<р+1 = 0. (11.2.2)
Отображение ср является автоморфизмом эл-
липтической кривой, его степени образуют груп-
пу порядка 6 по умножению.
Теоретически возможны два случая: 1) отобра-
жение ср действует внутри подгруппы (Q) порядка
г; 2) отображение ср действует из одной подгруп-
пы порядка г в другую подгруппу порядка г. Од-
нако в криптосистеме вторая ситуация на практи-
ке невозможна, так как число г по порядку величи-
ны должно быть близко к числу точек (см. гл. 15).
Поскольку бесконечно удаленная точка оста-
ется неподвижной под действием ср, то из (11.2.2)
заключаем, что г - 1 = 0 (mod 6). Таким образом,
все аффинные точки группы (Q) разбиваются на
шестерки, которые являются орбитами группы
{Q) относительно группы автоморфизмов. Орби-
та, содержащая точку (х,у), полностью опреде-
ляется одним из значений х3 или у2. Логарифмы
точек орбиты связаны вычислимым соотношени-
ем, поэтому знание логарифма одной из точек Pi
орбиты позволяет вычислить логарифм любой
другой точки Р2 этой же орбиты. Для этого дос-
таточно решить показательное уравнение
ср'(Р]) = Р2 относительно t, где 1 < t < 5.
Поэтому при логарифмировании методом
Полларда (а также любым другим методом) можно
расширить понятие встречи, используя равенство
не для точек, а для орбит. Это расширение потре-
бует вычисления значения у для каждой точки
тА(Р). Поскольку эта операция значительно проще,
чем сложение точек, ее сложностью можно пре-
небречь. При достижении встречи орбит лога-
рифмы точек можно легко уточнить. Таким обра-
зом, можно получить снижение сложности лога-
рифмирования по сравнению с п. 11.1 в л/З раз.
При этом сложность алгоритма Полларда соста-
вит 1,99э/г операций вычисления отображения т.
Пусть теперь р = 1 (mod 4) — простое число.
Тогда существует элемент i е Fr такой, что
z2 = -1. Эллиптическая кривая с неполным урав-
нением у2=х3 + Лх с инвариантом 7= 1728, за-
данная над полем Fr, обладает комплексным ум-
ножением вида ср: (х, у) -> (-х, iy), причем
<p(Pco) = Р«>. Оператор комплексного умножения
удовлетворяет характеристическому уравнению
ср2 1. < - (11.2.3)
Отображение ср является автоморфизмом эл-
липтической кривой, его степени образуют груп-
пу порядка 4 по умножению.
241
Будем считать, что отображение ср действует
внутри группы (0. Тогда из (11.2.3) следует, что
г - 1 = 0 (mod 4). Таким образом, все аффинные
точки группы (0 разбиваются на четверки, ко-
торые являются орбитами группы (0 относи-
тельно группы автоморфизмов. Орбита, содер-
жащая точку (х. у), полностью определяется зна-
чением х2. Логарифмы точек орбиты связаны вы-
числимым соотношением, поэтому знание лога-
рифма одной из точек Рг орбиты позволяет вы-
числить логарифм любой другой точки Р2 этой
же орбиты. Для этого достаточно решить показа-
тельное уравнение срД/Д) = Р2 относительно t, где
1<;<3.
Проводя рассуждения, аналогичные случаю
р = 1 (mod 6), получаем снижение сложности ло-
гарифмирования по сравнению с л. 11.1 в у/2 раз,
то есть сложность алгоритма Полларда составит
1,99д/г операций вычисления отображения т.
Пусть E/Fp — эллиптическая кривая, рассмат-
риваемая над конечным расширением F£/ поля F/3,
где q=pn- Тогда на кривой £(F,;) эндоморфизм
Фробениуса ср: (х,у) (хр,ур), где ср(Рто) = Роо,
действует как комплексное умножение. Опера-
тор комплексного умножения удовлетворяет ха-
рактеристическому уравнению
ср2-Тср+р = 0, (11.2.4)
где Т=р + 1 - #E(FP)— след эндоморфизма
Фробениуса. Отображение ср является автомор-
физмом эллиптической кривой, оставляющим
неподвижными точки с координатами из F/3, сте-
пени этого автоморфизма образуют группу по-
рядка п по умножению. Один из двух комплекс-
ных корней уравнения (11.2.4) задает показатель,
на который умножается точка с помощью эндо-
морфизма Фробениуса.
Как и прежде, будем считать, что отображе-
ние ср действует внутри группы (0. Тогда из
(11.2.4) следует, что г - 1 = 0 (mod и). Таким об-
разом, все аффинные точки группы (0 разбива-
ются на орбиты относительно группы автомор-
физмов. Орбита, содержащая точку (х,у), опре-
деляется любой симметрической функцией отно-
сительно степеней автоморфизма <р, например,
следом х-координаты:
Тг(х) =х + хр + хр + ...+хр .
Чтобы вычислить логарифм точки Р? орбиты,
зная логарифм точки Р\ этой же орбиты, доста-
точно решить показательное уравнение ср'(Рi) = Р2
относительно t, где 1 < 1 < п - 1.
Сложность логарифмирования снижается по
сравнению с п. 11.1 в Уп раз, то есть сложность
алгоритма Полларда составит 2,82^ г/п опера-
ций вычисления отображения т.
Рассмотренные эллиптические кривые обла-
дают вычислимыми орбитами автоморфизмов,
что позволяет несколько снизить сложность ло-
гарифмирования. Список кривых, для которых
применим метод логарифмирования на орбитах
автоморфизмов, может быть расширен за счет
использования изогений малых степеней. На-
пример, если рассматриваемая эллиптическая
кривая изогенна кривой с j = 0, то можно перейти
от исходной кривой к кривой с j~ 0 и вычислить
логарифм с использованием орбит (см. п. 15.4 и
приложение).
11.3. Логарифмирование
с использованием функции Вейля
Пусть Е(К)— эллиптическая кривая, Р, Q,
R — точки этой кривой и Р№ — бесконечно уда-
ленная точка. Пусть fa nfP — функции Вейля на
эллиптической кривой с дивизорами
div(£) = Г(0 - r(Pro); divtf,) = г(Р) - г(Рго).
Выберем дивизоры нулевой степени
Do = (0 - 0Д Dp = (Р + R)- (Я).
Спаривание Вейля ер. £[г] {ц, }, отобра-
жающее группу кручения порядка г в группу
корней степени г из единицы для алгебраическо-
го расширения L/К, вычисляется как функция
е,(Л0
fo(Dp)
fp(DQY
где
fQ(DP) =
. fo(R) ,
— значения функций на дивизорах. Спаривание
Вейля может быть вычислено алгоритмом И.А. Се-
маева с использованием функций Вейля (см. ал-
горитм 7.11.1, а также гл. 7 работы [6]).
Пусть Q — точка порядка г на кривой £(Fg),
причем НО ДО', q) = 1. Тогда существует конеч-
ное расширение L поля Fq такое, что #L = О
(mod г), а спаривание Вейля задает вложение
£(F9) L . Задача логарифмирования на эллип-
тической кривой сводится к логарифмированию
в мультипликативной подгруппе конечного поля
L субэкспоненциальным алгоритмом (см. гл. 10).
Спаривание Вейля задает изоморфизм из группы
£(F£/) в подгруппу порядка г группы L .
242
Оценим степень расширения zzz = (Z:F?), при
которой не происходит снижения стойкости за
счет использования спаривания Вейля. Слож-
ность субэкспоненциальных алгоритмов типа
алгоритма Копперсмита оценивается формулой
6' = ’/3) (см. гл. 10). Приравняем сложности
алгоритмов Полларда и Копперсмита:
П" _ т In <7)(ln In qm )2
Возведем в куб логарифмы обеих частей с
учетом равенств In-Jr — lnr/2 и г « q:
(In g)3 * * * = 8c3(m In </)(ln In «у'")2
или
(ln^)2 = 8mc3(lnln9m)2.
Численное решение этого уравнения относи-
тельно т в зависимости от q для различных зна-
чений с приведено в таблице 11.5.2
Таблица 11.5
Степени расширения т исходного поля,
при которых использование спаривания
Вейля неэффективно
log2g 100 150 200 250 300 350 400
с= 1 71 141 232 342 470 617 782
с= 21 42 67 99 136 178 225
с = 1,92 12 24 39 58 78 103 129
Метод, основанный на спаривании Вейля,
особенно эффективен, если #E(Fp)=j>-l или
#E(Fp)=p + 1. Второй случай соответствует су-
первырожденной кривой, например, заданной
уравнением у2 = х3 + В (mod р), где р = 5 (mod 6),
или у2 = х3 + Ах (mod р), где р = 3 (mod 4).
Этот метод эффективен и для некоторых эл-
липтических кривых над расширенными полями.
Например, эллиптическая кривая E/Fy у2+у =
= х3 '+ 1 с нулевым J-инвариантом и нулевым зна-
чением следа отображения Фробениуса имеет
над 1F2„ число точек N„ = 2" + 1 - q + 1. Следова-
тельно, группа точек такой кривой вкладывается
в мультипликативную группу поля F^.
2 Вычисление логарифма в конечном поле мето-
дом решета поля функций или методом Копперсмита
требует большого объема памяти. Если объем памяти
значительно меньше требуемого, то временная слож-
ность увеличивается по сравнению с общепринятой
оценкой. При ограничении на объем памяти степени
расширения, указанные в таблице, снижаются.
Другим примером является эллиптическая
кривая E/Fy. у2+у = х3 + х+1 с нулевым j-
инвариантом, имеющая одну точку над F2 и, сле-
довательно, значение следа отображения Фробе-
ниуса, равное 2. Характеристическое уравнение
отображения Фробениуса имеет вид ср2 - 2ср + 2 = 0.
Его корни равны 1 ± z, где z2 = -1. Эта кривая над
полем из 2" элементов имеет число точек
N„ = 2" + 1 - (1 + i)" - (1 - z)'7.
Преобразуем последнее выражение:
Nn=2n 1 + 2-'!-| — | -f—|
( 2 ) ( 2 )
„ I 1 + Z 1 I 1-z)
Значения суммы 5 = 1 —I +1 —— \ степе-
ней сопряженных характеров степени 8 приведе-
ны в таблице 11.6. В первых двух случаях число
точек является квадратом целого числа, такие
кривые нецелесообразно использовать в крипто-
графии. В остальных случаях для логарифмиро-
вания можно использовать спаривание Вейля для
расширений степени 2, 4 и 4 соответственно.
Таблица 11.6
-\п (л -\п
jl + i]
Значения суммы 5 = I —— I +1 —— I
п (mod 8) 5 N„
0 2 7V„=2'’+l+22+I = (22+1)2
4 -2 11 (О s i - 1 A 1 м 1 b->la 1 1 I to 1
±2 0 N„ = 2'7 +1
±1 1 Д±1 N„=2"+l + 2 2
±3 -1 jh4 N„=2n +1-2 2
Таким образом, задача логарифмирования на
эллиптической кривой E/F2 с нулевым j-
инвариантом сводится к логарифмированию в
поле степени расширения не более 4, то есть та-
кие эллиптические кривые тоже не годятся для
криптографии.
Если порядок группы (0 равен р, то функция
Вейля позволяет установить вычислимый в обе
стороны изоморфизм группы (0 с аддитивной
группой поля Fp. Этот изоморфизм устанавлива-
ется с помощью логарифмической производной
[16]. Обратный изоморфизм вычисляется путем
умножения точки Q на элемент поля F/;. В основу
метода логарифмирования положены следующие
утверждения.
243
Теорема 11.3.1. Пусть К— поле характери-
стики р > 3 и Е(Ку. у2 = х3 + Ах + В — эллиптиче-
ская кривая, имеющая циклическую подгруппу
(Q) порядка р. Пусть fo— функция на кривой
Е(К) с дивизором div(/o) =/?(0-/>(А) и
, df0
fo =—— — полная производная. Тогда
dx
div(/g) = div(A) - div(y).
Доказательство см. в работе [16].
Теорема 11.3.2. Пусть R е (Q). Тогда функ-
f'
ция — (R) в точке R определена корректно,
/р
f f
—(Рю) = 0, функция — задает изоморфное
/о fo
вложение группы (0 в группу Fp.
Доказательство см. в работе [16].
Для вычисления логарифма строится цепочка
отображений
Jo
где fo— функция Вейля, —(7?) — значение ло-
/е
гарифмической производной функции Вейля в
точке R, причем точка R имеет ненулевую у-
координату. Логарифмическую производную
можно вычислить алгоритмом 7.11.2 (см. также
работу [6]). Для нахождения логарифма / такого,
что Р = IQ, нужно вычислить дробь
^(/?)
------(mod/?).
JQ
Таким образом, задача дискретного логариф-
мирования в случае г=р решается легко и не
может быть положена в основу безопасности
криптографических алгоритмов с открытым
ключом. Однако ее можно использовать при раз-
работке криптографических алгоритмов шифро-
вания с секретным ключом на эллиптической
кривой £(F,,) (ключом является уравнение кри-
вой и характеристика поля (см. п. 15.6.4)), для
построения корректирующих кодов, а также в
качестве сертификата того, что составное число
свободно от квадратов.
Если эллиптическая кривая рассматривается
над кольцом Z/hZ, где п = pq— произведение
двух различных простых чисел и = р,
#E(fr4) = q, то #£(Z/«Z) = п. К такой эллипти-
ческой кривой применим метод логарифмиче-
ской производной над Если #E(YP) = q,
#£(F,;) =р, то тоже #£(Z/«Z) = п. Однако в этом
случае метод логарифмической производной над
ТПпЕ. не работает, так как аффинные координат-
ные кольца кривых над не изоморфны.
11.4. Другие задачи, связанные
с логарифмированием
Покажем, что сложность вычисления лога-
рифма на эллиптической кривой зависит от
сложности решения двух задач. Первая зада-
ча — поднятие точки эллиптической кривой из
конечного поля в бесконечное (числовое поле
или поле рациональных функций). Вторая за-
дача— нахождение вычислимой функции на
эллиптической кривой, обладающей дивизором
с большим носителем и такой, что логарифмы
точек, входящих в дивизор функции, перечис-
лимы.
Эллиптическая кривая ?
Е(Кр.у=х3 + Ах + В, (11.4.1)
заданная над числовым полем К= Q(6|, ..., 0,„),
может быть приведена по модулю р, если 0, е F,,.
Действительно, переходя к проективной форме,
получим уравнение кривой Y2Z = X3 + АХ2Z + BZ3
с эквивалентностью (Х\, Y}, Z) = (Х2, Y2, Z2), если
A A y} y2 7
—L =—для ненулевых Z„ и
Z,j Zi 2 Z j Z2
A A z, z2 v
—L = —L = —- для ненулевых Y,. Умножив
Т] Y2 I] Y2
координаты точки на наибольший общий дели-
тель знаменателей, получим целочисленные ко-
ординаты, которые допускают редукцию по мо-
дулю р. Поскольку НОД(Л", Y, Z) = 1, то ситуация
Х= Y=Z=0 (modр) невозможна и отображение
£(£) E(Yp) определено корректно. Сложение
точек описывается рациональными функциями,
допускающими редукцию по модулю р. Если при
сложении точек знаменатель углового коэффи-
циента касательной или секущей делится на р, то
полученная сумма соответствует бесконечно
удаленной точке кривой £(FP). Таким образом,
редукция по модулю р определена и задает го-
моморфизм абелевых групп
<p:£(A)->£(IFp).
(11.4.2)
244
Обратно, кривая
£(Ff): у1 = х3 + Ах + В (modр) (11.4.3)
может быть вложена в кривую Е(К). Будем назы-
вать отображение точки Q е £(Ff) в точку
Q е Е(К) поднятием точки из поля Fp в поле К,
при этом сравнение (11.4.3) превращается равен-
ство (11.4.1). Сумме точек кривой Е(К) соответ-
ствует сумма точек кривой £(F;,). Поэтому задача
вычисления (векторного) индекса на кривой Е(К)
соответствует задаче вычисления индекса на
кривой £(FP) относительно образующих кривой
Е(К). Группа точек кривой Е(К) бесконечна, ка-
ждой точке кривой £(F;,) соответствует беско-
нечно много точек кривой Е(К).
Пусть #Е(^р) = г, где г — простое число. Если
бесконечная группа точек кривой Е(К) циклична
с образующей Pi, то ядро гомоморфизма (11.4.2)
имеет вид
Кег(<р) = пгР\,
где п е Z, а точке Р = кР\, где к е F,., на кривой
£(FP) будет соответствовать множество точек
к + пгР\ на кривой Е(К).
Пусть бесконечная группа точек кривой Е(К)
без кручения имеет две образующих Pi и Р2 и на
кривой £(Ff) выполняется равенство <р(Р2)= Mp(Pi),
где s е F,-. Ядро гомоморфизма включает в себя
целочисленные линейные комбинации образую-
щих, кратные г. Кроме того, в ядро входят ком-
бинации образующих, гомоморфный образ кото-
рых дает бесконечно удаленную точку, напри-
мер, sPi - Р2, (2s (mod r))Pi - 2Р2 и т. п. Тогда
Ker(<p) = nirP\ + n2rP2 + (ms (mod r))Pi - тР2,
где «1, п2 е Z и т е F,-.
Обобщим предыдущее рассуждение. Пусть
бесконечная группа точек кривой Е(К) без кру-
чения имеет к образующих Pi, ..., Рк и на кривой
£(F;,) выполняются равенства <p(Pt) = si<p(Pj) =
= ... = sk-i<p(Pk-i). Тогда
к к-1
Ker(<p) = ^«,rP/ +^(m;s;(modr))Pi -
?=] /=1
к—] Л
- ZX (modr)pfc»
0=1 J
где и, е Z, m, е F,..
Каждая точка эллиптической кривой Е(К) од-
нозначно (с точностью до точки кручения) опре-
деляется канонической высотой (см. п. 6.13).
Точка кручения имеет нулевую высоту. Группа
точек кривой Е(К) бесконечного порядка (группа
Морделла-Вейля) конечно порождена в соответ-
ствии с теоремой Морделла-Вейля [17]. Индекс
ind(P) каждой точки R е Е(К) может быть пред-
ставлен как вектор, число координат которого
равно рангу кривой.
Равенство (6.13.1) устанавливает связь задачи
логарифмирования на эллиптической кривой
£(FP) и задачи вычисления векторного индекса
поднятой точки кривой Е(К).
Пример 11.4.1. Индекс точки бесконечного
порядка.
Эллиптическая кривая у2 = х3 + 17 имеет над
полем Q ранг 2 [13]. Образующие групп беско-
нечного порядка равны Pt = (2, 5) и Р2 = (-2, 3),
индекс точки бесконечного порядка является
двумерным вектором. Точка R с координатами
<1466 56857^1
у 169~ * ~ 2197 J представляется в виде
R = 3Pi - 2Р2, ее индекс: ind(£) = (3, -2). При пе-
реходе к расширению Q^) кольцо целых
Jl + V^T
квадратичных чисел имеет вид Z ----------- ,
кривая обладает комплексным умножением на
число р = -— , задаваемое парой функции
(х, у) (р2х, -у). Поскольку число р не является
рациональным, то множество образующих уд-
ваивается, то есть образующими становятся так-
же точки
(2р2,5)^Г2-~1 + л/=^,51
У 2 )
Пусть Н= (hy) — квадратная матрица размера
к, где к — ранг кривой Е(К),
h(P, + Р^-КР.У-КР,)
и Pi, ...,Рк-— образующие циклических групп
бесконечных порядков. Тогда имеет место ра-
венство [17]
hy(niPl + ... + nkPk) = nEIn[, (11.4.4)
где п = («|, ..., «/.)— векторный индекс ind(P)
точки Р = п\Р\ + ... + пкРк. Определитель матри-
цы Н является положительным вещественным
числом и называется регулятором эллиптиче-
ской кривой Е(К). Выражение (11.4.4) устанав-
ливает связь между канонической высотой про-
извольной точки кривой Е(К) и ее индексом.
Задача поднятия точки требует указания всех
двоичных разрядов координат точки кривой
245
Е(К). Длина координат пропорциональна квадра-
ту показателя. Задача поднятия является слож-
ной, так как перечисление всех разрядов коорди-
нат требует экспоненциального времени (даже
без учета сложности собственно вычислений).
Однако, если ранг к кривой Е(К) достаточно ве-
лик, то на ней существует значительное число
точек с малой высотой. Ранг эллиптической кри-
вой, обладающей комплексным умножением,
может быть вычислен с помощью так называе-
мой L-функции в предположении, что верна ги-
потеза Берча и Свиннертона-Дайера [17].
Определим вес w = w(P) точки Р е Е(К) на то-
чечной решетке как сумму абсолютных величин
координат векторного индекса. Если ind(P) =
= (п\,пь), то w(P) = |И]| + ... + |/д]. Число точек
N(w) с весом w в соответствии с известным ре-
зультатом из комбинаторики равно
вд^(^|)...(^и.^)(1145)
w! У w J
Если k = O(w), то число точек с весом не бо-
лее w можно оценить числом точек с весом w.
Вес является вычислимой функцией точки, спо-
соб вычисления основан на минимизации кано-
нической высоты.
Оценим сложность нахождения индекса точки
к
Р е Е(К), Р = ^, , если ранг кривой Е(Х) ра-
<=1
к
вен к и вес точки Р не превышает w, и, | < w .
/=!
Из (11.4.4) следует, что каноническая высота
точки Р приближенно равна O(kw2).
Для нахождения индекса точки Р е Е(К) нуж-
но к точке Р прибавлять точки ±Р, до тех пор, по-
ка не будет получена нулевая каноническая высо-
та. После каждого сложения высота должна
уменьшаться. Число сложений точек в ходе вы-
числения индекса равно O(kw). Наиболее трудо-
емкой арифметической операцией при сложении
точек является умножение. Сложность умноже-
ния целых чисел методом Шенхаге-Штрассена
(см. п. 7.1.3) равна O(Aw2log(AM’2)). Пусть поле К
является конечным расширением поля Q, полу-
ченным присоединением квадратных корней из т
небольших по абсолютной величине чисел, каж-
дое из которых является квадратичным вычетом
по модулю р. Координаты точки представляют
собой полиномы от 2“ переменных. Сложность
умножения координат равна O(2mbv2log(hv2)).
Такую же оценку имеет и сложность сложения
точек. Поэтому сложность нахождения индекса
точки Р е Е(К) равна
S = O(2m^w3log(bv2)).
Предположим, по аналогии с теоремой Мазу-
ра [14], справедливой для случая A"=Q, что
группа кручения эллиптической кривой над по-
лем К может иметь только гарантированно ма-
лый порядок, меньший чем г. Тогда общий план
решения показательного уравнения P = IQ на
кривой E(Ff) может иметь следующий вид.
1. Поднять из поля F,, в поле К не менее к точек
Rt = а,Р + bjQ для некоторых а„ определив
при этом вид поля К. Не все а, и Ь, должны
быть нулевыми.
2. Найти образующие Р}, ..., Д свободных под-
групп группы Е(К) (в силу теоремы Мордел-
ла-Вейля множество образующих конечно).
3. Найти векторные индексы точек R, в группе
Е(К) путем последовательной минимизации
канонической высоты.
4. Методом гауссова исключения найти логарифм
точки Р относительно точки Q в поле F,..
Ранг и множество образующих группы Е(К)
вычислимы [19]. Найдем сложность шагов 3, 4.
Заменим в (11.4.5) факториалы по формуле
Стирлинга и приравняем logMM’) и log/' в пред-
положении, что к w. Получим
log г = log2V(w) =
= (к + w) log(k + w) - к logk - w logw «2к log2.
Тогда к - (log2 r)/2 .
Для нахождения логарифма I нужно найти
О(Е) индексов точек R,, сложность этой операции
(шаг 3) равна
<9(2'"A:3w3log(AM’2)) = O(2m(logr)6 log log/').
Если предположить, что значение т остается
ограниченным с ростом г, то сложность шага 3
оценивается полиномом степени не более 6 от
log/', сложность шага 4— полиномом степени 3
от logr. Итоговая сложность вычисления лога-
рифма равна
O(2m(log/')6 loglog/') + O(logr)
где Si — сложность поднятия точки из поля F;, в
поле К так, чтобы вес поднятой точки был ми-
нимален. Если сложность Sj полиномиальная
(субэкспоненциальная), то и задача логарифми-
рования может быть решена указанным методом с
полиномиальной (соответственно, субэкспонен-
циальной) сложностью. Получить гарантированно
большой ранг можно переходом к мультиквадра-
тичному расширению К - ..., где
D, — малые по абсолютной величине квадратич-
ные вычеты по модулю р.
Таким образом, доказано следующее утвер-
ждение.
246
Теорема 11.4.1. Задача дискретного логариф-
мирования на эллиптической кривой £(Ff) поли-
номиально сводится к задачам нахождения мно-
жества образующих группы Морделла-Вейля и
поднятия точки кривой из поля в числовое
поле К, при этом вес поднятой точки должен
быть минимальным.3
Предположим, что R— точка порядка г эл-
липтической кривой, и на этой кривой существу-
ет функция gR, причем:
1) функция gR вычислима с полиномиальной от
log/' сложностью;
2) функция gR обладает дивизором div(g7;) с
большим носителем;
3) логарифмы по основанию R точек, входящих
в div(g7?), перечислимы с полиномиальной от
log г сложностью.
Примером функции, обладающей свойствами
1 и 2, может являться разреженный полином от х,
у большой степени. Примером функции, обла-
дающей свойствами 2 и 3, является функция с
круговым дивизором вида
div(gP) = X&P)-k(P№),
/=о
где 2, — примитивный корень степени к из 1 по
модулю г и А] (г - 1).
Выберем случайным образом точку R] из
группы порядка г и свяжем с ней все точки, ко-
торые входят в div(gR]). Затем выберем из той же
группы произвольную точку Т?2, не входящую в
div(g77]), и свяжем с ней точки, входящие в
div(gR2), и т. д. Таким образом, множество из
г - 1 аффинных точек разбивается на непересе-
кающиеся классы. В этом случае задачу лога-
рифмирования можно решать в два этапа: на
первом этапе вычислить логарифмы алгоритмом
Полларда для классов эквивалентности указан-
ных точек, на втором — уточнигь значение лога-
рифма внутри класса эквивалентности.
Для построения функции gR могут использо-
ваться обычные арифметические операции, а
также операции композиции и дифференцирова-
ния. Однако сложность и даже возможность по-
строения такой функции в настоящее время не-
известна.
Стандарт цифровой подписи ECDSS (см.
п. 15.6.5) допускает использование эллиптиче-
3 Сложность решения задачи поднятия на сего-
дняшний день неочевидна. Возможно, поднятие точки
может выполняться с использованием техники диофан-
товых уравнений [8,18], например, систем уравнений
Пелля или форм от логарифмов алгебраических чисел.
ских кривых над расширенными полями харак-
теристики 2. Если степень расширения п = ml
является составным числом, то число точек мо-
жет иметь большой простой делитель, если в
уравнении кривой у2 + ху = х3 + ах2 + b коэффи-
циенты а, Ъ лежат в расширенном поле. В этом
случае задача дискретного логарифмирования в
группе точек кривой методом спуска (Weil de-
scent) [12] может быть сведена к задаче дис-
кретного логарифмирования на гиперэллипти-
ческой кривой рода 2т над подполем из 21 эле-
ментов. Задача дискретного логарифмирования
в якобиане гиперэллиптической кривой боль-
шого рода решается субэкспоненциальным ал-
горитмом (см. п. 11.6), поэтому задача лога-
рифмирования на кривой £(F ,„,) является срав-
нительно несложной.
11.5. Время жизни параметров
криптосистемы, основанной
на дискретном логарифмировании
Безопасность криптосистем с открытым клю-
чом часто определяется сложностью задачи дис-
кретного логарифмирования в циклической
группе вычислимого или трудновычислимого
порядка (в группе обратимых элементов кольца,
в якобиане алгебраической кривой и т. п.). В об-
щем случае эта задача формулируется так: в
группе G решить показательное уравнение d = b.
В защищенной компьютерной системе в этом
случае используются общие для всех участни-
ков параметры криптосистемы, задающие груп-
пу G и образующую а. Каждый пользователь
имеет персональный секретный ключ (логарифм
х) и парный ему открытый ключ (значение Ь).
Например, в стандартах цифровой подписи РФ
и США параметрами криптосистемы являются
эллиптическая кривая £(Fp), характеристика по-
ля р и образующая точка Q группы простого
порядка г.
Персональные ключи должны периодически
меняться в соответствии с установленным по-
рядком. При смене персонального ключа сим-
метричные криптографические алгоритмы допус-
кают сохранение параметров криптосистемы (на-
пример, блока подстановок в ГОСТ 28147-89).
Что можно сказать о времени жизни параметров
криптосистем с открытым ключом? Можно ли
продлить срок безопасной эксплуатации крипто-
системы с открытым ключом, периодически ме-
няя персональные ключи всех пользователей и
сохраняя ее параметры? Если смена персональ-
ного ключа решается в организационном плане
несложно, то смена параметров криптосистемы
247
сопряжена со значительными неудобствами в
эксплуатации. Кроме того, по истечении срока
действия параметров все цифровые подписи, со-
ставленные с их помощью, должны считаться
недействительными, а все сеансовые ключи —
вскрытыми.
Будем рассматривать только криптографиче-
ские ограничения на время жизни параметров
криптосистемы.
11.5.1. Мультипликативная группа поля
Задача логарифмирования d = b в группе Fr*
положена в основу стандарта подписи
ГОСТ Р 34.10-94 (см. п. 13.2.3); наилучший ме-
тод вскрытия персонального секретного клю-
ча— решето числового поля— обладает слож-
ностью O(exp(cy/ln p(ln In р)2)), где с » 1,92 при
условии удачного выбора простого числа р. Ана-
логичную сложность имеет и метод логарифми-
рования на основе решета поля алгебраических
функций для группы F9 .
Модифицируем алгоритм 10.2.1 логарифми-
рования методом решета числового поля для
случая, когда а и b изначально неизвестны.
Алгоритм 11.5.1. Логарифмирование мето-
дом решета числового поля с использованием
предвычислений.
Вход. Характеристика поля р; образующая а и
экспонента b (становятся известными после соз-
дания базы данных).
Выход. Логарифм х такой, что d = b.
Метод.
1. Создать базу данных из пар (с, d) требуемого
вида (см. п. 10.2.2).
2. Выразить логарифмы элементов базы разло-
жения в виде линейных комбинаций показа-
телей, найденных на шаге 1.
3. После того как стали известны образующая а
и персональный открытый ключ Ь, подобрать
показатели k, l fdZL такие, что произведение
ab1 (mod р) имеет малые простые делители.
4. Выразить ненулевые показатели, с которыми
элементы базы разложения входят в произве-
дение ab1 (modр), через векторы, найденные
на шаге 2 (число таких ненулевых показате-
лей пренебрежимо мало по сравнению с раз-
мером базы данных).
5. Решить систему линейных уравнений для
ненулевых координат вектора, найденного на
шаге 4, и вычислить логарифм х.
6. Результат: х.
Сложность шагов 3-5 составляет примерно
O(d) операций, где и~—Е_ (см. п. 10.1). Тради-
1п у
ционная оценка сложности вскрытия ключа рав-
на О(ниу3), сложность вычисления ключа при вы-
полненных шагах 1, 2 не превышает квадратного
корня из сложности этих шагов. Например, если
первоначально вскрытие ключа требует несколь-
ких лет вычислений, то в случае смены ключа
при заготовленной базе данных срок действия
нового ключа составит несколько секунд. Смена
образующей по сути ничего не меняет, так как в
этом случае шаг 3 нужно выполнить два раза.
Поэтому здесь, в отличие от симметричных
криптосистем, по окончании срока действия лю-
бого персонального ключа нужно менять харак-
теристику поля и, следовательно, ключи всех
пользователей независимо от срока ввода их в
действие.
В криптографии иногда используется задача
логарифмирования в группе трудновычислимого
порядка (Z/pgZ) обратимых элементов кольца
вычетов по модулю составного числа pq с неиз-
вестным разложением. Данная задача сводится к
разложению общего для всех участников состав-
ного числа. Очевидно, что и в этом случае исте-
чение срока действия любого персонального
ключа влечет за собой замену характеристики
кольца и, следовательно, замену всех персональ-
ных ключей. Попутно отменяются защитные ка-
чества всех криптографических алгоритмов, ис-
пользующих отмененные параметры криптоси-
стемы, независимо от даты начала действия пер-
сональных ключей.
Данное свойство криптосистем в сочетании с
быстрым падением стойкости — полтора деся-
тичных порядка в год для размера задачи 1
Кбит— демонстрирует неудобство популярных
криптографических алгоритмов, допускающих
субэкспоненциальные алгоритмы вскрытия клю-
ча. Кроме того, на сложность логарифмирования
существенно влияет способ выбора характери-
стики поля р.
Все изложенное справедливо и по отношению
к задаче дискретного логарифмирования в муль-
типликативной группе расширенного конечного
поля, к которой сводится задача логарифмирова-
ния на эллиптической кривой.
11.5.2. Группа точек эллиптической кривой
Пусть циклическая группа точек эллиптиче-
ской кривой E(F9) имеет простой порядок г и
субэкспоненциальный метод логарифмирова-
248
ния с помощью спаривания Вейля неэффекти-
вен (с учетом аномально быстрого падения
сложности задачи логарифмирования в конеч-
ном поле). В этом случае алгоритм Полларда
не работает, так как персональный открытый
ключ неизвестен.
Рассмотрим модификацию алгоритма встре-
чи на случайном дереве при известном общем
ключе (уравнение кривой и образующая Q) и
неизвестном персональном ключе (точка
Р = IQ). Предположим, что память вычисли-
тельной модели ограничена значением O(\hr),
что обычно имеет место на практике. Выберем
отображение т, зависящее только от образую-
щей Q и текущего значения R аргумента. На-
пример, для одной половины аргументов
г(7?) = Q + R и logr(7?) = Iog7? + 1, для другой по-
ловины — т(/?) = 2R и logr(/?) = 2 log/?. Алгоритм
предусматривает выбор случайных начальных
значений R,, логарифмы которых известны, по-
следовательное выполнение к отображений и
запоминание троек {/(7?,), Я,} с сорти-
ровкой по первой «координате». После того как
точка Р стала известна, выбираем поочередно
случайные точки вида а,Р + b,Q, делаем т ото-
бражений, на каждом шаге сравнивая результат с
базой данных, при совпадении приравниваем
логарифмы точек и находим секретный ключ /.
Анализ сложности алгоритма с использовани-
ем численных методов и указанных аппроксима-
ций показывает, что оптимальными являются
значения т = О(к) ~ O(log г) или к = 0(1),
т - 0{у!г} . Если доступная память не превыша-
ет O(-Jr), то алгоритм имеет ту же асимптотиче-
скую сложность, что и обычный алгоритм Пол-
ларда.
Таким образом, в криптосистемах на эллип-
тических кривых смена персонального ключа
при сохранении параметров криптосистемы по-
зволяет продлевать срок безопасной эксплуата-
ции. В этом проявляется их аналогия с симмет-
ричными криптосистемами.
11.6. Логарифмирование в якобиа>
гиперэллиптической кривой
Задача дискретного логарифмирования е
биане гиперэллиптической кривой формула
ся так. Пусть div(a, b) — элемент (дивизор)
биана, образующий группу простого поряд
Для дивизора div(c, d) нужно найти логари
такой, что div(c, d) = /div(a, b). Эта задача pt
ется теми же методами, что и задача дискрет!
логарифмирования на эллиптической кривс
учетом арифметики в якобиане; наилучшим )
версальным методом является алгоритм Полла{
Пример 11.6.1. Логарифмирование на гип
эллиптической кривой методом Полларда.
Пусть С — гиперэллиптическая кривая над
рода 2, заданная уравнением
у2 = х5 + 4х2 + х + 3.
Число аффинных точек этой кривой над п
лем F7 равно 4: (1, ±3), (2, ±2), а над полем F4g -
62. Дзета-функция кривой: Z(7) = 74 - 37’3
+ 1172 - 217 + 49: порядок якобиана: Z(l) = 37.
Вычислим алгоритмом Полларда [15] в як<
биане 7(C) логарифм / такой, что для двух дивг
зоров £)/ = ((!, 3)) - (Рю) и Д = ((2, 2)) - (Рт) вь
полняется равенство DK = IDA. Представим диви
зоры D/ и DB в виде HO)((div(<7), di v(7> -у)) (см
п. 6.18): Da = div(x + 6, 3), DB = div(x + 5, 2).
Выбираем для элементов D, = div(a,. Ь,) яко-
биана отображение вида
Dt + Da , если at = Ь, (х, 2),
,+1 Df + 4DB, если а, b, (х, 2).
Здесь сравнимость пары полиномов а„ bi по
идеалу (х, 2) означает сравнимость их свободных
членов по модулю 2 в Z|x], а поле F? представ-
лено числами О, 1, .... 6. Если a,, b, сравнимы по
указанному идеалу, то выполняется равенство
для логарифмов: /,+1 = /,+ 1, в противном случае
выполняется равенство /,+) = /, + 4/. В качестве 7>0
выбран дивизор DA = div(x + 6, 3), /0 = 1. Резуль-
таты решения представлены в таблице 11.7.
Таблица 11.7
Вычисление логарифма в якобиане гиперэллиптической кривой методом Полларда
i 1 2 3
D, div(x2 + 4x + 2, 5x + 6) div(x + 5, 2) div(x2 + x + 4, 3x + 3)
d2i div(x + 5, 2) div(x2 + 6x + 6, 4x + 1) div(x + 6, 3)
I, 1 + 4/ 2 + 4/ 2 + 8/
hi 2 + 4/ 2 + 12/ 2 + 20/
249
Продолжение таблицы 11.7
i 4 5 6
D, div(x2 + 6.т + 6, 4х + 1) div(x2 + 4x + 5, 4x + 6) div(x + 6,3)
d2i div(x + 5, 2) div(x2 + 6x + 6, 4x + 1) div(x + 6,3)
I, 2 + 12/ 2 + 16/ 2 + 20/
д. 3+24/ 3+32/ 3+3/
Получаем встречу при i = 6: £>б = О12. Записы-
ваем равенство для логарифмов: 2 + 20/ = 3 + 31
(mod 37), откуда находим искомое значение:
Ь 24 (mod 37).
Пусть J(C) — якобиан (или его подгруппа)
простого порядка г гиперэллиптической кривой
С(Х) и г отлично от характеристики р поля К.
Тогда на J(C) определено спаривание Вейля, ко-
торое задает вложение якобиана в мультиплика-
тивную группу поля L, являющегося расширени-
ем поля К таким, что r\#L . Эта аналогия эллип-
тических и гиперэллиптических кривых следует
из того, что поля функций на них являются квад-
ратичными расширениями поля рациональных
функций одной переменной.
Если г=р, то методом логарифмической про-
изводной устанавливается изоморфизм между
якобианом и аддитивной группой простого поля
Fp, содержащегося в поле К.
Таким образом, для обеспечения высокого
уровня стойкости кривую С(Л) следует выбирать
так, чтобы степень расширения (L'.K) была дос-
таточно велика (см. табл. 11.5) и чтобы выполня-
лось неравенство г Фр.
Кроме того, род кривой желательно выбирать
небольшим. Если род кривой С(К) велик (в пре-
деле стремится к бесконечности), то задача лога-
рифмировании в якобиане имеет субэкспоненци-
альную сложность. Алгоритм логарифмирования
основан на том, что координатное кольцо Fc[C]
факториально и случайный многочлен из F;,[C] с
большей вероятностью делится на данный мно-
гочлен малой степени, чем на данный многочлен
большой степени.
На гиперэллиптической кривой может суще-
ствовать комплексное умножение (см. п. 15.7).
Наличие комплексного умножения позволяет
снизить сложность логарифмирования по анало-
гии с эллиптической кривой.
11.7. Требования к эллиптической кривой
Пусть E(F9) — эллиптическая кривая над полем
из q=pn элементов, Q е E(F9) и #(0 = г. Для дос-
тижения максимального уоовня стойкости крипто-
системы, равного О(у/г), эллиптическая кривая
должна удовлетворять следующим требованиям.
1. Для обеспечения стойкости к анализу мето-
дом Гельфонда порядок г циклической груп-
пы должен быть большим простым числом
(для задач аутентификации достаточно
200-250 бит, для шифрования долговремен-
ных секретов достаточно 400-500 бит).
2. Для обеспечения стойкости к анализу на ос-
нове спаривания Вейля порядок г группы не
должен быть делителем ни одного из чисел
q - 1, q2 - 1, ..., q' - 1 для значений т, ука-
занных в табл. 11.5. Практически для задач
аутентификации достаточно проверить это
для т ~ 100. Проверка может быть выполне-
на рекуррентно: если Ф 1 (mod /'), то
//'' Ф 1 (mod г), при этом достаточно прове-
рять только те показатели, на которые делит-
ся число г - 1. Поскольку сложность лога-
рифмирования в конечном поле падает ано-
мально быстро, не исключено, что значение
т может быть увеличено.
3. Для обеспечения стойкости к анализу мето-
дом логарифмической производной должно
выполняться неравенство г Ф р.
Заметим, что если эллиптическая кривая об-
ладает комплексным умножением на число 6 с
малым порядком т группы автоморфизмов, об-
разованной 0, то возможно снижение стойкости в
Vm раз по сравнению с первоначальным значе-
нием. Метод логарифмирования на орбитах ав-
томорфизмов можно применять не непосредст-
венно к данной эллиптической кривой, а к изо-
генной кривой (см. п. 15.4). При этом нужно от
исходной кривой с помощью несложной изоге-
нии перейти к другой кривой, на которой орбита
автоморфизмов вычислима, и решать задачу
дискретного логарифмирования на этой новой
кривой (изогенные кривые определяются корня-
ми модулярных полиномов над соответствую-
щим конечным полем).
250
При выполнении указанных условий стой-
кость лежит в диапазоне от до
а наилучшим методом логарифмирования явля-
ется метод Полларда (решается задача о встрече
в цикле графа случайного отображения для ор-
бит группы автоморфизмов).
Аналогичные требования предъявляются и к
гиперэллиптическим кривым.
Упражнения к главе 11
1. Почему выбор сжимающего отображения при
вычислении логарифма на эллиптической
кривой методом Полларда не принципиален?
2. Оцените срок безопасной эксплуатации крип-
тосистемы на эллиптической кривой по от-
ношению к методу Полларда, если характе-
ристика поля и порядок группы имеют длину
160 бит.4 Оцените срок действия ключа в на-
чале и в конце срока эксплуатации. Считать,
что вычислительная модель позволяет вы-
полнять I О20 арифметических операций в год
и производительность вычислительной моде-
ли каждый год удваивается.
3. Пусть E(FP)— эллиптическая кривая и г —
простой порядок группы точек этой кривой.
Покажите, что граф сжимающего отображе-
ния Р хн°Д(л-1>''-1) р _ где Р = (хр,уг) и
НОД(р - 1, г - 1) » 1, состоит из значитель-
ного числа несвязных частей.
4. Можно ли продлить срок действия общего
открытого ключа криптосистемы на эллип-
тической кривой по отношению к логариф-
мированию методом «giant step — baby step»,
меняя персональные открытые ключи?
5. Чему равен ранг вырожденной кубической
кривой у2 = х3 + х2 над полем Q?
6. Поднимите точку (8, 4) эллиптической кри-
вой у2 = х3 + 17 из поля F19 в поле Q.
7. Оцените емкостную сложность метода лога-
рифмирования с помощью поднятия точки
кривой в числовое поле К, если ранг кривой
равен т.
8. Оцените оптимальное число шагов алгорит-
ма встречи на случайном дереве, если запо-
минать не конечные точки траекторий, а са-
ми траектории.
9. Предложите способ вычисления орбиты эн-
доморфизма Фробениуса на эллиптической
кривой над расширенным конечным полем.
10. Пусть К — поле из р" элементов и
(х, у) е Е(К) — точка эллиптической кривой.
2
Какие симметрические функции от (х, хр, хр ,
4 Размер задачи в стандартах США.
...,хр ), кроме следа и нормы, принимают
значения в поле F,,?
11. Пусть эллиптическая кривая £(F^) с большим
простым числом точек г рассматривается над
числовым полем К. Покажите, что Е(К) не
имеет точек кручения.
12. Сравните сложность логарифмирования на
эллиптических кривых E(Z/hZ) и £(F/7), где
разложение числа п неизвестно, р~п,
#Е(Ж/пЖ) является произведением двух боль-
ших простых чисел, #Е(^Р) является простым
числом.
13. Какую кривую С можно использовать для
логарифмирования в F;, с помощью отобра-
жения поля Fp в точки кривой С и поднятия
точек в числовое поле К1 Кривая С(К) долж-
на иметь достаточно большой конечный
ранг, то есть быть неособой, и допускать изо-
морфизм Fp C(Fp).
14. Исследуйте экспериментально зависимость
сложности алгоритма Полларда от числа
ветвлений в отображении т (см. п. 11.1.3).
15. Пусть г — нечетное простое число. В квадра-
тичном расширении К поля Q имеет место
разложение г = ля, где л е Ок. Почему нель-
зя снизить сложность логарифмирования в
группе из г элементов, используя это разло-
жение, по аналогии с алгоритмом Гельфонда?
16. Покажите, что сложность вычисления лога-
рифма / на эллиптической кривой с простым
порядком группы г при условии, что выпол-
няется неравенство I < -Jr , не превышает
O(y[r log г) для алгоритма «giant step — baby
step». Какова будет сложность логарифми-
рования, если / < г“, где а < 1 ?
17. Пусть г — большой простой делитель порядка
группы точек эллиптической кривой, q — де-
литель числа г - 1 и g— образующая группы
порядка q в (Z/rZ) , причем 1 «q «г. По-
кажите, что если можно легко вычислить
функцию fp с «круговым» дивизором d iv(/}.) =
= (Р) + (gE) + • • • + (gq }P) ~ (qPf) в произволь-
ной точке, то сложность логарифмирования
снижается в O(fq) раз.
Литература к главе 11
1. Айерлэнд К., Роузен М. Классическое введение в
современную теорию чисел. М.: Мир, 1987.
2. Ван дер Варден Б.Л. Алгебра. М.: Наука, 1979.
3. Колчин В.Ф. Случайные отображения. М.: Наука,
1984.
4. Нечаев В.И. Элементы криптографии. Основы
теории защиты информации. М.: Высшая школа,
1999.
5. Прасолов В.В., Соловьев Ю.П. Эллиптические
кривые и алгебраические уравнения. М.: Изд-во
«Факториал», 1997.
6. Ростовцев А.Г. Алгебраические основы крипто-
графии. СПб.: Мир и Семья, Интерлайн, 2000.
7. Ростовцев А.Г. О времени жизни общего и персо-
нального открытого ключа И Проблемы инфор-
мационной безопасности. Компьютерные систе-
мы. 1999. №4. С. 57-61.
8. Спринджук В.Г. Классические диофантовы урав-
нения от двух переменных. М.: Наука, 1987.
9. Степанов С.А. Арифметика алгебраических кри-
вых. М.: Наука, 1991.
10. Феллер В. Введение в теорию вероятностей и ее
приложения. В 2-х томах. М.: Мир, 1984.
11. Fulton W. Algebraic curves. New York: Benjamin, 1969.
12. Galbraith S.D., Smart N.P. A cryptographic applica-
tion of Weil descent П Codes and cryptography. Lec-
ture Notes in Computer Science. Springer-Verlag.
1999. Vol. 1746. P. 191-200.
13. Husemoller D. Elliptic curves. Springer-Verlag, 1987.
14. Mazur B. Rational points on modular curves. Lecture
Notes in Mathematics. Springer-Verlag. 1976.
Vol. 601.
15. Pollard J. Monte Carlo methods for index computa-
tion (modp) // Mathematics of Computation. 1978.
Vol. 32. P. 918-924.
16. Semaev LA. Evaluation of discrete logarithms in a
group of p-torsion points of an elliptic curve in char-
acteristic p 11 Mathematics of Computation. 1998.
Vol. 67. P. 353-356.
17. Silverman J.H. The arithmetic of elliptic curves.
Springer-Verlag, 1986.
18. Zagier D. Large integral points on elliptic curves //
Mathematics of Computation. 1987. Vol. 48.
P. 425-436.
19. Zimmer H.C. Basic algorithms for elliptic curves I I
http.7/www.rzuser.uni-heidelberg. de/~hb3 /elleng.html.
Глава 12. ШИФРОВАНИЕ С ОТКРЫТЫМ КЛЮЧОМ
В основу шифрования с открытым ключом
положена вычислимая в одну сторону функция с
потайным ходом, знание которого позволяет вы-
числить обратную функцию. Например, в систе-
ме RSA вычислимой в одну сторону функцией
является отображение х хе (mod и), а потай-
ным ходом, позволяющим вычислить обратную
функцию, — показатель d такой, что ed = 1
(mod <р(и)), где (р — функция Эйлера.
В общем случае для зашифрования и расшиф-
рования используются разные ключи, которые
связаны взаимно однозначно, но эта связь вы-
числима в одну сторону: по известному ключу
зашифрования ключ расшифрования вычислить
легко, а обратную задачу решить трудно. К зада-
че шифрования с открытым ключом тесно при-
мыкает задача бесключевого шифрования, когда
ни отправитель, ни получатель сообщения не
имеют секретного ключа, а также задача шифро-
вания бита, используемая в протоколах предъяв-
ления битов (см. п. 14.1).
Шифрование с открытым ключом позволяет
облегчить управление ключами в системе, по-
скольку каждый пользователь должен обеспе-
чить конфиденциальность лишь своего персо-
нального ключа расшифрования.
Протоколы шифрования с открытым ключом
можно классифицировать по типу задач, поло-
женных в их основу:
- протоколы, использующие группу вычисли-
мого порядка (задача дискретного логариф-
мирования);
- протоколы, использующие группу трудновы-
числимого порядка (задачи разложения, дис-
кретного логарифмирования, решения алгеб-
раических уравнений);
- протоколы, использующие задачу об укладке
ранца.
Секретный ключ расшифрования имеет нуле-
вую шенноновскую энтропию; для вскрытия
ключа нарушитель при необходимости может
создать нужное ему число открытых и зашифро-
ванных текстов. Поэтому алгоритмы шифрова-
ния с открытым ключом не имеют криптографи-
ческих ограничений на объем данных, шифруе-
мых на одном ключе. Для сравнения: если из-
вестны один-два блока открытого и зашифро-
ванного текстов для DES, то сложность вскрытия
ключа равна 254, однако при наличии порядка 230
блоков открытых и зашифрованных текстов
сложность вскрытия ключа линейным методом
существенно ниже [11].
12.1. Шифрование с открытым ключом
для группы вычислимого порядка
В основу безопасности протоколов шифро-
вания с открытым ключом в группе G вычисли-
мого порядка положена задача дискретного ло-
гарифмирования и некоторые связанные с ней
задачи, в частности, задача Диффи-Хеллмана
(см. п. 10.6).
Эта задача используется в протоколе установ-
ления сеансового ключа [6]. Для того чтобы ус-
тановить общий ключ, участники протокола до-
говариваются о несекретных параметрах: группе
G простого порядка г и образующей а. Ключ ус-
танавливается в ходе диалога. Участник А выра-
батывает случайный показатель х, вычисляет
значение а" и посылает его участнику В. Участ-
ник В вырабатывает свой случайный показатель
у, вычисляет значение ау и посылает его участ-
нику А. Затем А и В возводят полученный текст в
степень, каждый со своим показателем, и оба
получают текст аху, который является секретным
сеансовым ключом.
Чтобы вычислить значение а\ число х пред-
ставляют в двоичном виде, находят последова-
2 4 8
дельность квадратов а, а , а , ... и перемножают
элементы этой последовательности. Число ум-
ножений (и, следовательно, длительность шиф-
рования) зависит от числа единичных разрядов в
двоичном представлении показателя х. Измере-
ние числа тактов, затраченных на шифрование,
дает некоторую информацию о показателе х, по-
этому программу шифрования имеет смысл раз-
рабатывать так, чтобы длительность вычислений
не зависела от показателя х.
Быстрое возведение в степень ах (modр) с
большим показателем х можно выполнить сле-
дующим образом. Записать показатель х в дво-
ичном виде. Для небольшого числа к вычислить
значения с?2, о3, ..., с?2-1. Разбить показатель х на
Л-битные слова: х = bt2kt + 6(-|2/;('и * + ... + Ьо. И,
наконец, вычислить рекурсивно для i, убываю-
253
ik ь
щего от t до 0, значения s,.=s,+]a', полагая
5/+1 = 1. Результатом является sq. Этот подход
можно использовать и при выполнении операций
в группе (Z/«Z) , группе точек эллиптической
кривой и т. п.
Оптимальный размер окна к определяется ми-
нимальной сложностью S вычисления экспонен-
ты:
S = (2fc_2)+l^ + log2x.
к
Здесь первое слагаемое учитывает сложность
„23 2*—I
вычисления степеней а , а , а , второе сла-
гаемое — сложность умножений с учетом разме-
ра окна (предполагается, что число умножений
не зависит от х, что исключает атаку на основе
измерения числа шагов работы программы),
третье слагаемое — сложность возведения в
квадрат. Вычисление обычным способом дает
сложность 2 log2x - 1. Оптимальные значения ктт
и минимальная сложность в зависимости от
максимального размера показателя х приведены
в таблице 12.1.
Таблица 12.1
Оптимальный размер окна
log2x 128 256 512 1024 2048 4096 8192
Аэпт 4 4 5 6 6 7 8
$мин 174 334 644 1256 2451 4807 9470
В протоколе Диффи-Хеллмана не использу-
ется непосредственно порядок группы. Поэтому
этот протокол может использовать группу
(Z/tzZ) или группу классов числового поля.
Обычно на практике используют протокол
шифрования с открытым ключом Эль-Гамаля
или протокол бесключевого шифрования, запа-
тентованный Дж. Месси и Дж. Омурой.
12.1.1. Бесключевое шифрование
Месси-Омуры
Протокол Месси-Омуры [10] требует диалога
между отправителем и получателем и, следова-
тельно, для его реализации необходим двуна-
правленный канал связи.
Отправитель и получатель договариваются о
параметрах криптосистемы: циклической группе
G порядка г и способе представления текста
m е М в виде элемента группы G, то есть о вы-
числимой в обе стороны функции f из множества
М сообщений в группу G.
Протокол 12.1.1. Бесключевое шифрование
Месси-Омуры.
Вход отправителя и получателя. Циклическая
группа G большого простого порядка г, вычис-
лимая в обе стороны функция f. M^G.
Результат. Зашифрование и расшифрование
сообщения.
Метод.
1. Отправитель вычисляет t <— fini) для сообще-
ния тп. Если t является единичным элементом
группы G, то результат: сообщение зашиф-
рованию не подлежит.
2. Отправитель генерирует случайный показа-
тель а е , вычисляет элемент ta группы G
и направляет f получателю.
3. Получатель вырабатывает случайный показа-
тель Ь, обратимый по модулю г, вычисляет
(ta)b = tab и посылает tab отправителю.
4. Отправитель возводит полученную шифро-
грамму в степень а~]: (tab)a = tb и посылает tb
получателю.
5. Получатель возводит шифрограмму в сте-
пень b~}: (tb)b = t и вычисляет m <— f\f).
Примечания.
1. Здесь шифрограммами служат ta, tab, tb.
2. Протокол будет работать и в том случае,
если порядок группы не является простым, но
имеет большой простой делитель.
3. Если порядок группы G кроме большого
простого делителя г имеет один или несколько
малых делителей р„ то нарушитель может из-
влечь некоторую информацию об открытом тек-
сте, вычислив для шифрограммы характер сте-
пени р,-. (ta)#Glp' (или (tb)#Glp'). Если характер
равен 1, то и характер для открытого текста ра-
вен 1. Поэтому желательно использовать группу
G простого порядка.
Оригинальный протокол Месси-Омуры ис-
пользует в качестве G мультипликативную груп-
пу F/? простого поля; в роли функции f может
выступать единичное отображение.
Этот протокол, как и протокол Диффи-
Хеллмана, очевидно, не обеспечивает аутентич-
ность, так как в общем случае ни отправитель, ни
получатель не знают, с кем ведут общение. Кро-
ме того, если нарушитель может включиться в
канал связи между отправителем и получателем,
то он может осуществить дешифрование, выда-
вая себя за получателя и отключив от канала
подлинного получателя. Иногда отсутствие ау-
тентичности не является помехой, например, если
нарушитель может только прослушивать канал
254
связи, но не вмешиваться в его работу. Для обес-
печения имитозащиты можно также применять
цифровую подпись.
Безопасность этого протокола основана на за-
даче Месси-Омуры: для заданных f, th, tab найти
t. Эта задача с полиномиальной сложностью сво-
дится к задаче дискретного логарифмирования.
Действительно, пусть известны образующая f и
логарифм b для экспоненты 1аЬ. Тогда, вычислив
расширенным алгоритмом Евклида /Г1 (mod г),
можно наити .
Кроме того, эта задача с полиномиальной
сложностью сводится к задаче Диффи-
Хеллмана. Предположим, что задача Диффи-
Хеллмана решена, то есть для заданных s, si*, sy
можно вычислить s*y. Полагая 5 = tab, / = ta,
sy = tb, получаем, что x = b~\ у = a~', откуда sxy = t.
Таким образом, сложность взлома протокола
Месси-Омуры не превышает сложности решения
задачи Диффи-Хеллмана.
Если порядок г группы G является простым
числом, то задача Месси-Омуры эквивалентна
задаче Диффи-Хеллмана. Для доказательства
этого предположим, что задача Месси-Омуры
решена, то есть для заданных ta, tb, tab можно
найти t. Поскольку число г простое и t не являет-
ся единичным элементом, то tab является обра-
зующей группы G. Полагая 5 = tab, s' = f, sy = tb,
получаем, что sxy = t. Сложность задач устанав-
ливает отношение порядка на множестве задач.
Таким образом, решение задачи Диффи-
Хеллмана влечет решение задачи Месси-Омуры,
и наоборот. Отсюда по свойству антисимметрич-
ности для отношения порядка заключаем, что
сложности указанных задач полиномиально эк-
вивалентны.
i i .5? j У •
12.1.2. Протокол Эль-Гамаля
шифрования с открытым ключом
Т. Эль-Гамаль предложил протокол шифрова-
ния с открытым ключом [7], основанный на за-
даче Диффи-Хеллмана.1 В протоколе Диффи-
Хеллмана оба показателя х и у случайны. В про-
токоле Эль-Гамаля один показатель фиксирован
и служит секретным ключом расшифрования, а
другой показатель является случайным. Рассмот-
рим обобщенный протокол шифрования с откры-
тым ключом, который иногда называют «мета-
протоколом» Эль-Гамаля.
Пусть М — множество сообщений и G —
группа. Открытым ключом, общим для всех
пользователей системы, являются группа G и
образующая а. Кроме того, существует общедос-
1 Этот протокол не требует знания порядка группы.
тупная функция f. MxG^G, обратимая по пер-
вому аргументу (если известны значение функ-
ции и второй аргумент, то можно легко вычис-
лить первый аргумент). Персональным секрет-
ным ключом является показатель х, персональ-
ным открытым ключом — экспонента b = cf.
Протокол 12.1.2. Обобщенный протокол Эль-
Гамаля шифрования с открытым ключом.
Вход отправителя. Группа G, функция
/: М х G -> G, образующая а, элемент Ь = а*.
Вход получателя. Группа G, образующая а,
логарифм х.
Результат. Зашифрование и расшифрование
сообщения.
Метод.
Для зашифрования сообщения т отправитель
выполняет следующие действия:
- генерирует случайный показатель у;
- вычисляет элементы d, Id g G и значение
с by).
Шифрограммой является пара (ау, с).
Для расшифрования шифрограммы (ау. с) по-
лучатель выполняет следующие действия:
- возводит ау в степень х, получает при этом
аху = Ь'\
- находит сообщение т <— f \c, hy).
Вид функции f зависит от группы G. Если
G = Fp — мультипликативная группа простого
поля, то в качестве/ могут использоваться функ-
ции flm, by) = mby (modр), flm, by) = т + Ьу
(modp),fim, by) = т - by (modp) и т. п. Сам Эль-
Гамаль первоначально предложил использовать
первую из указанных функций. Отметим, что в
этом случае можно извлечь некоторую информа-
цию о сообщении т, вычислив символы Лежандра:
[р/ W
< V Ь V
т b
Если а — квадратичный невычет, а b — квад-
ратичный вычет, то можно узнать, является ли т
квадратичным вычетом, что соответствует одно-
му биту информации о сообщении т.
Можно проверять характеры и более высоких
степеней по аналогии с протоколом Месси-
Омуры. Поэтому предпочтительнее использовать
вторую или третью из указанных функций.
Протокол 12.1.2 допускает атаку со стороны
отправителя на основе подобранных шифртек-
стов. Предположим, что группа G может быть
вложена в группу Н и принадлежность данного
элемента группы Н группе G неочевидна. Пред-
положим также, что #Н= t #G, где число t ма-
ло. Если отправитель шифрограммы отступит от
255
правил, в качестве образующей а выберет эле-
мент порядка t в группе Н и сумеет узнать у по-
лучателя результат расшифрования, то он может
перебором найти х (mod /). Для этого он, имити-
руя расшифрование, должен перебрать в качест-
ве х элементы от 0 до t - 1 до совпадения резуль-
тата с истинным расшифрованным значением.
Можно использовать и асимптотически более
быстрый алгоритм «giant step — baby step».
Если порядок группы Н имеет другой малый
делитель f, взаимно простой с t, то отправитель
может найти х (mod f), а затем восстановить х
(mod ft’) по китайской теореме об остатках. Эта
процедура обобщается на случай произвольного
числа малых простых делителей. Если порядок
группы G имеет, кроме большого простого дели-
теля, еще и малые делители, то для организации
атаки нет необходимости переходить к группе Н.
В частности, если G = F/? и число р имеет длину
512 бит, а большой простой делитель числа р - 1
имеет длину 160 бит, причем остальные делите-
ли числа р - 1 малы, то логарифм х можно легко
вычислить с использованием указанного метода.
Для противостояния такой атаке достаточно
модифицировать алгоритм расшифрования. До
начала расшифрования получатель должен убе-
диться, что элемент av принадлежит группе G и
имеет требуемый простой порядок г. Если это не
так, то отправитель нарушает протокол и, воз-
можно, предпринимает атаку, направленную на
вскрытие ключа.
Данный алгоритм шифрования является веро-
ятностным, поскольку использует генератор слу-
чайных чисел; одному и тому же открытому тексту
может соответствовать множество различных за-
шифрованных текстов. Следовательно, протокол
обладает скрытым каналом передачи зашифрован-
ной информации (см. п. 13.4), то есть дает возмож-
ность получить внутри шифра еще один шифр.
Вскрытие секретного ключа по открытому
ключу эквивалентно решению задачи дискретно-
го логарифмирования в группе G. Для того что-
бы затруднить вычисление логарифма методом
Гельфонда, порядок группы G должен быть
большим простым числом или иметь большой
простой делитель.
Отметим, что здесь при зашифровании и при
расшифровании порядок группы в вычислениях
не участвует, поэтому можно использовать груп-
пу как вычислимого, так и трудновычислимого
порядка.
Для взлома протокола Эль-Гамаля достаточно
решить задачу Диффи-Хеллмана. Действитель-
но, если для заданных а, ах, ау можно вычислить
аху, то легко можно вычислить и открытый текст:
т =f '\c, аху).
Если функция f такова, что по ее значению и
первому аргументу можно найти второй аргу-
мент, то справедливо и обратное: если по шиф-
рограмме и открытому ключу в протоколе Эль-
Гамаля можно найти открытый текст, то можно
найти и сеансовый ключ в протоколе Диффи-
Хеллмана. Для доказательства достаточно заме-
тить, что по известным т и с =fim, by) можно
найти Ьу = аху. В этом случае задачи вскрытия
ключей в протоколах Эль-Гамаля и Диффи-
Хеллмана эквивалентны.
Если функция f не обладает указанным свой-
ством (например, fpn, by) = m - h(by) (mod р\ где
h— вычислимая в одну сторону функция), то
такая эквивалентность отсутствует.2
Данный протокол шифрования похож на про-
токол цифровой подписи Эль-Гамаля (см.
п. 13.2.1). Однако в протоколе подписи к генера-
тору случайных чисел предъявляются сущест-
венно более жесткие требования. В случае шиф-
рования однократный сбой генератора или по-
вторное использование случайного числа могут
привести не более чем к возможности бесключе-
вого чтения одного сообщения; в случае подписи
указанный одиночный сбой или повтор приводит
к вскрытию ключа подписи.
Таким образом, безопасность протокола Эль-
Гамаля основана на следующих задачах:
1) задаче дискретного логарифмирования (по-
следствие ее решения — вскрытие секретно-
го ключа);
2) задаче Диффи-Хеллмана (последствие ее
решения — однократное дешифрование);
3) задаче вычисления случайного числа (по-
следствие ее решения — однократное де-
шифрование).
В качестве группы G может использоваться
мультипликативная группа конечного поля,
группа точек эллиптической кривой, якобиан
алгебраической кривой, циклические подгруппы
группы (Z/tzZ) или группы классов числового
поля и т. п.
12.2. Шифрование с открытым ключом
для группы трудновычислимого порядка
Обычно в качестве группы G трудновычис-
лимого порядка используется группа обратимых
2 Отметим, что такая модификация протокола
Эль-Гамаля не обязательно приведет к повышению
стойкости криптосистемы, так как могут появиться
новые направления атак. Модификация протокола
означает всего лишь неэквивалентность задачи Диф-
фи-Хеллмана и задачи дешифрования.
256
элементов кольца Z7hZ, где n=pq и р, q — раз-
личные большие простые числа. Классический
вариант такого шифрования — система RSA (см.
гл. 9). Существуют и другие варианты шифрова-
ния, например, протокол Эль-Гамаля, если
G = (Z.lnZ)'.
Отметим, что если используется общая для
всех участников группа G, порядок которой ни-
кому не известен, то желательно предусмотреть
механизм, позволяющий каждому из участников
убедиться, что число п имеет только два нетри-
виальных делителя, в противном случае задача
разложения облегчается (см. п. 9.1).
В качестве такого механизма можно предло-
жить доказательства с нулевым разглашением
(см. гл. 14). Здесь, однако, кроется некоторое
противоречие. Для доказательства того, что чис-
ло п выбрано правильно, необходима доверенная
служба, знающая разложение п = pq, то есть сти-
рание секретных простых делителей числа п по-
сле их автоматизированной выработки становит-
ся невозможным.
Рассмотрим некоторые варианты шифрования
с открытым ключом с использованием группы
трудновычислимого порядка.
12.2.1. Протокол шифрования Рабина
Протокол шифрования Рабина [13] похож на
протокол шифрования RSA. Отличие состоит в
том, что показатель зашифрования равен 2, а
расшифрование выполняется неоднозначно.
Персональным открытым ключом получателя
является составное число n=pq, персональным
секретным ключом — разложение этого числа на
множители.
Для зашифрования сообщения т е от-
правитель вычисляет шифрограмму с = т2 (mod и).
Для расшифрования шифрограммы получатель
извлекает квадратные корни тп = ±Vc(mod/>),
тд = ±4с (mod q) в полях Fp, F7 и объединяет их
по китайской теореме об остатках, получая че-
тыре различных значения квадратного корня из
с. Поскольку расшифрование неоднозначно, то
для выбора правильного квадратного корня не-
обходима дополнительная информация, то есть
открытый текст должен содержать избыточные
биты, например, нули в нескольких старших или
младших разрядах.
Вследствие необратимости открытого пока-
зателя по модулю ср(и) протокол Рабина оказы-
вается уязвимым по отношению к криптоанали-
зу на основе известных открытых текстов. Дей-
ствительно, вероятность того, что открытый
текст т будет расшифрован неправильно, нену-
левая. Если получатель сообщит неправильный
результат расшифрования т’ отправителю, то
последний, вычислив НОД(/и + т', п), найдет
делитель числа п.
Теорема 12.2.1. Задача нахождения всех че-
тырех решений сравнения у7 = с (mod и), где
с Ф 0, эквивалентна задаче разложения на мно-
жители п = pq.
Доказательство. Если известно разложение
числа и, то сравнение может быть решено вычис-
лением квадратных корней из с по модулям pviq
и восстановлением результата по китайской тео-
реме об остатках. Сложность вычислений оцени-
вается полиномом от log и степени не выше 3.
Обратно, если известны четыре корня, то они по
китайской теореме могут быть представлены в
виде
(4с (mod р), 4с (mod q)),
(4с (mod р), - 4с (mod q)),
(~4с(mod р), 4с (mod q)\
(~4c(modp), ~4c(modq)).
Тогда, если сумма по модулю и двух корней
не равна 0, то она имеет нетривиальный наи-
больший общий делитель с п, который может
быть вычислен бинарным алгоритмом Евклида с
квадратичной от log и сложностью.
Скорость зашифрования в протоколе Рабина
значительно выше, чем скорость расшифрова-
ния: для зашифрования нужно выполнить одну
операцию модульного умножения, а для рас-
шифрования — O(log«) таких операций.
12.2.2. Вероятностное шифрование
Примером вероятностного протокола шифро-
вания, отличного от протокола Эль-Гамаля, яв-
ляется протокол Голдвассера-Микали [8]. Здесь
доказуемо исключается возможность получить
какую-либо информацию об открытом тексте по
зашифрованному тексту. Однако платой за это
является увеличение длины шифртекста по срав-
нению с открытым текстом.
Открытым ключом зашифрования являются
составное число n=pq и квадратичный невычет
। У I
у по модулю п, причем — = 1 (это означает, что
k и J
= -1). Секретным ключом расшифро-
вания являются делителиpw.q числа п.
257
= 1.
Протокол 12.2.1. Вероятностное шифрование
с открытым ключом Голдвассера-Микали.
Вход отправителя. Составное число и, квадра-
тичный невычет у по модулю п, для которого
Гу
(и
Вход получателя. Простые делители р и q
числа п.
Результат. Зашифрование и расшифрование
сообщения.
Метод.
Для зашифрования сообщения т произвольной
длины отправитель действует следующим образом.
1. Представляет сообщение в виде двоичного
вектора:
2. Генерирует случайные элементы х, е ~ZJn7L,
О < i < к - 1, и вычисляет x,2(mod и) .
3. Для i = 0,1,..., к- 1 полагает ct <— x2(mod«),
если т, = 0, и с,- <— ух^ (mod и), если /и, = 1.
Шифрограммой является набор (с0, ..., q~i).
Для расшифрования шифрограммы получатель
вычисляет последовательность символов Лежанд-
( \ f X f X
I Q I С Q I
ра — . Если — -1, то и — = 1, то есть с,
\PJ \PJ V/ J
является квадратичным вычетом по модулю и.
Тогда т, <— 0. Если
есть с, является квадратичным невычетом по мо-
дулю п и т, <г~ 1.
Безопасность этого алгоритма определяется
сложностью распознавания того, является ли с,
f Cj „
квадратичным вычетом при — = 1. Эта задача
\п)
сводится к задаче разложения; для распознава-
ния квадратичного вычета достаточно вычислить
значение символа Лежандра
— . Обратная
\PJ
сводимость указанных задач неизвестна.
Этот алгоритм является, по сути, шифром гам-
мирования (см. п. 19.L2), в котором каждый «блок»
шифрограммы представляет один бит открытого
текста и не связан с другими битами. Следователь-
но, нарушитель может решать задачу дешифрова-
ния по частям, дешифруя отдельные биты.
Поскольку на сегодняшний день безопасным
считается число п длины не менее 1 000 бит, дли-
на зашифрованного текста не менее чем в 1000
раз превышает длину открытого текста, то есть
этот алгоритм непрактичен.
Более практичным является алгоритм вероят-
ностного шифрования Блюма-Голдвассера [3],
использующий генератор псевдослучайных битов
BBS (см. п. 12.4) и аналогичный алгоритму сим-
метричного шифрования в режиме гаммирования.
Отличие заключается в том, что в обычном шиф-
раторе гаммирования гамма вырабатывается на
передающей и на приемной стороне одинаково, а
в данном алгоритме на приемной стороне гамма
восстанавливается «задом наперед».
Открытым ключом зашифрования является
составное число n=pq, где p = q = 3 (mod 4) —
различные простые числа. Секретным ключом
расшифрования является четверка (р, q, а, Ь), где
а = р~х (mod q), b = qx (mod p), числа а и b можно
найти расширенным алгоритмом Евклида.
Протокол 12.2.2. Вероятностное шифрование
с открытым ключом Блюма-Голдвассера.
Вход отправителя. Составное число п.
Вход получателя. Четверка (р, q, а, Ь), где
p = q = 3 (mod 4) — простые делители числа и,
а = р~' (mod q), b = qx (mod p\
Результат. Зашифрование и расшифрование
сообщения.
Метод.
Для зашифрования сообщения т длины к бит
отправитель выполняет следующие действия.
1. Находит числа h <— [_log2[_Log2 пJJ, t«- \к/hJ.
2. Генерирует случайное число г е ~%JriZL и вы-
числяет начальное заполнение xq <— г2 (mod и)
генератора BBS.
3. Вычисляет последовательно х, <— x2(mod«),
х2 <-Xj2(modn), ..., xt xf_}(modn), берет из
каждого полученного числа h младших или
средних двоичных разрядов (по заранее ого-
воренному правилу) и получает t слов гаммы
длины h бит каждое.
4. Складывает полученную гамму поразрядно
по модулю 2 с открытым текстом, при этом
получается двоичный вектор (С|, ..., q).
5. Вычисляет х,+1 <-x2(modn).
Шифрограммой является вектор (С],..., ск, xw).
Для расшифрования сообщения получатель
выполняет следующие действия.
1. Находит числа h <- |_log2 |_Iog2 пJJ’f [Л/^J
2.
Вычисляет
/ iY+1
8/? <- (mod (р -1)),
К 4 J
258
3. Полагает и <— xf/j (mod р), v <— х^} (mod q).
4. Вычисляет х0 <- vap + ubq (mod и).
5. Находит последовательно Xj <— Xo(mod«),
х2 «-x^modw),...,xt <—x;2_|(mod«), берет из
каждого полученного числа h младших или
средних двоичных разрядов (по заранее ого-
воренному правилу) и получает I слов гаммы
длины h бит каждое.
6. Складывает полученную гамму поразрядно
по модулю 2 с вектором (су, ..., о) и получа-
ет двоичный вектор (тщ,..тк) сообщения.
Покажем, что начальное заполнение х0 при
расшифровании вычисляется корректно. В соот-
ветствии с формулой извлечения корня в конеч-
ном поле выполняется равенство х^+'^4 s
= ±yjxl+} = ±xz (mod p). Ho -1 является квадра-
тичным невычетом, a xt — квадратичным выче-
том по модулю р, поэтому х,(£+1)/4 = х, (mod р).
Точно так же х((/,+’^4 = x,_j (mod/?), то есть
x((p+i)/4) = Х/] (П10С] ру и т д Продолжая эту це-
почку сравнений в течение шагов, получаем
и s xf/j = х&+1)/4> s x0(mod р). Аналогичное срав-
8„
нение выполняется и по модулю qi v = xt^ =
= хЙ+1)/4) = х0 (mod q). Поскольку vap + ubq = x(!
(mod p), vap + ubq = x() (mod q), to vap + ubq = x()
(mod и).
Задача дешифрования эквивалентна задаче раз-
ложения числа п. Действительно, если разложение
известно, то дешифрование выполняется в соот-
ветствии с протоколом 12.2.2. Обратно, задача де-
шифрования требует вычисления предшествующе-
го заполнения генератора BBS по известному те-
кущему заполнению, то есть извлечения квадрат-
ного корня в кольце Z/zzZ. Тогда наибольший об-
щий делитель суммы или разности квадратных
корней дает собственный делитель числа п.
Этот протокол оказывается нестойким по от-
ношению к анализу на основе подобранных
шифртекстов.
12.3. Ранцевые алгоритмы
шифрования с открытым ключом
В основу ранцевых алгоритмов положена NP-
полная задача об укладке ранца\ дано множество
натуральных чисел W= {wi, ..., и,,}. Можно ли
данное натуральное число N представить в виде
суммы слагаемых из некоторого подмножества
множества W? Иными словами, существует ли п-
разрядный двоичный вектор (xj, ...,х„) такой, что
п
N = ]Гх,мл ? Эту задачу иногда называют зада-
>=i
чей о сумме подмножеств (subset sum problem).
Плотностью ранца называется вещественное
число
п
max{log2 w, 11 < i < п}
Непосредственно из определения следует, что
плотность ранца всегда меньше 1.
Назовем последовательность {by, ..., b,,}, где
k-l
b, е Z, сверхвозрастающей, если bk > bt для
/=1
всех к<п. Для сверхвозрастающей последова-
тельности задача об укладке ранца решается од-
нозначно с линейной сложностью. Для этого
число N сравниваем с Ь„. Если N > Ь„, то полага-
ем х„ = 1, в противном случае полагаем х„ = 0.
Далее находим N- Ь„хп, переходим к слагаемому
с номером п - 1 и т. д.
Для построения шифра на основе сверхвоз-
растающей последовательности Р. Меркль и
М. Хеллман предложили «замаскировать» эту
последовательность с помощью линейного пре-
образования [12].
Алгоритм 12.3.1. Генерация ключа для ран-
цевого шифра Меркля-Хеллмана.
Вход. Длина блока п.
Выход. Открытый и секретный ключи.
Метод.
1. Выбрать сверхвозрастающую последователь-
ность из п натуральных чисел: {Ь\,Ь„}.
2. Выбрать целое число и> by + ... + Ь„.
3. Выбрать случайное число г, взаимно простое с и.
4. Выбрать случайную перестановку л чисел I,
2, ..., п.
5. Вычислить последовательность {аь..., а,,}
вида а, <— vbrfj) (mod й).
6. Результат: {ау, ..., а„}— открытый ключ;
(л:, г, и, {by,..., Ь„}) — секретный ключ.
Протокол 12.3.2. Ранцевый шифр Меркля-
Хеллмана.
Вход отправителя. Открытый ключ
{щ, ...,ап} из алгоритма 12.3.1.
Вход получателя. Секретный ключ (л, г, и,
{by, ..., А,,}) из алгоритма 12.3.1.
Результат. Зашифрование и расшифрование
сообщения.
259
МеТОД.
Для зашифрования сообщения длины п бит,
представленного в виде двоичного вектора
in =(Ш], ..., т„), отправитель вычисляет сумму
fl
, которая и является шифрограммой.
' 1 . .****•.
Для расшифрования шифрограммы получа-
тель выполняет следующие действия.
1. Вычисляет d <— cv-1 (mod и).
2. Представляет число d в виде линейной ком-
бинации элементов Z»(: d= г\Ъх + ... + r„b„.
3. Вычисляет вектор m = (т\,in,,), где
т, <-
Алгоритм корректен, так как при расшифро-
вании используется цепочка сравнений:
п п
d = CV~' = ^171/2^ = ^7иД(;)(тобн).
(=1 /=1
Здесь открытый ключ может быть интерпрети-
рован как набор {иД из задачи об укладке ранца.
Тогда задача дешифрования является частным
случаем задачи об укладке ранца. В действитель-
ности же алгоритм шифрования определяет не
произвольную задачу об укладке ранца, а только
небольшой подкласс таких задач с линейным спо-
собом «маскировки» сверхвозрастающей после-
довательности (напомним, что сложность массо-
вой задачи выбора— это сложность наиболее
трудной задачи данного размера). Алгоритм
Меркля-Хеллмана вскрывается с полиномиаль-
ной сложностью с помощью алгоритма Ленстры-
Ленстры-Ловаша (LLL) (см. п. 7.3 и работу [9]).
Подобный принцип шифрования использова-
ли и некоторые другие авторы, поскольку ско-
рость шифрования здесь оказывается сравнимой
со скоростью симметричного шифрования. Од-
нако большинство ранцевых алгоритмов шифро-
вания оказываются нестойкими. Шифрование в
таких алгоритмах может быть представлено как
нахождение вектора «-мерной решетки. Методы
вскрытия ключа других ранцевых шифров также
основаны на алгоритме LLL.
Рассмотрим еще один пример ранцевого
шифра (протокол Шора-Ривеста [4]). Здесь ра-
нец представляет собой набор логарифмов в
мультипликативной группе расширенного поля и
обладает повышенной плотностью по сравнению
с ранцем Меркля-Хеллмана.
Алгоритм 12.3.3. Генерация ключа для про-
токола Шора-Ривеста.
Вход. Характеристика поля р.
Выход. Открытый и секретный ключи, .г
Метод.
I. Выбрать конечное поле F„ = РДх]/(Дх)) из
q - р элементов, задаваемое неприводимым
над полиномом Дх) и такое, что задача ло-
гарифмирования в F9 является несложной.
2. Выбрать образующую g(x) группы F9*.
3. Для i = 0, 1, ...,р- 1 вычислить логарифмы а,
по основанию g(x) элементов х + i.
4. Выбрать случайную перестановку л элемен-
тов ПОЛЯ Fp.
5. Выбрать случайное число d, 0 < d < q - 2.
6. Вычислить c,<-(a^,) + d) (mod (т/-1)), где
О < i < р - 1.
7. Результат: ((со,..., с7,р, h)— открытый
ключ; (Дх), g(x), л, d) — секретный ключ.
В отличие от протокола Меркля-Хеллмана
здесь последовательность логарифмов не являет-
ся сверхвозрастающей.
Протокол 12.3.4. Шифрование с открытым
ключом Шора-Ривеста.
Вход отправителя. Открытый ключ ((с0, ...,6^),
р, h) из алгоритма 12.3.3.
Вход получателя. Секретный ключ (Дх), g(x),
л. d) из алгоритма 12.3.3.
Результат. Зашифрование и расшифрование
сообщения. Г .
Метод.
Для зашифрования сообщения т, 0<т
И
— биномиальный коэффициент, отпра-
1.
где ,
витель выполняет следующие действия.
Преобразует сообщение в двоичный вектор
М = (М» содержащий в точности h
единиц, следующим образом. '
1.1. Полагает 1 <— h.
1.2. Для z = 1, 2, ...,р полагает M-i <—1,
при
/?-z
/
т >
; Мл <— 0 в противном случае.3
2. Вычисляет шифрограмму •
р-i
с<— ]ГЛДсДтоб(<7-1))
<=0 . .
3 Заметим, что =0 при / < 0.
260
Для расшифрования шифрограммы получа-
тель выполняет следующие действия.
1. Вычисляет г <— с- hd (mod (q - 1)).
2. Находит и(х) <- g(x)r в поле F9.
3. Вычисляет полином .s(x) <— w(x) +./(х) над по-
лем Fp и раскладывает его на линейные мно-
h
жители: s(x) - (х + .
7=1
4. Находит единичные компоненты вектора М:
их позиции имеют номера л-1(/,). Остальные
компоненты вектора М — нулевые.
5. Восстанавливает сообщение т следующим
образом.
5.1. Полагает т <^0,l <~h.
5.2.
Для i= 1,2,...,рполагает
( P~i'
т<— т + \
I I J
7 «— 7 — 1 при М-i = 1 •
Расшифрование выполняется существенно
медленнее, чем зашифрование, так как требует
вычисления экспоненты в расширенном поле на
шаге 2, то есть скорость расшифрования примерно
такая же, как в алгоритмах Эль-Гамаля, RSA и др.
В работе [14] предложен вероятностный алго-
ритм вскрытия ключа с полиномиальной слож-
ностью, основанный на нахождении кратчайшего
вектора решетки с помощью алгоритма LLL.
Этот алгоритм является модификацией алгорит-
ма [5], предложенного для решения произволь-
ной задачи об укладке ранца, обладающего
плотностью не более 0,9408.
12.4. Генераторы псевдослучайной
последовательности
Генерация случайной последовательности явля-
ется важным криптографическим примитивом.
Часто от характеристик генератора зависит безо-
пасность ключа (например, в протоколах цифровой
подписи Эль-Гамаля, Шнорра, протоколе установ-
ления сеансового ключа Диффи-Хеллмана) или
конфиденциальность открытого текста (например,
в протоколах шифрования Эль-Гамаля, Месси-
Омуры). На практике такие генераторы использу-
ются для шифрования в режиме гаммирования,
выработки ключей и параметров криптосистем,
выработки вспомогательных случайных чисел.
Генераторы случайной последовательности
обычно строятся с использованием физических
генераторов шума. В этом случае проверка слу-
чайностных характеристик генератора (включая
периодический автоматический контроль) со-
пряжена со значительными сложностями. Алго-
ритмические генераторы псевдослучайной по-
следовательности (ПСП) не нуждаются в таком
контроле; достаточно однажды провести иссле-
дования генератора и в дальнейшем убеждаться в
исправности программы и процессора.
Любой генератор ПСП должен содержать не-
которую недоступную для нарушителя конфи-
денциальную информацию (ключ), в противном
случае нарушитель, зная алгоритм работы гене-
ратора и ключ, может смоделировать его работу.
Объем ключа должен исключать атаку на основе
перебора, то есть практически должен составлять
не менее нескольких десятков бит.
Для криптографических приложений генера-
тор ПСП должен не только формировать последо-
вательность, удовлетворяющую статистическим
тестам, но и обладать рядом других качеств, на-
пример, непредсказуемостью последующих би-
тов, невозможностью «восстановления» преды-
дущих битов по известному отрезку ПСП.
Например, генератор Af-последовательности
(см. пример 1.4.2 и работу [1]) является «стати-
стически хорошим», но криптографически не-
стойким. Его автокорреляционная характеристи-
ка лучше, чем у случайной последовательности,
однако вскрытие (вычисление содержимого ре-
гистра) выполняется с линейной от п сложно-
стью. Восстановить предшествующие биты тоже
нетрудно. Это объясняется тем, что данный ге-
нератор является линейным конгруэнтным гене-
ратором над кольцом F2 [/]/(/(/))-
Легко раскрываются и другие линейные кон-
груэнтные генераторы над конечными кольцами
(см. пример 1.4.2).
Генератор, основанный на блочном шифре с
длиной блока т, работающем в режиме гаммирова-
ния, формирует случайную подстановку из 2"’ эле-
ментов. Длина цикла ПСП для заданной синхропо-
сылки равна длине цикла случайной подстановки,
то есть не является гарантированно большой.
Генератор, основанный на ключевой хэш-
функции, не допускает восстановления предше-
ствующей последовательности с полиномиаль-
ной сложностью, но характеризуется короткой
трудновычислимой длиной цикла, которая про-
порциональна 2п'^, где т — длина блока.
На практике часто используются генераторы,
имеющие простое алгебраическое описание и
обладающие вычислимой или гарантированно
большой длиной цикла. В общем случае для по-
лучения гарантированно большой длины цикла
можно использовать зависимость выхода генера-
тора от номера итерации, например, х,- =.Дх/-ь 0-
Безопасность генератора случайных битов
можно охарактеризовать его стойкостью как слож-
ностью наилучшего известного алгоритма, нару-
шающего непредсказуемость битов. Различают
сложность предсказания очередного бита, если из-
вестна конечная последовательность предшест-
261
вующих битов, но не известно состояние генерато-
ра, и сложность вычисления предшествующих би-
тов, если известно текущее состояние генератора.
Иногда генератор (псевдо)случайных битов
называют криптографически стойким, если не
существует или не известен алгоритм полиноми-
альной сложности, позволяющий по / известным
битам последовательности предсказать (/+ 1)-й
бит с вероятностью сушественно большей, чем
0,5 [11]. Однако это определение не оперирует
понятием количественной стойкости, что не по-
зволяет оценить, насколько ослабится итоговый
протокол шифрования (подписи) при использо-
вании данного генератора.
Криптографически стойкий генератор после-
довательности {х,} может быть построен по сле-
дующей схеме. Пусть р — большое простое чис-
ло, g— образующая группы F/; и h— обрати-
мый элемент кольца Z7(/? - 1)Z. Положим у0 = g,
j; = ypt (mod р), х, = 0 при y^p/l, х, - 1 при
у, > р/2. Длина цикла такого генератора равна
р - 1. Поскольку порядок группы четный, ве-
роятности появления нуля и единицы равны. За-
дача предсказания очередного бита сводится к
задаче вычисления текущего состояния генера-
тора. Задача вычисления предшествующих битов
по известному текущему состоянию генератора
решается с полиномиальной сложностью:
У,-1 =у'1 (mod/?).
Аналогичные генераторы можно строить и на
эллиптических кривых.
Л. Блюм, М. Блюм и М. Шуб предложили спо-
соб построения генератора BBS псевдослучайной
последовательности битов [2], основанный на
возведении в квадрат в кольце вычетов ~%Jn7L. Для
этого вырабатывают два случайных больших про-
стых числа p = q = 3 (mod 4), находят число и =pq-
Затем вырабатывают случайное число у0 и выпол-
няют рекуррентную процедуру yt =у,1 2_](тоби)
для z > 0. Из каждого у, выбирают младший бит,
который и является элементом последовательно-
сти {х/}. Заметим, что можно выбирать не один, а
О(1п1пи) младших битов. Сложность предсказа-
ния каждого из них (при известных остальных)
равна сложности предсказания младшего бита.
Безопасность генератора BBS основана на слож-
ности определения того, является ли квадратич-
ным вычетом по модулю п элемент, обладающий
единичным значением символа Якоби.
Статистически хорошие свойства у генерато-
ра получаются и при использовании в качестве х,
«средних» битов элемента у,.
Если у0 является образующей групп F/;*, F,/ и
числа р - 1, q - 1 имеют большие простые дели-
тели г, s, соответственно, и при этом число 2 яв-
ляется образующей групп F,*, F.v, то длина цикла
последовательности будет делить число
(г - !)(.$’ - 1). Это следует из изоморфизма групп:
(Z/hZ)* = F/ х F/. ‘
Порядок числа 2 в циклических группах F,.*,
Fs. вычисляется очевидным образом, если из-
вестны разложения чисел г - 1, s - 1. С другой
стороны, можно выбрать сначала г и s, для кото-
рых 2 является образующей группы большого
порядка, а затем найти по ним р и q. Сложность
выбора параметров р, q, у0 оценивается полино-
мом степени не выше 3.
Для восстановления предыдущего значения
у,_] по известному текущему значению у, необхо-
димо извлечь квадратный корень по модулю и и
выбрать из четырех значений корня то, которое
соответствует квадратичным вычетам по модулям
р w q. Поскольку -1 является квадратичным невы-
четом по модулям р, q, то квадратичным вычетом
по модулю /?, как и по модулю q, является только
одно из двух значений у или -у. Следовательно,
если у — квадратичный вычет по модулю п, то
—у— квадратичный невычет, одно из чисел у или
—у (mod и) четное. Задача извлечения квадратного
корня в группе (Z7hZ) полиномиально эквива-
лентна задаче извлечения корня в каждой из
групп Fp , F9, то есть сводится к нахождению
чисел pvtq (или к разложению числа и).
Задача «предсказания» полиномиально экви-
валентна нахождению числа п и текущего значе-
ния у,.
Упражнения к главе 12
1. Сравните безопасность протоколов шифро-
вания RSA и Эль-Гамаля при использовании
кольца Z7hZ.
2. Пусть G— конечная циклическая группа с
заданной образующей. Порядок группы G
известен и делится на простое число г. Как
найти образующую циклической подгруппы
порядка г? Как найти такую образующую,
если G — абелева группа?
3. Сравните безопасность протоколов Месси-
Омуры и Диффи-Хеллмана в случае, когда в
качестве группы G используется вся группа Fp .
4. Пусть открытый текст шифруется протоко-
лом Эль-Гамаля в подгруппе простого по-
рядка группы Fp, при этом используется
функция fi.m, by) = пгЬу (modр). Можно ли
получить информацию об открытом тексте с
помощью символов Лежандра?
5. Сравните сложность взлома протокола Диф-
фи-Хеллмана в группе (Z7«Z) и сложность
разложения числа п.
6. Пусть р = q = 3 (mod 4), п =pq и х е ~%JnZL,
1 п
причем — = 1. Покажите, что один из двух
\ п J
элементов х или -х является квадратичным
вычетом по модулю п.
7. Можно ли в протоколе шифрования Блюма-
Голдвассера использовать общее число п
для нескольких пользователей?
8. Предложите способ обеспечения имитоза-
щиты в протоколе Блюма-Голдвассера, от-
личный от цифровой подписи.
9. Предложите свой вариант генератора ПСП,
использующего вычисления в конечном поле
и обладающего вычислимой длиной цикла.
10. Пусть р и (j>-1)/2 — простые числа и
х,+] е= х*' (mod р). Оцените сложность нахож-
дения х,_1 по известному х,.
11. Предположим, что р — простое число, р = 5
(mod 6). Как найти неподвижные точки не-
линейного конгруэнтного генератора х,+) =
= х3 + Б (mod р) 2 Как нужно выбрать коэф-
фициент В, чтобы генератор не имел непод-
вижных точек?
12. Предположим, что р— нечетное простое
число, р Ф 1 (mod 10). Покажите, что генера-
тор х/+] = х,5 + В (mod р) задает подстановку
в Fp и может иметь не более пяти неподвиж-
ных точек.
13. Разработайте аналог системы RSA на эл-
липтической кривой E(Z7«Z), где n=pq и
#E(Fp) =/?', #E(F9) = q' — различные простые
числа. Предположим, что вычисления на эл-
липтической кривой выполняются корректно.
Будет ли группа E(Z7«Z) циклической?
14. (Продолжение). Будет ли группа E(Z7hZ)
циклической, если #E(F/J) = 2р', #EQFq) = 2q',
где /?', q' — различные простые числа?
Литература к главе 12
1. Варакин Л.Е. Системы связи с шумоподобными
сигналами. М.: Радио и связь, 1985.
2. Blum L., Blum М., Shub М. A simple unpredictable
pseudo-random number generator I I SIAM Journal on
Computing. 1986. Vol. 15. P. 364-383.
3. Blum M., Goldwasser S. An efficient probabilistic
public-key encryption scheme which hides all partial
information П Advances in Cryptology— Proceed-
ings of CRYPTO 84. Lecture Notes in Computer Sci-
ence. Springer-Verlag. 1985. Vol. 196. P. 289-299.
4. Chor B., Rivest R. A knapsack-type public key
cryptosystem based on arithmetic in finite fields H
IEEE Transactions on Information Theory. 1988.
Vol. IT-34. P. 901-909.
5. Coster M., Joux A., LaMacchia B., et al. Improved
low-density subset sum algorithms H Computational
Complexity. 1992. Vol. 2. P. 111-128.
6. Diffie W., Hellman M. New directions in cryptogra-
phy П IEEE Transactions on Information Theory.
1976. Vol. IT-22. P. 644-654.
7. ElGamal T. A public key cryptosystem and a signa-
ture scheme based on discrete logarithms H IEEE
Transactions on Information Theory. 1985.
Vol. IT-31. P. 469-472.
8. Goldwasser S., Micali S. Probabilistic encryption //
Journal of Computer and System Sciences. 1984.
Vol. 28. P. 270-299.
9. Lenstra A.K., Lenstra H.W., Lovasz L. Factoring
polynomials with rational coefficients // Mathema-
tische Annalen. 1982. Vol. 261. P. 515-534.
10. Massey J., Omura J. Method and apparatus for main-
taining the privacy of digital messages conveyed by
public transmission. Pat. USA 4,567,600, 28 Jan
1986.
11. Menezes A., van Oorschot P., Vanstone S. Handbook
of Applied Cryptography. CRC Press, 1997.
12. Merkle R., Hellman M. Hiding information and sig-
natures in trapdoor knapsacks // IEEE Transactions
on Information Theory. 1978. Vol. IT-24.
P. 525-530.
13. Rabin M. Digitalized signatures and public key func-
tions as intractable as factorization. Technical Report
MIT/LCS/TR-212, MIT Laboratory for Computer
Science, 1979.
14. Schnorr C.P., Homer H.H. Attacking the Chor-Rivest
cryptosystem by improved lattice reduction // Ad-
vances in Cryptology— EUROCRYPT ’95. Lecture
Notes in Computer Science. Springer-Verlag. 1995.
Vol. 921. P. 1-12.
Г л а в a 13. ЦИФРОВАЯ ПОДПИСЬ
До появления криптографии с открытым
ключом целостность и подлинность документов
в условиях взаимного недоверия контролирова-
лись, как правило, по материальным признакам.
Документы имели конкретное физическое во-
площение, например, были напечатаны на гер-
бовой бумаге или заверены печатью. Однако с
развитием информатизации они стали терять
уникальные физические качества, а печать те-
перь легко можно переснять сканером и вос-
произвести в любом масштабе на цветном
принтере.
Использование симметричных криптографи-
ческих алгоритмов не позволяет установить
подлинность и целостность электронного доку-
мента в условиях взаимного недоверия. Напри-
мер, если получатель сообщения утверждает,
что получил от отправителя некоторое заверен-
ное сообщение, а отправитель это отрицает, то
один из них лжет. Однако установить, кто
именно говорит неправду, затруднительно, так
как оба они обладают равными возможностями
в части формирования имитозащищенных со-
общений. Осуществить аутентификацию дан-
ных и их источника в этом случае позволяет
цифровая подпись.
Цифровая подпись в цифровых документах
играет ту же роль, что и подпись, поставленная
от руки в бумажных документах: это данные,
присоединяемые к передаваемому сообщению и
подтверждающие, что автор подписи (отправи-
тель) составил или заверил данное сообщение.
Получатель сообщения или третья сторона с по-
мощью цифровой подписи может проверить, что
автором сообщения является именно владелец
подписи и что в процессе передачи не была на-
рушена целостность данных.
Цифровая подпись предполагает два этапа:
формирование и проверку, то есть реализуется
некоторым протоколом. Часто способы форми-
рования и проверки цифровой подписи допуска-
ют некоторую свободу действий, которую нет
смысла строго регламентировать. Это позволяет
говорить о схеме подписи.
Таким образом, при разработке протокола
цифровой подписи нужно:
- создать пару сообщение/подпись так, чтобы
ее невозможно было подделать;
- уметь проверить, что подпись действительно
принадлежит указанному владельцу.
Кроме того, подпись должна быть построена
так, чтобы отправитель, подписавший сообще-
ние, не смог затем отрицать перед получателем
или третьей стороной факт подписания, утвер-
ждая, что подпись подделана.
Обычно, говоря о схеме цифровой подписи,
имеют в виду следующую ситуацию [15]:
- отправитель знает содержание сообщения,
которое он подписывает;
- получатель, зная открытый ключ проверки
подписи, может проверить правильность
подписи в любое время без какого-либо раз-
решения или участия отправителя;
- безопасность схемы подписи (то есть труд-
ность подделки, невозможность отказа от
подписи и т. д.) обеспечивается положения-
ми теории сложности.
При формировании цифровой подписи по
классической схеме [13] отправитель сообщения
сначала применяет к исходному тексту хэш-
функцию, а затем вычисляет собственно цифро-
вую подпись с помощью секретного ключа фор-
мирования подписи.
Получатель сообщения выполняет проверку
подписи: сначала вычисляет хэш-образ получен-
ного сообщения с помощью той же самой хэш-
функции, которую использовал отправитель, а
затем с помощью открытого ключа проверки
подписи проверяет, соответствует ли этот хэш-
образ полученной цифровой подписи.
Схемы подписи, как и шифрования с откры-
тым ключом, основаны на вычислениях в конеч-
ной группе, поэтому их можно разделить по типу
вычислимости порядка группы.
13.1. Подпись на группе
трудновычислимого порядка
Для этого класса подписей используется
группа, вычисление порядка которой эквива-
лентно труднорешаемой задаче разложения со-
ставного числа на простые множители (см.
ГЛ. 9). г ... ;; ;
264
13.1.1. Схема подписи RSA
Криптосистема с открытым ключом RSA мо-
жет использоваться не только для шифрования,
но и для построения схемы цифровой подписи.
Протокол 13.1.1. Схема подписи RSA.
Вход отправителя. Составное число п. секрет-
ный показатель d.
Вход получателя. Составное число п, откры-
тый показатель е.
Результат. Формирование и проверка подписи.
Метод.
Для формирования подписи для сообщения т
отправитель выполняет следующие действия.
1. Вычисляет хэш-образ г <— h(m) сообщения т
(за рубежом для подписи RSA часто исполь-
зуются хэш-функции MD4 и MD5).
2. Зашифровывает число г на своем секретном
ключе d, то есть вычисляет экспоненту s rd
(mod и).
Подписью для сообщения т является число s.
Для проверки подписи получатель выполняет
следующие действия.
1. Расшифровывает подпись s на открытом
ключе е отправителя, то есть вычисляет
I <— 5е (mod и), восстанавливая предполагае-
мый хэш-образ t сообщения т.
2. Вычисляет хэш-образ г <— h(m) сообщения т.
3. Проверяет равенство г = t. Если оно выполня-
ется, то результат: подпись подлинная, иначе
результат: подпись недействительна.
Схема подписи RSA может быть рассмотрена
как категория, объектами которой являются пары
сообщение/подпись, а морфизмами — отображе-
ния таких пар, удовлетворяющие проверочным
соотношениям. Очевидно, что если (т, s) — под-
линное подписанное сообщение, то пара (т', s')
тоже будет правильно подписанным сообщени-
ем, если h(m') = hk(m) (mod и) и s' s / (mod n) для
некоторого целого к. Новая пара (??/, s') может
быть создана следующим алгоритмом: выбрать
сообщение т', вычислить h(m'), найти логарифм
h(m’) по основанию h(m) и вычислить s'. Можно
наоборот, сначала найти г' = М(;и) (mod ri) для
известного к, а затем подобрать т' так, чтобы
выполнялось равенство h(m') = г'. Поэтому стой-
кость подписи RSA не может превышать слож-
ности вычисления логарифма в группе (Z7«Z)*
или сложности обращения хэш-функции.
Если нарушитель составляет текст для подпи-
си, то он может подготовить коллизию (/и, т')
такую, что h(m) = h(m'), дать на подпись сообще-
ние т, а затем подменить подписанное сообще-
2.
ние т сообщением т'. В этом случае стойкость
схемы подписи не может превышать сложности
вычисления коллизий хэш-функции. Приведен-
ные рассуждения показывают, что необходимо
согласовывать сложности разложения, логариф-
мирования и нахождения коллизий.
Если хэш-функция не используется, то мор-
физм подписи RSA можно легко вычислить. Это
обстоятельство положено в основу подписи
«вслепую» для электронных денег (подробнее
см. п. 13.5.2).
13.1.2. Схема подписи Рабина
Вариантом RSA является схема подписи,
предложенная в 1979 г. М. Рабином [14].
Протокол 13.1.2. Схема подписи Рабина.
Вход отправителя. Простые делители р и q
числа п.
Вход получателя. Составное число и.
Результат. Формирование и проверка подписи.
Метод.
Для формирования подписи для сообщения т
отправитель выполняет следующие действия.
1. Вырабатывает случайное число г и вычисляет
значение хэш-функции е <— /г(?и || г), е е ~ZJriZ..
Проверяет, является ли е квадратичным выче-
том по модулю и,1 для чего, например, вычис-
6 х /
е е
ляет символы Якоби
Если е—
квадратичный невычет по модулю и, то воз-
вращается на шаг 1 (генерирует новое значение
г и вычисляет новое е). В противном случае
вычисляет dp <^Je(modp), dq (mod q)
и восстанавливает d e (Z/«Z)*, d2 = e
(mod ri), по китайской теореме об остатках:
d <— dpq(q 1 mod p) + dgp(p 1 mod q) (mod ri).
Подписью для сообщения m является пара
(r,d).
Для проверки подписи получатель выполняет
следующие действия.
1. Вычисляет значение е <— d2 (mod ri).
2. Вычисляет хэш-образ е' <— h(m || г). Если
е = е', то результат: подпись подлинная, ина-
че результат: подпись недействительна.
Безопасность этого протокола основана на тео-
реме 12.2.1. Кроме того, схема подписи Рабина
1 При надлежащем выборе хэш-функции вероят-
ность того, что е является квадратичным вычетом по
модулю п, приблизительно равна 0,25.
265
подвержена атаке на основе подобранных сообще-
ний (например, извлечение квадратного корня из 4
не требует разложения числа и). Возможно также
нарушение «правильного» порядка вычислений,
при котором сначала ищется корень из сообщения
как целого числа, а потом подбирается число г.
13.1.3. Схема подписи Фиата-Шамнра
Эта схема подписи была предложена
А. Фиатом и А. Шамиром в 1986 г. [8]. Общим
открытым ключом здесь является составное число
n=pq-, персональным секретным ключом— на-
бор элементов 50,5*_j кольца Z/«Z; персональ-
ным открытым ключом — набор элементов
г0, v^i кольца Z/«Z таких, что г, ^,$72(mod«).
В отличие от RSA здесь можно использовать об-
щий модуль п, при этом ни один из участников не
должен знать разложение числа п. Организацион-
но это можно выполнить так: выработать два раз-
личных больших простых числа, затем вычислить
их произведение, а сами простые числа стереть.
Протокол 13.1.3. Схема подписи Фиата-
Шамира.
Вход отправителя. Составное число и;
So, ...,5а-_| е Z/nZ.
Вход получателя. Составное число п;
го,..., г^_] g Z/nZ, где г, ss/2(modn).
Результат. Формирование и проверка подписи.
Метод.
Для формирования подписи для сообщения т
произвольной длины отправитель выполняет сле-
дующие действия.
1. Выбирает произвольное целое число г,
1 < г < и - 1.
2. Полагает и <— г2 (mod п).
3. Вычисляет хэш-функцию /z(;w||w) и
представляет полученное значение в виде
двоичного вектора (е0, ek_i).
к-}
4. Вычисляет s <— гs^' (modп).
/=о
Подписью для сообщения т является пара
(е, s).
Для проверки подписи получатель выполняет
следующие действия.
1. Представляет число е в виде двоичного век-
тора^, ..., ек-]).
к-1
2. Вычисляет w<- ,у2 J”Jr,e' (mod«).
/=о
3. Полагает е' <— /г(т || и).
4. Проверяет равенство е = е'. Если оно выпол-
няется, то результат: подпись подлинная,
иначе результат: подпись недействительна.
Безопасность этой схемы подписи основана
на сложности извлечения корня в кольце выче-
тов ~ZJriZ.. При этом число п должно вырабаты-
ваться доверенной стороной. Для того чтобы ка-
ждый пользователь системы мог убедиться в
том, что число п выбрано правильно, в криптоси-
стеме необходимо предусмотреть процедуру до-
казательства того, что число п является произве-
дением двух различных простых чисел (см., на-
пример, п. 14.2.4).
Подпись Фиата-Шамира не обладает вычис-
лимыми морфизмами, присущими подписи RSA.
Использование стойкой (в смысле обращения и в
смысле нахождения коллизий) хэш-функции ис-
ключает атаку, связанную с подделкой подписи.
13.2. Подпись на группе
вычислимого порядка
В этих протоколах можно использовать про-
извольные группы вычислимого порядка г. В ка-
честве примера рассмотрим подгруппу группы .
13.2.1. Схема подписи Эль-Гамаля
Протокол подписи Эль-Гамаля [7] строится
следующим образом. Секретным ключом фор-
мирования подписи служит целое число х,
О < х < г, открытым ключом проверки подпи-
си — простое число р, образующая а подгруппы
простого порядка г мультипликативной группы
F,,* простого поля и экспонента b = ax (mod р).
Протокол 13.2.1. Схема подписи Эль-Гамаля.
Вход отправителя. Секретный ключ х.
Вход получателя. Характеристика поля р, об-
разующая а подгруппы простого порядка г, экс-
понента b = a' (modр).
Результат. Формирование и проверка подписи.
Метод.
Для формирования подписи для сообщения т,
О<т<г, отправитель выполняет следующие
действия.
1. Генерирует случайное число к, 0 < к < г.
2. Полагает и <— cf (mod р).
3. Находит число s, решая сравнение
т s xw + ks (mod г):
s <— (т - xm’)E ' (mod г).
Подписью для сообщения т является пара
Для проверки подписи получатель выполняет
следующие действия.
1. Проверяет неравенство w <р. Если оно не
выполнено, то результат: подпись недействи-
тельна.
2. Проверяет сравнение для экспонент:
d" = b"'w' (mod р). Если оно выполняется, то
результат: подпись подлинная, иначе резуль-
тат: подпись недействительна.
Поскольку число к, используемое на этапе
формирования подписи, взаимно просто с чис-
лом г, то к обратимо по модулю г, то есть число s
всегда существует и оно единственное.
При формировании подписи в протоколе Эль-
Гамаля можно использовать предвычисления.
Действительно, числа к и w никак не связаны с
сообщением и могут быть вычислены заранее, что
позволяет ускорить процедуру формирования
подписи. Проверка подписи является более тру-
доемкой. Протокол Эль-Гамаля положен в основу
стандартов подписи РФ и США (см. п. 13.2.3).
Протокол Эль-Гамаля можно модифицировать.
Например, использовать в сравнении m=xw + ks
(mod г) вместо сложения вычитание; менять мес-
тами s и h(m); умножать слагаемые на ненулевые
коэффициенты: am = bxw + cks (mod г); заменять
линейное сравнение алгебраическим уравнением,
имеющим единственное решение в поле вычетов
по модулю г. В частности, при r = 5 (mod 6) любое
сравнение третьей степени всегда имеет единст-
венное решение в F,-, поэтому можно использовать
сравнение т3 = xw3 + ks3 (mod г), тогда проверка
подписи сведется к проверке сравнения d" = b w'
(mod р). Можно возводить в степень не все коэф-
фициенты, а также использовать произвольную
нечетную степень t такую, что НОД(г - 1, t) = 1,
так как отображение х х (mod г) является взаим-
но однозначным и вычислимым в обе стороны.
Протокол подписи Эль-Гамаля тоже может
быть рассмотрен как категория, в которой пары
сообщение/подпись составляют множество объ-
ектов, а отображения между ними — морфизмы.
Покажем, что эти морфизмы могут быть легко
вычислены.
Пусть (т, w, .$) — правильно подписанное со-
общение. Создание нового формально правиль-
ного сообщения (т’, w', s') основано на умноже-
нии сравнения формирования подписи на число
р. Пусть к = ак (mod г). Обозначим w's ci
(mod p). Пусть w' = pvr (mod г). Тогда m' = рш
(mod r), s' s oT'ps (mod г). Таким образом, для
вычисления морфизма (ти, w, s) —> (id, w', s') дос-
таточно вычислить аир. Морфизм вычисляется
следующим алгоритмом.
Алгоритм 13.2.2. Вычисление морфизма про-
токола подписи Эль-Гамаля.
Вход. Тройка (т, w, s).
Выход. Тройка (»?', и', s'), удовлетворяющая
проверочным соотношениям.
Метод.
1. Выбрать произвольное число а, положить
w' <— (mod р).
2. Вычислить коэффициент р <— w'w] (mod г).
3. Положить id <— рт (mod г), s’ <— a 'ps (mod г).
4. Результат: (/д', w', s').
Нахождение данного морфизма основано на
нарушении порядка вычислений при генерации
подписи (сначала выбирается а, затем находятся
Р и т'). Для исключения подделки подписи без
вскрытия ключа необходимо использовать хэш-
функцию h, например, вырабатывать подпись не
для самого сообщения т, а для его хэш-образа
h(m). Эта хэш-функция должна быть стойкой в
части нахождения коллизий, в противном случае
возможна заготовка коллизий до формирования
подписи, как и в схеме RSA. Данный недостаток
можно устранить, если «связать» с помощью
хэш-функции2 независимые аргументы т и w,
например, вычислять подпись для h(m || и).
Указанный морфизм может быть положен в
основу подписи «вслепую», например, для элек-
тронных денег (см. п. 13.5.2).
Условие w < р, проверяемое получателем, яв-
ляется важным, так как в противном случае пра-
вильная подпись (и, s) для е = h(m) может быть
переделана в подпись для произвольного значе-
ния хэш-функции е' = h(m'). Для этого достаточ-
но вычислить элемент р = <?'<? ' (mod г). Тогда
а = Л“' = (mod/?). Полагая s' = Ps (modг),
w' = pw (mod r), w' = w (mod p), можно найти це-
лое число w' < pr по китайской теореме об остат-
ках, при этом (иД s') будет подписью для сооб-
щения е’ = h(vd).
Протокол подписи Эль-Гамаля может быть
очевидным образом перенесен из группы ОД в
произвольную циклическую группу вычислимо-
го порядка. Пусть G — циклическая группа про-
стого порядка г с образующей а и пусть b е G.
Секретным ключом формирования подписи яв-
ляется показатель х такой, что d = Ь; открытый
ключ проверки подписи содержит способ зада-
ния группы G, образующую а и элемент Ь. Кроме
того, необходимо иметь вычислимую в одну сто-
рону функцию f.G^> F, (функции / и h могут
2 Здесь хэш-функция должна обеспечивать сцепление
битов и блоков аргумента, то есть не должно существо-
вать пары т\, т2 такой, что /?(>И|||и-) = для всех w.
267
совпадать). Для формирования подписи для со-
общения т генерируется случайный показатель к
и вычисляются значения: w = </, Xw), Ырп\\~ю),
s = (h(m || и) - xflw))k 1 (mod г). Подписанное со-
общение представляет собой тройку (т, w, s).
Если в группе G выполняется равенство
то подпись подлинная.
В основу безопасности схемы подписи Эль-
Гамаля положены следующие предположения:
1) задача дискретного логарифмирования в
группе G является сложной;
2) энтропия генератора случайных чисел не
ниже энтропии генератора ключей;
3) вероятность повтора двух случайных чисел к
в течение срока действия ключа пренебре-
жимо мала;
4) хэш-функция h является вычислительно не-
обратимой;
5) коллизии хэш-функции h являются трудно-
вычислимыми;
6) функция f является вычислительно необра-
тимой;
7) коллизии функции / являются трудновычис-
лимыми.
Решение задачи логарифмирования в группе
G позволяет вычислить ключ формирования
подписи по открытому ключу. Если число к из-
вестно, то ключ формирования подписи вычис-
ляется решением линейного сравнения:
flw'i
Если среди множества подписей на одном
ключе встретились две с одинаковым значением w
(и, следовательно, с одинаковым значением к), то
ключ формирования подписи может быть вычис-
лен решением системы двух линейных сравнений:
//(/и, || w) = xw+kst (mod г),
<
h(m21| w) = xw + ks2 (modr).
Если задачи обращения или нахождения кол-
лизий функций/или h не являются сложными, то
возможна подделка подписи без вскрытия ключа
или замена подписанного сообщения другим.
Отметим, что если удастся вычислить к такое,
что /(и) = 0 (mod г), то пара (осмысленное) со-
общение/подпись может быть подделана даже
без наличия правильно подписанного сообще-
ния, независимо от секретного ключа. Такие зна-
чения к оказываются вычислимыми для некото-
рых функций/и некоторых эллиптических или
гиперэллиптических кривых. В этих случаях
протокол проверки подписи может потребовать
уточнений, например, проверки того, что эле-
мент w действительно принадлежит циклической
группе G порядка г (см. гл. 15).
Таким образом, сложностная неоднородность
обобщенного протокола Эль-Гамаля равна 7 (или
5, если/= й).
Оригинальный протокол Эль-Гамаля при ге-
нерации подписи использует не подгруппу по-
рядка г, а всю группу порядка р - 1, причем чис-
ло р и образующая а группы 0/, являются общи-
ми для всех пользователей. В этом случае воз-
можно встраивание потайного хода в протокол
выбором образующей [4].
Пусть р - 1 = сг, где с имеет только малые
простые делители. Если существует образующая
а' <р вида а' = dr, где 0 < d < с, и известен пока-
затель t такой, что (а'У = а (mod р), то подпись
можно подделать без знания секретного ключа.
Для формирования поддельной подписи нуж-
но выполнить следующие действия.
1. Решить показательное сравнение а™ = Ь'
(mod р) относительно переменной z путем
дискретного логарифмирования в подгруппе
порядка с. Для решения можно использовать
алгоритм Гельфонда.
Z2 — 3
2. Положить а <—ах (mod р\ t <-------. Тогда
Р-З Р-1
(а')' = (а') 2 = («')” («') 2 = -(«') = а (mod р).
3. Полагая w <— а', найти значение s <— t(e - drz)
(mod (/?-!)) для данного значения е хэш-
функции. При этом wsb" = (a'Yc~dr:}bdr =
= ae~d'~bdr = ае (mod р), то есть (w, s) — пра-
вильная подпись для е.
Таким образом, безопасность схемы подписи
Эль-Гамаля при работе в группе 0/, зависит от
существования заранее неочевидного набора
{а, а', с, d} с указанными свойствами; этот набор
может быть тайно создан нарушителем (разра-
ботчиком) на этапе выбора открытого ключа.
Поэтому более предпочтительным является ис-
пользование подгруппы простого порядка г.
13.2.2. Схема подписи Шнорра
В протоколе цифровой подписи К. Шнорра
[16] ключи формирования и проверки подпи-
си — те же, что и в протоколе Эль-Гамаля.
Протокол 13.2.3. Схема подписи Шнорра.
Вход отправителя. Секретный ключ х.
Вход получателя. Характеристика поля р, об-
разующая а подгруппы простого порядка г, экс-
понента b = ax (mod р). -> .г:
268
Результат. Формирование и проверка подписи.
Метод.
Для формирования подписи для сообщения т
отправитель выполняет следующие действия.
1. Генерирует случайное число к, 0 < к < г.
2. Вычисляет w <- с/1 (modр).
3. Находит е <- h(m || и), где h — хэш-функция.
4. Полагает s <— к - хе (mod г).
Подписью для сообщения т является пара
О, 5).
Для проверки подписи получатель выполняет
следующие действия.
1. Вычисляет w' cfbe (mod р).
2. Находит е' <— h{m || w').
3. Проверяет равенство е' = е. Если оно выпол-
няется, то результат: подпись подлинная,
иначе результат: подпись недействительна.
В основу безопасности схемы подписи Шнор-
ра положены следующие предположения:
1) задача дискретного логарифмирования в под-
группе простого порядка г является сложной;
2) энтропия генератора случайных чисел не
ниже энтропии генератора ключей;
3) вероятность повтора двух случайных чисел к
в течение срока действия ключа пренебре-
жимо мала;
4) хэш-функция h является вычислительно не-
обратимой.
Здесь, как и в протоколе Эль-Гамаля, повто-
рение одного и того же случайного числа к в те-
чение срока действия ключа х приводит к вскры-
тию ключа, для этого достаточно решить систе-
му из двух линейных сравнений. Случай одина-
ковых к выявляется сортировкой подписей по
значению w' (шаг 1 проверки подписи).
Среди возможных модификаций протокола
Шнорра: замена вычитания сложением; исполь-
зование вместо сравнения s = к - хе (mod г) ли-
нейной комбинации as = bk- схе (mod г) с нену-
левыми а, Ь, с; замена линейного сравнения ал-
гебраическим уравнением, допускающим един-
ственное решение по аналогии с протоколом
Эль-Гамаля.
Определим ограниченное обращение хэш-
функции как нахождение аргумента, часть кото-
рого фиксирована, то есть аргумент можно «на-
ращивать», начиная с некоторого фиксированно-
го отрезка. В протоколе Шнорра ограниченным
обращением будет нахождение сообщения т та-
кого, что h(m || w) = е при заданных w, е.
Задача ограниченного обращения хэш-фун-
кции h не проще задачи ее обращения. Действи-
тельно, в противном случае можно было бы за-
дать произвольно значение w и далее решать за-
дачу ограниченного обращения.
Категория схемы подписи Шнорра содержит в
качестве объектов множество пар сообще-
ние/подпись, морфизмами являются отображения
этих пар. Но поскольку в аргумент хэш-функции
входит неизвестный заранее элемент w, то мор-
физм трудновычислим, а предварительная заго-
товка коллизий затруднена. Это обстоятельство
накладывает менее жесткие требования на хэш-
функцию по сравнению с подписью Эль-Гамаля.
13.2.3. ГОСТ Р 34.10-94 и DSS
По принципу протокола цифровой подписи
Эль-Гамаля созданы отечественный стандарт
цифровой подписи ГОСТ Р 34.10-94 [1] и аме-
риканский стандарт DSS (Digital Signature Stan-
dard) [10], основанные на задаче дискретного
логарифмирования в подгруппе простого по-
рядка г простого поля характеристики р. В
ГОСТ Р 34.10-94 число г имеет длину 256 бит,
для формирования и проверки подписи исполь-
зуется хэш-функция ГОСТ Р 34.11-94 [2]. В DSS
длина числа г — 160 бит, используемая хэш-
функция — SHA-1 [9].
Параметрами алгоритма цифровой подписи в
указанных стандартах являются:
1) р — простое число, 2Л 1 <р<2'\ где510<£<512
или 1022<£<1024 для ГОСТ Р 34.10-94; L
кратно 64 и 512 < L < 1024 для DSS;
2)
3)
4)
5)
г — простой делитель числа /?-1,
2255 <г< 2256 для ГОСТ Р 34.11-94
где
и
о 159 q 160 псс*
2 <г<2 для DSS;
а — образующая циклической подгруппы
порядка г группы ;
х — случайное целое число, 0 < х < г;
b = d (mod р).
Целые числа р, г и а являются открытыми и
могут быть общими для группы пользователей.
Число х— секретный ключ формирования под-
писи, b — открытый ключ проверки подписи.
Протокол 13.2.4. Схема подписи ГОСТ Р 34.10-94
и DSS.3
Вход отправителя. Секретный ключ х.
3 В настоящее время стандарт подписи
ГОСТ Р 34.10-94 заменен стандартом подписи
ГОСТ Р 34.10-2001 (изменения по сути касаются типа
группы, в новой версии используется группа точек
эллиптической кривой). В США несколько раньше
разработана аналогичная версия стандарта ECDSS
(Elliptic Curve Digital Signature Standard).
269
Вход получателя. Характеристика поля р, об-
разующая а подгруппы простого порядка г, экс-
понента b = d (mod /?).
Результат. Формирование и проверка подписи.
Метод.
Для формирования подписи для сообщения т
отправитель выполняет следующие действия.
1. Генерирует случайное целое число к,
О <к< г.
2. Полагает w <— (</ (mod р)) (mod г).
3. Вычисляет e<—h(m), где h— хэш-функция
ГОСТ Р 34.11-94 (для ГОСТ Р 34.10-94) или
SHA-1 (для DSS).
4. Находит s <— (ке + xw) (mod г) (для ГОСТ
Р 34.10-94) или s <— к~\е +xw) (mod/') (для
DSS).
Подписью для сообщения т является пара
(w, 5), при этом не допускается 5 = 0.
Для проверки подписи получатель выполняет
следующие действия.
1. Проверяет неравенства w < г, 5 < г. Если хо-
тя бы одно из них не выполняется, то резуль-
тат: подпись недействительна.
2. Находит е <— h(m), где h — хэш-функция
ГОСТ Р 34.11-94 (для ГОСТ Р 34.10-94) или
SHA-1 (для DSS).
3. Вычисляет t <— е] (mod г) (для ГОСТ Р 34.10-94,
при е = 0 полагает t <— 1) или t <— 5-1 (mod г)
(для DSS).
4. Вычисляет u<-st (mod г), v<—-wt (mod г)
(для ГОСТ Р 34.10-94) или u-^et (mod г),
v <—wt (mod г) (для DSS).
5. Полагает w' <— (avbv (mod /?)) (mod r).
6. Проверяет равенство w' = w. Если оно вы-
полняется, то результат: подпись подлинная,
иначе результат: подпись недействительна.
Для затруднения закладки потайного хода
при выработке открытого ключа, общего для
всей системы, в ГОСТ Р 34.10-94 предусмотрен
механизм проверки того, что открытый ключ
вырабатывался «по правилам». Напомним, что
такой потайной ход (по отношению к методу
решета числового поля) может быть создан, ес-
ли сначала выбрать неприводимый над Z раз-
реженный полином с малыми по абсолютной
величине коэффициентами и алгебраическое
число а как корень этого полинома, а затем —
простое число р такое, что образ т = a (mod р)
является гладким.
Здесь, как и в протоколе Эль-Гамаля, исполь-
зование дважды одного и того же числа к ведет к
вскрытию ключа формирования подписи реше-
нием системы сравнений:
5] =xw + keA (mod/'),
<
52 = xw + ке2 (mod г).
В протоколах ГОСТ Р 34.10-94 и DSS аргу-
ментом хэш-функции является только сообщение
т, а не пара /?/||w, поэтому используемая хэш-
функция должна быть стойкой в части нахожде-
ния коллизий. Коллизии могут заготавливаться
заранее, то есть сложность нахождения коллизий
должна соответствовать сложности вскрытия
ключа или даже превышать ее, если в системе
предусмотрены механизмы смены общего клю-
ча подписи и не предусмотрены механизмы
смены параметров хэш-функции. Поскольку в
ГОСТ Р 34.10-94 порядок группы имеет длину
256 бит, то на практике вскрытие ключа подпи-
си, по-видимому, является более простой зада-
чей, чем заготовка коллизий.
Как было показано в гл. 10, 11, в протоколах
ГОСТ Р 34.10-94 и DSS срок действия ключей
подписи (в том числе персональных, которые
еще не выработаны) следует отсчитывать от мо-
мента выработки характеристики поля р. Смена
персональных ключей при сохранении характе-
ристики поля практически продлевает срок дей-
ствия ключа лишь на несколько секунд. Таким
образом, можно считать, что в системе все клю-
чи формирования и проверки подписи прекра-
щают действие одновременно. По окончании
срока действия ключей все подписи на их основе
считаются недействительными. Это необходимо
учитывать при формировании цифровой подписи
документов длительного пользования.
Протоколы ГОСТ Р 34.10-94, DSS, как и про-
токолы ГОСТ Р 34.10-2001, ECDSS (см. п. 15.6.5),
предъявляют жесткие требования к генератору
случайных чисел. Энтропия ключа формирова-
ния подписи не превышает энтропии генератора
случайных чисел.
Сложностная неоднородность протокола под-
писи равна 5. Стойкость подписи не превышает
минимума сложностей дискретного логарифми-
рования, нахождения используемого случайного
числа, обращения хэш-функции, вычисления
коллизий хэш-функции.
13.3. Сравнительный анализ
представленных схем подписи
Сложность задачи разложения составного
числа и сложность задачи логарифмирования в
мультипликативной группе простого поля по от-
ношению к асимптотически наилучшим универ-
сальным алгоритмам разложения и логарифми-
рования (метод решета числового поля [11]) по-
линомиально эквивалентны (см. п. 10.1), если
270
длины характеристики поля р в системе Эль-
Гамаля и характеристики кольца и в системе
RSA одинаковы. Эта сложность оценивается
субэкспонентой ехр(сд/(log /?)(log log р)2) для
с» 1,923.
Проверка подписи в протоколе Эль-Гамаля
выполняется медленнее, чем в RSA. Размер под-
писи в протоколе Эль-Гамаля больше, чем в
RSA, однако, если использовать вычеты состав-
ляющих подписи по модулю порядка группы,
как в стандартах DSS и ГОСТ Р 34.10-94, то
подпись оказывается короче, чем в RSA. В сис-
теме DSS, в отличие от RSA, алгоритм формиро-
вания подписи работает быстрее, чем алгоритм
проверки подписи.
Проверка подписи в протоколе Шнорра тре-
бует вычисления двух экспонент, поэтому фор-
мирование подписи в этом протоколе выполня-
ется примерно в 1,5 раза быстрее, чем в протоко-
ле Эль-Гамаля, так как обычно хэш-функция вы-
числяется быстрее экспоненты.
Требования к генератору случайного числа в
схемах Эль-Гамаля, Шнорра, DSS, ECDSS,
ГОСТ Р 34.10-94, ГОСТ Р 34.10-2001 одинако-
вы и являются более жесткими, чем требования к
генератору секретных ключей формирования
подписи. Требования к хэш-функции в части
коллизий наименее жесткие в алгоритме Шнор-
ра. Однако остальные протоколы могут быть
усилены, если в качестве аргумента хэш-функции
использовать /и||и’ вместо т (с соответствующим
изменением протокола).
Схемы подписи Эль-Гамаля и Шнорра могут
быть легко адаптированы для группы точек эл-
липтической кривой или якобиана гиперэллип-
тической кривой, что позволяет обеспечить экс-
поненциальную стойкость. Схема RSA, даже бу-
дучи перенесенной на эллиптические кривые, не
позволяет повысить стойкость (см. гл. 15).
Схемы подписи RSA и Рабина требуют ин-
дивидуального составного числа п для каждого
отправителя. Однако сроки действия открытых
ключей при этом не зависят друг от друга. Про-
токолы подписи, использующие задачу дис-
кретного логарифмирования в конечном поле
или в кольце Z7«Z, а также протокол Фиата-
Шамира обладают тем свойством, что сроки
действия персональных открытых ключей за-
канчиваются практически одновременно, неза-
висимо от начала их действия. Переход к эллип-
тическим или гиперэллиптическим кривым не-
большого рода, обеспечивающим экспоненци-
альную стойкость, устраняет этот недостаток
(см. гл. 11) и позволяет многократно сократить
размер задачи.
13.4. Скрытый канал
Иногда к криптографическим протоколам
предъявляется требование, согласно которому
они должны выполнять определенные крипто-
графические примитивы и не выполнять ничего
лишнего, в частности, не должны допускать
скрытую передачу зашифрованной информации.
Скрытый канал (subliminal channel) позволяет
передавать постороннюю информацию, внешне
не нарушая ход установленного протокола [17].4
Необходимым условием существования скры-
того канала является наличие избыточной слу-
жебной информации. Скрытый канал таят в себе,
например, протоколы цифровой подписи, ис-
пользующие генерацию случайного числа. Рас-
смотрим ситуацию, иллюстрирующую сговор
двух участников протокола против третьего. От-
правитель создает сообщение и подписывает его.
Контролер проверяет, что сообщение не содержит
недозволенных сведений и передает его получа-
телю. Если протокол подписи предусматривает
генерацию случайного числа, то под видом этого
числа отправитель может передавать получателю
зашифрованную информацию. Контролер не мо-
жет знать, какая информация передается по скры-
тому каналу и передается ли она вообще.
Приведем пример скрытой передачи в прото-
коле подписи Эль-Гамаля. Открытый ключ — р,
а, Ь = ах. Секретный ключ — показатель х. Пусть
отправитель сообщения (то есть владелец ключа
формирования подписи) и получатель нарушают
алгоритм генерации ключа и оба знают ключ
формирования подписи х.
Протокол 13.4.1. Передача информации по
скрытому каналу в протоколе подписи Эль-
Г амаля.
Вход отправителя и получателя. Показатель х
такой, что b = d (mod р).
Вход контролера. Ключ {ц, а, Ъ} проверки
подписи.
Выход. Зашифрование и расшифрование ин-
формации, передаваемой по скрытому каналу.
Метод.
1. Отправитель генерирует произвольное сооб-
щение т и число к, представляющее собой
4 Скрытый канал в схеме подписи был открыт
американцем Г. Симмонсом. Примечательно то, что
он сначала предложил использовать схему подписи со
встроенным скрытым каналом для тайной передачи
зашифрованной информации против СССР в рамках
контроля за соблюдением договора о запрещении
ядерных испытаний. Когда советское военное руко-
водство отвергло предложения американцев, появи-
лась его статья о скрытом канале. . .. -- —..
271
нелегально передаваемую информацию и об-
ратимое по модулю г. Затем вычисляет значе-
ния w <— </, 5 <— (т - xw)k4 (mod г) и отправ-
ляет их контролеру вместе с «сообщением» т
для последующей передачи получателю.
Шифрограммой нелегально передаваемого
сообщения к является подпись (w, s) «сооб-
щения» т.
2. Контролер проверяет правильность подписи.
Убедившись, что все в порядке, он передает
подписанное «сообщение» (т, w, s') получателю.
3. Получатель, зная секретный ключ х, находит
число к <— (т - хи').<> ' (mod г).
Очевидно, скрытые каналы можно организо-
вать и в других протоколах подписи, которые
требуют генерации случайного числа. Например,
в протоколах Рабина, Шнорра, протоколах стан-
дартов ГОСТ Р 34.10-2001 и ECDSS и т. п.
Для протокола Рабина скрытый канал может
быть реализован, если отправитель и получатель
подписанного сообщения знают разложение числа
«. Шифртексгом может быть число е, а нелегаль-
но передаваемым сообщением — л/е (mod р).
Скрытый канал можно исключить, если кон-
тролер будет участвовать в формировании под-
писи. Вот, например, как можно модифициро-
вать в этом случае протокол стандарта
ГОСТ Р 34.10-94.
1. Отправитель генерирует случайное целое
число к, 0 <к<г, вычисляет значение
w <— (ак (mod р)) (mod г) и направляет w кон-
тролеру.
2. Контролер запоминает число w, генерирует
случайное целое число к, 0<к <г, и воз-
вращает его отправителю.
3. Отправитель вычисляет показатель кл <— кк
к
(mod г), значение Wj <— (а 1 (mod р)) (mod г),
находит подпись s <— (k]h(m) + xuj) (mod г) и
передает сообщение т с подписью (и’1т л)
контролеру.
4. Контролер проверяет, что подпись для сооб-
щения т правильная и что Wj = (vZ (mod р))
(mod г), и в случае успешной проверки пере-
дает подписанное сообщение (т, s) полу-
чателю.
Организация скрытого канала возможна и в
схемах шифрования. Пусть в схеме симметрич-
ного шифрования используется рандомизатор,
добавляющий к текстам случайные слова, кото-
рые при штатном режиме расшифрования не
учитываются (но могут быть легко найдены).
Отправитель готовит открытые тексты, согласо-
вывает их с контролером и посылает получате-
лю, вставляя в открытый текст вместо слов ран-
домизатора свою информацию. Получатель по-
лучает не только известный контролеру откры-
тый текст, но и скрытую от него информацию в
виде слов рандомизатора.
Если в схеме шифрования с открытым клю-
чом Эль-Гамаля отправитель выбирает случай-
ное число к так, чтобы ак было квадратичным
вычетом (невычетом), то получатель получает
один бит скрытой информации (0 для квадратич-
ного вычета, 1 для квадратичного невычета), ко-
торый может быть легко расшифрован.
13.5. Другие схемы подписи
Диапазон применения схем цифровой подписи
весьма широк, поэтому зачастую от них требуют-
ся дополнительные свойства. Иногда это достига-
ется за счет ослабления используемых теоретико-
сложностных положений. Существует множество
схем цифровой подписи, удовлетворяющих тре-
бованиям различных приложений, в том числе:
- схема подписи «вслепую», когда отправитель
не знает содержания подписанного им сооб-
щения;
- схема «неоспоримой» (undeniable) подписи,
решающая проблему отказа нечестного от-
правителя сообщения от правильной подписи;
- схема коллективной подписи, в которой по-
лучатель может проверить, что подписанное
сообщение пришло от некоторой группы от-
правителей, но не знает, кем именно из чле-
нов группы оно подписано;5
- схема разовой подписи, позволяющая ис-
пользовать данный секретный (и открытый)
ключ для подписи только одного сообщения;
- схема подписи, в которой проверка осущест-
вляется без участия отправителя, но с при-
влечением доверенной стороны— «адвока-
та» (designated confirmer) и др.
13.5.1. Схема «неоспоримой» подписи
Обычную цифровую подпись может прове-
рить каждый пользователь, имеющий открытый
ключ; подписанное сообщение допускает копи-
рование. Но иногда может понадобиться такая
подпись, проверить правильность которой можно
только с участием ее автора. В этом случае копи-
рование подписанного документа теряет смысл.
5 Эта схема может быть реализована на основе
обычной цифровой подписи и схемы разделения сек-
рета (см. и. 14.5). •••
272
Необходимость в таких подписях может воз-
никнуть, например, в следующей ситуации.
Компания А разрабатывает программное обеспе-
чение, подписывает его, утверждая, что продукт
подлинный, и продает пользователю В. Пользова-
тель В делает нелегальную копию программ и
продает ее пользователю С. При такой схеме под-
писи пользователь С не может проверить подлин-
ность этих программ (в частности, их безопас-
ность) без участия А. Это позволяет улучшить от-
слеживание нелегального копирования.
Другой пример— несекретное личное или
деловое письмо, которое в случае нелегального
копирования и опубликования может нанести
ущерб отправителю. Тогда для защиты тоже
можно применить указанную схему подписи.
Кроме того, в обычной схеме подписи в слу-
чае утраты владельцем секретного ключа им мо-
жет воспользоваться нарушитель, причем дока-
зать факт такого использования невозможно. В
рассматриваемой схеме владелец ключа форми-
рования подписи может доказать, что документ
подписан без его участия. Обратно, если доку-
мент подписан владельцем ключа, то отказаться
от подписи невозможно.
Проверка подписи здесь осуществляется при
участии отправителя сообщения и реализуется
посредством протокола «запрос — ответ», в тече-
ние которого получатель посылает отправителю
ряд запросов. Если ответы отправителя проходят
проверочные тесты, то получатель может быть
уверен, что подпись правильная (вероятность по-
лучателю ошибиться обратно пропорциональна
экспоненте от длины подписи). В противном слу-
чае получатель может с большой долей уверенно-
сти распознать, является подпись поддельной или
же отправитель дает заведомо неверные ответы
(то есть умышленно отказывается от подлинной
подписи и обманывает получателя).
Д. Шаум предложил и запатентовал ряд дос-
таточно эффективных и практичных протоколов
такой «неоспоримой» подписи на основе задачи
дискретного логарифмирования в подгруппе
простого порядка г мультипликативной группы
простого поля [6]. При этом порядок группы
знать кому-либо из участников не обязательно,
однако протокол остается безопасным и в том
случае, если кто-нибудь его все-таки узнает.
В основу безопасности этого протокола по-
ложены следующие утверждения.
Теорема 13.5.1. Даже при наличии компьюте-
ра бесконечной вычислительной мощности6 от-
6 Бесконечная вычислительная мощность компь-
ютера означает, что стойкость данной схемы подписи
не зависит от сложности задачи дискретного лога-
рифмирования.
правитель не может с вероятностью, большей г-1,
дать верный ответ для поддельной подписи.
Доказательство см. в работе [6].
Теорема 13.5.2. Даже при наличии компьюте-
ра бесконечной вычислительной мощности от-
правитель, дав два неверных ответа для подлин-
ной подписи, будет уличен во лжи с вероятно-
стью, большей 1 - г 1.
Доказательство см. в работе [6].
Протокол 13.5.1. Схема «неоспоримой» под-
писи.
Вход отправителя. Образующая а группы G
простого порядка г (не обязательно известного);
секретные ключи — целые числа х и у.
Вход получателя. Образующая а группы G
простого порядка г (не обязательно известного);
открытые ключи — ах и аху.
Результат. Формирование и проверка подпи-
си.
Метод.
Для формирования подписи s для сообщения
т отправитель вычисляет s <— т.
Для проверки подписи отправитель и получа-
тель выполняют следующие действия.
1. Получатель выбирает вероятностным алго-
ритмом из интервала (1, г) числа Л, В, С и D,
вычисляет и <г- sccfn, г тАав и посылает
пару {и, v) отправителю.
2. Отправитель вычисляет Ц <— sy, С <— иу,
1з <— v” и возвращает тройку (1Ь t2, Е) получа-
телю.
3. Получатель проверяет, выполняется ли ра-
венство (tifyaxy)/} = t2. Согласно теореме
13.5.1 он знает, что неправильный ответ бу-
дет выявлен с вероятностью 1 - г-1. Таким
образом, получатель на этом этапе убеждает-
ся, что первым компонентом тройки дейст-
вительно является
4. Получатель проверяет равенство (в/(аху/ = у.
Если оно выполнено, то результат: подпись
подлинная с вероятностью 1 - г~} (по теореме
13.5.1). В противном случае получатель выби-
рает тем же вероятностным алгоритмом, что и
на шаге 1, числа Е и F из интервала (1, г), вы-
числяет z <— и посылает z отправителю.
5. Отправитель вычисляет <— zy и возвращает
Е получателю.
6. Получатель проверяет равенство (^(«xy)-fi)£ =
= (/4(<7J|)_/)'4. Если оно выполнено, то резуль-
тат: подпись недействительна (по теореме
13.5.2). В противном случае результат: от-
правитель лжет.
273
В этом протоколе сообщение т не может
быть произвольным, а должно являться элемен-
том группы G.
13.5.2. Схема подписи «вслепую».
Электронные платежи
Схема подписи «вслепую» (blind signature) так
же, как и предыдущая, была предложена
Д. Шаумом [5]. При использовании этой схемы
отправитель, подписывающий сообщение, не
знает содержания этого сообщения.
«Вслепую» могут быть реализованы некото-
рые рассмотренные выше схемы подписи. Вот
как, например, это делается для схемы подписи
RSA [15]. Пусть, как и в обычной схеме RSA,
d— секретный ключ формирования подписи,
(и, е) — открытый ключ проверки подписи.
Пусть т — сообщение, для которого нужно по-
лучить подпись, не раскрывая его содержания.
В формировании подписи участвуют и отпра-
витель, подписывающий сообщение, и получатель
этого сообщения. Получатель генерирует случай-
ное число w такое, что НОД(и;, и) = 1, и посылает
отправителю значение т’ = weт (mod и). Содер-
жание сообщения т «скрыто» числом w. Отпра-
витель возвращает подписанное сообщение:
л' = (m')d = (win)'1 (mod и). Так как s' = wmd
(mod n), то получатель может найти значение
подписи: л = md (mod ri) для сообщения т, вычис-
лив s = s’w~' (mod п).
Подпись считается подлинной, если выполне-
но сравнение se = т (mod и).
Рассмотрим возможную реализацию подписи
«вслепую» в протоколах электронных платежей,
основанных на использовании электронной мо-
неты (electronic coin) — информации, в отличие
от обычных денег не имеющей трудноподделы-
ваемого физического воплощения. «Вслепую»
подписывается банком уникальный номер моне-
ты, известный только ее владельцу.
Участниками протоколов электронных плате-
жей являются клиент, банк и магазин. Кроме них в
систему электронных платежей иногда включают
арбитра для разрешения споров. Клиент получает в
банке электронные деньги, производит на них по-
купку товара в магазине, затем магазин погашает
электронные деньги в банке. Протоколы элек-
тронных платежей содержат три основных этапа:
создание электронных денег, передачу их магази-
ну и погашение. Рассмотрим общие принципы соз-
дания и использования электронных денег.
Электронная монета представляет собой пару
(т, Sb), где т — информация о монете (ее номи-
нал, индивидуальный номер, информация о вла-
дельце, включающая открытый ключ Рс провер-
ки подписи клиента), sb = S(m) — подпись банка.
Поскольку монета представляет собой информа-
цию, она может быть скопирована (например,
клиентом или магазином). Поэтому необходимо
исключить повторное использование монеты.
Это обеспечивает банк контролем неповторяемо-
сти номеров монет при погашении.
На этапе создания монеты клиент и банк дей-
ствуют совместно и имеют возможность убедить-
ся в том, что никто из них не обманывает партне-
ра, при этом банк не может узнать номер монеты.
После того как монета создана, банк не может от-
следить ее использование до момента погашения,
это обеспечивается подписью «вслепую».
На этапе покупки клиент предъявляет монету
магазину. Магазин убеждается, что подпись бан-
ка правильная. Для проверки того, что монета
действительно принадлежит данному клиенту,
магазин генерирует случайный текст t и посыла-
ет клиенту текст (t, т) для подписи, затем прове-
ряет правильность полученной подписи sc клиен-
та с помощью его открытого ключа Рс проверки
подписи, который содержится в монете. Если
подпись неправильная, то покупка запрещается.
В противном случае покупка разрешается, и ма-
газин запоминает тройку (/, т, s().
При погашении монеты магазин предъявляет
банку тройку (Z, т, sc). Банк проверяет неповто-
ряемость этой тройки, гасит монету, если она не
встречалась, и заносит тройку (г, т, sc) в базу
данных. В противном случае он выясняет, кто
использовал монету дважды. Если пара (t, т)
встретилась дважды, то это означает, что монету
повторно использует магазин; если только ком-
понент т встретился дважды, то монету повтор-
но использует клиент.
Существует много вариантов протоколов
электронных платежей, основанных на элек-
тронных подписях, доказательствах с нулевым
разглашением, с монетами фиксированного или
произвольного номинала, монетами, которые
можно разменять, и т. п.
Практически, если стоимость монеты не фик-
сирована, то протокол подписи «вслепую» вы-
глядит следующим образом.
Протокол 13.5.2. Создание электронной мо-
неты на основе подписи «вслепую».
Вход клиента. Открытый ключ Рь проверки
подписи банка; функция F наложения маски;
функция G снятия маски; число и.
Вход банка. Секретный ключ формирования
подписи; функция F наложения маски; число и.
Результат. Электронная монета.
Метод.
1. Клиент генерирует п сообщений mh 1 <г< п,
содержащих денежное выражение монет
274
(одинаковое для всех п сообщений), ключ Рс
проверки подписи клиента и, возможно, до-
полнительную информацию, накладывает на
каждое сообщение случайную маску а„ вы-
числяя значение F, = F(rnh а,), I < i < и, и от-
правляет все F, в банк.
2. Банк выбирает наугад и - 1 замаскированных
сообщений и просит клиента раскрыть их.
3. Клиент раскрывает значения (w„ а,) для каж-
дого из и - 1 выбранных сообщений.
4. Банк убеждается, что все они созданы пра-
вильно. Если число и достаточно велико, то
банк может быть убежден с достаточной ве-
роятностью, что и оставшаяся пара (т, а)
тоже создана правильно. Кроме того, банк
вычисляет Fj = F(m„ а,) для раскрытых зна-
чений (т,, а,), проверяя таким образом их
подлинность.
5. Банк генерирует подпись Sb для пары (т, а) и
отправляет sh клиенту.
6. Клиент с помощью ключа Рь проверяет, что
пара (т, а) подписана банком правильно. За-
тем он вычисляет значение G = G(si„ ос) так, что
подпись остается верной и для сообщения т.
7. Результат: электронная монета (т, хь).
В случае монет фиксированной стоимости
первые четыре шага не нужны. Отличие подписи
«вслепую» от обычной цифровой подписи со-
стоит в возможности вычисления маски и ее по-
следующего снятия так, что подпись остается
верной. Кроме того, наложение и снятие маски
должны выполняться без знания секретного
ключа формирования подписи. Снятие маски
должно исключать возможность изменения со-
общения. Для этого необходима вычислимость
функций F и G в одну сторону.
Функция F должна быть такой, что по данно-
му значению F, трудно подобрать пару аргумен-
тов (т„ а,) и трудно вычислить коллизию, то
есть найти две пары аргументов (mj, 09) и (пн, сц)
таких, что Fj = Fk.
Таким образом, для подписи «вслепую» требу-
ется наличие вычислимых функций F, G таких,
что для операции подписи S оказывается справед-
ливым выражение GSF — S. Это свойство можно
интерпретировать как существование вычислимо-
го морфизма схемы подписи, не требующего зна-
ния ключа. Объектами категории являются пары
сообщение/подпись, выдерживающие проверку.
Морфизмами категории являются вычислимые
отображения одной пары в другую.
На безопасность протоколов «вслепую» влияет
то обстоятельство, что в формировании подписи
участвуют две стороны, которые не могут абсо-
лютно доверять друг другу. В частности, клиент
может предлагать такие сообщения, которые по-
зволят ему вскрыть ключ подписи и получить воз-
можность самому делать монеты (атака на основе
выбранных сообщений). С другой стороны, слу-
жащие банка могут быть заинтересованы в раскры-
тии замаскированного сообщения клиента, чтобы в
дальнейшем самим воспользоваться этой монетой.
13.5.3. Схема подписи
с восстановлением сообщения
Схема подписи с восстановлением сообщения
[12] может использоваться для подписи коротких
сообщений (например, ключей). Подписывание
осуществляется несимметричным алгоритмом
без каких-либо хэш-функций. Ключ зашифрова-
ния является секретным ключом формирования
подписи. Ключ расшифрования является откры-
тым ключом проверки подписи (например, в сис-
теме RSA). Исходное сообщение дополняется
избыточными битами, включающими в себя при-
знак начала сообщения и число добавленных би-
тов, и зашифровывается на секретном ключе от-
правителя сообщения. Восстановление исходно-
го текста по подписи происходит в процессе
проверки подписи. Получатель сообщения рас-
шифровывает его и проверяет правильность из-
быточных битов, выполняя действия отправите-
ля в обратном порядке.
13.5.4. Инкрементальная подпись
Инкрементальная (наращиваемая) подпись [3]
показывает, как объединение задач цифровой под-
писи и представления данных, которые решаются
известными способами, дает новое качество.
Это в равной мере относится к подписи и к
хэш-функции, то есть к вычислимым в одну сто-
рону функциям. В основу инкрементальной под-
писи положено следующее свойство таких функ-
ций: если л(х) — подпись (хэш-функция) для тек-
ста х, то л(л(х)) тоже может служить подписью
(хэш-функцией).
Назовем алгоритм инкрементальным, если он
обеспечивает коммутативность диаграммы ри-
сунка 13.1.
х --------------> у
Рис. 13.1. Диаграмма вычисления
инкрементальной подписи
275
Здесь х, Ах, х' = х + Ах — входы алгоритма, у,
Ду, у’=у + Ду— выходы алгоритма (сложение
формальное). Стрелками обозначены вычислимые
отображения. Коммутативность этой диаграммы
позволяет организовать вычисления для извест-
ных х, х', у следующим образом: сначала для ма-
лого Ах вычисляется выход Ду, затем находится
выход у' для измененного входа. Если размер из-
менений мал по сравнению с размером текста, то
есть |Ах| «|х|, то вычисления можно ускорить.
Инкрементальная подпись может использо-
ваться в ситуациях, когда необходимо внести
малые изменения в большое подписанное сооб-
щение, послать близкие по содержанию сообще-
ния нескольким пользователям, отредактировать
текст большого объема с подписью каждого оче-
редного варианта и т. п.
Инкрементальная подпись (хэш-функция)
может быть организована следующим образом.
Подпись представляется в виде 2-3 дерева, то
есть дерева с фиксированным корнем, каждая
вершина которого, не являющаяся листом, имеет
двух или трех сыновей, расстояния от любого
листа до корня одинаковы. Такие деревья ис-
пользуются для представления данных. Высота
2-3 дерева с и вершинами равна O(log и).
Для формирования инкрементальной подписи
(хэш-функции) текст разбивается на блоки фик-
сированной длины. Для каждого блока вычисля-
ется обычная подпись (хэш-функция), которая
является листом. Пары или тройки листьев в
свою очередь опять подписываются, полученные
подписи «второго уровня» объединяются в пары
или тройки, каждая из которых вновь подписы-
вается и т. д. При введении (исключении, замене)
нового блока вычисляется обычная подпись для
этого блока как новый лист (исключается или
заменяется лист) и вычисляются новые подписи
для вершин дерева, лежащих на пути от нового
листа до корня.
Пример вычисления инкрементальной подпи-
си для пятиблочного сообщения приведен на ри-
сунке 13.2. Каждому блоку соответствует обыч-
ная подпись, являющаяся листом. Для пары под-
писей А и В формируется подпись АВ, для пары
подписей АВ, CDE формируется подпись
ABCDE. Инкрементальная подпись представляет
собой множество подписей {А, В, С, D, Е, АВ,
CDE, ABCDE}. Для измененного (вновь введен-
ного, исключенного) блока D пересчитывается
(вновь вводится, исключается) подпись D, пере-
считываются подписи для вершин CDE и
ABCDE, связанные жирными ребрами с изме-
ненным листом D. Если сообщение содержит п
блоков, то при изменении одного блока нужно
пересчитать O(logw) подписей.
ABCDE
Рис. 13.2. Инкрементальная подпись
на основе 2-3 дерева
Инкрементальная подпись представляет собой
совокупность вершин дерева, то есть длина под-
писи (хэш-функции) не меньше, чем длина со-
общения.
Упражнения к главе 13
1. Сравните безопасность схем подписи RSA,
Рабина и Фиата-Шамира.
2. Оцените безопасность схемы подписи Рабина
при повторении случайного числа.
3. Предложите способ передачи зашифрован-
ной информации по скрытому каналу в про-
токоле Рабина и способ устранения контро-
лером этого канала.
4. Предположим, что в компьютерной систе-
ме реализован алгоритм цифровой подпи-
си ГОСТ Р 34.10-94 с характеристикой
поля длины 1000 бит и предусмотрена
возможность смены характеристики поля.
Оцените периодичность смены характери-
стики поля на десятом году эксплуатации,
если алгоритмическая сложность дискрет-
ного логарифмирования падает со скоро-
стью 30 раз в год, а вычислительная мо-
дель вскрытия ключа выполняет 1О20 опе-
раций в год.
5. Оцените стойкость модифицированных про-
токолов Эль-Гамаля с уравнениями формиро-
вания подписи: a) h(m) = xs + kw, б) w =
= xh(m) + ks; в) л = хм - kh(m)-, г) h(ni) = dx(yv +
+ с) + eks — для обратимых констант с, d, е.
Все уравнения решаются по модулю простого
порядка группы.
6. Предложите свой вариант уравнения форми-
рования подписи на основе протокола Эль-
Гамаля.
276
7. Оцените стойкость модифицированных про-
токолов Шнорра с уравнениями формирова-
ния подписи: а) 5 = к - хе: б) 5 = к + d(x + с)е;
в) е = xs + к — для произвольных ненулевых
с nd.
8. Предложите свой вариант уравнения форми-
рования подписи на основе протокола Шнорра.
9. Можно ли в протоколах Эль-Гамаля и Шнор-
ра использовать нелинейные уравнения фор-
мирования подписи и при каких условиях?
10. Предложите свои способы использования и
устранения скрытого канала передачи ин-
формации в протоколе подписи ГОСТ
Р 34.10-94.
11. Предположим, что генератор случайного
числа в схеме подписи ГОСТ Р 34.10-94 вы-
рабатывает случайные биты с биномиальной
плотностью распределения. Как это влияет
на сложность вскрытия ключа (при заданной
вероятности успешного вскрытия)? Какую
максимальную вероятность появления нуля
можно допустить без снижения стойкости,
если длина характеристики поля равна 1024
бита?
12. В условиях предыдущей задачи оцените мак-
симальную вероятность появления нуля, если
число формируемых подписей равно N.
13. Сравните максимальные вероятности появ-
ления нуля на выходе генератора случайного
числа, при которых не происходит снижения
стойкости в протоколах ГОСТ Р 34.10-94 и
DSS.
14. Сравните производительность схем подписи
Фиата-Шамира и RSA при формировании
подписи и при ее проверке.
15. Предположим, что две подписи сформирова-
ны по схеме Эль-Гамаля с использованием
двух похожих случайных чисел к, различаю-
щихся в нескольких младших разрядах. Как
это обстоятельство можно использовать для
снижения стойкости?
16. Предположим, что с целью исключения по-
второв в случайное число в протоколе
Шнорра включается код времени, априорно
известный нарушителю. Увеличит ли это
стойкость схемы подписи?
17. * Рассмотрим модифицированный протокол
подписи Шнорра, в котором уравнение фор-
мирования подписи имеет вид л = к + хе (вы-
числения проводятся над кольцом Z, знание
порядка группы не требуется). Предложите
вариант атаки на этот протокол на основе по-
добранных сообщений, используя значения s
и е для оценки к и х.
Литература к главе 13
1. ГОСТ Р 34.10-94. Информационная технология.
Криптографическая защита информации. Система
электронной цифровой подписи на базе асиммет-
ричного криптографического алгоритма. М.: Гос-
стандарт России. 1994.
2. ГОСТ Р 34.11-94. Информационная технология.
Криптографическая защита информации. Функ-
ция хэширования. М.: Госстандарт России, 1994.
3. Bellare М., Goldreich О., Goldwasser S. Incremental
ciyptography: the case of hashing and signing // Ad-
vances in Ciyptology— CRYPTO ’94. Lecture
Notes in Computer Science. Springer-Verlag. 1994.
Vol. 839. P. 216-233.
4. Bleichenbacher D. Generating ElGamal signatures
without knowing the secret key // Advances in Cryp-
tology — EUROCRYPT ’96. Lecture Notes in Com-
puter Science. Springer-Verlag. 1996. Vol. 1070.
P. 10-18.
5. Chaum D. Blind signatures for untraceable payments
// Advances in Cryptology — Proceedings of Crypto
82. Plenum Press. 1983. P. 199-203.
6. Chaum D., van Antwerpen H. Undeniable signatures
// Advances in Cryptology — CRYPTO ’89. Lecture
Notes in Computer Science. Springer-Verlag. 1990.
Vol. 435. P. 212-216.
7. ElGamal T. A public-key cryptosystem and a signa-
ture scheme based on discrete logarithms 11 IEEE
Transactions on Information Theoiy. 1985.
Vol. IT-31. P. 469-472.
8. Fiat A., Shamir A. How to prove yourself: Practical
solutions to identification and signature problems //
Advances in Cryptology— CRYPTO ’86. Lecture
Notes in Computer Science. Springer-Verlag. 1987.
Vol. 263. P. 186-194.
9. FIPS 180, Secure Hash Standard, Federal Informa-
tion Processing Standards Publication 180, U.S. De-
partment of Commerce/ N.I.S.T., National Technical
Information Service, Springfield, Virginia, May
1993.
10. FIPS 186, Digital Signature Standard, Federal Infor-
mation Processing Standards Publication 186, U.S.
Department of Commerce/ N.I.S.T., National Tech-
nical Information Service, Springfield, Virginia, May
1994.
11. Gordon D.M. Discrete logarithms in GF(p) using the
number field sieve // SIAM Journal on Discrete
Mathematics. 1993. Vol. 6. № 1. P. 124-138.
12. 1S0/IEC 9796. Information technology— Security
techniques— Digital signature scheme giving mes-
sage recovery, International Organization for Stan-
dardization. Geneva, Switzerland, 1991.
13. Menezes A., van Oorschot P., Vanstone S. Handbook
of Applied Cryptography. CRC Press, 1997.
14. Rabin M.O. Digitalized signatures and public-key
functions as intractable as factorization. Technical
Report MIT/LCS/TR-212, Laboratory for Computer
Science, MIT, 1979.
15. RSA Laboratories’ Frequently Asked Questions
About Today’s Glyptography. Version 4.1 //
http://www.rsasecurity.com/rsalabs/faq/.
16. Schnorr C.P. Efficient identification and signatures
for smart cards // Advances in Cryptology —
CRYPTO ’89. Lecture Notes in Computer Science.
Springer-Verlag. 1990. Vol. 435. P. 239-252.
17. Simmons G. The subliminal channel and digital sig-
natures 11 Advances in Cryptology — Proceedings of
EUROCRYPT 84. Lecture Notes in Computer Sci-
ence. Springer-Verlag. 1985. Vol. 209. P. 364-378.
Глава 14. ДРУГИЕ КРИПТОГРАФИЧЕСКИЕ ПРОТОКОЛЫ
В настоящее время существует множество
криптографических протоколов, и их число по-
стоянно растет. В этой главе представлены неко-
торые наиболее популярные криптографические
протоколы, отличные от шифрования и цифро-
вой подписи.
Отличительной чертой сложных криптогра-
фических протоколов является участие в них не-
скольких сторон, при этом, вообще говоря, воз-
можно отступление некоторых сторон от пред-
писанных протоколом правил, в частности, сго-
вор нескольких сторон против какого-то одного
участника.
Задача анализа криптографического протоко-
ла в общем случае является более сложной, чем
задача анализа криптоалгоритма (или математи-
ческой задачи), положенного в основу протоко-
ла. Иногда уязвимости протоколов связаны с ис-
пользованием слабых мест соответствующих
криптоалгоритмов.
Однако уязвимости протоколов могут быть
вольно или невольно внедрены разработчиком в
систему даже при использовании стойких крип-
тографических алгоритмов. Поэтому задача ана-
лиза протоколов является в значительной мере
не только математической, но и инженерной. В
настоящей главе рассматриваются только мате-
матические аспекты безопасности протоколов.
14.1. Схемы предъявления битов
В основу протоколов предъявления битов (bit
commitment schemes) [6] положен принцип шиф-
рования одного бита информации, который мож-
но проиллюстрировать на примере подбрасыва-
ния монеты по телефону: участник Р подбрасы-
вает монету, а участник V угадывает, что выпа-
дет (выпало): «орел» или «решка». Предвари-
тельно Р и V договариваются о некоторой стой-
кой в смысле обращения и в смысле поиска кол-
лизий хэш-функции h.
Протокол 14.1.1. Подбрасывание монеты по
телефону.
Вход. Хэш-функция h, стойкая в части обра-
щения и вычисления коллизий.
Выход. Заключение о четности аргумента
хэш-функции.
Метод.
1. Участник Р генерирует случайный аргумент
X хэш-функции Л, вычисляет значение h(x) и
посылает его участнику V.
2. Участник V должен угадать, является число х
четным или нечетным, и посылает участнику
Р соответственно 0 или 1.
3. Участник Р раскрывает значение аргумента.
4. Участник V проверяет подлинность аргу-
мента, вычисляя значение h(x), и убеждается
в правильности или ошибочности своей
догадки.
Если участнику Р удастся вычислить колли-
зию, то есть пару аргументов (х, х') различной
четности таких, что /г(х) = Л(х'), то он сможет
предъявлять любой из этих аргументов и поэто-
му всегда выигрывать.
Значение хэш-функции в протоколе 14.1.1
представляет собой шифрограмму одного бита.
Зашифрованию подлежит младший бит аргумен-
та хэш-функции. Строится отображение
ф: {0, 1} х (Z/2"_|Z)
Тогда ф(0,х,)=)’(!>— шифрограмма нулевого
бита при случайном х„ ф(1,х7) = у|/— шифро-
грамма единичного бита при случайном х,.
Шифрограмму одного бита называют блобом
(от англ, blob — капля), если она удовлетворяет
следующим требованиям.
1. По значению блоба вычислительно невоз-
можно предсказать, какое значение бита он
представляет, то есть получатель блоба не
может найти значение бита с вероятностью
большей, чем 0,5.
2. Вычислительно невозможно подобрать пары
(0, х,) и (1,х7) такие, что Jo, =yi;, то есть от-
правитель блоба не может менять значение
бита.
3. Получатель блоба не может извлечь никакой
информации о значении бита.
4. Блоб не несет никакой посторонней инфор-
мации.
Использование блобов характерно для доказа-
тельств с нулевым разглашением (см., например,
п. 14.3).
279
Представляют интерес схемы предъявления
битов, в которых нет коллизий. Такие схемы
можно строить на основе хэш-функций без кол-
лизий с переборной сложностью обращения (см.
п. 15.6.7) или на основе системы RSA.
Схемы предъявления битов позволяют стро-
ить и более сложные протоколы, например, иг-
рать в покер по телефону. Рассмотрим такой
протокол с двумя игроками А и В, основанный
на бесключевом шифровании по методу Месси-
Омуры в группе Fp (см. п. 12.1.1). В этом про-
токоле ключ зашифрования и соответствующий
ключ расшифрования хранятся у каждого игро-
ка и не передаются партнеру.
Сначала каждый игрок вырабатывает пару
показателей зашифрования и расшифрования.
Игрок А (сдающий) зашифровывает на своем
персональном ключе 52 названия карт и посы-
лает колоду игроку В. Игрок В выбирает слу-
чайным образом пять зашифрованных карт, за-
шифровывает их на своем персональном ключе
и посылает игроку А. Игрок А расшифровывает
полученное сообщение на своем ключе и посы-
лает игроку В, который после расшифрования
узнает свои карты. Затем игрок В выбирает еще
пять зашифрованных карт и посылает игроку А.
Расшифрование этого сообщения дает карты
игрока й.1 При смене игроками некоторых карт
процедура повторяется. По окончании игры иг-
роки раскрывают свои карты (соответствующие
тексты), а также пары ключей зашифрования и
расшифрования, и проверяют их корректность.
Для обеспечения стойкости число р - 1
должно иметь большой простой делитель г и
каждая из карт должна представляться элемен-
том порядка г в группе IFZ,.
Аналогичным образом можно строить прото-
колы игры с более чем двумя участниками. В ка-
честве функции шифрования может использо-
ваться любое (вычислимое с помощью ключа и
трудновычислимое без ключа) отображение боль-
шого множества в себя, принадлежащее коммута-
тивной группе отображений. Симметричное шиф-
рование для этих целей не годится, поскольку оно
не обеспечивает коммутативности.
14.2. Диалоговые доказательства
с нулевым разглашением
Рассмотрим протокол с двумя участниками:
претендентом, который утверждает, что знает
решение некоторой частной задачи выбора, и
1 Это соответствует сдаче пяти карт сначала одно-
му игроку, затем другому. При желании можно обес-
печить поочередную сдачу игрокам по одной карте.
верификатором, знающим условие задачи и осу-
ществляющим проверку того, что претендент
действительно знает решение [8]. Назовем такой
протокол доказательством с нулевым разглаше-
нием (знании) (zero-knowledge proof), если ин-
формация, получаемая верификатором от пре-
тендента, может быть создана им самим с поли-
номиальной сложностью без взаимодействия с
претендентом, то есть если верификатор не по-
лучает (а претендент не разглашает) никакой со-
держательной информации (знаний) о решении
указанной задачи. Нужно различать доказатель-
ства с нулевым и с минимальным разглашением.
Во втором случае верификатор может получить
некоторую информацию о ключе претендента,
используя особенности протокола или математи-
ческой задачи.
Первоначально доказательства с нулевым раз-
глашением использовались как механизм для
реализации криптографического примитива опо-
знавания в системе с недоверенным верификато-
ром. Позднее были найдены доказательства с
нулевым разглашением, являющиеся самостоя-
тельными криптографическими примитивами,
например, доказательство того, что составное
число в схеме подписи Фиата-Шамира выбрано
правильно [7].
Рассмотрим некоторые протоколы диалого-
вых доказательств с нулевым разглашением.
14.2.1. Доказательство
знания изоморфизма графов
Рассмотрим протокол доказательства с нуле-
вым разглашением знания изоморфизма графов
(два графа изоморфны, если существует переста-
новка вершин, превращающая один из них в дру-
гой). Типичное применение такого рода доказа-
тельств — опознавание. Неориентированный
граф представляется в виде квадратной симмет-
рической матрицы (йу), где a,j = 1, если между
вершинами i и j есть ребро; а,/ = 0 в противном
случае. Открытый ключ опознавания, известный
верификатору, — два изоморфных графа G и Н.
Секретный ключ, известный претенденту, — пе-
рестановка <р вершин графа G такая, что
Ф(О=я.
Протокол 14.2.1. Доказательство знания изо-
морфизма графов.
Вход верификатора. Графы G и Н\ число по-
второв к.
Вход претендента. Изоморфизм <р: G -> Н-,
число повторов к.
Выход верификатора. Решение о том, что пре-
тендент знает требуемый изоморфизм, с вероят-
ностью ошибки первого рода не более 2~к.
280
Метод.
1. Верификатор и претендент полагают i <— 1.
2. Претендент генерирует случайную переста-
новку х|/ вершин графа G, вычисляет граф
F <— \>(G) и предъявляет его верификатору.
3. Верификатор генерирует случайный бит и
передает его претенденту.
4. Если претендент получает значение 0, то он
предъявляет верификатору изоморфизм гра-
фов F и G, то есть перестановку Г|/. Если он
получает значение 1, то предъявляет изомор-
физм графов F и Н, то есть перестановку цдр'1.
5. Верификатор проверяет, что полученная пе-
рестановка является изоморфизмом соответ-
ствующих графов. Если проверка не прохо-
дит, то результат: претендент не знает изо-
морфизма. В противном случае возможны
две ситуации. Если i < к, то верификатор со-
общает претенденту об успешной проверке,
претендент и верификатор полагают i <— i + 1
и возвращаются к шагу 2. Если / > к, то ре-
зультат: претендент знает изоморфизм.
Итерации на шагах 2-5 выполняются необхо-
димое число к раз, чтобы вероятность ошибки со
стороны верификатора не превышала заданной
величины. Например, для к =30 вероятность ус-
пешного обмана со стороны претендента не пре-
п-30 -I л-9
вышает 2 «10.
Претендент в ходе генерации графа F не знает,
какой бит он получит и, следовательно, какой из
двух изоморфизмов ему придется раскрыть. По-
этому, если он не знает изоморфизма <р, то он мо-
жет лишь пытаться угадать, строить ему граф F
изоморфным графу G или графу Н. Отсюда сле-
дует, что претендент может успешно жульничать
в ходе одной итерации с вероятностью 0,5 (пред-
полагается, что подбрасывание монеты — идеаль-
ный генератор случайных битов). Если претендент
может угадывать результат подбрасывания монеты
с вероятностью более 0,5, то число повторов необ-
ходимо соответствующим образом увеличить.
Верификатор не получает никакой2 информа-
ции об изоморфизме гр, так как он знает графы G
и Н и может сам создавать графы F, изоморфные
G или Н.
Протокол допускает очевидную реализацию,
при которой все к итераций выполняются парал-
лельно. При этом претендент на шаге 2 генери-
рует к различных графов Fj, ...,Fk, верификатор
на шаге 3 посылает ^-разрядное случайное число
ИТ. д.
На практике задача об изоморфизме графов
является неудобной, поэтому обычно использу-
ются те же задачи, что и для цифровой подписи.
14.2.2. Доказательство знания
разложения составного числа
Доказательство знания разложения составно-
го числа и на множители основано на сложности
решения сравнения второй степени по модулю п
(см. теорему 12.2.1).
Рассмотрим протокол доказательств с нуле-
вым разглашением на основе задачи разложения.
Верификатор знает число п, претендент знает
разложение n-pq и хочет доказать это верифи-
катору, не раскрывая делителей числа и.
Протокол 14.2.2. Доказательство знания раз-
ложения числа и = pq.
Вход верификатора. Составное число и; число
повторов к.
Вход претендента. Делители р, q числа и; чис-
ло повторов к.
Выход верификатора. Решение о том, что пре-
тендент знает разложение числа и, с вероятностью
ошибки первого рода не более 2~\
Метод.
1. Верификатор и претендент полагают /'<—!.
2. Верификатор генерирует число х, вычисляет
его квадрат у <- т2 (mod и) и направляет пре-
тенденту.
3. Претендент генерирует случайный показа-
тель т, вычисляет z <— у'" (mod и), вычисляет
квадратный корень из z по модулю п и на-
правляет число z верификатору.
4. Верификатор генерирует случайный бит и
направляет претенденту.
5. Если претендент получает 0, то он раскрывает
показатель т; если получает 1, то раскрывает
вычисленное значение квадратного корня.
6. Верификатор проверяет правильность полу-
ченного ответа. Если ответ не совпадает, то
2 На самом деле в ходе многократного выполне-
ния протокола верификатор может получить некото-
рые знания, если генератор случайной перестановки у
претендента «плохой». В вырожденном случае может
получиться F=G или F = H. Тогда верификатор вы-
бором бита на шаге 3 может узнать изоморфизм <р.
281
результат: претендент не знает разложения. В
противном случае возможны две ситуации.
Если i < к, то верификатор сообщает претен-
денту о правильности этого шага; верифика-
тор и претендент полагают i <- z + 1 и воз-
вращаются к шагу 2. Если i > к, то результат:
претендент знает разложение.
Если претендент не знает разложения, то он
может вычислить z либо как степень у, либо как
квадрат некоторого числа по модулю п. Посколь-
ку претендент не знает, какой бит он получит, то
он может успешно жульничать с вероятностью
0,5. В свою очередь, верификатор не может из-
влечь никакой информации о разложении числа п.
14.2.3. Доказательство
знания дискретного логарифма
Протокол доказательств с нулевым разглаше-
нием может быть основан и на задаче дискретно-
го логарифмирования в группе G. В роли G мо-
жет выступать мультипликативная группа ко-
нечного поля, группа обратимых элементов
кольца ILknZL, группа точек эллиптической кри-
вой, группа классов поля алгебраических чисел и
г. п. По условиям протокола верификатор не обя-
зан знать порядок группы G.
Протокол 14.2.3. Доказательство знания дис-
кретного логарифма в циклической группе G.
Вход верификатора. Группа G, образующая а
и ее образ Z>; число повторов к.
Вход претендента. Логарифм х такой, что
b = число повторов к.
Выход верификатора. Решение о том, что пре-
тендент знает логарифм, с вероятностью ошибки
первого рода не более 2~к.
Метод.
1. Верификатор и претендент полагают i <- 1.
2. Претендент генерирует случайное число у,
вычисляет с <- ау и направляет с верифика-
тору.
3. Верификатор проверяет, что с е G, генериру-
ет случайный бит и направляет претенденту.
4. Если претендент получает 0, то он раскрыва-
ет логарифм logac = у (mod #G); если получа-
ет 1, то раскрывает логарифм log,-,с = ух4
(mod #G).
5. Верификатор проверяет правильность полу-
ченного логарифма и его соответствие биту,
выработанному на шаге 3 (должно выпол-
няться равенство с = а' для нуля и с = Ъух
для единицы). Если соответствующее равен-
ство не выполняется, то результат: претен-
дент не знает логарифма. В противном слу-
чае возможны две ситуации. Если i < к, то
верификатор сообщает претенденту о пра-
вильности этого шага; верификатор и пре-
тендент полагают i <— i + 1 и возвращаются к
шагу 2; если i>k, то результат: претендент
знает логарифм.
Верификатор не может получить никакой ин-
формации о логарифме х, если показатели у вы-
бираются случайным (непредсказуемым) обра-
зом и не повторяются. Если верификатору извес-
тен порядок группы, то, в случае повтора показа-
теля у (то есть элемента с), он может один раз
послать претенденту 1, а в другой раз — 0, и вы-
числить х из у и ух~ .
14.2.4. Доказательство
правильности выбора составного числа
Если в криптографическом протоколе исполь-
зуются вычисления в кольце 2Lln2L и составное
число п является общим для всей системы, то его
разложение не должен знать никто. Однако от
правильности выбора этого числа зависит безо-
пасность каждого пользователя. Поэтому необ-
ходимо иметь возможность доказать, что число п
выбрано правильно, то есть представляет собой
произведение в точности двух различных про-
стых чисел, не разглашая никакой информации о
делителях этого числа.
Пусть р, q — неравные простые числа такие,
что p = q = 3 (mod 4), и n=pq. Тогда, согласно
квадратичному закону взаимности, -1 является
квадратичным невычетом по модулю р и по мо-
дулю q. Следовательно, из двух ненулевых чисел
а и -а всегда лишь одно является квадратичным
вычетом по модулю р. То же верно и для модуля q.
Для любого а, взаимно простого с п, выполня-
ется равенство для символов Якоби:
(аУ (-а\ „ ( иЛ
— = —— . Если — = -1, то для произволь-
\п) \ п ) \п)
него х е (Z/zzZ)* ровно одно из чисел х, -х, их,
-их является квадратичным вычетом по модулю
п. Каждое квадратное уравнение вида z = а име-
ет четыре решения в Z7zzZ, которые получаются
объединением по китайской теореме об остатках
двух пар решений: z = ±y/a (mod р) и
z = ±-/a(modq). Для двух из этих решений
— = 1, для двух других — = -1. Следующий
п) \п)
протокол использует указанное свойство [12].
282
Протокол 14.2.4. Доказательство правильно-
сти выбора свободного от кубов числа п =pq,
если p = q = 3 (mod 4).
Вход верификатора. Число и = 1 (mod 4); чис-
ла к и 7.
Вход претендента. Разложение числа и; числа
к и 1.
Выход верификатора. Решение о том, что чис-
ло и имеет ровно два различных простых делите-
ля, с вероятностью ошибки первого рода не бо-
лее 2-Лг.
Метод.
1. Претендент и верификатор полагают s <— 1.
2. Верификатор вырабатывает 7 произвольных
(Щ , ,,
чисел г/, таких, что — = -1 и посылает {ц,}
у и )
претенденту.
3. Претендент вырабатывает 7 произвольных
нечетных чисел d„ обратимых по модулю
<р(«), где ср— функция Эйлера, вычисляет
v, <— н/' (mod и) и посылает {v,} верифика-
тору.
[ V |
4. Верификатор проверяет равенства — = -1,
V п )
выбирает произвольные I - 1 чисел из {v,} и
посылает их претенденту.
5. Претендент посылает верификатору показа-
тели dj для полученных 7-1 чисел.
6. Верификатор проверяет, что показатели d,
нечетны и соответствуют парам (ы„ у). Если
проверка прошла успешно, то он заключает,
что оставшееся число v получено возведени-
ем заданного и в степень с неизвестным по-
казателем.
7. Верификатор вырабатывает I случайных чи-
сел w„ отличных от ±1, и посылает {иД пре-
тенденту.
8. Претендент вырабатывает I произвольных не-
четных чисел с„ вычисляет z; <— иД (modw) и
посылает {z,} верификатору.
9. Верификатор выбирает произвольные 7-1
чисел из {z,} и посылает их претенденту.
10. Претендент посылает верификатору показа-
тели с, для полученных 7 - 1 чисел.
11. Верификатор проверяет, что показатели с,
нечетны и соответствуют парам (ii'„ z,). Если
проверка прошла успешно, то он заключает,
что оставшееся число z получено возведени-
ем заданного w в степень с неизвестным по-
казателем.
12. Верификатор посылает претенденту случай-
ный бит 7>.
13. Претендент вычисляет квадратный корень х
из одного из чисел {z, -z, vz, -vz} такой, что
~ - (_ 1У и посылает верификатору.
\п )
14. Верификатор проверяет, что х (mod п) е
е {z, —z, vz, -vz) и что — = (-1/. Если это
(w J
так, то он сообщает претенденту об успеш-
ной проверке. Иначе результат: число п вы-
брано неправильно.
15. Если s<k, то претендент и верификатор ус-
танавливают s <— 5 + 1 и возвращаются на
шаг 2. Иначе результат: число и выбрано
правильно.
Данный протокол можно разбить на четыре
этапа. На первом этапе (шаги 2-6) претендент и
верификатор совместно вырабатывают число v
такое, что — = -1, причем верификатор не зна-
I п)
ет числа v, но может убедиться, что оно вырабо-
тано «по правилам». На втором этапе (шаги
7-11) претендент и верификатор совместно вы-
рабатывают число z, причем верификатор не зна-
ет числа z, но может убедиться, что оно вырабо-
тано «по правилам». На третьем этапе (шаг 12)
верификатор вырабатывает случайный бит Ь. На
четвертом этапе (шаги 13, 14) претендент дока-
зывает, что он знает квадратный корень из одно-
го из элементов множества {±z, ±vz}, обладаю-
щий заданным значением символа Якоби. На ка-
ждом этапе доказательства вероятность ошибки
первого рода равна 0,5.
Корректность протокола вытекает из сле-
дующих рассуждений. Предположим, что п име-
ет нечетное число простых делителей. Тогда хотя
бы один из простых делителей /?, числа п срав-
ним с 1 по модулю 4. В этом случае существова-
ние квадратного корня требуемого вида возмож-
( Л
v
— -1, и, следовательно,
но лишь тогда, когда
и
когда — = 1. Поскольку верификатор выбира-
ет число и случайно, то вероятность этого собы-
тия равна 0,5 (это соответствует вероятности
ошибки в ходе одной итерации доказательства).
Предположим, что п имеет четное число,
большее 2, различных простых делителей. Тогда
существует четное число т (включая 0) простых
делителей числа п, сравнимых с 1 по модулю 4, и
рассуждения сводятся к предыдущему случаю.
283
Если все простые делители числа п сравнимы с 3
по модулю 4, то существует нечетное число де-
лителей, для которых т (и, следовательно, и) яв-
ляется квадратичным невычетом. Квадратный
корень требуемого вида существует лишь в том
случае, если z или -z является квадратичным вы-
или если выполняется
четом по модулю п
— Z
для всех простых
делителей pi числа п. Вероятность такого собы-
тия не превышает 0,5.
Предположим, что число п не свободно от
квадратов и все его простые делители сравнимы
с 3 по модулю 4. В этом случае по китайской
теореме об остатках задача вычисления корня
требуемого вида сводится к вычислению этого
корня в кольцах вычетов по модулям максималь-
ных степеней простых делителей числа п. Из
теории чисел известно, что элемент у такой, что
НОД(у,//) = 1, является квадратичным вычетом
по модулю рк тогда и только тогда, когда у явля-
ется квадратичным вычетом по модулю р [1].
Рассмотрим случай п =pqr. Квадратный корень
из {z, -z, vz, -vz} по модулю п будет существо-
вать тогда и только тогда, когда будет существо-
вать такой же корень по модулю pqr. Для суще-
ствования указанного корня необходимо, чтобы
квадратичным вычетом по модулю pqr являлось
одно из чисел {z, -z, vz, -тс}. Вероятность этого
события равна 0,5, если z и v взаимно просты с п.
Случай п =p2sq7il тривиален, так как п являет-
ся квадратом. Осталось рассмотреть случай
п = ]Г"\], где p = q = 3 (mod 4) и g > 1. Число р не
может входить вне четным показателем, так как
тогда не выполнялось бы условие п = 1 (mod 4).
По китайской теореме об остатках имеет место
изоморфизм колец HUnTL = ZTp2g+1Z © TLIqZL. По-
скольку множества квадратичных вычетов по
модулю р и по модулю p2g+1 совпадают и
n2g+1
\Р 7
, то протокол 14.2.4 не может от-
2к+1 2г:-1 2 Аг 1
личить случаи и -р qun=p& q от случая
п =pq.
Способ создания сертификата того, что со-
ставное число свободно от квадратов (и, следо-
вательно, от кубов), приведен п. 15.6.6. Доказа-
тельство того, что число п свободно от кубов,
может быть выполнено также с использованием
сложного протокола, приведенного в работе [7].
Протокол 14.2.4 можно легко обобщить на
другие простые числа, для которых квадратич-
ным невычетом является не -1, а данное число d.
Например, если р = q s ±3 (mod 8), то 2 является
квадратичным невычетом. Тогда квадратичным
вычетом по модулю р является один из элемен-
тов а или 2а, то же справедливо и для вычетов по
модулю q. Если т — произвольный элемент
л \
кольца HUriZL такой, что — = -1, то квадратич-
\Р)
ным вычетом по модулю п является в точности
один из элементов a, 2xi, va, 2va, где НОД(а, и) = 1.
14.3. Бездиалоговые доказательства
с нулевым разглашением
Аппарат доказательств с нулевым разглаше-
нием позволяет обеспечить доказательства зна-
ния секретной информации и без диалога. Сле-
довательно, на базе таких доказательств можно
строить бездиалоговые протоколы опознавания.
Как и в случае диалоговых доказательств, здесь
обеспечивается защита от атак на основе подоб-
ранных открытых текстов. Кроме того, в основу
доказательств с нулевым разглашением можно
положить задачу о выполнимости и, следова-
тельно, задачу о вскрытии ключа симметричного
шифра, допускающую широкий спектр модифи-
каций.
Пусть претендент знает доказательство неко-
торой теоремы и хочет убедить верификатора в
том, что теорема верна, не предъявляя доказа-
тельства. Рассмотрим две возможности:
1) доказательство может быть представлено
только одному верификатору, и только он
может проверить его правильность; ?
2) доказательство может быть проверено каж-
дым, в этом случае говорят об открыто про-
веряемых бездиалоговых доказательствах.
Во втором случае есть некоторая аналогия с
цифровой подписью. Однако для доказательств
с нулевым разглашением можно использовать
гораздо более широкий круг задач, чем для под-
писи.
Пусть р и q — неравные простые числа такие,
что p = q = 3 (mod4), и n=pq. Тогда, с учетом
рассуждений п. 14.2.4, можно конструировать
блобы, свободные от коллизий, следующим об-
разом. Выбираем случайное целое число t такое,
что 0 < t < п, и вычисляем ? (mod и). Бит 0 пред-
ставляется как Г2 (mod и), бит 1 представляется
как -t~ (mod и). Раскрытие значения бита осуще-
ствляется предъявлением /. Согласно теореме
12.2.1 решение сравнения второй степени равно-
сильно разложению числа п. Такие блобы назы-
ваются QR-блобами [5].3
3 От quadratic residue problem — задача распозна-
вания квадратичного вычета.
284
Пусть b — вектор блобов, b' — вектор соот-
ветствующих битов. Назовем подмножество S
множества «-разрядных двоичных векторов кон-
струируемым, если для любого b' g S претен-
дент может построить вектор блобов b и без диа-
лога доказать, что b' g S, не раскрывая верифи-
катору значения Ь'. Например, существование
блобов означает, что множество S = {0, 1} триви-
альным образом конструируемо. Если на множе-
стве блобов определена бинарная операция и
существует вычислимый гомоморфизм этого
множества в группу F2, то множества
Е= {00, 11} и D = {01, 10} тоже конструируемы.
Назовем подмножество S множества п-
разрядных двоичных векторов сертифицируе-
мым, если для любого вектора блобов Ь, для ко-
торого b' g S, претендент может без диалога до-
казать, что b' g S, не раскрывая верификатору
значения Ь'. Разница между конструируемыми и
сертифицируемыми множествами заключается в
том, что во втором случае претендент не может
сам создавать блобы.
Лемма 14.3,1. В случае использования QR-
блобов любое подмножество S’ множества п-
разрядных двоичных векторов конструируемо и
сертифицируемо.
Доказательство см. в работе [5].
Таким образом, для <9/?-блобов понятия кон-
струируемого и сертифицируемого множеств
совпадают.
Лемма 14.3.1 позволяет строить бездиалого-
вые доказательства с нулевым разглашением,
основанные на задаче о выполнимости булевой
функции. Каждый бит аргумента представляется
соответствующим блобом. Например, булева
функция Х=А + В является сбалансированной, и
ей соответствует произведение блобов (в силу
изоморфизма групп: F2 = Z). Если нулевое зна-
чение бита Л представляется блобом /^(modn),
нулевое значение бита В — блобом /^(modn), то
нулевое значение функции X представляется
блобом /2/д(тоби). Этот подход обобщается на
произвольное число слагаемых.
Несколько сложнее можно установить соот-
ветствие между битами и блобами для булевой
функции Y = АВ [5]. С использованием такой же
техники можно построить соответствие между
блобами и произвольными булевыми функциями.
Чтобы доказать знание набора переменных,
удовлетворяющих заданной булевой функции/
претендент выполняет следующие действия:
1) переводит этот набор в 2^-блобы, представ-
ляет необходимые данные, позволяющие
убедиться, что набор элементарных булевых
функций соответствует функции/
2) для каждой операции композиции булевых
функций представляет информацию, позво-
ляющую убедиться в корректности подста-
новки переменных;
3) открывает значение функции / раскрытием
соответствующего блоба.
Верификатору остается убедиться, что все
данные корректны. Безопасность таких протоко-
лов основана на двух задачах: разложения и вы-
полнимости, причем для взлома протокола дос-
таточно решить любую из них. Очевидно, какой
бы ни была задача о выполнимости, ее добавле-
ние к задаче разложения не может усилить про-
токол.
Бездиалоговые доказательства могут быть осно-
ваны и на задаче дискретного логарифмирования.
Протокол 14.3.1. Опознавание на основе без-
диалогового доказательства знания логарифма.
Вход верификатора. Группа G, образующая а,
экспонента Ь, число к, вычислимая в одну сторо-
ну хэш-функция h.
Вход претендента. Группа G, ее простой поря-
док г, образующая а, логарифм х, число к, вычис-
лимая в одну сторону хэш-функция h.
Выход верификатора. Решение о том, что пре-
тендент знает логарифм, с вероятностью ошибки
первого рода не более 2~к.
Метод.
1. Претендент вырабатывает к случайных пока-
зателей ...,Ук, обратимых по модулю г, и
У1 Ук
вычисляете ,...,а .
2. Претендент вычисляет хэш-функцию от аргу-
мента, представляющего собой конкатенацию
найденных экспонент: е <- h(a>l ||...||аУк).
3. Претендент посылает верификатору текст до-
казательства — набор (аУ 1,..., аУк; z},..., zt),
где z,=y„ если е, = 0; z, =уХ1, если е, = 1;
(су, ..су.) — младшие к битов числа е.
4. Верификатор вычисляет хэш-функцию е <-
<— h(a 11|...||ак), находит биты е, и проверяет
их соответствие предъявленному тексту. При
л Ч У1
е, = 0 должно выполняться равенство а = а ;
при е, = 1 — равенство о = а .
5. Если все к проверок на шаге 4 проходят ус-
пешно, то результат: претендент знает лога-
рифм, иначе результат: претендент не знает
логарифм.
Протокол 14.3.2. Аутентификация сообщения
на основе бездиалогового доказательства знания
логарифма. , - — •
285
Вход верификатора. Группа G, образующая а,
экспонента Ь, число к, вычислимая в одну сторо-
ну хэш-функция h.
Вход претендента. Группа G, ее простой по-
рядок г, образующая а, логарифм х, число к, вы-
числимая в одну сторону хэш-функция h.
Выход верификатора. Решение о том, что со-
общение является подлинным, с вероятностью
ошибки первого рода не более Тк.
Метод.
1. Претендент вырабатывает сообщение т и к
случайных показателей jy, ...,уц, обратимых
М Ук
по модулю г, и вычисляет а а .
2. Претендент вычисляет хэш-функцию от ар-
гумента, представляющего собой конкатена-
цию сообщения и найденных экспонент:
е <— h(m, а] ||...|| ак).
3. Претендент посылает верификатору текст до-
казательства — набор (т, а}1,а\ ..., z*),
где z,=y„ если е, = 0; z,=ypc-1, если е,= 1;
(щ,...,<?/.) — младшие к битов числа е.
4. Верификатор вычисляет хэш-функцию е <—
<- h(m, ||...|| ак\ находит биты <?, и прове-
ряет их соответствие предъявленному тексту.
При е, = 0 должно выполняться равенство
а = а ; при е, = 1 — равенство b = а .
5. Если все к проверок на шаге 4 проходят ус-
пешно, то результат: сообщение подлинное,
иначе результат: сообщение не является под-
линным.
Этот протокол является аналогом протокола
цифровой подписи.
14.4. Передача информации со стиранием
Криптографический примитив передачи ин-
формации со стиранием (oblivious transfer)4 был
предложен М. Рабином [11]. Передача информа-
ции со стиранием может быть применена, на-
пример, в бездиалоговых доказательствах с ну-
левым разглашением. Рассмотрим принцип пе-
редачи информации со стиранием от пользовате-
ля А к пользователю В. Получатель В имеет два
ключа: открытый ключ Рв и секретный ключ Sb-
Отправитель А имеет два текста to и Ц. Шифро-
грамма вычисляется как функция от /0, h, Рв- Ис-
пользуя секретный ключ Sb, получатель В может
4 Такой небуквальный перевод термина лучше от-
ражает механизм данного криптографического при-
митива.
расшифровать только один из текстов t0 или
причем А не знает, какой текст расшифровал В.
Таким образом, один из двух переданных тек-
стов в ходе передачи стирается и не доходит до
получателя.
Формальная модель передачи со стиранием
может быть рассмотрена как канал со стирани-
ем, который представляет собой пару каналов
с ~ (с°, с1), удовлетворяющих следующим требо-
ваниям:
1) отправитель А может передать произвольное
число битов по каждому из каналов с° и с’;
2) получатель В может получать информацию
только по одному из каналов с° или с1;
3) А не знает, по какому из каналов В получает
информацию.
Приведем пример передачи информации со
стиранием, основанный на задаче дискретного
логарифмирования в простом поле.
Алгоритм 14.4.1. Генерация ключей получа-
теля для передачи информации со стиранием.
Вход. Характеристика поля р, образующая а
группы и элемент g & Fz,. Логарифм х, для
которого ах = g в поле Fz„ не известен никому.
Выход. Открытый и секретный ключи.
Метод.
1. Сгенерировать случайный бит ie{0, 1} и
случайное число х, 6 {0, 1, 2} и вы-
х х — 1
числить р, <— а ' и <— g - (а ') .
2. Результат: Р/, = (ро, Pi) — открытый ключ.
Sb = (z, х,) — секретный ключ.
Любой пользователь может проверить пра-
вильность открытого ключа: PoPi = g- Благодаря
тому, что дискретный логарифм от g неизвестен,
владелец секретного ключа не может знать оба
логарифма от р0 и рь Кроме того, открытый ключ
не несет информации о том, какой из дискретных
логарифмов — от р0 или от Pi — знает В, так как
пары (р0, Pi) распределены в Fz, равномерно.
В основу безопасности положен тот же прин-
цип, что и в протоколе Диффи-Хеллмана: если
известны ах. ау, то а^' вычислить трудно.
Передача со стиранием пары сообщений
(/о, б) выполняется следующим образом.
Протокол 14.4.2. Передача информации со
стиранием.
Вход отправителя. Характеристика поля р,
образующая а группы Fz,; пара сообщений (/0, б),
представленных в виде двоичных векторов; от-
крытый ключ Ph - (Ро, pi) из алгоритма 14.4.1.
Вход получателя. Секретный ключ Sh = (z, х,)
из алгоритма 14.4.1.
286
Результат. Передача со стиранием двух сооб-
щений, из которых получатель может получить
только одно.
Метод.
1. Отправитель выбирает пару показателей
Уо,И е {0, 1, -2}, вычисляет значения
ос0 <— а '0, ОС] <— а 1 и посылает их получателю.
2. Отправитель вычисляет у0 <—рр0,у] <—р,'1.
вычисляет суммы по модулю 2 двоичных
векторов: rQ <— to + у0, rj <- А + fi и отправля-
ет го, Г] получателю.
3. Получатель для принятой пары а0, Ct] с по-
мощью своего секретного ключа (i, х,) рас-
шифровывает значение у, <— а,*' и находит
сообщение /, <— г, + у,.
Таким образом, получатель может узнать
только одно из значений to или А в зависимости
от бита i своего секретного ключа. В соответст-
вии с предположением Диффи-Хеллмана он не
может вычислить второй текст, так как не знает
у 1,- Например, если р]_, = а то у]_, = а то
есть получатель знает а а г', но не знает ни
х,_„ ниу]_,.
Для многократного повторения передачи со
стиранием можно каждый раз генерировать но-
вые открытый и секретный ключи. Но если тре-
буется бездиалоговая передача, можно поступить
иначе. Отправитель сначала передает по каналу
со стиранием пару текстов tQ и А, причем он не
знает, какой из текстов расшифрует получатель.
Затем отправитель, используя /0 и h как обра-
зующие, генерирует криптографически стойкие
псевдослучайные последовательности H(to) и
77(A). Эти последовательности могут состоять,
например, из младших разрядов элементов по-
следовательности t*, t*, t* , .
Для передачи со стиранием очередной пары
сообщений (rQ, Г]) отправитель посылает получа-
телю суммы по модулю 2 двоичных векторов:
г0 + G(l0), ri + G(t\). В качестве слагаемых С(/,)
используются незадействованные при передаче
предыдущих сообщений разряды соответствую-
щих псевдослучайных последовательностей H(tj).
Получатель при первой передаче расшифровы-
вает только один из двух текстов, поэтому он зна-
ет только одну из образующих: /0 или А- Описан-
ная конструкция образует канал со стиранием.
Канал со стиранием позволяет строить без-
диалоговые доказательства с нулевым разглаше-
нием (и, следовательно, позволяет решать задачу
опознавания без диалога, в режиме off-line или
по симплексному каналу связи). Покажем, как
это делается для задачи об изоморфизме графов.
Протокол 14.4.3. Бездиалоговое доказатель-
ство знания изоморфизма графов на основе кана-
ла со стиранием.
Вход верификатора. Графы G и Н; секретный
ключ Si, канала со стиранием (с°, с1).
Вход претендента. Графы G и Н, изоморфизм
<р: G -> Н; открытый ключ Рь канала со стирани-
ем (с°, с1).
Выход верификатора. Решение о том, что пре-
тендент знает требуемый изоморфизм, с вероят-
ностью ошибки первого рода не более 0,5.
Метод.
1. Претендент выполняет следующие действия.
1.1. Генерирует случайную перестановку у»
вершин графа G и вычисляет F <— »|/(G).
1.2. Генерирует случайный ключ шифрова-
ния К для симметричного алгоритма,
зашифровывает на этом ключе граф F и
передает шифрограмму верификатору
по обычному (без «стирания») каналу.
1.3. Генерирует случайный бит Ь. Если
b = 0, то передает по каналу с° ключ К и
перестановку vjy, а по каналу с1 — ключ
К и перестановку <р~1. Если b= 1, то
меняет местами каналы <?° и с1.
2. Верификатор проверяет, что полученная пе-
рестановка является изоморфизмом соответ-
ствующих графов. Если проверка проходит
успешно, то результат: претендент знает
изоморфизм с вероятностью 0,5.
Протокол повторяется необходимое число
раз. Для второй итерации доказательства нужна
новая пара ключей. В противном случае претен-
дент может обманывать с вероятностью 0,5 не-
зависимо от числа повторов протокола. Дейст-
вительно, верификатор не может менять канал,
в котором он умеет расшифровывать информа-
цию. Если он умеет расшифровывать информа-
цию, переданную по каналу с°, и претендент в
первом круге протокола угадал канал, не зная
изоморфизма графов, то он может успешно об-
манывать при неограниченном числе повторов
протокола.
Однако и при использовании каждый раз но-
вой пары ключей претендент может жульни-
чать. Например, он может отправить по обоим
каналам одну и ту же информацию, для этого не
требуется знать изоморфизм графов. Верифика-
тор не знает значения случайного бита, который
будет создан претендентом на шаге 3, поэтому
он не может выяснить, жульничает ли претен-
дент. Если же верификатору будет представлен
287
отрезок случайной последовательности, соот-
ветствующей действиям претендента (результа-
там генерации случайного бита), то обман со
стороны претендента будет исключен. Таким
образом, претендент должен представлять на
каждой итерации протокола значение случайно-
го бита, которое передается по обычному (без
«стирания») каналу. Очевидно, можно переда-
вать соответствующий отрезок случайной по-
следовательности после завершения всех повто-
ров протокола.
Рассмотрим еще один вариант передачи со
стиранием, основанный на задаче разложения.
Пусть и =pq, где p = q = 3 (mod 4). Безопасность
протокола основана на следующей задаче: зная
символ Якоби — р= 1, вычислительно невозмож-
\п J
но распознать, является ли х квадратичным выче-
том по модулю и. В протоколе совмещены этап
генерации ключа для передачи одного бита и этап
собственно передачи, поэтому требуется диалог.
Протокол 14.4.4. Диалоговая передача одного
бита со стиранием, основанная на задаче разло-
жения.
Результат. Передача бита с вероятностью по-
лучения, равной 0,5.
Метод.
1. Отправитель выбирает случайные большие
простые числа р = q = 3 (mod 4), запоминает
их, вычисляет п <— pq, выбирает случайное
число t такое, что 0 < / < п и НОД(/, и) = 1, и
случайный бит b и посылает пару (и, (-l)V
(mod и)) получателю.
2. Получатель выбирает случайное число г,
0 <г < и, вычисляетх <— г2 (mod п) и посыла-
ет х отправителю.
3. Отправитель выбирает случайным образом
число л — один из четырех квадратных кор-
ней из х по модулю п — и посылает его по-
лучателю.
Если s = ±r, то получатель не может узнать
ничего о бите Ь. В противном случае он на-
ходит р = НОД(г + s, п) и вычисляет символ
(-1)*/2(тоби)
. При I = 1
Лежандра I
Р
полагает b <— 0, при I = -1 полагает b <— 1.
Здесь очевидный способ обмана со стороны
получателя — выбрать число х специальным об-
разом (без вычисления f (mod и)) и получить от
отправителя постороннюю информацию — квад-
ратный корень из х. Этот протокол можно улуч-
шить, введя еще несколько шагов, при выполне-
нии которых получатель мог бы доказать с нуле-
вым разглашением знание квадратного корня из х.
Доказательство можно организовать, напри-
мер, так. Получатель генерирует случайное чис-
ло и, вычисляет v = н2 и предъявляет его отпра-
вителю. Отправитель возвращает 0 или 1. При
нуле получатель посылает отправителю u = Jv ;
при единице — y[xv .
Возможный способ обмана со стороны отпра-
вителя — выбор составного числа и, которое не
является произведением двух различных про-
стых сомножителей. Например, если и является
произведением трех простых сомножителей, то
существование хотя бы одного квадратного кор-
ня из данного числа влечет за собой существова-
ние восьми корней. В этом случае в протокол
следует ввести доказательство с нулевым раз-
глашением того, что п является произведением
двух различных простых чисел [7].
На базе протоколов со стиранием можно
строить более сложные протоколы с участием
нескольких сторон.
14.5. Разделение секрета
Рассмотрим сеть шифрованной связи с сим-
метричным шифрованием, в которой возможны
компрометации (нарушение конфиденциально-
сти) ключей отдельных пользователей, причем
каждый пользователь доверяет остальным. Как
могут оставшиеся пользователи обеспечить воз-
можность ведения секретных переговоров? Один
из способов — построить такую ключевую сеть,
в которой каждой паре участников соответствует
свой ключ. Однако это требует большого объема
памяти, поскольку число ключей пропорцио-
нально квадрату числа пользователей.
Другой способ— использовать схему разде-
ления секрета (secret sharing) [10, 12], то есть
разделить секретную информацию между не-
сколькими пользователями. Разделение секрета
используется для управления ключами в прото-
колах, содержащих большое количество участ-
ников, и для коллективной подписи.
Принцип разделения секрета можно пояс-
нить на примере коллективной схемы подписи
RSA. Пусть и = pq — составное число. Если в
RSA есть два ключа е, d таких, что ed = 1
(mod <р(и)), то в общем случае может быть не-
сколько ключей k\, ...,kt таких, что k\ki...kt=\
(mod <р(и)). Пусть / = 3; ключ к\ известен поль-
зователю А, ключ к~, известен пользователю В,
третий ключ опубликован.
1. А генерирует подпись sA = mkl для сообще-
ния т и посылает хд пользователю В.
288
2. В подписывает сообщение sA своей подписью:
_ *2 _ „/1*2
3. Любой верификатор может убедиться, что
т = sABk3 и подпись пользователей Л и В верна.
Очередность подписывания может быть лю-
бой. Для исключения атаки на основе гомомор-
физмов можно подписывать не само сообщение,
а хэш-функцию от него. Для обеспечения разде-
ления секрета ни А, ни В не должны знать разло-
жение числа п, так как в противном случае, зная
ключи к} и kj, пользователь А легко может вы-
числить секретный ключ пользователя В:
кг = (к}кзУ] (mod <р(и)).
В общем случае в схеме разделения секрета
секретная информация распределяется между Т
участниками так, что они в результате некоторо-
го диалога могут ее восстановить. Уточнением
схемы разделения секрета является пороговая
схема (threshold scheme). В этом случае секрет-
ная информация разделена между Т участниками
так, что любые tQ<t < Т из них в ходе диалога
могут восстановить эту информацию, но если
число участников f < t0, то секретную информа-
цию восстановить невозможно. Идеальная поро-
говая схема не позволяет получить никакой ин-
формации о секрете для любых t' < to участников.
Для краткости вместо /0 будем писать /.
Пороговая схема разделения секрета может
быть построена на основе интерполяции поли-
номов. Пусть секретная информация представля-
ет собой совокупность коэффициентов приве-
денного полинома Дх) степени t - 1 над конеч-
ным полем F9. Полином/полностью определяет-
ся своими значениями для t любых попарно раз-
личных значений аргумента xb Тогда по
интерполяционной формуле Лагранжа [2]
ДХ)=У /(х) i )-(*"*/ )
Zi ' (x,-x1)...(x,-x,_i)(x,-x,+i)...(x,.-x()
Сложность вычисления коэффициентов поли-
нома по указанным значениям Дх,) — полиноми-
альная от log q.
Пусть секретным является значение Дхо) по-
линома /для некоторого х0. На этапе подготовки
выбираются поле F?, полином Дх) над этим по-
лем и попарно различные значения хо,
X], ..., хт 6 F9 и вычисляются значения
/(х|), ...,fixp). Каждый из Тучастников получает
четверку (х0, F9, х„ Дх,)). При восстановлении
секрета любые t участников, используя интерпо-
ляционную формулу Лагранжа, могут восстано-
вить коэффициенты полинома Дх) и вычислить
его значение в точке х0. Если число взаимодейст-
вующих сторон менее /, то найти все коэффици-
енты полинома Дх) невозможно. Например, для
t - 1 участников в зависимости от недостающей
/-й порции информации искомый секрет может
принимать равновероятно любое из q значений.
Поэтому t - 1 и менее участников не могут полу-
чить никакой информации о секрете.
Данная схема является идеальной и допускает
наращивание в виде добавления новых пользова-
телей. Кроме того, она безопасна в теоретико-
информационном смысле. Эта схема может быть
описана и в терминах квадратных матриц разме-
ра t над полем IF,r
Если положить Т = 2/ - 1, то пороговая схема
может быть положена в основу голосования
«большинством голосов». В этом случае разде-
ленным секретом является ключ формирования
подписи, а ключ проверки подписи является от-
крытым. Тогда г или более выборщиков могут
сообща выработать ключ формирования подписи
и подписать соответствующий документ.
Схема разделения секрета как протокол с не-
сколькими участниками может допускать обман
со стороны некоторых участников. Например,
один из участников раскроет остальным не ис-
тинное значение своей информации, а некоторое
ложное значение, чтобы получить информацию о
секретах других участников. Очевидный метод
защиты от таких нарушений— использование
подписи доверенной стороны для информации,
хранящейся у каждого участника.
14.6. Протоколы управления ключами
Введем ряд определений согласно работе [10].
Установление ключа — процесс, в результате
которого (разделенная) секретная информация
становится доступной двум или более сторонам.
Примером установления ключа является получе-
ние общего ключа группой пользователей с по-
мощью схемы разделения секрета или протокол
Диффи-Хеллмана.
Доставка ключа — протокол или механизм
установления ключа, при котором одна из сторон
производит или получает иным образом секрет-
ное значение (ключ) и передает его безопасным
образом другим участникам. Примером доставки
ключа является протокол, в котором центр рас-
пределения ключей передает каждому из участ-
ников сеансовый ключ, зашифрованный на пер-
сональном ключе этого участника.
Предварительное распределение ключа —
протокол установления ключа, при котором ре-
зультирующие ключи полностью определяются
исходными ключами. Примером предваритель-
ного распределения ключа является формирова-
ние разделенных между пользователями секрет-
ных данных. _ .
289
Производный ключ — ключ, вычисляемый
шифрованием на секретном ключе некоторой
информации. Примером производного ключа
является ключ, полученный как шифрограмма в
результате симметричного шифрования ключа на
себе.
По принципу протокола Диффи-Хеллмана
можно устанавливать сеансовый ключ для трех и
более участников. Рассмотрим пример такого
протокола с тремя участниками А, В, С на основе
задачи дискретного логарифмирования.
Протокол 14.6.1, Установление сеансового
ключа для трех участников.
Вход. Общая для трех участников А, В, С
циклическая группа G простого порядка и обра-
зующая а.
Выход. Общий для трех участников сеансо-
вый ключ.
Метод. ; >' ;
1. А генерирует случайное число х, вычисляет
ах и посылает его В.
2. В генерирует случайное число у, вычисляет
ау и посылает его С.
3. С генерирует случайное число z, вычисляет
az и посылает его А.
4. А вычисляет azx и посылает его В.
5. В вычисляет аху и посылает его С.
6. С вычисляет ау~ и посылает его А.
7. А вычисляет сеансовый ключ а^.
8. В вычисляет сеансовый ключ azxy.
9. С вычисляет сеансовый ключ axyz.
Многие протоколы установления ключа ис-
пользуют доверенный центр (это может быть
доверенная третья сторона, доверенный сервер,
центр распределения ключей и т. п.).
Безопасное установление ключа требует, что-
бы ключ был секретным и чтобы каждый из уча-
стников мог быть уверен, что общается именно с
тем, с кем нужно, то есть чтобы обеспечивалось
опознавание (аутентификация) участников и
имитозащита передаваемой информации. Необ-
ходимо также исключить возможность действия
одного из участников в ущерб другим.
При доставке ключа могут использоваться
симметричные и несимметричные методы шиф-
рования, а также хэш-функции.
14.6.1. Установление ключа на основе
симметричных методов
Система распределения ключей— это уста-
новление ключа, при котором доверенный центр
распределения ключей генерирует и распределя-
ет секретные данные между пользователями так,
что любые два из них могут вычислить свой сек-
ретный ключ, недоступный для остальных поль-
зователей, за исключением центра.
Если ключи для каждой пары пользователей
фиксированы, то система распределения ключей
является системой с предварительным распреде-
лением.
В простейшей системе распределения ключей
с п участниками каждой паре пользователей со-
ответствует свой ключ, а каждый пользователь
получает информацию, позволяющую ему выра-
ботать ключ для связи с остальными п - 1 поль-
зователями. Тогда, используя разделение секре-
та, можно обеспечить идеальную в теоретико-
информационном смысле секретность.
Система распределения ключей называется j-
безопасной, если для любой пары участников
любые / участников (в число которых не входят
участники из выбранной пары), объединяя свои
секреты, не могут получить никакой дополни-
тельной информации о секретном ключе указан-
ной пары.
Если система связи имеет ///-разрядные ключи
и все ключи различны, то для достижения j-
безопасности каждый пользователь должен
иметь не менее m(j + 1) бит информации [4].
Максимальная защищенность достигается при
j = п - 2, где п — число участников.
Способ Блома предварительного распределе-
ния ключей [4] основан на корректирующих ко-
дах. Каждый из п участников имеет несекретные
данные и персональную порцию секретной ин-
формации, на основе которой он может устано-
вить секретный ключ с каждым из оставшихся
п - 1 участников.
Общие для всех пользователей несекретные
открытые данные— порождающая матрица G
для (и, Л)-кода5 над полем IF,,, q ~ 2т.
Доверенный центр выбирает секретную сим-
метрическую матрицу D размера к х к над полем
F?. Затем доверенный центр выдает каждому
пользователю i часть общей секретной информа-
ции S„ определяемую как i-ю строку в матрице
5 = (DG)1 размера их к. Тогда S, имеет размер
к log2q бит. Секрет 5, позволяет участнику i вы-
числить /-ю строку матрицы (DG)TG.
Пользователи i и j вычисляют общий ключ
Ку = Ку длины т бит. Поскольку матрица (DG)TG
симметрическая, то j-й элемент в f-й строке ра-
вен /-му элементу в j-й строке, этот элемент и
является ключом Ку.
Здесь граница безопасности равнаj- к- 1.
5 (и, Л)-кодом называется множество из 2к двоич-
ных векторов длины и таких, что хэммингово рас-
стояние между любыми двумя векторами — не
менее и- к + 1 [10].
290
14.6.2. Доставка ключа
Способы доставки сеансового ключа от поль-
зователя А пользователю В различаются по ис-
пользуемому способу шифрования (симметрич-
ные, несимметричные, бесключевые) и по нали-
чию диалога в ходе доставки (бездиалоговые и
диалоговые). Если доставка ключа основана на
симметричном шифровании, то при доставке се-
ансового ключа от Л к В оба пользователя имеют
общий секретный ключ К.
В случае бездиалоговой доставки ключа от-
правитель А генерирует случайный ключ гА и
посылает получателю В шифрограмму Ек(гА) на
ключе К (можно одновременно заменять и
ключ К). Получатель В расшифровывает сооб-
щение и находит сеансовый ключ гА. Имитоза-
щита осуществляется с помощью хэш-функ-
ции, зависящей от ключа К. Для защиты от по-
второв в сообщение вставляется значение tA —
время или номер сообщения. Для того чтобы В
понял, что сообщение адресовано именно ему,
в сообщение включается идентификатор idB
пользователя В. Тогда шифрограмма имеет вид
Е).'(гл || tA || idB).
В случае диалоговой доставки ключа пользо-
ватель В генерирует случайное число пв и посы-
лает его пользователю А. Тот, в свою очередь,
вычисляет шифрограмму ЕД>/|1ив|1г'^в) и посы-
лает ее пользователю В, который расшифровыва-
ет это сообщение, убеждается, что оно адресова-
но ему, проверяет, что нужное число имеет вид
пв, то есть что сообщение подлинное, и исполь-
зует гА в качестве сеансового ключа. Диалог по-
зволяет обеспечить имитозащиту, защиту от по-
второв и проблем, связанных с рассинхрониза-
цией часов пользователей.
Если сеансовый ключ вычисляется из произ-
водного ключа путем зашифрования на этом
ключе некоторого несекретного общего для двух
участников открытого текста, то доставка ключа
сводится к доставке указанного открытого тек-
ста, который может не быть секретным. Тогда А
генерирует случайное число гА и посылает его В.
Сеансовый ключ имеет вид Ек(гА).
Этот протокол требует имитозащиты, в том
числе, защиты от повторов. Следовательно, необ-
ходимо добавить к гА код времени tA, при этом се-
ансовый ключ имеет вид Ep(h(rA || //)), где h — хэш-
функция.
Примером доставки сеансового ключа, не
требующей наличия секретного ключа шифрова-
ния ни у отправителя, ни у получателя, является
протокол Месси-Омуры, в котором сеансовым
ключом является передаваемая информация.
Участник А выбирает ключ К, генерирует
случайный показатель а, обратимый по модулю
р - 1, вычисляет К1 и посылает участнику В. Тот,
в свою очередь, генерирует случайный показа-
тель Ь, обратимый по модулю р- 1, вычисляет
значение (./С/ и посылает его А. Участник А вы-
числяет значение Kaha = КУ и посылает его В.
Участник В возводит полученное сообщение в
степень и вычисляет K?h = К.
В этом случае необходимо принять меры,
обеспечивающие аутентификацию полученной
информации, в том числе защиту от повторов.
Рассмотрим способы доставки ключа от Л к Б,
использующие шифрование с открытым ключом.
В этом случае отправитель А пользуется откры-
тым ключом зашифрования; парный ключ рас-
шифрования знает только получатель В.
При бездиалоговой доставке отправитель за-
шифровывает по схеме с открытым ключом се-
ансовый ключ и отправляет получателю. Полу-
чатель расшифровывает сеансовый ключ и ис-
пользует его в качестве ключа симметричного
шифра. Для того чтобы получатель мог распо-
знать, от кого пришло зашифрованное сообще-
ние, нужна аутентификация.
Примером диалоговой доставки ключа, осно-
ванной на шифровании с открытым ключом, яв-
ляется протокол Нидхама-Шредера [10], исполь-
зующий взаимное опознавание участников. В
этом протоколе отправитель А и получатель В
имеют секретные ключи расшифрования КА, Кв,
а соответствующие ключи кА, кв зашифрования
опубликованы.
Протокол 14.6.2. Диалоговый протокол Нид-
хама-Шредера доставки ключа.
Вход отправителя А. Секретный ключ КА, от-
крытый ключ кв, идентификатор idB, сеансовый
ключ к\.
Вход получателя В. Секретный ключ Кв, от-
крытый ключ кА, идентификатор idA.
Результат. Доставка ключа к\ от А к В.
Метод.
1. Отправитель посылает получателю шифро-
грамму Eikk} || idA) текста к\ || idA на ключе кв.
2. Получатель расшифровывает сообщение на
ключе Кв и находит к}, генерирует случайное
число к2, вычисляет шифрограмму ЕА(Е || к2 || idB)
текста к^ || к21| id в на ключе кА и посылает ее
отправителю.6
3. Отправитель расшифровывает сообщение на
ключе КА, выделяет к2, зашифровывает его на
6 По-видимому, на этом шаге вместо ключа kj
лучше передавать значение хэш-функции h(kt).
291
ключе кв и посылает шифрограмму Е^к-А по-
лучателю.
4. Получатель расшифровывает сообщение,
проверяет, что полученное значение к2 сов-
пало с исходным, и убеждается, что отправи-
тель действительно знает ключ расшифрова-
ния КА, то есть ключ к\ подлинный.
Обеспечить имитозащиту в этом протоколе
можно с помощью: а) подписи зашифрованного
сообщения; б) зашифрования подписанного со-
общения; в) раздельного зашифрования и подпи-
си. Доставляемым ключом можно также считать
пару (Ц, к2}.
Рассмотрим еще один вариант установления
ключа, использующий систему RSA, в которой
шифрование и вычисление подписи выполняют-
ся одинаково [10].
Протокол 14.6.3. Установление ключа с опо-
знаванием (протокол Х.509).
Вход отправителя А. Секретный ключ dA, от-
крытый ключ (ид, ев), идентификатор idB.
Вход получателя В. Секретный ключ dB, от-
крытый ключ (и/, еА), идентификатор idA.
Результат. Установление сеансового ключа.
Метод.
1. Отправитель генерирует случайное число гА,
выбирает ключевую информацию к\ и за-
шифровывает ее на открытом ключе (ив, ев),
вычисляет текст DA <- 1АЦгА || idB[[EB(ki), где
tA — код времени, вычисляет подпись SA для
Da с помощью своего секретного ключа dA и
зашифровывает DA || S/,(DA) на открытом клю-
че (ив, ед). Затем отправляет сообщение
Eb(Da || Sa(DaY) получателю.
2. Получатель проверяет подлинность и пра-
вильность сообщения с учетом подписи,
времени, имени и т. п.; проверяет, что число
гА ранее не использовалось. Выделяет число
к} и запоминает его. Генерирует случайное
число гд, выбирает ключевую информацию
к2 и зашифровывает ее на открытом ключе
(пА, еА), вычисляет DB <- tB || rB || idA || ЕА(к2\
вычисляет подпись SB для DB с помощью
своего секретного ключа dB и зашифровыва-
ет DB || SB(DB) на открытом ключе (пА, еА).
Затем передает сообщение EA(DB || Sn(Dn))
отправителю.
3. Отправитель проверяет подлинность и пра-
вильность сообщения с учетом подписи, вре-
мени, имени и т. п.; проверяет, что число гв
ранее не использовалось. Если аутентифика-
ция прошла успешно, то он выделяет к2.
4. Результат: к\ или (к}, к2) — сеансовый ключ.
При использовании этого протокола необхо-
димо иметь в виду, что задача разложения обла-
дает субэкспоненциальной сложностью, а задача
вычисления симметричного ключа— экспонен-
циальной сложностью. Протокол Х.509 согласо-
ван с RSA и DES с коротким ключом. В случае
использования российских стандартов следует
обеспечить согласование стойкости систем с от-
крытым и с секретным ключом.
В случае доставки ключа от А к В шаг 3 не
нужен.
14.7. Временная метка
На практике часто требуется, чтобы документ
содержал дату ознакомления (создания, измене-
ния), которую было бы невозможно изменить без
того, чтобы это не стало бы явным. Например,
если выпускник школы может предъявлять ре-
зультаты выпускного экзамена в электронном
виде (не оценки, а саму работу) для поступления
в институт, он может быть заинтересован в под-
мене своей работы путем исправления «задним
числом» допущенных ранее ошибок.
Защиту от подмены можно обеспечить ис-
пользованием временной метки (time stamp).
Установка и проверка временной метки явля-
ется одной из задач аутентификации. Временная
метка может быть реализована с использованием
электронной цифровой подписи двояко: центра-
лизованно (при наличии центра установления
меток) и децентрализованно, с распределенным
механизмом проверки временной метки.
14.7.1. Централизованная
реализация временной метки
При централизованной реализации временной
метки иногда требуется, чтобы обеспечивалась
конфиденциальность (центр не должен знать со-
держание документа) и анонимность (центр не
должен знать, кто прислал документ).
Протокол предусматривает участие трех ле-
гальных пользователей: претендента, который
хочет добавить к документу временную метку,
центра временных меток и верификатора, прове-
ряющего правильность документа и времени его
создания. Используемый криптографический
примитив — электронная цифровая подпись
центра временных меток. Достоинством этой
реализации является ее простота.
Протокол 14.7.1. Централизованное создание
и проверка временной метки.
Вход претендента. Документ т; открытый
ключ проверки подписи; хэш-функция h.
292
Вход верификатора. Открытый ключ провер-
ки подписи; хэш-функция h.
Вход центра временных меток. Код текущего
времени; секретный ключ формирования подписи.
Метод.
Для создания временной метки выполняются
следующие действия.
1. Претендент, создавший (изменивший) доку-
мент т, вычисляет хэш-функцию h(m) и по-
сылает ее в доверенный центр.
2. Центр вырабатывает подпись s(T) для прове-
рочного текста Т= h(m)\\t, где t— код вре-
мени, и возвращает сертификат, состоящий
из проверочного текста и подписи для него
претенденту.
3. Претендент проверяет правильность прове-
рочного текста, подписи и времени.
Для проверки временной метки выполняются
следующие действия.
1. Претендент посылает документ и сертификат
(т, Т, s(t)) верификатору.
2. Верификатор выполняет следующие дейст-
вия.
2.1. Вычисляет хэш-функцию h(m) и прове-
ряет ее соответствие проверочному тек-
сту Т.
2.2. Проверяет время t формирования под-
писи.
2.3. Проверяет правильность подписи.
При успешном прохождении всех проверок
документ и время его подписи считаются
подлинными.
Цифровая подпись может быть реализована,
например, по ГОСТ Р 34.10-2001 (см. п. 15.6.5).
Поскольку участники протокола не вполне до-
веряют друг другу, могут возникать ситуации сго-
вора некоторых из них между собой. Это требует
соответствующего усиления протокола 14.7.1.
Так, центр иногда может быть недоверенной
стороной и нарушать протокол, чтобы вместе с
претендентом Р, обмануть верификатора. Для
противодействия этому обычно применяется
сцепка нескольких документов [9]. Например, в
сертификат включается имя претендента и имя
следующего претендента P,+i или нескольких
следующих претендентов. Верификатор обраща-
ется к этим претендентам с просьбой предъявить
свои сертификаты. Если они верные, то и серти-
фикат проверяемого претендента верен.
Однако в этом случае число легальных участ-
ников данного этапа протокола увеличивается, и
приходится рассматривать дополнительные слу-
чаи сговора, то есть это может привести не к
усилению, а к ослаблению протокола. Например,
если претендент Рм откажется представлять
свой сертификат или преднамеренно предъявит
подложный сертификат, то он может отменить
аутентификацию претендента Р„ даже если до-
кумент и сертификат, предъявленные претенден-
том Р„ являются подлинными.
14.7.2. Децентрализованная
реализация временной метки
Децентрализованная реализация механизма
проверки временной метки была предложена в
работе [3]. Рассмотрим основные положения та-
кой реализации.
Предполагается, что число претендентов, под-
писывающих документы, достаточно велико для
того, чтобы они не вступали в сговор против како-
го-то претендента или против верификатора. В ос-
нову протокола положена цифровая подпись RSA.
Пусть n=pq — составное число, разложения
которого не знает никто. Предположим, что пре-
тендент Р, с участием претендентов Рь ...,Р,„,
обладающих документами хц ...,хт, хочет под-
писать свой документ так, чтобы можно было
соотнести подписанный документ со временем
подписи. Для этого на каждом цикле протокола
выполняются следующие действия.
Протокол 14.7.2. Децентрализованное созда-
ние и проверка временной метки.
Метод.
1. Претенденты по коду времени t вычисляют
х0 <— /2 (mod и).
2. Претенденты вычисляют значения хэш-
функции для своих документов: у, <— й(х,).
3. Претенденты вычисляют проверочный текст
(х0, а) для данного цикла протокола, где
а = Хд1 "Ут (mod и), и опубликовывают его.
4. Претендент Р, вычисляет свой сертификат
(Zj = Xg1 -Ут (modи), у,-).
5. Для проверки правильности документа х( и
времени подписи претендент Р, предъявляет
верификатору текст, сертификат и время t.
6. Верификатор вычисляет хэш-функцию й(х,) и
проверяет условия: /?(х,) = у,-; а = zy‘ (modи);
хо = /2 (mod и). Если все проверки проходят
успешно, то претендент Р, действительно
подписал документ в указанный момент вре-
мени.
Недостатком протокола 14.7.2 является необ-
ходимость совместных действий нескольких
претендентов. Кроме того, этот протокол уязвим
к атаке на основе эндоморфизмов (см. п. 9.4.3).
Упражнения к главе 14
1. ^Предложите цифровую подпись для двух
владельцев разделенного секретного ключа
на основе протокола Шнорра.
2. Предложите способ восстановления общего
ключа в группе из п пользователей, если из
них любые (не более) т пользователей, где
т<п, могут быть скомпрометированы.
3. *Исследуйте возможность доказательства
того, что составное число п свободно от ку-
бов, с помощью аппарата эллиптических кри-
вых над кольцом ILInZL
4. Предложите схему разделения секрета на ос-
нове китайской теоремы об остатках. Как
можно нейтрализовать «разрастание» длин
частей секрета?
5. Предложите схему разделения секрета на ос-
нове быстрого преобразования Фурье.
6. Предложите протокол открытого электрон-
ного голосования, в котором каждый участ-
ник может доказать арбитру, что его голос не
искажен.
7. ^Предложите способ тайного электронного
голосования, при котором каждый из участ-
ников может доказать арбитру, что его голос
не искажен.
8. Как должны быть связаны стойкость зашиф-
рования сеансового ключа, стойкость цифро-
вой подписи и сложность вычисления колли-
зий хэш-функции (используемой для подпи-
си) при установлении этого ключа?
9. При каких обстоятельствах нужно защи-
щаться от повторов при установлении сеан-
сового ключа?
10. Предложите способ защиты от повторов в
бездиалоговых протоколах опознавания на
основе цифровой подписи и на основе дока-
зательств с нулевым разглашением.
11. Предложите способ электронной цифровой
подписи на основе бездиалоговых доказа-
тельств с нулевым разглашением.
12. Почему протоколы 14.6.2, 14.6.3 безопаснее,
чем просто передача подписанного ключа
13. Предложите протокол игры в покер для трех
участников, основанный на задаче дискрет-
ного логарифмирования в циклической груп-
пе простого порядка.
14. Предложите протокол погашения монеты на
основе доказательств с нулевым разглашени-
ем.
Литература к главе 14
1. Айерлэнд К., Роузен М. Классическое введение в
современную теорию чисел. М.: Мир, 1987.
2. Ван дер Варден Б.Л. Алгебра. М: Наука, 1979.
3. Benaloh J., de Mare М. One-way accumulators: a
decentralized alternative to digital signatures // Ad-
vances in Cryptology — Proceedings of
EUROCRYPT ’93. Lecture Notes in Computer Sci-
ence. Springer-Verlag. 1994. Vol. 765. P. 274-285.
4. Blom L. An optimal class of symmetric key genera-
tion systems // Advances in Cryptology — Proceed-
ings of EUROCRYPT 84. Lecture Notes in Com-
puter Science. Springer-Verlag. 1985. Vol. 209.
P. 335-338.
5. Boyar J., Peralta R. Short discreet proofs // Advances
in Cryptology — Proceedings of EUROCRYPT ’96.
Lecture Notes in Computer Science. Springer-
Verlag. 1996. Vol. 1070. P. 131-142.
6. Brassard G. Modem cryptology: a tutorial. Lecture
Notes in Computer Science. New York: Springer-
Verlag, 1988. Vol. 325 [Книга издана на русском
языке: Брассар Ж. Современная криптология.
Пер. с англ. М.: Полимед, 1999].
7. Camenisch J., Michels М. Proving in zero-knowledge
that a number is product of two safe primes // Ad-
vances in Cryptology — Proceedings of
EUROCRYPT ’99. Lecture Notes in Computer Sci-
ence. Springer-Verlag. 1999. Vol. 1592. P. 107-122.
8. Goldreich O., Micali S., Wigderson A. Proofs that
yield nothing but their validity and a methodology of
cryptographic protocol design // Proceedings of the
IEEE 27th Annual Symposium on Foundations of
Computer Science. 1986. P. 174-187.
9. Just M. Some timestamping protocol failures // Pro-
ceedings of the Network and Distributed Security
System (NDSS’98) Symposium (www.isoc.org/isoc/
conferences/ndss/98/just.pdf).
10. Menezes A., van Oorschot P., Vanstone S. Handbook
of Applied Cryptography. CRC Press, 1997.
11. Rabin M. How to exchange secrets by oblivious
transfer. Technical Memo TR-81, Aiken Computer
Laboratory, Harvard University, 1981.
12. Schneier B. Applied Cryptography: Protocols, Algo-
rithms, and Source Code in C, 2nd edition. New
York: J. Wiley & Sons, 1996 [Книга издана на рус-
ском языке: Шнайер Б. Прикладная криптогра-
фия. Протоколы, алгоритмы, исходные тексты на
языке Си. Пер. с англ. М.: Изд-во ТРИУМФ,
2002].
Г л а в a 15. КРИПТОСИСТЕМЫ НА ЭЛЛИПТИЧЕСКИХ
И ГИПЕРЭЛЛИПТИЧЕСКИХ КРИВЫХ
Пусть Е(К)— эллиптическая кривая над ко-
нечным полем из q=p" элементов, char(A9 =/? —
характеристика поля К. Разработка криптоси-
стемы на эллиптических кривых заключается в
выборе поля, уравнения эллиптической кривой
и числа точек. Требования, предъявляемые к
эллиптической кривой для обеспечения высоко-
го уровня стойкости, приведены в п. 11.7. Кро-
ме того, выбранная эллиптическая кривая
должна обеспечивать высокую скорость вычис-
лений. Это достигается соответствующим вы-
бором характеристики поля, выбором полинома,
задающего расширение простого поля (если ис-
пользуется расширенное поле), а также выбо-
ром кривой, допускающей комплексное умно-
жение или иной способ быстрого умножения
точки на число.
Основной задачей при создании криптосисте-
мы на эллиптической кривой является расчет
числа точек. При этом для того чтобы выполня-
лись криптографические требования, нужно оп-
робовать в среднем O(log<7) эллиптических кри-
вых.
Пусть на эллиптической кривой Е(К), задан-
ной уравнением у2 выполняется равенство
для простого порядка группы: г -#E{K)/s , где
s — малый делитель числа точек. Генерация точ-
ки, образующей группу порядка г, не составляет
труда. Можно воспользоваться, например, сле-
дующим алгоритмом.
1. Подобрать элемент хс е К такой, что квадра-
тичный характер от fixo) равен 1.
2. Положить х-координату равной xq. Вычис-
лить у-координату извлечением квадратного
корня из/хо) (см. п. 7.7).
3. Умножить точку (хо, уо) на s.
4. Проверить, что точка, полученная на шаге 3,
отлична от Р№ и имеет порядок г.
15.1. Расчет числа точек
эллиптической кривой в общем случае
Вычисление числа #Е(К) точек эллиптической
кривой в общем случае является довольно слож-
ной задачей. Для расчета числа точек можно ис-
пользовать алгоритм «giant step — baby step».
Алгоритм 15.1.1. Расчет числа точек эллип-
тической кривой.
Вход. Эллиптическая кривая Е(К2у. у~ + cqxy +
+ сьу = х3 + агхг + а$х + аь.
Выход. Число N точек эллиптической кривой
ВД.
Метод.
1. Выбрать точку Q е Е(К). Для этого выбрать
случайную х-координату хо е К так, чтобы
существовала у-координата у0 е К, удовле-
творяющая уравнению кривой.
2. Найти целое число k <-1_^2^J.
3. Вычислить точки Q, 2Q, 3Q, ...,kQ и отсор-
тировать полученную базу данных по х-
координате (при этом оказываются извест-
ными и точки -Q, -2Q,-kQ).
4. Вычислить точки Р <г- (2к + l)Q, R <г- (q + 1 )Q,
после чего сравнить поочередно х-
координаты точек R, R±P, R± 2Р, ...,R±kP
с базой данных (равенство означает, что
R + dkQ = eQ для некоторых целых <7, е). От-
сюда найти предполагаемое число точек:
А <— q + 1 + dk - е.
5. Результат:?/.
В действительности алгоритм 15.1.1 находит
порядок циклической группы (0; число N кратно
#(0. Поэтому желательно уточнить порядок
группы Е(К) для нескольких точек Q. Кроме того,
желательно убедиться, что число точек на скру-
ченной кривой равно q + 1 - dk + е (см. шаг 4).
Алгоритм 15.1.1 требует выполнения O(%[q)
операций умножения точки на число, то есть
O(tfq (log q)3) операций умножения и сложения
чисел на процессоре с фиксированной разрядно-
стью, так как сложность умножения точки на
произвольное число равна O((log<?)3). Требуемый
объем памяти равен O(tfq).
А. Аткин и Ф. Моран [12] предложили способ
расчета числа точек на произвольной эллиптиче-
ской кривой, основанный на использовании мо-
дулярных форм. Выбирают дискриминант D та-
295
кой, что характеристика поля р = а2 + Db2 явля-
ется простой и число N=p + 1 ± 2а точек эллип-
тической кривой соответствует предъявляемым
требованиям (см. п. 11.7). Для построения эллипти-
ческой кривой находят гильбертово поле Кн классов
мнимого квадратичного поля К = Q(V-H) как
максимальное неразветвленное расширение, для
которого группа Галуа является абелевой. Поли-
ном, задающий поле Кн, является минимальным
полиномом для значения модулярной
функции j комплексного переменного. Редукция
указанного значения по модулю р дает j-
инвариант кривой. Вычислить коэффициенты
кривой по заданному j-инварианту нетрудно.
Значение модулярной функции /(-J-D) яв-
ляется целым алгебраическим числом, степень
которого равна числу классов поля К. Число
классов и норма числа увеличиваются с
ростом D. Например, для D = 403 норма целого
квадратичного j является числом длины 56 деся-
тичных знаков. Поэтому метод работы [12] явля-
ется практичным только для небольших значе-
ний дискриминанта и небольшого числа классов.
Асимптотически более быстрым, чем преды-
дущие, является алгоритм, предложенный Р. Чу-
фом [16]. Алгоритм Чуфа использует так назы-
ваемые полиномы деления (division polynomi-
als), которые задают операцию умножения точ-
ки на число над алгебраическим замыканием К
поля К.
15.1.1. Предварительные сведения
Оценку числа точек эллиптической кривой с
уравнением у2 = х + Ах + В над полем К = F„ дает
теорема Хассе (теорема 6.17.1). Если значение
кубического полинома х3 + Ах + В при некотором
х отлично от 0 и является квадратичным вычетом
в поле К, то этот х является х-координатой в точ-
ности двух точек эллиптической кривой. Если
указанный полином равен 0 при некотором х, то
этот х является х-координатой одной точки. Если
значение кубического полинома является квад-
ратичным невычетом, то соответствующее зна-
чение х не может являться х-координатой точки
кривой. Значит, для данного значения х число
точек с данной
х-координатой равно
х3 + Ах+ В^
, где
— значение квадра-
тичного характера, равное 1, если z является
квадратичным вычетом в поле К, равное -1, если
z является квадратичным невычетом в поле К;
равное 0, если z = 0. Функцию
(
можно рас-
сматривать как продолжение символа Лежандра
на поле К.
Таким образом, с учетом одной бесконечно
удаленной точки получаем следующую формулу
для числа точек
дг = 1 + ]Г 1 +
хеА^
хеК\
х3 + Ах + В
< Я
о \
х + Ах + В
<7
(15.1.1)
то есть подсчет числа точек сводится к вычисле-
нию суммы характеров.
Эндоморфизм Фробениуса эллиптической
кривой Е(К) удовлетворяет характеристиче-
скому уравнению с целыми коэффициентами
ф2-Тф + ? = 0 ' ' (15.1.2)
или
ф(ф(Р))-Лр(Р) + 9Р = Рю.
Здесь Т— след эндоморфизма Фробениуса;
выполняется равенство t ;
Алгоритм Чуфа вычисляет значение Т. Для
этого в соответствии с китайской теоремой об
остатках достаточно найти Т (mod 7,), где 7, —
малые попарно взаимно простые числа, произ-
ведение которых превышает 4-jq (так как нуж-
но рассмотреть случаи N> q и N < q). В некото-
рых случаях (например, при 1 = 2) найти Т (mod /)
легко.
Если эллиптическая кривая имеет точку по-
рядка 2, то есть точку вида (х, 0), то выполняется
сравнение N= 0 (mod 2). То, что кривая Е/К име-
ет точку с нулевой у-координатой, означает, что
полином х3 +Ах + В имеет нуль в поле К. При пере-
ходе к кривой Е(К) получаем
нод(х4 - х, х3 + Ах + в) & к г; w
в кольце К[х]. Для проверки этого условия мож-
но вычислить значение хд -х в кольце классов
вычетов 7Цх]/(х3 + Ах + В).
Основная идея алгоритма Чуфа заключается в
рассмотрении равенства (15.1.2) для кривой
Е(К) как сравнения по модулю I для малых про-
296
стых I. При этом подбором находится такое зна-
чение Т (mod /), что
ф2 + к = тф, (mod 1), (15.1.2')
где ф/ = ф (mod /), k = q (mod /), т = Т (mod /).
Сравнение (15.1.2') справедливо, если на кривой
Е{К) существуют точки кручения порядка I с
указанным свойством. Для нахождения значения
т с помощью (15.1.2') проводятся вычисления в
группе кручения £[/] порядка I эллиптической
кривой Е(К). Очевидно, что если группа £[/]
существует, то сравнение (15.1.2') может выпол-
няться лишь для одного значения т. Эллиптиче-
ская кривая Е(К) не содержит группы £[/], если
кривая Е(К) супервырождена и р = 1. Вероят-
ность этого очень мала и равна О(^р^2).
Сложность алгоритма Чуфа оценивается по-
линомом восьмой степени от log#.
15.1.2. Полиномы деления
Для эллиптической кривой Е(К) определим
полиномы деления (division polynomials) из £[х].
Если р = char(£) = 2 и уравнение кривой ErfJCy.
у + ху = х3 + В, где В е К, то полиномы деления
имеют вид:
/-1W = 1 ;/о(х) = 0;/(х) = 1 -,f2(x) = Х-,
f$(x) = x4 + x3 + В; f4(x) = x6 +В;
O) = fk Wk+2(x} + fk-i (x)fk+l(x), k>2;
Xf2k (X) = fk-l (X)fk Wk+2 (X) + fk-2 (X)fk (X)f3+, (x),
k>3.
Если p = 2, то высокую стойкость обеспечи-
вают только кривые вида Ед^Ку.
у2 + ху = х3 +Ах~ +В (см. п. 11.3). При Тг(Э) = 0
(где Тг(Л)— след коэффициента А в поле IF2)
кривая Eaj£K) изоморфна кривой Е^К) = Ев(Ку
Если Тг(Э) = 1, то кривая ЕАВ{К) является скру-
ченной по отношению к Е^К), при этом выпол-
няется равенство #EAJ3(K) + #ЕО,В(К) = 2q + 2. Та-
ким образом, для расчета числа точек достаточно
рассмотреть только кривую £ов(£); число точек
скрученной кривой равно 2q + 2 - #Е0^К). Чис-
ло точек (или след эндоморфизма Фробениуса с
точностью до знака) полностью определяется
коэффициентом В.
Полиномы fk являются приведенными,
deg(A) = (^-l)/2 для нечетных к.
Если р = char(£) > 3 и эллиптическая кривая
задана уравнением у2 = х3 + Ах + В, то определим
полиномы деления из Х[х, у]:
ф_1(х, у) = -1; фо(*, у) = 0; ф](х, у) = 1;
v|/2(x, у) = 2у; ф3(х, у) = Зх4 + 6>Ах2 + 12Вх - Л2;
ф4(х,у)=4у(х6+5Лх4+20Вх3 - 5ЭУ - 4Abx - 8В1 -А3);
Чф-н _ ЧФгЧД ЧД-1ЧД+Р к >2',
2yW =Vfc(44+2vLi - ЧД-гУл+Д к>3.
Полиномы для нечетного к и полиномы
i|/fc/(2y) для четного к являются полиномами от
(х, у2). Заменим у на х3 + Ах + В и обозначим полу-
ченные полиномы через ф'д, тогда полиномы деле-
ния убудут лежать в £[х] или ву£[х]. Положим
^(х) = ф;(х,у),
если к нечетное, и
А(*) = ч4Счу)/у,
если к четное. При этом, если НОД(/2, А) = 1, то
deg(/A) = (2с? —1)/2 при нечетном к, degC4) =
= (к2 - 4)/2 при четном к.
Теорема 15.1.1. Пусть к> 2 — целое число и
Р = (хл уР). Равенство кР = /Ч на кривой Е(К)
выполняется тогда и только тогда, когда^(хР) = 0
над полем К.
Доказательство см. в работе [16].
Полиномы деления позволяют умножать точ-
ку (х, у) кривой Е(К ) на целое число к\
2 2 У
ЧД-1ЧД+1 Vfc-iVfc+2-44-2Vfc+i
2 5 л 3
Wk 4уфд. J
Обозначим т = Т (mod /). Условие (15.1.2') вы-
полняется, если в кольце £[х, у] имеют место ра-
венства:
2 2
(х9 ,yq )+ х-
при т = 0 или
(хЛу^ч- X
к
2
Vfc-iVfc+2 4/fc-24/fc+i
4У^к
2 2 У
Vt-iV't+i ЧД-1ЧЧ+2 "ЧД-гЧФи
wl ’ 4уф3
( / У
„ ЧФ1ЧФ1
- X 2
^х J
при т ф 0.
/ 2 2 у
V'x-l Vfc+2 ~ Vx-2 V'x+l
< 4уф3
297
Переходя к полиномам fk (это позволяет про-
водить вычисления в кольце А]х]), получаем, что
условие <yj(P) = ±kP (modZ) выполняется, если
д,'/2 _ % — >k-\Jk+i
/к(х3 + Ах + В)
(15.1.3)
для четного к и
2
х^ -х = 2+ Ах + (15.1.4)
fk
для нечетного к.
15.1.3. Алгоритм Чуфа
Алгоритм Чуфа для вычисления числа N точек
эллиптической кривой Е над полем К использует
вычисления в полях функций K\x,y\/(E(K),fi(x)),
где (Е(К)) — идеал, задающий кривую, f(x) —
полиномы деления, и содержит три шага:
1) вычисление набора попарно взаимно про-
стых чисел {/,} и соответствующих полино-
мов деления в кольце К[х];
2) нахождение вычетов числа T=q+( -N по
модулям малых взаимно простых чисел /, со-
гласно (15.1.2');
3) восстановление числа точек по китайской
теореме об остатках.
Первый шаг не содержит принципиально
сложных вопросов и может быть выполнен в со-
ответствии с известными формулами для поли-
номов деления. Здесь надо оценить, сколько
нужно полиномов деления, чтобы однозначно
определить Т. Следовательно, произведение всех
It должно быть больше, чем 4^. Третий шаг
выполняется очевидным образом.
Второй шаг является наиболее сложным. Если
char(A9^2s то условия (15.1.3), (15.1.4) сущест-
вования точки Р такой, что <р2 (Р) = +кР (mod /)
можно записать в виде
НОД((х"2 - х)Д2(х)(х3 + Ах + В) + 5)
для четных к и
НОД((х"2 -х)Л2(х) + /м(х)Д+1(х)х (15 }
х(х3 + Ах + В), / (х)) g К
для нечетных к. Для ускорения вычислений
можно разложить fi на простые множители и вы-
числять наибольший общий делитель для каждо-
го из простых делителей полинома f.
Полином <р2 - x<pz + к от переменной <pz, соот-
ветствующий уравнению (15.1.2'), может быть
неприводимым или раскладываться на множите-
ли над Fz. Во втором случае говорят, что эндо-
морфизм Фробениуса имеет собственное значе-
ние в группе £[/].
Если в группе £[/] существует аффинная точка,
для которой выполняется условие = -к (mod /),
то из (15.1.2') следует, что x<pz = 0 (mod/). По-
скольку <р/(Р) * Рю, то т = 0 (mod /).
Если в группе £[/] существует аффинная точка,
для которой выполняется условие <р2 = к (mod Z),
то из (15.1.2') следует, что т^О и 2Л — xcpz = О
(mod /), откуда <pz = 2 кх ' (mod /). Подставляя это
значение в (15.1.2') и сокращая на к ф 0, получаем:
т2 = dk (mod /). Тогда эндоморфизм Фробениуса <pz
должен иметь собственное значение в группе £[/].
Обозначим w = -fk(mod I). Тогда w или -ю явля-
ется собственным значением эндоморфизма Фро-
бениуса в группе £[/], при этом т = 2w или т = -2w
в зависимости от знака w.
При <pz =±&(modZ) случай <р2 =-к (modi)
можно легко распознать, вычислив символ Ле-
жандра; при этом должно выполняться равенство
Если
= 1. то должны существовать собст-
венные значения эндоморфизма Фробениуса, и
вместо (15.1.5), (15.1.6) получаем следующие
условия.
Случай т = 0 (mod /) распознается, если
НОД((х" - x)f;(х)(х3 + Ах + В) +
для четных w и
НОД((^-х)/1.2(х) + Л_1(х)Л+1(х)х
(15.1.8)
x(x3+Ax + B),f,(x))gK
для нечетных w. . -
Случай <р2 = к (modi) распознается, если
НОД(4(х3 + Ах + B)^f3(x) -
для четных w и
НОД(4(х3 + Лх + Б)(9+3)/2Л3(х)- 5 i
298
для нечетных w. Тогда т = 2w или т = -2w в зави-
симости от знака w.
Если ни одно из условий (15.1,7)-( 15.1.10) не
выполняется, то не выполняется и равенство
ср, = +к (mod 1), то есть эндоморфизм Фробениу-
са не имеет собственных значений в группе £[/].
В этом случае для нахождения т 0 нужно ис-
пользовать закон сложения точек на эллиптиче-
ской кривой. Координаты суммы точек
ф2(Р) + ЕР в группе £[/] кривой Е(К) можно
записать в виде:
-x^-x + M^ + Z2,
-j/ -zf-2x?2 -x + ^^l
I J
где
z = ^+2vLi -4/2~'Ул
4y^k ((* - ~ ЧД-i
Вычисления проводятся в кольце классов вы-
четов К[х,у\Ку -х3 - Ах-B,fi(x)). При этом по-
сле каждого умножения полиномов значение у2
заменяется на х3 + Ах + В, затем для полиномов
от х находятся вычеты по модулю /Ух).
Если т2 - Ук является квадратичным вычетом
по модулю I, то вычисление упрощается, так как
существуют собственные значения эндоморфиз-
ма Фробениуса. Число ±w, 1 < |w| < (Z -1)/2, явля-
ется собственным значением эндоморфизма
Фробениуса ф/ тогда и только тогда, когда суще-
ствует точка Р е E[Z] такая, что ф/(Р) = ±w£.
Пример 15.1.1. Расчет числа точек эллипти-
ческой кривой алгоритмом Чуфа.
Пусть у2 = х3 + х + 5 над полем Е;, = Е257- Все
вычисления проводятся в кольце Fp[x, у]Куг - х3 -
-Ах-В) для А = 1, В = 5.
Полиномы деления имеют вид:
фо = 0; ф] = 1; ф2 = 2у; ф3 = Зх4 + 6х2 + 60х - 1;
ф4 =у(4хб + 20х4 + 143х3 + 237х2 + 177х + 224);
ф'5 = 5х12 + 62х10 + 1 Olx9 + 152х8 + 172х7 +
+ 125х6 + 118х5 + 191х4 + 60х3 + 118х2 + 198х + 83,
а после разложения на множители над F257:
/_1=-1;/о = О;/1 = 1;/2 = 2;
/з = 3(х + 99)(х + 188)(х2 + 227х + 23);
/4 = 4(х3 + 92х2 + 215х + 149)(х3 + 165х2 + ЗОх + 9);
/ = 5(х12 + 218х10 + 123х9 + 236х8 + 240х7 + 25х6 +
+ 75х5 + 141х4 + 12х3 + 75х2 + 91х + 68).
Находим вычет числа точек кривой по моду-
лю 2. Уравнение х3 + Ах + В = 0 имеет решение
тогда и только тогда, когда его дискриминант1
является квадратичным невычетом. Поскольку
здесь справедливо
(4Д3+27Б2)/108"
257
= -1, по-
лучаем N = Т = 1 (mod 2).
Теперь находим вычет Т (mod 3). Полагаем
7=3, к-2 и проверяем наличие собственных
значений эндоморфизма Фробениуса в Z73Z
(они могут быть равны 0. 1 или -1). Для этого
вычисляем (хр - х)/и2 + fw_Jw+x (mod /3) для
w = 0 и w = 1. Вместо полинома / подставляем
поочередно его простые делители. Собственное
значение существует, если вычет по модулю хотя
бы одного делителя равен нулю. Получаем для
делителя х + 99: для w = 0 вычет ненулевой; для
w = 1 вычет нулевой. Следовательно, w = 1 или
w = -1 является собственным значением.
Уточнять знак собственного значения нет не-
обходимости. Из сравнения vv2 - xw + к = 0
(mod 3) находим дискриминант т2 - 8 = т2 + 1
(mod 3). Собственные значения существуют, ес-
ли дискриминант является квадратичным выче-
том по модулю 3, то есть т = О, Т= 0 (mod 3).
Находим вычет Т (mod 5). Полагаем 1 = 5,
А = 2 и проверяем наличие собственных значений
эндоморфизма Фробениуса в Z/5Z (они могут
быть равны 0, ±1 или ±2). Для этого вычисляем
(х'' -х)/и2 +/,M/„,+I(mod/5) для w = 0, w = 1 и
w = 2. Полином / на множители не раскладыва-
ется. Для и1 = 0, и’ = 1 и и’ = 2 вычеты по модулю
/ ненулевые. Следовательно, собственных зна-
чений не существует.
Находим вычеты по модулю/ для хр , ур :
хр2 = 193х" + 26х10 +11 Зх9 + 85х8 + 40х7 + 202х6 +
+148х5 + 215х4 +153х3 + 243х2 +160х +139,
ур2= у(136х’1 +165х10 + 21 Ох9 +1 Зх8 +15х7 +149х6 +
+11 Ох5 +146х4 + 230х3 +169х2 + 96х +100).
Проверяем возможность Т= 0 (mod 5). Срав-
нение
x)fk (х3 + Ах + В) + fk_} fl+] = 0 (mod f5)
не выполняется, следовательно, 7V 0 (mod 5).
1 Дискриминант уравнения вычисляется по фор-
муле Кардано и отличается от дискриминанта кривой.
299
Находим точку кР для к = 2. Здесь проще вос-
пользоваться обычными формулами сложения.
Получаем
. _Зх2+Л
2у
2х, У2 р —^2г(^ * Х2рУ Д'"
Находим х-координату точки ф2(Р) + 2Р. В
соответствии с законом сложения точек имеем:
х -к2-хр -х2Р,
i^IP'i+ZP
где к— угловой коэффициент секущей, прохо-
дящей через точки ф2(Р) и 2Р:
Х-.У^ УгР .
\2(Р)~Х2Р
Подставляя в последнюю формулу получен-
ные значения, находим
48х' 1 +124х10 + 53х9 + 248х8 +101х7 +
~ У 256х’1 +153х10 +114х9 +174х8 + 76х7 +
+157х6+ 45х5+ 143х4+189х3+ 54х2+ 255х + 37
+145х6 + 248х5 +170х4 + 52х3 + 52х + 3
Находим х-координату точки ф2(Р) + 2Р, за-
меняя у~ на х3 + Ах + В'.
_ 210х" + 134х10 +161х9 +138х8 +
\2(Г)+2Г " 212дл + 72л.10 +51*9 +229х8 +
+ 50х7 +19бх6 +60х5 +142х4 +
+ 201х7 +192х6 + 62х5 +143х4 +
+ 127х3 +250х2 +140х + 182
+ З1х3+70х2+108х + 124
Вычисляем х-координату точки ±тф(Р):
f^f^ + Ax+B)
Х+^(Р)-Х f2p
Ji
для т = 1 и
fp fp
v _ VP__________/т-l./t+l
±Тф(Р) /т2Р(х3 +Ах + В)
для т = 2.
Сравниваем х-координаты точек ф2(Р) + 2Р и
±тф(Р) как рациональные функции от х. Они
совпадают при т=1. Следовательно, Г=±1
(mod 5).
Найденные сравнения для Т по модулям 2, 3,
5 показывают, что возможны два случая: Т=-9
(mod 30) или Т= 9 (mod 30). Для того чтобы най-
ти знак числа Т по модулю 5, можно проверить,
какое из равенств выполняется для у-координат в
группе кручения порядка 5: У^2Р =У(р(П или
^<р2(/’)+2д =Можно также просто уточнить,
какое из равенств выполняется на эллиптической
кривой £(Е257): (257 + 1 + 9)Q = Рх или (257 + 1 -
- 9)Q = Рю. Проверка показывает, что правильным
является значение 7=9, тогда N=267.
Для некоторых эллиптических кривых число
точек может быть определено проще, чем алго-
ритмом Чуфа. Это возможно по крайней мере в
двух случаях: если эллиптическая кривая Е/К с
известным числом точек над К рассматривается
над конечным расширением К\ поля К и если
рассматриваются эллиптические кривые над про-
стыми полями, обладающие комплексным умно-
жением над полем С.
15.2. Расчет числа точек эллиптической
кривой над расширенным полем
Если эллиптическая кривая Е/К с коэффици-
ентами из поля K=iFq, рассматривается над ко-
нечным расширением К] = F9 поля К и qA = <7'",
то имеет место равенство
—/и
#E(Kl) = qm +1-6'” -0 , (15.2.1)
где 6, 6 — комплексно сопряженные корни ха-
рактеристического уравнения эндоморфизма Фро-
бениуса:
<р2 + (#Е(К) - q - 1)ф + q = 0. (15.2.2)
Уравнения (15.2.1) и (15.2.2) устанавливают
связь между #Е(К) и #E(Ki).
Заметим, что - 0т - 0м = -2 Re(0"'), величина
Ке(6"')/| 6'” | является косинусом угла, задающе-
го число 6'” в тригонометрической форме. По-
этому можно выразить #E(Ki) непосредственно
через #Е(К), используя полиномы Чебышева
первого рода Tm(x) = cos(m arccosx):
#Е(К})
#Е(К)
[гп / 2 j
qm+l+m W”~J
j<>
j\{m-2j^
q + \+k
где k = q + 1 - #E(K). Это соотношение позволяет
легко реализовать алгоритм генерации эллипти-
ческой кривой над расширенным полем.
Из уравнения (15.2.1) следует, что #Е(КУ) де-
лится на #Е(К), где K2 = ^q2, qi = q\ l\m. Это
объясняется тем, что кривая Е(Кр> как многооб-
300
разие содержит в себе кривую Е(АГ2), в том числе
кривую Е(К). Поэтому число #Е(Х'|) не может
быть простым. Для того чтобы число ri было
простым, необходимо, чтобы степень т расши-
рения была простым числом.
Пример 15.2.1. Эллиптические кривые над
расширениями поля F2 с большой подгруппой
простого порядка.
1. Эллиптические кривые E/F2 имеют вид
у2 + ху = х3 + а2х2 + 1 или у2 + у = х3 + аух + 1.
Во втором случае задача логарифмирования на
эллиптической кривой E(F2,„) сводится с помо-
щью спаривания Вейля к задаче логарифмиро-
вания в мультипликативной группе расширен-
ного поля F2j„„ где d < 4 (см. п. 11.3). Поэтому
на практике используются только кривые, зада-
ваемые первым уравнением. В диапазоне степе-
ней расширения 96 < т < 256 существует всего
11 эллиптических кривых, для которых ЧИСЛО Г1
простое.
т для кривой у + ху = X +1
97 39614081257132074233778707191
103 2535301200456459535862530067069
107 40564819207303335604363489037809
131 680564733841876926932320129493409985129
233 3450873173395281893717377931138512760570940988862252126328087024741343
239 220855883097298041197912187592864814948216561321709848887480219215362213
т , — — — — А А А Г] для кривойу + ху = X + х~ + 1
101 1267650600228230886142808508011
107 8112963 8414606692182851032212511
109 324518553658426701487448656461467
113 5192296858534827627896703 833467507
163 5846006549323611672814741753598448348329118574063
2. Пусть кривая Е/К задана над полем
К=F8 = F2p]/(Z3 +1 + 1). Для полей К\ простой
степени расширения над К существуют следую-
щие четыре кривые с различными числами то-
чек:
Еу.у2 + ху = х3 + t, Еу у2 + ху = х3 + t + 1,
Еу. у2 + ху = х3 + х2 + / + 1,
Еу. у2 + ху = х3 +х2 + t.
Как обычно, расширение поля из восьми эле-
ментов строится присоединением корня непри-
водимого над К полинома соответствующей сте-
пени. Для степени расширения т = (К\.Ку
29<т< 103, существует восемь эллиптических
кривых, для которых число Г] является простым.
т Г1 для кривой Е2
31 825293359523603415337631131
73 70208194445704791131945351789113626814156914745347160559455187521
т ri для кривой Е3
37 4326914048779022859742068773 83297
41 1772303994379887831408089032440014057
47 46459885830272131544916643423 83 823 80989717
59 31926990434706017882465563211521159723534715689440269
т Г| для кривой Е4
47 278759314981632789268903181396173621874561
59 19156194260823610729479337915747318375048137080701777
Эллиптические кривые над полями характе-
ристики 2 могут быть использованы в амери-
канском стандарте подписи ECDSS. Рассмот-
ренные примеры используют поля простой
степени расширения. В общем случае коэффи-
циенты уравнения эллиптической кривой над
таким полем могут лежать в расширенном по-
ле, а степень расширения не обязана быть про-
стой. Однако если степень расширения являет-
ся составной, то логарифм на эллиптической
кривой может быть быстро вычислен методом
спуска (см. п. 11.4).
301
15.3. Расчет числа точек эллиптических
кривых с / = 0,1728 над простыми полями
Рассмотрим случаи, когда эллиптическая кри-
вая над простым полем задается неполным урав-
нением, то есть случаи j = 0 и j = 1728. Такие эл-
липтические кривые не допускаются отечествен-
ным стандартом подписи ГОСТ Р 34.10-2001,
однако могут быть использованы согласно аме-
риканскому стандарту ECDSS.
Здесь все суммы равны 0, кроме той, в кото-
рой показатель при х равен р - 1. В частности,
последняя сумма равна 0, так как содержит р
одинаковых элементов. Так как xr~' = 1 (modр)
для ненулевых х, получаем у . д \ ;
ceF,,
7 з nA
х +В
< Р ,
Дб-П/6,
Г-1
В 6 (mod р).
Теорема 153.1. Если р = 3 (mod 4), то число
точек кривой с j= 1728 равно р+ 1. Если р = 5
(mod 6), то число точек кривой с j = 0 равно р + 1.
Доказательство. Случай j= 1728. Функция
х3 + Ах является нечетной. В соответствии с
квадратичным законом взаимности число -1 яв-
ляется квадратичным невычетом по модулю р.
Следовательно, если х3 + Ах — квадратичный
вычет, то (-х)3 + А(-х) — квадратичный невычет.
Сумму символов Лежандра в (15.1.1) можно вы-
числять, суммируя по х от — (/? —1)/2 до
(у> -1)/2; она равна 0.
Случай j = 0. Отображение х -> х3 является би-
екцией поля Fp, так как порядок мультипликатив-
ной группы поля не делится на 3, следовательно,
отображение х -> х3 + В — тоже биекция (так как
сдвиг на Б — биекция). Среди образов этого ото-
бражения есть один нуль и поровну квадратичных
вычетов и невычетов. Следовательно, сумма сим-
волов Лежандра в (15.1.1) равна 0.
Остается вычислить этот биномиальный ко-
эффициент.
Аналогично, в случае j = 1728 получаем
xeF,,
х3 + Ах
< Р ,
р-1
А 4 (mod р).
В общем случае, если оба коэффициента А и В
отличны от нуля, то сумма символов Лежандра
равна некоторой сумме биномиальных коэффи-
циентов, вычисление которых по модулю р со-
пряжено со значительными сложностями.
Рассмотрим другой способ подсчета числа то-
чек для кривых с неполным уравнением.
Следствие 15.3.2. Задача логарифмирования
на эллиптической кривой у2 = х3 + В (mod р), где
р = 5 (mod 6), и на эллиптической кривой
у2 = х3 + Лх (mod р), где р = 3 (mod 4), сводится с
помощью спаривания Вейля к задаче дискретно-
го логарифмирования в квадратичном расшире-
нии простого поля.
15.3.1. Кривая у2 = х3 + В
Обозначим число решений уравнения fix, у) = 0
над полем Fp через N(fix, у) = 0). Число точек на
кривой у2 = х3 + В можно определить следующим
образом [1]:
N = Д'(у2= х3+ В) +1 = 1 + N(y2= u)N(x3= -v) =
UA-V-B
= £ (1 + РО))(1 + x(-v) + х2 (-v)) =
u+v=B , 1 .
=л+1+ £p(w)x00+ ЕрООх2^),
u+v-B u+v=B
Таким образом, кривые из следствия 15.3.2 не
годятся для целей криптографии.
При р > 3 возможны случаи р = 1 (mod 6) или
р = -1 (mod 6), поэтому остается рассмотреть
случай р = 1 (mod 6) для кривой у2 = х3 + В. При
р > 2 возможны случаи р = 1 (mod 4) или р = -1
(mod 4), поэтому остается рассмотреть случай
р = 1 (mod 4) для кривой у2 = х3 + Ах.
Вычислим для кривой с j = 0 сумму символов
Лежандра по модулю р.
г- X + В 't-ч з / j \
X --------- = 2^(х +В) 2 (modp) =
«F Д Р J xeF
где р— мультипликативный характер второго
порядка (то есть символ Лежандра), х— муль-
типликативный характер третьего порядка (по
аналогии с символом Лежандра x(v) ~ I> если
у — кубический вычет по модулю р; множество
значений этого характера: {1, со, со2}, где со —
комплексный корень уравнения со2 + со + 1 = 0,
следовательно, х(т) и комплексно сопряже-
ны).2 Здесь учтено то, что х(_1)= Ъ так как ~1
является кубическим вычетом по модулю р.
Замена переменных u <— Ви, v <— Bv дает:
2V=P+1+PX(B) J(p, Х)+РХ< й) J (Р, X) • (15.3.1)
\р-^
3(р-1) п_1 3<Р-3) £4
-Вх 2 +...+ ^В 2 (modp).
xeFp xeFp 2 xeFp
2 В общем случае характер циклической группы G
порядка г представляет собой гомоморфизм группы G
в группу комплексных корней степени г из единицы.
302
Действительно,
£ p(w)xO') = X Р(£г/')Х(^') =
U+v=B u'+v’=]
= p(^)X(^) % PO ')XO') = p№)J(p, x).
lZ+v’=l
Для дальнейшего нам понадобится следую-
щая лемма.
Лемма 15.3.3. Пусть р — нечетное простое
число, р — характер порядка 2 группы Fp ,
£ — произвольный нетривиальный (то есть не
всюду равный 1) характер группы Fp . Тогда
Др, ^) = Д4Ж О-
Доказательство [1]. Имеем:
ДрЛ) = ^0+P(w)X(v).
l/-f-V=l l/+V=]
Равенство справедливо, так как сумма харак-
теров Дг) по всем г равна нулю. Тогда
ЛрЛ) = N(t2 = г/) Ду) . Это сумма характеров
ZZ + V=]
£ с коэффициентами 0 или 2. Поскольку сумма
характеров с коэффициентами 0 равна нулю, то
остается просуммировать характеры с коэффи-
циентами 2. Сумма берется по таким г, для кото-
рых 1 - г является квадратом в поле Fp. Но
Дх2) = Д>')2- Поэтому
ЛрЛ)= ^(t)2 = ^-t)2 =
1-ZeF^ /eF р
=«4) z я V X X11=
/eFr < 2 ) < 2 J
Теперь можно переписать (15.3.1) в виде
N - р +1 + рх(45) J (X, X) + РХ(45) J (х, X) •
Пусть £ — характер порядка 6, тогда р = £3,
X = ^2. Простое число р раскладывается на мно-
жители в кольце Z[<b]:
р = а2 - ab + Ъ2 = тгл = (а + Ь(о)(а+Ь(о) =
= (g+Zxb)(g+Z><b2),
где a s 2 (mod 3), b = 0 (mod 3).
В качестве характера До) порядка 6 можно
f г: ч
взять символ — вычета степени 6. 1огда
w6
Сумма Якоби— ком-
плексное число, модуль которого равен 4~Р = л .
Таким образом, доказана следующая теорема.
Теорема 15.3.4. Если р = 1 (mod 6), то число
точек эллиптической кривой у = х3 + В над по-
лем Fp равно
Для того чтобы выбрать кривую у2 = х3 + В с
большим простым числом точек, нужно разло-
жить число р на множители или сразу выбрать
пару чисел а, b таких, что а - ab + Ь2 =р — про-
п -1+7^3
стое число. 1 юскольку со =-----, то суще-
ствует представление
р = с2 + 3d2 =(c + dy/-3)(c-d4~3).
Тогда с = а - b/2, d = b/2 (здесь не обязатель-
но а = 2 (mod 3), 6 = 0 (mod 3), так как разложе-
ние на множители в Z[o] выполняется с точно-
стью до обратимого элемента, а таких элементов
всего шесть). Кроме того, кольцо не об-
ладает однозначным разложением на множители
(например, 2• 2 = (1 + 4~3)(1 -4~3), все сомно-
жители простые), тогда как кольцо Z[<b] этим
свойством обладает. Однако любое простое чис-
ло/? = 1 (mod 6) может быть разложено на множи-
тели в кольце Z[-/-3] единственным образом.
Поскольку символ вычета степени 6 может
принимать шесть различных значений: ±1, ±<в,
±со2, то число точек на кривой тоже может
принимать шесть различных значений в зави-
симости от разложения числа р. Имеем оконча-
тельно
а + Ь
N - р + \ + <2а-Ь
а-2Ь
Алгоритм 15.3.1. Генерация эллиптической
кривой cj = 0.
Вход. Длина I характеристики поля; параметр
безопасности т (максимальная степень расшире-
ния, при которой использование спаривания
Вейля становится неэффективным), где т выби-
рается в соответствии с табл. 11.5.
Выход. Эллиптическая кривая E(FP); обра-
зующая точка Q простого порядка г.
303
Метод.
1. Найти простое число р s 1 (mod 6) длины I
бит с единичным старшим двоичным разря-
дом.
2. Разложить число р на простые множители в
кольце Z[V-3] алгоритмом 7.10.1:
р = (с + dy[^3)(c - dy[^3) = с2 + 3d2 .
3. Проверить, что хотя бы для одного из чисел
N=p+\+T, где Te±{c + 3d, с-3d, 2с},
выполняется одно из условий: N=r, N=2r,
N=3r, N= 6r, где г— простое число; запом-
нить такие р, N и г. Если ни для одного из
шести возможных N указанное условие не
выполняется, то вернуться на шаг 1.
4. Проверить, что р^г и р' Ф 1 (mod г) для
i = 1,2, ...,т. Если условия не выполняются,
то вернуться на шаг 1.
5. Сгенерировать произвольную точку (х0, у0)
такую, что х0 0, у0 0, вычислить коэффи-
циент В yl - А'о (mod р) . Проверить, что
выполняется условие: В— квадратичный и
кубический невычет для N=r, В— квадра-
тичный и кубический вычет для N= 6г, В —
квадратичный невычет и кубический вычет
для N= 2г, В — квадратичный вычет и куби-
ческий невычет для N= Зг; в противном слу-
чае вернуться к началу шага 5.
6. Проверить, что N (х0, у0)= Р«= (знаменатель
углового коэффициента в формуле сложения
обращается в 0); в противном случае вер-
нуться на шаг 5.
N
7. Положить Q<------(х0, у0).
г
8. Результат: (р, В, Q, г).
Вместо разложения на множители простого
числа р можно подбирать пару целых чисел с, d
таких, что р = с2 + 3d2 — простое число и число
точек на кривой имеет большой простой дели-
тель. Вместо вычисления коэффициента В по ко-
ординатам точки можно сначала выбрать коэф-
фициент В, затем подобрать х-координату так,
чтобы выполнялось равенство
= 1, и
найти у-координату извлечением квадратного
корня.
Сложность шагов 1 и 3 при использовании
теста Миллера-Рабина или Соловэя-Штрассена
равна O((logp)3), сложность шага 2 равна
O((logy)3). Шаги 1-3 повторяются OQogp) раз.
Сложность шагов 4-7 не превышает O((log/?)3).
Таким образом, алгоритм 15.3.1 имеет сложность
O((log^)4).
Пример 15.3.1. Генерация эллиптической
кривой с j = 0.
Пусть /= 16, /и = 5. Выбираем р = 64033 —
простое число. Раскладываем р на множители:
р = с2 + 3d2, где с - 239, d= 48. Проверяем вари-
анты для числа точек, получаем: N=p+\-
- с+ 3d =3-21313. Коэффициент В должен быть
квадратичным вычетом и кубическим невыче-
том. Подбираем координаты хо, Уо так, чтобы вы-
полнялось равенство N • (хо, уо) = Р«,: х0 = -1,
Уо= Ю, В = 101. Находим образующую Q группы
порядка г = 21313, умножая точку (хо,уо) на 3:
б = (27774,44241). •-
15.3.2. Кривая у2 = х3 + Ах
Будем рассуждать так же, как и в предыдущем
случае. Для этого преобразуем кривую Е:
у2 = х3 + Ах в кривую Е' степени 4 с уравнением
1Г = г4 - 4А [1]. Бирациональный изоморфизм
ф(г/, г) =
/ 2
г/ +v
Г2“
v(u + v2)
2
отображает Е' в Е, при этом точка (0, 0) не явля-
ется образом какой-либо точки кривой Е' (А Ф 0,
поэтому -4А = и2 - г4 = (и — г2)(г/ + г2) Ф 0 и
и + v2 0). Бирациональный изоморфизм
( 2 А
у У
v|/(x,y)= 2х—,
Ч XX;
отображает Е (за исключением точки (0, 0)) в Е'.
Тогда ф1|/ = 1/л(о.о) и \|/ф = 1&. Обозначим через
к характер порядка 4 поля fy. Тогда Z2 = р. По-
лучаем
N(u2 = г4 - 4А) = = r^N(A = =
г+.у=-4/
= ^(1 + Р(И)(1 + л(.Д + л2(5) + 2.3(5)) =
л-+.¥=-4Л
= Р+ ^p(r)^(s)+ £p(r)Z(s)+ £p(r)Z3(s)=
r+s=~4A r+s=~4A r+s=-4A
= p-\ + р7.(4Л) ./(p, Z) + pZ(4J) J(p, Z) =
= p -1 + Z(4J>7(p, Z) + Z(4 Л)J(p,Z).
Здесь учтено, что pZ(o) = Z(o). По лемме
15.3.3 имеем ./(р, Z) = Z(4)J(Z, Z). Тогда
М4ЯУ(р, Z) = X(jy(Z, Z).
Поскольку p = 1 (mod 4), то по квадратичному
закону взаимности -1 является квадратичным вы-
304
четом. Следовательно, существует t, 1 <t <р - 1,
такое, что ? + 1 = (I + i)(t - f) = sp. Если предпо-
ложить, что р — простой элемент в Z[z], где
z2 = -1, то t + i или I - i должно делиться на р, но
этого нет. Следовательно, р раскладывается на
множители в Z[z]. Тогда делители числа р долж-
ны быть сопряженными:
р = пп = (а + Ы\а - bi) -а2 + Ь2.
Отождествим поле Fz, с кольцом Z[z]/nZ[z].
Поскольку тг — простой элемент, то ttZ[z] —
максимальный идеал, и кольцо классов выче-
тов по нему является полем. Если мы перейдем
к норме идеала, то увидим, что это поле со-
держит р элементов, то есть изоморфно полю
Fp. Выберем в качестве Z. символ биквадратич-
ного вычета:
Х(а) = |-| .
Ы4
Тогда из биквадратичного закона взаимности
следует, что ./(Л, Л) = -л. Получаем следующую
теорему.
Теорема 15.3.5. Если р = 1 (mod 4), то число
точек эллиптической кривой у2 = х3 + Ах над по-
лем Fp равно
„ 1 Ri
7V = /? + l- — л-
w4
>0 -
— л.
л Л
Подставляя один из четырех возможных сим-
волов вычета степени 4 (1, -1, z, -z"), получаем
N = p +1 ±-
2а
2Ь
Алгоритм 15.3.2. Генерация эллиптической
кривой cj = 1728.
Вход. Длина I характеристики поля; параметр
безопасности т (максимальная степень расшире-
ния, при которой использование спаривания
Вейля становится неэффективным), где т выби-
рается в соответствии с табл. 11.5.
Выход. Эллиптическая кривая £(FP); обра-
зующая точка Q простого порядка г.
Метод.
1. Найти простое число р = 1 (mod 4) длины 1
бит с единичным старшим двоичным разря-
дом.
2. Разложить число р на простые множители в
кольце алгоритмом 7.10.1:
p-{a + b^-\){a-b^-\) = a2 + Ь2.
3. Проверить, что хотя бы для одного из чисел
N=р + 1 + Г, где Т е ±{2а, 26}, выполняет-
ся одно из условий: N=2r или 7V=4r, где
г — простое число; запомнить такиер,Анг.
Если ни для одного из четырех возможных N
указанное условие не выполняется, то вер-
нуться на шаг 1.
4. Проверить, что ptr и р' ф 1 (mod г) для
i = 1, 2, Если условия не выполняются,
то вернуться на шаг 1.
5. Сгенерировать произвольную точку (хо,уо)
такую, что хо 0, уо * 0, вычислить коэффи-
циент А <г- (уо - Хд )х01 (mod р) . Проверить,
что выполняется условие: -А — квадратич-
ный невычет для 7V= 2г, -А — квадратичный
вычет для N = 4г; в противном случае вер-
нуться к началу шага 5.
6. Проверить, что N • (хо, уо) = Ра> (знаменатель
углового коэффициента в формуле сложения
обращается в 0); в противном случае вер-
нуться на шаг 5.
N
7. Положить Q <-----(х0, Уо ).
г
8. Результат: (р, A, Q, г).
Вместо разложения на множители простого
числа р можно подбирать пару целых чисел а, b
таких, что р = а +Ь2 — простое число и число
точек на кривой имеет большой простой дели-
тель. Вместо вычисления коэффициента А по ко-
ординатам точки можно сначала выбрать коэф-
фициент А, затем подобрать х-координату так,
чтобы выполнялось равенство
= 1,
и найти у-координату извлечением квадратного
корня.
Сложность алгоритма 15.3.2 равна O((log/?)4).
Пример 15.3.2. Генерация эллиптической
кривой с/ = 1728.
Пусть 7=16, т = 5. Выбираем р = 65129-—
простое число. Раскладываем р на множители:
р = а + Ь2, а = 205, b = 152. Проверяем варианты
для числа точек, получаем: N=p + 1 - 26 =
= 2 • 32413. Коэффициент -А должен быть квад-
ратичным невычетом. Подбираем координаты хо,
Уо так, чтобы выполнялось равенство
N (х0, уо) = х0 = 1, уо = 2, А = 3. Находим об-
разующую Q группы порядка г = 32413, умножая
точку (х0, уо) на 2: Q = (48847, 56987).
305
15.4. Эллиптические кривые
с комплексным умножением
В п. 15.3 число точек эллиптической кривой
определялось с помощью разложения простого
числа на множители в кольце Z[V-jD]. Этот же
подход используется и для нахождения числа
точек некоторых других эллиптических кривых,
а также для генерации эллиптической кривой.
Предположим, что простое число р может
быть разложено на простые множители в порядке
OD мнимого квадратичного поля К = Q(4~D).
Тогда при использовании дискриминантов £),
дающих число классов hK поля К, равное едини-
це, число точек эллиптической кривой E(F/;) вы-
числяется легко. Такое число классов обеспечи-
вают дискриминанты D е {1, 2, 3, 4, 7, 11, 12, 19,
27, 28, 43, 67, 163}, при этом /-инвариант являет-
ся целым рациональным числом (если hK> 1, то
/-инвариант является целым алгебраическим).
Все указанные значения дискриминантов могут
быть использованы согласно стандарту ECDSS;
согласно ГОСТ Р 34.10-2001 могут использо-
ваться любые значения дискриминантов, кроме 1
и 3, то есть не допускается/ = 0 и/ = 1728.
При hK = 1 разложение характеристики поля
на множители в мнимых квадратичных порядках
OD связано с комплексным умножением на эл-
липтической кривой. Значение /-инварианта и
вид уравнения кривой у2 =/(х) для разных значе-
ний дискриминанта приведены в табл. 15.1. Если
вид функции/не указан, то//) = х3 + 3kt2x + 2А?.
Кольца Z --------—
и Z
сов-
падают. Коэффициент к и /-инвариант связаны
соотношениями:
. / . 123&
£ =—г—> 7 =------
123-/ к + 1
Других кривых £(С) с комплексным умноже-
нием, как показал Ж. Серр, не существует [13].
Таблица 15.1
Параметры эллиптических кривых над простыми полями с вычислимым числом точек
D о» j fix) или к P p + 1 -N
1 12J fix) = x3 + Ax + b2 +2a, ±2b
4 Z[T^4] 66J 3372 cr + 4/r +2a
2 Z[V^2] 203 2-72 </ + 262 +2a
3 z -1+4^3 2 0 /(x) = C + £ a -ab + b2, a = 2 (mod 3), 6 = 0 (mod 3) ±(a + b), ±(2a - b), +(2b - a)
12 Z[V-12] 2 • ЗО3 ll2 о2 + 1262 ±2a
27 z -1 + 7-27 2 -3 •1603 2953 k = — 112232 a2 + 27b2, 7 a + 27ab + 27b2 ±2a, +a
7 z -1 + лр7 2 -153 ^4 337 a2 + 7b2, 2a + 7ab + 7b2 ±2a, +a
28 Z[V-28] 2553 53173 357-192 a2+ 28b2 ±2a
11 z -1+7ЛТ 2 -323 k = ~^- 7211 a2 + llb2, 3a2 + llab + 1162 +2a, ±a
306
Продолжение таблицы 15.1
D OD J /fx) или к Р p^l-N
19 -1 + Тч9 2 -963 З319 а2+ 1962, 5а2 + 19ab + 19b2 ±2а, ±а
43 -1 + 7^43 2 -9603 ^12г 3 k=-n1- 35 *7243 сГ + 4362, 1 la2 + 43а6 + 4362 ±2а, ±а
67 -1 + 7^67 2 -52803 -2953113 ~ 337231267 а2 + 61b1, 17а2 + 67ab + 61b2 ±2а, ±а
163 -1+7-163 2 -6403203 -21253233293 ~ З3721121921272163 а2 + 16362, 41а2 + 163а6 + 16362 ±2а, +а
Таким образом, комплексным умножением
над полем С обладают не только кривые, у ко-
торых характеристика поля раскладывается на
множители в максимальном порядке Z[0] всех
мнимых квадратичных целых данного поля, но
и кривые, у которых характеристика поля рас-
кладывается на множители в мнимом квадра-
тичном порядке Од = 2[/и0]. Немаксимальные
квадратичные порядки являются евклидовыми
кольцами, если зона точки (0, 0) расположена
внутри единичного круга (см. подробнее рабо-
ту [5])-3
Между указанными эллиптическими кривыми
существуют изогении малых степеней над С.
Так, изогенными для изогении степени 2 являют-
ся кривые с j = 0 и j = 2- ЗО3; j - 123 и j = 663;
j = -153 и j = 2553; кривая с j = 203 изогенна сама
себе. Кривая с j = 0 изогенна сама себе для изо-
гении степени 3. Другие кривые из табл. 15.1 не
имеют изогении степени 3 над С.4
Таким образом, для кривых, изогенных кри-
вым с j = 0 и j = 1728, возможно логарифмирова-
ние с помощью орбит автоморфизмов. Для этого
нужно от исходной кривой с помощью изогении
степени 2 перейти к кривой с j = 0 или j = 1728,
вычислить на ней логарифм для орбит автомор-
физмов точек (см. п. 11.2) и уточнить значение
логарифма внутри орбиты.
Сложность логарифмирования на указанных
кривых равна сложности логарифмирования на
соответствующих изогенных кривых с j = 0 и
7= 1728.
3 Зона точки целочисленной плоской решетки оп-
ределяется как множество точек комплексной плоско-
сти, расположенных ближе к данной точке решетки,
чем к остальным ее точкам.
4 Отсутствие изогений над С между данной кри-
вой и кривой с j = 0 (или 1728) не означает их отсут-
ствие над конкретным конечным полем .
15.4.1. Генерация эллиптических кривых
с комплексным умножением
Комплексное умножение позволяет легко ге-
нерировать эллиптические кривые с хорошими
криптографическими свойствами. Для этого
можно, используя разложение на множители в
OD, подобрать число р так, чтобы число точек на
кривой удовлетворяло необходимым требовани-
ям (см. п. 11.7). При D Ф 3 (mod 4) разложение
имеет вид:
р~{а + ь4-Й~У){а-Ь4^15) = a2 + Db2. (15.4.1)
Если такое разложение существует, то -D яв-
ляется квадратичным вычетом по модулю р.
Действительно, если имеет место разложение
(15.4.1), то числа а, b взаимно просты с р. Тогда,
перейдя от (15.4.1) к сравнению по модулю р и
умножив обе части сравнения на Ь~\ получим
-D = ab~2 (mod р), то есть -D — квадратичный
вычет. Обратное утверждение справедливо для
идеалов. Если —D — квадратичный вычет по мо-
дулю р, то существуют числа s, t е Z такие, что
s2 +D = tp. Имеем в OD: --J-D) = tp.
Если предположить, что (р)— простой идеал
кольца OD, то один из сомножителей в левой час-
ти должен делиться на (р). Поскольку этого нет,
то идеал (р) раскладывается на простые множи-
тели в О,,.
В случае использования формулы (15.4.1)
число точек р + 1 ± 2а всегда четно. Поскольку
при D = 3 (mod 4) мнимый квадратичный поря-
док имеет вид
, то для получения
нечетного числа точек можно воспользоваться
другим разложением числа р:
307
_ a + (26 + dyl-D a - (2b + a)-J-D _
2 * 1 2 (15.4.2)
= Db2 +Dab + ^-a2,
4
где число a—нечетное. Нетрудно заметить, что в
этом случае число 4р может быть представлено в
виде: 4р = п2 + П(26 + о)2. Поэтому для нахожде-
ния числа точек эллиптической кривой нужно
разложить на множители в мнимом квадратичном
порядке D] числор или 4р (см. п. 7.8).
Тогда число точек будет равно N=p + 1 +а.
Если N— простое число, то существует эллип-
тическая кривая £'(Р/.) с тем же /-инвариантом и
числом точек р. Такой «дуализм» является мощ-
ным тестом на простоту обоих чисел р и N. Если
а = ±1, то получается N=p [15] — эллиптическая
кривая, задача логарифмирования для которой
решается легко.
Алгоритм 15.4.1. Генерация эллиптической
кривой, обладающей комплексным умножением
над С [6].
Вход. Длина I характеристики поля; параметр
безопасности т (максимальная степень расшире-
ния, при которой использование спаривания
Вейля становится неэффективным), где т выби-
рается в соответствии с табл. 11.5.
Выход. Эллиптическая кривая ДЕД; обра-
зующая точка Q простого порядка г.
Метод.
1. Выбрать D е {1, 2, 3, 4, 7, 11, 12, 19, 27, 28,
43, 67, 163} и мнимый квадратичный порядок
OD в соответствии с табл. 15.1 (для ГОСТ Р
34.10-2001 значения D= 1, 3 недопустимы). С
помощью квадратичного закона взаимности
найти общий вид простого числа р, для кото-
рого -D является квадратичным вычетом.
2. Найти простое нечетное число р длины I бит.
3. Используя алгоритм 7.8.1, разложить число р
или 4р на простые множители в кольце OD
так, чтобы выполнялось равенство (15.4.1)
или (15.4.2).
4. Методом пробного деления проверить, что
хотя бы для одного из чисел N=p + 1 + 2а в
случае формулы (15.4.1) или хотя бы для од-
ного из чисел N=p + 1 ± а в случае формулы
(15.4.2) число точек имеет вид: N = cr для
малого с, где г— простое число; запомнить
такие p,N, с и г. Если это условие не выпол-
няется, то вернуться на шаг 2.
5. Проверить, что р^г и р' Ф 1 (mod г) для
i = 1, 2, ..., т. Если условия не выполняются,
то вернуться на шаг 1.
7.
Вычислить коэффициент к в поле Fp и коэф-
фициенты уравнения кривой согласно табл.
15.1.
Положить t <г- 1; выбрать элемент хо 6 Fr*
< о А
х0 + Зкх0 + 2к
такой, что
; вычислить у-
координату уо извлечением квадратного кор-
ня из Xq + 3kxG + 2к. Проверить, что
сг (хо,уо) = Рх- Если это не так, то перейти к
скрученной кривой, положив I <— и, где и —
произвольный квадратичный невычет;
брать элемент х0 е такой,
вы-
что
у-
+ 3kt2xG + 2kt3
вычислить
координату уо извлечением квадратного кор-
ня из Xq + 3kt2xG + 2kt3.
8. Положить Q <- с • (х0, уо), А <- 3kt2, В <г- 2к13.
9. Результат: (р, А, В, Q, г). ;
Альтернативный алгоритм имеет следующий
вид.
Алгоритм 15.4.2. Генерация эллиптической
кривой, обладающей комплексным умножением
над С [6].
Вход. Длина I характеристики поля; параметр
безопасности т (максимальная степень расшире-
ния, при которой использование спаривания
Вейля становится неэффективным), где т выби-
рается в соответствии с табл. 11.5.
Выход. Эллиптическая кривая £(FP); обра-
зующая точка Q простого порядка г.
Метод.
1. Выбрать D е {1, 2, 3, 4, 7. 11, 12, 19, 27, 28,
43, 67, 163} и мнимый квадратичный порядок
Он в соответствии с табл. 15.1 (для ГОСТ
Р 34.10-2001 значения 0=1,3 недопустимы).
2. Подобрать пару чисел а, b так, чтобы выпол-
нялись следующие требования.
2.1. Число р, определенное по формулам
(15.4.1) или (15.4.2),— простое и имеет
требуемую длину.
2.2. Число N=p + 1 ± 2а в случае формулы
(15.4.1) или N=p + 1 ±а в случае фор-
мулы (15.4.2) имеет вид N=cr для ма-
лого с, где г— простое число требуе-
мой длины.
2.3. р‘ Ф 1 (mod г) для i = 1,2, ..., т.
2.4. р^г.
3. Вычислить коэффициент к в поле F;, и ко-
эффициенты уравнения кривой согласно
табл. 15.1.
308
4.
Положить t<- 1; выбрать элемент х0 е F;,
такой, что
х(3 + 3£х0 + 2к '
Р
; вычислить у-
координату _И) извлечением квадратного корня
из х(3 + Зкх0 + 2к. Проверить, что сг (х0,у0)=Ра>
Если это не так, то перейти к скрученной
кривой, положив t <— и, где и — произволь-
ный квадратичный невычет; выбрать элемент
Хо 6 F/ такой, что
Xq + 3kt2x0 + 2kt3>
Р
вычислить j-координату у0 извлечением
квадратного корня из Xq + 3k/2x(l + 2kt3.
5. Положить Q <- с • (хо, уо), А <- 3kt2, В <- 2kt3.5
6. Результат: (р, А, В, Q, г).
Сложность алгоритмов 15.4.1, 15.4.2 при ум-
ножении «в столбик» равна O((log/?)5). Действи-
тельно, сложность проверки числа р на простоту
тестом Миллера-Рабина равна O((log/?)3). Веро-
ятность того, что число р будет простым, по тео-
реме Чебышева примерно равна 1/1п р. Вероят-
ность того, что число N будет иметь большой
простой делитель, примерно равна 1/1п р.
Пример 15.4.1. Генерация эллиптической
кривой, обладающей комплексным умножением
над С.
1. Рассмотрим квадратичный порядок
OD=Zh/=28] и разложение (15.4.1). Тогда
р = а + 2862, г - Р + ^ - ^а , vj\c v = j или v = 2.
2V
Ясно, что а=1 (mod 2). Подбираем пару коэф-
фициентов а, b так, чтобы р было простым чис-
лом и число точек N имело большой простой де-
литель г: а = 1, Ъ = 4. Получаем: р = 449, г = 113,
к = 2. Уравнение эллиптической кривой:
у2 = х3 + бГх + 4?. Проверка показывает, что для
получения нужного числа точек коэффициент t
должен быть квадратичным невычетом, напри-
мер, t-З. Для степеней расширения, меньших
16, число г не делит порядок мультипликативной
группы расширенного поля.
2. Рассмотрим кольцо OD = 72
и
разложение (15.4.2). Тогда р = За + 1 lab + 1162,
г -р + 1 ± а. Подбираем пару коэффициентов а, b
5 Кроме того, можно использовать изоморфизмы
эллиптических кривых, чтобы упростить формулы
арифметики.
так, чтобы р было простым числом и число точек
N имело большой простой делитель г: а = 3, b = 5.
Получаем: /? = 467, £ = 408, N=3r = 3 157 = 471.
Уравнение эллиптической кривой: у2 = х3 +
+ Зкх + 2к. Минимальная степень расширения,
при которой порядок мультипликативной группы
расширенного поля делится на г, равна 13.
1+7^27
2
3. Рассмотрим кольцо
и
разложение (15.4.2). Тогда р = 7<? + 21аЬ + 27б2,
г =р + 1 ± а. Подбираем пару коэффициентов а,
b так, чтобы р было простым числом и число то-
чек N имело большой простой делитель г: а = 5,
Ь = 3. Получаем: /7 = 823, £=168, 7V=r = 829.
Проверка при t = 1 показывает, что следует пе-
рейти к скрученной кривой с уравнением
у2 = х3 + Зкх - 2к.
4. Рассмотрим кольцо OD = 72
Ге-
нерируем эллиптическую кривую с числом то-
чек, равным р. Выбираем разложение (15.4.2) и
<7=1. Подбираем коэффициент b так, чтобы р
было простым числом, р = 5 + 19b + 19b2. При
6 = 3 получаем р = 233 — простое число. Тогда
£=118 и эллиптическая кривая у2 = х3 + Зкх + 2£
имеет 233 точки.
15.4.2. Влияние комплексного
умножения на скорость вычислений
Скорость криптографических алгоритмов оп-
ределяется скоростью умножения точки Р на
число d. Вычисления можно ускорить, если ис-
пользовать комплексное умножение.6
Эллиптические кривые cj = 0 и j = 1728 обла-
дают комплексным умножением. Соответст-
вующие группы автоморфизмов имеют порядок
6 и 4 (см. п. 6.14.5). Рассмотрим еще один вари-
ант комплексного умножения. Если 0 = 2, то
р = а + 262, и -2 является квадратичным выче-
том по модулю р. Для удобства комплексного
умножения запишем уравнение кривой в сле-
дующем виде [12]:
у2 = х(х2 - 4/х + 2?), (15.4.3)
где t— соответствующий произвольный квадра-
тичный вычет (невычет). При этом формула
6 Программа становится конкурентоспособной,
если она хотя бы на 10 % быстрее аналогов. Однако
скорость программы определяется не только искусст-
вом программиста, но и квалификацией математика.
309
сложения двух различных точек сохраняется, а
удвоение точки можно выполнять с помощью
комплексного умножения. Число точек кривой
равно N=p + 1 ± 2а. Если найдена кривая с од-
ним из двух возможных вариантов числа точек,
то, умножая коэффициент t на произвольный
квадратичный невычет, получаем скрученную
кривую. Нетрудно заметить, что всегда N=0
(mod 2).
Разложим на множители правую часть урав-
нения (15.4.3). Получим
у2 = х(х -1(2 + V2))(x -1(2 - V2)).
Отсюда следует, что N=Q (mod 4), если на
кривой существуют три аффинные точки поряд-
ка 2 (с нулевой у-координатой), что равносильно
существованию л/2 (mod р).
Случай N =2 (mod 4) получается, если 2 явля-
ется квадратичным невычетом, то есть р = +3
(mod 8); это возможно лишь при нечетных а, Ь.
Можно сразу выбирать а = ±1 (mod 6), b = 3
(mod 6), t = ± 1, при этом N не будет делиться на 3.
Кривые вида (15.4.3) над алгебраически замк-
нутым полем обладают нетривиальным эндо-
морфизмом, который можно вывести из изоге-
нии степени 2. Этот эндоморфизм соответствует
кратному корню модулярного уравнения (см.
п. 6.15.4). Комплексное умножение точки (х,у)
кривой (15.4.3) на у/- 2 имеет вид
ф:(х,у)—>
ч2х2 ’
у(х2 — 2t2)
2у[--2х2 ,
(15.4.4)
(р(х,у~)-уГ^2(х,у). (15.4.5)
Здесь каждому из двух значений корня из -2
по модулю р, участвующих в (15.4.4), взаимно
однозначно соответствует свое значение корня
из -2 по модулю г в (15.4.5). В случае проектив-
ной кривой Y2Z = X' - 4lXzZ + 2dXZ2 формулы
комплексного умножения примут вид
ф(ВДЛ) = уГ2(Х, Л ,Zi) = (X2,Y2,Z2),
где
х2 =~y2zu
Y2=(4-Xy[Y[(X2-4t2Z2),
Z2=2X2Z}.
Это позволяет вместо удвоения точки дважды
использовать комплексное умножение на V-2 ,7
7 Здесь нужно учесть, что <р2(Р) = -2Р.
При умножении точки на число d вместо
обычного двоичного представления показателя d
можно использовать представление в системе
счисления с основанием 7-2 , заменив порядок
группы г его простым делителем в кольце
Z[V- 2]. Это позволит заменить удвоение точек
комплексным умножением и тем самым уско-
рить вычисления на эллиптической кривой [7].
Представить порядок группы в виде полинома
степени не более log2r от 7-2 с коэффициентами
из поля F2 можно так. Сначала найти разложение
порядка г группы точек алгоритмом 7.8.1 и вы-
полнить приведение показателя d по модулю ре-
шетки алгоритмом 7.9.1: d = dG + <7,7-2 (mod/л),
где |<70|<у/r,|б7]|<у/г . Затем выписывать пооче-
редно двоичные разряды чисел do, d\, начиная с
младших, и заменять соответствующим образом
знаки двоичных коэффициентов с учетом того,
что 2 = -(7-2)2 .
Можно использовать не только положитель-
ные, но и отрицательные степени числа 7-2 .
Положим (и, г) = ф(х, у). Заменив в (15.4.4) у2 на
х t2
х3 - 4lx~ + 2tlx, получим ф(х) =--+ 2t-----, от-
2 х
куда
(Отсюда следует, что и может быть только
квадратичным вычетом.) Извлечение корня в ко-
нечном поле выполняется значительно быстрее,
чем умножение точки на число. При этом возни-
кает неопределенность, связанная с неоднознач-
ностью извлечения корня, если (и, у) Ф (0, 0) (эта
точка остается неподвижной под действием ком-
плексного умножения). Если число точек на кри-
вой равно 2г, то одна из найденных точек лежит
в циклической группе порядка г, а другая — нет.
Каждая из этих точек получается сложением дру-
гой точки с точкой (0, 0). Таким образом, эти
точки совпадают в факторгруппе E(F;,)/((0,0))
порядка г.
Пример 15.4.2. Представление показателя в
системе счисления с основанием 7-2 .
1. Пусть эллиптическая кривая 7r(Fi63) задана
уравнением у2 = х3 - 4/х2 + 2?х. Характеристика
поля р = 163 раскладывается в кольце Z[7-2]:
р = а + 262 = I2 + 2 • 92. При t = -1 кривая имеет
7V=/?+l+2n=166 точек, простой делитель
г = 83. Пусть показатель <7=61. Представим его в
310
системе счисления с основанием V- 2 . Для этого
вычисляем значение 0 = 4-2 = 9(mod83) и рас-
кладываем на множители число г в кольце
Ё[4-2]: 83-(9-VZ2)(9 + VZ2) = тгл, причем
л = 0 (mod 83). Представляем число d как вычет
по модулю л: d = dG + dfi s -4 + 20 (mod л). На-
ходим представление числа d в новой системе
счисления с учетом равенства 2 = -(Т^2)2 • При
этом ненулевые двоичные разряды числа do оп-
ределяют коэффициенты при четных степенях 0,
а ненулевые двоичные разряды числа d} — ко-
эффициенты при нечетных степенях 0. Получаем
<7|0 = 03, do = -04. Тогда
d — do + d]Q —
= 0 • 0° + 0 0 + 0 02 + 1 03 - 1 • 04.
Для проверки подставляем 0 = 9, получаем
<7=93-9 =61 (mod 83).
2. Рассмотрим ту же кривую £(F163). На кривой
лежит точка (-1, -1). Тогда V— 2(—1, -1) = (81,86).
Выполняя обратное преобразование, получаем
е {(-1,-1), (-2,2)}. При этом (-1,-1) +
V-2
+ (0, 0) = (-2, 2) и 7^2(-1, -1) = Ж2(-2,2) =
= (81,86).
Для эллиптической кривой с комплексным
умножением на 4-2 представляется возмож-
ной атака, связанная с разбиением множества
точек на классы эквивалентности, совпадающие
со смежными классами группы F,. по подгруп-
пе, образованной элементом 4-2 , и определе-
нием принадлежности данной точки некоторому
классу эквивалентности. Для исключения атаки
имеет смысл выбирать эллиптическую кривую
так, чтобы элемент 4-2 был образующей всей
группы Fr или достаточно большой ее под-
группы.
Аналогично можно использовать эллиптиче-
ские кривые с комплексным умножением на
1 + 4-7
0 =-------, задаваемым изогенией степени 2.
При этом 00 = 2. Для таких эллиптических кри-
вых j = -153 (см. табл. 15.1), и можно получить
7V=4r. Кроме того, можно использовать ком-
1±л/ЛТ
плексное умножение на -у-З или --------, оп-
ределяемое изогенией степени 3.
Пример 15.4.3. Умножение точки на число с
помощью комплексного умножения.
Умножим точку эллиптической кривой из
примера 15.3.1 на целое число d= 12345 с помо-
щью комплексного умножения. Параметры кри-
вой: р = 64033, В = 101, г = 21313, N- Зг. Найдем
представление d = do + р<7] (mod г), где
— i+4— з .
р =--------, а коэффициенты «0 и d\ имеют
минимальную абсолютную величину.
Раскладываем число г в кольце Z[p]:
г = mt = (159 +128р)(159 +128р2).
Вычисляем р = 15817, тогда л = 0 (mod г).
Находим вычет числа d по модулю л над по-
лем F,, минимизируя норму числа <7= <70 + <7ip ал-
горитмом 7.9.1. Получаем <7=d0 + р<7| = 11 - Юр.
Минимизация двоичных цепочек показателей
do и <7; ничего не дает.
Для умножения точки Р на число d достаточ-
но вычислить 1 OP = 2Р + 2(2(2Р)), 1 \Р = ЮР + Р,
-ЮрР, ПР - 10рР. Умножение на -р выполня-
ется с помощью комплексного умножения:
, . '-1+V-3
-р(х,у) = ------х,-у
\ 2 7
Всего требуется три операции удвоения точек,
три операции сложения точек и одна операция
комплексного умножения. Для сравнения: при
обычном умножении точки на число выполняет-
ся 13 удвоений и пять сложений. Комплексное
умножение в данном случае позволяет ускорить
вычисления в три раза.
Пример 15.4.4. Умножение точки на число в
арифметике Монтгомери.
Координаты точки можно изначально пред-
ставлять в виде образов преобразования Монт-
гомери (см. п. 7.1) и умножать точку на число, не
выполняя прямое и обратное преобразование
Монтгомери.
Пусть £(FP): у2 = х + 92 (mod 211) — эллип-
тическая кривая, заданная в обычном (не по
Монтгомери) виде, Р = (1, 84) е £(FP), г = 241,
нужно найти точку 100Р. Положим R = 256, то-
гда R' = R* l (mod р) = 136.
Находим 211-вычеты координат точки Р (см.
п. 7.1.4), домножив ее проективные координаты
на R: Хм s XR (mod р\ YM= YR (mod p), ZM = ZR
(mod p). Домножение всех трех координат на од-
но и то же число точку не меняет, поэтому мож-
но считать Рм = (Хм, YM, ZM) = (1, 84, 1). Находим
со = zl±2EI = и (mod 211),
311
co/? 208 (mod 211)— образ преобразования
Монтгомери для комплексного умножения;
р = —1+-— ^- = 15 (mod 241). Минимизируем по-
казатель: d= 100 = 7р - 5.
Находим точку Р7М с использованием проек-
тивной арифметики в форме Монтгомери (мо-
дульное умножение чисел выполняется по фор-
мулам умножения Монтгомери, модульное сло-
жение выполняется обычным образом):
X2U = 2YMZMR’(9X*R'3 -*XMY2ZMR'3yt = 9\,
Y2U = 4Y2ZmR'2(9X3mR'2-2Y2ZmR'2)R'-
-27X6mR'5 =107,
Z2M=8T^A5=177.
Чтобы умножить число на константу по фор-
мулам Монтгомери, ее следует предварительно
перевести в 211-вычет. Например, константа 27 в
формуле для Yim заменяется на 27R =160
(mod 211).
Точка Ам лежит на проективной кривой, то
есть удовлетворяет равенству
Y2Zm = Х3м +92ZI (modр).
Аналогично вычисляем Pw = (199, 171, 44),
= (130, 92,94). По формулам сложения точек
находим Р1М = Рш - А/ = (16, 16, 129), Р5М = Pw +
+ Ас = (18, 107, 90).
Выполняем комплексное умножение для точ-
ки Р7М. Для этого умножаем методом Монтгоме-
ри А-координату точки на число со/?: рР7м =
= (13,16,129). Вычисляем Т’юод/=(Адослг» Ziajw) =
=-Р5м+рАм=(47,31,185).
Для нахождения соответствующей аффинной
точки умножаем Z]00W на 1 методом Монтгомери
(при этом получается ZWomR' = 51), вычисляем
[7 = (Zjooa/A)-’ (mod/?) =120 расширенным алго-
ритмом Евклида и умножаем методом Монтго-
мери координаты Асом, Аю/о на U. Результат:
100Р = (55, 153).
Комплексное умножение позволяет свести
вычисление dP к вычислению суммы d<P + QdyP,
где |<70) < 4г, Щ < 4г , при этом комплексное ум-
ножение на число 6 выполняется быстро. Для
расчета точек d^P и dyP используется одна и та
же база точек 2Р, 22Р, .... Доля ненулевых цифр
в троичном представлении чисел d0 и dy состав-
ляет в среднем 4- Если традиционное умноже-
ние точки на число методом знакового двоично-
го окна (см. п. 7.10) требует в среднем '
сложений (удвоений) точек, то в случае ком-
плексного умножения при использовании обшей
базы удвоенных точек требуется
log2r , log2'J _51оё2г
2 3 6
сложений (удвоений) точек, то есть скорость ум-
ножения точки на число увеличивается примерно
на 50 %.
15.5. Эллиптические кривые
над расширенными полями
специальных характеристик
В примере 15.2.1 были рассмотрены эллипти-
ческие кривые P/F2, обладающие хорошими
криптографическими свойствами. Однако ариф-
метика поля характеристики 2, требующая мо-
дульного умножения и обращения полиномов
над Р2, неудобна для реализации на серийных
процессорах. Кроме того, число кривых с ука-
занными свойствами очень невелико.
Значительное увеличение скорости может
быть достигнуто за счет использования эллипти-
ческих кривых над расширенными полями ха-
рактеристик вида р = 2'" ± с, например, указан-
ных в табл. 15.2. Знаком «+» помечены простые
числа, знаком «±» — числа вида Зр', где р' —
простое число.
Таблица 15.2
Простые числа вида 2я' + с
1 -1 3 -3 -5 7 9 11 13 15 -15 -17 -19
7 + + + + + +
8 + + + + + + + +
14 + +
15 + + + +
16 + + + + + + +
29 + +
30 + + + +
31 + + + + +
32 + + +
312
Например, число 231 + 1 имеет малый простой
делитель 3. Кубическая кривая у2 = х3 + 2х + 2
имеет единственную проективную точку (Рх) над
F3, тогда из китайской теоремы об остатках сле-
дует, что можно работать непосредственно с
кольцом Z7(231 + 1)Z. Длина характеристики по-
ля (кольца) выбирается равной длине машинного
слова.
Если К- Fg, где q =р", то эллиптическая кри-
вая Е(К) = E/Fp всегда содержит в качестве «бал-
ласта» кривую Поэтому, если Е(К) — эл-
липтическая кривая над полем из q элементов и
/7(Е;,') — эллиптическая кривая над простым по-
лем из р' элементов, причем обе эти кривые
обеспечивают одинаковый уровень стойкости, то
длина числа q должна на одно машинное слово
превышать длину числар'.
Если характеристика поля вдвое меньше, чем
размер машинного слова, то в качестве «исход-
ной» можно использовать эллиптическую кри-
вую Е/F 2, коэффициенты которой лежат в квад-
ратичном расширении простого поля. Все приве-
денные рассуждения остаются справедливыми и
в этом случае с заменой р на р2.
Отметим, что кривая Е(К)~ Е/К, заданная
уравнением у2 = х3 + Ах + В, может не содержать
кривую Е(Е;,), а #Е(К) может не делиться на
#E(Fp). В частности, tfE(K) может быть простым
числом. Например, эллиптическая кривая у2 = х3 +
+ х + 2/ над полем [/]/(? +2) имеет 17 точек,
тогда как число точек произвольной эллиптиче-
ской кривой над Fs принадлежит множеству {2,
3, 4, 5, 6, 7, 8, 9, 10}. Кроме того, для получения
эллиптической кривой с требуемыми свойствами
не обязательно использовать простую степень
расширения. Для того чтобы число #Е(К) было
простым, полином х3 + Ах + В не должен иметь
корней в поле К, то есть должно выполняться
равенство
(А3 В2} 2 .
— + — = -1.
127 4 J
Увеличение скорости вычислений на эллип-
тической кривой Е(К) достигается в результате
использования трех факторов [3].
1. Характеристика р имеет специальный вид,
что позволяет реализовать быстрое умноже-
ние в простом поле Fp.
2. Неприводимый над F;, полином fit), задающий
расширенное поле X = Fz,[/]/(/(/)), имеет спе-
циальный вид: fit) = t"-t-a, что позволяет
реализовать быструю арифметику в расши-
ренном поле. Число таких полиномов асих
птотически равно О(р/п) [2].
3. Эллиптическая кривая Е(К) обладает ком
плексным умножением на собственное зна
чение эндоморфизма Фробениуса, что позво
ляет ускорить умножение точки эллиптиче-
ской кривой Е(К) на число.
Наиболее трудоемкой операцией в расширен-
ном поле при сложении точек эллиптической
кривой является модульное умножение полино-
мов. Вычисление модульного произведения
u(t)v(fi) (ywoAfit)) выполняется следующим обра-
зом. Так как 0 < deg(w), deg(v) < и, то произведе-
ние w(/) = u(t)v(t) будет иметь степень не выше
2(и-1).
Пусть
Н’(/) = 1 + 2 + ... + Wit + Wo,
где коэффициент w^n-i - 0 добавлен только для
симметрии.
Разделим w(t) с остатком на f, тогда
w(t) = 1 + w^t" 2 + ...+ w„) +
+ (w„~it"~l + w„_2^2 + ... + WO). (15.5.1)
Поскольку t"st + a (mod ДО), выражение
(15.5.1) можно переписать в виде:
w(f) - EwiH-it" 1 + 2 + ... + w„) +
+ ((w„-i + aw2n-\)t" 1 + (w„_2 + 2 + ... +
+ (W| + <7W,„ ,)/ + (w0 + ow,,)) =
= (w„_! + W2,,-2 + aw2„-i)tn~x +
+ (w„-2 + W2„-3 + OW2n~2)tn 2 + ... +
+ (wj + w„ + aw„+i)t + (w0 + aw„). (15.5.2)
С учетом того, что ~ 0, получаем иско-
мый полином степени не выше п - 1. Все опера-
ции над коэффициентами полиномов выполня-
ются по модулю р.
Выражение (15.5.2) определяет алгоритм де-
ления с остатком на fit).
Алгоритм 15.5.1. Нахождение остатка от де-
ления на трехчлен f — t — а.
Вход.
w(t) = w2n-2t‘Jl 2 + W2„-3r2'' 3 + ... + w0 6 Fp[/],
fit) = f -t-a.
Выход. r(Z) = w(/) (mod fit)).
Метод.
1. Для i = n - 1, n - 2,..., 1 вычислить r, <-
«- W; + w,+„_j + aW;+„ (mod p).
313
2. Положить r0 <— и'о + <Ж (mod р).
3. Результат: r(t) = + rrb-it"~2 + ...+r0.
Нахождение остатка алгоритмом 15.5.1 требу-
ет п умножений в простом поле на постоянный
коэффициент а и 2п сложений в простом поле.
Комплексное умножение позволяет увеличить
скорость умножения точки Р на число d. Для
этого нужно число d записать в виде полинома от
собственного значения 6 эндоморфизма Фробе-
ниуса: d = do + d\ 6 + J262 + • • • + Дч-|6х1 (mod г),
причем числа |J,| должны быть гарантированно
малы, например, не превышать . Значение 6
является одним из двух корней характеристиче-
ского уравнения эндоморфизма Фробениуса для
кривой Е/Ру. (р2-Тср+р = О (mod г), где
Т=р+ 1 - #EQFp). Чтобы уточнить, какой из двух
корней совпадает с 6, достаточно положить 6
равным одному из корней и проверить для лю-
бой точки равенство 6 • (х, у) = (хД уг).
Оценим оптимальное значение s, обеспечи-
вающее максимальную скорость вычислений. В
поле К выполняется равенство
а__ г?_ - - - -
Z4 — Z1 — Z "
для всех z. Поэтому, очевидно, s<n. Будем счи-
тать, что умножение точки на 6 выполняется
значительно быстрее, чем сложение или удвое-
ние точек, поскольку имеет место равенство
О=о у <=о
Предварительно созданная база данных вида
t'p (mod /(/)) позволяет свести умножение точки
на 6 к О(и2) сложениям и умножениям в поле
Используя так называемый нормальный базис
поля К над (Fp, состоящий из степеней 1Р
(mod/(0), можно получить линейную сложность
умножения точки на 6.
Будем считать, что вычисление dP выполня-
ется следующим алгоритмом.
Алгоритм 15.5.2. Умножение точки на число
в расширенном поле.
Вход. Точка Р; значение 0, число d= do +
+ J]0 + ... + <7,-16s”1 (mod г). а. :
Выход. Точка dP.
Метод.
2 max [log 2 rf, J
1. Вычислить базу данных 2P, 2Р,..., 2 1 Р
путем последовательного удвоения точек.
2. Провести минимизацию коэффициентов d, за
счет троичного представления: 0, 1,-1 (см.
п. 7.10).
3. Вычислить точки djP сложением соответст-
вующих точек из базы данных.
4. Вычислить точки d$P применением соот-
ветствующей степени отображения Фробе-
ниуса к точкам, полученным на шаге 3.
5. Сложить точки, полученные на шаге 4.
6. Результат: <7Е. .
Алгоритм требует (log2 r)/.s удвоений точек
на шаге 1, (log2 г)/3 сложений точек на шаге 3, s
сложений точек на шаге 5; всего
(log2 r)/s + (log2 r)/3 + x операций. Поэтому же-
лательно выбирать х ® -Jlog2 г . Например, если
разрядность процессора равна 16 и степень рас-
ширения п = 16, то logo/’ = 240. Оптимум при ис-
пользовании «фробениусовой» системы счисле-
ния достигается при s = n.
Поскольку представление целого показателя d
во «фробениусовой» системе счисления по мо-
дулю г с ограничениями на длину d, неочевидно,
можно изначально пользоваться указанным
представлением. В этом случае сложность умно-
жения точки на число равна примерно (log2 г)/3
операций сложения точек, то есть в 2-4 раза
меньше, чем для эллиптических кривых над про-
стыми полями.
Если используется 16-разрядный процессор
и порядок группы имеет длину 160-300 бит,
то криптоалгоритмы на эллиптических кривых
над расширенными полями 16-разрядной ха-
рактеристики работают в 8-15 раз быстрее,
чем на эллиптических кривых над простыми
полями.
Поскольку коэффициенты эллиптической
кривой лежат в поле BFr и число точек кривой
Е(К), где A = полностью определяется чис-
лом точек кривой Е^), то число эллиптических
кривых, неизоморфных над К как абелевы груп-
пы, равно O(tfp). Однако кривые, изоморфные
как абелевы группы, могут быть неизоморфны
как эллиптические кривые. На практике это оз-
начает, что сложность вычисления изоморфизма
между абелевыми группами близка к сложности
вскрытия ключа.
Если Ей Е' — изоморфные кривые, то для ло-
гарифмирования на кривой Е можно воспользо-
ваться базой данных, составленной для кривой
Е'. Поэтому при выборе эллиптической кривой
(общего открытого ключа криптосистемы) жела-
тельно исключить возможность выбора изо-
морфных кривых.
№f
Пример 15.5.1. Изоморфные эллиптические
кривые над полем характеристики 216 + 1.
Согласно (15.1.1) число точек эллиптиче-
ской кривой E(IFp) определяется следом Т эндо-
морфизма Фробениуса. В таблице 15.3 приведе-
ны допустимые значения -Т для кривых с раз-
личным числом корней в правой части уравнения
(см. п. 6.14.6) для р = 216 + 1 и различных степе-
ней расширения п.
Число кривых ДРД удовлетворяющих требо-
ваниям п. 11.7, с указанными значениями -Т для
различных степеней расширения приведено в
таблице 15.4. Число неизоморфных кривых оп-
ределено с учетом теорем 6.14.6-6.14.9.
Таблица 15.3
Значения следа эндоморфизма Фробениуса для р = 216 + 1
Уравнение кривой п -Т
у1 = х(х - 1)(х - X.) и -510; -370; -358; -274;466;502
13 -290; -246; -142; -30; 134; 206; 230; 238; 282; 286; 354; 394; 466
17 -426; -162; -46; 282; 366; 406; 510
19 -470; -302; -250; -182; -22; 134; 174; 226; 306; 310; 446
У2 = (X - Рз)(х2 + 3), у2 = (х-р27)(х2 + 27) 11 -510; -404; -370; -358; -274; -136; -128; -20; 104; 144; 148; 236; 240; 324;464; 466; 502
13 -340; -290; -280; -256; -246; -142; -88; -30; 28; 52; 134; 192; 206; 230; 238;282;286;354;394; 466
17 -512; -426; -372; -236; -162; -84; -46;124;176;208; 282; 366; 406; 510
19 -480;-470; -416; -400; -304; -302; -250; -240; -232; -182; -120; -92; -22; 112; 116; 134; 174; 226; 232; 252; 306; 310; 400; 446
у2 =х5 + А\х+ 1, у2 = х3 + А-зХ + 3 И -447; -303; -279; -273; -259; -251; -217; -139; -137; -49;13; 43; 49; 59; 75; 79; 95; 351; 433;505
13 -485; -379; -285; -255; -251; -225; -197; -193; -21; -19; -15; 87; 107; 153;205;219;245;285; 349; 387; 441
17 -495; -491; -429; -355; -325; -317; -237; -219; -215; -157; -135; -61; -43; -33; 163; 199; 311; 429; 449; 453; 467; 475
19 -509; -503; -499: -479: -383; -381; -291; -281; -265; -223; -221; -181; -101; -57; 9; 63; 139; 247; 257; 283; 287; 309; 359; 501
Число эллиптических кривых над полем характеристики р = 216 + 1,
удовлетворяющих требованиям и. 11.7
Таблица 15.4
Уравнение кривой Общее число кривых Число неизоморфных кривых
и= 11 п= 13 п= 17 п= 19 п = 11 п= 13 17 п = 19
у2 = х(х - 1)(х - А) 728 3036 1634 2184 202 936 449 640
Скрученные кривые 484 2580 1060 1656 162 804 362 526
у2 = (х - р3)(х2 + 3) 1556 2692 1534 2738 778 1346 767 1369
у2 = (х-р27)(х2 + 27) 1556 2692 1535 2738 778 1346 768 1369
у2 = xJ + Арс + 1 762 1027 801 955 762 1027 801 955
у2 =х2 + Я_3х + 3 796 1062 779 970 796 1062 779 970
15.6. Протоколы 15.6.1. Встраивание открытого текста
на эллиптических кривых в координату точки
Эллиптические кривые над конечными поля-
ми позволяют реализовать широкий спектр крип-
тографических протоколов.
При разработке криптографических алгорит-
мов на эллиптической кривой Е(К) иногда требу-
ется сопоставить данному открытому тексту не-
которую точку кривой, при этом обратное ото-
бражение должно позволять однозначно опреде-
лить открытый текст. Такое сопоставление мож-
315
но выполнять различными способами. Очевид-
ный способ — для фиксированного уравнения
кривой у2 =J(x) с размером задачи п бит над по-
лем К в качестве х-координаты использовать
(п - ^-разрядный текст, дополненный к двоич-
ными разрядами так, что число Дх) — квадра-
тичный вычет в поле К. Варьируя число к, можно
изменять скорость шифрования и вероятность
успешного зашифрования текста. Такой способ
целесообразен для кривых над простыми полями,
поскольку для нахождения «добавки» к откры-
тому тексту нужно вычислять значения квадра-
тичного характера, а эта операция удобно вы-
полняется в простом поле— достаточно найти
символ Якоби.
Пусть К — расширенное поле и число точек
кривой Е(К) нечетно. Тогда число аффинных
точек четно, и кривая не содержит точек с нуле-
вой у-координатой. Действительно, возможны
случаи, когда ни одна точка не имеет нулевой у-
координаты, одна точка имеет нулевую у-ко-
ординату или три точки имеют нулевую у-коор-
динату. В соответствии с геометрической ин-
терпретацией закона сложения (удвоение точки
определяется касательной к данной точке), уд-
воение точки с нулевой у-координатой дает бес-
конечно удаленную точку. Следовательно, если
предположить, что в группе нечетного простого
порядка г лежит хотя бы одна точка вида (х, 0),
то эта точка должна иметь порядок 2, что при-
водит к противоречию.
Определим квадратичный характер % поля К
так же, как символ Лежандра: %(а) = 1, если а —
квадратичный вычет в поле К; %(о) = -1, если
а— квадратичный невычет в поле К, %(0) = 0.
Тогда %(Дх)) Ф 0 для всех х. Следовательно, при
нечетном числе точек каждый элемент х е К яв-
ляется х-координатой некоторой точки, принад-
лежащей одной и только одной из скрученных
кривых у2 =fix) или у2 = -Дх). Встраивание тек-
ста в координату точки сводится к нахождению
обратимого отображения подмножества точек
скрученной кривой у2 = -Дх) в исходную кривую
Рассмотрим такое отображение для поля К=
характеристики 2. В этом случае криптографиче-
ски стойкой является только кривая Е(Е^,) с урав-
нением у2 + ху = х3 + Ах2 + В, где Тг(Л) g F2; для
перехода к скрученной кривой нужно изменить
Тг(Л). Уравнение у2 + ху + С = 0 заменой пере-
менной у <— ху сводится к уравнению
у2 + у + С/х2 — 0. Уравнение у2+у + С имеет
решение в тогда и только тогда, когда
Тг(О = 0 [5].
Пусть (F7:F2) = п — нечетное число (как пра-
вило, в криптографии используются именно та-
кие поля характеристики 2). В этом случае
Tr(l) = 1 и Тг(х + 1) = Tr(x) + 1. Если для текста
х е выполняется равенство Тг(х + А + Вх~2) - 0,
то х является х-координатой точки кривой E(F7).
Если Tr(x + А + Вх~2) = 1, но при этом
Тг(х) = Тг(Л), то х заменяется элементом х' таким,
что Вх'~2 = 1 + Вх 2. Поделив обе части последне-
го равенства на В, получаем: 1/х'2 = l/R+1/х2 . В
поле характеристики 2 любой элемент является
квадратичным вычетом. Отсюда находим равен-
ство 1/х' = 1/-/б + 1/х, определяющее замену пе-
ременной. При этом в силу того, что
(В“ ) = В2 = В, получаем \В~В2
Условие Тг(х) = Гг(Л) выполняется, если сво-
бодный член полинома х = x(t) не несет инфор-
мационного содержания и может быть выбран
любым. Для изменения Тг(х) достаточно заменить
х нах + 1.
Соответствие х«-»х' является взаимно одно-
значным и легко вычислимым.
Пример 15.6.1. Встраивание открытого текста
в координату точки кривой над F32.
Пусть эллиптическая кривая E(F32) задана
уравнением у2 + ху = х3 + Г, поле F32 задано поли-
номом t5 + Д + 1. Кривая имеет 16 точек. Откры-
тый текст /3 + 1 не является х-координатой точки
кривой. Вычисляем -Jt = ti6 = t4 + /3 +1 +1. За-
меняем элемент г +1 на элемент, заданный
11 1
уравнением — = ------з-----+ . Отсюда
х t +1 +1 +1 t +1
получаем необходимую х-координату точки кри-
вой: х = Д + ? + ? + / + 1.
15.6.2. Аналог криптосистемы RSA
На эллиптические кривые над кольцом вычетов
ИЛ для составного числа п =pq, где р, q — раз-
личные простые числа, можно переложить боль-
шинство криптографических протоколов, первона-
чально разработанных в рамках системы RSA.
Эллиптические кривые вида у2 = х3 + В (mod /?)
при р = 5 (mod 6) и у2 = х3 + Ах (mod р) при р = 3
(mod 4) имеют порядок группыр + 1 (см. п. 15.3).
Поэтому эллиптические кривые E(ZJri£) вида
у2 = х3 + В (modri) при p~q~5 (mod6) и
у2 = х3 + Ах (mod ri) при р = q = 3 (mod 4) имеют
порядок группы (р+ 1)(? + 1). Оригинальная сис-
тема RSA имеет порядок группы <р(и) = (р- IX?- 1)-
Поэтому такие эллиптические кривые позволяют
строить криптосистемы, аналогичные RSA. Если
316
безопасность системы RSA связана с вычислением
функции ср(тг), то в случае эллиптических кривых
она связана с нахождением числа (р + l)(g + 1).
Рассмотрим аналог шифрования с открытым
ключом на эллиптической кривой у2 = х3 + В
(mod и). Открытым ключом является пара (и, е),
секретным— показатель d=e~l (mod(p+ l)(g + 1)).
Для зашифрования сообщения т отправитель ге-
нерирует случайное положительное число у < п,
вычисляет шифрограмму, умножая точку
(т, у) е £(Z/«Z) на показатель е и посылает шиф-
рограмму получателю. Получатель умножает по-
лученную точку на число </, находит точку (т, у) и
восстанавливает сообщение т. Отметим, что в
этом случае длина шифрограммы вдвое больше
длины открытого текста, при этом уравнение эл-
липтической кривой не фиксировано.
Аналогичный протокол может быть использо-
ван и в случае эллиптической кривой у2 = х3 + Ах
(mod п). Для удвоения точки нужно предвари-
тельно вычислить коэффициент А. Это вычисле-
ние не требует разложения числа п и может быть
выполнено расширенным алгоритмом Евклида.
Эллиптические кривые £(Z/wZ) позволяют
строить протоколы, аналогичные протоколам
Рабина и Фиата-Шамира. При этом аналогом
задачи извлечения квадратного корня в кольце
Z/«Z является следующая задача: найти на эл-
липтической кривой все точки, удвоение кото-
рых дает точку ±Р с заданной х-координатой. В
силу изоморфизма £(Z/z?Z) = £(F,,) © £(FV) для
каждой из кривых ДЕД, £(F„) существует по две
таких точки (одна для Р и одна для -Р). Объеди-
нение этих точек по китайской теореме об остат-
ках дает четыре точки кривой £(Z/«Z). Протоко-
лы Рабина и Фиата-Шамира на эллиптической
кривой строятся так же, как и соответствующие
оригинальные протоколы с заменой элементов
кольца HJriZL на точки кривой EQLIriZPj и опера-
ции умножения в 7UnZ- на операцию сложения
точек кривой.
В общем случае использование алгоритмов
RSA, Рабина, Фиата-Шамира и т. п. для эллип-
тических кривых ведет к появлению отличий от
соответствующих оригинальных протоколов в
части их безопасности. Первое отличие связано
с проблемой сводимости к соответствующей
массовой задаче выбора. Оригинальный прото-
кол Фиата-Шамира основан на задаче разложе-
ния числа п, которая полиномиально эквива-
лентна задаче вычисления порядка группы об-
ратимых элементов кольца TJnZ.. В случае же
эллиптических кривых этот протокол основан
на сложности разложения порядка группы точек
эллиптической кривой £(Z/wZ). Задача вычис-
ления порядка группы точек полиномиально
сводится к задаче разложения числа п. Действи-
тельно, для известных р и q можно найти алго-
ритмом Чуфа число точек для каждой из кривых
£(Ер) и £(F„) и по китайской теореме об остат-
ках восстановить число точек кривой £(Z/wZ).
Обратная полиномиальная сводимость пробле-
матична. Отсюда следует, что для нахождения
#£(Z/«Z) могут использоваться методы, отлич-
ные от разложения числа п, то есть протокол
Фиата-Шамира на эллиптической кривой по-
тенциально более слабый (с точностью до
сложности алгоритма Чуфа).
Второе отличие имеет алгебраическую при-
роду и связано с тем, что группа £(Z/rZ) может
быть циклической, тогда как группа (Z/rZ) цик-
лической быть не может. Например, группа
£(Z/hZ) циклична, если #£(0РД и #£(F„) являются
различными простыми числами.
Поэтому механическое переложение протоко-
лов из (Z//?Z) на эллиптические кривые £(Z/z?Z)
должно сопровождаться их криптографическим
анализом.
Использование особой кубики С: у2 = х2(х + 1)
позволяет построить криптосистему, изоморф-
ную криптосистемам RSA, Рабина, Фиата-
Шамира. Изоморфизм \|/ группы неособых точек
этой кубики и группы (Z/hZ) легко вычислим в
обе стороны и задается формулами:
; v ‘О)=
- 4z - 4z(z -1)
? +1)2 ’ (z+ I)3
Для зашифрования информации можно ис-
пользовать как арифметику кубических кривых,
так и следующую цепочку действий: вычисление
изоморфизма C(Z/z?Z) -> (Z/hZ) , возведение в
степень, вычисление обратного изоморфизма
(Z/hZ)‘ -> C(Z/hZ).
15.6.3. Установление сеансового ключа
Адаптация протокола Диффи-Хеллмана для
установления сеансового ключа осуществляется
почти очевидным образом. Два абонента А и В
договариваются о (несекретных) параметрах:
безопасном уравнении эллиптической кривой
£(£) над конечным полем К и точке Q, образую-
щей группу большого простого порядка г. Дого-
воренность может быть предварительной, или
эллиптическая кривая может создаваться непо-
средственно в ходе сеанса связи. В последнем
случае абонент, который получает параметры
кривой, может эффективно проконтролировать
ее безопасность, проверив соответствие требо-
ваниям п. 11.7.
Для установления сеансового ключа абонент
А генерирует случайное число а, вычисляет точ-
317
ку aQ и посылает ее абоненту В. Абонент В гене-
рирует случайное число Ь, вычисляет точку bQ и
посылает ее абоненту А. Затем А умножает точку
bQ на а, В умножает точку aQ на Ъ, и таким об-
разом оба получают точку abQ, которая опреде-
ляет сеансовый ключ.
Если нарушитель может подавлять подлин-
ные сообщения и формировать вместо них свои,
то протокол Диффи-Хеллмана допускает «атаку
гроссмейстера». При этом нарушитель устанав-
ливает свой сеансовый ключ с абонентом А, вы-
давая себя за В, и свой сеансовый ключ с абонен-
том В, выдавая себя за А, после чего в ходе сеан-
са может оставаться незамеченным. Для этого он
расшифровывает шифрограмму, отправленную
от А к В, на ключе, установленном с А, зашифро-
вывает полученный текст на ключе, установлен-
ном с В, и отправляет новую шифрограмму або-
ненту В.
Для исключения таких атак можно использо-
вать цифровую подпись. При этом ключ подписи
может обладать значительно меньшей стойко-
стью, то есть основываться на задаче меньшего
размера, чем сеансовый ключ.
15.6.4. Шифрование
Бесключевое шифрование на эллиптической
кривой в соответствии с протоколом Месси-
Омуры выполняется следующим образом. От-
правитель А и получатель В, как и в протоколе
Диффи-Хеллмана, договариваются о (несекрет-
ном) безопасном уравнении эллиптической кри-
вой Е(К) таком, что группа Е(К) содержит под-
группу’ большого простого порядка г ~ #Е(Ку
Для передачи зашифрованного сообщения т
отправитель А встраивает сообщение в точку R
эллиптической кривой, например, так, чтобы не-
сколько старших разрядов х-координаты точки R
в совокупности давали т и чтобы порядок точки
R делился на г. Затем он генерирует случайное
число а, обратимое в кольце Z7#E(X)Z, вычисляет
точку aR и посылает ее получателю В. Тот, в
свою очередь, генерирует случайный показатель
Ь, обратимый в кольце 2U#E(Kj2L, вычисляет точ-
ку b(aR) и возвращает ее отправителю. А умно-
жает полученную точку на а и посылает точку
a]baR = bR получателю. В умножает получен-
ную точку на Ь~} и из точки b~]bR = R выделяет
сообщение т.
Вместо сообщения т отправитель может пе-
редать сеансовый ключ, на котором зашифрова-
но сообщение.
В общем случае протокол Месси-Омуры не
обеспечивает имитозащиты, а если передается
сеансовый ключ, то отсутствует и конфиденци-
альность. Если нарушитель может подавлять не-
которые шифрограммы и формировать собст-
венные, то здесь возможна та же «атака гросс-
мейстера», что и в протоколе Диффи-Хеллмана,
для защиты от которой может использоваться
цифровая подпись.
Рассмотрим протокол шифрования с откры-
тым ключом [9, 10], основанный на протоколах
Диффи-Хеллмана и Эль-Гамаля.
Открытый ключ зашифрования включает в
себя кривую Е(К), образующую Q простого по-
рядка г и точку Р = IQ. Секретным ключом рас-
шифрования служит показатель I. Кроме того,
общедоступной является хэш-функция Ь. Для
зашифрования сообщения т, 0 <т < г - 1, от-
правитель генерирует случайное число к,
2<к<г—\, вычисляет точку R = kQ, значение
хэш-функции h(kP) и часть шифрограммы:
с = т + h(kP) (mod г). Здесь можно использовать
и сложение по модулю 2, если разрядность зна-
чения хэш-функции соответствует разрядности
числа г. Зашифрованный текст представляет со-
бой пару (R, с).
Для расшифрования получатель вычисляет
точку IR - l(kQ) = k(lQ) = кР, значение hflR) и
находит сообщение т = с — h(lR) (mod г).
Значение h(lR) играет роль гаммы шифра,
поэтому точка R не должна использоваться
дважды, так как это может привести к бесклю-
чевому дешифрованию одного блока сообщения
(но не к вскрытию ключа, в отличие от прото-
колов цифровой подписи). Хэш-функция и
арифметика по модулю г при шифровании не-
обходимы для перемешивания и практического
устранения избыточности, имеющейся в коор-
динатах точки эллиптической кривой. Эта из-
быточность обусловлена тем, что длина двух
координат точки равна 21og2</, а длина мощно-
сти множества точек— log2r, причем, как пра-
вило, г по длине не больше q.
Этот протокол осуществляет шифрование в
режиме, аналогичном режиму простой замены
симметричного шифра, но может быть очевид-
ным образом преобразован и для шифрования в
режиме гаммирования (см. п. 19.1.2). Для этого
можно, например, использовать х-координату
точки кР в качестве исходной информации для
формирования псевдослучайной последователь-
ности, например, с помощью обычного симмет-
ричного шифра, у которого стартовый вектор
фиксирован, а ключ определяется точкой кР = IR.
Эллиптические кривые над конечными поля-
ми позволяют реализовать симметричное шиф-
рование. Алгоритм симметричного шифрования
на эллиптической кривой — не шенноновский,
способ его описания и анализа безопасности не-
318
типичен для большинства симметричных шиф-
ров. Несмотря на то, что данный алгоритм про-
игрывает по скорости обычным симметричным
шифрам, он может представлять интерес для ис-
пользования совместно с корректирующим ко-
дированием.
Секретным ключом являются уравнение эл-
липтической кривой /f(SFp), характеристика поля р
и образующая точка Q, причем #E(FP) =р. Откры-
тый текст представляет собой часть (несколько
младших разрядов) х-координаты некоторой точ-
ки Р & EQFp); шифртекст — логарифм I этой точки
относительно точки Q. Для обеспечения имито-
защиты старшие разряды х-координаты точки Р
должны иметь произвольный заранее определен-
ный вид, который должен храниться в секрете на
приемной и передающей сторонах.
Логарифм I при зашифровании вычисляется с
помощью логарифмической производной (см.
п. 7.11). Открытый текст по логарифму вычисля-
ется умножением точки Q на число I. Сложность
алгоритма зашифрования и расшифрования рав-
на O((logp)3).
Этот способ шифрования не претендует на
практическое применение и просто иллюстриру-
ет принципиальную возможность использования
эллиптических кривых для шифрования и коди-
рования.
Эллиптическая кривая со свойством #Е^Р^ —р
может быть легко найдена алгоритмом 15.4.1 или
15.4.2.
Искажение одного бита в процессе передачи
шифрограммы соответствует сложению точки,
представляющей открытый текст, с точкой вида
±2'Q для некоторого натурального числа I. Факт
искажения принятого текста выявляется путем
его расшифрования и проверки того, что стар-
шие биты х-координаты имеют заданный вид.
Для исправления одиночной ошибки необходимо
к найденной точке, представляющей открытый
текст, прибавить точку вида +2‘Q.
15.6.5. Цифровая подпись
На эллиптических кривых можно реализовать
протоколы подписи, аналогичные протоколам
Эль-Гамаля, Шнорра и др. (см. гл. 13).
В протоколе подписи Эль-Гамаля открытый
ключ проверки подписи содержит уравнение эл-
липтической кривой Е(К), образующую Q про-
стого порядка г и точку Р = IQ. Секретным клю-
чом формирования подписи является показатель
/. Кроме того, в протоколе подписи используется
хэш-функция h и функция f
Для подписи сообщения т отправитель вы-
числяет хэш-функцию h(m), вырабатывает слу-
чайное целое число к, 0 <к<г, вычисляет точку
R = kQ, R = (х7{, yR), и находит число .$ решением
сравнения
h(m) = IflJE) + ks (mod г). (15.6.1)
При этом необходимо, чтобы выполнялось
неравенство flR) Ф 0 (mod г), в противном случае
нужно выбрать другое число к (если f(R) = О
(mod г), то подпись не зависит от персонального
ключа).
Подписанное сообщение представляет собой
тройку (m, R, s). При этом можно сократить объ-
ем подписи, задав вместо R только координату xR
и знак координаты yR (0, если yR < р]2, и 1, если
yR> р/2). Тогда при проверке подписи необхо-
димо будет восстановить координату yR решени-
ем квадратного уравнения в поле К.
При проверке подписи левая и правая части
сравнения (15.6.1) используются в качестве пока-
зателей. Получатель сначала восстанавливает
точку R и убеждается, что она лежит на эллипти-
ческой кривой Е(К), а затем проверяет равенство
h(m)Q =flR)P + sR.
Как и в оригинальном протоколе Эль-Гамаля,
использование показателя к дважды или одно-
кратное использование известного показателя к
приводит к вскрытию ключа I. В качестве функ-
ции ДА) могут использоваться функции от коор-
динат: xR, yR, xR + yR и т. п.
Сравнение (15.6.1) требует, чтобы хэш-
функция была стойкой в части нахождения кол-
лизий, причем нарушитель может заготавливать
коллизии до начала формирования подписи. Ес-
ли в сравнении (15.6.1) связать сообщение т и
точку R через хэш-функцию (заменить h(m) на
/?(ш||А)), то заготовка коллизий до момента под-
писи станет невозможной.
Протокол подписи стандарта ГОСТ Р 34.10-2001
предусматривает использование эллиптической
кривой у2 =fix) над простым полем (F/7 со сле-
дующими параметрами:
1) р — простое число длины 256 бит;
2) полином Дх) не имеет кратных корней (дис-
криминант полинома f отличен от нуля по
модулю рУ
3) /-инвариант кривой отличен от 0 и 1728;
4) число точек ЙДВР/,) имеет простой делитель г
длины от 254 до 256 бит;
5) #Ефр)*р-
6) рк Ф 1 (mod/') для к= 1, 2,..., 31.
319
Выбор эллиптических кривых по стандарту
США ECDSS отличается тем, что не преду-
смотрено ограничение по п. 3 (можно использо-
вать кривые с j = 0 и 1728); число г должно
иметь длину 160 бит; разрешается использовать
эллиптические кривые над полями характери-
стики 2.
В основу протокола электронной цифровой
подписи ГОСТ Р 34.10-2001 положен протокол
Эль-Гамаля. Пусть т— подписываемое сообще-
ние, h— хэш-функция по ГОСТ Р 34.11-94 (см.
п. 19.12), {E((Fp), Q, г}— параметры цифровой
подписи; число / — секретный ключ, P = IQ —
открытый ключ.
Протокол 15.6.1. Схема подписи ГОСТ
Р 34.10-2001.
Вход отправителя. Секретный ключ I, пара-
метры подписи, сообщение т.
Вход получателя. Открытый ключ Р, пара-
метры подписи.
Результат. Формирование и проверка подписи
для сообщения т.
Метод.
Для формирования подписи для сообщения т
отправитель выполняет следующие действия.
1. Вычисляет хэш-функцию е <— h(m) (mod г);
при е = 0 полагает е <— 1.
2. Вырабатывает случайный показатель к,
0<к<г, и вычисляет точку R <— kQ,
R = (xR, yR), причем xR 0 (mod г).
3. Вычисляет часть подписи8
5 <— {lxR + кё) (mod г), (15.6.2)
причем 5 Ф 0.
Подписанное сообщение представляет собой
тройку (т, xR (mod г), s').
Для проверки подписи получатель выполняет
следующие действия.
1. Проверяет условия 0 < xR (mod г) < г и 0 < 5 < г.
2. Вычисляет е <— Ыт) (mod г); при е = 0 пола-
гает е <— 1.
3. Вычисляет точку
R' <— (.$<? '(mod r))Q - (хце~1 (mod r))P.
4. Проверяет сравнение xR’ = xR (mod г). Если
оно выполняется, то подпись верна.
Если в протоколе подписи используется эл-
липтическая кривая с комплексным умножением
на -J-2 и г = рр = с2 + 2d2, то в (15.6.2) поле Fr
8 В стандарте ECDSS вместо уравнения (15.6.2)
используется s = k\lxR + е) (mod г).
можно задать в виде Z[V^2]/(p), что позволит
использовать систему счисления с основанием
V— 2 и заменить операцию удвоения точек ком-
плексным умножением [7]. В этом случае число
модульных умножений при проверке подписи
может быть сокращено примерно в 1,7 раза по
сравнению с «традиционной» арифметикой эл-
липтических кривых.
Безопасность протокола подписи непосредст-
венно зависит от сложности обращения хэш-
функции и сложности вычисления коллизий
хэш-функции, так как в первом случае можно
вычислить сообщение для имеющейся подписи, а
во втором — заготовить пару сообщений с оди-
наковыми значениями е, подписать одно из них,
а потом заменить одно сообщение другим.
Сложность вычисления коллизий хэш-функции
методом Полларда равна Se = О(у[г) . Однако
сложность вычисления коллизий шаговой функ-
ции хэширования, при помощи которой вычис-
ляется h, равна (см. п. 19.12).
Этот протокол предполагает жесткие требо-
вания к генератору случайных чисел (см.
и. 13.2.1).
Для вскрытия секретного ключа подписи дос-
таточно или предсказать случайное число, кото-
рое появится в будущем, или найти случайное
число, которое использовалось ранее. Например,
если нарушитель получил доступ к алгоритмиче-
скому генератору случайных чисел, допускаю-
щему восстановление предшествующих состоя-
ний из текущего состояния, то все электронные
цифровые подписи, сформированные на дейст-
вующем ключе, должны считаться недействи-
тельными! Поэтому если к компьютеру, реали-
зующему формирование подписи, возможен не-
санкционированный доступ (например, при от-
правке компьютера в ремонт в результате по-
ломки) и генератор случайных чисел реализован
алгоритмически, то алгоритм генерации случай-
ных чисел должен быть вычислительно необра-
тимым.
Для нахождения секретного ключа / по от-
крытому ключу достаточно решить одну из задач
дискретного логарифмирования — найти сам
показатель I по точкам Q, Р или один из показа-
телей к по точкам Q и R (xR легко восстанавлива-
ется по xR (mod г), a yR можно вычислить как
\]f(xR) (modр)). Таким образом, требования,
предъявляемые к генератору случайных чисел,
оказываются более жесткими, чем к генератору
ключей: нарушителю все равно, что искать: к или
/, но повтор числа к в течение срока действия
320
ключа приводит к вскрытию ключа I.9 Таким об-
разом, справедливо следующее утверждение.
Теорема 15.6.1. Энтропия10 11 ключа формиро-
вания подписи ГОСТ Р 34.10-2001 не превышает
энтропии случайного числа, вырабатываемого
генератором. 1
Пример 15.6.2. Неудачная реализация генера-
тора случайных чисел.
Пусть генератор вырабатывает числа вида
к1+у = ик, + v (mod г), причем параметры и, т, а
также два последовательных подписанных со-
общения (ту, %] (mod г), sy) и (m2, -Ъ (mod г), s2)
известны нарушителю. Соответствующие урав-
нения формирования подписи имеют вид:
л , = Ъсу + key (mod г), s2 s lx2 + (ик + v)<?2 (mod г). В
этих уравнениях все параметры, кроме к и I, из-
вестны нарушителю. Поскольку уравнения ли-
нейны относительно указанных неизвестных,
секретный ключ I может быть вскрыт решением
системы двух линейных уравнений.
Аналогично, если генератор реализует рекур-
рентное соотношение
=g(^)(modr),
где g— алгебраическая функция, то задача
вскрытия ключа / сводится к решению системы
алгебраических уравнений над полем (F,.:
= (1хцх + key) (mod г), s2 s (lxRi + g(k)e}) (mod г)
относительно к, I. Поскольку переменная I может
быть исключена, задача вскрытия ключа сводит-
ся к решению уравнения вида g(k) = ак + b
(mod г) при известных а, Ъ. Отметим, что алгеб-
раические уравнения над конечными полями, в
отличие от уравнений над С, решаются сравни-
тельно легко.
Очевидно, что это качество присуще обоб-
щенному протоколу Эль-Гамаля над любой груп-
пой вычислимого простого порядка. В
Сложностная неоднородность протокола
ГОСТ Р 34.10-2001 определяется пп. 1-5 слож-
9 Отсюда следует, что если пользователю систе-
мы, в которой применяется электронная цифровая
подпись, разрешается генерировать случайные числа
к в ходе формирования подписи, то запрет самому
генерировать секретные ключи / формирования под-
писи является бессмысленным.
10 Имеется в виду колмогоровская энтропия.
11 Отсюда вытекает потенциальная уязвимость
устройств, реализующих электронную цифровую
подпись, по отношению к атакам, провоцирующим
различного рода сбои компьютера с целью нарушить
безопасную работу генератора случайных чисел.
ностной неоднородности протокола Эль-Гамаля
(см. п. 13.2.1 и работу [9]) и равна 5. Можно счи-
тать, что стойкость подписи не превышает ми-
нимума сложностей дискретного логарифмиро-
вания, нахождения используемого случайного
числа, обращения хэш-функции, вычисления
коллизий хэш-функции.
Сложностную неоднородность протокола
подписи можно уменьшить, если генератор слу-
чайных чисел реализовать алгоритмически так,
чтобы его безопасность основывалась на задаче
дискретного логарифмирования на этой же эл-
липтической кривой (см. п. 15.6.8).
Протокол цифровой подписи Шнорра на эл-
липтической кривой Е(К) имеет следующий вид.
Открытый ключ проверки подписи содержит
уравнение эллиптической кривой Е(К), обра-
зующую Q простого порядка г и точку Р = IQ.
Секретным ключом формирования подписи яв-
ляется показатель I. Здесь тоже используется
хэш-функция h.
Для подписи сообщения т отправитель выра-
батывает случайное целое число к, 0 <к<г, вы-
числяет точку R = kQ и хэш-функцию е = h(m, R),
проверяет, что е Ф 0 (mod /') (в противном случае
нужно выработать другое число Л), а затем нахо-
дит число
5 = 1е + к (mod г). (15.6.3)
Подписанное сообщение представляет собой
тройку (т, е, s).
Для проверки подписи получатель вычисляет
точку R' = sQ - еР (то есть использует левую и
правую части сравнения (15.6.3) в качестве пока-
зателей) и хэш-функцию е' = h(m, R') и проверяет
равенство е = е' (mod г).
Протокол Шнорра допускает модификации.
Например, при сохранении сравнения (15.6.3)
подписанное сообщение может представляться
тройкой (т, s, R). Точку R можно задавать х-
координатой и знаком у-координаты, как и в
протоколе Эль-Гамаля. Тогда при проверке под-
писи получатель сначала должен убедиться, что
точка R лежит на кривой, затем вычислить хэш-
функцию е = h(m, R) и проверить равенство
sQ = еР + R.
Эллиптические кривые позволяют реализо-
вать скрытый канал передачи информации в
схеме цифровой подписи Эль-Гамаля, Шнорра,
ГОСТ Р 34.10-2001. Как и раньше, рассмотрим
протокол цифровой подписи, в котором участ-
вуют три стороны: отправитель, получатель и
контролер. Протоколы формирования подписи
на эллиптической кривой предполагают этап ге-
нерации отправителем случайного показателя к,
неизвестного другим лицам, под видом которого
321
можно создавать информацию и передавать ее по
каналу, скрытому в уравнении формирования
подписи.
Например, для протокола Эль-Гамаля расшиф-
рование информации, переданной по скрытому
каналу, осуществляется решением сравнения
к = (Л(т) - IflRJjs4 (mod г).
Данное сравнение всегда имеет единственное
решение, которое может быть вычислено с поли-
номиальной сложностью.
Скрытый канал может быть устранен, если в
генерации точки R будет участвовать контролер.
В этом случае этап формирования подписи в
протоколе Эль-Гамаля выглядит так.
1. Отправитель генерирует показатель к, вы-
числяет точку R = kQ и направляет ее кон-
тролеру.
2. Контролер запоминает точку R, генерирует
случайный показатель к и направляет его от-
правителю.
3. Отправитель вычисляет показатель к\=кк'
(mod г), вычисляет точку R\ = kiQ, вычисляет
подпись s решением сравнения h(m) = IflRi) +
+ кр (mod г) и передает подписанное сообще-
ние (т, Ri, s) контролеру.
4. Контролер проверяет, что подпись соответ-
ствует сообщению и что R\ = k'R. Если про-
верки выполнены успешно, то он передает
сообщение получателю.
На эллиптических кривых можно строить и
специальные протоколы цифровой подписи, в
том числе протокол «неоспоримой» подписи.
Общим открытым ключом для этого протокола
является эллиптическая кривая Е(К) и образую-
щая точка Q простого порядка г. Персональным
секретным ключом является пара показателей и и
v, персональным открытым ключом— пара то-
чек U, Т, где U= uQ, Т~ wQ.
Подписью для сообщения m является точка S
такая, что выполняется равенство S = vh(m)Q, где
/?(щ) — значение хэш-функции для аргумента т.
Для проверки подписи участники протокола
выполняют следующие действия.
1. Получатель сообщения проверяет, что вы-
полняются условия 5 е Е(К) и rS = Рт, и по-
сылает отправителю запрос, содержащий па-
ру точек Z = aS + ЬТ, Z' = cS + dT для случай-
ных а, Ь, с, d.
2. Отправитель умножает обе точки запроса на
число г-1 (mod г): W = v~}Z, W' = v~1Z' и посы-
лает (IV, W) получателю.
3. Получатель проверяет равенства W= ah(m)Q +
+ bU и W = ch(m)Q + dU Если они выпол-
няются, то результат: подпись подлинная. В
противном случае получатель вычисляет две
точки: C = c(W-bU) и D = a(W'-dU). Если
С = D, то результат: подпись недействитель-
на, иначе результат: отправитель лжет (на-
рушает протокол).
Корректность этого протокола основана на
следующих равенствах:
Z = aS + ЬТ= avh(m)Q + buvQ',
W= v-1Z = ah(m)Q + buQ-,
c(W- bU) - cah(ni)Q + cbU- cbU= cah(m)Q;
Z’ = cS + dT= cvh(m)Q + duvQ',
W' = i“’Z' = ch(m)Q + duQ-,
a(W — dU) = ach(m)Q + adU- adU= achQn)Q.
15.6.6. Опознавание, канал co стиранием
и доказательства с нулевым разглашением
Эллиптические кривые позволяют решать за-
дачу (диалогового) опознавания. Открытым
ключом (информацией верификатора) в соответ-
ствующих протоколах является эллиптическая
кривая Е(К), образующая точка Q большого про-
стого порядка г и точка Р такая, что Р = 1Q. Сек-
ретным ключом претендента является логарифм
1. Если логарифм 1 известен только одному из
участников протокола, то можно реализовать
шифрование с открытым ключом, цифровую
подпись и диалоговые доказательства с нулевым
разглашением. Если логарифм не известен ни
одному из участников протокола, то можно реа-
лизовать канал со стиранием.
Протокол опознавания, основанный на шиф-
ровании с открытым ключом, имеет следующий
вид. Верификатор вырабатывает случайный
текст, зашифровывает его и посылает претенден-
ту для расшифрования (см. п. 15.6.4). Претендент
расшифровывает текст и возвращает верифика-
тору. Верификатор сравнивает полученный текст
с исходным; в случае совпадения опознавание
считается успешным.
Этот протокол допускает атаки со стороны
верификатора. Предположим, что число точек
эллиптической кривой имеет вид #Е(К) = р\...р,г,
где pt— малые различные простые числа. Тогда,
отступая от установленного протокола зашифро-
вания Эль-Гамаля, верификатор выбирает обра-
зующую Q] порядка pi и посылает претенденту
пару (ci, Qi), где щ — шифрограмма, найденная с
помощью точки Qi для произвольного текста т}.
По полученному от претендента тексту
mi = ci - h(lQi) (mod г) верификатор перебором
322
по множеству {0, 1, ...,р\ - 1} находит значение
1 (modу?]), поскольку h(lQ{) может принимать
лишь р\ возможных значений. При следующем
опознавании верификатор точно так же находит 7
(mod р2) и восстанавливает по китайской теореме
об остатках 7 (mod p\Pi) и т. д. Действуя таким
образом, верификатор может получить дополни-
тельную информацию о ключе претендента.
Для затруднения указанной атаки претенден-
ту следует проверять, что точка R, полученная от
верификатора, лежит на кривой Е(К) и что вы-
полняется равенство rR = Рт.
Протокол опознавания, основанный на циф-
ровой подписи, выглядит так. Верификатор вы-
рабатывает случайный текст и посылает его
претенденту для подписи. Претендент выраба-
тывает подпись (см. п. 15.6.5) и возвращает
подписанное сообщение верификатору. Тот, в
свою очередь, проверяет подлинность подписи.
Если подпись подлинная, то опознавание счита-
ется успешным.
Для опознавания на основе диалоговых дока-
зательств с нулевым разглашением можно ис-
пользовать следующий протокол.
Протокол 15.6.2. Опознавание на основе диа-
логовых доказательств с нулевым разглашением.
Вход верификатора. Эллиптическая кривая
Е(Ку, образующая точка Q большого простого
порядка г; точка Р е Е(К).
Вход претендента. Эллиптическая кривая
Е(Ку, образующая точка Q большого простого
порядка г; точка Р е Е(Ку, число 7 такое, что
P = 7g.
Выход верификатора. Решение о том, что пре-
тендент знает логарифм 7, с вероятностью ошиб-
ки первого рода не более 0,5.
Метод.
1. Претендент генерирует случайный показатель
к, вычисляет показатель к =kl (mod г) и точку
R = кР и посылает R верификатору.
2. Верификатор убеждается, что rR = Pa и
R Ф Рт генерирует случайный бит (0 или 1),
запоминает его и посылает претенденту.
3. Если претендент получает 0, то он предъяв-
ляет верификатору показатель к, если полу-
чает 1, то предъявляет показатель к.
4. Верификатор проверяет, что R = кР, если на
шаге 2 он посылал 0, или что 2? = к Q, если он
посылал 1. Если проверка проходит успешно,
то результат: претендент знает логарифм I. В
противном случае результат: претендент не
знает логарифм I.
Претендент при генерации точки R не знает,
какой бит — 0 или 1 — он получит, поэтому, не
зная логарифм 7, он может успешно жульничать с
вероятностью 0,5. Протокол повторяется необ-
ходимое число раз т, для того чтобы вероят-
ность 2~'" обмана со стороны претендента была
гарантированно мала.
Рассмотрим пример передачи информации со
стиранием, основанный на задаче дискретного
логарифмирования в группе точек эллиптиче-
ской кривой. Для получения точки P-1Q такой,
чтобы логарифм 7 не был известен ни одному из
участников протокола, достаточно сгенерировать
произвольную точку Р’ е Е(К) и найти
гдеТУ = #ВД,г = #<0.
Для получения открытого и секретного клю-
чей Рв и Sb получатель выбирает случайный бит
i е {0, 1} и случайное число 7, е {0, 1, ..., г - 1} и
вычисляет R, - 1,Q, R\-, = Р - l,Q.
Открытым ключом Рв служит пара (Д;,/?,),
секретным ключом Sb — пара (7, /,). Отправитель
может проверить правильность открытого клю-
ча: Ro + Ri = Р. Благодаря тому, что дискретный
логарифм от Р неизвестен, получатель не может
знать оба логарифма: от /?0 и от R\. Кроме того,
открытый ключ не несет информации о том, ка-
кой из дискретных логарифмов — от Ro или от
7?i — знает получатель, так как пары (Ro, /?|) рас-
пределены в группе точек кривой равномерно.
В основу безопасности положен тот же прин-
цип, что и в протоколе Диффи-Хеллмана: если
известны точки aQ, bQ, то точку abQ вычислить
трудно.
Передача со стиранием пары текстов, пред-
ставленных в виде положительных чисел (/0, 6),
каждое из которых не превышает г - 1, выполня-
ется следующим образом.
Отправитель выбирает пару случайных пока-
зателей ко, кл е {0, 1,..., г - 1}, вычисляет точки
So = koQ, Si = k]Q и посылает их получателю. За-
тем отправитель вычисляет То = koRo, Д — kR],
находит суммы по модулю 2 двоичных векторов:
,$о = /о + h(TQ), 5i = 7] + 7г(Д) и отправляет 50, 5j по-
лучателю.
Получатель с помощью своего секретного
ключа (z, 7,) раскрывает значение Д, = 7,5, и вы-
числяет значение /, = 5, + /?( Д).
Таким образом, получатель может узнать
только одно из значений t0 или t\ в зависимости
от бита z своего секретного ключа. В соответст-
вии с предположением Диффи-Хеллмана он не
может вычислить второй текст, так как не знает
Д_,. Например, если Rl4 = Ц-iQ, то Д_, = Hfa-iQ,
323
поэтому получатель знает l\-iQ и k_,Q, но не зна-
ет НИ /р/, ни к]Ч.
Для передачи со стиранием пары длинных
текстов можно разбить их на блоки длины не бо-
лее log?(r- 1) бит и каждый раз генерировать
новые ключи Рв и SB. Однако можно поступить
так же, как и в случае простого поля (см. п. 14.4).
Сначала отправитель передает по каналу со сти-
ранием пару коротких текстов to, t}, причем он не
знает, какой из текстов расшифрует получатель.
Затем, используя to, t] как исходную информа-
цию, отправитель генерирует псевдослучайные
последовательности G{tQ, G(jd, состоящие, на-
пример, из младших разрядов элементов после-
довательности t2jQ, t3Q, l*Q, ... . Для передачи
со стиранием пары длинных сообщений (и0, и\)
отправитель направляет получателю суммы по
модулю 2 двоичных векторов: и0 + G(to),
щ + СД/,). Поскольку получатель знает только
один из двух текстов to или t\, он может расшиф-
ровать только одно из зашифрованных сообще-
ний.
На основе задачи логарифмирования в группе
точек эллиптической кривой можно строить и
бездиалоговые доказательства с нулевым раз-
глашением. Чтобы доказать знание логарифма 7
такого, что P = IQ, претендент выполняет сле-
дующие действия:
1) генерирует случайное число k, 1 <к<г-\,
вычисляет к Ik (mod г) и точку R <— кР',
2) генерирует случайный ключ шифрования z
для симметричного алгоритма, зашифровыва-
ет на этом ключе точку R и передает шифро-
грамму по обычному (без стирания) каналу;
3) генерирует случайный бит 7е {0, 1}. Если
i = 0, то передает по каналу с° ключ z и пока-
затель к, а по каналу с1 — ключ z и показа-
тель к. Если i = 1, то меняет местами каналы
с и с1.
Верификатор проверяет, что полученная точ-
ка R лежит на кривой и имеет порядок г. Затем
он проверяет, что R = kP (если получен показа-
тель к) или R = kQ (если получен показатель к).
Выполнение равенства означает, что претендент
знает логарифм 7 с вероятностью 0,5. Протокол
выполняется (параллельно) необходимое число
раз, причем каждый раз с новой парой ключей.
В п. 14.2.4 был приведен протокол доказа-
тельства с нулевым разглашением того, что со-
ставное число и содержит в точности два раз-
личных простых делителя p = q = 3 (mod 4). Од-
нако этот протокол не распознает случай, когда
один из простых делителей входит в п в степени 3.
Эта проблема может быть решена следующим
образом.
Если простые числа р, q выбрать так, чтобы
они имели разложения в виде (15.4.2) при а= 1,
то существуют эллиптические кривые Е^р) и
E£;(F9), имеющие числа точек, соответственно, р
и q. Объединение этих кривых по китайской тео-
реме об остатках даст кривую E(ZJnZP) с числом
точек п. На этой кривой задача логарифмирова-
ния решается методом логарифмической произ-
водной (см. п. 11.3).
Если совместно с составным числом п предъ-
являть сертификат— кривую E(Z7«2Z) с числом
точек п, — то этот сертификат легко может быть
проверен. Если выполняется равенство nQ = Рт и
случайный логарифм может быть найден мето-
дом логарифмической производной, то число п
свободно от квадратов.12
Протокол доказательства может быть реали-
зован по следующей схеме. Претендент предъяв-
ляет верификатору эллиптическую кривую
E(Z/hZ). Претендент совместно с верификато-
ром выбирают х-координату точки кривой, пре-
тендент находит у-координату этой точки и
предъявляет верификатору. Верификатор прове-
ряет равенство nQ = Рт, выбирает произвольный
логарифм 7 > 4п и находит точку Р = 1Q. После
этого он методом логарифмической производной
вычисляет логарифм точки Р и сравнивает с 7.
Протокол может повторяться несколько раз.
Если #E(FP) = Np, то #E(Z/p2Z) = Npp. Дейст-
вительно, число аффинных точек E(FP) равно
Np — 1. Поскольку ненулевой элемент кольца
Тир-'Ё. является квадратом тогда и только тогда,
когда он является квадратом по модулю р, каж-
дая аффинная точка с ненулевой у-координатой
кривой EQEIp27Z) соответствует аффинной точке
кривой E(FP). При этом каждой точке кривой
E(F„) соответствуют р точек кривой E(ZJp'ZLY
Если точка кривой E(FP) имеет нулевую у-
координату, то ей тоже соответствуют р точек
кривой Ep(Z/p2Z). Эти точки имеют одну и ту же
х-координату и р различных у-координат, крат-
ных р.
Бесконечно удаленной точке кривой E(FP) со-
ответствуют р бесконечно удаленных точек кри-
вой E(Z7p2Z). Действительно, рассмотрим про-
ективное уравнение кривой: Y2Z = X3+AXZ2 +
+ BZ3 (mod/?2). При поднятии бесконечно уда-
ленной точки из Fp в ZTp2Z обязательно полу-
чится Z = 0 (mod /?2), в противном случае все три
12 Поскольку верификатор не может сам найти та-
кую кривую, этот протокол обеспечивает не нулевое,
а минимальное разглашение.
324
координаты должны делиться на р, что невоз-
можно (на проективной плоскости над IF;, такой
точки не существует). Поскольку число К долж-
но быть обратимым по модулю р1 (и, следова-
тельно, по модулю р), получаем X3 = О (mod /?2),
то есть Х-координата при Y= 1 может принимать
значения {0,/?, 2р, ...,(р - })р}.
Поэтому #EQ^/pl'7E) = Npp. Группа точек эл-
липтической кривой EQE/p27E) не циклична. С
вероятностью, близкой к 1, вычисленное значение
логарифма 7 не совпадет с истинным значением
(эти значения будут сравнимы по модулю р).
15.6.7. Вычислимая в одну сторону
функция, свободная от коллизий
Эллиптические кривые позволяют строить
вычислимые в одну сторону функции, свободные
от коллизий, с переборной сложностью обраще-
ния. Для эллиптической кривой Е(К) с цикличе-
ской группой (0 большого простого порядка г
функция h:k-> xko, ставящая в соответствие не-
отрицательному целому числу к < г/2 х-коорди-
нату Хю точки kQ, является вычислимой в одну
сторону и не имеет коллизий. Докажем это ут-
верждение.
Очевидно, что эта функция вычислима в пря-
мом направлении с полиномиальной сложно-
стью. Для решения обратной задачи по извест-
ному значению функции, то есть по х-координате
точки kQ, можно с полиномиальной сложностью
вычислить у-координату с точностью до знака
решением квадратного уравнения в поле К и тем
самым найти точку ±kQ эллиптической кривой.
Обращение функции полиномиально сводится к
решению задачи дискретного логарифмирования
в группе точек эллиптической кривой простого
порядка г, при этом в силу неравенства к < г/2
решение единственное. Эта задача является об-
щепризнанно сложной при правильном выборе
кривой. Следовательно, рассматриваемая функ-
ция вычислима в одну сторону.
Поскольку для каждой х-координаты точки
kQ существуют два значения у-координаты, ко-
торые различаются знаком и соответствуют точ-
кам kQ и -kQ эллиптической кривой, и порядок
группы г— простое нечетное число, то в этой
группе не существует точки с нулевой у-
координатой (см. п. 15.6.1). Кроме того, никакие
две точки, кроме kQ и -kQ, не имеют одинако-
вых х-координат. Действительно, в поле К квад-
ратное уравнение не может иметь более двух
корней. Следовательно, для данного х существу-
ет не более двух Значений у, а поскольку х явля-
ется х-координатой некоторой точки эллиптиче-
ской кривой, значений у ровно два. Отсюда за-
ключаем, что функция к-> kQ для 1 < к < г/2
является взаимно однозначной, то есть не имеет
коллизий.
Пусть максимальное значение аргумента рав-
но кт!№. Обращение функции h сводится к вычис-
лению логарифма к и при соответствующем вы-
боре эллиптической кривой имеет сложность
O(^Jkmax). Сложность обращения может быть
сделана переборной, если изменить алгоритм
следующим образом.
Алгоритм 15.6.3. Вычисление функции, сво-
бодной от коллизий, для аргумента длины и бит.
Вход. Параметры функции h — эллиптиче-
ская кривая Е(К) и точка Q большого простого
порядка г, где log2r > 2и + 2; аргумент функции
h — число к длины п бит; функция f
Выход. Значение h(k).
Метод. '
1. Вычислить точку kQ.
2. Положить е <-fikQ) (mod 2").
3. Найти точку R <- (2пк + e)Q, R = (хд, yR).
4. Результат: h(k) = xR.
Теорема 15.6.2. Функция h, вычисляемая ал-
горитмом 15.6.3, не имеет коллизий.
Доказательство. Координатах1{точкиR = uQ
однозначно определяется показателем и = 2" к + е
с точностью до знака показателя. Поэтому един-
ственно возможная коллизия (щ, и2) Для функции
h задавалась бы уравнением 2”к] + е\ +
+ 2”£2 + е2 = г. Но это невозможно, так как в силу
неравенств log2 к < (log2 г -1)/2 и log2r > 2п + 2
получаем тах(2" кл + ех, 2" кг + е2 ) < г/2 .
Очевидно, что выходными данными алгорит-
ма 15.6.3 может быть пара, состоящая из xR и зна-
ка координаты уК. Используемая на шаге 2 функ-
ция flkQ) может представлять собой хкО, ykQ,
Хко+УкО и т. п.
Задача обращения функции h сводится к вычис-
лению логарифма 2?к + е. Сложность вычисления
логарифма пропорциональна OQ^r), что соот-
ветствует перебору всевозможных значений к.
Пример 15.6.3. Вычисление функции, сво-
бодной от коллизий.
Эллиптическая кривая X(FI27), заданная урав-
нением у1 = х3 + Зх + 23, имеет 131 точку. Пусть
входной аргумент к имеет длину п = 3 бита, а в
качестве функции f используется х-координата
соответствующей точки. Пусть Q = (5, 6). Для
к = 5 получаем 5Q = (17, 62). Тогда е = jQ>Q) =
= 17 s 1 (mod 2"). Точка R определяется показа-
325
телем 2пк + е: Я = (23 5 + 1)£> = 41£> = (112, 13).
Результат: хК = 112.
15.6.8. Генераторы псевдослучайной
последовательности
KojmpoMemaijueii генератора псевдослучай-
ной последовательности назовем несанкциони-
рованный доступ нарушителя к секретным пара-
метрам генератора. Назовем компрометацию яв-
ной, если о случае несанкционированного досту-
па становится незамедлительно известно службе
безопасности, в противном случае компромета-
ция называется неявной.
Эллиптические кривые позволяют реализо-
вать криптографически стойкие генераторы
ПСП. Стойкость в данном случае означает, что
по известным т битам последовательности вы-
числительно невозможно предсказать после-
дующие или вычислить предыдущие биты. Та-
кой генератор является безопасным по отноше-
нию к протоколам шифрования с открытым клю-
чом, электронной цифровой подписи, доказа-
тельств с нулевым разглашением, если его ком-
прометации являются явными. В случае компро-
метации (например, передачи сломанного ком-
пьютера в ремонт) для дальнейшей безопасной
работы нужно сменить параметры генератора.
Для генератора ПСП характерно то, что, на-
чиная с некоторого шага, генерируемая последо-
вательность начинает повторяться. Если генера-
тор реализует отображение хж =fix^, где размер
состояний х, постоянен и составляет к бит, а ото-
бражение f не является взаимно однозначным, то
длина цикла и длина последовательности до вхо-
да в цикл равны <Э(2^2). Если отображение f
взаимно однозначное, то оно задает подстановку
и возникает задача вычисления длины цикла
этой подстановки. Наиболее просто длину цикла
можно вычислить, если генератор ПСП исполь-
зует алгоритмы криптографии с открытым клю-
чом, например, генератор Блюма-Блюма-Шуба
(см. п. 12.4). Аналогичный генератор можно по-
строить и на эллиптической кривой или на вы-
рожденной кубической кривой над £Jri£, где
n=pq — произведение больших простых чисел.
Построим аналогичный генератор ПСП на су-
первырожденной эллиптической кривой. Урав-
нение кривой имеет вид у2 = х3 + Ах (mod п), где
p = q = 3 (mod 4), или у2=х3 + /3 (mod п), где
p = q = 5 (mod 6). Число точек кривой равно
N=(p+ 1Х<7+ !)• Генератор вычисляет х-коор-
динаты точек Р, 2Р, 22Р,... и использует в каче-
стве элементов ПСП один или несколько млад-
z- тт р + 1 q + 1
ших битов этих координат. Числа —- , -
должны быть простыми, а элемент 2 должен
быть образующей для обеих групп
Г_^/»+1_'l Л __ / «-ь 1 __ Л
I £.1 - £ I , I £1 I • ° этом случае клю-
чом для предсказания последующих битов явля-
ется тройка (и, х,у): ключом для вычисления
предшествующих битов является четверка
(р, q, х, у). Длина цикла равна наименьшему об-
щему кратному порядков указанных групп.
Получив доступ к генератору, можно узнать
параметры генератора и текущую точку Т.
Сложность обращения такого генератора (вы-
числение предшествующих точек) основана на
сложности разложения составного числа п. Дей-
ствительно, если разложение известно, то можно
вычислить показатели
к = 2 1 ( mod 1 к = 2 1 f mod
р I 2 J “ I 2
для известной точки Т найти ТР=Т (mod /?),
Tq = T (mod q), вычислить kpTp, kqTq и восстано-
вить предыдущую точку по китайской теореме
об остатках.
Поскольку сложность задачи разложения бы-
стро снижается во времени, размер числа п при-
ходится выбирать большим (несколько килобит).
Предположим, что в информационной систе-
ме возможны только явные компрометации клю-
чей и аппаратуры, то есть обо всех случаях не-
санкционированного доступа к ключам и инфор-
мации, определяющей стойкость ключа, стано-
вится известно. Допустим, что текущее состоя-
ние генератора хранится в компьютере.
В этом случае алгоритмический генератор
случайных чисел для подписи по стандарту
ГОСТ Р 34.10-2001, обеспечивающий мини-
мальную неоднородность, должен удовлетворять
следующим требованиям:
1) задача вычисления случайного числа при из-
вестных параметрах генератора должна быть
безусловно безопасна или эквивалентна за-
даче дискретного логарифмирования на эл-
липтической кривой;
2) вероятность повторения одинаковых случай-
ных чисел в выборке объема 3 • 109 не долж-
на превышать 109;13
13 Этот объем выборки соответствует генерации
десяти подписей каждую секунду круглосуточно в
течение 10 лет, а вероятность выбрана достаточно
малой, чтобы ею можно было пренебречь.
326
3) задача вычисления предыдущего случайного
числа по известному текущему состоянию
генератора должна быть эквивалентна задаче
дискретного логарифмирования на эллипти-
ческой кривой.
Указанным требованиям удовлетворяет сле-
дующий рекуррентный генератор, выполняющий
вычисления на той же эллиптической кривой,
которая используется для цифровой подписи. В
качестве начального состояния можно взять про-
извольную аффинную точку (х, у) эллиптической
кривой. Пусть R, = (х„ у,) — текущая точка кри-
вой. Последующее состояние задается уравнением
Выходом генератора являются несколько
младших битов х-координаты очередной точки.
Отображение, вычисляемое генератором, обла-
дает сжимающими свойствами и, следовательно,
не имеет гарантированно большой длины цикла.
Для исключения зацикливания вводится сложе-
ние с номером i итерации (которое можно заме-
нить умножением по модулю г). Очевидно, что
необходимо исключить появление бесконечно
удаленной точки и нулевой х-координаты, на-
пример, пропуская такие точки.
Текущее состояние генератора является сек-
ретным. Поскольку на каждом шаге текущее со-
стояние меняется, то анализ сигналов, несущих
информацию о секретном параметре генератора,
методом накопления и выделения их из шума
невозможен.
Если в результате явной компрометации те-
кущее состояние 2?,+1 генератора стало извест-
ным, то восстановление предыдущих состояний
эквивалентно дискретному логарифмированию:
для точек Q и Rl+1 нужно найти показатель хЛ. + i
(mod г) в уравнении (15.6.4). Поэтому третье
требование к генератору выполнено.
Для эллиптических кривых над малыми поля-
ми закон распределения текущих состояний ге-
нератора близок к равномерному. В силу того,
что эллиптические кривые над малыми и боль-
шими простыми конечными полями описывают-
ся одинаковыми алгебраическими выражениями,
можно предположить, что распределение со-
стояний генератора близко к равномерному и в
случае большого поля. Тогда второе требование
к генератору выполняется с большим запасом.
Вычисление очередного случайного числа эк-
вивалентно определению текущего состояния
генератора, а состояния распределены примерно
равномерно и начальное состояние безопасно.
Предсказание такого генератора эквивалентно
перебору начальных состояний, генератор в этом
смысле является теоретически безопасным. По-
этому и первое требование выполнено.
15.6.9. Протоколы для электронных платежей
Как отмечалось в п. 13.5.2, для электронных
платежей можно использовать подпись «всле-
пую». Эллиптические кривые позволяют реали-
зовать эту подпись для групп вычислимого и
трудновычислимого порядка.
Для подписи «вслепую» на основе протокола
Эль-Гамаля открытым ключом банка является
уравнение эллиптической кривой Е(Ку обра-
зующая точка Q простого порядка г, точка
Р е (0. Оба участника протокола умеют вычис-
лять функцию f
Секретным ключом банка является показатель
I такой, что Р = 1Q. Подпись вырабатывается для
сообщения т, 0 < т < г.
В протоколе подписи Эль-Гамаля на эллипти-
ческой кривой, как и в общем случае, используя
морфизм схемы подписи, по данному правильно
подписанному сообщению т можно сконструи-
ровать другое правильно подписанное сообще-
ние т' следующим образом (здесь уравнение
формирования подписи: т =flR)l + ks (mod г)):
1) выбрать произвольный показатель а, «поло-
жить» к <— ик (поскольку к неизвестно, то и
к тоже неизвестно). Этому показателю будет
соответствовать точка R' = ukQ = о./?;
2) вычислить показатель р <— fiK)f(R')(mod г);
3) вычислить новое сообщение и'<-рт и под-
пись s' <— of'p.s.
Здесь существует односторонняя вычисли-
мость коэффициента Р из показателя а и, следо-
вательно, односторонняя вычислимость нового
сообщения т' из сообщения т. Применительно к
электронным платежам это можно рассматривать
как маску, накладываемую банком на сообще-
ние. Но для подписи «вслепую» требуется, чтобы
маска накладывалась клиентом. Поэтому изме-
ним протокол Эль-Гамаля следующим образом.
Протокол 15.6.4. Создание электронной мо-
неты на основе протокола Эль-Гамаля на эллип-
тической кривой.
Вход клиента. Открытый ключ: уравнение эл-
липтической кривой Е(К), образующая точка Q
группы простого порядка г, точка Р е (0; функ-
ция f
Вход банка. Открытый ключ: уравнение эл-
липтической кривой Е(К), образующая точка Q
группы простого порядка г, точка Р е (0; сек-
ретный ключ: показатель 1 такой, что P = 1Q,
функция/ s?
327
Результат. Электронная монета.
Метод.
Для создания электронной монеты, определяе-
мой сообщением т (см. п. 13.5.2), участники про-
токола выполняют следующие действия.
1. Банк выбирает случайный показатель к,
О < /с' < г, и вычисляет точку R' <— k'Q. При
fiR') = 0 заменяет случайный показатель, при
/й') Ф 0 посылает R' клиенту.
2. Клиент проверяет, что R' е Е(К). Если это не
так (то есть, возможно, банк пытается узнать
некоторую информацию о монете), то прото-
кол прерывается; иначе клиент выполняет
следующие действия.
2.1. Выбирает случайный показатель а та-
кой, что 0 < а < г.
2.2. Вычисляет точку R <— а/?' и проверяет.
что/(7?) Ф 0. Если это не так, то возвра-
щается к шагу 2.1.
2.3. Вычисляет коэффициент Р <— fiK)f(R')
(mod г).
2.4. Накладывает на сообщение т маску:
т' <—аР”’?« (mod г) и посылает т' бан-
ку.
3. Банк проверяет, что т' Ф 0. Если это не так,
то протокол прерывается (формирование
подписи немедленно ведет к вскрытию клю-
ча). При успешной проверке банк вычисляет
подпись s' <- l f(R’) + кт' (mod г) для сооб-
щения т’ и посылает ее клиенту.
4. Клиент проверяет равенство s'Q =flR)P + m'R'
для замаскированного сообщения. Если оно
не выполнено, то результат: подпись s' не-
действительна; если выполнено— снимает
маску с сообщения т' и полагает s <— ,$'Р
(mod г).
5. Результат: электронная монета (?и, R. s).
При погашении монеты (т, R, s) магазин вы-
полняет следующие действия.
1. Проверяет, что т ф 0. Если это не так, то ре-
зультат: подпись s недействительна.
2. Вычисляет функцию flR) и проверяет, что
/7?) Ф 0. Если это не так, то результат: под-
пись s недействительна.
3. Проверяет равенство sQ=j{R)P + mR. Если
оно выполняется, то результат: подпись s
подлинная, иначе результат: подпись s не-
действительна.
Рассмотрим кратко безопасность этого прото-
кола. Здесь может быть несколько направлений
атак: вскрытие ключа подписи; подделка подпи-
си без вскрытия ключа, например, подменой со-
общения; и, наконец, вскрытие подлинного тек-
ста сообщения (такая атака может быть предпри-
нята со стороны банка).
Для вскрытия ключа подписи банка достаточ-
но найти логарифм 7. Подделка подписи без зна-
ния ключа, в отличие от протокола, основанного
на логарифмировании в конечном поле, пред-
ставляется не менее сложной, чем логарифмиро-
вание в группе точек эллиптической кривой при
условии, что ключ выбран правильно. Непра-
вильный выбор параметров криптосистемы (на-
пример, использование в качестве К не поля из q
элементов, а кольца с делителями нуля из q эле-
ментов, использование группы составного поряд-
ка и т. п.) может быть легко выявлен с помощью
известных тестов проверки на простоту. Вариан-
ты нарушения протокола, связанные с тем, что
точка R' может не лежать на кривой, выявляются
в ходе протокола. Возможны атаки, связанные с
выбором точки R' не из группы (Q). Если число
точек на кривой имеет вид rl, где г— большое
простое число, г е Z, то для исключения такой
атаки следует проверить, что tR^ ТС, и tR' Ф Рт.
Клиент может попытаться изменить значение
подписанного сообщения под маской, используя
указанный морфизм подписи. Этот недостаток
неустраним, так как наличие морфизма — основа
подписи «вслепую». Поэтому сообщение т
должно содержать достаточно большой избы-
точный отрезок, априорно известный магазину и
банку. Если сложность подмены положить рав-
ной сложности вскрытия ключа, то длина избы-
точного отрезка должна быть равна (log2 г)/2 .
Избыточность может быть введена, например,
заменой сообщения т на конкатенацию w||g(m)
с соответствующим сокращением длины сооб-
щения, где g— хэш-функция, стойкая в части
обращения и в части вычисления коллизий.
Протокол 15.6.5. Создание электронной мо-
неты на основе протокола Шнорра на эллиптиче-
ской кривой.
Вход клиента. Открытый ключ: уравнение эл-
липтической кривой Е(К), образующая точка Q
группы простого порядка г, точка Р е (0; функ-
ция f
Вход банка. Открытый ключ: уравнение эл-
липтической кривой Е(К), образующая точка Q
группы простого порядка г, точка Р е (0; сек-
ретный ключ: показатель 7 такой, что Р = IQ\
функция f
Результат. Электронная монета.
Метод.
Для создания электронной монеты, опреде-
ляемой сообщением т, участники протокола вы-
полняют следующие действия. •,
328
1. Банк генерирует случайный показатель к,
0<к <г, и вычисляет точку R' <— кQ. При
flR') = 0 заменяет случайный показатель; при
flR') Ф 0 посылает точку R' клиенту.
2. Клиент генерирует случайный показатель а,
О < а < г, и вычисляет точку R <— а/?'. При
flR) = 0 заменяет случайный показатель; при
flR) * 0 вычисляет коэффициент р <—fiR)flR')
(mod г), полагает т' <— оГ’ри? (mod г) и посы-
лает сообщение т' банку.
3. Банк вычисляет подпись для сообщения под
маской: s' <- к +1 m'flR) (mod г) и возвраща-
ет ее клиенту.
4. Клиент проверяет равенство s'Q = R + m'flR)P.
Если оно не выполнено, то результат: подпись
s' недействительна; иначе клиент снимает мас-
ку с сообщения т' и полагает s <— as' (mod г).
5. Результат: электронная монета (т, R, s).
При погашении монеты (т, R, s) магазин вы-
полняет следующие действия.
1. Проверяет, что т Ф 0. Если это не так, то ре-
зультат: подпись s недействительна.
2. Вычисляет функцию flR) и проверяет, что
7г(А) ф 0. Если это не так, то результат: под-
пись s недействительна.
3. Проверяет равенство sQ = R + mh(R)P. Если
оно выполняется, то результат: подпись s
подлинная, иначе результат: подпись s не-
действительна.
В основу безопасности этого протокола также
положена задача логарифмирования в группе
точек кривой. Для вскрытия ключа подписи бан-
ка достаточно найти логарифм 7.
Подделка подписи без знания ключа требует
вычисления точки, координаты которой находят-
ся в требуемом соотношении с ее логарифмом.
Эта задача представляется такой же сложной, как
логарифмирование.
Для того чтобы защититься от подмены со-
общения, в него следует внести избыточность,
как и в протоколе Эль-Гамаля.
Протокол подписи «вслепую» на группе труд-
новычислимого порядка основан на том, что
функция шифрования RSA является мультипли-
кативной, то есть если .S |, .s2 — подписи для со-
общений mi, т2, то ,S|.s2— подпись для mqvh. Ес-
ли о-— функция, вычисляющая подпись s для
сообщения т, и множество подписей совпадает с
множеством сообщений, то о является эндомор-
физмом группы (2ZJri2E) .
Открытым ключом является эллиптическая
кривая E(Z7«Z), где n=pq и р, q — различные
простые числа, #E(jPlri2E) = N. Кроме того, от-
крытый ключ содержит показатель е, обратимый
по модулю N. Секретным ключом служит пока-
затель d такой, что ed = 1 (mod N). Сообщение т
представлено точкой М е E(Z/«Z).
По китайской теореме об остатках кривая Е
изоморфна прямой сумме кривых: E(flJn?E) =
Ф E(F(y), следовательно, число N не может
быть простым. В кольце есть делители ну-
ля, поэтому точки кривой E(flJn7E) не образуют
группу относительно обычной операции сложе-
ния точек. Это обусловлено тем, что каждая точ-
ка кривой E(flJri£) имеет две составляющих —
по модулю р и по модулю q. Поэтому, если две
точки S и Т кривой £(Z/«Z) имеют составляю-
щие Sp, Sq и Тр, Тч, vtSp = Тр, Sq Ф Тд, то по модулю
р нужно применять формулы удвоения точки, а
по модулю q — формулы сложения двух разных
точек. Следовательно, обычные формулы сложе-
ния могут давать ошибку (для ее исключения
нужно вычислять НОД (,л\ - хт, «)). Однако веро-
ятность такого события пренебрежимо мала и
1
равна О
. Порядки групп E(FP) и
^mm(/?,9)J
E(F9) должны иметь большие простые делители.
Протокол предусматривает следующие дейст-
вия.
1. Клиент генерирует случайную точку
R е E(7ZJri2E), вычисляет по сообщению
М е E(Z7nZ) точку М' <— М+ eR и посылает
М' банку.
2. Банк вычисляет для точки М' подпись
S'<-dM' = d(M+ eR) = dM+ R
и возвращает подписанное сообщение (М', S')
клиенту.
3. Клиент проверяет подлинность подписи (если
M' = eS', то подпись подлинная) и снимает
маску с подписи, вычисляя S = S' - R = dM.
Подписью для точки М является точка S.
Для проверки подписи S магазин вычисляет
точку eS и сравнивает ее с точкой М. Если они
совпадают, то подпись считается подлинной.
Для того чтобы банк мог проверить правиль-
ность сообщения М (по аналогии с протоколом
13.5.2), клиент должен предъявить точку R.
Безопасность протокола в части вскрытия
ключа подписи основана на сложности разложе-
ния составного числа и и сложности нахождения
порядка N группы. Поэтому размер задачи в этом
случае оказывается в несколько раз больше, чем,
например, в протоколе Эль-Гамаля. Следователь-
329
но, использование эллиптических кривых в таком
протоколе приводит к снижению скорости вычис-
лений в десятки раз по сравнению с протоколом,
использующим группу вычислимого порядка.
В силу морфизма схемы подписи теоретиче-
ски возможна подмена пользователем подписан-
ного персонального номера монеты (например,
на больший номинал). Использование вместо М
хэш-функции, стойкой в части вычисления кол-
лизий и в части обращения, устраняет указанный
морфизм, но одновременно делает невозможной
подпись «вслепую». Действительно, замена со-
общения М на значение хэш-функции h(M) в
уравнении шифрования приводит к тому, что
снять маску будет нельзя.
Чтобы это исключить, можно, например, вве-
сти избыточность в текст сообщения. Отметим,
что в обычной подписи RSA недопустимо вво-
дить избыточность путем использования нуле-
вых младших или старших разрядов. Если млад-
шие разряды нулевые, то атака может строиться
на основе гомоморфного вложения кольца Z/hZ
в кольцо Z. Если старшие разряды нулевые, то
для атаки можно использовать алгоритм LLL
минимизации базиса решетки (алгоритм 7.3.1).
Однако в случае эллиптических кривых этот не-
достаток отсутствует. ! - • • - '
15.7. Криптосистемы
на гиперэллиптических кривых
Основная трудность, возникающая при разра-
ботке криптосистем на гиперэллиптической кри-
вой, — это выбор кривой С(К), где К = F^„, такой,
что задача логарифмирования в якобиане J(Q
является сложной. Требования к порядку яко-
биана и полю К приведены в пп. 11.6, 11.7: поря-
док якобиана должен иметь большой простой
делитель г Ф char(A'); char(/Qfr * 1 (mod г) для не-
больших значений к\ род кривой должен быть
небольшим. Для выбора кривой необходимо ре-
шить задачу расчета порядка ее якобиана.
Гиперэллиптическая кривая С/К может рас-
сматриваться над различными расширениями L
исходного поля К. При этом могут меняться чис-
ло точек кривой и порядок якобиана. Для того
чтобы уточнить, о каком именно поле идет речь,
якобиан будем также обозначать J(C(Z)) или,
короче,./(/.). • •
Пусть кривая C/Fp рода g задана уравнением
I? + h(u)v =flu). (15.7.1)
Рассмотрим метод вычисления порядка яко-
биана кривой над расширенным конечным полем
с помощью последовательности N\, Ni, ... (где
Nk = #J(F ,,) — число элементов якобиана), за-
ключающийся в подсчете F ^-аффинных точек
кривой (15.7.1) для к = 1,2, ..., g [14].
Пусть Мк = #C(F- рк, где #C(F^)— число
аффинных точек (и, т) кривой. Если р > 2, то
можно считать в (15.7.1) h = 0, тогда Мк является
суммой квадратичных характеров полинома flu)
в поле F t.
р
По аналогии с эллиптическими кривыми
можно ввести дзета-функцию Z(T)— полином
степени 2g с целыми коэффициентами:
Z(T) = T2g + аА T2g~' + ... + ag-t Г+| + afl* +
+/Wg-iZ*”1 + /?2ag_27^“2 + ... + р^~'а}Т+]fl =
П(7 «,)('/ а;),
2=1 . е ч„ь
гдеа|, е 2 и а;а;
ПуСТЬ . 'Г' ' —,
Z(T’) = T2gz(j = 1 + а}Т + а2Т2 +... + pgT2g,
тогда коэффициенты полинома Z(T) связаны с
числами Мк соотношением
_ 00 Kf
; lnZ(7). • (15.7.2)
к=\ к
2 3
X X
Так как 1п(1 + х) = х---1------..., то, подстав-
2 3
ляя в (15.7.2) х = щТ + (рТ2 + ... + ]flT2g и при-
равнивая коэффициенты при одинаковых степе-
нях Т, получаем выражения для коэффициентов
полинома Z(T). Заметим, что для этого достаточ-
но первыхg величинМ\, Mg. Отсюда находим
g । |2
w»=nli-«;l
7=1
где |... | — модуль комплексного числа. Нетруд-
но видеть, что Л) = Z(l).
Представим симметрическую функцию
Sj =t{ + ... + t}m в виде полинома от элементар-
ных симметрических функций [4]:
+... + (-1)7-ijo7-, при j<m,
+ при j>m.
330
Применительно к задаче вычисления якобиа-
на эта формула означает, что для каждого и чис-
ло Nn элементов якобиана можно выразить как
полином над кольцом Z от коэффициентов по-
линома Z(T).
Тогда для любого п = 1,2,... справедливо
g-i
Н)А(1+)^и) +(-l)g5’|"), (15.7.3)
к=0
Пример 15.7.1. Вычисление порядка якобиана.
Пусть кривая С(К) задана уравнением
у2 = х5 + х2 + 17х + 35 над полем характеристи-
ки/? = 257. Найдем порядок якобиана этой кри-
вой для 7C = F;, и K=F 13. Для этого сначала
вычислим Z(7). Находим суммы квадратичных
характеров над полями из 257 и из 2572 эле-
ментов:
где =1,
к
M2= Е XU5+x2+17x + 35) = 89.
хе^6049
при к > 2,
S'7’1’^4-^7^^'’^..^-!)7’’^^, при j<2g,
cU) J 2g
1 xh)^7"'^1’,
npHj>2g.
Кроме того, S*n = (-!)' а, при z<g;
5,(1) =p'~8 Sg_, npng<z<2g.
Например, порядок якобиана кривой рода 2
над кубическим расширением основного поля
задается формулой:
N3 = 3p4nj + р3(а3 -За}а2) + 3р2(2а2 -а2)+
+ 3p(at - а2а2) +1 + а3 - За{а2 + а2.
Для обеспечения стойкости криптосистемы
необходимо, чтобы порядок N„ = #J(K) якобиа-
на J(K) был простым числом либо имел боль-
шой простой делитель г и чтобы спаривание
Вейля не позволяло легко вычислить лога-
рифм. В этом случае стойкость равна O(-Jr}.
Само N„ редко оказывается простым, так как
J(F^) есть подгруппа группы J(K) для любого
делителя d числа п, и, значит, Nd I N„. Поэтому
целесообразно использовать только простые
расширения поля Ну, и только кривые с непри-
водимым над полем рациональных чисел поли-
номом Z(T).
Для некоторых гиперэллиптических кривых,
например, у2 = х5 + Вс/>^±1 (mod 10), число то-
чек найти легко: М\ = М2 = 0. Однако такие кри-
вые не позволяют обеспечить стойкость по от-
ношению к логарифмированию на основе спари-
вания Вейля.
Эти значения полностью определяют дзета-
функцию. Находим коэффициенты функции
Z(T). Полагаем
Z(Z) = T4zl 11 = 1 +а}Т+а2Т2+252а{Г3+2522ТА
и
х = а}Т+ а2Т2 + 257а\Т3 + 2572Т4.
Вычисляем логарифм дзета-функции:
InZ(T) = ln(l + х) = х - + у- -... .
Достаточно рассмотреть коэффициенты при Т
иГ:
1 к т (щТ + а2Т2 +...}
In Z(T) = (ар + а2Т ------—
= М}Т + ^-Т2 +....
1 2
Приравниваем коэффициенты при одинако-
т1 л f ^2 Му гт
вых степенях Г: а\=М}, а2=—^ + -^~. Под-
ставляя сюда найденные значения М\ и М2, полу-
чаем «1=3, су= 49. Дзета-функция имеет вид:
Z(7) = Т4 + ЗГ3 + 49Т2 + 771Г+66049. Этот по-
лином неприводим над полем Q и А'| = #J(^2i2) =
= Z(1) = 66873.
Из (15.7.3) находим #13 = #J(F^13):
7V13 =1 + р26 ~(l + p'3)S^ + |((51(13))2 -S<26)) =
=455261795236548565733691886171487\
443711849618087383281840609793.
331
Тогда
= 68078566123330576725089630519261
598832291801146761522316041.
Для гиперэллиптической кривой справедлив
аналог теоремы Хассе:
|p/c + l-#C(Fpj|<277
для всех к = 1, 2,... . Поэтому, если поле К вели-
ко, то для расчета значений ЛД, ...,МЯ можно
воспользоваться аналогом алгоритма Чуфа для
гиперэллиптических кривых [11, 16, 18].
На практике желательно использовать гипер-
эллиптические кривые небольшого рода, так как,
раскладывая на множители пары полиномов, со-
ставляющих дивизор, можно снизить стойкость
криптоалгоритма.
В якобиане гиперэллиптической кривой, как и
на эллиптических кривых, может существовать
комплексное умножение на целое алгебраическое
число 6. Это позволяет ускорить умножение ди-
визора на целое число z, если представить z в виде
полинома от 0. Если кривая С/F,, рассматривается
над полем из рп элементов, то на ней действует
отображение Фробениуса <р: (и, у) (ир, vp), со-
ответствующее умножению элемента якобиана на
комплексное число [18].
Криптографические протоколы на гиперэл-
липтических кривых аналогичны протоколам на
эллиптических кривых. Общая несекретная ин-
формация: кривая С(К) (то есть поле К и пара
полиномов^ И) и дивизор D, образующий группу
большого простого порядка г. В основу крипто-
графических протоколов положена задача Диф-
фи-Хеллмана: для якобиана J(K), дивизора D и
дивизоров ID, sD найти дивизор tsD.
В общем случае строение якобиана как абеле-
вой группы может отличаться от строения груп-
пы точек эллиптической кривой. Например,
группа точек кривой над конечным полем цик-
лична или является прямой суммой двух цикли-
ческих групп, большой и малой, при этом поря-
док большой группы делится на порядок малой
группы. Якобиан может иметь более сложное
строение. Это обстоятельство следует учитывать
при разработке протоколов.
Так, представляются возможными атаки, ос-
нованные на посылке «фальшивых» дивизоров,
не являющихся элементами якобиана данной
кривой. Для защиты от такой атаки желательно
ввести проверку того, что полученный дивизор
div(a(w), b(u)) является приведенным и соответ-
ствует кривой С(К), то есть проверять делимость
а | (/г + hb -f) в кольце К[п].
15.8. Криптосистемы на изогениях
эллиптических кривых
На основе задачи вычисления изогении мож-
но строить протоколы шифрования с открытым
ключом и цифровой подписи.
15.8.1. Задача вычисления изогении
и квантовый компьютер
Недостатком криптосистем, основанных на
задаче определения структуры и порядка абеле-
вой группы и задаче дискретного логарифмиро-
вания в циклической группе, является их уязви-
мость по отношению к квантовому компьютеру.
Если удастся создать квантовый компьютер дос-
таточно большой разрядности, то задача разло-
жения составного числа и задача дискретного
логарифмирования в произвольной циклической
группе могут быть решены с полиномиальной
сложностью.
Рассмотрим массовую задачу вычисления
морфизма в категории абелевых групп.
В качестве категории будем рассматривать
категорию изогенных эллиптических кривых над
конечным полем. Тогда задача вычисления мор-
физма представляет собой задачу вычисления
изогении: для эллиптических кривых E|(F;;) и
/’^(F;-,) найти изогению ср: £i(Fp) -> Е^р). Со-
гласно теореме Тейта две эллиптические кривые
Ei(F/;) и Ет_(^р) являются изогенными тогда и
только тогда, когда они имеют одинаковое число
точек [20].
Результирующую изогению ср будем задавать
в виде композиции изогений малых степеней, по
аналогии с построением симметричного шифра в
виде композиции несложных отображений, а эл-
липтическую кривую будем задавать ее J-
инвариантом.
Зададим изогению в виде композиции изоге-
ний малых взаимно простых степеней Компо-
зицию удобно представить в виде графа. Верши-
ны графа — эллиптические кривые, для которых
определяются изогении степеней Z,, а ребра —
сами изогении. Граф изогений можно считать не-
ориентированным, так как для каждой изогении
существует дуальная изогения той же степени.
Например, для эллиптической кривой
у2 = х3 + х + 18 над полем из 1009 элементов чис-
ло точек равно 22 • З2 • 29, j = 117. Связный ком-
понент графа изогений содержит 42 вершины.
Изогенные кривые для изогении степени I за-
даются корнями модулярного полинома Ф/, рас-
332
сматриваемого над полем Fp. Модулярный поли-
ном Ф/ для нечетного I имеет 0, 1, 2 или I + 1 кор-
ней в поле Fp (см. п. 6.15.4). Случай одного корня
соответствует тому, что вершина является листом.
В криптографии целесообразно использовать
изогении малых простых степеней 7, для которых
модулярный полином имеет два корня, при этом
необходимо, чтобы дискриминант характеристи-
ческого уравнения эндоморфизма Фробениуса
был квадратичным вычетом по модулю I для не-
четных I.
Связный компонент графа изогений супервы-
« « «14
рожденной эллиптической кривой содержит все
изогенные кривые для изогении данной степени
[20]. Таким образом, все изогении являются сте-
пенями какой-то одной изогении.
Аналогично, если модулярный полином для
изогении степени / имеет два корня в основном
поле, то связный компонент графа изогений яв-
ляется циклическим. Изогении других степеней
задают перестановку вершин этого графа; ком-
позиция изогений коммутативна и ассоциативна.
Для того чтобы за несколько шагов по графу
изогений можно было добраться до произволь-
ной вершины, число образующих изогений
должно быть достаточно велико. Пусть число
изогенных кривых равно N и пусть п — число
изогений, задающих циклическую перестановку
на множестве из N элементов, причем каждая
изогения может применяться не более т раз.
Пренебрегая совпадающими вершинами графа
для различных путей, число достижимых вершин
можно оценить значением т (объем «-мерного
параллелепипеда). Положим N=m\ тогда
т = А17". Для достижения произвольной вершины
графа нужно сделать не более пт шагов. Найдем
соотношение между числами т и п, при котором
суммарное число шагов S = mn минимально.
Имеем: S = «A17'’, In 5 = In п+(In N)/n. Минимум
сложности достигается при п «In А и т к е, где
е — основание натурального логарифма.
Модулярные полиномы над полем Fp можно
найти с использованием результатов Лерсье и
Морана [19]. Для ускорения вычислений можно
искать не модулярный полином двух перемен-
ных над Z, а непосредственно полином Ф^и,])
(mod р).
Задача вычисления изогении между двумя
изогенными кривыми сводится к задаче нахож-
дения цепочки /-инвариантов для изогений сте-
пеней Zj, ..., Ik- Эта задача является частным слу-
чаем задачи нахождения пути между двумя вер-
шинами неориентированного графа.
14 Супервырожденная эллиптическая кривая £(11у,)
имеет р + J точек, то есть след эндоморфизма Фробе-
ниуса равен 0.
Задача вычисления изогении, образованной
цепочкой изогений различных степеней, пред-
ставляется сложной по отношению к квантовому
компьютеру. Действительно, для достаточно
длинной цепочки изогений степень уравнения
задающего результирующую изогению оказыва-
ется экспоненциально большой, и задание соот-
ветствующего модулярного уравнения и уравне-
ния изогении требует экспоненциально большого
объема работы. Это не позволяет составить про-
грамму для квантового компьютера. Оперирова-
ние с изогениями малых степеней приводит к
случайному блужданию на графе изогений и к
многократному повторению одной и той же про-
цедуры с переменными параметрами. Свойство
квантового компьютера— вычисление скрытых
периодов функций — не облегчает задачу нахо-
ждения пути на графе изогений.
15.8.2. Криптографические
протоколы на изогенных кривых
В основу безопасности протокола опознава-
ния положена задача нахождения цепочки изоге-
ний между двумя изогенными эллиптическими
кривыми. Поскольку произведение изогений
коммутативно, можно реализовать протокол
Диффи-Хеллмана. В этом случае пользователи
выбирают эллиптическую кривую E(F/;) такую,
что все модулярные полиномы имеют два корня
в Fp. Тогда изогении степеней 7, будут образовы-
вать циклы.
Пользователь А генерирует цепочку jA = \|/л(/о)
изогений (/-инвариантов модулярных полино-
мов) и посылает jA пользователю В. Пользователь
В генерирует цепочку у/ = \j/»(7o) изогений (/-
инвариантов модулярных полиномов) и посыла-
ет j'b пользователю А. Затем каждый пользова-
тель вычисляет свою цепочку /-инвариантов для
полученной кривой. Пользователь А получает
Ч'лОв)= 4W«(/o), пользователь В получает
VX/л) = 4W/(/o); в силу коммутативности произ-
ведения изогений они получают одинаковый /-
инвариант.
Для повышения стойкости протокола целесо-
образно выбрать кривую £(F;;) так, чтобы наи-
больший общий делитель длин циклов изогений
был большим простым числом.
По аналогии с протоколом Эль-Гамаля можно
построить протокол шифрования с открытым
ключом на изогениях. При этом в качестве эле-
ментов группы могут выступать /-инварианты
эллиптических кривых. На основе шифрования с
открытым ключом легко реализовать диалоговый
протокол опознавания «запрос-ответ». При этом
верификатор вырабатывает случайный запрос,
зашифровывает его на открытом ключе и посы-
333
лает претенденту. Претендент расшифровывает
шифртекст на своем конфиденциальном ключе и
возвращает открытый текст верификатору. Ве-
рификатор проверяет, что полученный текст сов-
падает с запросом.
Если длины циклов изогений для всех чисел I
вычислимы, то можно реализовать и протоколы
цифровой подписи, аналогичные протоколам
Эль-Гамаля, Шнорра, DSS.
Однако цепочки изогений позволяют найти не
только /-инварианты эллиптических кривых, но и
гомоморфизмы между кривыми, то есть получа-
ется новый криптографический примитив для
построения протоколов. Поскольку задача вы-
числения изогении между эллиптическими кри-
выми является сложной, то и гомоморфизмы мо-
гут быть секретными. В основу таких протоколов
можно положить коммутативную диаграмму изо-
морфизмов групп простого порядка г (рис. 15.1).
£i(Fp)---------------> ВД
\т\ [т]
Е^р)-----------------> £2(IFp)
Рис. 15.1. Коммутативная
диаграмма изоморфизмов групп
Здесь <р — изогения (композиция изогений
простых степеней, взаимно простых с г), [/и] —
операция умножения точки на показатель т, вза-
имно простой с г.
На основе этой диаграммы можно реализо-
вать протокол цифровой подписи, который по-
зволяет проверить, что документы подписыва-
лись в заданном порядке. Этот протокол является
аналогом временной метки. Предполагается, что
претендент, вырабатывающий подписи для до-
кументов, подготовленных различными пользо-
вателями, является доверенной стороной.
Как и в стандарте ГОСТ Р 34.10-2001 пара-
метрами протокола являются эллиптическая кри-
вая £|(F/,) и точка Q простого порядка г. Секрет-
ным ключом является логарифм I, открытым
ключом — точка P = IQ. Здесь, в отличие от
ГОСТ Р 34.10-2001, модулярный полином Ф для
эллиптической кривой £|(Fp) имеет ровно два кор-
ня над полем IFP (отсюда следует, что deg/Ф) > 4 и
степень изогении не менее 3). При этом изогении
должны образовывать цикл большой длины.
Протокол подписи на изогенных эллиптических
кривых аналогичен протоколу ГОСТ Р 34.10-2001.
При формировании очередной подписи меняется
эллиптическая кривая. Инвариант очередной эл-
липтической кривой определяется как корень
модулярного полинома Ф. Однозначное соответ-
ствие эллиптической кривой /-инварианту легко
обеспечить выбором минимального по абсолют-
ной величине коэффициента А или В. В состав
подписи можно включить инвариант текущей
эллиптической кривой. Для проверки подписи
претендент вычисляет цепочку /-инвариантов и
соответствующих изогений до тех пор, пока не
получит заданный инвариант. Проверка подписи
осуществляется согласно ГОСТ Р 34.10-2001.
При этом очередность подписи документов соот-
ветствует очередности /-инвариантов и может
быть легко проверена.
Оценим число вершин графа изогений. Число
неизоморфных эллиптических кривых над полем
равно О(р). Изогенные кривые должны быть
неизоморфными и иметь одно и то же число то-
чек. В соответствии с теоремой Хассе количест-
во вариантов для числа точек на кривой равно
O(Jp) Поэтому число изогенных кривых мож-
но оценить частным от деления числа неизо-
морфных кривых на количество вариантов для
числа точек, то есть числом
Наилучшим алгоритмом вычисления изоге-
нии представляется алгоритм встречи посере-
дине. Для каждой из двух помеченных вершин
Е] и Г2 графа изогений, соответствующих эл-
липтическим кривым £’i(Fp) и £’2(F;;), ищем
О(7Ё) вершин, ближайших к помеченной вер-
шине, и вычисляем ребра графа (изогении) ме-
жду помеченной вершиной и данной верши-
ной. Затем сортируем базу данных, состоящую
из пар (вершина V, путь из помеченной верши-
ны в вершину Г), по второй координате и в ней
ищем равные элементы. Если найдены пути в
некоторую вершину V из вершин V\ и Г2 (в ба-
зе данных найдены одинаковые элементы), то
путь из Г] в Г2 является композицией найден-
ных путей.
Временная и емкостная сложность задачи вы-
числения изогений методом встречи посередине
равна О(\Гр ~). , . , , -у
334
Упражнения к главе 15
1. Найдите число точек эллиптической кривой
у2 = х3 +х + 1 над полем из 5П элементов.
2. Найдите число точек эллиптической кривой
у1 = х3 + 2х над простым полем характеристи-
ки /? = (264+9)/125.
3. Найдите число точек эллиптической кривой
у2 = х3 + 5 над простым полем характеристи-
ки/? =261 - 1.
4. Найдите число точек эллиптической кривой
у2 = х3 - 4т2 + 2х над простым полем характе-
ристики р = 261 - 1.
5. *Можно ли алгоритмом Чуфа найти число
точек кривой £(2/и2), где n = pq — состав-
ное число с неизвестным разложением? Изо-
морфизм £(Z/nZ) = £(FP) ® £(F9) позволяет
рассматривать характеристическое уравнение
для обоих эндоморфизмов Фробениуса над
ILIriZL, контролируя наибольший общий дели-
тель промежуточных результатов и числа п.
6. *(Продолжение). Можно ли снизить слож-
ность разложения составного числа, исполь-
зуя алгоритм Чуфа?
7. Как связаны сроки действия ключа подписи и
параметров хэш-функции в протоколе цифро-
вой подписи Шнорра на эллиптической кривой?
8. Сравните сложности формирования и про-
верки подписи в протоколах Эль-Гамаля и
Шнорра на эллиптической кривой.
9. Предложите свой вариант алгоритма шифро-
вания с открытым ключом на эллиптической
кривой.
10. Оцените сложность вскрытия ключа подписи
в протоколе Эль-Гамаля на эллиптической
кривой, если генератор случайных чисел вы-
рабатывает числа, у которых половина дво-
ичных разрядов известна заранее.
11. Пусть случайное число вырабатывается на
основе такого генератора случайной после-
довательности, у которого вероятности нуля
и единицы заметно различаются. Как можно
ускорить вскрытие ключа подписи на эллип-
тической кривой?
12. Предложите способ нарушения безопасности
протокола подписи Эль-Гамаля, если допус-
кается ./(7?) = 0 (mod г). Покажите, что воз-
можна атака, при которой смена персональ-
ного ключа не позволяет продлить срок дей-
ствия общего ключа.
13. Предложите свой вариант построения вычис-
лимой в одну сторону функции, свободной от
коллизий, на эллиптической кривой.
14. Сколько бит зашифрованной информации
можно передать по скрытому каналу в про-
токоле ГОСТ Р 34.10-2001 в течение оди-
ночной реализации цифровой подписи?
15. Предположим, что в протоколе подписи Эль-
Гамаля функция У(7?) имеет многочисленные
коллизии, причем логарифмы точек R вычис-
лимы. Как это влияет на безопасность подпи-
си?
16. Предположим, что в протоколе подписи
«вслепую» для числа точек выполняется ра-
венство N=tr, где г— большое простое чис-
ло, f е Z. Рассмотрите возможные атаки, ес-
ли точка Q образует всю группу порядка N.
17. Пусть n=pq и £(2/и2)— эллиптическая
кривая. Установите связь между разложе-
ниями чисел #£(FP) и #£(FQ) и цикличностью
группы £(2/и2) (предполагается, что вычис-
ления на кривой выполняются корректно).
18. *Сравните стойкость протокола Фиата-
Шамира на эллиптических кривых со стойко-
стью оригинального протокола.
19. *Предложите вариант атаки на аналог систе-
мы шифрования RSA на эллиптических кри-
вых на основе пары шифрограмм, для кото-
рых открытые тексты связаны с помощью
аффинного преобразования (см. п. 9.4.2). Ка-
ким должен быть минимальный размер от-
крытого показателя?
20. *Пусть £/F;, — эллиптическая кривая, задан-
ная над полем из q = pn элементов и содер-
жащая группу простого порядка г. Тогда
£(F9) обладает комплексным умножением на
собственные значения степеней эндомор-
физма Фробениуса от 0 до п - 1. Разработай-
те алгоритм перевода показателя I е ILlriZL во
фробениусову систему счисления так, чтобы
абсолютная величина каждой цифры была
минимальной.
21. Может ли число точек на кривой #£(Z7pAZ)
быть простым?
22. Пусть #£p(Z//?2Z) — эллиптическая кривая.
Оцените сложность вычисления логарифма
на этой кривой.
23. *Разработайте набор алгоритмов, реализую-
щих быстрое умножение дивизора гиперэл-
липтической кривой на число с использова-
нием комплексного умножения. Набор алго-
ритмов должен содержать вычисление собст-
венного значения оператора комплексного
умножения, разложение порядка якобиана в
кольце целых элементов числового поля, ми-
нимизацию показателя для комплексного
умножения.
24. Пусть кривая £/(Fp обладает над полем F9,
q =р , комплексным умножением на собст-
венное значение (р эндоморфизма Фробениу-
са, где <р — целое квадратичное число. Опре-
делите, какой из двух корней характеристи-
ческого уравнения для эндоморфизма Фро-
бениуса является собственным значением в
F9, не умножая точку на целое число.
25. *Разработайте протокол диалогового опозна-
вания с нулевым разглашением на изогениях
эллиптических кривых (разглашение должно
быть на самом деле нулевым, не допускается
предъявление даже части результирующей
изогении).
Литература к главе 15
1. Айерлэнд К., Роузен М. Классическое введение в
современную теорию чисел. М.: Мир, 1987.
2. Лидл Р., Нидеррайтер X. Конечные поля. М.:
Мир, 1988.
3. Маховенко Е.Б., Ростовцев А.Г. Быстрая арифмети-
ка для эллиптических кривых над расширенными
полями // Проблемы информационной безопасно-
сти. Компьютерные системы. 1999. № 2. С. 50-54.
4. Мишина А.П., Проскуряков И.В. Высшая алгебра.
М.: Наука, 1965.
5. Ростовцев А.Г. Алгебраические основы крипто-
графии. СПб.: Мир и Семья, Интерлайн, 2000.
6. Ростовцев А.Г. О выборе эллиптической кривой
над простым полем для построения криптографи-
ческих алгоритмов // Проблемы информационной
безопасности. Компьютерные системы. 1999.
№ 3. С. 37-40.
7. Ростовцев А.Г., Маховенко Е.Б. Класс самых бы-
стрых эллиптических кривых для стандарта циф-
ровой подписи // Сб. тезисов конференции «Ме-
тоды и технические средства обеспечения безо-
пасности информации». СПб. 2002. С. 100-101.
8. Ростовцев А.Г., Маховенко Е.Б. Криптосистема
на категории изогенных эллиптических кривых //
Проблемы информационной безопасности. Ком-
пьютерные системы. 2002. № 3. С. 74-81.
9. Ростовцев А.Г., Маховенко Е.Б. Подпись и шиф-
рование на эллиптической кривой: анализ безо-
пасности и безопасная реализация // Проблемы
информационной безопасности. Компьютерные
системы. 2003. № 1. С. 73-83.
10. Ростовцев А.Г., Маховенко Е.Б. Реализация про-
токолов на эллиптических кривых // Проблемы
информационной безопасности. Компьютерные
системы. 1999. № 4. С. 62-67.
11. Adleman L., Huang М. Counting rational points on
curves and abelian varieties over finite fields // Algo-
rithmic number theory. H. Cohen (ed.). Lecture Notes
in Computer Science. Springer-Verlag. 1996.
Vol. 1122. P. 1-16.
12. Atkin A.O., Morain F. Elliptic curves and primality
proving // Mathematics of Computation. 1993.
Vol. 61. P. 29-68.
13. Cassels J., Frohlich A. Algebraic number theory.
Proceedings of an International Congress by the
London Mathematical Society. Washington,
1967.
14. Koblitz N. Hyperelliptic curve cryptosystems 11 Jour-
nal of Cryptology. 1989. Vol. 1. P. 139-150.
15. Miyaji A. Elliptic curves over Fp, suitable for crypto-
systems // Advances in Cryptology— AUSCRYPT
’92. Lecture Notes in Computer Science. Springer-
Verlag. 1993. Vol. 718. P. 479-491.
16. Schoof R. Counting points on elliptic curves over
finite fields // Journal de Theorie des Nombres de
Bordeaux. 1995. Vol. 7. P. 219-254.
17. Silverman J.H. The arithmetic of elliptic curves.
Springer-Verlag, 1986.
18. Smart N. On the performance of hyperelliptic
curve cryptosystems // Advances in Cryptology —
EUROCRYPT ’99. Lecture Notes in Computer
Science. Springer-Verlag. 1999. Vol. 1592.
P.165-175.
19. Lercier R., Morain F. Algorithms for computing
isogenies between elliptic curves // Computational
perspectives on number theory. AMS/IP Studies on
Advanced Mathematics. Vol. 7.
20. Tate J. Endomorphisms of abelian varieties over fi-
nite fields H Inventiones Mathematicae. 1966. Vol. 2.
P. 134-144.
Глава 16. ОБЩИЕ СВЕДЕНИЯ ОБ ИТЕРИРОВАННЫХ
КРИПТОАЛГОРИТМАХ
16.1. Основные понятия
классической криптографии
Симметричным шифром будем называть со-
вокупность взаимно однозначных преобразова-
ний множества открытых данных в множество
зашифрованных данных, осуществляемых по
определенным правилам с помощью секретного
изменяемого параметра — ключа, причем знание
ключа на передающей стороне позволяет вычис-
лить ключ на приемной стороне, и обратно.
Если шифр осуществляет обратимое отобра-
жение слов фиксированной длины п бит в слова
фиксированной длины т бит, то этот шифр на-
зывают блочным, а число п — длиной блока.
Чтобы можно было обратимым образом зашиф-
ровать любое слово длины п бит, необходимо
выполнение неравенства т>п. К блочным от-
носятся шифры ГОСТ 28147-89, RIJNDAEL
(см. гл. 19).
Часто блочный шифр реализуется последова-
тельным выполнением несложных процедур,
включающих в себя сложение блока текста с
блоком ключа, подстановку (замену) слов текста,
перестановку или сдвиг и т. п. Последователь-
ность этих процедур обычно чередуется. Оди-
ночное повторение таких чередующихся проце-
дур будем называть итерацией или циклом шиф-
рования.'
В множестве итерированных шифров наряду с
блочными различают поточные шифры. Поточ-
ный шифр осуществляет поэлементное зашифро-
вание открытого текста, однако способ шифро-
вания зависит от нескольких предшествующих
(последующих) разрядов открытого текста. Ти-
пичная схема поточного шифрования представ-
ляет собой сдвиговый двоичный регистр с нели-
нейными обратными связями. На вход регистра
подается открытый текст, на выходе получается
шифртекст.
Итерированным назовем симметричный
блочный шифр, полученный путем выполнения
нескольких итераций (циклов шифрования), как
1 Термин «цикл шифрования» правильно передает
смысл понятия, хотя один цикл может отличаться от
другого, например, используемым блоком ключа.
правило одинаковых или незначительно разли-
чающихся. Каждая итерация содержит набор не-
сложных обратимых операций преобразования
шифруемого текста.
16.2. Некоторые положения теории
секретности Шеннона
Принято считать, что научная криптография
начинается с доклада К. Шеннона «Математиче-
ская теория криптографии», представленного в
1945 г., который позднее был изложен в его ста-
тье [7].
Секретной системой (или просто системой)
Шеннон называет конечное множество взаимно
однозначных отображений множества открытых
текстов (сообщений) в множество шифрограмм.2
Вид отображения полностью определяется спо-
собом шифрования и ключом.
Для обмена информацией по незащищенным
каналам связи отправитель и получатель предва-
рительно выбирают общий секретный ключ из
множества возможных ключей. Нарушитель зна-
ет способ шифрования, имеет доступ к шифро-
граммам, но не знает ключа (и открытых тек-
стов). П,ель нарушителя— нарушение конфи-
денциальности, то есть вскрытие ключа или на-
хождение открытых текстов.
Шеннон одним из первых ввел понятие ком-
бинации секретных систем. Взвешенной суммой
систем R и Т называется такая система
S - pR + qT, что S совпадает с R с вероятностью р
и S совпадает с Т с вероятностью q = 1 -р. Вы-
бор в пользу R или Т определяется частью сек-
ретного ключа системы S. Операция взвешенно-
го сложения ассоциативна и коммутативна. По
2 Секретная система и криптосистема— разные
понятия. Криптосистема включает в себя, кроме спо-
соба шифрования, способы генерации ключей, их
доставки, ввода в действие, вывода из действия и
уничтожения, а также криптографические протоколы,
хэш-функции, способы аутентификации. Таким обра-
зом, понятие секретной системы по Шеннону анало-
гично понятию шифра или даже одной итерации
шифра. * '
337
индукции взвешенная сумма распространяется
на любое число слагаемых.3
Другой способ комбинации— произведение,
или композиция, — заключается в последова-
тельном применении секретных систем R и Т к
множеству входных текстов (записывается RT—
сначала выполняется Т, затем 7?).4 Композиция
систем ассоциативна: (QR)T= Q(RT), но в общем
случае некоммутативна: RTф TR.
Системы, у которых множества открытых и
зашифрованных текстов совпадают, называются
эндоморфными. Для эндоморфных систем с оди-
наковыми множествами входных текстов опре-
делены произведения и степени. При этом п-й
степенью эндоморфной секретной системы Т яв-
ляется Тп — последовательное «-кратное приме-
нение системы Т. Далее будем рассматривать
только эндоморфные системы.
Шифр Д определяемый ключом z, обознача-
ется Д. Чистым называется шифр, у которого
для любых трех ключей z, j, к существует такой
ключ 7, что ДД~1 Д = Д и все ключи равновероят-
ны, в противном случае шифр называется сме-
шанным.
В чистом шифре множества открытых тек-
стов, как и множества зашифрованных текстов,
распадаются на такие непересекающиеся под-
множества (области транзитивности), что дан-
ный открытый текст может быть переведен в
любой из текстов, лежаших в области транзитив-
ности, выбором соответствующего ключа.5 При
полном переборе ключей каждый элемент данно-
го подмножества открытых текстов может быть
переведен в любой элемент соответствующего
подмножества зашифрованных текстов такой же
мощности. При этом число ключей, осуществ-
ляющих перевод любого открытого текста из
данного подмножества в каждый из элементов
подмножества зашифрованных текстов, одина-
ково для всех открытых текстов и является дели-
телем мощности множества ключей.
Предположим, что нарушитель имеет беско-
нечные вычислительные возможности и не знает
ни ключа, ни открытых текстов; ключ (открытый
текст) выбирается случайно из множества клю-
3 Примером взвешенной суммы является опера-
ция обратимой замены слова текста словом такой же
длины. Такая замена описывается подстановкой, яв-
ляющейся частью ключа или параметром шифра, как
в ГОСТ 28147-89 (см. п. 19.6).
4 Для задания композиции RT необходимо, чтобы
множество выходов системы Т совпадало с множест-
вом входов системы R.
5 Понятие транзитивности аналогично можно оп-
ределить и для смешанного шифра.
чей (открытых текстов). В этом случае наилуч-
шим способом атаки является изучение вероят-
ностей того, что данный открытый текст перехо-
дит в данную шифрограмму.
Секретная система называется совершенной,
если зашифрованный текст не дает никакой ин-
формации об открытом тексте. Если Р(Х) — ап-
риорная вероятность открытого текста X и
Р(Х| Y) — условная вероятность того, что шиф-
рограмме Y соответствует открытый текст X. то
совершенная система задается равенством
Р(Х) = Р(Х\ Y).
Это равенство эквивалентно равенству
P(Y) = P(Y\X) для шифрограмм, где P(Y)— ап-
риорная вероятность шифрограммы Y и
Р(У|Л) -— условная вероятность того, что шиф-
рограмма Y соответствует открытому тексту X. В
совершенной системе число ключей должно
быть кратно числу открытых текстов, а каждый
открытый текст должен переводиться в каждый
зашифрованный текст одним и тем же числом
ключей. Например, если чистый шифр содержит
единственную область транзитивности, то он
является совершенным.
Естественные языки обладают избыточно-
стью, в них не все открытые тексты являются
равновероятными, что позволяет ввести в рас-
смотрение условную энтропию.6 Ненадежно-
стью ключа называется условная энтропия
Н(К | Y) ключа К при известной шифрограмме Y,
ненадежностью сообщения — условная энтро-
пия Н(Х\ Y) открытого текста X при известной
шифрограмме Y. Эти энтропии определяются
следующим образом:
Н(К I У) = X P(Y,K)\ogP(K IY),
г,к
Н(Х\Y) - XP(F,X)logPG¥| Y),
г.т
где P(Y, К) — вероятность появления ключа К и
шифрограммы Y при заданном распределении
вероятностей открытых текстов, Р(К\ Y)— веро-
ятность того, что для ключа К появилась шифро-
грамма Y при заданном распределении вероятно-
стей открытых текстов.
Ненадежность ключа и ненадежность сооб-
щения являются невозрастающими функциями
от числа N известных символов шифрограммы. В
связи с избыточностью языка ненадежность
ключа и ненадежность сообщения быстро стре-
мятся к нулю с ростом числа известных симво-
лов шифрограммы. Если избыточность языка на
6 В данном параграфе под энтропией всюду по-
нимается шенноновская энтропия.
338
одну букву равна D, то ненадежность ключа ста-
новится практически нулевой при ND = С)(Н(К)).
Нулевая ненадежность означает, что существует
практически единственное значение ключа,
удовлетворяющее заданной шифрограмме. Ми-
нимальный объем шифрограммы, соответст-
вующий практически единственному значению
ключа, называется точкой единственности. При
нулевой ненадежности нарушитель с неограни-
ченными вычислительными возможностями мо-
жет вскрыть ключ.
Если язык обладает нулевой избыточностью
(все символы равновероятны, все слова заданной
длины равновероятны и т. п.), то ненадежность
ключа и сообщения не зависит от длины шифро-
граммы, известной нарушителю. Такие секрет-
ные системы называются идеальными. Если на-
рушитель знает только шифрограммы, то вскры-
тие ключа идеальной системы невозможно. Для
того чтобы система приблизилась к идеальной,
следует максимально уменьшить избыточность
языка.7
Если нарушитель обладает конечными вычис-
лительными возможностями, необходимо учи-
тывать трудоемкость вскрытия ключа. Средний
объем работы по нахождению ключа Шеннон
называет рабочей характеристикой шифра.8 Это
среднее значение берется по всем открытым тек-
стам и всем ключам с учетом их вероятностей.
Обеспечить высокую рабочую характеристику
можно даже при практически нулевой ненадеж-
ности ключа.
После того, как объем шифрограммы пре-
взойдет точку единственности, ключ можно
вскрыть перебором. Однако этот метод (по су-
ти — метод проб и ошибок) практически нереа-
лизуем из-за большой трудоемкости.9 *
7 Если нарушитель знает открытые и соответст-
вующие зашифрованные тексты, то понятие идеаль-
ности теряет смысл. Ключ определен однозначно,
если шифр реализует случайное отображение множе-
ства текстов в себя и нарушитель знает 1,368Н(К)
символов открытых и соответствующих зашифрован-
ных текстов (см. п. 16.2.1).
8 По сути этот термин аналогичен понятию стой-
кости шифра.
9 На практике в криптоанализе используют усо-
вершенствованные методы проб и ошибок, среди ко-
торых можно выделить два класса. Первый класс ме-
тодов характеризуется тем, что множество ключей
упорядочивают по вероятности ключа быть истинным
и опробование выполняют, начиная с наиболее веро-
ятных ключей.
Второй класс характеризуется тем, что в резуль-
тате опробования отбраковывается не один ключ, а
подмножество ключей. Например, если в результате
каждого опробования исключается фиксированная
При разработке шифра следует максимизиро-
вать минимальный объем работы, которую должен
проделать нарушитель для нахождения ключа. Для
этого не достаточно быть уверенным в том, что
никаким известным методом вскрыть ключ не-
возможно. Надо быть уверенным в том, что этого
нельзя достичь вообще никаким методом. Дейст-
вительно. история криптографии показывает, что
часто за появлением нового шифра следует появ-
ление нового метода криптоанализа, вскрываю-
щего этот шифр. Проблема создания шифра за-
ключается в отыскании наиболее сложных задач,
удовлетворяющих определенным условиям.10
При разработке шифра с малым ключом не-
обходимо стремиться к тому, чтобы при шифро-
вании каждого малого элемента открытого тек-
ста использовалась значительная часть ключа.
Некоторые методы криптоанализа, например,
частотный метод анализа моноалфавитной под-
становки (см. подробнее п. 16.7.1), основаны на
использовании избыточности открытых текстов,
которая определяется статистическими свойст-
вами шифрограмм. Рассматривая статистические
методы криптоанализа, Шеннон приписывает
каждой статистике S (набору шифрограмм) неко-
торую «разрешающую мощность». Пусть
Н(К\ S) — ненадежность ключа при статистике S.
Взвешенное среднее P(S)H(К | S) (сумма бе-
рется по всем шифрограммам) дает среднюю не-
надежность ключа при известном S. «Разре-
шающей мощностью» статистики S называется
разность Н(К) -Yj\S)H(K 15).
Различают хорошие и плохие статистики. Хо-
рошая статистика характеризуется следующими
свойствами:
- ее легко вычислить;
- она зависит от ключа К больше, чем от от-
крытого текста X, изменения по X не маски-
руют изменения по X;
- те значения статистики, которые могут быть
распознаны, несмотря на размытость, созда-
ваемую изменениями по X, разбивают мно-
жество ключей на несколько подмножеств,
доля ключей, то сложность вскрытия оценивается
полиномом от длины ключа.
10 Имеются два подхода к решению этой пробле-
мы. Первый заключается в изучении всех методов
криптоанализа, которыми пользуется нарушитель, опи-
сании их в общих терминах и принятии мер противо-
действия этим методам. Второй подход состоит в том,
чтобы свести задачу вскрытия шифра к некоторой хо-
рошо известной общепризнанно сложной задаче.
339
причем статистика позволяет распознавать
подмножество, в котором лежит правильный
ключ;
- информация, даваемая статистикой, проста и
удобна в использовании.
Для противостояния статистическому крип-
тоанализу Шеннон предлагает в шифре обеспе-
чить рассеивание (диффузию, diffusion) и переме-
шивание (confusion). При рассеивании статистиче-
ская структура открытых текстов, приводящая к
избыточности шифрограмм, «распыляется» по
шифрограммам большой длины, в результате ста-
тистика становится трудновычислимой. При пе-
ремешивании соотношения между простыми ста-
тистиками в множестве шифрограмм и простыми
подмножествами в множестве ключей делаются
весьма сложными и беспорядочными.11
Шеннон предлагает строить шифр с использо-
ванием несложных, не коммутирующих между
собой операций по аналогии с перемешиванием
теста: сначала тесто раскатывается тонким слоем,
затем скатывается, затем опять раскатывается и
т. д. Для зашифрования открытый текст, записан-
ный на естественном языке (русском, английском
и т. п.), разбивается на блоки фиксированной дли-
ны. Шифр представляет собой композицию опе-
раций перестановки букв в блоке, замены подбло-
ков из нескольких букв и сложения букв по моду-
лю числа букв в алфавите (практически склады-
ваются номера букв в алфавите при их естествен-
ном упорядочении). При этом операция замены
должна быть определена на небольшом числе
символов, а операция перестановки должна рас-
пределять изменения равномерно по всему блоку.
16.2.1. Объем текстов, однозначно
определяющих ключ
Если открытые тексты не обладают избыточ-
ностью (каждый блок данных выбирается слу-
чайно и равновероятно из множества всех воз-
можных блоков одинаковой длины), то наруши-
тель никогда не сможет вскрыть ключ на основе
зашифрованных текстов [7]. Если же открытые
данные обладают избыточностью или если на-
рушитель знает открытые и зашифрованные тек-
сты, то ключ может быть вскрыт. При этом вы-
числительные возможности нарушителя предпо-
лагаются бесконечными.12
11 Термин «простая» применительно к статистике
следует понимать как эффективно распознаваемая, а
«простые» применительно к подмножествам клю-
чей — как эффективно перечислимые.
12 Отсутствие ограничений на вычислительные
возможности нарушителя ведет к тому, что перебор
ключей может быть проведен мгновенно.
Оценим объем открытых и зашифрованных
текстов, необходимых для однозначного опреде-
ления ключа шифрования (без учета сложности
вычислений). Предположим, что длины блоков
открытых и зашифрованных текстов и длина (эн-
тропия) ключа совпадают, а шифратор реализует
случайное отображение множества ключей в
множество пар блоков открытых и соответст-
вующих зашифрованных текстов. Для опреде-
ленности будем считать, что нарушитель знает
открытый текст и соответствующую шифро-
грамму. Если длина ключа отличается от длины
блока, то можно перейти к «увеличенным» бло-
кам. Поскольку мощности множества ключей и
множества зашифрованных блоков одинаковы,
то шифрование можно рассматривать как ото-
бражение множества блоков открытых текстов в
себя.
Пусть длина блока и ключа равна п бит.
Множество ключей задает отображения откры-
тых текстов в зашифрованные. Если отображе-
ние является случайным, то произвольный от-
крытый текст с равной вероятностью переходит
в любой зашифрованный текст.
Отображение множества открытых текстов в
множество зашифрованных текстов можно за-
дать таблично. Зафиксируем N = 2" открытых
тестов и зашифруем каждый из них на каждом из
N ключей. Если среди N зашифрованных текстов
шифртекст, соответствующий данному ключу,
встречается однократно (или не встречается ни
разу), то для определения ключа достаточно од-
ного текста. Если данный шифртекст встречается
дважды, то для определения ключа достаточно
двух текстов и т. д.
Аппроксимируя случайное отображение пуас-
соновским процессом, легко найти вероятность
того, что данный открытый текст встретится в
точности к раз. Эта вероятность приблизительно
1
равна —, где е — основание натурального ло-
ек\
гарифма. Математическое ожидание числа пар
открытых и соответствующих зашифрованных
текстов, необходимых для вскрытия ключа,
можно оценить выражением
1-- + 1-- + 2——+ 3-—!—
е е е • 2! е•3!
= 1 + 1 «1,368.
е
Поэтому для однозначного определения клю-
ча, шенноновская энтропия которого равна п бит,
требуется примерно 1,3 68п бит открытого текста
(в предположении, что все зашифрованные тек-
сты нарушителю известны).
340
16.2.2. Теория аутентификации Симмонса
По аналогии с теорией секретности Г. Сим-
монс предложил теорию аутентификации13 со-
общений [13]. Как и в теории Шеннона, предпо-
лагается, что нарушитель не знает ни сообщения,
ни ключа.
Пусть к получателю поступают шифрограм-
мы Y от подлинного отправителя и Y' от наруши-
теля. Цель нарушителя— навязать ложное со-
общение, которое будет принято как подлинное.
Обозначим через Pi вероятность успешного на-
вязывания ложной информации, а через Ps—
вероятность успешной подмены подлинного сооб-
щения ложным. Определим вероятность обмана
Р£/ = тах(Р/,Л).
Пусть #{Y}, #{Л], #{К} — мощности мно-
жеств соответственно шифрограмм, открытых
текстов и ключей, обладающих ненулевой веро-
ятностью. Из условия однозначного расшифро-
вания следует, что для каждого ключа существу-
ет не менее #{Х] различных шифрограмм Y, для
которых Р(У| К) > 0, так как любой текст X мо-
жет быть зашифрован и расшифрован. Следова-
тельно, если нарушитель выберет Y случайно из
множества шифрограмм с ненулевыми вероятно-
стями, то вероятность Р, успешной имитации
определяется неравенством
г ад
। Поэтому для защиты от обманов необходимо,
чтобы #{X}«#{Y}. При этом полная защита
(Pi = 0) невозможна.
«Совершенная аутентичность» определяется
как наибольшая защита, достижимая при задан-
ной мощности множества допустимых шифро-
грамм. Пусть h— такая функция аутентифика-
ции, что h(Y, К)= 1, если Y — шифрограмма, до-
пустимая при данном секретном ключе К, и
h(Y, К) = 0 в противном случае. При данном
ключе К получатель примет шифрограмму Y как
истинную только тогда, когда h(Y, К)= 1. Тогда
вероятность успешного навязывания задается
равенством
P(Yдопустимо) = ^h(Y,K)P(K).
к
Справедливо неравенство
^2 P(Y) log P(Yдопустимо) > -I(Y, К),
13 Обобщенная схема аутентификации включает в
себя двух легальных участников— претендента и
верификатора, причем верификатор по определению
не доверяет претенденту. Кроме того, предполагается
существование нарушителя, действующего автономно
или в сговоре с верификатором (см. рисунок 8.2).
где I(Y, К) = H(Y) - H(Y| К) — взаимная инфор-
мация шифрограммы и ключа. Справедливо не-
равенство IogP/>-Z(F, К), причем равенство
достигается при одновременном выполнении ус-
ловий:
1) вероятность P(Y допустимо) не зависит от Y
(то есть попытка имитации оптимальна при
случайном выборе У);
2) для каждой шифрограммы Y вероятность
P(Y\K) одинакова для всех К, при которых
h(Y,K) = 1.
Аналогичными рассуждениями можно полу-
чить logPrf> -I(Y, К), причем достижение равен-
ства соответствует совершенной аутентичности.
Задачи обеспечения секретности и аутентич-
ности противоречат друг другу: малая вероят-
ность обмана Pd достижима лишь тогда, когда
1(У, К) велико, то есть когда шифрограмма дает
нарушителю большую информацию о ключе.
16.3. Булевы функции и булевы формулы
Любую булеву функцию можно (по крайней
мере, теоретически) задать в виде таблицы. Если
число аргументов булевой функции равно п, то
таблица содержит 2й наборов аргументов. Для
каждого из наборов функция может принимать
значения 0 или 1. Все булевы функции можно
перечислить, выписывая всевозможные двоич-
ные слова длины 2”. Число таких слов (то есть
различных булевых функций) равно 22.
Переменная х,- называется существенной для
булевой функции flx}, ...,х„), если равенство
/(х],...,х(,...,х„) = f(x\,..., хп...,х„) выполняется
не для всех наборов переменных, в противном
случае она называется несущественной, или фик-
тивной.
Далее будут рассматриваться следующие бу-
левы функции:
1) константы 1 и 0, существенно зависящие от О
переменных (нуль-арные);
2) тождественная функция fix) = х и инверсия
(функция НЕ) f(x)-x, существенно зави-
сящие от одной переменной (унарные);
3) функция © сложения по модулю 2: fix, у) =
= х © у, существенно зависящая от двух пе-
ременных и принимающая значение 1 при
х * у и значение 0 при х = у;
4) функция И (конъюнкция): Дх, у) = ху (запи-
сывается также х л у), существенно завися-
щая от двух переменных и принимающая
значение 1 при х = у = 1 и значение 0 в ос-
тальных случаях; г
341
5) функция ИЛИ (дизъюнкция): fix, у) = х v у,
существенно зависящая от двух переменных
и принимающая значение 0 при х=у=0 и
значение 1 в остальных случаях.
Функции © и И задают соответственно сло-
жение и умножение в поле F2 и поэтому ком-
мутативны, ассоциативны, умножение дистри-
бутивно относительно сложения. Элементы
поля F2 образуют аддитивную группу с опера-
цией сложения по модулю 2, каждый элемент
противоположен сам себе. Функция И идемпо-
тентна: хх = х.
Функция ИЛИ коммутативна, ассоциативна,
идемпотентна и дистрибутивна относительно
функции И; функция И дистрибутивна относи-
тельно функции ИЛИ. Каждая из операций И,
ИЛИ задает на поле F2 структуру коммутативно-
го моноида, который не может быть вложен в
группу. Поэтому пара бинарных операций И,
ИЛИ образует коммутативное полукольцо. Лю-
бая из них может считаться сложением, а остав-
шаяся операция — умножением. Если сложение
задано операцией ИЛИ (И), то нулем полукольца
является 0 (1). Нетрудно убедиться, что оба ва-
рианта задают изоморфные полукольца, поэтому
обычно в качестве сложения используется опе-
рация ИЛИ, а в качестве умножения— И. Для
обеспечения функциональной полноты (возмож-
ности записать любую булеву функцию с помо-
щью указанных операций) к рассмотренному
множеству операций обычно добавляется унар-
ная операция НЕ.
Из 16 возможных булевых функций двух пе-
ременных только две пары функций задают
структуру кольца на множестве {0. 1}. Это рас-
смотренные выше функции сложения и умноже-
ния по модулю 2, а также инверсия функции сло-
жения по модулю 2 (сложение) и функция ИЛИ
(умножение). В этом случае нулем кольца явля-
ется 1, а единицей— 0. Полученное кольцо яв-
ляется полем, изоморфным полю F2; изоморфизм
задается инверсией.
Функции ©, И, ИЛИ по индукции определя-
ются для произвольного числа аргументов.
Булева функция может быть также задана
формулой (в некотором базисе В). Определим
булеву формулу индуктивно:
1) каждая переменная х, — формула;
2) если g(xZp..., х,п) е В и fi,..,,fi„ — формулы,
тоg(/i, — формула.
Базисом может служить набор нуль-арных,
унарных или бинарных булевых функций, позво-
ляющих реализовать произвольную булеву фун-
кцию. Существуют базисы, состоящие из одной
функции, например, х v у, ху.
Обычно используются базисы из функций, за-
дающих на множестве формул алгебраическую
структуру поля или полукольца. Например, базис
с бинарными операциями сложения и умножения
по модулю 2 и нуль-арной операцией— кон-
стантой 1, задающий на паре {true, false} струк-
туру поля, изоморфного полю F2. Другой часто
используемый базис состоит из бинарных опера-
ций И (умножение), ИЛИ (сложение) и унарной
операции НЕ и задает полукольцо булевых фор-
мул, изоморфное дистрибутивной решетке с от-
ношением порядка 0 < I.14
Используя законы де Моргана: ху = х v у,
х\/ у = х /\у и свойство дистрибутивности, лю-
бую булеву функцию в базисе И, ИЛИ, НЕ можно
записать в виде дизъюнктивной нормальной
формы (ДНФ):
/(%],..., Х„) = V ,
или в виде конъюнктивной нормальной формы
(КНФ):
/(%],..., хп ) = А(хУ| V xl2 V ... v xJn) ,
где символ означает, что соответствующая пе-
ременная входит в выражение с инверсией или
без инверсии.
Законы де Моргана определяют алгоритм пе-
рехода от ДНФ к КНФ, задающий изоморфизм
полуколец булевых функций, поэтому все свой-
ства ДНФ автоматически переносятся на КНФ.
Представление булевой функции формулой,
записанной в ДНФ, неоднозначно. Например,
формулы xyz v xyz v xyz и xyv xz задают одну и
ту же функцию. Поэтому в множестве ДНФ суще-
ствуют классы эквивалентности, представляющие
одни и те же булевы функции, и возникает про-
блема поиска представителей этих классов.
Булева формула, записанная в ДНФ и пред-
ставляющая некоторую булеву функцию, может
быть минимизирована по числу дизъюнкций и
среднему числу элементов в конъюнкциях.15 По
14 Здесь под решеткой понимается частично упо-
рядоченное множество, в котором каждая пара эле-
ментов имеет точную верхнюю и точную нижнюю
грани (см. п. 3.14).
15 После минимизации не все «слагаемые» имеют
одинаковую степень, поэтому минимизированная бу-
лева функция в общем случае не является формой,
тогда как до минимизации степени всех слагаемых
Одинаковы.
342
аналогии с несущественной переменной опреде-
лим нестандартную конъюнкцию, имеющую вид
aab, где а, b — произвольные формулы. Не-
стандартные конъюнкции представляют нулевую
константу и могут быть исключены. Если в ДНФ
входит выражение вида cd\/cd, где с и d—
произвольные формулы, то в силу_дистрибутив-
ности получаем: cd\/ cd = c(d v d) = c . Кроме
того, справедлив закон поглощения'.
c\/cd=cl vcd= с(1 vd)=c для произвольных
формул с, d. Минимизация выполняется с ис-
пользованием свойств идемпотентности, дистри-
бутивности и поглощения и основана на исклю-
чении несущественных конъюнкций.
Минимизированное представление булевой
функции в виде ДНФ может быть различным.
Например, булева функция f четырех перемен-
ных, принимающая на двоичных наборах
(хо,Х1,х2,х3) вида (0,0,0,0), (0,0,0,!),...,
(1, 1, 1, 1) значения соответственно 1, 0, 1, 1, 1, 1,
0, 1, 0, 1, 0, 1, 0, 0, 0, 0, имеет минимальные
представления:
f - Х0Х2Х3 V А'0А'| А'з V А'оА'^2 v ^оХ}Х-
И
ф — XqXjX2 V XqX^X^ \/ AqA^X3 \/ XqXjA3 .
Полукольцо ДНФ от п переменных с суммой
в виде точной верхней грани и произведением в
виде точной нижней грани иногда называют по-
лукольцом L„ решеточных полиномов. В полу-
кольце L„ единственным обратимым элементом
является константа 1.
Определим идеал полукольца L,, как множест-
во, замкнутое относительно операции нахожде-
ния точной верхней грани, причем точная ниж-
няя грань произвольного элемента из L„ и эле-
мента идеала является элементом идеала. Глав-
ный идеал полукольца L„, образованный поли-
номом f состоит из полиномов вида fg, где
g £ L„.
Булевы функции и булевы формулы являются
одним из основных инструментов описания ите-
рированных шифров. Например, любую п-
разрядную подстановку и вообще любое отобра-
жение множества Z/2'’Z в себя можно задать с
помощью п булевых функций. Задача вскрытия
ключа итерированного шифра сводится к задаче
решения булева уравнения (см. п. 16.5.2).
16.4. Аффинно эквивалентные булевы
функции и подстановки
Определим сбалансированную булеву функ-
цию как функцию, принимающую значения 0 и 1
одинаково часто. В соответствии с п. 3.15.2 сба-
лансированный полином f е G„ имеет в точности
2'7-1 различных неразложимых делителей.
В кольце Gn полином вида Xj@J(x], ...,x,_i,
А'/+|, ..., а'„) задает сбалансированную булеву
функцию. Действительно, функция х, сбаланси-
рована, и переменная х,- не входит в полином f
Поэтому, если на некотором наборе из п - 1 пе-
0 0 0 0 /
ременных х,,..., х,_)5х/+),..., хи полином j прини-
мает значение 0, то на паре наборов
0 0 л 0 О.о 0,0 о
Х],...,Хм,0,Х,+),...,Х„ И X, ,...,X,_J,1,X,+],...,X„
полином х, © f принимает по одному разу значе-
ния 0 и 1. Если на некотором наборе из п - 1 пе-
ременных Xj1,...,х’_],х,,,х* полиномf прини-
мает значение 1, то на паре наборов
X], ..., Xt_], 0, Х;+1, ..., Х„ И X],..., X;_j, 1, х,+1,..., Х„
полином xt+f тоже принимает по одному разу
значения 0 и 1. Это рассуждение справедливо и в
том случае, когда полином f зависит от меньшего
числа переменных.
Назовем булеву функцию аффинной, если она
задается формулой вида а0 @'^а1х1 >. Булева
функция называется линейной, если а0 = 0. Заме-
на переменных х, аффинными булевыми функ-
циями дает аффинную булеву функцию. Непо-
стоянная аффинная булева функция всегда сба-
лансирована.
Подстановку, действующую на множестве из
2" элементов, можно задать строкой из 2" п-
разрядных двоичных чисел. Каждый из п разря-
дов подстановки является булевой функцией п
переменных и может быть задан полиномом Же-
галкина.16
Назовем «-разрядную подстановку линейной
над OF2 (или просто линейной), если она задается
уравнением у = £х, где L — невырожденная над
F2 матрица размера «х« (то есть det£=l). В
линейной подстановке каждый разряд описыва-
ется линейной булевой функцией.
Композиция линейных подстановок соответ-
ствует умножению матриц этих подстановок,
поэтому линейные подстановки, как и невырож-
денные матрицы одного размера, образуют под-
группу симметрической группы, действующей
на множестве Z/2'’Z.
Назовем «-разрядную подстановку аффинной
над F2 (или просто аффинной), если она задается
уравнением у = £х © а, где L — невырожденная
над F2 матрица размера « х «, а — вектор сдвига.
16 См. также п. 3.15.
343
В аффинной подстановке каждый разряд описы-
вается аффинной булевой функцией.
Подстановка, обратная к аффинной, тоже яв-
ляется аффинной: х = £чу © £ 'а = £'у © а'.
Композиция двух аффинных подстановок явля-
ется аффинной подстановкой: если у = £х © а,
z = Му © Ь, то z = MLx © Ma © b = М'х © Ь', где
матрица М' невырождена. Поэтому аффинные
подстановки также образуют подгруппу симмет-
рической группы, действующей на множестве
Z/2'’Z.
Аналогично определяются линейные и аф-
финные подстановки над произвольным конеч-
ным коммутативным кольцом R с единичным
элементом. Очевидно, что определитель матри-
цы обратимой подстановки должен являться об-
ратимым элементом кольца R. Такие подстанов-
ки образуют подгруппу симметрической группы,
действующей на «-разрядных словах #А-буквен-
ного алфавита.
Теорема 16.4.1. Подстановка 5’ «-разрядных
двоичных слов задается « полиномами Жегалки-
на, степень которых не превышает « - 1.
Доказательство. Подстановку можно за-
дать « булевыми функциями. Объединим одно-
именные коэффициенты булевых функций в «-
разрядные векторы:
У = ао ®&Л ® ® -®а1.../Л -*«•
Выразим векторные коэффициенты через зна-
чения подстановки. Полагая xj = ... = х„ = О, на-
ходим а0 = 5(0). Полагая все х, = 0 при / i и
х, = 1, получаем:
а, = 5(0) ©ЭД,
a,j = 5(0) © 5(i) © 5(j) © 5(ij),
а12..." = 5(0) © 5(1) © S(2) © ... © 5(12...п).
Сумма в правой части содержит слагаемые от
00...О до 11...1, переставленные в соответствии с
подстановкой S, и поэтому равна нулевому век-
тору. Поскольку единственный коэффициент
а12..„, описывающий нелинейность порядка «,
равен нулю, то подстановка 5’ имеет порядок не-
линейности не выше « - 1.
Определим максимальный (минимальный) по-
рядок нелинейности подстановки как максимум
(соответственно минимум) степеней полиномов
Жегалкина, представляющих эту подстановку.
Аналогично можно определить и порядок нели-
нейности произвольного отображения множества
Z/2'’Z в себя.
Назовем обратимой аффинной заменой пере-
менных полинома fix\, ...,х„) е G„ обратимое аф-
финное отображение у = £х © а, где х = (хь ..., х„),
у = (у,, ..., у,,), при котором полином /Х],..., х„)
переходит в полином/уь ...,у„). Аффинную заме-
ну переменных можно представить как аффинную
подстановку, действующую на множестве наборов
аргументов.
Назовем булевы функции fix^,..., х„) и
g(V], ,)’,,) е Gn аффинно эквивалентными, если
существует обратимая аффинная замена пере-
менных у = £х © а, переводящая g в/или в/© 1:
f f (х)>
g(£x © а) = (
1/(х)©1.
Поскольку аффинные подстановки образуют
группу, это отношение рефлексивно, симметрич-
но и транзитивно. Тогда для каждого класса эк-
вивалентности существует канонический пред-
ставитель. Например, каноническим представи-
телем аффинных полиномов естественно назна-
чить полином хь
Теорема 16.4.2. При любой обратимой аф-
финной замене переменных степень полинома
Жегалкина не меняется.
Доказательство. Пусть g— полином, по-
лученный из полинома Жегалкина f при помощи
обратимой аффинной замены переменных. Тогда
deg(/) < deg(g), так как каждый одночлен степени
d полинома/заменяется произведением d линей-
ных полиномов, а получение степени, большей d,
потребует более d сомножителей. В этом случае
и полином / получается из полинома g обратной
заменой переменных, то есть полиномы/и g аф-
финно эквивалентны. Поэтому deg(g) < deg(/) и,
следовательно, deg(/) = deg(g).
Назовем подстановки 5' и Т аффинно эквива-
лентными, если существуют аффинные подста-
новки А, В такие, что ASB = Т. Последнее равен-
ство эквивалентно равенству AS = ТВ }. Аффин-
ная эквивалентность подстановок рефлексивна,
симметрична и транзитивна. Множество А аф-
финных подстановок является подгруппой сим-
метрической группы.
Пример 16.4.1. Аффинно эквивалентные под-
становки.
Пусть подстановка 5 задается таблицей
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
8 3 1 15 12 11 0 6 14 2 7 5 10 4 13 9
344
Выберем аффинные подстановки
д 0 о о> m
0 10 0 1
Дх) = • х +
10 10 0
<° 1 1 Z А
'1110' гг
0 10 0 0
ад= -х +
10 11 1
L0 1 1 ь Л
Если умножить двоичные векторы (0, 0, 0, 0),
(0, 0,0, 1),(1,1, 1, 1) на матрицу подстановки
А и прибавить соответствующий вектор сдвига,
то подстановку А можно записать в виде табли-
цы:
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
12 13 15 14 9 8 10 11 6 7 5 4 3 2 0 1
Аналогично для подстановки В:
0 1 2 3 4 5 6 7 8 9 10 И 12 13 14 15
11 8 0 3 6 5 13 14 1 2 10 9 12 15 7 4
^Произведение подстановок T = ASB будет
17
иметь вид
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
8 0 6 1 12 4 9 2 14 13 11 15 5 7 10 3
Оценим вероятность того, что случайная под-
становка будет аффинной. Аффинная подстанов-
ка задается произвольным вектором сдвига и не-
вырожденной над F2 матрицей размера их и и
поэтому может быть сгенерирована следующим
вероятностным алгоритмом.
1. Выбрать произвольный вектор сдвига.
2. Выбрать произвольную ненулевую первую
строку матрицы.
3. Выбрать произвольную ненулевую вторую
строку матрицы, отличную от первой строки.
4. Выбрать произвольную ненулевую третью
строку матрицы, отличную от первой и вто-
рой строк и суммы этих строк.
5. Далее по индукции, пока не будут выбраны
все строки.
Этот алгоритм порождает все аффинные под-
становки. Число векторов сдвига равно 2”. Число
17 Сначала выполняется подстановка В, затем S и А.
первых строк равно 2"-1, вторых строк —
2й - 2, третьих строк — 2" - 22 и т. д. Поэтому
число невырожденных аффинных подстановок
равно
#А = 2Л(2" - 2°)(2'’ - 2])(2" - 22)...(2" - 2'"1).
Вынесем 2” за скобки и изменим порядок со-
множителей:
#А = 2"2+"
1 2 Z
2'4 8
Т -1
Произведение дробных сомножителей схо-
дится к ненулевому значению при неограничен-
ном увеличении п, что легко показать, переходя
к натуральному логарифму этого равенства и
раскладывая логарифмы в степенной ряд. Это
произведение примерно равно 0,288, отсюда
#А = 0,288 2"21'', In #А = О(пг).
Общее число «-разрядных подстановок равно
2'’!. Выражая факториал по формуле Стирлинга,
получаем 2''!« ^2" 2 /е2 вероятность аф-
финной подстановки примерно равна
(2" +ге2 . Например, при п = 4 вероятность
аффинной подстановки равна 1,5 • 10-8, при
« = 5-1,2- 10~27.
16.5. Задача вскрытия ключа и
математические задачи
Безопасность криптографических алгоритмов
основана на сложности некоторой математиче-
ской задачи. Поскольку число таких задач вели-
ко, введем их классификацию, согласованную с
методами криптоанализа.
Существуют универсальные методы крипто-
анализа, применимые ко всем или многим крип-
тоалгоритмам, и специальные методы, примени-
мые к отдельным (неудачно спроектированным)
криптоалгоритмам. Очевидна аналогия между
универсальными и специальными методами
криптоанализа и методами решения массовых и
частных математических задач.
Примером специального метода является ме-
тод встречи посередине, применимый для замк-
нутых шифров (см. подробнее п. 17.2.1). Для вы-
яснения применимости этого метода необходимо
распознать, является ли шифр замкнутым (более
общо: обладает ли шифр заданным свойством).
Решение такой задачи сопровождается сертифи-
катом, представляющим собой «таблицу умно-
жения» подстановок, индуцированных шифром.
Очевидно, что сложность проверки этого серти-
фиката может быть сверхполиномиальной.
345
Примером универсального метода анализа
блочного шифра является дифференциальный
метод (см. п. 18.2). Для оценки стойкости к это-
му методу требуется указать наиболее вероятный
дифференциал — разность шифртекстов при не-
которой разности открытых текстов. Задача вы-
числения наиболее вероятного дифференциала
требует найти вид дифференциала и дать оценку
его вероятности для случайных или определен-
ным образом выбранных открытых текстов. От-
вет должен сопровождаться сертификатом, на-
пример, парами открытых и зашифрованных тек-
стов при переборе ключей, при этом сложность
проверки сертификата может быть сверхполино-
миальной.
16.5.1. Задача вскрытия
ключа и NP-полные задачи
Рассмотрим связь задачи вскрытия ключа ите-
рированного шифра с некоторыми NP-полными
задачами выбора, удобными для решения как на
обычном, так и на молекулярном и квантовом
компьютерах.
Если задача А размера п сводится к задаче В
размера п со сложностьюи задача В сводится
к задаче С того же размера со сложностью g(w), то
А сводится к С со сложностью не более g(/(»)).
Если f,g— полиномы, то их композиция — тоже
полином. Бинарное отношение полиномиальной
сводимости рефлексивно (тривиальная своди-
мость) и транзитивно. Кроме того, это отношение
антисимметрично с учетом полиномиальной эк-
вивалентности. Поэтому отношение полиноми-
альной сводимости на множестве массовых задач
выбора является отношением частичного порядка.
Криптография с открытым ключом, как пра-
вило, имеет дело с алгебраическими структура-
ми, обладающими определенными алгебраиче-
скими свойствами, например, с конечными абе-
левыми группами. Это позволяет использовать
для их анализа асимптотические оценки сложно-
сти, устремляя размер задачи к бесконечности.
Поскольку при этом все алгебраические свойства
математической структуры сохраняются, то кон-
кретная задача вскрытия ключа «подобна» асим-
птотически большой задаче, и есть основания
полагать, что полученные оценки будут справед-
ливы и в конкретном случае.
Для итерированных шифров указанный прин-
цип подобия не работает. Действительно, что со-
бой представляет «асимптотически большой» ал-
горитм шифрования DES? Для этого нужно уве-
личивать не только длину блока и длину ключа,
но и число циклов шифрования. В результате по-
лучится шифр, имеющий мало общего с исход-
ным шифром. Для сравнения: если рассмотреть
процедуру возведения в степень в простом конеч-
ном поле IFP как итерированную (итерациями яв-
ляются операции модульного умножения), то рост
размера задачи— числа р— сопровождается и
пропорциональным ростом числа итераций.
Отношение полиномиальной сводимости за-
дач, лежащее в основе теории сложности, опреде-
лено только для асимптотически больших разме-
ров этих задач. Поскольку, как правило, для ите-
рированных шифров увеличение размера задачи
невозможно, использование аппарата теории
сложности при их анализе обычно неэффективно.
16.5.2. Задача о выполнимости
Пусть булева функция и переменных задана в
виде нескольких наборов несложных булевых
функций, подставляемых друг в друга и связан-
ных с помощью обычных логических функций
И, ИЛИ, НЕ.18 NP-полная задача о выполнимо-
сти булевой функции состоит в том, что требует-
ся найти набор переменных, на котором эта
функция принимает значение «true» [1].
Рассмотрим алгоритм, вычисляющий компо-
зиции несложных наборов булевых функций от
нескольких переменных, например, подстановок.
Частным случаем такого алгоритма является
итерированный шифр.
Пусть разряды выходного текста описывают-
ся уравнениями
yi = Fi(xi, Лк), (16.5.1)
где х, — разряды открытого текста, к, — разряды
ключа, н — длина блока открытого текста, N—
длина ключа. Размером задачи будем считать
число N. Булевы функции F, заданы компози-
циями наборов булевых функций и не имеют
аналитической записи в виде ДНФ (она очень
сложна), но их значения могут быть вычислены
для произвольного набора аргументов.
Моделируя процесс шифрования на компью-
тере, выполняющем операции И, ИЛИ, НЕ, мож-
но вычислить значение функции F, с полиноми-
альной от N сложностью. Действительно, каждая
из операций сложения по модулю 2, подстанов-
ки, перестановки может быть записана в виде
булевых формул с полиномиальной от N слож-
ностью. Поскольку число композиций таких
операций в итерированном шифре равно 0(1), то
итоговая сложность вычисления функции F, по-
линомиальна.
18 Такое задание булевой функции не позволяет
записать ее в дизъюнктивной нормальной форме или
в виде полинома Жегалкина. ” и.-
346
Если известно Ада 1,368ЛГ открытых и зашиф-
рованных текстов, то система уравнений (16.5.1)
имеет единственное решение, которое и является
ключом [6]. Подставляя в уравнение (16.5.1) вме-
сто разрядов открытых текстов их значения и
представляя процесс зашифрования как компо-
зицию наборов булевых функций, получаем
функцию зашифрования, описывающую i-й раз-
ряд шифртекста. Приравняем эти функции к ис-
тинным значениям разрядов шифртекста:
ж, ...ДЛ)=у„ 7=1,2,...,/?. (16.5.2)
Система (16.5.2) имеет единственное реше-
ние, которое, следовательно, может быть записа-
но в виде булевой формулы, содержащей един-
ственную конъюнкцию:
к}к2 ... kN =1, (16.5.3)
где к означает, что переменная входит с инвер-
сией или без инверсии. Но булева функция
(16.5.3) может быть записана и в виде конъюнк-
ции булевых формул:
Я = д/,=1. (16.5.4)
(=1
Если у, = 1, то f входит в формулу (16.5.4) без
инверсии, в противном случае— с инверсией.
Поскольку выражения (16.5.3) и (16.5.4) прини-
мают значение 1 на одном и том же наборе аргу-
ментов, они представляют одну и ту же булеву
функцию аргументов кь kN, которую назовем
целевой, при этом (16.5.4) дает способ вычисле-
ния целевой функции для произвольного ключа.
Каждая функция / вычисляется с полиномиаль-
ной сложностью, поэтому и целевая функция Н
вычисляется с полиномиальной сложностью.
Предположим, что все функции / вычисляют-
ся с одинаковой сложностью, шифр содержит г
циклов, сложность выполнения каждого цикла на
компьютере равна R. Тогда сложность вычисле-
ния функции И равна 1,368Л7?г. На практике
числа R и г сравнительно невелики.
Таким образом, доказана следующая теорема.
Теорема 16.5.1. Задача вскрытия ключа ите-
рированного шифра с длиной ключа N бит на
основе известных открытых текстов полиноми-
ально сводится к задаче о выполнимости булевой
формулы (16.5.4) N переменных.
Пример 16.5.1. Сложность вычисления целе-
вой функции Н.
Пусть итерированный шифр имеет длину
ключа 256 бит, размер подстановки 4 бита, 32
цикла шифрования. На каждом цикле над блока-
ми длины 32 бита выполняются операции сложе-
ния по модулю 2 блока с ключом, замены слов
текста (четырехразрядной подстановки),19 пере-
становки битов в блоке и сложения блоков по
модулю 2. Сложность будем измерять как сум-
марное число конъюнкций и дизъюнкций фор-
мулы, заданной в ДНФ с использованием компо-
зиций наборов булевых функций. Сложность вы-
числения одноразрядной суммы равна 4, слож-
ность перестановки в расчете на один разряд
равна 1 (заменяется имя операнда), сложность
булевой функции, реализуемой подстановкой, с
учетом минимизации в среднем равна примерно
7. Итого, сложность вычисления всех функций F,
для одного блока на одном цикле равна
32 • (4 + 1 + 7 + 4) = 512, на 32 циклах— 16384.
Для вычисления функции Н из найденных / не-
обходимо выполнить 1,368 • 256 = 350 конъюнк-
ций в формуле (16.5.4). Это соответствует
10,94 да 11 блокам по 32 бита. Итоговая слож-
ность вычисления целевой функции составляет
16384- 11 = 180224 указанных операций.20
Формула (16.5.4) задает способ вычисления
булевой функции, которая равна 1 только для
набора аргументов, совпадающего с ключом.
Минимизируя правую часть формулы (16.5.4),
получаем уравнение (16.5.3). Это уравнение ре-
шается легко (см. алгоритм 17.3.1). Таким обра-
зом, справедлива следующая теорема.
Теорема 16.5.2. Задача вскрытия ключа ите-
рированного шифра с длиной ключа N бит на
основе известных открытых текстов полиноми-
ально сводится к задаче минимизации булевой
формулы N переменных, заданной в ДНФ.
Любая булева функция может быть задана в
виде полинома Жегалкина. Поэтому целевую
функцию (16.5.4) можно представить как компо-
зицию полиномов Жегалкина, а функцию
(16.5.3)— как результат упрощения (минимиза-
ции) итоговой композиции полиномов. Поэтому
справедливо следующее утверждение.
Теорема 16.5.3. Задача вскрытия ключа ите-
рированного шифра с длиной ключа N бит на
основе известных открытых текстов полиноми-
ально сводится к задаче минимизации полинома
Жегалкина от N переменных.
19 Здесь под подстановкой понимается замена од-
ной четверки битов другой четверкой, а не подста-
новка одной формулы в другую.
20 Найденная оценка справедлива, если отображе-
ние ведет себя как случайное. ?-2 -кз? u.
347
Свойство NP-полноты [1] означает полиноми-
альную сводимость задачи о выполнимости ко
всем остальным NP-полным задачам.
16.6. Требования к шифрам
Во второй половине XIX века на основе об-
ширного опыта использования методов крип-
тографии А. Керкхоффс в статье «Военная
криптография» сформулировал следующие ос-
новные требования к разработке шифроваль-
ных систем:
1) система должна быть нераскрываемой. если
не теоретически, то хотя бы практически.
Это значит, что на основе шифртекста невоз-
„ 21
можно вскрыть ключ или открытый текст;
2) знание открытой и соответствующей зашиф-
рованной информации не должно позволять
нарушителю вскрыть ключ или другую от-
крытую информацию;
3) криптосистема должна обеспечивать воз-
можность запоминания (хранения) и смены
ключа;
4) шифрованный текст должен допускать пере-
22
дачу по каналу связи;
5) шифровальная аппаратура должна быть удоб-
ной для переноски;
6) криптосистема должна быть простой в экс-
плуатации.
Эти требования справедливы и поныне.
История криптографии показывает, что зада-
чи вскрытия ключа шифра решаются с использо-
ванием всех имеющихся у нарушителя средств.
Мы будем рассматривать только криптоаналити-
ческие атаки, реализуемые с использованием ал-
гебраических и статистических свойств шифра, в
предположении, что нарушителю известен алго-
ритм шифрования.
Различают криптоанализ на основе:
1) шифртекстов (нарушитель знает только
шифртексты и статистические свойства мно-
жества открытых текстов);
2) открытых текстов (нарушитель знает от-
крытые тексты и соответствующие шифртек-
сты);
21 Заметим, что если множество ключей конечно,
то ключ всегда можно найти перебором. Однако
сложность перебора должна быть достаточно велика,
чтобы обеспечить практическую безопасность.
22 По Керкхоффсу, должна быть предусмотрена
передача по телеграфу — основному виду связи в то
время.
3) подобранных открытых текстов (наруши-
тель имеет доступ к шифровальной аппара-
туре, может задавать открытые тексты для
зашифрования и знает соответствующие
шифртексты);
4) адаптивно подобранных открытых текстов
(нарушитель имеет доступ к шифровальной
аппаратуре, может задавать открытые тексты
для зашифрования так, что последующий от-
крытый текст выбирается в зависимости от
результата зашифрования предыдущих тек-
стов, и знает соответствующие шифртексты);
5) подобранных шифртекстов (нарушитель
может подавать шифртексты для расшифро-
вания и узнавать результаты расшифрования
этих текстов);
6) адаптивно подобранных шифртекстов (на-
рушитель может подавать шифртексты для
расшифрования и узнавать результаты рас-
шифрования этих текстов, причем очередной
шифртекст выбирается в зависимости от ре-
зультатов расшифрования предыдущих тек-
стов);
7) связанных ключей (ключи К и К' =j(K) поль-
зователей не известны, но известна или даже
может быть выбрана функция f) [8].
Из широкого спектра задач криптоанализа
(вскрытие ключа, бесключевое чтение?3 навязы-
вание ложной информации, определение неиз-
вестного алгоритма шифрования и т. п.) будем
рассматривать только задачу вскрытия ключа
или обращения хэш-функции.
Шифры часто проектируют универсальными,
рассчитанными на различные условия эксплуа-
тации. Например, для стандарта шифрования
невозможно оговорить такие ограничения, как
коэффициент избыточности источника откры-
тых текстов, запрет шифрования априорно из-
вестных нарушителю открытых текстов или не-
возможность ознакомления нарушителя с от-
крытыми текстами. Поэтому стойкость таких
шифров должна обеспечиваться по отношению
к криптоанализу на основе подобранных, в том
числе адаптивно, открытых и зашифрованных
текстов. ..
Задача разработки шифра (как и других крип-
тоалгоритмов) характеризуется тем, что пра-
вильность ее решения трудно проверить. Напри-
мер, плохо сконструированный самолет не будет
летать и не пройдет испытания; программа, со-
23 Под бесключевым чтением будем понимать вы-
числение открытого текста по его шифрограмме, вы-
полняемое без вскрытия ключа.
348
держащая ошибки, будет неправильно работать
или давать сбои, что выяснится при ее тестиро-
вании или при эксплуатации. Однако плохие за-
щитные качества шифра никак не отражаются на
работоспособности информационной системы и
являются своего рода миной, которая может
быть задействована квалифицированным наруши-
телем по его усмотрению.
Оценка защитных качеств криптоалгоритма
является наиболее трудоемким этапом при его
разработке. Итерированные шифры отличаются
от алгоритмов криптографии с открытым клю-
чом значительно большим разнообразием, по-
этому задача криптоанализа итерированного
шифра обычно является новой научной задачей.
При разработке шифра криптоанализ сводится
к оценке его защитных качеств, при этом задача
практического взлома шифра не решается, но
лишь оценивается сложность ее решения.
При разработке криптоалгоритма перед разра-
ботчиком часто встает дилемма: делать ли алго-
ритм «прозрачным» для криптоанализа или по
возможности «запутать» его и тем самым предпо-
ложительно затруднить криптоанализ. Под про-
зрачностью следует понимать удобство описания
свойств криптоалгоритма с помощью известного
математического аппарата и, соответственно,
оценку стойкости по отношению к существую-
щим методам анализа. Например, если дифферен-
циалы шифра легко можно вычислить, то можно и
легко оценить стойкость к дифференциальному
методу криптоанализа (см. п. 18.2).
Под запутыванием следует понимать неудоб-
ство описания криптоалгоритма с помощью из-
вестного математического аппарата, сводимость
задачи вскрытия ключа к математической задаче,
принадлежащей недостаточно исследованной
области математики, или просто значительное
неудобство вычислений.
По сути, эти два подхода различаются тем,
что в первом случае задача оценки стойкости
криптоалгоритма решается легко, но задача
практического его вскрытия является сложной.
Во втором случае усложняется оценка стойко-
сти криптоалгоритма, хотя задача практическо-
го его вскрытия, возможно, тоже является
сложной.
Вряд ли можно однозначно ответить на во-
прос, какой из этих подходов лучше. В крипто-
графии встречаются оба подхода. В печати часто
описываются новые перспективные криптоалго-
ритмы, про стойкость которых сложно сказать
что-то определенное (это характерно для крипто-
алгоритмов, представляющих скорее научный, а
не практический интерес). В ходе публичного
обсуждения защитных качеств криптоалгоритма
картина иногда проясняется. Однако для практи-
ческого применения допускаются шифры, кото-
рые прошли всестороннее исследование, то есть
шифры, разработанные в соответствии с первым
подходом.
Стойкость шифра как сложность наилучше-
го известного алгоритма, вскрывающего ключ,
или как срок, в течение которого невозможно
вскрыть ключ, должна быть достаточной для
хранения информации в секрете в течение задан-
ного срока. Иногда этот срок может составлять
десятки лет.
Сложность вскрытия ключа обусловлена тем,
что небольшие изменения ключа или открытого
текста приводят к большим изменениям шифро-
граммы. Поэтому на множестве троек {открытый
текст, ключ, шифрограмма} трудно установить
вычислимую метрику (функцию, показываю-
щую, насколько тестируемый ключ близок к ис-
тинному). Следовательно, становится сложным
или даже невозможным использование методов
последовательных приближений для вскрытия
ключа.
Статистические методы криптоанализа ис-
пользуют в качестве такой метрики некоторые
статистические зависимости, которые для истин-
ного ключа имеют место чаще, чем для других
ключей. Алгебраические методы криптоанализа
основаны на использовании алгебраических
свойств шифра, что позволяет отбраковать клас-
сы ключей или непосредственно вскрыть ключ.
Это разделение в значительной мере условное.
Могут применяться комбинации алгебраических
и статистических методов.
Стойкость шифра к статистическим методам
криптоанализа существенно зависит от объема
известных открытых и соответствующих за-
шифрованных текстов (см. гл. 18). С ростом
этого объема стойкость снижается. Учитывая
высокую производительность шифраторов, для
ограничения объема зашифрованных на данном
ключе текстов и для сохранения высокого уров-
ня стойкости в информационной системе при-
ходится периодически менять ключи. Напри-
мер, для каждого сеанса можно устанавливать
собственный сеансовый ключ и стирать его по
окончании сеанса. На практике требуемый срок
конфиденциальности открытых текстов может
многократно превышать срок действия ключа.
Например, история показывает, что многие ар-
хивы становятся доступными для историков
только спустя многие десятилетия после их соз-
дания.
Алгебраические методы криптоанализа (см.
гл. 17) обычно не требуют большого объема ста-
тистики; здесь периодическая замена ключей не
позволяет усложнить атаку.
349
Стойкость шифра часто может определяться
особенностями протоколов управления ключа-
ми — процессами выработки, доставки, установ-
ления, ввода в действие, вывода из действия, заме-
ны и уничтожения ключей. Поэтому стойкость
шифра должна соответствовать стойкости прото-
колов управления ключами. Например, если отече-
ственный стандарт шифрования ГОСТ 28147-89
при разумных ограничениях на объем зашифро-
ванных на одном ключе текстов обеспечивает
сложность вскрытия ключа, по порядку величи-
ны близкую к переборной (то есть порядка Ю70),
то использование для установления ключа про-
токола Диффи-Хеллмана в случае мультиплика-
тивной группы простого поля с характеристикой
длины 1024 бита обеспечивает стойкость поряд-
ка 1026. Поэтому и стойкость шифра с указан-
ным протоколом не может превышать 1026. Ги-
потетический специализированный компьютер
для вскрытия ключа по состоянию на начало
1990-х годов мог выполнять порядка 102° опе-
раций в год [12]; каждый год производитель-
ность вычислительной техники удваивается.
Экстраполируя эту зависимость на будущее,
даже без учета развития математических мето-
дов криптоанализа, получаем, что в 2000 г. ма-
шина может выполнять 1023 операций в год, а в
2030 г. — 1032 операций в год. Падение сложно-
сти задачи дискретного логарифмирования при-
водит к дополнительному снижению срока, в
течение которого ключ невозможно вскрыть.
Поэтому указанный способ установления ключа
вряд ли можно признать удовлетворительным,
если информация должна храниться в секрете в
течение хотя бы 10 лет.
Стойкость бесключевых хэш-функций опре-
деляется двояко: как сложность обращения и как
сложность вычисления коллизии. Для хэш-
функции с переборной сложностью обращения
легче найти коллизии, чем вычислить аргумент.
Требуемый уровень стойкости для хэш-
функции обычно меньше, чем для шифра. Это
определяется тем, что зачастую обращение хэш-
функции или поиск коллизий представляет инте-
рес только в течение срока действия параметров
хэш-функции. Однако могут встречаться и ис-
ключения. Например, если текст завещания вы-
полнен на компьютере и подписан автором с ис-
пользованием электронной цифровой подписи
(при этом необходимо использовать хэш-
функцию), то подмена завещания может быть
сопряжена с обращением хэш-функции. В этом
случае задача обращения хэш-функции может
представлять интерес в течение всего срока дей-
ствия завещания.
Ключ любого шифра имеет конечную длину.
Поэтому теоретически его можно вскрыть пере-
бором. В действительности это затруднительно
даже при длине ключа в десятки бит. Для того
чтобы вскрыть ключ DES перебором, нужно в
среднем опробовать 254 ключей.24 Типовой ком-
пьютер потребует для зашифрования на одном
цикле не менее 60 тактов (перестановка— не-
удобная для компьютера операция), а для 16
циклов — не менее 1000 тактов, то есть опробо-
вание ключа при тактовой частоте 100 МГц зай-
мет 10 мкс, а опробование 254 ключей— 5712
лет. Стандартный чип шифрует по алгоритму
DES со скоростью примерно 1 блок в микросе-
кунду, то есть в 10 раз быстрее. Сконструировав
для перебора ключей специализированный «ком-
пьютер» из 1000 таких чипов, получим, что ключ
можно вскрыть за несколько месяцев. Этот при-
мер иллюстрирует нецелесообразность исполь-
зования универсальных компьютеров для вскры-
тия ключей «силовым» методом.
Обычно методы криптоанализа симметрич-
ных шифров и ключевых хэш-функций включа-
ют два этапа. На первом этапе устанавливается
вычислимое отношение порядка, связывающее
множество открытых и зашифрованных текстов
и множество ключей, при этом множество клю-
чей упорядочивается по вероятности ключа быть
истинным. На втором этапе осуществляется оп-
робование ключей, начиная с наиболее вероят-
ных.
Сложность опробования зависит от распреде-
ления вероятностей ключей. Предположим, что
удалось найти такой способ упорядочения, при
котором для последующего ключа длины п бит
вероятность быть истинным в а > 1 раз меньше,
чем для предыдущего. Тогда список вероятно-
стей будет иметь вид: Р, а'Р. аГ2Р, ..., причем
Вероятность вскрытия ключа с одной попыт-
ки будет равна 1 - а-1, с двух попыток — 1 - а-2,
и т. д. Здесь вероятность успеха на втором этапе
практически не зависит от длины ключа.
Таким образом, одна из основных задач крип-
тоанализа состоит в том, чтобы найти вычисли-
мое упорядочение ключей по их вероятности
быть истинными. Для решения этой задачи необ-
ходимо ввести вычислимый способ нахождения
24 DES как фейстелев шифр обладает свойством
дополнения (см. п. 16.8), поэтому ключи можно опре-
делять с точностью до инверсии, то есть объем пере-
бора составляет 255 ключей. I
350
«расстояния» между данным ключом и неизвест-
ным истинным ключом (метрику). Если оста-
ваться в рамках традиционного представления
шифра, это вряд ли возможно, поскольку поле Е2
не упорядочено.
Один из возможных подходов— «вложить»
шифр как алгебраическую структуру над Е2 в
структуру над упорядоченным кольцом R. При
этом решение уравнения Н= 1 для целевой
функции Н над Е2 должно совпадать с решением
этого же уравнения над R. Тогда по вычисленной
целевой функции можно судить о том, насколько
тестируемый ключ близок к истинному, и найти
ключ методом последовательных приближений.
Этот подход ведет к алгебраическим методам
криптоанализа (см. гл. 17).
Другой возможный подход — определение
новой метрики, которая проявляется не для оди-
ночного открытого и зашифрованного текстов, а
«в среднем», на большом объеме статистики.
Этот подход ведет к статистическим методам
криптоанализа (см. гл. 18).
16.7. Шифры замены и перестановки
В этом параграфе рассматриваются наиболее
простые шифры, использовавшиеся для защиты
открытых текстов на естественном языке, и час-
тотный метод криптоанализа согласно работе [11].
V 16.7.1. Моноалфавитная замена
Шифр моноалфавитной замены — шифр, в
котором каждая буква алфавита (как правило,
небольшого) заменяется буквой этого же алфа-
вита по фиксированному правилу, не зависящему
от других букв текста. Таким образом, шифры
моноалфавитной замены представляют собой
совокупность подстановок, действующих на бу-
квах алфавита. Если — буквы соответствен-
но открытого текста и шифрограммы, то уравне-
ние зашифрования имеет вид у, = Е(х,), где F—
подстановка.
Простейший пример моноалфавитной заме-
ны — шифр Цезаря?5 В этом шифре моноалфа-
витная подстановка реализуется циклическим
сдвигом алфавита, записанного в естественном
порядке. Значение сдвига является ключом. На-
пример, для 32-буквенного алфавита (А, Б, В, Г,
Д, Е, Ж, 3, И, Й, К, Л, М, Н, О, П, Р, С, Т, У, Ф,
X, Ц, Ч, Ш, Щ, Ъ, Ы, Ь, Э, Ю, Я) шифрограмма
слова ШИФРЫ при циклическом сдвиге вправо
на четыре буквы имеет вид ЬМШФЯ.
25 Таким шифром пользовался Ю. Цезарь при пе-
реписке с Цицероном.
Для усложнения вскрытия иногда исключа-
ются символ пробела и знаки препинания. От-
крытый текст записывается как одно большое
слово, например:
ОТКРЫТЫЙТЕКСТДЛЯЗАШИФРОВАНИЯ
и разбивается на слова фиксированного размера,
например, четырехбуквенные:
ОТКР ЫТЫЙ ТЕКС ТДЛЯ ЗАШИ ФРОВ АНИЯ.
После этого открытый текст зашифровывает-
ся с помощью циклического сдвига вправо (на
четыре символа):
ТЦОФ ЯЦЯН ЦЙОХ ЦИПГ ЛДЬМ ШФТЖ ДСМГ.
Для расшифрования выполняется цикличе-
ский сдвиг шифрограммы влево на столько же
символов.
Если буквы пронумеровать от 0 до 31 и обо-
значить: х — номер буквы открытого текста, у —
номер буквы зашифрованного текста, к — ключ,
то шифр Цезаря можно задать формулой:
у = х + к (mod 32).
Для практического использования шифр Це-
заря является слабым: вскрытие ключа сводится
к перебору 32 возможных сдвигов. Некоторое
усложнение этого алгоритма заключается в аф-
финном преобразовании множества текстов: у, =
= ax, + b (mod 32), где а— обратимый и b —
произвольный элемент кольца Z732ZL
В общем случае ключ (вид подстановки, ис-
пользуемой в шифре моноалфавитной замены)
может быть произвольным. Для расшифрования
используется обратная подстановка.
Вскрытие шифра моноалфавитной замены
при известных открытых текстах выполняется
очевидным путем — надо восстановить таблицу
подстановки. Если известны только зашифро-
ванные тексты, то вскрытие выполняется час-
тотным методом, который основан на разли-
чии вероятностей появления букв естественного
алфавита.25 26 Каждая буква имеет свою безуслов-
ную вероятность появления. Например, про-
бел— один из наиболее часто встречающихся
знаков, Ф — наиболее редко встречающаяся
буква в русском языке, Z— наиболее редко
встречающаяся буква в английском языке (таб-
лицы 16.1, 16.2 [4]).
Частота букв существенно зависит от вида
текста. Например, в данной главе буквы А, Б, В,
26 Примеры вскрытия шифров моноалфавитной
замены приведены в приключенческих рассказах
Э. По «Золотой жук» и А. Конан-Дойля «Пляшущие
человечки».
351
Г, Д, Е, Ж, 3, И, К встречаются соответственно с
частотами 0,074; 0,014; 0,0447; 0,0098; 0,0264;
0,0804; 0,0086; 0,0164; 0,0787; 0,034. Чаще всего
встречается буква О, ее частота равна 0,104, реже
всего — буквы Э и Щ с частотой 0,0036; частота
буквы Ф равна 0,0135, то есть в 6,5 раз больше,
чем положено согласно таблице 16.2.
Таблица 16.1
Относительные частоты встречаемости букв английского алфавита
Буква Частота Буква Частота Буква Частота Буква Частота
А 0,0856 Н 0,0528 О 0,0797 V 0,0092
В 0,0139 I 0,0627 Р 0,0199 W 0,0149
С 0,0279 J 0,0013 Q 0,0012 X 0,0017
D 0,0378 К 0,0042 R 0,0677 У 0,0199
Е 0,1304 L 0,0339 S 0,0607 Z 0,0008
F 0,0289 М 0,0249 т 0,1045
G 0,0199 N 0,0707 и 0,0249
Таблица 16.2
Относительные частоты встречаемости букв русского алфавита
Буква Частота Буква Частота Буква Частота Буква Частота
А 0,062 И 0,062 Р 0,040 Ш 0,006
Б 0,014 Й 0,010 С 0,045 Щ 0,003
В 0,038 К 0,028 Т 0,053 Ъ,Ь 0,014
Г 0,013 Л 0,035 У 0,021 Ы 0,016
д 0,025 м 0,026 ф 0,002 э 0,003
Е,Ё 0,072 н 0,053 X 0,009 ю 0,006
Ж 0,007 о 0,090 ц 0,004 я 0,018
3 0,016 п 0,023 ч 0,012
В зашифрованных текстах эти же частоты со-
ответствуют другим буквам. Остается найти эм-
пирическую частоту появления данной буквы
шифртекста и сопоставить ей букву открытого
текста с такой же или близкой частотой появле-
ния. Однако это не позволяет вскрыть весь
шифр, например, буквы Р, Y в английском языке,
а также буквы А, И в русском языке встречаются
почти одинаково часто. Уточнение вида подста-
новки выполняется методом последовательных
приближений на основе избыточности естест-
венного языка для сочетаний нескольких букв
или слов.
Шифр моноалфавитной замены действует как
набор подстановок на множестве букв открытого
текста. Поэтому такие шифры, как и подстанов-
ки, образуют группу по композиции. Это значит,
что зашифрование текста сначала одним, а затем
другим шифром моноалфавитной замены экви-
валентно зашифрованию этого же текста каким-
то третьим шифром моноалфавитной замены.
Композиция таких шифров ассоциативна, еди-
ничным элементом группы является шифр, ос-
тавляющий все буквы неподвижными. Число
шифров моноалфавитной замены равно q\, где
q — число букв алфавита.
16.7.2. Полиалфавитная замена
Усложненным вариантом шифров замены яв-
ляются шифры полиалфавитной замены, в кото-
рых каждая буква алфавита заменяется некото-
рой буквой этого же алфавита, но вид замены
зависит от других букв. Подробный обзор таких
шифров сделан в работе [11]. При этом откры-
тый текст, рассматриваемый как одно слово, раз-
бивается на слова длиной п символов («-граммы,
п > 2), которые заменяются обратимым путем на
«-граммы. Таким образом, шифры полиалфавит-
ной замены представляют собой подстановки,
352
действующие на «-граммах (длиной 2, 3 или бо-
лее символов).27 Совокупность шифров полиал-
фавитной замены, действующих на «-граммах
одинаковой длины, образует группу.
Если использовать произвольную подстанов-
ку на словах из п букв, то ключ становится слиш-
ком длинным. Например, для п = 3 в 32-буквен-
ном алфавите (А, Б,..., Я) нужно предусмотреть
всевозможные замены вида
ААА, ААБ, ААВ, ..., ЯЯЯ,
то есть при табличном задании подстановка бу-
дет иметь длину З23 = 32768 букв или свыше 150
Кбит. Хранить такой ключ неудобно, поэтому
используют ключи специального вида. Напри-
мер, если буквы пронумеровать от 0 до 31 и п-
граммы открытого текста представить как векто-
ры х, то линейную подстановку можно задать
невырожденной матрицей L над кольцом Z732Z
(определитель матрицы должен быть взаимно
простым с характеристикой кольца, то есть не-
четным). Зашифрованная «-грамма имеет вид
у = Lx (mod 32). Расшифрование выполняется ум-
ножением векторов шифрограммы на обратную
матрицу Z-1.
Пример 16.7.1. Полиалфавитная замена с по-
мощью шифрующей матрицы.
Для « = 3 и шифрующей матрицы вида
'19 4 8
z = 10 И 24
28 20 23
зашифрование задается уравнением у = Lx над
кольцом Z732Z, где х, у— векторы, состоящие
из номеров букв 3-грамм соответственно откры-
того и зашифрованного текста. Открытый текст
ЗИМНЕЕСОЛНЦЕ разбивается на 3-граммы:
ЗИМ НЕЕ СОЛ Е1ЦЕ. После перехода к номерам
букв в алфавите этот текст примет вид: X] =
= (7,8,12), х2 = (13,5, 5), х3 = (17, 14, И), Х4 =
= (13, 22, 5). Поочередно умножаем эти векторы
на матрицу. Получаем векторы зашифрованного
текста: У1 = (5,30,24), у2 = (19,17,3), у3 = (19,12,17),
у4 = (23, 12, 23), которым соответствует текст
ЕЮШ УСВ УМС ЧМЧ. Матрица расшифрования
имеет вид:
27 Принципиально шифр полиалфавитной замены
не отличается от шифра моноалфавитной замены: и
тот и другой задаются подстановкой. Если «буквой»
нового алфавита считать последовательность из и
символов обычного алфавита, то полиалфавитную
замену можно рассматривать как моноалфавитную в
новом алфавите. ,
'19 28 24"
6 27 24
J2 12 7 ,
В результате расшифрования получаем от-
крытый текст.
Такой шифр для любого ключа сохраняет
неподвижным нулевой вектор. Для исключения
этого недостатка можно перейти от линейных
преобразований к аффинным, описываемым
уравнением у = Lx + а, где а — вектор сдвига.
Обратное преобразование описывается уравне-
нием
x = Z-l(y-a).
Шифр с шифрующей матрицей, как и шифр
аффинного преобразования, легко может быть
вскрыт методами линейной алгебры, если из-
вестно несколько линейно независимых откры-
тых и соответствующих зашифрованных текстов.
Пример 16.7.2. Вскрытие ключа шифра аф-
финного преобразования.
Открытый текст имеет вид КРИ ПТО ГРА
ФИЯ, соответствующий шифртекст имеет вид
ПЮП РОЙ ИШЛ ЕЮШ. Матрица L имеет раз-
мер 3x3. Находим цифровое представление век-
торов открытого и зашифрованного текстов в
кольце Z732Z. Открытый текст: X] = (10, 16, 8),
х2= (15,18,14), х3 = (3, 16, 0), Х4 = (20, 8, 31);
зашифрованный текст: у| = (15, 30, 15), у2 =
= (16, 14, 9), уз = (8, 24, 11), у4 = (5, 30, 24).
Для вычисления вектора сдвига находим ли-
нейную комбинацию входных векторов, пред-
ставляющую нулевой вектор. Решаем над Z732Z
систему линейных уравнений относительно а, Ь,
с, d: аХ] + 6х2 + сх3 + dx< = 0, где 0 — нулевой
вектор.
Получаем b = 8а, с = 10а, d = 24а, где а —
произвольный ненулевой элемент кольца Z732Z.
Тогда уравнение зашифрования для такой ли-
нейной комбинации входных текстов можно за-
писать в виде
(23а\
ау)+6у2+су3+б/у4 = 14а =(а + 6 + с + rf)a = (11а)а,
^5aJ
откуда в Z732Z
а = 1Г’ 14
10
J5,
353
Теперь находим матрицу L. Для этого перехо-
дим к центрированным выходным векторам
у/ = у( -а: у/= (10, 20,0), у2'= (11, 4, 26), у3'=
= (3,14,28), уд'= (0,20,9). Решаем системы
уравнений:
^]1X1 + ^12X2 +^13X3 ~
62]х1 +^22Х2 +^23Х3 —
631xt + 632х2 + 633х3 =
0
ГО'
1
<0,
о
Л
Тогда первая строка матрицы L равна (бпу/ +
+ 612У2' + ^1зУз')Т = О, 2, 4); вторая строка равна
(621У1' + Мг + /?2зУз')Т = (Ю, П, 12); третья стро-
ка равна (631у 1' + 632у2' + й33у3')т = (20, 22, 23).
Аффинное преобразование характеризуется
хорошим рассеиванием (каждый элемент шиф-
рограммы зависит от всего блока открытого тек-
ста), но перемешивающие качества его невелики,
так как зависимость шифрограммы от открытого
текста подчиняется простым законам. Поэтому
для повышения стойкости шифра в соответствии
с предложениями Шеннона желательно исполь-
зовать композицию аффинного преобразования и
подстановки, описываемой нелинейным уравне-
нием над ТЛпЯ., где п — объем алфавита. Много-
кратное повторение таких композиций позволяет
задать полиалфавитную подстановку с использо-
ванием сравнительно короткого ключа, причем
будут выполняться требования Шеннона к шиф-
ру в части практической стойкости.
Другим известным примером шифра полиал-
фавитной замены является шифр Виженера [11].
Ключ представляет собой /7-грамму (Ао, ..., А,,-]).
Открытый текст разбивается на /7-граммы вида
х = (х0, ...,х„_1). Каждая «-грамма преобразуется
в «-грамму шифртекста у = (у0, ...,y„-i) следую-
щим образом: у, = х, + kj (mod 32).
Обобщенный шифр Виженера осуществляет
обратимую замену символа /7-граммы, то есть
задается набором из п подстановок.
Вскрытие ключа шифра полиалфавитной за-
мены на основе зашифрованных текстов тоже
выполняется частотным методом. Составляется
таблица частот допустимых n-грамм входного
текста, на которых действует подстановка, инду-
цированная шифром. Далее определяется эмпи-
рическая частота появления n-грамм шифртекста
и по этой частоте восстанавливаются слова от-
крытого текста. Вскрытие шифра значительно
облегчается, если известна часть открытых и со-
ответствующих зашифрованных текстов.
Криптоанализ шифров полиалфавитной заме-
ны на основе зашифрованных текстов подробно
описан в работе [ 11].
Очевидно, что чем больше п, тем сложнее
вскрыть ключ, так как сложнее найти вероят-
ность п-граммы.
Шифр перестановки не изменяет значения
букв в тексте, но переставляет их, то есть выпол-
няется замена не букв, а их позиций. В этом слу-
чае открытый текст разбивается на блоки фикси-
рованной длины «, и буквы в блоке переставля-
ются в соответствии с некоторой перестановкой,
которая является ключом. Мощность множества
ключей составляет п!, поэтому длина блока
должна быть достаточно велика, чтобы исклю-
чить перебор. Например, перестановка вида
(10,3,8, 9, 5,2, 1,7, 4, И, 12, 6)
переводит открытый текст КРИПТОГРАФИЯ в
шифртекст ФИРАТРКГПИЯО.
Криптоанализ шифра перестановки на основе
известных открытых текстов выполняется оче-
видным путем.
Криптоанализ шифра, представляющего собой
композицию шифров перестановки и моноалфа-
витной замены, на основе подобранных и извест-
ных открытых текстов читателю предлагается про-
вести самостоятельно (см. упражнения 1,10,11).
16.8. Операторы, используемые
при построении блочных шифров
Рассмотрим некоторые типичные операто-
ры, применяемые в итерированных шифрах
(алфавит входных и выходных данных — дво-
ичный). Если не оговорено особо, то линей-
ность и нелинейность оператора рассматрива-
ется над полем Г2-
1. Перестановка битов в блоке. Этот опера-
тор является линейным не только над IF2, но и в
любой алгебраической конструкции (не обяза-
тельно в кольце) с любыми одноразрядными
операциями. Перестановка описывается матри-
цей, в которой в каждой строке и в каждом
столбце содержится единственная единица, а ос-
тальные элементы — нулевые. Пример записи и
действия перестановки на блоке длины 8 бит:
вход 1 2 3 4 5 6 7 8
выход 51732684
ПЕРЕСТАНОВКА( 10110001 ) = (00111010).
354
Характерной особенностью перестановки яв-
ляется то, что она сохраняет вес входного векто-
ра (число единиц).
2. Сложение по модулю 2. Этот оператор яв-
ляется аффинным, точнее — сдвигом, поскольку
его матрица является единичной.
3. Подстановка п-разрядного слова вместо п-
разрядного входного слова (операция замены).
Этот оператор в общем случае при п > 2 нели-
нейный, но при п е {1, 2} он является аффин-
ным. При этом шифруемый блок разбивается на
«-разрядные слова, которые заменяются в соот-
ветствии с кодом подстановки.
4. Циклический сдвиг (фиксированный). Этот
оператор является частным случаем перестанов-
ки и поэтому линеен. При этом непостоянный
циклический сдвиг не является линейной опера-
цией.
5. Умножение на невырожденную матрицу.
Если элементы матрицы лежат в кольце R, то
этот оператор является линейным над R. Он ис-
пользуется в качестве рассеивающего оператора
в шифрах SAFER, RIJNDAEL (см. пп. 19.9,
19.10).
6. Сложение по модулю 2". Этот оператор яв-
ляется «слабо» нелинейным и используется во
многих шифрах (ГОСТ 28147-89, RC5, FEAL).
Матрица коэффициентов нелинейной части пре-
образования является разреженной, нелиней-
ность обусловлена наличием и длиной переноса
из предыдущего разряда в последующие при вы-
полнении сложения.
7. Умножение по модулю простого числа
Ферма. Этот оператор является нелинейным и
используется в шифре IDEA для простого чис-
ла/? = 2м + 1. При этом вычисления проводятся
в группе Ер порядка 216. Для обеспечения об-
ратимости умножения множитель 0 заменяется
на 216, а произведение 216 заменяется на 0. Об-
ратной операцией является умножение на
мультипликативно обратный элемент по моду-
лю р.
8. Нахождение обратного элемента в рас-
ширенном поле характеристики 2. Пусть р(1) —
полином степени п, задающий расширенное ко-
нечное поле из 2" элементов. Вход «-разрядной
подстановки представляется элементом x(t) это-
го поля. Выходом подстановки является эле-
мент y(f) поля такой, что x(t)y(f) = 1 (mod p(t))
(такая подстановка вычисляется расширенным
бинарным алгоритмом Евклида). При этом по-
лагают О-1 = 0. Данный оператор является нели-
нейным и используется в стандарте шифрования
RIJNDAEL.
Эта подстановка обладает хорошим распреде-
лением дифференциалов.28 Если число п четное,
то наиболее вероятный дифференциал имеет ве-
роятность 2~"'2, если п нечетное — то 2~',+1 (то
есть все дифференциалы, обладающие ненулевой
вероятностью, равновероятны). Представление
двоичных разрядов подстановки в виде п поли-
номов Жегалкина дает для каждой булевой
функции слагаемые со степенью нелинейности
п - 1 как для четного, так и для нечетного числа
п — это максимально достижимая степень нели-
нейности. ч ,?
9. Возведение в степень по модулю простого
числа Ферма р. Эта операция у = cf (mod р) явля-
ется нелинейной и используется в шифре SAFER
для р = 28 + 1. Для обратимости этой операции
необходимо, чтобы основание а являлось обра-
зующей группы . Обратной операцией являет-
ся дискретное логарифмирование. После вычис-
ления экспоненты выполняется замена -1
(mod р) на 0, а перед вычислением логарифма —
обратная замена.
10. Фейстелев шифр (рис. 16.1) назван по
имени американского математика X. Фейстеля,
который запатентовал соответствующую схему
шифрования [9]. На каждом цикле шифрования
входной блок х зашифровываемого текста длины
2п бит разбивается на два полублока: х = х' || х"
длины п бит каждый. Блок х" шифруется с по-
мощью (не обязательно обратимой) шифрующей
функции F,. Выходом первого цикла зашифрова-
ния является блок Xj = х" || (х' Ф F](x")). Для рас-
шифрования на этом цикле выполняется опера-
ция разбиения: xj = х1'||х1" и последующее шиф-
рование блока х/ с помощью той же функции F\.
Выходом является текст х = (Х) " Ф Fi(xi'))||x,'.
Обычно цикловые операторы шифрования
F, = F,(x„ kJ осуществляют подстановку, завися-
щую от ключа.
Фейстелев шифр обладает свойством дополне-
ния, если выполняется равенство Fk(x) = Ek(x),
где Ек(х)— итоговый оператор зашифрования
открытого текста х на ключе к, а черта означает
инверсию. Для шифра, обладающего свойством
дополнения, ключ можно искать с точностью до
28 Определение дифференциала см. в п. 18.2. Чем
меньше вероятность дифференциала, тем выше стой-
кость шифра к дифференциальному методу крипто-
анализа. .... . . . Л t
355
инверсии. Этим свойством, в частности, обладает
стандарт DES (см. п. 19.3).
Существует простой критерий для определе-
ния того, обладает ли фейстелев шифр свойством
дополнения.
Теорема 16.8.1. Если в операторе F, фейсте-
лева шифра происходит поразрядное сложение
входного (для F) текста с ключом по модулю 2,
то шифр обладает свойством дополнения.
Доказательство. Рассмотрим одиночный
оператор F,. Пусть х, — его вход и к, — его ключ.
Инверсия входного текста х,. = 1Ф х(. и ключа
k, = 1 © к, сумму не меняет: \ © к,. = 1 © х, ©
©1©к, = х, Фк,. Поэтому F,(x,,k,) = Е](х,,к,).
Рассмотрим шифрование первого блока, ин-
версного по отношению к (х0, Х]). После сложения
с текстом на выходе оператора F] получим инверс-
ный результат: х0 © F} (k,, Xj) = (1 © х0) © F(1 ©
© kj, 1Ф Xj) = 1Ф хо Ф Fj(ki, xj) = х0 © F^kpX,).
Свойство дополнения выполняется для первого
цикла и, следовательно, для второго и после-
дующих циклов шифрования.
У
Рис. 16.1. Фейстелев шифр
Обобщенное свойство дополнения означает
возможность инверсии не всех, а произвольных
одноименных разрядов в открытом тексте, ключе
и шифртексте. Свойство дополнения можно ин-
терпретировать как вычислимый автоморфизм
шифра: существуют такие отображения <рх, <pj;, <р/,
для открытого текста, шифртекста и ключа соот-
ветственно, что выполняется равенство
<ру(Е/,(х)) = £ф#)(<рДх)).
Из теоремы 16.8.1 следует, что этому уравне-
нию удовлетворяет инверсия произвольного чис-
ла одноименных битов в открытом тексте, шифр-
тексте и ключе.
Фейстелев шифр может быть рассмотрен как
сдвиговый регистр с обратными связями —
структура, типичная для поточных шифров. Ре-
гистр содержит две ячейки: для х' и х", то есть
сдвигает не биты, а полублоки. Содержимое
ячейки х" преобразовывается с помощью опера-
тора F, и складывается с содержимым ячейки х',
сумма поступает на вход ячейки х", а содержимое
х" переписывается в х'. Такой подход позволяет
адаптировать для анализа фейстелевых шифров
методы, первоначально предложенные для анали-
за шифров на основе сдвиговых регистров.
11. Подстановочно-перестановочные шифры.
Этот тип итерированных шифров характеризует-
ся тем, что в цикловой функции шифрования пе-
ремешивание и рассеивание реализуются с ис-
пользованием операций фиксированной или
ключевой замены (подстановки коротких слов
блока) и перестановки битов в блоке [10]. К та-
ким шифрам относятся DES, ГОСТ 28147-89
(см. пп. 19.3, 19.6). Часто размер подстановки
равен четырем битам. При этом для разных слов
блока иногда используются различные подста-
новки. Например, первое слово заменяется в со-
ответствии с подстановкой Si, второе — в соот-
ветствии с S2 и т. д.
Подстановочно-перестановочные шифры яв-
ляются наиболее хорошо изученным типом блоч-
ных шифров. Стойкость такого шифра в значи-
тельной мере определяется свойствами подста-
новки [14]. Вопросы выбора подстановок рас-
сматриваются в гл. 18.
12. Подстановка, задаваемая полиномом над
Z/2'”Z. Если размер подстановки равен длине
блока (полублока в фейстелевом шифре), то та-
кая подстановка совмещает в себе функции пе-
ремешивания и рассеивания. Табличное пред-
ставление такой подстановки требует экспонен-
циально большого объема памяти, поэтому инте-
рес представляет возможность задания подста-
новки полиномом невысокой степени. Например:
% <— ФХ4 + ар? + арх (mod 2'"), (16.8.1)
356
где а0, ai, at — обратимые (нечетные) элементы
кольца Z72mZ.
Теорема 16.8.2. Функция (16.8.1) описывает
подстановку в кольце Z72'"Z.
Доказательство. Очевидно, что (16.8.1)
отображает кольцо R в себя. Полиномиальная
функция не является подстановкой тогда и толь-
ко тогда, когда она принимает какое-нибудь зна-
чение дважды. Если предположить, что при пе-
реборе х функция (16.8.1) принимает дважды не-
которое значение Ь, то сравнение
а2х4 + а\Х + а^х - b = 0 (mod 2”) (16.8.2)
должно иметь двойной корень. Кратные корни
можно определить вычислением наибольшего
общего делителя левой части сравнения (16.8.2)
и ее производной. Поскольку в Z72'”Z каждый
элемент, не являющийся делителем нуля, обра-
тим, нужно рассматривать наибольший общий
делитель над каждым главным идеалом, который
является делителем нуля в кольце Z72'”Z. Доста-
точно рассмотреть кольцаТЛЖ, Z72"'Z.
Производная левой части равенства (16.8.2)
равна 4а2т3 + 2щх + а0. Нетрудно видеть, что ле-
вая часть этого равенства не делится на произ-
водную ни над одним из указанных колец. Кроме
того, производная не имеет корней ни в одном из
этих колец, так как коэффициент «о нечетный, а
коэффициенты при степенях х четные. Полином,
задающий производную, имеет степень 3, поэто-
му он может раскладываться на множители лишь
тогда, когда хотя бы один из делителей имеет
степень 1, то есть если производная имеет корень
в указанных кольцах. Поскольку корней нет, то
производная левой части равенства (16.8.2) не
раскладывается на множители ни над одним из
указанных колец. Следовательно, наибольший
общий делитель левой части равенства (16.8.2) и
ее производной над каждым из указанных колец
равен обратимой константе, и выражение (16.8.1)
задает подстановку в Z/2“Z.
Пронумеруем двоичные разряды входа и вы-
хода подстановки, начиная с младших разрядов.
Тогда i-й двоичный разряд подстановки (16.8.1)
зависит только от входных разрядов 1, 2, ..., i.
Поэтому данное отображение будет являться
подстановкой и в том случае, если к аргументу х
в формуле (16.8.1) приписать несколько произ-
вольных младших разрядов (соответственно уве-
личив число т), а после вычисления функции их
удалить. Коэффициенты я, и приписываемые
младшие разряды могут быть параметрами шиф-
ра или ключом.
Подстановка (16.8.1) эффективно вычислима и
при а0 = «1 = «2 = 1 требует двух операций возве-
дения в квадрат. Обратная подстановка тоже за-
дается полиномом над Z/2“Z, который, однако,
может содержать значительное число слагаемых,
поэтому подстановку (16.8.1) желательно ис-
пользовать в фейстелевых шифрах.
К недостаткам подстановки (16.8.1) относится
то, что два младших разряда являются аффин-
ными булевыми функциями, и подстановка
(16.8.1) сохраняет число подряд идущих нулей в
младших разрядах. Однако эти недостатки мож-
но устранить, если к аргументу приписать не-
сколько ненулевых младших разрядов, а после
вычисления подстановки их удалить.
16.9. Описание итерированных шифров
в терминах булевых функций
Результат зашифрования открытого текста
длины п бит с помощью итерированного шифра
задается композицией наборов несложных буле-
вых функций. Число композиций пропорцио-
нально числу циклов шифрования. Алгебраиче-
ские свойства булевых функций, записанных в
базисе И, ИЛИ, НЕ или в виде полиномов Же-
галкина, теоретически позволяют исключить
операцию композиции и представить итоговое
зашифрование в виде совокупности и булевых
формул, заданных в дизъюнктивной нормальной
форме или полиномами Жегалкина. Очевидно,
что для обеспечения стойкости шифра формулы,
описывающие итоговое зашифрование, должны
быть сложными.
Сложность булевой функции п переменных,
записанной в ДНФ, будем определять как число
конъюнкций (длину ДНФ) после минимизации.
Справедлива следующая теорема [5].
Теорема 16.9.1. Почти все булевы функции и
аргументов как дизъюнктивные нормальные фор-
мы и как полиномы Жегалкина имеют одинако-
вую сложность, асимптотически равную <9(2”/и).
Эта теорема обусловливает эффект Шеннона'.
почти все булевы функции имеют одинаковую
сложность, и эта сложность экспоненциально
велика. Этот результат означает, что уравнение
зашифрования практически невозможно записать
в виде стандартной булевой формулы, например,
в виде ДНФ, и выглядит пессимистическим для
нарушителя. Однако на практике не все так пло-
хо. Это обусловлено несколькими факторами.
Во-первых, булевы функции, с помощью ко-
торых строится шифр, не являются «случайны-
ми». Действительно, шифрование должно вы-
полняться быстро, а для этого наборы булевых
функций, композиция которых определяет шифр,
357
должны быть несложными (вычислимыми с по-
линомиальной сложностью). Однако почти все
булевы функции п переменных для достаточно
большого п не допускают представления в виде
набора небольшого числа композиций булевых
функций малой сложности. Действительно, если
сложность булевых функций, используемых при
шифровании, не превышает 2"' и т « п, а число
композиций не превышает г, то можно получить
всего Nc = (22 )' = 22 ' булевых функций. Число
же всевозможных булевых функций п аргумен-
тов, равное N„ = 22, несопоставимо больше:
Nc = Иными словами, почти все булевы
функции не являются вычислимыми.
Во-вторых, современные методы криптоана-
лиза не требуют представления итогового опера-
тора шифрования в виде набора булевых фор-
мул, не содержащих композиции (см. гл. 17, 18).
В-третьих, в ряде случаев описание шифра в
терминах булевых функций не является наилуч-
шим. Например, для шифра RIJNDAEL (см.
п. 19.10) более перспективным может быть опи-
сание в терминах кольца полиномов над IF256-
Упражнения к главе 16
1. Предположим, что шифр строится с помо-
щью «-кратных композиций коммутирующих
между собой отображений перемешивания и
рассеивания. Что можно сказать о стойкости
такой системы? Почему нужно использовать
не коммутирующие между собой операции?
2. Чем отличается булева функция от булевой
формулы?
3. Предложите методы вскрытия ключа крипто-
системы Виженера, а также шифрующей мат-
рицы и аффинного шифрующего преобразова-
ния на основе подобранных открытых текстов.
4. Оцените сверху объем известных открытых
текстов, необходимый для вскрытия 50 %
шифрограмм для шифра на основе замены
2-грамм и для шифра на основе замены
3-грамм (криптоанализ на основе известных
открытых текстов).
5. Оцените сверху объем подобранных откры-
тых текстов, необходимый для вскрытия
50 % шифрограмм для шифра на основе за-
мены 2-грамм и для шифра на основе замены
3-грамм (криптоанализ на основе подобран-
ных открытых текстов).
6. Пусть открытые тексты представляют собой
обычные тексты на английском языке, шиф-
рование осуществляется методом моноалфа-
витной замены. Используя таблицу частот
появления английских букв, оцените слож-
ность частотного метода криптоанализа и
сравните ее со сложностью перебора.
7. Пусть шифр представляет собой замену п-
грамм в Л’-буквенном алфавите для некото-
рого языка и вероятности появления всевоз-
можных «-грамм в этом языке образуют гео-
метрическую прогрессию. Покажите, что
шифр раскрывается частотным методом с
полиномиальной от N сложностью. Какова
емкостная сложность этого метода?
8. Пусть шифр представляет собой замену п-
грамм в Л'-буквенном алфавите для некоторого
языка, и вероятности появления всевозможных
«-грамм в этом языке образуют арифметиче-
скую прогрессию. Оцените сложность частот-
ного метода и требуемый объем статистики.
9. Пусть шифр представляет собой замену п-
грамм в Л'-буквенном алфавите. Какова дли-
на ключа, если совокупность всевозможных
ключей позволяет реализовать произвольную
подстановку?
10. Пусть шифр моноалфавитной замены А и
шифр перестановки В действуют на блоках
из п символов Л’-буквенного алфавита, и
АВ— применение к открытому тексту шиф-
ра В и затем применение к полученной шиф-
рограмме шифра Л. Покажите, что АВ = ВА и
что сложности вскрытия шифров АВ, АВАВ,
ABABA одинаковы.
11. Пусть А, В — шифры из предыдущей задачи.
Предложите способ вскрытия шифра АВ на
основе подобранных открытых текстов. Оце-
ните необходимый объем подобранных от-
крытых текстов.
12. Пусть шифры полиалфавитной замены А и В
действуют на словах длины пА и пв соответ-
ственно. Покажите, что композицию шифров
АВ можно рассматривать как шифр полиал-
фавитной замены, действующий на словах с
длиной пАВ, равной наименьшему общему
кратному пА, пв. Как можно задать действие
шифра Л на словах длины пАВ?
13. Приведите пример шифра с шифрующей
матрицей, в котором размер блока шифро-
граммы больше, чем размер блока открытого
текста, и вскройте ключ такого шифра. Если
L — шифрующая матрица размера п х (п + т)
и ранга и, то обратная матрица М имеет раз-
мер (п + т) х п, при этом ML = Еп.
14. Оцените вероятность того, что случайная квад-
ратная матрица будет невырожденной над F2.
15. Предложите несколько быстрых алгоритмов
генерации случайной невырожденной матри-
цы над F2 и над Z/2'’Z.
16. При каких условиях отображение, задавае-
мое полиномом степени 2 над Z72"'Z, являет-
ся подстановкой?
Литература к главе 16
1. Ахо А., Хопкрофт Дж., Ульман Дж. Построение и
анализ вычислительных алгоритмов. М.: Мир, 1979.
2. Гульден Я., Джексон Д. Перечислительная ком-
бинаторика. М.: Наука, 1990.
3. Колчин В.Ф. Случайные отображения. М.: Наука,
1984.
4. Нечаев В.И. Элементы криптографии. Основы тео-
рии защиты информации. М.: Высшая школа, 1999.
5. Нигматуллин Р.Г. Сложность булевых функций.
М.: Наука, 1991.
6. Ростовцев А.Г., Маховенко Е.Б. Введение в крип-
тографию с открытым ключом. СПб.: Мир и Се-
мья, Интерлайн, 2001.
7. Шеннон К. Теория связи в секретных системах / В
сб.: К. Шеннон. Работы по теории информации и
кибернетике. М.: ИЛ, 1963. С. 333-402.
8. Biham Е. New types of cryptanalytic attacks using
related keys // Advances in Cryptology —
EUROCRYPT ’93. Lecture Notes in Computer Sci-
ence. Springer-Verlag. 1994. Vol. 765. P. 398-409.
9. Feistel H. Cryptography and computer privacy // Sci-
entific American, 1973. Vol. 228. P. 15-23.
10. Kam J.B., Davida G.I. Structured design of substitu-
tion-permutation encryption networks // IEEE Trans-
action on Computers, 1979. Vol. C-28. P. 747-753.
11. Konheim A. Cryptography: A Primer. New York:
J. Wiley & Sons, 1981.
12. Odlyzko A. Discrete logarithms in finite fields and
their cryptographic significance // Advances in Cryp-
tology — Proceedings of EUROCRYPT 84. Lecture
Notes in Computer Science. Springer-Verlag, 1985.
Vol. 209. P. 224-314.
13. Simmons G.J. Authentication theory/coding theory //
Advances in Cryptology — Proceedings of
CRYPTO 84. Lecture Notes in Computer Science.
Springer-Verlag. 1985. Vol. 196. P. 411-431.
14. Webster A.F., Tavares S.E. On the design of S-boxes
// Advances in Cryptology — CRYPTO ’85. Lecture
Notes in Computer Science. Springer-Verlag. 1986.
Vol. 218. P. 523-534.
Глава 17. АЛГЕБРАИЧЕСКИЕ МЕТОДЫ КРИПТОАНАЛИЗА
В данной главе рассматриваются некоторые (в
том числе эвристические) методы криптоанализа
итерированных блочных шифров и хэш-фун-
кций, используюшие их алгебраические свойства
и не требующие знания большого объема откры-
тых и соответствующих зашифрованных текстов.
Для краткости под открытым (зашифрованным)
текстом будем понимать блок открытого (за-
шифрованного) текста.
Для решения одной и той же задачи, напри-
мер вскрытия ключа некоторого шифра, могут
использоваться различные методы. При этом
встает задача выбора наилучшего из них. Назо-
вем эффективностью метода число итераций,
определенных этим методом и необходимых для
решения данной задачи. Эффективность метода
является более грубым понятием, чем сложность
алгоритма, поскольку сложности одной итерации
(как число тактов некоторой вычислительной
модели) для различных методов существенно
различаются, хоть и являются обычно полиноми-
ально эквивалентными.
Рассматриваемые методы различны по своей
природе, поэтому при проектировании жела-
тельно проверить шифр (или хэш-функцию) на
стойкость по отношению к каждому из них, а
также по отношению к другим методам, предло-
женным разработчиком.
17.1. Метод обобщения и редукции.
Метод гомоморфизмов
Как правило, задача взлома шифра или хэш-
функции решается индивидуально. Однако спо-
собы ее решения имеют некоторые общие черты,
которые роднят варианты атак и позволяют го-
ворить о методах криптоанализа.
Использование отображений алгебраических
структур, сохраняющих их основные свойства
(«гомоморфизм»), является общепринятым ме-
тодом решения математических задач (см., на-
пример, книгу Д. Пойа [3]). Обычно использует-
ся вложение алгебраической структуры в объем-
лющую структуру (или иное продолжение ис-
ходной структуры на объемлющую структуру), а
также гомоморфное отображение большей струк-
туры в меньшую.
Первый подход применяется, если объемлю-
щая алгебраическая структура позволяет полу-
чить новые качества. Задача решается в два эта-
па. На первом этапе продолжают криптоалго-
ритм на некоторое объемлющее множество, по-
зволяющее облегчить вскрытие ключа за счет
указанных новых качеств и построить метод
вскрытия ключа продолженного криптоалгорит-
ма. На втором этапе параметризуют построен-
ный метод вскрытия с использованием данных,
присущих исходному (непродолженному) крип-
тоалгоритму и находят решение исходной зада-
чи. Такой ход рассуждений Д. Пойа называет
обобщением и редукцией.
Пример 17.1.1. Метод обобщения и редукции.
1. Для вычисления дискретного логарифма в
группе Fz, используется гомоморфное вложение
конечной группы Fz, в бесконечную полугруппу
Z*, обладающую однозначным разложением на
простые множители. Такое продолжение позво-
ляет использовать базу разложения для вычисле-
ния дискретного логарифма и за счет этого дос-
тичь субэкспоненциальной сложности логариф-
мирования (см. п. 10.1).
2. Гомоморфное вложение кольца Z7wZ, где
n=pq — характеристика кольца системы RSA, в
кольцо полиномов (Z7hZ)[z] позволяет найти
открытые тексты системы шифрования с откры-
тым ключом RSA, если известны параметры ли-
нейного соотношения между этими текстами (см.
п. 9.4.2).
3. Решеточный метод криптоанализа (см.
п. 17.3) основан на продолжении булевых функ-
ций с множества {0, 1} на конечное множество
рациональных чисел. Это продолжение является
гомоморфным вложением дистрибутивных ре-
шеток. Метод анализа позволяет отбраковать не-
сколько ключей за одно опробование и за счет это-
го снизить сложность по сравнению с перебором.
4. Метод криптоанализа на основе продол-
женных полиномов Жегалкина (см. пп. 17.6,
17.7) использует продолжение булевых функций,
заданных в виде полиномов Жегалкина над по-
лем F2, на упорядоченные множества рациональ-
ных или целых 2-адических чисел. Тем самым на
расширенном множестве ключей устанавливает-
ся вычислимое отношение порядка. ... .
360
Использование метода обобщения и редукции
иногда приводит к искажению свойств первона-
чальной математической структуры, в частности,
теряются некоторые ее алгебраические свойства.
Так, объемлющая структура из п. 1 примера
17.1.1 не содержит обратных элементов, из
п. 3 — не содержит решеточных дополнений, в
п. 4 теряется ассоциативность и однозначная
разрешимость уравнений. Из-за такого искаже-
ния соответствующий метод криптоанализа при-
обретает эвристический характер и до некоторой
степени утрачивает общность: иногда он эффек-
тивен, а иногда — нет.
Второй подход используется непосредственно
для снижения сложности задачи за счет умень-
шения ее размера. При этом задача разбивается
на несколько подзадач, решаемых поочередно. В
основе этого подхода лежат сжимающие гомо-
морфизмы алгебраических структур (групп, по-
лугрупп, колец и т. п.). Наличие таких структур и
существование гомоморфизмов в шифрах уста-
новить несложно (обычно разработчики стара-
ются исключить такие гомоморфизмы на этапе
проектирования криптоалгоритма). Поэтому дан-
ный подход на практике применим лишь для
плохо спроектированных шифров.
Пример 17.1.2. Методы, основанные на го-
моморфном отображении структуры, над кото-
рой определен криптоалгоритм, на меньшую
структуру.
1. Метод Гельфонда для вычисления дис-
кретного логарифма в циклической группе ис-
пользует эндоморфизмы исходной группы в под-
группы простых порядков (см. п. 11.1.1). Поэто-
му сложность логарифмирования в исходной
группе (с точностью до полинома от размера за-
дачи) равна сложности логарифмирования в под-
группе максимального простого порядка.
2. Если тексты и ключи, отображения которых
реализованы в шифре, можно разбить на непересе-
кающиеся классы так, что каждый класс содержит
только свои разряды текстов и ключей, то итого-
вый шифр можно представить в виде «прямой
суммы» небольших шифров по аналогии с китай-
ской теоремой об остатках. При анализе такого
шифра используется гомоморфное отображение
исходной структуры в аналогичную структуру
меньшего размера (например, гомоморфизм коль-
ца G„ в свое собственное подкольцо, см. п. 17.9).
3. Если шифр реализован для текстов в п-
символьном алфавите и использует алгебраиче-
ские преобразования, описываемые в терминах
кольца полиномов над TJnZL, где п — составное
число с известным разложением, то можно пред-
ставить кольцо Z/nZ в виде прямой суммы колец
простых характеристик (см. п. 17.9).
17.2. Замкнутые и чистые шифры
Эндоморфный блочный шифр, отображаю-
щий множество всевозможных блоков длины и
бит на себя, задает набор подстановок, дейст-
вующих на множестве из 2" элементов. Этот на-
бор зависит от ключа. Каждая из подстановок
зашифрования имеет обратную подстановку,
реализуемую расшифрованием на том же ключе.
Предположим, что для данного шифра после-
довательное шифрование на двух произвольных
ключах эквивалентно шифрованию на некотором
третьем. Это означает, что произведение двух
подстановок Е, и Ej, соответствующих зашифро-
ванию (расшифрованию) на ключах к, и kj, явля-
ется подстановкой Es, реализуемой зашифрова-
нием (расшифрованием) на ключе к. Такие
шифры будем называть замкнутыми.
В чистом шифре для любой тройки ключей к„
kj, к существует ключ к, такой, что справедливо
уравнение
E,EJXES = Е, .
Поскольку число всевозможных троек ключей
к, кр к значительно больше, чем мощность #К
множества ключей, то число таких троек для
фиксированных ключей к, к в среднем равно
О((#К)2).
Множества замкнутых и чистых шифров раз-
личны. Например, множество подстановок, дей-
ствующих на множестве букв русского алфавита
и отображающих А в Б, не замкнуто, но чисто,
так как подстановка Е^Е~' сохраняет букву А
неподвижной.
17.2.1. Вскрытие ключей
замкнутых и чистых шифров
Пусть К— множество ключей замкнутого
шифра. Тогда для каждого к G К существует
О(#К) пар (к, kj), эквивалентных ключу к,- Для
замкнутых шифров задача вскрытия ключа ре-
шается значительно быстрее, чем для шифров, не
обладающих этим свойством.
Пусть известны открытые тексты и соответст-
вующие шифрограммы, однозначно определяю-
щие ключ. Вместо того чтобы искать истинный
ключ к, будем методом встречи посередине ис-
кать пару ключей (к, к}) таких, что Es = EjE, [16].
Алгоритм 17.2.1. Вскрытие ключа замкнуто-
го шифра.
Вход. Замкнутый шифр с множеством ключей
К, открытый текст х и его шифрограмма у.
Выход. Пара ключей (к, I) таких, что искомый
ключ задает ту же подстановку, что и произведе-
ние подстановок, задаваемых ключами кмЛ.
361
Метод.
1. Для z=l, 2,..., О(4#К) выполнить сле-
дующие действия.
1.1. Выработать случайный ключ к,.
1.2. Зашифровать текст х на ключе к,-,
z, <- Екх).
2. Отсортировать базу данных (z„ Л,) по первой
«координате».
3. Для j = 1, 2,... выполнить следующие дейст-
вия.
3.1. Выработать случайный ключ
3.2. Расшифровать шифрограмму у на ключе
I,: Wj<r-Ej\y).
3.3. Сравнить w, с базой данных, получен-
ной на шаге 2. При совпадении z, = w,
положить к k,,l<— lj.
4. Результат: (к, /).
Число повторов шага 3 равно О(^]кК). Слож-
ность алгоритма 17.2.1 равна O(^EK \og(#K)),
множитель log(#K) обусловлен сложностью сор-
тировки. Емкостная сложность алгоритма 17.2.1
имеет такую же оценку. Для сравнения: слож-
ность вскрытия ключа замкнутого шифра пере-
бором равна О(#К).
Вскрытие ключа чистого шифра осуществля-
ется аналогично алгоритму 17.2.1, но вместо
ключа к, при составлении базы данных исполь-
зуются пары случайных ключей (Л„ kj), а сорти-
руются тройки (Л,, к , EjE^ty)) по третьей «ко-
ординате». Затем для случайных ключей кх и
шифрограммы у вычисляются и сравниваются с
базой данных тексты При совпадении
текста с элементом базы данных искомая тройка
ключей равна (£,, к,, ks). Можно, наоборот, при
составлении базы данных использовать пары
{к,, Е,(х)), а во встречном направлении — тройки
(ks, к , Е~1Е~\уУ). Сложность вскрытия ключа
чистого шифра тоже равна ()(^EK log(#A')), то
есть по порядку величины примерно вдвое
меньше, чем сложность перебора.
Этот же метод можно использовать и для
вскрытия ключа шифра, описываемого уравне-
нием вида
т
Гр,"'(*) = £,(х)
/=1
для небольших чисел п,, т е 7L В этом случае
искомый ключ к заменяется набором из т клю-
чей.
17.2.2. Проверка шифра -
на замкнутость и чистоту
Применимость метода встречи посередине
для вскрытия ключа замкнутого или чистого
блочного шифра определяется соответствующей
задачей распознавания. Множество подстановок,
реализуемых шифром, является подмножеством
симметрической группы, следовательно, опера-
ция композиции шифрования текстов на любых
ключах ассоциативна.
Поскольку в блочных шифрах операции за-
шифрования и расшифрования различаются не-
принципиально, то, дополнив множество под-
становок, индуцированных замкнутым шифром,
единичным отображением, получим некоторую
группу, которая является подгруппой симметри-
ческой группы, действующей на множестве тек-
стов. Таким образом, можно сказать, что замкну-
тый шифр является группой, тогда как незамкну-
тый шифр представляет собой набор случайных
подстановок, действующих на множестве блоков
открытого текста.
Для такого шифра определим для каждого от-
крытого текста х орбиту 5Д.. Множество откры-
тых текстов разбивается на непересекающиеся
орбиты. Если существует подгруппа Тх, остав-
ляющая неподвижным текст х,— стабилизатор
#К
текста х, — то # $ =----, где А — множество
ключей [16]. Число орбит теоретически может
лежать в диапазоне от 1 (транзитивная группа
или транзитивный шифр) до
Метод встречи посередине и метод Полларда
применительно к блочному шифру работают, если
шифр является замкнутым. Эти методы являются
вероятностными и дают результат с вероятностью,
сколь угодно близкой к 1, после 0(^1 #К) шагов.
Проверить шифр на замкнутость можно, контро-
лируя длину цикла подстановки, индуцирован-
ной шифром, и контролируя результат метода
встречи посередине и метода Полларда [14, 16].
При проверке длины цикла (cycling closure
test) выполняется псевдослучайное блуждание по
множеству для начального значения ль выбира-
ется ключ, совпадающий с Хо, затем вычисляется
х1 = Ех(хо), где Ех(1) — оператор зашифрования
текста t на ключе s, X2 = EXi(x\) и т. д. Рано или
поздно последовательность зациклится. Замыкание
цикла можно проконтролировать проверкой равен-
ства х, = хъ аналогично алгоритму Полларда. По-
лучение равенства служит индикатором того, что
Xi лежит в цикле, остается вычислить длину цикла.
362
Этот статистический тест позволяет выяснить,
индуцирует ли множество ключей шифра слу-
чайный набор подстановок или шифр является
группой.
Лемма 17.2.1 [16]. Пусть в блочном шифре
длины блоков открытого и зашифрованного тек-
стов равны М, а мощность множества ключей
равна т. Если шифр является группой, то число
индуцированных шифром пар отображений
(£„ Ej) таких, что EEj = Es для данного Е„ равно
т. Если шифр является случайным набором под-
становок, то число пар таких отображений близ-
ко к тп!(М\}.
Доказательство. Первое утверждение сле-
дует из рассмотрения группы порядка т (пред-
полагаем, что среди ключей нет эквивалентных,
число ключей равно порядку группы). Второе
утверждение следует из того, что число пар ото-
бражений (£„ £,) равно /и2, а число всевозмож-
ных подстановок из Мэлементов равно (А/!).
Тест встречи посередине также основан на
лемме 17.2.1. Если шифр является группой, то
для множества случайно выбранных пар ключей
(к„ к/) мощности ajm и случайных ключей ks
будет найдена тройка ключей такая, что
Е,Е^х) = Es(x) с вероятностью ошибки е “ ' для
всех х. Для шифра, являющегося набором слу-
чайных подстановок, вероятность нахождения
такой тройки ключей на указанном объеме ста-
тистики равна тг/M\kQ, если длина ключа
близка к длине блока. Тест можно проводить для
нескольких открытых текстов.
Аналогично можно проверить и чистоту
шифра. Действительно, шифр С является чистым
тогда и только тогда, когда хотя бы для одного
ключа к (и, следовательно, для всех ключей)
шифр Е^С является замкнутым [16]. Поэтому
любой замкнутый шифр является чистым. Об-
ратное, вообще говоря, неверно.
Таким образом, проверка шифра С на чистоту
сводится к проверке шифра Е^С на замкну-
тость для произвольного ключа к.
17.3. Решеточный криптоанализ
В большинстве современных шифров ис-
пользуются композиции наборов булевых
функций, каждая из которых имеет несложное
описание и может быть легко вычислена. При-
мерами являются DES, FEAL, ГОСТ 28147-89 и
т. п. Сложность вскрытия ключа таких шифров
обусловлена тем, что небольшое изменение
ключа или открытого текста приводит к значи-
тельному изменению шифрограммы, причем
неясно, каким именно разрядом ключа опреде-
ляется данный разряд шифрограммы — разряды
ключа «безымянны». Решеточный метод явля-
ется универсальным (применим к любому блоч-
ному шифру) и позволяет установить, каким
именно разрядом ключа определяется значение
шифрограммы.
Рассмотрим итерированный шифр без эквива-
лентных ключей. Предположим, что нарушитель
знает криптоалгоритм и некоторое количество
разрядов открытых и соответствующих зашиф-
рованных текстов, однозначно определяющих
ключ. Тогда согласно формуле (16.5.4) можно
составить целевую функцию, которая принимает
значение 1 тогда и только тогда, когда тестируе-
мый ключ равен истинному. Для простоты пред-
положим, что длины блока и ключа одинаковы и
равны п бит. Кроме того, в формуле (16.5.4) бу-
дем полагать, что h = n, пренебрегая возможной
неоднозначностью решения. - ,
17.3.1. Решеточные продолжения булевых
функций и решеточные полиномы
Решетка называется дистрибутивной, если в
ней выполняются законы дистрибутивности (см.
и. 3.14):
х(у V z) = ху V XZ', X V yz = (х V у)(х V z).
Дистрибутивной решеткой является любое
конечное линейно упорядоченное множество.
Дистрибутивная решетка {0, l,v, л} может
быть рассмотрена как полукольцо. В качестве
сложения используется операция v, в качестве
умножения — операция л. Присоединяя к полу-
кольцу {0, 1} новые элементы, можно получить
полиномы. По аналогии с тем, как полиномы над
коммутативным кольцом образуют кольцо, по-
линомы над полукольцом {0, l,v, л] образуют
полукольцо решеточных полиномов. При этом по
сложению элементы полукольца образуют ком-
мутативный моноид с нулем 0, а по умноже-
нию— коммутативный моноид с единицей 1,
которая является единственным обратимым эле-
ментом полукольца (из равенства min(n, «“') = 1
следует а = аЛ = 1).
Булевы формулы в функциональном базисе
И, ИЛИ, НЕ можно рассматривать не только как
элементы булевой алгебры, но и как решетки.
При этом множество {true, false} значений аргу-
ментов и функций интерпретируется как true = 1,
false = 0 с линейным упорядочением 1 > 0. Соот-
363
ветственно элементарные функции определяются
численно на множестве {0, 1} так:
avZ> = sup(a,Z>); алЬ = т((а,Ь);
а = 1 - а.
(17.3.1)
Здесь одной и той же буквой обозначено имя
аргумента и его численное значение. В дальней-
шем символы л и v будем понимать в решеточ-
ном смысле, символ л иногда будем опускать
для упрощения записи.
Выражения (17.3.1) позволяют формально
рассматривать произвольную булеву формулу
как решеточный полином, определенный на
множестве А'', где А — множество рациональ-
ных чисел, лежащих в интервале от 0 до 1. Здесь
О является наименьшим элементом, 1 — наи-
большим элементом решетки. В силу линейной
упорядоченности множества А имеем:
а\/Ь = max(a, b), a/ b = min(a, b). Множество А
может состоять из конечного числа элементов.
Отображение /1—>{0, 1}, переводящее числа,
меньшие 0,5, в 0, а числа, большие 0,5, в 1, явля-
ется гомоморфизмом решеток. При этом фор-
мальное представление булевой функции фор-
мулой сохраняется, но расширяется область ее
определения и, соответственно, область значений
(дистрибутивная решетка над {0, 1} вкладывает-
ся в дистрибутивную решетку над А). Будем на-
зывать такие функции решеточным продолже-
нием булевых функций (РПБФ), а бинарные опе-
рации a v b и а лЬ — дизъюнкцией и конъюнк-
цией по аналогии с булевыми формулами [5].
Соответственно определяется и дизъюнктивная
нормальная форма (ДНФ).1
Такой переход от булевых функций к их ре-
шеточным продолжениям обусловливает изме-
нение алгебраических свойств булевых функций
(элементы множества А не обладают дополне-
ниями).2
РПБФ обладает следующими свойствами:
1. Решеточные продолжения операций ИЛИ, И
сохраняют идемпотентность (по определе-
нию решетки): a v а = а, аа = а. Поэтому
РПБФ принимает значения одной из пере-
менных или ее инверсии.
1 Вообще говоря, с учетом минимизации булевых
формул и их композиций ДНФ не является формой в
алгебраическом смысле. Мы употребляем этот термин
как устоявшийся в области синтеза конечных автоматов.
2 Дополнением к элементу а е А называется эле-
мент b е А такой, что a v b = 1, а л Ъ = 0. Если пред-
положить, что для a g {0, 1} существует дополнение,
то по первому свойству дополнения b = 1, а по второ-
му свойству дополнения b = 0. Поскольку в Q выпол-
няется 1 Ф 0, получаем противоречие.
2. Решеточные продолжения операций И, ИЛИ
являются коммутативными, ассоциативными
(это следует из определения решетки) и ди-
стрибутивными (так как множество А линей-
но упорядочено). Для них выполняются за-
коны поглощения:
а'/ b = b \' a, ah ~ Ьа,
(avb)vc=av(bvc), (ab)c = а(Ьс),
a(b v с) = ab v ас, a v (be) = (av b)(a v с),
a v (ab) = а, а(а v b) = а.
3. Операция инверсии не является решеточной
операцией дополнения для нецелого аргу-
мента: аа Ф 0, a v а Ф 1, но представляет со-
бой инверсный изоморфизм решетки в себя.
Кроме того, выполняются законы де Морга-
на: ab = a v й, a v b = а а b.
4. Для решеточного продолжения операции
сложения по модулю 2 слагаемое, ближайшее
к числу 0,5, поглощает (с точностью до ин-
версии) другие слагаемые суммы. Число 0,5
является аннулятором для всех чисел:
0,5 © а = 0,5. Доказательство следует непо-
средственно из решеточного представления
операции сложения по модулю 2.
5. Округление а ->0 для 0 <а<0,5 и «-> 1 для
0,5 < а < 1 задает гомоморфизм из полуколь-
ца РПБФ в полукольцо булевых формул.
Кроме того, если интерпретировать введен-
ные понятия геометрически, определив булеву
функцию на вершинах TV-мерного единичного
куба, а РПБФ— на всех рациональных точках
этого куба, то выполняются еще два свойства:
6. Булева функция и ее решеточное продолже-
ние совпадают на вершинах единичного куба.
7. Множество РПБФ является расширением
множества (полукольца) булевых функций,
которое получается в результате присоеди-
нения нестандартных конъюнкций вида
klkt. Доказательство этого свойства следует
из рассмотрения РПБФ как полинома над
полукольцом А с учетом законов де Морга-
на и того, что в А отсутствуют дополнения.
Соответственно РПБФ разбивается на стан-
дартную и нестандартную части. Например,
если РПБФ представить дизъюнктивной
формой (см. также лемму 17.3.1), то в не-
стандартную часть входят нестандартные
конъюнкции g,k,k,, которые не превышают
0,5 на всем единичном кубе и равны 0 на
всех его вершинах (здесь g,— некоторая
формула). , . .
364
Лемма 17.3.1. Любая РПБФ, полученная пу-
тем применения конечного числа композиций и
операторов, описываемых в виде ДНФ, имеет
представление в виде решеточного продолже-
ния ДНФ.
Доказательство. Если не учитывать опера-
тор инверсии, то заключение леммы следует не-
посредственно из дистрибутивности операции v
относительно операции л. Таким образом, оста-
ется рассмотреть действие оператора инверсии на
ДНФ и показать, что в результате этого опять по-
лучается ДНФ. Инверсия дизъюнкции (конъюнк-
ции) РПБФ может быть исключена на основании
законов де Моргана. Поскольку число компози-
ций конечно, то повторение этой процедуры по
числу композиций через конечное число шагов
позволит исключить инверсии в формулах, то
есть даст ДНФ с элементарными конъюнкциями,
которая будет соответствовать РПБФ.
Лемма 17.3.2. РПБФ, не превышающая 0,5 на
всем единичном кубе, представима в виде ДНФ,
включающей только нестандартные конъюнк-
ции.
Доказательство. В соответствии с леммой
17.3.1 эта функция представима в виде ДНФ. По-
скольку по условию каждая конъюнкция не пре-
вышает 0,5, то в нее входит хотя бы одна пара
переменных вида kt к,. Эти конъюнкции являют-
ся нестандартными.
Следствие 17.3.3. Решеточное продолжение
целевой функции имеет вид
H = Cvg'kxk} v...\/g„knk„, (17.3.2)
где С — целевая конъюнкция (стандартная часть
РПБФ), представленная выражением (16.5.3),
g,— решеточные продолжения булевых функ-
ций.
Доказательство. Вынося за скобки нестан-
дартные конъюнкции вида k,kt в соответствии с
законом дистрибутивности, получаем требуемое
заключение.
Назовем конусом, ассоциированным с верши-
ной Т куба, множество точек куба, каждая коор-
дината которых отличается от соответствующей
координаты вершины Т меньше, чем на 0,5. Та-
ким образом, соответствие конус/вершина явля-
ется взаимно однозначным.
Удалением РПБФ (от значения 0,5) на дан-
ном наборе аргументов будем называть число
аргументов, расположенных к 0,5 ближе, чем
значение функции (как точки на вещественной
прямой). Удаление является естественной мет-
рикой для РПБФ и зависит от способа упорядо-
чения аргументов в данном конусе, а не от их
конкретных значений. Удаление целевой функ-
ции, равной конъюнкции нескольких булевых
функций (не все из которых превышают 0,5),
равно максимуму удалений тех функций, кото-
рые принимают значение меньше 0,5. Поэтому
увеличение числа РПБФ, входящих в конъюнк-
цию целевой функции, должно приводить к
увеличению удаления целевой функции. Удале-
ние (обозначаемое через rem) обладает следую-
щими свойствами:
1. rem(« Ф b) = rem(a) л rcm(/>). ’ ' ’
2. rem(«) = rem(a).
3. Если b<a<0,5, то rem(a7>) = rem(Z>) и
rem(a v b) = гет(а).
Поскольку каждое из преобразований шифро-
вания может быть легко вычислено, описываю-
щие это преобразование булевы формулы и их
решеточные продолжения также вычислимы.
Поэтому можно легко вычислить и решеточное
продолжение целевой функции.
Если целевая функция содержит только стан-
дартную конъюнкцию (с неизвестным уравнени-
ем), то ключ может быть легко найден следую-
щим алгоритмом.
Алгоритм 17.3.1. Нахождение набора пере-
менных, на котором стандартная конъюнкция
принимает значение 1.
Вход. Вычислимая конъюнкция С от п пере-
менных.
Выход. Набор переменных, на котором функ-
ция принимает значение 1.
Метод.
1. Придать переменным произвольные значе-
ния, отличные от 0,5, с попарно различными
удалениями.
2. Вычислить функцию С.
3. Если С < 0,5, то найти переменную, удаление
которой равно удалению функции, заменить
значение этой переменной на инверсное и
вернуться на шаг 2. Если С > 0,5, то резуль-
тат: вершина единичного куба, ассоции-
рованная с текущим конусом.
Отметим, что С Ф 0,5, так как С принимает
значение какой-либо переменной или ее инвер-
сии. Поскольку значение функции С превыша-
ет 0,5 в единственном конусе, а вероятность
угадать этот конус мала, то почти всегда будет
выполняться неравенство С < 0,5. Удаление
функции С равно удалению одной из перемен-
ных, неравенство С < 0,5 означает, что округ-
ление этой переменной было выбрано неверно.
365
После замены его на инверсное значение уда-
ление функции будет определяться другим
разрядом ключа. Алгоритм требует в среднем
и/2 шагов.
17.3.2. Метод криптоанализа
Алгоритм 17.3.1 можно адаптировать и для
случая, когда решеточное продолжение целевой
функции содержит нестандартные конъюнкции,
то есть С <Н.
Пусть для набора значений переменных {Д}
(К ф 0,5 — значение переменной к,) с попарно
различными удалениями из конуса, ассоцииро-
ванного с некоторой вершиной куба, выполняет-
ся равенство rem(/V) = гет(А,„) для некоторого т.
При этом во всех конусах, кроме конуса, ассо-
циированного с решением, Н<0,5. Поскольку
С < Н, то не все значения переменных с удалени-
ем не менее rem(A,„) выбраны правильно. Это
позволяет отбраковать сразу 2ге"’(А"') ключей. На-
пример, если тестируемый ключ, в котором раз-
ряды отсортированы по удалениям, имеет вид
(К:,..., К, ,...,К1 ), то при 77<0,5 и
rem(Z7) = rem(X, ) кроме тестируемого ключа
можно также отбраковать ключи вида
(К, , ..., К, , ..., К: ), (К: ,..., К, , ),
v '1 ’ ’ ’ 'и 7’ v '1 ’ ’ 'п-1 ’ 'л 7
(Ki,...,К, ,К, ),...,(К ,...,Ki ,Ki ,...,к,у
v '1 ’ ’ 'п-1 , 'п v '1 ’ ’ 'in ’ ',»+! ’ ’ п 7
Чем больше удаление целевой функции, тем
больше информации о ключе можно получить.
Целевая РПБФ может вычисляться как в раз-
ных конусах, так и в одном конусе с различным
упорядочением переменных. После серии таких
испытаний получается набор условий типа «хотя
бы одна переменная из данного набора опреде-
лена неправильно». Если удаление переменной
k,i не равно 0, то это позволяет отбраковать сразу
несколько ключей, которые не могут удовлетво-
рять целевой конъюнкции. Соответственно су-
жается и область перебора.
Алгоритм 17.3.2. Вскрытие ключа решеточ-
ным методом.
Вход. Алгоритм шифрования и набор откры-
тых и зашифрованных текстов, однозначно опре-
деляющих ключ.
Выход. Набор переменных, на котором целе-
вая функция Н принимает значение 1.
Метод.
1. По известным открытым и зашифрованным
текстам составить алгоритм вычисления ре-
шеточного продолжения целевой функции.
2. Разрядам ключа придать произвольные зна-
чения, отличные от 0,5, из (произвольно) вы-
бранного конуса с попарно различными уда-
лениями.
3. Вычислить целевую функцию Н. При Н > 0,5
результат: вершина, ассоциированная с те-
кущим конусом единичного куба. При
Н< 0,5 выполнить следующие действия.
3.1. Если удаление целевой функции равно
нулю, то выбор конуса неудачен или
метод не работает. В противном случае
вычислить множество возможных клю-
чей как пересечение найденного множе-
ства с пересечением найденных ранее
множеств.
3.2. Если мощность множества ключей дос-
таточно мала или если очередные ите-
рации не снижают мощности множества
возможных ключей, то искать ключ пе-
ребором.
Поскольку эффективность метода определя-
ется удалением целевой функции, но не ее зна-
чением, то разности между соседними значения-
ми аргументов могут быть произвольными. В
частности, значения аргументов могут образовы-
вать арифметическую прогрессию — это не
влияет на эффективность метода криптоанализа.
Корректность алгоритма следует из гомо-
морфизма решеток Л -> {0, 1}, заданного округ-
лением. Для повышения эффективности реше-
точного анализа можно использовать следую-
щие приемы:
1. Приравнивать не вычисленные значения раз-
рядов шифрограммы и их истинные значения,
а значения промежуточных текстов, которые
получаются зашифрованием открытого текста
на половине циклов и расшифрованием шиф-
рограммы на половине циклов на том же клю-
че (для этого нужно знать не отдельные раз-
ряды, а целые блоки открытых текстов).
2. Число отбракованных ключей для алгоритма
17.3.2 равно 2rem(W). Поэтому желательно вы-
бирать конус и упорядочение не случайным
образом, а использовать процедуры, обеспе-
чивающие максимум удаления.
3. Для снижения сложности метода целесооб-
разно учитывать распределение вероятностей
разностей удалений целевой функции и целе-
вой конъюнкции.
4. На сложность метода сильно влияют нестан-
дартные конъюнкции. С целью ослабления
их действия булевы формулы, описывающие
стандартную часть каждой операции шифро-
вания, желательно минимизировать.
366
Эффективность данного метода не зависит от
нелинейности криптоалгоритма. Метод не рабо-
тает, если в формуле (17.3.2) почти все g, больше
0,5. Например, g может содержать только не-
стандартные дизъюнкции вида \/к (этот слу-
чай неотличим от случая g, = 1). Тогда значение
целевой функции определяется переменной с
нулевым удалением, и алгоритм сводится к пере-
бору. Практически с ростом числа циклов шиф-
рования удаление целевой функции стремится к
0, то есть значения g, превышают 0,5.
Самой «неудобной» операцией для решеточ-
ного метода является сложение по модулю 2.
Действительно, удаление суммы к\ Ф ... Ф кп в
любом конусе равно нулю.
Влияние нестандартных конъюнкций можно
уменьшить, используя функцию округления. По-
скольку в алгоритме 17.3.2 переменные не могут
принимать значение 0,5, ни одна из булевых
функций не может принимать это значение. Ок-
ругление переводит РПБФ в двоичный вид.
Функции округления могут быть применены к
произвольным промежуточным РПБФ (входя-
щим в композицию функции шифрования).
Лемма 17.3.4. Функция округления сохраняет
решеточный гомоморфизм целевой РПБФ и це-
левой булевой функции, то есть решение уравне-
ния (16.5.4) для РПБФ соответствует решению
этого же уравнения для булевых функций.
Доказательство. Округление переводит
РПБФ в соответствующую булеву функцию.
При этом округление не меняет значения РПБФ
на множестве {0,1}, следовательно, функция
округления является решеточным гомоморфиз-
мом. В силу дистрибутивности решетки это
свойство выполняется и для композиции буле-
вых функций.
Функция округления является «неалгебраиче-
ской» в том смысле, что она не совпадает ни с
одним решеточным полиномом.3 Действительно,
значение решеточного полинома совпадает со
значением переменной или ее инверсии, значе-
ние же округления — всегда 0 или 1.
Основные свойства функции округления ф:
1. ф(о/>) = ф(«)ф(/>).
2. ф(а v Ь) = ф(«) v ф(/>).
3. ф(а) = ф(а).
Эти свойства позволяют сводить округление
РПБФ на выходе оператора шифрования к ок-
3 Поскольку единственным обратимым элементом
решетки над множеством А является 1, то рациональ-
ных функций над А не существует.
руглению переменных на входе этого оператора,
то есть к округлению аргументов РПБФ.
Рассмотрим композицию РПБФ: h о g = h(g(k)),
где h = (Ab ..., /гд), g = (gi, ..., g), k = (k{, ..., £„),
Й, = h,(a, k), gj - g,(k), и применим округление к
каждой координате вектора g. Тогда h о ф(о) =
= h ° g$(k)). Ясно, что g^(k)) не зависит от спо-
соба упорядочения переменных, то есть является
фиксированным двоичным вектором в каждом
конусе.
Поскольку целевая РПБФ без учета округле-
ния представима в виде ДНФ, то и с учетом ок-
ругления на начальных циклах шифрования це-
левая РПБФ тоже будет иметь представление в
виде ДНФ, хотя вид функции и изменится.
Лемма 17.3.5. Пусть gb ...,g„— решеточные
продолжения булевых функций и пусть
й =/gi, gn), const. Тогда
rem(A) > min(rem(gi), ..., rem(g„)),
причем функции h, g\, ..., g,, вычисляются на од-
ном и том же наборе аргументов.
Доказательство. Требуемое неравенство
выполняется, если функцию h записать в виде
ДНФ.
Из леммы 17.3.5 следует, что максимальное
удаление любого разряда выходного текста на
любом цикле шифрования не может превышать
максимального удаления входного текста. При-
меняя ее к итерированному шифру, получаем
следующее утверждение.
Следствие 17.3.6. Для того чтобы целевая
функция имела большое удаление, необходимо,
чтобы на каждом цикле шифрования конъюнк-
ция из соответствующих РПБФ, описывающих
шифрование на одном цикле, имела большое
удаление.
Таким образом, для повышения эффективно-
сти решеточного метода нужно, чтобы на каж-
дом цикле удаления разрядов промежуточного
текста принимали значения из всего спектра уда-
лений. Иначе говоря, совокупность решеточных
продолжений булевых функций, описывающих
каждый оператор шифрования, должна действо-
вать на множестве удалений как перестановка.
Удаление можно считать именем переменной.
После каждой операции в ходе шифрования один
из разрядов выходного текста должен принимать
имя первой переменной кх, другой разряд — имя
второй переменной кг и т. д. Данный метод ана-
лиза может быть реализован как на «обычном»
компьютере, так и на специализированном ана-
367
логовом устройстве, реализующем операции на-
хождения минимума, максимума и инверсии.
Это требование может достигаться введением
округления для тех аргументов промежуточных
булевых функций, которые гарантированно не
могут входить в стандартную конъюнкцию. На-
пример, для аргумента или значения булевой
функции к,к, можно применять округление. По-
этому, в частности, минимизация булевых функ-
ций и их композиций позволяет повысить эффек-
тивность метода (минимизация соответствует
введению округлений применительно к нестан-
дартным конъюнкциям).
Пример 17.3.1. Использование решеточного
метода для обращения хэш-функции.
Пусть 32-разрядная хэш-функция задана урав-
нением
у = Г4(х)Фх, (17.3.3)
где F— операция шифрования на одном цикле,
включающая в себя:
- сложение по модулю 2 текста х с константой
к= 1000 0111 0110 0101 0100 ООН 00100001;
- 32-разрядную перестановку битов текста:
(32, 5, 9, 13, 2, 6, 10, 14, 3, 7, 11, 18, 4, 8, 12,
16, 17, 21, 25, 29, 15, 22, 26, 30, 19, 23, 27, 31,
20, 24, 28, 1), пронумерованных от 1 до 32;
- 4-разрядную подстановку (блок разбивается
на 8 тетрад, каждая из которых заменяется в
соответствии с кодом подстановки: S = (0, 13,
11, 8, 3, 6,4, 1, 15, 2, 5, 14, 10, 12, 9, 7));
- циклический сдвиг блока на 15 бит влево.
Здесь 7,4(х) означает шифрование текста х на
четырех циклах.
Выбранная подстановка обладает экстремаль-
ными свойствами (максимальными нелинейно-
стью и диффузией, см. гл. 18). Для упрощения
моделирующей программы возьмем одну и ту же
подстановку для всех восьми тетрад. Все циклы
шифрования одинаковы, что соответствует сте-
пенному шифру (см. п. 18.5). Отметим, что ис-
пользование шифра с различающимися циклами
шифрования, например, с различными подстанов-
ками для каждой тетрады и различными переста-
новками, практически не влияет на стойкость
криптоалгоритма к решеточному методу анализа.
Пусть у = 0011 0100 0111 1010 1100 0000 1011
1001.4 Константа к, подстановка и перестановка
считаются известными.
4 Этому значению хэш-функции соответствует
х = 0111 0001 1101 0111 1100 0001 1100 0111;
F4(x) = 0100 0101 1010 1101 0000 0001 0111 1110.
Представим прямую и обратную подстановки
в виде наборов четырех РПБФ. Пусть векторы
(и\, иг, из, щ) и (vj, v2, V3, V4) соответствуют входу
и выходу подстановки. Найдем минимизирован-
ное представление булевых функций подстанов-
ки зашифрования:
( 0 1 ... 15
уф(0) <р(1) <p(15)J
0 1 2 3 4 5 6 7 8 9 10 И 12 13 14 15Л
0 13 И 8 3 6 4 1 15 2 5 14 10 12 9 7j‘
Для этого построим вспомогательную таблицу:
Каждой клетке таблицы соответствует набор
четырех входных переменных — число от 0 до
15. Например, элементу щи2й3й4 соответствует
число (1100)2=12 (здесь щ— старший двоич-
ный разряд), элементу й}й2и3й4 — число
(0010)2 = 2 ит. д.
Каждый элемент <p(z) подстановки S предста-
вим в двоичном виде:
<р(/) = (<р; <Р2 Фз <р4>2-
Для построения функции vk в клетку таблицы
с номером <р(7) записываем значение <р'д :
пх и3
ф!2 ф!4 Фл фа Щ
U2 ф!3 ф!5 ф! Фа
Фа фГ фа ф1 £>4
и2 ф! ф!° фа Фа- м4
и3 и3 и3
Каждую из функций vA представляем в виде
ДНФ — дизъюнкции конъюнкций вида щи^л3и^,
соответствующих ненулевым элементам <р'А..
Минимизируем булеву функцию, объединяя по-
парно (а если возможно, то по четыре или по во-
семь элементов) клетки таблицы, которые имеют
общие границы с учетом склеивания противопо-
ложных сторон таблицы. Объединять клетки
таблицы, вообще говоря, можно по-разному, по-
368
этому минимизированное представление подста-
новки в виде булевых функций неоднозначно.
Для функции v4 подстановки S таблица будет
иметь вид:
Записываем v4 в виде ДНФ и минимизируем
(соответствующие пары элементов в таблице за-
штрихованы):
V4 — 2 W3Z/4 X/ U3ll2ll3U4 V Tl^U2U3Tl4 V U3U2U3l{4 V
х/щй2й3и4 x/ii}u2u3u4 уй1в2и3й4 v щи2и3и4 =
= и}и2и3 \/й3и2и3и4 х/и2и3и4 х/ й}й2й3и4 х/
х/ г<}й2иА х/ й2и3й4.
Аналогично получаем для остальных разрядов:
v3 — и2й3й4 х/щи2й3 \/щи3и4 х/ щй2й3 vйхй2и3й4',
v2 = W]W2w3w4 и}и2и4 х/й}г13и4 х/щй2й4 х/и3и3и4',
Vj = i/1k2W4 v и3и2113 v и3113й4 х/ й2и3и4 х/
v и,й2и3 х/ щ й2и4.
Поэтому РПБФ для прямой подстановки име-
ют вид:
Vi = max(niin(i/t, и2, 1 - г/4), и2, 1 - г/3),
min(z/], 1 - и3, 1 - w4), min(l - w2, Щ, м4),
min(l - wb 1 - и2, щ), min(l - wb 1 - и2, и3)у,
v2 = max(min(l - U], u3, 1 - г/4), min(l - wb 1 - u3,
щ), min(z/|, U2, U4), min(z/|, u3, z/4),
1 - w2,1 - w4));
v3 = max(min(w2, 1 - w3, 1 - z/4), min(l - u3, z/2,
1 - z/3), min(wt, u3, щ), min(wb 1 - u2, 1 - z/3),
min(l - W], 1 - u2, u3, 1 - z/4));
v4 = max(min(z/|, z/2, u3), min(z/2, u3, щ),
min(z/b I - w2, 1 - w4), min(l - z/2, z/3, 1 - z/4),
min(l - U], U2, 1 - u3, 1 - w4),
min(l - wb 1 - u2,1 - u3. ufi).
Вычисляем минимизированные РПБФ для об-
ратной подстановки:
U] = max(min(vb 1 - v2,1 - v3, v4), min(l - v2, v3,
1 - v4), min(l - V|, v2, v4), min(vb v2, 1 - v4),
min(vb v2, v3));
u2 = max(min(v2, 1 — v3, 1 — v4), min(vb 1 - v2, v3,
1 - v4), min(l - v2, 1 - v3, v4). min(l - vb v3, v4),
min(l - vb v2, 1 - v4));
u3 = max(min(vb v2, v3,1 - v4), min(l - vb v2,1 - v3),
min(l - vb v2, v4), min(l - vb 1 - v3, v4),
min(vb 1 — v2, 1 — V3), min(vb 1 - v2, v4));
z/4 = max(min(] - vb 1 - v2,1 - v3, v4), min(l - vb
v2, v3), min(l - vb v3,1 - v4), min(vb v2,1 - v4),
min(V|, v2, 1 - v3), min(v], 1 - v3, 1 - v4)).
Из уравнения (17.3.3) следует, что
F4(x) = у Ф х, тогда, в силу обратимости шифро-
вания, умножая обе части этого уравнения слева
на F~2, можно записать
Р2(х) = р-2(уФх).
Целевая функция представляет собой конъ-
юнкцию поразрядных равенств битов в послед-
нем уравнении.
Выберем аргумент решеточного продолжения
хэш-функции так, чтобы компенсировать на-
чальную перестановку. Начальный конус и упо-
рядочение можно либо выбирать наугад, либо
расписать композицию нескольких операций
шифрования (не обязательно всех) и выполнить
минимизацию булевых функций; при этом на
выходе некоторых подстановок нужно получить
большие удаления. Например, для тестируемого
аргумента х= (хь ...,х32) (перечисление слева
направо и сверху вниз) вида
(0,68; 0,05; 0,09; 0,13; 0,98; 0,94; 0,90; 0,86;
0,97; 0,93; 0,89; 0,82; 0,96; 0,92; 0,88; 0,84;
0,17; 0,21; 0,25; 0,29; 0,85; 0,78; 0,74; 0,70;
0,81; 0,77; 0,73; 0,69; 0,80; 0,76; 0,72; 0,01)
после двух циклов решеточного продолжения
зашифрования получаем F2(x):
(0,32; 0,68; 0,68; 0,32; 0,21; 0,79; 0,31; 0,31;
0,21; 0,84; 0,16; 0,79; 0,21; 0,89; 0,18; 0,82;
0,11; 0,20; 0,28; 0,23; 0,72; 0,24; 0,31; 0,72;
0,69; 0,76; 0,72; 0,24; 0,72; 0,32; 0,32; 0,27).
Решеточное продолжение суммы х © у равно:
(0,68; 0,05; 0,91; 0,87; 0,98; 0,06; 0,90; 0,86;
0,97; 0,07; 0,11; 0,18; 0,04; 0,92; 0,12; 0,84;
0,83; 0,79; 0,25; 0,29; 0,85; 0,78; 0,74; 0,70;
0,19; 0,77; 0,27; 0,31; 0,20; 0,76; 0,72; 0,99).
Находим результат решеточного продолжения
расшифрования F~2(y Ф х):
(0,32; 0,83; 0,83; 0,71; 0,82; 0,86; 0,87; 0,29;
369
0,69; 0,86; 0,87; 0,82; 0,69; 0,83; 0,69; 0,82;
0,31; 0,83; 0,32; 0,74; 0,29; 0,30; 0,69; 0,32;
0,69; 0,31; 0,69; 0,74; 0,29; 0,30; 0.32; 0,69).
Вместо целевой функции, составленной как
конъюнкция поразрядных равенств одноимен-
ных разрядов в двух последних векторах, можно
найти вектор 1 - (F2(x) Ф F ~2(х Ф у)), соответст-
вующий элементам конъюнкции, как совокуп-
ность решеточных продолжений равенств одно-
именных разрядов в формуле (16.5.4):
(0,68; 0,68; 0,68; 0,32; 0,21; 0,79; 0,31; 0,69;
0,31; 0,84; 0,16; 0,79; 0,31; 0,83; 0,31; 0,82;
0,69; 0,20; 0,68; 0,26; 0,29; 0,70; 0,31; 0,32;
0,69; 0,31; 0,69; 0,26; 0,29; 0,68; 0,68; 0,31).
Значение целевой функции определяется ми-
нимальным (одиннадцатым) разрядом полученно-
го вектора и равно 0,16, то есть удаление равно
32- 100 - 0,16= 16. Значит, среди 16 разрядов
вектора х, имеющих значения в диапазоне от 0,01
до 0,16 и от 0,84 до 0,99 не все округления выбра-
ны правильно. Этим отбраковывается 216 возмож-
ных аргументов на первой итерации криптоанали-
за: неправильными являются аргументы (ху, ...;хз2)
вида(*; 0; 0; 0; 1; 1; 1; 1; 1; 1; 1; *; 1; 1; 1; 1; *; *; *;
*; 1; *; *; *; *; *; *; *; *; *; *; 1), где символом *
обозначено любое значение 0 или 1.
Аналогично выполняем вторую итерацию.
Для нового аргумента х:
(0,68; 0,05; 0,09; 0,13; 0,02; 0,06; 0,10; 0,86;
0,03; 0,07; 0,11; 0,82; 0,04; 0,08; 0,12; 0,84;
0,17; 0,21; 0,25; 0,29; 0,85; 0,78; 0,74; 0,70;
0,81; 0,77; 0,73; 0,69; 0,80; 0,76; 0,72; 0,01)
получаем вектор 1 - (F2(x) Ф F“2(x ф у)):
(0,32; 0,21; 0,68; 0,32; 0,69; 0,31; 0,31; 0,69;
0,31; 0,83; 0,84; 0,29; 0,21; 0,14; 0,31; 0,71;
0,69; 0,80; 0,68; 0,74; 0,29; 0,70; 0,31; 0,28;
0,69; 0,69; 0,31; 0,32; 0,29; 0,70; 0,68; 0,73)
с удалением 18. Этим отбраковывается 218 воз-
можных аргументов: неправильными являются
все аргументы (х,; ...; Х32) вида (*; 0; 0; 0; 0: 0; 0;
1; 0; 0; 0; *; 0; 0; 0; *; *; *; *; *; *; *; *; *; *; *; *;
*. *. *. Q)
Дальнейшие итерации позволяют получить
удаление порядка 15 + 17. Пренебрегая сложно-
стью нахождения пересечения множеств воз-
можных аргументов (или объединения множеств
отбракованных аргументов), получаем, что
сложность вскрытия аргумента равна примерно
216 итераций решеточного криптоанализа.
Отметим, что когда множество возможных
решений станет достаточно мало, аргумент хэш-
функции проще искать перебором. Кроме того,
как видно из данного примера, решеточный ме-
тод допускает распараллеливание.
17.4. Метод арифметического
продолжения булевых функций
Существует ряд других универсальных мето-
дов анализа, основанных на продолжении функ-
ций шифрования до функций над упорядочен-
ным множеством, поиске экстремума на продол-
женных функциях и обратном переходе к буле-
вым функциям. В 1982 г. американские матема-
тики Д. Андельман и Дж. Риде [9] предложили
для анализа дисковой шифровальной машины
«Энигма» времен Второй мировой войны ис-
пользовать представление продолженного шифра
в терминах векторного пространства над полем
(R вещественных чисел. При этом соответствую-
щим образом продолжается и множество преоб-
разований, выполняемых над текстами.
Дисковая машина состоит из набора к вра-
щающихся дисков (плоских цилиндров), каж-
дый из которых реализует однобуквенную под-
становку (замену) для входного алфавита. На
основаниях дисков расположены электрические
контакты, причем предыдущий диск может пе-
редавать электрический сигнал на последующий
диск, для каждой новой буквы осуществляется
поворот диска. Зашифрованная буква соответ-
ствует выходу последнего диска. Таким обра-
зом, дисковая машина реализует поточный
шифр, в котором каждая буква текста заменяет-
ся буквой из этого же алфавита, причем эта
подстановка зависит от времени и от предыду-
щих букв текста.
Пусть q — размер алфавита, X, — перестанов-
ка, реализуемая z-м диском, U— оператор еди-
ничного сдвига диска, при этом Uq+ = 1, г, —
сдвиг z-ro диска по сравнению с исходным со-
стоянием. Итоговая подстановка, реализуемая
машиной, содержащей к дисков, имеет вид:
S(r,X) = f]C/":^,C/';,
1=1
где г— вектор вращений дисков, X— вектор
перестановок.
Варьируемыми параметрами являются: набор
подстановок, реализуемых дисками, способ элек-
трического соединения дисков, способ вращения
дисков и т. и. Будем считать способ вращения
дисков известным. Тогда множество ключей
можно описать набором из к перестановок q-
буквенного алфавита, это множество имеет мощ-
ность (<?!)*. Перестановка представляется квадрат-
370
ной матрицей размера q, в которой каждый стол-
бец и каждая строка содержат единственный еди-
ничный элемент, остальные элементы — нулевые.
Андельман и Риде предложили заменить мат-
рицы перестановки матрицами, элементы кото-
рых— неотрицательные вещественные числа;
сумма элементов в каждой строке и столбце рав-
на 1 (такие матрицы называются дважды стохас-
тическими). Тогда расширенное множество клю-
чей состоит из к наборов всех указанных матриц.
Анализ выполняется на основе шифртекстов с
учетом того, что частота появления букв естест-
венного языка соответствует вероятности.
Пусть X = (Azt, ...,Хк) — вектор перестановок,
соответствующий набору к дисков, d(X, г) —
вектор вероятностей одиночных букв шифртек-
ста, р — «/-разрядный вектор вероятностей появ-
ления одиночных букв открытого текста. Тогда
d(X,r) = S(r,X)p =
Р
Нужно найти максимум функции
Z(X/{C,r}f)=n(ecWd(X,r(O)),
i=i
описывающей вероятность того, что при задан-
ной последовательности N символов c(z) шифр-
текста частота появления символов открытого
текста соответствует частоте появления букв ес-
тественного языка при некотором наборе дисков,
где е^,) — вектор символов шифртекста.
Для поиска максимума (вскрытия вектора
дисков) используется аппарат дифференциально-
го исчисления. Начальное приближение для два-
жды стохастических матриц, задающих «расши-
ренные» диски, выбирается произвольным. Ключ
вскрывается поочередно, начиная с первого диска.
Этот метод был опробован и на «маленьком»
подстановочно-перестановочном шифре с длиной
блока и ключа 27 бит, 3-разрядной подстановкой
и тремя циклами шифрования [9]. Для этого
арифметически продолженные булевы функции
рассматривались как полиномы над полем (R:
х л у ху;
х\/у-^х+у;
х-> 1 -х.
(17.4.1)
Заметим, что из равенства х v у = х а у сле-
дует:
х vy= 1 -(1 -х)(1 -у)=х + у-ху,
что противоречит продолжению (17.4.1). Однако,
если заменить х vу выражением х + у -ху, то не
будет выполняться дистрибутивность и множе-
ство продолженных булевых функций переста-
нет быть полукольцом. Поэтому переход к не-
прерывным функциям (17.4.1) вносит в вычисле-
ния погрешность, которую трудно учесть. Об-
ратный переход от непрерывных функций к дво-
ичным неочевиден. Например, для х = 0,4 и
у = 0,3 получаем xvy = 0,7, что значительно
ближе к 1, чем оба операнда. Для трех операндов
это еще заметнее. Операции сложения и умно-
жения не являются идемпотентными в отличие
от операций a, v.
Процесс поиска максимума целевой функции
для стартового значения (0,5; ...; 0,5) после 30
вычислительных итераций начинает сходиться к
истинному значению ключа.
По-видимому, этот метод не имеет преиму-
ществ по сравнению с перебором, если число
циклов шифрования и размер ключа велики. Это
обусловлено влиянием указанной погрешности
(целевая функция имеет множество локальных
максимумов, не связанных с решением), а также
тем, что сложность вычисления производной
растет по экспоненте от числа циклов шифрова-
ния. В частности, для DES с 16 циклами и 56 би-
тами ключа вычисление производной оказывает-
ся сложнее, чем перебор.
Обобщим метод криптоанализа на основе
арифметического продолжения булевых функ-
ций. Составим целевую функцию Н как арифме-
тически продолженную согласно (17.4.1) конъ-
юнкцию поразрядных равенств промежуточных
текстов для продолженного ключа по аналогии с
решеточным методом. Для однозначного опре-
деления ключа с помощью целевой функции в
среднем достаточно, чтобы число конъюнкций в
1,368 раза превышало энтропию ключа (см.
п. 16.2.1). Пусть и— число конъюнкций в целе-
вой функции.
Для дальнейшего изложения метода анализа
рассмотрим некоторые свойства продолженной
целевой функции.
Лемма 17.4.1. Если все разряды ключа равны
0,5 и каждая из операций шифрования описыва-
ется набором сбалансированных продолженных
булевых функций, представленных в виде пол-
ных дизъюнктивных нормальных форм, то каж-
дый продолженный разряд промежуточного тек-
ста равен 0,5. Для набора аргументов из интерва-
ла (0, 1) каждый разряд промежуточного текста
принимает значения из этого же интервала.
Доказательство. Сбалансированная про-
долженная булева функция т переменных может
быть записана в виде дизъюнкции 2'”-1 попарно
371
различных продолженных конъюнкций от т пе-
ременных. Следовательно, каждая из этих конъ-
юнкций принимает значение 2~т, а продолженная
дизъюнкция— значение 0,5 на любом наборе
переменных. Переход к объемлющим сбаланси-
рованным продолженным булевым функциям
выполняется по индукции.
Рассмотрим сбалансированную продолжен-
ную булеву функцию. Очевидно, что каждая
конъюнкция может принимать значение 0 или 1
на вершинах единичного куба и не может при-
нимать отрицательные или превышающие 1 зна-
чения. Следовательно, и значения продолженной
функции неотрицательны.
Покажем, что сумма продолженных конъ-
юнкций не может превышать 1. Сбалансирован-
ная продолженная функция не может принимать
значения, превышающие число конъюнкций. То-
гда можно найти экстремум этой функции, при-
равняв к нулю производную функции как поли-
нома над R. Поскольку в каждую конъюнкцию
каждая переменная входит в первой степени, то
внутри куба полная производная не может быть
всюду равной 0. Следовательно, экстремумы
функции возможны только на вершинах куба.
Существует вершина, на которой целевая функ-
ция и, следовательно, продолженная целевая
функция принимает значение 1, и вершина, на
которой эта функция принимает значение 0.
Продолженная функция внутри единичного куба
является гладкой, поэтому она принимает и все
промежуточные значения от 0 до 1.
Поскольку все операции шифрования обрати-
мы, то все промежуточные булевы функции, за-
дающие процедуру шифрования, являются сба-
лансированными. Таким образом, если каждый
разряд продолженной переменной равен 0,5, то в
целевую функцию будут входить продолжения
конъюнкций, равных 0,5. Поэтому продолженная
целевая конъюнкция от и продолженных двоич-
ных переменных равна 2”".
Очевидно, что если все разряды ключа опре-
делены правильно, то значение продолженной
целевой функции равно 1.
Теорема 17.4.2. Если целевая функция одно-
значно определяет ключ, то ее продолжение име-
ет единственный глобальный экстремум, равный
1, который достигается при совпадении продол-
женного ключа с истинным значением. Сущест-
вует окрестность вершины конуса, ассоцииро-
ванного с решением, в которой каждый элемент
целевой конъюнкции строго больше 0,5.
Доказательство. Согласно лемме 17.4.1
сбалансированная продолженная булева функция
принимает значения от 0 до 1. Если тестируемый
ключ является истинным, то все конъюнкции
равны 1 и значение продолженной целевой
функции равно I. Поскольку продолженная фун-
кция, описывающая равенство одноименных дво-
ичных разрядов, является сбалансированной, то
она принимает значения от 0 до 1. Следователь-
но, продолженная целевая функция на единич-
ном кубе принимает все вещественные значения
от 0 до 1. Целевая функция однозначно опреде-
ляет ключ, поэтому глобальный экстремум ее
продолжения является единственным и соответ-
ствует вершине единичного куба. В силу гладко-
сти продолженной целевой функции существует
окрестность вершины конуса, в которой каждый
элемент целевой конъюнкции строго больше 0,5.И
Приведенные рассуждения справедливы и в
том случае, если целевая функция определяет
несколько ключей— число глобальных макси-
мумов продолженной целевой функции равно
числу решений. Таким образом, нахождение точ-
ки глобального максимума продолженной целе-
вой функции эквивалентно вскрытию ключа
шифра на основе открытого и зашифрованного
текстов.
Нет необходимости рассматривать продолже-
ние (17.4.1) как непрерывное, можно ограни-
читься поиском максимума методом наискорей-
шего спуска [4] для трех значений разрядов клю-
ча: {0; 0,5; 1}. Кроме того, здесь не требуется
минимизация булевых функций. Действительно,
если к равенству булевых функций
(/Ag)v(/Ag) = /, (17.4.2)
соответствующему минимизации, применить
продолжение (17.4.1), то оно примет вид:
/g+Xi-g)=/g+/-/g=Z
Равенство (17.4.2) выполняется и для продол-
женных булевых функций.
Применим рассматриваемый метод к задаче
обращения хэш-функции.
Алгоритм 17.4.1. Обращение итерированной
хэш-функции с использованием арифметически
продолженных булевых функций.
Вход. Алгоритм вычисления хэш-функции/и
ее значение у.
Выход. Аргумент х = (у, ..., х„) хэш-функцииf
Метод.
1. Положить 77* <—2”", /<-1, х, <- 0,5 для
0 < i < п.
2. Положить <- 0 и вычислить продолженную
целевую функцию 77° = 77|* =0.
372
3. Положить <г-1 и вычислить продолженную
целевую функцию =1.
4. Если Н^<Н* < Н\ (то есть, вероятно, х, = 1),
то положить х}<— 1 и Н <— НУ. Если
НХ3<Н* < Hj (то есть, вероятно, Xj = 0), то
положить х} <- 0 и Н* . Если ни одно
из неравенств не выполняется, то положить
Xj <— 0,5.
5. Если все разряды аргумента найдены, то ал-
горитм заканчивает работу, иначе положить
j <—j + 1 и вернуться на шаг 2.
Разряд аргумента на шаге 4 можно определять
и по максимуму целевой функции, но это иногда
ведет к увеличению вероятности ошибки. Ис-
пользование двойного неравенства можно объ-
яснить тем, что высказывания «разряд аргумента
равен 0» и «разряд аргумента не равен 1» одина-
ково информативны. Если вероятно правильное
значение разряда аргумента соответствует уве-
личению целевой функции, то вероятно непра-
вильное значение должно соответствовать ее
уменьшению. При объединении этих условий
получаем двойное неравенство.5 * *
Для продолженных функций число 0,5 явля-
ется аннулятором для всех чисел по сложению:
0,5Фх = 0,5. Если число циклов шифрования
достаточно велико, то изменение одного разряда
аргумента перестает влиять на значение целевой
функции — оно всегда равно 2'". Поэтому есте-
ственным усилением метода представляется тес-
тирование на шаге 4 не одного, а одновременно
нескольких разрядов аргумента.
В ходе дальнейшего поиска разрядов аргумен-
та критерием правильности является рост теку-
щих значений Н. Это позволяет использовать
стратегию отбраковки найденных ранее разрядов
ключа, если Н не имеет тенденции к увеличению.
Хэш-функция характеризуется пороговым
числом г правильно найденных разрядов аргу-
мента, при достижении которого раскрытие оче-
редного разряда выполняется со сложностью
0(1) (одна итерация шага 4 алгоритма 17.4.1).
Таким образом, стойкость хэш-функции (слож-
ность ее обращения) пропорциональна 2': нужно
угадать г разрядов аргумента, тогда остальные
разряды определяются с линейной сложностью.
Поэтому число г задает экспоненциальную со-
ставляющую стойкости хэш-функции [4].
5 Можно использовать и просто максимум, а так-
же минимум целевой функции— для поиска «ин-
версного» ключа.
Пример 17.4.1. Оценка порогового числа раз-
рядов аргумента и стойкости хэш-функции.
1. Рассмотрим хэш-функцию из примера
17.3.1 при тех же значениях параметров и аргу-
мента, но для шести циклов шифрования. Тогда
у = 1010 1001 1010 1100 0001 ООП 0001 0111.
Используем неминимизированные булевы
функции, задающие прямую и обратную подста-
новки.
Операция вещественнозначного продолжения
суммы по модулю 2 одного разряда х текста с
разрядом z ключа задается равенством
г® z = x(l - z) + (1 - x)z = х + z - 2xz.
Продолженная прямая подстановка
(wb w2, Из, г/4) -> (vi, Иг, Уз, v4), где U], Vi — старшие
разряды двоичного представления входа и выхо-
да подстановки, имеет вид
У! = (1 - 2/0(1 - 2/0(1 - Мз>4 + (1 - MlX1 - W2) X
X 2/3(1 - 2/0 + (1 - 2/0(1 - Z22)Z23Z24 + U\ х
X (1 - 2/0(1 - 2/0(1 - 2/0 + l/](l - w2)w3w4 +
+ 22]222( 1 - W3XI - M4) + Wl«2(l - 22з)/24 +
+ 221Z22Z23( 1 - W4);
V2 = (1 - 2/0(1 - 2/0(1 - 223)224 + (1 - 220222 X
X (1 - w3)w4 + (1 - U^UQU-iO ~ +
+ 221(1 - 2/0(1 - W3)(l - 2/0 + 2/1(1 - 2/02/3 X
X (1 - 2/4) + 2/1(1 - 2/2)zZ32/4 + 2/12/2(1 - U3)U4 +
+ 2/i2/2z/3z/4;
V3 = (1 - 2/])(l - 2/2)2Z3( 1 — 220 + (1 — 220222 X
X (1 - ZZ3)(1 - 2/0 + (1 - 220ZZ2(1 - 270274 +
+ 2/1(1 -2/2)(l - 2Z3)(1 -2/4) +2/1(1 -2/0 X
X (1 - Z23)Z24 + ZZi(l - ZZ0223224 + Z/i2/2(1 - 2/3) X
X (1 - 2/0 + 2/]W2Z/32/4;
V4 = (1 - 221X1 ~ 2/0(1 - 2Z3)ZZ4 + (1 - 2/0(1 - 2/0 X
X 2/3(l - 270 + (1 - ZZ0ZZ2( 1 - 2/0(1 - 2/0 +
+ (1 - 220Z22223224 + Z/i(1 - 270(1 - 2/0(1 - 270 +
+ 221(1 - 222)223(1 - 2/0 + 22| г2222з(1 - 2/0 + ZZ1Z22223Z24.
Аналогично определяется продолженная об-
ратная подстановка. Выберем в качестве началь-
ного приближения значения 0,5 для всех разря-
дов аргумента.
Ищем целевую функцию Ft для начального
приближения аргумента (0,5; ...; 0,5), заменяя
логические операции арифметическими согласно
продолжению 17.4.1. Поскольку все булевы
функции, задающие разряды промежуточных
текстов, сбалансированы, получаем Н = 2“32 =
= 2,328306437- КГ10.
Вскрытие аргумента будем выполнять в не-
сколько итераций, используя алгоритм 17.4.1. На
первой итерации все разряды аргумента, кроме
373
одного, полагаем равными 0,5; этому одному раз- Целевая функция равна Н° = 2,32951-10“'°. ряду придаем поочередно значения 0 и 1. При этом проверяем, что if лежит между Н° и Н\, и Для Xl = ц х2 = ... =х32 = 0,5 получим по виду неравенства определяем оценку разряда н'= 2,32937 • 10“'°. Поскольку if не лежит меж- аргумента. На второй итерации тестируем пооче- ,.о ду Н, и Н,, то этот разряд не определен, редно остальные разряды, при этом в аргумент 1 ’ 1 ' подставляем оценки разрядов аргумента, найден- Аналогично получаем. ные на первой итерации. На третьей итерации — 2 32834-10-10 Н1 =2 32827-10”10, уточняем оценки второй итерации и тестируем ос- 13 13 тавшиеся нераскрытые разряды аргумента и т. д. = 2,32824 -10 , Н2А - 2,32838-10 ; Например, на первой итерации для аргумента = 2 32827-10“'° if =2 32834-10”10 х вида %] = 0; Х2-... =хз2=0,5 после трех циклов 32 32 ’ зашифрования получим F (х): Поэтому вероятные оценки разрядов аргумен- та равны: Х1з = 0, х24 = 1, хзг = 1 • Разряды тестиру- (0,5; 0,5; 0,5; 0,5; 0,5; 0,5; 0,5; 0,5; ем поочередно, чтобы исключить их взаимное 0,5; 0,5; 0,5; 0,5; 0,5; 0,5; 0,5; 0,5; влияние. 0,5; 0,5; 0,5; 0,5; 0,5; 0,501; 0,492; 0,492; На второй итерации подставляем найденные 0,5; 0,501; 0,492; 0,492; 0,5; 0,501; 0,492; 0,492). оценки в аргумент, остальные разряды полагаем равными 0,5, тогда if = 2,33142 • 10“10. Результа- ^После трех циклов расшифрования получим ты тестирования приведены в таблице 17.1 (д и F (х Ф у): — число одинаковых округлений в одноимен- (0 5- 0 5' 0 5’ 0 5’ 0 5’ 0 5’ 0 5’ 0 5’ ных Р^РЯД^ промежуточных текстов соответст- 0,493; оУ 0*493; 0*5; 0^508; оУ оУ о’У венно при нулевом и единичном значениях тес- 0,5; 0,493; 0,5; 0,5; 0,5; 0,5; 0,5; 0,5; тируемого разряда). 0,5; 0,5; 0,5; 0,5; 0,5; 0,5; 0,5; 0,484). Таблица 17.1 Результаты тестирования для примера 17.4.1
Разряд Я°-10'° 70 Н\ -1О10 7i Оценка Верно/Неверно • • - - I ‘ <73? <. ’ ‘ Й ?1 .. № a -s ''it'5 • i - -
' 1 2,32743 3 2,33346 4. 1 Неверно
2 2,33085 5 2,33176 6 1 Верно
3 2,32754 9 2,33315 6 0 Верно
4 2,328 5 2,329 8 — —
5 2,33867 4 2,32303 2 0 Верно
6 2,33299 6 2,32857 5 0 Верно
7 2,33486 7 2,32754 4 0 Верно
8 2,33702 5 2,32834 7 1 Верно
9 2,33702 5 2,32834 1 • .0 Неверно
10 2,32497 5 2,34141 7 1 Верно
11 2,33599 8 2,32828 7 0 Верно
12 2,32536 6 2,33871 8 1 Верно
13 — — — — 0 Итерация 1
14 2,33234 7 2,33175 7 — —
15 2,33058 6 2,33213 9 1 Верно
16 2,32716 6 2,33268 9 1 Верно
17 2,32853 8 2,33164 9 1 Верно
18 2,33332 7 2,33208 6 — —
19 2.32897 . 7 2,33446 8 д 1 Неверно
20 2,33759 7 2,32610 3 0 Верно
21 2,33435 8 2,32907 6 0 Верно
22 2,33443 5 2,3298 5 0 Верно
23 "л 2,32464 4 2,34146 7 1 Неверно
374
Продолжение таблицы 17.1
Разряд Я°-1О10 Jo 77} -1О10 J1 Опенка Верно/Неверно
24 —_ — — — 1 Итерация 1
25 2,3329 7 2,32962 7 0 Неверно
26 2.33285 8 2,32962 10 0 Неверно
27 2,33648 8 2,32858 8 0 Верно
28 2,32756 3 2,331563 7 1 Неверно
29 2,32954 5 2,33492 8 1 Неверно
30 2,33122 6 2,32924 5 — —
31 2,33511 6 2,33142 6 1 Верно
32 — — — — 1 Итерация 1
Тестирование по целевой функции if дает во-
семь ошибок. Поскольку принятие ложного раз-
ряда в качестве правильного ведет к ошибочно-
сти всех дальнейших вычислений, желательно
ужесточить критерий приема разряда аргумента.
Например, принимать тестируемый разряд при
выполнении двух условий: 1) <Н^-, 2)
jo > ft, если Hj > ifj, или jo < j), если 77° < . В
этом случае число ошибок сокращается до шести.
2. Зависимость порогового числа от числа
циклов шифрования той же хэш-функции имеет
вид:
Число циклов 6 8 10 32
Пороговое число «0 «9 «13 «27
Стойкость 2и 29 213 227
3. Рассмотрим 64-разряд ную хэш-функцию,
заданную уравнением: у = 7'’2А(х) Ф х, один цикл
шифрования которой содержит:
- сложение текста с константой по модулю 2;
- перестановку вида х, x23,(mo<i ед;
- подстановку (0, 13, 11, 8, 3, 6, 4, 1, 15, 2, 5,
14, 10, 12,9, 7);
- циклический сдвиг влево на 25 разрядов.
Зависимость порогового числа от числа цик-
лов шифрования имеет вид:
Число циклов 6 8 10 32
Пороговое число «32 «50 «58 «60
Стойкость 232 2-50 258 260
Таким образом, эта хэш-функция характери-
зуется определенным числом циклов шифрова-
ния, свыше которого стойкость по отношению к
данному методу практически не увеличивается.
Пороговое число для заданной хэш-функции
определяется с полиномиальной сложностью на
этапе предвычислений. Значение г в общем слу-
чае неточно и зависит от расположения найден-
ных разрядов. Для нахождения числа г достаточ-
но выбрать аргумент хэш-функции, вычислить ее
значение и потом увеличивать число угаданных
разрядов аргумента до тех пор, пока алгоритм
17.4.1 не начнет работать, а значение продол-
женной целевой функции if не начнет возрас-
тать. Можно двигаться и в другую сторону,
уменьшая число известных разрядов аргумента
до тех пор, пока алгоритм 17.4.1 не перестанет
определять очередной разряд аргумента с гаран-
тированно большой вероятностью.
Вскрытие ключа с учетом найденного поро-
гового числа выполняется следующим алгорит-
мом [4].
Алгоритм 17.4.2. Обращение хэш-функции с
помощью арифметически продолженных буле-
вых функций.
Вход. Значение хэш-функции.
Выход. Аргумент хэш-функции.
Метод.
1. Вычислить с помощью алгоритма 17.4.1 по-
роговое число г.
2. Выбрать произвольным образом г разрядов
аргумента.
3. Применить алгоритм 17.4.1 для вскрытия ос-
тальных разрядов аргумента, контролируя
значение 77*. Если значение 77* в ходе выпол-
нения алгоритма 17.4.1 (в среднем) возраста-
ет, то разряды на шаге 2 настоящего алго-
ритма выбраны правильно. В противном слу-
чае вернуться на шаг 2.
Сложность алгоритма 17.4.2 определяется
сложностью проверки того, что тестируемые
разряды ключа определены правильно. В общем
случае для снижения сложности можно исполь-
зовать и другие критерии: увеличение числа раз-
рядов, входящих в целевую функцию, с одинако-
выми округлениями; увеличение разности, обес-
375
печиваемой при изменениях аргумента, и т. п. На
очередной итерации целесообразно проверять
правильность разрядов аргумента хэш-функции,
найденных на предыдущих итерациях, по приня-
тому критерию. Это позволит корректировать
ошибки предыдущих итераций. Для повышения
точности метода желательно использовать мето-
ды проверки статистических гипотез.
Этот метод криптоанализа допускает распа-
раллеливание.
Алгоритмы 17.4.1 и 17.4.2 очевидным обра-
зом можно адаптировать и к задаче вскрытия
ключа итерированного шифра.
Пример 17.4.2. Использование арифметиче-
ски продолженных булевых функций для вскры-
тия ключа блочного шифра.
Рассмотрим степенной восьмицикловый блоч-
ный шифр с длиной блока 64 бита и цикловой
функцией шифрования А из п. 3 примера 17.4.1.
Выберем открытый текст x = 21d6 clc6 Ь579
0аЬ7 и шифрограмму у = 3518 7465 ff87 Ь527
(этому преобразованию текстов соответствует
ключ k= 86ed с328 270а 15а5).
Как и в случае хэш-функции, для вскрытия
ключа нужно угадать пороговое число разрядов
ключа, а оставшиеся разряды можно вычислить.
Например, если угаданы все разряды ключа, кро-
ме восьми (разряды 2-5, 8, 58,60, 61 равны 0,5), то
77* = 5,5147- Иг— целевая функция увеличи-
лась по сравнению со случаем, когда число уга-
данных разрядов невелико.
Зависимость порогового числа от числа цик-
лов шифрования примерно соответствует хэш-
функции из п. 3 примера 17.4.1.
По мере увеличения числа угаданных разря-
дов ключа увеличивается (в среднем) целевая
функция (таблица 17.2).
Таблица 17.2
Зависимость параметров алгоритма от числа угаданных разрядов в примере 17.4.2
Число правильно угаданных разрядов ключа Значение целевой функции II Число разрядов с одинаковыми округлениями Число разрядов с различными округлениями
4 5,4210108- 1О“20 0 0
8 5,4210108- 1О“20 0 0
12 5,4210108- 10 20 0 0
16 5,4210108- 1О“20 0 0
20 5,4210108- 1О“20 0 0
24 5,4210108- Ю"20 0 0
28 5,4364117- 1О“20 6 1
32 5,4324924 • Ю"20 6 3
36 5,4115101 • 10-2° 1 3
40 5,4395095 • Ю 2(1 5 0
44 5,4211892- 10 20 4 9
48 5,4911738- ИГ20 7 3
52 5,4214357- Ю ’20 5 9
56 5,5157845 • ИГ20 13 7
60 5,0686905 • КГ20 13 11
62 8,8367030 • ИГ20 14 6
17.5. Анализ шифров
с малым порядком нелинейности
В ряде случаев функцию шифрования удобнее
представлять композицией не булевых функций,
заданных в базисе И, ИЛИ, НЕ, а полиномов Же-
галкина. Это обусловлено тем, что G„ является
кольцом, тогда как множество булевых функций
в базисе И, ИЛИ, НЕ — только полукольцом. В
кольце Gtl определено дифференцирование, а ка-
ждая булева функция представляется полиномом
Жегалкина однозначно. Наиболее употребитель-
ная операция сложения текстов по модулю 2 при
описании ее в терминах кольца G„ является аф-
финной, тогда как при описании в базисе И,
ИЛИ, НЕ она таковой не является.
376
Ключ шифрования можно определить и как
содержимое памяти ключей, и как подстановку,
задаваемую блочным шифром.6
Каждую булеву функцию, описывающую со-
ответствующий разряд подстановки у =ХХ),
можно задать набором из 2” - 1 коэффициентов,
определяющих ее представление в виде полино-
мов Жегалкина:
Уь = «ЛО + X ahix, ahtix'xj + - •
i i>J
Тогда всю подстановку можно описать набо-
ром двоичных «-разрядных векторов, которые
соответствуют булевым функциям, задающим
разряды подстановки:
У = ао + £аЛ + £а<А*7 +-+а1...>Л-*и-
> »J
Для вскрытия ключа шифра (обращения хэш-
функции) составим целевую функцию как в ре-
шеточном методе. Если все операции предста-
вить полиномами Жегалкина, то целевая функ-
ция //над F2 тоже будет полиномом Жегалкина:
H = f[(b1®kl) + fjglkl(l®k1), (17.5.1)
/=1 <=1
где Ь,е {0, 1}, k = (ki, ...,к„) — ключ и g, — бу-
левы функции, представленные в виде полино-
мов Жегалкина. Если Ь, = 0, то соответствующий
разряд ключа равен 1, в противном случае этот
разряд равен 0. Целевая функция принимает зна-
чение 1 только на том наборе аргументов, кото-
рый является решением задачи криптоанализа.
п
Поскольку в действительности ^gAO ©&,) = 0
>=i
в G„, то и производная этой суммы по любой пе-
ременной равна нулю.
Между вычислением производной целевой
функции (17.5.1) и перебором ключей существу-
ет связь. Действительно, £>]£>2...£>„(//) = 1. По-
скольку функцию Н практически невозможно
записать в виде формулы, но можно вычислить,
то использование производных могло бы послу-
жить механизмом для вскрытия ключа. Напри-
мер, если выполняется равенство £>2...£>„(//) = 0,
то первый разряд ключа равен 0; если
£>2...£>„(Д)= L т° первый разряд ключа равен 1.
Остается то же проделать с остальными пере-
6 Любой блочный шифр не только реализует класс
подстановок, но и позволяет его компактно описать.
Вычисление собственно массива ключа сводится к вы-
числению искомой подстановки в «терминах» этого
шифра. Однако подстановку можно задать и на тради-
ционном языке описания подстановок.
менными. Таким образом, задача вскрытия клю-
ча сводится к вычислению многократной произ-
водной целевой функции.
Поскольку все переменные входят в полином
Жегалкина только в первой степени, дифферен-
цирование в кольце Gn сводится к исключению
переменной. Для испытываемого набора пере-
менных к\, к„ можно исключить переменную
kh если вычислить Н(кь ..^к^к^к,^, ...,к„) +
+ Н(к\, ..., к^\, F, км, ..., к,.). Исключение двух
переменных потребует четырех слагаемых и т. д.
Исключение всех переменных, кроме одной, по-
требует перебора.
Если итерированный подстановочно-
перестановочный шифр использует на каждом
цикле четырехразрядные подстановки (как в
примерах 17.3.1, 17.4.1, 17.4.2), то порядок нели-
нейности для одного цикла шифрования не пре-
вышает 3. При этом /j-мерные векторные коэф-
фициенты а„ а9, а,д,... являются «почти нулевы-
ми» и слабо зависят от ключа. После нескольких
циклов шифрования эта зависимость усиливается.
Пример 17.5.1. Изменение векторных коэф-
фициентов с ростом числа циклов шифрования.
Рассмотрим 64-разрядную хэш-функцию
у = F"'(x) ® х, каждый из т циклов шифрования
которой содержит операторы сложения по моду-
лю 2 текста с константой 86ed с328 270а 15а5,
перестановку вида х, -> x23/(mod бд, подстановку 5
из примера 17.3.1 и циклический сдвиг влево на
25 разрядов. Запишем хэш-функцию в виде по-
линомов Жегалкина:
64
у = а0 + ХаЛ + JX +•••
'=1 i>j
и вычислим векторные коэффициенты:
ао = у(О64), а, = а0 + у(1, 063),
а2 = ао + у(О, 1, О62),
ац = а0 + у(1, О63) + у(0, 1, О63) + у( 1, 1, О62)
и т. д. Пусть оператор шифрования /'"’(х) описы-
вается уравнением
64
F"’ (х) = Ьо + +....
/=1 i>J
Тогда а0 = bo, а, = b, + i, а,? = Ь„ и т. д.
Для того чтобы коэффициенты Ь,, описы-
вающие нелинейную часть преобразования, были
отличны от нуля, необходимо, чтобы соответст-
вующая конечная разность порядка j была от-
лична от нуля. Нелинейные свойства шифра про-
являются только при прохождении соответст-
вующих разрядов текста через блок подстановки.
377
Рассмотрим подробнее механизм появления
нелинейных свойств. Изменение z-ro разряда ар-
гумента вызывает изменение некоторых разря-
дов промежуточных текстов. Векторный коэф-
фициент Ь,, не равен нулю, если разряды проме-
жуточных текстов, обусловленные изменениями
входных z-ro и /-го разрядов, на некотором цикле
зашифрования пройдут через один и тот же блок
подстановки. Для того чтобы векторный коэф-
фициент by выглядел как случайный вектор, же-
лательно, чтобы после того, как он станет отлич-
ным от нуля на некотором цикле шифрования,
прошло еще несколько циклов, в ходе которых
этот коэффициент в результате операций пере-
мешивания и рассеивания (в данном случае —
операции подстановки) примет требуемый вид.
Для шифра можно определить число циклов,
при котором каждый разряд открытого текста
сцепляется при помощи нелинейного оператора с
каждым разрядом. Можно определить и число
циклов, необходимое для того, чтобы произволь-
ный текст стал похож на случайный.7 В данном
случае изменение одного разряда на входе под-
становки приводит к изменению двух-трех раз-
рядов на выходе подстановки. Следовательно,
для того чтобы каждый разряд сцепился с каж-
дым из остальных разрядов, необходимо от
log364 ~ 3,8 до log264 = 6 циклов шифрования.
Эксперимент показывает, что векторные ко-
эффициенты Ьцд, Ь2>4, Ь3;4, описывающие квадра-
тичную нелинейность, становятся отличными от
нуля только при т > 4. При т = 4 появляются
ненулевые коэффициенты, описывающие нели-
нейность порядка 3 и 4, но они, как правило, раз-
режены и явно не выглядят как случайные.
Если порядок нелинейности итогового урав-
нения шифрования невелик или векторные ко-
эффициенты полиномов Жегалкина, описываю-
щих подстановку, предсказуемы начиная с неко-
торой степени, то можно использовать следую-
щую атаку на основе подобранных шифртекстов.
1. Набрать необходимый объем открытых и за-
шифрованных текстов и вычислить непредска-
зуемые коэффициенты полиномов Жегалкина.
2. Представить дешифруемый шифртекст в ви-
де суммы найденных на шаге 1 векторных
коэффициентов полиномов Жегалкина.
3. Для нахождения открытого текста сложить
по модулю 2 найденные векторные коэффи-
циенты.
7 Поскольку изучать закон распределения 64-
разрядных блоков текста практически сложно, жела-
тельно изучить закон распределения некоторых раз-
рядов в блоке. Способ задания этих разрядов, очевид-
но, зависит от типа шифра.
17.6. Криптоанализ на основе
рационального продолжения
полиномов Жегалкина
Как и булевы функции, полиномы Жегалкина
можно продолжить до полиномов над полем Q
рациональных чисел, что позволит упорядочить
множество их значений.
17.6.1. Теоретические основы
Как и раньше, будем придавать переменным
значения из конечного множества рациональных
чисел и максимизировать целевую функцию как
продолженный полином Жегалкина. По анало-
гии с методом Андельмана-Ридса можно ис-
пользовать дифференцирование, если число цик-
лов шифрования невелико.
Отображения G„ -> IF2, вычисляемые путем
подстановки вместо переменных их двоичных
значений, являются гомоморфизмами колец. По-
скольку IF2 с G„, эти отображения можно рас-
сматривать как эндоморфизмы кольца G„. Соот-
ветственно отображения продолжения кольца Gn
в множество рациональных чисел можно рас-
сматривать как продолжения эндоморфизмов
кольца G„.
Определим два варианта продолжения опера-
ции сложения по модулю 2 и умножения:
х Фу ->х + у - 2ху, хлу—>ху, (17.6.1)
х©у-»[х-у|, хлу->ху, (17.6. Г)
где в левой части переменные и операции из по-
ля IF2, в правой — из множества А рациональных
чисел от 0 до 1. Продолжение сложения в
(17.6.1') получается из (17.6.1) с учетом идемпо-
тентности умножения:
х2 + у2 - 2ху = |х - у|.
Продолженная по формуле (17.6.1) операция
сложения задает на множестве А структуру ком-
мутативного моноида с нулем 0, так как она
коммутативна и ассоциативна и продолжения
сумм элементов из А лежат в А.
Противоположный элемент х' определяется из
равенства х Ф х' = 0, то есть х + х' - 2хх' = 0, от-
, х TJ
куда х =-------. Нетрудно заметить, что
2х-1
х' g (0, 1) для х^О, 1. Если расширить область
определения продолженных значений на все
множество рациональных чисел, то для всех эле-
ментов, кроме 0,5, будут выполняться свойства
378
абелевой группы. Элемент 0,5 при этом играет
роль «бесконечно большого» и является аннуля-
тором по сложению для всех элементов:
х Ф 0,5 -> х + 0,5 - 2 • х • 0,5 = 0,5.
По умножению продолженное множество об-
разует коммутативный моноид с единицей 1, так
как операция умножения коммутативна и ассо-
циативна и множество А замкнуто относительно
умножения.
Продолженные по (17.6.1) полиномы не обра-
зуют полукольцо, так как нет дистрибутивности:8
х а (у Ф z) -» ху + xz - 2xyz,
х лу® х лг -> ху + xz - 2xyz2.
Для двоичных переменных из А справедливы
равенства
1 Ф 1 -» 1 + 1 - 2 = 0,
0Ф0->0, 0Ф 1 -> 1, 1Ф0-> 1,
1 л 1 -> 1, 0 а0 0, 0 л 1 —> 0, 1а0—>0,
а также выполняется дистрибутивность. Поэтому
верна следующая теорема.
Теорема 17.6.1. Отображения (17.6.1),
(17.6. Г) определяют продолжение булевых
функций, заданных полиномами Жегалкина.
Множество А как подмножество поля Q явля-
ется упорядоченным. Вскрытие ключа сводится
к вычислению продолженной целевой функции
как композиции полиномов Жегалкина и нахож-
дению ее экстремума. Имеет место следующее
утверждение.
Теорема 17.6.2. Значения продолженного по
(17.6.1) и исходного полиномов Жегалкина сов-
падают тогда и только тогда, когда переменные
принимают двоичные значения.
Доказательство. Сначала докажем теорему
для единичных значений. Предположим, что су-
ществует набор переменных, на котором исход-
ный полином Жегалкина принимает значение 1.
В силу теоремы 17.6.1 продолженная целевая
функция на этом наборе переменных также при-
нимает значение 1. Докажем единственность это-
го набора. Очевидно, что для двух элементов
(значений продолженных полиномов) а и b усло-
вие ab = 1 выполняется только при о = 6 = 1.
Аналогично из условия а Ф b = 1 получаем
8 Отметим, что если бы для продолженных поли-
номов можно было задать условие х~ = х для всех х. то
дистрибутивность выполнялась бы.
b =-----. Нетрудно заметить, что это равенство
1 -2а
при 0 < a, b < 1 выполняется только для двоич-
ных значений а, Ь. Следовательно, продолжен-
ный полином Жегалкина принимает значение 1
только на двоичном наборе переменных. Однако
на этом наборе его значение совпадает со значе-
нием исходного полинома. Этим доказано, что
продолженный полином Жегалкина принимает
значение 1 только тогда, когда исходный поли-
ном принимает значение 1. Поскольку исходный
полином может принимать это значение только
на двоичных наборах переменных, продолжен-
ный полином принимает значение 1 на этих же
двоичных наборах.
Докажем теорему для нулевых значений. По-
скольку на остальных двоичных наборах исход-
ный полином принимает значение 0, то и про-
долженный полином на этих наборах принимает
значение 0. Предположим, что существует набор
недвоичных переменных, на котором продол-
женный полином Жегалкина принимает значе-
ние 0. Из равенства ab = 0 для значений двух
продолженных полиномов получаем а = 0 или
6 = 0, так как в поле Q нет делителей нуля. Из
равенства а Ф 6 = 0 получаем 6 = —-—. По-
2о-1
скольку это равенство при 0 < а, 6 < 1 выполня-
ется только для двоичных значений переменных,
теорема доказана. *
Любое пополнение поля Q является его рас-
ширением. В полном поле продолженный поли-
ном Жегалкина является непрерывным. Поэтому
продолженная целевая функция как конъюнкция
поразрядных равенств (см. п. 17.3) имеет гло-
бальные максимумы, равные 1, в точности на тех
наборах переменных из интервала (0, 1), которые
являются решениями задачи криптоанализа.
Таким образом, задача вскрытия ключа ите-
рированного шифра или обращения хэш-
функции сводится к поиску глобального макси-
мума продолженной целевой функции для пере-
менных из интервала (0. 1).
Продолжение (17.6.1) эквивалентно продол-
жению (17.4.1) полукольца булевых функций в
базисе И, ИЛИ, НЕ. Действительно, применяя
продолжение (17.4.1) к правой части равенства
X ф у = (х А у) V (х А у) , получим
XI -т)+Х1 -Х) = х+у-2ху,
что соответствует рассмотренному продолжению
для операции сложения по модулю 2. Поэтому
для криптоанализа можно использовать алгоритм
379
17.4.2. В этом случае часть разрядов ключа или
аргумента хэш-функции нужно угадать, а остав-
шиеся разряды — вычислить.
Множество А рациональных чисел из интер-
вала (0,1) замкнуто относительно операции аб-
солютной величины разности (17.6.1'). Эта опе-
рация коммутативна, но не ассоциативна:
||а -Ь\-с\ф\а-\Ь - с||. Число 0 является нулем,
каждый элемент противоположен самому себе
(аналогия с кольцом характеристики 2). Однако
уравнение \а - х| = b в общем случае имеет не
единственное решение. Например, при а = 0,5 и
b = 0,3 решением будет х = 0,8 и х = 0,2. Поэтому
А с операцией (17.6.1') не является ни полугруп-
пой, ни квазигруппой. Продолженная операция
сложения по модулю 2 дистрибутивна относи-
тельно умножения. Это означает, что в полиноме
Жегалкина, продолженном по варианту (17.6. Г)
и заданном в виде композиции полиномов, мож-
но «раскрывать скобки», однако его значение
зависит от порядка суммирования слагаемых.
Для уменьшения этой погрешности будем рас-
сматривать наряду с бинарными операциями
сложения и умножения унарную операцию ин-
версии. В ряде случаев это позволяет записать
булеву функцию с сокращенным набором сла-
гаемых. Отметим, что представление булевой
функции формулой с указанными операциями в
общем случае не единственно.
Очевидно, что целевая функция Н принимает
значение 1, если тестируемый набор переменных
совпадает с решением. Рассмотрим, в каких дру-
гих случаях продолженная по варианту (17.6. Г)
целевая функция Н может принимать значение 1.
Для a, b е А справедливо: а Ф b g A, ab G А.
Поэтому значение любого полинома Жегалкина
при подстановке вместо переменных элементов
из А принимает значения из Л.
Продолженная сумма а Ф b равна 1 тогда и
только тогда, когда <7 = 0, 6=1 или а = 1, 6 = 0.
Продолженная сумма а Ф 6 равна 0 тогда и толь-
ко тогда, когда а = 6. Продолженный полином
Жегалкина, представленный в виде суммы (с за-
данной очередностью суммирования), принимает
значение 1 тогда и только тогда, когда на по-
следнем шаге суммирования одно из слагаемых
равно 0, а другое 1.
Аналогично, ab = 1 для a, b е А тогда и толь-
ко тогда, когда <г = 6=1. Поэтому продолженный
полином Жегалкина, представленный в виде про-
изведения, принимает значение 1 тогда и только
тогда, когда каждый сомножитель принимает
значение 1.
Целевая функция представляет собой произ-
ведение продолженных равенств g = А,. Полином
Жегалкина с аргументами g и А„ принимающий
значение 1 тогда и только тогда, когда g^h,
(двоичные значения), имеет вид 1 Ф g, Ф А,. Про-
должать эту функцию можно по-разному:
1|1-&|-Ш1-А<|-&|;
l|l-g<|-|l-A,|-g,A,|;|]-!g,-A,.||
и т. д. В трех первых случаях функция равна 1
тогда и только тогда, когда операнды принимают
одинаковые значения из множества {0,1}. В по-
следнем случае функция равна 1 при g = А, (не
обязательно двоичные значения).
17.6.2. Метод криптоанализа
В основе метода криптоанализа лежит проце-
дура поиска максимума целевой функции Н, при-
нимающей значение 1 для истинного значения
ключа шифра или аргумента хэш-функции [6].
Для хэш-функции целевая функция Н пред-
ставляет собой продолженную конъюнкцию по-
разрядных равенств. Левая часть каждого равен-
ства— булева функция, описывающая выходы
хэш-функции в зависимости от аргумента; пра-
вая часть равенства— значение этой булевой
функции как значение соответствующего разряда
аргумента хэш-функции. В силу обратимости
операции шифрования можно составлять конъ-
юнкцию из равенств разрядов промежуточных
текстов по аналогии с решеточным методом.
Для шифра целевая функция Н представляет
собой продолженную конъюнкцию поразрядных
равенств булевых функций, описывающих зашиф-
рование известного открытого текста на полови-
не циклов шифрования и расшифрование соот-
ветствующей шифрограммы на половине циклов:
о(»)
67=П(ц,Фг,Ф1). (17.6.2)
1=1
Очевидно, что если все разряды аргумента
хэш-функции (ключа шифра) определены пра-
вильно, то значение продолженной целевой
функции будет равно 1. Поскольку продолжение
полиномов Жегалкина нарушает ряд алгебраиче-
ских свойств исходного кольца полиномов (нет
ассоциативности продолженного сложения и
идемпотентности умножения), у целевой функ-
ции появляются локальные экстремумы, не соот-
ветствующие решению задачи криптоанализа. 5'
При нахождении локального экстремума, как
и в п. 17.4, ограничимся тремя значениями раз-
рядов аргумента: 0; 0,5; 1. ;
Рассмотрим эвристический алгоритм нахож-
дения локального максимума целевой функции
на примере задачи обращения хэш-функции, где
380
х — неизвестный аргумент хэш-функции, у — ее
значение.
Алгоритм 17.6.1. Нахождение локального
максимума целевой функции для итерированной
хэш-функции.
Вход. Алгоритм вычисления хэш-функции f и
ее значение у.
Выход. Оценка разрядов аргумента х и ло-
кальный максимум целевой функции.
Метод.
1. Положить у<—0. Выбрать произвольным об-
разом начальное приближение (хь ...,х„) ар-
гумента х, близкое к вектору (0,5; ...; 0,5).
Для выбранного х, известного алгоритма вы-
числения хэш-функции и известного у вы-
числить продолженную целевую функцию Н
и положить if <— Н.
2. Для i = 1, 2,..., п выполнять следующие дей-
ствия.
2.1. Найти х' <— min(T\ {х,}), х" <— тах(Г\ {х,}),
где Т= {0; 0,5; 1} и вычислить значения
целевой функции Н' = Н” = Н^^".
2.2. При Н' < if < Н" положить Н, <- Н",
ji <— х"; при Н" < Н < Н' положить
Hi Н', j, <— х'. Если ни одно двойное
неравенство не выполняется, положить
H,^lf.
3. Для i = 1, 2, ..., п найти Нm.lx^rnaxA;. При
1</<и
Ятах> if ПОЛОЖИТЬ Н <- Hmm, Xj JДЛЯ
найденного максимума и вернуться на шаг 2.
При Hmax = if результат: if — локальный
максимум целевой функции, соответствую-
щий аргументу х.
Аналогичный алгоритм можно использовать и
для поиска локального максимума целевой
функции шифра. При этом вместо аргумента из-
меняется ключ.
Пусть Ну — суммарное число исходов, при
которых вскрытый бит аргумента равен i, если на
самом деле он равен j. По сути алгоритм 17.6.1
строит матрицу (АД; вместо целых чисел Ny
можно использовать нормированные величины
(частоты, которые на большой выборке пример-
но равны вероятностям).
Вскрытие аргумента хэш-функции выполня-
ется следующим алгоритмом.
Алгоритм 17.6.2. Обращение хэш-функции с
использованием рационального продолжения
полиномов Жегалкина.
Вход. Алгоритм вычисления хэш-функции f и
ее значение у.
Выход. Аргумент х хэш-функции f
Метод.
1. (Предвычисления.) Для произвольных аргу-
ментов и соответствующих значений хэш-
функции найти алгоритмом 17.6.1 для каждо-
го бита аргумента матрицы (АД (ру), (ду), где
ру — частота вскрытия бита аргумента как z,
если в действительности он равен у; qy —
частота того, что бит аргумента равен z, если
он вскрылся как j.
2. Для значения у хэш-функции и неизвестного
аргумента путем поиска максимума целевой
функции алгоритмом 17.6.1 найти вектор
Р = (Ро, Pi), где Р, — частота того, что бит
аргумента вскрывается как z.
3. Решая для каждого разряда аргумента урав-
нение Р = (р,у)л относительно л = (л0, 7Cj ) ,
где л, — вероятность того, что бит аргумента
равен z, упорядочить множество ключей по
вероятности ключа быть истинным. Тогда
я = (^)Р-
4. Опробовать аргументы, начиная с наиболее
вероятных, до выявления истинного значе-
ния. Результат: аргумент, для которого вы-
численное значение хэш-функции совпадает
с истинным. ’
Примечания.
1. Уравнение Р=(/г)л на шаге 3 следует из
формулы Байеса для условных вероятностей:
Pr(z,j) = ^Py=РДУ1 =
М
Noo + Ми + Мо +Mi
где Pr(zJ)— вероятность того, что оценка
бита аргумента равна z и его истинное значе-
ние равно у; Ау— числа, определенные на
шаге 1.
2. Элементы матрицы (ру) на шаге 1 можно оп-
ределить следующим образом:
Mo Aqj
Мо + Mo Mi + Ап
Mo Mi
Mo + Mo Mi+ M i
3. Аналогично определяется матрица (qyy.
_ Mo „ _ Mo
Mo+Mi’ V01 Alo + Au’
. Ml x Mi
Mo+Mi’ Mo+Mi’
381
4. Объем выборки, необходимый для того, что-
бы частоты были близки к вероятностям, оп-
ределяется методами математической стати-
стики.
5. Векторы частот тс могут быть рассмотрены
как функции двух аргументов: двоичного
аргумента и начального приближения. На-
зовем хэш-функцию l-эргодической, если
для разряда I аргумента знаки преобладаний
вероятностей л0 или Л] при изменении аргу-
ментов и при изменении начальных при-
ближений совпадают, а вероятность ошибки
мала. Менее формально: если оценка «по-
хожа» на аргумент при известном аргумен-
те, то она будет «похожа» на аргумент и при
неизвестном аргументе. Если частота появ-
ления нулевой (единичной) оценки для бита
аргумента равна
(0) =---^оо..^
TVoo+^io+^oi
то произведение (г/,,) (р(О), р(1)) дает вектор
вероятностей того, что бит аргумента в дей-
ствительности равен 0 или 1:
чМ)0 + ^0 + М), + ^11 М)0 + ^,0 + ^01 + ^п >
В основу алгоритма 17.6.2 положена гипотеза
об эргодичности хэш-функции.
6. Алгоритм 17.6.2 можно использовать и для
вскрытия ключа шифра.
7. Для некоторых шифров матрица (/?„) может
зависеть от ключа и открытого (зашифрован-
ного) текста, например, если перемешивание
обеспечивается за счет сложения с переносом
(FEAL, ГОСТ 28147-89, см. пп. 19.4, 19.6).
Тогда для разреженных ключей влияние пе-
реносов слабее, чем для случайных, и матри-
цу (/?у) можно рассматривать как функцию
числа единичных разрядов ключа для разре-
женных открытых текстов. При этом алго-
ритм 17.6.2 можно применять для проверки
гипотезы о том, что истинный ключ является
разреженным.
Вероятность ошибки алгоритма 17.6.2 в пред-
положении, что значения 7Vq;, распределены
по биномиальному закону, равна
2V0;+M;
min(7V0/,7V1;)
Механизм криптоанализа можно пояснить
следующим образом. Продолжение полиномов
Жегалкина по формуле (17.6. Г) приводит к то-
му, что после раскрытия скобок знаки слагаемых
в каждом из сомножителей в (17.6.2) становятся
случайными. Чем большее число композиций
полиномов Жегалкина применяется к данному
разряду неизвестного, входящего в целевую
функцию, тем заметнее эта случайность. Поэто-
му меньше всего она заметна для тех слагаемых,
степень которых мала.
Помимо того, что знаки слагаемых высоких
степеней являются более случайными, значение
каждого слагаемого по абсолютной величине
меньше, чем значение слагаемого малой степени.
В результате при изменении разряда переменной
наибольшее влияние на продолженную целевую
функцию оказывают слагаемые малой степени,
то есть наблюдается некоторая аналогия с линеа-
ризацией продолженных полиномов Жегалкина.9
Рассмотренный метод криптоанализа является
универсальным.
Пример 17.6.1. Криптоанализ на основе ра-
ционального продолжения полиномов Жегалки-
на.
1. Пусть хэш-функция с длиной блока п = 64
бита задана уравнением
у = К2"'(х)Фх, (17.6.3)
где F — подстановочно-перестановочный опера-
тор шифрования из примера 17.5.1, т = 4 или 8.
Выберем представление булевых функций
полиномами Жегалкина с уменьшенным числом
слагаемых и использованием инверсных значе-
ний аргумента. Обозначим через щ, и2, щ, щ
входы подстановки (выходы обратной подста-
новки), пронумерованные со старших разрядов, а
через V], 1’2, гз, 1’4 выходы подстановки (входы
обратной подстановки). Уравнения подстановки
имеют вид:
V] = (М](1 Ф M3I/4) Ф (1 Ф М?)) Ф (1 Ф М2)(1 Ф Мз)(1 ф 1/4),
9 По-видимому, для повышения точности метода
желательно снизить погрешность, обусловленную
отсутствием ассоциативности. Для этого булевы
функции целесообразно представлять так, чтобы чис-
ло слагаемых было небольшим (например, в виде
произведения неприводимых полиномов).
382
V2 — (W] Ф U2(l Ф (1 Ф W])(l Ф М3))) Ф Un(U2 Ф (1 Ф
Ф M2)(l Ф W3)),
V3 = (ZZ2( 1 Ф Ы3) Ф M|M4) Ф (1 Ф W2)(l Ф M4)(M| Ф М3),
V4 = (M2 Ф W1(1 Ф М3)) Ф (М3 Ф M4)(l ф M|M2),
Mj = (1’3 Ф (n Ф 1'з)(1'2 Ф V4)) Ф 1'21'4(1 Ф V3) Ф
Ф V1V4(V2 Ф V3),
M2 = (v2 Ф vl) ф V3(V1 Ф V2V4),
М3 = ((VjV2 Ф V3V4(V1 Ф V2)) Ф V1V2V2V4) ф (1 ф V3)(l ф
Ф (1 Ф v,)(l Ф V2XI Ф v4)),
M4 = ((Vi Ф V3) Ф V4(l Ф V2)) Ф 1’|1'з(1''2 ф 1'з)-
Из уравнения (17.6.3) следует, что
х ф у = г"'(х). В силу обратимости оператора F
можно применить к обеим частям последнего ра-
венства оператор F~'”. Тогда F"'(x) = F~"'(x Ф у).
Обозначим w = Я"(х), г = F ~т(х Ф у). Опреде-
лим целевую функцию Н как продолженную
конъюнкцию поразрядных равенств w, = z,. С
учетом функций поразрядного равенства можно
предложить два способа продолжения целевой
функции (17.6.2):
64
H = H|1-(w;+5,)|
/=1
(17.6.4)
Я = П(1-|и,-5,|). (17.6.5)
i=i
Для уравнения (17.6.4) условие w, = z, имеет
вид w, Ф г, Ф 1 = 1 или w, Ф (1 Ф z,) = 1. Переходя
к продолжению с учетом 11 - > О, получаем
|w, - (1 - z,)| = 1 или |1 - (w, + Zf)[ = 1.
Для входа х = 21(16 с1с6 Ь579 0аЬ7 определим
одиночное значение хэш-функции у = 14се Ь5аЗ
4afe bf90, затем «забудем» х и вычислим с по-
мощью алгоритмов 17.6.1, 17.6.2. Разряды аргу-
мента хэш-функции определим алгоритмом
17.6.2. Результаты анализа для т - 4 и различных
начальных приближений (целевая функция по
варианту (17.6.4)) сведем в таблицу:
Разряд | Оценка Верно/Неверно
Начальное приближение (0,5)64; начальное значение Я* = 5,13 • 10-42
3 0 4,55 • 10“35 Неверно
44 0 5,43 • 10“32 Неверно
2 1 1,09- 10“3! Неверно
41 0 3,28 • 1(Г30 Верно
59 0 5,25 НТ29 Неверно
Продолжение таблицы
Разряд Оценка Я’ Верно/Неверно
23 0 9,70- IO’29 Верно
22 0 1,86 10“27 Верно
4 0 6,74 • 1026 Верно
38 1 1,56- IO’25 Верно
Начальное приближение (0,5)151 (0,5)31 (0,5)44; начальное значение Я* = 1,48 • 10 37
53 1 2,40- 10“34 Верно
34 1 1,51 • 10”3’ Неверно
21 0 2,08- 10 29 Верно
56 0 7,54 • 10“29 Верно
24 1 1,08- 10ж Верно
1 1 2,24- I027 Неверно
45 1 4,04 I027 Верно
Первое начальное приближение позволяет
найти оценки для девяти разрядов аргумента,
второе — для семи разрядов. Для рассматривае-
мой хэш-функции средняя частота совпадения
найденных разрядов с истинным значением рав-
на 0,568, то есть е = 0,068 > ]/!5.
Для продолжений (17.6.4) и (17.6.5) большин-
ство разрядов вскрываются как нулевые. Если же
использовать целевую функцию вида
Н = (1 - z,.) + z, (l - и',)), то большинство
разрядов будут вскрываться как единичные.
(Этот вид целевой функции соответствует
Я = Л(и;Е, vx^,) в аппроксимации Андельма-
i
на-Ридса.)
2. Рассмотрим эту же хэш-функцию с целевой
функцией (17.6.5). Для начального приближения
(OjS)64, Ft = 1,68 - 10-15, начиная с третьей итера-
ции алгоритма 17.6.1, правильно определенными
оказываются все девять найденных разрядов ар-
гумента, для которых выполняется двойное не-
равенство (см. шаг 2 алгоритма).
Для начального приближения
1(0,5)41(0,5)41(0,5)41(0,5)48
и Я* = 2,38 10”’6 уже на первой итерации алго-
ритма 17.6.1 из 22 разрядов аргумента, для кото-
рых выполняется двойное неравенство (шаг 2
алгоритма), 18 оказываются правильно опреде-
ленными.
3. Рассмотрим степенной шифр с 16 циклами
шифрования, каждый из которых описывается
тем же оператором F, что и в уравнении (17.6.3).
Вскрытие ключа проведем для одного известного
блока открытого текста и соответствующей
383
шифрограммы. Сначала для выбранного ключа
(содержащего 34 единичных и 30 нулевых разря-
дов) и открытого текста вычислим шифрограм-
му, затем «забудем» ключ и вычислим его по
шифрограмме и открытому тексту. Целевая
функция имеет вид
64
н=+_ и<)) 5
>=]
где w = F8(x), г = F -8(у). Усредненная по всем
разрядам ключа матрица условных вероятностей
для уравнения л = (с/„)Р имеет вид
<0,41 0,39'
[о,59 0,61,
При вскрытии ключа (начальное приближение
для ключа: (0,5)1С12 * *(0,5)360(0,5)15, if = 6,07 1018)
алгоритм 17.6.1 дает следующие результаты:
Разряд Оценка Верно/Неверно
36 0 Верно
12 0 Верно
41 0 Верно
Эксперимент показывает, что зависимость
преобладания от числа циклов шифрования мо-
жет быть немонотонной.
Этот метод можно использовать для нахожде-
ния порогового числа правильно угаданных раз-
рядов ключа в начальном приближении.
17.7. Криптоанализ на основе
2-адического продолжения
полиномов Жегалкина
17 .7.1. Теоретические основы
Полиномы Жегалкина, заданные над множе-
ством {0, 1}, можно продолжить не только до
упорядоченного подмножества поля Q, но и до
упорядоченного подмножества кольца Z2 целых
2-адических чисел с 2-адическим нормированием.
Можно также говорить о соответствующем про-
должении эндоморфизмов кольца G„.
Напомним, что кольцо Z2 получается из коль-
ца 2 пополнением его бесконечными суммами
ОО
^о(2', at g {0, 1}. Конечные суммы в Z2 явля-
i=0
ются обычными целыми числами. Сложение и
умножение в Z2 выполняются так же, как в Z.
Для элементов из Z определим 2-адическое
показательное нормирование val: для п = 21с, где
с — нечетное число, val(w) = Таким образом,
нормирование в Z2 является дискретным, а его
значения— неположительными целыми числа-
ми.10 Для 2-адического нормирования справед-
ливы соотношения:
val(T^) = val(/) + val(g), ?
val(/±g)<max{val(/),val(g)}.
Будем рассматривать приближения 2-
адических чисел их редукцией по модулю 2т для
некоторого т (по аналогии с приближением ве-
щественных чисел конечными последовательно-
стями десятичных дробей). Из двух таких при-
ближенных целых 2-адических чисел, записан-
ных как обычные вычеты в кольце Z72'"Z, мень-
шим будет считаться то, которое содержит
больше нулей в младших разрядах. Например,
для целых двоичных чисел выполняются нера-
венства
val( 11110000) < val( 101000) <
< val(HOOlO) < val( 1011001).
2-адические нормы этих чисел равны соответ-
ственно -4, -3, -1, 0 как взятые со знаком «ми-
нус» числа нулей в младших разрядах.
Возможны два варианта продолжения кольца
Gr. В первом варианте используются продолже-
ния
a + b (mod 2) -> а + b (mod 2"'), (17.7.2)
ab (mod 2) -> ab (mod 2'”). (17.7.3)
Продолжения (17.7.2), (17.7.3) задают гомо-
морфное вложение кольца G„ в кольцо
!?„ = (Z/2"’Z)[xi, ...,х„]/21„г. Идеал порожден
элементами : ...... ,,;-
Х]'"(х2 -lXmod2'”), ...,х'”(х2 -l)(mod2w),
так как любой четный элемент кольца Z72"'Z
удовлетворяет сравнению х'" = 0 (mod 2"'), а лю-
бой нечетный элемент — сравнению
х2 -1 = 0(mod2'”)-11 Идеал 21,„ делится на иде-
ал Slt =(х2-X],...,х2-хй), а характеристика
10 Задание нормирования отрицательным значе-
нием показателя позволяет искать максимум целевой
функции, как и в методе рационального продолжения.
Нормирование можно эквивалентно задать положи-
тельным значением показателя, при этом необходимо
искать минимум целевой функции (см. п. 17.7.2)
11 Порядок группы обратимых элементов кольца
Z72"'Z равен 2'”'1, но эта группа изоморфна прямому
произведению двух циклических групп, одна из кото-
рых имеет порядок 2.
384
кольца R„ делится на характеристику кольца G„.
Имеет место следующая цепочка гомоморфиз-
мов колец:
Z[xi, ...,х„] -> (Z/2'"Z)[jci, х„] -> IF2[xi, хи].
Диаграмма гомоморфизмов колец рисунка
17.1 является коммутативной [7].
Рис. 17.1. Коммутативная
диаграмма гомоморфизмов колец
Для х е Z/2"'Z такого, что val(x) > -т, выпол-
няется равенство val(2x) = val(x) - 1.
Во втором варианте продолжения кольца G„
вместо (17.7.2) используется продолжение
а + b (mod 2) -> \а - 7>| (mod 2'"). (17.7.2')
Для такого отображения продолженная струк-
тура не является кольцом, так как нет ассоциа-
тивности. Однако для любого х е Z/2"'Z выпол-
няется равенство val(x + х) = -т.
17 .7.2. Метод криптоанализа
Метод анализа аналогичен рассмотренному в
п. 17.6.2— нужно найти локальный максимум
целевой функции
/7 = vail fj(l + w, + v,.) (mod2'”)],
I z=l J
(17.7.4)
где uh v,—- 2-адические продолжения разрядов
промежуточных текстов. Вместо (17.7.4) можно
использовать формулу
77 = val П<1+1
~ Ч |)(то^ 2m)
J
(17.7.4')
или другие аналогичные выражения. В кольце R„
в качестве переменных используются разряды
ключа. ... .
Если все разряды ключа (аргумента хэш-
функции) определены правильно, то все сомно-
жители в (17.7.4), (17.7.4') нечетны, и 77=0. В
противном случае Н является целым отрицатель-
ным числом.
Значения аргументов можно выбирать из
множества {0,1,2}. Поскольку val(l) = 0,
val(0) = -m, val(2) = -l, то значение 2 является
промежуточным между 0 и 1 так же, как значе-
ние 0,5 — промежуточное между 0 и 1 в п. 17.6.
На практике достаточно выбрать т несколько
большим, чем разрядность блока (ключа). По-
скольку значение нормирования дискретно и ле-
жит в интервале от 0 до —т, возможны случаи,
когда на очередном шаге «лучшими» оказывают-
ся несколько аргументов.
На результат анализа может влиять выбор по-
казателя т, поскольку G„ и его приближенное 2-
адическое продолжение описываются похожими
идеалами. Для получения максимального преоб-
ладания показатель т следует выбирать так, что-
бы при реализации процесса шифрования на-
блюдался «резонанс» между G,, и его прибли-
женным продолжением с учетом переносов, воз-
никающих при сложении и вычитании в Z72'"Z.
На практике, вероятно, показатель т следует
подбирать экспериментально.
Теорема 17.7.1. Пусть целевая функция одно-
значно определяет единственный ключ. Для про-
долженной по формуле (17.7.4) или (17.7.4') це-
левой функции равенство val(77) = 0 (с продол-
жением сложения согласно формуле (17.7.2) или
(17.7.2')) выполняется тогда и только тогда, ко-
гда тестируемый ключ является истинным.
Доказательство. Пусть val(77) = 0. Так как
диаграмма рисунка 17.1 коммутативна, а при пе-
реходе от Rn к G„ гомоморфизм по сложению
определяется формулой (17.7.2'), получаем, что
77= 1. Обратно, если в G„ выполняется равенство
77= 1, то поднятие целевой функции в R„ даже с
учетом неопределенности знака каждого слагае-
мого по формуле (17.7.2') даст val(77) = 0.
Пример 17.7.1. Поиск локального максимума
целевой функции.
1. Рассмотрим 8-цикловую хэш-функцию из
примера 17.5.1 с константой k = b6ed с368 af4a
15а5. Аргументу x = 21d6 clc6 Ь579 0аЬ7 соот-
ветствует значение функции у = 744b 5418 а9ее
7П2. Теперь «забудем» аргумент и будем ис-
пользовать его лишь в качестве «шпаргалки» для
проверки того, совпадет ли найденный разряд
аргумента с истинным значением.
Кольцо целых 2-адических чисел имеет ха-
рактеристику 0. Поэтому можно использовать
редукцию этого кольца, отбраковывая малые (в
385
2-адической метрике) числа. Достаточно выбрать
в формуле (17.7.4') такое т, которое не снижало
бы точность вычислений для начального при-
ближения. Зададим «наугад» т = 70 и будем
проводить вычисления по модулю 270. Разряды
аргумента вычислим по аналогии с алгоритмом
17.6.1. Для начального приближения (2, ...,2) по-
лучаем:
77 Разряд и оценка Верно/Неверно
-63 24-» 1 Верно
-46 30-» 1 Верно
-37 53 -» 1 Верно
-33 4 -> 0 46-»0 47-»0 Верно Верно Верно
1 -»0 15 -»0 28-»0 54-»0 56-»0 64-»0 40-»0 42-»0 Верно Неверно Верно Верно Верно Неверно Неверно Неверно
функции (17.7.4') получаем (<?,,) =
2. Аналогично ищется ключ 16-циклового
шифра с длиной блока 64 бита (см. пример 17.6.1,
п. 3). Для уравнения л = (^,)Р при целевой
0,47 0,39"
0,53 0,61,
(интегральные оценки для всех разрядов ключа,
без разбиения по разрядам). Округления для век-
тора л совпадают с истинными значениями для
63 % битов ключа.
Отметим, что сложность дифференциального
метода для данного шифра превышает перебор-
ную, сложность линейного метода близка к пе-
реборной, а анализ методом сдвига требует око-
ло 232 пар открытых и зашифрованных текстов
(см. гл. 18). Поэтому метод 2-адического про-
должения для этого шифра оказывается эффек-
тивнее, чем линейный или дифференциальный,
как по времени, так и по требуемому объему от-
крытых и соответствующих зашифрованных тек-
стов. Кроме того, для данного шифра этот метод
несколько эффективнее, чем метод п. 17.6.
2-адическое продолжение целевой функции
может быть использовано для оценки числа пра-
вильно угаданных разрядов ключа. Действитель-
но, в силу коммутативности диаграммы рисунка
17.1 можно записать продолженную целевую
функцию в виде
H = \{kigi + F,
/=1
(17.7.5)
где после редукции по модулю 2 множество ну-
лей полинома gj становится подмножеством ну-
лей полинома kj, и
F=X-/>°(mod2)-
J
Каждый сомножитель в правой части равен-
ства (17.7.5) является нечетным тогда и только
тогда, когда тестируемый ключ совпадает с ис-
тинным. В силу свойств (17.7.1) с учетом того,
что значение нормирования — неположительное
целое число, для нормирования продолженной
целевой функции (17.7.5) справедливо неравен-
ство
< max(val(//), val(F)).
На практике по значению val(/7) нужно оце-
нить число правильно угаданных битов ключа,
при этом значение val(F) неизвестно. По-
видимому, для увеличения информативности
последнего неравенства желательно искать не
максимум, а минимум продолженной целевой
функции алгоритмом 17.6.1, адаптировав его
очевидным образом.
Этот метод можно использовать и для нахож-
дения порогового числа правильно угаданных
битов ключа в начальном приближении.
17.8. Максимизация числа совпавших
разрядов промежуточных текстов
Этот эвристический метод в общем случае
менее эффективен, чем рассмотренные в пп. 17.6,
17.7 универсальные методы криптоанализа, и
отличается тем, что в качестве целевой функции
используется число совпавших разрядов проме-
жуточных текстов, полученных при зашифрова-
нии открытого текста на половине циклов шиф-
рования и при расшифровании шифрограммы на
оставшихся циклах шифрования.
Суть метода заключается в следующем. Для
произвольного исходного приближения искомо-
го ключа (двоичный вектор) вычисляется целе-
вая функция. Затем поочередно изменяются раз-
ряды ключа и для каждого из них вычисляется
целевая функция. Разряд ключа, обеспечиваю-
щий максимум целевой функции, считается
предположительно истинным. Поскольку значе-
ние целевой функции является целым числом,
несколько измененных разрядов ключа могут
386
давать одно и то же значение целевой функции,
то есть процедура нахождения локального мак-
симума целевой функции иллюстрируется дере-
вом. Для нахождения аргумента, дающего ло-
кальный максимум целевой функции, необходи-
мо просматривать все ветви дерева (включая по-
следующие ветвления), дающие максимальное
значение целевой функции на данной итерации
поиска.
На этапе предвычислений для различных
ключей, открытых текстов и найденных шифро-
грамм определяется преобладание 8, обеспечи-
ваемое данным методом при поиске ключа.
Собственно вскрытие ключа производится
после того, как станут известными открытые и
зашифрованные тексты, объем которых одно-
значно определяет ключ. Для этого процедура
повторяется примерно О(8-2) раз. Истинным
ключом считается наиболее вероятный.
Уязвимость шифра (хэш-функции) по отно-
шению к данному методу можно охарактеризо-
вать слабым сцеплением разрядов ключа между
собой в ходе шифрования. Например, для хэш-
функции из примера 17.7.1 существование поло-
жительного преобладания не установлено. Про-
тиводействие этому методу обеспечивается стро-
гим лавинным критерием (см. п. 18.1).
17.9. Анализ с использованием
сжимающих гомоморфизмов
Этот метод анализа, в отличие от предыду-
щих, не является универсальным и применим
лишь для некоторых (неудачно спроектирован-
ных) шифров. Атака использует гомоморфное
отображение шифра как алгебраической струк-
туры в другую структуру меньшего размера. На-
зовем отображение шифра S с уравнением шиф-
рования у = S(k, х), где х, у, к соответственно от-
крытый текст, шифртскст, ключ, в шифр Т с
уравнением шифрования Y=T(K,X) гомомор-
физмом, если существуют вычислимые отобра-
жения У= ср/у), Х= срх(х), К = ср^Л), Т = (рДЯ).
Сжимающий гомоморфизм позволяет перей-
ти от «большого» шифра S(k,x) к «малому»
шифру Т(К, X). Вскрытие ключа «малого» шифра
(перебором или иным методом) дает информа-
цию о ключе «большого» шифра по аналогии с
китайской теоремой об остатках.
Под сжимающим гомоморфизмом можно по-
нимать эпиморфизм колец, групп, полугрупп,
конечных автоматов и т. п. Вследствие сущест-
венного различия алгебраических свойств ука-
занных алгебраических структур описать этот
метод в общем случае вряд ли возможно, лучше
пояснить его на примерах.
Пример 17.9.1. Анализ на основе сжимающих
гомоморфизмов характеристики кольца.
Рассмотрим шифр, действующий на множест-
ве 10-буквенных блоков русского алфавита, до-
полненного пробелом; буквы Е и Ё, Ь и Ъ нераз-
личимы, то есть всего 32 буквы (размер блока
непринципиален— шифр взламывается с поли-
номиальной сложностью от размера блока). Бук-
вы пронумерованы в естественном порядке: про-
бел — О, А — 1, Б — 2, ..., Я — 31. Пусть шифр
содержит семь циклов шифрования, на каждом
из которых последовательно выполняются сле-
дующие три элементарные операции:
- сложение блока с ключом как 10-разрядных
векторов по модулю 32;
- подстановка букв, заданная уравнением
fix) = х4 + х1 + х (mod 32);
- операция рассеивания, заданная умножением
блока на циркулянтную матрицу12 над коль-
цом Z/32Z с первой строкой (3, 4. 6, 8. 10, 12,
14, 16, 18,20).
Зашифруем на ключе
(1, 2, 3, 4, 5, 6, 7, 8, 9, 10) = АБВГДЕЖЗИЙ
открытый текст
(6, 18, 19, 27, 0, 18, 3, 31, 8, 27) = ЕСТЬСВЯЗЬ.
После сложения получим г
(7, 20, 22, 31, 5, 24, 10, 7, 17, 5) = ЖУХЯДЧЙЖРД,
после подстановки —
(25,4,10, 1,15,24,30,25,19,15) = ШГЙАОЧЮШТР,
после рассеивания —
(11, 26, 0, 15, 1,6, 28, 31, 29, 5) = КЩ_ОАЕЫЯЭД.
Это результат шифрования на одном цикле.
После семи циклов получим шифрограмму
(5,18,22, 15, 31,6,10,15,11,25) = ДСХОЯЕЙОКШ.
Теперь «забудем» ключ и попробуем найти
его, зная открытый и зашифрованный тексты и
способ шифрования. Заметим, что мощность
множества ключей равна 3210 = 250, то есть пере-
бор ключей затруднен. Используем цепочку
вложенных гомоморфизмов колец
Z/32Z-»Z/16Z->Z/8Z-»Z/4Z-»Z/2Z. (17.9.1)
Шифр описывается полиномом из кольца
(Z732Z)[xj, ...,Хю]. Представим ключ в виде 10-
разрядного вектора над Z/32Z, а каждый разряд
12 В циркулянтной матрице каждая последующая
строка получается путем циклического сдвига преды-
дущей строки на один элемент.
387
этого вектора— в виде 5-разрядного двоичного
вектора. Будем искать ключ поразрядно, начиная
с младших двоичных разрядов каждого из десяти
слов ключа.
Сначала используем гомоморфизм
(Z/32Z)[xb ...,х10] -»(Z/2Z)[xb ...,х10].
В прообразе каждая координата 10-
разрядного вектора является 5-разрядным двоич-
ным числом, а в образе— одноразрядным дво-
ичным числом. Гомоморфизм ставит в соответ-
ствие 5-разрядной координате ее младший раз-
ряд. Гомоморфные образы открытого и зашиф-
рованного текстов имеют вид:
х2 = (0, 0, 1, 1,0, 0, 1, 1,0, 1),
у2 = (1,0,0, 1,1,0, 0,1, 1,1)
(индекс 2 означает, что рассматриваются двоич-
ные образы слов ключа и текста). Задавая подста-
новку и операцию рассеивания младшими разря-
дами, замечаем, что подстановка является тожде-
ственной, а операции рассеивания соответствует
единичная матрица. Тогда получаем уравнение
зашифрования х2 + 7к2 = у2 или к2 = х2 + у2 = (1, 0,
1, 0, 1, 0, 1, 0, 1,0). Младшие десять битов ключа
найдены.
Теперь используем гомоморфизм
(Z/32Z)[xi, ...,х!0] -»(Z/4Z)[X], ...,Х]0],
рассматривая по два младших разряда в каждом
пятиразрядном слове текста и ключа и учитывая
найденные младшие биты ключа. Гомоморфные
образы открытого и зашифрованного текстов
имеют вид
Х4 = (2, 2, 3, 3, 0, 2, 3, 3, 0, 3),
у4 = (1,2,2, 3, 3,2, 2,3,3, 1).
Подстановка задается уравнением fix) = х4 +
+ х2 + х (mod 4), то есть имеет вид (00, 11, 10, 01),
старший разряд на выходе 2-разрядной подста-
новки задается линейным над IF2 уравнением
у2 = X] + х-2, где Т| — младший, х2 — старший раз-
ряд в 2-разрядном слове на входе подстановки.
Первая строка матрицы рассеивания над Z/4Z
имеет вид (3, 0, 2, 0, 2, 0, 2, 0, 2, 0). Композиция
подстановки и рассеивания является нелинейной
операцией как над IF2, так и над Z74Z. В данном
случае десять старших разрядов в 2-разрядных
словах ключа проще всего искать перебором из
1024 вариантов. Решение с учетом найденных
ранее младших битов ключа имеет вид (1, 2, 3, 0,
1,2, 3,0, 1,2).
Далее ищем третьи биты в 5-разрядных сло-
вах ключа, используя гомоморфизм
(Z/32Z)[x,, ...,xI0] -»(Z/8Z)[x,, ...,х10]
с учетом найденных ранее 20 битов ключа, затем
следующие по старшинству биты и, наконец,
старшие биты ключа.
Для нахождения очередных десяти битов
ключа достаточно выполнить перебор из 1024
вариантов, то есть с помощью персонального
компьютера ключ может быть вскрыт за доли
секунды.
Слабость рассмотренного шифра обусловлена
существованием вложенных гомоморфизмов
(17.9.1). Именно поэтому сложность вскрытия
ключа несущественно зависит от вида подста-
новки и рассеивающей матрицы, а также от раз-
мера блока (при разумных ограничениях). При
использовании 26-буквенного латинского алфа-
вита и операций, действующих на этом алфавите,
существуют гомоморфизмы Z/26Z -> Z/2Z и
Z/26Z —> Z/13Z, обусловленные делимостью
характеристики кольца. Отсюда следует, что ес-
ли все операции шифрования описаны в терми-
нах некоторого кольца, то в качестве характери-
стики кольца следует выбирать простое число.
Пример 17.9.2. Редукция числа переменных.
Пусть шифр использует два частично пере-
крывающихся ключа т и с по 257 байт каждый
[2]. Каждое 16-разрядное слово ключа характе-
ризуется как своим содержимым, так и адресом
(указателем). Введем обозначения:
С1 — младший байт слова С;
Ffiufi Fc(y) — значения слов ключа т (соот-
ветственно с) с указателем и, (соответственно у,);
к — персональная константа;
Г„ С, — z-я пара двухбайтовых слов открыто-
го текста и шифртекста.
Зашифрование выполняется следующим ал-
горитмом.
1. Установить значение счетчика z = 1 и задать
начальные значения указателей г/0, у0, к как
составляющие ключа.
2. Осуществить преобразование z-ro слова тек-
ста.
2.1. Вычислить Di = (Г, - к) (mod 216).
2.2. Записать D, и Ffiujfi) в виде 16-
разрядных двоичных векторов и найти
вектор С' =(Pt +Fm(z/,_j))(mod 216).
3. Вычислить новые значения указателей:
3.1. г/, = z/,-i + (Fc(y,_j) (mod 28)) — сумма
двоичных векторов. . .г .
388
3.2. yt = У'_} + Cl’ (mod28).
4. Закончить преобразование слова:
Q =C' + w, (mod2!6).
5. Установить i = i + 1. Если блок закончился,
то зашифрование выполнено, если нет —
вернуться на шаг 2.
Этот шифр описывается нелинейными (над
IF2, Z/28Z и Z7216Z) уравнениями. Нелинейность
обусловлена зависимостью указателя очередного
слова ключа от предыдущего слова открытого
текста и использованных на предыдущем шаге
слов ключа. Для этого шифра, действующего на
16-разрядных словах, существует отображение в
шифр, действующий на 8-разрядных двоичных
словах (младших байтах слов), при этом 16-
разрядное слово ключа также заменяется млад-
шим байтом. Таким образом, задачу вскрытия
ключа можно решать поочередно: сначала найти
для гомоморфного образа шифра младшие байты
ключа, затем — старшие байты.
Возможно дальнейшее снижение числа пере-
менных, но при этом усложняется перечисли-
мость прообраза.
17.10. Поиск коллизий хэш-функции
В ряде случаев требуется, чтобы хэш-функция
была стойкой в части нахождения коллизий. На-
пример, если в схеме цифровой подписи ГОСТ
Р 34.10-2001 подготовить пару сообщений, даю-
щих одинаковое значение хэш-функции и предъя-
вить одно из них для подписи, а затем в подпи-
санном сообщении заменить это сообщение дру-
13
гим, то такая ситуация не распознаваема.
Для поиска коллизий (бесключевой) хэш-
функции с мощностью множества значений Y
используются следующие универсальные мето-
ды: метод встречи посередине со сложностью
O(TFlogT), метод Полларда со сложностью
О(э/К) и метод встречи на случайном дереве со
сложностью O(VrlogF).
Вероятностный алгоритм встречи посередине
позволяет найти коллизии осмысленных текстов
и работает следующим образом.
Алгоритм 17.10.1. Поиск коллизий хэш-
функции методом встречи посередине.
Вход. Хэш-функция h. 13 *
13 Способ защиты от таких нарушений описан в
работе [4]. .....
Выход. Пара аргументов и, v таких, что
h(u) = 7z(v).
Метод.
1. Для z’ = l,2,..., O(y/Y) выбрать произвольный
аргумент х„ вычислить пары (х„ Л(х,)) и от-
сортировать полученное множество по вто-
рой «координате».
2. Проверить в базе данных наличие элементов
с одинаковыми значениями h(x,). Если колли-
зий нет, то увеличить базу данных. В про-
тивном случае (коллизия /?(х,) = /?(х^)) поло-
жить и <— Xj, V <— Xj. л. ;
3. Результат: (и, г).
Если осмысленность текстов не требуется, то
можно воспользоваться алгоритмом встречи на
случайном лесе. Этот алгоритм отличается от
алгоритма 17.10.1 только тем, что в качестве ар-
гументов Xj используются хэш-образы после од-
ного или нескольких (не более O(log У)) последо-
вательных вычислений хэш-функции. В этом
случае длина текстов, дающих коллизию, равна
длине хэш-функции.
Алгоритм Полларда можно адаптировать для
нахождения корня ориентированного дерева (в
который по определению входят две стрелки,
начала этих стрелок дают коллизию). В этом слу-
чае длина текстов, дающих коллизию, также рав-
на длине значения хэш-функции. Алгоритм на
каждой итерации находит такую тройку вершин
(г/, v, w), что и лежит на дереве, v и w лежат в
цикле, причем расстояния между и и w, v и щ по-
следовательно сокращаются до 1.
Пусть объем памяти вычислительной модели
равен V. Алгоритм работает следующим обра-
зом. Определим начальное приближение хо и ре-
куррентную процедуру х,+1 = h(x,) для i > 0. На
первой итерации ищем такую тройку (z, х„х2,),
что Xj = х2/. При этом запоминаем пары (z, х,) по-
сле каждых zz = (7(л/г/к) шагов и сортируем ба-
зу данных по второй «координате». После того,
как указанная тройка найдена, вычисляем х,+1,
х,+2, ... до завершения цикла (получение равенст-
ва xi+j = х,), при этом на каждом шаге сравниваем
текущее значение с базой данных и помечаем в
ней встретившиеся позиции. Пусть к — наи-
большее значение z, соответствующее непоме-
ченной паре в базе данных, и I— наименьшее
значение i + j, записанное в базу данных, такое,
что 1>к- i. Тогда полагаем и <— х^, у <— X/,
w <— х^+1. Очищаем базу данных и на каждой по-
следующей итерации проходим пути от и до w и
от у до w, записывая в базу данных начальные
вершины и каждую ({к — i)/V) -ю вершину. Затем
находим новую тройку (г/, v, w) и т. д.
389
Пример 17.10.1. Поиск коллизии хэш-
функции как корня дерева.
Пусть хэш-функция задана уравнением
Л(х) = 1 (Г + х3 + 2т (modр), р = 2!6 + 3. Предпо-
ложим, что объем памяти вычислительной моде-
ли позволяет запомнить всего шесть чисел. Вы-
берем в качестве отправной вершины графа про-
извольное неотрицательное число, меньшее р,
например, Xj = 1. Предполагая, что хэш-функция
ведет себя как случайное отображение, находим
ожидаемую длину цикла и длину «хвоста»:
•J772/8 -160. С запасом выбираем оценку для
числа шагов алгоритма, равную 300, вычисляем
х,+] = Л(х,) для i от 1 до 300 и записываем каждое
50-е значение в базу данных. Получаем:
х50 = 57397, хюо = 39836, х150 = 1021,
*2оо = Ю480, х25о = 27126, х300 = 25967.
Далее, предполагая, что х3оо лежит в цикле,
продолжаем рекуррентные вычисления от хЗОо
до встречи с первым элементом базы данных:
это элемент х250 на 105-м шаге. Значит, корень
дерева лежит в промежутке между х2Оо и х250,
причем х25о лежит на дереве, а х2Оо — в цикле.
Длина цикла является делителем числа
300-250 + 105 = 155. Убеждаемся, что длина
цикла не является собственным делителем числа
155. Значит, длина цикла в точности равна 155.
Корень дерева лежит в цикле между верши-
ной х250 и вершиной, расположенной на 50 шагов
«назад» (эта вершина имеет порядковый номер
250 + 155-50 = 355), то есть между х355 и х250.
Вычисляем: х355 = 64671.
На второй итерации обнуляем базу данных,
берем в качестве начального значения х2Оо и
делаем 50 шагов до достижения х250, запоми-
ная в базе данных каждое 10-е значение. По-
лучаем х2ю = 211703, х220 = 31223, х230 = 30762,
*240 = 20026. Движемся по циклу от х355 до встре-
чи с элементом базы данных. Первый встретив-
шийся элемент — х24о. Значит, корень дерева ле-
жит между х230 и х240. Находим вершину из цик-
ла, отстоящую от х24о на 10 шагов «назад»:
х385 = 32228.
На третьей итерации обнуляем базу данных,
берем в качестве начального значения х230 и дела-
ем 10 шагов до достижения х24о, запоминая в базе
данных каждое 2-е значение. Получаем
*232 = 47341, х234 = 39518, х236 = 56975, х238 = 17723.
Движемся по циклу от х385 до встречи с элементом
базы данных. Первый встретившийся элемент —
*238. Значит, корень дерева лежит между х236 и х238.
Находим корень дерева: *238 = х393 = 17723. Колли-
зию составляют элементы х237 = 37126 и
*392 = 44978, /?(х237) = /г(*39г) = *238-
Как показывают рассмотренные методы крип-
тоанализа, вопреки распространенному мнению,
задача обращения хэш-функции не обязательно
сложнее, чем задача поиска коллизий.
17.11. Компромисс время/память
Компромисс время/память (time-memory trade-
off), предложенный в открытой печати М. Хел-
лманом (см. работу [17]), позволяет ускорить
процесс вскрытия ключа за счет использования
таблиц предвычислений. Составление таблиц не
требует знания открытых или зашифрованных
текстов и может выполняться однократно.
Например, если допустима атака на основе по-
добранных открытых текстов, то можно составить
базу данных из пар ключ/шифрограмма для одно-
го и того же открытого текста и отсортировать ее
по шифрограммам. Для вскрытия ключа доста-
точно зашифровать указанный открытый текст на
искомом ключе, найти для полученной шифро-
граммы равную ей в базе данных и прочитать зна-
чение ключа в найденной ячейке базы данных.
Сложность предвычислений равна 0(2"), где
п — разрядность ключа; требуемый объем памя-
ти примерно такой же. Сложность вскрытия
ключа после составления базы данных равна
0(1). Таким образом, увеличивая объем памяти,
можно снизить сложность вскрытия индивиду-
ального ключа. Отметим, что начать создавать
базу данных можно сразу же после опубликова-
ния алгоритма шифрования. Если алгоритм
шифрования неизвестен, то базу данных создать
невозможно. Вот почему алгоритм шифрования
целесообразно хранить в секрете.
В общем случае можно обойтись базой дан-
ных меньшего размера, не перебирая все ключи
[17]. Правда, тогда снижается вероятность нали-
чия искомого ключа в базе данных. Предполо-
жим, что длина блока не меньше, чем длина
ключа (в противном случае можно перейти к
блоку кратной длины).
Метод анализа заключается в следующем.
Определим отображение S шифртекста у = Е(к, л-)
в ключ к', к = S'(y). Примером такого отображения
является замена ключа шифртекстом с отбрасы-
ванием лишних битов или линейное над F2 пре-
образование шифртекста. Пусть х° — некий от-
крытый текст. Тогда для у0 = Е(к°, х°) отображе-
ние у = E(S'(y'“1), х°) не является взаимно одно-
значным и ведет себя как случайное, то есть об-
ладает сжимающими свойствами. Рекурсивное
применение такого отображения с последующим
преобразованием S' для некоторого начального
ключа дает последовательность ключей к?, Е".
390
Граф такого отображения для множества ключей
К представляет собой лес, корни которого связа-
ны в циклы, при этом почти все вершины графа
лежат на одном дереве, высота которого близка к
длине цикла и асимптотически равна О(у/#К).
Сжимающие свойства графа позволяют сокра-
тить объем базы данных за счет увеличения тру-
доемкости представления ключа.
На этапе предвычислений для выбранного от-
крытого текста х° вычисляется матрица из mt
элементов Лу. Элементы матрицы ищутся рекур-
сивно:
Лу = 5(£(Л/;н,х0)), 0<у<1-1,
^ = ВД£(^_ьх°)),Л
начальное значение к,& —Н— произвольно. Та-
ким образом, последний элемент /-й строки мат-
рицы является шифртекстом для открытого тек-
ста х° и ключа, полученного из к' после t рекур-
сий. В строке матрицы каждый последующий
элемент вычисляется по детерминированному
алгоритму из предыдущего, поэтому каждую
строку можно задать первым и последним эле-
ментами (введение последнего элемента строки
позволяет ускорить вскрытие ключа). Затем база
данных, представленная строками матрицы, сор-
тируется по последнему элементу строки. Со-
ставление базы данных не требует знания шиф-
рограммы для текста х° и может быть начато не-
посредственно после опубликования алгоритма
шифрования.
На этапе вскрытия ключа для открытого тек-
ста х° и неизвестного ключа ищется шифрограм-
ма у0, которая сравнивается с элементами базы
данных. Алгоритм определения ключа содержит
два шага. На первом шаге проверяется совпаде-
ние у° с каким-либо элементом базы данных kJit.
Если совпадение есть, то для известного началь-
ного значения ключа к! вычисляется которое
равно искомому ключу. Если совпадения нет, то
выполняется второй шаг: у° <- E(S(y°), х°) и осу-
ществляется переход на первый шаг.
При m = t = О(Ц#К) вероятность успеха со-
ставит О$/#К)“! [17]. В действительности веро-
ятность успеха будет несколько выше благодаря
сжимающим свойствам случайного отображения.
17.12. Сочетание перебора
и вычисления ключа
Очевидно, что если нарушитель владеет дос-
таточной информацией о ключе (шенноновская
энтропия нулевая), то ключ можно вскрыть пе-
ребором. Однако иногда «тупой» перебор можно
заменить более производительным: часть ключа
подобрать, а оставшуюся часть вычислить (или
проверить, существует ли для нее решение). Ес-
ли решение для оставшейся части существует и
найдено, то вскрыт весь ключ, в противном слу-
чае подобранная часть ключа оказалась непра-
вильной и нужна новая попытка. Естественно,
вычисляемая часть ключа должна допускать эф-
фективную проверку на соответствие «угадан-
ной» части. Данный метод пригоден для анализа
алгоритмов, в которых ключ не является моно-
литным и может быть вскрыт «по частям». При-
мером такого подхода является криптоанализ с
использованием арифметического продолжения
булевых функций (п. 17.4), при котором для
вскрытия ключа нужно угадать пороговое число
битов ключа, а остальные можно вычислить.
Проиллюстрируем этот прием на примере по-
точного шифра А5/1 стандарта GSM (см.
[10, 11]). Шифр реализован на трех двоичных
сдвигающих регистрах с обратными связями
(рис. 17.2). Запись 22(21) означает, что регистр
имеет длину 22 бита, и на вход регистра (22-й раз-
ряд) поступает сумма по модулю 2 содержимого
0-го и 21-го разрядов. Работа такого регистра зада-
ется неприводимым над IF2[/] полиномом вида
fit) = Г2 +1 + 1. Если состояние регистра равно
ЛАО, то на выходе генератора формируется ли-
нейная над IF2 рекуррентная последовательность
битов, определяемых как старшие разряды Xt'
(тоёД/)) Для i > 1. Таким образом, последователь-
ность состояний регистра можно описать подгруп-
пой циклической группы 1F * 22. Порядок этой груп-
пы равен 3 • 23 • 89 683, t— образующая этой
группы, то есть начальное ненулевое заполнение
регистра является некоторой степенью элемента t.
Поэтому период последовательности равен поряд-
ку группы. Неприводимый полином fit) задает
расширение поля IF2, которое является 22-мерным
линейным векторным пространством над Т2 [1].
Поэтому работа одиночного регистра описывает-
ся системой линейных над F2 уравнений.
Рис. 17.2. Схема алгоритма шифрования А5
391
Аналогичные рассуждения справедливы и для
двух других регистров, задающих расширения
поля Р2 степеней 19 и 23 и описываемых непри-
водимыми полиномами t>9 +15 +1~ +1 + 1 и
?3 + ?5 + ? + Г + 1 соответственно. Для групп
[Fj19’^3'»23 поРяДк°в 524287 и 47- 178481, соот-
ветственно, с указанными неприводимыми поли-
номами элемент t также является образующей.
Выходы регистров складываются по моду-
лю 2. Поскольку порядки трех мультипликатив-
ных групп взаимно просты, в случае работы ре-
гистров без пропусков длина последовательно-
сти на выходе сумматора равна произведению
порядков групп.
На самом деле регистры работают с пропус-
ками тактов. Содержимое управляющих разря-
дов ut (9 для 19-разрядного регистра и 11 для ос-
тальных регистров) подается на схему голосова-
ния «два из трех». Если содержимое соответст-
вующего разряда регистра совпадает с результа-
том голосования, то этот регистр тактируется
(выполняется сдвиг, и в младший разряд записы-
вается сумма разрядов согласно неприводимому
полиному), в противном случае такт пропускает-
ся и состояние регистра сохраняется. Это усло-
вие можно задать нулями полинома Жегалкина
щ © щи2 © © U2U3. Таким образом, на каж-
дом такте каждый регистр работает с вероятно-
стью 1 /2, а все три регистра не имеют пропусков с
вероятностью ’/4. Этим обеспечивается нелиней-
ность уравнения шифрования. Выходная после-
довательность шифратора складывается пораз-
рядно по модулю 2 с шифруемой информацией.
Поскольку последующее состояние трех регист-
ров полностью определяется их предыдущим
состоянием, то в качестве ключа можно рассмат-
ривать состояние регистров в любой предшест-
вующий момент времени.
В общем случае текущее состояние регистра
может быть получено более чем из одного пред-
шествующего состояния, то есть шифратор реа-
лизует сжимающее отображение; граф отобра-
жения содержит лес, корни которого связаны в
циклы. Для исключения входа шифратора в ко-
роткий цикл предусмотрены меры защиты.
Шифрование проводится кадрами. На каждом
кадре вырабатывается 428 бит последовательно-
сти. Первые 100 бит отбрасываются, последую-
щие 114 бит являются гаммой для передачи от
абонентаИ к абоненту Б, затем очередные 100 бит
отбрасываются, последние 114 бит являются гам-
мой для передачи от В к А. При этом на каждом
кадре ключ модифицируется номером кадра.
Если состояния двух регистров известны, то
неопределенности, связанные с пропуском так-
тов, не возникают, и состояние третьего регистра
может быть вычислено решением системы ли-
нейных уравнений.
На этом основан алгоритм криптоанализа
[10, 11]: для известного отрезка последователь-
ности на выходе шифратора содержимое двух
коротких регистров угадывается, а содержимое
более длинного регистра рассчитывается (с уче-
том пропусков тактов). Таким образом, на каж-
дой итерации поиска ключа выбирается содер-
жимое регистров длиной 19 и 22 бита и решается
система линейных уравнений для третьего реги-
стра. Если система имеет решение, то ключ
вскрыт, в противном случае попытка неудачна.
Поскольку сложность решения системы линей-
ных уравнений асимптотически пропорциональ-
на квадрату размера задачи (то есть решить сис-
тему из 23 уравнений проще, чем выполнить пе-
ребор из 223 элементов ключа), то этот метод ра-
ботает быстрее, чем перебор. С учетом того, что
сложность решения системы линейных уравне-
ний пропорциональна кубу числа переменных,
получаем итоговую сложность 250 (в то время как
перебор требует в среднем 263 опробований).
Для данного шифра рассмотренный метод не
претендует на то, чтобы быть наилучшим.
17.13. Отбраковка классов ключей
Суть этого метода заключается в том, что на
определенном этапе вскрытия ключа можно про-
водить опробования, в результате которых от-
браковываются не одиночные ключи, а классы
ключей. При этом опробование класса ключей,
очевидно, по своему механизму отличается от
опробования одиночного ключа и часто требует
нетривиальных вычислений.
Отбраковка классов ключей возможна, если
множество ключей можно разбить на попарно
непересекающиеся классы (по крайней мере на
два класса), то есть если можно задать эквива-
лентность на множестве ключей. При этом не
исключено, что на разных итерациях разбиения
будут различными, как в решеточном методе.
Иногда такое разбиение неочевидно и определя-
ется творческим подходом криптоаналитика. По-
ясним это на примерах.
Пример 17.13.1. Подстановочно-перестано-
вочный шифр с ключевой подстановкой.
Предположим, что в подстановочно-переста-
новочный шифр для повышения стойкости вклю-
чены 32 случайные подстановки.14 Мощность
множества подстановок равна (16!)32« 10426. Тогда
14 Такой способ построения шифра был предло-
жен К. Шенноном [8].
392
вероятность того, что выбранные подстановки
являются аффинными, ненулевая. В этом случае
итоговое преобразование блока открытого текста
длины п бит в шифрограмму длины п бит тоже
будет аффинным. Проверка того, что преобразо-
вание является аффинным, выполняется так.
Пусть у = Zx © а — уравнение аффинного пре-
образования. Тогда шифрограмма для нулевого
текста: у0 = L0 © а, то есть а = у0. Таким образом,
легко перейти к центрированному преобразова-
нию заменой шифрограмм у -> у © у0. Далее, для
пары текстов должно выполняться равенство
yi © у2 = Z(xi © х2). Это условие легко проверяется.
Если преобразование является аффинным, то ключ
может быть задан матрицей L и вектором сдвига а.
Если в ходе тестирования шифра установлено,
что преобразование не является аффинным, то
можно отбраковать множество ключей, индуци-
рующих аффинные преобразования. Число аф-
финных подстановок из 16 элементов равно
16 15 • 14 • 12 • 8 ® 3 105. Число наборов из 32
таких аффинных подстановок равно 2 • 10177.
В данном случае множество ключей разбива-
ется на два класса эквивалентности: класс аф-
финных подстановок и класс неаффинных под-
становок.
Пример 17.13.2. Отбраковка с использовани-
ем списка ключей.
Рассмотрим шифр с 32 циклами шифрования,
использующий список ключей {К, ....Ку} с че-
редованием (Ко, К\,..., Ку)\Ку, К6, ..., Ко) (на-
пример, ГОСТ 28147-89, см. п. 19.6). Если все
ключи Ко, ...,Ку одинаковы или чередуются с
«центральной симметрией», то шифр является
степенным. Например, если выполняются равен-
ства К^К^К^Ку и К1 = К2 = К5 = К6, то
шифр является степенным с периодом 4. Если
ключи чередуются: Ко = Ку, К\ = К6, Ку = Ку,
Ку = ZT4, то шифр является степенным с периодом
8. Для того чтобы определить, имеет ли место
такое чередование, можно предположить, что
шифр является степенным, и попытаться вскрыть
ключ соответствующего степенного шифра ме-
тодом сдвига (см. п. 18.5). Если гипотеза не под-
твердится, то этим можно отбраковать широкий
класс ключей указанного вида.
Множество ключей разбивается на четыре
класса. К первому классу относятся ключи, не
обладающие центральной симметрией. Ко вто-
рому, третьему и четвертому классам относятся
ключи с центральной симметрией и периодами 1,
4, 8 соответственно. Второй класс входит в тре-
тий, а третий класс — в четвертый. Поскольку
третий класс значительно шире, чем второй, а
четвертый значительно шире, чем третий, доста-
точно рассмотреть два класса ключей— обла-
дающих и не обладающих центральной симмет-
рией. Распознать, является ли ключ симметриче-
ским, можно, используя метод сдвига (см.
[12, 13] и п. 18.5).
Пример 17.13.3. Отбраковка ключей для фей-
стелева шифра.
Рассмотрим фейстелев шифр, в котором на
каждом цикле выполняется поразрядное сложе-
ние по модулю 2 векторов обрабатываемого тек-
ста и ключа (например, DES, см. п. 19.3). В таком
шифре выполняется свойство дополнения: если
у = F(k, х), то 1 © у = F(1 © k, 1 © х). Предполо-
жим, что пара блоков открытого и зашифрован-
ного текста однозначно определяет ключ (в про-
тивном случае можно перейти к парам или трой-
кам блоков). Благодаря свойству дополнения
ключ можно определять с точностью до инвер-
сии. Множество ключей разбивается на классы
эквивалентности, каждый из которых содержит
два ключа: прямой и инверсный.
Для вскрытия ключа на основе подобранных
открытых текстов сначала зашифровываем два
инверсных блока открытого текста: X] и
х2 = 1 © X]. Их шифрограммы равны соответст-
венно у, и у2. Затем выполняем собственно опро-
бование. Выбираем ключ к, находим шифро-
грамму F(k, Xi) и сравниваем ее с шифрограмма-
ми yi и у2. При F(k, х0 = у] искомым ключом
является к, при Г(к, Х|) = у2 — 1 © к. Если ни
одно из равенств не выполняется, то переходим к
опробованию следующего ключа. Сравнивание
выполняется значительно быстрее, чем вычисле-
ние шифрограммы Г(к, х,). Поэтому можно счи-
тать, что за одно опробование отбраковываются
сразу два ключа: прямой и инверсный.15
17.14. Задачи, к которым
сводится задача вскрытия ключа
Теперь можно составить список математиче-
ских задач, к которым полиномиально сводится
задача вскрытия ключа итерированного шифра
при наличии одного или нескольких открытых и
соответствующих зашифрованных текстов, одно-
значно определяющих ключ. Формулировка за-
дачи должна подсказывать пути к ее решению,
поэтому в этот список не нужно включать из-
вестные NP-полные задачи (задача о гамильто-
новом цикле, задача о клике, задача об укладке
ранца и др.), число которых составляет несколь-
ко тысяч.
15 Используя обобщенное свойство дополнения,
можно инвертировать не все биты ключа, а некоторое
их подмножество. Поэтому ключ можно искать с точ-
ностью до автоморфизма.
393
1. Задача о выполнимости.
2. Минимизация целевой функции и представ-
ление ее в виде стандартной конъюнкции
(см. п. 17.3).
3. Гомоморфное вложение группы подстановок
в множество (группу?) решеточных продол-
жений подстановок, при котором множества
удалений входных и выходных разрядов сов-
падают (см. п. 17.3).
4. Рациональное или 2-адическое продолжение
кольца полиномов Жегалкина такое, что ка-
ждый разряд ключа (вектор п) вскрывается с
положительным преобладанием 8, причем
преобладание удовлетворяет неравенству
О < 8 <8, где 8 оценивается полиномом от
(log #К)~1 (см. пп. 17.6, 17.7).
17.15. Вскрытие ключа
на квантовом компьютере
Задача вскрытия ключа к по нескольким из-
вестным открытым текстам и задача обращения
хэш-функции сводятся к задаче о выполнимости
булевой функции п переменных, где п— разряд-
ность ключа. Как показал Л. Гровер (см., например,
работу [15]), задача о выполнимости может быть
решена на квантовом компьютере со сложностью
0(2 '’/2 ), тогда как перебор дает сложность 0(2').
Таким образом, задача вскрытия ключа и задача
обращения хэш-функции могут быть решены на
квантовом компьютере со сложностью порядка
квадратного корня из сложности перебора.
Алгоритм Гровера аналогичен алгоритму «gi-
ant step — baby step». Предположим, что целевая
булева функция Н принимает единственное еди-
ничное значение на некотором наборе из п дво-
ичных переменных (искомом ключе к). Функцию
Н(г) можно вычислить на квантовом компьютере
для произвольного аргумента z. Пусть N=2!' и
число k(z) соответствует вектору k(z).
Зададим квантовое отображение квадратной
матрицей R = (А„) размера N, где RtJ = 0 при i Ф j,
Ra = е' = cos ф, + i sin ф,.
Это отображение меняет фазу только для ис-
комого значения ключа и не имеет аналогов в
классическом компьютере, так как искомое зна-
чение ключа ненаблюдаемо. Легко заметить, что
матрица R унитарна и поэтому может быть реа-
лизована на квантовом компьютере.
Зададим второе квантовое отображение квад-
ратной матрицей А = (Ау) размера N с элемента-
ми Ay =2/N при i^j и Alt --1 + 2/N. Матрица
А также унитарна и поэтому может быть реализо-
вана на квантовом компьютере.
Алгоритм 17.15.1. Алгоритм Гровера.
Вход. Целевая булева функция, однозначно
определяющая ключ.
Выход. Искомый ключ.
Метод.
1. Нормализовать состояние регистра путем
когерентной суперпозиции и привести N-
разрядный вектор амплитуд к виду
2. Выполнить O(2h'2) раз следующие действия.
2.1. Применить к регистру отображение R.
2.2. Применить к регистру отображение А.
3. Измерить состояние регистра и опробовать
найденный ключ на обычном компьютере.
Если найденное решение не удовлетворяет
целевой функции, то вернуться на шаг 1.
Анализ этого алгоритма проведем согласно
работе [15]. Сначала покажем, что отображение
А задает инверсию вектора состояний относи-
тельно среднего значения координат. Справед-
ливо равенство А = -Е + 2Р, где Е — единичная
матрица, Р— матрица из элементов 1/А, при
этом Р1 =Р.
Рассмотрим действие матрицы А на вектор v:
Av = (-Е + 2P)v = -v + 2Pv,
где
v. +... + VN
Pv ~(a,a, .... a), a =------.
N
Поэтому Av = {-V] + 2a, -v2 + 2a, ..., -vN + 2a).
Каждая координата вектора состояний Av имеет
вид а + (а - г,), то есть является инверсией отно-
сительно среднего значения координат.
Аналогично в векторе Rv сохраняются все ко-
ординаты вектора v, кроме равной к, которая за-
меняется на -к.
Теперь покажем, что алгоритм увеличивает
вероятность того, что измеренное состояние ре-
гистра совпадет с искомым ключом к.
Теорема 17.15.1. Если состояние квантового ре-
гистра, соответствующее искомому ключу, имеет
амплитуду к, а остальные состояния — амплитуду
z, то после применения отображения А получатся
соответственно состояния с амплитудами
(2 Y 2(А-1) , 2 А-1
к =----1 кН-------z и z =—к Л----z.
\N ) N NN
Доказательство проводится непосредст-
венным вычислением.
Если отображение R делает амплитуду со-
стояния к отрицательной, то после применения
отображения А получается к' >0, z' > 0. При
этом все состояния, отличные от искомого, име-
ют одинаковую амплитуду.
394
Теорема 17.15.2. Однократная итерация шага
2 алгоритма Гровера дает увеличение амплитуды
состояния, соответствующего искомому ключу,
на величину Лк > -Jn/2 .
Доказательство проводится непосредст-
венным вычислением.
Таким образом, повторение шага 2 алгоритма
Гровера O(-Jn) раз дает амплитуду искомого
состояния, близкую к 1. Это означает, что хотя
бы одно из состояний регистра, измеренных на
шаге 3, будет соответствовать искомому ключу с
вероятностью, близкой к 1.
Упражнения к главе 17
1. Предположим, что подстановочно-перестано-
вочный шифр использует четырехразрядную
подстановку, каждый разряд которой опи-
сывается полиномом степени 3 и содержит
пять слагаемых. Оцените сложность вычис-
ления производной целевой функции в мето-
де Андельмана-Ридса от числа циклов шиф-
рования. Сколько циклов шифрования нужно
использовать, чтобы (временная) сложность
метода Андельмана-Ридса превышала слож-
ность перебора?
2. Что собой представляет целевая функция при
вскрытии ключа шифра методом анализа на
основе арифметического продолжения буле-
вых функций?
3. Докажите, что функция округления задает
гомоморфизм полукольца решеточных поли-
номов над А в полукольцо решеточных по-
линомов над Г2.
4. *Предложите способ последовательной ми-
нимизации булевой формулы, заданной в виде
многократной композиции наборов неслож-
ных формул. Очевидно, способ должен быть
проще, чем перебор.
5. Почему алгебраические методы анализа итери-
рованных шифров с использованием аппарата
булевых функций неэффективны для крипто-
графических алгоритмов с открытым ключом?
6. *Исследуйте возможность (алгебраического)
определения операции дифференцирования
решеточных полиномов над А, пригодного
для решеточного анализа, с учетом того, что
множество А с операцией точной верхней
грани является моноидом, который не может
быть вложен в группу.
7. *Рассмотрите возможность использования
дифференцирования продолженных полино-
мов Жегалкина для нахождения экстремумов
булевых функций.
8. Предложите способ усиления шифра из при-
мера 17.9.1, исключающий атаку на основе
редукции характеристики кольца.
9. Предложите способ вскрытия ключа шифра
из примера 17.9.2, обладающий полиноми-
альной сложностью, на основе адаптивно по-
добранных открытых текстов.
10. *Исследуйте сложность вскрытия ключа
шифра ГОСТ 28147-89 (см. п. 19.6) по отно-
шению к методам, основанным на продолже-
ниях гомоморфизмов полиномов Жегалкина.
11. *Исследуйте сложность методов, основанных
на продолжениях гомоморфизмов полиномов
Жегалкина, на примере какого-либо шифра в
зависимости от способа представления под-
становок полиномами Жегалкина (число
сложений, очередность сложений и т. п.).
12. *Исследуйте эффективность алгоритма поис-
ка экстремума продолженной целевой функ-
ции на основе перебора не одной перемен-
ной, как в алгоритме 17.6.1, а пар или троек
переменных.
13. *Предложите и исследуйте способ построе-
ния шифров, стойких по отношению к мето-
ду анализа на основе рационального и 2-
адического продолжения гомоморфизмов
кольца G„. Способ должен быть конструк-
тивным, а не типа «предложили что-то и
проверили, если плохо— предложили дру-
гое, опять проверили и т. д.».
14. Как изменится свойство дополнения в фей-
стелевом шифре, где цикловая функция шиф-
рования содержит операции замены (подста-
новки) коротких слов полублока, сложения
над Г2 полублока с ключом и перестановки
битов в полублоке? Как изменится это свойст-
во, если будут выполняться сначала переста-
новка, затем сложение и подстановка; пере-
становка, подстановка и сложение?
15. *В шифре А5/1 нелинейная функция голосова-
ния «два из трех» имеет вид /= 1\Л + 6А + hh,
где /|, Z2, (j — значения разрядов регистров, оп-
ределяющих сдвиг. Для подстановки Z, = Д /17,
имеем/= ДДб/з + T1T3U2 + T2T3U]. После де-
ления на ДДГз получаем, что функция f про-
ективно эквивалентна линейной функции
И1 + и2 + Из (см. п. 6.15.5). Можно ли построить
«проективное продолжение» шифра так, что-
бы он был проективно эквивалентен аффин-
ному над F2 шифру? Если оставаться в рам-
ках полиномов Жегалкина, то обычно эта
функция не определена. Поможет ли переход
к продолженным полиномам?
16. Предложите шифр небольшой разрядности
и постройте его нетривиальное проективное
продолжение (проективные переменные Z,
должны быть отличны от константы, требу-
ется доопределить их преобразование). Од-
нозначно ли оно? Что собой представляет
класс AG-эквивалентных шифров?
17. Укажите достаточное условие стойкости
шифра по отношению к анализу методом
продолжения полиномов Жегалкина. Каким
соотношениям должны удовлетворять числа
Аоо, Аоь М<ъ Mi?
18. Предложите и проверьте метод анализа на
основе 2-адического продолжения булевых
функций с использованием порогового числа
правильно угаданных разрядов ключа по
аналогии с методом арифметического про-
должения.
19. Каков должен быть объем базы данных для
нахождения коллизии хэш-функции методом
встречи на случайном дереве?
20. Почему методы криптоанализа на основе ра-
ционального и 2-адического продолжения
кольца G,, в общем случае не гарантируют
вскрытие ключа быстрее, чем перебором, а
при оценке стойкости дают ответ типа «/-й
бит ключа может быть вскрыт быстрее, чем
перебором, с вероятностью р»?
21. * Автоморфизмы кольца полиномов Жегал-
кина (см. п. 3.15) позволяют поставить в со-
ответствие каждой сбалансированной буле-
вой функции аффинную булеву функцию.
Можно ли это обстоятельство использовать
при анализе шифров?
22. *Можно ли усилить метод, описанный в
п. 17.8, если использовать продолжение
кольца G„ до кольца tF9[xi, ..., х„]/21, где q = 2"
и21 = (х]9 + х1, + х„)?
23. *Методы, рассмотренные в этой главе, бази-
руются на архимедовом (пп. 17.3, 17.4, 17.6)
и 2-адическом (п. 17.7) нормировании про-
должения кольца G„. Предложите метод ана-
лиза, основанный на дискретном нормирова-
нии кольца полиномов в точке по аналогии с
нормированием функций из ОР на алгебраи-
ческих кривых (см. п. 6.16).
Литература к главе 17
1. Ван дер Варден Б.Л. Алгебра. М.: Наука, 1979.
2. Молдовян А.А., Молдовян Н.А. Новый принцип
построения криптографических модулей в систе-
мах защиты ЭВМ // Кибернетика и системный
анализ. 1993. № 5. С. 42-50.
3. Пойа Д. Математическое открытие. М.: Наука, 1976.
4. Ростовцев А.Г. Метод обращения итерированной
хэш-функции // Методы и технические средства
обеспечения безопасности информации. Тезисы
докладов. Под ред. П.Д. Зегжды. СПб.: Изд-во
СПбГТУ, 2001. С. 114-117.
5. Ростовцев А.Г. Решеточный криптоанализ // Безо-
пасность информационных технологий. М.: Изд-
во МИФИ(ТУ), 1997. Вып. 2. С. 53-55.
6. Ростовцев А.Г., Маховенко Е.Б. Исследование
стойкости криптоалгоритмов методом продолже-
ния многочленов Жегалкина // Проблемы инфор-
мационной безопасности. Компьютерные систе-
мы. 2001. №3. С. 43-50.
7. Ростовцев А.Г., Маховенко Е.Б. Криптоанализ с
использованием 2-адического продолжения мно-
гочленов Жегалкина // Научно-технические ведо-
мости СПбГТУ. 2002. № 3. С. 89-93.
8. Шеннон К. Теория связи в секретных системах / В
сб.: К. Шеннон. Работы по теории информации и
кибернетике. М.: ИЛ, 1963. С. 333-402.
9. Andelman D., Reeds J. On the cryptanalysis of rotor
machines and substitution-permutation networks //
IEEE transactions on information theory. 1982.
Vol. IT-28. P. 578-584.
10. Anderson R., Roe M. A5 // http://jva.com/crack-a5.1994.
11. Biryukov A., Shamir A. Real-time cryptanalysis of
the alleged A5/1 on a PC (preliminary draft) //
http://cryptome.org/a51 -bs.htm. 1999.
12. Biryukov A., Wagner D. Advanced slide attacks //
Advances in Cryptology — EUROCRYPT 2000.
Lecture Notes in Computer Science. Springer-
Verlag. 2000. Vol. 1807. P. 589-606.
13. Biryukov A., Wagner D. Slide attacks // Fast Soft-
ware Encryption FSE ’99. Lecture Notes in Com-
puter Science. Springer-Verlag. 1999. Vol. 1636.
P. 245-259.
14. Campbell K., Wiener M. DES is not a group // Ad-
vances in Cryptology— CRYPTO’92. Lecture
Notes in Computer Science. Springer-Verlag. 1993.
Vol. 740. P. 512-520.
15. Hayward M. Quantum computing and Grover’s algo-
rithm //http://alumni.imsa.edu/~matth/quant/473/473proj
/473proj.html.
16. Kaliski B., Rivest R., Sherman A. Is the Data En-
cryption Standard a group? (Results of cycling ex-
periments on DES) // Journal of Cryptology. 1988.
Vol. l.P. 3-36.
17. Konheim A. Cryptography: A Primer. New York:
J. Wiley & Sons, 1981.
Глава 18. СТАТИСТИЧЕСКИЕ МЕТОДЫ КРИПТОАНАЛИЗА
Статистические методы анализа (дифферен-
циальный, линейный и др.) характеризуются тем,
что на множестве ключей устанавливается вы-
числимое отношение порядка, которое справед-
ливо «в среднем», для большой выборки. Поэто-
му для противодействия таким методам следует
периодически менять ключи, не позволяя нару-
шителю набрать необходимый объем статистики.
18.1. Некоторые определения
Для описания статистических методов крипто-
анализа определим некоторые свойства шифров.
Понятие полноты шифра в открытой печати
было введено М. Мацуи [21]. В полном шифре
каждый выходной бит зависит от каждого вход-
ного бита. Если шифр неполный, то можно найти
такую пару входной бит / выходной бит. что из-
менение входного бита не приводит к изменению
выходного бита при произвольных значениях
остальных входных битов.
Пусть блочный шифр переводит блок откры-
того текста длины п бит в блок шифртекста той
же длины. Для пары открытых текстов х и х„ от-
личающихся значением z-ro бита, определим
лавинный вектор отображения (подстановки) S
как поразрядную сумму шифрограмм
<Г = 5(х)© 5(х,) = (<...,<), е {0,1}.
Определим для j-го разряда лавинного векто-
ра целочисленную сумму W(dj) = ^\ij, где х
X
пробегает все множество открытых текстов. Зна-
чение W(d’j)l2n можно интерпретировать как
вероятность изменения J-го бита в шифртексте
при изменении z-ro бита в открытом тексте.
Говорят, что подстановка удовлетворяет лавин-
ному критерию (avalanche criterion) [14], если ля
всех i выполняется равенство
7-1 . _ ' ,1«. I ..
На практике лавинный критерий применяется
при выборе блоков подстановки (.S-boxes) под-
становочно-перестановочных шифров. В качест-
ве открытого текста используется вход подста-
новки, в качестве шифртекста— выход подста-
новки. В этом случае, очевидно, суммы в форму-
ле (18.1.1) можно легко вычислить.
Понятия полноты и лавинного критерия были
объединены в работе [25] в виде строгого лавин-
ного критерия (strict avalanche criterion). Подста-
новка удовлетворяет строгому лавинному кри-
терию, если для всех z и j выполняется усилен-
ное по сравнению с (18.1.1) равенство
W')_l
2й ~ 2 '
Подстановка удовлетворяет строгому лавин-
ному критерию, если каждая из п булевых функ-
ций, задающих подстановку, удовлетворяет ему.
Очевидно, что подстановка, удовлетворяющая
строгому лавинному критерию, удовлетворяет и
лавинному критерию, обратное в общем случае
неверно.
Строгий лавинный критерий также часто ис-
пользуется при выборе блоков подстановки. Ес-
ли строгому лавинному критерию удовлетворяет
подстановка у = 5'(х), то ему удовлетворяет и
подстановка у = P(5(j0(x) © а)) © Ь, где Р, Q —
произвольные матрицы перестановок и а, b —
произвольные векторы сдвига (соответствующие
аффинные преобразования выполняются над F2)-
Критерий независимости битов (bit independ-
ence criterion) [25] означает, что при изменении
одного входного бита все двоичные разряды ла-
винного вектора d' попарно независимы.
Взаимная корреляционная функция для
двух сбалансированных двоичных векторов
х = (х], ...,х„), у = (Уь ,Уп) показывает степень
их схожести в зависимости от циклического
сдвига t и определяется как
Qy(0 = ^Z(2-A-, -D(2y,+<(mod„) -1). (18.1.2)
Каждый сомножитель в формуле (18.1.2) ра-
вен 1 или -1, поэтому и каждое слагаемое под
знаком суммы равно 1 или -1. Аналогично опре-
деляется автокорреляционная функция Схх(/).
Коэффициент корреляции двоичных сбаланси-
рованных векторов длины п бит равен р(х, у) =
= Сху(0). Выполняется неравенство -1 < р(х, у) < 1.
Чем меньше по абсолютной величине коэффици-
ент корреляции, тем ближе доли совпадающих и
несовпадающих битов в векторах.
Булевы функции f и g одного числа перемен-
ных, заданные таблично, можно рассмотреть как
двоичные векторы f, g и определить для них ко-
эффициент корреляции: p(f, g) = Cfjg(0).
Параметр независимости битов В1С(5) под-
становки S’ определяется как максимум коэф-
фициентов корреляции соответствующих булевых
функций. При этом таблично заданные булевы
функции рассматриваются как векторы. Справед-
ливо неравенство 0 < BIC(.S') < 1. Обычно при вы-
боре блока подстановки стараются сделать этот
параметр минимальным. Отметим, что выбор мак-
симума коэффициентов корреляции в качестве па-
раметра независимости битов не всегда оправдан.1
Определим (хэммингов) вес w(Az) разности
Az = Z] @ z2 векторов и z2 как число несовпа-
дающих в них разрядов (число единичных разря-
дов вектора Az). Шифр обладает коэффициентом
диффузии kd = I, если для 1 < w(Ax) < I выполня-
ется неравенство и(Ах) + и(Ау) >1 + 2, где Ах —
разность открытых текстов, Ду— разность за-
шифрованных текстов.
Коэффициент диффузии является уточнением
лавинного критерия и характеризует зависимость
веса разностей выходов подстановки от веса раз-
ностей входов. Чем больше коэффициент диффу-
зии какого-либо оператора, тем лучше его рассеи-
вающие свойства.
Коэффициент диффузии используется при
выборе блоков подстановки шифров (в частно-
сти, при определении дифференциальных харак-
теристик подстановки). При этом в качестве от-
крытого текста используется вход подстановки, а
в качестве зашифрованного текста — ее выход.
Непосредственно из определения коэффици-
ента диффузии следует, что у прямой и обратной
подстановки он одинаков. Поскольку операции
сложения по модулю 2 и перестановки битов со-
храняют вес разности, то коэффициент диффузии
сохраняется при замене подстановки у = S'(x)
подстановкой у = P(S(Q(x) © а)) © b для произ-
вольных матриц перестановок Р, Q и векторов
сдвига а, b (соответствующие аффинные преоб-
разования выполняются над (F2). Иными словами,
преобразования, заключающиеся в перестановке
битов и сложении с произвольным вектором для
входа и выхода подстановки, не меняют коэффи-
циент диффузии.
18.2. Дифференциальный криптоанализ
Дифференциальный метод криптоанализа был
предложен Э. Бихамом и А. Шамиром в 1990 г.
[7] и представляет собой попытку вскрыть сек-
ретный ключ итерированного шифра, исполь-
зующего r-кратную цикловую операцию шифро-
вания. При этом предполагается, что шифрова-
ние на каждом цикле осуществляется на своем
ключе. Метод может использовать как подоб-
ранные, так и известные открытые тексты, одна-
ко в первом случае анализ выполняется проще.
18.2.1. Конечные разности
Пусть R— коммутативное кольцо с единицей,
А = А|х,,..., x„]/2i — его расширение, представ-
ляющее собой кольцо классов вычетов кольца
полиномов над R по некоторому идеалу 21. Пусть
х = (хь ..., х„) и Ах = (Axi, ..., Ах„). Определим
(первую) разность Af функции f е А как
bf=f& + Дх) -Дх).
В соответствии с алгебраическим определе-
нием производной [1] получаем:
Л/=Х Л Д*/ +£ fx„x, i+...+fMx, ,-,х„ АХ)... Ах,„
где Д, f” ,fWx},...,x„ —частные производные.
Например, если R = (F2, S=G4 и
f= Xi © Х2Хз © х2х4, то
fx =!> fx =*з®х4, Л' = х2, f' — х2,
1 Действительно, коэффициент корреляции является
лишь одной из возможных функций, определенных на
открытых и зашифрованных текстах; выбор именно этой
функции никак не связан со свойствами ши(|)ра и совре-
менными определениями случайности. По-видимому,
этот выбор ведет историю от поточных шифров, кото-
рые строились с использованием сдвиговых двоичных
регистров (для них коэффициент корреляции является
естественной мерой случайности), а также от расхожего
мнения, согласно которому некоррелированность после-
довательностей означает их независимость.
Поэтому
bf= Ах] © (хч © х4)Ах2 © х2(Ахз © Ах4) ©
© Ах2(Ах3 © Ах4).
Оператор разности А обладает следующими
свойствами. .....
1. A(/+g)=A/+Ag. .
398
2. В соответствии с правилами умножения по-
линомов разность произведения определяет-
ся разностью одночленов сомножителей.
3. Если/— аффинный полином, то его разность,
очевидно, является линейным полиномом от
Axi,..., Ах„ и не зависит отхь ...,х„.
Если S=G„ — кольцо полиномов Жегалкина,
то каждый полином из £ имеет степень не более
1 по каждой переменной и переход к разности
ведет к снижению степени полинома на 1.
Аналогично можно определить разности
высших порядков. Пусть а, = Ах, а2 = А2х, ... .
Тогда А'О1 а./(х) = АО; /(х)).
Разность порядка i для кольца G„ вычисляется
как сумма 2' слагаемых:
Д'О1,/(*)= Е/(*®г),
Ye/Xcq
где а,) — всевозможные линейные ком-
бинации над Е2 векторов а, ,..., а,. Если эти век-
торы линейно зависимы, то разность любой
функции равна нулю.
Пример 18.2.1. Разность второго порядка для
кольца G4.
Для булевой функции /= X] © х2 © © Х1Х3Х4
аргумента х = (Х],..., х4) разность второго порядка
А2 /(х), определяемая векторами а, = (1, 0, 1,
1), а2 = (1, 1, 0, 0), равна
ДП|,а2 /(х)=/(х©а1 Фа2)Ф/(хФа1)Ф/(хФа2)Ф/(х).
Подставляя соответствующие значения с уче-
том И] © а9 = (0,1, 1, 1), получаем
д2«, ,«2 /О) = f(xi Л ® xi Л ® хз J ® *4 ) ®
© /(1 ©Xj,X2,l©X3,l©X4)©
© /(1®Х|,1®Х2,Лз,Х4)Ф /(Х],Х2,Х3,Х4).
Вычисляем:
/х1з 1 © х2, 1 © х3, 1 © х4) =
= Хз © Х]Хз © Х2Хз © Х]Х4 © Х1Х3Х4;
/1 © X], Х2, 1 © Хз, 1 © х4) =
= Х3 © Х4 © Х|Хз © Х2Хз © Х]Х4 © ХзХ4 © Х1Х3Х4;
/1 © Х1, 1 © Х2, Хз, х4) =
= X] © х2 © х3 © х2хз © Хзх4 © Х]Хзх4;
<.a2//) = -V3©-V4.
Разность порядка i ведет к снижению степени
полинома Жегалкина на z. Поэтому, если
А'П1 ...а./(х)ёЕ2, то степень полинома/х) боль-
ше Z.
18.2.2. Метод криптоанализа
В основу дифференциального метода крип-
тоанализа положена неравномерность распреде-
ления поразрядных разностей по модулю 2 пар
открытых и соответствующих зашифрованных
текстов.2
Сложность вскрытия ключа г-циклового
шифра зависит от существования дифференциа-
лов (г - 1 )-го цикла, которые имеют достаточно
большую вероятность [7—9].
Дифференциал для i циклов шифрования (z-
цикловый дифференциал) определяется как пара
векторов [а, 0]; такая, что пара открытых текстов
х, х' с разностью а может перейти после z-ro
цикла в пару выходных текстов у, у' с разностью
р (для соответствующего понятия разности).
Вероятность z-циклового дифференциала
[а, р], — это условная вероятность
P(Ay(z) = p| Ах = а)
того, что разность Ay(z) пары шифртекстов у, у'
после z-ro цикла равна р при условии, что раз-
ность Ах соответствующих открытых текстов
равна а, когда открытый текст х (или, что то же
самое, х') и ключи А'П), используемые
соответственно на циклах 1,2,..., z, независимы
и равновероятны.
На практике функция зашифрования на одном
цикле обычно является криптографически сла-
бой. В данном случае это означает, что по задан-
ной паре текстов на выходе одного цикла шиф-
рования и заданной разности входов этого же
цикла можно найти цикловый ключ (один или
несколько). Это ограничение не является прин-
ципиальным, так как обычно при необходимости
цикл можно разбить на более мелкие операции,
которые будут удовлетворять этому свойству.
Вероятности наиболее вероятных дифферен-
циалов используются для определения нижней
границы сложности атаки дифференциальным
методом и могут показать, когда г-цикловый
шифр устойчив к таким атакам.
Наряду с понятием z-циклового дифферен-
циала используется понятие (дифференциальной)
характеристики, представляющей собой после-
довательность одноцикловых дифференциалов, в
которой выходная разность текстов предыдуще-
2 Поразрядная (по модулю 2) разность совпадает с
суммой по модулю 2, поэтому можно говорить и о
распределении сумм.
399
го цикла совпадает с входной разностью текстов
последующего цикла. Характеристика задает
представление многоциклового дифференциала в
виде последовательности одноцикловых. Одному
и тому же многоцикловому дифференциалу мо-
гут соответствовать несколько характеристик.
Основная процедура дифференциального ме-
тода анализа r-циклового шифра с использовани-
ем подобранных открытых текстов может быть
следующей.
Алгоритм 18.2.1. Дифференциальный крип-
тоанализ.
Вход. Алгоритм шифрования, подобранные
открытые и соответствующие зашифрованные
тексты.
Выход. Ключ.
Метод.
1. На этапе предвычислений ищем множество
(г-1)-цикловых дифференциалов [«7, Р
такое, что вероятность Р(Ау(г - 1)=Р71 Ах=ау)
максимальна или близка к максимальной.3
При этом открытый текст х и все ключи
для г - I циклов независимы и
равновероятны. Упорядочиваем это множе-
ство дифференциалов по убыванию их веро-
ятностей.
2. Для произвольного открытого текста х вы-
числяем х' так, чтобы разность между х и х'
была равна щ. Зашифровываем тексты х и х'
на искомом ключе и после г циклов получаем
пару шифртекстов у(г), у'(г). Предполагаем,
что на выходе (г - 1 )-го цикла разность шифр-
текстов равна наиболее вероятной:
Ду(г-1) = Р1. Для тройки (Ду(г- 1), у(г),
у'(г)) находим все возможные (если их не-
сколько) значения ключа к<г>.
3. Повторяем шаг 2 до тех пор, пока одно или
несколько значений ключа kfl> не станет появ-
ляться значительно чаще других. Берем этот
ключ или это небольшое множество ключей в
качестве криптографического решения для
ключа последнего цикла шифрования.
4. Находим (г - 2)-цикловые наиболее вероят-
ные дифференциалы и выполняем шаги 2, 3
для предпоследнего цикла, при этом значения
y(r- 1), у'(г - 1) вычисляем расшифрованием
шифртекстов на найденном ключе к^. Далее
действуем аналогично, пока не будут вскрыты
ключи всех циклов шифрования.
3 Задача поиска наиболее вероятных дифферен-
циалов является нетривиальной, однако решить ее все
же значительно проще, чем вскрыть ключ перебором.
Таким образом, дифференциальный метод
вскрывает ключи независимо для каждого цикла
шифрования. При этом асимптотическая слож-
ность метода практически не зависит от того,
один и тот же ключ используется на всех циклах,
или все ключи попарно различны.
Подчеркнем, что если при вычислении наибо-
лее вероятных дифференциалов открытый текст
и все цикловые ключи независимы и равноверо-
ятны, то при проведении атаки все ключи фикси-
рованы (шифрование ведется на искомом клю-
че), и только открытый текст может быть произ-
вольным. В основу алгоритма 18.2.1 положена
гипотеза стохастической эквивалентности', для
(г - 1 )-циклового дифференциала [а, спра-
ведливо равенство ...
Р{ Ау(г -1) = р | Ах = а) « --
®Р(Ау(г-1) = р| Ах = а, А(1) = <В],..., k{r~v> =<»,._])
почти для всех значений ключей ад, ..., со,—;.
Если выполняются следующие условия:
- гипотеза стохастической эквивалентности
верна;
- цикловая функция шифрования является
криптографически слабой;
- существует (г - 1 )-цикловый дифференциал
[а, р],._1 такой, что:
P(Ay(r-l) = p| Ах = а)»2-",
где п— длина блока шифруемого текста в
битах,
то шифр с независимыми цикловыми ключами
является уязвимым по отношению к дифферен-
циальному методу анализа [8].
Сложность S(r) вскрытия ключа г-циклового
шифра не меньше, чем число итераций алгорит-
ма 18.2.1:
S(r)>-----------—
Р---------'—
max п -
где /;пах = max(a) тах(Р)Р( Ау (г -1) = р | Ах = а).
Чем больше Ртга по сравнению с (2" - I)”1, тем
легче вскрыть ключ, и наоборот. В частности,
при Ршах« (2" - 1 )-1 атака не будет успешной.
Здесь наблюдается аналогия с выделением сиг-
нала из шума в теории связи: чем больше соот-
ношение сигнал/шум, тем меньше требуется по-
второв для приема передаваемого сигнала.
Емкостную сложность дифференциального
метода (как число открытых и соответствующих
зашифрованных текстов, необходимых для вскры-
тия ключа) иногда можно снизить, если исполь-
400
зовать не единственный наиболее вероятный
(г - 1)-цикловый дифференциал, а класс таких
дифференциалов, обладающих одной и той же
входной разностью Ах. При этом в ходе вскрытия
ключа приходится решать дополнительную зада-
чу определения (г - 1)-циклового дифференциала.
На практике часто наиболее вероятный диф-
ференциал не является единственным, можно
использовать большой класс дифференциалов с
большими вероятностями. Такой подход позво-
ляет проводить криптоанализ на основе извест-
ных (а не подобранных) открытых текстов.
Поскольку вычисление ключа часто более
трудоемкая операция, чем шифрование, то еди-
ницей измерения сложности дифференциального
метода может служить сложность нахождения
возможных ключей одного цикла по известным
значениям (Ау(г - 1), у(г), у'(г)).
Отличительной чертой дифференциального
метода является то, что он практически не ис-
пользует алгебраические свойства шифра (ли-
нейность, аффинность, транзитивность, замкну-
тость и т. п.). В этом смысле линейный и нели-
нейный шифры, имеющие соответствующие
одинаковые распределения вероятностей диффе-
ренциалов, одинаково стойки по отношению к
дифференциальному методу. Различной может
быть лишь трудоемкость вскрытия ключа для
одного цикла, но это не принципиально и в итоге
приводит не более чем к полиномиальному раз-
личию сложностей вскрытия ключа.
Поиск наиболее вероятных (г- 1)-цикловых
дифференциалов можно упростить, если исполь-
зовать неподвижные дифференциалы или диффе-
ренциалы с небольшим периодом повторения [8].
Предложенный впервые для анализа шифра
DES, дифференциальный метод оказался приме-
нимым к широкому классу марковских шифров
[9,19]. Марковским (в честь русского математика
А.А. Маркова) называется шифр, у которого веро-
ятность дифференциала на каждом цикле не зави-
сит от выбора открытых текстов, если все ключи
равновероятны.4 Если цикловые ключи в таком
шифре независимы, то последовательность разно-
стей текстов после каждого цикла представляет
собой марковскую цепь, где последующее состоя-
ние определяется только предыдущим. Примерами
марковских шифров являются DES, FEAL, IDEA
(см. пп. 19.3-19.5). Такие шифры удовлетворяют
гипотезе стохастической эквивалентности. Для
марковского шифра поиск наиболее вероятного
(г- 1)-циклового дифференциала можно выпол-
4 Имеется в виду, что шифр является марковским
в части распределения дифференциалов. Аналогичное
понятие существует и в части распределения линей-
ных равенств в линейном криптоанализе (см. п. 18.4).
нять с использованием теории марковских цепей.
Дифференциал данного цикла здесь не зависит от
предыдущих циклов, а задание многоциклового
дифференциала характеристикой является кор-
ректным. Это позволяет упростить процесс оценки
стойкости шифра— достаточно найти наиболее
вероятный дифференциал для одного цикла. Одна-
ко, как показал Л. Гранбулан [11], это предположе-
ние выполняется не всегда, что приводит к сущест-
венной корректировке оценок стойкости шифра.
Для противостояния дифференциальному мето-
ду анализа может возникнуть соблазн использовать
такие шифры, в которых число наиболее вероят-
ных дифференциалов велико (в пределе все диф-
ференциалы с ненулевой вероятностью равноверо-
ятны). Однако этот метод можно усилить за счет
использования невозможных дифференциалов,
которые позволяют отбраковывать классы ключей
для данных дифференциалов [5] или сокращать
объем перебора. Это обстоятельство позволяет ус-
корить вскрытие ключа, даже если все допустимые
дифференциалы имеют одинаковую вероятность.
Дифференциальный криптоанализ по существу
является методом, который может быть адаптиро-
ван (это требует определенного искусства от крип-
тоаналитика) к конкретному шифру. Например,
можно использовать не первые, а вторые конечные
разности между входами и выходами одного цикла
шифрования. В этом случае для известных четырех
выходов и второй разности на входе задача нахож-
дения множества возможных ключей должна быть
несложной. Очевидно, что способ вскрытия цик-
лового ключа по набору выходов и разности
входов для каждого шифра индивидуален.
Пример 18.2.2. Дифференциальный анализ
шифра (короткий блок).
Пусть в 16-разрядном подстановочно-переста-
новочном четырехцикловом блочном шифре ис-
пользуется подстановка А = (14, 4, 13, 1, 2, 15, И,
8, 3, 10, 6, 12, 5, 9, 0, 7) и перестановка Р = (1, 5,
9, 13, 2, 6, 10, 14, 3, 7, 11, 15, 4, 8, 12, 16). На ка-
ждом цикле производится сложение текста с
ключом данного цикла шифрования [13].
Последовательность шифрующих операций
такова: три раза выполняется цикл (сложение,
подстановка, перестановка), затем сложение,
подстановка, сложение.
Одним из наиболее трудных этапов диффе-
ренциального анализа является поиск наиболее
вероятного (г - 1)-циклового дифференциала,
который удобно задать в виде характеристики.
В качестве разности будем использовать по-
разрядную сумму текстов по модулю 2 (XOR-
разность). Сложение текста с ключом не влияет
на величину дифференциала. Перестановка явля-
ется линейной операцией, поэтому операторы Р
4oi
и А перестановочны: из Р(Х] © х2) = P(x.i) © Р(*2)
следует Р(Ах) = АР(х).
Для построения наиболее вероятного одно-
циклового дифференциала воспользуемся раз-
ностными характеристиками подстановки. Со-
поставим вектору х = (Х|, х2, хз, х4) входа под-
становки число 8х] + 4х2 + 2хз + х4, а вектору
у = (yi, у2, уз, у4) выхода подстановки — число
8.У1 + 4у2 + 2уз +у4. Запишем подстановку в виде
таблицы булевых функций четырех аргументов:
X] %2 Х2 Хд Уз ,Уз 74
0 0 0 0 1 1 1 0
0 0 0 1 0 1 0 0
0 0 1 0 1 1 0 1
0 0 1 1 0 0 0 1
0 1 0 0 0 0 1 0
0 1 0 1 1 1 1 1
0 1 1 0 1 0 1 1
0 1 1 1 1 0 0 0
1 0 0 0 0 0 1 1
1 0 0 1 1 0 1 0
1 0 1 0 0 1 1 0
1 0 1 1 1 1 0 0
1 1 0 0 0 1 0 1
1 1 0 1 1 0 0 1
1 1 1 0 0 0 0 0
1 1 1 1 0 1 1 1
Пусть х, х' — векторы входа подстановки и у,
у' — соответствующие векторы выхода. Составим
для подстановки матрицу дифференциалов. Для
удобства представим разности числами. Запишем
вектор разности Ах = atxi © о2х2 © 03X3 © 04X4 как
число а — 8«| + 4а2 + 2аз + а4. Всего может быть
16 различных разностей, каждой из которых соот-
ветствует 16 пар входных векторов х, х'. Анало-
гично запишем вектор разности Ay = byyi © Ьууг ©
© Ьзуз © Ь^4 как число b = 86] + 462 + 263 + 64.
Пусть вход х для заданной разности а пробе-
гает все 16 значений. Для каждого х и соответст-
вующего х' найдем пары выходов подстановки и
соответствующую разность Ь. Элемент саЬ мат-
рицы разностей равен числу появлений выход-
ной разности b для входной разности а. Сумма
элементов в каждой строке и каждом столбце
матрицы равна 16, так как для каждого аргумен-
та и входной разности существует некоторая вы-
ходная разность. Поскольку для каждой пары
входов х, х' одна и та же разность встречается
дважды (Ах = х © х' = х' © х), причем то же
справедливо и для выходов подстановки, то каж-
дый элемент матрицы является четным числом.
Кроме того, с00= 16 (из Ах = 0 следует Ау = 0).
Транспонированная матрица разностей соответ-
ствует обратной подстановке. Матрица разно-
стей полностью определяет дифференциалы под-
становки и частоту их появления (таблица 18.1).
Под дифференциалом подстановки будем по-
нимать пару разностей Ах, Ау над Т2, где х, у —
векторы входа и выхода подстановки.
. Таблица 18.1
Матрица разностей при дифференциальном анализе шифра (короткий блок)
Разности выходов, представленные числами
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
0 16 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
О 1 к 1 0 0 0 2 0 0 0 2 0 2 4 0 4 2 0 0
т 2 о 0 0 0 2 0 6 2 2 0 2 0 0 0 0 2 0
к 3 0 0 2 0 2 0 0 0 0 4 2 0 2 0 0 4
S 4 0 0 0 2 0 0 6 0 0 2 0 4 2 0 0 0
S 5 0 4 0 0 0 2 2 0 0 0 4 0 2 0 0 2
ё 6 0 0 0 4 0 4 0 0 0 0 0 0 2 2 2 2
5 s 7 0 0 2 2 2 0 2 0 0 2 2 0 0 0 0 4
с g 8 0 0 0 0 0 0 2 2 0 0 0 4 0 4 2 2
§ 9 0 2 0 0 2 0 0 4 2 0 2 2 2 0 0 0
s 10 0 2 2 0 0 0 0 0 6 0 0 2 0 0 4 0
« Н 0 0 0 0 2 0 2 0 0 0 0 0 2 0 2
«Л & JL1 0 2 0 0 2 2 2 0 0 0 0 2 0 6 0 0
g 13 0 4 0 0 0 0 0 4 2 0 2 0 2 0 2 0
I 14 0 0 2 4 2 0 0 0 6 0 0 0 0 0 2 0
15 0 2 0 0 6 0 0 0 0 4 0 2 0 0 2 0
Наиболее вероятным нетривиальным диффе-
ренциалом для подстановки будет [11,2] =
= [(1, 0, 1, 1), (0, 0, 1, 0)], его вероятность равна
8/1б = '/г- Кроме того, шесть дифференциалов об-
ладают вероятностью б/1б = % (выделены жир-
ным шрифтом). Подстановка обладает много-
численными невозможными дифференциалами,
вероятность которых равна нулю. С помощью
построенной матрицы дифференциалов нетрудно
определить одноцикловые дифференциалы шиф-
ра и их вероятности.
Перенумеруем блоки подстановки (.S'-блоки)
двойными индексами. Обозначим использование
подстановки на i-м цикле шифрования для раз-
рядов 0, 1, 2, 3 через S,i, для разрядов 4, 5, 6, 7
через Sa, для разрядов 8, 9, 10, 11 через S^, для
разрядов 12, 13, 14, 15 через S^. Назовем S-блок
активным, если он используется при составле-
нии характеристики. Обозначим входы z-ro цик-
ла шифрования через и = г/ц>, ..., w,i5, выходы z-ro
цикла шифрования через v = г10, ..., v,i5, выходы
подстановки на i-м цикле через w = и',0, ..., и', |5.
Назовем весом дифференциала [Ди, Ду] сум-
марное число ненулевых двоичных разрядов в
векторах Ди и Ду (вес дифференциала связан с
коэффициентом диффузии, который, в свою оче-
редь, определяется минимальным весом диффе-
ренциала, обладающего ненулевой вероятно-
стью). Для нетривиальных дифференциалов че-
тырехразрядной подстановки минимально воз-
можный вес равен 2 (пара входных и пара вы-
ходных векторов различаются в одном разряде
каждая), максимально возможный — 8 (пара
входных векторов и пара выходных векторов
различаются в четырех разрядах каждая).
Для того чтобы характеристика, составленная
из наиболее вероятных одноцикловых диффе-
ренциалов, имела большую вероятность, она
должна содержать минимальное число активных
S-блоков. Следовательно, она как результирую-
щий дифференциал должна иметь минимальный
суммарный вес (при этом не учитывается раз-
ность открытых текстов — вход итогового диф-
ференциала).
Составим трехцикловую характеристику
шифра в целом из активных S-блоков (рис. 18.1,
разряды с ненулевой разностью выделены): S12,
S23, S32, S33, S42, S44.
Рис. 18.1. Дифференциальный метод криптоанализа
Тогда характеристика с учетом перестановки
имеет вид:
Ли, =0000 1011 0000 0000,
Awi = 0000 0010 0000 0000,
Av’j = 0000 0000 0100 0000 (вероятность 8/]6);
Аи2 = 0000 0000 0100 0000,
Aw2 = 0000 0000 0110 0000,
Av2 = 0000 0010 0010 0000 (вероятность 6/i6);
Au3 = 0000 0010 0010 0000,
Aw3 = 0000 0101 0101 0000,
Av3 = 0000 0110 0000 0110 (вероятность (б/1б)2);
Au4 = 0000 0110 0000 0110.
Считая шифр марковским и используя матри-
цу дифференциалов подстановки, находим веро-
ятность трехцикловой характеристики: р3 =
= (8/]б)(6/1б)(б/1б)2 « 0,0264. Предположим также, что
криптоанализ проводится на основе подобран-
403
ных открытых текстов. При этом используются
пары открытых текстов, в которых первый текст
произволен, а второй отличается от первого раз-
ностью Aui = (О, Ь, 0, 0) (в шестнадцатиричном
виде).
Вскрытие ключа производим, начиная с клю-
ча к5 для активных S-блоков. Для каждой пары
шифртекстов, которым соответствуют открытые
тексты с одинаковыми разностями, моделируем
расшифрование с использованием всех возмож-
ных ключей к5 на последнем цикле. Истинный
ключ определяем с учетом того, что на входе S'-
блока четвертого цикла шифрования разности
между указанными парами дают искомую наи-
более вероятную разность Ди4. В действительно-
сти достаточно опробовать только разряды
А54, ...,^57 и Л5Д2, ..., Л5Д5 ДЛЯ ЛКТИВНЫХ S-блОКОВ
четвертого цикла.
Поскольку истинный ключ является наиболее
вероятным, ищем его следующим алгоритмом.
Для каждого тестируемого ключа все пары за-
шифрованных текстов складываем с тестируе-
мым ключом, выполняем обратную подстановку
и находим соответствующую XOR-разность вхо-
дов подстановки. Если разность совпадает с наи-
более вероятной разностью Ди4, то соответст-
вующий счетчик увеличиваем на 1. Ключ, для
которого частота появления искомого диффе-
ренциала максимальна, является наиболее веро-
ятным.
Найденный ключ к5 позволяет найти вход S'-
блоков четвертого цикла. Затем подбираем ключ
четвертого цикла пробным расшифрованием пар
шифртекстов так, чтобы выполнялось условие
Ди3 = 0000 0010 0010 0000 и т. д.
Если наиболее вероятный (г - 1 )-цикловый
дифференциал (характеристика) имеет вероят-
ность то дифференциальный криптоанализ с
использованием подобранных открытых текстов
требует 0(1/р,.^) текстов. Временная сложность
метода также равна О(}/ рг^) .
В этом примере для проведения анализа тре-
буется примерно 38 пар подобранных открытых
и соответствующих зашифрованных текстов.
Вскрытие восьми битов ключа к5 требует 76 опе-
раций расшифрования на одном цикле.
Непосредственно из способа построения мат-
рицы дифференциалов для подстановки следует,
что при переходе к обратной подстановке эта
матрица заменяется на транспонированную. Пе-
реход от подстановки S(x) к подстановке S(x) © а
не влияет на матрицу дифференциалов. Если
S'(x)— подстановка, обратная к S(x), то для
S(x) © а обратной будет подстановка S'(x © а).
Следовательно, подстановки S(x), S(x © а) и
S(x © а) © b для фиксированных а, b обладают
одинаковыми матрицами дифференциалов.
Пример 18.2.3. Оценка стойкости шифра
(длинный блок) к дифференциальному методу.
Для сравнения с алгебраическими методами
рассмотрим шифр с теми же операторами шиф-
рования на одном цикле, что и в примере 17.5.1,
с восемью циклами шифрования. На каждом
цикле в общем случае может использоваться
свой ключ. Стойкость будем оценивать по одно-
му 6-цикловому дифференциалу.
Составим матрицу дифференциалов подста-
новки (таблица 18.2; наиболее вероятные диффе-
ренциалы выделены жирным шрифтом).5
Данная подстановка имеет 18 наиболее веро-
ятных дифференциалов, обладающих вероятно-
стью ’/4. Отметим, что все дифференциалы веса 2
(в которых входная и выходная разности содер-
жат единственный ненулевой разряд) имеют ну-
левую вероятность, то есть коэффициент диффу-
зии подстановки равен 1.
Предполагаем, что шифр марковский. По-
скольку сдвиг, подстановка и перестановка фик-
сированы, по значению шифртекста можно най-
ти сумму входа восьмого цикла с ключом. Для
вскрытия ключа восьмого цикла используем
дифференциальные характеристики подстановки
седьмого цикла и характеристику, включающую
дифференциалы с первого по шестой циклы. Ис-
комая характеристика должна содержать мини-
мальное число активных S-блоков.
Естественно предположить, что на каждом
цикле число активных S-блоков невелико. По-
видимому, оптимальный вариант характеристи-
ки должен быть похож на «песочные часы» (воз-
можно, с несколькими «талиями» при большом
числе циклов шифрования). Назовем активным
разрядом дифференциала его ненулевой вход-
ной или выходной разряд, участвующий в ха-
рактеристике.
Перестановка выбрана так, что никакие два
разряда подстановки z-ro цикла не попадают на
вход одной и той же подстановки (z+l)-ro
цикла, даже с учетом сдвига. Поэтому один
активный S-блок на z-м цикле шифрования с
одним активным разрядом на входе активизи-
рует не менее двух различных S-блоков на
(z + 1 )-м цикле шифрования. И наоборот, S-
блок с единственным активным выходом на
(z + 1)-м цикле шифрования может быть акти-
визирован не менее чем двумя S-блоками на z-m
5 Данная подстановка обладает заметно лучшим
распределением дифференциалов, чем подстановка из
предыдущего примера.
404
цикле. Отсюда следует, что небольшое число
активных S-блоков (один-два) не может оста-
ваться постоянным в течение трех циклов
шифрования.
Для обеспечения максимума вероятности ха-
рактеристики (минимизации числа активных S'-
блоков) желательно использовать дифференциа-
лы подстановки, обладающие вероятностью ’/4 и
минимальным весом, для всех циклов характери-
стики, за исключением, может быть, первого и
последнего. Определим веса наиболее вероятных
дифференциалов подстановки:
Вес Дифференциалы данного веса
3 [1,5], [3,2], [4, 9], [8, 6], [9, 2], [12, 1]
4 [1,13], [2, 7], [2, 11], [10, 10], [11, 8], [13, 1]
5 [7, 9], [8, 5], [13, 12]
6 [7,11], [12,15]
7 [15,7]
Искомая характеристика из S-блоков для шес-
ти циклов шифрования использует одноцикло-
вые дифференциалы веса 3 (рис. 18.2).
Цикл 1
Цикл 2
Цикл 3
Цикл 4
Цикл 5
Цикл 6
Рис. 18.2. Обобщенная характеристика
из активных S-блоков
Активные S-блоки первого цикла могут со-
держать произвольное число активных входов, а
активные S-блоки шестого цикла— произволь-
ное число активных выходов. Если такая харак-
теристика существует,6 * * * * то она, по-видимому, яв-
ляется наилучшей и имеет вероятность
(1/4)4(1/4)2(1/4)(74)(’/4)2(1/4)4 = 2-28.
6 Существование характеристики следовало бы
доказать, но в данном примере требуется лишь оце-
нить стойкость шифра к дифференциальному методу,
не вскрывая ключ. Для оценки стойкости использует-
ся предположительно существующая характеристика.
Таблица 18.2
Матрица разностей при дифференциальном анализе шифра (длинный блок)
Разности выходов, представленные числами
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
кг 0 16 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
S 1 ей 1 0 0 0 2 0 4 2 0 0 0 0 2 0 4 2 0
1—» Z-) о 2 S 0 0 0 2 0 2 0 4 0 0 2 4 2 0 0 0
Е? 3 0 2 4 0 0 2 2 2 2 0 0 0 0 2 0 0
§ 4 0 0 0 2 0 2 0 0 0 4 0 2 2 0 2 2
X г о J 0 0 2 2 0 0 2 2 2 0 2 0 2 0 2 0
§ 6 0 0 2 0 2 2 2 0 2 0 0 0 2 0 2 2
£ 1 0 2 0 0 2 0 0 0 2 4 0 4 0 2 0 0
О о О 0 0 0 0 0 0 4 0 0 2 2 0 0 2 2 4
5 9 0 0 4 2 0 2 0 0 2 0 0 0 2 2 0 2
g 10 0 2 0 2 2 2 0 0 0 0 4 0 0 2 2 0
й II 0 0 0 0 2 0 0 2 4 2 0 2 0 0 2 2
S 12 0 4 2 0 2 0 0 0 0 0 2 0 2 0 0 4
° 1 о о 13 0 4 0 0 2 0 0 2 0 2 2 0 4 0 0 0
й 14 0 2 0 2 2 0 2 0 2 2 2 2 0 0 0 0
15 0 0 2 2 2 0 2 4 0 0 0 0 0 2 2 0
405
Это значит, что для вскрытия ключа требуется
примерно 228 пар подобранных открытых текстов
с заданными XOR-разностями и соответствую-
щих пар зашифрованного текста. Сложность
вскрытия ключа после набора статистики со-
ставляет примерно 229 опробований.
Аналогичные рассуждения для 16-циклового
шифра показывают, что для вскрытия ключа не-
обходимо более 263 открытых и зашифрованных
текстов — невозможный объем статистики. (Это
позволяет сравнить для такого шифра сложность
дифференциального метода и методов, рассмот-
ренных в гл. 17.)
Как видно из приведенных примеров, на стой-
кость подстановочно-перестановочного шифра к
дифференциальному методу анализа влияют ве-
роятность наиболее вероятного (одноциклового)
дифференциала подстановки и коэффициент
диффузии.7
Для противостояния дифференциальному ме-
тоду желательно использовать такие подстанов-
ки, у которых наиболее вероятные дифферен-
циалы имели бы минимальную вероятность. В
случае подстановочно-перестановочного шифра
желательно выбирать такие подстановки, у кото-
рых все дифференциалы веса 2 имеют нулевую
вероятность (как в примере 18.2.3).
Поскольку на каждом цикле есть хотя бы
один активный .S'-блок, в общем случае стойкость
шифра к дифференциальному методу растет экс-
поненциально с ростом числа циклов шифрова-
ния. Поэтому почти каждый шифр можно сде-
лать гарантированно стойким по отношению к
дифференциальному методу.
Существует целый ряд модификаций диффе-
ренциального метода криптоанализа: анализ с
помощью усеченных дифференциалов (truncated
differentials) [16,18] и дифференциалов высших
порядков [16]. атака «бумеранг» [24], атака
«прямоугольник» (rectangle) [6], потоки диффе-
ренциалов [11].
18.2.3. Анализ с помощью
усеченных дифференциалов
Усеченный дифференциал использует разно-
сти не между блоками (полублоками в случае
фейстелева шифра), а между их частями или да-
7 В общем случае коэффициент диффузии должен
быть согласован с наиболее вероятными дифференциа-
лами, то есть должен рассматриваться для тех разно-
стей, которые входят в наиболее вероятные дифферен-
циалы, но обычно это не выполняется (см. п. 18.1).
же отдельными битами, иначе говоря, усеченный
/-цикловый дифференциал представляет собой
подмножество полного /-циклового дифферен-
циала. Использование усеченных дифференциа-
лов для фейстелевых шифров позволяет сокра-
тить требуемый для вскрытия ключа объем от-
крытых и зашифрованных текстов.
Рассмотрим фейстелев шифр с длиной полу-
блока п бит (и нечетно), в котором на каждом цик-
ле выполняется операция х <- (х © к)-1, где обра-
щение выполняется в поле из 2й элементов и
(Г1 =0 [16]. Поскольку все поля из 2" элементов
изоморфны, и изоморфизм задается умножением
на матрицу над Р2, то способы задания поля тем
или иным неприводимым полиномом степени п
задают аффинную эквивалентность «-разрядных
булевых функций. Поэтому не будем уточнять
вид поля. Подстановка, индуцированная обраще-
нием в поле F2„, является нелинейной. Все диф-
ференциалы с ненулевой вероятностью для не-
четного п имеют вероятность 21 ”. Если в шифре
четыре цикла, то вероятность любого трехцикло-
вого дифференциала не превышает 23”2"— это
меньше вероятности того, что блок будет иметь
заранее определенный вид. Поэтому использова-
ние разностей длины п бит не позволяет вскрыть
ключ дифференциальным методом.
Однако двухцикловый дифференциал этого
шифра для любого полублока совпадает с одно-
цикловым дифференциалом, так как каждый по-
лублок шифруется в течение двух циклов только
однократно.
Поскольку одноцикловый дифференциал име-
ет вероятность 21-”, то каждой ненулевой разно-
сти входов соответствует 2й”1 различных разно-
стей выходов с одинаковой вероятностью, рав-
ной вероятности дифференциала. При этом в по-
ловине случаев выходные разности являются не-
возможными. Поэтому выходная разность (и,
следовательно, двухцикловый дифференциал)
при фиксированной ненулевой входной инфор-
мации содержит п - 1 бит информации, то есть
один бит о выходной разности известен. Это по-
зволяет построить двухцикловый дифференциал,
обладающий вероятностью 1, в котором один
бит информации известен.
Для вскрытия ключа пятициклового фейсте-
лева шифра с длиной полублока п бит и цикло-
вой функцией F методом усеченных диффе-
ренциалов нужно выполнить следующие дей-
ствия [16].
1. Выбрать такую ненулевую разность а вход-
ных текстов, что доля W возможных диффе-
ренциалов среди 2" выходных разностей
меньше 1.
406
2. Найти матрицу (T,j) для 0 < i, j < 2" - 1 такую,
что 2].’(i)eF(iea) = 1, а остальные элементы —
нулевые.
3. Выбрать произвольный открытый текст х]5
найти текст х2 <— х, © а. и вычислить соот-
ветствующие шифрограммы у 1, у2.
4. Для каждого возможного ключа к5 пятого
цикла:
4.1. Расшифровать шифрограммы уь у2 и
найти входы Wi, w2 пятого цикла (каж-
дый блок wz содержит левую w/ и пра-
вую w,' части).
4.2. Для каждого возможного ключа кд чет-
вертого цикла:
4.2.1. Вычислить Vi <— F(wi' © кд), v2 <-
<— F(w2' © кд).
4.2.2.
Если Т „ , , >0, то к5 и
V]®V2®w{®w2
кд — искомые цикловые ключи.
При этом оказывается, что для вскрытия клю-
ча пятициклового шифра достаточно 2L подоб-
ранных открытых текстов, а временная слож-
ность вскрытия ключа равна 22"£, где L— наи-
меньшее целое такое, что WL < 22'1. Анализ с по-
мощью усеченных дифференциалов применим к
фейстелевым шифрам с произвольным числом
циклов шифрования [16].
18.2.4. Анализ с помощью
дифференциалов высших порядков
Определим одноцикловый дифференциал по-
рядка i как строку из i + 1 разностей: [а,,..., а,; р],
где Д' а/(х) = р. В случае кольца Gn и поли-
номов степени не менее i векторы, соответст-
вующие числам ос„ должны быть линейно неза-
висимыми. Поясним механизм атаки на примере
пятициклового фейстелева шифра [16] с цикло-
вой функцией шифрования fix) = (х + k)2 (mod р)
для простого числа р и ключа к.
Дифференциалы будем рассматривать в поле
Ну,. Оказывается, что одноцикловые дифферен-
циалы первого порядка распределены равномер-
но. Действительно, рассмотрим равенство
/(х) ~ЛХ + а) =fix') ~AX’ + а\ означающее, что
для двух пар аргументов с входной разностью а
выходные разности совпадают. Раскрывая скоб-
ки, получим:
(х + к)2 - (х + а + А)2 = (х' + Л)2 - (х' + а + £)2;
—2ак - 2ах + а2 = —2ак - 2ах' + а2;
х = х'.
Поэтому совпадение выходных разностей для
разных пар входов (х Ф х') невозможно. Данное
обстоятельство обусловливает неэффективность
дифференциального метода криптоанализа.
Однако дифференциалы второго и более вы-
соких порядков для того же шифра имеют значи-
тельно более удобное (для криптоаналитика)
распределение. Одноцикловая разность второго
порядка A2] a /(х) при постоянных а ь ос2:
д2аьа2 /(*) = /(л- + а1+а2)-/(х + а1)-
-/(х + а2) + /(х) = 2а]а2
не зависит от х, а третья и более высокие разно-
сти вообще оказываются нулевыми (самая бла-
гоприятная ситуация для криптоаналитика).
Рассмотрим атаку на данный шифр с помо-
щью разностей второго порядка A2 a /(х), где
а, = 0. а2 = Л || 0. Дифференциал второго цикла
задается парой разностей (вход, выход): (а, 2аЬ)
и (b, 2аЬ). Соответствующий дифференциал вто-
рого порядка имеет вид [а, Ь; 2аЬ]. Атака строит-
ся следующим образом [16].
1. Выбрать произвольный текст Xj.
2. Положить Х2 <— Х| + ОС], Х3 <- X) + 0С2, Х4 <- Х1 +
+ 0.1 + а2.
3. Вычислить соответствующие шифрограммы
У1,У2,Уз,У4.
4. Для каждого возможного ключа к$ пятого
цикла:
4.1. Расшифровать шифрограммы yt,..., у4 и
найти входы Wj, ...,w4 пятого цикла
(каждый блок Wj содержит левую и'/ и
правую w! части).
4.2. Для каждого возможного ключа к4 чет-
вертого цикла:
4.2.1. Вычислить г, <- Ffwf + к4), 1 < i < 4.
4.2.2. Если (ij + г4 - (v2 + v3)) - (w/+w4 -
- (wj + w;')) = 2ab, то ks и k4 —
искомые цикловые ключи.
Эта атака требует только восьми подобран-
ных открытых текстов (две четверки). Слож-
ность вскрытия ключей равна О(р2).
18.2.5. Атака «бумеранг»
Если характеристика шифра имеет вероят-
ность р, то для вскрытия ключа дифференциаль-
ным методом требуется О(р~1) подобранных от-
крытых и соответствующих зашифрованных тек-
стов. Иногда эту оценку можно улучшить. Атака
«бумеранг» и аналогичная атака «прямоуголь-
ник» основаны на замене одиночного (г - 1)-
407
циклового дифференциала парой дифференциа-
лов для половины циклов шифрования, обла-
дающих вероятностью ~q каждая. Обе атаки
требуют O(q”4) открытых и зашифрованных тек-
стов и при q'»р являются более эффективны-
ми, чем обычный дифференциальный метод.
При атаке «бумеранг» сравниваются проме-
жуточные тексты, полученные зашифрованием
открытых текстов на половине циклов и рас-
шифрованием соответствующих шифрограмм на
оставшейся половине циклов.
Рассмотрим четверку открытых текстов х. х',
и, и' и соответствующие шифрограммы у, у', v, v'.
Пусть Дх = х © х', Ди = и © и', Ду = у © у',
Ду = v © v' — XOR-разности. Пусть £0 — опера-
тор зашифрования на первой половине циклов,
Ei — оператор зашифрования на второй половине
циклов. Пусть оператор Ео обладает характери-
стикой Д—>Л*, переводящей разность открытых
текстов Д в разность промежуточных текстов Л*,
а оператор Ef1 обладает характеристикой б> б,
переводящей разность шифрограмм б в разность
промежуточных текстов б*. При этом пара (х, х')
задает требуемую входную разность для Ео, а
шифрограммы пар (х. и) и (х', и') — требуемую
входную разность для Ef1 (рис. 18.3). Тогда пара
(Ео(и), Е0(и')) задает требуемую входную разность
для оператора расшифрования Ер1. Действительно,
E0(u)©E0(u') =
= Ео (х) © Ео (х') © Ео (х) © Ео (и) © Ео (х') © Ео (и) =
=Е0(х)©Е0(х,)©Е1''1 (у)@ЕГ' (v)©^-’ (y')©Ef1 (V>
= А*©б*©б*=А*.
Рис. 18.3. Атака «бумеранг»
Следовательно, если дифференциал [Л, Л*]
является наиболее вероятным для оператора Ео,
то дифференциал [А*, Л] — для обратного опе-
ратора Ер1. Поэтому разность и © и' = Л явля-
ется составляющей входной разности для наибо-
лее вероятного дифференциала оператора Ео.
Требуемые четверки текстов (х, х', и, и') мож-
но получить следующим образом.
1. Выбрать пару открытых текстов (х, х') с тре-
буемой разностью Л.
2. Вычислить шифрограммы у, у' для открытых
текстов х, х'.
3. Выбрать шифрограммы v, v', имеющие тре-
буемую разность б с шифрограммами у, у'.
4. Вычислить открытые тексты и, и' расшифро-
ванием шифрограмм v, v'.
Таким образом, для реализации атаки нару-
шитель должен иметь возможность как зашиф-
ровывать, так и расшифровывать подобранные
тексты. Вскрытие ключа, начиная со средних
циклов шифрования, выполняется так же, как и
при обычном дифференциальном анализе.
18.3. Криптоанализ на основе списка
ключей и связанных ключей
Часто в r-цикловом итерированном шифре
для шифрования применяется так называемый
список ключей (key schedule)8, который готовит-
ся из исходного ключа и представляет собой
набор цикловых ключей, используемых соот-
ветственно на циклах 1,2, Например, в
ГОСТ 28147-89 (см. п. 19.6) исходный ключ
состоит из восьми 32-разрядных слов, а список
ключей задает их порядок: 0, 1,2, 3, 4, 5, 6, 7, О,
1, 2, 3, 4, 5, 6, 7, 0, 1, 2, 3, 4, 5, 6, 7, 0, 7, 6, 5, 4,
3, 2, 1, 0; в DES (см. п. 19.3) набор 48-разрядных
цикловых ключей рекурсивно получается из
ключа длиной 56 бит. Регулярные свойства спи-
ска ключей могут быть использованы, напри-
мер, для ранней отбраковки неправильных клю-
чей при дифференциальном или линейном
криптоанализе.
В общем случае атака на основе списка клю-
чей [15] определяется способом получения цик-
ловых ключей из исходного ключа и может ис-
пользовать встречу посередине, выявляемые
классы ключей и др. Как правило, анализ на ос-
нове списка ключей не является самостоятель-
ным методом, а служит вспомогательным меха-
низмом, позволяющим усилить другие методы.
8 Используется также термин «развертка ключа».
408
Для того чтобы затруднить анализ на основе
списка ключей, при разработке шифра целесооб-
разно ввести (криптографически нетривиальную)
зависимость списка ключей от номера цикла
шифрования.
Метод анализа на основе связанных ключей
был рассмотрен Э. Бихамом [4] для шифров, в
которых ключ очередного цикла вычисляется из
ключей одного или нескольких предыдущих
циклов по одному и тому же правилу. Список
ключей, полученных из некоторого исходного
ключа, можно циклически сдвинуть на одну или
несколько позиций. Этот новый список ключей
может быть получен из другого исходного ключа.
Достоинством данного метода является то,
что сложность анализа не зависит от числа цик-
лов шифрования. Как и в дифференциальном ме-
тоде, предполагается, что функция шифрования
на одном цикле является криптографически сла-
бой. В данном случае это значит, что по входу и
выходу можно легко вскрыть ключ, а гипотеза о
свойствах текстов или цикловых ключей для
одиночного цикла эффективно проверяема.
Пусть /’-цикловый шифр построен так, что
цикловые ключи получаются из исходного клю-
ча по одному и тому же правилу А, причем если
к, — ключ z-ro цикла, то ki+i = А(к,). Следуя рас-
суждениям Э. Бихама, рассмотрим атаку на ос-
нове подобранного ключа и подобранного от-
крытого текста.9 Суть атаки заключается в том,
что нарушитель может по своему усмотрению
изменять разность между связанными цикловы-
ми ключами (не зная самих ключей) и подбирать
открытые тексты для зашифрования. При этом
ему нужно получить систему равенств
= К2, ,+1, где Ку — цикловый ключ z-ro цикла,
полученный из исходного ключа К\, Куцл—
цикловый ключ (z + 1 )-го цикла, полученный из
исходного ключа К2. Для этого достаточно обес-
печить выполнение указанного условия после
первого цикла. Поскольку алгоритм выбора цик-
ловых ключей степенной, то для остальных цик-
лов это условие выполняется автоматически.
Обозначим входы для соответствующих после-
довательностей ключей z-ro цикла шифрования
через xl h ху:
*1,1 *1,2 •• *1,,-2 *1,7-1 *1,1
Хц2 .. Д ,г-2 Xlz_i Х1
*2,1 х22 *2,3 • *2,г-1 %2,г
Ку Ку Х2д .. Х2,-1 Ку
9 Такая атака может быть эффективна для шифра
LOKI [4].
Получаются две последовательности цикловых
ключей, сдвинутые на одну позицию, при этом
ключи, записанные друг под другом, совпадают.
Пусть в шифре используется неизвестный
ключ К]. Цель нарушителя— найти вспомога-
тельный ключ Л’2 и открытые тексты Хщ, х2ц (вы-
числив соответствующие шифрограммы >j, у2)
так, чтобы выполнялось условие Хщ = х2;2. Тогда
в силу равенств Хц, = ,+1 будут выполняться и
равенства хц,-= x2.;+i- Следовательно, у2=ху-
Очевидно, что в силу обратимости функции
шифрования можно искать вспомогательный
ключ К2, который дает список ключей, отстаю-
щий от списка ключей, который дает Хр
Для нахождения такой пары открытых тек-
стов хщ, х2j можно воспользоваться парадок-
сом дней рождения. Тогда сложность нахожде-
ния этой пары будет равна 0(2"^), где п — раз-
рядность блока (для фейстелева шифра— по-
лублока).
Для того чтобы выявить искомую ситуацию,
необходимо проверить совместность системы
двух уравнений:
*1.1 = F(xy, X2.i), уг = F(y2; K2J,
где ji, у2 — соответствующие шифрограммы,
X— функция шифрования на одном цикле. По-
скольку функция F криптографически слабая,
совместность указанной системы эффективно
проверяется для каждой четверки (хщ,у1, х2д,у2).
В ходе проверки вычисляются ключи Ку и Ку.
Зная ключ первого и/или последнего цикла, легко
вскрыть ключи остальных циклов.
Для ускорения подбора вспомогательного клю-
ча и указанных текстов можно воспользоваться
отбраковкой классов ключей и текстов, заведомо
не удовлетворяющих указанному сдвигу. Отметим,
что разности между ключами и выходами для од-
ного цикла шифрования при известных входах мо-
гут быть легко вычислены, если известна одна из
этих разностей, по аналогии с дифференциальным
методом криптоанализа. Поэтому при атаке на ос-
нове подобранных открытых текстов нарушитель,
зная разность ключей, может получить требуемое
соотношение между входами циклов шифрования
для тестируемых ключей быстрее, чем с исполь-
зованием парадокса дней рождения.
18.4. Линейный криптоанализ
Метод линейного криптоанализа был впервые
опубликован М. Мацуи в 1993 г. [21] и развит
рядом авторов [12, 13, 17, 22]. Данный метод
требует знания открытых и соответствующих
зашифрованных текстов. Суть метода заключа-
ется в поиске линейных зависимостей вида
409
X, ©...©X,- ©у, ©...©у,- =
'1 '« J Ji J л
-к, © ... © к, ,
'1 'с ’
(18.4.1)
которые выполняются с вероятностью, заметно10
большей или заметно меньшей, чем 0,5. Здесь
{х,}, {yj}, {к/} — биты соответственно открытого
текста, шифрограммы и ключа; й,..., ia,ji,
li, — некоторые подмножества битов соот-
ветственно открытого текста, шифрограммы и
ключа.
После получения системы таких уравнений
ключ можно найти решением этой системы, по-
скольку биты х„ у, известны. Истинный ключ опре-
деляется как наиболее (наименее) вероятный, для
которого условия (18.4.1) выполняются наиболее
(наименее) часто. Поскольку решение системы ли-
нейных уравнений (18.4.1) не составляет труда,
вскрытие ключа сводится к нахождению уравне-
ний (18.4.1), выполняющихся наиболее часто, на-
бору статистики открытых и зашифрованных тек-
стов и выявлению наиболее вероятных ключей.
Очевидно, что для противодействия линейно-
му методу необходимо обеспечить выполнение
равенства (18.4.1) с вероятностью, как можно
более близкой к 0,5 для всех наборов битов от-
крытого текста, шифрограммы и ключа. Это воз-
можно лишь в том случае, если уравнение шиф-
рования является нелинейным.
Определим нелинейность NL(/) булевой
функции f зависящей от п переменных, как наи-
меньшее хеммингово расстояние между таблич-
но заданными функцией f и множеством аффин-
ных функций, то есть как число наборов аргу-
ментов, на которых булева функция не совпадает
с аппроксимирующей аффинной функцией. Не-
линейность булевой функции— неотрицатель-
ное целое число. Нелинейность аффинной буле-
вой функции равна нулю. Аффинно эквивалент-
ные булевы функции обладают одинаковой не-
линейностью.
Таблица 18.3
Значения булевой функции f и аффинной булевой функции g = х( © х2 © х3 © х4
0 1 2 3 ‘"С; 5 7 8 ' 9 10 и 13 14 15
f 0 I 1 0 0 0 1 1 0 0 0 1 i 1 1 0
g 0 1 1 0 1 0 1 1 ; 0 0 1 0 1 1 0
Пример 18.4.1. Нелинейность булевой функ-
ции, задающей подстановку стандарта DES.
Рассмотрим вторую подстановку в блоке S0
стандарта DES: 0, 15, 7, 4, 14, 2, 13, 1, 10, 6, 12,
11, 9, 5, 3, 8. Ее можно записать в виде четырех
булевых функций четырех переменных Х], х2, Хз,
х4. Значения булевой функции /, задающей
младший разряд этой подстановки, и аффинной
булевой функции g = X! © х2 © хз © х4 на множе-
стве аргументов (0, 0,0,0),..., (1,1, 1,1), приве-
дены в таблице 18.3.
Значения булевых функций/и g различаются
в четырех позициях, поэтому NL(/) = 4. Следова-
тельно, в 12 случаях из 16 аппроксимирующая
функция совпадает с аппроксимируемой.
Функция g является наилучшей аффинной ап-
проксимацией для функции f. В общем случае
может существовать несколько наилучших аф-
финных аппроксимаций. Другая аффинная булева
функция, аппроксимирующая функцию f с веро-
ятностью ошибки ’ /4, имеет вид 1 © Xi © х2 © х3.
10 Вероятность заметно отличается от 0,5 по крип-
тографическим меркам. На практике это означает, что
можно статистически отличить последовательность,
обладающую указанной линейной зависимостью, от
случайной двоичной последовательности.
Легко заметить, что нелинейность сбаланси-
рованной булевой функции является четным
числом.11 Нелинейность четырехразрядной буле-
вой функции может принимать значения 0, 2 или
4. В общем случае, как показали Дж. Себерри и
С. Жэнь [23], нелинейность «-разрядной сбалан-
сированной булевой функции f изменяется в пре-
делах:
0 <NL(/)<2"4 -2L(" -|)/2-l
Покажем, как для итогового криптопреобра-
зования можно найти линейные суммы (18.4.1),
выполняющиеся с наибольшей (наименьшей)
вероятностью, по соответствующим линейным
суммам для операторов шифрования.
Рассмотрим две случайные двоичные величи-
ны Xi и х2 такие, что х, @ х2 = 0 (это означает, что
X] = х2). Предположим, что эти величины распре-
делены по биномиальному закону P(xi =0)=р\,
P(xi = 1) = 1 -pi, Р(х2 = 0) =р2, Р(х2 = 1) = 1 -р2.
Событие, заключающееся в выполнении равенст-
ва X] = х2, произойдет, если обе величины примут
11 Обратимое преобразование переменных может
задаваться только сбалансированными булевыми фун-
кциями.
410
значение 0 или 1. Соответствующие вероятности:
Р(хА = х2 = 0) =р\ръ Р(хх =х2 = 1) = (1 -pi)(l -#>)-
Тогда
Р(Х] = х2)=р]у>2 + (1 -Pi)(l -М
Пусть pi = 0,5 + 8], р2 = 0,5 + 82, где 8, — соот-
ветствующие преобладания. Тогда Р(х\ = х2) =
= 0,5 + Бщ, где 8]>2 = 28)82.
Обобщим это рассуждение на случай п неза-
висимых двоичных величин хь прини-
мающих значение 0 с преобладаниями соответ-
ственно 8],..., 8„. Тогда
р(х, ф ... ф х„ = о)= о,5 + 2”4 fj 8;.,
1=1
то есть
е,.„=2"-'ПЕ.-
/=1
Эти два равенства составляют лемму Мацуи
(piling-up lemma [21]), положенную в основу на-
хождения вероятности итоговой аффинной ап-
проксимации. Если хотя бы для одного i выпол-
няется 8, = 0 (то есть р, = 0,5), то 8] .„ = 0 и
Р(хА ф ... Фх„ = 0) = 0,5.
Нелинейность всех разрядов булевых функ-
ций подстановки (в подстановочно-перестановоч-
ном шифре) является необходимым, но не доста-
точным условием стойкости шифра к линейному
методу. Класс подстановок, слабых по отноше-
нию к линейному методу, определяется следую-
щей теоремой.
Теорема 18.4.1. Линейная сумма для входов и
выходов подстановки выполняется с вероятно-
стью 0 или 1 тогда и только тогда, когда подста-
новка аффинно эквивалентна подстановке, со-
держащей аффинную булеву функцию.
Доказательство. Пусть подстановка Т аф-
финно эквивалентна подстановке S с аффинной
булевой функцией У1 ='^iaJxJ, T=ASB, где А,
j
В — аффинные подстановки. Тогда подстановка
SB тоже обладает аффинной булевой функцией
(вид которой может отличаться от одноименной
булевой функции подстановки S). Применяя аф-
финную подстановку А к выходу подстановки
SB, получаем равенство над IF2:
(18.4.2)
< j
Обратно, пусть для подстановки Т выполняет-
ся линейное равенство (18.4.2), левая часть кото-
рого отлична от нуля. Тогда существует аффин-
ная подстановка С, переводящая вектор ^6, у,
в вектор, все координаты которого, кроме одно-
го, нулевые. В этом случае подстановка СТ со-
держит аффинную функцию. Отметим, что левая
часть равенства (18.4.2) не может быть равна ну-
лю, так как в противном случае и правая часть
равенства (18.4.2) должна быть нулевой, что про-
тиворечит линейной независимости аффинных
функций х}.
Таким образом, неудачно выбранная подста-
новка может иметь все разряды нелинейными, но
среди булевых функций, задающих подстановку,
могут быть такие, что их сумма является аффин-
ной функцией.
Пример 18.4.2. Неудачная нелинейная под-
становка в смысле линейного криптоанализа.
Пусть четырехразрядная подстановка имеет вид
(3. 11.0,6, 13,14, 8, 5,2,4, 15, 12, 1.7,2, 9).
Зададим связь между двоичными векторами
входа и выхода подстановки и соответствующи-
ми целыми числами следующим образом: вход-
ному вектору х = (хь х2, хз, х4) сопоставим число
8xj + 4х2 + 2х3 + х4, выходному вектору у =
= (Уь У2,Уз,У4)— число 8yi + 4у2 + 2у3 +у4, где
х„у, & {0, 1}.
Запишем булевы функции для этой подста-
новки:
yi = X, © х2 © х4 © х2х4 © хзх4;
у2 = х2 © Х]Х2 © Х1Х3 © Х]Х4 © х2х3 © хзх4;
у3 = Х2 © Х3 © Х|Х3 © XjX4 © х2х3 © х2х4 ©
ф Х3Х4 Ф Х1Х2Х4 © Х1Х3Х4;
У4 = X] © Хз © Х)Х2 © Х2Х4 © Х1Х2Х4 © Х]ХзХ4;
Все разряды подстановки описываются нели-
нейными уравнениями, однако при этом всегда
выполняется линейное равенство
у2 ® Уз © у>4 © Xi = 1.
Если подстановка является «слабой» в смысле
линейного криптоанализа, то и обратная подста-
новка тоже является «слабой».
Теорема 18.4.2. Если подстановка содержит
аффинную булеву функцию, то и обратная под-
становка лежит в классе аффинно эквивалентных
подстановок, содержащих аффинную булеву
функцию.
Доказательство. Действительно, если
у, = хг, то аффинной заменой переменных
I
х, = У хг получим Xi = yi. Значит, подстановка.
411
аффинно эквивалентная обратной, содержит аф-
финную булеву функцию.
Следствие 18.4.3. Если подстановка содержит
такие булевы функции, что сумма некоторых из
них является аффинной функцией, то и обратная
подстановка обладает эти свойством.
Предположим, что шифр содержит нелиней-
ные операции перемешивания (/«-разрядная под-
становка) и линейные операции рассеивания. В
этом случае для проведения криптоанализа ли-
нейным методом требуется найти линейные
СуММЫ ВИДа X; © у, для входных и выход-
ных разрядов подстановки (не булевой функ-
ции!), которые равны 0 с максимальной (или с
минимальной) вероятностью. Это можно сделать
следуюшим алгоритмом.
Алгоритм 18.4.1. Поиск наиболее вероятной
и наименее вероятной линейных сумм для под-
становки.
Вход, w-разрядная подстановка.
Выход. Наиболее вероятная и наименее веро-
ятная линейные суммы и вероятности этих сумм.
Метод.
1. Записать подстановку в виде таблицы т вы-
ходных булевых функций, зависящих от т
двоичных аргументов каждая.
2. Перенумеровать всевозможные линейные
комбинации входов а^у ©... © <ад,„ где
а, е {0,1}, по наборам из т коэффициентов а,.
3. Перенумеровать всевозможные линейные
комбинации выходов Ьу\ ©... © Ь„ут, где
Ь е {0,1}, по наборам из т коэффициентов Ь,.
4. Составить квадратную матрицу (с,7) размера
2"’, где строки перечисляют всевозможные
наборы {а,}, а столбцы— всевозможные на-
боры {Ь,} так, что номер строки равен
^о',_12"'-' , а номер столбца— ^Z>M2"'-' .
<=1 /=1
Элемент матрицы равен s - 2"' ', где л — чис-
ло выполнений над F2 равенства:
Z = Z Ькук. (18.4.3)
.. *„+26„ч...+412”“,=/
5. В полученной матрице найти максимальный
и минимальный элементы. Индексы этих
элементов определяют наиболее вероятную и
наименее вероятную линейные суммы для
подстановки, а значения этих элементов —
вероятности этих линейных сумм. в
Сумма элементов в каждой строке матрицы
(су) равна ±2т~1; каждый элемент принимает зна-
чение от -2"’-1 до 2"’-1. Равенство (18.4.3) выпол-
няется с вероятностью 0,5 + сц /2'" . Непосредст-
венно из леммы Мацуи вытекает, что по этой
матрице можно найти также наиболее и наиме-
нее вероятные линейные суммы для шифра в це-
лом (поскольку «-разрядный блочный шифр реа-
лизует «-разрядную подстановку, для нее тоже
определены наиболее и наименее вероятные ли-
нейные суммы).
Линейный метод криптоанализа аналогичен
дифференциальному. Назовем {линейной) харак-
теристикой последовательность линейных сумм
для отдельных операторов шифрования, в кото-
рых множество выходных переменных в линей-
ной сумме предыдущего оператора совпадает с
множеством входных переменных в линейной
сумме последующего оператора.
Криптоанализ заключается в построении ха-
рактеристики по мере продвижения в процессе
шифрования от входа к выходу и определении ее
вероятности. Наиболее (наименее) вероятные
линейные суммы для каждой операции в ходе
шифрования находятся с помощью леммы Мацуи.
Отметим, что поиск характеристики— нетриви-
альная задача, однако она значительно проще, чем
перебор ключей.
Задание наиболее вероятных и наименее ве-
роятных линейных сумм для шифра в целом с
помощью характеристики возможно, если шифр
является марковским (в смысле линейного крип-
тоанализа): вероятность линейной суммы не за-
висит от входных переменных и ключа. Практи-
чески это означает, что для шифра выполняется
лемма Мацуи.
По аналогии с дифференциальным методом в
подстановочно-перестановочном шифре можно
определить активные 5-блоки и активные разряды
5-блоков. Суммарное число активных 5-блоков
характеристики с учетом их вероятностей долж-
но быть минимальным. Поэтому обычно линей-
ная характеристика, как и дифференциальная,
имеет вид «песочных часов» с «талией» в сере-
дине процесса шифрования. :
Пример 18.4.3. Линейный криптоанализ
шифра (короткий блок).
Рассмотрим шифр из примера 18.2.2. Обозна-
чим через X], ...,Х4 входы подстановки,
yi, ...,у4 — ее выходы. Составим таблицу, харак-
теризующую преобладания для линейных сумм
подстановки, используя алгоритм 18.4.1 (таблица
18.4).
412
Таблица 18.4
Матрица разностей при линейном анализе шифра (короткий блок)
Разности выходов, представленные числами
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
Разности входов, представленные числами 0 8 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
1 0 0 -2 -2 0 0 -2 6 2 2 0 0 2 2 0 0
2 0 0 -2 -2 0 0 -2 -2 0 0 2 2 0 0 -6 2
3 0 0 0 0 0 0 0 0 2 -6 -2 -2 2 2 -2 -2
4 0 2 0 -2 -2 -4 -2 0 0 -2 0 2 2 -4 2 0
5 0 -2 -2 0 -2 0 4 2 -2 0 -4 2 0 -2 -2 0
6 0 2 -2 4 2 0 0 2 0 -2 2 4 -2 0 0 -2
7 0 -2 0 2 2 -4 2 0 -2 0 2 0 4 2 2 2
8 0 0 0 0 0 0 0 0 -2 2 2 -2 2 -2 -2 -6
9 0 0 -2 -2 0 0 -2 -2 -4 0 -2 2 0 4 2 -2
10 0 4 -2 2 -4 0 2 -2 2 2 0 0 2 2 0 0
11 0 4 0 -4 4 0 4 0 0 0 0 0 0 0 0 0
12 0 -2 4 -2 -2 0 2 0 2 0 2 4 0 2 0 -2
13 0 2 2 0 -2 4 0 2 -4 -2 2 0 2 0 0 2
14 0 2 2 0 -2 -4 0 2 -2 0 0 -2 -4 2 -2 0
15 0 -2 -4 -2 -2 0 2 0 0 -2 4 -2 -2 0 2 0
Здесь наибольшая абсолютная величина пре-
обладания определяется элементами c2tu, Сз,ъ
Сед5, что соответствует аппроксимациям
Лз=У!®У2©Тз; x3©x4=yi©y4;
Х1 = © у2 © Уз © у4.
Как и в примере 18.2.2, перенумеруем 5-блоки
двойными индексами. Чтобы построить линей-
ную сумму для шифра в целом, рассмотрим ап-
проксимацию для характеристики, заданной под-
становками 512, $22, 532, S34, 542, 544, затрагиваю-
щую первые три цикла шифрования; соответст-
вующие активные разряды выделены жирным
шрифтом (рис. 18.4)?2
Линейную характеристику составляем с уче-
том того, что выходные переменные предыдуще-
го цикла шифрования должны служить входны-
ми переменными последующего цикла шифро-
вания.
Для блока 512 используем аппроксимацию
х, © х3 © х4 =у2, что соответствует элементу Сц,4.
12 Использование в характеристике линейных ра-
венств, которые выполняются с преобладанием -б/16,
ведет к увеличению числа активных 5-блоков по срав-
нению с указанным.
Преобладание равно 4/]6 = '/4. Вероятность вы-
полнения указанной аппроксимации равна
,/2 + 1/4 = 3/4.
Пусть utJ—j-й разряд входного блока на z-м
цикле шифрования, г,, — j-й разряд выходного
блока на z-м цикле шифрования, k,j — j-й разряд
ключа на z-м цикле шифрования, где i = 1, 2, 3, 4,
7 = 0,1,..., 15.
Для блока 512 выполняются равенства
X] = zzlj4 © ki,4, Хз = z/j 6 © к^6,
Х4 = Щд © /С1>7, у2 = Г1Д,
так как после перестановки 5-й разряд текста ос-
тается неподвижным. На втором цикле шифро-
вания переменная vi,5 переходит в г/2,5.
Для блока 522 составляем аппроксимацию с
максимальной абсолютной величиной преоблада-
ния, в которую входит только входная переменная
Х2, соответствующая разряду г/2,5- Это аппрокси-
мация х2 = у2 © ум с преобладанием -4/16 = -74, ве-
роятность ее выполнения: ’/2 - ’/4 = ’/4. Для пере-
менных в составе блока для второго цикла шиф-
рования эта аппроксимация имеет вид (см.
рис. 18.4):
1/2,5 © &2,5 © V2,5 © V2,]3 = 0.
413
«1,4 «1,6 Щ,1
III 1 1111 1111 1111
Сложение с ключом Аа ,
Illi Illi Illi 1111
$11 S12 S13 S14
Illi Illi Illi Illi
Перестановка
Illi Illi Illi Illi
Сложение с ключом A^i
1 1 1 1 Illi Illi Illi
$21 ^22 S23 *$24
Illi Illi Illi Illi
Перестановка
Illi Illi Illi Illi
Сложение с ключом A3,
Illi Illi Illi Illi
•S31 S32 $33 $34
Illi Illi Illi Illi
Перестановка
J IL J fill 111! 1111
Сложение с ключом fc4,
Illi Illi Illi JJII
s4i <$Д2 S43 $44
Illi Illi Illi Illi
Сложение с ключом A5,
Illi Illi Illi 1 1 1 1
Рис. 18.4. Линейный метод криптоанализа
Рассуждая аналогично, получаем на третьем
цикле шифрования:
- для блока 532 переменная хг соответствует
разряду 1/3 5; аппроксимация х2=у2 ©у4 с пре-
обладанием -*/4 и вероятностью ’/4 имеет вид
- для блока 534 переменная х2 соответствует
разряду 1/313; аппроксимация х2 =_у2 ©у4 с пре-
обладанием ~'/4 и вероятностью ’/4 имеет вид
2*3,13 © А3Д3 = V3J3 © У3Д5.
На четвертом цикле шифрования:
- для блока 542 переменные х2 и х4 соответст-
вуют разрядам г/45 и г/47; аппроксимация
Х2 © х4 = у>2 © уз (соответственно х2 © х4 =
= yi © уз) с преобладанием ’/4 и вероятностью
3/4 (соответственно ~/4 и ’/4) имеет вид
w4,5 © к4$ © г/дд © к42 = v4,5 © v4i6 (соответст-
венно г/4>5 © Ад,5 © г/4;7 © к4,з - у4,4 © т4>6);
- для блока 544 переменные х2 и х4 соответст-
вуют разрядам щд3 и w415; аппроксимация
х2 © х4 = у2 © уз (соответственно х2©х4 =
= yi © уз) с преобладанием '/4 и вероятностью
3/4 (соответственно —1/4 и ’/4) имеет вид
г/4дз © Ад,13 © г/4д5 Ф Ад,15 = т4дз © т4д4 (соответ-
ственно */4|з © Ад,13 ® 2/4.15 ® Аддз = Уд,12 © Уд 14).
Составим сквозную линейную аппроксима-
цию с учетом леммы Мацуи. Выразим выходы
первого цикла с помощью найденной аппрокси-
мации и подставим их в качестве входов в выра-
жения для аппроксимации второго цикла. Равен-
ство
у2 s © Vj, © и,, © г/,, © г/, 7 ©
(18.4.4)
Ф кх 4 © ку 6 © кх 7 © к2 5 = О
будет выполняться с вероятностью
1/2 + 2(3/4-1/2)(,/4-1/2) = 3/8,
то есть преобладание равно -’/8.
Переходим к третьему циклу. Объединяем
аппроксимации для блоков 532 и 534 в одну ли-
нейную сумму. Подставляем в аппроксимацию
блока S32 выражение г/3 5 = v2;5 © Аз,5, в аппрокси-
мацию блока 534 выражение г/3д3 = у2,7 © Аз,|3. По-
лучаем:
V, з ф Уз 7 © Уз ,з © У, , з ©
” V ,1. -.15 (18.4.5)
© v2 5 © к2 5 © v2 7 Ф к213 = 0.
Согласно лемме Мацуи эта аппроксимация
выполняется с вероятностью */2 + 2('/4 - ’/2)2 = 5/8.
Преобладание равно */8. Выражаем у2,5 © у2,7 из
(18.4.4) и подставляем в (18.4.5):
Уз 5 © Узд © Уздз © У3Д5 © И],4 ф //] 6 © Щд ©
© к\ 4 © kt# © к\ 7 © А2д © кз з Ф Аддз = 0.
Переходим к четвертому циклу шифрования.
Здесь г/д,5 = V35 © Ад,5, г/4д = у3дз © А4д,
2'4,13 =’’зд © А4;|3, 2/дд5 = узд5 © Адд5. Рассуждая
аналогично, получаем:
и4з Ф г/4д © г/4дз Ф г/дд5 © щ 4 © Щ (, © и42 ©
© А| д © к{ (, Ф k\ i © А2д © kj s © Аздз ©
© Ад,5 © Адд © Аддз © Адд 5 — 0.
Это равенство выполняется с вероятностью
3/2 + 23(3/4-'/^(’/д -’/2)3 = 15/32, то есть преобла-
дание равно - /32.
В зависимости от четности суммы разрядов
ключа равенство
414
Ил с © и. , © и. п © и. ,< ©
’ (18.4.6)
© щ 4 © г/; 6 © г/[ 7 =0
выполняется с вероятностью 15/32 или 17/32, то есть
преобладание равно ±’/32.
После составления линейных аппроксимаций
для всех циклов шифрования, кроме последнего,
приступаем к вскрытию ключа последнего цик-
ла. Биты зашифрованного текста, сложенные по
модулю 2 с битами ключа последнего цикла, да-
ют выходы v4i, подстановок S4j. Таким образом,
для данного ключа последнего цикла можно вы-
числить вход u4j подстановки Sy.
Для всех возможных ключей к5 последнего
цикла и всех зашифрованных текстов вычисляем
разряды г/41, и проверяем выполнение равенства
(18.4.6). Экспериментальное значение преобла-
дания для каждого тестируемого ключа сравни-
ваем с расчетным. Сортируем ключи по экспе-
риментальным значениям преобладания. Значе-
ние ключа к5, для которого экспериментальное
значение преобладания наиболее близко к рас-
четному, имеет наибольшие шансы оказаться
истинным.
В данном случае в равенстве (18.4.6) в заклю-
чительном сложении с ключом участвуют шесть
активных выходных разрядов (v4>4, v4 5, v4.6, v412,
v4>13, v4.i4) Для блоков подстановки 542, S44. По-
этому достаточно рассмотреть только шесть би-
тов ключа: kSA, к5А, k5fi, к5Л2, к5ЛЗ, к5М.
Процесс поиска облегчается тем, что истин-
ный ключ, как правило, обладает максимальной
абсолютной величиной экспериментальной час-
тоты преобладания. Найденное значение ключа
последнего цикла позволяет по известным шиф-
рограммам найти разряды текста щЛ, затем
вскрыть ключ четвертого цикла с использовани-
ем соответствующих аппроксимаций и т. д.
Для вскрытия ключа линейным методом не-
обходимо О(г~2) известных открытых и соответ-
ствующих зашифрованных текстов, где в— аб-
солютная величина преобладания. В рассмот-
ренном примере требуется примерно Кг блоков
открытого и соответствующего зашифрованного
текста, суммарная трудоемкость анализа состав-
ляет примерно 103 опробований. Дифференци-
альный метод в данном случае несколько более
эффективен, поскольку в используемой подста-
новке вероятности дифференциалов превышают
абсолютные величины преобладаний. Однако,
например, для шифра DES линейный метод яв-
ляется более эффективным, чем дифференциаль-
ный (это объясняется особенностями используе-
мых подстановок). В частности, для вскрытия
ключа с вероятностью 0,5 необходимо примерно
239 открытых и соответствующих зашифрованных
текстов.
Нетрудно заметить, что итоговое значение
преобладания зависит от преобладания для оди-
ночного блока подстановки и от минимального
числа блоков подстановки, участвующих в шиф-
ровании. Таким образом, для противодействия
линейному методу нужно:
1) выбирать подстановки так, чтобы минимизи-
ровать абсолютную величину максимумов
преобладаний для булевых функций, состав-
ляющих подстановку;
2) выбирать рассеивающее преобразование так,
чтобы обеспечить максимум из минимально
возможных активных блоков подстановок,
участвующих в шифровании. Согласно лем-
ме Мацуи это приводит к экспоненциально-
му снижению абсолютной величины преобла-
дания;
3) ограничить объем информации, шифруемой на
одном ключе, например, заменять ключ по-
сле зашифрования определенного числа бло-
ков;13
4) включать в открытый текст случайные биты,
не несущие никакой информации и стирае-
мые после расшифрования.
Пример 18.4.4. Оценка стойкости шифра
(длинный блок) к линейному методу.
Рассмотрим шифр из примера 17.5.1 с восе-
мью циклами шифрования.
Предположим, что точность аффинной ап-
проксимации каждого разряда на каждом цикле
шифрования не зависит от остальных разрядов и
от остальных циклов (шифр является «марков-
ским» в смысле линейного анализа).
Двоичные разряды подстановки представляют-
ся полиномами Жегалкина следующим образом:
У1 = X, © Х3 © Х4 © Х2Хз © Х2Х4 © Х3Х4 ©
© Х]Х2х3 © xix3x4;
у2 = X] © х4 © Х|Х2 © х2х3 © х3х4 © Х]Х2Хз © х2х3х4;
уз = X] © х2 © х3 © Х]Х2 © Хзх4 © xjx2x4 ф х2х3х4;
у4 = Х| © Х2 © Х3 © Х4 © Х]Хз © Х]Х2Хз © Х]Х2Х4.
Наилучшие аффинные аппроксимации этих
разрядов имеют вид:
yi = X] © х2 © х3 © х4 или у] = 1 © X] © х2;
у2 = X] © х3 © х4 или у2 = Х| © х2 © х4;
13 Для реальных шифров линейный криптоанализ
требует обычно не менее 230 блоков открытого и за-
шифрованного текста. Поэтому смена ключей не сни-
зит заметно скорость передачи информации.
уз = Xi © х2 © *з или уз = X] © х3 © х4;
у4 = Х2 © Х3 © Х4 ИЛИ Уь = X] © Х2 © Хз © х4.
Нелинейность используемой подстановки
равна 4. Это означает, что нелинейность каждой
булевой функции равна 4, то есть вероятность
того, что каждый разряд совпадет с аффинной
аппроксимацией, равна 12/16 = 3/4.
Составляем таблицу, характеризующую пре-
обладания для линейных сумм подстановки (таб-
лица 18.5).
Линейные суммы для подстановки с наи-
большей абсолютной величиной преобладания
определяются затемненными ячейками в табли-
це, всего их 32. Кроме того, подстановка облада-
ет линейными суммами веса 2, в которых един-
ственный разряд входной суммы и единственный
разряд выходной суммы равны 1 (показаны жир-
ным шрифтом). Число таких сумм равно 8, пре-
обладание для них равно +’/8. Линейные суммы,
соответствующие элементу atJ таблицы, будем
обозначать [z,j].
Таблица 18.5
Матрица разностей при линейном анализе шифра (длинный блок)
Разности выходов, представленные числами
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
Разности входов, представленные числами 0 8 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
1 0 -2 0 2 2 0 -2 0 0 2 '4' 2 -2 0 -2 Ж
2 0 2 -2 0 0 2 -2 0 0 2 -2 0 -2 2 ’ 4
3 0 0 -2 2 2 2 4 0 0 2 2 2 -2 0 0
4 0 0 0 0 0 ш 0 4 -2 2 2 -2 2 2 -2 -2
5 0 -2 0 2 -2 0 2 0 2 0 2 -4 0 2 Ч 2
6 0 -2 2 0 0 2 2 2 И 0 2 2 0 0 -2
7 0 4 2 2 -2 -2 4‘ 0 -2 2 0 0 0 0 -2 2
8 0 0 2 2 2 -2 0 2 2 0 0 0 2 -2
9 0 2 -2 0 -2 -2 0 2 0 0 2 2 ЭДк 0 -2
10 0 -2 0 -2 -2 0 2 ; 4; 2 0 -2 0 2 0 2
11 0 0 0 0 0 0 2 -2 -2 -2 2 2 -2 2
12 0 0 2 2 2 2 0 0 R 0 -2 2 -2 2 : V 0
13 0 2 -2 -2 2 0 0 2 2 0 0 2 2 0
14 0 2 эд -2 -2 0 -2 0 0 -2 ЭД 2 2 0 2 0
15 0 4 0 0 0 Ж' 0 0 0 0 0 31 0 0 0
Определим вес линейной суммы (с ненулевым
преобладанием) как число входящих в нее сла-
гаемых.14 Распределение линейных сумм с пре-
обладанием ±’/4 по весам имеет вид:
Вес Суммы данного веса
3 [1,10], [2, 12], [4, 5], [12, 8]
4 [3, 6], [3, 9], [4, 7], [6, 9], [7, 1], [8, 7], [8, 13], [9,3], [11, 2], [И, 4], [13, 4], [14, 2]
5 [1, 15], [2, 15], [5, И], [5, 14], [6, 7], [7, 6], [9,13], [10, 7], [10, 11], [12, 14], [13,3], [14, 10], [15,1], [15, 8]
6 [15, 5], [15, 12]
14 Вес линейной суммы характеризует стойкость
шифра к линейному криптоанализу. В этом смысле
минимальный вес линейной суммы подстановки ана-
логичен минимальному весу дифференциала подста-
новки, то есть коэффициенту диффузии.
Составляем характеристику из 5-блоков, актив-
ные разряды которых используются в линейной
аппроксимации. Длина характеристики, как и в
дифференциальном методе, равна шести циклам;
выходы активных разрядов 5-блоков предыдуще-
го цикла шифрования (с учетом перестановки и
сдвига) должны быть входами активных разрядов
5-блоков последующего цикла шифрования.
Для снижения сложности криптоанализа об-
щее число 5-блоков в характеристике должно
быть минимальным. Использование в характери-
стике линейных сумм веса 3, обладающих наи-
большей абсолютной величиной преобладания,
ведет к резкому возрастанию числа активных 5-
блоков, как показано на рисунке 18.2. Поэтому
на всех циклах, кроме, может быть, первого и
последнего, в характеристике должны использо-
ваться линейные суммы веса 2. Отсюда тп = 14,
итоговое преобладание составит +2-15, а для
416
вскрытия ключа потребуется 230 известных бло-
ков открытого и зашифрованного текста.15
Предположим, что в характеристике линейная
сумма 5-блока первого цикла содержит единст-
венный выходной разряд и имеет преобладание
±74, линейные суммы 5-блоков циклов 2-5 со-
держат по одному входному и одному выходно-
му разряду и имеют преобладание ±78, а линей-
ная сумма 5-блока шестого цикла содержит
единственный входной разряд и имеет преобла-
дание ±74. Тогда абсолютная величина итогового
преобладания равна
£ = 25(74)(78)4(74) = 2~6.
Таким образом, в характеристике на циклах
2-5 желательно по возможности использовать
линейные суммы веса 2. Поскольку 5-блок обла-
дает суммами веса 2 с ненулевым преобладанием
для каждого входного разряда, то существование
требуемой характеристики не вызывает сомнений.
Перенумеруем 5-блоки на z-м цикле от 5,д до
5,д6. Обозначим линейные суммы блока 5,„ ис-
пользующиеся в характеристике, через 5, ,[/, т},
где 1ит — наборы соответственно входных и
выходных переменных, входящие в линейную
сумму и представленные числами. Пример иско-
мой характеристики с положительным преобла-
данием:
№ цикла Код линейной суммы Преобладание
1 Si.i[7,1] 74
2 52]4[8, 8] 78
3 ^.7[1, И -78
4 54.8[8, 8] 78
5 ^5.13[1, 1] -78
6 56.2[8, 7] 74
Для составления линейного равенства на ос-
новании только этой характеристики требуется
Е-2 _ 2З2 известных блоков открытого и зашифро-
ванного текста. Сложность вскрытия ключа рав-
на примерно 232. Однако объем текстов можно
сократить, если воспользоваться несколькими
характеристиками, имеющими одинаковые вхо-
ды и выходы (линейные равенства могут выпол-
няться в нескольких различных вариантах).
Сложность вскрытия ключа аналогичного 16-
разрядного шифра линейным методом равна
примерно 253. Этот пример показывает, что в
подстановочно-перестановочных шифрах слож-
ность определяется не только преобладаниями,
но и весом линейных сумм.
15 Минимизация веса линейных сумм позволяет
минимизировать число S-блоков. Вопрос существова-
ния такой характеристики не рассматривается.
На сложность линейного метода могут замет-
но влиять следующие обстоятельства.
1. Линейные аппроксимации подстановки иногда
не являются независимыми. Это может приво-
дить к увеличению или снижению абсолютной
величины преобладания, оцененной согласно
лемме Мацуи, и к тому, что стойкость шифра
будет отличаться от теоретической оценки.
2. Может существовать не единственная харак-
теристика с наибольшим преобладанием, а не-
сколько характеристик, в том числе с общими
входами и выходами. Это увеличивает итого-
вое преобладание. Использование «пучка» ха-
рактеристик позволяет сократить требуемый
для вскрытия ключа объем открытых и соот-
ветствующих зашифрованных текстов.
3. Очевидно, что вместо линейной аппроксима-
ции над F2 можно использовать аффинную ап-
проксимацию над произвольным коммутатив-
ным кольцом (при этом необходимо корректно
обходиться с делителями нуля) [3]. Например,
для шифра IDEA (см. п. 19.5) может оказаться
перспективным линейный криптоанализ над
кольцом Z7216Z или над Z7(216 + 1 )ZL
4. Сходство линейного и дифференциального
методов позволяет их объединить, используя
преобладания линейных сумм для разностей
текстов (при условии, что активные 5-блоки
в характеристике совпадают). Это сделано в
дифференциально-линейном методе крипто-
анализа [20], который требует подобранных
открытых текстов. Такой метод может быть
несколько эффективнее, чем чисто линей-
ный, поскольку можно ослабить влияние 5-
блоков, использующихся на первых циклах.
Поскольку на каждом цикле в характеристику
входит хотя бы один 5-блок, в общем случае стой-
кость шифра к линейному методу растет экспонен-
циально с ростом числа циклов шифрования. По-
этому почти каждый шифр (за исключением вы-
рожденных случаев) можно сделать гарантирован-
но стойким по отношению к линейному методу.
18.5. Анализ степенных
шифров методом сдвига
Этот метод криптоанализа, опубликованный
А. Бирюковым и Д. Вагнером в 1999 г. [10], ос-
нован на сдвиге процесса шифрования на один
или несколько циклов («slide attack»)16 по анало-
гии с методом списка ключей.
16 Перевод слова slide как сдвиг представляется более
подходящим по сути метода, чем буквальный перевод.
417
Сложность дифференциального и линейного
методов криптоанализа возрастает с ростом чис-
ла циклов шифрования (см. п. 18.2). А поскольку
многие современные шифры имеют большое
число циклов шифрования (RC6— 20 циклов,
MARS — 32 цикла, CAST — 48 циклов), пред-
ставляют интерес методы криптоанализа, слож-
ность которых не зависит (с точностью до поли-
нома) от числа циклов шифрования. Криптоана-
лиз методом сдвига удовлетворяет указанному
требованию.
Предположим, что шифр является степен-
ным, то есть все г циклов шифрования реализуют
одинаковые подстановки. Обозначим через x,i
вход Тго цикла шифрования, х, = F(x,-i), где F—
оператор шифрования на одном цикле,
xr = Fr(x0). Предположим, что ключ шифрования
легко вскрыть по известным х,_] и х,.
В рассматриваемом методе ищутся такие па-
ры открытых и зашифрованных текстов (х0, х,.),
(х0', х,'), что хо = X] (открытый текст второй пары
совпадает с результатом зашифрования на одном
цикле открытого текста первой пары). Тогда
х/ = х,.+1. Согласно парадоксу дней рождения,
если число пар открытых и зашифрованных тек-
стов равно <9(2''^2), то такие пары найдутся с ве-
роятностью (9(1). Для фейстелевых шифров, в
которых обработка текстов ведется половинами
блока, нужно знать <9(2"^4) пар открытых и за-
шифрованных текстов. Если для вскрытия ключа
требуется несколько блоков открытого и зашиф-
рованного текста, то соответственно нужно най-
ти несколько указанных пар (это не меняет
асимптотическую емкостную сложность). Как
только такие пары найдены, вскрытие ключа од-
ного цикла легко выполняется с использованием
пары (хо, хо).
Таким образом, для быстрого вскрытия ключа
нужно уметь находить указанные пары. Их поиск
выполняется путем проверки одновременного
выполнения равенств
4 = ^(х0),
x'r = F(xr)
(18.5.1)
для одного и того же ключа и сортировки тек-
стов в соответствии с этим признаком. При этом
нет необходимости просматривать все пары тек-
стов (такой просмотр имеет переборную слож-
ность), достаточно отфильтровать большую до-
лю заведомо неподходящих пар (возможно, в
несколько приемов). Отметим, что для фейстеле-
ва шифра отбраковка таких пар выполняется
особенно легко: достаточно сравнить левые по-
лублоки открытых и зашифрованных текстов
одной пары с соответствующими правыми полу-
блоками другой пары. Такой фильтр отсеивает
подавляющее большинство ложных пар. Для ос-
тавшихся пар можно выполнять более подроб-
ную проверку способом (18.5.1).
Аналогично можно выполнять анализ некото-
рых других шифров, например, шифров с двумя
чередующимися ключами: на нечетных циклах
используется первый ключ, на четных — второй
[10]. Такой шифр является степенным относи-
тельно пары циклов шифрования. В этом случае
вскрытие ключа методом сдвига осуществляется
так же, как и для обычного степенного шифра,
но для двух первых циклов. Данное рассуждение
может быть обобщено на случай трех и более
чередующихся ключей.
На практике список ключей, используемых на
различных циклах шифрования, делается не
вполне периодическим, но и не очень сложным.
Известны разновидности метода сдвига — сдвиг
с кручением (sliding with a twist) и сдвиг с допол-
нением (complementation slide) [10, 15], что дела-
ет этот метод применимым для более широкого
класса шифров.
Сдвиг с дополнением используется в том слу-
чае, когда цикловые ключи повторяются, напри-
мер, с периодом 2. Предыдущий вариант атаки
предусматривает сдвиг на два цикла шифрова-
ния, что усложняет вскрытие ключа, так как в
случае фейстелева шифра требуется 2"^2, а не
2"/4 блоков текста. Данный вариант позволяет
обойтись сдвигом на один цикл. Это значительно
сокращает требуемый объем статистики для
фейстелева шифра, а также упрощает распозна-
вание случая сдвига (случая равенств (18.5.1)).
Пусть фейстелев шифр использует операцию
поразрядного сложения с ключом ko||ki по мо-
дулю 2, то есть перед зашифрованием с помо-
щью цикловой функции шифрования F полублок
х" складывается с ключом к« или к! (ключи к« и
к] чередуются).
Рассмотрим зашифрование двух блоков (х' || х"
и и'|| и") на первых четырех циклах, где блок
и' || и" «похож» на результат зашифрования бло-
ка х'||х" на первом цикле. Обозначим ко © к]
через к, а результат зашифрования указанных
блоков на четырех циклах через у' || у" и v' || v"
соответственно. Если
и' = х" © к;
(18.5.2)
и" = х' © F(k0 © х") © к,
то после четвертого цикла с учетом равенства
к] © к = ко получим
v' = y"©k;
(18.5.3)
v" = у'© F(k0 © у") ® к.
418
Аналогичные равенства будут справедливы
после 8, 12, ...,4/и циклов шифрования для
т > 2. Поскольку обычно число циклов шифро-
вания кратно четырем, такие же равенства будут
справедливы и для шифртекстов.
Будем говорить, что пара открытых текстов х, х'
имеет сдвинутую разность d, если F(x) © х' = d. Та-
ким образом, в ходе шифрования сдвинутая раз-
ность (к) повторяется с периодом 4. Криптоана-
лиз такого шифра на основе известных открытых
текстов и соответствующих шифртекстов заклю-
чается в выявлении пар текстов (х' || х", и' || и") с
указанным свойством. Согласно парадоксу дней
рождения такие пары с большой вероятностью
могут быть выявлены на объеме статистики по-
рядка 2^2.
Ситуация, когда сдвинутая разность текстов
равна сдвинутой разности цикловых ключей,
может быть эффективно распознана. Для этого
необходимо проверить совместность систем
уравнений (18.5.2) и (18.5.3) для открытых тек-
стов и соответствующих шифртекстов.
После нахождения указанной пары текстов
ключ ко может быть вскрыт решением второго
уравнения в (18.5.2) для одиночного цикла шиф-
рования (предполагается, что функция F являет-
ся криптографически слабой и вскрытие ключа
для нее выполняется легко), затем ключ 1ц опре-
деляется решением первого уравнения в (18.5.2).
Для противостояния методу сдвига шифр не
должен быть степенным. Этого можно избежать,
если на разных циклах выбирать цикловые клю-
чи по нетривиальному закону или изменять
уравнения шифрования от цикла к циклу (на-
пример, ввести зависящую от номера цикла пе-
рестановку или подстановку).
18.6. Генерация экстремальных
подстановок для шифров
Некоторые шифры, например, ГОСТ 28147-89,
используют подстановки, которые не являются
фиксированными. Для того чтобы шифр имел
максимальную стойкость к линейному и диффе-
ренциальному методам криптоанализа, подста-
новка должна обеспечивать минимальную абсо-
лютную величину преобладания линейных сумм
и минимальную вероятность наиболее вероятных
дифференциалов. Это обусловливает актуаль-
ность задачи выбора подстановок, повышающих
стойкость шифра.
18.6.1. Экстремальные подстановки
Если диффузия шифра определяется подста-
новкой, то наиболее вероятные дифференциалы
подстановки и линейные суммы с наибольшим
преобладанием должны иметь по возможности
большой вес. Желательно, чтобы дифференциа-
лы веса 2 имели нулевую вероятность, а линей-
ные суммы веса 2 — минимальную абсолютную
величину преобладания (или наоборот: суммы
веса 2 — нулевое преобладание, а дифференциа-
лы веса 2 — минимальную вероятность). Если
перемешивающие свойства шифра в значитель-
ной степени определяются переносами при сло-
жении (как, например, в ГОСТ 28147-89), то
подстановка должна переводить слова веса 0 или
1 в слова большего веса.
Группа аффинных преобразований «-мерных
векторов содержит подгруппу РА, элементы ко-
торой соответствуют перестановке разрядов век-
тора и сложению его с константой. Согласно
п. 18.1 на нелинейность подстановки не влияют
аффинные преобразования, примененные к ее
входу и выходу. На коэффициент диффузии под-
становки не влияют операции из подгруппы РА
аффинных преобразований, примененные ко
входу и выходу подстановки. Произвольные аф-
финные преобразования могут изменять коэф-
фициент диффузии. Аффинное преобразование
входа (выхода) подстановки эквивалентно умно-
жению ее слева (справа) на подстановку, опреде-
ляемую указанным аффинным преобразованием.
Такие преобразования приводят к перестановке
строк и столбцов матрицы XOR-дифференциа-
лов. Поэтому аффинные преобразования входа и
выхода изменяют вид этих дифференциалов, но
сохраняют значение вероятности.
Назовем подстановку экстремальной, если
она:
- имеет минимально возможную абсолютную
величину преобладания линейных сумм;
- имеет минимально возможную вероятность
наиболее вероятных дифференциалов.17
Умножение экстремальной подстановки спра-
ва и слева на аффинные подстановки дает экстре-
мальную подстановку. Умножение подстановки
справа и слева на группу РА не меняет вероятно-
сти дифференциалов данного веса и абсолютной
величины преобладания линейных сумм данного
веса. Поскольку умножение входа и выхода экс-
тремальной подстановки на элементы группы РА
дает экстремальную подстановку (при этом со-
храняются вероятности дифференциалов веса 2 и
17 Желательно также, чтобы каждая булева функ-
ция, задающая подстановку, существенно зависела от
всех входных переменных. Кроме того, по результа-
там криптоанализа шифра на подстановку могут на-
кладываться дополнительные требования (см., напри-
мер, п. 19.6.1).
419
абсолютные величины преобладаний линейных
сумм веса 2), то множество экстремальных под-
становок можно разбить на классы. При этом экс-
тремальные подстановки S и Т будут РА-
эквивалентными, если S = ATB, где А, В е РА. По-
этому класс /’/-эквивалентных подстановок мож-
но задать подстановкой, переводящей 0 в 0.
18.6.2. Булевы функции
для экстремальных подстановок
Рассмотрим нелинейные свойства сбаланси-
рованных четырехразрядных булевых функций.
Для удобства будем рассматривать булевы
функции с точностью до аффинной эквивалент-
ности. Оказывается, что число аффинно неэкви-
валентных булевых функций четырех перемен-
ных {xj, ...,х4} невелико. Так, по определению
все аффинные функции аффинно эквивалентны,
поэтому любую аффинную функцию можно за-
дать представителем у = хр
Теорема 18.6.1. Множество сбалансирован-
ных булевых функций с нелинейностью 2 пред-
ставляется функцией f= Xi © х2х3х4 с точностью
до аффинной эквивалентности.
Доказательство. Существует аффинная бу-
лева функция fa, отличающаяся от f только на
двух наборах аргументов. С помощью аффинной
замены переменных можно получить fa = X\- С
учетом такой замены функция f принимает зна-
чение 0 в точности на одном из наборов вида
(1, а, Ъ, с), иначе она не будет сбалансированной.
Тогда с помощью обратимой аффинной замены
переменных можно сделать так, что функция f
будет принимать значение 0 для заданного набо-
ра (1, 1,1,1). Покажем, что существует обрати-
мая аффинная подстановка л, которая переводит
Xi в X] и заданный набор (1, а, Ь, с) в (1, 1, 1, 1).
Аффинной подстановкой, сохраняющей непод-
вижным аргумент хь является, например, единич-
ная подстановка. Такие аффинные подстановки
образуют подгруппу в группе аффинных подста-
новок. Пример искомой аффинной подстанов-
ки— подстановка (хь х2©а®1, х3®/>©1,
х4 ф с © 1). Таким образом, можно рассматривать
булеву функцию с таблицей истинности:
В незаполненной левой части таблицы долж-
но быть единственное нулевое значение. Пока-
жем, что обратимой аффинной заменой перемен-
ных таблицу можно привести к виду:
Для этого покажем, что можно перевести еди-
ничное значение в таблице истинности либо в
точку (0, 1, 1. 1), либо в точку (0, 0, 1, I), то есть
что существует аффинная подстановка л такая,
что л(хь *, *, *) = (хь *, *, *), л(1, 1,1,1) = (1,1,1, 1),
и выполняется только одно из двух условий:
л(0, d, e,g) = (0,1,1,1) или л(0, d, e,g) = (0,0,1, 1).
Поскольку четырехразрядная подстановка л со-
храняет неподвижным значение хь то достаточно
рассмотреть аффинную подстановку от трех пе-
ременных: л(х2, х3, х4). По второму свойству име-
ем: л(1, 1, 1) = (1, 1, 1). Поэтому если (d, е, g) =
= (1,1, 1), то л(0, d, е, g) = (0, 1,1, 1). Если (J,e,g)?b
(1,1, 1), то возможны семь случаев:
(d, е, g) Возможный вид подстановки л(х2, х3, х4)
(0, 0, 0) (х2, 1 ф Х2 ф Хз, 1 © х2 © х4)
(0, 0, 1) (х2, 1 ф х2 © х3, х4)
(0,1,0) (х2, 1 ф Х2 © Хз, 1 © х2 ф х4)
(0, 1, 1) (х2, Хз, х4)
(1,0,0) (х3, 1 © Х2 ф Х3, Х2 ф Хз ф Х'4)
(1, 0, 1) (х3, х2, х4)
(1,1,0) (х4, х2, Хз)
В каждом из этих случаев имеем л(1, 1, 1, 1) =
= (1, 1,1, 1). Таким образом, каждую сбаланси-
рованную функцию с нелинейностью 2 можно
свести к одной из двух функций:
/1 = Х1 Ф Х2ХзХ4
или
f = X] ф ХзХ4(Х]Х2 ф (1 © Х1)(1 © х2)).
Теперь покажем, что эти две булевы функции
аффинно эквивалентны. Раскроем скобки у
функции fi, получим /2 = Х| © (I © Х| © х2)хзх4. Де-
лаем обратимую аффинную замену переменных
л(хь х2, Хз, х4) = (xj, 1 Ф Xi © х2, Хз, х4) и получаем
формулу дляД.
Теорема 18.6.2. Существуют ровно две сба-
лансированные аффинно неэквивалентные буле-
420
вы функции с нелинейностью 4: /j = Xi ® х2х3 и
f2 = X] ф Х3 © Х(Х3 © Х2Х3 © Х3Х4 © Х|Х2Х3.
Доказательство. Выбираем аффинную ап-
проксимацию /й(Х|, Х2, Х3, Х4) = Х|. С помощью
аффинной замены переменных х2, хз, х4 делаем
так, что *,*,*) = 1 всюду, за исключением
двух точек: Д], 1, 1, 1) = 0 иУ(1, О, 1, 1) = 0. Воз-
можность такой аффинной подстановки указана
в теореме 18.6.1. Получаем таблицу истинности:
Если (0, d, е, g) = (0, 0, 1, 1), то канонический
представитель имеет вид х, © х2х3.
Предположим, что (0, d, е, g) Ф (0, 0, 1, 1). Ес-
ли d = 0, то, заменяя х2 на X] © х2 © х3 © х4,
Х1©х2©хз©1 или Х]©х2©х4©1, получаем
d- 1. Если е = 0, то, заменяя х3 на х2©х3© 1,
получаем е = 1. Следовательно, существуют
только две аффинно неэквивалентные булевы
функции:
- X] © х2х3, задаваемая таблицей
В незаполненной левой части таблицы стоят
две единицы, остальные элементы — нули.
Рассмотрим варианты приведения двух ос-
тавшихся единичных значений булевой функции
к стандартным наборам аргументов. Соответст-
вующая обратимая аффинная замена переменных
должна сохранять неподвижными элемент
вектор (1, 1, 1,1) и вектор (1, 0, 1, 1) или перево-
дить эти векторы друг в друга. Пусть единичные
элементы в левой части таблицы стоят на пози-
циях (0, а, Ь, с) и (0, d, е, g). Переведем вектор
(О, а, Ь, с) в (0, 1, 1, 1). Если Ь = 0, то, заменяя х3
на X] © хз © 1, получаем 6 = 1. Если (0, а, Ь, с) =
= (0,1, 1,1) или (0, а, Ь, с) = (0, 0, 1, 1), то вы-
полняем тождественное преобразование или за-
меняем х2 на 1 © х2. Если (0, а, Ь, с) = (0, 1, 1, 0)
или (0, а, Ь, с) = (0, 0, 1, 0), то заменяем х4 на
X] © х4 © 1 и при необходимости заменяем х2 на
1 © х2. Таблица примет вид
Здесь в незаполненной левой части осталась
единственная единица.
Для нахождения канонических представите-
лей аффинная замена переменных должна сохра-
нять неподвижными элемент Х| и векторы
(1, 1, 1, 1), (1, 0, 1, I) (или переводить их друг в
друга), а также сохранять неподвижным вектор
(0, 1,1,1) или переводить друг в друга векторы
(0, 1, 1, 1)и(0, d,e,g).
- Xi © хз © Х]Х3 © х2х3 © х3х4 © Х]Х2х3, задавае-
мая таблицей
Экстремальная подстановка может содержать
только булевы функции, определенные теоремой
18.6.2. Эксперимент показывает, что если одна из
булевых функций подстановки имеет вид
X] © х2х3, то невозможно подобрать три другие
булевы функции так, чтобы они задавали подста-
новку и имели нелинейность 4. Таким образом,
экстремальные подстановки можно строить толь-
ко с использованием булевых функций, аффинно
эквивалентных функции х, © х2х3 © Х]ХзХ4 © Х]Х2х3.
18.6.3. Примеры экстремальных подстановок
Приведем примеры экстремальных подстано-
вок. Поскольку порядок группы РА равен
16 • 4! = 3 • 27, то каждая экстремальная подста-
новка задает от 3 • 27 до З2 - 214 подстановок из
соответствующего класса. Верхняя оценка полу-
чается, если среди подстановок ASB при А,
В е РА нет одинаковых, нижняя оценка — если
для каждой подстановки А е РА и экстремальной
подстановки S существует подстановка В & РА
такая, что AS = SB.
421
Каждая экстремальная подстановка также по-
зволяет получить широкий класс подстановок ум-
ножением их справа и слева на вспомогательные
аффинные подстановки, не принадлежащие груп-
пе Ра- Выбором указанных аффинных подстано-
вок можно уменьшить число дифференциалов
веса 2 с ненулевой вероятностью и число линей-
ных сумм веса 2. Такие подстановки могут быть
рекомендованы для стандарта ГОСТ 28147-89
(см. п. 19.6). При этом желательно выбрать вспо-
могательные аффинные подстановки так, чтобы
входные слова веса 0 или 1 переводились в слова
большего веса, а взвешенная сумма дифферен-
циалов веса 2 с учетом их вероятностей и линей-
ных сумм веса 2 с учетом абсолютной величины
их преобладания была минимальна.
Заметим, что при сложении над IF2 входа или
выхода подстановки с произвольным вектором
распределение вероятностей дифференциалов и
линейных сумм не меняется. Поэтому можно ог-
раничиться рассмотрением линейных подстано-
вок А, В из группы невырожденных матриц
GL4(F2). Поиск указанных линейных подстано-
вок можно ускорить с учетом следующих сооб-
ражений.
1. Если L— искомая линейная подстановка
(невырожденная матрица), Р— группа мат-
риц перестановки, то PL и LP — тоже иско-
мые линейные подстановки. Поэтому поиск
матрицы L можно вести в пересечении пра-
вых и левых смежных классов группы
GL4(F2) по подгруппе Р, содержащих еди-
ничный элемент.18
2. Умножение матрицы L справа и слева на
группу Р не меняет число единиц как в
столбцах, так и в строках. Поэтому элементы
смежного класса можно задать парой спи-
сков: единиц по строкам и единиц по столб-
цам. Поскольку L отлична от матрицы пере-
становки и невырождена, множество списков
единиц по строкам и по столбцам имеет вид:
(2,1, 1,1); (3,1, 1,1); (4,1, 1,1); (2, 2, 1, 1);
(3,2,1,1); (3,3,1,1); (4, 2, 1,1); (4, 3, 1,1);
(2,2,2,1); (3,2,2,1); (3, 3,2,1); (3, 3,3,1);
(4,2,2,1); (4, 3,2,1); (4, 3, 3,1); (3, 2, 2, 2);
(3,3, 2, 2); (3,3, 3,2); (4, 3, 2, 2); (4, 3, 3, 2);
(3,3, 3,3); (4, 3, 3, 3). Здесь каждое из четырех
чисел списка означает число единичных раз-
рядов в соответствующей строке (столбце).
Одному и тому же списку по строкам может
соответствовать несколько различных спи-
18 Здесь удобно было бы рассмотреть фактор-
группу GL4(F2)/P. Однако GL4(F2) не имеет нормаль-
ных подгрупп [2], поэтому такой факторгруппы не
существует.
сков по столбцам. Перечисление матриц,
удовлетворяющих парам списков с учетом
действия группы Р, не составляет большого
труда. Например, у класса, соответствующе-
го списку строк (2, 1, 1, 1), есть единствен-
ный представитель:
41 1 О О'
0 1 0 О
0 0 10'
<0 0 0 1,
Аналогично классы, соответствующие спи-
скам строк (3, 1, 1, I) и (4, 1, 1, 1), имеют по од-
ному представителю.
Обозначим NL(,S) — нелинейность подста-
новки, s(5)— максимальную абсолютную вели-
чину преобладания; k/S)— коэффициент диф-
фузии, PCI(S) — вероятность наиболее вероятного
дифференциала. Для четырехразрядной подста-
новки выполняется неравенство NL(5)<4 [14].
При этом равенство достигается только тогда,
когда нелинейность каждой булевой функции,
задающей подстановку, равна 4.
Пример 18.6.1. Экстремальные подстановки.
1. Подстановка S] = (0, 13, 11, 8, 3, 6, 4, 1, 15, 2,
5, 14, 10, 12, 9, 7) из примеров гл. 17, 18.
Тад) = 4, 8(50 = 74, Ш>) = 1, ^i) = 74, Диф-
ференциалы веса 2 являются невозможными, од-
нако существуют линейные суммы веса 2 с пре-
обладанием ±’/8 (см. пример 18.4.4). Эта подста-
новка обеспечивает максимальную стойкость
подстановочно-перестановочных шифров к диф-
ференциальному методу анализа.
2. Подстановка, заданная над конечным по-
лем уравнением >S'2(x) = х-1 (mod /4 + t + 1) в поле
IF16, причем >S'2(0) = 0. В табличном виде = (0,
1, 9, 14, 13, 11, 7, 6, 15, 2, 12, 5, 10, 4, 3, 8). Здесь
NLCS2) = 4, s(S2) = '/4, PdtSz) = V4. Отметим, что
>S22(x) = х — единичное отображение (подста-
новки с таким свойством называются инволю-
циями). Переход к заданию поля F]6 другим не-
приводимым полиномом дает подстановки, аф-
финно эквивалентные подстановке S2. Эта экс-
тремальная подстановка имеет дифференциалы
веса 2 с ненулевой вероятностью и поэтому не
является идеальной для подстановочно-
перестановочных шифров. Из свойства S2 = S2~l
и того, что при переходе к обратной подстанов-
ке матрица дифференциалов заменяется на
транспонированную, следует, что S2 обладает
симметрической матрицей дифференциалов.
Аналогично можно показать, что матрица пре-
обладаний для линейных сумм тоже является
симметрической. .
422
Дифференциал [1,1] веса 2 имеет вероятность
’/4. Линейные суммы веса 2 встречаются с преоб-
ладанием ±'/8.
3. Подстановка, заданная над конечным полем
уравнением 5'3(х)^х7 (mod? + /+ 1) в поле IF16,
причем А’з(О) = 0. Здесь S32 3 * = S2 (см. предыдущий
пример). В табличном виде S3 = (0, 1, 11, 13, 9,
14, 6, 7, 12, 5, 8, 3, 15, 2, 4, 10). Имеем NL(53) = 4,
e(S3) = ]/4, PJS-i) = '/4. Эта экстремальная подста-
новка имеет дифференциалы веса 2: один диф-
ференциал, обладающий вероятностью 1/4, и че-
тыре дифференциала, обладающие вероятностью
*/8. Коэффициент диффузии равен 0. Кроме того,
подстановка S3 имеет линейную сумму веса 2, ко-
торая выполняется с преобладанием '/4. Эта же
подстановка может быть задана аналитически
над другим полем: >S4(*) = %5 (mod 17 1),19 причем
19 Другие показатели степени, отличные от 5, не
дают экстремальной подстановки.
нулевой аргумент перед возведением в степень
заменяется на -1, а значение функции -1 заменя-
ется на 0.
4. Экстремальная подстановка (0, 1, 2, 4, 3, 5,
8, 10, 7, 9, 6, 13, 11, 14, 12, 15) обладает диффе-
ренциалами, вероятность которых не более /4.
Среди таких дифференциалов три имеют вес 2.
Абсолютная величина преобладания для линей-
ных сумм не превышает ]/4, но три из них имеют
вес 2.
Еще шесть экстремальных подстановок, обла-
дающих дифференциалами с вероятностью не
более ’/4 и линейными суммами с абсолютной
величиной преобладания не более '/4, перечисле-
ны в таблице 18.6.
? Таблица 18.6
Экстремальные подстановки, обладающие дифференциалами с вероятностью не более */4
и линейными суммами с абсолютной величиной преобладания не более '/4
Подстановка Число дифференциалов веса 2 Число линейных сумм веса 2
Erf=74 Pd='/g е = */4 е — '/8
(0, 1, 11, 2, 8, 6, 15, 3, 14, 10,4, 9, 13, 5, 7, 12) 0 7 2 7
(0, 1, 11,2, 8, 3, 15, 6, 14, 10, 4, 9, 13, 5, 7, 12) 1 6 2 7
(0, 4, 11, 2, 8, 6, 10, 1, 14, 15, 3, 9, 13, 5, 7, 12) 0 9 3 8
(0, 4, 11,2, 8, 3, 15, 1, 14, 10, 6, 9, 13, 5, 7, 12) 1 7 2 8
(0, 11, 15, 9, 1, 5, 6, 8, 3, 10, 4, 12, 14, 13, 7, 2) 2 4 1 9
(0, 7, 10, 14, 9, 1, 13, 8, 12, 2, 11, 15, 3, 5, 4, 6) 2 4 2 И
Упражнения к главе 18
1. Предположим, что шифр реализует на одном
цикле шифрования операции сложения по
модулю 2 и подстановку, заданную форму-
лой у = кх (mod 2"), где к — нечетное число.
Покажите, что такой шифр будет нестойким
к линейному анализу.
2. Можно ли повысить эффективность линей-
ного метода, если при составлении линейных
сумм двигаться к середине от открытого тек-
ста и от зашифрованного текста, по аналогии
с решеточным методом?
3. Предложите пример шифра, в котором ха-
рактеристика, задающая наиболее вероятные
дифференциалы, описывается периодической
зависимостью.
4. Приведите пример нелинейной подстановки,
в которой наиболее вероятный дифференци-
ал неподвижен.
5. Два шифра используют операции сложения с
ключом по модулю 2, одну и ту же подста-
новку в качестве нелинейного перемеши-
вающего оператора и различаются только
операторами рассеивания. Первый шифр ис-
пользует перестановку битов в блоке, а вто-
рой — умножение блока как вектора над Е2
на квадратную матрицу общего вида. Объяс-
ните, почему второй шифр в общем случае
будет более стойким к линейному и диффе-
ренциальному анализу.
6. Приведите пример шифра с нелинейным
уравнением шифрования, уязвимого по от-
423
ношению к линейному методу над кольцом,
отличным от IF2.
7. Предложите свой вариант подстановки, ко-
торая описывается нелинейными уравнения-
ми, но характеризуется большим преоблада-
нием для линейной суммы.
8. Определите коэффициент диффузии для
квадратной матрицы размера 2и, содержащей
нули на главной диагонали и остальные эле-
менты — единичные.
9. Определите, удовлетворяет ли блок подста-
новки из примеров гл. 17 требованию строго-
го лавинного критерия.
10. *Предположим, что в подстановочно-пере-
становочном шифре все дифференциалы
имеют вероятность 0 или р. Предложите алго-
ритм поиска характеристики, обеспечиваю-
щей максимум вероятности (г - 1)-циклового
дифференциала.
11. Почему в линейном методе итоговое преоб-
ладание умножается на степень двойки (со-
гласно лемме Мацуи), показатель которой
пропорционален не числу битов в линейной
сумме, а числу .S-блоков?
12. Предложите свои варианты экстремальных
подстановок, аффинно не эквивалентных
подстановкам из примера 18.6.1.
13. Является ли композиция инволюций инво-
люцией? Что можно сказать о длинах циклов
подстановки, полученной как композиция
двух инволюций?
14. Оцените зависимость стойкости шифра к
дифференциальному методу от коэффициен-
та диффузии.
15. *Может ли нелинейная подстановка иметь
нулевое преобладание для всех линейных
сумм веса 2?
16. *Подстановку как набор полиномов можно
записать в проективной форме (см. п. 6.15.5).
Назовем эквивалентными подстановки, кото-
рые описываются изоморфными проектив-
ными полиномами (с точностью до переста-
новки элементов {X,} u {ZJ). Что собой
представляет множество классов эквивалент-
ности для симметрической группы?
17. Адаптируйте атаку «бумеранг» к линейному
методу. ; ...
Литература к главе 18
1. Ван дер Варден Б.Л. Алгебра. М.: Наука, 1979.
2. Каргополов М.И., Мерзляков Ю.И. Основы тео-
рии групп. М.: Наука, 1982.
3. Berson Т.А. Differential cryptanalysis mod 232 with
applications to MD5 11 Advances in Cryptology —
EUROCRYPT ’92. Lecture Notes in Computer Sci-
ence. Springer-Verlag. 1993. Vol. 658. P. 71-80.
4. Biham E. New types of cryptanalytic attacks using
related keys П Advances in Cryptology —
EUROCRYPT ’93. Lecture Notes in Computer Sci-
ence. Springer-Verlag. 1994. Vol. 765. P. 398-409.
5. Biham E., Biryukov A., Shamir A. Cryptanalysis of
Skipjack reduced to 31 rounds using impossible dif-
ferentials. Technion - Computer Science Depart-
ment-Technical Report CS0947. 1998 // http://
www.simovits.com/archive/cs0947.pdf.
6. Biham E., Dunkelman O., Keller N. The rectangle
attack— rectangling the Serpent // Advances in
Cryptology — EUROCRYPT 2001. Lecture Notes in
Computer Science. Springer-Verlag. 2001.
Vol. 2045. P. 340-357.
7. Biham E., Shamir A. Differential cryptanalysis of
DES-like cryptosystems // Advances in Cryptol-
ogy — CRYPTO ’90. Lecture Notes in Computer
Science. Springer-Verlag. 1991. Vol. 537. P. 2-21.
8. Biham E., Shamir A. Differential cryptanalysis of
FEAL and N-hash // Advances in Cryptology —
EUROCRYPT’91. Lecture Notes in Computer Sci-
ence. Springer-Verlag. 1991. Vol. 547. P. 1-16.
9. Biham E., Shamir A. Differential cryptanalysis of the
full 16-round DES 11 Advances in Cryptology —
CRYPTO ’92. Lecture Notes in Computer Science.
Springer-Verlag. 1993. Vol. 740. P. 487-496.
10. Biryukov A., Wagner D. Slide attacks // Fast Soft-
ware Encryption FSE ’99. Lecture Notes in Com-
puter Science. Springer-Verlag. 1999. Vol. 1636.
P. 245-259.
11. Granboulan L. Flows in differential cryptanalysis of
Skipjack // http://eprintiacr.org/ 2001/038/.
12. Harpers C., Kramer G.G., Massey J.L. A generaliza-
tion of linear cryptanalysis and the applicability of
Matsui’s piling-up lemma П Advances in Cryptol-
ogy— EUROCRYPT’95. Lecture Notes in Com-
puter Science. Springer-Verlag. 1995. Vol. 921.
P. 24-38.
13. Heys H.M. A tutorial on linear and differential crypt-
analysis // http://www.engr.mun.ca/~howard/Research/
Papers/.
14. Heys H.M., Tavares S.E. Substitution-permutation
networks resistant to differential and linear cryptana-
lysis // Journal of Cryptology. 1996. Vol. 9. P. 1-19.
15. Kelsey J., Schneier B., Wagner D. Key-schedule
cryptanalysis of IDEA, G-DES, GOST, SAFER, and
Triple-DES 11 Advances in Cryptology —
CRYPTO ’96. Lecture Notes in Computer Science.
Springer-Verlag. 1996. Vol. 1109. P. 237-251.
16. Knudsen L.R. Truncated and higher order differen-
tials // Fast Software Encryption. Second Interna-
tional Workshop. Lecture Notes in Computer Sci-
ence. Springer-Verlag. 1995. Vol. 1008. P. 196-211.
17. Knudsen L.R., Robshaw M.J.B. Non-linear approxima-
tions in linear cryptanalysis H Advances in Cryptol-
ogy— EUROCRYPT ’96. Lecture Notes in Computer
Science. Springer-Verlag. 1996. Vol. 1070. P. 224-236.
18. Knudsen L., Rijnmen V. Truncated differentials of
IDEA // ftp://ftp.esat.kuleuven.ac.be/pub/COSIC/
knudsen/idea trunc.ps.z.
19. Lai X., Massey J.L., Murphy S. Markov ciphers and
differential cryptanalysis 11 Advances in Cryptology —
EUROCRYPT’91. Lecture Notes in Computer Sci-
ence. Springer-Verlag. 1991. Vol. 547. P. 17-38.
20. Langford S.K., Hellman M.E. Differential-linear
cryptanalysis // Advances in Cryptology —
CRYPTO ’94. Lecture Notes in Computer Science.
Springer-Verlag. 1994. Vol. 839. P. 17-25.
21. Matsui M. Linear cryptanalysis method for DES cipher
// Advances in Cryptology — EUROCRYPT ’93. Lec-
ture Notes in Computer Science. Springer-Verlag.
1994. Vol. 765. P. 386-397.
22. Ohta K., Aoki K. Linear cryptanalysis of the Fast
Data Encipherment Algorithm // Advances in Cryp-
tology — CRYPTO ’94. Lecture Notes in Computer
Science. Springer-Verlag. 1994. Vol. 839. P. 12-16.
23. Seberry J., Zhang X.-M. Highly nonlinear 0-1 balanced
Boolean functions satisfying string avalanche criterion //
Advanced in Cryptology — AUSCRYPT ’92. Lecture
Notes in Computer Science. Springer-Verlag. 1993.
Vol. 718. P. 145-155.
24. Wagner D. The boomerang attack // Fast Software
Encryption. 6th International workshop, FSE’ 99.
Lecture Notes in Computer Science. Springer-
Verlag. 1999. Vol. 1636. P. 156-170.
25. Webster A.F., Tavares S.E. On the design of S-boxes
// Advances in Cryptology— CRYPTO ’85. Lecture
Notes in Computer Science. Springer-Verlag. 1986.
Vol. 218. P. 523-534.
Глава 19. ПРИМЕНЕНИЕ ИТЕРИРОВАННЫХ ШИФРОВ
И ХЭШ-ФУНКЦИЙ
В данной главе рассматриваются вопросы
применения шифров, а также некоторые попу-
лярные отечественные и зарубежные итериро-
ванные криптоалгоритмы. Способ описания
криптоалгоритмов выбран таким, чтобы лучше
просматривалась их алгебраическая структура (а
не удобство программной или аппаратной реали-
зации).
а) Зашифрование б) Расшифрование
19.1. Режимы шифрования
Под режимом шифрования будем понимать
способ получения шифртекста из открытого тек-
ста или расшифрованного текста из шифртекста
с помощью блочного шифра.
19.1.1. Режим простой замены
При шифровании в режиме простой замены
(в зарубежной литературе — электронная кодо-
вая книга (electronic codebook, ЕСВ); рис. 19.1)
текст разбивается на блоки, каждый из которых
шифруется независимо от других на одном и том
же ключе: у = ЕДх) при зашифровании,
х = Д'(у) при расшифровании. Таким образом,
одинаковые блоки открытого текста переходят в
одинаковые блоки зашифрованного текста. По
сути, этот режим аналогичен полиалфавитной за-
мене, зависящей от ключа. Например, если длина
блока — 64 бита, а длина одной «буквы» в ASKII-
кодах — 8 бит, то шифрование в режиме простой
замены текста, написанного на естественном язы-
ке, — это восьмибуквенная подстановка.
Источник открытых текстов часто обладает
большой избыточностью. Далеко не все блоки
открытого текста являются равновероятными.
Это позволяет применять для дешифрования
шифрограмм, полученных с помощью режима
простой замены, частотный криптоанализ. Воз-
можен также криптоанализ «со словарем», когда
составляется словарь из наиболее употребитель-
ных открытых и зашифрованных текстов. По-
этому режим простой замены желательно ис-
пользовать тогда, когда избыточность источника
сообщений на уровне блоков невелика (вероят-
ность появления пары одинаковых блоков в те-
чение срока действия ключа пренебрежимо ма-
ла), например, при шифровании ключей.
Рис. 19.1. Режим простой замены
Поскольку при шифровании в этом режиме
блоки текста шифруются независимо, изменение
(в том числе введение нового или исключение)
одного или нескольких блоков шифртекста при-
водит к изменению соответствующих блоков
расшифрованного текста. Поэтому здесь легко
можно навязать ложную информацию, если про-
верка подлинности выполняется по смыслу рас-
шифрованного текста. Соответственно, наруши-
тель может формировать осмысленные ложные
сообщения, составленные из кусков шифро-
грамм.
В то же время искажение отдельных битов
зашифрованного текста в результате воздействия
помех в канале связи приводит к непредсказуе-
мому искажению соответствующих блоков рас-
шифрованного текста. Поэтому для передачи
информации, зашифрованной в этом режиме, по
каналу связи с помехами после зашифрования
необходимо использовать корректирующее ко-
дирование.
19.1.2. Режим гаммирования
В режиме гаммирования (рис. 19.2) можно
зашифровать текст произвольной длины, даже в
один бит.
Предположим, что блочный шифр в режиме
простой замены реализует подстановку Е^. С по-
мощью ключа к из начального текста s, называе-
мого синхропосылкой, вырабатывается гамма
шифра — псевдослучайная последовательность
z = (Ek(s), El(s), El(s),...), то есть отрезок цик-
ла подстановки для начального состояния х.
Уравнение зашифрования имеет вид у = х ® z,
уравнение расшифрования — х = у ® z. Расшиф-
426
рование требует знания синхропосылки, которая
может включаться в состав шифртекста или до-
пускать вычисление на приемной стороне. В за-
рубежной литературе режиму гаммирования со-
ответствует режим обратной связи по выходу
(output feedback, OFB).
а) Зашифрование
Рис. 19.2. Режим гаммирования
Для обеспечения надежного зашифрования
гамма шифра должна иметь большой период. В
противном случае различные отрезки открытого
текста могут быть зашифрованы одним и тем же
отрезком гаммы, и, зная один из отрезков откры-
того текста, можно легко вычислить остальные,
то есть выполнить бесключевое чтение.
Случайная подстановка Ек имеет длину цикла
в среднем 2"~1, если длина блока равна п бит [27].
Однако не всегда можно гарантировать, что
шифр реализует действительно случайную под-
становку и имеет большую длину цикла. Для
увеличения длины цикла можно использовать
типовые приемы, например, складывать пораз-
рядно текущий блок гаммы с его порядковым
номером и полученную сумму подавать на вход
шифратора. Шифр DES (см. п. 19.3) допускает
подачу на вход шифра т<п бит текущего вектора
z, что ослабляет шифр, поскольку отображение
z, = Е^(г,_1) становится необратимым (случайным),
а длина цикла гаммы составляет и2'"/2 бит.
Повторение синхропосылки по своим послед-
ствиям аналогично повторению гаммы. Поэтому
вероятность повторения синхропосылки в тече-
ние времени действия ключа должна быть пре-
небрежимо мала. В качестве синхропосылки
можно использовать код текущего времени или
его шифрограмму в режиме простой замены.
При шифровании в режиме гаммирования ис-
кажение одного бита шифртекста приводит к ис-
кажению одного бита расшифрованного текста.
Здесь предъявляются менее жесткие требования
к корректирующему кодированию. Поэтому ме-
тод гаммирования является перспективным при
шифровании речи или изображения в реальном
масштабе времени и передаче по каналу связи с
помехами.
19.1.3. Режим гаммирования
с обратной связью
Режим гаммирования с обратной связью
(рис. 19.3) используется для шифрования много-
блочных текстов. Под действием различных син-
хропосылок одинаковые открытые тексты будут
переходить в различные шифрограммы. Поэтому
здесь также желательно обеспечить неповторяе-
мость синхропосылки.
Рис. 19.3. Режим гаммирования с обратной связью
Этому режиму соответствует режим обратной
связи по шифртексту (cipher feedback, CFB), при
этом перед зашифрованием (расшифрованием)
очередного блока осуществляется его цикличе-
ский сдвиг.
Искажение одного бита шифрограммы приво-
дит к случайному искажению соответствующего
блока гаммы и соответствующих битов расшиф-
рованного текста. Поэтому при передаче зашиф-
рованной информации по каналу связи с поме-
хами необходимо использовать корректирующее
кодирование. ...... :
19.1.4. Режим сцепления блоков.
Выработка имитовставки
В режиме сцепления блоков (cipher-block
chaining, СВС) результат зашифрования первого
блока открытого текста суммируется по модулю
2 с синхропосылкой. На каждом последующем
шаге блок у, шифртекста вычисляется по форму-
ле у, = Ел(х; @ У/-1). Расшифрование выполняется
аналогично (рис. 19.4).
Если в зашифрованном тексте поменять
местами блоки с номерами i и i + 1, то в рас-
шифрованном тексте изменятся блоки с номе-
рами i, i + 1, i + 2, а остальные блоки останутся
без изменений. Это свойство следует непосред-
427
ственно из способа сцепления блоков и не зави-
сит от типа шифра. Действительно, пусть шиф-
руется многоблочное сообщение (хо, х/), ко-
торому соответствует шифрограмма (у0, ..., yz),
где у/ - Е(х, ® У/-1), Е = Ек — оператор зашиф-
рования, и в ней переставлены местами блоки
у, и у„]. Обозначим расшифрованный текст для
искаженной шифрограммы (u0, ...,U/). Очевид-
но, что По = хо, ..., и,_] = х,_]. Для расшифро-
ванных блоков с номерами i и далее можно за-
писать:
и,- = Е '(у,+1) ® y,_j = Е 'Е(хн1 ® у,) ф у,_, =
= х,+1 Фу,-Фу,_ь
и,+1 = Е~'(у,) © у,+1 = Е“’Е(х, © у_,) © у,+] =
= х, © у,-1 © у,+];
и,+2 = Е~'(у1+2) © у,- = E^E(xi+2 © у,+1) © у, =
= х,+2 © у,+] © у,;
и,+3 = Е~\ум) © у,+2 = Е~1Е(х,+3 © у,-+2) © у,+2 =
= Х/+3-
а) Зашифрование б) Расшифрование
Рис. 19.4. Режим спепления блоков
Последующие расшифрованные блоки совпа-
дают с соответствующими блоками открытого
текста.
Искажение отдельных битов зашифрованного
текста приводит к искажению двух блоков шиф-
рограммы: искаженного блока и следующего за
ним. Поэтому здесь также необходимо приме-
нять корректирующее кодирование после за-
шифрования.
В стандарте ГОСТ 28147-89 в режиме сцеп-
ления блоков вырабатывается имитовстав-
ка — отрезок информации фиксированной
длины, добавляемый к зашифрованным дан-
ным для обеспечения имитозащиты [1]. Опера-
торы Ек (см. рисунок 19.4) при шифровании и
выработке имитовставки различаются, поэтому
отмеченный недостаток (возможность переста-
новки блоков в пакете) не характерен для рос-
сийского стандарта.
19.2. Некоторые вопросы
применения шифров
Блочные шифры могут выполнять следующие
защитные функции:
1) обеспечение секретности данных;
2) генерация криптографически стойких псев-
дослучайных чисел;
3) опознавание участника протокола;
4) контроль подлинности данных;
5) контроль целостности данных; ’
6) контроль неповторяемое™ данных.
Генератор псевдослучайных чисел можно
реализовать с помощью шифрования произволь-
ной информации в режиме гаммирования.
Защитные функции 3-6 являются вариантами
аутентификации и могут быть реализованы толь-
ко в том случае, если претендент доверяет вери-
фикатору. Действительно, если верификатор за-
являет, что получил сообщение от претендента, а
претендент утверждает, что не посылал этого
сообщения, то ясно, что один из них лжет. Одна-
ко кто именно обманывает, установить невоз-
можно— в случае симметричного шифрования
оба они обладают одинаковыми возможностями.
Симметричные шифры позволяют осуществлять
многократную аутентификацию, как диалого-
вую, так и бездиалоговую.
Бездиалоговое опознавание претендента мо-
жет быть выполнено шифрованием блока неко-
торой информации, заранее известной верифика-
тору. При этом претендент передает зашифро-
ванное сообщение верификатору. Верификатор
расшифровывает сообщение и проверяет его
правильность. Для защиты от повторов можно
использовать блок открытого текста, состоящий
из двух частей: фиксированной и переменной. В
качестве фиксированной части можно использо-
вать имя претендента и (или) фиксированный
код, в качестве переменной части — порядковый
номер сеанса аутентификации или код текущего
времени. Например, в 64-разрядном блоке пер-
вые 24 бита блока — фиксированный код, после-
дующие 16 бит— имя претендента, последние 24
бита— код времени. Верификатор, расшифровав
сообщение, устанавливает правильность имени и
фиксированного кода и проверяет, что код време-
ни, указанный в сообщении, и код, имеющийся у
него, различаются гарантарованно мало.
Диалоговое опознавание не требует защиты
от повторов и может выполняться различными
протоколами:
1. Верификатор формирует случайный запрос
и посылает его претенденту. Претендент зашиф-
ровывает запрос и возвращает верификатору.
Верификатор расшифровывает принятое сооб-
428
щение и сравнивает с запросом. При совпадении
опознавание считается успешным.
2. Верификатор вырабатывает случайное чис-
ло, зашифровывает его и посылает претенденту.
Претендент расшифровывает сообщение и посы-
лает верификатору. Верификатор сравнивает по-
лученный текст с первоначальным. При совпаде-
нии опознавание считается успешным.
3. Верификатор вырабатывает случайное чис-
ло, зашифровывает его и посылает открытое
случайное число претенденту. Претендент за-
шифровывает это число и возвращает верифика-
тору шифрограмму. Верификатор сравнивает
полученное сообщение с вычисленной шифро-
граммой. При совпадении опознавание считается
успешным. В этом варианте вместо шифра мож-
но использовать ключевую хэш-функцию— ее
обратимость не требуется.
Контроль подлинности и целостности данных
осуществляется введением избыточности в от-
крытый или зашифрованный текст.
Если избыточность вводится в многоблочный
открытый текст, то необходимо исключить воз-
можность нераспознаваемого изменения шифро-
граммы. Отсюда следует, что избыточность в
виде заранее известной верификатору информа-
ции должна вводиться в последний блок откры-
того текста. При этом нельзя использовать опи-
санные выше режимы шифрования: необходимо,
чтобы изменение любого блока шифрограммы,
включая замену, введение новых блоков или их
исключение, приводило к непредсказуемому из-
менению последнего блока расшифрованного
текста. Иначе говоря, последний блок расшиф-
рованного текста должен зависеть от каждого
блока зашифрованного текста, и эта зависимость
при неизвестном ключе должна быть трудновы-
числимой. В этом случае помогло бы двойное
шифрование многоблочного текста: сначала за-
шифрование в режиме гаммирования с обратной
связью, затем выполнение рассеивающего пре-
образования и повторное зашифрование. В каче-
стве рассеивающего преобразования можно ис-
пользовать умножение зашифрованного текста
как «длинного» вектора на невырожденную мат-
рицу такое, чтобы каждый блок на выходе зави-
сел от каждого блока на входе. Элементами мат-
рицы могут быть не только биты, но и более
крупные части блока, например, байты или двух-
байтовые слова.
Если избыточность вводится в шифртекст, то
он должен содержать значение ключевой хэш-
функции, аргументом которой является откры-
тый текст. В качестве хэш-функции можно ис-
пользовать шифрование в режиме гаммирования
с обратной связью на специальном ключе хэши-
рования, отличном от ключа шифрования. Зна-
чением хэш-функции является шифрограмма по-
следнего блока или ее часть. Отметим, что этот
режим работает только тогда, когда сообщение
передается в зашифрованном виде, так как в про-
тивном случае можно переставить местами два
блока открытого текста, и эта перестановка не
будет распознана.
Для защиты от повторов в текст сообщения
следует включать его порядковый номер для
данного претендента или код времени отправле-
ния. Для этого претендент и верификатор долж-
ны иметь нумераторы сообщений, причем если
существует несколько претендентов, то нумера-
ция сообщений должна быть индивидуальной
для каждого из них, и в сообщение необходимо
вставлять также имя (идентификатор) претен-
дента. Верификатор проверяет, что номер приня-
того сообщения больше, чем номер предыдущего
сообщения, отправленного данным претенден-
том. Альтернативный вариант— использовать
систему единого времени у претендента и вери-
фикатора. Причем, если нарушитель может тай-
но изменить код времени у претендента или ве-
рификатора, то это позволяет ему задерживать
информацию, передаваемую претендентом, и эту
задержку невозможно выявить.
При использовании шифра возникает вопрос
о времени жизни ключа. С одной стороны, смена
ключей в системе — хлопотное занятие, с другой
стороны, отсутствие смены ключей может при-
вести к снижению стойкости ключа по отноше-
нию к статистическим методам криптоанализа.
Для того чтобы эти методы были неэффективны,
ключ нужно менять, не давая нарушителю на-
брать необходимый объем статистики (см.
гл. 18).
Чем меньше объем информации, зашифро-
ванной на одном ключе, тем меньше выгоды из-
влекает нарушитель при вскрытии ключа (пред-
полагается, что вся шифруемая информация рав-
ноценна и каждый ее бит имеет конечную цену).
Поэтому существует пороговый объем информа-
ции, зашифрованной на одном ключе, ниже ко-
торого задача вскрытия ключа становится эко-
номически невыгодной.
Стойкость шифра, как и пороговый объем
информации, меняется во времени. Это обуслов-
лено следующими обстоятельствами.
1. Развитие математики и криптоанализа при-
водит к тому, что стойкость шифра (слож-
ность математической задачи, положенной в
основу безопасности шифра) постоянно сни-
жается.
2. Производительность вычислительной техни-
ки увеличивается каждый год примерно в два
раза.
429
3. Специализированные компьютеры, решаю-
щие задачу криптоанализа, дешевеют.
Почти все итерированные шифры разрабаты-
ваются так, чтобы первоначально обеспечива-
лась переборная сложность вскрытия ключа. При
этом каждый бит, добавляемый к длине ключа
(при разумных ограничениях на длину) дает уд-
воение сложности. Поэтому скорость падения
стойкости шифра (то есть снижение логарифма
сложности математической задачи) в течение
времени t будем оценивать в относительных
единицах по формуле
х(/,Т) =
logS(T)-logS(T + Z)
Ноё5(Т)
(19.2.1)
где S(T)— стойкость в начальный момент вре-
мени Т. Выражение (19.2.1) можно интерпрети-
ровать как снижение первоначальной перебор-
ной стойкости криптоалгоритма в расчете на
один бит ключа. Обычно величина s(t, Г) в тече-
ние достаточно большого промежутка времени
сохраняется примерно постоянной, поэтому ес-
тественно предположить, что так будет продол-
жаться и в дальнейшем. Например, для DES (см.
п. 19.3) величина s(t, Т) (в основном обусловлен-
ная появлением дифференциального и линейного
методов криптоанализа) для достаточно больших
значений t слабо зависит от t и равна примерно
0,015 год"1.
Преобразуем выражение (19.2.1) к виду
log.S'(7+f) = (1 - ts(t, T))logS(T),
S(T+ f) = S(T)
откуда
7) = e(l-foy,7))InS(7)
Следовательно, если s(t, Т) меняется слабо, то
зависимость S(T +1) для симметричного итериро-
ванного шифра или итерированной хэш-функции
можно приближенно описать падающей экспо-
нентой.
Некоторые неудачные шифры характеризуют-
ся повышенной скоростью падения стойкости. В
целом, по-видимому, для симметричных шифров
можно считать разумной оценку s(t, Т)«0,015,
найденную для DES.1
В зависимости от аппаратно-программного
устройства шифратора периодичность смены
ключей, определенная по отношению к «идеаль-
ному» шифру, для статистических методов крип-
тоанализа может только снижаться.
1 Для задач разложения составного числа и лога-
рифмирования в конечном поле (при размере задачи
103 бит), а также для задачи логарифмирования на
эллиптической кривой скорость падения сложности
составляет соответственно 0,047; 0,047; « 0.
19.3. DES
DES (Data Encryption Standard) [29] разрабо-
тан в середине 1970-х гг. сотрудником корпора-
ции IBM X. Фейстелем и представляет собой
блочный шифр, использующий подстановки, пе-
рестановки и сложение по модулю 2, с длиной
блока 64 бита и длиной ключа 56 бит.2 Подста-
новки и перестановки, используемые в DES, яв-
ляются фиксированными.
Список цикловых ключей, получаемых из
первоначального ключа, фиксирован и определя-
ется следующей последовательностью операций:
- разделение 56-разрядного ключа на два по-
лублока по 28 бит, с0 и d(i;
- циклический сдвиг блоков с0 и do влево на
сфД битов, результатом которого являются
полублоки С] и d], и далее по индукции:
С/+1 = cr[z + 1] • с„ dl+] = с>[/ + 1] di, 1 < i< 15
(число ст [г] зависит от номера итерации i и опре-
деляется соответствующей таблицей).
Цикловый ключ К,, i = 0, 1, ..., 15, длины 48
бит, используемый на z-м цикле, выбирается по
определенному правилу из конкатенации блоков
С/+], d/ \}.
Рассмотрим основные этапы алгоритма за-
шифрования DES (рис. 19.5).
1. К блоку входного текста применяется началь-
ная перестановка IP.
2. Для каждого цикла i = 0, 1, ..., 15 выполняет-
ся операция зашифрования , при которой:
- 64-разрядный блок разбивается на полу-
блоки х' и х" по 32 бита;
- полублок х" разбивается на 8 тетрад по 4
бита. Каждая тетрада по циклическому
закону дополняется крайними битами из
соседних тетрад до 6-разрядного слова;
- полученный 48-разрядный блок суммирует-
ся по модулю 2 с 48 битами циклового клю-
ча, биты которого выбираются на каждом
цикле специальным образом из 56 бит клю-
ча, а затем разбивается на 8 слов по 6 бит;
- каждое из полученных на предыдущем
шаге слов 48-разрядного блока поступает
на вход одного из восьми фиксированных
S'-блоков, который выполняет нелинейную
замену наборов 6-разрядных слов тетра-
дами. При этом два крайних разряда 6-
2 Вообще говоря, в DES используется 8-байтный
ключ, каждый байт которого состоит из семи битов
фактического ключа, непосредственно используемых
в алгоритме, а восьмой бит служит контрольным би-
том четности остальных семи битов.
430
разрядного слова задают одну из четырех
подстановок, на вход которой подаются
средние четыре бита 6-разрядного слова.
Выходом операции являются выходы
восьми четырехразрядных подстановок;
- полученные 32 бита подвергаются фик-
сированной перестановке, результатом
которой является полублок F,(x");
- компоненты полублока F(x") суммиру-
ются по модулю 2 с компонентами полу-
блока х', после чего полублоки меняются
местами, то есть (х', F,(x'')) преобразуется
в (х' ® F,(x"), х').
3. К блоку текста, полученному после 16 цик-
лов, применяется обратная перестановка IP-1.
Результатом является выходной зашифро-
ванный текст.
Итоговое уравнение зашифрования имеет вид
(порядок следования операторов — справа налево):
DES = Ip-'^]5^]4...n,0IP.
При расшифровании порядок следования опе-
раторов меняется на обратный.3
Каждый из S-блоков содержит четыре фикси-
рованных подстановки из 16 элементов. Эти под-
становки не всегда являются экстремальными.
Длина S'-блоков довольно велика — 32 • 16 4 =
= 2048 бит, поэтому в них теоретически можно
было бы встроить потайной ход, который позво-
лил бы разработчику снизить сложность дешиф-
рования (по этому поводу высказывались опасе-
ния [23]).
128 булевых функций, задающих подстановки
из S'-блоков, имеют нелинейность 2 или 4. Соот-
ветственно ту же нелинейность имеют и подста-
новки. Примером подстановки с нелинейностью
2 является первая подстановка из блока S4:
<0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15^1
^2 1241 7 10 11685 3 15 13 0 14 9/
3 Использование фиксированной перестановки IP
для открытого текста и IP-1 для шифрограммы не мо-
жет считаться защитной операцией.
Рис. 19.5. Схема шифра DES
Оператор F,
431
Старший разряд подстановки имеет нелиней-
ность 2. Соответствующая булева функция имеет
вид:
0 1 0 0 0 1 1 0 1 0 0 1 1 0 1 1
Пусть вход подстановки задан числом
х4 + 2л'3 + 4х2 + 8хь Аффинная булева функция
%! ® х3 ® х4 имеет вид:
0 1 1 0 0 1 1 0 1 0 0 1 1 0 0 1
Эти функции различаются в двух позициях и
совпадают с вероятностью 7/8.
Стойкость DES к линейному методу состав-
ляет примерно 241 известных открытых и соот-
ветствующих зашифрованных текстов [26].
Стойкость к дифференциальному методу не-
сколько выше, что обусловлено выбором S-
блоков: подстановки обладают дифференциала-
ми довольно большого веса, но нелинейность их
зачастую равна 2 [7, 9]. Метод списка ключей не
позволяет дополнительно снизить стойкость, по-
скольку цикловые ключи выбираются нетриви-
ально. DES как фейстелев шифр обладает свой-
ством пополнения', из равенства у = Ек(х) сле-
дует у = Ек(х). Поэтому перебор ключей можно
выполнять с точностью до инверсии (и даже до
инверсии произвольного числа разрядов).
Эксперименты по исследованию циклового
строения отображений, индуцированных различ-
ными ключами, показали, что DES не замкнут и
не является чистым шифром (то есть смежным
классом по замкнутому шифру) [19].
DES обладает коротким ключом. Однако
шифрование на двух или на трех ключах не по-
зволяет заметно увеличить стойкость. Например,
для вскрытия ключа двойного DES (цикловые
ключи шифрования постоянны на первых 16
циклах и на вторых 16 циклах, суммарная длина
двойного ключа — 96 бит) требуется 232 извест-
ных открытых текстов и 233 вычислительных
операций. Если возможна атака на основе подоб-
ранных открытых и зашифрованных текстов, то
для вскрытия ключа двойного DES требуется
лишь 217 подобранных текстов и 217 вычисли-
тельных операций [11].
DES используется для шифрования данных в
системе BestCrypt.
Попытка устранить недостаток DES, обуслов-
ленный малой длиной ключа, при использовании
существующих аппаратных средств была пред-
принята Р. Ривестом [36]. Полученный шифр на-
звали DESX. В отличие от оригинального DES в
DESX введены два дополнительных ключа. От-
крытый текст перед зашифрованием складывает-
ся поразрядно по модулю 2 с первым дополни-
тельным ключом, а полученный шифртекст
складывается поразрядно по модулю 2 со вторым
дополнительным ключом. Вскрытие ключа
DESX методом сдвига требует 232’5 известных
открытых и соответствующих зашифрованных
текстов, временная сложность составляет 287,5
[11]. DESX используется для шифрования дан-
ных в операционной системе WINDOWS 2000.
19.4. FEAL
Алгоритм FEAL (Fast Data Encipherment Algo-
rithm, рис. 19.6), предложенный японскими крип-
тографами А. Шимицу и С. Миягучи в 1987 г.
[34] как альтернатива DES, ориентирован на 8-
разрядный процессор. Длина блока и ключа в
FEAL — 64 бита. Обычно число циклов шифро-
вания N варьируется от 4 до 32. Существуют и
обобщенные версии алгоритма с более длинным
(128-разрядным) ключом и с большим числом
циклов. Основные операции в алгоритме
FEAL— сложение по модулю 2 и по модулю
256, сдвиг.
До начала шифрования из 64-разрядного клю-
ча формируется список цикловых ключей сум-
марной длины 2N + 16 байт: Хо,..., K2JM5.
Зашифрование происходит в три этапа:
1. Входной 64-разрядный блок открытого тек-
ста суммируется по модулю 2 с восемью бай-
тами списка ключей. Полученный блок раз-
бивается на два полублока х' и х" по 32 бита.
2. Для каждого цикла выполняется операция
зашифрования, при этом каждый новый 32-
разрядный полублок задается уравнением:
х,+2 = А,(х,+1) © х„ / = 0, 1, ..., N- 1,
где оператор F зависит только от двух бай-
тов списка ключей: Х2, и Х2,+1, а значение
у = Ff(x ), где х и у — 32-разрядные полу-
блоки, определяется следующим образом:
- полублок х разбивается на четыре 8-
разрядных слова Хо, Хь Х2, Х3;
- вычисляются 8-разрядные слова:
Ej = Sj(X0 © А] © К2„ Х2 © Хз © Х2/+1);
Y2 = Sg(Yx, Х2 © Хз © Х2,+1);
Е0=ад,К1);
Уз = ^(Х3,У2),
где Sf^a, b) — циклический сдвиг на два бита
влево числа a + b+j (mod 256), j g {0,1};
- полублок у представляет собой конкате-
нацию слов Ео, Уь У2, У3.
432
3. Блок выходного зашифрованного текста оп-
ределяется сложением по модулю 2 64-
разрядного блока (х№ xM1), полученного на
последней итерации, с восемью байтами спи-
ска ключей.
При расшифровании порядок выполнения
операций меняется на обратный, вид оператора
F, сохраняется.
Для анализа 8-циклового FEAL линейным ме-
тодом требуется 224 известных открытых текстов,
дифференциальным методом— 27 пар подоб-
ранных открытых текстов, при этом длитель-
ность вскрытия ключа составляет несколько ми-
нут на персональном компьютере [8, 27].
Оператор F,
Рис. 19.6. Схема 8-циклового шифра FEAL
19.5. IDEA
Алгоритм шифрования IDEA (International
Data Encryption Algorithm) [24] предложен С. Лаи
и Дж. Месси в 1991 г. и применяется в пакете
программ Pretty Good Privacy (PGP). IDEA пред-
ставляет собой блочный шифр, в котором 64-
разрядные блоки открытого текста последова-
тельно зашифровываются на 128-разрядном
ключе. Этот шифр не является фейстелевым и
удобен для программной реализации на процес-
сорах с аппаратным умножителем.
Для процедуры зашифрования используются
пятьдесят два 16-разрядных цикловых ключа,
которые получаются следующим образом. Сек-
ретный 128-разрядный ключ разбивается на во-
семь 16-разрядных слов, образующих первую
восьмерку цикловых ключей К\, затем
вектор сдвигается циклически на 25 бит влево и
разбивается на восемь 16-разрядных слов
К9, ...,К]6. Далее операции циклического сдвига
и разбиения повторяются до тех пор, пока не бу-
дут получены все 52 цикловых ключа.
Основными операциями алгоритма шифрова-
ния являются умножение по модулю 216 + 1, сло-
жение по модулю 2 и по модулю 216. Для того
чтобы умножение по модулю 216 + 1 было обра-
тимой операцией, нулевой сомножитель рас-
сматривается как 216, а произведение, равное 216,
заменяется на 0.
433
При зашифровании 64-разрядный блок от-
крытого текста разбивается на четыре 16-
разрядных подблока х2, х3, х4. На каждом цик-
ле используются шесть цикловых ключей. После
восьмого цикла выполняется выходное преобра-
зование, в котором используются четыре цикло-
вых ключа. Итоговые четыре блока у<, у2, уз, у4
сцепляются и образуют 64-разрядный блок шифр-
текста (рис. 19.7).
Рис. 19.7. Схема шифра IDEA
При расшифровании выполняется та же самая
последовательность операций, но с другим мно-
жеством цикловых ключей. Ключи расшифрова-
ния вырабатываются из ключей зашифрования и
являются обратными по модулю 216 + 1 или про-
тивоположными по модулю 216. Операцией, об-
ратной сложению по модулю 216 слов текста и
ключа, является операция сложения с противопо-
ложным цикловым ключом. Операцией, обратной
умножению слов текста и ключа, является опера-
ция умножения на обратный цикловый ключ.
Произведение с = ab (mod 216 + 1) вычисля-
ется следующим образом. Сначала выполняет-
ся целочисленное умножение 16-разрядных
слов: ab = 216J + В, затем вычитание: с = В - А
(mod216 + l). Ветвление при вычитании (обу-
словленное выполнением неравенства В < А)
приводит к тому, что, измеряя длительность
шифрования, можно получить информацию о
промежуточных текстах (timing attack). Это
представляет потенциальную опасность, по-
этому желательно строить программу шифро-
вания так, чтобы длительность вычислений не
зависела от ключа, открытого текста и шифро-
граммы.
В настоящее время наилучшим известным ал-
горитмом вскрытия ключа полной версии IDEA
является перебор. Для вскрытия ключа 3’/2-
циклового шифра требуется 256 открытых тек-
стов, а сложность вскрытия равна 267 [13]. Ско-
рость падения стойкости IDEA согласно формуле
(19.2.1) практически нулевая. Но для этого алго-
ритма существует перечислимый класс слабых
ключей [14].
Анализ IDEA методом продолженных поли-
номов Жегалкина вызывает сложности, которые,
однако, не представляются принципиальными:
операции модульного сложения и модульного
обращения необходимо представить в виде по-
линомов Жегалкина.
19.6. ГОСТ 28147-89
Алгоритм блочного шифрования ГОСТ
28147-89 [1] предусматривает три режима шиф-
рования: простой замены, гаммирования и гам-
мирования с обратной связью, а также режим
выработки имитовставки.
Шифр имеет длину блока 64 бита и длину
ключа 256 бит. Ключ составлен из восьми 32-
разрядных слов Ко, ..., К7. Основные операции —
сложение по модулю 2 и 232, перестановка, цик-
лический сдвиг.
При реализации алгоритма зашифрования в
режиме простой замены (рис. 19.8) открытый
текст разбивается на два полублока х' и х" по 32
бита, к которым применяется оператор цикличе-
ской итерации i = 0, 1, ..., 31, включающий в
себя:
- суммирование по модулю 232 полублока х" с
32 битами ключа;
- преобразование результата суммирования в
блоке подстановки, представляющем собой
набор из восьми 4-разрядных подстановок S),
..., Kg. Каждая из восьми тетрад, поступаю-
щих на вход блока подстановки, заменяется в
соответствии со своей подстановкой;
- циклический сдвиг на 11 бит в сторону стар-
ших битов.
434
Оператор F,
Рис. 19.8. Схема шифра ГОСТ 28147-89 в режиме простой замены
Результат циклической итерации F,(x") сум-
мируется поразрядно по модулю 2 с полублоком
х', полученные полублоки меняются местами, то
есть (х', F,(x")) преобразуется в (х", х' © F,(x")).
Всего реализуется 32 цикла, которые разли-
чаются используемым словом ключа К,. При за-
шифровании порядок выбора слов ключа сле-
дующий:
К^К^К^К^,
К.,КХ,К2,К2, К4,К5,К6,К2,
Ki,K6,K5, К4, К}, К2, К^, Ко.
Благодаря такому выбору слов, итоговый опе-
ратор зашифрования не является степенным. При
расшифровании слова ключа используются в об-
ратном порядке. Рассеивающие качества этого
шифра обеспечиваются операторами сложения
по модулю 232, подстановки и фейстелевой ите-
рации. Сложение по модулю 232 можно описать
полиномами Жегалкина следующим образом.
Пусть
32 32 32
а - И; 2'-1, b = bj 2'-1, с = с, 2'1, а + Ъ = с.
1=1 /=1 1=1
Обозначим через р, перенос в i-й разряд. Тогда
Р\ = 0 и рекуррентные соотношения с, = а, © Ь, ©
р,\ = a,b, ®ap, © bph где 1 < i < 32, задают опера-
цию сложения по модулю 232 в виде композиции
полиномов Жегалкина.
Если рассматривать сумму по модулю 232 как
функцию только одного из слагаемых, то два
младших разряда суммы описываются аффин-
ными функциями. Если рассматривать сумму по
модулю 232 как функцию обоих слагаемых, то
только младший разряд суммы является аффин-
ной функцией, а остальные разряды имеют вы-
сокую нелинейность (i-й разряд — как функция
2г переменных).
Для шифрования данных используются ре-
жимы гаммирования и гаммирования с обратной
связью. При этом в режиме гаммирования левый
и правый полублоки на каждом цикле складыва-
ются соответственно по модулю 232 - 1 и 232 с
константами.
Для обеспечения аутентификации сообщений
предусмотрен режим выработки имитовставки
(ключевой хэш-функции, аргументом которой
является текст, состоящий не менее чем из двух
блоков). Открытый текст зашифровывается по
схеме, приведенной на рисунке 19.4, при этом в
качестве синхропосылки s используется первый
блок открытого текста, а в качестве оператора
Ек— зашифрование по ГОСТ 28147-89 в режиме
простой замены на первых 16 циклах шифрова-
ния. Имитовставкой является отрезок полублока
шифрограммы, содержащего младшие разряды.
При длине имитовставки в т бит вероятность
навязывания ложной информации равна 2~т [1].
Заметим, что использование имитовставки дли-
ной более 32 бит за счет присоединения к ней
части старшего полублока ведет к увеличению
вероятности навязывания ложной информации
435
(при длине имитовставки 64 бита ложную ин-
формацию можно навязать с вероятностью 1).
Шифр ГОСТ 28147-89 используется в паке-
тах программ Arj, BestCrypt.
19.6.1. Стойкость шифра ГОСТ 28147-89
Число публикаций с результатами криптоанали-
за шифра ГОСТ 28147-89 в отличие от DES неве-
лико. На сегодняшний день не опубликованы ме-
тоды, снижающие стойкость ГОСТ 28147-89 по
сравнению с перебором. В отдельных публика-
циях исследуется стойкость искаженного шифра
(при использовании «слабых» блоков подстанов-
ки, уменьшенном числе циклов шифрования, за-
мене сложения по модулю 232 поразрядным сло-
жением по модулю 2 и т. п.) [11, 21 ]. Линейный и
дифференциальный методы криптоанализа тре-
буют недостижимого объема открытых и зашиф-
рованных текстов, который превышает 2е4 —
число всевозможных блоков открытого текста.
Атака на основе списка ключей на 20-цикловый
ГОСТ 28147—89 (взяты промежуточные 20 цик-
лов, для которых список ключей, начинающийся
с Кд, обладает центральной симметрией) требует
233 известных текстов и обладает сложностью 2™
[21]. По-видимому, этот подход не годится для
32-циклового варианта.
Существуют классы ключей, при которых
ГОСТ 28147-89 становится степенным шифром:
это ключи, определяемые равенствами Ко = Къ
К = Кь, Кг = К, К = Кд. Период повторения клю-
чей равен 1, 2 или 4. Для степенных шифров воз-
можен анализ методом сдвига на один период че-
редования ключей [11,12]. Однако эти равенства
эффективно проверяемы только при достаточно
малом периоде повторения ключей (1 или 2) и при
наличии примерно 233 открытых и соответствую-
щих зашифрованных текстов. Это обстоятельство
затрудняет использование свойства периодично-
сти на практике. Кроме того, вероятность перио-
дического ключа пренебрежимо мала.
Можно утверждать, что ГОСТ 28147-89 явля-
ется одним из лучших шифров не только в части
стойкости, но и в части скорости ее падения.
ГОСТ 28147-89 обладает обобщенным свой-
ством дополнения. Для задания этого свойства
достаточно описать коллизии, возникающие при
сложении с ключом. Пусть фх— отображение
шифруемых полублоков, соответствующее до-
полнению, ф*— отображение ключа, F— цик-
ловая функция шифрования, Х| — левый полу-
блок, х2 — правый полублок. Свойство дополне-
ния определяется равенством:
<рх(лд ф F(x2 + к)) = фДх1 Ф Г(фДх2) + фДА))).
Сокращая на обратимые операторы фх и F,
получаем условие автоморфизма шифра:
х2 + к = фх(т2) + ф^(А) (mod 232).
В частности, этому условию удовлетворяют
операторы ф/х) = х + 231 (mod 232), фДЛ) = к + 231
(mod 232), означающие инверсию старшего бита в
слове ключа и полублоке.
Перемешивающие и рассеивающие свойства
шифра в значительной мере определяются пере-
носами при сложении по модулю 232. Использо-
вание разреженных открытых текстов в сочета-
нии с разреженными ключами позволяет осла-
бить влияние переносов, если подстановка со-
храняет свойство разреженности. Это экспери-
ментально подтверждается результатами анализа
стойкости шифра к методам, описанным в
пп. 17.6, 17.7 (см. также работу [4]). Аналогичная
ситуация возникает, если ключ и открытые тексты
состоят почти из одних единиц, а подстановки
сохраняют свойство «разреженности по нулям».
Для повышения стойкости шифра можно ре-
комендовать следующие меры. Все подстановки
блока подстановок ГОСТ 28147-89 должны
обеспечивать малую вероятность наиболее веро-
ятных дифференциалов и малую вероятность
выполнения линейных равенств (см. п. 18.4).
Пусть Wtj — множество тетрад веса i или j. Каж-
дое из требований:
^0,1) £ {Wj}, £(м?од) ё. {и;3,4(>
А(и’з4) £ {ши ^'(и’зд) ё {и’34}
должно выполняться хотя бы для одной подста-
новки S из блока подстановок.
19.6.2. Стойкость шифра ГОСТ 28147-89
при наличии у нарушителя
лабораторных возможностей
Предположим, что ГОСТ 28147-89 реализо-
ван программно на персональном компьютере и
обработка ведется 32-разрядными словами (в
действительности разрядность не имеет принци-
пиального значения). Пусть нарушитель, обла-
дающий лабораторными возможностями, может
подавать произвольные тексты для зашифрова-
ния, знает, как работает программа зашифрова-
ния на данном процессоре, и имеет специализи-
рованную аппаратуру, позволяющую определить
хэммингов вес операнда (результата) на данном
такте работы процессора.4
4 Поскольку переключение логического элемента
компьютера с 0 на 1 и с 1 на 0 происходит с разными
скоростями, то такая аппаратура представляется тех-
нически реализуемой. Для выделения сигналов из
шума можно использовать несколько повторов одной
и той же программы.
436
Вскрытие ключа может выполняться следую-
щим образом. Нарушитель поразрядно подбира-
ет полублок х" открытого текста так, чтобы на
первом цикле шифрования вес результата на вы-
ходе блока подстановки, измеряемый аппарату-
рой, был минимальным (нулевым или близким к
нулю). Затем он поразрядно подбирает полублок
х' или х” открытого текста так, чтобы на втором
цикле вес результата на выходе блока подста-
новки был минимальным, и т. д.
В результате таких действий нарушитель мо-
жет (приближенно) определить ключ. Действи-
тельно, пусть х" — значение полублока х", обес-
печивающее нулевой вес на выходе блока под-
становки (Аь ...,А8) на первом цикле шифрова-
ния. Пусть z = (АГ'(О),..., .S's^O))— вектор на
входе блока подстановки, которому в алгоритме
шифрования соответствует целое число z. Тогда
первое слово К\ ключа определяется как
К\ = z - х" (mod 232). Аналогично можно найти и
последующие слова ключа.
В результате возможных ошибок измерения
веса нарушитель вычисляет не истинное значе-
ние ключа, а некоторое приближение к нему, по-
этому на заключительном этапе криптоанализа
требуется уточнить истинное значение ключа
вблизи найденного приближения.
Данная атака, очевидно, может быть реализо-
вана для любого шифра, в том числе гипотетиче-
ского «асимптотически большого». Если указан-
ной ошибкой пренебречь, то окажется, что дан-
ным методом ключ можно вскрыть с линейной
сложностью, а все криптографические ухищрения
по повышению стойкости шифра бессмысленны.
В качестве технических мер защиты от по-
добных атак наряду с физическим зашумлением
или случайным изменением тактовой частоты
процессора можно использовать преобразования
(автоморфизмы) шифрующей программы, кото-
рые затрудняли бы нарушителю проведение из-
мерений: случайное встраивание отдельных так-
тов шифрования в работу других сложных про-
грамм, динамический случайный порядок вы-
полнения операций (например, можно сначала
сложить младшую тетраду текста с тетрадой
ключа, применить подстановку к этой тетраде,
затем сложить вторую тетраду текста с тетрадой
ключа и т. д.). Аналогично можно использовать и
случайные автоморфизмы конечных автоматов
при аппаратной реализации шифра.
> 19.7. RC5
Быстрый алгоритм блочного шифрования
RC5 [32], предложенный Р. Ривестом в 1994 г.,
представляет собой параметризованный алго-
ритм с переменной длиной блока (32, 64 или 128
бит), переменным размером ключа (от 0 до 255
байт) и переменным числом циклов (от 0 до 255).
Из ^-байтного (0 < Ъ < 255) ключа KS форми-
руется список цикловых ключей Ао, ..., Аг^м, где
R— число циклов, а размер W слова А, может
быть 16, 32 или 64 бита. При построении списка
ключей выполняются следующие операции:
- представление ^-байтного ключа KS в виде
последовательности fT-разрядных слов
Zo,...,£)Ч, где г = 8(6-1)/1Т + 1;
- построение фиксированной (не зависящей от
ключа KS) псевдослучайной последователь-
ности Ао, , <$2/г+1 на основе чисел
«=2,7182... (основание натурального лога-
рифма) и ср = 1,6180... (золотое сечение);
- формирование цикловых ключей из последова-
тельностей Lj и St по алгоритму, аналогичному
алгоритму шифрования, в котором на каждом
шаге выполняются следующие операции:
a (S, + а + Ь) «< 3; S, «— а;
b<—(Lj + а г Ь) «< (а + b); Lj <— Ъ,
где «+» — сложение по модулю 2W, ««< /» —
циклический сдвиг в сторону старших разря-
дов на t бит.
Исходными значениями для а, Ъ, i,j являются
нули, а число итераций определяется размером
ключа АА.
При зашифровании (рис. 19.9):
1) блок входного открытого текста длины 2W бит
разбивается на два полублока х' и х" по W бит;
2) первые два цикловых ключа Ко и А] сумми-
руются по модулю 2 й с полублоками х' и х"
соответственно;
3) выполняется циклическая итерация:
х'<—((х'© х") <« И7*’) + A2i,
х" ((х" © х') «< + А2Ж, 1=1,2, ..., R.
Выходным зашифрованным текстом является
конкатенация итоговых значений полублоков
после R циклов.
При расшифровании операции выполняются в
обратном порядке с теми же цикловыми ключами.
Этот шифр использует управляемые цикличе-
ские сдвиги (вращения) fT-разрядных слов. От-
метим, что существуют векторы, нечувствитель-
ные к сдвигу, например, нулевой или единичный.
Периодичные векторы с периодом 2i переходят в
себя при сдвиге на четное число разрядов; векто-
ры с периодом 4 переходят в себя при сдвиге на
2i разрядов. Теоретически это свойство можно
положить в основу атаки на шифр с управляв-
437
мыми сдвигами, что позволяет свести изучение
шифра к изучению его периодов. Для того чтобы
противостоять этой атаке, в RC5 используется
сложение с непериодическими векторами ключа.
Управляемый сдвиг входного вектора х' в за-
висимости от пяти младших битов смежного век-
тора х" является подстановкой— нелинейной
операцией (тогда как фиксированный сдвиг, оче-
видно, линейная над [F2 операция). Ее можно за-
писать показательным уравнением для 32-
разрядного векторного пространства над 1F2:
У = х, где С] — матрица единичного сдвига,
х" — целое число, соответствующее пяти млад-
шим битам двоичного вектора х".
Рис. 19.9. Схема шифра RC5
При W= 32 каждый изх32 разрядов этой под-
становки зависит от 32 бит своего блока и пяти
младших битов смежного блока, то есть является
разреженной булевой функцией 37 переменных,
линейной над IF2 по 32 переменным своего блока.
Однако по отношению к пяти переменным
смежного блока операция управляемого сдвига
является нелинейной.
Это свойство само по себе не дает стойкости
по отношению к линейному методу криптоана-
лиза. Поскольку любой циклический сдвиг (даже
на переменное число разрядов) сохраняет число
нулевых и единичных разрядов, то наиболее ве-
роятное линейное равенство над [F2 для этой под-
становки имеет вид
W W
=о
/=1 /=1
и выполняется с вероятностью 1 (здесь х, и у, со-
ответственно входные и выходные разряды
управляемого циклического сдвига). Поэтому
шифр с операциями поразрядного сложения век-
торов по модулю 2 и операциями циклического
сдвига следует дополнить нелинейной операци-
ей, что и сделано в RC5 (сложение по модулю 2й).
Первоначальная переборная оценка стойкости
RC5 к дифференциальному и линейному мето-
дам [20] была снижена: для вскрытия ключа 12-
циклового RC5 требуется 244 подобранных от-
крытых текстов [10].
Для вскрытия ключа RC5 предложен метод
анализа по модулю 3, а также по модулям про-
стых чисел Ферма [22]. Этот метод пригоден и
для анализа других шифров, использующих опе-
рации сложения по модулям 2, 2ГУ и управляемых
циклических сдвигов. Поясним суть метода.
Пусть W= 32. Поскольку
31
2х, еслих < 2 ;
<
2х + 1-232, еслих>231;
и 232 s 1 (mod 3), то
х «< 1 = 2х
х «< 2 = х (mod 3). Тогда
(mod 3),
2х (mod3),
х (mod3),
если и четное;
если и нечетное
Если х s 0 (mod 3), то х «< п = х (mod 3) при
любом п. Следовательно, вероятность того, что
х «< и = х (mod 3), равна 4/6 при случайном х.
Кроме того,
(х + у) (mod232) =
х + у; |x + y(mod3);
х + у —232 [х + у — 1 (mod3)
в зависимости от того, появляются ли переносы
при сложении. Поскольку при сложении 32-
разрядных слов переносы возникают с вероятно-
стью 0,98, то нижнее равенство выполняется с
этой вероятностью. Таким образом, линейные
равенства х «< п = х (mod 3) и х + у (mod 232) =
= х + у - 1 (mod 3) выполняются с заметным пре-
438
обладанием, что позволяет для вскрытия ключа
использовать аппарат линейного над F3 метода.
Стойкость RC5 к этому методу в зависимости
от числа циклов шифрования [22]:
Число циклов шифрования 8 10 12 14 16
Требуемое число открытых текстов 229 237 245 253 261
Сложность вскрытия ключа 237 245 253 261 269
19.8. Blowfish
Алгоритм шифрования Blowfish, разработан-
ный Б. Шнайером в 1993 г. [33], представляет
собой фейстелев шифр с переменной длиной
ключа. Размер блока — 64 бита. Эксплуатацион-
ными особенностями этого шифра являются:
- скорость (при шифровании на 32-разрядном
процессоре выполняется 26 единичных ко-
манд на один байт данных);
- компактность (реализация алгоритма требует
менее 5 Кбайт оперативной памяти);
- простота (используются операции подстанов-
ки, сложения по модулю 2 и по модулю 232).
Для построения списка цикловых ключей
длиной 4168 байт из секретного ключа, длина
которого не превышает 448 бит, 521 раз приме-
няется сам алгоритм зашифрования. Поэтому
желательно использовать Blowfish в таких при-
ложениях, где не требуется частая смена ключей.
32-разрядные цикловые ключи К\, ...,KiS и 32-
разрядные подстановки (.S'-блоки)
*S”i = (5],о, «S'],255); S2 = (5г,о, • 5*2,255),
Рис. 19.10. Схема шифра Blowfish
<$3 ~ №,0, •••, 5з,255); 5д — (54,0, ..., 54,255)
могут быть сформированы на этапе предвычис-
лений.
При зашифровании 64-разрядного блока от-
крытого текста (рис. 19.10) выполняются сле-
дующие действия.
1. Блок разбивается на два 32-разрядных полу-
блока х' и х".
2. На i-м цикле (i = 1, 2, .... 16):
- левый полублок х' суммируется по моду-
лю 2 с соответствующим цикловым клю-
чом К,;
- полученная сумма х разбивается на четыре
8-разрядных слова а, Ъ, с, d, каждое из ко-
торых является адресом элемента соответ-
ствующей подстановки 5У, 1 <j < 4. 32-
разрядный результат обработки полублока
х оператором F, формируется так:
F,(x) = ((51; о + 52, л) © 53, с) + 54, d,
где «+» — сложение по модулю 232;
- полублок F,(x') суммируется по модулю 2
с полублоком х";
- полученные полублоки меняются места-
ми (на последнем цикле этот шаг не вы-
полняется).
3. После 16 циклов полученные полублоки тек-
ста суммируются по модулю 2 с цикловыми
ключами -Fir и ТС17, получаются полублоки у'
и у" соответственно.
Выходным зашифрованным текстом является
конкатенация полублоков у' и у".
Оператор F
439
Расшифрование осуществляется аналогично, с
обратным порядком использования цикловых
ключей: Кх$, К\.
Ключи Кх,Л'18 и «S'-блоки «$) У2, У3, У4 выра-
батываются из исходного ключа KS следующим
образом:
1) начальный массив К цикловых ключей и «S'-
блоков инициируется фиксированной 128-
разрядной строкой (дробной частью числа
л = 3,14159... в шестнадцатиричном пред-
ставлении): «Ki = 243f6a88, Кг - 85a308d3,
Ki = 13198а2е, Кх = 03707344, ...;
2) Кх суммируется по модулю 2 с первыми 32
битами ключа KS, К2 суммируется по модулю
2 со следующими 32 битами ключа KS и т. д.
Если ключ KS короткий, например, длиной
64 бита, то для построения массива К, ис-
пользуется конкатенация ключа вида:
KS\\KS,KS\\KS\\KSmt. д.;
3) 64-разрядный блок 0 = (0, ..., 0) зашифровы-
вается алгоритмом Blowfish на цикловых
ключах, полученных на шагах 1 и 2;
4) Кх и К заменяются полученным на шаге 3
результатом зашифрования Со = Blowfish(O);
5) шифртекст Со зашифровывается алгоритмом
Blowfish на модифицированных цикловых
ключах;
6) К и К заменяются полученным на шаге 5
результатом зашифрования Ci = Blowfish(C0);
7) процедура повторяется до тех пор, пока не
будут получены сначала девять пар цикло-
вых ключей, а затем 512 пар элементов S-
блоков. Таким образом, всего выполняется 521
цикл зашифрования, на каждом из которых
происходит модификация ключей.
Этот шифр обладает слабыми ключами, для
которых отображение F, обладает коллизиями
[35]. Наличие коллизий позволяет ускорить
вскрытие таких ключей по сравнению с перебо-
ром, а также распознать, дает ли ключ коллизии.
Шифр Blowfish используется в системах
BestCrypt, KREMLIN, GnuPG.
19.9. SAFER
SAFER— r-цикловый (r = 6 4- 10) блочный
шифр с длиной блока 64 бита, предложенный
Дж. Месси [25]. При зашифровании открытого
текста блок разбивается на восемь байтов, про-
нумерованных от 1 до 8, и составляется список
цикловых ключей. Далее на каждом цикле вы-
полняются следующие операции:
- сложение блока текста с цикловым ключом
(нечетные байты складываются поразрядно
по модулю 2, четные — по модулю 256);
- подстановка байта— для нечетных байтов
выполняется подстановка «S', задаваемая воз-
ведением в степень: х <— 45А (mod 257) с за-
меной 256 на 0, где 45 — образующая груп-
пы S~257 - Для четных байтов выполняется об-
ратная подстановка «S-1;
- сложение со вторым цикловым ключом (для
четных байтов — по модулю 256, для нечет-
ных — по модулю 2);
- рассеивающая операция— псевдоадамарово
преобразование, реализованное при помощи
операции над парами байтов: (х, у) <— (2х + у
(mod 256), х + у (mod 256)). Всего выполня-
ется 12 таких операций, что эквивалентно
умножению 8-разрядного вектора на матрицу
Мс определителем 1 над кольцом Z/256Z:
г8 4 4 2 4 2 2 Г
4 2 4 2 2 1 2 1 •
42214221
2 12 12 12 1
М =
44222211
22221111
2 2 112 2 11
J 1 1 1 1 1 1 1,
После r-го цикла шифрования выполняется
сложение блока текста с цикловым ключом (не-
четные байты складываются по модулю 2, чет-
ные— по модулю 256). Всего используется
2r + 1 цикловых ключей.
Список ключей для шифрования формируется
из исходного ключа длиной 64 бита. Пусть К, —
j-й байт z-го блока ключа. Первый блок ключа
совпадает с исходным ключом (К1,..., А8). Второй
и последующий блоки вычисляются рекуррентно:
К’ = ((Kj «< (3/ - 3)) + в!) (mod 256),
где «В/ = S(S(9i + j)).
Для этого криптоалгоритма с 8 и 10 циклами
шифрования не найдено практически реализуе-
мых атак, позволяющих снизить стойкость по
сравнению с перебором. С. Мэрфи предложил
рассматривать этот шифр как модуль над коль-
цом Z размерности 8, гомоморфизмы которого
определяются матрицей М [28]. Для некоторых
подмодулей это отображение является изомор-
физмом. Использование специфических свойств
этого гомоморфизма создает предпосылки для
снижения стойкости шифра.
Совмещение дифференциального метода и
атаки на основе связанных ключей показывает,
что для вскрытия ключа 6-циклового шифра
SAFER требуется 224 229 подобранных откры-
тых текстов [21].
440
Шифр SAFER используется в системе KREM-
LIN.
19.10. RIJNDAEL (AES)
Криптоалгоритм RIJNDAEL был разработан
В. Рейменом и Й. Даманом и в 2000 г. выбран
Национальным институтом стандартов США в
качестве стандарта [5]. В отличие от таких «при-
вычных» шифров как DES и ГОСТ 28147-89, он
не является фейстелевым, то есть операции за-
шифрования и расшифрования используют раз-
личные перемешивающие и рассеивающие пре-
образования.
Характерной чертой этого шифра является то,
что здесь нет подстановок, сконструированных не-
понятным образом по непонятным критериям.
Шифр достаточно прозрачен, чтобы математически
подготовленный пользователь мог убедиться в том,
что в него не заложены «мины»,— все операции
шифрования описываются в терминах поля из 256
элементов и кольца полиномов над этим полем.
Длина блока составляет 128 бит, длина клю-
ча— 128, 192 или 256 бит. Число циклов шиф-
рования зависит от длины ключа и равно 10, 12
или 14 соответственно.
Открытый текст представляется в виде квад-
ратной матрицы размера 4. Элементы матрицы
рассматриваются двояко: как векторы над Е2 (при
описании способа получения подстановки) и как
элементы расширенного поля [Е256 ~ гДе
полином Д/) = Xs + х4 + х3 +1+ 1 неприводим над F2.
Над элементами матрицы определены следующие
операции:
- сложение в поле tF256;
- умножение в поле tF256;
- обращение в поле Е25б-
Строки матрицы рассматриваются как эле-
менты кольца (с делителями нуля) классов выче-
тов: А = Р25б[м]/(^4 + О- Над строками выполня-
ются операции сложения и умножения как над
элементами кольца А.
На каждом цикле зашифрования выполняются
четыре операции:
1) подстановка S байтов;
2) циклический сдвиг строк матрицы влево со-
ответственно на 0, 1, 2, 3 позиции (или, что
то же самое, умножение полиномов из А на
и ,и,и, и );
3) перемешивание столбцов матрицы путем ум-
ножения на невырожденную над F256 цирку-
лянтную матрицу L размера 4 х 4;5
4) поразрядное сложение по модулю 2 блока
текста с цикловым ключом.
При расшифровании те же операции выпол-
няются в обратном порядке.
Подстановка S имеет простое алгебраическое
описание. Сначала для байта х вычисляется об-
ратный элемент х-1 в поле Е256 (для нуля обратным
считается нуль).6 * Затем эти байты представляются
как векторы над F2, и вычисляется подстановка
как аффинное преобразование у = <S'(x) = ЛА-' © с,
где М— циркулянтная матрица с первой строкой
(10001111) и с = (11000110). Поскольку число не-
нулевых элементов в строке нечетно, матрица М
невырождена.
Обратная подстановка .S’-1 определяется урав-
нением х ’ = ЛС'у © d, где М~л — обратная к
матрице М циркулянтная матрица над Р2 с пер-
вой строкой (00100101), d = (10100000). Затем
вычисляется х расширенным алгоритмом Евкли-
да по отношению к полиному Х0- Например, для
у = 0 получаем х-1 = (10100000), то есть
х-1 = t2 + 1, откуда х = X6 + X4 + /, х = (01001010).
Наиболее вероятные дифференциалы прямой
и обратной подстановки, задающей обращение в
Е256, имеют вероятность 3/64, что всего в 4 раза
больше, чем «естественная» вероятность ’/256.
Циркулянтная матрица L задается первой
строкой (х, t + 1, 1, 1) или в шестнадцатиричном
виде (2, 3, 1, 1). Обратная матрица 7Г1 также цир-
кулянтна и задается первой строкой (X3 +t2 + t,
г + t + 1, t3 + Г + 1, t3 + 1) или в шестнадцатирич-
ном виде (е, b, d, 9).
Очевидно, что каждый раз вычислять подста-
новку неудобно, поэтому прямую и обратную
подстановку лучше хранить в памяти шифрато-
ра. Компактность алгоритма вычисления подста-
новки (колмогоровская энтропия подстановки
мала) снижает опасения, что в подстановке спря-
тан потайной ход, позволяющий тем, кто его зна-
ет, быстрее вскрывать ключ — в коротком алго-
ритме спрятать постороннюю информацию
сложнее.
Список 128-разрядных ключей для шифрова-
ния готовится из ключа длины 128 (192, 256) бит
на основе операций подстановки S и циклическо-
го сдвига с учетом номера цикла шифрования.
Алгоритм построения списка ключей не является
циклическим, что исключает возможность атаки
на основе связанных ключей и атаки методом
сдвига (см. пп. 18.3, 18.5).
Криптографическое преобразование RIJNDAEL
удобно записать в алгебраическом виде [18]. Под-
становка может быть задана над Г25й уравнением
5 В оригинале эта операция называется «сдвиг
строк» и «перемешивание столбцов», но эти две опе-
рации эквивалентны умножению вектора на матрицу.
6 Обратный элемент может быть найден расши-
ренным алгоритмом Евклида или возведением в сте-
пень 254 в кольпе F2[x]/(/8 + X4 +13 +1 + 1).
441
S(x) = Ws + ±WdX^
d=0
Поскольку на каждом цикле шифрования
выполняется сложение байтов с ключом, учтем
константу wg в составе ключа (это приведет к
модификации списка ключей). Поскольку
Л'255 = 1 в поле ^256, то подстановку можно запи-
сать в виде
S(x) = j\>dx-2d . (19.10.1)
d=0
На каждом цикле шифрования каждый байт
шифруемого текста является элементом квадрат-
ной матрицы размера 4. Обозначим этот элемент
для r-го цикла шифрования . Здесь индексы i,
/ можно рассматривать по модулю 4. Тогда в
уравнении (19.10.1) коэффициенты wd и показа-
тель d будут зависеть от номера цикла шифрова-
ния: d = d(r). Подстановка для блока в целом
описывается уравнением
М?)= ЬЖ’
J(r)=0
Операции сдвига строк матрицы с учетом
подстановки соответствует уравнение
</(г)=0
Операцию перемешивания столбцов учтем в
виде дополнительной суммы:
MTS(a^) = X •
e(r)=0d(r)=0
Теперь можно записать уравнение шифрова-
ния для одного цикла:
ф-)=0</(г)=0
Если выполнить рекурсивную подстановку
(У)
элементов о, ; согласно этому уравнению, то
получим уравнение зашифрования на нескольких
циклах в виде непрерывной дроби. Все операции
описываются в терминах поля F256- Такое пред-
ставление уравнения шифрования является
предпосылкой для построения алгебраических
методов анализа, поскольку поле F256 является
расширением полей F16, F4 и F2, а теория непре-
рывных дробей — достаточно хорошо изученная
область математики.
Для вскрытия ключа 6-циклового шифра
RIJNDAEL требуется 235 подобранных открытых
текстов, сложность вскрытия ключа составляет
244 [17].
Шифр RIJNDAEL используется для шифро-
вания данных в системах Rar, GnuPG, BestCrypt.
19.11. MD5
Хэш-функция MD5 была разработана
Р. Ривестом в 1991 г. [30] как усиленный вариант
хэш-функции MD4 [31]. Необходимость замены
была вызвана тем, что для хэш-функции MD4
сложность вычисления коллизий оказалась не-
высокой— около 1 минуты на персональном
компьютере [15]. Длина аргумента хэш-функции
может быть произвольной, длина значения —
128 бит (отсюда следует, что сложность нахож-
дения коллизии не может превышать 264 опера-
ций вычисления хэш-функции).
В ходе вычислений используются следующие
функции 32-разрядных аргументов u, v, w:
/Ди, v,w) = uvvuw; /2(u,v,w) = uw v vw;
/3 (и, v, w) = и ® v © w; /4 (u, v, w) = v © (u v w).
Здесь символом © обозначено поразрядное
сложение векторов по модулю 2, символом v —
поразрядная дизъюнкция векторов, символ по-
разрядной конъюнкции опущен для однозначной
очередности операций.
С учетом равенства avb = a©b©ab эти
функции можно записать в терминах кольца Gn:
fi = w © u(v © w); / = v © w(u © v);
/ = u © v © w; f = 1 © v © w(l © u).
Каждая из этих булевых функций является
сбалансированной. Булевы функции f,f,f име-
ют нелинейность 2, булева функция / аффинная
(имеет нелинейность 0).
На этапе предвычислений определяются сле-
дующие параметры:
1) 64 константы по 32 бита каждая:
j[/] = |sin(/+ 1)| для 0 <j< 63; ' !
2) три перестановки z[-] на множестве
(0,1,..., 15) как арифметические прогрессии
в Z716Z: Д16...31]— прогрессия с первым
членом 1 и разностью 5, Д32...47]— про-
грессия с первым членом 5 и разностью 3,
Д48...63] — прогрессия с первым членом 0 и
разностью 7; «-•
3) четыре массива, которые задают параметры
циклических сдвигов: ДО... 15] = {(7,12,17,22)4},
442
s[0...15] = {(5,9, 14, 20)4}, s[0...15] = {(4, 11,
16, 23)4}, s[0...15] = {(6, 10, 15, 21)4}.
Пусть исходный аргумент m задан t-
разрядной строкой /Ир.ли,. Эта строка дополня-
ется до длины, сравнимой с 448 по модулю 512
(то есть длине аргумента «не хватает» ровно 64
битов, чтобы быть кратной 512), а именно: к ар-
гументу присоединяется одна «1», а затем необ-
ходимое количество нулей. Причем дополнение
строки выполняется даже в том случае, если ее
длина уже сравнима с 448 по модулю 512 (в этом
случае к аргументу добавляется одна единица и
511 нулей).
К полученной строке присоединяется 64-
разрядное представление числа t. При t > 264 ис-
пользуются только младшие 64 бита числа Л
Пусть дополненный аргумент имеет вид
М = М\...М„, где М— блок, состоящий из 16
слов по 32 бита каждое, 1 < i < п, а /? кратно 16.
Стартовый вектор хэширования длины 128 бит
представляет собой конкатенацию четырех кон-
стант: 012345671| 89abcdef || fedcba981| 76543210.
При вычислении используется накопитель,
содержащий четыре 32-разрядных слова А, В, С,
D. Исходным заполнением накопителя являются
слова стартового вектора хэширования.
Обработка 16-словного блока Mt, 1 < i < и,
осуществляется за четыре цикла, каждый из ко-
торых включает в себя 16 шагов.
На каждом шаге j-го цикла, 1 <j < 4, выпол-
няются операции:
t<r- В + (А +ДВ, С, D) + +у[Л),
(А, В, С, D)^(D,B + t «< 5[z], В, 0,
где — слово, выбранное из М, в соответ-
ствии с перестановкой z; X «< к— циклический
сдвиг слова X влево на к бит; «+» — операция
сложения по модулю 232. Таким образом, на каж-
дом шаге выполняются четыре операции сложе-
ния и одна операция сдвига, вычисляется значе-
ние одной цикловой функции.
Выходом каждой итерации является конкате-
нация текущих значений четырех слов накопите-
ля. После обработки блока Мп итоговым сжатым
образом аргумента будет 128-разрядная строка
из четырех слов: А || В || С || D.
Поскольку нелинейность операций f мала,
нелинейные свойства итогового преобразова-
ния определяются влиянием переносов при
сложении.
Коллизию для MD5 можно вычислить за не-
сколько часов на персональном компьютере [16].
Кроме того, этот алгоритм, по-видимому, уязвим
по отношению к дифференциальному анализу с
операцией разности по модулю 232 [6].
Хэш-функция MD5 используется в системах
MSOffice, PDF.
Вариантами хэш-функции MD5 являются
хэш-функция SHA, используемая в американ-
ском стандарте цифровой подписи ECDSS, и
хэш-функция R1PEMD.
19.12. ГОСТ Р 34.11-94
Отечественный стандарт хэш-функции
ГОСТ Р 34.11-94 [2] предназначен для использо-
вания в криптографических методах обработки и
защиты информации, в том числе в алгоритмах
цифровой подписи ГОСТ Р 34.10-94 и
ГОСТ Р 34.10-2001. В ходе вычисления хэш-
функции используется стандарт шифрования
ГОСТ 28147-89.
Длина аргумента х произвольная, длина зна-
чения h(x)— 256 бит. Варьируемыми парамет-
рами являются стартовый вектор длиной 256 бит
(выбирается произвольным) и блок подстановок
для шифра ГОСТ 28147-89 (выбирается уста-
новленным порядком). Хэш-функция вычисляет-
ся на основе шаговой функции хэширования с
длиной аргумента 256 бит, при этом аргумент
разбивается на блоки длиной по 256 бит. По-
следний блок при необходимости дополняется
нулями.
Шаговая функция хэширования вычисляется в
три этапа. На первом этапе вычисляются четыре
ключа К], К2, К3, Кд для шифра ГОСТ 28147-89
по 256 бит каждый. На втором этапе стартовый
вектор разбивается на четыре блока по 64 бита
каждый, и эти блоки зашифровываются на клю-
чах Кд, Ki, Кд, Кд по ГОСТ 28147-89. На третьем
этапе выполняется рассеивающее преобразова-
ние стартового вектора, аргумента хэш-функции
и полученных шифрограмм.
Рассмотрим подробнее этапы вычисления ша-
говой функции хэширования h (u, w) блока ар-
гумента и и стартового вектора w.
Для вычисления ключей Кд, Кг, Кд, Кд выпол-
няются аффинные над [F2 преобразования. Опре-
делим над F2 квадратную блочную матрицу:
'0 £ 0 О'
0 0 Е 0
А =
0 О 0 Е
чЕ Е 0 0,
где Е — единичная матрица размера 64 х 64, 0 —
нулевая матрица. Пусть вектор сдвига
c=l808l16024l1V(08l8)2l808(08l8)4(l808)4 и опера-
тор Р перестановки байтов представляет собой
блочную матрицу над DF2 из 1024 блоков размера
8x8 бит, каждый блок — нулевая или единич-
443
ная матрица: Р = (1, 9, 17, 25, 2, 10, 18, 26, 3, 11,
19, 27, 4, 12, 20, 28, 5, 13, 21, 29, 6, 14, 22, 30, 7,
15,23,31,8, 16,24, 32).
Ключи получаются выполнением аффинных
над F2 преобразований:
K!=P(u@w);
К2 = Р(А2и © Aw) = РА(Аи © w);
К3 = Р(А4и © A2w © с);
К4 = Р(А6и © A\v © Ас) = РА(А5и © A2w © с).
Ключи К, обозначены полужирным шрифтом,
поскольку они на этом этапе рассматриваются
как векторы над F2.
Полиномы от матрицы А образуют поле из 16
элементов, изоморфное полю F2[/]/(/4 + t+ 1). Это
утверждение вытекает из равенства А4 + А + Е = 0,
где полином в левой части неприводим.
На втором этапе стартовый вектор w разбива-
ется на четыре блока: w = (wb w2, w3, w4), каж-
дый блок w, зашифровывается на ключе К, в ре-
жиме простой замены с результатом s,. Четыре
шифрограммы образуют 256-разрядный двоич-
ный вектор s = (si, s2, s3, s4).
На третьем этапе выполняется рассеивание
для аргумента и хэш-функции, стартового векто-
ра w и вектора шифрограмм s как аффинная над
F2 операция. Определим над F2 блочную квад-
ратную матрицу с размером блока 16 х 16:
'0 Е 0 0 0 0 0 0 0 0 0 0 0 0 0 0"
00Е0000000000000
0 0 0 £ о о о о о о о о о о о о
0000Е00000000000
00000Е0000000000
000000Е000000000
0000000Е00000000
00000000Е0000000
в=
000000000Е000000
0000000000Е00000
00000000000Е0000
000000000000Е000
0000000000000Е00
00000000000000Е0
000000000000000Е
^ £ £ £ 0 0 0 0 0 0 0 0 £ 0 0
Полиномы от матрицы В образуют поле из 216
элементов.
Значение шаговой функции хэширования:
/г*(и, w) = B61(w © B(u © Bl2s)). (19.12.1)
Собственно хэш-функция вычисляется по ре-
куррентной формуле: w <— h (u„ w), 1 < i < w - 1.
Для последнего блока u„ значение шаговой
функции хэширования определяется так:
1) вычисляется w <— h (u,„ w);
2) вычисляется длина аргумента / в битах по
модулю 2256 с учетом возможного неполного
последнего блока; вычисляется w <— h (1, w);
3) вычисляется сумма q всех блоков по модулю
2256, вычисляется шаговая функция хэширо-
вания h (q, w), которая и является значением
хэш-функции.
Хэш-функция ГОСТ Р 34.11-94 характеризу-
ется следующими свойствами.
1. Не существует аргумент шаговой функции
хэширования, для которого совпадают три из
четырех ключей, вырабатываемых на первом
этапе. Это утверждение следует из того факта,
что полиномы от матрицы А образуют поле. Од-
нако существует множество пар стартовых век-
торов и аргументов, для которых два из четырех
аргументов совпадают, например, u = w = 0 дают
К] = К2 = 0. При этом для каждого стартового
вектора существует единственный аргумент, для
которого выполняется заданное равенство
К, = К;. Обратно, для заданного стартового век-
тора w существует единственный аргумент и,
позволяющий выработать заданное значение
ключа К,.
2. Коллизию для хэш-функции в целом можно
найти со сложностью примерно 2128 процедур
вычисления хэш-функции методом, описанным в
п. 17.10.
Коллизию для шаговой функции хэширования
быстрее можно найти методом встречи посере-
дине [3], если совместить заготовку коллизий с
выбором стартового вектора хэширования. При
равенстве левых частей в формуле (19.12.1) пра-
вые части можно сократить на обратимый опера-
тор В61. Поэтому коллизия (и, и') шаговой функ-
ции хэширования задается условием
w © B(u © B,2s) = w © B(u' © B12s').
Упрощая это равенство, получаем
s © s' = Bl2(u © u').
Матрица В~'2 (рассматриваемая как блочная)
имеет вид
% B2i В31 в.г
В-12 = В2] В22 В2] В4А
В21 0 В22 в 43
0 0 0 J
444
То обстоятельство, что в нижней строке один
блок единичный, а остальные нулевые, позволяет
разбить задачу поиска коллизий на две части:
сначала выбрать произвольные ключи Л?4, Кд,
блок w4 стартового вектора, вычислить s4 © s4',
U] © и/ = s4 © s4'; затем с помощью варьируемых
разрядов векторов w, u. u' найти коллизию для
оставшихся трех блоков методом встречи посе-
редине. Сложность поиска коллизий для шаговой
функции хэширования этим способом равна при-
296
ж
Аналогично можно искать пару аргументов,
дающих не нулевую, а заданную разность значе-
ний шаговой функции хэширования.
Упражнения к главе 19
1. *Шифр IDEA использует операцию умно-
жения слова текста на слово ключа по моду-
лю р = 21б + 1, ключи зашифрования и рас-
шифрования — взаимно обратные по моду-
лю р. Как найти ключ расшифрования для
продолженного ключа зашифрования при
анализе методом продолжения полиномов
Жегалкина?
2. *Оцените стойкость DES к анализу методом
продолжения полиномов Жегалкина.
3. *Оцените стойкость RC5 к анализу методом
продолжения полиномов Жегалкина.
4. *Оцените стойкость RIJNDAEL к анализу
методом продолжения полиномов Жегалки-
на. Сравните эффективность рационального
и 2-адического продолжения.
5. Предложите вариант атаки на ГОСТ
28147-89 для случая, когда одноблочные
тексты зашифрованы в режиме простой за-
мены и дополнены 32-разрядными имито-
вставками.
6. Предложите способы получения гаммы с га-
рантированно большой длиной периода.
7. Предложите свой режим шифрования длин-
ных сообщений, отличный от режимов гам-
мирования и гаммирования с обратной свя-
зью.
8. *Предложите свой вариант блочного шифра
с размером блока и бит и совмещенными опе-
рациями перемешивания и рассеивания.
Примером такой операции является подста-
новка х + х2 + х (mod 2") и перестановка би-
тов. Оцените требуемое число циклов.
9. *Исследуйте сложность обращения одно-
блочной хэш-функции MD5 методом про-
должения полиномов Жегалкина.
10. Предложите способ построения блочного шиф-
ра на основе блочной хэш-функции, например,
MD5. Очевидно, длина блока шифра должна
быть кратна длине блока хэш-функции.
11. *Исследуйте стойкость шифра IDEA с по-
мощью дифференциалов второго порядка над
2/(2,6 + 1)2.
12. *Насколько «усеченный вариант» шифра
IDEA (с заменой умножения по модулю
216 + 1 умножением по модулю 28 * + 1 или
24 + 1, 22 + 1 и пропорциональным сокраще-
нием длины блока) похож на полный шифр?7
Можно ли использовать «усеченный» шифр
для вскрытия ключа полного шифра?
13. *По аналогии с предыдущей задачей можно
определить «усеченный вариант» шифра
RIJNDAEL (более общо— вычислимый го-
моморфизм шифра в шифр меньшего разме-
ра, используя подполе поля Е25б)- Можно ли
использовать «усеченный» шифр для вскры-
тия ключа полного шифра?
14. Оцените стойкость шифра ГОСТ 28147-89 к
методу на основе 2-адического продолжения,
если сложение по модулю 232 заменить сло-
жением по модулю 2. Повлияет ли на стой-
кость свойство разреженности ключа и тек-
ста?
15. Предположим, что в шифре блок и ключ име-
ют длину п бит. Покажите, что если по ана-
логии с режимом гаммирования (рис. 19.2)
шифртекст использовать в качестве ключа, а
открытый текст оставить неизменным, то
длина цикла формируемой последователь-
ности составит 0(2”^) блоков.
16. *Каким требованиям должны удовлетворять
32 подстановки из S-блока шифра типа DES,
чтобы цикловая функция шифрования F, (см.
рис. 19.5) была биекцией на множестве 32-
разрядных слов?
7 Мультипликативные группы вычетов по модулю
простых чисел Ферма и кольца 2/2162, 2/282,
гомоморфны, причем эти гомоморфизмы «похожи».
445
Литература к главе 19
1. ГОСТ 28147-89. Системы обработки информа-
ции. Зашита криптографическая. Алгоритм крип-
тографического преобразования. М.: Госстандарт
СССР, 1989.
2. ГОСТ Р 34.11-94. Информационная техноло-
гия. Криптографическая защита информации.
Функция хэширования. М.: Госстандарт Рос-
сии, 1994.
3. Ростовцев А.Г., Дук Т.Г. Ускоренный способ по-
иска коллизий в стандарте на хэш-функцию //
Труды российской научно-технической конфе-
ренции «Методы и средства обеспечения безо-
пасности информации». СПб., 1996. С. 204-205.
4. Ростовцев А.Г., Маховенко Е.Б., Филиппов А.С.,
Чечулин А.А. О стойкости ГОСТ 28147-89 //
Проблемы информационной безопасности. Ком-
пьютерные системы. СПб., 2003. № 2.
5. Announcing the advanced encryption standard
(AES). Federal Information Processing Standards
Publication, 2001.
6. Berson T.A. Differential cryptanalysis mod 232 with
applications to MD5 // Advances in Cryptology —
EUROCRYPT ’92. Lecture Notes in Computer Sci-
ence. Springer-Verlag. 1993. Vol. 658. P. 71-80.
7. Biham E., Shamir A. Differential cryptanalysis of
DES-Iike cryptosystems // Advances in Cryptol-
ogy— CRYPTO’90. Lecture Notes in Computer
Science. Springer-Verlag. 1991. Vol. 537. P. 2-21.
8. Bihain E., Shamir A. Differential cryptanalysis of
FEAL and N-hash // Advances in Cryptology —
EUROCRYPT ’91. Lecture Notes in Computer Sci-
ence. Springer-Verlag. 1991. Vol. 547. P. 1-16.
9. Biham E., Shamir A. Differential cryptanalysis of the
full 16-round DES // Advances in Cryptology —
CRYPTO ’92. Lecture Notes in Computer Science.
Springer-Verlag. 1993. Vol. 740. P. 487-496.
10. Biryukov A. Cryptanalysis of RC5 // DREI ’97
Workshop on Cryptography and Network Security
(Abstracts). July28-Aug 15, 1997.
11. Biryukov A., Wagner D. Advanced slide attacks //
Advances in Cryptology— EUROCRYPT 2000.
Lecture Notes in Computer Science. Springer-
Verlag. 2000. Vol. 1807. P. 589-606.
12. Bityukov A., Wagner D. Slide attacks // Fast Soft-
ware Encryption FSE ’99. Lecture Notes in Com-
puter Science. Springer-Verlag. 1999. Vol. 1636.
P. 245-259.
13. Borst J., Knudsen L., Rijmen V. Two attacks on re-
duced IDEA // http://link.springer.de/link/service/ se-
ries/0558/bibs/1233/12330001 .htm.
14. Daemen J., Govaerts R., Vandewalle J. Weak keys
for IDEA // Advances in Cryptology —
CRYPTO ’93. Lecture Notes in Computer Science.
Springer-Verlag. 1994. Vol. 773. P. 224-231.
15. Dobbertin H. Alf Swindles Ann // CryptoBytes.
1995. Vol. 1(3). P. 5.
16. Dobbertin H. Cryptanalysis of MD5 compress //
http://www.ioc.ee/home/helger/crypto/htmls/hash.htm.
17. Ferguson N., Kelsey J., Lucks S., et al. Improved crypt-
analysis of RIJNDAEL // http://www.coimterpane.com/
rijndaeLhtml.
18. Ferguson N., Schroepel R., Whiting D. A simple al-
gebraic representation of RIJNDAEL // http://www.
xs4all ml/ ~vorpal/pubs/rdalgeq .html.
19. Kaliski B., Rivest R., Sherman A. Is the Data En-
cryption Standard a group? (Results of cycling ex-
periments on DES) // Journal of Cryptology. 1988.
Vol. l.P.3-36.
20. Kaliski B.S., Yin Y.L. On differential and linear
cryptanalysis of the RC5 encryption algorithm // Ad-
vances in Cryptology — CRYPTO ’95. Lecture
Notes in Computer Science. Springer-Verlag. 1995.
Vol. 963. P. 171-184.
21. Kelsey J., Schneier B., Wagner D. Key-schedule
cryptanalysis of IDEA, G-DES, GOST, SAFER, and
Triple-DES // Advances in Cryptology —
CRYPTO ’96. Lecture Notes in Computer Science.
Springer-Verlag. 1996. Vol. 1109. P. 237-251.
22. Kelsey J., Schneier B., Wagner D. Mod n cryptanaly-
sis, with applications against RC5P and M6 //
http://www.counterpane.com/mod3.html.
23. Konheim A. Cryptography: A Primer. New York:
J. Wiley & Sons, 1981.
24. Lai X., Massey J.L. A proposal for a new block en-
cryption standard // Advances in Cryptology —
EUROCRYPT ’90. Lecture Notes in Computer Sci-
ence. Springer-Verlag. 1991. Vol. 473. P. 389-404.
25. Massey J.L. SAFER K-64: A byte-oriented block-
ciphering algorithm // Fast Software Encryption.
Cambridge Security Workshop. Lecture Notes in
Computer Science. Springer-Verlag. 1994. Vol. 809.
P. 1-17.
26. Matsui M. Linear oyptanalysis method for DES cipher
// Advances in Cryptology — EUROCRYPT ’93. Lec-
ture Notes in Computer Science. Springer-Verlag.
1994. Vol. 765. P. 386-397.
27. Menezes A., van Oorschot P., Vanstone S. Handbook
of Applied Cryptography. CRC Press, 1997.
28. Murphy S. An analysis of SAFER // Journal of Cryp-
tology. 1998. Vol. J1. P. 235-251.
29. National Institute of Standards and Technology
(NIST). FIPS Publication 46-2: Data Encryption
Standard (DES). Dec 1993.
30. Rivest R.L. RFC 1321: The MD5 message-digest
algorithm // Internet Activities Board, April 1992.
31. Rivest R.L. The MD4 message digest algorithm //
Advances in Cryptology — CRYPTO ’90. Lecture
Notes in Computer Science. Springer-Verlag. 1991.
Vol. 537. P. 303-311.
32. Rivest R.L. The RC5 encryption algorithm // Fast
Software Encryption. Second International Work-
shop. Lecture Notes in Computer Science. Springer-
Verlag. 1995. Vol. 1008. P. 86-96.
33. Schneier B. Description of a new variable-length key,
64-bit block cipher (Blowfish) // Fast Software En-
cryption. Cambridge Security Workshop (Dec 1993).
Lecture Notes in Computer Science. Springer-
Verlag. 1994. Vol. 809. P. 191-204.
34. Shimizu A., Miyaguchi S. Fast data encipher-
ment algorithm FEAL // Advances in Cryptology —
EUROCRYPT ’87. Lecture Notes in Computer Sci-
ence. Springer-Verlag. 1988. Vol. 304. P. 267-278.
35. Vaudenay S. On the weak keys of Blowfish // Fast
Software Encryption. Third International Workshop.
Lecture Notes in Computer Science. Springer-
Verlag. 1996. Vol. 1039. P. 27-32.
36. ftp://ftp.replay.com/pub/replay/mirror/ftp.ciyptography.
org/ DESX/desx. algorithm.description.
ОТВЕТЫ И УКАЗАНИЯ К УПРАЖНЕНИЯМ
Глава 1
13. Закон исключения третьего g является вы-
сказыванием и должен быть или истинным, или
ложным. Пусть .S' — множество высказываний,
истинных тогда и только тогда, когда g ложно.
Тогда должно быть истинным в точности одно из
высказываний: g е S или g ё S. Однако ни одно
из них не является истинным.
Глава 2
2. Аддитивная группа Z абелева, все ее под-
группы имеют вид где п — неотрицательное
целое число.
3. Эндоморфизмы аддитивной группы Z име-
ют вид а па.
5. Если группа некоммутативная, то
{ab)~x = b 'a } Ф а Ь~\
6. Группа некоммутативна:
(1,3, 2X2, 1,3) = (3, 1,2);
(2, 1,3X1, 3,2) = (2,3, 1).
Перенумеруем подстановки (1,2,3), (1,3,2),
(2, 1, 3), (2, 3, 1), (3, 1, 2), (3, 2, 1) от 1 до 6. Таб-
лица умножения имеет вид
1 2 3 4 5 6
1 1 2 3 4 5 6
2 2 1 5 6 3 4
3 3 4 1 2 6 5
4 4 3 6 5 1 2
5 5 6 2 1 4 3
6 6 5 4 3 2 1
Группа S3 образована двумя подстановками
(1,3, 2), (2, 3,1).
Нормальными являются следующие группы:
{е}; сама симметрическая группа S3; знакопере-
менная группа, образованная степенями подста-
новки (2, 3,1).
7. Гомоморфный образ циклической группы
определяется образом образующей, то есть цик-
личен.
8. Элементами группы являются положитель-
ные и отрицательные числа вида 2'"3П, где т,
n&'Z..
9. Множество простых целых чисел и -1.
10. (а5) = {е, a5, a10}, G/{a5} = {е, а, а2, а3, а4}.
11. Любую обратимую матрицу можно пред-
ставить в виде произведения матрицы с единич-
ным определителем на скаляр.
12. Изоморфизм ср переводит единичный эле-
мент в единичный элемент, то есть ср(0)=1,
(р(1) = -1.
13. Рассмотреть множество транспозиций и
порожденную ими группу.
14. Рассмотреть множества подстановок, не
сохраняющих неподвижным элемент 1, не со-
храняющих неподвижным элемент 2 и т. д., за-
тем найти мощность объединения этих множеств
с учетом всевозможных их пересечений.
15. Результат следует из разбиения группы по
подгруппе.
16. Мультипликативная группа Q образована
простыми числами, а аддитивная группа Q не
имеет образующих.
17. Пусть G — группа и Н — ее подгруппа
индекса 2. Тогда существует элемент х е G та-
кой, что G = IHjxH, xH=G\H. Кроме того,
G = IGjНх, Hx = G\H, поэтомухН = Нх.
18. Если a g G — неединичный элемент, то
разложение G по подгруппе (а) совпадает с {а}.
Поэтому (а) = G.
Глава 3
1. Нет, поскольку не всегда существует про-
тивоположный элемент.
3. Рассматриваемые числа лежат в поле ком-
плексных чисел, поэтому аксиомы кольца вы-
полняются. Произведение чисел рассматривае-
мого вида является целым рациональным числом
тогда и только тогда, когда сомножители сопря-
жены. Кольцо целостное, если D не является
квадратом.
4. Рассмотреть квадрат модуля комплексного
числа.
5. Положить х = а G Ж. Ядро составляют по-
линомы с корнем а. При равенстве х2 = -1 гомо-
морфизма нет.
6. Сравнение a = b (mod 0) означает, что
а - Ъ = 0. Имеет место изоморфизм 7?/(0) = R.
7. Не будет, так как идеал не имеет противо-
положного.
448
9. (10) +(15) = (5), (10X15) = (150), (10)n(15)=
= (30); (2) + (3) = (1), (2X3) = (6), (2) n (3) = (6).
13. x + 6, x — 2x, 9.
14. В кольце Z[x] идеал (0) простой, а в коль-
це (Z735Z)[xj — нет.
15. Возможный гомоморфизм: положить
х„ = 1. Ядром этого гомоморфизма являются по-
линомы вида/(Х|,..., x„_i)+ х,Дхь ...,х„ч).
17- Q; Q; Q; рациональные функции
вида fix) + Ь(х)у, где а, b е С(х).
21. Нет, в поле все элементы обратимы.
22. xy+xz+yz = (l + х(1 +у)(1 +?))(! +у(1 +
+х)(1 +z)Xl +41 +хХ1 +J)X1 +(1 ++Х1 +
+JX1+*))-
Глава 4
2. Не существует, так как в противном случае
объемлющее поле содержало бы делители нуля.
4. Поле Q не содержит числа л, которое не
является корнем ни одного алгебраического
уравнения.
5, в). Построить неприводимый над С(х) по-
лином степени 2 от новой переменной у,
fix, у) = у2 + fix), дискриминант которого свобо-
ден от квадратов в С(х) (например, deg(g) = 3 и
fix) не имеет кратных корней), и присоединить
корень полинома/^ У)-
9. Рассмотреть полином хр - х и степени его
делителей.
11. Для этих полиномов в группе F)9 элемент
-а не является квадратом, то есть его порядок не
делится на 2, а порядок элемента -Ъ не делится
на 3.
12. Полиномы и рациональные функции, в ко-
торые переменная входит в степени р.
17. Порядок мультипликативной группы поля
характеристики 2 нечетный. Поэтому корень
единственный и имеет кратность 2. Корень урав-
нения имеет вид aq^2.
18. Рассмотреть сумму а2 +а2 +а2 +... из
слагаемых, входящих в след, взятых через одно.
Глава 5
3. Рассмотреть сравнение по модулю 3.
4. Воспользоваться формулой для геометри-
ческой прогрессии.
5. Да.
6. Рассмотреть норму квадратичного числа
N(a + b^-2) = а2 + 2Ъ2.
7. 17 = (3 + 2др2)(3 - 2-7-2). То, что сомно-
жители простые, следует из мультипликативно-
сти нормы.
8. -3 квадратичный вычет для простых чисел
р = 1 (mod 3).
6 квадратичный вычет, если 2 и 3 оба квадра-
тичные вычеты или оба квадратичные невычеты,
то есть если р = ±1 (mod 12) и р = ±1 (mod 8) или
если р = ±5 (mod 12) и р = ±3 (mod 8). Объедине-
ние этих условий дает р = ±1 (mod 24) или р = ±5
(mod 24).
21 квадратичный вычет, если 3 и 7 оба квад-
ратичные вычеты или оба квадратичные невыче-
ты, то есть если /?={1, 19, 25, 31, 37, 55}
(mod 84).
9. Число -72 + Js является корнем полинома
fix) = х4 - 14х2 + 9 с целыми коэффициентами.
Группа Галуа абелева, имеет порядок 4 и изо-
морфна прямому произведению групп порядка 2.
Группу Галуа составляют операции замены кор-
ня -72 + Js полинома fix) на сопряженные кор-
ни д/2 -45,—72 + V5, - д/2 -4$ и тождествен-
ная замена.
Глава 6
5. Нет. Эллиптическая кривая содержит четы-
ре точки порядка 2: (а, 0), (Ь, 0), (с, 0), Рх.
6. Рассмотреть прообраз произведения эле-
ментов, соответствующих узлам решетки.
12. Нет. - , г
13. Нет.
18. Ошибка заключается в том, что нужно ис-
кать кратность нуля функции на эллиптической
кривой, а не рациональной функции при х = 0.
Функция х имеет на эллиптической кривой нуль
кратности 2, так как х = 0 задает вертикальную
касательную в точке (0,0) с дивизором
2((0, 0))-2(Рю).
х(х—1)
19. f =-------. Дивизоры линейных функ-
2.У
ций: div(x) = 2((0,0)) - 2(РЮ); div(x - 1) = 2((1, 0)) -
- 2(РЮ); div(y) = ((0, 0)) + ((1,0)) + ((-1,0))-
- 3(РХ). Поэтому div(/) = div(x) + div(x - 1) -
- div(y) = ((0, 0)) + ((1, 0)) - ((-1,0)) - (Рю). Нор-
мирование в точках Р, Q равно 1.
21. Нулями функции являются точки пересече-
ния кривой у = —х2 и эллиптической кривой, всего
четыре точки пересечения: Р} = (0, 0), Р2 = (1, -1),
Р3 = (2, -4), Р4 = (-2, -4). Для нахождения кратно-
сти нулей построим дивизор функции. Проводим
секущую Zj через Р3, Р4. Получаем третью точку
пересечения Р5 = (-4, -4). Секущая задана нулями
функции у+ 4; div(Zi) = (/Д) + (ZJ4) + (7%) - 3(РК).
Проводим секущую Z2 через Ps, -Р5, заданную ну-
лями функции х + 4; div(Z2) = (Р5) + (-Р5) - 2(РД.
449
Проводим секущую Z3 через Рг, -Р5. Получаем
третью точку пересечения Pt = (0,0). Дивизор се-
кущей равен div(Z3) = (Л) + (~Л) + (Л) - 3(Р«>).
Тогда div(Zi) - div(Z2) + div(Z3) = (Pi) + (P2) + (P3) +
+ (P4) - 4(РЮ). Проверка показывает, что = f.
^2
25. Точка имеет нулевую у-координату.
26. Да, если Р — точка перегиба.
28. Если идеал, задающий алгебраическую
кривую, не является простым, то координатное
кольцо имеет делители нуля. Если идеал макси-
мален, то координатное кольцо целостное.
30. Представить f как рациональную функ-
цию, в числителе и знаменателе которой стоят
линейные функции, задающие прямые. Функция
определена с точностью до константы, но при
делении константы сокращаются, то есть можно
считать, что константа равна 1.
Глава 7
10. Пусть q = 3" •— число элементов поля. По-
скольку а‘‘ = а, решение уравнения х3 = а имеет
Зп—I
вид х = сг
Глава 8
2. Защита от несанкционированного воздейст-
вия включает в себя защиту от непреднамерен-
ного воздействия.
3. Если нарушитель вскрыл ключ, с помощью
которого вырабатывается ключевая хэш-
функция, и создал с его помощью сообщение,
это будет нарушением подлинности, но не цело-
стности.
4. Это будет нарушением подлинности и, воз-
можно, нарушением конфиденциальности (внут-
ри системы безопасной связи), если сообщение
должно храниться в секрете от пользователя В.
6. Предписание является частным случаем
разрешения (разрешается делать только то, что
предписано).
10. Для того чтобы гарантировать безопас-
ность, нужно, в частности, показать, что предпо-
лагаемые недокументированные возможности не
могут быть использованы для построения атак.
15. Транспозиция является инволюцией, а
любая подстановка может быть представлена как
композиция транспозиций.
Глава 9
4. Асимптотическая временная сложность ме-
тодов примерно одинакова. Разложение на эл-
липтической кривой требует полиномиального
объема памяти, а разложение квадратичным ре-
шетом — субэкспоненциального.
8. (р - 1 )-метод является частным случаем раз-
ложения на эллиптической кривой, если в качест-
ве кривой использовать вырожденную кубику.
9. Полином из [Fr[/] может быть разложен с
полиномиальной сложностью (см. алгоритм
7.4.1). Кроме того, вскрытие такой криптосисте-
мы требует не разложения полинома, а лишь на-
хождения степеней его простых делителей, так
как конечные поля одной и той же степени рас-
ширения эквивалентны.
15. Показать, что существует кривая Ер
у2 = х3 + В] (modр\) с числом точекр.
16. Эллиптическая кривая E(FP) определяется
своим полем функций и может быть описана как
квадратичное расширение поля рациональных
функций. Квадратный корень V х3 +Ах + В мо-
жет быть описан с помощью непрерывных дро-
бей над кольцом ТДх], так как из
, и , а
1 ч-------= X следует 1ч-----= X, то есть
1 + — х
1ч-...
X2 — X— а = 0. Замена в непрерывной дроби а на
кубический полином от х даст эллиптическую
кривую.
Глава 10
3. Идеалы (1+0 и (1 - /) порождаются ассо-
циированными элементами, а идеалы (1 + 2/) и
(1 - 2z) — нет.
12. Поскольку наилучшим известным мето-
дом как дискретного логарифмирования, так и
разложения является решето числового поля (от-
личия при логарифмировании и разложении не
принципиальны), асимптотические сложности
задач равны.
Глава 11
1. Такие отображения ведут себя как случай-
ные.
5. Группа точек вырожденной кубики над Q
изоморфна Q . Поэтому ее ранг бесконечно ве-
лик.
9. Любая симметрическая функция автомор-
физмов поля, например, след.
10. Все.
12. Для логарифмирования в группе E(Z7«Z)
нужно сначала разложить число w, а затем лога-
рифмировать в подгруппах. Задача разложения
значительно проще, чем задача логарифмирова-
450
ния на эллиптической кривой. Поэтому найти
логарифм на кривой E(Z7«Z) значительно легче,
чем на кривой E(FP).
13. Кривую с числом точекр - 1. Изоморфизм
с мультипликативной группой поля устанавлива-
ется спариванием Вейля.
15. Потому что Ok/(ti) = Z7rZ.
17. Логарифмирование выполняется так же,
как для орбит автоморфизмов.
Глава 12
1. Рассмотреть множества задач, решение каж-
дой из которых ведет к нарушению безопасности.
5. Поскольку разложение и логарифмирование
выполняются одним и тем же методом решета
числового поля, сложности взлома протоколов
примерно одинаковы.
11. Отображение х -> х3 + В (mod р) является
биекцией поля Fr. Неподвижная точка задается
уравнением х3 - х = -В (mod р), где В ё {-1, 0,1}.
Глава 13
15. Решить несколько вариантов системы
двух линейных уравнений с двумя неизвестными
х, к и опробовать найденное решение по откры-
тому ключу.
16. Нет.
Глава 14
7. Использовать подпись вслепую.
11. Использовать протокол 14.3.1, в котором
хэш-функция зависит и от сообщения.
12. Обеспечивается защита от повторов.
Глава 15
1. Найти число точек над F5 и след эндомор-
физма Фробениуса.
2. Вычислить V-Т (mod р) и разложить число
р на простые множители в
3. Вычислить V-3 (mod р) и разложить число
р на простые множители в ^[Т^З].
4. Вычислить V“2 (mod р) и разложить число
р на простые множители в Ж[уР2].
17. Достаточное условие цикличности группы
E(Z7«Z)— взаимная простота чисел #E(Ff) и
ад.
20. Использовать равенство <р" = 1.
21. Нет.
I
22. Не выше O(-jp), так как точки кривой
В(Х/р2Х) сравнимы по модулю р с точками
кривой E(FP). Поэтому можно вычислить лога-
рифм для редуцированных по модулю р точек
кривой E(Fp), а затем уточнить его значение по
модулю р.
Глава 16
1. Если шифр выполняет операции А и В, комму-
тирующие между собой, то для двух циклов шиф-
рования (ВА)2 = ВАВА = В(АВ)А = ВВАА = В2А2. То
же справедливо и для произвольного числа цик-
лов шифрования. Если А — короткая подстанов-
ка, В— перестановка битов в блоке, то такой
шифр эквивалентен одноцикловому шифру (с
измененными операциями подстановки и пере-
становки).
7. Пусть р— максимальная вероятность по-
явления одного символа. Поскольку р+ р2 +
+ ... +pN = 1, то ————- = 1. Отсюда следует,
\-р
что сложность дешифрования наиболее вероят-
ного символа полиномиальна. Далее процесс по-
вторяется для алфавита изА-1 символов.
10. Поскольку операции однобуквенной заме-
ны и перестановки букв в блоке действуют на
одиночных буквах, достаточно рассмотреть, во
что переходит буква X на позиции i. Пусть шифр
А заменяет Xна X, а шифр В перемешает букву с
позиции i на позицию j. Тогда АВ и ВА действу-
ют одинаково и переводят рассматриваемую бу-
кву в букву X на позиции j.
14. Треугольная матрица над F2 невырождена
тогда и только тогда, когда она содержит еди-
ничные элементы на главной диагонали. Остает-
ся сгенерировать случайные невырожденные
верхнюю и нижнюю треугольные матрицы и пе-
ремножить их.
15. Матрица над Z72"Z невырождена тогда и
только тогда, когда ее определитель не является
делителем нуля (является нечетным числом).
Такая матрица может быть получена как произ-
ведение верхней и нижней треугольных матриц,
содержащих нечетные элементы на главной
диагонали, а остальные элементы — произволь-
ные.
16. Достаточно рассмотреть полином вида
ах2 + Ьх = х(пх + Ь). Он является подстановкой,
если значение 0 встречается лишь однажды, то
есть полином ах + Ъ не имеет корней в Z72"!Z.
Для этого нужно, чтобы а было четным, а Ъ —
нечетным.
Глава 17
1. Для того чтобы сложность метода Андель-
мана-Ридса превышала переборную, достаточно,
чтобы сложность вычисления производной пре-
вышала сложность перебора. Сложность вычис-
ления производной для операции подстановки
равна 5. Сложность вычисления подстановки для
блока в целом равна 64 • 5/4 - 80. Сложность вы-
числения производной для двух циклов равна 802
и т. д. Если в качестве критерия правильности
вычисления ключа использовать условие равен-
ства промежуточных текстов, зашифрованных и
расшифрованных на половине циклов шифрова-
ния, то сложность вычисления производной оп-
ределяется половиной числа циклов. После 20
циклов сложность дифференцирования будет
примерно равна сложности перебора.
3. ф(йб) = ф(й)ф(6), ф(<7 v Ь) = ф(й) v ф(6),
ф(о) = ф(о).
5. В основу безопасности криптосистем с от-
крытым ключом положены задачи: определения
структуры и порядка абелевой группы, дискрет-
ного логарифмирования, вычисления категорно-
го морфизма. Эти задачи решаются со сложно-
стью, не превышающей квадратного корня из
сложности перебора.
8. Самый простой путь — изъять из алфавита
одну букву так, чтобы характеристика кольца
стала простым числом. Другой вариант — ввести
зависимость между двоичными разрядами, на-
пример, управляемый циклический сдвиг.
14. Пусть <pv, <р/.— отображения обрабатывае-
мого текста и ключа, индуцирующие свойство
дополнения, F— оператор одноциклового за-
шифрования полублока. Тогда свойство допол-
нения можно записать в виде
cpX^i ® к)) = срДх]) © F(<pXx2), <?к(к))-
17. Нужно, чтобы в матрице элементы в
каждой строке были равны между собой. Для
этого должны выполняться соотношения:
Мю ~ Mo Ми ~ Mi
Мю+Мп Mo + Mi Mo+Mi Mo + Mi
19. .
Глава 18
1. Младший разряд подстановки описывается
линейной булевой функцией.
2. Это будет атака, аналогичная атаке «буме-
ранг», с теми же критериями эффективности.
Атака может быть эффективной, если удастся
сократить суммарное число активных S-блоков в
характеристике по сравнению с обычным линей-
ным методом. При этом итоговая характеристика
может иметь вид пары «песочных часов». Если
линейная сумма имеет вес 2, то атака не будет
эффективной.
4. Такую подстановку можно получить из
произвольной подстановки, умножив ее слева и
справа на аффинные подстановки.
5. Предположим, что разрядность подстанов-
ки значительно меньше, чем разрядность блока.
Шифр с перестановкой имеет характеристику,
аналогичную приведенной на рисунке 18.2, тогда
как шифр с перемешивающей матрицей в общем
случае будет содержать значительно большее
число активных S-блоков.
6. Например, шифр из примера 17.9.1.
8. и/2 + 1.
11. Число битов в сумме учтено при вычисле-
нии преобладаний для подстановки.
Глава 19
5. В этом случае оказался бы известен от-
крытый текст, шифртекст и полублок промежу-
точного текста, являющийся имитовставкой.
Для пар открытый текст/промежуточный текст
и промежуточный текст/шифртекст можно при-
менить метод продолженных полиномов Жегал-
кина.
6. Гарантированно большую длину периода
дают (криптографически стойкие) генераторы
псевдослучайной последовательности, реали-
зующие вычисление элементов циклической
группы. Например, если Rx — точка эллиптиче-
ской кривой над конечным полем, имеющая про-
стой порядок г, и 2 — образующая группы IF,., то
последовательность младших битов х-координат
точек вида 7?,и = 27?, будет иметь длину г - 1.
10. Использовать схему Фейстеля с хэш-
функцией в качестве циклового оператора шиф-
рования.
15. Такой шифр задает случайное отображе-
ние, обладающее сжимающими свойствами. По-
скольку почти все случайные отображения
больших конечных множеств статистически
одинаковы, то псевдослучайная последователь-
ность будет содержать непериодический отрезок
и цикл длины О(2'^2) каждый.
Приложение
Эллиптические кривые для стандарта подписи ГОСТ Р 34.10-2001
В приложении приведены эллиптические кривые, допускаемые стандартом ГОСТ Р 34.10-2001
для использования в протоколах электронной цифровой подписи. Эллиптические кривые построены
согласно методике, указанной в главе 15. Эллиптическая кривая в форме Вейерштрасса
у2 = х3 + Ах + В задана над простым полем Fp, характеристика р которого — ближайшее к 2256 простое
число, позволяющее построить требуемую эллиптическую кривую, число точек имеет большой про-
стой делитель г.
П.1. D = -2
Эллиптические кривые с вычислимым числом точек, для которых характеристика поля представ-
ляется в виде р = а + 2/?, задаются уравнением у2 = х3 - 4/х2 + 2?х. Для того чтобы число точек было
удвоенным простым числом, должно выполняться сравнение р = 3 (mod 4). Замена переменной
4/ 2 з Ю 2 56 з гл Г,
х<— хч---дает эллиптическую кривую у =x-—tx- —t . 1 юлагая t = А± —, получаем уравне-
£±1
ние кривой в форме Вейерштрасса с коэффициентами А = ±1 и В = 14 • 15'1 - (2 • 15“’) 4 (mod р). Для
3
р= {1, 11, 13, 17, 23. 29, 31, 37, 43, 47, 49, 59, 67, 79, 101. 113} (mod 120) число является квадра-
тичным вычетом по модулю р и А = 1, в противном случае А = -]. Переход к скрученной кривой
осуществляется заменой знака коэффициента В.
Таблица П.1
Эллиптические кривые для р = а2 + 2b1, число точек равно 2г, А = ±1
2256 -р 2255 -г А В хо Уо
45717 -24863408365670231 860983643442574971 571203 -1 -1741781031181342258471981 850342194607249056846678321 966521244768988454459108583 5 745610396279665810568578751 573048444245925609260826101 1288149115076529326510279
155853 —22398292639384431 179550907487749281 924545 1 -7185976792694793920668021 941064086581579078161787661 830442728167637740455861353 4 910532079121699467786324521 733256447746342654487175201 0404087744034005591294990
294669 236001912694604151 824260438544056661 08679 1 -52289996177851192108920601 805532077259764234842243981 15237507522470460794360376 1 247759781829281287795827731 946681010959429399875540451 5573081603636358824635743
624429 125289213797550351 47787045322594781\ 35501 1 4599569958990904624701441\ 22928056428564362160812181 36103452302970636034583465 5 41646985714943908734535601 76365285278761148066499151 4499806432044948884031261
752445 -24345790607647741 081314267520416831 495305 -1 -3331219554100604343486901 096573996049738420398396771 701668805205643554975116159 5 51976928646419867977515491 22437439398851276780424691 010589176787022382012376107
789117 31495440210522451 144761762033363821 090291 -1 65142825228723235205274891 57205281395234157865533 84\ 981841002955913170905720081 8 72421467839195168390680051 92375937038892607234962681 431088173642846501524773051
953517 81305455637282919\ 383950344435274001 9437 -1 80869283464988815583279411 83010938791665017220641561 144103012648542005831261204 2 87488792632688131158442341 379272813967885628794917491 7828082600675456098560117 0
1031733 32376822076042615\ 236797158711232821 3615 1 370751465917068683 81373111 42981528770240406572780771 921512136541815921012057766 1 70847577499353838178738161 57884658731085124979359611 196586807472118029204067693
453
Продолжение таблицы П.1
О 256 2 -р 2255 - г А В XQ Уо
1063749 -4099156348372528Х 41188616798157597Х 88793 1 8457328746926381522469820Х 0122893630696762480089254\ 939953573566349964915374442 1 6224551393545006851822776А 6918847703979979640073931\ 443673403860723123190930731
1267029 29022759085966299Х 25036851333833065Х 72701 1 -465713005807060842460334Х 47146095131076464617656864Х 236527484944625437653944222 2 4378828887803262539932213Х 2245346332955199731591532\ 622815982274443197291734847
1340373 —1582432648268963Х 01364925528774115\ 36435 1 -1012665606515131957522341\ 99061648763169400382912397\ 267193879622116688245112749 4 9603376960956023990036778Х 2576146960021036817559305Х 196613121503339900869205411
1352205 23204515768527578Х 69598040090541593Х 34559 -1 -6317107686079422647835437\ 2118966201894427290143205Х 500162397641717217269997168 2 1041224277416516425114015\ 8277493627106758174677085Х 5801055652358951404838888 1
1358325 32261850039201125\ 88572417964141434Х 03445 -1 -6608543297415199784526060Х 15926535119520430982044880\ 12142818096197656702611736 4 271831313 8704006772914855\ 6540561317395184583681177\ 008530904356530795094774855
1378845 -3037023596646169\ 26163299283579572Х 020049 -1 -5017432325246128335992654Х 87650383521242157500737910Х 91947707827738004147922512 8 1042889001217944462206594Х 2287423791851330089285356Х 110186592332273232658893563
1531149 -1020244536181793Х 77803407331227029Х 093563 1 7409151137832277113975841\ 2131533639754761282206802Х 805180885360252639613347593 1 2546454685220176056863258Х 1602856683993312459792617\ 308868119318643653628598030
1582629 —3401328905606465Х 67099330454510663Х 444209 1 9628487269027973483516408\ 8235577308662412978248217\ 767140288257087272029770084 1 7146212900337769869894426Х 8033415599100379284237579Х 929427990738649850944444118
П.2. D = -4
Эллиптические кривые с вычислимым числом точек, для которых характеристика поля представ-
*7 2 2 3 2 ^ 11
ляется в виде р = сС + 4b , задаются уравнением у = + ЗкГх + 2кг, где к = ———
Поскольку р = 1
(mod 4), то -1 является квадратичным вычетом по модулю р, то при 3kt2 = 1 можно обеспечить А = 1,
в противном случае A =t2 для некоторого t. Число точек на кривой кратно 4.
Эти эллиптические кривые изогенны кривой cj = 1728, которая стандартом ГОСТ Р 34.10-2001 не
допускается.
Таблица П.2
Эллиптические кривые для р = я2 + 4Л2, число точек равно 4г » й-
О256 2 -р о 254 2 -г А В XQ Уо
90983 14743833257207118\ 90837166346533113\ 29787 3 34390778264990488403408089\ 71407844022638609228793300\ 0197748802842577482514971 6 11238560492870238837383361Х 09124869021842049152229961\ 76475643755103862941092056
101027 —1631458928808785Х 74383727781440101Х 058645 2 11287703231698444800901207\ 26856598990720307459502312\ 0121732749266735635065018 1 10730883075254907777892378\ 50729971098956095022181896\ 19141163367080229598221047
139515 82183354317676830Х 10060664656879258\ 7423 2 10366985147989829161774610\ 77904247777759937753721598\ 54564370491263415139826889 46 81292489056065840012392349Х 02961024173770630603456975V 4271331141385224373132837
169275 14842130233604673Х 53685018292100910Х 26871 2 84873128975653673665462058Х 10747703I96502339432754088X 6352949036700735058910932 5 10018753223128576502249213\ 48202786382865666281162309Х 03586295587393880421130065
454
Продолжение таблицы П.2
2™-р 2254-г А В Хо Уо
179183 —5884802690407868Х 93502890062958131Х 66213 9 94443682445053440467199076Х 79745504939568828732099097\ 1641504199016568293341755 16 62252548171945218964692630Х 35275382888000579524854807\ 62702489227243263 80467698
190239 —7112128161820191V 94346224067613441\ 49885 25 81489647217457299797888289Х 40361623146281486562000730Х 1448682595965189673939166 16 78709542784278695538061854\ 03851690545128598947566473Х 0259075118594408975244407
212555 -8329526038119998\ 12800867335343145\ 56969 2 42210445352079941645511695Х 90762518642697685131242995Х 6865127516464368442598845 16 90815795420149494315496984Х 78169909402755470362248740Х 430528083474354692980854
220247 61635422327721611\ 63003886322194210Х 3695 1 77773208948293988519623716\ 73678776936100774509747527Х 6280983279337959413389308 4 44714997549423484081867197\ 67659748020061449274938197Х 4884280839805880451508330
232019 16619802067438825\ 63709843649411794Х 60475 2 68327677192167372166265802Х 91759455710630968973638305\ 2624810517007727963272303 2 36114012281207804701383085Х 97886584963171735246722091\ 2450268901552269437427832
264935 14721549947194681Х 65766017893339731\ 04583 9 71312039749891848820348340Х 75478626287753899664065540Х 0358308579652107721720390 10 11323082348399026813978049Х 74629861628861413116992266Х 01989815020721243 865523 808
293039 -5605782868741979\ 31849552327585389Х 81785 27 59532686451761423054568545Х 79519663 878963056558704226Х 6054227145897852277344249 7 59643121778805098156661509Х 76871991353405591332533259Х 21532785155320944868681
429219 -1533797307026822Х 68125694158443261Х 120125 2 42509368609890754625741393\ 57211025357962847078681782Х 4117148271667675834610379 9 72201357130151007568024980\ 63123529583453323213723999Х 1689499059664499183555516
453675 13170050223368737Х 45425990377289475Х 08311 8 51481982846671448067605354\ 95673915078233805290401189\ 6666383067076738692578505 6 89126637818168980528854704Х 49031380569574051007545765Х 0555001025998482171921249
463379 -3156519232024768Х 40591576690435402\ 95405 1 14366560473624713969746950Х 79917846650549650049801017\ 5620424616381632278186280 И 84575564730966254623531415\ 11636437391617773920298287\ 5153235673929714640175431
472595 98412100121113376Х 44912610136386245Х 3971 8 57980108275386721207537268Х 84375746230919899603037142Х 2133115799079940776924074 14 21680681783935986284311254Х 62125282162628770485728211\ 74780002287063 51974190300
515387 14725457712601468Х 0946437520440792IX 65143 1 41044643075194244654083015\ 76664528519187276651199686Х 7034604165964832299499707 7 89033449188360469766338787Х 83401583110833694005691875\ 5906792640209107789752612
П.З. D = -3
Эллиптические кривые с вычислимым числом точек, для которых характеристика поля представ-
ляется в виде р = сг + ЗА2, задаются уравнением у2 = х3 + 3kt2x + 2кг. где к -
53
II2
Поскольку р = 1
(mod 4), то -1 является квадратичным вычетом по модулю р, то есть случай А = ±1 в общем случае
невозможен. Число точек на кривой кратно 4.
Таблица П.З
Эллиптические кривые для р = я2 + ЗА2, число точек равно 4г
2256-р ~254 2 ~г А В Хо Уо
62703 —1248754294576226Х 94264379308769150Х 12425 5J 56913011281336358855717569\ 45018050084078422784567395\ 1136660193904459684623824 14 77089865091439371310603048\ 92823174211I54028441036482\ 3475959978294088562720208
455
Продолжение таблицы П.З
2256-р О 254 2 - г А В XQ Уо
95385 -3910594134594038\ 50387498871926181\ 01423 1 -1028832443119287308254300Х 27885321254696601372180004Х 049216640507955002432558081 5 80752985092019104150507560\ 94065139201942916330751267\ 3773279214043142018424823
117993 -8897516304826794Х 68755465801913699Х 05455 -1 —5610205958802009423807665Х 94718051035019092355022951\ 7046194265569554376573827 3 17641537354796589006531660Х 58694606544572255095038997\ 0843346690132402720889929
213549 -1632071973292739Х 88957947583064782Х 80049 1 63335585118893127465502010\ 84072282961661279119779271Х 2174672009611173982313600 11 49349929033480519321933415\ 74449221927176343310502827Х 4267400970140714240035928
219465 14801105692119561\ 70688494410728960\ 02323 1 -5545051320446321318043133\ 42838424981554990491567220Х 27419744703939370605518329 19 66330462241537008352098797\ 17391702817641331446933417\ 5849100195750196509075893
231459 16833353011205453Х 67022176176598595Х 45101 8 37996804289649820416494709Х 39999844436303446006583883Х 7701521575646901651137181 13 47258069870340517878487298\ 52259407710453859943040653Х 5105709234954198566414509
238377 -1468687929123193\ 06888369440766207Х 152333 1 61244367724787781035208106Х 22507740837337774642734926Х 3833558994290949880227806 2 83592002088008369308491464\ 10588769659595751955548131\ 6639549934098609445647125
257037 -1496285344888158\ 33866786700974100\ 539943 1 -4242926719479501561311283\ 07889523950805301795431546\ 50029826292345996086282297 12 32000379479181298422542676Х 44398729496352659367391179\ 2457456518958411024510417
260013 -1679551425039547Х 09707286653776999Х 754489 -1 69126893891251862487193883Х 85204694732561431327193701\ 6636695107842858034562217 6 69864115437180019886687260Х 84952740888065918689298558Х 5480749308749391862138672
321189 16957293303105859Х 57203261152095653Х 66087 -1 90680125006691089571922219\ 50998402443005500993194178\ 8790737077620724733806545 4 50267549154303147315612341\ 22691663972281900767544423Х 1615667526739542181584178
330657 16977948996529911\ 63114608391848024Х 32011 1 -9265605337964124569058900Х 68453568025983094536902736Х 762096320281705715512870 10 57933119098008231467326991\ 06278578275721271165398356Х 7828764946763952586063282
379653 -1318983820132904Х 95524466052736677Х 154435 -1 -1028696179503823400593204Х 38355714914807740642911865Х 028209070880466356486564753 9 61181630965561307561395639Х 90129531522619240278997784Х 4886897777973684748046317
389757 17012550483742204Х 54714519314027158\ 07951 1 -9754762175156586887504344Х 79018695803867629083415110\ 65155712668796355820826234 2 21180070047659303013629807Х 94890720289552774952973884Х 5099585373166583617007987
394815 16914824354757107\ 78391903223220262Х 64347 1 20306799441477403380550934Х 46492549695248065945328364Х 4230242188060878205152227 4 11169624099331291169413248\ 90863113033610406391457239Х 8245939274122052279082387 0
434265 -4317710254083992Х 58298555418486495Х 10255 1 45243504256379360460208313\ 82589946100440588392475541Х 7116426662449933940662855 10 85045181826419141659536821\ 64758758832480454606039608\ 3468690695180523723837673
453543 -1673544245412488Х 55930016090621838\ 503869 5; 11212713579390414101294328Х 47233204317736113286841191\ 71640747518831808892536378 7 91375786152233456623759981\ 30376004860798267116803064Х 4896145898862632335132440
П.4. D = -7
Эллиптические кривые с вычислимым числом точек, для которых характеристика поля представ-
1 53
ляется в виде р = а2 + 7b\ задаются уравнением у = х + Зкгх + 2кР, где к = • Поскольку р = 1
(mod 4), то -1 является квадратичным вычетом по модулю р, то есть случай А = ±1 в общем случае
невозможен. Число точек на кривой кратно 4.
456
Таблица П.4
Эллиптические кривые для р = я2 + 7Л2, число точек равно 4г
2256 -р 2254-г А В Уо
64967 -1330967813620250V 27119606853567945V 675065 1 28387972031714775692393191V 18302484189733090027965529V 7738176714347407617818180 7 49245750382567663461020848V 81029604944482956737660774V 4908285536120563655190584
79647 -5784006770953001V 00319642880274495V 99653 и2 72225183367830918495196105\ 88017202786408187206268553V 9756465666847654014296040 1 24464938484036688032869753V 04916825094500090889483550V 2455395540914260100734508
91635 11491366607911365\ 28994704607020785Х 57105 4 57924860862554806464835545V 17802730579787126591184517\ 7613722308454454450707768 3 29184572007960748394486636V 51379973375018049409608041V 3464131116540144359641489
130383 15071073133937916\ 77862787413249621\ 01623 5J 92684534874350524825754961V 04673302693144149316071803V 7434748205731088127082063 2 10581683391867010229907741V 60783850381695787311405879V 5618318523639901597072581
207347 33307988092523116V 46951107119350604Х 1353 1 89085409626589763683729653V 85842553703074634839204537V 403 576036105983360971304 17 94794315860127441877996055V 24628582531858264448533849V 2499414075160522647403677
216287 11541561857393525Х 0318232495711521IV 98843 9 70136286761399630798014945V 42592387922165968573997954V 5561163026349081706857823 1 74381657711116190512234411V 62989671993119119616615600V 9289719897342204328839244
283619 16999886793208592Х 97288601872798983Х 54273 2 29139877655185727094092058\ 14911592475044329969732436V 4140616567076013954140712 6 33043917800991321043596653V 53327848473415293409042791V 0915611315079481487643749
309275 78785975345956091V 09419218673490030V 1053 4 74781486275684229519306015\ 08422007208848833344327913\ 4192444716543036854097302 10 30486905793918813688948444V 63580043380224386687799922V 6528893035838863044472628
429219 14939355983376488V 33591902879449959V 3561 8 89747789553986161602780786V 25457703702206531707660793V 9045631694693934151915138 4 60609701776525282373039028V 08661388196336162085281738V 7413294565465036325308661
482727 15921693248382816V 04038732872677544V 39111 121 15126616411682981954453566Х 70553439930847528229055308V 3999755590777031227162436 6 73416700516842565237205663V 41776161108514323242050955V 7222924982459295280921345
490127 16996916160130541V 17783926769438541V 69027 1 11099325613288191775364870V 09601104791043683302641419V 09735050505508634771789771 23 84959092383454289632178223V 58789830077988727212897535V 6461376920994392298265867
691299 —5726417747570395V 94524603347922062V 94279 2 77118539255676417938650833V 92059447953829296248986114V 468795501950645224573597 10 33522597315065140305397780V 33952075319781837001415427V 5616975700903060139085402
704235 —1496539304534962V 54880031286269859\ 336363 4 92124216359641030749842126\ 40683214568283511056333403V 636612700591221212186552 41 21322944229167524350510719V 50949101502373586719944091V 6804888500217193239634547
717963 11356186316470898V 59890719881994067V 8741 8 85218325813799902653439050V 7052583215758593620517609IV 5673977074482996005579794 14 79666562254116250975583648V 96016941531542570279012459V 2410510780072758630890782
738899 —1568910650654872V 84279604241108455Х 592543 2 43709237324117649916207266V 97141621591896605241540637V 0261848713032228676688721 2 71164375274306595479632930V 93745678152301913 840266743V 2705519209200330011888608
782327 —1296426307535822V 88951672493631887\ 505733 9 16833468548813179128824967V 66291526022831963538242172V 581294088536285554881581 7 84142509010701179801856847V 27610206541317472944159674V 770635069323442754595981
457
П.5. D = -11
Эллиптические кривые с вычислимым числом точек, для которых характеристика поля представ-
ляется в виде р = 3а 1 \ab + 1 \Ъ , задаются уравнением у = х + 3ktx + 2kt, где к = —-—. Для этих
7211
кривых число точек является простым. Если существует эллиптическая кривая E(FP) с числом точек г,
то существует и «двойственная» кривая £(F,) с числом точек р.
Таблица П.5
Эллиптические кривые дляр = 3«2 + llab + 11 b2, число точек равно г
О256 2 -р 2256 -г А В Уо
11932201199\ 89167196601Х 763 11933708036Х 56406066632Х 473 2 74939643494622884499000791 \ 53598742115488586052436260Х 3456260258241995009869271 3 27987454718750433616107360Х 12660339672011731862635562Х 4230610758309922887925573
11933708036Х 56406066632Х 473 11932201199\ 89167196601Х 763 1 91828618638450877742778734Х 29384325283736015866872594Х 4495140169505059898796779 1 42248938039502771428666723Х 93945599307828563407543813\ 6975215594202190588968216
31370394273Х 70590426363Х 663 31371901110\ 37829296368Х 573 25 64826859477311563151204522Х 86331932643084030524533819\ 3925271593930336205234454 2 11258458927084367265568298Х 51609086172819526581087321\ 96224990503641632074529679
31371901110\ 37829296368Х 573 31370394273Х 70590426363Х 663 1 54507142450020364936097446Х 06993286733375219831248100\ 6313469693567888447156914 1 10212602126962272897366235\ 39304645966565083277597938Х 93333089139886774367378828
35235430338Х 38291982381Х 153 35236937175Х 05530852380Х 933 -1 -1034298926787428920914805\ 01214514092142237722515877\ 443557851426501575937846510 3 39003845687666710235642721Х 09924574741188329616465018\ 8220002897292484281503997
35236937175\ 05530852380\ 933 35235430338Х 38291982381Х 153 1 12497568779037137727875992Х 50864730970220202198639078Х 0994968927933527114236583 1 62739372213125977369901449Х 26739002078435569247654603\ 184393094862343550543836
75196738890Х 13123673262Х 873 75198245726Х 80362543209Х 613 -1 74417596245655060395400428Х 55643224154059636077389390Х 7306986956375769968926600 1 43424520435456678390081059Х 03245755376572253938180367\ 7359331907058763408635522
75198245726\ 80362543209Х 613 75196738890Х 13123673262Х 873 1 58367671822063441915696533\ 73790690725750859981480886\ 6483 817346698428737912190 1 12570427447764547970326338Х 85255144858956410414747084Х 9504588086701827961768989
78180275501Х 46086163889\ 653 78181782338Х 13325033832Х 433 1 -6059713796361171475939947\ 01117745654264508001777608Х 59085941838082351906668419 1 24959754950210735235757775Х 42444438521482455010816167Х 7547992744553398467535186
78181782338Х 13325033832Х 433 78180275501Х 46086163889Х 653 -1 -1057303292575036655467419Х 49855712273227349215722520Х 264188291501695582467536946 2 10635298392030334533404555Х 76208343532314932292267077Х 0027206322174893469345297
95968482419\ 00945699061\ 333 95969989255Х 68184568980Х 503 1 80241703116102673993606451\ 15119754968719743004942633Х 3537323949725321860654234 1 14404324443765726679094089Х 58416654301735544051842333Х 9274751284795333231230625
95969989255Х 68184568980Х 503 95968482419\ 00945699061\ 333 25 82407390533495886104235405\ 67247250064084463842399179Х 8001375127930948252064762 2 55698897535291027942610355\ 55812858762388890516988373Х 8174748424551031409632373
72547989196\ 88479152318\ 27 72570303251\ 19703465664Х 07 8 63647237311356853045755549Х 26822250685690388727994844Х 3366802560024090103748134 6 78755747049779939530140972V 43I390274850840135944857I2X 6607649960631249680931102
72570303251\ I9703465664X 07 72547989196\ 88479152318\ 27 49 10248845357281994930457322Х 68407902149552903279367084Х 02480482910133383176035587 1 10570960246544597645284412\ 30310516186379436090336122Х 37818007453145632110312431
14551494679Х 79198368618Х 797 14553726085Х 22320799946Х 837 1 -4014571012729031028497079Х 00181786054750008585261049\ 3 8256417178543468159049904 3 62628336310919158286986817\ 83107594543328417568425222Х 9447238186298359049626409
458
Продолжение таблицы П.5
О 256 2 -р 225б-т А В Xq Уо
145537260851 223207999461 837 145514946791 791983686181 797 1 339313592570326204418362941 427222947619884418109070231 2462696320442522071121706 2 24935825182101937836016911\ 750352330355116235525472261 1067412447782905123492250
П.6./)=19
Эллиптические кривые с вычислимым числом точек, для которых характеристика поля представ-
ляется в виде р = 5сГ + \9ab + 19/Д задаются уравнением у2 = х3 + 3kt2x + 2к/\ где к
скольку р = 1 (mod 4), то -1 является квадратичным вычетом по модулю р, то есть равенство
А = +1 в общем случае невозможно. Для этих кривых число точек является простым. Если суще-
ствует эллиптическая кривая £((ЕД с числом точек г, то существует и «двойственная» кривая £(F,) с
числом точек р.
Таблица П.6
Эллиптические кривые для р = 5«2 + 19яА + 19b1, число точек равно г
2256-р 2256 - г А В Хо УО
187929661 010522291 59087807 188015376362652371 7750135 1 654035586478268617068051371 807670622061334791934214371 9323018232764097154749567 2 108379822284004794273062221 398599628956233102026427961 43728187192694668306605177
188015371 636265231 77750135 187929660105222951 9087807 9 597031258687012138432564981 210823462501559535475133351 703423062055993111225463 2 512686243547403988177472531 691353497834859112568372391 9308604251926111527947542
192215471 297669381 92201757 192301189234123311 0863985 -1 157504347886039937831889661 569936360277846554431432471 0061781177996492429719154 4 799092276896678893572427271 719455340028606724486107081 363321348907259904667711
19230118\ 923412331 10863985 192215472976693891 2201757 1 880855942498365441984324841 282406831194543944441190571 4508994522960389293886290 1 105459086327474203818182811 133735826593712866661421011 70921826865219487791603911
503708351 247520121 97535987 503794068732630711 6190947 8 111256242922520063165053881 788873156548593297087773191 47051117962370719320279988 5 430719137457836589989436471 200208594696903043631757331 6904511028262501040228751
503794061 873263071 16190947 503708352475201291 7535987 8 767568985608537695635519781 106915205788413252970945011 607071278504961382131677 2 316265565460832651003841991 119203395103630687810259421 812275066791944359791215
13279558Х 839164901 991173507 132804160017392041 09809235 8 114006729233478838740189041 499680167615427136304836741 53276643003986123847437941 1 100859635300558497313794191 319812651829696198312837881 75572414163466977213912334
13280416\ 001739201 409809235 132795588391649091 91173507 8 559254632709379688776064611 293387532698010355103962991 229718853233265078674357 1 985947527286919630400875181 141803796669300055969107081 5890892680953870397570044
201874321 025401751 711566037 201882891879760511 30185647 -1 -10592406733897379547652231 214424432581017634885001311 890392265370849301323943233 1 584846495188833 827951755431 625486086125876450569149591 3232873057581112110161005
201882891 187976051 130185647 201874320254017571 11566037 -1 349913022273848737506933001 424841087659240159890640531 05215742243924696048077 1 688627347834798978470542251 691566229205729924813829801 3731584519750619667893289
216566081 677741991 222641495 216574658403162861 41257677 9 323188938328683545309892571 152589844685031054677680531 6562671333685665873 579762 3 872384816966563601593177161 584332478859768810935702261 9622534901554247472908435
459
Продолжение таблицы П.6
п256 2 -р *-) 256 2 - г А В Уо
21657465Х 84031628Х 641257677 21656608677741992Х 22641495 -1 10769953066998068180789504Х 34043973724885013208966993Х 50547978871165908781552821 2 30974982917502976421275833\ 03884240190272450721452747Х 678774415272344148722095
26487576Х 94646402' 511684387 26488434109038319\ 30289297 2 23965997553000355623653117\ 83401482316481351543395598Х 7698157208107901886442584 1 990379469461I3502621980036Х 23754391756107652539252772Х 3158261171643772640244908
26488434Х 10903831\ 930289297 26487576946464025Х 11684387 1 10673989893487297902750872Х 14681828211223442702533996Х 25006997178213152016772759 1 53944095238070949365585584Х 57195159707757458990006175Х 2050467328127140687352405
31022824Х 12705456Х 322273807 31023681289628857Х 40868135 9 28027032891175022838627523Х 36501778947321075657738393Х 5485279302733863312423747 2 58716162547590255718595260Х 40296851876465800844598079Х 5813798827733820924303988
31023681\ 28962885Х 740868135 31022824127054563Х 22273807 28 9 98293388174138137451989377Х 01804774693431474504038503Х 3553392344509699771798919 1 77029755678491228218869215\ 76579777499851531282005518\ 3389307027580391861378988
П.7. D = -27
Эллиптические кривые с вычислимым числом точек, для которых характеристика поля представ-
2 2 2 3 2 3
ляется в виде р = 7а + 27ab + 21b , задаются уравнением у = х + ЗкГх + 2kt, где
2953
к =----Для
112232
этих кривых число точек является простым. Если существует эллиптическая кривая E(fy) с числом
точек г, то существует и «двойственная» кривая E(F,.) с числом точек р.
Таблица П.7
Эллиптические кривые для р = 7д2 + 27ab + 27Ь2, число точек равно г
э256 2 -р ^256 2 - г А В Уо
47761081\ 85498073Х 97062963 47772045463597401 \4170027 1 83937657404054016551071594\ 88802594963747283243333017\ 6554919199091551264909182 1 36722202423905344914985326Х 61959579764439273860157652Х 0810379390734641727007536
47772045Х 46359740Х 14170027 47761081854980739 \7062963 8 58285095293935385165553335Х 55050154142897631067292719\ 2348032514817236315971550 3 39835405772332827502342845Х 39510615862467013259448368Х 2641927917569860448570672
17468677Х 88100733Х 511527539 17469774241869001 \28611449 4 33465069114053148008749901Х 47439333532522355201682919\ 1194880198241751740698830 4 20378960863265025549146635Х 23948447390836095811200786Х 5961227618421399371140527
17469774Х 24186900Х 128611449 17468677881007335 \ 11527539 -1 51801464849882314462188590V 62423567773490478704601056Х 6471071741695180339006063 1 28659309998367342298058536Х 54531547151281460632122664Х 8396637540393455092299950
33489799Х 15253508Х 745179213 33490895513396753 \62233897 1 -2708506590547965432077703Х 14865643124221647072640036'. 38734948847142794138460037 1 48901475503066218258156897\ 74579691178096191604594727V 3450432516191200865340257
33490895Х 51339675Х 362233897 33489799152535087 Х45179213 1 —1385014122604552431834637\ 76312212881573286791671888Х 13302832115919160259525458 2 15938117425631610302565702\ 63579016526396454093640258Х 8119157082995069750548680
43021560\ 48386077 343024967 43022656844722439 \60062263 1 45707446639647009582159912\ 32406539780551724063444939Х 8656011455631742706378083 1 64895516214228729382510234Х 24998604013616449924703855Х 54134556811674740073743
43022656Х 84472243Х 960062263 43021560483860773 \43024967 5 93500234902717860553197658Х 93207075176829703266294980Х 9210109935959412698369351 4 40376845562260217581034970Х 38883654968538304515591564Х 7881058244732185001015325
460
Продолжение таблицы П.7
п256 2 -р О256 2 -г А В Уо
64015774Х 62390626Х 623541019 64016870984767932 \40540017 1 31560492077362040596253984Х 45218294744005944325271434\ 0370507469381893822220749 3 15628105264641478486464405Х 22351448570263463280516494\ 194382232555800914211777
64016870Х 98476793Х 240540017 64015774623906266 \23541019 1 9431520266405388I648763529Х 15338998033071405547566027Х 2641401873891002895565754 3 30981252101225097980738662\ 06551432033633316274796503Х 8478329106450509145094574
64548606Х 00267602Х 484818337 64549702363537691 \01816363 1 94832908577893991825630864Х 81620401655517379998715851\ 0541937380789313384292296 1 24171207542536384589026038Х 22824862635453074027433696Х 590298322509832044350256
64549702Х 36353769Х 101816363 64548606002676024 \84818337 4 30563829269741676863517728\ 84008330107718661835346105\ 6108589056518155888860439 2 13092586645719217753973454Х 34644029410635364143520039Х 5667264842258204233018679
67199606Х 56618482Х 380200899 67200702927046489 \97194089 1 71165876748687180636073608\ 41861775497028821481382459Х 8983907132927695331242516 4 10241009105816723309787051\ 17363520970874259756168722Х 10686837470113075889079145
67200702Х 92704648V 997194089 67199606566184823 \80200899 1 91306296025088518048347844Х 37627536402770236078997270Х 1287718775835013051166905 1 59136879174088851298890080Х 29426295033366359107915325\ 6347695975383479841421684
69455917\ 21949380Х 147952613 69457013580355467 \64941687 1 99015033315912934I42496842V 01758127832987546284033064Х 1599182344602535912877792 1 10926240328570195581876757\ 70981269531118008551065963V 19998680389348081171414981
69457013\ 58035546Х 764941687 69455917219493801 \47952613 1 27129182272983772894322327\ 04207129261002113290116165Х 0128271786737936822191015 1 18912189680558812148022201\ 34444808515000850286968026Х 086937004164889591222281
П.8./7 = 43
Эллиптические кривые с вычислимым числом точек, для которых характеристика поля представ-
21253
ляется в виде р = 1 \ а + 43аЬ + 43/Д задаются уравнением у2 = х3 + 3кгх + 2Л/3, где к ---—
357243
Для
этих кривых число точек является простым. Если существует эллиптическая кривая с числом
точек г, то существует и «двойственная» кривая £(Т,) с числом точек р.
Таблица П.8
Эллиптические кривые дляр = На2 + 43аЬ + 43Л2, число точек равно г
2256-р 2256 - г А В хе Уо
43952937Х 13084825Х 68648515 43957218382503620Х 8648233 4 10977430155645996945677413\ 09434790712171675225585591Х 25315345623917315593182200 1 68679572286912878225379801Х 90810333051984786290994899' 2957140048972544432583625
43957218\ 38250362Х 08648233 43952937130848256Х 8648515 -1 -5887677967791018219835296Х 36693084537377562946335508Х 31802134254257254784167085 3 29793317986476943147183498Х 81752985689738600509926970Х 8892857098010533259208105
55019972Х 65996419\ 61239905 55024253911619560Х 1234453 1 -4881315731510520810497091\ 87196995603795046250127944Х 3969677662423706376956879 1 44960396060041551514798996Х 64936281255169046628054206Х 0632033072998717526374252
55024253Х 91161956Х 01234453 55019972659964196\ 1239905 -1 -1008129164725065681144673Х 35687593586931923090689512\ 243775365807764043250702568 6 79603919469259218934732499Х 23330400481862284554971733\ 0567175193980846223426659
56462754Х 46782186\ 39289349 56467035719477227Х 9283223 -1 —5394257247463882787546538Х 47816929136374420567364024Х 87098669177598707700434023 6 83672738787737197838551959Х 62482291071169968988249256Х 1374023598833016556098238
461
Продолжение таблицы П.8
О 256 2 -р 2256 —г А В XQ Уо
56467035\ 71947722\ 79283223 56462754467821863\ 9289349 5 22866564805792335548698158\ 87402121645165761634650923\ 6273087841896266234837283 3 10962650927424463075885979\ 54174479130968820736038957\ 12574693323233 856101020941
65294976\ 63283779\ 42397505 65299257884493158\ 2387253 1 -64123664216495859048963 81\ 42746402733141784590527554\ 74418 876836985052808922531 6 67666827395516866716009456\ 91942306101883139536225081\ 5736486676648030368696071
65299257\ 88449315\ 82387253 65294976632837794\ 2397505 -1 47731995509994757464524897\ 82587752893896863501148699Х 2000359282836329108116941 1 28411728311113887390890897\ 42013458220743918032048075\ 6576420731775658748117478
86808266\ 20104188\ 65635605 86812547452697250\ 5615303 1 -9312393557217675178763879\ 14548499785602871980643463\ 01426681654884714229405055 9 95108224117527094539466352\ 16696191287216032917940802\ 9355701175153417058114294
86812547Х 45269725\ 05615303 86808266201041886\ 5635605 3 65276505829477987527523959\ 85126116742974921577962649\ 2988560599206488649616600 3 77072047028750361434318986\ 79883064518385937745709269\ 6388260094282750986386099
89355610\ 93598346\ 53202485 89359892187638829\ 3180993 1 19979354022454995634506354\ 01429238888393929797156761\ 71643023 52446563151743259 1 10702187787031439860713735\ 48946092625041620630724656\ 70612290677619035906194669
89359892\ 18763882\ 93180993 89355610935983465\ 3202485 -1 -3508097772267293184566399\ 17657188243539033133601673\ 87153321568588491943567587 2 19958105211681122802209332\ 26537478849706814175714596\ 3583695452490089365374323
99104020Х 95524728\ 79082749 99Ю8302206902651\ 9056703 -1 -1062361639524618940958757\ 10742098694995444466564508\ 437366681536183810144444350 3 96966293542451081110138018\ 82676514238851373 897004176\ 8213044879287414474793793
99108302Х 20690265\ 19056703 99104020955247287\ 9082749 5 98347026422055012946318116\ 35402408212187476310265177\ 624314805834590162721172 1 24307116072454381912721467\ 12815116331666623418294334\ 91222806172026024761164
10915211\ 85903865Х 892446725 10915639984204195\ 32415985 1 27809108918565957132649511\ 51987494607558885717217759\ 3792754741029377864760770 1 26893705871674917130266805\ 31975391695726267927927976\ 6414702495419697931053424
10915639\ 98420419\ 532415985 10915211859038658\ 92446725 1 92582008908640584545081422\ 25486947196820416889702863\ 243716878555404596865068 1 51537646170950141752680608\ 10099712565137093020622438\ 4186297650074744797227502
П.9. D = -67
Эллиптические кривые с вычислимым числом точек, для которых характеристика поля представ-
-> 2953113
ляется в виде р = 17а2 + бПаЪ + 67Z>2, задаются уравнением у = х3 + ЗкГх + 2кг, где к - —.
З37331267
Для этих кривых число точек является простым. Если существует эллиптическая кривая £(Fr) с чис-
лом точек г, то существует и «двойственная» кривая £(F,) с числом точекр.
Таблица П.9
Эллиптические кривые для р = Па2 + 67ab + 67Л2, число точек равно г
2256-р 2256 - г А В хе Уо
15264309\ 67824330\ 325370855 15265580120257617\ 11828747 1 49462865371616207614513729\ 74958347508063658115642737\ 1859573823832199482803251 1 17746017927026477136229140\ 97764984402340423199431898\ 98523309430840999745207
15265580\ 12025761\ 711828747 15264309678243303\ 25370855 1 10338046749661243022438720\ 10391640941020338461171901\ 49504913425975138576768379 1 50893880104489355587594798\ 16921458511320090259797528\ 07500545 86120974474079424
462
Продолжение таблицы П.9
О25б 2 -р 2256-г А В х<2 Уо
16022763\ 56078868\ 040376567 16024034002802994\ 26833265 27 27753357652553387433887044\ 60904020556923992588579354\ 0200328921329177595457584 2 43629728293083903880716309\ 3 8907029715722746688846014\ 6006668324413951717113204
16024034\ 00280299\ 426833265 16022763560788680\ 40376567 -1 58728425167286476224069294\ 04382336954961609269557944\ 6943755573083710281783443 1 76477490060809706133093097\ 87423 855505126452984907978\ 956951557049500477713711
19440252\ 57929297\ 601660777 19441523021307289\ 88112095 1 10388754240281453371824142\ 17118654971848631432378603Х 63855802422831861117905349 2 52335657519920847188301792\ 87024864981860191664648387\ 5236752065724961075832132
19441523\ 02130728\ 988112095 19440252579292976\ 01660777 9 11193849646933689719981336\ 13435965189133286533996018\ 95494266794412499950874015 3 10452651123852378450484700\ 00365071421754599855658699\ 80126835249105981841754089
26656363\ 22059572\ 612890297 26657633662610039\ 99330255 -1 77753809394040345292881216\ 93497828248789519760713463\ 9003300057865899481079067 3 81018561938462701120054773\ 02716057699516240091801885\ 5116841394394252176754730
26657633\ 66261003\ 999330255 26656363220595726\ 12890297 3 13175222410955884663924511\ 90699747565850938894350288\ 3523584848748539585263126 3 48993425545112771556344807\ 97663131434331421529779232 7717482153102363722141066
3168096П 38720705\ 967286117 31682231829221373\ 53718165 -1 40943081019283543839177987\ 97559355679928988320743134\ 1595749438872790074848421 1 78067757952239471564072399\ 97208049549674014858664797\ 7279381249324208165812915
31682231\ 82922137\ 353718165 31680961387207059Х 67286117 -1 99689952912126673036312551 \ 98674051670159323866872419\ 715937316725721299776096 2 32362732071105131321722382\ 80347690174300694216761705\ 9898689090851370508178137
33774649\ 82679630\ 804586965 33775920268810621\ 91015717 1 95323211076850016878020690\ 45943726806049358693516295\ 2534847755320456020669493 8 91169339858397818411938773\ 59060741150513025173026002\ 0567821212163173631165916
33775920\ 26881062\ 191015717 33774649826796308\ 04586965 -1 10322167160987134955549641\ 18444713777936730607876858\ 85619910091983530963896896 1 10710094734058609285767921 \ 06079267284495556599632714\ 03227313564150387763018936
38158945\ 21819345\ 358304167 38160215660207767\ 44726017 27 10317487330096191295861293\ 78402615102869770114997760\ 59468566442939299081132234 2 12836465677215448627168948\ 09080669559890489934698303\ 4600727118776479021342568
38160215\ 66020776\ 744726017 38158945218193453\ 58304167 -1 -9056195888906339656398879\ 00560655831030065439241114\ 69300240064817796388962321 1 73323085727772237582275664\ 92068969276529932068331793\ 697710789018115031856238
3981560IA 60485873\ 250697455 39816872046873046\ 37116697 II3 97567013678549290124566818\ 43577901847407239349732188\ 4128845950742650952905210 2 43248724563291194710399533\ 29408761237243039960502792\ 9426634143253914724007003
39816872\ 04687304\ 637116697 39815601604858732\ 50697455 1 1073222723320421905137652\ 40021592471536609197245789\ 319788287257353344879822008 1 20950740768688138169122542\ 06888328053144889464483416\ 60905187629476143 82338509
П.10. D =163
Эллиптические кривые с вычислимым числом точек, для которых характеристика поля пред-
ставляется в виде р = 41о2 + I63ab + 163Z?2, задаются уравнением у2 = х3 + 3kt2x + 2kt3, где
21253233293
к = ———-— -----------. Для этих кривых число точек является простым. Если существует эллип-
З3731121921272163
тическая кривая £(FP) с числом точек г, то существует и «двойственная» кривая £(F,) с числом
точек р.
Таблица П. 10
Эллиптические кривые для р = 41п2 + 163«й + 163Л2, число точек равно г
2256-р q256 2 ~г А В XQ Уо
63875528\ 42267958\ 2721855 63942173955984089\ 183283 17J 11602378773616822525463164\ 55622907355389332860210191\ 1259045730985155554960935 2 25278088159801497478039748\ 29332220738121281481992055\ 5512983401882438524923413
63942173\ 95598408\ 9183283 63875528422679582', 721855 2 18560378032518851078394783\ 41008803248782189907075250\ 01489322539664637996809 2 61242802886505009539781103\ 08226919049812500489718533\ 9116088698366875653013401
21282829\ 53582515\ 19020445 21289494089155602\ 5477403 1 11524881406340006321410850\ 67077468359448972631575155\ 2581591924028208876490121 2 98082602054975313366391043\ 62925909716980762089398691\ 7112303855451657928766484
21289494\ 08915560\ 25477403 21282829535825151\ 9020445 4 50534328592881227333216938\ 90361634557672818818281460\ 500938466266582837700610 2 77817373833099656649268554\ 96596288784590120823107339\ 5683327652262988054180585
22162550\ 57544463\ 71321609 22169215128775087\ 7778303 1 -5830683601944702366983490\ 94814971536759032325455865Х 63088191686222596964079025 2 18623775726701630407509260\ 58161906882342346718049607\ 9523687966817355699417139
22169215\ 12877508\ 77778303 22162550575444637\ 1321609 1 87151893941671681785683564\ 89827985807023223282465659\ 7957645129471462360856197 1 95696730116829271986581800\ 49904020578265518449269979\ 1412198745319385403368432
25121612\ 25416472\ 37897053 25128276807495174\ 4352859 1 35594514456813990512730999\ 41797627446381080695370408\ 8056214425074772111100367 4 55749324595633890958988077\ 70932497119738400130482936\ 8658747524024123783737222
25128276\ 80749517\ 44352859 25121612254164723\ 7897053 1 11564778716509527961262084\ 09686360211716173427842866\ 8797120151377728026523524 4 73381352979837061915083306\ 90956187172879380480535425\ 0803938429823257037621176
60550377\ 75884035\ 28707209 60557042312170803\ 5152383 -1 3232371039403 8809117153095\ 43423143665811381651077293\ 1441963 804892008869254212 1 80418851890853459260848483\ 14388503387711063172868482\ 0170754254420701556597439
60557042\ 31217080\ 35152383 60550377758840352\ 8707209 5 77894274605938273883243911\ 56862002715925235603798952\ 4694071924519090798302692 2 76563402047306352621387942V 49330538367202528083011659\ 4778635578550493761185827
70727150\ 69443848\ 68157705 70733815247768937\ 4599825 1 -5464913461230752006063759\ 89123284655957558616018234\ 36782180700236710873 875603 1 55484233620214628184160371\ 42344490399529144864642821\ 4823747634273804807442090
70733815\ 24776893\ 74599825 70727150694438486\ 8157705 1 34904080981655970357999518\ 14254162489032377308434298\ 8784614763832689488382130 3 62684645129623174652405920\ 18021589687564861420358759\ 8415353727599873131944430
83503099\ 42891237\ 14028773 83509763982242822\ 0467059 -1 -1031409381077126626314048\ 95987528369720557016431301\ 817444784747869073050518849 1 70210808358762247202756876\ 476381О419848696789912656О\ 7235946543799830530431999
83509763\ 98224282\ 20467059 83503099428912371\ 4028773 4 28997343434832669408933439\ 89158893863235410427300306\ 3686181558809089817675866 6 34078610225966969675649709\ 03526349628259449394235202\ 2570575300375243965609792
87521825\ 08717410\ 95952225 87528489640504560\ 2389305 -1 10417238978105067295428354\ 47652011028960549509978145\ 06431796633388117311136415 1 86268388505360671374170591\ 20539547459605669661188495\ 3378101665801053147140440
87528489\ 64050456\ 02389305 87521825087174109\ 5952225 1 53497435212484525882475740\ 79760452779907230756739085\ 7330706304255281987402895 3 85805813656947248421241713\ 12608722107983454417303350\ 4582587391055541213066588
471
- Якоби, 84
— алгоритм вычисления, 165
синхропосылка, 425 - ' *
система распределения ключей, 289
-/-безопасная, 289
скрытый канал, 270
- в схеме симметричного шифрования, 271
- в схеме цифровой подписи, 270
— на эллиптической кривой, 320
— Рабина, 271
— устранение, 271
— Эль-Гамаля, 270
- в схеме шифрования с открытым ключом, 271
след, 69, 71
сложение точек
-коники, 102
- кубики, 103
сложностная неоднородность, 184
случайное дерево
-путь, 237
- сжимающее свойство, 18
смежный класс
- левый, 24
- правый, 25
собственный делитель, 44
совершенная аутентичность, 340
спаривание Вейля, 138, 148
-свойства, 138
список ключей, 407
сравнение, 39
степень
- расширения, 62
- трансцендентности, 62
стикер, 13
сумма
-Гаусса, 87
- Якоби, 88
теорема
- Безу. 104
- Вильсона, 82
- китайская об остатках, 40
— для кольца 2, 82
- Морделла-Вейля, 117
— о гомоморфизмах групп, 27
- о гомоморфизмах колец, 39
- о примитивном элементе, 72
- об ассоциативности отображений множества в
себя, 7
— основная об абелевых группах, 32, 233
- основная теории Галуа, 71
- Ферма
— великая, 79, 99
— малая, 66, 210
— Хассе, 139
-Чебышева, 79
Чуфа,/71 :•
текст •
-открытый, 191
- зашифрованный, 191 ' £
тест псевдопростоты ..
-Миллера-Рабина, 165 г’'"
- Соловэя-Штрассена, 166
точка
- бесконечно удаленная, 100 '' ~
— вес на точечной решетке, 245 '‘
-возврата, 106 “а
- высота, 118
— каноническая, 119
-кручения, 117 ';‘
- локальное кольцо, 130 '
- неособая,/05
- особая, 105 '
- перегиба, 107 " '
- самопересечения, 105 -
транзитивная безопасность, 187
угроза, 179 : 1
-доступности, 180
- подлинности, 180
- раскрытия, 179 . • .
- целостности, 179
умножение Дирихле, 80
упорядоченность
-атак, 182
- безопасных информационных систем, 182
- моделей нарушителя, 182
уравнение Пелля, 91
установление ключа, 288
- на основе протокола Диффи-Хеллмана, 289
— на эллиптической кривой, 316
- на основе симметричных методов, 289
- протокол Диффи-Хеллмана, 252
- протокол Х.509,291
факторгруппа, 25
факторкольцо, см. кольцо классов вычетов
фундаментальная единица, 91
фундаментальный параллелограмм, 110
функция, 6 •
-Вейерштрасса,//2
-Вейля, 139 ’
— алгоритм вычисления, 172
— вычисление логарифмической
производной, 173
- взаимная корреляционная, 396
- вычислимая, 10
- вычислимая в одну сторону с потайным
ходом,252 £
-двоякопериодическая, 110
- криптографически слабая, 398 -:: '
-Лукаша, 229
-Мебиуса, 80 =• - ~
- мультипликативная, 81 7f ~
- рациональная, 46 -
— на кривой, 130
-----значение в точке, 130 м •-
-----значение на дивизоре, 137 ’’
-----нуль, 134
-----ПОЛЮС, 135 V' ' - •'
УКАЗАТЕЛЬ
абсолютная величина, 75
активный 5-блок, 403
алгебраическая кривая, 100
- степень, 99
алгоритм, 8
- вероятностный, 9
- Гровера, 393
- деления в кольце Z, 157
- детерминированный, 9
- Евклида бинарный для кольца Z, 158
— расширенный, 159
- Евклида для кольца Z, 158
— расширенный, 158
- Евклида для кольца F2[Z], 159
- инкрементальный, 274
- Ленстры-Ленстры-Ловаша (LLL), 160
- решения квадратного уравнения в поле из 2"
элементов, 164
- сложность, 10
— временная, 10
— емкостная, 10
— полиномиальная, 10
— субэкспоненциальная, 10
— экспоненциальная, 10
- умножения
— Карацубы-Офмана, 151
— Монтгомери, 156
— Шенхаге, 151
— Шенхаге-Штрассена, 155
-эффективный, 10
атака, 180
«атака гроссмейстера», 193,317
аутентификация, 179
— защитные функции, 196
— координаты, 196
— упорядоченность, 197
- корреспондента (пользователя), см. опознавание
-сообщения, 179
базис
- минимальный, 97
- нормальный, 313
-решетки, 160
— минимальный по Ловашу, 160
бесключевое чтение, 347
бесключевое шифрование Месси-Омуры, 253
— на эллиптической кривой, 317
бинарная операция, 6
— ассоциативность, 6
- дистрибутивность, 6
- коммутативность, 6
бинарное отношение, 7
- антисимметричность, 7
-рефлексивность, 7
-симметричность, 7
-транзитивность, 7
булева формула, 341
булева функция, 51
- арифметическое продолжение, 370
— аффинная, 342
- аффинная эквивалентность, 343
- инверсия, 51
- линейная, 342
-минимизация, 367
- нелинейность, 409
— максимальная, 420
- представление полиномом Жегалкина, 52
- решеточное продолжение, 363
— свойства, 363
— удаление, 364
- сбалансированная, 342
— сложность, 356
верификатор, 195,279
вес
- дифференциала, 402
- линейной суммы, 415
- полинома, 48
- слагаемого, 48
- хэммингов, 397
вложение, 26
временная метка, 291
- децентрализованная реализация, 292
- на изогенных эллиптических кривых, 333
- централизованная реализация, 291
вычет
- квадратичный, 83
- кубический, 83
- степени п, 82
генератор псевдослучайной последовательности, 260
- Блюма-Блюма-Шуба (BBS), 261
— на супервырожденной эллиптической
кривой, 325
- компрометация, 325
— неявная, 325
— явная, 325
- криптографически стойкий, 261
- на блочном шифре, 260
- на ключевой хэш-функции, 260
- на эллиптической кривой, 325
- пример неудачной реализации, 320
гиперэллиптическая кривая, 141
- норма функции, 142
465
- род, 141
- сопряженная функция, 142
гипотеза
- - Берча и Свиннертона-Дайера, 141
- Римана для эллиптических кривых, 140
- стохастической эквивалентности, 399
граф случайного отображения, 17
— глубина, 18
- ширина, 18
группа, 22
- абелева, 22
— индекс, 24
- автоморфизм, 26
- автоморфизмов, 26
- алгебраическая, 130
- аддитивная, 22 ••
- без кручения, 24
- бинарная операция, 22
-Галуа, 70
- гомоморфизм, 26
— ядро, 26
-Гротендика, 31
- дважды транзитивная, 31
- действие на множестве, 28
-дивизоров, 135
- единиц кольца, см. группа обратимых
элементов кольца
- знакопеременная, 30
- изоморфизм, 26 ,, -
- интранзитивная, 31
- кватернионов, 23
- классов идеалов, 93
- коммутант, 27
— коммутатор, 27
- конечно порожденная, 24
— кручения, 24
- модулярная, 24
- Морделла-Вейля, 244
- обратимых элементов кольца, 35
-полинома, 70
- порядок, 23
— прямое произведение, 31 : '
- разложение по подгруппе, 25
- свободная, 24
- симметрическая, 29
- система образующих, 24
- сопряжение, 28
- транзитивная, 31
- характеров абелевой группы, 28
- центр, 23
- циклическая, 23
— дискретный логарифм, 24
— образующая, 23
— порядок элемента, 23
— свободная, 23
- эндоморфизм, 26
данные, 189
делимость
- идеалов, 41 . -
- на идеал, 41
- относительно нормирования, 75
дешифрование, 191
дзета-функция кривой, 140 .
диаграмма
— коммутативная, 7
— вычисления инкрементальной подписи, 274
— гомоморфизмов групп, 27
— гомоморфизмов групп идеалов, 97 :=
— гомоморфизмов, индуцированная
изогенией, 333
- точная, 27 . t ,-и
дивизор Г '. ЬС..'
- на кривой, 135 /ч •' .:
— главный, 136 ’У Л; .рцч
- носитель, 135 < -
-положительный, 135 -j-тчг1
- полуприведенный, 144
- приведенный, 145
-степень,/55
- функции, 136
дивизоры
-линейно эквивалентные, 136
- наибольший общий делитель, 144
- сравнимость, 135
дискретное логарифмирование
- метод базы разложения, 219
- метод встречи на случайном дереве, 235
- метод встречи посередине, 234
- метод Гельфонда, 233
- метод Копперсмита, 227
- метод логарифмической производной, 242
- метод Полларда, 235, 248
- метод решета числового поля, 225
— оценка сложности, 226
— с использованием предвычислений, 247
— метод «giant step — baby step», 234
- на квантовом компьютере, 239
- с помощью орбит автоморфизмов, 240, 306
- через поднятие, 245
дифференциал, 398
- активный разряд, 403
— одноцикловый порядка i, 406
-подстановки, 401
- усеченный, 405
дифференциальный оператор, 54
диффузия, см. рассеивание
доказательства с нулевым разглашением, 279
— бездиалоговые
— знания дискретного логарифма, 284 ,
— знания набора переменных, .
удовлетворяющих заданной булевой
функции, 284
— на основе канала со стиранием, 286
— на эллиптической кривой, 323
- диалоговые
— знания дискретного логарифма, 281
— знания изоморфизма графов, 279
— знания разложения, 280
— правильности выбора составного числа, 282
466
— на эллиптической кривой, 322
дополнение к элементу, 363
доступ к информации, 7 78
- несанкционированный, 7 78
дробь
- непрерывная, 207
— бесконечная, 208
— конечная, 208
- подходящая, 208
задача
- выбора, 71
— класс co-NP, 12
— класс NP, 12
— класс Р, 12
— о выполнимости, 71
— о простом числе, 11
— о составном числе, 77
— об изоморфизме графов, 11
— полиномиальная сводимость, 12
— полиномиальная эквивалентность, 12
— решаемая, 11
— труднорешаемая, 11
- вычисления изогении, 331
— оценка сложности, 333
- вычисления категорного морфизма, 331
- дискретного логарифмирования
— в группе F/, 218
— в группе точек эллиптической кривой, 233
— в группе функций Лукаша, 229
— в якобиане гиперэллиптической кривой, 248
- Диффи-Хеллмана, 229
-массовая, 11
— сложность, 11
- математическая
— основная, 200
— унифицированная, 199
- Месси-Омуры, 254
- о выполнимости булевой функции, 345
- об укладке ранца, 258
- поиска, 200
- разложения на множители, 203 г •
-размер, 10
- распознавания, 200
- сертификат, 11
закон
- взаимности Вейля, 137
- исключения третьего, 20
- составления подходящих дробей, 208
зашифрование, 191
защита информации, 178
- от агентурной разведки, 178
- от непреднамеренного воздействия, 178
- от несанкционированного воздействия, 178
- от несанкционированного доступа, 7 78
- от технической разведки, 7 78
- от утечки, 178
- средство, 7 79
-цель, 179
-эффективность, 179
игра в покер по телефону, 279
идеал, 38
- аффинного алгебраического многообразия, 9<.
-базис, 39
- главный, 38
- дробный, 92 k •
- единичный, 38
— квадратичного порядка, 92
— возведение в квадрат, 175
— дробный, 92
— приведение, 175
— разветвление, 93 v" зк
— разложение, 93
— умножение, 7 74
- левый, 38 :>,
- максимальный, 41
- нулевой, 38
- порожденный элементами, 39
- правый, 38
- приведенный, 93
- простой, 41 .
- £>-гладкий, 223
идеалы
- пересечение, 40
- произведение, 40
-сумма, 59 .р' ’ -
идемпотентность, 22 's-
идентификатор, 179
извлечение корня
— квадратного в F6/
— q = 0 (mod 2), 163
— q= 1 (mod 2), 163
— q= ] (mod 4), 162
— q=3 (mod4), 762
— q=5 (mod 8), 162 "
- кубического в F9
—p = ] (mod 3), 164
—p = 19, 37 (mod 54), 164
—p = 7, 13 (mod 18), 164
изогения, 132
-дуальная, 132
-нулевая, 132 .
- степени 2,133
- степени 3,133
- степень, 132
-ядро, 132
изоморфизм
- бирациональный, 722
- торов, 114
- эллиптических кривых, 119
имитозащита, 190
инволюция, 201
информационная система, 178
-безопасная, 181
— доказуемо безопасная, 181
- доказуемо уязвимая, 181
- транзитивная, 185 '
-уязвимая, 181
информация, 178
467
-безопасность, 179 cf.
-доступность, 179 •
-защищаемая, 178 >= :
-конфиденциальная, 178 :
- подлинность, 179 w
-секретная, 178 ?•
- целостность, 179 - >
исчисление, 9 . г.•
- атак, 182 а--.
- порождающие правила, 9
канал со стиранием, 285
канал утечки, 178 ' ,
касательная к проективной кривой, 106
категория, 32
- морфизмы, 32 ’ ; '
- объекты, 32
- функтор, 32
квадратичная форма, 94 •
- главная, 94
- нормальная, 94
- положительно определенная, 94
- приведенная, 94
— эквивалентность, 94
квадратичный порядок, 90 * •
- максимальный, 90
квазигруппа, 22 -
квантовый регистр, 75 ' -
ключ, 189
- доставка, 288
— протокол Нидхама-Шредера, 290
- предварительное распределение, 288
- производный, 288 '
- шифрования, 191, 336
когерентная суперпозиция, 14
количество информации, 16
кольцо, 54
- ассоциативное, 34 ;
- главных идеалов, 42
- гомоморфизм, 36
- делители нуля, 35 --
- дискретного нормирования, 75
- дифференциальных операторов, 55
- евклидово, 42
- единица, см. обратимый элемент
- изоморфизм, 36
— классов вычетов, 39
- коммутативное, 54 ' "•
- координатное, 128 v’ -- - '
— норма элемента, 128
- полиномов Жегалкина, 51
— однозначность разложения, 55
— симметрические функции, 54
- присоединение переменной, 38
— прямая сумма, 41 $ <
- с единичным элементом, 34
- факториальное, 44 ; «лаг
- характеристика, 55
- целозамкнутое, 65
- целостное, 55
- целых алгебраических чисел, 95
— целых квадратичных чисел, 89 ..
— целых 2-адических чисел, 383 : -
- целых р-адических чисел, 76
- частные, 36 . я . . .
- частных, 57 :
- эндоморфизмов модуля, 45 i
комплексное умножение, 123
- влияние на скорость вычислений, 308
- влияние на сложность логарифмирования, 240
композиция . - . .
— алгоритмов, 10 й
-дивизоров, 173
- квадратичных форм, 95
— отображений, 7 «
компьютер .
-квантовый, 14
-молекулярный, 13
кондуктор .е -
- квадратичного порядка. 90
- квадратичной формы, 94
коника, 101
конус, ассоциированный с вершиной куба, 364
координаты лг
- аффинные. 99
-проективные, 100
корень степени п из единицы, 72 . /.
коэффициент •• •
- диффузии, 397 в-.
- корреляции, 396 -
кратность пересечения, 102 -л4-.-
криптоалгоритм, 190 с,
-безусловно стойкий, 192 -
- доказуемо стойкий, 192 .
- итерированный, 4
-предположительно стойкий, 192
криптоанализ, 190
- алгебраические методы, 348, 359 .
- дифференциальный, 397, 399 ..
— атака «бумеранг», 406
— использование дифференциалов высших
порядков, 406
— использование усеченных : л--
дифференциалов, 405 г-;- »qr - л •
— пример, 400, 403 •
- линейно-дифференциальный, 416 .
- линейный, 408 , -
— лемма Мацуи, 410
--пример, 411,414 ,
-метод сдвига, 416
- на основе адаптивно подобранных открытых
текстов, 547 •
- на основе адаптивно подобранных
шифртекстов, 547
- наоснове арифметического продолжения, 369
— обращение хэш-функции, 371
— пороговое число, 372 ъ
— пример, 372,374
— на основе гомоморфизма характеристики
КОЛЬЦа, 386 Л;.:;:--
468
- на основе компромисса время/память, 389
- на основе открытых текстов, 347
- на основе подобранных открытых текстов, 347
— на основе подобранных шифртекстов, 347
- на основе рационального продолжения, 380
— примеры, 381
- на основе редукции числа переменных, 387
— на основе связанных ключей, 347, 408
- на основе списка ключей, 407
- на основе шифртекстов, 347
- на основе 2-адического продолжения, 384
— примеры, 384
- решеточный, 362
— вскрытие ключа, 365
— пример, 367
- сочетание перебора и вычислений, 390
- статистические методы, 348, 396
- частотный, 350
- шифров с малым порядком нелинейности, 377
- эффективность метода, 359
криптографический примитив, 189
- бесключевой, 189
-вскрытие, 190
-несимметричный, 189
-симметричный, 189
- стойкость, 190
криптографический протокол, 190
криптография, 177
криптосистема, 190
кубика, 102
-/-инвариант, 115
— дискриминант, 115
кубит, 14
кубическая кривая, см. кубика
лавинный вектор, 396
- параметр независимости битов, 397
лавинный критерий, 396
— строгий, 396
минимальная подсистема безопасности, 182
многообразие
- аффинное алгебраическое, 99
- неприводимое, 100
множества
- равные, б
множество, 6
- декартово произведение, 6
- дополнение, б
- задач, положенных в основу безопасности, 184
- замкнутое относительно операции, 6
- линейно упорядоченное, 8
- мощность, 8
- объединение, б
- пересечение, б
- пустое, б
- разность, б
- симметрическая разность, б
- счетное, 8
- упорядоченное, 50
— верхняя грань, 50
----точная, 50
— нижняя грань, 50
----точная, 50
модели нарушителя
- однотипные, 182
модель нарушителя, 181
-максимальная, 182
- тривиальная, 184
модуль, 22
- над кольцом, 45
моноид, 22
— вложимость в группу, 31
нарушитель, 180
- возможности, 181
— вычислительные, 183
— криптоаналитические, 183
— лабораторные, 183, 435
— математические, 183
— организационные, 183
— технические, 183
- стратегия . 5
— активная, 180
— пассивная, 180
невычет
- квадратичный, 83
- кубический, 83
- степени п, 82
ненадежность
-ключа, 337
- сообщения, 337
нестандартная конъюнкция, 342
норма, 69,7/ р
-дивизора, 146
- идеала
— квадратичного порядка, 92
— числового поля, 97
- квадратичного числа, 90
нормальная форма
- дизъюнктивная, 341
— конъюнктивная, 341
нормирование, 74
-архимедово, 75
-дискретное, 75 . t-z, г.
— неархимедово, 75 .....
-недискретное, 75
-показательное, 75 .... ....
-тривиальное, 74
-jo-адическое, 74
- ф-адическое, 75
нуль-последовательность, 76
область транзитивности, 337
округление, 363
оператор • —
- возведения в степень по модулю простого
числа Ферма, 354
- обращения в расширенном поле
характеристики 2, 354 .
469
- перестановки битов в блоке, 353
— подстановки «-разрядного слова, 354
- сложения
— по модулю 2, 354
— по модулю 2", 354
- умножения
— на невырожденную матрицу, 354
— по модулю простого числа Ферма, 354
- циклического сдвига, 354
опознавание, 179
- диалоговое на изогенных эллиптических
кривых, 332
— на основе диалоговых доказательств с нулевым
разглашением, 322
- на основе шифрования с открытым ключом, 321
- по аргументу хэш-функции, 196
- по паролю, 196
основная теорема безопасности Белла-Лападулы, 177,
185
отображение, 6
- биективное, 7
-инъективное, 7 -
- кривых
— рациональное, 131
— регулярное, 129
— степень, 131
- область значений, 6
- область определения, 6
- образ, 6
- ограничение, 6
- продолжение, 6
- прообраз, 6
— полный, 6
- сюръективное, 7
парадокс дней рождения, 234
парадоксы теории множеств, 8
- логические, 8
- семантические, 8
параметризация окружности, 101
передача информации со стиранием, 285
- генерация ключей получателя, 285
- на основе задачи разложения, 287
- на эллиптической кривой, 322
- протокол, 285
переменная
- существенная, 340
- фиктивная, 340
перемешивание, 339
плоскость
- аффинная, 99
- проективная, 100
подбрасывание монеты по телефону, 278
подгруппа, 23
— нормальная, 25
подкольцо, 38
подмножество, 6
- собственное, 6 ? 1
подполе, 58
подстановка, 28
- аффинная, 342 :
- аффинная эквивалентность, 343
- беспорядок, 30
- задание набором циклов, 29
- задаваемая полиномом над Z/2"'Z, 355
-инволюция, 421
- линейная, 342
- неудачная в смысле линейного •
криптоанализа, 410
- нечетная, 30
- нормализатор элемента, 30
- поиск наилучших линейных сумм, 411
- порядок нелинейности, 343
- стабилизатор элемента, 30
- транспозиция, 29
- четная, 30
-экстремальная, 418
— аффинная эквивалентность, 418
— примеры, 421
поле, 35
— алгебраически замкнутое, 62
- алгебраическое замыкание, 62
- Галуа, см. поле конечное
- деления круга, 72
- квадратичное
— вещественное, 89
— дискриминант, 89
— мнимое, 89
— классов вычетов нормирования, 75
— конечное, 65
— автоморфизмы, 67
- мультипликативная группа, 58
- нормированное, 74
- полное относительно нормирования, 75
- порядок, 65
— максимальный, 65
- присоединение, 59 ••
- простое, 58
- разложения полинома, 63 5 .
- расширение, 59 ; ?
— автоморфизмы, 70 - \
— изоморфное, 61 : : s *;
— простое, 60
-----алгебраическое, 61
-----трансцендентное, 60
-упорядоченное, 74
- характеристика, 59 < : *. <.
- частных, 36 ~ 5 - к
- числовое, 95
полином, 37 >. ;;
-деление, 38
— деления круга, 72 • : ? ,
- дискриминант, 48
-значение, 38 .
-корень, 47
- коэффициенты, 37
— минимальный, 96 ’ ч- -» .
— модулярный, 132 V ~
— над кольцом, 46
- однородный, 46 • . \ :г.
470
- от нескольких переменных, 38
— степень, 38
-производная, 47
— простой корень, 47
- свободный от квадратов, 47
- симметрический, 47
- содержание, 49
-степень, 37
полином Жегалкина, 51
— неразложимый, 53
- проективная эквивалентность, 134
- производная, 54
- разности высших порядков, 398
-рациональное продолжение, 377
- тривиальное разложение, 53
— 2-адическое продолжение, 384
полиномы деления, 296
полугруппа, 22
— коммутативная, 22
полукольцо, 50
- булевых формул, 341
- решеточных полиномов, 342, 362
пороговый объем информации, 428
последовательность
- сверхвозрастающая, 258
- случайная, 16
— количественный подход, 16
— по Колмогорову, 16
— сложностный подход, 16
— частотный подход, 16
- фундаментальная, 75
предъявление бита, 278
-блоб, 278
преобразование данных
- несимметричное, 189
-симметричное, 189
преобразование координат
- аффинное, 101
- проективное, 101
преобразование
- Монтгомери, 156
— алгоритм вычисления, 156
- Фурье
— быстрое, 74,154
----алгоритм вычисления, 154
— дискретное, 73
— квантовое, 15, 213
претендент, 195,279
приведение
- дивизора, 174
- идеала мнимого квадратичного порядка, 175
- квадратичной формы, 94
- числа по модулю решетки, 169
принцип максимальной однородности, 184
произведение Монтгомери, 156
пространство
- аффинное, 99
- проективное, 100
прямая, 99
-аффинная, 100
- проективная, 100 -
— бесконечно удаленная, 100
разглашение знаний, 196
-минимальное, 196,279
-нулевое, 196,279
- полное, 196 .
-частичное, 196
разделение секрета, 199, 287
— пороговая схема, 288 \
— идеальная, 288
разложение на множители
- метод диофантовой аппроксимации, 206
- метод квадратичного решета, 209
- метод непрерывных дробей, 208
- метод пробного деления, 204
- метод Ферма, 205
- метод «giant step — baby step», 205
- на квантовом компьютере, 213
- на эллиптической кривой, 211
- неоднозначное, 43
- однозначное, 44
- по известным показателям RSA, 204
- полинома над F^, 161
- простого числа в мнимом квадратичном
кольце, 167
- схема Крайчика, 206
- тривиальное, 44
- p-метод Полларда, 207 •
- (р - 1 )-метод, 210
разность функции, 397
рандомизатор, 193 - . =
рассеивание, 339
расширение
- абелево, 70
- Галуа, 70
- конечное, 62
- мультиквадратичное, 64
- несепарабельное, 65
- нормальное, 64
- сепарабельное, 65
-циклическое, 70
расшифрование, 191 'ии?* _;
решетка, 50,160
- бинарные операции, 51
- гомоморфизм, 51
- дистрибутивная, 51, 362
- комплексная, ПО
-полная, 5/ -*>'<- j
- с дополнениями, 51
свертка, 153
- отрицательно обернутая, 153
- положительно обернутая, 153
секретная система, 336
- идеальная, 338
- совершенная, 337
-эндоморфная, 337
символ
- Лежандра, 83 л v
471
- Якоби, 84
— алгоритм вычисления, 165
синхропосылка, 425
система распределения ключей, 289
-/-безопасная, 289
скрытый канал, 270
- в схеме симметричного шифрования, 271
- в схеме цифровой подписи, 270
- - на эллиптической кривой, 320
— Рабина, 271
~ - устранение, 271
— Эль-Гамаля, 270
- в схеме шифрования с открытым ключом, 271
след, 69, 71
сложение точек
- коники, 102
- кубики, 103
сложностная неоднородность, 184
случайное дерево
- путь, 237
- сжимающее свойство, 18 •
смежный класс
- левый, 24
- правый, 25
собственный делитель, 44
совершенная аутентичность, 340
спаривание Вейля, 138, 148
- свойства, 138
список ключей, 407
сравнение, 39
степень
- расширения, 62
- трансцендентности, 62
стикер, 13
сумма
-Гаусса, 87
- Якоби, 88
теорема
- Безу, 104
- Вильсона, 82
- китайская об остатках, 40 -
— для кольца Z, 82
- Морделла-Вейля, 117
- о гомоморфизмах групп, 27
- о гомоморфизмах колец, 39
- о примитивном элементе, 72
- об ассоциативности отображений множества в
себя, 7
- основная об абелевых группах, 32, 233
- основная теории Галуа, 71
- Ферма
— великая, 79, 99
— малая, 66, 210
-Хассе, 139
- Чебышева, 79
- Чуфа, 141
текст
- открытый, 191
- зашифрованный, 191
тест псевдопростоты
- Миллера-Рабина, 165
- Соловэя-Штрассена, 166
точка
- бесконечно удаленная, 100
- вес на точечной решетке, 245
- возврата, 106
- высота, 118
— каноническая, 119
-кручения, 117
-локальное кольцо, 130
- неособая, 105
- особая, 105
-перегиба, 107
-самопересечения, 105
транзитивная безопасность, 187
угроза, 179
— доступности, 180
- подлинности, 180
- раскрытия, 179
- целостности, 179
умножение Дирихле, 80
упорядоченность
- атак, 182
— безопасных информационных систем, 182
- моделей нарушителя, 182
уравнение Пелля, 91
установление ключа, 288
- на основе протокола Диффи-Хеллмана, 289
— на эллиптической кривой, 316
- на основе симметричных методов, 289
- протокол Диффи-Хеллмана, 252
- протокол Х.509, 291
факторгруппа, 25
факторкольцо, см. кольцо классов вычетов
фундаментальная единица, 91
фундаментальный параллелограмм, ПО
функция, 6
- Вейерштрасса, 112
- Вейля, 139
— алгоритм вычисления, 172
— вычисление логарифмической
производной, 173
- взаимная корреляционная, 396
- вычислимая, 10
- вычислимая в одну сторону с потайным
ходом, 252
-двоякопериодическая, ПО
- криптографически слабая, 398
- Лукаша, 229
- Мебиуса, 80
- мультипликативная, 81
- рациональная, 46
— на кривой, 130
-----значение в точке, 130
-----значение на дивизоре, 137
-----нуль, 134
-----полюс, 135
472
регулярная в точке, 130 - трудновычислимая, 10 - целевая, 346 - Эйлера, 80 - элементарная симметрическая, 48 -эллиптическая, 770 . s, — порядок, 777 -RSA, 264 ЧИСЛО — алгебраическое, 95 . .. — степени п, 96 ' t — целое. 95 ' -гладкое, 206 .. •. — квадратич ное, 89
характер, 27 - аддитивный, 87 - мультипликативный, 87 характеристика - дифференциальная, 398 — линейная, 411 хэш-функция, 190 - бесключевая, 190 — стойкость, 349 - вычислимая в одну сторону, 190 -ГОСТ Р 34.11-94, 442 - ключевая, 190 - коллизия, 190 .... — вычисление, 388 — пример, 389 -обращение, 190 — ограниченное, 268 - свободная от коллизий, 190 — на эллиптической кривой, 324 . - 7-эргодическая, 381 • . -MD5, 441 - классов поля, 93 >. , >. > - Мерсенна, 79 - решений уравнения над FP, 88 „.г: — свободное от квадратов, 79 — сильное простое, 272 - сопряженное, 90 -Ферма, 79 — D-гладкое. 206. 208 - р-адическое у ‘ €. — дробное, 76 д -д*-; .«=». — целое, 76 шифр, 191 . .«j зйсй-» - блочный, 336 - Виженера, 353 - гамма, 17, 425 — гомоморфизм, 386 г. .<•.> — сжимающий, 386 - ГОСТ 28147-89, 433 — выбор блока подстановок, 435 г — свойство дополнения, 435 л,- СТОЙКОСТЬ. 435
цикл шифрования, 336 , ... циркулянтная матрица, 386 цифровая подпись, 263 -вслепую, 271, 273 — на эллиптической кривой, 326 - ГОСТ Р 34.10-2001,318, 319 . — безопасность, 319 — сложно стная неоднородность, 320 - ГОСТ Р 34.10-94, 268 — на изогенных эллиптических кривых, 333 - инкрементальная, 274 — коллективная, 271,287 ... - неоспоримая, 271,272 — на эллиптической кривой, 321 -Рабина, 264 -разовая,27/ - с восстановлением сообщения, 274 - Фиата-Шамира, 265 - Шнорра, 267 — на эллиптической кривой, 320 — безопасность, 268 - Эль-Гамаля, 265 — безопасность, 267 — встраивание потайного хода выбором образующей, 267 — морфизм, 266 — на эллиптической кривой, 318 — передача информации по скрытому каналу, 270 -ECDSS, 319 ; J - замкнутый, 360 — вскрытие ключа, 360 .у. - итерированный, 336 •<. - марковский, 400, 411 - моноалфавитной замены, 350 «4 - неполный, 396 у > / - перестановки, 353 - подстановочно-перестановочный, 355 - полиалфавитной замены, 351 < — полный, 396 , /j — поточный, 336 лани - рабочая характеристика, 338 • н, - симметричный, 336 - смешанный, 337 -у — степенной, 417 - стойкость, 348 — скорость падения, 429 - фейстелев, 354 : . — свойство дополнения, 354 обобщенное, 355 . - Цезаря, 350 - чистый, 337, 360 - эндоморфный, 191 .. .«.««едг - Blowfish, 438 - DES, 429 — свойство дополнения, 431 д.у — стойкость, 431 . ..г -DESX, 431 -YML,431 -IDEA., 432 . . . ..... ..
- RC5,436
— стойкость, 438
-RIJNDAEL, 440
— алгебраическое уравнение зашифрования, 440
- SAFER, 439
— стойкость, 439
шифратор, 191
шифрование, 191
режим, 425
- - выработки имитовставки, 427, 434
— гаммирования, 425
— гаммирования с обратной связью, 426
— простой замены, 425
— сцепления блоков, 426
-симметричное на эллиптической кривой, 317
шифрование с открытым ключом
-протокол Блюма-Голдвассера, 257
-протокол Голдвассера-Микали, 257
- протокол Рабина, 256
- протокол Шора-Ривеста, 259
- протокол Эль-Гамаля, 254
- ранцевый шифр Меркля-Хеллмана, 258
- RSA, 203
— атаки на основе эндоморфизмов, 215
— бесключевое дешифрование, 214
— на эллиптической кривой, 315
скорость падения стойкости, 204
шифртекст, 191
эквивалентность, 7
- дробных идеалов квадратичного порядка, 93
- полиномиальная, 10
- проективная, 134
электронные платежи, 273
- создание электронной монеты, 273
— на основе протокола Шнорра, 327
— на основе протокола Эль-Гамаля, 326
— на основе протокола RSA, 328
- электронная монета, 273
элемент, 6 ,, ,
- алгебраический над полем, 61, 63
— максимальный, 50
- минимальный, 50
- наибольший, 50
- наименьший, 50
- неразложимый, 44
- обратимый, 35
- обратный, 35
- орбита относительно группы подстановок, 30
— отрицательный, 35
-примитивный, 72
- простой, 41
- с однозначным разложением, 44
- трансцендентный над полем, 60
- целый над кольцом, 64
элементы .
- алгебраически зависимые, 62
— алгебраически независимые, 62
— ассоциированные, 44
— несравнимые, 50
— перестановочные, 23
- сопряженные, 25, 96
— сравнимые, 50
эллиптическая кривая, 107
— встраивание открытого текста в координату
точки, 314
— в простом поле, 315 _
— в расширенном поле, 315 '*-
- генерация кривой
— над расширенным полем, 299
— с j = 0, 302
— с j = 1728, 304
— с комплексным умножением, 307
-----примеры. 308
- генерация точки, 294
-группа кручения, 117 '
— закон сложения точек, 116
- поднятие точки, 244
- проективная арифметика
— в форме Вейерштрасса, 171
— в форме Гессе, 171
-ранг, 117
- расчет числа точек. 294
— алгоритм Чуфа, 297, 298
— над простым полем с j = 0, 301, 302
— над простым полем cj = 1728, 301. 304
— над расширенным полем, 299
— регулятор, 244
— супервырожденная, 140
— умножение точки на число
— в арифметике Монтгомери, 310
— в расширенном поле, 313
— с помощью комплексного умножения, 310
- в форме Вейерштрасса, 107
- в форме Гессе, 108
- в форме Дойринга, 107 ' f
- в форме Лежандра, 107
эндоморфизм Фробениуса 123, 241
- след, 241,295
- собственное значение, 297
- характеристическое уравнение, 124,295
энтропия • ’ •
-колмогоровская, 16
— шенноновская, 16
якобиан алгебраической кривой, 136
2-адическое показательное нормирование, 383 ’
/.-функция Хассе-Вейля, 141
А-вычет, 156 1.
477
12.4. Генераторы псевдослучайной
последовательности.................260
Упражнения к главе 12....................261
Литература к главе 12....................262
ГЛАВА 13. ЦИФРОВАЯ ПОДПИСЬ................263
13.1. Подпись на группе трудновычислимого
порядка............................263
13.1.1. Схема подписи RSA..........264
13.1.2. Схема подписи Рабина.......264
13.1.3. Схема подписи Фиата-Шамира..265
13.2. Подпись на группе вычислимого
порядка............................265
13.2.1. Схема подписи Эль-Гамаля....265
13.2.2. Схема подписи Шнорра.......267
13.2.3. ГОСТ Р 34.10-94 и DSS......268
13.3. Сравнительный анализ представленных
схем подписи.......................269
13.4. Скрытый канал......................270
13.5. Другие схемы подписи...............271
13.5.1. Схема «неоспоримой» подписи.271
13.5.2. Схема подписи «вслепую».
Электронные платежи..........273
13.5.3. Схема подписи с восстановлением
сообщения..........................274
13.5.4. Инкрементальная подпись.....274
Упражнения к главе 13....................275
Литература к главе 13....................276
ГЛАВА 14. ДРУГИЕ
КРИПТОГРАФИЧЕСКИЕ
ПРОТОКОЛЫ................................278
14.1. Схемы предъявления битов............278
14.2. Диалоговые доказательства
с нулевым разглашением....................279
14.2.1. Доказательство знания
изоморфизма графов..................279
14.2.2. Доказательство знания разложения
составного числа....................280
14.2.3. Доказательство знания
дискретного логарифма...............281
14.2.4. Доказательство правильности
выбора составного числа.............281
14.3. Бездиалоговые доказательства
с нулевым разглашением....................283
14.4. Передача информации
со стиранием.............................285
14.5. Разделение секрета.................287
14.6. Протоколы управления ключами.......288
14.6.1. Установление ключа на основе
симметричных методов...............289
14.6.2. Доставка ключа.............290
14.7. Временная метка....................291
14.7.1. Централизованная реализация
временной метки....................291
14.7.2. Децентрализованная реализация
временной метки....................292
Упражнения к главе 14....................293
Литература к главе 14....................293
ГЛАВА 15. КРИПТОСИСТЕМЫ
НА ЭЛЛИПТИЧЕСКИХ
И ГИПЕРЭЛЛИПТИЧЕСКИХ КРИВЫХ............294
15.1. Расчет числа точек эллиптической
кривой в общем случае..................294
15.1.1. Предварительные сведения..295
15.1.2. Полиномы деления..........296
15.1.3. Алгоритм Чуфа.............297
15.2. Расчет числа точек эллиптической
кривой над расширенным полем...........299
15.3. Расчет числа точек эллиптических кривых
cj = 0, 1728 над простыми полями........301
15.3.1. Криваяу2 = х3 + В.........301
15.3.2. Криваяу2^х3 + Лх..............303
15.4. Эллиптические кривые с комплексным
умножением..............................305
15.4.1. Генерация эллиптических кривых
с комплексным умножением..........306
15.4.2. Влияние комплексного умножения
на скорость вычислений............308
15.5. Эллиптические кривые над расширенными
полями специальных характеристик.......311
15.6. Протоколы на эллиптических кривых....314
15.6.1. Встраивание открытого текста
в координату точки................314
15.6.2. Аналог криптосистемы RSA..315
15.6.3. Установление сеансового ключа.316
15.6.4. Шифрование................317
15.6.5. Цифровая подпись..........318
15.6.6. Опознавание, канал со стиранием
и доказательства с нулевым
разглашением......................321
15.6.7. Вычислимая в одну сторону
функция, свободная от коллизий....324
15.6.8. Генераторы псевдослучайной
последовательности................325
15.6.9. Протоколы для электронных
платежей..........................326
15.7. Криптосистемы на гиперэллиптических
кривых..................................329
15.8. Криптосистемы на изогениях
эллиптических кривых....................331
15.8.1. Задача вычисления изогении и
квантовый компьютер...............331
15.8.2. Криптографические протоколы
на изогенных кривых...............332
Упражнения к главе 15..................334
Литература к главе 15..................335
ГЛАВА 16. ОБЩИЕ СВЕДЕНИЯ
ОБ ИТЕРИРОВАННЫХ
КРИПТОАЛГОРИТМАХ.......................336
16.1. Основные понятия классической
криптографии............................336
16.2. Некоторые положения
теории секретности Шеннона..............336
16.2.1. Объем текстов, однозначно
определяющих ключ.................339
16.2.2. Теория аутентификации Симмонса.... 340
16.3. Булевы функции и булевы формулы......340
СОДЕРЖАНИЕ
ВВЕДЕНИЕ................................3
ГЛАВА 1. МНОЖЕСТВА, АЛГОРИТМЫ,
СЛУЧАЙНЫЕ ОТОБРАЖЕНИЯ...................6
1.1. Сведения из теории множеств.......6
1.2. Сведения из теории алгоритмов.....8
1.2.1. Алгоритм и исчисление.......8
1.2.2. Сложность алгоритма........10
1.3. Нестандартные вычислительные модели... 12
1.3.1. Молекулярный компьютер.....13
1.3.2. Квантовый компьютер........14
1.4. Случайные последовательности
и случайные отображения..........16
1.4.1. Понятие случайности........16
1.4.2. Свойства случайного отображения... 17
Упражнения к главе 1...................20
Литература к главе 1...................20
ГЛАВА 2. ГРУППЫ........................22
2.1. Понятие группы...................22
2.2. Подгруппы........................23
2.3. Гомоморфизмы и изоморфизмы.......26
2.4. Действие группы на множестве.....28
2.5. Группа подстановок...............28
2.6. Вложимость коммутативной полугруппы
в группу..........................31
2.7. Прямые произведения групп........31
2.8. Категории........................32
Упражнения к главе 2...................33
Литература к главе 2...................33
ГЛАВА 3. КОММУТАТИВНЫЕ КОЛЬЦА..........34
3.1. Понятие кольца...................34
3.2. Гомоморфизмы колец...............36
3.3. Частные..........................36
3.4. Предварительные сведения о полиномах... 37
3.5. Идеалы и классы вычетов..........38
3.6. Делимость идеалов................41
3.7. Евклидовы кольца и кольца главных
идеалов...........................42
3.8. Разложение на множители..........43
3.9. Кольцо эндоморфизмов модуля.
Модули над кольцами...............45
3.10. Свойства полиномов...............46
3.11. Производная и кратные корни......46
3.12. Симметрические функции...........47
3.13. Разложение на множители полиномов
от нескольких переменных..........48
3.14. Полукольца и решетк! i...........50
3.15. Кольцо полиномов Жегалкина.......51
3.15.1. Полиномы Жегалкина........51
3.15.2. Разложение на множители
в кольце Gn.......................53
3.15.3. Симметрические функции
кольца G„.........................54
3.15.4. Кольцо дифференциальных
операторов кольца G„..............54
3.15.5. Эндоморфизмы кольца G„.......55
Упражнения к главе 3......................56
Литература к главе 3......................57
ГЛАВА 4. ПОЛЯ.............................58
4.1. Общие сведения о полях. Простые поля.58
4.2. Расширения полей.....................59
4.2.1. Простые расширения............60
4.2.2. Конечные расширения...........62
4.2.3. Целые элементы поля...........64
4.3. Конечные поля........................65
4.3.1. Строение конечных полей.......65
4.3.2. Автоморфизмы конечных полей...67
4.3.3. Норма и след в конечных полях.69
4.4. Элементы теории Галуа................70
4.5. Поля деления круга...................72
4.6. Дискретное преобразование Фурье......73
4.7. Нормирования.........................74
4.8. Пополнения поля Q ир-адические числа ...75
Упражнения к главе 4....................77
Литература к главе 4....................78
ГЛАВА 5. СВЕДЕНИЯ ИЗ ТЕОРИИ ЧИСЕЛ.. .79
5.1. Однозначное разложение на множители
в кольце Z...........................79
5.2. Некоторые числовые функции...........79
5.3. Кольцо Z/hZ..........................81
5.4. Квадратичные и кубические вычеты.
Квадратичный закон взаимности........83
5.5. Суммы Гаусса и Якоби.................87
5.6. Квадратичные числа и квадратичные
формы................................89
5.6.1. Кольцо целых . *
квадратичных чисел................89
5.6.2. Идеалы квадратичных порядков..91
5.6.3. Квадратич ные формы...........93
5.7. Алгебраические числа.................95
Упражнения к главе 5....................98
Литература к главе 5....................98
ГЛАВА 6. ЭЛЕМЕНТЫ АЛГЕБРАИЧЕСКОЙ
ГЕОМЕТРИИ. ЭЛЛИПТИЧЕСКИЕ КРИВЫЕ ...99
6.1. Аффинные алгебраические многообразия ...99
6.2. Проективная плоскость
и проективное пространство.............100
475
6.3. Сложение точек на конике............102
6.4. Кубические кривые. Закон сложения...102
6.5. Особые и неособые кубики............105
6.6. Касательные и точки перегиба
алгебраической кривой...............106
6.7. Нормальные формы
эллиптической кривой................107
6.8. Группа неособых точек кубики........108
6.9. Невозможность рациональной
параметризации эллиптической кривой.109
6.10. Параметризация эллиптической кривой
с помощью эллиптических функций.....110
6.10.1. Эллиптические функции........НО
6.10.2. Функция Вейерштрасса........112
6.10.3. Параметризация эллиптической
кривой над полем С..................113
6.11. Дискриминант иу-инвариант...........115
6.12. Закон сложения точек
эллиптической кривой................115
6.13. Эллиптические кривые
над числовыми полями................117
6.14. Изоморфизмы и эндоморфизмы
эллипти ческих кривых...............119
6.14.1. Изоморфизмы над полями
характеристики, отличной от 2 и 3 .. 119
6.14.2. Изоморфизмы над полями
характеристики 3....................120
6.14.3. Изоморфизмы надполями
характеристики 2....................121
6.14.4. Бирациональный изоморфизм
кривых..............................121
6.14.5. Эндоморфизмы эллиптических
кривых..............................123
6.14.6. Изоморфизмы эллиптических
кривых над алгебраически
незамкнутым полем...................124
6.15. Отображения алгебраических кривых...128
6.15.1. Регулярные функции и
отображения.........................128
6.15.2. Рациональные функции и
рациональные отображения............130
6.15.3. Проективные кривые..........131
6.15.4. Изогении эллиптических
кривых..............................132
6.15.5. Полиномы Жегалкина как
функции на поверхности
единичного куба.....................133
6.16. Дивизоры на алгебраических кривых...134
6.16.1. Локальное кольцо точки и
нормирование........................134
6.16.2. Дивизоры....................135
6.16.3. Спаривание Вейля............137
6.17. Эллиптические кривые
над конечными полями................139
6.18. Гиперэллиптические кривые...........141
6.18.1. Функции на кривых
6.18.2. Якобиан
Упражнения к главе 6......................148
Литература к главе 6......................149
ГЛАВА 7. ВЫЧИСЛИТЕЛЬНЫЕ АЛГОРИТМЫ
АЛГЕБРЫ И ТЕОРИИ ЧИСЕЛ.....................151
7.1. Алгоритмы умножения...................151
7.1.1. Алгоритм умножения
Карацубы-Офмана....................151
7.1.2. Умножение в классах вычетов..151
7.1.3. Умножение с помощью быстрого
преобразования Фурье...............153
7.1.4. Модульное умножение. Метод
Монтгомери.........................155
7.1.5. Деление.......................157
7.2. Алгоритмы обращения и вычисления
наибольшего общего делителя..........158
7.3. Минимизация базиса решетки............160
7.4. Разложение над конечным полем
полиномов от одной переменной........161
7.5. Извлечение квадратных и кубических
корней в конечном поле...............161
7.5.1. Извлечение квадратного корня
в случае q = 3 (mod 4)..........162
7.5.2. Извлечение квадратного корня
в случае q s 5 (mod 8),
q = 9 (mod 16)..................162
7.5.3. Извлечение квадратного корня
в общем случае для нечетного q.163
7.5.4. Извлечение квадратного корня
в случае четного q.................163
7.5.5. Решение квадратного уравнения.163
7.5.6. Извлечение кубического корня
в конечном поле....................164
7.6. Вычисление символа Якоби..............165
7.7. Проверка чисел и полиномов
на простоту..........................165
7.8. Разложение чисел в мнимом
квадратичном порядке 166
7.9. Приведение числа по модулю решетки....169
7.10. Умножение точки
эллиптической кривой на число........171
7.11. Вычисление функции Вейля.............172
7.12. Сложение элементов якобиана
гиперэллиптической кривой............173
7.13. Арифметика группы классов мнимых
квадратичных порядков................174
Упражнения к главе 7.......................175
Литература к главе 7.......................176
ГЛАВА 8. КРИПТОГРАФИЯ И ЗАЩИТА
ИНФОРМАЦИИ.................................177
8.1. Основные понятия защиты информации.... 178
8.2. Исчисление атак.....................181
8.2.1. Упорядоченность моделей
нарушителя и безопасных систем ... 181
8.2.2. Множества возможностей
нарушителя.....................182
8.2.3. Тривиальная модель нарушителя.... 184
8.2.4. Нетривиальная модель
нарушителя............................186
8.2.5. Место криптографии
в защите информации...................188
476
8.3. Основные понятия и определения
криптографической защиты данных...........189
8.3.1. Криптографические примитивы..189
8.3.2. Хэш-функция....................190
8.3.3. Шифр...........................191
8.3.4. Понятие стойкости
криптографических алгоритмов..191
8.4. Шифрование............................192
8.4.1. Симметричное и несимметричное
шифрование.........................193
8.4.2. Способы шифрования.............194
8.5. Аутентификация........................195
8.5.1. Опознавание....................197
8.5.2. Контроль целостности и
подлинности данных.................198
8.6. Управление ключами....................198
8.7. Задачи, положенные в основу
безопасности криптографических
алгоритмов............................199
Упражнения к главе 8......................201
Литература к главе 8......................202
ГЛАВА 9. СИСТЕМА RSA И ЗАДАЧА
РАЗЛОЖЕНИЯ..................................203
9.1. Безопасность системы RSA и задача
разложения на множители.............203
9.2. Детерминированные методы разложения.. 204
9.2.1. Метод пробного деления............204
9.2.2. Метод «giant step — baby step».205
9.2.3. Метод Ферма....................205
9.2.4. Метод диофантовой
аппроксимации...................206
9.3. Вероятностные методы разложения.......207
9.3.1. p-метод Полларда
(метод «Монте-Карло»)...........207
9.3.2. Метод непрерывных дробей.......207
9.3.3. Метод квадратичного решета.....209
9.3.4. (р-1)-метод....................210
9.3.5. Разложение на эллиптической
кривой..........................210
9.3.6. Разложение на квантовом
компьютере......................212
9.4. Атаки на систему RSA, не требующие
разложения............................213
9.4.1. Случай малого секретного
показателя......................213
9.4.2. Случаи специальных открытых
показателей........................214
9.4.3. Атаки на основе эндоморфизмов.... 215
Упражнения к главе 9........................216
Литература к главе 9........................217
ГЛАВА 10. ДИСКРЕТНОЕ
ЛОГАРИФМИРОВАНИЕ В КОНЕЧНОМ ПОЛЕ
И СМЕЖНЫЕ ЗАДАЧИ......................218
10.1. Метод базы разложения...........218
10.2. Логарифмирование в простом поле
методом решета числового поля.........222
10.2.1. Подготовительные
теоретико-числовые результаты....222
10.2.2. Метод решета числового поля.223
10.3. Логарифмирование в расширенном поле.227
10.4. Группа классов мнимого квадратичного
порядка.................................228
10.5. Логарифмирование в группе
функций Лукаша..........................229
10.6. Связь между задачами Диффи-Хеллмана
и дискретного логарифмирования..........229
Упражнения к главе 10....................230
Литература к главе 10....................231
ГЛАВА 11. ЗАДАЧА ДИСКРЕТНОГО
ЛОГАРИФМИРОВАНИЯ f
НА ЭЛЛИПТИЧЕСКОЙ КРИВОЙ.................233
11.1. Универсальные методы
логарифмирования.......................233
11.1.1. Метод Гельфонда...........233
11.1.2. Методы встречи посередине и
«giant step — baby step».........234
11.1.3. Метод Полларда............235
11.1.4. Метод встречи
на случайном дереве..............235
11.1.5. Сравнение сложности
логарифмирования на эллиптической
кривой и в конечном поле..........238
11.1.6. Логарифмирование с помощью
квантового компьютера.............239
11.2. Влияние комплексного умножения на
сложность логарифмирования..............240
11.3. Логарифмирование с использованием
функции Вейля...........................241
11.4. Другие задачи, связанные
с логарифмированием.....................243
11.5. Время жизни параметров криптосистемы,
основанной на дискретном
логарифмировании.......................246
11.5.1. Мультипликативная группа поля ....247
11.5.2. Группа точек
эллиптической кривой.......247
11.6. Логарифмирование в якобиане
гиперэллиптической кривой..............248
11.7. Требования к эллиптической кривой.249
Упражнения к главе 11...................250
Литература к главе 11...................251
ГЛАВА 12. ШИФРОВАНИЕ С ОТКРЫТЫМ
КЛЮЧОМ..................................252
12.1. Шифрование с открытым ключом
для группы вычислимого порядка..........252
12.1.1. Бесключевое шифрование
Месси-Омуры.................253
12.1.2. Протокол Эль-Гамаля шифрования
с открытым ключом.................254
12.2. Шифрование с открытым ключом
для группы трудновычислимого порядка...255
12.2.1. Протокол шифрования Рабина.256
12.2.2. Вероятностное шифрование..256
12.3. Ранцевые алгоритмы шифрования с
открытым ключом........................258
477
12.4. Генераторы псевдослучайной
последовательности..................260
Упражнения к главе 12.....................261
Литература к главе 12.....................262
ГЛАВА 13. ЦИФРОВАЯ ПОДПИСЬ................263
13.1. Под пись на группе трудновычислимо го
порядка.............................263
13.1.1. Схема подписи RSA...........264
13.1.2. Схема подписи Рабина........264
13.1.3. Схема подписи Фиата-Шамира..265
13.2. Подпись на группе вычислимого
порядка.............................265
13.2.1. Схема подписи Эль-Гамаля....265
13.2.2. Схема подписи Шнорра........267
13.2.3. ГОСТ Р 34.10-94 и DSS.......268
13.3. Сравнительный анализ представленных
схем подписи........................269
13.4. Скрытый канал.......................270
13.5. Другие схемы подписи................271
13.5.1. Схема «неоспоримой» подписи.271
13.5.2. Схема подписи «вслепую».
Электронные платежи...........273
13.5.3. Схема подписи с восстановлением
сообщения..........................274
13.5.4. Инкрементальная подпись.....274
Упражнения к главе 13.....................275
Литература к главе 13.....................276
ГЛАВА 14. ДРУГИЕ
КРИПТОГРАФИЧЕСКИЕ
ПРОТОКОЛЫ.................................278
14.1. Схемы предъявления битов............278
14.2. Диалоговые доказательства
с нулевым разглашением....................279
14.2.1. Доказательство знания
изоморфизма графов..................279
14.2.2. Доказательство знания разложения
составного числа....................280
14.2.3. Доказательство знания
дискретного логарифма...............281
14.2.4. Доказательство правильности
выбора составного числа.............281
14.3. Бездиалоговые доказательства
с нулевым разглашением....................283
14.4. Передача информации
со стиранием.............................285
14.5. Разделение секрета..................287
14.6. Протоколы управления ключами........288
14.6.1. Установление ключа на основе
симметричных методов...............289
14.6.2. Доставка ключа..............290
14.7. Временная метка.....................291
14.7.1. Централизованная реализация
временной метки....................291
14.7.2. Децентрализованная реализация
временной метки....................292
Упражнения к главе 14.....................293
Литература к главе 14.....................293
ГЛАВА 15. КРИПТОСИСТЕМЫ
НА ЭЛЛИПТИЧЕСКИХ
И ГИПЕРЭЛЛИПТИЧЕСКИХ КРИВЫХ.............294
15.1. Расчет числа точек эллиптической
кривой в общем случае...................294
15.1.1. Предварительные сведения...295
15.1.2. Полиномы деления...........296
15.1.3. Алгоритм Чуфа..............297
15.2. Расчет числа точек эллиптической
кривой над расширенным полем............299
15.3. Расчет числа точек эллиптических кривых
cj = 0, 1728 над простыми полями.........301
15.3.1. Криваяу2 = х3 +7?..........301
15.3.2. Кривая у2 = х3 + Ах...........303
15.4. Эллиптические кривые с комплексным
умножением..............................305
15.4.1. Генерация эллиптических кривых
с комплексным умножением..........306
15.4.2. Влияние комплексного умножения
на скорость вычислений............308
15.5. Эллиптические кривые над расширенными
полями специальных характеристик...311
15.6. Протоколы на эллиптических кривых....314
15.6.1. Встраивание открытого текста
в координату точки................314
15.6.2. Аналог криптосистемы RSA...315
15.6.3. Установление сеансового ключа.316
15.6.4. Шифрование.................317
15.6.5. Цифровая подпись...........318
15.6.6. Опознавание, канал со стиранием
и доказательства с нулевым
разглашением......................321
15.6.7. Вычислимая в одну сторону
функция, свободная от коллизий.....324
15.6.8. Генераторы псевдослучайной
последовательности.................325
15.6.9. Протоколы для электронных
платежей...........................326
15.7. Криптосистемы на гиперэллиптических
кривых...................................329
15.8. Криптосистемы на изогениях
эллиптических кривых.....................331
15.8.1. Задача вычисления изогении и
квантовый компьютер...............331
15.8.2. Криптографические протоколы
на изогенных кривых...............332
Упражнения к главе 15...................334
Литература к главе 15...................335
ГЛАВА 16. ОБЩИЕ СВЕДЕНИЯ
ОБ ИТЕРИРОВАННЫХ
КРИПТОАЛГОРИТМАХ......................336
16.1. Основные понятия классической
криптографии...........................336
16.2. Некоторые положения
теории секретности Шеннона.............336
16.2.1. Объем текстов, однозначно
определяющих ключ...........339
16.2.2. Теория аутентификации Симмонса.... 340
16.3. Булевы функции и булевы формулы..340
478
16.4. Аффинно эквивалентные
булевы функции и подстановки.......342
16.5. Задача вскрытия ключа
и математические задачи............344
16.5.1. Задача вскрытия ключа
и NP-полные задачи.................345
16.5.2. Задача о выполнимости......345
16.6. Требования к шифрам................347
16.7. Шифры замены и перестановки........350
16.7.1. Моноалфавнтная замена......350
16.7.2. Полиалфавитная замена......351
16.8. Операторы, используемые
при построении блочных шифров.......353
16.9. Описание итерированных шифров
в терминах булевых функций.........356
Упражнения к главе 16.....................357
Литература к главе 16....................358
ГЛАВА 17. АЛГЕБРАИЧЕСКИЕ МЕТОДЫ
КРИПТОАНАЛИЗА............................359
17.1. Метод обобщения и редукции. Метод
гомоморфизмов............................359
17.2. Замкнутые и чистые шифры...........360
17.2.1. Вскрытие ключей замкнутых
и чистых шифров....................360
17.2.2. Проверка шифра на замкнутость
и чистоту..........................361
17.3. Решеточный криптоанализ............362
17.3.1. Решеточно продолженные булевы
функции и решеточные полиномы ..362
17.3.2. Метод криптоанализа........365
17.4. Метод арифметического продолжения
булевых функций..........................369
17.5. Анализ шифров с малым
порядком нелинейности....................375
17.6. Криптоанализ на основе рационального
продолжения полиномов Жегалкина..........377
17.6.1. Теоретические основы.......377
17.6.2. Метод криптоанализа........379
17.7. Криптоанализ на основе 2-адического
продолжения полиномов Жегалкина..........383
17.7.1. Теоретические основы.......383
17.7.2. Метод криптоанализа........384
17.8. Максимизация числа совпавших
разрядов промежуточных текстов...........385
17.9. Анализ с использованием сжимающих
гомоморфизмов............................386
17.10. Поиск коллизий хэш-функции........388
17.11. Компромисс время/память...........389
17.12. Сочетание перебора и вычисления ключа... 390
17.13. Отбраковка классов ключей.........391
17.14. Задачи, к которым сводится задача
вскрытия ключа...........................392
17.15. Вскрытие ключа
на квантовом компьютере..................393
Упражнения к главе 17....................394
Литература к главе 17....................395
ГЛАВА 18. СТАТИСТИЧЕСКИЕ МЕТОДЫ
КРИПТОАНАЛИЗА...........................396
18.1. Некоторые определения.............396
18.2. Дифференциальный криптоанализ.....397
18.2.1. Конечные разности.........397
18.2.2. Метод криптоанализа.......398
18.2.3. Анализ с помощью усеченных
дифференциалов....................405
18.2.4. Анализ с помощью дифференциалов
высших порядков...................406
18.2.5. Атака «бумеранг»..........406
18.3. Криптоанализ на основе списка ключей и
связанных ключей.......................407
18.4. Линейный криптоанализ.............408
18.5. Анализ степенных
шифров методом сдвига..................416
18.6. Генерация экстремальных
подстановок для шифров.................418
18.6.1. Экстремальные подстановки.418
18.6.2. Булевы функции для
экстремальных подстановок....419
18.6.3. Примеры экстремальных
подстановок.......................420
Упражнения к главе 18...................422
Литература к главе 18...................423
ГЛАВА 19. ПРИМЕНЕНИЕ ИТЕРИРОВАННЫХ
ШИФРОВ И ХЭШ-ФУНКЦИЙ....................425
19.1. Режимы шифрования.................425
19.1.1. Режим । ,ростой замены....425
19.1.2. Режим гаммирования........425
19.1.3. Режим гаммирования
с обратной связью.................426
19.1.4. Режим сцепления блоков.
Выработка имитовставки.......426
19.2. Некоторые вопросы
применения шифров.................427
19.3. DES...............................429
19.4. FEAL..............................431
19.5. IDEA..............................432
19.6. ГОСТ 28147-89.....................433
19.6.1. Стойкость шифра ГОСТ 28147-89....435
19.6.2. Стойкость шифра ГОСТ 28147-89
при наличии у нарушителя
лабораторных возможностей.....435
19.7. RC5...............................436
19.8. Blowfish..........................438
19.9. SAFER.............................439
19.10. RIJNDAEL (AES)...................440
19.11. MD5..............................441
19.12. ГОСТ P 34.11-94 ................ 442
Упражнения к главе 19...................444
Литература к главе 19...................445
ОТВЕТЫ И УКАЗАНИЯ
К УПРАЖНЕНИЯМ...........................447
ПРИЛОЖЕНИЕ. ЭЛЛИПТИЧЕСКИЕ КРИВЫЕ
ДЛЯ СТАНДАРТА ПОДПИСИ ГОСТ P34JG-2001 .452
УКАЗАТЕЛЬ...............................464
Ростовцев Александр Григорьевич
Маховенко Елена Борисовна
ТЕОРЕТИЧЕСКАЯ КРИПТОГРАФИЯ
Издание подготовлено в АНО НПО «Профессионал»
191023, Санкт-Петербург, ул. Садовая, 28-30, корп. 35
Тел.: (факс) 321-67-38, 110-59-91, 115-14-35
www.naukaspb.ru,www.npomis.com
mail@naukaspb.ru, mis@npomis.com
Ответственный за издание: Полуда А. А.
Ответственный за подготовку: Емельянова Н.В.
Ответственный редактор: Белканова Л.В.
Редактор-корректор: Чудновская Э.И
Компьютерная верстка: Бойченко Т.А.,
Коробова НВ., Филина Т.А.
Ответственный за выпуск: Жадобина Т.Н.
Оператор цифровой печати: А.В. Кеда
Отпечатано в центре цифровой печати АНО НПО «Профессионал»
191023, Санкт-Петербург, ул. Садовая, 28-30, корп. 35
Тел.: (факс) 321-67-38; 110-59-91; 110-57-93; 115-14-35.
Сдано в набор 16.08.2004. Подписано к печати 18.10.2004
Формат 60x90/8. Бумага офсетная, плотность 80 г/м2
Объем 35 п. л. Тираж 1000 экз.