Релятивистские квантовые поля. Том 2 - Дрелл С.Д., Бьёркен Дж.Д.

Автор: Дрелл С.Д. Бьёркен Дж.Д.
Теги: физика квантовая физика
Год: 1978
Похожие
Квантовая теория поля. Том 1. Общая теория
Теория калибровочных взаимодействий элементарных частиц
Термополевая динамика и конденсированные состояния
Теория перенормировок
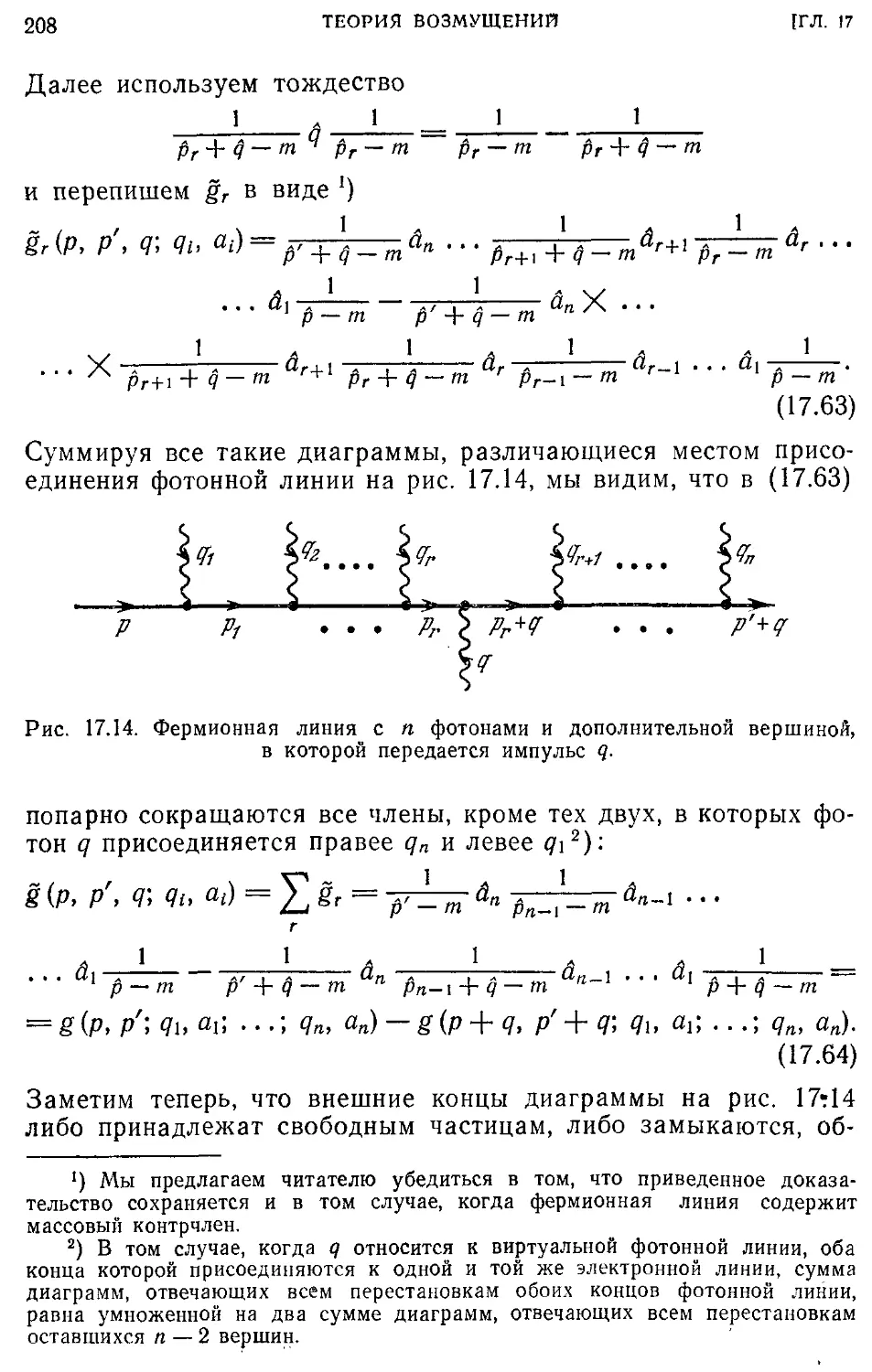
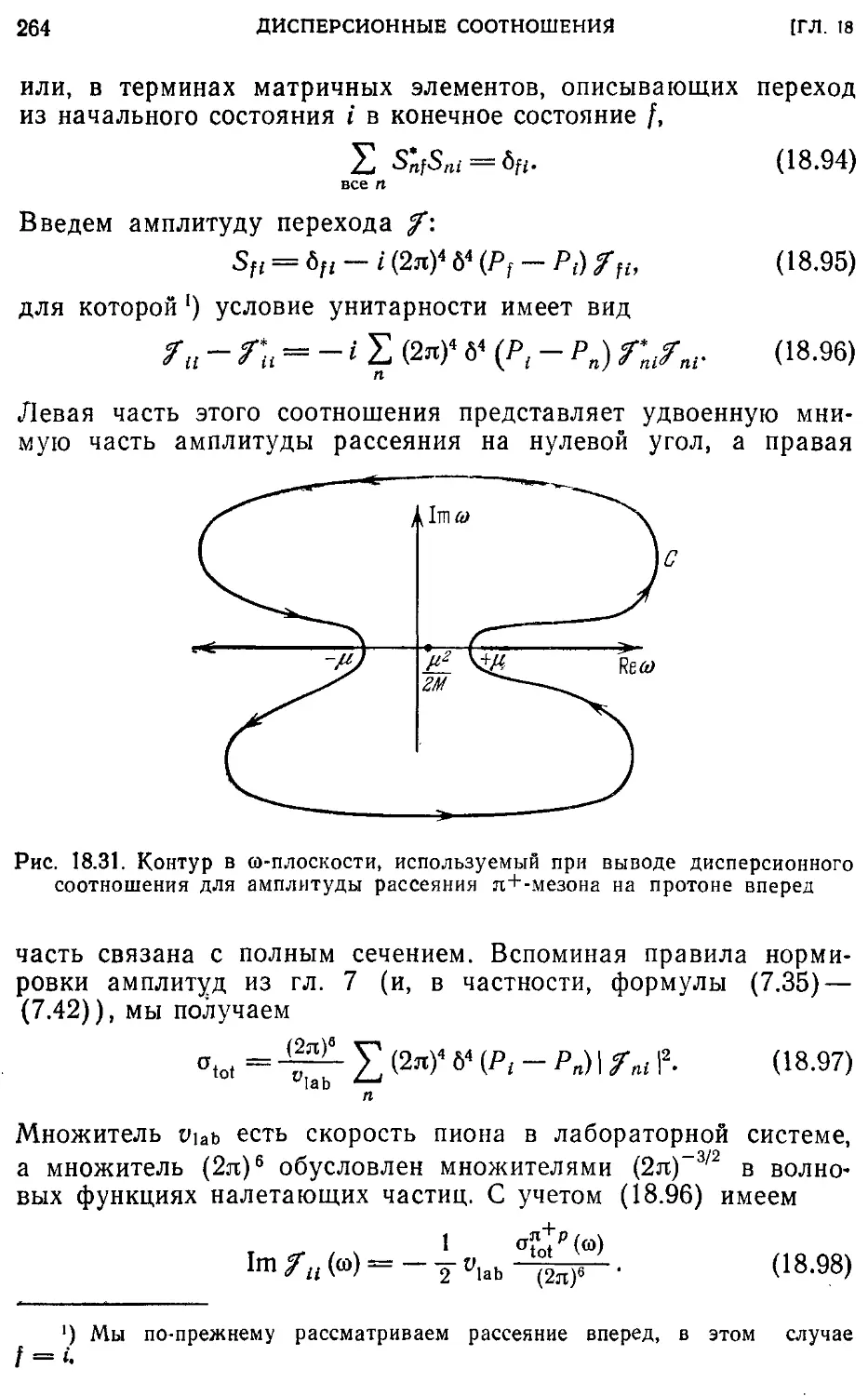
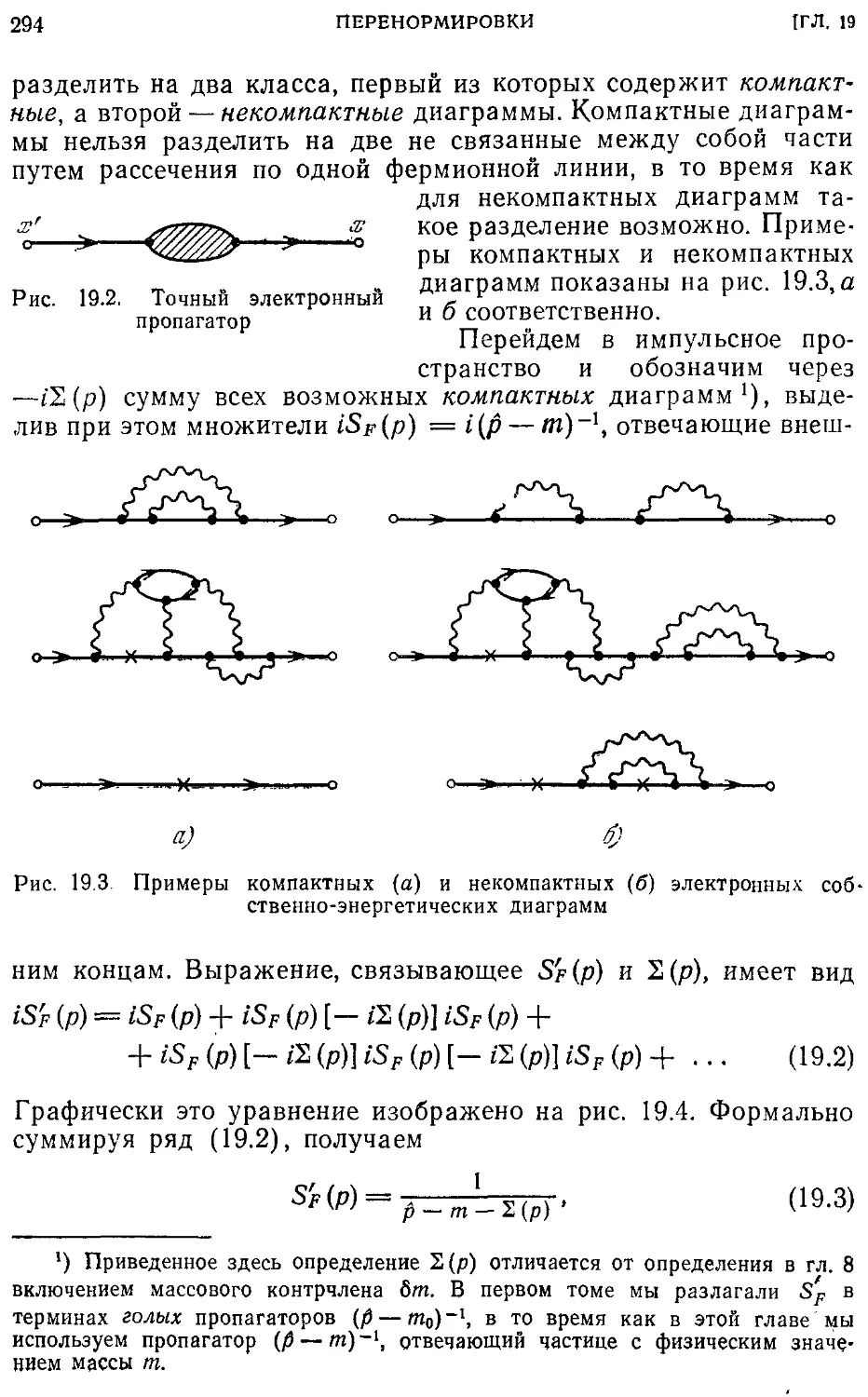
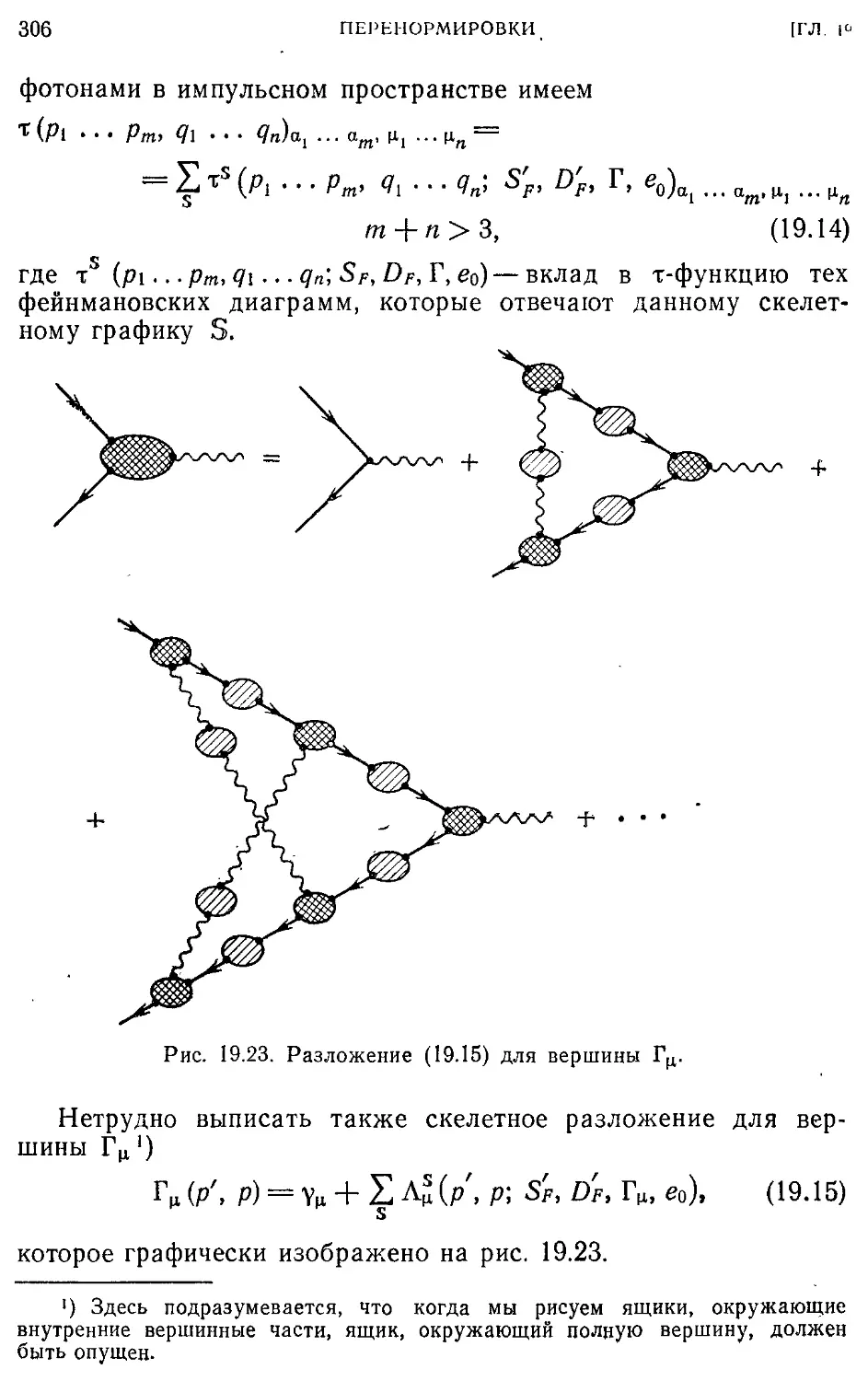
Текст
                    Дж.Д.Бьёркен, С.Д.Дрелл
РЕЛЯТИВИСТСКАЯ КВАНТОВАЯ ТЕОРИЯ
т. 2. Релятивистские квантовые поля
Настоящая книга является вторым томом двухтомника по квантовой теории. В
нем последовательно и продуманно изложены основы квантовой теории поля, а
также ряд специальных вопросов, включающий методы ренорм-группы и методы
дисперсионных соотношений.
В конце каждой главы помещены задачи, способствующие пониманию
изложенного.
ОГЛАВЛЕНИЕ
Предисловие	7
Глава 11. Общий формализм	9
§ 65. Следствия полевого описания	10
§ 66. Канонический формализм и квантование для частиц	12
§ 67. Канонический формализм и квантование полей	18
§ 68. Преобразования симметрии и законы сохранения	25
§ 69. Другие формулировки	31
Задачи	31
Глава 12. Поле Клейна — Гордона	33
§ 70. Квантование и интерпретация в терминах частиц	33
§ 71. Симметрия состояний	40
§ 72. Измеримость поля и принцип микропричинности	42
§ 73. Вакуумные флуктуации	43
§ 74. Заряженное скалярное поле	45
§ 75. Фейнмановский пропагатор	49
Задачи	51
Глава 13. Вторичное квантование поля Дирака	52
§ 76. Квантовая механика п тождественных частиц	52
§ 77. Представление чисел заполнения для фермионов	54
§ 78. Теория Дирака	63
§ 79. Разложение в импульсном пространстве	65
§ 80. Релятивистская ковариантность	71
§ 81. Фейнмановский пропагатор в теории Дирака	73
Задачи	74
Глава 14. Квантование электромагнитного поля	75
§ 82. Введение	75
§ 83. Квантование	76
§ 84. Ковариантность и процедура квантования	80
§ 85. Разложение в импульсном пространстве	82
§ 86. Спин фотона	85
§ 87. Фейнмановский пропагатор для поперечных фотонов	86
Задачи	89
Глава 15. Взаимодействующие поля	90
§ 88. Введение	90

§ 89. Электромагнитное взаимодействие	90
§ 90. Лоренцева инвариантность и инвариантность при трансляциях	95
§ 91. Разложение в импульсном пространстве	96
§ 92. Собственная энергия вакуума; нормальное упорядочивание	98
§ 93. Другие взаимодействия	101
§ 94. Симметрия взаимодействий	104
§ 95. Сильная связь между ж -мезонами и нуклонами	106
§ 96. Свойства симметрии странных частиц	108
§ 97. Несобственные преобразования симметрии	115
§98. Четность	115
§ 99. Зарядовое сопряжение	120
§ 100. Обращение времени	126
§ lOl.CPT-теорема	132
Задачи	136
Глава 16. Вакуумные средние и S -матрица	138
§ 102. Введение	138
§ 103. Свойства физических состояний	138
§ 104. In-поля и in-состояния; асимптотическое условие	141
§ 105. Спектральное представление для вакуумного среднего от	146
коммутатора и функция распространения скалярного поля
§ 106. Out-поля и out-состояния	150
§ 107. Определение и общие свойства S-матрицы	152
§ 108. Редукционная формула для скалярных полей	155
§ 109. In- и out-поля и спектральное представление в теории Дирака	159
§ 110. Редукционная формула для дираковских полей	168
§ 111. In- и out-состояния и редукционная формула для фотонов	172
§ 112. Спектральное представление для фотонов	175
§ 113. Связь спина со статистикой	179
Задачи	181
Глава 17. Теория возмущений	182
§ 114. Введение	182
§ 115. S-матрица	183
§ 116. Теория возмущений для т-функций и S-матрица	187
§ 117. Теорема Вика	190
§ 118. Графическое представление	193
§ 119. Вакуумные амплитуды	196
§ 120. Спин и изотопический спин; ж -мезон-нуклонное рассеяние	198
§ 121. л—71 -рассеяние	201
§ 122. Графическая техника в квантовой электродинамике	206
§ 123. Излучение мягких фотонов и инфракрасная катастрофа	211
Задачи	216
Глава 18. Дисперсионные соотношения	217
§ 124. Причинность и соотношения Крамерса — Кронига	217

§ 125. Приложение к физике высоких энергий	221
§ 126. Аналитические свойства вершинных диаграмм в теории возмущений 224
§ 127. Обобщение на случай произвольных диаграмм и аналогия с	228
электрическими цепями
§ 128. Пороговые особенности функций распространения	235
§ 129. Особенности произвольных диаграмм и правила Ландау	239
§ 130. Аналитическая структура вершинных диаграмм; аномальные пороги 244
§ 131. Дисперсионные соотношения для вершинной функции	250
§ 132. Сингулярности амплитуд рассеяния	253
§ 133. Применение к % -мезон-нуклонному рассеянию вперед	261
§ 134. Аксиоматический вывод дисперсионных соотношений для пион-	271
нуклонного рассеяния вперед
§ 135. Динамические расчеты %—% -рассеяния с использованием	278
дисперсионных соотношений
§ 136. Электромагнитная структура пиона	287
Задачи	290
Глава 19. Перенормировки	292
§ 137. Введение	292
§ 138. Свойства диаграмм собственной энергии и вершинных частей и	293
электрон-позитронное ядро
§ 139. Интегральные уравнения для собственно-энергетической и	299
вершинной частей
§ 140. Интегральные уравнения для т-функций и ядра К; скелетные
графики	302
§ 141. Топологическая теорема	307
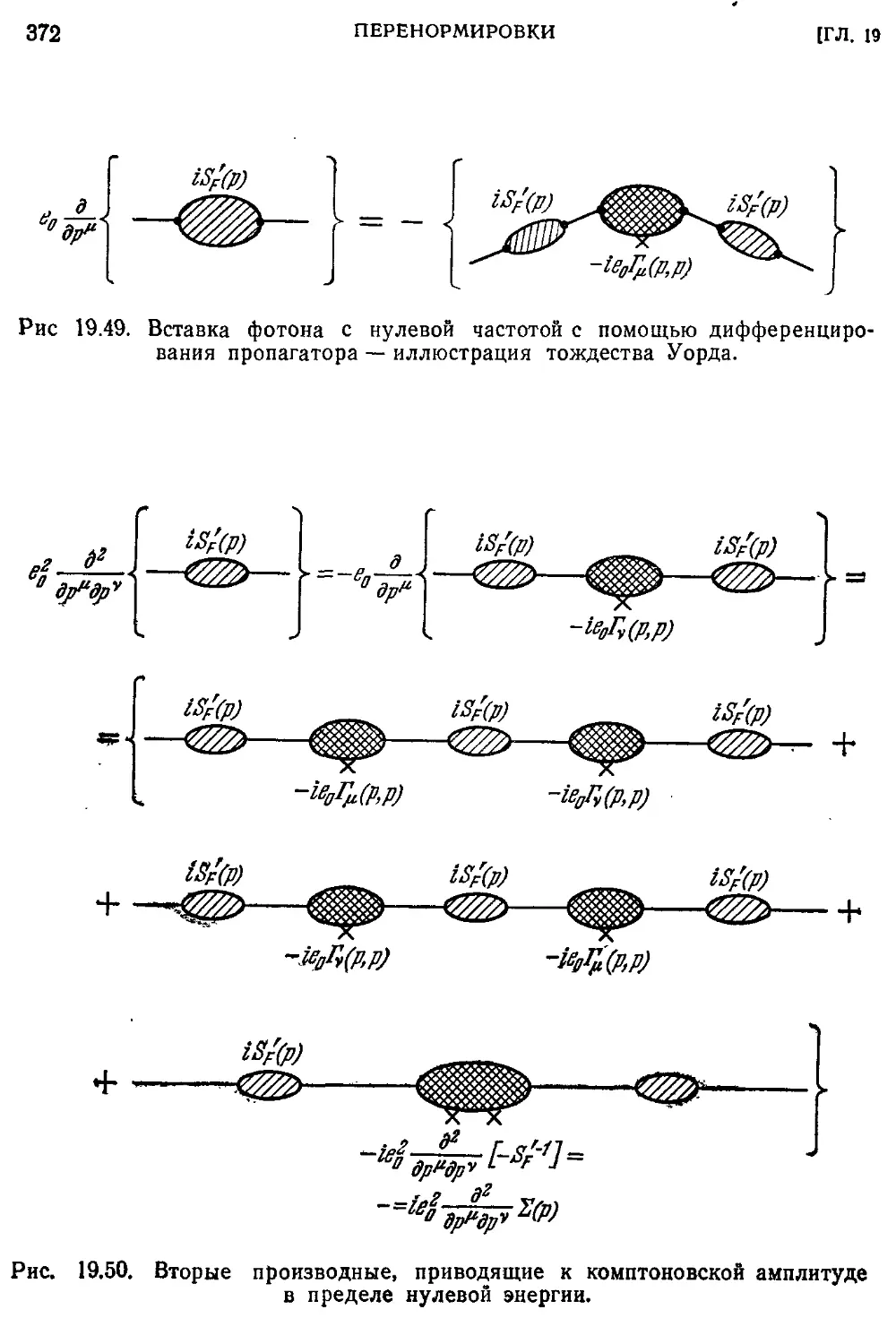
§ 142. Тождество Уорда	308
§ 143. Определение перенормировочных констант и правила	312
перенормировки
§ 144. Сводка формул: перенормированные интегральные уравнения	319
§ 145. Аналитическое продолжение и промежуточная перенормировка	322
§ 146. Степень расходимости и критерий сходимости	327
§ 147. Доказательство конечности перенормируемой теории	341
§ 148. Пример перенормировки заряда в четвертом порядке	357
§ 149. Низкоэнергетическая теорема для комптоновского рассеяния	370
§ 150. Асимптотическое поведение фейнмановских амплитуд	378
§ 151. Ренормализационная группа	382
Задачи	390
Приложение В. Коммутаторы и функции распространения	392
Дополнения редактора перевода	396
Литература	401
Предметный указатель	405

ПРЕДИСЛОВИЕ
Эта книга представляет собой перевод второго тома двух-
двухтомной монографии известных американских физиков-теорети-
физиков-теоретиков Джеймса Бьёркена и Сиднея Дрелла. На английском языке
книга появилась в 1965 году и с тех пор является за рубежом
одним из основных учебников по квантовой теории поля. В боль-
большинстве статей по теории элементарных частиц, если авторам
надо сослаться на основы теории, обозначения или нормировки,
которые они используют, они обычно ссылаются на книгу Бьёр-
Бьёркена и Дрелла. Книга играет роль как бы своеобразного эта-
эталона. Многочисленные ссылки на эту книгу содержатся и в це-
целом ряде монографий, написанных за рубежом уже после ее
выхода, и переведенных на русский язык в 70-х годах. Поэтому
настоящее издание монографии Бьёркена и Дрелла является
более чем желательным. Инициатором этого издания и редакто-
редактором перевода был профессор Владимир Борисович Берестецкий
A913—1977)—автор известных монографий по квантовой элек-
электродинамике и квантовой теории поля, ставших настольными
книгами физиков-теоретиков во всем мире. Владимир Борисович
высоко ценил книгу Бьёркена и Дрелла и считал, что ее пере-
перевод на русский язык заполнит существенный пробел в отече-
отечественной литературе.
Первый том монографии представляет собой введение в тех-
технику работы с фейнмановскими диаграммами. При этом диа-
диаграммы вводятся на основе наглядных физических соображений
и упор делается на то, чтобы продемонстрировать, каким обра-
образом, используя их, можно количественно описать широчайший
круг явлений физики элементарных частиц.
Второй том содержит теоретико-полевое обоснование тех на-
наглядных и простых правил, которые в первом томе формулиро-
формулировались на полуинтуитивном уровне. Он начинается с квантова-
квантования свободных полей, затем описывается взаимодействие между
квантованными полями. Заканчивается книга рассмотрением
процедуры перенормировок в произвольном порядке теории воз-
возмущений и изложением основных идей ренормгруппы. Наряду
с этим в книге большое внимание уделено S-матричному

g	предисловие
подходу, не использующему теорию возмущений: дисперсионным
соотношениям, особенностям Ландау (исследованию которых
была посвящена диссертация Бьёркена), применению диспер-
дисперсионных соотношений к я — N- и я — я-рассеянию.
Со времени написания книги теория элементарных частиц
изменилась до неузнаваемости. Центральными объектами в ней
стали калибровочные поля и механизмы спонтанного нарушения
симметрии, о которых в книге ничего не говорится. Важную
роль в этом преобразовании облика современной физики эле-
элементарных частиц сыграли авторы книги. Достаточно упомя-
упомянуть о бьеркеновском скейлинге, чарме, модели партонов Фейн-
мана — Бьёркена, механизме образования лептонных пар в
столкновении адронов, предложенном Дреллом и Яном, работах
Дрелла, посвященных моделям мешков и решеток.
Было бы совершенно неправильно думать, что новейшее раз-
развитие теоретической физики делает неважными или неинтерес-
неинтересными те вопросы, которым посвящена эта книга. Новейшие
теоретические идеи и открытия, несмотря на всю их необыч-
необычность, это новые ветви все той же квантовой теории поля. Чем
интенсивнее будут разрастаться эти ветви, тем чаще все более
широкому кругу физиков придется обращаться к основам тео-
теории, которым посвящена эта книга.
Л. Б. Окунь

ГЛАВА 11
ОБЩИЙ ФОРМАЛИЗМ
В первом томе этой книги при изложении метода функций
распространения и при выводе практических правил для вычис-
вычисления (в рамках теории возмущений) взаимодействия релятивист-
релятивистских частиц использовались интуитивные аргументы, основанные
на принципе соответствия. Теперь мы обратимся к систематиче-
систематическому выводу этих правил, используя формализм квантовых
полей. Наша цель заключается в том, чтобы, во-первых, «зашто-
«заштопать все дыры» в теории пропагаторов, и, во-вторых, развить ме-
метод решения задач, для которых неприменима теория возмуще-
возмущений. Примером таких задач является расчет реакций с участием
сильно связанных мезонов и нуклонов.
Идея нового метода лучше всего иллюстрируется на примере
электромагнитного поля. Потенциалы А^(х) удовлетворяют
уравнениям Максвелла и описывают динамическую систему с
бесконечным числом степеней свободы. Под этим мы подразу-
подразумеваем то, что в каждой точке пространства поле Av-(x) можно
рассматривать как независимую обобщенную координату. Для
перехода от классической теории к квантовой необходимо, со-
согласно общим принципам, сформулированным в главе I1), за-
заменить координаты и соответствующие обобщенные импульсы
на операторы, действующие в гильбертовом пространстве допус-
допустимых физических состояний, а также наложить на эти опера-
операторы квантовые условия. В результате мы приходим к канони-
канонической процедуре квантования, представляющей собой непосред-
непосредственное обобщение метода квантования в нерелятивистской
механике на случай полевых функций, которые удовлетворяют
дифференциальным уравнениям, выведенным из лагранжиана.
При этом возникает интерпретация электромагнитного поля в
терминах частиц — в смысле боровского принципа дополнитель-
дополнительности.
') Ссылки на гл. 1—10 и соответствующие формулы означают ссылки на
первый том этой книги (М., «Наука», 1978) (прим. перев.).

10	ОБЩИЙ ФОРМАЛИЗМ	[ГЛ. It
Поскольку фотоны естественным образом возникают при
квантовании максвелловских полей, естественно ожидать, что и
другие частицы, наблюдаемые в природе, также можно связать
посредством аналогичной процедуры с соответствующими по-
полями. Основываясь на этой идее, Юкава предсказал существо-
существование я-мезонов из самого факта существования ядерных сил.
И наоборот, с этой точки зрения естественно связать с каждой
наблюдаемой частицей поле ср(х), удовлетворяющее некоторому
полевому уравнению. После же квантования возникает интер-
интерпретация поля ф в терминах частиц.
При квантовании поля необходимо сначала определить им-
импульсы п{х), сопряженные полевым координатам ср(х). Это
удобно сделать, используя лагранжиан, из которого выводятся
уравнения для каждого из полей q(x) и их сопряженных им-
импульсов. Проквантовав поля с помощью коммутационных соот-
соотношений гл. 1, мы получим кванты, подчиняющиеся бозе-стати-
стике, например фотоны. Оказывается, что для описания в теории
квантованных полей ферми-частиц, удовлетворяющих прин-
принципу исключения, достаточно только заменить коммутационные
соотношения на антикоммутационные. Таким образом, мы по-
получаем единый метод описания обоих сортов частиц. Другим
преимуществом лагранжевого формализма является то, что, как
мы скоро убедимся, он непосредственно приводит к законам со-
сохранения.
§ 65. Следствия полевого описания
Прежде чем перейти к детальному рассмотрению квантова-
квантования классических полей, имеет смысл, возможно, обсудить от-
отличительные черты намеченной программы. Прежде всего, мы
имеем дело с локальной волновой теорией. Полевые функции
являются непрерывными функциями непрерывных же перемен-
переменных х и t, поэтому изменение поля в точке х определяется его
свойствами в соседней точке, бесконечно близкой х.
Для большинства волн (например, звуковых или волн упру-
упругих колебаний струн и мембран) такое описание представляет
идеализацию, справедливую для расстояний, много больших, чем
некоторая характерная длина, которая определяет масштаб зер-
зернистости вещества. Для меньших расстояний эти теории суще-
существенно модифицируются.
Электромагнитное поле представляет замечательное исклю-
исключение. До тех пор, пока специальная теория относительности не
устранила необходимость введения механистической интерпре-
интерпретации, физики потратили немало усилий для того, чтобы полу-
получить описание поля излучения в терминах механического движе-
движения. Однако когда отказались от понятия «эфира», в котором

§ 65]	СЛЕДСТВИЯ ПОЛЕВОГО ОПИСАНИЯ	11
распространяется свет, стало естественным распространить ос-
основные идеи теории электромагнитного поля для описания на-
наблюдаемых волновых свойств электрона и сопоставить ему свое
поле ty(x) Действительно, не существует никаких причин счи-
считать, что электронная волна -ф (х, t) распространяется в каком бы
то ни было эфире. Однако предположение о том, что волновое
описание, справедливое для «больших» расстояний (т. е. атомных
длин « 10~8 см), применимо для сколь угодно малых расстояний
(например, меньших, чем ядерные длины «10~13 см), представ-
представляет по существу ничем не оправданную экстраполяцию суще-
существующих экспериментальных данных.
Мы уже видели, что в релятивистской теории предположение
о справедливости полевого описания для сколь угодно малых
пространственно-временных интервалов приводит — в теории
возмущений — к расходящимся выражениям для собственной
энергии электрона и «голого» заряда. Теория перенормировок
позволяет обойти трудности с расходимостями, что, возможно,
указывает на недостатки теории возмущений. Тем не менее рас-
распространено мнение, что эти расходимости симптоматичны и не
связаны с применением теории возмущений, а указывают скорее
на хронический недостаток теории при описании малых про-
пространственно-временных интервалов.
Естественно задать вопрос, почему локальные теории, т. е.
теории полей, которые подчиняются дифференциальным законам
распространения волн, повсеместно признаны и столь широко
используются. Для этого существуют несколько причин, и важ-
важнейшая из них та, что именно в рамках полевой теории было
получено большое число предсказаний, согласующихся, как уже
отмечалось в первом томе, с экспериментом. Однако основная
причина очень проста: не существует какой-либо приемлемой
формы теории, которая обходилась бы без дифференциальных
уравнений.
Теория релятивистских частиц должна с очевидностью быть
очень сложной с математической точки зрения. Из-за существо-
существования процессов рождения и уничтожения она с самого начала
есть задача многих тел. В настоящее время известно только, как
построить приближенное решение этой задачи, поэтому предска-
предсказания любой теории подобного рода неполны и в лучшем случае
не лишены неопределенностей.
В этой ситуации самое разумное — это сохранить при по-
построении новой теории те общие принципы, которые ранее при-
применялись для более ограниченного класса задач. В этом случае
для формулировки правил квантования мы должны исходить из
существования гамильтониана Н. Поскольку Н генерирует, со-
согласно уравнению Шредингера, бесконечно малые временные
смещения, мы приходим к дифференциальному описанию

12	ОБЩИЙ ФОРМАЛИЗМ	[ГЛ. 11
временной зависимости, а тогда инвариантность относительно
лоренцевых преобразований требует, чтобы координатная зави-
зависимость также описывалась дифференциальным образом. В не-
нелокальной, «зернистой» теории гамильтониан может и не суще-
существовать; если это так, то теряется связь с методом квантова-
квантования в нерелятивистских теориях.
Допуская лоренц-инвариантное микроскопическое описание
в терминах непрерывных переменных х и t, следует ожидать, что
влияние взаимодействия в пространстве-времени не может рас-
распространяться со скоростью, большей с. Такое представление о
«микропричинности» является серьезным аргументом в пользу
полевой концепции. Если пространство на малых расстояниях
зернисто, и мы хотим сохранить микропричинность, то воздей-
воздействие одной «гранулы» на другую должно быть запаздывающим.
Наиболее естественно это обстоятельство можно было бы опи-
описать, вводя дополнительные поля; в результате наша задача еще
более усложнилась бы, не став от этого сколько-нибудь
яснее.
В настоящее время не существует никаких эксперименталь-
экспериментальных доказательств дискретности пространства при малых рас-
расстояниях1). Под этим понимается только то, что имеются не-
несомненные указания на применимость специальной теории
относительности при высоких энергиях и, если угодно, на спра-
справедливость принципа микропричинности2). Поскольку не суще-
существует сколько-нибудь приемлемой альтернативной теории, мы
ограничимся в дальнейшем формализмом локальных причинных
полей. Любая модифицированная теория, без сомнения, должна
содержать теорию локального поля как предел для описания
больших расстояний. Тем не менее еще раз подчеркнем, что рас-
рассматриваемый формализм пригоден лишь в пределе больших
расстояний (например, расстояний, больших 10~13 см), в то вре-
время как истинные свойства физического мира на субмикроскопи-
субмикроскопических расстояниях могут быть совсем иными.
§ 66. Канонический формализм и квантование для частиц
Мы начнем с напоминания обычного способа квантования
классической динамической системы в квантовой механике. Для
иллюстрации рассмотрим частицу, совершающую одномерное
движение в консервативном поле сил. Пусть q — обобщенная
') В квантовой электродинамике согласие между теорией и эксперимен-
экспериментом проверено с большой точностью, как в низко- так и в высокоэнергетиче-
высокоэнергетической области (см., например, [1—4]).
2) Под этим мы понимаем экспериментальную проверку дисперсионных
соотношений для пион-нуклонного рассеяния вперед, которые мы рассмотрим
в гл. 18.

66]
КАНОНИЧЕСКИЙ ФОРМАЛИЗМ И КВАНТОВАНИЕ ДЛЯ ЧАСТИЦ
13
координата, q = -jjL — скорость частицы, L (q, q) — лагранжиан.
Согласно принципу Гамильтона динамика системы определяет-
определяется из условия
67
t2
= 6 jj L(q,q)dt = O.
A1.1)
Уравнение A1.1) означает, что истинная траектория q(t), по ко-
ко( t) ( ) б	й
торой частица движется от (q\,
ством, что вдоль нее действие
/ стационарно. Таким образом,
малые вариации этой траекто-
траектории q{t) ~*q{t)-\- 8q(t), пока-
показанные на рис. 11.1, оставляют
действие неизменным с точно-
точностью до членов второго поряд-
порядка малости.
Принцип Гамильтона непо-
непосредственно приводит к урав-
уравнениям движения в форме Эй-
Эйлера — Лагранжа ])
рр q()
до (^2. h), обладает тем свой-
свойt
Рис. 11.1. Допустимая вариация траек-
траектории с фиксированными концами,
рассматриваемая при формулировке
принципа действия.
Чтобы применить канониче-
каноническую процедуру квантования,
перепишем это уравнение в
гамильтоновом виде. Для этого определим импульс р, сопря-
сопряженный q,
Р = 4г-	A1-3)
и введем с помощью преобразования Лежандра гамильтониан
H(p,q) = pq-L{q,q).	A1.4)
В терминах Н уравнение движения A1.2) приобретает следую-
следующий вид:
где символ { }рв означает скобки Пуассона.
При квантовании уравнений A1.5) мы будем считать, что q
является эрмитовым оператором, действующим в гильбертовом
') См. [5]. Уравнение A1.2) справедливо в том случае, когда L не содер-
содержит производных выше первого порядка,

J4	ОБЩИЙ ФОРМАЛИЗМ	1ГЛ. 11
пространстве, и заменим р на — ty", при этом сопряженный
импульс и координата удовлетворяют коммутационному соотно-
соотношению
[p,q] = -i,	A1.6)
которое заменяет классические скобки Пуассона {р, <?}рв=1-
По определению р также является эрмитовым оператором. Ди-
Динамика частицы содержится в уравнении Шредингера
i^-t	(Ц.7)
где \F означает волновую функцию или вектор состояния в гиль-
гильбертовом пространстве. Если задать начальное состояние W в
произвольный момент времени, скажем, t = О, то уравнение
Шредингера определит состояние и, следовательно, средние зна-
значения, имеющие физический смысл, в любой другой момент вре-
времени.
Такое описание изменения состояния частицы во времени,
когда от времени зависит волновая функция W, а операторы р
и q постоянны, называется представлением Шредингера. Можно,
однако, описывать временную эволюцию системы и по-другому,
а именно, считать, что от времени зависит не вектор W, а опе-
операторы p(t) и q(t). Это описание известно как гейзенберговское
представление. Оба представления эквивалентны, что может
быть формально продемонстрировано построением унитарного
преобразования, связывающего одно представление с другим.
Действительно, интегрируя уравнение Шредингера A1.7), полу-
получаем
(Ц.8)
В случае эрмитового гамильтониана Н оператор е~'ш унитарен
и описывает изменение во времени функции ^(О- В момент
времени t = О вектор *?s совпадает с гейзенберговским векто-
вектором состояния 40/ss \Fs@). Не зависящие от времени опера-
операторы Os связаны с зависящими от времени гейзенберговскими
операторами соотношением
",	A1.9)
причем унитарное преобразование A1.9) не меняет вида мат-
матричных элементов и тем самым физических наблюдаемых.
В квантовой теории решение динамической задачи заклю-
заключается в нахождении матричных элементов операторов, которые
сопоставляются физическим наблюдаемым, в произвольный мо-
момент времени, если эти матричные элементы заданы в некото-
некоторый предшествующий момент времени, скажем t = 0. В пред-
представлении Шредингера для этого нужно решить уравнение

§ 66J	КАНОНИЧЕСКИЙ ФОРМАЛИЗМ И КВАНТОВАНИЕ ДЛЯ ЧАСТИЦ	15
A1.7), описывающее изменение во времени волновой функции.
В представлении же Гейзенберга нужно решить уравнения дви-
движения, описывающие развитие во времени гейзенберговских опе-
операторов. Эти уравнения, согласно A1.9), имеют вид1)
^l=i[H,OH{t)\-	(НЛО)
До тех пор, пока мы имеем дело с нерелятивистской теорией,
указанные два подхода почти совпадают. Действительно, в силу
A1.9) HH(t) — Hs = H, и если зависящие от времени внешние
силы отсутствуют, то из уравнения A1.10) следует, что dH/dt —
= 0. Тогда в представлении Шредингера мы получаем для соб-
собственных функций оператора энергии ф„(<7, t) = e~mntun(q), а со-
соответствующий вектор состояния в представлении Гейзенберга
есть un{q).
Мы увидим, однако, что в релятивистской теории поля более
удобен гейзенберговский подход. Это объясняется тем, что в ре-
релятивистском случае неудобно работать с явным видом вектора
состояния W и гораздо легче описать развитие во времени опе-
операторов, нежели вектора состояния. Кроме того, лоренцева
инвариантность теории в представлении Гейзенберга более на-
наглядно прослеживается, поскольку в этом представлении поле-
полевые операторы зависят, наряду с пространственными координа-
координатами, также и от времени.
Из уравнений A1.6) и A1.9) следует, что фундаментальное
коммутационное соотношение сохраняет свой вид
q(t)] = ~i	A1.11)
для произвольного времени /, и мы можем написать
и i®i
Таким образом, уравнениям A1.10), записанным для канони-
канонических координат и импульсов
<Ш 1[Н.р@\, ^ = i[H,q(t)],	A1.12)
= 1[Н.р@\, ^ = i[H,q(t)],
можно придать вид классических уравнений движения, записан-
записанных, однако, уже для операторов
dp @ _ дН	dq(t) __ дН
dt ~~ dq (t) ' dt ~ dp (t) '
') Для операторов, явно зависящих от времени, имеем вместо A1.10)
dOH{i)	дО„

16	общий формализм	[гл. м
Такая формулировка квантоводинамической задачи очень напо-
напоминает исходную классическую постановку задачи. В дальней-
дальнейшем мы будем часто обращаться к классическим уравнениям и
брать их за образец при построении квантовой теории. Динами-
Динамические переменные p(t) и q{t) в квантовой механике являются
эрмитовыми операторами, которые удовлетворяют уравнениям,
в точности совпадающим с классическими уравнениями A1.5).
Для того чтобы полностью определить задачу, мы должны еще
задать матричные элементы операторов р и q в некоторый на-
начальный момент времени. При этом начальные условия для
р@) и ^@) должны быть дополнены требованием, чтобы соот-
соотношения коммутации A1.11) при t = 0 выполнялись для любого
физического состояния. Поскольку мы постулируем, что физиче-
физические состояния системы, например состояния с фиксированной
энергией, образуют полный набор, условие коммутации при
t = 0 можно рассматривать как операторные уравнения вида
A1.11).
В качестве примера мы проквантуем простой одномерный
гармонический оператор в гейзенберговском представлении.
В этом случае гамильтониан равен
И = 1/2(р*+ <%?),	A1.13)
и уравнения движения имеют вид
Для того чтобы решить эти уравнения, введем удобные линей-
линейные комбинации:
а=Vi ^+гр)> а+=Vi((ад ~ ip)> A1Л4)
для которых уравнения движения есть
a (t) = — iaoa (t), a+ (t) = + «о0«+ @-
Решением последних является
a (t) — аое~ ^, а+ (/) = а+е^,	A1.15)
где aQ, aj" — не зависящие от времени операторы, которые удо-
удовлетворяют коммутационным соотношениям, следующим из
A1.11):
[a it), а+ (/)] = [а0) а+] =1, [a (t), а «)] = [а0, а0] - 0, }
[+@+@] [<<] 0

5 661	КАНОНИЧЕСКИЙ ФОРМАЛИЗМ И КВАНТОВАНИЕ ДЛЯ ЧАСТИЦ	17
В терминах операторов а и а+ гамильтониан равен
Я = 72»0 (а+а + аа+) = Ч2% (а+а0 + аоа+). A1.17)
Поскольку любое состояние *Р может быть разложено в ряд
по стационарным собственным функциям Ч'п гамильтониана Н,
достаточно выяснить свойства 4fn. Из A1.17) имеем
+] = + «А+.	A1.18)
Таким образом, если Н^п = ©А, то Hat^n — (©„ + щ) at^n,
и мы получаем бесконечный набор состояний с возрастающей
энергией, действуя последовательно оператором at на состояние
*Fn с энергией со„: aty?n== Уп+и Наоборот, так как
то мы получим набор состояний с меньшей энергией, действуя
на состояние Wn оператором а0: ao^n^^n-i- Этот последний
ряд, однако, должен оборваться, поскольку гамильтониан A1.13)
равен сумме квадратов эрмитовых операторов и, следовательно,
не может иметь отрицательных собственных значений. Основное
состояние с наинизшей энергией определяется из условия
= 0- Его энергия равна
o = Ч&о К> «о+] ^о = V^o^o.
а энергия «-го состояния
^„ = (ао+)>о	A1.19)
равна
юп = (« + '/2) «>о-
Энергетический спектр одномерного осциллятора не вырож-
вырожден и различные состояния A1.19) взаимно ортогональны1)
(?„, Ч.'т) = Ьпт (п!) (%, %).	A1.20)
Можно вычислить матричные элементы оператора at в гей-
гейзенберговском представлении, если заметить, что
? I ?><^ I I w> I <Ч'''ао+1 ^«> I2 = л +1 ¦
Поэтому можно положить
Vl7T	A1,21)
') Отметим, что состояния Wn не нормированы-

18	ОБЩИЙ ФОРМАЛИЗМ	[ГЛ. II
В произвольний момент времени матричный элемент гейзенбер-
гейзенберговского оператора равен
0F»+i I а+ @1 Wn) = еш°* (Wn+l | at I Wn) =
= <<Гto«+'4+. I at I e-'ra«' ?„>. A1.22)
В этом частном случае только те матричные элементы отличны
от нуля, которые меняют п на ±1. Уравнения A1.13) — A1.22)
дают полное квантовомеханическое решение рассмотренной за-
задачи. Эти уравнения описывают развитие во времени операто-
операторов, допустимых физических состояний, а также матричных эле-
элементов операторов в энергетическом представлении.
Сформулированный подход непосредственно обобщается для
системы с п степенями свободы. В этом случае мы вводим в
картину Гейзенберга п эрмитовых операторов qi(t), i— l,...,n,
и п сопряженных импульсов pi(t). Динамическое описание си-
системы по-прежнему дается 2м классическими уравнениями дви-
движения:
дН dpt	дН dqi
~'Щ = ~1Г> ~Щ = ~йТ' г=1> ••¦>«• (П-23)
Определив матричные элементы операторов р,- и qt в момент
времени 1 = 0 и потребовав, чтобы они подчинялись коммута-
коммутационным соотношениям
[Pi @), q, @)] = - ii,,, [pt @), Pi @)] = 0, [q, @), <// @)] = 0, A1.24)
мы полностью формулируем квантовомеханическую задачу.
Квантовомеханический аналог уравнения A1.23), как в случае
A1.12), есть
р, @ = / [Я, р, (/)], qt (/) = I [H, q, (/)]	A1.25)
для каждой из п независимых координат и импульсов, опи-
описывающих систему с п степенями свободы.
§ 67. Канонический формализм и квантование полей ')
Переходя к пределу п -> оо, мы получим теорию, в которой
поле в каждой точке пространства-времени рассматривается как
независимая переменная. Простым примером такого перехода в
классической физике является поле колебаний массивной стру-
струны. Если рассматривать струну как N материальных точек, то
нужно решать систему W уравнений для связанных осциллято-
осцилляторов. Взяв же предел N-^-oo, мы получаем непрерывную струну,
смещение которой описывается полем <р(дс, t), которое непре-
') См. [6, 7].

i 67]
КАНОНИЧЕСКИЙ ФОРМАЛИЗМ И КВАНТОВАНИЕ ПОЛЕЙ
рывно зависит от х и t. По своему смыслу <р означает смещение
струны относительно состояния покоя, а производная по времени
д<р (*. t) /dt есть скорость в точке (х, t).
Следуя этой аналогии, можно ожидать, что при динамиче-
динамическом квантовании поле ф(лс, t) играет роль координаты qi(t), a
производная ду{х, t)/dt отвечает обобщенной скорости qi(t). При
этом дискретный индекс i заменяется непрерывной координатой
х; в результате поле в представлении Гейзенберга является
функцией как пространственных, так и временных координат
х = (х, t). При таком подходе координата и время входят на
равных основаниях, и мы видим преимущество гейзенберговской
Световой конус \y\=t
Рис. 11.2. Произвольная пространственно-подобная поверхность а с нор-
нормалью Т)ц.
картины, в которой явным образом подчеркнута лоренц-инва-
риантность формализма. Единственным упоминанием о выде-
выделенной роли времени является задание начальных условий и
коммутационных соотношений в некоторый момент времени, на-
например t = 0. Гиперповерхность t = 0 является единственным
нековариантным элементом теории. Эту трудность, однако, лег-
легко преодолеть, если заменить гиперповерхность t = 0 ковариант-
ной пространственно-подобной поверхностью и задать на поверх-
поверхности начальные условия и коммутационные соотношения. Эта
пространственно-подобная поверхность представляет собой трех-
трехмерную поверхность а, нормаль к которой ц^ всюду временипо-
добна: т)^ = 1 > 0. Условимся всегда выбирать вектор ц*1
лежащим в переднем световом конусе, так что т]° > 0. В даль-
дальнейшем мы будем подразумевать, что выражения «в данный мо-
момент времени» и «на цространственно-временнои поверхности а»,
означают одно и то же; таким образом, мы можем придать
выбранным начальным условиям ковариантную формулировку.
Путь к квантованию классических полей начинается с рас-
рассмотрения полевых уравнений. Исходя из этих уравнений, мы
ищем лагранжиан, который в силу принципа Гамильтона приво-
приводит к этим уравнениям. Построив лагранжиан, можно затем

20	ОБЩИЙ ФОРМАЛИЗМ	[ГЛ. И
определить канонические импульсы и выполнить квантование
согласно уравнению A1.24). В результате поля q>i(x,t) и кано-
канонические импульсы т{х, t) становятся операторами в гильберто-
гильбертовом пространстве, которые действуют на векторы состояния Ф.
Как и в одночастичной теории, упомянутой в самом начале гл. 1,
мы постулируем, что физические состояния Ф образуют полный
набор в гильбертовом пространстве. Наиболее часто мы будем
сталкиваться с векторами состояния в гейзенберговском пред-
представлении, т. е. с собственными векторами гамильтониана, по-
построенного из полей фг и импульсов т по аналогии с одноча-
одночастичной теорией:
Напомним сначала способ нахождения лагранжиана L из
уравнений движения в классической механике. Затем мы повто-
повторим те же самые выкладки, чтобы построить лагранжиан в тео-
теории поля. Начнем с уравнений Ньютона
умножим их на 6<jv и просуммируем по i = 1,
t-l	t-\ l
Интегрируя затем по времени от t\ до U и полагая 8ql(tl)=^
= bqi{ti) = 0, т. е. что концы траекторий частиц закреплены,
получим после интегрирования по частям
tl 4i = l	'
Это уравнение и представляет собой принцип Гамильтона для
лагранжиана
t
Теперь, рассматривая поле <p(x), мы в точности следуем той
же процедуре. Пусть, для примера, <р(х) удовлетворяет уравне-
уравнению Клейна — Гордона
r-V2+m2)cp = 0.	A1.26)
Сумма по i, которая встречалась выше, в этом случае заменяет-
заменяется трехмерным интегралом по пространственной координате х.

§ 67]	КАНОНИЧЕСКИЙ ФОРМАЛИЗМ И КВАНТОВАНИЕ ПОЛЕЙ	21
Умножим вначале уравнение A1.26) на бесконечно малую ва-
вариацию амплитуды в точке х:
и проинтегрируем по всем координатам х и по всем временам
от /i до t2:
dt
На вариацию 6<jf снова наложим условие бф(^) = бф(^) = 0.
Предположим также, что система локализована в простран-
пространстве, так что вклад от граничной поверхности при х-
отсутствует1). Тогда имеем
ИЛИ
где
л ( ф,—т| = — I—т,	mY •	A1.27)
V дх*) 2 V дх^ dXp	)
Величина % представляет собой лоренц-инвариантный функ-
функционал, зависящий от полей ф и первых производных ду/дх»;
эта величина называется плотностью лагранжиана. Ясно, что
лагранжиан L, играющий ту же роль, что и в классической
механике, равен объемному интегралу от плотности
В общем случае мы будем всегда полагать, что уравнения
могут быть выведены из некоторой плотности лагранжиана 2.
По аналогии с принципом Гамильтона в классической механике
A1.1) потребуем, чтобы действие было стационарно для полей,
удовлетворяющих уравнениям движения
dt
\>d3x2'=0.	A1.28)
') Этого можно также достигнуть, заключив систему в ящик и наложив
периодические граничные условия.

22	ОБЩИЙ ФОРМАЛИЗМ	[ГЛ. II
Варьируя поля таким образом, чтобы их граничные значения
при t\ и t2 оставались, как в классической механике, фиксиро-
фиксированными, мы получаем из A1.28) уравнения Эйлера — Лаг-
ранжа для полей. В частности, в том простом случае, когда
система описывается единственным полем ф и лагранжева плот-
плотность 3? зависит только от ф и ду/дх»-, получаем из A1.28)
= \dt \ сРх № бф + - ,а* b(*L\\ = 0.
Интегрируя по частям и используя соотношение
имеем
Поскольку вариации бф произвольны, отсюда получаем уравне-
уравнение для поля
* а*	^ = 0.	A1.29)
д {dq>/dxu) дф
В том частном случае, когда 3? определяется из A1.27), урав-
уравнение A1.29) приводит в точности к уравнению Клейна — Гор-
Гордона A1.26).
Полевые уравнения, полученные таким образом, являются
дифференциальными уравнениями и отвечают локальной теории.
Если & содержит производные полей выше первого порядка, то
порядок полевого уравнения больше двух1). До тех пор, пока 3?,
содержит производные конечного порядка, сами поля удовлет-
удовлетворяют дифференциальным уравнениям и теория является «ло-
«локальной». Мы примем гипотезу локального действия, в связи
с чем уместно напомнить оговорки, сделанные в § 65. Весьма
вероятно, что в том случае, когда пространство нелокально и
зернисто на малых расстояниях, описанный здесь канонический
') В дальнейшем мы всегда будем подразумевать, что 9? есть функцио-
функционал, зависящий только от полей и их производных. Кроме того, 9? не будет
явно зависеть от пространственно-временных координат. Это означает, что
мы рассматриваем только «замкнутые» системы, т. е. такие системы, которые
не обмениваются энергией и импульсом с внешними источниками.

§ 67]	КАНОНИЧЕСКИЙ ФОРМАЛИЗМ И КВАНТОВАНИЕ ПОЛЕЙ	23
формализм применим только на больших расстояниях в духе
принципа соответствия.
В любом случае выбор конкретной формы лагранжиана оп-
определяется видом полевого уравнения, которое мы рассматри-
рассматриваем. Плотность лагранжиана вида A1.27) выбрана так, чтобы
она приводила к уравнению Клейна — Гордона; другими инте-
интересующими нас примерами являются лагранжианы Дирака и
Максвелла. Для системы, описываемой более чем одним незави-
независимым полем, скажем, набором полей фг(х), г = 1, ..., п, мы
получаем п уравнений
A1.30)
которые выводятся из принципа Гамильтона независимой вариа-
вариацией по каждому из полей.
Возвращаясь теперь к каноническому формализму и кванто-
квантованию, мы, как и в механике частиц, используем для определе-
определения канонического импульса лагранжиан S'. Чтобы выявить пол-
полную аналогию между теорией поля и теорией частиц, мы рас-
рассмотрим поле как систему с конечным числом степеней свободы,
разбив трехмерное пространство на ячейки объема AF,- и опре-
определив i-ю координату ф*(^) как среднее значение <р(х) в i-й
ячейке
\ d*xtf(x,t).
Обозначив ф;@ среднее значение dq>(x,t)/dt в i-й ячейке, пере-
перепишем лагранжиан в виде
), ...)• 01.31)
Различные ф; отвечают независимым степеням свободы, кроме
того, <p;+s(O содержит координаты Si, отвечающие соседним
ячейкам, поскольку для вычисления градиента Уф необходимо
вычислять соответствующие разности. Так как каждый член 3:\
содержит только одну производную по времени ф.@. канониче-
канонические импульсы равны просто
01-32)
Тогда, согласно A1.4), гамильтониан равен
И = ? Ptii - Z, = ? AF, (я,ф, - Si).	A1.33)
i	i

24	ОБЩИЙ ФОРМАЛИЗМ	[ГЛ. II
Возвращаясь к непрерывным обозначениям, определим им-
импульс, сопряженный ф(лг, /), соотношением
я(Ж|/)ду(ф-Ф).	A1.34)
у ' ' дер (х, t)	ч	'
Усредняя этот импульс по /-й ячейке, получим как раз ni(t)
в формуле A1.32). Гамильтониан теперь записывается в виде
объемного интеграла от гамильтоновой плотности Ж{п, ср), кото-
которая выбирается, как подсказывает нам равенство A1.33), в виде
(х,/),ф(л;,/)), Ж=яф — Z. A1.35)
Определив канонические импульсы, мы следуем далее обыч-
обычной процедуре квантования, заменяя динамические переменные
Ф«@> Р« @ эрмитовыми операторами с коммутационными соот-
соотношениями вида A1.24)
[ф« (О, Ф/ @1 = [Pi (t), р,- (/)] = о, [pi @, Ф/ @1 = - й//
или в терминах яг (?)
На языке непрерывных обозначений эти соотношения приобре-
приобретают вид
[Ф (х, 0, Ф (*', t)\ = [я (х, t), л {xf, ()] = 0,
[я(х, 0, Ф (*', 01 = - гб3 (х - х'),	{П-6Ь)
где дираковская б-функция возникает как предел бц/AVi при
AVj->-0 в соответствии с определением
Уравнения A1.34) — A1.36) вместе с уравнениями движения
представляют основу канонической квантовой теории поля.
Обобщение для физической системы, описываемой несколькими
независимыми полями qr(x, t), получается, если ввести импуль-
импульсы, сопряженные каждому полю,
»'<*'«=adSir	AL37)
и плотность гамильтониана
38(яг,...,Фг...) = 2]ягфг-а'.	A1.38)
Коммутаторы, необходимые для квантования, имеют вид:
[<рг (х, /), ф, (х\ t)\ = 0, К (х, 0, я, (*', 01 = О,
[я, (*, 0, Ф. (*'> 0] = - гб«б3 (х - х'),	U >С>У;

§6S)	ПРЕОБРАЗОВАНИЯ СИММЕТРИИ И ЗАКОНЫ СОХРАНЕНИЯ	25
Наконец, чтобы закончить наше полное аналогий сопоставле-
сопоставление механики частиц и квантовой теории поля, укажем, что из
A1.37) —A1.39) следует, что аналог A1.25) есть
§ 68. Преобразования симметрии и законы сохранения
Лагранжева формулировка очень удобна для последова-
последовательного определения констант движения в классической теории
поля, а также при выводе явных выражений для этих констант.
Исходя из скалярного лагранжиана, можно показать, что каж-
каждому непрерывному преобразованию симметрии, оставляющему
инвариантными плотность лагранжиана 3 и уравнения движе-
движения, отвечает некоторая теорема сохранения и константа движе-
движения. Соответствующая теорема1) (теорема Нетер), позволяю-
позволяющая описывать наблюдаемые в природе правила отбора в терми-
терминах условий симметрии, налагаемых на лагранжиан, оказывается
весьма полезной при конструировании новых лагранжианов
со взаимодействием. Мы рассмотрим поэтому, как эта теорема
работает в квантовой теории поля.
Рассмотрим вначале законы сохранения, связанные с транс-
трансляционной инвариантностью в классической теории. При беско-
бесконечно малом смещении
х' =х 4- е	П1 4П
плотность лагранжиана 3 изменяется на величину
а о? — ср'	ар	р °-^	/11 дп\
ох — х х — г11дх^.	(liAZ)
С другой стороны, если плотность лагранжиана трансля-
ционно инвариантна, то она не зависит от координат: 3 =
= 3 (фг, дфг/(?фц), так что
где
Приравнивая два выражения для ЪЗ и используя уравнения
Эйлера — Лагранжа
J^L	i	UEL	= 0,	A1.45)
') Подробное обсуждение этой теоремы дано, например, в статье [8] (см.
Также [9], прим. перев.)

26	ОБЩИЙ ФОРМАЛИЗМ	[ГЛг 11
получаем
д rv^ ds дФг!	(П46)
A1.47)
"¦ дхц, дх„ I Lj д
Так как смеа^ение е^ произвольно, то
где /"^у есть тензор энергии-импульса
Из дифференциального закона сохранения A1.47) можно полу-
получить сохраняющиеся величины
^j -^ = 0. A1.49)
В предыдущем параграфе мы уже видели, что /оо есть плот-
плотность гамильтониана
-2' = 5»	A1.50)
поэтому мы можем рассматривать Pv как сохраняющийся 4-век-
тор энергии-импульса.
Аналогичным образом можно построить выражения для со-
сохраняющегося углового момента, рассматривая бесконечно ма-
малое лоренцево преобразование
A1.51)
Для проверки лоренцевой инвариантности нужно подставить в
уравнения движения')
Фг(х)->5Г1!F)ФЛ^)	A1.52)
и выяснить, сохраняют ли они в штрихованной системе коорди-
координат ту же форму, что и в исходной системе. Здесь 5„(е) — мат-
матрица преобразования полей <рГ) которая отлична от единицы,
если поля не скалярны. Мы уже сталкивались с такой ситуацией
') Здесь и далее по повторяющимся индексам компонент поля res под-
подразумевается суммирование.

§ 68]	ПРЕОБРАЗОВАНИЯ СИММЕТРИИ И ЗАКОНЫ СОХРАНЕНИЯ	27
при рассмотрении уравнения Дирака. Из уравнения Дирака мы
можем заключить, что ')
Подставим теперь A1.52) в лагранжиан и потребуем, чтобы
плотность лагранжиана была скаляром и не менялась бы при
этой подстановке, т. е.
(s;sl% (/), -J- s;s\ (*')) = 2 (ф, СО. -^А) -(и
.53)
Последнее равенство гарантирует инвариантность уравнений
движения, которые получаются из 9? с помощью инвариантного
принципа действия. Для бесконечно малого смещения
6Ф, (х) = S-1 (е) % {х') - Фг (х) = Фг (хО - Фг (х)
причем
A1.54)
Раскладывая A1.53) вблизи точки х и используя уравнения Эй-
Эйлера— Лагранжа A1.45), получаем
[4?] (.1.55)
Уравнения A1.54) и A1.55) приводят к закону сохранения
- /Г') + ^щ *.] = 0. A1.56)
Сохраняющийся угловой момент равен
Действуя в том же духе, можно получить дополнительные за-
законы сохранения, если лагранжиан обладает «внутренними
снмметриями», т. е. если при локальных преобразованиях
фЛ (х) -> Фг (х) - ieXrscps (x)	A1.58)
') В теории Дирака аналогичное уравнение имеет вид B.11).

28	ОБЩИЙ ФОРМАЛИЗМ	ГГЛ. Л
плотность лагранжиана остается инвариантной. В формуле
A1.58) Xrs — постоянные коэффициенты, не зависящие от х^ и
е — бесконечно малый параметр. Диагональные элементы мат-
матрицы К отвечают просто изменению фазы полей, в то время как
недиагональные элементы перепутывают различные поля, вхо-
входящие в 3? симметрично. Если S инвариантно при подстановке
A1.58), то, повторяя те же выкладки, которые привели нас к
уравнению A1.46), получаем
Таким образом, для каждой «внутренней симметрии» вида
A1.58), оставляющей S инвариантной, существует сохраняю-
сохраняющийся в дифференциальном смысле ток
^Г^==0,	A1.60)
где
а также сохраняющийся «заряд»
rXrS%, Д^ = 0.	A1.62)
Обращаясь теперь к квантовой теории поля, нужно выяснить,
остается ли при этом справедливым тот факт, имеющий место
для классических полей, что скалярность 9? гарантирует лорен-
цеву инвариантность теории и приводит, в силу теоремы Нетер,
к сохраняющимся величинам энергии-импульса и углового мо-
момента. В квантовой теории поля амплитуды qv(x) приобретают
смысл операторов, действующих на функции состояния, которые
представляются векторами в гильбертовом пространстве. Если
наложить условия лоренцевои ковариантности на матричные эле-
элементы этих операторов, через которые выражаются наблюдае-
наблюдаемые в двух различных лоренцевых системах, то мы придем к
некоторому операторному условию для ($г{х). В квантовой тео-
теории поля скалярность еще недостаточна для релятивистской ин-
инвариантности; нужно еще проверить, что поля удовлетворяют
дополнительным операторным условиям.
Чтобы показать, как возникают эти дополнительные условия,
возьмем матричный элемент полевого оператора <$г(х) между
двумя функциями состояния
(Фа;фг(л:)Фр).	A1.63)

5 68]	ПРЕОБРАЗОВАНИЯ СИММЕТРИИ И ЗАКОНЫ СОХРАНЕНИЯ	29
Всевозможный набор таких матричных элементов, нумеруемых
значками аир, образует полный набор амплитуд в квантовой
теории поля, который заменяет классические полевые ампли-
амплитуды (fr(x). Аналогичную роль в шредингеровской квантовой
механике играют матричные элементы оператора q{t). Для на-
наблюдателя в другой лоренцевои системе, связанной с исходной
преобразованием координат
амплитуды A1.63) равны
(Ф>г(ж')Ф^),	A1.64)
где векторы Фа и Фр представляют те же самые физические со-
состояния а и р, но в штрихованной системе координат, причем
сами операторы qv(x') вычисляются в новой точке х'. Ампли-
Амплитуды A1.64) представляют квантовомеханическое обобщение
классических полей q>'r (х') = Srs<ps (х) в штрихованной системе ко-
координат. Классическое правило преобразования полей может
быть теперь записано в виде
(Ф'а, Фг (*') 0>з) = Sra (а) (Фа, % (х) Ф„).	A1.65)
Это уравнение представляет собой математическое выражение
правила, устанавливающего связь между двумя лоренцевыми
наблюдателями. Кроме того, мы требуем существования унитар-
унитарного оператора U(a,b), который устанавливает связь между
векторами состояний в двух лоренцевых системах. Последняя
дается уравнением
ф'а = и(а,Ь)Фа.	A1.66)
Как следует из A1.65), полевые операторы преобразуются со-
согласно
U (а, Ъ) Ф, (х) U~l (а, Ь) = S7,1 (а) % (ах + Ъ). A1.67)
Рассматривая вначале трансляции, мы, в частности, полу-
получаем
иф)ъ{х)и-х{Ь) = ч>г{х + Ь),	A1.68)
где U(Ь) — унитарный оператор, генерирующий смещения коор-
координат. Для бесконечно малых смещений хР' = х^ + е^ можно
написать
U (е) = ехр (йдР") « 1 + i^,	A1.69)
где ри — эрмитов оператор. Уравнение A1.68) в этом случае
приводится к виду
[Ч>гШ = ^-.	A1.70)

30	ОБЩИЙ ФОРМАЛИЗМ	[ГЛ. II
Сравнение с классической канонической механикой и нереляти-
нерелятивистской шредингеровской теорией (уравнение A1.10)) позво-
позволяет отождествить р^ в A1.69), A1.70) с 4-вектором энергии-
импульса Р^ s= Рй. Поскольку мы уже вывели явное выражение
A1.49) для Р^, мы можем теперь в любой теории проверить, со-
согласуется ли это тождество с коммутационными соотношениями
при квантовании. Таким образом, можно установить, является
ли равенство A1.69) операторным уравнением и коммутируют
ли компоненты р с гамильтонианом
[Я, Р] = 0,	A1.71)
т. е. остается ли Р константой движения.
Если уравнения A1.70) и A1.71) не противоречат коммута-
коммутационным соотношениям, то квантовая теория трансляционно-ин-
вариантна. В противном случае либо оператор Р>\ удовлетво-
удовлетворяющий уравнениям A1.70), A1.71), следует определять каким-
либо другим способом (при этом нужно изменить условия на
коммутаторы), либо теория оказывается противоречивой и ее
следует отбросить. Для теорий, которые мы рассматриваем, пра-
правильные значения Рц и M^v могут быть найдены из теоремы
Нетер.
Аналогичным образом можно точно сформулировать, что оз-
означает инвариантность квантовой теории поля относительно ло-
ренцевых преобразований. Унитарный оператор, генерирующий
инфинитезимальное лоренцево преобразование х^' = дЯ -f- e^xv,
записывается в виде
^(e,v)=l-yeJVr,	A1.72)
где М^— эрмитов оператор, удовлетворяющий операторному
уравнению
Фл (х) ~ \ в„„ [IVT, Фг (*)] = S7sl (е^) <р, (х + гх),
которое следует из A1.67).
Используя A1.54), это уравнение можно привести к виду
I [NT, Фг (х)-] = х» U - х" |^ + О* <*)¦ A1.73)
Далее мы снова используем связь с классической и нереляти-
нерелятивистской теорией, чтобы отождествить оператор ЬЛ^, генерирую-
генерирующий лоренцевы преобразования, с тензором углового момента
A1.57) : М*"= Mv-V. Пространственные компоненты в уравнении
A1.73) выражают просто-напросто обычные коммутационные
соотношения в нерелятивистской механике для оператора
углового момента L = (М12, М23, Msl), который генерирует трех-
трехмерные пространственные вращения. Согласованность подобного

ЗАДАЧИ	31
отождествления тензора MliV с тензором углового момента и с
коммутационными соотношениями есть дополнительное условие
в теории, инвариантной при лоренцевых преобразованиях. Непо-
Непосредственная проверка производится здесь так же, как и для
оператора р*1.
Для большинства полевых теорий, которые чаще всего об-
обсуждаются сейчас в физических приложениях, лагранжев подход
и теорема Нетер могут быть непосредственно применены в кван-
квантовой области без каких-либо дополнительных трудностей.
Именно в квантовой формулировке эти теории и обнаруживают
свою практическую ценность, как это будет иллюстрировано в
последующих главах.
§ 69. Другие формулировки
Описанный выше подход использует как исходный пункт
классический лагранжиан, позволяющий вывести непротиворе-
непротиворечивые уравнения поля и коммутационные соотношения. Под-
Подчеркнем здесь, что физика заключается не в самом лагран-
лагранжиане, а в уравнениях поля и их решениях, а также в коммута-
коммутационных соотношениях и свойствах векторов состояний системы.
Можно сформулировать теорию ah initio в терминах кван-
квантового принципа действия, в этом случае лагранжиан играет бо-
более важную роль. Этот мощный, но более абстрактный подход
к квантовой теории поля широко обсуждался в литературе, осо-
особенно Швингером [10, 11].
Наоборот, возможна такая формулировка теории, которая
не требует использования лагранжианов. Общий подход такого
типа с аксиоматической точки зрения был сформулирован Лема-
ном, Шиманчиком и Циммерманном [12, 13].
ЗАДАЧИ
Волновое уравнение для массивной частицы со спином 1 имеет вид
дх- дху
откуда следует, что
o
dxv
1. Построить из этого уравнения плотность лагранжиана

32	ОБЩИЙ ФОРМАЛИЗМ	[ГЛ. II
2. Построить плотность гамильтониана
2 ' 2 V о; 2 VdW 2 ° 2 У 2
где
3.	Проверить, что гамильтоновы уравнения движения
дЖ _ . ц, дЖ _ .
1 —— (р j ————— ^_ — JXu
с дополнительным условием
воспроизводят первоначальное волновое уравнение.
4.	Предполагая, что SS не инвариантна относительно некоторого преобра-
преобразования внутренней симметрии, связать изменение 2 с дивергенцией соот-
соответствующего тока.

ГЛАВА 12
ПОЛЕ КЛЕЙНА-ГОРДОНА
§ 70. Квантование и интерпретация в терминах частиц
Простейшим примером поля является действительное ска-
скалярное поле ср(х), которое удовлетворяет свободному уравнению
Клейна — Гордона
{П+т2)у(х) = 0.	A2.1)
Это поле рассматривалось ранее в целях иллюстрации. Лаг-
ранжева плотность, из которой выводится уравнение A2.1),
записывается в виде
¦-тУ).	A2.2)
а сопряженный импульс равен
я = 4^=ф.	A2.3)
уф
При квантовании я и ср становятся эрмитовыми операторами,
которые удовлетворяют одновременным коммутационным соот-
соотношениям
[ср (х, t), ф (хг, I)] = [л (х, t), я {хг, /)] = О,
[я (х, /), ф (*', /)] = - id3 (х - х').	A2'4)
В результате мы получаем квантовую теорию, инвариантную
относительно трансляций и лоренцевых преобразований коорди-
координат, что можно непосредственно проверить прямым вычислением
коммутаторов A1.70) и A1.73). Из A2.2) и A2.3) получаем
выражение для гамильтониана
Ж (я, Ф) = шр - SB = \ [я2 (*, 0 + I V<P (*, 0 I2 + mV (*, 0] A2.6)

34	ПОЛЕ КЛЕЙНА — ГОРДОНА	[ГЛ. 12
и оператора импульса
A2.6)
Используя A2.4), можно убедиться; что
как и должно быть. Аналогичным образом можно вычислить
M&v в A1.57) и проверить выполнение условия A1.73), причем
для скалярного поля SrJ = O.
Для дальнейшего рассмотрения нам потребуется ввести пол-
полный набор векторов состояния Ф. Этот набор можно построить,
используя алгебру операторов, которая задается коммутацион-
коммутационными соотношениями; при этом удобно работать с собствен-
собственными функциями оператора энергии-импульса.
Заметим, что любое решение уравнения A2.1) может быть
разложено в интеграл Фурье по плоским волнам
[а (ft) в1*"-"*' + а+ (ft) «-'••*+'•*'] в
J [а (k) fk (x) + а+ (ft) /; (*)], A2.7)
где
Ф(,, t) = \
В классической теории амплитуда a+{k) комплексно сопряжена
a(k), поскольку поле у(х) действительно. В квантовой теории
эти амплитуды являются эрмитово сопряженными операторами.
Алгебру операторов a(k) и a+{k) можно получить, если перепи-
переписать коммутационные соотношения для <р A2.4) в терминах
коэффициентов a(k).
Из A2.7) получаем1)
\ /; (х, t)Ф (*, t) d3x = ~Va (k) + a+ (- k)*"«*'],
p	к	A2.8)
\ fl (x, t) ф [x, t) d3x = -j [a (ft) - a+ (- ft) е2г^]>
J) Функции /ft и fA удовлетворяют условию ортогональности (9.6):
- ft').

§ 70]	КВАНТОВАНИЕ И ИНТЕРПРЕТАЦИЯ В ТЕРМИНАХ ЧАСТИЦ	35
откуда
a (k) = ^ d3xfI (х, t) Kq> (x, t) + Щ (х, t)] =
t).	A2.9)
<-¦>
В последней строке использовано обозначение д0, которое имеет
следующий смысл:
а @%Ь (t) = а @ -|f - Dт
Правая часть в A2.9) по теореме Грина не зависит от времени,
поскольку и fk{x,t) и q>(x,t) являются решениями1) уравнения
A2.1). Выражение A2.9) представляет аналог внутреннего про-
произведения, которое мы рассматривали в гл. 9 при обсуждении
метода функций распространения в применении к уравнению
Клейна — Гордона.
Искомые коммутационные соотношения получаются теперь
из A2.4) и A2.9). Поскольку a(k) не зависят от времени, мы
можем при вычислении коммутатора в A2.4) взять операторы
Ф и п в один и тот же момент времени; в результате получим
[a (k), а+ (*>')] = J d?x d3y [ffc (*, О^Ф (*, 0, fv (у, t)%f (у, Щ =
= + i] dH\\(x, f)%rk,(x, t) = 63(k~k').
Аналогичным образом имеем
[a(k), a{k')\ = (if J d3xd3y [Гк (x, t)d*<p(x, t), Ц,(y, t)djf (y, 0] =
= -i\d3xfl(x,t)%f*k,(x,t) = 0
и
++	0.	A2.10)
Оператор энергии-импульса для свободного поля Клейна — Гор-
Гордона имеет простой вид в терминах коэффициентов a(k) и &)
') Это утверждение справедливо и в более общем случае, когда в каче-
качестве ортогональных функций, по которым производится разложение полевого
оператора ф(дс, f) в A2.7), используются волновые пакеты, составленные из
плоских волн (см. [12]),	~=

36	ПОЛЕ КЛЕЙНА — ГОРДОНА	[ГЛ. 12
Непосредственное вычисление по формулам A2.5) — A2.7) при-
приводит к следующему результату1):
Я = \ \
d3k щ [а+ (k) a(k) + a (k) a+ (k)],
A2.11)
rf3a [a+ (k) a(k) + a (k) a+ {k)\.
Мы получаем, таким образом, представление гамильтониана
в форме непрерывной суммы членов
Hk = \ Щ[а+ (k)a{k) + a(k) a+ (k)},
каждый из которых имеет вид гамильтониана простого гармони-
гармонического осциллятора с частотой ои. В самом деле, а+(?) и a(k)
есть повышающие и понижающие операторы, которые уже об-
обсуждались на примере с осциллятором в гл. 11, причем эти опе-
операторы удовлетворяют, с точностью до нормировки, тем же са-
самым коммутационным соотношениям. Чтобы пояснить различие
в нормировке и выявить полную аналогию с предыдущим рас-
рассмотрением одномерного осциллятора, мы снова вернемся к ди-
дискретным обозначениям. Разбивая ^-пространство на ячейки
объема AVk, имеем
?	k')-*^.	A2.12)
') Желая сохранить формальную ковариантность, мы можем переписать
разложение по плоским волнам в инвариантном виде, используя тождество
Обозначив A (k) = д/2<вА a (k), получим
~ т2) е (ko) [A (k) e~ikx + A+
\
где а — плоская пространственно-подобная поверхность, % — нормаль к этой
поверхности. Аналогичным образом имеем
! - /n2) в (k0) ka [A+ (k) A (k) + A (k) A+ (k)l
причем коэффициенты A(k), подобно <р, являются лоренцевыми скалярами.

§ 70]	КВАНТОВАНИЕ И ИНТЕРПРЕТАЦИЯ В ТЕРМИНАХ ЧАСТИЦ	37
Тогда Н имеет вид суммы гамильтонианов осцилляторов Hk, со-
соответствующих набору ячеек импульсного пространства:
Е	Е)К	)	/	A2.13)
к	k
причем
К. «Я = ***- К- **-] = К+- *Я = 0-	A2-14)
Указанной аналогии с гармоническим осциллятором не сле-
следует удивляться, поскольку классическое поле Клейна — Гор-
Гордона может быть представлено в виде разложения по своим
собственным частотам. Коэффициенты в этом разложении a(k)
и являются гармоническими осцилляторами. Все, что мы сде-
сделали, — это проквантовали каждый из осцилляторов a (k).
При квантовании мы ожидаем, что классическая энергия
поля станет равна сумме энергий отдельных осцилляторов.
Чтобы вычислить собственное значение оператора энергии и по-
построить соответствующие собственные функции, рассмотрим
каждый гамильтониан Нц по отдельности. Поскольку Я имеет
вид суммы взаимно коммутирующих для каждого волнового
числа k и частоты % = д/&2 + т2 операторов Hk, то его соб-
собственные функции представляются в виде произведения соб-
собственных функций Фк, отвечающих каждому из Hk- Произволь-
Произвольный вектор состояния Ф может быть далее записан в виде су-
суперпозиции таких произведений со всевозможными значениями
k в соответствии с. постулатом полноты, гл. 1.
Решение задачи на собственное значение для осциллятора с
данным волновым числом k характеризуется целым индексом
Пк = 0, 1,2, ..., который нумерует собственные функции и соб-
собственные значения
НкФк (я*) = щ (я* + j) Фк (я*),	A2.15)
"	A2.16)
Здесь Фк @) — основное состояние, определяемое из условия
а,ФА@) = 0.	A2.17)
Состояния в A2.16) нормированы согласно
(ф*(«*).ф*К)) = \.;.
Аналогично можно записать оператор импульса
Мах+ал+). 02.18)

38	ПОЛЕ КЛЕЙНА — ГОРДОНА	[ГЛ. 12
где
(пк + у) Фк (я*), «ft = 0, 1,2,...
Собственные функции оператора энергии-импульса ф записы-
записываются в виде произведения функций Фи, отвечающих отдель-
отдельным импульсным ячейкам; они характеризуются набором пи для
каждого значения k:
A2Л9)
В основном состоянии, т. е. в состоянии с наинизшей энергией,
все пк — 0:
Фо=ПФ*(О).	A2.20)
к
В этом состоянии, которое имеет физический смысл вакуума, не
возбуждена ни одна из мод нормальных колебаний.
Энергия вакуума
расходится, представляя по своему смыслу сумму энергий ну-
нулевых колебаний бесконечного числа осцилляторов, по одному
на каждую нормальную моду или степень свободы поля. Это
первый пример в ряду бесконечностей, с которыми мы будем
еще сталкиваться в теории поля. В данном случае от бесконеч-
бесконечности в A2.21) проще всего избавиться, вычитая из Н бесконеч-
бесконечную константу так, чтобы сократить член V — соА. Подобная
k
процедура является оправданной, поскольку физический смысл
имеют не абсолютные энергии, которые неизмеримы, а лишь их
разности. Согласно A2.17) и A7.20) вычитаемая константа
равна вакуумному среднему оператора энергии; она автомати-
автоматически исчезает, если переписать оператор энергии-импульса
в виде
К=р»- (фо> РЛ) = ? V*а*	<12-22)
или, используя непрерывные обозначения,
Чк^а+{к)а{Щ.	A2.23)

§ 70]	КВАНТОВАНИЕ И ИНТЕРПРЕТАЦИЯ В ТЕРМИНАХ ЧАСТИЦ	39
До тех пор, пока поля не подчинены коммутационным соотноше-
соотношениям, операторы Рц. и Р^ тождественны, поскольку классиче-
классические амплитуды нормальных колебаний коммутируют; при этом
нулевая энергия отсутствует.
В квантовой же теории замена Р^ и Рц эквивалентна записи
всех полевых операторов в выражениях для 2s и Рд таким об-
образом, чтобы положительно-частотная часть ср:
A2.24а)
всегда стояла бы за отрицательно-частотной частью
ф(-) (х) = J d3k a+ (k) fl (x).	A2.246)
Такой порядок множителей называется нормальным порядком
и обозначается символом
:фф: = <p<-)<pH> + 2ср<-у+> + ф<+у+>.	A2.25)
Из формулы A2.17) и эрмитово сопряженного ей выражения
следует, что вакуумное среднее любого оператора равно нулю,
если только этот оператор выражается через величины, записан-
записанные в нормальном виде. В данном случае единственным эффек-
эффектом, к которому приводит нормальное упорядочивание, является
избавление от бесконечной энергии нулевых колебаний; при
этом нуль энергии определяется как энергия вакуумного состоя-
состояния ф0.
Из A2.19) и A2.22) получаем собственные значения опера-
оператора Р'р.:
A2.26)
Собственные векторы для каждой нормальной моды k несут
4-импульс, отвечающий Пк квантам, каждый из которых имеет
4-импульс № и массу т, причем, согласно соотношению Эйнш-
Эйнштейна, kyk* = т2. Мы видим здесь, как при канонической про-
процедуре квантования возникает интерпретация поля в терминах
частиц. Целые числа Пк называются числами заполнения для
k-vo импульсного состояния; при этом задание наборов Пк пол-
полностью определяет вектор состояния Ф (... Пк ...).
Удобно ввести оператор числа частиц
tf*-«K	A2.27)
с целыми собственными значениями
.л*...). «* = 0, _1, 2, .... A2.28)

40	ПОЛЕ КЛЕЙНА - ГОРДОНА	[ГЛ. 12
через который можно выразить оператор энергии-импульса')
P^=Y,^Nk.	A2.29)
к
С помощью A2.14) можно проверить, что
[tf*.«a=<wtf и [^-^]=-<wv (l2-3°)
Сравнив с A2.29), мы видим, что а? есть оператор рождения
кванта с импульсом №. Этот оператор, действуя на состояние,
содержащее пь квантов с импульсом k*1, образует состояние с
п/г -f- 1 квантами, поскольку
Аналогичным образом оператор аь уничтожает квант с импуль-
импульсом k и, в частности, действуя на состояние, не содержащее та-
таких квантов вообще, дает нуль, поскольку а*Фь@) = 0 согласно
A2.17).
Единственными отличными от нуля матричными элементами
операторов ак и а\ являются те, которые, как и в примере с ос-
осциллятором (гл. 11), связывают состояния с п'к = пк±. 1:
nk'nk~i>
§ 71. Симметрия состояний
При каноническом квантовании классического поля Клей-
Клейна — Гордона возникает многочастичная интерпретация поля в
терминах чисел заполнения пь- Для свободного поля операторы
Nk и Н коммутируют, поэтому число квантов сохраняется. Ин-
Интересная физическая задача возникает, если ввести члены с
взаимодействием, которые меняют Пи- Для свободного же поля
остается только показать, что кванты представляют систему
тождественных частиц, т. е. подчиняются статике Бозе — Эйнш-
Эйнштейна.
Любое состояние представляет суперпозицию базисных со-
состояний
Ф ( • • • "*а • • • ) " П
') Здесь и далее мы опускаем штрихи при записи операторов с нормаль-
нормальным порядком множителей.

S 71]	СИММЕТРИЯ СОСТОЯНИЙ	41
Вектор A2.32) полностью определен набором чисел заполнения
Пк для каждого k. Отдельные кванты не различимы, поскольку,
согласно A2.14), все операторы а% взаимно коммутируют и их
порядок несуществен. Это обстоятельство находит отражение в
свойствах симметрии коэффициентов разложения произвольного
вектора по базисным векторам A2.32). Возвращаясь снова к
непрерывной нормировке, запишем это разложение в виде1)
Г °°
Xа+ (ft,)a+ (k2) ...a+ (?„)]Фо. A2.33)
Множитель l/V«i выбран из соображений удобства; при этом
условие нормировки для сп имеет простую форму:
... d3kn\cn(ku k2, .... kn)\\ A2.34)
Коэффициенты сп описывают распределение по импульсам ком-
компоненты вектора состояния, содержащей п квантов. Они имеют
смысл волновой функции в импульсном пространстве системы
тождественных частиц, которая характеризуется заданным набо-
набором импульсов ka. В силу коммутативности операторов a+{k)
в A2.33) эти функции есть симметричные функции своих аргу-
аргументов
e(...kt...k,...) = + c(...kt...kt...). A2.35)
Как отмечалось выше, состояние характеризуется только
числами квантов с различными k. Кванты неразличимы, и ве-
вероятность состояния, в котором квант а имеет импульс &,-, а
квант b импульс kj, равна вероятности состояния, в котором
кванты а и Ъ переставлены:
\с(... ki ... ^...)|2 = |c(... kt... k, ...)|2. A2.36)
Условие симметрии A2.35), которое является следствием алгеб-
алгебры коммутаторов операторов a+(k), означает, что частицы, воз-
возникающие при квантовании, подчиняются симметричной (или
бозе-эйнштейновской) статистике.
') Мы предполагаем здесь, что вероятность нахождения двух частиц в
одном и том же состоянии k бесконечно мала, т. е. в непрерывном пределе
га* -*¦ 1 или пк ->- 0. В случае сильно вырожденных систем, таких, как основ-
основное состояние свободного бозе-газа, когда все частицы находятся в одном
и том же состоянии с k — 0, удобно сохранить дискретную нормировку.
В теории поля нас интересуют произвольные состояния рассеяния, для кото-
которых вопроса вообще не возникает.

42	ПОЛЕ КЛЕЙНА — ГОРДОНА	1ГЛ. 12
§ 72. Измеримость поля и принцип микропричинности
В классической теории поле ср(лг) является наблюдаемым и
его величина может быть измерена в любой точке х. В гл. 11
мы ввели, с некоторыми оговорками, понятие локального поле-
полевого оператора <р(х), в квантовом смысле определенного в точ-
точке х.
Коммутационные соотношения в квантовой теории наклады-
накладывают некоторые ограничения на точное измерение величин поля.
Так, например, точное измерение полей в двух различных про-
пространственно-временных точках х и у возможно только в том
случае, если коммутатор [ср(х), ср((/)] обращается в нуль.
Полевой коммутатор можно вычислить, используя явное ре-
решение A2.7) для свободного поля Клейна — Гордона. С учетом
A2.10) получаем
[Ф (х), Ф(у)] = \ „ fk,p^- ([a (k), a+ (k')\ в-
J BяK у2й>А2соА,
(k), а (*')] в'**-'*'«) = J Bд^т> (в"'* <*-*) - в'* <*-*)) =
уо)^/Л(х~у)> A2-з7)
В теории поля мы постоянно сталкиваемся с целым зверинцем
инвариантных функций, к которому принадлежит и Л(х — у).
Сводка формул, относящихся к этим функциям, дана в прило-
приложении В. Лоренцева инвариантность Д непосредственно следует
из выражения A2.37), в котором инвариантная экспонента ин-
интегрируется по инвариантному же фазовому объему
Вводя нечетную функцию
+1, &о>О,
-1, *о<О,	<12-38>
которая также лоренц-инвариантна для времениподобного век-
вектора k2 > 0, можно представить Д в более компактной форме:
¦А (х - У) = - i \ -Цг S (k? - m2) e (k0) е-'* <*-*>. A2.39)
Из определения функции Д посредством коммутатора в левой
части равенства A2.37) следует, что Д есть решение свободного

§ 73]	ВАКУУМНЫЕ ФЛУКТУАЦИИ	43
уравнения Клейна — Гордона, причем она является нечетной
функцией своих аргументов
(ах + т2)\(х-у) = 0, А(х-у) = -А(у-х). A2.40)
Поскольку одновременный коммутатор в A2.37) зануляется,
Л (а; — у, 0) = 0. Тогда из лоренцевой инвариантности получаем
А(х — у) = 0 для всех {х — уJ <0,	A2.41)
т. е. два поля, разделенные пространственноподобным интерва-
интервалом, коммутируют. Таким образом, напряженности полей <р, рас-
рассматриваемые как физически наблюдаемые, могут быть изме-
измерены однозначно и независимо друг от друга в любых двух точ-
точках х и у, которые нельзя связать световым или каким-либо дру-
другим физическим сигналом, (х — уJ > 0. Производная по вре-
времени функции Д сингулярна в начале координат
(х - у)
= - S3 (x ~- у),	A2.42)
в результате, комбинируя A2.42) и A2.37), мы воспроизводим
канонические коммутационные соотношения A2.4).
Условие обращения в нуль коммутаторов для любых, даже
сколь угодно малых пространственно-временных интервалов со-
составляет содержание принципа микропричинности. Для того
чтобы придать какой-либо физический смысл этому математи-
математическому утверждению, следует придать смысл процедуре изме-
измерения поля в точке — недостатки подобной концепции уже об-
обсуждались в предыдущих параграфах1).
§ 73. Вакуумные флуктуации
Мы уже отмечали, что квантование поля представляет не что
иное, как квантование бесконечного набора гармонических ос-
осцилляторов. При этом энергия вакуума оказывается аналогом
нулевой энергии осцилляторов. Если осциллятор находится в со-
состоянии с фиксированной энергией, то его координата не яв-
является строго определенной величиной, т. е.
(?„, Л) > 0Р,ЛJ = 0.	A2.43)
Аналогичное положение имеет место и в полевой теории — ко-
координаты ф(х) флуктуируют. Например, в основном состоянии
А+ (х, У) = <01 ф (х) ф (у) 10) ф 0,	A2.44)
') Детальный анализ коммутационных соотношений на языке процессов
измерения был выполнен для квантовой электродинамики Н. Бором и Л. Ро-
зенфельдом [14].

44	ПОЛЕ КЛЕЙНА - ГОРДОНА	(ГЛ. 12
несмотря на то, что
(О | ф (jc) 10> = 0.	A2.45)
Функцию А+(л;, у) можно вычислить, используя выражения
A2.7), A2.10) и A2.17); в результате получаем
J3k d3k'
Bя):
При «/->¦* это выражение переходит в квадратично расходящий-
расходящийся интеграл для вакуумных флуктуации:
@1 ф2 (*) 10) = А+ @) = \ -щ$^ •	A2.46)
В отличие от нулевой энергии, расходимость в A2.46) не может
быть полностью устранена простым вычитанием. Мы уже знаем,
что вакуумные флуктуации приводят к наблюдаемым конечным
физическим эффектам в лэмбовском сдвиге, которые обсужда-
обсуждались именно с такой точки зрения в гл. 4.
Расходимость в A2.46) не вызывает, однако, беспокойства,
поскольку на самом деле квадрат амплитуды поля в любой точ-
точке не является измеримой величиной. Локализация изолиро-
изолированной точки в пространстве и времени требует бесконечной
энергии и соответственно бесконечно малой длины волны, что не-
недостижимо при конечных энергиях. При практических вычисле-
вычислениях расходимость в A2.46) также не приводит к серьезным за-
затруднениям. Тем не менее то обстоятельство, что аппарат теории
поля постоянно оперирует с выражениями типа 3? и Р&, кото-
которые, подобно A2.46), содержат произведение полевых операто-
операторов, вычисляемых в одной и той же пространственно-временной
точке, не может считаться удовлетворительным.
При этом следует иметь в виду, что с формальной матема-
математической точки зрения строго определено лишь произведение
полей, усредненное по некоторой пространственно-временной
области; только оно и имеет смысл физической наблюдаемой.
К расходящимся результатам вида A2.46) следует относится,
как к указанию на ограниченность концепции непрерывного
поля, которая представляет идеализацию, описывающую физи-
физическую реальность для больших пространственно-временных
интервалов в смысле принципа соответствия. Задачей экспери-
эксперимента остается установить, насколько малы интервалы, для
которых требуется количественная модификация теории.

i 74]	ЗАРЯЖЕННОЕ СКАЛЯРНОЕ ПОЛЕ	45
§ 74. Заряженное скалярное поле ')
Обсудив квантовую теорию действительного скалярного
поля, мы можем обобщить полученные результаты для описания
заряженных частиц, которые рассматривались в гл. 9. Эти
частицы описываются комплексной волновой функцией
где ф1 и фг — действительные величины. Рассмотрим вначале
два одинаковых невзаимодействующих действительных поля та-
такого вида. Полевые уравнения
(П* + т2)ф1 (*) = (), (П* + т2)ф2 (*) = (), A2.47)
получаются из лагранжевой плотности
^=Hf^-m2tf+f^-m2#- A2-48)
где : ... : означает нормальное произведение, определенное вы-
выражениями A2.24), A2.25). Канонические импульсы, как и
прежде, равны
Я1 = фь я2 = ф2,	A2.49)
а канонические коммутационные соотношения записываются
в виде
[ф* (*), фу (у)} = ibk,A (x - у).	A2.50)
Поскольку гамильтониан равен сумме двух членов типа A2.23),
состояния с фиксированной энергией записываются в виде пря-
прямого произведения собственных векторов гамильтонианов, отве-
отвечающих квантам 1 и 2. В отсутствие членов с взаимодействием
число частиц типа 1 и 2 сохраняется по отдельности, поэтому
снова удобно нумеровать состояния собственными значениями
операторов числа частиц
tf,(Jfe) = a+(Jfe)a,(Jfe), N2(k) = a+(k)a2(k). A2.51)
Как и в A2.30), A2.31), операторы af (k), at{k) соответственно
рождают и уничтожают кванты типа i с импульсом k и связы-
связывают, таким образом, состояния, различающиеся числами за-
заполнения на ± 1.
Все сказанное до сих пор справедливо для произвольных
масс mi и м2 в A2.47). В случае же равенства масс т\ = т.ч. =
') См. [15].

46	поле клейна - гордона	[гл. 12
= т можно заменить два уравнения A2.47) одним уравнением
для комплексной волновой функции
Ф = —т=- (ф1 + «Р2)> Ф* = —;=• (ф1 — «Рг)>	A2.52)
которая также удовлетворяет уравнению Клейна — Гордона
(?+т2)ф = 0, (П+я12)ф' = 0.	A2.53)
В терминах комплексных координат ф и ф* плотность лагран-
лагранжиана приобретает следующий вид:
_
Канонические импульсы, соответствующие этим координатам,
равны
д2 . * ф, — щг
Я =	 = ф ——	~—
д^	л/2
В результате для гамильтоновой плотности получаем
36 = яф + я*ф* - & = л*я + (V) (V<P) + т2ф*ф.	A2.55)
При этом коммутационные соотношения записываются	в виде
1ф (х), Ф (у)] = 0 = [Ф* (jc), Ф* (у)], [Ф (jc), ф* (у)} = /A (jc - у).	A2.56)
При равных временах выражения A2.56) переходят в канони-
канонические коммутаторы
[я (х, О, Ф (*', /)] = № (*, О, Ф* (*', t)] = - ifl3 (дс - *').
Взяв фурье-преобразование решений, мы получим анало-
аналогично A2.7)
VBjlK:
d3k
где
a+ (k) = J= [a, (ft) + ia2 (ft)],	a+ (ft) = -^= [a+ (ft) - ia+ (ft)],
1	,	A2.58)
a_ (ft) = ~= [a, (ft) - ia2 (ft)],	ai (ft) = ± [o+ (ft) + Ш+ (ft)].

§ 74]	ЗАРЯЖЕННОЕ СКАЛЯРНОЕ ПОЛЕ	47
Уравнения A2.7) и A2.57) различаются тем, что ф(л;) — теперь
комплексное поле, и, следовательно, при квантовании ему сопо-
сопоставляется неэрмитов оператор; согласно A2.58) a+(k) ф а| (&)•
Коммутаторы для a±(k) легко вычислить, повторяя выклад-
выкладки, которые привели нас к A2.10):
[о+ (k), а+ {Щ — \а_ (k), at (?')] = б3 (fe - k'),
[о+ (k), at (*')] = [«_ (k), a+ (*')] = 0,	A2.59)
[a± (k), a± (*')] = [a+ (Й), a+ {Щ = 0.
Поскольку алгебра операторов a±(k) и ai(fe), аг(/г) одинакова,
операторы числа частиц, записанные в терминах а+ и а_, долж-
должны иметь один и тот же вид и одинаковые собственные значе-
значения. Запишем, возвращаясь к дискретной нормировке, опера-
операторы числа частиц для ± квантов
i\fe := w+ fec*+ fe, iVfe •=== cz	 ka~• k*	i i^rf.ou)
Тогда
Рц= IX (#»¦ + #»)•	A2.61)
ft
Мы видим, что существует полная аналогия с теорией эрми-
эрмитова скалярного поля (§ 70). Например,
nt
nt
при этом, вакуумное состояние с наинизшей энергией не содер-
содержит квантов любого вида, так что
а±.йФо = О.	A2.62)
Операторы a±,k имеют смысл операторов уничтожения '+ и —
квантов с импульсом k, а а+ к представляют соответствующие
операторы рождения. При нормальном упорядочении операторы
уничтожения стоят справа от операторов рождения, как в
A2.60).
Из сказанного ясно, что не существует никакого различия
между описанием полей в терминах эрмитовых амплитуд ф1 и
ф2 и описанием посредством комплексно-сопряженных амплитуд
Ф, ф*. Состояния с равным успехом могут характеризоваться
числом квантов типа 1 и 2 или -}- и —¦.
Уравнение A2.53) для комплексного поля ф наводит на
мысль, что можно определить сохраняющийся ток, который мы
рассматривали в гл. 9:

48	ПОЛЕ КЛЕЙНА - ГОРДОНА	[ГЛ. 12
причем
и
= i\ d3x (ф*ф — фф*) = const.	A2.63)
Легко проверить, что в рассматриваемой квантовой теории с
лагранжианом A2.54) оператор Q остается константой движе-
движения. С этой целью достаточно записать Q в /г-пространстве и
убедиться, что Q коммутирует с Н. При этом мы получаем
Q=\d4 [a+ (k) a (k) - at (k) a_ Щ
или, в дискретных обозначениях,
- Nk),	A2.64)
причем, согласно A2.59), [Q, PJ —0.
Из A2.64) следует, что + и — кванты несут заряды соот-
соответственно + 1 и —1. Поскольку [Р^, a+(k)J\ = + k]la+(k) и
[Q, a+ (k)~\ = + #+ (&)> оператор а+(/г) увеличивает энергию на
№ и заряд на + 1, другими словами, а+ (k) — оператор рождения
кванта с 4-импульсом № и зарядом + 1. Аналогично a+(k) —
оператор уничтожения такого кванта, a at (k) и а_ (k) — опера-
операторы рождения и уничтожения квантов с импульсом № и заря-
зарядом — 1.
Согласно формулам A2.59), A2.61) и A2.64) кванты с за-
зарядом ± 1 возникают в рассматриваемой теории симметричным
образом. Для того чтобы придать какой-либо физический смысл
заряду Q, необходимо ввести взаимодействие, которое разли-
различает знак и величину заряда. В теории уравнения Клейна —
Гордона, гл. 9, ток jv- был связан с электромагнитным полем, а
величина Q отождествлялась с электрическим зарядом. В более
общем случае мы можем считать кванты, отвечающие положи-
положительным собственным значениям оператора Q, частицами, а
кванты, отвечающие отрицательным собственным значениям,
античастицами. Зарядовая симметрия в квантовой теории поля
при этом сводится к утверждению об инвариантности теории
при замене частицы на античастицу. Комплексные амплитуды
удобны для построения собственных векторов оператора заряда.
Таковыми могут быть, например, я+- и я~-мезоны, которые по-
получаются действием на вакуум операторов at(k) и at (k) coot-

5 75]	ФЕЙНМАНОВСКИЙ ПРОПАГАТОР	49
ветственно. В то же время описанный аппарат применим и для
описания электрически нейтральных скалярных частиц, таких,
например, как К0- и /("-мезоны, которые различаются «стран-
«странным» зарядом.
§ 75. Фейнмановский пропагатор
При рассмотрении в первом томе заряженной клейн-гордо-
новской частицы мы сталкивались с фейнмановской функцией
Грина, которая удовлетворяет физическому граничному усло-
условию: в отсутствие взаимодействия только положительно-частот-
положительно-частотная часть решения движется вперед во времени. Посмотрим
теперь, какая величина играет роль фейнмановского пропага-
тора в том случае, когда заряженная клейн-гордоновская ча-
частица рассматривается в формализме теории поля. Рассмотрим
с этой целью пространственно-временное поведение состояния,
содержащего 1 квант. Для того чтобы образовать (не нормиро-
нормированное) одночастичное состояние с зарядом +1, подействуем
на вакуум оператором
У+ (х, t) = Ф* (х, t) Фо = Ф* (х, 0 10).	A2.65)
В A2.65) вносит вклад только отрицательно-частотная часть
оператора ф*(х), содержащая операторы рождения. Поэтому
можно написать:
w+ (*: о=Ф* <->(*,
где отрицательно-частотная часть определена следующим об-
образом:
Ф* <-) (х, 0 = \ J^- а+ (k) e'**,
J д/BяK2и +
Г d>k	A2'67)
ф(-) (х t) = \ .	а+ (k) eikx.
Соответствующие положительно-частотные части полей в A2.57)
будем обозначать через ф*(+) и ф<+).
Вероятность обнаружить состояние A2.65) в момент времени
f >• t в точке (*', V) равна
е(?-t)<w+ (*', о|?+ (*, о> ==
= <0|ф(*', Оф*(*. 010)9(^-0 =
= (о | Ф(+) (*', о ф* (-»(х, о I о) е (f - /). A2.68)
Это выражение представляет собой матричный элемент, опи-
описывающий рождение кванта с зарядом -\-1 в точке (х, t) и

50	ПОЛЕ КЛЕЙНА - ГОРДОНА	[ГЛ. 12
поглощение его в точке х' в некоторый более поздний момент
времени f> t. Другой способ увеличить заряд на +1 в точке
(х, t) и уменьшить его на —1 в точке (х/, t)—это создать квант
с зарядом —1 в точке х', f, который, достигая затем точки х,
будет поглощен вакуумом в момент времени t > f. Амплитуда
этого перехода равна
в (/-О ОМ*, 014L(*', t')) =
= <о | Ф*<+>(*, о ф'-' {хг, о | о) е (/ -1% A2.69)
Фейнмановский пропагатор равен сумме амплитуд A2.68) и
A2.69)
iAF (х' - х) = <0 | Ф (*') Ф* (х) | 0N (f -1) +
+ <0 | Ф* (jc) Ф (х') 10> в (/ — О- A2.70)
Используя A2.57), можно проверить, что это выражение совпа-
совпадает с обычным выражением для фейнмановского пропагатора
(9.10), (9.11) из гл. 9
*' - х) = \2Jk\lny [8 (f -1) е-*(*'-*) + 0 (/ - С) X
е	J — l 3 BL k> 2 + / б	'
(D,- + m2) AF (*' - jc) = - б4 (*' - x).
При записи AF в виде A2.71) непосредственно проявляется
лоренцева инвариантность фейнмановского пропагатора. По-
Поскольку полевые операторы коммутируют для пространственно-
подобных интервалов, их произведение в A2.70) может быть
упорядочнено по времени лоренц-инвариантным образом. Удоб-
Удобно обозначать такое упорядочение, вводя хронологический опе-
оператор Т, определенный согласно
Т(а(х)Ь(х1)) = а(х)Ь(xf)B(t — f) + b(*')а(хH(f - t). A2.72)
Оператор Т означает, что поля надо располагать справа налево
в порядке возрастания времени. Хронологическую операцию
можно применить к произведению любого числа операторов.
Фейнмановский пропагатор при этом записывается в виде
/А, (*' - х) = <01Т (Ф (*0 Ф* (jc)) 10),	A2.73)
или, в терминах эрмитовых полей,
ib4 AF (хг -х) = ф\Т (% {х') Ф/ (jc)) 10).	A2.74)

ЗАДАЧИ	51
Фейнмановский пропагатор в квантовой теории поля, как
в одночастичной теории, играет главную роль при вычислении
амплитуд перехода. Функция Af(jc', х) описывает распростране-
распространение частицы из точки х в точку х', если f > t, если же t > f,
то kF(x',x) описывает распространение античастицы из точки
х' в точку х. В результате мы получаем ту же самую физиче-
физическую картину, которая обсуждалась в гл. 6, 9 при рассмотрении
решений, отвечающих частицам и античастицам.
ЗАДАЧИ
1.	Проверить, что для скалярного поля — (г/2) euv [М^,, ф] = бф,
2.	Вычислить
(О I Ф21 0),
где
ф = -у' \
v
и V — сферическая область радиуса R.

ГЛАВА 13
ВТОРИЧНОЕ КВАНТОВАНИЕ ПОЛЯ ДИРАКА
§ 76. Квантовая механика я тождественных частиц
В предыдущих параграфах мы рассмотрели те следствия, ко-
которые возникают при каноническом квантовании поля. В резуль-
результате было получено непротиворечивое описание частиц, подчи-
подчиняющихся статистике Бозе— Эйнштейна. Описанный форма-
формализм, достаточно гибкий, чтобы включить процессы рождения
и уничтожения частиц, успешно устранил также трудности од-
ночастичной теории, связанные с решениями с отрицательной
частотой и отрицательными вероятностями.
Представляется естественным обсудить с этой точки зрения
и другие примеры многочастичных задач, рассматривая лагран-
лагранжианы, приводящие либо к уравнению Шредингера либо
к уравнению Дирака для частиц со спином 1/2. При этом, од-
однако, мы сталкиваемся с той трудностью, что при квантовании
возникают бозе — эйнштейновские частицы, в то время как из-
известно, что частицы со спином 1/2, например электроны и про-
протоны, описываются статистикой Ферми — Дирака и удовлетво-
удовлетворяют принципу запрета. Мы сталкиваемся, таким образом, с не-
необходимостью изменить некоторые промежуточные этапы кван-
квантования. Эти изменения необходимы, как мы вскоре убедимся,
и с другой точки зрения. Мы имеем в виду связь между спином
и статистикой — один из наиболее значительных результатов
квантовой теории поля.
Для того чтобы наиболее естественно ввести в метод кванто-
квантования необходимые изменения, мы временно вернемся назад
и рассмотрим многочастичную теорию фермионов, основанную
на n-частичном уравнении Шредингера, которое мы постараемся
переформулировать на языке теории поля. Другими словами,
вместо того чтобы получить многочастичную теорию в резуль-
результате квантования классического поля, как это было сделано
в предыдущей главе, мы начнем сразу с задачи п частиц, имея
при этом целью найти такую форму полевой теории, которая не
противоречит принципу запрета [16—18].

$ 76]	КВАНТОВАЯ МЕХАНИКА л ТОЖДЕСТВЕННЫХ ЧАСТИЦ	63
Рассмотрим уравнение Шредингера для п тождественных
невзаимодействующих частиц
i-^-(*i	xn;t) = №,	A3.1)
п
где Н = 2 Я (xh pi) — сумма одночастичных гамильтонианов
(=1
одинакового вида. Переменные в задаче разделяются и частное
решение имеет вид произведения
п
V (хи .... х„; t) = Д "а, (*/, t)	A3.2)
решений иа(х, t) одночастичного уравнения Шредингера
Hua(x,t) = idtt*?t) .	A3.3)
Общее решение уравнения A3.1) представляет суперпозицию
частных решений A3.2) и может быть записано в виде
	*„;/) =
с(аь .... а„)ыа1 (*i, 0 ••• «а„(ж», 0. A3.4)
где множитель 1/дЛг! выбран из соображений удобства. В фор-
формуле A3.4) N есть число одночастичных уровней. Если функ-
функции ип( (xit t) образуют ортонормированную систему, то условие
нормировки коэффициентов разложения имеет вид
N
к (а,	а„)|2=1.	A3.5)
Набор коэффициентов с в A3.4) определяет «-частичное состоя-
состояние и должен удовлетворять принципу неразличимости тожде-
тождественных частиц. Другими словами, плотность \W(х\,...,хп; t) \2
должна быть инвариантна при перестановке аргументов, т. е. W
сама по себе может быть либо симметричной, либо антисиммет-
антисимметричной функцией1). Коэффициенты c(a,i, ...,an) соответственно
симметричны или антисимметричны при перестановке индексов
с(	щ ... а/ .. .)= ± с(. ... а/ ... at...). A3.6)
Конкретный выбор знака в A3.6) ведет либо к статистике
Бозе — Эйнштейна, либо к статистике Ферми—Дирака.
') В том случае, когда сам вектор Ч? записывается в виде столбца, воз-
возможен более общий вид статистики (см. в этой связи [19—21]).

54	ВТОРИЧНОЕ КВАНТОВАНИЕ ПОЛЯ ДИРАКА	[ГЛ. 13
Уравнение A3.6) несет в себе огромное количество инфор-
информации, поскольку из него следует, что если известен какой-либо
один коэффициент с(оц, ...,ал) в A3.4), то из A3.6) получаются
остальные п\ — 1 коэффициентов. Поэтому разложение A3.4)
можно записать в более компактной форме, если упорядочить а
и определить новые коэффициенты
Г с (а,	а„), а, <а2< ... < а„,
@	в остальных случаях.
При этом разложение A3.4) в случае статистики Ферми — Ди-
Дирака может быть записано в виде
.,*„;/) =
N
^Г	(*1, 0 ••• "а„(*л, *) =
(аь .... а„)	 , A3.7)
|| «а, (хп, 0 • •. «о„ (*»> О |
где 2j — сумма по всем перестановкам Р индексов аг, 8р — чет-
четность перестановки Р.
§ 77. Представление чисел заполнения для фермионов
Информация, которую несет в себе волновая функция A3.4)
или A3.7), заключается не в том, какие именно частицы имеют
определенные квантовые числа, а в том, сколько тождествен-
тождественных частиц находится на том или ином квантовом уровне.
В этом обстоятельстве и заключается аналогия с квантово-по-
левым описанием уравнения Клейна — Гордона. Состояние
поля как n-частичной системы описывается числом квантов,
или частиц, занимающих определенный одночастичныи уровень.
Разница при этом заключается лишь в том, что в случае анти-
антисимметричного решения числа заполнения для каждого со-
состояния равны 0 или 1. Имея в виду указанную аналогию, мы
рассмотрим теперь динамику и-частичной фермионной системы
на языке квантовой теории поля.
Для начала изменим обозначения в A3.7) и вместо сумми-
суммирования по уровням аь ..., ал = 1, ..., N будем суммировать
по числам заполнения па, которые указывают, свободен (па=0)
или занят (иа=1) уровень а. Обозначим через W (хи ..., хп;
nv ..., nN; /) n-частичный детерминант Слэтера (вида A3.7)),
составленный из одночастичных волновых функций иар где
символы а(- обозначают занятые уровни. Пусть столбцы детер-

§ 77]	ПРЕДСТАВЛЕНИЕ ЧИСЕЛ ЗАПОЛНЕНИЯ ДЛЯ ФЕРМИОНОВ	55
минанта упорядочены естественным образом, т. е. сц < <х% < ...
... < а„, причем
1, если а = аг для некоторого /,
О в остальных случаях.
Например, если в системе, содержащей семь уровней, частицы
находятся на 2-м, 4-м и 5-м уровнях (ai = 2, схг = 4, аз = 5),
то
х2х3; 0101100; /) =
«2 (*1, t) «4 (*1, 0 «5 (*1, 0 II
М*а. 0 «4(дг2, 0 «6(дг2, 0 . A3.8)
«2 (*3, 0 «4 (*3. t) «5 (*з. 0 II
В новых обозначениях волновая функция A3.7) записывается
в виде
x2, ..., хп\
1
IN
A3.9)
где
с'(tt,, ..., nN) = c(a,, a2> ..., ап)	A3.10)
и числа па определены, как и раньше.
Условие нормировки теперь имеет вид
? \c'(nv .... nN)P=l,	A3.11)
откуда следует, что коэффициенты c'(nj, ..., ttN) можно интер-
интерпретировать как амплитуду вероятности появления данного
набора {ftp ..., nN}.
Для описания «-частичной фермионной системы на языке
теории поля нужно ввести удобный способ построения, исходя
из вакуумного состояния, «-частичной волновой функции. Из
предварительного рассмотрения дырок в теории Дирака (т. 1)
ясно, что центральную роль при динамическом описании си-
системы играют процессы рождения и уничтожения частиц.
Включение взаимодействия между частицами в A3.1) приведет
к переходам между состояниями с различными квантовыми чис-
числами. Поэтому нас интересует амплитуда перехода частицы из
состояния а в состояние а'.
С этой целью, следуя рецепту, сформулированному при рас-
рассмотрении теории Клейна — Гордона, введем операторы рожде-

56	ВТОРИЧНОЕ КВАНТОВАНИЕ ПОЛЯ ДИРАКА	[ГЛ. 13
ния и уничтожения, в терминах которых можно построить и свя-
связать между собой состояния а и а'. Прежде всего определим
вакуумное состояние Фо. Вакуум не содержит частиц вообще,
поэтому его импульс и энергия равны нулю. Это следует и из
решений уравнений A3.1) или A3.3). Оператор рождения опре-
определяется таким образом, что, действуя на Фо, он образует одно-
частичное состояние Фа с квантовыми числами а:
а+Ф0 = Фа = Ю0... 1 ...).	A3.12)
Прежде чем связать эти состояния с волновой функцией
в A3.1), построим простое и удобное представление. В силу
принципа запрета состояние а либо занято, либо пусто. Пред-
Представим эти две возможности столбцами „ и . соответ-
соответственно. Тогда вакуумное состояние есть произведение столб-
столбцов, отвечающих всем пустым состояниям
A3.13)
а одночастичное состояние имеет вид
°*-[Ц П [?]„¦
афа'
афа'
Оператор рождения а+, может быть поэтому представлен 2X2-
матрицей, действующей в пространстве а'-го состояния, которая,
действуя на столбец Г.] , дает Гп 1 . Эта матрица имеет вид
L 1 Ja'	L U Ja'
Г* п 1 с произвольными х и у. В силу принципа Паули опера-
оператор а+,, действуя на занятое состояние 0 ,' дает нулевой
вектор. Поэтому мы положим х — у = 0, тогда
-	03.15)
Аналогичным образом из условий аа' [0] , = [ j ] , и аа' Г j J ,=0
находим оператор уничтожения
па-
-[? II-

§ 77]	ПРЕДСТАВЛЕНИЕ ЧИСЕЛ ЗАПОЛНЕНИЯ ДЛЯ ФЕРМИОНОВ	57
эрмитово сопряженный а+.. Из A3.15) и A3.16) получаем набор
антикоммутационных соотношений') для аа, и а+,
{а*>,аа'} = 0,	A3.17a)
К'. а+} = 0,	A3.176)
К'. <'} = [о ij^1-	A3Л7В)
Таким образом, принцип Паули приводит вместо коммута^
торов A2.10) в теории бозонов к антикоммутационным соотно-
соотношениям для операторов рождения и уничтожения. Уравнения
A3.17а) и A3.176) выражают тот факт, что нельзя создать или
уничтожить два фермиона в одном и том же состоянии. Соб-
Собственные значения произведения «?«„' = 0 0 Для занятого
и пустого состояний равны 1 и 0 соответственно. Это произве-
произведение имеет смысл оператора числа частиц, который обозначим
Na, = а+аа,.
Оператор Na> отличается от оператора числа частиц для
бозонов, поскольку его собственные значения равны 0 и 1.
Теперь можно простым образом связать результаты, полу-
полученные на языке одночастичных волновых функций иа(х), с на-
нашим операторным формализмом. Определим полевые опера-
операторы:
N	N
%(х, t)= ? иа(х, t)aa, %*(х, 0= Z u'a(x, t)a+. A3.18)
а=1	' а=1
Тогда волновая функция uai (x, t) равна матричному элементу
поля %(х, t) между вакуумным состоянием Фо и одночастичным
состоянием Фа;:
(Фо, %(*, t), Фа,)«ич(X, t).	A3.19)
Действуя в том же духе, можно получить из поля «-частич-
«-частичную волновую функцию A3.8), а также гамильтониан, соб-
собственные значения которого совпадают со спектром оператора Н
в A3.1). С этой целью рассмотрим состояния, содержащие не-
несколько частиц. Операторы аа и а+ в A3.15), A3.16) комму-
') Матрицы A3.15), A3.16) и соотношения A3.17) показывают, что су-
существует полная аналогия между операторами аа>, aj и матрицами Паули
Ох—iOg, Ox-\-iOy. Вакуумное состояние A3.13) отвечает спиновому состоя-
состоянию, в котором все спины направлены вниз; оператор aj переворачивает
спин a'-го состояния; таким образом, занятое состояние отвечает спину, на1
правленному вверх.

58	ВТОРИЧНОЕ КВАНТОВАНИЕ ПОЛЯ ДИРАКА	[ГЛ. 13
тируют с аа , а+, \ф1, поскольку они действуют в различных
подпространствах состояний. Например, если 1ф\, то
П [?Х, =фв/«?- (!3.20)
Действуя на вакуум различными операторами а+, мы получим
волновые функции, которые характеризуются некоторым поряд-
порядком состояний а. При этом Фа^а, в A3.20) симметричны при
перестановке индексов а» и а/, в то время как состояние W,
определенное выражением вида A3.8), антисимметрично. По-
Поэтому с математической точки зрения удобно изменить опера-
операторы аа, а+ таким образом, чтобы они удовлетворяли антиком-
антикоммутационным соотношениям [17] как в том случае, когда они
действуют на одинаковые состояния, так и в том случае, когда
они действуют на различные состояния. Это, в частности, озна-
означает, что для различных состояний а и а' модифицированные
операторы Ь+ удовлетворяют соотношениям
btba'\O)== — ba'bt\O),	A3.21)
а не а+а+, | 0) = + at'at I ^)- Для того чт°бы обеспечить знак
минус в формуле A3.21) и в то же время сохранить интерпре-
интерпретацию bt как операторов рождения, положим
где Tia — диагональный в пространстве чисел заполнения опе-
оператор. Подставляя A3.22) в A3.21), мы видим, что для выпол-
выполнения условия A3.21) необходимо, чтобы
а+г\а = — Лва+, а+ца=х]аа+ для а,<ау. A3.23)
Диагональный оператор A — 2Na) антикоммутирует1) с а+,
поэтому
"J о°]а	<13-24>
а-1	а=»1
Оператор
Ьа = iiaaa
J) Оператор A — 2JVa) аналогичен матрице Паули —

§ 77]	ПРЕДСТАВЛЕНИЕ ЧИСЕЛ ЗАПОЛНЕНИЯ ДЛЯ ФЕРМИОНОВ	59
эрмитово сопряжен bt; его можно интерпретировать как опе-
оператор уничтожения. Оператор bt., действуя на свободное со-
состояние 1,1 , дает состояние „ с фазой +1 или —1,
которая зависит от того, четное или нечетное число частиц
находится на уровнях а < аг, поэтому состояние, в котором
заняты уровни щ и а/; антисимметрично при перестановке
индексов а,- и а;-. Операторы Ьа и bt удовлетворяют тем же
антикоммутационным соотношениям, что и аа и а+
{bt , bt} = {&«, ba} = 0, {&„, bt} = 1.	A3.25)
Более того, справедливы и более общие коммутационные соот-
соотношения
{Ьа, bt'} = б„«', {ba, ba'} = {bt, bt'} = 0,	A3.26)
которые могут быть проверены непосредственным вычислением.
Например, при а > а'
&А' + К'К = ^ЛАЛ' + \'аа'ааПа =
К'К
Оператор числа частиц в терминах 6 и J+ равен просто
Na = aiaa = biba.	(I3.27)
Состояния
Г---Ю'в---(*.+)в1Фо-Ф(».. ••-. «n) A3.28)
являются собственными функциями оператора Na и образуют
полный ортогональный набор
(Ф {п[, ..., п'н), Ф (пр ..., nN)) = Ц Ч»«-
Образовав произвольную суперпозицию, получим
0)"N (Г)"фо' A3.29)
причем коэффициенты с'(я,, ..., rtN) имеют смысл соответ-
соответствующих амплитуд вероятностей:
(ф, ф)= Z К (я,	О|2 Aз.зо)

60	ВТОРИЧНОЕ КВАНТОВАНИЕ ПОЛЯ ДИРАКА	[ГЛ. 13
и могут быть поэтому отождествлены с коэффициентами
в сумме A3.9). Неисчезающие матричные элементы операто-
операторов 6а и bt равны
«р ••¦» ftN)) =
(-)"'"*'. если па = п'а для a=^aft и «aft = 0; <fe=L (J3 g
О в остальных случаях,
О в остальных случаях,
(—)" , если па = п'а для а^ай и п'а = 0; па =1,
N	N
где п = 2 na, я' = X rta> aft ~ ^"" член упорядоченного набора
a=l	a=l
{a1( a2, ..., an}, aft, — k'-ft член набора {a[, ..., a^,J.
Точно так же как были построены одночастичные волновые
функции A3.19), можно построить и антисимметричные «-час-
«-частичные волновые функции. С этой целью введем полевой опера-
оператор q>(x,t), который отличается от A3.18) тем, что операторы
аа заменены в нем на взаимно антиком мутирующие опера-
операторы Ьа:
N	N
Ф (*, 0 = S «а (*, О К, Ф* (Ж, 0 = S < (Ж, 0 *+. A3.32)
а-1	а=1
Образовав матричный элемент между вакуумом и произволь-
произвольным состоянием Ф вида A3.29) от произведения п полевых
амплитуд ф(дс,-, t), получим с учетом A3.31)
-j=r (Фо, Ф(*ь 0 • • • Ф(ж„, О Ф) = ^ (ж,, ..., *„; 0, A3.33)
где W — антисимметричная волновая функция A3.9) системы
п частиц.
С помощью антикоммутационных соотношений для операто-
операторов рождения и уничтожения можно получить антикоммута-

§ 77]	ПРЕДСТАВЛЕНИЕ ЧИСЕЛ ЗАПОЛНЕНИЯ ДЛЯ ФЕРМИОНОВ	61
ционные соотношения для операторов ') ф и Ф*:
{<р(*. 0, ф (*',*)} = о,
{Ф*(ж, 0, ф*(х',0} = 0,
N
{ф (*, О, Ф* (*', 0} = S К, &?} «а (*, 0 "а' (*', /) =
а, а'=1
= Z иа (*, 0 < (*', 0 = б3 (х - х'). A3.34)
а=1
Используя построенные операторы и векторы состояния,
можно теперь сняться с якоря, оставив язык волновой функции,
и перейти к формулировке Xf-частичного уравнения Шредин-
гера A3.1) в теории квантовых полей. Перепишем уравнение
A3.3) в терминах полевого оператора A3.32)
t) = idv{*t't) .	A3.35)
По аналогии с теорией Клейна — Гордона это уравнение можно
рассматривать как уравнение для классического поля ф, полу-
полученного из соответствующего лагранжиана. Наложив коммута-
коммутационные соотношения A3.34),мы интерпретируем далее A3.35)
как операторное уравнение, причем главное его отличие от урав-
уравнения Клейна — Гордона заключается в использовании анти-
антикоммутаторов вместо коммутаторов. Это отличие приводит
к статистике Ферми — Дирака вместо статистики Бозе — Эйн-
Эйнштейна. Описанная процедура носит название вторичного кван-
квантования. При первом квантовании координаты классической
частицы заменяются на квантовомеханические операторы, дей-
действующие в пространстве волновых функций. После этого одно-
частичное уравнение Шредингера само рассматривается как
полевое уравнение, причем, налагая квантовые условия на
амплитуды поля, мы получаем операторы, удовлетворяющие со-
соотношениям A3.14). Выше мы показали, что новый подход при-
приводит к тем же результатам, что и многочастичное уравнение
Шредингера. Коэффициенты разложения с' (п{, ..., nN) как
в A3.9), так и в A3.29) описывают состояние и-частичной систе-
системы в том или ином формализме. Полная энергия, выраженная
') Здесь мы видим преимущество введения операторов 6J вместо а*.
Уравнения A3.33) и A3.34) не имеют столь простого вида, если использовать-
р	) (
в A3.28) операторы а+.

62	ВТОРИЧНОЕ КВАНТОВАНИЕ ПОЛЯ ДИРАКА	[ГЛ. 13
через волновые функции, равна, согласно A3.9),
п
H (*„ Pi) У (ж,, ...,*„; О =
N \
A3.36)
Это выражение можно рассматривать также как среднее зна-
значение оператора гамильтониана
(дс, р)<р(дс, 0 =
N
М .«.=Е^.	A3<37)
о=1
в состоянии A3.29), причем Н, как и следовало ожидать, имеет
смысл гамильтонового оператора поля.
В заключение построим функцию Грина, описывающую рас-
распространение частицы от точки (х, t) до точки (х\ t') (f > t)
и сравним ответ с результатами гл. 6. Для этого нам нужна
амплитуда вероятности рождения частицы из вакуума в точке
(х, t) и последующего ее уничтожения при (х\ ?).
Волновая функция частицы, локализованной в точке х, про-
пропорциональна
% {х', 0 = б3 (х - х') = Z иа {х', 0 < (х, t). A3.38)
a=l
Из сравнения A3.38) с A3.9) и A3.29) получаем аналог
A3.38) в методе вторичного квантования
N
?,(*, 0= Е«а(*. О^Фо = Ф*(*, ОФо.	A3.39)
а=1
Функция Грина получается, если спроектировать Wi {x, t)
для частицы, образованной в точке (x,t), на одночастичное со-
состояние Vi {x1, ?) в более поздний момент времени t' > t:
G (xr, t'\ x, t) = - i (T, (*', f), V, (x, t)) 9 (*' - 0 =
= _ /e (r - о (o | Ф (х', о Ф* (*, t) | o).
Используя A3.31) и A3.32), мы приводим это выражение к виду
G (*', f; x,t) = - iQ (f - 0 Z ио (*', О < (ДС, t),
который совпадает с результатом F.28), полученным для за*
паздывающей функции Грина в гл. 6.

§ 78]	ТЕОРИЯ ДИРАКА	63
Мы закончим наше сопоставление многочастичной теории
и вторично-квантованного уравнения Шредингера, отметив два
преимущества теоретико-полевого описания. Эти преимущества
проявляются при вычислении матричных элементов, представ-
представляющих физический интерес, и привели в последнее время
к широкому использованию методов теории поля в нерелятиви-
нерелятивистской задаче многих тел. Во-первых, операторы Ьа и bt по
своему построению автоматически обеспечивают антисимметрию
волновых функций. Во-вторых, в терминах этих операторов мы
получаем достаточно гибкий и в то же время простой и есте-
естественный язык для описания физических систем с переменным
числом степеней свободы.
§ 78. Теория Дирака
Вернемся теперь к основному содержанию настоящей главы,
а именно — к уравнению Дирака. Чтобы подчеркнуть близкую
аналогию с теорией Клейна — Гордона, перейдем вначале
к лагранжиану. Будем рассматривать 4 компоненты поля if>a
и 4 компоненты сопряженного поля "фа как 8 независимых пе-
переменных.
Построим лагранжиан, исходя из свободного уравнения Ди-
Дирака
(/V - т) ф = 0.	A3.40)
Умножив это уравнение слева на бф и проинтегрируем по про-
пространственно-временным координатам от t\ до t%-
0 = \ й*х бф (jc) (/V - m) ф (jc) = в J d*x ф (jc) (iV - /га) ф (*). A3.41)
Из A3.41) следует выражение для плотности лагранжиана
= i> (x) (iV - /га) ф (х).	A3.42)
Варьируя действие в A3.41) по if), получим сопряженное урав-
уравнение
¦ф (- iV - т) = 0.
Канонический метод дает импульс, сопряженный ifi:
Я'*	A343)
Поскольку A3.41) не содержит производных ty, импульс, со-
сопряженный 1|)ц, равен нулю, а из уравнения A3.41) следует, что

64	ВТОРИЧНОЕ КВАНТОВАНИЕ ПОЛЯ ДИРАКА	[ГЛ. 13
ity* есть импульс, сопряженный г|>а. В результате получим га-
мильтонову плотность
Ж = mj> - % = if+ (- /а • V + pm) г|) = ф+f-^ ф, A3.44)
причем последнее выражение в A3.44) следует из уравнения
Дирака. Такой вид — одночастичный гамильтониан, зажатый
между двумя спинорами, — согласуется с результатом в A3.37),
полученным из нерелятивистского рассмотрения.
Из инвариантности & при трансляциях и лоренцевых пре-
преобразованиях следует полный набор законов сохранения энер-
энергии, импульса и углового момента. Из A1.48) и A1.49) находим
4r-b	A3.45)
откуда, с учетом A1.49), получаем выражения для операторов
энергии и импульса
Н= \ /00 d\= \ г|э+ (- /а • V + рт) г|) с?х,
03-46)
+V Л
Оператор плотности углового момента ж и сохраняющийся
зого моме*
M.VA.	 .-. а ,
оператор углового момента Mvl равны
где Sv^ = 'AlV. Y^] — спинорная матрица лоренцевых враще-
вращений, которая добавляется к спиновому угловому моменту в ЗЯ^.
В частности, для пространственных компонент получаем
03.48)
Это выражение имеет обычный вид суммы орбитального и спи-
спинового углового момента, / = L -f S.
Для свободного уравнения Дирака можно определить еще
один закон сохранения, если вспомнить, что из этого уравнения
A3.49)
следует \ = 0 и что поэтому величина
ОХ

§ 79)	РАЗЛОЖЕНИЕ В ИМПУЛЬСНОМ ПРОСТРАНСТВЕ	65
имеет смысл постоянного полного «заряда». Этот заряд анало-
аналогичен сохраняющемуся заряду A2.63) в теории Клейна — Гор-
Гордона с неэрмитовыми полями.
Далее, чтобы получить полную квантовую теорию, нам
остается только наложить коммутационные соотношения. Мы
уже знаем, однако, что использование коммутационных соотно-
соотношений A1.39) приводит к системе многих частиц, которые под-
подчиняются статистике Бозе — Эйнштейна. Поэтому, чтобы при
построении квантовой теории электронов учесть принцип Паули,
мы должны, как в предыдущем разделе, использовать не ком-
коммутаторы, а антикоммутаторы.
§ 79. Разложение в импульсном пространстве
Обратимся теперь к квантованию уравнения Дирака. Вна-
Вначале перейдем в импульсное пространство и введем операторы
рождения и уничтожения. После этого мы сможем непосред-
непосредственно применить метод, обсуждавшийся в начале главы, при-
причем для квантования нам нужны операторы вида A3.32), ко-
которые рождают частицы с учетом принципа Паули.
Общий вид разложения по плоским волнам для решения
свободного уравнения Дирака A3.40) в соответствии с резуль-
результатами гл. 3 имеет вид
ф (х, t) = Yj \ ^'з/2 y-jT № fa' s) " fa' s) e~iPX +
+ d+ (p, s) v (p, s) eipx\
- *>=z S
A3.50)
dip, s)v(p, s)yoe~ipxl
где Ep = po — + Vl P I2 + ot2 • В гл. З были выведены следую-
следующие полезные соотношения для спиноров') и (р, s) и v (p, s):
а) Уравнение Дирака
{р-т)и(р, s) = 0, п(р, s)(p-—m) = 0,
{Р + т) v (p, s) = 0, v(p,
') См., например, C.16) и C.30). Напомним, что u{—p,s) означает
« (Vp2 + т2' ~ Р> s)< т- е- знак энергии в аргументе спинора всегда выби-
выбирается положительным. Нормировка амплитуд Ь и Ь+ выбрана так, чтобы
кванты поля имели заряд ±1.

66	ВТОРИЧНОЕ КВАНТОВАНИЕ ПОЛЯ ДИРАКА	(ГЛ. 13
-б) Ортогональность
п (р, s) и (р, s') = 6SS> = — v(p,s)v (р, s'),
и+(р, s)u(p, s') = ^-6SS'=u+(p, s)v(p, s'), A3.51)
v (p, s) и (p, s') = 0 = v+ (p, s) и (— p, s').
в) Полнота
Z [«a (P, S) Up (/>, S) - Va (p, S) Op (p, S)] = 6ap)
«a (P. S) п, (p, S) = (-4^-) - (A+ (P))ap,
- E u° (^>s) u"a </>'s)=
При вторичном квантовании дираковского поля коэффи-
коэффициенты разложения b(p,c), b+(p,s), d(p,s) и d+(p,s) стано-
становятся операторами, которые уничтожают и рождают частицы.
Поскольку в нашем случае необходимо учесть требования прин-
принципа Паули, эти операторы следует подчинить антикоммута-
антикоммутационным соотношениям вида A3.26). В непрерывных обозна-
обозначениях A3.50) имеем
{Ыр, s), Ь+(р', s')} = bSS'V{p-p'),
{d(p,s), d+{p', S')} = 6^63(p-p'),
{b (p, s), b (/>', s')} = {d (p, s), d {pr, s')} =0,
{b+ (p, s), b+ (//, s')} = {d+ (p, s), d+ (p', s'j} = 0, •
{b(p, s), d{pr, s')) = {b{p, s), d+(p', s')} = 0,
{dip, s), Ыр', s')} = {dip, s), b+ipr, s')} = 0.
Отсюда легко вывести антикоммутационные соотношения
для полей A3.50). Например, с учетом A3.51) находим
±s, ±s'
X [ua (p, s) 6t 0»', s0 Y°pe"-<*-*'> + oa (p, s) уг (р', s') vSp
(W W «(^ + m> Y°]a3 e"'<*-^ - [(m - p) Y°]a3 e

§ 79]	РАЗЛОЖЕНИЕ В ИМПУЛЬСНОМ ПРОСТРАНСТВЕ	67
Аналогичным образом можно получить
(х, О, Ч> (*', П) = 0, {ф+ (х, t), г|)+ (ж', О} = 0. A3.54)
Как и в шредингеровской теории, мы интерпретируем Ь+ и d
как операторы рождения для электронов. В теории Дирака
мы сталкиваемся, однако, с той трудностью, что операторы d
рождают состояния с отрицательной энергией. Это легко уви-
увидеть, если выразить энергию и импульс в терминах операторов
b, d, b+ и d+. Подставляя A3.50) в A3.46) и используя A3.51),
получаем
)) [2п/ Vxfc Ep'X
±s, ±s'	и н
X[b+(p, s)u(p, s)yoeipx+d(p, s)v(p, s)yoe-tpxlX
X [b (/>', s') и (p't s') e~ip'x - d+- (//, s') v (pr, s') eip'x]
= 2 \<?pm [b+ (p, s) b (p, s') u+ (p,s)u (p, s') -
±5, ±5'
- d (p, s) d+ (p, s') v+ (p, s) v (p, s')] =
ip's)b{p>s)~d{p>s)d+ (p's)]- A3>55)
Аналогичным образом
(P, s)b(p, s)-d(p, s)d+(p, s)l A3.56)
±s
Из этих выражений и из A3.52) следует, что d(p,s) рождает
частицу с отрицательной энергией —Ер и импульсом —р,
a b+(p,s) рождает частицу с положительной энергией Ер и им-
импульсом р, что же касается операторов d+(p,s) и b(p,s), то они
имеют смысл соответствующих операторов уничтожения.
Отметим также, что гамильтониан в A3.55) не является
положительно определенным оператором. Это приводит к оче-
очевидной трудности в теории, поскольку в этом случае всегда
можно построить состояние с энергией, меньшей любой наперед
заданной, добавляя необходимое количество частиц с отрица-
отрицательной энергией. Тем не менее эту трудность можно устранить,
используя теорию дырок, которая обсуждалась в гл. 5. Со-
Согласно этой теории вакуум определяется как состояние, в кото-
котором заполнены все состояния с отрицательной энергией и сво-
свободны лишь уровни с положительной энергией. Тот факт, что
подобное определение вакуума в принципе возможно, суще-

68	ВТОРИЧНОЕ КВАНТОВАНИЕ ПОЛЯ ДИРАКА	(ГЛ. 13
ственным образом опирается на принцип Паули и метод кван-
квантования с антикоммутационными соотношениями. При попытке
квантования поля Дирака с коммутаторами мы немедленно
столкнулись бы с фундаментальными неразрешимыми противо-
противоречиями. Согласно статистике Бозе — Эйнштейна, в любое дан-
данное состояние всегда можно добавить неограниченное число час-
частиц, при этом для гамильтониана A3.55) не существует основ-
основного состояния с наименьшей энергией. Связь между антиком-
антикоммутаторами и теорией Дирака является частным случаем
фундаментальной теоремы в теории локального, лоренц-инва-
риантного поля. Эта теорема, впервые доказанная Паули
в 1940 г., утверждает, что частицы с полуцелым спином подчи-
подчиняются статистике Ферми — Дирака, а частицы с целым спином
подчиняются статистике Бозе — Эйнштейна1). В гл. 16 мы рас-
рассмотрим этот вопрос с более общей точки зрения.
Возвращаясь к теории дырок, перепишем 4-вектор энергии-
импульса в виде
Pu=?$d3ppw!>+(P, s)b(p, s) +
±s
+ d+ (p, s) d (p, s) - {d (p, s), d+ (p, s))l A3.57)
При действии на вакуум первые два члена в A3.57) дают нуль,
поскольку в состоянии вакуума нет электронов с положительной
энергией и дырок с отрицательной энергией. Последний же член
в A3.57) дает бесконечную константу. Эту константу можно
не учитывать, если все энергии и импульсы отсчитывать от
энергии и импульса вакуума. Выполнение же последнего усло-
условия можно обеспечить, переопределив Р& в терминах нормаль-
нормальных произведений полевых амплитуд. Произведение операторов
полей в нормальной форме пишется так, что положительно-
частотные части
') См. [22]. Если нарушить связь спина со статистикой в выражениях
A2.14) и A2.15) для квантов со спином 0, то 4-вектор энергии-импульса не
будет более представлять собой оператор, собственные векторы которого опи-
описывают физические состояния системы, а сведется лишь к бесконечной кон-
константе.

§ 79]	РАЗЛОЖЕНИЕ В ИМПУЛЬСНОМ ПРОСТРАНСТВЕ	69
стоят всегда справа от отрицательно-частотных частей
Для антикоммутирующих полей нормальное произведение опре-
определяется так, что каждый член меняет знак при каждой пере-
перестановке, необходимой для приведения полей к нормальной
форме, например:
При таком определении билинейная форма 4-вектора энергии-
импульса только с-числом отличается от
" (р, s) b (p, s) + d+ (p, s) d (p, s)]. A3.59)
±s
Оператор b(p,s) уничтожает, а опеоатор b+(p,s) рождает
электроны с положительной энергией; по аналогии с теорией
Клейна — Гордона можно ввести оператор числа частиц
iV(+> (p, s) = b+ (p, s) b (p, s).
Собственные значения оператора N<-+){p,s)d3p равны числу
электронов со спином s в интервале импульсов dzp. Оператор
d+(p,s) уничтожает электроны с отрицательной энергией; этот
процесс в теории дырок рассматривается как рождение пози-
позитрона. Аналогично d(p,s) уничтожает позитрон, и
iV*"' (p, s) = d+ (p, s) d (p, s)
есть оператор числа частиц с положительной энергией. Выраже-
Выражение A3.59) содержит вклад частиц обоих сортов
яр рц О(+) (р, s) + N{~] (p, s)].	A3.60)
j
±s
Аналогичным образом можно построить оператор заряда.
Подставляя A3.50) в A3.49) и учитывая нормальный порядок
операторов, получим прямым вычислением
У* \ d%p : b+ (p, s) b (p, s) -f- d (p, s) d+ (p, s): =
±s
= ?$d3p[iV(+)(p, s)-N{-)(p, s)l A3.61)
±s

70	ВТОРИЧНОЕ КВАНТОВАНИЕ ПОЛЯ ДИРАКА	[ГЛ. 13
Нормальное упорядочивание в A3.61) позволяет избавиться от
бесконечной константы — полного заряда всех электронов с от-
отрицательными энергиями. В выражениях A3.60) и A3.61) про-
проявляется симметрия квантовой теории поля Дирака относитель-
относительно перестановки электронов и позитронов, имеющих одинаковые
массы, но противоположные заряды. В гл. 5 мы уже обсуждали
зарядовую симметрию в применении к теории позитрона. При
этом сохраняющийся ток фу^г)) был связан с электромагнитным
полем и заряд A3.61) рассматривался именно как электриче-
электрический заряд. Такое отождествление основывается на классиче-
классической аналогии, тем не менее возможна и более общая интерпре-
интерпретация сохраняющегося заряда — мы обсудим ее в гл. 15.
Рассмотрим теперь оператор углового момента. С учетом нор-
нормального порядка операторных множителей в A3.48), легко по-
показать, что состояние, в котором позитрон находится в покое и
имеет проекцию спина +1 на ось г
Wi positron = d+ (р, S) | 0),
p = (m, 0,0,0), s = @, 0,0,4-1)	A3.62)
есть собственное состояние оператора
отвечающее собственному значению +1/2, и поэтому действи-
действительно описывает частицу с проекцией спина +1/2. Запишем
далее
JJVl positron = [/„ d+(p, S)]|O),
где использовано соотношение /2| 0) = 0, и вычислим коммутатор:
*г » 1 positron ==
Vf	, 7
Так как оператор углового момента Ьг = —/(гХ^)г эрми-
эрмитов, мы можем подействовать им налево, при этом для частицы
в покое Lz->0'). Поскольку при нашем выборе s в A3.62) спи-
спинор v(p, s) равен
0-
— Jл ТЯ* Vf '-""* <*• s> [(' X 7
о(р, s)= I .
') Для строгого доказательства возможности проведения интегрирования
по частям лучше использовать вместо плоских волн волновые пакеты.

§ sol	Релятивистская ковариантность	71
мы получаем
v+(p, s)az=-v+(p, s),
Wi positron = + \\ dZ)C-^e~i
= '/2d+ (p, S) | 0) = + 7^1 positron.
Таким образом, метод вторичного квантования в сочетании с
теорией дырок приводит к разумному результату: спин позит-
позитрона противоположен спину дополнительного электрона с отри-
отрицательной энергией.
§ 80. Релятивистская ковариантность
Квантовая теория поля Дирака инвариантна при трансля-
трансляциях и преобразованиях Лоренца. Чтобы убедиться в этом, до-
достаточно проверить совместность антикоммутационных соотно-
соотношений A3.53) и A3.54) и гейзенберговских уравнений A1.70)
и A1.73):
A3.63)
Эта проверка с использованием выражений A3.46) и A3.47)
для Р» и М^ производится непосредственным вычислением, ко-
которое мы оставляем читателю в качестве упражнения.
Поскольку явное решение A3.50) для свободного поля Ди-
Дирака известно, можно вычислить антикоммутационные соотноше-
соотношения и для неравных времен, причем результат может быть запи-
записан в ковариантном виде. Рассматривая A3.53) при неравных
временах, получим
, 0, <(*', t')} =
?	*) - [(т - Р) Y°]
= \
где А(х — х')—инвариантная сингулярная функция, определен-
определенная выражением A2.37).
Умножив антикоммутатор на y°> приведем его к виду
(Фа (х), % (х')} = i {Ях + т)ч Л (х - х') =э - /Sap (х - х'). A3.64)

72	ВТОРИЧНОЕ КВАНТОВАНИЕ ПОЛЯ ДИРАКА	[ГЛ. 13
Проделав аналогичные вычисления для антикоммутаторов
A3.54), получим
{4>а (X), % {X')} = Й« (X), % {X')} = 0.	A3.65)
В ковариантности этих выражений можно убедиться, подей-
подействовав на поля лоренцевым преобразованием A1.67)
U (а, Ь) ф (х) U (a, b)~l -¦= S~x (а) г|) (ах + Ь),
причем для спинорного поля матрица S удовлетворяет условию
Правая часть в A3.64) есть с-число и не изменяется при пре-
преобразовании U (а, Ь) ... U~l (a, b) с унитарными операторами U.
В левой же части получаем
U(а, Ь){%(х), фр(*')} и'1 (а, Ь) =
= Sax (а) {ЧЧ (ах + Ь), ^ (ах1 + Ь)} $ч (а) =
*= Sex1 (a) (- Vax + im),k Sk& (а) Д (ах - ах') =
Где учтено, что Д(ж — х') — инвариантная функция и
S~\a) WaxS(a) — Vx. Тем самым мы видим, что выражение A3.64)
ковариантно, поскольку обе части его преобразуются при лорен-
цевых преобразованиях одинаковым образом. Аналогичный ре-
результат сразу же получается для антикоммутаторов в A3.65).
В § 72 мы уже показали, что функция А(х — у) равна нулю для
пространственно-временных интервалов (х — уJ < 0; то же са-
самое относится, следовательно, и к S(x — у). Поэтому, хотя сами
по себе поля при (х — г/J<0 и не коммутируют, билинейные
формы, локальным образом построенные из полей, коммути-
коммутируют, если только координаты разделены пространственно-по-
пространственно-подобным интервалом:
[Фа М % (X), ^ (-0 Фх (*')] = ^а (X) {% (X), ^ (*')}
- Йа (X), Ук (X')} % (X) фх (X') + ^ (X') t« (X) {% (X),
х), Цх(х')}%(х) = 0 для (x~x'f<0. A3.66)
Так как все амплитуды, которым можно придать тот или иной
физический смысл, например плотность заряда или импульса,
содержат билинейные произведения операторов и удовлетво-
удовлетворяют условию A3.66), то теория Дирака, так же как и теория
Клейна — Гордона, согласуется с нашим интуитивным представ-
представлением о микропричинности.

§ 81]	ФЕЙНМАНОВСКИЙ ПРОПАГАТОР В ТЕОРИИ ДИРАКА	73
§ 81. Фейнмановский пропагатор в теории Дирака
В заключение построим одночастичную функцию Грина, со-
соответствующую фейнмановскому пропагатору в позитронной тео-
теории. Амплитуда, описывающая рождение позитрона в точке
х = (х, t), равна
где индекс а = 1, 2, 3, 4 нумерует спинорные	компоненты.
Амплитуда, описывающая распространение этого	электрона в
точку х' (при V>t), описывается спин-тензором
WIW-0-	A3.67)
Согласно результатам гл. 6 фейнмановский пропагатор не зану-
ляется при ? < t, поскольку наряду с распространением элек-
электрона он описывает также распространение позитрона с положи-
положительной энергией, рожденного в точке х' и движущегося вперед
во времени в точку х, где он уничтожается. Как и в уравнении
Клейна — Гордона, соответствующая амплитуда получается пе-
перестановкой операторов в A3.67):
<0Ц>+(/I|>э(х)|0>.	A3.68)
Каждая из амплитуд A3.67), A3.68) увеличивает на еди-
единицу заряд в точке х' и уменьшает его на единицу в точке х;
взяв их разность, мы получим полную функцию Грина. Опреде-
Определим далее функцию SP(x',x) соотношением
(SF (х', х) у\а	?<0|Ч>р (*') tf (х) | 0) Э (/' - 0 +
+ / @ I < (х) % (х') 10) 9 (/ - ?), A3,69)
Легко проверить, что
(»"V*'-/n)Jl(,(S,(*/. *)YV =
= у% <° 1 {% (*'), i? (х)} 10) б (/' - о = yLs4 (*' - х).
или
(ЯХ' - т) SP {xr -х) = Ь* (х' - х).	A3.70)
Функция Sf(x' — х) совпадает с фейнмановским пропагатором,
который мы уже определили и постоянно использовали в первом
томе при рассмотрении позитронной теории. Непосредственное
вычисление матричных элементов в A3.69) приводит к знакомой
сумме по волновым функциям F.48).
В квантовой теории поля мы приходим к функции Грина,
рассматривая электроны и позитроны с положительной энергией.

74	ВТОРИЧНОЕ КВАНТОВАНИЕ ПОЛЯ ДИРАКА	[ГЛ. 13
которые всегда движутся вперед во времени. Действительно, и
те и другие симметрично содержатся в выражении A3.69), при-
причем относительный знак двух членов в A3.69) выбран так, что-
чтобы получить затем антикоммутатор в формуле A3.70). В по-
зитронной же теории мы рассматриваем распространение за-
заряда, который движется либо вперед, либо назад во времени в
зависимости от знака энергии. Подобное отождествление пози-
позитрона с положительной энергией, движущегося вперед по вре-
времени с электроном с отрицательной энергией, движущимся на-
назад во времени, уже встречалось в гл. 5.
Фейнмановский пропагатор A3.69) играет центральную роль
при различного рода вычислениях в теории поля. Его можно
выразить в более компактной форме, если ввести хронологиче-
ски-упорядоченное произведение полей, которое уже встречалось
в A3.69) на примере уравнения Клейна — Гордона. Для того
чтобы учесть знак минус в A3.69), мы изменим определение
Г-операции, вводя минус для каждой перестановки полей, ко-
которые квантуются с антикоммутаторами. Другими словами, для
двух полей Ферми — Дирака а(х) и Ъ(х)
Т (а (х) b {х')) = а(х)Ь (xr) Q(t-t')-b (x') а (х) 9 {f -1) =
= -T{btf)a(x)). A3.71)
В результате фейнмановский пропагатор равен
Sf(*'. x\a = -i@\TOp(*'), &(*)I0).	A3.72)
ЗАДАЧИ
1. Выписать л-частичный гамильтониан в уравнении Шредингера и в
квантовой теории поля с учетом двухчастичных потенциалов взаимодействия.
р	у	у
2.	Доказать, что -^— Эй1^ = 0 и что оператор MvK = \ d3x SKOv71 равен
Здг	J
не зависящей от времени константе.
3.	Проверить A3.54) и A3.56).
4.	Вывести уравнения A3.63); получить соответствующий результат в
р-пространстве.

ГЛАВА 14
КВАНТОВАНИЕ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ
§ 82. Введение
Поскольку электромагнитное поле является классической
наблюдаемой, казалось бы, что его квантование следует рас-
рассмотреть в первую очередь. По иронии судьбы, однако, из всех
рассматриваемых полей это поле наиболее трудно для кванто-
квантования. В частности, наиболее распространенный метод кванто-
квантования электромагнитного поля, развитый Гупта и Блейером
[23], противоречит одному из важнейших принципов теории
поля, которого мы до сих пор неукоснительно придержива-
придерживались, — постулату положительной вероятности. Возможен тем не
менее и канонический метод квантования. В действительности
именно каноническим способом и было в 1929 г. впервые про-
квантовано электромагнитное поле [24]. Однако этот способ об-
обладает тем недостатком, что процедура квантования не обладает
явной ковариантностью. Метод Гупта — Блейера, возникший
лишь двадцать лет спустя, был стимулирован развитием совре-
современной техники ковариантного вычисления в теории поля. Этот
метод обеспечивает ковариантную формулировку квантования,
хотя и ценой потери ясной физической интерпретации.
В.нашем изложении мы будем следовать канонической схе-
схеме квантования. Метод Гупта — Блейера изложен во многих
учебниках, например у Швебера, Яуха и Рорлиха, Боголюбова
и Ширкова, Ахиезера и Берестецкого [25—28].
Трудности при квантовании возникают из-за использования
числа переменных большего, чем число независимых степеней
свободы. Электромагнитное поле обычно описывается в терми-
терминах четырех компонент вектора потенциала Ап. Хотя непосред-
непосредственный физический смысл имеют напряженности поля, опре-
определяемые тензором

76	КВАНТОВАНИЕ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ	[ГЛ. 14
именно потенциалы А^ естественным образом входят в члены с
взаимодействием и в амплитуды перехода. Мы уже сталкива-
сталкивались с этим обстоятельством при выполнении расчетов в пер-
первом томе. Но четыре компоненты Ап не могут одновременно
рассматриваться как независимые переменные. Поэтому канони-
каноническая схема квантования приводит к ряду трудностей. Именно
с этими трудностями мы уже сталкивались при попытке приме-
применить классический канонический формализм для максвеллов-
ского поля.
Все вышесказанное непосредственно связано с тем обстоя-
обстоятельством, что разложение электромагнитного поля по плоским
волнам содержит только поперечные компоненты, т. е. волны, век-
вектор поляризации которых пространственно-подобен и ортогона-
ортогонален волновому вектору. Условие поперечности накладывает огра-
ограничения на ориентацию вектора-потенциала. Динамическими же
переменными являются только две поперечные компоненты век-
вектора-потенциала, только их и нужно рассматривать при кванто-
квантовании. С другой стороны, не существует какого-либо инвариант-
инвариантного способа выбрать два независимых поперечных вектора по-
поляризации, отвечающих данному волновому вектору, поскольку
всегда существует набор выделенных лоренцевых систем, в ко-
которых зануляется временная компонента каждого вектора поля-
поляризации. Именно в этом месте и начинаются трудности с лорен-
лоренцевои ковариантностью. Вскоре, когда мы детально рассмотрим
квантование, это обстоятельство станет даже слишком оче-
очевидным.
При последующем рассмотрении мы отбросим требование яв-
явной лоренцевои ковариантности и выберем векторы поляризации
фотона каким-либо специальным образом. При этом мы исхо-
исходим, однако, из лоренц-инвариантных уравнений для максвел-
ловского поля, и в конце концов, когда дым рассеется, мы полу-
получим те же самые ковариантные правила вычислений, которые
были уже выведены в гл. 7, 8 с помощью более или менее ин-
интуитивных соображений. Эти правила дают одинаковый резуль-
результат во всех лоренцевых системах.
§ 83. Квантование
Компоненты напряженностей электромагнитного поля Е и В
образуют антисимметричный тензор второго ранга, обозначае-
обозначаемый через
x	Ey Ег
pv-v	 I — cx 0	Bz	— By
1 " -Bz	0 Bx
By	~BX 0 -I
A4.2)

§ 831	КВАНТОВАНИЕ	ff
Связь F»v(x) с векторным потенциалом А»-(х) — (ф, А) дается,
согласно A4.1), уравнениями
А, B = VXA.	A4.3)
Эти уравнения можно написать в виде двух уравнений
Максвелла
VXE=-B, V.B = 0.	A4.4)
Два оставшихся уравнения Максвелла в отсутствие источников
зарядов и токов имеют вид
dxv
или
V.2? = 0, VXB = ?.	A4.5)
Ясно далее, что все компоненты поля удовлетворяют волновому
уравнению
D^VW = O.	A4.6)
Для данных напряженностей поля F^v(x) существует много
потенциалов, отличающихся друг от друга градиентным преобра-
преобразованием
Л I \\ _^ Л I \\ I ^ \ I	I \ \ F7\
™ц\л) — ^*|л \л) I ~я~1ь '	\^^•'/
где А(х) —произвольная функция х и t. Уравнение A4.7) выра-
выражает градиентную свободу в выборе векторного потенциала:
если Ац.(х) удовлетворяет уравнению A4.1), то ему удовлетво-
удовлетворяет и А^(х). Вопрос о конкретном выборе калибровки мы пока
оставим открытым.
Для того чтобы с помощью принципа Гамильтона вывести
уравнения A4.5) из лагранжиана, умножим это уравнение на
бесконечно малую вариацию ЪА^х), которая исчезает при t\ и
t2, и проинтегрируем по всему пространству и по времени в ин-
интервале {t\, <г):
и
= -1 \ Л F»y 6/vv = -1 б \ A F^\ A4.8)
и	и
и	и
Отсюда видно, что подходящей плотностью лагранжиана для
свободного максвелловского поля является выражение

78	КВАНТОВАНИЕ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ	[ГЛ. 14
При таком выборе & принцип Гамильтона воспроизводит поле-
полевые уравнения A4.5), если каждая из четырех компонент век-
вектора А^(х) рассматривается как независимая степень свободы.
Далее, используя стандартные правила, построим сопряжен-
сопряженные импульсы
i^	^	^ k. A4.10)
дА0	dAk	dxk
В результате для плотности гамильтониана получаем
з
М^ (?2+В2) + ?
у	A4.11)
а сам гамильтониан равен
Н= \d3x28 = ^d3x(E2 + B2),	A4.12)
причем последний член в A4.11) исчезает при интегрировании
по частям с использованием уравнения Максвелла
При квантовании максвелловского поля мы рассматриваем
() как оператор и вводим коммутационные соотношения ме-
между А» и каноническими импульсами пк. Попробуем близко сле-
следовать каноническому методу и рассмотрим зануляющиеся од-
одновременные коммутаторы
[A»{x,t), Лу (*',*)] = 0,
[я*(«,/), я'(*', f)] = 0,	A4.13)
[я*(*. 0,
Мы видим, что скалярный потенциал оказывается выделен-
выделенным, в результате теряется явная ковариантность теории. По-
Поскольку импульс п°(х), сопряженный А°(х), равен нулю, А°(х)
коммутирует со всеми операторами и, следовательно, является
не оператором, а с-числом в противоположность пространствен-
пространственным компонентам Ak(x). В этом месте нам приходится пожерт-
пожертвовать лоренцевой ковариантностью. Продолжая рассмотрение
канонического метода квантования, мы, однако, имеем в виду,
что исходные уравнения лоренц-коварианты. И хотя в дальней-
дальнейшем мы будем сталкиваться со многими выражениями, которые
не лоренц-, не градиентно-инвариантны, в конце концов мы об-
обнаружим, что наши физические результаты — амплитуды пере-
перехода (S-матричные элементы)—лоренц-инвариантны и не зави-
зависят от выбора калибровки.

5 83]	КВАНТОВАНИЕ	79
Для одновременных коммутаторов между потенциалами
Aj(x',t) и сопряженными импульсами nk{x,t) канонический ме-
метод дает')
[л'(х, 0, Aitf, t)] = -[El(x, t),
= - 1би63 (х - х'). A4.14)
Однако эти уравнения противоречат уравнениям Максвелла. За-
Закон Гаусса
не содержит производных по времени и накладывает ограниче-
ограничение на электрическое поле. Поэтому дивергенция от левой части
A4.14) равна нулю, а дивергенция от правой части, содержа-
содержащей б-функцию, нулю не равна. Удобно записать эту диверген-
дивергенцию, переходя к импульсному пространству:
t	\
t 4rt б3 <* - *') =' \
Отсюда видно, что для того, чтобы получить равную нулю ди-
дивергенцию от правой части A4.14), необходимо модифицировать
величину 6<у63(* — х'), вводя в ее фурье-разложение член, про-
пропорциональный kj. На самом деле этот член должен быть про-
пропорционален kikj — единственному тензору второго ранга, кото-
который (помимо б,/) имеется в нашем распоряжении. Коэффициент
при kikj однозначно определяется из условия обращения в нуль
дивергенции, в результате рецепт получения «поперечной б-функ-
ции», т. е. функции с равной нулю дивергенцией заключается
в замене
6,/63 (x - x') -> 6Y} (x - *') = J -j^r e'*-^-*')^ - -jJ-). A4.16)
При этом коммутаторы A4.14) заменяются на
[я' (х, t), А1 (х' 0] = + й</ (* - х').	A4.17)
Отсюда следует, что величина V -А коммутирует со всеми опе-
операторами, поскольку дивергенция по х' от правой части A4.17)
равна нулю. То, что V-A является с-числом, следует уже из оп-
определения Е через А и Ф и закона Гаусса
0 = У.?==-У2Ф-У- А.	A4.18)
Поскольку мы уже знаем, что Ф есть с-число, таковым являет-
является и V-A, за исключением, быть может, вклада членов, отве-
отвечающих нулевой частоте.
') Согласно уравнениям A4.10) и A4.11) л1 сопряжен А; = —А1,

80	КВАНТОВАНИЕ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ	1ГЛ. 14
Таким образом, продольная часть вектора А (т. е. компо-
компонента А в фурье-пространстве, параллельная волновому век-
вектору) и скалярный потенциал в действительности не являются
динамическими степенями свободы. И действительно, при под-
подходящем выборе калибровки величины \ -А и Ф можно сделать
равными нулю. Опишем соответствующее градиентное преобра-
преобразование, причем выполним его в два этапа. Вначале выполним
преобразование
t
^\t')dt',	A4.19)
в результате которого обращается в нуль скалярный потенциал.
Для того чтобы устранить затем продольный потенциал, найдем
функцию А(х), удовлетворяющую уравнению
Выбрав Л в виде
Л (х) = \ —J-^—rr- V' • А' (х\ t),
мы обращаем продольную часть потенциала в нуль, причем с
учетом равенств A4.18) и Ф'= 0, получаем
^ = 0 и ф" = ф' = 0.
Калибровка, в которой
ф = 0, У-Л = 0,	A4.20)
называется калибровкой излучения. В дальнейшем мы будем ра-
работать именно в этой калибровке, теряя при этом лоренцеву и
градиентную ковариантность теории. Преимуществом же калиб-
калибровки излучения является то, что формализм теории содержчт
только две поперечные степени свободы поля излучения.
§ 84. Ковариантность и процедура квантования
Рассмотренный выше метод квантования может считаться
удовлетворительным только в том случае, если коммутационные
соотношения A4.13) и A4.17) сохраняют инвариантность тео-
теории при пространственных вращениях и трансляциях. Что же
касается лоренцевых преобразований, то неинвариантные отно-
относительно этих преобразований члены должны компенсироваться
в результате изменения калибровки,

§ 84]	КОВАРИАНТНОСТЬ И ПРОЦЕДУРА КВАНТОВАНИЯ	81
Трансляционная инвариантность будет гарантирована, если
выполнено условие A1.70), где Р^ определяется из теоремы Не-
тер A1.49)
ро = н = ±.\ d3x: Е2 + В2: = -i \ d3x: А2 + (VX АJ:,
з	04.21)
Р = J d3x: Е X В: = - J d3x ? : A,VAt:.
Двоеточия в A4.21), как и в теории скалярного поля, озна-
означают нормальное упорядочивание. Аналогичным образом можно
проверить выполнение условия A1.73), подставив для простран-
пространственных компонент М1', i, /= 1, 2, 3, определенных согласно
A1.57), выражения
з
Ar(xl-^r-xl^Ar-(AiAi-AlAi):, A4.22)
причем тензор ~Zlrs в A1.57), согласно A1.54), равен
Яг1 = 8'гВ'а-818'г-	A4.23)
Наконец, преобразование, описывающее переход между двумя
лоренцевыми системами, генерируется операторами
о
\х° ? АТЩ^ - -? (Л2 + (V X ЛJI:. A4.24)
В действительности при лоренцевых преобразованиях А^
преобразуется не как 4-вектор, но приобретает дополнительное
калибровочное слагаемое1). При бесконечно малом лоренцевом
преобразовании с генераторами Мок A1.72) и A1.73)
U (е) А» (х) U-1 (е) = А» {х') - в»уАу (*') + дА{*/ в) . A4.25)
гдеЛ^', е)—операторная калибровочная функция2). Ясно, что
калибровочный член в A4.25) необходим, поскольку, если
ФМ = Ло(*) = О,
то
UO(x)U~l = 0	A4.26)
для любого унитарного преобразования U. Структура выраже-
выражения A4.25) гарантирует лоренцеву ковариантность градиентно-
') Несмотря на это, мы будем по-прежнему называть преобразования, ге-
генерируемые операторами A4.24), лоренцевыми,
2) См. задачу 2 к данной

82	КВАНТОВАНИЕ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ	[ГЛ. 14
инвариантных уравнений Максвелла. Единственное дополнитель-
дополнительное требование заключается в том, что
Т-А'(х') = 0	A4.27)
и что одновременные коммутационные соотношения A4.13) и
A4.17) остаются по-прежнему справедливыми в штрихованной
системе координат. Выполнение этих условий может быть про-
проверено непосредственным вычислением. Таким образом, резуль-
результаты, полученные для квантовой электродинамики в калибровке
излучения двумя наблюдателями, находящимися в движущихся
друг относительно друга системах О и О', могут быть связаны
между собой, поскольку всегда существует унитарное преобразо-
преобразование, связывающее состояния в системах О и О'.
Нетривиальные вычисления, ведущие к выражениям A4.21) —
A4.27), а также проверку ковариантности одновременных ком-
коммутационных соотношений мы оставляем читателю в качестве
упражнения.
§ 85. Разложение в импульсном пространстве
Разложив потенциалы по плоским волнам и наложив комму-
коммутационные соотношения A4.13) и A4.17), мы можем интерпре-
интерпретировать, как и в теории Клейна — Гордона, коэффициенты раз-
разложения как операторы рождения и уничтожения. Отличитель-
Отличительной чертой максвелловской теории является, однако, то, что эти
кванты несут целый спин.
В калибровке излучения вектор А(х, t) чисто поперечен.
В разложении A(x,t) по плоским волнам:
2
А (х, t) = J d3k ? в (k, к) A (k, к, t) elk-*	A4.28)
для каждого значения k два единичных вектора z(k, Я), X — 1,2,
ортогональны k
e(k,X)-k = 0,	A4.29)
так что V-A = 0. Удобно выбрать эти векторы также ортого-
ортогональными друг другу для каждого k
z{k,\)'Z(k,k') = bxv.	A4.30)
Тогда векторы e(k, I), e{k, 2) и k = kl\k\ образуют трехмерный
ортогональный базис, показанный на рис. 14.1. Условимся также
считать, что, как показано на этом рисунке,
е (- kx 1) = - е (k, 1), е (- k, 2) = + е (kt 2). A4.31)

§ 85]
РАЗЛОЖЕНИЕ В ИМПУЛЬСНОМ ПРОСТРАНСТВЕ
83
С учетом A4.30) это означает, что
е (к, А) • е (- к, К') = (- 1)х 6U'.	A4.32)
Из уравнений Максвелла следует, что А(х) в калибровке
излучения по-прежнему удовлетворяет волновому уравнению
? Л = 0,
поэтому можно записать
l. /\ 	 V 	 ' 	¦- \ p I h 7 ^ \ n
A,= l
e~ikx
A4.33)
где
= (D = |jk| и k2 = k^ = 0.
Далее, так же как и в теории Клейна — Гордона, мы можем
разрешить A4.33) относительно a(k, Я). Используя A4.30) и
Щ2)
г(-*,2)
Рис. 14.1. Единичные векторы поляризации фотонов с импульсами k и —ft.
A4.32), получим вначале
г
со \ d3xeikxe(k,
, к)-А(х) =
(-if fl+ (- к, Я)
откуда
а(к, Я) =
/2© BяK
[о Л (дс) + /А (*)] ¦
= i \ d,Xe -ъ дог (k, к) • А (х),
а+^ = -1\^^7^к'К)-А^
A4.34)

$4	КВАНТОВАНИЕ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ	[ГЛ. 14
Для коммутационных соотношений между a(k,K) и a^{k,X) по-
получаем из A4.13) и A4.17)
[а (к, Я), а+ (к', Я')] ==
__ I d_xdjc_e__—(ш/_|_ш) У e.(k, X)e,(k', Х')Ь\их — х').
При вычислении интеграла используем определение 6{) A4.16),
тогда, учитывая соотношения ортогональности для векторов по-
поляризации, получаем
[а (к, к), а+ (к', К')) = 63(k- k') 6U'.	A4.35)
Аналогично получаем
[a(k, I), a(k', X')] = [a+{k, Я,), a+(k', Я,'I = 0. A4.36)
Таким образом, коэффициенты разложения для двух попе-
поперечных компонент векторного потенциала квантуются с теми же
коммутационными соотношениями, что и в теории Клейна — Гор-
дона. Поэтому мы можем интерпретировать a+(k,X) и a(k, к)
как операторы рождения и уничтожения квантов с энергией со
и импульсом Л. Действительно, с учетом A4.3), A4.21) и A4.33)
гамильтониан A4.12) может быть записан в импульсном про-
пространстве в виде
Н = \ ^~:{Е2 + В2): =J йЧсо ?а+ (k, X)a(k, %). A4.37)
Аналогичным образом для полного импульса получаем
2
Р= J d3x : Е X В : = J d3k k ? а+ (k, к) а (к, к). A4.38)
Вакуумное состояние, т. е. состояние с наинизшей энергией,
есть собственный вектор операторов Н и Р и удовлетворяет урав-
уравнению
a(k, А,)Ф0 = 0	A4.39)
в полной аналогии с уравнением A2.17) для теории Клейна —
Гордона. Оператор а+(к, I) интерпретируется как оператор рож-
рождения фотона с 4-импульсом k^, причем k2 = к^Ш- = 0. Для того
чтобы убедиться в этом, достаточно построить состояние
®1.ы^а+(к, Я)Ф0 = а+(?, А,)|0> '	A4.40)

5 86)	спин фотона	85
и показать, что
2
^ */и ха+ <*'»*'>а (*'•я')а+ <*»^ °>=АЦф1. «I
A4.41)
§ 86. Спин фотона
Фотоны отличаются от квантов клейн-гордоновского поля в
нескольких отношениях. Поскольку они удовлетворяют соотно-
соотношению Эйнштейна k^kv = О, их масса покоя равна нулю. Кроме
того, векторный потенциал А (х) действителен и при квантовании
становится эрмитовым оператором. Поэтому фотоны не несут
заряда и похожи в этом отношении на нейтральные мезоны, ко-
которые возникают при квантовании действительного поля Клей-
Клейна—Гордона. Другой отличительной чертой является наличие
у каждого фотона вектора поляризации e{k,X), который связан
со спиновым угловым моментом. В частности, векторный харак-
характер потенциала А ведет к тому, что фотоны имеют единичный
спин; при этом условие поперечности устраняет одну из степеней
свободы. Проекция спинового углового момента на направление
распространения фотона не может равняться нулю, а равна
только ±1. Чтобы показать это, рассмотрим оператор углового
момента A4.22) и вычислим компоненты углового момента од-
нофотонного состояния
М12Фи kK = [М12, а+ (к, Щ 10),	A4.42)
причем будем считать, что импульс фотона параллелен третьей
оси, т. е. kx = o)(t — я3). М12 состоит из двух членов, первый из
которых можно отождествить с орбитальным угловым момен-
моментом. Его проекция вдоль направления движения равна нулю,
что можно проверить прямым вычислением коммутатора. Остает-
Остается только вклад спиновых членов, который с помощью A4.22) и
A4.33) приводится к виду
[А*'*, а+ (k, Щ =
d3xe~ikx
-\
[г1 (k, X) д0А2 (х) - е2 (k, X) д0А1 (х)]. A4.43)
Используя A4.34) и определение векторов поляризации
(рис. 14.1), получаем
' [М12, а+ (k, Я)] = /е1 (к, Я,) а+ (к, 2) — /е2 {k, К) а+ (к, 1). A4.44)

86.	КВАНТОВАНИЕ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ	[ГЛ. 14
Образовав линейные комбинации
ja+(k, \) + ia+(k, 2)],
,	A4.45)
которые описывают право- и левополяризованные волны, имеем
[М12, а+ Щ = + а+ (k), [М12, а+ Щ = - а+ (k), A4.46)
откуда следует, что проекция спина вдоль направления движе-
движения для право-поляризованного фотона равна +1, а для лево-
поляризованного равна —1.
§ 87. Фейнмановский пропагатор для поперечных фотонов
Для того чтобы описать развитие в пространстве и во вре-
времени состояния, содержащего поперечно поляризованный фо-
фотон, мы рассмотрим фейнмановский пропагатор. Так же как
в § 75, где мы рассматривали клейн-гордоновские кванты, по-
построим амплитуду для поперечного фотона, который рождается
в точке х с проекцией поляризации ц и движется вперед во вре-
времени в точку х', где он поглощается, имея при этом проекцию v:
(О | Av {х') А» (х) | 0) 9 (f - 0.	A4.47)
Если t > V, то мы строим амплитуду для фотона, рожденного
в точке х' с проекцией v и поглощенного в точке х с проекцией ц:
@ | Лц (х) Av (x') \O)Q(t- П.	A4.48)
Сумма выражений A4.47) и A4.48) определяет фейнмановский
пропагатор
ш? (*', *)v(l = <о | av (xf) А» (х) | о) е {? - о +
+ <0 | Л,, (х) Av {х') | 0) 9 (t - t') = <0 | Т (Av {x') Л„ (х) |0>, A4.49)
где Т означает хронологический оператор, определенный в
A2.72) и A3.71).
Далее найдем явный вид D1f(x', x)vil, используя разложение
полей по плоским волнам
? ^{k x) e^{k'x) [e {f ~t] e~ik {x'~x
9 (/-О elft <*'-*>]. A4.60)

§ 87]	ФЕЙНМАНОВСКИЙ ПРОПАГАТОР ДЛЯ ПОПЕРЕЧНЫХ ФОТОНОВ	87
В калибровке излучения временная компонента векторов ev(k, I)
равна нулю
в*(*. Л) = @, в{к, А))
и условие поперечности фотона G.54) зависит только от направ-
направления вектора k, а не от частоты со. Фиксируя систему отсчета,
можно записать фейнмановский пропагатор в виде четырехкрат-
четырехкратного интеграла
-S %,	? ev (k, к) е, (k, I). A4.51)
Функция распространения, записанная в виде A4.51), кото-
который мы впервые ввели в гл. 6, а затем использовали в гл. 12,
будет часто встречаться в последующих вычислениях. Выраже-
Выражение A4.51) не лоренц-инвариантно, поскольку пространственные
компоненты векторов ev(k,K) определены в фиксированной си-
системе отсчета. Для того чтобы явным образом отделить коорди-
координатную зависимость, введем в той системе отсчета, в которой мы
выполнили квантование, единичный времениподобный вектор
т^ = A, 0, 0, 0). Тогда для данного № имеется четыре незави-
независимых ортогональных единичных вектора su(k, I), e^(k,2), r\v и
a»-*!-<*">"".	A4.52)
*J(kr\J—k2
Далее получаем
2
2] ev (k, к) г^ (k, I) = —gvil	?^
Подставляя A4.53) в A4.51), имеем
Dp (x' - x)VVL = gvilDF {/ -x)-
fe2 + ie
В этом выражении первый член
gVilDF (xf — x)= lim (— gv(l) Af (/ — ж, m)
m!->0
есть обычный фейнмановский пропагатор, который использо-
использовался при расчетах электромагнитных эффектов в гл. 7, 8, 9,
причем Af(x' — х, т)—пропагатор бозона с нулевым спином,
введенный в гл. 9.'
Зависимость Df от ц^ содержится во втором члене выра-
выражения A4.54). Как показывает последующее рассмотрение, при

88	КВАНТОВАНИЕ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ	(ГЛ. 14
вычислении физических амплитуд в теории поля пропагатор
Df (х' — x)VVi всегда стоит между сохраняющимися токами, ко-
которые являются источниками электромагнитного поля. В резуль-
результате члены, пропорциональные ku и kv, исчезают в силу сохране-
сохранения тока. Это обстоятельство было отмечено нами ранее (см.
G.61)) и использовалось при вычислении поляризации вакуума
(8.9). Остающийся в A4.54) член, зависящий от ц, в системе
координат, где г\^ = A,0,0,0), равен
г
BяL (кг\)*-к* ^Ч)»— 4п\х'-х\
A4.55)
Это выражение имеет вид обычного статического кулоновского
взаимодействия между двумя зарядами. При вычислении пол-
полного взаимодействия между двумя зарядами в точках х и х'
A4.55) сокращается с кулоновским взаимодействием, которое
необходимо учесть в дополнение к полю излучения. В результате
пропагатор сводится к лоренц-ковариантному первому члену
в A4.54).
Указанное обстоятельство, которое будет строго доказано в
гл. 17 для произвольных 5-матричных элементов, позволяет по-
получать на самом деле лоренц- и градиентно-инвариантные выра-
выражения при вычислении физических амплитуд рассеяния. Допол-
Дополнительные, зависящие от калибровки члены в Df (х' — x)vll вно-
вносят вклад в ненаблюдаемые величины, такие, как константы
перенормировки Z\ и Z2, введенные в гл. 8, которые не градиент-
но-инвариантны. Их появление в функции D%^ является распла-
расплатой за квантование уравнения Максвелла каноническим мето-
методом. Все эти нежелательные члены, однако, исчезают при
вычислении скоростей перехода и сечений, которые непосред-
непосредственно могут быть измерены на опыте.
ЗАДАЧИ
1. Вычислить коммутационные соотношения между напряженностями
поля и показать, что они обращаются в нуль для пространственно-временных
интервалов.
Ответ.
[Bt (*'), Bj (х)] = f6(/V'V - А —1 ID (x' - х),
L	дх, дх,]
(*'), Bj (x)) = - Лу. ? eilk JL ID (x' - x),
\Et (x'l E, (x)} = (Ьц-^-r ~ Л-ЛЛ iD (*' ~ *fc
V дходхц дх дх' J

ЗАДАЧИ	8§
2. Вывести выражения для операторов энергии-импульса и углового мо-
момента A4.21), A4.22) и A4.24). Проверить, что при лоренцевых преобразо-
преобразованиях потенциалы Аи (х) действительно преобразуются по формуле A4.25) и
построить явные выражения для Л (л:', е) и ?/(е). Дополнить доказательство
ковариантности максвелловских уравнений, проквантованных в калибровке
излучения, проверив равенство A4.27), а также ковариантность одновремен-
одновременных коммутаторов. Учесть, что если e^v = 8oft. то
дАк
Непосредственным вычислением показать, что Мц и Мок коммутируют с Н.
3. Рассмотреть лагранжиан Максвелла с (нековариантной) «фотонной
массой», т. е. членом —Х2А2(х) (А,2 мало). Проквантовать электромагнитное
поле в этом случае, используя только одно дополнительное условие Ао = 0.
Построить вначале гамильтониан и показать, что из гамильтоновых уравне-
уравнений
дН ¦. дН	.и
	 = Ak, 	= — пя
dnk	dAk
при к -> 0 получаются уравнения Максвелла с единственным исключением —*
добавлением членов с нулевой частотой в формулу Гаусса:
Наложить канонические коммутационные соотношения, например
/ [я* (х, /), А, (х', /)] = 6*,63 (х - х"?
и проквантовать как лродольные, так и поперечные составляющие. Показать,
в частности, что возникающие при этом кванты поля подчиняются дисперсион-
дисперсионному закону ш2 = Я,2.
4. а) Решить уравнение Максвелла для того случая, когда электромаг-
электромагнитное поле заключено между двумя бесконечными параллельными проводя-
проводящими пластинами, расстояние между которыми равно а. Проквантовать элек-
электромагнитное поле с учетом граничных условий.
б) Вычислить энергию нулевых колебаний Еа на единицу площади, ис-
используя обрезание, зависящее только от частоты. Показать, что Еа имеет вид:
где Cj и Сг — величины, зависящие от обрезания, В4 = —Узо — четвертое число
Бернулли.
в) Показать, что сила, действующая между (нейтральными) пластинами,
обусловлена только последним членом, и вычислить ее величину (см. [29]).

ГЛАВА 15
ВЗАИМОДЕЙСТВУЮЩИЕ ПОЛЯ
§ 88. Введение
Теория одних только свободных полей лишена какого-либо
физического содержания. Физическая реальность раскрывается
только посредством взаимодействия между полями, к рассмот-
рассмотрению которых мы теперь и приступаем.
При построении лагранжианов взаимодействий различного
вида мы будем руководствоваться аналогией с электромагнит-
электромагнитным полем. Поэтому вначале обсудим теорию электромагнит-
электромагнитного взаимодействия заряженной частицы в методе вторичного
квантования.
В случае же неэлектромагнитных взаимодействий структуру
членов со взаимодействием лучше всего выяснять, используя
факт существования экспериментально наблюдаемых законов
сохранения. Последние могут быть введены в теорию посред-
посредством требования, чтобы лагранжиан обладал определенного
вида симметрией, поскольку для каждого непрерывного преоб-
преобразования симметрии теорема Нетер автоматически приводит
к некоторой сохраняющейся величине.
§ 89. Электромагнитное взаимодействие
Ранее в качестве рецепта введения электродинамической
связи мы использовали «минимальную» подстановку
Рц-+Рц — eV	A5.1)
которая отвечает классическому взаимодействию точечного за-
заряда. Можно сохранить эту аналогию и подставить A5.1) в
лагранжеву плотность для полей электрона и фотона; в резуль-
результате получим
2{х) = Ъ (х) (tV - е0А (х) - гщ) ф (х) - 'Д F^ (*) F»" (x). A5.2)
Плотность лагранжина A5.2) описывает локальное взаимодей-
взаимодействие между электроном и фотоном в одной и той же точке х.

§ 89]	ЭЛЕКТРОМАГНИТНОЕ ВЗАИМОДЕЙСТВИЕ	91
Независимо варьируя A5.2) по полям г|з и А, получим систему
связанных уравнений
A5.3а)
).	A5.36)
Первое из этих уравнений имеет ту же форму, что и уравнение
одночастичной теории. Теперь, однако, поле А^(х) не является
внешним полем, а включено в рассматриваемую динамическую
систему, поскольку оно связано с электронным током в A5.36).
Этот ток в свою очередь определяется из решения уравнения
A5.3а), которое описывает движение электрона под действием
поля А й.
Ясно, что при включении связи между полями мы сталки-
сталкиваемся с очень сложной нелинейной задачей. Эта задача сложна
уже в классическом случае, как это видно из рассмотрения ра-
радиационного затухания и решений, отвечающих расходящимся
электромагнитным волнам в задаче о движении классических
зарядов под действием либо их собственного поля, либо каких-то
других полей (см., например, [30]). Очевидно, что в квантовом
случае задача не становится легче.
Система связанных уравнений A5.3) неявно уже использова-
использовалась нами при вычислении электрон-электронного рассеяния,
комптоновского эффекта и собственной энергии электрона (см.
гл. 7, 8). В случае рассеяния электронов мы вычислили движе-
движение каждого из зарядов под действием поля другого заряда. Для
комптоновского рассеяния было вычислено изменение поля из-
излучения, обусловленное присутствием электрона. Наконец, в за-
задаче о собственной энергии рассматривалось взаимодействие
электрона со своим собственным полем излучения.
Когда рассматривается движение электрона под действием
внешнего электромагнитного поля, необходимо только добавить
в A5.1) в дополнение к полю излучения потенциал внешнего
поля ApXi (х). Тогда уравнения приобретают вид
дх
В формулах A5.4) мы приписали индекс массе т0 и заряду
е0, предвосхищая то обстоятельство, что эти величины не равны
физически наблюдаемым значениям т и е. Мы уже видели в
гл. 8, как возникают поправки к то и «о в теории возмущений.
При этом обнаружилось, что в низшем порядке по е поправки

92	ВЗАИМОДЕЙСТВУЮЩИЕ ПОЛЯ	(ГЛ. 15
к массе и заряду логарифмически расходятся. Мы не будем
здесь обсуждать вопрос о том, останутся ли константы перенор-
перенормировки /п0—т и Zjj бесконечными при точном вычислении.
Более важно осознавать то, что логическая необходимость пе-
перенормировки сама по себе никак не связана с величиной пере-
перенормировочных констант. Тем не менее ввиду трудностей, воз-
возникающих в теории возмущений, необходимо тщательно отде-
отделить все бесконечности от конечных наблюдаемых физических
величин. Начиная с 1948 г. в этом направлении был достигнут
большой прогресс и в настоящее время квантовая электроди-
электродинамика представляет теорию, в которой имеющиеся бесконечно-
бесконечности не препятствуют вычислению с любой желаемой степенью
точности физических амплитуд, причем точность вычислений на
практике ограничивается только объемом работы, которую при
этом необходимо выполнить [31].
Для обобщения классической теории на квантовый случай
определим вначале канонические импульсы и выпишем одно-
одновременные коммутационные соотношения. Член со взаимодей-
взаимодействием в A5.2), введенный по классической аналогии,
#mt = - ео'Ф (х) уцф (х) А11 (х)	A5.5)
не содержит производных от полей по времени. Поэтому кано-
канонические импульсы не меняются по сравнению с теорией сво-
свободных полей и в калибровке излучения (кулоновской калиб-
калибровке) по-прежнему даются выражениями A3.43) и A4.10)
V»A = 0.	A5.6)
В указанной калибровке скалярный потенциал уже не равен
нулю; из теоремы Гаусса и A5.6) следует, что
V • Е (х) — - V • А (х) — ^Ф (х) =
= - У2Ф (х) = eot+ (х) Ч> (х) Ф 0. A5.7)
Тем не менее скалярный потенциал все еще не является неза-
независимой динамической переменной, поскольку он определяется
мгновенным распределением заряда р (лс, t) = ф+ (x, t)ty(x, t):
Так как независимые переменные остаются такими же, как
и в теории свободных полей, мы примем для них перестановоч-

$ 89]	ЭЛЕКТРОМАГНИТНОЕ ВЗАИМОДЕЙСТВИЕ	93
ные соотношения вида A3.53), A3.54), A4.13) и A4.17):
{фа (х, 0, < (*', t)} = ба0б3 (х - х'),
{\ (х, 0, % (х', 0} = {< (х, t), < (*' 0} = 0,	(^ ^
[At (х, t), А/ {х', 0] = - ibfi (х - О, /, /=1,2,3,
[At (х, t), А, (х\ 0] = [At (х, t), A, (*', /)] = 0.
Чтобы дополнить этот набор, потребуем чтобы одновременные
коммутаторы между полями Дирака и Максвелла также равня-
равнялись нулю:
[фа (х, t), At (x', t)] = 0, [% (х, t), At {xr, t)) - 0. A5.10)
Эти соотношения непротиворечивы, поскольку г]за и А{ есть не-
независимые канонические переменные. Как уже было отмечено,
скалярный потенциал Ф не является независимым, а опреде-
определяется через ф посредством соотношения A5.8) и потому удов-
удовлетворяет коммутационным соотношениям
[Ф (*, t), At (*', /)] = [Ф (*, 0, А\ (х', ()] =0,
Р	A5.11)
[Ф (Ж, 0, Фа (*', 0] = - 4л\х-х'\ ^ Р' V-
Переходя, согласно каноническому методу, к гамильтониану
и повторяя те же выкладки, что и в теории свободных полей,
получаем
Ц1И*-^ A5Л2>
откуда следует, что
Ж = ф+ (- т ¦ V + рш0) ф + 1/а (?2 + S2) + Е	ц
A5.13)
В результате находим выражение для гамильтониана:
Н = J d3x Ж =
= J d3* { t|)+ (ж) [«• D V - еол) + рто] Ф (*) + у Ш2 (х) + В2 (х)} },
A5.14)
причем в A5.14) учтено, что член Е-УФ при интегрировании

94	ВЗАИМОДЕЙСТВУЮЩИЕ ПОЛЯ	[ГЛ. 15
по частям дает — еоф+фФ и, кроме того, опущен несущественный
поверхностный член 1).
Выражение A5.14) на первый взгляд кажется удивительным,
поскольку оно явно содержит только связь тока электронов с по-
поперечным векторным потенциалом. Возникает вопрос, где же со-
содержится электромагнитное взаимодействие между зарядами. На
самом деле оно включено в член с электрической энергией
Чтобы пояснить это, разложим Е на поперечную и
продольную составляющие:
Б = Б1 + Еи Ei^bt- УФ, Et = -A.	A5.15)
Тогда полная энергия поля представляется в виде суммы двух
членов
1 J d3x (Е2 + В2) = 1 \ Л El + 1 J Л (El + В2), A5.16)
причем член с ErEt после интегрирования по частям обращает-
обращается в нуль. Первый член в первой части выражения A5.16) равен
энергии, связанной с кулоновским полем. Действительно, ис-
используя теорему-Гаусса и выразив его через заряды, получим
е f з ,з ^+ (*• О * (*• О ^+ (У' 0 * (У' О
p (x, t) p (t,, /)•
\х-У\ ¦
Второй член в A5.16) равен полной энергии поперечного поля
излучения, связанного с током / = ф+аф, и имеет тот же вид,
что и в случае свободного поля.
') Квантовая теория связанных электромагнитного и клейн-гордоновского
заряженного полей во многих отношениях похожа на теорию фотонов и элек-
электронов, и мы не будем ее здесь обсуждать (см., например, [7]). Отметим
только, что в этой теории возникает то неприятное обстоятельство, что под-
подстановка A5.1) приводит к членам в лагранжиане взаимодействия, содержа-
содержащим производные; при этом лагранжева плотность имеет вид
Поскольку второй член в &, описывающий взаимодействие, содержит произ-
производные, выражение для канонических импульсов в этом случае изменяется:
п	ф* — ie0A0($*, я*=-^гг

$ 90]	ЛОРЕНЦЕВА ИНВАРИАНТНОСТЬ	95
§ 90. Лоренцева инвариантность
и инвариантность при трансляциях
С помощью канонической процедуры мы получили оператор
энергии Н A5.14). Аналогично можно определить оператор им-
импульса
Р= J d3* (-n|>+V4> + Я* X В).	A5.17)
Поскольку взаимодействие не содержит производных, это вы-
выражение совпадает с суммой операторов импульса свободных
полей A3.46) и A4.21).
Соотношения Гейзенберга
A5Л8)
выполнение которых необходимо в трансляционно-инвариантной
теории, могут быть выведены из коммутационных соотношений
A5.9), A5.10) и уравнений поля A5.3). Коммутационные соот-
соотношения и уравнения поля, таким образом, образуют самосо-
самосогласованный набор уравнений, на которых основывается наша
теория.
Чтобы проверить лоренцеву инвариантность, рассмотрим тен-
тензор углового момента, который можно построить, используя тео-
теорему Нетер (см. A1.56) и A1.57)). Пространственные компо-
компоненты М11 (i, /= 1, 2, 3) совпадают с суммой операторов угло-
угловых моментов для свободных частиц. Поскольку коммутацион-
коммутационные соотношения также не изменяются по сравнению с теорией
свободных частиц, соотношения A1.72) и A1.73) для трехмер-
трехмерных вращений сохраняют свой вид. Взаимодействие приводит
к дополнительным членам в генераторах MOk (k = 1, 2, 3) ло-
ренцевых преобразований, связывающих между собой движу-
движущиеся системы. Имеем
Mok = Pkt _ ^ #х |>^ (Х) _ L ф (Ж) Y*^ (д)] t A5.19)
где 96 — гамильтонова плотность A5.13). Выполнив бесконечно
малое преобразование Лоренца, генерируемое операторами МОк
в A1.72), мы снова обнаруживаем, что электромагнитные потен-
потенциалы
, А(х))
претерпевают градиентное преобразование, которое восстанав-

9Й	ВЗАИМОДЕЙСТВУЮЩИЕ ПОЛЯ	(ГЛ. 15
ливает поперечную калибровку в новой координатной системе
[33]. Аналогично уравнению A4.25) для свободного поля полу-
получаем
U (в) А» (х) U-1 (е) = А» (*') - е^Лv (*') + дА[х'; б) ,
где1)
\^Щ^Ш^1.	A5.20)
Дираковский оператор ty(x) в дополнение к лоренцеву преобра-
преобразованию также подвергается фазовому преобразованию:
U (е) ф (*) СГ1 (е) = [1 - ie0A (x, в)] S (в) фв (*'), A5.21)
которое необходимо для того, чтобы уравнения поля преобразо-
преобразовывались под действием оператора U ковариантным образом,
например;
U (е) ф {х) [iV — е0А (х)] ф (ж) f/ (е) = ф(ж') [iV*- — е0Д (ж')] Ф (^).
Чтобы дополнить проверку лоренцевой инвариантности кван-
квантовой теории поля, необходимо еще проверить инвариантность
одновременных коммутационных соотношений2) A5.9) и A5.10).
Соответствующие вычисления весьма громоздки и не совсем
тривиальны, мы оставляем их читателю в качестве упражнения.
Мы не выписываем здесь результатов, поскольку заранее из-
известно, что правило «минимальной» подстановки A5.1) обеспе-
обеспечивает градиентную инвариантность и гарантирует релятивист-
релятивистскую ковариантность физических результатов даже в том слу-
случае, если при квантовании используется специальный выбор ка-
калибровки.
§ 91. Разложение в импульсном пространстве
При включении взаимодействия разложения в импульсном
пространстве A3.50) и A4.33) для ф(л:) и А(х) следует моди-
модифицировать, поскольку их координатная зависимость не имеет
больше вида плоских волн. Более того, так как точные решения
системы связанных уравнений A5.3) неизвестны, мы вообще не
знаем явного вида координатной зависимости решений. В этой
') При вычислении этого выражения полный дифференциал V -(ЕФ) в A5.13)
дает нуль, в отличие от члена Ef ¦ Ei = V • (АФ).
2) Мы не можем, как в теории свободных полей, выписать явный вид ко-
вариантных коммутаторов для времениподобных интервалов, поскольку ре-
решения уравнений движения неизвестны.

§ 9i]	РАЗЛОЖЕНИЕ В ИМПУЛЬСНОМ ПРОСТРАНСТВЕ	9?
ситуации удобно перейти к трехмерному интегралу Фурье, счи-
считая время фиксированным, например t = 0, и описывать разви-
развитие амплитуд во времени гейзенберговскими уравнениями
A5.18). Формально интегрируя эти уравнения, получаем
1>(ж, t) = eIHt$(x, 0)е~Ш{, А(х, t) = eiHtA(x, 0)e~tm, A5.22)
после чего можно использовать разложения по плоским волнам
вида A3.50) и A4.33):
V> s)u{p' s^e+ip'x+
+ d+(p, s)v(p, s)e-ipxl
+ d(p, s)v(p, s)yoe+ip'»l
2	A5.23)
4
. 0)=\
J
V2co Bя)
где ?р = Vl Р-Р + »г2, a = \k\, u(p, s) и &{k, К) определены
выражениями A3.51) и A4.29) и т. д. Коэффициенты b(p,s),
d(p, s), a(k, X) в операторном разложении и эрмитово сопряжен-
сопряженные коэффициенты удовлетворяют тем же перестановочным со-
соотношениям A3.52), A4.35) и A4.36), что и в теории свобод-
свободных полей. Кроме того,
[a(k, к), b(p, s)] = [a+(k, к), Ь[р, s)] = [a(k, I), d(p, s)] =
= [a+(?, Я), d{pt s)] = 0. A5.24)
В результате канонические коммутационные соотношения A5.9)
и A5.10) справедливы при t = 0 и, более того, согласно A5.22),
выполняются в любой момент времени /.
Поля, из которых выделена их временная зависимость, ис-
используются в шредингеровском представлении. Они совпадают
с гейзенберговскими полями A5.22) при / = 0.

98	ВЗАИМОДЕЙСТВУЮЩИЕ ПОЛЯ	[tn. 15
Формальная связь между разложениями A2.7), A2.57),
A3.50), A4.33) и A5.23) может быть суммирована следующим
образом:
Свободные поля	Взаимодействующие поля
a{k, Х)е-ш->	eima{k, Х)е~т,
a+(k, к)еш->	eiHta+(k, К)е~ш,	(I5l25)
b(p, s)e~/wi->	eiHtbip, s)e~iHt.
Коэффициенты в полученных операторных разложениях теперь
уже, однако, не имеют простого смысла операторов рождения
и уничтожения одиночных квантов с фиксированной массой, как
это было, например, в A4.41).
§ 92. Собственная энергия вакуума;
нормальное упорядочивание
В квантовой теории поля на каждом шагу можно столкнуть-
столкнуться с противоречием — вот одно из них. Возьмем теорему Гаусса,
записанную в операторной форме A5.7), и вычислим среднее
значение по вакууму
где сумма берется по всем возможным состояниям. Мы видим,
что вакуум обладает зарядовой плотностью, которая к тому же
еще и бесконечна. Физический смысл заряда вакуума очеви-
очевиден — это бесконечный электростатический заряд моря электро-
электронов с отрицательной энергией.
Возникающую при этом неприятную ситуацию можно, од-
однако, легко устранить. Изменим нашу теорию, добавив внешний
однородный заряд противоположного знака, который нейтрали-
нейтрализует заряд вакуума. С формальной точки зрения для этого до-
достаточно во всех предыдущих уравнениях, включая и уравнения
Максвелла, сделать замену
Ч^Ф^'Ш, У,Л1	A5.26)
т. е. антисимметризуя электрический ток относительно переста-
перестановки дираковских полей, что приводит к вычитанию бесконеч-
бесконечной с-числовой константы из оператора тока •фуцф. Указанная
модификация фактически эквивалентна использованию нор-
нормального порядка в операторных множителях. Для того чтобы
убедиться в этом, рассмотрим снова поля A5.22) и их разложе-
разложения A5.23) и заметим, что произведение взаимодействующих
полей, каждое из которых взято в один и тот же момент вре-

§ 92]	СОБСТВЕННАЯ ЭНЕРГИЯ ВАКУУМА	99
мени /, может быть применением оператора eiHt ... e~iHt приве-
приведено к моменту времени t — 0. Но, согласно A5.24), при / = 0
алгебра взаимодействующих полей совпадает с алгеброй свобод-
свободных полей. Поэтому нормальное произведение для взаимодей-
взаимодействующих полей может быть определено так же, как и раньше,
например,
: Ъ (р, s) d+ {;/, s') + b+ (p, s) b (//, s') + d (p, s) a+ (k, A): =
= -d+(//, s')b{p, s) + b+(p, s)b(p', s') + a+(k, l)d{p, s).
Тогда в A5.26) получаем
V2 N> (x), Y^ (x)] = -Ф (x) v^ (x) - '/2 (ф (x), y^ (x)} =
= : $ (x) y^ (x): + W+) (x), y^ (x)} - '/2 (^ (jc), Y^ (x)} =
= : ф (x) yfl (x): + 263 @) ^0 - 263 @) g^ A5.27)
При выводе A5.27) мы использовали коммутационные соотно-
соотношения для свободных полей, которым удовлетворяют операторы
a, b, d и т. д. Таким образом, сингулярные члены в операторе
плотности, который отвечает ц = 0 в A5.27) сокращаются.
Знаки (-)-) и (—) в A5.27) означают, что соответствующее вы-
выражение сводится к той части оператора в A5.23), которая со-
содержит либо a, b, d, либо а+, 6+, d+. Последние же, как это сле-
следует из A5.25), совпадают с операторами рождения и уничто-
уничтожения для свободных полей.
Хотя мы строго и не показали, что замена A5.26) устраняет
фоновый заряд и нейтрализует вакуум, уместно напомнить, что,
как было отмечено при обсуждении свободного поля Дирака,
вакуумное среднее от нормального произведения всегда равно
нулю. В § 99 мы рассмотрим зарядовую инвариантность в кван-
квантовой электродинамике и убедимся в том, что равенство
<0 |: ф (ле) УдЧ» U): I 0> = 0
есть следствие этой симметрии. В настоящий же момент мы при-
примем это равенство без какого-либо дополнительного обсужде-
обсуждения, тогда
Н= $ d3x Ж (х) = J d3x : ф+ (х) [а • (- /V - е0А (х)) + $гщ] ф (х) +
Далее вычтем из гамильтониана его вакуумное среднее, другими
словами, будем отсчитывать все энергии от энергии вакуума.

100	ВЗАИМОДЕЙСТВУЮЩИЕ ПОЛЯ	[ГЛ. 15
Условие
<0|Я|0) = 0
позволяет избежать рассмотрения некоторых неприятных расхо-
димостей в выражении A5.28). Первая из них — это нулевая
энергия осцилляторов поля, которая, как и в теории Клейна —
Гордона (см. A2.46)), равна
<0|Л2(л;)|0)=оо.
Кроме того, имеется еще одна расходимость, обусловленная
последним членом в A5.28). Эта расходимость возникает из-за
того, что плотность заряда :р(х): не коммутирует с гамильто-
гамильтонианом, несмотря на то, что полный заряд Q= \ :p(x):d3x ком-
коммутирует с Н:
[Q, я] = о.
В результате в теории возникают флуктуации плотности заряда
вакуума, причем обусловленная этими флуктуациями кулонов-
ская энергия равна бесконечности.
Возникает вопрос об истинной природе указанных вакуумных
флуктуации. Точные решения системы связанных полевых урав-
уравнений не известны и, более того, до сих пор не удалось пока-
показать, исходя из формализма теории, что вакуум, как наинизшее
энергетическое состояние гамильтониана, действительно суще-
существует. Однако если допустить, что спектр гамильтониана не ог-
ограничен снизу, любая попытка построения физически разумной
теории заранее обречена на неудачу. Вопрос о существовании
вакуума отнюдь не является тривиальным, что можно увидеть
уже из следующего простого примера. Рассмотрим теорию, в
которой частицы и античастицы отталкиваются друг от друга.
В такой теории энергетически выгодно рождение пар, причем
необходимая для этого энергия возникает за счет изменения
потенциальной энергии, поскольку образующиеся частицы и
античастицы разлетаются в разные стороны [34].
Если ввести нормальное упорядочивание в операторах энер-
энергии-импульса и углового момента, то все полевые уравнения
можно записать в нормальной форме, например вместо A5.3)
имеем
дР^) = е0: ^ (х) у^ (х): A5.29)
В дальнейшем будем подразумевать, что все операторные выра-
выражения автоматически имеют нормальный порядок множителей.
Что же касается вычитания вакуумных средних, то эта про-
процедура не влияет на результаты, поскольку она сводится к вы-
вычитанию из гамильтониана с-числа (возможно бесконечного).

§ 93]	ДРУГИЕ ВЗАИМОДЕЙСТВИЯ	101
§ 93. Другие взаимодействия
Представляется естественным обобщить рассмотренный выше
лагранжев формализм для описания взаимодействия других ча-
частиц, например мезонов и нуклонов. Первое, хотя и не слишком
оригинальное, что приходит в голову — это сопоставить каждой
частице свое поле, удовлетворяющее волновому уравнению, ко-
которое описывает спин, массу и заряд частицы. Взаимодействие
между частицами можно строить по образцу известного взаи-
взаимодействия дираковских или скалярных частиц с электромаг-
электромагнитным полем. При этом предполагается, что взаимодействие
должно быть локальным и, кроме того, может быть выведено
из некоторой лагранжевой плотности. Мы будем требовать так-
также инвариатность взаимодействий при пространственно-времен-
пространственно-временных смещениях и собственных однородных преобразованиях Ло-
Лоренца, другими словами, лагранжева плотность должна быть
лоренцевым скаляром. Если взаимодействие оказывается инва-
инвариантным относительно несобственных преобразований симмет-
симметрии таких, как четность, обращение времени или зарядовое со-
сопряжение, то на лагранжиан накладываются дополнительные
ограничения. Наконец, законы сохранения числа нуклонов, леп-
тонов, электрического заряда, а также приближенные законы
сохранения изотопического спина и странности в свою очередь
накладывают дополнительные ограничения на вид взаимодей-
взаимодействия.
Решающим, хотя и не слишком физическим принципом, ко-
которым мы будем руководствоваться в дальнейшем, является со-
соображение простоты. Именно так мы поступили, например, при
обсуждении мезон-нуклонного рассеяния в гл. 10. В этой главе
мы рассмотрели в предположении зарядовой независимости вол-
волновые уравнения A0.33) и A0.34)
где нуклонное поле рассматривается как изотопический спинор
а мезонное поле — как изотопический вектор —
+ (*) + Ф_ W	. Ф+ («) - Ф_ (*)

T02	ВЗАИМОДЕЙСТВУЮЩИЕ ПОЛЯ	[ГЛ. 15
Эти уравнения могут быть выведены из лагранжевой плотности
+ тШШ-«-•]-<**v*¦ * <1Ы0>
независимой вариацией по W(х) и ф(л;). В A5.30) мы опять
приписали индекс массам и константе связи с тем, чтобы под-
подчеркнуть, что эти параметры не связаны непосредственно с экс-
экспериментально наблюдаемыми величинами и изменяются при
перенормировке, подобно тому, как это имеет место при взаи-
взаимодействии фотонов и электронов, которое было рассмотрено
в гл. 8.
Следует отметить ту легкость, с которой связанные уравне-
уравнения поля получаются в лагранжевом методе. Утонченные аргу-
аргументы, касающиеся выбора знака в уравнениях A0.17), A0.19),
A0.21) и A0.24), заменяются здесь требованием, чтобы при
go->O лагранжиан сводился бы к сумме свободных лагранжиа-
лагранжианов, знаки которых определяются из условия положительной оп-
определенности гамильтоновой плотности для свободных частиц.
Связь в A5.30) однозначно определяется следующими требова-
требованиями:
1)	отсутствие производных в лагранжиане взаимодействий;
2)	линейность по мезонному полю и билинейность по нуклон-
ным полям, что приводит к элементарным процессам, изобра-
изображенным на рис. 10.4 и 10.5;
3)	связь сохраняет изотопическую инвариантность свобод-
свободного лагранжиана.
Подчеркнем снова, что лагранжиан A5.30) можно в лучшем
случае рассматривать как грубое приближение. В частности,
можно было бы дописать члены
или
Первый из них, однако, обычно считается неприемлемым, по-
поскольку он приводит к выражениям теории возмущений, рас-
расходящимся даже после перенормировки массы и константы
связи. Второй же член нарушает «принцип максимальной про-
простоты»; этот член нужно вводить в дополнение к последнему
члену в A5.30), а не вместо него, поскольку сам по себе он не
описывает процессы с образованием одного мезона1).
') «Максимальная простота», однако, может оказаться обманчивой. На-
Например, («простой») эйнштейновский лагранжиан гравитационного поля со-
содержит квадратный корень из детерминанта метрического тензора и приво-
приводит к ряду трудностей,

§ 93]	ДРУГИЕ ВЗАИМОДЕЙСТВИЯ	ЮЗ
Сингулярное поведение при высоких энергиях теории с произ-
производными можно было попытаться устранить, вводя формфактор,
который размазывает взаимодействие, например:
' (х) = J Фу d*z gW (г) YsY^ (у) ¦ Ц®- F ((x - yf, (x - zJ).
Это выражение сохраняет свой вид при смещениях, а также
при преобразованиях Лоренца. Однако оно нелокально, по-
поскольку изменение пионного поля в точке z вызывает изменение
нуклонного поля в другой пространственно-временной точке; при
этом нарушаются основные принципы, на которые мы опираемся
при построении теории поля, сформулированные в гл. 11. Кроме
того, нелокальные лагранжианы приводят к дополнительным
математическим трудностям1).
Что же касается более сложных лагранжианов взаимодей-
взаимодействия, то они практически не исследованы. К тому же не имеет-
имеется убедительных физических соображений, с помощью которых
можно было бы дать предпочтение одному из них. Тем не менее
возможность использования таких лагранжианов нельзя ис-
исключить полностью.
Отметим еще, что подход, в котором каждой частице сопо-
сопоставляется свое поле и свой член в лагранжиане взаимодей-
взаимодействия, вряд ли может считаться удовлетворительным, его в
лучшем случае следует рассматривать как феноменологический
способ описания взаимодействий. Неясно, в частности, какие
частицы являются «связанными» или «возбужденными» состоя-
состояниями более фундаментальных полей2). В настоящее время из-
известны попытки переформулировать теорию поля без привлече-
привлечения лагранжианов, опираясь только на фундаментальные ак-
аксиомы теории поля. Вместо введения с помощью лагранжиана
«голых» частиц, которые затем «одеваются», т. е. приобретают
структуру в результате своих взаимодействий, аксиоматический
метод сразу исходит из существования физических частиц и за-
затем постепенно «раздевает» их, рассматривая пространственную
структуру теории. Можно думать, что по своим физическим
следствиям аксиоматический метод, являясь по самой своей сути
феноменологическим подходом, вполне эквивалентен лагран-
жеву формализму [38].
') Некоторые проблемы, возникающие в нелокальной квантовой Теория
поля, обсуждаются в статье [35] (см. также [135], прим. перев.).
2) Хотя составные частицы могут быть описаны локальными полями [36,
37], получающиеся при этом волновые уравнения оказываются весьма слож-
. ными, а сам лагранжев формализм в лучшем случае неудобным.

104	ВЗАИМОДЕЙСТВУЮЩИЕ ПОЛИ	[ГЛ. 15
§ 94. Симметрия взаимодействий
При рассмотрении взаимодействий мы руководствуемся сооб-
соображениями простоты и экспериментальными фактами. Кон-
Конструируя лагранжианы физических систем, мы сопоставляем
каждому наблюдаемому закону сохранения то или иное свой-
свойство симметрии 3?. С этой точки зрения мы обсудили в гл. 11
законы сохранения энергии, импульса и углового момента, при
этом соответствующие лагранжианы строились таким образом,
чтобы они были трансляционно- и лоренц-инвариантными.
Кроме того, сохранению заряда, числа нуклонов, изотопического
спина и т. д. также можно сопоставить некоторые «внутренние»
симметрии лагранжиана. Как было показано в гл. 11 (см.
A1.58) и ниже), инвариантность 2? при локальном преобразо-
преобразовании полей
<рг (х) -*¦ <pr (x) — ieKs<Ps (x),	A5.31)
где е—бесконечно малый параметр, ведет к сохраняющемуся
току
S
dJ^	(lb.62)
и сохраняющемуся «заряду»
« J
A0.00)
Используя это обстоятельство, мы смогли построить электромаг-
электромагнитный ток заряженных частиц. Например, лагранжиан элект*
ронов и фотонов инвариантен при фазовом преобразовании
1>(х)-»Ч)(х)-йи|)(*), А11(х)->А11(х),	A5.34)
Поэтому, согласно A5.32), существует сохраняющийся электро-
электромагнитный ток
д
h (х) — ~ i dm/dXll) * W = * (х) Yn1> W-	A5.35)
Аналогичный результат имеет место и для заряженных бесспи-
бесспиновых частиц.
При переходе к квантовой механике ток /д(х) становится
оператором. Удобно считать его нормально-упорядоченным опера-
оператором (см. A5.26) и A5.27))'), т. е. сделать следующую замену
') Здесь и в дальнейшем при рассмотрении сохраняющихся величин мы
предполагаем, что вакуумное среднее всех операторов равно нулю.

S 94]	СИММЕТРИЯ ВЗАИМОДЕЙСТВИИ	105
Jii(x)-*- '¦ ty(x)Vixty(x):- Эта замена не нарушает закона сохране-
сохранения, поскольку она сводится к вычитанию (возможно, бесконеч-
бесконечной) константы, не зависящей от координат и времени:
(О I /„ (х) | 0) - @1 е№% @) e-iPx | 0) = @ | ^ @) 10).
Сохраняющаяся величина Q в A5.33), подобно Рц и М^,
имеет смысл генератора преобразования. Образовав унитарный
оператор
?/() '«l + Q	A5.36)
где е — бесконечно малый параметр и Q — эрмитов оператор, по-
получим с учетом A5.31)
U (в) Фг (х) и~1 (е) = Фг (х) + ie [Q, Фг (х)] = <р, {x)-leXr#t (х), A5.37)
или.
[Q, фг (х)] = — Xrsq>s (x).
Результат находится в соответствии с A1.69) и A1.70). Исполь-
Используя коммутационные соотношения A1.39) и A5.37), получаем
:nr (x) Я„ф, (х):	A5.38)
в согласии с A5.33). Можно проверить, что A5.38) сохраняет
смысл генератора преобразования и в теориях, квантуемых с ан-
антикоммутаторами, при условии, что матрица Xrs связывает ме-
между собой одни только ферми-поля, удовлетворяющие одновре-
одновременным перестановочным соотношениям:
{¦|. а (*. 0. ¦,!в (*'- 0} = бар6г/б3 (X - Х>),
В A5.39) индексы а, р = 1, 2, 3, 4 нумеруют спинорные компо-
компоненты, a t, /=1, 2, ... относятся к различным ферми-полям,
например к полям протона и нейтрона.
В дальнейшем мы будем всегда требовать, чтобы различные
ферми-поля не коммутировали, а антикоммутировали друг
с другом. Кроме того, потребуем чтобы различные бозе-поля
коммутировали друг с другом и чтобы при равных временах
ферми-поля коммутировали с бозе-полями'). Для свободных
полей указанные правила коммутации означают только согла-
соглашение о выборе фазы. Однако для взаимодействующих полей
отказ от антикоммутаторов приводит к противоречиям уже при
') В случае фотонов электромагнитные потенциалы не независимы и вме-
вместо A1.39) мы используем коммутационные соотношения A5.9) в калибровке
излучения. Правила же коммутации электромагнитных потенциалов с другими
полями не изменяются.,

106	ВЗАИМОДЕЙСТВУЮЩИЕ ПОЛЯ	[ГЛ. 15
рассмотрении гейзенберговских уравнений движения. Действи-
Действительно, для мезон-кулонного взаимодействия A5.30) гамильто-
гамильтониан равен
Я = J й3х\ч+{- i* • V
+ 1 (я • я + Щ ¦ Щ + ц2ф • ф) + 1ёоУу5т ¦ фУ]; A5.40)
при этом уравнение для протонного поля имеет вид
(N - Мо) г|)р (х) = igQy5 (л/2" <р+ (х) % (х) + % (х) г|)р (х)).
Для выполнения соотношения Гейзенберга
dtyn (х)
[Н, ър(х)] = -1-Щ-
необходимо потребовать, чтобы оператор г|)р(дг, t) коммутиро-
коммутировал с билинейной формой г|)* (х, t) ... г|)ге (х, t), а также чтобы
выполнялось условие
{%(*, t), Ф+(*> t)\{x, /)} = 0.	A5.41)
При указанном выше выборе перестановочных соотношений оба
эти условия, как легко видеть, выполняются. Отметим также,
что антикоммутаторы в A5.39) инвариантны под действием
преобразования A5.37), другими словами, теория, построенная
в терминах преобразованных полей
q>fr(x) = U(e)(fr(x)U~1(e),	A5.42)
не отличается от исходной теории, оперирующей с полями уг(х).
§ 95. Сильная связь между я-мезонами и нуклонами
Свойства симметрии особенно важны при рассмотрении
сильных взаимодействий. В случае я-мезон-нуклонных взаимо-
взаимодействий модельный лагранжиан A5.30) инвариантен при од-
одновременном изменении фазы у нейтронного и протонного полей
Чг->Ч — Ш.	A5.43)
Это преобразование отвечает выбору Xrs = 8rs (г, s=l,2)
в выражениях A5.37). Оно приводит к сохраняющемуся току
вида A5.32)
•С (х) = Ч^Д = Jl (х) + II (х)	A5.44)
и к константе движения вида A5.33)
N = J d3x 1%(х) = J йъх{tf% + Ф>п} = Np+ Nn, A5.45)

§ 95]	СИЛЬНАЯ СВЯЗЬ МЕЖДУ л МЕЗОНАМИ И НУКЛОНАМИ	Ю7
которую можно назвать числом нуклонов. Ранее мы уже рас-
рассматривали этот закон сохранения (см. A0.39) и A0.40)).
В теории без взаимодействия оператор N имеет смысл числа
протонов и нейтронов минус число антипротонов и антинейтро-
антинейтронов. Если включить взаимодействие, то N уже нельзя вычис-
вычислить в явном виде. Тем не менее при тех предположениях о
состояниях взаимодействующей системы, которые будут обсуж-
обсуждаться в § 106, этот оператор сохраняет свой смысл при усло-
условии, конечно, что он все еще остается константой движения.
Модельный лагранжиан A5.30) допускает также преобразо-
преобразование симметрии, отвечающее сохранению заряда. При этом
преобразовании только заряженные частицы приобретают об-
общую фазу:
Ф+-*Ф+ —*«р+,	A5.46)
Ф_ = Ф+ -* Ф_ + /е<р_,
Фо -*• фо-
В изотопическом формализме эти соотношения имеют вид
', ф->ф-е(фХФо), A5.47)
где вектор фо — @, 0, 1) был определен выражениями A0.36).
Инвариантность 3? при преобразовании A5.47) может быть
проверена непосредственным вычислением; согласно A5.32),
A5.33) эта инвариантность приводит к сохраняющемуся элек-
электромагнитному току:
k (*) = ^ (-4^-) Ч - (-Ц- X Ф) • Фо,	A5.48)
Q = J /о (*) d3x = J Л [г|)+ (х) г|)р (х) + Ф, (х) ф2 (х) - ф2 (х) ф, (х)].
Вид тока в A5.48) согласуется с выражениями A0.37) и A0.38),
полученными с помощью метода функций распространения.
Инвариантность & в A5.30) при вращениях в изотопическом
пространстве ведет к сохранению изотопического спина. Мы ос-
оставляем читателю непосредственную проверку того, что выра-
выражение A5.30) инвариантно при вращении
V -> W - is '/2 т ¦ ф>, ф (х) -> ф (я)' - е (ф (х) X ф), A5.49)

108	ВЗАИМОДЕЙСТВУЮЩИЕ ПОЛЯ	[ГЛ. 15
где ф —набор единичных векторов: ф[ = A,0, 0), ф2 = @, 1,0),
фз=@, 0, 1). Сохраняющийся изотопический ток
(ф X -0-
A5.50)
который получается из A5.32) и A5.49), и три компоненты изо-
изотопического спина
5^[{+]	A5.51)
являются константами движения. Эти выражения согласуются
с A0.43) и A0.44). Сложив JV/2 в A5.45) и третью компоненту
вектора A5.51), получим с учетом A5.48) соотношение
Q = 4 + /3>	A5.52)
которое также было выведено в гл. 10 (см. A0.41)). Используя
коммутационные соотношения, можно проверить, что три ком-
компоненты вектора / удовлетворяют тем же коммутационным со-
соотношениям
Ut, Il] = itk,	A5.53)
что и компоненты углового момента. Поэтому, как и в гл. 10,
мы можем нумеровать состояния собственными значениями опе-
операторов /3 и Р.
Мы обнаружили, таким образом, что наш модельный лагран-
лагранжиан A5.30) допускает преобразования симметрии A5.43),
A5.47) и A5.49), которым отвечают законы сохранения числа
нуклонов, заряда и изотопического спина. Хотя лагранжиан
A5.30) слишком прост, чтобы описать полное я-мезон-нуклон-
ное рассеяние, мы в дальнейшем при обсуждении более общих
лагранжианов сохраним указанные симметрии, а также рас-
рассмотрим другие преобразования симметрии, существование ко-
которых обусловлено экспериментально наблюдаемыми прави-
правилами отбора.
§ 96. Свойства симметрии странных частиц
При построении лагранжианов для гиперонов и К-мезонов,
которые также принимают участие в сильных взаимодействиях,
удобно учитывать требования симметрии, приводящие в свою
очередь к тем или иным законам сохранения. Экспериментально
было известно, что эти частицы группируются в зарядовые
мультиплеты и что их сильные взаимодействия подчиняются
определенным правилам отбора. Поэтому естественно рассмат-
рассматривать лагранжианы, инвариантные при тех преобразованиях

§ 96]
СВОЙСТВА СИЛМЁТРИИ СТРАННЫХ ЧАСТИЦ
№
1400
7Ж
WHO
*•"
I
симметрии, которые генерируются операторами, связанными
с наблюдаемыми.константами движения.
В дальнейшем термином «странные частицы» будем назы-
называть те частицы, которые в дополнение к лептонам, я-мезонам
и нуклонам стабильны при
выключенном слабом взаи-
взаимодействии'). Энергетиче-
Энергетические уровни всех этих частиц
указаны на рис. 15.1. Как
обычно, при обозначении
барионов (N, 2, Л, Н) и леп-
тонов ((х, е, v, v') мы ука-
указываем только частицы, а
не античастицы. Различие
между последними обычно
ясно проявляется в экспери-
эксперименте. Законы сохранения
барионного и лептонного
числа, надежно установлен-
установленные в настоящее время, по-
позволяют в схеме на рис. 15.1
отождествить с барионом,
например Н--гиперон, а не
его положительно_заряжен-
I
800
500
ZOO
-Л
-п,р
\Ги/?ерош
\Нуюю//ы
-It'-
¦Мезоны
¦Лептоны
Рис. 15.1. Диаграмма энергетических
уровней низколежащих барионов, мезо-
мезонов и лептонов.
ную античастицу B~. В слу-
случае же мезонов на рисунке
указаны как частицы, так и
античастицы. Для п~- и К~-
мезонов античастицами яв-
являются противоположно за-
заряженные я+- и К+-мезоны; я°-мезон, который не обладает заря-
зарядом, является своей собственной античастицей. В то же время
К°-мезон отличается от своей античастицы Я0, поскольку реакция
я-4-р->Л°+К°	A5.54а)
разрешена, а реакция
К° + р-»Л° + я+	A5,546)
запрещена.
Из эксперимента известно, что спин К-мезона равен нулю.
Спины всех барионов, за исключением 2° и 5°, измерены
и равны 1/2; мы будем считать, что спины 2° и S0 также
') К странным частицам относится и 2°-гиперон, хотя его распад 20-*
-*-Л° + у обусловлен электромагнитным взаимодействием; в то же время Q--
гиперон по нашей терминологии не относится к странным частицам.

110	ВЗАИМОДЕЙСТВУЮЩИЕ ПОЛЯ	[ГЛ. 15
равны 1/2) '), поэтому барионы (в отсутствие взаимодей-
взаимодействий) описываются уравнением Дирака с соответствующей
массой, а я- и К-мезоны — уравнением Клейна — Гордона2).
Мультиплетная структура уровней на рис. 15.1 указывает
на то, что к странным частицам применима концепция изотопи-
изотопического спина, введенная первоначально только для я-мезонов
и нуклонов. Поскольку эксперимент указывает на то, что изо-
изотопический спин во всех сильных взимодействиях между мезо-
мезонами и барионами сохраняется, удобно с самого начала рас-
рассматривать изотопически симметричные лагранжианы. Тем са-
самым мы гарантируем изотопическую инвариантность теории
при условии, что электромагнитные потенциалы выключены.
В изотопическом пространстве поле 2, подобно я-мезонному
полю, является вектором:
q + (х) + -ф (х) Ц +(x)-q (х)
V2"	' '	V2	' **(
В теории свободного поля оператор ^s+ (х) уничтожает ча-
частицу Е+ и рождает античастицу S+, в то время как оператор
i])s_ (х) уничтожает 2~- и рождает 2~-частицы. Так как гипе-
гипероны отличаются от антигиперонов (например, 2+ не совпадают
с 2~), то поле ^SW, подобно изотопическому вектору я-мезона,
не является эрмитовым. Для A5.55) эрмитово сопряженное
поле есть
<+(*) +1>+ (*)	1>++(*)-!>+ (х)
,	фъ—
Волновая функция Л-гиперона является скаляром в изотопиче-
изотопическом пространстве, а каскадный Н-гиперон и К-мезон, подобно
нуклону, описываются изотопическими спинорами
>„_(*) J-	A5.56)
A5-57)
При бесконечно малом вращении в изотопическом пространстве
вокруг произвольного единичного вектора и различные поля
') В настоящее время спины 2° и Е° измерены из угловых корреляций
в распадах 20-»-Л + у и Е°-»-Л + я0 и равны tys (см. [139]) {прим. перев.).
2) Обсуждение теоретических схем, описывающих симметрию между во-
восемью барионами и мезонами (включая Т)-мезон), содержится в книге [39]
(см. также [40, 41], прим. перев.).

§ 96]	СВОЙСТВА СИММЕТРИИ СТРАННЫХ ЧАСТИЦ	IJ ]
преобразуются следующим образом:
Фя -»¦ Фя — еФя X U,
Фк -* Фк — -у-1 ¦ иФК)
да _> да 	_iL т . и \if
в	в 2	a
С учетом A5.58) и A5.32) или A5.37) получаем следующее
выражение для сохраняющегося изотопического тока1):
A5.59)
причем сохраняющийся полный изотопический спин равен
Эти формулы являются обобщением выражений A5.50) и
A5.51), которые справедливы только для нуклонов и д-мезо-
нов. В частности, вычислив третью компоненту /, получаем
+ 72г(фк+Фк+ — Фк+Фк+ ~ Фк°Фк° + Фк0(Рк0)] =
= 72 (Np -Nn + N3o - Л/а_ + NK+ - NKo) + Ns+ - Nx- + Nn+.
A5.60)
Легко снова убедиться, что оператор / по своим коммутацион-
коммутационным свойствам аналогичен оператору углового момента A5.53),
') Формула A5.59) справедлива в том случае, когда S не содержит
связей с производными.

112
ВЗАИМОДЕЙСТВУЮЩИЕ ПОЛЯ
[ГЛ. 15
поэтому состояния системы могут быть характеризованы одно-
одновременно собственными значениями операторов /з и /2.
Закон сохранения изотопического спина является прибли-
приближенным. Он справедлив для сильных взаимодействий и нару-
нарушается электромагнитными взаимодействиями. В частности,
небольшая разница в массах между членами каждого мульти-
плета на рис. 15.1 обусловлена электромагнитными эффектами.
При написании зарядово-симметричного лагранжиана, инва-
инвариантного при преобразо-
ваниях A5.58), этой раз-
ницей масс мы пренебре-
гали.
Если включить в рас-
рассмотрение реакции со
странными частицами, то
число нуклонов A5.45)
больше не сохраняется.
Соответствующий закон
сохранения заменяется те-
теперь на точный закон со-
сохранения полного барион-
ного числа, который носит
Рис. 15.2. Примеры реакций, в которых абсолютный характер
сохраняется разность барионов и антиба- Этот	он утверЖдаеТ)
рионов.	,, „ J "	'
что в любой реакции со-
сохраняется число барионов
минус число антибарионов или, на языке фейнмановских диа-
диаграмм, что барионная линия не может оборваться или возникнуть
в вершине (рис. 15.2). При этом плотность лагранжиана & дол-
должна быть инвариантна при одновременном фазовом преобразо-
преобразовании всех барионных полей:
A5.61)
— «Wg.
Для сохраняющегося оператора барионного числа В получаем
B = NN + NA + Nz + Na,	A5.62)
что и является обобщением A5.45).
Наконец, закон сохранения заряда можно связать с требо-
требованием, чтобы 3? была инвариантна при одновременном фазо-
фазовом преобразовании вида A5.47) только заряженных частиц.

§96]	СВОЙСТВА СИММЕТРИИ СТРАННЫХ ЧАСТИЦ	113
При этом плотность лагранжиана должна быть инвариантна
при изотопических вращениях вокруг вектора из ^ @,0,1):
Фя -*¦ Фл — еФя X U3,
Фк -»¦ Фк —Y О + тз) Фк.
^n-*^n — — 0 +4Ln>	A5.63)
что приводит к следующему выражению для оператора заряда:
= J
A5.64)
Преобразование A5.63) состоит из вращения вокруг 3-й оси
в изотопическом пространстве и фазового преобразования К.-,
и N- и 3-полей:
Фк->Фк--^Фк, ?*-*?*--?-?*, Чг3-+чгв + 1±.уЕ. A5.65)
Поскольку плотность лагранжиана инвариантна при вращениях
вокруг 3-й оси изотопического пространства (напомним, что
отсюда следует сохранение h в A5.60)), преобразования
A5.65) также представляют некоторую операцию симметрии.
Эта операция связана с сохранением величины У, которая на-
называется «гиперзарядом»
Y = NK+NN-N3.	A5.66)
С учетом A5.60) и A5.64) получаем соотношение
Q + 7	<1567)
С гиперзарядом У тесно связана «странность» S, определяе-
определяемая как
S = Y-B.	A5.68)
Странность также сохраняется в сильных ваимодействиях. Так
как константы движения S, У, В, /з и Q можно выразить в тер-
терминах операторов числа частиц, мы можем приписать соответ-
соответствующие квантовые числа каждой из частиц, для которой

114
ВЗАИМОДЕЙСТВУЮЩИЕ ПОЛЯ
[ГЛ. 15
справедливы обсуждаемые аддитивные законы сохранения.
В таблице указаны квантовые числа для барионов и мезонов,
квантовые же числа антибарионов противоположны по знаку
квантовым числам барионов.
зт
К
N
Л
у
g
Q
1, 0, —1
1,0
1,0
0
1, 0, -1
0,-1
Гз
1, 0, —1
'/2,-72
Чг-Чг
0
1, 0, -1
'/2,-72
в
0
0
1
1
1
1
к
0
1 .
1
0
0
-1
S
0
1
0
-1
—1
	2
Законы сохранения гиперзаряда У и странности S есть след-
следствия сохранения Q, /3 и В. Они приводят к экспериментально
наблюдаемым правилам отбора в реакциях ассоциативного
рождения. Например, К-мезоны могут рождаться только вместе
с Л- или 2-гиперонами (см. реакцию A5.54а)), в то время как
реакция A5.546) нарушает закон сохранения S и У на две еди-
единицы [42—44].
До сих пор мы рассматривали только сильные взаимодей-
взаимодействия. Если при включении электромагнитных взаимодействий
использовать минимальную подстановку
то В, У и S по-прежнему сохраняются, поскольку электромаг-
электромагнитная связь не зависит от барионного числа, гиперзаряда или
странности. В силу A5.67) сохранение Q означает сохранение
/3. Другими словами, та часть лагранжиана, которая содержит
электромагнитное взаимодействие, должна быть инвариантна
при вращениях вокруг 3-й оси в изотопическом пространстве.
Что же касается полной симметрии лагранжиана при изотопи-
изотопических вращениях, то она, разумеется, нарушается электро-
электромагнитными взаимодействиями. Это обстоятельство приводит,
например, к тому, что в реакциях фотообразования
конечное состояние содержит как / = 72, так и / = 3/2 каналы.
В слабых взаимодействиях /3 не сохраняется, поэтому из
A5.67) и A5.68) следует, что нарушаются также законы сохра-
сохранения странности и гиперзаряда. Именно слабая связь обус-
обусловливает распады странных частиц такие, как, например,
А -> я -+- я .

§98]	ЧЕТНОСТЬ	П5
При этом абсолютно сохраняются только заряд Q и барионное
число В (а также лептонные числа Le и Lu (см. задачу A5.22)).
Никаких нарушений этих законов сохранения в настоящее
время не обнаружено.
§ 97. Несобственные преобразования симметрии
Рассмотренные до сих пор преобразования симметрии гене-
генерировались операторами бесконечно малых преобразований.
Существуют, однако, и «несобственные» или дискретные преоб-
преобразования, которые нельзя получить последовательным приме-
применением бесконечно малых преобразований. Эти преобразования
также играют важную роль, поскольку они приводят к опреде-
определенным правилам отбора и, следовательно, содержат инфор-
информацию о виде лагранжианов взаимодействия. К дискретным
преобразованиям относятся: инверсия пространства или преобра-
преобразование четности ^, операция отражения времени f и зарядо-
зарядовое сопряжение С.
§ 98. Четность
Чтобы определить смысл операции четности, добавив в плот-
плотность лагранжиана член, описывающий взаимодействие (обычно
электромагнитное) квантовой системы с измерительным при-
прибором
2-*2-Ь(х)АЪЛх).	A5.69)
В A5.69) Aext(x) представляет классическое внешнее поле, ко-
которое взаимодействует с оператором тока системы ]^(х). Если
обратить измерительный прибор, т. е. рассмотреть новую физи-
физическую систему, для которой внешнее поле, приготавливающее
и анализирующее ее состояния, равно
Л«й (*) = Uext (- *, t), - Лех( (- *, t)) = A? (- X, t), A5.70)
то, если четность сохраняется, динамическое поведение новой
системы будет таким же, как и у исходной системы. В частно-
частности, если действие новой системы
связано с действием исходной системы / унитарным преобразо-
преобразованием &, то уравнения движения не изменятся. Потребуем,
чтобы оператор 5s удовлетворял следующим соотношениям:
l = S?(-x, t),	A5.71)
1 = Г (-*, 0,	A5.72)

116	ВЗАИМОДЕЙСТВУЮЩИЕ ПОЛИ	[ГЛ. 15
и чтобы 0> не менял перестановочные соотношения. В этом слу-
случае динамика новой и исходной квантовых систем одинакова,
и мы говорим, что четность сохраняется.
Рассмотрим вначале теорию свободного поля и построим
оператор & в явном виде. В случае поля Клейна — Гордона
(см. A2.2), A2.4) и A2.63)) равенство A5.71) выполняется,
если оператор д* удовлетворяет условию
= ±<р (-*,/).	A5.73)
При этом, очевидно, не меняются и коммутационные соотно-
соотношения.
Выбор знака в A5.73) определяется тем, что называется
«внутренней четностью» частицы, связанной с полем; знак
плюс выбирается для скалярных частиц, знак минус для псев-
псевдоскалярных (например, для я-мезонов в лагранжиане A5.30)).
Этот знак определяет фазу одночастичного состояния
<р(*)|0>	A5.74)
и может быть однозначно определен только при рассмотрении
всевозможных связей между различными частицами1). Внут-
Внутренняя четность отличается от пространственной четности, свя-
связанной с четностью волновой функции частицы в состоянии
с данным орбитальным моментом. Обозначим одночастичное
состояние с угловым моментом I через |п=1;/>, а соответ-
соответствующую волновую функцию через (Fi(x), тогда
(-l)'iT, (-*,/). A5.75)
Это равенство по существу содержит лишь утверждение о чет-
четности или нечетности функции &~i{x). С другой стороны, чет-
четность состояния \п=\\Г) по отношению к вакууму, четность
которого по определению положительна:
= |0),	A5.76)
можно определить, рассмотрев следующую цепочку равенств:
= ±<«=1; Лф(-ж,/)| 0>=±(-1)'?-,(*,/). A5.77)
Мы видим, что эта четность равна произведению внутренней
четности ±1 и орбитальной четности (—1)'. Например, псевдо-
псевдоскалярный я-мезон в р-состоянии имеет положительную чет-
четность.
') В A5.73) можно добавить произвольную фазу el<t, для нашего рассмо-
рассмотрения это несущественно.

5 98]	ЧЕТНОСТЬ	117
Перейдем в A5.73) к разложению в импульсном простран-
пространстве (см. A2.7) или A2.57)), тогда получим1)
= ±a+(-k). A5.78)
Действуя на состояние с заданным импульсом, оператор & об-
образует новое состояние, в котором импульсы к\, ..., kn заме-
заменяются на —ki, ..., —kn, а все остальные квантовые числа —
заряд, число частиц и т. д. не меняются.
Уравнения A5.73) или A5.78) для оператора & проще всего
решить в импульсном пространстве. Положив
& = eiP,	A5.79)
перепишем A5.78) в виде
д>а(кH>-x = a(k) + i[Р, a(к)] + ? [Р. [Р, a(k))} + ...
?	. =-а(-Л). A5.80)
Для определенности рассмотрим псевдоскалярное поле и в пра-
правой части A5.80) выберем знак минус. Тогда
[Р, a(k)] = ±r[a(k)±a(-k)},	A5.81)
причем величину X и знак плюс или минус в уравнении еще
следует определить. Имеем, далее,
и, в силу A5.80),
= ±[a(k) =f c(- k)\ + 1^ [a(k)±a(- k)]. A5.82)
Выбрав в A5.81) знак плюс и положив Х = п, получим2)
PPs = - y \ <?k [a+ (k) а (к) + а+ (к) а (- к)] = Р?
a(-k)]}. A5.83)
') Замена k->-—k в аргументе операторов рождения и уничтожения от-
относится только к пространственным компонентам импульса.
2) См. [45]. Отметим, что в координатном пространстве операторы ?и?
являются нелокальными, как и должно быть для преобразований, переводя-
переводящих частицу из точки х в точку —ж.

118	ВЗАИМОДЕЙСТВУЮЩИЕ ПОЛЯ	(ГЛ. IS
Для скалярного поля (в этом случае в правой части формулы
A5.80) нужно взять знак плюс) имеем
9>s = ехр {- Щ- J d3k [а+ (к) а (к) - а+ (к) а (- к)]}. A5.84)
Унитарность оператора 9s гарантируется эрмитовостью Р в
A5.83) и A5.84), а соглашение A5.76) о четности вакуума
обеспечивается нормальным порядком операторных множите-
множителей в Р.
Аналогичным образом можно построить оператор <?, удовле-
удовлетворяющий условию A5.73), и для взаимодействующих полей.
При этом, если выполняются соотношения A5.71) и A5.72),
т. е. если 9* как оператор симметрии коммутирует с гамильто-
гамильтонианом
[&>, Я] = 0,	A5.85)
то четность 9* является константой движения.
Чтобы построить общий вид оператора 9*, построим вначале
оператор 9*0, удовлетворяющий A5.73) в момент времени / = 0.
Оператор 9*й строится так же, как и в теории свободных полей,
поскольку при t = 0 коэффициенты разложения взаимодей-
взаимодействующих полей удовлетворяют алгебре коммутаторов свобод-
свободных полей (см. A5.23)). Поэтому для 9*0 по-прежнему справед-
справедливы выражения A5.83) или A5.84), в которых операторы
рождения и уничтожения нужно рассматривать как коэффи-
коэффициенты разложения взаимодействующего поля при t = 0. Далее
применим гамильтонов оператор, чтобы выполнить смещение
во времени. Если
0»оф(*. О)^о~1 = ±ф(-лг, 0),	A5.86)
то оператор
д>ц) = е1нгр0-ш	A5.87)
удовлетворяет A5.73) в произвольный момент времени t. Нако-
Наконец, если оператор 9* коммутирует с гамильтонианом, то немед-
немедленно получаем, что
9>(t) = 9> @) = 9>а.
Фундаментальные соотношения A5.71) и A5.72) для поля
Дирака будут выполнены, если потребовать, чтобы вместо
A5.73) выполнялось условие
(х, t) 9>~х = ?оФ (- *, t),	A5.88)
причем коммутационные соотношения A3.53) и A3.54) при
таком преобразовании не меняются. Инвариантность уравнения
Дирака относительно преобразования A5.88) была показана

§ 98]	ЧЕТНОСТЬ	П9
в гл. 2 (см. B.33)). Снова удобно перейти в формуле A5.88)
к разложению по плоским волнам. Имеем
1
t Z t* <*
e~iEpt~ipx
+ d+ (p, s) yov (p, s) eiEpt+ipxl A5.89)
Заменив р на — p и используя свойства спиноров и и v:
yQu(—p,s) = u(p,s), yov(—p,s) = — v(p,s), A5.90)
получим
SPb(p, sH>-l = b(~p, s), Pd+(p, s)^~[ = -d+(~p, s) A5.91)
и аналогичные соотношения для операторов b+ и d.
Вспомнив, что оператор Ь+, действуя на вакуум, образует
одноэлектронное (или барионное) состояние, a d+ уничтожает
позитрон (антибарион), мы видим, что четности электрона
и позитрона в одном и том же орбитальном состоянии противо-
противоположны. Независимо от выбора фазы A5.88) электронные
состояния под действием оператора &> преобразуются как ска-
скаляры, а позитронные — как псевдоскаляры. Поэтому электрон-
позитронная пара в s-состоянии имеет отрицательную четность.
Точно так же в любой теории, в которой !? является операто-
оператором симметрии, четность барион-антибарионной пары отрица-
отрицательна:
!?\dzpf{p2)b+(p, s)d+(p, s) | 0> =
= - \ d'p f (p2) b+ (p, s) d+ (p, s) | 0). A5.92)
Для того чтобы построить явный вид оператора четности
для дираковского поля, нужно только повторить все выкладки,
ведущие к выражению A5.84). В результате получим
гас = - y \ d3p [b+ (р, s) b (р, s) - b+ (р, s) b (- p, s) +
+ d+ (p, s) d (p, s) + d+ (p, s) d (- p, s)l A5.93)
Так как оператор четности содержит матрицу уо, величина
^ является псевдоскаляром:
t)у5Ц(х, t)&-х = -у(-х, t)Y5t|>(-x, t). A5.94)

120	ВЗАИМОДЕЙСТВУЮЩИЕ ПОЛЯ	[ГЛ. 15
Это обстоятельство играет важную роль в теории мезон-нуклон-
ного рассеяния. Например, наш модельный лагранжиан A5.30)
только в том случае удовлетворяет условию A5.71), в котором
оператор & действует на все мезоны и нуклоны:
когда &>л псевдоскалярный оператор A5.83). Этот выбор на-
находится в согласии с экспериментальными данными.
Внутренняя четность электромагнитного поля определяется
принципом соответствия, поскольку оно может быть связано
с классическими токами. Поэтому для фотонов мы полагаем
SPA (x, t) 0>~l == - А (- лг, /).	A5.95)
Это преобразование оставляет уравнения Максвелла инвариант-
инвариантными. Явный вид оператора 5s находится так же, как и в тео-
теории Клейна — Гордона.
§ 99. Зарядовое сопряжение
Операция зарядового сопряжения связана с перестановкой
частиц и античастиц. В гл. 5 было показано, что в частном слу-
случае поля электронов эта операция сводится к изменению знака
электрического заряда и электромагнитного поля. Если снова
рассмотреть модельный лагранжиан A5.69), включающий
внешнее поле А™\ которое описывает измерительный прибор,
то такая интерпретация сводится к утверждению, что в заря-
дово-симметричной теории существует унитарный оператор Ci
такой, что
1	, C/,WC4=-/,W, A5.96)
где /р, — электромагнитный ток. Чтобы законы сохранения
странности, числа барионов и изотопического .спина были инва-
инвариантными при зарядовом сопряжении, нейтральные частицы,
описываемые неэрмитовыми полями, под действием опера-
оператора С должны переходить в соответствующие античастицы.
Например, действуя на К0, п и Л, оператор С переводит их в К°,
п и Л. Фотоны и я°-мезоны, которые описываются эрмитовыми
полями, не отличаются от своих античастиц, поэтому при С-пре-
С-преобразовании эрмитово поле может самое большое приобрести
множитель —1. Электромагнитное поле под действием оператора
С- должно преобразовываться следующим образом:

5 99]	ЗАРЯДОВОЕ СОПРЯЖЕНИЕ	121
при этом член j(x)-A(x) в лагранжиане взаимодействия ос-
остается инвариантным. Из A5.97) следует, что
Са+ (k, к) С = - а+ (k, к).	A5.98)
Повторяя выкладки, аналогичные выкладкам предыдущего Па*
раграфа, получаем
С = ехр от J d3k ? а+ (k, X) a (k, к) .	A5.99)
Если включены взаимодействия, то .Со в выражении A5.99) мо-
может и не быть оператором симметрии теории. В этом случае мы
определим .С: соотношением, аналогичным A5.87) для опера-
оператора 3>, а именно:
m,	A5.100)
где Со удовлетворяет условию A5.97) в момент времени ? = 0
и имеет вид A5.99), причем под а+, а нужно понимать коэф-
коэффициенты взаимодействующего фотонного поля при t = 0.
В теории свободного поля вакуумное состояние |0> не вырож-
вырождено, поэтому оно является собственным состоянием оператора
симметрии О. Будем считать, что вакуум есть не только чет-
четное (см. A5.76)), но и зарядово-четное собственное состояние:
С|0) = + |0).	A5.101)
Тогда, с учетом A5.97), собственное значение оператора С, для
я-фотонного состояния равно (—1)". В дальнейшем будем на-
называть собственные значения оператора С. зарядовой четностью
состояния. В случае, когда в лагранжиане присутствуют члены
со взаимодействием, мы по-прежнему будем считать вакуум не-
невырожденным и зарядово-четным.
Зарядовую четность я°-мезона можно определить из самого
факта существования распада п°->2у. Если сильные и элек-
электромагнитные взаимодействия инвариантны под действием опе-
оператора С, то я°-мезон должен быть зарядово-четным, поскольку
он связан с зарядово-четным состоянием двух фотонов.
Перейдем далее к заряженным д-мезонам. Рассмотрим поля
Ф и <р*, которые рождают отрицательно и положительно заря-
заряженные частицы. Поскольку при замене <р<^ф* имеем 9?{х)-+
-*-3? (х) и /р. (х) -> — /ц (х), то оператор С с точностью до произ-
произвольной фазы должен удовлетворять соотношениям
СГ'^ф'М, Сф*(х)С~' = <р(*). A5.102)

125	ВЗАИМОДЕЙСТВУЮЩИЕ ПОЛЯ	[ГЛ. 15
В терминах операторов рождения и уничтожения я+- и я~-мезо-
нов A2.57), эти соотношения имеют вид
CaX(k)C~i = a±(k), Cat(k)C~l^aX(k). A5.103)
Переходя к эрмитовым полям (pi и <р2, получаем
Сф,(ж)С-1 = ф,и), Сф8(*) (Г1 = -%(*), A5.104)
или
Cai(k)C~l=ai(k), Ca2(k)C~l = -a2(k). A5.105)
Эти соотношения показывают, что С, имеет смысл оператора
отражения в A,3)-плоскости изоспинового пространства. От-
Отсюда следует, что собственные векторы оператора С, должны
содержать равное число д+- и я~-мезонов и, следовательно,
должны быть электрически нейтральными. Формально это сле-
следует из соотношения
CQ = -QC.	A5.106)
При построении явного вида оператора зарядового сопряжения
следует помнить, что .Q не коммутирует только с ср2. Поэтому
С = ехр[/я \d3ka+(k)a2(kj\.	A5.107)
В том случае, когда С. не является константой движения он
определяется формальным выражением A5.100).
Аналогичное рассмотрение применимо и к К-мезонам. Все
сказанное выше непосредственно относится к К+- и К~-полям.
Поскольку для К+-мезонов QK+ = SK+ = YK+ (см. A5.64),
A5.66), A5.68)), то из A5.105) следует, что С антикоммутирует
с S и У. Кроме того, под действием оператора С. состояния К0
и К0 должны переходить друг в друга. В этом смысле система
К°К° аналогична системе К+К", единственная разница заклю-
заключается в том, что заряд Q теперь равен нулю. Что же касается
операторов S и У, то они по-прежнему антикоммутируют с С:.
Поскольку операторы ф^„ и фк0 рождают К0- и К°-мезоны, ко-
которые есть собственные векторы оператора странности, эрмито-
вые линейные комбинации ')
Ифср) чж.^-тгС^ + ФкО A5Л08)
по аналогии с ф1 и ф2 в A5.104) рождают соответственно заря-
дово-четные и зарядово-нечетные состояния. Эти состояния иг-
') Известно, что К0 имеет отрицательную внутреннюю четность. Поэтому
согласно A5.108), состояние Ki четно относительно комбинированной опера-
операции ОР, а состояние Kq нечетно.

§ 99]	ЗАРЯДОВОЕ СОПРЯЖЕНИЕ	123
рают важную роль в теории слабых распадов нейтральных
К-мезонов ').
Зарядовое сопряжение для дираковской частицы уже об-
обсуждалось в первом томе. Напомним, что свободное уравнение
Дирака инвариантно при замене
$(x)-+Ci}T(x),	A5.109)
где С — 4X4 матрица, удовлетворяющая условиям
CY^-^-vJ, или С^С-' = -У^ A5.110)
В уравнении E.6) мы выбрали эту матрицу в виде
C = tv2Y°= —С"' = —С+—— Сг	A5.111)
в представлении, где Yo —Yo> V2 = vl- В теории поля мы ищем
унитарный оператор С, генерирующий преобразование A5.109):
Сг|)а (х) (Г1 = Са&% (х) = (CY°)ag < (х)
и
С%(х)С-1 = -%(х)С^,	A5.112)
где матрица С по-прежнему определяется соотношениями
A5.110), A5.111) с точностью до несущественного фазового
множителя. Порядок матриц в A5.112) явно указан индексами,
и его нужно тщательно придерживаться.
Легко проверить, что при С-преобразовании перестановоч-
перестановочные соотношения A3.53) и A3.54), а также уравнение Дирака
остаются инвариантными. Что же касается плотности лагран-
лагранжиана Я? в A3.42), то она изменяется только на несуществен-
несущественную полную дивергенцию.
Подействуем далее оператором G на $ (х) у uty (х); при этом
получим
С* (х) Y4 (х) С = - г|)а (х) С;1у^С1%% (х) = фа (х) v^t (х).
A5.113)
В § 92 мы отмечали, однако, что отождествление величины
¦фМТм-ФМ с электромагнитным током приводит к ряду труд-
трудностей и что поэтому для тока следует использовать выражение,
антисимметризованное по фермионным полям, или, что эквива-
эквивалентно, выражение с нормальным порядком операторных мно-
множителей. Если
') См. [46, 47].

124	ВЗАИМОДЕЙСТВУЮЩИЕ ПОЛЯ	[ГЛ. 15
то непосредственно из A5.113) следует, что
CU*) (Г1 = -/„(*).	A5.114)
Таким образом, электромагнитный ток меняет знак при
С-преобразовании, как и должно быть. Отметим также, что
если вакуум не вырожден и является собственным вектором
оператора С, то <О|/ц.(лг) j0> = 0.
Чтобы построить явный вид оператора С для фермионного
поля, вспомним (см. гл. 5), что электронные и позитронные спи-
спиноры связаны соотношениями
Переходя к A5.112) к разложению по импульсам, получаем
Cb(p, s)C~1
Cd+(p, s)C-l
Эти выражения показывают, что, в согласии с определением,
преобразование зарядового сопряжения переставляет операторы
частиц и античастиц. Явный вид оператора С можно построить
так же, как и в случае бозонных полей. Удобно сначала пред-
представить .С: в виде произведения двух унитарных преобразовании
С = С2С,,	A5.115)
причем Ci выбрать так, чтобы устранить фазовый множитель <j>:
Непосредственным вычислением находим
С, = ехр |— / J d3p ? Ф (р, s) [Ь+ (р, s) b (p, s) - d+ (p, s)d(p, 5)]|.
A5.116)
Для С2, используя ту же технику, что и при вычислении опе-
оператора четности A5.84), получаем
С2 = ехр I f \ d3p ? [b+ (p, s) - d+ (/>, s)] [b (p, s)-d(p,s)}\.
A5.117)
Если Ci не является константой движения, то выражения
A5.116) и A5.117) справедливы при / = 0, в произвольный

§ 99]	ЗАРЯДОВОЕ СОПРЯЖЕНИЕ	125
же момент времени оператор .С; определяется выражением
A5.100).
Проверку того факта, что введение я-мезон-нуклонной связи
в лагранжевой модели A5.30) не нарушает зарядовую инва-
инвариантность теории при условии, что С-преобразование приме-
применяется одновременно ко всем полям, входящим в 3?, мы остав-
оставляем читателю в качестве упражнения. В случае электромаг-
электромагнитной связи симметрия сохраняется; в действительности
именно с помощью этой связи мы определили само понятие
зарядовой симметрии.
Чтобы проиллюстрировать, как зарядовая инвариантность
приводит к определенным правилам отбора, рассмотрим распад
позитрония. Как и в случае нейтральных К-мезонов, мы можем
образовать зарядово-четные и зарядово-нечетные состояния по-
позитрония. С этой целью построим вначале состояние позитро-
позитрония с данным угловым моментом, образовав суперпозицию элек-
трон-позитронных пар с различными спинами и импульсами
g(p, s; p', s')b+(p, s)d+(p', s')|0>. A5.118)
s,s'
Хотя в присутствии электромагнитной связи состояние A5.118)
не является точным собственным вектором гамильтониана, оно
в силу инвариантности электромагнитных взаимодействий отно-
относительно С-преобразования имеет те же свойства симметрии, что
и точное физическое состояние. Поэтому нужно только выяс-
выяснить, какие из амплитуд ^(p,s; p',s') отвечают зарядово-четным
состояниям, распадающимся на два фотона, и какие — зарядо-
во-нечетным состояниям, распадающимся на три фотона. По-
Подействуем на A5.118) оператором С; используя алгебру анти-
антикоммутаторов для операторов Ь+ и d+, получим')
С?в+в- = J d*p d*p' ? g (p, s; p', s') d+ (p, s) b+ (//, s') 10) =
s,s'
= - J d?p d*p' ? § (p'f /; p, s) b+ (p, s) d+ (pf, s') 10).
s,s'
Отсюда следует, что состояние, четное при перестановке элек-
электрона и позитрона,
s; p', sO = + g(p', s'\ p, s)
является нечетным при .(^-преобразовании и наоборот. Таким
образом, позитроний в триплетном состоянии 35i распадается
1 ') Мы опустили здесь фазу </)(p,s); для обоснования см. задачу 23 этой
главы.

126	ВЗАИМОДЕЙСТВУЮЩИЕ ПОЛЯ	[ГЛ. 15
с испусканием трех фотонов, синглетное же 'So состояние рас-
распадается на два у-кванта.
Симметричное состояние бозона и антибозона четно при
С-преобразовании, поскольку в этом случае отсутствует знак
минус, связанный с антикоммутационными соотношениями.
Уместно сформулировать здесь и более общее правило, утверж-
утверждающее, что зарядовая четность пары частица — античастица
равна +1, если частицы находятся в состоянии, разрешенном
для двух тождественных частиц (это состояние четно для бозо-
бозонов и нечетно для фермионов). Для состояний с зарядовой чет-
четностью — 1 ситуация в точности противоположна.
§ 100. Обращение времени
Операция обращения времени заключается в замене направ-
направления времени t на f = —t. При рассмотрении одночастичного
уравнения Дирака мы обнаружили, что обращение времени яв-
является преобразованием симметрии только в том случае, когда
оно включает, наряду с заменой t на f, комплексное сопряже-
сопряжение волновой функции и умножение ее на матрицу Т = iyly3
(в представлении, где только матрица у2 является мнимой).
В теории поля мы строим оператор f, который преобразует фи-
физические состояния, развивающиеся вперед во времени, в со-
состояния, развивающиеся назад во времени, которые выглядят
так, как если бы запустить фильм задом наперед ? = —t.
Из A1.70) ясно, что этот оператор, как и в одночастичной тео-
теории, не может быть линейным. Действительно, рассмотрим, на-
например,
[Я, Фг(*,/)] = -/ аф'а(*'° ¦	A5.119)
Для унитарного оператора Щ, который оставляет действие ин-
инвариантным и преобразует поля q>r(x,t) в Wrsq>s(x,t') =
= B6q>r(x,t)<Zl~K должно выполняться соотношение
,фя(*,О] =+/аф'?;</). A5.120)
Для того чтобы это соотношение совпадало с A5.119), необхо-
необходимо чтобы оператор Щ переводил Н в —Я. Это, однако, яв-
является неприемлемым с физической точки зрения, поскольку
как до, так и после преобразования собственные значения га-
гамильтониана должны оставаться положительными, по отноше-
отношению к вакууму. Поэтому, как и в уравнении E.14), следует
отказаться от требования унитарности f, вводя, в дополне-
дополнение к оператору °Ы, оператор комплексного сопряжения К,

§ 106]	ОБРАЩЕНИЕ ВРЕМЕНИ
действующий на все с-числа1). При этом, если
= Н,	A5.121)
то перестановочное соотношение A5.119) под действием преоб-
преобразования f остается инвариантным. На языке лагранжевой
плотности A5.69), включающей взаимодействие с внешним по-
полем, инвариантность теории при обращении времени означает,
что в этой теории существует оператор f, оставляющий комму-
коммутационные соотношения неизменными и удовлетворяющий ус-
условиям
fS (х, t)f~x = g (x, -t),	A5.122)
АЛ*, 0/"' = />, -t).	A5.123)
Отметим, что в правиле преобразования электромагнитных то-
токов A5.123) заряды не меняют знака при обращении времени,
в полной аналогии с классической теорией. Действительно, при
обращении времени внешнее электромагнитое поле преобра-
преобразуется как
ДД*. f)-*A*{x, —t)	A5.124)
поэтому, если ток преобразуется по A5.123), то
/„ (х, О А» (х, 0 -* + /„ (х, - О ЛЙ (х, -1).
Найдем далее изменение действия:
= J d3x dt ?{x, -t)= J d3x dt S(x) = J (- /,, -12). A5.125)
Новое действие /(—1\,—12) отличается от J{t2,t{) только сдви-
сдвигом по времени — операцией, которая также является преобра-
преобразованием симметрии теории. Мы видим, таким образом, что
выполнение соотношений A5.122), A5.123) достаточно для ин-
инвариантности при обращении времени.
Построим явный вид оператора f для различных полей, об-
обсуждавшихся до сих пор. В случае электромагнитного поля
?А{х, t)f-1 = -'A(x, -0.	A5.126)
поскольку, согласно A5.123), токи, генерирующие поля, меняют
знак. Соотношение A5.122) выполняется для максвелловского
лагранжиана A4.9) в поперечной калибровке. Преобразование
f благодаря наличию оператора К оставляет инвариантными
') Оператор К является нелинейным; оператор f называется поэтому анти-
антилинейным или антиунитарным оператором. См. [48—50].

128	ВЗАИМОДЕЙСТВУЮЩИЕ ПОЛЯ	[ГЛ. 15
перестановочные соотношения A4.13) и A4.17). Переходя
в импульсное пространство и подставляя разложение A4.33)
в A5.126), имеем
А==1
+ <Ua+ (к, X) <и-1ё-ш+л'*] = - А (ж, - 0 =
= - \ -. d3k У г (k, Я) [а {к, К) еш+*-* + а+ (к, X) е-*»«-'*-*].
A5.127)
Вспомнив наше соглашение A4.31) о векторах поляризации
e(fe, l) = _e(-fe, 1), г(к,2) = + г(-к,2),
получаем
^/а (Jfe, 1) <U~l = + а (- fe, 1), ^/а (Jfe, 2) ^"' = - а (- ft, 2).
A5.128)
Эти уравнения по своей форме совпадают с уравнениями A5.78)
для оператора четности, поэтому их решение по аналогии
с A5.83), A5.84) выписывается немедленно:
+{к, \)a(k, \)-a+(k, l)a(-k
+ а+ (k, 2) a (k, 2) + а+ (k, 2) а (- к, 2)] A5.129)
В случае невзаимодействующего эрмитового поля Клейна —
Гордона уравнения A5.122) и A5.123) выполняются, если по-
положить
/ср(*, О/~' = ±Ф(*. -О-	A5.130)
Для заряженного же поля правило преобразования тока
A5.123) означает, что
/ср(*, 0/~' = ±Ф*(*, -0-	A5.131)
Объединяя эти два уравнения, получаем
[ф| (х, t)-l	Г + ф1 (х, - t) "I
ф2 (x,i) /-' = ± - «pi (*.-/),	A5.132)
Фз (л, .0 J	L + ф3 (х, - t) J
причем фаза в правой части может быть выбрана произвольно.
При построении явного вида оператора f нужно повторить вы-
выкладки, которые были сделаны для электромагнитного поля.

§ 1001	ОБРАЩЕНИЕ ВРЕМЕНИ	129
Рассмотрим далее спинорное поле. Оператор / определяется
следующим образом:
Я>«(*. 0Г' = ЗД(«, -0."	A6.133)
Кроме того, он должен удовлетворять соотношениям A5.122)
и A5.123) и оставлять инвариантными антикоммутаторы A3.53)
и A3.54). Легко проверить, что все эти условия можно выпол-
выполнить, если матрицу Т выбрать в том же виде, что и в одночас-
тичной теории (см. E.15)), а именно:
= yJ = V1*
= Т+ = Т~* = -Г, A5.134)
причем используется представление, в котором мнима только
матрица у2. Проверим, например, уравнение A5.123)
= Ф+ (х, - t) T~l (ycAV)* 74 (x, - t) - @ | H^ 10) =
= $(*,-1) y4 (*. — 0 — <o I ФуЛ 1°) = /д (*. - 0-
Отметим, что правило преобразования A5.133) отличается
от аналогичного правила в одночастичной теории: ty(x, t)—*
-+Tty*{x,—t). В теории поля преобразование г|з->Га|)+ является
неприемлемым, поскольку оно переводит, например, покоящийся
электрон в позитрон.
Переходя в A5.133) к импульсному пространству, получаем
Ш+(р, s)<U~1v*(p, s)
+ d+(p, s)Tv(p, s)e-tEt-tp-*]. A5.135)
Из рассмотрения одночастичной теории (см. E.16)) мы знаем,
что
Ти(р, s) = M*(-p, ~s)ela+{p's\ Tv(p, s) = v*(~p, ~s)eia-{p-s\
A5.136)
где а — фазовые множители, зависящие от спинового состояния.

13Й	взаимодействующие поля	(Гл. is
Подействуем еще раз оператором Т на обе части уравнений
A5.136). Поскольку Т2= 1, получим
а±(р, s) = n + a±{-p, -s).	A5.137)
Поэтому из A5.135) и A5.136) следует, что
Ш(р, s)<U-1 = -b(-p, - s)eia+ip-s\
Ш+(Р, sLl-1 = -d+(-P, -s)eia-»-sK {1
Представим далее °Ы в виде произведения двух унитарных пре-
преобразований
<М = <W2<W,.	A5.139)
Оператор Ш\ выберем так, чтобы устранить фазовые множи-
множители
^1b(ps)W' = eia+{p-s)b(p,s),
la(''-s)d+{)	K	}
Явный вид этого оператора есть
<UX = ехр / - i J d3p 2 [а+ (р, s) Ь+ (р, s) Ь (р, s) -
V	±s
- а^ (р, s) d+ (p, s) d (р, в)] }. A5.141)
Оператор Ш2 удовлетворяет уравнениям
<Uib (p,s)U2l = -b(-p,- s), <U2d+ (p, s) U? = - d+ (- p, - s).
A5.142)
Используя ту же технику, что и при построении оператора
четности, получаем
(p, s) b (p, s)
±s
+ b+(p, s)b{—p, —s) — d+(p, s)d(p, s) —
~d+(p,s)d(-p, -s)]}. A5.143)
Равенство A5.138) означает, что обращенное по времени со-
состояние электрона или позитрона с энергией-импульсом Ер, р
и спином s представляет состояние с собственными значениями
Ер, —р, —s, т. е. состояние с обращенными спином и импульсом,
но по-прежнему с положительной энергией. Соответствующие

§ 100]	ОБРАЩЕНИЕ ВРЕМЕНИ	131
волновые функции связаны при этом следующим образом'):
$вр, р, s (*> 0 = <01Ф (*> t) 11 электрон; р, а) =
= (КО | /Ct (х, I) 1 электрон; р, а)* =
= {K0\aU~X(UKi>{x, t) 1 электрон; р, а)* =
= @|/г|5(*, t)f~l\f A электрон; р, «))* =
= — е'а+(Pl в)Г <0 | ф (*, -01 1 электрон; - р, — «)* =
= eia+{p'sWEp ,_р ._,(*• "О-	A5-144)
Это уравнение показывает, что волновые функции обращенных
по времени состояний, как и в одночастичной теории, ком-
комплексно сопряжены.
Мы можем воспользоваться построенными операторами и
в теории взаимодействующих полей, несмотря на то, что разло-
разложение полевых амплитуд возможно лишь в фиксированный
момент времени, например, t = 0. Поскольку при t = 0 все ком-
коммутаторы совпадают с коммутаторами свободных полей, можно
построить оператор fo, удовлетворяющий соотношениям
A5.145)
foA(x, O)fol = -A(x, 0),
foA(x,	1	A
/оФ (х, 0) /о = ± Ф (х, 0),
совпадающими по своей форме с аналогичными соотношениями
для операторов свободных полей. Решения уравнений A5.145)
совпадают с соответствующими решениями в теории свободных
полей с заменой операторов а+, Ь, d и т. д. на коэффициенты
операторного разложения в A5.23), вычисленные при ^=0.
Чтобы найти f в произвольный момент времени t, положим2)
m.	A5.146)
') Отметим, что во второй строке цепочки равенств A5.144) мы, совер-
совершив комплексное сопряжение, явно выделили нелинейный оператор К- В силу
A5.134) Г* = —Г.
2) Знак в первой экспоненте отличен от знака в аналогичных формулах
Для ЯР и С. Это связано с тем, что при обращении времени нужно рассматри-
рассматривать смещение аргумента t -*¦ 0 ->—t, а не t-*-O-*-t, как при остальных пре-
преобразованиях симметрии.

132	взаимодействующие поля	[гл. is
Легко видеть, что такой вид оператора f приводит к выполне-
выполнению всех требуемых условий. Проверим, например, выполнение
равенства A5.133):
X mt ф (ж, 0)/~Уя' =
^(х, 0)е"" =
= ?VM*' -О-
Точно так же получаем, что
Яр (ж, t)f-l = ±q>(x, -/) и fA(x,t)f-] = -A(x,-t).
Если / удовлетворяет условиям A5.122) и A5.123), то он пред-
представляет оператор симметрии теории. В этом случае
[/, Я]==0	A5.147)
и
§ 101. /С^-теорема
Легко проверить, что электромагнитные взаимодействия,
а также модельный лагранжиан A5.30) я-мезон-нуклонного
взаимодействия инвариантны относительно каждого из преоб-
преобразований симметрии /, .С: и 53, рассмотренных в предыдущих
параграфах на примерах различных взаимодействий. Разумеется,
всегда можно ввести в члены со взаимодействием несколько
чисто мнимых констант или матриц ^5 и тем самым нарушить
инвариантность какого-либо дискретного преобразования сим-
симметрии, сохранив при этом инвариантность теории относительно
преобразований Лоренца и пространственно-временных смеще-
смещений. Замечательным фактом, однако, является то обстоятель-
обстоятельство, что произведение f', С; и 9* по-прежнему остается преоб-
преобразованием симметрии в любой теории, для которой выполнены
следующие условия:
1)	теория должна быть локальной, инвариантной относи-
относительно собственных лоренцевых преобразований, и в ней должна
быть определена нормально-упорядоченная эрмитова лагран-
жева плотность;
2)	при квантовании полевых уравнений используется обыч-
обычная связь между спином и статистикой, например поля Макс-
Максвелла и Клейна — Гордона должны квантоваться с коммутато-
коммутаторами, что приводит к квантовой статистике Бозе — Эйнштейна,
а дираковское поле должно квантоваться с антикоммутаторами,
что приводит к принципу запрета.
Сформулированное утверждение составляет содержание
ff?,^-теоремы, доказанной Людерсом и Зумино, Паули и Швин-
гёром [50]. В этом параграфе мы докажем эту теорему для

§ 101]	УСТ*-ТЕОРЕМА	133
взаимодействующих полей Клейна — Гордона, Максвелла и Ди-
Дирака. Конкретно мы покажем, что при последовательном при-
применении операторов /(/), ,С.(/) и &*(t), взятых в один и тот
же момент времени t, гамильтониан Н удовлетворяет условию
С"^-1^//.	A5.148)
Поскольку наши исходные предположения относятся к свой-
свойствам лагранжевой плотности, удобно проводить все рассужде-
рассуждения именно для 3? и лишь в конце доказательства вернуться
к гамильтониану. Итак, покажем вначале, что
9>Cf&(x, t)f-lC-l9>~l = 2(-x, -t),
где все операторы вычисляются в момент времени t.
Лоренцева инвариантность лагранжевой плотности означает,
что 9? является эрмитовым оператором, который содержит ска-
скаляры, построенные из полей <рг(х), А^(х), их производных д/дх^
и билинейных форм ^дГЧ|зв спинорных полей или их производ-
производных, преобразующихся как тензоры. Индексы А я В относятся
к различным фермионным полям (р, е~, v и т. д.), а Г — одна из
шестнадцати линейно независимых матриц Дирака: /, i'ys, Yn>
T5Yii> а\>у- При действии оператора ?PCf на скалярное эрмитово
поле фг получаем
0>Cf<tr(x, 0/"'С^"' = ±Фг(-«. -0, A5.149)
где знак плюс или минус определяется выбором знака в A6.132).
В терминах операторов, образующих состояния с определенным
зарядом, уравнение A5.149) имеет вид
v-1 = ±?*(-*) -о,
0(-1 = ±ф(-*, -0.
Для спинорных полей, используя уравнения A5.88), A5.112)
и A5.133), получаем
- *. - о=+1№+ (- *. - о
-! = - i^(-x, -t)(y5y0\a. A5.150)
Отсюда можно найти правила преобразования для билинейных
форм спинорных полей
= _ фА (_ х> _ t) (Y5Y0
(-x, -t),	A5.151)

134	ВЗАИМОДЕЙСТВУЮЩИЕ ПОЛЯ	[ГЛ. 15
где
Г' = Г для Г=1, гу>5. ffnv»
Г' = — Г для Г = уц, YsYn-
Вспомнив, что различные фермиевские поля г|И и $в анти-
коммутируют друг с другом и что 3? представляет нормальное
произведение спинорных полей, приходим к следующему ре-
результату:
9>Cf : ^ (х, t) ТаХ (*, 0 : Г1С~V =
= +:$?(-*, _ог;^(-д, -о:. A5.152)
Отметим, что при переходе от A5.151) к A5.152) наше согла-
соглашение о нормальной форме операторов существенно только для
случая векторной связи Г = уд и одинаковых спинорных полей
А = В, поскольку в остальных случаях в силу A5.39)
- itf (- х, - 0 r;xttB (- х, - t) =
= + #(-*,- О Г;,^ (- *,-/)- блвбз @) Sp (Yor').
Напомним, однако, что при рассмотрении дискретных преобра-
преобразований необходимо знать именно свойства векторного тока
(см. A5.72), A5.96) и A5.123)). При комбинированном дей-
действии 9>, .С: и / имеем
PC ft1 (x, t) f ""С" V = - f (- x, -1) =
= -:$(-*, -0y^(-*> -*):• A5.153)
Для электромагнитного поля аналогичная формула полу-
получается с помощью уравнений A5.95), A5.97) и A5.126)
PCfA(x, t)f-{C~l^~l = -A(-x, -t). A5.154)
PCfAQ{x,
Применив ^.С^-преобразование к уравнению A5.8) для
А0(х, t), получим
(-У. —0	Ло(—ж, -0,
что непосредственно следует также из A5.152). Поэтому
*) /"'C'V = - Лд (- х).	A5.155)
В том случае, когда плотность лагранжиана содержит произ-
производные полей, мы используем равенство
^ = -аАо-	05-156)

$ 101]	JC0»-ТЕОРЕМА	135
Таким образом, эффект ^С^-преобразования сводится
к следующему:
1. Все координаты х^ заменяются на •*? = —л^; при этом
д	д
2.	Эрмитовы скалярные поля <рг(х) переходят в -\-<рг(х'), где
для определенности мы выбрали фазу равной +1. Электромаг-
Электромагнитное поле Ац(х) переходит в —А^.{хг).
3.	Все тензоры четного ранга, содержащие билинейные фор-
формы фермиевых полей и их производных, переходят в эрмитово
сопряженные величины, а тензоры нечетного ранга — в эрми-
эрмитово сопряженные тензоры со знаком минус.
4.	Все с-числа заменяются комплексно-сопряженными.
Так как 9? — скалярная величина, тензорные индексы в каж-
каждом члене сворачиваются; при этом получается четное число
знаков минус, связанных с условием 3, которые, тем самым,
оказываются несущественными. Чистый эффект ^С^-преобра-
зования сводится к эрмитовому сопряжению плотности лагран-
лагранжиана. Вопрос порядка множителей устраняется благодаря
записи операторов в нормальной форме. Именно в этом месте
и проявляется связь между спином и статистикой, поскольку
операция нормального упорядочивания вносит знак минус
(см. A3.58)) для антикоммутирующих полей со спином 1/2
и знак плюс для бозевских полей со спином 0 и 1 (см. A2.25)).
Поэтому, если 9? — эрмитов оператор, то
<РСчГ9?(х\ 2"ГТ1<5а'"'1 = tptx') — Si	ж 	t) П5 157Ъ
Переход от 2? к гамильтоновой плотности выполняется обыч-
обычным способом
Ж (х) = - 2 (х) + ? : пг (х) фг (*):,	A5.158)
г
где сумма берется по всем ферми- и бозе-полям, входящим
в 3?. Поскольку каждое из преобразований /, С и ^ по по-
построению оставляет инвариантными коммутационные соотноше-
соотношения для бозе-полей
[я, (х, о, ф, (*', т = - /бз (х - х') 6rs
и коммутационные соотношения для ферми-полей
{яг (х, О, Ф5 (*', 0} = + г63 (* - *') 6rs,
то из
'C'V=Ti^r(-«, -/) A5.159)

ВЗАИМОДЕЙСТВУЮЩИЕ ПОЛИ	[ГЛ. 15
= — Ъг д (_ t) Фг (— X, — t) = — Т1гфг (— X, —t)
Х-О-
Отсюда заключаем, что
PCfMix, 0/""С^-1 = #?(-*, -0,
откуда следует A5.148), и /С^-теорема доказана1).
ЗАДАЧИ
1.	Показать, что в калибровке излучения DA = etftr, и построить опера-
оператор поперечного тока.
2.	Показать, что в низшем порядке по е0 зарядовая плотность вакуума
кубично расходится.
3.	Проверить, что в квантовой электродинамике полный заряд сохра-
сохраняется, т. е. что [Q, Н] = 0.
4.	Проверить гейзенберговские уравнения A5.18).
5.	Проверить формулы A5.20) и A5.21) преобразования полевых опера*
торов при преобразованиях Лоренца.
6.	Дополнить доказательство лоренцевой инвариантности квантовой элек-
электродинамики в калибровке излучения, проверив инвариантность одновремен-
одновременных коммутаторов A5.9) и A5.10).
7.	Проквантовать поле заряженной скалярной частицы, выбрав калиб-
калибровку Ао = 0 и добавив в лагранжиан, как и в задаче 14.3, член с массой
фотона —%2А2(х), где к2 мало. Соответствующий лагранжиан выписан в при-
примечании на стр. 94 и в приложении Б (см. т. 1).
8.	Проделать те же выкладки для заряженной дираковской частицы.
9.	Используя условие A5.41), проверить справедливость гейзенбергов-
гейзенберговских уравнений движения для изотопически-инвариантного мезон-нуклонного
взаимодействия A5.40). Что получится при попытке построить теорию с этим
гамильтонианом, в которой поля протона и нейтрона коммутируют друг с
другом?
10.	Проверить, что для модельного лагранжиана A5.30) число нуклонов,
изотопический спин и заряд сохраняются; в явном виде построить соответ-
соответствующие константы движения, используя теорему Нетер.
11.	Выписать общий вид лагранжиана 2, билинейного по восьми барион-
ным полям, линейного по бозонным полям (без связей с производными) и
инвариантного при преобразованиях, генерируемых операторами барионного
числа, изотопического спина, заряда и странности. Ввести в этот лагранжиан
электромагнитную связь и вычислить сохраняющиеся токи.
12.	Разложив поле по сферическим волнам и используя свойства сфери-
сферических гармоник, проверить уравнение A5.75).
13.	Вывести уравнение A5.93) для оператора четности поля Дирака.
14.	Построить оператор четности для электромагнитного поля и проверить
инвариантность лагранжиана и перестановочных соотношений в квантовой
электродинамике при пространственных отражениях.
') В аксиоматическом методе доказана изящная теорема о связи ?
преобразования, спина, статистики и слабой локальной коммутативности [51].

ЗАДАЧИ	137
15.	Проверить инвариантность уравнения Дирака и коммутационных соот-
соотношений A3.53) и A3.54) при зарядовом сопряжении. Вывести формулы
A5.116) и A5.117).
16.	Показать, что при зарядовом сопряжении векторный и тензорный токи,
построенные из билинейных форм дираковских полей, нечетны, а скалярный,
аксиальный и псевдоскалярный токи четны. Обсудить СР-инвариантные ла-
лагранжианы для C-распада.
17.	Построить оператор С для лагранжиана A5.30).
18.	При классификации сильно взаимодействующих частиц удобно исполь-
использовать преобразование G = е'л/2С. Выяснить, как барионы и мезоны преобра-
преобразуются под действием этого оператора. Показать, в частности, что п-пионное
состояние с Q — 0 имеет G-четность, равную (—1)".
19.	Построить оператор / для я-мезонного поля, удовлетворяющий соот-
соотношениям A5.132).
20.	Как при обращении времени преобразуется состояние, содержащее
право-поляризованный фотон?
21.	Проверить уравнения A5.141) и A5.143).
22.	Построить феноменологический слабый лагранжиан для лептонов, ну-
нуклонов и мезонов, основываясь на идеях, обсуждавшихся в гл. 10. Обсудить
соответствующие законы сохранения и свойства симметрии лагранжиана.
23.	Как зависят фазы Ф(р, s) в формулах преобразования операторов Ъ
и d+ при зарядовом сопряжении (см. стр. 124) от импульса р и спина s? По-
Показать, что при вычислении на стр. 125 функции S, описывающей состояние
позитрония с данным L и S, этими фазами можно пренебречь.

ГЛАВА 16
ВАКУУМНЫЕ СРЕДНИЕ И S-МАТРИЦА
§ 102. Введение
Цель квантовой теории поля как физической теории состоит
в динамическом описании наблюдаемых на опыте взаимодей-
взаимодействующих частиц. В предыдущих главах мы уже видели, как
при формальном квантовании классических полей возникает ин-
интерпретация в терминах частиц и как при построении лагран-
лагранжианов учитываются свойства симметрии взаимодействия и
определяются константы движения. Нам остается теперь задача
изучения и вычисления различных матричных элементов, опи-
описывающих динамику взаимодействующих частиц.
Мы интересуемся как амплитудами, отвечающими распро-
распространению в пространстве-времени одной частицы, т. е. одночас-
тичными функциями Грина, так и амплитудами перехода между
различными начальными и конечными состояниями, т. е. 5-мат-
рицей. Одним из главных результатов здесь является обоснова-
обоснование, исходя из формализма теории поля, фейнмановских пра-
правил, обсуждавшихся в первом томе этой книги.
§ 103. Свойства физических состояний
Задача построения точных решений для системы связанных
нелинейных уравнений вида A5.4), описывающих взаимодей-
взаимодействующие поля, до настоящего времени не решена. Поэтому,
прежде чем рассматривать приближенные методы ее решения
имеет смысл выяснить, как далеко можно продвинуться в опре-
определении свойств точных состояний Ф и пропагаторов, исходя
только из принципов инвариантности. Особенно важную роль
при таком рассмотрении играют лоренцева инвариантность и
инвариантность при пространственно-временных смещениях, по-
поскольку эти две симметрии являются общими для всех случаев,
представляющих физический интерес.
Начнем с рассмотрения собственных векторов Ф оператора
энергии-импульса. Эти векторы действительно существуют, по-

§ 103]	СВОЙСТВА ФИЗИЧЕСКИХ СОСТОЯНИЙ	139
скольку мы предполагаем инвариантность теории при простран-
пространственно-временных смещениях. В дальнейшем мы будем рабо-
работать в гейзенберговском представлении, нумеруя векторы Ф соб-
собственными значениями оператора Pw и всех остальных взаимно
коммутирующих сохраняющихся операторов.
Из физических соображений можно наложить некоторые ог-
ограничения на спектр оператора />•*. В отсутствие точных реше-
решений эти ограничения остаются, конечно, недоказанными. Тем не
менее мы сделаем следующие предположения.
1.	Собственные значения операторов энергии и импульса ле-
лежат внутри переднего светового конуса
Р2 = РAР'1>0, Р°>0.	A6.1)
2.	Существует невырожденное лоренц-инвариантное основное
состояние с наинизшей энергией, называемое вакуумным состоя-
состоянием	\
)Фо^Ю>.
По определению начало /отсчета энергии выбирается так, что
/ р°|0> = 0.	A6.2)
Тогда из A6.1) следуете/ что
^-^ Р|0) = 0.
Условие A6.2) лоренц-инвариантно, поэтому вектор |0) являет-
является вакуумным состоянием во всех лоренцевых системах.
3.	Для каждой частицы с массой /п,- существует стабильное
одночастичное' состояние
где pWPW^m.
Временно игнорируя «инфракрасные» усложнения, связан-
связанные с существованием систем фотонов и нейтрино с полной ну-
нулевой массой, добавим четвертое предположение.
4. Вакуум и одночастичное состояние образуют дискретный
спектр операторов Р». На фиг. 16.1 в качестве примера изобра-
изображен спектр для л-мезонов. Конечно, я-мезон в действительности
не является стабильной частицей, он распадается в основном
по каналу
причем наблюдаемое время жизни ~2-10~8 сек. Эта величина
гораздо бвльще естественной частоты h/rtinC1 ~ 5-10~24 сек, по-
поэтому в первом приближении разумно пренебречь слабой связью
и рассматривать я-мезон как стабильную частицу. Далее можно
сопоставить п-мезону поле ф и построить лагранжиан и соответ-

140
ВАКУУМНЫЕ СРЕДНИЕ И S-МАТРИЦА
[ГЛ. 16
ствующий 4-вектор энергии-импульса, спектр которого и указан
на рис. 16.1.
Аналогичным образом каждому дискретному (или почти ди-
дискретному) состоянию в спектре оператора Я" можно сопоста-
сопоставить свое поле <р(х) или я|з(х). Такой подход по существу осно-
основывается на предположении о возможности использовать теорию
возмущений. Действительно, рассматривая поля, отвечающие
стабильным частицам, мы предполагаем, что взаимодействия
Рис. 16.1. Спектр оператора энергии-нмпульса для я-мезонов
Этих частиц не слишком сильно искажают спектр затравочных
состояний. Это предположение является весьма сильным, в ча-
частности оно автоматически исключает рассмотрение связанных
состояний. Хааг, Нишиджима и Циммерманн [52] в рамках ак-
аксиоматического метода несколько продвинулись в понимании
того, как можно построить локальное поле, определенное в каж-
каждой пространственно-временной точке х и описывающее связан-
связанное состояние двух элементарных полей, например, как пред-
представить дейтрон, образованный из двух нуклонов'). Однако
точная связь между составным полем и лагранжианом взаимо-
взаимодействия элементарных полей остается при этом неясной2).
') Рецепт весьма прост. Для скалярного одночастичного «составного» со-
состояния а, связанного с бесспиновыми полями А(х) и В(х), полевой оператор
<ра можно выбрать в виде
Фа
е)В(х-е)
e'<0
a BяK ф\ А (х + е) В (х - е)\а)
*) См. в этой связи замечания С. Вейнберга и А. Салама [53].

§ 104]	tn-ПОЛЯ И in-СОСТОЯНИЯ	141
§ 104. In-поля и in-состояния; асимптотическое условие
Поскольку мы интересуемся главным образом задачами рас-
рассеяния, попытаемся прежде всего построить состояния, которые
описывают физическую систему в начальный момент времени
t -> — оо. В этот момент времени рассеивающиеся частицы еще
не взаимодействуют и распространяются под влиянием своего
собственного поля. Поэтому прежде всего нужно построить опе-
операторы рождения частиц с физическим значением массы. Как
обычно, мы предположим, что всевозможные состояния, разли-
различающиеся числом частиц и их импульсом, образуют полный
набор.	-""^
В случае невзаимодействующих частиц одночастичное состоя-
состояние получается при действии на вакуум одного из операторов
рождения, в разложении свободного поля. Действуя последова-
последовательно на вакуум п операторами рождения, мы получаем п-ча-
стичное состояние. Напомним, что указанная интерпретация
поля в терминах частиц возникает при рассмотрении спектра
оператора энергии-импульса Я" с учетом алгебры операторов
рождения и уничтожения. Построим теперь аналогичные опе-
операторы рождения в теории взаимодействующих полей. Рассмот-
Рассмотрим вначале простой пример эрмитового мезонного поля q>(x),
удовлетворяющего уравнению
(П+т*)<р (*) = /(*)	A6.3)
и одновременным перестановочным соотношениям
[Ф (х, t), Ф (у, ()] = [л (х, t), л (у, ()] = 0,
Будем считать, что ток }(х) в A6.3) представляет оператор, ло-
локальным образом построенный из поля ф(лг). В том простом
случае, когда ток не содержит связь с производными, имеем
л (х) = ф (х).
В остальном форма тока может быть произвольной. Он может
содержать связь с нуклонным источником или, например, само-
Действие вида
/ (х) = V (х).
В последнем случае уравнение поля может быть выведено из
лагранжевой плотности
™	 1 / dtp д<р	п о I 1а лЛ
2 \дХц дх^	2 )
Обозначим оператор, который генерирует одночастичные фи-
Зические состояния, через фй(л)_, Оператор фщ представляет

14?	ВАКУУМНЫЕ СРЕДНИЕ И S-МАТРИЦА	[ГЛ. 16
Собой функционал, зависящий от ф(х) и любых других полей, вхо-
входящих в /(я); существование этого оператора будет продемон-
продемонстрировано ниже явным построением. Для того чтобы <$\п(х)
можно было интерпретировать как оператор рождения физиче-
физического мезона, потребуем выполнения следующих условий, ко-
которые уже встречались в предыдущих главах при рассмотрении
свободных полей.
1. При преобразованиях Лоренца и пространственно-времен-
пространственно-временных смещениях ф1П(*) преобразуется так же, как и соответ-
соответствующее поле ф(х). Это условие гарантирует ковариантность
одночастичного состояния, построенного с помощью оператора
(рт(х). Из инвариантности при трансляциях, в частности, сле-
следует, что
[^Ф1„М] = -;%^.	A6.5)
2. Пространственно-временная зависимость оператора фш (х)
описывается уравнением Клейна — Гордона с физическим зна-
значением массы
(П+т2)Ф).п(х) = 0.	A6.6)
Покажем, что из A6.5) и A6.6) следует, что оператор ццп{х)
действительно генерирует физическое одночастичное состояние.
С этой целью рассмотрим произвольный собственный вектор
) = Р„1«>	A6.7)
и вычислим матричный элемент
~^<П\Ф,„ WI 0> = (ft I[Р*, <Pin (*)]I 0) = р*п(п|ф,п(х) 10).
Дифференцируя еще раз это выражение и используя A6.6),
получим
(? + т2) (п | ф1п (х) 10) = (т2 - р2) (п | ф1п (х) 10) = 0, A6.8)
откуда следует, что состояния, полученные из вакуума примене-
применением оператора фт(*), удовлетворяют условию р2п = т2 и яв-
являются, таким образом, одночастичными состояниями с массой
т. Поскольку ($ш(х) удовлетворяет уравнению Клейна — Гор-
Гордона, его фурье-разложение имеет такой же вид, как и для сво-
свободного поля (см. A2.7)):
Фт М = \ йЧ [аш (*) fk W + < W fl Щ
где
? / A	*		Ibv

§ 104]	In-ПОЛЯ И in-СОСТОЯНИЯ	143
И
причем
ain (k) = / J d3x f*k (x) X Ф,„ (*),
как в уравнении A2.9). Операторы aln(k) удовлетворяют пере-
перестановочным соотношениям
«in
которые следуют из уравнения A6.5).
Последовательно действуя операторами afn(k) на вакуум,
мы получаем произвольное n-частичное состояние. Используя
выражение A6.10) и предположение о существовании вакуум-
вакуумного состояния с нулевой энергией, получаем
Е
причем
(р! ... рм in \k{ ... kN in) = 0,
если М Ф N и набор (рь ..., рм) не совпадает с {k\, .... /глг).
Как отмечалось выше, мы предполагаем, что набор состояний
с различными N н $ является полным.
Для того чтобы выразить оператор щп(х) через поле ф(х),
перепишем уравнение A6.3), добавив к обеим частям его мас-
массовый контрчлен
^(т2-т2)ф(х),	A6.12)
при этом получим
(? + т2) Ф (х) = / (х) + бт2Ф (х) ^ Дх).	A6.13)
Новый ток f(x) теперь является источником, который приво-
приводит к рассеянию. Вычитая из ф(х) рассеянные волны, мы полу-
получим невозмущенное решение с массой т, т. е. оператор q>m(x).
Поэтому1)
VZ ф1п
п (х) = ф (х) - J Л/ Лге1 (х - у; m) Г(г/), A6.14)
') Константа Z обычно обозначается через Z3; мы сохраним, однако, обо*
значение Z3 для фотонов.

144	ВАКУУМНЫЕ СРЕДНИЕ И S-МАТРИЦЛ	[ГЛ. 16
где Aret(* — у; т) есть запаздывающая функция Грина (см. при-
приложение В)
(П* + т2)Дге4 (*-*/; т) = 6*(х-у),	A6.15)
Aret (х — у; т) — 0 для х0 < у0.	A6.16)
Оператор ф!П(л:) в A6.14) удовлетворяет, очевидно, обоим
условиям A6.5) и A6.6) для in-полей. Например, так как/"(у) —
скалярный оператор, то
ш (х + а) = ф (х + а) - J d*y Aret (дс + а — у) Дг/) =
«= eiPaq> (x) e~iPa - J dy Aret (jc - у') J(y' + а) =
= e№« [Ф (*) - \ dV Aret (* - yf) J(y')]e-»>" =
= eiPa л/Z <pin(x) e~iPa.
Константа л/Z в A6.14) определяется из того условия, чтобы
матричный элемент оператора ф!п(л:) между вакуумом и одно-
частичным состоянием был нормирован на единицу. Эту кон-
константу мы вскоре вычислим. На первый взгляд кажется, что при
хо->—оо член с взаимодействием в A6.14) исчезает:
ф(л;)—>л/гц>1П(х) при хо-+ — оо,	A6.17)
т. е. что, в соответствии с интуитивным представлением о при-
причинности, оператор поля при х0 = — оо равен невозмущенному
оператору.
Асимптотическое условие вида A6.17) справедливо в одно-
частичной квантовой механике и рассматривалось, в частности,
в первом томе этой книги (см. гл. 6, 9) как гипотеза. Мы ис-
использовали это условие, чтобы выключить взаимодействие в на-
начальном и конечном состояниях. Другими словами, эта адиаба-
адиабатическая гипотеза утверждает возможность построения лока-
локализованных волновых пакетов, которые как до, так и после
рассеяния находятся на большом расстоянии друг от друга и не
взаимодействуют.
Выражение A6.17) является, однако, операторным уравне-
уравнением. Внимательное рассмотрение показывает, что оно приводит
к противоречию, связанному, по существу, с тем фактом, что
невозможно разделить вклады операторов ф(д;) и j(y), посколь-
поскольку последний содержит все собственные взаимодействия при
хо~*—оо. В квантовой теории аналогом волновой функции яв-
являются матричные элементы операторов поля, поэтому асимпто-

§ 104]	In ПОЛЯ И In-СОСТОЯНИЯ	145
тическое условие следует формулировать непосредственно для
матричных элементов. Мы приведем корректную формулировку
асимптотического условия, следуя Леману, Шиманзику и Цим-
мерманну [12]. Пусть qpf (t) представляет оператор ф(х), усред-
усредненный по пространственно-подобной области
Ф? @ = i J d3x Г (х, t)%q> (х, t),	A6.18)
где f(x, t) — произвольное нормируемое решение уравнения Клей-
Клейна — Гордона
= 0,	A6.19)
и пусть |а) и |р) — два нормированных вектора состояний.
Тогда асимптотическое условие означает1)
lim <а|фф)|р> = У2<а|ф{п|Р>,	A6.20)
где оператор
Ф[п = / J d3xГ (х, t)X%n (x, t)	A6.21)
по теореме Грина (см. A6.6) и A6.19)) не зависит от времени.
Уравнение A6.20) носит название «слабого асимптотического
условия». Оно накладывает ограничения на локализованные па-
пакеты, описывающие частицы в начальном состоянии. Состояния
A6.11), образованные in-операторами
IV- К ™) = <{*№*••• К'™) =
в дальнейшем будут пониматься как предел нормированных со-
состояний, образованных операторами ф^п в A6.21), причем вол-
волновые пакеты f*(x,t) в A6.21) заменяют монохроматические
плоские волны f*k (x) в A6.9). Полный набор in-состояний и
асимптотическое условие — это все что требуется, чтобы задать
начальное состояние в эксперименте по рассеянию.
Уравнение A6.14) определяет оператор фщ при условии, что
у Z Ф 0. К сожалению, мы не можем быть заранее уверены в
том, что константа Z не равна нулю, поскольку рассматривае-
рассматриваемая теория с локальными лагранжианами и локальными поле-
полевыми операторами является математической идеализацией и
') Смысл уравнения A6.20), который существенно отличает его от A6.17),
заключается в том, что в этом уравнении нужно сначала построить нормиро-
нормированные волновые пакеты и образовать матричный элемент, а затем перейти
к пределу /->-— оо (см. [37], а также [54]).

146	ВАКУУМНЫЕ СРЕДНИЕ И S-МАТРИЦА	[ГЛ. 16
приводит к выражениям, расходящимся с ростом энергии. Ука-
Указанная неприятная ситуация действительно может возникнуть,
если наше рассмотрение представляет предел некоторой более
утонченной теории. Тем не менее ниже мы рассмотрим фор-
формальный вывод общего выражения, определяющего константу z,
основываясь только на предположениях A6.1), A6.2) о спектре
оператора Р^ и канонических коммутационных соотношениях
A6.4).
§ 105. Спектральное представление
для вакуумного среднего от коммутатора
и функция распространения скалярного поля
Для вычисления константы Z построим общее выражение для
вакуумного среднего от коммутатора двух полей
/А' (*, х') = @ | [Ф (х), ф (х')] 10).	A6.23)
В гл. 12 этот коммутатор был вычислен для случая свобод-
свободных полей. Теперь же коммутатор в A6.23) нельзя вычислить
явно, поскольку решения полевых уравнений неизвестны. Тем не
менее, основываясь только на аргументах, связанных с трансля-
трансляционной инвариантностью теории, и используя свойства спектра
оператора Р*, можно найти общий вид функции А' в A6.23).
Вставим между двумя операторами в A6.23) полный набор
состояний A6.7). Трансляционная инвариантность означает, что
(п | ф (*) | т) — (п | e"*q> @) e~iPx | т) =
= е'("«-"«> *<я|ф@)|т>, A6.24)
поэтому
А'(х, jc') == — / X <01Ф @) | я> <п | ф @) 10> X
п
X (e~ipn <*-*') - eipn {х-х']) = А'(х- х'). A6.25)
Удобно далее объединить состояния, отвечающие одному и тому
же значению рп- С этой целью используем тождество
тогда A6.25) можно переписать в виде
Д' {х - х>) = -=^ J #q ГBпK ? б4 (ра - <7) | <01Ф @) | п) р j X
Х (e-lq {х-х') _ eiq (х-х')^	A6.26)

§ 105]	СПЕКТРАЛЬНОЕ ПРЕДСТАВЛЕНИЕ	147
Величина в квадратных скобках называется спектральной
функцией')
р (q) sa BпK Ц б4 (рп - </) | <0 | <р @) | п) |2.	A6.27)
п
Эта величина определяет вклад в А' всех состояний с 4-импуль-
сом q. Из лоренцевой инвариантности следует, что p(q) есть
функция только q2. Действительно, поскольку
?/(а)|0> = |0>
и
(/(а)ф@)(/-1(а) = Ф@),
то
Р (д) = BяK Z S4 (р„ - 9) КО IФ @) | U (а) п) \\ A6.28)
п
где а — матрица коэффициентов собственного лоренцева преоб-
преобразования. Лоренцева инвариантность б-функции очевидна из
ее фурье-разложения, поэтому
ЬЧРп-я) = &[{Рп-я)а-'\.	A6.29)
Наконец, выполнив суммирование по полному набору векторов
\т) = U(а) \п) с импульсами
fM = <« IРI т) = {п | С/ (а) Р"?/ (а) | п) = ^„аI*. A6.30)
приходим к следующему результату:
Р (q) = BяK Z б4 (рт - qa~l) | <0 | Ф @) | /п) |2 = р (^а).
m
Так как в силу предположенного свойства спектра оператора
Р» спектральная функция р(^) обращается в нуль вне перед-
переднего светового конуса, то
Р(?) = р(?2)еы,	A6.31)
причем р(<?) равна нулю для q2 < 0 и вещественна и неотрица-
неотрицательна при q2 ^ 0. Уравнение A6.26) может быть поэтому
записано в виде интеграла от инвариантной функции свободного
поля с весовой функцией р
Д' (Х -х') = - -JLg- J d*q p (q2) 6 (q0) (
оо
*= - Wf \ d°2 P (or2) S d
- ^ е
J da2 р (а2) А (х - х', а), A6.32)
о
') В терминах неперенормированных полей.

14й	Вакуумные средние и s-MAft>i-iUA	[гл. ш
где 0(<7о), е(<7о) и инвариантная функция А с массой а опреде-
определены в приложении В.
Выражение A6.32) называется спектральным представле-
представлением вакуумного среднего от коммутатора. В квантовой элек-
электродинамике оно было получено Челленом в 1952 г., а для рас-
рассматриваемого случая — Леманом в 1954 г.1). Приведенный
выше вывод применим без каких-либо изменений и для различ-
различных функций Грина в теории поля. Например,
d2p(o!)bP(x-x'. а)
A6.33)
или, в импульсном пространстве,
причем функция р здесь та же, что и в A6.32).
Хотя спектральная амплитуда A6.27) не вычисляется в яв-
явном виде, мы можем, выделив в ней вклад одночастичного со-
состояния, доказать условие
O<Z<1,	A6.34)
а также показать противоречивость выражения A6.17) как
операторного уравнения. Для этого заметим.что в силу наших
предположений о свойствах спектра оператора Р» (см. рис. 16.1)
функция р(а2) при а2 — пг2 определяется только одночастичным
матричным элементом <0|ф(л;)|/?> в A6.27). Согласно A6.14)
<0 | Ф (х) | р) = -y/Z @ | ф1п (х) \р)+\ d*y Aret (x - у; m) <0 | f(y) \ р).
A6.35)
Но второй член в этом выражении обращается в нуль в силу
A6.13):
= (т2-р2)<0|ф(г/)|р> = 0.	A6.36)
Поэтому
<01Ф (х) I р) = л/Т{01 ф1п (х) | р).	A6.37)
') См. [55—57], а также A. Wightman (не опубликовано, 1953), цитируется
в книге [25]. При нашем выводе мы, не задумываясь, меняли порядок инте-
интегрирования и суммирования. Для обоснования возможности этой замены см.
цитированную литературу.

§ 105]	СПЕКТРАЛЬНОЕ ПРЕДСТАВЛЕНИЕ	149
По определению оператор фт(*) нормирован так, что матрич-
матричный элемент @1 ф1п (л:) \р) совпадает с матричным элементом
свободного поля. Используя A6.9) и A6.11), получим
(О IФ1П (*) 1 р) = $ ^ 7gLr @ | ain (*) | Р) = -;ff= . A6.38)
Соответствующий матричный элемент для q>(x) отличается от
A6.38) множителем л/Z .
Таким образом, вклад одночастичного состояния в p(q)
равен
BяK J d3p б4 (р - q) Bя)!2Юр = Z6 (^ - т2) 6 Ы. A6.39)
Отделив этот вклад в спектральной функции, перепишем A6.32)
в виде
со
Д' (х - х') *=Zb(x- х', т) + J da2 р (а2) А (* - л;'; а), A6.40)
где пороговое значение mf определяется квадратом массы наи-
наинизшего состояния континуума; для п-мезонов, например, т =
= тп и т\ = 4т2.
Взяв в A6.40) производную по времени и полагая t = t', мы
получаем требуемый результат. Действительно, используя опре-
определения A6.23) и A2.42) функций 4' и Д, а также канонические
перестановочные соотношения A6.4), получаем
Jim (/ -§fbf(x- x')) = <0 | [ф (*, t), Ф (х', /)] 10) -
= - /б3 (« - *') = lim (i 4r А (* - ^'; отL). A6.41)
откуда
со
1 = Z+ J p (or2) dor2.	A6.42)
Поскольку р (а2) не отрицательна, из A6.42) следует, что
0<Z<l	A6.43)
при условии, что наши вычисления имеют смысл и интеграл
в A6.42) существует. Интуитивно представляется естественным,
что Z=j?l, если имеется связь с континуумом. Действительно,
можно ожидать, что амплитуда рождения одночастичного со-
состояния из вакуума полем ф(д;) меньше единицы, поскольку это

150	ВАКУУМНЫЕ СРЕДНИЕ И S-МАТРИЦА	[ГЛ. 16
поле рождает еще и состояния континуума. Однако константа Z
не может равняться и нулю, так как в этом случае уравнение
A6.14), определяющее поле ф|П(*)> с помощью которого строят-
строятся произвольные многочастичные состояния A6.22), теряет
смысл. Поэтому было бы весьма неприятно обнаружить, что от-
отдельные члены в ряду теории возмущений нарушают усло-
условие Z ф 0.
Покажем далее, что в присутствии взаимодействия условие
Z < 1 находится в противоречии с сильным асимптотическим
условием. Предположив, что условие A6.17) справедливо
и проводя вычисления, аналогичные вычислениям в A6.41),
получим
t limjO | [ф (х, t), Ф (*', t)\ 10) = - /б3 (х - *') =4
=L lim Z <0 | [ф.п (x, t), <pln (*', 0] I 0). A6.44)
t -> —oo
С другой стороны, взяв производную от коммутатора двух
in-полей
<0 I [Ф1п (х), Фт (*')] 10) = Ш (х - х')	A6.45)
и сравнив с A6.44), мы приходим к заключению, что Z= 1.
Очевидно, что в рассматриваемом случае возможность переста-
перестановки операций суммирования и интегрирования не может
быть строго обоснована.
§ 106. Out-поля и out-состояния
Точно так же, как мы рассмотрели динамическое описание
системы при t-+—оо в терминах in-полей, можно рассмотреть
предел *->+<х> и ввести подходящим образом определенные
out-поля q)Out(*). Состояния при /->+оо представляют конеч-
конечные состояния в рассеянии, поэтому целесообразно иметь про-
простой аппарат для описания физической системы в этот момент
времени.
Свойства оператора фои^я) вполне аналогичны свойствам
ф1п(л;). Этот оператор, по аналогии с A6.5) и A6.6), удовле-
удовлетворяет соотношениям
A6.46)
(П+/п2)фои4 (*) = (),	A6.47)
откуда следует, что, действуя на вакуум, фои^я) образует
только одночастичные состояния. Из разложения, аналогич-
аналогичного A6.9),
Tout W = J М [aout (k) fh (x) + a+t(k) ft (*)] A6.48)

§ 106]	Oul-поля и out-СОСТОЯНИЯ	151
получаем
(k), A6.49)
что находится в полной аналогии с A6.10).
Теперь, однако, в противоположность A6.20), мы рассматри-
рассматриваем асимптотическое условие в виде
lim (a |cpf @10> = Уг" <а | tf | р>	A6.50)
+
или просто
<р(*)-*> У2" Фапг (*) при /-> + оо, ¦ A6.51)
где последнее выражение понимается в смысле слабой опера-
операторной сходимости. Для определения оператора qpout(*) мы
вместо A6.14) используем уравнение
V2~q>0Ut (х) = Ф W — J d*y Aadv (x - у; т)](у), A6.52)
где Aadv (* — У; tri) — опережающая функция Грина:
у;т) = б4 (х - у),
если х0 — г/о > 0.	A6.53)
Нормировочная константа V^ снова вводится для того, чтобы
амплитуда образования из вакуума одночастичного состояния
с помощью оператора фошМ была равна единице. Используя
уравнения A6.36) —A6.38), можно показать, что эта константа
тождественна с д/Z в A6.14):
A6.54)
Поэтому вакуумные средние от коммутаторов <pin(x)
и a?out(.x:) выражаются через функции А для свободных полей
@ I [Ф,п W, Ф1П ЩI 0) = /А (х - у),
/Д()
На самом деле указанные коммутаторы сами по себе представ-
представляют с-числа [37]; другими словами, уравнения A6.55) ос-
остаются справедливыми и без вычисления вакуумного среднего
в левой их части
Проверку этого факта мы оставляем читателю в качестве
увлажнения.

152	ВАКУУМНЫЕ СРЕДНИЕ И 5-МЛТРИЦА	[ГЛ. 16
§ 107. Определение и общие свойства S-матрицы
В предыдущих параграфах мы рассмотрели свойства опера-
операторов ц>т(х) и qpout(x). Теперь, используя развитую технику,
можно перейти к рассмотрению и изучению амплитуд перехода,
или 5-матричных элементов, непосредственно наблюдаемых на
опыте. Рассмотрим начальное состояние « невзаимодействую-
невзаимодействующих (т. е. пространственно разделенных) частиц с квантовыми
числами ри ..., рп:
\pi ... р„ in) = | a in).	A6.57)
Индекс р означает, помимо импульса, все квантовые числа, ха-
характеризующие частицу, такие, как заряд, странность и т. д.
Отметим, что in-состояние действительно можно характеризо-
характеризовать дополнительными квантовыми числами, отвечающими раз-
различным преобразованиям симметрии системы, поскольку, со-
согласно определению A6.14), поле фт(*) при преобразованиях
симметрии имеет те же трансформационные свойства, что и
ф(л;). Например, если
[Q, фг (*)] = — ЯГ5ф5 (х),
то
[Q, I (х)} = (? + от2) [Q, Фг (х)] = - KsU (*),
поэтому из A6.14) следует
Таким образом, мы можем интерпретировать константы дви-
движения для взаимодействующей системы в терминах квантовых
чисел начальных и конечных состояний. В частности, систему
свободных частиц в in- и out-состояниях можно характеризо-
характеризовать квантовыми числами операторов, введенных в гл. 15 при
рассмотрении сильно взаимодействующих частиц. 5-матричный
элемент для перехода из «-частичного состояния A6.67) в /п-ча-
стичное состояние
| р[...р'т out) = | pout)	A6.58)
дается амплитудой вероятности
5ра = (pout lain).	A6.59)
Это уравнение определяет pa-элемент S-матрицы.
Поучительно сравнить A6.59) с определением 5-матричного
элемента в нерелятивистской теории. В уравнении F.16) мы
определили
Sft = lim \ cfx q>; (х, t) Y+ (х, t) = lim (<p. (x, t), W+ (*, /)), A6.60)

§ 107]	ОПРЕДЕЛЕНИЕ И ОБЩИЕ СВОЙСТВА S-МАТРИЦЫ	153
где 47 (х, t) — точное решение уравнения Шредингера F.74)
с граничным условием, которое заключается в том, что при t =
= — оо Wi совпадает с плоской волной. Величина Sfi равна
скалярному произведению 47 (при /->+оо) и q)f(#, t), где
Ф/(#, 0 — плоская волна с квантовыми числами / конечного со-
состояния. Для того чтобы переписать A6.60) в виде, аналогич-
аналогичном A6.59), рассмотрим точное решение 47 (*> 0 уравнения
Шредингера с граничным условием при t->-\-oo: tyf (x, t)->
->q>f(x, t). Функция 4*7 (ж, t) состоит из плоской волны и из су-
суперпозиции сферических волн, сходящихся при /—*—оо к рассеи-
рассеивающему центру и исчезающих при t-*- + °°- Эта функция пред-
представляет решение уравнения Шредингера F.14), в котором за-
запаздывающая функция Грина заменена на опережающую
47 ОО - «pf ОО + \ ctx[Gt (x; х[) V (х{) 47 U)> A6.61)
где
Goadv (*', t'\ x\, t[) = 0 при ? > t[.
Так как 4rf (x', t')-> щ (х', t') при t'-++oo, то из A6.60) по-
получаем
S/(-lirnD7(*, t),4t(x,t)) =
= lim J d3xWf* (x, 0) elHte~iHtWt (x, 0) =
*=(W(x, 0), Wt(x, 0)),	A6.62)
где W(x, 0) — волновая функция в гейзенберговском представле-
представлении, из которой выделена ее временная зависимость. Уравнение
A6.62) представляет аналог A6.59) с волновыми функциями,
удовлетворяющим in- и out-граничным условиям.
Из A6.59) и предположения о полноте in- и out-состояний
следуют выражения для матричных элементов оператора 5
<pin|S = <pout|, <pout|5"' = <|5in|,	A6.63)
откуда
Spa ==<Pin| S|<xin>.
5-матрица играет центральную роль в динамических вычис-
вычислениях, поскольку ее матричные элементы непосредственно свя-
связаны с измеряемыми на опыте физическими амплитудами. Ис-
Используя наши предположения о спектре состояний, а также свой-
свойства операторов цчп(х) и (pout(я), сформулируем далее важней-
важнейшие ее свойства.

154	ВАКУУМНЫЕ СРЕДНИЕ И S-МАТРЙЦА	[ГЛ. 16
1.	Стабильность вакуума означает, что |Soo| = 1 или
<0 in 15 = @ out | = егч>°<0 in |.
По определению вакуумное состояние единственно. Полагая
фазу ф0 равной нулю, получим
<0 out | = <0 in | = <01	A6.64)
и 5оо= 1.
2.	Стабильность одночастичного состояния в свою очередь
означает
<р in 151 р in> == </? out | /7 in> == <р in | р in> = 1, A6.65)
поскольку, согласно A6.54), \pin) = \poixt) = \p).
3.	S-матрица преобразует in-поля в out-поля:
Чтобы доказать это, рассмотрим матричный элемент
<р out | фои1 (х) | a in) = <p in 1Sq>out (х) | а in).
Поскольку ф out | qpout (x) есть out-состояние, то в силу A6.63)
<Р out | qpout (x) = (Р in | ф,п {х) S, откуда
(Рin |Ф,п (x)S\ain) = фin |Scpout (x) \a in).
Поскольку in-состояния образуют полный набор, то из послед-
последнего равенства следует выражение A6.66).
4.	S-матрица унитарна. Действительно, из A6.63) получаем
5+|ain) = |aout).	A6.67)
Следовательно,
<р in 155+1 a in) = ф out | a out) = 6pa	A6.68)
и
SS+ = S+S=l.	A6.69)
5.	S-матрица трансляционно и лоренц-инвариантна'), т. е.
U {а, Ь) SU'1 (а, Ь) = S,	A6.70)
') Следует иметь в виду, что в квантовой электродинамике выполнение
одного только условия A6.70) еще недостаточно для градиентной инвариант-
инвариантности теории. Действительно, чтобы восстановить в новой системе координат
калибровку излучения, каждое лоренцево преобразование нужно дополнить
соответствующим градиентным преобразованием. Поэтому в квантовой элек-
электродинамике следует дополнительно установить градиентную инвариантность
S-матрицы.

§ 108J	РЕДУКЦИОННАЯ ФОРМУЛА ДЛЯ СКАЛЯРНЫХ ПОЛЕЙ	155
где U(a,b) — определенный выражениями A1.66), A1.69) и
A1.72)—унитарный оператор, генерирующий преобразование
координат
Для доказательства подставим A6.66) в уравнение A1.67), вы-
выражающее закон преобразования полевых операторов
ф1п (ах +b) = U (а, Ь) «р,п (*) СГ1 (а, Ъ) =
= US<poJx)S-'f/-1 = USU-\at(ax + b)US^V1. A6.71)
Учитывая далее, что qpin (ах -f b) = 5cpout (ax -f b) S~l, немедленно
получаем A6.70).
§ 108. Редукционная формула для скалярных полей
Сформулировав общие свойства 5-матрицы и интересуясь
далее ее матричными элементами, квадрат которых |5ра|2 имеет
смысл вероятности экспериментально наблюдаемых переходов
между in-состояниями а и out-состояниями р, мы сталкиваемся,
однако, с весьма нетривиальной задачей их реального вычис-
вычисления.
До 1954 г. единственный систематический метод вычисления
5-матрицы основывался на использовании рядов теории возму-
возмущений по степеням тока/(л:) в A6.13). После проявления работ
вначале Лоу [58], а затем Лемана, Шиманзика и Циммермана
[12, 13] (LSZ) возник новый подход к этой проблеме, основан-
основанный не на разложении по степеням малой константы связи, а
на использовании общих свойств 5-матрицы. Асимптотические
условия A6.20) и A6.50) позволяют выразить интересующие
нас матричные элементы в терминах вакуумных средних поле-
полевых операторов. Мы уже видели преимущества такого подхода
при вычислении полевого коммутатора в A6.40). При этом мы
получили общее выражение для функции А'(л: — х'), используя
только лоренцеву инвариантность и некоторые весьма общие
свойства теории.
Ниже мы рассмотрим вычисление вакуумных средних от про-
произведения полевых операторов. Эти величины в некотором
смысле более удобны, чем матричные элементы вида A6.59).
Далее мы разложим операторы ф(д;) в ряды теории возмущений
и получим таким образом общий вид разложения 5-матричных
элементов в терминах вакуумных средних свободных in-полей.
Соответствующие формулы в точности совпадают с фейнманов-
скими правилами, введенными при рассмотрении функций рас-
распространения. Отметим еще, что требования инвариантности,
аналогичные тем, которые использовались при вычислении функ-

156	ВАКУУМНЫЕ СРЕДНИЕ И S-МАТРИЦА	[ГЛ. 16
ции А'(х-х'), наиболее легко сформулировать для матричных
элементов гейзенберговских операторов ф(л;) между единствен-
единственным образом определенным и инвариантным вакуумным состоя-
состоянием. Этот подход приводит к ряду новых результатов, которые
не связаны с использованием теории возмущений.
Приступим теперь шаг за шагом к построению общей «ре-
«редукционной техники». Эта техника позволяет извлечь всю ин-
информацию, заключенную в определении физических состояний
A6.59) и перенести ее на произведение полевых операторов, за-
зажатых между вакуумными состояниями.
Рассмотрим 5-матричный элемент
Sp.ар = (Pout \ар in),	A6.72)
где индекс р означает частицы в out-состоянии |р out), a \apin)
означает совокупность частиц а в in-состоянии плюс еще одну
налетающую частицу с импульсом р.
Используя асимптотическое условие, мы можем извлечь из
in-состояния частицу р, вводя вместо нее подходящий полевой
оператор. С учетом A6.22), A6.9) и A6.48)') имеем
ф out | ар in) = ф out I а+ (р) | а in) =
= ф out | а+1 (р) | а in) + ф out | а+ (р) - a+ut (p) | а in) =
= <Р ~ Pout I а in) - * (Р out | J dh fp (х)Х Ош W ~ Tout (*)] I «in>-
A6.73)
Здесь |р — pout) есть состояние, из которого в том случае, когда
частица р содержится в наборе р, нужно удалить эту частицу,
в противном случае первый член в A6.73) равен нулю. Если
\<хр in> представляет начальное двухчастичное состояние, то пер-
первый член в A6.73) вносит вклад только в амплитуду упругого
рассеяния на нулевой угол, причем в ту ее часть, которая отве-
отвечает сохраняющимся квантовым числам налетающей частицы
и частицы мишени. Правая часть в A6.73) по теореме Грина
не зависит от времени. Используя асимптотические условия
A6.20) и A6.50), можно заменить q>in{x,x0) при хо->—оо и
<Pouf(*,*o) при лго-^гЬ00 наО/У^ )ф(дс, х0); при этом получаем
(Р out | ар in) = (р — р out | a in) +
+ —lj=r( Hm — lim ) \ d3x L {x, x0) d0 (p out | qp (x, x0) | a in).
		A6.74)
') Строго говоря, следует работать с нормированными состояниями и ис-
использовать операторы ф{п, определенные в A6.21), вместо ащ(р). Тем не ме-
менее при практических вычислениях мы будем использовать, с известной осто-
осторожностью, простые плосковолновые решения.

§ 108]	РЕДУКЦИОННАЯ ФОРМУЛА ДЛЯ СКАЛЯРНЫХ ПОЛЕЙ	157
Тем самым выполнен первый этап в редукционном разложении.
Желая сохранить ковариантную форму вычислений, мы перепи-
перепишем выражение A6.74) в виде четырехкратного интеграла, ис-
используя тождество
го
f	¦<->¦	f	д	¦<->
( lim — lim ) \ d3x g, (*) д0 g2 {x) = \ d4x -^— [g, (x) dQ g2 {x)] =
— OO
oo
= \ d'x \gl (x) ¦?? g2 (x) - ^fi- g2 (x)] . A6.75)
_i I	dxo	dxo	J
Учтем далее, что fp(x) удовлетворяет уравнению Клейна —
Гордона
д " * =(V2 — m2)fp(x).	A6.76)
Интегрируя член с V2 по частям '), получим искомый результат
(р out | ар in) = (р — р out | a in) +
+ —l— \ d4x fp (x) (? + т2) <р out | ф (*) | а in). A6.77)
Далее можно последовательно применять описанную процедуру
до тех пор, пока мы не вытащим все частицы из обкладок мат-
матричного элемента и не представим наше выражение в виде ва-
вакуумного среднего от произведения полевых операторов. Пусть,
например, в A6.77) $ = ур'. Повторяя предыдущие выкладки
и используя при этом там, где нужно, эрмитовое сопряжение,
мы можем исключить out-частицу р' из набора ур\ в резуль-
результате получаем
<Р out | ф {х) | a in) = <y out | ф (х) \ а — р' in) +
+ (y out |aoui (p') Ф (x) — ф(x)aia(pf) Iain) = <y out \q>(x)\a — p'in) —
- i J d3y (y out | youX (у) ф (*) — ф (*) Ф1П (у) | a in) d^f/ («/)• A6.78)
Асимптотическое условие снова позволяет заменить в матрич-
матричном элементе A6.78) in- и out-поля при г/0->—оо и г/0-> -f00
соответственно на (l/V^) ф(г/), в результате A6.78) записывает-
записывается в виде хронологического произведения A2.72):
(Y out | фои( (у) ф (х) - ф (х) ф!п (у) | a in) =
= ^U( lim - lim ) (у out | T (ф (у) ф (х)) \ a in). A6.79)
') Поскольку физическая система локализована в пространстве, при та-
таком интегрировании не возникает никаких поверхностных членов.

]58	ВАКУУМНЫЕ СРЕДНИЕ И S-МАТРИЦА
Используя A6.75) и A6.76), получаем
>' out | ф (х) | a in) = (y out | ф (х) | а — р' in) -f
-<
out 1Т (ф (у) ф (л:)) | а in)
1ГЛ, 16
2) f*p, (у). A6.80)
Теперь ясно, какой вид имеет окончательный результат:
(Pi ... рпout|^ ... 9m in) =
Х<о|Г(фЫ ... фЫфМ... Ф(*т))!0>х
X (Oyt + /n2) Гр (г//), если все р1Фц1. A6.81)
В формуле A6.81) мы предположили для простоты, что все
Ф Ц\, и опустили члены, отвечающие рассеянию на нулевой
угол, которые содержатся в
выражениях A6.77) и
A6.80). Учет этих членов не
представляет никаких труд-
трудностей, поскольку к ним мо-
может быть также применена
описанная редукционная
техника.
Уравнение A6.81) яв-
является основой всех вычис-
вычислений в современной кван-
квантовой теории поля. Уместно
в этой связи сделать сле-
следующее замечание. Величи-
Величина @|Г(фB]) ... ф(zr)) 10)
равна точной r-частичной функции Грина (см. рис. 16.2), пред-
представляя по своему смыслу сумму всех феинмановских графиков,
в которых частицы рождаются или уничтожаются в точках
(zb ..., zr). При этом операторы (Oi-{-m2) в A6.81) устраняют
пропагаторы внешних линий, поскольку в импульсном простран-
пространстве каждый из них равен ш2 — р?и сокращается с соответствую-
соответствующим пропагатором ij(p2t — m2). Таким образом, 5-матричный
элемент в силу редукционной формулы A6.81) равен просто
функции Грина для г ==. п + m частиц, в которой нужно выде-
выделить внешние концы, а все внешние импульсы взять на массовой
Рис. 16.2. Полная г-частичния функция
Грина.

$ 109]	In- И out-ГЮЛЯ В ТЕОРИИ ДИРАКА	159
поверхности, р2 —<72. = /п2. Этот факт будет широко использо-
использоваться в дальнейшем.
Отметим еще близкую аналогию редукционной формулы
A6.81) с представлением для 5-матрицы, полученным в методе
функций распространения (см. F.30)). Эта аналогия стано-
становится особенно ясной, если переписать объемные интегралы в
F.30) в четырехмерной форме. Используя свойства запазды-
запаздывающей функции Грина, а также уравнение Шредингера
получаем
Stl = - i lim \ d4 \ d4x ф* (*', П -^ [G (х'\ х) Ф/ (х, t)] =
= \\ха^ \ й3х' \ й'х Ф; (/) G (*'; х) (- / ~ + -Ц
= - / \ dV J Л Ф; (*0 (г ^г + -^) G (л;', х) X
Сравнивая A6.81) и A6.82), мы видим, что в одночастичной
теории полная r-частичная функция Грина с точностью до нере-
нерелятивистской подстановки
заменяется на запаздывающую одночастичную функцию Грина
G(xf, x) в заданном внешнем поле. Мы предлагаем читателю
показать, что аналогичный результат имеет место и в позитрон-
ной теории (см. F.56)), где роль функции G играет точный фейн-
мановский пропагатор.
§ 109. In- и out-поля и спектральное представление
в теории Дирака
Продолжим наше обсуждение, включив в рассмотрение спи-
норное и электромагнитное поля. При этом мы сталкиваемся
лишь с формальными трудностями. Спин усложняет алгебру
в дираковском случае, а градиентная инвариантность вносит
некоторые усложнения при рассмотрении уравнений Максвелла.
Основные же идеи, использовавшиеся при построении in- и
out-состояний и при обсуждении спектрального представления

160	ВАКУУМНЫЕ СРЕДНИЕ И S-МАТРИЦА	[ГЛ. 16
вакуумного среднего от коммутаторов, а также при выводе ре-
редукционной формулы, остаются при этом неизменными [56, 59].
Рассмотрим уравнение Дирака с физической массой т,
вводя, по аналогии с A6.13), массовый контрчлен
(N - т) ф (*) = Г(х), ft*) =} (х) -{т~ тй) ф (*). A6.83)
Поля ${х) удовлетворяют обычным одновременным перестано-
перестановочным соотношениям A5.9)
{Фа (*, 0, % {У, t)} = 0, {% (X, t), ^ (У, t)} - б3 (х - у) бар.
Снова определим in-поле фтСх) как неоднородный член в ин-
интегральном уравнении, соответствующем уравнению A6.83), т. е.
(х) = ф (х) - J dAy 5ret (х ~ у; т) J(y), A6.84)
где SretM — запаздывающая функция Грина:
(iVx — т) 5ret (* — у;т) = б4 (х — у),
5ret (x — y) = Q при х0 < у0.
Константа V^7 по-прежнему выбирается из условия, чтобы
матричный элемент оператора ifinC*:) между вакуумом и одно-
частичным состоянием был равен единице.
Из определения следует, что оператор ^цп(х) удовлетворяет
свободному уравнению Дирака с массой т:
(iV-/nHin(x) = 0	A6.86)
и обладает теми же трансформационными свойствами, что и
поле o|)in(*)> B частности
->~~-	A6.87)
Так как каждая компонента спинора а|)т(*) удовлетворяет урав-
уравнению Клейна—Гордона, то, как и в A6.8), можно показать,
что г|IП(л:), действуя на вакуум, приводит к одночастичному
состоянию с массой т.
Фурье-разложение поля tym{x) имеет тот же вид, что и раз-
разложение свободного дираковского поля (см. гл. 13). Запишем
его в виде
%п (*) = J d3p ? [bin (p, s) Ups (x) + dtn (p, s) Vps (x)], A6.88)
±5
где

109)	In- И ouf-ПОЛЯ В ТЕОРИИ ДИРАКА	161
и Ер = -\- VI Р I2 + гп'2. Обратив уравнение A6.88) и эрмитово
сопряженное уравнение, для коэффициентов разложения по-
получим
A6-89>
Эти коэффициенты удовлетворяют перестановочным соотноше-
соотношениям
О", bin (p, s)] = - р»Ьы (р, s),
[Я", ЬГп (Р, S)] = + P4tn (Р, S),
[Р*> din(p,s)]=-p»dln(p,s),	¦ *
[Р\ di+n(p>S)]=-f p4t{p, s),
которые следуют из A6.87).
Выражения A6.90) совпадают с перестановочными соотно-
соотношениями для свободного поля. Поэтому мы можем построить
произвольное «-частичное состояние, последовательно действуя
на вакуум операторами bin и dtn по аналогии с A6.11). При
этом мы снова предположим, что вакуум представляет един-
единственное состояние с нулевой энергией и что набор состояний,
полученный применением in-операторов, является полным.
Асимптотическое условие, как и в случае скалярного поля,
имеет вид
1|з (х) -> д/22 1|э,п (х) при / -> — оо,
причем это уравнение понимается в смысле слабой операторной
сходимости. Другими словами, мы предполагаем выполнение
условия
lim <а 1 ^f @ | Р> = д/Z^ <а | ф[п | р>,	A6.91)
где 1|з[п определяется первым из уравнений A6.89), в котором
U$s нужно заменить на локализованный пакет. Оператор i|>f(/)
определяется тем же уравнением с заменой ^т(х) на ${х).
Аналогичным образом можно ввести out-поля, описывающие
физическую систему при /-> + °°- Вместо A6.84) имеем
v (х - У) I (У),	A6.92)

J62	ВАКУУМНЫЕ СРЕДНИЕ И S-МАТРИЦ,	[ГЛ. 16
где
(iVx - т) Sadv (х-у) = б4 (х - у),
Sauv(x — у) = 0 для лг0 > Уо-	A6.93)
При этом уравнения A6.86) — A6.90) по-прежнему справедливы
для out-операторов, причем асимптотическое условие имеет те-
теперь вид
lim (а | ф' @ | р) = л/г7 (« I 4>?ut I P>.	A6.94)
+
Уравнение, определяющее Z2 — вероятность образования од-
ночастичного состояния с массой т из вакуума, •— выводится в
полной аналогии со случаем скалярной теории. Определим
SU (х, х') = i <0 I {фа (х), % {х')} 10).	A6.95)
Вставим далее полный набор состояний
и сместим операторы поля в начало координат
')^
Ф„ @) | я> (п ! ^р @) 10)e~ipn *-*'> +
+ ф\^@)\п)(п\Ца@)\0)е{рп<х-х'Ч. A6.96)
Введем снова спектральную амплитуду, объединив в сумме
по п состояния с данным 4-импульсом q
Paf5(q) = BяK Z б4(р„ - с?)@ |фа@) |д><«|%@) | 0). A6.97)
п
Используя соображения, связанные с лоренцевой инвариант-
инвариантностью, можно выяснить общий вид функции pap (q). Она пред-
представляет 4 X 4-матрицу и может быть, таким образом, разло-
разложена по шестнадцати линейно независимым матрицам Дирака
Paf5 (<7) = Р (?) баР + Р„ (<?) Y?e + P^v (Я) а$	^p „	„р
A6.98)
Коэффициенты в этом разложении можно найти из условия ло-
лоренцевой ковариантности1). Действительно, отдельные члены
') Излагаемые в этом параграфе аргументы неприменимы, когда поле
¦ф(л:) связано с полем излучения. В этом случае необходимо дополнить ло-
ренцево преобразование градиентным преобразованием с тем, чтобы восста-
восстановить поперечную калибровку, используемую при квантовании. В то же время
функция S (х,х') не градиентно-инвариантна (см задачу 8 этой главы).

S 109]	In- И out-ПОЛЯ В ТЕОРИИ ДИРАКА	163
в A6.98) должны преобразовываться так же, как и рар в A6.97).
Напомним в этой связи, что при преобразовании Лоренца
U (а) % @) [Г1 (а) = Sal! (a) ^ @),
U (а) $а @) ?/"' (а) = ^ @) Ska (а),	A6.99)
где 5 — матрица, определенная в гл. 2,
S-yS = ay.	A6.100)
Тогда, в предположении лоренцевой инвариантности вакуума
?/|0) = |0>,
Pap (я) = I BяK б4 (р„ - <?) S^1 (a) Sep (a) X
X<0|%@)|f/(a)«)(t/(a)«|ta@)|0). A6.101)
Используя инвариантность б-функции (см. A6.29)), перепишем
A6.101) в виде суммы по полному набору состояний \т) =
= \U(a)n):
Раз (Я) = Sal W 2 BяK б1 (Pm - qa~{) X
X @1 ^ @) | т)(т | ф6@) | 0M6р (а).
Таким образом,
1(l)S(a).	A6.102)
Это уравнение определяет вид коэффициентов p(q), рц(<7) и
т. д. в выражении A6.98). Если подставить A6.98) в A6.102),
то получим, например,
т. е. что p(q) преобразуется, как скаляр. Аналогичным образом
находим, что
преобразуется, как 4-вектор, и т. д. Так как рар зависит только
от q и обращается в нуль вне переднего светового конуса,
то р и р в A6.98) зависят только от q2. Поэтому р^^) и рд (q)
можно представить в виде скалярных функций от q2, умно-
умноженных на q^, точно так же р^ пропорционально q^q^. В ре-
результате получаем
Раз (Я) = Р, (Q2) Яа, + Р2 (V2) баЭ + р, (<72) WY5)ae + Р2 (Я2) Yae. A6.103)
Далее используем инвариантность теории при пространствен-
пространственном отражении
^,@)^"' = У0Д@).	A6.104)

164	ВАКУУМНЫЕ СРЕДНИЕ И S-МАТРИЦА	[ГЛ. 16
Подставив A6.104) в A6.97) и выполнив выкладки, аналогичные
тем, которые были проделаны при рассмотрении лоренцевых
преобразований, получим
Раз (?- Чо) = Y>m(- Ч, Яо) Y°p6.	A6.105)
Подстановка A6.103) в A6.105) приводит к результату
Pi = P2 = 0,	A6.106)
поскольку матрица у5 антикоммутирует с у0. В результате полу-
получаем окончательное выражение для pa$(q)'-
Pap (q) = Pi {<f) q4 + P2 (q2) V	A6.107)
Дальнейшее рассмотрение основывается на представлении
p в виде A6.107). В том случае, когда включены слабые взаи-
взаимодействия, отражение пространства уже не является преобра-
преобразованием симметрии теории, и для рар нужно рассматривать бо-
более общее выражение A6.103). При этом константа перенорми-
перенормировки Z2 является матрицей вида а + Ьу5. Соответствующие вы-
вычисления можно найти в оригинальных статьях [60, 61].
Спектральная амплитуда для второго члена в A6.96) может
быть выражена непосредственно через A6.97) с помощью
^С^-преобразования. Действительно,
@ I % (*') % (х) 10) = {КО I К% (*') фа (*) 0)* = {К% (*') % (х) 0 | #0),
где К — оператор комплексного сопряжения, который содержит-
содержится в операторе обращения времени ? = 'UK. Используя &С
инвариантность вакуума
и учитывая, что 1 = {SPQ,%L)-X {PCU), получаем
<о 1 -фр (л:') 4v W1 о> =	'	'
С учетом правил преобразования A5.150) дираковских поле'й
под действием оператора tPCf
а (д) б = - i (YoYe* (~ *))a = I
и учитывая, что ys = Y5' находим
@ I фр (х1) Ф« (*) 10) = - (y5H, @ |ф, (- х) $х (- х') 10> (Y5)^. A6.109)

i 109]	In И out-ПОЛЯ В ТЕОРИИ ДИРАКА	165
Подставляя A6.109) вместе с A6.107) в A6.96), получаем окон-
окончательно
9 (q0) ([q9l (q2) + р2 (^)]ор
- (Y5 [#i <<72) + Р2 (	p
(^} + р2 (^)]а» (е~Шх~х') ~ eiq{x-x>))- A6.110)
Поскольку р обращается в нуль для пространственно-подобных
q2, это выражение с помощью подстановки
р (^2) = J rfM2p (М2) 6 (<г - М2)
о
может быть записано в виде интеграла по массам
_*') = -$ dM2[i9l (M2) V, + Р2(М2)]а&Ь(х-х'; М) =
l{M2)S4{x-x'; M) +
2)-92(M2)]a^(x-x'; M)}, A6.111)
где инвариантные функции Д и 5 определены в приложении В.
Приведенный выше вывод спектрального представления
практически не меняется для вакуумного среднего от упорядо-
упорядоченного по времени произведения дираковских полей, при этом
нужно только заменить 5 и Д в A6.111) на фейнмановские
пропагаторы SF и Д^:
Чр <* ~ *') = + \ dN[2 UPi (^2) V, + Р2 (М2)]аа Д„ (* - х'; М)
A6.112)
или, в импульсном пространстве,
00
S'P (р) = \ dM2 \fipi (М2) + р2 (М2)] p2_J2+.e .
о
Аналогичный результат может быть выведен и для остальных
функций Грина.
Сопоставляя A6.111) и A6.32), мы видим, что учет спиновых
степеней свободы в уравнении Дирака приводит к тому, что
спектральное представление записывается в виде интеграла, со-
содержащего не одну, а две скалярные функции pi и рг. Свойства
этих функций аналогичны свойствам 9{q2)-
1)	Pi(M2) и р2(М2) вещественны,
2)	Р,(М2)>0,	A6.113)
3)	Alp, Щ2) - р2 (М2) > 0.

166	ВАКУУМНЫЕ СРЕДНИЕ И S-МАТРИЦА	[ГЛ. 16
Условие 1) проверяется непосредственным вычислением:
Р;р (Я) = I BлK б4 (рп - q) {п\ % @) | 0) v^YJU @ | 4>я @) | п) =
= [YoP (q) Volga = lPi (Я2) f + P2 (q2)U-
Чтобы доказать 2), рассмотрим Sp(vop); используя A6.97) и
A6.107), получаем
I BяK в4 (/>»-?) 1<0|фа@)|п)<«|ф+@)|0> =
4 (р„ -q)?\ <0 ) Ч>« @) I л)
Отсюда, поскольку q0 > 0, следует pi (q2) > 0.
Условие 3) доказывается аналогичным образом, для этого
нужно рассмотреть квадрат модуля (t'V — M)ty. Конкретные вы-
выкладки мы оставляем читателю в качестве упражнения.
Теперь, как и в случае скалярного поля, можно выделить из
спектральных амплитуд вклад одночастичного состояния и вы-
вывести условие для Z2, аналогичное A6.42). Для этого вычис-
вычислим матричные элементы операторов в правой и левой части
уравнения A6.83) между вакуумом и одночастичным состоя-
состоянием \ps}:
(N - т) @1 ф (х) | ps) = (р - т) @1 ф @) | ps) е'1" =
= @\]@)\ps)e-ipx. A6.114)
Из A6.99) следует, что (О|яр(О) \ps) при лоренцевых преобра-
преобразованиях преобразуется как спинор с импульсом р и спином s:
@1фа@)| ps)==@ |f/(a)%@)U~l (a)\U(a)ps)=S-* (a)@ | % @)| />V>.
Поэтому ')
= au(p, s) + bv(p, -s) = (a + by5)u(p, s). A6.115)
Потребовав, чтобы теория была инвариантна при отражении
пространства, мы устраним член с b в A6.115). Действительно,
из A5.88) и A5.91) получаем
<0Ж0)|р0) -Р, s) = (a
= Yo (a + 6yS) и (р, s) = (a - 6у5) и (- р, s), A6.116)
J) См. задачу 9 этой главы.

§ 109]	tn- И out-НОЛЯ В ТЕОРИИ ДИРАКА	167
где учтено, что в силу уравнения Дирака и{—р, s) = уои(р, s) ' ).
Поэтому Ь = 0. Из A6.114) имеем
@\т\Р*) = а(р-т)и(р, 5) = 0	A6.117)
и
(О | ф (х) I ps> = У Г2 <0 | thn (jc) I ps) =
Jruip's)e~lpx' A6Л18)
По аналогии с A6.55) отсюда следует, что
(О I К" (х), ^п (у)} | 0) = - /Sae U - у),	A6.120)
а также, что антикоммутаторы в A6.120) являются сами по
себе с-числами, т. е.
Непосредственную проверку этих утверждений мы оставляем чи-
читателю. Используя A6.118), выделим вклад одночастичного со-
состояния в спектральную амплитуду A6.97); этот вклад равен
Подставив в A6.111), найдем
со
- J <Ш2 [iPl (M2) Vx + р2 (М2)Ц А (х - х'; М), A6.122)
где спектральный интеграл начинается от порогового значения
т\ непрерывного спектра.
При t = t' левая часть A6.122) выражается через антиком-
антикоммутатор полей ty(x):
S'a?> (х — х'\ 0) = /@[ {г1>а (х, t), ^в (xr, t) 10} = /YafjS3 (х — х').
A6.123).
Отсюда получаем уравнение для Z2:
оо
1=Z2+ $<Ш2р,(М2)	A6.124)
') Напомним используемое обозначение: и(—p,s)^u(po.—p,s).

168	ВАКУУМНЫЕ СРЕДНИЕ И S-МАТРЙЦА	A\Л. 18
или, с учетом A6.113),
0<Z2<l	A6.125)
в полной аналогии с A6.34).
При выводе неравенства A6.125) для вероятности образова-
образования дираковской частицы из вакуума использовалось только
свойство лоренцевой инвариантности. Как известно, в том слу-
случае, когда теория содержит электромагнитную связь, каждое ло-
ренцево преобразование следует дополнить соответствующим
градиентным преобразованием. Поскольку функция S'{x— х')
не градиентно-инвариантна, условие A6.125) не выполняется в
квантовой электродинамике; при этом Z% зависит от калибровки
и не имеет простой физической интерпретации.
§ 110. Редукционная формула для дираковских полей
В § 108 мы использовали общие свойства 5-матрицы для вы-
вывода редукционной формулы в случае скалярных полей. Обоб-
Обобщение на случай матричных элементов между дираковскими час-
частицами требует лишь небольших технических усложнений.
Из выражений A6.88), A6.90) и A6.121) видно, что п-час-
тичное in- (или out-) состояние может быть, как и в случае сво-
свободного поля Дирака, получено последовательным применением
операторов
A6.126)
Например, произвольное in-состояние может быть записано
в виде
Квантовые числа этого состояния записаны в порядке, который
при чтении справа налево в точности соответствует последова-
последовательности, в которой частицы рождаются из вакуума, при этом
частицы (piSi) предшествуют античастицам (piSi). Указанное со-
соглашение фиксирует фазу состояний и помогает разобраться в
кухне, связанной с алгеброй антикоммутаторов в случае фер-
миинных полей.
Как обычно в редукционной процедуре, мы извлекаем сна-
сначала дираковскую частицу из in-состояния и заменяем ее мат-
матричным элементом соответствующего полевого оператора. Для

§ ПО)	РЕДУКЦИОННАЯ ФОРМУЛА ДЛЯ ДИРАКОВСКИХ ПОЛЕЙ	169
этого повторим выкладки, которые мы проделали в A6.73),
A6.74). Используя асимптотическое условие в форме A6.91) и
A6.94), получим
(Р out | (ps), a in) = (р — (ps) out | a in) +
+ ф out | bt (ps) - bom (ps) | о in) = <p — (ps) out | a in) +
<fx <p out | [*+ (*) - 4>o+ut (x)] | a in) Ups (x) -
= (p — (ps) out I a in) —
- -J=. J d^<pOut I -^- (ij> (*) v°t/ps W la in).	A6.128)
Поскольку Ups(x) есть решение свободного уравнения Дирака,
подставим
Y0 ~ Vps (х) = (- Y • V - im) Ups (x)
и проинтегрируем по частям член с —y-V. В результате второй
член в правой части A6.128) приобретает вид
	jL \ d*x Ф out 11 (x) I a in) (- iV - m) <7ps (*). A6.129)
В том случае, когда in-состояние содержит не частицу, а ан-
античастицу, имеем
-j= [ d'xVps (»V - от) <р out | ф (х) | a in).	A6.130)
Для out-состояний при извлечении из обкладок частицы и ан-
античастицы получаем соответственно
- т) Ф out | ф (*) | a in), A6.131)
рг ( Л <р out | $ (*) | a in) (- /V - т) V^ (x). A6.132)
Отметим, что выражение A6.129) для амплитуды, описываю-
описывающей взаимодействие электрона с квантовыми числами ps в на-
начальном in-состоянии, и выражение A6.132) для амплитуды,
описывающей взаимодействие позитрона p's' в конечном out-со-
out-состоянии, тесно связаны друг с другом: одно получается из дру-
другого заменой UpS(x) на —Vp'§'(x), т. е. и(р, s)e~ipx на
— v(p', s') e~i(~p')x. Это обстоятельство, которое является теоре-
теоретико-полевой формулировкой нашего старого результата, полу-
полученного в гл. 6 при обсуждении метода функций распростра-
распространения, позволяет нам рассматривать позитрон как электрон с от-
отрицательной энергией, движущиеся назад во времени. Аналогич-

170	ВАКУУМНЫЕ СРЕДНИЕ И S-МАТРИЦА	[ГЛ. 16
ная связь имеет место между амплитудами A6.130) и A6.131),
отвечающими электрону в конечном и позитрону в начальном
состояниях.
Мы можем продолжить редукционную процедуру до тех
пор, пока не извлечем все частицы из in- или out-состояний.
В результате мы получим вакуумное среднее от хронологически-
упорядоченного произведения полей. Рассмотрим, например, слу-
случай, когда in-состояние содержит дираковскую частицу, а сам
матричный элемент вычисляется от произведения скалярных и
спинорных полей. Имеем
(pout |Г(лгь •••, zp)Oi_p |(ps)ain) =
X Ф6, B,) ... Ф6р (zp) I (ps) a in) =
= (— II"-" <p — (ps) out l Г (JC! ...zo)ei...Bp|ain> +
+ (p out 17* (jf, ... zp)a^pbtn{p, s)|ain>-
- <pout| (-l)m+pb+1 (p, s)T(Xl... zp)ei... зр I a in), A6.133)
где знак (—\)m+p определяется числом перестановок фермион-
ных полей (см. A3.71)), как это следует из определения хроно-
хронологического произведения фермионных полей:
Т (Фа (*) % (У)) = Фа (*) % (У) 9 {Хо - г/о) - % {У) Фа (*) 9 (УО - Х0).
Во втором члене используем асимптотическое условие; тогда,
повторяя выкладки, приведшие к выражению A6.129), получаем
, (Рхф out | T (Ф (*,) ... ф (у,) ... ф (Zp) фл (х) I a in) X
X(—iVx — m)kxUpS(x)x. A6.134)
Если in-состояние содержит не частицу, а античастицу, то
A6.134) заменяется на
=r \ d*x Vps (х)х (Ях-т)л X
...%p(zp))\am). A6.135)
В том случае, когда частица и античастица извлекаются из
out-состояния, имеем соответственно
-У- \
Up>s> (ж), (iVx - m)u X
X <P out I T (ф„ (*) Ф (*,)... фйр(гр)) |ain), A6.136)

§ 110]
РЕДУКЦИОННАЯ ФОРМУЛА ДЛЯ ДИРАКОВСКИХ ПОЛЕЙ
171
IT, J
d*x <p out | Т (Ф
, (Zp) 4>x (*) I a in) X
Y(	nm + pf	 /V 	tn\ V-,-,(y\	Cifi \%7\
/\ \ i) \ i vx — 1*Чх% v ps \X)x'	^lи. lot)
Описанная процедура приводит в конце концов к вакуумному
среднему
A6.138)
В следующей главе будет показано, что выражение A6.138)
представляет сумму всех феинмановских диаграмм, отвечающих
рождению и уничтожению бозонов в точках xit рождению фер-
мионов и уничтожению антифермионов в точках z< и рождению
антифермионов и уничтожению фермионов в точках iji. Опера-
Операторы Клейна — Гордона и Дирака в редукционной формуле
\ dAx fp(x)(Dx + m\ \ d*x Up's' (x) (iV - т) и т. д.
исключают концы диаграмм, отвечающие внешним частицам, и
сажают эти частицы на массовую поверхность. Множители
//д/Z, — j/V^2 и '/V^2 Для каждой бозонной, фермионной
или антифермионной линии
обеспечивают перенорми-
перенормировку соответствующей вол-
волновой функции, в результа-
результате окончательный результат
непосредственно равен ам- ps ^	~^p's'
плитуде перехода.
В качестве примера МЫ Рис 16 3 Мезон-протонное рассеяние,
рассмотрим рассеяние ме-
мезона на протоне. Кинематика указана на рис. 16.3, где i озна-
означает зарядовое состояние мезона. Применяя редукционную тех-
технику, получим
Sft = {q'\ p's' out | q; ps in) =
x
X [UP's' (zO (NX' - m)]a @ | T (% {z') фт (z) Ф/ (x) Фг (*')) I 0) X
A6.139)
где ц, m — масса мезона и протона соответственно, a bft ф 0
только в том случае, когда in- и out-состояния совпадают, т. е.
Для рассеяния вперед. При практических вычислениях в A6.139)
(NX' - m)]a @ | T (% {z') фт (z) Ф/ (x) Фг (*')
X[ (- fix - m) Ups (z)]r (Dx+|x2) fq (x),

172	ВАКУУМНЫЕ СРЕДНИЕ И S-МАТРИЦА	[ГЛ 16
обычно используются плоские волны A6.9) и A6.88):
f ( v) — 	!	g-<<7*
A6.140)
представляющие предельный случай нормированных волновых
пакетов, при этом б/(- в A6.139) имеет вид
§ 111. In- и out-состояния и редукционная формула
для фотонов
В заключение применим формализм, обсуждавшийся в этой
главе, к полю излучения. Указанный случай требует отдельного
рассмотрения ввиду трудностей, обусловленных нековариантным
выбором калибровки при квантовании уравнений Максвелла.
Напомним, что в калибровке излучения векторный потен-
потенциал поперечен и описывается уравнением
аЛ = е/,	A6.141)
где
еоЦ^ео] + ,
а поперечный ток определяется из условий
V • Е = еор = во/о, V./tr = O.
Продольная часть векторного потенциала в этой калибровке
равна нулю, при этом скалярный потенциал определяется из
формулы Гаусса
VM0 == еор.
Таким образом, имеются две независимые компоненты век-
векторного потенциала, каждая из которых удовлетворяет A6.141).
Одновременные перестановочные соотношения для этих компо-
компонент имеют вид (см. A5.9))
[At (х, (), Ak (*', /)] = [At (x, t), Ак (х', 0] = 0,
[A t (x, t), Ak (*', /)] = ih% (x - *')•
Ситуация вполне аналогична канонической теории свободных
полей, отличаясь от последней лишь в том отношении, что мас-
масса квантов равна нулю и поле поперечно, так что в A6.142)
входит лишь поперечная часть б-функции.

§ 111]	In- И out-СОСТОЯНИЯ ФОТОНОВ	173
По аналогии с теорией скалярного поля введем поперечные
in- (и out-)поля, удовлетворяющие, в соответствии с A6.5) и
A6.6), соотношениям
[Р\ А1п (х)] = - i -?- Aln (x), D Л,„ (х) = 0. A6.143)
Поле Ащ(х), действуя на вакуум, рождает только1) однофо-
тонные состояния с Р\ = 0. Это можно показать тем же спосо-
способом, каким мы получили уравнение A6.8). Поскольку масса фо-
фотонов равна нулю, уравнение A6.143) теперь не содержит мас-
массового контрчлена.
Выпишем далее фурье-разложение оператора Ат(х):
]YJi	кЛ(х) + а+(к, к) A'k>Л«], A6.144)
Л = 1
где
Ak К (х) = . ' е~'кхг (к, к).
Обратив A6.144), получим
ain (k, к) = i \ d?x Л; х (х) • % А.т (х) =
?xAlK(x)u%Aln(xr.	A6.145)
Последовательно действуя операторами а+ (k, к) на вакуум, мы
получаем in-состояние, содержащее п фотонов, в полном соот-
соответствии с A6.10) и A6.11). Аналогичные результаты имеют ме-
место для out-полей и out-состояний. Как обычно, мы предпола-
предполагаем, что in- и out-состояния образуют полный набор.
Выпишем уравнения, связывающие А\п{х) и AOut(*) с А(х).
Эти уравнения в точности аналогичны уравнениям A6.14) и
A6.52) для скалярного поля:
<sJTz Aln(х) = А{х)-еЛ dly Dre, (x - у)/*(у),
_	г	A6.146)
VZ3 AoUi (x) = А (х) - е0} d4y Dadv (x - у) /tr (у).
Здесь Dret и Dadv — предельные значения соответствующих функ-
функций Грина при т->-0, а константа -\/Z3 определяется из усло-
') Мы не обсуждаем здесь усложнения, связанные с инфракрасной расхо-
расходимостью, которая возникает при рассмотрении многофотонных состояний
с нулевой частотой. Мы уже убедились (гл. 8) в том, что при конкретных
вычислениях эту проблему следует каждый раз рассматривать отдельно. Мы
еще вернемся к этому вопросу в гл. 17.

174	ВАКУУМНЫЕ СРЕДНИЕ И S-МАТРИЦА	[ГЛ. 16
вия единичной нормировки матричного элемента in- и out-опера-
out-операторов между вакуумным и одночастичным состоянием.
Пока что все напоминает формулы скалярной теории. Похо-
Похожий вид имеют и асимптотические условия, понимаемые, как
обычно, в смысле слабой операторной сходимости A6.20):
A (x, /)—>V%ч Aln (x, /) при t-> — oo
._!	F	A6.147)
Л (л;, 0~* VZ3-Dout (д:, /) при /->+оо.
Лишь редукционная формула для фотонов немного отличается
от выражения A6.81) для скалярного поля
^+™2) <0 I ... q>(*,) ... |0>-
->-^-Л,.,А.(х,)П,;-@|... A(Xi) ... |0)==
= - —=• Ait. Kt (x{) Dx. @1 ... Л, (xt) ...|0). A6.148)
Например, если фотон с квантовыми числами k"k' «вытаскивает-
«вытаскивается» из out-состояния, A6.80) заменяется на
<Y' {k"k') out | ф (x) | a in) = <v out | ф (x) | a - {k'X') in) +
\ d*y (y out \T (A^y) у (x))\ a in) П у A»k;l'(y), A6.149)
причем дополнительный по сравнению с A6.80) знак минус в
A6.149) связан с тем обстоятельством, что единичный вектор
поляризации пространственно-подобен:
е^е" — — е • е — — 1.
Таким образом, потеря явной ковариантности при квантова-
квантовании не приводит к каким-либо новым трудностям при рассмот-
рассмотрении редукционной техники. В следующей главе, анализируя
член за членом в ряду теории возмущений, мы установим, что
5-матрица в присутствии электромагнитных взаимодействий гра-
диентно-инвариантна, а потому в силу A6.70) также и лоренц-
инвариантна. В низших порядках по константе связи этот факт
был проверен явным вычислением (см. гл. 7 и 8). Здесь же мы
укажем только, что нормировочная константа Z3, равно как и
остальные члены в уравнении A6.146), градиентно-инвариантны.
Предвосхищая дальнейшее обсуждение, отметим важное
свойство константы Z3, которое отличает ее от соответствующих
констант для заряженного фермионного и бозонного полей Z2 и
Z. В гл. 8 мы обнаружили, что если собрать воедино различные
поправки порядка е3 к вершинной функции, то единственной ве-

§ 112J	СПЕКТРАЛЬНОЕ ПРЕДСТАВЛЕНИЕ ДЛЯ ФОТОНОВ	175
личиной, зависящей от радиуса обрезания является Z3> кон-
константа перенормировки волновой функции и заряда (е = Vz3 во)-
Вскоре мы убедимся, что Z3 из гл. 8 совпадает с Z3, обсуждав-
обсуждавшейся в настоящей главе. Таким образом, свойство градиентной
инвариантности физического заряда определяется градиентной
инвариантностью Z3 в A6.146).
§ 112. Спектральное представление для фотонов
Продолжим наше сопоставление с теорией скалярного поля
и рассмотрим вакуумное среднее от коммутатора
iD'n (х, x'f s= @ | [А, (х), А, (х')] 10).	A6.150)
Тот факт, что при квантовании максвелловского поля теряется
явная лоренцева инвариантность, приводит к некоторым труд-
трудностям. Рассмотрим вначале матричный элемент
@ | At (х) А, (*') 10) = 2 *"'"" {Х~Х/) <-° IЛ* (°> 1«><«М/@I0> =
ВМе-^ЛД?) A6.151)
-J-
и обычным образом определим спектральную амплитуду:
9ц (Я) ^ I @ I At @) | п) (п | Л/ @) | 0} BяK б (рп - q). A6.152)
п
Выделив, как в A6.37), однофотонное состояние
@ \А(х)\ РХ) = У2~з @1 А1п (х) | рХ),	A6.153)
получим
9ii (q) = Z36 (q2) t d A, Л) в, (q, Я) + щ, (q). A6.154)
А= 1
Второй член в A6.150) также можно выразить через A6.154),
если использовать /С^-инвариантность электродинамики. При
преобразовании 0 = f&P
BA(x)Q~1 = -A(-x) и 9|0) = |0>.
Поэтому, записывая f = cUK, где К — оператор комплексного
сопряжения, получаем
@1 А, {х') A i (х) 10) = (/СО | КAj {x') At (x) 0)* =
= @1QAj{х')е-'ЭЛу(х)б 10)* = @1 At (- x)At (-х')\ 0>.
A6,155)

176	ВАКУУМНЫЕ СРЕДНИЕ И S-МАТРИЦА	[ГЛ. 16
В последней строчке этого равенства использовано тождество
(А\В)* = {В\А) и учтена эрмитовость поля А(х). Отсюда сле-
следует, что тензор рц(д) симметричен относительно перестановки
индексов; учитывая A6.152), заключаем также, что рц— дей-
действительная функция
A6.156)
Выражение A6.150), с учетом A6.151) и A6.154), приво-
приводится к виду
~ 1 \ -Щ* Э (<?о) (в-"(*-*') - в*-*'О щ, (q), A6.157)
Dil(x-x'f =
где
= ~' \ W 6
При выводе общего выражения для спектральной функции
ni,-(q) мы, следуя Эвансу и Фултону [62], рассмотрим вначале
градиентно-инвариантный лоренцев тензор
^v (q) = I @ I k @) I я) <" I /v @) I 0) BяK б4 (рп -q). A6.158)
Операторы тока в A6.158), которые являются источниками элек-
электромагнитного поля, удовлетворяют дифференциальному закону
сохранения
и являются, таким образом, градиентно-инвариантными 4-векто-
рами. Например, для дираковского электрона
V W = * W Y^^ W - <0 I ф (*) У^Ф WI 0).	A6.160)
Из A6.158) следует, что /^v есть лоренцев тензор второго ранга
и не меняется при градиентном преобразовании, которое сопут-
сопутствует лоренцеву преобразованию, отвечающему переходу к но-
новой системе отсчета. Уравнение непрерывности накладывает
дальнейшие ограничения на вид тензора Jnv{q). Из A6.159) сле-
следует, что
/?<0IU*)|n> = 0.	A6.161)
Поэтому
?Чп-= <7V-Vv = 0-	A6.162)

§ 112]	СПЕКТРАЛЬНОЕ ПРЕДСТАВЛЕНИЕ ДЛЯ ФОТОНОВ	177
Таким образом, 4-дивергенция тензора J^viq) равна нулю. Ис-
Используя те же аргументы, с помощью которых мы определим
структуру тензора поляризации вакуума (8.16), получаем
(<72).	A6.163)
Для того чтобы связать J (q2) с интересующей нас спектральной
функцией pa(q), достаточно вычислить J^viq) в данной лорен-
цевой системе, используя при этом для потенциалов калибровку
излучения. Согласно определению pi/(q) в A6.152) и волновому
уравнению A6.141), достаточно рассмотреть только поперечную
часть электромагнитного тока:
41 (о I /'/ @) I «> <« I i)r @) I о) « б4 (р„ -я) =
= (q2J 9ц (q) = (q2Jnil(q). A6.164)
Последнее равенство в A6.164) следует из A6.154) и формулы
ХЦ (х) = 0.
Вид тензора nij(q) можно найти из условия инвариантности
при трехмерных вращениях
nii{q) = bijn(qQ, \qf)~j^n{qu, \qf).	A6.165)
Поскольку
V./*(*) = 0,
то
qi^ii (q) = q^n (q) = о
и, следовательно,
«*/ (Ф = (»*/ - jff) " to» I я I2)-	A6.166)
Заметим далее, что поперечные части Jiu(q) и J^viq) про-
простым образом связаны между собой. Действительно, рассмотрим
в выбранной системе координат две величины
Wjniiiq) и e,,evyuv (q),
где
еA = @, е), е • ? = - е^ = 0.	A6.167)
Так как, согласно A6.141),
;)|n}> A6.168)
то
Для любого состояния \п), удовлетворяющего условию

178	ВАКУУМНЫЕ СРЕДНИЕ И S-МАТРИЦА	[ГЛ. 16
Интересующие нас матричные элементы удовлетворяют именно
этому условию. В результате, используя A6.158), A6.164) и
A6.168), находим искомую связь между я</(<7) и J^viq)
|0)BяK64
n
A6.169)
Сравнив с общим видом J^v и р(/, получим
)^- <16Л70>
Таким образом мы выразили тензор щ(д) через скалярную,
градиентно-инвариантную функцию J(q2)- Подставим далее
A6.170) в A6.157), тогда, используя равенство
= J dM2 б (q2 - М2) / (М2)
и вводя поперечную функцию Д(;у с произвольной массой М:
•pHF 9 (Ао) б (б2 - М2) = [6Ч - -щг/е-'к <*-*') - е« («-Л),
A6.171)
приходим к компактному виду спектрального представления
D'u (x - x'f = Z3Di; {x - x'f + J dM2 Д„ (jc - л;', M2)tr II (M2),
A6.172)
где
ЩМ2) = е2^Ш.	A6,173)
В импульсном пространстве фейнмановский пропагатор равен
/~T7Fr
Для того чтобы, как в A6.42), выразить константу Z3 через ин-
интеграл от спектральной функции П(ЛР), достаточно вычислить

§ 1131	СВЯЗЬ СПИНА СО СТАТИСТИКОЙ	179
производную в A6.171) при t = V и использовать коммутаторы
A6.142) и определение Ю'ц {х, х')Хт, в результате находим
оо
1 = Z3+ \ dM2 П (М2).	A6.174)
м2
Инвариантность величины Z3 при градиентных и лоренцевых
преобразованиях теперь очевидна. Из A6.169) и A6.170) сле-
следует, что весовая функция П(М2) всюду неотрицательна
0 ^ е(-е;я(/- (q) =	5— = л (у2)-
Поэтому
0<Z3=l- \dM2U(M2)< 1.	A6.175)
Таким образом, вероятность образования фотона полем А(х)
из вакуума заключена в пределах между нулем и единицей в
полном соответствии с результатами, полученными для бозонных
и фермионных полей в отсутствие электромагнитной связи ').
§ 113. Связь спина со статистикой
Обсудим теперь, используя спектральные представления, по-
полученные в этой главе, некоторые вопросы, касающиеся связи
спина со статистикой [51], отмеченные ранее в гл. 15. Мы рас-
рассмотрим только поля со спином 0 и 1/2. В локальной, лоренц-
инвариантной теории поля, обладающей единственным основным
состоянием, существует теорема, устанавливающая, что поля с
целым спином должны квантоваться как бозе-поля, а поля по-
полуцелым спином — как ферми-поля, при условии, что выполнено
условие микропричинности. Последнее означает, что локальные
плотности наблюдаемых операторных величин
а вз [d3x а (х, л
не интерферируют и поэтому должны коммутировать для про-
пространственно-подобных интервалов:
[О(х),О(у)] = 0 для (х-уJ<0.	A6.176)
Покажем, что это условие несовместимо с квантованием по-
полей Клейна — Гордона с антикоммутаторами и дираковских по-
полей с коммутаторами.
') Обсуждение случая 1г = 0 дано в работе [63].

180	ВАКУУМНЫЕ СРЕДНИЕ И S-МАТРИЦА	(ГЛ. 16
Наблюдаемые в этих теориях, такие как заряд и плотность
тока, в общем случае представляют квадратичные формы поле-
полевых амплитуд. С помощью простых алгебраических выкладок
нетрудно убедиться, что A6.176) справедливо для билинейных
форм
<?(*)= Фа (*)ф*М
при условии, что поля коммутируют или антикоммутируют для
пространственно-временных интервалов:
[фг(*),Ф. @I = 0, (х-уJ<0	A6.177а)
или
Шх), ЧЛУ)) = О, (х-уТ<0.	A6.1776)
Здесь фг(я) и (fs(y) означают различные комбинации клейн-гор-
доновских полей ф и (или) ф* или различные спинорные компо-
компоненты 1(з и ф дираковских полей.
Для взаимодействующего поля Клейна — Гордона соотноше-
соотношение A6.177а) выполняется, если рассматриваемая теория ло-
ренц-инвариантна и квантуется с коммутаторами. Использова-
Использование же антикоммутаторов при квантовании немедленно ведет
к противоречию. Действительно, рассмотрим вакуумное среднее
@1 (ф, (*), Ф5 (у)} I 0) ^ Д; (* - у).	A6.178)
Используя ту же технику, котроую мы применяли при выводе
выражения A6.32), получим
д{ (х-у) = ZA, (* - у; m2) + J da2 p (ег2) А, (* - у; а2),
где	.
\
Функция Д] (х — у) по-прежнему удовлетворяет уравнению Клей-
Клейна — Гордона, но не обращается в нуль для пространственно-по-
пространственно-подобных интервалов (л; — //J<0. В самом деле, для интервалов
Л Cv / тЛ exp(-mV[x|2-/2)
^1 V*> '» 'П I	I v 12 	 /2
1*1	'
Отсюда для больших х
со
7 -m\x\	Г	-о |дг|
, 0)
m?
\
Поэтому выражение A6.1776) не может быть справедливым и
условие микропричинности нарушается. Этим и устанавливает-
устанавливается связь спина со статистикой.

ЗАДАЧИ	181
При попытке квантовать фермиевское поле с коммутаторами
происходит то же самое. Изменение относительного знака двух
членов, отвечающих различному порядку операторов, приводит
к замене функции Д в спектральном представлении A6.111) на
функцию Af, в результате снова возникает противоречие с прин-
принципом микропричинности. Укажем, что приведенные соображе-
соображения носят весьма общий характер и применимы к полям с про-
произвольным спином, поскольку последние всегда могут быть по-
построены из произведения полей со спином 1/2.
В заключение имеет смысл отметить, что при квантовании,
скажем, бозе-полей с антикоммутаторами, нарушение принципа
микропричинности происходит на расстояниях порядка компто-
новской длины волны частицы ~10~13 см. Поэтому эксперимен-
экспериментальное согласие с принципом микропричинности — одним из
наиболее важных следствий локальной теории поля — указывает
на применимость концепции локального поля, по крайней мере
вплоть до расстояний, сравнимых с комптоновской длиной вол-
волны элементарных частиц.
ЗАДАЧИ
1.	Рассмотреть выражение
d*x J d*y fa (х) /* (у)(пх + т2) (оу + т2) Т (<р (*) <р (у))
и показать, изменяя порядок интегрирования, что
[<PlnW> «Pin (#)] = [«Pout М' «Poutte)]-
Рассмотреть затем тот же самый интегральный оператор, содержащий произ-
произведение трех полей ц>(х)<р(у)(р(г) и показать, что
[[<Pin(*)> ФшМ]. Ф (*)]=-О-
(Обоснование возможности изменения порядка интегрирования см. в работе
[37].) Аналогичным образом доказать соотношение A6.121).
2.	Показать, что S-матрица F.56) может быть непосредственно выражена
через фейнмановский пропагатор SP по аналогии с A6.82).
3.	Предполагая сдвиг массы бт2 в скалярной теории конечным, выра-
выразить его через спектральную весовую функцию р(р2) в A6.27).
4.	Показать, что S = б^'О, где в = /С0>.
5.	Показать, что @ | [ф1п (х), фои1 (у)] | 0) = + /Д (х — у, т).
6.	На примере фермионных и неэрмитовых скалярных полей проверить
выполнение условий 1—5 для S-матрицы, сформулированных в § 107.
7.	Доказать неравенство 3 в формулах A6.113).
8.	Построить спектральное представление для электрона в квантовой
электродинамике и обсудить свойства спектральной функции.
9.	Доказать A6.115).
Указание. См. § 9 первого тома.
10.	Установить связь спина со статистикой для фермионных полей, ис-
используя при этом закон сохранения четности (который подразумевается в
A6,111)).

ГЛАВА 17
ТЕОРИЯ ВОЗМУЩЕНИЙ
§ 114. Введение
В настоящее время известно два общих подхода к вычисле-
вычислению амплитуд перехода и матричных элементов, которые позво-
позволяют сравнить предсказания квантовой теории поля с экспери-
экспериментом. Первый из них основывается на разложении по степе-
степеням константы связи. В этом методе точные поля у(х) выра-
выражаются через in-поля фт (-*:), временная зависимость которых оп-
определяется гамильтонианом свободных частиц. При этом мы
снова приходим к тем же диаграммам и феинмановским прави-
правилам (а вместе с ними к расходимостям), которые рассматрива-
рассматривались в гл. 7, 8, 9 в формализме одночастичной теории. Второй
подход основывается на редукционной технике, с помощью ко-
которой вакуумное среднее от коммутаторов выражается через
вакуумное среднее от произведения трех и более полей, после
чего можно применить аппарат теории аналитических функ-
функций. При этом не используется малость константы связи, кото-
которая играет важную роль при построении теории возмущений.
Этот метод мы детально обсудим в следующей главе; в на-
настоящей же главе рассмотрим ковариантную теорию возму-
возмущений.
Наша задача заключается в том, чтобы записать амплитуды
перехода и матричные элементы в виде (бесконечной) суммы по
степеням константы связи и установить правила, с помощью ко-
которых может быть вычислен каждый отдельный член в этой
сумме. Для этого следует выразить точное поле ср(х) через
асимптотические поля фш(л:), свойства которых известны. Фун-
Фундаментальным предположением, на котором основывается вся
теория возмущений, является предположение о том, что спектр
точных состояний находится во взаимно однозначном соответ-
соответствии со спектром невозмущенных состояний. В частности, пред-
предполагается, что для каждого поля ф(х) в лагранжиане суще-
существует свое in-поле ф1П(*). Аналогичное условие имеет место и

§ П5]	U-МАТРИЦА	183
в нерелятивистской потенциальной теории: борновский ряд для
амплитуды рассеяния может расходиться, если в потенциале
имеется связанное состояние.
Представляется весьма сомнительным, чтобы теория возму-
возмущений была применима в теории сильных взаимодействий. Если
быть оптимистом, то можно предположить, что ряд теории воз-
возмущений сходится в квантовой электродинамике, поскольку в
этом случае параметр разложения а = V137. Напомним, что
в гл. 7, 8 мы обнаружили впечатляющее количественное согла-
согласие с экспериментом уже первых приближений теории возму-
возмущений в электродинамике. Применимость же теории возмуще-
возмущений к слабым взаимодействиям остается в настоящее время
весьма проблематичной.
Исходным пунктом, для разложения полевых операторов в
терминах in-полей, являются интегральные уравнения вида
A6.14), A6.84) и A6.146), в которых оператор тока j{x) сле-
следует выразить через in-поля. Указанная процедура не приводит,
однако, непосредственно к фейнмановским диаграммам [64], по-
поскольку вместо Af (x) при этом появляется функция Aret(x). По-
Поэтому для вывода фейнмановских правил непосредственно из
теории поля мы, следуя Дайсону [65, 66], сформулируем теорию
возмущении, основанную на формализме ^/-матрицы.
§ 115. {7-матрица
Одновременные перестановочные соотношения для взаимо-
взаимодействующих полей (f(x,t) и сопряженных импульсов л(х, t) со-
совпадают1) с соответствующими величинами для in-полей2)
Фт(*, t) и itin(x,t). In-поля образуют полный операторный на-
набор, поскольку, согласно нашему предположению, последова-
последовательным действием на вакуум операторами ф или фщ можно по-
построить полный набор состояний. Если предположить далее, что
поля ф и ф1п находятся во взаимно однозначном соответствии,
то связь между ними выражается3) с помощью унитарного
') Мы не рассматриваем здесь случай связей с производными. Примером
таких теорий являются взаимодействия заряженного бозона или векторной
частицы с электромагнитным полем. Обсуждение теории возмущений в этом
случае см. в [67—69].
2)	Здесь <р(х) означает бозонное или фермионное поле. Специфические
свойства поля, такие, как спин и изоспин, не играют сколько-нибудь сущест-
существенную роль в нашем рассмотрении.
3)	Хотя это утверждение представляет известную теорему обычной кван-
квантовой механики, ее нельзя доказать для систем с бесконечным числом степе-
степеней свободы (см. [70, 71] и задачу 2 этой главы). Здесь мы просто предполо-
предположим существование оператора U{t).

184	ТЕОРИЯ ВОЗМУЩЕНИЙ	[ГЛ. 17
оператора') U(t):
1	A7.1)
A7.2)
Поскольку уравнения движения для q>(x) и ф!П(*) известны,
нетрудно получить уравнение, описывающее изменение опера-
оператора U(t) во времени. Это уравнение следует, в частности, из
перестановочных соотношений, которым удовлетворяют in-поля:
\Х = i[//in((Pin> "in)' Фш].
Здесь //щ(ф1п, пт) — гамильтониан свободных полей, содержа-
содержащий физическую массу т. Для точных гейзенберговских полей
трансляционная инвариантность означает, что
1[Н(ч,п),ч(х)]	A7.4)
?	n),n(x)].	A7.5)
Поэтому
Ф,п (*) = •!¦ ^ @ ф («.Of/ (О =
= [п (t)U-l(l), Ф1П(*)]+ /[//(ф1п, nin), Ф,.ПМ] =
= ф,„ (х) + [ии~х + Ш, (ф1п> я1п), Фь (х)] A7.6)
и
А,„ W = А1п (х) + [UU-1 + Ш, (ф1п, я1п), я1п (ж)],
где
Я/ (Фщ. ят) = Н (Ф,п, я1п) - Я(п (ф1п, я,п) в Я7 @ A7.7)
есть гамильтониан взаимодействия, выраженный через in-поля.
В A7.7) мы явно выписали зависимость гамильтониана от вре-
') Оператор U может быть ковариантно определен на произвольной про-
странственноподобной поверхности, что не приводит, однако, к каким-либо
преимуществам (см. [72, 73]).

S 118]	f-МАТРИЦА	185
мени t. Напомним, что Hi(t) содержит массовый контрчлен (см.
гл. 7) '). Из A7.6) получаем
где E0(t) коммутирует с ф1П(ж, 0 и mn(x,t) и является, таким
образом, с-числом. Определив
находим уравнение, определяющее U:
Jtgtl '	A7.8)
Решение этого уравнения в терминах in-полей представляет
основу для разложения в ряд теории возмущений. С помощью
оператора U можно выразить вакуумное среднее от произведе-
произведения полевых амплитуд, через которые выражаются 5-матричные
элементы, в виде бесконечного ряда, содержащего in-поля. По-
Последние же могут быть вычислены в явном виде, поскольку свой-
свойства свободных полей нам известны.
Продолжим рассмотрение и выпишем итерационный ряд для
A7.8). При этом нужно задать начальное условие, которое удоб-
удобно ввести с помощью оператора
U(t,t')^U(t)U-l(t'),	A7.9)
который также есть решение для A7.8). При t = f U(t,t') ра-
равен единичному оператору2)
A7.10)
U(t,t)=l.
Уравнение A7.10) уже встречалось при рассмотрении неста-
нестационарной теории возмущений в нерелятивистской квантовой
') Для модели самодействующего скалярного поля
имеем
И
s, («Pin) - - */ (Фш) - Т
Для фермионных полей массовый контрчлен в 261 (<pIn) имеет вид
К-т):+111*111:-
2) В дальнейшем будем писать Hi(t) вместо Hi((fia(x,t)).

186	ТЕОРИЯ ВОЗМУЩЕНИЙ	[ГЛ. 17
механике, поэтому решение этого уравнения нам уже известно.
Записав A7.10) в форме
t
/, 0=1 — / $
f
получаем итерационное разложение для U (t, f):
t	t	и
U (t, t') =\~i\ dh Hf,(h) + (- if \ dt\ Щ (t{) J dh W (t2) + ...
r	r	v
... +{-i)n\dh\ut,... \ dtnH',(t0... H'i(tn)+ ... (i7.il)
Г t'	V
Поскольку tx^t2'^ .. .~^tn, каждый член в A7.11) хронологи-
хронологически упорядочен. Поэтому вместо Я/ (t\) ... Я/ (/„) можно
написать T(H/(ti) ... Hj(tn)), в результате имеем
U(t,f) =
со	t	*1	1п~\
-=l + ?(-*rS<«i$^2-.- \ dtn T (Hi (/,)... Н\ (/„)). A7.12)
Хронологическое произведение симметрично относительно пере-
перестановки аргументов t\, ..., tn, поскольку каждая такая пере-
перестановка включает четное число перестановок фермионных по-
полей и, следовательно, четное число знаков минус. Это свойство
симметрии подынтегрального выражения можно использовать,
чтобы промежуток интегрирования в каждом интеграле рас-
распространить вплоть до t. Для п = 2
t и	* и
J dh \ йк(Г (Я/' (*,) Я; (h)) = J Л2 $ dh Т (Н, {U) H\ (t2)) =
г
Для произвольного п можно аналогично выполнить п\ переста-
перестановок п индексов и распространить область интегрирования "на
n-мерный куб. Так как каждый из п\ членов вносит равный
вклад, то	t	t
u(t, o= l +21^г"S*• • • • Sdt*T№^) ¦¦¦H>C*)H
n=l
-/^;@лП=7'ехр1-/^4д;5»/(ф1п(*)) .
A7.13)

§ 116]	ТЕОРИЯ ВОЗМУЩЕНИИ ДЛЯ t-ФУНКЦИЙ И S-МАТРИЦА	187
где 7"-экспонента означает символическую запись суммы упоря-
упорядоченных по времени членов, с которой она совпадает при раз-
разложении по степеням константы связи.
Отметим полезное мультипликативное правило, следующее
либо из определения A7.9), либо из A7.13)
U(t,t') = U{t,t")U{t",tf).	A7.14)
В частности,
t') = U~](t',t).	A7.15)
§ 116. Теория возмущений для т-функций и S-матрица
Используя A7.1) и A7.13), можно выразить 5-матричные
элементы через вакуумные средние от in-полей. Из предыдущей
главы известно, что 5-матричные элементы выражаются через
одну фундаментальную величину — вакуумное среднее от Т-
произведения гейзенберговских полей q>(x):
т (*,	хп) = <0 | Т (Ф (*,) . . . Ф (jej) | 0).	A7.1 fi)
Из A7.1) и A7.9) получаем
= <0 I Г (?Г! (/,),,,,,(*,)?/(/,, B)%n(x2)U(t2, /,)...
= <о | т (и-1 (о и (/,/,) Ф1П (Xl) и (/„ t2)...
где аргумент времени t мы в дальнейшем устремим к <х>. В этом
пределе t больше, чем все tt, a —t меньше, поэтому U~l (t) и
U (t) можно вынести из хронологического произведения. В ре-
результате находим
x(xv ...,*„) =
A7.17)
где использована символическая запись A7.13).
Уравнение A7.17) выражает т-функции и, следовательно,
S-матричные элементы через in-поля. Зависимость от U~l (t) и
U(—t) на самом деле исчезает, поскольку вакуум является соб-
собственным состоянием этих операторов при t-+oo. Действитель-
Действительно, рассмотрим произвольное состояние |apin>, содержащее

188	ТЕОРИЯ ВОЗМУЩЕНИЙ	(ГЛ. 17
частицу р и произвольный набор а других частиц. Пусть р—
клейн-гордоновская частица; тогда из A6.9) и A6.73) следует
= -i\cPxf*p(x, -?)(-±-—±.)(а1п\щп(х, -t')U(
A7.18)
Используя A6.126) и A6.145), получаем аналогичное выраже-
выражение в случае фермионов и фотонов. Далее, в силу A7.1) выра-
выражение A7.18) приобретает вид
\Гр (х, -OXia in | U (- f) Ф (x, - f) U~l (-/') U (-/) | 0),
где
Согласно асимптотическому условию A6.20) при / = //->оо
получаем
\p(x, -t)X
-t)O~i(-t)U(-()\0).
A7.19)
Очевидно, что
ат(р)|0> = 0,
поскольку вакуумное состояние не содержит in-частиц. Поэтому
первый член в A7.19) равен нулю. Простые выкладки показы-
показывают, что и второй член в этом выражении также обращается
в нуль:
Здесь мы использовали A7.1), A7.8) и предположение о том,
что Hi не содержит связей с производными; общий аргумент t
опущен. Поэтому
<ap in | U (—010)-+ 0 при /->оо
для всех in-состояний ар, содержащих частицу. Отсюда
U(-()\0) = l_\0) при /->оо.	A7.20)
Аналогичным образом убеждаемся в том, что
k+\0) при t-*oo.

§ 116}	ТЕОРИЯ ВОЗМУЩЕНИЙ ДЛЯ X ФУНКЦИЙ И S МАТРИЦА	189
Константы Я,-, Х+ входят в A7.17) в виде произведения А_Я,+ .
В пределе /->оо это произведение равно
Я-Л+ = <0 | С/ (/) | 0><0 | ?/ (— О I 0> =
= <0 | G (-/)(/-'(О Ю> = <0| ?/(-/, /)|о> =
— <0 | Г Гехр I « \ dt'H1(t')\)\O) =
= @ | Т ГехрГ —/ \ dt' //; (Г)! JI О).
Таким образом, т-функция A7.17) может быть записана в виде
х(хи ..., хп) =
- i \ dt' н\ (/') J j |
,„(*,) ... ф1п (х„) ехр | — f \ dt H,(t)\ j|0>
-, A7.21)
(О | Т ( ехр - / J dt' H'j W) J I 0)
где /->-оо. Наконец, сократим с-числовой множитель
ехр
-/ J d?E0(t') \,
заменив Hi{f) на Hi(t), и возьмем предел при /->оо:
х(хи ..., хп) =
@1 Т ^ф!п (*,)••• Фщ (*п) е^Р [-' ] dt
н! W J JI
-/
X @ | Г (Ф|п (Xl) ... Фт (*„) Ж; (Ф|в (у,)) • • • Ж, (Ф,п (уи))) | 0) X
m=0
X(O\T {Ж1 (Ф,п (г/,)) ...Ж1 (ф1п (г/т))) 10> }"'. A7.22)

190	ТЕОРИЯ ВОЗМУЩЕНИЙ	[ГЛ. 17
Уравнение A7.22) представляет фундаментальный результат.
S-матрица в уравнениях, например, A6.81) или A6.139) вна-
вначале выражается через т-функции, а затем, согласно A7.22),
в виде ряда, целиком содержащего только in-операторы. Теперь
диаграммная интерпретация уравнения A7.22) и вывод фейнма-
новских правил вычисления представляют чисто алгебраическую
задачу.
§ 117. Теорема Вика
Для того чтобы представить каждый член в A7.22) в виде,
удобном для вычисления, переставим каждый оператор уничто-
уничтожения шаг за шагом направо, а каждый оператор рождения на-
налево; при этом в конце концов мы приходим к выражению, в
котором операторы рождения и уничтожения действуют непо-
непосредственно на вакуумное состояние и дают в результате нуль.
Указанная процедура нормального упорядочивания хронологи-
хронологического произведения, из которой непосредственно получаются
фейнмановские амплитуды, была впервые выполнена в 1949 г.
Дайсоном [65, 66], а позднее Виком [74], которые сформулиро-
сформулировали и доказали следующую теорему:
(*,) ••• Ф,„Ю) =:Ф,„(*,)••• Ф,„(*„)= +
+ [<0 IТ (ф1п (*,) Ф1П (х2)) 10): ф1п (*3) ... ф1п (*„): +
+ перестановки] -|-
+ [<о \т (ф1п (*,) ф,п (*,)) I о) <о | т (Ф,п (*3) ф1п (*4)) I о) х
X : ф1п (х6) .. . Ф,„ (*„) : + перестановки] + ... +
017- (Ф,„ (*,) Ф1п (х2)) I 0) ... <0 | Т (ф,п (х„_,) Ф!п (хп)) | 0) +
+ перестановки], (п четно),
... <0 | Г (ф1п (хп_2) ф1п (xn_.) | 0> Ф1П (*я) +
+ перестановки], (п нечетно).
A7.23)
Вакуумные средние, или свертки полей в A7.23) возникают
при (анти) коммутации полей, необходимой для приведения
произведения полей к нормальному порядку множителей. Как
мы убедились при рассмотрении свободных полей, эти сверт-
свертки представляют теоретико-полевой аналог фейнмановских ам-
амплитуд. Напомним в этой связи определение нормальною

4 П71	Теорема вика	191
произведения операторов:
:Ф,п(*.) ••• Ф|„К):-
Разложим каждый оператор на положительно- и отрицательно-
частотную части
Ф,„(*) = Ф^(*) + ф{й)(*),	A7.24)
где ф|+> (х) содержит ператоры уничтожения, а ф<~> — опе-
операторы рождения. Затем переставим операторы так, чтобы все
операторы рождения оказались слева от операторов уничтоже-
уничтожения. Учтем также, что при каждой перестановке ферми-полей
возникает знак минус; тогда получим:
= Ф.. (*.) ••• Ф.пК)= » ?ДДТ Ф^) П. W(x,), A7.25)
где сумма вычисляется по всем наборам А и В п индексов (при-
(причем каждый индекс входит в сумму один раз), а бр означает
четность перестановки ферми-полей. Вакуумное среднее от нор-
нормального произведения всегда равно нулю, поскольку
Ф(+)|О) = <О|Ф(-) = О.	A7.26)
Именно это свойство оказывается весьма полезным при рас-
рассмотрении дайсоновского упорядочивания хронологического про-
произведения. В силу A7.22) при вычислении S-матричных элемен-
элементов нужно рассматривать только вакуумные средние. Из A7.23)
следует, что
1.	Если п нечетно, то @| Г(фт(л:1) ... фт(*„)) |0) = 0.
2.	Если п четно, то
| Т (Ф
|п
перестановки
Х<0| Г (Ф|п (*„_,) Ф1п(хя))|0>. A7.27)
Последнее равенство и есть требуемый результат. Оно выражает
5-матрицу через известные фейнмановские пропагаторы сво-
свободных частиц с физическим значением массы.
Теорема Вика, из которой следует A7.27), может быть дока-
доказана по индукции. Выражение A7.23), несомненно, справедливо
для п = 1; проверим его справедливость для п = 2. Пусть фщ —
эрмитово бозонное поле. Имеем
Т (Ф>п (*i) Ф«„ (*2)) = : Фш (*i) Фщ (х2) ¦ + с-число,
так как хронологическое упорядочивание отличается от нормаль-
нормального лишь порядком следования операторов рождения и уничто-
уничтожения, причем коммутаторы, возникающие при перестановке

192	ТЕОРИЯ ВОЗМУЩЕНИЙ	[ГЛ. 1?
операторов, представляют собой с-числа. Взяв вакуумное сред-
среднее, получим
= • Ф.п (*,) «Pin (*2) •• + (О I Т(щп (ж,) <pin (х2)) | 0>, A7.28)
поскольку вакуумное среднее от нормального произведения опе-
операторов равно нулю. Легко видеть, что аналогичный результат
получается и для фермиевских полей:
Т Н\п (*,) %п (х2)) = : 4-ш (xi) tm (х2): + <01Г (i\n (*,) %n (x2)) 10).
A7.29)
Таким образом, A7.23) справедливо для п = 2. Предполо-
Предположим теперь, что A7.23) выполняется для п множителей, и по-
покажем, что отсюда следует его справедливость для п + 1 мно-
множителей. С этой целью рассмотрим выражение
Пусть для определенности /„+1 меньше tu ..., tn, тогда
= : ф1п (*,)••• Фш (*») •• 4>in (*n+i) +
+ 2 <0|Г(Ф1п(*,)Ф1п(*2))Ю>Х
перестановки
X : Ф1п (дс3) • • • Фт (*„) = Ф,„ (*„+,) + • • • A7.30)
Для того чтобы переписать это выражение в виковской форме,
нужно внести поле q>m(xn+i) внутрь нормального произведения
п полей. Используя A7.25) и A7.26), получаем
= Ев V II ф}-'(ж,) Пв ф};»(ж,) ф{
A7.31)
где бр, — четность перестановки, необходимой для упорядочива-
упорядочивания множителей в каждом отдельном члене A7.31). При введе-
введении (pin(*n+i) внутрь нормального произведения мы получаем
Плф|„->(х,) ф}-> (ж^,) Пв ф!+> (ж,) +
V Д ф&} W ft?B Пй ф!п+» (ж7) (о I ф|+> (ж4) ф }-) (як+1), о),

§ 118)	ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ	193
цепочку членов (последняя строчка в A7.31)), которые содер-
содержат коммутатор (или антикоммутатор) ф'п'С^я+О с П0ЛЯМИ
ф!п^ (xk) из набора В. Этот коммутатор затем заменяется вакуум-
вакуумным средним. Используя далее A7.26), можно выразить эти
вакуумные средние через фейнмановские пропагаторы:
= <° I Фш (**) Фщ (*я+.) I 0) = @ I Т (ф1п (xk) ф1п (*„+1)) | 0).
Здесь учтено, что /п+1 < 4. Наконец, переписав A7.31) в виде
: Фщ (*i) • • • Ф.„ (*») ¦ Фщ (*»-н) = : Фш (*i) • • • Фш (*»+i) : +
+ Z бр : Фш (л-,) ... Ф|п (**_,) ф1п (xk+l) ... ф1п (хя) : X
мы видим, что выражение A7.30) совпадает с A7.23), записан-
записанным для п + 1 множителей. Тем самым теорема Вика доказана.
Мы рекомендуем читателю тщательно проделать все выкладки
для п = 3 и п = 4, после чего станут ясными детали доказатель-
доказательства и в общем случае.
Применим теперь теорему Вика к A7.22). Напомним, что
плотность гамильтониана взаимодействия <Ж/(фш(г/)) уже имеет
нормальную форму1). Поэтому при упрощении хронологических
произведений не появляется сверток, содержащих произведение
полевых амплитуд, взятых в одной и той же точке у. Указанные
произведения входят в A7.22) уже нормально упорядоченными,
причем очевидно, что
Т: Ф,п (у) Ф!п (у): = : Ф1п (у) Ф1п (у):.	A7.32)
§ 118. Графическое представление
При рассмотрении A7.23) появляется три типа не равных
нулю сверток: для эрмитового A2.74) или комплексного A2.70)
поля Клейна — Гордона
<° I Т (Ф1а (х.) Ф1п (у)) | 0) = iAF (х - у, (х2) =
d*k e~ik(x-y)
(W~ k2 - ц* + is ' A7-33a)
<0 | T (ф,п (х) Ф;п Щ | 0) = i\ (x - y, v?);	A7.336)
') Исключение представляет статическое кулоновское взаимодействие в
A5.28) (см. также § 127). Однако и в этом случае не возникают свертки, со-
содержащие произведение амплитуд, взятых в одной и той же пространственно-
временной точке.

194	ТЕОРИЯ ВОЗМУЩЕНИЙ	1ГЛ, 1?
для поля Дирака A3.72)
(О IТ ($? (х) $• (у)) 10} = iSp (х - у, m)ap = i\-^jc ^-"Гч-t*0
A7.33b)
и, наконец, для электромагнитного поля A4.51), A4.53)
@ | Т (Л|Г (х) А\я (у)) | 0) = Ф$ (х - у)^ =
~ ' 3 BлL k2 + /8 L~ ^v ~~ '
_ ^4% 1
В последнем выражении вектор ц = A, 0, 0, 0) определен в той
лоренцевой системе, в которой производится квантование. Ука-
Указанные свертки можно, как и в фейнмановском подходе, пред-
представить графически; правила соответствия указаны на рис. 17.1.
/
Рис. 17.1. Пропагаторы для полей Клейна — Гордона, Дирака и Максвелла.
В дальнейшем при записи функции распространения мы будем
опускать аргумент массы во всех случаях, когда это не ведет
к недоразумению.
Теперь, рисуя каждый раз для сверток, возникающих при
разложении Дайсона — Вика для т-функции, линии, указанные
на рис. 17.1, мы можем графически изобразить каждый член
в A7.22). Поскольку рассматриваемые гамильтонианы содержат
произведения полей, взятых в одной и той же точке, пропага-
пропагаторы, сопоставляемые сверткам этих полей, должны «стягивать-
«стягиваться» в те же самые точки; сами же эти точки называются вер-
вершинами.
Проиллюстрируем графическую технику на конкретном при-
примере самовзаимодействующего скалярного поля:
**1 (Ъп W) = - 7Л: ф?» W = + 7* (К - и2): Ф2П W: • 0 7-34>

118]
ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ
195
Во втором порядке по Ко и первом по бц2 вклад в x(xi, х2, х3,
равен
Ф
|„
«Pin Ы X
>. A7.35)
Применяя теорему Вика и используя диаграммную технику, по-
получаем набор графиков, типичный вид которых показан на
рис. 17.2. Взаимодействие, содержащее константу Ко, изобража-
изображается 4-лучевой вершиной, а взаимодействие, содержащее массо-
массовый контрчлен — 2-лучевой вершиной (рис. 17.3). Каждая линия,
x2
P
,4
ф
Xg 3?j
?" V
к
Рис. 17.2. Типичные диаграммы, содержащиеся в уравнении A7.35).
выходящая из вершины, отвечает свертке полей в Жи Ти-
Типичная диаграмма, которая не содержится в разложении Дай-
сона—Вика, изображена на рис. 17.4; она исключается из рас-
рассмотрения, поскольку гамильтониан Ж\ имеет нормальный вид
и не содержит сверток двух полей, взятых в одной и той же
вершине.

196	ТЕОРИЯ ВОЗМУЩЕНИЙ	[ГЛ. 17
Таким образом, мы получаем соответствие между отдель-
отдельными членами в разложении т-функции и фейнмановскими гра-
графиками. Для того чтобы прийти к фейнмановским правилам,
остается только решить простую комбинаторную задачу и вы-
выяснить, сколько раз каждая диаграмма входит в разложение
Дайсона — Вика (различаясь при этом только нумерацией вер-
вершин). Например, для диаграмм, отвечающих A7.35), имеется
3! перестановок вершин ух, у2, уъ, при этом каждый график, от-
отличающийся только перестановкой аргументов, дает один и тот
Q
ч
Ч
ч
л
to*'
i i
Рис. 17.3. Вершины для мезон-мезон-	Рис. 17.4. Собственно-энер-
ного рассеяния и массового контр-	гетическая диаграмма с «го-
члена,	ловастиком», не содержа-
содержащаяся в уравнении 17.35.
же вклад в т. В общем случае существует т! диаграмм, отли-
отличающихся перестановкой вершин у\, ..., ут, причем возникаю-
возникающий отсюда ml сокращается с I/ml в A7.22). Точно так же для
диаграмм, указанных на рис. 17.2, имеется 4! перестановок по-
полей в 4-лучевой вершине 1/^\ '. q>4la: и 2! перестановок в 2-луче-
вой вершине — '/гОЦ2 : ср^ :. Общее правило гласит: если взаимо-
взаимодействие содержит оператор поля в степени г, соответствующая
диаграмма умножается на rl,
§ 119. Вакуумные амплитуды
На рис. 17.5 показаны некоторые диаграммы, возникающие
при разложении знаменателя в A7.22). Точно такие же диа-
диаграммы содержатся и в разложении числителя (см. рис. 17.2,в),
Как мы увидим, вклад вакуумных петель в числителе и знаме-
знаменателе сокращается и выпадает из полного ответа.
Графики, связанные с числителем, отличаются от графиков,
связанных со знаменателем, тем, что они обладают внешними
концами. Эти внешние линии отвечают операторам cj>in(*i) ...

5 119]	ВАКУУМНЫЕ АМПЛИТУДЫ	197
... фшСхп), которые содержатся в т(хх	хп). Назовем со-
совокупность графиков, не связанных с внешними концами диа-
диаграммы несвязанной частью. Графики, не содержащие несвязан-
несвязанной части, назовем связанными. Каждый график в числителе_
может быть отнесен либо к связанной, либо к несвязанной части,
?Д	/"	n	<	\
* * i-	•
\—v
Рис. 17.5. Вакуумные петли.
Точно так же на две части разбивается и аналитическое выра-
выражение для функции т.
Суммарный вклад связанных графиков s-ro порядка в числи-
числитель функции т равен
p-0
X @ ] T (ф1п (*,) ... %a (xn) Ж, (*/,) ...Ж, (ys)) 10)c X
X sl{pP!_s)l <01T (Ж, (ys+1) ...9fgj (yp)) | 0), A7.36)
где значок с означает, что вакуумное среднее вычисляется толь-
только от связанной части. Комбинаторный множитель	—
fM =	Р!
V, s / . s! (р — s)!
Означает число способов, которым можно извлечь 5 множителей

198	ТЕОРИЯ ВОЗМУЩЕНИИ	[ГЛ. 17
из полного числа р множителей Ш'/. Выражение A7.36) можно
переписать в виде
)^ (</,)••• */(*.)) Ю>вХ
оо
X ? -^ J rf42i ... d% <0 | Т (Ж, (г,) ... Я, (гг)) \ 0>. A7.37)
0
г-0
Это выражение имеет вид связанной амплитуды s-ro порядка,
умноженной на бесконечную сумму вакуумных петель, изобра-
изображенную на рис. 17.5. Последняя в точности сокращает знамена-
знаменатель в A7.22). Таким образом,
>?(*,	x) A7-38)
I \Л1> • • • > ¦'¦nit
I
где G* — вклад связанных, a Dk — несвязанных диаграмм. Дру-
Другими словами, при вычислении т-функции несвязанные графики
выпадают из ответа, и последняя сводится к сумме всех связан-
связанных фейнмановских диаграмм.
§ 120. Спин и изотопический спин;
я-мезон-нуклонное рассеяние
В большинстве вычислений, представляющих физический
интерес, мы рассматриваем гамильтонианы, содержащие поля
со спином и изотопическим спином. Примером является л-ме-
зон-нуклонное взаимодействие, рассмотренное в гл. 15:
$$j = g ; tyiy5T • <|)i|); — '/2 6fi2 I ф • ф '. — 6M '• ijiil)'. . A7.39)
В A7.39) явно выписан массовый контрчлен. Для того чтобы
разобраться в кухне индексов, рассмотрим вклад графиков пер-
первого отличного от нуля порядка. Соответствующее выражение
A6.39) для я-мезон-нуклонного рассеяния содержит
<01Т (ф (z2)ar Ч> (z,)^ <р< (*,) Ф/ (х2)) | 0),	A7.40)
где индексы а, E и г, s означают соответственно спин и изо-
изотопический спин нуклонов, a (I, j) — изотопические индексы

120]
СПИН И ИЗОТОПИЧЕСКИЙ СПИМ
я-мезонов. В первом неисчезающем порядке получаем
/, «в, rs
d% d% X
Х@|Г(^»(г2)^
2)) 10>ef A7.41)
где индекс с снова указывает на то, что рассматриваются толь-
только связанные диаграммы, а диа-
диаграммы, изображенные на ty>J &*1*
рис. 17.6, не учитываются.	?
Массовые контрчлены в J
A7.39) порядка g2, поэтому при
вычислениях с точностью g2 каж-
каждый из них должен учитываться
только один раз. Эти контрчлены
модифицируют диаграммы соб-
собственной энергии (рис. 17.7).
В гл. 8 мы уже обсуждали
диаграммы собственной энергии
в связи с вычислением радиацион-
радиационных поправок к рассеянию элек-
электронов. Учет контрчленов в диаграммах рис. 17.8 приводит к
тому, что физические частицы имеют (с точностью g2) наблю-
наблюдаемую массу. Ниже мы рассмотрим рассеяние на угол, не
J
J
Рис. 17.6. Несвязанные диаграммы,
которые не дают вклад в я-мезон-
нуклонную амплитуду.
6
г2)аг
о
12,ХР
Pa
Рис. 17.7. Диаграммы собственной энергии в я-мезон-нуклонной амплитуде.
равный нулю; в этом случае диаграммы рис. 17.7 и 17.8 вклада
не дают.
Остающаяся часть выражения A7.41) отвечает диаграм-
диаграммам, указанным на рис. 17.9. Эти диаграммы отвечают пере-
переходам с изменением квантовых чисел я-мезонов и нуклонов.

200
ТЕОРИЯ ВОЗМУЩЕНИЙ
(ГЛ. 1?
Соответствующие аналитические выражения имеют вид
(х у ? ? \ —
-.Bа)
1Ц,
d<y2 (x,xt)r3 /Af (у, -
X [iSF (z2 - y2) iy5iSF (y2 — г/,) tVslSp (y
тBб)
l<7, a/3,
(	 Л2
X [/SF (z2 — y2) i^iSp (y2 - г/,) /Y5iSf (г/i —
(x2 - y2) X
)Ц, A7.42a)
(x2 — yt)X
i)]ap. A7.426)
Ничто не заменяет опыта! Мы настоятельно рекомендуем чи-
читателю самому вывести формулы A7.42), внимательно прове-
проверить все множители и спи-
спиновые И ИЗОСПИНОВЫе ИН-
дексы.
Для того чтобы вычис-
лить амплитуду перехода,
подставим A7.42) в редук-
редукционную формулу, связы-
i
в
Х-,,1
ч
\
>N
/
2„08
а)
Ф
Рис. 17.8. Массовые контр-
члены в л-мезон-нуклонной
амплитуде.
Рис. 17.9. Вклад второго порядка
в я-мезон-нуклонное рассеяние. Соот-
Соответствующие амплитуды определены
выражениями A7.42а) и A7.426) со-
соответственно.
вающую т-функцию с 5-матрицей. Отбрасывая при этом член,
отвечающий рассеянию вперед, получаем
s<2> (p2, я2;
(~j \
d%
'21 x
X+ B) tfl ap, rs (xt, x2, zlt z2) X
X Ъ CD[(-^~
Hf„ (x,), A7.43)

S 121]	Я-Я-РАССЕЯНИЕ	201
где fq — нормированная волновая функция бозона с импульсом
д, Ups — нормированная волновая функция фермиона, ф; и /г —
изотопические волновые функции.
При вычислении с точностью g2 следует, в соответствии с под-
подходом теории возмущений, положить Z2 = Z3=1. Операторы
Клейна — Гордона и Дирака устраняют внешние линии, по-
поскольку
(	2))	V(
(iVx - М) SP (x-y) = SF (х - у) (- Я у -М) = б*(х- у). A7.44)
Другими словами, пропагаторы заменяются на волновые функ-
функции частиц в начальном и конечном положениях. Выполнив
интегрирование с учетом б-функций, получим
X ф <*+*> у, J-JJ+ B) т • ф> • ф1% A)] X
X [п (р2, s2) iy5iSF (г/2 - yt) iy5u (рь s,)] e~< <"•+'?'» у +
+ ei «й-?.»», [Х+ B) t • ф,т. ф;% A)] х
X [й (р2, s2) /Ys^f (г/2 - г/i) JY5« (Рь st)] e~l 0»--й »•. A7.45)
Выполнив далее фурье-преобразование и переходя в импульсное
пространство, мы снова приходим к выражению A6.54).
Отметим, что из редукционной формулы непосредственно сле-
следует кроссинг-симметрия амплитуды, отмеченная ранее в A0.54)
и A0.55). Выражение A7.40), очевидно, не меняется при замене
i<-*-j, X\ ¦*->• х2. Поэтому, если в A7.43) заменить фн-*-*-фо(- и
^л (xi) ч~у f- г (^О' то ^"матРиЦа не изменится. Гелл-Манн и Голд-
бергер показали, что в пределе qi = q2~>-0 амплитуда я — ./V-
рассеяния не зависит от изотопического спина, в этом случае
5,7 = 8ijS. Подробности доказательства мы оставляем читателю
в качестве упражнения. Другим важным результатом, следую-
следующим из кроссинг-симметрии, является теорема Померанчука [75]
lim (ТЫ(А + В->А + В) = lim etot{A + ?->А + В).
В гл. 18 мы обсудим эту теорему при рассмотрении дисперсион-
дисперсионных соотношений для амплитуды рассеяния на нулевой угол.
§ 121. я — я-рассеяние
Приведем еще один пример применения редукционной тех-
техники Дайсона —Вика. Снова рассмотрим взаимодействие
A7.39) и вычислим в низшем порядке амплитуду л — л-рассея-
рия. Графики, отвечающие вкладу ~g4 в эту амплитуду,

202
ТЕОРИЯ ВОЗМУЩЕНИЯ
to,
\i.
"~\
t
i
/
/
i
X
/ л
i
\
\
\
/
1
\
\ ,
A
1 ^
1
1 l J
/
&2-
Рис. 17.10. Диаграммы четвертого лорядка для я — я-рассеяния.

§ 121]	Я-п-РАССЕЯНИЁ	203
изображены на рис. 17.10. Диаграммы, показанные на рис. 17.11,
дают вклад только в амплитуду рассеяния вперед; их мы рас-
рассматривать не будем. Для графиков рис. 17.10 полагаем Z3 = 1
ф ф ф1
*
II	II
А А	А	А
Рис. 17.11. Диаграммы четвертого порядка для я — я-рассеяния вперед.
и не учитываем массовый контрчлен; тогда
-X
X ] ^4-ti • • • Лс4 {exp / [?з^з + qAXi — qxxx — q2x2]} X
где фг — изотопические функции и
Кх=Пх + \12.
В рассматриваемом порядке
X @ | Г (Ф/ (д:2) ф, (г/2)) 10} @ | Т (щ (х3) Ф< (г/3)) I 0} @ | Т (Ф, fo) Фы (г/4)) I >Х
X <01Г (: -ф (г/,) /у6ТгФ («/О : Ф (г/2) ^.Ф Ы :: * Ы ^/Ф Ы : X
— Уз) X
X Л^ (jc4 — г/4) Sp Tjt^t, Sp iy5iSF (г/i — г/2) 'Ys^f (гу2 — Уз) X
X iYe'S/» (г/з — г/4) 'Ys'-S^ (г/4 — У\) +
5 членов, получаемых перестановкой внешних линий. A7.47)

204	ТЕОРИЯ ВОЗМУЩЕНИЙ	[ГЛ. 1?
Отметим знак минус в A7.47). Он обусловлен тем, что при
вычислении свертки if (t/4) с ty(y\) необходимо выполнить нечет-
нечетное число перестановок. В общем случае произвольной диаграм-
диаграммы при вычислении замкнутой электронной петли вклад соот-
соответствующей диаграммы умножается на —1. Действительно,
Рис. 17.12. Замкнутая фермионная петля как часть некоторой произвольной
диаграммы.
виковское произведение для замкнутой петли, изображенной на
рис. 17.12, равно
+ @1Т (ф Ы ГЧ|» Ы ф Ы Гф (у2) ... ф (уп) Гф (уп)) | 0) =
= - <0 | Т (ф (?/„) ф (?/,) Г ф (?/,) ф (?/2) Г . . . ф (?/„_,) ф (уп) Г | 0> =
= (- 1) Sp i SP {yn - ?/,) YiSP (у, -у2)Г ... iSp (yn_x -yn)Y +
+ перестановки. A7.48)
Объединив A7.46) и A7.47), получаем в импульсном простран-
пространстве
п. п ч	* BяL 6«
^4, <7ь ^ - -
Bя)в
где
Ш = - fg4 Sp т • ф,т. ф2т • ф^т • ф' X
X J 72nF Sp iY5/» + <?i-M + /e ^5 ^ + ^i + & - М + /в
X jfr^ + ft «Ye р-м + ь + 5 перестановок. A7.49)
Выражение A7.49) в точности согласуется с выражением,
полученным по фейнмановским правилам (см. прил. Б, т. 1).

§ 121]	Л-Я-РЛССЁЯНИЁ	205
К сожалению, интеграл по внутреннему импульсу р лога-
логарифмически расходится1). Для того чтобы устранить эту рас-
расходимость, необходимо ввести дополнительный контрчлен в
лагранжиан мезонного взаимодействия. Простейший контрчлен
имеет вид
-^1==^1(Ф) = 1/4бЯ:(ф.фJ:,	A7.50)
где 6Я—бесконечная константа, которая сокращает расходи-
расходимость в A7.49); при этом конечный ответ для амплитуды я — я-
рассеяния получается после вычитания бесконечных контрчле-
контрчленов. Вычисление интегралов и шпуров в A7.49) требует гро-
громоздких выкладок; помимо всего прочего, такое вычисление не
слишком полезно, поскольку трудно ожидать, что ряд теории
возмущений сходится (g2/4n= 15). Установим далее некоторые
общие свойства амплитуды рассеяния, определяемые требова-
требованиями симметрии.
1.	Ш — скалярная функция инвариантов
s = 07. + <72J, / = (<71-<7зJ, и = (<7,-<74J, A7.51)
где
s + t + « = V.
В физической области рассеяния qt + <72-><7з-Ь' q* s~^A\n2,
t < 0, и < 0.
2.	В предположении зарядовой независимости Ш имеет сле-
следующую изоспиновую структуру:
=(и • Ф2) (ф; • ф:) a (s, t, и) + ($, • ф1) (ф2. ф в (s, t, и) +
/>М). A7.52)
3. Амплитуда Эй обладает свойством кроссинг-симметрии, т. е.
не меняется при перестановке любой из внешних частиц:
— <73> Ф2 *"'¦ Фз*> s "*-* *>
Это свойство следует из A7.46) и симметрии т-функции. От-
Отсюда
A (s, t, м) = В (/, s,u)=C (и, t, s) = A (s, и, t) =
= В (и, s,t) = C (t, и, s). A7.53)
') Эта расходимость не возникает в квантовой электродинамике, где в
силу градиентной инвариантности на амплитуду рассеяния света на свете на-
налагаются дополнителньые условия. Дальнейшее обсуждение этого пункта
см. в § 146.

206	ТЕОРИЯ ВОЗМУЩЕНИЙ	[ГЛ. 1?
В приложениях часто используется амплитуда с данным изото-
изотопическим спином. Для того чтобы получить выражения для этих
амплитуд, введем изотопические инварианты Р,, которые отве-
отвечают определенному изотопическому спину в реакции 1+2->
3 + 4
ф2)
= '/2 [(Ф, • Фз*) (Ф2 • Ф0 - А * Й)
»='/2 [(ф, •*;)($,-$;)+
(ф, • ф;) (ф2 • ф^)] - 7з (ф, • ф2) (ф; • ф;). A7.б4>
Определив
A7.55)
легко проверить, что
з
Е Pi Щтп) Р,' (mnkl) = Р, (ijkl) б;/.	A7.56)
т, п=\
Подробные выкладки мы оставляем читателю. Далее имеем
Щ<7з, ад <7ь q2) = A0P0 + AlP] + A2P2,
где
Л0 = ЗЛ + В + С, Л, = В-С, Л2 = В + С, A7.57)
причем Л/ — искомые амплитуды рассеяния с полным изоспи-
ном /. В симметричной точке s = t = и = 4(х2/3, согласно
A7.53), Л = В = Си
А) = 72^2, ^i==0, s = t = u.	A7.58)
Эти соотношения будут использованы в § 135 при рассмотре-
рассмотрении техники дисперсионных соотношений.
§ 122. Графическая техника в квантовой электродинамике
В предыдущих параграфах мы вывели фейнмановские пра-
правила вычисления диаграмм, суммированные в приложении Б
1-го тома и уже использовавшиеся в первом томе. Однако слу-
случай квантовой электродинамики требует отдельного рассмотре-
рассмотрения. В квантовой электродинамике имеется два типа диаграмм.
Первый из них содержит обмен поперечным фотоном. Соответ-
Соответствующая вершина равна —/еоуц, а пропагатор, согласно
A7.33), равен
iDp(q, TiVv =
<7ц<?у	(дц) (gn'Hv + т)ц?у)	<72Т1ц% "I
+	~q2	~ Ш* - q2 J '
A7.59)

§ 122]	ГРАФИЧЕСКАЯ ТЕХНИКА	207
где вектор г\ = A, 0, 0, 0) определен в той лоренцевой системе,
в которой выполняется квантование. Второй класс диаграмм со-
содержит мгновенное кулоновское взаимодействие A5.28)
	4п\х-х'\	•	A7-6°)
Докажем утверждения, сформулированные в § 87.
1.	Из сохранения тока следует, что члены в A7.59), пропор-
пропорциональные <7ц или <?v, не вносят вклад в амплитуду рассеяния ').
2.	Последний член в A7.59) сокращается с кулоновским
взаимодействием A7.60).
Отсюда следует, что при практических вычислениях можно
использовать ковариантный пропагатор
Тем самым гарантируется ковариантность электродинамических
амплитуд.
Рис. 17.13. Фермионная линия с и реальными или виртуальными фотонами.
Докажем вначале 12). Рассмотрим фермионную линию, кото-
которая соединена с п фотонными линиями (рис. 17.13). Соответ-
Соответствующая амплитуда равна
g(p, />'; <7ь аи ... qn, an) =
Вставим еще один фотон, реальный или виртуальный с импуль-
импульсом <7 и вершиной 4. тогда получим диаграмму, изображенную
на рис. 17.14. При этом g заменяется на gr:
gr(p, p', q; qh fli) =
A7.62)
') В гл. 7 мы уже использовали это обстоятельство (для случая реаль-
реальных фотонов) при вычислении поляризационных сумм с помощью фейнманов-
ской техники.
2) Приведенные ниже аргументы неприменимы в случае, когда рассматри-
рассматриваются радиационные поправки к внешним электронным линиям (см. [140]).
В общем случае неперенормированные 5-матричные элементы зависят от ка-
калибровки и становятся градиентно-иивариантными только после умножения
Ва зависящую от калибровки константу Z. (Прим. перев.)

208	ТЕОРИЯ ВОЗМУЩЕНИЙ	[ГЛ. 17
Далее используем тождество
11	1	1
pr + Q — m4 рг — m Pr — m pr + Q —
и перепишем gr в виде ')
gr(p, p', q; qh ад = р,+ \_тйп... pr+s^_jr+l
••• йх J=^T ~~ p' + q-m йп* • • •
ч/ 1 А	1.1,
4-m ar+i Pr + q_mar pr_x _ т аг_! ... а, р _т .
A7.63)
Суммируя все такие диаграммы, различающиеся местом присо-
присоединения фотонной линии на рис. 17.14, мы видим, что в A7.63)
Рг }Рг+?	. . .	р'+
Рис. 17.14. Фермионная линия с я фотонами и дополнительной вершиной,
в которой передается импульс <?•
попарно сокращаются все члены, кроме тех двух, в которых фо-
фотон <7 присоединяется правее qn и левее <7i2):
Й(Р, Р', Я\ Яи at) =
л J
• • • l р - т p' + Q-m п рп-х + q-m а"-1 " ' ' fl' р + 4 - т
= g (p, p'\ qu ах\ ...; qn, an) — g(p + q, p' + q\ qu «ь . . •; <7„, ап).
A7.64)
Заметим теперь, что внешние концы диаграммы на рис. 17?14
либо принадлежат свободным частицам, либо замыкаются, об-
') Мы предлагаем читателю убедиться в том, что приведенное доказа-
доказательство сохраняется и в том случае, когда фермионная линия содержит
массовый контрчлен.
2) В том случае, когда q относится к виртуальной фотонной линии, оба
конца которой присоединяются к одной и той же электронной линии, сумма
диаграмм, отвечающих всем перестановкам обоих концов фотонной линии,
равна умноженной на два сумме диаграмм, отвечающих всем перестановкам
оставшихся п — 2 вершин.

5 122]
ГРАФИЧЕСКАЯ ТЕХНИКА
209
разуя петлю (см. рис. 17.15). В первом случае 5-матричный
элемент равен
XI Hm (Pf + q-m)g(p,p',q;ql,al)(p-m)}u(p) = O. A7.65)
*2
Для электронной петли имеем
Sd4p
,9т\4 Sp aog (р, р , q; qt, a{) =
7! qt, a^]. A7.66)
Во втором из интегралов A7.66) сделаем замену переменных,
обращаясь с этим интегралом так, как если бы он был сходя-
сходящимся. Для обоснования этой процедуры необходимо, как и при
вычислении поляризации вакуума, сначала регуляризовать под-
подынтегральное выражение, а затем сделать замену перемен-
переменных. В результате получим $ = 0.
Таким образом, утверждение 1
доказано, и при вычислении S-мат-	-	jq
ричных элементов Dp можно за-
заменить на
Юг
¦(я)-
- q2 ¦
A7.67)
В координатном пространстве (см.
A4.55)) имеем
A7.68)
Рис. 17.15. Замкнутая фермион-
ная петля, содержащая п фо-
тонных линий.
Последний член в A7.68) имеет тот
же вид, что и кулоновское взаимо-
взаимодействие в A7.60). Покажем, что на самом деле указанные два
члена в точности сокращаются (утверждение 2).
Для доказательства нужно лишь тщательно пересчитать гра-
графики. Гамильтониан взаимодействия содержит как член с попе-
поперечными фотонами
Щ @ dt =
in (у) Y^In (у) : Al (у) = е0 \ d*y ft (у) Л'/п (у),
A7.69)

210	ТЕОРИЯ ВОЗМУЩЕНИЙ
так и мгновенное кулоновское взаимодействие
1ГЛ. 17
dt = l
Mb (z0 - z'o) Р* (г') -
Рассмотрим отдельный член в разложении A7.22), содержащий
2п множителей Я*г и т множителей Я/ул. Порядок этого члена
есть N = 2п -\- т. Однако его статистический вес в формуле
Вика равен не [NI]'1 = [Bл + т)\]~\ а [{2п)\т\]-\ поскольку
Легко видеть, что статистические множители сокращаются, если
просуммировать все топологически эквивалентные графики. Дей-
Действительно, имеется Bп\)т\ тождественных диаграмм, получен-
полученных перестановкой аргументов г/г друг с другом и аргументов zt
V777/
>/////
V/77/
а)
Ф
Рис. 17.16. Произвольная диаграмма, содержащая обмен поперечным фото-
фотоном (а), мгновенное кулоновское взаимодействие (б).
друг с другом. Кроме того, имеется 2т топологически эквива-
эквивалентных графиков, полученных перестановкой пар аргументов
zi и z\, в результате сокращаются множители '/г в Я/ул.
Таким образом, статистический вес каждого топологически
неэквивалентного графика равен единице. Любой диаграмме,
содержащей обмен поперечным фотоном (рис. 17.16, а), можно
сопоставить диаграмму с тем же самым статистическим весом,
отвечающую мгновенному кулоновскому взаимодействию
(рис. 17.16,6). Используя A7.68) и A7.17), найдем вклад этих
диаграмм в т-функцию. Для поперечных фотонов этот вклад
равен
\ фх dV (- teoYll) Г + i^DP (x - х') - i6^~x~Sf] (- /e"Vv).
A7.71)

§ 1231	ИЗЛУЧЕНИЕ МЯГКИХ ФОТОНОВ	211
а для кулоновских сил
Таким образом, кулоновское взаимодействие сокращает неприят-
неприятный член в правой части A7.71), в результате мы приходим к
ковариантному фотонному пропагатору.
§ 123. Излучение мягких фотонов
и инфракрасная катастрофа
Мы завершим эту главу рассмотрением взаимодействия поля
излучения с классическим распределением токов. Эта интерес-
интересная с физической точки зрения задача допускает точное реше-
решение. Вычислим, в частности, число испускаемых фотонов и их
распределение по частоте. С этой целью мы явно построим опе-
оператор 5 и проведем вычисление интересующих нас матричных
элементов.
В калибровке излучения уравнение для поля имеет вид ¦)
? Л (*) = /(*),	A7.73)
где ](х) — заданная с-числовая функция, причем
V./(x) = 0.	A7.74)
Перепишем A7.73) в интегральной форме:
А (х) = Ain (х) + J d*y Dret (x-y)j (у) =
= Aout (x) + J d*y Dadv (x - у) j (у), A7.75)
где положено Z3 = 1, поскольку А, А\п и Aout отличаются только
на с-число и удовлетворяют одним и тем же перестановочным
соотношениям. Согласно A6.66), 5-матрица удовлетворяет со-
соотношению
5"'Л1п(л;M = Лои((л;)	A7.76)
или
S~lAln (x) S = Aln (x) +\d<yD(x- у) / (у), A7.77)
где
- D (г) = Dadv (г) -Dret(z) = -/ \ -0ре-'Ь*6(к*)е(k0) A7.78)
(см. приложение В).
') Величина заряда включена в определение тока /.

212	ТЕОРИЯ ВОЗМУЩЕНИЙ	[ГЛ. 1?
Удобно перейти в импульсное пространство, разложив j(y)
в интеграл Фурье:
, Я)[/(k, X)e~ik* + Г(k, Я)е'*«], A7.79)
тогда A7.77) приобретает вид
amt(k; X) =	jff
S~latn (k, K)S = at (k, к) - ?ЩМ, k2 = 0.
V2|*|
Уравнение A7.80) можно решить в явном виде, поскольку
поля ат(&Д) под действием оператора 5 смещаются лишь на
с-число. С этой целью используем тождество
евАе~в = А + [В, А],	A7.81)
справедливое в том случае, когда коммутатор [В, А] есть с-число.
Выражение A7.81) наводит на мысль, что В следует выбрать
в виде линейной комбинации операторов а1п и ata- Условие уни-
унитарности позволяет записать следующее общее выражение для
оператора S:
, X)a+(k, K)+f(k, X)aln{k, A.)]l. A7.82)
)
Подставив A7.82) в A7.80), получим
х)=Ш-	A7-83)
Для вычисления матричных элементов между in-состояниями
удобно представить S-матрицу в нормальной форме. При этом
оказывается полезной следующая теорема.
Теорема.
Если [Л, В] = С есть с-число, то
= еА^-ъ [А, В]>	A7>84)
Доказательство.
Определим
F (Я) —
Тогда

§ 123)	ИЗЛУЧЕНИЕ МЯГКИХ ФОТОНОВ	213
Непосредственно из A7.81) следует, что
«» и
Поскольку /7@)=1, F (Я) является с-числом, в частности
Применяя эту теорему, получаем
s=ехр
2
X ехр Г/ J -^=- 2 Г (*, Я) am (Л, ЯI X
Г/
-тS
2
Xexp|-i\-^-2J^'X)lT (l7-85>
\-i	J
Теперь мы можем вычислить вероятность Рп процесса, в ко-
котором при взаимодействии с током испускается п фотонов
с заданными импульсами и поляризацией:
ki в я
= Е KM-i • • • КК in I S10 in) |2, A7.86)
где 31—некоторая область в Зп-мерном фазовом пространстве.
Обращаясь к A7.85), мы замечаем, что вклад в S дает только
член, содержащий п операторов рождения и не содержащий
операторов уничтожения вовсе. Поэтому
„) = | ехр Г—
| X
X
в .
0	2	.ч
-^ ^ / (k, Я) а+ (Л, Ы 10 in) p. A7.87)
Если мы интересуемся вероятностью испускания фотонов с
произвольной поляризацией в заданный интервал импульсов R

214	ТЕОРИЯ ВОЗМУЩЕНИЙ	[ГЛ. 17
(т. е. k\ e R, ..., kn^R), то выражение A7.87) можно упро-
упростить. Запишем сначала:
9
г, в R
2	-.га
—f= Ya i (k> Л) atn (k< x) M °in) I2> A7.88)
где
Г	Г ЛЗЬ т—1	П
A7.89)
[
есть вероятность того, что не испускается ни один фотон1). По-
Поскольку интеграл в A7.88) вычисляется по ограниченной обла-
области R, внешнее суммирование может быть формально выполнено
по всем kr, при этом очевидно, Pn{R) не изменится. В результате
получим
0
(i7-9o)
В том случае, когда R есть все импульсное пространство, ве-
вероятность Рп излучения п фотонов имеет вид распределения
Пуассона
A7.91)
') При рассеянии на внешнем потенциале, например при рассеянии элек-
электронов в кулоновском поле (гл. 7), для получения конечного результата не-
необходимо учитывать графики с виртуальными фотонами в промежуточном со-
состоянии. Вклад таких графиков содержится в Яо = @ out 10 in) , поскольку
в этом случае электронное состояние включено в |0 in) и |Oout).

$ 123]	ИЗЛУЧЕНИЕ МЯГКИХ ФОТОНОВ	215
где среднее число испускаемых фотонов п равно:
2
=Z
л=0
Очевидно, ?Лг=1> что отвечает сохранению полной ве-
роятности.
То обстоятельство, что для числа испускаемых фотонов спра-
справедливо распределение Пуассона, означает, что фотоны излу-
излучаются статистически независимо. Статистическая независи-
независимость в свою очередь есть следствие сделанного предположения
о классическом характере источников тока, на которые излу-
излучение не оказывает обратного воздействия; в результате каждый
фотон испускается в одинаковых условиях.
Для вычисления полной энергии излучения используем
A7.86):
Ё= Ё Е \(kih ...?,Ain|S|0in>|2X
п=° *Л	*n\,
X(*i + *2+ .-. +*B) = <Oin|S-I#oDin)S|Oin>f A7.93)
где
— гамильтониан свободного поля излучения. Учитывая A7.80),
получаем
A7.94)
в согласиц с известным результатом классической электродина-
электродинамики.
Поскольку источник тока излучает конечное количество энер-
энергии на единичный интервал частот при k-*-0, то /(?Д)~ l/k
при &->0. Например, для точечного заряда, который мгновенно
меняет направление своего движения,
где Р(р')—скорость до (после) излучения. Если ток ведет себя
указанным образом, то среднее число испускаемых фотонов

216	ТЕОРИЯ ВОЗМУЩЕНИИ	[ГЛ. 17
равно бесконечности, поскольку, согласно A7.92), бесконечно
число фотонов с частотой k ~ 0. Мы сталкиваемся, таким об-
образом, с «инфракрасной катастрофой», обсуждавшейся ранее
в гл. 7 и 8. В том случае, когда свойства тока приближаются
к классическим, имеется конечная вероятность испустить любое
число фотонов с k ~ 0; например, если выбрать R в виде
Os^|A|s^ А, то
2	П
i/(*. А.)|2 . A7-95)
J
Г
= ехр -
L
Отношение вероятности излучения я + 1 фотонов к вероятности
излучения п фотонов равно
1 f d3, | / (k, X) |2 ^
n + 1 J	2\k\ ~
и расходится при ?->0. Таким образом, теория возмущений,
основанная на разложении по степеням а, неприменима в пре-
предельном случае больших длин волн. Близкий к нашему изложе-
изложению анализ возникающих при этом расходимостей был дан
Блохом и Нордсиком [76] (см. также [77]) в 1937 г.
ЗАДАЧИ
1.	Вывести формулу A7.5), описывающую развитие во времени канони-
канонического импульса.
2.	Вычислить [/-матрицу для клейн-гордоновской частицы, связанной
с постоянным с-числовым током: (D + т2) q> = f. Обсудить результат в связи
с теоремой Хаага (см. примечание на стр. 183), согласно которой в данном
случае оператор U(t) не существует. Построить 5-матрицу.
3.	Показать, что вакуумные петли, содержащиеся в ^ft Dfe в A7.38),
можно собрать в exp | j —^i\> где ^' — связанные петли, a r\i — их по-
рядок.
4.	Выписать общую спиновую и изоспиновую структуру яЛ^-амплитуды.
5.	Проверить, что 5-матрица я-мезон-нуклошюго рассеяния в пределе
9~>0 (q — 4-импульс пиона) не зависит от изотопического спина (см. § 120).
6.	Вычислить расходящуюся часть в A7.49) и показать, что расходимость
можно устранить подходящим выбором контрчлена в A7.50).
7.	Доказать свойство кроссинг-симметрии A7.53) для амплитуды я — я-
рассеяния.
8.	Показать, что результат A7.64) не изменится, если учесть массовый
контрчлен.
9.	Вычислить q>in и cpout для лагранжиана
Ds	i^,
где 2?'D и 3?s — свободные лагранжианы для дираковскои и скалярной ча-
частиц, и показать, что S = 1. Совпадает ли в этом случае точный фейнманов-
ский пропагатор для дираковскои частицы со свободным: Sp — Sp?

ГЛАВА 18
ДИСПЕРСИОННЫЕ СООТНОШЕНИЯ
§ 124. Причинность и соотношения Крамерса—Кронига
Обсуждавшийся до сих пор метод вычисления амплитуд
перехода ограничивается случаем малой константы связи, ко-
которая является параметром разложения рядов теории возмуще-
возмущений. Например, в квантовой электродинамике этот параметр
равен а = 1/137. В предыдущей главе, исходя из формализма
теории поля, мы развили систематический (хотя и формальный)
метод, основанный на использовании диаграммной техники, а
также сформулировали правила вычисления фейнмановских
диаграмм.
Указанный подход оказывается, однако, совершенно беспо-
бесполезным в том случае, когда мы рассматриваем сильные взаимо-
взаимодействия. В гл. 10 при обсуждении мезон-нуклонного и нуклон-
нуклонного рассеяния мы убедились в необходимости привлече-
привлечения иной, более адекватной техники. В настоящее время наибо-
наиболее плодотворным методом в теории сильных взаимодействий
является метод «дисперсионных соотношений», который осно-
основывается на экстраполяции в комплексную плоскость. Локаль-
Локальная структура коммутационных соотношений и полевые урав-
уравнения накладывают некоторые ограничения на поведение ампли-
амплитуд рассеяния, рассматриваемых как функции энергии и пере-
переданного импульса, при аналитическом продолжении амплитуд
по этим переменным от физических значений в нефизическую
комплексную плоскость. При этом оказывается возможным
установить ряд соотношений, позволяющих либо вычислить эти
амплитуды, либо выразить их через другие наблюдаемые вели-
величины [78, 79].
Метод дисперсионных соотношений в теории поля был инспи-
инспирирован соотношениями Крамерса — Кронига в оптике [80],
которые мы кратко рассмотрим для иллюстрации основных идей
дисперсионного подхода. Соотношения Крамерса — Кронига вы-
выражают действительную часть амплитуды рассеяния вперед

218	ДИСПЕРСИОННЫЕ СООТНОШЕНИЯ	[ГЛ. 18
света на атомах через интеграл от сечения поглощения. В макро-
макроскопическом смысле это соотношение устанавливает связь
между показателем преломления в веществе и интегралом (по
всем частотам) от коэффициента поглощения. При выводе
соотношений Крамерса — Кронига нужно прежде всего убедиться
в том, что амплитуда рассеяния на нулевой угол ана-
литична в верхней полуплоскости комплексной со-плоскости.
Этот факт в свою очередь является математическим выраже-
выражением того обстоятельства, что электромагнитные сигналы не мо-
могут распространяться со скоростью, большей скорости света.
Переходя к выводу соотношений Крамерса — Кронига, рас-
рассмотрим монохроматическую волну с амплитудой а|пс, которая
распространяется вдоль оси х и падает затем на рассеивающий
центр:
Амплитуда рассеянной вперед волны aScatt линейно связана с
амплитудой падающей волны
где / (со) — амплитуда рассеяния на нулевой угол. Асимптоти-
Асимптотически
,-lait-x)
(X, t) -> aScatt (со) '
X-> oo
Взяв суперпозицию волн с различными частотами, получим
оо
Г
Aiac(x,t) = \ don alnc (со ) e~ia <*~х>,	A8.1)
— 00
со
А
scatt
(х, t) -» 1 \ d»7(«0a.nc(«>')e-to'«-*> A8-2)
для падающей и рассеянной на нулевой угол волн соответствен-
соответственно. Учтем далее, что A8.1) представляет световой сигнал, по-
поэтому A\az{x, t) = 0 при х > t. Этому требованию, вытекающему
из физических соображений, можно придать математическую
формулировку, рассмотрев фурье-амплитуды
И = гП dx A
где верхний предел выбран в соответствии с условием
Air.c(x, 0) = 0 при л:>0. Из A8.3) следует, что ащс(ю) может

5 124]	ПРИЧИННОСТЬ И СООТНОШЕНИЯ КРАМЕРСА - КРОНИГА	219
быть аналитически продолжена в верхнюю часть комплексной
©-плоскости. Действительно, при ©->-© +/| у |
о
A8.4)
и интеграл абсолютно сходится. Принцип причинности озна-
означает, что
ЛзсаН (X, 0 = 0 ПрИ X > t,
т. е. что световой сигнал не может достигнуть точек, лежащих
впереди фронта падающей волны. Используя те же аргументы,
что и выше, мы заключаем из A8.2), что функция атс(со)/(сй)
к-с
г
Ш@'
\
С\
\
\
Rev'
Рис. 18.1. Контур в верхней полуплоскости to', используемый в формуле Коши.
также аналитична в верхней полуплоскости. Следовательно1),
функция Дсо) сама по себе является аналитической в верхней
полуплоскости. Запишем для нее формулу Коши:
которая справедлива для любого z = co + /|y| в верхней полу-
полуплоскости. Контур С в A8.5) указан на рис. 18.1. Если z стре-
стремится к физическому значению а», оставаясь при этом в верхней
полуплоскости, то
оо
/(со)= lim /(«> + «)= JL-P \ У-ш* +т/(<о) + |Со, A8.6)
е»0+
е-»0+
где Р \ .., означает главное значение интеграла. Второй член
в этом выражении возникает при интегрировании по полуокруж-
полуокружности, окружающей полюс о»' = со, а комплексная константа
') Амплитуда f не имеет полюсов, связанных с нулями в ашс(и), по-
поскольку функция Щпс(в>)—фурье-компонента волнового пакета — совершенно
произвольна,

220	ДИСПЕРСИОННЫЕ СООТНОШЕНИЯ	[ГЛ. 18
Coo = Coo + iC'x, есть вклад интеграла по полуокружности бес-
бесконечно большого радиуса. Разделяя действительную и мнимую
части, получаем
Im / (со) = - IP ld^L(:] + С.	A8.76)
— Оо
Легко видеть, что уравнение A8.7а) есть действительная часть
от выражения
оо
/(«)= Ига f(co + /e) = Hmi J ffl" ^ + Сте> A8.8)
которое и представляет наиболее общий вид дисперсионного
соотношения.
Величина С«х не равна нулю в том случае, когда /(со) не
исчезает при со-хэо. Вклад большого полукруга можно устра-
устранить, сделав «вычитания». С этой целью запишем теорему Коши
не для /(со), а для /(со)/со; в этом случае подынтегральная функ-
функция имеет дополнительный полюс при со = 0, но зато лучше
ведет себя на бесконечности. Если /(со) при <в->оо ограничена
константой, то вместо A8.7а) получаем
оо
Re f (со) _ Re f @) 1 f rfco' Im f (со')	„. .
со ~ со ~*~ я J со'(со'-co) •	<ie'y'
— oo
Эта формула называется дисперсионным соотношением с одним
вычитанием. В том случае, когда /(со)—>0 при сй-»оо, величина
С» = 0 и вычитания не нужны.
Дисперсионные соотношения в форме A8.7) или A8.9)
позволяют вычислить амплитуду рассеяния, если известна ее
мнимая часть. Если необходимо одно вычитание, то нужно до-
дополнительно задать функцию /(со) при со = 0, если же требуется
несколько вычитаний, то нужно задать еще и производные /(со)
при со = 0. Отметим, что для вычисления амплитуды при какой-
либо одной частоте нужно знать мнимую часть при всех часто-
частотах — этот факт является до некоторой степени компенсацией
за преимущества дисперсионного метода.
На практике, однако, это обстоятельство не приводит к за-
затруднениям, поскольку мнимая часть амплитуды рассеяния впе-
вперед с частотой со > 0 связана, в силу оптической теоремы, с
полным сечением поглощения света с той же частотой
Im/(co) = ^-atQt(»),	A8.10)

§ 125]	ПРИЛОЖЕНИЕ К. ФИЗИКЕ ВЫСОКИХ ЭНЕРГИЙ	221
Далее, можно избавиться от области отрицательных со в диспер-
дисперсионном интеграле A8.7), заметив, что поскольку амплитуды
падающей и рассеянной волн вещественны, то
«шс(- <°) = <„<»> f (-©) = /*(«>)
Im f (— со) == — Im f (со).
Поэтому дисперсионный интеграл содержит только положитель-
положительные частоты
оо
Re / (со) = If ^ ®'2d&' 2 Im / (соО	A8.11а)
о
или
Re / (со) = Re / @) + — Р\ da', ГТf-(<i>'\ ¦ A8.116)
я J со'(о)'2 — со2)
Таким образом, принцип причинности распространения световых
сигналов в сочетании с оптической теоремой, которая выражает
сохранение вероятности при рассеянии, позволяет сформулиро-
сформулировать следующее утверждение. Действительная часть когерент-
когерентной амплитуды рассеяния света вперед на атомах вещества, т. е.
коэффициент поглощения может быть вычислен из дисперсион-
дисперсионных соотношений, если в последних задать более простую
величину, измеренную на опыте, либо вычисленную независимо,
которая описывает поглощение света в веществе. Выражение
m,»_m>	A8.12)
о
и представляет соотношение Крамерса — Кронига.
§ 125. Приложение к физике высоких энергий
Метод дисперсионных соотношений находится в близкой ана-
аналогии с соотношениями Крамерса — Кронига. Этот метод цели-
целиком основывается на принципе причинности, который позволяет
сделать определенные утверждения о свойствах аналитичности
амплитуд. После того как область аналитичности установлена,
амплитуды по теореме Коши выражаются через вычеты в полю-
полюсах и скачки на разрезах («абсорптивные части») вида A8.8)')
lim [/ (со + /е) - / (со - /в)] = 2г Im / (со).	A8.13)
8-»0+
') Мы используем принцип отражения Шварца f(co*) — j* (со), позволяю-
позволяющий определить / в нижней полуплоскости, которая отделена разрезом от
верхней полуплоскости.

222	ДИСПЕРСИОННЫЕ СООТНОШЕНИЯ	1ГЛ. 18
Чтобы затем получить соотношения между измеренными вели-
величинами, нужно использовать унитарность S-матрицы. Это свой-
свойство позволяет выразить абсорптивные части через другие
величины, непосредственно измеряемые на опыте. Хотя проб-
проблемы, с которыми приходится сталкиваться при конкретной реа-
реализации указанной программы, гораздо более серьезны, чем в
примере с соотношениями Крамерса — Кронига, основные идеи
остаются при этом теми же самыми.
Отправной точкой при строгом доказательстве дисперсион-
дисперсионных соотношений в теории поля являются аксиомы, сформули-
сформулированные в гл. 16, и особенно важнейшая из них, утверждаю-
утверждающая, что коммутаторы бозе-эйнштейновских полей и антикомму-
антикоммутаторы ферми-дираковских полей равны нулю для простран-
пространственно-подобных интервалов
О,	A8.14)
= О- (х-уJ<0.
Выписанные соотношения локальной коммутативности заменяют
условие причинности, использованное в предыдущем параграфе
при обсуждении рассеяния света на атомах. Эти соотношения
действительно выражают свойство микропричинности в теории
поля, поскольку из них следует, что измерения амплитуд бозе-
эйнштейновских полей независимы, коль скоро эти поля разде-
разделены пространственно-подобным интервалом. То же относится
и к билинейным формам полей Ферми — Дирака, посредством
которых выражаются локальные плотности физических величин
таких, как заряд или энергия.
Условие микропричинности позволяет установить область
аналитичности функций Грина и S-матричных элементов, когда
один или несколько их аргументов аналитически продолжаются
от своих физических значений. Нахождение области аналитич-
аналитичности представляет главную проблему в дисперсионном методе;
при этом мы сталкиваемся с задачей, несравненно более слож-
сложной, чем рассмотренный выше случай рассеяния света на свете
на нулевой угол. Пожалуй, простейший пример строгого доказа-
доказательства такого рода основывается на рассмотрении представ-
представления Челлена — Лемана для функций распространения.
В гл. 16 мы показали, что из аксиом теории поля, в частности
из перестановочных соотношений A8.14), можно вывести спект-
спектральное разложение для функции Грина (например, бозонных
полей):
A'F(x-y)=-i@\T((p(x)cS>(y))\0)=\da2P(a2)AF(x-y,a). A8.15)

§ 1251	ПРИЛОЖЕНИЕ К ФИЗИКЕ ВЫСОКИХ ЭНЕРГИЙ	223
Выполнив фурье-преобразование
мы видим, что Af аналитична всюду в <72-плоскости, за исклю-
исключением разреза вдоль положительной вещественной полуоси.
Поэтому tsfp полностью определяется через скачок на разрезе,
т. е. спектральную функцию A6.27)
р (о2) = BяK Е б4 (рп - о) | @ | Ф @) | п) |2.	A8.16)
п
Эта функция практически, конечно, может быть вычислена лишь
приближенно. Выражение A8.16) имеет тот же смысл, что и
оптическая теорема в примере Крамерса — Кронига. Это урав-
уравнение выражает скачок 2зхр(о2) через вероятность распада вир-
виртуального мезона ср(О) |0> с массой о в энергетически разре-
разрешенные физические состояния \п}. Структура выражения
A8.16) типична для всех выражений, определяющих скачки в
дисперсионных задачах.
При обобщении дисперсионного подхода на случай вычисле-
вычисления вершинных функций и амплитуд рассеяния мы сталки-
сталкиваемся с огромными математическими трудностями; при этом
приходится иметь дело с большим числом переменных, причем
число сингулярностей быстро растет, а их структура становится
все более и более сложной. В этом случае не только задача
исследования комплексной плоскости оказывается весьма труд-
трудной, но и найденные сингулярности имеют весьма необычный
вид и находятся при нефизических значениях аргументов, недо-
недоступных непосредственному измерению. В такой ситуации воз-
возникает необходимость аналитически продолжать само условие
унитарности, позволяющее вычислить скачки амплитуд. Не-
Несмотря на указанные трудности, в теории дисперсионных соот-
соотношений был получен ряд строгих результатов, в частности
были доказаны дисперсионные соотношения по переданному
импульсу для я-мезон-нуклонного рассеяния [81, 82].
Ниже мы ограничимся более скромной задачей. Мы рас-
рассмотрим положение особенностей отдельных фейнмановских
диаграмм. Тем самым мы сможем сделать определенные
утверждения об области аналитичности суммы всех фейнманов-
фейнмановских диаграмм, хотя последняя может иметь и дополнительные
сингулярности [83]. Объединяя далее эти свойства аналитич-
аналитичности с унитарностью 5-матрицы, мы проиллюстрируем полез-
полезность применения дисперсионного метода для вычисления вер-
вершинных функций и амплитуд.

224	ДИСПЕРСИОННЫЕ СООТНОШЕНИЯ	[ГЛ. 18
§ 126. Аналитические свойства вершинных диаграмм
в теории возмущений
Чтобы пояснить метод нахождения особенностей произволь-
произвольных фейнмановских диаграмм, рассмотрим вклад простейших
диаграмм в электромагнитный форм-фактор л-мезона. Будем
полагать, что форм-фактор обусловлен связью я-мезона с ну-
клон-антинуклонной парой. Соответствующая диаграмма изо-
л-
Рис. 18.2. Вклад нуклонной петли в электромагнитный форм-фактор заряжен-
заряженного пиона.
бражена на рис. 18.2, а отвечающая ей амплитуда с точностью
до несущественных множителей равна
^Spvs^Ys^Y»-~м ¦ A8.17)
Импульсы указаны на рисунке, причем
Р2 = р1 + <7з, Ръ = Р\ — Яъ <7 = — <72 — <7з, A8.18)
а внешние импульсы удовлетворяют условию
Предполагается, что масса нуклона М имеет бесконечно малую
отрицательную мнимую часть.
Векторная форма выражения A8.17), равно как и зависи-
зависимость Fn только от переменной q2, обусловлены лоренцевой ин-
инвариантностью. Кроме того, в силу сохранения тока (гл. 10)
член, пропорциональный q^ = —(<72 + <7з)ц, отсутствует. Нас
интересуют свойства аналитичности функции Fn(q2). Для их
исследования введем вначале фейнмановские параметры ait a2,
аз так, чтобы знаменатели в A8.17) можно было записать в
виде, удобном для последующего интегрирования по импульсу.

S 126}	СВОЙСТВА ВЕРШИННЫХ ДИАГРАММ	22В
Используя формулу')
имеем
ABC
о о о
'
, 94	Г 4	f	/	V	1
<7з)ц рп (<7) ~ \ d Pi \ d«i da2 da361 1 — > a,- I X
X
О	ч	i = l
Sp Ys (pi + M) Ys (рз + Л1) Yh {рг + M)
Интеграл в A8.17) или A8.20) расходится на верхнем пределе,
что отвечает бесконечной перенормировке вершины (см. гл. 8),
и приобретает смысл либо после обрезания при больших им-
импульсах, либо с помощью регуляризации. Эта расходимость, од-
однако, несущественна при рассмотрении аналитических свойств
Fn(q2)-
Изменим порядок интегрирования2) и вычислим вначале ин-
интеграл по импульсу. С этой целью введем новую переменную ин-
интегрирования /:
Pi = *, + *, p2 = k3 + l, рз = Ьз + 1,	A8.21)
где векторы ki снова удовлетворяют соотношениям вида A8.18),
вытекающим из сохранения импульса:
ki = k2-q3=k3+q2.	A8.22)
Знаменатель подынтегрального выражения в A8.20) равен кубу
выражения
+ /2Еаг + 2/?бА. A8.23)
Для того чтобы устранить последний член в D, положим
з
Z k,nt = 0.	A8.24)
') Напомним формулу (8.58). Отметим, что эта формула верна при ус-
условии, что мнимые части А, В и С имеют один и тот же знак.
2) Такая перестановка возможна, поскольку после регуляризации инте-
интеграл абсолютно сходится.

226	ДИСПЕРСИОННЫЕ СООТНОШЕНИЯ	[ГЛ. 18
Четыре уравнения A8.24) совместно с восемью уравнениями
A8.22) позволяют однозначно определить импульсы kc
и
«1 =дд
?, = 1.	A8.25)
Выполнив интегрирование по d4/, получаем ')
11	.	3
- ? a, ] X
Величины Ni и Л/2 возникают из числителя в A8.20), они сво-
сводятся к полиномам по q2 с коэффициентами, зависящими от ад
Л2 есть параметр обрезания. Аналитические свойства Fn(q2) оп-
определяются функцией J(q2,at), которая остается в знаменателе
после интегрирования по d.4:
a, =
n2ai(l-a1)-M2.	A8.27)
Последнее выражение в A8.27) следует из A8.25); в A8.27)
учтено также, что я-мезон находится на массовой поверхности
Ц\ == <7з = й2.
Из A8.26) следует, что особенность в Fn(q2) может возник-
возникнуть в том и только в том случае, когда / обращается в нуль
в некоторой точке, лежащей внутри-области интегрирования по
а. Поскольку нули / определяют аналитическую структуру функ-
функции Fn (q2), последняя имеет те же аналитические свойства, что и
1 1 1
da2 [ da3 —	6A - «.-«2 - a3)	(J 2g)
J J J J 6 <72a2a3 + H2a, A — си) — M2 + is y	'
000
Здесь мы опустили несущественные численные множители и вы-
выписали в явном виде бесконечно малую мнимую добавку, кото-
которая возникает из мнимых добавок в массах фейнмановских про-
пагаторов.
') Вычисления производятся как и в гл. 8, см. примечание на стр. 172
первого тома.

§ 126]	СВОЙСТВА ВЕРШИННЫХ ДИАГРАММ	227
Функция I(q2), а вместе с ней и Fn(q2), аналитична в верх-
верхней полуплоскости комплексной переменной q2. Действительно,
интеграл A8.28) существует для всех q2 = и -f iv с и > 0. Если
I (q2) вещественна для некоторых вещественных q2, то с помощью
принципа отражения Шварца форм-фактор Fn(q2) может быть
аналитически продолжен в нижнюю полуплоскость:
Из физических соображений можно ожидать, что функция Fn(q2)
в некоторой области переменной q2 должна быть вещественной.
Действительно, рассмотрим пространственно-подобные значения
q2 (q2 < 0). В этой области Fn(q2) дает вклад в амплитуду элек-
трон-пионного рассеяния, причем в борновском приближении по
электрическому заряду этот вклад чисто вещественный, что мож-
можно проверить явным вычислением. При q2 = 0 знаменатель /
отрицателен:
/@, ai) = ii2at(\~a1)-M2^^~-M2<0, 0<а,<1,
если (i2 < AM2, что действительно имеет место для пионов и
нуклонов1). В результате мнимая часть A8.28) в пределе е->-0+
равна нулю, причем этот результат, очевидно, справедлив и для
q2 < 0.
В рассматриваемом случае Fn(q2) можно аналитически про-
продолжить в нижнюю полуплоскость q2, в результате F^ (q2) ока-
оказывается аналитичной во всей комплексной плоскости, за исклю-
исключением, быть может, разреза вдоль вещественной положитель-
положительной оси. Положение разреза можно найти, вычислив максимум
/ по отношению к параметрам а,-. Максимизируя по осг и а3, по-
получаем
1 -а,
а2= аз — —о—
/ < q2 ("Ц^J + (A»i A - а,) - М2.	A8.29)
Правая часть в A8.29) может достигать максимального значе-
значения либо при а; = 0, либо при некотором 0 ¦< ai < 1. Прямым
вычислением можно убедиться в том, что при q2 > 2ц2 макси-
максимальное значение достигается на конце интервала: ос\ = 0. Для
физических значений масс я-мезона и нуклона ц2/М2 « 0,022
¦J ртметим, что соотношение ц2 < 4М2 представляет собой как раз усло-
условие стабильности я~-мезона по отношению к распаду на пр.

228	ДИСПЕРСИОННЫЕ СООТНОШЕНИЯ	1ГЛ. 18
и функция / все еще отрицательна при q2 = 2ц2. Поэтому поро-
пороговое значение q2, при котором начинается разрез, равно')
q2 = 4M2. Это значение отвечает точке
ai = 0, a2 = a3=l/2, q2 = 4M2	A8.30)
в пространстве параметров а,-, в которой / = 0. Пороговая энер-
энергия q2 = 4M2 представляет собой как раз то значение энергии,
при котором виртуальный времениподобный фотон, образован-
образованный при столкновении электрон-позитронной пары, может пе-
перейти в реальную нуклон-антинуклонную пару, которая затем
аннигилирует в пару я+ + п~. Указанный процесс также изобра-
изображается диаграммой рис. 18.2, на которой в этом случае необхо-
необходимо изменить направление пионных линий. Мы видим, таким
образом, что при обсуждении аналитических свойств вершинной
функции Fn(q2) необходимо одновременно рассматривать обра-
образование пар и рассеяние я-мезонов. В случае рассеяния я-мезо-
нов переданный импульс пространственноподобен, а в случае
образования пар — времениподобен.
Результат A8.30) означает, что сингулярности функций
Грина лежат при тех же значениях импульсов, при которых раз-
разрешены процессы поглощения. Установление подобной связи ме-
между сингулярностями и вероятностью абсорптивных процессов
является большим достижением дисперсионного подхода.
§ 127. Обобщение на случай произвольных диаграмм
и аналогия с электрическими цепями
Переходя от рассмотренного примера к произвольным диа-
диаграммам, полезно отделить существенные факторы от несуще-
несущественных и ввести стандартные обозначения для импульсов
и параметров интегрирования. Некоторые пункты ясны уже
сейчас.
1.	Произвольный матричный элемент имеет вид
3K*E<V,(<7.. .... qm),	A8.31)
где 0i — произведения внешних импульсов, спиновых матриц и
волновых функций, а Ft — зависящие от скалярных произведе-
произведений внешних импульсов, инвариантные функции, аналитической
структурой которых мы интересуемся.
2.	Числители в подынтегральных выражениях (например,
шнур в A8.20)) несущественны, поскольку после параметриза-
') Если ц2 > 2М2, то разрез начинается при q2 — 4ц2 ( 1 — ^ 2 ).
В этом случае, который мы обсудим позднее, разрез называется аномальным.

S 127]
ОБОБЩЕНИЕ НА СЛУЧАЙ ПРОИЗВОЛЬНЫХ ДИАГРАММ
229
ции подынтегрального выражения и вычисления интеграла по
внутренним импульсам они сводятся к полиномиальным множи-
множителям. Эти множители входят в F,- только в виде полиномов,
зависящих от скалярных произведений qiqt.
3. Проблема ультрафиолетовой расходимости здесь не суще-
существенна. Если для сходимости интеграла необходимо иметь не-
некоторую степень в знаменателе, этого всегда можно добиться,
продифференцировав нужное число раз по внешним импульсам
или массам внутренних линий. Такое дифференцирование не из-
изменяет аналитические свойства функции, определенной интегра-
интегралом. Например, дополнительная степень знаменателя в выра-
выражении A8.20) приведет к схо-
сходимости интеграла по д}р\, при
этом его сингулярности, кото-
которые определяются нулями /
в A8.27), не изменятся.
Удобно рассматривать внеш-
внешние импульсы всегда входящи-
входящими в диаграмму; обозначим их
через qu — qm. Будем рас-
рассматривать только связные ди-
диаграммы, для которых
s=0
Рис. 18.3. Произвольная фейнманов-
ская диаграмма, в которой внутрен-
внутренние линии обозначены своими им-
импульсами р., а внешние, входящие
в диаграмму линии — импульсами qs.
Каждой внутренней линии мы
приписываем импульс р,- и
массу /п/, как показано на
рис. 18.3. В каждой вершине выполняется закон сохранения им-
импульса
hsqs = о,
A8.32)
где
+ 1, если внутренняя линия / входит в вершину /,
ег/ = < —1, если внутренняя линия / выходит из вершины i,
О в остальных случаях.
Величина ёи аналогичным образом определяется для внешних
линий, которые, по определению, всегда входят в вершины.
Каждая диаграмма имеет определенное число k внутренних
петель или замкнутых контуров интегрирования. Обозначим пе-
переменные, по которым выполняется интегрирование в замкнутых
петлях, через 1Г. Хотя число независимых 1Г определено одно-
однозначно, конкретный выбор этих переменных можно осуществить

230
ДИСПЕРСИОННЫЕ СООТНОШЕНИЯ
[ГЛ. 18
разными способами. Например, на рис. 18.4 указаны два раз-
различных способа выбора замкнутых контуров для диаграммы
18.3. Выбрав определенным образом контуры и направления их
обхода, нужно определить переменные 1Г таким образом, чтобы
можно было выполнить интегрирование по импульсам. В при-
примере A8.20) мы выбрали переменные так, чтобы дополнить D
Рис. 18.4. Два возможных способа выбора контуров интегрирования.
до полного квадрата (см. A8.21) — A8.24)). Аналогично следует
выбирать переменные для каждой петли и в общем случае.
Положим
г=\
A8.33)
где
1,
— 1,
если /-я внутренняя линия входит в r-ю петлю
и векторы pi и 1г параллельны,
если /-я внутренняя линия входит в r-ю петлю
и векторы pj и 1Г антипараллельны,
О в остальных случаях.
Оптимальный выбор векторов kj можно сделать после введения
фейнмановских параметров. Опишем эту процедуру в общем
случае.
Для определения аналитической структуры скалярного
«форм-фактора» Ft в A8.31) для каждого данного графика до-
достаточно рассмотреть интеграл
dH, ... d4.

127|	ОБОБЩЕНИЕ НА СЛУЧАЙ ПРОИЗВОЛЬНЫХ ДИАГРАММ	231
1
.. . d4k \dax ... dan 6 (\ — ]Г аЛ X
о	\	/ /
, kJ l у 	jyY' A8-34)
T	ui	i,r,r'	J
Чтобы устранить в знаменателе A8.34) член, содержащий 1Г1Г<,
положим
~	=0	A8.35)
для каждой петли г=1, ..., ^. Диагонализовав эрмитову
матрицу
можно выполнить интегрирование по 1Г> при этом имеем
A8>36)
где
A=det||z||.
Импульсы k/ зависят от внешних импульсов gs и фейнмановских
параметров. Они определяются уравнениями A8.35) и законами
сохранения импульса A8.32) в каждой вершине, в которых р/
нужно заменить на kt:
„, Ев7,
/-1	s=l
Легко видеть также, что из определения еA и ц!г следует
A8.37)
Уравнениям A8.35) и A8.37) можно придать форму, кото-
которая обнаруживает их полную аналогию с уравнениями электри-
электрических цепей. Опустив в некоторых случаях знак минус, полу-
получаем
Z
ft, в петле
0,	A8.38а)
Z	(k, + q,) = O.	A8.386)
i
Z
ft., <?s входят в вершину i

232	Дисперсионные соотношения	(гл. is
Эти уравнения естественно интерпретировать, сопоставив фейн-
мановским диаграммам электрическую цепь, а импульсам— ток.
Тогда импульсы k; имеют смысл внутренних токов в цепи, а
qs — внешних токов, втекающих в рассматриваемый контур. Со-
Сопоставим далее параметрам ос/ сопротивления /-го участка цепи;
тогда уравнения A8.38) в точности совпадают с уравнениями
Кирхгоффа1). Уравнение A8.38а) означает, что полное «падение
напряжений» на замкнутом контуре равно нулю, а уравнение
A8.386) означает, что равна нулю алгебраическая сумма, «то-
«токов», входящих в каждую вершину2).
Поучительно снова рассмотреть выражения A8.34) — A8.36),
имея на этот раз в виду аналогию с электрическим током. Если
пренебречь постоянным членом — X /я;а/( выражение ? р]а}
в знаменателе A8.34) можно рассматривать как мощность, вы-
выделяющуюся в цепи. По закону сохранения энергии эта мощ-
мощность равна сумме мощностей, обусловленных внешними и внут-
внутренними источниками qs и 1Г:
Здесь kj — токи в цепи в отсутствие внутренних источников 1Г.
Эти токи определяются из законов Кирхгоффа.
Таким образом, токи и сопротивления сопоставляются им-
импульсам и фейнмановским параметрам. Чтобы дополнить сопо-
сопоставление, нужно найти физическую аналогию «падению напря-
напряжения». Поскольку «напряжение» есть потенциал и очевидным
образом связан с вершиной, естественно связать напряжение
с координатой вершины х^. Тогда первый закон Кирхгоффа
A8.38а) сводится к утверждению, что сумма разностей коорди-
координат вершин в любом замкнутом контуре диаграммы равна
нулю.
Смысл обсуждаемой аналогии раскрывается глубже при вы-
выяснении физического смысла закона Ома
На нашем языке этот закон имеет вид
Ьхц^/г^а,	A8.39)
где йц — импульс некоторой линии, а — соответствующий фейн-
мановский параметр, Ах^ — разность координат вершин, которые
соединяются этой линией. Уравнение A8.39) можно интерпрети-
1)	Параметры а/ действительны, поэтому рассматриваемая цепь не содер-
содержит емкости и индуктивности.
2)	При этом предполагается, что импульсы kj определены однозначно.

§ 1271	ОБОБЩЕНИЕ НА СЛУЧАЙ ПРОИЗВОЛЬНЫХ ДИАГРАММ	233
ровать как уравнение движения свободной частицы; это стано-
становится особенно ясным, если написать A8.39) отдельно для про-
пространственных и временной компонент:
A* = fta, A/ = koa, ~ = -L.	A8.40)
Поскольку параметр а всегда положителен, уравнения A8.40)
согласуются с нашими представлениями о причинности
Д//&о = а > 0.
Действительно, частица, распространяющаяся в направлении fe,
движется либо вперед, либо назад во времени в зависимости от
знака энергии k0. Аналогичную интерпретацию мы использовали
в теории феинмановских функций распространения в гл. 6. Тот
факт, что а ^ 0, есть прямое следствие наличия мнимой отрица-
отрицательной добавки ie к массе в фейнмановском пропагаторе. Что-
Чтобы наглядно продемонстрировать это обстоятельство, вернемся
назад к (8.12) и (8.18). Имеем
**.
Сформулируем окончательно правила соответствия, на которых
основывается наша аналогия с теорией электрических цепей:
координата <->¦ напряжение,
импульс <->ток,
. „ „ собственное время
феинмановскии параметр а =	¦*->
•*-»¦ сопротивление > 0,
уравнения движения свободной частицы •*-> законы Ома,
причем условие положительности «сопротивления» а связано с
принципом причинности в распространении частиц.
Указанная аналогия оказывается весьма полезной, поскольку
при изучении феинмановских диаграмм мы можем пользоваться
наглядной картиной и теоремами теории цепей. Рассмотрим,
например, вершинную функцию с тремя внешними линиями

234
ДИСПЕРСИОННЫЕ СООТНОШЕНИЯ
[ГЛ. 18
и произвольным числом внутренних линий. Такой черный ящик
с сопротивлениями всегда можно заменить эквивалентной цепью
с сосредоточенными сопротивлениями [84] (см. рис. 18.5). Мощ-
Мощность Р, выделяемая в такой цепи, равна
р = ?1<?2 + l2q\ + ?3<7з> li>Q>	A8.42)
где эквивалентные сопротивления ?,- есть неотрицательные функ-
функции исходных сопротивлений а,-. При этом выражение A8.36)
может быть записано в виде
A8.43)
,2
2_2
1-9k
где явно выписана мнимая добавка /е. Уравнение A8.43) пред-
представляет обобщение результата, найденного для диаграммы ни-
нижайшего порядка (рис. 18.2), на случай произвольного порядка
Рис 18.5 Эквивалентная сосредоточенная цепь для вершины с тремя внеш-
внешними линиями
теории возмущений. Поскольку ?/ неотрицательны, функция
I (q], q\, <7з) как функция любого из трех внешних импульсов
аналитична в верхней полуплоскости q\, когда остальные два
ее аргумента положительны и вещественны. Можно показать,
что / (<7р ц\, <7з) при одновременном продолжении всех трех
своих аргументов в верхнюю полуплоскость по-прежнему остает-
остается аналитичной.
На первый взгляд кажется, что обсуждавшийся в этом параг-
параграфе метод исследования аналитических свойств никак не свя-
связан с условием причинности, использованном при выводе соот-
соотношений Крамерса — Кронига. Тем не менее именно свойство
причинности в уравнении A8.40), которое выражено в форме
а ^ 0, обеспечивает выполнение неравенств в A8.42), что ве-
ведет в свою очередь к установлению требуемых аналитических
Свойств.

§ 128]	ПОРОГОВЫЕ ОСОБЕННОСТИ ФУНКЦИИ РАСПРОСТРАНЕНИЯ	235
§ 128. Пороговые особенности функции распространения
Выведем теперь необходимые условия для появления осо-
особенностей произвольных диаграмм. Вначале рассмотрим функ-
функции распространения. Снова будем использовать отмеченную в
предыдущем параграфе аналогию с теорией электрических це-
цепей. Эта аналогия поможет нам разобраться с множеством внут-
внутренних линий произвольной диаграммы и найти положение осо-
особенностей форм-факторов Ft из рассмотрения знаменателей
J=T.(k*-m*)al	A8.44)
в выражениях вида A8.36) или A8.43).
Аналитические свойства пропагатора частицы со спином О,
а также частиц с ненулевым спином, выражаются представле-
представлением Челлена — Лемана. Поучительно, однако, заново устано-
установить положение сингулярностей пропагатора, используя нагляд-
наглядную картину электрических цепей, поскольку аналогичная тех-
техника может быть затем применена при рассмотрении вершин-
вершинных функций и амплитуд рассеяния. Для диаграммы собствен-
собственной энергии имеется только один внешний импульс, при этом
аналитические свойства форм-факторов Z7,- совпадают с аналити-
аналитическими свойствами интеграла в A8.36)
(q2)=\
A8.45)
Величина t,q2 в знаменателе A8.45) представляет мощность, вы-
выделяемую в блоке с двумя внешними линиями, отвечающем
графику собственной энергии, поэтому эквивалентное сосредото-
сосредоточенное сопротивление не может быть отрицательным. Используя
те же аргументы, что и при рассмотрении простейшей вершин-
вершинной диаграммы, мы заключаем ') из A8.45), что:
1)	/ — аналитическая функция в верхней полуплоскости q2;
2)	/ — вещественная функция для вещественных отрицатель-
отрицательных q2;
3)	в силу принципа отражения Шварца / также аналитична
и в нижней полуплоскости, обладая, самое большее, точками,
ветвления при q2 ^ 0.
Чтобы найти начало разреза q\, найдем наименьшее значе-
значение q2, для которого знаменатель / в A8.45) обращается в нуль.
Будем увеличивать q2, начиная от нуля, до такого значения q2,
при котором имеется хотя бы одна точка (а°г ..., а°\ в п-мер-
') Отметим, что Д > 0 для aj > 0, если 2ctj > 0 (см. задачу 1). При об-'
суждении аналитических свойств I(q2) величина А2 несущественна.

236
ДИСПЕРСИОННЫЕ СООТНОШЕНИЯ
(ГЛ. 18
ном а-пространстве, для которой
/(<7f, а?,ао	ао) = О.	A8.46)
Поскольку / удовлетворяет масштабному закону
J(Xaj) = M(a,),	A8.47)
эту точку всегда можно выбрать так, чтобы удовлетворить усло-
условию 2 <х,= 1. Справедливость A8.47) следует либо из A8.44),
либо из того факта, что мощность, выделяемая в цепи, линейно
связана с величинами всех сопротивлений цепи. Поэтому мы мо-
можем игнорировать 6-функцию в A8.45) и рассматривать / как
функцию п неотрицательных независимых параметров а,-.
*J
0
> =qf~A
Рис. 18.6. Обращение в нуль «действия» У (а) в точке пороговой сингуляр-
сингулярности q2= (ff. В первом случае У имеет максимум при а;- = cty, во втором
случае У = 0 на границе области интегрирования.
Хотя / = 0 при q2 = q2t и a; = aj, функция / ввиду непре-
непрерывности по переменной q2 не может быть положительной в ос-
остальной области интегрирования по а/:
,.., а°)<0 для всех
A8.48)
Значения a^a1^, при которых / имеет максимум, лежат либо
внутри области интегрирования, либо на ее границе. Другими
словами, для каждого а/ либо
?	«/	О
да,
либо
V"?
= 0, если а» ф О,
= 0.
A8.49а)
A8.496)

250	ДИСПЕРСИОННЫЕ СООТНОШЕНИЯ	[ГЛ. 18
Как отмечалось выше, необходимое условие для возникнове-
возникновения аномального порога имеет вид
Ц2 > X tn2,
i
где \i — масса внешней частицы, /л,- — массы внутренних частиц.
В теории сильных взаимодействий форм-факторы я- и /(-мезонов
и нуклонов не содержат аномальных порогов, хотя эти пороги
существуют для Л-, Е- и Н-гиперонов. В физической области
времениподобных переданных импульсов аномальные пороги в
форм-факторах стабильных частиц отсутствуют, и особенности
определяются только одномерными приведенными диаграм-
диаграммами. Следует подчеркнуть, что вопрос о существовании обсуж-
обсуждаемых порогов тесно связан с величинами масс и правилами
отбора в вершине взаимодействия. Тем самым этот вопрос
окончательно нельзя выяснить, не привлекая дополнительных
физических аргументов.
§ 131. Дисперсионные соотношения для вершинной функции
Поскольку во всех порядках по сильному взаимодействию
единственной сингулярностью электромагнитного форм-фактора
Fn(q2) является разрез от q2 = 4ц2 до q2=oo, мы можем вы-
выписать следующее дисперсионное соотношение:
где q2 — произвольная точка в комплексной ^-плоскости, лежа-
лежащая внутри контура С, указанного на рис. 18.18. Поскольку
функция Fn(q2) действительна при q2 <. 4ц2, то используя
принцип отражения Шварца, можно выразить скачок на раз-
разрезе через мнимую часть Fjx{q2). Когда q2 стремится к действи-
действительной оси, оставаясь при этом в верхней полуплоскости,
lim Fx (<72 + ie) = Re Fn (q2) + i Im Fn (q\
e->0+
откуда
lim [Fn (<72 + ie) - Fn (q2 - ie)] = 2/ Im Fn (q2). A8.69)
e-»o+
Разделим в дисперсионном интеграле вклады от интегрирования
по разрезу и по бесконечно большому кругу Со
,. м=л» *. «>+,, - i ш I «ум? +
A8.70)

238	ДИСПЕРСИОННЫЕ СООТНОШЕНИЯ	[ГЛ. 18
где б/г — вариации переменных интегрирования во внутренних
петлях. Знаковые множители г\,г определены в A8.33). Подста-
Подставив A8.51) в A8.50), получим, с учетом законов Кирхгоффа,
требуемое сокращение. В результате
б/ = ? (?2 _ т2) бау = 0 при ^. = 0@.	A8.52)
Таким образом, для каждой линии редуцированного графика
k2 = т2,. При этом необходимые условия существования порого-
пороговых особенностей ф== qj функции I (q2) можно сформулировать
следующим образом.
1.	Диаграмма должна быть представлена в виде блоков,
внутри которых все а/ = 0 и которые соединены между собой
линиями, изображающими частицы на массовой поверхности,
для которых Щ = щ2,.
2.	Уравнения Кирхгоффа A8.38) должны быть выполнены
для положительных значений «сопротивлений» а,-, что отвечает
правильному причинному поведению теории.
Поясним физический смысл условия 1. Сингулярности ам-
амплитуды отвечают случаю, когда взаимодействие не ограничено
в пространстве и (или) во времени. Обычно пространственно-
временной интервал, на котором разыгрываются события, огра-
ограничен принципом неопределенности. Однако может возникнуть
ситуация, в которой промежуточные частицы становятся «ре-
«реальными», т. е. удовлетворяют кинематическим соотношениям
для свободных частиц. При этом взаимодействие неограниченно
растет, а соответствующая амплитуда имеет особенность. Усло-
Условие же 2 положительности сопротивлений гарантирует тот факт,
что реальные промежуточные частицы распространяются в со-
соответствии с принципом причинности; при этом законы Кирхгоф-
Кирхгоффа выражают геометрические и кинематические ограничения,
которым подчинено распространение частиц.
Сформулированные результаты оказываются весьма полез-
полезными, если дополнить их какими-либо диаграммными или ин-
интуитивными критериями для нахождения реальных промежуточ-
промежуточных состояний. Эта задача особенно просто решается для функ-
функций распространения. Для времениподобного q2 выберем си-
систему координат, в которой дц = (q, 0, 0, 0). Поскольку источник
тока имеет только временную компоненту, у внутренних
токов k/, удовлетворяющих законам Кирхгоффа, отлич-
отличны от нуля также только временные компоненты. Для
возникновения сингулярностей необходимо, чтобы диаграммы
содержали реальные промежуточные состояния. Примеры
таких диаграмм изображены на рис. 18.8. Законы Кирх-
Кирхгоффа позволяют приписать каждой вершине редуцированного

§ 129]
ОСОБЕННОСТИ ПРОИЗВОЛЬНЫХ ДИАГРАММ
графика свое «время». При этом в силу «причинности» закона
Ома (все а,- положительны) ток течет в одном и том же направ-
направлении от /, до U и затем от t2 до t3- Величина тока равна массе
Рис. 18.8 Некоторые редуцированные графики, дающие вклад в функцию
распространения
промежуточного состояния, поэтому сингулярности возникают
при тех значениях, для которых
где сумма берется по всем частицам в промежуточном состоя-
состоянии. При этом пороговое значение qt определяется массой лег-
легчайшего промежуточного состояния, в которое могут перейти
внешние частицы. В гл. 16 мы получили этот результат, исходя
из более общих аргументов1).
§ 129. Особенности произвольных диаграмм
и правила Ландау
Следует ожидать, что при переходе от графиков, дающих
вклад в функцию Грина, к произвольным фейнмановским диаг-
диаграммам выражения A8.52), определяющие положение особен-
особенностей диаграмм, не изменятся. Ниже мы покажем, что это
действительно так. Условия A8.52) не только имеют простой
и наглядный смысл, но и были выведены, исходя из весьма об-
общего интегрального представления A8.36), справедливого и для
более сложных диаграмм:
I(qu
<7m) =
da'
[?(
*?-
n-2k
A8.53)
') В действительности в гл. 16 мы продвинулись немного дальше и по-
показали, что если при вычислении электронного пропагатора S'p пренебречь
калибровочными членами (что всегда можно сделать, если мы интересуемся
только S-матричными элементами), то пропагатор удовлетворяет спектраль-
спектральному представлению.

240	ДИСПЕРСИОННЫЕ СООТНОШЕНИЯ	1ГЛ. 18
где импульсы k,- линейно зависят от внешних импульсов qs, см.
A8.3?). Знаменатель / в A8.53) можно записать в виде
/ = I (Щ - т)) а, + /е = Д | iiflfli - I m)a. + is, A8.54)
где коэффициенты ?,-,- снова выражаются через параметры а/.
Уравнения A8.53) и A8.54) известны под названием интеграль-
интегрального представления Намбу [85]; частными случаями этого пред-
представления являются выражения A8.45) для функции Грина и
A8.43) для вершинной функции. Поскольку представление Нам-
Намбу справедливо для произвольной фейнмановской амплитуды,
рассматриваемой как функции комплексных переменных </;9/.
мы можем теперь, исходя из этого представления, в общем слу-
случае сформулировать необходимые условия появления сингуляр-
ностей в любом фейнмановском графике.
1.	Каждой сингулярности отвечает «редуцированный» гра-
график, полученный стягиванием в точку некоторых внутренних
линий.
2.	Промежуточные частицы в редуцированном графике долж-
должны быть реальными:
Щ = т),	A8.55)
где kj — кирхгофовские импульсы, которые, наряду с фейнманов-
скими параметрами а/, сопоставляются каждой внутренней ли-
линии. Эти импульсы связаны соотношениями Кирхгоффа A8.35)
и A8.37).
Сформулированные утверждения называются условиями Лан-
Ландау [86]. Они позволяют свести задачу нахождения особенностей
произвольных фейнмановских диаграмм к простой алгебраиче-
алгебраической задаче. Если мы рассматриваем особенности по перемен-
переменным <7<<7/ на первом «физическом» листе, то справедливо допол-
дополнительное ограничение, вытекающее из причинности:
а^О, Im<X/ = 0 для всех /.	A8.56)
В том случае, когда функция / аналитически продолжается в
область комплексных значений qiq/, доходя при этом до далеких
нефизических листов, уравнения Ландау по-прежнему сохра-
сохраняют свой смысл при условии, что параметры а/ могут прини-
принимать комплексные значения.
Представление Намбу оказывается, однако, не столь удоб-
удобным, когда оно применяется для рассмотрения диаграмм с более
чем тремя внешними концами, например для диаграмм, описы-
описывающих рассеяние. Причина этого заключается в том, что в
этом случае число различных комбинаций qiq,- превышает число
независимых инвариантов, которые можно составить из импуль-

§ 129]	ОСОБЕННОСТИ ПРОИЗВОЛЬНЫХ ДИАГРАММ	241
сов. Тем не менее ряд предсказаний (см. § 132) может быть
получен и в этом случае. Отметим, что формулы A8.53) и
A8.54) позволяют выполнить аналитическое продолжение ам-
амплитуды из области вещественных значений инвариантов неза-
независимо от того, являются ли эти значения физическими или нет.
Поэтому все амплитуды, полученные с помощью правила под-
подстановки, например, амплитуды комптоновского рассеяния, ан-
аннигиляции пары в два фотона и образования пары фотонами,
описываются одной и той же аналитической функцией, но при
разных предельных значениях своих аргументов.
Вернемся теперь к нашей основной задаче и выведем необхо-
необходимые условия появления сингулярностей функции в A8.53).
Прежде всего устраним ограничения, налагаемые б-функцией
на область изменения параметров а. Для этого используем
масштабные свойства A8.47).Выполним в A8.34) и A8.36) од-
однородное масштабное преобразование
а,-
Перепишем далее A8.53) в виде
оо doti ... dan
._j_j±?i)
Очевидно, что / в A8.34) не зависит от X, поэтому б-функцию
можно устранить с помощью следующего приема:
dai ••• dart(Za/)exP(~Zaf) ,,„„„,
Выполним вначале интегрирование по ai при фиксированных
значениях а2, ..., ап, причем инварианты qtqj будем считать
чещественными:
?7", (а2, .. ., а„; qtqt) —
= \ 	±1—1	\/ > = \ dax Tx (а, ... а„; qt4l). A8.58)
Очевидно, функция ?Г2 определена до тех пор, пока при неко-
некотором ai величина / в знаменателе не станет равна нулю, т. е.
пока функция W\ не сингулярна. Однако даже в этом случае
особенность в подынтегральном выражении можно обойти, сме-
сместив контур интегрирования в комплексную плоскость а\, как
показано на рис. 18.9. В результате функция 5^2 не будет иметь

242
ДИСПЕРСИОННЫЕ СООТНОШЕНИЯ
[ГЛ. 18
особенностей, В этом случае малые изменения импульсов qs или
параметров ct2, ..-, аи приведут к малому изменению положе-
положения величин сингулярностеи в а\ плоскости, что есть следствие
существования самого интеграла и его производных. Функция
3~ч становится сингулярной лишь в том случае, когда особен-
особенность <х\ находится в граничной точке <х\ = 0, либо когда две
Re a-i
Контур интегрирования
Рис. 18.9 Контур при интегриро-
интегрировании по cd Деформация контура
позволяет избежать особенности
Пира особенностей
I
Re а,
Рис 18.10. Пара особенностей, зажи-
зажимающих контур интегрирования
в точке а
сингулярности <7"i совпадают и зажимают контур интегрирова-
интегрирования, как показано на рис. 18.10. Поэтому необходимые условия
для появления сингулярностеи в 0~2 имеют вид
/(а?, а2, .... ап; qtq,) = O,	A8.59a)
причем либо
а? = 0, либо -г-	= 0,
A8.596)
1 1
поскольку в последнем случае / имеет двойной нуль при a, =aj.
Мы получили, таким образом, правила Ландау; в действитель-
действительности выражение A8.59) имеет тот же вид, что и A8.49).
Перейдем далее к интегрированию по а2".
A8.60)
Снова функция ?ГЪ будет сингулярной, если ?7~2 имеет двойную
особенность либо если ее сингулярность находится в граничной
точке сиг = 0. В первом случае
/(о?, < <х3	ап; qtqt) = O	A8.61а)
и
dJ
= 0.
A8,616)

129]
ОСОБЕННОСТИ ПРОИЗВОЛЬНЫХ ДИАГРАММ
243
Уравнение A8.616) включает также вариацию по а?, по-
поскольку в силу A8.59а) а? определяется через а2 и остальные
фейнмановские параметры. С учетом A8.596) получаем
dJ
да2
da2
Эту процедуру можно по индукции продолжить до тех пор, пока
мы не исчерпаем все а-интегрирования. В результате получаем
требуемые условия
либо
Vе?
Мы видим, таким образом, что полученные ранее уравнения
A8.52) представляют в точности уравнения Ландау. Отметим,
Re a
Рис. 18.11 Траектории нулей функции /. Начальные точки отвечают веще-
вещественным значениям qtq,, конечные — комплексным.
что в том случае, когда переменные <7<<7/ принимают веществен-
вещественные значения, не возникает необходимость деформации конту-
контуров интегрирования по переменным а, поскольку мнимая до-
добавка ie предохраняет от появления любого нуля в функции /,
лежащего на расстоянии ближе чем О(е) от вещественной оси.
Поэтому для возникающих при этом сингулярностей справед-
справедливо условие а/ ^ 0, следующее из принципа причинности. Ксин-
гулярностям такого вида относится большинство случаев, пред-
представляющих физический интерес.
Если же переменные qiq, принимают комплексные значения,
то нули / могут пересекать контуры интегрирования, при этом

244	ДИСПЕРСИОННЫЕ СООТНОШЕНИЯ	[ГЛ. 18
последние необходимо деформировать так, как показано на
рис. 18.11. Сингулярность интеграла снова появляется лишь
тогда, когда сингулярности подынтегрального выражения зажи-
зажимают контур интегрирования либо совпадают с граничной точ-
точкой щ = 0. Таким образом, правила Ландау применимы и в
этом случае при условии, однако, что область определения па-
параметров а включает комплексные значения1).
§ 130. Аналитическая структура вершинных диаграмм;
аномальные пороги
Применим теперь уравнения Ландау для нахождения осо-
особенностей вершинных графиков, аналитическая структура кото-
которых может быть гораздо сложнее, чем у функций Грина. Вер-
Вернемся к рассмотренному ранее примеру с электромагнитным
форм-фактором я-мезона. Используя интегральное представле-
представление A8.43), мы заключаем, что функция F Ля2) во всех поряд-
порядках теории возмущений аналитична в верхней полуплоскости q2.
Более того, следует ожидать, что F:i(q2) действительна при
q2 < 0 во всех порядках по сильному взаимодействию, поскольку
простые физические соображения, приведенные в § 126 для тре-
треугольной диаграммы, должны быть справедливы и в более об-
общем случае. Для строгого доказательства достаточно заметить,
что при q^ = 0 вершинная диаграмма кинематически эквива-
эквивалентна одночастичной функции Грина. Применяя результаты
§ 128, мы заключаем, что поскольку |i < ?/гаг, где 2] ть —
i	i
масса любого промежуточного состояния, связанного с я-мезо-
ном, знаменатель / в интегральном представлении любой диа-
диаграммы отрицателен на массовой поверхности q22 = q2— ц2. От-
Отсюда, в частности, следует, что знаменатель J(q2) в фейнманов-
ском интеграле, отвечающем любой диаграмме, которая вносит
вклад в Fn, отрицательно определен при q2 = 0 и, тем самым,
при q2 <. 0. Поэтому с помощью принципа отражения Шварца
можно определить Fn(q2) в нижней полуплоскости. Таким обра-
образом, мы заключаем, что единственными сингулярностями Fn(q2)
являются точки ветвления на положительной вещественной по-
полуоси.
Чтобы найти начало разреза и остальные точки ветвления,
следует рассмотреть все редуцированные графики, дающие
вклад в сингулярную часть Fn(q2). Редуцированный график для
') Уравнения Ландау, являясь по своей структуре алгебраическими урав-
уравнениями, имеют лишь конечное число решений. Поэтому они не приводят к
появлению естественной границы области аналитичности при аналитическом
продолжении по переменным qiq/ на другие листы. Сингулярности, отвечаю-
отвечающие случаю а = оо, обсуждаются в статье [87].

130]
АНАЛИТИЧЕСКАЯ СТРУКТУРА ВЕРШИННЫХ ДИАГРАММ
245
треугольной диаграммы изображен на рис. 18.12; он приводит
к особенности при q1 = 4М2. При этом мы снова можем дать
наглядную физическую картину рассматриваемого процесса в
координатном пространстве. Времениподобный фотон с <7ц =
= (<7, 0, 0, 0) распадается при t = t\ на нуклон-антинуклонную
пару, которая через некоторое время при t = t2 переходит в два
ч
\
N
H
/
N
(x,
3
7t~
X
Phc. 18.12. Редуцированная диаграмма для пионной электромагнитной вер-
вершины и соответствующая пространственно-временная картина.
реальных пиона. Ясно, что указанный распад происходит только
при <7о ]>2Л1
Существуют, однако, и другие редуцированные графики, от-
отвечающие более сложным диаграммам, которые понижают зна-
значение порога от q2t = 4M2 до ^ = 4ц2. Эти графики, например,
изображенные на рис. 18.13, включают перерассеяние пионов
.--«Г
X
Рис. 18.13. Редуцированная диаграмма высшего порядка, приводящая к по-
пороговой особенности в точке <$ = 4ц .
в конечном состоянии. Тогда
акции
е~ + е+
'¦ = 4ц2 является порогом для ре-
в. которой можно измерять ^л (q2) при q2 > 0. Для простран-
ственноподобных значений q2 < 0 форм-фактор Fn(q2) опреде-
определяется из упругого электрон-пионного рассеяния. Между указан-
указанными двумя областями лежит нефизический интервал 0 ^ q2 <g;

246
ДИСПЕРСИОННЫЕ СООТНОШЕНИЯ
[ГЛ. 18
Перейдем к рассмотрению редуцированных диаграмм в нефи-
нефизической области. Сделаем импульсы внешних пионов <?2 и <?з
комплексными и посмотрим, какие редуцированные графики при
этом появляются. Для удобства выберем координатную систему,
в которой компоненты импульсов равны
q = (q, О, 0, 0),
Яг = { - -f •
9з=(~т- -1л/^2-^' °. °)-
A8.63)
Законы Кирхгоффа означают, что все внутренние «токи» или
импульсы имеют вид
k = (k0, iku 0, 0),	A8.64)
где kQ и k\ вещественны. Другими словами, вторые и третьи
компоненты внутренних токов равны нулю, если равны нулю эти
компоненты у внешних токов. Далее,
если компоненты внешних токов чисто
мнимы, таковыми являются и первые
компоненты всех внутренних токов.
Поскольку пространственные компо-
компоненты импульсов в A8.63) и A8.64)
чисто мнимы, можно с помощью оче-
очевидной замены переменных перейти к
вещественным векторам с евклидовой
метрикой. Условия Ландау, согласно
которым сингулярности произвольной
\ диаграммы появляются при k2. = tri2,,
Рис. 18.14. Двумерная ре- применимы в этом случае и в силу ев-
дуцнрованная диаграмма. клидовости пространства векторов
имеют простую геометрическую интер-
интерпретацию. Сингулярности возникают только в том случае, когда
можно нарисовать редуцированный график с двумерными век-
векторами, отвечающими внутренним частицам на массовой поверх-
поверхности и удовлетворяющими законам сохранения импульса в каж-
каждой вершине, другими словами, когда существует двумерный
редуцированный график. Рассмотрим, например, треугольную
диаграмму и предположим, что для нее возможен двумерный
редуцированный график, изображенный на рис. 18.14. Угол 6
определяется из сохранения импульса и условия «реальности»
промежуточных частиц:
qj = ц2 = ^ _ k^2 ==к2 + к2_ 2kxk2 cos (я - в) = 2М2 A + cos 6),
A8.65)

130]
АНАЛИТИЧЕСКАЯ СТРУКТУРА ВЕРШИННЫХ ДИАГРАММ
•247
Для того чтобы замкнуть такой треугольник, необходимо вы-
выполнение условия 6 < я/2 или (х2 > 2М2. Поскольку в случае
я-мезонов и нуклонов эти условия не выполняются1), указан-
указанный редуцированный график не дает вклада в сингулярности
Fn{q2). Отметим, что в общем случае углы замкнутых много-
многоугольников, отвечающих двумерным редуцированным диаграм-
диаграммам, определяются законами сохранения импульса в каждой
вершине, а длины сторон опреде-
определяются разностью напряжений
(или током, умноженным на со-
сопротивление) вершин, которые
эти стороны соединяют.
Рассмотрим теперь произволь-
произвольную диаграмму, отвечающую
высшим порядкам по взаимодей-
взаимодействию. Чтобы найти сингулярно-
сингулярности, обусловленные двумерными
редуцированными графиками
(<72^4ц2), заметим, что любой
такой график должен целиком со-
содержаться в треугольнике, вер-
вершины которого х\, х2 и х3 равны
координатам точек, в которых
взаимодействуют внешние части-
цы. Стороны этого треугольника
не должны иметь изгибов, други-
ми словами, ни одна из внутрен-
внутренних линий не должна проходить через сторону треугольника,
как показано на рис. 18.15. В противном случае эта линия вый-
выйдет за пределы треугольника, поскольку не существует такого
внешнего импульса, после встречи с которым внутренняя линия
могла бы повернуть назад к вершине и поглотиться. Построив
такой треугольник, мы замечаем, что по крайней мере в одной
из его вершин угол 6 должен быть острым. В этой вершине
внешний пион диссоциирует, образуя ливень частиц с импуль-
импульсами ki и массами mi, причем
ваНной стороной (невозможный
случай)
= Z
i
A8.64)
Таким образом, сингулярности (если она существует) отвечает
связанное с я-мезоном состояние, для которого
') См. A8.29) и примечание на стр. 227,

248
ДИСПЕРСИОННЫЕ СООТНОШЕНИЯ
[ГЛ. 18
Сташрорд
Такое состояние, однако невозможно, если мы не рассматри-
рассматриваем слабые и электромагнитные взаимодействия. Отметим да-
далее, что при учете только сильных взаимодействий ни один
одномерный редуцированный график не вносит вклад в Fn(q2)
в области 0 ^ q2 <. 4ц2, поскольку легчайшим состоянием, со-
составленным из сильно взаимодействующих частиц и связанным
с я-мезоном, является состояние 2л. Поэтому мы заключаем,
что Fn(q2) аналитична во всей
плоскости q2 с разрезом, который
начинается от порога q2 = 4[i2
и отвечает приведенным графи-
графикам, содержащим промежуточное
состояние 2я.
Сингулярности, связанные с
двумерными приведенными диа-
диаграммами, называются аномаль-
аномальными порогами». Хотя эти сингу-
сингулярности отсутствуют в рассмат-
рассматриваемом случае, они интересны
сами по себе. Аномальные осо-
особенности могут возникать в форм-
факторах слабо связанных со-
составных частиц, удовлетворяю-
удовлетворяющих условию A8.65), и также в
форм-факторах нестабильных ча-
частиц, для которых это условие
заведомо выполняется. Например,
при учете слабых взаимодействий
в Fn(q2) появляется аномальный
разрез, причем он находится в
физической области q2 < 0. Этот
разрез отвечает редуцированному графику на рис. 18.16. При
этом возникает следующая картина: пион, образованный в Берк-
Беркли с импульсом q/2, распадается на покоящийся ц,-мезон и ней-
нейтрино с импульсом q/2, которое летит в Станфорд, где оно рас-
рассеивается на -у-кванте и возвращается в Беркли с импульсом
—q/2, после чего, захватив ц-мезон, снова превращается в пион.
Импульс q, при котором Fn становится сингулярным, равен
Рис. 18.16. Пример редуцирован-
редуцированной диаграммы, которая имеет ано-
аномальный порог в физической об-
области, отвечающий нестабильной
частице
причем
т2 + \i2 — 2тЕл = О,
где т — масса ц-мезона. Отсюда получаем
т
A8.66)

130]
АНАЛИТИЧЕСКАЯ СТРУКТУРА ВЕРШИННЫХ ДИАГРАММ
249
Эта сингулярность, разумеется, весьма слабая, но в принципе
она существует.
При переходе от нестабильных частиц к стабильным ано-
аномальный порог смещается из области пространственно-подобных
q2 в область времениподобных. В результате для систем, по-
подобных дейтрону, должен существовать двумерный редуциро-
редуцированный график в евклидовой области. Два таких графика
J?'
а)
Рис. 18.17. Редуцированные диаграммы, приводящие к аномальному порогу
в дейтронном форм-факторе:
^
-Ж(а); cos б.
\\ - М2 - (М 4
2ЛГ (Af + ц)
¦'-%<»
указаны на рис. 18.17. Для графика рис. 18.17, а угол 8 весьма
мал, что связано с малостью энергии связи дейтрона е:
cos 8 « 1	g"
BА1 - еJ - 2Мг
2М2
м ¦
Из этого рисунка заключаем, что сингулярность находится при
<7 = 2Msine<v2Me«4VMe-	A8.67)
В пределе нулевой связи дейтрона q-*-0. Таким образом, форм-
фактор дейтрона становится сингулярным при времениподобных
переданных импульсах, равных по порядку величины среднему
импульсу k в дейтроне k2/2M ~ е.

250	ДИСПЕРСИОННЫЕ СООТНОШЕНИЯ	[ГЛ. 18
Как отмечалось выше, необходимое условие для возникнове-
возникновения аномального порога имеет вид
ц2 > X /и2,
где \i — масса внешней частицы, mi— массы внутренних частиц.
В теории сильных взаимодействий форм-факторы я- и /(-мезонов
и нуклонов не содержат аномальных порогов, хотя эти пороги
существуют для Л-, Е- и Н-гиперонов. В физической области
времениподобных переданных импульсов аномальные пороги в
форм-факторах стабильных частиц отсутствуют, и особенности
определяются только одномерными приведенными диаграм-
диаграммами. Следует подчеркнуть, что вопрос о существовании обсуж-
обсуждаемых порогов тесно связан с величинами масс и правилами
отбора в вершине взаимодействия. Тем самым этот вопрос
окончательно нельзя выяснить, не привлекая дополнительных
физических аргументов.
§ 131. Дисперсионные соотношения для вершинной функции
Поскольку во всех порядках по сильному взаимодействию
единственной сингулярностью электромагнитного форм-фактора
Fn(q2) является разрез от q2 = 4ц2 до q2 = °о, мы можем вы-
выписать следующее дисперсионное соотношение:
A8.68)
q — q2
где ^ — произвольная точка в комплексной ^-плоскости, лежа-
лежащая внутри контура С, указанного на рис. 18.18. Поскольку
функция Fn(q2) действительна при q2 <. 4ц,2, то используя
принцип отражения Шварца, можно выразить скачок на раз-
разрезе через мнимую часть Fn(q2). Когда q2 стремится к действи-
действительной оси, оставаясь при этом в верхней полуплоскости,
lim Fx (q2 + is) = Re Fn (q2) + i Im Fa (q2),
e->0+
откуда
lim [Fn (q2 + /e) - Fn (q* - is)] = 2i Im Fn (q2). A8.69)
e-»o+
Разделим в дисперсионном интеграле вклады от интегрирования
по разрезу и по бесконечно большому кругу Со
F. („ = Ы Р. V + /., - ^ «ш ] 'У^? + С
A8.70)

131]
ДИСПЕРСИОННЫЕ СООТНОШЕНИЯ
251
В том случае, когда Fn(q2) на бесконечности стремится к нулю,
мы получаем дисперсионное соотношение без вычитаний
F (Л = _L
Im
&д'г
'	9
A8.71)
Поскольку, однако, в теории возмущений Fn(q2) на бесконеч-
бесконечности к нулю не стремится, то, проявляя известную осторож-
осторожность, следует записать дисперсионное соотношение с одним
\
Рис. 18.18. Контур в комплексной q' -плоскости в дисперсионном интеграле
для Fn (q1).
вычитанием. Записывая его для функции Fn{q2)/q2, снова полу-
получаем Сх, = 0. Повторяя выкладки, которые мы проделали при
выводе формулы A8.9), находим окончательно
dq'2 Im Ря (д'2)
A8.72)
4JJL2
Уравнения A8.71) и A8.72) аналогичны соотношениям Кра-
мерса — Кронига. В то время как последние с учетом требова-
требования унитарности — оптической теоремы — связывают между со-
собой экспериментально наблюдаемые величины в A8.12), смысл
дисперсионных соотношений A8.71) и A8 72) заключается в
том, что с помощью этих формул задача вычисления форм-фак-
форм-фактора /гп(?2) сводится к вычислению его скачка для положи-
положительных q2 > 4fjA Практическая ценность этого результата

252	ДИСПЕРСИОННЫЕ СООТНОШЕНИЯ	[ГЛ. 18
заключается в следующем. Было показано, что для возникнове-
возникновения сингулярности в Fn необходимо существование редуцирован-
редуцированного графика, в котором виртуальный времениподобный фотон
связан с реальными промежуточными состояниями. Поскольку
пионный форм-фактор не содержит аномальных порогов, все
редуцированные графики для него одномерны. Таким образом,
вычисление \т Fn(q2) сводится к вычислению амплитуды пере-
перехода фотона в реальное состояние |п> и вычислению амплитуды
последующего перехода |#> в пару п+п~. Соответствующее ана-
аналитическое выражение, в точности аналогичное формуле A8.16),
выражающей скачок функции Грина на разрезе, мы подробно
обсудим позже при рассмотрении конкретных расчетов в рамках
дисперсионного метода. Здесь же отметим только, что в
спектральную сумму в области
BцJ «^ q2 s=r DцJ вносят вклад
только двухпионные состояния,
^	поскольку трехпионные состоя-
^^^	ния не могут перейти в пару
пионов в силу законов сохра-
сохранения.
Практически дисперсионные
Рис. 18.19. Редуцированная диа- расчеты всегда основываются на
грамма лля^лектромагнитнои вер- ?риближешш> в котором учиты.
вается вклад простейших проме-
промежуточных состояний. Например, при использовании диспер-
дисперсионных соотношений A8.72) с одним вычитанием для вычисле-
вычисления Fn(q2) при малых q2 можно в первом приближении учесть
только состояние 2л, масса которого меньше всех других состоя-
состояний, поскольку, из-за подынтегрального множителя l/q'4 основ-
основной вклад в дисперсионный интеграл вносит пороговая область.
В этом приближении уравнение A8.72) устанавливает связь
между электромагнитным форм-фактором пиона и амплитудой
я—я-рассеяния, которая может быть проверена эксперимен-
экспериментально. Подробные выкладки мы проделаем в § 136. Здесь же
уместно подчеркнуть, что дисперсионные соотношения связы-
связывают различные физические амплитуды и представляют поэтому
основу для развития ряда приближенных схем, не связанных
с разложением по степеням большой константы связи.
К сожалению, связь с наблюдаемыми величинами часто ока-
оказывается не столь непосредственной, как в рассмотренном выше
примере. Например, при рассмотрении электромагнитного форм-
фактора протона нужно учитывать редуцированный график, изо-
изображенный на рис. 18.19. Вклад его пропорционален пионному
форм-фактору, умноженному на амплитуду перехода л+ + я-->-
-*р-\-р. К несчастью, этот график имеет смысл в евклидовой
нефизической области, в частности при q2 = 4ц2, в то время как

132]
СИНГУЛЯРНОСТИ АМПЛИТУД РАССЕЯНИЯ
253
процесс аннигиляции разрешен лишь выше порога 4М2. В ре-
результате возникает необходимость аналитического продолжения
амплитуды аннигиляции, равно как и условия унитарности, ис-
используемого при вычислении скачков в дисперсионном методе.
Вернемся теперь к непосредственному рассмотрению этих вопро-
вопросов и обсуждению аналитических свойств амплитуд рассеяния.
§ 132. Сингулярности амплитуд рассеяния
При выводе ряда аналитических свойств амплитуд рассея-
рассеяния мы можем использовать развитые выше методы. Однако,
как отмечалось выше, и в рассматриваемом случае эти методы
не столь плодотворны, поскольку инварианты, составленные из
внешних импульсов qt, оказы-
оказываются теперь линейно зависи-
зависимыми. Вместо скалярных про-
произведений qiq-, удобно , ввести
следующие переменные:
и = (<7i + <?4J- A8.73)
Кинематика указана на рис.
18.20. Величина s равна квад-
квадрату энергии в системе центра
масс «s-канала» для которого
начальные импульсы равны q\
и q2, а конечные импульсы рав-
равны —<?з и —<74- Величины / и и имеют аналогичный смысл в
«кроссинговых» каналах. Согласно правилу подстановки одна
и та же фейнмановская амплитуда описывает все три реакции
в s-, t- и ы-каналах. Для этой амплитуды снова справедливо
представление Намбу
Рис. 18.20. Кинематические перемен-
переменные для амплитуды рассеяния.
оо
dan6(
\ -
dai
мнимая добавка ie в котором позволяет аналитически продол-
продолжить / от действительных значений инвариантов s, t и и. Од-
Однако поскольку величины s, t и и не независимы, а связаны
соотношением
4
s + / + K=Z/nj,	A8.75)

254
ДИСПЕРСИОННЫЕ СООТНОШЕНИЯ
[ГЛ. 18
проблема установления аналитических свойств, исходя из пред-
представления A8.74), является теперь более трудной. Например,
из A8.75) следует, что если s изменяется в верхней полупло-
полуплоскости при фиксированном значении t, то и меняется в нижней
полуплоскости. Поэтому, хотя и можно показать, что величины
?i, ?2 и ?3 в A8.74) положительны1), это представление еще не
4ftL
Рис. 18.21. Физические области s-, t- и «-каналов в я — я-рассеянии.
гарантирует отсутствия сингулярностей всюду в комплексной
s-плоскости.
В результате мы сталкиваемся с гораздо более сложной
задачей, чем в случае вершинных функций. Эта задача до на-
настоящего времени полностью еще не решена. Положение сингу-
сингулярностей существенно зависит от масс частиц, участвующих
в реакции, и, чтобы свести кинематические усложнения к мини-
минимуму, мы рассмотрим я — я-рассеяние.
В этом случае физическим областям s-, t- и ы-каналов отве-
отвечают заштрихованные области на рис. 18.21. Значения инва-
инвариантов s, t и и могут быть выражены через импульс k в си-
системе центра масс и угол рассеяния 9 в s-канале:
s = 4(k2-f Ц2), / = -2*2A -cos9), ы = -2*2A +cos6),
A8.76)
') См. задачу 2 этой главы.

§ 132]	СИНГУЛЯРНОСТИ АМПЛИТУД РАССЕЯНИЯ	255
Прямая / = 0 отвечает я — я-рассеянию вперед, которое мы
и рассмотрим в первую очередь. Перепишем интегральное урав-
уравнение A8.74) для амплитуды A(s,t) в более компактной форме:
A8.77)
Так как величины ?, ?' и о2 не обязательно положительно опре-
определены, разобьем A(s, 0) на два слагаемых:
A (s, 0) =
A8.78)
Первое слагаемое Л+ аналитично в верхней полуплоскости s
при е -> 0+, а второе аналитично в нижней полуплоскости. Если
существует некоторая область действительных переменных s,
для которых знаменатель / в A8.78) не равен нулю, то функции
А+ и А- в этой области действительны. Тогда, согласно прин-
принципу Шварца, можно аналитически продолжить Л+ в нижнюю
полуплоскость и Л_ в верхнюю полуплоскость. Если указанное
обстоятельство действительно имеет место, то можно показать,
что A(s, 0) аналитична в комплексной s-плоскости всюду, за
исключением разреза вдоль той части вещественной оси, где
знаменатель в представлении Намбу обращается в нуль, после
чего сразу можно выписать дисперсионные соотношения.
Таким образом, основная проблема заключается в том, что-
чтобы найти такую область действительных значений s, для кото-
которой знаменатель в интегральном представлении амплитуды
A(s, 0) не равен нулю и через которую можно выполнить ана-
аналитическое продолжение A+(s) и Л_(я). Из рис. 18.21 мы за-
заключаем, что единственно подходящей областью для аналити-
аналитического продолжения является отрезок 0 ^ s ^ 4ц2. При s 2== 4ц2
мы попадаем в физическую область s-канала. В этой области
амплитуда комплексна и равна сумме членов вида <?i6sin6 для
каждой парциальной волны. При s ^ 0 имеем и ^ 4ц2, и мы
находимся в физической области ы-канала, причем в этой об-
области амплитуда, согласно правилу подстановки, описывается
той же аналитической функцией A(s,t), что и в s-канале. Ин-
Интервал 0 ^ s ^ 4ц2, равно как и треугольник s ^ 0, I ^ 0,
и ^ 0, обозначенный на рис. 18.21 буквой С, является нефизи-
нефизической областью Анализ амплитуды в этой области может быть
выполнен так же, как и анализ евклидовой области в случае
Диаграмм, отвечающих вершинной функции.

256	ДИСПЕРСИОННЫЕ СООТНОШЕНИЯ.	(ГЛ. 18
Покажем, что знаменатель / в A8.77) отрицательно опре-
определен в С и не может иметь здесь особенностей. В результате
окажется возможным аналитическое продолжение функций А+
и Л_. Как и в предыдущем разделе, введем в С евклидову
метрику. Поскольку каждая из переменных s, t и и положи-
положительна в рассматриваемой области, можно выбрать импульсы
следующим образом:
<71 = 72(У«. /"УГ, /У«, 0),
<fe = 72(Vs". -*У7, -»Уй, о),
(/ —	/ —	/ — \	( 10» / У^
	V s, i\ t, —/-Vй. °Л
<74 == '/2 (— л/s, - i УТ, / ^и, О),
в полном соответствии с A8.73). Убрав затем с помощью за-
замены переменных множитель i из пространственных компонент
векторов qt, мы тем самым изменим метрический тензор g^v на
8Ну Применяя законы Кирх-
^	л у гоффа, снова убеждаемся в
х=< д	s'' том, что все внутренние им-
s_^. ^^ш 1*"ZZZ.1C	пульсы диаграммы веществен-
у^ ~(Масса)г>4и2 ^^^ ны, причем аналитические свой-
s'it	>s	^^^ ства амплитуды в новой мет-
метрике остаются неизменными.
Рис. 18.22. Одномерная редуцирован- Критерий существования син-
ная диаграмма.	гулярностей в области С оста-
остается по существу неизменным
с тем, однако, различием, что теперь импульсы и тем самым
координаты («напряжения») в вершинах трехмерны и реду-
редуцированный график может быть уже не плоским, а объемным.
Одномерные редуцированные диаграммы, указанные на
рис. 18.22, мы можем немедленно исключить из рассмотрения,
поскольку масса легчайшего состояния, связанного с двумя
я-мезонами, равна 2\а, и, таким образом, это состояние в силу
законов сохранения не может быть построено для s, t, и <С 4ц2
в A8.79). Аргументация при этом такая же, как и в случае
электромагнитного форм-фактора пиона, поскольку два внешних
пиона, сходящихся в вершине А, кинематически эквивалентны
фотону с массой У« < 2ц. В этой области форм-фактор Fп не
содержит сингулярностей. Аналогичные соображения показы-
показывают, что двумерные редуцированные графики (рис. 18.23) не
приводят к аномальным порогам в евклидовой области С; на-
напомним, что такие сингулярности отсутствуют и в вершинной
функции.
При рассмотрении трехмерных редуцированных графиков мы
должны заключить все линии во внутренность тетраэдра, к вер-

§ 132]	СИНГУЛЯРНОСТИ АМПЛИТУД РАССЕЯНИЯ	257
шинам которого присоединяются внешние частицы (рис. 18.24).
Как и в случае вершинных функций, мы снова можем исключить
возможность выпуклости граней тетраэдра. Благодаря евклидо-
вости геометрии по крайней мере в одной из вершин все три
плоских угла являются острыми. Поэтому тетраэдр можно по-
построить только в том случае, когда массы промежуточных
частиц таковы, что указанная вершина с острыми углами дей-
действительно существует. Пусть, например, это будет вершина А
на рис. 18.24. Тогда направления импульсов любых двух частиц,
ж" !!
*
Рис. 18.23. Двумерная редуциро-	Рис. 18.24. Трехмерная редуциро-
редуцированная диаграмма.	ванная диаграмма.
на которые диссоциирует пион в точке А, должны образовывать
острый угол. В этом случае должно было бы выполняться нера-
неравенство A8.65)
Z2>I>?,	08.80)
которое, однако, не может быть выполнено. Поэтому амплитуда
п — я-рассеяния не имеет сингулярностей в евклидовом тре-
треугольнике С на рис. 18.21. Чтобы завершить наше доказатель-
доказательство нужно еще показать, что амплитуды A±(s, 0) вещественны
при 0 ^ s ^ 4ц,2. Тогда, используя принцип симметрии Шварца,
мы сможем аналитически продолжить А+ в нижнюю полупло-
полуплоскость s, а А- в верхнюю полуплоскость. Для того чтобы убе-
убедиться в вещественности знаменателя, будем равномерно умень-
уменьшать внешние импульсы
начав с некоторой точки в евклидовой области, например, 5 =
= t — и. Поскольку условие A8.80) при такой однородной
деформации тем более невыполнимо, ни в одной точке при этом
не возникает особенностей. В точке Я, = 0 знаменатель
/ = — X/ /"/«/ < 0- Возвращаясь теперь обратно к исходным
значениям импульсов, мы видим, что знаменатель всюду

258	ДИСПЕРСИОННЫЕ СООТНОШЕНИЯ	[ГЛ. 18
остается отрицательным, поскольку если бы в некоторой про-
промежуточной точке / обратился в нуль, то должен был бы суще-
существовать редуцированный график, отвечающий этому условию.
Мы показали, однако, что такие графики отсутствуют.
Выпишем теперь дисперсионные соотношения для ампли-
амплитуды я— л-рассеяния вперед. Действительность A (s, 0) на от-
отрезке 0 ^ s ^ 4ц2 позволяет аналитически продолжить А+ и Л_
через «брешь», в результате мы заключаем, что единственными
особенностями A(s,0) являются разрезы от s = 4ц,2 до s = оо
и от s = 0 до s = —оо, изображенные на рис. 18.25. Временно
,1ms
Re s
Рис. 18.25. Разрезы в s-плоскости амплитуды я — Л-рассеяния на нулевой
угол
игнорируя вопрос о вычитаниях, запишем дисперсионное соот-
соотношение в следующем виде:
V^ilV-^+C- 08.81,
4цг	-с»
Уравнения A8.81) по своему смыслу и форме очень напоми-
напоминают оригинальные соотношения Крамерса — Кронига A8.8),
с которых начинается вся дисперсионная техника. Эти уравне-
уравнения позволяют выразить амплитуду рассеяния вперед A (s, 0)
через интеграл от ее мнимой части. Последняя обладает теми
же притягательными свойствами, что и абсорптивные части в со-
соотношениях Крамерса — Кронига и дисперсионных соотноше-
соотношениях для электромагнитного форм-фактора Fn(q2), а именно:
она отлична от нуля только в физической области рассеяния.
Поэтому можно использовать оптическую теорему и выразить
lmA(s, 0) через полные сечения в s- и и-каналах. Тем самым
мы получаем соотношение между измеримыми (в принципе)
величинами. Явная связь между lm A (s, 0) и полным сечением
получается из условия унитарности 5-матрицы: SS+=1; при
этом нужно только правильно учесть нормировочные множи-
множители. Конкретные вычисления будут проделаны в § 135, где мы
используем свойства аналитичности, унитарности и кроссинг-
симметрии для динамического описания л — я-системы.

§ 132]
СИНГУЛЯРНОСТИ АМПЛИТУД РАССЕЯНИЯ
259
До сих пор мы обсуждали дисперсионные соотношения при
t s= 0, используя вещественность A (s, 0) на границе евклидо-
вого треугольника и представление A8.77). Используя это пред-
представление, мы можем получить другой чрезвычайно полезный
результат, а именно, доказать дисперсионные соотношения для
Рис. 18.26. Линии cos 9 = const, которые рассматриваются при выводе дис-
дисперсионных соотношений для парциальной амплитуды я — я-рассеяния.
парциальных амплитуд. Парциальные амплитуды определяются
следующим образом:
A(s, /)=? B1 +l)At(s) Pi (cos 6),
;=o
Ai(s) = j )d (c°s 6) Pi (cos 6) A (s, cos 9),
-l
A8.82)
где Л (s, cos 8) s=A(s,t) и 8 — угол рассеяния в системе центра
масс. Для того чтобы установить аналитические свойства Ai(s),
необходимо выяснить аналитические свойства A(s, cos 0) при
фиксированном cos 0. Выразив t через cos 0 и s, получим
/=_i/2(s-4fj,2)(l —cos 9).
Подставляя это выражение в интегральное представление
A8.77) для A(s,t), мы видим, что знаменатель / можно запи-
записать в виде
J = ?s-62 + ie,	A8.83)

260
ДИСПЕРСИОННЫЕ СООТНОШЕНИЯ
[ГЛ. 18
где величины ? и а2 зависят теперь от cos 6 и «сопротивлений»
а/. Поэтому для амплитуды A(s, cos 0) справедливо то же самое
интегральное представление A8.78), что и для амплитуды рас-
рассеяния вперед. Фиксированным значениям cos 8 отвечают в
s^-шюскости прямые линии, пересекающие евклидовыи треуголь-
треугольник С (рис. 18.26), в котором, как мы показали, знаменатель /
не равен нулю. Поэтому можно разделить A(s, cos 0) на две
части, подобно тому, как мы сделали это для A (s, 0) и, повто-
повторяя рассуждения, приведенные ранее при переходе от A8.78)
к A8.81), показать, что амплитуда A(s,cos0) при любом зна-
значении cos 0 аналитична в s-плоскости, за исключением, быть
может, разрезов от s = 4ц2 до
lms	оо и от s = 0 до S ——оо.
¦«?——		В результате снова оказывает-
оказывается возможным применить тео-
теорему Коши
Res
A {s, cos 8) =
	 1 f ds'A (s', cos
2яг J s' — s — L
cos 6)
A8.84)
Рис. 18.27. Контур s-плоскости в дис-
дисперсионном интеграле для парциаль-
парциальной амплитуды я — я-рассеяния.
где С — любой контур, не пере-
пересекающий разрезов и окружаю-
окружающий точку s (рис. 18.27). Умно-
Умножим затем правую и левую
части A8.84) на P/(cos0) и
проинтегрируем от —1 до +1.
тогда слева мы получим парци-
парциальную амплитуду At(s). Поскольку интегралы в правой части
сходятся абсолютно, можно изменить порядок интегрирования;
в результате приходим к выводу, что для Ai(s) также приме-
применима теорема Коши
л (с\— ' [ ds'Ai(s')
с
s'-s-Ы
A8.85)
где с — тот же контур, что и в A8.84). Таким образом, Ai(s)
имеет те же аналитические свойства, что и амплитуда рассеяния
вперед и удовлетворяют дисперсионному соотношению, анало-
аналогичному A8.81). Этот факт имеет большое практическое зна-
значение.
Описанную выше технику можно применить для изучения
аналитических свойств и вывода дисперсионных соотношений в
других случаях, например для рассеяния я-мезонов на нуклонах
вперед или для парциальных амплитуд нуклон-нуклонного рас-

§ 1331	Я-МЕЗОН-НУКЛОННОЕ РАССЕЯНИЕ ВПЕРЕД	261
сеяния. Следует при этом отметить, что когда в рассеянии уча-
участвуют частицы с разными массами, кинематические усложне-
усложнения и трудности, связанные с аномальными порогами, значи-
значительно усложняют существо вопроса.
§ 133. Применение к л-мезон-нуклонному рассеянию вперед
Наиболее важным и плодотворным примером применения
техники дисперсионных соотношений является анализ пион-
нуклонной амплитуды рассеяния на нулевой угол [88]. Как и
во всех вычислениях, в рамках дисперсионной теории для та-
такого анализа необходимо следующее:
1.	Выделить скалярные функции Ft, зависящие только от
инвариантов (см. A8.31)), отделив при этом все спиновые и
изоспиновые множители.
2.	Изучить	аналитические	^	" \t
свойства форм-факторов, выявляя #NVr+ * яг+ ^
для этого с помощью техники ^^^	^^^ г
редуцированных графиков либо s—*- \%4fffl
другими алгебраическими спосо- ^S	^
бами сингулярности, происходя- ^"Лротон /Гратон
щие от знаменателя J.	pJtsr	p^,s3
3.	Из оптической теоремы вы-	/Г )-?
числить скачок на разрезе, после	-(?2~w
чего можно вывести соотноше-
соотношения, аналогичные соотношениям Рис 18.28. Кинематика я-мезон-
Крамерса — Кронига A8.11) и протонного рассеяния.
A8.12).
Рассмотрим рассеяние п+-мезона на протоне. В этом случае
усложнения, обусловленные изоспиновой кинематикой, отсут-
отсутствуют. Обозначим амплитуду через 5Ш(^2, />2, s2; Яи Ри si), где
спины и импульсы указаны на рис. 18.28. Разложение амплитуды
по инвариантным лоренцевым скалярам сводится к выражению
ЭД(<72. Ръ Ч, Ц\, Ри «1) =
= й (р2, s2) [A (s, I) + % Di + h) В (s, t)] и (Рь Sl). A8.86)
Действительно, используя уравнения Дирака, легко проверить,
что члены, содержащие р\ и рг. снова приводятся к виду A8.86),
например
u si).
Инварианты s и t определяются так же, как и в случае п — я-
рассеяния (см. рис. 18.28):
§ = (Р1 + Яд2, t-={q%~qxf.	A8.87)

262	ДИСПЕРСИОННЫЕ СООТНОШЕНИЯ	[ГЛ. 18
В том частном случае, когда рассматривается рассеяние вперед,
более удобно вместо s использовать лабораторную энергию
пиона со:
	 Р\д\ _ s — М2 — ц2 .	П8 88)
Ai	2M	'
при этом амплитуда выражается через один форм-фактор Т,
представляющий линейную комбинацию форм-факторов А а В:
Ш ((/,, р,, s,) = 4яп (р,, s,) Т (со) и (р,, sO,	A8.89)
где	4nT(a) = A(s, 0) + &B(s,0).	A8.90)
Нашей задачей является вывод дисперсионных соотношений
для Г (со).
ЯГ	Я	ЯГ
\	/	s
S —*- Ч	у	С ¦ ¦—	^
7г \
я"
Рис. 18.29. Полюсные члены в рассеянии я-мезона на нуклоне.
Прежде всего необходимо выяснить аналитические свойства
Г (со), что можно сделать тем же способом, который был ис-
использован для амплитуды я — it-рассеяния. Вклад любого гра-
графика в Г (со) можно записать в виде, аналогичном A8.78),
со
... dan г \\ь\	unj	ляо1\
Для доказательства аналитичности функции /(со) в разрезан-
разрезанной со-плоскости снова нужно найти интервал вещественных
значений со, на котором знаменатель J не обращается в нуль и,
следовательно, Т(со) действительна.
Амплитуда Г (со), без сомнения, комплексна при со >-jj. или
s>(M + |iJ. поскольку при этом мы попадаем в физическую
область п+ ~ р-рассеяния. Точно так же Г(со) комплексна в
физической области ы-канала: и = {р2 — <?J > {М + jj.J или
со <Г—ц, которая, согласно правилу подстановки (см. A7.45)),
отвечает рассеянию л~-мезона на протоне. Поэтому единствен-
единственной областью, где амплитуда Т(со) может быть вещественной,
является интервал —\i ^ со ^ ц.
Полюсной вклад в этой области был вычислен в гл. 10, ему
отвечают диаграммы, изображенные на рис. 18.29. В случае

§ 133]	Я-МЕЗОН-НУКЛОННОЕ РАССЕЯНИЕ ВПЕРЕД	263
я+ — р-рассеяния вклад вносит только вторая из этих диа-
диаграмм. Выясним, имеются ли здесь какие-либо дополнительные
сингулярности. Рассмотрим систему координат, в которой
" Pl = p2 = (,W,0,0,0),
9i = <7г = (Iх cos cp, /usinqp, 0, 0),
и, как обычно, перейдем к евклидовой метрике. Легко видеть,
что в рассматриваемом случае, как и в случае я— я-рассеяния,
не существует двумерных редуцированных графиков, изобра-
изображенных на рис. 18.30, и, таким образом, единственная особен-
особенность дается графиком «однонуклонного обмена», как это было
/я
а)
Рис. 18.30. Редуцированные диаграммы для рассеяния я-мезонов на протоне:
двумерная диаграмма (а), одномерная диаграмма (б).
отмечено выше. Снова аналитически продолжая внешние им-
импульсы piqi^kpi^qi^O, мы получаем, что знаменатель /
отрицательно определен при —\х < а» < \х, за исключением по-
полюсного вклада в точке
(Pi — q2J—M2 или со = + -~^г = -+- сов.	A8.93)
Мы приходим к выводу, что во всех порядках теории возму-
возмущений амплитуда Г (со) аналитична в плоскости со, за исключе-
исключением разрезов от -\-\i до +00 и от —ц до —оо и полюса в точке
со = +ц2/2М. Поэтому, используя контур С, указанный на
рис. 18.31, можно выписать для Г(со) дисперсионные соотноше-
соотношения, связывающие эту амплитуду с ее абсорптивной частью и
вкладом полюса.
На этом этапе нужно использовать условие унитарности, ко-
которое позволяет выразить мнимую часть амплитуды рассеяния
вперед через полное сечение и тем самым установить связь
между измеренными на опыте величинами. В силу унитарности
S-матрицы (см. A6.69))

264
ДИСПЕРСИОННЫЕ СООТНОШЕНИЯ
[ГЛ. 18
или, в терминах матричных элементов, описывающих переход
из начального состояния i в конечное состояние /,
? S'nfSni = 6fi.	A8.94)
A8.95)
Введем амплитуду перехода /:
Sft = t>i,-tBn)*V(P{-Pt)fft,
для которой') условие унитарности имеет вид
ftl -П^-iI, BлL б* (р, - рп) rnifni.
A8.96)
Левая часть этого соотношения представляет удвоенную мни-
мнимую часть амплитуды рассеяния на нулевой угол, а правая
Рис. 18.31. Контур в ш-плоскости, используемый при выводе дисперсионного
соотношения для амплитуды рассеяния л+-мезона на протоне вперед
часть связана с полным сечением. Вспоминая правила норми-
нормировки амплитуд из гл. 7 (и, в частности, формулы G.35) —
G.42)), мы получаем
0(о.=
•'lab
A8.97)
Множитель t»iab есть скорость пиона в лабораторной системе,
а множитель BяN обусловлен множителями Bя)~3/2 в волно-
волновых функциях налетающих частиц. С учетом A8.96) имеем
A8.98)
') Мы по-прежнему рассматриваем рассеяние вперед, в этом случае
/ = «".

§ 133,	я-МЕЗОН-НУКЛОННОЕ РАССЕЯНИЕ ВПЕРЕД	265
Свяжем далее амплитуду /,¦; с инвариантной амплитудой Г (о»),
выделяя все нормировочные множители и спиновые функции
нуклонов. Из определений A8.86) и A8.89) получаем, в полной
аналогии с A8.89),
Ш^ Р s)	^4л(Р S)r((O)«(p S)]
Bя)«2т Ш^и Р»' sl)= Bп)°2со ^4л»(Рь Si)r((O)«(pb S,)],
A8.99)
поэтому
At	^=	A8.100)
Легко видеть, что амплитуда Г весьма просто связана с сече-
сечением упругого рассеяния на нулевой угол; из оптической тео-
теоремы, с учетом используемой нормировки, следует
'2-	08.101)
Этот результат может быть также непосредственно выведен из
формул A0.54) и A0.68).
Уравнение для скачка A8.100) справедливо только в физи-
физической области со ^ ц. Поэтому необходимо еще вычислить
вклад от левого разреза со ^ —ц и полюса. Поскольку левый
разрез отвечает физической области «-канала, т. е. реакции
я~ — р-рассеяния, мы можем, используя свойство кроссинг-сим-
кроссинг-симметрии амплитуды, выразить скачок на этом разрезе через се-
сечение яг— р-рассеяния. Как обсуждалось в § 120, точная ам-
амплитуда it-мезон-нуклонного рассеяния инвариантна при одно-
одновременной перестановке изотопических индексов пионов
(частица ¦*-»- античастица) и 4-импульсов пиона в начальном
(qi) и конечном (—<7г) состояниях. Для рассматриваемого слу-
случая рассеяния вперед эта замена сводится к замене со -*-»• —си
и л+ ¦*-> лг:
Т (со) = г("+р) (со) = Г("~"> (- со).	A8.102)
Аргумент амплитуды it+ — протонного рассеяния лежит на верх-
верхнем берегу разреза «в ^ ц, а аргумент амплитуды it~ — протон-
протонного рассеяния лежит на нижнем берегу разреза со ^ —ц. Дей-
Действительно, амплитуда A8.91) может быть, как и в случае
я — я-рассеяния вперед, разделена на две части, одна из кото-
которых отвечает вкладу ? > 0, а другая — вкладу 5 < 0- Подчерк-
Подчеркнем это обстоятельство, записав A8.102) в виде
у("+р)(—со — ге) = Т{-я~р) (со + ie),

266	ДИСПЕРСИОННЫЕ СООТНОШЕНИЯ	[ГЛ. 18
поэтому
1га Т^+р] (- со) = -^ [r(«+"> (- со + fe) - Т^п+Р] (-со - /в)] =
После того, как мы выразим скачок на левом разрезе через
сечение, нам остается только вычислить вычет в полюсе со =
= (os = \i2l2M. После этого амплитуда рассеяния вперед цели-
целиком будет выражена только через экспериментальные величины.
Покажем, что вклад полюсных членов по-прежнему дается вы-
выражением, полученным в гл. 10, с заменой голой константы
связи go перенормированным значением g.
Для этого нужно вычислить вклад всех фейнмановских гра-
графиков типа, изображенных на рис 18.29, т. е. имеющих вид двух
вершинных блоков, соединенных нуклонным пропагатором.
Согласно сказанному перед формулой A8.93) о приведенных
графиках эти диаграммы достаточно вычислить лишь вблизи
полюса нуклонного пропагатора. Как было отмечено выше, в
it+ — р-рассеяние вносит вклад только один график (см.
рис. 18.29,6). Инвариантная амплитуда, сопоставляемая ука-
указанной диаграмме, равна
-tf»poie(?i. P.- Si) = Z2Z(-tg0 V2J X
Х«(Р„ OtT^p,; p)iS'p(p)ir6(p, р,)и(р„ s,), A8.104)
Кинематика в A8.104) отвечает рассеянию вперед: р2 — pi и
q2 = qu Множители Z2 и Z возникают при перенормировке вол-
волновых функций нуклона и пиона, как это следует из редукцион-
редукционных формул A6.81) и A7.43). Множитель -\fz A8.104) полу-
получается при выделении пропагаторов внешних частиц. Действи-
Действительно, выделяя внешние концы, например в A7.43), получим
О,) OX, -M)S'p(x-y)...= дД; еЧчУп (р,) ...
Согласно спектральному представлению A6.122) точный про-
пагатор §'Р(рЛ при переходе на массовую поверхность равен
22/(р1 — М) и в точности сокращается оператором Дирака, так
что в результате мы получаем множитель -y/Z2 в числителе.
Аналогичный результат имеет место для пионного пропагатора
и волновой функции. Отметим еще, что функция Грина S'p(p)

§ 133]	Я-МЕЗОН-НУКЛОННОЕ РАССЕЯНИЕ ВПЕРЕД	267
промежуточного нуклона в A8.104), согласно представлению
Челлена — Лемана, вблизи полюса также ведет себя как
Z2/(p-M).
Величина Г5(рг, р) представляет сумму всех компактных,
вершинных диаграмм, т. е. таких вершинных диаграмм, которые
не могут быть разделены на несвязанные части мезонной или
нуклонной линией. При р\ —*М, т. е. в полюсе, отвечающем
промежуточному нуклону, Г5(р1,р) должна быть пропорцио-
пропорциональна матрице у5, что можно показать так же, как мы вывели
формулу A0.157). Все множители pi в Г5 следует перемещать
налево или направо до тех пор, пока они не окажутся рядом
со спинорами п{р{) или и(р\), после чего их можно заменить
на М. Поправки, пропорциональные р— М, исчезают, коль
скоро мы интересуемся поведением вершинной функции вблизи
полюса. Инвариантные форм-факторы в Гб зависят от
р2 = р21 = М2 и q] = (p — рЛ2=цЛ Поэтому коэффициент при
матрице у5 равен просто числу. Мы определим его следующим
образом:
^М2.	A8.105)
Подставляя A8.105) в A8.104), мы воспроизводим старый ре-
результат A0.56) теории возмущений с заменой голой константы
go на g:
72 U (pi, Si) V5 (Pi — <?1 + М) у5» (pi, Si) __
(Pi - <?iJ - М2
при {Pl-qi?->M\ A8.106)
где
4л ) 4М2 ~
есть рационализованная и перенормированная константа пион-
нуклонной связи.
Используя далее формулу Коши и контур С в интеграле,
изображенный на рис. 18.31, мы можем выписать дисперсионные
соотношения, аналогичные соотношениям A8.81) для я — я-рас-
сеяния вперед, с той лишь разницей, что теперь добавляется
вклад полюсного члена. Объединяя выражения A8.100),

268	ДИСПЕРСИОННЫЕ СООТНОШЕНИЯ	[ГЛ. 13
A8.103) и A8.106), получаем
у/ \_J_ Г сГ(о'1тГ((о') 1 ^ da'lmT(d)') .	2\_
п j <o' — <в — ге	я J <в' — со — ге со —
—оо
-I
= 1я^ J
" rf<D' У@'2 - Ц2 O?ot Р(-«') _
1
со' — со — ie
1 Г
4я2 J
— <а —
°°'
Взяв действительную часть этого выражения и скомбинировав
первый и второй члены, получим окончательную форму диспер-
дисперсионных соотношений для я+ — р и п~ — р-рассеяния
Re Г(я+") (о) =
+ со \а^Р (со') — а^~
Re Г(«-") («>)=--?--
_ _L р С ^У^-ц2 уг^+р (со0 + Стя+Р (со01 _
4л2 J ш' — ш2 I L tot v ' i tot v П
- со [<*?р (со') - ofo/ (со')]} + С^. A8.107)
Эти соотношения удобно записать, введя полусумму и полураз-
полуразность амплитуд:
Г+ = 7, [Т (со) + Т (- со)] = 7, [Г("+Р) И + 7*0) (со)],
Г~ = — 7г [Г И — Г (— со)] = 72 [Г(я~р) (со) — Г(п+Р> (со)].
Полагая, в частности, что для нечетной амплитуды Т~ справед-
справедливо дисперсионное соотношение без вычитании, получим важ-
важное соотношение
Ш
"Г
1 Г da V«'2 - И2 Г<Т" («О ~ <ТР («01
^р\	1	и L/2tot \ 	tot '\ A8.109)
4л2 J	со — (о4

§ 1331	я МЕЗОН-НУКЛОННОЕ РАССЕЯНИЕ ВПЕРЕД	269
Формула A8.109) связывает между собой экспериментально
измеримые величины и содержит лишь один свободный пара-
параметр при условии, что
lim К!" («О - ст?о7Р И] "* °-	A8.110)
Экспериментальные данные указывают на то, что соотношение
A8.110) по-видимому выполняется. При энергиях -~ 10 Гэв
разница сечений составляет ')
Др- <^И-<^(ц) 2-Ю-27 см2 QQg
Выражение A8.109) позволяет экспериментально определить
величину /2, она оказалась равной [89]
Р = 0,080 ±0,001.	A8.111)
Этот результат является наибольшим достижением метода
дисперсионных соотношений.
Результат A8.111) мало чувствителен к поведению сечения
при со—юо. Если, однако, будущие эксперименты покажут, что
условие A8.110) не выполняется, то в дисперсионных соотно-
соотношениях нужно будет сделать вычитание, записав их для ампли-
амплитуды Т~ (со)/*» (со2 — со2), где со2 ^ ц2— вычитательная точка.
Тогда, выбрав, например, «во = ц> мы получим вместо A8.109)
Re Т~ (со)	 Т~ (ц) ,	if (a2 — \i2)
ш	ц	(со2-ш2)(ц2-ш|)
(В — [А
Дисперсионный интеграл в A8.112) теперь сходится на беско-
бесконечности гораздо быстрее. Однако A8.112) в этом случае содер-
содержит дополнительную величину — амплитуду рассеяния на по-
пороге T~(\i), которую необходимо определять из опыта.
') В исследовании рассеяния адронов при высоких энергиях с момента
написания книги был достигнут существенный прогресс, связанный с введе-
введением в строй больших ускорителей в СССР и США и ускорителя на встречных
пучках в ЦЕРН'е. Интересующегося читателя мы отсылаем к недавним обзо-
обзорам [136, 137], где имеется также исчерпывающая библиография. Отметим
здесь только, что малость отношения Дст/ст при энергии 10 Гэв, которая по
современным представлениям весьма далека от асимптотической, имеет место
только для я* — р-рассеяния. Тем не менее измерения в широком интервале
энергий ?5^200 Гэв показали, что разности полных сечений взаимодействия
частиц и античастиц в исследованной области энергий убывают степенным
образом, что согласуется с теоремой Померанчука (прим. перев.).

270	ДИСПЕРСИОННЫЕ СООТНОШЕНИЯ	(ГЛ. 18
Нарушение условия A8.110) —асимптотического равенства
я+ — я- и я~ — р-сечений— ведет к странному и противореча-
противоречащему нашей физической интуиции результату, хотя строго
исключить его возможность и нельзя. Предположим, например,
что сечения о%*р и о^~р остаются конечными при со—>оо, как
это имеет место при достижимых в настоящее время энергиях
и, более того, что остается конечной разность сечений До. Тогда
из A8.112) следует, что
оо
Re Г" (со) ~--^ Да Д-—^	 _ «-2L да in JL, A8.113)
4я2	J <в' (ш'2 - со2) 4я2	со
где со Э> ц и со/со Э> 1, причем значение со выбирается так, что-
чтобы сечения могли быть аппроксимированы своим асимптотиче-
асимптотическим пределом. Однако из оптической теоремы следует, что при
со ^> ц мнимая часть амплитуды рассеяния л± мезонов на про-
протоне ведет себя как
В результате мы приходим к выводу, что при со -> оо действи-
действительная часть амплитуды упругого я+ — р-рассеяния домини-
доминирует над ее мнимой частью. Это заключение, безусловно, проти-
противоречит нашей физической интуиции. Наблюдаемые полные
сечения [90] ') при энергиях порядка десятков Гэв превосходят
упругие сечения более чем в три раза. Поэтому следует ожи-
ожидать, что при таких энергиях преобладает дифракционное рас-
рассеяние пиона, сопровождающееся поглощением в различные не-
неупругие каналы, вклад которого в упругую амплитуду чисто
мнимый. Эксперименты при высоких энергиях подтверждают
эту интуитивную картину [90].
Изложенные аргументы привели Померанчука [75] к выводу
о том, что должно выполняться условие A8.110) и тем самым
безвычитательные дисперсионные соотношения A8.109). Это
утверждение, называемое теоремой Померанчука, было позднее
доказано при некоторых более слабых предположениях Вайн-
бе,ргом и др. [91—93]. Аналогичный результат выведен и для
других сечений, например:
о?Г'(<о)-а&-'(«>)-> 0, СО'
причем эти соотношения, по-видимому, также подтверждаются
на опыте.
') См. также [138] (прим. перев.).

§ 134]	ВЫВОД ДИСПЕРСИОННЫХ СООТНОШЕНИЙ	271
Тем же способом, которым мы получили дисперсионное соот-
соотношение для амплитуды Г~(со), можно вывести и дисперсион-
дисперсионное соотношение для четной амплитуды Г+(со). В этом случае
дисперсионный интеграл содержит сумму сечений of~P (со) +
+ сг^р (со) и вычитания заведомо необходимы. Складывая два
дисперсионных соотношения в A8.107) и сделав вычитания при
и = ц, получаем
ПВТ+/,.'1_Т+/|Л	/V ((О2 — Ц2)
Ке 1 (со) — 1 (ц)	——	2\Т~2	гТ ~
М (со2 - со2,) {у.2 - со2,)
Было показано [94], что это соотношение не противоречит
эксперименту '). Аналогичные результаты можно получить и для
амплитуды рассеяния вперед с переворотом спина [95].
§ 134. Аксиоматический вывод дисперсионных соотношений
для пион-нуклонного рассеяния вперед
Дисперсионные соотношения A8.109) и A8.114) указывают
на вполне однозначную связь между наблюдаемыми величи-
величинами. Поэтому вполне уместно задать вопрос: что будет озна-
означать противоречие этих соотношений с экспериментом, если та-
таковое обнаружится? Чтобы ответить на этот вопрос, нужно про-
проанализировать основные постулаты, на которых основывается
наша теория. При выводе дисперсионных соотношений мы ис-
использовали общие свойства S-матрицы, обсуждавшиеся в гл. 16,
в частности трансляционную инвариантность, из которой сле-
следует существование 4-вектора энергии-импульса Рц, и инва-
инвариантность при преобразованиях Лоренца. Далее мы предполо-
предположили существование единственного и нормированного основного
состояния, вакуума, а также полного набора in- и out-со-
out-состояний. Наконец, мы использовали локальность теории, т. е.
тот факт, что поля удовлетворяют дифференциальным уравне-
уравнениям, а генераторы Рм выражаются через соответствующие ло-
локальные плотности. При этом коммутаторы бозе-полей и анти-
антикоммутаторы ферми-полей обращаются в нуль для простран-
пространственно-подобных интервалов, равно как и коммутаторы всех
локальных плотностей, построенных из полей и отвечающих
«наблюдаемым» величинам. Напомним, что это свойство теории
мы называем микропричинностью.
>) См. также [137] (прим. перев.).

272	ДИСПЕРСИОННЫЕ СООТНОШЕНИЯ	[ГЛ. 18
Указанные постулаты все имеют фундаментальный характер
и отказаться от них можно было бы только в крайней случае.
В нашей теории имеется, однако, одно слабое место, а именно,
вопрос о сходимости ряда теории возмущений. Действительно,
нельзя заранее исключить возможность того, что бесконечная
сумма фейнмановских диаграмм имеет дополнительные сингу-
сингулярности, которые не содержатся ни в одном ее члене. Тем не
менее возможность появления дополнительных особенностей сле-
следует исключить, поскольку можно строго доказать дисперсион-
дисперсионные соотношения для мезон-нуклонного рассеяния вперед, не
прибегая к анализу аналитических свойств отдельных фейнма-
фейнмановских диаграмм [97, 27]. Ниже мы обсудим это доказатель-
доказательство, следуя Шиманчику и Боголюбову.
Рассмотрим S-матрицу A6.77) для рассеяния вперед. Вы-
Выражение A6.77) записано в виде, в котором редукция выпол-
выполнена наполовину, и в in- и out-состояниях оставлены мезонные
состояния:
out | qiPlSl in) = 6,,,, - г ^ {2л)Ч4щоь - X
(x))\PlSlm) =
где амплитуда WI определена в A8.99) и равна
/ BяL б4 (<?2 — <7i) cww	\ /in 1 11-\
Bя)«2т	Ш^1' Р'» Si), A8.115)
A8.116)
Поле ф сопоставляется я+-мезону и, действуя на произвольное
состояние, увеличивает заряд на +1. В формуле A8.116) ис-
использована трансляционная инвариантность теории, которая по-
позволяет заменить q>(x) на ф@), благодаря чему можно явно вы-
вычислить один из четырехмерных интегралов. Выразив Г-произ-
ведение полей через коммутатор:
= 8 @ [а @, 6@)]+ 6@) а @, A8.117)
приведем все выражение к виду, удобному для исследования его
аналитических свойств:
X {6 Ы (PS I [Ф (у), Ф+ @)] I ps) + (ps | ф+ @) Ф (у) | ps)}. A8.118)
Покажем, что второй член в A8.118) равен нулю в силу ста-
стабильности протона. Действительно, вставив между операторами

§ 134]	ВЫВОД ДИСПЕРСИОННЫХ СООТНОШЕНИИ	273
полей полный набор состояний \п) и выполнив интегрирование
по dAy, получим
J d*y е+<« (П у + И2J (ps | Ф+ @) | п) {п | Ф (у) | ps> =
2 - V??1 (PS IФ+ @) I п) |2 BяL б4 (q + pn- p). A8.119)
Поскольку до > 0. не существует такого состояния |л), для ко-
которого р = q + pn-
Уравнения A8.118) и A8.116) совпадают на массовой по-
поверхности я-мезона, т. е. при q2 = \i2. Тем не менее аналитиче-
аналитические свойства функций, определенных этими уравнениями, раз-
различны, когда мы рассматриваем их продолжение в комплексную
плоскость q0 = со. Запаздывающий коммутатор в A8.118) имеет
причинную форму, которую удобно использовать при выводе
дисперсионных соотношений. Напомним, что при обсуждении
дисперсионных соотношений в классической теории мы исполь-
использовали тот факт, что рассеянные волны не могут распростра-
распространяться со скоростью, большей скорости света. Причинное усло-
условие теперь имеет вид
Ф+@)] = 0, у2<0.	A8.120)
Как мы покажем ниже, условие A8.120) позволяет выполнить
аналитическое продолжение амплитуды.
С этой целью перейдем в систему покоя нуклона, в которой
р = (М, 0, 0, 0). Поскольку 2Л — скалярная амплитуда, то в слу-
случае рассеяния вперед она не зависит от спина s. Поэтому мат-
матричный элемент зависит только от \у\2 и г/о, и в A8.116) можно
выполнить интегрирование по угловым переменным. При этом
получаем из A8.118)
со
7» = -^-Щ<7,р, s)=\dyyY(«>, у),	A8.121)
о
где Г (со) определена выражением A8.99) и
К («о, y)^-^™^E^JL J
X (Ms | [Ф (у), ф+ @)] | Ms). A8.122)
Функция У (со, у) аналитична в верхней полуплоскости со. Точка
со = щ не является особой, поскольку функция (l/*Jz) sin -y/z
зависит не от -y/z, а от z. Роль ступенчатой функции 6(уо).как
и в случае соотношений Крамерса — Кронига, сводится к тому,

274	ДИСПЕРСИОННЫЕ СООТНОШЕНИЯ	[ГЛ. 18
что подынтегральное выражение, как функция у0, экспоненци-
экспоненциально затухает, когда «в уходит в верхнюю полуплоскость. Дей-
Действительно, если бы 0 (г/о) в A8.122) стояла слева от оператора
Клейна — Гордона, то интеграл по dyo вычислялся бы по обла-
области положительных значений 0 ^ у0 < оо
A8.123)
В действительности же интеграл по dy0 в A8.122) отличается
от A8.123) на некоторое число б-функций и их производных,
возникающих в результате коммутирования 6(г/0) с оператором
Клейна — Гордона; при этом d/dy0 Э (у0) = б {у0). В результате
появляются дополнительные члены, которые, однако, представ-
представляют собой лишь безобидные с-числа, поскольку они сводятся
к коммутаторам полей при равных временах:
, 0), Ф+@)], [ф(у, 0), Ф+(О)] = -Й3(У). A8.124)
Эти члены приводят к добавлению к 7"(со) в A8.121) функций,
растущих не быстрее, чем полином, поэтому при аналитическом
продолжении по «в их можно просто игнорировать. Далее, усло-
условие причинности A8.120) обеспечивает быстрое убывание функ-
функции У (со, у) при сй->оо в верхней полуплоскости. Действительно,
экспонента в A8.122) не опасна, если мы находимся внутри пе-
переднего светового конуса у0 ^ у. Выражение
ехр [г (он/о ± Ущ2 — Ц2 у)] да {ехр [/со (у0 ± у)]} ехр (+ i -^- у)
A8.125)
для |со|-+оо
не приводит к трудностям, если Im со > 0 и у0 ^ у. Хотя второй
множитель для больших у может расти экспоненциально
~ехр(+ц2#/2|со|), его можно подавить, вводя под знак инте-
интеграла множитель е~ги\ причем после вычисления интеграла
следует положить е = 0.
Учитывая вышесказанное, мы можем вычислить интеграл
A8.121) для всех со, лежащих в верхней полуплоскости; тем са-
самым устанавливается аналитичность амплитуды в этой обла-
области. В результате можно выписать дисперсионное соотношение
для Г (со):
оо	оо
Re Т (со) = -1 Р \ -J^ \ dy ye->«! Im Y (со', у) + С„, A8,126)

§ 134]	ВЫВОД ДИСПЕРСИОННЫХ СООТНОШЕНИЙ	275
где С»— вклад интегрирования по большому полукругу. Этот
вклад можно устранить, сделав достаточное число вычитаний1).
Чтобы завершить доказательство, нужно еще вычислить пре-
предел е->-0 под знаком дисперсионного интеграла A8.126) при
] со} ^ ц, что не приводит к каким-либо трудностям, поскольку
в этом случае множитель (sin Vю2 — й2 I/W^2 — й2 осциллирует
и интеграл в A8.121) существует для вещественных значений со.
В этой области, по существу, вовсе не требуется вводить е~гу"
для подавления экспоненциального роста второго множителя в
A8.125). Однако, и это является камнем преткновения при вы-
выводе любых дисперсионных соотношений, в нефизической обла-
области |<й| <; ц мы не можем положить е->0, поскольку этот мно-
множитель реально необходим, чтобы подавить рост sh Vh<2— ®2У-
С другой стороны, из рассмотрения фейнмановских диаграмм
известно, что абсорптивная амплитуда в нефизической области
имеет простой вид, а именно Im Г (со) и обращается в нуль всю-
всюду, кроме полюса при со = ц2/2М. Посмотрим теперь, как можно
получить этот простой результат в рассматриваемом подходе.
Вернемся к A8.122) и вычислим Im У(со, у) в нефизической
области | со | < ц. Будем считать, что, как обычно, «в стремится
к вещественной оси из верхней полуплоскости. Вставив полный
набор состояний 1 = ^ \п){п \ между полями ср и ср+ в коммута-
п
тор^е, сместим поле ср в начало координат и выполним интегри-
интегрирование по d2)
+ M - En + fe ~ a - M + Ea + is )\ ¦ A
Мнимая часть отлична от нуля там, где знаменатели обращают-
обращаются в нуль, что имеет место только при
Еп = М±а>.	A8.128)
Состояния \п) в A8.127) могут быть связаны либо с состоянием
qp+|.Ms) с нуклонным числом +1 и зарядом +2, либо с состоя-
состоянием qp|Als) с нуклонным числом +1 и зарядом 0. Единствен-
') Гораздо хуже дело обстоит в том случае, когда коммутатор в A8.122)
при (/->0 имеет существенную особенность, при этом возникающая добавка
к Т(а) уже не сводится к полиному.
2) Производная по времени от 9(г/о) в A8.122) ведет лишь к полиномам
по си и поэтому не содержится в A8.127). Множитель (sin pny)/Pn возникает
после усреднения по проекции спина s.

276	ДИСПЕРСИОННЫЕ СООТНОШЕНИЯ	[ГЛ. 18
ным состоянием с указанными квантовыми числами и с энергией
Еп < М + Ц.1) является дискретное состояние нейтрона, причем
это состояние содержится во втором члене в A8.127). Вклад
в нефизическую область от непрерывного спектра нуклонов и
пионов, порог которого равен М + Н-. отсутствует. Вклад же од-
нонейтронного состояния, очевидно, приводит к полюсному члену
в 7*(со), вычисленному в предыдущем параграфе.
При попытке вычислить Im У(со, у) в нефизической области
непосредственно из A8.127) мы сталкиваемся со сложными и
запутанными вычислениями2). Оказывается, однако, возможным
избежать трудности, если воспользоваться приемом, предложен-
предложенным Боголюбовым [27]. Im У (со, у) при со < ц равна
Im У (со, у) = J d3k f (k, у)б(<а~М
?kF(k, у) й(е>-<*-№), A8.129)
где k — импульс нейтрона. Все несущественные множители вклю-
включены в функции f(k,y) и F{k,y) и 2j B A8-127) заменена на
п
\ d?k. Боголюбов заметил, что можно избежать вычисления
A8.129), если ввести вспомогательную амплитуду f (со), которая
определяется через функцию F(co, у), обладающую всеми же-
желательными свойствами, позволяющими доказать дисперсионные
соотношения, и отличающуюся от У(со, у) лишь заменой
F (k, y)->F (k, у) = (со - м2~Д*12) F (k, у) A8.130)
в A8.129). Поскольку х8{х) = 0, Т(со) не вносит вклада в нефи-
нефизическую область.
Функция f (со) не содержит нейтронного полюса, поскольку
Т (со) = (со -J?-) T (со),	A8.131)
что легко проверить, повторяя предыдущие выкладки с учетом
дополнительного множителя. Действительно, амплитуда Ш (q, p, s)
в A8.116) умножается на
ц2	ш2 - [ q |2
') Это неравенство следует из A8.128) при |со| < ц.
2) " "" "
2) См. [97—99]. Трудности еще более возрастают при рассмотрении дис-
дисперсионных соотношений для рассеяния на ненулевой угол.

% 134]	ВЫВОД ДИСПЕРСИОННЫХ СООТНОШЕНИЙ	277
Этот множитель может быть внесен внутрь интеграла в правой
части A8.116) и заменен затем локальным дифференциальным
оператором, действующим на ср(г/)
а2 + VI
*	A
Поэтому все выкладки, ведущие от выражения A8.116) к дис-
дисперсионным соотношениям A8.126), могут быть повторены для
Т(со) с заменой
()	A8.133)
При вычислении Im У(со, у) в A8.127) единственное изменение
заключается в появлении дополнительного множителя со —
— (со2 — \k\2)/2M. Следовательно,
Im У (а, у) = 0 при |со|<ц.	A8.134)
Поэтому Т(со) удовлетворяет дисперсионным соотношениям, вы-
выражающим ее свойства аналитичности в комплексной со-шюско-
сти с разрезом
й	A8.135)
Разумеется, чтобы компенсировать лишнюю степень со в A8.132)
и устранить вклад <?<х>, необходимы дополнительные вычитания.
Наличие вычитательных членов не приводит, однако, к каким-
либо дополнительным трудностям.
Физическая амплитуда
г/.л— Н)
1 W — а -
обладает теми же аналитическими свойствами, что и ?(со), но
имеет дополнительный полюс при со = \$/2М. Вычет в нем
выражается через матричный элемент (V&2 + Al2s'|ф@)| Ms),
относящийся к я-мезон-нуклонной вершине. Проверку этого фак-
факта мы оставляем читателю. Ответ при этом согласуется с ре-
результатом, полученным из анализа редуцированных диаграмм.
Таким образом, мы вновь воспроизвели все выводы предыду-
предыдущего раздела, не используя предположение о сходимости ряда
теории возмущений. Поэтому противоречие дисперсионных соот-
соотношений для пион-нуклонного рассеяния вперед с эксперимен-
экспериментом, если таковое обнаружится, будет иметь более глубокие
последствия.

278	ДИСПЕРСИОННЫЕ СООТНОШЕНИЯ	[ГЛ. 18
§ 135. Динамические расчеты я — я-рассеяния
с использованием дисперсионных соотношений
Одним, притом весьма впечатляющим, примером использо-
использования техники дисперсионных соотношений для пион-нуклонного
рассеяния вперед является вывод соотношений, связывающих
экспериментально наблюдаемые величины, проверка которых
позволяет сделать вывод о справедливости основных постула-
постулатов в теории поля. В последнее время много усилий уделялось
также и другому аспекту метода, а именно, использованию дис-
дисперсионных соотношений для выполнения динамических вычис-
вычислений основных характеристик взаимодействующих частиц. В ча-
частности, в области сильных взаимодействий, где теория возму-
возмущений неприменима, дисперсионный подход представляется в
настоящее время наиболее плодотворным.
Возможность динамических вычислений подобного рода свя-
связана с применением весьма грубых приближений, которые ча-
часто подвергаются критике. Справедливость этих приближений
весьма редко обоснована теоретически. При этом поправочные
члены не только трудно оценить, но и, вообще говоря, практи-
практически невозможно вычислить, а справедливость приближений
может быть оправдана только путем сравнения результатов рас-
расчета с экспериментом [100—102]. Поэтому мы не будем здесь
слишком подробно обсуждать детали вычислений. Наша цель
заключается лишь в том, чтобы дать обзор основных идей ме-
метода с тем, чтобы у читателя сложилось некоторое представле-
представление о дисперсионной картине, такой, как она представляется с
наиболее оптимистической точки зрения.
Рассмотрим случай с простейшей кинематикой, а именно,
пион-пионное рассеяние и вычислим фазы рассеяния и пионную
электромагнитную вершину. Как и в дисперсионных соотноше-
соотношениях для пион-нуклонного рассеяния вперед, динамические вы-
вычисления основываются на использовании аналитических
свойств, а также унитарности (или сохранении вероятности) и
кроссинг-симметрии амплитуды рассеяния.
Отделив кинематические и изоспиновые множители, получим
для амплитуды я — я-рассеяния в системе центра масс налетаю-
налетающих пионов следующее выражение:
2
bfi — bft	)в B(оJ	2-lA'{s' l> u>pi- A8Л36)
Кинематика указана на рис. 18.32, где со= V<72 + V\ изотопиче-
изотопические проекционные операторы Pi определены формулами A7.54)
и A7.55). Рассмотрим реакцию в s-канале, физическая область
которого задана неравенствами 4ц.2 ^s^ooni, и^О. Ампли-

135]
ДИНАМИЧЕСКИЕ РАСЧЕТЫ Л-Я-РАССЕЯНИЯ
279
туды реакций в t- и «-каналах при необходимости могут быть
построены с использованием кроссинговых соотношений A7.52)
и A7.53).
Хотя аналитические свойства амплитуды рассеяния A (s, t, и)
как функции переданного импульса t (или и) неизвестны, тем
не менее в § 132 мы обнаружили (см. A8.84)), что амплитуда
A(s, cos 0) &з Ai(s,t, и) при фиксированном cos 0 аналитична в
s-плоскости с разрезами — оо ^ s ^ 0 и 4j^2 ^ s =g; oo. Из выра-
выражений A8.82) и A8.85) следует, что парциальные амплитуды
а = (%-
A\{s) = y ) d (cos 6) Pi (cos 6) A, (s, cos 9) A8.137)
-l
имеют те же самые аналитические свойства. Ниже мы исполь-
используем это обстоятельство, равно как и
свойства унитарности и кроссинг-сим-
кроссинг-симметрии.
Чтобы применить условие унитарно-
унитарности, нужно обобщить формулу A8.96),
использованную ранее для пион-ну-
клонного рассеяния на нулевой угол,
на случай переходов в различные ко-
конечные состояния. При этом мы полу-
получим выражение для скачка парциаль-
парциальных амплитуд At (s) на разрезе s^4jx2, .
аналогичное A8.100). Введем времен- f &
но обозначение:
S<+> = (п out | / in) =
= 6п{ - Bя)« Л* (Рп - Р,) /<+> A8.138)
для обычных S-матричных элементов и амплитуд перехода. Если
|л> и |i> представляют двухпионные состояния, то /<+) сводится
к амплитуде упругого я—л-рассеяния и отличается от A(s, cos 9)
множителем, пропорциональным s~1. В частности, при s ^ 4jx2
амплитуда /<+' определяется представлением Намбу как пре-
предельное значение аналитической функции, когда аргумент s
приближается к разрезу на действительной оси, оставаясь при
этом в верхней полуплоскости:
cos 9) s f As + is, cos 6).
Рис. 18.32. Кинематические
переменные для я — я-рас-
сеяния.
Определив аналогичным образом
A8.139)

280	ДИСПЕРСИОННЫЕ СООТНОШЕНИЯ	[ГЛ. 18
запишем условие унитарности S-матрицы в виде
Es{fn)SlnV = (>l{.	A8.140)
п
Введем по аналогии с A8.138)
SfcT* = 6fn + ' W б4 (Pf - Рп) f\~h	A8.141)
тогда, с учетом A8.140), условие унитарности приобретает вид
f\T) = -i ?BяL6<(Р„-Р()/?>/<+>. A8.142)
Из определения A8.139) следует, что /(~> связана с физической
амплитудой fw соотношением
с учетом которого A8.142) в случае, когда i = f, сводится к
A8.96).
Мы можем вывести и более полезный результат, согласно
которому амплитуда /\Т] получается аналитическим продолже-
продолжением f\V в точку s — ie под разрезом s ^ 4ц.2 в s-плоскости.
Тогда левая часть в выражении A8.142) представляет скачок
амплитуды ?(s) на разрезе. Этот результат можно доказать,
используя редукционную технику, рассмотренную в гл. 16. По-
Повторим выкладки § 108, ведущие от уравнения A6.72) к A6.81),
меняя при этом всюду местами in- и out-состояния. Такая за-
замена отвечает изменению направления времени на противопо-
противоположное; в результате хронологический оператор Т(АВ ...) за-
заменяется во всех выражениях на антихронологический оператор
Т(АВ ...). Например, вместо A6.78) — A6.80), получаем
<YP in | ф (х) | a out) = <y in | qp (х) | а — р out) +
-f <y in | а|п (p) ф (x) — Ф (x) aout (p) | a out) = <y in | q> (x) | а — p out) —
- -±=- \ d*y (y in | Г(Ф(x)Ф(у)) |aout)(П, + m2) f*p (y), A8.143)
где
f (Ф (x) ф (y)) = Ф (x) ф (y) 0 (y0 - x0) + Ф (у) 4>(х)д(х0-у0). A8.144
Взяв свертку по всем частицам, получим A6.81) с заменой
in -> out, T -> Т и (i)m+n->(—i)m+n. Аналог формулы A7.21), вы-
выражающей т-функцию в терминах in-полей, получается взятием
эрмитового сопряжения. При этом единственный эффект, свя-
связанный с антихронологическим оператором, заключается в за-
замене —i на -\-i в выражении ехр(—i \ Hjdtj. Поэтому можно

$ 1351	динамические расчеты л-л-рассеяния	281
непосредственно повторить виковскую редукцию, описанную в
гл. 17, вводя всюду антихронологическое произведение полей
-у) = @\Т(Ф1п(х)Ф(п(у))|0) = -
A8.145)
Антипричинная функция Грина &f(x — у) отличается от фейн-
мановской Af(x — у) общим знаком и заменой в знаменателе
ie—*—ie. Аналогичный результат может быть получен для спи-
норных и векторных полей. Поэтому мы заключаем, что, с точ-
точностью до знака, переход от f^ к f^ сводится к замене ie на
—ie во всех фейнмановских пропагаторах.
Что же касается фазовых множителей, то в силу A8.145) мы
имеем дополнительный множитель —1 для каждой функции
Грина. Кроме того, имеется дополнительный множитель —1 для
каждой вершины, обусловленный заменой
,dl).	A8.146)
Наконец, согласно A8.143), имеется еще множитель —1 для
каждой внешней линии, подходящей к вершине, приводящий к
разности операторов (а1пф ...) — (qpaOut ...), которая отличается
знаком от соответствующей разности в A6.79). Эта комбинация
знаков минус дает в результате +1, и мы приходим к представ-
представлению Намбу A8.74). Для взаимодействия ^ф3 вершины и фер-
мионные пропагаторы в высших приближениях всегда комби-
комбинируются парами1). Каждый дополнительный бозонный пропа-
гатор приводит к дополнительной замкнутой петле. Интегриро-
Интегрирование по 4-импульсу петли йЧ приводит к дополнительному
знаку —1, который обусловлен изменением знака у мнимой до-
добавки ie (поскольку при этом контур интегрирования повора-
поворачивается в противоположном направлении), в результате мы
имеем четное число знаков минус. Таким образом, нужно выяс-
выяснить только общий знак амплитуды ^(~) по отношению к ^"(+).
Знак минус, связанный с внешними концами т-функций, сокра-
сокращается с минусом в волновой функции (см. формулу A8.143)).
Поэтому, чтобы установить относительный знак f^ и fw, до-
достаточно рассмотреть диаграмму нижайшего порядка; в резуль-
результате мы устанавливаем, что амплитуды У(~> и fM имеют оди-
одинаковую фазу, что и отражено в определениях A8.138) и
A8.141). Тщательную проверку сделанных утверждений мы ос-
оставляем читателю в качестве упражнения.
') Для теории Хер* мы получаем аналогичный результат, поскольку при
подсчете общего числа знаков минус мы можем рассматривать эту теорию
как предел теории с трехлучевой связью.

282	Дисперсионные соотношения	(гл. is
Таким образом, мы показали1), что амплитуда f^ полу-
получается из ^"<+> изменением знака у ie в представлении Намбу
A8.74), т. е. переходом от верхнего берега разреза в s-плоско-
сти к нижнему2). Учитывая этот результат, применим теперь
условие унитарности A8.142) к изотопическим амплитудам
Ai(s, cos 0) с «хорошими» аналитическими свойствами. Особенно
просто выглядит условие унитарности при 4ц2 =g: s ^ 16ju2, по-
поскольку в этом случае в сумму ? в правой части A8.148) вно-
п
сят вклад только двухпионные состояния. В этой области усло-
условие унитарности сводится к нелинейному уравнению для упру-
упругой амплитуды
BjtN s \Ai (s + ie, cos Qfi) — At (s — is, cos 9f <)] =
~ k2) x
XAj(s — ie, cos Qfk) A, (s + ie, cos6w), A8.147)
где использовано свойство полноты A7.56) изотопических проек-
проекционных операторов. Множитель 1/2 в A8.147) возникает при
переходе от суммы по промежуточным состояниям к интегралу
и связан с тождественностью двух пионов с импульсами k\ и йг-
В системе центра масс
= (Vs\ 0)
cosef*-
При этом правая часть в A8.147) сводится к следующему ин-
интегралу по углам:
tm Л/ (s, cos6f,) =
1
128я2
, cosefcf), A8.148)
где подразумевается, что s имеет бесконечно малую положи-
положительную мнимую добавку. Для парциальных амплитуд A8.137)
условие унитарности сводится к
imAiM — ^sv/^-Wis)?.	A8.149)
') Местоимение «мы» в данном случае включает и читателя.
2) Отметим, что этот результат получен без использования свойства ин-
инвариантности теории при отражении времени.

§ 135]	ДИНАМИЧЕСКИЕ РАСЧЕТЫ П-Я-РАССЕЯНИЯ	283
Поэтому в упругой области амплитуда A\{s) имеет вид
Ali(s) = - 32я д/t^V" Ьхр Ш E)]} sin 6{ (s), A8.150)
где фазы b\ вещественны.
Выше порога образования 4-пионов s= 16ja2 условие унитар-
унитарности уже не имеет столь простого вида, поскольку в формуле
, ,1ms
О 4/гг
Res
Ims
Res
а)
в)
Рис. 18.33 Аналитические свойства парциальной амплитуды рассеяния: правый
разрез функции D\ (s) (а), левый разрез функции N[(s) (б).
A8.42) содержатся, наряду с упругими, также и неупругие ка-
каналы. В этом случае		_
^l^^\[\2S[(s), A8.151)
где S\ (s) — вещественный множитель, который при s <? 16ц2
равен тождественно единице. При s > 16ц2 этот множитель ра-
равен отношению полного сечения с моментом /, т. е. вкладу всех
упругих и неупругих каналов, к упругому сечению:
<&/<*>
(s)
-1,1,
Tinel'
J, I
'(s)
A8.152)
В духе дисперсионного подхода амплитуду рассеяния следует
параметризировать в терминах аналитических и слабо меняю-
меняющихся в рассматриваемой области функций. С помощью такой
параметризации можно построить теорию эффективного радиуса,
которая наилучшим образом отражает свойства аналитичности,
унитарности и кроссинг-симметрии теории. Покажем, как это
можно сделать на примере амплитуды зх — я-рассеяния вблизи
порога (рис. 18.33). Как известно, At(s) имеет точку ветвления
при s = 4(д,2, причем скачок на разрезе 4ц2 < s < оо опреде-
определяется из условия унитарности. Если нам удастся выразить
A'i (s) через функцию, не имеющую этой точки ветвления, то мы

284	ДИСПЕРСИОННЫЕ СООТНОШЕНИЯ	[ГЛ. 18
можем предсказать основные черты энергетической зависимости
амплитуды А1[ (s) вблизи порога s — 4ц2.
Фредгольмовская теория потенциального рассеяния наводит
на мысль, что для этого амплитуду следует представить в виде
отношения двух функций
<18Л53)
Числитель N'i аналитичен в s-плоскости с левым разрезом
—оо ^s^O и веществен при s > 0, в то время как функция
Dj (s), представляющая аналог детерминанта Фредгольма,1) ана-
литична всюду, за исключением правого разреза 4ц2 ^ s ^ оо, и
вещественна при вещественных s < 4ц2. Если функция N[ (s)
задана, то D^s) определяется из условия унитарности. Согласно
A8.153)
Im A\ (s) = ~ *,' ^ Im D[ (s), 5>4ц2, A8.154)
Im A\ (s)
а из A8.151) следует, что
s>4n2. A8.155)
Зная аналитические свойства функции D' (s) и выражение для
ее скачка на разрезе, мы можем выписать дисперсионное пред-
представление для D'i(s). При этом число необходимых вычитаний
определяется асимптотическим поведением N'(s) и S?\(s). В не-
нерелятивистской потенциальной теории аналог N\ (s) стремится
при s->oo к борновскому члену; в результате при s->oo
N'i (s) ->¦ 0 и D\ (s) -> 1. Если, для простоты, предположить, что
3?\{s) -> const,
то
(s) = 1 +1 $ s, Jss'_ .e ^/^P^-N't (s')S\{s'\ A8.156)
') См. [103]. Функция D называется функцией Иоста. Возможность пред-
представления A8.153) сразу становится ясной, если определить
1 Г b\(s')ds'
Тогда функция
вещественна в области 0 < s < 16ц2, т. е. ниже неупругих порогов.

§ 135]	ДИНАМИЧЕСКИЕ РАСЧЕТЫ Я-Я-РАССЕЯНИЯ	285
где использовано условие нормировки DJ (оо)=1, которое, ко-
конечно, является произвольным. Подставляя A8.156) в A8.153),
мы приходим к представлению парциальной амплитуды в виде
i^(s) =	-	 Nl {S) 	. A8.157)
s	s — s — te
4Ц.1
Следует помнить, однако, что это выражение, как и A8.156),
получено при определенных оптимистических предположениях об
асимптотическом поведении амплитуды А\. Преимущество пред-
представления A8.157) заключается в том, что оно обладает
правильными аналитическими свойствами и автоматически обес-
обеспечивает унитарность амплитуды. Для фактического же вычисле-
вычисления А\ необходимо задать функцию Nj, которая не имеет осо-
особенностей вблизи порога s = 4(х2. В качестве первого грубого
приближения можно аппроксимировать N[ вкладом простейшей
диаграммы, описывающей взаимодействие я-мезонов. Если кон-
константа связи стремится к нулю, то А\ (s)—>32яЛА/ (s); при этом
амплитуда вещественна. Представление же A8.157) подправ-
подправляет этот результат в случае произвольных констант связи, по-
поскольку оно содержит поправки, возникающие из знаменателя,
которые и обеспечивают унитарность амплитуды. Вводя фазу
рассеяния A8.150), из A8.157) получаем
;V-S ¦
J
4ц»	J
Поскольку функция N'i(s) имеет только левый разрез, можно1)
разложить правую часть этого выражения в степенной ряд вок-
вокруг точки s = 4(х2 с радиусом сходимости 4|j,2. При этом мы при-
приходим к обобщенной формуле эффективного радиуса.
Чтобы получить более точный результат, нужно задать до-
дополнительную информацию о числителе Nt (s). На левом раз-
разрезе существует множество особых точек, отвечающих различ-
различным редуцированным графикам и сингулярностям Ландау. Од-
Однако точно так же, как низкоэнергетическая часть правого
разреза отвечает простому одномерному графику, указанному на
') См. задачу 10 этой главы.

286
ДИСПЕРСИОННЫЕ СООТНОШЕНИЯ
[ГЛ. 18
рис. 18.34, а, низкоэнергетическая часть левого разреза обуслов-
обусловлена соответствующими кроссинговыми диаграммами (см.
рис. 18.34,6). Скачки указанных особенностей можно получить,
рассматривая аналитически продолженное соотношение упру-
упругой унитарности в t- и м-каналах. Эти скачки вновь выражаются
через амплитуду упругого я — п-рассеяния, поэтому, в предпо-
предположении, что указанные особенности играют доминирующую
а)
\ /
11
Ij
к
/
U
Рис. 18.34. Одномерные редуцированные диаграммы в я — я-рассеянии.
роль, мы получаем замкнутую систему интегральных уравнений
для вычисления А\ (s). Несмотря на то, что решение этих урав-
уравнений неоднократно обсуждалось в литературе, еще раз под-
подчеркнем, что приближение, в котором учитываются особенности,
отвечающие только графикам рис. 18.34, не может считаться
удовлетворительным. Асимптотическое поведение амплитуды,
равно как ее вид в достаточно удаленной от порога области на
левом разрезе, остаются полностью неопределенными. Любое
рассмотрение здесь связано с необходимостью проводить вычис-
вычисления в глубоко нефизической области, где математические ме-
методы становятся ненадежными, а качественные аргументы —не-
—неприменимыми.

$ 136]	ЭЛЕКТРОМАГНИТНАЯ СТРУКТУРА ПИОНА	287
Из A8.157) вытекает возможность существования связанных
состояний или резонансов, которые определяются поведением
функций D'i(s). Если D'i(s) такова, что ReZ)/(Si?) = 0 в некото-
некоторой точке s = sR > 4ц2, то фаза 6; проходит в этой точке через
90°, и мы имеем резонанс. Если же D/(s) = 0 при s < 4ц2, то
амплитуда Ai (s) имеет полюс, отвечающий связанному состоя-
состоянию. Динамические вычисления я — п-амплитуды, если они от-
отвечают действительности, должны, очевидно, приводить к пер-
первой возможности, т. е. к существованию р-волнового резонанса,
сопоставляемого р-мезону.
§ 136. Электромагнитная структура пиона
Описанный выше подход может быть использован также для
вычисления электромагнитного форм-фактора пиона [104, 105].
Как было показано в § 131, особенности Fxiq2) при q2 <С 16(х2
определяются только редуцированными диаграммами, указан-
указанными на рис. 18.35. Эти диаграммы сводятся к произведению
Im
*4
¦* >
Рис. 18.35. Электромагнитная вершина пиона.
электромагнитной вершины пиона и амплитуды я — я-рассея-
ния. Используя условие унитарности, можно получить соответ-
соответствующее аналитическое выражение, необходимое для последую-
последующего вычисления форм-фактора пиона.
В § 131 были установлены аналитические свойства Fn(q2),
которые использовались затем при обсуждении дисперсионных
соотношений для амплитуды it — п-рассеяния на нулевой угол.
Напомним, что в Fn(q2) отсутствует левый разрез и единствен-
единственной его сингулярностью является правый разрез от 4|х2 до оо.
Повторяя теперь для вершинной функции выкладки, проделан-
проделанные в § 133 (см. A8.136) —A8.142)), получим
К+) = <"+ (9+) "" (?-) out | V (?) I 0) =
-М2^-^=Ь)

288	ДИСПЕРСИОННЫЕ СООТНОШЕНИЯ	[ГЛ. 18
где1) йЛд(х) = е/ц(*)> /ц(<7)-~Фурье-компонента тока /ц(*) и
кинематика указана на рис. 18.35. Ниже порога вершина равна
in 1
Условие унитарности имеет вид
{f out | /д| 0) - (f in | /; | 0) = - Z [<f in | n out) - flf„] (n out | /^ 10).
A8.161)
Если в Yj ограничиться вкладом п+ — п~-состояний и перейти
п
в систему центра масс двух пионов, то из A8.141) и A8.159)
получаем
= — * J d3k+d3k_ BixL б4 (q - k+ - k_) X
X (~ i)f\~n\k+ - k_fFn(q2+ie). A8.162)
После интегрирования по углам правая часть в A8.162) содер-
содержит только р-волновую амплитуду. Эта амплитуда отвечает чи-
чистому изотопическому спину I = \, как это следует из стати-
статистики Бозе для пионов. Выделим в A8.136) член с /= 1 и уч-
учтем, что
<я+хГ|Р,|я+я->=1/2
(см. A7.54)); тогда, умножив A8.162) на пространственно-по-
пространственно-подобный вектор поляризации е*1 = @, е), получаем
cos 9 Im Ря (д2) =
qA	I I VX-TT" ~ ~ * \7	' ~	~ I It/	if di\7	i *" / • \*O. l\JXJj
В формуле A8.163)
R =
После интегрирования по углам получаем
= {ехр[- /б! (^2)]} sin 6l (q2) Fn (q2 + is). A8.164)
1( Поскольку мы рассматриваем первый порядок по электромагнитной
связи, то е ~ е0 и Z3 = 1

136]
ЭЛЕКТРОМАГНИТНАЯ СТРУКТУРА ПИОНА
289
Это простое выражение и представляет собой аналитическую
запись графического соотношения, указанного на рис. 18.35. По-
Поскольку Im Fn(q2) вещественна, то из A8.164) следует, что
Fn (q2 -j- te) имеет ту же фазу, что и р-волновая амплитуда
я — я-рассеяния. Этот результат известен в теории потенциаль-
потенциального рассеяния как теорема о взаимодействии в конечном со-
состоянии [106].
Формула для скачка A8.164) вместе с дисперсионными со-
соотношениями A8.72) позволяют определить Fn(q2). При этом
решение [107—109] удовлетворяет следующим условиям:
1) функция Fn(q2) аналитична в плоскости q2 с правым раз-
разрезом оо ^ q2 42
2)	при q2
3)	при q2
4)	М0)
4ц2;
4(х2 фаза Fn(q2) равна б';
4(x2 функция FK(q2) вещественна;
1
В § 135 мы построили функцию l/D\(q2), удовлетворяющую
условиям 1—3. Поэтому решение для Fn(q2) дается, с точностью
до полинома P(q2) с вещественными коэффициентами, в терми-
терминах этой функции:
Z)j(O)
P(q2)
D\(q2) P@)
P(q2)
A8.165)
Более удобное представление для Fn, не зависящее от произвола
в выборе N\ (s), получается, если выразить Fn непосредственно
через фазу б} (^2). Действительно, так как
+ '») = ехо Г2;б|
— )рЛ ехР LZ*01
то скачок In Fn (q2) равен б! (q ). Поэтому функция
4Aг
A8.166)
A8.167)
имеет по крайней мере ту же область аналитичности, что и
Fn (q2). Далее, Р вещественна при q2 > 4|x2, и поэтому сводится
к целой функции. Поскольку мы не рассматриваем случай, когда

'290	ДИСПЕРСИОННЫЕ СООТНОШЕНИЯ	[ГЛ. 18
на бесконечности имеется существенно особая точка, P(q2) пред-
представляет собой полином [ПО]. Поэтому при условии
б' (q2)/q2 -»¦ 0 при q2-+oo
форм-фактор Fn{q2) равен
^]*^]	08..68,
Снова подчеркнем, что выражения A8.165) и A8.168) спра-
справедливы лишь в той степени, в какой можно пренебречь вкла-
вкладом масс q2 ^ 16jj,2 в условие унитарности. В результате мы по-
получили выражение, которое в лучшем случае может иметь тот
же смысл и ту же область применимости, что и формулы теории
эффективного радиуса. Отметим, что выражение A8.168) можно
рассматривать как точное, если допустить, что функция P(q2)
имеет разрез 16ц2^72^°°- В результате Fn(q2) выражается
через фазу1) b\(q2) и неизвестную функцию P(q2), которая, как
мы надеемся, плавно меняется в области q2 ^ 16(х2. Полученное
выражение имеет простой вид и его можно непосредственно
сравнить с экспериментом, хотя мы по-прежнему не можем обос-
обосновать сделанные предположения. В частности, A8.168) и
A8.165) предсказывают пик в Fn(q2) в области энергий л/q2,
близких к экспериментально наблюдаемому р-волновому я — я-
резонансу (р-мезону). Экспериментальная проверка этого ре-
результата представляет большой интерес.
Техника, описанная выше, может быть применена также и
для изучения электромагнитных форм-факторов нуклонов. Мы
не будем здесь обсуждать эти вопросы и рекомендуем интере-
интересующемуся читателю обратиться к специальной литературе [1111.
ЗАДАЧИ
1. Показать, что детерминант Д для произвольной фейнмановской диа-
диаграммы может быть записан в виде
где сумма берется по всем наборам S, состоящих из k внутренних линий /
(где k — число независимых внутренних импульсов, по которым производится
') При q ^ 16ц фазу б[ можно определить разными способами, на-
например
еШ	1	,л
А =	^	 или А = це sin й. г\ вещественно.
Конкретный выбор представления для фазы — дело вкуса.

ЗАДАЧИ	291
интегрирование), которые обладают следующим свойством: при исключении
внутренних линий / е S график остается связанным. Этот результат показы-
показывает, что Д > 0 до тех пор, пока хотя бы одно а/ ф 0.
2. Показать, что в представлении Намбу A8.74)
где S' — всевозможные совокупности контуров, содержащих k + 1 внутрен-
внутреннюю линию (в то время как Д представляет сумму различных произведений k
множителей а,), таких, что исключение линии isS' приводит к двум и
только двум несвязанным графикам, один из которых содержит внешние ли-
линии р\ и рч, а другой ръ и pi. Этот результат показывает, что ?i > 0, как и
предположено в наших рассуждениях после формулы A8.75).
3.	Доказать, что амплитуда я — я-рассеяния A(s,t) во всех порядках
теории возмущений не имеет особенностей при s < 4|х2, / < 4|х2 и и < 4|х2, и
тем самым установить дисперсионные соотношения по s при фиксированном
0 < / < 4ц2.
4.	Тщательно проанализировать утверждения, сделанные после формулы
A8.91) и устанавливающие аналитичность амплитуды пион-нуклонного рас-
рассеяния вперед во всех порядках теории возмущений.
5.	Вывести дисперсионные соотношения для амплитуды я+ — р-рассея-
ния вперед с переворотом спина. Обсудить, как можно измерить абсорптив-
ную часть этой амплитуды.
6.	Доказать дисперсионные соотношения для амплитуды К+ — р-рассея-
ния на нулевой угол. Какие величины, помимо амплитуды рассеяния в физиче-
физической области и полных сечений, следует задать, чтобы экспериментально про-
проверить эти соотношения?
7.	Рассмотреть аксиальный векторный ток /"„ в (З-распаде нуклона (см.
A0.151)). Предполагая, что дивергенция тока удовлетворяет дисперсионному
соотношению без вычитаний, вывести соотношения Гольдбергера — Треймана
A0.161).
8.	Показать, не прибегая к анализу диаграмм теории возмущений, что
форм-фактор пиона Fn(q2) веществен при q2 < 0 (если пренебречь слабыми
взаимодействиями).
9.	Найти точки ветвления для электромагнитного форм-фактора 2-гипе-
рона.
10. Используя дисперсионные соотношения для N^is), вывести формулу
теории эффективного радиуса, которая обсуждалась после формулы A8.158).
Аппроксимируя Л/q полюсом, вычислить Aq (s) и параметры разложения эф-
эффективного радиуса.

ГЛАВА 19
ПЕРЕНОРМИРОВКИ
§ 137. Введение
В гл. 8 при вычислениях в низших порядках теории возмуще-
возмущений мы выделили расходимости в диаграммах, отвечающих соб-
собственной энергии и вершинной части, и показали, как, перенор-
перенормируя заряд и массу электрона, можно выделить из этих
диаграмм конечные выражения. При этом в приближении е2 раз-
разность между экспериментально определяемыми зарядом и мас-
массой электрона и их затравочными значениями в уравнениях дви-
движения равна бесконечности, в то время как физические вели-
величины, выраженные в терминах перенормированных заряда и
массы, оказываются конечными.
Как мы убедились на примере вычислений гл. 8, перенорми-
перенормировка необходима в любой физической теории взаимодействия
полей. Единственное требование, налагаемое на физически ра-
разумную теорию, заключается в том, чтобы после перенормировки
5-матрица была конечной.
В дальнейшем мы предположим, что ряд теории возмущений
для 5-матрицы сходится и 5-матрица конечна в каждом порядке
разложения по степеням константы связи. При этом возникает
другая важная проблема, а именно, проблема доказательства
сходимости перенормированного ряда теории возмущений. Мы,
однако, не будем здесь обсуждать этот вопрос и сосредоточим
усилия на том, чтобы показать, что все зависящие от обрезания
множители, появляющиеся в разложениях т-функций и 5-мат-
5-матрицы, можно выделить в константы перенормировки. Наше рас-
рассмотрение основано на использовании методов теории возмуще-
возмущений и фейнмановских правил, выведенных в гл. 17, а также
общих свойствах перенормировочных констант 22 и Z3, обсуждав-
обсуждавшихся в гл. 16. В качестве применения полученных результатов
мы рассмотрим в конце этой главы квантовую электродинамику
электронов и фотонов.

§ 138]	СВОЙСТВА ДИАГРАММ СОБСТВЕННОЙ ЭНЕРГИИ	293
Программа '), которую предстоит выполнить, состоит из трех
частей. Вначале мы обсудим различные диаграммы с топологи-
топологической точки зрения и введем терминологию, удобную при клас-
классификации и анализе произвольных фейнмановских диаграмм.
Далее будет дан рецепт перенормировки произвольной диаграм-
диаграммы «-го порядка. Наконец, мы по индукции покажем, что этот
рецепт позволяет устранить все расходящиеся (т. е. зависящие
от обрезания) величины2) из разложения 5-матрицы.
§ 138. Свойства диаграмм собственной энергии
и вершинных частей и электрон-позитронное ядро
Начнем с установления в общем случае соответствия между
константами перенормировки Zb Z2, Z3, 8m и фейнмановскими
графиками, которое в приближении е2 было найдено в первом
томе. Напомним, что константы Z2 и Ьт относятся к диаграмме
собственной энергии (рис. 19.1, a), Z3 появляется при вычислении
а)	б)
Рис. 19.1. Диаграммы второго порядка для собственной энергии электрона (а),
поляризации вакуума (б) и вершинной части (в).
поляризации вакуума (рис.19.1, б), a Z\— при вычислении вер-
вершинной части (рис. 19.1, в). Все эти величины в приближении е2
логарифмически расходятся, фактическое их вычисление в этом
порядке было дано в гл. 8.
Диаграмма рис. 19.1, а появляется при разложении электрон-
электронного пропагатора
iS'P (х - х') = <0 | Т (г|э (х) ф (х')) | 0>,	A9.1)
который изображается заштрихованным блоком на рис. 19.2 и
представляет сумму всех связанных графиков с двумя внеш-
внешними электронными линиями, одна из которых входит в точке х,
а другая выходит в точке х'\ эти графики не содержат внешних
фотонных линий. Структура функции S'f подробно обсуждалась
в гл. 16. Все графики, содержащиеся в S'F, можно однозначно
') Эта программа, вывод соответствующих уравнений и формулировка
критерия перенормируемости теории были впервые даны в статьях [65, 66,. 112].
2) Инфракрасные особенности при этом следует рассматривать отдельно
(см. [77]).

294	ПЕРЕНОРМИРОВКИ	[ГЛ. 19
разделить на два класса, первый из которых содержит компакт-
компактные, а второй — некомпактные диаграммы. Компактные диаграм-
диаграммы нельзя разделить на две не связанные между собой части
путем рассечения по одной фермионной линии, в то время как
для некомпактных диаграмм та-
такое разделение возможно. Приме-
Примеры компактных и некомпактных
„тот.	ч диаграмм показаны на рис. 19.3, а
Рис. 19.2. Точный электронный е v
пропагатор	и б соответственно.
Перейдем в импульсное про-
пространство и обозначим через
—1'2 (р) сумму всех возможных компактных диаграмм1), выде-
выделив при этом множители iSF(p) = i(p — от), отвечающие внеш-
а)	ф
Рис. 19.3 Примеры компактных (а) и некомпактных (б) электронных соб-
собственно-энергетических диаграмм
ним концам. Выражение, связывающее S'f{p) и 2(р), имеет вид
iS'P (р) = iS, (p) + iSF (p) [- CL (р)\ iSF (p) +
+ iSF (р) [- /2 (р)] iSF (р) [- а {р)\ iSF (p) + ... A9.2)
Графически это уравнение изображено на рис. 19.4. Формально
суммируя ряд A9.2), получаем
A9.3)
') Приведенное здесь определение S(p) отличается от определения в гл. 8
включением массового контрчлена 6т. В первом томе мы разлагали SF в
терминах голых пропагаторов (fi — /no)~\ в то время как в этой главе мы
используем пропагатор (/3 — /п)-1, отвечающий частице с физическим значе-
значением массы т.

138]
СВОЙСТВА ДИАГРАММ СОБСТВЕННОЙ ЭНЕРГИИ
295
где величина Ъ{р), сумма всех компактных собственно-энерге-
собственно-энергетических диаграмм с исключенными внешними линиями
(рис. 19.5), называется массовым оператором электрона.
= iSF
iSF[-iZ]iSF
iSF[-HjiSF[-H]iSF
Рис. 19.4. Графическое изображение ряда A9.2) для электронного пропагатора,
который представляет сумму компактных собственно-энергетических вставок.
Аналогичным образом рассмотрим фотонный пропагатор.
Диаграмма рис. 19.1, б содержится в разложении точного фо-
фотонного пропагатора
Юр (х - хТ = @1Т (л* (х) Av (Л) I 0) +
+ градиентные и кулоновские члены, A9.4)
который представляет сумму всех связанных диаграмм с двумя
внешними фотонными линиями и не содержит внешних элек-
Рис. 19.6. Точный фотонный пропа-
пропагатор.
Рис. 19.5. Электронная компакт-
компактная собственно-энергетическая
часть (массовый оператор 2).
тронных линий. Функция D'f может быть представлена заштри-
заштрихованным блоком на рис. 19.6.
Как и в случае электрона, можно снова выделить компакт-
компактную часть, к которой относятся те графики, которые нельзя раз-
»/v\/4/4 e/"v/'v\/« •'"v/'vyv* '\/v4 «/w{ k/N/\jf	«/4/^j
а)	Ф
Рис. 19.7. Примеры компактных (а) и некомпактных (б) фотонных	собственно-
энергетических диаграмм.
Делить на две несвязанные части путем рассечения	по одной
фотонной линии. Некоторые компактные диаграммы	показаны
на рис. 19.7, а, примеры некомпактных диаграмм	даны на

296	ПЕРЕНОРМИРОВКИ	1ГЛ. 19
рис. 19.7,6. Сумму всех компактных диаграмм, из которых вы-
выделены внешние фотонные линии, обозначим через ie^l^, эта
.величина называется фотонной собственно-энергетической ча-
частью. Тензор nuv по своему смыслу аналогичен массовому опе-
оператору 2 (р); в гл. 8 тмы называли его также тензором вакуум-
вакуумной поляризации. По аналогии с A9.2) можно установить связь
точного фотонного пропагатора с nuV (рис. 19.8):
A9.5)
Как известно, Df (q)^ в A6.172) включает также члены, содер-
содержащие т)|л — времениподобный вектор, который напоминает нам
Рис. 19.8. Разложение A9.5) для фотонного пропагатора в виде суммы ком-
компактных собственно-энергетических частей И^ (известных также под назва-
названием тензора вакуумной поляризации)
об использовании поперечной калибровки в той системе, в кото-
которой выполняется квантование. Воспользовавшись, однако, ре-
результатами § 122, можно опустить члены, содержащие q^v,
ЦуУ\ч, q^Qv, поскольку мы знаем, что эти члены не вносят вклад
в S-матричные элементы. Формально суммируя ряд A9.5), по-
получаем
Df foVv = - -^ + |- IV (q) D'P (qfv
и по аналогии с A9.3)
(У^ - *оЧ* Щ D'F (д% = - ^v.	A9.6)
Наконец, третья величина, которая уже встречалась при вы-
выполнении перенормировки во втором порядке теории возмуще-
возмущений, есть треххвостка, рис. 19.1, в, связанная с константой Z\.
Снова определим компактную треххвостку, которую будем назы-
называть также вершинной частью, как сумму всех связанных диа-
диаграмм с двумя внешними фермионными линиями и одной внеш-
внешней фотонной линией, которые компактны в указанном выше
смысле, т. е. не могут быть разделены на несвязанные диа-
диаграммы рассечением либо по электронной, либо по фотонной

S 138]
СВОЙСТВА ДИАГРАММ СОБСТВЕННОЙ ЭНЕРГИИ
297
линиям. Примеры компактных и некомпактных треххвосток изо-
изображены на рис. 19.9, а и б соответственно. Из этих примеров
ясно, что вставка во внешних линиях вершинной части электрон-
электронной или фотонной собственно-энергетических частей превращает
компактную вершинную диаграмму в некомпактную. Обозначим
а)	6)
Рис. 19.9 Примеры компактных (а) и некомпактных (б) вершинных диаграмм.
сумму всех вершинных частей в импульсном пространстве через
Ги(р', р), где р и р' — 4-импульсы входящего и выходящего элек-
электронов. Отметим, что в определение Г^(р', р) не включены про-
пагаторы внешних электронных и фотонных линий, а также мно-
множитель —ie0. Таким образом, вершинная часть определена так,
что в первом порядке Гц(р', р) = у11, в общем же случае
', p).
A9.7)
При рассмотрении ренормализационной программы необхо-
необходимо ввести дополнительную величину, которая не возникает

298
ПЕРЕНОРМИРОВКИ
[ГЛ. 19
при вычислениях с точностью е2. Эту величину мы будем назы-
называть электрон-позитронным ядром, или, для краткости, просто
ядром. Графически ядро изображено на рис. 19.10, обозначим
его через
А' (Р, Р'> Я)а$,чЬ-
К состоит из диаграмм с двумя внешними электронными и
двумя внешними позитронными линиями; —р и р' есть импульсы
p'-q
позитрона и электрона в на-
начальном состояниях, q — пере-
переданный электрону импульс, а а,
Р, у и б — спинорные компонен-
компоненты, указанные на рис. 19.10. В
ядро К включены все четырех-
хвостки, изображенные на
рис. 19.10, за исключением гра-
графиков двух типов. Мы не вклю-
включили в К графики, в которых две внешние линии (р, а) и (//, р)
объединяются в блок А, а две другие внешние линии (р — q, у)
и (// — q, 8) объединяются в блок В, причем блоки А и В
Рис. 19.10. Ядро К электрон-пози-
тронного рассеяния.
Рис. 19.11. Два класса диаграмм, исключенных из определения ядра К-
Р
Рис. 19.12. Несвязанные собственно-энергетические части, исключенные из
определения ядра К-
соединяются только одной фотонной линией или электрон-пози-
тронной парой (рис. 19.11). Точно так же исключаются диаграм-
диаграммы, изображенные на рис. 19.12, состоящие из двух несвязан-
несвязанных собственно-энергетических частей. На рис. 19.13 приведены
некоторые диаграммы, которые включены в К. В низшем порядке

§ 139]	ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
ядро К сводится к диаграмме рис. 19.13, а
(Р, Р\
3. Ye
299
A9.8)
По аналогии с S, П^ и Гц, из определения К исключаются
пропагаторы внешних фермионных линий, при этом не нужно
Р'
Р	Р-?
а)
Р'
Р'-<Г
6)
Р-?
p-q
Рис. 19,13. Примеры диаграмм, содержащихся в ядре К.
также,учитывать собственных частей в свободных концах диа-
диаграммы.
§ 139. Интегральные уравнения
для собственно-энергетической и вершинной частей
В предыдущем параграфе мы определили величины S, П^
и Гц. Выпишем теперь интегральные уравнения, связывающие
эти величины друг с другом. Например, компактная электрон-
электронная собственно-энергетическая часть удовлетворяет интеграль-
интегральному уравнению, которое графически изображено на рис. 19.14,
- /2 (р) = (- teg)
Г (р, p-k) iS'P (p - k) Yv. A9.9)
Это уравнение описывает образование в вершине v электрона
и фотона, которые, прежде чем фотон поглощается в вершине \к,
взаимодействуют всеми возможными способами. Отметим, что
поскольку A9.9) содержит точные функции Грина электрона
и фотона, Tv в этом уравнении должно быть сопоставлено вер-
вершинной части, а не полной вершинной функций, в противном

300	ПЕРЕНОРМИРОВКИ	[ГЛ. 19
случае, например, диаграмма рис. 19 15 учитывалась бы
дважды.
Фотонная компактная собственно-энергетическая часть удов-
удовлетворяет уравнению, аналогичному A9.9). Это уравнение
Рис. 19.14. Графическое представление A9.9) для компактной электронной
собственно-энергетической части 2()
графически изображено на рис. 19.16:
SpY^Wr^fc, k + q)-iS'F(k + q). A9.10)
Если бы вершинная часть Гц была известна, уравнения
A9.9) и A9.10) совместно с уравнениями A9.3) и A9.6) для
S'f и D'f образовывали бы замкнутую
систему нелинейных интегральных
*	уравнений, которую можно было бы
решать, например, методом итерации
Рис. 19.15 Вклад в s (р) по степеням константы е\. Оказы-
Оказывается, что для Ги можно выписать
дополнительное интегральное уравнение, ядром которого яв-
является введенная выше функция К:
. Я) +
X КаЪ_ хк (р + 92, / + 92, 72 - 9,) ^ (Р' + 9,)ал X
/p + «71)Kp/C№Ye(p + ^1, p' + qv qt)+ ... A9.11)
Y А (Р + ^2)]ра X
Графически это уравнение изображено на рис. 19.17. В даль-
дальнейшем мы часто будем использовать сокращенную запись
Г = y ~ J ySiS'pK + J J ySpS'pKS'pS'pK + ...

139]
ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
301
Это выражение описывает превращение внешнего фотона в элек-
трон-позитронную пару, которая перерассеивается всеми воз-
возможными способами. При этом каждому члену в разложении
Рис. 19.16- Уравнение A9.10) для фотонной компактной собственно-энергети-
собственно-энергетической части ~
A9.11) отвечает различное число виртуальных электрон-пози-
тронных пар. Ряд A9.11) может быть формально просуммиро-
просуммирован1) точно так же, как борновский ряд в теории нерелятивист-
Рис. 19.17 Последовательные члены в ряду A9.11) для вершины Гц, выра-
выражающиеся в терминах ядра К-
ского потенциального рассеяния суммируется в интегральное
уравнение Липпмана — Швингера. В результате получаем
') Этот ряд аналогичен ряду многократного перерассеяния для функции
Грина, полученному в гл. 6. Соответствующее уравнение, которое связывает
полную электрон-позитронную амплитуду вне массовой пооверхности Т с яд-
ядром К, имеет вид
- Ц = К + \ K'SpiSpK + \ KiSpiSpKtSpiSpK +...==
и называется уравнением Бете —Солпитера. Оно представляет релятивистский
аналог интегральной формы двухчастичного уравнения Шредингера, при этом
величина iK аналогична потенциалу V (см. [113]).

302	ПЕРЕНОРМИРОВКИ	[ГЛ. 19
(рис. 19.18)
J J&	' Р + q) iS'p {P + q)\° X
fsyu q,p' + q,q) A9.12)
или в символической форме
Г = y
Естественно задать вопрос, в чем заключается польза полу-
полученных интегральных уравнений. С точки зрения практических
Рис. 19.18. Интегральное уравнение A9.12) для вершинной части.
вычислений мы достигли немногого—выразили неизвестные вели-
величины S'f, D'f и Гц через неизвестное же ядро К. Однако с точки
зрения метода перенормировок связь S'P, D'f и Гц с К чрезвы-
чрезвычайно полезна. Причина этого заключается в том, что расходи-
расходимости в ядре К возникают только из-за собственно-энергетиче-
собственно-энергетических и вершинных вставок во внутренних линиях; позднее мы
обсудим этот пункт более подробно. Поэтому перенормировка
ядра К выполняется относительно легко, а обсуждение более
сложных вопросов об устранении расходимостей в S, П^ и Гц
облегчается, если использовать интегральные уравнения, свя-
связывающие каждую из этих величин с ядром К-
§ 140. Интегральные уравнения для т-функций
и ядра К; скелетные графики
Центральную роль в программе устранения расходимостей
играют функции 2, nuv и Г^, введенные в §§ 138, 139. Все
остальные величины в теории: 5-матричные элементы, т-функ-
ции и, в частности, ядро К — выражаются через эти три вели-
величины, точнее, через S'f, D'f и Ги. Однако для т и К не существует
замкнутых уравнений, аналогичных тем, которые были рассмот-
рассмотрены в предыдущем параграфе. Вместо этого мы соберем вместе
диаграммы, дающие вклад в т и К, которые различаются
только собственно-энергетическими и вершинными вставками;

§ 140]
ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ ДЛЯ Т-ФУНКЦИЙ И ЯДРА К
303
эти вставки существенны при получении конечных ответов
в теории.
Рис. 19.19. Пример произвольной диаграммы, на которой каждая собственно-
энергетическая и вершинная вставки окружены ящиками.
Вначале рассмотрим графики, которые содержатся в ядре К,
и выделим в каждом из них собственно-энергетические и вер-
вершинные вставки. С этими вставками легче всего разобраться,
если заключить каждую из них в
ящик, как это показано на рис. 19.19.
Из этого рисунка заключаем, что
ящики, содержащие внутри себя
различного рода вставки, либо пол-
полностью разделены, либо заключены
один внутри другого с единственным
исключением: в случае собственно-
энергетических вставок ящики могут
перекрываться. Указанное тополо-
топологическое свойство оказывается спра-
справедливым и для произвольных диаграмм: ящики, содержащие
вершинные и собственно-энергетические вставки, могут быть все-
всегда выбраны таким образом, чтобы они не пересекались, за ис-
исключением случая вершинных вставок в собственно-энергетиче-
Рис 19.20. Скелетная диаграм-
диаграмма, отвечающая диаграмме
рис. 19.19.

304
ПЕРЕНОРМИРОВКИ
{ГЛ. 19
ские части. Доказательство этого утверждения мы приведем
в§ 141.
Используя сформулированный результат, можно однозначно
сопоставить каждому графику 2?, содержащемуся в К, другой
Рис. 19.21. Отдельные члены в разложении A9.13) для ядра К-
график S, который будем называть скелетным. Скелетные диа-
диаграммы получаются стягиванием всех ящиков, содержащих
внутри себя собственно-энергетические и вершинные вставки,
в точку; другими словами, эти диаграммы не содержат указан-
указанных вставок вообще. На рис. 19.20 изображен скелетный гра-
график, отвечающий диаграмме 19.19. Наоборот, любой график,
входящий в К, можно построить из соответствующего скелетного

НО]
ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ ДЛЯ t-ФУНКНИП И ЯДРА К
305
графика, вводя в последний различного рода вершинные и соб-
собственно-энергетические вставки.
Обозначив через Ks (p,p',q; SF, DP, y^, e0) вклад тех фейнма-
новских диаграмм &, которые совпадают со своими скелетными,
мы можем записать полное ядро К в виде суммы по всем ске-
скелетным графикам, в которой, однако, каждой электронной и фо-
фотонной линиям нужно сопоставить точные функции Грина
Sf и Df, а каждой вершине — точную вершинную функцию Гд:
(р, р', Я) —
, V»
f> Df,
^, е0) —
A9.13)
Графическая запись уравнения A9.13) представлена на
рис. 19.21. Отметим, что скелетные графики, изображенные на
рис. 19.22, не включены в
разложение для ядра К, по-
поскольку эти графики мож-
можно разделить на две части,
соединенные либо фотонной
линией, либо электрон-пози-
тронной парой, и они в соот-
соответствии с определением,
сформулированным в § 138,
не содержатся в указанном
разложении.
Для того чтобы убедить-
убедиться в справедливости разло-
разложения A9.33), достаточно
заметить, что любой гра-
график &, содержащийся в К,
появляется в разложении по
скелетным диаграммам один
и только один раз, поскольку, во-первых, соответствующий $?
скелетный график S определен однозначно и, во-вторых, в
графическом разложении К существует одна и только одна
диаграмма, отвечающая &. Последнее утверждение есть след-
следствие того обстоятельства, что вершинные и собственно-энерге-
собственно-энергетические вставки в диаграммы можно определить однозначным
образом.
Скелетные разложения для произвольных т-функций (вклю-
(включая пропагаторы и собственно-энергетические части) могут быть
получены тем же способом, что и в случае ядра К. Для т-функ-
ции с т внешними фермионными концами и п внешними
Рис. 19.22. Скелетные диаграммы, не
включенные в разложение для К на
рис. 19.21

306
ПЕРЕНОРМИРОВКИ
[ГЛ.
фотонами в импульсном пространстве имеем
f(Pl ••• Рт, Я\ ••¦ <7п)а, ...ат, ц, ...Ц„ =
= I т8 (р, ... рт, q, . .. дп; S'F, D'F, Г, е,)^ ___ ^^ __ ^
т + «>3,	A9.14)
где ts (pi... рт, <7i • • • <7«; 5/г, D/r, Г, е0) — вклад в т-функцию тех
феинмановских диаграмм, которые отвечают данному скелет-
скелетному графику S.
Рис. 19.23. Разложение A9.15) для вершины Г^.
Нетрудно выписать также скелетное разложение для вер-
вершины Гц ')
Гц (//, Р) = Уц + I K(P, Pi Sf, d'f, Гц, во), A9.15)
S
которое графически изображено на рис. 19.23.
') Здесь подразумевается, что когда мы рисуем ящики, окружающие
внутренние вершинные части, ящик, окружающий полную вершину, должен
быть опущен.

141]
ТОПОЛОГИЧЕСКАЯ ТЕОРЕМА
307
Для собственно-энергетических частей скелетное разложение
оказывается не столь полезным ввиду существования перекры-
перекрывающихся расходимостей. Напри-
Например, для диаграммы, изображен-
изображенной на рис. 19.24, радиационные
поправки сводятся к вершинной
поправке либо к блоку А, либо
к блоку В (но не к обоим бло-
блокам вместе). Поэтому полную
собственно-энергетическую часть
нельзя однозначно построить, ис-
ходя из скелетных диаграмм1).
Эту трудность, однако, можно
обойти, рассматривая вместо ске-
скелетного разложения непосредственно
A9.10) для IV
А
Рис. 19.24. Пример перекрываю-
перекрывающихся собственно-энергетической
и вершинной вставок.
интегральное уравнение
§ 141. Топологическая теорема
При рассмотрении в предыдущем параграфе собственно-
энергетических и вершинных вставок мы установили, что окру-
окружающие их ящики могут быть нарисованы таким образом, что
они не перекрываются во всех
случаях за исключением вер-
вершинных вставок в собственно-
энергетические части. Тот факт,
что ящики, окружающие соб-
собственно-энергетические встав-
вставки, либо полностью разделены,
либо лежат один внутри дру-
другого, но никогда не перекры-
перекрываются, является самоочевид-
самоочевидным. Прежде чем в общем слу-
случае показать, что вершинные
вставки могут перекрываться только тогда, когда они содер-
содержатся внутри собственно-энергетических блоков, рассмотрим
простой пример, иллюстрированный рис. 19.25. Стенки каж-
каждого ящика, содержащего вершинную вставку, по определению
пересекают только две электронные и одна фотонная линия.
Предположим, что на рисунке указаны все линии, пересекаю-
пересекающие неперекрывающиеся стенки; тогда остальные линии можно
нарисовать так, как это показано на рис. 19.26, а. При этом,
Рис. 19.25
Пример
вставки.
вершинной
') Единственными скелетными диаграммами, содержащимися в
являются диаграммы второго порядка.
и 2,

308
ПЕРЕНОРМИРОВКИ
[ГЛ. 19
однако, мы получаем несвязанные собственно-энергетические и
вершинные части (рис. 19.26,6).
Покажем теперь, что вершинные части перекрываются
только внутри собственно-энергетических вставок. С этой целью
прямым графическим построением мы убедимся в том, что
можно последовательно устранить перекрытие между вставками
во всех остальных случаях. Соответствующее графическое по-
построение выполнено на рис. 19.27 для всех случаев, кроме тех,
f
а)
Рис. 19.26. Попытка нарисовать перекрывающиеся вершинные вставки внутри
вершинной части диаграммы приводит либо к несвязанной собственно-энерге-
собственно-энергетической вставке (а), либо к несвязанной вершинной вставке (б). Переста-
Перестановка фотонной и входящей электронной линий приводит к аналогичному
результату.
которые уже рассматривались в примере рис. 19.26. Ящики, во-
вообще не содержащие линий, проходящих через неперекрываю-
неперекрывающиеся части, либо содержащие одну такую линию, невозможны,
а собственно-энергетические ящики, содержащие две такие ли-
линии, рассматривать не следует.
§ 142. Тождество Уорда
При устранении расходимостей в квантовой электродинамике
важную роль играет обобщенное тождество Уорда [114—115],
которое позволяет связать Sf непосредственно с Гц. Это тож-
тождество является непосредственным следствием дифференциаль-
дифференциальной формы закона сохранения тока и утверждает, что
(pf - р^ I* {f/, p)
A9.16)
Очевидно, что голая вершина Yn и свободный пропагатор-
SF(p) = (р— т)~1 удовлетворяют A9.16), поэтому, используя
A9.3) и A9.7), это выражение можно переписать в виде соот-

142]
ТОЖДЕСТВО УОРДА
309
-*—
v/W/ЧУ
-»—
ч/V/W
1
-К
J
ч
Рис 19.27. Перечень диаграмм, показывающий, как можно избежать расхо-
димостей во всех случаях, за исключением случая вершинных вставок внутри
собственно-энергетических частей (рис. 19.24).

310
ПЕРЕНОРМИРОВКИ
[ГЛ. 19
ношения между вершинной частью и компактной собственно-
энергетической частью:
Ъ(р)].	A9.17)
Смысл этого выражения заключается в том, что Лц(//, р)
можно получить из —2(р), добавляя вершину уц (с передан-
Р-*
¦*— р
¦ГУ
Рис. 19.28. Фотонные вставки в собственно-энергетическую диаграмму четвер-
четвертого порядка.
ным импульсом р' — р) в каждый фермионный пропагатор, со-
содержащийся в 2(р), и суммируя по всем возможным вставкам
(см. рис. 19.28, где изображены диаграммы собственной энер-
энергии четвертого порядка).
Для доказательства явно вычислим дивергенцию от АУ-(р', р),
т. е. величину (// — p)ilA^(p', p), и воспользуемся результа-
результатами, полученными в гл. 17, в частности формулами A7.64)

§ 142]	ТОЖДЕСТВО УОРДА	311
и A7.66). Первая из них утверждает, что сумма всех вставок
в замкнутые электронные петли равна нулю, а по A7.66) сумма
всех вставок в электронную линию, которая не образует замк-
замкнутой петли, дает в точности разность двух членов в правой
части A9.17). Тем самым тождество Уорда доказано.
Из A9.16) можно вычислить SfF (p) и тем самым 2(р),
взяв предел р->т. Напомним, что в гл. 8 и 16 мы установили,
что')
S'r(p)-+jir^	09.18)
при р-+т. Поэтому при р = т и произвольном р'
= S71 (//) и (р) - Z2-' (р-т)и (р) = S'F~l (//) и (р). A9.19)
В силу лоренцевой инвариантности и сохранения четности функ-
р— 1
ция Sf {p') имеет следующий вид:
Скалярные функции А(р'2) и В(р'2) непосредственно выра-
выражаются через Гц, если в левой части A9.19) вычислить коэф-
коэффициенты при р'и(р) и и(р) соответственно.
Тождество Уорда позволяет не только вычислить Sp (p) при
заданном Гц(//, р), но и определяет Гц через SF в том частном
случае, когда р'-*р, т. е. когда импульс, переданный электро-
электромагнитному полю, равен нулю. В этом пределе A9.19) сво-
сводится к
dS'F~l (p)	32 (р)
Мр, Р)= Fgpii или AVi(p,p) = --^-. A9.20)
Именно эти выражения были получены в оригинальной работе
Уорда. Общий результат A9.16) был получен Такахаши в
1957 г., который исходил непосредственно из полевых уравнений
без обращения к анализу фейнмановских диаграмм.
Важным следствием тождества Уорда, которое стоит здесь
отметить, является установление общей структуры тензора по-
') Мы не рассматриваем здесь инфракрасную расходимость в Zi. В дей-
действительности привносимую этой расходимостью трудность можно избежать
при помощи метода промежуточной перенормировки (§ 145) или явно вводя
массу фотона. Мы не рассматриваем также проблему калибровочной инва-
инвариантности константы Z%.

312	ПЕРЕНОРМИРОВКИ	1ГЛ. 19
ляризации вакуума ПцУ(<?)- Взяв дивергенцию от A9.10) и ис-
используя A9.16), находим
q-П^ (q) = i \ -Цг Sp Ytl [5^ (k) - S'P{k + q)\ A9.21)
С интегралом в правой части мы неоднократно сталкивались
ранее, см., например, (8.10) и A7.66). Снова предполагая1),
что этот интеграл может быть регуляризован, после чего в нем
можно сделать замену переменных, получим
(<7) = 0.	A9.22)
Отсюда в общем случае следует результат, полученный ранее
в (8.20) при вычислениях во втором порядке теории возму-
возмущений
П^ (q) = (<7n<7v — ?nv<72) П (q2).	A9.23)
Более того, в любом конечном порядке по е\ функция П(<72)
не имеет полюса при q2 = 0, как это следует из рассмотрения
ее аналитических свойств2) (гл. 18).
Подставив A9.23) в A9.6), получим
<72[1 +e$l(q2)~]D'p(q)vy-
откуда
При практических вычислениях член с q^qv в A9.24) не вносит
вклада, поскольку Df связана с сохраняющимся током. В лю-
любом случае, однако, вид DP полностью определяется скалярной
функцией П(<72) в A9.23). Так как U(q2) не имеет полюса при
q2 = 0, выражение A9.24) показывает, что фотонный пропага-
тор описывает кванты с нулевой массой покоя.
§ 143. Определение перенормировочных констант
и правила перенормировки
В этом параграфе мы приступим к фактическому рассмот-
рассмотрению метода перенормировки. Используя определение кон-
констант Z\, Z2 и Z3 (см. гл. 16) и наш опыт вычислений во втором
порядке теории возмущений (см. гл. 8), мы переопределим про-
') См. также [116].
г) В действительности П (q2) имеет разрез при 0 ^ д3 < оо. О возмож-
возможности существования полюса в точной (т. е. просуммированной по всем сте-
степеням бц) функции П(</2) и об интерпретации этого полюса см. [63].

i 143]	КОНСТАНТЫ И ПРАВИЛА ПЕРЕНОРМИРОВКИ	313
пагаторы S'f и D'f, вершину Г р. и заряд ео> причем после такого
переопределения константы перенормировки можно снова свя-
связать с 2, П и Гц. В результате этой процедуры все интеграль-
интегральные уравнения, выведенные на предыдущих страницах этой
главы и являющиеся основой метода перенормировки, могут
быть переписаны в терминах перенормированных величин. Да-
Далее мы покажем, что константы перенормировки и определяю-
определяющие их уравнения конечны в каждом порядке по перенормиро-
перенормированному заряду е, т. е. что все зависящие от обрезания мно-
множители исчезают при перенормировке, как это было явно
продемонстрировано в первом томе при вычислении во втором
порядке теории возмущений.
Величина Z2, определенная в A6.84), представляет, согласно
A6.118), вероятность обнаружения «голого» электрона в состоя-
состоянии, описывающем физический электрон Из общего выражения
A6.122) для S'f следует, что
ПРИ Р~*т.	A9.25)
Для массового оператора ? (р) получаем
S(p)->-(j9-m)(Z2~1- 1) при р-+т, A9.26)
откуда следует, что при р->т 2(р) обращается в нуль. Вы-
Выполнение этого условия обеспечивается введением массового
контрчлена Ьт = т — то, который, согласно правилам, сфор-
сформулированным в гл. 17, явно содержится в гамильтониане взаи-
взаимодействия. Величина Ьт в каждом порядке определяется из
A9.26):
203 = m,6m) = 0.	A9.27)
Отметим, что A9.26) имеет тот же вид, что и вычисленное во
втором порядке теории возмущений выражение (8.42), за ис-
исключением того, что массовый оператор 2(р), используемый
в настоящей главе, включает в себя Ьт.
Константа Z3 определяется аналогично, как вклад однофо-
тонного состояния в фотонный пропагатор; она равна, согласно
A6.172), вычету пропагатора в полюсе q2 — 0:
+ градиентные члены при <72->0. A9.28)
Градиентные члены, как обычно, несущественны, поскольку
они не вносят вклада в S-матрицу1). Тогда из соотношения
') Следует подчеркнуть, что, как это следует из A9.14), градиентные
члены с необходимостью модифицируют т-функции, через которые в свою
очередь выражаются S-матричные элементы. Соответствующие поправки, од-
однако, можно полностью игнорировать.

314	ПЕРЕНОРМИРОВКИ	[ГЛ. 19
A9.24), связывающего Df с тензором поляризации вакуума, на-
находим
воП(О) = гГ' —1.	A9.29)
Сравнив с результатом вычислений во втором порядке теории
возмущений (8.23), получим
5
где М — масса, на которой производится обрезание.
Наконец, константа Zu связанная с вершинной функцией,
определяется так же, как в примере (8.50), а именно как пре-
предел Гц, когда переданный импульс стремится к нулю, а элек-
электронные линии лежат на массовой поверхности
«(Р) г!х (р, Р) и (р) = Zf'u (p) у„и (р).	A9.30)
Правая часть в этом выражении, как показано в A0.88), пред-
представляет наиболее общий вид вершинной функции при нулевом
переданном импульсе. Используя тождество Уорда, мы можем
в общем случае доказать весьма полезное равенство
Zi = Z2,	A9.31)
которое было установлено ранее в теории возмущений. Дей-
Действительно, положив в A9.19) р2 = т2 и обозначив р' = р + q,
получим
п (р) ^Г„ (р', р) и (р) = б (р) S'i1 (рО и (р).	A9.32)
Взяв производную djdqa, в пределе q^—»-0 получаем, с учетом
A9.30) и A9.25),
^Г'й (р) УцМ (р) = 22~'й (р) УцИ (р),
откуда и следует A9.31).
Идея метода перенормировки заключается в том, чтобы
переопределить пропагаторы и вершинные функции таким обра-
образом, чтобы вблизи массовой поверхности или (в случае верши-
вершины) при нулевом переданном импульсе эти величины совпадали
с соответствующими выражениями для свободной частицы.
С этой целью введем, следуя Дайсону [65, 66], перенормиро-
перенормированные пропагаторы и вершинные функции Sf, Dp и Гц и пе-
перенормированный заряд е:
>==Z3t>W	A9.33)
)=*ZT%(p',p),

5 143]	КОНСТАНТЫ И ПРАВИЛА ПЕРЕНОРМИРОВКИ	315
для которых
Sp (р) -» _ т при р-^-т,
Dp (<7)цу ->	^~ + градиентные члены при q2 -> 0, A9.34)
Гц (р, р) -¦ Y(x при р -> т.
Основная проблема в методе перенормировок заключается
в том, чтобы показать, что величины S'f, d'f и fu, выраженные
через перенормированный заряд е, конечны, т. е. не зависят от
Рис, 19.29 Первые два члена в скелетном разложении для ядра К-
радиуса обрезания. Эта проблема сильно усложняется расходи-
расходимостью констант Z; напомним, что в гл. 8 мы обнаружили, что
все эти величины зависят от обрезания.
Доказательство того факта, что SF, Ь'Р и Г^, а также выра-
выражающиеся через них т-функции конечны, основано на исполь-
использовании интегральных уравнений и разложении по скелетным
диаграммам, которые обсуждались в начале этой главы. По-
Поэтому желательно переписать эти уравнения в такой форме,
чтобы они содержали только перенормированные величины.
В результате вместо разложения по e\f можно использовать
разложение по перенормированному заряду е2. К счастью для
теории, указанное переопределение не затрагивает структуру
интегральных уравнений.
Начнем с рассмотрения ядра К, которое выражается через
Sp, Dp, Г и во. Выпишем в символической записи первые два
члена в разложении по скелетным диаграммам A9.13)
(рис. 19.29):
К = ielYD'pY + el \ [TSfГ] DPDF [Г5^Г] + ... A9.35)

316	ПЕРЕНОРМИРОВКИ	[ГЛ. 19
В терминах перенормированных величин A9.33) это выражение
приобретает следующий вид:
К = ielZ^ZsVDpf + etZT*ZlZ23 $ [fSFf]Ь'рЪ'р\_YS'ff] + ... =
ie2TD Ff + e4 J [fSPT] DfD f [fSFT]
Таким образом, в результате замены A9.33) все перенормиро-
перенормированные величины в первых двух членах разложения ядра ока-
оказались выраженными через перенормированные величины и,
кроме того, появился общий множитель Z^2.
Нетрудно показать, что указанное свойство имеет место
для любого члена в разложении по скелетным диаграммам
A9.13), в результате это разложение можно записать в виде
К (р, р', q) = Z2~2 Z KS (p, p', q\ S'f, Dp, f, e). A9.36)
скелетные
диаграммы S
Сопоставим далее каждой вершине скелетной диаграммы
половину множителей, относящихся к фотонной линии и к двум
фермионным линиям. Остальную половину множителей отнесем
к другой вершине или к внешним линиям. В результате каждая
вершина содержит множитель ZT , возникающий при перенор-
перенормировке Ги (см. A9.33)), множитель (д/%г~J> связанный
с электронными линиями, и множитель -\fz~3, связанный с фо-
фотонной линией, причем предполагается, что все эти линии —
внутренние. Поэтому полный коэффициент в вершине равен
Если же в вершину входят внешние электронная или позитрон-
ная линии, множитель -\JZ2, связанный с каждой из таких ли-
линий, следует опустить, поскольку пропагаторы внешних линий
не включены в определение К- В результате возникает полный
множитель ZJ2, как и указано в A9.36). Этот результат поз-
позволяет ввести перенормированное ядро К:
= Z KS{p,p',q\ Sp, 5'р,Г, e). A9.37)
скелетные
диаграммы S
Аналогичное масштабное преобразование может быть вы-
выполнено для фейнмановских амплитуд с произвольным числом

5 ИЗ]	КОНСТАНТЫ И ПРАВИЛА ПЕРЕНОРМИРОВКИ	317
внешних линий. Например, для т-функции с т внешними фер-
мионными и п внешними фотонными линиями получаем
Т(р, ...Pm,ql •¦•^)а,...ат,!х1...ц„ =
х^ х (pi ... рп, qt . .. qn\ Sp, DF, f, e)a , =
етные	'	я
скелет
диаграммы S
= ?2
'2т(р, ...рт, <?,... qn)ai...^ (m + n>3). A9.38)
Доказательство проводится аналогично A9.36) с той лишь
разницей, что теперь нужно учесть, что в т-функцию включены
пропагаторы внешних концов, которые не содержатся в опре-
определении К- В этом случае для перенормировки вершин доста-
достаточно множителя <\lz ; в результате в A9.38) возникает мно-
множитель л/Z для каждой внешней линии.
Для S-матричных элементов ситуация еще проще. Из редук-
редукционной формулы (см. A6.139) и A6.148)) следует, что инва-
инвариантный S-матричный элемент получается из т-функции умно-
умножением на (р— m)I^JZ2 для каждой электронной линии и на
<72/V^3 Для каждой фотонной линии, после чего следует пе-
перейти на массовую поверхность: р-+т, q2-*Q — и подставить
волновые функции свободных частиц, отвечающие внешним
линиям (не забывая при этом о множителях /). Поскольку пере-
перенормированные пропагаторы внешних линий на массовой по-
поверхности равны (р — т)~х и —(<72)~Igruv, мы приходим к за-
замечательно простым правилам вычисления S-матричных эле-
элементов, которые заключаются в следующем.
1.	Нарисуем все скелетные диаграммы.
2.	Вычислим по фейнмановским правилам соответствующие
амплитуды, подставляя ef ц для вершин и Sp и Df для внут-
внутренних линий.
3.	Подставим свободные волновые функции
Vm / т
	и(р), и(р) Л/	 и т.д.,
ЕBяK И V ?BяK
¦\/2k BлK
отвечающие внешним концам диаграммы, причем в этих функ-
функциях не нужно учитывать множители Z или собственно-энерге-
собственно-энергетические вставки, поскольку л/z в A9.38) сокращается с -\fz
в редукционной формуле. Мы видим, что вопрос о конечности
S-матричных элементов ни коим образом не связан с расходи-
расходимостью множителей Z, а сводится лишь к изучению конечности
функций Sp, Df и Гц и условий сходимости интегралов, отве-
отвечающих скелетным диаграммам.

318	ПЕРЕНОРМИРОВКИ	[ГЛ. 19
Интегральные уравнения, определяющие, вершину Гц, равно
как и тождество Уорда, позволяющее вычислить пропагатор
электрона Sf через вершину Гц, также подлежат перенорми-
перенормировке. Подставив A9.33) в A9.12), получим для вершины
Гд = ZiV». - \ TvS'pSfK,	A9.39)
где константа Z\ определяется из условия A9.34)
Г»(р,р)\^т = У»-	A9.40)
Поскольку Z\ = Z2, тождество Уорда при перенормировке не
меняется
(р' - Р)» Гд {р\ Р) = S71 (р') - Sf~1 (p).	A9.41)
В частности, выражение A9.19) справедливо и для перенорми-
перенормированных величин
S^ (//) = (р' - pi Г»(//, р) \.=т,	A9.42)
где обозначение \fi=m указывает на то, что р2 = т2 и каждый
множитель р в вершине следует заменить на т.
Поскольку тождество Уорда позволяет выразить Sf непо-
непосредственно через Гц,, не возникает необходимости рассматри-
рассматривать отдельно уравнение для электронной собственно-энергети-
собственно-энергетической части. Перенормировку этого уравнения мы оставляем
читателю в качестве упражнения.
Рассмотрим еще, как перенормируется фотонный пропага-
пропагатор и тензор вакуумной поляризации. Сделав замену A9.33)
в уравнении A9.24), получим
Вспомнив определение A9.29) константы Z3 и отделяя значение
П(<72) при <72 = О
где
Пс@) = 0
и
получим
г]-
[1+е2П
A9.45)

§ 144]	ПЕРЕНОРМИРОВАННЫЕ ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ	319
Напомним, что в силу сохранения тока члены, пропорцио-
пропорциональные qnqv не вносят вклада в S-матричные элементы. По-
Поэтому при вычислении 5-матрицы в A9.45) выживает только
первый член и пропагатор Df(<7)m.v фактически определяется
лишь функцией Пс(<72). Согласно A9.10), A9.23), A9.33) и
A9.44) выражение последней через перенормированные вели-
величины таково:
= (W, ~ g^q2) [П @)
-gr Sp Y^ (ft) \\ (k, k + q)SF(k + q). A9.46)
§ 144. Сводка формул:
перенормированные интегральные уравнения
Мы в основном закончили построение формального аппа-
аппарата, используемого в методе перенормировок. Ниже мы вы-
выпишем сводку формул, необходимых для вычисления S-матрич-
ных элементов.
Для неперенормированных величин имеем ')
t(p\ ... рт, qi ... qn)ai ...nn —
= I x\Pl...pm,qx... qn- S'P, D'P, Г eQ)	, A9.47a)
скелетные	ai ••• Vn
диаграммы S
Kafi, Y6 (P, p', q)= Z ^«3, Y6 (p, p', Ц\ Sp, Dp, Гцво), A9.476)
скелетные
диаграммы S
w tiS'F {p + q) г*(р' + 41P + U iS'F {р + ?> V х
X /С„з. «v (Р + </. Р' + </> <7) = Y^ - $ r^Sr/C ^
^ Y» + Лц (р', р), A9.47b)
Sf'1 (Pf) = (Pf - P), Ги (p', p) |,_m,	A9.47r)
ЧЛеНЫ С
П (<72) =
Sp Y^(Й)Г^(&' b + 4)SP(b + Я). A9.47e)
') См. уравнения A9.14), A9.13), A9.12), A9.19), A9.24) и A9.10) для
случаев A9.47 а, б, в, г, д, е) соответственно.

320	ПЕРЕНОРМИРОВКИ	ГГЛ 19
Эти уравнения поволяют полностью определить т-функции
в виде разложения по степеням е\. В первом неисчезающем
порядке по е\ для вычисления функций т, К и П в A9.47а) —
A9.476) и A9.47в) величины Sf, Df и Гц следует заменить на
Sf, Dp и уц. После этого, используя A9.47в) и A9.47г), можно
вычислить в том же порядке Г р. и Sf. Функцию Df можно вы-
вычислить с точностью е^ если подставить в A9.47д) нулевое
приближение для П в A9.47е). Указанные вычисления были
фактически проделаны в гл. 8. Полученные при этом значения
Sf, Dp и Гц, которые содержат поправки порядка el, можно
затем подставить обратно в A9.47а), A9.476) и A9.47е), после
чего описанную процедуру следует повторять до тех пор, пока
не будет достигнута желаемая точность.
Отметим, что в A9.47) не выписаны уравнения, определяю-
определяющие электронную собственно-энергетическую часть
= iel \ W Dp {k)^ Г"(Р' P~k)S'p(p- k) YV- A9.48)
Эти уравнения не нужны, поскольку тождество Уорда A9.47г)
позволяет определить Sf непосредственно через Гц.
Производя в A9.47) перенормировку1)
l e,
D'f fa)i»v =
Pm, <7l ••¦ <7n)Ol ...ц„
(p, ... Pm, gi... qn)ai _ ^ A9.49)
и учитывая, что вследствие тождества Уорда
ZX = Z2,	A9.50)
1) См. A9.31), A9.33), A9.37) и A9.38)..

144]
ПЕРЕНОРМИРОВДННЫЕ ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
321
мы получаем вместо A9.47) следующую систему уравнений1):
т(р, ... рт, <7, ... <7„)а| ...цп =
= ? ts (р, ... рт, <?,... «?„; S;, D;, f ltl e)	, A9.51a)
скелетные	а1 ••• М-
диаграммы S
)
а
1 •••
, р\ q)=
скелетные
диаграммы S
, р', q; Sf, 6'f, fu, e\ A9.516)
Y	hy6
f (P + g)\a X
или
К ^ z\\ - 5 f Ц5да
vu+к if/, p),
члены с
A9.51b)
(I9.51r)
A9.51д)
= (<7m.Gv - <?^<72) П (<72) =
= /Z,
где
Sp YuS^(*) fv(*. * + q)S'F{k + q), A9.51e)
^П@) + ПЛ<72), Пс@) = 0.
Используя эти шесть уравнений, можно вычислить все
S-матричные элементы, заменяя в перенормированных т-функ-
циях A9.51а) внешние пропагаторы Sf и uf волновыми функ-
функциями свободных частиц, причем, как было указано выше,
в волновых функциях не нужно учитывать множителей Z.
Уравнения A9.51) вместе с граничными условиями2) для
определения констант Z\ и Z3
h(P>P)\fi-m = V» 4 = 4--П@) = % A9.52)
ео е	е
составляют замкнутую систему, из которой можно вычислить
все т-функции и 5-матрицу в виде разложения по степеням пе-
перенормированного заряда е. Эти уравнения позволяют выпи-
выписать также разложение по степеням неперенормированного за-
заряда. Действительно, подставим в A9.51 в) ядро Я, вычис-
') См. A9.38), A9.37), A9.39) и A9.42), A9.45) и A9.46).
2) См. формулы A9.40) и A9.44).

322	ПЕРЕНОРМИРОВКИ	[ГЛ. 19
ленное в низшем порядке по е, и Sf « {р — т)~'; тогда, исполь-
используя A9.52), получим Гц и Zj с точностью е2. Далее, из тожде-
тождества Уорда A9.51г) можно вычислить Sf с точностью е2, a Df
в том же порядке определится из A9.51д), если подставить
в это уравнение нулевое приближение для П^- Используя зна-
значения величин Sf, Df, f ^ и Zb вычисленные в приближении е2,
можно затем вычислить Я и т в следующем приближении по е,
после чего описанная процедура повторяется1).
До сих пор мы, однако, не выяснили, существует ли решение
перенормированных уравнений A9.51). Появление Z\ в свобод-
свободном члене уравнения для вершины A9.51 в) не слишком опасно,
поскольку бесконечный свободный член можно устранить вычи-
вычитанием расходящейся части интеграла в правой части этого
уравнения. Более серьезная трудность связана с появлением
множителя Z\ перед интегралом, определяющим Hlxv(q). В дей-
действительности эта проблема представляет наиболее трудную из
тех, с которыми мы столкнемся при проведении программы пе-
перенормировок. Аналогичная трудность возникает при прямом
вычислении электронной собственно-энергетической части непо-
непосредственно из A9.48). В последнем случае, однако, вместо ин-
интегрального уравнения можно использовать тождество Уорда
и тем самым отмеченную трудность удается избежать. Именно
в этом пункте и проявляется практическое преимущество ис-
использования тождества Уорда.
§ 145. Аналитическое продолжение
и промежуточная перенормировка
В предыдущих параграфах мы ввели алгебраический и то-
топологический аппарат, необходимый для выполнения перенор-
перенормировки. В частности, в § 144 мы выписали полный набор урав-
уравнений, определяющих Sf, Df, Гц, Ка&, у& и т, итерация кото-
которых позволяет вычислить эти величины в любом порядке по
перенормированному заряду е в виде конечной суммы фейнма-
новских интегралов. Подчеркнем, что при этом мы получаем
не замкнутое выражение, а ряды по степеням е. В этом месте
мы приходим к узловому пункту метода перенормировок. Мы
должны теперь член за членом перебрать все фейнмановские
интегралы и показать, что они конечны и что поэтому перенор-
1) Наиболее смелым предположением этой главы, о котором не следует
забывать, рассматривая топологические свойства различных фейнмановских
диаграмм, является следующее: мы предполагаем, что оба разложения, как
по степеням е2, так и е2, равномерно сходятся, несмотря на то, что величины
Zu SF, Dp и Гц все выражаются расходящимися интегралами и зависят от
обрезания.

S 145]	АНАЛИТИЧЕСКОЕ ПРОДОЛЖЕНИЕ	323
мированный ряд теории возмущений представляет ряд конеч-
конечных, т. е. не зависящих от обрезания, членов. Вопросы же, свя-
связанные с установлением сходимости полного ряда, мы здесь во-
вообще не будем рассматривать.
В этом параграфе мы обсудим одну техническую проблему,
не связанную непосредственно с теорией перенормировок,
а возникающую при установлении критерия сходимости для
фейнмановских интегралов. Как мы обнаружили в гл. 18, зна-
знаменатели (р2 — т2)~' в фейнмановских интегралах могут при
некоторых значениях кинематических переменных обращаться
в нуль. Это обстоятельство приводит к дополнительным трудно-
трудностям при анализе расходимостей. В методе перенормировок, од-
однако, мы интересуемся лишь ультрафиолетовым поведением по-
подынтегральных выражений при р2->оо,а не сингулярностями, ко-
которые ведут к появлению абсорптивных частей. Последние были
рассмотрены в связи с дисперсионной теорией1) в гл. 18. Ниже
мы покажем, как с самого начала можно избежать указанных
трудностей путем аналитического продолжения по внешним им-
импульсам фейнмановской амплитуды в область, где знамена-
знаменатели не обращаются в нуль. После установления сходимости
интегралов в этой области можно аналитически продолжить
амплитуду обратно к физическим значениям инвариантов. При
этом мы можем быть уверены в том, что при таком продолжении
интеграл существует почти всюду, за исключением конечного
числа особенностей Ландау.
Для аналитического продолжения амплитуды удобно исполь-
использовать представление A8.53) и выражения A8.35) и A8.37)
для действия / A8.44) в знаменателе A8.53). Согласно A8.34) —
A8.36) фейнмановский интеграл, отвечающий диаграмме с т
внешними импульсами qs и п внутренними импульсами р/,
имеет вид
da,
... danb A - ? a Л Q («/> <7S)
dax ...rfa/t6(l-?a/)Q(ay, gs)
—F-s	И	W'	A9.53)
') В гл. 18 мы не рассматривали инфракрасные расходимости, которые,
как мы вскоре убедимся, могут быть устранены при помощи метода, изложен-
изложенного в этом разделе.

324	ПЕРЕНОРМИРОВКИ	[ГЛ. 19
где Р и Q — полиномы, в общем случае зависящие от внутрен-
внутренних и внешних импульсов, а также матриц у и векторов поля-
поляризации. Кирхгофовские импульсы kj линейно связаны с qs,
причем коэффициенты линейного преобразования зависят от ос,
(см. A8.35) и A8.37)). Коэффициенты ?у также зависят от ос
(см. A8.35)).
Наша задача заключается в том, чтобы путем замены пере-
переменных в A9.53)
перейти к евклидовой области, в которой все знаменатели отри-
отрицательно определены и в которой потому не возникают указан-
указанные выше неприятные сингулярности. Прежде всего заметим,
что из линейных соотношений, связывающих р,-, k,- и /, в A8.32),
A8.33) и A8.37) следует, что любой поворот внешних импуль-
импульсов qs подразумевает такой же поворот импульсов kj и 1Г. За-
Заменим внешние импульсы
<7°-»<#"<¦>, 0<Ф<я/2, qs-*qt.
Легко видеть, что в результате такой замены интеграл / остается
конечным. Действительно, кирхгофовские импульсы kj при этом
заменяются на
а знаменатель в A9.53) приобретает вид
п
J = ? а/ (?J — т) + /е) =
п
= Z {[(^J cos 2ф - k) — mj] а, + /[(A:°J sin2(p + е] ау}. A9.54)
Поскольку
Im/>0
для всех ос/ ^ 0 в A9.53), / существует для всех 0 < ф < -^
при условии, конечно, что интеграл регуляризован на верхнем
пределе. Положим теперь в A9.54) ф = я/2, тогда получаем
для 7(^1	qm)
С h	P(qs, Ir)	nfl,n
A955)
где Рм = (фо>Р)> Р2== — (Po "I" P2) < 0 и интеграл вычисляется
по евклидовому четырехмерному пространству.

S 145]	АНАЛИТИЧЕСКОЕ ПРОДОЛЖЕНИЕ	325
В выражении A8.55) знаменатели отрицательно определены,
и потому это выражение более удобно при анализе расходимо-
стей. Если нам удастся показать, что интеграл I(q) существует,
то тем самым будет показано, что и исходный интеграл /(</),
определенный для физических импульсов q существует всюду,
за исключением тех частных значений импульсов, для которых
интеграл имеет сингулярности Ландау (см. гл. 18). Действи-
Действительно, обратное аналитическое продолжение от евклидовых qs
к физическим значениям q всегда возможно; для этого нужно
только сделать замену qo-*qoe~l<Sl и положить ф = я/2. По-
Поскольку мы работаем с хорошо определенными аналитическими
функциями, их аналитическое продолжение возможно до тех
пор, пока мы не подойдем к естественной границе аналитично-
аналитичности. Однако рассуждения § 127 показывают, что при аналити-
аналитическом продолжении мы можем встретить лишь сингулярности
Ландау. Отметим, что указанное обстоятельство было установ-
установлено в § 127 только для вершин с одним внешним импульсом q.
Однако этот факт легко обобщить и для произвольных диа-
диаграмм, содержащих несколько внешних линий; для этого до-
достаточно рассмотреть значения инвариантов, не лежащие на
массовой поверхности и продолжить затем импульсы в евкли-
евклидову область. Поскольку число сингулярностей Ландау меньше
или равно числу всевозможных редуцированных диаграмм,
а число последних конечно, мы приходим к выводу, что инте-
интеграл I(qs) существует почти всюду для физических qs, если су-
существует I (qs) ¦
При последующем рассмотрении мы не будем делать разли-
различия между импульсами qs и qs и предположим, что аналитиче-
аналитическое продолжение от физических значений импульсов к евкли-
евклидовым может быть выполнено всякий раз, когда в этом возни-
возникает необходимость.
Фейнмановские интегралы, определяющие константы пере-
перенормировки Z\ и Z2, требуют специального рассмотрения, по-
поскольку они вычисляются при р2 = /и2. В этом случае критерий
сходимости, справедливый только для евклидовых 4-векторов
с /?2<01) неприменим. Поэтому в интегралах для Z\ и Z2 мы
сначала сделаем вычитания, необходимые для того, чтобы пре-
превратить интегралы в сходящиеся, причем вычитания сделаем
в точке Рц = 0, которая лежит на границе евклидовой области.
Эта процедура носит название промежуточной перенормировки.
После промежуточной перенормировки пропагатор и вершина
уже не будут должным образом нормированы на массовой
поверхности р2 = пг2. Однако мы достигнем нашей цели и
') Таких проблем не возникает с 23, поскольку фотонный пропагатор уже
перенормирован в точке д* == 0.

326	ПЕРЕНОРМИРОВКИ	[ГЛ. 19
покажем, что Sf и Df конечны, если мы сможем показать,
что:
1)	теория, в которой пропагатор и вершина перенормируются
в точке /?ц = 0 (а не в точке р2 = т2), сходится;
2)	константы перенормировки, связывающие пропагаторы
и вершины, перенормированные в точке р^ = 0, с функциями
Sf и Гц, перенормированными в точке р2 = т2, конечны (т. е.
не зависят от обрезания).
Таким образом, наш подход заключается в том, чтобы вы-
выполнить перенормировку в точке р^ = 0, после чего можно ис-
использовать любые теоремы о сходимости интегралов, вычисляе-
вычисляемых по евклидовым областям. Далее мы обсудим смысл про-
промежуточной перенормировки в уравнениях A9.51) и A9.52)
и ее физическую интерпретацию и, наконец, покажем, что до-
дополнительная перенормировка, необходимая для вычисления
Sf и Df, конечна.
Введем константы промежуточной перенормировки:
Sf (р) = Z'2~1S'F (р) = 22% (р),	A9>56)
Г„ (//, р) = г[г„ (//, р) = z,f „ (//, р),
определенные так, что
%(р)-+\Цр-т) при Р|1->0,
~	(ly.oYJ
Гц(р, р)-+Ч»	при Рц-»0.
Исходные уравнения A9.51) и A9.52) могут быть теперь запи-
записаны в терминах промежуточно перенормированных величин;
для этого достаточно лишь добавить еще одну тильду в Sf и
Гц, заменить Zb Z2 на Z\, Z2 и заменить граничное условие
\р_т на \р _0. После указанных замен по-прежнему сохраняется
тождество Уорда, а вместе с ним равенство
7>' —7'
поскольку выражения A9.20) и A9.57) в пределе Рц-^О сво-
сводятся к
(КГ1 -j^(fi-m) = (Z[)~l у, при Р|1 -> 0,
откуда
7' — 7'
В оставшейся части этой главы мы займемся установлением
того факта, что теория с промежуточной перенормировкой ко-
конечна. После того, как мы убедимся в этом, для доказательства
конечности Sf и Гц достаточно будет,согласно A9.56) и A9.57),

§ 146]	СТЕПЕНЬ РАСХОДИМОСТИ И КРИТЕРИЙ СХОДИМОСТИ	327
лишь показать, что конечны z\, z2 и т. Последнее же утвержде-
утверждение следует из обобщенного тождества Уорда
1я(/>)-1Г1@) = р»Г|1(р, о).
~/—1
Поскольку Sf (p) равна нулю при р = т, параметр in равен
m = pj* (р, 0) !,_„,.	A9.58)
Далее, из условия нормировки Гц и из A9.56) заключаем, что
= 2,Г, (р, р) \р=т = Г, (р, р) |.=т.	A9.59)
Таким образом, если вершина Гц конечна, то конечны и кон-
константы Z\ — г2 и т. Поэтому истинно перенормированная тео-
теория (с одной тильдой) конечна, если конечна промежуточно-
перенормированная теория (с двумя тильдами). Более .того,
если мы покажем, что Гц(р', р) конечна для евклидовых значе-
значений р' и р, то тем самым мы установим конечность этой вели-
величины и для физических значений р' и р. Последнее утвержде-
утверждение следует из возможности аналитического продолжения ам-
амплитуды от евклидовых значений импульса к физическим их
значениям, которая обсуждалась в начале этого параграфа.
В дальнейшем при обсуждении сходимости интегралов мы
не будем каждый раз обращаться к утонченному приему анали-
аналитического продолжения к евклидовым значениям 4-векторов и
последующей промежуточной перенормировке, поскольку эта
процедура всегда может быть выполнена в случае необходимо-
необходимости. Отметим еще, что в квантовой электродинамике метод про-
промежуточной перенормировки имеет непосредственное отношение
к проблеме инфракрасной расходимости. Поскольку фотон имеет
нулевую массу покоя, нормировка волновых функций в точке
ветвления (при обычной перенормировке в точке р2 — т2) пред-
представляет с математической точки зрения некорректно постав-
поставленную задачу. Мы убедились в этом уже при вычислении соб-
собственно-энергетической части второго порядка в (8.40) и при
проверке равенства Z\=Z2 в (8.42). В обоих случаях мы об-
обнаружили инфракрасные расходимости при р2-*-т2. Эти расхо-
расходимости, однако, не возникают в методе промежуточной пере-
перенормировки при р^-уО.
§ 146. Степень расходимости и критерий сходимости
В настоящем параграфе мы детально рассмотрим вопрос об
установлении признака сходимости фейнмановских амплитуд и
покажем, как можно устранить расходимости в квантовой элек-
электродинамике [65, 66]. В гл. 8 при вычислениях во втором порядке

328	ПЕРЕНОРМИРОВКИ	(ГЛ. 19
теории возмущений было обнаружено, что в интегралах для соб-
собственной энергии и вершины вопрос о характере сходимости ин-
интеграла решается простым подсчетом степеней внутренних им-
импульсов. При этом оказалось, что сумма степеней импульсов в
числителе плюс четыре степени от интегрирования по внутрен-
внутреннему импульсу d4 равна или больше суммы степеней импульсов
в знаменателе, в результате все указанные интегралы содер-
содержали ультрафиолетовую расходимость при ^->оо. После вычи-
вычитаний эти интегралы приобрели дополнительные импульсы в
числителе и в результате оказались сходящимися.
При переходе к высшим порядкам теории возмущений, когда
фейнмановские диаграммы содержат несколько независимых
контуров интегрирования, возникает вопрос, достаточен ли ука-
указанный подсчет степеней внутренних импульсов в числителе и
знаменателе интеграла для установления его сходимости. Есте-
Естественно предположить, что подсчет степеней, по-видимому, все-
таки имеет некоторое отношение к вопросу о характере расхо-
расходимости. Поэтому, желая выяснить общий критерий сходимости,
мы детально рассмотрим систематический способ подсчета сте-
степеней виртуальных 4-импульсов, входящих в подынтегральные
выражения интегралов, отвечающих диаграмме произвольного
порядка.
Вначале определим степень расходимости графика 9 как
число степеней внутренних 4-импульсов в числителе (включая
четыре степени, отвечающие каждому интегрированию по d4lr)
минус число степеней в знаменателе; обозначим степень расхо-
расходимости через D(&). Пропагаторы каждой внутренней фотон-
фотонной или бозонной линии содержат импульс в степени —2, а про-
пропагаторы каждой внутренней электронной или фермионной ли-
линии— импульс в степени —1. Поэтому в квантовой электродина-
электродинамике имеем
D = 4k-2b-f,	A9.60)
где b — число внутренних фотонных линий, / — число внутрен-
внутренних фермионных линий, k — число переменных интегрирования.
Замечательным свойством соотношения A9.60), которым
фактически и обусловлена плодотворность метода перенормиро-
перенормировок в квантовой электродинамике, является то обстоятельство,
что величина D не зависит от внутренней структуры фейнманов-
ских диаграмм, а определяется только числом и сортом (фотоны
или электроны) внешних частиц. Этот факт непосредственно
связан с безразмерностью константы связи е. При этом един-
единственным размерным параметром в теории является масса элек-
электрона /л, зависимость от которой в ультрафиолетовом пределе
/ц->>оо исчезает. Поэтому вставка в данную фейнмановскую
диаграмму все большего и большего числа внутренних фотон-

§ 1461¦
СТЕПЕНЬ РАСХОДИМОСТИ И КРИТЕРИИ СХОДИМОСТИ
329
ных линий не меняет ее размерность. Прямое доказательство
сделанного утверждения состоит в следующем. Вставка каждой
фотонной линии в диаграмме автоматически влечет за собой
вставку двух фермионных линий и дополнительное интегриро-
интегрирование по d4lr- Из A9.60) следует, что полное изменение D равно
при этом
AD = 4A/e — 2A6 — Д/= 4 — 2 — 2 = 0.	A9.61)
Таким образом, мы подтвердили соображения, основанные на
анализе размерностей и устанавливающие, что D зависит только
\
Рис. 19 30. Упрощение компактной диаграммы путем удаления дополнитель-
дополнительных линий, которое удобно при вычислении степени расходимости D.
от числа внешних линий. В теориях, содержащих связи с произ-
производными и размерные константы связи, изложенные аргументы
неприменимы, в таких теориях нарушается также вся схема пе-
перенормировок.
Используя A9.61), можно вычислить D для любого компакт-
компактного графика, последовательно упрощая его до тех пор, пока
мы не получим достаточно простой график, например вида, ука-
указанного на рис. 19.30. Если теперь добавить к этому графику
одну внешнюю фотонную линию, то появится дополнительная
внутренняя фотонная линия, в результате D увеличится на 1.
Отсюда OD/dB = —1, где В — число внешних фотонных или бо-
зонных линий. Точно так же добавление к диаграмме двух
внешних фермионных концов влечет за собой появление внут-
внутренней фермионной и внутренней фотонной линий. При этом D
увеличивается на 3 или, в расчете на одну дополнительную внеш-
внешнюю фермионную линию F, на 3/2, т. е. dD/dF = —3/2. Отсюда
выводим связь D с числом В и F:
D = 4-3/2F — B,	A9.62)
где константа, равная 4, получается из рассмотрения любого
данного графика. Например, для электромагнитной компактной

330	ПЕРЕНОРМИРОВКИ	[ГЛ. 19
вершины в нижайшем порядке по е имеем F = 2, В = 1 и
D = 0, поскольку эта вершина сводится к постоянной и не со-
содержит интегрирования по импульсам.
В методе перенормировок мы обычно рассматриваем фейн-
мановские интегралы с одним или несколькими вычитаниями.
Примеры такого рода интегралов встречались при вычислениях
в приближении е2. В гл. 8 мы убедились, что, вводя каждый раз
дополнительные внешние импульсы в числитель подынтеграль-
подынтегрального выражения, мы зарабатываем дополнительную степень
внутренних импульсов в знаменателе. Это, очевидно, справед-
справедливо не только для интегралов ~е2, но и в общем случае; дру-
другими словами, справедливо следующее правило: каждое вычита-
вычитание по отношению к некоторому набору внешних импульсов qs
ведет к уменьшению степени расходимости D этого интеграла
на единицу.
Если D < 0, то фейнмановский интеграл имеет достаточное
число 4-импульсов в знаменателе и на первый взгляд сходится.
Однако этот интеграл перестает быть сходящимся, если, напри-
например, вставить внутрь диаграммы вершинную часть, хотя при
этом D не изменится. Приведенное рассуждение показывает, что
условие D < 0 для диаграммы в целом, вообще говоря, еще не-
недостаточно для сходимости фейнмановского интеграла; его
нужно дополнить требованием конечности интегралов, отвечаю-
отвечающих каждому из внутренних блоков, которые можно выделить
из диаграммы.
Если, с другой стороны, для данной диаграммы D ^ 0, то
она почти наверняка расходится. В квантовой электродинамике,
однако, имеется ограниченное число расходящихся диаграмм,
соответствующих следующим значениям неотрицательной сте-
степени расходимости D:
а)	электронная компактная собственно-энергетическая часть
2(/>) D=l;
б)	компактная вершинная часть Гц(р', р) D — 0;
в)	фотонная компактная собственно-энергетическая часть
или тензор вакуумной поляризации 11^(^H = 2;
г)	компактная трехфотонная вершина D = 1;
д)	амплитуда рассеяния фотона на фотоне D = 0.
Эти диаграммы изображены на рис. 19.31.
В действительности из указанных пяти случаев достаточно
рассмотреть только случаи б) ив). Собственная энергия элек-
электрона а) определяется через Ги посредством тождества Уорда, и
ее можно отдельно не рассматривать. Трехфотонная вершина г)
тождественно равна нулю, поскольку она нечетна при зарядо-
зарядовом сопряжении. Напомним в этой связи (см. A5.96) и A5.97)),
что в квантовой электродинамике существует унитарный опера-
оператор С, коммутирующий с гамильтонианом, под действием ко-

146)
СТЕПЕНЬ РАСХОДИМОСТИ И КРИТЕРИЙ СХОДИМОСТИ
331
торого электромагнитное поле преобразуется как нечетный опе-
оператор:
СЛ^ (х) С	Л„ (х).
Вакуумное состояние, которое, как обычно (см. A6.2)), предпо-
предполагается единственным, является собственным вектором опера-
оператора С, т. е. С|0) = |0), поэтому
(О | Т (А» (х) Av (у) Ак (z)) 10) = <0 | Т (СА„ (х) Av (у) Ах (z)) | 0) =
= -(Q\T(All (x) Av(у) Ах(г)) 10) = .0,
и трехфотонная вершина тождественно равна нулю. Обобщение
этого результата на случай произвольных замкнутых электронных
Рис. 19.31. Диаграммы в квантовой электродинамике с неотрицательной сте-
степенью расходимости.
петель с нечетным числом фотонных концов (теорема Фарри
[117]) было получено в 1937 г.
Хотя для фотонной собственно-энергетической части D — 2,
квадратично расходящийся член, который следовало бы связать
с массой фотона, на самом деле должен быть тождественно
приравнен нулю в силу тождества Уорда (см. A9.21) и A9.22)).
Две степени импульса в U^viq) на самом деле затрачиваются,
чтобы образовать тензор q^q? в A9.51), и не вносят вклада в
степень расходимости D на верхнем пределе. В результате
Deff = 0 и расходимость П(</2) всего лишь логарифмическая.
Для амплитуды фотон-фотонного рассеяния (е) ситуация еще
лучше. В этом случае четыре внутренних импульса в фейнманов-
ском интеграле затрачиваются, чтобы образовать четыре элек-
электромагнитных тензора F^iq) ~ (q^v — <Л>8ц)> по одному на

332	Перенормировки	[гл. 19
каждый внешний фотон. Это есть следствие требования гра-
градиентной инвариантности. В результате эффективная степень
расходимости Deu = —4, а не 0, что ведет к конечной (в теории
возмущений) амплитуде. Этот вывод был подтвержден Карплу-
сом и Нейманом [118] явным вычислением. Истинное сечение фо-
фотон-фотонного рассеяния чрезвычайно мало; при низких энер-
энергиях
а4 о6
orvv ~ —5—г > ш — энергия в системе центра инерции, со -С т,
при релятивистских энергиях ш 3> т сечение падает как 1/ш2.
Таким образом, остаются лишь две расходящиеся величины:
Гц и Пцу, которые обе имеют эффективную степень расходимости
Deff = 0. Именно с этими двумя величинами и связаны все рас-
расходимости в квантовой электродинамике. Напомним, что расхо-
расходимость Гц и Пцу в теории возмущений всего лишь логарифми-
логарифмическая.
Как отмечалось выше, не все амплитуды с D < 0 конечны,
в действительности любая собственно-энергетическая или вер-
вершинная вставка не изменяет D, но приводит к расходимости
всей диаграммы. Поэтому необходим более утонченный крите-
критерий сходимости, чем простой подсчет степеней. При этом кое-
что нужно сказать и об интегрировании по некоторому подклас-
подклассу внутренних импульсов внутри фейнмановской диаграммы.
Указанный критерий был впервые сформулирован Дайсоном
[65, 66] в 1949 г., дополнен затем Саламом [112] в 1950 г. и, на-
наконец, строго доказан Вайнбергом [119] в 1960 г. Теорема Вайн-
Вайнберга, к рассмотрению которой мы сейчас приступаем, дает
строгий критерий сходимости фейнмановских интегралов и яв-
является основой для применения метода перенормировок Дай-
сона — Салама'). Теорема Вайнберга, однако, оказывается по-
полезной не только при обосновании метода перенормировок, эта
теорема определяет также, с точностью до степеней логарифмов,
асимптотическое поведение фейнмановских интегралов в обла-
области, когда любой фиксированный набор внешних импульсов стре-
стремится к бесконечности. Здесь мы обсудим только часть, относя-
относящуюся к перенормировкам, а рассмотрение асимптотического
поведения отложим до § 150.
Чтобы сформулировать и пояснить основные идеи, относя-
относящиеся к теореме Вайнберга, необходимо ввести понятие субгра-
субграфика диаграммы и внутреннего интегрирования. Будем называть
внутренним интегрированием интегрирование по некоторому на-
набору 5 внутренних замкнутых контуров 1Г. Часть диаграммы, по-
') Между тем Боголюбов с соавторами доказал перенормируемссть, ис-
используя несколько другую технику (см. [27]).

§ 146]
СТЕПЕНЬ РАСХОДИМОСТИ И КРИТЕРИЙ СХОДИМОСТИ
333
лученную удалением тех линий, которые не зависят от импуль-
импульсов /,, входящих в набор S, будем называть субграфиком. На-
Например, диаграмма рис. 19.32 имеет три возможных субграфика,
изображенных на рис. 19.33. Эти субграфики отвечают внутрен-
внутреннему интегрированию по /] при фиксиро-
фиксированном /г(а)> внутреннему интегрирова-
интегрированию по /2 при фиксированном U (б) и, f\/\/\/\/v\/v
наконец, интегрированию по 1\ при фик-
фиксированном /) — 12 (в). Мы можем сопо-
сопоставить каждому субграфику и связан-
связанному с ним внутреннему интегрированию f\/\/\/\/\/\/\>
свою степень расходимости D(S), кото-
которая определяется так же, как степень
расходимости диаграммы в целом. В рас-
рассмотренном примере D = —3, 0 и —5
ДЛЯ субграфиков {а), (б) и (в) СООТвет- Рис. 19.32. Диаграмма
ственно. Следует отметить, что полное с ДВУМЯ внутренними им-
т	г	пульсами 1\ и 1ъ по ко-
вычитание в диаграмме 9, вообще го- т^рым прОизводигся ин-
воря, не уменьшает значения D(S), за	тегрирование.
исключением случая, когда импульсы,
отвечающие внутренним линиям данного субграфика, непосред-
непосредственно связаны с внешними импульсами в аргументе вычита-
тельного члена.
ffi-'"i-'~i-/~'-'"\-'*i-'"'-'*t--t
\/\/\/\/\S\S\S\l
a)	6)	v)
Рис. 19.33. Три субграфика диаграммы на рис. 19.32 с фиксированными им-
импульсами 1г (a), h (б) и I, — k (в). Подразумевается, что интегрирование
по импульсам пунктирных линий субграфика не производится.
Отметим еще дополнительную проблему, возникающую при
попытке приписать степень расходимости какому-либо субгра-
субграфику и связанную с наличием вычитательных членов в фейнма-
новских интегралах, которые возникают при разложении пере-
перенормированных уравнений A9.51) по степеням е. Напомним, что
вычитательные члены необходимы, чтобы удовлетворить усло-
условиям A9.51в), A9.51д) и A9.52), которые определяют перенор-

334
ПЕРЕНОРМИРОВКИ
(ГЛ. 19
Г{? (р, р + /,) ~ \ d%yvSF (р - /2) y»SF (p
- J d42yvSF (p - k) y
мированные значения Ги и Dp. Поясним сказанное на примере
диаграммы 19.33. Выпишем явно вершинную вставку
h- h) yvDF (/,) -
(p - l2) уЮР (l
Знаменатель первого члена в этом выражении содержит одну
степень импульса 1\, которая вносит вклад в степень расходи-
расходимости D(l]) = —3 для внутреннего интегрирования по /ь Вто-
Второй член, однако, не зависит от 1и поэтому вклад в степень рас-
расходимости, привносимый этим членом, равен D(l^) = —2. В об-
общем случае будем рисовать в диаграммах ящики с пунктирными
«¦'.'--.-¦--•-\.<-\.---.---.---.т
i ¦:' I
I	""
i	.'
a)
Рис. 19.34. Ящики с пунктирными линиями, окружающие те части двух воз-
возможных субграфиков в диаграмме рис. 19.32, которые содержат вычитатель-
ные члены.
линиями, окружающие ту часть диаграммы, в которой выпол-
выполняется вычитание, как это показано на рис. 19.34, а и б. Изобра-
Изображенные там диаграммы представляют собой два единственно
возможных субграфика с вычитательными членами в вершине,
их степень расходимости равна D = —2 и 0 соответственно.
Процедура подсчета степени расходимости при внутреннем ин-
интегрировании, отвечающем диаграмме с вычитаниями, такова:
1.	Нарисуем ящики с пунктирными линиями вокруг всех вер-
вершинных и собственно-энергетических вставок с вычитаниями.
2.	Для внутреннего интегрирования по импульсам, целиком
содержащимся внутри ящика (см., например, рис. 19.34,6) под-
подсчет степеней производится обычным образом.
3.	При подсчете же степени расходимости при интегрирова-
интегрировании по замкнутому контуру, не содержащемуся целиком внутри
ящика (см. рис. 19.34, а), этот ящик следует стянуть в точку и

146]
СТЕПЕНЬ РАСХОДИМОСТИ И КРИТЕРИЙ СХОДИМОСТИ
335
л=о
б)
/Л=-5 /
а)
забыть о нем вообще. Последнее утверждение эквивалентно сле-
следующему: часть диаграммы, заключенную внутри ящика с пунк-
пунктирными линиями, можно не рассматривать, поскольку импуль-
импульсы линий, входящих и выходящих из этого ящика, фиксированы
при вычитании.
Действительно, рассмотрим вычитательные члены в вершин-
вершинной части и электронной и фотонной собственно-энергетических
частях, пропорциональные соответственно уц. Р и	2
Степени расходимости, отве-
отвечающие этим вставкам, равны
О, +1 и +2. Однако эти сте-
степени в точности компенсируют-
компенсируются при учете фермионных и бо-
зонных пропагаторов, содержа-
содержащихся в собственно-энергетиче-
собственно-энергетических вставках, в результате
ответ будет такой же, как если
бы ящики с пунктирными ли-
линиями не учитывать совсем.
Сформулируем теперь тео-
теорему Вайнберга: фейнманов-
ский интеграл сходится, если
степень расходимости диаграм-
диаграммы, а также степень расходи-
мости, связанная С каждым
субграфиком диаграммы, отри-
отрицательна. По этой теореме диа-
диаграмма на рис. 19.32 расходится из-за вершинной вставки
(рис. 19.33,6) с D(S) = 0. После регуляризации вершины путем
вычитания ее расходящейся части с D = 0 (рис. 19.34,6) (на-
(напомним, что от последней можно целиком избавиться, перенор-
перенормируя вершину) остается лишь конечная часть с D(S) = —1;
теорема Вайнберга утверждает, что полный интеграл, отвечаю-
отвечающий диаграмме 19.32, после регуляризации вершины также ста-
станет сходящимся.
Обсудим на примере той же диаграммы рис. 19.32 основную
идею, лежащую в основе доказательства теоремы Вайнберга.
Интегрирование d4\d4i в этих диаграммах производится по
восьмимерному 1\ — ^-пространству, которое схематически изо-
изображено на рис. 19.35. Полная степень расходимости, согласно
A9^62), равна D = —2; действительно, при интегрировании по
радиусу-вектору в h—/г-пространстве интеграл для большин-
большинства направлений ведет себя как
ч
Рис. 19.35. Области в 1\ — /г-про-
странстве и соответствующие степени
расходимости.
f d4

336	ПЕРЕНОРМИРОВКИ	[ГЛ 19
причем фактор /10 в знаменателе возникает из четырех фермион-
ных и трех фотонных пропагаторов. Однако можно выделить
4-мерные «трубы» в области интегрирования, в которых подын-
подынтегральное выражение ведет себя иначе. Эти трубы отвечают
следующим трем областям:
а)/2малои/~(
ограниченная область
D(a) = -3;
б) /, мало и /
ограниченная область
в) U-k мало и /	J
ограниченная область
D (в) = - 5.
Очевидно, внутренние интегрирования по этим областям свя-
связаны с субграфиками (а), (б) и (в) на рис. 19.33. Точно так
же, субграфики с вычитаниями (рис. 19.34, а и б), отвечают об-
областям
а)	12 мало и /	\
ограниченная область
D(a) = -2,
б)	h мало и /~(	J
ограниченная область
D (б) = 0.
Проблема эффективного разбиения фейнмановского интеграла
на части, отвечающие различным областям интегрирования,
в каждой из которых интегралы могут быть оценены, в общем
случае была решена Вайнбергом. В частности, с помощью теоре-
теоремы Вайнберга можно строго обосновать оценки интегралов, ос-
основанные на вычислении интегралов по конечным областям.
Идеи, рассмотренные в предыдущем примере, можно обоб-
обобщить и на высшие порядки, что послужит более глубокому по-
пониманию содержания теоремы Вайнберга. Пусть имеется k
внутренних импульсов; тогда размерность пространства инте-
интегрирования равна 4k. При интегрировании по радиальному на-
направлению в 4&-мерном пространстве подынтегральное выра-
выражение ведет себя как lD~4k, где D — полная степень расходимо-
расходимости диаграммы. Однако снова можно выделить «трубы» раз-

146]
СТЕПЕНЬ РАСХОДИМОСТИ И КРИТЕРИИ СХОДИМОСТИ
337
личной размерности, отвечающие тем субграфикам, которые со-
содержат пропагаторы, не зависящие от переменных соответствую-
соответствующего внутреннего интегрирования. Эти пропагаторы во всей
г*
а,,
''Ч Ь
\ЛЛЛЛЛЛЛЛЛЛ
п)
	1
V-----'-'*
Г
К
К
f,-%'%^.--^
Рис. 19.36. Субграфики (б) диаграммы (а), отвечающие расходящимся вну-
внутренним интегрированиям.
области интегрирования остаются малыми и не помогают схо-
сходимости интеграла в целом. При подсчете степени расходимо-
расходимости D(S) для такой трубы необходимо учитывать только линии,

338
ПЕРЕНОРМИРОВКИ
[ГЛ. 19
целиком содержащиеся внутри данного субграсрика, а осталь-
остальные линии не нужно учитывать вообще. Доказательство этого
утверждения, данное Вайнбергом, существенно основывается на
а)
^../-../-•-'--'¦•...-..'--"-.."-..¦¦•¦'^
_ j	_i-_j
7
Рис 19.37. Член с вычитанием в вершинной вставке (а) и связанные с ним
расходящиеся внутренние интегрирования (б), (в) и (г).
использовании теоремы Гейне — Бореля. За деталями доказа-
доказательства мы отсылаем интересующегося читателя к оригиналь-
оригинальной статье [119].
Теорема Вайнберга позволяет свести задачу установления
сходимости членов в перенормированном ряду теории возмуще-
возмущений к выявлению всех субграфиков 5, для которых D(S)^0.
Более того, поскольку, согласно A9.62), неотрицательные сте-
степени расходимости имеют только вершинная и собственно-энер-
собственно-энергетическая вставки, мы можем сразу выделить те субграфики,
которые являются потенциальными источниками расходимостей
в фейнмановских интегралах. Эти субграфики фактически пред-
представляют те части диаграмм, которые в § 140 мы заключали
в ящики, выделяя тем самым вершинные и собственно-энергети-

146]
СТЕПЕНЬ РАСХОДИМОСТИ И КРИТЕРИЙ СХОДИМОСТИ
339
ческие вставки. Как было обнаружено выше, эти вставки можно
однозначно определить так, чтобы они не перекрывались. Ис-
Исключение представляют вставки в собственно-энергетическую
часть.
На рис. 19.36,6 указаны все субграфики для диаграммы
19.36, а, которым отвечают расходящиеся внутренние интегриро-
интегрирования. Некоторые из этих субграфиков содержат несвязанные
диаграммы. Достаточно, одна-
однако, рассмотреть только связан-
связанные субграфики; действитель-
действительно, если степень расходимости	\ ~ " /	/
всех связанных субграфиков
отрицательна, то и степень рас-
ходимости несвязанных суб-
субграфиков тоже отрицательна.
Член с вычитанием в вершин-
/П-~
S
л=о
Рис. 19.38. Фотонная собствен-
собственно-энергетическая диаграмма
четвертого порядка
Рис. 19.39. Области в /, — /2-прост-
ранстве и соответствующие степени
расходимости.
ной функции1) изображен на рис. 19.37, а. Этот член окружен
пунктирной линией, соответствующие расходящиеся внутрен-
внутренние интегрирования указаны на рис. 19.37,6, в я г. Отметим,
что внутреннее интегрирование, указанное на рис. 19.37,6, ко-
которое сходится в том случае, когда вершина не содержит вы-
вычитаний (см. рис. 19.36), с учетом вычитаний расходится, при-
причем расходимость возникает при интегрировании внутри вер-
вершинной вставки. Этот результат, очевидно, имеет общий харак-
характер: рассуждения на стр. 334 показывают, что вычитания при-
приводят к расходящимся внутренним интегрированиям только в
том случае, когда они производятся внутри вершинных и соб-
собственно-энергетических вставок.
Отдельная проблема возникает при рассмотрении вершинных
субграфиков, перекрывающихся внутри собственно-энергетиче-
собственно-энергетических частей. Примеры таких субграфиков изображены на
рис. 19.38 в случае фотонной собственно-энергетической части
четвертого порядка. Полная степень расходимости, согласно
A9.62), равна нулю, поскольку две степени импульсов в подын-
') Учет субграфиков, содержащил вставку вакуумной поляризации не
приводит к каким-либо новым следствиям или проблемам: эти субграфики мы
здесь не рассматриваем.

340
ПЕРЕНОРМИРОВКИ
ГГЛ. 19
тегральном выражении необходимо изъять для образования тен-
тензора <7n<7v в выражении A9.51) для U^v. Кроме того, существуют
а)	ф
°> —
тА
I	J
ж)
Рис. 19.40 Субграфики, отвечающие фотонной собственно-энергетической
диаграмме четвертого порядка
три области, указанные на рис. 19.39, которым отвечают три
субграфика на рис. 19.40, а, бив:
а)	/, — /2 мало'), D (а) = — 2,
б)	12 мало,	DF) = 0,
в)	h мало,	D (в) = 0.
•) Поскольку внешние импульсы могут быть выбраны так, чтобы от них
зависел каждый внутренний нмпульс субграфика (а), степень расходимости
D(a) уменьшается при вычитаниях, содержащих внешние импульсы.

§ 147)	КОНЕЧНОСТЬ ПЕРЕНОРМИРУЕМОЙ ТЕОРИИ	341
На рис. 19.40 указаны также субграфики (г, д, е и ж), завися-
зависящие от вычитательных членов, возникающих при перенорми-
перенормировке вершинных вставок. Этим субграфикам отвечают следую-
следующие области в /i — 4-пространстве
г)	/i мало, D(a) = 0,
д)	/2 мало, D(d) = 0,
ё) U мало, D(e) = 0,
ж) 12 мало, Б(ж) = 0.
При вычитании расходящихся выражений в вершинных
функциях степень расходимости каждого из указанных субгра-
субграфиков становится отрицательной. Точно так же после вычита-
вычитания в собственно-энергетических частях становится отрицатель-
отрицательной и полная степень расходимости всей диаграммы. Детальное
обсуждение случая перекрывающихся расходимостей впервые
было дано Саламом [112].
§ 147. Доказательство конечности
перенормируемой теории
Мы можем теперь приступить к доказательству конечности
5-матрицы в квантовой электродинамике в любом порядке раз-
разложения по перенормированному заряду е. Итерация уравне-
уравнений A9.51) позволяет вычислить перенормированные функции
Гц, Sf, Df и т и 5-матричные элементы в виде рядов по степе-
степеням е, при этом в каждом порядке по е результат выражается
конечной суммой фейнмановских интегралов. Вопрос о сходи-
сходимости этих интегралов решается с помощью теоремы Вайн-
берга, а именно: интеграл, отвечающий данной диаграмме, схо-
сходится, если степени расходимости всех субграфиков, равно как
и степень расходимости диаграммы в целом, отрицательны.
Наше доказательство основано на методе математической
индукции. В нижайшем порядке по е2, как было проверено
в гл. 8 явным вычислением, степени расходимости функций Гц
и Uc(q2) = U(q2) — П@) отрицательны, поэтому эти величины
определяются сходящимися (т. е. не зависящими от обрезания)
интегралами. Аналогичное утверждение справедливо для функ-
функций Sf и Df, которые выражаются через Гц и Пс(<72). Пред-
Предположим, что сделанные утверждения справедливы с точностью
до членов порядка п — 2, т. е. предположим, что в порядке п— 2
степени расходимости всех субграфиков в Гц и Uc(q2) отрица-
отрицательны, и потому эти величины, а также Sf и Df конечны.
Далее, итерируя уравнения A9.51) и используя теорему Вайн-
берга, мы покажем, что сделанные утверждения справедливы

342	ПЕРЕНОРМИРОВКИ	[ГЛ. 19
с точностью до членов порядка п. Тем самым мы установим тот
факт, что S-матричные элементы конечны в любом порядке по
заряду е.
Начнем с рассмотрения скелетных разложений A9.51а)
и A9.516) для функций т (с четырьмя и более внешними ли-
линиями) и для ядра К. При вычислении функций т и К в дан-
данном порядке по е их скелетные разложения содержат конечное
число диаграмм. Более того, поскольку функции Я и г вклю-
включают по крайней мере две вершины взаимодействия, то они
являются величинами порядка по крайней мере е2 (при е2—>0).
Поэтому при вычислении т и К в приближении е" достаточно
рассмотреть пропагаторы и вершинные функции, перенормиро-
перенормированные лишь в приближении еп. Так как скелетные разложе-
разложения A9.51а) и A9.516) содержат перенормированные вершин-
вершинные и собственно-энергетические части, а последние, в силу
предположения индукции, конечны в приближении е"~2, мы ви-
видим, что соответствующие вставки S в диаграммы я-ro порядка
имеют D(S)<.0. Так как субграфики 5 с ЬE)>0 могут воз-
возникать только от вершинных и собственно-энергетических час-
частей '), функции т и К в я-м порядке вообще не содержат расхо-
расходящихся субграфиков. Далее, заметим, что т и К не содержат
расходящихся внутренних интегрирований, связанных с вычи-
тательными членами в Гц, Uc(q2),Sp и Dp, поскольку, как было
отмечено ранее, указанные расходимости могут возникать
только в том случае, когда соответствующий субграфик цели-
целиком лежит внутри некоторой вершинной или собственно-энер-
собственно-энергетической части. Что же касается полной степени расходимости
интегралов для т-функций и ядра К, то она заведомо отрица-
отрицательна, поскольку сомнительным преимуществом иметь D > О
обладают только вершинная и собственно-энергетическая функ-
функции (см. § 146). Приведенные рассуждения показывают, что
функции К и ? и S-матричные элементы конечны в порядке еп,
так как в указанном порядке эти величины содержат конечное
число диаграмм 9 с D(&) < 0, все субграфики 5 которых также
имеют отрицательную степень расходимости D(S)<. 0.
Наше доказательство, однако, не закончено, поскольку ос-
остается еще установить конечность функций Гц и Пс(<72) или
Dp в порядке е", что удобно сделать с помощью уравнений
') Принимая во внимание градиентную инвариантность квантовой элек-
электродинамики, мы можем снова не рассматривать блоки фотон-фотонного рас-
рассеяния. Эти блоки в произвольной диаграмме можно выделить однозначным
образом, причем соответствующие субграфики не перекрываются (что можно
показать способом, аналогичным изложенному в § 141). При суммировании
диаграмм с четырьмя внешними фотонными линиями, отличающихся переста-
перестановкой фотонов, эффективная степень расходимости уменьшается с D = 0
до D = — 4.

§ 147]	КОНЕЧНОСТЬ ПЕРЕНОРМИРУЕМОЙ ТЕОРИИ	343
A9.51 в) и A9.51е). В силу тождества Уорда конечность Sf
следует из уравнения A9.51 г), коль скоро доказана конеч-
конечность Гц.
Для вычисления Гц в п-м порядке подставим в A9.51ш)
функции SF, Гц и К, вычисленные с точностью до еп~2:
'(»-2)s(n-2)V(»-2)^(B-2| _(П)	р(«)_ д(п) /1QfiQ\
где значок п указывает порядок по е, в котором производятся
вычисления. Наша задача заключается в том, чтобы показать,
что после одного вычитания, которое необходимо для перенор-
перенормировки вершины Гц, функция ЛцП) остается конечной, т. е. что
выражение
л;'(р', р) = л<"> (р', р) -лГ (р, р) |,_т
представляется суммой не зависящих от обрезания интегралов.
Чтобы применить теорему Вайнберга, выясним вначале, может
ли какой-либо субграфик в A9.63) иметь отрицательную сте-
степень расходимости. Согласно гипотезе индукции субграфики
с DE)^0 не содержатся в членах порядка еп~2, относящихся
к вершине Гц1), пропагаторам Sf и ядру К- Поэтому остается
рассмотреть только те внутренние интегрирования 3?, которые
содержат импульс / пропагаторов Sf (рис. 19.41).
Два электронных пропагатора в субграфике рис. 19.41, а при-
привносят по крайней мере две степени импульса в знаменателе.
Поэтому этот субграфик расходится только в том случае, когда
часть его, относящаяся к ядру R, имеет степень расходимости
D(K)$z —2. Посмотрим, в каком случае это может быть. Подо-
Подозрительными с указанной точки зрения являются, во-первых,
диаграммы нижайшего порядка, а во-вторых диаграммы, содер-
содержащие вычитания (см. рис. 19.41,6). Все эти диаграммы имеют
D(K) = —2. Кроме того, возникают аналогичные диаграммы
высших порядков, в которых все линии, входящие в К, отно-
относятся к рассматриваемому субграфику (за исключением, быть
может, тех, которые целиком лежат внутри ящика, отвечающего
вычитаниям). Эти диаграммы, согласно правилу подсчета сте-
степеней A9.62), также имеют D(R) — —2. Далее рассмотрим суб-
субграфики, содержащиеся в R с D(K)^—2 и не содержащие
безвредных вычитательных членов. Степень расходимости та-
таких субграфиков нельзя понизить, делая полное вычитание
') Напомним, что выражение A9.63) содержит сумму конечного числа
фейнмановских диаграмм, каждая из которых в свою очередь содержит ко-
конечное число вершинных и собственно-энергетических вставок.

344
ПЕРЕНОРМИРОВКИ
[ГЛ. 19
в A9.63). Примеры этих субграфиков изображены на
рис. 19.42, а, они отвечают случаю, когда ядро разбивается на
две части А и В, причем блок А содержит все линии субгра-
субграфика') &, в то время как остальные линии2) либо содержатся
в В, либо соединяют блоки А и В. Субграфик 9?, очевидно, рас-
расходится только в том случае, когда вклад в D(R) — —2 дают
1	I
Рис. 19.41. Внутренние интегрирования в вершине, содержащие импульсы
пропагаторов Sp
линии из блока Л, однако правило подсчета степеней показы-
показывает, что это невозможно. Действительно, степень расходимости
D{R)^—2 имеют только диаграммы, в которых блоки А и В
соединяются либо двумя фермионными линиями, либо одной,
двумя или тремя фотонными линиями. Случай двух фермионных
и одной фотонной линии исключается, поскольку такие гра-
графики не содержатся в определении R (см. рис. 19.11). Диа-
') Легко показать, что случай, когда все внешние линии присоединяются
к блоку А, можно не рассматривать.
2) При этом нужно рассматривать только связанные субграфики
1см. стр. 339j.	Y '

Конечность перёнормируёмой теории
345
грамма с двумя фотонами равна нулю в силу зарядовой инва-
инвариантности, поскольку, являясь частью вершинной функции,
она сводится к замкнутой петле с тремя внешними фотонными
линиями. Наконец, в последнем случае диаграммы с тремя фо-
фотонными линиями, указанном на рис. 19.42,6, полная степень
¦--» В
а)
Рис. 19.42 Потенциальные опасные субграфики.
расходимости понижается на четыре единицы, что связано с об-
обсуждавшимся ранее законом сохранения тока1).
Таким образом, мы убедились в том, что субграфики 9?, со-
содержащие ядро R, все имеют ?)B')^—2, причем степень рас-
расходимости D(R) = —2 имеют только те диаграммы, которые
целиком содержатся в R (за исключением диаграмм, содержа-
содержащихся внутри блоков с вычитаниями). Поэтому, в том случае,
когда субграфик Я? расходится, вклад в степень расходимости
его части, заключенной внутри вершины fjf~2>, равен нулю. По
гипотезе индукции, однако, все внутренние интегрирования
внутри Г{Г~2) имеют D <. О, в результате мы приходим к един-
единственной возможности: субграфик 9? вообще не содержит
') При этом, конечно, нужно включить субграфики фотон- фотонного рас-
рассеяния, необходимые для обеспечения градиентной инвариантности полной
амплитуды.

346	ПЕРЕНОРМИРОВКИ	[ГЛ. 19
линий, относящихся к fjj1'. Поэтому этот субграфик может
только целиком лежать внутри блока с вычитаниями
(см. рис. 19.41,в). После вычитания в A9.63), которое затра-
затрагивает все линии ядра R, его степень расходимости уменьшается
на единицу. При этом уменьшается также на единицу и полная
степень расходимости, поэтому, согласно теореме Вайнберга, ве-
величина ')
KW (Р', р) = <> (р', р) - A<f> (р, р) \р=т	A9.64)
однозначно определена и не зависит от обрезания. Так как по
построению
где L(n) — константа, зависящая от обрезания, из A9.52) и
A9.63) получаем
Z(r> = 1 - L(n)	A9.66)
с точностью до членов порядка е". Следовательно, в указанном
порядке
f?V, p) = v» + Kw(p', p)
конечная величина. Согласно A9.51 г) то же относится и к элек-
электронному пропагатору S'F.
Все, что нам теперь осталось, это обсуждение вакуумной по-
поляризации Uc(q2). Этот случай более труден для рассмотрения
ввиду проблемы перекрывающихся, расходимостей. Как было
показано в § 141, ящики, окружающие вершинные части, могут
перекрываться в том случае, когда они находятся внутри соб-
собственно-энергетических вставок. Указанная трудность, оставав-
остававшаяся долгое время в тени, теперь выходит на передний план.
Типичный пример графика вакуумной поляризации изображен
на рис. 19.43. На этом рисунке расходятся те субграфики, кото-
которые либо сводятся к вершинным вставкам в конце диаграммы,
либо перекрываются. Очевидно, что указанные субграфики
нельзя выделить по отдельности, один за другим. Кроме того,
ряд субграфиков, сходящихся до вычитаний, при учете вычита-
вычитаний становится расходящимся — такие субграфики получаются
заменой одного или нескольких ящиков на рис. 19.43 ящиками
с пунктирными линиями2). Необходимо поэтому тщательно
рассмотреть указанные субграфики и показать, что все они
') Напомним, что условие \р=*т означает, что р, действуя направо,
дает т.
2) При этом ящики с пунктирными линиями можно считать неперекры-
неперекрывающимися.

147]
КОНЕЧНОСТЬ ПЕРЕНОРМИРУЕМОЙ ТЕОРИИ
347
имеют отрицательную степень расходимости. Для функции Sf
аналогичное рассмотрение не нужно, поскольку в этом случае
можно использовать тождество Уорда. При обсуждении же
функции Пс нам предстоит выдержать настоящее сражение
с проблемой перекрывающихся расходимостей, которое мы
предвидели заранее, когда вводили ядро К-
Рис. 19.43. Диаграмма вакуумной поляризации.
Эффект перекрывающихся расходимостей приводит к тому,
что в уравнении A9.51е) исчезает множитель Z\. Чтобы пока-
показать, как это происходит, вернемся к уравнению A9.51в), вы-
выразим из него Ziyv- и подставим в A9.51е). В сокращенной за-
записи получим ')
(Я) = i \ iVSj&fv + / \ V^Sf
A9.67)
Покажем, что сумма двух членов в правой части A9.67) не со-
содержит перекрывающихся расходимостей (эту сумму более ес-
естественно записывать в виде разности, вводя к"аждый раз вме-
вместо Ъ'Р комбинацию (iS'F\ как это предписывается фейнманов-
скими правилами). С этой целью полезно построить итерацион-
итерационный ряд для вершинных вставок, содержащий разложение по
степеням ядра К, а не е2. В нулевом приближении Г<0) ж у^,
в первом приближении из A9.51в) получаем
- z,
- 5
A9.68)
1) Порядок спиновых индексов и аргументы в A9.69) легко могут быть
восстановлены в случае необходимости из уравнений A9.51в) н A9.51е).

348
ПЕРЕНОРМИРОВКИ
1ГЛ. 19
Субграфики в A9.68) сходятся по тем же причинам, что
и субграфики в A9.63). Исключение составляют субграфики,
отвечающие блокам фотон-фотонного рассеяния, сходящиеся
только после сложения всех членов, отвечающих различным
порядкам в итерации по степеням ядра R. На рис. 19.44 показан
пример, в котором необходимо учесть две итерации по степе-
степеням е. Однако графики фотон-фотонного рассеяния можно здесь
вообще не рассматривать. Действительно, в полном разложении
по степеням е 1*ожно однозначно выделить набор субграфиков,
Рис. 19.44 Примеры субграфиков фотон-фотонного рассеяния, отвечающие
различным порядкам в итерации по степеням К
содержащих диаграммы фотон-фотонного рассеяния, в кото-
которых расходящиеся члены сокращаются, и полная эффективная
степень расходимости которых Detf = —4, причем сказанное от-
относится к вставкам фотон-фотонного рассеяния как в вакуум-
вакуумную поляризацию, так и в вершинную функцию.
Таким образом, в дальнейшем мы можем забыть о фотон-
фотонных вставках и сосредоточить все внимание на более за-
запутанной картине вершинных субграфиков Здесь и ниже мы
используем термин «сходящийся» субграфик в смысле «сходя-
«сходящийся по отношению к внутреннему интегрированию в вер-
вершине». Отдельные члены в разложении на самом деле могут
расходиться из-за вставок блоков фотон-фотонного рассеяния
и сходятся лишь после сложения всех членов в данном по-
порядке по е, но различных порядков по R. Все это не имеет отно-
отношения к тому, что мы собираемся делать, поскольку нашей за-
задачей является применение критерия Вайнберга к каждой диа-
диаграмме в отдельности. При этом поведение подынтегрального

5 147)	КОНЕЧНОСТЬ ПРРЕНОРМИРУЕМОП ТЕОРИИ	349
выражения по отношению к остальным внутренним интегриро-
интегрированиям можно не рассматривать?).
Вернемся к выражению A9.68). Согласно гипотезе индукции
ядро R в порядке е" не содержит расходящихся субграфиков.
Анализ, проведенный на стр. 334 с некоторыми, отмеченными
выше оговорками, применим также к функции Sp. Поэтому одно
вычитание в A9.68) приводит к сходящемуся результату:
- J y»S'FS'FK = Lxt + AUp', P),	A9.69)
где Л]1 (р', р) — «конечная» с точностью до членов первого по-
порядка по R величина. Вычитание делается, как обычно2), при
Р'= р = т, так что'
Л?(Р, P)Um = 0.	A9.70)
Тогда в A9.68) в первом порядке по К имеем
Гй)(р', р) = Bп1,+ «уЧЛ?(р', р),	A9.71)
где, согласно условию нормировки A9.52),
Z1A, = l-L,.	A9.72)
Подставляя A9.71) обратно в A9.51в), получим во втором по-
порядке по К
Л Р) = 2, B) у» - \ [у* + А*? (//, р)] SFS'FK =
= Z, B^ + Uy^ + Л? (р', р) - J Л? (р', р) S'fS'fK ¦
По аналогии с A9.69) имеем
- \ A^S'fSfK = L2y» + Л? (р', р),
где Л? (р, р) \^т = 0.
') Читателю следует ясно осознать все разнообразие вопросов, которые
необходимо выяснить при исчерпывающем обсуждении проблемы перенорми-
перенормировок. Это является отличительной чертой всех доказательств путем «пере-
бирания всех возможностей». Можно было бы, как это часто делают многие
авторы, не рассматривать некоторые специальные случаи вообще. Аналогич-
Аналогичная ситуация возникает при построении общего вида амплитуды, совместного
с заданными требованиями симметрии с привлечением аргументов типа «что
еще может быть?». Если вы при этом не будете достаточно внимательны,
всегда найдется некто, который укажет вам то, что вы упустили.
2) См. § 143.

350	ПЕРЕНОРМИРОВКИ	[ГЛ. 19
Используя те же аргументы, что и в предыдущем случае,
можно убедиться в том, что функция Лг (//, р) конечна и что
во втором порядке по К
Т%) (//, р) « у* + ЛГ (//, р) + Л? (р\ р)
и Z] B) да 1 — L} — L2.
Очевидно, что после п итераций мы получим
f U (р\ р) = у" + ? Л? (р', р),	A9.73)
где
2, (В) = 1 - Е L,, Л? (р, р) \р_т = 0	A9.74)
+ Ab.,, A^s/.	A9.75)
Таким образом, мы получили для Г^(р',р) ряд сходящихся
интегралов. Роль констант L,-, через которые определяется кон-
константа перенормировки Z\, заключается в устранении расходи-
расходимости в полном вершинном интеграле A9.75), для которого
Рис. 19.45. Диаграммное разложение для П^ (q).
D = 0, а также в расходящихся субграфиках, связанных с теми
вычитательными членами, которые целиком содержатся внутри
этого интеграла. Подставим теперь A9.73) в выражение A9.67)
для Il^v(q), в результате получим графическое разложение, изо-
изображенное на рис. 19.45. Нашей задачей является показать, что
в каждом члене этого разложения все внутренние интегрирова-
интегрирования дают конечный результат. Тогда, используя теорему Вайн-
берга, мы получим, что полное вычитание в A9.51 е) приводит
к тому, что функция Пс (<72) = П (<72)—П@) конечна и опреде-
определяется интегралом, эффективная степень расходимости которого
равна D = —1.

5 H7I	КОНЕЧНОСТЬ ПЕРЕНОРМИРУЕМОЙ ТЕОРИИ	351
Подставив A9.73) в A9.67), сгруппируем члены, содержащие
одну и ту же степень К; тогда получим
+ лГ + ...] = пГ + пГ + п!Г+ .... A9.76)
где
$	? \	A9.77)
r+s=*n
Каждый график в П^ содержит п итераций ядра К, как это
показано на рис. 19.46. В силу A9.75) Лг содержит г итераций
ядра R, поэтому каждый член в правой части A9.77) содержит
ядро R п раз.
Чтобы убедиться в том, что IL(<72) сходится, необходимо по-
показать, что степени расходимости всех субграфиков, входящих
в Не отрицательны. По гипотезе индукции те субграфики, кото-
которые целиком содержатся внутри Лм или R, сходятся. Поэтому
любой расходящийся субграфик с необходимостью содержит не-
некоторую совокупность внутренних линий, принадлежа-
принадлежащих SF (см. рис. 19.46). Обозначим импульсы, относящиеся
к этим линиям, через /,-. Назовем далее внутреннее интегри-
интегрирование, относящееся к субграфику, целиком содержащемуся в
первом ящике, ^-интегрированием, внутреннее интегрирование
в субграфике, содержащемся во втором ящике—Ы2-интегриро-
ванием и т. д. Точно так же определим, например, /2/з-, /2/3/4-ин-
тегрирования. При этом, однако, рассматривать интегрирования
вида hkUk не нужно, поскольку соответствующие субграфики
не связаны. Выписав явно импульс U и опустив обозначения
всех остальных импульсов в К и Л, а также спиновые индексы,
перепишем A9.77) в следующем виде:
X Sf (lr+l) SF (lr+i + q) Л? (lr+u lr+i + q)
E
E
r+s-*n—\
X KS'r (/r+2) S'P (lr+2 + q) Л? (lr+2, lr+2 + q). A9.78)

со
to
Э
И
•о
и
о
¦о
S
¦о
о
W
Рис. 19.46. Субграфики, содержащие импульсы 1% электронных пропагаторов Sp

§ H7]	КОНЕЧНОСТЬ ПЕРЕНОРМИРУЕМОП ТЕОРИИ	353
Рассмотрим вначале ^-интегрирование. В этом случае доста-
достаточно рассмотреть только член с г = О и Ло = у'\ поскольку
при г ^ 1 график, отвечающий /i-интегрированию, целиком со-
содержится внутри Л? (lr+i, lr+\ + ф и по построению сходится
(см. A9.73)). Подозрительный член в A9.78) с г = 0 в симво-
символических обозначениях равен
где мы использовали A9.75). Константа вычитания Ln, хотя и
расходится, не имеет отношения к вопросу о сходимости ^-ин-
^-интегрирования, поскольку эта константа представляет интеграл,
зависящий от остальных переменных 12, ..., 1„. Интеграл в-
A9.79), как и следует ожидать, имеет D = -(-2. Однако после
вычитания двух степеней импульсов, необходимых для воссоз-
воссоздания тензорной структуры q^v, эффективная степень расходи-
расходимости понижается до D = 0. Образовав разность Пе(<72) =
= П(?2) — П@) (см. A9.51е)), мы понижаем D до —1.В ре-
результате приходим к выводу, что /i-интегрирование сходится,
поскольку сходятся все внутренние интегрирования, содержа-
содержащиеся в функции Sf в A9.79).
Перейдем к обсуждению /^-интегрирования. По аналогии
с предыдущим случаем достаточно рассмотреть только члены с
г = 0 и 1, поскольку для г^2 /^-интегрирование целиком со-
содержится внутри Лг и тем самым автоматически сходится.
Соответствующие члены в A9.77) равны
i \ tSrFS'PAl + I \ A'tSpS'pAX-i +
+ i J y^SFSpKSrSFAl-i + i J A^SpSpKSPSpAVn-2 =
= -i\ y»SFSFy4La - i \ ArSrF~S'FyvU-i,
где снова учтено выражение A9.75). Выписав явно аргументы
импульсов и опустив спинорные индексы, получим
F У1' ^ ' + ^ ^
X [К Ф, Р, Р- 4) S'F A2) % (fe) Л^_, (/2, «]« _т —
- i \ -§^A»y (h + q, к) SF {k) S'P (l2 + q) YvLrt-i, A9.80)

354	ПЕРЕНОРМИРОВКИ	[ГЛ. 19
В A9.80) явно выписан расходящийся интеграл по /2. При под-
подсчете степеней импульсов при /i-интегрировании из первого чле-
члена нужно вычесть 2 (по тем же причинам, что и в предыдущем
случае) и еще 1, отвечающую полному вычитанию1) содержа-
содержащемуся в nc(q2)- При подсчете числа степеней импульса 1% в вы-
выражении, заключенном в квадратную скобку, мы можем быть
заранее уверены в том, что соответствующая степень расходимо-
расходимости неположительна, поскольку это выражение сводится к вер-
вершинной вставке2). В результате степень расходимости для 1\12-
интегрирования в первом члене не превосходит —1. Точно так
же полное вычитание во втором члене понижает указанную сте-
степень расходимости по крайней мере до —1. Следует подчерк-
подчеркнуть, что ни первый, ни второй члены в A9.80) сами по себе
не приводят при интегрировании по 12 к конечному результату.
Это обстоятельство, однако, не затрагивает наши рассуждения,
поскольку мы интересуемся степенью расходимости /^-интегри-
/^-интегрирования, а не внутреннего интегрирования по 1%. Ответ же на
интересующий нас вопрос утвердительный: степень расходимо-
расходимости субграфика, отвечающего /^-интегрированию, отрицательна.
В свою очередь можно рассмотреть и каждое внутреннее интег-
интегрирование по отдельности, не обращая внимания на остальные;
вопрос о сходимости каждого из них решается с помощью тео-
теоремы Вайнберга.
Теперь ясно, как обобщаются полученные результаты для
произвольного h ... /^-интегрирования. Все члены в A9.77),
содержащие Л?(/й+1 + ?, h+\) с k^r, по гипотезе индукции
автоматически сходятся, поскольку для этих членов 1\ ... /г-ин-
тегрирование целиком содержится внутри Л^. Остающиеся чле-
члены можно записать в виде
*=0
r-1
r-1	fe=0
ft=O
') При этом следует помнить, что выражение в квадратных скобках в
формуле A9.80) представляет константу, умноженную на матрицу у.
2) Следует понимать, что полное вычитание в П не уменьшает./) для всех
/i/г-субграфиков. Однако единственными субграфиками, для которых это вы-
вычитание необходимо, является субграфик, содержащий все линии ядра К, н
субграфнки, указанные на рис. 19.40, а. Для этих субграфиков вычитательная
процедура на самом деле уменьшает D, поскольку они содержат внешний им-
импульс q, который течет только внутри них. Остальные субграфики уже имеют
Л«1

§ 147]	КОНЕЧНОСТЬ ПЕРЕНОРМИРУЕМОИ ТЕОРИИ	355
Интегрирования по h ... lk целиком содержатся внутри Ль а
интегрирования по /*+2 • • ¦ U, если таковые существуют, содер-
содержатся в константе перенормировки Ln~k- Степень расходимости
при lk+2 ¦ ¦ ¦ /г-интегрировании неположительна, поскольку Lr,-k—
вершинная вставка. С другой стороны, степень расходимости
при U ¦ ¦ • /^-интегрировании понижается от +2 до —1, по-
поскольку нас интересует не U(q2), а Пс(<72). Поэтому и полное
1\ ... /^-интегрирование приводит к сходящемуся результату.
Аналогичным способом следует рассматривать /2-, Ыъ-, • • • ,-
интегрирования. Наша задача — привести соответствующие вы-
выражения к виду, удобному для проведения полного вычитания
в n^v! при этом мы установим сходимость рассматриваемых
субграфиков. Начнем с /г-интегрирования. Единственно подозри-
подозрительными с точки зрения расходимости являются те члены в
A9.77), в которых ^-интегрирование не содержится целиком
в Лг или As. Выпишем эти члены, подчеркивая множители, со-
содержащие импульс 12:
[Подозрительные члены], =
i + I \ yfS'PS'FKSfFS'PK-\ +
+ / J A^SfSfKSfSpK- 2 =
= - iU \ i"S'is'FAl-x + i \ A$SFSFKSPSFK-2. A9.81)
Используя снова A9.75), представим последний член в A9.81)
в виде
i \ A^SFSFKSFSFAn-2 = - Их \ yuSrSFKSFSFAl-2 -
- i J y»SFSFKSFSFKSFSFAl-2. A9.82)
Ясно, что в последнем члене в этой формуле ^-интегрирование
сходится, поскольку четыре подчеркнутых множителя дают
D ('г) ^ —2 для любого ^-интегрирования. Комбинируя первые
члены в формулах A9.82) и A9.81), получаем для оставшихся
подозрительных членов
[Подозрительные члены], =
= - /L, J <fs'p&Al-i - iU \ fSFSF

356	ПЕРЕНОРМИРОВКИ	[ГЛ. 19
Это выражение, очевидно, сходится по отношению к /г-интегри-
рованию, если в нем сделать полное вычитание, отвечающее
вычислению Пс(<72)-
Аналогичная техника применима для исследования произволь-
произвольного h ¦ ¦ ¦ /3-интегрирования. Те члены в A9.77), которые от-
отвечают неотрицательной степени расходимости при этом интег-
интегрировании, с помощью A9.75) приводятся к виду
[Подозрительные члены], , =
= ? i \ AlS'FS'FAl-u + i ? J AlSFS'FKS'FSFAvn-k-{ =
k=\	fe=0
= - i Yj Lk\ ¦fS'pS'pAl-k + i \ A^s'FSFKSFSFAl-s. A9.83)
Снова, как и при рассмотрении ^-интегрирования, обратим
внимание на последний член в A9.83). Используя A9.75), вы-
выразим As-i через Л^-г и Ls-i, затем As-2 через Aj_3 и Ls_2 и
т. д. В результате получим
s-i
+ i (-l)s~l 5 yy%S'FKSFSF ... KSpS'pAIs,	A9.84)
где мы подчеркнули члены, зависящие от импульсов !) 12, ..., ls.
Последний член в A9.84), очевидно, имеет отрицательную
степень расходимости и его можно опустить. Члены под знаком
суммы могут быть упрощены, если с помощью A9.45) выразить
A^-s через A^_s+i, A^_s+2 и т. д. до тех пор, пока мы не изба-
избавимся от множителей К. Получающиеся при этом члены, содер-
содержащие вычитательные константы, все имеют структуру
Lk J ^SfS'fR .. . S'FSPyvL,.
Полное вычитание в П(^2) уменьшает степень расходимости
подынтегрального выражения до —1, и, поскольку все внутрен-
внутренние интегрирования внутри констант перенормировки Lk имеют
D ^ 0, /2 ... /s-интегрирования, содержащиеся в этих членах,
Подразумевается, что Ц в сумме подчеркивать не нужно.

§ 148]	ПЕРЕНОРМИРОВКА ЗАРЯДА В ЧЕТВЕРТОМ ПОРЯДКЕ	357
все имеют отрицательную степень расходимости. Поэтому A9.84)
упрощается и приводится к виду
S-1
* J A^SfSfKSfSfAI-s = *?*.*$ V^SfSfAI-ь + члены с D< 0.
fc-i
A9.85)
Члены, явно выписанные в A9.85), сокращаются с такими же
членами в A9.83); тем самым доказательство того, что /2 • • • U-
интегрирование приводит к конечному результату, закончено.
Точно так же можно показать, что степень расходимости произ-
произвольного /, ... /^-интегрирования с 1 < г < s < n тоже отрица-
отрицательна. Это мы оставляем читателю в качестве упражнения.
Таким образом, внутренние интегрирования в U(q2), связан-
связанные с вершинными и собственно-энергетическими вставками,
сходятся и полная степень расходимости в Ylc(q2) отрицательна:
D = —1. Более того, на первый взгляд расходящиеся блоки фо-
фотон-фотонного рассеяния на самом деле сходятся и имеют
D ^ —4, если рассматривать градиентно-инвариантные комби-
комбинации этих блоков. Это можно показать, используя аргументы,
аналогичные приведенным выше. Поэтому из теоремы Вайнберга
следует, что функция Пс(<?2) конечна в любом порядке е2. Из
A9.51 д) следует, что йр(ф^ также конечна в любом порядке
по е2. Таким образом, наше доказательство закончено. Мы по-
показали по индукции, что Гц, Sp, Df^m и S-матричные элементы
конечны в п-м порядке, коль скоро они конечны в порядке п—2.
Конечность этих величин в приближении е2 нам уже известна
из непосредственных вычислений.
В заключение этого параграфа снова подчеркнем, что наш
результат ничего не говорит о сходимости перенормированного
ряда теории возмущений. Например, при высоких энергиях, как
отмечено в гл. 8, параметр разложения ряда теории возмуще-
ний может быть не a, a a In — .В этом случае разложение яв-
является асимптотическим и сходится в лучшем случае при низких
энергиях.
§ 148. Пример перенормировки заряда
в четвертом порядке
Фактические вычисления перенормированных величин в низ-
низшем порядке теории возмущений были выполнены в гл. 8. При
этом, однако, не возникала рассмотренная в предыдущем пара-
параграфе проблема перекрывающихся расходимостей, поскольку
эти расходимости впервые проявляются лишь в порядке е*. Для

358
ПЕРЕНОРМИРОВКИ
[ГЛ. 19
того чтобы проиллюстрировать детали приведенного выше ана-
анализа, мы вычислим здесь явно тензор вакуумной поляризации
и покажем, что величина Uc(q2) (а вместе с ней и Ь'р) конечна
с точностью е4 [120].
Р+7
а)
р+1? ' р+Л+дг
Рис. 19.47. Два члена порядка е4 в уравнении A9.86) для W^ (q).
Вернемся к выражению A9.67)
I^v (q) = i \ fVSf&fv + / \ Y^S'fS'fKS'fS'fV^ A9.86)
и выделим в нем с помощью A9.51) все члены порядка е4. Диа-
Диаграмма, отвечающая первому слагаемому в правой части
а)
Рис. 19.48. Собственно-энергетические и вершинные вставки второго порядка,
которые в приближении е4 нужно учесть в диаграмме 19.47, а.
A9.86), указана на рис. 19.47, а. В приближении е4 для соб-
собственно-энергетических и вершинных частей этой диаграммы
нужно оставить графики, указанные на рис. 19.48. Отметим, что
каждая из вершинных вставок дает один и тот же результат,
поскольку замена q **•—q, \i *-> v не изменяет H^iq), но пере-
переводит (а) в (б) и наоборот. По той же причине равны и соб-

§ 1481	ПЕРЕНОРМИРОВКА ЗАРЯДА В ЧЕТВЕРТОМ ПОРЯДКЕ	369
ственно-энергетические вставки (в) и (г). Поэтому достаточно
учесть только одну вершинную и одну собственно-энергетиче-
собственно-энергетическую вставку и результат умножить на 2. Разложение второго
слагаемого в A9.86) начинается с члена порядка ё2, этот член
вместо Гц и Sp содержит уд и Sp соответственно, а для ядра К
в нем подставлена скелетная диаграмма рис. 19.47,6. Собирая
все члены порядка е4 и используя A9.51), получаем
ЛК -sF]SpVv +
+ 2;^SA?[f<2>-Yv] +
= 2i\y6SF{2)Spyv-2i\
- i J y^SpSpK^SpSpy,, A9.87)
где L<2) e= 1—Z\ (cm. A9.65), A9.66))—константа перенорми-
перенормировки вершины, вычисленная во втором порядке, a 6Sp =SF —
— Sp. Используя A9.63), можно выразить последний член в
A9.87) через перенормированную вершинную функцию по-
порядка е2:
после чего A9.87) приводится к виду, удобному для вычислений,
n^v (q) = 21 \ -2 .4 Sp y^fS'F (p) yvSF (p + q)-\-
- 21 \ -gfr Sp y^Sp (p) yvSF (p + q) L<2>.	A9.88)
Определение кинематических переменных дано на рис. 19.47 и
19.48. Первый член в A9.88) включает собственно-энергетиче-
собственно-энергетические вставки и не содержит перекрывающихся расходимостей.
Следует ожидать поэтому, что вклад этого члена в Пс(<72) коне-
конечен, в чем мы скоро убедимся непосредственным вычислением.
Два последних члена в A9.88) содержат неперенормированные
вершинные вставки A(v2). При их вычислении необходимо вычесть
два возможных расходящихся субграфика, относящихся к каж-
каждой из вершин в IInv Фактические вычисления при этом слож-
сложнее, чем в первом случае, но в конце концов и здесь получается
конечный результат.

360	ПЕРЕНОРМИРОВКИ	[ГЛ. 19
Начнем с более легкой задачи и обсудим вклад собственно-
энергетических вставок (рис. 19.48,3 и г). Имеем
1С (?)= 2/ $ -J^- Sp Y(i6S;B) (р) yA (P + q). A9.89)
При вычислении этого интеграла удобно использовать СПеК-
яо'B). .
тральное представление для ог>р (р), которое было получено в
гл. 16 и 18. Напомним спектральное представление A6.122) для
перенормированного пропагатора:
Fхг' р — т
После перенормировки имеем
-
я
1. \ *»М»р.(«') + р,(о'I , A9.90)
я J	р2 — а2 + te	K '
где p^Zj'p- Спектральные функции порядка е2 могут быть не-
непосредственно получены из результатов1) гл. 8 (см., в частно-
частности, уравнение (8.34)):
1 Г-
-т L
BлL (fe2 - Я2) [(р - feJ - m2]
A9.92)
Выражение A9.92) включает массовый контрчлен, поскольку го-
голый пропагатор [р — т]~1 содержит физическую массу2). Кон-
Константа перенормировки волновой функции LB> в A9.92) возни-
возникает при перенормировке Sf . Вычисление интеграла по импуль-
импульсам A9.92) было выполнено в (8.38); в результате для поправки
второго порядка получаем
[?$ k fe A ) + ] у» X
Г
A9.93)
') Выражения A9.90) и A9.91) содержат массу фотона %, которая вве-
введена для того, чтобы отделить непрерывный спектр в Sp от одночастичного
полюсного вклада. Подобный прием уже использовался в гл. 8 при обсужде-
обсуждении инфракрасной расходимости.
2) См. сноску на стр. 294.

§ 148]	. ПЕРЕНОРМИРОВКА ЗАРЯДА В ЧЕТВЕРТОМ ПОРЯДКЕ	361
В приближении е2 спектральные функции р[ и р2 получаются
взятием абсорптивной части в A9.93):
- [ppi (р2) + р2 (р2)] = -?¦ -^^г J dz Y|l \p A - г) + /n] у X
о
X я0 [р2г A - г) - т2г - Я2 A - z)\ ф^т, A9.94)
где 9 — знаковая функция
Подставляя вычисленные спектральные амплитуды A9.94) в
A9.91) и A9.89), получим вклад собственно-энергетической
поправки в тензор вакуумной поляризации; этот вклад обо-
обозначим II^v':
3 Р2 - а2 + /в
(т+Я.)"
Интересующий нас коэффициент ПBа'(?2) при g^q^ в П^ может
быть выделен с помощью обычной процедуры введения фейнма-
новских параметров и последующей замены переменных в ин-
интеграле по импульсам:
(
Интеграл по d4// в A9.96) логарифмически расходится, что яв-
является напоминанием о равной нулю степени расходимости в
диаграмме вакуумной поляризации. Перенормированное значе-
значение Il>v(<72) содержит, однако, разность Пс(q2) = П(q2) — П@),
которая представляется уже сходящимся интегралом:
1
П'2а> (q2) = ^ \do2 p, (a2) \ dz z A - z) X
m'Z-Hr»(l~z)	I	П997)
z + а^ A - г) - 92г A - z) J' Uy-y/^

362	ПЕРЕНОРМИРОВКИ	[ГЛ. is
В сходимости этого интеграла легко убедиться, если заметить
что при (т2->оо логарифм ведет себя как 1/а2 и что при этом,
согласно A9.94), pi (о2) также порядка 1/а2. Спектральный ин-
интеграл в пределе —q2 ^> т2 может быть выражен через элемен-
элементарные функции, в результате получим
„2
+ члены порядка единицы при -Ц- > 1. A9.98)
Таким образом, мы убедились в том, что собственно-энерге-
собственно-энергетическая вставка дает конечный вклад в Uc(q2)- Это обстоятель-
обстоятельство не удивительно, поскольку в рассмотренном случае не воз-
возникает проблемы перекрывающихся расходимостей. Результат
A9.98) можно было бы получить и другим способом: выполнить
вначале перенормировку собственной энергии и результат под-
подставить затем в интеграл для вакуумной поляризации.
Ситуация не столь проста для последних двух членов в
A9.88), возникающих из вершинных вставок. Перекрываю-
Перекрывающиеся расходимости во втором члене
^ i \ "(Ёуг Sp VV (Р) А® (Р, p+q)SP(P+ Я) A9.99)
сокращаются с расходимостями, возникающими от двух вер-
вершинных внутренних интегрирований в
A9.100)
Выполнив еще общую перенормировку, т. е. сделав вычитание
при q2 = 0, мы ожидаем, что величина П<,26) (q2) — 2П<,2в) (q2) опре-
определяется уже сходящимся интегралом. Рассмотрим подробнее,
как происходит указанное сокращение.
Согласно фейнмановским правилам для П*2^ получаем
(> (а) = еЛ
Г Уц (Р + т) уд (р +
ЬР L (р2 - т2) [(р + feJ - m2] [(р + А + <?J - т2] (р +
Г Уц (Р + т) уд (р + к + т) уу {р + к + 4 + *п) уа (/> + ^ + т) ~|
L	- m2 J '
A9.101)
где кинематика указана на рис. 19.47, в. Выделим вначале коэф-
коэффициент ПBб)(<72) при тензоре q^qv, тем самым устранив кажу-
кажущуюся квадратичную расходимость в A9.101). Скомбинировав

§ 148]	ПЕРЕНОРМИРОВКА ЗАРЯДА В ЧЕТВЕРТОМ ПОРЯДКЕ	363
четыре знаменателя, возникающих от петель с заряженными
частицами, получим
1	»
A9Л02)
где at — электронные знаменатели, указанные на рис. 19.47,6.
Интеграл по d*p вычисляется с помощью замены переменных 1)
p' = p+k(z2 + z3) + q (z3 + z4),
которая дополняет знаменатель до полного квадрата; при этом
в знаменателе исчезают нечетные по р' члены. Шпур в числи-
числителе можно разложить по степеням р'\ тогда члены, содержащие
нечетные степени р', при интегрировании дают нуль, а члены,
содержащие четыре степени р', дают вклад, пропорциональный
gnv, и могут быть также опущены — эти члены представляют
единственную расходящуюся часть интеграла. Члены, квадра-
квадратичные по р\ с помощью громоздких алгебраических выкладок
приводятся к виду2) р'2{кукч — q^qv) плюс несущественные
члены, содержащие g^- Выполнив в A9.101) интегрирование по
dAp', получим
B>
/a Г d*k Г
= -^Г ) B^4 )
( 16(feuyfev
^	^- члены с g^, A9.103)
где
— z224) — m2 + /e
= k2 {zx + z4) (z2 + Z3) + q2 (z, + г2) (z
SP Yn [- ^ fe + Za) - 4 B3 + z4) + m] Ya X
X [k (zi + Z4) - tf (z3 + Z4) + m] Yv [^ B1 + z4) +
z2) + m] Ya [~ ? (z8 + 23) + ^ (z, + z2) + m\. A9.104)
Далее необходимо выполнить интегрирование по dik. Отме-
Отметим важнейшие промежуточные этапы.
') Интеграл по импульсам следует регуляризовать, с тем чтобы получить
конечное и однозначно определенное с математической точки зрения выраже-
выражение. В первом томе мы использовали градиентно-инвариантный метод регу-
регуляризации (см. (8.20)), который может быть применен и в рассматриваемом
случае.
2) При этом члены, антисимметричные при замене (zi, z2)<—>Bз,г4), можно
опустить.

364	ПЕРЕНОРМИРОВКИ	[ГЛ. 19
1. Вначале перепишем .2 _ . 2 в следующем виде:
_ (z, + Zt) (z2
к2 - X2 (г, + z4) (z, + z3) (fe2 - Я2) '
имея в виду дальнейшую параметризацию A9.102), в которой
мы сопоставим фейнмановский параметр ^ с Di и (/=1—х с
фотонным пропагатором.
2.	Регуляризуем фотонный пропагатор
k2 - х2 ~^ k2-K2 ~ k* - А2'	A9.105)
с тем, чтобы сделать конечным интеграл в A9.103), логарифми-
логарифмическая расходимость которого возникает от слагаемых, пропор-
пропорциональных fe2/Di и k^JDx. При этом возникают зависящие от
обрезания члены, которые окончательно исчезают при полном
вычитании в Uc(q2).
3.	Сделаем замену переменных
и' __ и г qx\z,z3 —
к "f
к "f (z, + z«) (z, + z8) '
чтобы дополнить выражение в знаменателе до полного квад-
квадрата. Тогда после интегрирования по d4k' получаем три члена.
Первый из них возникает из первого слагаемого в A9.103), про-
пропорционального Dr\ назовем его П^1'. Два других члена —
II^v!) и njfv' — возникают при интегрировании слагаемого с Df2
и отвечают членам нулевого и второго порядка по k' в Л^у
Член в Nyy, пропорциональный /г'4, приводит к несущественному
множителю g^y.
Коэффициент при q^q^ в П^) равен
dz,...dz«efl2z0
nB6l) (а2) = — \ dx \	v '	I у
11 W > 4Лз J пХ ) (Zl + г4) (г2 + 23) Л
о о
?>2 (Л2, <?2)	,. „ . .„
D2(l\ q2) • A9Л06)
где
D2 {К2, q2) = К2 (I - *) (г, + г4) (z2 + г3) +
{ + г2) (г3 + z<) - j
Интеграл по параметрам в A9.106) не приводит к расходи-
расходимости, поскольку при 2i + z4-*0, z2-\-z3->l он ведет себя как
в в
+ Zi .-e In в.	A9.108)
о

§ 148]	ПЕРЕНОРМИРОВКА ЗАРЯДА В ЧЕТВЕРТОМ ПОРЯДКЕ	365
Однако если знаменатель содержит дополнительные степени zt,
возникают, как мы вскоре убедимся, трудности. После вычита-
вычитания получаем выражение
которое сходится; явное вычисление интегралов представляет
хорошее упражнение для энергичного студента. Здесь мы при-
приведем лишь асимптотическое значение при —q2 ^> т2:
0A).	A9.109)
Рассмотрим далее выражение для ПBб2), которое отвечает не
зависящей от k' части Л?дУ в A9.104). Подынтегральное выра-
выражение в этом случае ведет себя как d^k'jk'6 при больших k'2 и
несомненно, сходится без всякой регуляризации фотонного про-
пагатора. Для коэффициента при q^qy получаем
dzx
где D2(k2, q2) определено выражением A9.107). В пределе
—</2-»-оо получаем
Ю("Н? (?)	A9.111)
Теперь остается только вычислить тензор 1$'\ отвечающий
членам с k'2 в A9.104). Этот тензор не только логарифмически
расходится при интегрировании по d4k', но и содержит перекры-
перекрывающиеся расходимости и сходится только после включения
контрчленов A9.100), связанных с перенормировкой вершины.
Вычислив все шпуры и выполнив, с учетом регуляризации
A9.105) фотонного пропагатора, интегрирование по d4k', для
коэффициента при q^qv получим
1
о
X (zi - z3) (z4 - z2) In DD22[%' ^-, A9.112)
где величина D2 определена в A9.107). После вычитания в
точке q2 = 0 в выражении A9.112) исчезает зависимость от Л2,
однако взамен появляется расходимость при внутреннем интег-
интегрировании по параметрам. В этом пункте как раз и проявляется

366	ПЕРЕНОРМИРОВКИ	[ГЛ. 19
трудность работы с перекрывающимися расходимостями. При
22 + 23->0 (и 2i + Z4« 1, как это предписывается б-функцией)
в A9.112) получаем выражение
A—Zi — г\ {z2+z)
о
A2 A — x) (z2 + z3)
которое, как и A9.106), сходится для конечных X и Л. Однако
вычитание при ^2 = 0 приводит к замене логарифмического
множителя в A9.112) на \n[D2(X2,0)/D2(k2, q2)]. В результате
при z2, z3->0
Ш
2, 0)
In
8
dz2
и в A9.113) возникает расходящийся интеграл \
о
Логарифмическая расходимость в ПBбз), возникающая от ин-
интегрирования по области z2 -f z3 < е, очевидно, связана с внут-
внутренним интегрированием в вершинной вставке v. Используя ана-
аналогию с теорией электрических цепей из гл. 18, эту расходи-
расходимость можно интерпретировать в терминах токов, текущих по
линиям с импульсами p+knp+k+q на рис. 19.47,6. В рас-
рассматриваемом случае сопротивления этих линий становятся ис-
чезающе малыми, в результате по петле в вершинной вставке v
течет бесконечно большой ток. Аналогичная расходимость от об-
области (z\, z4) » 0 связана с внутренним интегрированием в вер-
вершине \л. Обе расходимости устраняются двумя вычитаниями
вида A9.100), необходимость которых предписывается програм-
программой перенормировок.
Чтобы продемонстрировать сокращение расходимостей, мы
заново рассмотрим контрчлены в A9.100), которые ранее были
вычислены в гл. 8. Здесь мы проведем выкладки способом, мак-
максимально близким тому, которым была вычислена функция
ПBбз)(<72)-
Подставим в A9.100) определение IB)Yv из A9.65). По фейн-
мановским правилам находим

148]
ПЕРЕНОРМИРОВКА ЗАРЯДА В ЧЕТВЕРТОМ ПОРЯДКЕ
367
Кинематика для вершины v указана на рис. 19.47,6. Переменная
р не есть переменная интегрирования; протаскивая р направо
или налево, мы всегда получим р2 = т2 и р = т, поскольку вы-
вычитание в вершине каждый раз приводится на массовой поверх-
поверхности. В результате получаем ')
d*kdlp
Уп (Р + k + m) Yv (p + k + т) у
а "I I
J |
Р + Я +
(Р + 9J ~
A9 114)
Несмотря на то, что р не есть переменная интегрирования, удоб-
удобно скомбинировать четыре знаменателя в точности так же, как
в выражениях A9.101) и A9.102); при этом выкладки макси-
максимально похожи на выкладки при вычислении тензора П^. После
замены переменных
Н	Н ' *1 + 24 '
дополняющей выражение в знаменателе до полного квадрата,
выполним интегрирование по d4p'; тогда получим
т<2в)
—	— J2- \ dk \
—	2я ) BяL )
л Sn /5 Г
Vn эр </ [ [(j5
2 (z, + z3)
/Bi + 24)
+ члены с
ya	"I I
- m2]2 J |«
A9.115)
Чтобы выполнить интегрирование по d4k, перепишем фотонный
пропагатор в виде
1			22 + 23
k2 -
(Z2 + 23) (й2 - Л2)
и скомбинируем его с помощью параметра к со знаменателем
в A9.115). Интеграл по импульсу вычисляется затем с помощью
замены переменных
k'— k + рх,
после чего, взяв шпур, мы получаем два члена, nBBl)(</ ) и
ПBвг)(<72). которые представляют собой коэффициенты при
в ПBв>(<?).
') Выражение в квадратных скобках в числителе не следует раскрывать
до тех пор, пока мы не заменим его константой, умноженной яа Yv

368	ПЕРЕНОРМИРОВКИ	[ГЛ. 19
Функция nBBlH/2) содержит часть числителя в A9.115), не
зависящую от k', и равна
0	0
О 	 О» 	 vi
X
(Zi + Z4L (Z2 + Z3)
2 — 2x - x2
' т?х -m2x(\-x) (z2 + z3) — <?2*zi24/(zi + z4) + Л2 A - x) (z2 + z3) "
A9.116)
Интеграл A9.116) расходится при интегрировании по z\t zA
\dZl (d24 *i?4 = {**. \ У*У
J ' J 4 (zi + z4L J z, J A + j/L
oo	oo
и сходится после вычитания в точке q2 = 0. Согласно аналогии
с теорией электрических цепей (см. рис. 19.47,6) мы связываем
эту расходимость с интегралом вакуумной поляризации, умно-
умноженным на конечную часть вставки LB) в вершине v. Хотя функ-
функция Пс2"'1 (q2) сходится на верхнем пределе, она расходится в ин-
инфракрасной области, поскольку в этой области расходится вер-
вершина перенормировки ?<2\ В пределе —q2 3> т2 выражение
A9.116), умноженное, как и A9.88), на —2, равно
Функция ПBВ1> (д2) возникает при учете членов в числителе
выражения A9.115), пропорциональных (k'J, и логарифмически
расходится. Используя регуляризацию A9.105), получаем
п<2^' (п2) — _^_
П {q )-4п3
о	о
X In {[Л2 A - х) (z2 + z3) + m2x -
- т2х A - *) (z2 + 23) - q2x ZizJizi + zt)] X
- x) (z2 + 23) + m2x -m2x(\-x) (z2 + z3) -
-</2Jcz,z4/(zl + z4)]~1'}. A9.118)
Это выражение расходится даже после вычитания из него
дBвг) ^ Расходимость возникает при интегрировании по z2, z%
при 2г, z3->0. Ее можно связать с расходимостью константы пе-
перенормировки ?B), умноженной на интеграл вакуумной поляри-
поляризации (конечный после вычитания в нуле).
В точности такая же расходимость была найдена нами в
A9.112). Указанные две расходимости сокращаются, если взять

§ 1481	ПЕРЕНОРМИРОВКА ЗАРЯДА В ЧЕТВЕРТОМ ПОРЯДКЕ	369
разность выражений A9.112) и A9.118), как это предписывается
правилами перенормировки в A9.88). Сделав вычитание в нуле,
получаем
- Z2) X
)	(	tf (zs
0	0
Z3J 1 (Zl -
n2 — ,
Л. ¦, \f* Л.*\ X (ZjZ, — Z2Z4J
1 T Z2) IZ3 ~\~ Zi)	;	;	r—	;	Г-
(z, + z4) (z2 + z3).
ZiZ4
где мы пренебрегли фотонной массой X, поскольку A9.119) уже
не содержит инфракрасной расходимости, и положили Л->оо,
поскольку это выражение не зависит от Л. Мы также симмет-
ризовали член с вычитанием в Пс2вг)(<72) относительно замены
zi, Z4-*-»-z<i, Zz- Эта замена отвечает тому, что вершинная вставка
вычисляется по одному разу в каждой из двух вершин в диа-
диаграмме вакуумной поляризации. Выражение A9.119) свободно
от перекрывающихся расходимостей; при z%, 2з->0 и zi + г4—> 1
расходимости в первых двух членах сокращаются, поскольку
\	(
о о
"" ZlZi 1П т* -q*zxzi + ° ^' ZA ~ Е ПРИ Е "*" 0>
а третий член конечен. Точно так же при z\,Zi->-0, 2г + гз->1
сокращаются расходимости в первом и третьем членах, а второй
член конечен. Таким образом, вычитательные члены обеспечи-
обеспечивают желаемое сокращение расходящихся частей вершинных
вставок внутри функции Пс2бз)- Сделав затем полное вычитание
при q2 = 0, мы получим для вакуумной поляризации конечный
ответ. На приведенном выше примере можно убедиться в том,
что метод перенормировок неизбежно приводит к успеху, однако
требует при этом весьма громоздкой вычислительной работы.

370	ПЕРЕНОРМИРОВКИ	1ГЛ. 19
Для фактического вычисления A9.119) введем удобные пе-
переменные
Zl + Z4 = Z, Z\ = ZU, Z2=(l— Z)V, 0^.2, U, У^1,
тогда в пределе — q2 Э> т2 получим
Сложив вместе выражения A9.98), A9.109), A9.111), A9.117)
и A9.120), мы получим полную вакуумную поляризацию четвер-
четвер2 2
у
того порядка; в пределе —q2 ^> т2 она равна
0A).	A9.121)
В A9.121) сократился член с In2 (—q2/m2), равно как сократи-
сократились инфракрасные члены в собственно-энергетических встав-
вставках в ПBа> и в вершинных вставках в ПBб) и П<2в). Подставляя
в фотонный пропагатор A9.51е) вакуумную поляризацию вто-
второго порядка (см. (8.29)) и только что полученный результат
A9.121), приходим к следующему выражению (справедливому
с точностью до е4):
X' ( 2\ _	^ЦУ Г	1		"I
Up \q J^v — q2 - a ( ~jf\ a2 . / qT\~.	'
1 —r-ln( —-VI— 1-5 n I — -Ц- I -4- ... I
L Зя \ m2 J 4л2 \ m2 J~ J
-?2»m2, A9.122)
где мы опустили градиентные члены. Этот результат был впер-
впервые получен Иостом и Латтинджером [120] в 1950 г. Оба попра-
поправочных члена имеют знак минус и поэтому увеличивают взаимо-
взаимодействие между частицами на малых расстояниях. К аналогич-
аналогичному выводу, справедливому, однако, уже во всех порядках по
а, можно прийти, рассмотрев спектральное представление для
Dp(q) из гл. 16. Этот вывод следует из положительной опре-
определенности весовой функции в выражениях A6.172) и A6.173).
§ 149. Низкоэнергетическая теорема
для комптоновского рассеяния
Тождество Уорда и теория перенормировок позволяют сфор-
сформулировать теорему о низкоэнергетическом поведении ампли-
амплитуды комптоновского рассеяния, которая оказывается справед-
справедливой во всех порядках по е2. Как впервые было показано Ти-,
рингом [121] в 1950 г., амплитуда рассеяния фотона на электроне

§ 149]	НИЗКОЭНЕРГЕТИЧЕСКАЯ ТЕОРЕМА	371
в пределе малых частот стремится к классическому комптонов-
скому пределу и равна а/т, где а= 1/137 и т— перенормиро-
перенормированные значения заряда и массы электрона'. Во втором порядке
возмущений этот результат был получен в гл. 7 (см. формулу
G-74)).
Доказательство сформулированной выше теоремы основы-
основывается на том факте, что, согласно тождеству Уорда, полная вер-
вершинная функция Гр.(р, р) при нулевой передаче импульса может
быть получена дифференцированием точного фотонного пропа-
гатора Sf (р)
Г>> p) = -^rS'F~'(p).	A9.123)
Другими словами, добавление к заряженной линии фотона с ну-
нулевой частотой приводит к дифференцированию по импульсу
этой линии, что легко понять, используя одну только градиент-
градиентную инвариантность, т-функция для свободного заряженного
электрона равна
x(p)^iS'P(p).	A9.124)
Чтобы получить т-функцию заряженной частицы (с затравочным
зарядом е0) в постоянном электромагнитном поле, достаточно
сделать в A9.124) градиентно-инвариантную подстановку
При этом х{р) заменяется на
т (р) -> х (р — е0А) =
—*</>)- ъА'уг ' <Р> + j elA»A" -^г * (р) + ¦ ¦ • A9.115)
Коэффициент при Лд в этом выражении
- ео-^г * (р)=fcos; (р) [-^г S7l (
= iS'F (p) e.Y^ (р, p)S'F(p) A9.126)
представляет, с точностью до множителя е0, некомпактную вер-
вершинную часть при нулевом переданном импульсе, которая со-
содержит электронную собственно-энергетическую вставку, но не
содержит фотонных концов (рис. 19.49). Коэффициент1) при
Va^n^v равен т-функции, описывающей комптоновское рассея-
рассеяние. Этот член содержит взаимодействие второго порядка, при-
причем оба фотона как до, так и после рассеяния имеют нулевую
') Множитель '/г учитывает тот факт, что АцАу содержит два двух-
фотонных состояния: А^А^-у А^А^ + +*^\

372
ПЕРЕНОРМИРОВКИ
Рис 19.49. Вставка фотона с нулевой частотой с помощью дифференциро-
дифференцирования пропагатора — иллюстрация тождества Уорда.
tS/ф)
13/0»
tS/(p)
-iegTv(p,p)
ts/(p)
~iejfi(p,p)
Рис 19.50. Вторые производные, приводящие к комптоновской амплитуде
в пределе нулевой энергии.

5 H91	НИЗКОЭНЕРГЕТИЧЕСКАЯ ТЕОРЕМА	373
энергию. Как обычно, электронные концы включены в опреде-
определение т-функции, а фотонные концы исключены (рис. 19.50).
Имеем
^(Pr-iel^^S'Ap).	A9.127)
Графическую связь с комптоновской амплитудой легче всего
проследить, рассматривая тождество, следующее из A9.48):
с'"'/ \	д'2
¦SP (р) = —
дрцдрч	г	dppOpv
Подставляя это тождество в A9.127) и учитывая A9.123) и ра-
равенство
= -S'P(p)[~SF \p)]sF(p),
получим
т(с) (рГ = + [iSP (р)] [(- /е0) Г* (Р, Р) ^ (р) (- ie0) Tv (p, p) +
+ (- ie0) Tv (p, p) iS'P (р) (- 1е0) Та (р, р) - ie20 ^^] №
A9.128)
Три члена в A9.128) представляют сумму всех диаграмм, полу-
полученных добавлением к электронной линии с зарядом е0 и им-
импульсом рц двух фотонов с нулевой частотой. Пропагаторы
вдоль электронной линии имеют вид (р + ?,• — m)~l, где ki из-
изменяется при каждом взаимодействии с фотоном внутри блока
собственной энергии. Поскольку
е0 -?- AJ_! = - тт-Г	(~ /e<>Yu) 7ТТ	' (! 9-!29)
<5р.и Р + ki — m	p + k{ — m	p + ki — m
мы заключаем, что дифференцирование пропагаторов каждый
раз отвечает добавлению фотона с нулевой частотой. Вставки
же фотонов в замкнутые электронные петли дают нуль1) в силу
причин, уже обсуждавшихся в § 146. Действительно, градиентно-
инвариантная амплитуда для замкнутой петли пропорциональна
<7ц8у — 9Чец и равна нулю при q^ = 0. В результате приходим к
выводу, что выражение A9.127) содержит все фейнмановские
графики при нулевой энергии. Поэтому можно вычислить S-мат-
ричный элемент, выделив в этом выражении внешние элект-
электронные концы и умножив его на волновые функции фотонов и
') То есть в рассматриваемом пределе \й4р-т—F (p, kh ..., kn) — 0,
где F — вклад замкнутой петли.

374	ПЕРЕНОРМИРОВКИ	(ГЛ. 19
электронов в начальном и конечном состояниях (см., например,
A7.43)). В результате получаем
S(p', k\ в'; р, k, e)= Bп*^шЖ^(р', k'\ p, k), A9.130)
где кинематика указана на рис. 19.51, а амплитуда 3Wav в пре-
пределе k, &'->0 равна
ЭГ>, 0;р, 0) =
(P +	)(p)
fi opv
d"Sl{Pd+Dk) ku{p). <19Л31>
В последнем выражении мы учли правила перенормировки
A9.49). Для дифференциального сечения рассеяния фотона с
данной поляризацией получаем
ИуМ3^ md3p' BnY bUp + k-p' - k')
I
ИЛИ
^ i|B/vrf при fe, fe'->0.	A9.132)
Очевидно, что сечение doldQ при нулевой энергии конечно, если
конечна амплитуда 50UIV. Поэтому в A9.131) необходимо вычис-
вычислить d2Sf (р + ?)/<Эрц dpv с точностью до членов порядка kr2.
Рассмотрим общее выражение для
перенормированного пропагатора
Л(т2) = В(т2)=1. A9.133)
Вычисление производных упрощает-
упрощается, если выбрать поперечную калиб-
Рис. 19.51. Кинематика для ровку в системе покоя электрона,
кочптоновского рассеяния. Тогда
ер = 0, е'р = 0,	A9.134)
и члены, пропорциональные р^ и pv, можно опустить. Выполнив
дифференцирование, получим
-f paOv + PVO" + pV- A9.135)

S 149]	НИЗКОЭНЕРГЕТИЧЕСКАЯ ТЕОРЕМА	375
Величина Ф^ в этом выражении представляет сумму многих чле-
членов, не превосходящих ОA/&2), но не существенных для нас в
силу выбора калибровки A9.134). Величина / возникает от вто-
второй производной знаменателя
(p+kJ-m2 = 2pk
и имеет порядок O(l/k3). Отсюда, в частности, видно, насколько
существен для получения правильных результатов в электроди-
электродинамике точный закон сохранения электромагнитного тока. Здесь
мы сразу избавились от сингулярного поведения в знаменателе,
выбрав удобную калибровку A9.134). Результат, разумеется,
останется тем же и в любой другой калибровке.
При оценке порядка величины различных членов в A9.135)
предположим, что производные функций А и В существуют в
точке р2 = т2, что можно показать, используя спектральное
разложение A6.112) для S'p (p) (при этом следует приписать
фотону массу Я, с тем чтобы отделить вклад разреза (т + AJ sg
=g; p2 =g: оо от полюса р2 = т2). Радиус сходимости в разложе-
разложении А (р) и В (р) по степеням р2 в окрестности точки р2 = т2
имеет порядок 2тк. Вопрос предельного перехода Л—»-0 мы об-
обсудим в конце этого параграфа.
Подставляя A9.135) в A9.131) и учитывая A9.134), получим
" (p, 0; p, 0) = 2ie2e . e' lim * (p) *(/+ ff *"
k->o	* \PRi
A9.136)
что представляет собой в точности комптоновскую амплитуду,
зависящую от физического заряда е и массы т. Для дифферен-
дифференциального сечения из A9.132) получаем
-|^-=J^-(e.g'J при й->0.	A9.137)
Таким образом, константа тонкой структуры а = 1/137, которая
входит в перенормированное разложение 5-матрицы, может
быть экспериментально определена как томпсоновский предел
комптоновского рассеяния при нулевой частоте. Обобщение этой
теоремы, позволяющее вычислить члены в Ш^у, линейные по k,
через статические характеристики фермиона, а именно, через
его заряд и магнитный момент, было дано Лоу, Гелл-Маном
и Гольдбергером'). Например, для нейтральной частицы с
') См. [122, 123]. Для обсуждения близких вопросов см. также статью
[124], где впервые выведена низкоэнергетическая теорема для реакций фото-
фотообразования мезоиов, и [125, 126].

376	ПЕРЕНОРМИРОВКИ	1ГЛ. 19
магнитным моментом ц (нейтрона) дифференциальное сечение с
точностью до членов порядка k2 равно
у sin2 б) при k-*0.
2
В случае заряженных частиц интерференция между томпсонов-
ским и релеевским рассеянием не выражается только через ста-
статические свойства частиц и имеет порядок k2. Поэтому ее нель-
нельзя отделить от вклада магнитного момента, который сам имеет
порядок1) k2. Полный анализ й2-членов, таким образом, требует
изучения динамических деталей взаимодействия и может быть
выполнен, например, с помощью соотношений Крамерса —
Кронига.
Нам остается еще отделаться от инфракрасной проблемы,
встретившейся в проведенном выше анализе. При доказатель-
доказательстве равенства A9.136) необходимо было предположить глад-
гладкое поведение (р'* — mf)Sp(pf) в A9.133). Это предположение
справедливо, однако, лишь в области р'2 — т2 ^<-2т%, где Я —
фиктивная масса фотона, откуда получаем ограничение на энер-
энергию фотона
(р + kf — m2 = 2mk0 + Я2 ^ 2тЯ или k0 < Я.
Однако если фотон имеет массу Я > 0, предел A9.132) никогда
не достигается, поскольку наблюдаемое физическое сечение обя-
обязано обращаться в нуль для k0 < Я. Чтобы придать выражению
A9.137) какой-либо смысл, следует расширить область его при-
применимости и считать, что оно выполняется при m>4, k' 3> Я.
Основанием для такого обобщения служат эвристические
аргументы, основанные на анализе инфракрасной проблемы в
модели Блоха — Нордсика (§ 123). Аналогичные результаты в
приближении е2 были получены в гл. 7, 8. Согласно A7.89) и
A7.95) амплитуда упругого комптоновского рассеяния при
Я -> 0 имеет вид
2L, i 2qa
A9.138)
где
Р' = — р' = — (k — k') = скорость электрона отдачи,
') Для неполяризованной мншени.

НИЗКОЭНЕРГЕТИЧЕСКАЯ ТЕОРЕМА	377
и стремится, таким образом, к нулю. Выражение A9.138) полу-
получается при классическом рассмотрении тока электронов умноже-
умножением томпсоновской амплитуды на вероятность того, что при
рассеянии не испускается ни одного дополнительного фотона.
Эта вероятность равна @out10 in) и дается формулой A7.89).
При этом мы приходим к результату, согласующемуся с выра-
выражением (8.62) для вершинной поправки и с вычислением радиа-
радиационных поправок второго порядка к комптоновской амплитуде,
выполненными Броуном и Фейнманом [127].
При рассеянии вперед р' = 0 и экспонента равна единице, в
результате выражение A9.138) не содержит инфракрасной осо-
особенности. Однако для любого |р'| ф О и любого k инфракрасная
особенность в экспоненте приводит к тому, что ЭДцу-^О при Л->0.
При этом нарушается низкоэнергетическая теорема A9.137), ко-
которая была доказана в предположении, ko/X ->¦ 0 при k0 -> 0, в то
время как здесь мы имеем обратную ситуацию: к/ko -> 0.
Из опыта работы с инфракрасными расходимостями мы
знаем, однако, что обращение в нуль упругой амплитуды Wl^
компенсируется неупругой амплитудой испускания произволь-
произвольного числа мягких фотонов с (/< Д?. Если учесть это обстоя-
обстоятельство, экспонента A7.89) заменяется на A7.95), а для диф-
дифференциального сечения вместо A9.138) получаем
Л
?J
J
-!^'2ln(^)], A9.139)
где р' = B&/m)sin2@/2). Нижний предел обрезания <~Д& равен
разрешению по энергии в детекторе, т. е. той максимальной энер-
энергии, уносимой мягкими фотонами, которую еще нельзя детекти-
детектировать измерительным прибором. Верхний предел в интеграле
по dq равен1) 1/Д/ ~ т, где At—интервал времени, в течение
которого скорость электрона возрастает от нуля до Э'. Отметим,
что обрезание на верхнем пределе необходимо здесь только по-
потому, что для простоты использовалась классическая модель
электронного тока.
Согласно A9.139) для любой энергии фотона k0 можно в
принципе проводить измерения со столь малым разрешением
Afe, что результаты измерения дифференциального сечения бу-
будут значительно отличаться от томпсоновского предела за счет
радиационных поправок. Однако если относительное энергети-
') Напомним, что комптоновская амплитуда содержит промежуточные
состояния с отрицательной энергией, которым в нерелятивистском пределе
отвечают энергетические знаменатели ~2ш.
13 Дж. Д. Бьёркен, С. Д. Дрелл, т. 2

R78
ПЕРЕНОРМИРОВКИ
[ГЛ. 19
ческое разрешение Ak/k фиксировано, то A9.139) при k-+0
действительно приближается к томпсоновскому пределу. В рас-
рассматриваемом случае, как впрочем и для большинства электро-
электродинамических процессов, прежде чем придавать определенный
смысл каким-либо количественным предсказаниям эксперимен-
эксперимента, необходимо тщательно проверить все экспериментальные ус-
условия.
§ 150. Асимптотическое поведение
фейнмановских амплитуд
Теорема Вайнберга, [119], обсуждавшаяся в связи с вопросом
о сходимости фейнмановских интегралов, содержит гораздо
больше результатов, чем мы до сих пор использовали. В дей-
действительности эта теорема дает простые
правила для вычисления асимптотического
поведения любой фейнмановской амплиту-
амплитуды в случае, когда некоторые из внешних
импульсов (или все импульсы одновремен-
одновременно) стремятся к бесконечности. Для форму-
формулировки этих правил, вывод которых осно-
основан на идеях, обсуждавшихся в § 146,
удобно немного изменить введенное ранее
определение субграфиков. Рассмотрим не-
некоторый набор {Qs} внешних импульсов qs,
входящих в данную диаграмму; в дальней-
дальнейшем положим Qs->oo. Тогда, выбрав ка-
каким-либо способом внутренние импульсы
{1г}, мы определим субграфик, отвечаю-
отвечающий данным внутренним линиям {Lr} и
внешним импульсам {Qs}, как набор всех
линий, содержащих по крайней мере один
импульс из наборов Lr и Qs, при условии, конечно, что получаю-
получающаяся при этом диаграмма является связанной. Рассмотрим,
например, диаграмму шестого порядка для электрон-позитрон-
ного рассеяния (рис. 19.52). Пусть нас интересует асимптотиче-
асимптотическое поведение амплитуды при qu qs->oo. Этому случаю отве-
отвечают субграфики, изображенные на рис. 19.53.
Каждому субграфику, определенному указанным .выше спо-
способом, мы припишем «асимптотический коэффициент» а, кото-
который является аналогом введенной в § 146 степени расходимости
D. Коэффициент а получается подсчетом степеней импульсов для
всех линий, входящих в субграфик. При этом каждая фотонная
и фермионная линии вносят вклад —2 и —1 соответственно, а
каждое интегрирование в субграфике вносит вклад
Рис. 19.52. Диаграмма
шестого порядка для
электрон-позитронного
рассеяния

§ 1501
ПОВЕДЕНИЕ ФЕИНМАНОВСКИХ АМПЛИТУД
379
где Ъ — число фотонных линий в субграфике g, f — число ферми-
онных линий в субграфике gf k — число интегралов по внутрен-
внутренним линиям в субграфике g. Например, если считать диаграмму
а)
f
i
i \S\J\S\SSS\s\i
Ф
а---5
ос=-2
'V,
f
I
a=-ff
3)
а=-д
«WWVVVi
| \Л/ЧЛЛЛА
а=-5
ж)
Рис. 19.53. Субграфики диаграммы рис. 19.52 и их асимптотические коэф-
коэффициенты.
на рис. 19.52 компактной (т. е. исключить из рассмотрения внеш-
внешние концы), то асимптотические коэффициенты субграфиков,
изображенных на рис. 19.53, равны —1, —3, —5, —2, —6, —8
и —5 соответственно.

380	ПЕРЕНОРМИРОВКИ	[ГЛ, 19
Теорема Вайнберга утверждает, что если:
1)	внешние импульсы qs и внутренние импульсы /, продол-
продолжены в область с евклидовой метрикой (см. § 145) и
2)	импульсы {Qs} некоторых из внешних линий стремятся
к бесконечности:
Qs-^xQs, x->°°.
то при X"-*0 амплитуда Wl(%Qi ... %Q/, qju ... qm) асимптоти-
асимптотически ведет себя как
где
а = max а (g),
субграфики g
и a(g)—асимптотический коэффициент субграфика g. Коэффи-
Коэффициент р теоремой Вайнберга не определяется.
В рассмотренном выше примере (рис. 19.52) амплитуда ве-
ведет себя как
причем этот результат возникает из области интегрирования, в
которой малы импульсы всех внешних линий, за исключением
внутренней электронной линии, изображенной жирной линией
в субграфике а) на рис. 19.53.
Идея доказательства сформулированных утверждений анало-
аналогична той, которая использовалась при доказательстве теоремы
о сходимости фейнмановских интегралов. Каждый субграфик,
отвечающий данному асимптотическому режиму, содержит ин-
интегрирование по импульсам {Lr}, которые велики при %->оо;
остальные внутренние импульсы U в интеграле малы. Внутрен-
Внутреннее интегрирование обрезается большими импульсами %QS, со-
содержащимися в субграфике; при этом величина вклада опреде-
определяется размерными соображениями, т. е. путем подсчета числа
импульсов в диаграмме. Каждая линия в субграфике в том слу-
случае, когда она находится в асимптотическом режиме, может да-
давать вклад либо —1, либо —2. Асимптотическое поведение ам-
амплитуды затем получается перебором всех возможных субгра-
субграфиков (отвечающих, как и в § 146, «трубам» в 4/>-мерном
пространстве) и выделением доминирующего вклада.
Последующая перенормировка не изменяет выводов теоремы:
асимптотическое поведение определяется по сформулированным
правилам') ив том случае, когда диаграмма содержит перенор-
перенормированные вершинные и собственно-энергетические вставки
(необходимые, чтобы придать смысл интегралу в целом!!). В ча-
') Это можно доказать по индукции.

§ 150]	ПОВЕДЕНИЕ ФЕИНМАНОВСКИХ АМПЛИТУД	381
стности, согласно теоремеВайнберга, асимптотическое поведение
вершинной и собственно-энергетической частей в любом порядке
по е совпадает с точностью до логарифмических множителей с
поведением их затравочных выражений
при р2->-оо,
1п (— q2)f при ф -» — «>,
при р2-^~оо,	A9.140)
(Р. Р\Я)^\ ^(In (~pY" при /->-«>,
^ фиксировано.
Аналогичный вид имеют асимптотические формулы и в том слу-
случае, когда другие комбинации импульсов р, р' и q стремятся к
оо. Мы могли бы заранее угадать это поведение S, П и Гд, ис-
исходя из требования перенормируемости; действительно, при дру-
другом асимптотическом законе степень расходимости диаграммы
увеличивалась бы при добавлении все нового и нового числа
вершинных и собственно-энергетических вставок. Асимптотиче-
Асимптотическое поведение, предсказываемое теоремой Вайнберга, согла-
согласуется с результатами, полученными во втором порядке в § 148.
Значение этой теоремы ограничено, однако, двумя обстоя-
обстоятельствами. Первое из них заключается в том, что теорема Вайн-
Вайнберга ничего не предсказывает об асимптотическом поведении
точных функций, просуммированных во всех порядках по заряду.
Например, рассмотрим гипотетическое разложение для 5'f~' (p)
(безусловно, неправильное для всех членов, кроме второго по-
порядка):
-?)+¦¦¦]=
Это разложение приводит к асимптотическому поведению Sf ,
совершенно отличающемуся от того, которое было получено в
конечном порядке по е.
Другое обстоятельство, ограничивающее полезность теоремы
Вайнберга, заключается в том, что она формулируется для нефи-
нефизических значений импульсов, которые возникают при аналити-
аналитическом продолжении в евклидовую область (§ 145). Желательно
было бы оценить, например, асимптотику физических амплитуд

382	ПЕРЕНОРМИРОВКИ	[ГЛ. 19
рассеяния в том случае, когда внешние импульсы остаются
на массовой поверхности q2s = m2s, а энергия s и переданный им-
импульс t стремятся к бесконечности. Обсуждение этой более труд-
трудной и до сих пор полностью не решенной задачи имеется в ли-
литературе [128—131].
§ 151. Ренормализационная группа
Метод теории перенормировок основывался на переопределе-
переопределении пропагаторов, вершинных функций и т-функций, т. е. на
возможности замены по формулам A9.49) затравочных значе-
значений этих величин их перенормированными значениями. Помимо
этой (возможно бесконечной) перенормировки, все величины в
теории поля допускают также конечную перенормировку, с при-
примером которой мы уже сталкивались в § 145. Возможность ко-
конечной перенормировки отражает произвол в выборе точки нор-
нормировки пропагаторов и вершинных функций, поскольку физи-
физические 5-матричные элементы не зависят от выбора этой точки.
С существованием указанных масштабных преобразований
(известных под названием ренормализационной группы) свя-
связана возможность получения информации о степени роста диа-
диаграмм высшего порядка без какого-либо реального вычисления
самих этих диаграмм. При этом оказывается возможным, зада-
задавая поведение амплитуд в низших порядках теории возмущений,
получить результаты относительно их поведения в следующих
порядках. Кроме того, метод ренормализационной группы позво-
позволяет получить ряд интересных результатов, относящихся к струк-
структуре точной теории, и, в частности, к связи между голым и пе-
перенормированным зарядами [27, 59].
Ниже мы проиллюстрируем метод ренормализационной груп:
пы на примере рассмотрения точного фотонного пропагатора и
перенормировки заряда. Согласно A9.51д) перенормированный
пропагатор имеет вид
e2Dp (q)^ =	~?- d (q2, О, е2) + градиентные члены,
где скалярная функция d(q2,0,e2) равна
d{q\ 0^2)-T+e^.0,eV	A9Л41>
Первый аргумент в d и П есть переменная импульса. Второй
аргумент равен тому значению импульса, при котором произво-
производится вычитание:
Uc (q\ О, е2) в П (q2, О, е2) - П @, 0, е\ Пс @, 0, е2) = 0. A9.142)

§ 1511	РЁНОРМАЛЙЗАЦИОННАЯ ГРУППА	383
Третий аргумент, е2, представляет собой параметр в перенорми-
перенормированном ряду теории возмущений. Величина е2 равна физиче-
физически наблюдаемому заряду
и экспериментально определяется из кулоновского сечения при
q2-*O. Согласно A9.141), A9.142) и результатам § 149, относя-
относящимся к томпсоновскому пределу комптоновского рассеяния,
d@, 0, е2) = е2.	A9.143)
Предположим, что мы изменили всю схему перенормировки,
описываемую уравнениями A9.51), и производим вычитание не
в точке ц2 = О, а в некоторой другой точке ц2 = к\ Ф 0. (Для
того чтобы обеспечить вещественность функции d, мы выберем
к2 < 0; при этом мы по-прежнему остаемся в той области, где
абсорптивные амплитуды в спектральном представлении A6.172)
равны нулю.) Выясним, к каким следствиям приводит такое из-
изменение.
Согласно A9.49) комбинация
e2Dp{q)^ = e2Dp{q)^	A9.144)
инвариантна при перенормировке заряда. Поэтому при вычита-
вычитании в произвольной точке q2 = к2 < 0 для e2D'P имеем
e2bF (q)^ =	^- d (q2, 0, е2) + градиентные члены =
=	т-d (q2, Ц, ё>) + градиентные члены, A9.145)
где
»>• e')=^,"WA%4AA^rA9Л46)
Новый «заряд», или параметр разложения е\, равен
ОД. 4 е?) = 4	A9Л4?)
С точностью до градиентных членов
d(q2, 0,e2)*=d(q2, к2, е2),	A9.148)
откуда следует уравнение, связывающее заряды е\ и е2=4я/137
в точке q2 =» 0:
e2 = d@, к2, е\).	A9.149)
Мы можем также выполнить перенормировку, вычитая рас-
расходящиеся величины в какой-либо третьей точке к\ < 0; при этом

384	ПЕРЕНОРМИРОВКИ	ГГЛ. 19
снова получаются соотношения, аналогичные A9.147) — A9.149),
Тогда для двух произвольных точек X2 и х\ имеем
Выписанные два уравнения могут быть объединены в одно функ-
функциональное уравнение
d{q\ Х\, e]) = d(q\ Х% d{%% Ц, е\)),	A9.150)
справедливое для всех Х\.
Посмотрим теперь, чего мы достигли. Функциональное урав-
уравнение A9.150) связывает пропагатор d с самим же пропагато-
ром, правда, ценой введения дополнительного параметра X2.
Само по себе это обстоятельство еще не приводит к новым фи-
физическим результатам. Для того чтобы получить какие-либо
следствия из функционального уравнения, необходимо задать
дополнительную информацию о поведении функции d. Эта ин-
информация заключается в следующем: предположим, что в пре-
пределе — Х2^>пг2, —Х\~^>т2 и —q2 ^> m2 зависимостью функции
d от массы т можно пренебречь. Ниже мы постараемся обос-
обосновать это предположение, а сейчас посмотрим, какие следствия
могут быть из него получены.
Первое следствие основывается исключительно на анализе
размерностей. Если постулировать отсутствие зависимости про-
пагатора от массы, то d является функцией только двух пере-
переменных, <72Д2 и е2. Однако функциональное уравнение A9.150)
накладывает ограничение на возможный вид зависимости d от
q2/X2 и е2 и, следовательно, на поведение асимптотических чле-
членов в разложении функции d по степеням е2.
Согласно сделанному предположению при —q2, —Х\~^>т2
d{q\ X2, e\)^d^, ef).	A9.151)
Поэтому уравнение A9.150) можно переписать в виде (пола-
(полагаем Хг = X)
СИ-'СМЗ-'О) <19л52)
с граничным условием
d(l, e\) = e2v	A9.153)
справедливым при всех е\. Замечательно, что решение уравне-
уравнений A9.152) и A9.153) можно сразу выписать. Для этого про-

§ 151]	РЕНОРМАЛИЗАЦИОННАЯ ГРУППА	gg5
дифференцируем A9.152) no q2 и положим q2 = X2, тогда по-
получим
(%)>((%)) A9л54)
где в силу A9.153)
Ф(е3) = ^й(х, е2)[=г	A9.155)
Уравнение A9.154) при фиксированных е\ и К\ можно проин-
проинтегрировать
*(<W*?)
J я2	ф
,2
откуда
i ф	\	du
Разрешив это уравнение относительно d, получаем общее реше-
решение функционального уравнения A9.152)
Если Z7 существует, то отсюда следует, что функция d, зави-
зависящая при больших импульсах от двух переменных, именно от
<72Д2 и е2, в действительности является функцией только от од-
одной переменной, представляющей некоторую комбинацию этих
двух переменных. Это обстоятельство не удивительно, посколь-
поскольку при —q2 ^> т2 зависимости от импульса и заряда связаны
между собой.
Используя вычисленные ранее первые несколько членов в
разложении функции d по степеням е2, мы можем теперь при-
применить метод ренормализационной группы для вычисления
членов высшего порядка. Процедура заключается в следующем.
1.	Подставим затравочное значение d (л:, е2) и найдем Ф(е2)
из A9.155).
2.	Проинтегрируем A9.156) и вычислим исправленное зна-
значение d(x, е\) по формуле A9.157).
Чтобы проиллюстрировать метод, предположим, что вся ин-
информация о функции d заключается лишь в том, что эту функ-
функцию можно разложить в степенной ряд по е\:
d (х, е\) = ё\ + е\ / (х) + О (еЧ).	A9.158)

386	ПЕРЕНОРМИРОВКИ	[ГЛ. 19
Тогда, используя A9.155), получаем
ф (О = <
Подставляя в A9.156), находим
, 92	Г	du
ln-^- =
ИЛИ
-Чг = "Г - Г (О In x + О f In4
d(x, ef) =	z-,	!—-Г7-7	r.	A9.159)
Таким образом, не вычисляя никаких фейнмановских интегра-
интегралов, мы установили, что вакуумная поляризация во втором по-
порядке асимптотически ведет себя как 1п(<72А2) и что в четвер-
четвертом порядке она растет также не быстрее 1п(<72Д2). Тем самым
без всяких вычислений мы показали, что член \n2(q2/m2), воз-
возникающий в четвертом порядке, в конце концов должен сокра-
сократиться. В § 148 мы убедились в этом непосредственно с по-
помощью весьма громоздких вычислений (см. A9.121)).
Аналогичным образом можно начать с выражения для пропа-
гатора d с учетом всех вычисленных членов четвертого порядка
d(x, е*) =	р	^	¦• A9Л6°)
1 —ш 1пх~ ш^ 1ах + ° О?)
Тогда, вычислив Ф из A9.155) и d из A9.156), получим
d(x, е]) =
1	lT In х +	т In 1	Ц- In * I + О I в? In ——-j I
12я2	16я2 V. 12я2 / \	1 + ef/
при ^2пл;<1. A9.161)

§ 15!]	РЕНОРМАЛИЗАЦИОННАЯ ГРУППА	387
Таким образом, мы видим, что уравнения ренормализационной
группы позволяют найти главный асимптотический член функ-
функции d в шестом порядке; при этом мы определяем не только
функциональную зависимость этого члена, но численный коэф-
коэффициент ').
Другим замечательным свойством уравнения A9.157) яв-
является то обстоятельство, что
Lt ef\->F~l (oo) при -G2-»оо. A9.162)
Это соотношение показывает, что при больших импульсах про-
пропагатор стремится к пределу, не зависящему как от точки пере-
перенормировки Х\, так и от заряда е\. Однако из спектрального
представления для фотонного пропагатора следует, что при
больших импульсах функция d имеет смысл голого заряда е2й.
Согласно A6.172), полный неперенормированный пропагатор
удовлетворяет спектральному представлению
[°°	п
z3 . Г dM2H{M2) .
Y + ) 2_V + градиентные члены,
о	-I
A9.163)
где П(М2)Г>0. Более того, если спектральный интеграл суще-
существует, то справедливо правило сумм
со
1 = z3 -|- 5 dM2 U (М2) при <72-*оо.
о
Поэтому точный пропагатор при больших импульсах должен со-
совпадать, с точностью до градиентных членов, с неперенормиро-
ванным пропагатором, т. е.
^F^l)v.i~>	^-+ градиентные члены при'<72-*оо. A9.164)
Сравнивая A9.162) и A9.164) и вспоминая, что произведение
e\p'F (<7) инвариантно при перенормировке, получаем
е2 = /г-'(оо).	A9.165)
В этом пункте мы сталкиваемся со следующей дилеммой. Исполь-
Использовавшиеся в этом параграфе аргументы основывались на воз-
возможности перенормировки рядов теории возмущений, которая,
') Аналогичный подход применим и для исследования рядов теории воз-
возмущений для вершинных функций и фермионных пропагаторов как в ультра-
ультрафиолетовой, так и в инфракрасной областях. Подробное обсуждение см. в ци-
цитированной выше книге Боголюбова и Ширкова.

388	ПЕРЕНОРМИРОВКИ	[1Л. 19
в частности, подразумевает возможность разложения пропа-
гаторов, вершинных функций и т. д. в ряды по степеням как
перенормированного, так и затравочного зарядов. Однако урав-
уравнение A9.165) означает, что значение е0 должно удовлетворять
некоторому соотношению и тем самым не может быть выбрано
произвольно. Это обстоятельство является совершенно чуждым
самому духу теории возмущений и приводит нас к заключению,
что по крайней мере одно из предположений, заложенных в на-
нашей теории, неправильно1). Например, можно думать, что тео-
теория возмущений неприменима при q2-+oo, поскольку уравнение
A9.161) показывает, что последовательные члены этого разло-
разложения растут, когда
A9.166)
Закончив на этом с примерами применения ренормализа-
ционной группы, вернемся к основному предположению, с по-
помощью которого мы смогли получить физические следствия из
группового уравнения A9.150), а именно, к предположению о
том, что пропагатор не зависит от т2 при —q2 >¦ т2, —К2 ^> т2.
Чтобы убедиться в правдоподобности этого предположения, мы
покажем здесь, что решение перенормированных интегральных
уравнений A9.51) нечувствительно к величине массы т при ус-
условии, что перенормировка выполнена в точке —X2 ^> т2. С этой
целью мы используем теорему Вайнберга об асимптотическом
поведении фейнмановских амплитуд (§ 150) и применим метод
индукции.
Рассмотрим перенормированные при некоторой большой мас-
массе —Я2>/л2 функции Т^(р', р, A), S'F(p_, А) и DF(q, А). Пусть
при р, р', q-+oo эти величины с точностью до членов порядка
gjf~ могут быть аппроксимированы функциями, не зависящими
от т. Используя теорему Вайнберга, мы покажем, что это
утверждение справедливо также и для членов порядка el- На-,
пример, согласно теореме Вайнберга,
Sf (/>,'А,)-> (постоянная) р (логарифм) при /}-*оо. A9.167)
Предположим, что с точностью до е?~2 асимптотическая часть
Sp (p> ^) не зависит от т, т. е. что постоянная и логарифм в
A9.167) конечны при —к2 3> т2 и т-»-0. Наша цель заклю-
заключается в том, чтобы показать, что это предположение справед-
справедливо с точностью до членов порядка е". Конечность Sf в при-
') См. в этой связи, помимо ссылок, указанных на стр. 382, работу Лан-
Ландау [132], а также [133, 134].

§ 151]	РЕНОРМАЛИЗАЦИОННАЯ ГРУППА	389
ближении el следует из уравнения (8.39), если в нем выпол-
выполнить перенормировку в точке —к2 >> т2. Предположим также,
что при —X2 Э> т2 вершинная и фотонная собственно-энергети-
2	~' —1
ческие части в порядке е\ ведут себя так же, как и Sf .
В справедливости этого предположения во втором порядке тео-
теории возмущений легко убедиться непосредственно, используя')
результаты, полученные в гл. 8.
Начнем с вершинной функции. Для вычисления ее в порядке
el используем уравнения A9.51), в которых, однако, сделаем
вычитание не на массовой поверхности, а при некотором боль-
большом к. Нас интересует только асимптотическая часть, которая,
согласно теореме Вейнберга, ведет себя как (постоянная) X (ло-
(логарифм) (см. A9.140)). Этот результат получается из рассмот-
рассмотрения тех внутренних интегрирований, асимптотические коэффи-
коэффициенты которых равны а = 0. Единственно возможными субгра-
субграфиками с неотрицательными асимптотическими коэффициентами
являются, очевидно, вершинная и собственно-энергетическая
части. Однако если эти субграфики целиком содержатся внутри
вершинной диаграммы, то по крайней мере два из их внешних
концов, присоединяющие субграфики к остальной части диа-
диаграммы, несут большой импульс и приводят к отрицательному
асимптотическому коэффициенту. Поэтому единственная диа-
диаграмма с а = 0 это сама вершинная диаграмма2), имею-
имеющая нулевой асимптотический коэффициент (напомним, что
внешние линии этой диаграммы не включены в определение
компактной вершинной части). Вершинная часть имеет также
степень расходимости, равную нулю, при этом соответствующая
область интегрирования состоит из тех внутренних импульсов,
которым отвечают большие внутренние пропагаторы. Поэтому
для пропагаторов и вершинных вставок внутри Ги можно под-
подставить их асимптотические выражения. Отсюда следует, что
масса т не входит существенным образом в интеграл для вер-
вершинной функции и что этот интеграл существует после перенор-
перенормировки. Более того, асимптотическая часть Гц существует при
1) Отметим, что если использовать нормировку
1
SF (р, X) =
р~т(Х)
Гц (р, р, Я) 1^ = уу,
то тождество Уорда Zx(X) = Z2(k) не изменится. Ниже мы воспользуемся
этим результатом.
2) За исключением субграфиков, содержащихся внутри вычитательных
членов; ситуация здесь в точности аналогична той, которая возникает при
обсуждении метода перенормировки.

390	ПЕРЕНОРМИРОВКИ	[ГЛ. 19
m—*0, поскольку логарифмически расходящиеся интегралы обре-
обрезаются либо величиной —X2 Э> т2, либо внешними импульсами.
Полностью пренебрегая математической строгостью дока-
доказательства, мы можем продолжить наше рассмотрение и обра-
обратиться к тождеству Уорда с тем, чтобы вычислить^ (р, X) из Гц;
при этом мы заключаем, что Sf также не зависит от т. Нако-
Наконец можно использовать приведенные выше аргументы для рас-
рассмотрения фотонного пропагатора. В этом случае, согласно
A9.140), следует выделить субграфики с асимптотическим коэф-
коэффициентом -(-2. Такими графиками являются только сами эти
графики, что можно показать, используя аргументы, аналогич-
аналогичные тем, которые использовались при рассмотрении вершинной
функции. Таким образом, гипотеза индукции доказана.
Используя приведенные выше рассуждения, мы можем оп-
оправдать применение методов ренормализационной группы для
улучшения асимптотических результатов теории возмущений.
При этом молчаливо подразумевается, что, перебрав член за
членом в ряду теории возмущений и вычислив асимптотическое
поведение каждого из этих членов, мы получим асимптотическое
поведение всей амплитуды в целом. Конечно, не следует забы-
забывать о возможности того, что опущенные как относительно ма-
малые при больших импульсах члены, при суммировании рядов
теории возмущений окажутся доминирующими. Поэтому вы-
выводы, основанные на методе ренормализационной группы и от-
относящиеся к величинам, просуммированным во всех порядках
по е, могут оказаться ненадежными и к ним следует относиться
с осторожностью.
Впрочем, так обстоит дело со всеми результатами, полу-
полученными из локальных релятивистских теорий поля.
ЗАДАЧИ
1.	Доказать обобщенное тождество Уорда A9.16), рассмотрев вакуумное
среднее от произведения трех полей
<0 I 7- <ч|> (х) + (У) /ц (г)) I 0)
и используя сохранение тока и полевые уравнения.
2.	Выписать общую структуру вершинной функции Т*1 (р', р) и обсудить
ограничения, накладываемые тождеством Уорда, а также /-, С- и ^-инва-
^-инвариантностью.
3.	Дополнить доказательство перенормируемости (§ 147) и показать, что
произвольное 1Г... k-внутреннее интегрирование приводит к сходящемуся ре-
результату.
4.	Проверить результаты в уравнениях A9.109), A9.111), A9.117) и
A9.118).
5.	Проверить уравнения A9.120) и A9.122) и получить аналогичные ре-
результаты в пределе —ф/ш2 -С 1.
6.	Проверить уравнение A9.131).

. ЗАДАЧИ	39]
7.	Проверить уравнение A9.135) и вычислить Фи/.
8.	С помощью представления Челлена — Лемана доказать существование
обратной функции F-1 в A9.157).
9.	Проверить уравнение A9.161).
10. Выписать общее выражение для амплитуды образования реальных
электрона и фотона на массовой поверхности (р2 = т2, I2 = 0). Используя
обобщенное тождество Уорда, показать, что эта амплитуда может быть выра-
выражена в терминах четырех скалярных функций Fi(W2), где W2 = (р + 1)г. Вы-
Выписать дисперсионное соотношение для Ft(W2) и связать их с неприводимыми
вершинными функциями задачи 2. В частности, обсудить и объяснить физи-
физический смысл появления заряда е как необходимой константы вычитания в
дисперсионных соотношениях для этой амплитуды.
П. Доказать перенормируемость теории псевдоскалярных мезонов, вза-
взаимодействующих с нуклонами посредством связи без производных. Учесть то
обстоятельство, что, поскольку эта теория не обладает градиентной инвариант-
инвариантностью, при доказательстве необходимо дополнительно рассмотреть субгра-
субграфики я — я-рассеяния.

ПРИЛОЖЕНИЕ В
КОММУТАТОРЫ И ФУНКЦИИ РАСПРОСТРАНЕНИЯ1)
Ниже собраны выражения для инвариантных функций, встречающихся в
этой книге.
Фейнмановский пропагатор для свободного уравнения Дирака имеет вид
gr -f [e(t' -1) a+
- n a-
Величину ?е в знаменателе следует понимать в смысле предельного значе-
значения е->-0+. Это означает, что при вычислении интеграла по dpa следует ис-
Ыр0
-*-
Рис. В. 1.
пользовать контур интегрирования, указанный на рис. В.1. 6(/' — /) есть еди-
единичная ступенчатая функция:
0 f < t
2ni
ш + IB
Пропагатор Sc удовлетворяет дифференциальному уравнению для функции
Грина
(Nx, - т) Se (х' — х) = б4 (*' - х).
Приложения А и Б см. в первом томе.

ПРИЛОЖЕНИЕ В	393
В импульсном пространстве
о , ._ р + т =	1
Фейнмановский пропагатор для уравнения Клейна — Гордона равен
(х' — х) — — / \ .3 — [9 (/' — t) e~ik{x'~x) + 9 (/ — ;
\
BяL
и удовлетворяет уравнению
(П^ + т2) Д,,. (х' — х) = — б4 (л/ — л;).
В импульсном пространстве
Функции Д/> и Sp связаны соотношением
SF(x' - х) = + («f x, + m) AF (л' - x).	(В. 1)
Определим функцию Грина для уравнения д'Аламбера о т-*-0:
ах Dt (x' — х) = + б4 U' — ж)
(отметим изменение знака по сравнению с Д/>). Фейнмаяовский пропагатор
для фотонов равен
F \v	^Dp [q) = - -^T+IT-
Функцию Д^ можно представить в виде
2Л,, (л' - дг) = — <Д, (х' — x) + e(t' — t)b (x' — х),
где Ai и Д — четное и нечетное решения однородного волнового уравнения
А' (*' ~ Х) - J
(П^ + тг) Д, (л' - *) = 0. Д, (х' --х) = + Д, (х - х'),
(Пх, + т2) Д (*' - х) = 0 Д (х' — х) = - Д (дс - *').
в(/'_0ив2в(//-0-1-|_1( </<<.
Нечетная функция Д обращается в нуль вне светового конуса
Д (х' — х) = 0 для всех (х' — х)г < Q;

394	ПРИЛОЖЕНИЕ В
на световом конусе Д имеет особенность
= - б3 (х' - х).
дх'о
U
Общее выражение для функции Д таково:
/0 (т V*2 — г2),
где
г = | х — х |, / = х'о — х0
и /о — регулярная функция Бесселя.
Четная функция Ai не обращается в нуль вне светового корпуса, при
г > \t\ она падает экспоненциальным образом:
С
Г„ (т л]Р - г«),	| /1 > г,
V* л/ 4яг аг (_ -±.Ko{m^/-^—fl\ r>\t\,
где Уо и Ко — цилиндрические функции (см. Г. Н. Ватсон, Теория бесселевых
функций, М., ИЛ, 1949).
Для электромагнитного поля т -*¦ 0 и
-D(x'-x)= lim \(х'-х) = - -1~ [б (г - /) - 6 (г + <)],
— D, (л' — х) = lim Д, (л' — х)= —^ (я —Ц- + Р —!—г).
J
где г^|х — jc |, t = х0 — х к Р означает главное значение.
Можно рассмотреть также положительно-частотные и отрицательно-ча-
отрицательно-частотные части функций Д и Д^которым соответствуют два члена в интегра-
интегралах, определяющих эти функции:
Д, (х' — x) = ^+ (х' — х) + Д- (х' — х),
/Д (х' — х) = 1±+ (х' - х) — Д_ (х' — х).
Для уравнения Дирака определим
S(x'-x) = - (fix + m)/i (x' - х),
2Sp (xr -x) = + iS{ (x' -x)-e(t'-t)S (x' - х).
Различие в знаках в уравнениях (В.1) и (В.2) есть следствие нашего согла-
соглашения о фазовых множителях, которое приводит к тому, что при практиче-
практических вычислениях возникает минимальное число знаков минус. Функции Д/,

ПРИЛОЖЕНИЕ П	395
Dp и Sf, связаны с Г-упорядоченными произведениями свободных полей Клей-
Клейна — Гордона, Максвелла и Дирака:
<0 | Т (ф. (*') ф/ (*)) | 0) = Д^Д, (*' - х).
@ | Т (Ф (*') ф* (дс)) | 0) = Шр (х' - х),
@ | Т (Av (х') А^ (х)) | 0) = Ю$ (х' - Х)^ =
2
d4k e
~ik (х'~х
= ig^Dp (*' — *) + градиентные члены — кулоновский член
@ | Т (fy (дс') ^а (дс)) | 0> = iSP (x' - *).
Определим еще запаздывающую и опережающую функции Грина:
Aret (х' - х) = - Д (*' - *) 9 [f - t),
Aadv (дс' - х) = + Д (х' - дс) Э (/ - Г).
Aret равна нулю внутри переднего светового конуса, в то время как Aa<jv ис-
исчезает внутри заднего светового конуса. Эти функции удовлетворяют неодно-
неоднородному волновому уравнению
(?«. + т2) Д$у (х' -х) = 6* (х' - х).
Аналогично
Sre' (х' -х)=- (Ях, + т) А{% (х' - х)
adv
% (х' - х) = + lim ДЙ, (*'-*)¦
0
Наконец приведем выражения для различных вакуумных средних свобод-
свободного эрмитового бесспинового поля:
<0 | [ <р (*'). ф (дс)] 0) = /Д (х' - дс),
<0|{<р(дс'). <р (*)} | 0> ¦= Ai (*'-*).
<0 | ф (х') ф (х) | 0> = Д+ (х' - дс),
<0|<р(дс)ф(дс')|0> = А-(д!'-х).
<0 | Г (ф(
(о | [Ф](*'). <р W1 I о) е (Г -1) = - iAret (*' - л),
@ | [Ф (*'). Ф (дс)] | 0N (*-/')=. + iAadv (x' - х).
Аналогичные формулы можно выписать для полей Дирака и Максвелла.

ДОПОЛНЕНИЯ РЕДАКТОРА ПЕРЕВОДА
1. Рассеяние мюона на электроне (к § 27). В § 27 рассмотрена задача о
рассеянии электрона на бесструктурной дираковской частице (тяжелом
электроне). Как там отмечалось, такое рассмотрение неприменимо к про-
протону, поскольку оно не учитывает его структуру и его аномальный магнит-
магнитный момент, связанные с сильными взаимодействиями. Но эта задача бук-
буквально соответствует задаче о рассеянии мюона на электроне, так как мюон
в смысле его электромагнитных свойств действительно отличается от элек-
электрона толькр массой и не подвержен сильным взаимодействиям. Таким
образом, формулы § 27 остаются справедливыми, т. е. описывающими рас-
рассеяние мюона на электроне, если в них заменить еР на е, а под М подразу-
подразумевать массу мюона.
Дифференциальное сечение рассеяния определяется формулой G.42), а
квадрат матричного элемента для случая неполяризуемых частиц — форму-
формулой G.43). В системе центра инерции выражение для дифференциального
сечения имеет следующий вид:
da =
a2 do
-Q- Г(е? + p2J + (e? + p2 cos2 OJ - 2 (m2 + M2) p2 sin2 ^-1,
где р —импульс в системе центра инерции,8 ='•
энергия электрона и мюона, О — угол рассеяния, do— элемент телесного угла
(все в системе центра инерции).
2. Превращение электронной пары в мюонную пару (к § 32). При'столк-
При'столкновении электрона и позитрона, кроме упругого рассеяния, может произойти
их аннигиляция с превращением в мюонную пару (положительно и отрица-
отрицательно заряженные мюоны). Этот процесс описывается второй диаграммой
(рис. 7.12,6), а амплитуда — формулой G.86), в которой надо опустить пер-
первый член в квадратных скобках, заменить т2 на тМ и считать р{ и q^ соот-
соответственно импульсами ц~- и ц+-частиц (pi и q\ — по-прежнему импульсы
электрона и позитрона). Из законов сохранения следует, что превращение
возможно при Е ^ М, где Е — энергия электрона (позитрона) в системе
центра инерции.

Дополнения редактора перевода	^
Полное сечение превращения равно
4я а2 (. М* \ Г "Ж
Заметим, что эта формула неприменима непосредственно вблизи порога
процесса, где образующиеся мюоны нельзя считать свободными.
3. Неупругое рассеяние электрона на протоне (к § 56). В § 56 рассматри-
рассматривалась задача об упругом рассеянии электрона на реальном протоне. Для
этого было модифицировано выражение для тока G.34), отвечающее «дира-
ковскому» протону. Эта модификация сводилась к замене / на (Pf\J\Pi) —
матричный элемент точного оператора тока протона, учитывающего сильные
взаимодействия (но первого порядка по электромагнитным взаимодействиям).
Как было показано в § 56, этот матричный элемент может быть представлен
феноменологически в виде
п (Pf) ГцВ (Pt),
где Гц — вершинная функция протона, выражающаяся согласно A0.88) через
два инвариантных форм-фактора F\, F% являющихся функциями от квадрата
переданного импульса q2. Таким образом, амплитуда рассеяния может быть
определена на основании простой диаграммы Фейнмана (рис. 7.3) с заменой
в протонной вершине У1 на Г11.
Аналогично можно рассмотреть задачу о неупругом рассеянии электрона
на протоне, т. е. процесс, в котором электрон теряет импульс q, а протон
превращается в некоторую совокупность адронов. Для этого надо использо-
использовать диаграмму рис. 7.3 или формулу G.31), заменив протонный ток /л йа
матричный элемент тока
<я I ^ I Pt),
где \Pi) —начальное состояние простона с импульсом Р,-, а \п) —конечное
адронное состояние.
Элемент матрицы рассеяния S/t, отвечающий этому процессу, будет со-
содержать амплитуду
где, как и в § 27, pi и р/ — импульсы электрона до и после рассеяния, а
u(pt) и u(Pf)—соотвегствующие дираковские амплитуды (мы опустили для
краткости спиновые индексы), q = pi—¦ pf.
Дифференциальное сечение рассеяния с образованием адронного состоя-
состояния л, вычисленное по обычным правилам, имеет следующий вид:
(в этой формуле и далее мы пренебрегаем массой электрона).

398	ДОПОЛНЕНИЯ РЕДАКТОРА ПЕРЕВОДА
Просуммировав это выражение по спиновым состояниям электрона в ко-
конечном состоянии, усреднив по спиновым состояниям электрона в начальном
состоянии и просуммировав по всем конечным адронным состояниям п, мы
получим сечение рассеяния электрона на протоне при данном угле рассеяния
и данной потере энергии (инклюзивное сечение).
В качестве независимых переменных удобно выбрать инварианты
Мы получим
v
где
«V = ? BяL б<4> (рп ~ pi ~ Я) (pi I /ц I я> (Я I /v I РД
Тензорная структура l^v определяется только двумя векторами, Pt и </.
Из этих векторов и метрического тензора g^v можно построить всего пять
независимых тензоров. Требования инвариантности относительно обращения
времени и сохранение тока накладывают три условия. Поэтому W^ опре-
определяется двумя инвариантными функциями от двух переменных: q2 и v. Мы
можем записать W^ в следующем виде:
Ц7„л, = 4яМЦ7,
Выражение для сечения мы запишем в системе покоя протона, в которой
<72 = 4e,e2sin2 — , v = M qQ, Pipl = Me,
где ei, 82 — соответственно начальная и конечная энергии электрона, а О1—¦
угол рассеяния электрона,
da = de2 daMOTT ( Г2 + Г, tg2 4)•
Здесь Й0мотт — сечение рассеяния релятивистского электрона в кулоновском
поле:
,		 . a2 cos2 Ф/2
4ef sin2 0/2
Таким образом, неупругое рассеяние определяется двумя структурными
функциями двух инвариантов, W\ и W2. Если при больших энергиях адронная
структура такова, что не зависит от дополнительных размерных параметров
(типа масс), то W\ и U^2 могут зависеть только от безразмерных отношений
q2j\ (автомодельность или масштабная инвариантность). Тогда W\, W2 должны

ДОПОЛНЕНИЯ РЕДАКТОРА ПЕРЕВОДА	399
иметь вид
Заметим, что общее выражение для W^v может быть представлено
в виде
гДе Ни. (*)> !ч (у)] — коммутатор операторов тока в двух мировых точках.
4. Аннигиляция электронной пары в адроны и адронная поляризация ва-
вакуума (к § 140). Электрон и позитрон могут аннигилировать, испустиив вир-
виртуальный фотон, а последний—образовать из вакуума совокупность адронов
в некотором состоянии п. Обозначим импульс электрона р_, импульс пози-
позитрона р+, импульс виртуального фотона q, а импульс (суммарный) адронов
рп; при этом
Р- + р+ = q = pn-
Ток перехода пары в вакуум есть v (р+) у и (р_), ток перехода ва-
вакуума в адронное состояние мы обозначим как в § 110, через (я | /ц | 0). Процесс
аннигиляции описывается, следовательно, амплитудой
Определим полное сечение 0 аннигиляции во всевозможные адронные со-
состояния. Будем считать, что энергия пары значительно превышает массу
электрона и последней будем пренебрегать. Тогда
* = i У. I ЭЛ« I2 BяL 6<4) (р„ - q).
После подстановки сюда выражения для Ш1„ и усреднения по спиновым со-
состояниям электрона и позитрона получим
о*
_ яе*	(n) ^
где
a 1$ определено A6.158), A6.163):
J] « (pn - <?) <0 | / J n> < n | /v I 0),
с тем отличием, что здесь под токами подразумеваются адронные токи.
Подставляя эти выражения, получим

400	ДОПОЛНЕНИЯ РЕДАКТОРА ПЕРЕВОДА
Заметим, что функция J{q2), согласно A6.173), определяет поляризацию
вакуума U(q2). Таким образом, измеряя сечение аннигиляции в адроны, мы
определяем (в первом приближении по е2) адронный вклад в поляризацию
вакуума
Аналогичным образом мы можем определить мюонный вклад в поляриза-
поляризацию вакуума. Действительно, формулу для сечения аннигиляции мы можем
применить и к образованию мюонных пар
где /'^ также выражается по формулам A6.158), A6.163) через мюонные
токи. Использовав вычисленное в дополнении 1 выражение для 0 > найдем
где
Заметим, что эта же формула определяет и соответствующую функцию
J(e)(q2) (с заменой М на т).
Таким образом, спектральную плотность, определяющую адронный вклад
в поляризацию вакуума, можно записать в виде (при f(q2) ~ 1)
где
— отношение сечений образования адронов и мюонов при аннигиляции элек-
электронной пары.

ЛИТЕРАТУРА >)
1. R. P. Feynman, Rept. Solvay Conrg., Brussels, New York, Interscience
Publishers, Inc., 1961.
2*. P. Гатто, в книге «Электромагнитные взаимодействия и структура эле-
элементарных частиц», «Мир», 1969, стр. 43; Д. Йенни, там же, стр. 123.
3*. 5. L Brodsky, S. D Drcll, Ann. Rev. Nucl. Science 20, 147 A970).
4*. B. E. Lautrop, A. Peterman, E. de Rafael, Phys. Rev. 3C, 193 A972).
5.	Г. Гольдстейн, Классическая механика, «Наука», 1975.
6.	W. Heisenberg und W. Pauli, Z. Physik 56, 1 A929). (Русский перевод:
В. Паули, Труды по квантовой теории, «Наука», 1977, стр. 30.)
7.	О. Wentzel, Quantum Theory of Field, New York, Interscience Publishers,
Inc., 1949. (Русский перевод: Г. Венцель, Введение в квантовую теорию
волновых полей, Гостехиздат, 1947.)
8.	Е. L. Hill, Rev. Mod. Phys. 23, 233 A957).
9*. Э. Шмутцер, Симметрии и законы сохранения в физике, «Мир», 1974;
Э. Шмутцер, Основные принципы классической механики и классической
теории поля, «Мир», 197в
10.	Л Schwinger. Phys. Rev. 9f, 713 A953).
11.	R. E. Peierls. Proc. Roy. Soc. (London) A214, 143 A952).
12.	H. Lehman, K- Symanzik and W. Zimmermann, Nuovo Cimento 1, 1425
A955).
13.	H. Lehman, K. Symanzik and W. Zimmermann, Nuovo Cimento 6, 319
A957).
14.	N. Bohr and L. Rosenfeld, Kgl. Danske Videnskab. Selskab. Mat.-Fyz.
Medd. 12, 8 A933); Phys. Rev. 78, 794 A950) (Избранные научные труды,
т. 2, «Наука», 1971, сто 120, 434).
15.	W. Pauli and V. F. Weisskopf, Helv. Phys. Acta. 7, 709 A934). (Русский
перевод: В. Паули, Труды по квантовой теории, «Наука», 1977, стр. 194.)
16.	P. Jordan and О. Klein, Z Physik 45, 751 A927).
17.	P. Jordan and E. P. Wigner, Z. Physik 47, 631 A928).
18.	V. Fock, Z. Physik 75, 622 A932).
19.	H. S. Green, Phys. Rev. 90, 270 A953); A. M. L. Messiah and
O. W. Greenberg, Phys. Rev. 136, B248 A964).
20.	O. W. Greenberg and A. M. L. Messiah, Phys. Rev. 138, B1155 A965);
J. Math Phys. 6,500 < 1969).
21*.Д. В. Волков, ЖЭТФ 36, 15 A959); ЖЭТФ 38, 518 A960).
22. W. Pauli, Ann. Inst. Henri Poincare 6, 137 A936); Phys. Rev. 58, 715
A940). (Русский перевод: В. Паули, Труды по квантовой теории, «Нау-
«Наука», 1977, стр. 244, 354)
23 S. ,V. Gupta, Proc. Phys. Soc. (London) A63, 681 A960); К. Bleuer, Helv.
Phys. Acta 23,567 A950).
') Литература, помеченная звездочкой, добавлена при переводе. Работы,
изданные на русском языке, цитируются по последним изданиям, {прим.
перев.).

402	ЛИТЕРАТУРА
24.	Е. Fermi, Rev. Mod. Phys. 4, 87 A932). (Русский перевод см. в книге
Э. Ферми, Научные труды, т. I, «Наука», 1971, стр. 375.)
25.	С. Швебер, Введение в релятивистскую квантовую теорию поля, ИЛ,
1963.
26.	J. M. Jauch, F. Rohrlich, The Theory of Photons and Electrons, Cambridge,
Mass., Addison — Wesley Publising Company, Inc., 1955.
27.	H, H. Боголюбов, Д. В. Ширков, Введение в теорию квантованных по-
полей, «Наука», 1976.
28*. А. И. Ахиезер, В. Б. Берестецкий, Квантовая электродинамика, «Наука»,
1969.
29.	Н. Casimir, Koninkl. Ned. Akad. Wetenschap, Proa, Ser. B, 793, A948);
M. Fierz, Helv. Phys. Acta 33, 855 A960).
30.	P. A. M. Dirac, Proc. Roy. Soc. (London) A167, 148 A938); G. N. Plass,
Rev. Mod. Phys. 33, 37 A961).
31.	J. Schwinger, Quantum Electrodynamics, Dover Publications, Inc., New
York, 1958.
32*. P. Фейнман, Квантовая электродинамика, «Мир», 1964; Е. М. Лифшиц,
Л. П. Питаевский, Релятивистская квантовая теория, часть 2, «Наука»,
1971.
33.	В. Zumino, J. Math. Phys. 1, 1 A960).
34.	F. J. Dyson, Phys. Rev. 85, 631 A952).
35.	M. Chretien and R. E. Peierls, Proc. Roy. Soc. (London) A223, 468 A954).
36.	K. Baumann, Z. Physik 152, 448 A958); K- Nishijima, Progr. Theor. Phys.
(Kyoto) 11,995 A958).
37.	W. Zimmermann, Nuovo Cimento 10, 567 A958).
38.	G. F. Chew, Physics 1, 77 A964).
39.	M. Gell-Mann and Y. Ne'eman, The Eightfold Way, New York, W. A. Ben-
Benjamin, Inc., 1965.
40*. Л. Б. Окунь, Слабое взаимодействие и унитарная симметрия, ВИНИТИ,
1965.
41*. Нгуен Ван Хьеу, Лекции по теории унитарной симметрии элементарных
частиц, Атомиздат, 1967.
42.	A. Pais, Phys. Rev. 86, 633 A952).
43.	М. Gell-Mann, Phys. Rev. 92, 833 A953).	;
44.	К. Nishijima, Progr. Theoret. Phys. (Kyoto) 12, 107 A954).
45.	P. Fererbush and M. Grisaru, Nuovo Cimento 9, 1058 A958).
46.	XII Международная конференция по физике высоких энергий, Дубна,
1964, Атомиздат, 1966.
47*. Ц. Ли и Ц. By, Слабые взаимодействия, «Мир», 1968.
48.	Е. P. Wigner, Gottinger Nachr. 31, 546 A932). (Русский перевод в книге
Е. Вигнёр, Этюды о симметрии, «Мир», 1971, стр. 262.)
49.	W. В. Pauli (ed.), Niels Bohr and the Development of Physics, New York,
Me Graw-Hill Book Company, 1955. (Русский перевод «Нильс Бор и раз-
развитие физики», ИЛ, 1958.)
50.	G. Luders, Ann. Phys. 2, 1 A957).
51.	R. F. Streator and A. S. Wightman, PCT, Spin and Statistics and All That,
W. A. Benjamin, Inc., New York, 1964. (Русский перевод: Р. Стритер и
А. Вайтман РСТ, Спин и статистика и все такое, «Наука», 1966.)
52.	К- Nishijima, Phys. Rev. Ill, 995 A958).
53.	S. Weinberg and A. Salatn, Proc. 1962 Intern. Conf. High-energy Phys.,
CERN, Geneva, p. 683—687.
54.	O. W. Greenberg, Doctoral dissertation, Princeton University, Princeton,
N. Y., 1956.
по. G. Kallen, Helv. Phys. Acta 25, 417 A952).
56. H. Lehman, Nuovo Cimento 11, 342 A954). (Русский перевод см. в сб.
«Проблемы современной физики» № 3, ИЛ, 1955, стр. 133.)
57*. Г. Бартон, Дисперсионные методы в теории поля, Атомиздат, 1968,

ЛИТЕРАТУРА	403
68 F. Low, Phys. Rev. 97, 1392 A955).
59.	M. Gell-Mann and F. Low, Phys. Rev. 95, 1300 A954). (Русский перевод
см. в сб. «Проблемы современной физики», № 3, ИЛ, 1955, сто 195)
60.	К. Sekine, Nuovo Cimento 11, 87 A959).	"' ''
61.	К. Hiida, Phys. Rev. 132, 1239 A963); 134, B174 A964).
62.	L. Evans and T. Fulton, Nucl. Phys. 21, 492 A960).
63.	/. Schwinger, Phys. Rev. 125, 397 A962).
64.	F. J. Dyson, Phys. Rev. 82, 428 A951).
65.	F. I. Dyson, Phys. Rev. 75, 486 A949). (Русский перевод в книге «Сдвиг
уровней атомных электронов», ИЛ, 1950, стр. 94.)
66.	F. Dyson, Phys. Rev. 75, 1736 A949). (Русский перевод в книге «Новей-
«Новейшее развитие квантовой электродинамики», ИЛ, 1954, стр. 205)
67.	Р. Т. Matthews, Phys. Rev. 76, 684, 1489 A949).
68.	F. Rohrlich, Phys. Rev. 80, 666 A950).
69.	T. D. Lee and С N. Yang, Phys. Rev. 128, 885 A962).
70.	R. Haag, Kgl. Danske Videnskab. Selskab. Mat.-Fys. Medd 29 112)
A955).	'	* '
71*. #. H. Боголюбов, А А. Логунов, И. Т. Тодоров. Основы аксиоматиче-
аксиоматического подхода в квантовой теории поля, «Наука», 1969.
72.	/. Schwinger, Phys. Rev. 74, 1439 A948); 75, 651 A949); 76, 790 A949).
(См. русский перевод в книге «Новейшее развитие квантовой электроди-
электродинамики», ИЛ, 1954, стр. 12.)
73.	S. Tomonada, Progr. Theoret. Phys. (Kyoto) I, 27 A946). (Русский пе-
перевод в книге «Новейшее развитие квантовой электродинамики», ИЛ,
1950, стр. 1).
74.	G. С. Wick, Phys. Rev. 80, 268 A950). (Русский перевод в книге «Новей-
«Новейшее развитие квантовой электродинамики», ИЛ, 1954, стр. 245.)
75.	И. Я. Померанчук, ЖЭТФ 34, 725 A958).
76.	F. Bloch and A. Nordsieck, Phys. Rev. 52, 54 A937).
77.	D. Yennie, S. Frautschi and H. Suura, Ann. Phys. (N. Y.) 13, 379 A961).
78.	M. Gefl-Mann, M. L. Goldberger and W. Thirring, Phys. Rev. 95, 1612
A954).
79.	M. L. Goldberger, Phys. Rev. 99, 979 A955).
80.	R. Kronig, J. Op. Soc. Am. 12, 547 A926); H. A. Kramers, Atti Congr.
Intern. Fisici Como A927).
81.	N. Bogolyubov, B. Medvedev and M. Potivanov, Fortschr. Physik 6, 169
A958).
82.	H. Bremermann, R. Oehme and J. G. Taylor, Phys. Rev. 109, 2178 A958).
83.	G. Kallen and A. S. Wightman, Kgl Danske Videnskab. Selskab. Mat.
Fys. 1, F) A958); R. lost, Helv. Phys. Acta 31, 263 A958).
84.	E. Guiliemin, Introductory Circuit Theory, New York, John Wiley and Sons,
Inc., 1953.
85.	Y. Nambu, Nuovo Cimento 9, 610 A958).
86.	L. D. Landau, Nucl. Phys. 13, 181 A959); ЖЭТФ 37, 62 (J959);
/. D. Bjorken, Doctoral dissertation, Stanford University, 1959.
87.	Fairlee et al., J. Math. Phys. 3, 594 A962).
88.	M. L. Goldberger, Phys. Rev. 97, 508 A955); 99, 979 A955).
89.	U. Haber-Schaim, Phys. Rev. 104, 1113 A956); T. D. Spearman, Nuovo
Cimento 15, 147 A960).
90.	S. A Lindenbaum, в книге «XII Международная конференция по физике
высоких энергий», Дубна, 1964, т. 1, Атомиздат, 1966, стр. 188.
91.	S. Welnberg, phys. Rev. 124, 2049 A961).
92.	D. Amati, M. Fierz and V. Glaser, Phys. Rev. Letters 4, 89 A960).
93.	H. H. Мейман, ЖЭТФ 43, 227 A962).
94.	H. L. Anderson, W. С Davidon and U. W. Kruse, Phys. Rev. 100, 339
A955).
95.	/. Hamilton, Phys. Rev. 110, 1134 A958).

404	ЛИТЕРАТУРА
96.	W. С. Davidon and M. L. Goldberger, Phys. Rev. 104, 119 A956).
97.	/(. Symanzik, Phys. Rev. 105, 743 A957).
98.	И. Lehmann, Nuovo Cimento 10, 579 A958).
99.	H. Lehmann, Nouvo Cimento, Suppl. 1, 14, 153 A959).
100. G. F. Chew, S Matrix Theory ot Snrong Interactions, New York,
W. A. Benjamin, Inc., 1962.
101*. Дж. Чью, Аналитическая теория S-матрицы, «Мир», 1968.
102.	S. Mandelstam, Rept. Progr. Phys. 25, 99 A962).
103.	R. Jost and A. Pais, Phys. Rev. 82, 840 A951).
104.	P. Federbush, M. Goldberger and S. Treiman, Phys. Rev. 112, 642 A958).
105.	W. Frazer and J. Fulco, Phys. Rev. 117, 1609 A960).
106.	M. Гольдбергер, К. Ватсон, Теория столкновений, «Мир», 1967.
107.	R. Omnes, Nuovo Cimento 8, 316 A958).
108.	//. И. Мусхелишвили, Сингулярные интегральные уравнения, «Наука»,
1968.
109*. Е. Ferrari, La Rivista del Nuovo Cimento 6, 199 A976).
110.	L. Casiilleio, R. Dalitz and F. Dyson, Phys. Rev. 10,, 453 A956).
111.	С. Д. Дрелл, Ф. Захариазен, Электромагнитная структура нуклонов, ИЛ,
1962.
112.	A. Salam, Phys. Rev. 82, 217; 84, 426 A951).
113.	Е. Salpeier and И. Belhe, Phys. Rev. 84, 1232 A951).
114.	/. С Ward, Phys. Rev. 78, 1824 A950).
115.	Y. Takahashi, Nuovo Cimento 6, 370 A957).
116.	K. Johnson, Nucl. Phys. 25, 431 A961).
117.	W. H. Furry, Phys. Rev. 51, !25 A937).
118.	R. Karplus and M. Neumann, Phys. Rev. 80, 380; 83, 776 A950).
119.	S. Wetnberg, Phys. Rev 118, 838 A960).
120.	R. Jost and J. M. Luttinger, Helv. Phys. Acta. 23, 201 A950).
121.	W, Thirring, Phil. Mag. 41, 1193 A950).
122.	F. Low, Phys. Rev. 96, 1428 A954).
123.	M. Gell-Mann and M L Goldberger, Phys. Rev. 96, 1433 A954).
124.	N. M. Kroll and M, A. Ruderman, Phys. Rev. 93, 233 A954).
125.	A. Klein, Phys. Rev. 99, 998 A955).
126.	E. Kazes, Nuovo Cimento 13, 1226 A959).
127 L. M. Brown and R. P. Feynman, Phys. Rev. 85, 231 A952).
128. /. Polkinghome, J. Math. Phys. 4, 503 A963).
B9. P. Federbush and M. Grisaru, Ann. Phys. (N. Y.) 22, 263 A963).
130.	/. Bjorken and Т. Т. Wu, Phys. Rev. 130, 2566 A963).
131.	G. Tiktopolous, Phys. Rev. 131, 480 A963).
132.	Л. Д. Ландау, Собрание трудов, т. 2, «Наука», 1969, стр. 228, 302.
133.	P. J. Redmond, Phys. Rev. 112, 1404 A958).
134.	P. J. Redmond and J. L. Uretski, Ann. Phys. (N. Y.) 9, 106 A960).
135*. Л В. Ефимов, Нелокальные взаимодействия квантованных полей, «Нау-
«Наука», 1977.
136*. Л. С. Золин и др., УФН 117, 119 A975).
137*. А. Б. Кайдалов, Труды международной конференции по физике высоких
энергий, Тбилиси, 1976, AI—27.
138*. Л. S. Carrol et all. Phys. Lett. 61 В, 303 A976)
139*. Review of particle properties, Phys. Lett, 75B, No 1 A978).
140*./. Bialynsky-Birula, Phys. Rev. 155, 1414 A967); 166, 1505 A968).

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Аксиоматическая теория поля 31
Аналитическая структура вершинных
диаграмм 224—228, 244—250
Аналитическое продолжение в евкли-
евклидову область 322—327
Аналогия с электрическими цепями
228—231
Аномальные пороги 248—250
Античастицы 48
Антиунитарный оператор 127
Асимптотическое повеление фейнма-
новских амплитуд 378—382
—	условие 144—145
	 слабое 145
Вакуумные амплитуды 196—198
—	средние 138—181
—	флуктуации 43—44
Взаимодействующие поля 90—137
Внутренние симметрии 27, 104—106
Внутренняя четность 116, 120
Вторичное квантование бозонов 37,
46—48
	фермионов 54—63
Гармонический осциллятор 16—18
Гейзенберговское поле 97
Генератор преобразования 105
Гильбертово пространство 20, 28
Гиперзаряд ИЗ
Гипероны 109
Графическое представление сверток
полей 193—196
Группа ренормализационная 382—390
Диаграммы компактные 267, 294—297
—	редуиированные 240, 244—248, 256,
263, 287
—	Фейнмана 182—183, 196, 198, 224,
239—240
	 в квантовой электродинамике
206—211
Дисперсионные соотношения 217—291
—	— для вершинной функции 250—
253
	я — JV-рассеяния 261—271
	—, аксиоматический вывод
271—277
	Крамерса — Крояига 217—221
—	— — —, приложение к физике вы-
высоких энергий 221—223
Законы Ома 232—233
—	сохранения 25—31
Зарядовая четность 121
Зарядовое сопряжение 120—126
Заряженное скалярное поле 45—49
Излучение мягких фотонов 211—216
Измеримость поля 42—43
Изотопический спин III, 107—108, 198
—	ток 111, 107—108
In-поля 141—146
In-состояния 141—146
Инвариантные функции 392—395
Интегральные уравнения для соб-
собственно-энергетической и вершин-
вершинной частей 299—302
	т-функций и ядра К 302—
307
	перенормированные 319—322
Инфракрасная катастрофа 211—216
Калибровка излучения 80, 92
Канонический формализм 12—25
Квантование 12—18	"_
—	вторичное бозонов 37, 46—48
	фермионов 54—63
—	полей 18—25
—	поля Дирака 52—74
—	электромагнитного поля 75—89
Квантования процедура 80—82
Квантовый принцип действия 31
Ковариантность 80—82
—	релятивистская 71, 72
Конечность перенормированной тео-
теории 341—357

406
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Крамерса — Кронига	соотношения
217—221, 234
Критерий сходимости	327—341
Кулоновское поле 94
Локальные теории поля 10—12
Лоренцева инвариантность 12, 26, 28,
71, 76, 78, 95—96
Лэмбовский сдвиг 44
Массовый контрчлен 143
Метод перенормировки Дайсона —
Салама 332
Микропричинность 43, 179
Мягкие фотоны 211—216
Несобственные преобразования сим
метрии 115
Низкоэнергетическая теорема 370—
378
Нормальное упорядочивание 31 68
134—135, 98—100
Обращение времепи 126—132
Общий формализм 9—32
Оператор антиунитарный 127
—	Гамильтона 62
—	рождения 40, 47, 48, 56, 57, 58,
66—67, 69, 84
—	уничтожения 17, 47, 48, 56, 57 59
66—67, 69, 84
—	числа нуклонов 107, 112
	частиц 39, 47, 57, 59, 69
Особенности произвольных диаграмм
231—235
Out-поля и out-состояиия 150—155
Перенормировка заряда в 4-м порядке
357—370
Перенормировки 292—390
—	метод Дайсона — Салама 332
—	правила 312—319
Перенормировочные константы 312—
319
л — мезон-нуклонное взаимодействие
101—102, 106—108, 261—278
я —я-рассеяние 201—206, 278—287
Плотность гамильтониана 24
—	лагранжиана 21
Позитроний 125—126
Поле Бозе 105, 135—136
—	Бозе — Эйнштейна 222
—	Дирака 63—65, 98—99, 118, 129, 133
	, вторичное квантование 52—74
	, редукционная формула 159—
172
<	, спектральное представление
159—172
Поле Клейна — Гордона 33—51, 54,
73, 94, 128, 133
	.редукционная формула 155—
159
—	Максвелла 78, 93, 133
—	свободное 91
Поля взаимодействующие 90—137
Поперечная 6-функция 79
Представление Гейзенберга 14—15,
19—20, 139
—	Намбу 231, 240, 246, 234
—	Челлена —Лемапа 148, 222, 235
—	Шредингера 14, 97
Преобразования Лоренца 80—82, 95—
96, 101, 103, 142
—	симметрии 25—3!
Принцип Гамильтона 13, 19—21, 77
—	микропричинности 42—43
—	Шварца 244, 250. 255
Причинность 217—221, 234
Промежуточная	перенормировка
Q25	327
Пропагатор 49—51, 73—74, 86—88
Пространственно-подобная поверх-
поверхность 19
Псевдоскалярные частицы 116
Разложение в импульсном простран-
пространстве 65—71, 82—85, 96—98
—	Дайсона —Вика 194, 195
Редукционная формула для поля Дн-
рака 168—172
	Клейна — Гордона 33—
51, 54, 73, 94, 128, 133
	скалярного поля 155—159
—	— — фотонов 172—175
Релеевское рассеяние 376
Релятивистская ковариантность 71—
72
Ренормализационная группа 382—390
Свертка полей 190, 194
	, графическое представление
193—196
Свойства физических состояний 139—
140
Связанные состояния 140
Связь спина и статистики 179—181
Скелетные графики 304—307
Слабая локальная коммутативность
136
S-матрица 292
—.общие свойства 152—155
—, определение 152—155
—.теория возмущений 187—190
Собственная энергия вакуума 98—
100

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
40?
Собственно-энергетическая часть
293—295, 299
Соотношения Гейзенберга 95
—	Крамерса — Кронига 221, 251, 258,
376
Спектральная функция 147, 162, 167,
175
Спектральное представление 146—150,
159—168, 175—179
Статистика Бозе — Эйнштейна 41, 52,
61, 65, 68, 132
—	Ферми —Дирака 52—54, 61, 68
Спин фотона 85—86
Степень расходимости 327—341
Странные частицы 108—115
Субграфики 332—341, 378—380
Тензор энергии-импульса 26
Теорема Вайнберга 332, 335—338, 341,
346, 348, 378—381, 388
—	Вика 190—193
—	Гаусса 79, 92, 94, 98
—	Гейне — Бореля 338
—	Грина 35
—	Коши 260
—	Нетер 25, 31, 81, 90
—	топологическая 307—308
—	?9>С 132—136
Теории поля локальные 10—12
Теория возмущений 182—216
	для т-функций 187—190
—	потенциального рассеяния Фред-
гольма 284
Тождественные частицы 52—54
Тождество Уорда 308—312, 371, 390—
391
Трансляционная инвариантность 95—
96
Унитарность S-матрицы 279—280
Уравнение Бете — Солпитера 301
Уравнение Гейзенберга 71
—	Дирака 63—65, 123
—	Клейна — Гордоиа 33, 46, 142
—	функциональное 384—385
—	Шредингёра 53, 61
—	Эйлера —Лагранжа 13, 22, 25, 27
Уравнения Кирхгоффа 232, 237—238,
246
—	Максвелла 77, 82, 83
Условия асимптотические 144, 145
—	Ландау 240
[/-матрица 115
Флуктуации вакуумные 43—44
Фейнмановский пропагатор 49—51,
73—74, 86—88
Фредгольмова теория потенциального
рассеяния 284
Функции Грина 62, 73, 228, 392—395
—	инвариантные 392—395
—	цилиндрические 394
Функция спектральная 147, 162, 167,
175
Частицы псевдоскалярные 116
—	странные 108—115
—	тождественные 52—54
Четность 115—120
—	зарядовая 121
—	внутренняя 116
Электромагнитная структура пиона
287—290
Электромагнитное взаимодействие
90—95
—	поле-10
Электрон-позитронное ядро 293—299
Энергии-импульса тензор 26
Энергия вакуума 38
	 собственная 98—100

ОГЛАВЛЕНИЕ
Предисловие		7
Глава 11. Общий формализм		9
§ 65. Следствия полевого описания		10
§ 66. Канонический формализм и квантование для частиц ...	12
§ 67. Канонический формализм и квантование полей		18
§ 68. Преобразования симметрии и законы сохранения		25
§ 69. Другие формулировки		31
Задачи		31
Глава 12. Поле Клейна — Гордона		33
§ 70. Квантование и интерпретация в терминах частиц		33
§ 71. Симметрия состояний		40
§ 72. Измеримость поля и принцип микропричинности		42
§ 73. Вакуумные флуктуации		43
§ 74. Заряженное скалярное поле		45
§ 75. Фейнмановский пропагатор		49
Задачи		51
Глава 13. Вторичное квантование поля Дирака		52
§ 76. Квантовая механика п тождественных частиц		52
§ 77. Представление чисел заполнения для фермионов		54
§ 78. Теория Дирака		63
§ 79. Разложение в импульсном пространстве		65
§ 80. Релятивистская ковариантность		71
§ 81. Фейнмановский пропагатор в теории Дирака		73
Задачи		74
Глава 14. Квантование электромагнитного поля		75
§ 82. Введение		75
§ 83. Квантование	,		76
§ 84. Ковариантность и процедура квантования		80
§ 85. Разложение в импульсном пространстве .........	82

4	ОГЛАВЛЕНИЕ
§ 86. Спин фотона	85
§ 87. Фейнмановский пропагатор для поперечных фотонов	86
Задачи	89
Глава 15. Взаимодействующие поля	90
§ 88. Введение		90
§ 89. Электромагнитное взаимодействие		90
§ 90. Лоренцева инвариантность и инвариантность при трансляциях	95
§ 91. Разложение в импульсном пространстве		96
§ 92. Собственная энергия вакуума; нормальное упорядочивание . .	98
§ 93. Другие взаимодействия		Ю'
§ 94. Симметрия взаимодействий		104
§ 95. Сильная связь между я-мезонами и нуклонами . ,		106
§ 96. Свойства симметрии странных частиц		108
§ 97. Несобственные преобразования симметрии		45
§ 98. Четность	,		И5
§ 99. Зарядовое сопряжение		120
§ 100. Обращение времени		126
§ 101. /С^-теорема		132
Задачи		136
Глава 16. Вакуумные средние и S-матрица	138
§ 102. Введение	138
§ 103- Свойства физических состояний	138
§ 104. In-поля и in-состояния; асимптотическое условие	141
§ 105. Спектральное представление для вакуумного среднего от ком-
коммутатора и функция распространения скалярного поля . . .146
§ 106. Out-поля и out-состояния	«	150
§ 107. Определение и общие свойства S-матрицы	152
§ 108. Редукционная формула для скалярных полей	155
§ 109. In- и out-поля и спектральное представление в теории Дирака 159
§ 110. Редукционная формула для дираковских полей	168
§ 111. In- и out-состояния и редукционная формула для фотонов . .172
§ 112. Спектральное представление для фотонов	175
§ 113. Связь спина со статистикой	,	179
Задачи	181
Глава 17. Теория возмущений	182
§ 114. Введение		182
§ 115. {/-матрица		183
§ 116. Теория возмущений для т-функций и 5-матрица		187
§ 117. Теорема Вика		190
§ 118. Графическое представление		193

ОГЛАВЛЕНИЕ	5
§ 119. Вакуумные амплитуды	196
§ 120. Спин и изотопический спин; я-мезон-нуклонное рассеяние . ,198
§ 121. я—я-рассеяние	201
§ 122. Графическая техника в квантовой электродинамике .... 206
§ 123. Излучение мягких фотонов и инфракрасная катастрофа . . .211
Задачи	216
Глава 18. Дисперсионные соотношения	217
§ 124. Причинность и соотношения Крамерса — Кронига	217
§ 125. Приложение к физике высоких энергий	221
§ 126. Аналитические свойства вершинных диаграмм в теории воз-
возмущений 	224
§ 127. Обобщение на случай произвольных диаграмм и аналогия
с электрическими цепями	228
§ 128. Пороговые особенности функций распространения	235
§ 129. Особенности произвольных диаграмм и правила Ландау . . . 239
§ 130. Аналитическая структура вершинных диаграмм; аномальные
пороги	244
§ 131. Дисперсионные соотношения для вершинной функции .... 250
§ 132. Сингулярности амплитуд рассеяния	253
§ 133. Применение к я-мезон-нуклонному рассеянию вперед . . . 261
§ 134. Аксиоматический вывод дисперсионных соотношений для пион-
нуклонного рассеяния вперед 	 271
§ 135. Динамические расчеты я—я-рассеяния с использованием дис-
дисперсионных соотношений	278
§ 136. Электромагнитная структура пиона	287
Задачи	290
Глава 19. Перенормировки	292
§ 137. Введение	292
§ 138. Свойства диаграмм собственной энергии и вершинных частей
и электрон-позитронное ядро	293
§ 139. Интегральные уравнения для собственно-энергетической и вер-
вершинной частей	299
§ 140. Интегральные уравнения для т-функций и ядра К; скелетные
графики	302
§ 141. Топологическая теорема	307
§ 142. Тождество Уорда	308
§ 143. Определение перенормировочных констант и правила пере-
перенормировки 	312
§ 144. Сводка формул: перенормированные интегральные уравнения . 319
§ 145. Аналитическое продолжение и промежуточная перенормировка 322
§ 146. Степень расходимости и критерий сходимости	327
§ 147. Доказательство конечности перенормируемой теории .... 341

ОГЛАВЛЕНИЕ
§ 148. Пример перенормировки заряда в четвертом порядке .... 357
§ 149. Низкоэнергетическая теорема для комптоновского рассеяния . 370
§ 150. Асимптотическое поведение фейнмановских амплитуд .... 378
§ 151. Ренормализационная группа	,	382
Задачи	; 390
Приложение В. Коммутаторы и функции распространения	392
Дополнения редактора перевода 	 	 396
Литература	401
Предметный указатель	405