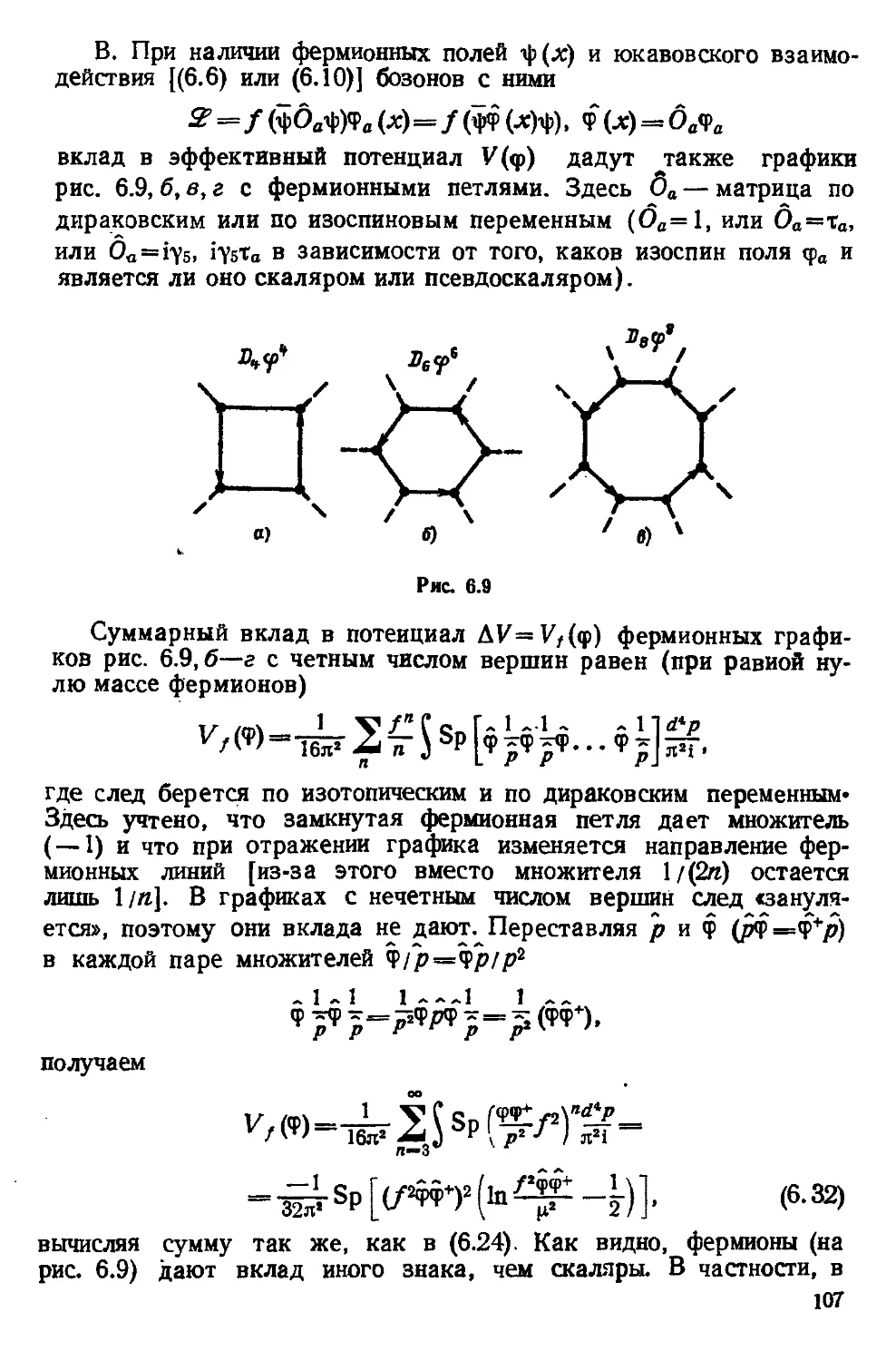
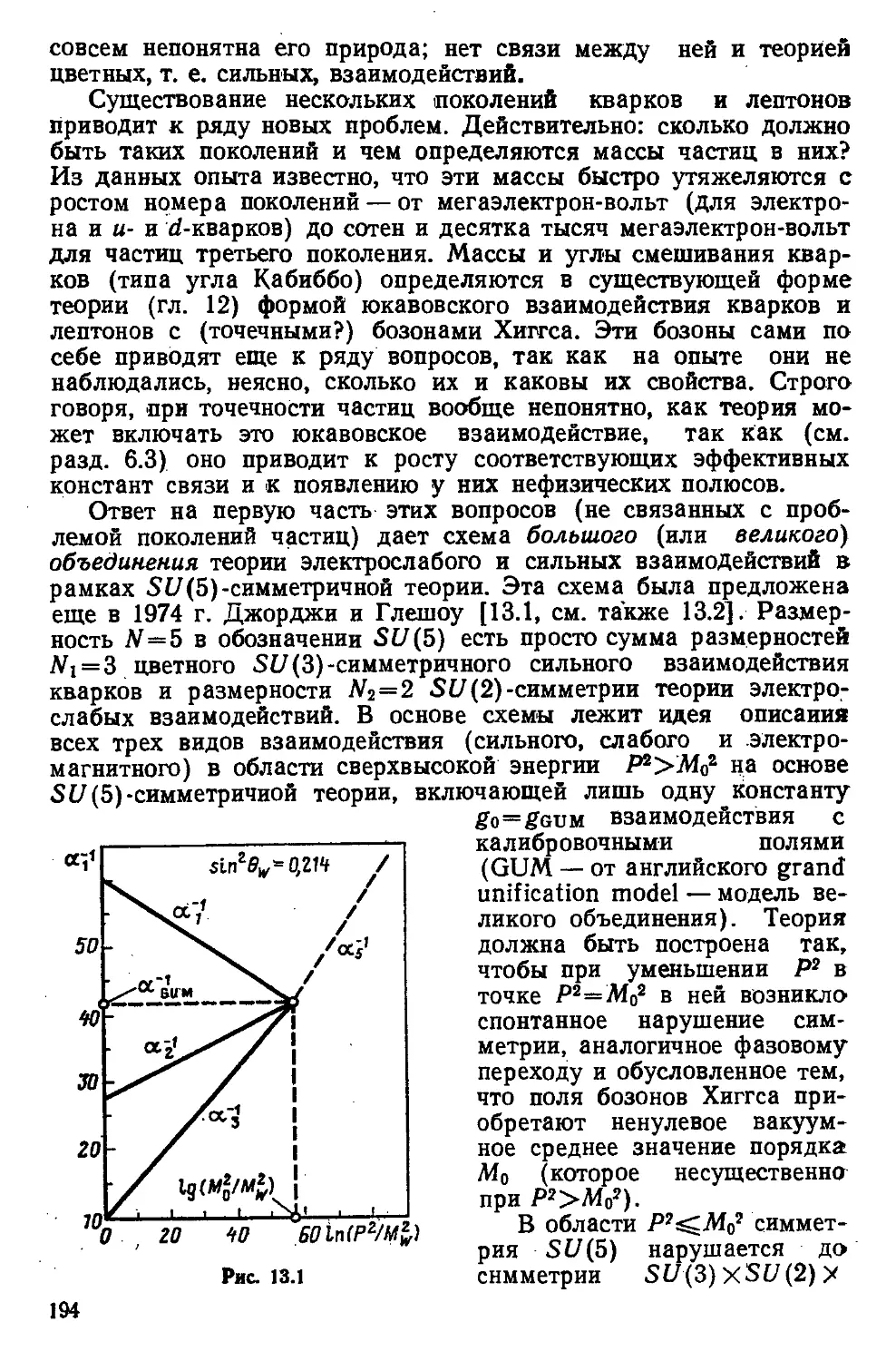
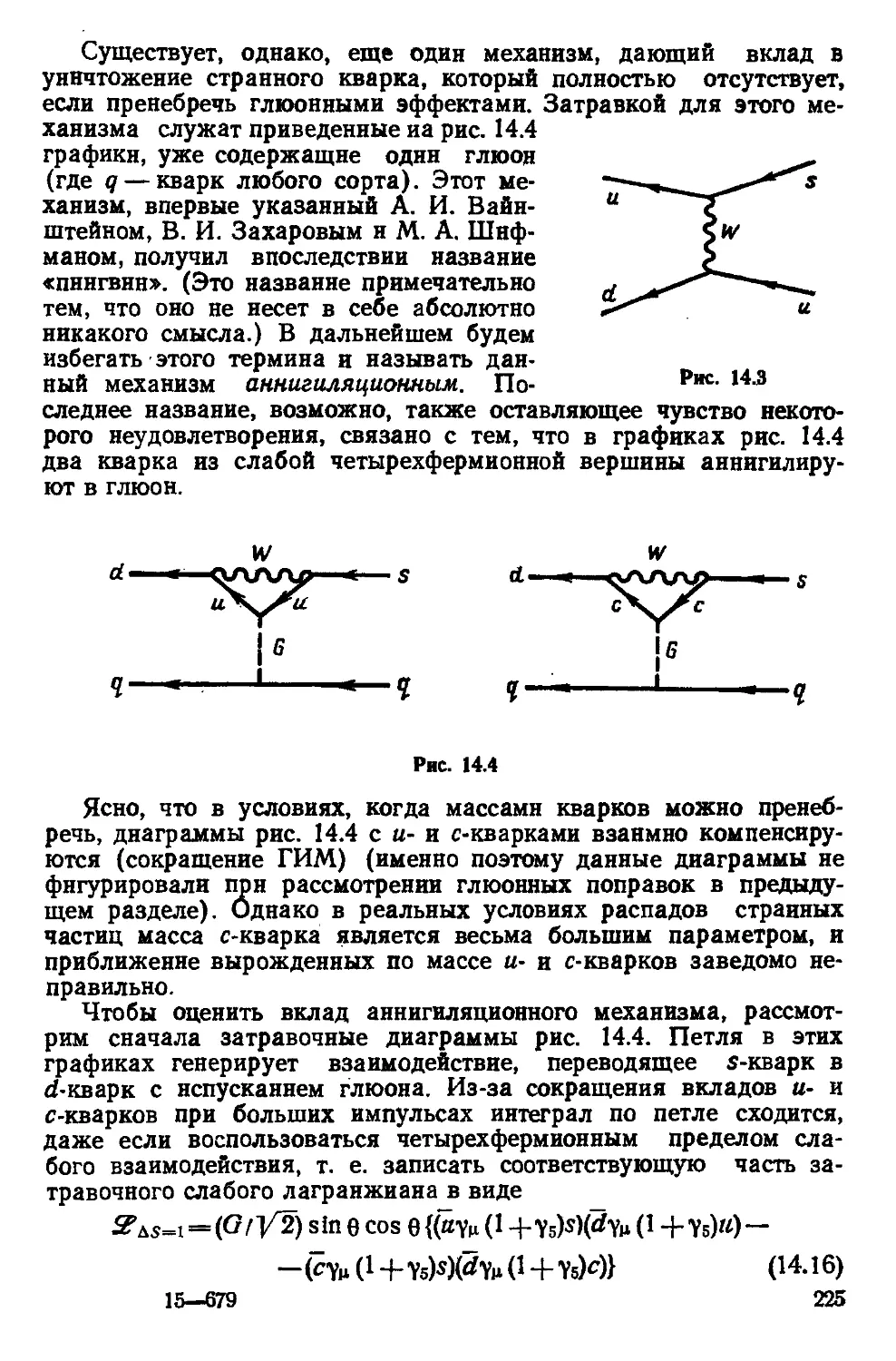
Автор: Волошин М.Б. Тер-Мартиросян К.А.
Теги: математика ядерная, атомная и молекулярная физика физика квантовая механика
Год: 1984
Текст
М. Б. ВОЛОШИН, К. А. ТЕР-МАРТИРОСЯН
ТЕОРИЯ
КАЛИБРОВОЧНЫХ
ВЗАИМОДЕЙСТВИЙ
ЭЛЕМЕНТАРНЫХ
ЧАСТИЦ
МОСКВА
ЭНЕРГОАТОМИЗДАТ
1984
УДК 519.4:539.12
Волошин М. Б., Тер-Мартиросяи К. А. Теория калибро-
калибровочных взаимодействий элементарных частиц. М.: Эиерго-
атомиздат, 1984, 296 с.
Излагаются теории калибровочных взаимодействий эле-
элементарных частиц — электромагнитного и слабого, а также
сильного взаимодействия, описываемого квантовой хромоди-
иамнкой. Обсуждаются вопросы перенормировок, спонтанного
нарушения симметрии и схем объединения- взаимодействий.
Описываются приложения квантовой хромодннамнкн к процес-
процессам с участием адроиов.
Для научных работников, аспирантов и студентов.
Табл. — Ил. 84. Библногр. 119.
РецеизеитА. А. Аисельм
1704070000-464
В—05K0D-84 " ® Энергоатониздат, 1984
ПРЕДИСЛОВИЕ
Цель этой книги — дать в краткой и по возможности простой
форме современную картину теории электромагнитного, слабого
и сильного взаимодействий элементарных частиц, которая стронт-
ся на общей основе теорий с так называемой калибровочной сим-
симметрией. Авторы также видели свою цель в том, чтобы научить
Читателя методам конкретных расчетов физических процессов, ос-
основанных на теории возмущений. Большинство интересных при-
приложений расчетов по теории возмущений требует выхода за рам-
рамки борновского приближения, что неизбежно приводит к пробле-
проблеме перенормировок. В связи с этим в первой части книги приве-
приведен обзор схем перенормировок и способов суммирования
главных логарифмов в простейшей из калибровочных теорий —
квантовой электродинамике. В дальнейшем эти методы с мини-
минимальными модификациями переносятся на более сложный случай
так называемых неабелевых калибровочных теорий, к которым
относятся современная теория сильного взаимодействия — кванто-
квантовая хромодинамика, единая теория электромагнитного и слабого
взаимодействий — теория Глешоу—Вайнберга—Салама, а также
модели так называемого большого (или «великого») объединения
этих трех взаимодействий. Изложению основ этих теорий посвяч
щена часть II книги. В эту же часть включены различные аспек-
аспекты взаимодействия скалярных полей. Введение таких полей в тео-
теорию электрослабого взаимодействия и модели большого объеди-
объединения необходимо для спонтанного нарушения калибровочной
симметрии и генерации наблюдаемого на опыте спектра масс
кварков, лептонов и промежуточных бозонов слабого взаимодей-
взаимодействия. До настоящего времени частицы — кванты элементарных
скалярных полей — не обнаружены на опыте. В большой степе-
степени это связано со сложностью их поиска и с неопределенностью
теоретических предсказаний их масс и других свойств. Поэтому
нельзя исключить того, что в ближайшие годы большое внимание
в экспериментальных и теоретических исследованиях будет уде-
уделено поиску и изучению элементарных скалярных частиц.
В часть III книги вошли некоторые приложения квантовой
хромодинамики к описанию свойств адронов. На этих приложени-
приложениях проиллюстрированы методы вычислений в калибровочных тео-
теориях, такие как использование уравнений реиормгруппы и опера-
1* 3
торного разложения, а также феноменологические методы учета
эффектов, не описываемых теорией возмущений. В конкретных
расчетах, приводимых в книге в качестве примеров применения
общих методов, авторы стремились доводить вычисления, что на-
называется, «до числа», чтобы убедить читателя в том, что речь
идет не об абстрактных теоретических построениях, а о реально
существующих в природе явлениях.
Авторы полагают, что такое сочетание достаточно углубленно-
углубленного изложения теоретических основ с физическими приложениями,
которое отличает данную книгу от ряда других монографий на
близкие темы, весьма полезно для понимания общей картины
современной физики элементарных частиц.
В основу книги положен курс лекций, прочитанный авторами
в Институте теоретической и экспериментальной физики для сту-
студентов Московского физико-технического института. Этим об-
обусловлен несколько конспективный характер изложения материа-
материала (особенно в части I) и его выбор, при котором авторы стара-
старались включить в книгу описание лишь тех аспектов теории,
относительно которых можно уже сейчас полагать, что дальней-
дальнейшее развитие на них принципиально не скажется (в меньшей сте-
степени это относится к гл. 13). При этом естественно, что многие воп-
вопросы современной теории элементарных частиц остались за рам-
рамками изложения. Однако авторы надеются, что данная книга
может быть полезной на определенных этапах работы в этой об-
области. ¦..:¦.
1 Главы 1—6 и 10—13 написаны К- А. Тёр-Мартиросяном, гла-
главы 7—9 и 14—17—М. Б. Волошиным. Раздел 4.6 иаписан в тес-
тесном сотрудничестве с А. В. Смилгой. Авторы благодарны своим
друзьям и коллегам, в особенности А. И. Вайнщтейну, В. И. За-
Захарову, Б. Л. Иоффе, Я. И. Когану, И. Ю. Кобзареву, Ю. М. Ма-
кеенко, В. А. Новикову, Л. Б. Окуню, А. В. Смилге и М. А. Шиф-
ману; Дк В. Ширкову, за многочисленные обсуждения затро-
затронутых в книге вопросов. Мы также глубоко признательны
Н. А. Волчковой и Е. А. Ильиной за большую работу по оформ-
оформлению рукописи книги.
Часть I
Перенормировка КЭД. Ренормгруппа.
Главные логарифмы
Глава 1
ЛАГРАНЖИАН. S-МАТРИЦА. ПРАВИЛА ФЕЙНМАНА В КЭД
1.1. Калибровочная инвариантность. Лагранжиан
Эта глава—вводная; в ней дан конспективный обзор основ
квантовой электродинамики (КЭД) и определены основные обо-
обозначения, используемые далее в книге. Материал ее носит спра-
справочный характер и содержится в учебниках по квантовой элек-
электродинамике — в книгах А. И. Ахиезера и В. Б. Берестецкого
[1.1], В. Б. Берестецкого, Е. М. Лифшица и Л. П. Питаевского
[1.2] или Н. Н. Боголюбова и Д. В. Ширкова [1.3, 1.4],
Дж. Д. Бьеркена и С. Д. Дрелла '[1.5]. В какой-то мере, это же
относится и к следующим трем главам (гл. 2—4), в которых про-
проведен анализ структуры вкладов феймановских графиков и рас-
рассмотрена общая схема перенормировки КЭД.
Квантовая электродинамика (КЭД) —это теория взаимодейст-
взаимодействующих полей: векторного электромагнитного поля Ац(х)=
— (А0(х), A(jc)) и дираковского биспинорного поля электронов-
/ф /х)\
позитронов tya(x)=LfJh здесь <P(jc) и х{х)—двухкомпонентные
спинорные поля.
Уравнения КЭД не меняются по форме (т. е. инвариантны)
при локальных калибровочных преобразованиях, т. е. при измене-
изменении фазы поля т})а(л:) в любой точке x=(xo=act, x) и добавлении
при этом к 4-вектору Ац(х) градиента фазы:
У (х) = ехр [ - to (х)] Ч> (ж);
1
Здесь (о(х)—произвольная фаза; dli.^=d/dxll=^(d/dx0, —v)—опе-
—v)—оператор частной производной; е—заряд электрона. Различный выбор
&{х) называют различной калибровкой полей Ац(х) и ij> (jc).
Теизор напряженностей электромагнитного поля
A.2)
и лоренц-инвариантные формы (в которых
.(¦*)-(¦(.*)*(*)). (^(x)yll[id^~eAli(x)]^(x)) A.3)
не меняются при этом преобразовании, т. е. не зависят от выбора
калибровки (само слово калибровка означает подстраивание вида
A.1) вектор-потенциала А»(х) под данный выбор произвольной
фазы <о(х) поля if(x)). Поэтому лагранжиан КЭД, инвариантный
относительно калибровочных преобразований A.1) и преобразо-
преобразований Лоренца, может быть выбран в виде
3S (х) = <?„+<?' (х) = - A /4) Fl, (jc) +
+ (¦(*) [Yi»(W|i- eAi» (*))-«H(Jc)), 0-4)
где от—масса электрона.
Здесь и далее использованы сокращенные обозначения (Фейн-
мана): по дважды повторяющимся векторным индексам v, ц=0, 1,
2,3 всегда подразумевается суммирование, причем пишем для
краткости у^Ац—А = у0А0—уtAt, i = \,2, 3 вместо более точной
формы ¦A = YAgiiv-Av с метрическим тензором вида
Точно так же F^V=F?A — 2Flit где всюду латинские индексы про-
пробегают значения i, ?=1,2,3. Так как дц = (д0, —\), то всюду
¦yM<?,, = Yodo-f-YiV>. Матрицы Yn Дирака антикоммутируют друг с
другом: {Yii, Yv} = YuYv + YvYw = 2g^v и с матрицей Ys = — i
«^^5= — Y5Yw. и могут быть выбраны в следующем виде:
. /1 0\ о / 0 оЛ @ 1
при этом Yn=PYMP^Y(i- Здесь a, —матрицы Паули 2x2:
/О IV /0 —1\ (I 0\
°i = il OJ' a2=\t О)' аз==^0 -lj-
Возможны и другие представления матриц Yn. которые следуют
из A.5) при замене ¦ф = 1/^/, yii->-Yw = ^Yii^+. где V— любая
унитарная матрица 4x4 C/V+ = V+V = l). Иногда, например,
пользуются представлением Вейля, которое следует из A.5) при
, @ \\ , I 0 аЛ
H-x)\
A.6)
Удобно считать, что все величины умножены на нужные степе
яи постоянных^ Л и_ с (например, &=$ihc, Aw = A^lYTc, т =
=meclh, e—eiYhc)> так что они имеют размерности только сте-
степеней длины I:
После этого постоянные h и с из всех формул выпадают.
В A.4) 9?0 — сумма лагранжианов свободных полей А№(х)
и tJ)(jc), a
2>'=2>-2>0=-е${х)у^(х))А»(х)~-и(х)А»{х) A.7)
—хорошо известный в электродинамике лагранжиан взаимо-
взаимодействия; здесь
и(х)=е(#(х)у^(х)) ' A.8)
—4-вектор плотности тока электрон-позитронного ..поля, удовлет-
удовлетворяющий закону сохранения dlijli(x)~0.
1.2. Уравнения движения.
Спектральные разложения полей. Энергия-импульс
Равенство нулю, вариации & по полю Ау(х) (т. е. величины
) = [d1lFw,v—j4(x)]8Av) дает вторую пару уравнений Макс-
Максвелла:
^dlAy (х)-дч (д№ A»(x))=/v (x), A.9)
которые при калибровке Лоренца <?цЛц=О эквивалентны, как
следует из A.9), так называемым уравнениям для запаздываю-
запаздывающих потенциалов
dlAv (х)-А (*)=«(¦(*) W* («)). (ЫО)
Напомним, что первая пара уравнений Максвелла есть тождество
Бианки di.F^-^-dyFi.n-^-dvFMi — O, которому удовлетворяет всякий
тензор вида A.2).
Условие F2')^-=0 (или F2%=0) дает уравнение Дирака
I*fti(Wii—«^,»)-«l^(je)—0 A.11)
и комплексно-сопряженное к нему
(здесь Y^=ifYw; yJ—матрица, транспонированная по отношению
к уц), которое можно представить в форме
ЫЙи+еА,»)—«JlfC*) —0, A.12)
где ^с(х)=С^(х)-- поле, зарядово-сопряженное по отношению
к. tJ)(jc); 6=ia2=(j q2] —матрица зарядового сопряжения;
c5c
Общим решением этих уравнений при е=0 будут следующие
разложения полей в ряды Фурье:
-f# х«с (/>, *) ехр (\рх)\,
где и<=Сп(рЛ); шА=^к2=|к|; 8/,=Кр2+яГ2; ck|V, Op,* и & + *-
амплитуды плоских волн; Sp=\ d3plBnK; ew(k, v)==g^v—вектор-
орт поляризации фотонов; он равен gwv в системе координат
с 0Z||k, причем значения v = l, 2 в Ck, v — физические» а продоль-
продольная и скалярная компоненты поляризаций v=3,0 не дают вклада
в значения физических величин.
Амплитуда и(р,Х) (и ас(р, Щ есть решение (при е=0) урав-
уравнения A.11) Дирака: (у».р».—т)и(р,Х)=0; она нормирована усло-
условием (ии)=*2т и в представлении A.5) имеет вид
AЛ5)
где Пр«=р/| р |, а г»(Я)—двухкомпонентный спинор. Его состояния
«A/2)«=(q), г)(—1/2)=A) отвечают проекциям Х=±\/2 спина
на ось квантования 0Z, а все остальные состояния спина можно
получить из них поворотом системы координат вокруг произволь-
произвольной оси п на произвольный угол ю, что соответствует преобразо-
преобразованию г»в = ехр[—A/2)аю]г»(Я,), где ю=<оп. Если 0Z||p, то такие
состояния г»(А,) называют спиральными [для них (anp)v{X)=
=2Ад)(А,)= ±v(K)]. В представлении Вейля A.6) амплитуда A.15)
содержит лишь верхние компоненты при 8Р//ге-> оо в правоспи-
ральном состоянии, в котором anpv (A) = -j-v(k), и только нижние—
в левоспиральном, где апрг;(Я,)=—v(X).
Полные 4-импульсы электромагнитного поля Pi=)T^tOdv и
электрон-позитронного поля Р* =J T^Qdv (где тензоры энергии
импульса Т^у и Тет этих полей определяются в известном виде
[1.1 — 1.5] через лагранжиан) являются квадратичными функциями
амплитуд полей CkV, <ц%, bv,\ вида
2
k.v
Определяющими в Р? являются вклады поперечных поляризаций-
v=l, 2, а члены с v = 3 и v=0 взаимно сокращаются, так как:
в калибровке Лоренца д1ХА11=0 имеет Ск,з=Ск.о [член с v==O
входит в A.16) со знаком минус].
4-вектор тока /w (х) и полный заряд поля (в единицах е) также
квадратичны по амплитудам:
где Уо(-*)=/о (•*)/«.
1.3. Квантово-механическая теория. 5-Матрица
В квантовой электродинамике амплитуды Ck,v, аРд и bv,%
являются операторами, действующими на волновые функции Ф№
состояний. Эти операторы коммутируют или антикоммутируюг
между собой:
\Ck,s, ?|c'.v']=O; ,
_i_ о 11 • 1 / К
{Орд, аР'Д'}='0
(^ аналогично для операторов 6рд, b^w, которые антикоммути-
руют с Орд и с Др*;д.). дают хорошо известные [1.1, 1.4, 1.5] соот-
соотношения коммутации и антикоммутации для операторов А11(х),.
И?{х), определенных в виде A.13), A.14).
Формулы A.JN—A.12) классической теории остаются справед-
справедливыми ив КЭД, однако в выражениях для операторов полного»
4-импульса поля и оператора тока удобно подставить Ск,ус?у =
= l+ciJivCk,v. 6рд6р"д=1 —6р"д6рд, что дает, с точностью до по-
постоянных слагаемых,
2 2
k,V рД
Q=2 Ид'-
РД
гДе Мк,ч=с?уСк,ч, N$=a.p,i, Яр* и N^l^b^bf,}, имеют смысл,
чисел фотонов, электронов и позитронов в состояниях k, v и р,.
^ соответственно. Неучтенные справа в A.18) постоянные сла-
слагаемые (Ро).«2 1Ш*' (ро)«=— 2 ЪР' (Q)o=2 J характеризуют
k,v рД рД
свойства вакуума и являются соответственно энергией нулевых,
колебаний электромагнитного поля {PV)t, а также полной энергией.
P) и полным зарядом (Q)o всех электронов дираковского вакуума
(электронов с отрицательной энергией). Эти постоянные бесконечныз
к
\
(
м не наблюдаемы, однако их изменение при изменении внешних
условий, например при включении внешнего поля, в принципе
физически наблюдаемо.
Собственные состояния Ф„ системы свободных полей (при е=0)
удобно характеризовать числами частиц Nu,?, Л^рд, Л^рд в эле-
элементарных ячейках [объемом BяйK] с заданными импульсами и
поляризациями (v=l, 2, или Я= + 1/2 для ет), причем в силу
принципа Паули числа Nffi могут иметь лишь значения 0 и 1.
Таким образом, индекс п у Ф„ есть совокупность чисел {^Vk.v.
¦Мрд.Мрд'} для всех «ячеек» k, v и р, I.
Состояния с одним фотоном с данными к, v или с одним
электроном или позитроном получаются из волновой функции
вакуума Фо при действии на нее операторов рождения с?ч, а+к,
или Ь$х-
причем Ck,v%=Op,K%=bp,i(D0='0. (Состояние вакуума Фо со-
содержит любые числа скалярных и продольных фотонов с Nu,y и
v=0, 3, поэтому условие ек^Ф0=0 выполняется только для по-
поперечных поляризаций v=l,2).
Таким же образом можно получить и волновые функции не-
нескольких свободных частиц, например: Q>2y — c?t VfC+ У1Фо; Фпие=
с?,уа+хФ0; Ф2е = «р<;д,«рЬ11,Фо и т. д. Отметим! 'что вообще
МУ7^1к^'ь а c?№VW;h
При включении взаимодействия между полями, т. е. при
все эти состояния Ф„ перестают быть собственными состояниями
системы и между ними возникают переходы: из состояния Ф, при
t-+ — ao (где заряд е можно считать выключенным) возникает при
.t-+-\-oo (где опять е—0) состояние V,, отличное от всех Ф„. Его
разложение по полной ортонормированной системе функций Фп
дает >Р,=2ф'п5тГ, где Smt— амплитуды перехода из состояния I
в состояние т, квадрат модуля которых определяют наблюдаемые
на опыте вероятности этого перехода: Wi^.n=\Smt\2. Можно по-
показать, что >Р,=5Ф/, где ^—оператор E-матрица) вида
5==Гехр I J 2"rf4JC =
=Гехр \-ie ] ${х)ъ${*)) A№(x)d*x\, A.20)
т. е. что
5т/=(Ф^)=(Ф^Ф,). A.21)
ю
Интеграл в A.20) есть предел суммы 2У- (ф (х}) у»$ (xj)) X
X A»(Xj)Л4яу по всем A*Xj, а экспонента от него—произведение
соответствующих экспонент Еу=ехр [—le (ip/Yufy) А1ЧА*х]], которые
между собой не коммутируют. Символ Г-произведения в A.20)
означает, что множители Ej=E(Xj) должны быть упорядочены по
времени, т. е. операторы Е(Х]), зависящие от большего времени
¦x<n=clj, стоят в A.20) левее операторов, зависящих от меньших
значений х0.
Приведенная в A.20) форма 5-матрицы отвечает так назы-
называемому представлению взаимодействия, в котором операторы
А»(х) и tp(je) имеют простой вид A.13), A.14), такой же, как в
случае е=0. Поэтому, если заряд е мал, то разложение экспо-
экспоненты A.20) в ряд по его степеням дает
...Фхп, A.22)
где А — у»А»(х), a W>Aij>)y=(ij>(jCy) A(Xj)ty(Xj)), и позволяет с по-
помощью A.13), A.14) непосредственно вычислить матричные эле-
элементы перехода A.21) в виде релятивистски инвариантного раз-
разложения теории возмущений по степеням малого параметра
а=е2/4/г= 1/137 (вклад в Sml дают только четные или нечетные
степени е—в зависимости от общего числа фотонов в начальном
и конечном состояниях I и in).
' _ В теории возмущений в КЭД каждую из скобок
(i|) (х) А (х) ij) (x))=%е (х) (A (jc))f ^ (х) можно записать без измене-
изменения матричных элементов Sm[ в виде ^V-произведения соответст-
соответствующих операторов, т. е. в виде (ty(x)A(x)ty(x))v=
—N {tya{x)tf(x)){A (д:))р. В ./V-произведении по определению
операторы поглощения Орд, йРд переставлены так, что стоят
справа от операторов рождения Орд, й^"д; при этом при пере-
перестановке двух операторов Ферми-частиц (Орд и Ор-д- или bPw)
их произведение меняет знак, а в случае бозе-частиц—не
меняет. Например: (ордОрд—йрдй^д)лг=а?хард-Ирдйрд, a
(ck.*cj?v+c?vCk,v)w=2c?vckiV. Замена каждой из скобок в A.22)
¦W-произведением (^А^)-^(^А^)^ не изменяет в КЭД матричных
элементов оператора S, но сильно упрощает их вычисление.
Поэтому обычно предполагают, что все скобки в A.22) являются
такими Л^-произведениями и что поэтому среднее по состоянию
вакуума от них исчезает: (<1^ (фДф) Фо)=0.
Отметим, что такая замена произведений операторов их
^-произведениями в классических формулах A.16), A.16а) для
энергии-импульса и заряда поля и дает непосредственно их зна-
значения A.18) с нулевым средним в состоянии вакуума. Как уже
было отмечено, это, вообще говоря, может дать неправильный pe-
pell
зультат в специальных условиях, возникающих при включении
внешних полей, приводящих к перестройке структуры вакуума
(такие эффекты, как правило, ускользают в рамках теории воз-
возмущений).
1.4. Правила Фейнмана
Результаты вычисления Sm, в (.1.21) сводятся к простым гра-
графическим правилам Фейнмана ![1.6] (см. [1.1—1.5] и дают:
о __ Bя)М«(*ж—**) , Т
/2222?2°4
где Nq = N, и N=Nm — число частиц в начальном и конечном со-
состояниях; е*° и ъ( — их энергия; ff>t и &т — их суммарные 4-им-
пульсы; i Tm, — так называемая Г-матрица, представляемая вкла-
вкладом бесконечного числа графиков Фейнмана.
Все графики в КЭД содержат Nt линий входящих электронов
и фотонов и Nm линий выходящих частиц в конечном состоянии и
п-вершин —по степени п в сумме A.22) (см. рис. 1.1), к каждой
Рис- !•! Рис 1* Рнс. 1.3
из которых примыкают две электронные и одна фотонная линии.
Электронные линии имеют определенное направление — от вхо-
входящей до выходящей —и тянутся вдоль всего графика, не обры-
обрываясь, или же являются замкнутыми петлями. Фотонные линии
начинаются и обрываются в вершинах. Всем линиям отвечают
определенные 4-импульсы частиц, причем в каждой вершине
4-импульс сохраняется.
Вклад в Тт, графика (диаграммы) с п вершинами пропорцио-
пропорционален еп и определяется приведенными ниже правилами Фейн-
Фейнмана.
Соответственно A.20) или A.22) каждой вершине рис. 1.1 от-
отвечает множитель
-ieyVL{2nf6*(pl--P2-k), A.24)
где pi и р2 — 4-импульсы входящего в вершину и выходящего из
нее электронов; Л —4-импульс выходящего фотона; ц — его поля-
поляризация. Каждой внутренней линии электрона с 4-импульсом р
(см. рис. 1.2) отвечает множитель iO°{p), где (G0)^ — дираков-
ская матрица вида:
/jp/дЛ . * Р г "* Л "^ч П
12'
причем:1 р—УиРн* Функция (?°(р) является образом Фурье функ-
функции Грина или пропагатора
j4 A-26)
уравнения Дирака
(Y^-w)Go(jc)=6*(jc). A.27)
Поэтому G~°(p) часто называют пропагстором электрона.
Каждой внутренней фотонной линии (рис. 1.3) с 4-импульсом k
отвечает множитель — Ю%(Щ, где
/>^v (А)=^nv / (*2—Я2+10) A.28)
— фотонный пропагатор. Здесь Я,=0 масса фотона, а тензор d^ за-
зисит от выбора калибровки и в простейшей, так называемой
лоренцевой калибровке (^-калибровка) имеет вид
A.29)
где С—произвольное число. Выбор С=1 отвечает фейнмановской
калибровке, в которой </цу=?му, а выбор С=0—калибровке Лан-
Ландау, в которой rfnV=g^v, где
iv A-30)
—поперечный тензор, т. е. ^^=^^^=0. Величина D^ify есть
¦фурье-образ^функцйи Грииа электромагнитного поля
n)\ A731)
удовлетворяющей уравнению (подробнее см. разд. 1.5):
Ы»Л- A -1 /С) с?Ж1 Bis (ж) - g^V (x), A.32)
в котором, строго говоря, нужно считать ^~*"°°- Однако физиче-
физичер, р р, у ^ ф
ские результаты не зависят от ? и поэтому этот параметр можно
выбрать любым. г :
Каждой внешней линии электрона (с импульсом рис проек-
проекцией спнна %), входящей в график, нужно сопоставить спинор
«(р, А) A.15), а выходящей из графика — величину п(р, К).
Внешней входящей фотонной линии следует сопоставить орт по-
поляризации фотона е,Дк, v), а выходящей г—величину е,,* (причем
в случае линейной пр'ляризацнн фотона е^*=е^).
Вклад графика в величину-- Bя)*84Х&т—&'1IТш получается
перемножением вкладов всех вершин и линий и интегрированием
по 4-нмпульсам рх всех внутренних линий Твида 2Р/ = \ ]
1 Вместо i6, где в>0, в—»-0, всюду ниже пишем сокращенно 10.
13
Вклады электронных линий и вершин перемножаются как матрицы;
в порядке от конца линии к началу. Если эти линии образуют
петли, то в результате суммирования по дираковским индексам:
возникает след от произведения всех вершин и пропагаторов
каждой петли. Кроме того, каждой такой петле нужно приписать
множитель (— 1), возникающий из-за антикоммутации фермионных
операторов у(х), у(х).
Удобно устранить б-функции, возникающие от вершин A.24).,
проводя во вкладе каждого графика интегрирование по 4-импуль-
сам внутренних линий. В результате останется лишь общая
б-функция BяLб4(^т—^j), которая записана в виде отдельного
множителя в A.23), а 4-импульсы будут сохраняться в каждой
вершине. При этом если график не содержит петель (из элек-
электронных и фотонных линий), то 4-импульсы всех внутренних
линий в нем определяются однозначно при задании импульсов
внешних линий. Вклад \Тт1 графика с одной петлей определяет-
определяется однократным интегралом по импульсу одной из линий в пет-
петле fd*p/Bп)*, двухпетлевой график —таким двукратным интег-
интегралом и т. д. Эти интегралы называют фейнмановскими. После
устранения б-функций вклад вершин рис. 1.1 определится мно-
множителем —ieyr
Например, вклады беспетлевых графиков (рис. 1.4,а,о) для
амплитуд уе и ее-рассеяния не содержат совсем интегралов по
4-импульсам, а вклады однопетлевых и двухпетлевых графиков
(рис \.Ъ,а,б, 1.6,а,б и \1,а,б) для поправок порядка е2 и е* к»
№
а) V «) Тп
Рис. 1.4
14
a)
Рис. 1.5
Рис. 1.6
к1
ЛллллГ ; _W\/vw*
Рис. 1.7
Рис. 1.8
вкладу соответственно вершины, электронного и фотонного про-
пагаторов определяются однократными и двукратными интегра-
интегралами Фейнмана.
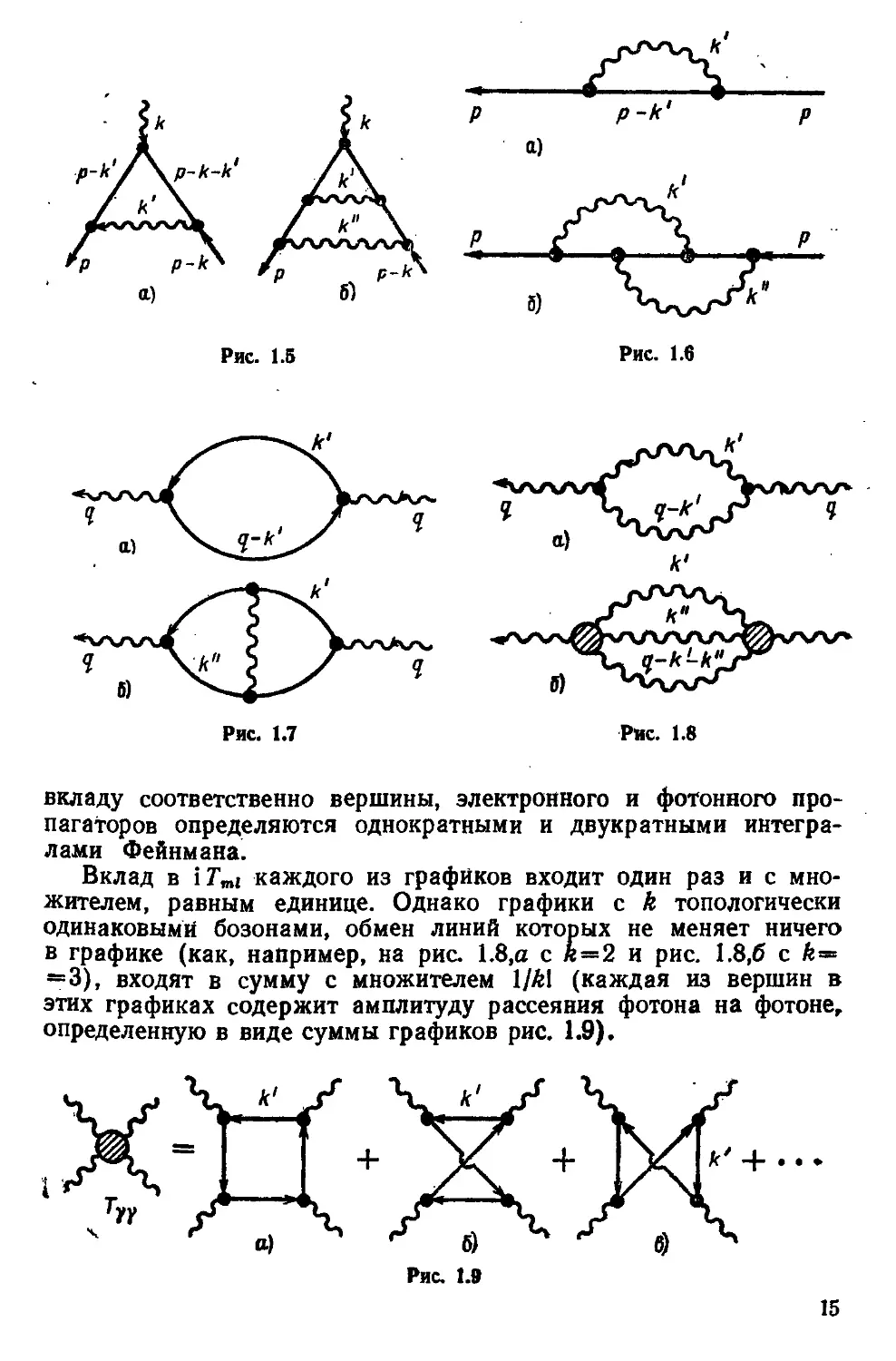
Вклад в \Тт1 каждого из графиков входит один раз и с мно-
множителем, равным единице. Однако графики с k топологически
одинаковыми бозонами, обмен линий которых не меняет ничего
в графике (как, например, на рис. 1.8,а с «=2 и рис. 1.8,6 с ?=
—3), входят в сумму с множителем IJkl (каждая из вершин в
этих графиках содержит амплитуду рассеяния фотона на фотоне,
определенную в виде суммы графиков рис. 1.9).
Рис 1.9
15
Отметим, что пропагаторы электрона A.26) и фотона A.30)
жожно представить в виде среднего по состоянию факуума Фо
(вакуумного среднего) от Г-произведений операторов полей
A.33)
В этом виде они удовлетворяют уравнениям A.27) и A.3);
это — следствие уравнений свободного движения (см. § 1.2) со-
ютветствующих полей и определения понятия Г-произведения
операторов. .
1.5. Фотонный пропагатор в различных калибровках.
Продольные фотоны
Пропагаторы Б°ю(х) и б°(л:) [см. A.26), A.31)] являются функ"
алиями Грина классических уравнений движения A.9), A.11)
•т. е. они удовлетворяют этим же уравнениям, но с б-функциями
8 правых частях:
(Yi*tfй-«) 0°(х)-в* (jc); {g^dl -д»да)&„ (х) gw64 (х).
, В импульсном представлении (где 1дк~>к\, б4(л:)->-1) они дают
{p-mNo(p)=l, (Pgn-lbbdDliW-g,». ^ A.34)
Непосредственно видно, что электронный пропагатор С°(р) в
виде A.25) удовлетворяет этому уравнению, однако с фотонным
яропагатором дело обстоит сложнее: в виде A.28), A.29)
(в калибррвде Лоренад) он удовлетворяет не этому, а немного
¦отличному^,о/г него уравнению A.32). Попытаемся удовлетворить
уравнению (i.34), выбрав Do»0 в виде тензора следующего обще-
общего вида:
,()Е„ A.35)
где g^v—^единичный поперечный тензор A.30) (для него ggxext^
' —««• «OT—3i' Йх**^="°)' а А и 5—некоторые функции №.
•Это дает ЛМ*;,?^+М/*2
Как видно, член, пропорциональный В, вообще выпал, и при
любом А уравнение A.34) не удовлетворяется. Причина этого в
том, что Ц„°(&) должно быть матрицей (т. е. тензором), обрат-
обратной матрице k2g»v—kvk4, а она является вырожденной (ее детер-
детерминант равен нулю) и обратной не имеет. Чтобы обойти эту
трудность, добавим к лагранжиану A.4) калибровочно неинвари-
неинвариантный член :
2 A.36)
16
я параметр ? устремим к бесконечности. При наличии этого чле-
.«а вариация лагранжиана по полю А»(х) дает вместо A.9) урав-
уравнение
д„Рп+ A /С) ds (д„ Ар) = Л (х), A.37)
функция Грина которого удовлетворяет выписанному выше урав-
уравнению A.32). В импульсном представлении оно вместо условия
A.34) дает равенство
что при ?-м>° совпадает с A.34) (так как gv*r'+k»k4f№=gv,v).
В отличие от A.34) матрица в левой части этого уравнения не
вырождена и при подстановке Ц,»°(&) в виде A.35) дает A = l(k2;
?=>?,/№. Это решение точно совпадает с A.28), A.29), но теперь
видно, что формально все самосогласованно при 5-*"°°. когда
А3?-*Ъ. Ясно, что к этому пределу можно перейти и на конечном
этапе вычислений, устремив ?-»-оо в их физическом результате.
Однако эти результаты калибровочно инвариантны и от ? вообще
не зависят, так как ? входит лишь в продольную часть пропага-
торов A.28), A.29). Поэтому переход к пределу ?-»-оо можно и
не делать, оставив ? произвольным.
Применение к обеим частям уравнения A.37) оператора ду дает
O/C)^Tj(jc)=d»yv(jc)=O, где 1\(х)=*дцАц(х)—продольная часть
поля Ац(х). Как видно, в силу сохранения 4-вектора тока
<V/v(jc)=O «продольные» фотоны ц(х) удовлетворяют уравнению
свободного движения д^г]=О, т. е. не взаимодействуют с полем
электронов. Поэтому, если в начальный момент величина i\(x)—
=др.Ац{х) была постоянной г\(х)=С0, то это значение сохранится
во времени, а добавок к действию Af = §&2?d*x от члена A.36)
есть эффективно несущественная постоянная. Таким обра-
образом, член Д57 A.36) (его называют членом, фиксирующим ка-
калибровку) всегда может быть добавлен к лагранжиану без каких-
либо физических следствий, так как поле ц(х) продольных фо-
фотонов полностью свободно и не оказывает никакого воздействия
на физические процессы.
Кроме лоренцевой калибровки (или ^-калибровки) можно
ввиду свободы выбора фазы в A.1) пользоваться большим чис-
числом калибровок других типов. Из них следует упомянуть часто
используемый (особенно в квантовой хромодинамнке, о которой
речь пойдет в следующих главах) класс аксиальных калибровок.
Они определяются заданием в некоторой лоренцевой системе от-
отсчета 4-вектора &„. Для фиксации этих калибровок к лагранжиа-
лагранжиану следует добавить вместо A.36) член вида
^(^' О-38)'
где величину d нужно устремить к бесконечности. Его изменение
при вариации Ац-*А» + 8Аи. поля А» есть
2—679 17
Поэтому вариация всего лагранжиана SB -\-tsS' дает вместе
A.9) уравнение <V>»—(l/Ct&j[)M|(VAn) =/»(•*). для ФУНКВД;
Грина которого ?>Jv(ife) (в импульсном представлении) тепер!
получим:
Wg^~KK~{k4Ub\) M«l ?>J?(*)«ft«. A.39)
Общий вид решения этого уравнения, _зависящего от k» и fr,
(и линейного по компонентам орта йц/к b\), есть
Подстановка показывает, что уравнение A.39) тождественно^
удовлетворяется при A — —B=\/k2, C=(\ — ?i)/k2, что опреде-
определяет D°v(k) в виде A.28) с
Параметр ?t входит лишь в продольную часть пропагатора и по-
поэтому может быть выбран произвольно. Как показано ниже, и
здесь продольная часть фотонного поля r\(x)=bv.A)h(x) удовлетво-
удовлетворяет уравнению для свободного движения dlr\(x)—0. Поэтому до-
добавок к действию от члена Д5", т. е. величина Д/' = \ bSB'tfx,
является несущественной постоянной и его всегда можно ввести
в лагранжиан без изменения физических следствий при любом.
•¦" Последний член в A.40) отсутствует при выборе Ci = l; эта
так называемая планарная калибровка. Так как Ь„с1сч =
= (— bc/b\k),)^ikv, то при выборе ?х=0 имеем bcdCv=daVby=0^
Из A.33) видно, что при этом Ь»Ац{х)=0; именно эту калибровку
и называют собственно аксиальной. При ?t=0 еще остаются
разные варианты аксиальной калибровки, различающиеся выбором
4-вектора Ь».
Выбору,: 6ц=A,0) в данной лоренцевой системе координат
отвечает радиационная калибровка, в которой Л0(л:)=0. Если
же выбрать &^ = @, к) или в Jc-пространстве йц = (О, — iy), то по-
получим широко известную кулоновскую калибровку, в которой.
<**/=¦-(б*/-^*//k2), i, 7 = 1,2,3. A.41) ¦
В этой калибровке фотон имеет только поперечные типы колеба-
колебаний и выполняется условие divA(*)=0.
Все виды аксиальных калибровок иногда используют в кван-
квантовой хромодинамике, где они удобны тем, что не приводят к
появлению духовых состояний (см. гл. $). Однако они одновре-
одновременно и неудобны из-за сложного вида пропагатора A.40) и тем,
18
что формально лоренц-неинвариантны, так как связаны с той
системой отсчета, в которой определен 4-вектор &*.
Покажем, что при добавлении к лагранжиану члена Д2" вида
A.38) продольная часть г\=Ь^Ац(х) фотонного поля действительно
удовлетворяет уравнению d\i\(x)=O свободного движения. Для
этого рассмотрим вариацию суммарного лагранжиана 5?-|-А2"при
вариации поля 6Av = A'y — Ау=дч(а(х)/е вида калибровочного
преобразования A.1). При этом основной лагранжиан SB не изме-
изменяется, а условие б(Д2")=0дает согласно (\.38)(8АчЬ<,)д1ц(х)=О,
т. е. dJrj(jc)=O. Поэтому поле ц(х) аналогично случаю лоренце-
вой калибровки является свободным, и если оно постоянно в на-
начальный момент t)(jc)=C0, то останется постоянным и позже.
В этом случае, добавок вида A.38) можно без всяких физических
последствий ввести в лагранжиан при любом выборе постоянной ?,.
1.6. Амплитуды и сечения
Приведем для справок и уточнения обозначений вклады неко-
некоторых из графиков рис. 1.4—1.9.
Амплитуды уе- и ее-рассеяния определяются (в калибровке
Фейнмана) в низшем порядке по е2 графиками рис. 1.4 в виде
Tf <V ТЯ где
rA) _ f
причем а — е2/4я; "ек=У^ек11; А=1,2; и,=«(р,Д,); Я,, —проекция
спина i-ro электрона.
Сечения процессов уе- и ее-рассеяния определяются квадрата-
квадратами этих амплитуд, просуммированных по направлению Я< спинов
электронов в конечных состояниях и усредненных по спинам %{°
начальных состояний:
= { | T
ml I
) VI,
A.43)
Для числа частиц # в конечном состоянии, равного двум. Здесь
dxit — фазовый объем частиц в конечном состоянии, который в
общем случае имеет вид
¦*—W»(>.-i») А, (^„ ...^. 0-44)
а р ®—5V=^ >^IS - (mi+^zJ] [« - (Щ - w2J] - импульс |р| двух
Z у S
сталкивающихся частиц в системе их центра инерции; s=*W2=m
""(PfJ—квадрат общей энергии в этой лоренцевой системе.
2* 19
Подробности вычисления сечений ув- и ее-рассеяния на основе
этих формул даны в ряде монографий [1.1, 1.2]. Мы их н.е при-
приводим, а отметим лишь, что суммирование по проекциям спинов
электронов проводится с помощью, соотношений
? Д) Ир (р Д) == (р -f /ге)вр;
i-±m...
к . ¦ .
и сводится,к вычислению шпуров от некоторого числа матриц у„.
Графики рис. 1.4 называют беспетлевыми, древесными или
полюсными. Вклад одно- и двухпетлевых графиков рис. 1.5—1.9
рассмотрен в следующих главах.
Глава 2
ПРИВОДИМЫЕ И СКЕЛЕТНЫЕ ГРАФИКИ. ПРОПАГАТОРЫ
И ВЕРШИНЫ. МНИМЫЕ ЧАСТИ ВКЛАДА ГРАФИКОВ
2.1. Приводимые и скелетные графики
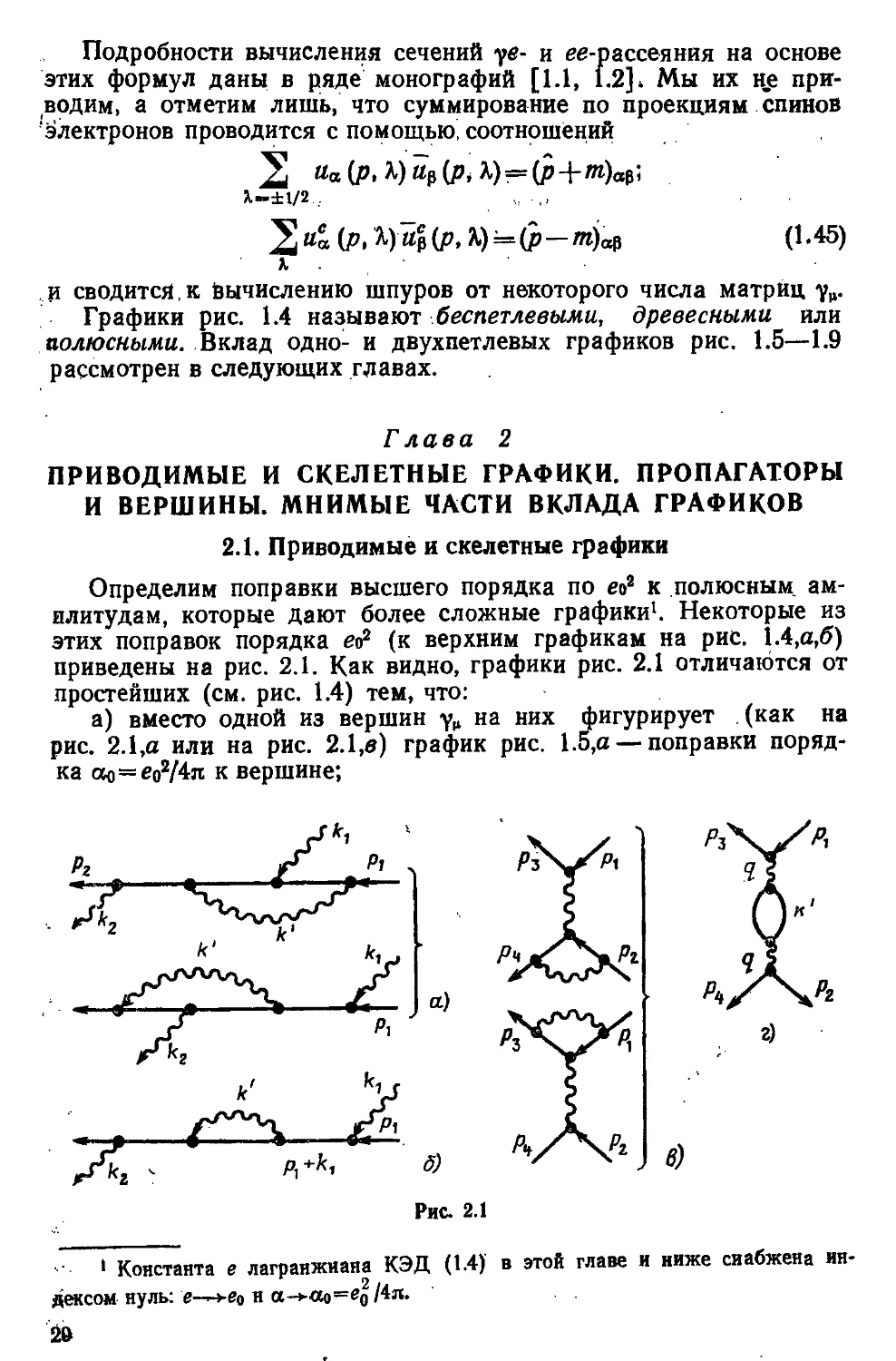
Определим поправки высшего порядка по ео2 к полюсным ам-
илитудам, которые дают более сложные графики1. Некоторые из
этих поправок порядка ео2 (к верхним графикам на рис. 1.4,а,б)
приведены на рис. 2.1. Как видно, графики рис. 2.1 отличаются от
простейших (см. рис. 1.4) тем, что:
а) вместо одной из вершин уц на них фигурирует (как на
рис. 2.1,а или на рис. 2.1,в) график рис. 1.5,а — поправки поряд-
порядка оо=ео2/4я к вершине;
в)
1 Константа е лагранжиана КЭД A.4) в этой главе и ниже снабжена ин-
индексом нуль: е-**-е0 н а-*-ао=е0 /4я.
б) электронная линия.заменена (см. рис. 2.1,6) поправкой
рис. 1.6,а порядка cto к этой линии;
/ в), фотонная' линия заменена (как на рис. 2.1,г) поправкой
рис. 1.7,а порядка ао к этой линии.
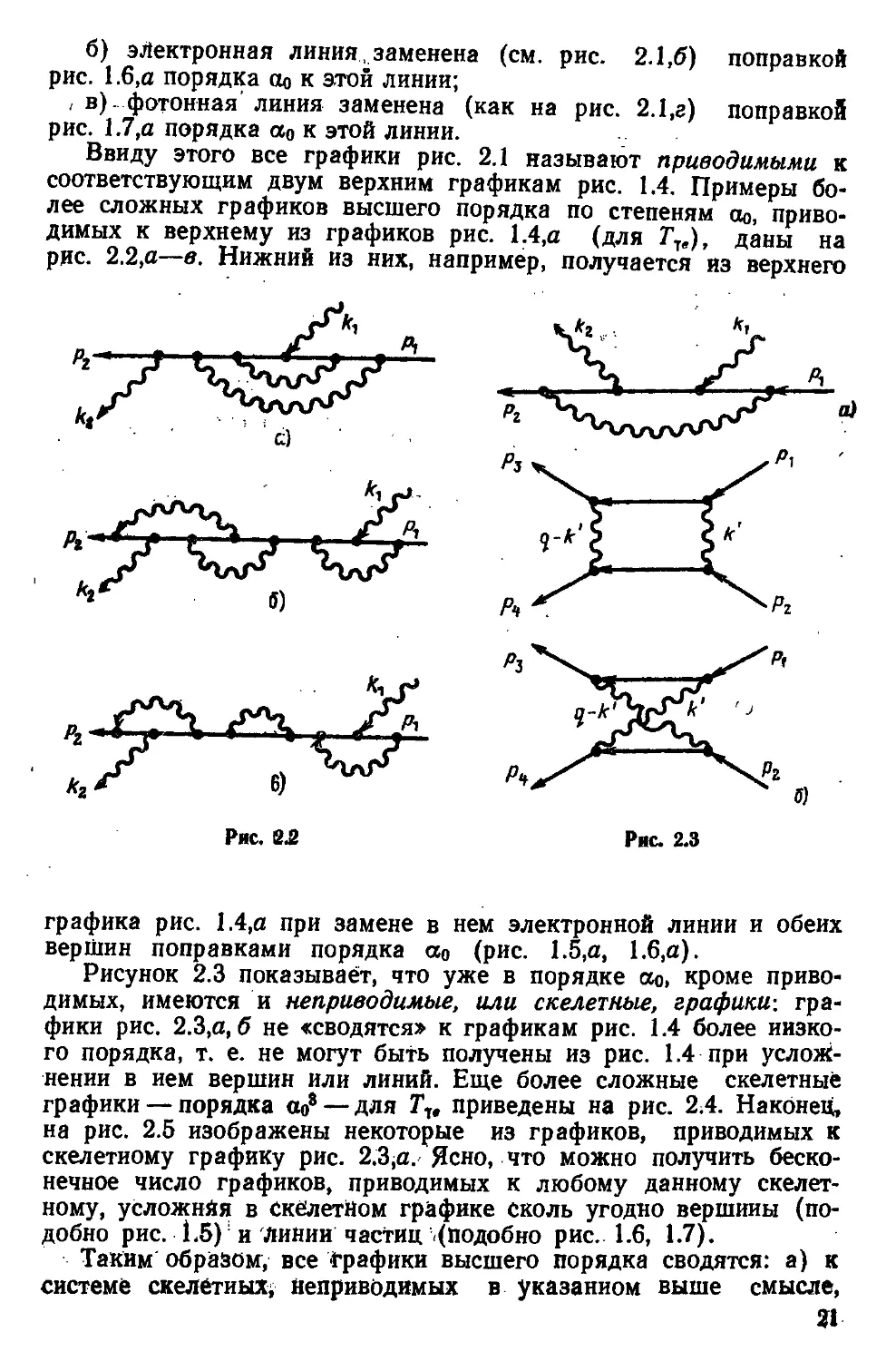
Ввиду этого все графики рис. 2.1 называют приводимыми к
соответствующим двум верхним графикам рис. 1.4. Примеры бо-
более сложных графиков высшего порядка по степеням ао, приво-
приводимых к верхнему из графиков рис. 1.4,а (для Т1в), даны на
рис. 2.2,а—в. Нижний из них, например, получается из верхнего
6)
Ряс. asi
X
Ряс 2.3
графика рис. 1.4,а при замене в нем электронной линии и обеих
вершин поправками порядка ао (рис. 1.5,а, 1.6,а).
Рисунок 2.3 показывает, что уже в порядке сю, кроме приво-
приводимых, имеются и неприводимые, или скелетные, графики: гра-
графики рис. 2.3,а, б не «сводятся» к графикам рис. 1.4 более низко-
низкого порядка, т. е. не могут быть получены из рис. 1.4 при услож-
усложнении в нем вершин или линий. Еще более сложные скелетные
графики — порядка ао8 — для Ти приведены на рис. 2;4. Наконец,
на рис. 2.5 изображены некоторые из графиков, приводимых к
скелетному графику рис. 2.3,а. Ясно, что можно получить беско-
бесконечное число графиков, приводимых к любому данному скелет-
скелетному, усложняя в скелетном графике сколь угодно вершины (по-
(подобно рис. 1.5) и Линии частиц (подобно рис. 1.6, 1.7).
Таким образом, все Графики высшего порядка сводятся: а) к
системе скелетных; неприводимых в указанном выше смысле,
Я
ч /
Ряс 2.4
Ряс 2.5
графиков; б) к бесконечно большому числу графиков, приводи-
приводимых к каждому скелетному усложнением в нем вершин и линий.
Поэтому, как было замечено Дайсоном [2.1], сразу же после
выявления описанной выше техники графиков Фейнмана [1.6],
задача о суммировании вклада графиков в любой амплитуде есте-
естественно решается в два этапа:
1) суммируются все поправки высшего порядка ко вкладу
A.24), A.25), A.28) вершин и линий и представляются в виде:
(р, p-
B.1)
где Лр, Gll)(p), D$l (ft)—поправки порядка а^\
2) рассматриваются и суммируются лишь вклады скелетных
графиков, в которых вместо Yt». G@)(p) и D$(k) подставлены
соответственно Г„(р, р—п), G(p) и A»v(?)- Величину Г„(р, р — k)
называют точной вершинной частью, a G(p) и D^ (k)—точны-
(k)—точными пропагаторалш, или функциями Грина электрона и фотона.
Точным значениям Гй, О(р) и D^ik) ставят в соответствие на
графиках жирные точки и жирные линии.
Так, для получения точной амплитуды 7\, достаточно просум-
просуммировать вклады лишь скелетных графиков рис. \А,а, 2.3,а и 2.4
(и всех таких более сложных «скелетов»), построенных на жир-
жирных точках и линиях. Все приводимые к ним графики рис. 2.1 и
2.2 можно при этом вообще не рассматривать.
2.2. Уравнение Дайсона—Швингера
Суммирование поправок всех порядков к вершинной части и
к пропагаторам проводится следующим образом [2.1!].
1. Суммируются вклады графиков всех поправок к вершинной
части рис. 2.6,а; они могут быть приводимыми (см. рис. 1.5,6,
22
который отличается от рис. 1.5,а усложненными вершинами) и
.неприводимыми. Последние указаны справа на рис. 2.6
(рис. 2.6,5—г и др.). Достаточно рассматривать лишь эти непри-
неприводимые или скелетные графики, построенные на жирных линиях
Ряс 2.6
и вершинах. Учет их дает уравнения с бесконечным числом сла-
слагаемых:
?»{Р. р — к) = Ч»+А»{р, р — Щ\ A,i{p,p—k) =
=-л?1А(р, р - ft)+ ЛГ(Р,/>-*)+..., B.2)
тде в низшем порядке по el (т. е. при тонких линиях и вершинах
на рис. 1.5, а)
Л?4' (р, р- *)=? \ ук -з-г; VI» - г \, X
p—k—k'—m*
B.3)
м, если линии и вершины на рис. 1.5, а жирные,
Л?1} (р, р-А)=(«о/4я) j Гх(р, p-k')
XT»(p-k', Pi-kJCfiPt-k^TaiPi-k
где px—p—k. Обход полюсов пропагаторов при взятии интеграла
по k' должен всегда отвечать правилу, указанному в A.25),
A.28): т0 и Я,о=О должны быть заменены величинами щ—Ю,
-Х2- Ю.
Аналогично, для вклада следующего члена Лд2), отвечающего
рис. 2.6, в, правила Фейнмана (сформулированные выше) дают:
#t-*9) (*""-*3)
B.5)
23
Для сокращения этот вклад записан для тонких линий и вер-
вершин; переход к точным вершинам и пропагаторам ^тривиален,,
такой же, как переход от А$у к Л^'. Складывая все^величинь»
А$\ ползаем вершину Лц.
2. Суммируются все графики для функции Грина электрона
0{р), приведенные на рис. 2.7; они являются цепочками петель,,
связанными линией одного электрона. Вклад свободной линии,
к1
о) в) в)
Рис 2,7
(рис. 1.2 или 2.7, а) есть 1C@)(р)=1(р — тоуг, а первая поправка
к нему определяется графиком рис. 1.6, а в виде I(/°(pJA)(р)Х
Хб°{р), где
—вклад петли в средней части графика рис. 1.6, а [более точно:
этот вклад есть —12A) (р)]. Обозначим Юа(рJ,(рH°(р) суммар-
суммарный вклад всех графиков вида рис. 1.6; они характеризуются тем,
что кроме двух тонких электронных линий по краям содержат в
центре «компактные» графики, не состоящие (как рис. 2.7, в) из
двух или более частей, связанных только электронной линией..
Единственным скелетным графиком среди них является простей-
простейшая петля в центре рис. 1.6, а; все остальные можно получить и*
нее, усложняя на рис. 1.6, а одну из двух вершин или внутренние
линии частиц. Так, график рис. 1.6,6 получается усложнением
(вида рис. 1.5,а) одной из вершин на рис. 1.6 а. Поэтому 2(/>)
получим, заменив в интеграле для 2ш(/>) оба пропагатора
G°(p—k'), D#v°(k') и одну из вершин у# или yv их точными значе-
значениями:
Замена обеих вершин точными привела бы к переучету числа-
графиков: так, вклад графика рис. 1.6,6, как легко заметить,
появился бы дважды. Величина B.7) отвечает вкладу петли »
центре на рис. 2.7,6, в которой лишь одна из двух вершин жир--
ная. Ее называют собственной энергетической электронной
частью (или кратко — собственной энергией электрона); это ре-
релятивистски инвариантная матрица Дирака вида
(p) (f)+pf) р B.8>
где А и В — скалярные функции р2, зависящие от вида калибров-
24
ки. Несмотря на простоту записи, уравнение B.7) неудобно для*
практических вычислений, так как оно несимметрично по отно-.
шению к вершинам Vh и Гт; это приводит к появлению дополни-,
тельных расходимостей—.так называемых перекрьшающихся.
Чтобы избежать их анализа, будем для вычислений использовать-
другую форму 2(р), в которой обе вершины фигурируют равно-
равноправно.
Кроме вклада iG°(pJ(p)G°(p) графика рис. 2.7,6 вклад в
Ш (р) дают также и некомпактные графики вида рис. 2.7, в и дру-
другие, в. которых петля Б(р) повторяется много раз. Так, график,
рис. 2.7,в с двумя петлями дает вклад iG°(p)[S(p)G°(p)]2. Про-
Просуммировав все эти вклады, получим:
ft-0
где учтено, что [G^^^p—Щ [см. A.25)]. Вместе с B.7) эта
выражение определяет G(p) через [функции Гц, G(p) и ?>^(?).
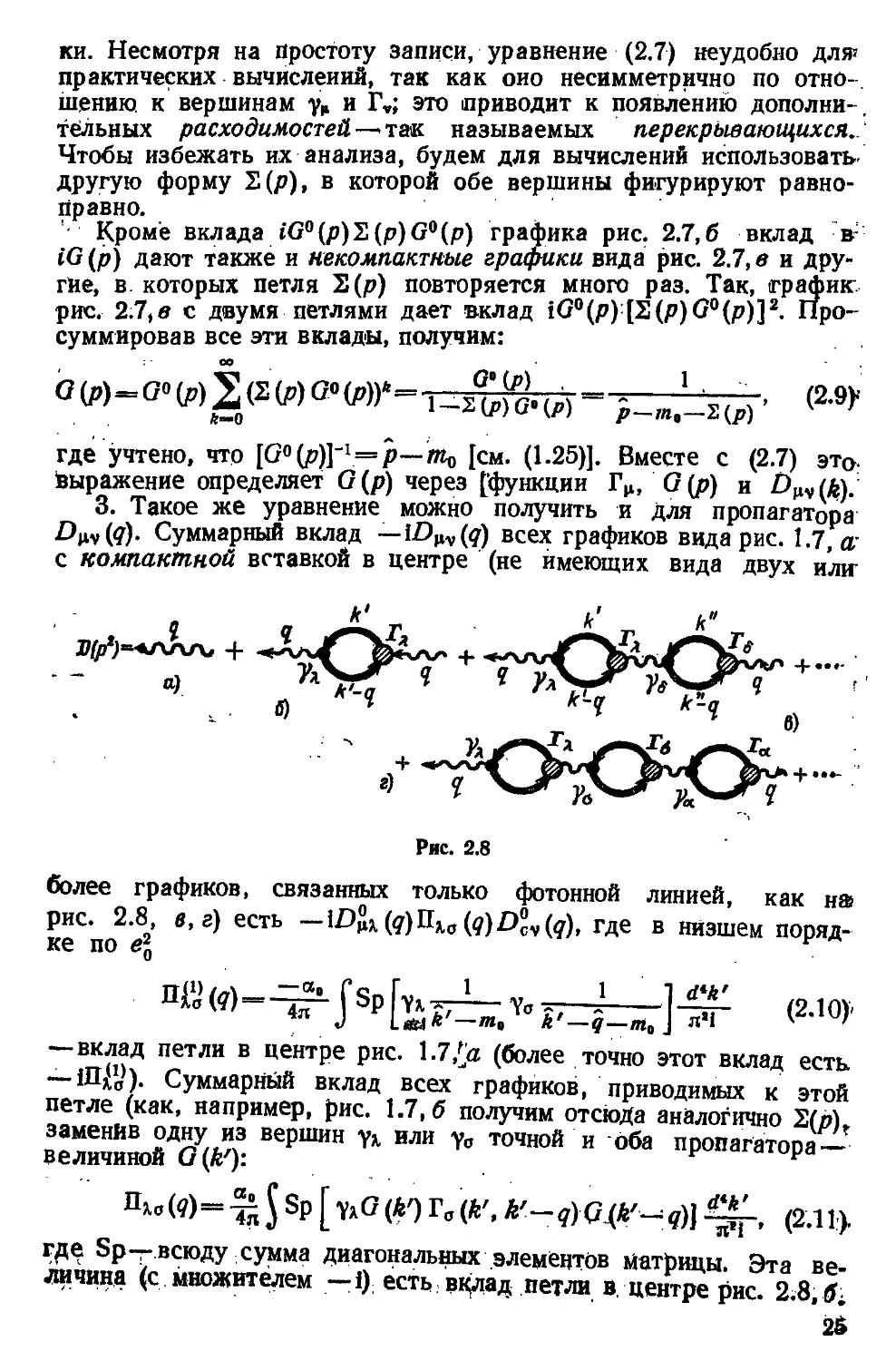
3. Такое же уравнение можно получить и для пропагатора
Dw(q). Суммарный вклад —\D^{q) всех графиков вида рис. 1.7, а
с компактной вставкой в центре (не имеющих вида двух илнг
в)
Рис. 2.8
более графиков, связанных только фотонной линией, как на
рис. 2.8, в, г) есть — lDpx(q)nKo(q)D°cv(q), где в низшем поряд-
порядке по eg
ке по
—вклад петли в центре рис. 1.7//I (более точно этот вклад есть
— Ш/У). Суммарный вклад всех графиков, приводимых к этой
петле (как, например, рис. 1.7,5 получим отсюда аналогично 2(/>)t
заменив одну из вершин у*, или у0 точной и оба пропагатора —
величиной G{kr):
l[X'^q)]^-, B.11 >
где Sp-r-всюду сумма диагональных элементов матрицы. Эта ве-
величина (с множителем —1) есть вЦлад петли в центре рис. 2.8,^
Чтобы построить точный пропагатор — lDm(q), нужно к вкладу
— lD%(q) свободной линии фотона рис. 2.8, а добавить вклад
графика рис. 2.8, tf — lDpb(q)Uxo(q)D0ov(q), в котором последний
множитель Dlv(q) заменен точным пропагатор ом Dov(q):
Dm(q)=D% (?)+D0^ (q) Щ„(?) Д,у(?), B.12)
*де последний член дает сумму вклада цепочек всех петель иа
рис. 2.8: она генерируется при последовательных итерациях,
т.е. при подстановке справа вместо D^(q) сначала D%,{q), a
потом всей правой части равенства. Полученное уравнение ана-
аналогично уравнению B.9) для (?(/?), его усложняют лишь векторные
индексы, от которых можно легко избавиться. Действительно,
тензор собственной энергии фотона Щ,с(?) поперечен
Пяо(?)=1%2)#и, B.13)
[П(q2)—скалярная функция q2, a q'ttO=g\o—qi.qoiqi—поперечный
единичный тензор A.30)], так как он определяет амплитуду Ап
превращения виртуального фотона с 4-импульсом q и поляризацией
ео(\) в фотон с поляризацией е\B) в виде
Ап=е1B)ПКо(д)ее(\).
Как и все остальные амплитуды Атп превращения я фотонов в т.'
эта амплитуда не изменяется при калибровочных преобразованиях»
яри которых еоA) заменяется e0{\)-\-cq0, где с—произвольный
коэффициент [и аналогично меняется е*,B)]. Ясно, что только
условие попеоечности Щ0(я) в виде ^„=^^„=0, т. е. в виде
B.13), обеспечивает калибровочную инвариантность амплитуды Ап.
Так как gu=3, то из B.13) следует
B.14)
лоэтому B.10) при о=Л определяет эту величину (которую часто
называют поляризационным оператором) в порядке е02, а B.11)
дает ее точное значение.
Отделяя в DnV(q) подобно A.35) поперечную часть от продоль -
ной
получаем, подставляя в B.12) D^K(q) в виде A.35) [в ?-калибров-
же, в которой Л = 1/(?2—Я,2), B=ll{q2—A$] и учитывая, что
B.15)
и D/(^2)=5=g/(^2—Ц), где Ц=0 есть масса фотона.
Равенства B.2), B.6), B.9) и B.11), B.14), B.15) являются
замкнутой системой уравнений, позволяющих, в принципе, вычис-
26
лить точные функции Тт G(p) и D{q2). Их называют уравнения-
уравнениями Дайсона—Швингера [2.1, 2.2].
В заключение отметим, что в x-представлении точные функции
Грина
?>nv (л:, — х2) = J ехр [ — lq (хх—х2)] A,v (q) d*q/ Bя)
определяются такими же средними по вакууму, как и свободные
A.33), но Г-произведение в них включает дополнительным сомно-
сомножителем S-матрицу A.20), т. е.
i-Ъ) =1 (ФЗГ(Л^ (хх) Av(х2M)Фо), J
причем 5-матрица A.20) должна быть «расщеплена» под знаком
Г-произведения следующим образом:
при tx>t2, где
S(*2, i^T ехр I- \е01 гёИ Y.»*(л:)) А»(х)d*x
есть «неполная» 5-матрица: S"=5(oo, ti)S(tu t2)S(t2, — оо).
В справедливости формул B.17) проще всего убедиться, раз-
разлагая S-матрицу в ряд A.22) по степеням во2 и убеждаясь в том,
что при этом B.17) точно воспроизводит вклады всех графиков.
2.3. Тождество Уорда и теорема Фарри
Дифференцирование по р^ свободной функции Грииа О" (/>)=¦ 1/(р—л»р)
дает (—d/дрц) О» (р) = 6* (р) у^Ф (р). Представим 2(/>) в виде суммы вклада
всех графиков рис. 2.9, а, приводимых к петле, и возьмем от них почленно
производную д/дрц. Учитывая последнее равенство, получаем при этом
Ряс 2.9
27
в точности вклад всех графиков рис. 2.9' для Л^ {р, р), т. е.
pA^p.p). . B.1.8)
или согласно B.9) '
(д/дрр) G-' (/>)•= т„ + А„ (р, р) - Гй (р, р). B.19>
Это соотношение называют теоремой У орда [2.3]; оио является следствием ка-
калибровочной инвариантности теории (из-за которой, лагранжиан КЭД A.4) со-
содержит 4-потенцнал лишь в простой комбинации id^—eA^; последнее и есть
внутренняя причина появлении равенства B.19) в графиках Фейнмаиа). В от-?
личие от B.6) левая часть этого (или предыдущего) равенства содержит все
вершины 1\ симметрично, поэтому им удобно пользоваться для вычисления
функции 2(р).
Следующее замечание относится к графикам, содержащим замкнутые элек-
электронные петли (см., например, рис. 1.7). Вклад каждого из таких графиков
возникает в теории как полусумма вклада двух таких графиков, различающих-
различающихся направлением электронных линий. Замена направления электронной линии'
отвечает в КЭД замене электронов позитронами, т. е. так называемому преоб-
преобразованию зарядового сопряжения. При этом изменяется знак каждой вершины,
лежащей на линии, т. е. заряд электрона е в вершине заменяется зарядом —е.
Поэтому если число вершин в электронной петле четное, как иа рис. 2,10,аг
то вклад графика не меняется при изменении на обратное направления элект-
электронной линии, и полусумма вкладов двух графиков с разными направлениями
линий совпадает с вкладом одного из графиков. Если же число вершии нечетное,
то суммарный вклад двух таких графиков (как иа рис 2.10,6) равен нулю. Это
утверждение называют [2.4] теоремой Фарри: графики с замкнутыми электрон-
электронными петлими дают нулевой вклад, если нечетно общее число подходящих к
петлям фотонных линий. Иными словами, четность чисел фотонов в начальном
и конечном состояниях должна быть одинакова. Это свойство—следствие ин-
инвариантности КЭД по отношению к преобразованию зарядового сопряжения
(или С-преобразоваиию), из-за чего сохраняется полная С-четиость системы
п фотонов, равная (—1)"*.
2.4. Мнимые части вклада графиков1
н величин П(<72)>
Вычислим мнимые части величии 2(р) и H{q*). Это даст для них уравне-
уравнения, содержащие, в отличие от B.6), B.11), только точные вершины, весь-
весьма удобные для практического вычислении этих функций.
Напомним, как вычисляется мнимая часть вклада любого графика на при*
мере величины 1гаП(у'). Для этого график делят пунктирной линией так,
чтобы отделить всеми возможными способами линии входящих частиц от линий
выходящих (как на рис. 2.11, а, б). При этом яз одного графика для \
г)
Рис 2.11
получается, вообще говоря, несколько для 1тП(?:)(см. рис. 2.11, б). Линии,
которые пересекают пунктир, будем называть линиями частиц на массовой
поверхности. На них поставлены крестики и им нужно поставить иа графике
в соответствие вместо б'(р) или D*V(A) величину—2 Im Ф (р) —
— 2я6(/>'—т*) (/Н- т) дли электронной линии илн —2ImZ)Jv(ft) —
=-2яб(А*—Хр*)^ для фотонной, где йцу зависит от выбора калибровки
{см. A.40), A.29)], причем так как на массовой поверхности **=0, то в
^-калибровке имеет смысл лишь выбор ?=1 (когда «*|»v ¦»?,»„)». т. е. калиб-
калибровка Фейнмана. В правые части этих формул нужно еще включить множи-
множители 8(/>р) или 8 (Ар), отбирающие лищь положительные р, и ft,:
мы их не выписываем для сокращения записи, но при вычислениях о них
не следует забывать.
1 Материал этого раздела нужен в основном для строгого доказательства
переиормируемости КЭД, данного ниже. Он несколько сложен по форме (хотя
крайне прост по существу)' и может быть опущен при первом чтении книги.
29
Позитронные линии с крестиками имеют на графиках направление, проти-
противоположное электронным, справа налево, импульсом позитрона является
минус 4-импульс р такой линии />— — р\ им нужно ставить в соответствие1
2я6(/>"— и») в (>.)(>—да) =2im 5» (р), где 9 (р.) = в (—/>,).
Имей дело с мнимыми частями вклада графиков, удобно с самого начала
рассматривать физические массы частиц да и & вместо «затравочных» т»
и Х„ т.е. полагать, что G"(/>) = l/(j»—т + Ю), ?>• (д2) = ll(q*—Xs+ 10),
где р = т и ys=Xs—0—полюсы точных функций Грина B.9) и B.15).
При этом G°(p) получается из точной функции Q(j>), если в ее знаменателе
пренебречь величиной 2(р)—2(/я), пропорциональной е<?. Не меняя ничего по
существу, это значительно упрощает анализ. В остальном вклад графиков, пе-
пересеченных пунктиром (графиков с частицами иа массовой поверхности), полу-
получается иа основе обычных правил Фейимаиа, только всем элементам графика
по одну из сторон пунктира, например справа от него, нужно сопоставить ве-
величины, комплексио-сопряжеикые по вкладу вершин и линий. Суммарный вклад
таких графиков дает значение 2 lmH(qs) (или, вообще, значение удвоенной
мнимой части вклада любой другой рассматриваемой величины). Учитывая это*
получаем в низшем порядке по е0* из рис. 2.11, а:
—е2
B-20)
= ТГ ^—J J
Ai,X3
где и, = и(р„ К); и%-ие{pt, А,,); Л« —А-—(/>! + Я)—4-импульс пози-
позитрона, a dT,-Bя)(/>j—т*)Ь{р\—mi)d*pllBn)*--фазовый объем A.44) при
п = 2 [так как Ь(р\—mi)dlp1lBny = dtp1/Bn)>2e1, в, = Vv\ + «']• Права»
часть равенства B.20) равна средней1 в силу соотношений A.45). Вычислив-
dx* = (P?<* I Pi I dai)/BnLSiSidW в системе центра ииерцни, где Pj=—Pi,
a q* = s = l^s—квадрат полной энергии lF-e,+es, dW/d|p, |-|pi 1
получим
причем в нашем случае Wi = jns —«, т. е. ^, = A/2) У^^'—4вд! н drs отлично-
от нули лишь при 0s>4ms. Интеграл для 21тПA)(у») берется лишь по на-
направлениям вектора pi = (/>i, ©i, q>i), dQi= sin ©id^^qi,, легко вычисляется m
дает
^ B.21).
1 Так как для позитронов jriuco,(p,'b)uL(p,'k) = (p—»0ag, a для элек-
_ \
тронов 2 иа(Р> а>
30
причем Imllf1) (^s) = 0 при g'<4m2. Это означает, что q* = 4m* есть корневая
точка ветвления функции П'1' (q*): для ее однозначного определения в пло-
плоскости рис. 2.12, а комплексной переменной s = q* следует сделать разрез ог
s = 4/я* до бесконечности, например,
направо до s-»- + oo. Левее этой
точки s = 4ms ПС) вещественно, а
правее, над и под разрезом (в точ-
точках s = gs+ 10, ql>4m?) принимает
комплексно-сопряженные значения.
Поэтому скачок функции ПA) (q3)
через разрез, т. е. величина
г, Л-0
б)
Рис 2.12
B.22У
совпадает с ее мнимой частью над разрезом (с Im '*' (^s + i0)). Ввиду этого,
всюду ниже будем рассматривать именно эти скачки через правые разрезы
вместо мнимых частей вклада графиков и функций П(<72) и 2(р). При этом не-
непутаются мнимости, не связанные с точками ветвления рассматриваемых функций
переменной q2 или s=p* (возникающие, например, от матриц ¦ух или из-за точек,
ветвлення по другим переменным тогда, когда они есть).
Построим скачок 6П(<72) точной функции П(<72) на правом разрезе. Для
этого рассмотрим все графики, определенные выше, для 2бП(<72)=2 ImII(g2) и.
мысленно наложим их друг на друга так, чтобы совпали пунктирные линии на
них. Выделяя диаграммы вида рис. 2.11 с определенным числом электронов и
фотонов на массовой поверхности и складывая по обе стороны пунктира вкла-
вклады всех графиков, получаем справа и слева точные амплитуды Тц = (Тцг-е%У
рождения одного фотона с импульсом q и с поляризацией е% из любого физи-
физического состояния / (в котором Af« = 2v, электронов-позитронов и AfT—1 фото-
фотонов). Суммируя по всем этим состояииям l=l(N,, N-,), получаем
Ne,
С,, V/
где dxn—фазовый объем A-44); n=Ne+Ny— I — число частиц на массовой-
поверхности; q
ft/+
(Pi+Pi)—сумма их импульсов; 20
сумма по проекциям спинов электронов, позитронов и по поляризациям фото-
иов-. Каждый член BбП)^ N в сумме по Ne и Ny в B.23) отвечает вкладу
графика рис. 2.13, а с Ny — 1 фотонами и Ne электронами-позитронами на мас-
массовой поверхности. Он отличен от нуля лишь при энергии \V=Yq* выше-
порога рождения этих частиц, т. е. при 0s>(/n//e + A,(//Y— l))s~mW^,
^я отвечает точке ветвления gs = (/nNe)s функции П(?').
ЗМ
a) 26
б) 28 ^
в) 2i,
Рис. 2.13
5Представвм точную амплитуду Г,/ в виде
B.24)
тде uCi = ue(pt); иь = и(рь)—дираковские амплитуды (pt—4-импульсы входя-
входящих позитронов, а рь—входящих в вершину электронов); e0(/)«=e0(v/)—
поляризации, а
— соответствующая вершина (матрица Дирака, действующая на щ) с ^-фо-
^-фотонными и А^о-электрониыми лннвямн; при N,—2 и JV-j|=l оиа превращается
в вершину e0Ti(pi,pi). Предполагаем, что по определению энергии е* (и~е<) у
всех электронов и позитронов положительны. Тогда замена pt величиной —р<«=
= (—8i, —pi) в B.24) отвечает переходу от входищего в вершину позитрона к
выходящему электрону (вс(—Pi)^u{pi))l а при замене ki на — kj=(—cdj, —kj)
вместо входищего фотона получим выходищий. Меняя знаки 4-импульсов р<, рь
и kj, можно из B.24) получить физические амплитуды Tm',i' переходов /'•^-m'
в любых каналах с участием всего N. электроиов-позитроиов и N% фотонов.
32
Член суммы B.23) с N,=Z, JV,»*O отвечает точке ветвления q*
26<2W)= D/3) 2 J ( «г** (Рг, />«)«,) CS|rx 1Л. Р.) «•)**, B.26)
At. *«
и отлячен от 26П(Т) (?*) лишь заменой ул точными вершинами Гл (ps, Pi) (где
Р* — — Рг)-
Заменим в B.24) pi величиной —р«=(—е, —р) (е>0), a q—величиной
kN и запишем полученную амплитуду Ту {, рождення"электрона с 4-импуль-
сом р из состояния /', содержащего Ne—I электронов-позитронов и Ny
фотонов в виде
Tv.i—{\lP)V?:r). B.27)
где V"i [>—произведение всех множителей в B.24) кроме (^*i)e""^*e(P);
при N,-2, //,= 1 имеемVf,f г-=(Гх(р, р,) щ)ае% (А,)-
После сделанных выше замечаний ясно, что скачок 62 = б-А(рг) + рбВ(рг)
на правом разрезе функции 2Q?) определяется вкладом графика рис. 2.13, в
в таком же виде, как B-23):
j ^Г „, B.28)
е 7
причем p~Pi+ 2 (?*+iP'+>) + 2*^' Член с ^«"=2, 7/v=l имеет вид
*2 ;i
,==р—ft,; rfT2•= г—/~~ g^"—фазовый объем системы электрон—фотои
(см. выше общую формулу для dx, при nti — m, /п» = Я, = О и Wi'=pt). В низ-
It»
3-679 33
шем порядке по вд имеем 6(tJ-62(t) (р), где 6S(t)—скачок (рис. 2.14, а)
вклада B.6) простейшей петли рис. 2.9, а на правом разрезе в плоскости
рис. 2.12, б\
262<'> {р) = -е\ lyx(p-k + m) т Ao*»r B.29)
Этот скачок отличен от нули лишь при рг> (т+Л,)г->тг и существенно за-
зависит от выбора калибровки. В простейшей фейнмановской калибровке1
tf получаем
причем а>1 = (р'—m*)l2Yp*—энергия фотона-в системе центра инерции, в
торой р = ytW, W">y~jp—полнаи энергия.
/J t _f Подставляя вершины
Jr J* JT (Pi, kj) в B.24) в виде вклада ripoc-
¦ i ¦ * м г . г тейших, т. е. полюсных, графиков
с с рис. 2.15, а (именно этот вклад про-
с с порционалеи степени заряда е оv • »
• ^i * i ' ц выделенной в B.25)), а затем—одио-
s 5 > петлевых рис.) 2.15, б) и т. д., мож-
S 5 5 но получить скачки 6u(qf) и 62 (р)
ш ? t > > на правых разрезах рис 2.12, а, б в
/J" виде рядов по степеням ej. Зная
а) ^* $) эти скачкн, можно построить и сами
функции П(?2), 2 (р) при помощи
формулы Коши:
Рве 2.15
J ? ) s-q*
4m» +Я)»
Последний формула фактически справедлива ве для 2(р), а для функций
и В(р*), определяющих ее в виде 2(p)=A{p*)+*pB{p*). Хорошо взвестно, чт»
если интегралы не сходится, то следует сделать нужное число вычнтаиий, опре-
определяй, например, вместо величины Щд1) разность П(^—ЩЯ,2)—[q*—Л.а)П'(й,*>
и т. д. так, чтобы получить сходящийси ответ.
2.5. Общее условие унитарности
В заключение рассмотрим произвольную амплитуду Тт1 рождении ЛГ° фо-
тоиов и Ng электронов или позитронов (это состоиние т) при столкновении
Ny—Ny фотонов н Ne—Ng электронов или позитронов (это начальное со-
1 В аксиальвых калибровках для 6SA>(p) получим более сложное выра-
выражение. Остальные g-калябровки с s#l использовать при ftj=0 нельзя. Поправ-
Поправки к B.29) порядка еь4 указаны на рис. 2.14, б.
34
«тоиние /). Ее можно получить, заменяй в B.24) N^—1 4-импульсов фото-
фотонов ki на —kt и N° импульсов pi электронов нли р/ позитронов на —pi и
—PI- Амплитуда Тт[ зависит от многих переменных, в частности от s = W' =
-Р,. где Pi—суммарный 4-импульс всех сталкивающихся (или рожденных)
частиц. В зависимости от числа электронов (и позитронов) в начальном и ко*
иечном состояниях она имеет точку ветвления при s«=/C*m2, где
JC*=min {W°, ме—№е). Проиедем от этой точки разрез направо (как на
рис. 2-12) и найдем ее скачок 6Тт1 по переменной s через этот разрез. Рас-
Рассматривая все графики дли ЬТШ, замечаем, что подобно 6П и б? скачок
определяется вкладом графика рис. 2.13, в в виде, аналогичном B.23), B.28):
2бГт/ = 2 2 lTmnT\ndxn. B.32)
Здесь N—NS+N/ — полное число частиц иа массовой поверхности иа
рис. 2,13, в; о/, v/—проекцви вх спииои в поляризации; Тпп и Тщ — амплиту-
амплитуды (такве же» как Tmi) перехода этих частиц из промежуточного состояния в
соответственно в конечное состояиве /пив начальное /. Это соотношение мож-
можно получить я как следствие условия унитарности SS^«= 1 S-матрицы A.20),
записывая S=l+f/ и учитывая, что i^mf'Smi вмеет вид A.23). Рассматри-
Рассматривая это же соотношение для амплитуды 7»(р'. р) упругого ряссеяння двух ча-
частиц (с заданными проекциями спвнов и поляризаций) на нулевой угол при
р/=р, получим, разделив обе части равенства на ip{s)T/s:
т 6Т" (Р' Р) " 2 1da" (S) = a'Ot (S)' B>33>
где atot = 2 адг (s)—полное сечение взаимодействия двух частиц; 0^E) —
полное сечение рождения N частиц (электронов, фотонов) при взаимодейст-
взаимодействии двух сталкивающихся, а йодг™ < I Тш |г > dxNHp (s) Y^—дифференци-
Y^—дифференциальное сеченве этого же процесса.
Это соотношение является хорошо известной оптической теоремой.
Задача 2.1. Выписать матричные элементы распада нейтральной векторной
частицы V-t-e+er и скалярной частицы S->-«+?- (с массами My и Me) и полу-
получить вероятности этих распадов W*=Tfh в первом порядке по го2=4яа<).
Ответ. График рис. 2.6, а вершинной части (или рис. 2.11, а, справа
°т пунктира) дает в случае вектораой частицы—тижелого фотона 7"^«=
" ~е*еа 0*iYaa2)' «i-b(jPi). «4-««(?,), Pi+p~i°*q, Ч* = М\., откуда (при
^¦= I Pi I = I P. I
35
В случае скалярной частицы Г|,«. — /, (и,^), откуда
Задача 2.2. Указать, как связана полная ширина Г^' распада векторной
нейтральной частицы V-*e+e-AT, где X—любая система частиц (во всех по-
ридках по ejj) с величиной [6П (?*)] ,=Л?2 - 1ш П (М\) мнимой части B.23]
оператора П (q*).
Ответ. Так как
где 7?, —матричный элемент превращения векторной частицы (тяжелого
л
фотона) в систему л любых частиц, то согласно B.23)
Г4,°1=-A/Л!к)[еП(?г)] .. B.34)
" у
Глава 3
ПЕРЕНОРМИРОВКА ПРОПАГАТОРОВ И ВЕРШИН.
ОБЩАЯ СХЕМА ПЕРЕНОРМИРОВОК
3.1. Перенормировка пропагаторов и вершин
Физической массой электрона является то значение р=т, при
котором знаменатель функций G(p) B.9) обращается в нуль. Ана-
Аналогично масса ротона определяется нулем знаменателя D(k?)
B.15). Для положения этих нулей получаем уравнения /)=mo+i
+S(p), когда р=т, и ft2=V+II(ft2) при А2-=Я2, т. е. тп=
=»mo+S(m), Д/п-=2(/п)—добавка к массе электрона, возни-
возникающая от взаимодействия с электромагнитным полем. Появ-
Появление массы у фотона нарушит калибровочную инвариант-
инвариантность теории, поэтому в равенстве №=№+П(№) не только
Ло=О, но и %=0, т. е. должно быть П@) =0.
При р-*-т и k*-*-).2 пропагаторы имеют полюсы G(p)ca
<~Z2/(P—m); D(k2)=Zt/(&—№), где числа Zj н Zt являются вы-
вычетами в полюсах и имеют важное физическое значение: чем они
больше, тем больше эффективный физический заряд электрона
¦ег, который, вообще говоря, отличен от параметра во.
Удобно (перестроить схему теории, вводя в нее вместо пара*
метров од и е<> реальную массу т электрона и его реальный
заряд ег. После этого амплитуды физических процессов, выражен-
выраженные через т и еТ, никаких расходящихся интегралов содержать
не должны. Такую перестройку называют схемой перенормировки.
Для пропагаторов и вершин она сводится к следующему.
36
Вместо функций Е(р) и П(<72) введем величины
где штрихи означают производные по соответствующим аргумен-
аргументам и где
ZT1 —1-2'(ж); ZF1 ==1-П'(Х2) = 1-П'@) C.2)
есть некоторые постоянные. Находя отсюда Е(р) и П(^) и под-
подставляя их в знаменатели точных функций Грина B.9) и B.15),
получаем
(j'p)=Z2Gf(p); Z)(<?2)=Z8Dr(^), C.3)
где
Gr{p)=(i>-m-2.r{p)r; Dr(<?)-[t-V-Tlr(f)\-i C.4)
называют перенормированными пропагаторами, или функциями
Грииа. Они удобны тем, что при /J-wn и q2-*-).2 соответственно
имеют простые полюсы с единичными вычетами Gr(p)->-(/)—tn)~\
Dr(<72)-*(#2—Я2), так как из C.1) видно, что в этом преде-
пределе величины Sr(p) и П,(<72) убывают заведомо быстрее, чем
Р—т и q2—X2, Кроме того, как показано ниже, в них, в отличие
от G(p) и D(q2), сокращаются все расходящиеся на верхнем
пределе части фейнмановских интегралов.
Чтобы аналогично преобразовать вершину Гц == уд+Лц. (р, р—fc),
введем 4-импульсы электрона на массовой поверхности ро=(гр, р)„
Р?=(вр. Pi). гДе P?==P-k» 6/,=yrp2+7PI &Pt=Vpffm?, т. е.
^рр н pou(pf)=mu{p»), p\u(pb=mu(p\). Обозначим
(P°> PU оператор ЛцО?0, /??), в котором матрицы p°=Yn/$ и р?
заменены величиной т (как было бы, если бы он был «зажат»
между спинорами и(р°) и и{р%; его общий вид, как легко пока-
заты есть: А^{р°, р\) =*&(&)У»—bik^o^kv^m, где \(k2) и
Ь (k2)—некоторые функции k2; k=p\—pP, <TnV=(l/2I)(YnYv—YvYh)
Если еще и р\*=р°, т. е. А=0, то Л°(/>°, P°)=YnA@). Учитывая
это, определим аналогично C.1)
ZTl^r{p, p-k)=\»(p, p-k)-Al(ifi, po), C.5)
где Z-I = l-fA@). Находя отсюда A|4=Z-IA^r+Y(iA@), получаем
Гц(р, Р-Щ=ZrT^(p, p-k), C.6)
где Гц,(/>, р—fc)=Yu+AnrQ?t p—А)—перенормированная вер-
вершинная часть. При Л-»-0 и р-*-р° величина (a(p)IVa (p—k)) имеет
простой предел, равный согласно C.5) (и (jp0) Yh« (jfi)), т. е. Гцг-^уи*
В jc-пространстве перенормировка пропагаторов B.17) опреде-
определяется теми же соотношениями C.3): G (JCj — jc2)=Z2Or(jCi—x2),
fi)ZP,,(xi—X2). Здесь Gr и Duv.r определены
37
формулами B.17) с заменой в них Ц(х) и А»{х) на уг(х) и
Ац,г(х), где
C.7)
причем ij>r(jc) и А»,г(х) имеют общий вид A.13), A.14), где вместо
и(р), ец(к) записаны иг(р). *и,г(к), для которых
e(p)-Zpttr(p). ^(k)-ZJ«e№i,(k). C.8)
После перенормировки формулы содержат иг(р) и eM.,r(k) вместо
и{р) я ец(к1.
Отметим, что если перенормнровэнные пропагаторы и вершины
представить в форме
C.9)
и в таком же виде представить их до перенормировки
2, k\ p$-bJ%J)omkv, (ЗЛО)
то равенства C.3), C.6)
C.11)
вместе с условием Г,, (от2, 0, fft2)=sr(fft)=d/.(Xs)=l дают
, О, да2); Z2=s(/n); Z8=d(X2). C.12)
3.2. Ультрафиолетовые расходимости вклада графиков
Интегралы Фейнмана, определяющие вклады скелетных гра-
графиков, могут быть приведены в области больших значений им-
импульсов интегрирования к виду
C.13)
где а—число интегрирований по компонентам k\ 4-импульсов,
а р~ степень роста знаменателя с ростом |^'|1/2 (вместо степени
знаменатель может содержать произведение целого числа р/2 раз-
различных членов подобного вида). В области \k'%.\-*-oo эти интегра
лы могут быть расходящимися, так как они содержат параметры щ
и е0, но не физические величины т и еТ, где ег—физический заряд
(это так называемые ультрафиолетовые расходимости). Поэтому
38
интеграл обрезан на верхнем пределе условием |^'|<М2, где
предполагается, что Ж2-»-с». При переходе к перенормированным
величинам все расходящиеся члены, пропорциональные In Ж или
степеням величины М, сокращаются*
Ясно, что степень расходимости интеграла C.13) определяется
разностью v=a—р, т. е. при Ж-»- с» /ep~Af, причем при v=>0
расходимость логарифмическая, т. е. /a, a~lnM.
Как было показано Дайсоном [2.1], еще в конце 40-х годов,
сразу же после появления графической техники Фейнмана, сте-
степень v расходимости вклада графика не зависит от числа п вер-
вершин в нем, а определяется числами Ne внешних электронных и
N., внешних фотонных линий в виде
Nr C.14)
Теории поля, подобные КЭД, в которых степень расходимости
вклада графика не растет с ростом его порядка, т. е. числа п,
называют перенормируемыми- В них константа связи безразмер-
безразмерна и все расходимости, как показано ниже, могут быть сокраще-
сокращены переопределением (перенормировкой) масс частиц и зарядов.
Чтобы, получить результат C.14), нужно подсчитать число 4JV
компонент 4-импульсов ft/, по которым ведется интегрирование
во вкладе графика: a=4W=4(/?,+rT—я+1), и число степеней
импульсов в знаменателе в C.13) ,р—fe+2FT, где Fe, /\—соот-
/\—соответственно числа внутренних электронных и фотонных линий.
Так каквсе графики в КЭД (построены на вершинах рис. 1.1, то
легко заметить, что
n=Ny+2F4=Ne/2+Fe. C.15)
Поэтому если выразить отсюда аир через числа N, и #т внеш-
внешних линий, то получим: а—2(п—N,—#т)+4, а р=2п—#т—N,/2.
Это и дает формулу C.14).
Из формулы C.14) видно, что расходятся (т. е. имеют
только графики с малым числом внешних линий Ne/2 и
1) графики собственной энергии фотона TL(qs) с N,=0, #т=2
(рис. 1.7,а,б). Для них v=2 и интегралы B.10), B.11) формально
расходятся квадратично, т. е. П(#г) ~aAI2+6gr2ln(Al?/?!!) + ...
Однако в силу калибровочной инвариантности КЭД, как было
показано выше, П@)=0. Поэтому обрезание интегралов для
П(<72) нужно сделать так, чтобы постоянная а обратилась в нуль
(см. об этом ниже, гл. 4). В результате П(<72) ~bq2\n{M*/<p) бу-
будет содержать лишь логарифмически расходящиеся члены;
2) графики собственной энергии электрона Е (р) (петли в
центре рис. 1.6, а,б). Для них v=-l, однако при интегрировании
по, направлениям 4-вектора k' линейно расходящиеся члены исче-
исчезают и остаются лишь логарифмические расходимости Ъ{р\
>~р\п{М*/р*);
3) графики вершинной части рис. 1.5 с Л^т=1, N,12=1; для иих
•v=0 и вклад их Лц(р, р—k) ~ln {M'Jp2) логарифмически расхо-
расходится.
39
Графики всех остальных типов — сходящиеся» Формально v=»O
и для графиков рис. 1.9 для амплитуды"ГТТ(АЬ й2, fa, fa) рассея-
рассеяния фотона на фотоне. Однако аналогично амплитуде Пх. величи-
величина Гп должна обращаться в нуль при й«=0 из-за калибровочной
инвариантности теории. Поэтому члены !~1пЛ! в ней во всех по-
порядках по е02 должны строго сокращаться. Так, в порядке во2 они
взаимно сокращаются во вкладе трех графиков рис. 1.9. Отме-
Отметим также, что графики с N.=0 и #т=3 в силу теоремы Фарри
вообще вклада не дают.
График всех остальных типов, с большими NJ2 и #т, отвеча-
отвечают v<0, и вклады их определяются сходящимися интегралами;
например, это именно так для графиков рис. 2.3 для амплитуд
Гт. и Г...
Таким образом, расходимости (логарифмические) имеются
только во вкладе графиков собственной энергии и вершинной
части.
3.3. Общая схема перенормировок
После сделанных выше замечаний (принадлежащих, в основ-
основном, Дайсону [2.1]) общая схема перенормировки КЭД выглядит
весьма просто. Амплитуда любого физического процесса опреде-
определяется суммой вклада ряда скелетных графиков, построенных на
точных пропагаторах G{p), D(q2) и на точных вершинах
Г„(р, р—k). При |р2|-»-оо и |?2|-»-оо эти пропагаторы согласно
C.10) отличаются от свободных лишь множителямиs(p),d(q2),
Т(р, k), которые никак не влияют на оценку C.14) расходимости
вклада графика, так как они логарифмически изменяются с рос-
ростом |р2| и \q2\ (как некоторые степени 1п|р21, In|<712; это подроб-
подробно показано в гл. 5).
Сказанное означает, что вклады скелетных графиков, постро-
построенных на точных пропагаторах и вершинах, в амплитуду Ттп лю-
любого физического процесса (например, графиков рис. 2.3 и 2,4
для амплитуд рассеяния Гт„ Гтт) определяются сходящимися ин-
интегралами по 4-нмпульсам внутренних линий. Согласно формулам
C.3) и C.6) все расходимости оказались выделенными в множи-
множителях Z\~l, Z<i, Z%, определенных в C.12), при условии, конечно,
что в перенормированных функциях Gr(p), D^q1) и Т„{р, p—k)
все расходящиеся части интегралов точно сокращаются, т. е. что
эти функции также определяются лишь сходящимися интеграла-
интегралами по 4-импульсам.
Таким образом, для доказательства перенормируемости КЭД
[2.1] покажем: а) что множители Z\~l, Zt и Z3, содержащие lnM2,
где М — предел обрезания расходящихся интегралов по импульсу,
собираются во вкладе любого скелетного графика в виде произве-
произведения вместе с затравочным зарядом е0 в некоторую величину ег,
которая имеет смысл физического заряда; б) что в функциях Grr
Dr и Г„г все расходимости точно сокращаются и эти функции мо-
могут быть получены в виде рядов по степеням того же физическо-
физического заряда еД Последнее означает, что любая физическая ампли-
40
туда Ттп определяется вкладом скелетных графиков в виде рядов
по степеням физического заряда е,2 и не зависит от 1пЛ12 в преде-
пределе при М*-*-оо, т. е. определяется лишь сходящимися при MWoo.
интегралами.
Рассмотрим первое из этих двух утверждений (т. е. пункт «а»).
Пусть произвольный скелетный график для амплитуды Тг=Тт
физического процесса включает: п вершин, т. е. п множителей*
воГц—е^-Тц/-, где е0—затравочный, или перенормированный,,
заряд; Fe—внутренних электронных линий, т. е. множителей
G (p)*=Z2Gr(p); Fy—внутренних фотонных линий, т. е. множите-
множителей D{k^)=ZzDr(k2); Ne—внешних электронных линий, т. е. мно-
множителей u{p)=zy2ar(p); Ny—внешних фотонных линий, т. е.
множителей вц. (k)=Z3/2eM, r (к).
Вклад его Г(п> символически запишем в виде
Т(n) _«g J (Гц)» (G (p)f* {D (fc*))Fv (a (p)f* fafy (dk'f. C.16>
Выражая все величины через перенормированные и учитывая, что*
в силу равенства C.15) имеет место соотношение e"ZT"Zp^+N*12 X
XZ^Ny'2^(e0Z7lZ2zy2)\ получаем [2.1]:
Т (п>=епг \ (Т»ГУ {Qr (p))F<(Dr WP (в, (P)f< (e»rfv {dk'f, C.17>
где величина
er=eoZT%Zl/2 C.18).
имеет смысл физического, или перенормированного, заряда, для ко-
которого в КЭД е2/4я=аг = 1/137.
Как видно, вклад графика Г(п) выражен только через перенор-
перенормированные величины, в частности через ег и физические массы
m и 1=0, а интеграл J {dk')a по 4-импульсам внутренних линии
как был сходящимся до перенормировки [согласно оценке C.14)],.
так и остался сходящимся.
3.4. Конечность перенормированных величин IV, Gr, Dr
Покажем, что вклады всех графиков в величины IV, G, и Drt.
т. е. в Ар,, S, и П„ действительно не содержат расходимостей
(это второе из сделанных выше утверждений, т. е. пункт «б»
в разд. 3.3).
По определению [см. C.5I] Д». есть разность
Где Лц—сумма вкладов скелетных графиков рис. 2.6 с точными
пропагаторами и вершинами. Подставляя в них rV=Z~4V,.
G==Z2Gr, D = ZaDr и умножая на Zx, замечаем, что во вкладе
каждого из графиков el заменяется e2==eoZT2ZlZ3. Это справед-
справедливо для вклада B.4) треугольника (рис. 2.6, б) и всех остальных
41
графиков рис. 2.6: автоматически на каждую лишнюю фотонную
линию D (k2) в графике появляются две вершины (т. е. elvl) и две
электронные линии l~(GJ), т. е. появляется лишний множитель
e*=e\ZT2Z\Z3. Поэтому вклад каждого из графиков рис. 2.6, б, в,...
в ZjAji определяется теми же формулами, что и для Лц (напри-
(например, вида B.4)], но с заменой всех величин перенормированными.
В отличие от C.17) интегралы, определяющие вклады гра-
графиков в Л„(р, р—k) [типа B.4)], логарифмически расходящиеся:
для них v=0 в C.14). При обрезании их на верхнем пределе
|й'г|<Л12 возникает вклад вида С1пМ2 от области очень больших
импульсов интегрирования — вклад, ие зависящий от внешних
импульсов р, k. Ясно; что в разности C.19) этот вклад сокра-
сокращается. Поэтому во всех порядках по е,г для Л^г получаем конеч-
конечные (при ЛР-мю) значения, равные нулю при А=0 и р=т.
Остается показать, что конечны при Af2-»-oo также величины
2г(р) и TL,{q2), определенные согласно C.1) в виде разностей
где Л2=0, a 2,(p)=Z22(p) и П, (?2) =Z,II (q2).
Для доказательства этого неудобно пользоваться общим ви-
видом B.7), B.11) функций 2(р) и Щ^2), так как из-за их несим-
несимметрии по отношению к вершинам у*, и Г„ величины 2i(p) и Ui{q2)
не выражаются только через перенормированные величины.
В них остается1 еще множитель Zu содержащий расходящиеся
члены ~1пЛ12, которые фактически сокращаются в разностях
C.20). Чтобы избежать анализа этих сокращений, удобно по-
построить значения 2г(р) и Пг(<72) непосредственно с помощью фор-
формул Коши B.31), которые дают:
4m' C.21)
где 6ni(<72)=Z36n(<72); 62ieZ26Z(p), а бЩя2), б2(р)-скачки
B.23), B.28) функций П(^2) и t{p) = A{p^)-\-pB{pJ) на правых
разрезах [плоскостей переменных q2np2\ так как 2г(р)=Лг(р2) +
-f рВг(р2)—спинориый оператор, то речь идет здесь о скачках
функций АДр2), Bffjp2), для которых и записано фактически пра-
правое из соотношений C.21)].
1 Действительно, переход к перенормнруемьш величинам дает: Si (/>)«=
{2)l
{)lvsrilVtr
- -Z,(e2f/4n)J[7XGr (*') rx,f (k/k'-q) Gr (k'-q)] dW/яЧ, и в раз-
разностях C.20) расходимости сокращаются лишь при учете членов, пропор-
пропорциональных 1пМ* в Z,.
42
Несмотря на громоздкость формул B.23) и B.28) для скачков
6П(G2) и 62(/>), идея доказательства конечности величин C.21)
очень проста: после умножения их соответственно на постоянные
Z3 и Z2 и перехода к перенормированным величинам происходит
полная перенормировка, т. е. справа в B.23) и B.28) заряд eg за-
заменяется перенормированным е? C.18), а амплитуды Гц и V™,r.
определяющие скачки 6П(^2) и 62 (р), выражаются в теории воз-
возмущений только через перенормированные величины Гйг, Ог{р),
Dr(q2) и т. д. (более полно об этом—см. ниже). Все интегрирова-
интегрирования в B.23) и B.28) по фазовым объемам dxn проводятся в конеч-
конечной области изменения импульсов, разрешенной законами сохра-
сохранения 4-импульса, и не дают расходимостей. Поэтому скачки
№\ {<?*) и 62j (p) конечны и определяются в виде рядов по степеням
е\ [в первом порядке—формулами B.21), B.30) с е\-+е\, в сле-
следующем порядке—формулами B.23), B.28), в которых использова-
использованы конечные величины ^(q2) и 2?1)(р), вычисленные согласно
C.21) в порядке е2 и т. д.].
Расходимости в вещественных частях функций П,.^2) и 2г(р)
могли бы появиться из-за интегрирования по 5 в C.21). Однако и
эти интегралы во всех порядках—сходящиеся из-за роста в них
знаменателя пропорционально s3 при s-y со. Действительно, вклад
простейших петель в 6II(s), 62 (s) [см. B.21), B.30)] растет лишь
пропорционально s [в 6П или постоянен в случае 62(s)=6A(s)+
-\-p6B(s)], а вклад в них более сложных графиков растет с рос-
ростом s или—так же (с логарифмической точностью), или еще мед-
медленнее. Это легко проверить, увеличивая число внутренних линий
в B.21), B.30) и подставляя в иих полюсные амплитуды Тц, V?r
рис. 2.15, а или более сложные—рис. 2.15,5.
Расходимости при Я-»-0 (также логарифмические) возникают
в правом интеграле в C.21) не на верхнем, а на нижнем пределе
интегрирования s-+-m2. Это инфракрасные расходимости, нужные
в 2г(р) для устранения реальных расходимостей при яА-оо в
матричных элементах реальных физических процессов. Они обу-
обусловлены при Я-»-0 возможностью реального испускания фотонов
•сколь угодно малой энергии. Способ их устранения в теории воз-
возмущений хорошо известен (см. гл. 4).
Покажем теперь более полно, что скачки бЛ^2) и 62 (р)
в C.21) остаются конечными при Л12->оо. Рассмотрим сначала
величину S&iiq2), которая выражается через амплитуды Г* раз-
разчных физических процессов, определенных в B.24) вкладом
^у\ графиков рис. 2.15, имеющих Ne электронных и Ny фо-
фотонных внешних линий. Вклад простейшего Г^*^^—полюсного
графика рис. 2.15,а можно символически представить произведе-
произведением /1=ЛГв+Му—2 вершин Гц, числом F°=>Ny+Nei2—2
43
электронных пропагаторов 0{р) и числом F* =Nel2 — \ фотонных
пропагаторов в виде
то*е?у)!к ~(rn)JV«+/y"'-2G/vv+iV«/2-2?>iV«/2-1# C.22>
Соответствующий член в амплитуде Ти B.24)
Т°и ~ (e0rv)^+^-\ulf'GNy+N^2-2 {etfWW-1 C.23)
полностью перенормируем, т. е. при переходе к перенормирован-
перенормированным величинам становится тождественно равным
без появления множителей Zu Z%, Z3. Таким же свойством обла-
обладают и вклады в 7ц и более сложных скелетных графиков, на-
например вида рис. 2.15,6. Действительно, легко заметить, что при
всяком усложнении такого графика во вкладе его появляется
множитель вида степени величины e<?YfG*D, которая полностью
перенормируема. Петли в таких более сложных скелетных гра-
графиках (вида рис. 2.15,6) приводят согласно оценке C.14) к схо-
сходящимся интегралам, т. е. не дают новых расходимостей.
Амплитуды Т\г квадраты которых определяют скачок B.23
2), отличаются от Ти тем, что не содержат одного множителя
ZJ/2en,r(q), и для полной перенормировки им не достает
множителя Zl3/2. Поэтому величина 6Ki=Z?R(q2) полностью пере-
перенормируема.
Это же относится и к величине 62i=Z262(p), так как скачок
B.28) 62 (р) определяется квадратом амплитуд V™,,,, которые
отличаются от Ти тем, что не содержат одного множителя иа(р)
и для полной перенормируемости им недостает как раз множи-
множителя Z2.
Таким образом, скачки бП,^2), 62i(p), входящие в C.21),.
могут быть выражены только через перенормированные величины
(через ег, Гцг, Gr, Dr) и остаются конечными в пределе при
да-х». Иными словами, в равенствах C.3) и C.6) при М2-*ао
от 1пЛР зависят лишь постоянные Zf1, Z2, Z3, но не перенорми-
перенормированные функции Гцг, Gr и Dr Это завершает доказательство
перенормируемости КЭД.
Отметим в заключение, что в КЭД теорема Уорда B.18),
2.19) справедлива и для перенормированных величин, т. е.
(д1дР11)О7Чр)=Т»г(р, р), C.24)
что следует точно так же, как B.18), B.19), из рассмотрения
вклада в G, и IV всех переномированных графиков. Но так как
G=Z2-Gr, Гц=^-'-Гцг, то B.19) и это соотношение дают
Z^^Z-\ т. е.
ZX=Z2, C.25)
44
и поэтому в C.18) эти величины сокращаются:
C.26)
3.5. Преобразование перенормировки в контрчлены в лагранжиане
Простое и полезное для дальнейшего представление о схеме
перенормировки, немного отличное по форме от изложенного выше
подхода,< можно получить, рассматривая ее [1.3] в лагранжевой
ф В КЭД A4) ()
у рр [] р
формулировке теории. Введем в лагранжиан КЭД A.4) поля $()
и А»{х) в виде C.7): q{x)=Zl'\(x), A^x)^Z^AVr{x) и
перепишем его тождественно в форме
2 (х) = -A /4) Z3 (d»Avr - dvA»ry-\-Zrtr (p~m) qr -
-Zie^Avrb+ZzAmftrt,), C.27)
где p=i%dp, er—ZYlZ2Z3/2e0, а Ат=т—щ, причем здесь е0
и /По—параметры, которые содержал исходный лагранжиан A.4),
а величины т, Zi=Z2, Z3 пока произвольны. Лагранжиан C.27)
тождественно равен начальному A.4), вообще говоря, при любых
значениях этих величин, причем при условии Zt»Z2 выполняется
теорема Уорда. В теории возмущений величины т, ZJt / = 1,2,3
удобно определять в виде рядов по степеням аг/4я=е*/DяJ
]' '-ЬЗ. 3; ^f-I.
и коэффициенты Zf] и (А/п)« подобрать так, чтобы в каждом по-
порядке все расходимости сокращались. Чтобы увидеть, как это
можно сделать, представим &(х) в виде суммы
где 2Г (х) A/4) (<?„А,г- d'^A^f+фг (р -т) уТ)- ет ($гъ»Ь)
есть лагранжиан точно вида A.4), но записанный через перенор-
перенормированные величины, а добавок
- (Z, -1) еТ {& ъА»гЪ) +AmZi &#r) C.29)
определяет так называемые контрчлены, коэффициенты C.28) в ко-
которых подбираются так, чтобы в каждом последующем порядке
сократить логарифмические расходимости расходящихся интегралов.
Для этого лагранжиан взаимодействия следует выбрать в виде
'j?e«=— er(tyTyv,Av.r'§r)-\-b3?f и, считая все члены в AS" величинами
порядка аг = е*/4п (или порядка erar~ef) и разлагая 5-матрицу
вида A.20) ^=Гехр i \2"г</4д:1 в ряд по степеням S"r, последова-
45
тельно выполнить программу теории возмущений, описанную выше.
При этом величины всех физических амплитуд T(Nelvv^ определят-
определятся суммарным вкладом скелетных графиков, содержащих перенор-
перенормированные функции Грина и вершины вида C.4) ГцГ=Уи4-
-f-Лц, г (р. р—Щ> причем, как видно из графиков, Лц, т и операто-
операторы 2г(р) и Пг(й2) в C.4) определятся в форме
C.30)
Ац.,(p. p-*)=Ai1}(p, p-ft)+(Z,-l)Y,x;
причем Zx{p)=Z?,(p), n1(*2)==Z3n(*2), и члены (Zj—l)Yn, (Z2—1)
и (Z3—I) появляются за счет вклада контрчленов C.29). Величина
A^iz=Z1A1l{p, p—А) определяется суммарным вкладом скелетных
графиков (рис 2.6, б,«...), содержащих функции IV г, Ог и Dr
и перенормированный заряд ег, a nj(#) и 2i(p) определены дис-
дисперсионными соотношениями B.31), в которых бП(й2) и 62 (р2)
выражаются через неперенормированные физические амплитуды
[формулами B.23) и B.28)J, перенормированный заряд ег и массу
tn—m.Q-\- Am электрона.
Формулы C.30) позволяют в последующих порядках теории
возмущений однозначно определить постоянные Лт=2(т) и Zi»=
=Z2, Z3 в виде рядов C.28) по степеням <х,/4я и получать в каж-
каждом порядке конечные значения величин 2г(р), Пг(*г) и Л„г и
всех физических амплитуд.
Соответственно тому, как это было сделано выше, величины
Zb Z2, Z% можно нормировать на точки А2=Яг=0, р=т, отвечаю-
отвечающие физическим массам частиц. Это отвечает выбору в каждом
порядке теории возмущений в C.30)
где YiCP^p)
Из C.30) видно, что, в принципе, возможна и другая норми-
нормировка, например на любую пространственно-подобную точку
—jt?2== —А2=|*2, где ц—произвольно:
p—Kl
n2), C.32)
т. е. на точку, в которой пропагаторы заведомо не имеют полю-
полюсов. Значения Zb Z2, Z3 в этой нормировке отличны от их значе-
значений в нормировке C.31) на конечные множители (или в теорий
возмущений — на конечные слагаемые, см. ниже).
46
Глава 4
ФЕПНМАНОВСКИЕ ИНТЕГРАЛЫ. ВЕРШИНЫ
Л ПРОПАГАТОРЫ В ТЕОРИИ ВОЗМУЩЕНИЙ
4.1. Логарифмическая асимптотика
фейнмановских интегралов
Рассмотрим некоторые способы вычисления интегралов Фейн-
мана.
Начнем с простейшего, предложенного Л. Д. Ландау
А, А. Абрикосовым и И. М. Халатниковым [4.1] (в 1954 г.
для выделения главных логарифмически больших членов
~In {М21 {р\ |) ~ In (| р\ 11т2) > 1 в логарифмически расходящихся
интегралах при больших импульсах \p\\ytri1 (АР—предел обре-
обрезания интегралов). Поясним его на примере вычисления вершины
1, р—k) при \р2\~\(р—*J1>!*2!> т2. В интеграле B.3) по
=—(/feb, k'), определяющем ее значение, удобно повернуть контур
интегрирования в .комплексной плоскости переменной k'o (—<» <
<А^<оо), рис. 4.1, на угол я/2 против часовой стрелки^
? ... к'„А
В результате интеграл J
ог
анц
— 00
too оо
перейдет в j dtio — 1 )dk\, где ftj = ~r
-loo -oo \
= ik^, T; e. получим интеграл в >^
4-мерном евклидовом пространст-
пространстве: Рнс. 4.1
1/7 VC
\
i dQ^KftdKft, причем dQi=2 sin2a</a sin 9d»*t —
элемент телесного угла в 4-мерном евклидовом пространстве
(в нем |k|=/<r'sina; ft4==^'cosa; 0<а<я; §dSk*=2n2, a
</(%'*)) =J/(#') d^/2n2—среднее от функций /(/Г') по на-
направлениям 4-вектора К')-
При таком повороте контура рис. 4.1 (его называют ваков-
ваковским поворотом) интеграл не изменится, если: а) он быстро схо-
47
дится при &о'-*-±°9; б) при повороте контура не пересекаются
полюсы подынтегральной функции. Первое из этих условий вы-
выполняется с большим запасом, а второе — зависит от расположе-
расположения в плоскости ko рис. 4.1 полюсов подынтегральной функции в
D.1), которые перемещаются при изменении «внешних» импуль-
импульсов в интеграле по kof в D.1). Всегда имеются такие значения
этих импульсов (см., в частности, разд. 4.4), при которых положе-
положение полюсов при тг+т,—Ю имеет вид, указанный на рис. 4.1.
Тогда контур можно повернуть, а ответ, будучи аналитической
функцией внешних импульсов, будет справедлив для всех их зна-
значений.
После поворота контура внешние импульсы р, px*=p—k
также удобно считать еквлидовыми, обозначая Po—iPi и вводя
{вместо р) 4-вектор P={V,р\)> для которого Р2=р2-\-р2=—р2
[я аналогично, вводя вместо рх 4-вектор ?\=(Pi, —1рю)»
В области больших К'%, за счет которой в интеграле
\" У»"'1 => 4К'*/К'* возникает большой, логарифмически зави-
зависящий от Р2, вклад, в знаменателях B.3) можно пренебречь
всеми импульсами Р, РХ^Р—К по сравнению с К'- В резуль-
результате под интегралом Г k [я i ¦ в B.3) появится величина
с/ \к )
t t
MS-1I-^г1,
где правая часть записана для случая 5-калибровки: dlo=g\<3-\-
-f-(S—tykykls/k'*. Таким образом,
/• К* К. ^ та а в . а.
, D-2)
/ft У
т
где osq—e2i4n (здесь и далее вместо е будем писать е0), а
Р2т~тях[Р2, Р\), т. е. Р2т равно любой из величин Р2, Р?=
*=(P—Kf, если они одного порядка или же если одна из них
намного больше другой, то Р2т— наибольшая из них.
Как видно, после поворота контура задача сведется к вычис-
вычислению интеграла
pi pi
m tn
где учтено D.1) и то, что < K%Ka > —К'гЬ%о1^=~К' g%al^
It. е. что < kike > =(l/4)ft'1^a> где giw=— б^. причем справа Я,
48
0 пробегают евклидовы значения 1,2,3,4]. Произведение gt,a
на квадратную скобку в D.2) есть Yi»'?, поэтому, в результате,
лолучим:
^). D.4)
Это — логарифмическая асимптотика B.3), справедливая с точ-
точностью до членов порядка единицы по сравнению с большим ло-
логарифмом '[фактически в D.4) следовало бы писать 1п(М2/Рт2) +
+ С, где С~1—неизвестная в этом приближении постоянная].
В калибровке Ландау, т. е. при ?=0, как видно, Л(^в асимптотике
исчезает.
Вычислим в этом приближении ЕA)(р) и Wl)(q2), определен-
определенные в B.6) и B.10).
Если пренебречь в знаменателе в B.6) всеми величинами по
сравнению с k', то это приведет к интегралу J Yn^'Yv^vX
Y^(dAk'jj&\)l(kf*Y, который обращается в нуль при интегрировании
по направлениям 4-вектора k' (т. к. < К'у. > =0). Поэтому пропа-
гатор \l(p—k'—т)^ — \l(k'—p) в B.6) нужно разложить в ряд
по степеням pik' (при PV.<KV.—в евклидовой метрике). Это
удобно сделать прямо в операторном виде
+ — Р ~ + • • • • где первый член вклада не дает, следующий
я R
важен, а остальные приводят к сходящимся на верхнем пределе
интегралам, дают конечные, не содержащие большого логарифма
члены, н в пределах рассматриваемой точности ими нужно пре-
пренебречь. Второй член дает результат
)=> («о/4я) S In (Р*1Щ;-\ D.5)
отличающийся от Лц{р, р) лишь множителем — р^ [это следствие
теоремы Уорда —d?,{p)ldpv.=\.v.(p,p)\.
Для вычисления R{l)(q*) пропагатор 1/(й'—q—mo)^l/(ife' — q)
в B.10) разложим в ряд по q:
Первый член приводит в B.10) к квадратично расходящемуся ин-
интегралу вида аМа, где а зависит от способа обрезания (а=
=— 2ао/3я, если просто интегрировать до К'2^М2). Для сохране-
сохранения калибровочной инвариантности способ обрезания нужно
выбрать так (см. гл. 3), чтобы а=0; это не повлияет никак на
интересующие нас логарифмические члены, которые «набирают-
4—679 49
ся» не на верхнем пределе, а на всей области интегрирования
Q2</C'2<M2, (Q2=—q2). Поэтому первый член вклада не дает;
второй также не дает, так как он обращается в нуль при усредне-
усреднении по направлениям 4-вектора k'. Третий член дает:
где До —интеграл D.3). Подставляя сюда его значение, получаем
ПA) {q2) = (оо/Зя) q2 In (С?2/ЛР). D.6>
Асимптотики D.4) — D.6) справедливы с рассматриваемой точ-
точностью (в пренебрежении постоянными порядка единицы по срав-
сравнению с большим логарифмом) и в области малых Р2, Q2->-0, ког-
когда под логарифмом остается большая величина М21т2. Здесь уч-
учтено, что под знаком логарифма фактически имеются не выписан-
выписанные в D.6) члены порядка т2, которыми при Q2~^m2 в D.6)
было пренебрежено.
4.2. Асимптотика вершины и пропагаторов
в КЭД в порядке е02
Представляя вершину и пропагаторы в виде C.9)
(p) = s(P2)l(p—m)] D{q2)=^d{Q2)iq2, находим таким образом:
следующие асимптотики функций Г(Р„), s{P2) и d(Q2) в первой
порядке по е2=4
s @ = 1 + SA) Ср)//Г= 1 + (ао/4л) U\ D.7).
где l=\n(P2IM2) и где для удобства записи переменная q2 в
D(qa) заменена величиной р2. Заменив всюду р2-»-//»2, получим
отсюда (см. замечание в конце разд. 4.1) для констант перенор-
перенормировки C.12):
D.8).
где /o=ln(M2/m2), причем всюду второй член ао//4я или ао1о/4я
считается малым по сравнению с единицей (это область примени-
применимости обычной теории возмущений; напомним, что М2 — предел
обрезания, am — масса электрона).
Для перенормированных величин Tr=ZiT, sjr=Zis, dr=ZJldt.
отсюда получим с той же точностью:
-1-^'4^ 1 D.9>
(«г /4я) U/, dT (/,) == 1 + (а, /Зя) /„}.
50
где /r=/o+/=ln(P2//ns). Эти функции по определению обраща-
обращаются в единицу при Р2=т2. Отметим, что по данному выше опре-
определению функция dr=\ при Р2=0, но не при Р2=т2, однако в
пределах нашей точности между этими условиями фактически
нет разницы, так как для нужного смещения точки нормировки
достаточно заменить в dT величину /r=ln(P2/m2) на //=1п[(Р2+|
+т2)/та] (а при Р2^т2 между l/^lr+m^/P2 и /г практически
нет разницы).
Функции D.7) Г(/), s(l) и d(t) нормированы иначе: они равны
единице при Р2—М2, т. е. на верхнем пределе обрезания.
4.3. Общая форма асимптотик вершин и пропагаторов в КЭД
Рассмотрим вклады графиков высших порядков по е03 в вер-
вершину Г„ и пропагаторы. Начнем с вершины Г„(р, р—k), вклад в
которую дают скелетные графики рис. 2.6 и целый ряд графиков,
приводимых к каждому из них.
Ограничимся сначала теми графиками (вида, например,
рис. 1.5,6, приводимыми к простейшему скелетному треугольнику
рис. 2.6,6), переход от более простого к более сложному, в кото-
которых происходит путем добавления одной или нескольких не пере-,
секающихся фотонных линий или электрон-позитронных петель.
Можно заметить, что при каждом таком усложнении на каждый
множитель ао/4я=ео2/16я2 появляется лишняя степень величины
|/| = |1пР2/М2|>1. Например, вклад графика рис. 1.5,6 при Р2~]
~ | Р—К |2 ~ /С2Э> т2 определяется логарифмическим интегралом
от вершины Д,A):
м' dfC2 '
где lx =ln [k\iM2). Поэтому в асимптотике сумма всех графиков
этого типа, приводимых к треугольнику рис. 2.6, б, есть величина
^' где
DO
Л» (9 =2 4(ао*)л=2^"' DЛ0)
л—'0
причем ?=а</, а Я° —некоторые числовые коэффициенты.
Переход к более сложным скелетным графикам связан каж-
каждый раз с появлением лишней степени малого параметра а0 без
большого множителя |/| — |1пР2/М2|>1. Так, в следующем ске-
скелетном графике рис. 2.6,в с двумя пересекающимися фотонными
линиями интегрирование по одному из двух 4-импульсов k\ или
k2 дает сходящийся интеграл, т. е. не приводит к появлению
большого множителя /. Поэтому вклад такого гра-
графика (при тонких линиях и вершинах) пропорционален ao-(d(/)=a
=ao-g. Суммарный вклад всех приводимых к нему графиков
4* 51
(полученных из него путем добавления не пересекающихся с дру-
другими фотонных линий или электрон-позитронных петель) составляет
. где ГA) (^-величина вида D.10): ГA) (Е)—2
"- Асимптотика вклада еще более сложного скелетного
л
трафика с тремя пересекающимися фотонными линиями (вместе
со всеми графиками, приводимыми к нему в указанном выше
смысле) равна аналогично Уйао^B)Ш и т- Д- Поэтому в асимпто-
асимптотике суммарный вклад всех вообще графиков рис. 2.6 (скелетных
и всех приводимых к ним) имеет общую форму Гц(/?, />1)Г@
где [4.1,5.2]
причем
2
я—О
включают все степени величины g==a0ln(P2/AI2), которая даже
при очень малом ао<1 может быть не малой, а Яя*;—некоторые
числовые коэффициенты. В теории возмущений при § < 1 функции
Г(Л) определяются первыми членами рядов D.12): ^^
+ Г(*)'@)/
()(/
Ряд вида D.11) очень быстро сходится при малом Oq<1 и при
любом \, поэтому он очень удобен для исследования асимптотики
функции Г(/). Член Г°(?)=1-[- А°(§) называют главным логариф-
логарифмическим приближениим (ГЛП)\ в нем отсуммированы все степени
(Ор/)"; в следующем члене учтены степени a.Q+1tn и т. д.
К такой же форме аналогично можно привести (суммируя
вклады всех графиков) и асимптотики функций Грина s(l) и
2 2 DЛЗ)
*-0 ft-0
причем при Оо<1 основным здесь будет вклад ГЛП, т. е. функ-
функций s<°>(§) и rf@)(i)-
При l-+—lr функции D.11)—D.13) определяют постоянные
перенормировок, в частности Z3«=rf(— /0)—rf@)(—a</0), где /0=
«ln^/ni2). Теорема Уорда в КЭД, согласно которой ZX=*Z%
(при Z71=r(— /0), -?2=«(— ^о)). Дает Г(— 10) = s-1(Iq) при всех
/0>=1п(ЛР/от2)>1. Это означает, что, вообще, при всех />1
в КЭД
Перенормировка заряда определяется соотношением C.26):
w D.15)
52
Если ао<1, а РМ-АР (т. е. 1=\п(Р2/М2)-+0), то применима
теория возмущений и функции Г@), s@), и d{0) имеют согласно
D.7) значения, близкие к единице: r(O)«s(O)=*=</(O)<=*l+O(ao).
Асимптотика перенормированных величин Г,(/,), sT(l,), dT{lT)\
определяется вкладом тех же графиков и может быть представле-
представлена в форме, аналогичной D.11)—D.13):
DЛ6>
и в таком же виде для Yr(lr)*=s?(tr), где /,—In^/»2), причем
*#*'(?/¦) в D-15) суммирует все степени величины gr=a^r- ана-
аналогично D.12).
Способ построения всех функций Г<*>(&), s<4) (g), d<*>(?)
(и Г<*>(?г), sM(&), dW(&)) на основе теории возмущений и мето-
метода ренормгруппы указан в гл. 5.
4.4. Метод параметров Фейнмана
Метод Фейнмана [1.6] вычисления интегралов по 4-импульсам
сейчас хорошо известен (см. [1.1—1.4]). Кратко напомним его для
сравнения с формулами размерностной регуляризации, использу-
используемыми далее.
В качестве примера рассмотрим оператор B.10) поляризации
)(i)=A/3I11$ (я2), Для которого после вычисления шпура
получим
mi) ttfli - ^» С 2m*-pq-p* d*p
~-=^{2m4+qJ«-h>\, D.17)
где для удобства записи вместо k' введены 4-импульс интегри-
интегрирования р и использованы обозначения
D18)
причем Lx=ml—xq'i. Последнее выражение есть следствие равент
dx
ства1
аЬ )
D.19)
1 Оно является частным случаем более.общего соотношения:
П 1I О \1 ~~"•* | ' Л f ^"~ * • # •—JCл/
... + влх„)п
о •
53
где cl—(p—qJ—rn2, b — p2—m2, которое вместе с его производны-
производными по а и по Ь позволяет привести произведение большого числа
знаменателей к n-й степени (л=2, 3...) величины вида
р1—2qxp—Lx. В D.18) три равенства представлены для сокраще-
сокращения записи в виде одного, так что каждый член в скобке слева
равен интегралу от соответствующего члена справа.
Чтобы вычислить расходящиеся при |ра|-»-оо интегралы D.18)
[(причем Д„ расходится квадратично, а /„ — логарифмически), их
нужно регуляризовать, т. е. ввести в них обрезающий множитель
Л(/>*) = [М 1(м2—р*)]2, где М2 сколь угодно велико. Это—про-
Это—простой, но не очень удобный способ, так как обрезание в импульс-
импульсном пространстве отвечает наличию в я-пространстве сложного
нелокального взаимодействия (со сколь угодно малым размером
нелокальности го~1/М) вида
2'(х)=-е\(f (х+*,)А»(х)*(¦*+*»))Ч(*ь *»)
где г\(ги г2) — функция, близкая к 64BiN4(z2). Но легко заметить,
что при этом основное свойство теории — инвариантность SB' по
отношению к калибровочному преобразованию — заведомо нару-
нарушается; в результате у фотона появляется масса, а у амплитуд,
которые должны быть поперечными (к 4-импульсу фотонов q),
могут появиться малые продольные составляющие. К таким же
следствиям приводит и прямое обрезание всех интегралов D.18)
по Р2 при Р2<М2, где М2 очень велико, после виковского поворо-
поворота (рис. 4.1) переменной ро-*лрь Однако все эти нарушения лег-
легко исправить в конечном результате, поэтому вычислим интегра-
интегралы D.12), введя в них тем или иным способом обрезание по им-
импульсу t)(p2).
Рассмотрим сначала интегралы еще более простые, чем
D.18):
f У-г*) (')
)p*—2qp-Ln4 р
где p'*=p—q\ A=Z.-f-?2; L—произвольная величина, такая же,
как в D.18).
Проще всего последний интеграл вычислить при t]=l, произ-
производя виковский поворот рис. 4.1 по переменной ро=Щ и обрезая
интеграл при Р'2<.ЛР. Это дает, очевидно,
\р'ж
-0.fr) (ЛЫ^-ЛР). D.20)
Несмотря на грубость подхода, этот результат, как мы уви-
увидим, наиболее прост и правилен.
54
Вычисление этого интеграла с обрезающим множителем г\(р2)
[М2/(М2—р2)]2 немного более сложно и дает
)]
где е —основание натурального логарифма Aпе=1).
При вычислении было использовано соотношение D.19) [про-
[продифференцированное один раз по a—NP—(p'+qJ] и следующее
значение сходящегося интеграла:
* — 2qp—Ly яЧ — *l' Ча1)(Р'2+цK~~ 2Д '
где Д имеет то же значение, что в B.20), B.21), т. е. A^
Сравнение величин D.20) и D.21) показывает, что от способа
обрезания зависит коэффициент при М2, который «набирается» на
верхнем краю интегрирования, и малые добавки к М2 (вида сщгЦ-
+&А), которые появляются при интегрировании. От обрезания
йе зависит коэффициент при большом логарифме ln(Afs/A) в ло-
логарифмически расходящемся интеграле и, конечно, сходящаяся
часть интеграла, которой совсем нет в D.21), но которая только
и есть в D.22).
Дифференцируя обе части равенства D.20) [или же D.21)]
по q% или по L, легко найти нужные интегралы D.18) /, 1„ /*„.
Например, при обрезании из D.21) получаем
Интегралы D.18) отсюда получаются при замене q->x-q, L-*LX.
Подстановка их в D.17) дает после простых алгебраических
образований
представить в виде C.20), т. е. записать ^
'@)+ ПРЦ2), то ПA)(О)=(-2ао/Зя)(Ж2-/я2);
)[1п(^2/та2)-7/6)], a
о
D.25)
55
где у=2х— 1, причем величина ПA)@), равная квадрату массы
фотона, должна быть положена равной нулю для сохранения кали-
калибровочной инвариантности, нарушенной из-за введения обрезающего
множителя t\(fr).
Отметим, что если обозначить s=4/n2/(l— у2), т. е. «/=1 —
—4да2/$, то R$l) (д2) можно тождественно переписать в виде
4т»
точно совпадающем с дисперсионной формулой C.21), если в нее
для скачка 6HA)(s) подставить найденное выше значение,
[см. B.21)]: 6nA)(s)=(—Oo/3Ks)Ks-4ot2(s+2ot2). Как видно
дисперсионный подход дает още одни наиболее простой способ вы-
вычисления nj1' (^2). Интеграл D.25) берется в элементарных функ-
функциях и дает
=(ао/я){1/9—[(l--a2/3)(l-aargth(l/a))]}, D.27)
где a2=l—4ni2/^2=ch2»/sh2d, причем sh2&=— ?2/4ot2=Q2/4ot2.
Аналогично просто вычисляются с помощью D.20) или D.21)
величины 2A)(р) и Л?* [р, р—Щ.
4.5. Размерностная регуляризация т'Хофта— Вельтмана
Очень удобен калибровочно-инвариантный метод размерност-
ной регуляризации т' Хофта—Вельтмана [4.2, 4.3], в котором все
интегралы по импульсам р, берутся в n-мерном пространстве,
где они сходятся при п<по=4, и далее производится аналитиче-
аналитическое продолжение п к л=4. Дифференциал импульса d*p'/n*i =
= 16n2c4p7BrtLi в п-мерном пространстве принято [4.3] записы-
записывать в виде
где множитель р," с произвольной массой ц введен для сохране-
сохранения у интегралов той же размерности, которую они имеют
при п=4, и где предполагается, что по переменной р'0=1р'4 сделан
виковский поворот, т. е. Р''=р''+р1=—р'\ При любом п
в евклидовом пространстве, как несложно показать, rf"P' =
= [я"''2/Г(л/2)](Я/>/2^/1- Поэтому интегралы вида D.21)—D.23)
вычисляются элементарно:
56
Г
Г(я/2)
где в последнем интеграле произведен переход к евклидовому
пространству и где учтено, что
для любых целых и нецелых n<2k.
Метод основан на утверждении, что для вычисления перенор-
перенормированных величин достаточно знать аналитическую функцию
и, стоящую справа, при л-И. Поэтому, полагая я=4—2е, где е-*
->О, получим, в.частности, для k=l:
Здесь учтено, что ГA— я/2)=ГB — я/2)/A— я/2)*= — Г(в)/A — в>
(так как Г(л:+1)=.*Г(л:)) и что при 8-+0
), D.31),
так как ГA +в)^1 — у^в, Ye=— (rfr 0 -f-Jc)/rfJc)x-o== 0,5772—по-
0,5772—постоянная Эйлера, причем было введено обозначение <ц
° D.32)=
так что Af02-»-oo при 8-М). Всюду, как н ранее, A^L+q2. Простой-
значение D.30) является аналогом формул D.20), D.21), кото-
которые более сложны, но приводят к тем же значениям перенорми-
перенормированных величин.
Дифференцируя D.30) по qx или L [или полагая k=2 в D.29)
и используя D,31)], получаем простой аналог формул D.23):
f (Ь Лт. РхРа) (IE.) (. аа,ек* а \Т1
, 0, вив)[1п(Л^/Д) + 1] А, D.33)
где в нижней строке произведен переход к пределу 8-»-0 соот-
соответственно D.31), D.32). В пределе е-М) интегралы D.30), D.33)
не зависят от выбора \i, но зависят от величины Мо, которая*
аналогична пределу обрезания интегралов по импульсам.
Дифференцируя обе части D.33) по L (т. е. по b=L+q2),
легко получить значения таких же интегралов с ббльшей;
57
•степенью знаменателя:
Г О-Ра.РьРа) rd
J (p*-2qP-Ly W
(i. *. ш+[о. о, Щ г (в) Dт)
Г A. Ру РьРу) ldp\ _
J W-29P-1-)* \«Ч )я~
-(о, о. ^
D.34)
¦где, как и всюду, выше (dp/n2i)»=16nsrfnp/Bn)"i, причем
Г(е)(|Д/4яц2)-«~1п(Л10а/А) при в-*О.
Преимущество формул размерностной регуляризации состоит
в том, что они немного проще полученных обрезанием по им-
импульсу и, главное, сохраняют калибровочную инвариантность тео»
рии: в КЭД они, в частности, автоматически дают П@)=0, т. е.
"П(<72)~<72 и q*-+0. Однако, чтобы не ошибиться, надо все вычис-
ления со спинорами и тензорами проводить не в 4-мерном, а в
л-мерном пространстве и далее считать п=4—2в |члеи 2в после
умножения на 1/е в D.31) даст конечный вклад при 8-*-0]. Так,
пнужно учесть, что A/4)-у„2= A/4)^,ц,=п/4ч=1—«/2.
При любом n YfYv+YvYe— Igv», отсюда следует, что
D.35)
¦Этих соотношений практически достаточно для выполнения всех
вычислений (величину vn=Sp-l, равную фактически 2л—4, можно
люложить равной четырем).
В качестве примера вычислим в размерностной регуляризации тот же
-оператор B.10) поляризации |ЦA)(в'*)'=11я,я,(9'1)/3- Первое из равенств D.35)
.дает в л-мерном пространстве
A/8) Sp [ук (р + т) ук (p—q—m)] - (я/2) от' + (я/2-1) (pq—p1).
я-4) рг
т. е. И*1» (?') = (-2а,/3я) [(я/2) тЧ + (я/2-1) ^/„-(я/2-1)
«где /, 1С и 1%<3—интегралы D.33). Используя их значения, получим, обозна-
обозначив аналогично D-24) pjj .= Д-г/ц1 = от1/^1 + Jr A— дг)(—q1/».1):
Зл
-*Iп
:Б8
где в последнем равенстве был выполнен переход к в-+0 и где ^
есть величина D.32). Масса фотона оказалась теперь равной нулю Х' =
= Ш ' @) = 0, а для постоянной Z, перенормировки получаем значение!
отличное от найденного в разд. 4.4
Z, = 1 +П*1»' @) = 1—(а,/3я) [In (Alg/n')-2/3] D.37)
из-за различия величины М^- предела обрезания интегралов по импульсу —н
сходной с ией величины Mo, определенной в D.32)). Для
П«> (?«)/?«= П<х> (?')/?'-(Z,-l) D.38)
получим точно то же значение D.25), D.26), что и при обрезании интегралов
по импульсам. Ясно, что конечное значение разности Wi)(qt)lq'^(Zi—1) можно
получить, выбирая Zs и многими другими способами, отличными на постоянную
от D.37).
В связи с этим следует упомянуть о других способах перенормировок
(или вычитания), отличных от схемы гл. 3, которые обсуждаются в литературе
[4.5] в применении к теориям, в которых и фермионы—безмассовые1. Наибо-
Наиболее простой способ—это так называемая минимальная схема вычитания
minimal subtraction зсЬете, сокращенно MS), в которой Zs = Z^s, причем
т. е. в отличие от D.32) In (Afj^s/nJ) ¦=. l/e-«-oo. Ясно, что в этой схеме
правая часть D.38) отличается от D.25) малой постоянной (—а,/Зя)Х
ХAп4я—\в—2/3)). По аналогии с М^ величину Мщ, определенную
в D.32), обозначают М—§. причем, как следует из D.32),
In («Jg/AIj,s) -= In 4n-YE - 1.954. D.40)
В схеме вычитания MS величину Zt •= Z^s также удобно определить в стан-
стандартном виде D.39) 2ri*s.= l— (os./Зя) In(All^/ц1), М_=Л1„ немного от-
отличном от D.37).
Еще один способ—считать, что Zt—1 ¦—[(I/ji)II(ji)]4i-_p(M где ц—не-
ц—некоторая фиксированная масса [именно этот способ и был использован в D.37)
при ц* = А,»-=0]. Это иипульная схема вычитания, сокращенно mom (от
слова momentum, т. е. импульс); в ней Zt =» Zg10, где, как и в D.39),
= \—(<х,/ЗяIп(А!^от/ц«), причем, как следует из D.36),
D.41)
1 В этом случае в D.36) величина р»=1+жA—ж)— qVai2 (сц-=/п) обра-
обращается в бесконечность при /п=0.
59
где
i
А, - In 4я— ув—B/3)—6 Jх (I — *) In [ю'/Ц1 + л A — *)] Ас. D.42*
Так как 1/в = 1п(А!^8/ц»), то при
ln (
1
где учтено, что J лгA—лгIплг (I—дг)rfjc -= — 5/18.
Во всех трех схемах перенормированный заряд е* = 4яа определяется
в стандартном виде C.26):
_ а,-а <|»«)-«А (ц«), D.44)
т. е. а*18, ое^15 и а™ош различаются (уже в порядке а*) членами, не содержа-;
щими большого логарифма. Например,
р -1 -(«./Зя) In (Л*^/<5)~
~l-(a*s/3n)(ln4n-Ye), D.45)
где справа было использовано D.40) и величина а. с точностью до членов
порядка а\ была заменена константой a^s. Точно так же
amom/Q,MS = ZmomlZWS = j_^aMS/3n). Л, (цг), D.46)
где Ло (от2) =-0,96. Как видно, эти различия в определении чувствуются только
в высших порядках ~Ог* по степеням величины а,.
В КЭД, где тФШ, удобно нормировать на точку ц=га и использовать ка-
каноническое определение C.26) перенормированного заряда аг=*а<?3 @), где
Z9@)—величина D.37). Однако в рассмотренных ниже теориях поля, в кото-
рых все частицы безмассовые, приходится пользоваться одной из указанных
выше схем вычитания. \
Задача 4.1. При нецелой размерности п=»4^-2в вычислить элемент фазового
объема системы двух безмассовых частиц
Bя)"-* 2?,
для заданной полной энергии системы W=» W-
Ответ. При размерности я—I чисто пространственной части вектора р»
(угол между которым и осью OZ есть в: р,пг= J5icos6) имеем:
я-1
_ 2
я-2
_ 2
или ~Ш 1п-2\ Е"~ dEl <sinв>Я~3
г(-г-)
60
я-4
где (sine)"-8de-2n-*[y(l— у)] 2 dy, если у~A—cos6)/2 н
с
о
1
f)]*,—r(;_2)—Ж
rl~2~j
Последнее равенство справа есть следствие теоремы удвоения [4.4], согласно
Так как (q—p,)f = TF1—2ТР?„ то отсюда получаем
"^ (п—2\
п2т[—)
Bл)я-*2Г(п— 2) w 8я Г B—2е)
Замечание. Фазовые объемы¦ нужны для вычисления мнимых частей
графиков Фейнмана (см. разд. 2.4) при нецелом п *=4—2s.
Задача 4.2. в этих же условиях вычислить элемент фазового объема
трех безмассовых частиц dRt - Bя)* *-• dxt •= ^?Х 2?^* 6 ((?—Р»—PiI) B
зависимости от энергий ?, = |pi|, ?t-!Pil двух из них и от угла 6„ между
р, и р,.
Ответ-решение. Подставляя значения dP~xpx и dn"*/>i из предыду-
предыдущей задачи, находим:
BЯJ8ГB-2в) '
где учтено,-:что (?— pi—лI" ^—21^ (?, + ?,) + 2?,?, A— cosв„) и что
поэтому J6((^—pi—pi)*)dcose,i=»l/2?i?s, причем в°2 то значение угла,
при котором аргумент б-функции исчезает, т. е. для которого
у » (i -cos в?2)/2 = [2TF (?, + ?,)-Г»]/4?1?1.
Задача 4.3. Интегрируя по ?, = дг,ТГ/2 и ?f = xtW/2, иычислить полный
фазовый объем Л» =¦ J dRt = Bя)*n J dt, системы трех безмассовых частиц
предыдущей задачи.
О т в е т. Подставляя ?, и ?t в указанном виде, находим из результатов
предыдущей задачи, что у(хх+х%—l)/xtxt. Поэтому, введя вместо
xt = (l—xt)l(l—хгу) переменную у, получим d?,d?,-= (TF»/4)xx (I— Xi)dxtX
Xi}—Xiy)-*dy, причем обе переменные, xl'=2El/W и y-»(l/2)(l— cos6j2),
взиеняются независимо в пределах от 0 до 1. Это дает
S 1
1 . вГ'A-Е) ч
U^f ГB-2е) /¦
ГB-2е)
61
ак как [4.4] 1кк. (дг,)= J
о
"* Г(Г+*/—2е) A~~-у')~~*+8. т> е- оба интеграла по у и по лг, вы-
вычисляются точно.
Задача 4.4. Вычислить ширины распада тяжелого кванта (векторной части»
цы с массой Мг=Уо*) и скалярной частицы на безмассовый фермион и анти-
фермион в пространстве нецелой размерности п—4—2е.
Ответ. Используя матричные элементы задач 2.1, 2.2 и фазовый объев*
dxt из задачи 4.1 (лрн W**Mv, или W=Ms), получаем:
D.48)
Ts [' > - 2/*JW§, Fs - A/2MS) I < | rs |«) rft,
- (/*/4я) Msr(l-e)/rB-28),
2
где а8- Dя/^2и)8а; /
4.6. Сокращение инфракрасных расходимостей
и дважды логарифмическая асимптотика
Мягкие фотоны в КЭД и физические сечения. Помимо ульт-
ультрафиолетовых расходимостей в фейнмановских интегралах, опре-
определяющих радиационные поправки (одио- и миогопетлевые) к
амплитудам различных процессов, встречаются инфракрасные
расходимости, возникающие за счет области интегрирования по
очень малым импульсам виртуальных фотонов. Хорошо известно,
что они обусловлены равенством нулю массы фотона (А=0) и
связаны с тем, что реально процессы рассеяния заряженных час-
частиц идут лишь в том случае, если они сопровождаются испуска-
испусканием («стряхиванием») бесконечного числа мягких фотонов — со
сколь угодно малой энергией. Эти расходимости должны точна
сокращаться во всех физически осмысленных величинах, напри-
например в суммарном сеченин рассеяния электрона во внешнем поле
Лц с испусканием им при этом любого числа мягких фотонов
о?Офи3 = da0 -f 2 dan, D.49)-
«—1
где rfao=rfaei—сечение чисто упругого рассеяния, а dan—сечение-
рассеяния с испусканием п фотонов с суммарной энергией coY =
л
= 2 ю*> меньшей некоторой заданной малой величины toY<co0.
*—i
Выберем ©о^-Е, где Е—характерная энергия процесса, в;
данном случае Е — энергия электрона.
62
Вычислив вероятность излучения такого мягкого (длинновол-
(длинноволнового) фотона dWl=daildao, получим в первом порядке по e=i
=е2Dя) за счет вклада графиков вида ряс. 4.3 с п= 1
dWt = -(«/BлJ) (p'^lp'k-p»ipkfd*kl<s>, D.50),
так как при ш<соо<^? эти графики дают для амплитуды рассея-
рассеяния электрона с излучением Тх = еуТу„ где е»—вектор поляриза-
поляризации фотона.^ a Til=e(p'fl/p'k-Pil/pk)T^ (р'г р), Тр(р',р)~
—¦ — е (и (/?') А (?) и (р)) — амплитуда упругого рассеяния. Отсюда
для среднего числа длинноволновых фотонов ло= j dWlt излу-
Х<ш<ш,
ченных при рассеянии, получим хорошо известное значение (см.
[1.1, 1.2. 1.5]):
(О,
Л0(со0, Ь) = Bа/пM(/?', р) \ dc3/c3 = {2a/n)B{p', /7) In (о>о/Я), D.51).
где при she=VQ2/4m2
In V*+i*+V* -1,D.52)
причем Q2=—(p—p'J=(P—P'J—импульс, переданный при рас-
рассеянии электрона B6 совпадает с логарифмом в D.52), actg B0)—
с коэффициентом перед логарифмом). В D.51) расходящийся
интеграл по импульсу |к|=со фотона обрезан иа некотором ииж-
ием пределе со=Я, что эквивалентно введению фиктивной массы1
фотона, а верхним пределом является заданное значение шо мак-
максимальной энергии фотонов.
Ясно, что испускание каждого такого мягкого фотона происхо-
происходит независимо от излучения остальных, поэтому распределение
по числу п этих фотонов должно быть пуассоиовским
%n=l D.53).
л—0
и каждое из сечений dan в D.49) пропорционально соответствую-
соответствующей вероятности Wn. В результате при А,->0, когда /ig-^-oo, все
члены с любым конечным п в сумме D.49) обращаются в нуль;.
суммарное сечение а?ОфИЗ в силу условия Jt, Wn*=\ остается ко-
л=-0
1 Прн введении массы фотона Я., вместо D.50) получим
: а ( Р'ц Pv. \ <Pk
что дает прн интегрировании по всем к (с |к|<ш») и прн Я., —сХ значение п,г
отличающееся от D.51) членами, не сингулярными прн А.-+0 (онн обращаются
точно в нуль для нерелятнвистского электрона [1.1], если с=«2ехр (—5/6)].
63"
нечным и при Х=0. В частности, при А,->0 первый член в D.49)
получим в виде
rf<ro=rf<roexp(—/io)=rfo0exp[—{2a/n)B\n{E/X)]t D.54)
где da0—величина, не сингулярная при X-+Q, и где вместо ш0
подставлена энергия Е, поскольку этот члеи обусловлен вкладом
графиков лишь с вертуальными фотонами и отвечает отсутствию
реальных фотонов (энергия которых только и была ограничена
выше условием cov<coo).
Теория возмущений неприменима, если «z^l, но при Я-»-0,
когда а1п(ю<А),>1 (или aln(E/X)>l). Тем не менее экспоненци-
экспоненциальную зависимость D.54) dao от а\пХ можно получить иа ее ос-
нове (без всякой связи со всем сказанным выше), выбирая малое
X, но такое, чтобы еще выполнялось условие aln (?Д)<1, и сум-
суммируя главные логарифмы, т. е. все степени [aln(E/X)]h [4.7].
Задача 4.5. Показать в первой 'порядке теории возмущений, что da,
-при 1п(?Д)>1 (но при aIn(?A)<l) имеет вид D.54), т. е. что
da, - (rfa.).|[l —Bа/я) В In (Е/А.)], D.55)
где (da,), =- < |7^0>|f/16nf )dQ—сечение рассеяния, вычисленное без радиа-
радиационных поправок.
Решение. В первом порядке по а амплитуда упругого рассеяния есть
Tt*=T^ +Т$К где 7^0) было приведено выше, а Т^ определяется вкладом
графиков рис. 4.2 в виде
ТР- A/21) J Dp, (*) 7$ (Р1, Р\ к, -к) d*k/Bn)*. D.56)
Здесь в калибровке Фейнмана Ditv(k)<^gilv/k*{cM. рис. 4.3 при п—2)
p-p-q
Рис. 4.2
! {Р', р; *., *t) - •« (рд/р'А,-VP*O [р'ч/Р'кш—Ру/рк,) Т^[Р', Р) D-57)
—амплитуда излучения двух мягких фотонов, сингулярная как при ftt-*0, так
и при fcf-t-О (множитель 1/2 в 7^ компенсирует удвоение интеграла по k,
отвечающее *-•-—k). Подстановка 7",^ в интеграл дает при р*=,р'2*=т*
б*
О ва' 0 " ' Р ) ~9Г
_j??l_ ?!!/
(p'k){pk) J A»+ 10 '-s
и после взятия интеграла no k, (путем замыкаиня контура вокруг полюса
А,=-|к|—10) приводит к D.55), так как
rju.-rf — [ f Ipp') _ mtJ2t_ тЧ\ 1
4я|к|
-Т{Р (Р\ Р) («/я) В (р', р) In (?Д).
Здесь учтено, что
/(Р'. />) - (РР;) fc1 ^ (p/fe* (p^) ¦=¦ (Рг
D.58)
-х)Ф °2ecth26'
где pp' = m1 + Q!/2; px-Xp + (\—x)p' и /(p, p)«=I. Первый член слева
в D.58) отвечает вкладу треугольного графика рис. 4.2, а.
Задача 4.8. Формулу D.57) для
сингулярной при k,, &2-»-0 части ам- X, В„ (а)
плитуды излучения обобщить на слу- " ^
чай испускания п мягких фотонов при
рассеянии.
Решение. Сингулярная по каж-
каждому из импульсов фотонов при ki-*-
-«-О часть амплитуды излучения лрн
рассеянии определяется суммарным
вкладом графиков вида ряс. 4.3, раз-
различающихся лишь всеми перестанов-
перестановками фотонов, и имеет вид, аналогич-
аналогичный D.57):
Рис. 4.3
'' р> *»• ** *«)"*
¦епТ.(р',
(-1)"
m
где 2р включает лишь перестановки фотонов, испущенных из начальной
tit
и конечной фермионных линий [но не включает перестановки внутри каждой
из этих двух групп т и п—т фотонов, которые учтены уже в каждом
члене в D.59)]. Амплитуда Т,(р', р) включает радиационные поправки лишь
с большими виртуальностями внутренних фотонных линий (с|к/|^? и с
^ и остается конечной при А.-*0.
Задача 4.7. Используя решение предыдущей задачи, найти суммарно по-
поправки всех порядков по а1п(?А) к амплитуде Ta(j/,p) упругого рассеяния и
получить соотношение D.54).
6—679 65
Решение. При учете всех этих поправок амплитуда упругого рассеяния
определяется формулой, аналогичной D.56):
D.60)
где ft(p', p) включает радиационные поправки лишь от «жестких» внутрен-
внутренних фотонных линий (с со/^Е) и несингулярна при Х->-0. Подставляя сюда
амплитуду излучения иягкнх фотонов в виде D.59), получаем
Т, {pf, P) -Т. (/>', р) 2 ЦР (-^1^)" - Т„ (р', р) ехр [-л, (?, к)/2],
D.61)
где п,—величина D.51) с заменой со, на В. Отсюда для сечения рассеяния
rfa, ~ 17\, |* получаем значение D.54).
Таким образом, первый член в сумме D.49) имеет вид D.54),
где множитель dao несингулярен при Я-»-0 и сам может быть пред-
представлен в виде ряда по степеням а.
В таком же виде может быть представлено сечение dao' лю-
любого процесса в КЭД (ее-, -уе-рассеяния, рассеяния электрона на
внешнем поле с испусканием любого числа жестких фотонов и др.):
rfa;=rfa;exp [-Ba/nM1п(Е/Щ, D.62)
где da'o определяется суммарным вкладом графиков лишь с жест-
жесткими внутренними линиями виртуальных фотонов, а В теперь
зависит не от одного инварианта (p'p)=m?-\-Q2/2, построенного
из импульсов р', р электронов (находящихся на массовой поверх-
поверхности р2=р''=т2), а от всех комбинаций таких инвариантов
(p'iP/)> (p'iPj) и (PiP))> гДе штрихом обозначены выходящие, а без
штриха —входящие импульсы всех заряженных частиц.
Формула D.58) в задаче 4.5 показывает, что величину В можно
записать в следующем общем виде:
в IVС чт/(PjP/) а*ь у ШЖ.]П i + hi
4^0 (Pik)(Pik) 2я|к[— *f 4pi/ l-p;/'
где для входящей частицы ti,= —1, а для выходящей x\l=-ir\r
а р^ = [1—т^/(/?;руJ]1/2—-скорость i-ro электрона по отношению
к /-му (р\г=О). В частном случае рассеяния на внешнем поле
члены с i=j, относящиеся к импульсам входящего илн
выходящего электрона, дают в сумме (—1), а член,
в котором р(=р', Pj=p, дает первый член справа в D.52).
В этом виде величина В определена для любого процесса с любым
числом импульсов Ри Рг РгР2--- входящих и выходящих
заряженных частиц, и именно в этом виде [4.7,4.8], независящем
от X при А,->о, она входит в D.62).
66
Найдем следующие члены в сумме D.49), т. е. все сечения
dan испускания п мягких фотонов при рассеянии. Соответствую-
Соответствующие амплитуды излучения, сингулярные по импульсам kt всех
мягких фотонов, были получены при решении задачи 4.6 и имеют
факторнзованный вид, аналогичный D.59):
'. Р> kU *2»
Т (в' п\е» У / IV-
Zi 2л {P'k1)...{p'km)(pknHl)...(pkn)-
т—и гя
Эти амплитуды отличаются от D.59) тем, что при заданном
числе п реальных фотоиов содержат полную амплитуду Т0(р',р)
упругого рассеяния, включающую все виртуальные инфракрасные
расходимости, а не только жесткофотонную часть ее То, как
в D.59) [в виде D.59) амплитуды 7\ц...»1в были нужны для решения
задачи 4.6, в которой все эти расходимости были исключены
ъзТ0(р',р)].
Возводя в квадрат модуль амплитуды D.63), суммируя его
по поляризациям и интегрируя по фазовому объему п мягких фо-*
тонов, получаем с учетом множителя 1/л! от тождественности фо-
фотонов: 'л\
^ РЩ^"№$><»„-»,-...-<,,), D.64,
где В(р', р) — величина D.52), несингулярная при Я-И), а
9-функция вырезает нужную область, в которой энергия фотонов
не превышает заданное малое значение соо<сЕ. Интеграл справа
легко вычислить, используя для 8-функции фурье-представление
ft—I
00
что дает физическое сечение da^m'=^idan D.49) в виде
л-0
а?афиз=daof (аВ) ехр [Bа5/л) In (%/&)], D.65)
где / (аВ) = —- \ s/"q da' ехр { ° \ --^- [ехр (Ico'a') — 111 (здесь
а'=асоо, а со'=со/о>„—несингулярная при А,->0 величина).
Подставив сюда da0 в форме D.54), получим для физического
сечения значение [4.7, 4.8]
>> р) In±], D.66)
несингулярное при Л-»-0 и зависящее от велнчны Шо, определя-
определяемой лишь условиями эксперимента.
5* 67
Как видно, инфракрасные расходимости, возникающие при Я-»-.
I в физическом сечении D.49), D.66), точно сокращаются.
Этот результат легко обобщается на случай любого процесса в
(КЭД): его физически осмысленное сечение определится суммой
вида D.49)
^2i D.67)
я«-0
сечений da'n этого же процесса, идущего в сопровождении испус-
испускания любого числа п мягких фотонов Bщи<що]| и может быть
приведено к виду D.64)—D.66):
ln X ] »
eifi^(ав)ехр [ -Л5Ё.In±]. D.68)
[ ]
Особенно просто сокращение инфракрасных расходимостей
выглядит в теории возмущений — при разложении всех членов
суммы D.49) в ряды по степеням а=е*/4я. Дело в том, что се-
сечения dan (или da/) в D.67) исчезают пропорционально а" при
а-*-0 [за исключением общего множителя а*, входящего в йа</,
который есть и во всех членах D.49), D.67) и который мы усло-
условимся сейчас во внимание не принимать].
Поэтому:
а) в нулевом порядке по ada^u3 — da0',
б) с точностью до членов первого порядка по a rfa^3==rfaW +
-f- doM+de[l\ где индекс сверху указывает порядок по а. Так
как rfff(I'=efa<°)Ba/nM1n(cu0/A,), то первый член в сумме D.49)
должен обязательно содержать a In Я,. Из D.55) видно, что ои,
действительно, его содержит и в точности сокращает;
в) в следующем, втором порядке по а в аа0 нужно удержать
три члена: doo^doW+do^+do^, в dat—два: rfai^daW-f
-frfo{2>, а в rfa2—один: da2^dafK По сравнению с предыдущим
порядком остается сумма членов порядка а2, а именно do№-\-
_j_rfcr<2)^da<2>, в которых все 1п\ точно сокращаются.
Этот рецепт распространяется иа любой следующий порядок
теории возмущений и очень удобен для практических вычислений
в теории до или после перенормировки.
Формулы D.65) и D.68) демонстрируют, как In Я, сокращается
вие рамок теории возмущений. Это сокращение инфракрасных
расходимостей, возникающее при суммировании сечеиий процес-
процессов с испусканием различного числа мягких фотонов, является
•следствием общей теоремы, установленной Ли и Науенбергом
[4.9] и в менее общем виде Киношитой [4.10]. Теорема Ли—Нау-
енберга—Киношиты относится к общей (не ограниченной только
•случаем КЭД) ситуации, когда имеются вырожденные по энер-
68
гий состояния, причем это вырождение можно снять, введя неко-
некоторый параметр ц. F рассмотренных выше примерах вырожде-
вырождены состояния с различным числом бесконечно мягких фотонов, а
роль параметра ц, снимающего вырождение, играет масса фото-
фотона Л). В этом случае при вычислении S-матрицы по теории воз-
возмущений матричные элементы S,<, вообще говоря, сингулярны
при стремлении ц к нулю. Обозначим D(E{) множество состоя-
состояний, вырожденных при ц=0 с начальным состоянием i, a D(Ef) —
такое же множество для конечного состояния f. Теорема Ли—
Науенберга—Киношиты утверждает, что величина
W(Ef,Et)= 2 2l5/<l2. D-69)
где суммы берутся по вырожденным по энергии начальным и ко-
конечным состояниям, конечна при ц-»-0 в каждом порядке теории
возмущений. Заметим, что в D.69) стоит сумма вероятностей пе-
переходов из всех начальных состояний с одинаковой энергией Et
во все конечные состояния с одинаковой энергией Et. Ли и Нау-
енберг также показали, что в частном случае вырождения со-
состояний с различным числом мягких фотонов для получения ко-
конечного значения достаточно суммировать вероятность только по
начальным состояниям (или только по конечным). Отметим, что
в электродинамике можно рассматривать в качестве параметра ц
также и массу электрона. Прн /я,-»-0 становятся вырожденными
по энергии состояния с различным числом бесконечно мягких
эЛектрон-познтронных пар. В этом случае для получения ко-
конечного при те-»-0 результата необходимо суммирование в D.69)
также и по вырожденным начальным состояниям фотонов и элек-
трон-позитронных пар.
Мы не приводим здесь доказательство теоремы Ли—Науенбер-
Ли—Науенберга—Киношиты, исчерпывающее изложение которого дано в их
работе [4.9]. В ней также разобраны примеры применения дан-
данной теоремы к инфракрасной проблеме в КЭД с массивными и
безмассовыми электронами.
Коллинеарные расходимости и дважды логарифмическая
асимптотика. Формулы D.66)—D.68) особенно интересны в облас-
области больших энергий н больших переданных ипульсов при Q2>wi2.
Из D.52) видно, что при этом B^ln(Q2/mz)> 1, т. е. 4о'4ла~
~ехр[(— 2a/n)ln(Q2/m2)ln(E/<o0)]1 причем в системе координат
Брейта (в которой р'= — p)?"=>/rQ2/2 и rfa^,3 — exp[(— а/я)Х
Xln(Q2/m2)ln(Q2/4©o)]. Эта формула описывает весьма сильную
зависимость сечения от Q2 при Q2>m2: как видно, в разложении
' экспоненты на каждую степень а приходится две (а не одна, как
обычно) степени большого логарифма. Поэтому эту асимптотику
называют дважды логарифмической. Из решения задачи 4.5 вид-
видно, что логарифм B«"=ln(Q2/m2) возникает во вкладе треугольного
графика рис. 4.2,а за счет области, где импульс виртуального фо-
фотона к параллелен импульсу электрона в начальном или конеч-
69
ном состоянии. Действительно, оставляя в D.58) лишь первый
член, получаем для вклада графика рис. 4.2,а значение
In D) / (Pr, P), D.70)
где в системе Брейта, в которой cos&„* = 2, cos ЬР'„= — z при
Q242 и p2=l-m2/E2==l-4m2/Q2,
Г
V(pp')dQk/{4n) Г <fa . Q'
(p'k)(pk) )
— ) (i_pV)—m mi
Как видно, интеграл по z расходится при m?/Q2=Q на верхнем и
нижнем пределах, т. е. при &р*-»-0 или при ЬР'к-*-0. Эти так на-
называемые коллинеарные расходимости и приводят к появлению
квадрата логарифма в формфакторе упругого рассеяния:
Определенный так формфактор (с электронными линиями на
массовой поверхности p2=p'2=nfi) является нефизической вели-
величиной и обращается в нуль при \-»-0. Поэтому удобно определить
амплитуду Т0(рг, р) вне массовой поверхности в так называемой
судаковской кинематической области [4.11]:
D.72)
в которой вклад треугольного графика рис. 4.2, а [определяющий
отклонение отношения D.71) от единицы, т. е. То/Т — 1 =
=S(I)(Q2, Ц2)] согласно D.58) равен
{р'р)
Интегрируя по k0 путем замыкания контура в нижней полу-
полуплоскости на полюс fto = |k| —10, получаем в системе Брейта
В 1
а С rflkl С dz
л
0. ' -1
1 I
A,
где учтено, что основной вклад в интеграл (при ц2^то2) дает об-
область l>p=|k|/?1>n2/Q2, &pft<L Отсюда следует [в пренебре-
пренебрежении членами 0(aln(Q2/n2))], что
Соответственно этому суммарный вклад всех инфракрасных син-
70
гулярных графиков дает в кинематической области D.72) для от-
отношения D.71) с учетом всех членов вида (l^Q22))"
-? In» (-?)) +0 (а- щь-, ?). D.73)
= ехр
ВЛКЭД эта асимптотика была получена В. В. Судаковым
[4.11] в 1956 г. В квантовой хромодинамике, в которой констан-
константа а. относительно велика (a,«0,2-f-0,3), экспонента в D.73)
превышает единицу уже при достижимых значениях 1п(<2/ц)<=*
«3—4.
Задача 4.8. Вычислить ширину Г(У-*-е+е-у) трехчастичного распада
тяжелого фотона—векторной частицы на фермион-аитифермион с нулевыми
массами и на реальный фотон при нецелом л =4—2в.
Ответ-решение. Матричный элемент распада У^-*е*е~у^, отве-
отвечающий вкладу двух графиков рис. 4. 3 с B^-4-V^ «•=!, —р=Ри р'=Рь есть
где заряд в вершине испускания фотона с k,^p, и с поляризацией^ обо-
обозначен g (чтобы отличить его, если это надо, от заряда е распада вектор-
векторной частицы). Возводя модуль Г* в квадрат и использовав калибровку Фейи-
мана, в которой (е^ед) — — gya, подучаем после простых, ио длинных
вычислений при
0,0'
РгРг)+
где My"q1{pip1 + piP,+p1p,) и где использованы формулы D.35). При
интегрировании по фазовому объему J < 17*? | *) dR, члены, отличающиеся
лишь заменой импульсов местами pi+tpn, дают одинаковый вклад. Поэтому
первый член в квадратной скобке дает то же, что 2A—в) piPt/ргР» а вто-
второй член—то же, что ^{PiPtYl(P\Pi)(PiPt)+^P\PtlPiPn и эта скобка может
Г 2tPiPi)* ptp. I
быть представлена в виде , ., ;+2C—r) ~z-r-—2в . В результате,
используя dRt из задач 4.2,4.3 (при W = MV) и учитывая, что. р, — —pi—ра,
M2V Xi(\-xt)y M2VXl(i_y) M2V
т. е. что^1Л = -2 l—xiy—' ЛЛ'Т 1— xiy ' P*P*~~2~*- *''
71
находим:
f
< I Г? I1 ><*/?.-—3—^ г~B-2в)' [A + C-e)J,-8
где /*- J**-*¦ (I —Jet)^2"/*., (*•)**i. * = 1.2; /,«}[*, A— д;,)]2"^
X'»«(Jfi)rf*iF a /ft(ft-(*i)—интегралы по у, указанные в задаче 4.3. Под-
Подставив их значения1, подучим Г {V-* е*е-у) => ^jfi— I < 1 7^ | *) Bn)"-» B виде
«ё Г* A-е) гB—в) A — 8) C—в)A—в)
—F5=iL $ ~
где *««FE=3i)L$~ё
причем ae = g/4n = (g44n) Dя/Л*?)8, а г? = (аеМк/3) Г B—е)/ГB—2в)быд©
найдено в задаче 4.4. Значение величины r(V-»-e+e-y) расходится при е-*-(У
из-за нулевой массы рожденных частиц.
Задача 4.9. Вычислить оператор 2(/>) собственной энергии электрона
с нулевой массой в пространстве нецелой размерности.
Ответ. В калибровке Лоренца O^^-fl/*1) («Г,
—l)Si(^). Использование формул D.33), D.34) дает после несложных вы-
вычислений
где a,= a/<i2c; цт— произвольный масштабный фактор. Отсюда 2(р)=?2о(р) я
2(р)»=0 в калибровке Ландау прн ?=0. Отметим, что 2(р)/р исчезает в любой
калибровке, если р*-»-0 и если (—е) выбрано положительным.
Задача 4.10. Вычислить поправку Л?(—рг, pi) к вершине распада тяжелого
фотона на пару безмассовых фермионов (например, иа e+е-), отвечающую об-
обменом виртуальным фотоном—вида графика рис. 1.5, а —в пространстве с не-
нецелым п«=4—2е, ?=pi+ps.
О т в е т. В произвольной калибровке Лоренца
а Г
= 4я J
ft?ift,,/*') (dk
U*i
(см. рис. 1.5, а, где f—pt, p—k=>px), причем р\~ р\ = ®, а
i l
AW)_* frfrfov Г WaT»Wit*i,*i» + Yx (У^ + Я) Ту(У/У-A) Tx.
p\ qxx(\—x)\
' f_ Г ('-«) f 1-8 I" A-8) B_8)(l-8) ()
1 Г(З-Зе) • 7'= _8 Г(З-Зе)' У» 7* ГC-38) '
72
Используя эти равенства и формулы D.34), D.35), подучаем после некоторых
вычислений для Л° = ("й|??и1) на массовой поверхности:
Л<?> = -J- ехр (-Ш) Г (е) J х~г A -х)~е dx J Vl-2tdy X
о о
+ у*х{1 — X)q* VX (УЛ: + Л) Гц (УРх—Рг) YX J и>) -
X (^2 [ —
где о8 = о/цЕ, (—у1/4яц1)~8 = ехр(—1яе), так как ц1 было выбрано равным
Му/4п, My = q* = (fi +р»)г = 2/»i/>i. При нулевой массе фермионов
a f (А1 + *->i) Уц (**—Р* •*) /¦ \
^ ) PaBHa «У™1 TaK KaKB
А-Л можно заменить k-pt + pt'k = 2(kpt), a ?•/>!—значением 2(fe/>i), что
дает л"'= Гц ^" } (feiZTcjT (iJiTj,,1 гДе c==0- Ho nPH C-+Q этот интеграл
исчезает пропорционально С—2е [если (—в)>0]. Таким образом, Л^1' =0, т. е.
для безмассовых частиц вершина Л^зЛ^ не зависит от выбора калибровки.
Замечание. При ?=0, т. е. в калибровке Ландау вершина А» вообще
ие содержит в графике рис. 1.5, а ультрафиолетовых расходимостей, поэтому
все полученные выше расходимости Л„ при е-»-0, пропорциональные Г(е)е»Л/е к
¦ 1 /е2, чисто инфракрасные, т. е. появляются при нулевых массах частиц за счет
очень малых импульсов интегрирования.
Задача 4.11. Используя результаты двух предыдущих задач, вычислить
амплитуду распада векторной частицы (с массой Mr) с учетом всех однопет-
левых поправок от обмена виртуальным фотоном.
Ответ. Учитывая, что 2(/>)//= 0 на массовой поверхности для частиц
с нулевой массой (при (—е)>0) и что Л^= ("a^Yji11»)^ С0"- задачи 4.6, 4.7),
находнм в однопетдевом приближении
17L
»Л«/\^^ + «Л/\/Ч^5 + W4/VH^ + «ЛЛЯШ^ в
где Л-W - 2L ехр (_1Я8) ^_^) г (е) (l - 8(lL2e))- По9™му, исполь-
используя результат задачи 4.4, получаем ГG-*в+в-) = Г^-A + Д2), где
ае Г1 A—e)cos«e I 2
— ГA J28) Г(е) (!_ e,(i_2e
Значение этой величины расходится в пределе при 8-ьО за счет только
инфракрасных расходимостей.
73"
Задача 4.12. Вычислить полную ширину т[м\) = Г(У-*е+<г) +
(У-*е+е-у) распада векторной частицы на е+е- и на е+е~у. Учитывая,
¦что 1тП {My} = — MVT {Mv), найти ТтЩд1) в порядке а* •= (е1 /4лI в теории
возмущений.
Ответ. Складывая полученные в задачах 4.11 и 4.8 значения, находим
где
"'ПИ „Л ! Г 0-«/2) A-8)
1ГПA-в)|ГA_зв) [ A_38/2)A-38)8» -
A-в/3)A-8) 3 I ГA+8)СО5Яе Г-1 3 11
- A-38/2)(l-3e) 2e"+0(8)J+ ГA-2е) |_"i*—гГ+°(e>J}-
Разложение в ряд по в функций [ГA— Зв)]-* и /(8)=r(l + e)cos«8/r(l—2в)
доказывает, что до членов порядка 81 эти ряды совпадают: /(в)~
~[ГA-Зе)]-> = 1—Ve38 + A/2) (у|-я»/б) (Зе)« + .... где уЕ = 0,5771 —
постоянная Эйлера (она появляется, так как ГA+-*) = 1—Уе-* +
+ (v|+я1/б) Jfl/2+•••)• Кроме того, разложение в ряд по 8 первой квад-
фатной скобки дает для нее 1/в1 + 3/28 + 19/44-0(8), где всюду 0(8)—члены
порядка е, исчезающие при 8-+0. Поэтому с точностью до этих членов при
•е-ьО
А а* Г' A-8) Г/ 1 3 19\ /-1 3 \л За
д -« Terser \w + s+1)+ It* ~2i -• я - 4^ •
'В сумме все инфракрасные расходимости сократились, как это и должно быть.
В результате при в-»-0 получаем Г [Mv\•= (аМу/Щ(\ +3о/4я) н
ImlK?1)»-— У7*Г (?*) = (—aq1/3)(l+3a/4n). D-75)
Задача 4.13. Используя найденное значение 1тП(?2), иайти асимптотику
функции П(<72) при больших \q*\'>m2 в двухпетлевом приближении, отвечаю-
отвечающем вкладу графиков рис. 1.7, а, б.
Ответ. Дисперсионный интеграл вида D.26) дает для U(qs)fq2 значение
о
о-де ц: произвольно и определяется выбором постоянной С
Глава 5
ИНВАРИАНТНЫЙ ЗАРЯД И РБНОРМГРУППА
5.1. Перенормировка пропагаторов, вершин
и физических амплитуд
Выше было показано, что вся зависимость функций Грина и
вершины от импульса обрезания М расходящихся интегралов мо-
может быть выделена в виде множителей (Z3, Z2 или Z\~x),
•74
зависящих от М, например:
d (/». АР, el) =Z3 {т2, АР. el) dT {P2, m2, e2) E.1)
и аналогично для s[P2, АР, e2) и Г(Р2, АР, eg). Здесь т—физи-
т—физическая масса электрона, а
в? = egzr2Z|Z3=egZ3 (w2, М el) E.2)
—квадрат его физического заряда. В равенстве E.1) наиболее
важно то, что перенормированная величина dT(P2,m2,e2) при
М-+СХ) от М вообще не зависит (см. гл. 3). Это же относится и
к тгеренормированным величинам sr (Я2, т2, е2\ и Гг (Р2, т2, е2),
•определяющим функцию Грина электрона и вершинную часть [см.
<3.9), (ЗЛО)]; Гг(Р2)-функция Тг{р.к) при Я»«|р*|~|*«|.
Напомним, что величины s(P2) и Т(Р2), как и sr, Tr, были
определены в C.9), (ЗЛО), вообще говоря, как спинорные матрицы,
например s(/?)=$(/«)+/к?,(Я2), где s(/«) и s^P2) (P2=—pP)—
числовые функции. Однако в области больших Р2^>т2, которая
будет нас в основном интересовать, спинорные члены в них малы
,[т. е. sl~m2lP2^s(P2), "s<^s(P2)\ и они являются числовыми
функциями, связанными теоремой Уорда D.14) T(P2)==s~1(P2). Для
них имеют место равенства вида E.1): s(Р2. АР, ё$ =
=Z2{m2,, Ai, e2^sr(P2,m2,e2). Напомним также, что функция
Грина фотона была нормирована условием rfr=l при Я2=0, a sr
и Гг—условиями $71==ГГ=1 при —Р2=рР=т2.
Для дальнейшего удобнее нормировать все функции единым
условием
dr = sr = rr=l при Р2=т\ E.3)
Разница в этих двух нормировках несущественна, чисто условна
и сводится лишь к небольшим (порядка аг/Зл~0,1%) переопре-
переопределениям постоянных Z\, Z2 и Z? в равенствах E.1) и таких же—
для s и Г. Будем всюду ниже полагать, что в этих равенствах dn
sr и Гг уже переопределены (умножением иа постоянные,
близкие к единице), так что выполнено условие E.3). Поэтому,
лолагая в E.1) Ра=т2, получаем вместо C.12)
Z3=d{m2, АР, е2); Z2=Z^s{m2, АР, е2), E.4)
-t. e. dt{P2, m2, e2)=d(P2, АР, e*fid(m2, АР, е$ и аналогично
для sr==T~K
Рассмотрим теперь (см. гл. 4) большие Р2, в частности, пусть
Р2-+АР. Значение ЛР-v оо всегда можно выбрать так, чтобы при
pi=AP перенормированная функция d(P2, ./W2, е2) обратилась
в единицу, т. е. d{AP, АР, е^) = 1. Аналогично и 5=Г = 1 при
Р2=АР1, где разница между APl=tiM2 (a— постоянная порядка
«единицы) и АР для дальнейшего не важна, и мы эти величины
75
ниже различать не будем. Поэтому, полагая в E.1) Р2=М2, получаем^
Z^dj^M2, m2, ?2r) E.5>
и аналогично Z2 = Zl = sj1(M2, т2, е\).
Соотношения перенормировки, подобные E.1), можно записать
и для амплитуд Тт любых физических процессов, которые выра-
выражаются через соответствующие спинорные операторы—вершины
^о!№\(Рь kj)~B виДе B-24). Сами эти амплитуды Тт„ как мы=
видели, в пределе ЛР-+<х> от Ж2 не зависят [см. C.22), C.23)],
однако от М2 зависят множители Z\<2 и Zy2, определяющие-
согласно C.8) перенормировку дираковских спиноров и (pft =
^Zy2uT{pi) и ортов поляризаций е^Ц) = Zy2ei,r(j). Здесь
ur(pj) и ех.гU)— физические спиноры и орты, не зависящие от
выбора М2. Поэтому из B.24) [или из C.23)—для соответствую-
соответствующих полюсных членов] следует, что перенормированной вершиной,,
не зависящей от М2 при М2-+ оо, является величина
Рййх (Л. */>], =Z?'^/2nNe<:N$ (Pi. *>)• («4-
где Ne и JVT — общее число электронных и фотонных линий, под-
подходящих к вершине.
Формулы E.1)—E.6) определяют характер изменения основ-
основных величин при перенормировке. Затравочный заряд е0 в них
можно считать зависящим от АР.
5.2. Инвариантный заряд, функции Гелл-Мана—Лоу
Функцию
е2 (P2)=eld {Р2, АР, е\) ^ е2 dr {P\ m2, е2) E.7>
называют квадратом аффективного (или инвариантного) за-
заряда; правая часть этого равенства есть следствие E.1) и E.2)-
Так как d(AP, М2, e$=dr(m2, т2, е2)=1, то е2(М*)=е2, а
e2(mi)=e2r. В КЭД (см. ниже) эффективный заряд есть растущая
функция е2=у(Р2/т2) вида
рис. 5.1,а от Р2, т. е. от
1п(Р2//). Кривую рис. 5.1,а:
можно рассматривать и как опре-
определяющую обратную функцию-
P2fm2=f(e2), Существуют тео-
теории, в которых эффективный за-
заряд g2(P2) убывает с ростом Р2,.
как на рис. 5.1,б. Если все ча-
частицы в теории — безмассовые,,
то #2=<р(Ра/Л2), где Л—некоторая характерная для теории кон-
константа размерности массы, определяющая ход эффективного»
заряда.
Понятие эффективного, или инвариантного, заряда было фак-
фактически использовано в работе Гелл-Мана и Лоу [5.1] в 1954 г.
76
Рис 5.1
Они же заметили, что производная сЦпе2(Р2)/сИпЯ2=
—dlndr(P2, т2, e2r)/dlaP2, где т и ег—фиксированные величины
(физические масса и заряд электрона)—есть функция лишь пере-
переменной Р21т2=/ (е% т. е. функция только е2:
d\Re2/dln[P2=-fi(es)=dlnd(P2, M2, eft/dlnP2. E.8)
Левую часть этого равенства иногда называют уравнением Гелл-
¦Мана—Лоу, а р(е2) —функцией Гелл-Мана—Лоу. Фактически в
их работе [5.1] это уравнение было введено с ссылкой на
Т. Д. Ли в интегральном виде (см. ниже), а в дифференциальной
форме E.8) оно было впервые записано Н. Н. Боголюбовым и
Д. В. Ширковым 1[5.2] в 1955 г. (они же и назвали е(Р2) —инва-
—инвариантным зарядом).
Вид функции ^(е2) Гелл-Мана—Лоу зависит от лагранжиана
рассматриваемой теории. При малом заряде, т. е. в теории воз-
возмущений, она определяется рядом по степеням малой величины
(Я2L 2(Я2)DJ< 1
E.9)
и исчезает пропорционально е2 при е?-*О. Величина и знак коэф-
коэффициента р2 имеют особо важное значение; всюду ниже будем его
-обозначать, как это принято в литературе, —6=,р2. В разных тео-
теориях поля, включая и КЭД, возможны следующие случаи.
а. Если J52=—Ь>0 или, точнее, если Р(е*) положительно
(рис. 5.2,а), т. е. сйпе2/ЛпР2>0, то инвариантный заряд е2(Р2)
растет, как на рис. 5.1, а, с ростом Р2, т. е. с уменьшением рас-
расстояния г2~1/Р8 до центра источника поля. К теориям такого
типа относится КЭД; как мы увидим, они не противоречивы лишь
гпри очень малом значении аг—етЩл=а(т2).
р
0
а)
0
А
Р
0
\1ЧЯ
»*/«Г 1?
PSc. 5.2
б. Если р(е2)<0, причем достаточно, чтобы р2=—Ь<0 (см.
рис. 52,6), то ^(Р2) убывает, как на рис. 5.1,6, с ростом
Р2. К таким теориям относится квантовая хромодинамика
(КХД): в них эффективное взаимодействие между заряда-
зарядами, пропорциональное e^l/r2), исчезает на малых рас-
расстояниях— при Р2 ~ 1/г2-»-оо. Это теории с асимптотической сво-
свободой иа малых расстояниях. В этих теориях на больших расстоя-
расстояниях, т. е. малых Р2, заряд е?=е?(Р8) становится большим,
т. е. связь — сильной (рис. 5.2,6).
77
в. Возможны теории, в которых Р(е2) обращается в нуль, при
некотором ei=e12 и вблизи этой точки р(е2)«6'- (ехг—е2). Если
коэффициент Ь' положителен 6'>0 (как на рис. 5.2,в), то такую
теорию поля называют теорией с фиксированной точкой. В ней
эффективный заряд ^(Р2) при Р2-^-оо стремится к в\2. Действи-
Действительно, если e2<eJ2 при каком-либо Р2, то производная
dlne2[ci[nP2'=$(e2) положительна, т. е. заряд е2(Р2) растет, стре-
стремясь к eia при Р2-^оо. Если же e2>ej2 при данном Р2, то в этой
точке производная dlnePfdlnP2 отрицательна, т. е. функция е2(Р2)
убывает, стремясь при Р2-»-оо к ер.
В теориях, в которых Ь'<0 (рис. 5.2,г), точка #=ei2 неустой-
неустойчива. В них заряд еР^Р2) растет, отдаляясь от этой точки вправо,
если e2(P2)>ei2- Наоборот, если сначала было дано, что е2(Р2)<
<ег2, то с ростом Р2 заряд уменьшается, отдаляясь от точки ер
влево.
Эти результаты ясно видны, если из левой части E.8) опре-
определить dln/e=dlne2/p(e2) и проинтегрировать обе части получен-
полученного равенства по Р2, например, в пределах от .Р2=|12 (где \i
произвольно) до Р2. Это даст
1п(Я2/ц2)= j
т. е. определит кривые рис. 5.1 в виде обратной зависимости
iniP2^2) от эффективного заряда \n(P2/m2)=f(e2) (при выборе
ц=т)—после подстановки явного вида функции Pfe2) и вычис-
вычисления интеграла.
В частности, подстановка Ще2) в виде ряда E.9) дает при
а(Р2)<1
а(Р')
. Ра_4я С ftf.J, о , \
1п Т ) ^¦11 + 1?Г+ ]-
^f^i^ E.11)
или
Если а(ц)<1, a (a(\i2)/4n)ln(P2/\i2) ~l, то последний член
справа мал (при Р4~&) по сравнению с первыми двумя (а(ц2) =
=аг= 1/137 при выборе ц=т). Поэтому с точностью до членов
(а(ц2)/4яJ<1 вместо а(ц2)/а(Р2) в аргумент логарифма можно-
подставить сумму первых двух членов в E.12). Это даст:
78
где
gA)(<ii)E.14).
есть эффективный заряд, определенный в первом порядке по па-
параметру а(ца)/4я<1 (и во всех порядках по степеням величины
[о(ц2)/4я]1п(/>2/и2). которая может быть не малой при;
а(A2)/4ж1, если 1п(Р2/у?) очень велик). Выбирая ц=т или ц=
=М и вспоминая, что a(m)=ar, a(M)=a0, выразим эффективный;
заряд через а, или oto:
a
Полагая здесь Р2=М2 (или Р2=т2), найдем связь между а0;
и аг:
*) ' E'16)'
"""
аг= \—Ь(а,/4яIп(МЧт*)' "о"" 1 + Ь (ог/4я) In {М*/т*)
Ясно, что такие же формулы, справедливые в следующем, втором
порядке по а(ц)/4я, можно получить из E.12) [или из E.13)],.
полагая там непосредственно р=т (или ц=М) и Р2=М2 или
Р2=т*.
Согласно E.7) фотонный пропагатор dr(P2)=a(P2)/a(m2)
или d(P2) =a(P2)/a(M2) определяется, очевидно, этими же форму-
формулами E.12) в виде1
в первом порядке по а/4я вместо dj1 (P2) или d~l (P2) можно-
подставить сумму двух первых членов в правой части.
Так как d(P2)=Z3dr(P2), причем d(M2)=dr(m2) = l, то Z3=
—d(m2)=d7l{AP). Поэтому в первом порядке по а/4я имеем,.
учитывая в E.17) лишь первые члены:
Z3 (т2, М2, в»)-[1 -Ь (Оо/4л) In {ЛР/т*)]-1 -
= 1+6 (аг/4я) In (M2/m2), E.18>
и равенство ar = Z3a0 в точности воспроизводит соотношения E.16).
Легко построить этим же способом и функцию Грина элект-
электрона s(P2,M2,e2)=Z2(m2,M2,e§sr(P2,m2,e2), если учесть, что
производная от ее логарифма d\ns(P2)/d\nP2=dInsr{P2)/dInР2'
1 Эти формулы двухпетлевого приближения были получены впервые
Н. Н. Боголюбовым и Д. В. Ширковым [5.2] в 1955 г. Соответствующие одно-
петлевые значения вида E.16) [или E.17), но без последнего члена] были
построены ещ« ранее, в 1954 г., Л. Д. Ландау, А. А. Абрикосовым и И.М.Ха-
латниковым [4.1] путем решения системы упрощенных уравнений Дайсона —
Швннгера (гл. 2).
79
аналогично E.8) есть функция лишь [5.2, 5.3] P^fm2—/^2), т. е.
зависит только от е2(Р2):
dins(Р2,М2, e$/d InР2=у(е2) E.19)
и в теории возмущений определяется рядом по степеням е2/DяJ:
У(е2)=Ъ-е2/DяJ-Н4.[е2/DяJ12+ ••• E-20)
Коэффициент у2 называют аномальной размерностью функ-
функции s(P*). Находя отсюда rfhsG^-YH|^Tr-${g4r и
интегрируя, получаем аналогично E.10):
еЧЯ») о(Р»)
Здесь обе функции у(е2) и р(е2) представлены рядами E.9),
E.20), где Рг——&> и учтены лишь линейные члены по а/Dя).
Интегрируя, получаем, избавляясь от лографимов в том же ли-
линейном приближении по а/4л [5.2, 5.3]
s(P*) sr(P*) fg(n')vW> г. у. (U , Р«^ «(Р')-а(ц') 1
где а(|12)/а(/J) и а(Р2) определяются соотношениями E.11),
{5.12) и где второй член является лишь малой поправкой. Пола-
Полагая здесь \i=M или \i—m, получаем, пренебрегая этой поправкой,
E.22)
яричем из E.16) видно, что ао/аA)(Р2)=1 + 6(ао/4яIп(Р2/Л12),
а аг/аП>(Я2) = 1+?(аг/4яIп(Р2/ю2).
Так как Z2 — s(m2)—s-1(M2), то отсюда и из E.16) получаем
аналогично E.18):
Таким образом, уравнения E.8), E.19) [или в интегральном ви-
виде— E.10), E.21)] позволяют построить с помощью рядов тео-
теории возмущений при ог/4я<1 или при <ю/4я<1 '[но при
(аг/4яIп(-Р2/'я2)~1] функции Грина и вершину, а также все по-
постоянные перенормировки Zu Z2, Z3 в любом порядке по степеням
14 (или —ао/4я).
5.3. Ренормгруппа
Соотношения перенормировки вида E.1) для функций Грина
и вершины удобно обобщить, введя вместо dT, sr, Г, функции d=
=d(Pi, р,2, e2(p,2))=tf(P2/|i2, ^(ц2)), s и Г, нормированные не в
точке Р2=тп2, где m — физическая масса электрона, а на произ-
80
вольную массу \i, т. е. при Р2 = |х2. Вместо er2=e2(m2) эти функции
будут зависеть от эффективного заряда е2(ц2), определенного
при Р2=ц3, и вместо E.1) получим
d \P\ М2, «»)-=Z, {v?, АР. е2) d (Я2, ^ ег (^ E.24)
причем ео2 = е2(М2) и функция d(P2, ЛЯ, е02) та же, что ив E.1);
она отличается от функции d(P2, ц,2, ^(ц2)) в правой части лишь
выбором точки нормировки, причем обе они нормированы усло-
условием d(M2, М2, е?(М*))=й№, у*, е5!(ц2)) = 1 >[т. е. функция
d(P2/y?, е2(ц2)) двух безразмерных переменных x=P2f\i2 и е2
нормирована условием d{\, e2)=sl]. Поэтому, полагая Р2=цг, на-
находим
Z3 (ii2, АР, el) =rf (i*a, М\ el). E.25)
Два точно таких же равенства получим для функций s(P2) —
= s(P2, ц\ е*№)) и Н(Я)=5(Р2).
Подставляя это значение 23(ц2, Л12, е02) в E.24), а E.24) —в
левое из равенств E.7), находим
E.26e
где согласно E.7) в8(!*¦) = ejrf(jia, M2, e\) = e\dr (|д,2, М2, в»). Средне
или правое из значений E.7) получаются отсюда, если выбрать
в E.26) [1=Л1 или [i=/n.
Эти соотношения являются обобщением равенств E.1), E.4),
E.7) и показывают, что перенормировку можно рассматривать
как переход от одной нормировки функций d, s и Г на точку Р2=
=М3 к другой — на точку Р2=|х2, причем обе точки фигурируют
совершенно равноправно (точка Рг=Мг, в частности, может быть,
а может и не быть пределом обрезания расходящихся интегра-
интегралов). Если этот переход М-*-ц выполняется в два приема — от М
к ць а потом от ц\ к цг, то ясно, что каждое из результирующих
равенств E.24) — E.26) будет произведением двух таких же пре-
преобразований — ОТ М К (LJ.1 И ОТ |Xi К |Л2.
Совокупность таких преобразований, обладающих тем свой-
свойством, что два последовательных преобразования определяются
их произведением и являются одним из этих же преобразований,
называют в математике группой (или группой преобразований),
а каждое из 'преобразований называют элементом группы. Груп-
Группа должна содержать и единичный элемент: он действительно
входит в E.24) при ц=-М, когда коэффициент Z% обращается в
единицу.
Эффективный заряд E.26) является инвариантом группы: он
не меняется при изменении точки нормировки (т. е. при любом
. преобразовании группы), оставаясь равным стандартной функции
e*(P2)=er2dr(P2/m2, er2), которую, как было показано выше, мож-
можно построить при аг = ег2/4я<1 на основе теории возмущений.
Иногда эффективный заряд записывают в виде функции без-
безразмерной переменной Х2=/J/ц2, где ц—произвольная точка иор-
6—679 8 1
мировки ez(Pz)=e2(kz, е2(ц2)), удовлетворяющей уравнению E.8)
д1пё21дШ2=$(ё*) и граничному условию ё"A, е*{ур))шше*(р*)
[при выборе ц=Л1, например, ePiP2) <=e2{P2fM2, e02)]. Этот способ
записи отражает лишь то, что е2(Р2) есть функция одной только
переменной Р2:
ё E.27)
и не зависит от выбора точки \i нормировки; выбор \i—P2 дает,
в частности, е2(Р2)=ё2A, е2{Р2)).
Г бй E24) (
()(, {))
Группу преобразований E.24) —E.26) '[и таких же преобразо-
преобразований функции s (Р2) =Г~1 (Р2), а также различных физических
амплитуд], называют ренормгруппой. Ее наличие в теории поля
было замечено Штюкельберном и Петерманом [5.4] в 1953 г. и
эффективно использовано Гелл-Маном и Лоу [5.1] в 1954 г. (см.
выше). Систематическое применение ренормгрупповых свойств в
комбинации с теорией возмущений было использовано в 50-х го-
годах для построения функций Грина в работах Н. В. Боголюбова
и Д. В. Ширкова [5.2] и В. В. Судакова [5.3, 5.5]. Они записы-
записывали преобразования E.24) — E.26) с учетом перенормировки
также и массы электрона (которой мы пока пренебрегли, см. об
этом ниже) и заметили, что эти соотношения, ограничивая воз-
возможный вид функций d{P2), s(P2) =Г~:(^2Ь полностью их опре-
определяют при сшивке с рядами теорий возмущений.
Если обозначить Т(Р(Рк, ц2; е2^2)) физические амплитуды
E.6), нормированные на точку Р2=ц2, где для упрощения записи
отброшены векторные индексы а, е,..., Я и числа частиц Ne, JVT, a
зависимость от 4-импульсов их ри ks обозначена в виде зависи-
зависимости от инвариантов PiPh= — (PiPk), то соотношение ренормгруп-
пы, следующее из E.6), запишется в форме
t (Р{Рк, М\ e*(M*)) = Z-* ([д.2, АР, el) f (PtPk, \x\ e^% E.28)
в которой оно аналогично равенству E.24); здесь согласно E.6)
Z=Z2e Zzy _• Это соотношение существенно ограничивает воз-
возможный вид зависимости амплитуд от иивариаитов РгРк-
Сделаем два замечания чисто формального характера, полез-
полезные для дальнейшего (и для понимания литературы по ренорм-
группе). Отметим, во-первых, что дифференциальные уравнения
вида E.8), E.19) могут быть получены формально простым диф-
дифференцированием по Р2 общих функциональных уравнений E.27)
или E.24) и такого же уравнения для пропагатора s(P2) элек-
электрона
s (PJ/ЛР, e2)=Z2 {y*iAP, el) s [Р2/ц*. i2 {v?l№, eg)], E.29)
где этот пропагатор записан подробно E.27) в виде функции без-
безразмерной переменной Р2/ц2 (или Р2/АР). Действительно, диф-
дифференцируя обе части логарифма равенства E.27) по_ In Я2 и
полагая потом ^2=Я2, получаем уравнение E.8): д,Прг — Р(е2).
82
где Р(е2)=| ь ^
\
Jx«-i есть ФУНКЦ-ИЯ лишь пере-
переменной е2=е2(Р2). Такое же дифференцирование логарифма ра-
равенства E.29) воспроизводит при ц,2=Я2 уравнение E.19):
\el), где ч[ег)=\
(всюду Х2=Р2/у,2; учтено, что Z2(P2/ji2, e2) = s(A,2, е2)).
Заметим, во-вторых, что это же уравнение E.19) можно по-
получить, дифференцируя логарифмы обеих частей равенства E.29)
не по lnP2, а по параметру ц2 (по 1пц2), полагая потом ц2=Р2.
Так как левая часть E.29) от ц2 не зависит, то дифференциро-
дифференцирование правой дает
' д In Z2 \ Г д In s
In Ц1 /ц»=Я» L
где учтено, что (^1п5(Х2, ~e2)ldln\i2)-t ^—dlns/дЫР2. Пер-
вый член слева есть по определению функция yfe2) = у(е2(Р2))„
т. е. правая часть уравнения E.19), а величина в скобке есть его
левая часть, так как она равна частной производной
[dlns(P2/]i2,e2(P'))jdlnP2\-^cotat, совпадающей при ц,2=Р*
с производной [dlns(V, \Ц™
5.4. Аномальные размерности физических амплитуд.
Зависимость от массы
Соотношение E.28) ренормгруппы аналогично равенству
E.29) и позволяет получить уравнение (которое называют урав-
уравнением Овсянникова [5.6], Каллана [5.7] и Симанчика [5.8] —
уравнением ОКС), определяющее зависимость произвольных амп-
амплитуд T=T^*'Jfe) от 4-импульсов частиц в простом слу-
случае, когда все они масштабно увеличиваются в X раз, т. е. при
изменении Р^ъ-^-МР^к-
Чтобы получить его, продифференцируем логарифм обеих час-
частей равенства E.28) то 1пц2 и после этого заменим ц2 на Я2'ц2.
Учтем при этом, что амплитуда Т является размерной величиной
вида .„ i
Т (pPtPk, v2, e2 (yP))=^F (WPiPb/tf, ~e2 (ц2)) E.31)
и поэтому ((?1пГ/(?1пц2)_ =(&/2) — (?ln77dlnk2, где число k
называют канонической размерностью амплитуды. Так как
левая часть равенства E.28) от \i2 не зависит, то, приравнивая
нулю производную от правой части, получаем, аналогично E.30):
-7Й +k/2-[dlnT/dlnk2-{dlnTldlne~2)fi(e~2)]v..+il.,x.=0, E.32)
б* 83
где (д In Т/д In е-) есть частная производная функции Т=Т
е2 при %2PlPki)x2 = zonsi, а
— (—~—дя'»в !„ ,—некоторая функция переменной е2 =
= i2(H2). Так как в E.28) Z = zfe/2zfv/2, то
При замене [12->-Х2^2 переменная e2=e2(jx2) заменяется ё2=
= е2(Я2, е2(ц2)) = е2(Л2(л2). Как видно непосредственно, величина
в скобке в E.32) есть частная производная [{д/д\пХ2)х
ХЬГ^Р^/^.ё2^2, е2(ц2)))]- , совпадающая при ц2->Я2ц2
{согласно E.28)] с производной д lnT(k2PtPk, М2,е,?)/д In Я2. Поэтому
уравнение E.32) сводится к виду, сходному с E.8) и E.19):
(НпГ(Я2РгЯй)/д1пЯ2=-уЙ + ?/2 E 34)
с ё2=е2(Я2|л2), и решением его будет экспонента вида E.21):
[е»(Х«ц«) _
- S Ш
(Ц)
(как и в E.21), в интеграле J у{е2[ц1)) rflnjx? была сделана
Inj
подстановка rflnjij = [P(e2(n2))]-irfe2(|i2)/e2(ii2)). В области
а=е2/4я<1 можно использовать разложение, подобное E.20):
Y И = Y2 • [е2/ DяJ] + Y~4 • [е2 /DлJ]2+ .... E.36)
где коэффициент ^2 называют аномальной размерностью ащли-
туди Г=7^,1',..?,*,. Подстановка ^(е2) в виде такого же разложе-
разложения E.9) дает для экспоненты в E.35) простое значение вида E.22)
(а(|12)/а(ЯУ))-у>/6 с точностью до членов порядка а([12)/4л.
Поэтому с зтой точностью
fb, у.2, а (ц2)) = WT (PtPk, ix2, а (\х2)) (а (ц2)/ а (ВДрЛ E.37)
где отношение а(ц2)/а(Х2ц2) определяется равенством E.12) (при
эд
Эти результаты нашли широкое применение не столько в КЭД,
сколько в физических приложениях квантовой хромодинамики
(КХД) (см. гл. 14—16).
Ясно, что уравнения E.19) —E.21) для пропагатора электро-
электрона s(P2) являются частным случаем общих уравнений ОКС
E.32) —E.35) при k=0, Х2?Р2
84
Учет конечности масс частиц вносит небольшие изменения в
соотношения ренормгруппы. Напомним, что знаменатель G"'(/5)'=*
—р—то—2(р)^ точной функции Грина электрона B.9) [где
1,(р)=А(р2)-\-рВ(р2)] имеет нуль при р=т(—р2):
Поэтому функцию [5.9]
m(-p*)=m(P*) = {mQ+A{p*))i{\-B(p>)) E.38>
называют оператором массы или бегущей массой электрона. Фи-
Физическая масса электрона р=Шфт определяется полюсом функ-
функции^ Грина, т. е. значением т(—рг) при р2=т2, величина то=
==т(М2) есть затравочная масса электрона А(М2) =В(М2) =0, а
m(m2)— величина, очень близкая к Шфт=т.
Функция Грина электрона s(P2)c^0G(p) до перенормировки
зависит от т0: s=s(P2, пц, М2, eo2)=s(P2/Afi, то/М, е02), а при
нормировке на произвольную точку Р2=цг — от т(ц2): s=>»
=s(P2/n2, т(ц.2)/ц, е2(ц2)), и учет массы в E.29) дает [5.2]
s[P2iM2,m0/M,e2) =
=Z2[tf/AP, rrio/M, el) s {Р2/ц2, mbi2)/», e2(ц2)). E.39)
В этом виде преобразования ренормгруппы1 справедливы для
всех Р2, а ие только в асимптотике Р2>т2, где они практически
используются.
В принципе, s(P2) зависит также от выбора калибровки, т. е.
от постоянной ? в калибровке Лоренца (в которой Du4°(k) ~^v+
+ (?—1)?,А/*2), и сама постоянная ? может изменяться в каж-
каждом следующем порядке теории возмущений из-за радиационных
поправок к D^ik), получая добавки, пропорциональные
(а/4я) In (F/M2). Как было пояснено выше, в КЭД эти поправки
во всех порядках исчезают из-за поперечности тензора поляриза-
поляризации П^Щ, однако в КХД они отличны от нуля (см. гл. 8 и 9) и
там ?=?СР2). Поэтому в общем случае соотношение перенорми-
перенормировки пропагатора электрона s(P2) имеет вид
=Z2 [tf/M2, mo/M, So, el)s{P2i)L\ mfr2)/?2, ОД, е2^2)). E.40)
Дифференцируя его по ln\i2 и полагая ц2==Р2, получаем вмес-
вместо E.30) уравнение
Аналогично при учете массы вместо ^5.24) получаем [5.2] соотношение
2
ренормгруппы (, )(^ )И (ц
справедливое для всех Рг~^-т?. Общее решение этих уравнений было проведено
Л. В. Овсянниковым [5.6].
85
где Y(m) (e2)=^Inm (ц2)/^ 1пц2, y(C) (e2) = dln?(p2)jdln\i.2—функции
e2 = e2(\i2), которые легко построить в виде рядов E.20)—E.36)
по степеням е2/DлJ. Как и E.30), это уравнение непосредствен-
непосредственно сводится к равенству E.19), если, используя свободу выбора [i2
справа в E.40), представить s(P2) в виде функции
s(A.2,7rc(P2), Z{P2),e2(P2)) при А,2->1, что отвечает выбору ц,2=Р2
!при этом_величина слева в E.41) равна частной производной
при tf_/-^_l. „сяорая в силу
dliP^
<5.39) совпадает с i^]
Такое же соотношение перенормировки произвольной амплиту-
амплитуды Т =Гст,е*..У,^1 имеющее в общем случае вид
Т {WPiPblAP, щ/М, С* e»)-
=Z {^/М2, Щ1М, ?0, <?) Т (WPfklv?, m И/Ц. Е И. е2 И). E.42)
дает вместо E.32) уравнение ОКС вида [5.7, 5.8, 5.6]
где ^^e2(\i2), а ё2=ё2(Л,2, e»(|i2))-e«(XV)- Запись функции Г в
виде, указанном справа в E.42) с р.2-*~к2ц2, показывает, что левая
часть в E.43) есть в точности производная [<Jlnr(A,2/Vfc/|i2,-m(e2),
К?), 12)/^1пХ2],1=1=(д1пГ/д1пЯ2),=ь где справа Т=Т(КРлРн1М\
triolM, go, e02). Поэтому и в общем случае E.43) сводится к про-
простому уравнению ОКС E.34).
5.5. Функция Гелл-Мана—Лоу и эффективный заряд в КЭД
Полученные выше общие формулы E.13), E.17) применимы
к случаю КЭД, в которой теория возмущения дает [см. D.7) и
задачу 4.10]:
/ + ...,E.44)
где ? = 1п (Р2Ш2) и, в обозначениях D.43), М=ММОЫ-
Взяв производную вида E.8), E.19) этих функций при Р2=Л12
?де 2(М2)е2] ом
зв прдую в
?где е2(М2)=е20], получим
dd{e) \ _ а,
d(t)dt J/_
при любом ао=е2/4я. Заменив е2 в обеих частях этих равенств
величиной е2=е2(Р2), найдем Р(е2) и у(е2) в виде рядов E.9),
E.20), в которых — Ь=Р2 = 4/3; р4=4; Ъ = Ъ, причем С—произ
86
вольная постоянная калибровку. Отсюда находим квадрат эффек-
эффективного заряда в виде ряда
в
по степеням малого параметра аг=\/1Ъ7=а№(т2)
«о,(^_«шМ/A-Р>»9)-с.,/(>-? h&). E-46)
Всюду параметр ц может быть выбран произвольно.
Формулы E.11) и E.12) определяют функцию d(P2, \i2, а(ц,2))=
=а(Р2)/а(ц2) в виде рядов типа D.13)
d{P\ v*. o0i«))-rf«>(E)+[o(|i?)/4«]rfA)(9, E.47)
где
g/ ( б/)
—функции величины ?=а(ц2Iр(Р2/^2), которая может быть
не малой (при а<?1). Аналогично найдем из E.12) константу пере-
перенормировки E.25):
[см. E.18) при Ь= —4/3], где инжияя строка получена из E.12)
при р.*-*-М2, Р2-*~ц2, а верхняя — просто подстановкой Р2-*-М2.
При выборе \i=m функции а(Р2) и d(P2) выражаются через
перенормированный заряд ar=a(m2), а при р=М — через затра-
затравочный заряд ao=a(Af2).
Выпишем также асимптотику функции Грина электрона
s(P2) =T~1(P2) и константу перенормировки Z2=ZU которые
определяются формулами E.21)—E.23):
Z2 Ox», M\ e*)=s (у,2, № ao)= (l +g- In ^L E.51)
в низшем порядке по степеням a<1)~a0~ar<l.
5.6. Нуль заряда в КЭД и область ее применимости
Константа Z3 перенормировки, определенная в E.49) при ц=
= m [или в E.18)],
Z,(««, АР. eg)=(l +^ ta^-l-g ln? E.52)
87
задает связь E.16) между затравочным и перенормированным за-
зарядами:
E.53)
Полученные выше формулы не приводят к противоречию лишь
до тех пор, пока Р2<ЛР, а (аг/ЗпIп(АР/т2)<. 1, т. е. в области
М2. E.54)
В ней постоянная перенормировки E.52) остается величиной по-
порядка единицы (Z3<1), a ao=Or/Z3 — того же порядка малости,,
как и аг= 1/137. Однако если, увеличивая предел обрезания ин-
интегралов М2, довести его до огромного значения
e, E.55)
то формулы E.47)—E.53) теряют смысл {5.10, 5.11]. Постоян-
Постоянная Z3(m2, М2, во2) E.52) при М=М\ обращается в нуль, а квад-
квадрат эффективного заряда а(Р2) E.45), E.46) имеет полюс при
Р2—М2 (см. рис. 5.1,а) и становится отрицательным в области
Р3>М\2. Это совсем недопустимо, так как заряд ei^P2) и затра-
затравочный заряд во=е(М2) оказываются мнимыми и теории вообще
не существует, потому что при мнимом е=е0 S-матрица A.20) не-
неунитарна. Положение ие улучшается при P2>Mi2 за счет учета
следующих членов1 в ряду E.45) по степеням <хг — при
(аг/ЗяIп(/>2/пг2)>1, но при аг<1, так как в этих условиях ряд
E.45) дает для а(Р2)—4пе2(Р2) отрицательное значение [с не-
небольшой мнимой частью, см. E.17)].
Положение в КЭД спасает лишь малость физического заряда
ar= 1/137 и связанное с ией огромное значение верхнего предела
E.55) области применимости P2<g.Mi2 теории. Для огромных
энергий вблизи этого предела могут быть важными другие виды
взаимодействий (например, слабое или гравитационное), кото-
которые могут кардинально изменить ход E.45), E.46) эффективного
заряда. При малом ar«Cl имеется большой иитервал энергий 0<
<P2<g.Mi2, где ряды теории возмущений быстро сходятся и опре-
определяют амплитуды физических процессов. При немалом а, не
только эти ряды не сходились бы, но вообще ие было бы области
применимости теории, например при аг~3я ее верхний предел
E.5) есть величина порядка те.
Эту, характерную для КЭД, ситуацию, когда коэффициент
р2=—Ь в разложении E.9) положителен, эффективный заряд
имеет полюс и вся теория имеет смысл, строго говоря, лишь при
нулевом заряде (при ar=0) или в ограниченной области энергии
E.45) —E.55), при очень малом аг<1 называют ситуацией с ну-
нулем, заряда. Обращение в нуль перенормированного заряда при
1 Вблизи полюса прн Р2—>-т2ехр [2я-137], где согласно E.46) а(Р2)~
—а( >)(/») не мало и где теория возмущений неприменима, эта картина могла
бы существенно измениться. Однако последовательную теорию сильной связи
в этой области построить никому ие удалось.
М2-*-оо в КЭД есть следствие формулы E.53): из нее видно (как
заметили Л. Д. Ландау [5.10] и И. Я. Померанчук [5.11]), что
при любой зависимости а0 от М2 величина аг уменьшается при
In (M2/m2)-voo как llln(M2Jm2) или быстрее (так будет, напри-
например, если ao=const при Af2-»-»). Теория поля с нулем заряда,
т. е. с —Ь = Рг>0, подобные КЭД (примеры их рассмотрены ни-
ниже), имеют область применимости E.54) лишь при слабой связи,
т. е. при Or'Cl. Как уже было отмечено, они совершенно непри-
непригодны для описания сильных взаимодействий, так как при боль-
большом заряде при аг>1 вообще не имеют области применимости.
Как показано ниже, для этого нужны теории поля, в которых Рг<
<0, т. е. теории с асимптотической свободой на малых расстоя-
расстояниях.
Если в теории фигурирует не один, а несколько сортов Nf за-
заряженных частиц — фермионов, таких же, как электроны-по-
электроны-позитроны, например ц,+-, у-мезоны, протоны-антипротоны и др.,
то будем иметь N, графиков рис. 1.6, а типа фермион-антиферми-
онных петель. Каждая из этих петель дает одинаковый вклад в
D.6) при высокой энергии P2>msmax, где ттах — масса самого
тяжелого фермиоиа, и суммарный вклад всех фермионов ПA)(<72)
будет в Nf раз больше, чем в D.7). В результате во втором и в
третьем членах в функции d(t) в E.44) появятся множители Nt:
d @=1 +(«о/3л) NJ + (ао2/4я2) N/ +...;
b=-DiZ)Nf; р4-4ЛГ, E.56)
и вместо E.46) эффективный заряд определится в виде
a(P2)=ar/[l _(аг/3я) Nfln(P'/m% E.57>
что уменьшает верхнюю границу М* применимости КЭД:
Тем не менее при не очень больших Nf ^ 10 область примени-
применимости КЭД Mi(Nj)<^\0 Ime все еще остается огромной.
5.7. Оператор массы электрона в КЭД
Для некоторых применений представляет интерес поведение
функции E.38) т(Р2) при больших Р2>т2. Ее можно построить
в КЭД с помощью теории возмущений, которая определяет т(Р*)
в виде рядов типа D.13) или E.47):
да(Я2)=я1<>Ы+(а(ц2)/4л)то> (]*) + (а({х2)/4лJтB) (&,)+ • • •. E-58>
где ?„=(а(ц2)/4яIп (Я2/ц2)—тот же параметр [порядка едини-
единицы при 1п(Р2/ц2)>1 и а(р2)/4я<1], что и в E.47). Производ-
Производная логарифма функции т(Р2) аналогично функциям d(P2) к
s(P2) [см. E.8), E.19)] есть функция только инвариантного
89
заряда es=ei(Pa):
dbim {P2)/d In P2 = Y(m) (e2) = Y^m) ¦ («{Р^/Щ -f
+ Y]m) • (а(Р2)/4лJ + .... E.59)
где Y2m)> Y4m) —некоторые числа; коэффициент •уг' называют
аномальной размерностью оператора массы.
Учитывая в E.59) лишь первый член и интегрируя обе части
этого равенства в пределах от ц,2 до Р2, получаем совершенно
аналогично E.22) (или E.50))
7*. E.60)
Коэффициенты у^т\ у[т)... просто вычисляются в теории воз-
возмущений. Действительно, в порядке е2 из D.5) следует, что
5(/>2)==(а0/4л)?1п(Р2/И» а функцию А{р2) в S(p) = A(jt72)+/>5(/?2)
можно определить, учитывая в электронном пропагаторе в B.6)
член, пропорциональный затравочной массе электрона: \/(р—У —
—то)=(р—?'-|-/гс0)/[(/?—ft7J—/n2] [при получении асимптотики
4.5) вкладом зтсго члена было прекебрежеио]. Это дает в том же
(порядке eh
Поэтому из E.38) получаем
+ ;Iп(Р'/Ж') Л 3«.
^ I1 Г1п
т. е. зависимость от ? (от калибровки) сокращается и
Сравнение с E.59) при Р2=ЛР дает Y^m)=— 3, т. е. [5.9]
Ъ(Р2)^т(ц2)[1 — {а(у,2)/Зп)ЩР2/ц2)]9^, так как Ъ = — 4/3. В част-
частности, при ц=т, а(т)=аг т(т2)=т, т. е. получаем
т (Р2)=т [1 —(а,/3л) In (Р21т?$'\ E.62)
Как видно, в КЭД оператор массы электрона убывает с ро-
ростом Р2; в гл. 12 показано, что убывание с ростом Р2 «бегущих
масс» частиц является характерным свойством всех реалистиче-
реалистических теорий.
90
Часть II
Скалярные поля. КХД. Слабые взаимодействия.
Единые теории
Глава 6
ВЗАИМОДЕЙСТВИЯ И САМОДЕЙСТВИЕ СКАЛЯРНЫХ
ПОЛЕЙ. ВАКУУМНЫЙ КОНДЕНСАТ
6.1. Скалярные поля
Следующие главы посвящены взаимодействиям и полям, от-
отличным от изучаемых в КЭД и важным в современной физике
элементарных частиц.
Начнем с простейших — скалярных полей — бозонов (мезонов)
с нулевым спином. Теория их имеет длинную историю (см. [6.1]
или старую книгу Г. Вентцеля [6.2]). Отметим кратко лишь са-
самые основные ее положения.
Поле <ро(*) таких нейтральных свободных бозонов веществен-
вещественно' фо+(*)=<ро(*). Свободное скалярное поле описывается лагран-
лагранжианом
2^.-0/2) КдхФ^-да^Й. F-1)
который при вариации по <ро приводит к уравнению Клейна—Гор-
Клейна—Гордона дк\о+т2ц>'=0. Его общее решение представляется разложе-
разложением вида A.13) по плоским волнам
•где k={kQ, к)—4-вектор импульса бозона; Ло=сой
(т. е. ?2=/я2); т—масса бозона.
Амплитуды С** являются операторами рождения бозонов:
С?Флгк_1=УNkQNk, Ск"Ф0=Фцс—точно как для фотонов, и как
для них [Cic, C^]=6k,k', a JVk=Ck"Ck—число бозонов с дан-
данным к.
Полный 4-импульс поля Р%= \ до% д д 9' d3x определяется
подобно A.16) суммарным вкладом частиц во всех импульсных
91
ячейках:
Рь= \ (<W (<W &х = 2 Ь (CfCk +1 /2)=
k
2
k
причем Р1 — A>кЩ/2, 0) — энергия нулевых колебаний вакуума
(ее изменение под действием внешних полей — реально наблюдае-
наблюдаемая величина).
Заряженные скалярные частицы (условно будем называть
их здесь п-мезонама) описываются парой таких же полей:
], a—1.2, F.3)
причем поле я+ комплексно
F.4)
а поле л"—комплексно-сопряженная к нему величина
Здесь ak=(l/1^2)(Ck,i — iCk,г)—оператор поглощения л+, а ftk=
=A/>/Л^~)(Ск,1 + 1Ск, 2)—оператор поглощения я" (причем at=
={С?л-\-\С?,2IУ^фЬъ). Отметим, что из соотношений коммута-
коммутации [Ck,aC?,/]=6k,ic'8aJ (а,й = 1,2) следует, что [ак) ак"] =
= [*к, *к']=бк,к'- Поэтому at является оператором рождения я+,
а ftf—я" и акьФ0=Ф1+,к, &кФо==ф1-,к.
Лагранжиан свободных заряженных полей
2 [(^aJ-mVa]^dxrd^-m^^ F.5)
k,a-l,2
есть сумма лагранжианов вида F.1). Он определяет 4-импулье поля
7 J [(^оФ+) ^яФ+дь<Р+доч] Фх
и 4-вектор плотности тока частиц j\ = -4- Г Ф+ ¦,,, +.—^ ^ ф|
и дает
92
где е — заряд зт+-частицы, причем dj,j\(x)=Q. Для вещественного
поля (ф+=ф) 4-вектор j\(x) исчезает.
i Скалярные поля могут взаимодействовать с другими полями:
с фермионами, с фотонами н т. д. и сами с собой.
6.2. Юкавовское взаимодействие с фермионами
Лоренц-инвариантный лагранжиан взаимодействия нейтраль-
нейтрального скалярного поля (линейный по этому полю) с фермионами
может быть выбран в виде
Шх) F.6)
]или в виде i/l^Ys^)^» если пОле <?(-*)—псевдоскалярное, т. е-
меняет знак при инверсий х->—х осей координат]. Более сложные
лагранжианы 2", содержащие производные, например, вида
/'(¦Wm^kVPo или /'4*<Wft(<VPo)(dv<Po). Cuv = (l/2i)(YnYv — YvYu)
приводят к неперенормируемым теориям. Константы взаимодей-
взаимодействия f'~ 1/m и f"~l/m2 в них размерные, и степень расходимости
интегралов Фейнмаиа в таких теориях быстро растет с ростом
числа вершин в графиках. С ними мы работать практически не
умеем и рассматривать их не будем.
Лагранжиан системы нейтральных бозонов и фермионов опре-
определяется суммой
S^S^+S^+S", F.7)
где З'Ч'^^^Чцдц—т0})^) — лагранжиан свободных фермионов (они
могут быть, например, электронами, а также и-, d-кварками).
Квантование такой системы проводится точно так же, как
в К?Д, и приводит к 5-матрице вида A.15)
F.8)
Правила построения графиков Фейнмана сходны с КЭД (см.
рис. 6.1, а—в): каждой внутренней фермионной линии отвечает
множитель iG°(p)=i/(p—/п/°+
+Ю), внешним фермионным ли- Р », j
ниям соответствуют спиноры Ди- ' ™(р' ~ Й-т° + iO
рака A.15), внутренней бозон- а) '
ной линии отвечает множитель к
1
) /(mz+i0) F.9)
— пропагатор бозона.
Вершинам фермион—ферми- ' гу сили
он—бозон (рис. 6.1) нужно со- ^-^^s^ гя-г-Уили
поставить множитель if в случае Р, J
скалярных бозонов или — /vs.—
Рис. 6.1
93
если они псевдоскалярны [а также б*-функцию Bn)*6*(pi—pa—
—k), отвечающую сохранению 4-импульса].
Теория, основанная на взаимодействии F.6), пернормируема
и подобно КЭД имеет нуль заряда (см. ниже задачи). Поэтому
при jf~l она совершенно непригодна для описания сильных взаи-
взаимодействий элементарных частиц. В первом порядке по f2f4a
вместо кулоновского потенциала она приводит к потенциалу
Юкавы
статического взаимодействия фермионов. Поэтому взаимодействие
вида F.6) часто называют юкавовским.
Взаимодействие заряженных скалярных полей с фермио-
нами. Так как при поглощении или испускании кванта такого заря-
заряженного поля общий заряд системы должен сохраняться, фермион-
ные поля \j>(jt) и ty(jt) [в лагранжиане типа F.6)] должны быть
различными, т. е. иметь разный заряд. Пусть, например, имеются
два типа полей фермионов — нейтральное у„(х) и поле %(х), несу-
несущее заряд +|е|; в остальном они одинаковы. По аналогии с тео-
теорией спина 1/2 их можно рассматривать как одну частицу—нуклон,
который может находиться в одном из двух этих состояний, и
описывать столбцом ф (х) =(')=» ур (х) %р+% (х) Ъ, где %р—
/1\ * /0\
= [п)—собственное протонное состояние, а Хл = 1 )—нейтронное
(при этом поля УР(х), уп(х) являются дираковскими биспинорами
и имеют по 4 составляющих). Тогда в том же формализме лагран-
лагранжиан, сохраняющий заряд, можно записать в следующем компакт-
компактном виде:
/О 1\ /0, —1\
где x± = (l/2)(T1 + iT2), причем fi —L 0J и т2= I } Q I—матри-
/0 1\
цы Паули, действующие на спинор $(х). Так как т+=1лл). а
/0 0\ _ _
т"=1 j 0J, то (фт+^)=(^л), (¦ут-у)=%Ур, т. е. 2"' устроен так,
что в нем при поглощении л+ и нейтрона рождается протон
(за счет первого члена слева), а при поглощении я" и протона —
нейтрон. Заряд при этом автоматически сохраняется.
Если ввести третье нейтральное поле <рз(х) [определенное в
F.5) членом с с=3], то лагранжиан &" можно считать частью
более симметричной величины
&* =2"'+/ (^зФзФ) -/ б (х) тафв (х) * (х)), F.10)
94
1 0
где з=10 — 1)~матРица ПаУЛИ. а таФв==#
Известно, что обычный спинор х—( ') при любом вращении
системы координат, например на угол со вокруг оси n=(<VP)
(по правилу буравчика), преобразуется определенным образом,
превращаясь в новой системе координат в спинор
K'=exp(-iW2)x, F.11)
где й) = ©п=(©1, ©2» Юз)'» ча—матрицы Паули. При этом билиней-
билинейная форма (х+тах) преобразуется как обычный вектор. Поэтому
удобно ввести некоторое фиктивное пространство, которое назы-
называют пространством изоспима, и считать, что три величины
?=(Ф1. Ч>2> Фз) определяют в нем вектор (и преобразуются при его
(л \
I преобразуется как
¦фл/
Х=( I, т. е. является спинором. Отметим, что при этом заряд
\Х2/
нуклона в единицах ер=\е\ определится формулой
F.12)
где К=1 называют гиперзарядом дублета I ."I. a fs*=-z3/2—
оператором третьей проекции изоспина G*зХр=0/2)Хр>
= —A/2)Хл)- При вращениях пространства изоспина формы
¦§(х)тау(х)) преобразуются как компоненты облч.чого вектора t
поэтому лагранжиан F.10) инвариантен по отношению к любому
такому вращению. Подобно спину можно ввести понятие изоспи-
изоспина частицы и системы частиц: изоспин нуклона равен 1/2, мезона
<Р„—единице, и при лагранжиане F.10) суммарный изоспин дол-
должен сохраняться (подобно полному моменту количества движе-
движения). Поэтому, в частности, сохранение проекции его Т3 ведет в
силу F.12) к сохранению заряда <3 при лагранжиане 2".
Отметим, что два последовательных поворота системы коорди-
координат являются также некоторым поворотом: он описывается матри-
матрицей Uzi^UiUi, где Ui и U2 имеют вид матрицы F.11):
?/"=ехр(—-к^ш с @=©! илио)=оJ. При этом последовательность
двух поворотов вокруг разных осей ni^=n2 отличается от обратной
последовательности, т. е. f72i^=t/i2=i7if/2, и результирующие
повороты различны (лишь при ni=n2 имеем l/n — U^i). Поворот
на нулевой угол (оэ=0) отвечает единичному преобразованию
#(со=0)=1.
Совокупность операций или преобразований, обладающих такими
свойствами, называют группой (а каждую из них—элементом-
95
группы). С понятием группы мы уже встречались при анализе
преобразований перенормировки. В данном случае О — ехр (—iia>/2) =
cos(co/2) + i((jn)sin(co/2) является матрицей 2X2; она унитарна
=U+U = \ и детерминант ее, как можно непосредственно
проверить, равен единице: cos2(со/2) + sin2(со/2) = 1, т. е. матрица О,
как говорят, унимодулярна. Группу таких преобразований спино-
спинора х или ijj= " ) называют группой SU B): символ S озна-
чает, что матрицы преобразований унимодулярны, a U — что они
унитарны. Элементы группы SUB) между собой, вообще говоря,
не коммутируют — такую группу называют неабелевой; группа
поворотов вокруг одной и той же оси абелева — все ее элементы
коммутируют. Более подробные сведения о группах Ли [частным
случаем которых является SUB)] даны в гл. 7.
Система взаимодействующих заряженных мезонов и фермио-
нов описывается суммой лагранжианов вида F.7), в которой
лагранжиан 2?* свободных бозонов есть сумма членов вида сред-
средней части F.5) по всем трем значениям индекса а:а = \, 2, 3, а
взаимодействие частиц определяется изотопически инвариантным
[т. е. SUB) -инвариантным] лагранжианом 2"=i?V F.10). Кван-
Квантование и правила построения графиков Фейнмана для этой си-
системы те же, что в случае нейтральных мезонов, и 5-матрица
имеет тот же вид F.8) с 2"=2'ч,'. Только теперь вершине взаи-
взаимодействия скалярный бозон—фермион—фермион следует сопо-
сопоставить матрицу ifxa, где а — проекция изоспина бозона, подходя-
подходящего к вершине, а пропагатор бозона
Dab(k) = 8abi(k*-m?+i0) F.13)
сохраняет эту проекцию [это видно, например, при вычислении
его фурье-образа в ^-пространстве Дл(*1—л^)=<7'(<рв(*1)<Рй(*2))>,
который пропорционален бвь].
Если бозоны псевдоскалярны, то вершине взаимодействия со-
соответствует fygta-
Реальным примером точечных фермионов, взаимодействующих
с бозонами, может быть изотропический дуплет кварков q(x)=
"С*!"*!) с заРЯДОм 2/3 для к-кварков (в единицах ер=\е\) и
—1/3 для d-кварков. В этом случае поле т|?(х) в F.10) следует
заменить изоспинором q(x) и положить в F.12) У=1/3.
SUB) -инвариантная теория с 2" вида F.10) перенормируема
я так же, как теория нейтральных мезонов, имеет нуль заряда
(см. ниже задачи) и из-за этого непригодна для описания силь-
сильных взаимодействий.
Функции Грина, вершины и пропагаторы в этих теориях
удовлетворяют уравнениям ренормгруппы, таким же как в
96
Задача 6.1. Найти поправки порядка f\ к вершине Г5 взаимодействия
мезон-"-пук л он—нуклон, к функциям Грина D (k*) и G(p) мезона и иуклона
в асимптотике при In (М*/Рг)>1 [или при 1п(Р*/и2)>1] в случае скалярных
нейтральных и заряженных мезонов. Вычислить в этом же порядке эффек-
эффективные заряды o/(P2)«=«?Z72Zf(P2)Z,(P2), где о? = /^/4л, af{P*) =
Реше ние. Записывая вершину и пропагаторы в виде C.9) Г(р, р—k)m
~Г(/); G{p) = s{l)/Cp-mN); Р (p*) = d(l)/(.p*—m*) [где / = ln(P2/Af*),
Я2 =—р3], получаем, так же как это было сделано в D.7), из однопетлевых
графиков вида рис. 1.5,л, 1-6,а, 1.7,а при а?<1, \а^1 |~1 в случае нейт-
нейтральных мезонов:
(/»)/4n-ag[l+Ea?/4j»)/]-of [l + Eа?/4л) ln(P2/m2)],
причем aJ = 4(Z-2z|Z,)pl=mt~o$[l —Ea^/4rt)ln(Af2/«1)] и I =ln(P2/Af2).
Аналогично, вводя в вершины матрицы ха и используя F.13), получаем
для SUB) схемы заряженных мезонов:
о' (Р*) = af0[l+ Eо{/4п) /] - о; [1 + Eа?/4я)
Всюду aJ = af(M*); а^ = а^(и2); и—масса мезона; /-=1п(Р2/Мг). В обеих
теориях эффективный заряд /*(Я*) = 4яа-^(Р2) од икаксво ргстет с рсстсмР2
как и в КЭД. Однако здесь в отлнчие от КЭД Zt^Z2 (из-за отсутствия
аналога локальной калибровочной симметрии).
Задача 6.2. Используя результаты предыдущей задачи, построить (в обеих
теориях) методой ренормгрушш эффективный заряд и функции Г @, я(/), d{l)
в главном логарифмическом приближении, суммируя все члены вида (fl)n
(А. Д. Галаиия, Б. Л. Иоффе, И. Я. Померанчук, 1956 г. [6.Э], см^ также
[5.3, 5.5]).
Решение. Дифференцируя /*(Р2) по InP2(dl = dInP2) и полагая
Р2 = М2, т. е. / = 0[а a^(Af*) = a,], находим в порядке а^~^ функцяю
Гелл-Мана — Лоу. В случае нейтральных мезонов
3 (oj) = (dlna-(P')ldInР2)Р,_д,.- 5с^/4я+0 (aj').
Поэтому, [учитывая члены порядка aj, имеем rfa'"(P*)/a' (Р2) dl = р (а') —¦
= 5а^/4я, т. е.
97
где а? = а?/[1 + Eа?/4я) ln(Af*/»i2)J. Величины Г8> s, d удобно считать
функциями af (Р2)-+а?(I), г не I (ясно, что это одно и то же), и так как
т<5) (af) = (d\nTb(af)/dl)l_0 = af0/4n + 0 (о^), то с точностью до/*уE)(«') =
(
а'/4п, и поэтому, интегрируя, находим
О 7-0
Так как Г5@) = 1, то прн 1т=ЩМ2/т2)
ZT1 @ = г, @ = [г
*i <-1я) = (/02//2гI/5=
Точно так же получим [6.3] функции s (I) и
Ясно, что, как и должно быть, произведение Z^~2(l)Zl(l)Zt(l) есть отно-
отношение/*(Z)//g.
В SU B)-ннварнантной схеме взаимодействия заряженных мезонов эф-
эффективный заряд тот же, т. е. а'(/") = /*(Р*)/4я=а? Д1—"^"«0') =
Л 5 Р2 \
1—4я~а/1п^г)' но Функции Г5, s и d имеют другие значения:
Как видно, теория имеет ненулевую область применимости лишь при усло-
условии E/4л}Ог'<1, иначе у эффективного заряда появляется полюс уже в обла-
области In (P*lm*)~\.
Задача 6.3. Показатель, что точно те же значения асимптотик функций
Г5@. ¦<№• d(l) и а{1) справедливы и в случаях нейтральных или SU B)-сим-
B)-симметричных псевдоскалярных мезонов [это — общее следствие у*~инвариантности
теории — инвариантности ее относительно замены ty(x)-*-yity{x) в случае, когда
массами частиц можно пренебречь).
Задача 6.4. Построить лагранжиан системы заряженные скалярные мезоны
в электромагнитном поле; найти лагранжиан взаимодействия и вид вершин взаи-
взаимодействия заряженных мезонов с фотонным полей.
Решен и е. Лагранжиан системы имеет вид:
2 4" F&, + К*№ + 1*ЛМ) <р]+ [(dM + ieAJ Ф] —яЛрф+.
Он отличен от лагранжиана s\ F-5) свободных заряженных скалярных мезо-
мезонов добавочным членом 35% = —A/4) ^j(v—лагранжианом свободных фотонов
и заменой производной 1дд, ковариантной производной id^-t-ld^—еЛм; где
е—заряд бозонов (как мы видели, такая замена проводит к калибровочной
инвариантности теории). Разность 2' = S~Sy—2?\ есть лагранжиан
взаимодействия мезонов с электромагнитным полем:
•2" 2 »
98
где Ум (х)—плотность тока (е/2) [<p+idMq>—(idMq>)+ ф] бозонов. Член, пропор
циональиый eM^(x), приводит к возможности испускания бозонами сразу
двух фотонов; без его учета теория не будет калибровочно инвариантной.
Лагранжиан 5" приводит к двум
типам вершин взаимодействия мезо-
мезонов с электромагнитным полем: трех-
частичной (рис 6.2. в), которой соот-
соответствует вклад —ie(*i,,+k&), где kt
м ki — 4-импульсы соответственно
входящего и выходящего из верши- -ъеСк +к 1
ВЫ мезонов (k2=ki+q; q — импульс г /*
фотона) и четырехчастичиой (рис. а>
6.2,6), вклад которой есть ie^,,, где
(I, v — поляризация фотонов. Рис 62
Константа связи е безразмерна, поэтому теория перенормируема. Амплиту-
Амплитуда комптои-эффекта на мезоне определяется, например, графиками
рис 6.3, а — в.
Ч"
кг
0}
А в)
Рис. в.3
6.3. Самодействие скалярного поля.
Появление вакуумного среднего поля
Потенциал самодействия. Самодействие скалярного поля появ-
появляется, если в свободном лагранжиане F.1) заменить массовый
член (т2/2)<ро2 некоторой нелинейной функцией ?/(<ро)» которая
есть гамильтониан или энергия самодействия поля. Это дает в;
случае нейтрального поля
2>*.=Р12)(да%Г-и(Ч0). F.14)
Соответствующее выражение для гамильтониана имеет вид
Рассмотрим наиболее низкое, т. е. вакуумное, состояние в тео-
теории с этим гамильтонианом. В классическом приближении, в ко-
котором <ро(*) —числовое, а не операторное поле, минимум гамиль-
гамильтониана достигается при <ро(*), не зависящем от *„ и минимизи-
минимизирующем функцию ?/(<ро) • Отсюда видно, что функция Г/(фо)
должна быть ограничена снизу и иметь минимум при конечном
Фо. В противном случае минимум гамильтониана достигался бы
при |д>о|->-°о и в теории не было бы устойчивого вакуумного со-
состояния. Такая неустойчивость, проявляющаяся на классическом
Уровне, не устраняется за счет квантовых эффектов, так** как
|<ро|-»-оо отвечает бесконечно большим числам заполнения, и в
этом пределе справедливо классическое рассмотрение. Так, из
простейших потенциалов к неустойчивому решению (что экви-
7* 99
валентно отсутствию решения) приводит ?/(<ро) = (V3)<po8 при лю-
любом знаке постоянной Я, или потенциал
?/(Ф0)=(/тг2/2)ф?-[-(^/4)Фп F.15)
приЛ<0. Однако если X положительно, то этот потенциал при-
приводит к устойчивой задаче, которая при Я<1 может быть иссле-
исследована методами теории возмущений: в ней появляются графики
¦Фейнмана, основанные на вершине рис. 6.4,с четырехбозонного
взаимодействия (вклад этой вершины рис. 6.4, с есть—61 Л.). Эта
теория перенормируема и приводит к нулю четырехбозонного за-
заряда К [т. е. Kj>ocry и к логарифмическому полюсу эффективно-
эффективного заряда i "
\
= -iA
Рнс 6.4
X -и'
/ s
S) k*>b
К интересным результатам приводит потенциал F.15) при
Я>0 в случае, когда параметр т2 отрицателен, т. е. при т?=
=—\ч2. Этот потенциал
^(Фо)=(Я/4)(ф2-ц?/ЯJ-^/4Л. F.16)
имеет минимум Umla= — |aJ/4X как функция поля %(х) в двух
точках: при фо= ±"|/м|Д= ±v, где ¦o=|j,i/yT (рис. 6.5). Клас-
Классическая система «свалится» в одну из этих ям, а в квантовой
механике поле фо(.ж) будет флуктуировать около одного из этих
\
ИГ'**-
Рнс. 6.5
значений, т. е., например, %(x)=v+r\(x), где r\(x)<?v—поле
малых флуктуации. Так как f/ (ф0) = (Я / 4) (tj2 -j- 2<dti (jc)J—цJ / 4Л,
то движение поля г\(х) опис&вается лагранжианом вида 9?ц(х) =
— \}l2)[(dar[y+2%tf-r?\~Ul(r[), где потенциал Ul(x])=(Xr4)r\* +
-^-vkrf-irXvhf имеет минимум при т|=0. Как видно, кванты поля
100
t](jc) имеют массу
да»—2^—211», F.17)
а среднее по вакууму от него равно нулю. Поэтому
(ФоФо(*)Фо) = < ФоD> •=*. F18>
т. е. при потенциале вида F.16) у поля <ро(х) самопроизвольно
(как говорят «спонтанно») возникает отличное от нуля среднее
значение <<ро(*)> = и, которое может быть немалым. Этот эффект
появления (или выпадения) бозонного конденсата хорошо изве-
известен в теории Бозе газов и жидкостей [6.4]; он был впервые ис-
использован Л. Д. Ландау и В. Л. Гинзбургом [6.5] в феноменоло-
феноменологической теории сверхтекучести и сверхпроводимости. Он приво-
приводит к ряду следующих любопытных свойств поля фо(лг) и систем,
взаимодействующих с ним.
«Стенка». В квантовой механике возможны «подбарьерные»
переходы системы с определенной энергней из одной ямы рис. 6.5
в другую. Предположим, что в какой-то момент времени t=xofc
в некоторой области Vo пространства, ограниченной замкнутой
поверхностью So, система находилась в одной яме, например в
правой на рис. 6.5 «<ро>=и)> а вне этой поверхности она была в
другой яме «фо>=—v). Переход системы (т. е. поля <р0) из одной
ямы в другую связан с большим изменением функции фо(*) (на
значение 2 v), поэтому в области вблизи поверхности So функция
Фо(*) должна иметь огромные градиенты в направлении, пер-
перпендикулярном к So. Это означает, что вблизи So очень вели-
велика энергия Е=Ро поля <ро(*) или, другими словами, что поверх-
поверхность раздела So (ее называют стенкой) несет с собой большую
потенциальную энергию, которую всякая система всегда стремит-
стремится уменьшить. Поэтому переходы системы из одной ямы в другую
происходят так, чтобы уменьшить эту поверхность — она сама по
себе приближается к форме сферы и стремительно уменьшается,
стягивая объем Vo в точку [6.6]. При этом энергию, которая осво-
освобождается из-за уменьшения поверхности So, система будет
сбрасывать в виде излучения нейтральных бозонов — квантов по-
поля ti(*).
Генерация масс. Лагранжиан нейтральных самодействующих
бозонов, взаимодействующих с фермионами, получим из F.1) и
F.6) в виде
¦5--Д?+5-ф.+/Фо (*)(*(*) *(*)).
где 3?q>t — лагранжиан F.1), а ^"^Оуцдц —m?) ¦$ — лагранжиан
свободных фермионов. Если у поля фо(-*) спонтанно возникает
среднее вакуумное значение F.18), то, переходя к квантованному
полю т]=ф0—v, получаем
+/ W*) Ч> (х) п (х)),
101
где S'n — лагранжиан поля r\(x), a
m'=—vf 'F.19)
—изменение массы фермиона за счет взаимодействия с вакуумным
средним поля скалярных бозонов.
При m°f=0 вся масса фермиона mf—m' генерируется этим
эффектом; если эта масса гп' согласно F.19) отрицательна, то это
лишь означает, что физическим фермионным полем является не
Ц (х), a $' (х) = Ys4> И, так как (ф (^ддр+т') if) = (ip (iYn<?n — т') у').
Таким образом, эффект появления не равного нулю вакуумно-
вакуумного среднего F.18) поля <ро(*) приводит из-за юкавовского взаи-
взаимодействия к генерации масс фермионов. Кроме того, и у самих
бозонов появляется масса F.17), причем обе генерированные
массы—и фермионная m'=fv, и бозонная п\=^2% v — пропорци-
пропорциональны вакуумному среднему »=|<<ро>| поля фо(*) (его называ-
называют иногда плотностью бозонного конденсата).
Потенциал Коулмена—Вейнберга [6.7] самодействия бозонов.
Учет поправок высшего порядка теории возмущений в квантован-
квантованной теории приводит к тому, что потенциал самодействия ?/(фо)
поля фо вида кривой рис. 6.5 с минимумом при фо#=О появляется
даже в том случае, когда «затравочно» это самодействие опре-
определяется в лагранжиане самым простым потенциалом ?/(фо)=*
= (V4)<po4=(V/4!)<p04 вида F.14) (с Я=Г/6>0 и с т25*0 — см.
лунктир на рис. 6.5).
а] б) б) г)
Рис. 6.6
Действительно, за счет петлевых графиков рис. 6.6,с—г само-
самодействие ?/(фо) = (?//4!)фо4 приводит к амплитудам процессов
превращения двух мезонов в четыре, шесть, восемь и т. д., т. е.
к тому же, что дали бы члены потенциалы вида <р06, <ро8 и т. д.
Найдем вклад этих графиков и тот суммарный потенциал
V (Фо) = с2Ф|5+сз(Ро+С4<^—•, которому они эффективно соответ-
соответствуют. Практически это просто сделать в однопетлевом прибли-
приближении, т. е. без учета двух, трех и т. д. петлевых графиков
рис. 6.7, а—г, вклад которых отличается от однопетлевых малым
множителем (Я'/ 16л2)*, где k = 1,2..., и поэтому мало существе-
существенен при Я/^1.
Итак, рассмотрим лагранжиан простейшего вида
2'=(с?иФJ/2—/и2ф2/2—Я'Ф4/4! F.20)
102
Ъ Г $
'«• ' 5) ^
Рис 6.Г
скалярного нейтрального поля <р (обозначаемого так вместо фо
для упрощения записи) и остановимся сначала на графике рнс.
6.6, а второго порядка по А/. Он определяет в сумме с вкладом
двух таких же графиков (отличающихся от рис. 6.6, а заменой
импульсов 2=s=t3 и 2=s=t4 частиц) поправку к амплитуде А/=6А,
рис. 6.4, а рассеяния бозона на бозоне в виде
-41 (Г/2)»
¦— 4 16я*
и отвечает эффективно потенциалу Д?/(ф)=ДА/ф*(.х)/4! (более
точно Д^' есть 1/3 суммы трех таких членов, из которых первый
записан выше, а два других отличаются от него заменой &,2 =
=ki+k2 соответственно kl3 и &14). При больших ^2~^»'w*i4=='
= —К2 интеграл, определяющий ДА/, в главном логарифмическом
приближении равен 1п(ЛР//Г2), где М2—импульс обрезания. Поэто-
Поэтому в этом приближении в порядке А/2 4-бозонная вершина есть
2, АР. ?10)=л;[14-C/2)Л^1б1:Мп(/Г2Ш2)]. F.22)
Отметим попутно, что так как в порядке А,„1п(Л12//Г2) нет по"
правок к функциям Грина бозона [эта поправка, как нетрудно за-
заметить, величина порядка А,^* 1п(М2/К2), т. е. мала, если Х'о<1, а
А,ц щ(М2/ЛТ2)~1], то эффективный заряд 4-бозонного взаимодейст-
взаимодействия определяется [6.8, 6.9] отсюда в виде следукшей растущей
функции ^ЛР)
и /A
1 -| T^in^). F.23)
где fi2—произвольный параметр. Для получения ее нужно ре-
решить ура внение Гелл-Мана—Лоу (d\ru! (WI/dlnK2) =
= C/2)V(/СJ/16я2; оно и дает это значение X'(/С2), соответствую-
соответствующее эффекту нуля-заряда [5.10, 5.11].
Аналогично F.21) графики третьего порядка рис. 6.6, б дают
для амплитуды превращения двух частиц в четыре (при равных
нулю импульсах внешних линий) такой же вклад, как потенциал
^ \-piIItf) 1?f#
103
Действительно, вклад графика рис. 6.6, б буквально есть
(* * ?)[(^2K23162] х
X \ {{p2-mP) \(p+kl2y-m?] [(p-k56y-
При ^i2=0, A56=0 он и дает указанное значение с3=с3@,0,0),
а вся зависимость Сз(&12> кы, kse) от импульсов приводит (при раз-
разложении в ряд по степеням импульсов) к членам в потенциале,
содержащем производные д„ф(х). Эти члены нас не интересуют,
поскольку наша задач здесь — найти лишь ту часть эффективно-
эффективного потенциала, которая зависит только от <р(х) (но не от произ-
производных д„<р(*)), и мы их будем всюду ниже опускать.
Действуя аналогично, находим, что однопетлевой график я-го
порядка вида рис. 6.6 дает в общем случае такой же вклад, как
и потенциал с„(ф2)", где с„=—^—Гбя»Л( 8— ») ~~ч~' Множитель
1/BпЧ%) возник здесь как следствие правил Фейнмана: 2п+1п
есть число перестановок и отражений вершин в графике, оставля-
оставляющих вклад его неизменным (они включают п циклических пере-
перестановок вершин, п отражений графика относительно прямых, де-
делящих график на две одинаковые части, и замену направления
импульсов в петлях).
Таким образом, суммарный вклад всех графиков рис. 6.6, б—г
[вместе с «затравочными» рис., 6.4, а, отвечающими ?/(<р) =А,\р4/4!]
соответствует эффективному потенциалу:
Vi
п—3
^Учитывая, что 2 (—jc"/ft)—ln(l— jc)+jc+jc2/2, и производя в
интеграле виковский поворот контура интегрирования по р0 (см.
гл. 4), а также переходя к евклидовой метрике d4p/n4-+P2dPz
(где Я2= —р2), получаем:
Отметим, что интеграл от величины в фигурной скобке здесь —
сходящийся (при т2Ф0), однако в нем верхний предел заменен
конечной величиной NP- для удобства вычисления интегралов от
отдельных членов (которые расходятся и в сумме все расходи-
расходимости сокращаются, так как вклад каждого из графиков
рис. 6.6,б"—г конечен). Учитывая, что \ xln(x-\-a)dx =
-»^-y^-ln(.x-fa)-fa(jc-fa)— *"*"][ , получаем после простых
104
вычислений:
F.26>
Как видно, предел обрезания Af*-»-oo вообще выпал из ответа.
Особый интерес представляет наиболее простой случай без-
безмассовых поначалу бозонов (т2=0), тогда масса у них появляет-
появляется именно в результате действия потенциала V(<p). В этом случае
последний член справа в F.25) приводит к логарифмически рас-
расходящемуся интегралу. Для устранения этой инфракрасной рас-
расходимости заменим (в интеграле от последнего члена) нуль —
нижний предел интегрирования в F.5) — некоторым значением
\х??=0 и положим в F.25) т2=0. При этом все вычисления еще
более упрощаются, и для V(<p) получаем значение F.26) с то2=
= 0 (и с m^-i-ji2 в знаменателе логарифма):
F-27>
Этот потенциал был получен Коулменом и Е. Вейнбергом
[6.7]; различному выбору постоянной ц,2 в нем отвечает добавка
членов, пропорциональных 1/(<р) =А/<р2/4!, т. е. небольшому из-
изменению постоянной Я'. Поэтому [А2 можно считать здесь неко-
некоторым фиксированным, но теоретически неизвестным параметром.
Потенциал Коулмена—Вейнберга V(<p), который иногда запи-
записывают также в виде
P^M <6-28>
где \ii — величина порядка ц (в этом виде он не симметричен от-
относительно замены ф->—ф), имеет пологий минимум при )
= — 1/4, т. е. при ф=т>=ц,1ехр(—1/4) с
-¦ (^iI
32я2 A/4) . -j-, , и сам по себе обеспечивает спонтанное
появление ненулевого вакуумного среднего (и спонтанное наруше-
нарушение симметрии, см. гл. 11); ход его схематически показан на рис. 6.8..
Полезно отметить несколько
простых обобщений этих формул.
А. Если затравочный ' потен-
потенциал в лагранжиане U(<p) имеет
вид более сложный, чем А/ф4/4!,
то все записанные выше соотно-
шения останутся, как нетрудно
проверить, в силе при замене
А/<р2/2 в них величиной U"(<p) —
й ф
р (p)
второй производной функции
Е/(<р). Таким образом, в общем
случае
Рис 6.8
105
Б. Если имеется не одно, а несколько бозонных полей <рв (х)
Цнапример, с SU B)-симметричным лагранжианом вида F.5), где
сумма по а пробегает значения а = 1,2,3], то все сказанное выше
остается в силе. Только теперь ?/"(ф) будет матрицей ??"(ф)=
={^в*(Ф)}. где и"аь—д2и{$Iдчад4ь, и так как пропагаторы частиц
имеют вид Dab{p)=babi{p2—wP), а вклады графиков рис. 6.6, б—г
определяются суммой вкладов всех частиц в промежуточных со-
состояниях (в линиях петель), то они будут иметь вид следов от
величин F.24)
яЧ ~
F.30)
тде вторая строка относится в случаю то=0.
Покажем, как вычисляется такой след на примере 5?/^-инва-
5?/^-инвариантного взаимодействия ?/(ф)=(Л/8)(ФвФвJ. В этом случае
=6«»—Ф«Ф»/Ф*—тензор, ортогональный к т]^=фвфй/Ф2 (т. е.
¦&'аЬ\с=0), причем б'б'=б', а т]'Л' = 'П'и Sp6'=2e6^a=2, Sprj' — 1.
Таким образом, в матричных обозначениях ^У"=ЯФ2 Г^-6'.f j-ti'].
а (??")л = (А,ф2/2)в[6'+3'г'Г]'1 и
= (Ядр|/2)«[2+Зя]. Отсюда
"Г
8 "Г i^s ^ jj 2п (р2—т*)п пЧ
т. е. согласно F.30) при то=0
В общем случае вместо Л'' полей Фв нужно ввести их линей-
мые комбинации 4a=2iKoc4'c и унитарную матрицу К=*{Кас}
с
здыбрать так, чтобы матрица U"^ в новых полях ф^, была диаго-
жальной: f/^=f/*6e*- После этого след в F.30) определится
гпросто в виде суммы диагональных членов матрицы, что дает
406
В. При наличии фермионных полей ty(x) и юкавовского взаимо-
взаимодействия [F.6) или F.10)] бозонов с ними
вклад в эффективный потенциал V(<p) дадут также графики
рис. 6.9, б, в, г с фермионными петлями. Здесь ба — матрица по
дираковским или по изоспиновым переменным (ба=1, или ба=ха,
или 6a = iys, iy5ta в зависимости от того, каков изоспин поля фо и
является ли оно скаляром или псевдоскаляром).
а)
Суммарный вклад в потенциал ДУ=У,(<р) фермионных графи-
графиков рис. 6.9,6—г с четным числом вершин равен (при равной ну-
нулю массе фермионов)
где след берется по изотопическим и по дираковским переменным*
Здесь учтено, что замкнутая фермионная петля дает множитель
(— 1) и что при отражении графика изменяется направление фер-
фермионных линий [из-за этого вместо множителя 1/Bге) остается
лишь 1/л]. В графиках с нечетным числом вершин след «зануля-
ется», поэтому они вклада не дают. Переставляя р и Ф (^+)
в каждой паре множителей Ф}^2
-. 1 ~
1 1 1 ~л
ФРЛФ
получаем
вычисляя сумму так же, как в F.24). Как видно, фермионы (на
рис. 6.9) дают вклад иного знака, чем скаляры. В частности, в
107
случае одного скалярного поля ф=ф+=ф
vf D0-iJ l/W (ь^Ч) -&rf^ln й • F'33)
Этот потенциал имеет максимум, а не минимум при <p = (ii/(eI/4.
Отметим, что не включенный в V/(<p) [в F.32)] член с /г = 4 —
вклад рис. 6.9,а — дает поправку ДА,/ к взаимодействию (Л'/4)ч>*,
аналогичную F.21): ДХ/= D!f4/16n2)ln(Af2/K2). что изменяет урав-
уравнение F.22) и дает при наличии фермионов
Это изменит эффективный заряд Я'(^2)=Лю'Г(/С2) четырехбозонно-
го взаимодействия по сравнению с F.23); однако он по-прежнему
остается растущей [6.8] функцией In К2.
Глава 7
ПОЛЯ ЯНГА—МИЛЛСА
7.1. Группы SU(N)
Квантовая электродинамика — наиболее простая из широкого класса теорий,
обладающих калибровочной инвариантностью. Калибровочные преобразования в
КЭД порождаются локальный фазовым преобразованием волновых функций
заряженных частиц ф(х)->ехр[ив(х)]ф(х). Такие фазовые преобразования об-
образуют группу, называемую С/A). Простота 'КЭД обусловлена тем, что в U(l)-
группе любые два преобразования коммутируют между собой. Группу, элемен-
элементы которой обладают этим свойством, называют абелевой, в отличие от неабе-
левых групп, в которых результат последовательного применения двух преоб-
преобразований зависит в общем случае от того, в каком порядке эти преобразования
совершаются.
Рассмотрим теории, обладающие калибровочной инвариантностью относи-
относительно преобразований, образующих иеабелевы группы, — теории Янга —
Миллса1. В построении реалистических теорий калибровочных взаимодействий
элементарных частиц основную роль играют схемы, основанные на группах
SU(N). Здесь приведем необходимый для чтения последующего материала на-
набор сведений о группах SU(N) и получим ряд соотношений, которые будут
полезны в дальнейшем.
Простейшим объектом, над которым можно совершать преобразования
группы SU{N) (в фундаментальном представлении группы), является столбец
из N комплексных полей:
G.1)
1 Янг и Миллс впервые предложили [7.1] в 1954 г. калибровочную теорию
ыгой 5?/B)-ннвариантностью; современное понимание построения неа-
мы G 91 калибР°вочных теорий появилось во многом благодаря работе Утия-
108
Преобразование описывается соотношением
Y-SY, G.2)
где S—унитарная
S+S = SS+ = I G.3)
и унииодулярная
detS = l G.4)
матрица" размером NXN. Условие унитарности G.3) означает, что при пре-
преобразовании G.2) сохраняется квадрат модуля W:
(обычно такой вид имеют вероятности, наблюдаемые иа опыте, что обусловли-
обусловливает важную роль SC/(АО-групп в физике частиц). Уиимодулярность G.4) озна-
означает отсутствие свободы в выборе общей фазы Ч^из G.3) следует, что |detS| =
= 1, поэтому G.4) есть условие только на фазу определителя]. Преобразования
общей фазы составляют отдельную группу U A); калибровочная инвариантность
относительно нее может быть использована отдельно, например для описания
электромагнитного взаимодействия полей *F.
Матрица размера NX.N, удовлетворяющая условиям G.3) и G.4), описы-
описывается N*—1 независямыми вещественными параметрами ю", д->1, 2, .... АР—1.
В частности, эти параметры всегда можно выбрать так, чтобы записать произ-
произвольную матрицу S, удовлетворяющую условиям G.3) и G.4) :
S = exp(lco°/fl) G.5)
(по дважды повторяющимся индексам здесь всегда подразумевается сумми-
суммирование), где Р—фиксированный набор из №—1 независимых матриц разме-
размером NXN. Подстановка G.5) в условие унитарности G.3) приводит к требо-
требованию эрмитовости матриц t":
(*•)+-*", G.6)
а подстановка G.5) в соотношение G.4) приводит к условию равенства нулю
следа:
Sp*e=O. G.7)
Подсчетом числа параметров убеждаемся, что матрицы Р образуют пол-
вый набор матриц, удовлетворяющих условиям G.6) и G.7). Это означает, что
любую эрмитову матрицу размером NXN с равным нулю следом можно пред-
представить в виде линейной комбинации матриц ta с вещественными коэффициента-
коэффициентами. Так как произвольную матрицу F можно представить в виде суммы эрмито-
эрмитовой и антиэрмитовой (эрмитовой, умноженной на i), то возможно также разло-
разложение по матрицам Р любой (не обязательно эрмитовой) матрицы с равным
нулю следом: F^caf, но лри этом коэффициенты са разложении будут, вооб-
вообще говоря, комплексными.
Далее будем работать с матрицами /", удовлетворяющими стандартному
условию нормировки:
Spt"tb- A/2)8°*. G.8)
Такой выбор аналогичен выбору ортогональных координат, коэффициент же
1/2 в правой части есть просто результат соглашения. При выборе нормн.
ровки G.8) коэффициенты разложения са легко определяются: ca=-2Sp(taP).
109
Поэтому, выписывая явно матричные индексы, можно записать Flk =
=¦ 2 (tay F4 (*")!• Применяя это соотношение к бесследовой матрице вида
(F'm)ill = btafilk~(llNNik61in [здесь / и ft—матричные индексы, а(ии просто
обозначают матрицу [Р'т)]> приходим к следующему полезному тождеству:
которое играет роль тождества Фирца в группе SU(N). Свертывая в этом
соотношении индексы т и i, находим
W-[(tf1—l)/2N]I G.10)
//—единичная матрица). С помощью формул G.9) и G.8) также легко
вычислить
Sp(Ptbftc)=—A/4A06»». G.11)
Коммутатор двух матриц t: [P, tb] является аитиэрмитовой матрицей с
равным нулю следом. Поэтому можно записать: ^ „л- . :, -, ^ -,.
If, t>] =lfb°t', ' 7 ¦' Z 1 "т ¦'¦¦'¦ " ; G.12)
ГДС f»« 2 iSp (.[<-, <«-]<"). G.13)
Коэффициенты febc, называемые структурными константами группы, веществен-
вещественны я антисимметричны по каждой паре индексов.
Используй определение G.12) и свойство антисимметрии структурных кон-
констант, для следа, входящего в G.11), можно записать следующую цепочку
преобразований:
Sp t*t*t*te - Sp tatatbtc + Sp t" [tb, ta] tc - Sp tat<*t*te—lfab* Sp tat'tc =
= Sp tat"tbtc + {l/2) /ab'faed sp tdtc = (ЛГ2—1) 6bc/4N—(l/4) fabeface
[на последнем шаге использованы также формулы G.8) и G.10)]. Отсюда
с учетом равенства G.11) получаем следующий важный для дальнейшего
результат:
Можно рассмотреть также действие преобразований группы SU(N) иа бо-
более сложные объекты, чем столбцы вида G.1), которые с необходимостью воз-
возникают при рассмотрении свойств преобразования произведений нескольких
объектов1 типа G.1). В этом случае матрицы преобразований SU(N) образуют
(Л^—1)-параметрическое семейство матриц размером КХК (где К>Ю, удов-
удовлетворяющих условиям G.3) и G.4), и их также можно выразить через N*—1
фиксированных эрмитовых бесследовых матриц Т' размером КхК формулой,
аналогичной G.5):
S=exp(i<flTe). G.15)
Из-за большего, чем #Х#, размера матрицы Та уже не образуют полного на-
набора всех матриц КХК, удовлетворяющих условиям G.6) и G.7). Определяю-
Определяющим свойством набора матриц Т", генерирующих преобразования именно SU(N)-
группы, в этом случае является замкнутость данного набора матриц относи-
относительно операции коммутирования, т. е. выполнение соотношений
[Г", Ть] -1 р'Т* G.16)
с теми же коэффициентами, что и в G.12). . _
' См. формулу G.31) и текст перед ней.
Важную роль в теории групп играет оператор
«2-ГТ-, G.17>
называемый квадратичным оператором Казимира. Этот оператор коммутирует
со всеми генераторами Г":
[<&!, 7"«] = [Т6ТЬ, 7"«] = 1/с [ТЬТС + ТСТ*\ = 0.
Поэтому значение 'ёз одинаково для всех компонент неприводимого представ-
представления, или, другими словами, в представлении R размерностью K(R) оператор,
'ёг имеет вид матрицы, пропорциональной единичной матрице размера K(R) X
Из формулы G.10) следует, что в фундаментальном представлении
F)»C* = (JV*—1)/2ЛГ. Через Ct(R) можно выразить величину
которая обобщает G.8) на случай произвольиого представления:
Г(Я)-С2(Я)Ш)/(ЛР-1). G.20>
Отметим следующее соотношение для структурных коистаит:
fadcfbce _|_ fbdcjace _ xabcfcdt^ G.21У
оторое сразу следует из G.12) и тождества Якоби для коммутаторов:
[[*«. t"], tc\ + \[tb, Щ, t*] + l[t", t*], tb] =0.
Соотношение G.21) означает, что матрицы размером (N*—1)(Я—1), эле-
элементы которых определяются самими структурными константами
(Гв)*"=— I/***, G.22)
удовлетворяют коммутационным соотношениям G.12) и потому образуют на-
набор генераторов группы SU(N) в некотором неприводимом представлении.
Представление, в котором действуют генераторы G.22), называют присоединен-
присоединенным. Размерность этого представления, очевидно, равна N*—1. Значение опера-
оператора Казимира в этом представления, обозначаемое C2(G) или Су, согласно'
G.14) составляет
C2(G) = VV=JV. G.23)
Отметим, что матрицы S=преобразований группы в этом представлении ве-
вещественны и ортогональны [ср. G.3), G.15) и G.22)]. Поэтому присоединен-
присоединенное представление вещественно я объекты, на которые действуют матрицы груп-
группы в этом представлении, можно записать в виде вещественного вектора Ф"»
а=»1, 2, .... Л^—1. Формула G.22) в этой записи означает следующий закон
преобразования:
AГ») :Ф»-/«»ефс. G.24)
Закон преобразования Ф" можно записать также в другой форме, еслн
рассмотреть матрицу вида
Ф=Ф»Г«, G.25)
. где Та — генераторы группы в некотором представлении. :,'
' Формула G.24) эквивалентна закону преобразования матрицы Ф:
®-*-S©.S+, G.26)
где 5 —матрица преобразования в том же представлении, в котором выбраны
матрицы Г«. Последнюю формулу можно переписать в терминах действия
111
генераторов Та на матрицу Ф:
Г«:Ф=.1!Г»,Ф]. G.27)
Эквивалентность формул G.24) и GJ27) очевидна.
Заметим, что если в фундаментальном представлении преобразование груп-
группы имеет вид G2), то эрмитово-сопряжениый объект V* преобразуется по
формуле
4+-+W+S+ G.28)
{в квантовой теории эрмитово-сопряжеиными волновыми функциями обычно
описывают античастицы). Правила преобразования G.2) и G.28) с матрицей S
вида G.5) удобно записать в виде действия генераторов, приписывая элемен-
элементам объектов типа ЧГ верхние индексы: ф*, а элементам объектов типа W+ —
нижние индексы ф<. При этом формулам G.2) и G.28) соответствуют:
Т°: tf-if)}p; G.29)
Т«: фг = -(^)*ф*. G.30)
Представления групп Slf(N), отличные от фундаментального -[правила
преобразования G.29)] и эрмитово-сопряженного к нему [правила преобразо-
преобразования G.30)], получаются при рассмотрении объектов, преобразующихся как
произведения некоторого числа объектов типа ? и Y+. Элементы такого
произведения можно представить в виде объекта с л верхними индексами и
m нижними ф},"К «= ф /'"" ,п . Из рассмотрения этого объекта как произве-
(¦* fnf Jt*""Jm
дения л функций ф' и m функций фу сразу следует закон действия на него
генераторов группы:
Смысл этой формулы очевиден: матрицы ta действуют поочередно на все
индексы, причем на верхние—по правилу G.29), а на нижние—по правилу
G.30) [отметим, что формула G.27)—частный случай G.31)].
В общем случае наборы элементов !!>},% с заданными 'п и m образуют
\J ml
приводимые представления группы, т. е. их можно разбить на меньшие
н аборы элементов, преобразующихся друг в друга. Чтобы выделить непри-
неприводимые представления, заметим, что ^генераторы действуют одинаково на
все верхние (и иа все нижние) индексы независимо от того, каким по счету
стоит этот индекс. Поэтому 'преобразования группы не меняют свойств
симметрии фЬ 1 относительно перестановки верхних (или нижних) индексов,
если такая симметрия имеется. Это означает, что в неприводимых представ-
представлениях ФЬ% обладают определенным типом симметрии относительно переу-
переустановок верхних и (отдельно) нижних индексов. Типы симметрии относитель*
но перестановок, в свою очередь, классифицируются по неприводимым пред-
представлениям дискретной группы перестановок, которые определяются так
называемыми схемами Юнга. В дальнейшем изложении встречаются только
простейшие случаи, так что рассматривать здесь общую схему нет необхо-
112
димости. Отметим лишь в связи с вышесказанным, что абсолютно антисиммет-
антисимметричный символ ранга N s^ , инвариантен в группе Slf(N): Та:&„ . =0.
Данное свойство следует из того, что при преобразовании SU(N) тензор
переходит в объект, также полностью антисимметричный по N индек*
сам. Однако такой объект пропорционален в,.», так как каждый из нндек-
'сов принимает всего N значений. Константа же пропорциональности равна
единице в силу унитарности (сохранение нормировки) и унимодулярностн
{отсутствие фазового множителя) преобразования. Аналогично инвариантен
символ $' N с верхними индексами.
Таким образом, с помощью символов ъ„ » и г' N> можно поднимать я
опускать индексы у объектов ф}/ \> не меняя их свойств преобразования.
V mi
В частности, отсюда видно, что полная антисимметричность Wjn\ no N
верхним илн нижним индексам эквивалентна отсутствию этих индексов, так
как зависимость от них описывается инвариантным тензором е.
Очевидно также, что символ б' инвариантен в группе SU(N): re:5j=»0
[это следует непосредственно из G.31)]. Поэтому если свертка щ}п\ по
Vmi
одному верхнему и одному нижнему индексу отлична от нуля, то можно
выделить бесследовую часть и чистый след по данным индексам:
Последнее слагаемое в правой части преобразуется как объект, у которого
на один верхний и один нижний индекс меньше.
Таким образом, набор элементов ф»» ¦>, преобразующихся по неприво-
V' /я/
димому представлению группы SU(N), должен обладать определенным типом
симметрии относительно перестановок индексов и не иметь ненулевых сверток
по любой паре иэ верхнего и нижнего индексов. Можно показать, что этих усло-
условий также и достаточно для выделения иеприводимого представления.
Формула G.31) позволяет построить генераторы SU(N) в любом пред-
представлении, если известны генераторы в фундаментальном представлении ta.
Стандартный их выбор аналогичен выбору генераторов в группе SUB): t°-=
=т«/2, где т» — матрицы Паули:
О 1\ @ —
Именно, запишем *e =
В качестве N(N—1) независимых матриц Ка выбирают матрицы размером
WXN, у которых отличны от нуля лишь два иедиагоиальных элемента, сим-
нетричио расположенных относительно главной диагонали. Эти два элемента
либо оба равны единице, либо элемент под диагональю равен 1, а над диаго-
диагональю —i. Остальные матрицы к' диагояальны (их число N—1). Стандартному
8-679 113
выбору отвечают следующие наборы элементов этих матриц на диагонали:
/ 2 \i/2
A. -ь ° °)-- (-Щ+ТТ) (ЬЬ^Ь -*• о 0),...
к элементов
\1/2
) A, 1,...,!.—(ЛГ—1)).
Очевидно, что указанный набор генераторов удовлетворяет соотношениям
ортонормированности G.8).
Отметим в заключение, что, как вндио из приведенного построения, в груп-
группе SU(N) имеется ЛГ—1 взаимно коммутирующих генераторов (диагональные
генераторы). Максимальное число взаимно коммутирующих генераторов назы-
называют рангом группы. Следовательно, ранг SU{N) равен ЛГ—1.
Приведем в заключение этого параграфа сводку формул, нужных для
практических вычислений. Большинство из них уже фигурировало в данном раз-
разделе, вывод остальных оставляем читателю в качестве несложного самостоятель-
самостоятельного упражнения:
1
¦. -=- 6е*;
¦«?;
2N
N
fadgfbedfcge = — fabc',
fabc4
__
G.32)
7.2. Классическая теория полей Янга—Миллса
В теориях Янга—Миллса реализуется локальная калибровоч-
калибровочная инвариантность относительно преобразований неабелевой груп-
группы подобно тому, как в электродинамике — калибровочная инвари-
инвариантность относительно абелевой U A) группы фазовых преобразо-
преобразований. Рассмотрим построение лагранжиана теории с калибровоч-
калибровочной инвариантностью относительно группы SU(N). (Данное
рассмотрение легко переносится также иа общий случай любой
неабелевой группы).
Инвариантность квантовой электродинамики относительно ло-
локальных фазовых преобразований достигается тем, что всюду В
ее уравнениях производная ?„=<?/<?*„ заменена ковариантной произ-
производной:
114
>?>„
<?„—i
где Q — оператор заряда в единицах
\е\ ![генератор ?7A)-преобразований]; Л„—потенциал электро-
электромагнитного поля. Название сковариантная> обусловлено тем, что»
применение оператора ?>„ не меняет свойств функции по отноше-
отношению к локальному фазовому преобразованию. Так, если преобра-
преобразование имеет вид YM-^exppeofAOQFPf*), то D,??(x)-*-
^^txp[i(o(x)Q]D^?(x), если одновременно поле Л„(*)» входящее в;
Dw подвергается преобразованию Л„(х)-»-Л|1(л;) +A/еMца)(дс).
Для построения производной, ковариантиой относительно пре-
преобразований неабелевой группы SU(N), запишем по аналогии с
КЭД
D»=d»-lgAZr°, G.33>
где g — безразмерная постоянная (играющая роль, аналогичную'
заряду е в КЭД); Л„"(дс)—набор из N2—1 векторных полей:
(а=1, 2,..., N2—1), a T — генераторы группы SU(N) (их кон-
конкретный вид зависит от того, по какому представлению преобра-
преобразуется функция, на которую они действуют). Оператор G.33)
является оператором ковариантной производной, если он не меня-
меняет закона преобразования объекта, на который действует.
Пусть W(x) принадлежит некоторому представлению группы
SU(N) и преобразуется по правилу
4(x)-*S(xyP(x). G.34>
Для того, чтобы найти закон преобразования полей АЦ(х) обеспе-
обеспечивающий ковариантный смысл оператора G.33), подействуем этим!
оператором на обе части G.34):
ZVF (х) -»(d»-l
- S
(на последнем шаге введен слева множитель /=SS+J. Отсюда
видно, что DJ? преобразуется так же, как Y, если имеет место-
закон преобразования
S+ (<?MS) - igS*AfT'S -+ - lgA$Ta
или, в эквивалентном виде,
AlT'-ySAlT'S*+(i/g-)Sd,xS+ G.35>
[здесь мы воспользовались тождеством S(dvS+) + (djS)S+=u'
=6^(SS+)=0]. Эта формула и определяет искомый закон преоб-
преобразования полей Д,,. Заметим, что ковариантность оператора Д»
можно также сформулировать в виде закона преобразования са-
самого оператора ?>„:
Dv-fSDuS* G.36>
и прийти к формуле G.35), исходя из этого условия.
\ Заметим также, что при глобальных преобразованиях, т. е.
когда 5^5=0, поля Л„в преобразуются по закону G.26) для при-
присоединенного представления. Поэтому можно говорить о действии
генераторов группы SU(N) на поля А/ в смысле формул G.24)
и 7.27).
8* 115
С помощью оператора ?>„ локализация симметрии превращает-
превращается в автоматическую процедуру: везде, где в лагранжиан сво-
свободного поля входит обычная производная <?,,, ее следует заме-
заменить ковариантной Д,. Так, если W описывает 5С/(Л/)-мультиплет
спинорных полей, то лагранжиан, обладающий калибровочной
^[/(^-инвариантностью имеет вид:
&v=4(iy»D)l—m)W=4(iylidll+gyilAZra-m)W. G.37)
Как должен выглядеть кинетический член полей А?, описываю-
описывающий их распространение, который следует добавить к лагран-
лагранжиану S?ygi В случае электродинамики он содержит тензор напря-
напряженности Fm, который, в свою очередь, выражается через ком-
коммутатор двух ковариантных производных: [?>ц, Z)v]=—iQF
Рассмотрим,аналогичный коммутатор в неабелевом случае:
В силу закона преобразования ковариантных производных G.36)
определяемый отсюда антисимметричный. тензор
S G.39)
преобразуется по присоединенному! представлению группы:
Ffl4TaS'SFfi4TaS+ и поэтому выражение
^kai=-A/4)^^v G.40)
инвариантно относительно калибровочных преобразований. Это в
есть необходимое выражение, содержащее кинетический член по-
полей Л„°. Коэффициент 1/4 в G.40) есть просто результат выбора
системы единиц.
Уравнения движения, как обычно, получаются из требования
исчезновения первой вариации действия I=S3?dAx при варьиро-
варьировании полей.
Найдем выражение для вариации действия, отвечающего ла-
лагранжиану G.40):
J G.41)
где F%(x) определяется формулой G.39). Имеем
6/ka( = -A/2)J^v(^?v)^4JC. G.42)
Из G.39) находим
8Fk-<VFAS)-д&ЬА$ +gfab*lAl {ЬА%) + (бЛ*) А%]-
=?>» [ЬА%) -?>v (SA?) G.43)
{при действии7ковариантной производной на поля А % подразумевает-
подразумевается, что генераторы; Та действуют на А% Согласно G.24)]. Отсюда
6/Гуи«= -A12) I F& [А*
116
=J FЛ?) (?>Л) Лс- J Д» (^6Л
Здесь использовано следующее свойство оператора ?у. /)М(АВ) =
=(?>МЛ)В+Л(?>МВ). Величина FMev6^$ является SU. (N)-cmrле-
(N)-cmrлетом (она не содержит внешних групповых индексов), поэтому для
нее ковариантная производная совпадает с обычной: Dn[F^6A") =
^=dn{F^bA^). Объемный же интеграл от полной дивергенции
сводится к поверхностному интегралу. Отбрасывая, как обычно,
поверхностные члены, имеем
81 ум=J
* х.
Отсюда следует, что в случае чистой теории Янга—Миллса (беа
полей «материи») уравнения движения имеют вид:
=O. G.45)
В отличие от уравнений свободного электромагнитного поля
6^4=0 они нелинейны из-за наличия ненулевых структурных
констант fabc (как следствие неабелевости группы симметрии).
Поэтому даже без спинорных и скалярных полей калибровочные
поля имеют весьма интересную «собственную жизнь>. В частно-
частности, для полей Янга—Миллса несправедлив принцип суперпози-
суперпозиции.
В случае же, когда имеется спинорное поле, описываемое
лагранжианом G.37), к вариации действия G.44) добавляется
член с вариацией действия, отвечающего G.37):
W. G.46)
Вариация действия по Y приводит к уравнению Дирака для Y*
iY»A^=^- G.47)
Если положить g=0, то G.46) превращается в N2—1 незави-
независимых волновых уравнений дц(дцА%—<?уА?)=О, каждое из кото-
которых аналогично уравнению движения для свободного безмассового
Поля. Таким образом, в пределе g=0 поля А? описывают N2—1
независимых безмассовых векторных полей типа фотонного. При
g*?0 эти поля взаимодействуют между собой и с полями материи*
Уравнение G.46) можно записать в виде
DtFb — Л. G.48)
где Jy— ковариантный ток спинорных полей. Это уравнение анало-
аналогично уравнениям Максвелла в электродинамике
<?Л,= -А, G.49)
которые в силу асимметрии F^ приводят к равенству
17.50)
117
означающему сохранение электрического заряда
, t)d>x G.51)
{интеграл берется по всему трехмерному пространству при
t =const).
Применим оператор Z)v к обеим частям уравнения G.48) и за-
запишем
Здесь оба слагаемых в правой части равны нулю в отдельности:
второе равно нулю как произведение симметричного тензора на
антисимметричный, а равенство нулю первого следует из опреде-
определения F$v как коммутатора в асимметрии fabc- [Z)v> D^Fy.*—
= igFwTbF?4=gfal":F{l4Fpv=O. Следовательно, для /? имеем ра-
равенство
=O. G.52)
Это равенство, однако, не означает сохранения заряда, отвеча-
отвечающего току /„". Отсутствие сохраняющегося ковариантного тока,
порождаемого только спинорными и скалярными полями, не уди-
удивительно, так как групповые заряды переносятся также и самими
полями Л„в и, следовательно, могут «перетекать> с одних полей
ла другие. Основываясь на G.48), можно построить нековариант-
ный ток, сохраняющийся в обычном смысле. В качестве такового
можно выбрать, например,
jZ=JZ + gf""A>Fcw, G.53)
для которого дцу'Л=О. Выбор этот не однозначен—к у? можно
прибавить дивергенцию антисимметричного тензора, например
gdvfabcA4,Ap> которая сохраняется автоматически. Однако некова-
риантный ток, как правило, никогда не приходится рассматривать
(в этом курсе он, во всяком случае, больше не встретится). Оста-
Остановились на этом вопросе здесь лишь для того, чтобы подчерк-
подчеркнуть отличие уравнений для полей Янга—Миллса от электроди-
электродинамики.
В электродинамике, как известно, кроме G.49) имеется также
уравнение
dxFw+dtFvK+dvFb^O, G.54)
которое можно записать в другом эквивалентном виде:
<?»((! ^«^«Л^-О. G.55)
где e^v>io — абсолютно антисимметричный тензор. Уравнение G.54)
[или G.55)] выражает тот факт, что F^ можно выразить через
потенциалы Л„. Имеется аналог этих уравнений и в теории полей
Янга—Миллса, который следует из тождества Якоби, примененно-
примененного к ковариантным производным:
Ря, [Ai, ?
118
что дает
А/^+АЛ+?>Л==О, G.56)
или
At @/2)8^/^=0. G.57)
Последние уравнения называют тождествами Бианки; они играют
важную роль в теории зшстантонов (ом. гл. 17).
Название тождества Бианки заимствовано из дифференциаль-
дифференциальной геометрии и теории гравитации. Читатель, знакомый с этими
теориями, вероятно, заметил в этом и в предыдущем разделах
много параллелей между дифференциальной геометрией и теори-
теорией гравитации, с одной стороны, и теориями Янга—Миллса — с
другой. Такие параллели не случайны, и теории Янга—Миллса
можно рассматривать как основанные на дифференциальной гео-
геометрии в так называемом расслоенном пространстве (такой под-
подход подробно обсуждается в книге Н. П. Коноплевой и В. Н. По-
Попова [7.2]). С другой стороны, теория гравитации может быть по-
построена как теория Янга—Миллса, реализующая локальную ин-
инвариантность относительно группы Пункаре (см., например, ра-
работы Утиямы и Киббла в сборнике [7.3]).
Задача. Пусть Ф описывает комплексные скалярные поля (см. гл. 8), пре-
преобразующиеся по некоторому представлению rpynnnSl/(AO.Найти калнбровочно-
инвариантное выражение для кинетической части лагранжиана этих полей и их
вклад в /ц.
Ответ:
t й 1] — g'OH- (T°Tb + ТьТа
7.3. Правила Фейнмана в теориях Янга—Миллса
Основное свойство теорий Янга—Миллса — калибровочная ин-
инвариантность, позволяющая придать теории элегантный и ком-
компактный вид, с другой стороны, означает, что в теории имеются
лишние, нефизические переменные, от которых наблюдаемые яв-
явления не зависят. В квантовой теории, учитывающей флуктуации
полей, флуктуации нефизических переменных вносят, если с само-
самого начала о них не побеспокоиться, несуразные бесконечности.
Так как действие от этих переменных не зависит, то ничто не огра-
ограничивает амплитуду их флуктуации, что и приводит к бесконеч-
бесконечностям. Поэтому при построении квантовой теории необходимо
каким-либо образом ограничить амплитуды флуктуации нефизи-
нефизических переменных, т. е. сделать действие от них зависящим и
тем самым «испортить» калибровочную инвариантность. Эту про-
процедуру обычно называют выбором дополнительного калибровоч-
калибровочного условия.
С трудностями, вносимыми калибровочной инвариантностью,
мы уже сталкивались в гл. 1 при обсуждении построения пропа-
119
гатора фотона. В неабелевых теориях все проблемы с определе-
определением пропагатора полей А„а повторяются, и они также могут
быть решены добавлением к лагранжиану калибровочно-неинва-
риантного выражения, например, вида, аналогичного A.36):
SS A/2С) (<?АаJ. G.58)
В отличие от электродинамики, в неабелевом случае эта добавка
вносит свои проблемы (см. разд. 7.4). Здесь же приведем правила
Фейнмана, которые генерируются основным лагранжианом и до-
добавкой G.58). При этом будем для определенности иметь в виду
теорию, описывающую взаимодействие калибровочных полей и
опинорного мультиплета с массой т, так что лагранжиан 2"' —
=2?+А2 с учетом добавки G.58) имеет вид
Среди членов этого лагранжиана выделяются следующие слагае-
слагаемые: _
квадратичное по спинорным полям: ¦^(iyv,dVi—m)'^]
квадратичное по полям А^: (—\/4)(дцА"~дчА$,J—A/2?)Х
кубичное по Лй: -(l/2)gfabc [д»А?—д?А
(<VUMSA$;
член четвертого порядка по полю Aw: —
i
и, наконец, член с взаимодействием А и •$: gA
Соответственно этим слагаемым образуются следующие эле-
элементы фейнмановских диаграмм: пропагатор спинорной частицы
(рис. 7.1,а); пропагатор векторной частицы (рис. 7.1,6); трех-
векторная вершина (рис. 7.1,в); четырехвекторная вершина
(рис. 7.1, г) и вершина взаимодействия спинорной и векторной
частиц (рис. 7Л,д).
Чтобы найти вклад того или иного графика в амплитуду про-
процесса, умноженную на i, следует перемножить все образующие
график элементы в порядке следования фермионных линий и, ес-
если в графике имеются замкнутые петли, проинтегрировать по не-
нефиксированным импульсам (с?4&/Bя4)). Добавки Ю в знаменате-
знаменателях пропагаторов определяют правило обхода полюсов при ин-
интегрировании в петлях.
Вывод данных правил Фейнмана из лагранжиана вполне ана-
аналогичен рассуждениям в электродинамике. Возможно, некоторого
пояснения требует вывод выражений для трехвекторной и четы-
рехвекторной вершин, специфических для неабелевых теорий. По-
Поясним этот вывод на примере трехвекторной вершины.
При квантовании теории вводятся операторы уничтожения с? (А)
и рождения (с+)? (А) квантов векторных полей с импульсом k, по-
поляризацией ц и групповым индексом а. Поле AUx), рассматривае-
рассматриваемо
4 J p
*
c,A
У N
V
* ь~~°
яс)
Рйс.7.1
мое как. оператор, представляется через операторы рождения и
уничтожения следующим образом:
К(х) =2 [^(*) ^ W ехр(-i
iL G.60>
[()—амплитуды векторных полей в соответствующих состоя-
состояниях]. Операторы с имеют следующие коммутационные свойства:
[с?(,Ь),(с+%A1']]=Вц8аь6лл-; [с, с]=0; [с+, с+]=0, из которых для
вакуумного состояния 10 > получаются соотношения:
< 01 с« (А) (с+) j
121
Трехвекторная вершина, в которой все импульсы для опред е
ленности считаются «выходящими», отвечает матричному элементу
J
< 01 с- (*0 с» (?2) с? (*3) 1&ш 10 > =
»'c' (<?д, А*) Ад'. Л$: 10 > G.62)
<) — кубичное по А слагамое лагранжиана). Подставляя сю-
сюда разложение G.60) для полей А, находим, что вследствие соот-
соотношений G.61) из сумм вида
G.60) отбираются лишь члены
с операторами рождения соот-
ветствующих состояний. При
этом 1д,-+—1ь так как произ-
производная действует на exp(iib:),
причем имеется всего шесть спо-
способов, которыми можно выбрать
три оператора рождения из
\/ iazaFa(Taf+TbTa)ti СУММ Для тр^ операторов А,
•> •> входящих в G.62). Соответст-
венно возникают шесть членов
в приведенном выше выражении
Рнс 7kfc для трехвекторной вершины.
Задача. Какие элементы графиков Фенймана описывает вза-
взаимодействие скалярных частиц с калибровочными полями (см.
задачу к разд. 72)?
Ответ. (См. рис. 7.2).
7.4. Поля «Духов» Фаддеева—Попова
Рассмотрим вариацию действия, связанного с членом G.58),
при бесконечно малом калибровочном преобразовании (остальная
часть действия инвариантна). Подставляя в формулу G.35) мат-
матрицу калибровочного преобразования с бесконечно малыми пара-
параметрами <о" (х):
5 = / + 1©вГ«, G.63)
находим в первом порядке по ©
А?Т°-у А%Г°,+to>Mj \Т", Т«1+A /g) (д»<**) Т;
откуда
АЛ-^Аг + О/йА^илибАЦ^О/ЙД^- G.64)
Следовательно, вариация действия при преобразовании G.63)
Ы = ~ Т $ (д»А® 8 &А
t22
Если ввести обозначение ца=дцА», то для rf(x) получим урав-
уравнение движения
O. G.65)
Отсюда видно, что в отличие от электродинамики условие
>dlAlk"?S'r)*=0 в начале процесса не означает, что поле tj" не воз-
возникает с течением времени, так как согласно G.65) оно может
генерироваться полем А. На квантовом языке G.65) означает, что
;поле А генерирует т)-частицы или, другими словами, возбуждает
.флуктуации tj-поля, которые затем могут оказывать влияние на
.физический процесс. Поэтому G.58) —не безобидная константа,
л ее добавка приводит к возможности появления rj-частиц как в
конечных продуктах процесса, так н, что самое неприятное, в
петлях.
С таким положением, вообще говоря, можно было бы смирить-
смириться и просто каждый раз вычеркивать вносимый членом G.58)
вклад rj-частиц. В конечном состоянии Tj-частицы устраняются
довольно просто — для этого достаточно матрицу плотности каж-
каждого конечного глюона выбирать поперечной, что означает нало-
наложение условия дуЛ/—О в конечном состоянии. Однако с устране-
устранением нефизического вклада в петлях, т. е. в промежуточных состо-
•яниях, ситуация существенно сложнее. Действительно, возмож-
возможность рождения и поглощения rj-частиц уже «упрятана» в пра-
правила Фейнмана, обсуждавшиеся выше, и на первый взгляд не-
неясно, что именно следует вычитать из приведенных на рис. 7.1,а—д
элементов графиков Фейнмана.
Изящный способ устранения вклада Tj-частиц в петлях, най-
найденный Л. Д. Фаддеевым, В. Н. Поповым [7.4] и де Виттом
[7.5] в 1967 г., состоит в том, что из рассмотренных правил Фейн-
Фейнмана ничего вычитать не надо, а следует ввести дополнительный
•мультиплет полей (Ф+)в, называемых теперь духами Фаддеева—>
Попова, которые удовлетворяют такому же уравнению, как и
tj-поля:
(?>д(?1гФ+)о = <?2(Ф4)о+§/о»сЛ^1г(Ф+)с=0, G.66)
ai считать, что (скалярные) поля Ф+ квантуются по статистике
Ферми, т. е. что каждой замкнутой петле с Ф+ следует приписать
дополнительный множитель (—1). (Мы пишем Ф+, а неФ, чтобы
•следовать общепринятым обозначениям.) При этом, поскольку по-
поля Tj и Ф+ удовлетворяют одному и тому же уравнению, на каж-
каждую Tj-петлю найдется точно такая же Ф-петля с противоположным
знаком. Поэтому нефизические tj- и Ф-поля взаимно уничтожают
вклады друг друга (разумеется, Tj-петли не надо учитывать от-
отдельно, они уже содержатся в рассмотренных выше правилах
'Фейнмана).
Формально введение Ф-полей можно описать лагранжианом
S%yx = (<ЭдФ+)° (?ДФ)°=(<?дФ+)°<?дФв+gfabc (д»Ф+)аAl®° G.67)
123
и правило квантования по статистике Ферми обеспечить, считая
Ф, Ф+ аитикоммутирующими полями.
Таким образом, полный эффективный лагранжиан, который
позволяет стандартным способом проквантовать теорию, имеет
вид
<?,*-.2'+A*+**7Jt- G.68)
Введение лагранжиана 2^ вида G.67) вносит новые эле-
элементы в графики Фейнмана: пропагатор духа (см. рис. 7.1, е) в
вершины дух—дух—вектор (см. рис. 7.1,ж). Отметим, что по-
последняя вершина выражается через импульс только выходящей
скалярной «частицы», в отличие от обычной вершины взаимодей-
взаимодействия физических скалярных частиц с векторной, которая выра-
выражается через сумму импульсов входящей и выходящей скалярных
частиц.
Напомним, что по построению духи распространяются лишь в-
замкнутых петлях, которым присваивается дополнительный мно-
множитель (—1).
После всех изложенных построений встает вопрос: что проис-
происходит с неабелевой калибровочной инвариантностью после всех
модификаций лагранжиана полей Янга—Миллса? Ответ на этот
вопрос известен сравнительно давно: амплитуды физических про-
процессов калибровочно инвариантны (в частности, не зависят от
параметра калибровки ?). Изящный способ увидеть это на уров-
уровне лагранжиана был найден в 1975 г. Бекки, Рюэ и Стора, кото-
которые заметили, что лагранжиан вида G.68) инвариантен (с точ-
точностью до полной дивергенции) относительно следующего нели-
нелинейного преобразования, содержащего инфинитезимальный анти-
коммутирующий параметр Я+ (такого же типа, как поля Ф):
J
(Я+ не зависит от х). Здесь в последней строчке проявляется ан-
тикоммутирующий характер полей <р: выражение /вЬсФ*Фе не рав-
равно нулю, так как ФЬФС—фсф1>=2Ф1'Ф<!=74:0. Заметим также, что
первая строчка в G.69) описывает обычное бесконечно малое
калибровочное преобразование полей Л„ [см. G.64)] с парамет-
параметрами <вв=Я+Фв (произведение двух антикоммутирующих чисел
есть обычное число) и инвариантность относительно преобразова-
преобразований G.69) в секторе физических переменных эквивалентна обыч-
обычной калибровочной инвариантности. Что же касается последних
двух строчек в G.69), то в них решается вопрос о законе калиб-
калибровочного преобразования полей духов.
После того, как преобразования Бекки—Рюэ—Стора G.69)
выписаны, проверка инвариантности действия, отвечающего лаг-
лагранжиану G.68), превращается в простое упражнение, которое
предоставляем читателю проделать самостоятельно.
124
Глава 8
ПЕРЕНОРМИРОВКИ В ТЕОРИЯХ ЯНГА-МИЛЛСА
8.1. Перенормировка пропагаторов, вершин и заряда
Как видно из предыдущей главы, правила Фейнмана в неабе-
левых теориях Янга—Миллса во многом аналогичны диаграмм-
диаграммной технике квантовой электродинамики. В частности, поведение
пропагаторов и вершин при больших импульсах такое же, как в
электродинамике спинорных и скалярных частиц. Это позволяет
доказать перенормируемость неабелевых калибровочных теорий,
повторяя ту же линию рассуждения, что и в КЭД. Не приводя
здесь доказательства перенормируемости теорий Янга—Миллса,
нриведем стандартную схему перенормировок в неабелевых тео-
теориях, которая понадобится в дальнейшем для конкретных вычис-
вычислений.
Напомним, что свойство перенормируемости означает незави-
независимость соотношений, получаемых в теории между наблюдаемы-
наблюдаемыми амплитудами, от параметров обрезания, вводимых для регу-
регуляризации графиков Фейнмана. (Для определенности будем иметь
в виду регуляризацию в импульсном пространстве, при которой
фейнмановские интегралы обрезаются тем или иным образом при
больших импульсах порядка М). Как и в случае КЭД (гл. 2),
при исследовании общих свойств теории (например, перенорми-
перенормируемости), а также на промежуточных этапах вычислений удобно
обсуждать отдельные элементы графиков Фейнмана с учетом пет-
петлевых поправок к ним (точные пропагаторы я вершины). С уче-
учетом поправок эти элементы зависят, вообще говоря, от параметра
М. Однако в перенормируемой теории эта Ъависимость собирается
в мультипликативные факторы Z, после выделения которых оста-
остаются конечные величины — перенормированные пропагаторы и
вершины. В окончательных выражениях для физических ампли-
амплитуд факторы Z комбинируются вместе с затравочным зарядом в
перенормированный заряд.
Введем обозначения перенормировочных факторов Z для про-
пропагаторов н вершин в неабелевых теориях:
для поперечного пропагатора векторного поля А»;
Dg, (k) |* ft
для пропагатора духа:
для пропагатора спинориой частицы:
ЗД|*.—I* =Z2S@) (k) |*.—д.;
для трехвекторной вершины:
г*D„ К ?3Wlft2__jii=zr1(iw(*i. К ^
125
для вершины дух—дух—векторное поле:
для вершины взаимодействия спинорной частицы с векторный
полем:
для четырехвекторной вершины:
rv! <*<) 1Й?._^-*г' (г; (*о)т 1^^,.
Здесь в правых частях с индексами @) стоят затравочные
выражения для пропагаторов и вершин, приведенные на рис. 7.1,
а слева — выражения для соответствующих элементов графиков
Фейнмана, которые получаются при непосредственном вычислении
с учетом поправок (неперенормированные, пропагаторы и вер-
вершины). Все пропагаторы и вершины в приведенных определени-
определениях факторов Z рассматриваются в условиях, когда все внешние
имлульсы в них пространственно-подобные (евклидовы величины
одного порядка ~ц). Необходимость рассмотрения евклидовых
импульсов диктуется тем, что гори временинподобных импульсах
амплитуды приобретают абсорбтивные части, которые отличны
по своей структуре от затравочных выражении. Все приведенные
множители Z являются функциями затравочного заряда g пара-
параметра обрезания М, точки нормировки р, и калибровочного пара-
параметра ?: Zi—Zi(g2, М2, р,2, ?). Введение точки нормировки ц —
удобный технический прием для того, чтобы при обсуждении от-
отдельных элементов графиков Фейнмана сопоставить им конечные
величины — перенормированные пропагаторы и вершины. Пере-
Перенормированные пропагаторы выражают через неперенормирован-
ные делением на соответствующий множитель Z, а вершины—»
умножением. Например, перенормированный пролагатор вектор-
векторного поля имеет вид
b # f, АР, ц2, Q,
а перенормированная трехвекторная вершина
rJ$T(fti, k2, кд = Т$Цкг, k2, kb)Z,{g\ NP, у?, Q.
В точке ц все перенормированные величины совпадают с затра-
затравочными. В перенормируемой теории все Dr и Р" не зависят от
параметра М (но зависят от точки нормировки р,). Последнее
свойство особенно легко проследить на однопетлевом уровне, за-
заметив, что зависимость неперенормированных величин от М в ка-
калибровочной теории — логарифмическая. В частности, факторы Z
имеют в однопетлевом приближении вид
Zi (g2, АР. V-2, &) =
где Ct{l) —численные коэффициенты.
126
Заметим теперь, что неперенормированные величины в точке
j*_ могут быть воспроизведены в первой порядке по следующему
эффективному лагранжиану (ограничиваемся случаем чистой тео-
теории Янга—Миллса, включение спинорных и скалярных полей оче-
очевидно):
5%ф A /4Z3)(ддА%-дуА-Y
l $+A /Z3) (<
+(gfZ1) fabc (д»Ф+а) А* Ф< - A /2C) (ддЛ«J (8.1)
(последнее слагаемое остается без модификаций, так как про-
продольная часть пропагатора векторного поля не перенормируется)»
Переход к лангранжиану, дающему в точке р. перенормирован-
перенормированные величины, осуществляется заменой исходных полей А и Ф
перенормированными A-*-Zy2A; Ф-*-2\/2Ф; <!>+->Z'>'2e>''. В терминах
этих полей
«;Aк. (8.2>
Этот лагранжиан дает элементы графиков Фейнмана, совпа-
совпадающие в точке р с исходными, если определить перенормиро-
перенормированный заряд ?2(р2) (эффективный заряд при импульсе ц) со-
согласно
(8.3>
Если же учесть спинорные поля, то в эту цепь равенств следу-
следует добавить <n—g2Z$Z#/Z$4. Ясно, что данная цепь равенств га-
гарантируется калибровочной инвариантностью теории, так как
только при условии выполнения указанных соотношений обыч-
обычные производные «соберутся» в ковариантные с константой"
#2([л2). Поэтому попутно получаем соотношения между множите-
множителями Z (тождества У орда):
ZbiZ^ZbiZ, ^ZFizF-ZiiZ*. (8.4)
Из перехода от (8.1) к (8.2) следует правило для перенорми-
перенормировки параметра ? ^^/^з-
Исходный лагранжиан в терминах перенормированных полей:
можно записать в виде (см. разд. 3.5);
<?= -A /4)(«Mj-^Ajp-g,/-"(<М$)(А* АЗ-
А%
с перенормированными параметрами gr и ^г, определяемыми фор-
127
мулами (8.3) и (8.5). При этом процедура перенормировок в про-
процессе вычислений не отличается от рассмотренной в разд. 3.5 для
электродинамики. Именно, при вычислении петель, генерируемых
данным лагранжианом, последние два слагаемых в ием следует
рассматривать как возмущение и в каждом порядке подбирать
множители Z% и Zs, а также ?r=g0i2) и g2. чтобы элементы гра-
графиков Фейнмана в точке ц совпали с затравочными. Последний
лагранжиан является исходным лагранжианом теории, записан-
записанным в терминах других (перенормированных) переменных, тогда
как эффективный лагранжиан (8.1) [а также (8.2)] представляет
собой лишь удобную компактную запись пропагаторов и вершин,
вычисленных с учетом петлевых поправок, в точке ц. При этом
нетрудно заметить, что точный лагранжиан SB отличается от
З'аф (8.2) лишь последними двумя слагаемыми.
Так же, как и в КЭД, с помощью несложного анализа графи-
графиков Фейнмана легко убедиться, что при вычислениях физических
амплитуд множители Z всегда входят в комбинации с затравоч-
затравочным зарядом вида (8.3), т. е. амплитуды зависят лишь от эффек-
эффективного заряда. Другими словами, вся зависимость от затравоч-
затравочного заряда и параметра обрезания собирается в эффективный за-
заряд. Поэтому лишь последний является физически наблюдаемой
величиной. Перенормируемость означает, что если эффективный за-
заряд определен в одной точке ц, т. е. ?2(ц2), то он может
быть вычислен в любой другой точке ц', причем связь между
g2(\i2) и g2(i*'2) не содержит параметра обрезания М, Если точ-
точки ц и р' таковы, что массовыми параметрами теории (напри-
(например, массами снинорных полей) можно пренебречь, такая связь
имеет вид g2(\i2) =f (?2(!*/2)> (vPfyS2). Продифференцировав это
функциональное соотношение по In р,2 и положив затем ц/е=ц, при-
приходим к уравнению Гелл-Мана—Лоу:
Смысл уравнения (8.5) состоит, очевидно, в том, что эволю-
эволюция эффективного заряда в точке ц зависит только от его зна-
значения в этой точке.
Функция Гелл-Мана—Лоу может быть вычислена по теории
возмущений в виде ряда по g2:
(8.6)
В разд. 6.4 обсуждалось поведение пропагатора электрона и
вершинной функции в КЭД при больших импульсах. Эффектив-
Эффективным средством для изучения асимптотики этих величин служат
дифференциальные уравнения Овсянникова—Каллана—Симан-
чика (ОКС). На практике часто приходится рассматривать зави-
зависимость от импульсов не только основных элементов графиков
Фейнмана, ио и матричных элементов операторов, внешних по
отношению к теории, построенных из полей векторных бозонов,
128
спинорных полей и т. д. (например, матричные элементы тензора
энергии-импульса, аксиального тока и т. д.). Такой матричный
элемент, вычисленный по состоянию с внешними импульсами ри
можно рассматривать как некоторую вершинную функцию Г(р4),
вычисленную с учетом поправок, вносимых калибровочным взаи-
взаимодействием, описываемым константой g (Г может обладать
групповыми и лоренцевыми индексами, которые для простоты за-
записи опускаем). Учет петель, возникающих за счет калибровоч-
калибровочного взаимодействия, приводит к тому, что неперенормированная
величина Г содержит зависимость от затравочной константы g и
параметра обрезания М. Предположим, что структура неперенор-
мированной величины Г совпадает с структурой затравочной, т. е.
такова, что можно ввести перенормировочный множитель Z:
Г (a; g\ т %2r_»,=Z-> (g2, №, у?, С)Г@) ЫЦ_Д,.
Величиной, не зависящей от М, при этом будет перенормирован-
перенормированная амплитуда
Г' (Pi; g2, V2, tr)=Z (g2, M\ р\ С) Г {Pi; g2, Ж2, С), (8.7)
которая при импульсах, выбранных в точке нормировки ц, совпа-
совпадает с Г@). Важно, что Гг определено в терминах перенормирован--
ного заряда gV2(n2)-
Нетрудно получить уравнение для Р, гарантирующее то, что
вся зависимость от М соберется в множитель Z и в эффективный
заряд g ([х2). Для этого можно, например, воспользоваться тем,
что неперенормированная амплитуда Г не зависит от выбора
ц: dTfdln\j?~O. Отсюда, пользуясь связью (8.7), для Гг полу-
получаем
ХГ'0^2.И2.?)=0, (8.8)
где P(g2)=(l/g2)^g20*2)/<?ln(i2; Y(g2,9==<?lnZ/<?lnn2; 6(g2, C)=
ЭГ12
Все производные в последних определениях вычисляются при
фиксированных затравочных g2, ? и фиксированном параметре
М. В уравнении (8.8), в отличие от рассмотрения в разд. 5.4,
разделена зависимость от ц и g (именно в таком виде данное
уравнение встречается в литературе). При фиксированном затра-
затравочном заряде
так что можно вернуться к виду уравнения, обсуждавшемуся в
разд. 5.4.
Таким образом, повторен вывод уравнений ОКС, рассмотрен-
рассмотренных для КЭД в разд. 5.4. Как показано в разд. 5.4, уравнения.
ОКС позволяют определить зависимость Г при масштабном
9—679 129
преобразовании импульсов р1-*-Яр1. Именно, если Г имеет размер-
размерность (масса)*, в калибровке Ландау [?=0, при этом и Г=0. и
bB Z)=®1 находим
Показатель экспоненты в этой формуле можно переписать в тер-
терминах интеграла по заряду:
(
-
Выше уже говорилось, что р-функцию можно найти в теории
возмущений в виде ряда по g2; то же самое справедливо и для
у-функций. При малых g2
где Ь и y—числа (у, естественно, зависит от того, какая величи-
величина Г рассматривается). В этом приближении интеграл в (8,9)
легко вычисляется:
Таким образом, при v^O помимо тривиального множителя Я*
имеется нетривиальная зависимость от масштабного множителя
к, описываемая последним сомножителем. Величину k по понят-
понятным причинам называют канонической размерностью. Величину
у [а также ^(g2)] называем аномальной размерностью, хотя в
литературе этот термин часто употребляют в более узком смыс-
смысле (в применении к теории с фиксированной точкой).
Имеется класс величин (сохраняющиеся тензоры), для кото*
рых нетривиальная зависимость от к исключена с самого начала.
Рассмотрим для примера простейший из таких объектов—электро-
объектов—электромагнитный ток Уд- Сохранение тока означает неизменность во вре-
времени заряда Q(O=w'o(x> t)dzx. Если выполнить масштабное
преобразование х-*-хА, t-+t/k, то Q(t) переходит в Q(t/k)>
но в силу закона сохранения Q(tlX)—Q(t) и поэтому /о может
иметь только каноническую размерность, равную трем. В силу
лоренц-инвариантности то же справедливо и для остальных ком-
компонент /„. Еще одним важным примером сохраняющегося тензо-
тензора является тензор энергии-импульса 6„у, аномальная размерность
которого также равна нулю.
В начале раздела мы предположили, что одевание петлями
не изменяет затравочной структуры Г рассматриваемой величины.
Если это не так, то следует совместно рассмотреть несколько
величин Гв, так что после петлевого одевания можно выразить
130
эффективные Га в виде линейной комбинации затравочных: Га—
*=2 (Z'^abTf*.- При этом множители Z образуют матрицу и
ь
соответственно y(g2) также является матрицей. На однопетлевом
уровне в этом случае удобно перейти к таким линейным комби-
комбинациям Г„, для которых матрица коэффициентов у диагональна.
8.2. Вычисление функции Гелл-Мана—Лоу
в SU(N) калибровочной теории
Вычислим коэффициент Ъ в первом члене разложения P(g2)
по g2 в SU(N) -теории. Согласно определению $(g2) —
==dlng2(n2)/dlnn.2. Для вычисления ?2(ц2) можно воспользоваться
любым из эквивалентных определений (8.3). Выберем третье из
них g2(ii2)—g2Z3Z3i/Zi2, в этом случае вычисления наиболее про-
просты.
Множители Z зависят от отношения М2/ц2, поэтому можно за-
записать:
Отсюда видно, что достаточно следить лишь за зависимостью,
множителей Z от 1п М2.
Перейдем к конкретному вычислению этих множителей.
Вычисление 2%. Множитель 23, описывающий перенорми-
перенормировку пропагатора духа, определяется на однопетлевом уровне
из графического соотношения, приведенного на рис. 8.1. Для ле-
левой части этого соотношения имеем выражение
где iPcd(p2)—вклад петли. Используя правила Фейнмана (см»
рис. 7.1), находим выражение для Р в виде интеграла
<8ЛЗ>
Заметим теперь, что если следить только за параметром обре-
обрезания М2 по импульсу интегрирования к, то импульс р можно
считать произвольно малым и разложить подынтегральное выра-
выражение в ряд по р2. Из (8.13) легко видеть, что член (р2H отсут-
— .z3()
a. b р р+к р a. J p
Рис 8.1
9* 131
ствует, поэтому первый член разложения пропорционален р2.
Удерживая лишь этот член, имеем:
Г — П 16Я2 O^JIJirU' + iO (ft»+ 10)» /Х
- <8Л4>
(Здесь мы попутно воспользовались равенством G.14), /<»<**/««» =
= —Л^ба6.] Оставшийся интеграл может быть выражен только
через guv, поэтому кц1ь, эффективно заменяется (l/4)&2gnv. Следо-
Следовательно,
*"--*т?г**±тЧ-?ч*ЬоГ-' (8л5)
Интеграл здесь логарифмически расходится, и на верхнем преде-
пределе его следует обрезать при —fe*=AP. (На нижнем пределе точ-
точный интеграл, не разложенный по р2, естественно, автоматически
обрежется на импульсе р). Таким образом, имея в виду только
зависимость от М, можно записать
Отсюда, возвращаясь к определению Z3, получим
Z8—l+W(gs/16rf)C/4._E/4)liiAft (8.16)
Вычисление Z\. Для Z\ имеем графическое определение,
приведенное на рис. 8.2. Так как нас интересует только
Рис 8.2
зависимость Zx от Af, мы положили импульс глюона рав-
равным нулю, а зависимость от импульса духа учитываем лишь в
первом неисчезающем (линейном) приближении. Последняя вер-
вершина на линии духа пропорциональна р, поэтому фактически в
петле можно положить р=0. После этого для вклада второй диа-
диаграммы ва рис. 8.2 имеем выражение
fbaefoafffee J **. [kX&v+k,&v-^2kvg^\ X
132
X gvK —A — 5) —— g^ff — A — 5) -. ,— | AГг,Ж|
' fbdefadfffecn
я° J J J P
=~ЩГ f*defadff/ecPll (% ta№). (8.17)
Аналогично для третьей диаграммы находим:
(8Л8>
Произведение трех символов / в этих формулах «распуты
вается» с помощью предпоследнего из соотношений G.32
fbdefadfffec^N/Pjfabc, Подставляя это равенство в (8.17) и
(8.18) и складывая окончательные выражения с затравочной
вершиной, получаем эффективную вершину в виде
jgl) откуда
Jin АР. (8.19)
Вычисление Z3. Вычисление множителя Z3, отвечающег01
перенормировке поперечной части пропагатора глюона, аналогично
вычислению Z3, проведенному выше. Обозначим, петлевой вклад
iHjivG?)- Тогда поперечная часть пропагатора глюона с учетом
петлевого вклада примет вид
Основанные на калибровочной инвариантности рассуждения,
повторяющие известную аргументацию из квантовой электродина-
электродинамики, приводят к выводу, что поляризационный оператор П имеет
следующую структуру
ЩЦр)~в»Р (р2) (Л* -рх/ы).
где 6a*P(p2)=(l/3)Il2*Q?2)//72. Отсюда находим
Z3=l + P(-n2). (8.20)
Графическое представление П приведено на рис. 8.3. (Корот-
(Короткие внешние глюонные линии означают, что отвечающих им про-
пагаторов писать не надо, а следует вычислить лишь вклад пет-
петли.) Первые два графика входят с коэффициентом 1/2. Он появ-
р+к Ъ,/1 a,ji р+к р*к
Рис 8JS
133
ляется из-за того, что при выводе правил Фейнмана все
глюоны, выходящие из вершины, считались различными. В петле
же глюоны неразличимы. Напомним также, что диаграмма с ду-
духовой петлей имеет дополнительный коэффициент (—1), как
если бы дух был фермионом.
Как и в случае вычисления Z3, здесь существен член, пропор-
пропорциональный р2, в разложении П№ в ряд по проходящему импуль-
импульсу р. При этом вторая диаграмма выпадает из рассмотрения, так
как она не зависит от р. (Роль этой диаграммы сводится к со-
сокращению вклада остальных графиков при /7=0.)
Для вклада первого графика в Д|* из правил Фейнмана полу-
получаем следующее выражение:
-I is? facdfbcd \ Sr I -
Х (*•+ 10) [(p+k)* + 10] '
В этом выражении следует свернуть лоренцевы индексы и найти
член разложения, пропорциональный р2. Вычисления несколько
упрощаются, если, имея в виду дальнейшее интегрирование по
d*k, производить попутно замену (pkJ/k2-*-p2/4. При такой замене
Полезно также рассматривать отдельно члены разных степеней
по ?. При этом легко видеть, что член, пропорциональный g2, об-
обращается в нуль. Для оставшихся в результате все же довольно
длинного вычисления можно из (8.21) получить:
(8.22)
Вклад духовой петли в П„, вычисляется по сравнению с пре-
предыдущим совсем просто и составляет
161<Г )Ч
=NT^P2[ilnM2)- (8-23)
Рассмотрим теперь вклад фермионной петли в Пдд:
134
Напомним, что все рассматриваемые импульсы считаются намного
большими массы фермионов, поэтому последней пренебрегаем.
Воспользовавшись формулой G.19) для входящего сюда сле-
следа от генераторов, вклад фермионной петли можно записать в
виде
—AT (R) 8ab (g2/16л2) ? In М2. (8.24)
Складывая окончательные выражения в (8.22)—(8.24) для различ-
различных вкладов в Щд i вычисляя Р, а затем согласно (8.20) множи-
множитель Z3, находим:
z*-l+&[N $--%)-&М]\йЮ. (8.25)
(J- Функция. Собирая вычисленные множители Z [форму-
[формулы (8.16), (8.19) и (8.25)] в комбинацию, входящую в (8.12), с
точностью до членов порядка g2\nM2, находим
Z?\iZ\=1 + (g*/ 1бя2) [1Ш/3 - D/3) Т (R)] In М2,
откуда согласно (8.12) первый член разложения ^-функции имеет вид
р = -•*g*/16n*+O(g4); b=UN/3-D/3)T{R). (8.26)
Из приведенных вычислений видно, что нетривиальную задачу
представляет нахождение первого слагаемого в выражении для
Ь, которое связано с самодействием векторных полей. Вклад фер-
фермионов возникает лишь за счет последнего графика рис. 8.3 и вы-
вычисляется весьма просто. Очевидно также, что если имеется не-
несколько мультиплетов фермионов, преобразующихся по представ-
представлениям \RU то каждый из мультиплетов дает свой отдельный вклад
в Д^ за счет графика типа последнего на рис 8.3. Наконец, за-
заметим, что если имеются также мультиплеты комплексных скаляр-
скалярных полей R/, их вклад в четыре раза меньше вклада аналогич-
аналогичных спинорных мультиплетов (проверить это утверждение пред-
предлагаем читателю в качестве самостоятельного упражнения).
Поэтому коэффициент Ъ в достаточно общем случае наличия муль-
мультиплетов Rt дираковских фермионов и мультиплетов R/ скаляр-
скалярных полей можно записать [8.1—8.3] в виде
Приведем также для справок выражение для р-функции в сле-
следующем (двухпетлевом) приближении [8.4] для случая, когда
нет скалярных полей:
135
![напомним, что для SU(N) C2(G)=N]. Заметим, что и в двух-
петлевом приближении вклады мультиплетов спинорных частиц
аддитивны. Это легко объяснить, так как неаддитивность может
возникнуть за счет графиков, содержащих одновременно две фер-
мионные петли, которые бы исчерпали рассматриваемое число
петель. Однако единственный имеющийся график такого типа
(рис. 8.4) является итерацией однопетлевого приближения и не
входит в ^-функцию. Трехпет-
/'-"~-чч /""^^ч левая р-функция в неабелевых
/ \ / \ теориях также вычислена [8.5].
[ /?t )—{ r- j Однако на трехпетлевом уров-
V J V J не результат зависит от
^~^У \^^/ конкретного способа регуляри-
регуляризации фейнмановских интегра-
Р*с %А лов, эта же зависимость появ-
появляется и в самом перенормиро-
перенормированном заряде. Соотношения же между физическими наблюдаемы-
наблюдаемыми амплитудами от способа регуляризации не зависят во всех
порядках теории возмущений.
Рассмотрим интересный для дальнейшего частный случай,
когда теория включает Nf различных полей фермионов, причем
все они находятся в одном и том же, например в фундаменталь-
фундаментальном, представлении Rt=F группы G=SU(N). При этом в (8.28)
C2(G)=N; Cj(J?«)-=(JV»— l)/2N; Г(Я,)=1/2, и, обозначая
g2/Dn,)=as, получаем (без учета вклада скалярных полей):
<8-29>
причем при W=3 6=11— B/S)Nf, а р=102—CS/S)Nr При этом
из определения (8.5) функции ^(g2) следует уравнение Гелл-Мана—
Лоу:
в котором второй член справа при «^(ц2)^! приводит лишь к ма-
малым поправкам.
В заключение рассмотрим влияние массовых параметров лаг-
лагранжиана на эволюцию эффективного заряда. Именно вклад в
коэффициент Ь, вычисленный по формуле (8.28), дают лишь по-
поля с массами т2<ц2 (в этом случае величиной т можно пренеб-
пренебречь по сравнению с характерными импульсами в графиках
Фейнмана, определяющих множители Z). Графики, содержащие
поля с массой т2»ц2, зависят от ln(Af2/m2), а не от In (М2/ц,2),
поэтому вклада в р-функцию не дают (степени свободы тяжелых
частиц «заморожены» при ц8<ст2 и не дают вклада в перенор-
перенормировку заряда). Поведение ^-функции в переходной области
136
т~ц зависит от определения и для многих практических расче-
расчетов достаточно приближения, при котором вклад частиц с мас-
массой т в коэффициент Ь с ростом ц включается скачком при
Задача- Вычислить перенормировочные множители Z,, Z4> Z, и 2^, в од-
иопетлевом приближении в убедиться в справедливости тождеств Уорда (8.4)
на однопетлевом уровне.
Ответ. Z1 = 1+^f[n(^- + ^)—j7-(*)]lnA««;
? Г ЗЛГ !
^ = 1 - ife- [— A -С) + Сг (/?) С I Ш Af«,
где СгС/?)—значение квадратичного оператора Казимира в представлении Нг
по которому преобразуются спинориые поля.
8.3. Асимптотическая свобода и размерный параметр Л
Для достаточно малых значений заряда можно ограничиться
первым членом разложения р-функции (8.26)—(8.29) и решить-
уравнение Гелл-Мана—Лоу (8.5), т. е. найти перенормированный
заряд g*(n8) как функцию ц:
1/в?И-1/8*(!4)«(*/16я?IпО*»/11в). (8.31)
Это соотношение позволяет найти заряд ^(ц2), если известен
заряд ?2(цо2)> причем оба должны быть достаточны малы:
¦(*B)/16»)<1 BB)/162)<1
(в(|)/), (§(ц))
Из формул (8.27) — (8.29) видно, что вклады самодействия
векторных полей и полей «материи» в коэффициент Ь имеют раз-
разные знаки. Первый (положительный) вклад называют антиэкра-
антиэкранировкой заряда, а второй (отрицательный) — экранировкой
заряда. Поэтому если вклад экранировки не превосходит вклад
антиэкранировки, то коэффициент b положителен '[например, в
случае чистой теории калибровочных полей или когда имеются
лишь фермионы в фундаментальном представлении, T(F) = \/2
(см. G.8) и число таких мультиплетов п<11 N/2]. Тотда, если
имеется точка щ, в которой ?2(цо2) достаточно мало, при всех
ц>ц,о можно пользоваться формулой (8.31), так как с ростом ц
заряд #2(ц2) убывает и при цЯ-^оо логарифмически обращается
в нуль. Такое поведение называют асимптотической свободойг
так как при асимптотически больших импульсах (т. е. на асимп-
асимптотически малых расстояниях) взаимодействие в теории выклю-
выключается. Видно, что асимптотическая свобода возникает за счет
137
антиэкранирующего вклада самодействия векторных полей, ко-
которое является следствием неабелевости калибровочной группы.
Формулу (8.31) можно переписать в виде
(8.32)
где
(8.33)
Постоянная Л в (8.32) формально отвечает точке, в которой
?2(ц2) обращается в бесконечность. Однако сама формула (8.32)
применима лишь при малом заряде и применять ее для области
ц~А нельзя. Тем не менее формулы (8:32) и (8.33) показывают,
что, изучая поведение перенормированного заряда ?2(ц2) в обла-
области, где этот заряд мал, можно из величин ц и ?2(ц2) построить
размерную величину Л, которая от точки нормировки ц фактиче-
фактически не зависит. [При изменении ц изменяется также и ?2(ц2).
¦причем так, что значение Л остается постоянным^ Величину Л
можно определить и тае ограничиваясь первым членом разложе-
разложения для р-функции:
( S k) <884>
Таким образом, даже в отсутствие массовых параметров в
-лагранжиане в теории возникает массовый параметр Л. (Это яв-
явление иногда называют размерностной трансмутацией.) Ясно
вместе с тем, что точное значение Л зависит от способа регуля-
регуляризации фейнмановских интегралов, который влияет на нелога'
рифмические члены в множителях Z (см. разд. 4.5, обсуждение
¦перенормировки в КЭД).
Уравнение Гелл-Мана—Лоу (8.30) легко проинтегрировать
при аг(ц2)<1 и с учетом поправки от второго члена в правой ча-
части, т. е. от вклада двуяпетлевых графиков. Для этого вместо
>ес,(ц2) в этот член в (8.30) следует подставить решение (8.31) и
(8.32):
^^Ь^ (8.35)
тде ц0—произвольное начальное значение переменной ц, а справа
мод знаком логарифма gj(tii) а?Н 4л— j?=—4Н—lnSV ПРИ
учете этого соотношения формулу (8.35) можно записать в виде
С + F/4яIп (Ц2/Л2)+ф/4я&Iп [In ((х2/Л2)], (8.36)
причем постоянную С выбирают равной нулю. При С=0 при
1п(ц2/Л2)>1 последний член представляет собой лишь малую до-
добавку, поэтому, разлагая в ряд по его отношению к l^A2)
138
получаем
а ЛЛ« ^ h P'n(in((i
*VJ *l(»/A«)L i2 1п(цг/
Это равенство (или уравнение (8.36) с С=0) используют для
определения постоянной КХД Л в двухпетлевом приближении
[через значение а,(ц2) при каком-либо импульсе ц] в виде
(8-38
Это же значение А2/ц2 следует и из соотношения (8.34), кото-
которое при подстановке в него $(g2) в виде первых двух членов ря-
ряда (8.29) в точности воспроизводит уравнение (8.35).
Второй член оправа в (8.38) является [при малом а.(ц2)]
лишь малой добавкой, однако учет его при не совсем малом а.
весьма существенно увеличивает постоянную КХД Л (она увели*
чивается почти в два раза при а«(ц2) «0,2). Поэтому при определе-
определении этой постоянной следует обязательно указывать, как она оп-
определена—с помощью соотношения (8.32) или (8.38).
Глава 9
КВАНТОВАЯ ХРОМОДИНАМИКА. КВАРКИ,
ГЛЮОНЫ И АД РОНЫ
9.1. Лагранжиан квантовой хромодинамики.
Кварки и глюоны
В настоящее время можно с уверенностью утверждать, что в
природе реализуется теория с нарушенной калибровочной инва-
инвариантностью относительно преобразований группы SU C). Эта
теория описывает сильное взаимодействие элементарных частиц.
Соответствующую группу SU C) называют цветовой, а теорию —
квантовой хромодинамикой (КХД). Дираковские спинорные час-
частицы в КХД, называемые кварками, преобразуются по фундамен-
фундаментальному (триплетному) представлению калибровочной SU C)-
группы. Векторные частицы, отвечающие калибровочным полям и
преобразующиеся по присоединенному (октетному) представле-
представлению SU C), называют глюонами (от английского glue —клей;
глюоны «склеивают» кварки в адронах).
Существуют кварки различных сортов, обозначаемые и (up),
d (down), s (strange), с (charm), b (bottom), t (to^) (не исклю-
исключено, что этот ряд следует продолжить). Сорта кварков опреде-
определяют их свойства по отношению к электрослабому взаимодейст-
взаимодействию, например электрический заряд кварка Qu=Qc=Qt=+2/3,
Qd = Q, = Qb=—1/3, где Q — заряд в единицах \е\. Кварки раз-
различных сортов также различаются по маосе: и-, d-, s-юваркн на-
называют легкими, а с-, Ь-, f-кварки — тяжелыми. По отношению же
к сильному взаимодействию, являющемуся калибровочным взаи-
взаимодействием в цветовой группе SU(S), свойства всех кварков
одинаковы. Другими словами, волновое поле карка q—q(x) мож-
139
но записать в виде (<7/)\ где /—сорт кварка, a i — цветовой ин-
индекс группы SC/C); часто сорта кварков называют ароматами
(flavors). Сильное взаимодействие действует на индекс i. Такое
разделение индексов (т. е. факторизация взаимодействия), несом-
несомненно, имеет место при доступных энергиях. Не исключено одна-
однако, что при сверхвысокой энергии происходит объединение
взаимодействий, и пара индексов / и i представляет собой один
общий индекс для опонтанно нарушенной группы симметрии.
Модели этого явления, называемого великим объединением^
см. в гл. 13.
Лагранжиан КХД имеет вид, стандартный для SU{3) калиб-
калибровочной теории:
2 AУйОй-и,) qf, (9.1)
где сумма берется по всем сортам /; mf—масса кварка сорта /-
Напомним, что ковариантная производная имеет вид Dnq=
= (dn — lgA$.ta)q, где га—генераторы группы SU C). В фундамен-
фундаментальном представлении SU C) генераторы определяются матри-
матрицами Гелл-Мана №: ta=№/2 (индекс а пробегает значения
от 1 до 8). Для полей кварков qf здесь опущены цветовые
индексы (матричная запись). Наконец, F?v— тензор напряженности)
калибровочного (глюонного) поля А%
Fb=.dtAi-dvAl + gf»<AlAl. (9.2>
где /°be — структурные константы группы SUE): \[F, tb]—ifabctc.
Разумеется, для квантования теории к лагранжиану (9.1) сле>-
дует добавить член, фиксирующий калибровку и духовую часть.
Кроме того, (9.1) описывает собственно сильное взаимодействие;
для описания других взаимодействий (электрослабого, гравита-
гравитационного) в лагранжиан добавляют соответствующие члены.
Константу связи g, определяющую интенсивность сильного»
взаимодействия, принято обсуждать в терминах величины g2/4n—
= а„. Пользуясь результатами предыдущей главы, легко найти
однопетлевую функцию Гелл-Мана—Лоу в КХД, определяющую
эволюцию эффективного заряда,
Ъ=\\-\п}, (9.3>
где щ — число сортов кварков с массой, меньшей рассматрива-
рассматриваемых значений импульсов, при которых вычисляется эффективный
заряд. Для эффективной константы a.(q2) можно соответствен-
соответственно записать [в области, где a,(q2) достаточно мало]
<M?2)=4jx/Mii(?2/Aqco). (9.4)
Отсюда видно, что КХД — асимптотически свободная теория, ес-
если число сортов кварков nf не превышает 16. Открытие этого»
свойства в 1973 г. Политцером [8.1] и Гроссом и Вильчеком
'[8.2] послужило главным толчком к развитию КХД как реали-
реалистической теории сильного взаимодействия. Именно, при передан-
переданных импульсах больше 1 ГэВ константа a,(q2) благодаря свой-
140
ству асимптотической свободы достаточно мала, и применима тео-
теория возмущений КХД. * [Забегая несколько вперед, укажем, что
.«. A ГэВ)«0,3. В этом случае в перенормировку заряда дают
вклад лишь и-, й- и s-иварки и коэффициент Ъ равен 9.}. Это об-
обстоятельство позволяет рассчитывать по теории возмущений КДХ
целый ряд характеристик процессов, в которых участвуют силь-
сильно взаимодействующие частицы—адроны. Все такие расчеты под-
подтверждаются в области их применимости экспериментальными
данными, и нет оснований сомневаться в правильности КХД как
теории сильного взаимодействия. (Детальное обсуждение физи-
физических процессов в рамках КХД ом. в части III.)
9.2. Адроны и инфракрасная проблема КХД
Основные объекты КХД—кварки и глюоны—не наблюдают-
наблюдаются непосредственно на опыте; наблюдаются лишь их связанные
состояния — адроны. Известен обширный спектр кварковых свя-
связанных систем — барионов и мезонов. Барионы имеют полуцелый
спин, и их квантовые числа соответствуют связанным состояниям
трех кварков. Мезоны обладают целым спином, и их квантовые
числа отвечают состояниям типа кварк—антикварк. Вместе с тем
до сих пор не найдены адроны, которые можно было бы не-
недвусмысленно интерпретировать как глюоний — связанное состо-
состояние глюонов, однако ожидаемые свойства таких адронов ожив-
оживленно обсуждаются в последнее время.
Адроны являются синглетами по цветовой группе 5?/C).
Другими словами, по принятой терминологии кварки и глюоны —
цветные, а адроны — бесцветные. Например, цветовую часть
волновой функции мезона М и бариона В можно представить че-
через волновые функции кварков (qty [и антикварков (<?)$:
1 (9.5)
Напомним, что индексы i, J, k—\, 2, 3—цвета кварков, а /—их
сорт (/=и, d, s, с, Ь . *.); по дважды повторяющимся индексам
производится суммирование, и г1]к — абсолютно антисимметричный
символ [инвариантный в группе SU(S)]. Адроны не имеют
«внешних» цветовых индексов (этим выражается тот факт, что
адроны бесцветны), но имеют внешние индексы /, относящиеся
к сортам кварков (а также спиновые индексы, которые здесь
опущены). Внешние индексы / определяют квантовые числа адро-
адронов по отношению к электрослабому взаимодействию (например,
электрический заряд бариона, составленного из кварков #,, qt,,
qft, равен сумме зарядов кварков Qd + Qf.+Qf,), а также по
отношению к пространственным вращениям (спиновые переменные).
По индексам f мезоны и барионы также могут обладать свой-
свойствами симметрии и образовывать мультиплеты. Наиболее из-
141
вестны из таких симметрии изотопическая SUB)-симметрия, по
которой и- и d-кварки образуют фундаментальный дублет, и уни-
унитарная симметрия SUC), которой обладают адроны, содержащие
легкие и-, й- и s-кварки. В отличие от точной цветовой SUC) по-
последние симметрии — приближенные. Нетрудно проследить в рам-
рамках КХД причины возникновения приближенных изотопической
и унитарной симметрии адронов. Действительно, в лагранжиане
сильного взаимодействия (9.1) кварки разных сортов различают-
различаются лишь массами. Если бы массы Nt сортов кварков были оди-
одинаковыми, то лагранжиан (9.1) обладал бы глобальной SU(Nf)-
симметрией относительно перемешивания Nf кварков данных сор-
сортов. Массы и-, й- и s-кварков не одинаковы, однако все они малы
по сравнению с массами адронов и с величиной, обратной харак-
характерному размеру адрона. Забегая вперед, укажем, что массы и- и
d-кварков в данном обсуждении можно считать равными пример-
примерно 4 и 7 МэВ соответственно, а тв<**\50 МэВ, тогда как харак-
характерный размер адрона г можно определить, например, по зарядо-
зарядовому формфактору протона F(q2) = 1—q2<r2>/6=O((r^L). На опы-
опыте <ra>/6^mp-2, где тр=*780 МэВ — масса р-мезона. Поэтому в
некотором приближении массами легких кварков можно пренеб-
пренебречь по сравнению с характерными адронными параметрами и
прийти к приближенным SUB)- и 5?/C)-симметриям. Для и- и
d-кварков такое приближение весьма точное, и соответствующая
изотопическая симметрия выполняется очень хорошо. Для
s-кварка, масса которого больше масс и- и d-кварков, приближе-
приближение более грубое и унитарная (SU) C)) /-симметрия имеет худ-
худшую точность. Масса остальных кварков более 1 ГэВ, и продол-
продолжение этого ряда приближенных симметрии лишено смысла.
Свойства кварков и глюонов образовывать бесцветные адроны
и невозможность извлечения отдельных цветных кварков или
глюонов из адронов называют невылетанием цвета (или кон-
файнментом). Свойство невылетания не доказано, и последова-
последовательное динамическое описание внутренней структуры адронов в-
рамках КХД отсутствует. Основной причиной такой неполноты
описания адронов современной теорией является то, что при
уменьшении переданного импульса, т. е. с ростом расстояний в
так называемой инфракрасной области, эффективная константа
взаимодействия растет и на расстояниях порядка характерного
размера адронов КХД перестает быть теорией слабой связи, так
что методы теории возмущений для описания структуры адронов,.
как правило, неприменимы. При более внимательном рассмотре-
рассмотрении ситуация в КХД выглядит следующим образом. Если начи-
начинать с вычисления амплитуд в КХД на малом расстоянии, где
применима теория возмущений, и затем расстояние увеличивать
(например, рассматривая меньшие переданные импульсы), то с
ростом расстояния развивается неустойчивость, уводящая ампли-
амплитуду безнадежно далеко от значения, даваемого теорией возму-
возмущений, так что даже суммирование бесконечного ряда теории
возмущений не приводит в инфракрасной области к правильным
142
физическим результатам. Возможность возникновения масштаба
передаваемых импульсов, при котором образуется неустойчивость
теории возмущений, можно увидеть уже в самой теории возмуще-
возмущений. Действительно, если при некотором переданном импульсе
<72=—ц2 константа а,(ц2) мала, то можно образовать размерную-
величину ЛГхар. аналогичную параметру Л в формуле (8.32), ко-
которая фактически не зависит от параметра ц:
Л*хар=соп81цехр
^const [x exp ( - Ь^Ш) )= const Л. (9.6)
Из этого выражения видно, что все коэффициенты разложения
ЛГхар в ряд по g2 равны нулю. Поэтому если в некоторой ампли-
амплитуде имеются члены вида {М1Я921ф)к (q— характерный импульс;
k—некоторая степень), то их нельзя найти ни в каком порядке
теории возмущений. С другой стороны, эти члены становятся
главными при уменьшении q2. Можно полагать, что для масс и
характерных размеров легких адронов имеют место выражения
типа (9.6), неаналитичные по константе связи. Величины и эф-
эффекты, не описываемые теорией возмущений, удобно для крат-
краткости называть непертурбативными (несмотря на некоторую не-
неблагозвучность этого слова). Последовательный метод для вычис-
вычисления непертурбативных эффектов отсутствует. Имеются лишь
способы их полуфеноменологического учета в отдельных ампли-
амплитудах (см. гл. 17).
Можно ожидать, что проблемы больших расстояний, в частно-
частности, проблема невылетания, носят чисто технический характер и
могут быть решены (правда, это потребует выхода за рамки
теории слабой связи). В принципиальном же отношении КХД
представляется «настоящей и правильной» теорией сильного взаи-
взаимодействия. В это высказывание вложен смысл, аналогичный
тому, что электродинамика и нерелятивистская квантовая меха-
механика дают «настоящую и правильную» теорию атомных спектров.
Мало кто сомневается в последнем, однако фактически рассчи-
рассчитать спектр достаточно сложного атома д&реко не просто. Дру-
Другим примером может служить гидродинамика в области турбу-
турбулентности. В правильности этих теорий убеждаются, изучая про-
простые объекты типа атома водорода или ламинарного течения.
В КХД нет своего «атома водорода» (может быть, его роль сы-
сыграют адроны, состоящие из очень тяжелых кварков), поэтому
приходится изучать теорию сильного взаимодействия на совсем
не простых примерах.
9.3. Тяжелый кварконий и константа а8
Как уже отмечалось, массы легких кварков малы в масштабе
характерных адронных параметров. Поэтому при обсуждении
адронов, содержащих эти кварки, необходимо, вообще говоря, рас-
143
сматривать релятивистские эффекты, такие как рождение кварк-
антикварковых пар, излучение и поглощение глюонов и т. д. По-
Поэтому говорить о том, например, что барион состоит нз трех
кварков, а мезон—из кварка и антикварка, в отношении легких
кварков можно лишь в смысле соответствия «внешних» кванто-
квантовых чисел, сохраняемых сильным взаимодействием1- Эти пробле-
проблемы в значительной мере снимаются при обсуждении адронов, со-
состоящих из тяжелых ^кварков (с, b, t), поскольку движение их в
адронах в первом 'приближении можно считать нерелятйвистским.
На опыте наблюдаются мезоны, состоящие из тяжелых квар-
кварка и антикварка: се и ЬБ. По аналогии с позитронием, состоящим
из электрона и позитрона, такие системы называют кварконием
(ее чармоний, bb-боттоний). Изучение свойств таких систем поз-
позволяет фиксировать ряд параметров КХД, в частности дает наи-
наиболее надежную оценку константы связи as. Рассмотрим здесь
оценку константы а„ которая получается из сравнения вероятно-
-стей (ширин) распада тяжелого кваркония на пару е+е~ и на
легкие адроны. (Детальное обсуждение свойств тяжелого кварко-
кваркония см., например, в [9,1].)
Подобно уровням позитрония уровни кваркония характеризу-
характеризуются орбитальным моментом L=6, 1, 2, 3,..., обозначаемым S,
Р, D, F..., спиновым моментом s, для которого указывается
мультиплетность 2s+l, полным моментом / и номером радиаль-
радиального возбуждения. Эти квантовые числа компактно записываются
в виде символа (nr+l)i2s+1)Lj. Например, l'Sx означает основное
радиальное состояние Пг=0 с L=Q (S-волна), параллельными
спинами кварка и антикварка S=|Si + Sa| =1 и полным момен-
моментом /=1. Орбитальный и спиновый моменты определяют прост-
пространственную и зарядовую четности состояния Р—-(—1)L+1, C=
= (—1)L+S (при выводе этих соотношений необходимо помнить,
что четности фермиона и антифермиона противоположны). Отсю-
Отсюда видно, что квантовые числа ^-состояний /рс=1— совпадают
с квантовыми числами фотона и поэтому кварки из ^-состояния
могут аннигилировать в пару е%~ через один виртуальный фотон
(рис. 9.1). На опыте этот процесс выглядит как распад 35гуров-
ня кваркония на пару е+е~ (или ц+рг или т+т~). Большой инте-
1 Для описания целого ряда свойств адронов все же применима нереля-
нерелятивистская кварковая модель (в конечном счете именно благодаря этому об-
обстоятельству появились понятия о кварках и цвете). Прн этом, однако, речь
идет не о тех кварках, которые входят в лагранжиан КХД (их называют иног-
иногда токовыми кварками), а об эффективных кварках называемых блоковыми.
По-видимому, блоковый кварк представляет собой токовый кварк,
окруженный глюонным полем н кварк-антикварковымн парами. Массы
каждого из блоковых и- н d-кварков составляют примерно 1/3 массы
протона, а s-кварка примерно на 150 МэВ больше Успех нерелятивнетской
кварковой модели, например, в объяснении магнитных моментов барионов,
по-видимому, означает, что <шуба> из глюонов и пар не меняет квантовых
чисел кварка н что блоковые кварки в значительной мере сохраняют свою ин-
индивидуальность внутри адроиа, т. е. что их шубы перекрываются слабо. Одна-
Однако в настоящее время не существует какого-либо последовательного динами-
динамического объяснения иерелятивистской кварковой модели в рамках КХД.
144
pec представляет также обратный процесс — рождение 35[-уровня
в е+е~-аннигиляции. На опыте этот процесс выглядит как весьма
заметный резонанс в е*ег-аннигиляции. Так, сечение е+е~-анни-
гиляции в пике г|з-резонанса (основного ^-уровня системы ее-
чармония) с массой 3095 МэВ в сотни
раз превышает сечение в нерезонансном
фоне. Именно благодаря этим резонан-
сам известны из опыта остальные (не
8Si) уровни чармония и боттония, кото-
которые наблюдаются при переходах с воз-
возбужденных ^-уровней с испусканием риа gj
фотона.
Наиболее замечательным свойством кваркониевых резонансов
в е+е~-аннигиляции является их малая полная ширина. Так, пол-
полная ширина основного состояния чармония—г|з-резонанса—рав-
чармония—г|з-резонанса—равна 63±9 «эВ, тогда как ширина резонансов, состоящих из легких
кварков, как правило, более 100 МэВ. Причина столь сильного
подавления распада тяжелого кваркония на легкие адроны в ко-
конечном счете связана с малостью константы а, на малых рас-
расстояниях.
Рассмотрим механизм адронного распада тяжелого кваркония
и, в частности, г|з-мезрна. Чтобы такой распад произошел, тяже-
тяжелые кварк и антикварк должны аннигилировать. В КХД кварки
связаны непосредственно лишь с глюонами, но не друг с другом.
Поэтому кварконий сначала аннигилирует в глюоны и лишь за-
затем глюоны превращаются в адроны, состоящие из легких квар-
кварков. Важным замечанием, принадлежащим Аппельквисту и По-
литцеру [9.2], является то, что полная вероятность аннигиляции
тяжелых кварков в адроны определяется лишь вероятностью
первого процесса — аннигиляции в глюоны. В теории возмущений
этот вывод может быть обоснован с помощью теоремы Ли—Нау-
енберга—Киношиты (см. разд. 4.6). Действительно, в полной
вероятности суммируются все конечные состояния, поэтому если
вероятность вычислена в терминах константы а„ нормированной
при полной энергии (массе кваркония), то она не содержит ин-
инфракрасных сингулярностей. Другими словами, характерный ад-
ронный масштаб ЛГхар в полной вероятности распада ф-мезона
может входить лишь в виде положительных степеней отношения
Мхяр/Мф. Масса ф-мезона обусловлена в основном массами со-
составляющих его кварков и является весьма большим параметром.
Поэтому можно полагать, что члены, содержащие отношение
•Мхар/Л(«, описывают лишь малые поправки, которыми можно пре-
пренебречь. В любом случае роль таких членов можно выяснить,
сравнивая вероятности распада г|з-мезона и Т-мезона. Последний
является основным состоянием 6&-кваркония и имеет массу
9,46 ГэВ.
Найдем вероятность аннигиляции 3SrnapH из тяжелого квар-
кварка и антикварка в глюоны. Кварконий—бесцветный объект, по-
поэтому переход его в один (виртуальный) глюон запрещен сохра^
10—679 145
нением цвета. Распад на два глюона из ^-состояния запрещен
С-четностью. Действительно, цветовая часть волновой функции
двух глюонов в бесцветном состоянии имеет вид АаАа=А1А1 +
Н-1... \+АгАъ и не изменяется при С-преобразовании. С другой
стороны, 8Si-cocTOHHHe кваркония С-нечетно. Поэтому минималь-
минимальное число глюонов, на которые может идти распад, равно трем.
Одна из диаграмм, описывающих аннигиляцию в три глюона, при-
приведена на рис. 9.2. Остальные графики получаются перестанов-
перестановкой глюонов.
Б
6е
If у ллллплллл
у "wrv/vx/ww
у *\ллл/\лллл
Ptac 9? Рис 9.3
Для того, чтобы найти вероятность распада на три глюона,
можно воспользоваться известным результатом для вероятности
распада ^[-позитрония на три фотона, полученным Ором и Пау-
эллом в 1949 г. [9.3] (см. также [16.2]):
Г ((e+e-).s,-*3Y) = F4/9) (п*-9) (tf/AP) | ф @) |2, (9.7)
где Ме*2т. — масса позитрония; г|з(г) ¦—волновая функция отно-
относительного движения электрона и позитрона в позитронии. Для
распада позитрония на фотоны аналогом графика рис. 9.2 яв-
является график рис. 9.3. Сравнивая эти графики, нетрудно пере-
пересчитать формулу (9.7) на интересующий нас распад кваркония.
Действительно, отличие заключается в том, что в вершинах
для распада позитрония на фотоны стоят факторы еууац, где
Оц—амплитуда фотона, а в графиках для распада кваркония—
факторы g<aYna?> где а?—амплитуда глюона, описывающая его
поляризационное и цветовое состояние. Произведения матриц
Гелл-Мана, стоящих в вершинах испускания глюонов, действуют
на цветовую часть волновой функции кваркония. Нормированная
на единицу цветовая волновая функция имеет вид
fo/K3"-(??i+?fc+^»>/K3\ (9.8>
Поэтому на каждом графике для распада кваркония следует
взять след от произведения генераторов, входящих в вершины,
деленный на У^З. Таким образом, различие в константах связи
и цветовая структура приводят в вероятности распада к пере-
пересчетному фактору
2 MtJrF ^
а.Ь.с а,Ь,с
146
где фигурные скобки означают полную симметризацию произве-
произведения цветовых матриц (т. е. следует сложить все перестановки
и поделить на число перестановок: 3!=6). Симметризация произ-
произведения генераторов возникает из-за перестановок глюонов, а
делить на число перестановок необходимо потому, что сравниваем
вероятность трехглюонного распада с трехфотонным, в котором
диаграммы с перестановками фотонов суммируются в матричном
элементе без дополнительных (цветовых) факторов. Суммирова-
Суммирование по цветам глюонов а, Ь, с отвечает вычислению полной веро-
вероятности, а не парциальной вероятности перехода в конкретное
цветовое, состояние конечных глюонов.
Для вычисления следа сим метризованного произведения А,-мат-
риц достаточно произвести симметризацию по индексам а и Ь:
A/2) (X«k*+VX*j— {2/3)bab=dabcXc, (9.10)
где ^' — полностью симметричный символ в группе SUC).
'[Заметим, что соотношение (9.10) всегда имеет место для генера-
генераторов группы SU(N), так как слева стоит бесследовая эрмитова
матрица и символы <f" являются вещественными коэффициента-
коэффициентами ее разложения по полному набору бесследовых эрмитовых
матриц Х\. Отсюда получаем
Sp {KaK*kc}=dabc Sp №=2dabc.
Для суммы квадратов коэффициентов d0 можно найти
2 (dabcf=AOiZ, (9.11)
а.Ь.с
поэтому для пересчетного фактора (9.9) находим
E/18)К/а)* (9.12)
и из формулы (9.7) получаем для вероятности аннигиляции
^-состояния кваркония в три глюона
Г ((qq).St -^ЗО)-A60/81) (я2-9) (а^/Щ | ф @) |2, (9.13)
где теперь М — масса кваркония, а ф(г)—координатная часть
волновой функции относительного движения кварка и антикварка.
Наличие г|з(О) в формуле (9.13) отвечает тому факту, что
кварки аннигилируют на расстояниях порядка комптоновской дли-
длины волны кварка 1/т, которые намного меньше характерных раз-
размеров области, занимаемой волновой функцией нерелятивистского
связанного состояния. Поэтому как отсюда, так и из теоремы
Ли—Науенберга—Кииошиты можно полагать, что константу а,
в формуле (9.13) следует нормировать при массе кварка или
массе кваркония. Более точное определение возможно лишь пос-
после вычисления петлевых поправок к формуле (9.13) (см. ниже).
Входящая в формулу (9.13) волновая функция -ф (г) опреде-
определяется внутренней механикой кваркония, и ее теоретическое вы-
вычисление привело бы к дополнительным неопределенностям. Что-
10* 147
бы этих неопределенностей избежать, можно сравнить вероят-
вероятность аннигиляции в адроны с другим процессом, идущим на
расстояниях порядка \Jm, например с упомянутой выше анниги-
аннигиляцией в пару е+е~ через один фотон. Вычисляется вероятность
этого процесса легко. Предоставляем читателю самому убедиться
в том, что ширина аннигиляции связанного ^-состояния ц+ц~ в
пару е+е~ выражается формулой
b) |^k()| (9.14)
где М=*2ту, — масса распадающего состояния (массой электрона
пренебрегаем). Пересчетный коэффициент для распада кваркония
{QSIV~3rSQ2 (9.15)
где Q, — заряд кварка. Коэффициент SpZ/УЗ возникает из-за того,
что электромагнитная вершина является единичной матрицей в
"пространстве цветов и действует она на цветовую волновую функ-
функцию (9.8). Таким образом, для отношения вероятностей распада
^-состояния кваркония на адроны (через три глюона) и на пару
е+е~ имеем
^ЗР ю (Я«—9) «' ,q 1fi.
,q 1fi
Поправки к этой формуле следующего порядка по а. вычис-
вычислены недавно Маккензи и Лепажем [9.4]. Результат сводится к
тому, что если производить вычисление в схеме MS (см. разд. 4.5)
и нормировать в (9.16) константу а. на половине массы кварко-
кваркония, то поправка следующего порядка приводит к тому, что вы-
выражение (9.16) умножается на коэффициент 1+@±0,5) а./п.
Другими словами, при такой нормировке поправка обращается в
нуль с указанной точностью. (Неопределенность связана с при-
'ближенным вычислением фейнмановских интегралов на ЭВМ)*
На опыте для г|з-мезона отношение в левой части (9.16) близко к
10,. поэтому из (9.16) находим (напомним, что Qc = 2/3)
as(mc)^O,l9. (9.17)
При таком значении as неопределенность в поправке несуществен-
несущественна, важно лишь, что поправка мала. Для Г-мезона—35х-уровня
боттонйя (bb) с массой .Mr=9,46 ГэВ обсуждаемое отношение
вероятностей составляет на опыте 22 ±4, что дает при Qb=—1/3
a, {M?l2)^as (/?16)^O,155 ± 0,010. (9.18)
Если определять as (Mr/2) не прямо из данных опыта и фор-
формулы (9.16), а основываясь на (9.17) и пользуясь решением урав-
уравнения Гелл-Мана—Лоу с однопетлевой р-функцйёй:
148
то при 6 = 25/3, что отвечает вкладу четырех сортов кварков
аЛ(Мг/2)^0Д49, (9.19)
что вполне согласуется с (9.18) в пределах погрешностей.
Таким образом, представление об адронной аннигиляции квар-
кония как аннигиляции в глюоны очень хорошо согласуется с экс-
экспериментальными данными .позволяет фиксировать константу
а, и установить из данных опыта факт убывания константы на
малых расстояниях в согласии с формулой асимптотической сво-
свободы.
Записывая константу связи КХД a, (<f) в виде (8.32) [(см. (9.4){
с 6=9, отвечающему Л^=3 [см. 9.3)], находим при q2=m\i
ал(/и^)=4я/Ып(/и2/Л2)=0,19±0,01, откуда 1п(/гсс/Л) =
=2я/Fс^(/ге?))^3,6. Это дает для Л=Л<?со весьма малое значе-
значение Л=@,04 ±0,01) ГэВ; очень близкое к этому значение Л
получается и из данных (9.19) об as при половине массы ипсило-
ния Mrl2.
В литературе чаще всего для определения A=A<?cd=A^
используют не (8.32), а формулу (8.37) двухпетлевого приближе-
приближения, которая дает для 1п/ис/А (при том же о^ (/7^)^0,19) меньшее
значение (8.38) 1п(/гес/Л)^3,6—1п2, т. е. дает примерно в два раза*
большее Л=@,08 + 0,02) ГэВ [это же Л следует и изданных
(9.19) от as(Mrl2)]. Как видно, при данном as(mf) можно получить
разные значения Л в зависимости от того, учитывается или нет
второй член справа в (8.37), т. е. используются ли формулы одно-
или двухпетлевого приближения. В этом смысле определение Л
весьма условно, и иногда предлагают вместо Л задавать значения
«Л?2) ПРИ определенном д2 (равном, например, т%). При Л = 80МэВ
формула (8.37) двухпетлевого приближения дает при q2=l ГэВ2
«^(l ГэВ)=:0,22. Эти значения Л=Л^ и as A ГэВ) используются
далее всюду, так как они хорошо соответствуют всей совокуп-
совокупности известных данных опыта.
Глава 10
СИММЕТРИЧНАЯ СХЕМА СЛАБЫХ ВЗАИМОДЕЙСТВИИ
ГЛЕШОУ, ИЛЛИОПУЛОСА, МАИАНИ. ПРОМЕЖУТОЧНЫЕ
ВЕКТОРНЫЕ МЕЗОНЫ
10.1. Феноменологический лагранжиан
Большое число распадов элементарных частиц (в том числе
Р-распад ядер, распад ц-мезонов, /(-мезонов, гиперонов и т. д.) и
реакций в пучках нейтрино v«, vM происходит из-за слабого взаи-
взаимодействия. Экспериментальные и теоретические исследования, в
основном конца 50-х годов [10.1—10.9], показали, что процессы,
которые наблюдаются при не очень высокой энергии, обусловлены
прямым, контактным взаимодействием четырех фермионнь^
149
полей вида
2V=DG/K2)/+(.*)/a(.*), A0.1)
где Ja(x)—так называемый заряженный ток;
2/a(Jc)=(e0ave)+(ir0aV^)+(rf0aa) + ... A0.2)
HOa-Y«0 + Y5). Ys —(l о)'!!
Здесь е=е(х); р(х); ve, v^—волновые поля A.14) фермионов,
соответственно электрона, [х-мезона, а также двух типов нейтрино:
электронного \е, которое рождается лишь при поглощении электро-
электрона, и ц-мезонного (у?). Ток ja(k) A0.2) является оператором, при-
применение которого к какому-либо состоянию изменяет (уменьшает)
заряд на единицу, поэтому его и называют заряженным током.
Матрица [_Ys= —(i o)=iYoYiY2Y3. Ys=l меняет пространствен-
пространственную четность (Р-четность) состояния фермиона, из-за этого опера-
оператор взаимодействия фермионов A0.1), в который Ys входит в сумме
с единицей, нарушает Р-четность.
Если ввести левошральные компоненты полей eL, p,?, vu, uL,
dL, применяя к полям оператор Pi—(l + Ys)/2, например
«I - 0/2) A + Ye) в (*),?««(*) (l + Y8)/2f A0.3)
и учесть, что A + y8J=2 A + yM, A + Y5) A — Y5)=0, то ток /a (x)
можю выразить только через них [10.1, 10.2]:
(e^IA0.4)
Физически это означает, что в процессах, вызванных слабым вза-
взаимодействием, частицы рождаются только в левокиральных со-
состояниях. Такое состояние для свободной частицы получается при
применении оператора Яг=A+7б)/2 к волновой функции A.15)
е(х) =ы(/>, Я) exp (—ipx) в виде
A0.5)
где пр=р/|р| и значениям А,—±1 отвечают два разных спираль-
спиральных состояния: с проекцией спина по (А, = -}-1) и против (Я,= —1)
импульса р частицы; для них (mp)v{k)=Kv{K), X=±l. Справа
в A0.5) спинор ei записан для ультрарелятивистского случая
(е»т, в частности, при т=0). Как видно, он в этом случае не
равен нулю лишь при левой спиральности, при Я=—1, когда спин
частицы направлен против импульса. Рождение только таких ча-
частиц и наблюдалось в процессах слабого взаимодействия. Обра-
150
зование частиц в правокиральных состояниях еяг=A/2)Х
ХA—уъ)е{х), волновая функция которых (при ъ>т) отличается
от «уля лишь при Я,= + 1, в эти ^взаимодействиях не наблюдалось
(они фактически могут рождаться лишь за счет нейтральных то-
токов, см. гл. 12).
При подстановке заряженного тока в виде A0.2) в лагранжи-
лагранжиан A0.1) возникает ряд членов, дающих вклад в первом поряд-
порядке по константе взаимодействия Ферми G в матричные элементы
72, ~ (Ф2*2%/Ф0 различных физических процессов. Член лагран-
лагранжиана
дает вклад в матричный элемент Т21 распада n->-eveV|i, отвечаю-
отвечающий графику рис. 10.1. Этот вклад такого же вида по форме, как
и A0.6), но в нем е, ve, \i, vp—не операторы полей, а волновые
функции A0.5) соответствующих частиц. Член
(О/К2)йаA+у5)<0Й«A+ъК) A0.7)
определяет амплитуды ^-распада нейтро-
нейтрона, идущего в результате перехода в нем
«-кварка в d-кварк (d-*~u+e+vt). В A0.1),
A0.2) содержится гипотеза, что эти члены
определяет одна и та же универсальная
константа G/V2. Эта гипотеза Фейнмана и
Гелл-Мана [10.3] A958 г.; см. также
[10.4, 10.5]) получила блестящее под-
подтверждение на опыте 1[10.6—10.9]. В част-
частности, вычисление полного времени жизни
¦ц-мезона с помощью матричного элемен- „ 1П,
та A0.6) дает [10.2, 10.3] Рис- 10Л
l/^ = r^V(i = G%S/192fct3, (Ю.8)
и так как на опыте Тц точно измерено (тй^ 2,197 «10 с), то отсюда
можно найти константу Ферми слабого взаимодействия:
G/rc2 = l,03-10-8, A0.9)
где G= 1,1664-10-» ГэВ; т„=938,28 МэВ — масса протона.
Постоянную G можно также получить, вычисляя с помощью
матричного элемента A0.7) вероятность ^-распада так называ-
¦емых зеркальных (сверхразрешенных) ^-переходов атомных ядер
и сравнивая ее с данными опыта. В вероятность этих переходов
вклад дает только член с^в первой скобке в A0.7) (т. е. только
векторная ее часть), а член ^«75 этой скобки вклада не дает. Эта
(векторная) часть матричного элемента A0.7) вообще не изме-
изменяется под действием сильного КХД-взаимодействия между
кварками из-за сохранения1 векторного тока dll(u(x)yad(x))=0
1 Равенство dIL(u(x)yv4(x) =0 имеет место как следствие уравнения
Дирака для свободных полей и(х) и d(x), если массы mu н пц одинаковы.
Оно выполняется приближенно с большой точностью из-за малости та—
—*я«~1 МэВ.
151
аналогично тому, как не меняется электромагнитный заряд квар-
кварков из-за сохранения электромагнитного тока. Значение постоян-
постоянной G, полученное из данных о сверхразрешенных р-распадах
ядер, оказалось очень близким к A0.9)—меньше его примерно
на 3%.
В р-распад нейтрона вносят вклад оба члена и уа и 7^5 в
первой скобке в A0.7), причем влияние сильного КХД-взаимодей-
ствия кварков на аксиальную часть ?а?5 матричного элемента
можно довольно точно учесть на основе гипотезы '[10.11] частич-
частично сохраняющегося аксиального тока. Она приводит к соотноше-
соотношению Гольдбергера—Треймана [см. A7.6)], которое определяет
матричный элемент распада п-*-рехе в виде, сходном с A0.7):
Тп = @/1/2") {руа (I + OoYs)a) (eYa A + Ъ) v.). A0.10)
где со=1,26О±О,ОО5 — некоторая постоянная '[10.12], причем ряд
членов, не существенных для вероятности распада, здесь опущен.
Для времени жизни нейтрона отсюда следует ![10.10]:
где x=Ee/A; A=mn—mp^l,293 МэВ; me=0,511 МэВ. При зна-
значении A0.9) константы Ферми отсюда следует значение т„^910 с*
хорошо соответствующее данным опыта (т„)эксп^877-^918 с.
Если в лагранжиане (ЮЛ), A0.2) поле d-кварка заменить ли-
линейной комбинацией полей d- и s-кварков d-+d°(x)=d(x)cos&c-\-
-)-s(x)sin&c, где"&с—некоторый числовой параметр (его называют
углом Кабиббо [10.13]), то вместо последнего члена в A0.2) по-
появится сумма (dWau)=(dOau)cosbll-\-(sOau)sinul.. JB результате
в лагранжиане (ЮЛ) появятся члены @/1/2) sin&c(ttYa(l+Y5) S)X
X еуа О + Ys) v«). которые приведут к ненулевой вероятности рас-
распада д-мезонов и гиперонов (включающих s-кварк—так называе-
называемый странный кварк) в обычные адроны, не содержащие s-квар-
s-кварка, например к распаду K-^neVg, h-+peve и т. д. Прн этом не-
немного изменится член вида A0.7), определяющий амплитуду
обычного р-распада: вместо G в нем появится величина G=
G
р-Распады странных частиц в обычные идут с относительно
малой вероятностью и хорошо описываются лагранжианом
A0.1) с константой Ферми A0.9) при sin*,.^0,23. Это как раз
соответствует значению G, на 3% меньшему, чем A0.9), т. е. имен-
именно тому, что требует эксперимент.
152
10.2. Симметричная схема Глешоу, Иллиопулоса, Майани.
Смешивание кварков
Успех идеи Кабиббо ![10.13] о замене поля d-кварка комбина-
комбинацией A0.9) привел Гелл-Мана '[10.14] и Глешоу, Иллиопулоса и
Майани [10.15] в 1970 г. к мысли, что может существовать еще
Один сорт кварков, с-кварк типа и-кварка (с зарядом +2/3), ко-
который входит в заряженный ток A0.2) совершенно симметрично
с и-кварком в виде '[10.15]
{d°Oau) + {3>Oac), A0.11)
где d° и s°—линейные ортогональные комбинации указанного выше
вида полей d- и s-кварков:
rf°=rfcos&c-l-ssin&(,; s°= —rising+s cos &c, A0.12)
причем (d°f-\-{s<sf^d2-\-s2. Замена последнего члена в A0.2) сум
мой A0.11) дает ток /а(х) в симметричном виде:
Выражение для }а(х) и для лагранжиана SBw' можно сделать
еще более простым и симметричным, введя в него сколько угодно
(природе) сортов лептонов и кварков, если распределить их ес-
естественным образом по парам:
I
где Ь — тяжелый кварк с зарядом 1/3, a t—еще не открытый
?-кварк с зарядом 2/3, и считать, что эти пары преобразуются как
компоненты спиноров Si/B) при глобальных вращениях в неко-
некотором изотопическом пространстве. Каждую пару (//, qf) лепто-
лептонов и кварков, масса которых становится все большей с увели-
увеличением номера f, называют поколением элементарных частиц, а
f — номером покол ения.
Из билинейных комбинаций этих изоспиноров можно постро-
построить векторные токи, которые одновременно будут и 3-векторами
в изопространстве:
У-1,2.3
причем т"—матрицы Паули, действующие на столбцы A0.14), а
индекс 0 над q\L означает, что нижние компоненты пар кварков
"di., sL, bi замены некоторыми линейными комбинациями их вида
A0.12):
/KuK12Kl3\/dL\
Т21 #22 #231 lsL \ A0.16)
^31 #32 #33/ \bl./
153
где {ktt,}=*K — некоторая унитарная матрица КК+=1 (ее назы-
называют матрицей Кобаяши—Маскава) >[ 10.17]. В случае двух поко-
поколений этим преобразованием является A0.12). Таким образом,
00.17)
Аналогично A0.1) лагранжиан слабого взаимодействия можно пред-
представить в виде SU B)-инвариантного произведения двух таких
токов:
^)]> A0Л8)
где /i±)(Jc)=(yi1)±iyi2)(Jc))/2. причем ja(x)=Д->(^-заряжен-
вый ток1 A0.13), a Д8> (*)—его третья (а=3), нейтральная компо-
яента:
где в последнем члене учтено, что
^j A0.20)
2
ввиду унитарности матрицы Ktr в (Ю.16); vfL, efL, ufL и dfL —
здесь и всюду далее верхние и нижние компоненты дубле-
дублетов A0.14).
Характерной особенностью нейтрального тока A0.19) является
то, что он не содержит недиагональных переходов v^-^v^z.;
BfL-+ef4.', UfL-^-itfL и dfL-^dfi с f=hf между частицами разных
поколений в отличие от заряженного тока
который за счет недиагональных членов матрицы Кц A0.16)
такие переходы включает. Разные типы кварков называют разными
ex ароматами и говорят, что нейтральный ток не изменяет
аромата кварков: не приводит, например, к переходам d-*-s или
s-+b, d-+b; соответствующие члены сократились в левой части
•суммы по ароматам / в A0.20). Это отвечает данным опыта,
так как на опыте отсутствуют все распады адронов, связанные
1 Так как г- L 0) н, например, (*и?вт-/и) = (<?хтв^?)' а (
PS)
154
такими переходами в них кварков. Так, /С+-мезон является
связанным состоянием и- и s-кварков, а я+-мезон —ю- и ^-кварков.
За счет перехода s->d+(ee) [который шел бы, если бы нейтраль-
нейтральный ток включал члены (dLyaSi)] могли бы с заметной вероят-
вероятностью идти распады К-+пее, К-+щ>-1». или K-+nvv. Однако на
опыте эти распады не наблюдаются, —они замедлены по сравне-
сравнению с тем, что следовало бы ожидать [при значении A0.9) кон-
константы G], по крайней мере, на 10 порядков. Точно так же
нейтральный ток A0.19) диагоналей по ароматам лептонов—«элект-
лептонов—«электронов» разных поколений и «нейтрино». В частности, он не включает
переходов \i->-e, которые могли бы привести к ненаблюдаемым
на опыте распадам ц->-еу, \i-+e(ee). В этом смысле описанная
выше симметричная схема Глешоу, Иллиопулоса и Майани (ГИМ)
{10.15] автоматически дает именно то, что в секторе нейтральных
токов требует опыт. Однако, как показано ниже, форма A0.19)
й б В jg>(x)
ру фр
нейтрального тока—не самая общая. В принципе, этот ток g
мог бы содержать члены, пропорциональные обычному электромаг-
электромагнитному току (он, конечно, также нейтральный): Jgm)(x)=*
). где
2 ////,/ (Ю.22)
который: а) пропорционален зарядам частиц
Qe=-U QB=+2/3; Q,= -l/3 (Qv=0); A0.23)
б) сохраняет /'-четность и поэтому содержит не левые компоненты
полей частиц, а сами эти поля е, и, а. Поэтому самая общая
форма нейтрального тока есть
/i0) <*)=/<?> (*)-ЕЛ (*). (Ю.24)
где | — некоторый вещественный коэффициент (далее показано,
что |=sin28w — число, меньшее единицы).
При трех поколениях лептонов и кварков заряженный ток
A0.21) включает 12 членов (три лептонных и девять кварковых)
и столько же членов включает нейтральный ток A0.19) или
A0.24). Поэтому феноменологический лагранжиан слабых взаи-
взаимодействий A0.18) приводит к 144 вершинам взаимодействия ви-
вида рис. 10.1 за счет заряженных токов и к стольким же — за счет
нейтральных токов. На основе этих вершин он удивительно точ-
точно описывает практически всю известную из данных опыта ин-
информацию о слабом взаимодействии элементарных частиц в об-
области небольших энергий уже при простейшем виде A0.12) мат-
матрицы Кобаяши—Маскава A0.16):
( ci Si 0\
-*» *° •
V 0 0 1/
<1а25)
155
где Ci=cos<h, Si = sin<h, Otx—Qe — угол Кабиббо, a |
«0,21.
Однако эта простейшая форма унитарной матрицы A0.16) —
не самая общая. Она, в частности, не включает возможности пе^
рехода ^-кварка в с- или в ы-кварк, т. е. не приводит к р-распаду
6-кварка за счет заряженных токов (вида b-*-c+ef+vt или 6-*-с+,
+d+u), который наблюдался на опыте уже вскоре после откры-
открытия (в 1976 г.) связанной системы (ЬБ) —Т-мезона [10.16] и ча-
частиц с открытым бьюти, т. е. включающих единичный ?-кварк
кроме и- и d-кварков.
Каков наиболее общий вид унитарной матрицы K={Kff) Ko-
баяши—Маскава A0.16) и каким числом параметров она опреде-
определяется? Нетрудно найти ответ в общем случае [10.17]. Унитарная
матрица К размером Nx^N содержит N2 комплексных элементов;
Kff=\Kff |ехр(»ф#')> т. е. включает 2N2 вещественных парамет-
параметров, удовлетворяющих N2 уравнениям Kfr-K*f,r=6ff (число этих
уравнений есть N при /=/' и N2—N при /?•/', т. е. всего-
их, действительно, Лг). Поэтому такая матрица содержит 2N2—
—N2=N2 произвольных вещественных параметров. Из них Гд^
=(N2—N)i2 являются параметрами ортогональных преобразова-
преобразований полей кварков, a N2—vN={N2-\-N)i2 параметров опреде-
определяют фазы ф//' вращений этих полей [матрица N)>iN ортогональ-
ортогонального преобразования \Kfc\ действительно содержит (N2—N)i2.
параметров]. Из этих фаз 2N—1 произвольны и определяются
произвольным выбором фаз cry, / = 1,2,... волновых функций
кварков dL, sL, bL и т. д. справа в A0.16) и фаз %f, кварков d°L,
sf, b°L и т. д.—слева в A0.16) [при замене dfz.—dfiexp(—iq^)»'
?*/'?-*"?^'лехР (—Щ-) к Фазам Ф//' добавляется слагаемое1
%(,—фу]. Кроме этих фаз ф//-, которые можно, в частности, вы-
выбрать равными нулю, элементы Kff матрицы К содержат
nN=(N2+N)l2— BЛГ—l)=(AT2_3iV-f2)/2 = (iV — \){N—2)/2
физических СР-нарушающих фаз. При двух поколениях кварков,
т. е. при N=2, ^2=0—этих фаз нет ^=A'0=(_511 с]}) и СР~
четность в теории сохраняется. Однако уже при трех поколениях
кварков [как в A0.16]) при ЛГ=3 получаем Л3=1, т. е- матри-
матрица К содержит одну СР-нарушающую фазу. При этом v3=3,
т. е. R содержит три физических угла смешивания, определяющих,
матрицу \Kff\ типа угла Кабиббо &j в A0.25). Наиболее просто-
ее параметризовать в виде, предложенном Кобаяши и Маскава
[10.17]:
(
0
\0 —s
156
p() 223p () A0.26)
— c2s3 exp(i<P) — +^)/
где s/=sinfy; c/=cos^; f = l, 2, 3. При Ф^вз—О и <p=0 эта мат>
рица сводится к простому виду #=?<> A0.25). Однако в общем
виде она содержит четыре параметра Фь Фг, Фз и <р и автоматиче-
автоматически приводит при крФО к нарушению СР-четности из-за комп-
комплексности вершин рис. 10.1 слабого взаимодействия.
В секторе s- и d-кварков [в верхней левой части матрицы R,
см. A0.16) —A0.26] это нарушение происходит также автомати-
автоматически за счет малого мнимого члена s1s3sin«p~ Itf-*—10 (в Кц),
если все углы Фь Фа, Фз, <р— величины одного порядка, такого же,
как угол Кабиббо di—Ge^lO рад. Именно это и дают данные
опыта отри обработке их на основе "матрицы A0.26), приводя,
как сейчас хорошо известно, при 51~8тфе~0,23 к значениям
Sj~s2>s3 и к значениям порядка 10~3 параметров, определяющих
нарушение СР-четности в распадах JC-мезоиов.
Уже отмечалось, что описанная выше схема слабых взаимо-
взаимодействий очень точно Описывает все данные опыта о рождении и
распаде частиц при слабом взаимодействии. Однако в ней отсут-
отсутствует главное—понимание природы этого взаимодействия и
причины симметрии его структуры вида A0.18).
.Важными для понимания этих вопросов были попытки, сде-
сделанные в работах еще 60-х годов [10.18—10.21], представить сла-
слабое взаимодействие как результат обмена между фермионами
и тяжелыми векторными бозонами.
10.3. Массивные векторные поля.
Векторные промежуточные бозоны
, Теория массивных (нейтральных) векторных полей может
быть построена аналогично описанному в гл. 6 случаю скаляр-
скалярных полей, если лагранжиан свободного поля выбрать сходным
с F.1):
l
где Мв—масса поля, а — 5? = В2—Щ—квадрат значения поля
[аналогичный чЦх) в F.1)].
Векторное нейтральное поле определяется заданием в каждой
точке Хр. 4-мерного пространства трех величин, например вектора
В(х). При этом компонента поля В0(х) должна быть выражена
через В (х) при помощи некоторого дополнительного условия. Если
в качестве него выбрать условие Лоренца дцВ11(х)=0, то энергия
поля будет положительно определена в том же виде A.16), как
для электромагнитного полярно с k0=(ok, где a>fe=l/k2+Af^. Это
соотношение—следствие уравнений Клейна—Гордона—уравнений
157
движения для поля В»(х):
{х)^0, A0.27)
которые получаются из лагранжиана &\^ при варьировании его
по Вр(х).
Гораздо лучше, однако, слегка изменить основной лагранжиан,
добавив к нему член (д5)(д5J
AО28)
таккак (^5ц—<?^J/2s(dx5nJ—(а^)(<?ц5л). В этом виде он
отличается от лагранжиана — rf^/A электромагнитного поля лишь
массовым членом (М%/2)В^, и вариация его по др'Щприводит
к известным уравнениям Прока
которые, в частности, при применении к ним оператора дц дают
М!(дц2?и)=0, т. е. при Мв^О автоматически ведут к условию
Лоренца: <?ц2?ц=0. При этом уравнения до-прежнему эквивалентны
уравнениям Клейна—Гордона A0.27), т. е. в импульсном простран-
пространстве также дают сой=Ук2+М|.
Заряженные векторные бозоны отличаются от нейтральных лишь
тем, что их поле (будем его обозначать Wjj) имеет векторный изо-
изотопический 5^/B)-индекс а=1, 2, 3, т. е. аналогично A0.28)
A0.29)
причем 9?Wp является суммой лагранжианов ^заряженных полей
1Г*—(Я^ФЯ^)/УТ и нейтрального поля W*(jc). Как"и A0.28),
он автоматически приводит к дополнительному условию дц№?=0 и
к уравнениям Клейна—Гордоиа (d\-\-M\^W^{x)=Q для всех ком-
компонент векторного поля.
Взаимодействие поля W*(x) с изотопическими дублетами
левых фермионов A0.14) естественно выбрать в наиболее^простом
виде, аналогичном F.10):
/(+) (л) W+ (х)+/(-) (*) W- (х)+^ /• (х)Wl (x)], A0.30)
где g—безразмерная константа связи, а /?(*)—ток A0.15) левых
фермионов. При этом лагранжиане взаимодействия теория инва-
инвариантна по отношению к глобальным вращениям в изопространстве,
в котором определены дублеты A0.14).
158
Вариация по W?(X) лагранжиана S==SvVb+^'Vr дает
ния Прока с правой частью
Применение к обеим частям его оператора дифференцирования
др. показывает, что Mw(dxW$* (g/2) дйу2. Поэтому это уравне-
уравнение можно переписать в виде
ш - (g/2) (&„+d^lMV) Ji {x). A0.31)
Ясно, что его общее решение есть
где AГ? (^-свободное решение ((дх+2Иг)(НРЗо—0), а
exp [-ik (x-y)] D$ (k) d*klBn)*
—функция Грина W-бозона, которая в импульсном пространстве
имеет, как следует из A0.31), вид
A0.32)
Как видно, пропагатор массивных векторных полей содержит
в числителе kuk^/Mw вместо k^k^lk2 в теории безмассовых бозонов
[см. A.29) или (8.18) для случая глюонов в калибровке Лаидау,
т. е. при С=0], в результате он не имеет иефизического полюса
при ?2=0. Этот вид D$, обеспечивает его поперечность kp?)f&(k)=O
иа массовой поверхности (при k2=Mw), однако член
в пропагаторе приводит к появлению нело-
нелогарифмических неперенормируемых расходи-
мостей в теории возмущений. Поэтому тео-
теория массивных векторных бозонов неперено-
рмируема.
Однако полюсные графики теории возму-
возмущений рис. 10.2 дают для амплитуды взаи-
взаимодействия фермион—фермион конечный,
т. е. иерасходящийся, вклад. Этот вклад
такой же, как и от феноменологического
лагранжиана A0.18), но с множителем
g2/8(Mir—tf2) вместо G/V2, т. е. как отла-
гранжиана
gi(s-W/Mvr) ,а, , *
где правая часть записана для случая \q2\<?Mw, когда массы всех
фермионов также много меньше Mw [в правильности этого выраже-
выражения легче всего убедиться на примерах_ конкретных процессов:
например, для амплитуды реакции vd-+ev, для которой A0.30)
и график рис. 10.2 дают Tyd^ey^^S-^-^^—-^{e1yvyL) ^tLyvdi)
и точно то же самое дает лагранжиан 2?w A0-33)].
Правая часть A0.33) совпадает с лагранжианом A0.18) при
A0.34)
т. е. при
ШМ?Г- Aа36>
где справа представлено значение A0.9) константы Ферми G,
причем тР=0,98 ГэВ — масса протона.
Таким образом, феноменологический лагранжиан A0.18) вос-
воспроизводится при малых ц2 взаимодействием A0.30) фермионов с
векторным (так называемым промежуточным) бозоном при лю-
любой константе связи g.: для этого достаточно выбрать массу Mw-
бозонов в виде A0.35). Особо интересен случай малых g
(#2/4л<1), когда эффекты высших порядков по g2 несуществен-
несущественны. Так, положив в A0.35) g=e/sw, где е—заряд электрона;
€2/4л= 1/137, a sw—некоторое число, получим
Mw=Z9,7mpjSw, A0.36)
где 39,7 = [я/уг2"»137О11/2//пр. Это означает, что при Mir порядка
нескольких десятков гигаэлектрон-вольт все эффекты слабых
взаимодействий можно описать [10.18], по крайней мере в области
\q2\<?Mw, на основе лагранжиана A0.30), с константой g почти
такой же, как в КЭД. Численная малость константы A0.9) Ферми
(т. е. величины Gm2) оказывается при этом просто следствием
относительно большого значения Mw—массь?№-мезонов, рождение
которых на опыте из-за этого затруднительно i[10. 19, 10.20].
Вся теория приобрела бы стройный и элегантный вид, объеди-
объединяя КЭД и слабые взаимодействия, если бы удалось понять
смысл множителя Sw в A0.36) и в равенстве e=gsw, и, главное,
понять, как следует ее перестроить, чтобы она была перенорми-
перенормируемой и позволила вычислять поправки порядка любой степени
gz. Это было достигнуто в модели Глешоу—Вайнберга—Салама,
которая рассмотрена ниже. Однако до этого кратко рассмотрим
интересный эффект спонтанного нарушения симметрии, о котором
упоминалось еще в гл. 6.
160
Глава 11
СПОНТАННОЕ НАРУШЕНИЕ СИММЕТРИИ.
МЕХАНИЗМ ХИГГСА
11.1. Безмассовые бозоны при спонтанном нарушении
глобальной симметрии
Эффект спонтанного появления вакуумного среднего приводит
к интересным физическим следствиям в случае, когда исходный
лагранжиан обладает свойствами симметрии. Рассмотрим снача-
сначала случай, когда эта симметрия глобальная (не калибровочная).
Нарушенная U A)-симметрия. Рассмотрим лагранжиан F.5)
заряженного поля ф (х) = A /У 2 ) (Ф! (х) + 1ф2 (х))=р (х) ехр [ко (х)\
при потенциале самодействия этого поля вида F.15) (см. рис. 6.5):
U (ф)= — ц.^ф+ф + Я (ф+фJ=Я [р2 (jc)—ц2/2Я]2 + const, A1.l)
где const= — [а*/4Я; [А2>0; Я,>0. При этом лагранжиан поля есть
Как видно, потенциал ?/(Ф) зависит лишь от модуля поля
\<9(x)\ = pjx) и _имеет минимум_ (в состоянии вакуума) при
p=fAi/|/r2A, =©/^2 , где ъ^рх/Ук . Фаза а>(х) поля при этом
неопределенна, однако в наиболее низком по энергии состоянии
она не должна зависеть от х
< (о(х) > 0=co0=const, чтобы не
увеличивать кинетическую часть
лагранжиана (<?оФ)+(<?оФ) =(<?арJ +
-f (г (х)(дааJ- Поэтому она мо-
может быть выбрана равной нулю, так
как лагранжиан A1.1) инвариантен
по отношению к U (^-преобразова-
(^-преобразованию поля Ф (х) -+ ехр (—1сооф (х)], т. е.
по отношению к движению вдоль
окружности в плоскости фь Ф2
(рис. 11.1).
Таким образом, в состоянии вакуума
< ф (х) > ^(Ф^(х)Ф0)^\11/У2Т=ю/У2, A1.3)
или <Фг(л:) > =©, <Ф2(л:)>=0, и малые отклонения поля от
этого его среднего можно записать в форме
Рис- "л
Ф
), A1.4)
т. е. р(л)НФ(х)|=(в/УТ)A-Н(х)/в) и л(*)/«<!•
Из двух вещественных полей |(jc) и г\(х) потенциал A1.1)
зависит лишь от г\(х):
U (Ф) = (>,/4)B©r]+T12J+const, A1.5)
11—679 161
а лагранжиан A1.2) этих полей есть
3—A,t]4/4+const, A1.6)
где слагаемое r\(x)fv в первом члене—малая поправка, которой
в первом приближении можно пренебречь.
Как видно, у поля г\(х) появляется масса
/712=2^=2^, A1.7)
а поле !(*) остается безмассовым.
Состояние вакуума A1.3) нарушает U(\) -симметрию теории,
так как в нем фаза со(х) поля ср(х) фиксирована равной нулю.
Как видно, в результате этого спонтанного нарушения симметрии
лагранжиана A1.2) возникло два типа нейтральных бозонов
(вместо ф! и фг), один из которых, •—т) (д:), оказался массивным,
а другой, |(х), —безмассовым. Это так называемый голдстоунов-
ский бозон; причина того, что ои безмассовый, ясна: изменению
%(х) отвечает движение вдоль окружности на рис. 11.1, которое
является свободным и поэтому не приводит в A1.5) к членам,
пропорциональным ?*(х): потенциал ?/(<р) от ?(*) вообще не за-
зависит. Таким образом, из двух бозонов ?(*) и г\(х) безмассовым
оказывается ?(*), изменение поля которого отвечает симметрии
?/A), нарушенной вакуумным состоянием A1.3).
Последние два члена справа в A1.6), кроме несущественной
константы, определяют потенциал самодействия поля т\(х):
^(tO-W+V/4- A1-8)
Нарушенная SU (ЛО-симметрия. Рассмотрим еще одну группу
лагранжианов, на примере которых более полно видны простые
следствия спонтанного нарушения глобальной симметрии. Пусть
комплексное поле ? С*)=BJ/"у является 5?/B)-спинором, описы-
описывающим дублет бозонов (типа, например, К*, А"°-мезонов: Ф1=^Г+»
Ф2=ЛГ°); комплексно-сопряженное поле Ф+(.х) описывает соответст-
соответствующие античастицы (9lf"=Ar°, ф2* = — ЛГ~).
Лагранжиан системы выберем в 5?/B)-иивариантном виде A1.1),.
A1.2), где ф+ф заменено сверткой (Ф+)гф' [причем (ф')+г=(Ф+)г], а
л?оф)+(<?оф) — величиной (^оФ0+(^аФ0- Тогда минимум потенциала
U(Vi)=UB4>f4>t) достигается при р(х)=фг+ф'='О2/2 (v=\i/Vfy
за счет Su B)-неинвариантной конфигурации поля вида < Ц>(х) ) =
=-^=р), причем вблизи минимума поле может быть представле-
представлено аналогично A1.4) в виде
[l H
где то—матрицы Паули, ^—вещественные поля, и равенство
справа справедливо при &,/г><С1. Но при этом 2q>t?=*(p+i\(x)J*
162
и поэтому ?/Bф+ф') имеет точно вид A1.5), а дифференцирование
правой части A1.9) дает
^^-^М, (п.ю)
3
где ?/i^n)—потенциал самодействия A1.8), a 2'= 2* Как видно,
а а—1
положение здесь сходно с предыдущим примером: только мезоны
г\(х) получили массу A1.7), а все остальные три мезона gota)
остались безмассовыми. Три—это число генераторов то в A1.9),
инвариантность по отношению к преобразованиям которых нару-
нарушается состоянием < ф (х) > =—т=- ( ) вакуума: под их действием
это состояние изменяется.
Если поле ф'(лс) является SU (З)-триплетом ф(д;)=(ф!! , то со-
Ф(л:)=^],
стояние вакуума при потенциале AЫ), с заменой ф+ф-^-ф^ф' оп-
определится конфигурацией
Напомним, что 8 генераторов группы S?/C) %a=h?=2ta
удобно записать в виде матриц 3X3, выделяя в них верхний ле-
левый блок 2x2. Первые четыре генератора Ха получим, подставляя
всюду нули, кроме одного из элементов правого столбца и ниж-
нижней строки, в качестве которых возьмем 1 или —i (и 1 и i соот-
соответственно):
ft
\1о|оУ \t о
Следующие три запишем в виде Яо+4=»(-^.р 1, где а =1,2, 3, и;
\о 0| о/
наконец, последний—в диагональном виде ^8="ij7f"( 1 )> в ко-
котором SpX8=0; БрЯ,о=2. Полученные 8 матриц Гелл-Мана удов-
удовлетворяют соотношениям антикоммутации {яД,4}=218г4,Я,. Легко-
видеть, что три из этих генераторов Яо+4=|—\-\ дают нуль в
\оо|о/
применении к < ф (х) > , а остальные 5 можно использовать, чтобы
построить поле вблизи минимума потенциала аналогично A1.9) в
виде
163
w
¦где 2i —сумма по индексам только этих пяти генераторов, прй-
а
чем поле—BjY~3)%s(x) обозначено 1ъ(х). Используя этот вид
спинора Ц>(х), легко заметить, что лагранжиан и в этом случае
в точности имеет вид A1.10), где записано g8(jc) вместо g^(jc).
Поэтому мезон т\(х) и здесь получает массу A1.7), а 5 мезонов
%а(х)> генераторы которых преобразуют состояние поля в вакууме
< Ф (х) > , остаются безмассовыми.
Ясно, что сказанное легко обобщить на случай SU (Л/Асим-
(Л/Асимметрии лагранжиана A1.2), когда поле У(х) в нем—суперспинор
¦<P(jc)={9'(jc)}, i = \,2, ...,N, а среднее его по вакууму есть
< Ф (х) > = A iYY)<obi,N. Подгруппа SU(N—\) группы SU(Щ
содержит (iV—1J—1 генераторов %b=2tb, под действием которых
преобразуются N— 1 верхних строк i = 1, 2, 3,..., N — 1 столбца
ф(дг). В применении к <Ф(.х) > они дают нуль, поэтому состояние
вакуума <Ф(х)> не изменяется под действием оператора—
экспоненты expii^^eEeC*)/*7]» содержащей только эти генерато-
генераторы. Остальные n'={N2—1)—((N—lJ—l) = 2N—1 генераторов
Ka=2ta из общего числа их vN=N2— 1 для группы SU(N) не
обращают <Ф(лс)> в нуль и подобно A1.11) могут быть исполь-
использованы для построения поля ф (х) вблизи вакуумного значения
< ()>
A1.12)
где 2 —сумма только по этим генераторам, причем cn—
а
y^l)/iV—несущественная для дальнейшего постоянная.
Подстановка ф(х) в A1.1) и A1.2) в виде первого из этих
равенств определяет лагранжиан точно в виде A1.10) [в котором
cn\\n(х)-*¦ §удгС*)] и показывает, что только поле г\{х) получает
массу A1.7), а остальные n'*=2N—l полей %а(х) [из общего
числа 2N вещественных полей в ф (х) = {Ф' (х)}\ остаются без-
безмассовыми.
Теорема Голдстоуна. Сделаем общий вывод из рассмотренных
примеров. Пусть имеется набор и вещественных полей ф={ф'(д;)},
которые преобразуются друг через друга при любых преобразо-
преобразованиях некоторой группы G по закону ф-»-ф' = A — шо4)Ф. т.е.
<р' =ф*—i(aa (ta)j4>J, coe<^ 1—малые параметры преобразований.
164
Этой группой могут быть U(\), SU(N), как в рассмотренных выше
примерах, или любая другая группа Ли [SO(N), Sp(Af) и т. д.],
ta=27ia—генераторы группы; поле ф={ф'(л:)} определяет веще-
вещественное представление группы размерности ги Если компоненты
полей комплексны, то через q>'(jc) будем обозначать вещественные
величины, являющиеся совокупностью вещественных и мнимых
частей всех полей [поэтому в примере O=SU(N) было n=2N\.
Пусть лагранжиан теории вида A1.2) и потенциал ?/(Ф) инва-
инварианты по отношению ко всем преобразованиям группы О, т. е.
U(<p')~UD>k) — iaa(ta)fP>(dUid<pk)=sUD>i°) для всех еов<1. Это
означает, что
ЁИШо A1.13)
для всех генераторов группы ta. Кроме того, полагаем, что по-
потенциал имеет минимум при ф(*)=фо=<<р(*)> = {фо'}, где компо-
компоненты <ро' поля вакуума можно найти из условия минимума по-
потенциала
Гв' частности, в примере с SU (ЛГ)-симметрией ф^= ?
Поле вблизи минимума потенциала представим в виде ф(л:) =
'"{Ч^+Л7 (¦*)}, где i\t(x)—малые отклонения компонент полей от
их вакуумных значений.
Появление вакуумного среднего < Ф(-я) > ={Ф^} нарушает
инвариантность теории по отношению к преобразованиям группы О,
так как некоторые из них изменяют это среднее—переводят ф0
в фо=A—и»в?в)Фо. Для этого нужно, чтобы соответствующие ге-
генераторы не обращали ф0 тождественно в нуль: (<0Ф0)/='П^о?=0.
Обозначим п' число линейно независимых наборов величин
¦Чао=@а%У> из которых нельзя построить линейные комбинации,
равные нулю (^ СаЦ^оХ В этих условиях из равенств A1.13) и
AГ.14) следует, что п' полей r\J-(х) из общего их числа п.—без-
п.—безмассовые.
Физически это почти очевидно: действительно, п' — это число
тех преобразований группы G, т. е. поворотов в n-мерном прост-
пространстве векторов ф(*) = {ф'(*)}, которые, оставляя потенциал
fr(<p) неизменным, меняют вакуумное среднее поля {фо''}> т. е. со-
соответствуют некоторым линейно независимым отклонениям от
него фо'-яфо'+V (*) типа движения вдоль окружности на рис. 11.1.
Потенциал при этом не меняется и никаких членов, пропорцио-
пропорциональных i\}(xJ, за счет него в лагранжиане A1.2) не появляет-
появляется, поэтому массы этих п' полей равны нулю.
165
Чтобы доказать это строго1, отметим, что равенство нулю ва-
вариации лагранжиана A1.2) по полям ф^б.З'/бф*^—д«2Ф*—
—<Э?//дф*Nф*] приводит к следующим уравнениям для малых откло-
отклонений т]*=ф*(^)—<ро* от вакуумного состояния:
д-де учтено, что при малых »!*(.*
причем из (П.14) видно, что первый член здесь равен нулю.
Подставляя в A1.15) т]*(л:)=т]*ехр(—\px), где /?2=w2—квад-
/?2=w2—квадрат массы соответствующего бозона, получаем систему уравнений
т. е. т2—собственные значения матрицы m\.
Чтобы найти #' нетривиальных решений этого уравнения
С Л12=О, продифференцируем равенство A1.13) по Ф*ЭД и поло-
положим в нем Ф*=Ф*. Это дает (<?С/(ф)/<?ф%.(<оI+*я4=0, так
как первый член слева согласно A1.14) равен нулю. Но среди ве-
величин т]?о=(<в){фо по условию п'—не равные нулю независимые
векторы; поэтому уравнения A1.16) имеют заведомо столько же
нетривиальных решений с нулевой массой т2=0. В общем виде
это утверждение называют теоремой Голдстоуна ;[11.1, 11.2].
Нарушение киральной симметрии. Если теория включает так-
также безмассовые фермионы, т. е. в лагранжиане—член вида
то возникает еще один тип глобальной симметрии—инвариантность
по отношению к преобразованию
я|)' (х) = ехр (—1у5а/2Щх)\У'(х) =^(jc)exp(—iYsa/2), A1.18)
где матрица у5 антикоммутирует со всеми у^, и поэтому экспо-
экспонента в A1.17) сокращается. Такую симметрию называют кираль-
киральной, а лагранжиан—кирально инвариантным. Если ввести лево-
киральное и правокиральное поля ¦»j)i=(l/2)(l-f Ys) 'ф; 4л = A/2)Х
,ХA—Ys)^; ¦ф='ф1-т-Фд. то З'Ч будет суммой лагранжианов этих
полей:
[так как (^iY«i^«i1l)^)=OJ» и вращения^A1.18)^[можно выполнять
отдельно для лево-: H.J правокиральных полей. Отметим, что (<фф)а=*
() + ('фГфд). поэтому введение в лагранжиан массового члена
заведомо нарушает его киральную инвариантность. Точно
1 Авторы благодарны И. Ю. Кобзареву, обратившему вх внимание на ука-
указанный здесь общий вывод теоремы Голдстоуна для случая скалярных полей.
166
так же появление отличного от нуля вакуумного среднего
< t|> (х) i|> (х) > невозможно в кирально инвариантной теории (где
< i|> (х) тE (х)) =0), а если оно появляется, то это свидетельствует
о нарушении киральной инвариантности. Причиной такого наруше-
нарушения может быть взаимодействие фермионов с бозонами. Пусть,
например, это взаимодействие определяется юкавовским лагран-
лагранжианом
A1.20)
где Ц>0(х) и Ф0(л:)—вещественные скалярное и псевдоскалярное
поля, лагранжиан которых имеет форму, подобную A1.2):
)
где р2=A/2Нф2+Ф2). а ?/(р2) имеет вид функции A1.1) с миниму-
минимумом p=v/V2 .
Обозначая <po + i1YB<Do=P(-*)exp[i1Ys§(J<:)I> Удобно ввести поля
р(х) и g (jc) вместо ф0 (х) и Ф0(х) и считать, что одновременно
с киральным преобразованием A1.18) эти поля преобразуются по
закону p'(jc)=p(jc), ?'(х)=%(х)-\-а. Легко заметить, что при
этом лагранжианы S'yuk и &у,ф будут кирально-инвариантны, так
как (Vt|)') = H)exp(-iaYB)i|)), а (<VPoJ+(^00J-(<W+pWJ-
Минимуму потенциала U (р2) в A1.21) отвечает появление
вакуумного среднего поля р(х): < р > =©/1/^2", v=\ii/K, причем
вблизи минимума р(л:)=A/уг2~) (©+t)(jc)). При этом у фермионов
появляется масса F.19) mf=fv, у поля г\(х)—масса A1.7)
Wi,=|/r2~[A1, а псевдоскалярное поле %(х) остается безмассовым,
так как потенциал U(\^-{-1у5Ф\2)=и{^!) от него вообще не зависит.
Из-за появления массы фермионов, т. е. члена—/^(ф^) в
лагранжиане, его киральная симметрия нарушается. Лагранжиан
перестает быть инвариантным по отношению к преобразованию
A1.18): соответственно этому появляется один безмассовый псев-
псевдоскалярный бозон Ф(х). Теорию можно сделать более реали-
реалистичной (с реальным безмассовым триплетом я-мезонов), введя
вместо одного поля ij5(jc) дублет фермионных полей i|)(jc)=I ^ I
и триплет Фа(х) псевдоскалярных мезонов при юкавовском взаимо-
взаимодействии вида A1.20)
(х) (Ф (х) + 175тоФо (х) !|) (х)). A1.22)
Кроме обычной SU B)-кнваркантности такая теория инвариантна
по отношению к киральнсму преобразованию A1.18) дублета i|>(jc
и к группе киральных SUB) вращений—преобразований вида
У{х)=ех?[-Aаа/2)т*у5]${х), A1.23)
сходных с обычными SU B) -вращениями. Ясно, однако, что для
реального изучения взаимодействия я-мезонов и кварков мо-
167
дельный лагранжиан A1.22) непригоден. Поэтому оставляем
анализ до гл. 17, где он проведен на основе гипотезы частичного
сохранения аксиального тока (разд. 17.1).
11.2. Механизм Хиггса поглощения скаляров
векторными полями и генерации масс
Спонтанное нарушение не глобальной, а калибровочной сим-
симметрии приводит к несколько иным следствиям. Рассмотрим его-
сначала на простых примерах.
Лагранжиан A1.2) комплексного скалярного поля при нали-
наличии взаимодействующего с ним калибровочного (электромагнит-
(электромагнитного) абелева поля А»(х). Чтобы ввести его, нужно заменить
производную dt. в A1.2) «длинной производной» Dk=dk+ieAk(x)
и добавить лагранжиан свободного электромагнитного поля
F2/
-U BФ+Ф) -
(П.24>
Этот лагранжиан инвариантен по отношению к калибровочным пре-
преобразованиям A.1)
ф' (х)=ехр [—ieco (*)] ф (х);
. (И.25>
где со (х) произвольно. Поэтому, выбирая eco(jc) = g(jc)/© и под-
подставляя ф(д;) в виде средней части равенства A1.4), получаем
Ф'(x)=(v+v\(x))/V%, причем 2Ф+Ф=2Ф'+Ф'=(©+'ПJ. После этога
лагранжиан (записанный в полйх ф' и A^—Wy) вообще поля 1(х)
не содержит—оно входило лишь в виде фазы в средней части
A1.4) и сократилось при калибровочном преобразовании. Так как
Ф' = [<?дт] + ie (v + r\) W*] /1/2 , то
+ [(g2/2) B-oti + rf)Wl-Ux (г])], A1.26)
где члены в последней скобке описывают взаимодействие полей ц
и Wp. и само действие поля г\, причем Wnv—dpWv— dyWy., а
?/i От)—потенциал A1.8).
Поле Ъ(х)—комплексная фаза в A1.4)—поглотилось и
«упрятано» в продольную составляющую калибровочного поля
W^x) =Ali(x) +ац|/и, которое из безмассового теперь стало мас-
массивным: член eWWfl2 в лагранжиане отвечает Тем. (Ю.29)] era
массе mw2=e2o*/2, а поле х\(х) получило массу A1.7): тц2=2ц12.
Число степеней свободы системы после нарушения симметрии не
изменилось: вместо поглощенного скалярного поля \(х) появи-
появилась продольная составляющая массивного векторного поля А/=
168
= №„(*). Этот результат часто называют эффектом Хиггса или
механизмом Хиггса [11.3] появления массы у поля Лц(х).
Замечательно, что калибровочное преобразование A1.25) ни-
никак не может повлиять на расходимости теории в области боль-
больших значений импульсов. Поэтому если теория была перенорми-
перенормируемой :[с лагранжианом A1.24)] до спонтанного нарушения сим-
симметрии, то она должна остаться переиормируемой и после ее на-
нарушения, несмотря на то что лагранжиан A1.26) содержит мас-
массивный векторный мезон1.
Случай SU(N)-симметрии исходного лагранжиана. В этом
случае лагранжиан
y
9fA
сходен с рассмотренным выше. Он отличается от A1.2) введением
неабелева калибровочного поля;#"?у—напряженности G.39) этого
поля. Как и в A1.12), предположено, что скалярное поле ф1 нахо-
находится в фундаментальном представлении группы SU(N). Лагран-
Лагранжиан ^ф'^о инвариантен по отношению к замене
ф* {х)=ехр (—mat а)Ч>(х), A1.27)
при которой калибровочное поле преобразуется согласно G.35):
Л{1г->-Ар=W$.. Поэтому, заменяя в лагранжиане ф'-»-ф", A$.-+W$.
и подставляя ф(л:) в виде средней части A1.12), для которой
2ф)+Ф'?=2ф]ф'=('Р+'П(-*)J. получаем, выбирая o>ai()
О
<п-28)
Как видно, после этого все поля 1-а(х) поглотились, потенциал
самодействия опять оказался зависящим лишь от поля t)(jc):?/=
=?/((© + Т]J), а лагранжиан имеет вид
z AL29>
где (W?vJ содержит «кинетический» член (duWv—dyW^J и члены
самодействия векторного калибровочного поля. Третий (пред-
1 Пропагатор его D^4{k)=[gllv—*u*v/m|-)/(A*—m2^), как уже обме-
обмечалось в гл. 10, медленно сходится при Ад-»-оо за счет его продольной
части, которая не убывает при ?д-»-оо. Возникающие нз-за этого лишние
расходимости при т^^О должны точно сократиться во всех порядках (си.
об этом подробнее в гл- 12).
последний) член лагранжиана определяет массу компонент калибро-
калибровочного поля W%,, для которых соответствующий генератор ta=
=Ло/2 дает ненулевой результат при действии на поле ф'(.х)
A1.28) [т. е. которые входят в экспоненту в A1.12) и A1.27)].
У поля ф' всего 2N вещественных компонент [т. е. jV-комплексных
компонент ф'(.х), г = 1,2 ...], из которых в A1.28) осталась лишь
одна, поэтому при калибровочном преобразовании A1.27) погло-
поглотилось 2N—1 полей ф'. Столько же, т. е. 2N—1, компонент
поля №? получают массу.
Наиболее просто дело обстоит в случае группы SUB): в ней
всего три поля W$., и так как 2iV—1=3, то все эти три компо-
компоненты получают одну и ту же массу: /7i2r=g2©2/4—вдвое мень-
меньшую, чем в рассмотренном выше абелевом случае. Действительно,
для группы SUB) 7а—ха/2, где ха—матрицы Паули, и так как
W^wiiatb^=(\lA)WlWbv.(xaxbJ!rxbxa)^(\i2)(^lJ, а ф;+ф"=A/2)Х
X(©+tiJ» то в лагранжиане появляется член (g2/4) ю2 (№?J, отве-
отвечающий указанному выше значению массы.
В общем случае группы SU(N) -генераторы ?"=Л«/2 удобно
выбрать (см. разд. 7.1) следующим образом. Первые 2N—2 из
-лих запишем в виде
iW-з
A1.30)
•остальные (iV —1J—1 — в виде, в котором они дают нуль,
.действуя на функцию A1.28):
V-4
.0...0
.где AlN~1]—генераторы группы SU(N—1)), и, наконец, послед-
лий (N2 — \)-u генератор Л=Л(Лг«_1) — в диагональном виде:
A1.31)
170
где I{N ^—единичная матрица размером (N— l)x(N— 1). Теперь
легко проверить, что величина . ., (ф'* (AaAft) ф^ равная ниж-
нижнему правому элементу матрицы ЛоЛй, отлична от нуля и равна
единице лишь при индексах a=b<2N—2 [т. е. лишь для квад-
квадратов матриц A1.30)], а также при a=b = N2—1, когда
(AaA*)a-ft-w«-i=A2=2(JV— \)jN. Поэтому BN—2)-компоненты
поля Wl, отвечающие матрицам A1.30), получают массу лг^=
=g2t>2/4, а одно поле W^N'~l) отвечающее матрице Ayv«-i =
= Л, —массу т? =(g2v2/2)X{N—l)/N. Симметрия SU(N) ока-
оказывается нарушенной до SU(N — \)xU(l): 2N—1 скалярных
полей %а{х) поглощаются 2N—1 компонентами полей W? теми,
генераторы которых имеют отличные от нуля элементы в самом
правом столбце и в нижней строке. Остальные (N2—1)—
—B./V—1)=(N—IJ—1 полей W$.=A'u остаются безмассовыми.
Теория как была перенормируемой до нарушения симметрии,
так и остается такой же при лагранжиане A1.29) после калиб-
калибровочного преобразования A1.27) и нарушения симметрия. Свой-
Свойство ее перенормируемости, связанное с поведением всех величин
в области очень больших виртуальностей А2 частиц, не меняется
при появлении небольших вакуумных средних и масс частиц
mj~mf~v*<\k2\, где \k*\-+oo.
Общий вывод. Как показывают эти примеры, при спонтанном
нарушении калибровочной симметрии [за счет потенциала вида
A1.1), имеющего минимум] не возникает безмассовых скалярных
полей — так называемых голдстоунов. Соответствующие поля
поглощаются тем же числом компонент векторных калибровочных
полей, которые при этом становятся массивными. Это те компо-
компоненты полей, которые отвечают генераторам с нарушенной симмет-
симметрией. Описанный механизм, замеченный Хиггсом [11.3] в 60-х го-
годах, широко используется в современной теории элементарных
частиц (см. также статью Л. Ли [11.4] и обзор Аберса и Б. В. Ли
[11.50).
Отметим в заключение, что скалярные частицы могут быть
введены с самого начала в лагранжиан не в фундаментальном,
а в любом другом представлении основной группы симметрии Q
лагранжиана. В случае, например, группы O*=SU(N) скаляры
можно ввести в присоединенном представлении, в котором поле их
определяется тензором Ч{=(*а){Ча(х). В этом случае потенциал
?/(Ф) может зависеть не только от (Ф2)г=Фа(л:)/2, например,
в виде A11) Ux=— (Ц?/2)(Ф2)| + (Я/4)|(ф'')гг]2 но содержать также
в виде A1.1) Ux=— (Ц?/2)(Ф2)| + (Я/4)|(ф'')гг]2, но содержать также
член, пропорциональный (Ф4I=(ф2){ (?2)':f/2=(V/4)($4)j. Среднее
ло иаинизшему состоянию системы—по вакууму—от поля ф'Длс)
определяется симметричным тензором D{(х)) = const с нулевым
следом (так как ф|=0). Вид этого тензора может зависеть
Ш
от соотношений между константами к и к'. Например, в случае
JV=5 для группы SUE) при к>0 и Я'>0 наиболее низкой энер-
энергии отвечает [11.4]
I \V A
-3/2 J
—3/2/
и соответственно этому симметрия SUE) разрушается до SUC)x
XSUB). Если же (—100)к/17 <к' <0, то наиболее выгодно
когда SUE) разрушается до SUD)xUQ)- (Подробнее о0 этом—
см. гл. 13).
Глава 12
МОДЕЛЬ ЭЛЕКТРОСЛАБЫХ ВЗАИМОДЕЙСТВИЙ
ЛЕПТОНОВ И КВАРКОВ
12.1. Лагранжиан
Предыдущие разделы (начиная с гл. 10) близко подвели к
единой теории электромагнитных и слабых взаимодействий, раз-
развитой Вейнбергом [12.1] и Саламом [12.2] в 1967 г. (важная
часть ее была сформулирована Глешоу ![10.8] еще в 1961 г.).
Для построения теории слабых взаимодействий, содержащей
безразмерную константу связи g (см. гл. 10), нужны массивные-
векторные мезоны и при их массе Mw порядка десятков гигаэлек-
трон-вольт эта константа — порядка заряда электрона | е \ =
=У4я/137. Однако теория, содержащая в лагранжиане затравоч-
но массивные векторные поля, как уже отмечалось, вообще не-
непригодна из-за ее неперенормируемости. Выход из этой трудности
указан в гл. 11: ввести сначала все поля, включая векторное, с
нулевой массой (при этом, как мы видели, теория векторных по-
полей перенормируема), но ввести также в некоторой группе калиб-
калибровочной симметрии скалярное поле с потенциалом самодействия
A1.1) и, далее, за счет спонтанного нарушения симметрии полу-
получить массы векторного и спинорных полей. Такая теория с само-
самого начала перенормируема; она остается перенормируемой и после
спонтанного нарушения симметрии вследствие того, что в области;
очень больших импульсов интегрирования, где формируются рас-
172
зодящиеся интегралы, массы частиц и все вакуумные средние ро-
роли не играют.
Так как кванты электромагнитного поля также являются век-
векторными (нейтральными) бозонами с нулевой массой, то теория
чугабых взаимодействий, о которой здесь идет речь, могла бы од-
одновременно описывать и электромагнитные взаимодействия. Для
этого нужно, по крайней мере, чтобы кроме триплета векторных
нолей WV"(x), часть из которых получает массу и приводит к
появлению лагранжиана слабых взаимодействий вида A0.30),
теория содержала еще одно векторное нейтральное поле В„(х),
за счет которого могло бы возникнуть электромагнитное поле.
Кроме того, необходимо, чтобы кроме левых фермионов еь, vL,
«ь, dL и т. д. лагранжиан теории содержал правые поля этих ча-
частиц: ея, vB, ur, ds и т. д., так как в электромагнитное взаимодей-
взаимодействие поля входят в комбинации е(х) =eL(x)+eK(x), utt=uL(x)+]
+ия(х) и т. д.
Слабые взаимодействия содержат только левые поля, поэтому
лагранжиан единой теории нужно строить так, чтобы левые и
правые поля входили в него по-разному. Например, левые поля
•он может содержать в виде дублетов A0.14) (и иметь калибро-
калибровочную SUB)-симметрию), а правые — в виде синглетов по отно-
отношению к 517B)ь-поворотам. Все это почти однозначно определяет
вужный лагранжиан единой теории. Рассмотрим сначала для
упрощения мир, в котором из фермионов имеются только поля
электронов е(х) и нейтрино v(x), т. е.:
а) дублет лептонов /z.(jc)=(Vi^j и два синглета ец(х) и vR(x);
б) триплет W$l (х) и синглет В»(х) векторных безмассовых полей;
в) дублет полей бозонов 9=L1|Jj, где Vi(x)*=<P+(x) — положи-
положительно заряженное поле, аф2=Ф0(д:)—нейтральное поле. Эти поля
подобны изодублету полей /С-мезонов К=\ко}х)Ь они комплексны
и изменяются при зарядовом сопряжении, переходя в фс(лс) =
((^)> гдеФ_=ф? С=1<г2 = (_?о)-матрвда за-
зарядового сопряжения.
Будем считать, что SU B)-симметрия теории—калибровочная.
Для такой симметрии лагранжиана необходимо, чтобы при введении
векторного калибровочного (безмассового) поля W$.(x) все произ-
производные 1дц=1д/дХц были заменены инвариантными производными
idii+g(ta /2)W$.(x). Если же, кроме того, в лагранжиан введено
синглетное поле векторных безмассовых мезонов Вц(х), то все
производные id» следует заменить операторами
iDll=idll+g'(r/2)BVL+g(Taj2)Wl A2.1)
где g'—константа связи с полем В», a y=2(Q> —гиперзаряд,
т. е. удвоенный средний заряд мультиплета фермионов или бозо-
173
нов; теория при этом также локально U(l) инвариантна, т. е.
инвариантна по отношению jk замене eL,R-+e'LR, Вц-уВ^, где
Чя (*)=ехр[1-у-Ую(л:)]ел,Л и В'11(х)=В11.(х)+д11.а>(х), так как
() A2.2)
Отметим, что гиперзаряд связан с оператором заряда частиц,
соотношением Q=f3+Y/2, где Т3—проекция изоспина (Г3=т3/2
для дублета частиц), и что для лептонного дублета lL имеем
YiL=—\, для eR имеем YtR= — 2, a У\^=0, в то время как
Тф=1 для дублета полей q> = f'+). Поэтому лагранжиан рас-
рассматриваемой системы полей содержит две константы связи g, gr
и имеет следующий вид:
где
2V= -A/4) {W
( ' У
есть лагранжиан векторных безмассовых калибровочных полей.
и W%. (а, Ь, с всюду пробегают значения 1, 2, 3);
— лагранжиан фермионов, а
Ф]*-
—лагранжиан дублета ф = |(р+| скалярных полей. Чтобы обеспечить
эффект спонтанного нарушения SU B)-симметрии теории, потен-
потенциал самодействия поля ф следует выбрать в виде A1.1):
U B (Ф+Ф)) = — ц? (Ф+Ф)+^ (Ф*ФJ, A2.7>
с Ц?>0 и ^>0, причем (Ф+ф) = ффФ++Ч)о"(Ро- ^Роме этих Тчастиц
лагранжиан & содержит член SVuk, определяющий юкавовское-
взаимодействие поля ф с фермионами
h) + K-lc, ?<12.8)
где /е, /v—константы связи (к. с—величина, комплексно-сопря-
комплексно-сопряженная к предшествующей ей). Поле фс(.а;)=( ° х )—зарядо-
во-сопряженное к ф, введено вместо ф во второй член для того,
чтобы весь лагранжиан SVuk сохранял электрический заряд. За
174
счет взаимодействия S'yus (см. гл. 6) генерируется масса фермио-
иов при спонтанном нарушении симметрии.
Лагранжиан & A2.3) инвариантен по отношению к локальный
SU B)- и ?/A)-вращениям—отдельно для левых и правых полей
[см. A2.2)] и локально сохраняет гиперзаряд У-частиц. Поэтому,
в частности, он не допускает введения затравочной массы фермио-
нов в виде /no(ie)=mo(iftei+Jie^)—эта величина изменяется при
калибровочных вращениях дублета ?/.=(/); массы фермиоиов могут
появиться лишь в результате нарушения симметрии.
При лагранжиане A2.3) — A2.8) теория содержит безмассо-
безмассовые калибровочные поля векторных бозонов и скалярное поле
<р — самодействующее 1[по закону А(<р+<рJ] и взаимодействующее
с фермионами. Все эти типы полей включают только безразмер-
безразмерные константы связи [g, gr, fn f4 и Я в случае лагранжиана
A2.3)], и теория их перенормируема. Специально для лагранжиа-
лагранжиана A2.3) перенормируемость теории была доказна Т' Хофтом
'[12.3] в 1971 г. Не приводя здесь этого доказательства, рассмот-
рассмотрим, к чему ведет в этой теории спонтанное нарушение симметрии
в рамках механизма Хиггса при потенциале U(<q) вида A2.7) с
минимумом при 2<р+<р=о2=цгД. Для этого удобно, пользуясь
свободой калибровки [см. A1.9)], выбрать поле <р(х) в виде
A1.28):
где ti(jc) вещественно, и считать, что калибровочное поле
~~ /v \
и дублет tL = I ? I определены всюду именно в этой, так назы-
называемой ^/-калибровке. [Это означает согласно A1.9), что в лагран-
лагранжиане & вместо полей 4>(х), Il(x) и Ац(х) в существенной обла-
области вблизи минимума потенциала ?/(ф) подставлены q>'(jc) =
7 ' C &' 0&0
где ^=(to/2)W'J[(x), U(x)=exp(-ixalt(x)lv), причем la(x)
.определены согласно A1.9). После этого для упрощения записи
штрихи у всех полей не пишем).] Как видно из сравнения с пра-
правой частью A1.9) при этом у поля 4>(х) исчезают три компоненты
h(x), h(x), 13(jc) и нарушается SUB)-симметрия теории за счет
появления вакуумного среднего лишь у нижней компоненты дублета
(ф(лс)> «=—тг=-гМ. Эффекты, к которым это приводит, рассмот^
рены ниже.
12.2. Генерация масс лептонов и бозонов.
Нейтральные токи
Появление массы у трех векторных полей и у поля ]()
Подстановка Ф(*) в виде A2.9): Ф(*)=A/]/2 )Co+ti(jc))Xi, где
175
Xi=(j)—единичный орт в лагранжиан S"s A2.6), дает:
A2.10)
где
A2.11)
и учтено, что (х+ (f В*
+{К)'1> (tf*.*W--vj. а [(П)таН
Кроме того, потенциал U [(ti+*>J] подставлен в виде A1.5).
Если выделить в S's члены с постоянными коэффициентами при
поле z\ и при WfyPp., то можно записать
2W1/2) [(д^Г —I*?»]2] +ZlMz/2+MtrWiWZ+&'s. A2.12)
где 2^=2?5('П3» Л-^д • ••)—члены третьего и четвертого порядков
по степеням полей r\, Zu, Wjt, описывающие их взаимодействие,
а множители
^?)У A2.13)
имеют смысл масс трех векторных полей Zp. и W? (см. гл. 10),
которые появились у них в результате спонтанного нарушения
симметрии. Видно также, что остаточное поле г\(х) хиггсовских
бозонов приобрело массу A1.7):
mri=V2~[>.1=Vl&v, A2.14)
определяемую параметрами потенциала ?/(Ф).1
Лагранжиан A2.12) не включает «кинетической» части, квадра-
квадратичной по производным d|iZv> dyWy от калибровочных полей.
Однако она содержится в члене S'y A2.14), который можно запи-
записать в виде
2V_ -A/4) [{WbY+&] + Xv.
где &v—члены кубические и третьего порядка по полям W?, Bp.
(которые в удобном виде выписаны ниже). Если обозначить
и определить нейтральное векторное поле Ац
в виде комбинации полей Вц (х) и W^(x), ортогональной к Z».(x),
т.е. i4u(x)=[g5u(Jc)+o/w2.(A:)]/(]/g2+g'2), то легко понять, что
{W^f+BlysZly-^-F^, где /7nv=d^v—дуА^ имеет смысл, как
176
сейчас увидим, тензора напряженности обычногб электромагнит-
электромагнитного поля (а Ар.—его потенциала). Поэтому
<2V= -A /4) [Fl+Zl + {WlvJ+ {WlvJ] +3>v. A2.15)
Ортогональность линейных комбинаций полей Z» и Лц ясно видна,
если ввести обозначения
w, A2.16)
где Bw — так называемый угол Вейнберга. В этих обозначениях
данные выше определения полей имеют вид:
— 5Д (jc) sin бит+W? (jc) cos виг, J
причем при в5г-»-0 поле Ад(д;) совпадает с Вц(х), a Z,j(jic)—
с W^(^:). Как видно, суммарный лагранжиан содержит все эти
поля в виде
Ss +2V = - A /4) Flw + [(-1 /4) Z2m+A /2) M%Zl] + .
2
e-1,2
+ 7«^ЛJ-<т|2)+2'5 + 2'7, A2.18)
т. e. Mz и Mw действительно имеют смысл масс соответствующих
векторных бозонов [см. A0.28), A0.29)]; векторное нейтральное
поле Ар(х), определенное в A2.17), остается безмассовым: оно
имеет все свойства обычного электромагнитного поля и его взаи-
взаимодействие с заряженными частицами, которое содержится в
лагранжиане 3? A2.3), приводит, как мы увидим, к обычной
КЭД. Из A2.13) и из определения угла бтг следует, что Mw/Mz~
=cos0w, т. е.
Mz=Mwlcos бит. A2.19)
Можно показать, что это соотношение справедливо для широкого
класса теорий [содержащих не один, как в A2.3), а несколько
дублетов полей Хиггса]. Таким образом, спонтанное нарушение
SU B) -симметрии привело к поглощению трех скалярных полей
[ii. is, h — в обозначениях A1.9)] и к появлению массы A2.13)
у трех векторных полей WV", НР„~ и Z,,. Образно говоря, они «по-
«поглотили» скалярные поля и при этом стали «тяжелыми>. Попутно
масса появляется и у других частиц, например у самого поля
Хиггса г\{х) за счет его <<р(х)>. Важный для теории параметр —
угол Вейнберга виг, задающий отношение констант g/g=tgQWr
так и остается произвольным и определяется экспериментально;
опыт дает для него значение sin26Tr^0,225. Это означает, что
теория Вейнберга—Салама является частью какой-то более об-
общей (см. гл. 13) теоретической схемы, которая, фиксируя бтг,
12—679 177
дает более глубокое понимание физики элементарных взаимо-
взаимодействий. .
Вакуумное среднее zj= <ф(л:)> и массы Mw, Mz. Очень
важно, что взаимодействие векторных полей W? [в лагранжиане 3?f,
см. A2.5)] имеет место лишь с левыми фермюнами, как того
требует феноменология слабых взаимодействий (см. гл. 10), и опре-
определяется той же калибровочной константой g, которая задает
взаимодействие W%, с полем Хиггса ф(л). Кроме того, для полей
W$ [т. е. для а=1,2 в A.5)] оно имеет точно такой же вид
в лагранжиане &f, как в феноменологическом лагранжиане, введен-
введенном в гл. 10 [справа в A0.30)]:
в—I, 2
__ S 11 (+) /r\ П7~ _i /(—) / r\ \ХУ^^\ /19 9ГЛ
где jl~] =Сеу„У1); №] = {yi4v.eL), а №^ —поля A2.11). Поэтому
лагранжиан A2.3) воспроизводит за счет графиков вида рис. 10.2
[точнее, см. ниже рис. 12.1, а], четырехфермиоиное взаимодействие
заряженных токов A0.18) —дает в области низких энергий такой же
результат, как лагранжиан 2?w=(bGlY2)(eLyv.vi){yiyv.ei) при усло-
условии A0.34), т. е. если g2/2M^=4G/]/27 Так как 4Mw=g2v2
[см. A2.13)], то константа g2 отсюда вообще выпадает и это усло-
условие сводится к равенству <о2==1/(]/г2 С?), которое определяет ваку-
вакуумное среднее v поля ф(лс) через константу Ферми A0.8) и дает
для него значение
p=(l/]/2GI/2= . 10> = /те. =262 /и.^245,8 ГэВ, A2.21V
1/103/2" р
определяющее физические массы всех частиц, возникающие после
нарушения симметрии. В частности, массы векторных бозонов
Mw=gv/2 и Mz=MvtrtcosQw [см. A2.13)] можно найти отсюда,.
подставляя для константы g полученную ниже величину g=ejsinQw
[см. J12.29)]. Это дает для Mw значение вида A0.36) Mw=
=У па v I s in Qw—C8,5 / s in Qw) ГэВ. Здесь вместо аг = 1 /137 постав-
поставлено «бегущее» значение a(Afvr)^l/128 величины а(Р2) = е2/4л
(см. подробнее раздел 12.4) и, тем самым, учтены главные радиа-
радиационные поправки к массе М.
При sin?eTr=0,22 отсюда следует Mw**82,\ ГэВ, a Mz*=*
~93,0 ГэВ.
Как видно, векторные частицы — тяжелые, однако их наблю-
наблюдение возможно1 на ускорителях нового поколения.
1 Рождение W±- и Z'-бозонов наблюдалось (?ЛА-1-коллаборацией) а
1983 г. на /7/7-коллайдере в ЦЕРНе, и первые оценки масс дали: Л4Г=>81±
±2 ГэВ, А^„-.95±2,5ГэВ.
178
Массы фермионных полей появляются за счет лагранжиа-
лагранжиана A2.8) юкавовского взаимодействия. Подстановка в него поля
Ф (х) в_виде A2.9) дает: 2Чпк=[ — (v +ц (х))/УЩ [Л (ё (х) е (х)) +
. так как ^+h) = \('o + r\)/V2]eL(x), (фс+^) =
a eReL + eLeR = ee (и аналогично для v =
В сумме с лагранжианом 9?f фермионов это дает Sf
=(s(yv.idv.—me)e)-ir(:v(yv.idv.—mv)v)-irS''Yuk+S'r, где массы элект-
электрона и нейтрино
me=fev/V2\ m4=f4viV2 A2.22)
определяются безразмерными константами fe и /v;
&'уЛ= —(mttv) (е (х) е (х))г\ (х) — (mv/v) (v(x) v(x)) r\(x) A223)
сть лагранжиан взаимодействия лептонов с остаточным полем
хиггсовских бозонов г] (л), а
A2.24)
— лагранжиан взаимодействия лептонов с калибровочными по-
полями. Как видно, константы взаимодействия легких лептонов с
полем г\(х) хиггсовских бозонов численно очень малы /е/У2=
=т<»/и~ 10~5, fv/f2 = mJv=0 или mv/u~10~10, если масса нейтри-
нейтрино — величина порядка десятков электрон-вольт (как, возможно,
показывают данные о спектре р-распада ядер трития [12.4]). Эти
константы пропорциональны массам тех лептонов, с которыми
взаимодействует поле t|(x).
КЭД и нейтральные токи. Лагранжиан &' A2.24) содержит
в себе взаимодействие A2.20) 2" ± с заряженными бозонами (за
счет члена xaW$. с а=1,2). Остальная его часть
A2.25)
определяет взаимодействие лептонов с нейтральными векторными
бозонами Вц и №д. Здесь каждая из внутренних скобок содержит
одну и ту же величину [фигурирующую в A2.1) для а = 3]:
где Y—гиперзаряд соответствующего мультиплета фермионов
(XiL — — \, YeR=— 2—см. выше); Г3=т3/2—проекция изоспина
на ось квантования (причем 7V/? = 0), a Q = Tz-\-Yi2—оператор
заряда частиц в единицах \е\ — заряда протона. Из A2.17) сле-
следует, что
д sin Qw; В„.= —Zu sin Qw + A^cos Qw. A2.26)
Подставляя отсюда значение 5„ в Лд и замечая, что gW%.—g'Bn=*
12* 179
где g=Yg*+g' [см. A2.11)], получаем:
A^=(g' cos Qw) QA» (x)+g(T3-Q sin2 ftr) Z» (jc). A2.27)
При подстановке в A2.25) первый член этого выражения в точ-
точности воспроизводит лагранжиан A.4) электромагнитных взаимо-
взаимодействий &"w~-\e\j<«»(x)Av(x), где ДвЯ1> =Q,(*Yi»e) [см.
A0.22)]; Qe=—I, e=|e|Qe—заряд электрона, если g' выбрать
так, чтобы
g'cos Qw=gslnQw=gg'/yg2 + g''=e. A2.28)
Действительно, он дает вклад в &'о [см. A2.25)] j
+ (i*YuOe*)Mu= — е(ёъе)Аи.(х) точно равный д
Из A2.28) и определения A2.16) угла %w следует, что
g'=elo.osQw\ g=e/sinew; g=g/cos 6w=e/(sin6wcos6w) A2.29)
и что
l/g2+l/g''=l/e2. A2.30)
Второй член в A2.27) дает при подстановке в 2*„ лагранжиан
взаимодействия лептонов с нейтральным Z^ бозоном:
&Z, = [е I (s in Qw cos 6^)] [(?yh (t3/ 2 — Q s in2 Qw) lL) —
— (?i&4v.eR) s in2 Qw] Z.». =
x). A2.31)
Таким образом, «зарядом» лептона по отношению к полю Zp. (x
является оператор ^z=(—e/slnQwrCosQw)(T3—Qsiri*Qw) в том
смысле, что лагранжиан 2^.= — {(къегк^^Ъегвц^^х)
переходит в лагранжиан электродинамики ^эд, если Zu заменить
в нем полем Ар., a ez—обычным зарядом e=\e\Q.
Из окончательного выражения для 2"zo также видно, что в
сумме 2''z'+S'w± с лагранжианом A2.20) S'v± он приводит к
графикам рис. 12.1 четырех-
фермионных слабых взаимодей-
ствий, которые содержат обмен
^-бозонами (рис. 12.1, а) или
?°-бозонами (рис. 12.1,6) в зави-
зависимости от зарядов фермионов.
Т 2/NP ?8 2/M2
Так как g
р
g2/M
w,
Рйс 12.1
то в низкоэнергетическом пределе
(AfV^I^I) эти графики в обо-
обоих случаях дают вклад с одним и
тем же коэффициентом перед
180
фермионными скобками — таким же, как феноменологический
лагранжиан A0.18) с нейтральным током вида квадратной скоб-
скобки во второй строке A2.31):
К (*) = JI (*) ~ 1\?т) (*) s in2 6r. A2.32)
т. е. вида A0.24) с ?=5т2вг. Однако при высокой энергии, когда
\q2\ становится сравнимым с М^, вклад этих графиков немного
отличается от вклада четырехфермионного лагранжиана A0.18):
вместо g2/8Mwr=G/]/2 график рис. 12.1,а приводит, очевидно,
к коэффициенту g2/8(M2v — q2), a график рис. 12.1,5—к немного
отличающемуся от него значению
g2/8 (М| -^cos2 6tr=g2/8 (M2v~q2cos2Qw).
Взаимодействие векторных бозонов. Кроме части З^+ЗЧик,
все члены в которой были выписаны выше, полный лагранжиан
A2.3) включает часть 2V+2Vi записанную в виде A2.18) и
содержащую члены взаимодействия полей 3?'s -\-3?'v—кубические
и четвертой степени по этим полям. Выпишем их в явном виде,
так как они важны в ряде конкретных вычислений.
Лагранжиан S's включает взаимодействие и самодействие
хиггсовского остаточного поля г\(х) и, как видно из A2.10) и
A2.12), имеет вид
!V]( |)t, A2-33)
где const=—Hi4/4X, a g2 я g2 имеют значения A2.28). Это взаи-
взаимодействие приводит к графикам теории возмущений, основан-
основанным на трех- и четырехбозонных вершинах рис. 12.2, о—г. На
Z0 |д/ уО и/* ?0 7O
U у V- ** V j" V U ~V
а.) б) В) г)
Рис 12.2
этом же рисунке указаны значения, соответствующие каждой из
этих вершин — вкладу их в i T21.
По определению 3?'w есть разность [см. A2.15)] 2"w=
= — 0/4)[(»v(ivr—(M'liv) ]i где W|iv=** nv+gee&cH'Jl \vv. Учитывая,
что (#2vJ=2^il-v^v+(^vJ и что
181
получаем
+tl+2 <^wz-
. A2.34)
Чтобы перейти к полям реальных частиц Z^ и Лц, сюда нужно
подставить поле Wl в виде A2.26): ^ = ZM (a;)cos Bw + A^sin QF.
Отметим, что при этом электромагнитное поле Ац(х) всюду вхо-
лит здесь, как это и должно быть, вместе с множителем e=g sin Qw.
Лагранжиан S?'v приводит к графикам, основанным на трех- и
четырехбозонных вершинах рис. 12.3, а—б, 12.4, а—в—на вер-
вершинах превращения фотона или Zn-бэзона в пару заряженных бэ-
зонов W$, или же на четырехбозонных вершинах рис. 12.4, a—в
рассеяния фотона, или Z^, W» на W$.
.*
& > ч ?/ ч^ Ч
у х \
Рис 1218 Рис. 13.4
. 12.3. Несколько поколений лептонов и кварков.
Кабиббовское смешивание
Несколько поколений кварков. Теорию легко обобщить на
реальную ситуацию, когда имеется несколько поколений A0.14)
лептонов и кварков. Однако сначала полезно понять, что происхо-
происходит в случае, когда вместо электрона и нейтрино имеется только
несколько поколений левых и правых кварков q'iiL=*(u'L
\diij
dj.R, где i, / = 1, 2, 3—номера поколений, причем левые кварки
q\,L указаны в нижней строке в A0.14), а и},^; d'j,R—синглеты
таких же правых кварков. Все поля кварков снабжены штрихами по
причинам, которые ясны из дальнейшего. Так как для левого дуб-
дублета V9i =2/3—1/3 = 1/3, а для правых кварков Г„,я=4/3;
Yd,R= —2/3, то вместо лагранжиана A2.5) получим согласно A2.1):
2
/-1,2,3
Взаимодействие с заряженными и нейтральными векторными бэ"
зонами в результате останется прежним—вида A2.20), A2.27),
182
A2.31). В частности, заряженный ток Jn — ji ' имеет вид A0.21):
A2.36)
где оба поля du и «и—штрихованные.
Вместо лагранжиана A2.8) юкавовского взаимодействия полу-
получим (заменив в нем li-+qu, й)
2
I. /=1,2,3
где на месте констант fe и /v юкавовского взаимодействия теперь
появились матрицы flj, fj этих констант (по значкам ij поколе-
поколений). Если эти матрицы самосопряженные, то 2"уик сохраняет
СР-четность, иначе он ее нарушает. Ниже будем пользоваться
матричной формой записи, в которой, например, первая строка в
S'f.k есть -р«/ДФ+ф + &Ф)/ЗД- Так как (Ф+?и)=A/К2)Х
X(v+4(x))dtL, а (Фс+^?)==A/К2)('о + л(л:))и/?. то в результате
спонтанного нарушения симметрии получим
v + r\(x) —г
= - yg- [(^
где учтена возможность записи произвольной матрицы /а в виде
произведения самосопряженной матрицы fd=f'd и унитарной
^r<i(Vi/Vrj"=l), т. е. что fd—fdVd, и где d'L==Vad'i. Аналогично
fu=faVa, где /ц=/ц+, VaVt^=\.Учтено также, что ~d'nJdd'L-\-
-\-difddji^d'fdd', где d'=d^-{-di (и аналогично и'==Ид+И?,
где UL — Vua'i), и введены массовые матрицы m4=f'dVlV^" ^и3»
—?'„р1У~2. Эти матрицы самосопряженные. Удобно диагонализо"
вать их, так как после этого их диагональные элементы приобре-
приобретают смысл физических масс кварков. Представив для этого поля
кварков d't и iii в виде линейных комбинаций новых полей
и i=^lijU ijU j, U1=2jjU ijll], (IZ.oo)
т. e. d'=Dd, u'—C/u, где D и t?—унитарны DD+=UU*=\,
выберем их так, чтобы
" + ~ л (mdl \ f + ~ f^ ^
\ mdj " \ maj
В результате лагранжиан 5Руик запишется в диагональном виде:
2
i-I.2,3
183
Кинетический член кварковых полей в A2.35) не изменится при*
указанном унитарном преобразовании, так как (d'y^d^d')^
= {d\dt,.d) и (tt'Y^utt') = (пу^дциу Поэтому 2"Я[ в сумме с 2"^
дает 27+^=2; (п; {у^-т^) и,) + EУ (y^-m^) ^) +
+2'/'4-2'уп|[, откуда видно, что смысл физических полей кварков
с определенными массами та1 и md/ имеют именно поля ut и d/,
а не их линейные комбинации A2.38), которые поначалу входили
в лагранжиан. Здесь S'y'uk обозначен подобный A2.23) лагран-
лагранжиан взаимодействия этих кварков с остаточным полем_т](л:) хиг-
гсовских бозонов: 3?hk=—2j[(mujlv)(u.jU))i\-(mdj/v)(d]dJ)]r\(x)r
а &] =i?o -\~&'w± — лагранжиан взаимодействия кварков с век-
векторными бозонами. Как видно, 2"?Uk вносит вклад в переходы,.
в которых не меняются ни заряды, ни поколение (т. е. ароматы)
физических кварковых состояний1. Этот вклад на опыте пока не
наблюдался.
В лагранжиане взаимодействия кварков с нейтральной компо-
компонентой калибровочного поля [вида A2.31)] Si' —
матрицы О и D вообще сокращаются. Видно, что соответствую-
соответствующий нейтральный ток не изменяет поколений и имеет точно вид
A0.24) с ij = sin2e^;
Лагранжиан S4^± взаимодействия с заряженным током имеет
вид A2.20), но в самом токе /ц = Ум~)(л:) A2.36) матрицы if ъ D
не сокращаются:
j Г> (х) = (ЗЛГХ%) - 2у CW л) a S^ [diL y/jL), A2.40>
где d°—Rd, а и°=К+и, причем K=W+l3—матрица Кобаяши—
Маскава.
Как видно, в заряженном токе участвует либо комбинация
d°JL='S,iKjida(x) физических нижних кварковых полей, либо [как
справа в A2.4)] сходная комбинация
^* A2.41)
верхних полей. Общий вид унитарной матрицы Кц Кобаяши—
Маскава для случая трех поколений был выписан ранее [см.
A0.26)].
1 Если теория включает не один, а несколько дублетов бозонов Хиггса, то>
приходится принимать специальные меры, чтобы подавить такого рода пере-
переходы, не наблюдаемые на опыте.
184
Замечательно, что каОиббовское перемешивание кварковых
полей возникло в теории Глешоу—Вейвберга—Салама как неиз-
неизбежное следствие общего недиагонального вида матриц констант
flj, flj юкавовского взаимодействия кварков. Интересно также,
что уже при трех поколениях кварков автоматически появляется;
эффект нарушения СЯ-четности за счет появления комплексной
фазы в A0.26). Фактически же (см. гл. 10) все углы смешивания
невелики—порядка 10, а нарушение СР-четности очень незна-
незначительно—порядка 10~3 рад; в результате матрица Кобакши—
Маскава оказывается почти диагональной; она была бы в точ-
точности диагональна, если бы матрицы констант flj и flj были;
одинаковы или пропорциональны друг другу. В настоящем виде
теория не определяет зти матрицы; их происхождение остается
до сих пор загадкой, решению которой посвящено большое число»
работ (см. гл. 13).
В реальном случае, когда имеется три или более поколений
и кварков, и лептонов, фермионный лагранжиан 3'f в A2.3)>
нужно взять в виде суммы кварковой и лептонной частей, т. е-
3f=.3?-\-3\, где 3\—сумма членов типа A2.5) по всем поко-
поколениям лептонов, а к 3%иь добавляется член того же вида, как
в A2.37):
и
описывающий взаимодействие лептонов со скалярами, где l'L=
— \е' )» a flj и /^—матрицы констант, аналогичных входящим
в A2.37). Теория может вообще не включать полей правых
нейтрино v^ (если нейтрино не имеют дираковских масс); тогда
в A2.42) не будет второго члена и ни к чему новому S'yu*
не приведет.
Если же поля \iR существуют, то аналогично случаю квар-
кварков заряженный ток, имея вид A0.21) j() Jj)()
будет включать не поля нейтрино
viL с определенной массой, а линейную комбинацию их вида
A2.41): v°i = 2(^+)i/v/i' гДе К1 ~ лептонная матрица A0.26).
2
Кобаяши—Маскава. Это может привести к наблюдаемым эффек-
эффектам в реакциях, идущих под действием массивных нейтрино,—
к так называемым нейтринным осцилляциям.
12.4. Радиационные поправки
Эффективные константы электрослабых взаимодействий—
величины a'(/J2)=g/'(P2)/4n и a2(/>2)=g2 (P2)/4n—связаньв
185'
«с квадратом эффективного заряда электрона а(Р2)=е2(/Э2)/4я
«соотношением A2.30)
а-1 (Я2) = а'" (Р2) + «71 {Р2)- A2.43)
В КЭД величина а (Р2) определяется в первом порядке по е2
формулой E.11): а-1(Я2)=а'1(ц2) + F/4яIп(/>2/ц2), причем в той
эке форме определяется [см. (8.31)] и эффективный заряд а2
группы SUB):a~i(Р^^а-1 Ь>.2) + (Ь2/4п)Ы(Р2Ц».2). Здесь ц — про-
произвольная точка нормировки, а Ь и &2—известные коэффициенты
{см. ниже). Рассмотрим область P2^>v2yMw, т2, mf, где
можно пренебречь всеми массами, не учитывать спонтанного
нарушения симметрии и использовать непосредственно ту калиб-
калибровку, в которой записан лагранжиан A2.3) — A2.8), не делая
унитарного преобразования A1.9). На нижнем пределе этой
¦области можно выбрать p2=Mw, где от1 (Л&)^ or1 ^137;
-а' (М^)=а-1 cos26«r; aj1 (М2г) = а sin2 6w [см. A2.29)]. Напомним,
"чему равны Ь и Ь2 в этих формулах.
а. Если бы рассматриваемая система частиц включала лишь
электроны (разных поколений) с зарядами eQf, то согласно
рис. 12.5 а и E.56) имели бы Ъ=—D/3J/N,Q,2. Однако кроме
лих теория электрослабых «взаимодействий включает еще NB= 1
заряженных скалярных полей (рис. 12.5,6) и Nv=l заряженных,
т. е. комплексных векторных полей (ИРД Рис- 12.5, в или N=2Nr
вещественных векторных полей). Поэтому согласно рис. 12.5
NfQf-(l/S)ZsNsQl A2.44)
По сравнению с E.56) но-
новое здесь — вклад B2/3) N,v
заряженных векторных по-
полей; он другого знака, чем
E.56), и равен (см. гл. 8)
11/8 — на каждую веществен-
вещественную компоненту векторного
поля, или 22/3 — на каждую
заряженную №±-компоненту.
Это и дает первый член в Ь.
Считая, что теория элек-
электрослабых взаимодействий
включает v поколений квар-
кварков и лептонов (с массами
не больше Mw), для которых
•ZfNfQi2 = A+4/3+ l/3)v = 8v/3,
где первый член в скоб-
скобках — вклад электронов (каж-
Рис. 12.5 дого поколения), второй —
трех ы-кварков с Q=2/3, a
186
6)
в)
третий —трех d-кварков с Q= —1/3, и что NV=NS=1, Qs = l,
лолучаем:
6=22/3-D/3)(l+5/3)v-l/3. A2.45)
б. В общем случае группы SU(N) величина b2=(bN)Nms2 опре-
определяется формулой (8.27)
Ъы = A1 /3) N - D/3) 2fl,NfT (Rf)-(\ /3) 2sOsNsT (Rs), A2.46)
тде Nt и NB — число мультиплетов фермионов и скаляров, нахо-
дйщихся в представлениях Rf и Rs группы SU(N), причем T(RF) =
= 1/2, если эти представления являются фундаментальными, а
«ели частица — синглет группы (как правые частицы eR, vH), то
•она вообще вклад не дает, т. е. Г8=0. Для киральных, т. е. ле-
левых или правых, частиц Х,= \/2, а для некиральных Я>=1. Анало-
Аналогично ав—У2 для вещественного скалярного поля и as— 1—для
комплексного.
В каждом поколении теории электрослабых взаимодействий
с группой 517B) имеются четыре дублета левых фермионов, по-
поэтому А., = 1/2, Nt=4, T(Rf) = 1/2, и один дублет заряженных ска-
скаляров, т. е. <ts=1, Ne=\, T(RB)~lj2. В результате для v поколе-
поколений фермионов в ней (N=2) получим:
62=22/3-4v/3-l/6, A2.47)
тде последний член ;[как и в A2.44)] —малый вклад бозонов
Хиггса. Наличие в теории, кроме SUB) -калибровочного поля
"W/, еще одного 17A) поля В#(х) не изменяет это значение Ь^,
так как лагранжиан A2.3)—A2.6) не содержит прямого взаимо-
взаимодействия этих полей.
Из A2.43) для заряда «' (Р2), связанного с полем Зц, (х), полу-
получаем а''1 (Р2) = а (Р2) — аГ1 (Р2) = а' (ц2) + *' h» (Р2/Ц2)/4я, где
коэффициент
6' = 6_62 = —D/3)Ev/3) —1/6 A2.48)
¦отрицателен при любом числе v поколений фермионов. Соответ-
Соответствующий рост заряда <х/(Р2) с ростом Р2 и появление у него не-
нефизического полюса в области очень больших Р2 означает лишь,
что теория электрослабых взаимодействий сама по себе не яв-
является внутренне замкнутой, а есть часть более общей теорети-
теоретической схемы (см. гл. 13).
Отметим, что это же значение а' (Р2) и коэффициента Ъ'
можно получить, рассматривая непосредственно радиационные по-
поправки к вершине g'(K/2MnYii взаимодействия фермионов (или
бозонов) с полем В» (х). Как видно, это поле взаимодействует не
с зарядом Q, а с гиперзарядом F/2 частиц. Поэтому коэффициент
Ь' определится такой же формулой, как A2.44) для Ь, но без пер-
первого члена (его нет, так как поля 5ц и W» не взаимодействуют
в лагранжиане) и с заменой NfQJ величиной KfNf(Y/2J, a NsQis
величиной ст5Л'5(}'/2J, т. е.
Ь' = -D/3) 2/^/(Г//2J-A/3J5о5Л^5 (К5/2J.
187
где сумма берется по всем частицам мультиплета. В КЭД, т. е. в
A2.44), множитель kf отсутствует, так как вклад правых и левых
фермионов одинаков и, складываясь дает 2к,= \. Для двух скаля-
скаляров <р+ и фо ys = <Xs=l, поэтому SsorsiV's(ys/2J=l/2; немного менее
простой расчет дает для v поколений фермионов I>f\fNf(Yf/2J=-
= 5v/3. В результате записанное выше выражение для Ь' в точ-
точности воспроизводит A2.48).
В дальнейшем вместо квадрата заряда «/(/>2)=§/2(/Э2)/4я всю-
всюду будем использовать пропорциональную ему величину «1(/>2)=
= E/3)а'(Р2) или a-1(P^{3/5)a'~i(P^); множитель 3/5 удобен
для перехода к большому объединению SUE) (см. гл. 13). Для
него а-1(Р2) = а710А2) + (й1/4тгIп(Р2/ц2), где 61=36'/5= — 4v/3 —
— 1/10.
Эффективные заряды а{(Р2) и пересечение прямых хода
«^(Р2). Напомним, что такой же, как «^(Р2), линейной (расту-
(растущей) функцией переменной 1пР2 является квадрат эффективного
глюонного заряда кварков a~1=aj1(P2) (8.32) в SU (З)-симметрич-
ной КХД:
ari(P2) = a-i(H2) + F3/4^ 1п(Р2/ц2) = F3/4яIп(Р2/Л2). A2.49>
где Л=0,08±0,02 ГэВ — характерная для КХД константа^ а ко-
коэффициент 6з = П—4v/3 определяется общей формулой A2.46)
при N=3 и Nf=2v [в каждом поколении два 517C)-триплета
кварков с Kf=l и T(Rf) = lJ2] и при отсутствии цветных скаля-
скаляров, взаимодействующих с полем глюонов. Таким образом, при
включении взаимодействия КХД между кварками имеем три за-
заряда частиц электрослабой теории: а^Р2); ац{Р2) и аз{Р*). Их
обратные величины удовлетворяют очень сходным уравнениям
(однопетлевого приближения):
daj1 (Р2)/d InР2=6г/4я, / = 1,2, 3, A2.50)
где
4v I 22 4v 1 ii 4v
—полученные выше постоянные коэффициенты, зависящие от чис-
числа v поколений, и являются линейными функциями 1пР2 вида A2.49)
„-1 (р2) _ „-, (,,2) + {Ь[ /4я) 1П (^2^2). A2.52)
Ход трех прямых: a-](P2), a-^P2), aj^P2) приведен ориенти-
ориентировочно для -v=3 на рис. 12.6; a (P2) линейно уменьшается срос-
сростом 1пР2, а а-^Р2) и «д-1 (Р2) линейно растут. При заданном v
(например, при v=3) все параметры прямой aj1(P2) однозначно
определены в A2.49). Однако положение прямых «-'(Р2) и а-^Р2)
при этом зависит от параметра sin26nr, который определяет поло-
положение начальных точек (при P2=^Mw) этих прямых: a^x{Mw) =
= Ca-1/5)cos2e^, aT1(M2r) = a-1sin2ew, где a-'^lS?. С уменьше-
188
нием sin26ir обе эти прямые сдвигаются параллельно самим себе:
нижняя для «^(Р2) вниз, а верхняя для ^"'(Р2) вверх так, что
точка нх пересечения на рис. 12.6 смещается направо (как указано
стрелкой иа рис. 12.6). Ясно, что значение siu2Qw можно выбрать
так, чтобы точка пересечения прямых а^1(Р2) и a-J(P2) легла на
нижнюю прямую «^(Р2), т. е. чтобы все три прямые пересеклись
в одной точке Р2=»Ж?:
ai\Mo)=cb2\Mo) — au \/K1oJ = Яоим« A2.53)
При этом получим картину
рис. 13.1 (гл. 13). Значение Мо,
которое называют массой боль-
большого объединения, огромно —
лорядка 10м ГэВ, а соответству-
соответствующее значение параметра sin26Tr
очень близко к найденному из
данных опыта.
Если теория такова, что в
точке Р2=М0* происходит фазо-
хый переход, то правее этой
точки при Р2>М(? все три за-
]ряда могут быть одинаковыми и
изменятся с ростом Р2 вдоль
.некоторой кривой, указанной
справа на рис. 13.1. Это означа-
означало бы, что в области Р2>М02 в
теории произошел переход к бо-
более высокой группе симметрии-
симметрии, которая спонтанно
нарушена левее точки /и=М02. Такая возможность (см. гл. 13)
привела бы к объединению теорий электрослабых и сильных
взаимодействий.
Из сказанного ясно, что в области очень больших Р2 все три
заряда аг(Р2), as(P2) и <z3(jP2) имеют близкие друг к другу зна-
значения. Поэтому при вычислении функции Гелл-Мана и Лоу каж-
каждого из них fl4=da{(P2)/ai{P2)dlnP2 следует в высших порядках
учитывать вклады калибровочных полей, отвечающих трем за-
зарядам. Так, в двухпетлевом приближении при учете вклада гра-
графиков вида рис. 12.7, с—г в правой части равенства A2.50) появ-
R 1//Ь Д° " -'8
го чо во 1п(рг/м$
Рис 12.6
г)
Рве 12.7
189
ляются малые добавки, пропорциональные зарядам a.j(Pz):
A2.54)
причем для постоянных р\;- были получены [12.5] (без учета очень
малого вклада хиггсовских скаляров) следующие значения:
19v 3v 44v\. R /v — 136 + 49v , \
j PU—'4vb
A2.55);
где величины в скобках соответствуют / = 1,2, 3.
Эти уравнения легко проинтегрировать, подставив справа
arjl{P'2) в виде линейных функций A2.52) однопетлевого приблк
жения, что дает:
В результате получаем последовательное разложение функций
а»(Рг) по степеням малого параметра (ln(P2/l*2))~1J ПРИ
In {P2/^2) > 1 последний член справа приводит лишь к малым по-
поправкам, причем основной вклад в него дает член с /=3. Учет в
формуле для аз-Ч/52) лишь этого члена (с Рзз=Р) в точности вос-
воспроизводит выражение (8.35) двухпетлевого приближения для
«1(/J)=аз(/52) вКХД.
Зависимость масс кварков и лептонов от импульса. Как мы
видели, массы mq лептонов и кварков определяются значениями
констант fg лагранжиана A2.8) [или A2.37)] юкавовского взаимо_
действия mg=—j=-fq (см. рис. 12.8, а), где значение q=u, d, e,v
определяет сорт частицы (в случае нескольких поколений в него
можно включить также и индексы i, j поколений). При учете
радиационных поправок, возникающих в порядке a,l=g\i4n за счет
однопетлевых графиков рис. 12.8, б, в, г, величины fq становятся
о)
Рис 12.8
190
эффективными зарядами—функциями квадрата 4-импульса?
—р2=Р2 фермионов
/, (Р2) = flZTj (Р2) Zli2 {Р2) Zi "
Здесь /^=/в(ЛР) и a°=aJ(M2)—затравочные значения этих
констант; М2—импульс обрезания логарифмически расходящихся.
,интегралов; y?—числа—аномальные размерности фермионных масс»
Множители Z2i=5z(P2) и Z2^==sji(P2) являются коэффициентами:
перенормировки функций Грина правых и левых фермионов [подоб-
[подобными E.25)], a Z~q (Р2)=Г „ (Р, Р, 0)—фактором перенормировки-
юкавовской вершины, т. е. соответствующей вершинной частью
(рис. 12.8,6) при одинаковых импульсах обоих фермнонов р\=
= р%=р, —р2=Р2 и при нулевом импульсе к=рх—р2 = 0 поля Хиг-
гса скалярных частиц. Масса фермионов определяется именно та-
такой конфигурацией импульсов частиц в вершине рис. 12.8, так
как часть поля бозонов Хиггса, которая выпадает в конденсат и
приводит к генерации фермионных масс, описывается полем q> (х) —
= const, т. е. несет нулевой импульс /С=0. Из-за этого в средней
части равенства A2.36) отсутствует множитель ZZ(K?) перенорми-
перенормировки поля этих бозоиов, равный единице при K?-+Q. При его от-
отсутствии вершины A2.37) fq(P2), а следовательно, и «бегущие»
массы фермионов
могут зависеть (при р2Фтя2) от выбора калибровки. Можно пока-
показать, однако, что в одиопетлевом приближении эта зависимость-
всегда исчезает {при учете в уравнениях ОКС E.43) членов, зави-
зависящих от калибровки].
Будем пользоваться поперечной калибровкой Ландау, полагая
постоянную ? лоренцевой калибровки равной нулю. Это значитель-
значительно упрощает все вычисления, так как при ?=0 вклады графиков
рис. 12.8,в и г обращаются в нуль, т. е. Z%u~Z2R=\, a Ziq~l—\
определяется вкладом лишь суммы трех графиков вида рис. 12.8, б,
в которых волнистой линии отвечают пропагаторы или U{\) поля-
В„(х), или SUB)-поля WJ(x), или глюониого SUC)-поля А/(х).
Дифференцируя равенство A2.58) по 1пР2 и полагая Р2=м2,.
получаем:
~ 2
/2
2 j/
/-1.2.3
где в обеих частях вместо переменной Мг записано Р2. Под-
Подставляя ат1^2) справа в виде линейных функций A2.52), легко
проинтегрировать эти уравнения, как это было сделано с послед-
последним членом в A2.54). Так как (v^/4n)o;.(P2)rflnP2=»
191
=(y^bJ)dlnaj1(P2), то это дает
(^;^) A2.60)
где \i—произвольный параметр.
Числа y^ определяются (при ?=0) вкладом графика рис. 12.8, б%
который вычислим в области />2>Af|r, где можно не учитывать
ни масс частиц, ни вакуумных средних < <р > ~v~Mw [однако
¦считаем Р2<^М$>, так что заряды а](Р2) различаются]. На этом
графике один из фермионов — левый, а другой — правый. Поэто-
¦му поле 517B), взаимодействующее лишь с левыми фермиона-
ми, вклада в него не дает и Ye =0 Для всех Q, т. е. для всех фер-
фермионов. Вклад ?/A)-поля В^х), взаимодействующего с гиперзаря-
гиперзарядами YL/2 и Уд/2 фермионов, в вершину рис. 12.8, б есть
"I 3 ( YL \ ( Y* \ Г., ( -1
где под знаком интеграла пренебрежено величиной /? по сравне-
сравнению с k, а интегрирование по K2=—k? ограничено логарифми-
логарифмической областью -Р^А/^Л/2, дающей главный вклад (учтено
также, что g'2/4n=3o?/5).
Вклад поля глюонов SUC) в этот же график в случае квар-
кварков получим отсюда при замене 3aJ/5-»-a!> и (К?/2)(Кл/2)->-
-¦•(МгУ'^^/З, где ^=^„/2—генераторы группы SUC). В случае
лептонов поле Sf7C) вклада в график рис. 12.8,6 не дает.
Поэтому в сумяе от всех калибровочных полей ZT
?
о?
n'Ap-' и так kwcZm-Zm-I.to срав-
нение с A2.57) дает y?= — 5"а~1>—Г"» Y?=—4, причем в случае
лептонов Yj=0- Дл8 Дублет кварков К?/2 = 1/6, для леп-
лептонов VL/2= — \l2, а для синглетов правых кварков и лептонов
Уц/2 совпадает с их электрическим зарядом. Поэтому аномальные
размерности масс y}Q = (y\, "fq, Y|) имеют значения
4J'
A2.61)
\ — »
192
Так как они отрицательны, то массы всех фермионов в
слабой теории согласно A2.60) убывают с ростом Р2:
электр
т, И A -^ $ inf
A2.62)
Масса нейтрино остается неизменной: оно не взаимодействует с
St/(З)-полем глюонов, кроме того, ?/A)- и Sf/B)-вершины взаи-
взаимодействия правого нейтрино на графике рис. 12.8,6 также обра-
обращаются в нуль. Из-за малости заряда ен» 1/137 основным фак-
фактором, определяющим ход «бегущих» масс кварков, является
«глюонный» множитель в A2.62), в котором заряд аз~Ч^2) КХД
записан в виде A2.49) с Л=*0,08 ГэВ. При большом 1п(Р2/А2)
он приводит к существенному
ходу масс кварков (вида рис.
12.9).
Отметим, что аномальные
размерности A2.61) [и фор-
формулы A2.62)] немного отлич-
отличны от известных в литературе
J13.2], вычисленных непосредст-
непосредственно путем исследования мас-
массового оператора 2e(/J) фер-
мионов [и ошибочно включаю- Рис 12.9
щих вклад Sf/B)-полей]. Гра-
Графики вида рис. 12.8, б фактически дают тот же результат, что и
вычисление оператора 2e(/J), однако в случае киральных f/(l)- и
SUB)-взаимодействий рассмотрение эффективных кжавовских
констант A2.57), определяющих значения спонтанно генериро-
генерированных масс, позволяет избежать ошибок и учитывать лишь ре-
реальные взаимодействия. В- частности, 51^B)-взаимодействие, как
уже отмечалось, никакого вклада в «бегущие» массы A2.62) не дает.
Глава IS
МОДЕЛИ БОЛЬШОГО ОБЪЕДИНЕНИЯ
13.1. Большое объединение SUE).
Заряды оь О2, о3 и sin Qw
Теория электрослабых взаимодействий, прояснив многие воп-
вопросы физики слабых взаимодействий, оставила нерешенными ряд
проблем. В ее рамках параметр sin6w остается произвольным и
13—679 193
совсем непонятна его природа; нет связи между ней и теорией
цветных, т. е. сильных, взаимодействий.
Существование нескольких поколений кварков и лептонов
приводит к ряду новых проблем. Действительно: сколько должно
быть таких поколений и чем определяются массы частиц в них?
Из данных опыта известно, что эти массы быстро утяжеляются с
ростом номера поколений — от мегаэлектрон-вольт (для электро-
электрона и и- и d-кварков) до сотен и десятка тысяч мегаэлектрон-вольт
для частиц третьего поколения. Массы и углы смешивания квар-
кварков (типа угла Кабиббо) определяются в существующей форме
теории (гл. 12) формой юкавовского взаимодействия кварков и
лептонов с (точечными?) бозонами Хиггса. Эти бозоны сами по
себе приводят еще к ряду вопросов, так как на опыте они не
наблюдались, неясно, сколько их и каковы их свойства. Строго
говоря, при точечности частиц вообще непонятно, как теория мо-
может включать это юкавовское взаимодействие, так как (см.
разд. 6.3) оно приводит к росту соответствующих эффективных
констант связи и к появлению у них нефизических полюсов.
Ответ на первую часть этих вопросов (не связанных с проб-
проблемой поколений частиц) дает схема большого (или великого)
объединения теории электрослабого и сильных взаимодействий в
рамках SUE) -симметричной теории. Эта схема была предложена
еще в 1974 г. Джорджи и Глешоу [13.1, см. также 13.2]. Размер-
Размерность N=5 в обозначении SUE) есть просто сумма размерностей
#1 = 3 цветного Sf/C)-симметричного сильного взаимодействия
кварков и размерности N2=2 SUB) -симметрии теории электро-
электрослабых взаимодействий. В основе схемы лежит идея описания
всех трех видов взаимодействия (сильного, слабого и электро-
электромагнитного) в области сверхвысокой энергии Р2>М02 на основе
SU E) -симметричной теории, включающей лишь одну константу
go=gGUM взаимодействия с
калибровочными полями
(GUM — от английского grand
unification model — модель ве-
великого объединения). Теория
должна быть построена так,
чтобы при уменьшении Р2 в
точке Р2=М02 в ней возникло
спонтанное нарушение сим-
симметрии, аналогичное фазовому
переходу и обусловленное тем,
что поля бозонов Хиггса при-
приобретают ненулевое вакуум-
вакуумное среднее значение порядка
Мо (которое несущественно
при Р2>Мо2).
В области Рг^.М0* симмет-
симметрия SUE) нарушается до
симметрии SUC)X$UB)y
194
20 W ,Б0ШРг/ф
Рис 13.1
XU(l), часть полей фермионов (кварки) с симметрией - SC/C)
взаимодействуют со своими калибровочными полями [с глюонным
полем Af(x)] с константой аз(Р2), а с другими видами калибро-
калибровочных полей (WJ> и By) —с константами а,2(Р2) и oi(P2). Ясно,
что все калибровочные поля должны быть частью общего Sf/E)-
калибровочного поля В„а(х), где а —векторный индекс St/E).
В этой схеме ход зарядов ^(Р2), ct^iP2) и Оз(Р2) должен:
определяться картиной вида рис. 13.1. Правее точки P2=M\t
где теория SU E)-симметрична, имеется лишь один заряд
oouM(jP2)=go(-P2)/4n, а левее ее—три расходящиеся с уменыне-
нием Р2 прямые: «-1 (Р2), «^(Р2) и аъ1(р2)- Условие, что все
три прямые совпадают в точке Р2=А%, определяет (см. гл. 12}
величину sin26w, если ^(Р2) задано в виде «1(Р2)=со/(/J)=!
= cg/2(/>2)/4n, причем ниже показано, что 5С/"E)-симметрия теории
в области Р2>Щ дает с=5/3.
Учитывая это, найдем Мо, ординату aovt\=aout\{Ml) =
=Oj (Жо)=а2 (Л1о)=аз(^о) точки пересечения, а также значение
sln26w, при котором три прямые рис. 12.6 пересекаются в одно*
точке [13.3—13.5]. Для этого, полагая в A2.52) \l = Mw, прирав>
няем величины а-1 (Я2) и а.-1 (Р'г) = C/5)а'~1 (Р2). При «'"'(Ж^)^
(?) 71—137) это дает для абсг
a
циссы Р2=м1 точки пересечения прямых а-1 и а-1 на рис. 12*6:
и для ординаты этой точки
Остается найти значение sin26ir, при котором эта точка пере-
пересечения ляжет на прямую aj^P2) A2.52), т. е. будет выполнено'
условие a^1(Ml)=a^1 + (b3l^n)ln{MliMw)=aT1{Ml), где ак —
=«з (М\?)— величина, известная из A2.49). Подставляя сюда
In (Жо/Af») и «Г1 (-Мо) из двух предыдущих равенств, получаем.
где
t «. • п /, i 1 \ 23
не зависят от числа v поколений, причем bi=Zb'lb=—4v/3—1/10,
b2 и Ьз определены в A2.51).
13* 195.
Поэтому из A3.1) получаем для Мо значение, также не зави-
зависящее в рассматриваемом порядке по ат от числа v поколений:
так как 8&32+5&2i= F6+1)— 67 [малые добавки в скобках здесь
л в A3.4) обусловлены вкладом бозонов Хиггса и практически не
важны]. Аналогично из A3.2) и A3.3) находим ординату точки
Пересечения всех прясыхва рис. 13.1:
W 8
Для получения численных значений величину а7г=аг1(М&)
«ужно аккуратно «протянуть» с помощью формул гл. 5 от значе-
значения аг1(—т%=\Ъ7 к точке Р2=Mw, где она равна 128, а ai5J =
=a^\Mw) можно найти из A2.62), при известном из опыта
Лаг0,1 ГэВ. Это дает «^ = №±1, т. е. a,»-1 ^ 1/12,8. Поэтому
из A3.5) для Мо получаем огромное значение 1п(Мо/Ж^)=57,О,
т. е. Мо=2,40-lOKMv^ 1,9-10м ГэВ, а из A3.5) для v=3
«(при 3ft3=2l, 5ft2i—8*2=11) следует
]~4l,8, A3.6)
шричем, как видно из A3.6), эта величина уменьшается с ростом
*числа v поколений [так как в A3.6) 3ft3a^1 + Eft2i—8?2)азо1==1
.=3(llari-7a^)-Dv/3)Ca7l-8a-i), т. е. a^M^59,9(l-v/9f9)].
Для величины sin29ir, определенной согласно A2.28) в виде
isin26ir=g/i/(g2+rt)=3g?/Cgf+5g^ и равной 3/8 в точке Р2=Щ,
<где gi=g2=go. получаем [13.5] при Р*=М% из A3.3) значение
sin26w=O,2lO+6i — 0,214, где бх^ 0,04—вклад малых добавок
в A3.4) от бозонов Хиггса. Это значение удивительно хорошо со-
соответствует данным опыта (о реакциях в пучках нейтрино), кото-
которые дают sin26w=0,215±0,010, причем учет радиационных по-
поправок еще более улучшает согласие.
Отметим, что учет двухпетлевых поправок A2.56) в ходе эф-
•фективных зарядов ^(Р2) еще немного увеличивает теоретическое
значение sin'O^r (примерно на бг^О.ОЗ) и приводит к слабому ро-
росту ln(M02/Mwz) с ростом числа v поколений — примерно на 0,5
¦на каждое новое поколение фермионов.
Задача 13.1. .Найти, как изменяются по сравнению с A3.3)—A3.6) вели-
величины sin:6ir, ln^Afo/AI2^) и «оим при учете двухпетлевых (нелинейных)
(поправок A2.56) к ходу эффективных зарядов а (/>*).
Решени'е. Приравнивая правые части A2.53) для a (Af2,) и "oif1
три p = Mw, находим аналогично A3.1) и A3.2):
а 96
GUM Sn ¦- Л-l,-2i3
где Li«In 1 + f ln 7JF*) • a *» "° **~*»= 22/3- Приравн™88 «ouw
к аГЧлф, при указанном здесь значении 1а(М%/Мф) получаем
У—1.2.3
где 5; = (p,/fttl + p,/ft,j + fr/*ii)/(*n + (8/5) ft,,); коэффициенты Р// = зависят
от числа v поколений и определены в A2.55), a (sin!er)e есть значение A3.3>
однопетлевого приближения. Подставляя это значение sin2 6^ в первые два
равенства, находим-{13.6]:
,.2 Г ч2 I \»1
где Aй[мЬМф))9 и («оим)в—величины A3.5), A3.6) одиопетлевого прибли-
приближения. С ростом числа v поколений величина Д sin* dw убывает (от 0,003 пр»
V —3 до 10'* при v«=8), a
Ala(Ml/Ml) растет от —0, 91
при v«=3 до 0,72 при v-6 и до ^
2,3 при v=8, что соответствует ^ .
увеличению М„ примерно в 2,3 °^>
раза при переходе от трех к ше- ^
сти поко дениям фермионов. Зави. ^
My Мф\
от v, полученная из этих фор-
формул, приведена на рис.13.2.
13.2. Фермионы, скаляры и калибровочные поля
в 5?/E)-симметричной теории
Чтобы построить SU E) -симметричную лагранжеву схему
взаимодействия частиц, нужно прежде всего выбрать представ-
представления этой группы, в которых находятся поля всех частиц.
Напомним, что в SU B) х^A)-симметричной теории электро-
электрослабого взаимодействия Глешоу—Вейнберга—Салама скаляры были
представлены дублетом Ф=($*). а векторы 5?/B)-синглетом В*
и присоединенным представлением 1^ц=(тй)^л. Некоторая «хит-
«хитрость» нужна была там для выбора представления фермионов;
в электродинамике правые и левые фермионы фигурируют равно-
197"
лравно, а в ¦ слабых взаимодействиях участвуют лишь левые
компоненты фермионов. Поэтому в теории электрослабого •взаимо-
•взаимодействия фигурировали и левые, и правые фермионы, но в разных
представлениях: левые в виде четырех дублетов группы SU=2:
м-2'3 A3л0)
'[i—значок цвета группы S?/C)], а правые в виде синглетов
группы SUB):
v*. ея, ajj, dlR, i = 1,2,3 A3.11)
в каждом поколении, включающем, как видно, 16 частиц.
Это различие привело к несохранению четности в слабых вза-
взаимодействиях, а электромагнитные взаимодействия содержали
лишь некиральные частицы е=еь+е„, u=ut+uBt d=dt+aH.
Эту идею можно целиком перенести на случай SU E) -симмет-
-симметрии лагранжиана, введя в него левые и правые поля фермионов
•в различных представлениях. Напомним предварительно про-
простейшие представления этой группы.
Простейшие представления и генераторы SUE). В группе
SU E) единичный антисимметричный тензор вертел—eepvfln имеет
¦5 значков; простейшие неприводимые ее представления могут быть
•симметричными иантисимметричными по индексам:
яра=5, i])a=5a—фундаментальное представление, пятиплет
{квинтету, антипятиплет, «=1,2,3,4,5;
^|иЭ1 = Ю1аР}=10|7в»1} —тензор, антисимметричный по индексам
<х, р—декуплет A0=E-4/2));
^{ар}=15{а>р}—симметричный тензор 15-плет A5=5+E-4/2));
ярР =24Pj=24a — 24-плет, определвпощий присоединенное пред-
представление"^» =0, 24=5-5—1);
^ар1==45|а,р1_45-Плет D5 = 10-5—5), я|>ааР1=0.
Более сложные представления нам не понадобятся.
24 генератора группы SUE) удобно построить по принципу,
указанному в гл. 7. Записывая их в виде ta=Aal2, выделим в
¦5x5 матрицах Ла левый верхний блок 3x3 и подставим в него
или 8 матриц Я,а-генераторов группы SU C), или нули. Аналогично
в нижний правый блок 2X2 подставим нули или 3 матрицы
Паули та. В правую верхнюю колонку 3x2 (как и в нижнюю
•3X2, расположенную горизонтально колонку) подставим нули или
в один из элементов этой колонки — 1 или — i (соответственно
ь нижнюю 3X2 горизонтальную колонку 1 или +*)• Это даст
^следующие 24 матрицы, удовлетворяющие условиям SpAe=0;
198
000
^00 1
oJ];Ai = ^|-|), * = 13, 14, 15;
"=(т|-2)'с=16> 17 23;
'-1/3
-1/3
-1/3
A3.12)
1/2
1/2.
Ранг группы SUE) равен четырем (r—N~ 1=4), поэтому среди
этих генераторов четыре диагональных коммутирующих между
собой: Ям. Л22» Л2з и Л24« В векторном представлении 24-плет
задается вещественным вектором Gy. Фа = (Ф)а = (<"Фа)а =
=A /2) (Ла)? Фа, причем ф? Ф? =Sp Ф2=4 2 ^ •
а—1
Фермионы в SUE). Каждое поколение частиц содержит восемь
левых лептонов и кварков A3.10) (два левых лептона и шесть
левых кварков) и столько же—восемь правых лептонов и кварков
A3,11). Из них правое нейтрино \ц, не участвующее ни в слабых,
ни в сильных взаимодействиях, можно вообще не вводить в лаг-
лагранжиан, если нет необходимости иметь дираковскую массу1
нейтрино. Тогда в каждом поколении остается 15-частиц-фермио-
нов, которые можно поместить в правый пятиплет у% и в левый
десятиплет Wfft (декуплет). При этом вместо полей некоторых
правых частиц удобно рассматривать левые доля соответствующих
античастиц; например, поле (ёк)с = С (ёя)=[(\— ys)/2]Ce=*(ec)L
является левым (так как у5 антикоммутирует с матрицей р из
в=ре*). Удобно вместо е* и Ur в A3.11) рассматривать левые
поля (ec)i и (uc)L [значок i группы SU C) опускается вниз при
зарядовом, т. е. при комплексном, сопряжении] и, наоборот,
вместо левого поля
ввести его зарядово-сопря-
1 Если данные опыта требуют введения этой массы в виде /nv(w), то
правое нейтрино vR можно ввести в лагранжиан [и в юкавовское взаимодейст-
взаимодействие типа A2.42)'] в виде сииглета группы SUE).
199
( ee \
женное правое поле (lc)R=[ _vC . В результате частицами 1-го
\ e/R
поколения, точно эквивалентными A3.10), A3.11), будут
Л JR
(знак минус перед v.e несуществен и отброшен для удобства за-
записи). Отбросив Vb, получим пять правых частиц d/ и lRe, кото-
которые естественно образуют б-плет 1[три верхних значка t=l, 2, 3
у него цветные, это значки группы SUC), а два нижних —знач-
—значки группы Sf/B)]:
d3e , a = 1, 2, 3, 4, 5, A3.13)
а остальные десять—левый 10-плет
ul d1'
ЛсУ '. - \_J, _5. ZTd> _^о / L A3.14)
где мюжитель 1/1^2 введен для удобства нормировки.
Отметим, что при этой форме 5-плета матрица, стоящая мно-
множителем перед 2V3/5 в Л24 в A3.12), есть точно К/2, где
К-^гиперзаряд частиц, т. е.
*24=A / 2) Л24=У 3/5 К/ 2. A3.15)
Действительно, половина гиперзаряда трех верхних частиц в
A3ЛЗ) rf-кварков равна их заряду, т. е. (—1/3), а пбловина ги-
гиперзаряда двух нижних равна 1/2 и именно эти числа стоят на
диагонали в матрице Лг*.
В каждом из поколений (которые ниже будем нумеровать
значком /7=1,2,3...) 5-плет ij>j* и 10-плет ^i"/1 повторяют
тот же.вид A3.13), A3.14) при замене полей u-d-кварков и е-,
v^-лептонов соответствующими полями следующих поколении
A0.14) (при /7=2 ир=с, dp—s, а ер=р v/,=vJi и т.д.).
Калибровочные поля и скаляры в SUE). Сказанное выше
почти однозначно определяет простейшие мультиплеты векторных
полей и скаляров.
Векторные—калибровочные, поля образуют присоединенное
представление 24? аналогично 5?/C)-хромодинамике и SUB)-jw-
намике Глешоу—Вейнберга—Салама: (B,i)^ = (ta)^B^(x), Эр5ц=0.
Как видно, при этом в представлении A3.12) восемь полей
200
Вр=Ар(х) с а=с, где с = 16, 17, ..., 23, соответствует цветным
глюонам; три поля а—Ь и 6 = 13, 14 и 15 отвечают SU B)-век-
торным полям В^=ТР^ теории Глешоу—Вейнберга — Салама, а
поле с а=Оо=24 является SL/C)- и -SU B)-синглетом ?ц =
= ??'(л:) этой же теории. Остальные 12 вещественных полей ??
с а<12 группируются в шесть комплексных—заряженных:
причем соответствующая часть матрицы
12
_ ¦ л г. г -ж
A3.16)
при действии ца столбец Y" переводит .лептоны в кварки.
Поэтому поля X^.+=Xfi-., Уц± иногда называют лептокваркалш.
Скалярные поля частиц Хиггса "можно поместить в различ-
различные представления группы SU E). Скалярное поле в присоединен-
присоединенном представлении 24&: (Ф)о=Фа=(ОаФв интересно тем, что
его вакуумное среднее может иметь вид диагональной матрицы,
пропорциЪнальной генератору
Г* Л
> 0= ¦ 1 V- -К15 ^f-V, A3.17)
\ —3/2 I
\ -3/2
где V — некоторая величина размерности массы. При таком
<Фа*>о симметрия SUE) нарушена, как видно, до симметрии
SUC)XSUB). В результате остается симметрия SUB) модели
Глешоу—Вейнберга—Салама. Чтобы и эта симметрия оказалась
спонтанно нарушенной, нужно ввести еще одно поле скаляров —
5-плет '[т. е. фундаментальное представление 5?/E)]:
*;>
*•
Его пятая компонента hb(x) аналогично крмпоненте vce фермионов:
в A3.13) электрически нейтральна и может иметь отличное от
201
нуля вакуумное среднее < А5(лг) > =viV2 , т. е.
( °°Л
<А«(х)>0= 0 , A3.18)
что нарушает симметрию SUB) (симметрию двух последних ин-
индексов).
Обсудим кратко форму, которую имеют малые отклонения
полей Аа (х) и ф?(л:) от их вакуумных средних [13.5].
Поле ha{x) удобно представить подобно A1.12) в виде
«•w-l jjq j-
\v/V2+b(x).
| 15
=exp i^J
I 0-7
0
x)/v\\ .0 . |. A3.19)
где экспонента содержит сумму по тем 9 генераторам Лв в A3.12)
<с а—7,8 15), которые не дают нулевой результат1 при
действии на < Ав (х) > 0; здесь hl(x)==(\/V2Wb+b(x)> .'...A4 —
()(S13+Si4) (g5+g())K где все Е.(-«) и 6(ж) ве
щественны и гораздо меньше v. Преобразование калибровки
позволяет почти полностью избавиться от оператора-экспоненты
в A3.19).
Такая же параметризация поля ф? немного более сложна.
Действие генераторов Та на него определяется формулой
ff%W' где (ГЛЭД-Й'Р.Й—РвЙ'Ф, т- е-
(^Ф-Ф/Х A3.20)
где справа—обычное произведение матриц ?в=A/2)Лв A3.12) и
матрицы поля ф={Фа} [см. формулу G.27)]. Не равное нулю
значение ТаФ0 дают лишь первые 12 генераторов в первой стро-
строке в A3.12): для них матрицы Лв не коммутируют с Фо.
1 Генератор Лм также не обращает (А(дг)> в нуль, однако его вклю-
включение в экспоненту A3.21) приводит к несущественному изменению поля ?()
всюду считаем, что exp {i 2Авбл/»}— 1 + &aAl
а -•
202
Применение к Фо оператора 5?/E)-вращения, содержащего
эти генераторы Аа—2Та, дает лишь часть матрицы ф?:
где 7—единичная матрица 3x3, а
Коэффициент —)^2/5 в экспоненте—следствие того, что ре-
результат действия A3.20) каждой из входящей в нее матриц Аа=
г=2Та на Фо равен матрице Aa=2ia, умноженной на (— 5/2) V.
Все поле Ф* можно получить (около его вакуумного значения),
добавляя к этому значению матрицу, включающую остальные ге-
генераторы Лв(а>12) с произвольными вещественными коэффи-
коэффициентами т]в(х)IV2 (где |Tje(x) |<V):
0—13
П,+УГГ^г1(хI
л
V
_Ч?_ 1
1/2"
0
_¦¦*
1-
—1/
Здесь tig (л;) = 2 AjTjc (jc)/K2—произвольная матрица 3x3 с ну-
с-16 _
левым шпуром; n*=Tlis(-x); П±=A/К2)(^з±Itii4>. a ti(jc)=
= —124 (•*)• В результате поле Ф| вблизи его вакуумного сред-
среднего A3.17) определяется суммой этих матриц:
A3.21)
203
24
X
\
Ja
где учтено, что при действии на второй- член экспонента эквива
лентна единице.(с точностью до членов, линейных по На, т|а).
f 15 - )
Преобразование калибровки Ф-> ехр I — i 2 А*.юв (¦*)\ф» в кото-
ром аа{х) при а<12 выбраны равными (—Y2/5)Ha/V,
а при а=13,14,15—равными \a{x)iv, позволяет полностью из-
избавиться от оператора-экспоненты и выбрать
где V(Ar)=V+|/2/15Tj(j:). Вакуумное среднее второго члена
слева обращается в нуль, поэтому < Ф ) ==Ф0 1см. A3.17)].
Таким образом, физическими полями являются: поле tj(jc)=
=*\У(х)—V]/V2/15, восемь (глюоноподобных) полей т]с(д:), поля
W) и т|±(х).
При этом преобразовании экспонента в A3.19) полностью
не сокращается; в ней исчезают лишь члены с а =13, 14, 15,
( 12 1
ноостаютсяса<13ввидеехр|12 Лв&,(л:), ~„ -„_ М\~/-ъп"/
¦ _ У ~7 J.
+ (}//5)(t)/V)^e(j:). Поэтому после преобразования калибров]
вместо A3.19) будем иметь:
A3.23)
где А'(л;)=А1(д:L-A/'2/5)('0/К)Я^_(д:). Как видно, среди всех:
полей h (х), а также Н1Х±, Н1У± физическими являются лишь три.
цветных поля Ъ1(х) и поле Ъ(х).
В заключение этого раздела приведем значения инвариантов
Sp$2; Sp<S«; (Sp6^; A+Aa. (A+A«f; (A+A«)SpO2; А+(ф2)«Аэг
составленных из полей A3.22), A3.23) и нужных для дальнейшего.
Не выписывая для упрощения записи члены третьего и более
204
высоких порядков по малым физическим полям, получаем
h+k={\l2)v2(x)+h*h\
(А+АJ—A /4) v* (х) + *>2А+А +...;
A3.24)
где (Ф2)?
2 Чс+2
»Ч». причем индек-
с
сы с и & пробегают указанные выше значения (&—13, 14, 15,
с=16, 17 23), а К(л;)==К+К2/151](х), ч>(х)-*+Е(*).
Отметим, что инвариант (k*fahf лишь постоянным множителем
отличается от (А+АJ и поэтому ниже нигде не фигурирует.
13.3. Лагранжиан. Свойства бозонов Хиггса
в 5?/E)-симметричной теории.
Массы бозонов и фермионов
Лагранжиан системы фермионов (пока — одного поколения),
бозонов и векторных калибровочных пол её имеет следующую
SUE)- и калибровочно-инвариантную форму [13.1]:
A3.25)
где
/2) 0й
A3.26)
причем
^ A3.27)
—ковариантная производная; g0—, единственная константа калиб-
калибровочного взаимодействия; '¦Fp,m=d»fivr-d\B»-{-gafabclftBcv.—напря-
'¦Fp,m=d»fivr-d\B»-{-gafabclftBcv.—напряженность глюонного поля;
2'уак=-/(?ГI«р,Ч.-Ар-|8артвп?1«Р'№тв1АГ1+к. с. A3.28)
—лагранжиан юкавовского взаимодействия; / и х—константы
этого взаимодействия; С=О2—дираковский оператор зарядового
205
сопряжения
?/(ф, A) = [(-
A3.29)
—потенциал взаимодействия скалярных полей Хиггса Oo(jc) и
Aa(jc). Этот потенциал построен из инвариантов A3.24), имеет
минимум при Ф=Ф0, Аа= < Aa(jc)) 0 (при положительных ц2, а, Ь,
v2, \ и при ^<0 — см. ниже) и содержит, кроме членов само-
самодействия полей Ф и Л, член взаимодействия этих полей, пропор-
пропорциональный константам с1 и с2. Этот член появился бы автомати-
автоматически, даже при С1=сг=0, за счет графиков вида рис. 6,9, a, ~g<?
с замкнутыми петлями калибровочных бозонов (вместо фермио-
нов, указанных на рис. 6.9, а) и с внешними линиями бозонов
Фа* и Ла. Это же относится и к остальным членам ~Ф4 и ~Л4 в
?/(Ф, А), к которым графики вида рис. 6.9,а и более сложные
с большим числом внутрених линий дают поправки, пропорцио-
пропорциональные go4, go6 и т. д.
Взаимодействие фермионов с калибровочными полями опре-
определяется вторым членом goTaB$. в ковариантной производной Шц—
=°=*д»-\-ёФуТа в лагранжиане &'f, т. t. одной константой g0. Как
Уже отмечалось, 8 из 24 полей ?? с а=с, с = 16,17,.. .,23-
ВЬ=Ар(х) соответствуют цветным глюонам, 3 поля с а—Ь>
6=13,14, 15, 2#=№?—векторным бэзонам SU B) теории Гле'
шоу—Вейнберга —Салама (см. гл. 12), а поле ?$' с с=24 является
SU ^)-синглетом В^—В^х) этой же теории. Учитывая, что /24—
=/3/5У72 [см. A3.15I, где
1/2,
—оператор половины гиперзаряда, получаем, что в лагранжиане
Sf, в A3.26) взаимодействие полей ?? с фермионами я|)? опреде-
определяется производной
^^, A3.30)
где последний член—вклад полей В» с а<12, т. е. полей Х»±,
Y\l±, определенных в A3.16). Физические следствия, к которым он
206
приводит (распад протона), рассмотрены в разд. 13.4. Матрицы
Ль и Лс [см. A3.12)] точно соответствуют в секторах St/B) и
SU C) трем матрицам ть и восьми матрицам Гелл-Мана %с. Срав-
Сравнение с такими же членами взаимодействия (в производной D
электрослабой теории A2.1) показывает, что .в области
из SU(б)-симметрии теории следует: gf = VSJ5g0, g=g2 — go*
причем, в отличие от теории электрослабых взаимодействий, в-
A3.30) включено также взаимодействие с глюонами с той же кон-
константой g3=go- Таким образом, в области SU (б)-симметрии три
константы ?/A)-, SU{2)- и SU (З)-взаимодействия gi = V5/3g'f
g2=g и g3=gs одинаковы и равны g0. Как видно, коэффициент
3/5, связывающий «Г1 и а'-1:аГ1=C/5)а'-1_!_использованный в.
разд. 13.1, возник из-за соотношения t2i—1^3/5^12, специфичес-
специфического для теории с SU E)-симметрией.
Как показано ниже, с уменьшением Р2 в области Р2<М&
(левее точки Ml на рис. 13.1) происходит нарушение S?/E)-chm-
метрии. Здесь три заряда git g2 и g3 становятся различными в
изменяются соответственно левой части рис. 13.1.
Отметим, что генераторы Та в производной Dp. совпадают с
матрицами ta=2A.a лишь в случаях, когда они действуют на поля
$я или Аа-частиц в фундаментальном представлении. Если же по-
поле Фа присоединенного представления, то действие на него гене-
генератора Та определяется в виде A3.20) или же, в случае поля
YfPI представления 10, в сходном виде (faYL)i^r=(ta^LJt^Lia)m\f
-что есть следствие общего соотношения G.31).
Свойства системы бозонов Хиггса определяются формой по-
потенциала ?/(Ф, h) их взаимодействия. Если в A3.29) константы
ц2, v2, а, Ь и к положительны, то U (ф, А) имеет минимум вблизи
значений A3.17), A3.18) полей Ф~ф0 и А«= < А° ) = А™. Найдем
значения v и V, при юторых' достигается этот минимум, сначала
при Ci=c2=O, т. е. в отсутствие взаимодействия полей Ф и А.
Так как
; SpФ< = C/8)ЗоУ4;
то условия минимума потенциала A3.29) dU/dV2=dU/dv2=0 дают
H2=(l5c/2+7*/2)Vr2; v2=^2/2, A3.32>
откуда и определяются вакуумные средние V и v.
Будем считать, что параметры ц2 и v2 выбраны так, что \12~>
>v2, т. е. что V2»»2. При уменьшении квадрата импульсов час-
частиц Р*=—р2 симметрия SC/E) нарушается в области Р2<У2, так
как здесь проявляется отличное от нуля вакуумное среднее
A3.17) поля Фа*. Она будет нарушенной до симметрии
(S?/C))CX (SUB))w~ останется точная цветная симметрия
(S?/C))e и изотопическая симметрия (SUB))W теории электро-
207
слабых взаимодействий. С дальнейшим уменьшением виртуально*
, сти импульсов частиц при P2<v 2 становится важным также ва-
вакуумное среднее A3.18) поля ha(x) и симметрия нарушается до
¦Щ1) -симметрии, как в теории электрослабых взаимодействий
(см. гл. 12). Значениям P2~V и P2~v2 отвечают точки наруше-
нарушения симметрии (фазового перехода) в теории. Как показано в
разд. 13.1, для получения разумной теоретической схемы необхо-
необходимо, чтобы V было порядка Мо«1014—1015 ГэВ, a v~MW??
«^lO2 ГэВ, т. е. должна соблюдаться огромная иерархия этих
величин V/vcxlO*2—Ю13.
Покажем, что при первом нарушении симметрии в области, где
/>2<V2, но Р2^'»2, остаются без массовыми: глюоны В^=А^(х) и
SUB) векторные поля Вц, W\u теории электрослабых взаимодей-
взаимодействий, а поля A3.16) Хц± и У1ц± получают огромную массу'Мх~
—My~V. Действительно, лагранжиан полей ф—первый член в
3?н [см. A3.26)] содержит кроме квадрата производной поля
¦A3.29)—кинетического члена
24
A/2)(<VI>)?+ (^Ф)| = A/2) 2 PrtaJ, 03.33)
а—13
где г\а (х)—вещественные физические поля, определяющие Фа, так-
также слагаемое
{\12)ё1в?В&[(ТаФГ(ТьФ)]> • A3-34)
обусловленное вторым членом в производной /)ц—дц
(перекрестные члены ig0Sp[(^nO)+GrflO)—(ГаФ)+дцф] В?
-щаются). Главная часть этого слагаемого, возникающая от ваку-
вакуумного среднего поля Ф—СЦ), содержит только члены с а<12 (так
как только для них ГаФ0=?0), т. е. содержит лишь поля Xji± и
Yl± [см. A3.16)], и дает1
ri_), A3.35)
что согласно A0.29) определяет массу Хц±- и Кц±-мезонов [13.5]
в виде
A3.36)
1 Это следствие правила A3.20) действия генераторов Та на поле Ф,
которое дает
Отсюда
208
т/о V Т
и получаем
Ф.*? =(А
равенство
A3
Гц) Ф. =
.35).
1
^0
1ц |
0
пропорциональном V. Остальная часть A3.34), обусловленная вкла-
вкладом физических полей Хиггса т|в(л:) в Ф—Фо (см. A3.24)], дает чле-
члены взаимодействия этих полей с калибровочным полем и сейчас не
важна. Глюоны i?(i=.A? и поля теории электрослабых взаимодей-
взаимодействий Wl, Вц=В»{х) остаются безмассовыми в области <о2
Ясно, что нарушение SUE) -симметрии возникает фактически
«три Р2=МХ3, Муй, так как в области Р*<М*, М/ обмен бозонами
Хц, У„ дает вклад в амплитуду физических процессов ; [из-за на-
наличия массы в их пропагаторах "(Ръ+М,?)-1), отличный от
вклада, обусловленного обменом другими безмассовыми калибро-
калибровочными полями. Это заведомо нарушает SUE) -симметрию, по-
поэтому Мо=Мх—Му и есть масса большого объединения.
Аналогично этому второй член фрЛ)а (Dp/if в 3?н приводит
к появлению массы полей W%, Z^ в области малых Р2<Ми? с
Mxr~Mz—gl'D2/4:—там, где появляется вакуумное среднее A3.18)
поля ha{x) и где нарушается 5?/B)-симметрия—точно так же,
как в теории электрослабых взаимодействий. Напомним, что при
этом фотоны остаются безмассовыми.
Рассмотрим подробнее, что происходит в системе хиггсовских
бозонов после первого нарушения SU E)-симметрии, т. е. в обла-
области Л&<Р2<Мо.
Из трех триплетов полей Нх, Ну и А,, входящих в 24-плет
Ф& A3.21) и в 5-плет ka(x) A3.23), поля Нх и Н1У исчезают при
калибровочном преобразовании—поглощаются полями А'Д и У», ко-
которые при этом становятся массивными. Триплет полей А7 в A3.23)
не поглотился, однако при подстановке 5-плета ha(x) в потенциал
A3.29) [в виде средней части равенства A3.23)] он сокращается
всюду, кроме последнего члена в потенциале, пропорционального
постоянной с2.
Для упрощения будем оставаться пока в рамках случая с$=
= с3—0, когда взаимодействие между нолями Фа* и fta выключе-
выключено. При этом поля &(х) не дают вообще никакого вклада в по-
потенциал и—ио(Ф, Л), т. е. они остаются безмассрвыми. Все ос-
остальные поля i)c(x)'t г\ь(х) == {t\z> ти) и *](*)— 24 (*) получают
большие массы. Это легко увидеть при подстановке равенств
A3.24) в A3.29). Используя равенства A3.31), получаем с точ-
точностью до членов квадратичных по полям:
23
C-16
?,...), A3.37)
прячем [?/(Ф0, Ao|]Cl-c,_o=-A5/16) V4A5a+7ft)-'O4A/16.
Отсюда получаем следующие значения порядка Мо для масс всех
14—679 209
физических полей, определяющих ф?:
т? =E/2) bV2; т\ =/n*
да2=A5а+76)К2 и m\^v4.l2. A3.38)
Наличие в теории безмассового триплета полей типа Я'(х)
(или таких полей с массой, меньшей 10м ГэВ) недопустимо, так
как эти поля привели бы к быстрому распаду протона на лепто-
иы и мезоны, которого на опыте нет.
Включение членов взаимодействия полей Ф& и ка [во второй
строке в A3.29)] с сь с2=^0 и с2<0 устраняет эту трудность.
Однако следует учесть, что при этом появляется отличное от нуля
вакуумное среднее поля г\г(х). Удобно обозначить его — V6/]/!§==
= < ik(jc) >, где 6—малое число, и включить в определение Фо,
считая, что вместо A3.16) оно определено в виде
Ф0=<Ф>=| 1 I. A3.39)
\ —3/2-6/2 /
\ —3/2+8/2/
В этом виде среднее по вакууму Фо= <Ф > нарушает не только
SUE)-±SU(S)XSUB), но и SUB)-+U(\). Будем считать, что
именно оно фигурирует справа в A3.21) или в средней части ра-
равенства A3.22); тогда ясно, что в этих формулах 1\г(х) нужно
заменить отклонением ее от своего среднего по вакууму, т. е.
lr Vt для к070?010 < vi,i*) >==0-
Будем считать, что это уже сделано и что штрих у поля r\'(z)
отброшен для сокращения записи. Это небольшое изменение дает
где считалось, что 6 — величина порядка о*/У"<.1 (это сейчас
будет видно). Подстановка этих значений в A3.29) дает вместо
A3.31) следующие условия минимума потенциала [13.5]:
^=-A /2) Хг^+З [5^ +C/2) с2] V2—!
причем условие -^=0 дает
210
Как видно, величина У«*«2|12/A5а+7Ь) ~Af02 при этом прак-
практически не изменяется [по сравнению с A3.32)]. Однако учет
взаимодействия полей Ф и Л полностью изменил уравнение для
о2: теперь эта величина определяется как разность двух огром-
огромных чисел v2 и ЗУ*Eс1+Зс2/2), каждое из которых иа 25 порядков
(!) больше юс разности Цравной о2(Я/2—Зс22/Eс+9Ь)I. Более
того, для достижения огромной иерархии Vs/»2 ~ 10м—1б*в во всех
порядках теории возмущений следует в каждом ее порядке, когда
числа v2, си с2 получают добавки порядка ?о2/4я, так изменять
-их начальные значения — с точностью порядка 10-*5, чтобы эта
иерархия всегда сохранялась. В принципе, это возможно, но та-
такая структура теории не представляется красивой, или «нату-
«натуральной». Однако за неимением лучшей возможности с этим по-
пока приходится мириться. _
Заменяя в соотношениях A3.24) Tjx-^-ri» (jc) + (V7V2) в, учиты-
учитывая равенства A3.40) и выписанное выше значение б, получаем
для потенциала Хиггса A3.29) при учете членов, пропорциональ-
пропорциональных с\ и с2:
где [?/(Ф, ft)—?/(Фо> Ло)]с.-с,-о имеет выписанное выше значе-
значение, а С/(Фо, Ао)=1[С/(Фо, Ао)].'-.,-о—C/4)Eci+3c2/2)o2Vs. Kai?
видно, теория самосогласоваиа, если постоянная с2 отрицательна;
при этом у поля Я появляется огромная масса /п»2= E/4) (—с2) V
и за счет членов, пропорциональных tj| и г\г%, немного меняется
масса скаляров ц, т), и |. Квадраты масс тлг и т* изменяются
(при учете членов порядка сь с2) ничтожно мало по сравнению с
выписанными выше значениями порядка V: к ним добавляются1
слагаемые порядка у2. Заметно изменяется1 лишь тъ2, оставаясь
и после этого величиной порядка с2. Кроме того, ничтожно мало'
(на слагаемые порядка и2) изменяются массы тяжелых бозонов
М* и Му2.
Эти результаты были получены впервые Ё. С. Фрадкиным и
О. К- Калашниковым 1[13.7] (в 1976 г.) и Бурасом, Гайяр, Элли-
сом и Нанопоулосом [13.5] (в 1977 г.) (см. также обзор С. Г. Ма-
1 Для получения явных значений всех этих масс нужно, очевидно,
диагонализовать квадратичную форму: W=(l/2)[Av*tt+BV*ri2. + CV*Ti* +
+ 2QvVr\l—2#»Ут)га, в которой А-A/2) [Я + Зс|/Eл+9*)]; B-10J;
С-15а+ 7*; Л-3 У?(—с1); Q-2-/30(c,+6c,/5) и где w«<y«. Эго дости-
достигается при |^|' + (#,+#i#i)Ti^+#1»i/; ч~т)' + (#,— *1*«Iг—#iS'; ч'г"
: Q v —R v RQ v* ,
Ы' O-g- ^-р ^^В)^ н дает: тч'~
^ т?-(А—ОЧС—R*fB)v*.
U* 21t
тиняна [13.8]). Как видно, за исключением ненатуральности усло-
условий A3.40) (вместе.с требованием иерархии V^2^— lO^6 о2) система
связанных друг с другом полей Хиггса Фв* и А" удовлетворяет
всем нужным физическим условиям:
1) приводит к нарушению SC/E)-»-S?/C)XS?/B)-cHMMeTpHH
в области P~M0~V н вторично к нарушению SUB)-+U(l) в об-
области Pc*Mw~v\
2) калибровочные поля Хц и Y^ поглощают поля Хиггса Н1Х
и Нд [точнее, комбинацию Н'у =Нв—~— -рг А1, ортогональную к
А1 (х)—см. выше] и получают огромные массы МхшМу^М0, а
глюоны [и фотон в секторе SUB)] остаются строго безмассовыми.
3) все физические компоненты «большого» поля Хиггса т\а(х)
'[входящие в A3.24)] и компоненты Я'{х) малого поля получают
такие же массы — порядка V~M0. Одна из компонент «малого»
поля Хиггса A3.25) ?(*)—точный аналог поля Хиггса теории
электрослабых взаимодействий — получает массу порядка v~Mw,
т. е. такую же, как в этой теории.
Массы лептоиов и кварков в модели 527E) возникают за
счет взаимодействия Юкавы A3.28) только после второго фазо-
фазового перехода, т. е. после появления вакуумного среднего A3.19)
у хиггсовского поля ha(x). Подстановка этого среднего в A3.28)
дает
. с,
где значки i,k,l,m пробегают значения 1,2,3,4. Использование
явного вида A3.13) и A3.14) полей ?[aB1 и i$ показывает, что
первый член дает вклад в массу нижних кварков и электрона,
а второй—только в массу верхних кварков:
2'= -(fv/2) (d[dlR+?L e%)+{w/V2) ((a%,Cai +ai& («?.,)) +
+к. с. -> -(|/|«/2)[(ie)+Eirf0]->/r2"M<o(a>i). A3.41)
т. е. для масс частиц (в области Р2 вблизи М%)
inS=fn°=[/|«/2, m°u=V2~\H\v=-mu{Ml). A3.42)
С уменьшением Р2 массы изменяются, растут согласно рис. 13.7
в основном за счет сильного взаимодействия, поэтому массы физи-
физических d-кварков, равные примерно md{M^), будут больше массы
электрона me^me[Mw).
Только левое нейтрино (т. е. правое антинейтрино) входит
в A3.13) и в лагранжиан Sf в A3.26), который поэтому приводит
к нулевой дираковской массе нейтрино. Однако соответствующие
члены (у\)=(уя\ь+^я) можно получить в лагранжиане &f, если
ввести в теорию поле правого нейтрино, т. е» левого антинейтрино
^=(\?р?, в виде синглета группы SU E). При этом в лагранжиане
212
A3.28)
появится дополнительный член
который при подстановке вместо ha(x) его вакуумного среднего
A3.20) дает
« -(«/2) [/v RJl (
(| /v 1o/2) IveiveJ?+ frtvrt]- - (| /v | «/2) veve, A3.43)
т. е. приводит к дираковской массе нейтрино mv=(|fv|o)/2, отли-
отличающейся множителем |/v//| от массы электрона.
13.4. Распад протона [13.5]
Большой интерес представляет часть лагранжиана, отвечаю-
отвечающая взаимодействию полей тяжелых векторных бозонов Х„ У„ с
фермионамн. Последний член в A3.30) определяет ее в виде
A3.44)
где Хц+Yfi—матрица A3.16). Действуя иа фундаментальное
представление д|>?, она переводит лептоны в кварки:
4] +к. с.
Первый член отвечает поглощению позитрона и Х_-бозона (а вто-
второй — правого антинейтрино и У_-бозона) и испусканию d-квар-
ка. Как видно, закон сохранения заряда выполняется, если заряд
Xt-бозонов Qx равен ±4/3 (в единицах е„=|е|),а заряд У±-бо-
зонрв Qy равен 1/3. Учитывая, что согласно A3.14)
—Иг —Иг
О — еР
"? о
и используя явный вид A3.16) матрицы
?1 ^ Л YJIaB1) - -
получаем:
. с.
213
Таким образом, лагранжиан A3.44) [13.5]
г - (go/ V2) Xl
+ {go/V2) Yl ^
A3.45)
де сохраняет число лептонов L и бариоиное число В, равное 1/3
для кварков и —1/3 для аитикварков. Легко заметить, что каж-
каждая из фермионных скобок изменяет величину B—L на —2/3,
т. е. в начальном состоянии ее значение во всех случаях иа 2/3
больше, чем в конечном. Поэтому обмен Х^±- и У„±-бозонами не
изменяет квантового числа В—L (при испускании Х^ или Уй+
оно уменьшается на 2/3, а при поглощении — на столько же уве-
увеличивается). Это свойство специфично для St/E)-теории.
Обмен этими бозонами (см. гл. 6) приводит к эффективному
4-фермиоииому взаимодействию вида произведения квадратных
скобок в A3.45). В нем наиболее интересны члены (см. подроб-
подробнее1[13.10])
с] A3.46)
приводящие к поглощению двух кварков (например, из трех квар-
кварков в нуклоне) и рождению позитрона или аитииейтрино и анти-
антикварка. Это отвечает процессу распада нуклона, например ней-
нейтрона, в позитрон и в мезои (п^, р~ и т. д.) или в антинейтрино и
з я?-, р°- и т. д. мезоны. Отметим, что в St/E)-теории не -идет
распад нейтрона в электрон и я+-, р+-мезоиы — это запрещено
законом сохранения В—L. Константа взаимодействия в A3.46)
GxlY2 =go/8Mx=go/8iMp= (О-/У2) Mw/ Ml=mtavM/2M%
на множитель Mw2JMo2~lQr2S—10-86 отличается от коистаиты
Ферми A0.8) слабого взаимодействия. Поэтому время жизни про-
протона по отношению к распаду р-+е+ии? определится формулой,
отличающейся от A0.8) лишь численным множителем Л о порядка
единицы [обусловлениым не столько отличием формы взаимодей-
взаимодействия A3.46) от универсального 4-фермионного слабого взаимо-
взаимодействия A0.1), A0.18), сколько тем, что и- и ис-кварки рожда-
рождаются в виде мезонов] и заменой т„ иа тт и G-*-Gx:
96at* 2я 96я» 4 | —« i i A3 47)
где Gx2=2Mo/n2b^VM; оБим—42 [см. A3.6)]. Множитель Ао трудно
оценить из-за влияния сильного взаимодействия между протоном
и рожденным мезоном, в результате он может быть численно
большим — достигать значения Ло^Эбл2 порядка тысячи (за счет
!214
Возможности ![13.9] испускания протоном я-мезоиа с последую-
последующим переходом виртуального протона, рис. 13:3, в позитрон).
При этом формула A3.47) дает приЛ10г^З-1014ГэВ, 1//пр~B/3)Х
X Ю-2* с= B/Зя) • Ю-41 лет: хр= D/я) D3 М08/тр*)*(l/m )~
^ (8/3 я2) D,3J-1029 лет~0,5-1030 лет.
В 1 т вещества A06 г) около 6,02- 10м- Ю^О.б- 10м нуклонов,
поэтому при такой оценке в 1 т можно наблюдать в среднем 1 рас-
распад в год или в 1 тыс. т вещества около 10* распадов в год.
Трудность наблюдения таких
распадов (в веществе, проложен-
проложенном детекторами частиц) связа-
связана с большим фоном от косми-
космического излучения. Поэтому пла-
планируемые и проводимые опыты
ставятся на большой глубине, в
туннелях гор, для уменьшения
этого фона. В иих уже достиг- Рис-
иут [13.11Ц предел хт>\0Р° лет.
Ясно, что небольшое увеличение массы Мь=*Мх большого объеди-
объединения может существенно увеличить время т„ и вывести его да-
далеко за пределы возможности наблюдения.
13.5. Несколько поколений фермионов.
Горизонтальная симметрия
Обсудим очень кратко возможность введения в модель больших
объединений нескольких v поколений (семейств) кварков и лепто-
нов, т. е. полей t|$'? и T^J1, q=l,2,...,v, лагранжиан которых
<?,=2<?«, где все 2] имеют вид A3.26). Ясно, что форма ла-
Я— I
гранжиана юкавовского взаимодействия S'yuk зависит от того,
какие скаляры Хиггса Аа:р>?'" содержит теория.
Простейшее предположение—ввести те же скаляры A3.19) и
A3.22) ha и Ф|, что и при одном поколении, а константы связи /
и х в A3.28) снабдить индексами поколений, полагая 24uk=
= — /p»(Yi)fe,pnj)S1*Ap-f-|uieH, пропорциональный vP4. Тогда массы
кварков и лептонов (и углы их смешивания) определятся путем
диагоиализаций массовых матриц mepq=mpg= (v/Y2) \fp4\, mpq==
=V^2 v I v.pq I. Никаких сведений о массах частиц отсюда реально
получить нельзя, так как все константы /р9 и хР« неизвестны,
кроме неправильного, с точки зрения данных опыта, утверждения,
будто отношения масс электронов и нижних кварков во всех поко-
поколениях одинаковы. Чтобы избавиться от этого заведомо неправиль-
неправильного вывода, в теорию вводят, кроме 5-плёта ha(x) группы 5GE),
еще 45-плет скаляров ф1а-Р1(.зс) с нулевой свертк6й-Ч>?вР1=ф1аР1=0.
Его вакуумное среднее (ЭС), нарушая, подобно A3.19) SUE)- и
SU B)-симметрию теории электрослабого взаимодействия, имеет вид
(х)
A3.48)
где «'—величина порядка постоянной v в A3.19). При учете
этого скаляра первый член в i?yUk в A3.28) можно записать
в форме
..+к. с, A3.49)
что даст для масс электронов и ^-кварков в разных поколениях
теперь заведомо разные значения, так как mdpv=\vfpq+
+ <orfM\/V2, *Jf-|t»/,f-3«'/;j/V5". причем /и-новый
набор постоянных юкавовскрго взаимодействия.
Эстетически более привлекателен другой вариант теории,
в котором S'Yvik включает лишь две константы, /их, как
в A3.28), ио где индексы поколений несут сами поля скаляров
ha-+h*q(x), a <pi*W-»-q>?*J(x). Тогда вместо A3.49) будет
где сумма берется как по а, р4, у, так н по индексам поколений
р, q. Поскольку теперь все члены лагранжиана имеют вид свер-
сверток по индексам поколений, то можно считать, что и по ним
имеется непрерывная (калибровочная) симметрия, например вида
[SU (v)]g (где индекс g—от английского generation—поколение) —
это симметрия .поколений или так называемая горизонтальная
симметрия. Лагранжиан фермионов SBj с такой SUE)xlSU(\)]ir
симметрией должен включать длинную производную /)й вида
более сложного, чем A3.27): Dv.=dVL—\gataBi.—lg'^e,Bltg, где
tsr—генераторы горизонтальной группы [5?/(v)]g (онн равны Яг/2
для v=3), a Bp, g—новые семейные (или горизонтальные) компо-
компоненты калибровочного поля.
Чтобы фактически поколения различались, в теорию следует
ввести семейные бозоны Хиггса, зависящие только от семейных
значков: g^, r\«, %р9 и т. д., которые получают вакуумные средние
вида, например, < \р > =Vg6PiV и спонтанно нарушают симметрию
поколений. Почти все компоненты этих полей поглощаются семей-
семейными калибровочными полями B^,g, которые при этом приобретают
массу AiBg~Vg, причем следует выбрать Vg~V (r,je V^1012z>—
вакуумное среднее 24-плета ф?). Из-за большого значения Мве
.новое взаимодействЕе фермнонов через поля Bg совсем несущест-
216
веино и не приводит к нежелательным переходам фермионов (с
изменением типа кварков в нейтральных токах). В результате
разрушения симметрии поколений возникает иерархия масс фер-
фермионов разных поколений, что приводит, как было показано
3. Г. Бережиаии и Дж. Л. Чкареули [13.12], к ряду интересных
соотношений между массами кварков и лептоиов и углами их
смешивания (в матрице Кобаяшн—Маскава), разумно соответст-
соответствующих даииым опыта.
Обсуждение этих соотношений выходит за рамки настоящей
книги. Отметим лишь, что для реального построения такой схемы
горизонтальной симметрии необходимо, чтобы массы физических
полей Хиггса, остающихся после нарушения симметрии и изме-
изменяющих поколения А^=й^+ < А«? > (с p^q), были на 5—6
порядков больше Mw—массы W±-6o3ohob теории электрослабого
взаимодействия. Действительно, иначе переходы за счет обмена
квантами этих полей приведут в противоречии с данными опыта
к изменению ароматов (т. е. типов) кварков в нейтральных токах.
В то же время вакуумные средние этих же полей < А™ > =
= vpQ6a,5 должны быть малыми величинами (порядка Mw~f'od)T
так так они определяют массовую матрицу кварков wp?~/-o/,?.
Оказывается, именно это и имеет место [13.12] при наличии
потенциала Хиггса, зависящего1 от всех скалярных полей
Ф? & 9 k кК
Следует подчеркнуть, что для реального построения теории,
так же как ив случае одного поколения, должно быть выполнено
одно «ненатуральное» условие огромной иерархии V|~V2~
~ 1(РЧ>? между вакуумными средними полей фв, §р, г\*, %pq, с одной
стороны, и полей А«? и АР—с другой. Трудность остается точно
та же, что и в случае одного поколения: если даже это условие
ввести произвольно в уравнение A3.40), то видно, что оно сразу
же будет нарушено при учете радиационных поправок в каждом
высшем порядке по константе g2 калибровочного взаимодействия.
В настоящее время энергично развивается подход, основан-
основанный на суперсимметрии — симметрии фермионных и бозонных
состояний (целиком отсутствующий в этой книге), в рамках ко-
которого большое объединение взаимодействий выглядит иначе,
чем это было описано выше, и где, в частности, условие иерархии
V~ 1O1S v автоматически выполняется во всех порядках по gz.
Возможно, что нарушенная симметрия поколений может быть
естественно вписана в эту новую форму теории.
1 Включающего линейные по А„» члены вида ф?йрХм'h%q •
217
Часть III
ПРИМЕНЕНИЕ КВАНТОВОЙ ХРОМОДИНАМИКИ
К ОПИСАНИЮ ФИЗИЧЕСКИХ ПРОЦЕССОВ
Г лава 14
ЭФФЕКТЫ СИЛЬНОГО ВЗАИМОДЕЙСТВИЯ
В НЕЛЕПТОННЫХ СЛАБЫХ РАСПАДАХ
14.1. Эффективный лагранжиан слабого взаимодействия
кварков (большая виртуальность)
Эта часть посвящена анализу в рамках квантовой хромоди-
яамикн физических процессов. Мы будем применять как методы
теории возмущений, изложенной в гл. 7 и 8, так и, где это воз-
возможно, те соотношения, не связанные с теорией возмущений, ко-
которые удается получить из первых принципов. Общим обстоя-
обстоятельством, присущим применениям КХД к физическим процессам
и препятствующим во многих случаях получению достаточно
точных количественных результатов, является то, что исходная
теория формулируется в терминах кварков и глюонов, а на опы-
опыте же наблюдаются бесцветные адроны. Переход от соотношений
в терминах кварков и глюонов к результатам для физических
адронов требует, как правило, знания того, как адроны «устрое-
«устроены» из кварков и глюонов. Другими словами, этот переход су-
существенным образом зависит от динамики на больших расстоя-
расстояниях, которая практически неизвестна. Поэтому в большинстве
"случаев приходится прибегать к эвристическим методам, а также
к модельным представлениям, что, естественно, вносит неопреде-
неопределённость в численные оценки. По этой же причине ниже рассмот-
рассмотрены процессы, которые не.являются чисто сильными, а обуслов-
обусловлены слабым или (и) электромагнитным взаимодействием. По-
Поскольку вид этих взаимодействий известен, они являются хорошо
определенными пробниками адронной структуры и позволяют
изучать возникающие на их фоне эффекты сильного взаимодейст-
взаимодействия.
В этой главе рассмотрены эффекты, которые вносит сильное
взаимодействие в нелептонные слабые распады адронов. На
опыте эти эффекты весьма существенны. Пожалуй, наиболее яр-
ярким примером их проявления служит известное эмпирическое
правило ДГ=1/2 в нелептонных распадах странных частиц, со-
218
гласно которому переходы с изменением изосшгаа ДГ=3/2 подав-
подавлены по сравнению с переходами с АТ=>1/2. Это подавление не
содержится в затравочном (без учета сильного взаимодействия)
лагранжиане иелептонного слабого взаимодействия, поэтому ясно,
что мы имеем дело с динамическими сильными эффектами. Здесь
приведены основные этапы анализа в рамках КХД иелептонных
распадов странных частиц, принадлежащего большей частью
А. И. Вайнштейну, В. И. Захарову и М. А. Шифману [14.1 J, в
результате которого возникает почти количественная теория этих
распадов. Оговорка «почти» относится здесь к тому, что рассмот-
рассмотрение неизбежно «затягивается» в область динамики иа больших
расстояниях и поэтому подвержено неопределенностям, о которых
уже говорилось выше.
Приводимый здесь анализ нелептонных слабых процессов яв-
является весьма характерным примером применения КХД в ее со-
современном состоянии — использование обсуждавшихся выше ме-
методов теории возмущений иа малых расстояниях и применение
эвристических приемов и (или) модельных представлений для
больших расстояний.
Слабое взаимодействие (см. гл. 12) обусловлено испусканием и
поглощением W-бозоиов. Однако, когда импульсы взаимодейству-
взаимодействующих частиц намного меньше массы W, пропагатор W-бозона
стягивается в точку и взаимодействие приобретает знакомый че-
тырехфермиоииый вид. Ясно, что 4-фермионный лагранжиан, ко-
которым описываются слабые распады, даже без учета сильного
взаимодействия (например, для распада мюона), не является
«настоящим», а служит, как говорят, эффективным лагранжианом,
который в первом порядке генерирует амплитуды распадов, а
также слабого рассеяния при не слишком высоких энергиях. Ис-
Использование таких эффективных лагранжианов, справедливых
лишь в первом порядке в определенной области импульсов, часто
весьма удобно, что иллюстрируется, в частности, богатой феноме-
феноменологией слабого взаимодействия. (В гл. 8 применялся эффектив-
эффективный лагранжиан, генерирующий иеперенормированные амплитуды
в точке нормировки ц.) Нашей задачей в этом и следующем раз-
разделах будет нахождение эффективного лагранжиана иелептонно-
го слабого взаимодействия с учетом глюонных поправок при им-
импульсах, насколько возможно близких к тем, которые имеют квар-
кварки в распадах странных частиц.
Начнем с рассмотрения вершины для
слабого рассеяния. кварков Ц\Цг*-ЧъЧк в
области, где и входящие, и выходящие
кварки имеют нефизические евклидовы
импульсы Pi одного порядка р<2«—ц2.
Величину \i будем "предполагать большей
всех масс кварков (от этого предположе-
предположения откажемся в следующем разделе) и
меньшей массы W-бозоиа. При этом так-
также предполагаем, что константу а,(ц) Рве 14.1
219
можно считать малым параметром. Без учета глюоиных допра-
вок амплитуда рассматриваемого процесса описывается диаграм-
диаграммой, изображенной на рис. 14.1, и в рассматриваемых условиях
генерируется 4-фермиовным лагравжианом
#m«C(fcY|i-0 +YbWi)(?4YmA + Ye) Я»). A4.1>
где константа С представляет собой произведение фермиевской
константы G/V2 на соответствующую комбинацию параметров
смешивания кварков в слабом лагранжиане, зависящую от сортов:
кварков. Здесь и далее для цветовых индексов ^пользуются
матричные обозначения, так что выражения типа (дОд) означают
в развернутой записи Ц&йК где i, /=1,2,3—цветовые индексы
[Конкретно, в билинейные формы в A4.1) в качестве 0' входит
бесцветная матрица тДИ-Тв), поэтому в данном случае ее цве-
цветовая структура есть 6Д в дальнейшем встретятся также били-
билинейные формы с нетривиальной цветовой зависимостью.] Отме-
Отметим также, что здесь и далее, если не оговорено особо, обознача-
обозначаем в диаграммах пропагатор глюона пунктирной линией, а про-
пагаторы W-бозона и фотона — волнистой.
Рассмотрим теперь глюонные поправки первого порядка по-
сс, к этой амплитуде, описываемые десятью диаграммами, при-
приведенными на рнс. 14.2. Вычислять все эти диаграммы точно не
будем, а рассмотрим лишь поправки, пропорциональные
а.1п(туг*/\12), которые более важны, чем поправки порядка а,У
Рас 14.г
220
так как \n(mw2/\i2)>l. При этом из рассмотрения выпадают
первые шесть диаграмм.
Действительно, рассмотрим отдельно первые три диаграммы.
Они описывают поправку к оператору слабого тока /m=(?3YmA+J
+fsLi)- Но этот ток сохраняется (массами кварков пренебрег-
пренебрегли), т. е. его аномальная размерность равна нулю (см. разд. 8.2).
Это означает, что в сумме первых трех графиков зависимость от
ультрафиолетового параметра обрезания М выпадает и остаются
лишь конечные члены порядка а,. Такое же рассуждение справед-
справедливо и для суммы графиков во втором ряду на рис. 14.2.
Рассмотрим теперь последние четыре графика, представляю-
представляющие реальный интерес. Если пользоваться для затравочной ампли-
амплитуды слабого рассеяния лагранжианом A4.1), т. е. заменить про-
пагатор W точкой, то для суммы вкладов этих графиков в ампли-
амплитуду получим следующее выражение:
!
?4 [ух p- Yix — Ъ р- Ух] A-f Y5) if I*} X
X (?
X [**-<» -t)*Sr]/ (»+Щ A4.2)
![индекс A) указывает на однопетлевое приближение]. Здесь k —
импульс интегрирования в петле. Ясно, что поскольку нас инте-
интересует только коэффициент перед In (mw2/iia), то существенна об-
область интегрирования &2»ц2, и поэтому внешними импульсами
мы'пренебрегли. Заметим теперь, что член в пропагаторе глюо-
на, пропорциональный &А> вклада не дает, так как в результате
свертки выражения в первой квадратной скобке с 6, (а также во
второй с kKj получается нуль. Член же с ?»* приводит к следую-
следующему выражению:
А <0 в С Т&" {^31WaYv ~ YvYaYix] A + Ys) Ц- я] X
X -ffc [YvYaYix -YixYeYv] (I + Ys)
(Напомним, что под интегралом выражение kJh эффективно за-
заменяется k2gaf/4). Остающийся логарифмический интеграл расхо-
расходится на нижнем и верхнем пределах, что связано со сделанными
приближениями. Ясно, что снизу точный интеграл обрезается на
ц*, а сверху — на mw2, так как при ks>mws «оживает» пропагатор
^-бозона н интеграл по петле сходится. Поэтому с рассматрива-
рассматриваемой здесь точностью
d*k , mW ,\ л л\
-1п_-. A4.4)
Произведения у-матриц «распутываются» с помощью формулы
YnYoYv—YvYoYn = — 21бцаУр YbYs*
221
Подстановка этого соотношения, а также A4.4) в A4.3) дает
окончательно
О4-6)
Таким образом, наряду со структурой затравочной амплитуды
A4.1), в которой цвет передается неизменным от первого кварка
третьему и от второго четвертому, в порядке c^ln^m^/n2) воз-
возникла цветовая структура, которая перемешивает цвета кварков
(это неудивительно, так как в рассмотренных диаграммах глюон
передает цвет от одной фермионной линии к другой). В следующем
порядке (а* 1п (/я^/ц2)J возникают обе структуры. Когда параметр
as\n(ni*pl]i?) не мал, а порядка единицы, необходимо суммировать
его во всех порядках, и разобраться в переплетении этих двух
цветовых структур было бы весьма трудно, если бы не общий
метод, основанный на уравнениях Овсянникова—Каллана—Симан-
чика (см. гл. 5,8). Чтобы его применить, рассмотрим два оператора:
<5"=(ftYu(l+Ys) ft) Mu О +Ys) ft)- 04.8>
Эти операторы мы рассматриваем как точечные до размера по-
порядка /га^1, т. е. ntw служит ультрафиолетовым параметром обре-
обрезания при вычислении петлевых поправок к матричным элементам
этих операторов по кварковым состояниям. Если бы не было цвета
кварков, то операторы О' и б" были бы равны друг другу в силу
тождеств Фирца для у-матриц. При наличии же цвета переста-
перестановка Ц\ и q2 превращает произведение бесцветных токов в про-
произведение цветных [см., например, A4.10)].
Вычислим теперь с учетом поправки матричные элементы этих,
операторов по состоянию четырех кварков. Затравочный (т. е. бе»
учета поправки) матричный элемент О' совпадает по форме с видом,
оператора A4.7), а затравочный матричный элемент оператора Ь'
отличается от вида A4.8) знаком, так как б" отличается от О'
перестановкой qY и д2, и если оба оператора усредняются по одному
и тому же состоянию, то перестановка фермионов меняет их от-
относительный знак (общий же знак—неопределенный). С учетом,
вычисленной поправки матричные элементы имеют вид:
| б' | gtg2 > =63Yn (I + Ys) ?i) (Wn A + Y5) ft)—
а/2) q2] =
— (ftYix A + Ys) ft) (ftYn A + Ys) ft) A + r/6) +
232
Здесь r«=Fg2/16rt2)ln(m^./|*2) и использовано тождество Фйрца
для Я-матриц [см. G.9)] и для у-матриц, которые дают, например:
)ТЯil I?4Yu(! + Ys)Г ?з1 =
A /6) fartu A + Ys) <Ji] I?4Yii A + Ys) Я*] —
(Это соотношение записано для числовых амплитуд, так что при
перестановке спиноров qx и qz дополнительного по отношению
к «фирцевскому» знака минус не возникает).
Из A4.9) и A4.10) видно,^ что матричные элементы разности
Ъ.=О'—СУ и суммы О+=Ъ'-\-Ъ" выражаются только через за-
затравочные:
О4-11)
Эти равенства — операторные, т. е. их следует понимать так,
что матричные элементы левой и правой частей по состоянию с
виртуальностью ц берутся уже без одевания глюоном. При этом
получаем правильный результат с точностью до однопетлевого
приближения.
Теперь установим связь рассмотрения с уравнениями Овсянни-
Овсянникова— Каллана—Симанчика, обсуждавшимися в гл. 5 и 8. Для
этого заметим, что операторы Ъ(- и <$+' в терминологии разд.
8.1 —эффективные операторы в точке т^, в. б, к О+—ъ точке ц.
Поскольку отношение этих эффективных операторов в двух раз-
разных точках нормировки (mw и р) вычислено (это эквивалентно
вычислению отношения множителей Z в двух точках), можно
найти соответствующие аномальные размерности:
-1 4 ** In "V)~4 g' • v le\— 2 g'
+ 16я» ш ц1^ 1бя" Y+ISJ== * 16я*
16я» ц
или соответствующие коэффициенты в записи y{g)=yg2l{l6n2):
у.=4, Y+==—2.
Отсюда, пользуясь уравнениями ОКС для перенормированных
0. й О+, получаем результат для отношений перенормированных
223
операторов [см. E.38)]:
A4.12)
в котором суммируются все члены вида \as\xx (я1^/ц2))". Если
в эти формулы подставить явное выражение для отношения
эффективных констант, as(p)/as(*V) = 1+*0и,/4л) In («&/!*), то
в первом порядке по as\n [m^i^ воспроизводится результат
A4.11), определяющий, как мы видели, все решение A4.12). Та-
Такая простая проверка правильности алгебраических действий, в
данном случае тривиальная, в более сложных случаях бывает
весьма полезной (см., например, разд. 14.3).
Теперь можно вернуться к обсуждению амплитуды слабого
рассеяния кварков и записать ее с помощью эффективного лаг-
лагранжиана, перенормированного в точке ц:
где операторы О^ и О(+ имеют фиксированное выражение в тер-
терминах кварковых полей, а зависимость матричных элементов от ц
перенесена на коэффициенты с+ и с_:
"*)Г 1
( '
Теперь осталось выяснить, чему равны коэффициенты c±(mw).
Нетрудно видеть, что, за исключением поправок порядка a,(mw),
онн равны единице: c±(mw) = l+Ofa.(mw)]. Действительно, при
импульсах порядка mw из поправок исчезает логарифм, и они со-
составляют величину порядка а,. Дальнейшее же одевание глюонно-
го пропагатора и вершин приводит к замене а, перенормирован-
иой константой a.(mw), поскольку в этой кинематической области
нет другого, кроме mw, массового параметра. Итак, окончательно,
пренебрегая поправками порядка a,(mw), можно записать соот-
соотношение
которое определяет глюонную перенормировку слабого взаимодей-
взаимодействия A4.1) в той области, где параметр р больше масс тяжелых
(с, Ъ\ ..) кварков.
14.2. Аннигиляционный механизм
В распадах странных частиц слабое взаимодействие превра-
превращает один странный кварк (или антикварк) в нестранный. Такой
процесс может генерироваться затравочным слабым взаимодейст-
взаимодействием, отвечающим диаграмме, изображенной на рис. 14.3.
224
Существует, однако, еще один механизм, дающий вклад в
уничтожение странного кварка, который полностью отсутствует,
если пренебречь глюонными эффектами. Затравкой для этого ме-
механизма служат приведенные иа рис. 14.4
графики, уже содержащие одни глюон
(где q — кварк любого сорта). Этот ме-
механизм, впервые указанный А. И. Вайн-
штейном, В. И. Захаровым н М. А. Шнф-
маном, получил впоследствии название
«пннгвнн». (Это название примечательно
тем, что оно не несет в себе абсолютно
никакого смысла.) В дальнейшем будем
избегать этого термина и называть дан-
данный механизм аннигиляционным. По-
Последнее название, возможно, также оставляющее чувство некото-
некоторого неудовлетворения, связано с тем, что в графиках рис. 14.4
два кварка из слабой четырехфермионной вершины аннигилиру-
аннигилируют в глюон.
Рис. 14.3
<?-—*
Рис. 14.4
Ясно, что в условиях, когда массами кварков можно пренеб-
пренебречь, диаграммы рис. 14.4 с и- и с-кварками взаимно компенсиру-
компенсируются (сокращение ГИМ) (именно поэтому данные диаграммы не
фигурировали при рассмотрении глюонных поправок в предыду-
предыдущем разделе). Однако в реальных условиях распадов странных
частиц масса с-кварка является весьма большим параметром, и
приближение вырожденных по массе и- и с-кварков заведомо не-
неправильно.
Чтобы оценить вклад аннигиляционного механизма, рассмот-
рассмотрим сначала затравочные диаграммы рис. 14.4. Петля в этих
графиках генерирует взаимодействие, переводящее s-кварк в
d-кварк с испусканием глюона. Из-за сокращения вкладов и- и
с-кварков при больших импульсах интеграл по петле сходится,
даже если воспользоваться четырехфермионным пределом сла-
слабого взаимодействия, т. е. записать соответствующую часть за-
затравочного слабого лагранжиана в виде
2'д5=1=(G/1/2) sin в cos в (Йц A + y5)s)(dyv. A + у5)и)-
0 + YsK)}
15—679
A4.16)
225
a
Рис 14.5
(в — угол Кабиббо; смешиванием с Ь- и f-кварками пренебрега-
пренебрегаем). Для вычисления dsG-вершины (G-глюон) удобно в этом лаг-
лагранжиане сделать преобразование Фирца (только для у-матриц),
после чего вершина выражается через вклад петель, изображен-
изображенных на рис. 14.5, следующим образом:
^ js] ASO^ik), A4.17)
где iIIM,(ft) —вклад петель на рис. 14.5 (А-импульс глюона). Цве-
Цветовая структура вершины уже учтена в A4.17) и петли вычисля-
вычисляются как для бесцветных кварков (т. е. след по цветовым пере-
переменным в петле брать не нужно). Заметим также, что при преоб-
преобразовании Фирца, приводящем к A4.17), кварковые операторы в
A4.16) считали антикоммутирующими, поэтому знак «—» в
A4.17) не возникает, однако в этом случае дополнительный знак
«—» возникает из-за фермионной петли (т. е. в нашем определе-
определении он содержится в П„»). Можно было бы считать кварковые по-
поля коммутирующими. Тогда бы петля дополнительного знака не
давала, но он возникал бы при преобразовании Фирца.
Итак, рассмотрим вычисление Пм,. Легко видеть, что вклад
аксиального тока из левой вершины на графиках рис. 14.5 обра-
обращается в нуль. Петля же с векторными токами в вершинах напо-
напоминает хорошо известный поляризационный оператор в электроди-
электродинамике, н поэтому можно сразу записать Ц«(?), выделив попереч-
поперечную тензорную структуру:
^ A4.18)
Величину jP^2) можно вычислить, воспользовавшись дисперсионным
соотношением
в котором мнимая часть, отвечающая графикам рис. 14.5, вычис-
вычисляется элементарно и составляет (массой а-кварка пренебрегаем)
ImP(s)=A/12ji){6(s)-1/i —Amlis(I +2ml/s)Q(s-4ml)} A4.20)
[6E)—ступенчатая функция]. Здесь первое слагаемое обусловлено
вкладом а-кварка, а второе—вкладом с-кварка. Из A4.20) видно,
что эти два слагаемых компенсируют друг друга при s>4/7t|,
поэтому интеграл в A4.19) сходится при s~m?c. Следовательно,
при ?2</»с (тс формально считаем большим параметром) с лога-
226
рифмической точностью
Р(А2)=A/12я2Iп|^/Л2|. A4.21
С другой стороны, при ?2>4/Ис величина Р{№) быстро вымирает
из-за сокращения ГИМ.
Величина Пм,(^) пропорциональна А2, поэтому прн подстанов-
подстановке dsG-вершины в графики рис. 14.4 полюс при 62=0 в пропага-
торе глюона сокращается. С помощью формул A4.17), A4.18) и
A4.21) графики A4.4) вычисляются без труда, и прн внешних
импульсах порядка ц, ц2<4тс2 находим эффективный лагранжи-
лагранжиан для аннигиляцнонного вклада:
S'ann (G//2)sinecos Ote'/Wi^lnCmJ/i^X
A4.22)
На первый взгляд, вклад аннигиляционного механизма в распады
странных частиц должен быть невелик из-за малого значения
коэффициента g2/(l2j&). [Что здесь следует подразумевать под
константой g, можно выяснить, лишь «одев» графики рис. 14.4
следующими глюониыми поправками. Соответствующий резуль-
результат приведен в следующем разделе. Однако качественно малость
коэффициента ?2/A2я2) ясна заранее.] Тем не менее выражение
A4.22) содержит структуру, которая принципиально отсутствует
в затравочном лагранжиане слабого взаимодействия, т. е. вторая
фермионная скобка в A4.22) содержит левые н правые кварко-
вые поля. Часть, содержащая правые поля, приводит к появле-
появлению структур типа qRSL, которые обладают квантовыми числами
псевдоскалярных мезонов. Матричные элементы таких кварковых
операторов по мезонным состояниям усилены (см. разд. 14.4) по
сравнению с матричными элементами операторов, содержащих
только левые поля. Количественные оценки этих матричных эле-
элементов приведены в разд. 14.4.
14.3. Полный эффективный лагранжиан
для нелептонных распадов странных частиц
Как было показано выше, глюонные «одевания» приводят к
появлению в эффективном лагранжиане операторных структур,
которые отсутствуют в затравочном слабом взаимодействии.
Можно задаться вопросом о перечислении полного набора возни-
возникающих таким образом операторов в эффективном лагранжиане
для нелептонных распадов странных частиц. Такой полный набор
операторов имеет вид [14.1]:
u, ({8,}, АГ = 1/2);
dL) -f
), ({Sd}, AT = 1 /2);
15* 227
. ({27}, ДГ=1/2);
({27}, ДГ=3/2);
), ({8}, ДГ —1/2);
). ({8}, Д7* = 1 /2).
Здесь индексами L и R отмечены левые и правые фермионные
поля: i|>i=(l/2) (l+7s)t|j; фя=A/2)A—Vs)^- В скобках после
каждого оператора указано, какому представлению (унитарной)
группы 5?/C) он принадлежит^ а также его изотопические свой-
свойства. Указание этих характеристик весьма полезно, так как глюо-
ны являются синглетами по изоспину и по унитарной группе и
поэтому глюоиные поправки не приводят к перемешиванию опе-
операторов с разными 51/C) и изотопическими свойствами.
Алгоритм построения операторов, преобразующихся по непри-
неприводимым представлениям группы сортов кварков (SU C) в случае
трех кварков), основан на разложении произведений токов вида
Tff,=^~qf>Oqt. [В случае SU C) /, f=a, d, s.] Например, анти-
антисимметричный оператор, преобразующийся по представлению {8},
имеет вид 7*р7*|,—Tff,Tffl и элемент этого произведения, перево-
переводящий jf-кварк в cf-кварк (/=s, /Г=Ф1 имеет вид: (du)(us) +
+ (dd) (ds) + (ds) (Is) — (ds) \(m)+Cd)+(ss)]=(du) (us)—(ds) (пи),
который с точностью до знака совпадает по структуре с опера-
оператором 0i. Аналогично находятся и остальные неприводимые струк-
структуры. Так, оператор О, получается из cfs-элемента произведения
Ц.Т\. + ЦЦ* т. д.
Одним из критериев при отборе операторов является их (ка-
(каноническая) размерность d. Все перечисленные операторы име-
имеют d—б, как и операторная структура, входящая в затравочный
лагранжиан. Операторы меньшей размерности за счет петель
появиться вообще не могут, а операторы большей размерности
(например, содержащие производные кварковых полей) могут
появиться в лагранжиане лишь будучи поделенными на большие
массы (в данном случае mw или тпс).
Нетрудно проследить причины возникновения в лагранжиане
всех перечисленных операторов Ot. Так, оператор Ох имеет такую
же структуру, как и оператор ©_ (см. разд. 14.1). Оператор Ъ5
содержится в выражении A4.27) для вклада аннигиляционного
механизма. Оператор О6 возникает при одевании О5 глюонами
аналогично тому, как при одевании обсуждавшегося в § 14.1 опе-
228
ратора б' возникает & (и наоборот). Наконец, линейная комби-
комбинация
A/5H2+B/15)д3-ЬB/3H4 A4.23)
совпадает по структуре с О+, а расщепление этой комбинации
на отдельные операторы происходит за счет вклада чисто левой
части аннигнляционных графиков, которая подмешивается к опе-
операторам 0, и 02. [В действительности, как будет видно далее,
отщепляются не отдельные операторы 03 и О4, а комбинация
B/15) 03 + B/3) О4.1
Эффективный лагранжиан для нелептонных слабых распадов с
А5=1 записывается в виде линейной комбинации операторов Ot
б
2>as,.i = ]/2~G sin 6 cos в 2 c A A4.24)
с коэффициентами с,-, зависящими от точки нормировки ц.
Коэффициенты Ci прн \ica.mw находятся из условия равенства
A4.24) и A4.16): C1(mw)=—I; c2(»M = l/5; C3(mw) =2/15;
Ci(mw) =2/3; c5,6(mw)=0. Для анализа же распадов странных ча-
частиц необходимо знать этн коэффициенты прн ц порядка импуль-
импульсов кварков в адроне. Эволюцию с<(ц) от ц2«т^2 до точки Ц2<
<?.тс2 естественно разбить на два этапа: от mw до тс и ниже те.
На первом этапе (|i>mc) эволюция констант весьма проста; коэф-
коэффициенты с5 н с6 в этой области равны нулю нз-за сокращения
ГИМ. Коэффициент С\ определяется формулой A4.14) для с_:
cl(y.) = -(as(i»,)ias(mv))*'6, ц>отс. A4.25)
Коэффициенты же съ сг н сА эволюционируют подобно друг другу
по формуле A4.14) для с+. Действительно, из изотопических и
унитарных свойств операторов О2—О* следует, что каждый из
этих операторов перенормируется мультипликативно (т. е. нет
перемешивания). С другой стороны, их линейная комбинация A4.23)
совпадает с оператором О+, который также перенормируется
мультипликативно (см. разд. 14.1). Поэтому множители Z для
операторов О2—О\ одинаковы и совпадают с Z+. Следовательно,
из результатов разд. 14.1 имеем
A4.26)
V2/3J-
Указанная зависимость коэффициентов от точки нормировки
сохраняется до ц^тс. При меньших значениях ц закон эволюции
изменяется ввиду включения аннигиляционного механизма, и зна-
значения с( при ц«тс служат начальными для этих новых уравне-
уравнений. Как следует из унитарных свойств операторов О, закон эво-
229
люции с3 и с4 остается неизменным (аннигиляция в них вклада не
дает), н при (i2=m2<me2:
Vc«(»)J xi И2 {2/3)' \1*-*°)
где
3t,=a,(ffic)/ai(fftff'); Х2 = аД/л)/аЛдае)- A4.29)
При ц</тсс в коэффициент 6 дают вклад только a-, cf- и s-квар-
ка, поэтому в этой области 6=9.)
Вычисление матрицы аномальных 'размерностей, описывающей
совместную перенормировку ^операторов Ои б2, б5 и <56, вполне
аналогично вычислениям, приведенным в разд. 14.1 н 14.2. Про-
Процесс нахождения этой матрицы Hvll можно символически изобра-
изобразить в виде графического соотношения, приведенного на рнс. 14.6
Рис. 14.6
(в записи у* k — номер строки, i— номер столбца). Здесь в левой
части изображены два типа глюонных поправок: обмен глюоном
(графики типа рассеяния; на рисунке изображен один из таких
графиков) и анннгнляцнонные графики. Точка обозначает четырех-
фермионную вершину, генерируемую соответствующим операто-
оператором О. Наконец, —1пц2 в правой части отвечает тому, что доста-
достаточно следить лишь за коэффициентом при логарифме нижнего
предела обрезания в фейнмановском интеграле.
Результат вычислений представим в виде суммы двух матриц,
описывающих соответственно вклады рассеяния и аннигиляции:
—2/9 10/9 4/3 0\
1/9 —5/9 -2/30\
1/6 -5/6 —1 0 =
0 0 0 0/
llYlh
/4 0 0 0
0-2 0 0
0 0 7 3/2
КО 0 16/3 0
/34/9 10/9 4/3 0
/1/9 —23/9 —2/3 О
¦И/6 —5/6 6 3/2
\0 0 16/3 0
A4.30)
(Нумерация строк и столбцов в матричной записи отвечает записи
операторов в следующем порядке: 6и Оъ б5, б6.)
В левом верхнем 2X2 блоке первого слагаемого в матрице
Н\|| легко узнать аномальные размеркости операторов (?_ и О+,
230
найденные в разд. 14.1. Стоящие в этой матрице на антидиаго-
антидиагонали 2х2-блоки равны нулю, так как при рассеянии спираль-
ность кварка не изменяется, а поэтому за счет рассеяния опера-
операторы 01,2 не перемешиваются с Os.g. Лишь правый нижний блок
первой матрицы, описывающий эволюцию ©5,6 за счет рассеяния,
требует вычисления заново, что предоставляется читателю в каче-
качестве самостоятельного упражнения. Аннигиляционная матрица
устроена еще более просто. Легко видеть, что элементы в каждом
из ее столбцов пропорциональны коэффициентам в следующем
операторном разложении:
(dty^st) (пу^аи+dy^'d+Iy^s) = — D/3) бх+B /3) 62+Ов,
что вполне понятно, так как за счет аннигиляции возникает лишь
такая структура. Общий же коэффициент в каждом столбце лег-
легко пересчитавается из результата разд. 14.2. Очевидно также,
что оператор О6 в аннигиляции не участвует и не возникает
при ней, поэтому на соответствующих местах в аннигиляционной
матрице стоят нули.
Возвращаясь к задаче определения коэффициентов с( в точке
ц—m<titnc, запишем решение уравнений ОКС с помощью матрич-
матричной экспоненты:
(Здесь в правой части подставлены значения коэффициентов при
ц=тс.)
Матричную экспоненту можно вычислить преобразованием к
базису, в котором ||v|| диагональна, а затем вернувшись к исход-
исходному базису. Возникающие в результате выражения для коэф-
коэффициентов с{(т) с достаточной для приложений точностью мож-
можно записать в виде
с2=0,20х72/* @,96х7°'30+0,ОЗз<^-0-12) — 0,02х*/* («°-42—V30)
cs=0,01x*/* C,Зх°2-« + 0,3«-о.зо_3)9иО,80+0CиГо.^ +
+0,01«Г2/» (-0,1хМ2+2,9и-0-30-1,4*».»—l,
Здесь проверка того, что разложение данных формул по g2 вос-
воспроизводит, с точностью до погрешностей округления, результаты
A4.11) и A4.22), вовсе не тривиальна и позволяет избежать ариф-
арифметических ошибок.
231
Приведем также собственные значения матрицы \\y\\, необхо-
необходимые для проверки приведенных результатов: %у=— 2,679702;
Яг=—1,076123; Яз=3,755918; ^=7,222131.
Для полноты картины следует сказать, что в предыдущем рас-
рассуждении был «утаен» еще один оператор размерности d=6: f—
==1яг,C1,<1кДв5я)/ц,в (F№V° — глюонный тензор). Данная структура
возникает в эффективном лагранжиане, только начиная с двух-
петлевого уровня, например, за счет диаграмм вида, изображен-
изображенного на рис. 14.7. Поэтому коэффициент, с которым входит опе-
оператор Т в лагранжиан, весьма мал, и
мы здесь вслед за авторами работы
[14.1] пренебрегаем этим оператором.
Чтобы получить пригодное для
конкретных вычислений выражение
эффективного лагранжиана, описыва-
рис |4.7 ющего нелептонные распады странных
частиц, например /С-мезонов, следует
решить, какие значения пг отвечают импульсам кварков в адроне.
А. И. Вайнштейи, В. И. Захаров и М.. А. Шифман предположили,
что характерное пг отвечает а,(пг)<=*1 и что формулы A4.36) те-
ории возмущений можно «протянуть» в эту область. При этом
также предполагается, что кварковые поля, входящие в определе-
определение операторов (токовые кварки), при таких значениях пг отвеча-
отвечают полям кварков, из которых в наивном смысле состоят адроны
(блоковые кварки), т. е. считается, что в мезоне кроме кварка и
антикварка ничего нет. Эта гипотеза рассматривается в конце
гл. 15 при обсуждении глубоконеупругого рассеяния (при этом
смысл данного предположения будет несколько более прозрач-
прозрачным). Здесь же просто примем ее и проследим, к каким она при-
приводит результатам.
Как показано в гл. 9, при \i=mc a,(me)«0,2, откуда a,(mw)<=*
^О,!. Поэтому в интересующей нас области \i<=*m %\=*2, хг^б,
подставляя эти значения в формулы A4.28) и A4.31), находим
выражение для эффективного лагранжиана с численными коэф-
коэффициентами:
-х~ — l/2Gsinecose[—
+ 0,075б>з+0,375О4—0,141О5—0,045О6]. A4.32)
При вычислении значений х\*/ь и хг2/ь принято Ь=*Ъ, т. е. сред-
среднему между значениями Ъ для четырех F = 25/3) и для пяти F =
= 23/3, учитывается 6-кварк) кварков. Вкладом ^-кварка в пере-
перенормировку константы а, при me<\i.<mw можно пренебречь, так
как в логарифмической шкале масса t-кварка (mt>20 ГэВ)
близка к mw. В любом случае численные значения коэффициен-
коэффициентов с,- мало изменяются при таких изменениях 6.
232
14.4. Матричные элементы и распады /С~~*2я
Если вычисление коэффициентов в эффективном лагранжиане-
по теории возмущений представляет лишь техническую задачу, та
нахождение матричных элементов кварковых операторов по ад-
ронным состояниям, необходимое для того, чтобы превратить зна-
знание лагранжиана в результаты для конкретных адронных процес-
процессов, требует привлечения модельных предположений о кварковом
устройстве адронов. Как уже говорилось, примем гипотезу, что-
в процессе участвуют лишь те кварки, из которых в наивном
смысле состоят рассматриваемые адроны, т. е. что не происходиг
испускания и поглощения дополнительных глюонов и кварк-анти-
кварковых пар. Предположим также, что эти кварки отвечают
кварковым полям теории возмущений в точке нормировки т та-
такой, что <х,(т) = 1. В рамках этой гипотезы распад К~-*-п~п° опи-
описывается пятью кварковыми диаграммами, приведенными на
рис. 14.8, в которых точка означает взаимодействие, генерируемое-
Рис 14.8
эффективным лагранжианом A4.32). Поскольку в распаде К~-*~
-»-я-я° конечное состояние имеет изоспин Т=2, то вклад в амплитуду
распада дает лишь оператор Ъ\—единственный, входящий в A4.32)"
оператор, имеющий ДГ=3/2. Рассмотрим подробно вклад этого
оператора. Начнем с диаграммы рис. 14.8, а. В этой диаграмме-
я°-мезон рождается током левых и-кварков, поэтому сковка
(iiiy^u-i) заменяется матричным элементом (nP\UiynUi\O) =
= —ifKqll/2Y2, где q»,—4-импульс я-мезона; /я—константа рас-
распада rt+-*fi+v; /я~130МэВ. Это равенство получается изотопи-
изотопическим преобразованием из соотношения, описывающего матричный
элемент распада n+-+-n+v: ( n+\aiyndi\ 0 > = — qv\fal2.
Можно также записать матричный элемент со свободными цве-
цветовыми индексами кварков i, J:
A4.33>
233
<С помощью этого соотношения и явного вида оператора О4 нахо-
находим вклад диаграммы 14.8, а:
ll0[? + ^/+(^/] i^* 04.34)
Здесь мы воспользовались соотношением, известным из феномено-
феноменологии /С-»-я|^-распада: < я"| Hl4».Sl\K- > = A l2)[(p + ql)ll/+ +
+ (/>—?ita/-]. где р, q1—импульсы К- и я'-мезонов, а /+и /_ —
формфакторы #-*-яр,у-распада. Мы также пренебрегли в A4.34)
п& по сравнению с т?к и положили /+~1, /_~0.
Легко видеть, что диаграммы 14.8, б, в дают одинаковые вкла-
вклады, равные вкладу диаграммы 14.8, а; при этом в диаграмме
.рис. 14.8,6 «работает» третье слагаемое в операторе ©4» и следует
учесть два возможных способа объединения конечных кварков
в я-мезоны. Диаграммы 14.8, г, д вклада в амплитуду распада не
дают по следующей причине. В этих диаграммах п-мезоны рож-
рождаются векторной частью тока (uLy^Ut). С другой стороны, мат-
матричный элемент ^[пьу^^К^У пропорционален импульсу /С-мезо-
ла. Поэтому вклад данных диаграмм пропорционален диверген-
дивергенции изотопического векторного тока (ду*и), которая равна нулю
«с точностью, с которой справедлива изотопическая симметрия.
.Другими словами, вклады диаграмм рис. 14.8, г,д в распад
К-*-2п взаимно сокращаются, что связано с тем, что я-мезоны
рождаются оператором dy^u, изотопический спин которого равен
единице. За счет этих диаграмм система 2л должна образовы-
образовываться в состоянии с Г=1 и в S-волне (так как спин /С-мезона
.равен нулю). Однако такое состояние системы запрещено со-
сохранением G-четности.
Таким образом, суммируя ненулевые вклады диаграмм
рис. 14.8, а, б и в, оцениваем амплитуду распада:
I < я-яо^Я" > |=*Ы Gm%fn sin ecos 6^0,08 Gf»m% A4.35)
[здесь подставлены sine=0,23 и коэффициент с4 из A4.32)].
Амплитуда, извлекаемая из экспериментальной ширины распада,
•отвечает численному коэффициенту в записи A4.35), равному
¦0,05, т. е. примерно в полтора раза меньше теоретической оценки.
Причиной такого расхождения может быть использование фор-
¦мул теории возмущений в области относительно больших значе-
значений константы связи или грубость модельного вычисления мат-
матричных элементов. Отметим однако, что если не учитывать глюон-
ных поправок, то расхождение возрастет еще примерно в два раза.
Оценим теперь с помощью кварковых диаграмм ампли-
амплитуду разрешенного правилом Д7"=1/2 распада^ Ks-*-n+n~.
-Матричные элементы операторов Оъ О2, О3, О4 находятся
234
с помощ ь ю соотношений
< я+я" |(&/М?)(Й?7цИ?)+э. с: |JCs >
=*A /3) < я+я" | (e^ftA) (З^Ил) + э. с. | Ks > ^i%
(+э. с. означает добавление оператора, эрмитово-сопряженного
указанному), вклады же остальных слагаемых в этих операто-
операторах в принятой модели равны нулю. Следовательно,
by+dt | Ks > «-1/.Л&/
Линейная комбинация этих матричных элементов с коэффициента-
коэффициентами, указанными в A4.37), дает
4
> *±—Ют?/я-0,28.A4.36)
—Y2G sine cose <
Экспериментальное значение ширины распада отвечает коэффи-
коэффициенту, в этой записи равному 1,07. Поэтому даже с учетом не-
неопределенностей данного теоретического анализа видно, что опе-
операторы Ъъ и Ъ6 играют весьма существенную роль в обсуждае-
обсуждаемом распаде. Приведем оценку их вклада.
С помощью преобразований Фирца для у- и Я-матриц, а также
в рамках факторизации матричных элементов кварковых опера-
операторов, следующей из кварковых диаграмм, можно получить
< я*я- \б5 +Ot | Ks > =A6/3) < я*я-106+dt | Ks > ~
-f < я+я-1 dRdL 10 > < 0 \~sLdR | К0 >}. A4.37)
В последнем слагаемом без труда можно узнать вклад диаграм-
диаграммы, в которой аннигилируют кварки из /С-мезона (типа диаграмм
рис. 14.8, г, д). Однако поскольку кварки аннигилируют за счет
псевдоскалярного оператора, вклад этого процесса не обращает-
обращается в нуль, и соответствующий матричный элемент можно вычис-
вычислить, воспользовавшись следующей цепочкой равенств:
% 01 swfcrfIК° > - < 01дд(lyrfsd)\K°) =
(s+d) (\Jy 5d\K°) -=-2i(i»,+m*)< 0| ~Sidn\K* >.
Здесь ms и md—массы 5- и d-кварков; /к—константа распада
К-*\ю; /л-~1,25/«. Отсюда
< 01 sLdR | К° > —i/jr»tir/2 (ms-\-md)^ifKm%/2щ. A4.38)
,, помощью аналогичного приема получаем также
l; j
\
235
Оценка матричного элемента < я+я~ | urUl | 0 > требует не-
несколько более глубокого рассуждения. Чтобы ее пояснить, запи-
запишем цепочку равенств:
< ri?n-\muuu-\-md~dd\O > = < jCn~\{ma-\-m,d)dd\Q > =
=2(mu+md) < я+я"\dRdL10 > . A4.40)
Здесь на первом шаге мы воспользовались тем, что разность
ии— dd не рождает пару п-мезонов из вакуума, так как этот
оператор имеет изоспин 7"=1, запрещенный для 5-волновой си-
системы яп, а на втором шаге учли, что система я+п~ рождается
лишь скалярной (но не псевдоскалярной) частью оператора dpdL.
В начальное выражение в A4.46) входит матричный элемент
массового члена и- и d-кварков, «ответственного» за массу п-ме-
зона [да2 = 0, в пределе ma,d*=Q (см. гл. 17)]. Если описывать
я-мезоны феноменологическим (эффективным) лагранжианом, то
ему отвечает массовый член я^(я+п- + A/2)я°я°)- С Другой сторо-
стороны, исходный и феноменологический лагранжианы должны давать
одинаковые матричные элементы по л-мезонным состояниям.
Поэтому < n+n'\mttua-\-mddd\O > *=п&. Это соотношение, строго
говоря, верно лишь при (q+-\-q_J=c0 (т. е. при нулевом передан-
переданном импульсе в канале рассеяния). При не слишком больших зна-
значениях {д+ + Я-J можно воспользоваться линейным приближением
по этой переменной, учитывая вклад а-мезона (mo^70Q МэВ), что
дает
|0 > =*[mll2(ma+mdj] [\
Собирая оценки для матричных элементов в формулу A4.37),
получаем
t | Ks > —у- < я+я-1 Э6 + О6+1 Ks > ~
Здесь мы воспользуемся оценкой для масс кварков, которую наи-
наиболее надежно можно получить из сравнения с эксперименталь-
экспериментальными данными правил сумм для е+е--аннигиляции в адроны
(см. гл. 17). Масса кварка имеет аномальную размерность (рав-
(равную 4 в единицах g2/lfm2) и поэтому зависит от точки нормиров-
нормировки. В точке нормировки, отвечающей а.^1, mu + md~ 10ч-15 МэВ.
Масса странного кварка также находится из этой оценки с по-
помощью соотношения tnK»2lmx2=(m^+md)l(mu+md)ca.ni,/(mu +
+md), которое получается применением гипотезы частичного со-
сохранения аксиального тока как к я-, так и к /С-мезонам. Отсюда
tn.cn 13 (mui+md)~ 130—200 МэВ. Подставляя значения масс
236
кварков в A4.41), приходим к оценке:
< я+я" | О5+О? | Ks > =A6/3) < я+я-1
^A0-20) 1/ят%/У2. A4.42)
Нетрудно проследить, что усиление матричных элементов опе-
операторов 05 и б>6 обусловлено малостью масс кварков.
Возвращаясь к численной оценке амплитуды распада Ks-^^n~
и комбинируя соотношения A4.32), A4.36) и A4.42), получаем
| < +l&lK > Н0,28+@,33-к0,66)]G/«wt^@,6-к 0,95)Qf%
что с учетом всех имеющихся неопределенностей разумно согла-
согласуется с экспериментальным значением A,07 в тех же единицах).
Заметим, что в этом случае теоретическая оценка меньше экспе*
риментальной, тогда как для распада К~-*-п~п° ситуация обрат-
обратная. В обоих случаях теоретические оценки изменяются в пра-
правильном направлении, если точку нормировки для эффективного
лагранжиана понизить по сравнению с выбранным значением,
дающим <х, = 1. При этом коэффициент С4 уменьшается, а сумма
Cs+ C/16) cs увеличивается. Однако законность такой процедуры
не ясна. Тем не менее из приведенных оценок видно, что учет
глюонных поправок модифицирует эффективный лагранжиан в
правильном направлении.
А. И. Вайнштейн, В. И. Захаров и М.. А. Шифман 1[14.1] про-
проанализировали также амплитуды распадов гиперонов с помощью
эффективного лагранжиана вида A4.32) и нашли во всех случаях
удовлетворительное согласие численных оценок с данными опы-
опыта, а также что во всех случаях эффективный лагранжиан дает
правильные относительные знаки амплитуд.
Глава 15
ГЛУБОКОНЕУПРУГОЕ РАССЕЯНИЕ
ЛЕПТОНОВ НА НУКЛОНАХ
В этой главе рассмотрено глубоконеупругое рассеяние лепто-
нов на нуклоне. Этим термином называют процессы электромаг-
электромагнитного рассеяния электронов (мюонов) и слабого рассеяния
нейтрино на нуклонах в условиях, когда передаваемый от лепто-
нов к адронам 4-импульс q велик, так что на расстояниях порядка
(q2)~m применима теория возмущений квантовой хромодинами-
ки. В этих реакциях лептон выступает в качестве пробника струк-
структуры адрона на малых расстояниях, поэтому изучение глубоконе-
упругих процессов на опыте, проводимое с конца 60-х годов, слу-
служит важным источником информации о внутреннем устройстве
адронов. Уже в первых опытах было обнаружено, что процесс
рассеяния на адроне выглядит так, как если бы лептон рассеи-
рассеивался на (почти) свободных точечных объектах внутри адрона,
названных Фейнманом партонами. Согласно партонной модели,
при описании глубоконеупругого рассеяния нуклон представляется
237
в виде ансамбля невзаимодействующих партонов, распределенных
по импульсу, и рассеяние на нуклоне является некогерентной
суммой рассеяний на партонах. Впоследствии было выяснено, что
квантовые числа партонов совпадают с квантовыми числами квар-
кварков.
С открытием асимптотической свободы в квантовой хромоди-
намике стало ясно, что с помощью КХД можно объяснить на-
наблюдаемое на опыте почти свободное поведение кварков-парто-
нов на малых расстояниях, что дало решающий толчок развитию
этой теории. КХД описывает также отклонения от партонной
модели при больших q, однако эти отклонения лишь логарифми-
логарифмически зависят от ц. Существующие экспериментальные данные не-
недостаточно точны, чтобы надежно количественно выявить эту
слабую логарифмическую зависимость. В области же сравнитель-
сравнительно небольших q, где логарифм является «живой» функцией, про-
проявляются эффекты больших расстояний, не описываемые теорией
возмущений, и в настоящее время имеются лишь более или менее
феноменологические попытки описания этих эффектов. Во всяком
случае, количественное сопоставление КХД с данными по глубо-
конеупругим процессам представляется сейчас преждевременным,
и речь может идти лишь о качественном сравнении, результаты
которого, впрочем, весьма впечатляющи.
15.1. Определения и кинематика
Рассмотрим сначала для определенности рассеяние нейтрино
на нуклоне за счет взаимодействия слабых заряженных токов:
vm vN-+V.-X, A5.1)
где X — адронное состояние, образо-
образовавшееся в результате реакции. Этому
процессу отвечает диаграмма рис.
N(p) 15.1, где в скобках указаны импуль-
импульсы частиц, р' — суммарный импульс
состояния X. Сечение данного процес-
процесса определяется формулой
Рис. Г5.1 A5.2>
Здесь т — масса нуклона; E(Ef)—энергия начального (конеч-
(конечного) лептона в лабораторной системе; L,,,— произведение мат-
матричного элемента лептонного тока на комплексно-сопряженный:
0
где ejtvxo—абсолютно антисимметричный тензор; q=l—l'-. Массой
мюона пренебрегли, так что можно также записать Q2s=—^2 =
238
=2 {IV). Наконец, входящая в A5.2) величина Нт есть вклад
адронной вершины
tfW=Bjr)«6D)(/;+<7-/'/)<W|/ji@)|*> (X]JV(O)\N), A5.4)
где /„(я) — ток в адронной вершине, например для реакции A5.1)
это в основном ток /ц==ы7цA+75)^ (смысл оговорки «в основном»
будет ясен из следующего раздела).
Постановка опытов по глубоконеупругому рассеянию состоит
в том, что измеряются лишь кинематические характеристики ко-
конечного лептона. При этом в измеряемом сечении складываются
все возможные конечные адронные состояния. Определенное та-
таким образом сечение называют инклюзивным. Ясно, что сечение
рождения каждого конкретного адронного состояния определяет-
определяется, помимо прочего, структурой самого этого состояния и, следо-
следовательно, зависит от динамики на больших расстояниях. Поведе-
Поведение же инклюзивного сечения (см. ниже) позволяет выделить
информацию о взаимодействии на малых расстояниях. Таким об-
образом, характеризующая адроны величина, входящая в выраже-
выражение для инклюзивного сечения, получается суммированием по
всем возможным конечным состояниям:
^^ > X
X(X\JV(O)\N) A5.5)
(суммирование по X подразумевает суммирование по всем ко-
конечным каналам и в каждом канале — по поляризациям и интег-
интегрирование по фазовому объему). Здесь будем рассматривать
лишь рассеяние на неполяризованйых нуклонах, поэтому в A5.5)
будем также подразумевать усреднение по поляризациям нукло-
нуклонов. В этих условиях величина Н^ описывается тремя инвариант-
инвариантными функциями, зависящими от двух переменных
Q2=—g-2 и х==рд; A5.6)
viq2)W1(Q', v) +
-ipq) q»iq*) ips - ipq) q^iq2) w2 (Q\ x)im?-
—(l*ma/2m2)pbqoW3(Q2,v). A5.7)
To, что инвариантных функций всего три, легко понять, заме-
заметив, что из имеющихся в распоряжении 4-векторов р и q можно
составить лишь три входящих в A5.7) тензора, ортогональных qv
, (ортогональность Н и q требуется сохранением тока /„).
Значения переменных Q2 и v в каждом конкретном акте рас-
рассеяния можно определить, измеряя лишь кинематические харак-
характеристики вылетающего лептона — угол вылета 0 и энергию Е'.
В лабораторной системе
Q2=4??/sin2(e/2), v = m(E—E'). A5.8)
Выражение для дифференциального по этим переменным инклю-
инклюзивного сечения получается из формул A5.2), A5.3) и A5.7) и
239
имеет вид
d2a (xN -*¦ ц- + все) /dQ2dv=
-ИРТ [2^sin2 i+W,cos^-^±^Wssin^] A5.9)
(где «все» обозначает любые адронные состояния).
Физическая область изменения переменных Q2 и v следует из
очевидных неравенств Q2^0, v^O, v<mE и неравенства р/2=
= (p+?J=m2+2v—Q2S*m2=*Q2/Bv)=sSl, которое выражает тот
факт, что масса рождаемого адронного состояния не может быть
меньше массы нуклона. 1[3аметим, что равенство Q2/Bv) = l от-
отвечает упругому рассеянию]. Таким образом, если ввести безраз-
безразмерные переменные
(;t=Q2/2v;J y=\ — E'jE = x/mE, A5.10)
то в этих переменных физическая область отвечает квадрату в
плоскости (х, у):
0s?*s?l, O^i/^l. A5.11)
Дифференциальное по переменным хну сечение при Е^пг име-
имеет вид
d2o (xN ->р- + все)/ dxdy=(G2s ft^^F^ [х, Q^-f
+(L-y)F,(x, Q^-xyil-yWF^x.Q2)), A5.12)
где введены обозначения
/^ = 1^; F2=xW2/m?; Fs=xW3/m? A5.13)
и s= (p+lJ=*2mE. Функции F4 (а также Wt) называют струк-
структурными функциями нуклона.
Обсудим в заключение модификацию формул A5.9) и A5.12)
на случаи других процессов, кроме A5.1). Для рассмотрения
рассеяния антинейтрино следует выполнить С-сопряжение над
лептонным тензором /.„„, что сводится к изменению знака перед
последним слагаемым в A5.3). Что касается адронного тензора
#„„ то входящий в него ток изменится. Это будет в основном
Иур(\+уь)и. Соответственно изменятся и структурные функции
W{, определяемые формулами A5.5) и A5.7). Однако сами эти
формулы останутся неизменными, поэтому для рассеяния анти-
антинейтрино знак перед последним слагаемым в формулах A5.9) и
A5.12) изменится на обратный. Общую формулу типа A5.12) за-
записывают при этом в виде
d2o^W/dxdy=(G2sj2n) [xy2Fx + A —у) F2 + xy A —у/2) F3]. A5.14)
При этом, когда речь идет о конкретном процессе, функции F
снабжают соответствующим значком, например, для ^-рассея-
^-рассеяния Ffp.
В случае электромагнитного рассеяния электронов на нуклонах
в определение Н^ входит электромагнитный адронный ток /д =
= 2 QfQ/Wf где Q/—заряд кварка сорта / в единицах \е\.
t
240
Этот ток сохраняет С- и Р-четности, поэтому тензорная струк-
структура с символом Щч1.а возникнуть в //цу не может. Следова-
Следовательно, WiN=0. Аналог формулы A7.14) для еЛ/-рассеяния имеет
вид
d2ae I dxdy={4na?iq*) slxytF^iX —y)F2]. A5.15)
15.2. Партонная модель
Функции Ft безразмерны и зависят от двух переменных: без-
безразмерного отношения х и размерной величины Q2. Если предпо-
предположить, что в области, где кинематические параметры Q2 и v на-
намного превышают массу нуклона, не остается размерных парамет-
параметров, характеризующих нуклон, то зависимость от Q2 исчезнет,
так как Q2 нечем «обезразмерить». Другими словами, можно бы-
было бы полагать, что выполняются следующие предельные соот-
соотношения:
Поведение структурных функций вида A5.16) называют бьерке-
новским скейлингом. Скейлинговое поведение оказалось хорошим
приближением к экспериментальным данным.
Обсудим предложенную Фейнманом модель устройства нукло-
нуклона, которая объясняет поведение A5.16). Начнем с того, что за-
заметим, что если бы нуклон был аморфным образованием с непре-
непрерывным распределением заряда, то структурные функции просто
падали бы степенным образом с ростом Q2, так как в рассеянии
когерентно участвовали бы каждый раз лишь «куски» нуклона
размером порядка 1/Q. В этом случае предел A5.16) выполнялся
бы тривиально — правая часть обращалась бы в нуль. Однако
такое поведение явно противоречит экспериментальным данным.
Фейнман предположил, что в нуклоне заряд сосредоточен в то-
точечных объектах — партонах, и рассеяние лептона на нуклоне
происходит через упругое рассеяние на одном партоне, а затем
через превращение состояния партонов, образовавшегося после
рассеяния (оно отличается от начального изменения импульса
партона, на котором произошло рассеяние) в наблюдаемое конеч-
конечное адронное состояние. При инклюзивном подходе последнее со-
состояние не рассматривается и, по существу, изучаются характе-
характеристики лишь первого процесса.
Не вдаваясь в подробный обзор развития нартенной модели,
перечислим ее основные положения, установившиеся в результате
накопления экспериментальных данных.
Рассмотрение удобно вести не в лабораторной системе, где
нуклон покоится, а в системе, в которой он имеет большой им-
импульс р |р|^>/п; во многих случаях удобно пользоваться так на-
называемой брейтовской системой, в которой 4-импульс q чисто
пространственный: q=@, q). Поперечные по отношению к р им-
16—679 241
пульсы партонов ограничены и, следовательно, малы по сравне-
сравнению с |р|; также малы и массы партонов. Партоны распределены
по продольному импульсу. Это распределение удобно описывать
в терминах отношения
*=|р„шфт|/|р|. A5.17)
Легко убедиться, что переменная х, введенная в предыдущем раз-
разделе, равна величине х из A5.17) для партона, на котором про-
произошло рассеяние. Действительно, записывая условие того, что
лептон рассеивается на партоне с импульсом хр и вылетающий
в результате партон имеет ту же массу, что и начальный (либо
пренебрегая этими массами вовсе), имеем: (xp + qJ=(xp)a отку-
откуда 2хх—Q2—О или x=Qa/2v, что совпадает с определением
A5.10).
Важнейшим положением партонной модели, представляющим-
представляющимся сейчас более чем естественным, является то, что партоны обла-
обладают квантовыми числами кварков. Сюда относятся: спин, сорт
(и, d, s...), электрослабые заряды, а также цвет (хотя послед-
последний в самой партонной модели для глубоконеупругого рассеяния
не слишком существен). Поэтому далее часто будем говорить не
о партонах, а о кварках. Кварковые распределения по х, кото-
которые обозначаются и(х), d(x),..., п(х), 3(х),..., показывают
плотность числа кварков при данном х.
Чтобы найти сечение рассеяния лептона на нуклоне, следует
вычислить сечение рассеяния на кварке каждого сорта, а затем
проинтегрировать по х с соответствующим кварковым распреде-
распределением. Так, процесс A5.1) может идти либо на d-кварке, либо
на антикварке п (углом Кабиббо пренебрегаем). Соответствую-
Соответствующие сечения на кварках при (l+pxJ=sx имеют вид *_
do{\u-+}i-d)/dy=G2sx(l—yJ/n.
Соответственно для сечения, например, на протоне
где d(x) л~и(х)—кварковые распределения в протоне. Сравнивая
эту формулу с A5.12), находим:
(x)=d(x)+u(x);
FY(x)=2x(d(x)+u(x));
Если бы мы интересовались рассеянием на нейтроне, то в эти
формулы следовало бы подставить4 распределения кварков в
нейтроне. Однако из-за изотопической симметрии распределение
d-кварков (и антикварков) в нейтроне такое же, как и ы-кварков
(и антикварков) в протоне, и наоборот;•распределения же s-квар-
ков (и антикварков) в протоне и нейтроне одинаковы. И теоре-
242
тически, и экспериментально часто бывает удобно говорить об
усредненных по протону и нейтрону распределениях (распределе-
(распределения в среднем нуклоне). Теоретически это удобно для сокраще-
сокращения числа оговорок, о каком именно нуклоне"идет речь, а экспе-
экспериментально— поэтому, что во многих экспериментах (особенно
нейтринных) используют в качестве мишени тяжелые ядра с при-
примерно равным числом протонов и нейтронов. Распределение и- и
^-кварков в среднем нуклоне N обозначим q(x) =u(x),.+d(x), a
антикварков q(x)=u(x)+3(x) [здесь и(х) и dfx), а также
п. и d определены по отношению клротону]. В этих обозначениях
структурные функции для \N- и vJV-рассеяния (в пренебрежении
вкладом s-кварков) имеют_вид
A5.19)
Подробное обсуждение экспериментальных данных по глубоконе-
упругому рассеянию и теоретических соотношений в партонной
модели приведено в обзорах [15.1], [15.2]; здесь же рассмотрим
схематический график распре-
распределений q(x) и q(x), умножен-
ный на х, как они представля-
представляются на основе современных
экспериментов (рис. 15.2/. Важ-
Важным обстоятельством, видным из
этого графика, является то, что
суммарный импульс кварков в
нуклоне намного больше, чем ан-
антикварков. Естественно связать
этот факт с тем, что в наивном
смысле нуклон состоит из квар-
кварков (эти кварки в партонной мо-
модели называют валентными), а
антикварки появляются лишь за счет рождения кварк-антиквар-
ковых пар (это называют морем пар). В разд. 15.8 показано, что
в КХД этой картине можно придать разумный количественный
смысл. Качественно убедиться в том, что кварков в нуклоне
больше, чем антикварков, можно рассмотрев полные сечения vN
и \N:
Рис. 15.2
xq(x)+(M3) xq(x)] dx;
1
= (&s/2n) j [(l/S)xq(x)+xq{x)] dx.
A5.20)
Если бы антикварков не было вовсе, то отношение сечений
a*/v/avJV составляло бы 1/3. На опыте это отношение несколько
16* 243
больше и равно примерно 0,5, что отвечает малому вкладу
антикварков.
Еще одним существенным обстоятельством является то, что
экспериментальные значения интегралов, входящих в A5.20),
которые очевидным образом связаны с полной долей импульса
нуклона, несомого кварками и антикварками, даже приближенно
не отвечают тому, что весь импульс нуклона переносится кварка-
кварками и аитикварками. С учетом s-кварков, которыми мы пренебрег-
пренебрегли, импульс, сосредоточенный в кварках и антикварках, составля-
составляет лишь примерно 0,5 полного импульса нуклона. В рамках КХД
естественно считать, что весь остальной импульс переносится
глюонами и, как показано ниже (в разд. 15.7 и 15.8), можно ко-
количественно оценить распределение полного импульса нуклона
между кварками и глюонами.
15.3. Операторное разложение
В этом и следующем разделах проиллюстрируем применение
формального аппарата теории поля к рассмотрению глубоконе-
упругого рассеяния, во-первых, чтобы придать читателю уверен-
уверенности в возможности строгого обоснования ряда утверждений,
сделанных ранее, в частности о том, что в инклюзивных реакци-
реакциях доминируют малые расстояния (и в терминах каких величин
эта доминантность, строго говоря, проявляется), и тех, которые
будут сделаны в последующих разделах, и, во-вторых, чтобы свя-
связать задачу описания глубоконеупругих процессов с общими ме-
методами уравнений ренормгруппы, изложенными в гл. 5 и 8 и уже
использовавшимися в гл. 14. Также по ходу изложения будет
введено разложение произведения операторов на малых расстоя-
расстояниях, на общность и важность которого в теории поля указал
Вильсон и которое обычно называют разложением Вильсона (от-
(отметим, что в гл. 14 мы фактически пользовались этим разложе-
разложением, не акцентируя его общий характер).
Те из читателей, у кого эти два раздела вызовут трудности
или неудовлетворение, могут без особого ущерба для понимания
дальнейшего перейти к разд. 15.5, где все интересные результаты
будут получены более простым способом, не апеллирующим к
операторному формализму.
Вернемся к определенному формулой A5.5) адронному тензо-
тензору Нф. В силу соотношения унитарности этот тензор равен (де-
(деленному на 2i) скачку на разрезе при физических значениях
переменной s'= (p + qJ следующей амплитуды:
> A5.21)
(здесь 2К—4-мерные координаты);
#»v(Q2, v)=(l /20 [Ttf (Q8, v)-7V (Q», v)l, A5,22)
<тде Т$]—значения амплитуды ГКУ на берегах разреза по пере-
244
менной s'=2v—Q2. Чтобы пояснить эту связь, напомним, что #Kv
согласно A5.5) есть сумма по всем состояниям X произведений
матричного элемента тока /v@) и комплексно-сопряженного, a 7VV —
амплитуда рассеяния тока / на нуклоне вперед. Ток можно свя-
связать с (виртуальным) фотоном или HP-бозоном, так что в более
привычных терминах Н^, есть поляризационная матрица для веро-
вероятности полного поглощения (виртуальной) векторной частицы
нуклоном, а ГЦУ — амплитуда рассеяния вперед этой векторной
частицы на нуклоне. Можно еще для наглядности изобразить со-
соотношение A5.22) графически (см. рис. 15.3, где на левом гра-
N-
к!
1
—1-
4=
-r
X
p
off<-
(Jfc=
p
/>
Рис. 15.3
фике пунктиром показано разрезание по физическим промежуточ-
промежуточным состояниям). Разумеется, соотношение A5.22) можно уста-
установить и чисто формально, насыщая произведение токов в A5.21)
полной системой состояний и воспользовавшись свойством / отно-
относительно трансляций:
У (г)=exp (iPz) J @) ехр (- \Pz). A5.23)
Таким образом, рассмотрение #MV сводится к исследованию по-
поведения амплитуды TV,,. На формальном уровне это исследование
удобно проводить, воспользовавшись операторным разложением
для произведения токов, входящего в A5.21). В общем случае это
разложение для произведения операторов А и В можно записать
в виде
Л(г)Я@)=2 С?(г2)гк,...г11л01|1--11л(О), A5.24)
I, п
где ц* — лоренцевы индексы; индекс i нумерует операторы Ot с
данным числом лоренцевых индексов, а СУ(г2) — с-числовые ко-
коэффициенты. С разложениями типа A5.24) приходится сталки-
сталкиваться весьма часто. Так, в теории слабого взаимодействия ампли-
амплитуды генерируются произведением операторов слабых токов, ум-
умноженным на пропагатор №-бозона, который отбирает лишь
вклад расстояний между точками, где действуют токи, порядка
mw~x- Поэтому в случае слабого взаимодействия главный вклад
при невысоких энергиях дают первые члены разложения вида
A5.24), и возникает эффективная четырехфермионная теория, ко-
которой мы занимались в предыдущей части. Операторное разложе-
разложение полезно всякий раз в ситуациях, когда имеются два различ-
различных масштаба расстояний, и оно позволяет получать разложение
по степеням отношения меньшего масштаба к большему. В сла-
245
бом взаимодействии меньшим масштабом является mF-', а боль-
большим— дебройлевская длина волны взаимодействующих частиц
порядка s~I/2. Отметим еще из знакомых примеров, что, по суще-
существу, на операторном разложении основано разложение излучения
атомных систем по мультиполям. Разложение по степеням отно-
отношения характерных масштабов возникает в терминах A5.24) в си-
ситуациях, когда операторы А и В действуют на состояния, харак-
характерный размер которых велик по сравнению с характерным рас-
расстоянием г между точками, в которых эти операторы действуют.
В случае глубоконеупругого рассеяния характерные значения г2,
как видно из A5.21), порядка Q-2, матричные же элементы опе-
операторов Ot определяются структурой нуклона, т. е. имеют фикси-
фиксированный, не зависящий от Q2 масштаб.
Прежде чем перейти к более детальному обсуждению приме-
применения разложения A5.24) к глубоконеупрутому рассеянию, сде-
сделаем еще несколько замечаний общего характера. Наиболее не-
нетривиальным свойством разложения A5.24), которое следует осо-
особо подчеркнуть, является то, что оно есть истинно операторное
равенство, не зависящее от того, между какими состояниями бе-
берутся матричные элементы его левой и правой частей. Это озна-
означает, что коэффициенты С{ можно вычислять, взяв, например,
матричный элемент обеих частей A5.24) между кварковыми со-
состояниями, а затем использовать это разложение с уже известны-
известными С, для нахождения адронных матричных элементов произве-
произведения операторов, стоящих в левой части. При этом, разумеется,
последние матричные элементы будут выражаться через извест-
известные коэффициенты С< (определяемые лишь свойствами операто-
операторов) и адронные матричные элементы операторов О{ (определя-
(определяемые свойствами адронов на больших расстояниях). Последние,
как правило, не поддаются вычислению и входят в качестве фе-
феноменологических параметров.
Операторное разложение A5.24) доказано строго, исходя из
аксиом теории поля, только в теории возмущений. Вне ее рамок
доказательства нет, но физические аргументы, стоящие за этим
разложением, столь естественны, что многие (и мы вслед за ни-
ними) без колебаний применяют его в ситуациях, где существенны
также и эффекты, не описываемые теорией возмущений. Есть все
основания полагать (см. гл. 9), что структура вакуума К.ХД и
тем более адронов определяется эффектами, лежащими далеко
от теории возмущений. Поэтому, по существу, все интересные
результаты, основанные на разложении A5.24), связаны с ис-
использованием этого равенства в непертурбационной области.
15.4. Применение операторного разложения к глубоконеупругому
рассеянию и моменты структурных функций
Применяя разложение A5.24) к Г-произведению токов, входя-
входящему в A5.21), для амплитуды Т^ можно записать следующее
равенство (для сокращения записи лоренцевы индексы токов /
246
опускаем):
z*)zltl...zltn (N\Q*1 Кл|ЛО A5.25)
i,n
(общий множитель i включен в ' определение С?). Здесь удобно
перейти к таким операторам Qi ", которые не имеют следа по
любэй паре индексов \i. [Если начать с произвольного набора
операторов, то из каждого оператора можно выделить бгсследовую
часть и члены, содержащие g^1*11*'; последние при умножении на
г*кг»к' Д8101" множители г2, которые можно убрать в переопре-
переопределение коэффициентов Ct(z2).] В этом случае фактор гм,...2^я
сводится к применению оператора 2qVLt...2qv.n(d/diq2)n к скаляр-
скалярному интегралу j d*z exp (iqz) С" (г2). Определяя новые коэффициен-
коэффициенты C?(Q2)=(Q2)"(<?/<?i?2)n J d*z exp (iqz) С, (г2), получаем:
74Q2, v)-2 (Q2)"^- • -2^BC7(C?«) (N\O^ й"|N > .
Рассмотрим теперь матричные элементы операторов О{. Для
¦бесследовых операторов зависимость от лоренцевых индексов ji
может выражаться только через импульс нуклона />„ (усредняем
по спину нуклона, поэтому зависимость от спиновых переменных
выпадает):
<W|<# *"\N)-pb...p»nKl, A5.26)
где К1—скалярные в общем случае размерные множители, опре-
определяемые структурой нуклона. Таким образом, для амплитуды Т
получаем разложение:
2 A5.27)
I, п . . ¦
в каждом члене которого, как легко видеть, факторизуются зави-
зависимости от х, Q2 и от структуры нуклона.
Сделаем, наконец, последнее усилие, чтобы выяснить связь
произведений C(n(Q2)/C,n с введенными выше структурными функ-
функциями F(x, Q2). Для этого вспомним, что при фиксированном Q2
амплитуда Т как функция (комплексной) переменной х имеет
разрез при физических значениях х. Этот разрез идет от *=—1
до х= + 1 (для амплитуды рассеяния Т отрицательные значения
х, |*|^1 также являются физическими из-за кроссинговой диа-
диаграммы с переставленными токами /+ и /), и амплитуда Т ана-
дитична при |х| >1. Поэтому ряд A5.27) по х сходится при
|х|>-1. Следовательно, коэффициенты при х~п в разложении
A5.27) можно найти, умножая Т на хп~1 и интегрируя по доста-
247
точно большому контуру Г (см. рис. 15.4):
gl-, $ dxJF-T {x, Q2) = 2 С» (Q2) К*. A5.28)
Г i
Стягивая контур так, чтобы он прошел по берегам разреза, полу-
получим интеграл от скачка амплитуды на разрезе:
1
A/2я) J dxxn-4T(х, Q2)=2 C1 (Q2) К" • С15-29)
-1 i
В силу кроссинговой сим-
симметрии амплитуда Т четна по
х. Поэтому при нечетных п
интеграл A5.29) равен нулю, а
при четных ¦—удвоенному ин-
интегралу от нуля до +1. По-
Поэтому, пользуясь соотношением
A5.22) и восстанавливая зави-
зависимость от лоренцевых индек-
Рис. 15.4 сов токов, находим при чет-
четных п:
l(х, (Р)-%СЦ1Р)К*, A5.30)
о i
где F(x, Q2) есть xF\, Fz или xFs.
Величины Мп называют моментами структурных функций.
Формула A5.30) относится только к четным моментам. Это, разу-
разумеется, не означает, что нечетные моменты не существуют, просто
они не связаны с операторами, появляющимися в разложении
амплитуды Т. В этой ситуации обычно поступают так. Из A5.30)
определяют изложенным ниже методом зависимость Мп от Q2 и
п при четных п, а затем пользуются этой зависимостью и при не-
нечетных п, имея в виду возможность аналитического продолже-
продолжения по п.
Из A5.30) видно, что зависимость Mn(Q2) определяется зави-
зависимостью от Q2 коэффициентов Cy(Q2) в операторном разложении
при операторах с числом индексов (неприводимых, т. е. таких,
по которым след равен нулю), равным п; это число называют
лоренцевым спином. Ясно, что в A5.30) при больших Q2 дают
основной вклад лишь члены в правой части с минимальной разг
мерностью величин К", которая согласно A5.26) равняется раз-
разности между размерностью оператора с^" ••••*/» и его лоренцевым
спином п. Эту разность называют твистом и обозначают т:
"»)—я. A5.31>
Главная последовательность операторов, определяющая асимп-
асимптотику моментов при Q2-* оо, имеет т=2 и включает следующие
операторы: qy^q; ?[YmA>— (l/4)gnv?]?.--.; ЙкАч- • -Dv.n4~еле-
248
ды),... Эта последовательность дает асимптотику ^„(Q2), не
падающую степенным образом при Q*-»-oo. (В справедливости
этих утверждений можно прямо убедиться, используя явный вид
токов / в КХД и пройдя по цепочке рассуждений, намеченной »
этом разделе). Поэтому моменты Мл являлись бы константами
при больших Q2 (это бы отвечало точному бьеркеновскому скей-
лингу), если бы не аномальные размерности операторов. Из-за
того, что операторы Ои появляющиеся в операторном разложе-
разложении, имеют аномальные размерности, а аномальные размерности
токов, для произведения которых это разложение применяется^
равны нулю, коэффициенты C((Q2) обладают логарифмической
зависимостью от Q2 (это мы знаем уже из опыта работы с .лаг-
.лагранжианом слабого нелептонного взаимодействия):
С1 (Q2) = С" (ц2) (a, (Q2)/a, №)у"'» ~ [In (Q^/A^". A5.32)
Поэтому моменты логарифмически зависят от Q2 и, следователь-
следовательно, скейлинг все-таки нарушается. (При произвольно большом
Q2 остается логарифмическое «воспоминание» об инфракрасном:
параметре КХД Л.)
15.5. Эволюция кварковых и глюонных распределений в адроне
В этом и последующих разделах рассмотрим вычисление мо-
моментов Мп в терминах кварк-партонов и глюонов-партонов, сле-
следуя методу работы [15.3]. Отличие от простой партонной модели
будет заключаться в том, что партоны-кварки и партоны-глюоны
взаимодействуют друг с другом, и будем интересоваться именно-
эффектами, обусловленными этим взаимодействием. Явления,,
приводящие к нарушению скейлинга, состоят в следующем. Наря-
Наряду с простым рассеянием лептона на кварке возможен также про-
процесс, когда кварк до рассеяния излучает глюон и участвует в
рассеянии, имея импульс меньше исходного. Поэтому измеряемое
в опыте по рассеянию лептонов распределение кварков не совпа-
совпадает с исходным, а является так сказать, эффективным распре-
распределением с учетом излучения. Ясно также, что само излучение
происходит за счет возмущения движения кварка рассеянием и
вероятность излучения зависит от передаваемого кварку импуль-
импульса q. Поэтому измеряемые на опыте эффективные распределения:
зависят от Q2 или, как говорят, эволюционируют с изменением Q2.
Вероятность излучения вычислим в следующем разделе, здесь
же воспользуемся лишь тем результатом, что эта вероятность
логарифмически зависит от Q2. Именно, вероятность того, что-
из-за излучения глюона кварк при рассеянии имеет.импульс, со-
составляющий долю z начального, можно записать в виде
dw=(asi2n)P,,<l(z)dzlnQ2, A5.33>
где Рчч{г)—так называемая функция расщепления (splitting
function), явный вид которой будет найден в следующем разделе.
Подчеркнем, что речь идет все время о продольном по отноше-
24»
яию к исходному импульсе. Поперечные импульсы при излучении
малы: Px2<Q2<^Pii2- Отметим также, что в нашем главном лога-
логарифмическом приближении несущественно, чем «обезразмери-
шается» Q2 под логарифмом, хотя, разумеется, это интересный
(и сложный) вопрос, который к тому же до сих пор не решен.
Используем формулу A5.33) для того, чтобы сравнить резуль-
результаты измерения эффективного кваркового распределения q(x, Q2)
три <?2 и при Q2+dQ2. Различие q(x, Q2) в этих двух случаях
«описывается соотношением
^y Q2)- о5-34)
Здесь подставлена эффективная константа связи a,(Q2), так как
различие кварковых распределений обусловлено лишь испускани-
испусканием глюонов с поперечными импульсами порядка Q2. Вклад из-
излучения глюонов с р^-^.02 сокращается <ъ разности q(x, Q2 +
+dQ*)-q(x, Q2).
\
\
,.,_^ B
Ptac. 15.5
Формула A5.34), вооб-
вообще говоря, неполная: в ней ^G6: \
отсутствует вклад процесса, \
¦обратного рассмотренному. ? "* L ¦^¦—6
Именно, кварки, участвую-
участвующие в рассеянии, могут Рис. 15.6
возникнуть также из-за превращения в кварк-антикварковые па-
пары партонов-глюонов, имеющихся в начальном состоянии, т. е.
за счет процессов типа изображенного на рис. 15.5 (напомним,
что волнистой линией обозначен виртуальный фотон или W-бо-
зон). Поэтому если так же, как в A5.33), ввести функцию рас-
расщепления P<,g{z), которая описывает возникающую за счет этого
процесса вероятность найти вместо глюона с импульсом р кварк
с импульсом zp, то полную формулу для эволюции q(x, Q2) сле-
следует записать в виде
Oidq(x, Q')_
1
=«И0!) С dy Тр | х_\ q (y> Q2) +pfl0 {Х1у) q {yt Q2)l (i 5.35)
X
где G(x, Q2)—распределение глюонов.
250
Ясно, что для того, чтобы замкнуть эволюционные уравнения
сюда следует добавить закон эволюции распределения G(x, Q2):
Q2)}, 05.36)
где pGq(x) и Pee(z) — функции расщепления, отвечающие про-
процессам, изображенным на рис. 15.6.
На рис. 15.6 волнистые линии обозначают (фиктивный) проб-
пробник глюонного распределения (а не фотоны или ТР-бозоны, по
отношению к которым глюоны нейтральны). Отсутствие простых
пробников глюонов в природе не означает, что глюонное распре-
распределение G(x, Q2) вовсе неизмеримо. Так, фоторождение и лепто-
рождение тяжелых кварков чувствительно к этому распределе-
распределению. Для обсуждения эволюции G(x, Q2) удобно считать, что
каким-либо образом введен фиктивный пробник глюонов. (Явный
вид взаимодействия глюонов с этим пробником нам не потребует-
потребуется.)
Эволюционные уравнения A5.35) и A5.36) называют уравне-
уравнениями Альтарелли—Паризи [15.13]. С их помощью легко найти
асимптотическое поведение моментов кварковых и глюонных рас-
распределений:
1 1
MM (Q2) = J dxx^q (х, Q2); Л*<°> (Q2) = f dxx«-'G (x, Q2).
о о
Интегрируя обе части уравнений A5.35) и A5.36) с весом Xя'1,
переставив порядок интегрирования в правых частях и переходя
к переменным у и z=x/y, находим
A5.37)
Где матрицу
(Чп)ва 2 V dzz^PBA (z) A5.38)
oJ
{А, В означают q или G), очевидно, естественно назвать матри-
матрицей аномальных размерностей,
Чтобы решить уравнения A5.37), следует подставить в них
явную зависимость а, от Q2: a,(Q2) =4я/Ып (Q2/A2). В матрич-
матричной записи решение имеет вид
A5.39)
что совпадает с поведением A5.32), которое мы ранее аргументи-
аргументировали на основе операторного формализма.
251
15.6. Вычисление функций РВА (z)
и аномальных размерностей
Вычисление вероятностей расщепления партонов удобно про-
проводить не с помощью фейнмановских графиков, а по обычной
нековариантной теории возмущений квантовой механики (в тео-
теории поля это называется старой или гайтлеровской теорией воз-
возмущений). Это связано с тем, что
в одном фейнмановском графике
содержатся, как правило, процессы
с разной упорядоченностью по вре-
времени. Например, фейнмановскому
графику рис. 15.7 отвечают два
гайтлеровских, в которых имеется
направление оси времени (справа
Рис. 15.7 налево) (рис. 15.8). Первый иа
графиков рис. 15.8 отвечает излу-
излучению глюона до рассеяния, а второй — рождению пары (проб-
(пробником кварков) и последующей аннигиляции антикварка с на-
начальным кварком в глюон. Главную логарифмическую зависи-
зависимость от Q2 дает лишь первый график, и поэтому удобно сразу
перейти к гайтлеровским диаграммам и только этот график к
рассматривать.
Рис 15.8
Вычислим сначала функцию Рт(г) при z<l, т. е. когда кварк
рассеивается на пробнике, имея импульс меньше начального (в от-
отличие от случая z=l, когда глюон уносит бесконечно малый им-
импульс). При этом из рассмотрения выпадают диаграммы с излу-
излучением глюона кварком после рассеяния (которые, вообще гово-
говоря, необходимо рассматривать при z=l, наряду с графиками
рис. 15.8, чтобы обеспечить калибровочную инвариантность).
Рассмотрим амплитуду процесса, изображаемого первым гра-
графиком на рис. 15.8. Согласно теории возмущений квантовой ме-
механики эта амплитуда имеет вид:
-En), A5.40)
где Vnt — матричный элемент гамильтониана кварк-глюонного
взаимодействия между начальным состоянием i— |кварк> и про-
252
межуточным |/г> = |кварк+глюон>; V/n'— матричный элемент
гамильтониана взаимодействия с пробником (фотоном или W-бо-
зоном) между состояниями промежуточного и конечного кварка;
Е{, Еп — энергия соответствующих состояний. В квантовой меха-
механике теория возмущений строится над собственными состояниями
невозмущенного гамильтониана, которым являются в данном слу-
случае свободные частицы на массовой поверхности. Поэтому для
внешних и внутренних линий в гайтлеровских диаграммах выпол-
выполняется соотношение
Также в каждой вершине сохраняется импульс, но ие энергия. По-
Поэтому в A5.40) знаменатель не обращается в нуль. Вычислим его
в первую очередь.
Обозначим энергию начального кварка Е. Тогда его 3-импульс
можно записать в виде р=(Е, 0, 0) (массами кварков пренебре-
пренебрегаем). Трехмерный импульс кварка в промежуточном состоянии
запишем в виде Pi=(z?', рх), а глюона: к=(A—z)E, —р±). Тог-
Тогда энергии промежуточного кварка и глюона находятся из усло-
условия A5.41) (т=0):ш
откуда находим знаменатель в A5.40):
?,_?„= _p2±/2?z(l-z). A5.43)
Сумма в A5.40) означает суммирование по поляризациям
промежуточного кварка и интегрирование по его фазовому объ-
объему <Рр\1Bп)г. Это интегрирование, однако, снимается fi-функ-
цией, обеспечивающей сохранение 3-импульса, так что остается
лишь сумма по поляризациям. Для вклада обсуждаемого процес-
процесса в вероятность рассеяния на пробнике, используя A5.43), по-
получаем выражение
Bя)'2со' (">•'**)
где сумма относится к спиновым переменным, опущены индексы
у V и для наглядности модифицировано обозначение матричного
элемента V. Появление множителя 2Е2Е\ (а также 2со) в зна-
знаменателе обусловлено желанием сохранить релятивистскую нор-
нормировку матричных элементов V и V, которая отвечает волновым
•функциям частиц, нормированным на 2Е частиц в единичном
объеме.
Через введенные выше переменные элемент интегрирования в
A5.44) выражается следующим образом:
^й/BяK2со^A/ 16л2) dp\dzl(\ — z). A5.45)
'Поскольку мы не интересуемся спиновыми эффектами, квадрат
«суммы по поляризациям произведений матричных элементов в
253
A5.44) заменим произведением | V |21 V(q-+q + G) |2, где черта
означает суммирование по поляризациям конечного кварка и усред-
усреднение по спину начального кварка. С учетом этого замечания и
A5.45) выражение A5.44) можно переписать в виде
jfe-gl. A5.46)
Следующее замечание состоит в том, что при вычислении мат-
матричного элемента V следует учитывать лишь физические поля-
поляризации глюона (только они входят в невозмущенный гамильто-
гамильтониан). Легко понять поэтому, что матричный элемент V(q-*q+)
+ G) исчезает при pj_=O, так как при этом глюон испускается
параллельно импульсу р и ток перехода в этом случае также про-
пропорционален р. С другой стороны, физические поляризации глюо-
глюона ортогональны его импульсу и, следовательно, току перехода.
По этой причине выражение, стоящее в скобках в A5.46), конеч-
конечно при pj.8-*^). Его нетрудно найти явно:
~??- ?- < age > i
где а?—поляризационная амплитуда глюона; §2/4я=а/, %а—цве-
%а—цветовые матрицы Гелл-Мана. Для физических поляризаций глюона
матрица плотности < а«а* > —чисто пространственная:
<в«в{>«в«(вм-А1А*/к8); eg-O, A5.48)
и ее подстановка в A5.47) дает
^р A5.49>
(напомним, что ЯаЯа=A6/3)- /). Отсюда
2
^lV^g- iт=7dz-^-. A5.50»
Матричный элемент V зависит, вообще говоря, от р^_. Однако,,
имея в виду лишь логарифмическую точность, можно пренебречь
этой зависимостью при р2± ^ Q2 и обрезать интегрирование по р^
сверху при р^—Q2. В результате приходим к выражению
dW^JW^dw, A5.51)
где dw определяется формулой A5.33) с функцией Pqq(z), имею-
имеющей следующий явный вид:
Ряя{г)=\±±?-, г<\. A5.52)
Ясно, что формула A5.51) допускает использованную в пре-
предыдущем разделе интерпретацию dw как дифференциала вероят-
вероятности расщепления кварка с импульсом р на кварк с импульсом
zp и глюон с импульсом A—z)p.
254
Функция расщепления Pe<,(z) при z>0 получается очевидным
образом заменой z-»-(l—z) в формуле A5.52):
/>OvB)=PM(l-z)=D/3)[l + (l-zJ]/z. A5.53>
Формулы для функций расщепления PqG{z) и Pgg(z) при
получается тем же методом из вершин G-+q-\-~q и
Например,
а* Р /,\_ ! gU-g)l^(G
Явные выражения имеют вид:
+* Az)], 2<1. A5.54>
Прямое вычисление функций расщепления при z=l требует
рассмотрения диаграмм, описывающих поправки к волновой функ-
функции кварка и к вершине его взаимодействия с №-бозоном или е-
фотоном за счет не только реальных глюонов, но также и вирту-
виртуальных. Вклад этих диаграмм сокращает бесконечность в приве-
приведенных выше функциях расщепления, возникающую за счет ис-
испускания мягких глюонов (при z-И) либо при z-*-l). Паризи иг
Альтарелли нашли способ, позволяющий избежать этих вычис-
вычислений, основанный иа законах сохранения, которые должны вы-
выполняться при перераспределении кварков и глюонов по импуль-
импульсам.
Первым из таких законов сохранения рассмотрим сохранение-
фермионного числа (или закон сохранения заряда) при расщеп-
расщеплении кварка на кварк и глюон. Этот закон означает, что в ре-
результате расщепления кварка на кварк и глюон число кварков не-
неизменяется:
Jef(«)—0. A5.55>
о.
Это соотношение означает, что сколько вероятности нахождения
кварка прибавилось в области г<1, столько же следует вычесть,
при z=V. Выражение A5.52) для Р„(г) сингулярно при z=lr
поэтому его надо каким-либо образом регуляризировать, чтобы
выполнялось соотношение A5.55). Паризи и Альтарелли ввели
функцию 1/A—z)+, определенную так, что для любой регуляр-
регулярной функции f(z)
о
В терминах этой функции выражение для Ря,(г), удовлетворяю-
удовлетворяющее A5.55) и совпадающее с A5.52) при г<\, можно записать
1 При г=1 функция Pqq(z) не является положительно определенной н в.
действительности отрицательна [вида—абA— г)].
255.
в виде
доопределяющем Pgg(z) при z=l.
Ф P() РЛг)
рдщ gg() р
Функции P&(z) и РвЛг) регулярны, при z=l и доопределения
яе требуют, a Pce(z) доопределяется с помощью условия сохране-
сохранения полного импульса при расщеплении глюона, т. е. в процессах
<l-+q+q и G^-G+G:
1
^ flfez [Яоо (z) +2п,Рда (z)] — 0, A5.58)
о
где Лу—число сортов кварков с массами /ra/<?Q2. (Множитель 2tij
при втором слагаемом возникает из-за учета кварков и антиквар-
антикварков всех существенных сортов.) Удовлетворяющее этому условию
выражение для Pgg(z) имеет вид
(^-^)S(l-z). A5.59)
Интересно заметить, что коэффициент при fi-функции в этом
выражении равен половине коэффициента Ь в функции Гелл-Ма-
на—Лоу в КХД. Этот факт имеет свое объяснение, однако его об-
обсуждение увело бы в сторону от основного изложения.
Приведем в заключение выражения для аномальных размер-
размерностей A5.38), которые получаются интегрированием приведенных
выше выражений для PBa(z) [при интегрировании 1/A—z) +
следует использовать правило A5.56)]:
A5.60)
/-2
15.7. Применение логарифмической теории
к наблюдаемым процессам
Феноменология глубоконеупругих процессов, к которой можно
применить формулы предыдущих двух параграфов, весьма об-
обширна. Здесь приведем лишь несколько примеров такого приме-
применения.
Наиболее просто выглядят предсказания для моментов так
называемых несинглетных функций. Этим термином называют та-
такие комбинации кварковых распределений, в которые не дает
вклад расщепление глюонов на кварки. Эволюция таких функ-
256
ций описывается одним только уравнением A5.34). Примером
функции такого рода может служить разность и(х)—d(x). Второй
момент этой разности определяет разность сечений рассеяния
нейтрино за счет заряженного тока на нейтроне и на протоне:
d (х)] xdx—^Mlr** (Q2) A5.61)
1индекс (n—s) означает «несинг летный»]. Эволюция несинг летных
моментов с изменением Q2 определяется аномальными размерно-
размерностями Yjjv. Согласно A5.60) при л=2 ^=32/9, поэтому в асимп-
асимптотике следует ожидать поведения
^""^(Q^ — ^nQ2)2781. A5.62)
Поскольку средние значения Q2 в нейтринных реакциях про-
пропорциональны s=*2mNEy, из асимптотики A5.62) следует, что при
высокой энергии отношение разности полных сечений vp- и
vn-реакций к энергии нейтрино логарифмически ладает:
{o™—o*p)/Ev~(lnE)-32'*\ A5.63)
В реальных условиях соотношение A5.36) не очень удобно,
так как статистика данных по взаимодействию нейтрино с водо-
водородной и дейтериевой мишенями недостаточно велика, чтобы
уловить слабую логарифмическую зависимость A5.63). Для экс-
экспериментаторов более удобно изучение моментов структурной
функции F3 для «среднего» нуклона. [Согласно A5.19), F3— не-
синглетная функция.] Наблюдаемая на опыте зависимость мо-
моментов этой функции от Q2 хорошо согласуется с предсказаниями
логарифмической теории.
В качестве примера расчета поведения моментов функций, в
которые дает вклад процесс расщепления глюона, рассмотрим
предсказания для асимптотики вторых моментов распределений
q(x)=u(x)+d(x) и q(x)=u(x)+3(x), которые согласно форму-
формулам A5.20) определяют полное сечение взаимодействия нейтрино
и антинейтрино со средним нуклоном (тяжелым ядром). Обозна-
Обозначим
1 1
М2=§ dxx[u(x)+d(x)]; M2=J
\ ' \ \ A5-64)
М\=I dx х [s (x)+s (x)]; М°=J dx xG (x).
о о
17—679 257
Из формул A5.60) для аномальных размерностей при га = 2
находим систему эволюционных уравнений для этих моментов;
~М2~\
М2
м2
4я
32/9 0 0 —2/3"
О 32/9 0 —2/3
О 0 32/9 —2/3
-32/9 —32/9 —32/9 2
•м2
М2
Ml
A5.65)
Распределения s-кварков необходимо включить в рассмотре-
рассмотрение, так как глюоны «утекают» также в пары s+s. Отметим,,
что элементы матрицы в A5.65), стоящие в последнем столбце
(кроме Tee)i вдвое больше значения, даваемого формулой A5.60)
для yqG при п=2. Это происходит потому, что в каждый из квар-
ковых моментов в A5.64) входят две функции распределения, и.
следует учесть вклад расщепления глюона в каждую из них.
Рассмотрим сначала следующие из A5.65) связанные уравне*
ния для суммы
A5.66)
и
П2 а (Мр<\ q,(Q») / 32/9 -2\(Mq2+
QW\M? Г 45Г-1-32/9 2){м?
Из определений очевидно, что М2+я есть доля импульса ну-
нуклона, содержащегося в кварках, а-Л*?—доля импульса, несомого»
глюонами. Поэтому неудивительно, что из уравнений A5.67) следует
независимость суммы М2+ч +М2 от перераспределений импульса
между кварками и глюонами: 5gr(^+* +M$)=0. Более того,
поскольку здесь систематически пренебрегаем вкладом тяжелых
кварков, эта сумма должна равняться единице при всех Q2:
Mq2+V+M2=\. A5.68)
Общее решение уравнений A5.67) можно записать в виде
2+32/9
2+32/9
A5.69)
258
{здесь использован тот факт, что начальные условия при Q2=fi2
должны удовлетворять соотношению A5.68)]. Отсюда видно, что
каковы бы ни_были начальные моменты AfjOi2), асимптотические
значения Мф* и М° составляют 9/25 и 16/25, однако приближе-
приближение к асимптотике крайне медленное.
По данным различных экспериментов при Q2«5-*-20 ГэВ2 зна-
значения моментов группируются около
-М2^0,44; Л*2^М2^0,04, A5.70)
так что Жг+*—0,52, и видно, что изучаемая в настоящее время
область значений Q2 еще далека от асимптотической.
Общее решение уравнений A5.65) не очень наглядно, поэтому
ограничимся тем, что приведем в следующем разделе решение
при некоторых специальных начальных условиях. Здесь лишь
отметим, что асимптотика общего решения отвечает равномерному
распределению доли импульса Ml+q по всем кваркам и анти-
антикваркам:
Ж2=ЛГ2=Л^ = A/3)М2+?=3/25, Q2-*oo, A5.71)
откуда также видно, что значения A5.70) весьма далеки от асим-
асимптотических. Эффекты приближения к асимптотике можно наблю-
наблюдать иа опыте. Так, одним из следствий равнораспределения.
A5.71) является равенство сечений взаимодействия нейтрино и.
антинейтрино с нуклоном [см. формулы A5.20)]. Поэтому прибли-
приближение к асимптотике должно выражаться в медленном росте
отношения <pN I<PN с энергией, который и наблюдается в нейтрин-
нейтринных экспериментах.
15.8. Модель валентных кварков
При обсуждении в гл. 14 матричных элементов кварковых
операторов по адронным состояниям мы воспользовались гипоте-
гипотезой, что если точка нормировки операторов т отвечает as(m) = l,
то матричные элементы можно оценивать, считая, что в адроне
имеются лишь те кварки, из которых он состоит в смысле наив-
наивной кварковой модели (валентные кварки). Здесь мы применим
эту гипотезу, чтобы оценить моменты Мъ При этом сравнение с
экспериментальными значениями A5.70) может служить допол-
дополнительной проверкой данной гипотезы, которую иногда называют
моделью валентных кварков [15.4].
В терминах эволюционных уравнений Альтарелли—Паризи
модель валентных кварков: означает, что при Q2=m2, as(m2)~l
эффективные распределения всех партонов, кроме и(х, тг) и
d(x, тг), равны нулю, а весь импульс нуклона сосредоточен в и-
17* 259
и ^-кварках:
о
М2 (m2)=Mi (/re2) = Ж? (m2)—0.
Эти соотношения служат начальными условиями для эволюцион-
эволюционных уравнений A5.65) и предполагается, что сами эти уравнения
можно «протянуть» до таких значений т2.
Отметим для связи с операторными методами, что в рамках
операторного формализма, описанного в разд. 15.3 и 15.4, момен-
моментам М2 отвечают соответствующие слагаемые в операторе тензо-
тензора энергии-импульса в КХД:
A5.73)
При этом модель валентных кварков отвечает предположению,
что в точке нормировки ц=т лишь слагаемые с и- и ^-кварками
имеют ненулевое среднее по нуклону:
2pv.pvUNuN з= < N | Guv IN ) =
= (N\ uiy^D„и + diy^Dyd |N ) , A5.74)
а матричные элементы всех остальных слагаемых в A5.73) равны
нулю.
Решения уравнений A5.65) с начальными условиями A5.62)
имеют вид:
3
A5.75)
где x=as(m2)/a,(Q2) и коэффициент b положен равным 9, имея в
виду обсуждение области значений Q2 порядка 5—20 ГэВ2. В
этой области эффективная константа a,(Q2) равна примерно
a,(Q2)— 0,2. Поэтому если полагать, что начальные условия
A5.72) относятся к точке as(m2)«l, то х^*5, и при таком значе-
значении
М2^0,56; M2=Ms2^0,02; M°^0,4O, A5.76)
что качественно согласуется с наблюдаемыми на опыте значения-
значениями моментов A5.70). Количественно согласие оставляет желать
лучшего, однако напомним, что значения A5.76) получены в ло-
логарифмической теории, которая не учитывает ни следующих (не-
(нелогарифмических) поправок теории возмущений, ни степенных
2
по Afzap/Q2 поправок, возникающих из-за операторов высших
твистов.
260
Любопытно отметить, что, если считать, что начальные усло-
условия A5.72) относятся к точке а,(т2), отвечающей а«(т2)^2, т. е.
в формулах A5.75) х^Ю, то для моментов получаются следую-
следующие значения:
М2 = 0,44; M2 = M^0,04; М?=*0,48, A5.77)
которые совпадают с приведенными в A5.70) характерными экс-
экспериментальными значениями. Предсказания для амплитуд не-
лептонн'Ых распадов также приходят в хорошее количественное
соответствие с данными опыта (см. разд. 14.4), если считать, что
кварковые диаграммы воспроизводят матричные элементы квар-
ковых операторов в точке нормировки т такой, что а,С)~2
l[a не at(m2)=*l]. Трудно ожидать, что за этим численным со-
согласием стоят глубокие причины, однако возможно, что и в дру-
других приложениях логарифмическая теория и наивная кварковая
модель, применяемая в точке ая(т2)~2, с хорошей точностью
воспроизводят также вклад неучтенных в эволюционных уравне-
уравнениях членов.
15.9. Процесс Дрелла—Яна. Рождение W-
и Z-бозонов в адронных реакциях
Процессом Дрелла—Яна называют рождение лептонных пар в
столкновениях адронов, например, реакции типа
рр+П+все. A5.78)
При этом, так же как и в глубоконеупругом рассеянии, конечное
адронное состояние не регистрируется, а изучаются лишь инклю-
инклюзивные характеристики лептонной пары. Если отвлечься от по-
поляризационных измерений, то такими характеристиками являют-
являются компоненты полного 4-импульса пары Р. В качестве независи-
независимых переменных принято выбирать инвариантную массу пары
М2=Я2, продольный по отношению к направлению сталкиваю-
сталкивающихся пучков в системе их центра инерции импульс Рл и попереч-
поперечный импульс Рх.
В рамках партонной модели такие процессы естественно опи-
описывать как идущие за счет аннигиляции пары кварков-партонов
из сталкивающихся адронов в пару лептонов. При этом все
остальные лартоны проходят «насквозь» и образуют конечное ад-
адронное состояние. ¦
Найдем выражение для сечения образования лептонной пары
в терминах распределений партонов в начальных адронах. Обо-
Обозначим р\ и р2 импульсы начальных адронов. Квадрат полной
энергии в системе центра инерции есть s= (Pi + p2J^2pip2. Обо-
Обозначим также полное сечение образования лептонной пары с мас-
массой М в столкновении партонов А и В
аАв (М2) = а {АВ -+ II). A5.79)
261
Сохранение 4-импульса в рождении пары партонами означает, что
должно выполняться равенство
x1p1+x2pi=P, A5.80)
где х:р1 и Х2Р2 — импульсы партонов А и В, откуда следует так-
также условие
x1x2s=M2. A5.81)
В этих обозначениях дифференциальное сечение процесса Дрел-
ла—Яна имеет вид
2 \Ai{x1)B2{x^+Aa{xa)В:(Xl)]X
А,В
X оАВ (М2) 6 (xtx2s—Щ dxxdx2dM\ (\ 5.82)
где AU2(x) и BUi(x)—распределения партонов Л и В в первом и
втором сталкивающихся адронах; два слагаемых в квадратных
скобках отвечают тому, что партоны Л и В могут находиться в
каждой из двух начальных частиц, а сумма берется по всем сор-
сортам партонов Л, В, которые могут аннигилировать в пару. Про-
Происхождение множителя 1/3 обусловлено соглашением о том, что
партонное сечение A5.79) вычисляется так, как если бы у квар-
кварков не было цвета. В адронное сечение A5.82) входит усреднен-
усредненное по цвету кварковое сечение (так как адроны бесцветны), по-
последнее же в три раза меньше сечения для бесцветных кварков.
Вероятность того, что кварк найдет из налетающего адрона ан-
антикварк цвета, подходящего для того, чтобы аннигилировать в
бесцветную леитонную пару, составляет 1/3.
Если интересоваться лишь распределением сечения по инва-
инвариантной массе М2, то по остальным переменным в A5.82) сле-
следует проинтегрировать:
Aji X
где x=M2js. Зависимость сечения от Я| выражают обычно
в терминах фейнмановской переменной хр=<2.Р \ lY~s > причем зна-
значения Xi и х2 находят из условий A5.80):
Xi,2=(\l2)[±xF + (x2F+4M2isy2]; хр=хх — хг, A5.84)
или в терминах быстроты у=(И2Iп[(Р0-{-Р^I(Р0— °и)]> пРи
этом хх = ]/гтеу; л^==|/те"у-
В случае у=0 из A5.82) следует:
dM*dy [y=o
262
{именно эту величину часто приводят в экспериментальных ра-
работах).
На опыте до настоящего времени изучают лишь электромаг-
электромагнитный процесс рождения е+е~- или ц+ц~-пар, возникающих за
«чет аннигиляции кварков и антикварков из сталкивающихся ад-
$>онов. Кварковое сечение A5.79) составляет
aq-q(MV)^Q2qbna?iZM\ A5.86)
где Q, —заряд кварка в единицах \е\. Поэтому в рамках пар-
тонной модели на основании приведенных выше формул можно
было бы ожидать, что величина M4da/dM2 (а также ее распреде-
распределение по яр или у) является функцией одного только отношения
т. Однако известно, что взаимодействие в КХД приводит к эво-
эволюции кварковых распределений. В рамках метода Альтарелли—
ТТаризи почти очевидно, что для того, чтобы учесть эволюцию
кварковых распределений в главном логарифмическом приближе-
приближении, следует в приведенных выше формулах заменить партонные
распределения эффективными, измеряемыми при Q2=M2: А(х)-*-
—>-А(х, М2), В(х)->~В(х, М2). Строгое обоснование такой замены
впервые привели Ю. Л. Докшицер, Д. И. Дьяконов и С. И. Троян
1[15.5], которые сделали также предсказания в рамках КХД от-
относительно распределения лептонных пар по поперечному импуль-
импульсу, возникающего за счет испускания глюонов.
Таким образом, имеется возможность, извлекая кварковые
распределения из опытов по глубоконеупругому рассеянию леп-
тонов, предсказывать сечение процесса Дрелла—Яна для нуклон-
ных соударений. С другой стороны, из изучения рождения лептон-
лептонных пар в яЖ-реакциях можно извлекать распределения кварков
"в я-мезонах, для которых невозможны опыты по рассеянию леп-
тонов. К сожалению, экспериментальная ситуация не такова, что-
'бы с хорошей точностью реализовать эту программу, не говоря
уже о том, чтобы уловить логарифмическую зависимость партон-
ных распределений от М2. Скажем, для иллюстрации этой ситуа-
ситуации, что до недавнего времени экспериментальные данные то сог-
согласовывались с наличием цвета у кварков ([коэффициент 1/3 в
A5.82)], то требовали бесцветных кварков, и лишь в последнее
время положение устоялось в пользу цветных кварков. Следует
отметить однако, что хотя опыты по рождению лептонных пар по-
пока еще не позволили количественно проверить КХД, они привели
тс ярким качественным открытиям J/ty- и Т-резонансов, которые
сильно изменили отношение многих к кварковой модели и кванто-
зой хромодинамике, заставив поверить в реальность этих теорий.
С пуском установки со встречными рр-пучками на энергии в
несколько сотен гигаэлектрон-вольт в системе центра инерции
стало возможным наблюдение рождения промежуточных W- и
.Z-бозонов слабого взаимодействия. Сечение рождения этих бозо-
бозонов можно предсказать на основе модели Дрелла—Яна. Так,
рождение №+-бозона происходит в основном за счет аннигиляции
263
сечение которой можно записать в виде
= a (ad-*¦№)*= л V2GM4 (Af2—Mw), A5.87)
где предполагается, что UP-бозон является бесконечно узким ре-
резонансом (учет его ширины приводит к тому, что б-функция за-
заменяется брейт-вигнеровской кривой). Подставляя это сечение в
A5.83), находим для полного сечения рождения №-бозона вы-
выражение
г .
а* = ¦? V2G J Ц- v [и, (jc, А&) d2 (V/ x, Mb) +
+ fc2 (V/*, Ml)dx [x. Ml)]. A5.88)
Если применить эту формулу к рр-столкновениям, то щ(х)=и(х)г
d2(x)=d(x) (распределение антикварков в антипротоне такое же,
как и кварков в протоне), а произведение «2(^1)^1(^2) =
= U(xiK(x2) мало по сравнению с первым слагаемым в A5.88).
В р//-столкновениях индексы 1 и 2 можно опустить, и оба
члена в A5.88) дают одинаковый вклад. Значение ri]/2G/3 равно
6,6-108 см2, а интеграл можно грубо оценить с помощью модель-
модельных параметризаций кварковых распределений. Более подробное
обсуждение характеристик процессов рождения промежуточных
бозонов в рамках такого подхода см. в [15.6]. Здесь же укажем,
что типичное значение интеграла в A5.88) при Ут=*0,1 составляет
примерно 0,4 для рр-реакций и около 0,2 для pp. Поэтому харак-
характерные значения полных сечений — порядка 103 см2.
По предварительным данным, полученным к лету 1983 г. на
рр-коллайдере ЦЕРН, наблюдаемое на опыте сечение рождения
W- и Z-бозонов согласуется с этими теоретическими оценками.
Г лава 16
АННИГИЛЯЦИЯ ПАРЫ е+е~ В АДРОНЫ
16.1. Полное сечение е+е~-аннигиляции
в ц+|я~ и в адроны
Аннигиляция электрона и позитрона в адроны является одним
из наиболее интересных процессов. В настоящее время в мире
работает около десяти ускорителей с встречными е+е--пучками,
перекрывающих область энергий в системе центра инерции от
нескольких сотен мегаэлектрон-вольт до 38 ГэВ, основной зада-
задачей которых является изучение е+е~-аннигиляции в адроны. В тео-
теоретическом плане данная реакция представляет собой в опреде-
определенном смысле простейший адронный процесс и поэтому допу-
допускает весьма глубокое исследование в рамках КХД, включая
эффекты, не описываемые теорией возмущений. В данном разделе
264
рассмотрено вычисление в рамках теории возмущений КХД.
асимптотики полного сечения е+е~-аннигиляции в адроны.
В силу соотношения унитарности полное сечение аннигиляции*
определяется мнимой частью диаграммы, изображенной на-
рис. 16.1, в которой суммирование производится по всем адронным
состояниям X, а пунктир обозначает разрезание по физическим
(т. е. на массовой поверхности) состояниям. Жирные точки на
рис. 16.1 отвечают действию электромагнитного адронного тока
/»(*)=- 2 Qjfix)wf{x). A6.1).
f—a,d,s
где Q/—заряд кварка сорта / в единицах |е| ¦ (напомним, что-
Q«=Qc=Q,=2/3; Q«=Q.=Qb 1/3).
Поскольку суммирование на рис. 16.1 затрагивает только адрон^
ный блок, полное сечение пропорционально мнимой части ампли-
амплитуды вида
Hiiv (?) = - i J exp {iqx) < 01 Г (Ум (x) /v @)) 10 > d*x, A6.2>.
где |0>—адронный вакуум (в е+е~-аннигиляции адроны рожда-
рождаются из вакуума электромагнитным током /„). Величину A6.2)"
называют поляризацией вакуума током, /,,(*)•
В силу сохранения электромагнитного тока тензор И»ч(яУ
должен быть ортогонален 4-импульсу q, поэтому амплитуда A6.2)"
определяется лишь одной скалярной функцией P(q2):
A6.3)-
Для неполяризованных е+с~-пучков формула для полного сече^-
ния имеет вид
otot (eV ->адроны)=i^ll Im P (s), A6.4)>
где sssq2 — квадрат полной энергии в системе центра инерции;,
массой электрона везде пренебрегаем. Коэффициент пропорцио-
пропорциональности в последней формуле можно определить непосредствен-
непосредственно из соотношения унитарности или заменив адронный ток /,.
электромагнитным током мюонов \iyp\i и рассмотрев полное сече-
сечение процесса е+е~->-ц+ц~, которое при х^»тц2 составляет
а (е+е~-*- цV)=4jta2/3s. A6.5)
' f
Ряс 16.2
265-
Л1нимая часть мюонного аналога амплитуды A6.2) определяется
графиком рис. 2.11 (см. разд. 2.4) и вычисляется элементарно:
-J
0 \ру# | Г (*0 Ц+ (ftj) > < |Г (fti) Ц+ (ftj) | (TYvH 10 > =
поляр
J rfx2 Sp (ft, + «„) w (*2-«i») Yv = - J 4 (?2 +2»»
и iq) V\4ml/g4 (?4m) A6.6)
«(напомним, что dt2—элемент двухчастичного фазового объема).
^Отсюда
1шР№Ч*") E) = A / 12я)A +2mlIs) /l-4«»/se E-4л?) A6.7)
[0 (д;) — ступенчатая функция Хевисайда].
Сравнивая это выражение яри 5>4т,2 с A6.5), находим ко-
коэффициент пропорциональности в формуле A6.4).
Перейдем теперь к обсуждению адронной величины Il^(q).
Попытаемся вычислить ее в теории возмущений КХД. В низшем
порядке взаимодействие кварков с глюонами отсутствует, и диа-
диаП й 162 (
р р уу
грамма для Пц, имеет вид, приведенный на рис. 16.2 (в петле
распространяются кварк и антикварк сорта f). Поскольку сорта
кварков входят в ток A6.1) аддитивно, достаточно рассмотреть
вклад лишь одного сорта. Выражение для мнимой части графика
:на рис. 16.2 отличается от мюонного аналога A6.7) лишь заме-
заменой щ-*-т, и общим множителем 3Q>2, который возникает из-за
заряда кварка (фактор Q,2) и суммирования в поляризации ва-
вакуума вклада кварков трех цветов (фактор 3). Другими словами,
^коэффициент 3 возникает из-за цветового следа единичной мат-
матрицы в петле в графике на рис. 16.2: Sp(/) =3.
При обсуждении е+е~-аннигиляции в адроны принято говорить
:не об абсолютном значении сечения, а о R(s)—отношении дан-
данного сечения к сечению, определяемому формулой A6.5):
R(s) = Cs/4na2)a (е+е~->адроны). A6.8)
Чтобы иметь представление о реально измеряемом на опыте
-сечении, отметим, что определяемое A6.5) стандартное сечение
стСтанд=4ла2/35~86-10-33 см2/5, A6.9)
где s — квадрат полной энергии, ГэВ2.
Отметим следующее из A6.4) прямое соотношение между
J?(s) nP(s):
R(s)=\2nlmP(s). A6.10)
Таким образом, вычисляемый в низшем порядке КХД вклад квар-
кварков сорта /в R{s) составляет
+ 24-)]/ 1-^-6E-4^) « 3Q2. A6.11)
B)
266
{Здесь обозначение /?/0) отвечает тому, что величина R(s) вычис-
вычислена в низшем порядке теории возмущений.) Для нахождения
полного адронного значения R(s) следует просуммировать Rt
по всем сортам кварков, рождение которых кинематически воз-
возможно при данном s.
Однако на данном уровне рассуждений нет никаких оснований
доверять формуле A6.11) низшего порядка теории возмущений,
так как эффекты высших порядков, а также непертурбативные
явления могут полностью изменить поведение сечения по сравне-
сравнению с A6.11) (и это действительно происходит в области рожде-
рождения адронных резонансов). Особенно опасным представляется
вычисление мнимой части поляризации вакуума, так как при этом
¦считается, что в е+е~-аннигиляции рождаются не адроны, а квар-
кварки, уходящие на бесконечность (т. е. на большие расстояния, на
которых взаимодействие в КХД становится сильным). Поэтому,
чтобы придать смысл предсказнаиям теории возмущений, необхо-
необходимо дополнительное рассмотрение [16.1].
16.2. Оператор поляризации вакуума
в квантовой хромодинамике
Центральным пунктом данного рассуждения является исполь-
использование аналитических свойств оператора поляризации вакуума в
комплексной плоскости q2. Именно, амплитуда Р(Ф) аналитична
в плоскости ф с разрезом при положительных q2, при которых
происходит рождение физических промежуточных состояний, и
для P(q2) справедливо дисперсионное соотношение B.31) с од-
одним вычитанием:
[интеграл берется по всем значениям s, при которых ImP(s)
отлично от нуля]. Воспользовавшись соотношением A6.10), мож-
можно переписать формулу A6.12) в терминах измеряемой на опыте
величины R (s):
Рассмотрим теперь график рис. 16.2 не при физических значе-
значениях q2>0, а, наоборот, при отрицательном q2. При этом величина
P(q2) вещественна, и, как нетрудно убедиться, в фейнмановском
интеграле, отвечающем графику рис. 16.2, доминируют значения
импульсов кварка и антикварка ki и &2. лежащие в пространствен-
пространственно-подобной области и имеющие порядок q2: k^^k^^q2 (при
mt2^.\q2\). Другими словами, в диаграмме рис. 16.2 основную
роль играют расстояния порядка |?2|~1/2, на которых справедлива
теория возмущений КХД с константой a.(q2) малой постольку,
поскольку велико значение | q21.
Формально убедиться в том, что при евклидовых qa поправки
к поляризации вакуума описываются константой a,(q2), можно с
267
помощью уравнения Овсянникова—Каллана—Симанчика (ОКС)
(см. разд. 5.4, 8.1). Действительно, аномальная размерность тока
/„ равна нулю в силу его сохранения, поэтому зависимость от
константы а, входит лишь ъ виде эффективной константы a.(q2)
при реально рассматриваемом импульсе q. Строго говоря, рас-
рассуждение, основанное на уравнении ОКС, справедливо лишь,
если масса кварка мала по сравнению с qz. Для тяжелых квар-
кварков, массы которых существенны, характерные расстояния имеют
порядок 14m/2—q2\~u2. Это обстоятельство легко понять из рас-
рассмотрения графика рис. 16.2.
Отвлекаясь на время от обсуждения поправок по сс„ заметим,
что диаграмму рис. 16.2 можно вычислить как по правилам
Фейнмана, так и с помощью правил разрезания, т. е. по ее мни-
мнимой части с помощью дисперсионного соотношения, совпадающе-
совпадающего по виду с A6.12) или A6.13), но содержащего вместо физиче-
физической величины R(s) формальную величину A6.11). Поскольку
при больших значениях |G2| значение P(q2), вычисленное в низ-
низшем порядке, отличается от истинного на члены порядка a,(q2)*
можно записать (пренебрегая временно массами кварков)
,1fi ..
A6Л4>
Здесь в левую часть входит измеряемая на опыте величина
R$™(s), а в правую — #<°>(s), определяемая формулой A6.11).
Смысл соотношения A6.14) состоит в том, что истинная величина
?ФизE) в среднем совпадает с кварковой R{0)(s) с точностью да
поправок порядка а,. В частности, если в асимптотике при боль-
больших (положительных) s вклад кварка сорта f выходит на кон-
константу (именно такое поведение наблюдается на опыте), то и»
формул A6.11) и A6.14) следует, что эта константа равна 3Q>2:
Поправки порядка а, к этому результаты можно найти, рас-
рассмотрев диаграммы следующего порядка теории возмущений
(рис. 16.3). Здесь пунктирной линией обозначен глюон.
Если заменить кварки мюонами, а глюон — фотоном, то диа-
грамы рис. 16.3 ответят поправке порядка а к мюонной поляри-
поляризации вакуума, которая была вычислена в процессе развития
квантовой электродинамики (подробные вычисления см. в зада-
задаче 4.13 и в книге Швингера [16.2]). При q2^>m/ результат сво-
сводится к тому, что выражение низшего порядка следует
Рис. 16.3
268
умножить на коэффициент
A+За/4я). A6.16)
В КХД отличие состоит в том, что кварк-глюонные вершины вно-
вносят множитель
^Sp?x=4^ A6.17)
^fc™ множителя е*> который имеет место в КЭД. Коэффициент
A6.17) следует еще уменьшить в 3 раза из-за того, что диаграм-
диаграммы рис. 16.3, описывающие поправку, следует сравнить с затравоч-
затравочным графиком рис. 16.2, содержащим Sp(/)=3. Таким образом, в
/?/оП0Правка п0РЯДКа а« получается из A6.16) заменой а-»-
->D/3) а,. Внося эту поправку в A6.15), получаем [16.1]
Rt ®7Z?$ 0 +«,(«)/ * + О Ю)- A6.18)
Отсюда видно, что R,(s) должно приближаться при s-*-oo к пре-
пределу сверху, так как a,(s) логарифмически убывает с ростом s.
16.3. Правила сумм для R(s)
Экспериментальные данные о /?(s) приведены на рис. 16.4.
Из этого графика видно, что ниже yri"=3 ГэВ -вклад а-, й- и
s-кварков выходит на асимптотику, близкую к 3(Q?+Qi*+Q*)=2.
Выше 1/Т~4,5 ГэВ R(s) выходит на асимптотику вклад пар
се, добавляющий к R(s) еще 4/3, а затем при]/1>12 ГэВ добав-
добавляется еще и вклад пар ЪЪ, равный 1/3.
Рис. 16.4
На пороге рождения адронов, содержащих новые сорта квар-
кварков, имеются мощные резонансы: р, со, <р — вблизи порога и, d, s;
/ф, ф'... — вблизи порога ее и Т, Т'... — на пороге ЪЬ. Еестест-
гвенно задать вопрос о применимости формул типа A6.14) для
описания сечения е+е--аннигиляции в этой области. Ответ на
этот вопрос утвердительный, однако для случаев легких (и, d, s)
и очень тяжелых {b, t) кварков соотношение A6.14) не очень ин-
информативно. Проиллюстрируем это соотношение на примере
вклада в R(s) адроиных состояний, содержащих пару се, считая,
что масса с-кварка достаточно велика в том смысле, что
а. Dте2)«; 1 (реально а, Dтс2) =*0,2). Вклад электромагнитного
тока с-кварков в поляризацию вакуума может быть вычислен по
теории возмущений не только при больших евклидовых q2, но и
при |^|<с4тга2, т. е. при q2^0. В этой области q2 поправки опреде-
определяются малой константой <z,Dmc2). Вычисляя по дисперсионному
соотношению n-ю производную P(qz) no q2 при 92=0 и прирав-
приравнивая физическое выражение вычисленному в теории возмуще-
возмущений, находим [9.1, 16.3]:
j'J^l^)]. 0e.I9,
Интеграл в правой части нетрудно вычислить, если воспользо-
воспользоваться явным видом A6.11) для i?@'(s) и перейти к переменной
с
интегрирования v=(l—4mc2/sI/2, которая представляет собой ско-
скорость кварка в системе центра инерции при данном s:
Отсюда находим следующие правила сумм [16.3, 9.1J:
R*K3(s)ds 3(?
A6.21)
где
ОЯ /_ ¦ 1 \ /— 1\1
{1 + О[а^Dт2)]}. A6.22).
В эксперименте вклад тока с-кварков в сечение е+е~-анниги-
ляции проявляется в виде резонансов -ф C,095), i|/ C,684), ф" и
т. д. и континуума пар мезонов DD, FF,..., очарованных барио-
нов и т. д. Правила сумм A6.21) можно рассматривать в различ-
различных аспектах. Можно, сравнивая A6.21) с эксперименталь-
экспериментальными данными при некотором п, например п=\, определить
единственный неизвестный параметр — массу с-кварка; при этом
правила сумм A6.21) с другими значениями п будут предсказы-
предсказывать интегралы от RJ^is). Полученное таким образом значение
тс составляет [16.3, 9.1].
те=1,26±0,01 ГэВ. A6.23)
270
Другим возможным применением правил сумм A6.21) может
служить оценка ширины распада -ф C,095) на пару е+е~. Дейст-
Действительно, с ростом п в интеграле в левой части A6.21) домини-
доминирующим становится низшее физическое сс-состояние — резонанс
•ф C,095). В пределе малой полной ширины брейт-вигнеровскук*
кривую можно заменить б-функцией. При этом вклад резонанса
в R(s) определяется его шириной распада на е+е~ и записывает-
записывается в виде
/?Res(s)=(9n/a2)r(Res->e+O^fiE-M2). A6.24>
Анализ интегралов в левой части A6.21) показывает, что при.
п, равном 3 и 4, вклад резонанса -ф C,095) составляет 85—90%
полного значения интеграла. Поэтому если пренебречь вкладом
высших состояний, то можно записать два равенства
"КГ 4'
из которых можно исключить тс и найти связь между Г(ф-»-е+е~);
и массой ф:
кэВ A6.25>
[здесь мы воспользовались выражением A6.22) для А„]. Оцен-
Оценка A6.25) согласуется с экспериментальным значением ширины
T(i|>->e+e~)=4,8±0,5 кэВ лучше, чем можно было бы ожидать*
поскольку мы пренебрегли как поправками к Л„, так и вкладом
высших состояний в левую часть A6.21). Оказывается однако*
что последние два эффекта практически полностью компенсируют
друг друга и оценка A6.25) остается справедливой и при более
тщательном анализе [16.3, 9.1].
Выше уже говорилось, что смысл правил сумм типа A6.14)
состоит в том, что физическое сечение в среднем совпадает с
кварковым. С этой же точки зрения можно рассматривать прави-
правила сумм A6.21). Именно, интегрально вклад резонансов и физи-
физического континуума в Rc(s) равен вкладу пары кварков се. Дру-
Другими словами, кварковое сечение получается, если «размазать»
резонансы -ф, т|з',... Неудивительно поэтому, что кварковый
(нефизический) порог лежит согласно A6.23) ниже самого лег-
легкого физического сс-состояния — резонанса -ф C,095), так как для
согласования правил сумм A6.21) с разными п следует разма-
размазать резоиансный пик по обе стороны от его центра.
Идея о том, что физические резонансы интегрально отвечают
кварковому сечению, возникла до развития КХД; ее называли ги-
гипотезой дуальности — резонансы дуальны кварковому контину-
континууму. Правила сумм типа A6.14) и A6.21) в КХД придают ду-
дуальности точный смысл, определяя весовую функцию в интеграль-
интегральном соотношении; КХД нозволяет также вычислять поправки к
дуальности.
271-
Поправки в правых частях правил сумм растут с уменьшени-
уменьшением |<72| [в A6.14)] либо с ростом п [в A6.21)]. Это неудиви-
неудивительно, так как если бы, например, интегралы в левой части
A651) при всех п совпадали с кварковыми, то физическое се-
сечение поточечно совпадало бы с кварковым, что, разумеется, не
выполняется на опыте. [Именно рост поправок заставляет огра-
ограничиться в оценке A6.25) рассмотрением соотношения A6.21)
при л=3 и п=4, когда поправки еще малы]. Анализ правил
сумм A6.21) показывает [9.1], что рост поправок теории возму-
возмущений с увеличением п недостаточен для согласования правил
сумм с экспериментом, что приводит к выводу о необходимости
рассмотрения при больших п непертурбативных (т. е. не описы-
описываемых теорией) возмущений КХД эффектов. Эти эффекты (см.
гл. 17) обусловлены нетривиальной структурой вакуума в КХД, и
их учет в правилах сумм для е+е--аннигиляции позволяет извле-
извлекать из сравнения с экспериментом весьма важные характерис-
характеристики вакуумного состояния.
Глава 17
ВАКУУМ И АДРОНЫ В КВАНТОВОЙ ХРОМОДИНАМИКЕ
ВНЕ ТЕОРИИ ВОЗМУЩЕНИЯ
17.1. Частичное сохранение аксиального тока
и кварковый вакуумный конденсат
Рассмотрим некоторые результаты в КХД, выходящие за рам-
рамки теории слабой связи, методы получения которых комбинируют
адронную феноменологию и общие квантово-полевые свойства
КХД. Большое значение при этом имеет изучение основного со-
состояния теории — вакуума, возбуждениями над которым являют-
являются физические адроны.
Наиболее хорошо изученным проявлением непертурбативной
(не описываемой теорией возмущений) структуры вакуума в
КХД является так называемое частичное сохранение аксиального
тока (РСАСI, исследование которого привело еще до развития
КХД к появлению весьма обширной теории мягких я-мезонов (см.,
например, [17.1, 17.2]), результатами которой мы уже пользова-
пользовались в гл. 14.
Чтобы проследить связь РСАС со структурой вакуума, рас-
рассмотрим квантовую хромодинамику в секторе и- и d-кварков,
предполагая, что их массы тпи и гпл можно считать малыми пара-
параметрами. В пределе mu=md имеет место (см. гл. 9) изотопическая
симметрия (электромагнитным взаимодействием пренебрегаем).
^ пределе же mu—md=0 в КХД имеется дополнительная симмет-
симметрия, выражающаяся в сохранении изотриплетного аксиального тока
& О7-1)
1 От английского Partially Conserved Axial Current
272
где в данном случае q обозначает изотопический кварковый дублет
о7-2)
а * — матрщы Паули [по цветовым же переменным в A7.1) и
далее подразумевается суммирование]. _
Изотопические компоненты тока A7.1) ^^ЪУь^Я—^У^Ъ^ и
j^s=dy,iy5u входят в слабое взаимодействие, и матричные элементы
этих операторов измеряются на опыте. Так, из 0-распада нейтрона
известно, что матричный элемент j+s между нейтроном и протоном
< Р | j+51 ./V > содержит выражение
афр iPi) ЪЪи-N (pi) • A7.3)
где 00^1.25 — численная константа, а иР(р), uN(p)—биспинор-
ные амплитуды протона и нейтрона; р\, рг — импульсы нейтрона
и протона соответственно. Выражение A7.3), однако, не по-
поперечно:
где MN — масса нуклона, a q=pi—pi — 4-импульс, передавае-
передаваемый слабым током. К нетривиальным следствиям приводит пред-
предположение (самосогласованное в рамках КХД), что при ти=
=md=0 масса нуклона MN не обращается в нуль. Чтобы согла-
согласовать с сохранением аксиального тока A7.1) выражение A7.3)„
последнее следует принудительно сделать поперечным, т. е. за-
записать (в пределе mu—md—d) вместо A7.3)
(P\j+5\N) ^aoupip^y^ig^—q^^/q^ujvip!). A7.4)
Наличие полюса в этом выражении при ^ = 0 отвечает вкладу
безмассовой частицы, т. е. предположение о том, что М„Ф0 в
пределе mu=m.d—0, приводит к выводу о существовании безмас-
безмассовой в этом пределе частицы. Поскольку аксиальные токи обра-
образуют шотриплет A7.1), безмассоъые частицы также должны образо-
образовывать изотриплет. Таким образом, мы воспроизвели доказательст-
доказательство теоремы Голдстоуна (см. разд. 11.1) для рассматриваемого част-
частного случая. На опыте изотриплет голдстоуновых частиц ассоци-
ассоциируется с изотриплетом я-мезонов, массы которых отличны от
нуля лишь постольку, поскольку отличны от нуля массы и- и
d-кварков. При этом предположение о малости ти и тл эквива-
эквивалентно предположению о малости т„ в масштабе адронных масс.
Формулу A7.4) легко понять из графиков рис. 17.1. Первое сла-
слагаемое в ней отвечает прямому взаимодействию тока с нуклоном
(рис. 17.1,с), а второе — взаимодействию через я-мезонный по-
полюс. При этом константа яЛ^-взаимодействия gnrr я N i у$ - N и
константа перехода аксиального тока в л-мезон fn
<0|У+5(^)|я->=1/п^ A7.5)
18-679 / 273
31 +
N
a)
Рис. 17.1
(<7—импульс я-мезона, а |0>—адронный вакуум) оказываются
связанными соотношением
A7.6)
называемым соотношением Голдбергера—Треймана. На опыте
2
gnK определяют из данных по яЛГ-рассеянию (gnN^n^Hfi), а
/„ — из распада п+-+ц+\ (/„-130 МэВ). Таким образом, соотно-
соотношение A7.6) выполняется с погрешностью не хуже 10%.
То обстоятельство, что масса нуклона конечна при mu, md=Q
и, как следствие, появление безмассовых я-мезонов отвечает спон-
спонтанному нарушению симметрии относительно глобальных изото-
изотопических 75-преобразований:
?-*-exp(lY«"t)?. A7.7)
где ш — произвольный постоянный вектор [именно этой симмет-
симметрии, называемой киральной, соответствует в силу теоремы Не-
тер сохранение аксиального тока A7.1)]. Как мы видели при
изучении хиггсовского механизма, спонтанное нарушение сим-
симметрии связано прежде всего с перестройкой вакуумного со-
состояния, которое становится неинвариантным относительно пре-
преобразований симметрии. Поскольку теория возмущений КХД
¦строится над кирально-инвариантным вакуумом и аксиальный
ток A7.1) сохраняется во всех порядках по константе связи, то
ясно, что в теории возмущений с безмассовыми и- и d-кварками
•отсутствует спонтанное нарушение киральной симметрии, а вместе
с ним и безмассовые я-мезоны и массивные нуклоны. Неинвариант-
Неинвариантность вакуумного состояния видна уже из формулы A7.5). Поучи-
Поучительно проследить ее далее с помощью техники РСАС, считая
пги и md малыми, но отличными от нуля величинами и учитывая
их в первом неисчёзающем порядке.
Умножая соотношение A7.5) на' q^ и пользуясь явным видом
тока Jit5=U4ny5d, получаем < 0\(ma+md)U45d\n) =1/««н .
С другой стороны, стандартная техника мягких я-мезонов [см.,
например, [17.1JJ дает
- 0//-Х 01J d*y6 (Хог-удЦЩ) та (у)), (а (*) Ys<* (¦*))] 10 >
- S)d0
274
где использована редукционная формула
@\fu(x)y5d(x), ф„@)|0 > d4x,
причем /тс2 /ЯФЯ(л:)=<?д(йГ(л:)ъуьи(x))j= -i(ma-\-md)'d{x)y5u(x).
Вакуумный матричный элемент {0\и(х)и(х) -\- d(x)dxfi) не
зависит от х в силу трансляционной инвариантности вакуума.
Таким образом, приходим к соотношению
/>?»-(m« + »*)<0|ee+dtf|0>, A7.8)
которое содержит вакуумное среднее кирально-неивариантного
оператора пи+пй. Отличное от нуля это вакуумное среднее харак-
характеризует степень спонтанного нарушения киральной симметрии в
вакуумном состоянии. Его называют также кварковым вакуумным
конденсатом.
Отметим, что говорить о конкретном численном значении ваку-
вакуумного среднего <0|йи+3#|0> имеет смысл, лишь когда явно ука-
указывается точка нормировки операторов. (Оператор qq имеет ано-
аномальную размерность, сокращающуюся аномальной размерностью
массы в произведении tnjqq.) Вакуумное среднее <0|5«+5d|0>
можно определить независимо от масс и- и d-кварков, сравнивая с
экспериментальными данными правила сумм для е+е~-аннигиляции
в адроны в области р- и ю-резонансов, во многом аналогичные рас-
рассматриваемым в следующем разделе правилам сумм для рожде-
рождения сс-состояний. Результат этого сравнения ¦ [ 17.3] можно предста-
представить так, что в точке нормировке, отвечающей а«(|д.)^1, обсужда-
обсуждаемые вакуумные средние равны
<0|й"и|0> = <0|5cfj0> ^—B20—250 МэВK A7.9)
(первое равенство следует из изотопической симметрии). Отсюда,
в частности, следует i [см. A7.8I], что массы кварков в этой же точ-
точке нормировки составляют
mu+md2*.l0—15 МэВ. A7.10)
17.2. Глюоиный вакуумный конденсат
Отличное от нуля вакуумное среднее кварковых операторов
пи и eld можно представить как результат существования в ваку-
вакууме сильных флуктуации кварковых полей, амплитуды и длины
волн которых определяются инфракрасным массовым парамет-
параметром КХД .МХар Лкхд , не вычисляемым по теории возмущений.
Кварки сильно связаны с глюонами на расстояниях порядка раз-
размеров флуктуации, поэтому можно ожидать, что глюонное поле
также флуктуирует непертурбативным образом.
18* 275
Не располагая способом вычисления характеристик вакуумных
флуктуации, можно попытаться извлечь информацию об их силе,
изучая влияние вакуумных полей на движение кварков на малых
расстояниях. При этом взаимодействие бесцветной системы квар-
кварков с вакуумным глюонным полем тем слабее, чем меньше размер
системы. Действительно, в пределе нулевого размера бесцветная
система не взаимодействует с цветовым глюонным полем. В сле-
следующем приближении появляется цветовой дипольный момент
системы, пропорциональный ее размеру, который взаимодействует
с напряженностью глюонного поля вакуумных флуктуации. Сла-
Слабость взаимодействия с вакуумными флуктуациямй для кварко-
вых систем малых размеров приводит к тому, что в основном ди-
динамика системы описывается теорией возмущений и потому хо-
хорошо определена, а эффекты вакуумных флуктуации проявляются
в виде малых поправок на фоне теории возмущений.
Удобным объектом для изучения влияния глюонных полей на
динамику кварков является поляризация вакуума электромагнит-
электромагнитным током тяжелых с-кварков, для мнимой части которой в физи-
физической области имеются достаточно надежные экспериментальные
данные. В гл. 16 приведены вычисления данной поляризации ва-
вакуума в теории возмущений. Для учета взаимодействия с вакуум-
вакуумными полями пропагатор с-кварка следует заменить пропагато-
ром в случайном (вакуумном) поле. При этом эффекты вакуум-
вакуумных полей в обсуждаемом поляризационном операторе выражают
через их средние характеристики: Этими характеристиками яв-
являются вакуумные средние калибровочно-инвариантных (и пото-
потому, в частности, бесцветных) операторов, построенных из глюон-
глюонных полей. Такие операторы удобно классифицировать по их
канонической размерности. Вакуумное среднее оператора размер-
размерности d порядка Afxapd. где Afxap — непертурбативный инфракрас-
инфракрасный массовый параметр КХД. Как отмечалось в гл. 16, характерные
расстояния в поляризации вакуума током с-кварков при |^2|<
<С4т<:2—порядка Bтс)-1. Поэтому вклад вакуумного среднего
оператора размерности d в этой области значений q3 определяет-
определяется отношением (Afxap/2mc)л. Но поскольку массу с-кварка мож-
можно считать большим параметром, для начала достаточно
ограничиться вкладом оператора наименьшей размерности. Таким
оператором является F2-=F*Jf*v, имеющий сГ= 4 (следующие опе-
операторы имеют d=6, например,F' — f^F^^Fl^).
Имеется несколько способов вычисления вклада в поляриза-
поляризационный оператор вакуумного среднего <O|F*|Q>. Действительно,
так как этот оператор не содержит производных напряженности,
то коэффициент, с которым входит <0|F2|0>, можно вычислить,
рассматривая поляризационный оператор во внешнем поле по-
постоянной напряженности во втором порядке по полю. Приведем
здесь результат вычисления [17.4, 17.5] в терминах введенных в
разд. 16.3 величин Ап, входящих в правила сумм для рождения
сс-состояний в е+е--аннигиляции. С учетом поправки, пропорци-
276
ональной <0|772 jO>, формулу A6.22) следует переписать в виде
О'| (as/n) F* 10
1здесь также введена поправка теории возмущений первого по-
порядка по а,(тс2); численные коэффициенты ап невелики и изме-
изменяются от fli~0,73 до ав^—1,45}. Из этой формулы видно, что
вклад поправки на взаимодействие с вакуумными полями быстро
растет с ростом п. Естественно связать с этой поправкой упомя-
упомянутое в разд. 16.3 расхождение результата теории возмущений в
правилах сумм A6.21) при п>4 с экспериментом, которое также
быстро возрастает с ростом п. Анализ [17.4, 17.5] показывает,
что учет этой поправки действительно улучшает согласие вплоть
до п = 8 при вакуумном среднем
@\{a./n)F*\0) =*C65 МэВL. A7.12)
(Это уточненное значение вакуумного среднего, которое полу-
получается, если учесть также анализ системы Y-резонансов [17.6].)
Оператор а,/72 [точнее, p(as)f2] ренорм-инвариантен (не име-
имеет аномальной размерности — см. разд. 17.3). Поэтому величина
A7.12) является универсальной константой, имеющей фундамен-
фундаментальный смысл непертурбативной плотности энергии вакуума
(см. разд. 17.4).
17.3. Квантовая аномалия
в следе тензора энергии—импульса
Классическое действие чистой теории Янга—Миллса
A7.13)
инвариантно относительно глобального изменения масштаба длины
на множитель Я.. Рассматривая для простоты значение А., беско-
бесконечно мало отличающееся от единицы (l=l-j-g. ?<1), такое пре-
преобразование можно записать в терминах координат Хц и потенциа-
потенциалов А»(х):
xv+xv-tx», АЦх)-+АЦх)+1А?(х) A7.14)
<(напомним, что потенциалы имеют размерность L).
Альтернативно это преобразование можно определить, остав-
оставляя координаты и потенциалы неизменными, но преобразовывая
метрический тензор
^v^(l-2g)^v. A7.15)
При этом необходимо восстановить в выражении для действия
явную зависимость от метрического тензора (при этом следует
различать верхние и нижние лоренцевы индексы). С учетом этой
277
зависимости действие A7.13) записывается в виде
/гя- -A/4) J gWg»'F$Jb'V.}rZ&*x, A7.16)
где g—определитель матрицы g^ (не путать с константой связи!),
a g"*—матрица, обратная g^. Выражение для F^ через потен-
потенциалы А% остается прежним G.39) и не содержит зависимости от
метрического тензора. При преобразовании A7.15) g|lv-»-(l+2g)g|lv>
У — ?->-A—4gyj/—¦#, поэтому действие A7.16) явно инвариантно
относительно данного преобразования.
В общем случае вариация действия при изменении метриче-
метрического тензора определяется тензором энергии-импульса:
б/=A /2) J itoJbp^V^d4* A7.17)
(Данное определение тензора энергии-импульса, а также ковариант-
ную формулировку электродинамики (легко обобщающуюся на
случай общей теории Янга — .Миллса) см., например, в [17.7]).
Из формулы A7.17) видно, что вариация действия при масштабном
преобразовании A7.15) 6g|lv=2gg|Jv определяется следом тензора
8цг:6/=Д iQnvg^V — gd*x, а инвариантность относительно данного
преобразования означает равенство этого следа нулю:
= 0. A7.18)
(После этого экскурса в общековариантный формализм снова
возвратимся к обычным обозначениям в пространстве Минков-
ского и в дальнейшем не будем делать различия между верхними
и нижними индексами).
Инвариантность относительно масштабного ^преобразования,
выражаемую соотношением A7.18), можно сформулировать в
виде утверждения, что в классической теории Янга—Миллса нет
выделенного масштаба длины (или массы). Это свойство сохра-
сохраняется и при введении безмассовых кварков.
Соотношение A7.18), однако, неверно в квантовой теории.
Действительно, утверждение об отсутствии выделенного масшта-
масштаба с учетом всего изложенного выше о перенормировках выгля-
выглядит малоправдоподобным. Мы видели, что из точки нормировки
ц и констаты ?2(ц2) можно образовать характерную для теории
(в частности, для КХД) размерную величину Л [см. формулу
C.32)]. Поэтому в квантовой теории нет инвариантности относи-
относительно изменений масштаба длины, и соотношение A7.18) не
может быть точным операторным равенством.
Чтобы найти правильное выражение для в^, заметим, что из-
изменение масштаба длины в безмассовой теории ненаблюдаемо,
если одновременно с преобразованием A7.14) изменять ультра-
ультрафиолетовый параметр обрезания М : М->-A+1)М при неизменном
затравочном заряде g. Однако вместо того, чтобы изменять пара-
параметр М, можно изменить заряд g. Изменение М на 6М=%М при
278
неизменном затравочном заряде g эквивалентно изменению g3 на
Sg=— 2lg*$(gz) при неизменном М. Таким образом, эффекты
масштабного -преобразования эквивалентны изменению заряда на
22 A7.19)
()
(так как обратное изменение заряда компенсирует изменение масш-
масштаба).
Чтобы проследить за вариацией амплитуд при вариации заря-
заряда, переопределим поле А%. (х), введя a?(x)=*gA$.{x) и <??v(x)=**
^gFlv(x)^dvflSl{x)--d4c^.{x)->rfabcal(x)(?l(x). При этом лагран-
лагранжиан чистой теории Янга—Миллса переписывается в виде
/™= _ J A !4g*)9-b9bvd*x. A7.20)
Заметим, что SFp? не зависит от g явно, а также что в тер-
терминах полей а/ ковариантная производная также не зависит яв-
явно от g, поэтому явной зависимости от g нет и во всех членах,
описывающих спинорные поля. Сравнивая вариацию действия в
форме A7.20) при изменении g2 вида A7.19) с A7.17), находим:
x). A7.21)
Это и есть искомое выражение для 8„, в безмассовой теории
J17.8]. В теории с массивными кварками к A7.21) добавляются
обычные неаномальные слагаемые, так что полное выражение
имеет вид
8W - A /2)Р (g*)Fb (x)FZv {x) + 2 ™flflt> A7.22)
f
где сумма берется по всем сортам кварков.
В разд. 8.1 было показано, что аномальная размерность сохра-
сохраняющегося тензора, в частности в„», равна нулю. Отсюда следует,
что входящие в правую часть A7.22) операторы имеют нулевую
аномальную размерность.
Выражение A7.22) обладает следующей интересной особен-
особенностью. По смыслу приведенного выше рассуждения аномалия в
в„, возникает из вариации ультрафиолетового параметра обреза-
дия, по сравнению с которым массы всех кварков малы. Поэто-
Поэтому в р-функцию в A7.22) входит экранирующий вклад произволь-
произвольно тяжелых кварков. Рассмотрим матричный элемент оператора
A7.22) по состоянию с характерными импульсами, малыми по
сравнению с массой какого-либо из тяжелых кварков (обозначим
временно этот кварк Q). Такое состояние не содержит Q-кварков,
поэтому оператор, отвечающий вкладу Q в неаномальную часть
6да, т. е. mQQQ, дает вклад в матричных элемент лишь когда
рождаемые им кварки снова аннигилируют через время порядка
1/тс. «По пути» Q-кварки могут провзаимодействовать с глюона-
ми, что и приводит к отличному от нуля вкладу оператора mQQQ.
'Описанный механизм отвечает замене оператора m^QQ по отно-
279
шению к состояниям с характерными импульсами p<mQ беско-
бесконечным рядом глюонных операторов. Калибровочно-инвариантным
глюонным оператором наименьшей размерности (см. разд. 17.2)
является оператор Я. Вклады операторов более высокой размер-
размерности подавляются лишними степенями отношения (o/mcR По-
Поэтому можно записать
< Ь|mQQQIa )=С(Ь\F*\a > A + О(р2//^)), A7.23)
где коэффициент С не зависит от низкоэнергетических состояний
а и Ь. Этот коэффициент легко найти, рассматривая, например,
случай, когда а и Ь — одноглюонные
состояния. В этом случае коэффици-
ент С находится в низшем порядке по
а, из графика рис. 17.2:
-1 С= а,/12я. A7.24)
Подставляя этот коэффициент в фор-
мулу A7.23) и сравнивая с экраниру-
экранирующим вкладом кварка в однопетле-
Рнс. 17.2 ву10 Р-функцию, убеждаемся в том,
что неаномальное слагаемое mQQQ в
вда сокращает в данном порядке часть аномального члена, обуслов-
обусловленную вкладом данного тяжелого кварка в Р-функцию. Это со-
сокращение может быть прослежено во всех порядках по а,.
Таким образом, при вычислении матричного элемента бцц по
состояниям с характерными импульсами /?хар в аномальном слагае-
слагаемом в A7.22) можно оставить вклад в р-функцию лишь кварков
с массой /Гс/^рхар и только эти кварки учитывать в сумме
В заключение отметим, что аномалия в бцц—не единственный
пример такого рода. Более широко известна аномалия в дивер-
дивергенции аксиального тока (см., например, в [17.2]), которая,
в частности, приводит к тому, что в пределе та=та=0 изото-
пически синглетный аксиальный ток y^aYnYsK+^YnYs^ B кван-
квантовой хромодинамике не сохраняется (вопреки наивному ожида-
ожиданию): dv.jl = (as/4a)ev.v^aFS.vFxa-
Общая причина возникновения аномалий состоит в том, что
симметрия классического лагранжиана не может поддерживаться
при регуляризации, необходимой для обращения с расходимостя-
ми в квантовой теории.
17.4. Непертурбативная плотность энергии вакуума
и проблема невылетания
Вакуумное среднее оператора бцц представляет особый интерес
ввиду того, что оно определяет плотность энергии вакуума.
Действительно, в силу лоренц-инвариантности вакуума среднее
280
тензора энергии-импульса может выражаться только через метри-
метрический тензор: <0(euv|0> =eg,jv (коэффициент пропорциональ-
пропорциональности здесь равен плотности энергии е ввиду равенства
< 01 Boo 10 > =е). Поэтому
< 01 Эдм 10 > =4е. A7.25)
При вычислении вакуумного матричного элемента оператора
», определяемого формулой A7.22), мы сохраним согласно об-
обсуждению в предыдущем разделе вклад в A7.22) лишь легких и-,
d- и 5-кварков, так что P(g2)=—9<х./Dя)+О(«.»).
Согласно A7.22) и A7.25)
+ A /4) < 01m~uu+mjtd+msls10 >. A7.26)
Первое слагаемое здесь определяется вакуумным средним A7.12).
Вакуумные средние полей и- и cf-кварков оцениваем по форму-
формуле A7.8): < 01 mauu+mddd10 ) =A /2){та+та) < 0 fuu+dd\ 0 > =
= — Рят?к12, а вклад s-кварков можно оценить из аналога фор-
формулы A7.8) для /Г-мезонов: (ma+ms) ( 0|ии+?$|0 > =—/|л&.
Если_ для_ оценки положиться на SU (З)-симметрию и записать:
~@'\~iiu-{- ss j 0 > =*2 < 0 fss j 0 > ; /к—/«, то для вклада кварковых
операторов
A/4) < 01 т.Jut+mjid+m^ss \ 0 > ^ — (/?/8) {ml+т2к),
т. е. это величина существенно меньшая, чем первое слагаемое в
A7.26). В результате для е получаем оценку
еы— B65 МэВ)«. A7.27)
В связи с вышесказанным естественно задать вопрос: что яв-
является началом отсчета для только что оцененной величины 8.
Для ответа на этот вопрос заметим, что выражение A7.22) для
в„, требует доопределения. Именно, если вычислять диагональный
матричный элемент, например, оператора f?(je) по какому-либо
состоянию в теории возмущений (в частности, по вакууму), то
возникает бесконечный расходящийся вклад от графиков, в кото-
которых глюоны из оператора F9 аннигилируют друг с другом, ие
взаимодействуя ни с какими внешними частицами (такой же бес-
бесконечный вклад возникает из операторов mqq, когда кварки из
оператора взаимно аннигилируют, не взаимодействуя с внешними
полями). Этот бесконечный вклад не зависит от.того, по какому
состоянию вычисляется матричный элемент, и, следовательно,
сокращается во всех физических амплитудах. Физической яв-
является лишь разность между полным матричным элементом и
этой расходящейся частью. С другой стороны, расходящаяся
часть в б„, связана с энергией вакуума в теории возмущений.
19-679 281
(В теории возмущений полное вакуумное среднее в„, совпадает
с обсуждаемым расходящимся вкладом, так как в вакууме нет
«внешних» частиц.) Поэтому началом отсчета для найденной^ вы-_
б
рии возмущений, и сама величина s имеет смысл непертурбатив-
в5ГБ
щБш^яя-анерхии_вакухмаг
Естественно полагать, что отрицательное значение е связано с
тем, что крупномасштабные непертурбативные флуктуации полей
глюовов и легких кварков в вакууме КХД понижают энергию, по
сравнению с ее значением в теории возмущений. Также можно
ожидать, что собственные глюонные поля кварков в адроие частич-
частично подавляют непертурбативные флуктуации поля внутри адрона,
т. е. что «вакуум» внутри адрона ближе к теории возмущений, чем
вакуум вне адрона (это свойство можно качественно проследить
на модельных примерах, в частности, для бесконечно тяжелых
кварков, однако детальное обсуждение этих примеров требует
введения новых понятий и увело бы нас в сторону от линии изло-
изложения). Таким образом, кваркам и их глюонным полям энергети-
энергетически невыгодно занимать большой объем. Отсюда, как кажется,
недалеко до понимания (на качественном уровне) картины невы-
летання цветных объектов. Действительно, глюонное поле изоли-
изолированного цветного объекта, например кварка, как можно пола-
полагать, основываясь на аналогии с кулоновским полем электриче-
электрического заряда, простирается до бесконечности и поэтому занимает
бесконечный объем, и в принципе не исключено, что за счет по-
подавления непертурбативных флуктуации цветным полем энергия
такой конфигурации бесконечна (что и означает невозможность
образования изолированного цветного объекта). Однако последо-
последовательное рассмотрение данной ситуации в рамках исходных
принципов КХД отсутствует.
В описании спектра бесцветных адронов пользуются популяр-
популярностью феноменологические модели, возникшие до того, как бы-
была определена величина е, и использующие гипотезу о существо-
существовании некоторой положительной (по отношению к внешнему ва-
вакууму) объемной энергии в области, занятой полями кварков.
Речь идет, о так называемых моделях мешков и моделях струн.
Согласно первой из них адрон представляется сферической по-
полостью (мешком) радиусом R, в которой «заперты» кварки. Пред-
Предполагается, что внутри мешка кварки движутся как свободные,
а запирание обеспечивается соответствующим граничным услови-
условием. Для безмассовых кварков масса адрона складывается из
объемной энергии мешка 4яВ?3/3, где В — избыток плотности
энергии «вакуума» внутри адрона по отношению к внешнему ва-
вакууму, и из кинетической энергии кварков nx/R, где п — число
кварков в адроне (п равно 3 для барионов и 2 для мезонов), а
х — безразмерный фактор, зависящий от радиальных и орбиталь-
орбитальных чисел движения кварков в полости (значения х в каждом
конкретном случае получаются из решения свободного уравнения
Дирака с граничным условием на краю мешка, для основного
282
S-состояния лс=2,04). Радиус адрона Я и его масса М получают-
получаются минимизацией полной энергии
A7.28>
М=D/Щ4пВ)т{пх)т. (П.29}
Сравнение носледней формулы с массами адронов, состоящих из
и- и d-кварков (р-, to-мезонов, нуклона, Д-резонанса), позволяет
оценить величину В: В** A004-120 МэВ)*. Если сравнить эту
оценку с оценкой величины в A7.27), то видно, что В<еи непер-
турбативные флуктуации внутри адрона подавляются весьма
слабо.
Мы изложили здесь лишь основную идею модели мешков в
связи с оценкой величины е, опустив ее дальнейшее развитие, свя-
связанное с введением дополнительных членов в выражение A7.28) Т
предназначенных для улучшения согласия модели со спектром на^
блюдаемых адронов, объяснения спиновых эффектов и т. д. Не-
Неясно, насколько имеет смысл уточнять данную модель, так как
само предположение о резком крае полости, по-видимому, являет-
является весьма грубым приближением (более вероятным представляет-
представляется плавное изменение плотности энергии). Также маловероятно,
что в модели мешков можно правильно учесть спонтанное нару-
нарушение киральной симметрии и получить для безмассовых и- и
d-кварков безмассовый я-мезон. Кроме того, имеются трудности с
интерпретацией собственных степеней свободы мешка.
Другая модель, модель струн, предполагается применимой
для описания ситуации, когда кварк и аитикварк разведены друг
от друга на большое по сравнению с характерным адронным мас-
масштабом расстояние /. (Такая ситуация имеет место в адронах с
большим спином /, в которых кварки имеют большой орбиталь-
орбитальный момент относительного движения.) Предполагается, что а
этой ситуации силовые линии цветного поля, идущие от кварка к
антикварку, сжимаются в пучок толщиной порядка характерного
адронного размера. В пределе больших / толщиной пучка сило-
силовых линий можно пренебречь, и возникает образ одномерного об-
образования— струны, энергия которого пропорциональна /. (Вне
зависимости от теории адронов релятивистская квантовая дина-
динамика таких протяженных объектов представляет собой отдельную'
интересную область.)
Сжатие силовых линий в пучок также хорошо согласуется с
картиной подавления непертурбативных флуктуации цветным по-
полем. (Силовым линиям энергетически невыгодно рассеиваться па
большому объему, как это происходит в электродинамике. Дан-
Данную ситуацию можно сравнить со сжатием силовых линий маг-
магнитного поля в сверхпроводнике.)
Таким образом, во всех случаях знак A7.27), способ опреде-
определения которого можно считать строгим, хорошо согласуется с не-
нестрогими (но более амбициозными) представлениями о невылета-
невылетании цвета и структуре адронов.
19* 283
17.5. Инстантоны
, Структура флуктуации, приводящих к образованию вакуумной
Плотности энергии A7.27), неизвестна. Тем не менее известен яв-
яый вид одного класса непертурдативных вакуумных флуктуации
глюонного поля,' называемых инстантонами, которые, однако, да-
дают лишь.малый вклад в е. Наиболее естественным образом ин-
•стаитоны описываются не в привычном пространстве Минковско-
го, а в пространстве Евклида, отличающемся от первого заменой
t>-*-it (сравните это с поворотом Вика лри вычислении фейнманов-
<жих интегралов). Переход к пространству Евклида часто бывает
удобен при рассмотрении процессов и квантовых состояний, в ко-
которых не происходит рождения реальных частиц. Особенно удо-
удобен он при изучении структуры вакуумного состояния. Заметим,
в частности, что вакуумное среднее <0|/?2|0> не меняется при пе-
переходе в евклидово пространство. В пространстве Евклида инстан-
инстантоны, открытые в 1975 г. iA7.9], являются решениями классиче-
классических уравнений Янга—Миллса, обладающими конечным действи-
действием. [Интерпретация в пространстве Минковского более сложна —
в этом случае инстантоны являются подбарьерными квазикласси-
квазиклассическими траекториями, описывающими переходы между состояни-
состояниями вакуума с различной топологической (глобальной) структу-
структурой. Обсуждение данного вопроса выходит за рамки книги.]
: Необходимое аналитическое продолжение теории Янга—Милл-
Янга—Миллса из пространства Минковского в пространство Евклида проще
всего сделать, не затрагивая времени и потенциалов Л„а, а пере-
перенося преобразование на метрический тензор. Для этого в дейст-
действии Янга—Миллса в форме A7.16) следует заменить метрический
тензор gUv=(iiag A, —1, —1, —1) иа единичную матрицу би»=
=diag A, 1, 1, 1). (Заметим, что переходу к мнимому времени
отвечает знак ?„„ обратный по сравнению с последним выраже-
выражением, однако общее изменение знака всех компонент метрическо-
метрического тензора оставляет действие A7.16) инвариантным.] При этом
из-за члена У—g действие становится мнимым:
/гм-+Иум, где /^—евклидово действие:
A /4) J
A7.30)
¦суммирование по всем повторяющимся индексам здесь произво-
производится с положительным знаком. Полевые уравнения, обеспечива-
обеспечивающие минимальность евклидова действия и возможность выра-
выразить Fuv" через потенциалы, остаются прежними:
=0, A7.31)
ио с модифицированным (евклидовым) соглашением о свертке ин-
индексов.
Если выразить согласно G.39) тензор напряженности F?v через
потенциалы А?* то второе из уравнений A7.31) будет выполнено
тождественно, а первое превратится в нелинейное уравнение вто-
второго порядка относительно потенциалов, найти общее решение
которого не представляется возможным. Поэтому в дальнейшем
-речь пойдет лишь о классе частных решений уравнений A7.31).
Для получения этих решений заметим, что если найти потенциалы
А{1 такие, что соответствующее FjJv удовлетворяет одному из-
условий
A7.32>
или
F& = -A /2) B^xaFtc, A7.33)
то в силу второго из уравнений A7.31), которое выполняется
тождественно, будет удовлетворено и первое. Поля, удовлетворя-
удовлетворяющие условию A7.32), называют самодуальными, а условию*
A7.33)—антисамодуальными, соответственно A7.32) называют
уравнением самодуальности, а A7.33) —уравнением антисамоду-
яльности. По отношению к потенциалам Л„а каждое из этих урав-
уравнений имеет первый порядок и решение каждого из них является
одновременно и решением уравнений A7.31).
Рассмотрим простейшее так называемое одноинстантонное ре-
решение уравнения A7.32), открытие которого А. А. Белавиным»
А. М. Поляковым, А. С. Шварцем и Ю. С. Тюпкиным [17.9] поло*
жило начало активному исследованию уравнений дуальности
A7.32) и A7.33), в результате которого [17.10] найдено общее
решение этих уравнений для S {/-теории заметим, однако, что, по
.существу, все известные физические приложения основаны на
одноинстантонном решении).
Каждая группа SU{N) содержит в качестве подгруппы груп-
группу SUB). Поэтому, если решение уравнения A7.32) .(или A7.33)!]
найдено для St/B)-теории Янга—Миллса, то его можно «встро-
«встроить» и в более широкую SU(N) -теорию [хотя это, вообще говоря,
не исчерпывает всех решений уравнений дуальности для SU(N)-
теории]. Напомним, что в группе 51/B) индекс а у потенциалов
А№а и напряженностей F^" пробегает три значения A, 2, 3), а
структурные константы f"be совпадают с абсолютно антисимметг
ричным символом 8о*с Одноинстантонное решение уравнения
A7.32) для 5?/B)-теории компактно записывается через так на-
называемый символ т'Хофта -Паш, антисимметричный до индексам
ц и v и определяемый следующим образом:
eali, i, / = 1,2,3. A7.34)
Легко проверить, что символ %jiVl самодуален, [т. е.
(l2)
(/)^v».o%».o
Поле инстантона, являющегося решением уравнения A7.32),
можно записать в виде
К (*)= -B/er)-i|Sv(x,-i,)/I(**-J0L)»+p»l. A7.35)
285
где Ху — координаты произвольной точки в 4-мерном евклидовом
пространстве (координаты центра инстаитона), а р-т-произволь-
р-т-произвольный параметр — размер иистантона. То, что положение центра
инстантона произвольно, очевидно из трансляционной инвариант-
инвариантности уравнений A7.32), а наличие произвольного масштабного
параметра р отвечает обсуждавшейся в разд. 17.4 инвариантности
классической теории Янга—Миллса относительно выбора масшта-
масштаба длины. Тензор напряженности, отвечающий потенциалу
< 17.35), имеет вид (проверьте!):
A7.36)
Заметим, что квадрат этого тензора
F% (х) F% (*)=-16- 12р«/^ К*-*J+Р2]4. A7.37)
а интеграл от этой величины, определяющий евклидово действие
A7.30), конечен и равен
/&-8rf/g«. A7.38)
Аналогичное приведенному выше решение уравнения A7.33),
называемое антиинстамтонныл, получается заменой в форму-
формулах A7.35) и A7.36) символа Tionv символом Tiajivi отличающимся от
417.34) знаком О/'-компоиенты: т|яО/ =—fio/5 ~*\aij=zaii- Выражения
A7.37) и A7.38) для квадрата напряженности и для действия
остаются неизменными.
Классические решения «выживают» в квантовой теории по-
постольку, поскольку квантовые флуктуации искажают их слабо.
Критерием для такого поведения служит требование, чтобы дей-
действие для классического решения было велико по сравнению с
единицей (по сравнению с постоянной планка h в обычных еди-
единицах) , так как действие для квантовых флуктуации — порядка 1
(А ). Таким образом, обсуждение инстантонных решений в кван-
квантовой теории имеет смысл, если мала величина ?2/8я2. В кванто-
квантовой теории (см. гл. 8) константа g перенормируется пертурбатив-
ными флуктуацнямн. Анализ этих флуктуации на фоне поля
инстаитона, проведенный т'Хофтом '[17.11], подтверждает естест-
естественное ожидание, что при рассмотрении инстантонных эффектов
следует нормировать g2 на импульсах порядка обратного размера
инстантона: g*(l/p*). Так как ir(l/p2) растет с ростом р, обсуж-
обсуждение классических решений вида A7.35) при больших р теряет
смысл. Можно сказать, что инстантон большого размера разру-
разрушается квантовыми флуктуациями. Заметим, что условие клас-
классичности /(Г>»1 делает малым вклад инстантонов в физические
амплитуды. Действительно, вклад полевой конфигурации в ту или
иную амплитуду определяется ее действием й пропорционален
exp (i /). Для конфигураций в евклидовом пространстве действие
•чисто мнимое: exp(i/)=exp(—Im), поэтому вклад конфигураций,
для которых применимо рассмотрение, основанное на классиче-
классическом решении, экспоненциально мал. Заметим также* что под-
286
стаиовка в экспоненту инстантонного действия A7.38) с констан-
константой gu{p~a), определяемой формулой (8.30), дает ехр(—/(Ж>)»
=ехр(—8я2/52(р~2)) = (рЛ)ь. Поэтому квазиклассическое рас-
рассмотрение применимо лишь для инстантонов размера р<Л~', ко-
которые, однако, как уже говорилось, дают малый вклад в физиче-
физические амплитуды.
Задача 17.1. Показать, что лагранжиан теории Янга—Миллса инвариан-
инвариантен относительно преобразования инверсии с центром в произвольной точ-
точке х^:
{x_-r
еде Пд = (Хц—ХцI У (х —~х)*.
(Преобразования инверсии и изменения масштаба дайн называют конформ-
конформными.)
Задача 17.2. Показать, что потенциал вида
а) является решением уравнения A7.32) (несмотря на то, что сюда входит
¦символ ~riallv);
б) связан с решением вида A7.35) калибровочным преобразованием и пото-
потому физически ему эквивалентен.
Задача 17.3. Найти частное решение уравнения A7.32), предположив, что
потенциалы Лд имеют вид А%
Г ' " 1
Ответ: / (х) - In 1 + 2 *-«/(¦* — х1)* , где Я.;—произвольные числа;
L «-1 J
jc1—координаты проязвольных точек в пространстве; N—также произвольное
.натуральное число (число инстантонов). Заметим, что действие для этого
решения равно 8n*N/g* (попробуйте это доказать).
287
Список литературы
1.1. Ахиезер А. И., Берестецкий В. Б. Квантовая электродинамика. М.: Нау-
Наука, 1969.
1.2. Берестецкий В. Бч ЛифшиЦ Е. М., Питаевскнй Л. П. Квантовая электро-
электродинамика. М.: Наука, 1980!
1.3. Боголюбов Н. Н., Ширков Д. В. Введение в теорию квантованных полей,
М.: Наука, 1973.
1.4. Боголюбов Н. Н., Ширков Д. В. Квантовые поля. М.: Наука, 1980.
1.5. Бьеркен Дж. Д., Дрелл С. Д. Релятивистская квантовая теория, т. I, Пг
Пер. с англ. М.: Наука, 1978.
1.6. Feynman R. P. The theory of positrons. — Phys. Rev., 1949, vol. 76, No. 6,
p. 749—768.
Space-time approach to quantum electrodynamics. — Phys. Rev., 1949, v. 76,
No. 6, p. 769—789.
. 2.1. Dyson F. J. The S-Matrix in Quantum Electrodynamics.—Phys. Rev., 1949r
vol. 75, No. 11, p. 1736—1755.
2.2 Quantum Electrodynamics. N. Y., Schwinger J. (Ed.), Dovear, 1958.
'- 2.3. Ward J. С An Identity in Quantum Electrodynamics. — Phys. Rev., 1950,.
vol. 78, No. 2, p. 182.
2.4. Furry W. H. A Symmetry Theorem in the Positron Theory. — Phys. Rev.,,
1937, vol. 51, p. 125—129.
4.1. Ландау Л. Д., Абрикосов А. А., Халатников И. М. Асимптотическое вы-
выражение для гриновской функции электрона в квантовой электродинами-
электродинамике.—Докл. АН СССР, 1954, т. 95, № 4, с. 773—775.
Ландау Л. Д., Абрикосов А. А., Халатников И. М. Асимптотическое вы-
выражение для гриновской функции фотона в квантовой электродинамике. —
Докл. АН СССР, 1954, т. 95, № 6, с. 1177—1180.
4.2. t'Hooft G. An Algorithm for the Poles at Dimension Four in the Dimensio-
Dimensional Regufarization Procedure. — NucO. Phys., 1973, vol. B62, p. 444—460.
43. t'Hooft G. and Veltman M. Regularization and Renormalization of Gauge-
Fields. — Nucl. Phys., 1972, vol. B44, p. 189—213.
4.4. Градштейи И. С, Рыжик И. М. Таблицы интегралов, сумм, рядов и<
произведений. М.: ГИФМЛ, 1963.
4.5. Celmaster W., Gonsalves R. J. Reirormalizattoii-Prescription Dependence of
the Quantum-Cromodynamics Coupling Constant. — Phys. Rev. D, 1979,.
v. 20, No. 6, p. 1420—1434.
4.6. Bloch F., Nordsieck A. Note on the Radiation Field of the Electron.—
Phys. Rev., 1937, vol. 52, p. 54—59.
4.7. Yennie D. R., Frautschi S. C., Suura H. The Infrared Divergence Phenome-
Phenomena and High-Energy Processes. — Annal. Phys., 1961, vol. 13, p. 379—452_
4.8. Wemberg S. Infrared Photons and Gravitons.— Phys. Rev., 1965, vol. 140,.
No. 2B, p. 516—524.
4.9. Lee T. D., Nauenberg M. Degenerate Systems and Mass Singularities.—
Phys. Rev., 1964, vol. 133, N<x 6B, p. 1549—1562.
4.10. Kinoshlta T. Mass Singularities of Feynman Amplitudes. — J. Math, and-
Phys., 1962, vol. 3, No. 4, p. 650—677.
4.11. Судаков В. В. Вершинные части для сверхвысоких энергий в квантовой!
электродинамике. — Жури, эксперим. и теорет. физ., 1956, т. 30, вып. 1,.
с. 87—95.
•288
5.1. Gell-Mann M., Low F. E. Quantum Electrodynamics at Small Distances.—
Phys. Rev., 1954, voL 95, No, 5, p. 1300—Ш2.
5.2. Боголюбов Н. H., Ширков Д. В. Оренормализационной группе в кванто-
квантовой электродинамике. —Докл. АН СССР, 1955, т. 103, № 2, с. 203—206.
Боголюбов Н. Н., Ширков Д. В. Приложение ренормализациоиноб груп-
группы к улучшению формул теории возмущений. — Докл. АН СССР, 1955,
т. 103, № 3, с. 391—394.
Боголюбов Н. Н., Ширков Д. В. Группа мультипликативной ренормиров-
ренормировки в квантовой теории поля. — Жури, эксперим. и теорет. фнз., 1956,
т. 30, вып. 1, с. 77—86.
5.3. Судаков В. В. Следствия переиормируемости квантовой электродинамики
и мезонной теории. — Жури, эксперим. и теорет. физ., 1956, т. 31,
вып. 4A0), с 729—731.
5.4. Stueckelberg E. С G., Petermann A. La normalisation des constantes dans
la theorie des quanta. — Helv. phys. acta, 1953, vol. 26, p. 499—520.
5.5. Pomeranchuk Ya., Sudakov V. V., Тег-Martirosyan K. A. Vanishing of Re-
normalized Charges in Field Theories with Point Interaction. — Phys. Rev.,
1956, vol. 103 No. 3, p. 784—802.
5.6. Овсяиииков Л. В. Общее решение уравнений ренормализационной груп-
группы.—Докл. АН СССР, 1956, т. 109, № 6, с. 1112—1114.
5.7. Curtis G. Callan, jr. Broken Scale Invariance in Scalar Field Theory,—
Phys. Rev. D, 1970, vol. 2, No. 8, p. 1541—1547.
5.8. Syrnanzik K- — CommunSi Math. Phys., 1970, vol. 18, p. 227.
6.9. Ландау Л. Д., Абрикосов А. А* Халатнииов И. М. Масса электрона в
квантовой электродинамике. —Докл. АН СССР, 1954, т. 96, № 2,
с. 261—264.
5.10. Лаидау Л. Д., Померанчук И. Я. О точечном взаимодействии в кванто-
квантовой электродинамике. —Докл. АН СССР, 1955, т. 102, № 3, с. 489—492.
5.11. Помераичук И. Равенство нулю перенормированного заряда в квантовой
электродинамике.—Докл. АН СССР, 1955, т. 103, № 6, с 1005—1008.
6.1. Швебер С. Введение в релятивистскую квантовую теорию поля: Пер. с
англ. М.: Изд-во иностр. лнт., 1963.
6.2. Веитцель Г. Введение в квантовую теорию волновых полей. М.—Л.:
ОГИЗ—ГИТТЛ, 1947.
6.3. Галаинн А. Д., Иоффе Б. Л., Померанчук И. Я. Об асимптотике функ-
функций Грина нуклона и мезона в псевдоскалярной теории со слабым взаи-
взаимодействием.— Журн. эксперим. н теорет. физ., 19о5, т. 29, вып. 1G),
с. 51—63.
6.4. Лифшиц Е. М., Питаевский Л. П. Статистическая физика. Ч. 2. М.: Нау-
Наука, 1978.
6.5. Лаидау Л. Д., Гинзбург В. Л. К теории сверхпроводимости.—Жури,
эксперим. н теорет. физ., 1950, т. 20, с. 1064—1089.
6.6. Зельдович Я. Б., Кобзарев И. Ю., Окунь Л. Б. Космологические следст-
следствия спонтанного нарушения дискретной симметрии.—Журн. эксперим. в
теорет. фнз., 1974, т. 67, вып. 1G), с. 3—11.
6.7. Coleman S., Weinberg E. Radiative Corrections as the Origin of Sponta-
Spontaneous Symmetry Breaking. — Phys. Rev. D, 1973, vol. 7, No. 6, p. 1888—
1910.
6.8. Дятлов И. Т., Тер-Мартиросяи К. А. Асимптотическая теория рассеяния
мезона на мезон.—Журн. эксперим. и теорет. физ., 1956, т. 30, № 2Г
с. 416, 419.
6.9. Ширков Д. В. Двухзарядная ренормализационная группа в псевдоскаляр-
псевдоскалярной мезонной теории. —Докл. АН СССР, 1955, т. 105, № 5, с. 972—975.
7.1. Yang С. N., Mills R. L. Conservation of isotopic spin and isotopic gauge
invariance. — Phys. Rev., 1954, vol. 96, No. 1, p. 191—195.
7.2. Коноплева Н. П., Попов В. Н. Калибровочные поля. 2-е изд. М.: Атом-
издат, 1980.
7.3. Элементарные частицы и компенсирующие поля. Сб. статей: Пер. с
англ. / Под ред. Д. Д. Иваненко. М.: Мир, 1964.
7 4 Faddeev L. D., Popov V. N. Feyman diagrams for the Yang—Mills field. —
Phys. Lett., 1967, vol. 25B, No. 1, p. 30—31
28»
7.5. De Witt В. S. Quantum theory of gravity II. The manifestly covenant theo-
theory.— Phys, Rev., 1967, voL 162, No. 2, p. 1195—11239.
7.6. BeccW С, Rouet A., Stora R. —Communs. Math. Phys., 1975, v. 42, No. 2,
• p. 127.
4.1. Politzer H. D, Reliable perturbattve results for strong interactions? — Phys.
Rev. Lett., 1973, vol. 30, No. 26, p. 1346—1349.
8.2. Gross D. J., Wilczek F. Ultraviolet behavior of non^abelian gauge theo-
theories. — Phys. Rev. Lett., 1973, vol. 30, No. 26, p. 1343—'1346.
8.3. Gross D. J., Wflczek F. Asymptotically free guage theories. I. — Phys. Rev.,
1973, v. D8, No. 10, p. 3633—3651.
Asymptotically free gauge theories. II. —Phys. Rev., 1974, vol. D9, No. 4,
p. 980—992.
8.4 Jones D. R. T. Two-loop diagrams an Yang —Mills theory.—Nucl. Phys.,
1974, vol. B75, No. 3, p. 531—538.
Gaswell W. E. Asymptotic Behavior of non-abelian gauge theories to two-
loop order. — Phys. Rev. Lett., 1974, vol. 33, No. 4, p. 244—246.
8.5. Tarasov 0. V., Vladimirov A. A. Three-loop calculations in non-abelian
gauge theories. — Препринт ОИЯИ № E2-80-483, Дубна, 1980.
9.1. Charmonium and gluons / V. A. Novikov e. a.—Phys. Rep., 1978, vol. 4ftC,
No. 1, p. 1—133.
9.2. Appelquist Т., Polltzer H. D. Heavy quarks and e+e--annihilatk>n. — Phys.
Rev. Lett., 1975, vol. 34, No. 1, p. 43—45.
9.3. Ore A., Powell T. L. Three-photon annihilation of an electron-positron
pair. —Phys. Rev., 1949, vol. 75, No. 11, p. 1696—1699.
9.4. Mackenzie P. В., Lepage G. P. Quantum chromodynamic corrections to the
gluonic width of the T-meson. — Phys. Rev. Lett., 1981, vol. 47, No. 18,
p. 1244—1247.
10.1. Lee T. D., Yang С N. Question of Parity Conservation in Weak Interac-
Interaction.—Phys. Rev. 1956, vol. 104, No. 1, p. 254—258.
Lee T. D., Yang C. N. Parity Nonconservation and a Two-Component Theo-
Theory of the Neutrino. —Phys. Rev., 1957, vol. 105, No. 5, p. 1671—1675.
10.2. Ландау Л. Д. Об одной возможности для поляризационных свойств ней-
нейтрино.— Журн. эксперим. и теорет. физ., 1957, т. 32, вып. 2, с 407—408.
Landau L. On the conservation laws for weak interactions. Nucl. Phys.,
1957, vol. 3, p. 127—131.
10.3. Feynman R. P., Gell-Mann M. Theory of the Fermi Interaction. — Phys.
Rev., 1958, vol. 109, N6. 1, p. 193—198.
40.4. Sudarshan E. C. S., Marshak R. E. Chirality Invariance and the Universal
Fermi Interaction, — Phys. Rev., 1958, vol. 109, p. 1860—1861.
10.5. Sakural J. J. Mass Reversal and Weak Interactions. — Nuovo dmento, 1958,
vol. 7, No. 5, p. 650—660.
10.6. Garvin P. L., Lederman L. M., Weinrich M. Observation of the Failure of
Conservation of Parity and Charge Conjugation in Meson Decays: the Mag-
Magnetic Moment of the Free Muon. — Phys. Rev., 1957, vol. 105, No. 4,
? 1415—1417.
10.7. Friedman J. J., Telegdi V. L. Nuclear Emulsion Evidence for Parity Non-
conservation in the Decay Chain. — Phys. Rev., 1957, vol. 105, p. 1681—1682.
10.8. Wu С S. Parity Experiments in Beta Decays. — Rev. of Modern. Phys.,
.1959, vol. 31, No. 3, p. 783—790.
10.9. Алихаиов А. И., Елисеев Г. П., Любимов В. А. Измерение продольной
поляризации электронов, испускаемых при В-распаде. — Журн. эксперим.
и теорет. физ., 1958, т. 34, вып. 5, с. 1045—1057.
10.10 Окунь Л. Б. Лептоны и кварки.—М.: Наука, 1981 (см. также
Окунь Л. Б. Слабое взаимодействие элементарных частиц.—М.: Изд-во
физ.-мат. лит., 1963).
10.11. Gell-Mann M., Levy M. The Axial Vector Current in Beta Decay. —Nuovo
cimento, 1960, vol. 16, No. 4, p. 704—726.
10.12. Goldberger M. L., Trieman S. B. Phys. Rev., 1958, vol. 110, p. 1178—1182.
Goldberger M. L., Trieman S. B. Form Factor in 6-Decay and u-Capture.—
Phys. Rev., 1958, voL 111, No. 1, p. 354—361.
290
40.13. Cabibbo N. Unitary Synnnetry and Lepton Decays. — Phys. Rev. Lett,
1963, vol. 10, No. 12, p. 531—633.
10.14 Gell-Mann M. A Schematic Model of Baryons and Mesons. — Phys. Lett,
1964, voL 8, No. 3, p. 214—215.
10.15. Glashow S. L., Hliopoulos J., Maiani L. Weak Interactions with Lepton-
Hadron Symmetry. — Phys. Rev. D, 1970, vol. 2, No. 7, p. 1285—1292.
30.16. Observation of a Dimuon Resonance at 9,5 GeV in 400-Gev Proton-Nudeus
Collisions / L. M. Lederman e. a. —Phys. Rev. Lett., 1977, vol. 39, No. 5,
p. 252—255.
10.17. Kobayashi M., Maskawa Т. СР-Violation in the Renormalizable Theory of
Weak Interaction. — Progr. Theoret. Phys, 1973, vol. 49, No. 2, p. 652.
10.18. Glashow S. L. Partial-Symmetries of Weak Interactions. — Nucl. Phys.,
1961, vol. 22, No. 3, p. 579—588.
10.19. Schwinger J. A Theory of the Fundamental Interactions. — Ana Phys.,
1957, vol. 2, No. 5, p. 407—434.
30.20. Lopes J. 1» A Model of the Universal Fermi Interaction.— Nucl. Phys.,
1958, vol. 8, No. 2, p. 234—236.
10.21. Salam A., Ward J. С Weak and Electromagnetic Interaction. — Nuovo ci-
mento, 1959, vol. 11, No. 4, p. 568—577.
Salam A., Ward J. C. Electromagnetic and Weak Interaction. — Phys.
Lett., 1964, vol. 13, No..*, p. 168—171.
11.1. Goldstone J. Field Theories with «Superconductor» Solutions. — Nuovo ci-
mento, 1961, vol. 29, No. 1, p. >I54—164.
11.2. Goldstone J., Salam A., Weinberg S. Phys. Rev., 1962, vol. 127, p. 965.
11.3. Jiiggs P. W. Broken Symmetries and the Masses of Gauge Bosons.—
Phys. Rev. Lett., 1964, vol. 13, No. 16, p. 508—509.
Higg-s P. W. Spontaneous Symmetry Break down without Massless Bo-
Bosons. — Phys. Rev., 4966, vol. 145, No. 4, p. 1156—1163.
Higgs P. W. Broken Symmetries, Maesless Particles and Gauge Fields.—
Phys. Lett., 1964, vol. 12, No. 2 p. 132—133.
11.4. Lingf-Fongf-Li. Group Theory of the Spontaneously Broken Gauge Symmet-
Symmetries.—Phys. Rev. D, 1974, vol. 9. No. 6, p. 1723—1739.
11.5. Abers E. S., Lee B. W. Gauge Theories. — Phys. Rep., 1973, vol. 9, p. 1—
163. (Русск. пер. в сб.: Квантовая теория калибровочных полей. М.: Мир,
1977. Серия НФФ; Вып. 8).
112.1. Weinberg S. A Model of Leptons. — Phys. Rev. Lett., 1967, vol. 19, No. 21,
p. 1264—1266.
12.2. Salam A. Elementary Particles Theory. Stockholm, Ed.: N. Swartholm
Almquest and Weacsell, 1968, 367 p.
12.3. t'Hooft G. Renormalizatkm of Massless Yang—Mills Fields. — Nud. Phys.,
1971, vol. B33, p. 173—199.
t'Hooft G. RenormaJizable Lagratigians for Massive Yang-s-Mills Fields.—
Nucl. Phys., 1971, vol. B35, p. 167—188.
.12.4. An Estimate of the ve Mass from the 6-Spectrum of Tritium in the VaUine
Molecule / V. A. Lubimov e. a.—Phys. Lett., 1980, vol. 94B, No. 2,
p. 266—268.
12.5. Jones D. R. T. Two-Loop 6-Function for GiXG2 Gauge Theories. — Phys.
Rev. D, 1982, vol. 25, No. 2, p. 581—582.
13.1. Georgi H., Glashow S. L. Unity of All Elementary-Particle Forces. — Phys.
Rev. Lett., 1974, vol. 32, No. 8, p. 438—441.
13.2. Pati J. C, Salam A. Unified Lepton-Hadron Symmetry and a Gauge Theo-
Theory of the Basic Interaction. — Phys. Rev. D, 1973, vol. 8, No. 4, p. 1240—
1251.
Pati J. C, Salam A. Lepton Number as the Fourth «Color». — Phys. Rev. D,
1974, vol. 10, No. 1, p. 275—289.
13.3. Georgi H., Quinn H., Weinberg S. Hierarshy of Interactions in Unified
Gauge Theories. — Phys. Rev. Lett., 1974, vol. B3, No. 7, p. 451—454.
13.4. Marciano W. Weak Mixing angle and Grand Unified Gauge Theories.—
Phys. Rev. D, 1979, vol. 20, No. 1, p. 274-m
Goldman Т., Ross D. A. How Accurately can we estimate the Proton
291
Lifetime in an SUE) Grand Unified Model. —Nud. Phys., 1980.
13.5. Aspects of the Grand Unifications of Strong, Weak and Electromagnetic
Interactions / A. J. Buras e. a. —Nud. Phys., 1978, vol. В135, p. 66—91.
13.6. Uncertainties in the Proton Lifetime / J. Ellis e. a. —Nucl. Phys., 1980,.
vol. B176, p. 61—99
13.7. Fradkin E. S4 Kalashnikov О. К. Asymptotically Free SUE) Model of
Unified Interaction. — Phys. Lett., 1976, vol. 64B, No. 2, p. 177—180.
13.8. Матиняи С. Г. На пути к объединению взаимодействий.—Успехи фнз.
иаук, 1980, т. 130, вып. 1, с. 3.
13.9. Berezinsky V. S., loffe В. L., Kogan Ya. I. The Calculation of the Matrix
Element for Proton Decay. —Phys. Lett., 1981, vol. 105B No. 1, p. 33—37.
13.10. Ellis J., Gaillard M. K., Nanopoulos D. V. Baryon Number Generation
in Grand Unified Theories. — Phys. Lett, 1979, vol. 80B, No. 45, p. 360—364.
Ellis J., Gaillard M. K., Nanopoulos D. V. On the Effective Lagrangian.
for Baryon Decay. —Phys. Lett., 1979, vol. 88B No. 4, 5, p. 320—324.
13.11. Candidate Events for Nudeon Decay in the Kokr Gold Field Experi-
Experiment / S. Miyake e. a. —Phys. Lett., 1981, vol. 106B, No. 4, p. 339—346..
13.12. Чкареули Дж. Л. Кварк-лептонные семейства: SU{5) XSU(8) -симметрия. —
Письма в ЖЭТФ, 1980, т. 38, вып. 11, с. 684—686.
Бережнанн 3. Г., Чкареули Дж. Л. Масса f-кварка и число кварк-леп-
тонных поколений. — Письма в ЖЭТФ, 1982, т. 35, вып. 11, с. 494—497.
14.1 Вайиштейи А. И., Захаров В. И., Шифмаи М. А. Нелептониые распад»
Я-мезонов и гиперонов. — Жури, эксперим. и теорет. физ., 1977, т. 72,.
вып. 4, с. 1275—1297.
15.1. ФейимаН Р. Взаимодействие фотонов с адронами: Пер. с англ. М.: Мир,
1975.
15.2. Politzer H. D. Asymptotic freedom: an approach to strong interactions.—
Phys. Rep., 1974, vol. 14C, No. 4, p. 129—179.
Petermann A.Renormalization group and the deep structure of the pro-
proton.—Phys. Rep., 1979, vol. 53C, No. 3, p. 157—248.
Buras A. J. Asymptotic freedom in deep inelastic processes in the leading:
order and beyond. —Rev. of Modern Phys., 1980, vol. 52, No. 1, p. 199—276.
15.3. Alfarelli G., Paris! G. Asymptotic freedom in par ton language. — Nud.
Phys., 1977, vol. B126, No. 2, p. 298—318.
15.4. Naive quark model and deep inelastic scattering /V. A. Novikov—Ann,
of Phys. (N. Y. —Lond.), 1977, vol. 101, No. 2. p. 276—287.
Parisi G., Petronzio R. On the breaking of Biordken scaling. — Phys. Lett.,
1976, vol. 62B, No. 3, p. 331—334.
15.5. Докшицер Ю. Л., Дьяконов Д. И., Трояи С. И. Жесткие процессы а
квантовой хромодинамнке. — Материалы XIII школы физики ЛИЯФ. Л.,
1978, ч. 2, с 3—89.
15.6. Okun L. В., Voloshin M. В. Production of Intermediate Bosons in pp- and
pp-collisions. — Nucl. Phys., 1977, vol. В120, No, 3, p. 459—476.
Quigg C. Production •and_detection of Intermediate Vector Bosons and hea-
heavy Leptons in pp- and pp-colHsions. — Rev. of Modern. Phys., 1977, vol. 49,.
No. 2, p. 297—316.
Peierls R. F., Trneman T. L., Wang L. L. Estimates of production cross-
section and distribution for IP-bosons and hadronic jets in high-energy
pp- and pp-colllsions. — Phys. Rev., 1977, vol. D16, No. 5, p. 1397—1421.
16.1. Appelquist Т., Georgi H. e+e--Annihilation m Gauge Theories of strong
Interactions. —Phys. Rev., 1973, vol. D8, No. 11, p. 4000—4002.
Zee A. Electron-positron Annihilation in Stagnant Field Theories. — Phys.
Rev., 1973, vol. D8, No. 11, p. 4038—4040.
16.2. Швингер Ю. Частицы, источники, поля. Т. II: Пер. с англ. М.: Мир,.
1976.
16.3. Sum rules for Charmonium and Charmed Mesons in Quantum Chromodyna-
mics /V. A. Novikov. e. a, —Phys. Rev. Lett., 1977, vol. .38, No. 12,
p. 626—629.
292
17.1. Вайнштейн А. Ич Захаров В. И. Частичное сохранение аксиального то*
ка. —Успехи физ. наук, 1970, т. 100, вып. 2, с 225—276.
а 7.2 Трейман С, Джекив Р., Гросс Д. Лекция по алгебре токов: Пер. с
англ. М.: Атомиздат, 1977.
17.3. Eidelman S. I., Vainshtein A. I., Kurdadze L. H. e+e~-Annihilation into
Hadrons below 2 GeV. Test of QCD predictions. — Phys. Lett., 1979, vol.
82B, No. 2, p. 278—280.
17.4 Вайнштейн А. И., Захаров В. Ич Шифмаи М. А. Глюонныи конденсат
и лептонные распады векторных мезонов. — Письма в ЖЭТФ, 1978, т. 27,
вып. 1, с. 60—64.
Tic-Puzzle in Quantum Chromodynamics / M. A. Shifman, e. a. —Phys.
Lett., 1978, vol. 77B, No. 1, p. 80—83.
17.5. Shifman M. A., Vainshtein A. 1., Zakharov V. I. QCD and resonance Phy-
Physics.— Nud. Phys., 1979, vol. B147, No. 4, p. 385—448.
17.6. Voloshin M, B. Non-relatiyistic bottonium in the physical vacuum of QCD.
Mass of" the IP level. — Препринт ИТЭФ, № 21, 1980.
17.7. Ландау Л. Д., Лифшиц Е. М. Теория поля. 6-е изд. М.: Наука, 1973.
17.8. Crewther R. Nonperturbative Evaluation of the anomalies in low-energy
Theorems.—Phys. Rev. Lett., 1972, vol. 28, No. 21, p. 1421—1424.
Chanowitz M. S., Ellis J. Canonical Anomalies and broken scale Invarian-
ce.—Phys. Lett, 1972, vol. 40B, No. 3, p. 397—400; Canonical trace ano-
anomalies. — Phys. Rev., 1973, vol. D7, No. 8, p. 2490—2505.
Collins J. C, Dunkan A., Joglekar S. D. Trace and dilatation Anomalies
in gauge Theories. — Phys. Rev., 1977, vol. D16, No. 2, p. 438—449.
17.9. Pseudoparticle solutions of the Yang—iMiMs equations / A. A. Belavin e. a. —
Phys. Lett., 1975, vol. 59B, No. 1, p. 85—87.
17.10. Дриифельд.В. Г., Мании Ю.,И. Поли Янга—Миллса, инстантоиы, тензор-
тензорные произведения инстантонов. — Ядерная физика, 1979, т. 29, вып. 6,
с. 1646—1654. ' '
17.11. t'Hofft G. Computation of quantum effects due to a four-dimensional
pseudoparticle. — Phys. Rev., 1976, vol. D14, No. 12, p. 3432—3450.
ОГЛАВЛЕНИЕ
Предисловие , . . . . 3'
Часть I
ПЕРЕНОРМИРОВКА КЭД. РЕНОРМГРУППА. ГЛАВНЫЕ ЛОГАРИФМЫ
Глава 1. Лагранжиан. S-матрица. Правила Фейнмана в КЭД ... 5
1.1. Калибровочная инвариантность. Лагранжиан 5
1.2. Уравнения движения. Спектральные разложения волей. Эиергня-
импульс 7
¦1.3. Квантово-механическая теория. S-Матрица 9
1.4. Правила Фейнмаиа 12
1.5. Фотонный пропагатор в различных калибровках. Продольные
фотоны 16
1.6. Амплитуды и сечения 19
Глава 2. Приводимые и скелетные графики. Пропагаторы и иершииы
Мнимые части вклада графикой 20
2.1. Приводимые и скелетные графики 20
2.2. Уравнение Дайсона — Швингера . • 22
Ф.З. Тождество Уорда и теорема Фаррн 27
2.4. Мнимые части вклада графиков и величин П(<?2), 2(р) 29
2.5. Общее условие унитарности 34
Глава 3. Перенормировка пропагаторов и вершин. Общая схема пе-
перенормировок 3&
3.1. Перенормировка пропагаторов и вершин 36
3.2. Ультрафиолетовые расходимости вклада графиков .... Зв
3.3. Общая схема перенормировок 40
3.4. Конечность переиормнровавных величин Гщ-, GT, DT 41
3.5. Преобразование перенормировки в конгрчлеиьг в лагранжиане 45
Глава 4. Фейиманоиские интегралы. Вершины и пропагаторы в теории
возмущений 47
4.1. Логарифмическая асимптотика фейнмановских интегралов . . 47
4.2. Асимптотика вершины и пропагаторов в КЭД в порядке во2 50
4.3. Общая форма асимптотик вершин и пропагаторов в КЭД . . 51
4.4. Метод параметров Фейнмаиа 53
4.5 Размерностная регуляризация т Хофта — Вельтмана .... 56
4.6. Сокращение инфракрасных расходимостей и дважды логарифми-
логарифмическая асимптотика 62
Глава 5. Инвариантный заряд и реиормгрулпа 74
5.1. Перенормировка пропагаторов вершин и физических ' амплитуд 74
5.2. Инвариантный заряд, функции Гелл-Мана— Лоу .... 76
5.3. Ренормгруппа 80
5.4. Аномальные размерности физических амплитуд. Зависимость от
массы 83
294
5.5. Функция Гелл-Маиа — Лоу и эффективный заряд в КЭД . . 86
5.6 Нуль заряда в КЭД и область ее применимости ...... 87"
5.7. Оператор кассы электрона в КЭД ........ 89'
Часть II
СКАЛЯРНЫЕ ПОЛЯ. КХД. СЛАБЫЕ ВЗАИМОДЕЙСТВИЯ.
ЕДИНЫЕ ТЕОРИИ
Глава 6. Взаимодействия и самодействие скалярных полей. Вакуумный
конденсат . . . . , . 91
6.1. Скалярные поля 91
6.2. Юкавовское взаимодействие с фермиовами 9$
6.3. Самодействие скалярного поля. Появление вакуумного среднего
поля 99-
Глава 7. Поля Яига — Мнллса 10&
7.1. Группы SU(N) , 108
7.2. Классическая теория полей Янга —- Ми*1 са . . . . . . 114
7.3. Правша Фейнмана в теориях Яига—А\вллса 119
7.4. Поли сдухов» Фаддеева — Попова 122
Глава 8. Перенормировки в теориях Яига — Мкллса 125
вЛ. Перенормировки пропагаторов, вершии и заряда .... 125
8.2. Вычисление функция Гелл-Мана— Лоу в SU(N) калибровоч-
калибровочной теории .131
8.3. Асимптотическая свобода я размерный параметр А .... 137
Глава 9. Квантовая хромодниамнка. Кварки, глюоны и адроны . . 139
9.1. Лагранжиан квантовой хромодинашпсн. 'Кварки и глюоны \Ш
9.2- Адроиы н инфракрасная проблема КХД 141
9.3. Тяжелый кварконнй и константа о< . . 143
Глава 10. Симметричная схема слабых взаимодействий Глешоу, Иллио-
пулоса, Майани. Промежуточные векторные мезоиы 149
10:1. Феноменологический лагранжиан 149*
10.2 Симметричная схема Глешоу, Илляопулоса, Майанн. Смешивание
кварков . .- 153
10.3. Массивные векторные поля. Векторные промежуточные бозоны 157
Глава 11. Спонтанное нарушение симметрии. Механизм Хиггса . . 161
Г1.1. Безмассовые бозоны при спонтанном нарушении глобальной
симметрии 16Г
11.2. Механизм Хнггса поглощения скаляров векторными полями н
генерации масс 164
Глава 12. Модель электрослабых взаимодействий лептоиов и кварков 172:
12.1. Лагранжяаи 172
12.2. Генерация масс лептояов и бозонов. Нейтральные токи . . 175.
12.3. Несколько поколений лептоиов и кварков. Кабяббовское сме-
смешивание 182
12.4. Радиационные поправки 185
Глава 13. Модели большого объединения 193:
13.1. Большое объединение SUE). Заряды Oi, Ог, щ и sin6-w . . 193-
13.2. Фермионы, скаляры и калибровочные поля в SUE) -симетрич-
иой теории 197
13.3. Лагранжиан. Свойства бозонов Хиггса в Si/(S)-симметричной
теории. Массы бозонов и фермионов 20S
13.4. Распад протона 213-
13.5. Несколько поколений фермионов. Горизонтальная симметрия 215
295-
Часть III
ПРИМЕНЕНИЕ КВАНТОВОЙ ХРОМОДИНАМИКИ
К ОПИСАНИЮ ФИЗИЧЕСКИХ ПРОЦЕССОВ
Глава 14. Эффекты сильного взаимодействия в иелептоины* слабых
распадах 218
14.1. Эффективный лагранжиан слабого взаимодействия кварков
(большая виртуальность) 218
14.2. Аннигнляциоииый механизм .224
14.3. Полный эффективный лагранжиан для иелептоииых распадов
странных частиц , 227
14.4. Матричные элементы и распады /(-*-2я ... . . . . 233
Глава 15. Глубокоиеупругое рассеяние лептонов иа нуклонах . . . 237
15.1. Определения и кинематика 238
15.2. Партонная модель 241
15.3. Операторное разложение ... 244
16.4. Применение, операторного разложения к глубоконеупругому
рассеянию и моменты структурных функций 246
15.5. Эволюция кварковых и глюоииых распределений в адроие 249
15.6. Вычисление функций Рвл(г) и аномальных размерностей . . 252
15.7. Применение логарифмической теории к наблюдаемым процес-
процессам . . 256
15.8. Модель валентных кварков 259
15.9. Процесс Дрелла — Яна. Рождение W- и ?-<бозоиов в адроииых
реакциях . 281
Глава 16. Аннигиляция пары е+е- в адроны 264
16.1. Полное сечение е+е~-аинигиляции в (i+ft~ и в адроны . . 264
16.2. Оператор поляризация вакуума в квантовой хромодинамаке 267
16.3. Правила сумм для R(s) 269
Глава 17. Вакуум и адроны в кваитоиой хромодииамике вне теории
возмущений 272
17.1. Частичное сохранение аксиального тока и квартовый вакуумный
конденсат 272
17.2. Глюониый вакуумный конденсат . 275
17.3. Квантовая аномалия в следе тензора энергии — импульса . . 277
17.4. Непертурбатнвная плотность энергии вакуума и проблема ие-
вылетания 280
17.5. Инстантоиы 284
Список литературы 288
Михаил Борисович Волошин
Карей Аветикович Тер-Мартиросяя
ТЕОРИЯ КАЛИБРОВОЧНЫХ ВЗАИМОДЕЙСТВИЙ
ЭЛЕМЕНТАРНЫХ ЧАСТИЦ
Редактор 3. Д. Андреенко
Художественный редактор А. Т. Кирьянов
Технический редактор И. П. Собакина
Корректор М. Г. Гумма
ИБ № 1125
Сдано в набор 25.01.84 Подписано в печать 04.09.84 Т-17046
Формат 60x90'/ie Бумага типографская № 1 Гарнитура литературная
Печать высокая Усл. печ. л. 18,6 Усл. кр.-отт. 18,5 Уч.-нзд. л. 20 88
Тираж 3000 экз. Заказ 679 Цена 3 р. 60 к.
Энергоатокиздат, 113114, Москва, М-114, Шлюзовая наб., 10
Производственно-издательский комбинат ВИНИТИ
140010, Люберцы. 10. Моск. обл.. Октябрьский пр., 403