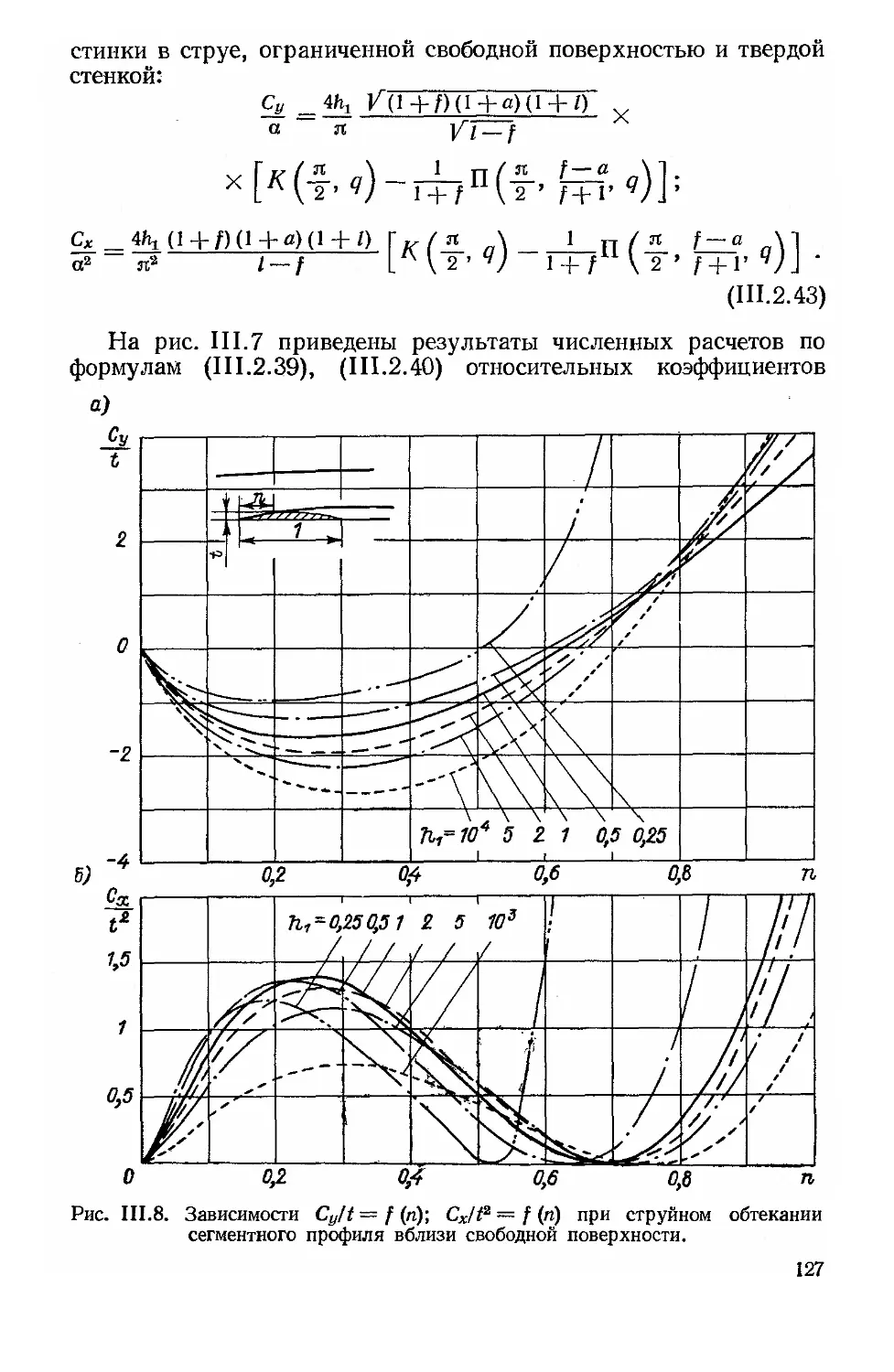
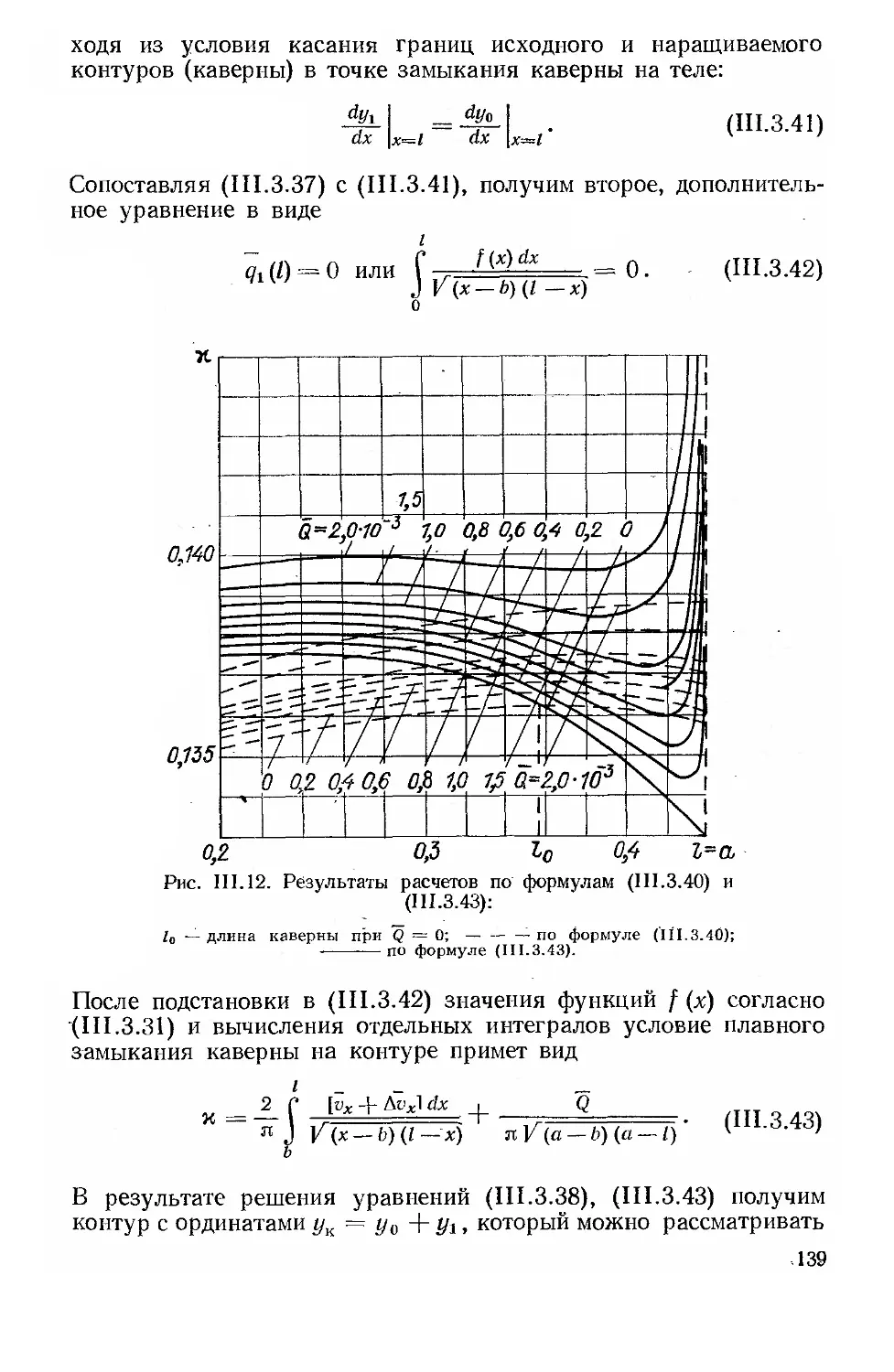
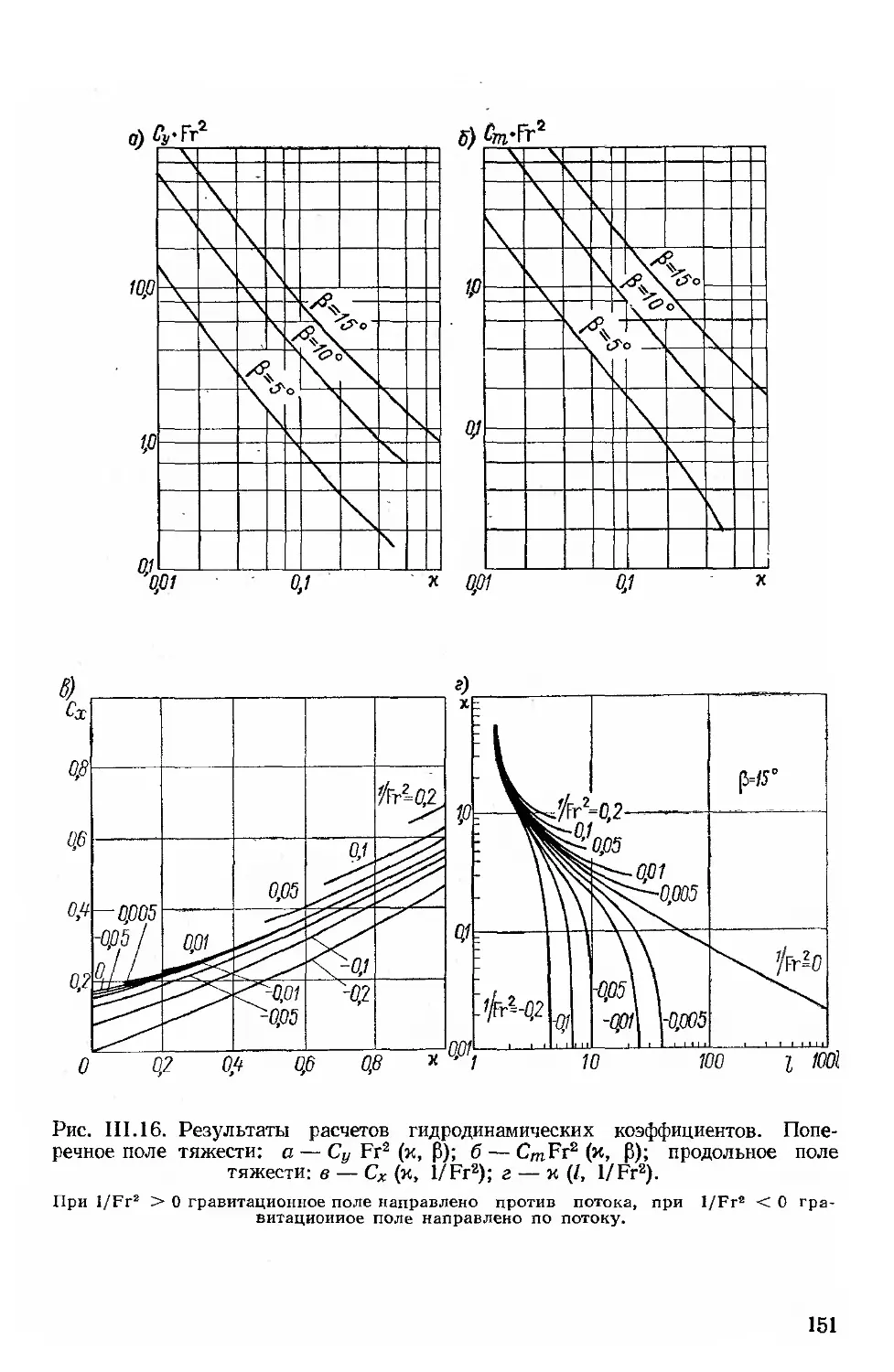
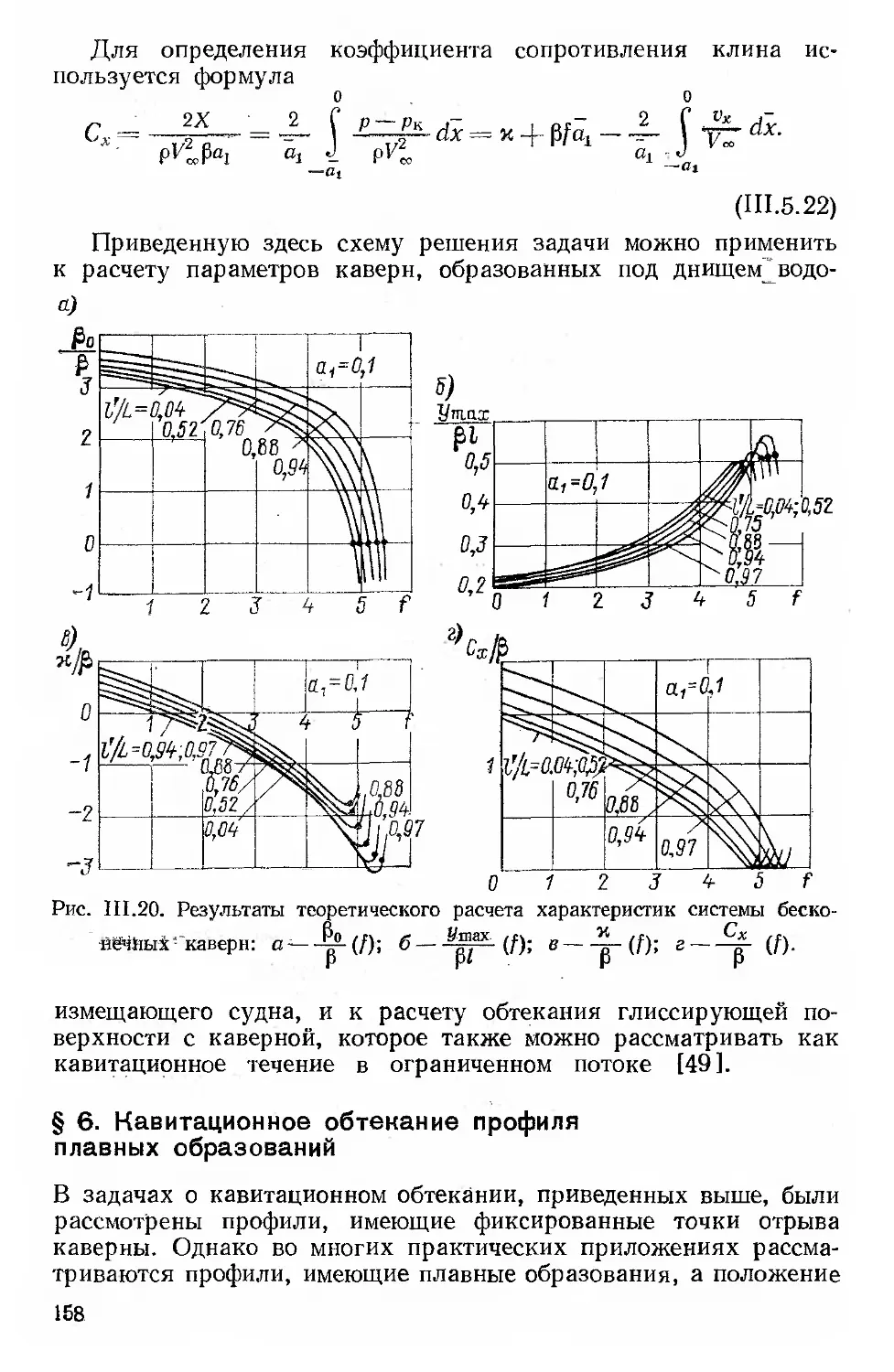
Автор: Рождественский В.В.
Теги: испытания материалов товароведение силовые станции общая энергетика аэродинамика
Год: 1977
Текст
в. в. Рождественски й
КАВИТАЦИЯ
Допущено Министерством высшего
и ореднвго специального]
образования СССР
в качестве учебного пособия
для студентоа вузов, обучающихся
ро специальности «Гидроаэродинамика»
Издательство
,Судоотроеннв"
Ленинград
1977
УДК 620.12.001.11 ; 532.628
Р62
Учебное пособие написано в соответствии с программой одноименного
курса лекций, читаемых автором в Ленинградском
кораблестроительном институте студентам специальности «Гндроаэродинамика».
В книге раскрывается физическая природа явления кавитации.
Рассматриваются начальная стадия кавитации (пузырчатая) и
развитая кавитация. Приведены схемы изучения начальной стадии кавитации
и показано исследование движения парогазового пузьфька в
безграничной жидкости и вблизи твердой стенки.
Основное внимание уделено изучению развитых кавитационных
течений при использовании методов нелинейной и линейной теорий.
Рассматривается решение задач о нестационарных кавитационных
течениях методом потенциала ускорения. Показано, что многие задачи о
стационарных и нестационарных кавитационных течениях сводятся
к задаче Римана — Гильберта для полуплоскости и успешно решаются
с помощью формулы Келдыша—Седова.
Рассматривается искусственная кавитация как метод физического
исследования явления, а также как способ изменения
гидродинамических характеристик различных тел. Приведены некоторые результаты
экспериментальных исследований искусственных каверн,
образованных на телах простых форм.
Учебное пособие предназначено для студентов кораблестроительных
институтов специальности «Гидроаэродинамика», может быть полезен
студентам других специальностей, а также аспирантам и инжене рам,
занятым исследованием проблем кавитации.
Реиензенты: канд. техн. наук А. С. Горшков,
докт. техн. наук проф. А. Н. Патрашев
Научный редактор докт. техн. наук проф. И. Т. Егоров
ρ 048Г0П—77 ^~^^ ® Издательство «Судостроение», 1977 г.
048@1)-77
ОСНОВНЫЕ
УСЛОВНЫЕ
ОБОЗНАЧЕНИЯ
ρ — давление жидкости в произвольной точке.
Рн — давление газа в каверне.
κ — число кавитации.
g — ускорение силы тяжести.
Η — глубина погружения тела.
Fr — число Фруда.
R — радиус кавитационного пузырька,
α — угол атаки.
β — половина угла раствора клипа.
μ — даиамическая вязкость.
V — кинематическая вязкость,
ρ — плотность жидкости,
σ — коэффициент поверхностного натяжения,
ш — комплексный потенциал скорости течения
(характеристическая функция),
φ — потенциал скорости.
ψ — функция тока.
-т— = V = I V |е'® — комплексная скорость
течения, где I VI — модуль функции; θ —
аргумент.
Voo — скорость потока на бесконечиости.
Vk — скорость частицы жидкости иа границе
каверны.
Vx, Vy — проекции вектора скорости иа оси
прямоугольной системы координат.
Vx, Vy — проекции вызванных скоростей.
ω — функция Η. Ε. Жуковского.
Χ — сила сопротивления.
Υ — подъемная сила.
Μ — гидродинамический момент.
Сх — безразмерный коэффициент сопротнвлення.
Су — безразмерный коэффициент подъемной силы.
Cm — безразмерный коэффициент момента.
Cq — коэффициент расхода газа.
Φ — потенциал ускорения.
F {г, /) = Φ -|- /Ψ — комплексный потенциал
ускорения.
ВВЕДЕНИЕ
Кавитация — явление разрыва капельной жидкости под
действием растягивающих напряжений, возникающих при
разрежении в рассматриваемой точке жидкости. При разрыве капельной
жидкости образуются полости — кавитационные пузырьки,
заполненные паром, газом или их смесью. Следовательно, разрыв
жидкости обусловлен изменением характеристик поля скоростей
и давлений.
Кавитационные пузырьки образуются в тех местах, где
давление в жидкости ρ становится ниже некоторого критического р^р.
-Если давление снижается вследствие возрастания местных
скоростей потока капельной жидкости, то кавитация называется
гидродинамической, если снижение давления вызвано
прохождением акустических волн, то кавитация называется
акустической.
Критическое давление, при котором происходит разрыв
жидкости, зависит от многих факторов: от чистоты жидкости,
содержания воздуха, состояния поверхности, на которой возникает
кавитация.
Кавитация может возникать в потоке жидкости, имеющем
переменное поле давления, а также вблизи и на поверхности тел
различной формы — в местах наибольшего разрежения.
Переменное поле давления создается различным образом: в результате
изменения скорости потока (движения тела), влияния формы тела,
вследствие механических воздействий на жидкость (вибраторы
гидроакустических станций).
Различают две стадии кавитации: начальную и
развитую.
Разрежение на теле зависит от скорости его движения
(скорости потока): при возрастании скорости оно увеличивается.
Поэтому явление кавитации характерно для больших
скоростей движения тел.
Начальная стадия появляется при больших разрежениях,
приводящих к разрыву жидкости. Существуют различные формы
начальной стадии кавитации: пузырчатая, пленочная, в виде
вихревых шнуров.
Если представить себе жидкость, свободную от примесей,
то при давлении, равном давлению ее насыщенных паров,
происходит вскипание жидкости. Это явление называется паровой
кавитацией. Образовавшиеся при этом пузырьки пара
переносятся потоком в область повышенного давления, пар
конденсируется, и пузырьки схлопываются.
В потоке жидкости, как правило, содержится некоторое
количество газа, мельчайшие пузырьки которого имеют радиус —10"® м
и невидимы для невооруженного глаза. Эти пузырьки воздуха —
нуклеоны (зародыши) — переносятся потоком жидкости и,
попадая в область более низкого давления, начинают расти. Через
поверхность пузырька происходит диффузия газа: внутрь
пузырька или из него в зависимости от концентрации газа в
пузырьке и окружающей его жидкости. Это явление называется
газовой кавитацией. Практически всегда наблюдается
парогазовая кавитация.
При попадании в область повышенного давления кавитацион-
ный пузырек не всегда схлопывается: он может лишь уменьшиться
в размере вследствие сжимаемости газа. При этом повышается
температура газа в пузырьке и при очень больших давлениях
возможно свечение газа.
Если пузырек содержит достаточно много газа, то, достигнув
минимальных размеров, он начинает снова расти и, таким образом,
совершает несколько циклов затухающих колебаний.
Если в пузырьке газа мало, то под действием повышенного
давления размеры пузырька быстро уменьшаются, а схлопывание
пузырька сопровождается звуковым импульсом и гидравлическими
ударами, способными разрушать поверхность обтекаемого тела
(кавитацнонная эрозия).
Однако в ряде случаев начальная стадия кавитации
сопровождается образованием на теле тонкой пленки (пленочная
кавитация). Экспериментальные исследования на моделях
профилей, тел вращения, винтов в кавитацпонных трубах показывают,
что форма начальной стадии кавитации зависит от многих
факторов (размеров модели, состояния ее поверхности, типа
экспериментальной установки).
Для выяснения картины начальных стадий кавитации на телах
вращения по решению Международной конференции ученых,
работающих в опытовых бассейнах разных стран мира, были
проведены кавитационные испытания стандартного тела вращения
с эллипсоидальной головкой и с полусферическим носиком в
кавитацпонных трубах. Было замечено, например, что при испытании
тела вращения с полусферической головкой пузырчатая
кавитация возникает в районе минимального давления по длине тела.
6
Пленочная кавитация в виде пояска возникает в районе,
значительно смещенном в корму модели от места минимального
давления па теле. Возможно возникновение пленочной кавитации
в виде пятен.
Таким образом, для тел вращения наиболее типичны три
формы начальной кавитации: пузырчатая; пленочная в виде
пояска; пленочная в виде пятен (рис. 1).
Рис. 1. Начальные стадии
кавитации на теле вращения: а —
пузырчатая; б — пленочная в
виде пояска; β — пленочная в виде
пятеи.
При рассмотрении начальной кавитации крыла конечного
размаха учитывают особенности ее возникновения и развития на
различных участках поверхности крыла и за крылом:
на поверхности крыла, удаленной от кромок;
на кромке крыла;
в концевых вихрях.
Кавитация, возникающая на поверхности крыла, удаленной
от кромок (профильная), может быть пузырчатой и пленочной;
7
пупырчатая сопровождается образованием пузырьков, пленочная—
образованием каверны, вытянутой в продольном направлении и
замыкающейся на профиле.
Кавитация на кромке крыла (кромочная) может быть
различной формы в зависимости от относительной толщины крыльевого
профиля, его кривизны, степени скругления носика и угла атаки.
Первая форма кавитации характеризуется образованием
пленочной каверны н возникает на засасывающей стороне относительно
толстых профилей с большим радиусом скругления 1юсика.
Рис. 2. Нячальиая стадия кавитации иа эллиптическом крыле
при κ= 1,64; п= 8, V= 15,4 м/с.
Вторая форма кавитации представляет собой полый шнур,
тянущийся вдоль входящей кромки на некотором расстоянии от
нее, и возникает на профилях с острым носиком, а также на
нагнетающей стороне изогнутых профилей.
Кавитация в вихревых шнурах, сбегающих с крыла конечного
размаха (вихревая), представляет собой в сущности кавитацию
в следе за крылом. При достаточном разряжении в центре
вихревого шнура нерастворимые пузырьки воздуха, попадая туда,
начинают интенсивно расти (первая фаза). Когда давление в центре
вихревого шнура достигает значения, близкого к упругости
паров воды, происходит разрыв жидкости и образуются сплошные
полости, тянущиеся на некотором расстоянии за крылом (вторая
фаза). На рис. 2 приведена фотография кавитнрующего
эллиптического крыла с вихревыми шнурами.
При развитой кавитации каверна имеет вид прозрачной
полости, замыкающейся на теле (частичная кавитация) или
оканчивающейся за телом (суперкавитация). В районе замыкания
каверны образуется струйка, которая, попадая в полость каверны,
8
вызывает разрушение ее хвостовой части и образование за
каверной следа, содержащего пузырьки пара и газа.
За один из основных параметров, характеризующих кавитацию,
принимают число кавитации
Рсо-Рк
κ =
Pi^i
где /7со, Vk — давление и скорость потока на бесконечности;
р^ — давление в каверне; ρ — плотность жидкости.
Описанная выше кавитация называется естественной, так
как ее возникновение связано с разрывом жидкости,
обусловленным изменением характеристик поля скоростей и давлений.
Если в какую-либо разреженную область жидкости подавать
воздух или иной газ, то возникает явление, называемое
искусственной кавитацией (вентиляцией). Искусственную кавитацию можно
создавать на телах различных форм: на крыльях, телах вращения,
гребных винтах. Вследствие образования искусственных каверн
(воздушных полостей) изменяются поле давления на теле и
гидродинамические силы, действующие на тело. Например, при
вдувании воздуха на поверхности крыла изменяются его подъемная
сила, момент, лобовое сопротивление.
Для создания на теле области разрежения предусматривают
местные конструктивные изменения формы тела — выступы, или
кавитаторы. Вдувание воздуха используют в лабораторных
условиях для исследования физических процессов, характеризующих
кавитацию, так как для получения естественной кавитации
необходимы весьма большие скорости потока жидкости, обтекающей
тело, а искусственную кавитацию можно получить при
сравнительно малых скоростях потока.
При развитой искусственной кавитации каверна имеет вид
прозрачной пленки, которая в хвостовой части либо сворачивается
в две вихревые трубки, либо заканчивается обратной струйкой
жидкости.
Кемпбел и Хильборн 176] предложили критерий перехода от
одной формы образования хвостовой части каверны за диском
к другой:
при κ > 1/Fr хвостовая часть каверны сворачивается в два
вихревых жгута;
при κ < l/Fr каверна заканчивается обратной струйкой,
здесь κ — число кавитации; Fr — число Фруда по диаметру
диска.
Из формулы, характеризующей число кавитации, видно, что
для получения одного и того же числа кавитации нужно либо
увеличить скорость потока (знаменатель), либо увеличить
давление р^ путем вдувания газа (уменьшить числитель). Поспедний
путь при проведении эксперимента оказывается значительно
дешевле, так как не требует создания высокоскоростных установок.
9
Впервые с явлением кавитации в судостроении встретились
в 1894 г. при испытании английского миноносца «Дэринг». На
режимах полного хода гребной винт резко изменял свои
характеристики, что приводило к падению скорости. Тогда же по
совету В. Φ руда был введен термин «кавитация». Известно также,
что примерно в то же время Рейнольде исследовал возможность
разрыва жидкости в трубках с пережатием.
Примерно до 40-х годов XX в. развитие исследований
кавитации гребных винтов и насосов шло очень медленно в связи
с трудностью создания экспериментальных лабораторных
установок, обеспечивающих большие скорости движения жидкости.
Кавитация рассматривалась только как вредное явление,
сопровождаемое шумом, вибрацией, эрозией и падением упора
гребного винта.
В 1939 г. В. Л. Поздюнин выдвинул идею создания суперка-
витирующего гребного винта: улучшения характеристик
профилей лопасти, а также винта в целом путем использования
развитой кавитации. Так выявилась положительная сторона
кавитации, а понятие о ней было значительно расширено. Появилась
необходимость в разработке теоретических методов расчета
супер кавитирующи χ профилей. В качестве расчетных стали
использовать разработанные ещ,е ранее методы теории струи идеальной
жидкости Кирхгоффа, Гельмгольца, Вагнера, Н. Е.
Жуковского, С. А. Чаплыгина, М. А. Лаврентьева, Л. И. Седова и др.)
применительно к известным схемам плоских кавитационных
течений. В дальнейшем были предложены новые схемы плоских
кавитационных течений, достаточно хорошо отражающ,ие
физическую картину явления. Так, в 1944 г. Д. А. Эфросом была
предложена схема обтекания с обратной струйкой, значительно
позже, в 1965 г., М. Тулиным предложены две схемы кавитацион-
ного обтекания (односпиральные и двухспиральные вихри).
Решение нелинейных задач кавитационного обтекания было
связано с вычислительными трудностями. Большой вклад в
теорию плоских кавитационных течений внес М. Тулин: в 1956 г.
он разработал теорию линейного приближения и свел задачу о ка-
витирующем профиле к задаче об обтекании некавитирующего
профиля, что значительно упростило численные расчеты.
А. Н. Иванов в 1962—1965 гг. предложил использовать метод
особенностей (источников, стоков, вихрей) для решения плоских
задач кавитационного обтекания, а в дальнейшем применил этот
метод для решения пространственных задач.
В 1944 г. Рейхардтом и независимо от него Л. А. Эпштейном
были начаты экспериментальные исследования искусственной
(воздушной) кавитации на дисках и телах различной формы.
Позднее аналогичные эксперименты были выполнены ^Клайде-
ном и Коксом.
В исследования искусственных кавитационных течений внесли
вклад советские ученые Л. А. Эпштейн, Г. В. Логвинович,
10
Α. Φ. Болотин; их работы в значительной степени раскрыли
физические процессы, характеризующие явление кавитации, и
позволили установить ряд закономерностей.
В связи с применением искусственной кавитации для
улучшения гидродинамических качеств быстроходных судов появился ряд
экспериментальных и теоретических работ в этой области. В
работах М. Тулина, Ларока, Стрита, М. А. Басина и других
получены решения задач о стационарном кавитационном обтекании
крыла вблизи свободной поверхности.
А. А. Бутузовым была разработана теория определения
параметров искусственных каверн, образованных под пластиной,
основанная на использовании метода особенностей. Согласно
этой теории задача сводится к приближенному решению интегро-
дифференциальных уравнений. А. А. Бутузов провел большую
серию лабораторных и натурных экспериментов. Одновременно
с этим рядом авторов были проведены исследования поля
давлений, а также характеристик пограничного слоя вдоль кавитатора,
вдоль каверны и .на пластине за каверной.
Движение подводных крыльев имеет неустановившийся
характер: ускоренное и замедленное — на режимах разгона и
торможения судна, в условиях волнения. В связи с этим ряд ученых
в СССР и за рубежом начал разрабатывать теорию расчета
нестационарных кавитационных течений. Линейное приближение
этой задачи с помощью метода потенциала ускорения было
исследовано в 1965 г. Сонгом и в дальнейшем развито в работах
М. А. Басина, А. В. Шалларя. Ряд задач нестационарных
кавитационных течений был решен в работах А. В. Кузнецова.
Развитие вычислительной техники позволило значительно
расширить возможности решения задач кавитационного
обтекания, особенно осесимметричных и пространственных. Следует
отметить работу Бреннена, использовавшего для расчета осе-
симметричного кавитационного течения в ограниченном потоке
метод конечных разностей, и работы А. Н. Иванова, сводящие
задачу к двум интегральным уравнениям, решение которых
выполняется численными методами.
Представляют интерес также работы Л. Г. Гузевского, в
которых предлагается численный метод расчета осесимметричных
течений, со свободными границами при использовании сплайн-функций.
Если теоретические методы решения задач о развитых
кавитационных течениях быстро совершенствуются, то теоретические
методы изучения начальных стадий кавитации развиваются
сравнительно медленно. В настоящее время достаточно хорошо
разработана статика и динамика одиночного кавитационного
пузырька в безграничной жидкости и вблизи стенки. Впервые
динамика парового пузырька была исследована в 1917 г. Рэлеем.
В дальнейшем в изучение этого вопроса внесли большой вклад
Плессет, Триллинг, Джильмор, Си Дин-Ю, А. Д. Перник,
Ю. Л. Левковский и другие.
И
Влиянием сжимаемости жидкости на нестационарное движение
стенки пузырька долгое время пренебрегали вследствие
трудностей математического решения задачи, несмотря на то, что этот
эффект имеет важное значение и в ряде случаев оказывает
существенное влияние на характер движения.
В 1941 г. Херринг при решении задачи о подводном взрыве
исследовал случай произвольного изменения давления внутри
каверны и ввел поправку первого приближения на ее
сжимаемость. Он принял известное из акустики допущение, что скорости
жидкости всегда малы по сравнению со скоростью звука. В 1952 г.
Триллинг принял условие, что потенциал скорости приближенно
удовлетворяет акустическому уравнению расходящихся
сферических волн, и получил на основе акустического приближения
более общее уравнение движения стенки газового пузырька.
Примерно в то же время Джильмор, отказавшись от
акустического приближения, принял гипотезу Кирквуда—Бете,
согласно которой возмущения распространяются со скоростью,
равной сумме местной скорости звука и скорости жидкости, и
составил приближенные уравнения движения стенки пузырька при
переменном давлении газа, а затем выполнил численные расчеты.
Кавитация возникает при движении жидкости вблизи тел
различной формы (поверхности крыльев и лопастей, стоек и т. д.),
в связи с этим Ю. Л. Левковским и Г. Г. Судаковой были
составлены уравнения движения газового пузырька вблизи стенки и
исследовано ее влияние на поле скоростей и давлений.
Однако в настоящее время нет достаточно хорошо
разработанных теоретических методов исследования движения нескольких
пузырьков, их взаимодействия и перехода от начальной стадии
к развитой кавитации.
Значительное число работ посвящено исследованию
начальной стадии кавитации на крыльях и телах вращения. Так, в
работах, А. С. Горшкова, О. Н. Гончарова, Ю. Н. Калашникова
выявлены разновидности кавитации, исследован масштабный
эффект и разработаны методы выбора масштабных экстраполяторов.
Результаты теоретических и экспериментальных
исследований кавитационных течений используются в различных отраслях
техники. Широкое применение находят они при решении задач
управляемости и ходкости современных скоростных судов.
Настоящее учебное пособие знакомит студентов с
теоретическими методами решения задач кавитационного обтекания и
с экспериментальными методами его исследования, т. е. с
основами знаний, необходимых в начале инженерной и
исследовательской работы в этой области.
Предполагается, что до изучения материала, изложенного
в пособии, студент ознакомился с курсами высшей математики
(включая численные методы решения задач), общей
гидромеханики, газодинамики и теории крыла в соответствии с учебными
программами по специальности «Гидроаэродинамика».
Глава I
НАЧАЛЬНАЯ СТАДИЯ
КАВИТАЦИИ
(ПУЗЫРЧАТАЯ КАВИТАЦИЯ)
1. Статическое равновесие пузырька в жидкости.
Критическое давление и критический радиус
Предположим, что газовый пузырек, находящийся в жидкости
в статическом равновесии, имеет сферическую форму (радиус
сферы R). В нем содержатся пары воды и газ, причем масса газа
остается постоянной и диффузия газа через поверхность пузырька
не происходит.
Уравнение статического равновесия имеет вид (рис. 1.1)
где ρ — давление в окружающей жидкости; р„ — давление
насыщенных паров воды; р^ — парциальное давление газа; σ —
коэффициент поверхностного натяжения.
Давление р„ и коэффициент σ зависят от температуры. Так,
например, для воды при Τ = 293 К (ί ~ 20° С) р„ == 2350 Па
B40 кгс/м^); σ = 7,35-10-^ Н/м G,5-10-^ кгс/м), а при Τ =
= 277 К (ί = 4° С) р„ = 785 Па (80 кгс/м^).
В частном случае при паровой кавитации (рг = 0) условие
равновесия:
P = P„-f· A.1.2)
Если ρ < р„ D-i то паровой пузырек растет (расширение),
^ 2σ
если ρ > Ра р- f то паровой пузырек сжимается.
Из формулы A.1.2) можно легко найти порядок величины
растягивающих напряжений, при которых происходит разрыв
жидкости. Пузырьки в жидкости имеют радиус /?= 10"* м^ 10"'' см;
так как |р„К I^L то р = —^=—147-10«Па(—1500кгс/см«).
При изменении радиуса парогазового (газового) пузырька
изменяется давление газа.
13
Как известно из газодинамики, давление совершенного газа
внутри пузырька связано с объемом и температурой уравнением
Клапейрона, которое для сферического пузырька может быть
представлено в виде
Рг = -^. A.1.3)
где Τ — абсолютная температура; В — постоянная, зависящая
от массы газа внутри пузырька.
Тогда уравнение статического равновесия без учета вязкости
жидкости можно записать так:
_ ВТ 2σ
Ρ Ра~Т рц ρ '
A.1.4)
Из A.1.4) расчетным путем легко определить зависимости
давления ρ (R) или (ρ — ρ„) {R) при постоянной температуре и
массе газа. В частном случае
изотермического или адиабатического
закона изменения состояния газа
форма записи уравнения
статического равновесия изменяется.
Образование кавитационных
пузырьков происходит в
различных условиях, определяющих
характер расширения (сжатия) газа
внутри пузырька. Если
выделяемое тепло при сжатии пузырька
быстро поглощается водой (что
происходит при небольших,
скоростях движения стенки пузырька,
а также из-за большой
теплоемкости воды и малой массы газа), то
процесс расширения или сжатия пузырька считается
изотермическим, т. е. изменение давлений газа и радиуса пузырька
связано законом Бойля—Мариотта:
Рис. 1.1. Силы, действующие на
поверхность парогазового пузырька
при статическом равновесии.
или
PrR^ = ProRo
о -о -^
Иг — А'го ps »
A.1.5)
где индекс О соответствует начальному состоянию пузырька.
Тогда условие статического равновесия для начального
состояния парогазового пузырька:
2σ
Po = Ριί + Pro — -^
или
Pro
, 2σ
A.1.6)
Подставив A.1.6) в A.1.5), получим давление газа в пузырьке
после изменения его радиуса от Rq до R:
7?»
Рг = Pro -^ = [Po-РиЛ'-щ)
A.1.7)
р,Па(кгс/м^)
5-10^(-^5-10^)
2-10^(--2-10^)^"
8 9 Р-10^м
Рис. 1.2. Зависимость равновесного давления в жидкости от начального и
текущего радиусов пузырька.
Используя это выражение затем в A.1.1), найдем зависимость
равновесного давления в жидкости от начального и текущего
радиусов пузырька:
P = P„+(po-p„ + ^)||-f-. A.1.8)
На рис. 1.2 формула A.1.8) представлена графически для
диапазона значений радиусов пузырька i?o = @,1-ь1,5)«10"* м.
15
в расчетах равновесное давление ρ о в жидкости при R = Rq
было принято равным 10^ Па A0 300 кгс/м^).
Если пузырек содержит большое количество газа, а движение
его стенки происходит настолько быстро, что рассеяние тепла
в жидкости можно рассматривать как медленно развивающийся
процесс, то закон изменения состояния газа в пузырьке следует
считать адиабатическим.
Если предположить, что начальное давление газа р^„, то,
полагая адиабатическим закон расширения и сжатия газа, получим:
££0 _ (βο_γν
A.1.9)
где γ — показатель адиабаты.
В этом случае зависимость давления в жидкости от радиуса
аналогично A.1.8) имеет вид:
2σ
R
(I.l.lO)
Как следует из формул A.1.4), A.1.8), A.1.10), пузырек
изменяет свой радиус под действием результирующей силы f {R, Τ),
которая для различных частных случаев закона изменения
состояния газа представляется таким образом:
по закону Клапейрона
fiR, T) = -p-fp„ +
ВТ
R^
2σ
R
по изотермическому закону
/(i?, Т) = -р + р„ + (ро-Рн + ^||
по адиабатическому закону
/(;?.T) = -p-fp,„(ff-f
Для парового пузырька
f{R, Т)^^р + р,~Щ-.
A.1.11)
ψ, A.1.12)
A.1.13)
A.1.14)
Если / {R, Т) > О, то пузырек растет; если / {R, Т) < О,
то он схлопывается.
Как видно из рис. 1.2, при давлениях р, больших р„,
[существует единственное значение радиуса, соответствующее
положению равновесия пузырька. При давлениях, меньших Рн
(действие растягивающих напряжений), существует два положения
равновесия. И наконец, при разрежении, которое больше
некоторого критического значения, равновесия нет.
16
Для того чтобы определить, какое из двух положений
равновесия (например, на рис. 1.2 точки А и В) устойчиво, необходимо
составить частные производные ^ в этих точках, а
устойчивость оценить по знаку производной.
Если 35" < О (точка Л), то пузырек находится в устойчивом
равновесии, если же ^ > О (точка В), то равновесие
неустойчивое.
Радиус пузырька R^p и давление р^р» соответствующие
минимуму функции / {R, Т) или / {RiRo), назовем критическими
(точка С).
rif
Выполняя условие ^π^ = О, получим после ряда
преобразований выражения критического радиуса для всех рассмотренных
случаев:
для закона изменения состояния газа A.1.3)
для изотермического закона A.1.5)
R.P = RoY^{po-p. + ^)-V~SRoY'^^ A.1.16)
Для адиабатического закона A.1.9) при показателе адиабаты
R., = RoY^· (I-1-17)
Для парового пузырька при постоянной температуре кривая
/ {R, Т) не имеет экстремума по 7? и равновесие всегда
неустойчиво. Радиус, соответствующий статическому равновесию, равен
критическому, он находится исходя из условия f {R, Τ) = О
и равен
^кр = ^р. A.1.18)
Подставляя затем выражения для критического радиуса
A.1.15)—A.1.17) в уравнения равновесия, найдем формулы для
определения критического давления:.
для A.1.3)
Ркр = Рн—4llv_.
17
для A.1.5)
— 4 σ -ι/ 2σ
_ __ 4 σ Γ 2σ
для A.1.9)
», пЗ / σ \4/3 2σ / σ \3/2
§ 2. Неустановившееся движение парогазового пузырька
Рассмотренное выше решение задачи не учитывает ряда
факторов, в первую очередь таких, как инерция, вязкость, диффузия
газа через поверхность пузырька, сжимаемость, суш,ественно
влияюш,их на радиус пузырька в течение времени его
расширения или сжатия. Поэтому рассмотрим неустановившееся
движение пузырька и определим характеристики этого течения.
Появление пузырька означает существование замкнутой
поверхности, делящей рассматриваемую область на две части,
каждая из которых заполнена однородной средой: вне пузырька —
жидкость с растворенным газом, внутри пузырька — смесь газа
и паров жидкости. Положение и форма стенки пузырька
неизвестны. Математически задача принадлежит к типу краевых
задач со свободной границей. При переходе через стенку пузырька
выполняются общие законы сохранения массы, импульса и
энергии.
В наиболее общем случае, когда нельзя ничего заранее
сказать о симметрии задачи, ее решение весьма затруднено. Общая
постановка задачи и ее математическое описание известны и даны,
например, в [54]. Для составления основных уравнений
используются известные законы газо- и термодинамики. Система
уравнений включает уравнения: неразрывности, движения частиц
жидкости и газа, баланса энергии, диффузии, теплопроводности,
а также условия на границе раздела двух сред. Эти уравнения
громоздки, и мы их здесь не приводим.
Из опытов известно, что большинство пузырьков имеет
сферическую форму. Примем допущение о сферической симметрии
пузырька, которое значительно упрощает задачу, однако она все
еще остается трудно разрешимой.
Дополнительно сделаем предположение о том, что внутренняя
область пузырька однородна. В таком случае будем исследовать
только поле течения вне пузырька, а параметры,
характеризующие внутреннюю область, считаем связанными непосредственно
с соответствующими величинами на движущейся стенке пузырька.
18
в дальнейшем для упрощения задачи примем также допущения
о том, что массовые силы отсутствуют, вязкость равна нулю,
эффект взаимодействия между сжимаемостью и вязкостью
пренебрежимо мал, так как жидкость, по существу, несжимаема,
а эффект вязкости мал.
Движение стенки пузырька определяется в основном тремя
факторами: инерционными, тепловыми и диффузионными
эффектами. Так как эти факторы не всегда равноценны, то,
рассматривая только превалирующие, можно значительно упростить
решение задачи. Если инерционный эффект оказывается основным
определяющим фактором движения пузырька (как, например,
при быстром смыкании пузырька пара), то можно пренебречь
тепловыми и диффузионными эффектами. В этом случае скорость
стенки пузырька иногда может превышать скорость звука, и
жидкость нужно рассматривать как сжимаемую. Если
преобладают тепловые и диффузионные эффекты, то скорость стенки
обычно мала по сравнению со скоростью звука в жидкости.
В этом случае сжимаемостью жидкости можно пренебречь.
Если инерционные силы являются определяющим фактором
движения пузырька и можно пренебречь всеми тепловыми и
диффузионными эффектами, то система уравнений, описывающих
движение пузырька, значительно упрощается: исключаются
уравнения теплопроводности, диффузии и баланса энергии.
Последнее обстоятельство объясняется тем, что для большинства
жидкостей, результаты исследования которых представляют
практический интерес в судостроении, существует зависимость ρ =
= ρ (ρ). В рассматриваемом частном случае система уравнений
для невязкой жидкости имеет следующий вид:
1) уравнение неразрывности
1+ div(pK) = 0, A-2.1)
где div—дивергенция векторного поля;
2) уравнение движения частиц жидкости (газа)
f = f+(V-V)V = F—^V/', A.2.2)
где V — вектор скорости; F — главный вектор напряженности
массовых сил; ρ — давление в произвольной точке жидкости;
ρ — плотность жидкости; SJ — оператор Гамильтона (набла);
divV = f^ + 5:^+t;
дх ' ду ' dz
3) уравнение состояния
Р = Р(рУ. A.2.3)
19
4) граничные условия
Ρ = ρ', A.2.4)
где ρ' — давление внутри пузырька; ρ — давление в жидкости,
окружающей пузырек.
Допущение о сферической симметрии течения позволяет
получить более простые уравнения, если принять сферическую
систему координат с началом в центре пузырька. В этом случае
каждая физическая величина в произвольной точке течения
зависит только от г — расстояния этой точки от начала координат,
и только радиальная составляющая скорости отлична от нуля,
т. е. уравнение стенки пузырька
г — /? (ί) - 0.
С учетом сказанного напишем уравнение A.2.1) в сферической
системе координат
f+|-(pl^.)+^==0. A.2.5)
Уравнение Эйлера A.2.2) в дальнейшем рассматривается
в форме Громеко, а первый интеграл берется в форме Коши—
Лагранжа; массовыми силами пренебрегают:
^ + -^ + Р = /^@, A.2.6)
ρ
где Ρ (р) ~ \ —^ функция давления; F (t) — произволь-
Ро
пая функция времени, определяемая исходя из граничных
условий.
Из термодинамики известно, что функция давления
представляет собой разность энтальпии для жидкости при давлениях ρ
и Pf). В дальнейшем функцию давления обозначим через
h{p) = P ip).
Если стенка пузырька движется медленно, то жидкость можно
рассматривать как несжимаемую. Тогда, полагая в A.2.5) и A.2.6)
Ρ (О = Ρ =" const, после преобразований получим:
уравнение неразрывности
r^ + 2F, = 0. A.2.7)
где V^ == -^; φ — потенциал скорости течения;
интеграл Коши—Лагранжа
20
Потенциал φ находим исходя из граничных условий.
Преобразуем A.2.7) к виду
■|r(rV,) = 0
или
rV, = D и 1/, = -^, A.2.9)
где D — постоянная величина, определяемая граничными
условиями.
На стенке пузырька
I/ _ d« _ ρ
r = R.
Тогда A.2.9) преобразуем к виду
D = /?2^ и 1/, = ^. A.2.10)
Потенциал скорости течения находим путем интегрирования
второго уравнения A.2.10):
Φ = |ΐ/,
dr=.—B^. A.2.11)
Используя выражение для потенциала φ, а также его частные
производные по ί и г, найдем формулу для определения давления
в произвольной точке течения:
ρψ ^ RR^ + 2RR^_^R^_^p (^) (J 2.12)
Формула A.2.12) позволяет найти поле давления в жидкости
вблизи пузырька переменного радиуса R (t).
Для вычисления величин R (t), R (t), R (t), входящих в A.2.12),
составим уравнение движения стенки пузырька. Полагая в A.2.12)
г = R, после преобразований получим:
RR-^±if==-^-^F({), A.2.13)
где ρ — давление внутри пузырька.
Величина ρ зависит от вида кавитации (паровая, парогазовая,
газовая) и от законов изменения состояния газа. При
изотермическом законе изменения состояния газа ρ определяется из
21
A.1.7). Тогда уравнение движения стенки парогазового пузырька
с учетом сил поверхностного натяжения преобразуется к виду
RR+^R - —(^р„-р„ + —j —+
9R
Рн
==^-Fit). A.2.14)
При адиабатическом расширении газового пузырька на
основании A.1.13) получим:
где γ = */з — показатель адиабаты для воздуха.
Уже указывалось, что в общем случае функция F (t) зависит
от времени. В качестве примера могут быть рассмотрены три
возможных закона ее изменения:
1) внезапное понижение давления в жидкости (растяжение)
или повышение давления (сжатие). В этом случае
F{t)==--f nnnFi^^f;
2) изменение давления на теле (профиле), обусловленное его
формой. В этом случае закон изменения давления определяется
эпюрой распределения давления на профиле
Fit)^^,
где X (t) — абсцисса . центра пузырька;
3) изменение давления по гармоническому закону, что
характерно для излучателей гидроакустических станций, у которых
возникает ультразвуковая кавитация. Если излучатель
расположен на некоторой постоянной глубине жидкости, то
f U) _ Ρα — Po Sin (üt
где Ρα — постоянное статическое давление; ро — амплитуда
ультразвукового давления; ω — частота колебаний.
При заданном законе изменения давления уравнения
A.2.14)—A.2.15) решаются методом численного интегрирования.
В качестве начальных при ί = О принимаются условия R = Rq,
Наиболее простое уравнение движения стенки получается для
парового пузырька при мгновенном изменении давления (расши-
22
рение или сжатие). Если в A.2.14) исключить третий член,
учитывающий влияние газа, то уравнение приобретает следующий
вид:
при растяжении пузырька (разрежение в жидкости)
RR +-|-^Ч 1¾ =^^=^ = f; A.2.16)
при сжатии пузырька (повышение давления в жидкости)
В уравнениях A.2.16) принято F (t) = — ^ = const, а
в A.2.17) — F(t) = ροΐρ = const и р„ С р^.
Для иллюстрации на рис. 1.3 приведена зависимость радиуса
парового сферического пузырька от времени с учетом сил
поверхностного натяжения в переменном поле давления. Рассматривалось
развитие пузырька в потоке, обтекающем тело вращения с ожи-
вальной формой носа. Профиль тела и распределение
коэффициента давления Ср по длине при отсутствии кавитации даны на
рис. 1.4. Кривая изменения давления ρ (t) получена по Ср при
постоянных скорости потока Voo и числе кавитации κ. Начальное
статическое давление р^ (t), при котором возникают пузырьки
заданного радиуса, определяется по формуле
Po (О = Рн - -^ ·
Расчет произведен [48] для значений начального радиуса
Ro = 0,01, 0,1 и 0,5 мм и при ρ = 1000 кг/м^ A02 κγ/cVm*); р„ =
= 2330 Па B38 кгс/м^); σ = 0,0735 Н/м @,0075 кгс/м); V^ =
= 21,3 м/с; κ = 0,30.
На рис. 1.5 проведено сравнение теоретических и
экспериментальных результатов. Некоторое расхождение экспериментальных
данных и теоретических кривых объясняется принятыми в теории
допущениями, а также тем обстоятельством, что распределение
давлений в эксперименте [92] было найдено неточно.
В ряде случаев уравнения движения стенки пузырька
приводят к безразмерной форме.
Введем безразмерные величины:
Тогда, пренебрегая в A.2.16) силами поверхностного
натяжения и вводя безразмерное время τ, после промежуточных
преобразований получим:
23
R^MM
<
Χι ι
Li- L·
ν/ /
^1 /
Ζ- ι
ι /
ι ι
.m
\1
1 1
•^ Б 8 ΙΟΙ 12 η 16 18 20
t-W, с
Рис. 1.3. Зависимость радиуса парового сферического пузырька
от времени (с учетом сил поверхностного натяжения) в
переменном поле давления.
Рис. 1.4. Профиль тела и распределение
коэффициента давления Ср по длине.
Р-Рсо
24
Для упрощенных уравнений (без учета вязкости и
поверхностного натяжения) часто используют формулы первых
интегралов. Подстановка их в A.2.12) для постоянных значений
F (t) при растяжении или сжатии позволяет нам составить
выражения для определения давления.
V(t)^üa,{Krc/M^)
2-(-10^^)-1--2-(-10^]
1,3 6 9/ 12 15 18 21
\
Рис. 1.5. Сравнение теоретических и экспериментальных
результатов работ [48] и [92].
Теоретические результаты: —·—,- — [48];
[92 ]; Экспериментальные результаты: X, О, Δ [92 ].
Действительно, замечая, что
получаем
/?/?44^=w^(^^'>=f'
d (R^R^ ==^ RЫR.
Проинтегрируем левую и правую части
R R
jd(R^R^^^ JR4R.
Но Но
A.2.20)
25
Предполагая начальные условия при ί=0; R = Rq, R =
Ro — О, после интегрирования находим
fa2 2 zo Л Rl\.
. ^ = -^11- (I-2-21)
Полагая в A.2.21) Zo = р„ + Ро. а затем Zo = —Ро, получим
формулы для определения скорости и ускорения при расширении
или сжатии парового пузырька соответственно.
Указанный выше прием решения уравнения A.2.16) можно
также применить и для случая расширения или сжатия газового
пузырька. Принимая во внимание A.1.5), для изотермического
закона изменения состояния газа внутри пузырька найдем:
/?/,· + 4- ^^ — ^ + ? {^У = W- ά т) A-2.22)
или
d {R^R^ = ^-P-2R'dR _^El^l^, A.2.23)
После интегрирования левой и правой частей A.2.23) получим
к R к
(diR'R^ = --^\R^R + ^-^\f
Ro Ro ^0
или
/^^2 = ^ J-£-(i?^_/^} + ?^inA.
Разделив на R^, получим
2
R'- 3
Для получения ускорения движения границы газового
пузырька продифференцируем A.2.24) по времени t.
После преобразований находим:
^ = --ί^[^-Ρ-(ΐ-31η^)]. A.2.25)
В случае постоянного растяжения следует принять в A.2.25)
ρ = —Po, а в случае постоянного сжатия ρ = Ро·
Анализируя исходное уравнение движения стенки газового
пузырька A.2.22), находим, что в начальный момент, когда ί = О,
R = Ro, R = О, знак ускорения определяется разностью
Pro — Ρο· Если эта разность больше нуля, то пузырек будет
расширяться, и, наоборот, если р^о—Ро<0, сжиматься.
26
Таким образом, газовый пузырек при давлении в нем,
отличающемся от внешнего, будет совершать незатухающие
гармонические колебания. Из уравнений A.2.24), A.2.25) легко найти
экстремальное значение радиуса пузырька {R φ Ro), при
котором скорость движения его границы обращается в нуль, а также
значение критического радиуса, при котором скорость сжатия
газового пузырька достигает максимума. В первом случае
необходимо положить в A.2.24) ^ == О, а во втором — в A.2.25)
JR = 0. Тогда после промежуточных преобразований
экстремальный радиус пузырька находится как решение уравнения вида
ρ (l - ^) + Pro In (-§^У = 0. A.2.26)
Решение уравнения A.2.26) легко получить графически как
точку пересечения кубической параболы /^(-^ j =-S- I—-— Л
и логарифмической кривой f^ {~р~) = '" (w) '
Критический радиус определяется по формуле
Аналогично можно получить выражения для R и R для
случая адиабатического процесса расширения и сжатия газового
пузырька. Принимая в этом случае, что
где γ — показатель адиабаты, после преобразования найдем
-4f['-(-in· 0-2-28)
Если показатель адиабаты принять равным % и пренебречь
внешним давлением ρ о по сравнению с Рго> то в результате
получим:
l^.^2f{fy{l-^). A.2.29)
Дифференцируя выражение для R^ по времени, найдем
ускорение в виде
э4
й__3рг(
(F)(f-')='f|- ('-2-^0)
27
Приравнивая A.2.30) нулю, получим выражение для
определения критического радиуса: ί^^ρ = %^ο·
Выражения A.2.24) и A.2.25) можно переписать в
безразмерной форме с учетом принятых обозначений A.2.18):
ή= [-3-(η~^—1) + δη 4ηη] ;
η = δ-γ* A _ 3 1ηη - δ-1). A.2.31)
Аналогично выводят формулы для η и η при адиабатическом
законе расширения или сжатия газового пузырька. Опуская
промежуточные преобразования, получаем:
ή = Ι2δη-Μ1-η-^)Γ;
η = 3δΐ]-* (η-1 -1) + δη-Б. A.2.32)
Подставив полученные значения скорости R и ускорения
движения R стенки пузырька в A.2.13), A.2.14) и введя безразмерные
величины, после преобразований получим зависимости
безразмерных давлений от двух безразмерных параметров.
Для паровой кавитации эти формулы приобретают следующий
вид:
при расширении пузырька
1 + ^^ = -^^ii-rf^) i- ε^ A - η-'); A.2.33)
при сжатии пузырька
ElZfl = -i- ε [η-a A _ ε^) - D - ε«)]. A.2.34)
Β формулах A.2.33), A.2.34) приняты следующие
обозначения:
ε— ^ ,
^0 — Ρο -l· Ри — растягивающие напряжения в жидкости;
Ро — давление на бесконечности.
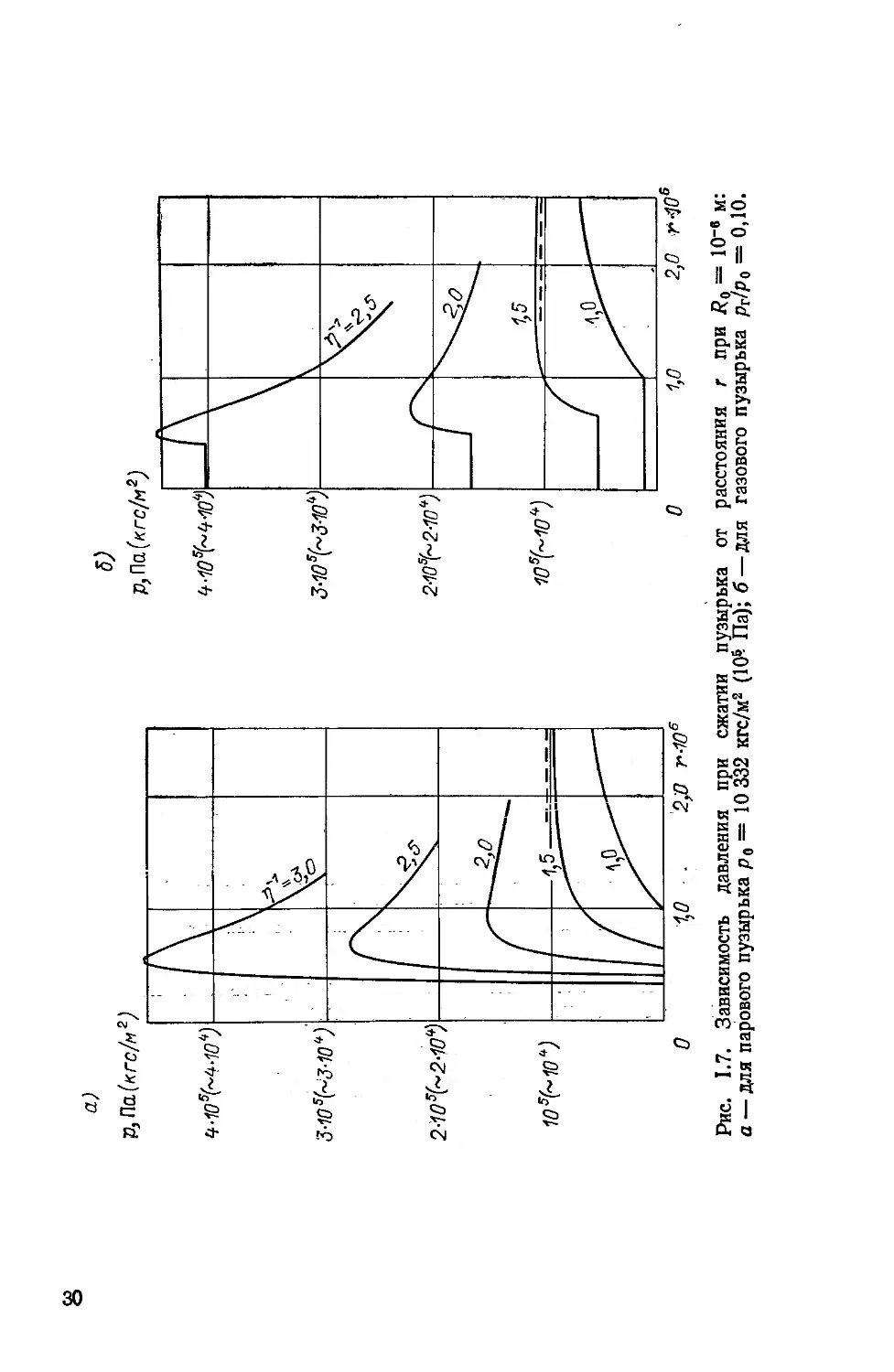
Результаты расчетов по формулам A.2.34) даны на рис. 1.6—
1.7.
Для газовой кавитации, полагая показатель адиабаты 7=*/з,
учетом A.2.27) получаем:
Ро
= ε/η-«[ΐ+^Dη-ΐ-3)] +
+ D-ε«){η-«[4-+^-°A-η-^)] —f})' 0-2-35)
28
где Po — изменение давления на бесконечности; знак +
соответствует расширению пузырька, знак — его сжатию.
Результаты расчетов для сжатия по A.2.35) даны на
рис. 1.7, б.
Время t, за которое радиус пузырька изменяется от Ro до R,
можно получить путем интегрирования первого уравнения
A.2.21) — для парового пузырька и выражений A.2.24), A.2.28) —
для газового пузырька.
7
1,25
Р'
1
1
1
1
■r/R
67
1
\
\ -1
^
*-
2.5
\Я^=50
ч
^Ί
г
25
J5
.9
v4
5
ОС
0,1 0,9 Ο,δ 0,7 0.6 0,5 0,4- Οβ 0,2 0,1 О
"*—е/г
Рис. 1.6. Распределение давлений вблизи схлопываю-
щегося пузырька.
геометрическое место максимальных значений p/Pq.
В результате после промежуточных преобразований получим:
при расширении парового пузырька
при сжатии парового пузырька
R^i^ dR
, _ ■\/±_ ±_ г R^'^ dR
^^ У 2 р„ J (Rl-R^/^
Rh
29
у/
С
1
ι
5C
R.
^o
v2
CM
so
Qi C5.
s «
et л
о.
•-S
η
>.
к с
s „
6β ρ
§§
0°
ο СП
се га
о.·"
SS
<« I
• с·
с«.
о
вС
в
X
в<м
t-eo
о
Sil
ё <=
с
3
СП
с
со о.
в I
30
Или, вводя значения безразмерного радиуса η = RIRo,
получим:
при расширении
Τ)
при сжатии
Τ)
Из второго выражения A.2.32) при η = О получим время
полного схлопывания τ. В этом частном случае интегрирование
можно выполнить с помощью Г-функций. Опуская
промежуточные выкладки, получим
В работе [31] приведена таблица значений безразмерного
времени f = tiRo VplPo в интервале η от О до 1,0, полученных
в результате численного решения второго уравнения A.2.36).
Время изменения радиуса газового пузырька, как и в
предыдущих случаях, находим по формуле
t- , -^,
где функция R определяется по формулам A.2.24), A.2.29).
На последних стадиях сжатия пузырька вязкость может
оказать существенное влияние на характеристики течения. Поэтому
рассмотрим способ учета вязкости в дифференциальных
уравнениях движения границы пузырька. В связи с тем что проявление
вязкости жидкости происходит сложным образом и связано с
сжимаемостью жидкости, рассмотрим сначала несжимаемую жидкость.
Из анализа уравнений Навье—Стокса 1681 можно показать,
что движение жидкости, вызванное сжатием или расширением
сферического пузырька, описывается уравнением невязкой
жидкости, а влияние вязкости учитывается граничными
условиями. Из курса динамики вязкой жидкости известно, что при
движении вязкой жидкости возникают касательные напряжения
и изменяются нормальные напряжения (по сравнению с невязкой
жидкостью). На основании гипотезы Ньютона при ламинарном
31
обтекании касательные напряжения в вязкой жидкости связаны
с градиентом скорости и динамической вязкостью зависимостью
dV
где μ — динамическая вязкость.
В невязкой жидкости нормальные напряжения одинаковы для
всех площадок, проходящих через данную точку, и равны
величине —р, абсолютное значение которой равно гидродинамическому
давлению в данной точке.
Будем Считать, что касательные напряжения, а также и
изменения величин нормальных напряжений не зависят от давления
в данной точке. Тогда нормальные напряжения при движении
вязкой жидкости представляются в виде суммы двух слагаемых:
одно равно —р, другое, обусловлено только вязкостью и не
зависит от р.
В декартовой системе координат получим:
Рхх = —ρ + Олх;
Pzz = —Ρ + ^ζζ.
где Оц — дополнительные нормальные напряжения, вызванные
вязкостью, находятся по формулам
σ -2μ^'·
"дгл: — ^V· Яд. >
<Jyy — ζμ ^^ ,
σ^ζ = 2μ-^.
В случае же сферической симметрии потока (сферическая
система координат)
а суммарные нормальные напряжения
Ргг = —Ρ + 2μ-^.
Так как давление внутри пузырька равно нормальному
напряжению с обратным знаком, т. е. р„ = —р, то для парогазо-
32
вого пузырька при учете сил поверхностного натяжения и
вязкости найдем:
или
P-A,-f + ..,.(tr-2>.fU. A.2.37)
Выразим градиент скорости через радиус пузырька и его
производные:
-оГ = ^'™<Р = Г· A.2.38)
Тогда после двойного дифференцирования A.2.38) по г получим
^^^ = _2.¾!. A.2.39)
дг
После подстановки A.2.39) в A.2.37) найдем давление на
границе пузырька
Подставляя затем это выражение в интеграл Коши—Лаг-
ранжа, получим дифференциальное уравнение движения границы
парогазового пузырька с учетом вязкости:
+ 4μ^ = ^-Ρ{1). A.2.40)
При заданном законе изменения возмущающей силы F (t)
уравнение A.2.40) решают численными методами на ЭВМ при
заданных начальных условиях. Применяя описанный выше прием
1см. A.2.20)], можно получить первый интеграл
дифференциального уравнения A.2.40).
Для оценки влияния вязкости и поверхностного натяжения
на величину радиуса пузырька на ЭВМ «Мир» были проведены
численные расчеты R (t), R (t) [A.2.40)] для парового и
газонаполненного пузырьков. В первом случае третий член
уравнения был опущен. Рассматривалось мгновенное повышение
давления в жидкости, т. е. F (t) = —Ро = —Ю'^ Па (—10 332 кгс/м^).
Кроме того, было принято: Ro = 10~^ и; Ro = 0; ρ = 1000 кг/м^
A02 КГМ-« с^); Г = 283 К (ί = 10° С); о = 7,35 10"^ Н/м G,57 X
X 10-3 кг/м); Рн = 1230 Па A25 ктс/м^); μ = 133-10^^ Па-с
[133-10-* (кгс-с)/мЧ и μ = 133-10-* Па-с [13310-« (кгс-с)/мЧ.
33
а) 10
0.5
\1=0;ΰ*ΰ'
I I
X
ft:
Ö
^=0;ϋ=0
^;0^
50
40
30
20
10
\^OiÖ*0'
π
и
/
y.iO;a*o\
/
<μ^Ο;σ^Ο
I I 1
0,05
MO
t-10^C
0,05
\10
ЪЮ.с
Рис. 1.8. Влияние вязкости и сил поверхностного натяжения при схлопы-
вании парового пузырька: а — на радиус пузырька; б — на скорость
движения границы пузырька.
ff и
0.5
ПH
10
к
Ч) ·>
-¾
5
\
\
\
Ж.
1
i33-io"'mcfi33-io~^-i
153-10'^
ire
М2
^)
0,05 0,10 0,15 t10U
/\
/
1/
V.'155-IO'^
133-10
/
-4
ас5
010
0,15 f10°c
Рис. 1.9. Влияние вязкости при схлопатыванин
парового пузырька: а — на радиус пузырька; б — на
скорость движения границы пузырька.
34
Первое значение μ относится к воде, второе — к гипотетической
жидкости.
Результаты расчетов даны на рис. 1.8—1.10. Как видно из
рисунков, поверхностное натяжение уменьшает время схлопы-
вания парового пузырька, а вязкость, наоборот, его увеличивает.
Рго= I 1
51ΒΒθηα.(τ5166κΓο/>η
I I
'20664 Πα (г20ЁБ,Чкгф^
Vro'D
О
0.1
0,2
Урго=516В0Па{51Б51<гс/м^)
_1 I I I
Рис. 1.10. Пульсация газонаполненного пузырька при различных
значениях начального давления газа: а — изменение радиуса пузырька; б —
изменение скорости движения границы пузырька.
Газонаполненный пузырек, в отличие от парового, под действием
сжимающих усилий совершает незатухающие колебания, частота
которых уменьшается с ростом начального парциального
давления газа Pro·
§ 3. Влияние сжимаемости жидкости
на развитие парогазового пузырька
В тех случаях, когда скорость движения стенки пузырька
(особенно парового) приближается к скорости звука в жидкости,
полученные выше решения будут неточными, так как влияние
сжимаемости может оказаться весьма существенным и тогда
необходимо решать полные уравнения A.2.1)—A.2.3).
Прежде всего необходимо выбрать зависимость между
давлением и плотностью. Внезапное сжатие жидкости не вызывает
существенного роста температуры, т. е. жидкость изоэнтропична
(энтропия сохраняет свою величину), и поэтому плотность
связана с давлением эмпирическим соотношением уравнением
состояния в форме Тэта
р = Ар" — В, A.3.1)
где
А^
Рв — В .
Ро и роо — давление и плотность жидкости на бесконечности.
35
Константы, входящие в A.3.1), для воды равны: В = 3-10^ Па
C000 атм), η = 7.
Скорость звука с определяется формулой
с^ = -|-. A.3.2)
После дифференцирования A.3.1) по ρ и подстановки
результата в A.3.2) получим
и—I
2 _ п{Р + В)
vJ^'+HiM)" ■ <··^^
в невозмущенной жидкости квадрат скорости звука при ρ = Ро
reo
После подстановки этого выражения в A.3.3) местная скорость
звука
п—1
'р + В\ 2п
^=-(Ш
На основании решения Римана [51 ] для плоских волн
конечной амплитуды представим уравнения неразрывности A.2.5) и
движения жидкости A.2.6), учитывая A.3.2), в следующем виде:
[i + iVr-c)j,]{v,--^) = ^. A.3.6)
Оператор в квадратных скобках показывает, что величина
(У^-|—^^j сохраняет свое постоянное значение при
распространении волн в положительном направлении г со скоростью
(Vr + с), а величина (v^ ΖΓτ) — "Ρ" распространении
волн в отрицательном направлении со скоростью (У,- — с).
Широко распространенным методом решения уравнений
сжимаемой жидкости является метод характеристик [54].
Введем характеристические координаты α {г, О и β (Л t)
такие, что
dr — (V^ + с) dt = О при β = const
или
^ = (F. + c)^ A.3.6)
36
v^'
К"-
η—1 J
2c \
η—1 У ~"
л öa
2VrC dt
И iir — (V^ — c) dt = 0 при α = const
либо
^-(Уг~с)^. A.3.7)
Уравнения A.3.6) и A.3.7) определяют два семейства
характеристических линий а = const и β = const, где а называется
«уходящей» характеристикой, а β — «приходящей». С учетом
A.3.6), A.3.7) выражения A.3.4), A.3.5) легко привести к системе
уравнений в частных производных:
д /,^. I 2с \ 2V,c dt _ ,τ о о\
A.3.9)
Неизвестными в этой системе являются характеристические
координаты а (г, ί) и β (г, t). Для решения системы A.3.8),
A.3.9) используются численные методы, в частности метод
конечных разностей, при заданных начальных и граничных условиях.
При смыкании пузырька кривые а {г, t) к ^ (г, t) будут
расходиться от стенки пузырька г = R (t). При расширении пузырька
с достаточно большой скоростью семейство характеристик β =
= const может стать сходящимся, что означает появление ударной
волны, при которой A.3.4) и A.3.5) оказываются неправомерными.
Вследствие сложности точного метода решения
рассмотренных выше уравнений рядом авторов были предложены различные
приближения. В частности, в [95] предлагается считать, что все
возмущения распространяются со скоростью звука. В этом
случае предполагается, что скорость течения жидкости мала по
сравнению со скоростью звука. На основании теории волн
потенциал скорости расходящихся сферических волн определяется
формулой
где г — расстояние рассматриваемой точки течения от центра
пузырька; f — произвольная функция аргумента It '—λ.
Как видно из формулы A.3.10) величина щ представляет
собой функцию двух переменных t и г.' Ее производная с учетом
условия на бесконечности
37
Используя A.3.11) и опуская промежуточные выкладки,
перепишем интеграл Коши—Лагранжа в виде
'■(^+^)=f(^-i-)' ^'-'-''^
где Сео — скорость звука на бесконечности.
Из уравнений A.3.11) и A.3.12) следует, что возмущения, ха-
рактеризуемые г(р и г \h -\--^j, распространяются в жидкости
со скоростью звука Соо. Такое приближение называется
квазиакустическим, так как обычно в акустике делается еще дальней-
шее допущение о том, что в A.3.12) -g- С /г, и таким образом
возмущение, характеризуемое rh, распространяется со скоростью
звука Соо. Если пренебречь вязкостью, массовыми силами и
поверхностным натяжением, то уравнение A.3.11), учитывая A.2.6),
после ряда промежуточных преобразований можно написать
следующим образом:
+ ..|^ + ..rF,|-' + °ff = 0. A.3.13)
Po
Уравнение A.3.13) дает связь между скоростью и давлением
в любой точке жидкости. Если принять
r^R, V, = R, ¾-' = ^^
то получим дифференциальные уравнения, связывающие скорость
и давление на стенке пузырька.
Для замены частных производных полными используем
соотношения:
dp__dp_ л Φ .
dt ~ dt 'Т'^ дг '
Уравнение неразрывности A.2.5) преобразуем к виду
ρ др dt ~^ ρ др дг дг ' г
или, принимая во внимание A.3.2), получим
38
Исключая из уравнений A.3.13), A.3.14), A.3.15) частные
производные от ρ и V^, получим с помощью A.2.6) уравнение
движения стенки пузырька
~ oR dt \с с2 "^ сЗ И- J
pR dt \с с^ er J Ρ
Ρο
Пренебрегая затем в правой части членами, содержащими
в знаменателе c^J и с1>, вследствие их малости,' напишем
приближенное уравнение:
/?/^(l_^\+ 3 ^.(l_i^U^^A+f^. A.3.16)
\ Coo j 2 \ Зс„ j ρ/? л с„ J ρ '
ρ
Если приближенно считать ρ «:^ р„, то j
dp _ ρ —Po
——^^^ j^
Ρ Poo
Po
решение A.3.17) может быть получено при помощи численного
интегрирования.
В частном случае при малых скоростях движения стенки
пузырька R/cco A.3.16) приводится к уравнениям A.2.13) для
несжимаемой жидкости.
Кроме квазиакустического приближения при решении задачи
используется приближение более высокого порядка,
основанное на гипотезе Кирквуда—Бете, предложенной в теории
подводного взрыва [34]. Согласно этой гипотезе возмущения
распространяются с переменной скоростью, равной сумме местной
скорости звука и скорости движения частицы жидкости, т. е.
величине (с -|- У^)· Или, иначе говоря, предполагается, что ве-
( ^^ \
личина г (^ + -^ I распространяется со скоростью (с + 1/^).
Тогда по аналогии с уравнением A.3.11) можно написать:
= 0. A.3.17)
'+^c+κ)-ί-][r{n + Щ
dt г х- Т^ ' г/ 0г
Так как энтальпия h, входящая в A.3.17), связана с
плотностью, давлением и скоростью звука формулами A.3.1), A.3.2),
A.3.3), то, опуская промежуточные преобразования, найдем:
h—T=:f- A.3.18)
39
Подставляя A.3.17) в A.3.18), получим:
[i+(^. + ^)^][i + ^fe^J-o. A.3.
19)
В соответствии с формулой A.3.6) введем характеристическую
координату α (г, f) и после преобразований перепишем A.3.19)
в виде:
да.
[ί+^4Ξ#]-.
в дальнейшем из A.3.4), A.3.5) с помощ,ью A.3.19) исключим
(dVr\ д / 2с \
величины С (—г.— ] и с ηΓ-{ _ j, в результате получим
одно уравнение
^Уг-С)±{Уг--^^)
A.3.20)
Полагая в A.3.20) г ~ R, V^ = R и обозначая прописными
буквами значение переменных на стенке, получим уравнение
движения стенки пузырька
(^-^^-(^-71^) —i-[^^^^?S^ +
-^-4^^4
A.3.21)
где С = С [р {R, t) ] — скорость звука на стенке пузырька,
а ρ (R, t) согласно § 2 гл. I определяется формулой
Rü \3v
piR, 0 = Р„-^+^?го(^)
4μ
R
Если пренебречь взаимодействием вязкости и с;;;имаемости,
то будет справедливо соотношение
С = C{R, R)
и движение стенки пузырька можно определять путем
интегрирования уравнения A.3.21), которое можно рассматривать теперь
как обыкновенное дифференциальное уравнение второго порядка,
не зависящее от поля скоростей жидкости.
40
Что же касается распределения скоростей внутри жидкости,
то гипотеза Кирквуда—Бете позволяет исключить с из
уравнения A.3.8). В результате получим
-ΊΓ = r4C~Vr) r(C-Vr) "PHß= const.
где С связана с V^ соотношением
Таким образом, поле скоростей можно определить
интегрированием обыкновенных дифференциальных уравнений вдоль
одного семейства характеристик β = const.
Первый интеграл выражения A.3.21) легко получить, полагая
в нем скорость звука на стенке пузырька постоянной величиной.
Г) 1
Используя очевидное равенство -^- = —^—τ о~~г' после
промежуточного преобразования A.3.21) получим
^ я— 1 я — 1
С2 — С^
Входящее в A.3.22) выражение ——-j— представляет собой
разность энтальпий жидкости между стенкой пузырька и
бесконечностью Н.
Для заданных значений С и Η интеграл A.3.22) может быть
вычислен численно или графически. В частности, если определить
корни кубического многочлена в знаменателе
подынтегрального выражения, а затем разложить последний на простейшие
дроби, то A.3.22) можно проинтегрировать аналитически.
В большинстве практических случаев замыкания пузырька
Η <ξ^€^ (для воды это соответствует условию | р,· — р„ | С 2 χ
X 10" Па B-10* атм), и подынтегральное выражение A.3.22)
можно аппроксимировать выражением, которое разлагается на
простейшие дроби
4 Η
1/2,, R 9с
A.3.23)
41
После подстановки A.3.23) в подынтегральное
выражение A.3.22) и последующего интегрирования находим:
= — 4-[4 In(ЗС - ^) + In (^^ + ^J^) —
в частном случае, если положить [ Я | <ξ^ С^, то последним
членом в A.3.24) можно пренебречь. В результате получим
логарифмическое уравнение, которое после подстановки пределов и
промежуточных преобразований преобретает вид:
Ro
(ЗC-^)«(^2 4.-2Ш-^
Если положить теперь, что R^ мало по сравнению с [Я], то
R V ж: ) V ^ 2\н\)'
Или принимая во внимание, что | Я | = \Р^ — Ро\ ^ получим
г со
(^r=('-4r('+4i^)· <·-3.25)
Выражение A.3.25) представляет собой обобщенное
уравнение Рэлея для сжимаемой жидкости. Как видно из рис. 1.11,
решения для сжимаемой и несжимаемой жидкости быстро
расходятся при числах Маха больших единицы.
В предельном случае несжимаемой жидкости, т. е. при R <^С,
находим:
т-
J 3_Р»^^ A.3.26)
На рис. 1.11 даны зависимости скорости движения стенки,
отнесенной к скорости звука, от относительного радиуса
газового и пустого пузырька при γ = 1,0 и 1,4 и при внешнем
давлении Ро = 10^ Па (—1,0 атм) и 10* Па (—10 атм). Как видно,
решение с использованием гипотезы Кирквуда—Бете хорошо
согласуется с точной теорией, за исключением последних стадий
42
р^=10^!)а.Aатм)
Рис. I.ll. Относительная скорость перемещения стенкн пузырька в зависимости
от относительного радиуса R/Rq при изменении содержания газа.
-^-Pro =104 Па A0-1 атм); 2 —рго=10^ Па (IQ-^ атм); 3 — Рго =
= 10^ Па A0"^ атм); 4 — рго = Ю Па A0~* атм); 5 — пустой пузырек.
несжимаемая жидкость; расчет с использованием гипотезы
Кирквуда—Бете; точное решение.
43
охлопывания пустого пузырька. В соответствии с точными
решениями уравнений движения скорость стенки пузырька в
сжимаемой жидкости стремится к бесконечности, как (-в~) ' ·
Согласно приближению, основанному на гипотезе Кирквуда—
Бете, как видно из формул A.3.26), величина R стремится к беско-
/ ;? \-о.5о ^
нечности, как (-5—) · В то же время скорость движения
стенки пустого пузырька в несжимаемой жидкости, как видно
из A.2.29), стремится к бесконечности, как \-р~)
Таким образом, сжимаемость среды приводит к замедлению
темпа роста скорости границы захлопывающегося пузырька.
§ 4. Влияние твердой стенки на развитие
парогазового пузырька
Выше было рассмотрено поведение парогазового пузырька в
переменном поле давлений в безграничной жидкости. Однако
в большинстве случаев пузырчатая кавитация возникает на
элементах судовых конструкций (стойках, крыльях, гребных вин-
Рнс. 1.12. Кавнтацнонный пузырек вблизи плоской твердой
стенки.
тах), поэтому большой интерес представляет влияние твердой
поверхности на поведение парогазового пузырька [41].
Рассмотрим влияние твердой стенки на развитие
изолированного пузырька. Пусть пузырек радиусом R расположен вблизи
плоской стенки на расстоянии b (рис. 1.12). Пузырек имеет
сложное движение: граница пузырька совершает радиальное
движение под действием постоянного давления Ро, а центр пузырька
имеет некоторое поступательное перемещение со скоростью и.
Будем считать, что движение пузырька происходит в
несжимаемой невязкой жидкости и имеет потенциал скорости φ.
Расширение или сжатие пузырька можно заменить источником или
44
стоком, расположенным в центре пузырька, а обтекание
пузырька — диполем, также приложенным в центре сферы, с
моментом, ориентированным вдоль оси перемещения.
Для учета влияния твердой стенки используется метод
зеркальных отображений, согласно которому симметрично
относительно стенки располагаются фиктивный источник и диполь.
Тогда с учетом A.2.11) суммарный потенциал течения имеет вид:
dR , п2 dR I ,
. ра d/? I . I uR^ cos (г^, χ) 1 uR^ cos (rg, x) A-4-1)
+ ^ Λ Га ' 2 rl "Τ" 2 /"Ι
где φ/} и фг — единичные потенциалы радиального и
поступательного движения соответственно; и — поступательная скорость
движения; г^, Га — расстояния от центров сфер до некоторой
произвольной точки А; cos (Гх, л;), cos(r2, л;) — косинусы углов между
осями диполей и осью х.
Из рис. 1.12 следует, что
cos (/-1, X) = -^; cos (/-2, χ) = —Р^;
'1 '2
Г1 = {х^ + уТ'; r,^[{2b-xf + yψ^. A.4-2)
Тогда с учетом A.4.2) формулы A.4.1) переписываются в виде:
fp^P^dR ( I 1 1
dt [(х^ + у^'' "^ [Bb-x)^+y^''j
R^ ( χ x~2b λ ПЛЗ)
В A.4.3) первый член определяет сумму потенциалов источников,
а второй член — сумму потенциалов диполей.
Для вывода уравнения движения пузырька вблизи твердой
стенки воспользуемся энергетическим методом.
Кинетическая энергия находится по значениям потенциала
скорости и его градиента по нормали к поверхности s:
S
Производные -^ должны удовлетворять граничным условиям
на сфере (пузырьке) и стенке:
для сферы
45
для стенки
-^Р«- = 0; ^==0. A.4.5)
дп дп ^
Выразим φ, входящие в подынтегральное выражение A.4.4),
через единичные потенциалы φ/^ и φ^ в соответствии с
формулой A.4.1). В результате получаем
Т-^ГГГсг, ^φ^ М^ ^' I fr) '^Ч'^ и ^^ I
S
Из теории потенциала известно, что
S
После подстановки A.4.7) и граничных условий A.4.5) в A.4.6),
выражение для кинетической энергии получим в виде:
[Dг)' J J Ф« ^s + 2ы— J J фг ds + ы' J |фгСо8 (Сх) ds],
\_ S SS
A.4.8)
~ 2
где ф/} и фг для сферы (поверхности пузырька) легко находится
из A.4.3):
'Р^ ^ \ (л:2 + (/^^I/2 + [B6 — xf + I/2J1/2 I'
Для произвольной точки на поверхности пузырька (сферы)
rf = /^=^ = (^:^+ «/=>);
/-i = {2b - χ)" + г/^ = /^=^ + 4Ь^ - 4Ь/? cos (/Сл:).
Как видно, величина Гг, а следовательно, и единичный
потенциал фг переменны по периметру сферы и зависят от угла R, х.
Для упрощения задачи примем некоторое среднее значение г^,
при котором LR, χ = 0. Тогда
^'^^'{f + 'ϊ
46
Или, используя формулу бинома Ньютона и ограничиваясь
первым членом ряда, найдем:
_26_
R '
r^^R-
Подставим значение единичных потенциалов φ/^ и φ^ в выражение
для кинетической энергии A.4.8).
После промежуточных преобразований выражение для
кинетической энергии приобретает вид:
3 R^
Для практических расчетов примем в дальнейшем -^—гг С Ь
тогда
Γ=.2π7?«ρ(ΐ +1) (^у+±д;?3р„2 (I 4.9)
Для вывода уравнений движения пузырька вблизи стенки
воспользуемся уравнениями Лагранжа, в которых в качестве
обобщенных координат примем радиус сферы R и расстояние
центра пузырька от стенки Ь. Далее, обозначая
запишем
n.^dR ,
d дТ
dt дк
d дТ
dt дЬ
ü db
дТ ρ
дЬ '
где Ffi — сила, действующая на поверхность пузырька по
направлению обобщенной координаты. Эта сила определяется
разностью давлений, действующих на поверхность сферы.
Согласно A.1.2) в предположении, что полость пузырька
заполнена парами жидкости и газа, а сжатие происходит по
адиабатическому закону, находим условие статического равновесия
Р = Рн + Рг —-^ = Рн~-^ + Рго(-^) . A.4.10)
где все обозначения прежние.
47
с учетом A.4.10) сила
F^ = AnR- [ρ _ р„ + .| _ р,„ (-^Υ'] , A.4.11)
где 7 = ^/3 — показатель адиабаты.
Составим производные от выражения для кинетической
энергии A.4.9) по обобщенным координатам и времени и подставим
их в уравнения Лагранжа. Опуская промежуточные выкладки,
получим, учитывая A.4.11), два нелинейных дифференциальных
уравнения:
-'ii>'-p^^b-^[-p+p.~^+Pro{-^y]; (I-4.12)
6b^bR + 2ЬтЬ + 3R^R^ = 0.
Первое уравнение соответствует радиальному движению
границы пузырька, второе — поступательному движению. Для
удобства вычислений приведем уравнения A.4.12) к
безразмерной форме и введем безразмерное время. Обозначим
_ R __R_ о_ 6
'^- Ro' ^- 2b' Р~Ж'
t = rR, (^)''' и di = dxR, (^^у\ A.4.13)
Po
Пренебрегая силами поверхностного натяжения, после
подстановки A.4.13) в исходные уравнения A.4.12), получим:
ηηA+ε) + νD + 26)--[β^-2ε^ηβ-Α + ι=θ;
ηβ -f 3ήβ -f 6ε2ή2 = 0; A.4.14)
здесь все производные составлены по безразмерному времени τ.
При бесконечном расстоянии пузырька от стенки, т. е. при ε -^ О,
β-^ О, β —» О, левая часть второго уравнения A.4.14) обращается
в нуль, а первое уравнение переходит в рассмотренное выше
уравнение радиального движения границы пузырька в
безграничной жидкости A.2.13). Дифференциальные уравнения A.4.14)
решаются численно с помощью ЭЦВМ. Для иллюстрации на
48
рис. 1.13—1.14 даны результаты расчетов системы A.4.14) на
ЭЦВМ с помощью метода Рунге—Кутта, приведенные в
работе [411. При численном интегрировании были приняты
следующие начальные условия:
при ί=0 η = 1, ß=ßo, ή=0,
β = 0.
-ρ.
10'
10'
10
ti
-10
-10'
■Ιΰ-ή
Ο
1-0,2
0,4
0,6
0,8
1,0
у5
,4
η
0 \ 0^ 0,3 0,40
<5
J^
50
/Ι
Λ\
Ηβ-λ
у
У
w
10'
10
1
7~ 6· 5- /Λ
-2^
J-
Ю
10'
ю'
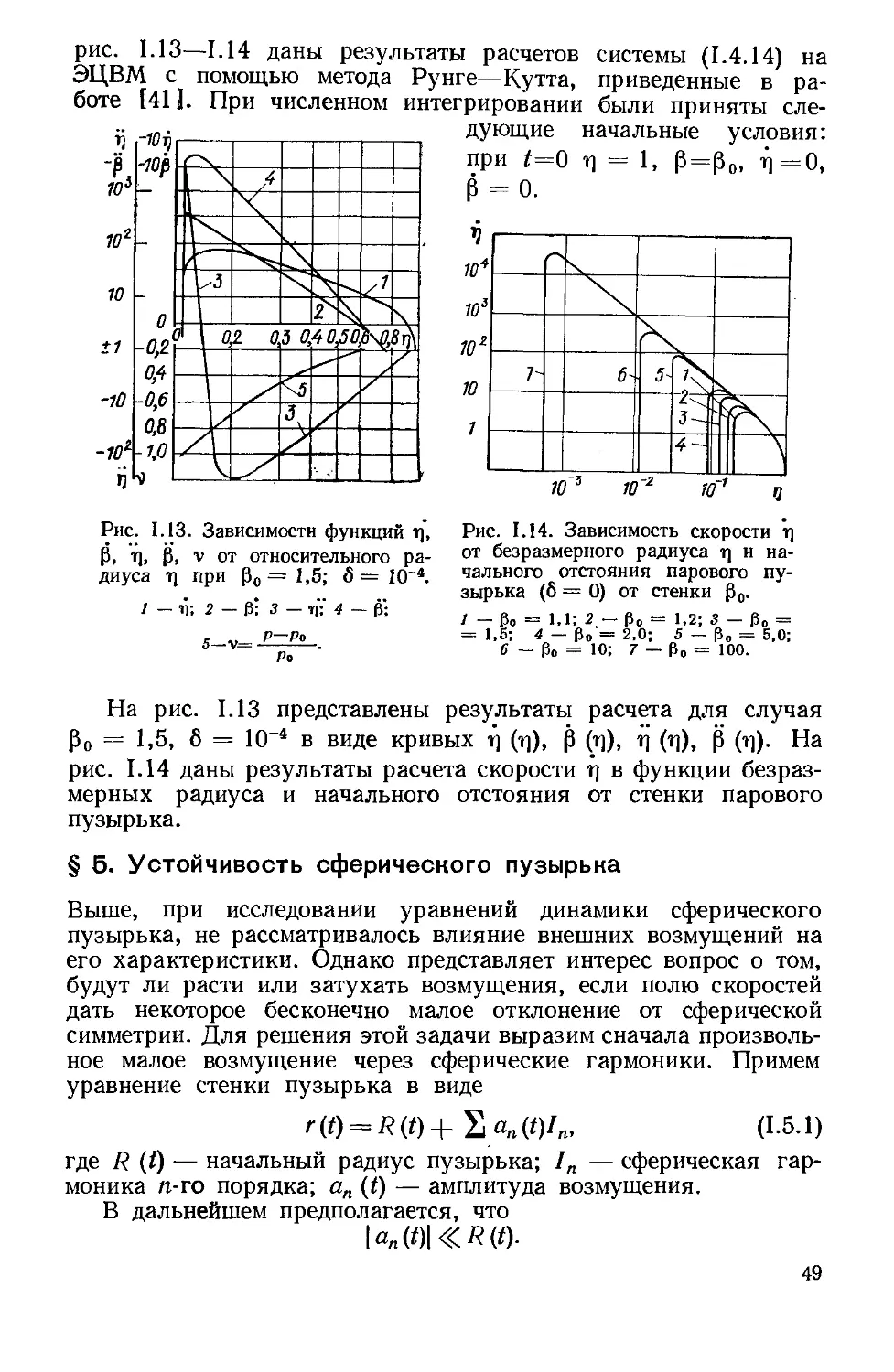
Рис. 1.13. Зависимости функций η. Рис. 1.14. Зависимость скорости η
от безразмерного радиуса η и
начального отстояния парового
пузырька (δ = 0) от стенки ßo·
/ — ßo = 1.1: 2 — ßo = 1.2; s - ßo =
= 1,5; 4 — ßo = 2.0; 5 — ß„ = 5,0;
6 _ ßo = 10; 7 — ßo = 100.
ß, η. β. ν ОТ относительного
радиуса η при ßo = 1,5; б = 10"*.
■η; 2 — β: 3 — η; 4
На рис. 1.13 представлены результаты расчета для случая
ßo = 1,5, δ = 10-* в виде кривых ή (η), β (η), η (η), β (η). На
рис. 1.14 даны результаты расчета скорости η в функции
безразмерных радиуса и начального отстояния от стенки парового
пузырька.
§ б. Устойчивость сферического пузырька
Выше, при исследовании уравнений динамики сферического
пузырька, не рассматривалось влияние внешних возмущений на
его характеристики. Однако представляет интерес вопрос о том^,
будут ли расти или затухать возмущения, если полю скоростей
дать некоторое бесконечно малое отклонение от сферической
симметрии. Для решения этой задачи выразим сначала
произвольное малое возмущение через сферические гармоники. Примем
уравнение стенки пузырька в виде
Γ@ = /?@+Σ«„@^η. A.5.1)
где R (t) — начальный радиус пузырька; /„ — сферическая
гармоника п-го порядка; а„ {t) — амплитуда возмущения.
В дальнейшем предполагается, что
\an{t)\^R(f)-
49
Уравнения для коэффициентов а„ образуют бесконечную
систему связанных уравнений, что затрудняет решения. Для
упрощения решения принимают, что невозмущенная стенка
пузырька г = R (t) есть поверхность раздела двух несмешиваю-
щихся несжимаемых невязких жидкостей.
Кроме того, будем считать, что составляющие амплитуды
возмущений малы и не зависят друг от друга, т. е. каждая
гармоника может рассматриваться отдельно. Составим потенциал
скорости возмущенного движения (для п-й гармоники) по обе
стороны от поверхности раздела, предполагая при этом, что
возмущение по мере удаления от поверхности раздела должно
уменьшаться:
Φι = \-bir"In при r<.R (внутри пузырька);
pap τ
Фг = \~^2~-^— при r>/? (вне пузырька). A.5.2)
Коэффициенты Ь^ и bg определяются из условия непрерывного
изменения скорости при подходе к границе раздела изнутри
и снаружи пузырька
Выражение в правой части A.5.3) получено путем
дифференцирования A.5.1) по времени.
Производная первого выражения A.5.2) по г имеет вид
¾- = -^ + nV"-^/n. A.5.4)
Приравнивая A.5.4) правой части A.5.3), подставляя г =
= Га = R -{- ünln и пренебрегая членами, содержащими а^,
получим
а + 2а —
^' ^ nR—4l+aR-4n{2R~' + n~l)]' ^^"^-^^
Здесь и в дальнейшем в а„ индекс η опущен. После
разложения в степенной ряд выражение A.5.5) с точностью до малых
высшего порядка примет вид
50
Аналогично легко найти выражение для Ь^· После
подстановки bi и &2 в формулы для потенциалов возмущенного
движения A.5.2) получим:
Найдем теперь давление по обе стороны от поверхности
раздела жидкости, используя решение уравнения A.2.8) в форме
Коши—Лагранжа:
р- = F, it) - Pi [(^-)^^+ 4-(grad Ф1)?з] ; A-5.6)
где ρ — давление вне пузырька; Fi,2 (t) — постоянные
интегрирования; р' —· давление внутри пузырька.
Составим затем выражения отдельных членов, входящих
в A.5.6). Опуская промежуточные преобразования, получим:
+ 7ГТГ ^'" + -Щ^ «^'" + 1ГТГ ^'" + 2«-!^ '«' (^-δ-δ)
(grad φι),^ - (grad φ,),^ ^f? + 2aRI,. A.5.9)
Возмущение поверхности раздела вызывает изменение ее
кривизны, а следовательно, и сил поверхностного натяжения.
Если обозначить через R' к R" главные радиусы кривизны
возмущенной поверхности раздела, тогда давления снаружи и внутри
пузырька связаны
/ = ρ-σ(^+^).
Выражение в скобках можно приближенно представить в виде
51
Тогда на основании формулы A.5.10) приближенно можно
написать
2σ
■P--R
(η-1)(η-2)
ααΙ„,
A.5.11)
После подстановки A.5.6)-A.5.9) в A.5.11) получим
нелинейное дифференциальное уравнение второго порядка относительно
амплитуды возмущения
о + ^а-Ла=0, A.5.12)
ГДЕ
А
[и (и — 1) Р2 — (и - 1) (и — 2) pi] ;? — (и — 1) η (и + 1) (и + 2) -
а)
а/Оц
4
3
2
1
п=6
rf'f'
и
1 /
Rlnp2+(n+l)Pi]
а I ар
RjRo
4
3
A.5.13)
/
J
ßy
л
^
П'б
0 -■
5^
-^
-^
■ч
^.
-д
Ο,Ζ o/t 0,6 Οβ 1,0 о 0,2 0,4 0,6
PoiR f>olP
Oß 1.0
Рис. 1.15. Развитие возмущений при расширении пузырька: а— Dq = 0;
б— Vq= ßo/3.
Из A.5.13) видно, что форма возмущения при η = 1
соответствует поступательному перемещению пузырька; таким образом,
нарушение сферичности обусловлено возмущениями при η > 2.
Если предположить, что ρχ < рз, т. е. рассматривать паровой
пузырек, то выражение A.5.13) получит вид
Л =
(п~\)
R-{n- 1)(п+1)(« + 2)-
Дифференциальное уравнение A.5.12) легко преобразуется
к двучленной форме с одним переменным коэффициентом, если
/ /?п \3/2 „
ввести подстановку ω == ( ~б^ ) С.
Опуская все промежуточные преобразования, найдем:
A.5.14)
dt
+ 5С=0,
где
5 = («-1)(п+1)(п + 2)
pR^
(η+1/2)/?
3 /_^\2
~ 4 \R ) ·
52
Как видно из A.5.12), A.5.14), амплитуда возмущений a{t)
или С (t) определяется путем интегрирования дифференциальных
уравнений при заданных начальных условиях и различных
значениях п. Обычно за независимые начальные условия принимают а^
и Ro-
Характер изменения функций а (t) или С (t), полученных
в результате интегрирования A.5.12) или A.5.14), определяет
закон развития начальных возмущений поверхности пузырька
во времени. Если возмущения с течением времени затухают до
нуля или до некоторого постоянного значения, то движение
стенки пузырька устойчиво асимптотически или
неасимптотически.
Если же возмущения неограниченно возрастают во времени,
то движение неустойчиво.
Коэффициенты А (t) к В (t) являются функциями R, R к R,
которые находятся в результате численного интегрирования
нелинейного дифференциального уравнения движения стенки
пузырька.
Если принять, как это было сделано выше, давление внутри
пузырька не зависящим от времени и равным давлению
насыщенных паров воды, а давление на бесконечности постоянным
(внезапное расширение или сжатие), το R к R, согласно A.2.21),
зависят от отношения Ro/R.
При такой постановке задачи выражения A.5.12) и A.5.14)
представляют собой линейные дифференциальные уравнения с
постоянными коэффициентами, решение которых в квадратурах не
вызывает затруднений.
На рис. 1.15 для иллюстрации приведена зависимость
безразмерного возмущения -нто от величины RJR при расширении
парового пузырька, имеющего устойчивую границу (возмущения
затухают). Зависимость получена по A.5.12) без учета
поверхностного натяжения для начальной скорости возмущения
3
; 0.
где
1/ _ ^0^0 . п* — п' ~ η
" ~ ί 2р* у/2 ^ Ρ — Ρ Ρ-
Глава II
РАЗВИТАЯ КАВИТАЦИЯ.
УСТАНОВИВШИЕСЯ
КАВИТАЦИОННЫЕ ТЕЧЕНИЯ
(НЕЛИНЕЙНАЯ ТЕОРИЯ)
§ 1. форма границы каверны, парадокс Бриллуэна,
схемы кавитационных течений
Форма границы каверны зависит от ряда факторов:
конфигурации и размеров тела, вида каверны (частичная или развитая),
скорости набегающего потока, влияния гравитации, степени
турбулентности потока и внешних возмущений.
Достаточно полное представление о форме и поведении
границы каверны дают экспериментальные исследования
искусственных кавитационных течений.
В настоящее время имеется большое число опытов с кавити-
рующими дисками, крыльями, телами вращения или близкими
к ним телами.
Визуальное наблюдение за поведением границы каверны
позволяет дать характеристику ее формы и установить ее
зависимость от ряда факторов.
Как показывают эксперименты,
а) при больших скоростях потока образуется развитая
каверна, в хвостовой части которой появляется обратная струйка,
при этом части каверны отрываются, вызывая пульсацию хвоста
каверны;
б) при уменьшении скорости обтекания образуется каверна,
хвостовая часть которой сворачивается в два вихревых жгута;
в) при малых скоростях потока и направлении его, перпенди-'
кулярном силе тяжести, последняя существенно влияет на
симметрию каверны относительно горизонтальной плоскости: с
уменьшением скорости всплывание каверны возрастает.
При направлении потока, совпадающем с направлением силы
тяжести, ее влияние проявляется в укорочении и расширении
каверны;
г) поверхность каверны негладкая, она имеет
малоамплитудные высокочастотные возмущения.
Таким образом, эксперименты указывают на нестационарный
характер границы каверны, причем наибольшая нестационарность
54
наблюдается в хвостовой части каверны и в следе за каверной.
Экспериментально доказано, что при кавитации за телом
образуется полость с постоянным давлением р^. Следовательно,
давление постоянно также и на границе каверны, которая представляет
собой свободную поверхность. Это обстоятельство учитывается
при построении теоретических методов решения плоских и
пространственных задач.
Рассмотрим уравнение движения частицы жидкости,
перемещающейся по границе каверны. Это даст нам возможность
установить знак кривизны границы каверны.
Если частица движется со скоростью У^ по границе каверны,
имеющей кривизну \IR, то
-X-=--^gradpn, (II.1.1)
где ρ — давление в жидкости; η — нормаль, направленная к
центру кривизны; ρ — плотность жидкости.
Так как V^IR > О и 1/р > О, то для соблюдения условия
(II. 1.1) векторы grad ρ и η должны быть направлены в разные
стороны.
Как правило, каверна образуется в тех областях потока,
где появляется минимальное давление, т. е. grad ρ направлен
из каверны в сторону жидкости, а нормаль η для получения
положительной величины правой части (II. 1.1) должна быть
направлена к центру кривизны. В этом случае число кавитации
2
Таким образом, при положительном числе кавитации граница
каверны имеет выпуклую форму (рис. ΙΙ.1, а). В то же время,
если давление в каверне оказалось бы больше давления в
окружающей ее жидкости, граница каверны имела бы вогнутую форму
(рис. II.2, б). Однако на практике такое течение не реализуется.
Чем меньше число кавитации κ, тем меньше кривизна границы
каверны (рис. ΙΙ.1, в).
При построении теоретической схемы кавитационного течения
принимают, что поверхность каверны гладкая.
Важное значение приобретает вопрос об устойчивости границы
каверны. Как показывают исследования, в большинстве случаев,
когда плотности соприкасающихся жидкостей существенно
различны (вода и газ), граница раздела устойчива. Однако при этом
возникают трудности представления формы хвостовой части
каверны.
На основании уравнения Бернулли скорость на границе
каверны должна быть постоянной и равна V^. Однако точка
смыкания струй в хвосте каверны, принадлежащая ее границе,
55
является критической, т. е. скорость в ней равна нулю. Это
противоречие называется парадоксом Бриллуэна.
Кроме того, в реально существующих кавитационных течениях
не происходит смыкания верхней и нижней границ каверны,
хвостовая часть каверны пульсирует, а в ряде случаев
периодически разрушается, образуя тонкий турбулентный след,
содержащий пузырьки воздуха, попавшие в каверну вследствие диффузии
газа из окружающей среды.
Рис. II.1. Зависимость формы каверны от числа
кавитации: а — κ > 0; б — κ < 0; β — κχ > κ2 > κ3 > 0.
Β СВЯЗИ С этим ряд ученых предложил различные теоретические
схемы кавитационных течений. Многие из этих схем построены
для частных случаев течений, и их применение весьма
ограничено.
Рассмотрим некоторые из этих схем, получивших применение
при решении кавитационных задач (рис. II.2).
Схема Кирхгоффа (рис. II.2, а) — одна из старых известных
схем —· предполагает струйное течение вблизи тела, уходящее
вниз по потоку на бесконечность, так что давление внутри
каверны Рк = р«,, скорость свободной струи на границе V^ = У«,,
а число кавитации κ = 0.
В дальнейшем схема Кирхгоффа была видоизменена
различными авторами для общего случая κ ^ 0. Так, в частности,
Н. Е. Жуковский и Рошко предложили схему замыкания струй
на две параллельные полубесконечные горизонтальные пластинки,
на которых скорость изменяется от V^ (рис. II.2, б) до У«,. Ря-
бушинский построил схему обтекания пластинки с замыканием
56
Рис. 11.2 Теоретические схемы плоских кавитационных течений: а —
Кирхгоффа (струйное течение); б — Н. Е. Жуковского — Рошко; в —
Рябушинского (схема с зеркалом); г — схема Т. By; д — Д. А. Эфроса
(схема обтекания с обратной струйкой); е ■— А. В. Кузнецова; ж-—М.
Тулина первая (с односпиральными вихрями); з — М. Тулина вторая (с двух-
спиральными вихрями).
57
струй на зеркально расположенную пластинку (схема с зеркалом).
На рис. II.2, β дана более общая схема Рябушинского.
В дальнейшем исследователем Т. By эта схема была
использована при рассмотрении более общего случая обтекания
произвольного профиля с замыканием струй на короткую вертикально
расположенную пластинку (рис. II.2, г).
Широкое применение находит схема обтекания с обратной
струйкой, предложенная в 1945 г. Д. А. Эфросом. По этой схеме
каверна заканчивается обратной струйкой, уходящей через сток
на вторую Риманову плоскость, а затем в бесконечность
(рис. II.2, Ö). Образование обратной струйки наблюдается
экспериментально, однако, попадая в каверну, обратная струйка
вызывает разрушение хвоста каверны.
Переход обратной струйки на вторую Риманову плоскость
представляет собой чисто математический прием, необходимый
для решения задачи.
А. В. Кузнецов, развивая схему Д. А. Эфроса, предложил
в 1964 г. схему, в которой жидкость за каверной затекает в
обратный канал с бесконечными стенками, но, в противоположность
схеме Д. А. Эфроса, течение в этом канале изменяет еще раз
направление так, что за каверной критической точки нет
(рис. II.2, е).
( В 1964 г. М. Тулин предложил для случая κ φ О две схемы,
довольно хорошо описывающие реальные кавитационные течения.
Обе эти схемы предполагают, что вниз по потоку за каверной
находится тонкий след, исчезающий на бесконечности.
В первой схеме М. Тулина каверна заканчивается односпи-
ральными вихрями, в центре которых скорость на границе скачком
изменяется от V^ ДО нуля, за каверной образуется*гладкий
тонкий след (рис. 11.2, ж).
Во второй схеме М. Тулина каверна заканчивается двух-
спиральными вихрями, в центре которых скорость на границе
скачком изменяется от 1^^ до V» — скорости на бесконечности
(рис. 11.2,0).
Применение той или иной схемы обусловлено граничными
условиями задачи: первая схема (с односпиральными вихрями)
целесообразна при рассмотрении случая кавитационного
обтекания в безграничной жидкости, вторая схема (с двухспиральными
вихрями) —- случая обтекания вблизи свободной поверхности при
больших числах Фруда.
Как показано в [7], двойной спиральный вихрь представляет
собой единственную форму соединения в одной точке двух линий
тока с разными скоростями. Одна из них образует границу
каверны, вторая соответствует границе следа за каверной.
Вблизи центра вихря (особая точка) струя закручивается
в спираль с бесконечным числом витков.
Для получения скачкообразного изменения скорости в центре
каждого вихря течение должно иметь особенности.
58
§ 2. Методы решения задач
Решение задачи о кавитационном обтекании тела может быть
выполнено различными методами, однако обычно выбирают тот,
который требует наименьшей затраты времени.
При решении задачи определяют форму границы каверны,
поле скоростей и давлений вблизи кавитирующего тела, и,
наконец, силы и моменты, действующие на тело со стороны жидкости.
Сравнительно простые решения получают для плоских задач.
Принятые в настоящее
время методы решения
задач могут быть сведены
к двум:
а) метод потенциала
скоростей; ^, „ ,,
б) метод особенностей ^ ·'
(источников и стоков,
вихрей).
При решении плоских
задач первым методом ис- Рис. П.З. Схема отрывного течения,
пользуют теорию струй
идеальной жидкости, а также решения краевых задач. Второй
метод более универсален, его применяют при рассмотрении как
плоских, так и пространственных кавитационных течений.
Ранее всего и наиболее полно были разработаны методы теории
струй, и поэтому они нашли наиболее широкое применение при
решении плоских задач кавитационных течений. При этом методе
используют математический аппарат теории функции
комплексного переменного. Суть метода состоит в том, что течение на
физической плоскости преобразуется на вспомогательную плоскость
с' помощью некоторой преобразующей функции, которую в
процессе решения необходимо найти. Вспомогательную плоскость
выбирают такой, чтобы можно было получить наиболее простое
решение. Способы определения преобразующей функции
отличаются различной формой представления преобразующей
функции (вспомогательной плоскости), и большинство из них известны
под именами их авторов — Кирхгоффа, Н. Е. Жуковского и
С. А. Чаплыгина и др.
Прежде чем перейти к рассмотрению этих способов,
остановимся на существе задачи о кавитационном течении. Для решения
задачи необходимо найти комплексный потенциал течения w =
= φ + ϊψ· Основываясь на теории струй идеальной жидкости,
легко представить себе плоскость комплексного потенциала.
Пусть Б потоке несжимаемой идеальной жидкости находится
тело АОВ, за которым образуется отрывное течение (рис. П.З).
Поток имеет линии разрыва ОАМ и ΟΒΝ, между которыми
образуется область //, заполненная газом или паром. Предположим,
что в этой области, называемой каверной, газ находится Б
состоянии покоя {Vf = 0) и давление постоянно.
59
в области /, занятой жидкостью, скорость и давление вверху
по потоку на бесконечности постоянны и соответственно равны
Vco и р„, поле скоростей непрерывно и потенциально. Положим,
что каверна простирается вниз по потоку до бесконечности, т. е.
^^1^^"?д происходит при нулевом числе кавитации (схема Кирх-
гоффа). Известно, что комплексный потенциал течения определяют
с точностью до произвольной постоянной. Поэтому, принимая
во внимание, что в точке разветвления потока О потенциал φ = О,
а)
®
®
УвгУгг
д)
S)
(W)
, 9<L
J
Рис. II.4. Плоскость комплексного потенциала при кавитационном
обтекании: с — в безграничной жидкости — по схеме Кирхгоффа-
б —в безграничной жидкости — по первой схеме М. Тулина· в —
в безграничной жидкости — по второй схеме М. Тулина; г — вблизи
свободной поверхности — при струйном обтекании.
МЫ вправе считать и функцию тока ψ = О вдоль линий QOAM
и QOBN. Так как на бесконечности (вверх и вниз по потоку)
скорость имеет конечное значение У„, то потенциал φ вдоль
линии тока изменяется от +оо до —оо.
Действительно, скорость V вдоль линии тока S связана с
потенциалом формулой
-£-, а Ига 1^ = 1/^ при ζ-*οο.
V =
Следовательно, для того, чтобы скорость на бесконечности
бьша конечна, должно быть выполнено условие φ = ±оо при
Кроме того, вследствие неограниченности течения на
физической плоскости функция тока ψ должна изменяться также от
оо до +00.
Таким образом, в рассматриваемом частном случае плоскость
комплексного потенциала представляет собой плоскость с
горизонтальным полубесконечным разрезом от начала координат
в сторону положительных значений (рис. 11,4, а).
60
При числах кавитации κ =jfe О длина разреза будет конечной
(первая схема М. Тулина). В случае же замыкания каверны на
параллельные стенки или окончания каверны двумя спиральными
вихрями с противоположным направлением вращения (вторая
схема М. Тулина) плоскость комплексного потенциала также
имеет полубесконечный разрез, однако берега разреза
соответствуют не только границам каверны, но и твердым горизонтальным
стенкам (рис. II.4, б и в).
В случае же кавитационного обтекания тела вблизи свободной
границы (при больших числах Фруда) плоскость комплексного
потенциала w будет иметь кроме полубесконечного разреза линию
постоянного значения -ψο, соответствующую заданной глубине
погружения (рис. II.4, г).
После того как установлен вид плоскости комплексного
потенциала скорости W кавитационного течения, выбирают формулу
преобразующей функции (вспомогательной плоскости) и
устанавливают соответствие между точками физической плоскости ζ
и плоскости W. Рассмотрим коротко различные способы
представления преобразующей функции.
1. Способ Кирхгоффа. При этом способе преобразующая
функция имеет вид
ζ=^=Τ' ^''-^-'^
где V = Vx — tVy — комплексная скорость течения.
Если ζ (ш) найдена, то
άζ = ζ{ΐΐ})άυϋ и 2~1ξ(ά')ίία). (II.2.2)
Таким образом, найден профиль каверны. Способ удобен
при рассмотрении задач о кавитационном обтекании тел, границы
которых состоят из отрезков прямых, так как здесь легко
определить граничные значения функции.
Так как скорость на твердых границах (на участках прямых)
имеет постоянное направление (угол), а на свободных границах
(каверна) — постоянное значение, то на плоскости ζ твердые
границы изображаются в виде лучей, а свободные границы —
в виде окружности.
Представим вспомогательную функцию в параметрическом
виде:
(ΙΙ.2.3)
где I ν I — модуль комплексной скорости; θ — аргумент
функции ζ (arg ζ).
В первом случае θ = const, τ, е. arg ξ = con§t, и мы
получаем уравнение луча.
61
Во втором I FI = const, т. е. | ζ | = const, — мы получаем
уравнение окружности.
2. Способ годографа. При использовании этого способа в
качестве вспомогательной выбирают плоскость годографа, а
преобразующая функция имеет вид:
По существу, этот способ не отличается от способа Кирхгоффа.
3. Способ Н. Е. Жуковского. При этом способе 122] вводится
новая функция ω, связанная с преобразующей функцией формулой
ω=^1ηζ = 1η/'-ζ^Ί==1π(^^); (ΙΙ.2.4)
в параметрическом виде
или
ω = In ξ = In
ω =: In ζ = In
е»е = In
Ч-ίθ
(^-К^)^
(II.2.5)
(II.2.6)
в параметрическом виде соответственно:
ω = In ζ = In
Ч-ίθ.
(ΙΙ.2.7)
Таким образом определяются оси координат вспомогательной
Комплексной плоскости ω.
Представление (II.2.7) удобно тем, что позволяет легко найти
границы области течения на вспомогательной плоскости,
основываясь на данных о форме тела и постоянной скорости на границе
каверны. Например, поскольку на границе каверны V = F^»
(II.2.7)
= 1п " '
то согласно (П.2.5),
Re ω = ш
Ι^κ
или
Re ω
= In 1 = 0.
= -^ln(l-fx)
Таким образом, свободные струи располагаются либо на
мнимой оси, либо на линиях, ей параллельных, а границы тела
(при постоянных Θ) на линиях, параллельных вещественной оси.
4. Способ С. А. Чаплыгина. Широкое применение при
решении задач о кавитационных течениях находит метод особых
точек. Он основан на известном представлении рациональной
функции в виде произведения линейных множителей, содержащих
62
комплексные координаты точек, в которых эта функция
обращается в нуль (нули функции), и точек, в которых эта функция
обращается в бесконечность (полюсы функции). Неизвестная
функция имеет вид:
/(z)^^^;-y/;-y/;~y---f-^"> (II.2.8)
'^' (г —έι) (ζ—&2)B —6з) ■·· B —ад ^ '
где ßi, ..., о„ — нули функции; bi, ..., b^ — полюсы функции;
А — постоянная.
С помощью (П.2.8) может быть составлено выражение
комплексной скорости (или комплексного потенциала) физического и
фиктивного течений.
В этом способе течение на физической плоскости ζ конформно
отображается;на какую-либо простую геометрическую фигуру:
полуокружность, квадрант, полосу, круг вспомогательной
плоскости (t). Причем отображающую функцию отыскивают в ходе
решения. Обычно этот способ несколько видоизменяется.
На физической плоскости и на плоскости фиктивного течения
(вспомогательной) находят особые точки (нули и полюсы).
Причем, если на физической плоскости особые точки находят на
основании физических представлений, например: точка разветвле-х
ния потока — нуль скорости; начало потока — источник, конец
потока — сток, то скорость в этих точках, согласно известным
формулам, обращается в О и оо, т. е. в этих точках находятся
нули и полюсы. Что же касается фиктивного течения, то для него
особые точки, кроме того, могут появиться:
а) как отображение особых точек течения на физической
плоскости;
б) как результат аналитического продолжения через границу
простейшей области;
в) из-за нарушения конформности в некоторых точках
течения.
Соответствие особых точек физической и вспомогательной
плоскостей устанавливают исходя из характерных черт течения.
Итак, составляем в общем виде комплексные скорости обоих
течений — заданного и на вспомогательной плоскости:
Разделив одно выражение на другое, получим:
dw
dz _ ΊΓ h(t)
dt dw fi (i)
dz
-fit).
откуда
= jfit)dt. (II.2.9)
63
при рассмотрении кавитационного обтекания тел часто
используют решения краевых задач. Под краевой (граничной)
задачей понимают такую задачу о нахождении функции внутри
некоторой области, когда известны предельные значения функции
на границе этой области.
При решении задач кавитационных течений наибольший
интерес представляет задача Римана—Гильберта для полуплоскости.
Рассмотрим постановку задачи. Пусть на действительной оси ох
даны раздельно лежащие конечные отрезки а^Ь^ (^ = 1,2, ..., т),
при этом Οχ < &1 < Ог < ^2 ··· «т < ^т·
Обозначим через D' совокупность этих отрезков, а через
D" —остальную часть действительной оси, так что D" состоит
из конечных отрезков ^^α+ι (k = 1, 2, ..., т — 1) и из
«бесконечного» отрезка Ь^а^ состоящего из двух полупрямых Ь^ <
< X < оо и —схз < X <; Οχ (рис. П.5).
-r^ö ^> Ь» ^ ^г ^f ^к ^та ^¢1 сю
^■^^ > 1 1 I I -А I.III..— I. ^
•Д.
Рис. П.5. К решению краевой задачи Римана—Гильберта для полуплоскости
(формула М. В. Келдыша—Л. И. Седова).
Задача состоит в том, чтобы найти функцию Φ (ζ) == « + iü,
голоморфную в верхней полуплоскости (г/ > 0) и ограниченную
на бесконечности, по смешанному граничному условию на оси ох:
, и* на D'
ш+ на D .
Решение этой задачи было получено М. В. Келдышем и
Л. И. Седовым [14, 29] для трех наиболее важных классов
функции.
1. Решение, не ограниченное вблизи всех концов щ, Ь^.
Π
где 7^ (г) = ϊ/ i 1 (ζ — ß^) {г — ЬЛ; τ — текущее значение коорди-
нат точек на действительной оси.
В случае если Φ (оо) = О, то полином Р^ {ζ) нужно заменить
полиномом Pm-l (^)-
64
2. Решение, ограниченное вблизи концов а^ и не ограничен-'
ное вблизи концов Ъ^, при условии, что Φ (оо) = 0:
со
0(,) = ^5i£L_U [р^Ш^Ах, A1.2.11>.
Π(ζ-α,); ^(ζ) = ΐ/ Π B-¾).
3. Решение, ограниченное вблизи всех концов, при условии,.
что Ф(оо) = О,
Φ (г) =/^ (г)-^ 1^^1^, A1.2.12).
причем в последнем случае должны выполняться условия
разрешимости
Οΰ
^(τ)
τ/-ΐ£ίτ = 0 (/= 1, 2, ...,m).
Функции Ц (ζ). На. ъ B^) многозначны, для полной их
определенности и однозначности в точках разветвления а^ и &^ на
вещественной оси проводится разрез и выбирается необходима*
ветвь функции.
При решении плоских задач о кавитационных течениях
широко используют теорему Кристоффеля—Шварца, позволяющук>
взаимно однозначно и конформно преобразовать течение внутри
или вне многоугольника на верхнюю полуплоскость и найти πρβ'
образующую функцию.
В случае преобразования внутренней области многоугольника
теорема формулируется так: пусть в плоскости переменного гг^
есть п-угольник (рис. II.6), внутренние углы которого равны
«ι^π, ttgn, адЯ, ..., α„π, где α^, а^, ag, ..., α„ — действительные
числа, причем каждое из них не должно превышать двух и, кроме
того,
«1 + ¾ + 1- «« = " — 2.
Функция ffi)= / (ί), конформно отображающая верхнюю Пблу'
плоскость 1 {ΐ) > О на внутреннюю область многоугольника,
имеет вид
W
о
Где üi, Ö2. ···· <^n —точки действительной оси, αχ — крайняя
точка слева, а„ — крайняя точка справа, соответствующие
вершинам многоугольника; С^ и Сг—некоторые постоянные числа.
На рис. ΙΙ.6, а, б даны обозначения вершин м^ногоугольника
на плоскостях w и t. В частном случае, когда одна из точек
действительной оси, например точка а„ (рис. II.6, в), удалена на
бесконечность, формула примет вид:
> =^^I (ί- a,fi-' ...{t- α„_ιΓ"-ι-^ dt + С,. A1.214)
w-
При рассмотрении задачи о конформном отображении
внешней по отношению к контуру многоугольника области, содержа-
6)
«А· л
а, η
а-н
СХпЛ=0
®
an
• ■■■
Рис. II.6. К формулировке теоремы Кристоффеля—Шварца.
1цей, бесконечно удаленную точку, преобразующую функцию
находят по формуле.
i
,α„-1
w ■
η г (<-^Л '■■■(<-«„)"" ,^ . _ .,. _ ,^.
■kf
Где k — координата точки верхней полуплоскости^^
соответствующая бесконечно удаленной точке на плоскости w\ k— величина,
сопряженная с k.
В этом случае углы измеряют так, как показано на рис. II.6, г,..
а сумму ^глов находят по формуле
α^μ + α^τι + · · · + a^ji = (η + 2) π.
Приведенные выше формулы выведены в предположении, что
Верхняя полуплоскость находится слева от положительного
направления оси абсцисс. В случае преобразования на нижнюю
полуплоскость в формулах должен быть изменен знак.
¢6
в последнее время для решения кавитационных задач
применяют метод особенностей. При использовании этого метода
предполагают, что на неизвестной поверхности (границе) каверны
располагаются особенности (источники, стоки, диполи, вихри),
интенсивность которых неизвестна. На основании граничных
условий на поверхности каверны составляют уравнения, которые
позволяют найти интенсивность особенностей и вызванные
скорости. В общем случае эта задача нелинейна... Для частичной
каверны, когда каверна заканчивается на теле, возможна
линеаризация задачи: каверна считается тонкой, а граничные условия на
каверне сносятся на поверхность тела.
Как известно, задачи гидромеханики разделяют на прямые,
обратные и.смешанные. Прямая задача состоит в том, что поле
скоростей и давлений при обтекании тела определяют по
.заданным координатам точек его. поверхности. В обратной, задэче по
заданным скорости и давлениям в функции выбранных координат
находят форму тела. В смешанной задаче в одной области течений
задается форма тела, а в другой — скорость и давление на
некоторой линии тока, форма которой неизвестна.
Задача о кавитационном течении относится к числу смешанных,
т. е. на контуре тела, свободном от каверны, решается прямая
задача, а на границе каверны — обратная задача.
Рассмотрим сначала случай плоского течения, в котором
применим метод вихревых особенностей. Поток, обтекающий плоский
контур, можно представить, накладывая на основной
поступательный поток возмущенный поток от системы вихрей, расположенных;
на контуре (см. рис. V.10) в его плоскости-. На основании
известных из кинематики ж;идкости формул (закон Био и.Савара)
составляющие скорости в любой точке потока, вызываемые вихрями»
расположенными на. участке, кривой /, определяются так:
йормальная (к контуру) .составляющая
ι
касательная (к контуру) составляющая
где γ (S) — интенсивность вихревого слоя в точке контура Si,
г — расстояние от точки S до произвольной точки S^, cos {r,_t),
sin (г, t) — косинус и синус угла между касательной к контуру
в точке Si и отрезком г. ν
Тогда интенсивностд> вихрей может быть найдена из
интегрального уравнения, для составления которого используется
.67
условие непроницаемости, т. е. равенство нулю суммы
нормальных составляющих скоростей (к контуру). Предполагая, что
чскорость поступательного потока равна К«,, получаем:
1
2π
|-^^^f^γ(S)dS + l/eoSinτ = 0. (Ι1.2.16)
где τ — угол между касательной в произвольной точке контура Sj^
Я направлением Vo.
Получаем сингулярное интегральное уравнение, справедливое
как для замкнутых, так и незамкнутых контуров.
В случае замкнутого контура, имеющего непрерывную
касательную, интенсивность вихревого слоя в каждой точке
контура равна модулю касательной скорости течения в этой точке,
что дает возможность получить интегральное уравнение Фред-
:тольма 2-го рода
у (Si) = ^ φ ^ypJL у (S) dS 4- 2Veo cos τ. (Π.2.17)
t
В общем случае кавитационного обтекания профиля можно
^рассматривать систему тело (крыло) — каверна как сложный
контур, составленный из контура профиля тела (к^), свободного
•от кавитации; границы каверны (Г); контура, на котором
замыкается каверна (Kg).
Выражение (П.2.17) представляет собой интегральное
уравнение Фредгольма 2-го рода, из которого определяется
неизвестная интенсивность циркуляции у (S). Уравнение (П.2.17) решают
методом последовательных приближений. Неизвестную границу
каверны определяют по уравнению (П.2.16), в котором у (S) —
:постоянная величина, найденная согласно уравнению A1.2.17).
В случае замены границы тела и каверны особенностями
типа источников и стоков используют известные из кинематики
.жидкости формулы для комплексного потенциала и
комплексной скорости. Составляют выражение для суммарной скорости,
чэбусловленной скоростью потока, присутствием тела в потоке,
а также распределенными по поверхности каверны неизвестными
источниками и стоками./С помощью граничных условий на ка-
.верне составляют интегральное уравнение для нахождения
неизвестной интенсивности особенностей и их распределения по
телу и каверне.
При распределении особенностей вблизи тела должны быть
учтены принцип аналитического продолжения и условие
непротекания.
Наиболее простые решения получают в случае тонких тел,
т. е. таких тел, у которых углы, образуемые между касательными
:;К контурам тела и каверны и осью х, малы.
т
§ 3. Струйное обтекание пластинки, решение задачи
с помощью способа Н. Е. Жуковского
Рассмотрим теперь решение задачи о струйном обтекании
пластинки с помощью способа Н. Е. Жуковского (рис. II.7, а). В этом
случае, согласно (II.2.4), преобразующая функция имеет вид
(ο = 1ηξ = 1η-^ (ΙΙ.3.1)
или в параметрической форме
ω = 1п
+ ίθ.
где V:
dw
dz
комплексная скорость течения; θ — угол между
касательной к линии тока в данной точке и осью абсцисс.
А С
о)
6)а
®
,27
@
г)
-оо -/
©
ж
-Ш.
TP
7оо
Ьп,
AJ)
Рис. II.7, Решение задачи о струйном обтекании
пластинки с помощью способа Н. Е. Жуковского: а —
физическая плоскость течения; б — плоскость комплексного
потенциала w; в — плоскость ω.
Согласно идее способа обе функции (ω и w) выражают через
параметрическое переменное t, изменяющееся в верхней
полуплоскости, а затем используют соотношение (П.2.4). После
преобразования перепишем:
(II.3.2)
,(,)=■ je. ш^Л
Как уже указывалось, при струйном обтекании пластинки
плоскость комплексного потенциала представляет собой плоскость
с полубесконечным разрезом вдоль положительной оси абсцисс
(рис. II.7, б).
Рассмотрим теперь вспомогательную плоскость ω = In
+
+ ίθ и проследим изменение функции ω на границах течения.
(Б9
= In 1 == о, ω = ιθ»
На границах каверны I VI = F„ = V«,, тогда функция ω имеет
чисто мнимые значения, а именно ш ^^
V
т. е. значения функций ω находятся на мнимой оси плоскости.
Аргумент же функции изменяется следующим образом:
на линии BD, как видно из рис. II.7, в, 0<ίθί^ί—;
на линии AD i -^ < ίθ < ш.
Таким образом, может быть найдено положение точек ABD
на плоскости ω. На пластинке AB скорость изменяется от О
до некоторого конечного значения, поэтому функция ω —
комплексная величина. Значение аргумента θ на пластинке постоянно
и равно:
на участке СВ — θ = 0;
на участке CA — θ = я.
Таким образом, на плоскости ω части пластинки
располагаются: ВС — на оси абсцисс, АС — параллельно оси абсцисс
на расстоянии равном π. Для дальнейшего решения задачи
преобразуем плоскости ш и ω на верхнюю полуплоскость t. При
соответствии точек, указанном на рис. II.7, г, функция w
преобразуется на плоскость t с помош,ъю формулы
w = φot^ (И.З.З).
W везде в верхней полуплоскости — аналитическая функция.
Конформность нарушается только в точках t = О и ί = схз, так
dw „ „ dw
как в первой точке -тт- ==0, а во второй -тт- = оо.
Преобразуем теперь на полуплоскость t функцию ω. Как
видно из рис. ΙΙ.7, е, область изменения ω представляет собой
полуполосу, которую можно рассматривать как треугольник, одна
из вершин которого — С находится в бесконечности. Для
преобразования воспользуемся интегралом Кристоффеля—Шварца,
рассматривая при этом отображение течения внутри треугольника,
на верхнюю полуплоскость (П.2.13).
Координаты точек Oj в (II.2.13) соответствуют рис. II.7, г,.
л \ л 1
Л: αι=1; па^^^—-; ^ = -
β: 02 = —!; Ji«2 = -y-; α2==-2-; A1.3.4)
С: «3 = 0; itttg = 0; 0½ = 0.
После подстановки условий (II.3.4) в (II.2.13) и
промежуточных преобразований получим:
« = C,J-p^4-C.. (II.3.5)
70
Дополнительные условия для определения постоянных С^ и С^.
в точке А ω A) = in; (П.3.6)
в точке В ω (^1) = 0.
Интеграл, входящий в (П.3.5), — табличный. Его решение
имеет вид:
С dt . 1 , π
\ —г — —arcsm -Г" + -^- ·
Тогда формулу A1.3.5) переписываем так:
i(i) = Q (-aresin ^+-|-)+С2. (II.3.7)
ω
Подставив первое и второе условия (П.3.6) в (П.3.7), после
преобразований получим:
Ci = —t и Ca = πι. (ΙΙ.3.8)
При учете выражения (П.3.7) функция ω (ΐ) приобретает вид
ω
(ί) = In (г aresin ^)+^- (II.3.9)
Используя известные соотношения между обратными
тригонометрическими и логарифмическими функциями, получим:
ω(^) = 1η(|/ΐ--1- +4)+^. (II.3.10)
Тождественность (П.3.9) и (II.3.10) легко проверить дифферен
2
цированием. Или, принимая во внимание, что Int =-^In— 1 =
1 .
= -ψ ш, найдем:
ω (t) == In '^ ~ [- ni при 0 < ί <: 1;
ω{ί)=-1ηϋ^ί^^ при 0>ί> - 1. A1.3.11)
Так как ΐπ= \п e^", то формулы (П.3.11) можно
преобразовать к виду:
ω (t) = In е''^ 1 Ч- Vi - Ρ jjpj^j О < ί <: 1;
0)@ = lni^t£i^^ при О >/> — !. (II.3.12)
71
Сопоставляя (II.3.12) и A1.3.1), получим:
, dw , l + VT^
— in ,. ■ = In ■ ;
ИЛИ
dw t
(II.3.13)
Из выражения (II.3.13) определяем функцию ζ {t), т. е.
профиль каверны
в выражении (П.3.14) первый сомножитель находим согласно
(II.3.13), а второй — путем дифференцирования выражения
(II.3.3). После подстановки получаем:
z(t)
= ^Y-±^^2^tdt==^^{\-^VT—F)dL (II.3.15)
Сопротивление пластинки вычисляем по формуле
На основании уравнения Бернулли выразим давления, входящие
в подынтегральное выражение (II.3.16):
Если учесть (Н.Э. 17), то формула для вычисления
сопротивления приобретает вид
I
X = 2рщУ^ J A - -^-,^==^-^ A +l/r~F") dt. (II.3.18)
о
Постоянную φο определяем по формуле (II.3.15) при заданной
половине ширины пластинки /
О О
2фо
откуда
72
Φο^τίττ- ("·2·^ο>
После интегрирования выражения (II.3.18) и ряда
промежуточных преобразований находим
X = npVeoCpo (П.3.20)
или после подстановки φ о получаем
^-РУ'^1·^- ("·3·21)
Коэффициент сопротивления пластинки при струйном
обтекании, отнесенный к ее ширине, определяем по выражению
С^ = -Ä^ ^ ^L_ -=. 0.88. (II.3.22)
§ 4. Навитационное обтекание пластинки
в безграничной жидкости (по схеме Д. А. Эфроса).
Решение задачи с помощью способа.
особых точек С. А. Чаплыгина
Методы решения плоских задач теории струй идеальной жидкости
были кратко описаны в § 2 гл. П. Рассмотрим в качестве
иллюстрации применение способа особых точек для решения задачи
о плоском кавитационном обтеканий пластинки, расположенной
поперек безг|)аничного потока идеальной несжимаемой жидкости.
Предположим, что замыкание каверны происходит с обратной
струйкой (схема Д. А. Эфроса) и число кавитации κ т^ 0.
Задача состоит в том, чтобы при заданных характеристиках
потока на бесконечности: скорости VOe, давлении р^, числе
кавитации κ, ширине пластинки / — найти на физической плоскости
форму границы каверны, поле скоростей и давлений вблизи
каверны, а также сопротивление пластинки. Схема обтекания дана
на рис. II.8, а.
В соответствии со способом особых точек внешнее течение на
физической плоскости преобразуется на некоторую простую
область вспомогательной плоскости t. В качестве такой области
примем полукруг единичного радиуса (рис. П.8, б), причем,
следуя [33], пластинку расположим на горизонтальном диаметре,
а границы каверны — на дуге полукруга. Расположение
характерных точек течения показано на рис. П.8, а и б.
Возможно иное расположение границ потока: границы
каверны — на горизонтальном диаметре, пластинка — на дуге
полукруга [17], что, однако, не повлияет на результат решения
задачи.
т, dw
Будем искать комплексные скорости -^ течения на пло-
, . » dw
скости t и течения на физической плоскости -^, используя
известное представление рациональной функции в виде линейных
73
множителей содержащих в числителе координаты точек, в
которых искомая функция обращается в нуль, а в знаменателе —
координаты точек, в которых функция обращается в
бесконечность [нули и полюсы функции, (П.2.8)].
Применительно к течению на плоскости t и найдем нули и
полюсы функции -^. Нули функции определяются
критическими точками физического течения, в которых скорость
обращается в нуль (точки О' и /С') и в точках, где нарушается конформ-
► В
δ)
'1-1
ΰ' i
tf^
ill
с'· ic
С"
к'
„π
л
С"·
0'
'-ic
i
©
Ύ
Рис. II.8. К решению задачи q кавитационном обтекании пластинки
по схеме Д. А. Эфроса; с — физическая плоскость течения; б —
вспомогательная плоскость t.
ность (точки А' и В'). Полюсы находятся в точках, где
располагаются особенности типа источника (стока) или диполя (точки
С и D').
Известно, что комплексные потенциалы течений, вызванных
источником (стоком) или диполем, можно представить в виде
DD = -^ In (ί — а), W
Μ
2π ""^- ^" "^ 2л (ί—β) '
а соответствующие им комплексные скорости — в виде
dw
1
_0_
2π t — a''
dw
~dt
Μ
2π {t — с)
_Ω^2 '
где Q — интенсивность источника или стока; Μ ■— момент
диполя; α — угол между осями диполя и Ох; а — координаты
источника (стока) или диполя.
Как следует из схемы течения (рис. П.8, б), особенности
располагаются следующим образом: в точке D' — сток, в точке С —
диполь.
74
Используя ^нал1™ческое__щодолжш^
течение на всю плоскость 1 и найдем симметричные особые точки.
На основании принципа симметрии [56] известно, что
координаты точки, симметричной относительно отрезка вещественной
оси, имеют комплексное сопряженное значение, а координаты
точек, симметричных относительно окружности радиусом R,
связаны соотношением
R^ = PiPa.
где р1 и ρ 2 — радиусы концентрических окружностей, на
которых расположены симметричные точки.
Для окружности единичного радиуса
На основании сказанного представим теперь все особые точки
течения на плоскости t (рис. П.8, б).
Таким образом, окончательно найдем следующее
распределение особых точек:
нули — в точках с координатами; ί = О, t = ik, t = —ik,
^^^ ~~k ' ^^ Ik ' ^^^ ^ ^^^
полюсы 1-го порядка — t = i, t — —i;
полюсы 2-го порядка — t = ic, t = —ic, t = — , t = — — .
Зная нули и полюсы функции -^, напишем ее выражение:
at
или
t(t-\){t+\){t~ik)(t-4rik) (i_-l)(i+-lj
{t~i){t + i){t~icY{t + ic^ ^i-_-i-)^(<+-Ly
U^+i) {t^ + (^)(^t^ + -^J
Составим теперь выражение комплексной скорости -у— также
при помощи метода особых точек. Для удобства выкладок рас-
^ dw
смотрим безразмерную комплексную скорость ■. у и найдем
границы течения на плоскости годографа. На границе каверны
du) I t
^ у =1. Т. е. получаем уравнение окружности единичного
задиуса. Рассмотрев течение на физической плоскости, найдем,
что нули функции находятся в точках О и К с координатами
t = О, t = ik.
75
Используя принцип симметрии, распространим течение на
всю плоскость. Тогда при зеркальном отображении через
окружность нули переходят в полюсы, а при отображении через
вещественную ось (диаметр) нули переходят в нули.
После аналитического продолжения находим:
нули функции —г в точках с координатами: t = О, t = ik,
t = —ik;
полюсы — t — -гг ί ==
k ' " k ·
^ , dw
Строим функцию ■ у по нулям и полюсам
' (^^ ρ t(t-ik)(t + ik) ρ t{t^ + k^ /ТТД9Ч
Постоянную в находим на основании следующих рассуждений.
При t = i в точке D (рис. П.8, а), соответствующей стоку, ско-
эость на границе каверны изменяет свое направление, т. е.
'^-.\ — —1. Подставляя это условие в (И .4.2), получим:
άζΥκ
-i^Bt^-'+P.^-Bik^
(-+^)
или
В--iL· = -1- ("·4.3)
При учете (П.4.3) формула (П.4.2) приобретает вид
Ук dz Ä2
Разделив (П.4.1) на (П.4.4), получим выражение для функции
■JT- (t)· Выполнив ее интегрирование, найдем границу каверны,
а затем характеристики течения. В результате получим
dz_ik^A (^'-1H' + "р-) A,4.5)
dt
^« iP+l)(P + c^(^t^-\.^y
dz
== Fco., Тогда на
Входящие в (П.4.5) неизвестные постоянные k, с, А должны
быть найдены на основании трех дополнительных условий.
1. Условие для скорости набегающего потока, состоящее
в том, что в точке С при t = ic скорость
основании формулы (II.4.2) получим
_^^__^^£i=l£!±i!L = ,fz_£! (II.4.6)
76
2. Условие однозначного соответствия ζ (t) в точках t = ic
вспомогательной плоскости t и ζ = oq физической плоскости. Это
условие означает отсутствие циркуляции на бесконечности. Из--
вестно, что циркуляция зависит от вычета функции, иначе говоря,
вычет функции -тт- в точке t = ic должен быть равен нулю.
Напомним, что если функцию f (ζ) разложить в ряд Лорана
по степеням ζ
f (ζ) = +b_,z~^ + b.iz-"- + bo + ...,
TO коэффициент b_j называется вычетом функции. На оснований
теоремы вычетов [56] условие, указанное в п. 2, сводится к
равенству
После подстановки (И.4.5) в (П.4.7) и промежуточных преобра-г
зований найдем
3. Условие задания ширины пластинки, которое можно ЗВ'
писать в виде:
I
il-^j^(t)dt. (П.4.9>
— 1
После разложения (П.4.5) на элементарные дроби и интв'
грирования в пределах от —1 до +1 находим длину пластинки,
а после интегрирования по бесконечно малой полуокружности
вокруг точки ί = t определяем толщину струи б.
Силу сопротивления находим по формуле С. А. Чаплыгина
после вычисления по (П.4.4) комплексного потенциала. Более
простым оказался прием определения силы сопротивления, осно-;
ванный на использовании теоремы количества движения [17Ь
Рассмотрим обтекание пластинки, расположенной между двумя
параллельными стенками, расстояние между которыми равно 2Н.
Проведем в бесконечности слева и справа от пластинки
прямолинейные сечения, параллельные пластинке, и в бесконечности слева
поперек обратной струйки, как показано на рис. П.9.
Давления рс, Pd, скорости Усу Кд связаны интегралом Бернулли
Очевидно, что расход жидкости в струйке равен
до - р2Я (Ус - Vo),
где q — объемный расход.
77
Применим теорему об изменении количества движения к
рассмотрению жидкости, заключенной между параллельными
стенками, пластинкой, свободными поверхностями и прямолинейными
сечениями, проведенными параллельно пластинке.
С
\
1
1
1
1
1
1
/
=t
Csl
!
ι
Α·
0
Β·
/·
'
V
'
ι
"iOj
ij
Ώ
~—~^ '
) ι
Γ^ Ι
ι
ь
27
Рис. 11.9. К выводу формулы A1,4.10).
Приращение в единицу времени количества движения
жидкости, заключенной внутри этого контура, равно
-К|р2Я-ЬК1,р2Я-КкДО,
а результирующая всех давлений на жидкость
Приравнивая оба эти выражения при учете (П.4.10), после
преобразования получим
X
= № (Vk +
УсЧ-Ур\
В случае безграничной жидкости, когда стенки удалены
в бесконечность и Кс = ^d = VOo, находим силу сопротивления
в виде
X = W (V^K + V^~).
а затем и коэффициент сопротивления
^.=^-^ = 1^A + ^-).
Выражая отношение
Vk
■ψ^ через число кавитации κ, найдем
а/
c.-^i{^-vV\-\-y)·
(П.4.11)
Входящий в (П.4.11) расход жидкости q связан с толщиной
обратной струйки δ формулой
78
Результаты расчетов по формуле (II.4.11) даны на рис. 11.10.
Как видно из рисунка, с ростом числа кавитации (уменьшение
длины каверны) коэффициент сопротивления увеличивается. '
В работе [53] рассмотрен более общий случай — обтекание
пластинки под углом атаки. В этом случае на плоскости
вспомогательной переменной t точки С и D'
смещены относительно вертикального
диаметра окружности, а для
определения шести постоянных составляют
mecTi} дополнительных условий.
В [53 ] приводятся также
результаты решения задачи о кавитацион-
ном обтекании решетки профилей.
Рассмотрим теперь несколько
видоизмененную задачу об
обтекании кавитирующей пластинки
поперечным потоком. Предположим, что
за пластинкой вниз по потоку на
оси симметрии в точке L (рис. 11.11)
расположен источник
интенсивностью Q. Так как источник
находится в плоскопараллельном потоке,
то его обтекание равносильно
обтеканию полутела [65],
Вследствие симметрии будем рассматривать верхнюю половину
течения. Схема течения на физической плоскости дана на
рис. 11.11, а. Для решения задачи воспользуемся также способом
особых точек. Преобразуем внешнюю область верхней поло-
6)
3 у4-
2 -/^
7 ^
Η
Рис. II. 10. Зависимость Схг (κ).
Рис. II.П. К решению задачи о кавитационном обтекании пла-·
стинки с источником, расположенным вниз по потоку: с —
физическая плоскость течения; б — вспомогательная плоскость t.
вины течения плоскости ζ на первый квадрант
вспомогательной плоскости t (рис. П.11, б) так, чтобы свободные струи
располагались^ на мнимой оси, а твердые границы потока — на
действительной оси. При этом зададим положение трех точек так,
чтобы на плоскости t точка D имела координату ί = О, точка
О — t = 1, точка А — t = оо.
79
По аналогии с- предыдущим решением построим зависимости
'Ж ^^^ ^ ~аг ^^^ способом особых точек, для чего найдем нули
Й полюсы функций.
Найдем особые точки функции -tj. комплексной скорости
вспомогательного течения. Рассмотрев течение на физической
плоскости (см. рис. 11.11, а), мы находим:
нули 1-го порядка в критических точках К, Н, где скорость
равна нулю, с координатами t = k я t = h;
полюсы 1-го порядка в точках D (сток) и L (источник) с
координатами t = О и t = b соответственно;
полюс 2-го порядка в точке С (диполь) с координатой t = с.
Так как функция регулярна, то воспользуемся аналитическим
,ее продолжением через мнимую ось. В этом случае согласно
принципу симметрии нули переходят в нули, а полюсы — в
полюсы.
Таким образом, после аналитического продолжения функ-
dw
НИИ -JT- через мнимую ось получаем следующее распределение
лсобых точек:
нули: при t = k, t = —fe, t = h, t = — h;
полюсы 1-го порядка: при t = О, t == b, t = —b;
полюсы 2-го порядка: при t = с, t = —с.
Зная нули и полюсы, получим:
dw ^ л {t — k){t + k){t—h){t-]-h)
dt ~ t\t — b)(t + b)(t — c)^(t + c)^
или после преобразований:
dw ,. ^-k?)(t^-h^) /114 191
dt ^ t{t^~-,b^)(t^—c^· χιι.^.ΐΔ)
Найдем теперь особые точки функции -^ (t). Как следует из
рис. 11.11, а, течение имеет две критические точки (скорость
равна нулю) Я и /С, в точке L расположен источник, а в точке С
особенность типа Y^t — 1. Рассмотрим здесь также относительную
dw
скорость ^jp-.
Как уже указывалось, при решении предьщущей задачи на
dw . .,
τΎτ- = 1, Т. е. на плоскости годографа,
это уравнение окружности единичного радиуса. При
аналитическом продолжении через окружность нули переходят в полюсы,
в полюсы—-в нули. На вспомогательной плоскости ί свободные
струи располагаются на мнимой оси, поэтому после аналитиче-
80
границе каверны
ского продолжения через нее получим следующее выражение для
относительной комплексной скорости:
dw ^^{t^h){t~k)]iT^^i{t-{-b) (II4 13>
(II.4.14)
Разделив (II.4.12) на (II.4.13), получим:
dz _ А (t + h)^ {t + k)^ νΤψϊ
dt ~ V^B t (t 4- fcJ (^2 ^.^2) ιΛ^ΤΤγ ■
В правой части выражения (II.4.14) — шесть неизвестных
параметров А, В, h, k, b, с. Для их определения необходимы
шесть дополнительных условий, причем четыре из них примем
такими же, как и при решении предыдуш,ей задачи.
1) В точке D (см. рис. 11.11) при ί = О отношение .^ —
= —1, так как скорость обратной струйки направлена в сторону,
противоположную направлению основного потока. Тогда после
подстановки этого условия в (II.4.13) получим:
или в — i.
2) Условие для скорости набегающего потока. В точке t —с
dz '^'=°·
После подстановки этого условия в (II.4.13) получим:
V.O ^ i{c-h){c-k)VF^ri^c + b) (II 4 15)
Vk (c + h){c.+ k)(c — b)Vc+l
3) Условие однозначного соответствия функции ζ (ί) в точках
t = ic и ζ = оо определяется (П.4.7).
4) Условие задания ширины пластинки определяется формулой
во
il = 2^~-{t)dt. (II.4.16)
I
5) Условие задания расстояния до источника L^ имеет вид:
ь
U^\^{t)dt. (II.4.17)
6) Условие задания интенсивности источника Q.
На рис. 11,12 приведены результаты расчетов
относительных параметров каверны /?^ и L^ при расположении за ней
полутела (точки на графике), и дано сравнение с соответствую-
81
к
It
,ci
I
τ
I/
\
\
о
1
1
L
/
л
/
Η
I
1
f
\^
у
/
f
ι
I
\
A
\
)
/
1
.-c^
1 ?
f- ^ -n
'^
с
V
Ί
-3
ÜH
1
—^
J
1
rt"
.
Ka
«■<1
^5
ίε>
ca
'"^ 7
II
Ö
\
\
/
/■
/
/
'
/
/3
,cf
t^
i
/
.^"
'
D
/\
*
/
1
1
1 *. *
l<J leaf
«
»
CI
/
-
4
V
,
^^
V
Pn -^
■»*
/
Μ
ί
ч/~
5С
l·
Г
1
■
.^а?
ζ
«л,
32
я
s
ев
s
Ια?
s
в
s
о.
s
а
о
с
S
>»*
>-3
II
üi
^
_
S
si
ч
о
с:
X
ч
<D
f-
Я
öi
о"
V/
V/
С5
о
II
■α
~«"
S
α.
с
1
1
Ö
ел
о
II
I
ь<"
:<
-t
I
■4
<
^-
со
■fl"
I
I
,Η
bi
a
^
1
•
о
"C
o^
V/
s
V/
Tt>
о
t>
—
II'
-5?
'S"
s
o.
Ε
1
1
vo
Ю
CO
о
C5
II
1
i<^
»
-J
1
■4
«d
άί"
"*
Ю
II
1
s<"
и
-t
1
•
О
I
CO
S
ЩИМИ параметрами без полутела (кривые на
графике). Как показывает рис. 11.12, а,
если за каверной расположено полутело,
ширина которого примерно равна ширине
пластинки, то полуширина каверны для
данного числа кавитации практически
совпадает с полушириной каверны,
образующейся при том же числе кавитации в
случае отсутствия полутела [65].
На длину каверны при малых числах
кавитации расположение за ней полутела
влияет незначительно, но при увеличении
числа кавитации (уменьшение длины
каверны) влияние усиливается. Так,
например, при κ = 0,5 (рис. 11.12, б) присутствие
полутела приводит к сокращению длины
каверны по сравнению со случаем Q = О
на 12%, если полутело далеко от каверны
Lk
5,48), и на 22%, если
расстояние от конца каверны до полутела
составляет 0,085 длины каверны.
§ 5. Кавитационное обтекание
пластинки в безграничной жидкости
(по первой схеме М. Тулина)
Рассмотрим пластинку АС (рис. 11.13),
расположенную в потоке несжимаемой
невязкой жидкости под некоторым углом атаки а
к направлению скорости потока Vco.
Предположим, что течение характеризуется
числом кавитации κ, каверна заканчивается
двумя односпиральными вихрями в точках
Ε и D, за которыми образуется тонкий
вихревой след, монотонно сужающийся
к бесконечности. Обозначим V^ —
скорость на границе каверны, w — ψ + i-ψ —
комплексный потенциал скорости течения,
точка В — точка разветвления потока на
пластинке.
Схема течения на физической плоскости
дана на рис. 11.13, а. Принята
прямоугольная система координат хОу с началом в точке
разветвления. При решении этой задачи
необходимо найти профиль каверны, силу
сопротивления и подъемную силу.
83
кроме физической плоскости рассмотрим еще две: плоскость
комплексного потенциала скорости w и плоскость функции
Н. Е. Жуковского ω. Как указывалось в § 2, функция ω связана
с комплексной скоростью V и скоростью на границе каверны V^
соотношением:
ω^
1πζ = 1π
ο—Ιβ
In
dw
dz
(II.5.1)
Рис. 11.13. К решению задачи о кавитационном обтекании пластинки в
безграничной жидкости (по первой схеме М. Тулина): а — физическая плоскость
течения г; б — плоскость комплексного потенциала w; в — вспомогательная
плоскость t.
Из выражения (II.5.1) видно, что —^ = ζ представляет собой
Vk
преобразующую функцию, зная которую, а также комплексный
потенциал, легко построить профиль каверны по формуле
dw
Ύ'
'" V, J
(II.5.2)
Плоскость комплексного потенциала рассматриваемого
течения представляет собой плоскость с конечным разрезом вдоль
положительного значения оси φ (рис. 11.13, б). Такое
представление возможно в случае предположения, что потенциалы скорости
в точках Ε и D равны φ^ = φ^, а также равны аргументы θ£ =
= θβ. .
84
Преобразуем конформно плоскость w на некоторую
вспомогательную комплексную плоскость t (рис. 11.13, в) так, чтобы
выполнялось следующее соответствие точек:
точка В: хюв = О, ί = 0;
точка С: Wc = ехр {2ni), t = —1;
точка D: w^ = φ^, ί = оо.
Связь между w и t установим при помощи интегрального
соотношения Кристоффеля—Шварца. Разрез ABCD вдоль оси φ
комплексной плоскости w примем за четырехугольник, внешность
которого преобразуем на верхнюю полуплоскость t [формула
(II.2.15)]-
В соответствии с рис. 11.13, б ив найдем для нашего случая
координаты а,- и а,·:
точка А: α^π = π, αϊ = 1, % = ί^ί
точка В: а^л = 2π, α2 = 2, α^ = 0;
точка С: а^п = π, ag = 1, Cg = —1;
точка D: α^π = 2π, α^ = 2, щ = сю.
Подставим эти координаты в (II.2.15), учитывая следствие
теоремы, касающейся случая ßj == сю:
tdt
^-C,\-j^,^^C,. (II.5.3)
После замены переменной и последующего интегрирования
получим:
Постоянные С^ и Cg найдем исходя из граничных условий:;
в точке В W = О и t = 0;
в точке D W = ЦI)И t = оо.
Подставляя эти значения в (II.5.4), получим^два уравнения;
для определения Cj и С^:
С^ = %.л и Сз^фд. A1.5.5)
2
После подстановки (II.5.5) в выражение для потенциала
скорости (П.5.4) получим:
= Фо12^^. откуда t = k{^-^^^y'\ (II.5.6)
W-
Входящий в (II.5.6) потенциал φ/, находится исходя из
граничных условий в точке С. После их подстановки в (II.5.6)
получим φο = 1 -Ь k^-
Согласно (II.5.1) функция ω представляет собой комплексное
число:
ω=-1π-1^-ίθ, (ΙΙ.5.7)
85
где
Κεω == In-Lr-L, a Im(o = —Θ.
' к
Рассмотрим теперь изменение функции ω на действительной
'ОСИ полуплоскости ί и на отдельных ее участках. Запишем
известные граничные значения функции ω:
! при ^л<^<оо|1^| = 1^и Кеш = In 1 = 0;
при О < ί < /^ Im ω = —(π — α) = α — π;
при —1 < ί < Ο Im ω = —(—α) = α;
при —οο < ί < —1 Ι VI == V« и Κβω = 1η 1 = 0. (II.5.8)
Таким образом, на вещественной оси для функции ω (t)
заданы смешанные граничные условия, которые позволяют найти
эту функцию на основании решения краевой задачи Римана—
Гильберта для верхней полуплоскости. Здесь мы предполагаем,
что функция ω (t) на концах % 6,¾ не ограничена, однако
ограничен интеграл от ω (t). Задачу можно решить при помощи
формулы (П.2.10) Келдыша—Седова, приведенной ранее в § 2 гл. II,
0@ =
R{t)
J_J^|Iliirf, + P„,„
A1.5.9)
где g(t)== Rero (t) на отрезках α^ b,^; g (τ) = i Im ω (τ) на
отрезках bk a/i+i, τ — переменная интегрирования.
Полином Рт (t), входящий в решение, принимается в виде
степенного ряда
Рт it) = AJ"^ + А^_г1'^~^ + - + Ло-
В дальнейшем при решении задачи согласно [85] ограничимся
только одним членом ряда Л о- Как следует из рис. 11.13,
вещественная ось, ограничивающая верхнюю полуплоскость t [см.
обозначения формулы (II.5.9)], имеет три отрезка: —ооЬ^, ^1¾.
Λχοο, причем &х = —1, «1 = tji- При учете сказанного формула
для определения функции ω (ί) получает вид:
ω@ =
R(t)
где
_L[A^lii,, + J, (П.5.10)
— оо J
^^'^=Vit+mt-u)' ^(-)-V-
1
(T+\){x~tA)
При составлении функции R (t) ветвь разреза действительной
оси принята в интервале —1 < ί < ^л- Интеграл, входящий
в формулу (II.5.10), может быть представлен как сумма
интегралов с пределами, равными координатам соответствующих точек
на вещественной оси t. Однако, так как g (τ) на отрезках (— оо
S6
—1) и {tji оо) равны нулю, то равны нулю также первый и
последний интегралы этой суммы. Учитывая сказанное, после
подстановки в (П.5.10) граничных условий (И.5.8) и дальнейших
преобразований формула (II.5.10) примет следующий вид:
ω(ί)=|/(ί+1)(ί^-ί)
άτ
" J Κ(τ+1)(ί^-τ)(τ-ί)
-1
ίίτ
V(X+l)(tA-X)(l~t)
+ Л
(II.5.11)
В формуле (II.5.11) неизвестны ί^ и А^, а в (II.5.6) неизвестна
k — координата бесконечно удаленной точки на плоскости t.
Таким образом, для решения задачи необходимо иметь три
дополнительных уравнения.
1. Первые два уравнения могут быть получены исходя из
условия, что для скорости набегающего потока при t — ik модуль
"^ — Voo, аргумент θ = 0. Учитывая это условие.
скорости
dz
получим на основании (II.5.7):
Re ω (ik) = In
dw
,-|ΐπA+κ);
Im ω (ik) = 0.
(II.5.12)
2. Третье уравнение получим исходя из условия замкнутости
системы тело—каверна. Известно, что расход жидкости при
истечении из какого-либо замкнутого контура С пропорционален
функции тока -ψ или Im фс ζ(ζ) dz, где ζ = у ^ .
Разложение функции ζ в ряд Лорана по степеням ζ
показывает, что для больших значений ζ функция ζ имеет те же
особенности, что и функция ω. Поэтому условие замкнутости имеет вид:
1т φ ζαζ==1ναφ ω dz-=1тф ω dw= О
или
Ιιη^ω(ί)-^^ίίί = 0.
(ΙΙ.5.13)
Входящую в (II.5.13) производную -гт- вычисляем путем
дифференцирования (II.5.6) по t:
dw _ 2k^(k^+\)t
dt (t + ik)^ {t — ik)^
(II.5.14)
После разложения ω (t) в ряд в точке t — ik при помощи теоремы
вычетов третье дополнительное условие приобретает вид
Im
i^L·.-'- ("·5-ΐ5)
Оно получено в предположении, что поток на бесконечности не
возмущен.
Условия A1.5.12)—(П.5.15) приводятся к трем уравнениям
[85], линейным относительно In A + κ), а, и Л,,, но нелинейным
относительно t^ и k. Поэтому в [85] эти зависимости представлены
в виде графиков ί^ (fe) при постоянных значениях а, κ я Aq.
Без потери общности примем скорость на границе каверны V^ =
= 1 м/с. Тогда для обтекания наклонной пластинки выражение для
функции ω (t) (П.5.11) после интегрирования приобретает вид:
■ωα)^ΐα + 1η ^'^~^/A!}+E- + A,V(tA-t){l+t). (П.5.16)
Формула (П.5.16) дает возможность определить длину пластинки,
коэффициенты подъемной силы и сопротивления, профиль
каверны. Так, на основании (П.5.2), (II.5.14) и (II.5.16) после
лреобразований найдем длину пластины
/ = 1р (-1, h),
где
^^ ^ l + tA \ [tA ~ (^) t + VHa {tA-t)il+ t)] Χ
Χ exp [— Ло VitA-t){l-i t)] (fe2^^f2J ·
Для определения коэффициентов подъемной силы и
сопротивления воспользуемся первой формулой С. А. Чаплыгина [681.
Гидродинамическая реакция, действующая на пластинку:
ί? = Χ + ιΤ== —i \(P-PUdz
'Ά
или на основании уравнения Бернулли
"А
Принимая во внимание, что
Г - 2^ ·
PVkI
'•Ш'-«·
88
после промежуточных преобразований получим:
c. + /c, = -i(l)j(|-s)
dw
dt.
(П.5.17)
где ζ =
С:
dw
'dzK
; ζ — величина, сопряженная ζ.
0,2
0,1
C6=iff°
20°
15"
I
10° ,,
ι
Δ
•
. —^
■9
ί.
—"νν
Ο
0,1
0,1
о,ъ
0,4 -κ
Рис. 11.14. Зависимость коэффициента подъемной силы Су
от числа кавитации κ.
теоретические результаты (по формулам, приведенным
в § 5 гл. II).
Δ —α = 20°; D —о: = 15°; ·, V — α = 10° (экспериментальные
результаты).
После разделения в (П.5.17) вещественной и мнимой части
найдем:
C.-(l + /c)sina, C^,= (l+/c)cosa, A1.5.18)
где /с==
}{-^л+(-Ц^)^ + К^л(^л-0A+0
4feg {ЬР- + 1)
/A+^л)
— 1
X ехр [Л V{tA-t){\-Vt)\ I
X.
dt
(fe2+ ^2J
Для определения профиля каверны используют (II.5.2) и
(II.5.16).
На рис. 11.14 приведены результаты расчетов коэффициента:
подъемной силы Су по изложенной выше теории [формула
(II.5.18)].
§ 6. Кавитационное обтекание пластинки вблизи
свободной повэрхности (по второй схеме М. Тулина)
Рассмотрим случай обтекания пластинки АС при больших числах:
Фруда, когда вызванная продольная скорость на свободной
поверхности равна нулю.
89-
Пусть пластинка расположена на некоторой глубине Η под
свободной поверхностью с углом атаки α к направлению
потока.
Примем в качестве модели обтекания вторую схему М.
Тулина, в которой каверна заканчивается двумя двухспиральными
вихрями (рис. П. 15). Скорость на границе каверны равна V^,
в точках £ и D происходит скачок скоростей от У,, до У „о. Для
упрощения задачи предположим, что в точках Ε и D потенциалы
скоростей равны фб = фд.
По аналогии с решением задачи, рассмотренной в § 5,
преобразуем с помощью конформного отображения плоскость
комплексного потенциала w на верхнюю вспомогательную
полуплоскость t. Затем исследуем поведение функции Н. Е. Жуковского ω
на действительной оси этой плоскости и найдем на ней граничные
значения функции.
Используя в дальнейшем решения краевой задачи Римана—
Гильберта с помощью формулы Келдыша—Седова по смешанным
краевым условиям на действительной оси, построим выражение
■функции ω.
Для этой задачи плоскость комплексного потенциала
представляет собой плоскость с полубесконечным разрезом вдоль
положительной вещественной оси, а свободная поверхность может
•быть представлена линией, параллельной этой оси, определяемой
постоянным значением функции тока ψο. Последнее, в свою
очередь, зависит от глубины погружения пластинки (рис. 11.15, б).
•Область течения между границей IF и берегами разреза FBI
представляет собой многоугольник, у которого два угла (при
вершинах / и F) равны нулю.
Конформно преобразуем эту область плоскости w на верхнюю
полуплоскость t так, чтобы все границы потока лежали на
действительной оси (рис. 11.15, в). Для установления связи между
плоскостями воспользуемся интегралом Кристоффеля — Шварца
{преобразование внутренности многоугольника на верхнюю
полуплоскость) [формула (П.2.14)].
В соответствии с рис. П. 15, б, в найдем а^ и а,- многоуголь-
лика для рассматриваемого случая:
точка В:
точка А:
точка Е:
точка F:
точка С:
точка D:
точка /:
90
Ωι == 0; «1 = 2
0^2 "= ^л! ct2 "^ 1
% = *е'> 0^3 ~ 1
Ω4 = β; α4 = 0
«5 = —1;«5= 1
О-в =^ *D'> ^'б ^
щ = ± со; ау =
= 1;
= 0.
δ)
ι ~tz
Ima)=a
-1
ilt.
Q
йеаЛ A">-/W-xJ
44
/^еш
^^Х/УТ^/'^^у'У^/'Уу*г'У/у'у>^у'1у'/уУ^Уу'у'у'/УУ'УУ/-'У'У/'/У^
ΒΙΑ £
1пьш=(х~п,
Рис. 11.15, К решению задачи о кавитационном обтекании
пластинки вблизи свободной поверхности (по второй схеме М. Тулина):
а — физическая плоскость течения; б — плоскость комплексного
потенциала; β — вспомогательная плоскость t.
9f
Подставляя эти выражения в интеграл Кристоффеля—Шварца
1формула (II.2.14)], получим:
W
== ^1 j ^_iß dt + Cz
или после интегрирования
гг, = Ci [ί+ß 1η(ί —β)] +С2. (ΙΙ.6.1)
Неизвестные С^ и Ca найдем исходя из граничных условий.
Из рис. 11.15 видно, что в точке В (критической точке потока)
W = 0. Это условие сохранилось и на плоскости t, ί. е. w (ί) = О
при ί = 0. С учетом этого выражения формулу (II.6.1) можно
лредставить в следующем виде:
Ci [ßln(-§)l +С2 = 0,
юткуда устанавливаем связь между Cj и Сг'·
С, = -Ciß in (-β).
Подставляя это условие в исходную формулу A1.6.1) и
выполняя преобразования, находим:
гг, = С1 [ί + β1η(ΐ --р-)]. (ΙΙ.6.2)
Найдем теперь постоянную С^. Рассмотрев течение на
плоскости t, установим, что при обходе точки F (/=ß) по полуокруж-
лости бесконечно малого радиуса и переходе с прямой IF на
прямую EF на плоскости w (см. рис. 11.15, в) комплексный
потенциал изменяется на заданную величину ι'-φο·
При этом аргумент точки F изменится на величину π.
Тогда
ίψο = Ciß In е~ '=^ = — Cjßin,
откуда
С, =.-^. (II.6.3)
Подставляя (II.6.3) в выражение для комплексного
потенциала (II.6.2), окончательно найдем:
^[ί + ρΐη(ΐ-|)]. (ΙΙ.6.4)
W ==-
Рассмотрим теперь изменение функции ω = In ^^^^ на
действительной оси плоскости t. Представим ω в параметрическом
виде:
ω = In -Φ- - ιθ.
S2
Найдем граничные значения функции ω на отрезках
вещественной оси верхней полуплоскости t (рис. 11.15, е):
— οο<ί<ίβ; Кеш=1п-^==1п1=:0;
—1 < t < 0; Im ω ~ α;
О < ί < ίχ. Im ω = α — π; (II.6.5)
tA<t<tE^ Реш = у ΙηA ~f κ);
ί£ < ί < β; Re ω = 1η 1 = 0;
β < ί < οο; Re ω = 1η 1 = 0.
Здесь, как и в предыдущем случае, надо найти функцию ω {t)
в верхней полуплоскости по смешанным граничным условиям на
вещественной оси t.
Воспользуемся A1.5.9). Как следует из рис. 11.15, в, если
исключить отрезки, содержащие нулевые граничные условия,
на вещественной оси останутся три отрезка: —схз Ь^, Ьхи^, а^оо,
причем Ь^ = —1, Ol = ί^.
Найдем функции R {t) я R (t), входящие в формулу Келдыша—
Седова A1.5.9):
Rit)-^Y-
1
{t+l)(t-fA)
R
(τ) = У
1
(τ+1)(τ~/^)"
(ΙΙ.6.6)
При составлении функции R (t) разрез сделан в диапазоне
I <t <tA.
После подстановки этих значений в (II.5.9) с учетом
граничных условий (II.6.5) получим
—1
ω(ί) = ΐ/(ί+1)(ί^-ί)
1
2π
In
A+ί<) J
dx
-to
K(T-f 1)ил-т)(т-0
+
άτ
+
(α-
+ ^ln(l+x)J^
-Л)Г
π J
άτ
V{T+\){tA-X){T~t)
+
άτ
т-Ь1)(^л —τ)(τ —ί)
+ ^
(ΙΙ.6.7>
—г . , , , , входящий Β A1.6.7),
V(X+\){tA~^)Kt-t)
определяют согласно [15].
93
После интегрирования (П.6.7) и промежуточных
преобразований найдем:
«(i) = ia + lnJ^^-=J^^S + ' 1пA+
+ κ)[π-|
dl СЬ111 — , , ,,—;—J—; 1-
Как следует из A1.6.4),A1.6.8), выражения для ω (ί) и ш (ί) имеют
пять неизвестных постоянных ί^, tß, ί^,Α, β, для определения
которых необходимо составить дополнительные пять условий.
Первое условие легко получить исходя из заданного соответствия
точек С при конформном преобразовании: при t = —1, w = \.
Подставляя это условие в (П.6.4), найдем связь между функцией
тока Tj5(, и параметром β. После преобразования получим:
Учитывая прийятое допущение о том, что потенциалы скорости
в точках Ε я D равны, найдем на основании (П.6.4) второе
условие в виде
т+'-т)=т+'Ч'-т)· <'"■"'>
Заметим, что функция ω может иметь только логарифмическую
особенность. Поэтому все отрицательные значения / исключаются.
Кроме того, вдали от профиля ω = О, что исключает все
положительные значения /. Таким образом, любое Aj в (П.6.7) равно
нулю.
Для получения двух недостающих уравнений испол^^зуют
условие о том, что поток жидкости на бесконечности горизонтален.
Это означает равенство нулю аргумента функций в точках F и /:
Im [ω (β)] = Im [ω (oo>] = 0; (II.6.11)
Re [ω(β)] = —ValnU +κ).
Учитывая (П.6.8) и (II.6.И), получим два недостающих
уравнения:
-^Ιη(ΐΗ-κ) 1п
2 V(l + to) (to - tA) A 4- β) (β - (a) +
+ (ί --tA + 2tD) β - A - ^^) to - 2tA
(tD-§){l + tA)
+
~2 V{1 + iE.) {ΪΕ - m (I -FßHß-^ iA) + (i~tA + 2tEJ ρ +
+ a + {-f^arcsin[.ß<'-^^^^^]}^0; (II.6.I2)
,^1 +(l-tA)tk-2tA ,
' ifi-tEUl + tA) -i>'^
?4
In
(!+«){
In
2V{l+tD)itD-tA) + il'-tA + 2tD) 1
-A + tA)
4-In
l+tA
l-tA
h
+«+[-! + --" (ΪΠ7)]
При выбранных значениях κ, α и грд уравнений (II.6.9) —
(II.6.13) вполне достаточно для определения параметров if,
ίο> ^А' β- Однако вследствие того, что каждое из уравнений транс-
ее
2,2
2.,0
1fi
7.4
Рис. 11.16. Результаты
расчета на ЭВМ.
Зависимость Cijla (^o//)
при постоянных
значениях относительных
погружений НЦ.
^Л
х=5\0.5
L=io''
1
Х^?,5
1
^= const
zlif
ι
5,0
г^ч —-Ч
ψοβ
цендентно и нелинейно относительно переменных, используем
графоаналитический метод решения в соответствии с [861:
1) из (II.6.9) находим β и строим график ψο (β);
2) используя ряд значений t^ и ί^, решаем уравнения
(II.6.12), (II.6.13) относительно Ιη(Ι + »<) и α. В каждом
случае tß находим из A1.6.10) для данных значений ί^ и β и строим
зависимости
^-D_Ae\.
3) строим график зависимости α и κ в функции от ί^ и t^
при ψο = const.
При известных значениях параметров t^-, t^, is и β
уравнение (ΙΪ.6.8) решается численными методами на ЭВМ.
После определения функции Н. Е. Жуковского ω вычисляем
комплексный потенциал течения, а затем по формуле С. А.
Чаплыгина находим коэффициенты сопротивления и подъемной силы.
Формулы для их определения аналогичны приведенным в § 5
этой главы.
На рис. 11.16 приведены результаты расчетов относительного
коэффициента подъемной силы для пластинки CJa в зависимости
от значений функции тока ψο/^ при я = 0,075 и разных значе-
лиях погружения Н/1 {I — длина пластинки).
Глава III
РАЗВИТАЯ КАВИТАЦИЯ.
УСТАНОВИВШИЕСЯ
КАВИТАЦИОННЫЕ
ТЕЧЕНИЯ
(ЛИНЕЙНАЯ ТЕОРИЯ)
§ 1. Кавитационное обтекание профиля
с фиксированными точками отрыва
Предположим, что кавитационное обтекание профиля у = У (х)
происходит в безграничном потоке по первой схеме М. Тулина при
числе кавитации κ, давление и скорость на бесконечности известны
и соответственно равны рс«, и V^. Физическая плоскость течения
дана на рис. III. 1, а. Как уже указывалось в гл. II, задача об
определении характеристик такого течения — нелинейная. В
нелинейной постановке граничные условия задачи даны на
горизонтальном разрезе плоскости комплексного потенциала
(рис. III.I. б). Как указывалось в гл. II, комплексный потенциал
равен W = (р -\- tip, комплексная скорость:
dz
а функция Н. Е. Жуковского:
^ к ^ к
где Υχ, Vy—проекции скорости на координатные оси; \V \ —
модуль комплексной скорости; θ — аргумент.
Как показал Т. By [118], лучшее приближение к нелинейной
теории получается, если в качестве характерной принять скорость
на границе каверны. В связи с этим разделим комплексный
потенциал на скорость жидкости на границе каверны V^, тогда
получим:
^ = ^ + '1^· . <"■■'·"
Члены, входящие в (III. 1.1), имеют размерность длины. Это
дает возможность выбрать масштаб длины так, чтобы в точке С
96
отношение φ/ν^ = Ь Граничные условия в нелинейной
постановке имеют следующий вид:
на профиле θ = θ (φ/Ι^κ);
на границе каверны In .. ■ =0;
»к
на бесконечности
θ==0; 1п-Ш- = 1п^==-^-1пA+х).
Условие замкнутости каверны
dm
Im mln-^- dw = 0.
BD
Для упрощения решения положим, что ширина каверны мала
по сравнению с ее длиной, так что граничные условия на профиле
и на каверне могут быть перенесены на горизонтальную ось Ох
{у = 0).
Примем, кроме того, что вызванные (дополнительные) скорости
Vx и Vy, обусловленные присутствием в потоке кавитирующего
профиля, — это малые величины первого порядка по
сравнению со скоростью основного потока, и их квадратами и
произведениями можно пренебречь. Будем также считать, что каверна
имеет фиксированные точки отрыва.
Сказанное выше дает основание произвести линеаризацию
задачи, т. е. разложить выражения In-^r;-! и θ в степенные ряды,
а затем ограничиться линейными членами. Тогда получим:
1п
IL - (SXL _ л _ 1 (АН _ 1V -L i AX1 _ Л
или в линейном приближении
'"^-^-'^ "»arctgl«*. (Ш.1.2,
Для упрощения решения введем новую комплексную
функцию V (ζ), связанную с проекциями скоростей формулой
97
ю
f
Jvl
к
(D
л
-(i) "(i-')
χ
Vk
в)
у
Vy Ά
^
Ъ
Οχ=|-
.J^-
—ч
'
Ί)
ι .
®
- ■ ' ^1
αχ
Vy =
С - Χ
χ 2
Рис. III.l. Кавитационное обтекание слабоизогнутого профиля с фикси
б — плоскость комплексного потенциала и граничные условия; в — ли
скость; д — контур
98
^)
π
κ
¾=2'
\
—·—
Α
1
©
y^'%<''
^c-1
-ък
- κ
^;
♦ ^3/
-^ ^
Θ
fi> ;γ——'
itl?
Γ
Ι
-φ·
ι ι
^r
С
®
27
I I
роваиными точками отрыва при κ =^0: а — физическая плоскость течения;
неаризованная физическая плоскость течения; г — вспомогательная пло-
интегрирования.
99
Учитывая далее, что F,^ = F» + ^ и Fj, = у^,, а также
принятые ранее допущения, граничные условия после
линеаризации перепишем в виде:
на профиле
Imv- = 5.= f„„„^=(l+^f;
на границе каверны
на бесконечности (при χ —^ оо)
Re V = -ρ 1 = -ψ- =: —g- или v^ = 0.
Условие замкнутости каверны
УК
BD
Легко также показать, что в линейном приближении плоскость
комплексного потенциала преобразуется в физическую плоскость ζ.
Используя известные соотношения между составляющими
скоростей, потенциалом скорости и функцией тока, а также условия
Коши—Римана, после преобразований получим
ψ
л, ., — у.
На основании лрннятых выше допущений найдем связи между
величиной безразмерного давления (коэффициента давления),
скоростью на бесконечности и скоростью в произвольной точке
кавитационного течения. При составлении формулы для
безразмерного давления его относят к скорости потока на границе
каверны или на бесконечности:
При помощи уравнения Бернулли выражения (П 1.1.3) легко
представить в виде
С -1-Л- с -г ^'
■'PK * „2 ' ^Р"" * у2
В наиболее общем случае кавитационного течения (κ =^ 0)
вследствие малости поперечных скоростей течения можно при-
160
нять |l/|sF;,. Тогда V^ ^Vl, + 2VooVx, a коэффициент
давления:
'к "^ к
Принимая затем во внимание, что V^ = V« 1^1 + κ и
используя линейную часть биномиального разложения, после
промежуточных преобразований найдем, что
Ορ, = χ-2A-χ)-^ = κ-2A-κ)^.
В частном случае струйного обтекания (κ = 0)
Срк =-^^-=-2-^ = -2¾. (III. 1.4)
В результате принятых выше допущений и преобразований
физическая плоскость течения ζ представляет собой плоскость
с конечным разрезом BD вдоль оси Ох. Граничные условия и
координаты характерных точек даны на рис. III. 1, в.
Разрез BD можно рассматривать как многоугольник, по
отношению к которому течение на плоскости ζ является внешним.
С помощью интеграла Кристоффеля—Шварца преобразуем
это течение на вспомогательную плоскость ζ так, чтобы вершины
многоугольника располагались на действительной оси ξ с
выбранными их абсциссами (рис. III.1, г), а бесконечно удаленная
точка находилась на мнимой оси η с ординатой η = —ik.
Аналогичное преобразование было выполнено в § 5 гл. П.
В соответствии с (П.5.6) преобразующая функция
^ = ~ik{-j~-y\ или ζ^Η[-^^γ\
где / — длина каверны, или
ζ^ + k^
Ьг. ("Ι-1.5)
Исходя из граничных условий легко установить связь между k
и / при ζ = \, ζο = 1· Поэтому на основании (II 1.1.5) получаем
k = {l— 1I/2.
Составляя дифференциалы левой и правой частей (II 1.1.5),
найдём после преобразований производную преобразующей
функции:
101
Как видно из рис. ΙΠ.1, г, в результате преобразования мы
получили на плоскости ζ задачу об обтекании тонкого некавити-
рующего профиля, решение которой известно.
Граничные условия на плоскости ζ приобретают вид
Re V (ζ) =^ О или ^ (ξ) == -2" при I < ξ < оо | на границе
Ιπΐν{ζ) = ί^(ξ) =-^ (ξ) при —1^<|< 1 — на поверхности
профиля.
В соответствии с принятой схемой обтекания (схема М.
Тулина с односпиральными вихрями) след каверны уходит на
бесконечность, а скорость в этой области имеет особенность вида
η {ζ — /)~'^^, где η—действительное число.
Следовательно,
ν(ζ)-^Αΐζ при ζ-»οο,
где А — действительная постоянная.
Условие замкнутости означает равенство нулю расхода
жидкости через контур тела — каверны. Это условие должно быть
выдержано на физической и вспомогательной плоскостях. В
результате находим:
lm(^v(z)dz=lm & ν(ζ)-|ίίζ = 0. (III. 1.7)
BD ζ=—/ft
Контуры интегрирования в (III.1.7) даны на рис. III. 1, д.
Как видно из рис. III.1, г, мы получили краевую задачу об
определении функции υζ по смешанным граничным условиям на
вещественной оси |. Решение этой задачи дается уже известной
нам формулой Келдыша—Седова (II.2.И), которая должна быть
дополнена членами, учитывающими в общем случае особенности
в точках отрыва каверны и носике профиля.
Применительно к функции ν (ζ) граничные условия на
отрезках AD и CDocH I обращаются в нуль, поэтому интеграл в (П.2.11)
необходимо взять в пределах от —|^ до единицы.
+в{^^У''^Аш+1М^-т'''. ("I-1-8)
Первый член выражения (II 1.1.8) удовлетворяет граничным-
условиям на вещественной оси при предположении, что в точке С
(Sc = 1) обтекание плавное, т. е. выполняется постулат
Жуковского—Чаплыгина о конечности скорости на задней кромке
профиля.
102
Второй и третий члены удовлетворяют однородным граничным
условиям для Vx вне профиля и для Vy на профиле.
Входящие в (III.1.5) и (III.1.8) константы А, В, k или А, В, I
определяются исходя из трех дополнительных условий:
условия на бесконечности
Rev(—iÄ) = -|-; (III.1.9)
Imv(—tyfe) = 0;
условия замкнутости
iin[-J(-f^)]=f·
Координата |д определяется заданной величиной х^.
Коэффициент подъемной силы на контуре, отнесенный к
скорости на границе каверны,
2Y
С„ =
^^ -2Re^vB)d2-2Re ^ ν(ζ)-|-ίίζ. (ΠΙ.1.10)
BD ζ=—tfc
Учитывая (III.1.6), представим контурный интеграл в (III.1.10)
следующим образом:
(III.1.11)
в дальнейшем для вычисления интеграла (III.1.11)
воспользуемся теоремой вычетов и разложением в ряд функции ν в точке
ζ = —ik. Тогда, учитывая условия на бесконечности (II 1.1.9),
найдем:
^=-ΐ + 1(ζ + ίΑ)+···
Вычет функции — подынтегрального выражения (III. 1.11) —
после преобразований
, /κ ilk dv
На основании теоремы Коши о вычетах получим:
После разделения этого выражения на вещественную и мнимую
части найдем:
Im ^ ν(ζ)-|.^ζ^„/[/^Ιπι(-^-κ)];
Re ^ v(C)_|_dS = n/yfeRe(-^). (III.1.12)
ς=—/ft
103
Подставляя второе из выражений A11.1.12) в (III. 1.10),
получим формулу для коэффициента подъемной силы:
C,=='^=2nlkRe(f)
Решение может быть также использовано при рассмотрении
профиля, имеющего переднюю острую кромку (|^ = 0), а также
профиля стоек На = 1. ^ (ξ) = -¾ (-^I-
Наиболее простые решения получаются для каверны при κ = О
(струйное течение), образованной на профиле с острыми
кромками. В этом случае точки А иВ совпадают. Функция,
преобразующая течение на физической плоскости на вспомогательную
плоскость ζ:
ζ =.-^1/2 или ζ ==ζ2 (ΙΙΙ.1.13)
Здесь также задача о кавитирующем тонком профиле сводится
к задаче о бескавитационном обтекании некоторого иного профиля
(рис. III.2, а—в). Например, если форма кавитирующего профиля
описывается уравнением у {х) ~ ах -\- Ьх^ при О < а: < 1, то
выражение для некавитирующего профиля на вспомогательной
плоскости ζ можно найти из равенства производных (условие
конформности):
dy ^ ац
dx dg
или при учете (III.1.13):
а = 2Ьх = а + 261^,
откуда после интегрирования
η = αξ + "з" ^S*·
Гидродинамические характеристики кавитирующего профиля
легко выразить через характеристики некавитирующего профиля.
В соответствии с принятыми допущениями граничные условия
переносим на верхний и нижний берега разреза. Обозначим
индексами 0_, 0+ ординаты точек на нижней и верхней сторонах
разреза в плоскости.
Сила сопротивления, подъемная сила и продольный
гидродинамический момент кавитирующего профиля, зависят от разности
гидродинамических давлений, действующих на профиль.
Следовательно,
подъемная сила
ь
Υ^\[ρ{χ, 0_) - ρ (л·, 0^)] dx; (III. 1.14)
о
104
5)
у
η
ι
в
л
\
®
fiev=vx=0 .
С
_
Rev^Vj^'^O
Jmv = -vy
Χ
д)
Йеу=ь^О
η.
О
Φ
1тп\}=-Ьц Reb-'V^^O
^=У5
Рис. III. 2. Струйное обтекание слабоизогнутого профиля с
фиксированными точками отрыва: а — физическая плоскость; б — линеаризованная
физическая плоскость; в — вспомогательная плоскость.
105
сила сопротивления
ь
Х=\{р{.х, 0_)-р(х, %)\-^άχ; (III. 1.15)
о
гидродинамический момент
ь
Л1 = j X [р (х, 0_) - ρ {χ, 0+)] dx. (III. 1.16)
о
Так как рассматривается обтекание при κ = О, то р^ ~ Ζ'"·
У^ =1/со и в формулах A11.1.14)-A11.1.16) ρ (х, 0+) = Рк =
= Рос. Позиционные гидродинамические характеристики профиля
определяются следующими выражениями:
Г .— ^ -г — ^
'"' 9Vl . ' ^^~ pVl
2 2
Cm--#-, (III.1.17)
где 6 — хорда профиля.
После подстановки в (III.1.17) формул (III.1.14) — (III.1.16)
и учета (III. 1.4) гидродинамические характеристики кавитирую-
щего профиля представим в виде
b Ь
г — _ ί ^ϊ^ ήγ· С — — ί -^ -^ dx-
о о
о
Выразим эти характеристики через вызванные скорости не-
кавитирующего профиля ν^, v-^. Принимая во внимание, что
χ == ξ^; dx = 2ξ di, получим:
Vb
о
:.,-?iÜils-°-K(i.°->-^; (Ш.1.19)
О "
Vb
Ρ __ f 4ξ4(ξ,0_)
'"~ J Уоо*2
О
106
в выражение для С^ входят две составляющие скорости v^
и v^. При решении линейной задачи, как известно из теории
тонкого крыла, на основании интеграла Коши можно получить связь
между ϋη и ü| в виде:
1 π J I' — I "S '
0
где ξ' —■ текущая координата.
После подстановки этой формулы в (ΙΠ.1.19) для С^ найдем:
ут, \гь
г _ |· 4ξϋξ(ξ. о,) .g f υ\{\', 0-) .е.
Принимая во внимание, что
I'
1~
Т- + 1.
после преобразований получим
о
КЗ
о
J πδν^ J
Так как первый двойной интеграл в этом выражении равен С;„
то в результате найдем:
а =
2π
l·^^
Vw^
J^(L 0_)ίίξ
Используя принцип симметрии, распространим течение также
на всю плоскость ξ. Тогда коэффициенты подъемной силы и
моментов некавитирующего искаженного профиля:
vv
^mS =
Cni^ = ■
bV„
J Iv^db
0
b^V„
0
(III.1.20)
107
Формулы (III.1.20) составлены по такому же принципу, как
и (II 1.1.18) для физической плоскости ζ, однако в плоскости ζ
длина пластинки равна Ύ Ь, г. интегрирование давления
производится по верхней и нижней сторонам профиля (безотрывное
обтекание).
В результате сравнения (III. 1.18) для кавитирующего
профиля с аналогичными выражениями (III. 1.20) получена связь
между гидродинамическими коэффициентами при струйном
обтекании заданного профиля и при безотрывном обтекании
искаженного профиля:
^г/ — Ст\\- Сх — "Ά^^^ΰί' Cm = Cml^. (III.1.21)
Формулы (III. 1.21) могут быть проверены для простых
случаев обтекания, для которых известно точное решение. Например,
для пластинки, обтекаемой безотрывно при малых углах атаки а,
как известно,
Су1 = 2зтоб; С ml = -γ ί Cmi^ == -gg- πα.
Сопоставляя эти выражения с (III. 1.21), получим для
струйного обтекания:
с,=
а
πα
е.-
Сх
πα^ .
2 '
"'
t^m —
Cm
_ α
5
-32-^°^
5
2 "·
ИЛИ
η ^ /^ „г-
(III. 1.22)
Рассмотрим теперь более общий случай обтекания тонкого
кавитирующего профиля вблизи свободной поверхности при
у, =h О [4]. Примем все рассмотренные в начале параграфа
допущения и ограничимся решением задачи по линейной теории.
Эта задача имеет практический смысл — позволяет
исследовать движение высокоскоростных судов На подводных крыльях
(обтекание кавитирующего профиля под свободной поверхностью).
Для упрощения решения задачи предположим, что обтекание
происходит при больших числах Фруда и поэтому на свободной
поверхности горизонтальная составляющая скорости равна
скорости потока на бесконечности.
В качестве схемы обтекания примем схему М. Тулина с двух-
спиральными вихрями. На рис. III.3 показана физическая
плоскость кавитационного течения и приведены граничные условия
на сторонах разреза и свободной, поверхности. Точка F
соответствует бесконечности, где происходит совпадение границы
турбулентной струи каверны и свободной поверхности.
108
a)
I
.
3:
'
У
.
В
0
.
Va: = 0
ι
κ I
[ , · 1 «—
®
f
vx=0 F
νχ=Ό I
f4\
■*~x
ϋ)
' f
F %
S)
η
_ X· _
-Oe λ
.
в
0
Vy
,^C%=T ^D
С D ^j.2=0
J
ξ
2,0 κ/ο£
Рис. III.3. Кавитационное обтекание тонкого профиля вблизи
свободной поверхности: а — линеаризованная физическая плоскость; б —
вспомогательная плоскость; β — отнесенные к углу атаки зависимости
коэффициента подъемной силы от числа кавитации.
10!
Рассмотрим линеаризированную физическую плоскость и
найдем граничные условия на сторонах разреза и на свободной
поверхности:
Верхняя сторона разреза при y=0^.
При О <х <хл профиль Vy== —^
— УС
» ХА <х <Хе кавериа Vy = -^
» хе <.х <.хр граница турбулентной струи
Нижняя сторона разреза при ί/ = 0_
При О < Λί < Λίο профиль Vy =-^
» хс <.х *C.xd каверна υχ = —^
* XD <х <xi граница турбулентной струи t>x=0
» у = Η свободная поверхность ^ = О
Течение на физической плоскости ограничено свободной
поверхностью, каверной и поверхностью профиля. Можно считать,
что течение находится внутри некоторого многоугольника, у
которого два угла равны нулю. С помощью интеграла Кристоф-
феля—Шварца преобразуем внутреннюю область этого
многоугольника плоскости ζ на верхнюю полуплоскость ζ так, чтобы
его вершины расположились на действительной оси | [см. (П.2.14)].
Коэффициенты щ и а^ имеют такие же значения, как и при
решении нелинейной задачи (§ 6, гл. II). Поэтому перепишем
выражение (П.6.1) так:
^1-άζ + 0„ (III. 1.23)
= cj.
где β — координата точки F на веш,ественной оси
вспомогательной плоскости ζ; Ci, Cg — постоянные, определяемые граничными
условиями.
После интегрирования (II 1.1.23) получим:
2 = Ci [ζ + β In (ζ - β)] + Ca- (ΠΙ. 1.24)
Постоянные €χ и Cg находим исходя из следующих условий.
В точке В на физической плоскости ζ — О, на вспомогательной
плоскости ζ — 0. Подставляя это условие в (III. 1.24), установим
связь между постоянными:
Cg = —Ciß In — β.
При обходе точки ζ = β по бесконечно малой полуокружности
выражение (III.1.24) изменится на величину ζ = Ш,
отсчитываемую от свободной поверхности до начала координат по
вертикали. Опуская промежуточные преобразования, найдем
^^^ πβ ·
НО
После подстановки значений постоянных выражение (III. 1.24)
окончательно приобретает следующий вид:
^ = -~^[ζ + βΐ"(^-τ)]· <"'·^·25^
Координату бесконечно удаленной точки β легко определить
из (III. 1.25), полагая 2 = схз. В результате преобразования
находим β = —1. После подстановки этого значения в (III.1.25)
получим:
2^^[ζ_1ηA + ζ)]. (III. 1.26)
Граничные условия на вещественной оси ξ полуплоскости ζ:
при ξβ < ξ < оо граница турбулентного следа g (τ) = 0;
при Ic<1<Id граница каверны: я(т) = -|-;
при О < ξ <; |с поверхность профиля: g (τ) = t -j^;
при ?A < Ε < О поверхность профиля: g{r) = i -^;
при |£ < I < 1а граница каверны: g (τ) = -^;
при β<Κξ£ граница турбулентного следа: я(т) = 0;
при — оо < ξ < β свободная поверхность жидкости
g(T) = 0. (III. 1.27)
Таким образом, задача сводится к отысканию функции ν
(безразмерной вызванной комплексной скорости) по заданным
смешанным граничным условиям. Как уже указывалось ранее,
это задача Римана—Гильберта. Для ее решения в данном случае
можно воспользоваться формулой Келдыша—Седова. Согласно
(ΙΙ.2.11) перепишем ее еще раз с учетом обозначений настоящей
задачи:
где
Г т Г т
Г *=1 Г fe=I
Ьк).
При составлении Ка,ь (ζ) разрез сделан в диапазоне Сл<?<?с»
g (τ) определяется по граничным условиям (III.1.27).
111
при решении задачи считаем, что скорость ν (|) в точках А
и С ограничена. Это допущение следует из постулата
Жуковского—Чаплыгина. Тогда на основании рис. III.3 находим с^ =
= 1с, Iä, Ьк =^ 0.
В дальнейшем, как это было сделано в § 5 гл. II, интеграл
(III. 1.28) представим как сумму интегралов с пределами,
равными координатам соответствующих точек на вещественной оси |.
Так как на отрезках FE и W граничные значения функции ν (ζ)
равны нулю, то первые два и последний интегралы обращаются
в нуль:
τάτ
ъ^Q^^V&^i¢MM
^ί
1^(-^-ёс)(^ + 1л)(^-й
+
υ.
ί
~iA
о
t —~τατ
αχ
/(-^-^0)(-^ +У (-^-ξ)
+
i^rdx
αχ
/(т-1с)('^+У (-^-0
τάτ
/(T-|c)(T-fy(T-Q
+
]
(III. 1.29)
Первый и третий интегралы, входящие в (III. 1.29), табличные
[15].
После ряда промежуточных преобразований получим:
ν{ζ) =
1 /(?-1с)(^-^л)
ί
dx
τάχ
ьёл
/(-^-^(-^+1^)(-^-0
+
+
dys
dx
τάτ
/(-^-1с)(-^.+ 1л)(-^-о
+
2πϊ
In
, п^^У{^р-^){^ + ^а) + У(^-^с)(^р + Ы ^
+ 2
Vih + Ic) (ζ + ^л) - Vii~ Ц i^E - Ia)
l/(e-gc)(c+y, ντ^=Τα-νϊ^ΤΪΑ
ι
In
VIe^IcW^e
±Ы. (III.
6д J
1.30)
уравнение (III.1.30) решается совместно с (III.1.25),
неизвестными в (III.1.30) являются ξβ и %ε·
112
Для их определения составим два дополнительных условия.
Первое из них определяется предположением о равенстве абсцисс
верхнего и нижнего спиральных вихрей. С помощью (III. 1.26)
можно получить условие
i + lß·"
In
i-i.
Второе дополнительное условие получаем исходя из замкнутости
системы тело—каверна—след. Это условие эквивалентно
предположению о равенстве нулю вертикальной составляющей
скорости üy = 1т V (ζ) при I = —1, соответствующей на физической
плоскости бесконечно удаленной точке. Подставляя это условие
в (III.1.30), после ряда промежуточных преобразований найдем
sc
1/A+?с)A-Ы J
-5л
dx
τάτ
A+^)/A0--^)(-^ + 5^)
κ iln
г/^l-ξ^.[^^/^(ξд-ξc)(^-gл)+·|/(^+ec)(ξD+u]
V^+^D iVi^E+У A - У -/A + Sc) (¾ - у]
+ /A+1с)A-Ы1п
Vlo-ic-V^D + ^A
Vh + lc + V^E-lAl
(III.1.31)
Таким образом, неизвестная комплексная скорость ν (ζ)
в произвольной точке потока определяется путем совместного
решения уравнений (III.1.30) — (III.1.31). Гидродинамические
коэффициенты вычисляют по формулам, составленным с учетом
A11.1.14)-A11.1.17), (III.1.24). Кроме того, принято Я = 1 м,
V«, = 1 м/с, ρ =^ 1 кг/м^.
Следовательно,
2 С ^(ς)ζ^.
Су = -
~^А
1с
[^-lii(l+lc)f
J ^(ζ)[ζ-ΐη(ΐ+α]χ
χ
1 + r
6c
c.=
Sc-in(» + y
J ^(Ö^(D
1+ζ
-1л
(III. 1.32)
lie
Наиболее простые решения получают для плоской пластинки.
В этом случае 2л = ^л = О, -^ = —а, где α — угол атаки.
Тогда уравнения (III.1.30)—(III.1.32) значительно
упрощаются:
υ{1)==αι 1 -" ^ ^ " ^1п-^^^ '
2π V ζ — !
an
где
(^£ + 1с)? + (?-У^£ + 2У(?-УМ£(^ + 1с)
ζ 2lE + lc + 2Vli,{li, + lc)'
-Γ T/^iß + lc+n^
-Inl^aÜ^^SiJ^^a?!; (III.1.34)
T/^i + U/iß + ic+1/^¾ A + ic)]j
2π
Из формулы (III. 1.35) путем предельных переходов легко
получить выражение для Су для частных случаев обтекания
пластинки:
для струйного обтекания вблизи свободной поверхности
(κ = 0, ^о = ^£ = оо)
С^^^{1с-2У1+1с-1) = п 4~^ν^Ι;^,^Τ' ; (ΠΙ.1.36)
а b 1с-1"(' + ^
Для обтекания в безграничной жидкости (^с == 0> ^d = ^ß —
(III. 1.37)
114
где
κ =■
Vh+^+ViE
Yh+^+Yh Yh-^ + Yh
Ha рис. III.3, в приведены результаты расчета по формулам
(III. 1.33)—(III. 1.35) относительного коэффициента подъемной силы
Cyla в функции от числа кавитации κ/α при различных
глубинах погружения h = ^/b, где b — длина пластины.
Как видно из рис. II 1.3, в, приуменьшении глубины
погружения коэффициент подъемной силы возрастает и одновременно
увеличивается число кавитации (уменьшается относительная
длина каверны).
§ 2. Кавитационное обтекание тонких профилей
ограниченным потоком
Рассмотрим струйное обтекание (по схеме Кирхгоффа)
слабоизогнутого криволинейного профиля ограниченным потоком
несжимаемой невязкой жидкости:
1) струей конечной ширины, ограниченной сверху и снизу
свободными поверхностями;
2) потоком жидкости, ограниченным сверху свободной
поверхностью, снизу — твердой стенкой;
3) потоком жидкости, ограниченным двумя твердыми
стенками (течение в канале с двумя параллельными прямолинейными
стенками).
Положим, что каверна образуется на верхней стороне профиля.
Хорду профиля, скорость натекающего потока примем равными
единице.
Ширину потока, углубление профиля, расстояние от нижней
поверхности, отнесенные к хорде профиля, обозначим L, h^, h^
соответственно. Безразмерные ординаты нижней поверхности
профиля заданы в виде некоторой функции у = f (χ), где χ —
безразмерная абсцисса профиля (отнесенная к хорде). Безразмерную
вызванную комплексную скорость обозначим ν = υχ — iVy.
Задачу будем решать в линейной постановке, принимая допущение,
сделанное в § 1 гл. III. В соответствии с этим линеаризованная
физическая плоскость в приведенных выше трех случаях
представляет собой полосу с полубесконечным разрезом вдоль
положительного направления оси Ох.
115
Схемы трех случаев струйного течения на физической плоскости
и линеаризованная плоскость течения даны на рис. II 1.4.
При решений задачи предполагаем свободную поверхность
невзволнованной. Тогда граничные условия имеют следующий
вид:
на свободной поверхности -¾ = 0;
на твердых стенках — ^ = 0;
на нижней поверхности профиля — Vy = §■ (χ) =
а)
dy_
dx'
Ώ
if
-^- ,
es)
Ώ 1
У·
(
ί
,
"Β
1
Vy
Щ-О ®
Va: =0 С
ι
Дт^оз:
ε
ν/////////////////////Λ
Β)
!/lt
'//////////.
Vy=0
®
■///////////////'^
Vx-0
VjtD χ
Vy
в)
Ώ
Ώ
«Μ
■
yi
,
®
С
Β ΑVx-0 С
Λ
Vy
υ
υχ=0 £"
х=Оили -Оу=0 Ε
Рис. III.4. Струйное обтекание профиля ограниченным потоком
несжимаемой невязкой жидкости: а — струей конечной ширины; б —
потоком жидкости, ограниченным сверху свободной поверхностью,
снизу — твердой стенкой; в — потоком жидкости, ограниченным двумя
твердыми стенками.
Линеаризованная плоскость течения (г).
Течение на линеаризованной плоскости внутри области DCBAE
преобразуем на верхнюю полуплоскость ζ с помощью интеграла
Кристоффеля—-Шварца (II.2.14) так, чтобы вершины
пятиугольника DCBAE располагались на вещественной оси ξ при
соответствии точек, указанном на рис. III.5.
Значения а^ и а^ (см. § 6 гл. II) найдем по рис. ΙΙΙ.4, г и III.5:
D : а^ = О, ßj = оо;
С : аг = О, а^ = С^;
В : а^ = 2, аз = 0;
«4 = 1, Й4 = —1;
А
Ε
«в = О, β.
116
Тогда
:=AJ
(^-¾) (ζ-с,) +^г,
(ΙΙΙ.2.1)
где Dj, Dg — постоянные, зависящие от начальных условий.
Используя табличные значения интегралов рациональных
функций и опуская промежуточные преобразования, получим:
2
^1+¾ 1„ ζ —С2
ζ^^[\η{ζ~ο,)(ζ-ο,)+^±^\η
ζ-
^]+D,. (III.2.2)
ΰ'
ε' Vor ο
A_gfX)
в' νχ-=0 С^Ьх=Оилииу^О d'
\C2 -7
Рис. 111.5. Вспомогательная плоскость и граничные условия.
Для определения постоянных D^ и D^ составим дополнительные
условия. Полагая в (III.2.2) в соответствии с рис. III.4, г и III.5
в точках ВиВ'г = ОиЬ, = 0, получим:
D.=
D,
(lnqc,+-|±^ln-|-). (III.2.3)
Как видно из рис. III.5, при обходе точки С (с^), лежащей
на вещественной оси полуплоскости ζ, по бесконечно малой
окружности величина ζ на физической плоскости ζ изменяется на Ш^.
Составляя разность значений ζ для двух точек на оси | слева и
справа от точки С', найдем после преобразований
А =
(ΙΙΙ.2.4)
После подстановки (III.2.4) в (III.2.3) найдем:
D,^
hl Ci-
2π Ca
ПпС^Са
Ci + Ca
In
-) (III.2.5)
или
Б2 = А1пС1-А^1.1пС2.
■'π 1 π Ca ^
(ίΙΙ.2.6)
117
Заменяя затем постоянные D^ и D^ в (III.2.2) выражениями
(III.2.4), (III.2.5), получим:
Α_^ιιζ^[ΐη(ζ_^ι)(ζ-^) + -|±^1η-|^]+
^^'2п
+ Alnq-A^lnc,. (III.2.7)
Преобразуем первый член (III.2.7) к форме, аналогичной форме
двух других членов суммы. Опуская промежуточные
преобразования, найдем:
Таким образом, формула для ζ приобретает вид:
ζ = -^ϊη-^ h-^-^ln ^~'' . (III.2.8)
Для определения координат с^ и с^ составим два дополнительных
условия:
1) в точках А и А', как видно из рис. III.4, г, III.5,
координаты должны иметь значения ζ = I и ζ = —1; тогда (II 1.2.8)
преобразуем к виду
l^i^Lin '^^ 4--^^1п--Ц^;
π — A + %) ' π Cg С2
2) при обходе точки Е' по бесконечно малой окружности
величина ζ изменяется на ih^.
По аналогии с предьщущим получим:
Dl
^1 ^2
1
Сравнив эту формулу с (III.2.5), найдем соотношение между
координатами с^ и с^:
h^Ci = — Я^Сг и Ci = — -¾^. (III.2.9)
Для решения задачи будем в дальнейшем считать, что задняя
кромка профиля в точке А обтекается плавно, и скорость в ней
имеет конечное значение, т. е. выполняется постулат
Жуковского—Чаплыгина. Таким образом, мы получим краевую задачу
со смешанными граничными условиями,- которые для
перечисленных выше случаев обтекания даны на рис. III.5. Учитывая
принятые допущения, рассмотрим решение, ограниченное вблизи
концов а^, и не ограниченное вблизи концов Ь^ [см. (III.1.28)].
Как уже указывалось, скорость ограничена в точке Л (задняя
кромка профиля), а также в точках С и Ε вниз по потоку на
бесконечности. Таким образом, абсциссы этих точек могут быть
обозначены через а^.
118
При составлении функции R^, t> (ζ) разрез сделан вдоль оси ξ:
при —1 < ξ < О — для первого случая обтекания, при ·—оо <
< ξ < Сг и —1 <ξ <0 — для второго случая обтекания, при
—оо < ξ < Cg, —1 < ξ < О, Ci < I < оо — для третьего
случая обтекания.
В результате формулы (ΙΠ.1.28) приобретают следующий вид:
1) струя конечной ширины (рис. 111.4, а)
—I
i (ζ) = _ γζ±Λ J_ Γ ^1^.^-^ (Ιίΐ.2.10)
2) поток жидкости, ограниченный сверху свободной
поверхностью, снизу —· твердой стенкой (рис. III.4, б),
—1
;;(Г)^-]/1 + 1)/^-^^)^Г ^ S(r)dr (III.2.11)
V '"δ^ |/(I±i)il=:^)(T-p'
3) поток жидкости, ограниченный двумя твердыми стенками
(рис. III.4, в),
— 1
Х_1_Г______£М^,^_ . (ΠΙ.2.12)
Jf
(τ+ 1)(τ —ci)(T —Cg)
(τ-ξ)
τ
Входящая в подынтегральные выражения (III.2.10), (III.2.11),
(III.2.12) функция g· (τ) =10^ находится в зависимости от формы
(уравнения) профиля, так как в линейной постановке
v^^^m. (III.2.13)
dx
Наиболее простые решения могут быть получены для плоской
пластинки, расположенной под углом атаки а к направлению
основного потока. Тогда в формулах (III.2.10), (ΠΙ.2.11), (ΠΙ.2.12)
следует положить g (τ) = —ία, a для получения решений
необходимо взять интегралы, содержащие иррациональные
подынтегральные функции вида:
— 1 —1
ас
J l/^+l .. .^ ' J
J j/£±i(,_0' J |/"^----(τ-ζ)
(τ—1)(τ—Ca)
— J
ί
1
(ΠΙ.2.14)
V
(τ+1)(τ —Сд)(т—Ca) /^_q
119
Согласно [15] решение первого интеграла выражается через
иррациональные функции, а второго и третьего интегралов — через
полные эллиптические интегралы первого и третьего рода.
Опуская промежуточные выкладки, получим первый интеграл
в виде:
— 1
άτ in
J |/^(τ-ζ) ζ|/,+-|-(|/",+|-,)
. (ίΙΙ.2.15)
Подставляя затем (III.2.15) в выражение (ΠΙ.2.10) с учетом того,
что g (τ) = —ί'α, получим для струи конечной ширины
^(ζ)= J^ г. (III.2.16)
ξ
Второй интеграл представим так:
άτ
(τ—Ca)
Используя (ΠΙ.2.17) и условие g {τ) = —ια, получим выражение
для вызванной комплексной скорости кавитационного обтекания
пластинки потоком жидкости, ограниченной сверху свободной
поверхностью, снизу — твердой стенкой, в виде:
"'ö=-;dfc>'2^?^[n(l. Ь ύ-ЧЬ ή]
или
1^.2 "'
я у с« ' ь
X
[/^(^, ?)-Π (f. -Т'^)]' ("^·2·ΐ«)
где /С и Π — полные эллиптические интегралы первого и третьего
рода;
120
-'Vi'
Третий интеграл имеет следующий вид:
— 1
ί
^ 1/(-^ + 1) (τ — Ca) (τ — c^) ^^ ^^
(III.2.19)
Подставляя (III.2.19) в выражение (III.2.12) и принимая также во
внимание, что g (τ) = —ia, получим выражение для комплексной
скорости при кавитационном обтекании пластинки потоком
жидкости, ограниченным двумя твердыми стенками:
(ζ+1)(ζ-^)
χ
-Г.
Для определения гидродинамических реакций, действующих
на плоский профиль, воспользуемся формулами С. А. Чаплыгина
168]. При этом будем рассматривать комплексную скорость
отнесенной к скорости, на бесконечности, а координату ζ
отнесенной к хорде профиля. В случае линейной задачи, когда
вызванные скорости считаются малыми, по сравнению со скоростями
набегающего потока, формулы С. А. Чаплыгина несколько
видоизменяются.
Учитывая принятые допущения и формулы (III. 1.4), представим
на основании уравнения Бернулли гидродинамические
коэффициенты в следующем виде:
Су = — 2Re jvdx = -— 2 j Όχάχ;
о о
1 1
С;,=^—2Im |ü-^dx==—2 J^-^-dx.
о о
Однако в силу линейности задачи (см. § 1 гл. III)
^ч άχ-
121
После преобразований окончательно получим:
1 1
С;, == — 21 m J ? dx = — 2 J 4 dx.
0 0
При переходе к плоскости ζ формулы переписываем в виде
— 1
C^ = -2Re |ϋ(ζ)-|-ίίζ; (ΙΙΙ.2.21)
о
-1
C, = -2Im \χ^(ζ)-^άζ. (ΙΙΙ.2.22)
Входящую в (ΠΙ.2.21), (ΠΙ.2.22) комплексную скорость ν (ζ)
определяем из выражений A11.2.10)—(III.2.12) в зависимости от
формы профиля и вида течения.
В частном случае кавитационного обтекания пластинки под
углом атаки α определение гидродинамических коэффициентов
значительно упрощается, так как входящая в (III.2.22)
вызванная комплексная скорость находится по формулам (II 1.2.16),
dz
(III.2.19), (III.2.20). Функция -^ определяется путем
дифференцирования выражения (III.2.8). Составляя дифференциалы левой
и правой частей выражения (III.2.8), получим
dz=.-!iL·-^ 1. A-S^ dg ^ (III.2.23)
Несколько более общее решение может быть получено для
профиля, указанного на рис. III.6, а. Такое течение может
служить аналогом для вентилируемого профиля, на верхнюю
поверхность которого подается воздух. Решение задачи для
струйного течения было получено в [101]. Рассмотрим его.
Пусть безразмерные ординаты верхней и нижней
поверхностей профиля заданы функциями yi (χ) и у^ {х). Тогда вызванные
вертикальные скорости на соответствующих поверхностях
профиля равны -~ и -j^.
Линеаризованная плоскость течения ζ преобразуется на
верхнюю полуплоскость ζ так, что все характерные точки
(вершины многоугольника) располагаются на вещественной оси ξ
(рис. III.6, б). При решении задачи будем в дальнейшем
предполагать, что в точках Аир происходит плавное обтекание и скорость
в них имеет конечные значения, т. е. выполняется постулат
Жуковского—Чаплыгина.
122
Связь между координатами ζ и ζ устанавливается формулой
Кристоффеля-Шварца (ΙΙΙ.2.2). ,„,„,, ,τττ г. ,^ч /тттопл
НаЬ^новании формул (ΙΙΙ.2.2), (ΙΙΙ.2.4), (ΙΙΙ.2.6), (ΙΙΙ.2.9),
полагая в них Ci = —1, с^ = е (см. рис. III.6, б), найдем:
,^^[ΐπ(ζ+1)(ζ-.) + ^Ιη-|±|] + /^. (Ш.2.24)
а)
J
В
■
у
В
1
®
%=ö или Vy = 0
Vy F %=ö
"^ Tb
Ί
Άυχ^Ο
Vx'^O или Dj,=ö
С
С
χε
Ε
ΰ)
Β Cvx-0 F
οο \'1 f
ь^=Оилиьу^О
в
0
Ρ
®
А vx=o ε If
a e / oo t,
Ух'=Оилииу=0
Рис. III.6. Общий случай струйного обтекания профиля
ограниченным потоком: а — линеаризованная плоскость течения;
б — вспомогательная плоскость.
ИЛИ
^1η(ζ+1) + 4Γ^η(ζ-β)-^1η-.. (ΙΙΙ.2.25)
Но так как согласно (III.2.9)
K=^h^e, (III.2.26)
то, подставляя (III.2.26) в (III.2.25), окончательно найдем:
^ = 2^[/ΐχ1η(ζ + 1) + /^η(-^ζ-ΐ)]+/Λ. (ΙΙΙ.2.27)
123
На физической плоскости координаты точек А я F известны
A ЯП соответственно), тогда из (III.2.27) получим два
дополнительных условия для определения координат α и / на плоскости ζ:
1=2^[^ι1η(α+1) + /ΐ2ΐη(|;-α-ΐ)+ί/ιφ (ΠΙ.2.28)
η--^ [/iiln(f+1) +/ι,In (-^/-1) + 1¾]. (ΙΙΙ.2.29)
Как видно из рис. III.6, б, получена краевая задача со смешанными
граничными условиями на вещественной оси. Воспользуемся
формулой Келдыша—Седова в предположении ограниченности
решения вблизи концов с^ и неограниченности вблизи концов Ь^.
В силу принятых выше допуш,ений концам а^ соответствуют
точки А я F. Тогда на основании (П.2.11) получим выражения
для вызванных скоростей, соответствуюш,ие трем случаям
течения:
1) струя конечной ширины
ς ιπ J ]/(τ;_^:)(τ_ο)(τ_ξ)
f
2) поток жидкости, ограниченный сверху свободной
поверхностью, снизу — твердой стенкой:
ν{ζ) ^(g-^)(g-")(g-^) ^ Г g{T)rdT
С g(i
J Ι^(τ-/)(τ-,
in J Κ(τ —/)(τ—ο)(τ—β)(τ —ξ)
(ΙΙΙ.2.31)
3) поток жидкости, ограниченный двумя твердыми
параллельными стенками:
X
а
-j-f , ^{τ)τατ (ΙΙΙ.2.32)
ш J νΛ(τ_^)(τ_ο)(τ-ε){τ+1)(τ-ξ)
f
В частном случае обтекания плоской пластинки g (τ) = —ia,
тогда для получения решения нужно взять интегралы:
а а
С τάτ . Г τάχ .
J V (τ-/)(τ-ο)(τ-ξ) ' J Ι^(τ-/) (τ-ö) (τ-e) (τ-ξ) *
f f
(III.2.33)
a
τάτ
ί
\^{τ~η{τ-α){τ-ε)(τ+ί)(τ-ζ)'
124
Для решения (III.2.33) воспользуемся также [15]. Опуская
промежуточные преобразования, получим следующие зависимости.
Первый интеграл
а
τ^τ ^ inW (ξ-/)(ξ-α)-ξ] ^ 34)
V (τ-ί)(τ-α)(τ-ζ) ν^(ξ_/)(ξ_β)
f
Подставляя затем (ΠΙ.2.34) в формулу для вызванной скорости
и полагая при этом, что g (τ) = —ia, получим для струи
конечной ширины
ϋ(ξ)=ία[]/(ΐ --^)A-1)- 1]. (III.2.35)
Второй интеграл
f
+ /((^, <?)]. (ΙΠ.2.36)
Используя (III.2.36) и полагая в (III.2.31) g· (τ) = —ia, найдем
выражение для вызванной скорости в случае обтекания
пластинки в потоке жидкости, ограниченном сверху свободной
поверхностью, снизу — твердой стенкой:
fig- -^ Kiw "
Гидродинамические силы находятся путем интегрирования
давления по контуру тело—каверна., ,
Для определения коэффициентов С^ и Су используются
формулы (ΙΙΙ.2.21) и (ΙΙΙ.2.22),Β которые подставляются комплексные
скорости, для трех рассмотренных случаев обтекания.
Так, например, для случая 1 — кавитационного обтекания
пластинки Б струе — получим гидродинамические коэффициенты
в виде
С^ - iCy = — 2iah^ [КA+/)(!+«) - 1 ] +
+ 2ία/.4ΐ/(ΐ -1)A-^-1
+
+ /ΐια4A+/)A-«)-2K(l+f)(l+«)-!] +
+ М^[A -I) A-Й-2УA-|)A-|)+ i].
(III.2.38)
125
Приравнивая вещественные и мнимые части в левых и правых
частях (III.2.38), после промежуточных преобразований найдем:
^ = 2/ii[I-]/(l+f)(l+«)] +
+ 2h,[l -У [ι --f) (l -I)]; (III.2.39)
Cx
^ = 2hAl- 1/A + /)A+0)] +
+ 2Λ,[ΐ -}/(l -i-) (l -±)] + Mf(l +1) (III.2.40)
Рис. III.7. Зависимости Cyla= f (η), Cxio? = f (η) при струйном обтекании
пластинки вблизи свободной поверхности (ftj =^ 0; ^2= о°)-
ИЛИ, подставляя (III.2.39) в (III.2.40), получим связь между
гидродинамическими коэффициентами
(III.2.41)
§ = ^+Mf(i+4)
в частном случае кавитационного обтекания пластинки под
свободной поверхностью /ig = е =оо, и формула (III.2.41)
приобретает вид
^:=-^+Vf. (III.2.42)
Аналогично могут быть найдены гидродинамические
коэффициенты для второго случая: для кавитационного обтекания пла-
126
стинки в струе, ограниченной свободной поверхностью и твердой
стенкой:
9ί .^^fci /A+/)A+й)A + гГ ^
απ Vl — f
Сх _ 4hl A + Л A + а) A + О Г 1^ / π Л 1 ττ ( η f-a\-\
а?~ п^ l-f [^\2' '^)~ΓfJ^^■\Ύ' rFv ^I ■
(III.2.43)
На рис. II 1.7 приведены результаты численных расчетов по
формулам (III.2.39), (III.2.40) относительных коэффициентов
Рис. III.8. Зависимости Cy/t = / (η); Cx/t^ — f (η) при струйном обтекании
сегментного профиля вблизи свободной поверхности.
127
подъемной силы и сопротивления пластинки единичной длины
в функции от абсциссы точки начала образования каверны при
различных значениях /ii и h^ = оо. Для профиля произвольного
образования при определении вызванной скорости Ъ используют
формулы A11.2.10)-A11.2.12), (III.2.30)—(ΠΙ.2.32). Интегралы,
входящие в них, вычисляют приближенно. На рис. III.8 при-
, ведены результаты расчетов гидродинамических коэффициентов
для сегментного профиля вблизи свободной поверхности с хордой,
равной единице, и при нулевом угле атаки. Принято, что на
верхней поверхности профиля
^ = ^ = 4^A-2^),
на нижней —
. rfi/2
^=d¥
§ 3, Обтекание тонких ненесущих тел в режиме
развитой кавитации. Применение метода
источников и стоков
Рассмотрим стационарное симметричное обтекание плоского
контура несжимаемой невязкой жидкостью в режиме развитой
кавитации при конечном числе кавитации κ [23].
Схема обтекания контура
У и система координат даны
на рис. III.9.
Задачу будем решать
'-»- о\^ ^>, )—»> в линейной постановке, т. е.
считаем, что контур и
каверна тонкие, а углы между
касательными к контуру
тела, каверны и осью χ
малы. Для решения задачи
используем метод особенностей
(источников и стоков). Так
как рассматривается тонкое
тело, то его обтекание (сов-
i
^
·*
л^_^
7
Ъ
-♦-
X
Рис. II 1.9. Симметричное кавитационное
обтекание плоского контура (метод
источников и стоков).
/ — контур; 2 — каверна.
местно с каверной) заменим обтеканием системы источников и
стоков, непрерывно распределенных по оси χ между передней
кромкой тела и задней точкой каверны.
Интенсивность источников связана с формой тела зависимостью
L681
(ΙΙΙ.3.1)
128
где q — интенсивность особенностей, отнесенная к величине
скорости на бесконечности; г/д — ординаты точек контура,
ограничивающего поперечное сечение тела.
Обозначим затем:
q (ξ) — неизвестная безразмерная интенсивность особенностей
в точке на оси с координатой ξ; ν^ = -г~ безразмерная ско-
со
рость, вызванная особенностями q (ξ), в точке на оси с
координатой х;
Χι, Χζ — безразмерные абсциссы носика профиля и задней
точки каверны соответственно.
Все линейные размеры, приведенные ниже, отнесены к длине
контура (тела).
Известно, что безразмерный комплексный потенциал скорости
течения, вызванного источником или стоком, определяется
формулой
а вызванная скорость соответственно равна
^". = f = i*«4|- (.3.2)
На основании (III.3.2) легко получить зависимость
распределения скоростей от интенсивности особенностей, распределенных
по оси х:
^JM|L = ^^(,)==J\^^,,. (III.3.3)
Xt Χι
Как указывалось в гл. II, кавитационную задачу можно
рассматривать как смешанную задачу: в одной части области
течения задана форма контура, а в другой — скорость на границе
каверны, форма которой заранее неизвестна.
При этом для определения точек схода каверны с тела и ее
замыкания необходимы два дополнительных условия, для
составления которых в дальнейшем введен ряд допуш,ений.
В соответствии с рис. III.9 xi =0, х^ = I, тогда (III.3.3)
получит следуюш,ий вид:
2ΐί J X
^ = ^ω· (ΠΙ.3.4)
Обозначим: b — абсциссу точки схода каверны с контура; V^ —
скорость на границе каверны.
129
Тогда при решении задачи положим:
^ = 2 -^ при О < X < 6; (III.3.5)
Vx — -γ^ при Ь <: л: < /,
где скорость V^ связана с числом кавитации κ:
Fk = Fco1/1+k. (III.3.6)
Решение уравнения (III.3.4) может быть получено с помощью
формулы обращения особого интеграла с ядром Коши для
замкнутого контура L [14]. Из теории интегралов с ядром Коши
известно, что если дан особый интеграл типа
то с помощью формулы перестановок [14] можно получить
зависимость
4^(^) = ^11^-^^^- ("I-3-8)
L
Формула (III.3.8) называется формулой обращения особого
интеграла. Решение интегрального уравнения (III.3.5) будем
искать в классе функций, обращающихся в нуль в носике тела
(х = 0) и в бесконечность— в точке замыкания каверны (х = I).
Представим в нашем случае
то с помощью формулы (III.3.8) легко получить
о
Разбивая пределы интегрирования на две части, соответствующие
смоченной части контура и каверны, найдем
\о ь у
где Vx„ — функция, характеризующая распределение скоростей
на смоченной части контура.
130
Используя формулу бинома Ньютона и ограничиваясь двумя
членами, вторую формулу (III.3.5) можно переписать так:
^=-^=1/147^5^14-4-^^ при κ<1. (Ш.З.Ю)
Подставляя это выражение в (III.3.9), после промежуточных
преобразований найдем
+4-4/^^7^)· ('"-з·")
о /
в формуле (ΠΙ.3.11) неизвестная функция ^„ характеризует
распределение скоростей на смоченной части контура. В
интервале значений О < | < Ь интенсивность особенностей известна,
так как на основании (III.3.5) она может быть представлена в виде
q =2 -^. Поэтому выражение(III.3.11) вновь можно
рассматривать как интегральное уравнение для определения функции (¾^ —
—-^/ί,κ). С помощью формулы обращения после преобразований
получим эту функцию:
ь
-^^--^^У^-^ШУН
X
Принимая длину кавитирующего контура равной единице, в
рамках линейной теории легко написать формулу для определения
коэффициента сопротивления:
где ρ = —2vx„ — безразмерное гидродинамическое давление
в произвольной точке контура, отнесенное к скоростному напору.
Подставляя это выражение в (III.3.13) и принимая величину ^
согласно формуле (III.3.12), окончательно найдем
о о
-^^4уЩж1^- <""■"'
о
131
Используя тождество
h fc'-i/ b — x
^ с у ι — χ
b b
о ϋ г I —
dyp dyp dx dl
J dx άζ il — x)
0 0
X
X
rfi/o dyo dldx
d| dx (I — л:) '
преобразуем последний интеграл и окончательно напишем:
(III.3.15)
С'-^-Л^^Т^^ + ^^^Т]
'dyo
dx
dx
V(l — x)(b~x)
(III.3.16)
Подставляя (III.3.12) в (ΠΙ.3.11), получим формулу для
вычисления интенсивности источников, заменяющих каверну:
ь
^—'•УЫ-^УШУт.
dyo dx
dx χ— I
при &<!<:/. (III.3.17)
Интегрируя A11.3.17) согласно (III.3.5) в пределах от b до ξ,
найдем формулы для определения ординат точек границы каверны
Ρ й
-il~b)
V
-y^Vii-Dil-b)^
Vodx
(l-x)\i{l-x){b-x)
при ξ > Ь.
(ΙΙΙ.3.18)
Координаты точек схода каверны b и замыкания I, входящие
в (III.3.18), неизвестны. Для их определения составим два
дополнительных условия. В качестве первого примем условие
равенства кривизны каверны и контура в точке схода при ξ —> Ь со
стороны каверны. Дифференцируя (III.3.18) по ξ, получим
( dyo\ _ d-\fl-b[^^ , 2 {-\f 1-х dyo dx \
\ d| Д=ь dl Υ i-i y^ η ] V b~x dx x-l j'
(III.3.19)
132
Второе условие характеризует течение в кормовой части каверны,
которое зависит от принятой стационарной схемы кавитационного
обтекания. Напомним, что в действительности в хвосте каверны
движение жидкости нестационарно, и именно поэтому прибегают
к схематизации кавитационных течений. Более подробно эти
схемы были рассмотрены в § 1 гл. П.
Сформулируем в линейной
постановке второе необходимое
нам условие. Положим, что сум-
■" марная интенсивность источни-
Рис. III. 10. Образование каверны на плоском контуре: α — схема
Н. Е. Жуковского; б — линейный аналог схемы Д. А. Эфроса; β — схема
Рябушинского.
ков и стоков, заменяющих каверну, равна некоторой постоянной
величине
]q{x)dx = 2y^{l)=.2k.
(III.3.20)
где Ук (О — ординаты границы каверны в месте ее замыкания.
Используя это условие в формуле (III.3.18) и принимая 1 = 1,
получим условие замыкания каверны:
Полагая
ь
yAl)^k = jYl^'-^dx-±Ml-b). (Ш.3.21)
о
получим, что (III.3.21) соответствует линейному аналогу схемы
Жуковского—Рошко (рис. III.10, а):
_ 2 ('Фо
dx
V(l — x){b — x)
(III.3.22)
133
Если величину k принять равной т"^^' ^° условие (ΠΙ.3.20)
будет соответствовать линейному аналогу схемы Д. А. Эфроса
(рис. ШЛО, б).
В этом случае в области, занятой каверной и контуром, есть
сток, расход жидкости в котором пропорционален сопротивлению
контура. Границы каверны при этом пересекаются и замыкаются
на две линии, уходящие в бесконечность. Показанные пунктиром
линии соответствуют течению на втором листе Римановой
поверхности. Подставляя значение k в (ΠΙ.3.21) и принимая во
внимание (ΠΙ.3.16), получим для этой схемы:
V
1 — х фо
b — X dx
dx
l — b
2π
- о
J dx
dx
V{l-x) (b~x)
4-u-
b)-
41Я
b — xdyg
dx
dx
(III.3.23)
Если каверна замыкается на эллиптический контур (рис. ΠΙ.10, в),
то суммарная интенсивность источников и стоков, заменяющих
каверну, равна нулю, т. е. k = 0. Такая картина замыкания
соответствует схеме с зеркалом или первой схеме М. Тулина.
В этом случае
пA — Ь)
w^
dx
dx.
(ΠΙ.3.24)
При больших значениях Ζ (Ζ > Ь) выражения (ΠΙ.3.23) и (Πι.3.24)
в пределе совпадают:
ь
dx
VV-
(III.3.25)
Таким образом, для развитой кавитации (каверна замыкается
далеко за кавитирующим контуром) схема Д. А. Эфроса и схема
с замыканием на эллиптический контур оказываются
равноценными.
Для решения задачи должно быть задано уравнение кавити-
рующего контура. Если уравнение контура задать в виде
полинома, то интегралы, входящие в формулы (ΠΙ.3.22)—(ΙΠ.3.25),
вычисляют элементарно. Задают также абсциссы точки
замыкания каверны I. Далее исключают параметр κ из (ΠΙ.3.19), и при
помощи одного из равенств (ΠΙ.3.22)—(ΠΙ.3.25), в зависимости
от принятой схемы кавитационного обтекания, определяют
абсциссу точки схода каверны Ь. После исключения аналогичным
1Э4
образом параметра κ из (III.3.16), (III.3.19) находят зависимость
Сх и у^ от I.
^Рассмотрим теперь другой метод решения: исходный некави-
тирующий контур наращивается дополнительным контуром так,
чтобы сумма вызванных скоростей исходного и дополнительного
контуров равнялась скорости на границе каверны.
При этом поле скоростей исходного контура может быть задано
с любой степенью точности, а условие «тонкости» добавочного
контура может быть выполнено и тогда, когда исходный контур не
является тонким. Это обстоятельство позволяет с помощью
метода «наращивания» решать также и нелинейные задачи. В
качестве примера, иллюстрирующего применение этого метода,
рассмотрим задачу об обтекании тонкого тела в режиме частичной
кавитации при наличии стока, расположенного за телом на оси
симметрии [1].
1 Поверхность комплекса тело—каверна будем рассматривать
как непрерывный контур, на котором выполняется условие
непротекания, а на поверхности каверны соблюдено условие
постоянства давления. Физическая плоскость течения дана на
рис. III.11, а.
Проекцию скорости на границе каверны на ось Ох представим
в виде
Ук>: = V^ + v^-^ Αν^ + ^ -f Δ^ + ^, (III.3.26)
где Fco — скорость потока на бесконечности; Vx — проекция
скорости, вызванной системой особенностей, заменяющей тело;
AVx — проекция скорости, вызванной влиянием стока на
систему особенностей, заменяющую тело; ^, — проекция скорости,
вызванной системой особенностей, заменяющей «наращиваемый»
контур; Δ^, — проекция скорости, вызванной влиянием стока
на систему особенностей, заменяющих «наращиваемый» контур;
Vx^ — проекция скорости, вызванной стоком.
Исходя из условий непротекания на контуре каверны и
учитывая допущения линейной теории и зависимость (ΙΠ.3.1), можно
найти
где Qi — неизвестная интенсивность системы источников и
стоков, заменяющих наращиваемый контур и расположенных на
отрезке Ы оси Ох.
Формула получена на основании следующих рассуждений: на
бесконечно малом участке длины dx направление скорости,
касательной к границе каверны V^., совпадает с секущей. Эта скорость
имеет проекции на координатные оси V^x и V^. Из рис. ΙΠ.11, б
видно, что
^к. = ^кх^-· (III.3.27)
135
Так как интенсивность источника или стока есть расход жидкости q^
через заданную поверхность (в рассматриваемом случае через
отрезок единичной длины), то при учете влияния стенки (исходного
тела) формула для интенсивности q^ получит вид ς^ = 21^,^^.-^,
как было показано выше.
Задача состоит в определении неизвестной системы
особенностей qi (ξ), поэтому в правой части интегрального уравнения
h
Рис. III. 11. К решению задачи об обтекании тонкого тела в режиме частичной
кавитации при наличии стока, расположеиного за телом на оси симметрии:
а—физическая плоскость течения; б — объяснение к формуле (III.3.27).
относительно этой неизвестной должны быть записаны скорости,
вызванные этими особенностями, т. е. (II 1.3.26) перепишем так:
V^^ - Fco - V:c - А^ - ^ == v^^ + Αν^^. (ΙΙΙ.3.28)
Тогда интегральное уравнение получим в виде
/
_L f 9ι(ξ)€
2π J χ —ξ
Ь
где ξ — текущая абсцисса.
136
: ^. -f Δ%. = Fk^ -V^-Vx- AVx - ^, (III.3.29)
Введем безразмерные величины:
^1 = 1^-; v, = ^, (ш.з.зо)
а все линейные размеры отнесем к длине тела L.
После преобразования найдем
1_ г ¢1 (I) rf| _ Ϊ7
2л
J q,^ .^у^^_^_-^^_ д^^ _ у^^ _ ;(ξ). (Ill 3.31)
Считая тело тонким, можно положить, что Vkx ^^ К^, а
принимая во внимание формулу (ΠΙ.3.10) и ее разложение по биному
Ньютона, для малых значений чисел кавитации κ получим
i^K. = V,= l+-f. (III.3.32)
При определении скорости ^ пренебрегаем величиной yj^ по
сравнению с (а—х)^, где у^ — ордината деформируемого контура,
а — абсцисса стока; Q — интенсивность стока, расположенного
за телом. Тогда в безразмерной форме получим:
где Q = -jf-.
V со
с помощью формулы обращения (ΠΙ.3.8) из выражения (ΠΙ.3.31)
легко получить уравнение для определения неизвестной
интенсивности q^ в виде
^.Μ-4Κ|=ϊί/ΪΞΪ^«. ,111.3.34)
Подставляя в (ΠΙ.3.34) формулы (ΠΙ.3.31) и (ΠΙ.3.33), получим
^ h
2 (а —χ)
IcrV^l (Ι"·3·35)
Ордината добавочного контура у^ определяется путем
интегрирования (ΠΙ.3.27)
X
Уг = -^\^ах. (Ш.3.36)
b
137
Принимая во внимание (III.3.32), напишем
1^
2 +
УЛх)=^]яЛх)ах. (III.3.37)
/
После подстановки в (III.3.37) формулы для вычисления Gi
(III.3.35) и вычисления отдельных интегралов найдем выражение
для ординат добавочного контура в виде
χ ' ι
2 Γ ί/1 — Ь {\ί 1~Χ Ъх (χ) + Δ^ W1 dx dl
~πB + κ) J V Ι-Ι J V x~b χ~1
(ΙΙΙ.3.38)
В (III.3.38) входит пять параметров: а, Ь, I, κ к Q. В
дальнейшем будем считать а, Ъ, Q заданными величинами. Для
определения κ я I составим два дополнительных уравнения. В качестве
одного из условий примем условие замкнутости каверны на теле
в точке X = I:
У1 (О = 0. (III.3.39)
Предполагая, что каверна направлена по нормали к телу
в точке замыкания, и принимая во внимание, что
arctg оо =^, легко приведем (III.3.38) к виду
b
Решение по формулам (III.3.38), (III.3.40) соответствует каверне,
граница которой совпадает в начальной и конечной точках с
поверхностью тела^ касается тела в начальной точке и направлена
по нормали к телу в точке замыкания. Следовательно, в точке
замыкания условие тонкости нарушается, и решение для
хвостовой части каверны следует считать формальным. В случае же
плавного замыкания условие тонкости не нарушается. Тогда
второе дополнительное уравнение может быть получено и ис-
138
ходя из условия касания границ исходного и наращиваемого
контуров (каверны) в точке замыкания каверны на теле:
dx
χ·=1
dye
dx
хЫ
(III.3.41)
Сопоставляя (ΠΙ.3.37) с (ΠΙ.3.41), получим второе,
дополнительное уравнение в виде
ι
^(/) = 0 или Г-^
о
f (χ) dx
b)(l —χ)
,= 0.
(III.3.42)
0,140
0.155
—
-^ '
^ --^
а^г
т—^
:^ =
7'
ΰ 0,
—
; -^ '
'?
fi-10
7
- /
''^
7
2 0,4 0,(
"\
7,5
-i
' .
ψ
I
7 0,
7,0
~4-
J 1,C
0,8 I
Ρ
16 0,
/\
6=.
1
1
4 ό,Ζ Ö /
^*~
1.0-10^
—
::;-^
l·
1
'
/
/ /1
\
\
4 1
0,2
о,ъ
0,4
i=a
Рис. III. 12. Результаты расчетов по формулам (III.3.40) и
(III.3.43):
ίο — длина каверны при Q = 0; — — — по формуле (ΙίΙ.3.40);
по формуле (III.3.43).
После подстановки в (III.3.42) значения функций / (х) согласно
"(III.3.31) и вычисления отдельных интегралов условие плавного
замыкания каверны на контуре примет вид
[vx 4- ίΛ'χ\ dx ι_ Q
^ ^_2_ г [% + Д^'л:1 dx _[_
η J K(x-b)(i-x)
в результате решения уравнений (III.3.38), (III.3.43) получим
контур с ординатами г/к ~ i/o + ί/ι. который можно рассматривать
.139
как каверну, образованную на теле, ординаты у тела
удовлетворяют следующим условиям:
У<Уи при Ь<х<1;
у == Уо при X <Ь·, х^1.
Таким образом, получим две формулы, связывающие
параметры /, Ь, а, Q, κ: первая из них — для случая замыкания
каверны по нормали к поверхности тела (III.3.40), вторая
предполагает плавное замыкание— [см. формулу A11.3.43I.
На рис. III.12 приведены зависимости числа кавитации κ
от длины каверны I при постоянных значениях мощности
источника, подсчитанные по этим двум формулам. Характер
изменения зависимостей κ A) различен.
Полагая в^формулах A11.3.38)-A11.3.40), (III.3.43)
интенсивность стока Q = О, получим зависимость для случая кавитацион-
ного обтекания тонкого тела без стока.
Полученные результаты могут быть использованы при оценке
влияния работающего гребного винта, установленного за кави-
тирующим телом, на характеристики каверны. Влияние потока
двухфазной жидкости за каверной на характеристики гребного
винта показано в работе А. А. Беспрозвания.
§ 4. Влияние весомости жидкости на характеристики
кавитационного обтекания тонкого клина
Приведенные выше примеры решения задач о кавитационном
обтекании тел рассматривались в предположении, что влияние
весомости жидкости на параметры каверны отсутствует. Однако такое
решение, вообще говоря, весьма приближенно, так как весомость
окружающей каверну жидкости вызывает деформацию границы
каверны в зависимости от направления вектора силы тяжести
по отношению к условной оси тела и скорости его движения. Для
установления этого влияния рассмотрим два предельных случая
кавитационного обтекания:
а) обтекание тела, при котором вектор силы тяжести
направлен перпендикулярно продольной оси тела, движущегося
параллельно свободной поверхности;
б) обтекание тела, при котором направление вектора силы
тяжести совпадает (или имеет противоположный знак) с
направлением продольной оси тела, что соответствует движению тела
перпендикулярно свободной поверхности.
Эти два случая движения имеют практическое значение. Задачу
будем рассматривать в линейной постановке. Рассмотрим
линейную задачу о кавитационном обтекании тонкого клина в
поперечном и продольном поле тяжести. Для упрощения возьмем клин
единичной длины. Вследствие тонкости клина и каверны
граничные условия на их поверхности будем переносить на продольную
140
ось клина. Физическая плоскость течения дана на рис. III. 13, а, б,
а плоскость после линеаризации — на рис. III. 14. В качестве
безразмерных величин, характеризующих кавитационное течение
с учетом влияния сил тяжести, примем:
число кавитации
и :.--"= ■
pvl
число Фруда Fr = ^г= , где 6—длина клина.
Задача состоит в определении вызванных скоростей,
обусловленных влиянием весомости жидкости.
6)
а)
У
Роо
v«o
6)
,
;
'71
-8
"^
1
1
1
V
ρ
Г^
Xfi
../1 з:
у'
if"»
0
г^
. 9
\ 1'
ρ ^^
-«—: >-
й ,
X
yk
Рис. II 1.13. Кавитационное
обтекание клина с учетом сил грави-
^ тации: а—физическая плоскость
X течения в поперечном
гравитационном поле; б — физическая
плоскость течения в продольном поле тяжести; в — связь между
параметрами клина и вызванными скоростями.
Рассмотрим сначала задачу о влиянии поперечного
гравитационного поля на кавитационное обтекание тонкого клина
(рис. III. 13, а) и составим уравнение Бернулли. В левой части
уравнения запишем члены, характеризующие давление и
скорости у основания клина, а в правой его части — аналогичные
члены для произвольной точки на границе каверны:
Ρκ + ^ = ρ+ν + Ρ^ί'- (ΙΙΙ-4.1)
где р,^, V-^ — давление и скорость потока на поверхности каверны
в невесомой жидкости; р, V — давление и скорость потока на
поверхности каверны в произвольной точке в весомой жидкости;
Ук — ордината границы каверны.
Учитывая предположение о малости вызванных скоростей,
можно написать, что
V = (Ι^κ -1~ Щ) - iVy и V^ = (I/, ~f v^f + li^y.
141
Пренебрегая квадратами малых величин, найдем
1/^ = 1/| + 2Ук^; V^-FS=2V^Kfx. (ΠΙ.4.2)
Тогда с учетом (III.4.2) выражение (III.4.1) представим в виде
Ρ - Рк = -f- (V^S - Ρ) - р§г/к = ~ pV^v, - pgi/κ. (III.4.3)
Из (ΠΙ.4.3) находим коэффициент давления:
г Р—Рк 2¾ 2gyK(х) (]-{] л л-\
Найдем теперь граничные условия на поверхности клина и
каверны. Учитывая малую толщину клина, а также то
обстоятельство, что суммарная вызванная скорость на клине должна быть
касательна к его поверхности (рис. III. 13, в), можно написать:
где β — половина угла раствора клина; νχ, Vy — безразмерные
вызванные скорости, отнесенные к скорости V^·
Однако вследствие тонкости клина и малости ^ по
сравнению с единицей первое граничное условие упрощается и
получает вид
ϊ^ = ztß при О < л; < 1, (III.4.5)
где ^ = β — на верхней поверхности клина; Vy = — β — на
нижней поверхности клина.
Давление на поверхности каверны равно давлению в каверне,
т. G. ρ = р^ и Ср = 0. Тогда, принимая во внимание (II 1.4.4),
получим второе граничное условие — на поверхности каверны:
или
Третьим граничным
Действительно,
при ζ
или
142
= схэ
Vx
ν.
~
>^Х '
Vx
v^
условием
L + %
ЕУк {x)
1^^A +
будет
= Vco; Vx =
1 =
1
νΐ + κ
1/2
κ)
условие
V^c»-
j-
-V,
^ —
на
κ
(HI.4.6
бесконечности
(ΙΙΙ.4.7]
Четвертое граничное условие—условие замкнутости — состоит
в том, что расход жидкости через контур тело—каверна равен
нулю.
Дальнейшие решения этой задачи вызывают определенные
трудности, так как функция, описывающая форму каверны у^ {х),
неизвестна. Выражение (III.4.6) для вызванной безразмерной
скорости может быть приведено к виду
S Ук Μ
(Ι+κ)
где δ = -ρ^ < 1 при Ь = I.
Разложим функцию ^^ (х) в степенной ряд по б:
У. (^) = Σ δ'>, (χ) = öVo (^) + by, {χ) + 6¾ W + · · · (ΠΙ-4.8)
t=0
Наиболее простой приближенный способ решения получается,
если ограничиться в (III.4.8) первым членом ряда. Тогда у^ {х) ^
^ Но (л;), что соответствует ординате каверны без учета
гравитации. Так как i/o {х) на большей части длины каверны
изменяется мало, то вызванная скорость на поверхности каверны
почти постоянна:
^ 14-κ '
а граничные условия имеют вид
Ух = —с при i/ = Ö+;
Уд:= +с при у== 0_. (III.4.9)
С учетом этого обстоятельства даны граничные условия на
плоскости ζ (рис. III. 14, а).
С помощью интеграла Кристоффеля—Шварца преобразуем
течение, внешнее по отношению к разрезу физической плоскости,
на вспомогательную верхнюю полуплоскость ζ с соответствием
точек, указанным на рис. III.14, б. Это преобразование
описывается выведенной в § 1 гл. III формулой
2 = -5¾ или l^k[-j^Y , (III.4.10)
где / — длина каверны; ik — координата точки М,
соответствующей бесконечно удаленной точке на плоскости ζ (ζ = схз).
Величину k находим исходя из граничных условий в точке А
k^ = l—l. (III.4.11)
ИЗ
Дальнейшее решение выполним при помощи метода
особенностей, при котором вызванная комплексная скорость
формируется как сумма комплексных скоростей, обусловленная
особенностями.
Для этой цели преобразуем течение на плоскости ζ на новую
вспомогательную плоскость t по формуле
i-ii'+i)
(III.4.12)
При этом щеки клина переходят на дуги единичного
полукруга, как показано на рис. III. 14, в. Найдем координату точки М,
сг)
2/*
Ur
Θ
S)
И
Imv=b Reii=-C
/ / f ß
В Rei;=C -1
l
X
-n
Imü=-p
В Rei) = C /-■;
*2'.
0.
K.M
Ιτηΰ=-ρ
®
Imv=p .
1\ Kev=-C В
IK
®
1 9ev=-C В
Ό\Α ^ Щ
А'
Рис. III. 14. Линеаризованная плоскость течения в поперечном гравига-
ционном поле (а), вспомогательная верхняя полуплоскость ζ (б),
вспомогательная полуплоскость t (в) и граничные условия.
соответствующей бесконечно удаленной точке на физической
плоскости. Для этой цели преобразуем первое из выражений
(III.4.10) к следующему виду:
/ 1
k^
■)·
ζ^ + k^
Подставляя затем вместо ζ его значение через t, получим
_ . /, 4W \
(III.4.13)
2A + 2^2)^2^, J
После подстановки k по формуле (III.4.11)
= '(
4(ί —1И2
i^ + 2{2l~])t^+\
■)■
(ΠΙ.4.14)
144
Найдем на плоскости t координату точки, соответствующей
ζ — оо.
Как видно из (III.4.14), ζ = оо, если выполняется условие
ί* + 2 B/ — 1) ί^ + 1 = О,
откуда
t*m^i{VT-VT^^)- (III.4.15)
Физический смысл имеет первое выражение (III.4.15), так как
точка лежит вне контура обтекания. Перейдем к построению
выражений для составляющих комплексной скорости, учитывая
при этом условия на границе потока на вспомогательной
плоскости t.
Из рис. III.14, β видно, что реальные части вызванной
скорости должны удовлетворять граничным условиям на оси х,
а мнимые части — граничным условиям на единичном круге.
Выражение для вызванной комплексной скорости представим
в виде
Ht)^-^^\n^ + iA{t-\)+B-\-iE\nt + iD^,
(III.4.16)
где А, В, Е, D—действительные постоянные, определяемые
из граничных условий. Постоянные В и Ε найдем исходя
из изменения ν (t) на вещественной оси плоскости t.
В точке А при ί = 1 на основании (III.4.16):
v{i) = -^ In 1±А-4- β -= --^ Ine' 2" + β = β - φ.
Принимая во внимание, что ^=¾ — iVy, найдем:
B-==v^-= — c.
В точке Л' при t = —1
^(^)^~"!Γ^"-!ί! +t^^"- 1 + β-= —с—π£ + ίβ,
откуда
ρ,
ϋ„ = с ·= — с — πΕ или Ε = .
* η
Для определения постоянных А vi D разложим искомую
функцию V (t) в ряд Лорана:
i(/) = ß« + -f+-^··-
145
Принимая во внимание условия на бесконечности (II 1.4.7), найдем
αο = υ^ =^-^:====---1-,
01 = О (условие отсутствия вихрей на бесконечности).
Используя второе из этих условий в (III.4.I6), найдем
значения постоянных:
^-=^47¼ и Ζ)===-^^^1η(ΐ/Γ + //^ΓΤ),
где Т = 2/-1+2//(/- 1).
Входящие в (III.4.16) особенности находим исходя из
следующих соображений:
1) особенность вида In _. соответствует скачку в Im с
в носике клина на единичном круге. Действительно,
при / =i ± 1 In -f^ = lir t -g-;
2) особенность вида ΐ (t τ-) характеризует вызванную
скорость V при обтекании полуокружности. Так,
при ί = zt 1 t {i — т) = 0.
т. е. в угловых точках скорость равна нулю;
3) особенность вида t In t соответствует скачку в Re t; при
переходе от верхней к нижней границе каверны (на плоскости t)
■ π, ί < О j'
fs ι
4) особенность вида ΐ ^ удовлетворяет условию на
бесконечности.
Практически более удобно искать решение в виде функции
V (ζ). Тогда (II 1.4.14) преобразуют к виду t (ζ) и раскладывают
в ряд по степеням Ι/ζ при ζ —* оо (ί —»t^), а полученный
результат подставляют в (II 1.4.16).
Коэффициент сопротивления, отнесенный к длине клина,
определяется путем интегрирования давления по поверхности
клина
C^=.2lc,^dy^^^^j±j, (III.4.I7)
о
где Ср^ определяется формулой (III.4.9).
146
., , 0,ί>0
tlnf =
Коэффициент подъемной силы, отнесенный к длине клина;
Q = -2(l+K)c(l+2i//(/-l) [l +
-\-^^^ln{VT + VT^=^)] - /}>. (Ш.4.18)
Коэффициент момента относительно носика клина,
отнесенный к квадрату длины клина:
с^ = -2A+к) οζ^ + ^ΐρ-νηι-ΐ) {ι +
r In {УГ+ νΤ^
(Г2—1)A —Γ)
(III.4.19)
Для определения формы границы каверны воспользуемся
зависимостями
^^-^^, dy^-^dx. (III.4.20)
Интегрируя (III.4.20) и принимая во внимание (III.4.9), получим
для физической плоскости:
AT\n{Vl +Vl~l \2Vl{l~\){\^T) ,._γ\\, /зЧ
Τ^ 1тг η CI τ\ Ι 2Ζ + 1 ^ ) /'
У κ W = ΤΤ7 j ^ ^^ + ίΌ A)
1_
- с
Ι
или
ί/κ W = — 7½ Im j ^ ^2 + ί/„ A),
Ι
где Hq = =tß; знаки «=t» относятся к ординатам верхней и
нижней границ каверны соответственно.
Рассмотрим теперь линейную задачу о кавитационном
обтекании клина в продольном поле тяжести. Так же, как и в
предыдущей задаче, будем считать клин тонким, а граничные условия
на поверхности клина и каверны перенесем на продольную ось
клина. Примем, что нуль потенциала гравитационного поля
находится в начале координат {х = 0). Тогда уравнение Бернулли
получит вид
Ρ.+-^ + Ρβ-Ρ^ψ- + Ρ§Χ, (ΙΙΙ.4.21)
где левая часть (III.4.21) соответствует точке у основания клина
(л: = 1), а правая — произвольной точке в произвольном
сечении X на границе каверны; g — ускорение силы тяжести;
остальные обозначения прежние.
147
Уравнение (III.4.21) преобразуем к виду
P~-p.-=i-iVl- νη + pgil - X).
Принимая во внимание (ΙΠ.4.2), после деления всех членов
преобразованного урав
коэффициент давления:
,,2
преобразованного уравнения на скоростной напор ^ "^ получим
Q _ Р —Рк 2g(l~x) 2¾
^¾ pV| VI Vk
или, используя связь Vk = Foe 1^1 + κ, напишем:
Чк-у2„A+х) v/„vAi-p^· A11.4.^^)
Здесь так же, как и в предыдущей задаче, найдем возмущенную
комплексную скорость ν = v^ — ϊυ^, обусловленную влиянием
продольного поля тяжести.
Граничные условия задачи следующие:
на клине (О < χ < 1)
Vy = ± β;
на границе каверны A < χ < I)
С„=0 и ^=-^ -^A-^)
Третье граничное условие — это условие на бесконечности
аналогично (II 1.4.7):
- 1 1 _ **
-- ^γψ^ 2 ·
Четвертое граничное условие — условие замкнутости контура
тело—каверна.
Линеаризованная физическая плоскость течения с
граничными условиями показана на рис. III. 15.
Так же, как и в предыдущей задаче, преобразуем с помощью
формул Кристоффеля—Шварца внешнюю область
многоугольника на физической плоскости ζ на верхнюю полуплоскость ζ,
а затем, используя преобразование (III.4.12), перейдем к
течению на вспомогательной плоскости t.
Вспомогательные полуплоскости ζ, ί и соответствующие
граничные условия представлены на рис. III. 15, бив. Точка М,
соответствукщая бесконечно удаленной точке ζ = схз, лежит
I4R
на мнимой оси полуплоскости ζ и Имеет ординату tk, а ордината
точки Mt,n полуплоскости t определяется формулой (III.4.15).
Неизвестную вызванную комплексную скорость ν найдем
как сумму скоростей, обусловленных особенностями. Решение
получим как частный случай выражения (III.4.16).
а)
S)
У
®
_ дп-х)
п ■
Imv- β /?еС=-]р
ΐλ
, Vi,
О 1
©
Ιί-Χ)
β
lTn.v~Tjy=P
/?e 1/=1),=
n—^
Рис. 111.15. Линеаризованная плоскость течения в продольном
гравитационном поле (β), вспомогательная верхняя полуплоскость ζ (б), вспомогательная
полуплоскость t (β) и граничные условия.
В этом случае решение представляем в виде двух частей
f = »1 + »2 И ί^ι = ^ — ivy^; V2 = Vx^ — ivy^,
которые удовлетворяют условиям
на клине
Vy, = ± β; Vy^ = 0;
на каверне
" к
IL
Сумма этих решений должна удовлетворять общим граничным
условиям.
Решение для v^ по аналогии с ранее изложенным будет иметь
следующий вид:
--_^inl+i.
η ι — ι
iA
(^-4-)+β.
где В = g/ί/κι a постоянная A пока неизвестна.
149
Получение решения для ν 2 оказывается более сложным, так
как согласно (III.4.14) х, входящая в граничные условия, —
сложная функция. Ее нельзя прямо использовать для
составления выражения комплексной скорости, так как üg имеет полюс
в точке t = t^.
В связи с этим в [74] подобрано решение для üg,
устраняющее влияние этой особенности, в виде
--,- 2R , t + i , . А /, 1\
-4(/-D + ^f^irr^-w]· ("^-^-^^^
Постоянная А находится из условия αϊ = О
Л-. Р^·^ Γι "g(^-')']
Коэффициент сопротивления, отнесенный к длине клина,
1
о
где Ср^ находится по формуле (ΠΙ.4.22).
В результате получим коэффициент сопротивления клина
с учетом продольных сил тяжести
^ ^ 8ß^ A + и) ί I \ I 2βΙ^7
(т^) +
Fr2
При Fr -^ оо получим Сх для случая кавитационного обтекания
клина в невесомой жидкости.
Связь между числом кавитации, длиной каверны и углом β
находится исходя из условия Gq = 0:
для поперечного поля тяжести
1- ^^ ^±{1П^л_ыУ'^^
для продольного ПОЛЯ тяжести
γ 1 /-1 _ β / 21^7 , ,„ 1^/^+Г'
VT^yi ~ 4ΡΓA+κ) - IT \1-Ϊ + "{Λ^_ι
Расчеты кавитационного обтекания клина с учетом
поперечного поля тяжести показывают, что коэффициент сопротивления
и длина каверны в рамках принятых допущений мало зависят
от числа Фруда (параметра с). Влияние тяжести проявляется
в деформации каверны (всплывание) и возникновении подъемной
силы и момента.
150
a) СуТг
юр
φ
ηι
\
^
\
\
\
^
ti^
ji>
v^
s-^^N
о
\ '
5^0-
\^
S) y-Fr
φ
φ
\
^
\
^
\
\
\ V
l'\
\^.: \
0Ч
0Ü/
ft/
κ β/?/
OJ
0.6
ой-
0.ί
0.005
-Οβ5/
QW^
0,05
<^-o.oi
-0,05
0,1
ν^α?
-C,2
^x
ίο
о/
ш/
: ι
W^ '/ft^ ΙΊ ''
ι ш^
\ \ν^
1 \\
:
'-^гЦг
-0}
$:--Qü/
^^Q0Ö5
-φί\ \0,О05
^-15°
\fFriO
ι 1 Τ I Μ ι ι
Q? 0,^ οβ 0,8 κ ' ;
W
100
Рис. III.16. Результаты расчетов гидродинамических коэффициентов.
Поперечное поле тяжести: а — Су Fr^ {κ, β); б — CmFr^ (κ, β); продольное поле
тяжести: в — Сх {к, l/Fr^); г — κ (/, l/Fr^).
При 1/Fr^ > О гравитационное поле направлено против потока, при 1/Fr^ < О гра-
витациоииое поле направлено по потоку.
151
На рис. 111.16, а, б приведены зависимости коэффициентов
Су Fr^ и С^ Fr^ от числа кавитации κ и половины угла раствора
клина β [98]. При рассмотрении продольного гравитационного
поля установлено, что длина каверны и коэффициент
сопротивления существенно зависят от числа Фруда. На рис. III.16, в
приведена зависимость коэффициента сопротивления от числа
кавитации и от функции 1/Fr^ [74]. На рис. III. 16, г даны
зависимости числа кавитации от длины каверны и от функции 1/Fr^.
§ 5. Влияние весомости жидкости на характеристики
кавитационного течения в ограниченном потоке
В § 4 была рассмотрена задача о влиянии гравитационного поля
на характеристики каверны, образованной за клином, в
безграничном потоке. Рассмотрим сначала случай, когда тонкий клин,
имеющий длину а и угол раствора β, расположен под
горизонтальной стенкой [10]. За клином образуется каверна, которая
замыкается на зеркально расположенный клин (схема Рябушин-
ского). Схема обтекания и система координат даны на рис. III. 17.
Рис. III. 17. Кавитацнонное обтекание тонкого клина под
горизонтальной пластинкой (схема обтекания и система
координат).
Жидкость считается невязкой, тяжелой, несжимаемой, движение
безвихревым.
Решение такой задачи имеет практическое значение при
расчете конструктивных элементов системы вдува воздуха под
днище судна с целью снижения его вязкостного сопротивления.
Задачу будем решать в рамках линейной теории, т. е. будем
считать толщину каверны и клина малыми, а граничные условия
с контура каверны перенесем на горизонтальную ось.
Задача состоит в отыскании вызванной комплексной
скорости 0=¾ — iVy, где ϋχ и Vy — горизонтальная и
вертикальная составляющие вызванной скорости. Составим граничные
условия течения:
на поверхности клина
ТГ = -£^ = Р прих>/их<-/; (III.5.1)
на поверхности каверны
Р" "= Рк + Ρί^"^ — Pgy при — Ζ < X < /, (III.5.2)
152
где у, Уо — ординаты контура каверны и твердых границ
соответственно; I — полудлина каверны.
При решении воспользуемся методом особенностей. Каверну
заменим источниками и стоками, интенсивностью q (ξ),
расположенными по оси Ох. Тогда скорость, вызванная источниками,
с учетом (III.3.3) примет вид
-(Но)
где
q{x)^2V.
-J^--^ß при х< — 1, х>1;
dx
dy ,^ ^, (И1-5.4)
При таком представлении условие (III.5.1) удовлетворяется
автоматически. Преобразуем условие (III.5.2). Учитывая (III.5.3),
найдем:
1+а
^-» = Рк + -^- ί ^~Pgy- (Ι"·5.5)
- (ί+α)
Введем безразмерные координаты:
— X ^ I — у — а
^'~~Т'' -~Т' ^^JT' """Τ'
j( = , ^"^ число кавитации, отнесенное к β;
2 Ρ
Fr = -^ - число Фруда; / = -J^ = ^.
Используя граничные условия, преобразуем далее (III.5.5)
к следующему виду:
-Рк I
(III.5.6)
Переходя к безразмерной форме и изменяя в (III.5.6) пределы
интегрирования, после промежуточных преобразований получим:
2^ "J 1-х ^ л (l+ß + x) π ]__j, Τ^'ί^
—I
153
или
где для клина
1
f+^ jÄ + /y_^-(«. χ), (ΠΙ.5.7)
(ΙΙΙ.5.9)
4>(α, χ) = ---1π ^ у ^ .
Интегродифференциальное уравнение (III.5.7) решается
относительно неизвестной ординаты границы каверны у. Параметры а
и / в расчете задаются. Число кавитации находим в результате
решения.
Искомая функция у (х) должна удовлетворять условию на
концах каверны
У(^) Ь=-1 -=У(х) fc=i = ^0 Й k^^il (ΙΠ.5.8)
У' W Ь=_1 = у' (X) Ь^, = yh (х) Ь_,.
В частном случае для клина
В формулах A11.5.7)-A11.5.9O = -^--
dx
Уравнение (III.5.7) аналогично уравнению Прандтля из
теории крыла конечного размаха.
Интегродифференциальное уравнение (III.5.7) в [10] решается
приближенно на ЭВМ путем его замены системой линейных
алгебраических уравнений. При этом функция у' (х) = q {х)
аппроксимировалась непрерывной ломаной линией. Так как
рассматривается обтекание по схеме Рябушинского, то
функция q {х) должна быть нечетной (рис. III.18). Длина каверны
(от —1 до +1) разбивалась на η —· 1 интервала. Уравнение
удовлетворялось в η точках в середине каждого интервала |,·|,+ι
(ί = О, 1, 2, ..., /г — 1). Соответствующая система
алгебраических уравнений содержала η неизвестных
q^i, 9_2, . . ., 9_(п-1), V-
В работе [10] приведены результаты расчетов по изложенной
выше схеме, а также выполнено исследование сходимости
приближенных решений на примерах систем линейных уравнений
с десятью и двадцатью неизвестными. Результаты исследования
позволяют сделать заключение о хорошей сходимости
приближенных решений уравнения (III.5.7), за исключением некоторой
узкой области параметров /.
154
Задача может быть использована при рассмотрении более
общего случая: бесконечной системы каверн, расположенных
друг за другом под горизонтальной стенкой [71]. Каверны
образованы за тонкими клиновидными насадками. Замыкание
каждой каверны осуществляется на некоторый клин. Схема
системы каверн дана на рис. III. 19. Длина клина а^, угол
раствора β, а также расстояние между двумя соседними клиньями
-A*0.) t-n 1-ιτι-ι) ξ-i, ξ-/Ή ί-ί
ξ? h-11 и ?7b-7 Sn A+ct)
H-i,i Χτί-ι,η
X
Рис. III. 18. Аппроксимация q (χ) непрерьшной ломаной линией.
(основаниями или вершинами) L приняты постоянными. Каждая
каверна замыкается на некоторый клин длиной Og с углом
раствора ββ.
Граничные условия практически останутся неизменными
[(III.5.1)—(III.5.2)], но границы их применения станут иными.
^(ϊ)
Рис. III. 19. Кавитационное обтекание бесконечной системы каверн,
расположенных друг за другом по горизонтальной стенке. Схема системы
каверн.
Граничные условия непротекания жидкости через границу
течения и постоянства давления на контуре каверны имеют
следующий вид:
^ = F,
dy
^ при — оо<л:<оо, (III.5.10)
pV^v^ — pgy = ρ« - р^; р„ = р^ -f pV„v^ — pgy (III.5.11)
при nL<Zx<nL + l или О < Хо < ^
155
где χQ --^ χ — nL — значение χ в пределах одного периода или
—Ö1 ^ Хо is^ L — α^; I — длина каверны; η — ряд целых чи-
сел, изменяющихся в диапазоне от —оо до оо.
Величины роо и V^ можно считать предельными значениями
давления и скорости потока на уровне горизонтальной стенки
в середине между кавернами при увеличении расстояния между
ними до бесконечности.
Кроме того, исходя из условия непротекания и периодичности
характера течения найдем:
на поверхности клиньев
q ■■= 21/οοβ при nL — ai<^Xt^ nL;
q = — 2V^% при nL + Kx<nL-\-l-^a^\ (III.5.12)
на поверхности каверны
q (Xq) = q{Xo-\- tiL) при nL ^ χ s^ tiL-{-1;
q = O при ftL + Z + ßa < л:<(/г+l)L — ai. (III.5.13)
Так же, как и в предыдущем случае, система клин—каверны
заменяется особенностями, расположенными по оси Ох, а
вызванная скорость в произвольной точке с координатой ζ определяется
формулой (III.5.3), в которой изменены пределы интегрирования:
оо
Интенсивность источника связана с формой границы каверны у {х)
зависимостью [см. (ΙΙΙ.3.1)]
q{x) = 2V^ -¾ (,χ) = 2V^y· {χ). (III.5.15)
Учитывая условие замкнутости каверны 1 q (ξ) dl·, = О,
вызванную скорость можно представить в следующем виде:
—со /1=—-©о —üi
Принимая во внимание известное разложение котангенса
в полубесконечный ряд [56]
156
выражение (III.5.16) можно легко преобразовать к виду
vAx)-~^ j 9 ih) ctg^ (X« - У dH„. (III.5.18)
-а
Ордината границы каверны на основании (III.5.15)
^ί^) = жг J 9 (^> ^^ = WT 1^ί^ο^ ^^0· ί"^·^·^^)
— со —Ωΐ
Далее подставляем (III.5.18), (III.5.19) в условие (III.5.10)
и в результате получаем интегральное уравнение относительно
интенсивности распределенных по оси Ох особенностей q (χ).
Предварительно введем безразмерные величины
(ΙΙ1.5.20)
Учитывая безразмерные величины (III.5.20), условие на
поверхности каверны (III.5.11) преобразуем к виду
Ρ „ _ _ _ R Sin -=-A —χ)
JL\gii)ctg^{x~l)dl--fln ^
χ =
«1 =
Ql .
CO
Xo
I
Я
' ε~ ι '
— 02 .
Q
2V^^ '
^ ι '
у ι '
3j ._ Р~—Рк
sin-y-(l +02—дг)
о ^
Г- - - π κ sm-^(x + ßi)
-л/U (ξ) dl-1^ = -In „ _ +"/%· (ΠΙ.5.21)
J ^ sin -ρ χ
Решаем (III.5.21) приближенно путем замены интегрального
уравнения системой линейных алгебраических уравнений.
Так же, как и для случая одной каверны, искомая функция
q {χ) аппроксимируется ломаной линией. Подробное изложение
численного метода решения дано в 171].
На рис. III.20, а—г для иллюстрации представлены
расчетные зависимости -|-(f), -^(f). |-(D. ^if) при
заданном значении длины клина а^ =0,1. Системы линейных
уравнений были рассчитаны на ЭВМ при соотношениях —=0,1
и 4:= ^ + + "^ =0,04; 0,52; 0,76; 0,88; 0,94; 0,97. При
численном интегрировании число участков на клине m = 5.
157
Для определения коэффициента сопротивления клина
используется формула
о о
2Х 2 Г ю —юк - , „.- 2 С ^
Сл-
рСР«
—Cj —Oj
dx.
(Ш.5.22)
Приведенную здесь схему решения задачи можно применить
к расчету параметров каверн, образованных под днищем^водо-
Jo
Ρ
J
2
1
D
-1
0.5Г
0,76
α
Τ
0-1=0,1
vaI
li
1
о ? 2 J 4^ 5 f
Рис. 111.20. Результаты теоретического расчета характеристик системы беско-
йВчйы! - ~кавер н: с -
Ро
β
(/); б-
ψ-(η; e~f(f); е-^Ш.
измещающего судна, и к расчету обтекания глиссирующей
поверхности с каверной, которое также можно рассматривать как
кавитационное течение в ограниченном потоке [49].
§ 6. Кавитационное обтекание профиля
плавных образований
В задачах о кавитационном обтекании, приведенных выше, были
рассмотрены профили, имеющие фиксированные точки отрыва
каверны. Однако во многих практических приложениях
рассматриваются профили, имеющие плавные образования, а положение
168
точки отрыва каверны неизвестно. Это обстоятельство усложняет
применение метода теории струй идеальной жидкости. В этом
случае более рационально использовать метод особенностей
(источников и стоков).
Следуя работе [24], рассмотрим на физической плоскости ζ
кавитационное обтекание профиля произвольной формы под
некоторым углом атаки а.
Преобразуем- течение на физической плоскости на
вспомогательную плоскость ζ. Будем считать, что ζ = / (ζ) — некоторая
известная функция, преобразующая внешнее течение около
профиля на плоскости ζ во внешнее течение около круга
единичного радиуса на плоскости ζ. Соответствие точек указано на
рис. ΙΠ.21.
Положим, что граница каверны представляет собой линию
тока, вдоль которой скорость постоянна и равна Ι^κ = F« ]/ΐ + и·
Скорость на границе каверны при течении на вспомогательной
плоскости Fg связана со скоростью F« формулой -
F. = l/„ ^^
к
я
{ΙΠ.6.1)
Задачу решаем в линейном приближении, т. е. считаем, что
граничные условия с поверхности каверны переносятся на
поверхность профиля и некоторой линии. При этом концевая точка,
где происходит смыкание верхней и нижней каверн,
представляет собой особую точку, влияние которой сказывается лишь
вблизи ее окрестности. Заменим каверну системой особенностей,
расположенных на дуге единичного круга А'С и отрезке С В'
(см. рис. ΠΙ, в).
На основании принципа симметрии внутри круга должны
быть размещены особенности, симметричные кругу и прямой.
Для обеспечения условия непротекания в центре располагают
стоки, интенсивность которых равна суммарной мощности
особенностей, заменяющих каверну. Задача сводится к отысканию
системы особенностей, удовлетворяющей заданному
распределению скорости, причем координаты начал^а каверны (точка А')
и конца каверны (точка В') неизвестны.
Обозначая через g (φ) и g (ξ) погонную интенсивность
источников (стоков) на дуге круга и отрезке прямой соответственно,
составим комплексный потенциал течения на плоскости ζ.
Комплексный потенциал особенности (источника) определяется
формулой -—- In (ζ — α), где а — координата особенности. На
дуге единичного круга α = е'*, где φ — текущий угол, а на
оси — α = ξ. Тогда комплексный потенциал особенностей
определится следующими выражениями:
на окружностл
-¾^ In (ζ-.'>);
159
η)
y>
0
л^У
А,
^
——-"^
■^
X
6) 7,
а'/"^^
1 ^^
ι ,^')/
\ '^У
,
^0
^"^х. ^
\ х«^
γ ^---
©
^в'
%
φ η η
©
'+ + + ft 1- 1-н--^ -H-^jt^Sf
5' ^
Рис. 111.21. К решению задачи о кавитационном обтекании профиля плавных
образований: а — физическая плоскость течения; б — вспомогательная
плоскость; β — схема распределения особенностей.
160
на оси ξ
Итак, на вспомогательной плоскости ζ рассматривается
обтекание единичного круга под некоторым углом а, имеющего
указанную выше систему особенностей.
В связи с тем что координаты начала и конца каверны
неизвестны (точки А' и В'), необходимо составить два дополнительных
условия.
Первое из них — требование о замкнутости каверны —
равносильно тому, чтобы интегральная интенсивность источников и
стоков была равна нулю, т. е.
Θ. 1
о I.
где li — абсцисса конца каверны на оси ξ; θχ — угловая
координата начала каверны.
Второе условие — касание границы каверны в начальной
точке:
de |θ=θ.
Суммарный комплексный потенциал определяется формулой
/ βία \ т,
θ, θ,
о о
+ -i^ig(ivnii-i')di'^^]gavn (ξ --f) dl' -
1 1
-^lnujga')dl'. (III.6.2)
1
где I' — переменная интегрирования.
Первый член (ΠΙ.6.2) представляет собой потенциал скорости
обтекания неподвижного единичного круга под некоторым углом
а. Второй член учитывает наличие циркуляции Г, третий
и пятый члены представляют собой потенциал скоростей,
вызванных источниками и стоками и расположенных на дуге круга и
на оси симметрии течения (в случае развитой каверны).
Четвертый и седьмой члены определяют условие непротекания через
круг и горизонтальную стенку, это потенциалы скоростей от
стоков, расположенных в центре круга, шестой член определяет
потенциал скорости зеркально отображенных источников
161
(рис. III.21, в). В частном случае частичной кавитации пятый,
шестой и седьмой члены равны нулю.
Комплексную скорость течения -^ находим путем
дифференцирования (II 1.6.2) по ζ:
dw 1/ irr (л ^^°'\ . г I
■ = Vcoe~^°' 1
'('-ΐ)+
θ, θ,
ξ- -
+ ii^(^') W+ii^(^'O^ - ik-i^(^')^^'
1~-γ
(ΙΙΙ.6.3)
Для определения циркуляции Г в (III.6.3) составляется
дополнительное условие. В силу принятого условия тонкости граница
каверны совпадает с поверхностью профиля и частично с
линией / — li. Критическая точка находится на границе каверны,
скорость на ней должна быть конечной и равна У«, что
соответствует постулату Жуковского—Чаплыгина. Скорость ^ должна
обращаться в нуль. В частном случае частичной каверны это
условие' имеет следующий вид:
d(f 1
+ ^/^(^^)-1^^-^1^(^^)^^^===°
при ζ = 1
или
ίίφ
Ι
ΐ
θ
θ, · "
θ.
— \g(^)d^ = 0, (ΙΙΙ.6.4)
где 02 — угловая координата конца каверны.
Выражая затем показательные функции через
тригонометрические, после промежуточных преобразований получим
уравнение для определения циркуляции
Г = -4лУ„8й1а + 1 [MM^JLd^.
' 2 J 1 — cos φ ^
θ,
162
Как видно из рис. III.22, комплексная скорость Υζ
может быть представлена через проекции так:
dw
V,
0
1
г /
d© //
Ут *
ί^ε =
= У|-/1/,;
Лг>
\хИ/?
^^хч:
ξ
1/^^1/,-
-»Уе.
У^г d^-^
-=^''
^n^v
-ίξ
*ϊ
Рис. ΙΙΙ.22. К выводу интегральных уравнений.
Как уже указывалось, мы считаем каверну тонкой, и поэтому
полагаем, что скорости V, и Κη малы так, что
^ε = ^θ при 1<.\\
F^ = F| при 1<|<|,.
(III.6.5)
Представим комплексную скорость Υ^ в параметрическом виде.
Учитывая (III.6.5), найдем
dw
.-'■ A-е)
е ■' 2 ' = — t
dim
οίθ
(ΙΙΙ.6.6)
После подстановки (III.6.3) в выражение (III.6.6), с учетом
(ΙΙΙ.6.4) и ряда промежуточных преобразований для частичной
каверны получим:
7ζ= 2V„ Sin (θ — α) — ^ —
-Ж]^^^^ l-'JsV-Φ) А^-^\&Ш^. (И1.6.7)
е« θ.
163
Сопоставляя (III.6.5) с (III.6.7), найдем
θ.
sin (θ — φ)
dcp;
Ve = 21/^ sin (θ-α)-J^ i_fg(cp)
" ^ ' 2л 4л J *^ ^^' I — cos (Θ — φ)
Принимая во внимание связь между скоростями на границе
каверны на физической и вспомогательной плоскостях (III.6.1),
hfl
0,5
«=
ψ'/ο"/
ЕЪТЫХ.
δ)
hfl
Oß
0,7485
^^__,^ό6°
-~_____-- —с
о/
^ о
0,5
W
0,5 . го
smci
Рис. 111.23. Результаты расчета относительной длины кавериы в
зависимости от угла атаки и числа кавитации.
а также выражения (III.6.5) и (III.6.6), получим интегральные
уравнения для определения неизвестной функции распределения
особенностей g (θ):
1^е = ^к|^| при/·=!; 0<:θ<2π; |<:1. (ΙΙΙ.6.8)
164
Выражение (III.6.7) можно написать для более общего случая —
развитой каверны. Интегральное уравнение (III.6.8) дополняется
тогда уравнением
n=-n = l^K'|f I· ("I-6.9)
Решая (III.6.9), найдем функцию распределения особенностей
g (ξ) вдоль оси ξ.
Зная распределение особенностей g (Q) Hg (ξ), легко
вычислить и форму каверны.
Исходя из положений геометрии можно установить по
рис. III.22 связь между скоростями и приращениями координат
каверны:
для части каверны, расположенной на профиле,
^•^ ^^ άθ —^^ άθ '
для части каверны, расположенной за профилем,
у _ν ^^1/^^
где Υζ определяется по выражению (III.6.7).
На рис. III.23 приведены результаты расчетов по
приведенной выше схеме для частичной каверны, образованной на плоской
пластинке, а также результаты экспериментов с симметричным
двояковыпуклым и плоско-выпуклыми профилями.
На рис. II 1.23, а дана зависимость относительной длины
каверны h/l от отношения —, где а — угол атаки; κ — число
кавитации; I — длина пластинки; h — длина каверны.
На рис. II 1.23 даны аналогичные зависимости для двух
профилей, образованных дугами круга. Там же нанесены
экспериментальные точки, полученные в работе [89] для профилей,
имеющих хорду 150 мм и толщину 6 мм. Как видно из рисунка,
совпадение теоретических данных с экспериментальными
наблюдается при h/l is£ 0,5. При увеличении этого отношения
получается резкое расхождение результатов теории и эксперимента,
что объясняется неправомочностью использования линейной теории
в диапазоне значений h/l = 0,75-f-1,0.
Глава IV
НЕСТАЦИОНАРНЫЕ
КАВИТАЦИОННЫЕ
ТЕЧЕНИЯ
§ 1. Понятие о потенциале ускорения
Исследование гидродинамических сил, действующих на тело
при нестационарном обтекании с отрывом струй, имеет
практическое значение: его результаты необходимы для различных
инженерных расчетов, в частности при проектировании
конструкций быстроходных судов.
Настоятельная потребность в достаточно простых способах
расчета вызвала появление теории, основанной на ряде
допущений, известных из решений линейной задачи о стационарном
обтекании. В частности, предполагается, что вызванные скорости
жидкости, обусловленные присутствием тела и его колебаниями,
малы по сравнению со скоростью основного потока. Весьма
плодотворным оказался метод потенциала ускорения, введенный в
аэродинамику Прандтлем.
Метод потенциала ускорения состоит в следующем. Из теории
невязкой жидкости известно, что нестационарное движение
определяется уравнениями Эйлера.
В случае плоского движения (ζ = 0), исключая массовые
силы, в декартовой системе координат получим:
dt ' дх ■^^"г ду У ρ дх '
Проекции скоростей, входящие в (IV. 1.1), легко представить так:
V^ = V^-\-v„ Vy = Vy,
где 1/^ — скорость на границе каверны при стационарном
обтекании; Vx, υ у— проекции вызванной скорости ν на оси Ох и Оу.
166
в дальнейшем Vx, Vy и их производные будем считать малыми
величинами. Тогда третьими членами в (IV. 1.1) можно
пренебречь. В результате найдем:
Svx , *д; Τ/ ^ 1 Φ .
dt ^^ дх ^^ ρ дх
Введем безразмерные величины
После подстановки (IV. 1.3.) в (IV. 1.2) получим:
^ = -^' ^ = Й- (ϊ^·ΐ·3)
у *^ 1
1 &ϋχ ,
Кк öi 1
1 *& ,
ν„ öt 1
dvy ,μ
дх ^^^^
dvx
дх
дх
1_ öp .
ρ дх '
\_др
Ρ Φ
1 φ.
pVl дх '
1 φ
pVl Φ'
ИЛИ
(IV. 1.4)
Как видно из (IV. 1.4), левые части этого выражения
представляют собой проекции вектора ускорения а = a^i + ^]» где
10¾. dvx 1 dp .
"■" Кк öi ' дх
I ^ 0¾
^ Ук öi ' öx
pVl дх '
1 φ
ру2 Ф'
Известно, что векторное поле потенциально,
няется условие
rot а = 0
или
дих day
ду дх
(IV. 1.5)
если выпол-
(IV. 1.6)
Составив частные производные правых частей (IV. 1.5) по у
и по X соответственно, убеждаемся, что в нашем случае
условие (IV. 1.6) выполняется и векторное поле ускорения
потенциально. Определение потенциала консервативного поля
167
равносильно задаче о вычислении функции Φ по ее полному
дифференциалу:
но
"■'''^ дх ' "^У'" ду '
Тогда потенциал поля ускорений находим по формуле
Φ = J ßy di/-j-J од: dx.
Подставляя вместо a^, üy их значения по формуле (IV. 1.5),
после интегрирования получим следующие выражения для
потенциала ускорения (для несжимаемой жидкости):
в размерной форме
ф==.
в безразмерной форме
_р_.
Ρ '
φ.
9Vl
или, так как потенциал определяется с точностью до постоянной,
Ф- —-^=|!^. (IV.1.7)
Если вызванные скорости отсчитывать от скорости основного
потока на бесконечности, т. е. считать, что
то выражение для безразмерного потенциала ускорения получим
в. виде
Ф:
или
pvl
Ф^—^ ^°° . (IV.1.8)
Покажем теперь, что потенциал Φ — гармоническая функция,
т. е. он удовлетворяет уравнению Лапласа.
Уравнение неразрывности течения:
*+f = 0. (IV.I.9)
168
Продифференцируем первое и второе уравнение (IV. 1.5) по χ
и у соответственно, а затем сложим их почленно:
_J д_(^ , ^¾ \ , д ί^χ övy \ _
Т7 dt\dx · ду )'^ дх [дх 'т' ду }~
Как видно, на основании (IV. 1.9) левая часть (IV. 1.10)
обращается в нуль. В результате получим уравнение Лапласа
■»+S = 0. (IV.l.U)
дх^ ' ду^
На основании (IV. 1.11) можно утверждать, что существует
комплексная функция F (ζ, ί) = Φ + ι'Ψ, удовлетворяющая
условиям Коши—Римана:
■аГ^-аГ^^"^^ -^Г==--йГ=^· (IV.1.12)
Назовем функцию F {ζ, t) комплексным потенциалом
ускорения. Легко установить связь между вызванной комплексной
скоростью V и комплексным потенциалом ускорения F.
Принимая во внимание, что ν — Vx — iVy, умножим второе
уравнение (IV. 1.4) на t и вычтем его из первого. После
преобразований с учетом (IV. 1.12) получим:
1 (dvx , dvy\ /dvx · ^у\ __
дФ . дФ дФ , . ΟΨ
дх ду дх дх ^
Рассмотрим теперь применение метода потенциала ускорения
к задачам нестационарного кавитационного обтекания.
§ 2. Ускоренное кавитационное обтекание
тонкого клина
Такая задача встречается в корабельной гидродинамике,
например, при нестационарных режимах движения крыльевой системы
быстроходного судна (колебания на волнении, разгон,
торможение). В ряде случаев отдельные элементы системы: стойки,
крылья—находятся в режимах кавитации (или вентиляции),
при которых с течением времени изменяются: скорость
набегающего потока, длина каверны, а также гидродинамические силы
169
сопротивления. Так как профиль стойки имеет большое
удлинение, то ее обтекание может быть уподоблено обтеканию тонкого
тела.
Рассмотрим тонкий клин АСВ единичной длины в
ускоренном потоке невязкой и невесомой жидкости при числе
кавитации κ =7^ О [78]. Предположим, что на бесконечности скорость
натекающего потока Va, изменилась на малую величину Vi (t)
так, что результирующая скорость имеет вид
Необходимо найти вызванные скорости, длину каверны и
силу сопротивления, обусловленные изменением скорости потока.
Физическая плоскость течения дана на рис. IV. 1, а. Здесь хАу —
прямоугольная система координат, связанная с клином; х'Оу' —
система координат, связанная с жидкостью на бесконечности.
Пусть давление на бесконечности равно р«., при
кратковременном изменении скорости Vi (t) ускорение потока равно а = —jj-·
Рассмотрим граничные условия задачи.
1. На поверхности клина
при О < χ < 1, у = О
Выразим это условие через потенциал ускорения. Так как Vy ==
= const, то из второго уравнения (IV. 1.5) получим, что —^— ==
= Im-^— = О или, принимая во внимание условие Коши—
Римана,
"* 1Л = ^^0. (IV.2.2)
ду '"dz дх
кроме того, примем Ψ = 0.
2. На границе каверны давление ρ = р^.
Принимая во внимание (IV. 1.7) для потенциала ускорения, получим
граничное условие в виде:
при 1 < л: < /, г/ = О
Φ = Re F (ζ, t) = О, (IV.2.3)
где ι — длина каверны.
Ζ. На бесконечности (при больших значениях |ζ|).
В настоящей задаче целесообразно представить систему
координат хАу как неподвижную. Тогда на основании принципа Далам-
бера необходимо учесть инерционные силы, обусловленные
ускорением потока на бесконечности, что достигается введением
в интеграл Коши — Лагранжа потенциала инерционных сил в виде
Ω = ах.
170
1/k
v=V^+Vj(t)
Φ=0
д)
®
%ίΞ
P=P/<
Θ
>M(Vm)
Рис. IV. 1. Ускоренное кавитацион-
ное обтекание тонкого клина: а —
физическая плоскость течения; б —
линеаризованная физическая
плоскость; в — вспомогательная
плоскость Q:
О в А с
г — вспомогательная плоскость ζ
Re F (ζ, ί) = φ = 0;
д — вспомогательная плоскость ν:
ν
Re f (ζ, ί) = Φ = О
Im —Γ- — -ζ— = 0;
αζ ду
ά дФ
lm~F (г, 0=-^ =0;
dz ^ ду
m = -i^f' + i('-i)'^^l·
171
Учитывая сказанное, представим потенциал скорости и
давление в следующем виде:
φ = У (ί) >^, ρ ^ р^ — ρ ах. (IV.2.4)
Подставляя выражение (IV.2.4) в (IV. 1.7), найдем величину
комплексного потенциала ускорения при больших значениях |ζ|:
^B· ^) TT" (Рк - Ρ" + Pß2)
или, принимая во внимание, что V^ = Vco \^\ + κ, получим:
F{z, ή ^-^ -οτΆ—τ- (IV.2.5)
В формуле (IV.2.5) первый член представляет собой вид
особенности на бесконечности.
Линеаризованная физическая плоскость течения и граничные
условия даны на рис. IV. 1, б. Преобразуем с помощью формулы
Кристоффеля—Шварца внешнее (по отношению к разрезу)
течение на плоскости ζ на вспомогательную верхнюю полуплоскость Q
(рис. IV. 1, в), при этом может быть использована известная нам
формула из § 1 гл. III.
Q-(l- 1)''^ {т^У^ или Q = Ä {т^У' · ί^^·2·6)
В результате получим задачу с заданными граничными условиями
на вещественной оси плоскости Q. Точка Μ {ik) на мнимой оси
этой плоскости соответствует бесконечно удаленной точке на
плоскости 2 (ζ = оо). Решение этой задачи выполним методом
особенностей, рассмотренным нами в § 4 гл. III. В этом случае
находим потенциалы ускорений, обусловленные каждой
особенностью, а затем суммируем их.
По аналогии с изложенным в § 4 гл. III преобразуем
течение на плоскости Q на вспомогательную плоскость ζ с помощью
формулы
ο = ^(ζ + -ξ-)· (IV.2.7)
Как видно из рис. IV. 1, г, поверхности клина располагаются на
полукруге единичного радиуса, а границы каверны — на
вещественной оси. Однако отметим, что если постоянные значения
граничных условий не изменяются при переходе от одной плос-
dp
кости к другой, то граничное условие —^— изменяется.
Действительно,
ΛΡ__άΡ_άζ_ dF _ dF dz
dz άζ dz αζ dz ίίξ *
172
Производные —Φ— или —^ легко определить путем
дифференцирования (IV.2.6) и (IV.2.7). Опуская промежуточные
выкладки, получим
άζ 4(Ζ-0ζ2_ΐ-(ζ2_ΐ-ΐJ
dz 8ί(ί-1)ζ(ζ*-1)
(ΐν.2.8)
Таким образом, граничное условие на поверхности
единичного круга плоскости ζ зависит от (IV.2.8). Координату точки
плоскости ζ, соответствующую бесконечно удаленной точке ζ —
= оо, аналогично решению стационарной задачи, находим при
помощи формулы (III.4.15):
ζ^=^ί[ί^^'+(ί-ΐγ'']. (IV.2.9)
Неизвестный потенциал ускорения F можно легко получить как
сумму потенциалов ускорений, вызванных особенностями:
Ρ{ζ, t) = ^ln^ + i^(t--^)+F„ (IV.2.10)
где первый член соответствует скачку вызванной скорости Vy
в носике клина; второй член характеризует вызванную скорость
при обтекании окружности единичного радиуса; третий член
определяется особенностью на бесконечности при ζ — оо; А (ί)—
действительная функция времени.
Асимптотическое приближение для потенциала ускорения на
плоскости ζ в точке ζ^ (ζ = оо) после подстановки в первый
член (IV.2.5) формул (IV.2.6), (IV.2.7) и последующих
преобразований имеет вид
2ν1A+κ)(ξ-ω
вблизи ζ==ζ^, (IV.2.11)
где ζη определяется формулой (IV.2.9).
В дальнейшем формулу для F удобнее получить в новой
вспомогательной плоскости V, связанной с плоскостью Q соотношением
v = (^)"·. (IV.2.12)
Вспомогательная плоскость, соответствующая этому
преобразованию, дана на рис. IV. 1, д.
С помощью (IV.2.7)—(IV.2.12) выражение (IV.2.11)
преобразуем так:
2Vi A + κ) Ζ'/»
вблизи ν = ν„ = -щ- [1 + t (/ — 1I/2 ]^
где ν — координата, сопряженная с v.
(IV.2.13)
173
Граничные условия (IV.2.1), (IV.2.2) и (IV.2.5) применимы
к мнимой и вещественным осям плоскости ν соответственно.
Решение для функции F при ζ = оо может быть выражено
затем через комплексную переменную ζ:
fc =
2Vt(l+X)
i-{l- 1)
'/2
'■ + α -1)
72
■ν —Vm
V — Vm
+
= ι
. ß(Z— 1)
'/£
4^1A+>ί)
(ΐ-ζ)
[
ε-<
V + Vm
ζ + ζηι
1 —
ζ^
1 +
ζ^
fem fem
Таким образом, окончательно решение для потенциала ускорения
имеет вид
^(ζ'^) = ΐΐ"ΤΤ^
+ i
(ΐ-ζ)
_1_
fem
ζ-ξ^
fem
ξ + ζ«
fem
ξ-
ζη
(IV.2.14)
Полученное решение удовлетворяет граничным условиям для F
dF
и —^—, а также граничным условиям для вызванной скорости Vy.
Скорость Vy может быть найдена из (IV. 1.5):
X
— оо
где G ■■
дх
— переменная интегрирования.
Решение (IV.2.14) для комплексного потенциала ускорения F
при заданных ускорении и форме клина содержит две
неизвестные функции: А (t) R I (f) — длину каверны. Найдем два
дополнительных условия для их определения.
Первое условие легко найти, если в (IV.2.14) положить ζ—*
—* ζ^, а затем вещественную часть полученного выражения
приравнять постоянному члену формулы (IV.2.5). Опуская про-,
межуточные выкладки, найдем
1''^~^\ Л(^)/-„.У+,'),. (IV.2.15)
1 к
2 1+κ
Am
π
ι" + 1
2^1A +κ)
174
Второе условие можно получить исходя из следующих
соображений. При больших значениях ζ можно принять условие,
что контур клин—каверна замкнут. Тогда, если представить
вызванную скорость ν в виде ряда Лорана, найдем:
-^ = ί-^^ 1+ L^ + ^lJ).+ ^. (IV.2.16)
В этом выражении в соответствии со сказанным выше вычет
ßi = 0. Отсутствие логарифмической особенности в выражении F^
dp
означает также, что вычет при разложении функции —^— в ряд
Лорана равен нулю. Используя (IV. 1.13) и (IV.2.16), получим,
что -^ = О, т. е. ßi не зависит от времени и поэтому равно
значению для стационарного потока.
В рассматриваемой задаче предполагается, что при
кратковременном изменении скорости потока каверна остается
симметричной относительно оси Ах, однако при этом изменяются
размеры каверны при сохранении ее площади — укорочение
каверны сопровождается увеличением ее ширины, удлинение —■
уменьшением ширины. При больших скоростях потока, когда
весомость жидкости проявляется слабо, это допущение
справедливо и подтверждается экспериментом. Согласно ί119] площадь
стационарной каверны для клина единичной длины находим по
формуле
S = —2яа^,
тогда в свете принятого допущения а^ = const.
Все сказанное выше дает основание считать с учетом (IV. 1.13)
dF
и (IV.2.16), что коэффициент при члене 1/z^ в выражении для ^^
должен быть равен нулю, а это, в свою очередь, значит, что равен
нулю коэффициент при члене \lz в выражении для определения F.
Учитывая эти обстоятельства и переходя к плоскости ζ, после
промежуточных преобразований из (IV.2.14) получим второе
условие для определения неизвестных Л (ί) и / (t):
2 " . ..,(^-^)'--¥-^'^'+^^'^4^- 1) = 0- (IV.2.17)
4V^> A + ^)
η
Сила сопротивления кавитирующего клина может быть
получена интегрированием давления по поверхности клина:
1 1
X = 21 (р - р,) di/ =-- 2β I (ρ (χ) - pj dx, (IV.2.18)
о о
где ρ {χ) — давление на стороне клина; Рк — давление в
каверне.
Разность давлений, входящая в (IV.2.18), может быть
получена на основании (IV. 1.7), (IV.2.14) и (IV.2.17).
175
После преобразования получим коэффициент сопротивления:
С.= , ^ =^"βγ+ΓΝ-2β-^. (IV.2.19)
I Полагая в (IV.2.19) ß = О, получим формулу для
стационарного кавитационного обтекания клина в невесомой жидкости.
Длина каверны I (t) определяется из (IV.2.15) и (IV.2.17) при
заданном значении ускорения а (t). Из этих двух уравнений
функция А {t) легко исключается. В результате получаем прямую
зависимость между I (t) и а it):
a{t) ^ 1+х / 1 у, ß_ , CI' + 1 __ ^ г'^°
4^1 -1^^ + 312 \-\-y, я си __ 1 π Ζ — 1
(IV.2.20)
где κ — число кавитации стационарного^ потока.
Уравнение (IV.2.20) решается графически для заданных κ и β.
После графического определения функции I (ί) по формуле
(IV.2.20) находят коэффициент сопротивления С^ по (IV.2.19).
§ 3. Нестационарное навитационное обтекание
тонкого профиля вблизи свободной поверхности
Рассмотрим тонкий кавитирующий профиль, совершающий вблизи
свободной поверхности колебания малой амплитуды по закону
h {χ, t) в потоке жидкости, имеющем постоянную скорость Vo=.
[69]. Предположим, что каверна замыкается далеко за телом,
что соответствует малым числам кавитации κ. Отрыв струй
происходит в произвольных фиксированных точках нагнетающей
и засасывающей сторон профиля. В качестве схемы замыкания
каверны примем схему М. Тулина с двойными спиральными
вихрями, уже рассмотренную в гл. П.
Течение рассматриваем в прямоугольной системе
координат хОу, нагнетающие и засасывающие стороны профиля
определяются уравнениями у^ = yi (χ) и у^—У^ {х) соответственно.
Предположим, что г/1,2 и ~^ настолько малы, что средняя
линия профиля незначительно отличается от отрезка прямой,
а вызванные скорости (обусловленные нестационарностью) ν =
— Vx — iVy малы по сравнению со скоростью основного потока У«·
При сделанных выше допущениях влияние нестационарных
составляющих движения можно рассматривать как малые
возмущения, а задачу представить в линейной постановке.
Физическая плоскость течения ζ показана на рис. IV.2, а.
Задачу также будем решать методом потенциала ускорения (см.
§ 1 этой главы). Рассмотрим граничные условия:
V76
1) на поверхности профиля задана вертикальная
составляющая скорости жидкости. Так, если профиль совершает
колебания по закону h == h{x, t), то вертикальная составляющая
скорости определяется формулой
у _ ду(х· t) τ/ ду(х, t)
'у яТ »'et
di
дх
(IV.3.1)
, β
Φ
®
Ф=Л
дф
ду А
Ф=0
/ F
— —■· ^-- у 7"
ф=
и
Vit
дФ
Τ -1 -^ε I -Ча'Щ
аЬ ·—, β 1 т ' ι
Г7 ε
©
дФ
4ι>
6
—·—}—·—
с л
Ф=-?г
Ф=0
7 L·
Рис. IV.2. Нестационарное обтекание тонкого профиля
вблизи свободной поверхности: а — физическая плоскость
течения; б — линеаризованная физическая плоскость;
в — вспомогательная плоскость.
где у {х, t) определяется формой профиля и законом колебания,
а граничное условие на профиле в соответствии с (IV. 1.1) имеет
вид:
дФ
ΟΨ
dVu
dV.
дх
dt f^ дх ^^°
при О < д; < χ^, у = 0+;
О < X <Хс, у == О'
177
2) на границе каверны давление ρ = р^, поэтому,
учитывая (IV. 1.8), получим:
ф =
pvt
к
2
при Ха < X < I, Хс < X < h
где / — длина каверны.
3) на свободной поверхности давление постоянно и равно роо,
поэтому граничные условия имеют вид:
при —оо < д: < оо, у = Н,
где Η — глубина погружения профиля.
4) в соответствии со второй схемой М. Тулина давление
в следе каверны ρ = р^, поэтому условие на границе следа
Φ = О при / < д: < оо, ^ = 0+.
5) на большом удалении перед профилем вызванные скорости
и ускорения пропадают, следовательно,
F B, ί) == О при л: = —оо. (IV.3.2)
6) в дополнение к перечисленным выше граничным условиям
в точках Л и С (см. рис. IV.2, а) должно удовлетюряться условие
плавности схода струй, что эквивалентно условию Чаплыгина—
Жуковского о конечности скорости и непрерывности
распределения давления в этих точках. Таким образом, функция F {ζ)
должна быть ограничена в этих точках в каждый момент времени.
В дальнейшем под χ νί у будем понимать безразмерные
значения координат, отнесенные к Я. В этом случае Я = 1.
Линеаризованная физическая плоскость течения и граничные
условия показаны на рис. IV.2, б. Как видно из рисунка,
течение находится внутри многоугольника BAEFIDC. Преобразуем
внутреннюю область этого многоугольника с помощью интеграла
Кристоффеля—Шварца на нижнюю полуплоскость ζ так, чтобы
вершины многоугольника лежали на вещественной оси ξ.
Подобные преобразования были нами уже сделаны при
решении стационарных кавитационных задач в § 1 гл. ΠΙ и
определялись формулой (ИГ. 1.26). Учитывая, что в рассматриваемом
случае используются безразмерные координаты, напишем
формулу, устанавливающую соответствие плоскостей ζ {χ, у) и ζ (I, η)
следующим образом:
Параметрическая плоскость ζ и соответствие точек плоскости
дано на рис. IV.2, е.
178
Задача сводится теперь к определению функции F (ζ),
регулярной во всей нижней полуплоскости ζ (за исключением точки
ζ = 0) и удовлетворяющей следующим граничным условиям:
1) Φ = О ■ при —оо < 1<—1е, η = О";
2) Φ = -^ при —ξ£ < ξ < - |л, η -= 0-; (IV.3.4)
δΦ
дг\
3) -^ = ^ηA. ί) при -Ел<1<1с. η = ο-
где Vrj (ξ, t) определяется с учетом формы профиля и закона
движения крыла;
4) Φ = ^ при 1с<1<Ы
5) Φ = О при |д < ξ < оо;
6) F (ζ) ограничена при ξ = —|^, ξ = Ig.
В верхней полуплоскости ζ в соответствии с принципом
аналитического продолжения
Следовательно,
Ref+ = Ф+ = —ReF- = — ф-;
ImF+ = ¥+==ImF- = ¥-.
дФ
Как следует из условия Коши—Римана, производная
дг\
связана с функцией Ψ интегральным соотношением
- Ψ (ξ, ί) = I -^ {ξ, t) dl - с (t), (IV.3.5)
где с (t) — постоянная интегрирования.
Таким образом, задача об определении потенциала ускорения
сводится к краевой задаче Римана—Гильберта для нижней
полуплоскости со смешанными краевыми условиями. Действительно,
на отрезке АС (см. рис. IV.2, е) границы полуплоскости задано
Im —,^ , что согласно (IV.3.5) равносильно заданию Im (ζ) =
= Ψ (ξ), на остальных отрезках задано Re F (ζ) = Φ (ξ). И здесь
может быть использована формула Келдыша—Седова (см. § 2
гл. II). Применение этой формулы было ранее рассмотрено при
решении стационарных кавитационных задач.
Функция F (ζ) ограничена вблизи концов отрезка (—ξ^, 1с)>
ζ
вблизи точки ξ = о ограничен интеграл J F (ζ) άζ.
о
Необходимо по заданным граничным условиям найти
потенциал ускорения во всей нижней полуплоскости ζ.
179
в § 2 гл. II уже указывалось, что есть несколько
разновидностей формулы Келдыша—Седова, которые определяются
условиями на концах отрезков вещественной оси.
В рассматриваемом случае функция F (ζ) ограничена на всех
ε
концах βκ. а вблизи концов Ьк ограничен интеграл J F (ζ) άζ.
о
Тогда в соответствии с (П.2.11) решение получит следующий вид:
оо
F(P = |£|)_U [/^М^Лт, (IV.3.6)
^^' Rb (ξ) πι J Ra (τ) (τ — ζ) ' ^ '
κοορ-
/ m / m
где R, = 1/ Π (ζ - ßj, 7?ь = у Π (ζ - bj; Ω,, Ь,
г ί;=1 Ύ k=l
динаты концов отрезков, имеющих мнимые граничные условия,
т. е. в рассматриваемом случае а^ = —ξ^, ξ^ί ^к = О·
В соответствии с (IV.3.6) получим:
/·
^@ „ι/ (S-y(s+y ^YlzMMM
функция g (τ) имеет следующие значения:
g- (τ) = О при —оо <1< ~1е,
g(T) = -|- при ^ξ^.<ξ<^ξ^; (IV.3.7)
g (τ) = —ΐψ при —Ια < ι < Ic;
δ'(τ)==-|- при ^c<I<Id;
g- (τ) = О при Ιο < ξ < оо.
Подставляя эти условия в (IV.3.6), получим:
Sc
F (ζ) = — T^(^"~^c)(g + y Г Ψ (τ, pTdT ^
"S J 1/(^-1с){^ + ^л)(^-й
κ 1/(?-У{? + ^л) Г Tdx
^ί
2 ш? J 1/(т;_у(т + у (τ-ξ)
+
+ Τ-- Щ J ΐ/(τ^|^)(τ + ^(τ-ζ) {IV.3.8)
Sc
180
После вычисления второго и третьего интегралов выражения
(IV.3.8) и преобразований получим
Sc
Ρ(ζ)
+
2πί
In
ζ + \
πζ
+ 2 In
ί
/(^-ад(^ + ?л)(^-Э
+
(IV.3.9)
Формула (IV.3.9) — общая для произвольного закона
неустановившегося движения; функция Ψ (τ, t) для каждого закона
колебания будет иметь свое выражение. Параметры ξ^ и ξ^ —
функции времени. В частном случае струйного обтекания (κ = 0)
F (ζ) определяется первым членом (IV.3.9).
В формулах (IV.3.9) абсциссы ξ^ и ξ^ известны. Они
определяются согласно (IV.3.3) по заданным значениям координат Ха
и Хс на физической плоскости течения. Величины же Ед и Ея
неизвестны, для их определения составим два дополнительных
условия.
В качестве первого дополнительного уравнения, связывающего
параметры ξ^ и Ед, можно использовать условие равенства
координат «двойных спиральных вихрей». Тогда, учитывая
формулы (IV.3.3), получим:
После преобразования найдем:
ξο + ?£ == In
1+Ь
1~1е
(IV.3.10)
(iv.a.u)
Второе дополнительное уравнение получаем исходя из
граничных условий (IV.3.2).
Точка F с координатой ζ (—1,0) в параметрической плоскости
соответствует аналогичной точке ζ (оо, 0) на физической плоскости.
Полагая поэтому в (IV.3.9) ζ = —1, F (—1) = О, получим:
6с
Ψ(τ,/)τ£ίτ κ
ί
1^(|с-т)(т + |л)A-Ьт)
4-2 In
УЗо-1с){1
2КA-Ыс)A-?л)
Ы + УA + 1с)(%р + 1а)
In
К(|£-ыс)A-;
-2/A4-1с)A+1лIп
;л)-КA-Ыс)(|я-Ы
К|р-|с-К|д-Цл
VlE + lc + VlE-U
(IV. 3.12)
181
Выражения (IV.3.9), (IV.3.11), (IV.3.12) позволяют получить
однозначное решение задачи.
Рассмотрим в качестве примера вертикальные гармонические
колебания кавитирующей пластинки ВС. Закон неустановившегося
движения при этом имеет вид
h{f)=^KeM, (IV.3.13)
где hfj — амплитуда колебапий; ω — угловая частота.
Учитывая угол атаки а, можно представить уравнение
траектории произвольной точки X пластины следуюш,им образом:
у(х, t)^—ax — h^i'^t. (IV.3.14)
Вертикальная составляюш,ая скорости находится по
формуле (IV.3.1):
Vy = — aV^ - jwtkieM^ (IV.3.15)
a ускорение Oy определяется путем дифференцирования (IV.3.15)
по времени:
Скорость и ускорение легко представить в виде
νς = -^ = -а - / -^ hoeM; (IV.3.16)
ау--^=--^кфМ. (IV.3.17)
оо со
На основании условия (IV. 1.12) находим, что
X
Принимая во внимание формулы (IV.3.17), получим:
X
— Ψ (д:, О = J -^ V'"' dx - с it), (IV.3.18)
о
а после интегрирования (IV.3.18)
Ψ (X, ί) == Й- ^'^'"'^ + ^ (^)- ί^^·^· ^^)
' оо
При переходе от физической Плоскости ζ к вспомогательной ζ
воспользуемся формулой (IV.3.3), в результате найдем:
Ψ(I, О = -^ V'-' [g-'";:' + ^) ] + '(О- (IV.3.20)
182
После подстановки (IV.3.14) в (IV.3.9) получим выражение
для потенциала ускорения F (ζ, t) при заданном законе
колебаний пластинки.
Коэффициент подъемной силы можно получить из выражения
для потенциала ускорения (IV. 1.8).
Действительно, если
Φ
то давление на внешней стороне контура
p^ — pVlO-^Pc..
Принимая во внимание, что давление в каверне постоянно
и равно рк, легко определить суммарное давление, действующее
на точку контура:
ρ — рк == — pVloO + Рсо — Рк
или
ρ-Ρκ = -ρνΐ(φ-^). (IV.3.21)
Интегрируя (IV.3.21) по контуру профиля, получим выражение
для суммарной силы, действующей на него:
Ρ = -1 J (р - Рк) ίίζ = -tpP„ J (φ - ^) dz,
"A "A
где Za, Zc— координаты точек отрыва каверны.
Проецируя силу Ρ на ось у, найдем подъемную силу
•«с
"А
И коэффициент подъемной силы
'Ά
где Ъ — длина хорды профиля.
Потенциал ускорения определим по формуле (IV.3.9).
Момент относительно передней кромки профиля
Μ
= —ρν^|(Φ γ)χάχ.
183
a коэффициент момента
"с
Cm = —ν? = шг Ι ι Φ Η-) Χ αχ.
pVlob" b^ } \ 2 /
Для определения потенциала ускорения Φ, а затем
гидродинамических коэффициентов Су и &„ необходимо предварительно
найти постоянную интегрирования с (t) в (IV.3.5). Рассматривая
гармонические колебания профиля, представим потенциал
ускорения и вызванные скорости в комплексной форме:
Φ = Φ (х, у) ei<^t; v^ = ϋχ {χ, у) еМ;
(IV.3.22)
Vy = Vy{x,y)ei<^t,
где Φ {χ, у); ν^ (χ, у); Vy (χ, у) — комплексные функции
координат, не зависящие от времени.
Тогда на основании (IV. 1.4), (IV. 1.2) и с учетом (IV.3.22)
после дифференцирования по времени получим
Исходя из граничного условия (IV.3.2) найдем, что при χ =
= —оо вызванная скорость ν — 0. Решая затем уравнение
(IV.3.23) относительно Vy на смоченной части профиля найдем
Хо
Vy, (X, y,t)=--e-jx^' J e/*^^ dx, (IV.3.24)
где Vy„ (x, y, t) — вертикальная составляющая скорости точки
профиля, имеющей абсциссу; Xf, = х/Ь; k = (шЬ)/^™.
Формула (IV.3.24) справедлива для любой точки профиля
и не зависит от пути интегрирования.
Для носика профиля Хд = О после интегрирования (IV.3.24)
по частям с учетом (IV.3.5) получим:
о
Vy„ (О, О, t) = —с (О -1- jk J β/'^*ψ {χ, t) dx, (IV.3.25)
где Vy @, 0, t) и Ψ (χ, t) определяются законом колебания
профиля и его формой. Функцию Ψ(λ:, t) находим из общего решения
задачи (IV.3.9) в предположении, что длина каверны велика.
184
Подставляя (IV.3.9) в (IV.3.25) и полагая, что длина каверны
велика, а амплитуды колебаний малы, после ряда
преобразований получим:
о
c{t) = —v,iO,0,t) + jk I е/*'
— со
У(т-|с)(т + |а)(т-|)
-6л
Здесь на основании приведенных выше допущений принято Ее =
= ξβ= оо. В случае установившегося движения полученные
выше решения совпадают с решением стационарной задачи,
изложенной в § 1 гл. III.
Глава V
ЧИСЛЕННЫЕ
МЕТОДЫ РАСЧЕТА
ПАРАМЕТРОВ
КАВИТАЦИОННЫХ ТЕЧЕНИЙ
§ 1. Применение метода конечных разностей
(метода сеток)
В связи с широким использованием ЭВМ для приближенных
вычислений появилась возможность решить ряд задач о кавита-
ционных течениях, не имеющих аналитических решений. Одним
из численных методов, применяемых при расчете кавитационных
течений, является метод конечных разностей. Для иллюстрации
применения этого метода рассмотрим осесимметричное кавита-
ционное обтекание тела по схеме с зеркалом в потоке,
ограниченном твердыми стенками (рис. V.1, а) [75].
Примем цилиндрическую систему координат {х, г), тогда
функция тока ψ и потенциал скорости φ будут связаны соотношениями
^ = J_^ = l/^; _^ = __L|!L==v„ (V.1.1)
дх г дг " дг г дх г» \ /
где Vx, Vr — проекции вектора скорости V на осях χ и г
соответственно. Направление вектора скорости составляет угол θ с осью г.
Удобно рассматривать задачу в безразмерном виде. Введем
относительные величины:
-' '■ . ν'— ■*^ · ν — ^'^ ·
л —гг' * —
где Vco — скорость однородного потока; ψ„ — функция тока
на границе AB (рис. V.1, а); φ^ — разность потенциалов между
точками Ε и D.
Тогда физическая плотность течения преобразуется так, как
указано на рис. V.1, б.
186
После подстановки (V.l.2) в (V.1.1) найдем:
1 дФ
а дх'
1 дф
1 ^^-Г·
α or'
or'
1 ^^V'
„ι "^ Γι
ол:'
(V.1.3)
1 и
где «^-^VOo—-. Так как функция тока равна объемному
расходу жидкости, то ^„ = -^ΗΨ„,
а =
Обычно при решении задачи основываются на уравнениях,
в которых функции φ и ψ связаны с независимыми переменными х.
ψ=ί; <Γ=ί
фЫ^^>-
том
ф=0 /^'' V^^^P»% 1"°
F ^1,,
f=0
Ψ=ί?
L.f^
Фг
φ
Рис. V.l. Осесимметричное кавитационное обтекание тела в потоке,
ограниченном твердыми стенками: а — физическая плоскость течения; б —
трансформированная плоскость.
плоскость симметрии; i — стенка трубы (ψ = ψ^); 2 — смоченная
поверхность. D — точка отрыва; Ε — критическая точка.
Г. Однако в этом случае возникают определенные трудности
при построении сетки вблизи криволинейных границ. Здесь
рассмотрим новую форму уравнений, в которых роли (φ, ψ) и {χ, г)
меняются.
На основании (V.1.1) легко получить соотношение
οφ οψ
дх дг
^Ф ^ _ ^/Т/2 I 1/84 _ ^1/2
Затем, определив χ и г и выполнив их дифференцирование по φ, ψ,
после преобразований получим:
дх
дψ ~
3ψ
дг
дх
~дг' .
дг _
6·ψ
дх
дг
dip
дφ
дх
(V.l.4)
187
Сопоставляя затем первое и четвертое, второе и третье
выражения (V.l.4) и учитывая (V.1.1), находим, что
дх 1 or
οψ г δφ '
дх _ дг _
Переходя к безразмерным величинам (V.l. 2) и опуская
промежуточные выкладки, получим:
α
дх'
дг'
дФ
οψ
Ух .
α-
дг'
дФ
дх'
^. (V.1.5)
Следуя работе [75], обозначим g· = (г')^ и г' =g'^^^. После
подстановки новых обозначений в выражения (V.l.5), найдем:
α
дх'
дФ
а dg
1 dg _ Ух _
2 ΟΨ У'2 '
дх' У'г
= -0-1/2
дψ
или
2gi/2 дФ
Из математики известно, что
g'@) ding (Φ)
у2
(V.l.6)
gm
дФ
(V.l.7)
dg
где §'(Ф)= оф ·
Продифференцируем первое из выражений (V.l.6) по Ψ, а
второе по Ф:
д^х' 1 0¾ . α 0¾ j,2 д^х'
о
α
ΟΦΟΨ
2 Οψ2 »
2ίΤ
1/2 Оф2
ΟΨΟΦ
02л;'
Исключая в этих уравнениях члены ^φβψ- > получим:
а2 a2g@) g2g(o)
g@) ОФ2 '^ οψ2 ^^
или
α'
_dg_
дФ
аФ V g J ' дψ^
Подставляя (V.1.7) в (V.1.8), напишем:
a'
d^lng . d^g
ОФ2
Οψ2
0.
(V.1.8)
(V.l.9)
188
Зная решение уравнения (V. 1.9) g· (Φ, Ψ), по приведенным ниже
выражениям легко найти значения V'x, V'r, V, θ и χ' в любой
точке. Получим формулы для определения этих величин.
Возведем в квадрат выражения (V.l.6) и сложим их левые и правые
части:
4 \дЧ ) '^ 4g \ дФ J ~~
Vj+Vr
1
уч у'2
Из (V.l. 10) можно определить V', Vx и V'y.
(V.l. 10)
а)
j
е
,-ϊ 1
1
'
\ψ
г
0
-t 'i
Л
1 Φ
Рис. V.2. Графическое представление метода конечных
разностей: а — элементы сетки; б — представление производных
через конечные разности.
Разделив левую часть второго выражения (V.l.6) на левую
часть первого выражения (V.l.6), найдем формулу для
определения Θ:
„ dg
tge =
ОФ
.1/2 dg
g·
οψ
Vr
v'x
Составив выражение для полного дифференциала
dx'--^
I dg
2α οψ
άΦ-
dg
2g дФ
dW,
iV.1.11)
(V.l. 12)
найдем абсциссу χ' путем интегрирования (V.l. 12).
Согласно методу конечных разностей (методу сеток) плоскость
течения разбивается взаимно перпендикулярными
параллельными линиями на прямоугольники (ячейки). Угловые точки
каждого прямоугольника называются узлами. В рассматриваемой
плоскости течения (Ф, Ψ) обозначено: расстояние между
параллельными вертикальными линиями сетки п, а расстояние между
горизонтальными линиями т (рис. V.2).
Смысл метода конечных разностей состоит в том, что при малых
значениях пит производные искомой функции в какой-либо
189
точке вычисляют приближенно, как разности значений функции
в соседних (сверху и снизу, слева и справа) точках, отнесенные
к соответствующим приращениям аргумента — центральные
разности.
Пусть функция / (х) представлена на рис. V.2, б. В
соответствии с [56] выразим ее первую и вторую производные через
центральные разности:
\ dx >— 2Δλ; ' V dx^ )o~ tSjc^ ^'i ^Ιϋ^Ι-ι),
где fi, /_i — значения функций в точках х^ + Δχ, х^ — Δχ
соответствен но.
1=1
t —'
ρ
Гф^«,-''«'^
η.
h
(Фу„~ф'*<х\
,, .^
S±
0
%
«
ίί
15
ίΟ
6^ г
J jo
7 U
/г
5
ί
β
iJ
9
iff
6/t
ff
5
. /ф.»^1 κ/ ^: фЛ г
у
off
1
^-^-^
UCK
'Ar
fT
\
./i-
Φ ¾
'«■i:(Ä)''f»f'
Рис. V.3. Разбивка трансформированной физической
плоскости на ячейки и граничные условия.
Φ,,_+4α^Ψ,
gQ-Ур Γ_^ν^
gp-Ψρ [(Φΐ/„-«
ρ
л2 + 4α2ψρ
3/2
В соответствии с [75] выразим частные производные,
входящие в (V. 1.9), через центральные разности. В качестве примера
рассмотрим точку с индексом О (рис. V.3):
\&ψ)ο~ίΐ[ (^2 й);
\ οψ2 jo — "^ (§2 + g'4 — 2gO);
(V.l.13)
190
Подставим второе и четвертое условие (V. 1.13) в уравнение
(V.l.9). В результате получим:
-^ (In gl + In g3-2 In go) + -^ (g2 + ^4- 2Ы - 0.
После преобразований найдем:
«'-ί ln-^+g,-fg,~2go-0. (V.1.14)
Обозначая левую часть (V.1.14) через Х^, легко определить
так называемые коэффициенты влияния:
(V.l. 15)
где
^4 = ^2+^4; gl, 3 = gigs-
Уравнения (V.1.14) составляют для каждого узла.
При решении задачи необходимо выписать столько уравнений
типа (V.l. 14), сколько внутренних точек (узлов) содержит
рассматриваемая область изменения переменных Φ и Ψ, разделенная
сеткой.
Присоединяя к этим выражениям еще зависимости,
полученные при удовлетворении граничным условиям, можно записать
систему алгебраических уравнений, определяющую значения
искомой функции в узлах сетки. Таким образом, в случае применения
метода конечных разностей интегрирование системы
дифференциальных уравнений сводится к решению системы алгебраических
уравнений. Точность решения зависит от размеров сетки: чем
гуще сетка, тем точнее решение.
Однако полученные выше уравнения нелинейны, и поэтому
их решение можно получить методом итерации (последовательных
приближений) Гаусса—Зейделя, смысл которого состоит в
следующем. В начале процесса итерации задаются значениями g во всех
узлах сетки. Затем, обозначая индексом i значения в узле после
i-й итерации, мы повторяем операцию для каждой точки по
формуле
^έ+' = ^έ + ω(-Χο)'·/(^)'·.
где Χς, — частное значение левой части уравнения (V.l. 14) в
какой-либо момент итерационного процесса; ω — выбранный
фактор релаксации.
191
Для составления системы алгебраических уравнений
предположим, что площадь прямоугольника на безразмерной
физической плоскости (Ψ, Ф) разбита на а-Ь ячейки, причем по
вертикали (в столбце) есть а ячеек, а по горизонтали (в строчке) —
b ячеек. Тогда общее число узловых точек равно /г = (й+1)х
Х(Ь+1). Нумерация узловых точек принята в соответствии со
схемой на рис. V.3.
Каберна
]]
^8=90"
Вц^^О
Диск ^"Р^Р"-
Рис. V.4. К выводу граничных условий.
Принимая центральную точку прямоугольника за исходную,
составим систему алгебраических уравнений:
1) точка О
9 '" I
а^—т In
gigs
2) точка /
3) точка 2
4) точка 3
а'
т'^
In
εΐ
α^—5- In
g^e
a"
In
gl
gogii
+ ί^2 + ί^4-2^0 = 0;
?e + g7- 2g3 = 0
(V.l. 16)
и т. д.
Рассмотрим теперь значения функции g на границах области
ABCDEFA плоскости (Ф, Ψ): на стенке AB
г' = -^-=1 и gr=r'2=.l; (V.l.17)
на оси симметрии потока χ на участке EF
г' =0 я g = Q. (V.l. 18)
На участке DE, соответствующем смоченной поверхности тела,
граничные условия зависят от его формы.
Рассмотрим два тела: диск и сферу (рис. V.4).
192
Для диска θ == 90°, т. е. в (V.l.И) tg θ = сю, тогда должно
выполняться условие
^ = 0; (V.Li9)
для сферы, исходя из положений геометрии, легко получить
соотношения
Переходя к функции g, найдем:
tge = Ai2!l^^__iL_. (v.1.20)
Приравнивая (V.l.И) выражению (V.1.20), после
преобразований получим граничные условия для сферы:
дФ а \cos^Gd ^) δΨ' {V.l.Al)
Производные, входящие в (V.1.21), дают возможность
составить следующие уравнения для узла О на границе:
Ш= ^ [8^« - й. - 7g. + 2 (-^)' Ш (if)];
(#)«--δτ (δ«· - ft - 2& - 3g,)
ИЛИ
(ж)о-=ж(-^з + Й1+.2ё^,4-ЗЫ. (ν.1:22)
Подставляя затем производные (V.l.22) в (V. 1.19) и (V. 1.21),
после преобразований получим граничное условие на поверхности
тела DE:
для диска
8g.-gio-'7go + 2(^yin(^)-^0; (V.1.23)
для сферы
^{6g,~g,^2g,-^3go)^~(-^~-g)
X ^ [Sg. - ^.0 -7^0 + 2 (ψγ in (Ä)].. (V.1.24)
193
На участке DC (см. рис. V.3), соответствующем границе
каверны, число кавитации определяется по формуле
""^iv^y-^ илих=(^:у--1.
принимая во внимание (V.l. 10), получим граничное условие
яа поверхности каверны
"-тш+тг-^· <v.,.25,
где gO — значение функции g в точке О на границе каверны.
После подстановки (V.l.22) в (V.l.25), найдем:
+ {i[8..-i„-7,. + 2(^/.n(^)]}y - I.
Известно, что в схеме с зеркалом (Рябушинского) каверна
симметрична относительно вертикальной оси ВС (см. рис. V.3),
положение которой необходимо найти. Это приводит к следующему
соотношению значений функции g в точках Τ (см. рис. V.3), R и S:
Bc+l)gr = 4cgs + il-2c)g,i.
Значение с получается для каждой итерации.
Если рассматривать границу AF перед телом на таком
расстоянии, где поток заведомо однородный, то граничное условие
определяется выражением g =Ψ· Однако для того чтобы уменьшить
объем вычислений, границу Л^ устанавливают там, где еще
возможны некоторые возмущения потока.
В связи с этим в [75] на основании изучения различных ана-,
дитических решений для осесимметричных неотрывных
обтеканий простых тел для двух точек Ρ и Q, принадлежащих линиям
тока, получено соотношение
gp-Ψρ ~\ (Φν/co - nf + 4aWp ) '
которое следует считать точным при условии, что в точках Ρ и Q
перед телом выполняется неравенство {gq — Ψρ) С Ψρ· Это
условие допускает небольшие возмущения однородного потока
перед телом.
Таким образом, окончательно решение задачи сводится к
совместному решению системы уравнений (V.l. 16) и уравнений,
характеризующих граничные условия (V.l. 17)—(V.1.19),,(V. 1.21),
или (V.1.26)—(V.1.28).
На рис. V.5.—V.9 приведены результаты численных расчетов
по предлагаемой ■ выше теории для диска, имеющего радиус С
194
''""~~-'^. ν.=0,δ
0,2 ОЛ 0,6 0,6 1
r/C
O,m5
fo,8W
^Ο,Βδδ
0,650
0,625
Ο,Β
0,6
0,2
О
-0,2
-0,^
Рис. V.5. Зависимость
распределения
коэффициента давлений Ср по
смоченной поверхности
диска для и = 0,3 и κ =
= 0,7 от г/С.
Ώ —экспериментальные
данные [116].
30 Н/С
Рис. V.6. Зависимость функции
коэффициента сопротивления Сх A -|- и) для
диска от отношения Н/С при различных
значениях числа кавитации κ.
О
экспериментальные данные Рейхардта
[113], [114].
(с/ву
0,Ш5
О 0,1 0,2 0,J ОЛ 0,5 0.6 X
Рис. V.7. Сравнение расчетных и
экспериментальных зависимостей
коэффициента сопротивления от
числа кавитации.
О — данные, полученные согласно
рассматриваемой теории для диска
при Я/С=со; данные [107];
данные [109].
C/l
0,7
0,6
0,5
0,4
О, J
0,2
0,1
О 0,1 0,2 Ο,δ D,'t 0,5 0,6 κ
-
- 4 .
" /^
^ ι
у
/ ,
/Α
т\
,/ ΐοΐ с=|
I II L
V ό>/,
/щ
/ж\
'&// / /
vi/T /
γ/ ' I
Ί
<=»! ^.
u-S\ sj-
1
1
0,2 0,3 0,4 0,5 Ο,Β 7ί
Рис. V.8. Зависимость параметра
ширины (С/BY от числа кавитации κ
при различных значениях Н/С.
— ·—·—результаты, полученные
согласно рассматриваемой теории;
D данные [114]; О
—данные [116]; — — — Δ— — —данные
[107].
Рис. V.9. Зависимость параметра
длины C/L от числа кавитации κ при
различных значениях Н/С.
— — — результаты, полученные
согласно рассматриваемой теории;
D — результаты [114]; Δ · ■
результаты [116]; О результаты
[107].
195
На рис. V.5 дана зависимость распределения коэффициента дав-
ления С„ = 5— или, что то же, С„== 1 — -r^j— 1 по смо-
pVJ, \v^ J
2
ченной поверхности диска для двух значений числа кавитации
κ = 0,3 и κ = 0,7, а также приведены экспериментальные данные
при κ == 0,24 [116]. Как видно, число кавитации слабо влияет
на картину распределения коэффициента давления, а совпадение
с экспериментальными данными вполне удовлетворительное.
На рис. V.6 даны зависимости С^ A + κ) от отношения HI С
для диска при различных значениях чисел кавитации κ. Эти
результаты точно совпадают с экспериментальными данными
[114].
На рис. V.7 приведена зависимость Сх A + κ) от числа
кавитации κ для диска при HIC — оо, рассчитанная по данной теории;
и дано сравнение с результатами работ [107], [109], анарис. V.8—
V.9 — зависимости параметров ширины (С/В)^ и длины C/L —
в функции κ при различных отношениях Н/С.
В [75] приведены аналогичные результаты для сферы, из
которых следует, что распределение коэффициента давления по
смоченной поверхности мало зависит от κ, за исключением района
точки отрыва каверны.
Что же касается Οχ A + κ), то здесь расхождение между
теоретическими и экспериментальными результатами значительно
больше расхождения этих данных, полученных для диска.
Экспериментальные данные о сопротивлении лежат значительно ниже
соответствующих теоретических кривых.
§ 2. Применение метода вихревых особенностей
для расчета плоских кавитационных течений.
Численное решение интегральных уравнений
с помощью метода последовательных приближений
В гл. II и III были рассмотрены методы решения плоских задач
о кавитационном обтекании тел, основанные на классической
теории струй идеальной жидкости и использовании аппарата
теории функции комплексного переменного применительно к
различным схемам, имитирующим течение в конце каверны. Однако
этот метод пригоден главным образом для решения задач об
обтекании тел, имеющих острые (срывные) кромки. Поэтому появилась
необходимость в разработке универсального метода, пригодного
для расчета характеристик профилей произвольной формы (в том
числе и гладких, имеющих непрерывную касательную) без каких-
либо ограничений, обусловленных формой профиля и формой
замыкания в конце каверны.
Ниже рассматривается метод вихревых особенностей для
решения плоских кавитационных задач, в котором использован
196.
способ последовательных приближений [6]. Ранее в § 2 гл. II
указывалось, что в методе вихревых особенностей обтекание
сложного контура тело — каверна можно определить путем
наложения на основной поступательный поток возмущенного потока
от системы вихрей неизвестной интенсивности у E), непрерывно
распределенных на сложном контуре К. Контур К состоит из.
части контура, свободного от кавитации Κι, границ каверны Г
и некоторого замыкателя /Сг (рис. V.10). Неизвестная
интенсивность у (S) определяется согласно (II.2.16) и (II.2.17) двумя ин>
Рис. V.iO. Применение метода вихревых особенностей для расчета
плоских кавитационных течений.
тегральными уравнениями, из которых первое составлено для
нормальной составляющей скорости, а второе — для касательной.
Перепишем эти уравнения
1 Г COS{r,t) ,с\ JC 1 1 Г COS(r,t) -ел JC I
Kl Кг
+ ^ Ι '"' ^r' ^^ dS = ~ Fco Sin τ (Si); (V.2.1)
г
ΥEι) =4- J^*i4^TE)dS^4- J^HLÖ •yiS)dS +
+
Ук Г sin ()
η J ■ г
r,i)
ii5 + 2VeoCOSTEi).
(V.2.2)
Выражения (V.2.1), (V.2.2) представляют собой интегральные
уравнения Фредгольма первого и второго рода соответственно.
В случае решения прямой задачи выражения (V.2.1), (V.2.2)
рассматриваются как линейные интегральные уравнения
относительно неизвестной интенсивности вихревой линии у. Eί). При
1W
Необходимости определения координат контура К решается
обратная задача, в этом случае (V.2.1) и (V.2.2) рассматриваются
как нелинейные интегральные уравнения.
Любое из приведенных уравнений или их комбинацию можно
использовать для решения кавитационной задачи. При этом
(V.2.1) и (V.2.2) следует рассматривать как интегральные
уравнения смешанного типа: в точках, лежащих на контурах Κι и iCg.
искомой величиной является функция γ (Si), относительно
которой интегральные уравнения линейны.
В точках, лежащих на границе каверны Г, интегральные
уравнения становятся нелинейными относительно искомых значений
координат границ каверны. Уравнения (V.2.1) и (V.2.2) могут
быть переписаны в безразмерном виде:
2π
φ у (S) F^ (Si, 5) dS == — sin τ (Si); (V.2.3)
к
yiS,)^2coST(S^)-}-~§yiS)FASuS}dS, (V.2.4)
где
F,iS„S)=^^^; F,(Si.S) = i5i^; y(S)^^
V.
Выражение (V.2.4) представляет собой интегральное
уравнение Фредгольма второго рода, оно используется для нахождения
неизвестной у (Sj).
При определении границы каверны исБользуют (V.2.3), в
котором вихревая интенсивность на границе каверны считается
заданной. Для решения применяют метод итерации
(последовательных приближений). Задаваясь в нулевом приближении какой-либо
зависимостью угла τ от координаты S^, можно путем обычного
интегрирования найти форму каверны — нулевого приближения.
Зная форму каверны, легко рассчитать значение функции Fg (Si, S)
для любой точки контура. Вычисляя интеграл в левой части ра-
Ьенства, получим значение τ для следующего приближения.
Для вычислений .исходные функции у (S) и τ (S) должны быть
каким-то образом аппроксимированы, причем выбор
аппроксимации влияет на точность и время расчета. Построив исходный
контур из (V.2.4) находим функцию у (S), характеризующую
распределение"' скоростей по его поверхности. Интенсивность
У (S) удобно определять методом последовательных приближений,
полагая, например, в первом приближении γE) = €08τ. Это
198
значение подставляют затем в правую часть выражения (V.2.4)
и вновь определяют γ E) в первом приближении.
Отметим следующее: так как искомая граница каверны в
нулевом приближении задана неточно, то и скорость, определенная
по расчету, будет переменной по длине каверны. Поэтому в
дальнейшем надо изменить форму каверны так, чтобы на границе
каверны было постоянное распределение скоростей. Для этого
необходимо задать значение скорости V^ на границе каверны;
она может быть принята равной скорости в точке схода.
Распределение скоростей на смоченной части контура остается
пока прежним. Подставив в (V.2.3) полученную из предыдущего
приближения зависимость у E) для смоченного контура, а также
выбранное значение V^, найдем τ E), т. е. ординаты границ
каверны в первом приближении. Пользуясь этими значениями τ (S),
можно снова рассчитать распределение скорости по
полученному контуру.
После этого процесс уточнения координат границ каверны
должен быть продолжен. В случае обтекания тела с острыми
кромками кривизна каверны в точках схода стремится к
бесконечности. Это обстоятельство необходимо учитывать при выборе
аппроксимации формы границы каверны вблизи точки схода.
Так, например [6], вблизи точки схода каверна
аппроксимировалась двояко:
у ^ ах"" + Ьх+ с (V.2.5)
и
у = [а(х~М) + Ь]{х~ М)У^ + уо. (V.2.6)
где Μ — координата точки схода; а, Ь, с — постоянные.
В (V.2.6) учтена бесконечная кривизна в точках отрыва.
При расчетах по формуле (V.2.6) процесс сходится быстрее и
результаты более точные. В контрольных расчетах оказалось
достаточным сделать три приближения, чтобы скорость на границе
каверны отличалась от постоянной не более чем на 1,5—2%.
Для иллюстрации изложенного выше метода ниже рассмотрим
пример расчета обтекания клина (единичной длины) по схеме с
зеркалом при произвольном числе кавитации (рис. V.ll).
Выбранные нулевые^риближения для γ (χ) и ~- (х) = tg τ
даны на рис. V.12. Функция у {х) аппроксимировалась: на клине ■—
наклонной прямой, на границе каверны — постоянной величиной;
функция -J- {х) = tg τ аппроксимировалась: на клине —
постоянной величиной, на границе каверны (до половины длины
каверны) — отрезком наклонной прямой.
199
Выберем вихревую систему так, как показано на рис. V.11.
Будем искать вызванную скорость в некоторой произвольной
точке контура Si с координатой χ от непрерывно расположенных
вихревых особенностей контура клин—каверны—клин.
Вследствие симметрии контура относительно продольной оси
(например, точки 5 и S') введем в рассмотрение два радиуса-вектора г^
и /-2, направленных от точек, содержащих вихревые особенности
(S и S') к точке Si. Прежде чем преобразовывать уравнения (V.2.3)
и (V.2.4) к форме, удобной для вычислений, получим некоторые
вспомогательные формулы. Обозначая dS^ и dS дифференциалы
Рис. V.11. К решению задачи о кавитационном обтекании клина по схеме
Рябушинского с помощью метода вихревых особенностей.
дуг контура вблизи точек Si и S соответственно (на основании
известной из математики формулы) и учитывая обозначение на
рис. V.11, получим
Первая из этих формул позволяет связать уравнение контура
у {х) с τ — углом между касательной к контуру в точке S^ и
направлением скорости потока V^ или в рассматриваемом случае
с осью X. На основании рис. V.U
dx dy dy dx dy
dx
dSl
200
Учитывая (V.2.7), напишем:
dy
dx
COS τ.
(V.2.8)
cos τ =
У'Л^У '
dSi
sin τ ==
dy
dx
F>+(ir
(V.2.9)
На основании рис. V. 11, принимая во внимание положения
геометрии, найдем:
sin (λ-1, t) = cos α cos τ (tg α — tg τ);
cos (r^t) = cos α cos τ A + tg α tg τ);
sin (λ-2, 0 = cos β cos τ (tg β — tg τ);
cos (λ-2, 0 = cos β cos τ A + tg β tg τ),
где α = /. Γι, χ; β = /. r^, χ.
Кроме того, исходя из рассмотрения треугольников (см.
рис. V.11) AS Si и AS'Si получим
cos« =^^::::^: cos β = ^^:=^-. (V.2.11)
'Ί ''a
/-1-= ^^^^; /-¾ = ^^^. (V.2.12)
^ COS α ^ COS β ^^ '
Принимая во внимание условие симметрии относительно оси
„ sin (/·, /) cos (г, t)
Ox, подынтегральные выражения ^^—- и ^^—-, входящие
в (V.2.3) и (V.2.4), перепишем в виде:
sin (t-j, t) _ sin (γι, t) sin (/-g, ^)
COS(/·). t) ^ COS (/-1, 0 COS (/-g, 0 ,y 2 134
/■ /Ί /'s
Тогда с учетом формул (V.2.9), (V.2. И)—(V.2.13) интегральные
уравнения (V.2.3) и (V.2.4) перепишем в виде
у(х) = , X
X
2 -4- ^ j lcos2a(tga — tg τ) -4- cos^ß (tg β — tg τ)] χ
А
D
ί'' W = - i· ί [COS'« A + tg α tg τ) +
Α
+ cos^ β A + tg β tg τ)] у (ξ) *^'^t!ξ '^^ dt ^ (V.2.15)
где ί/' (χ) = ^
201
Уравнения (V.2.14) и (V.2.15) решаются с помощью метода
последовательных приближений, при этом интегралы, входящие
в эти уравнения, заменяются конечными суммами по формуле
численного интегрирования и правилу трапеции с переменным
шагом.
Изложенный выше случай кавитационного обтекания клина по
схеме с зеркалом был рассчитан на ЭВМ (рис. V.12 и V.13^) [6].
^.
^/J
'
lx_i
γ ω'
~^2
Клин
■^ ^
rfi;
ι
%^^
1
^
2 / и/г 0
1,0
0,5
Рис. V.12. Первое A) и пятое (9)
приближение расчетов для функций у (х) и
dy
dx
(χ).
dy
dx
Οχ
1.5
V
0,5
y;iOx
ill
X
,y
Οχ
0
0,5
W
Рис. V.13. Результаты
ленных расчетов.
у
у = -,
X -
# — расчетные точки;
О—экспериментальные данные
М. Плессета и П. Шеффера.
b , ί^ —длина и ширина
каверны
§ 3. Применение метода
вихревых особенностей
для расчета осесимметричного обтекания тела
в режиме развитой кавитации
Рассмотрим осесимметричное кавитационное о 7екание твердого
тела произвольной формы. Для схематизации течения в хвосте
каверны примем обобщенную схему Рябушинского, согласно
которой каверна замыкается на фиктивное тело (рис. V.14). При
решении задачи необходимо найти форму каверны и распределение
скоростей на поверхности тела, свободной от каверны [2].
По аналогии с изложенным в § 2 будем рассматривать
обтекание комплекса тело—каверна как обтекание единого тела.
Распределяя по поверхности единого тела вихревой слой и
используя закон Био и Савара, можно составить два интегральных
соотношения, связывающих форму контура меридионального
сечения тела с интенсивностью вихревых колец.
^ Плессет М., Шеффер П. Кавитационное сопротивление плоских и
пространственных тел. — ЖПФ, 1949, т. 20, № 1.
202
При решении задачи примем прямоугольную систему
координат хОу с началом, расположенным посредине длины тела на
оси его симметрии. Положительные направления осей указаны
на рис. V. 14. Будем искать скорость У^, в некоторой точке
^ί i^i У)> вызванную продольным обтеканием тела потоком
жидкости со скоростью Усо и вихревыми особенностями,
расположенными на поверхности тела. Примем текущие координаты
элементарной вихревой особенности в некоторой точке S — ξ, η, ζ.
Рис. V.14. Осесимметричное кавитационное обтекание
твердого тела произвольной формы (обобщенная схема
Рябушинского).
— · —· — граница каверны.
Тогда вектор скорости Vsi в некоторой точке Si получает
следующий вид:
Vs. =Veo -f Vs., (V.3.1)
где Vs. — вектор скорости, вызванной вихревым слоем.
Для составления уравнений примем вспомогательную
прямоугольную систему координат tSxti с началом в точке S^ поверх-
ндсти тела так, чтобы ось Sii6bma касательна меридиональному
сечению тела и направлена вниз по потоку, а ось S^n
перпендикулярна оси S^t, как показано на рис. V.15, б.
Составим выражения для нормальной и касательной
составляющих скоростей Vs^n и Vs^i- Предварительно обозначим угол
между осью Si ί и направлением скорости Vc^, совпадающим с осью
Ох, через τ. Тогда (V.3.1) перепишем так:
Vs.n = Vccii -|- Vs.n;
Vs.i=V„„t + Vs.t, (V.3.2)
где η, t — единичные векторы в системе координат nSi^.
Скалярные произведения векторов, входящие в {V.3.2),
получают вид
Vooii = Fco cos (Fco, η) = Fco sin τ;
Vcot = Fco cos (fC t) = Fco cos τ. (V.3.3)
203
Рис. V.15. К выводу формул нормальной и тангенциальной
составляющих скорости (V.3.5), (V.3.6).
204-
Скорость dV|,, вызванная элементом вихревого кольца dS
в точке Si, находится на основании уравнения Био и Савара:
^^^'-~is—w~' (^-^-^^
где R — радиус-вектор, проведенный из точки S^ к элементу dS
вихревого кольца; γ — неизвестная интенсивность вихревого
кольца.
Принимая во внимание, что на теле расположен вихревой
слой переменной по длине интенсивности, представим выражения
для нормальной и касательной составляющих скорости в точке Si
с учетом {V.3.4) в виде:
Vs.„=FeoSinT + -^ f γ(ξ)|
ι_
2 2π -
R xdSn
L **
2
χ
χ
yi~j-r?dl; (V.3.5)
Vs,t =^ V^ cos τ-^-^ j γ(|)|
i_
2 2π
R xdSt
L ^ ■
2
X
X
Yi^r'Ui. (V.3.6)
Как следует из рис. V.15, радиус-вектор R связан с
координатами «точки 5i {χ, у) и точки S (ξ, η) соотношениями:
R= (χ —|)i + (r2COs\l5 —ricosq)) j +
-f (Г2 sin ψ — Γι sin φ) k; (V.3.7)
R' = {x- gf + (/-1 + r^f ~ 2Г1Г2 [ 1 4- cos (Ψ ~ φ)];
i?^ = (χ - Sf + r! + ri - 2ri/-2 cos (ψ - φ). (V.3.8)
Элемент dS вихревого кольца:
dS = Γι cos φ ίίφ| -f Г1 sin φ ίίφ1(, (V.3.9)
где i, J, к—единичные векторы — орты.
Для преобразования числителей подынтегральных выражений
в (V.3.5)—(V.3.6) необходимо воспользоваться формулой
смешанного векторного произведения, предварительно определив вхо-
дящ,ие в него проекции векторов Rh dS на координатные оси и
направляющ,ие косинусы. Для преобразования знаменателей
в (V.3.5)—(V.3.6) используется замена переменной по формуле
ψ _φ = π -Ь 2а [33].
205
Входящие в него проекции векторов R и dS на координатные
оси находятся по формулам
Rx = {x—^; /?ί^ = Γ2 8Ϊηψ —Γιδΐπφ;
R^ = —Гг cos ψ -}- Γι cos φ;
dS^ = О, dSy = Γι cos φίίφ; {V.3.10)
dS^ = Γι sin φίίφ.
Окончательно после промежуточных преобразований получим
следующие выражения.
Нормальная составляющая скорости
2
y,.„=V.sinx+-^ ],(ξ)/|±^
2
2
£
2
2
Χ
^^ ([''Λ + '-2'-2 + (^ - Ι)] £ (k^) ~ 2 [/-2^2 + (^ - ξ)] 4
Λ2 >^
Xl£(fe2)-fe'2x(fe2)]
>< k'^n.~iv+ir, + rl^ ^^· (^-^-^^)
Касательная составляющая скорости
j_
2
Fs.,=l/.coST + -^ j γ(ξ)|/|±^
2
2 Χ
^2 I [/-2 - (χ - I) /-2 + /-1 ] £ ik") + ^ ['-2 - (^ - ^ '■2] X
X
fe'2v^(x-|J + (ri + f,).2
(V.3.12)
где Ε (k^), К (k^) — полные эллиптические интегралы I и II рода.
Так как в рассматриваемом случае обтекания кривизна
каверны в продольном направлении мала, то для упрощения задачи
в дальнейшем положим ή^ = r'-i ^ 0.
Кроме того, для облегчения расчетов в дальнейшем будем
рассматривать безразмерные величины: скорости, отнесенные
к Усо, линейные координаты — к половине длины единого
тела Z/2.
Для определения неизвестной интенсивности вихрей γ (ξ),
входящих в {V.3.11) и {V.3.12) по аналогии с изложенным в § 2
этой главы воспользуемся двумя положениями: 1) условием не-
206
протекания, т. е. равенством нулю суммы нормальных
составляющих скоростей к контуру тело—каверна; 2) известным из
гидромеханики положением о том, что в каждой точке замкнутого
контура интенсивность вихревого слоя равна модулю касательной
скорости течения в этой точке. В результате после преобразования
(V.3.11) и {V.3.12) с учетом принятых допущений найдем:
1
-ϊ=4^ ί ^[i<ik')S, + E{k^)S,]d^; (V.3.13>
_1
1
YW= йЬ ^^[^<ik')Rl-l·E{kηR,]dξ + cos(τ, X), (V.3.14>
где
51=2[г2Г2 + (л:-5)];
52 =-- -^ 1^4^1^2 -f r/^ + {X - g)] - 2 [Г2Г2 + (X - ξ)]);
Ri=2[{x-l)r'2-r2]·,
R2 -- η^ {2 [Г2 - (χ _ ξ) Г2] - /г' [Г2 - (ЛГ - ξ) Г2 + Γζ]) ;
^'2=1- F; k^ =
(X-gJ+(ri + f2)^'
Гп =
COS φ ' ^ COS ψ
γ (ξ) — значение вихревой интенсивности, отнесенное к величине
скорости на бесконечности; τ — угол между касательной t
к контуру меридионального сечения тела в точке с абсциссой χ
и вектором Voo; χ, у, ξ, η —координаты фиксированной и
произвольной точек контура меридионального сечения тела.
Приведенные соотношения обычно используют для
определения вызванных скоростей на контуре меридионального сечения
твердого тела при его безотрывном обтекании. Выражение {V.3.13)
есть линейное интегральное уравнение Фредгольма первого рода,
а {V.3.14) — уравнение Фредгольма второго рода относительно
вихревой интенсивности.
Как уже указывалось, при решении плоской кавитационной
задачи (V.3.13) и {V.3.14) следует рассматривать как интегродиф-
ференциальные уравнения смешанного типа.
На смоченных частях контура, свободных от кавитации,
искомой величиной является у, и {V.3.13), (V.3.14) следует
рассматривать как упомянутые выше уравнения Фредгольма.
207
На границах каверны известна величина у, которая постоянна
в силу постоянства давления в каверне, а {V.3.13) и (V.3.14)
становятся нелинейными интегродифференциальными уравнениями
для определения формы меридионального сечения границы
каверны у = / (л:).
Для исследования кривизны контура меридионального
сечения каверны вблизи точки отрыва в работе [2] после ряда
промежуточных преобразований уравнения (V.3.13) произведен ряд
оценок интегралов.
В системе координат х^О^у^ с началом в точке отрыва при учете
этих оценок выражение для кривизны меридионального сечения
каверны вблизи точки отрыва, равное ^ ^ , легко может быть
представлено в виде
^^1 ^ ^1 , I ^2¾ I . . . iV3 15)
где В^, В^ — некоторые постоянные.
Таким образом, при Xi —> О кривизна может обращаться в
бесконечность.
По приведенным выше формулам на ЭЦВМ были произведены
расчеты кавитационного обтекания двух тел: шара и конуса —
на основе схемы Рябушинского [2]. Была принята следующая
процедура вычислений. Сначала задавалась форма
меридионального сечения так называемой пробной границы каверны. Она
принималась простейшей: для шара — в виде двух отрезков
параллельных прямых, касающихся окружностей (меридиональных
■сечений основного и фиктивного шара); для конуса эти отрезки
соединялись с кромками оснований основного и фиктивного конусов
отрезками кривых, обеспечивающих непрерывность касательной
при переходе от отрезков прямых к сечениям конусов.
Далее по формуле {V.3.i4) в первом приближении определяется
7 на поверхности тела, свободной от кавитации. Так как скорость
на границе каверны постоянна, то на пробной границе каверны
7 = const.
Вычисленные значения у подставляют затем в {V.3.13),
которое становится нелинейным относительно функции у (х). Из
(V.3.13) у {х) находится методом последовательных приближений,
путем последовательной подстановки в правую часть этого
выражения значений координат пробной границы каверны и т. д.
Определенные таким образом координаты границы каверны
использовались вновь для вычисления у по {V.3.14) и т. д.
При вычислениях на частях тела, свободных от кавитации,
была использована кусочно-постоянная аппроксимация функции
у1у. На меридиональном сечении границ каверны полагалось
у = const, а у {х) аппроксимировалось кусочно-линейной
зависимостью за исключением участков, непосредственно примыкающих
к точкам отрыва, где использовалась аппроксимация (V.3.15),
208
которая оказалась весьма удобной для определения положения
точек отрыва каверны от шара.
Так же, как и в случае плоского кавитационного обтекания
гладкого контура, при произвольном задании положения точек
отрыва кривизна меридионального сечения границы каверны
в этой точке, вообще говоря, бесконечно большая и при заданном
режиме течения, определяемом числом кавитации, становится
конечной только в одной точке.
Условие конечности кривизны сечения каверны для
определения положения точки отрыва (точки «гладкого» отрыва), сформу-
/P/Sr
0,50
0,25
/ о
?
о У^
^
Р=^5'
0.1
0,2
0,50
0,25
О
,
(
-^
2
9-—^"^
7
Шар
0,1
0.2
Рис. V. 16. Зависимость
относительного радиуса Rib от числа
кавитации κ.
/ — по формулам § 3 гл. V, шар;
О — эксперимент, шар [72 ]; 2 — по
формулам § 3 гл. V, коиус; ·— по
формулам § 1 гл. V.
Рис. V.17. Зависимость
коэффициента сопротивления Сх от
числа кавитации v..
1 — по формулам § 3 гл. V, шар;
2 — по формулам § 3 гл. V, конус;
3 — по формулам § 1 гл. V, шар;
9 — эксперимент, конус [72 ].
лированное Бриляуэном, использовано и при расчете обтекания
шара. Этой точке в данном случае соответствует равенство нулю
коэффициента В^ в {V.3.15).
Сначала положение точки отрыва задается произвольно..
Если она оказывается впереди точки «гладкого» отрыва, то В^
имеет отрицательное значение, если сзади — то положительное,
и монотонно уменьшается до нуля по мере приближения к
искомому значению координат точки «гладкого» отрыва.
Результаты расчетов контролировались с помощью решения
«прямой» задачи, т. е. путем определения γ из уравнения {V.3.14).
Оказалось, что почти на всей границе каверны γ имеет постоянное
значение и только на небольших участках, примыкающих к
точкам отрыва, отклоняется на величину, не превышающую 2% этого
значения.
Время, затрачиваемое на расчеты с помощью ЭЦВМ, невелика
и составляет для одного режима обтекания (каверна заданной
длины) 10—15 мин. На рис. V.16 даны зависимости отношения
радиуса шара и радиуса основания конуса к половине ширины
каверны от числа кавитации, полученные на основании
расчетов по формулам (V.3.13) и (V.3.14). Для сравнения приведены
209·
Pu,m^
экспериментальные данные Л. А. Эпштейна и расчетные данные,
лолученные по формулам § 1 этой главы [72].
Экспериментальные и расчетные данные для шара и конуса
удовлетворительно согласуются.
Результаты*расчетов для шара относились к обтеканию его
в трубе круглого поперечного сечения, а приведенные на
рис. V.16 данные получены путем
экстраполяции на условия обтекания шара
безграничным потоком.
На рис. V.17 приведены зависимости
коэффициента сопротивления шара и
конуса от числа кавитации.
Экспериментальные и расчетные зависимости для шара,
полученные по формулам (V.3.13) и
{V.3.14) также удовлетворительно
согласуются.
На рис. V.18 приведены
экспериментальные и расчетные данные о положении
точек отрыва каверны от поверхности
шара, определяемого углом β о
(отсчитываемым от передней критической точки) в
зависимости от числа кавитации. При
малых числах кавитации согласование
расчетных зависимостей с данными Л. А. Эпштейна можно считать
удовлетворительным. С ростом числа кавитации в эксперименте
заметно увеличение угла отрыва каверны, тогда как расчеты
показывают сравнительно слабое его увеличение.
ео
70
£0
in
J
1
I
ζ
Ό
0,1
к
о,г
Рис. V.18. Зависимость
угла β о от числа
кавитации κ.
/ — по формулам § 3 гл. V;
-2 — по формулам § 1 гл. V;
3 — эксперимент [72 ].
Глава VI
ИСКУССТВЕННАЯ
КАВИТАЦИЯ
§ 1. физические основы искусственной кавитации
Во введении уже было сказано о том, что развитые кавитацион-
ные течения можно получить, вдувая воздух или другой газ
в область разрежения за плохообтекаемым телом. При
экспериментальных исследованиях в качестве таких тел широко
используют простейшие тела: пластины, клинья, круглые цилиндры,
шары и конусы.
При многих экспериментальных исследованиях осесимметрич-
ных кавитационных течений в качестве тел (кавитаторов), за
которыми образуется каверна, приняты диски, сферические и
эллиптические головки. Эксперименты позволяют выявить ряд
особенностей кавитационных течений: таких, как нестационарность,
влияние весомости, а также установить зависимости между
расходами газа, числами кавитации и Фруда, коэффициентом
сопротивления воды и числами кавитации и т. д.
Каверна, образованная за диском, при определенных числах
Фруда имеет на большей части своей длины гладкую прозрачную
поверхность (рис. VI. 1). Однако это свойство существенно зависит
от степени турбулентности потока. При повышении
турбулентности потока (например, путем его искусственной турбулизации)
на поверхности каверны, образованной за диском, появляются
высокочастотные колебания — волны (рис. VI.2). На поверхности
сферических и эллиптических кавитаторов есть пограничный слой,
который вблизи точки отрыва каверны разрушается и служит
источником возмущения поверхности каверны. На небольшом
участке длины за точкой отрыва каверна имеет гладкую и
прозрачную поверхность течения. Однако сразу же за этой областью
появляется система поверхностных волн с амплитудой,
возрастающей вниз по потоку. Ряд исследователей предполагает, что эти
волны возникают вследствие роста неустойчивости отделенногс^
пограничного слоя кавитатора.
Эксперименты показывают, что для сглаживания поверхности
каверны необходимо обеспечить устойчивость ламинарного
211
Pu,m^
экспериментальные данные Л. А. Эпштейна и расчетные данные,
лолученные по формулам § 1 этой главы [72].
Экспериментальные и расчетные данные для шара и конуса
удовлетворительно согласуются.
Результаты*расчетов для шара относились к обтеканию его
в трубе круглого поперечного сечения, а приведенные на
рис. V.16 данные получены путем
экстраполяции на условия обтекания шара
безграничным потоком.
На рис. V.17 приведены зависимости
коэффициента сопротивления шара и
конуса от числа кавитации.
Экспериментальные и расчетные зависимости для шара,
полученные по формулам (V.3.13) и
(V.3.14) также удовлетворительно
согласуются.
На рис. V.18 приведены
экспериментальные и расчетные данные о положении
точек отрыва каверны от поверхности
шара, определяемого углом β о
(отсчитываемым от передней критической точки) в
зависимости от числа кавитации. При
малых числах кавитации согласование
расчетных зависимостей с данными Л. А. Эпштейна можно считать
удовлетворительным. С ростом числа кавитации в эксперименте
заметно увеличение угла отрыва каверны, тогда как расчеты
показывают сравнительно слабое его увеличение.
ео
70
£0
in
J
1
I
ζ
Ό
0,1
о, г
к
Рис. V.18. Зависимость
угла β о от числа
кавитации κ.
J — по формулам ? 3 гл. V;
-2 — по формулам § 1 гл. V;
3 — эксперимент [72 ].
Глава VI
ИСКУССТВЕННАЯ
КАВИТАЦИЯ
§ 1. физические основы искусственной кавитации
Во введении уже было сказано о том, что развитые кавитацион-
ные течения можно получить, вдувая воздух или другой газ
в область разрежения за плохообтекаемым телом. При
экспериментальных исследованиях в качестве таких тел широко
используют простейшие тела: пластины, клинья, круглые цилиндры,
шары и конусы.
При многих экспериментальных исследованиях осесимметрич-
ных кавитационных течений в качестве тел (кавитаторов), за
которыми образуется каверна, приняты диски, сферические и
эллиптические головки. Эксперименты позволяют выявить ряд
особенностей кавитационных течений: таких, как нестационарность,
влияние весомости, а также установить зависимости между
расходами газа, числами кавитации и Фруда, коэффициентом
сопротивления воды и числами кавитации и т. д.
Каверна, образованная за диском, при определенных числах
Фруда имеет на большей части своей длины гладкую прозрачную
поверхность (рис. VI. 1). Однако это свойство существенно зависит
от степени турбулентности потока. При повышении
турбулентности потока (например, путем его искусственной турбулизации)
на поверхности каверны, образованной за диском, появляются
высокочастотные колебания — волны (рис. VI.2). На поверхности
сферических и эллиптических кавитаторов есть пограничный слой,
который вблизи точки отрыва каверны разрушается и служит
источником возмущения поверхности каверны. На небольшом
участке длины за точкой отрыва каверна имеет гладкую и
прозрачную поверхность течения. Однако сразу же за этой областью
появляется система поверхностных волн с амплитудой,
возрастающей вниз по потоку. Ряд исследователей предполагает, что эти
волны возникают вследствие роста неустойчивости отделенногс^
пограничного слоя кавитатора.
Эксперименты показывают, что для сглаживания поверхности
каверны необходимо обеспечить устойчивость ламинарного
211
числа Фруда
Fr,=
Vgd
Fr ._ =
- для круглых дисковых и сферических кави-
таторов;
' 1А7л:"~ , /■ ^— —для дисковых эллиптических кавитаторов.
Кроме того, безразмерный расход зависит также и от
коэффициента сопротивления, определяемого формой кавитатора
(конус, диск, шар, эллипсоид).
npj£ относительных
погружениях Я > 4 безразмерный расход
не зависит от глубины
погружения:
Cq = Cq{k, Fr, С J.
Для кавитаторов
определенной формы расход Cq зависит
только от двух параметров: κ
и Fr.
На рис. VI.3 даны
зависимости Cq (κ) при разных числах Fr,
полученные Л. А. Эпштейном
[73] для дисков.
Там же нанесены
экспериментальные точки — результаты
работы Клайдена и Кокса [108].
Как видно, результаты
испытаний дисков разных диаметров
хорошо согласуются между собой.
_^ Для выявления влияния фор-
κ мы кавитатора на безразмерный
расход газа Cq на рис. VI.4
приведены результаты экспериментов
с конусами, имеющими различный
угол раствора β = 45, 90 и
180° (диск). Видно, что с
увеличением угла β при постоянном числе
кавитации κ расход Cq резко
возрастает.
При исследовании искусственных каверн, образованных за
кавитаторами, сделано много замеров силы сопротивления и
определена зависимость С^ (κ).
На рис. VI.5 дана зависимость С^ (κ) для конусов при
вариации угла β. Из рис. VI.5 видно, что в диапазоне чисел
кавитации О =5С κ sS 0,3 для диска С^, (κ) — линейная
зависимость. Результаты экспериментов [84] в диапазоне чисел
О =£С κ ΐζ 1,5 показывают, что с возрастанием числа кавитации,
214
Рис. VI.3. Зависимости
коэффициента расхода газа Cq от числа
кавитации κ при постоянных
числах Фруда, полученные для
диска.
• — rf = 12,7 мм; © — d = 19 мм;
О — d = 25,4 мм.
начиная с κ = 0,5, зависимость С^ (κ) становится нелинейной,
она хорошо аппроксимируется формулой:
Сх = Сх^ A + κ) при κ < 0,5,
Сх = Слг„ A + >< + 0,028κ2) при κ =^ 1,5
(где Сд:о = 0,8053 — коэффициент сопротивления при κ
Зависимость коэффициента
сопротивления от чисел кавитации
для эллиптических плоских ка-
0).
Рис. VI.4. Зависимость коэффициента
расхода газа Cq от κ для каверны,
образованной за конусом при
различных β.
— β = 45?;
,.β = 80°;
β = 180°.
Рис. VI.5. Зависимость
коэффициента сопротивления Сх от числа
кавитации κ при различных углах β.
/ —^ β ^ 180°, пластинка; 2 — β ^^
= 90°, — конус; 3 — β = 45°, —
конус, β — d = 100 мм; О — d = 35 мм.
Битаторов была экспериментально исследована И. Т.
Егоровым. Результаты испытания (паровая и воздушная каверны)
приведены на рис. VI.6.
Как видно, для насадков этого типа функция Q (κ) так же,
как в рассмотренном выше случае при значениях κ ¢£= 0,5 имеет
.зависимость, близкую к линейной, а при значениях κ > 1,5
коэффициент сопротивления остается постоянным.
Эксперименты показывают, что при осесимметричном кавита-
ционном обтекании полуэллипсоидов вращения коэффициент со-
лротивления возрастает с увеличением отношения а/Ь, где а —
длина большой полуоси; b — длина малой полуоси.
Такие эксперименты были проведены М. Ю. Цейтлиным [65]
с насадками, имеющими различные значения α/b (рис. VI.7),
лри числах Фруда Fr^ =-^=^ = 6,52; 7,83, 9,13 и погоужении
оси эллипсоида на глубину около пяти его диаметров. На
рис. VI.7 даны экспериментальные зависимости С^ (κ) при отно-
215
шениях α/δ = 0,25; 0,50; 1,0; 2,0. Эти кривые показывают, что
с увеличением чисел Фруда коэффициент сопротивления падает.
Эксперименты на эллипсоидах позволили также приближенно
установить положение точки отрыва струй.
Влияние гравитационных сил при кавитационных течениях
проявляется в том, что ось каверны деформируется и ее хвостовая
часть всплывает. Сила плавучести каверны уравновешивается
Рис. VI.6. Зависимость коэффициента сопротивления от числа
кавитации для эллиптических плоских кавитаторов.
т- — — расчет для пластины бесконечного размаха. Значения Ь1а:
О — 1; Δ — 2; D — 3; X — 4; β — 1 (с поддувом воздуха).
подъемной силой, обусловленной циркуляцией, и поэтому
деформация и всплывание каверны зависят от скорости
потока.
Эксперименты с искусственной каверной хорошо
иллюстрирует это явление.
На рис. VI.8 даны различные стадии образования каверн
за круглым диском при изменении скорости потока. Как
видно, при малых скоростях потока в результате подачи
воздуха за диск образуются всплывающие пузыри; с увеличением
скорости формируется каверна, несимметричная Относительно
оси диска-; при дальнейшем увеличении скорости несимметрия
каверны уменьшается.
Некоторые способы позволяют уменьшить всплывание каверны,
обеспечить бесциркуляционное кавитационное обтекание тела:
например, дифферентовка его на нос, установка кавитатора на
горизонтальной разделительной пластине. ·
На рис. VI.9 приведены результаты экспериментов с плоскими
кавернами, образованными на пластинке при различном ее
положении по отношению к направлению силы тяжести. Влияние
216
а) Cx
0,70
0,66
0,62
0,5 Ь
0,52
0,ЧЪ
0,40
б) Οχ
0,30
0,26
0,22
г) Cx
0,10
ο,η
0,10
a/b=0,5
a/b=Z,0
0
0,05
0,10
0,15
V.
Рис. VI.7. Зависимость коэффициента сопротивления от числа
кавитации для различных соотношений осей пслуэллипссида
вращения (alb).
О — I'oo = 5 м/с. Fr = 6,25; β — l'„ = 6 м/с, Fr = 7,83; Δ — l'^ =
= 7 м/с. Fr = 9,13.
217
.;,,
Ю
V
ч:;^'.- ^:
Рис. VI.8. Влияние скорости потока на образование каверны за
круглым диском: а—Ργ^=1,9, Cq = 10,5· 10"^; б — Fr^ = 4,3, Сп =^
= 4,6 10^3; е—Frd=6,8, Cq = 3,0 ΙΟ"'.
218
весомости хорошо иллюстрируется зависимостью числа
кавитации от угла наклона кавитирующей пластинки к направлению
линии горизонта κ (γ) при разных расходах газа Cq и числе
Фруда FTfj, ^ отнесенном к высоте выступа Н.
К
135 γ град
Рис. VI.9. 'Зависимость числа кавитации κ от угла
V
наклона кавитирующей пластинки при Fr// = ■- -_ - ==
VrHk
= 8,35.
Как следует из рис. VI.9, наибольшие числа кавитации
получаются при V = 90°, что соответствует вертикальному положению
пластинки. Для горизонтальных ее положений (каверна сверху
О 30 60
Рис. VI. 10. Зависимость
верны I
120 "^^град
относительней длины ка-
Як
от угла γ.
И каверна снизу) число кавитации уменьшается. Это же
подтверждает и визуальное наблюдение эксперимента.
На рис. VI. 10 даны зависимости относительной длины каверны
/ = l-Jliy^ от угла γ. Как видно, каверна наименьшей длины
219
образуется при у = 90°, что соответствует максимальному числу
кавитации. Благоприятное распределение давления на контуре
кавитирующего тела приводит к уменьшению всплытия каверны.
§ 2. Приближенные формулы для определения
параметров искусственной к^вита'ции
Чтобы оценить величину циркуЛяции скорости, возникающей
вокруг каверны при небольших числах Фруда (для случая
развитой каверны с вихревыми шнурами), составим уравнение Бер-
нулли для верхней и нижней границы каверны (рис. VI. 11):
Р1^^.
Рк
ρί^Ι
pvi
γ- -l· Pgi/„ = Рк + —2~ + Pgi/в, (VI.2.1)
где p„, Рк — давление на бесконечности и в каверне
соответственно; ]/„, !/„, Vb — скорость потока на бесконечности, на ниж-
У>
со .,
0
ItL —
— —'
^-"
-
_--^/β
"^ ^-i^^
т-х
Hi
"jE-·
Χ
Рис. VI. 11. К выводу формулы циркуляции скорости,
возникающей вокруг каверны.
ней и верхней границах каверн соответственно; ^/„, у^
нижней и верхней границ каверны.
После преобразования получим:
ординаты
Vi - vi = (V„ - V.) (Vh + Vb) = 2g (i/3 - ί/н).
Принимая приближенно, что l/„ + V^ = 2Vk, найдем:
^VAV^~V,)^2g{y^-y,). (VI.2.2)
Из курса гидромеханики известно, что циркуляция Г по
замкнутому контуру L определяется формулой
T^j)VaS,
(VI.2.3)
где V — проекция скорости в точке на направление элемента
контура as.
220
в рамках линейной теории, если считать каверну тонкой
и снести граничные условия с поверхности каверны на ось Ох,
то формула (VI.2.3) примет вид:
о
После подстановки в нее (VI.2.2) получим
'к
Г == -#- ί (г/в - ί/„) άχ = -^,
где S* — площадь диаметрального сечения каверны; Ук —
средняя скорость на границе каверны.
Или принимая во внимание формулу (III.3.6), напишем:
Г = S^=-. (VI.2.4)
ν^ν^ΐ + ίί
Систему диск — развитая каверна можно рассматривать как
П-образную вихревую линию, где расстояние между вихрями
равно расстоянию между наблюдаемыми вихревыми трубками
каверны Ь. Тогда на основании теоремы Жуковского подъемную
силу находим по формуле
Υ = pVV^b.
Приравнивая ее силе плавучести каверны, найдем:
рГУсоб-γν^*, (VI.2.5)
где V* — объем каверны.
Подставляя затем в (VI.2.5) выражение для циркуляции по
формуле (VI.2.4), после промежуточных преобразований получим
расстояние между вихревыми трубками:
Если приближенно считать, что форма каверны близка к
эллипсоиду вращения с длиной /^ и диаметром D, то
b =^^DYY^. (VI.2.6)
Один из существенных факторов, определяющих образование
и поддержание каверны (за плоским диском) — это расход газа Q.
Существуют полуэмпирические методы, позволяющие оценить Q
для развитой каверны с вихревыми трубками, в частности имеют
практическое значение методы Эпштейна, Клайдена и Кокса.
На основании наблюдений за каверной в процессе эксперимента
Л. А. Эпштейн предположил, что процесс уноса газа состоит в том,
221
что по мере движения тела образовываются все новые участки
вихревых трубок, содержащие газ, покоящийся относительно
частиц жидкости. Давление в каверне и вихревых трубках
одинаково и равно р^. Силы трения стремятся только уравнять
скорость газа и жидкости.
Согласно предположениям Кокса ц, Клайдена унос газа
происходит по вихревым трубкам вcлeдöfвиe f идростатического перепада
давлений.
Рассмотрим сначала метод Эпштейна. Предположим,
что скорость образования трубок равна скорости потока, тогда
расход газа найдем по формуле
В безразмерной форме согласно (VI. 1.1) найдем:
-f-J, (VI.2.7)
где а — диаметр вихревого шнура.
С другой стороны, применяя уравнение Бернулли для
абсолютного движения жидкости, пренебрегая квадратами малых
скоростей и считая размеры вихревых трубок малыми по
сравнению с расстоянием между ними, получим:
Рсс = /7к + Pg/i -f -|- ^, (VI.2.8)
где h — высота всплытия оси вихря в месте его сформирования
над осью тела.
Третий член (VI.2.8) содержит квадрат скорости,
индуцированной полубесконечным вихревым шнуром.
Из (VI.2.8) легко найти отношение
(Я-
^2^2у2 1^
1/2
где κ — число кавитации.
Высота всплытия оси вихря h возрастает при уменьшении
чисел κ и Fr настолько, что возможны такие их малые значения,
при которых скобка в знаменателе формулы (VI.2.15) обращается
в нуль, а диаметр вихревого шнура а — в бесконечность. В этом
случае формула (VI.2.9) неприменима. Кроме того, когда диаметры
вихревых трубок становятся соизмеримыми с расстоянием между
ними, трубки взаимодействуют и деформируются. Поэтому
формула (VI.2.9) рекомендуется для значений а <; Ь/2. В случае
невыполнения этого условия, т. е. при использовании формул
В большем диапазоне значений а, необходимо вводить поправочный
коэффициент ßi, учитывающий деформацию сечений [72].
222
На основании вышеизложенного, а также формул (VI.2.4),
(VI.2.7), (VI.2.9) напишем после промежуточного преобразования
следующее выражение для безразмерного расхода газа:
Cq —^ г г-. (VI.2.10)
Для выполнения расчетов (VI.2.10) необходимо знать величину
h (см. рис. VI.II). Известно несколько приближенных оценок
этой величины: в частности, если рассматривать каверну как крыло
малого удлинения, то согласно линейной теории подъемная сила
этого крыла равна
где α — угол атаки (всплытия), т. е. угол, образованный вектором
скорости и прямой линией, соединяющей середины тела и области
замыкания каверны; С" — позиционная производная
коэффициента подъемной силы; S — площадь каверны в плане.
Угол атаки определяется исходя из условия равновесия
каверны. Приравнивая подъемную силу крыла силе плавучести
каверны, найдем:
С«а^5 = р^Г. (VI.2.11)
Для крыла малого удлинения производная по углу атаки может
быть представлена в виде
C" = ^¾πλ^ (VI. 2.12)
где коэффициент k зависит от удлинения крыла λ* (каверны)
и угла атаки.
Для крыла при λ* = 5 -ь6 и α = 3 -ь6° fe ~ 1. Примем, что
каверна имеет форму эллипсоида вращения. Полагая λ* = D//«
получим из (VI.2.11):
Откуда находим
^-4гф-- (VI.2.14)
со
223
Результаты экспериментов с кавитирующими дисками
позволяют установить ряд приближенных зависимостей размеров
каверны от числа кавитации. В частности,
отношение диаметра каверны к диаметру диска
^-V^Щ^' (VI.2.15)
где Ωι —эмпирический коэффициент, равный 0,8—1,0.
Отношение длины каверны к диаметру
/к ^ к + 0да8 J 2.16)
Dk 1,7κ (κ+ Сз) ^ '
где no опытам Рейхардта а^ = 0,066; по данным Эпштейна
Ω2 = 0,040.
Необходимо подчеркнуть, что приведенные выше формулы
справедливы лишь для развитой каверны с вихревыми шнурами.
Область появления режимов, при которых прекращается
образование вихревых шнуров, может быть оценена эмпирической
формулой
где
4 ·
d
Если следовать теории Кокса и Клайдена, т. е.
считать что унос газа происходит по вихревым трубкам, то
(VI.2.9) скорость Уо» должна быть заменена скоростью газа Vr-
Скорость газа Vr определяется исходя из потери давления газа
при его движении по трубопроводу:
где / — длина вихревого шнура до свободной поверхности; а —
угол всплытия каверны; рг — плотность газа; λ — коэффициент
сопротивления вихревых трубок движению газа; Ар — перепад
давления между точками в начале вихревого шнура и на
свободной поверхности. Откуда находим, что
у2 2αΔρ
λ/рг
Если предположить, что угол всплытия вихревых шнуров α
постоянный, то на основании (VI.2.13), (VI.2.15) и (VI.2.16),
учитывая результаты исследований И. Т. Егорова, можно
получить
0,646 i/c7"
к== J;, "" . (VI.2.18)
^p^ä
224
Перепад давлений в формуле (VI.2.17)
PV^.
ΔΡ = Рк — (Роо — PgH) = pgH — -л —2
(VI.2.19)
где Я — глубина погружения насадка.
Подставляя (VI.2.18), (VI.2.19) в (VI.2.17), после
преобразований получим:
xFr2"
К
«•«1^^:ШШ[-^]
Xkf4
(VI.2.20)
13
12
11
10
9
е
7
6
5
J
2
0
Жд
\V^'^
^,¾
г
ь
к?
го
ςΐ6.
]б
>^5,8
^Ι'','* ,
о,и
tJii
I'i —
fe
ll„.
^^^-1
tF
U,L
'.0
0,20
p]5D
Ύ,υ
if
<.o
0,01 0,0't 0,0b Ο,ΟΒ 0,10 0,12 Ο,η st Ce-<«
Рис. VI. 12. Диаграмма для расчета характеристик каверны, образованной
за диском в безграничной жидкости.
Ьсли учесть, что Cq =-γ \~т) тг-> то после
подстановки в это выражение (VI.2.20) найдем:
25
(VI.2.21)
Для случая кавитационного обтекания круглых дисков, при
Сд;„ = 0,82 коэффициент сопротивления вихревых трубок в
формуле (VI.2.21) аппроксимируется зависимостью
λ = [0,194 (Fr^— 1,35) P.
225
Расход воздуха Cq в условиях безграничной жидкости
определяем по (VI.2.20) при Я = оо:
^ ^ 6Л2
^ ' Fi-2 (Fr^ - 1,35) >i'·'' {■>i' f4 - 1,955I-25 '
В работе [27] построена диаграмма для расчета
характеристик каверны, образованной за диском в безграничной жидкости
(рис. VI. 12). По оси абсцисс отложены числа кавитации, а по оси
ординат — числа Фруда, определенные по объему каверны
в расчетах за объем каверны принят объем эллипсоида
вращения. В качестве параметров на диаграмме приняты числа
Фруда по диаметру диска Fr^ и безразмерный расход газа Cq.
§ 3. Структура кавитационных потоков
Физическое представление о структуре кавитационных течений,
о структуре пограничного слоя, а также о природе
гидродинамических сил дает экспериментальное исследование поля· скоростей
и давлений.
Если исходить из задачи исследования, то наиболее общей
оказывается частичная кавитация, при которой каверн: замы-
а)
85 мм
^=.SSS^^^_.
^85 г·}η
Рис. VI. 13. Клиновидные кавитаторы, использованные при замерах
давлений.
кается на теле. В этом случае рассмотрим три участка на
поверхности тела: кавитатор (насадок), каверну, смоченную часть тела
за каверной. Эксперимент с искусственными кавернами —
наилучший и доступный способ исследования поля скоростей и давлений
на каждом из этих участков.
Такие исследования были выполнены рядом авторов на
простых телах (пластинах и крыльях). При экспериментах с
искусственными кавернами существенно проявляется весомость, поэтому
ниже приведем некоторые результаты исследований поля
скоростей и давлений кавитационного течения, образованного под
горизонтальной пластиной (длиной 2,5 м, шириной 0,6 м).
Пластину буксировали в бассейне со скоростью 3 м/с [20].
Были применены два клиновидных кавитатора, размеры
которых даны на рис. VI. 13.
226
Распределение давлений по длине на нижней поверхности
пластинки при кавитационном и бескавитационном обтекании
даны на рис. VI. 14, α (кавитатор Л) и рис. VI.14, б (кавитатор Б).
Там же указаны длины каверны /^, отстояния линии замыкания
каверны от передней кромки пластины 1^.
Как видно из рисунков, есть три характерные области
распределения давлений по длине пластины. Левая область — это
распределение давлений на клиновидном кавитаторе; в средней области
в пределах длины каверны давление постоянно; правая область —-
давление за каверной, для этой области характерен пик давления
сразу же за каверной.
Коэффициент давления в каверне Ср возрастает при уменьшении
ее длины в диапазоне его значений: —0,15 -.—0,05. Эти результаты
соответствуют уже рассмотренным нами зависимостям межцу
числами кавитации и длиной каверны.
В эксперименте было выявлено два случая замыкания каверны
на пластине:' а) при сравнительно большой высоте выступа
(кавитатор А) замыкание каверны сопровождается появлением
развитой обратной струйки и большим расходом газа; б) при
относительно малой высоте выступа (кавитатор Б) замыкание
происходит без обратной струйки и сравнительно малом расходе газа.
Характер изменения давления в конце каверны определяется
формой замыкания каверны на пластине (с обратной струйкой
или без нее). В первом случае изменение давления при переходе
от каверны к смоченной части пластины происходит сравнительно
плавно. В то же время при использовании кавитатора Б
наблюдается резкое изменение давления в районе замыкания
каверны.
Характеристику структуры пограничного слоя позволяют
получить экспериментальные исследования скоростей за
каверной. На рис. VI. 15, а, б приведены эпюры местных относительных
скоростей V (y)IVm в пограничном слое за каверной в сечении
на расстоянии 1250 мм от передней кромки пластины при
различных длинах каверны 1^.
Как видно, профили скоростей по форме соответствуют
турбулентному режиму течения. Однако для кавитатора А эпюры
скоростей вблизи района замыкания каверны имеют перегибы,
характерные для местного отрыва пограничного слоя. По мере удаления
от района замыкания эпюры скоростей для кавитационного и бес-
кавитационного режимов обтекания практически совпадают
(рис. VI. 15, б).
На рис. VI. 16 приведены кривые коэффициентов местного
трения Cf, определенные по замеренным касательным
напряжениям в функции от местного числа Рейнольдса для двух случаев
кавитационного обтекания (кавитаторы Л и Б). В первом случае
измерения производились в одной точке на расстоянии 1250 мм
от передней кромки пластины, во втором — в трех точках на
расстояниях 850, 1250 и 1650 мм.
227
I
(.'Z.
•q- >^
-——_
ff
^ ί
Oj J
i/ '
If 1
//
X /
X /
/ /
1
i 4—
Ϊ5 i
1
. 1
/
/
^
"-1=
J/ ^
///
' 1
1
1
\
:^-¾¾^^^^^
"
—•^
v^
"οι
csi
I
Ό
I
■*
er
I
228
га
ί£
О
η
χ
о
га
S
о
ί£
S
о.
с
ü:
S
11
^
=
Ε
(М
il
1
'Ч'
^
(X) О
СО CS"
|| -
:.:11
> "^
S 1
S 1
о «ад
со ·-
h 1
»-Ίο
СО
1 "^
^ II 1
.-J^^n
S UD
s if Ξ
ш
о
с
1- о
I-· _ Τ"*
S "^
S
S
^
о
с:
S
X
φ
*=?
i=t
II
^ЬЙ
s'
о
¢0
О
II
II Ξ
~=Ίι
s "^
s I
о Ό
to
Ц5 .-
II i
^
«"s-
I
CM
es'
1
I
cs'
1
s
äi
ι ι
229
Во время эксперимента варьировалась длина каверны так, что
расстояния от точки замера до конца каверны и соответственно
Ух
местные числа Рейнольдса Re^. = —- изменялись. При
замыкании каверны с обратной струйкой (кавитатор А) касательные
напряжения растут плавно от нулевых значений до напряжений
турбулентного трения, а при замыкании каверны без обратной
струйки (кавитатор Б) наблюдается резкое возрастание
напряжений. Это позволяет предположить, что при плавном замыкании
а;
у,нм
50
W
30
го
10
·—
7
'Li
0,6 0,8 1,0
v(y)/V,
1,г
,ΜΜ
W
30
20
10
η
w /II
2^/1
sjy/
0,6
0,8 1,0
V(y)/Vco
Рис. VI. 15. Эпюры
скоростей движения
жидкости в пограничном слое
за каверной для двух
случаев обтекания:
с — с обратной струйкой
(кавитатор А);
1 — без каверны: 2 — /ι =^
= 650 мм, ί^ =^ 165 мм, X =
= 600 мм; 3 — li = 1150 мм:
/ ^= 665 мм, X = 1Ό0 мм,
б — без обратной струйки
(кавитатор Б);
1 — без каверны; 2 — li —-
= 650 мм, 1^ = 165 мм, X =
= 600 мм; 3 — /ι = 1220 мм.
/„ = 735 мм, д; = 30 мм.
(кавитатор Б) за каверной зарождается новый турбулентный
пограничный слой, в котором касательные напряжения
определяются местным числом Рейнольдса (с характерной длиной —
отстоянием рассматриваемой точки χ от места замыкания каверны).
Что же касается случая замыкания с обратной струйкой
(кавитатор А), то вывод о появлении нового турбулентного пограничного
слоя можно сделать, если предположить, что в зоне замыкания
каверны наблюдается местный отрыв пограничного слоя.
Большинство задач о кавитационных течениях решается с
учетом основных положений теории струй, в которой внутреннее
движение газа в каверне не рассматривается и предполагается
разрыв скоростей на границе каверны.
Ниже приведены результаты [115] экспериментального
определения профиля скоростей течения газа в каверне, образованной
за клиновидным насадком под горизонтальной пластиной. Опре-
230
о 100 300 500
1200 χ
WOO Χ,,мм
Рис. VI. 16. Зависимость касательных напряжений от чисел Кел:
при кавитационном обтекании нижней части пластинки:
а — кавитатор А;
/—при кавитационном обтекании; 2— Сг при турбулентном обтекании
пластины (эксперимент); 3 — С с при турбулентном обтекании пластины
(расчет); 4 — Сс — при ламинарном обтекании пластины; 5 — Сг при
переходе от ламинарного к турбулентному режиму движения при
Re,
кр
1,5· 10»; 2,5· 10^ 3,5· 10^
б — кавитатор Б;
1,2,3 — Cr в трех точках по длине пластины при кавитационном обтекании
(850, 1250 и 1650 мм от передней кромки пластины); 4 — Cr при
турбулентном обтекании пластины (расчет).
231
деление производилось при скорости потока Vcc = 1,02 м/с,:
что соответствует числу Фруда по высоте выступа насадка
в трех сечениях по длине каверны: вблизи кавитатора, посредине
длины и в районе замыкания каверны (рис. VI.17); h — высота
каверны в данном сечении; и = α^ΙΥοο — местная скорость
течения газа на данной высоте. Вследствие малого перепада по
длине каверны для измерения давления использовали
микроманометр с уравновешенной каплей. Опыты проводили при
постоянных безразмерных расходах газа, отнесенных к высоте
выступа и ширине клина Cq == 2,23.
Результаты эксперимента в виде профилей скорости,
построенных в прямоугольных координатах h и и, даны на рис. VI. 17.
В гидромеханике рассматривается течение Куэтта — плоское
течение между двумя параллельными стенками, из которых одна
движется вместе с потоком. Считая границу каверны подвижной,
течение газа внутри можно рассматривать как течение Куэтта.
Сравнение результатов эксперимента с расчетными данными по
теории Куэтта показывает удовлетворительное их совпадение
1115].
Мы предполагаем, что параметры искусственной каверны,
образованной на каком-либо теле, при постоянном числе
кавитации и постоянной длине каверны такие же, как и для естественной
каверны. Однако эксперименты показывают, что от расхода
воздуха зависит не только число кавитации, но и форма границы
каверны.
Экспериментально было установлено [95], что при
определенных условиях подтверждается известная зависимость между
параметрами, характеризующими каверну: при увеличении расхода
газа Cq давление в каверне возрастает, а число кавитации падает.
Однако при этом для значения κ существует некоторый предел,
после которого при увеличении расхода воздуха число кавитации
остается постоянным. На поверхности каверны образуется одна
волна (первая стадия), и каверна начинает пульсировать,
сокращаясь и увеличиваясь в длину.
При дальнейшем увеличении расхода воздуха длина каверны
и давление в ней скачком увеличиваются, число кавитации
соответственно падает. Каверна продолжает пульсировать, а на ее
поверхности по длине образуются две волны (вторая стадия).
Если расход воздуха продолжает увеличиваться, то число волн
возрастает и возможно появление трех, четырех и пяти волн.
Таким образом, существуют два типа каверн: стационарные
и пульсирующие. Стационарные каверны возникают при малых
расходах воздуха, по своим параметрам они подобны
естественным кавернам.
2,32
:¾
^•^Й
•о_ ^
.—^%^__ο
• \
•а
s
§
о
<5Г -
•о
см
См
Q ir о «-у
У^ ' ^ °
о ·>«
«Χι
Id
С5
»о
*
3
О
О
CS
13
"S3-
1^ «N1
«О
«а
>s
So
s ϊ^
С)
%\\
с СУ
ЧО
О
£■1)
сок,
1
I
ч
Ш·
о
о,
t=;
S
о.
233
Для иллюстрации на рис. VI. 18 показаны пульсирующие
искусственные каверны, образовавшиеся за пластинкой,
установленной в вертикальной гидродинамической трубе [95].
Для того чтобы получить
представление о поведении и пара-
мет pax каверны в различных
стадиях ее развития целесообразно
рассмотреть схематизированную
зависимость Cq (κ), приведенную
на рис. VI. 19. Она построена на
основании экспериментальных
данных [95] и позволяет составить
представление о механизме
образования различных стадий
каверны.
Представим себе, что
начиная с некоторого критического
числа кавитации возрастает
расход газа, каверна, имеющая одну
волну, удлиняется, а число
кавитации падает. Когда расход
достигает некоторого порогового
значения Cq,, каверна удлиняется
(без изменения расхода) при
уменьшении числа кавитации, и
ее поверхность имеет уже две
волны (вторая стадия). Переход
от первой стадии ко второй
сопровождается изменением частоты
колебаний.
Дальнейшие увеличения
подачи воздуха в каверну приводят
опять при некотором пороговом
значении Cq^ к внезапному
изменению длины каверны,
сопровождаемому уменьшением числа
кавитации, а на поверхности
каверны образуется три волны. Таким
образом, в эксперименте можно
получить четыре, пять и более
волн.
При увеличении количества воздуха до некоторого предела
пульсирующие явления пропадают. Если затем расходы воздуха
уменьшать в обратной последовательности, то пороговые Cq
при переходе от стадии к стадии получают меньшие значения.
На рис. VI. 19 видно, что Cq^ < Cq, и C'q^ < Cq^. Таким
образом, схематизированная диаграмма Cq (κ) характеризуется
некоторой петлей типа петли гистерезиса,
234
Рис. VI. 18. Различные формы
пульсирующих каверн: а —
стационарная каверна; б — одна
волна; в — две волны; г — три волны;
д — четыре волны.
Представляет значительный интерес исследование
искусственной каверны при движении вблизи свободной поверхности.
Рассматриваются два случая: движение вблизи невозмущенной
поверхности, движение при волнении. Как показывают
экспериментальные исследования 127], возможны три вида деформации
каверны, обусловленной влиянием свободной поверхности и
весомости, каждый из которых проявляется в зависимости от чисел Фруда.
При малых числах Фруда весомость жидкости проявляется
весьма существенно: каверна сильно всплывает, а подаваемый
в каверну воздух за насадком
прорывается в атмосферу и не
позволяет создать замкнутую кавита-
ционную полость (рис. VI.20, а).
При умеренных числах Фруда
каверна формируется достаточно
хорошо: влияние весомости
жидкости проявляется весьма
существенно и приводит к
образованию волнового бугра над кавита-
ционной полостью (рис. VI.20, б).
При движении с очень
большими числами Фруда влияние
весомости жидкости практически
отсутствует, каверна может
оказаться несимметричной
относительно горизонтальной плоскости
(рис. VI.20, в).
Для судостроительной практики наибольший интерес
представляет режим движения при умеренных числах Фруда. Поэтому
все дальнейшие результаты относятся к этому случаю.
Близость свободной поверхности вызывает искажение формы
каверны и оказывает влияние на механизм подачи воздуха за
насадок.
Наблюдаются два режима поступления воздуха в каверну:
принудительная подача с избыточным давлением и поступление
самотеком из атмосферы. Первый режим наблюдается при
большом погружении каверны или при малом погружении и малой
относительной скорости гг^ = ,— .
Второй режим наблюдается при больших числах Ргя-
Количество подаваемого воздуха определяется площадью сечения,
через которое воздух поступает в каверну. Практически воздух
из атмосферы может поступать: либо по вихревым жгутам за
каверной, либо вдоль вертикальных стоек (у катеров на крыльях),
находящихся в отрывном режиме обтекания, либо по внутренним
трактам системы подачи воздуха. Для определения числа
кавитации в этом случае необходимо принять давление ро, = Ра
+ pgH, а р„ = р^.
235
Рис. VI. 19. Схематическая
зависимость расхода воздуха от числа
кавитации для пульсирующих
каверн.
/ — одна волна; 2 — две волны; 3 —
три волны.
■s..?
Рис. VI.20. Виды деформации Рис. VI.21. Зависимость числа ка-
каверны вблизи невзволнованной
свободной поверхности: а — при
малых числах Фруда; б — при
умеренных числах Фруда; в — при
больших числах Фруда.
витации от расхода воздуха и
относительной глубины погружения.
О 0,01 0,02 0,03 0,04 0,05 0,0В 0,07 Ο,ΟΒ 0,09 V.
Рис. VI.22. Зависимость коэффициента сопротивления Οχ =
X
= ——7¾ от числа кавитации при различных относитель-
ных глубинах погружения диска Н.
236
Тогда
κ = ^_ 2 . (VI.3.1)
Fr2
Такое значение число кавитации принимает при
неограниченном поступлении в каверну воздуха из атмосферы. Зависимость
(VI.3.1) не учитывает особенности подачи воздуха из атмосферы
по внутреннему тракту, один из концов которого находится за
насадком в зоне разряжения, а другой сообщается с атмосферой.
В этом случае скорость воздуха, поступающего в каверну,
зависит от перепада давления между этими концами, что, в свою
очередь, зависит от глубины погружения, скорости движения и формы
насадка.
Начало прорыва воздуха из атмосферы в каверну соответствует
резкому увеличению количества подаваемого в каверну воздуха
и приводит к существенному снижению числа кавитации. На
рис. VI.21 дана экспериментальная зависимость числа κ (Cq)
при разных значениях относительного заглубления Η = Hid.
Зависимость коэффициента сопротивления диска С^,
отнесенного к площади миделевого сечения каверны, от числа
кавитаций κ для разных относительных погружений Я дана на рис. VI.22.
Как следует из рисунка, коэффициент С^ при одном и том же числе
кавитации возрастает при уменьшении глубины погружения, что
объясняется волновыми эффектами, приводящими к увеличению
площади миделевого сечения каверны, а также к появлению
дополнительной волновой составляющей сопротивления.
ПРИЛОЖЕНИЕ
Ниже приведено решение некоторых интегралов, используемых в гл. II,
Согласно работе [15]
[-^ = -^^B1^^ + 2^ + ^)= [с>0]
J VR Ус
1 , 2СХ -\-Ь г ^ η А ^ m
arsh yrL·— = [с > О, Δ > 0]
2t
I . 2cx 4-b r ^ л Д ^ ni
=-arcsin— ' = [c<0, Δ<0]
= -^1пBсл; + й), [c>0, A = 0]
V с
где /? = сл:^ + te + с; Δ = 4ac — b^.
_^^Ja±bx + 2VL·^^ [β>0]
С dx 1_,^ 2a-{-bx + 2VaR
J хУн~"~У^
I . 2c +te r ^л Д ^ m
arcsin ^ = [c <0, Δ < 0]
l·^—с X Vb^ — Aac
\ , 2a -\-bx , ^ ni
-7=Γ arctg ^_Z ..- == [β < 0
238
1 . 2a-\-bx
—szrr arsh rrtzr—
I ,. 2a + bx
-arth — '-,
V^a 2 V^a V^R
I . X
in
у a 2a 4- bx
2 Vbx + CK^
bx
[β > 0, Δ > 0]
[α>0]
\a > О, Δ = 0]
(α = О, 6 =f 0]
УКАЗАТЕЛЬ
ЛИТЕРАТУРЫ
t. Адам И. В. Влияние стока, расположенного за каверной, на ее
параметры в случае двумерного обтекания тонкого тела в режиме частичной
кавитации.— Труды ЦНИИ им. Крылова, 1970, вып. 258, с. 82.
2. Амромин Э. Л., Иванов А. Н. Осесими{етричное обтекание тел
в режиме развитой кавитации.— Известия АН СССР. Механика жидкости и газа,
1975, № 3.
3. А м ρ о м и н Э. Л. Теория и расчет осесимметричного кавитационного
обтекания судовых конструкций.— Автореферат диссертации на соискание
ученой степени канд. техн. наук. ЦНИИ им. Крылова, Л., 1975.
4. А м фи л о X и е в Л. В., Басин М. А. Линейная теория тонкого
кавитационного профиля, движущегося вблизи свободной поверхности идеальной
невесомой жидкости.— Труды ЦНИИ им. Крылова, 1971, вып. 266, с. 29.
5. Айылчиев Α., Саламатов Д. К струйному обтеканию осе-
симметричных тел вращения. Материалы первой конференции молодых ученых
Академии наук Кирг. ССР. Фрунзе, «Илим», 1973.
6. Барабанов В. Α., Иванов А. Н. Применение «вихревого»
метода для расчета плоских кавитационных течений.— Труды ЦНИИ им.
Крылова, 1970, вып. 258.
7. Биркгоф Г., Сарантонелло Э. Струи, следы и каверны.
Пер. с англ., М., «Мир», 1964.
8. Болотин А. Ф. Исследование характера деформации каверны в
весомой жидкости. Доклад на 12-й конференции секции мореходных качеств судов.
Крыловские чтения. Л., 1962.
9. Бутузов А. А. Результаты эксперимента по созданию искусственных
каверн на моделях судна с плоским днищем.— Труды ЦНИИ им. Крылова.
Гидродинамика судна, 1965, вып. 218, с. 100.
10. Б у τ у 3 о в А. А. Влияние весомости жидкости на кавитациоиное
течение за телом, расположенным на нижней поверхности бесконечной
горизонтальной стенки.— Труды ЦНИИ им. Крылова. Гидродинамика судна, 1965,
вып. 218, с. 84.
11. Бутузов А. А. Об искусственном кавитационном течении за тонким
клином, помещенным на нижнюю поверхность горизонтальной стенки.— МЖГ,
1967, № 2.
12. Б у τ у 3 о в А. Α., Π а к у с и н а Т. В. Расчет обтекания
глиссирующей поверхности с искусственной каверной.—■ Труды ЦНИИ им. Крылова,
1970, вып. 258, с. 63.
13. В у д с Л. Дозвуковое плоское течение в кольцевой области или в
канале с периодическими по длине граничными условиями.— «Механика», 1956,
№ 2, с. 52.
240
14. г a χ о в Φ. Д. Краевые задачи. М., Физматиздат, 1958.
15. Градштейн И. С, Ρ ы ж и к И. М. Таблицы интегралов сумм,
рядов и произведений. Изд. 4-е. М., Физматиздат, 1963.
16. Г у ρ е в и ч М. И. Теория течений со свободньши поверхностями.—
В сб.: Итоги науки. Гидромеханика. Т. V. М., ВНИИТИ, 1971.
17. Гуревич М. И. Теория струй идеальной жидкости. М.,
Физматиздат, 1961.
18. Гуревич М. И. Кривизна струи в точке схода ее с конечной стеики.
Исследование по интегродифференциальным уравнениям. Фрунзе, «Илим», 1967.
19. Г у ρ е в и ч М. И., X а с к и н д М. Д. Струйное обтекание контура,
совершающего малые колебания.— ПММ, 1953, т. XVII.
20. Г ρ о м о в Р. С. Экспериментальное исследование пограничного слоя
на пластинке за каверной.— Труды ВНИТОСС. Экспериментальная
гидромеханика судна. Материалы по обмену опытом, 1968, вып. 118.
21. Д и а н о в Д. И. Влияние проницаемости тела, обтекаемого с отрывом
струй, на его сопротивление и размеры каверны.— Труды ЦНИИ им. Крылова,
1969, вып. 248, с. 77.
22. Ж у к о в с к и й Н. Е. Видоизменение метода Кирхгоффа для
определения движения жидкости в двух измерениях при постоянной скорости, данной
на неизвестной линии тока. Избранные сочинения. Т. I. М.—Л., Гостехиздат,
1948.
23. И в а н о в А. Н. Двумерное обтекание тел произвольной формы в
режиме развитой кавитации.— Труды ЦНИИ им. Крылова, 1963, вып. 200. с. 3.
24. И в а н о в А. Н. Симметричное кавитационное обтекание удлиненного
плоского контура.— Известия АН СССР. Механика и машиностроение, 1962,
№ 3, с. 61—66.
25. И в а н о в А. Н. Обтекание тел вращения в режиме частичной
кавитации и определение формы тела вращения, при обтекании которого давление
на участке заданной протяженности постоянно.— Труды ЦНИИ им. Крьшова.
Гидромеханика вязкой жидкости и отрывных течений, 1965, вып. 219, с. 70.
26. И в а н о в А. Н. Кавитационное обтекание профилей крыльев.—
«Механика и машиностроение», 1960, № 6, с. 117.
27. Искусственная кавитация. Л., «Судостроение», 1971.
Авт.: И. Т. Егоров, Ю. М. Садовников, И. И. Исаев,
М. А. Б а с и н.
28. Кавитационное обтекание подводного крыла неустановившимся
потоком.— Труды ЦНИИ им. Крылова. Гидродинамика быстроходных судов. 1971,
вып. 266, с. 25.
Авт.: М. А. Б а с и н, И. Т. Егоров, Ю. М. Садовников,
Л. В. Ш а л л а ρ ь.
29. К е л д ы ш М. В., Седов Л. И. Эффективное решение некоторых
краевых задач для гармонических функций.—ДАН СССР, 1937, т. XVI, № 1.
30. Киселев О. М. О кавитационном обтекании пластинки потоком
тяжелой жидкости.— Изв. вузов. Математика, 1963, № 6.
31. Кнэпп Р., Дейли Дж., Хеммит Ф. Кавитация. М., «Мир»,
1974.
32. К о ρ о в к и н А. Н., Левковский Ю. Л. Исследование
замыкания кавитационной каверны вблизи твердой стенки.— «Инженерно-физический
журнал», 1967, т. ХП, № 2.
33. К о ч н н Н. е., К и б е л ь И. Α., Ρ о з е Н. В. Теоретическая
гидромеханика. М., Гостехиздат, 1955.
34. Ко у л Р. Подводные взрывы. М., ИЛ, 1950.
35. К у 3 н е ц о в А. В. Нестационарная задача обтекания с отрывом
струй.— Труды семинара по краевым задачам, 1968, вып. 5, с. 137—160
(Казанский уи-т).
36. Кузнецов А. В. Нестационарные слабо возмущенные течения
жидкости со свободными границами. Автореферат докторской диссертации. Казань,
241
37. Кузнецов Α. В. Нестационарное обтекание с отрывом струй
препятствия под свободной поверхностью.— Труды семинара по краевым задачам,
1969, вып. 6 (Казанский ун-т).
38. Кузнецов A.B. Малые колебания контура, обтекаемого с отрывом
струй.— В сб.: «Современные вопросы гидродинамики». Киев, «Наукова думка»,
1964, с. 273—281.
39. Кузнецов А. В. Обтекание с кавитацией пластинки струей
конечной ширины.— Известия АН СССР. Отделение технических наук, 1962, № 1,
с. 174.
40. Л а м б Г. Гидродинамика. М., Гостехиздат, 1947.
41. Левковский Ю. Л., Судакова Г. Г. Влияние твердой стенки
на замыкание сферической кавитационной каверны.—«Инженерно-физический
журнал», 1968, т. XV, № 2.
42. Логвинович Г. В. Гидродинамика течений со свободными
границами. Киев, «Наукова думка», 1969.
43. Мальцев Л. И. Решение обратной задачи кавитационного
обтекания криволинейной дуги.— ПМТФ, 1966, № 3.
44. Μ и г а ч е в В. И. Исследование влияния движителя на
характеристики искусственных каверн, создаваемых на днище речных судов. ЛИИВТ.
Автореферат кандидатской диссертации. Л., 1971.
45. Μ и ш е л ь Ж· И. Вентилируемые каверны. К исследованию механизма
их пульсации.— «Механика», 1972, № 4.
46. Мусхелишвили Н. И. Сингулярные интегральные уравнения.
М., «Наука», 1968.
47. Некоторые способы управления кавитационным течением при малых
значениях чисел Фруда.— Труды Международного симпозиума по
неустановившимся течениям воды с большими скоростями.,М., «Наука», 1973.
Авт.: Г. С. Μ и г и ρ е н к о, Г. С. К о з ю к , Л. И. Мальцев,
В. И. Μ и к у τ а, Б. Г. Η о в и к о в.
48. О с и π о в а Н. П. Определение времени существования сферического
пузырька в воде.— Труды ЦНИИ им. Крылова, 1963, вып. 200, с. 43. J
49. Отрьшное кавитационное обтекание профилей в случае глиссирования
и в безграничном потоке.—Труды Международного симпозиума по
неустановившимся течениям воды с большими скоростями. М., «Наука», 1973.
Авт.: В. А. Барабанов, А. А. Бутузов, А. И. Иванов,
И. А. Τ и τ о в.
50. О влиянии искусственно создаваемых воздушных полостей на
гидродинамические характеристики глиссирующих поверхностей.^ Труды ЦНИИ
им. Крылова. Гидродинамика быстроходных судов, 1971, вып. 266, с. 80.
Авт.: А. С. Павленко, С. Д. Прохоров, СБ. Соловей,
В. П. Ш а д ρ и н.
51. Π е ρ н и к А. Д. Проблемы кавитации. Изд. 2-е. Л., «Судостроение»,
1966.
52. Π ы X τ е е в Г. Н. Общая и основная краевые задачи плоских струйных
установившихся течений н соответствующие им нелинейные уравнения.— ПМТФ,
1966, № 1, с. 32.
53. Седов Л. И. Плоские задачи гидродинамики и аэродинамики. М.,
«Наука», 1966.
54. С и - Д и н - Ю. Некоторые аналитические аспекты динамики пузыр ь-
ков.— Труды американского общества инженеров-механиков. Серия Д. 1965,
№ 4, т. 87, с. 157—174 (пер. с англ.).
55. С и д о ρ о в О. П. Решение задачи об обтекании тела вращения. ^
Труды Казанского авиац. ин-та, 1958, вып. XXXVIII, с. 23—42.
56. С м и ρ н о в В. И. Курс высшей математики. М., Гостехиздат, 1957.
57. Τ е ρ е н τ ь е в А. Г. Плоские стационарные задачи теорий струйных
и кавитационных течений. Казань—Чебоксары, Гос. университет им. И. Н.
Ульянова, докторская диссертация, 1972.
58. Τ е ρ е н τ ь е в А. Г. Струйное обтекание тонкого профиля
ограниченным потоком.— Известия АН СССР. Механика жидкостей и газа, 197-2, №2,
с. 137.
242
59. τ e ρ e Η τ ь e в Α. Г. К решению линейной задачи кавитационного
обтекания криволинейной дуги.— Известия АН СССР. Механика жидкостей
и газа, 1972, № 1, с. 34.
60. Τ ρ о е π о л ь с к а я О. В. Решение некоторых струйных задач
гидромеханики с учетом силы тяжести. Автореферат диссертации на соискание ученой
степени канд. техн. наук, Казань, 1972.
61. Троепольская О. В. Об одной схеме кавитационного течения
тяжелой жидкости.— Изв. вузов. Математика, 1963, № 6.
62. Труды семинара по краевым задачам, 1968, вып. 5 (Казань, изд-во
Казанского ун-та).
63. Труды семинара по краевым задачам, вып. 6, 1969 (Казань, изд-во
Казанского ун-та).
64. Труды ЦАГИ им. Н. Е. Жуковского. Статьи по вопросам кавитационных
течений, вып. 824, 1961.
65. Ц е й τ л и н М. Ю. Симметричное струйное обтекание пластины при
наличии источника, расположенного за каверной.— Технический отчет ЦАГИ,
вып. 170, 1960.
66. Ц е й τ л и н М. Ю. Исследование сопротивления эллипсоидов
вращения при осесимметричном струйном обтекании.— Труды ЦАГИ, вып. 801, 1960.
67. Ц я н Л. Ф,, Г и л ь б о М. Расчет и исследование суперкавитационных
крыловых профилей при гармоническом движении.— Труды Международного
симпозиума в Ленинграде. М., «Наука», 1973.
68. .Ф е д я е в с к ий К· Κ·ι В о й τ к у н с к и й Я. И., Фаддеев Ю. И.
Гидромеханика. Л., «Судостроение», 1968.
69. Ш а л л а ρ ь А. В. Исследование нестационарных гидродинамических
характеристик суперкавитирующих и вентилируемых подводных крыльев.
Диссертация на соискание ученой степени каид. техн. наук, Л., ЦНИИ им. Крьмова,
1970.
70. Ш а л л а ρ ь А. В. Подъемная сила и момент на суперкавитационных
и вентилируемых подводных крыльях в волновом потоке. — Труды ЦНИИ
им. Крылова, 1971, вып. 266.
71. Элл ер А. О. Определение параметров бесконечной системы искус-
ствеииых каверн, расположенных друг за другом на нижней стороне иеограни-
ченной горизонтальной плоскости.— Труды ЦНИИ им. Крылова, 1970, вып. 258.
72. Э π ш τ е й к Л. А. Определение количества газа, необходимого для
поддержания кавериы за телом, движущимся горизонтально при небольших
числах Фруда.—Труды ЦАГИ, 1961, вып. 824.
73. Э π ш τ е й н Л. А. Течение около тел вращения при малых числах
кавитации.— Труды ЦАГИ, 1961, вып. 817.
74. А с о S t а А. J. The Effect of Longitudinal Gravitational Field on the
Supercavitating Flow Over a Wedge.— «Trans. ASME», 1961, vol. 83, Series, E,
pp. 188—192.
75. Brennen Christopher. A numerical Solution of axisymmetrie
cavity flows.— <Journal. Fluid Mech.», 1969, vol. 37, part 4, pp. 671—668.
76. С a m ρ b e 1 1 I. J., Η i 1 b о r π e D. V. Air Entrainment Behind
Artificially. Inflated Cavities.— Second Symposium an Cavitation on Naval Hydro-
dymanics. Wachington, 1958.
77. Cumberbatch E. Cavitating Flow past a Large Aspect — Ratio
Hydrofoil.— «Journal of Ship Research», 1961, March, vol. 4, N 4.
78. Cumberbatch E. Accelerating, Supercavitating Flow Past a thin
two-dimensional Wedge.— «Journal of Ship Research», 1961, June.
79. G e u r s t J. A. and Verbrush P. J. A note on camber effects of
a partially cavitated Hydrofoil.— Int. Shipbuilding Progress», 1952, Sept., vol. 6,
N 61.
80. G e u r s t J. A. Linearized theory for partially Cavitated Hydrofoils.—
«Int. Shipbuilding Progress», 1959, Aug., vol. 6, N 60.
81. G i 1 b a r g B. D. Jets and Cavites.— «Handbuch der Physic», 1960, В. IX.
82. Kermeen R. W. Experimental invistigation of three-dimensional
effect on cavitating hydrofoils.— «Engineering Division», 1960, Sept., Rep. 47
(California, Institute of Technology).
243
83. к i m Jong Η. The Wall Effect for Unsteady, Choked Supercavitating
Flow.— «Journal of Ship Research», 1972, December, vol. 16, N 4.
84. Klose J., Acosta A. J. Some new measurements on the drag of
cavitating disks.— «Journal of Ship Research», 1965, Sept., vol. 9, N 2.
85. L a r о с к В. Ε. and Street R. L. A Riemann-Hilbert Problem for
Nonlinear Fully Cavitating Flow. — «Journal of Ship Research», 1965, vol. 9,
N 3.
86. L a r о с к В. Ε. and Street R. L. A Nonlinear Solution for a Fully
Cavitating Hydrofoil. Eensath a Free Surface. — «Journal of Ship Research», 1967,
June, vol. 11, N 2.
87. L e η a u Ch. W., Street R. L. A non-linear theory for symmetric,
supercavitating flow in a gravity field.— «Journal of Fluid Mechanics», 1965, 21,
pt. 2, pp. 257—280.
88. L u u T. S., О f f e r В., Τ s e η L. F. Etude theorique et experimental
des hydropteres, cent'iles, d'envergure finie munis d'un mat.—Bull, de I'A.T.M.A,
Paris, 1968.
89. Μ e i j e г Μ. С. Some experiments of Partly Cavitating Hydrofoils.—
«Int. Shipbuilding Progress», 1958, Aug., vol. 6, N 60.
90. Μ i 11 о η Μ a г 1 i η. Unsteady lift and moment of fully cavitating
Hydrofoils at zero cavitation number. — «Journal of Ship Research», 1962, 6,
N 1.
91. N i s h i ]■ a m a T. Lifting-line Theory of Supercavitating Hydrofoil of
Finite Span.— «Zeitschrift für angewandte mathematik und mechanik», 1970,
Band 50, Heft 11 (Akademie — Verlag GMBH, Berlin).
92. Ρ 1 e s s e t M. S. The Dymanics of Cavitation.^ «Journal Appl. Mech.,»
1949, v. 16, N 3.
93. Ρ 1 e s s e t M. S., Μ i t с h e 1 1 T. P, On the Stability of the Spherical
Shape of a Uapour Cavity in a Liquid.— «Quart, of Appl. Matem.», 1956, v. 13,
N 4.
94. S с h о t Steven H. The Hydrofoil with Finite Cavity in a Solid-
Wall Channel.— «Journal of Ship Research», 1971, June, vol, 15, N 2. "
95. S i 1 b e r m a η η Ε., S о η g С. S. Instability of Ventilated Cavities.—
«Journal of Ship» Research, 1961, June.
96. S о η g С. S. Two-Dimensional Supercavitating Plate Oscillating under
a Free Surface.— «Journal of Ship Research», 1965, June, vol. 9, N 1.
97. S о η g С. S. Supercavitating Flat Plate with an Oscillating Flap at zero
cavitation Number.— «Journal of Ship Research», 1967, March, vol. 11, N 1.
98. S t r e e t R. L. Supercavitating flow about a slender wedge in a transverse
gravity field.— «Journal of Ship Research», 1963, N 1.
99. S t r e e t R. L. A note on gravity effects in supercavitating flow.—
«Journal of Ship Research», 1965, N 4.
100. Sulmont P., Cordonnier J. P. Ecoulement Supercavitant
autour d'un profit souple Extrait, Annates, Ecole nationale superieure de mecani-
que, Nantes, 1971.
101. Tsen Li Fang, GuilbaudMichel. Influence de la pro-
fondeur d'immersion sur les caracteristiques d'un profit a ventilation provoquec a
lextrados.— С R. Acad.
Sc. Paris, 1968, t. 267, p. 575—578.
102. Τ u 1 i n, Marshall P. Supercavitating Flows—Small Perturbation
Theory.— «Journal of Ship Research», 1964, January, vol. 7, N 3.
103. Van Dyke M. Perturbation methods of fluid mechanics.—Applied
Mathematics and Mechanics. Academie Press, 1964, vol. 8, p. 175.
104. W i d η a 1 1 S. E. Unstady loads on supercavitating hydrofoils of
finite Span.— «Journal of Ship Research», 1966, N 9, p. 107.
105. Woods L. С A new relation treatment of flow with axial summetry.—
Quart. Journal Mech. and Applied Meth., 1951, vol. IV, pt. 3.
106. Wu — Th. Yac — TSU. Cavity and wake Flows.— Reprented from
Annual Review of Fluid Mechanics, 1972, vol. 4.
244
Дополнение к указателю литературы
107. Armstrong А. Н., D и η h а и J. Н. Axisymmetric cavity flow.—
Rep. Arm. Res. Est. G. В., 1953, 12/53.
108. Cox R. N., С 1 a у d e η W. A. Air entrainmentat the rear of a steady
cavity.— Cavitation in Hydrodynamics, London, 1956.
109. Fisher J. W. The drag on a circular plate generating a cavity in
water.— Underwater Ballistics Commun, 1944,
110. Meyer M. С Some Experiments of Partly Cavitation Hydrofoils.—
Int. Shipb. Progress, 1959, vol. 6, N 60.
111. O'Neill. Flow around Bodies with attached open cavities.—
Hydrodynamics Laboratory Report. NE—24.7.— Institute of Technology, California, 1954.
112. Ρ 1 e s s e t M. S., S h a f f e r P. A. Cavity drad.— «Journal of
Applied Physics», 1948, vol. 19.
113. R e i с h a r d t H. The Laws of Cavitation Bubbles at Axially
Symmetric Bodies in a Flow.— Map Reports and Translations, 1946, N 766, (Washington).
114. R e i с h a r d H. The physical laws governing the cavitation bubbles
produud behind solids of revolution in a fluid flow.— The Institute of Hyg. Res.
Gottingen, 1945, Rep. UM 6628.
115. Rogdestwensky V. V., Khlynpin A. I. Experimental
study of the Gas Velocity Profile the Ventilated Cavity. — Twelfth International
Towing Tank conference, Rome, 1969.
116. Rouse H., McNown. Cavitation and pressure distribution head-
forms at zero angles of yaw.— Bull. St. Univ. JOWA, Studies Engineernig, N 32.
117. Τ г i 11 i η g L. The Collapse and Rebound of a Gas Bubble.— Journal
of Applied Physics, 1952, vol. 23, N 1.
118. T. Y. W u. A note of the Linear and Nonlinear Theories for fully cavitated
Hydrofoil.—California Institute of Technology, Hydrodynamics Laboratory,
Report, N 21—22, 1956.
119. T. V. W u. A. Simple Method for Calculating the Drag in the Linear
Theories of Cavity Flows.— California Institute of Technology, Engineering Division,
Report N 85—5, 1957.
СОДЕРЖАНИЕ
Основные условные обозначения 3
Введение 5
Глава I. НАЧАЛЬНАЯ СТАДИЯ КАВИТАЦИИ
(ПУЗЫРЧАТАЯ КАВИТАЦИЯ) 13
§ I. Статическое равновесие пузырька в жидкости. Критическое
давление и критический радиус —
§ 2. Неустановившееся движение парогазового пузырька 18
§ 3. Влияние сжимаемости жидкости на развитие парогазового
пузырька , 35
§ 4. Влияние твердой стенки на развитие парогазового пузырька 44
§ 5. Устойчивость сферического пузырька 49
Глава II. РАЗВИТАЯ КАВИТАЦИЯ-
УСТАНОВИВШИЕСЯ КАВИТАЦИОННЫЕ ТЕЧЕНИЯ
(НЕЛИНЕЙНАЯ ТЕОРИЯ) 54
§ 1. Форма границы каверны, парадокс Бриллуэна, схемы кавитацион-
ных течений —
§ 2. Методы решения задач 59
§ 3. Струйное обтекание пластинки. Решение задачи с помощью способа
Н. Е. Жуковского , 69
§ 4. Кавитационное обтекание пластинки в безграничной жидкости (по
схеме Д. А. Эфроса). Решение задачи с помощью способа особых точек
С. А. Чаплыгина 73
§ 5. Кавитационное обтекание пластинки в безграничной жидкости (по
Первой схеме М. Тулина) 83
§ 6. Кавитационное обтекание пластинки вблизи свободной поверхности
(по второй схеме М. Тулина) 89
Глава ΠΙ. РАЗВИТАЯ КАВИТАЦИЯ-
УСТАНОВИВШИЕСЯ КАВИТАЦИОННЫЕ ТЕЧЕНИЯ
(ЛИНЕЙНАЯ ТЕОРИЯ) 96
§ 1. Кавитационное обтекание профиля с фиксированными точками
отрыва —
§ 2. Кавитационное обтекание тонких профилей ограниченным потоком 115
§ 3. Обтекание тонких ненесущих тел в режиме развитой кавитации.
Применение метода источников и стоков 128
246
§ 4. Ёлияние весомости н^идкости на Характеристики кавитационногО
обтекания тонкого клина 140
§ 5. Влияние весомости жидкости на характеристики кавитационного
течения в ограниченном потоке 152
§ 6. Кавитационное обтекание профиля плавных образований 158
Глава IV. НЕСТАЦИОНАРНЫЕ КАВИТАЦИОННЫЕ
ТЕЧЕНИЯ 166
§ 1. Понятие о потенциале ускорения —
§ 2. Ускоренное кавитационное обтекание тонкого клипа 169
§ 3. Нестационарное кавитационное обтекание тонкого профиля вблизи
свободной поверхности 176
Глава V. ЧИСЛЕННЫЕ МЕТОДЫ РАСЧЕТА
ПАРАМЕТРОВ КАВИТАЦИОННЫХ
ТЕЧЕНИЙ ■ 186
§ 1. Применение метода конечных разностей (метода сеток) ■—
§ 2. Применение метода вихревых особенностей для расчета плоских
кавитационных течений. Численное решение интегральных уравнений
с помощью метода последовательных приближений 196
§ 3. Применение метода вихревых особенностей для расчета осесимме-
тричного обтекания тела в режиме развитой кавитации 202
Глава VI. ИСКУССТВЕННАЯ КАВИТАЦИЯ .... 211
§ 1. Физические основы искусственной кавитации —■
§ 2. Приближенные формулы для определения параметров искусственной
кавитации 220
§ 3. Структура кавитационных потоков 226
Приложение 238
Указатель литературы 240