Автор: Adamek J. Trnkova V.
Теги: mathematics mathematical physics higher mathematics applied mathematics mathematics and its applications series kluwer academic publishers
ISBN: 0-7923-0010-6
Год: 1999
Текст
Mathematics and Its Applications
w Adamek and Vera Trnkova
Automata and
Algebras in Categories
Mathematics and Hi Applications (East European Series)
Muting Edkof:
M. HAZEWINKEL
Ctnmfor Mmrhamaha and Computer Sd**ct. Amsterdam. Tmt Netktrlnmdt
EiMuriil Bui*
A. BIALYNICKI BIKULA, Iralinilr ofMaktnwtia. Warier Vmrrmity. folaod
H. KURKE. Humboldt Unimily. fern*. CD*
J. KURZWEIL, UolKrmatkt Iralttwt. Aeodtmy ofStinm. humvt. Cnrhadovakia
L LEINDLER. tofyol Imliuu. Sitftd. Hm$ary
D. S. MITRINOVlt, Urilmhyaf Btitrwk. tugailarta
S. ROLEWICZ. Mil* Atadtmy of Stttim. Wmnmw. Pthnd
■L. H. SENDOV. BwlferitK Afdrmy ofSdtncn. Sofia. BWforio
I. T. TODOROV, tulgerima Aradtmy ofStumm. Sofia, fulmar*
H. TRIEBEL, Uidmtly of Ima. G.D.K.
Automata and Algebras
in Categories
by
JiRI adAmek
Faculty of Ottuitat Emgiimrimg. TtckiHcal Vnhmitj. Fromat. Cxtvhmbmkul
ind
V£RA TRNKOVA
Faculty of Malhtmatki aad Physki. Charks Untwrstty. Frag**. CirthoshnaUa
KLUWER ACADEMIC PUBLISHERS
DORDRECHT / BOSTON /LONDON
lAmr •» C^na Cttd^taj la PaNiottoa Datt
OE
Adamek. JIH. Dr.
Automata and algebras in categories/by JIH Adamek and Vera Trakova.
p. an. (Mathematics and lb application*. East European scries; 37)
Bibliography: p.
Includes Indei.
ISBN 0-7923-0010-6
I. Machine theory. 2. Categoric* (Mathematics) 3. Functor theory. I. Trakova, Verm. II. Title,
til. Strict: Mathematic* and Hs applications (D. Reidd Publishing Company). East European
•erics; v. 37.
QA267.A32 1909
311 -dcl9 M-297B0
Published by Kluwer Academic Publishers,
P.O. Boi 17. 3300 AA Dordrecht. The Netherlands
in co-edition with SNTL— Publishers of Technical Literature, Prague
Kluwer Academic Publishers incorporates
the publishing programmes of
D. ReMd, Maninus NIJhoiT. Dr. W. junk and MTP Press.
Sold and distributed In the U.S-A- and Canada
by Kluwer Academic Publishers,
101 Philip Drive. Norwetl. MA 02041, U.S-A.
Sold and distributed in Albania, Bulgaria. China. Ciechoslovakia, German Democratic Republic,
Hungary, Mongolia. Northern Korea, Poland. Rumania, U.S.S.R., Vietnam, and Yugoslavia by
ARTIA. Foreign Trade Corporatioa Tor the Import and Export of Cultural Commodities,
Vc Smeckach 30.111 27 Prague I. Czechoslovakia
In all other countries, sold and distributed
by Kluwer Academic Publishers Oroup,
P.O. Boi 322. 3300 AH Dordrecht. The Netherlands
All Rights Reserved
Copyright • 1990 by JiH Adamek and Vera Tmkova
No part of the material protected by this copyright notice may be reproduced or utilised in any
form or by any means, clearonlc, or mechanical including photocopying, recording or by aay u-
fornation storage and retrieval system, without written permitsioa from the copyright owners
Printed in Czechoslovakia
Scries E4ltor*i Preface
'Et mol si J'avah ■■ On* Krvtce mathematics
uhmiwih en revenir, jc n'y has rendered the haiaan
■crib point Bile.' nee. It has pot common
Jain Verne mam bncfc when it
belongs, on the topmost their
The series it divergent; neil to the dusty canister
IbereTon we msy be aNe la labelled 'discarded non-
do something with it. sense'.
O. Heavlside Eric T. Bell
Mathematia is a tool Tor thouiht. A highly necessary tool in a world where
both feedback and nonlineariliea abound. Similarly, all kinds or parts or
mathematics serve as tools for other parti and for other sciences.
Applying a simple rewriting rule to the quote on the right above one
finds such statement* as: 'One service topology has rendered mathematical
physics ...'; 'One service logic has rendered computer science ...'; 'One
service category theory has rendered mathematics ...'. All arguably true. And all
statements obtainable this way form part the raison d'etre of this series.
This series, Mathtmatki and In Applications, started in 1977. Now that over
one hundred volumes have appeared it seems opportune to reexamine its
scope. At the time I wrote
"Growing specialization and diversification have brought a host of
monographs and textbooks on increasingly specialized topics. How-
ever, the 'tree' of knowledge of mathematics and related fields does
not grow only by putting forth new branches. It also happens, quite
often in fact, that branches which were thought to be completely
disparate are suddenly seen to be related. Further, the kind and level of
sophistication of mathematics applied in various sciences has
changed drastically in recent yean: measure theory is used (non-trivi-
ally) in regional and theoretical economics; algebraic geometry
interacts with physics; the Minkowsky lemma, coding theory and the
structure of water meet one another in packing and covering theory;
quantum fields, crystal defects and mathematical programming profit
from homotopy theory; Lie algebras are relevant to filtering; and
prediction and electrical engineering can use Stein spaces. And In
addition to this there are such new emerging subdisdpllnes u
'experimental mathematics', 'CFD', 'completely IntegraMe systems', 'chaos
synergetics and large-scale order', which are almost impossible to fit
into the existing classification schemes. They draw upon widely
different sections of mathematics.*'
VI
Strict Editor'! Preface
By and large, all still applies today. It is still true that at Tint sight
mathematics seems rather fragmented and that to find, see, and exploit the deeper
underlying interrelations more effort is needed and so are books that can help
mathematicians and scientists do so. Accordingly MIA will continue to try to
make such books available.
If anything, the description I gave in 1977 is now an understatement. To the
examples or interaction areas one should add string where Riemann surfaces,
algebraic geometry, modular functions, knots, quantum field theory, Kac-
Moody algebras, monstrous moonshine (and more) all come together. And to
the examples of things which can be usefully applied let me add the topic
'finite geometry': a combination of words which sounds like it might not even
exist, let alone be applicable. And yet it is being applied: to statistics via
designs, to radar/sonar detection arrays (via finite projective planes), and to bus
connections of VLSI ehipt (via difference sets). There seems to be no part of
(so-called pure) mathematics that is not in Immediate danger of being
applied. And, accordingly, the applied mathematician needs to be aware of much
more. Betides analysis and numerics, the traditional workhorses, he may need
all kinds of combinatorics, algebra, probability, and so on.
In addition, the applied scientist needs to cope increasingly with the
nonlinear worid and the extra mathematical sophistication that this requien. For
that is where the rewards are. Linear models are honest and a bit tad and
depressing: proportional efforts and results. It is in the nonlinear worid that
Infinitesimal inputs may result in macroscopic outputs (or vice vena). To
appreciate what I am hinting at: if electronics were linear we would have no fun
with transistors and computers; we would have no TV; in fact you would not
be reading these lines.
There is also no safety in ignoring such outlandbh thing at nonstandard
analysis, supenpace and anticommuting integration, p-adk and ultrunetric
space. All three have applications in both electrical engineering and physics.
Once, complex numbers were equally outlandish, but they frequently proved
the shortest path between 'real' results. Similarly, the Tint two topics named
have already provided a number of 'wormhole' paths. There is no telling
where all this is leading—fortunately.
Thus the original scone of the series, which for various (sound) reasons now
comprises five subseries: white (Japan), yellow (China), red (USSR), blue
(Eastern Europe), and green (everything else), still applies. It hat been
enlarged a bit to Include books treating of the tools from one subdisdpline
which are used in others. Thus the series still aims at books dealing with:
— a central concept which plays an important role in several different
mathematical and/or scientific specialization areas;
— new applications of the results and ideal from one area of scientific
endeavour into another;
Serin Editor*! Prate*
VII
— influence! which the resulu, problems and concept* or one Held or
enquiry have, and have had, on the development of another.
Automata, more predtely, sequential automata, have their Importance In
logic, computer science and control and signal processing theory. They ad on
(input) strings (over a given alphabet) producing a 'behaviour map' and
important questions concern (minimal) realizations of behaviours and the recog-
nfctability or formal languages by deterministic and nondeterminlstic
automata.
In many situations, more general objects than strings need to be processed.
A most important class being trees (think. Tor example, of types). Just as
sequential automata act on strings, tree automata act on trees: more precisely
E-tree automata act on E-treet where £ is a given set of n-»ry operations (n not
necessarily constant over I). And or course there are the natural questions
concerning realization, behaviour, and recognizability also in this case.
Both classes of automata are a special case or the much more general idea
or /^automata where F is an endofunctor or some category. These objects and
the associated questions and old results concerning behaviour,
realization and recognuability (KJeene type theorems) from the subject matter of
this book, which therefore has something to offer to all mathematicians,
engineers and computer sdentists with an interest in automata, categories,
formal languages, or universal algebra.
Perusing the present volume is not guaranteed to tum you into an instant
expert, but it will help, though perhaps only in the sense of the last quote on
the right below.
Th< shortest pith between Never lend books, for oo
tws trails In the real do- one ever returns lAcm: the
mitn posset throofh die only booki I hive In my tlb-
complei domain. rai-y tre booki that other
J. Hadamari fob hive lent me.
Aiiatolc France
La physique nc neus donne
pas settlement 1'occssion de The function of an expert is
resoudra des pfobleaei ... not IB be more right than
clle aoaa fall pressentir la other people, hot to be
sontton. wrong for mora BopWstie-
H. Point-ant mod reasons
D-ntdBtrtkr
Butsum. January 1989
Michiel Hazewinkel
Contents
Sitor«iiiirwf«c» v
Preface XI
Chapter hSEQUTNTUL AUTOMATA I
1. Aalomata tad Behavior I
2. Minimal Ruination 7
3. Finite AbUhmia and Languajee 19
Nan In Chapter I 21
Chapter II i TUT AUTOMATA 29
1. Flimwy Tree Atrtomitt 2V
2. Minimal RullnUon 42
}. Inflatory Tree Aatomala 92
4. Flnim Amsrnata and Langnafa 69
NontoCkapltrll II
Ollll llli rVWTOMATA (2
1. Introduction 12
2. Automata m a Category II
3. FAIfeora 113
4. Sat Fuacton 121
9. Factmiiatlon Syurm 144
Nolo to Chapter III 197
CkantarlViCONSTIllCnONOrrUCALGIBaAS 191
1. Inuodacoon 191
2. liuW-AJfieraCoa«nj<non 199
3. Frcc-AJgnbraConalractioa 170
4. Cllarncterrarlon Theorem Ill
9. Abjeorea In Coacrett Cateaoriet 117
6. Flnlury Varfeton 199
7. Free-Completion Comtrocuon 210
I. CaleaoritiorAlfebrM 221
Nous to Chapter IV 242
X Content!
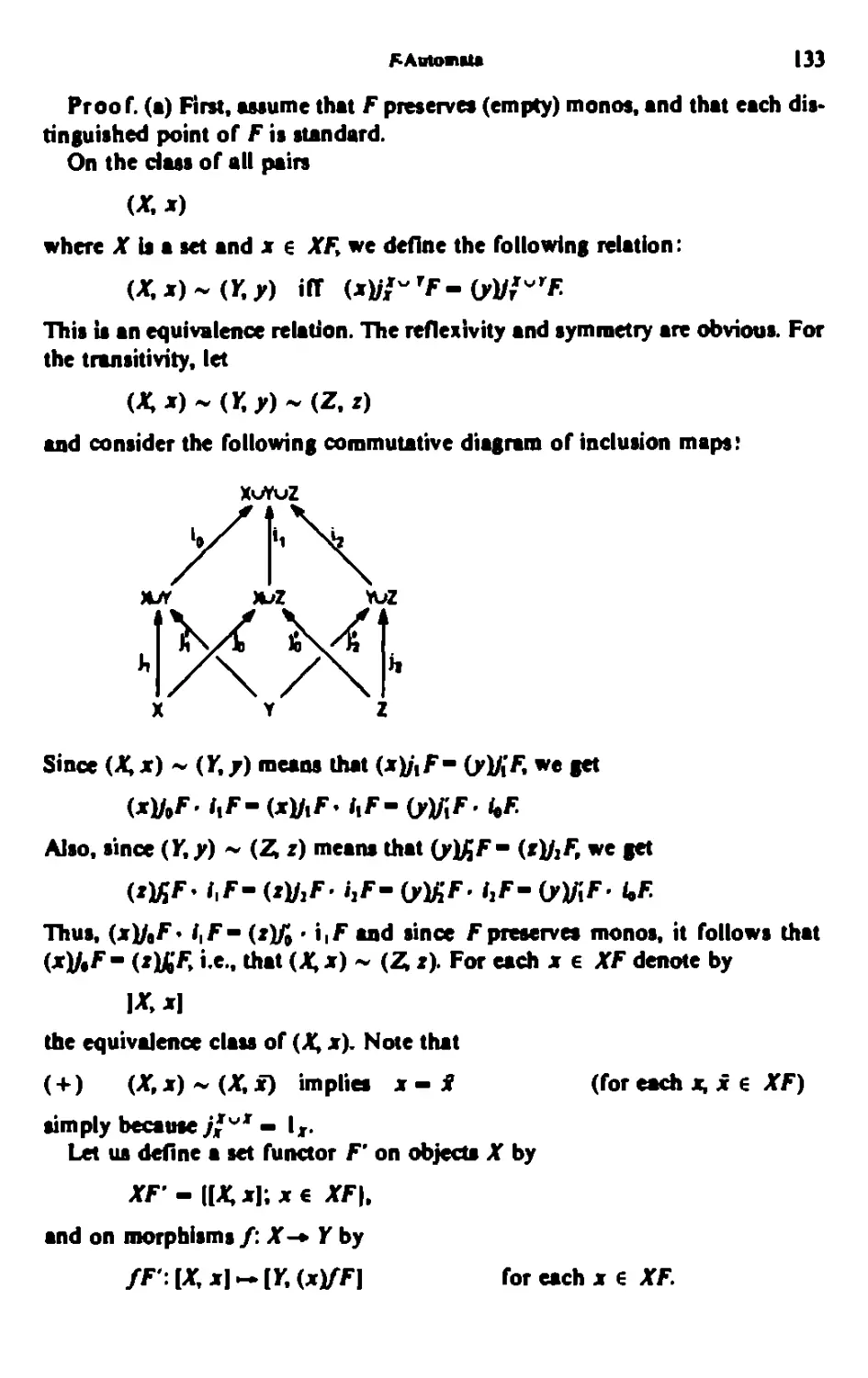
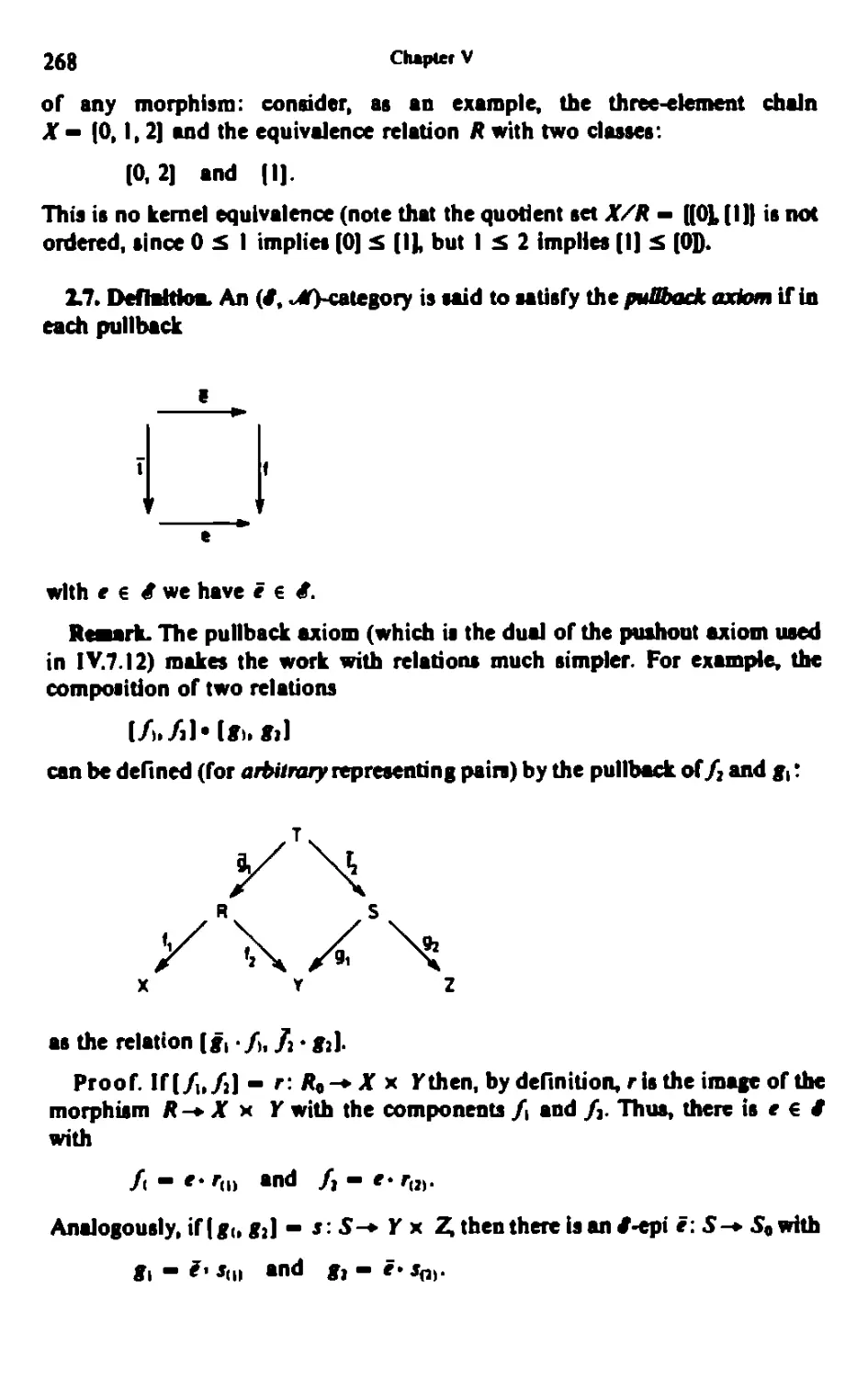
Chant* Vi MINIMAL REALIZATION AND REDUCTION 244
1. Minimal Reduction 244
2. Refattona In ■ Category 257
3. Unitary Functors 279
4. Consequence* of Minimal Reduction 302
5. Finns Automata 311
Note* io Chapter V 319
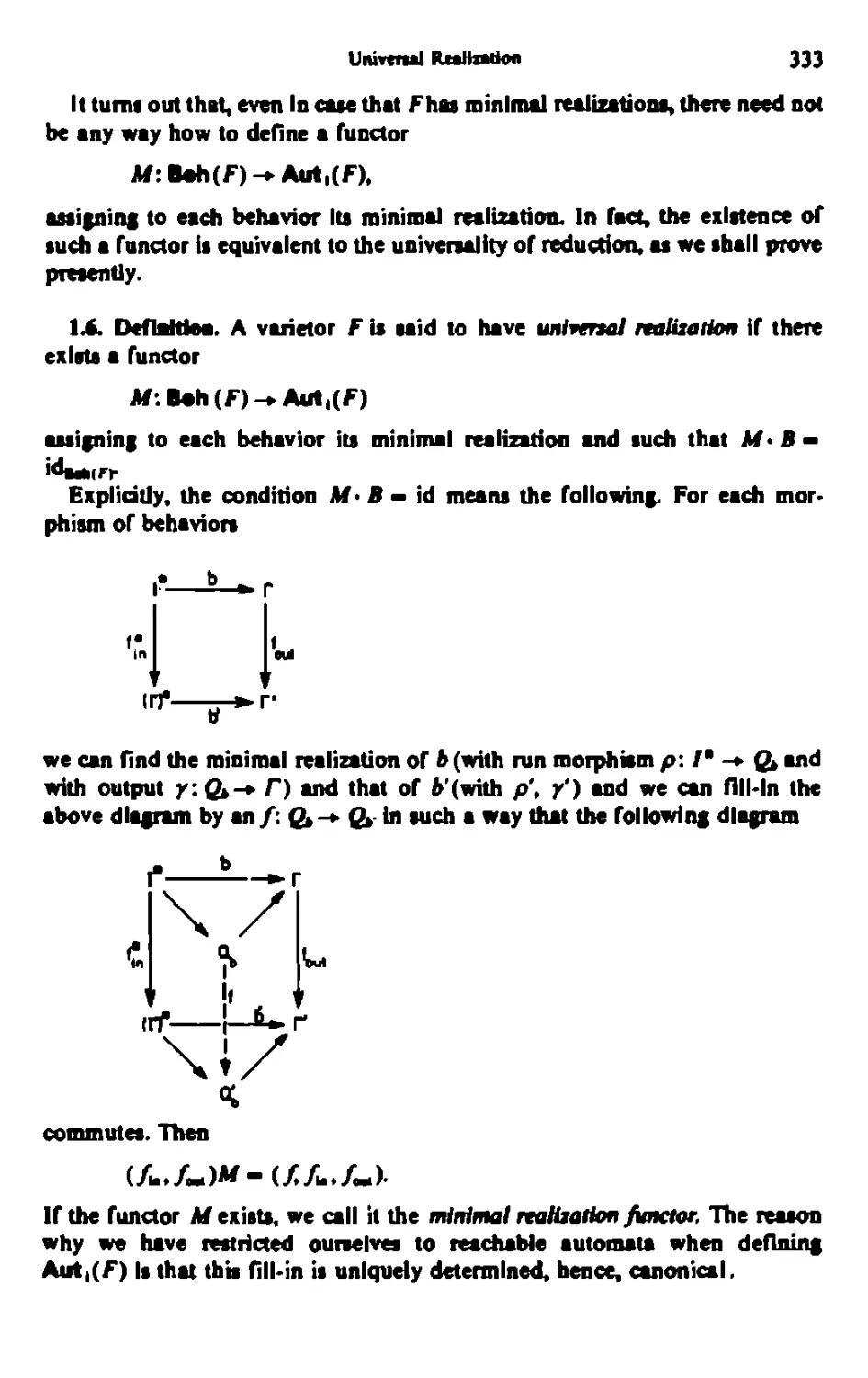
Owatar VI: UNIVERSAL REALIZATION 321
1. The Concept of Universality 321
2. Urrivenal Reduction Theorem 339
3- Nerode Equivalence! M3
Notes to Chapter VI 37*
ChaaMvVlliNONDETERMINISTICAUTOMATAANDKLEENETHEOREM MO
1. Nondctermlniiiic Behavior MO
2. Nondetermlntstic Languages In Rat 404
3. Kleene Theorem 430
Notes to Chapter Vll 462
An is Mm BET-THEORETICAL CONVENTIONS *M
UatefCnmtfStmMs 465
Irfitwn 467
Sat*et h**n 471
Preface
Wkat ta Geaerallnd
The theory or automata has developed rapidly in the last decades: from ihe
first endeavour to describe formally the input-output behavior, to a clear
algebraic insight into the basic concepts and their interrelationship. The original
notion of a sequential automaton has been generalized in a number of
directions. The motivating directions for the present monograph are two:
(i) linear sequential automata, arising from the theory of dynamical
systems, and
(ii) tree automata, the basic structure of which is an arbitrary algebra
(whereas the structure of a sequential automaton Is a unary algebra).
The first example shows that sets with structure and structure-preserving
maps play an important role; the latter indicates thai "types" more complex
than an input set and an output set are needed.
A model of automata based on categories and functors, and encompassing
the above examples, has been presented by M. A. Arbib and G. E. Manes in
a series of papers since 1974. They study automata in a category which will be
the category of sets for the sequential automata and the tree automata, or the
category ofmodules for the linear sequential automata. The fundamental idea
is to express the type of automata under study by a suitable functor. This
makes the basic notions concise and general. We present the concepts of
Arbib and Manes in the third chapter, and thereafter we develop a theory of
functorlal automata, based on the research of the Prague Seminar on Oeneral
Mathematical Structures since 1970. The first two chapters present the
motivation: the first one is devoied to standard facts concerning sequential
automat*, and in Ihe latter w« study tree automata (with some results appearing
for ihe first time in a book).
Wkat Reaalta are Obtained
Our monograph presents a study of functors motivated by automata-theoretic
concepts. An ^automaton in a category JT (where F: Jt -► Jf is a functor
expressing the type) is, roughly speaking, an algebra of type F endowed with an
output. We discuss
XII
Preftn
(a) the existence and construction or Tree f-algebras which play the role
that the monoid or words does Tor sequential automata (Chapter IV),
(b) the existence or minimal realizations Tor all behaviors (Chapter V), and
their construction and universally (Chapter VI), and
(c) the languages recognizable by finite deterministic and nondeterministic
automata (Chapter VII).
Each of these problems turns out to be very difficult when investigated in
a general category with a general type functor. We try, in each case, to obtain
not only sufficient conditions under which the individual construction can be
performed, but also necessary conditions on the functor. This serves to shed
new light on the boundaries of the automata-theoretic concepts. For example,
we prove that if F is a finitarity functor, then all behaviors have minimal
realizations. But we are interested also in the converse: does minimal realization
imply finitarity? We prove that it does, under additional hypotheses, which
shows e.g. the "handicap" of infinitary tree automata.
An analogous situations arises in each of the fields of problems we
investigate. We present necessary and sufficient conditions for
(a) the "constructive" and "finitary" existence of free algebras,
(b) the existence and universality of minimal realizations,
(c) the description of the languages recognized by finite automata using
rational operations, and the coincidence of these languages with those
recognized by nondeterministic finite automata.
The obtained results have diverse degrees of generality: in (a) the categories
and functors are quite general, in (b) we often have to assume restrictive
additional hypotheses, and (c) is studied only in the category of sets. Nevertheless,
in each case the presented condition shows boundaries beyond which
automata theory cannot be extended. Particularly sharp results are achieved for
the category Set of sets and A-Voot of vector spaces (over a field R). For
example, the main result of Chapter V is that ^automata have minimal
realizations iff F is a finitary functor; in case of S«t and A-Vect, this holds for all
functors, and otherwise additional hypotheses are needed. Analogously, the
main result of Chapter VI is that f-automata have universal minimal
realization iff F preserves unions: again, this holds for all functors in case of S«t
and A-Voct. And the free-algebra construction of Chapter IV also converges
for all functors in Set and A-Voct for which the free algebras actually exist;
these are just the functors with arbitrarily large fixed points.
The special case when the functor F has an adjoint subsumes the theory of
automata in closed categories investigated for example by J. A. Goguen,
L. Budach and J.-H. Hoehnke, and H. Ehrig el al. (sec References).
Preface
XIII
Orgaaltatloa
The interdependence or the chapters or our monograph can be depicted as
follows:
theory
We have endeavoured to make our book self-contained. All concepts or the
theory or automata we use can be found in the first two chapters. The reader
is expected to be familiar with the fundamentals of category theory.
Everything beyond "common knowledge" of categorists is carefully introduced in
the text.
Each chapter is numbered by a Roman numeral, and is divided into
sections numbered by Arabic numerals. Thus, III.5 denotes the fifth section of
Chapter III, Sections, listed in the contents, arc subdivided into numbered
subsections (for example, III.5.2 is the second subsection of the Section III.5)
and they are concluded by exercises, denoted by capital letters (for example,
Exercise III.5.B is the Exercise B. in the Section III.5).
All historical comments are concentrated at the end of each chapter. We
include a list of references which is very detailed as far as papers of the Prague
Seminar are concerned. Other references were chosen so as to cover all the
paper* we used, or were inspired by, but we have not provided an exhaustive
list of the extensive body of literature connected with our monograph.
Aduwwkdgeitita
We are deeply Indebted to the members of the Prague Seminar of General
Mathematical Structures, in particular to V, Koubek and J. Reiterman.
Although we have tried to be accurate in our references to their papers, their
work has influenced ours throughout the years beyond these bare facts.
XIV
Preface
Our thanks are due to M. A. Arblb and E. G. Manes Tor their interest and
stimulation or our work. On a suggestion or the latter we wrote a survey paper
which became the basis or our monograph. Also G. Grltzer rollowed our
work with a close interest. He has encouraged us on different occasions,
particularly during the lectures or the second author on this topic at the Algebra
Seminar or the University or Manitoba.
Chapter I; Sequential Automata
1.1. Aatoauta sad Behavior
I.I. A sequential automaton is, roughly speaking, a device which is at one or
its states and, receiving an input signal (from a specified set L, called the input
alphabet) changes its state to another state and emits an output signal (from
a specified set /~, called the output alphabet). Each state q and each input
signal a determine the next state q' - (q, 0)6, in which the automaton will be
after receiving the Input o-in the state q. Formally:
Deflattle*. Let Tbe a non-empty set, called the Input alphabet. A sequential
L-auumalon is a quintuple A — (ft S, r, y, <h), where
Q is a set, called the set of stales:
6: Q x £-» Qua map, called the next-stale map:
riia set, called the output alphabet:
y: Q-* Tis a map, called the output map;
q, is an element of Q, called the Initial slate.
The automaton A is supposed to start its work always in the state q*
Receiving the first input o-, e L, it changes its state to
q< - (*» d)«
and emits the output (q*)r- Receiving the second input o-j e I, It changes its
state to
«i - («. Ci)«
and emits the output (<?i)r- Etc.
1.2. Denote by L* the set of all words in the alphabet £ That is, the
elements of I' arc
(0) the empty word 8:
(1) all the one-letter words, i.e., elements of I;
(2) all the two-letter words a,a, (with o-„ a, e £);
(3) all the three-letter words 0-,0-jO-i (with a„ ab a, e I), etc.
(We write words without commas or brackets which leads to no confusion
provided that Tdoes not contain symbols d, a* ■.., a,such that the symbol
0-1O-] .. .a, is in I too, which we shall always assume.) There is a naturally de-
2
Chapter I
fined binary operation on the set I' called the concatenation which auigni to
wordj w - a,a, ...a, and w' - t,Ti ... t„ in X* the word **' = <t,it, ...
tr.TiT]... r„. This operation is associative, i.e. (»»')»" — w(w'w~) Tor all w,
w\ w" in I', and the empty word V Is a unit, i.e.
iw- w9 - w
Tor all w e 27*. Hence, the set 27* endowed with this operation is a monoid.
CoTftJ—. When writing a,a,... a. we consider n - 0,1,2,..., where the
case n — 0 describes the empty word.
I J, The reaction or an automation to sequences or input symbols, i. e„ to
elements or I', can be described formally as follows:
Defliltlon, The run map of « sequential ^automaton A - (ft 6, r, y, <f0) is
the map
defined by the following induction
(»)P - 9%:
(a,... a.)p - q. implies (a,... aja.. ,)p - (q„ a.. ,)S
for all <t„ ..., <r„ <r.,, e I and all q. e Q.
The behavior of >4 is the map
Thus, when receiving inputs a„ o-] a., the automaton terminates in the
state q, - (a,a, ... a,)p, and emits the final output (a,a,. ■. a.)fi - (<?.)r-
M, A "small" automaton can be depicted by a labelled graph, where
vertices correspond to the states (and are labelled by pairs (4, y), where q e Q
and y - (q)r E /") and arrows correspond to 6. That is, an arrow leads from
q to q' and carries a label a E i"ifT(<j, a)S - q'. The initial state q, is
indicated by a small arrow —.
Examples
Here Q - \p, q, r, j, r), I- \a) and /"- |a, b, c). The word monoid
I' - \a)' consists of the words 9, a, 00 - a1, aaa — <r>, etc.
Sequential Aulonuu
The run map p: \a\ • -► ft is given by the following table:
0 a a' a' a' o-1 o*
q r s I r s I
The behavior 0: \a\ • -► [a, b, c) is the following map:
a if n - 0
(c"W-
c ifn-2 + 3/t, * - 0. 1,2,.
6 else.
<"' W<®^<©#®
Here ft - \p, q. r), I- |c, r| and T- |0, l|.
The behavior j): [a, r| * -» |0, l| is the following map:
.. j odd and s, •
f I if n is (
■»-|o else.
IS. Automata art unary algebras. A unary operation on a set ft is a map of
ft into itself. A unary £algebra is a set ft with a collection of unary
operations indexed by the elements of T, say |5,|„, t- The next-state map 6: ft *
I-+ ft of a sequeniial ^automaton A — (ft 6, r, y, q,) defines a unary
algebra on ft with the operations
(-)«„-(-.c)«:e-C
Conversely, each unary £algebra can be obviously described by a map
5; ft x T-» ft.
The word monoid I' Is a unary £algebra, the cooperation of which is
defined by the concatenation:
o*iCi... am »-• atOi... ama.
This defines a map p: I' x Z-+ £ (which is a restriction of the
concatenation of words).
Given unary algebras (ft, 5) and (ft', <5'). a homomorphism f:(ft £)-»
(ft, 6~) is a map of ft into ft' which commutes with the operations:
((* o)S)f- ((q)f. a)S- (q e ft a e I)
or, equivalently, fulfils
S-f-l/x idr].fi'.
4 Chapter I
This can be expressed by the commutation of the following square
0.1
OH = 0'
1.6. Prapcalttoa. The £algebra (X*, «t) is the free unary algebra on one gen-
enter 0. That is, for each unary £algebra (ft S) and each element q, e Q
there exists a unique homomorphism p: (£*, e>) -»(ft S) with (ft)p — fa-
Proof. Let us verify that the map p of Definition 1.3 is a homomorphism:
for each w — a,a2... a. in I' and each a e I we have
((>»■ »»P - (C|Cl ■ ■ ■ <V)P
- ((<T,<T, . . . <T.)A <T)fi
- [(!». <T)(P X idr)15.
Hence, f> • p - (p x id,) • &
Conversely, any homomorphism assigning <j, to 0 clearly fulfils the
inductive condition of Definition 1,3. □
Thus, the run map of a sequential ^automaton can be defined as the
unique homomorphism which maps 0 to the initial state.
1.7. DeflaMea. A morphism from a ^automaton A - (ft 8, C y, q,) to a £■
automaton A' - (ft, S\ r\ y\ q',) is a pair of maps (//„): A -► A' with
/: C-» C "id /-■: r-» /" such that
(i) /: (ft 6) -»(ft, 6") is a homomorphism:
(ii) / and /M commute with the outputs, i.e., /«« ■ y - / • /;
(iii) /preserves the initial state, i.e., (qtif— qi-
The conditions (i) and (ii) just state that the following diagram
Seqttentitl Automita 5
Coataadam. In cue r- f and /» - id/-, we write/: >4-» /«' in place or
Examples, (i) Connder the following automita A and A' and the following
map / (denoted by ~»):
a
Then /:/«-•■/«' li • morphiim.
(li) Consider the following A, A' and /:
Here r- \a,b\ and /"' - |0,1); let/„: T-» i~ be the constant map with the
value 0, then (//„,): A-* A' It a morphiim.
I J. PutaalUta. For each morphiim (//„): A-» A" of ^automata, the run
map p of A is related to the run map p' of A' by
P' - P • /.
hence, the behavior f) of A it related to the behavior p~ of A' by
A"-£■•/-■
Proof. Put /< - (ft 5, T, r. (J.) and /«' - (Q\ A", /"', /. $,"). Since the run
map p:(I',f|-»(ft{) of >4 Is a homomorphum, the composite map Is
a taomomorphism
p/:(r«,y)-(e-,o~).
6
Chi (Her I
Moreover,
Wp ■ f-(<h)f-q,-
Hence, p ■ f is the run map or A'—indeed, the run map is the unique homo-
morphism mapping 0 to q'„.
The behavior of A is /) — p • y and the behavior of A' is /)' — (/>•/) • Y-
Since/- Y - Y'• /«.. we gel 0" - p- /■ Y - P- Y ■ f~ -Pf~- °
Corollarjr. Given ^automata A and A with a joint output alphabet, the
existence of a morphism f: A-* A' guarantees that A and A have the same
behavior.
13. Isomorphism of automata is a morphism (/,/_): A-» A' such that /
and/M are bijections. It is easy to see that the inverse maps form a morphism
(/-'./.i'M-^again.
If A and A have the same output alphabet and there is an isomorphism
f: A-* A', then A and A are called isomorphic By 1.8, isomorphic automata
have the same behavior.
Exerctaea 1.1
A. CoaiaoiHI— of ■torpahna. (i) Prove that, given morphia™ of £automa-
"(//»): A —A' and (g. g„): A' - A", then (/• »,/„ • g„): ><-» >4' u alao
a morphism.
(ii) Conversely, if (//„„): /«-►/«' is a morphism with both /and /«, surjec-
tive, and given a pair of maps (g, g„«) such that (/,/„)• (g, g„): >4 -» A" a
a morphism, prove that also (g, g„,): A' -* A" is a morphism.
B. Aotomata with a alagle laaat. (i) Let a ^automaton with £ - |o-| have fi-
nitely many states. Prove that the behavior fi: E'-* /"has a "cycle", i.e. there
exists k- 1,2,... such that(o")/)- (o" k)fi holds for all sufficiently large
n. (Hint: Consider the map (—, a)S: Q-* Q. since Q is finite, this map has
a cycle.)
(ii) Conversely, for each map fi: \o"\~.«-► r which has a cycle prove that
there is a finite-stale ^automaton with the behavior fL (Hint: If
(am)fi - (a"')0 for all n £ n„ there will be n, + k states and the next-sute
map returns from the (n„ + k)-th state to the (n0 + l>-sl one.)
(Mi) Prove that etery map fi: \a' I'., -» r is the behavior of a (possibly in-
finite) ^automaton. (Hint: Put C - £'■)
Sequential Automata
7
1.2. MlaJmll RealizarJoa
2.1. Given a behavior, i.e., a map
8: T*- T,
does it have a realization?, that is, can we find a sequential automaton whose
behavior is fll And can we Hnd the realization with the minimum number or
states? The answers to these questions are affirmative, and we proceed as
follows. We first present a 'Tree" realization (which is always infinite), and then
we show how to minimize each realization to obtain the (unique) minimal
one. The minimization takes two steps: we first discard all superfluous states,
and then we merge all pairs of states which behave in the same way.
12. Free realization. For each behavior map 8, we define the following
sequential automaton:
A{fl)-W. e>, r.A«)-
The states of A(fi) are words in X* and
p-.px r-r
is the concatenation map, the output is the given behavior, and 0 is the initial
state.
Reaurka. (i) A(fi) realizes 8 because the run map of A{fi) is idt.. In fact,
idj.: (r*, e>) -»(£*, <p) is a homomorphism mapping 0 to the initial state of
A(fi) and thus, p - id,.. Consequently, the behavior of A(fi) is id,. • 8 — 8.
Thus, we see that each behavior has an (infinite) realization.
(ii) For each realization A - ((?, 6, /", y, qt) of A the run map p: £*-* Q
defines a morphism
p:A(fi)-*A.
In fact, p is a homomorphism which commutes with the outputs because
8-p. r
(for A realizes 8), and p preserves the initial state:
Q)P - *■
2J. Reackakk part. By a subaulomalon of a sequential automaton (Q. S, T.
y, ft) is meant an automaton (Q\ 6'. /", y\ q,) where Q is a subset of Q
(containing qo), 6' is a restriction of <S, and Y is a restriction of y. Thus, a
subaulomalon is given by a set
t7c Q
8 Ctapurl
tuch that
(ftxDSc ft
and
The rtaehabk part or a sequential automaton >4 — (ft, <S, T, y, 9,) is the sub-
automaton on the image or p, i.e.,
ft - If e Q, q - (a,... a.)p Tor some c,... a. e l'\.
Thus, a state it in ft ifT it can be reached from the initial Kate a, — (S)p by
tome input sequence a,... a. f. £'. We have
l(?H £)8<z ft
became Tor each pair
(ft ff) 6 ft x T
we have an input sequence c,... a. 6 £' with f - (c,... a.)p and then
(q, a)S - ((c,... a.)p, a)S - (ff,... aja)p 6 ft".
An automaton it rtaehabk if ft* — ft, i.e., each state can be reached from the
initial state.
riattflit (i) The reachable part or the automaton in 1.1.3, Example (i), is
the subautomaton with
ft - (ft r, s, l\ - ft - \p\.
(ii) The Tree realization is always reachable.
Pupodtloa. The reachable part or a sequential automaton A a both the
unique reachable subautomaton or A, and the smallest subautomaton of A.
Further, it realizes the same behavior as A.
Proof. Let A' be an arbitrary subautomaton of A - (ft S, /", y, q,). The
inclusion map »: ft -► ft of the state set of A' is clearly a morphism
v. A—A.
By 1.1.8, we have p - p' • »(where p is the run map of A and p' that of /t"), in
other words, p' is just the restriction of p. It follows, that
(a) A' and A have the same behavior (1.1.8),
(b) ft contains the state set (2"*)p - (r')p' of the reachable part of A. and
(c) if A' is reachable, then ft - (r*)p and hence, A' Is the reachable part
of A. D
Sequential AotooflU
9
■•mark. The preceeding propoiition thowi that by restricting a given
automaton A to iti reachable part A', we obtain an automaton having no proper
subautomata. Thus, there are no Mates of A' we can simply discard.
14. Coigncaces. The next step or minimization is achieved by merging
pairs or states q and q' as Tar as it does not ruin the structure of the
automaton. Thus, we must expect that by merging q with q\ we shall have to
merge also
(q,a)S and (q',a)B (ere I),
and further, that two merged states must have the same output The first
condition indicates that we cannot consider the two states q and q isolated, but
we must work with an equivalence relation ~ on Q (where q ~ q' means that
q will be merged with q"). For each state q, we have the equivalence class of ill
states merged with q.
|f] - \q' 6 Q. q ~ q\.
We expect to obtain a new automaton A/~ from A — (Q, 6, T, y, qt) whose
state set is the quotient set of Q,
Q/~ - |M; q £ CI
and whose structure is derived from A. Thus,
A/~ -((?/-.8, r,f,lqj>
where
(l«U)*-[(*»)«l
and
<l«l)?-(«)r-
The following concept describes precisely what equivalences are "admissible"
Tor this approach.
Dcflattasm. A congruence on an automaton (Q. o\ H y. qj is an equivalence
relation ~ on Q such that
(a) q~ q' implies (q, a)S ~ (q, a)S for all a 6 £;
(b) q~ q' implies (q)y - (q")r-
For each congruence ~ we define the quotient automaton
A/~ -((?/-. 6. r,?.\qj)
as above. An automaton is rtduced if it has no congruence except the trivial
one (q ~ a' iff q — q").
10 Ctoptal
Exaaple. Consider the following automaton
The equivalence with two classes |/>, r| and I4, s\ it a congruence. The
quotient automaton is the following:
Rtsaark. Congruences are closely related to moronisms or automata:
(i) For each congruence ~ on an automaton A, the canonical map
c:Q-» Q/~, defined by
(«)« - l«l for a € Q,
is a moronism
c:A — A/-~.
(ii) For each moronism /: A -* A', the kernel equivalence
q ~ q ifr IqV- («')/
is a congruence.
15. Let 4 be > slate or an automaton A - (ft 6, f, y, q,). By changing the
initial state of A to q, we get a new automaton
A,-{Q,6,r,r.q)
whose behavior
is called the beharior of the state q in A. Explicitly, P,-p,-Y where (B)p ~ 9
[and thus, (B)ft - («)rl. and
(c,... 0-.0-,. ,)p, - ((a,... o.)p„ a. ♦ ,)£.
The best "merging procedure" is to merge two states iff they have the same
behavior:
S«qu«iilisl AolomMi 11
TbtoTML For each sequential automaton A, the equivalence
q, * q, iff />„ - />„
is the largest congruence on A (i.e., given a congruence ~. then q, ~ qt
implies q i * «j).
Proof. I. » is a congruence. Let
1" «'.
then (q)y - {.q")y because (8)/), - (9)0,. Given a 6 £ we put f, - (q, a)S
and q\ — (f', 0)6, and we verify that
fi» -/>*•
We prove by induction on n that
(d ... a.)pK - (our,... ff.)p.
Tor each a,... a. € I*. In Tact, for n — 0 we have
(8)P„ - «i - (9. ff)fi - (a)p,.
The Induction step follows from the inductive definition (of p„ as well as p,):
(o-,... o-.o-,, ,)ft, - ((a,... o.)p„ a., ,)*"
- ((oul...o.)p,.o.tl)S
- (OUT,... ff. ♦,)*>,.
Consequently,
la,... «j.V». - (ffff,... cV>, (for all c,... a. £ T*).
Analogously,
la,... c.V>„ - (ott, ... c)/>, (for all a,... a. € I*).
Thus, />, - />, implies />„-/>„.
II. <% it largest. Let ~ be a congruence on A. For each state q. we have
a quotient automaton of A, under the equivalence ~ (which, of course, is
a congruence on /«,, too). Let
c,:A,-*A,/~
be the canonical morphism. Then A,/~ has the same behavior as A,, viz., /I,
(1.1.8).
Given states q ~ f°, the two automata A,/~ and A,/~ coincide (because
they would differ only in the initial state, but \q\ - \qT). Hence, /), is the
behavior of A,/~, in other words, fi, — /),. G
12
Example. Consider the following automaton
6/
The behavior of p is the following map
{I if w - to-"' r"'o-"T"'... a"T"' with all m m,
even,
0 else.
The behaviors of q and r are constantly 0, and the behavior of s is
(H0ft-(rw)ft.
Hence, the largest congruence merges q and r, resulting in the following three-
state automaton:
— (JpJo)
./' ""
. (i) We shall prove below that the minimization of each automaton
is obtained by factoring its reachable part through the largest congruence.
(Ii) Since it is sometimes inconvenient to have equivalence classes ofstates
as new states, we introduce the following relaxation of the concept of quotient
automaton. A reduction of an automaton A is any surjective morphiam
c.A —A:
Thus, on the one hand, each congruence ~ defines the (canonical)
reduction
c:A—A/~.
On the other hand, each reduction e: A->- A' defines a congruence
q ~ q- iff (f)f - (q-)t
Sequential Aulomila
13
such that A' ii isomorphic to A/~. In fact, the map
J: Q/~ - Q
defined by
QlW - («)« for q £ (?,
i.e.. by
cj-e.
ii clearly one-to-one, and it ii luijcctive since t is. Thus, ,/ is a bijection and
because r and t — c • y are morphisms,
j:A/~ — A-
Is an isomorphism (see Exercise I.I .A).
2.6. D«naltioa. The minimal realisation of a behavior fiat reachable
realization At of fi such that any reachable realization A has a reduction
e:A-* At.
The minimal realization is obtained by applying the minimization
procedure to the free realization A(fi). Since A(fi) is a reachable realization of fi
(1.2.2), it is sufficient to merge states with the same behavior. Let us have
a look at the behavior of an arbitrary state (i.e., word) w e £*. The run map
of A(fi). is defined by
(c,... a,)p, — we/,... a. for a,... a. 6 £'
or, more symmetrically,
(»)p, - wv for v 6 £'.
In fact, we have (8)p. - w8 - w, which is the initial state, and it is easy to see
that p. Is a homomorphism on (£', e>). Thus, the behavior map Is »-* (ht)/1
Two words W| and mt have the same behavior In Aifi) i(T
(Hr,F)/l - (w2,)fi for all f E T*.
We now obtain the minimal realization by factoring A{fi) through the
corresponding congruence:
CotatracttM. For each behavior fi: £*-* r we define the Nerode
equivalence os on the set £' as follows:
w, w w, iff (wtr)fi- (w,i)fi for all v 6 T*.
14
Chapter 1
Then the following automaton
AtfV* -(TV*.6r.fl[0])
where
(Iff,... a.\. 0)9 - [c,... aja\
and
Off,... a.\)f- (0-1 • • • C)fi
is the minimal realization or fi.
Proof. Since w, w w, iff w, and *>j have the same behavior in A(fi), it
follows that <« is the largest congruence on A(fl). In particular, A(/))/» is
well-defined, and it has the same behavior as A(fl), viz, p\
For each reachable realization A — (Q,&, r, y,q,)o(p\ the run map is
a moronism
p:A(fi)^A
or automata, see 1.2.2. Therefore, the kemel equivalence ofp is a congruence
on A(0) and hence,
(w,)p — (wj)p implies *>, as w,.
We can define
*: Q-* f V»
by p- 1 — t. i.e..
((w)p)e- [w] for* e I'.
Then
e:A-*A{fl)/«i
is a morphism (since p is a surjective moronism, seel.l.A) and hence,
A(P)/<>i is the minimal realization. G
Exaaplc. (i) Find the minimal realization or the following behavior
fi:\o, r|*-» |0, \\:(w)f>- I ifT w contains at most two o-'x. To do so. we shall
go through all the words in [a, r|* (rrom smaller lengths to larger) and we
shall try to collect a set or representatives Tor the Nerode equivalence or ft.
First, the empty word 9 will correspond to the initial slate. The word a is
not equivalent to 0 since
(ooo)fl - 0 while (9oa)fl - I;
thus. |o-| will be another sute. The word ris obviously equivalent to 9, since
a word a, ...a. e [a, r|* has at most two o's iff so does to, ... a.. Next, 00
Sequential AulonteH I5
is not equivalent to 0:
(aao)f) - 0 while (Sir)/) - I
and neither to a:
(aaa)fi-0 while (aa)fi - \.
But
or ~ a, ra ~ a and it ~ 0.
Finally, the word aaa is not equivalent to 0 nor to a nor to aa: but each
word is equivalent to one or the words
0, a, aa and aaa.
Thus, the minimal realization has Tour states.
The next-state map is given by concatenation, and the output map is a
restriction of p. Thus, the following is a minimal realization of fl:
(ii) Find the minimal realization of the behavior
ft: \a\' - |a, *, c|
given by the following table:
0 a aa a' a4 a* a* a1 a* a* a" <r" a" a" a" ...
abcaabbccaa a b b b
We try again to find a set of representatives Tor the Nerode equivalence.
The initial state is (0): the words 0, a. a' are non-equivalent because fl has
distinct values on them: the word a' is not equivalent to 0 since
(a'a)P-a while (0<r)/»-6:
the word a* is not equivalent to 0, since
la*a*)fl - b while (ecr')fl - c
nor to a' since
(a'a)fl - b while (a'a)fl - a,
etc We Hnd out that ail the words in [a]* are palrwise non-equivalent. Thus,
the Tree realization is minimal:
16
CfctBWtl
Rtanrk. The above behavior has no finite realization.
2.7. The minimal realization or fi can be constructed from any realization.
Given an automaton A, let us call a reduction
*,: A -- A,
minimal if each reduction e: A->- A' can be further reduced to A* (That is,
there is a reduction e':A'-* A, with e, — e ■ *'.) The minimal reduction Is
unique up to isomorphism, and one or the possibilities is
c.A — A/k
where
q » q' iff q and q' have the same behavior.
Pupodtloa. Let A' be the reachable part of an automaton A. The minimal
reduction of A' is the minimal realization of the behavior of A.
Proof. Each reduction of a reachable automaton A' u dearly reachable.
Let A, be the mininul reduction of A', then A,\»t reachable realization of the
behavior fi o( A' (or, of A). Thus, A, can be reduced to the mininul realization
of fi But any minimal reduction is clearly reduced, hence. A, is the minimal
realization. _
ExasaaJes. (i) Find the minimal realization of the behavior of the following
automaton:
First, the reachable part is the following subautomaton:
Sequential Automats
17
The minimal reduction fives the required minimal realization; it is the
following automaton:
(ii) Given the input alphabet rand the output alphabet T, we define an
automaton realizing all behaviors (with appropriate initial states). Put
r. - hom(r*, D - |/»; />:£» -► *"]•
This will be the state set. The next-state map
v.r. x r-r.
auigns to each behavior fi € /". and each letter a € Z the behavior
(A<j)r - (o-)fi:Z* — rdefined by
»►* (ov)fi for » € r*.
The output map
Is given by
(fi)r-WP-
Thus, Tor each behavior fie /". we have a ^automaton
Its run map p: £* -* /". is defined by
(w)p - (w-)fi,
where (w-)fi-.L' -- r assigns to each isT the value (m) fi. In Tact, p is
a homomorphism with (B)p - /I It follows that no two distinct states
(behaviors) of Xt have the same behavior.
Consequently, the minimal realization of/lis just the reachable part oX A,.
This It the subautonuton with the following state set
\(w-)fi\ w £ f |.
We obtain another description of the Nerode equivalence: instead of the class
[w] we work with the map {w —)fi
18
Chapter I
U. Remark. Minimal realization is unique up to isomorphism: an
automaton A is a minimal realization of/lifT A is isomorphic with Aifiyi. In Tad,
if A is a minimal realization, then there is a reduction t:A(fi)/x -» A. and ris
one-to-one (and hence, a bijection) because the following equivalence
in, ~ w, iff (|H>,])r-([H'I])r
is a congruence on A{fi). This implies that m is larger than - and thus,
QwiD* - (|tij)f implies \w\ - [h>J.
Corollary. Let fi£' -* /"have a realization with a finite state-set Then its
minimal realization is characterized (up to isomorphism) as the realization
with the least possible number of states.
In fact, let A be the realization with the least number of states. Then A is
reachable (else, the reachable pan would have less states) and the reduction
t:A-+ Aip)/<n is one-to-one [else, A0)/k would have less states). Thus, A is
isomorphic to A(fi)/x.
Eitidscs IJ
A. MlakMl redactloa aad realization, (i) Prove that for each reachable
automaton A, the minimal realization or the behavior of A is the minimal
reduction of A. (This is a converse to 1.2.7.)
(ii) Verify that minimal reduction is unique up to isomorphism (commuting
with the corresponding morphisms).
(iii) Prove that an automaton is minimal (i.e., is the minimal realization of
its behavior) iff it is reachable and reduced.
B. ObacrTaMIHy sua, For each ^automaton A - (g, S, H y. q,) define
b.Q-t- T. (see 1.2.7) by [q)b - /),, the behavior of q. A is said to be observable
if b is one-to-one.
(i) Prove that an automaton is minimal iff it is both reachable and
observable.
(ii) Verify that b:A-*A,at morphism of automata (where /> is the behavior
of A) and prove that 6 is the unique morphism from A to A,.
(iii) For each behavior fi.I' -► I denote by
/>. :r«-r.
the observability map of the free realization A(0) (1.2.2.). Verify that the
minimal realization of /lis obtained by image factorization of fi,: it is (a) the sub-
automaton of A on the state set (£*)/>• and (b) the quotient automaton of
Aifi) under the kernel equivalence of/)..
Sequential Aelomtu
19
C. Construct the minimal realizations for each of the following behaviors
with I- |c, r|:
(i) r- |0. l| and (■*)/) - I iff w - <m>" Tor some n - I. 2, 3,...;
(ii) T- |0, l| and (w)0 - I ilT w - tmr for some n - 0. I, 2,...;
(iii) r - |0, I, 2,.. | and (w)/)is the number of leners in w.
13. Flate Aatotaata —t Laagaaga
3.1. We know that every behavior has a realization (111.)- In the present
section we study the question which behaviors can be realized by a finite
automaton, i.e., an automaton with finitely many states. First, we prove that,
instead of mappings fi: L* -► /", it suffices to study subsets of I'.
Cotfftarioa. Subsets of I' are called languages in the alphabet I.
3.2. DcflaMlaa. A language L c L* is recognisable if there exists a finite
^automaton with the output alphabet /" - |0,11, the behavior of which is the
characteristic function of L, i.e.,
p.Z'-*\0,\\;(w)P-\ ifT w e L.
Reaurk. Finite ^-automata with the output alphabet /"- |0, l| are called
acceptors; their output map
r.-e-io. n
is the characteristic function of the set
r-dlr'co
of so called terminal states. Thus, acceptors are usually described as
quadruples A - (ft 6, T. q) with 7"c Q the set of terminal states and q e Q the
initial state.
The behavior of an acceptor A is the language LA of all words in I' which,
received In the initial state of A, transfer A to one of iu terminal Mates. We say
that A accept* such words; globally, A recognizes the language L+ Note that if
there is no terminal state (7"- 0), then the recognized language Is empty.
3J. Preswaltlaa. A behavior /): £*-»/" has a finite realization IfT
(1) the language ly)P~' is recognizable for each >•€/";
(2) the set <£•)/> c /"is finite.
Proof, (a) Let fi have a finite realization, say A - (ft 6, C y, q).
(I) For each y e rdefine an acceptor
<*,-(Q.s.(y)r-'.«)-
20 Clupur I
We prove that 0>)/>-' is the language recognized by A,. Denote by p:r*-» Q
the run map of A; then
fi-PY-
Moreover, p u the run map of A, as well; iu output map y,: g-» |0,11 is
defined by
(q)yv- \\tt(4)y-y.
Thus, the behavior of A,,
A-P- »
maps w € r*to I iff> - ((i»)p)y- (w)fi. Therefore,
This proves that OOP""' is recognizable.
(2) The set (I')fi - (Q)y is finite, since Q is.
(b) Let fi have properties (I), (2). Put
<£•)/>-l>> *|.
By hypothesis, for each < — I n the language
*, - MP-'
has a finite realization, say,
A, - (ft. 6,. T,. q'). / - I n.
Define a finite automaton A - (Q.S, r, J", q*) as follows:
ft- ft, x ... x ft.;
«« «.). <T)« - ((«,. <T)fi (,., <T)tf.)
for all (4 4.) € ft and a a I;
y.Q, x ... x &-»T
Is an arbitrary map such that, for each (9 q.) € ft,
(4 ?.)y - >>, whenever q, z T, but (J, € Q, — 7" for ally * /;
nnally,
,•-(,?,...,«•.)€ ft
We shall prove that A realizes fi.
Denote by p,:Z'-*Q, the run map of A„ /-I n. The map
p: r*-» ft x ... x ft. defined by
Sequential Automiu 21
(w)P - ((w)p (w)p.) for all w e I'
is a homomorphism, since for each w € I' and a e T
(w)p - ((wo)p ,(m-Op.)
- (((w)P,. <t)« ((i»)p.. <r)tf.)
-«(W)P„. .,(W)P.).<T)«
- ((W)p, <T)&
Since (6)p - ((j° 1!) - <?". we •«* (bat p is the run map of A. Hence, the
behavior of A \t ff - y - p. for each w € T* there exists / - I n with
(w)f) — >■,; then w belongs to the language of A, and does not belong to the
language of any A,,j* L Thus
(w)p, € T, while (w)p/ « Qi — Ti for ally #t
Then ((wjpjy - ((w)p„ .., Wp,)r - y,- This proves that
(w)fi - y, implies (w)p*- {(w)p)r - y„
in other words, 0-0. O
Example. In I.2.6 we have exhibited a behavior f>: |c|* -+\a,b,c\ which
has no finite realization. It follows that at least one of the languages («)/>"',
(6)/)"' and (Op*-1 is not recognizable.
In fact, the language
(«)/»-' - |0, a1, o\ er\ <r'\ <r",...|
is not recognizable, tee Exercise I.I.B.
3.4. Next, we want to describe the recognizable languages. To do so, we
introduce nondeterministic acceptors.
First, recall that a relation with a domain X and codomain Y is a triple
(X,f, Y) where/is a subset of the cartesian product Xx Y. We write/: X-- Y
instead of (X,f,Y) and, for each x e AT, we put
(JrV-lje YAx,y)<if\.
Clearly, any relation/: X—• Y a determined by its domain and codomain and
by the collection |(x)/; x € X]. We denote by
/:Ar-»expK- |A#| A# <= K|
the map with (x)f- (x)f for all x € AT. Note that any map from X to exp Y
uniquely determines a relation AT-* Y.
The composition of relations is defined in the usual way: given relations
/: X-* Y and g: Y-* Z, their composition is the relation/- g: X-* Z with
<«)/"• I- U (j-)j for all x€ X.
22
Chapter 1
15. DeflaMoa. A nondettrministicL-acctptor'u a quadruple A — (fl 6, T, /)
where
g is a finite set (of states);
6:Qx I — C is a (next-state) relation;
Tc g is the set of terminal suits;
/ c Q is the set of initial states.
While a deterministic acceptor A accepts a word iff this transfers A from
the initial state to one of its terminal states, for nondeterministic acceptors we
can choose various possibilities and we are happy if at least one works.
IJk. DtfiaHlaa. The run rtlation of a nondeterministic 27-acceptor(Q 8, T, I)
is the relation p: I'—* Q, defined by the following induction:
<»)P - /:
(ff ff.)p - D implies (c,... ov.. i)P - U (a, a., ,)S
«* D
for arbitrary a a„ a,., e I and D c Q.
The language rttognhed by /< consists of precisely those words w € 27*
with (w)pr\ T+ 0.
Remark. Nondeterministic ^acceptors can be depicted by graphs
analogous to those we have used for ^automata. The nodes carry a single label (of
a state) and the terminal states are denoted by small out-comming arrows
(replacing the output labels, of course).
Example. Consider the following nondeterministic [a, r|-acceptor:
It accepts the word 0 (and r, rr,...) since ris initial as well as terminal; it
accepts a since from q we can go to r; it accepts m since we can remain in a
once and then go to r, etc. It does not accept nr since this word brings us to no
state at all. The language recognized by the given acceptor is
L- |<T'r-|n,m- 0. I.2....|.
Can L be recognized by a (deterministic) acceptor? We use the Nerode
equivalence of the characteristic function of L to construct the minimal
realization (see 1.2.6). The initial state is the equivalence class of 0. The word a is
equivalent to 0. since for each w € [a, r|.
we L iff aw € L.
Sequential Auloouta
23
The word ris not equivalent to 0, since
0<r € L while to i L.
The word re is not equivalent to 0 or r, since
to t L and 0 € i.
But each word is easily seen to be equivalent to 0, ror rcr: if w € |o~, r|* — L
then w ~ re; if w - c"r" with » *» 0 then w ~ 0 and if w - r" then w ~ t
Here is the resulting minimal realization:
T T
Remark. Observe that nondeterministic accepton can be smaller than the
deterministic ones: no deterministic acceptor recognizing the above language
has two states. In the proof of the next proposition we shall see that if an n-
state nondeterministic acceptor recognizes a language, then a 2"-state
deterministic acceptor can do the same.
3.7. ProtmcHkM. Each language, recognizable by a nondeterministic £ac-
ceptor, is recognizable by a deterministic one.
Proof. Let L be a langugae recognized by a nondeterministic ^acceptor
A - (ft S, r, /). Define a ^acceptor A~ - (exp ft S, t, q,\ where exp Q is the
set of all subsets of Q and
(A a)S - U (f, a)S for each D c Q and a € I:
T- |Ae 'Q\DnT+9\;
1.-1-
Letp: r*-* Q be the run relation of A, let 0: I'-- exp Q be the
corresponding map. We prove thai p ia Ihe run map of A. Indeed, by the inductive defini-
lion 1.3.6 we have
(0)1 -l-q,:
(o*„ ... a,)P — D implies
(<r, . o.o.,,)fi - U (« «,,■)£-(A «.»i)£
«« »
Thus, fl: (27*, p) -»(exp ft S) is a homomorphUm mapping 0 to the initial
state <f»-
We conclude that a word we X* is accepted by X iff (w)0 € exp g is
24
Chieur t
■ terminal Mate of A\ i.e., ifT (w)p r\T+t. This ii equivmleni to A
this word.
3A Operatives n accepters. The reason why nondetenniniatic acceptors
are useful In the study of languages is that some operations on them can be
easily described (and used to introduce the corresponding operations on
recognizable languages). We mention some examples needed below.
(A) Vnkm. Let A - (ft 6, T, /) and A' - (ft, 6", 7", f) be nondetcnnirds-
tic ^acceptors with Q <~> ft — 8. Their union is the nondetennlnistjc
acceptor A \j A' - (Cu ft, S\jS\ T\j 7", l\j /'). Note that tu 6" denotes the
set-theoretical union:
(ft<T)|o-wSl.
■(*«r)*«(*«r)*--{(*X
if«€ e
if«€ ft.
A
"~I 1
I I i T
i !
i 1
r ! ! r
AUX
It is easy to verify that the language recognized by A <j A' is just the union
of languages recognized by A and A':
(B) Serial connection. Let A and A' be as in (A). Their serial connection is
the nondeterministic ^acceptor A- A' — (Q\j ff% S, t. I) where, for each
(E Q <j ft and each Set,
{(a, o-)6 if? € Qand(a, a)8n T- 9
(a,<r)£u/' if q € Qand(a, ff)6"^ T+ 9
(a, <t)«' if q € ft.
Moreover,
f-r,
I - /in case lr\T- 9: I- Ikj /' in case /<-> T * 9.
t ► r • r
Snpaitial AMoauu 23
Pupsettlua. The language recognized by A- A it
LA-LA - |nr€ r«|»€ L^andw e LA\.
Proof. Denote by p and p the run relations of A and A', respectively. The
run relation p of A • A' assigns to each a, ...a. e r* the set
• <r.)p'.
(Oi... a.)p - (c,... c,)p <j U (01,,.
01... 0i < LA
This b easy to prove by induction on n (just distinguishing the cases 0 € L,
i.e., / r> 7" * 0, and 0 i» I).
Thus, <7,... cr. is accepted by A ■ A' ifT (a,... a.)pr\ T * 0, U, ifT there is
<7,... cr, € L, with a, ♦ i... c. e L^. Equivalent^, c,... a. e L., • t,. D
C—mtlia. Given languages L. L c I', the language L- L' —
I pw e r*|r€ L and w € LI is called their concatenation.
(C) Feedback of a nondetenninistic acceptor /< - (ft £7", /) is the nondeter-
ministic ^acceptor
A' -(Q.S\T,l)
where, for each q e Q and c € T,
KJ I
if (ft <r)«^ T-0;
if (4; o-)6" ^ 7" * 0.
The language recognized by A * is
tj - LA \j (LA• LA) \j (LA■ LA• LA) \j ...
- |w, HJ...W, € Z' | »,,.., w, € A,; *- 1,2,3, ...|.
Proof. Denote by pthe run relation of A. The run relation p* of/<* can be
described as follows:
&>P*-\
and
(o-|... o-,)p* - |J (c... c,)p for each a,... a. e J', n * 0,
where the union ranges over all < — I,.... nfor which there eiist
26 Chipur I
j,< J, <..<>,< i (*- 0.1.2....)
with
<r,... <r„ € LA: <r„,,... <r„ € t,;...; <T„,,... a, e Lt.
This is easy to prove by induction on n.
Thus, a,... a, it recognized ifT there exist j, < ... < jt < I with a,... 07,;
07, ♦,...o-,; ...; ?„.,... ?,; a,,,... a. in L4. Equivalent]?,
ff,... a. € L*j . a
C—miloa. Given a language L c I', the language
L' - |0|u f - |0|u Lkj(L-L)kj(LL-L)kj ...
Is called hi iteration.
3.9, Kleeae Theorem For each finite alphabet £, the clan of all recognizable
languages in 2"* is the smallest class of languages which
(i) contains the singleton languages |0| and \a\ for each a e 2" and the
empty language 0:
(ii) is closed under the formation of union, concatenation and iteration.
Beaark. The operations U. ■ and * are called rational oprrotkuu on
languages. A language L c L* is said to be rational if it can be expressed by a
finite expression using the letters of the alphabet £, the symbols 0, |, |, and the
rational operations. Example:
I-|<r|«w|rr.|<T|w|0|.
Kleene's theorem then states:
A language is recognizable ifT it is rational.
Proof, (a) Rational languages are recognizable. We use Proposition 1.3.7.
First, |0| and |<r| and 0 are recognizable languages:
By 1.3.8, the class of all recognizable languages is closed under rational
operations.
(b) Recognizable languages are rational. First, observe that every subset of
lu |0| is rational (since it is a finite union of singleton, one-letter languages).
For each ^acceptor
A - (Q. S,T, a,)
Sapiential Automata 27
we are going to prove that the language LA is rational. Put
Q - \<fr. 9 «-)•
For arbitary i.j-0 m we denote by L„ the set of all words in I' which
transfer A from « to q,. More precisely, for each a,... a, e I' we put
<o - q,: r, - (rfc a,)S;...; r, - (r._ „ c,)fi
and we define Lv ai follows:
c, ...c. € Z, ifT r. - q,.
Clearly,
«;« '
Hence, to prove that LA is rational, it suffices to prove the rationality of each
L,;. To do so, we denote by
tj, *-0,.... m+ I,
the set of all words in I' which transfer A from q, to q, without passing
through the states qt, ..., qm. More precisely, a, ... a. e ij ifT the above
states /»,..., r. fulfil
'i '.-i e I*. •••. ft-J-
Note that L,,- L~ *'. We are going to prove that 1} is a rational language by
induction on it
Fint, L'u is a rational language: here r r. _, e 0, thus n £ I, therefore
IJcTwiei.
Next, if L'" ' is rational then, to prove that L{ Is rational, we shall verify
the following formula:
Indeed, let c, ... c. € LJ and consider the above states r„ ..., r.. If all the
states r, r. _ , are distinct from ft, then 0,... c € £.{"'• Else, denote by
I, < h < ... < t, all of the indices r - I n — I with r, - qk. Then the
states r, r,, _, are distinct from q,, thus
c, ...o-„ e ti"'-
Analogously,
oil ♦ i • • • Oi|i oil ♦ i • • • a<» ■ ■ ■• °ii-1 ♦ i • • • a<,€ ^"Ir'
as well as
oi.. i ...a. € tj,-1.
28 Chapter I
This shows that
<t,...<t. € U-'•(!!,-')•-15,-'.
The reverse inclusion 1J-' <_i 11"' •(!£,-')■ • lj/"' c tj is obvious. This
proves the above formula, thus, L{is rational. D
Excretes IJ
A. laflakt alakaktii. Let Ibt an infinite input alphabet. Prove that all
recognizable languages in I' form the least class containing all language*
L c lu |0| and closed under the rational operations.
B. OpererloM yinmlng the recognlzibllltY. If L„ L, c I' are recognizable
languages, prove thai the following languages are also recognizable:
(I) I' — L,. Hint: Interchange the terminal and the nonterminal states,
(ii) L,nL,. Hint: Use (i).
(iii) rev L, - |c,... Ci I Ci... c, e L,\. Hint: reverie the arrows of Sand
interchange the terminal and initial states.
C. Find a rational expression for each of the following languages:
(i)r--|o-|:
(ii) |<r, r|« - |tT|«:
(iii)rev(|<T||r|'w|<T,p|«|pop|).
Notes 10 Chapter I
This chipler presents just ■ standard Introduction to sequential automata. The interested reader
can find more information for example In M. A. Arblb |IM9| or S. Elknberg 11974).
Chapter II: Tree Automata
Il.l. FlaJtary Tree AatoaaU
1.1. Tree automata ire devices which handle labelled trees analogously as
sequential automata handle sequences (words) of input symbols. The intemil
structure of a sequential automaton is a unary algebra; for a tree automaton,
it is an algebra of an arbitrary type.
A ftnitary type is • set X of operation symbols together with an ariry map
assigning to each a e I a natural number
lot -0, 1,2
The set of all n-ary operation symbols (such that \a\ — n) is denoted by I,.
A £algebra consits of a set Q and operations of the prescribed aritles:
«.: C" - Q « Q « • • « C- C (ff € 2; W - n).
For /i - I we have a unary operation S„: Q-» Q, for n — 2 a binary operation
S„:Q x g-» Q, etc For n - 0, the set g* has just one element, and a miliary
operation
s. o"-e
is usually identified with the element of Q which forms (OS,.
Operation-preserving maps are called homomorphisms. Thus, a map
/■' (C. (Ail.. x) -»(C \&A., i) is a homomorphism if for each a € 27.,
(«..... «.-i)«.- a implies ((«!/:.... (q..,)f)S. - («l/l
I J- DattaMioa. A I-iih automaton it a sixtuple /4 - (C, 14,)., r. r. y, /. A)
where
8 is a set, called the eel of Halts:
S.:Q"-*Q (c € 2T, |o| - n) are operations on Q;
/" is a set, called the output alphabet;
y: Q-* r is a map, called the output map;
I is a set, called the set ofrariablet;
X: /-» Q is map, called the initialization.
If all operations are unary (i.e., 2T - I,) and if / contains just one variable.
30
Chapter It
/ - |x|, then a X-tree automaton U precitely a sequential ^automaton with
the initial Mate (xlL
I J. Euapk Let I - I, - | +1 and let (Z, +) be the additive Salgebra of
Integers. Put T- |0,11. and let y be the parity map:
f I if r is odd
wr ~\0 if zis even.
Then we have a £tree automston
with
(x)A- -I ind(>)A- I.
The "action" of this automston (to be made precise below) consists of
taking any binary tree with leaves labelled by x and y, computing the tree and
giving an output. For example, the following tree
is computed as follows:
The resulting output is (3)y - I.
Tree Automata
31
The external behavior or the automaton A is expressed by the map fi
assigning to each of these trees / the value
(DP « r
of the output which results after the computation of /. In our present
automaton clearly (/)/)- 0 iff the number of x-labdled leaves is congruent to the
number of ^labelled ones modulo 2.
1.4. IMree automata act on finite trees labelled as follows: each node with it
successors (n > 0) is labelled by an it-try operation symbol, and each leaf is
labelled by a variable or a miliary symbol. We formalize these trees by
introducing a non-labelled "base" tree and defining its admissible libel lings.
Put
m- Vw,
i.e., m is the maximal arity if such exists, and m — o if arities are unbounded.
The nodes of the base tree are all sequences p,.., p\ of numbers smaller than
m (for * — 0, 1,2,..., where * - 0 stands for the empty sequence, the root).
More precisely, recall that m a the set of all natural numbers smaller than m
(i.e., m - |0,1,.. „ m — l| if m is finite, and a is the set of all natural
numbers). The nodes of the base tree form the set
of all words In m, with p,... p, e m' preceded precisely by
*• Pi. Pift Pi... Pi - i*
For example
2* - |0. I|«
is the complete binary tree:
Here 0 is the root, and each node p, ...p, € 2* has two immediate succes-
32 Chapm II
son: pi . ..p,Oandp,... Pi I. (In a' each element hu countably many
Immediate lucceuors.)
The binary tree or the above example can be considered as a partial
labelling of 2* by the labeli +, x and y, i.e., a partial map
»:2«-| + .*>|.
The map ii denned as follows
0 0 I 00 01 000 001 010 Oil
I + + y + + x y y y
The domain of derinition Z>, of / it |0,0,1,00,01,000,001,010,011|. In
general, Street will be partial maps from m* with values either in I or /. For
each partial map i: X-* Y, put
Z>,-|*€ X; (i)l it defined|.
Defuhlet), Let £ be a finitary type with m - V lot Let / be a set (of var-
«« x
iables) with / n I — 0. A flnht L-lrtt it a partial map
such that
(i) the domain of derinition D, it non-empty and finite;
(Ii) given p,... PtPt» i € m*, then
p, ...p,., € D, ilT (pi...pi)< € X. for tome n > p,»,.
The meaning of (ii) is that:
(A) Labels are assigned from left to right: if p,... PiPi., hat a label (Le, It
In D,), then alto p,... paO, p,... pi I,..., p,... PtPt., have labeli.
(B) Each node p, ...pk labelled by of- (p,...p,)l] In £ has precisely n
lucccssors, viz, p, ...p,0 p, ...p,(n — I).
(C) Each node p,...p, labelled by x[- (p,... p,)i| in / ia a fee/ (i.e..
Pi • • • PiPi ♦ i < D, for any p» * 0; the same holds for ^-labels, of course.
Furthermore,
(D) 0 always hat a label: there exists p,...p, € D, (because D, * 0) and it
follows that Pi... pt. i € D, and hence p,... p, _, € D„ etc.
13. Netetl—. (i) The set of all Slices over / is denoted by
/•.
This set carries a natural structure of a Salgebra. For each a € Z. we have
the operation
«..:(/•)"- /•
Trw Autonuu 33
of tree-tupling: given tree* /..../,., € /", we form the following tree
Ho-.U If. . J0\
/o\ /i\ AA
Formally, the tree
I- lU. ... I.-,)?.
hat the followim domain of definition
D, -IPrPj-Pi € m«;p, < n and p, ,,, p, € D,„| w |0|
and li defined by
(«)»- a;
(P\Pi.Pt)l-(ti..Pt)l„
for ill pi p,... p, with p, < n and p, ... p, € />,„. The conditionf (i) and (ii)
of III .4 are euily verified for (»«,...,»._ \) p.; in particular each ff € 2^
define! the ilngleton tree
®
(ii) We consider / u a iubtet of /• by identifying each variable x € / with
the singleton tree
©
(iii)The depth \t\ of a tree I € /'is the largest number * - 0, I, 2,... for
which there exists p,p, ... Pi € D,. Thus, each variable and each operation
symbol in t, have depth 0. The tree in Example II.1.3 has depth 3.
(iv) For each node w of a tree t. I.e., each
»-«,...«.€ D,
we define the branch
SJ
of I at •■ as the following tree:
(p,... p»Rf -(«,... «.p,... p,)f
(where the lefi-hand side is defined iff the right-hand one is). For example,
the following tree
34
Chipm II
'<&
has the following branches:
*•': («
*■"■© V: ©
»oo'=Q
(iv) We define sets or trees
W.<z /'(B-O. 1.2....)
by the following induction:
W.-l
and
W.,
i / ^ !(»„,..., »,-,)«>„: ff€ £|o1 - *,and»,,...,»,_, € IP,|.
We have
because for each I € /•,
|(| s n implies I € W..,.
[This is clear if n — 0. Each tree / of depth n + I has the form ( — ('■,...,
'i -i)W> for some a € £,, k > 0, where |/,| £ n and hence by induction
hypothesis, i, € W,., for i- 0 * — I.Thus, / € W.<,.\
PtfoaJtiM. The algebra of finite trees
(/M«,l..i)
is the free Salgebra generated by the set /. That is, for each Salgebra
Tit* Avtomali
35
(S lft>l) and each map/: /-» ft there u a unique homomotphiim
r ■(!•. |t>„|)- (ft |«.|)
extending /
Proof. We define/* on each W, by induction on ft Flnt,/*-/on / - If,.
Given /* on If., for each I i W,» , — / we have I - (la, .., »». ,)e>, with
'•.....»«-1 E If,, and we put
(0/* -((».)/* (».-,)/*)«■.•
It ii obvious that this is how/* has to be defined (i.e../* is unique) and that
J* is a homomorphism, provided only thit/* Is well-defined. Thus, the proof
is concluded by the following
Observation. The algebra (/", |e>,|) has the following Ptanopmptriies:
(i) Each element of /• — /has the form Co, .., 'i -1)*>„ for « unique
operation symbol a e Z, and a unique lot-tuple <*...,/,_, € /";
(ii) conversely, each element ((«,...,(»_ i)e>„ lies in /" — /.
In fact, given I € I' — I then (9)/ - a for some a € Z If |o| - k, it
follows that»-(»«,...,»!_ i)c>, iff i, - if for ( - 0 * — I. Conversely, the
root of each Co, . , 'i _ ,)»>„ is labelled by a and hence, this is not an element
of/.
Exetaale*. (i) Let I - £ and / - |jc| (the case of sequential automata). The
free algebra /" consists of the following trees:
36 Chiput It
This is just the algebra I', except Tor the (superfluous) symbol x.
If we consider an arbitary set /of variables, then words starting with
different variables act quite separately. Therefore,
/• - /x S"
with
(«, ff,... o-.)e>. ■h»,.„ oja) (x e / and a,... a. e £•).
(ii) Let r be an arbitrary type and / - B. Then the free algebra, known as
the initial Saigebra, consists of finite ^labelled trees : all leaves are labelled
in X, and each node with n successors is labelled in Z.. The characteristic
property of the iniiial algebra is thai each Salgebra A has a unique homomor-
phitm from the initial algebra 10 A.
\*. Defnltlon. Lei A - (Q, |5„|, /", v, /, A) be a Stree automaton. The
unique homomorphism
p:(/M»>.l)-(ftl«LI)
extending the initialization map X is called the run map of A. The map
fi-p.y.l'^r
is called the behavior of A.
For each tree t, the result of the computation of / (after interpreting the
variables x as the states (x)A| is the state (l)p. And the resulting output is (/)/).
Example. Let I consist of a binary symbol a and a nullary symbol r.
Consider the set
Z, - 10,1,2,31
with the addition a - + modulo 4 (which is the usual addition with 4
subtracted if the result would exceed 3) and with r - I: let
v:Z,-|0, II
be the parity map. Denote by
^-(Z„|+, 11. |0, l|, y. Uy\.X)
the automaton with
(x)A - I and (y)X - 0.
Tree Avloouu
37
For the tree
the computation in A yields
* ) ('
~©
(Op-3 and (l)fi- I.
In general, (Op - i iff the number of all leaves labelled by r or x is congruent
to i modulo 4. Thus,
!>■■{*. y)m~V>. i)
is given by
())fi - 0 ifT the number or leaves labelled by either x or r is even.
I.T. Eianple. Let I — Ii — |V, A| and Tor a non-empty set U, consider
the set
Q - exp U
or all subsets or U with the operations union <_> and intersection n. Define
an automaton
A - (exp U, |w, r>|. (<■» a„ 61. y, \x,y\. A)
where
a, ifr-9
(Dr- { a, VT-M
b if re expA/-|M,B|
38 Oupterll
and
(Jt)A. -0,iy)A- U.
The tree
ii computed as follows:
and hence, (»)/> — a,.
The tree
is computed as follows
and (f)fi - a*.
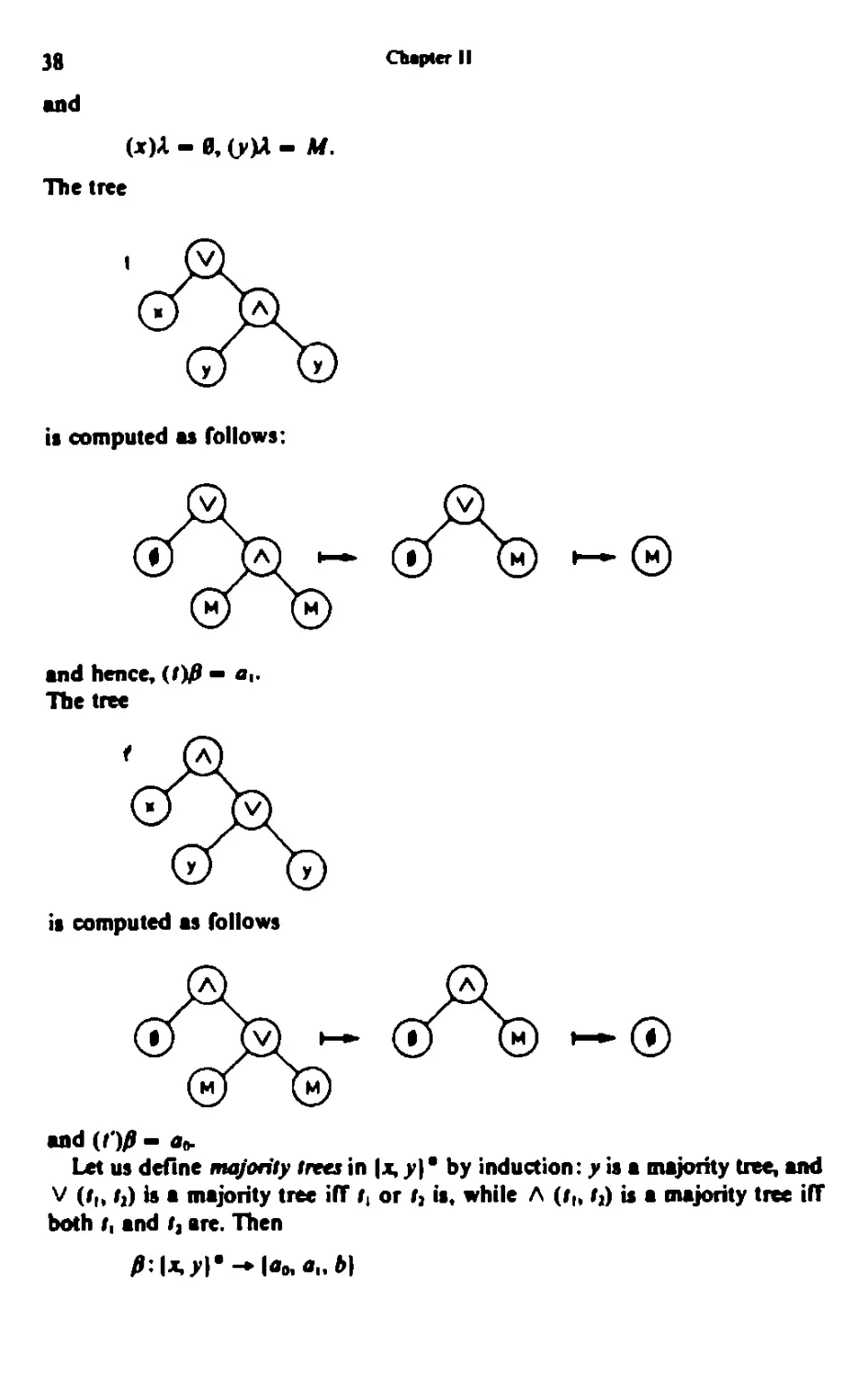
Let us define majority Irea in [x, y)' by induction: y is a majority tree, and
V (/,, /,) is a majority tree i(T f, or I, is, while A (/„ /,) is a majority tree ilT
both f, and f, are. Then
fi:\x.y)m-\a»a„b]
TfM Automata
39
majority tree
it defined by
ins- \"' ''•,m*Jori'
)p ™ [a, elie.
I.8. Let X be a flnitaiy type, and let
a-iQ. |«„|, r, r, /, A) and ^ - ((?•, i«;i, r. s; v. a-)
be Slice automata. A morpfiism from .4 to /*' is a triple
of maps such that
/:(ftl«.l)-(C'.l«.l)
is a homomorphiun and /„: /-» 1',/^,: /"-» /"' fulfil
/• Y • r-Am.
Incase /"- T'and/M = idraswellai /- /'and/. - id,, we write simply
f:A-»A\
Euatflo. (i) In II.1.6 we had the automaton ^ - (Z* | + , l|, |0, l|, y,
|j,>|. A). Define an analogous automaton
^-(Z1,|+,l|, |0,l|, y, \x,y\,X)
where + is the addition modulo 2 on Zj — JO, l|, y' U the identity map and
(x)A' — I, Cv)A' — 0. Then we have a morphUm
f:A—A'
denned by
0 12 3
/:
0 10 1
Note that A and A' have the same behavior ft.
40 Chapter II
(ii) Define ui automaton A' analogously as A in 11.1.7 except that the
output alphabet is /"' — I a, b] and
_ . fa ifr-IorM,
U)r~\b if Te exp At* — |A#. I|.
Let/„.: /"-» /"' be the following map
(«a/~ - («,V» - <> and (*VM - A.
Then
(l<W«, W ,*„, /->:<<-
'tis a morphism. The behavior of A' is the constant map to a.
1.9. PupcHtoa. For each morphism
f:A—A'
of £tree automata, A and /*' have the same behavior, and if p: I' -» Q is the
run map of A, then p • /: /• -» Qf is the run map of A'.
Proof. Proving the latter statement, the former follows:
fi-p-r-p-f-y -p-y -er.
It is sufficient to note that since p:(/\ l*v|)-»((?, |5.|) and /:(g|<,|)
— (C l£|) are both homomorphisms, p • /: (/', |t>.|) — (C, |£|) is also
a homomorphism. For each x € /, we have
(x)p-f-(x)Af-(x)A-
and hence, p -/is an extension of A': /-» Q'. But also the run map p'of A'it
an extension of A', and since A' hu a unique extension to a homomorphism,
we conclude that
p-f-p: O
l.U. We have seen in this section that there are dose analogies between
sequential automata and tree automata. We shall see more of these analogies in
the subsequent sections. Let us conclude by having a look on the role of the
variables.
Oiven a type £ of algebras and a set / ofvsriables(/<~> I—V), we can
extend I by "co-opting" the variables. Let r be the following type
£-1,^1 and r, - Z. forailn>0.
A £*-algebra on a set Q is given by a Salgebra on Q plus a map A: /-» Q.
Thus, ^automata with the set / of variables are precisely ^-automata with-
Trw Automali
41
out variables (i.e. with the empty set of variables). Also behaviors correspond
naturally:
OkacrvatJoa. The Tree Salgebra (/*, |e>„|) is precisely the initial £*-algebra
(11.1.5). In Tact, /" consists of finite Z-um with leaves labelled in
L, \j I - J£, and this Is precisely (0*, |*>„|) in the extended type I\
Reanrk. The concept of variables for tree automata is nevertheless useful,
since we want to consider a fined type L It will turn out that both for minimal
realizations (11.2) and for recognizability of languages (11.4) it is of crucial
importance that we can enlarge the set of variables. In the approach without
variables, this would change the type.
Exaaple. Sequential automata: Here £ - £, and / - |x|. We can consider
them as £*-automata without variables where r - £, <-> \x\. In fact, the nul-
lary operation x is just the initial state.
Eureka IL1
A. Conpotirioa of iwihlims Consider tree automata of a given type and
with given F and /.
(i) Prove that the composition of morphisms f:A-+ A' and %: A'-» A" is
a morphism f-%:A-+ A".
(ii) For a surjective morphism f:A-+ A', conversely, a map % is a
morphism g:A'-» A" whenever/- %:A-+ A" is a morphism.
(iii) Can (ii) be generalized to the morphisms (/,/„, fa)"!
B. Sabargebra of /'. A subalgebra of a Salgebra (Q, |5„|) is a subset
Q, c Q closed under the operations |i.e., (q,)S„ € Q, for all a € Z, q, e QJ.
(i) Prove that the set of all trees of depth £ 3 Is a subalgebra of /".
(ii) For each x € / prove that the set of all trees with x as a label of some
leaf is a subalgebra of /".
(iii) Prove that each subalgebra of /", containing all of /, is /".
C. Ualforai trees are trees such that all leaves have the same distance from
the root. Formulate this precisely. For which types I is each tree in /"
uniform? For which types I do all uniform trees form a subalgebra od /"7
D. Rm ansa aad awehliii (i) Generalize Proposition II.1.9 to morphisms
(f.f>..f~.):A~A:
(ii) Conclude that given a Stree automaton A - (ft |5„|, /", y, I. X) and
a subset U c A then the run map of the corresponding automaton A, - (Q,
||S„|, r, y, !„, X,) (where A, is the restriction of A) is the restriction of the run
map of A.
42
Ch.pMrll
E. StajftJal awtosaata with rents. A rtsel in a sequential automaton is an
input a such that the map (—, 0)8: g-» g is constant
(i) Let I - £, \j I, be a type (with arities 0 or I). Verify that Stree
automata are just sequential ^automata with resets in L+
(ii) Describe the initial algebra Tor the type in (i). (Hint: Using II.1.10, we
getB' -lix i;.)
II J. MMsaal Reallxatioa
2.1. Throughout this section, a fixed Unitary type I is considered.
Analogously to the case of sequential automata, we show that each behavior map, i.e.,
a map
fi: /• -. r
has a realization (i.e. there exists a Stree automaton with the behavior p~) and
we then apply the minimization procedure to get the minimal realization of A
We start by defining the free realization
Mfi)-U',\9.\..i,r, A /,n).
where 17: /-» /* is ihe inclusion map (see II.1.5 (ii)). Since the run map of
M(fi)\t clearly id,., it realizes A Let
a - (ft l«.|. r. r. 1, A)
be another realization of A The run map of A is a morphtsm
p:A(0)^A.
In fact,
(i) p: (/*, |«>„|) -»(ft |5„|) is a homomorphism
with
(ii)n.p-A,
and since A realizes A we also have
(ttt)py- fi.
Since (i) and (it) actually define the run map. we see that p is the unique mor-
phism A(fi)-»A.
IX We turn to the minimization procedure. As in the case of sequential
automata, the mintmization of a tree automaton is performed in two steps : the
first (easy) one Is to discard all superflouous states, and the latter is to merge
pairs of states which behave in the same way.
By a subautomaton of a J-tree automaton A - (ft |5„|, /", y, I. X) we
understand a J-tree automaton (with the same Tand /)
Tree Automiti
43
a- • iff. |*;i, r, y, i M
such that;
(I) ff ii a iubal|ebra (Exercise II.IB);
(ii) ff contains (/)A and A' is range-restriction or A;
(iii) Y is the restriction or y.
Shortly, A' is a subautomaton of A if ff c Q and the inclusion map
' ■ ff -* C >• • morphism
f:il'->il.
It follows that the behavior of an automaton A Is the same as that of each sub-
automaton (II. 1.9).
A £tree automaton is reachable if each state is the result of the
computation of a tree; in other words, if p is surjedlve. The automaton in II.1.3 is
clearly reachable.
Prspmhioa. Each L-tttt automaton has a unique reachable subautomaton
which is also its smallest subautomaton.
Proof. Let A ■ (Q, |5„|, /", y, I. A) be a X-trec automaton. The Image of Its
run map
is a subalgebra of(g |5„|). Indeed, given a e I. and q, e Q, (i < n), we have
trees t, e /'with
Ci)p-«i ri'<").
Put
'-(',)...«'.€ /'.
Since p is a homomorphlsm, we have
(Op - (C.)«>.)P
- «',)P)«.
-(«,)«.;
hence,(«,),<.5. E &.
Thus, we obtain a subautomaton A, of the automaton A with the state set
Q,. Then A, is reachable since its run map is a restriction of p (II. 1.9).
A. is the smallest subautomaton of A because for each subautomaton A',
with the state set ff, we have (/)A c ft. and this implies Q, - (/')p c ft
(because the run map of A\ Is also a restriction of p). Q
Remark. The subautomaton above is called the reachable pari of A. For
example, the automaton in 11.1.7 is not reachable (if M has more than I point).
The reachable part of A is the subautomaton with two states, 0 and M.
44
Chapter II
A reachable automaton has no proper subautomata. The Tree realization
A(fi) is an example or a reachable automaton.
For the next step or minimization, we need the concept of an "admissible"
equivalence ~ on a £tree automaton A. Our aim is to construct a new
(smaller) automaton A/~ with the state set Q/~ (or all equivalence classes
If 1 or states if e C), and with the structure derived from A. That is
*'~ -{Q'~.\o\\. r. 9, i,X)
where
(a) a«L ■ ■ -. Ift. iD*. = K*. ■■-.«. i)«.l:
(b)GW<«)r;
(c)(x)X-|(x)Al.
Thus, "admissible" are those equivalences Tor which (a) and (b) are
well-defined:
Definition. A eongrvtnee on a J-tree automaton A - (ft |5„|, /", y, I. A) is
an equivalence ~ on Q such that
(A) given gel, and q, ~ q \ in Q (i - 0,.. -, k — I), then
(»•.••■, q>-i)S.~ (»'„..., q',-,)S„;
(B) given q ~ q' in ft then
Wr ~ <«>■
For each congruence ~, we define the quotient automaton A /~ by (a), (b) and
(c) above.
Example. For the automaton or II.1.6, the equivalence with two "parity"
classes
|0, 2| and |l,3|
is a congruence (because the operation + respects parity, the miliary
operation r maices no difference, and y is the parity map). The quotient automaton
is
A/~ - (1101,111), l + .llll. |0, l|, y. \x,y\. X),
where
aoi)r - o and aiDr - i
and
(jtH-IH »n<l O0A-I0].
Note that A/~ has the same behavior as A.
Tree Autooim 45
Remark. Congruences are closely related to morphums:
(i) For each congruence ~ on a tree automaton A, the canonical map
c:Q-» Q/~ (with (q)e - |<;D is a morphism
c:A — A/~.
Hence, A has the same behavior as any quotient automaton (see II.1.9).
(ii) For each morphism
f-.A^A-
of £trec automata, the kernel equivalence
<f. ~ <h iff (q,\f- (<h)f
is a congruence on A.
13. The concept of two states having the same behavior was crucial in 1.2.
We consider the corresponding concept of Interchangeable states q, and q,:
these are states for which a substitution or if. for ft In the interpretation of
variables does not influence the behavior.
Dcflaltlea. Given states if,, if, E fiofi T-tree automaton A - (ft |<5.|, /", y,
I. A), choose a variable y t I, and put
A, - (ft |«.|, T, y, / w |H X,) for i - I, 2
where X, extends A by (y)\, - q,.i( A, and A, have the same behavior, we say
that $ and rf, are wterehmttabU.
Remark. Interchangeable states have the same output : if A is the behavior
of A, above, then
Mr-(J0A-(J0A-<*)>'■
Example. In the automaton of 11.1.3, any two even numbers are
interchangeable (and so are any two odd ones). The states I and 2 are not
Interchangeable because (l)v * (2)v.
ProaaattMa. For each congruence on a J-tret automaton, any two
congruent states are interchangeable.
Proof. Let ~ be a congruence on A. Then ~ is clearly a congruence on
each of the automata A, above (i - 1,2). Therefore, A, has the ume behavior
uA,/~. Since l<fi 1 - IfJ, clearly A, /— is the same automaton as A-,/-. Q
14. We are now ready to minimize reachable tree automata: we prove that
interchangeability is a congruence and hence, the largest congruence.
Consequently, the quotient automaton is minimal.
46 Ch.pur II
Dcflattloa. A reduction of a tree automaton A is a surjective morphism
t: A -» A'. The minimal reduction u a reduction et: A -» A, such that for each
reduction e: A -» A' we can further reduce /*' to /<», i.e., (here exists a
reduction/: A'-»Atmth t„ — ff.
Tkeoma. Let t be a finitary type. Each reachable J-tree automaton A has
a minimal reduction c:A-»A/~ obtained from the following congruence
q, ~ q, iff q, and iji are interchangeable.
Proof. I. The interchangeability equivalence ~ is a congurenoe. In fact,by
Remark II.2J we know that ~ respects the outpuu: it is sufficient to prove
that it respects the operations. Let a e £, and q, ~ q, in fibe given for i — 0,
.... a — I. To prove that
(ft. • ■. ft - ,)&. ~ («'* .. ■, «', _,)«.,
it is clearly sufficient to show (hat for each n - 0,..., k — I,
(ft....,».-1. ft, q'.t q\ - ,)6. ~ (ft. ■ ■ ■. ft- i. «'.. 1'. ♦ «i -1)«.-
Denote by J: g-» g the map defined by
(«)rf-(ft.---«.-■.««;. «'»-,)«» (« € fi).
The proof of I. will be concluded if we show that
(•) q ~ q- implies (q)d ~ («V (q, q' 6 Q).
For each state q denote by
the extension of X (the initialization map of A) with
(yM,-«.
The "extended" automaton has run map X' and behavior X * • y:
(/w |^D* -» r. Thus, (*) states that
A,* ■ r - A; ■ y implies A'M ■ y - Xfa • y.
Since /< is reachable, there exist trees i„ i\ e /* with
,,-(j,)A' and «;-(*;)*• (i-o,..,«- i).
Since each A, extends X, we also have q, - U,)X' """''J'i - (J'/M,* (see
Exercise HID). Put
*- U 4-i. y. '.-„■■, *',_,)?. € (/._> |v|)•.
Tree Aatonuli
47
Then Tor each q e Q,
(s)a; - (um; <*._,*;, »<*;.,) a; &;_,*;)«.- <«)<*■
Denote by
the unique homomorphism with
(x)A - x (x 6 /) and (y)A - >.
Then
*•■»;- A'„:(/uW)' -fi.
In fact, A • A* is a homomofphism which coincides with the homomorphism
A,*w on the set or all variables:
(x)A ■ A,' - (jt)A; - (x)A - (xJA'y (x 6 /)
and
(y)h ■ A,' - (j)A; - (q)d - {y)X?„.
Thus, if A * ■ y - A; ■ y, then
A,,w ■ y — A ■ A# ■ y — h ■ A#- • y ~ A,,w ■ p.
II. The reduction c:A-*A/~ is minimal. In Tact, Tor each reduction
e: A -» A', the kernel equivalence at of *is a con|urence on A and hence, by
Proposition 11.2.3,
q a, q- implies q ~ f (q, q' 6 fi).
Thus, we can define a map / by the condition
c-e-f.
I.e., Tor each q e Q,
((«)*!/■- [«1.
Since e is a surjective morphism, and c is a morphlsm, it follows that / is
a (surjective) morphism by Exercise 11.1. A. D
48 Chapur 11
Eianplt. The minimal reduction or the automaton II.1.3 has two states, (0|
(- the class or all even numbers) and (I) (- the class or all odd numbers).
Here
id + ioi - (o + oi - (oi in + in - ii + n - id;
ioi + in - io + n - m m +101 - n + 01 - in.
The output is given by (101))'-0 and QIDr- I. the initialization by
(x)A - OOA - 111.
15. We now apply the minimization procedure to the Tree realization A(ff)
of 11.2.1. Given a state (i.e., a tree) I £ /*, we consider the behavior of the
automaton
Alfi), - ((/ w \y\); \<p.\, r, A / w \y\, A,)
where
fjt for x £ /
[i for x - y.
The morphism
A.Vt/wM)'-/'
changes each tree i e (/ >_> |/|)" by substituting every /-labelled leaf by the
tree I. We use the notation
f-.j-(j)A;.
Thus, for each node we D, we have
{(w)j *Hw)s*y
(u)f if * - v • u and (v)J - >■
undefined else.
Example: For
(A
Tree Amoiuu 49
we have
The behavior of ><(£), is the map i -*{t;i)fi. Therefore, two trees t„ f, E /*
are interchangeable in A(fi) iff
(', ys)P - («, ;j)P for each t £ (/ w {.y|) •.
Ceaatnctlta of the minimal realization of a map
fi-.r — T.
We define the Ntnde equiralenci x on /* by
f, w f, ifT (f, -,s)P - (f, -,i)fi for all j « (/«-> Irl)'
(where y t I). The minimal realization of /) Is the J-lree automaton
a. -(/•/*, {^.|, r, A /.*)
with
(I'd. ■ ■., M.i-il)l». - [('« ..., <M-i)f>.).
and
(Jt)X-(xl.
Proof. Since the Nerode equivalence is just the interchangeability
congruence on A(fi), we know already that A, is a minimal reduction of A(fi), For
each reachable realization A of ft, the run map is a morphism
p\A(p~)^A
(see 11,2.1). Since p is surjedive, A\tt reduction of A(ft), and we can reduce A
to At. a
50 ChtpMr II
Exanale. Put
l- 2T, - \a, r|.
We construct the minimal realization of the behavior
/J: K u. »C —|0. I|
defined as follows:
r has the label a, and the left-most leaf is x
(')/>■
(I if t h
I 0 else.
We inspect the Nerode equivalence classes of the simplest trees.
First, clearly
I*] * |u] - M.
The class |u] consists of those trees which neither have the label a, nor have
their left-most leaf x. Further, the tree
V l«
is not equivalent to x or u because (i,)fi - I; the class |r,l is precisely (\)f>-
The next tree
is non-equivalent to x or u: given y € |x, u, v|, consider the following trees
Then(fi ;')P* l*;*)P and((, ;S~)P+ (x •, 3~)fi. The class |(J consUu of all
trees having the label o* but not having the left-most leaf x. Finally, (x) is the
class of all trees not having the label a but having the left-most leaf x. We see
that
|x,u.v|- - |x] v, \u\ v |f,] v, m.
Tm Automata 51
The minimal realization of fi has the itate set
C-IM.M.IM.KJI-
The operation a depends on the first variable only:
(1*1 -)<»- (I'll -)"- I'll
and
(l"l-)c-(l'J.-)<»-l%l-
Alto r depends on the first variable only: it is the first projection. Further, y
and X are given by the following tables
..MMMM K x u '
ooio 1*1 MM
Exeidttall.2
A. Mlalasal mlbarJoa. Find the minimal realization of the following
behaviors:
(i) I- £, - |<r|. 0:1*1'-|0. l|.(r)0- I ifrthe depth of I bat least 2.
(ii) Z, - Ict.I for all n - 0. I. 2,.... fi: \x\% -. (0. I|. (i)fi - I ifTthe root
has more immediate successors than any other node.
(iii) I - Z, - \a. r|. fi: \x, y\' -. (0.1.2|, 0)0 - 0 if t has only labels a
and x, (f)/l - I if t has the label r but not y, and else (i)fi - 2.
B. GeatrarJoa. A subalgebra C of a X-ilgebra (Q, \S.\) is said to be
generated by a set M c fi If fi' is the least subalgebra with At* c Q'.
(i) Verify that the reachable part of a J-lree automaton is just Ihe
subalgebra generated by (/)A c Q.
(ii) Describe the subalgebra of (/*. |«>„|) generated by |Jt| for a given
x 6 /. and that generated by ft.
C Cogtawatl—. A congruence * on a J-ilgebra (Q, \S„\) is said to be cc-
menmted by an equivalence ~ (on Q) If m it the lafgeat congruence
contained in ~ (i.e., such that q * q' implies q - q~).
(I) Verify that the Nerode equivalence of fi is cogenerated by the kernel
equivalence of/) (on /*).
(ii) Describe the congruence cogenerated by an arbitrary equivalence on an
arbitrary J-ilgebrt. (Hint: See 11-2.4.)
52 Oupur II
II J. laflaHary Tree Aateanta
3.1. In this section we consider types I with infinitary arities or operations.
The definition or X-tree automata is naturally extended to then type*, and the
run map is defined on the (free) X-ilgebrt /• of all finite-path £4rees. It turns
out, however, that minimization cannot be extended: there are behaviors
which do not have a minimal realization.
3.2. By a type we understand a set £ of operation symbols, together with an
arity map assigning to each ieIi cardinal number |e>L Again, L. denotes
the set of all n-ary symbols, t, - \a e S: \a\ - n|. A J-ilgebra is a set Q
equipped with operations
«.:C'-»C l«ai»l-«),
where the elements of the it-fold cartesian product Q' are all n-tuplea
(«■)■<.
with q, 6 C for each i < n. A homomorphism
/:(ai*.l..5)-(t3M*;i..i)
is a map such that for each o* E l„
(»).<•«.-« Implies ((filOi<.%-(«)/•
A l-tnt automaton is defined precisely as in 11.1.2: it is a £algebra
(ft ||S„|„, i) together with an output map v: fi-» T and an initialization map
A:/-fi.
fiasafli Let £ - |c| where a is at-ary. Put
y4-(«>w|«.|,«..|0. l|.r,|Jr|.A)
where 6, is the following operation on sequences in a \j | oo |:
(ft. *. <h....)«.-( V?. J + I
(I.e., S, is the maximum plus I if the sequence is bounded, else 5„ - <=).
Further.
f 0 if a 6 to
W"|l ifj--
and (Jt)A - 0.
3J. The construction of the free algebra /* (formed, for Military types, by
all finite X-treej over /) requires a revision.
Tm Antomita
53
If a 6 £ is an infinitary operation, then the trees in a free £algebra will no
longer be finite—consider the following tree:
Neither are they going to have finite depths—comider the following tree with
X unary:
It lunu out that the trees in a free X-algebrt are just those which have finite
paths.
As in the finitary case, we shall work with the complete m-ary tree
with m - V |cr|. (Remark: The case m - at can Indicate either that £it an
««i
infinitary type with all operations at most 0-ary. or that X is a finitary type
with unbounded arities.)
A path in.the tree m* (from the root t downwards) is a sequence of
elements of m* of the following form
•i Pi. PiPfc PiPlP* ■ ■■
where p„ pi, p%,... are elements of m (i.e.. ordinals smaller than m). An
example of a path in a':
34 CbapMr II
3A. DefbrirJoa. Let Z be ■ type and let / be ■ set (of variables) with
Zr\ I — t: put m — V \a\. A finite-path Z-trtt orer I (shortly. ■ L-lm) Is
a partial map t: m''-» I\j Z such that
(i) the domain of definition D, is non-empty and its Intersection with any
path in m* is finite:
(ii) given p,...p,p,. i e m', then
/>,.../>,»,€£>, iff (p, ...p,)t 6 Z. for some ■ > p,♦ ,.
Ksaaark. The condition (i) can pn view of (ii)] be reformulated as follows:
(B)r is defined, and for each path t. p,. p, pj,... there exists k, e a such that
O'iPi- ■ • >».)' 's defined iff J: £ *» Note that for T flnitary, the latter is
equivalent to the ftniteness of D„
The set ofall finite-path J-treo over / is. again, denoted by /*.
EJuaate. Let Z - |e>. A| with |o) - a and |A| - I. The following trees
Tree Aotomiu
55
■re element! or |Jt|*. In (,, Tor each pith we hive either k, — I or Jt* — 2. In
(,. for eich pith 0. p„ p,p,,... we hive k, - p, + I. In contrast, the following
trees
■re not element* of 11) ■: consider the pith 0.0,00.000,... for (, and the pith
0. I. 10. 100. I 000,... for I,.
33. The properties of /* are analogous in case of Infinllary types. The
branch of ■ tree I e /' with the root we D, is the tree <?.( defined by
(rtf.t- (wr)l for ill r 6 in*.
Cleiriy <?.( 6 /'. The operations *>,:(/*)'-> /*. for ill o- e £. are again
defined is follows: given I, e I'. I < n, denote by
'-(',),<.«>.
the tree with
D. - IPiPi • • • Pi 6 m': Pi < » and p,... p, 6 DJ «_< |0|
where
(0)1 - <r.
(PiPi--P»)'-(/>i--Pi)'„-
We must verify the condition (i): For each pith 0, p„ p,p,.... either (p,)' is
undefined (then k, — 0) or p, < ■; since (,, c /*. there is k, such that
(Pi • ■ ■ Pk)'„ is defined iff * & k+
Then
(PiPi - - - Pi)''» defined iff k S k,.
56
Chapter II
Thus, we get in algebra
(/'. I«».l)
which clearly hu the Peano properties (II.1.5). To prove that this is a free
algebra (u in 11.1.5), we use transfintte Induction; in order to deflne sets Wk for
all ordinals k. we must deflne
(a) W,:
(b) W,.,. given Wt;
(c) Wk, for each limit ordinal 4c, given W, (j < k).
Analogously, to prove a statement about each ordinal k. we must (a) prove
the statement for * - 0: (b) derive the cue k + I from the cue k and (c) for
each limit ordinal k. derive the case k from the preceding cases.
We now define sets Wt analogous to those in II.1.5:
W„- I.
"ti<1-'"l(i,)i-.».;»e £.',- W.l
and for each limit ordinal k,
Wt - U Wt.
i< i
Whereu In the flniury case we had /* - W„ in general we have /• - (f, for
some ordinal k, but the proof is more technical here.
We say that a L-tm I hu finite depth if it is an element of Wk,k finite.
Then the depth of I equals to the largest number k for which there exists
p.... pt 6 />,.
14. Theorni. The algebra of finite-path trees
is the free £algebra generated by the set /.
Proof. For each £>algebra (Q, |d°„|) and each map/: /-» Q. we are to show
that/has a unique extension to a homomorphism /•: (/'. |«>a|) -»(Q, [Sc[).
It is sufficient to prove that there exists a cardinal m with
/• - W-
Then we proceed by extending / to each Wt:
(D/'./onlf,.;;
(b) given /* on Wk and given I e Wt t „ we have ( — ((,), < .«>„ with
I, e Wk, and we put (i)f - «r,V),<.«.;
(c) the extension on the limit ordinals is clear.
Tm Attomu 57
The Peano properties guarantee that /* it well-defined, and (b) impliei that
/'ill homomorphism. Moreover,/* ii unique became the rule for the exten-
lion above it just a consequence of tbe expected properties of/".
We prove
/• - W.
wbere * is the first regular cardinal larger than
m- Viol.
9 f I
For each tree It /'we define sets
(OS, c m*
by transfinite induction as follows:
(OS, - m' - />„•
(OS,*, - \p,...p,e m*-, p,... p,p,., € (OS, for each/>,*, < m\;
(OSi - U (OS, if * is a limit ordinal.
/<»
We are going to prove the following statements for each tree I e /• and each
ordinal k:
I. (OS, c (OS, for each ordinal *' S *;
II. if(()S, - (()SW„ theog e (OS,;
III. if" 6 (t)S,,tben(€ Wt,
This will prove the proposition: for each * 6 /* we have by I. a monotone
chain of sets (OS. c (OS, c ... c (OS, c ... c m*: necessarily, there
exists an ordinal k of cardinality £ m (- card m*) with (OS, - (OS,.,.
Then II. and III. imply I € Wk. Since m < iftand lAis a regular cardinal, the
ordinal k is smaller than the ordinal ii) and hence, W, c Wm. Thu proves
/• c Wm.
I. (OS, c (OS,. We prove this by transflnite induction on k. This is clear if
* - 0, since than k' - k. Assume that k' & k implies (OS, c (OS,; to prove
that this also holds for k + I, It aufficas to prove (i)S, c (OS,. ,- Let
p,... p. 6 (OS,.
(a) If k * 0, then for each p,+ , e m there exists k' < k with
P\-P,P,+ \ 6 (OS,- c (OS,: this proves »,...», € (OS,*,.
(b) If k — 0. then (px... p.)l \i undefined and hence, for each p, + , e m
also (P\ ■ ■■ p,p,t\)l is undefined. Thus, Pi..-p,p,n e (OS* which proves
p,..p,e (OS,.
The proposition is obvious for each limit ordinal k, since (OS, — U (OS,.
,' <,
II. (OS, - (OS,* i implies t e (OS,. Assume the contrary: there exists
58
Chi pin II
a finite-path L-lnt I e /• and an ordinal k with
9 t (OS.-(»)«.♦ i.
The itatement 0 t (OS.* i means that there exists a p, < m such that
p, t (OS.. Hence, p, t (OS., ,: this means that exists a p, < m such that
ftft < (OS., etc. We obtain an infinite sequence p„ p* ph ... in m such that
p,...p.t (OS. for all j £ an It follow! that (p,... p,)i is defined for all
ie at: by I. if p,... p, e (OS. then p,...p, e (OS.. This contradicts to the
condition (i) in the definition of finite-path £trecs (IIJ.4).
III. 9 £ (OS. implies I £ Wt.
We first prove that given p,... p, £ m* with p, £ D„ then
p,... p, e (OS, implies pi...p. £ (<V)S,
by transfinite induction on k. (Remark: For s - 0. p, ... p, - 9 as well as
ft.--ft -■•)
Let * - 0. Then p,...p,e (OS. means that (p,... p.)lis undefined: this
Implies (ft ... ft)<V Is undefined (I.e.. Pi...p, £ (<V)S«) whenever p, e />,.
If the fUtemem holds for k (and all ( £ /*) then it holds for k + I :
p,...p,e (OS.., means that for all p,*, £ in we have ft ... p, p,.\
E (OS.: this implies p, ... p, p.., € (<?„0S. (for all p,.,) or p, ... p, 6
(<?„(>S,. i. whenever p, e />,. The situation with a limit ordinal k is dear.
Now, we prove that
9 e (1)5. implies I e W,
by transfinite induction again. This statement holds trivially for * - 0. since
9 E (OS. cannot occur. Assuming the statement holds for k. let ■ € (OS.» i.
Then for each p e in we have p E (0S», i.e., 9 e (<?,i)S,, whenever p E />,:
for these p we have <?,( e Wt by induction hypothesis. Now, either
* £ / c W» ♦ i. or (0)( - a £ Xwith |o-| - n and
Finally, the situation with a limit ordinal k Is clear. D
3.7. As in the finitary case, Z-tm automata work with the trees in /* :they
compute the trees and give a resulting output. But the computation can now
be infinitely long.
We define the run map of a £tree automaton A as the unique homomor-
phism p:(/*. |*>„|) -»(Q. \S„\) extending the initialization map, and the
behavior as
fi-p-r-i'-r.
Tree Automata
Enaple. For the automaton of II.J J, the following tree
59
yieldi the output 0:
®-i
The ume holds, evidently, for each £tree of finite depth (11.3.5). On the other
hand, the following tree
yieldi the output I (after • countable, computation):
© >-i»l
60
CtlipttTll
The same holds Tor each tree or infinite depth. Thus, the behavior of A is
defined as follows:
fO if (has finite depth;
18. The concepts of congruence, reduction, interchangeability and minimal
realization are defined for infinitary automata in the same way as for the finl-
tary ones. But interchangeability is no longer a congruence on each
automaton. In fact, any two states <?.. ift e a in the automaton of II J.2 are dearly
interchangeable, and oo is not interchangeable with any q € a. Yet, the
equivalence m with the dasses a and |oo | is not a congruence: we have
0 * 0. 0 a> 1.0 « 2,...
but
(0, 0, 0,...)«. - I • oo - (0.1, 2... .)«„.
It tums out that the behavior of this automaton does not have a minimal
realization :
Tktoreaa. For each type £, the following are equivalent:
(i) lit finiury;
(ii) each behavior fi:l'-+ /~has a minimal realization:
(iii) the behavior fi: |x| ■ -► |0,11 defined by (l)P - 0 ifT I has finite depth,
has a minimal realization.
Proof. (i)-»(ii) See 11.2.5.
(ii) -»(iii) This is clear.
(iii) -»(i) Assuming that I'm infinitary, we shall prove that the behavior ft in
(iii) does not have a minimal realization,
(a) Let I- |o-| with \a] - a. The automaton A of 11-3.2 realizes fi, see
11.3.7. And A is reachable : we have
0 - (*)A,
1 - (0, 0.0,.. .)«„,
2 -(I. I, l,...)6°„,
etc, and finally,
oo -(0, 1,2,...)«..
Suppose B is the minimal realization of fi. There is a morphism
f-.A^B.
Tree Automata
61
Since for q e a we hive (q)y - 0 * (oo)y, it is dear that J{q) * /{<»). We
•hall prove that
Al) - Al) for all q, q e a.
This is a contradiction: the kernel equivalence of/has just two classes, at and
| oo |, and we have observed above that this is not a congruence on A.
For each k — I, 2, 3, ... denote by ~» the following equivalence on
a\j |oo|:
q ~, q' iff q < k and q' < k, or q - q ■
This is a congruence on A (because for each bounded sequence ($>, q,, q>, ■ ■ ■)
in otu |oo|, all sequences (q'„ q„ q'„ ...) with f. ~>f'„ for n < <v are also
bounded]. Hence, the quotient automaton A / ~, is a reachable realization of fi
and consequently, there are morphisms
f,:A/~t—B for*- I. 2. J
Denote by c»: A-+ A/~t the canonical map, then
/- c,./,for*- 1,2. J
In fad. If p: |x|* -» ou |oo| is the run map of A, then p • /is the run map of
0(11.1.9). Since p ■ ti ■/, is • homomorphiim, p • c, • /, is also the run map of
A Hence, p • /- p • f, • /i. and since p is onto (because A is reachable), we
conclude / — e, ■ f,. Thus for arbitary q, q' e a we choose k such that q < k
and f' < *, and we have (q)c, - (q')c,; consequently,
<»)/- («)c,. /, - (,")c, • /, - (qY.
which was to be proved.
(b) Let I be arbitrary. Then the above automaton A Is readily adjusted:
choose o- € X of arity n fc cu, and put
<«).«A- (V«) + I.
All the remaining operations are chosen as the constant map to oo. The proof
then proceeds as above. D
Rctaarkf. (i) Even for I infinitary, each £tree automaton A for which the
equivalence
q, » q, iff q, and qt are interchangeable
is a congruence, has the minimal reduction A/as. (The proof is as in 11.2.4.)
This is in particular the case If A is finite.
(Ii) Each behavior fi with a finite realization does have a minimal
realization: it is the minimal reduction A/ * of (any) finite realization A of p\
62
Chapter II
3.9. Although minimal reductions exist Tor Unitary types £ they do no)
have an important "universal" property encountered in case or sequential
automata. This property can be formulated as the possibility to minimize not only
automata but also morphisms or automata.
MMtkM. Let Xbe a type. We say that X-tree automata have
mlrtnalminimal rrdticlion if Tor each morphiim
<//_,/«.):><- A'
or £tree automata with minimal reductions rA: A -► A, and r\ :A' -» A', there
is a morphism A, -» A', such thai the following square
IU„,.1,J ,
A «• A
a0 -n0
commutes.
Since r, abbreviates (r>,id,id,), the new morphism must have the form
(./•,/.,/»•) for the (unique, if any) m«p/, with
'A-ft-f- 'a-
In the categorical language, let
Aut,(X)
denote the category of reachable £tree automata and automata morphisms.
Composition or morphisms
(/,/.,/«.): *-» A' and (g. g,,, goul): A' —■ A"
is componentwise, i.e.,
(/• >./. • >!../« • !«.,): A-*A~.
(It is easy to check that the last triple is in fad a morphism.) The identity
morphisms are (ide, id,, id,). Then minimal reduction is universal ifTthe minimal
reduction r,: A -* A„ of each automaton is a universal arrow [and thus,
reduced automata form a full reflective subcategory of Aut,(X)|. We shall prove
that sequential automata with resets (Exercise I I.I .E) present the only case of
tree automata with universal realization.
Tkeoreai. If all arities in I are I or 0 (i.e., I — I, \j £,), then minimal
reduction is universal.
In particular, sequential automata have universal minimal reduction.
Tm Automsu 63
Proof. Let I — I, \j Ef We can view £tree automata A as sequential L-
automata with resets in Z, (Exercise II.I.E). Extending the minimization
procedure or 1.2.6, we introduce the behavior or a state q of A as
ft - p, ■ r *r- r
where p,.X,*-» G " defined by the following induction:
(•*>, - «;
(<r,... a., ,)p, - ((<t, ... a.)p,, a.. ,)S.
(We form words only from letters In I,.) It is easy to verify thai the results
concerning sequential automata generalize to our case: the equivalence
q « «• IfT ft - ft
is a congruence on A, and the minimal reduction is the canonical map
rA:A-A/*,lq)rA-\q\.
Let
be a morphlsm of automata. The behavior ft of a state q\n A \» related to the
behavior fi!„fot (q)/in A' by
ff„/-ft-/-:*.*-r.
This follows from fl'41/ - p, • /(which is easily proved by Induction):
p"w/ ~ fl'o/ • y'
-P,-f- Y
- p, • r<f~
-ft-/«r
Consequently, for arbitrary states q and q' of A,
ft - ft implies ff,,, - #,v.
Thus, if « is the congruence above for A. and m' the corresponding
congruence for A\ then
qaiq' implies («)/«>"(«•)/
Define
/•:(?/*-0/*'
by r^ • ft - /• r,,, i.e., by
<l«l)/. - l(«)/].
64 Chapter II
Then
(/../../»«): A/» -,4V*'
Is a morphism such that
(•) rA •(/../../-)-(/./«./.) t,.
In Tact, (a) is clear, and since rA is a surjective morpbism, it follows thai
(/•./-./«) >s a morphism (Exercise 1.1.A).
This proves the universality. D
Theorem IT minimal realization is universal, then all arities are I or 0.
Proof. Let I be a type with s symbol rof arity n > I. We define a £*rce
automston A and its subautomaton A such that the inclusion morphism
»: A-*A
cannot be "minimized".
Put
>4-(|0. I.2,J|, \S.\. |0. 11, y. 1*1. A)
where 6. is constant to 0 for all o- c I — | r| and
(«•. * )*. -«. + «>
(where + is the addition modulo 4). and
(Dr- l:(0)r-(2)y-(3)y-0
(*)A - 2.
We clearly have a subautomaton A of A on the set |0.2|: since the output
map of A is constant to 0, the minimal reduction
n,:A-»A,
is the constant map. On the other hand. A does not have any non-trivial
congruence: since 0)Y~' - I. one congruence class must be |l|. and then it Is
easy to verify that all congruence classes are singleton sets. Thus,
id: A-A
is a minimal reduction. There is no commutative square
i
*. -A
Tree Automsu 65
Corollary. Among tree automata, realization is universal just Tor sequential
automata with resets.
Eierdso IIJ
A. lafhttt-patk trees. Denote by /• the set of all (not necessarily finite-path)
trees, i.e., maps ( defined in 9 and satisfying (ii) in Definition IIJ.4. Define
the operations on /* analogously as on /*. Why is /' not the free algebra?
Hint: Try to extend the inclusion map /-» /*.
B. Ualmsaltty of atlalsaal raallzatioa. While behavior has a "functorisl"
nature (it defines a functor from the category of automata to the category of
behaviors), minimal realization is seldom "functorisl". We make these ideas
precise. Let I be a Unitary type.
(i) Let B*rt(X) be the category whose objects are (/,AO, where
fi:lm — r is a behavior, and morphisms (/.,/„): (/, A /") -► (/\ F, r) are
maps/,: /-► /', f„: /"-► /"' witb
Verify that the following behavior functor
0:Aut,(£)-»B«f)(X)
is well-defined: AB Is the behavior of A and (//„,/.)« - (/*,/..)-
(ii) In case I - I, <j ii. verify that there is a functor
/M:B«IXD-»Aut,(r)
which assigns to each behavior its minimal realization, and fulfils M ■ B = I
(i.e., for each morphism (/.,/_) there Is / such that (/.,/„)** -
Hint: Proceed as in 11.3.10 using the fad that the minimal realization of fi
is just the minimal reduction of the free realization A((t).
(Hi) Verify that M and B are adjoint functors.
(iv) Prove that whenever I contains ■ symbol of arity > I, then there does
not exist a functor M with the properties of (ii).
Hint: Try to find (Kld„idr)/M In 11.3.11.
IM. Flaltt Aatosuta eatj Laagaage*
4.1. Throughout this section, I denotes a fixed type of finitely many finitely
operational symbols; such types are called suptr-fmilary. We denote by m the
maximum arity in £
66
Oupler II
We want to characterize the behaviors or finite L-lrcc automata, i.e.,
automata with the sets Q (of states) and / (of variables) both finite. We proceed in
a close analogy to the case of sequential automata. First, we introduce
acceptors and languages, and we prove that instead of behaviors it sufTlces to study
recognizable languages.
Informally, a £tree acceptor is a £tree automaton such that:
(i) variables form a subset of the state set and A is just the inclusion map;
(ii) the output alphabet is T- |0, l|.
The first restriction means that we need not interpret variables as states,
since they are states already. The latter means that instead of a map
y: Q-+ |0, I) we can just consider the set T- (l)c'
AX DefnHtoa. A I-tree acceptor is a quadruple A - (ft |£.|., r. T, I)
where
0 is a finite set (of states):
S„: 0"-* 0 » *" operation for each ail,,
T and / are subsets of Q (of terminal and initial states, respectively).
The run map of A is the unique homomorphism p: /" -» Q with (q)p — q
for each initial state q. In other words, for each £.tree / £ /' (with leaves
labelled by initial states or nullary operations), (/)p is the result of the
computation of l The tree / is accepted if (/)p is a terminal state. The language
recognized by A is
L4-\te /';(/)p£ r|.
In general, languages are sets of £>trecs (i.e., subsets of /' where / is a set
of variables).
4.3. Defnttloa. Let / be a finite set (of variables). A language Lc I * is said
to be recognizable if there exists a £.tree acceptor A with L— L,.
Remark. In the above definition, it has not been required for the acceptor A
that the set / be the set of all initial states. Indeed, A can have a larger set of
initial states (none of which happens to be a label in any accepted tree, of
course).
4.4. PrepaaWoa. Let / be a finite set and /"be an arbitrary set. A behavior
p-. /• - r
has a realization by a finite £.tree automaton iff
(1) the language {y)P~' is recognizable for each y t T;
(2) the set (l')fi c T is finite.
Proof. I. Let fi be a behavior with a finite realization, say,
A - (ft |«.|, T. y, IX).
Tree Autonuu 67
(a) We prove thai f) has a finite realization
* - (C |o-.|, T, /. /. A")
•uch that / c Q' and (x)X' - x Tor all x € I.
First, assume that X: /-» g Is one-to-one. Then A' Is defined by a formal
"re-labelling" of the states of A. For each state q £ C? — (/W, choose an
element q' such that
q, * f, implies q\ * «,' « /;
the new state set will be
C- /w |,-;,£ {?-</H|.
For symmetry, given q £ (/)A, put f' - x Tor the (unique) x £ / with
(Jt)A - q. Define
«;:<(?y-G' (<T£ X.)
by
(flb. • • •. 1„-.)«; - Kft. •. 9.- i)«.l'
and put
r.Q^r-Aq)r-(q)r-
Finally, X': l-+Q"n the inclusion map. It is easy to see that this automaton
A' has the same behavior as A.
Next, let A be arbitrary. We shall find a realization of A
*-(Q.\S.ir, f.l.X)
with X one-to-one. Put m - card /; there clearly exists a map
X.l—Q* |0, I m- l|
which is one-to-one and such that
(x)X - (q, j) implies (x)X - q for all * £ /.
Put
Q- Qx |0. I m-\\
and define
S.Q'^Q (ff£ I.)
by
«*../.). (<?„>,) <». -1. A - .))*. - <«, 0)
where f - (ifr, fl„ ..., fl._ ,)*,. Finally define
r:e-r;((j.»r-(«)r.
(g Oupurtl
Denote by p: /* -» Q the run map or A and define
p:/*-G
by
(/)p-« iff (t)p-(<),J) for some y.
It is easy to check that p is a homomorphism; Tor each x € I, (x)p - (x)A
since, by the choice or X,
(x)p- (*)X- (q,j) implies (x)X-q.
Hence, p is the run map or A. Clearly,
p- yp- y:/"-»r,
hence A and A realize the urne behavior.
(b) We prove that (y)p~' is a recognizable language Tor each / e /"! We use
the realization A\ and we define an acceptor
*\ - ((?'. 141. T, /), where T- MrT'-
Let p': /* -► 0 be the run map of /< . then p' is the run map of A'r, too, and
since A' realizes p"(- p' ■ }0, clearly
(i)P-y iff (i)p' £ r (for each /£ /•).
Hence, A'7 recognizes (y)fi ~'.
(c) The set (/■# - ((/•)p)r c (Or is finite.
II. Let fi have the properties (I) and (2). The proof that fi has a finite
realization is quite analogous to the sequential case (1.3.3). Put
</•«»-1/ /.I:
the language
L,-{/,#-'V - I *)
has a realization by an acceptor, say,
*, - (e.. i«:i. t„ i,).
Define a finite L-lrtt automaton
A-lQ.\6.\,r.r.l.i)
as follows:
G - G. x (?, x ... x ft;
for each o- £ I., A", - o",J x ... x 61 — more exactly, given «*..., f.., £ G
|where « - («/ «/)),
Tree Automata 69
(«* •••.«.-,)«. - ((*' «! - ,)*i («.' «.'-,)«);
further,
is an arbitrary, map such that (a,,..., q,)y - y, whenever q, £ T, while
qt £ 0, — Tj Tor all j * I; finally
A: 1-+Q
is defined by
(«)* -(**•••.«) f«f «ch « « I-
(Note that since /<, realizes a language in variables /, we have / c /, Tor all i)
Let p,: /* -► ft denote the restriction or the run map of A„ i — I,.... t,
then the map
P-.I'-Q: C)P - «')P (Op.) (t £ /*)
is the run map of >4 (it suffices to verify that p is a homomorphism). The
behavior of A a p": given / £ /• with (/)/) - /„ then
(/)p, £ T and (t)pf £ (J - r, for all./ * f
(since / is accepted by A, but not by A,,j+ Q; hence.
Or-/,- n
4.3, We introduce nondeterministic acceptors similarly to the sequential
case, and we prove that they accept nothing more than their deterministic
relatives. We return to arbitrary variables (to which states are assigned in
a nondeterministic manner).
DeflaitML A nonieterminiatic I-tree acceptor it a quintuple
-<-((?. \S.\.,i,T,l, X)
where QUs finite set (of states), for each a e £.
6„: G*-" Qitt relation;
T c Q is a subset (of terminal states), / Is a finite set (of variables) and
X.I^Q
is a relation.
The ran relation of A is the relation
P:/'-{?
70 Chipler II
defined by induction (on *, where /* - U Wt, see 11.1.3):
»■ o
if* £ /then (x)p - (x)X\
if/£ K*i- IV,;/-(/». .../._,)♦>. then
(/)p- U (** • ••. J._i)4,
where the union ranges over all s, £ ((,)a •••,».-1 £ ('.- i)p. The language
recognized 6/ >4 is
/..,- |/ e /';|l|pn T+ 0|.
44. PropoaUhm. Each language, recognizable by a nondeterministic £tree
acceptor, is recognizable (by a deterministic one).
Proof. Let A — (ft 14,1, T, /, X) be a nondeterministic £tree acceptor,
recognizing a language L c /*. We define a £>tree automaton with the output
alphabet /"- |0, l| such that its behavior is the characteristic map of L; in
view of the preceding proposition, L is then recognizable.
Put
-J - (exp ft |&|, |0, 11, y, l,X)
where, for each a £ 2. and Do, D D._, £ exp ft,
<*V O O— i) S. - U(*. * <?.-i)4,
the union ranging over all 4, c ZV ..., fl._ 1 £ D._ 1, and
r.expg-IO, l|
is defined by (D)r - I ilT D n, T * 8. Moreover, the relation A : *— g yields
a map X~: /-»exp ft
It is easy to prove that the run relation of A,
p.l'-Q
yields the run map /$:/*-» exp Q of A. Thus, a tree / £ /'is accepted by A
iiHOp/-* r* e,i.e.,irr((/)/?)>'= i. □
4.7. Operation oa accepters aad laagaagea. We introduce now operations
on acceptors corresponding to the union, concatenation and iteration of
languages. While these notions are parallel to those used for sequential automata
(I J.8), the proofs for the last two operations are more technical.
Uatoa-Ut
A - (ft 14,1. T. /. X) and A - (ft, |4.|, T. I. X1)
be nondeterministic £tree acceptors with disjoint state sets, Q n, ft — 0, and
with a common variable set /.
Trtc Automata 71
Their union ii the following acceptor
Ayj A -(Qyj Q\ |6"„|. Tw r. /, A~)
where A", - A", w 5', and A" - A w A' (u tet-theoreticml union), i.e.. Tor each
a e Z.
f («. ,«.-l)«. If «..,«.-! « 0
(•.■■■.*..)4-^ («..,«..,w; if *...,«.-,« c
l 0 else
in cue n > 0, and
6, - 8, w A";,
in case n — 0.
Further,
(*Vf-(*)Aw(*)A' (*£ /).
It is easy to see that A w A' accepts a tree iff either A or A' does; hence,
l-A^r - Lt\j LA.
4.8, Serial x-c—ecrJoa. Let A and /<' be acceptors as above and let * e I.
The serial x-connection A ; A' is the acceptor resulting from connecting the
terminal Mates of A with the A'(jr)-itate» of A'. More precisely:
a-.a-iQuq; |6*„i. r, /, X).
where, for each 6 « Z.,
S. - 8. w S', w »/.
with
\W if (*....».-,)«.^ J>e
(*.•••,«„-.)»'.- \
and for each y € I,
l(/Hw(*H if (jr)iftr*«.
The operation on languages, corresponding to the serial connection, is the
concatenation (generalizing the substitution):
First, given a tree / £ /* and a language L c /*, denote by
L-.i
the language of all trees obtained from / by substituting each x-labelled leaf
by a tree in L
72 Chapter II
Example:
We define thii concept formally. Recall that m denotes the join or all
antics, m - V |<r|.
o* £
DeflaMoa. For each L c /" and / £ /* and Tor each x £ /, denote by
L; I c /'the language or all treea /such that Tor all a £ m*,
(i) (a)/ - x implies i, I £ L,
(ii) (a)/ £ lu /— |x| implies (a); - (a)/.
The x«mcatenation of two languages L. L' c /* is the language
L-, V - U *••„/.
f < I'
Proaosllloa. The language recognized by the serial x-connection A; A' is
the x-concatenation or the languages LA and L,:
l*A-MJl ~ **A •„ L4 .
Proof. Denote by p the run relation of A, and by p' that of A'. For each tree
/ £ /*, put
LJ,- |/~£ /•;/ £ Lt-,J\.
We are going to prove that the run relation of A ■, A' is defined by
(Hp-Wpu .U (Op
for each / £ /*.
Then a tree / is accepted by A ■, A' iff (/)p r\ 7" * I, i.e., ifT there exists
Tree Automat!
73
I £ ly, with (Op' r\ 7" * 0; equivalently, with i e LA. That will prove the
proposition.
First, we must prove that p extends X. For each / £ / — M, clearly
LA-,y- l/l »nd L,,-,*- /«■ On the other hand,/ t L-,/"for any i + x,y.
Thus,
(I) if/£ L^.then LV,= |*,/| and OOp-MpuO'lP'uf.JOp'-O')*:
(ii) if y t LA. then LJ, - \y\ and (j-)P - OOP" O-Jp' - 0-)*
Analogously with *: if* £ L,,, then LA i, - \x\; if Jt t LA, then L^?, - 0. In
both cues, (x)p - (x)X.
Next, we prove the inductive formula: if / - (fc..., /,. ,)p„ then
(Op- U.(v ■■■.!.-,)*.
Ml I UllP
for n > 0, and (<r)p — o'.for n — 0. The latter is clear since LA9„ — \a\. Let us
prove the former.
I. / t LA. Let us sun with the right-hand side. Since (OP-
(/,)p u |J (Op', and since (j«, ..., i. _ ,)£, - 0 unless all of »„..., j. _, are in
one of the sets Q and Q', the right-hand side equals to
U (v---.'.-.)*.". U U. (V.......,)*:.
* • IMP * t l^, m, I !/,)?'
Now, both p and p' satisfy the inductive formula. Moreover, 11 LA implies
(J*..., j..i)o"./-> T-0 for any i, £ (/,)p and hence (j„.. , i.. ,)& -
(«►•••. *. -1)<%. Thus, the right-hand side can be written as
l*u( JL Mi- ■■-'•- i)*.)?'-
To analyse the left-hand side, consider an arbitrary tree /" £ LA9,. Since
II LA, clearly /"( / and thus, /-(/"*..../._,)«>„ where t,—if for
* - 0 n — I. We claim that i, £ L,xV Indeed, since / £ L-,t, we obtain /
from /" by substituting x-labelled leaves by trees in LA and hence, the Mh
branch /, is obtained from i, by the same substitutions (In the nodes />,... Pt
with p, — 0. Conversely, given trees I, £ Ljlt, < — 0 n — I, then the tree
i - (is,.... £ - i)«V is in LAi,. Hence,
(/)p - (/)p w . U (iV
- (Op w U ((/* ., h- ,)«vlp".
We see that both sides are equal.
II. / £ LA. The proof is quite analogous, only both sides are "enlarged" by
(Jt)A': the left-hand side since / £ LA-,x, i.e., x £ Ljl,: the right-hand side,
since there exist i, £ (;)p, with (jfc ...,»._ ,)S. aTi> ». O
74
Chapter II
4.9. x-Fe*dback. Let A - (Q, |o°„|. 7; /, X) be a nondeterminiitic acceptor
with (Jt)A n T+ %. The x-feedback of A li the acceptor
A"-W.\S:\.T.I,X')
where for each a € Z.,
(*.■■■.«.-
and for each / £ /,
0-M
«• J <*.■■, *-i)'. if(ft-
'' ' I (ft.....«.-,)«.w(x)Atf(»1..
,«,.,)A,ftr-»
Jo-j/i ifi»>i/->r-e;
\Or)/lw(*)yl if(»/l/-> T+ ».
The corresponding operation on language* is the following:
Deftaitloa. For each language L c /• and each x £ / with * £ L, the
x-ittmiion is the language
l"-lu (L •, t)u((ta)\l)u •■■
Exaaate.
then
0
L":0
Rcaarfc. The x-concatenation is associative
H-AK-.L)- (H;K).L
(therefore, the brackets in the preceding deTinition can be omitted). Indeed, If
/ £ H -A.K -,L) then there exists i £ K •, L with / £ H -, x and there exists
r £ L with i £ K -, r. This implies
/£ (H;K);r
Tret Aulomui 75
■i followi:
If («)r — x. then S, s £ X and since / £ H -, J, we have
Ai £ »',Aic //-,*:
if (a)r£ (/- |*|) w 2; then (a)r-(a)j implies («)* £ (/- |jr|) w 2;
hence, (a)rm (a)> - (a)(.
Analogously, from / £ (H -, K) -, L we derive / £ W •, (AT •, L).
PropaeMoa. The language recognized by the x-feedback A " is the x-itera-
tion of the language LA:
Lt~ - (LA)".
Proof, If p is the run relation of A, then the run relation oM**is defined
by
</)P-(,Uj.-)p.
The proof Is quite analogous to the preceding one. Consequently, a tree I is
accepted by A •* ifT there exisu a tree I £ LJ'g, with (i)p n, T * 0, i.e., with
I £ LA. Thus,
/ £ Lj'itt i £ LJ* -,LA.
Since * £ LA (by the hypothesis on A), clearly LJ' -, Lt — LJ' and hence,
LA.. - Lf. O
4.10. Dtflatttoa. The class of rational languages is denned as the least dus
of languages in arbitrary (finitely many) variables, which contains all
singleton languages |0| and |/|. / £ /*, and the language 0, and is closed under the
formation of union, x-conotenatlon and ^iteration for all variables x
Remarks, (i) Every finite language Is rational.
(ii) Trees in Wt (see II.I.S) are called basic, thus, basic trees are of the
following kind:
76 Chapter II
0 0 0L
Every tree can be concatenated from baiic trees. Example:
Hence, in the above definition we could start with singleton languages |(|
where / e /* is a basic tree. This corresponds to the sequential case: basic
"sequential trees" ire 0 and a, for a € Z.
4.11. Kleet* Theorem For each super-Unitary type, a language is
recognizable ifT it is rational.
Proof. I. Rational implies recognizable. We know already that
recognizable language* are closed under rational operations, see 11.4,7—9. Both |l|
and B are clearly recognizable (compare I J.9). Thus, it suffices to prove that
each singleton language |'| is recognizable. Since / can be concatenated from
basic trees, we can restrict ourselves to these.
The language |z) is recognized by the acceptor
* - (l«|. I<U l«l. 1*1. *).
where 5„ Is nowhere defined (for all ail) and (Jt)A - »
The language |(xo,...,*._ ,)*>„| where a € I. (possibly with n — 0) is
recognized by the acceptor
-<-<G.I«,l,,i. T. I.X).
where
G - Ifo, . 9.1 with q, - »(iff *,-*,:
S, is nowhere defined for all r £ I — \a\;
(<h> ■■■.«.. ,)S. - «., else 6. is not defined;
Tm AulomiU 77
/- |ifc.... x.-,| and(*,)A- q,;
T- |«.|.
II. Recognizable implies rational. Let L c /* be a language recognized by
a (deterministic) ttree acceptor A - (Q, |<5„|, r, I). We shall prove thai L hu
a rational expression in variables Q.
Let
be the run map of the acceptor A - (Q, |S,\. T, Qy. Put
0 - Ift..... «.|.
and Tor each set U c g »nd each./ - 0,.., m, put
£*./-I'£ 0*;(')*>-ft and/£A/*|.
It sufTices to prove that each Ly, is rational language: clearly
L- U £«-/.
*« r
For each tree / € G * w* denote by A, c g the set of all "intermediate"
stales In the computation of t, l.e, states computed from the branches i.i of /
except a - 0 (where <?,/ - ') »nd the leaves [where (a)/ € / w Zy. That is,
'i ~ l(*)p: *-<?,/ for some a £ n'with a * 0 and («)/ £ X— £,|. For
example, for the following tree
the intermediate states are (fl)A and (a,(o)A)a. Given Vc g, >- 0,.... m
and ft - 0,.. , m, put
££,,-!/£ £,,,; fl,does not contain q, qm\.
We are going to prove that l^are rational languages (by Induction on *);
since LH/ - LJ,. this will prove the statement.
(i) * - 0. Since / £ H, implies B, - 0, all trees in LJ, t are basic. Hence,
LJi | Is a finite language.
(ii) For the Inductive step, we shall verify that
M - f*-'. rf'-'!•«■. M-'
78 Chapter II
with
M - «u|«|.
It is obvious that qh t L'yt' (because q, £ W and fl„ - »), hence, we can
form (Li;,'),«. Note that
t-*~l c ^x7' '«(Li7»')** '»^lr~.i'
Tor all M, k, j. Indeed, if q, e M. then q, £ I^lc Li",' and also
ft £ (A/k'i ')**•thu'. for "ch tr« ' <= C* we have
' £ 19.1 -1*1 ««c Li.-.' -.(^V)*" ■<•
If q, t M. then no tree in Li"' has any leaf labelled by q,, thus, / £ Li'}'
implies / £ Lg ■„/ for any language L».
Now, we are going to prove the above formula for Li t. First, let
/£ Li.-,'..(LiV)««../'
for some f £ Li;/. The langugae L, - Li ,' '„(Li7,') does not use the
variable ft, unless fk £ M: thus, L, c AC*. This implies / £ W, Further, for
each tree I £ La, clearly (i)p — q,; since / is obtained from /' by substituting
such trees /" for leaves labelled by q,, it follows that
(Op - (OP - %■
Thus, / £ Ly,. Finally, the intermediate states of / are, except possibly q,, all
the intermediate states of I or the substituting trees (from La)—the latter do
not include q,,..., qm. Hence, B, does not include q,, qm. I.e., / € Lir
Conversely, let
' « Li(.
Denote the "size" of / by
||/| - card|a £ n*; (a)/ is defined!;
we proceed by induction on )/||. If I'll — I, then / is a variable, thus
/ £ li.(c Li-- c Li.-,- •„</£:.')•• •„/£:/.
If |r| — d > I and the proposition holds for trees of a smaller size, choose
a node a € n* — |0| with (a)/ £ I — E, and 9j - q,. (If no such node exists,
then / £ Li")' and there is nothing to prove.) Substituting q, for the branch
S.i in I, we obtain a new tree /:
<«)'"- ««:
(ac)7 it undefined for all c £ n* —10|;
(ft)/'- (6)/ for all 6 £ n* with (6)/ defined and b* ac for any (i"».
Then m>8 implies lk?./|| < 4 and (a)/ £ X — Ji implies |/1 < </: hence, we
can use the inductive hypothesis on both
Ti« Automata 79
i€ Li,! and <?,/ £ Lj, t.
Thui.
u Liv -.(Li.;.-)" .„/£:/ c <«£:.')•■ -,/i:/
and
-v £ Li;.' -.(ti:.')- -.U-V c /£-.' •.(tt:.'),«.
Since clearly
it followi that
«« *-i.v •«k^:.'),« •.(it:.'),«i •.^■7/'
c ti-.'-.(^7.')'"-«^7/'- °
Eurcssrs IM
A. BteogutzaMe laaajsagta. Deacribe the language of the following acccpton.
(I) T- Z, - \a\:A - (|o,r|. fi„ |r|, |a|) where 5„ it given by the following
uble
6. q r
9 r q
far
(Hint: Count the leaves.)
(ii) X- |a. r| with |<j| - 2 and |r| - 0;
A - (|0,1,2, 3|, l-t-. I|. 0,0) where + it the addition modulo4 (i.e., the utual
addition with 4 subtracted if the retult exceeds 3).
(iii) I-U-lo-l;
* - (\p, q, r, s\, 6„ |/>, s|, \q, s\) where the operation it defined at followi:
IP ifa-p;
q ifa,»/>and b- q.
r Ua + p.b+qtndc-r.
s elte.
(Hint: Consider the left-molt leaf.)
B, Noaatetenalabtlc acccpton. Describe the languages of the following
nondeterminittic acceptors.
(i)T-i;-|c7|;
80 Chapter II
* - (I*. <h. ftl. 6.. |a,|, |*|, A)
where (x)k — |a,, a,, a,| and (a, b, c)S„ — a, if a, 6, care pairwise distinct, else
5„ is undefined.
(Hint: For each n - I, 2, 3, ... count the leaves with distance n from the
root.)
(ii) T- t,-\a. r|;
^ - (|0. I. 2. 3|. |fi.. fi,|, K y|. A) where (*)A - 0; 0-H - |0. U
and the operations are defined Tor each a, 6 - 0,1.2,3 as follows:
(a,b)S„- |0.1.2.31; (a,6)6, - |a + 6 + l| ife + 6< 3. else undefined.
(Hint: Consider the root only.)
C. Rarioaal eifusalui. Find the languages described by the following
rational expressions, where r » t, — |o*|.
(i) |js,i|" where t-(x,x)o.
(ii) \y, i\" Tor the same tree /;
(iii) |jt,f|".,|j(,t|" where f-(Jt.j>)<r;
(iv) I*, /)*' •,/' where I and /' are the following trees
D. Kites* Theorcn. The above proof that each recognizable language is
rational gives an algorithm for finding a rational expression which describes the
language of a given acceptor. Use this procedure to find a rational expression
for the languages of Exercise A above.
E. The Htenstoa of the set of variable* la accessary, (i) Recall Remark 11.4 J.
(ii) Put I - I, - |«r|. Consider the language L c |x| * formed by the
following sequence of £trees:
Tree Automata
81
(a) Construct a finite Z-tnt acceptor which recognizes the language L
(b) Express L a« a rational expression
(c) Prove that L cannot be expressed at a rational language using only -,
and •■.
F. A ■oa-reeofalzabk burgage. (I) Put I - t, - |o-|. Prove that the
language ^v c /* of all unirorm trees (Ex. II. I C) it not recognizable (for any let
/•» 0). Hint: Let A - (ft 6, T, I) be an acceptor with L, c LA. Since ft it
finite, there exist distinct trees /„ d £ L. with (/,)p - (/Jp £ 7". Since
(/„ ;,)o- £ L,,, it follows that (/,. h)o £ L,,—but (/,, i,)a t L,
(ii) Verify that
L. - |*| w lu (L -,L) w ((L -,L) .,*•) w ...
Tor the (finite) language L - |(x, x)a\. This gives a reason not to define L "
Tor languages L with x t L.
Notes lo Chspter II
The concept of flmtary lree etitoiiiaton has appeared In the late 19We in the papers of Afbib
•Ml Olve'oa |l9»li Braiaerd |I»W Doner 119701 Eileaberi and Wright |IW7], Meajdor and
Moran 11969). Meiei ami Wright |I9ATL and Tdialchei and Wright 119411 The material presented
m Chapter tt is. In one form or another, to he found In those papers. A detailed, systematic study
of fim'tary tree automata b presented in Ihe OMOOfrapb of Oecseg and Sternby |I9S4|- Tree
automata In a variety of algebras are dhcuned by Eilenbeig and Wright |l9e7) who. however, ab-
aadoa this lenerBHry when dealing whh Kleene Theorem. The reason will be seen in Chapter Vlt
below: the validity of Kleene Theorem In a variety will be shown to be a deep problem. The ani.
venality theorem 11.3.10 is due to J. A. Goguen |I97J|.
Infraltary tree automata have received but link attention, see Anderson. Arbrb and Manei
II97AI The results we have presented on Inflnhary tree automata are new.
Chapter III: ^Automata
III.I. Iitrotocrloa
We shall study a general theory of automata in a category JT. The main three
motivating examples are
(i) sequential ^automata in the category of sets:
(ii) tree ^automata in the category of sets;
(iii) linear ^-automata (i.e., linear discrete-time dynamical systems) in the
category of modules over a ring.
The idea or the investigated generalization, due to M. A. Aibib and C. E.
Manes, is to express the type I of automata under study by a functor
F: JT -* jr. The resulting concepts of ^automaton, behavior, minimal
realization, etc. are simply formulated but they often lead to non-trivial categorical
problems. For example, we know that L-mt automata have minimal
realizations Iff T is a Unitary type (11.3.8). It is interesting to know which functors
have the property that each behavior has a minimal realization.
The theory we present goes far beyond the three motivating examples
above, though not "too far", as we feel and as we hope to persuade the
reader. For example, ^automata in the category of sets are much more
general than the tree automata. Yet, we prove that the minimal realization
problem is solvable essentially only for itree automata with L Unitary and for
their "varieties".
The aim of the present chapter is to explain all of the basic concepts and
problems studied in the subsequent chapters, and to lay category-theoretical
foundations for the rest of the book. In the second section we introduce Pau-
tomata, free ^algebras (playing the role C* does for sequential automata),
behavior, and minimal realization. These concepts are illustrated on the
particularly simple case of a coadjoint functor F. The remaining sections present
some basic facts about algebras, factorization systems and set functors. After
reading the second section, the reader will know what to expect of the
subsequent sections (each of which can be skipped without breaking the continuity
of the text) and also of the following chapters.
We assume that the reader is familiar with the most basic concepts of
category theory, but we discuss in detail all more advanced notions. Categories tte
denoted by script letters Jtf, 2 or by the name of their objects. For exam-
^Automata
83
pie, Sat denotes the category of sets (as objects) and mappings (as mor-
phisms). Pot denotes the category of posets and order-preserving maps, etc.
Objects are denoted by capital letters and morphisms
f.A—B
by case letters; here A is the domain off, and B is the codomain. For a
category Jtr, the class of all objects is denoted by Jtr°, and the class of all morphisms
by JT". The composition of morphisms is written from left to right, i.e., for
two morphisms/: .4-» B and g: B-* C, we have/- g:A-» C The identity
morphism of an object A is denoted by 1, or id. Recall that an isomorphism is
a morphism/: A -» B for which an inverse morphism exists, i.e., a morphism
/-':*-» A with//-1 - l^and/-1-/- I (. A more general concept is that
of a monomorphism (shortly: mono) which Is a morphism f:A-*B such that
in each diagram
-B
Si
if g1 * *•] then g, • f + ft • / And an tpimorphlsm (shortly: epi) is a morphism
f:A-*B such that in each diagram
if h, * A, then/• h, * /■ *,. For example, let /: A -» B and g: B-* A fulfil
/■g— IA. Then /is a mono (called a split mono) and g is an epi (called t split
epi). (Each isomorphism is a split mono as well as a split epi.)
Functors are denoted by letters F.G.H,...; they are also written from left
to right, i.e., a functor F: JT -» *■ assigns to each object A of JT an object AF
of 2, and to each morphism f:A-*Bo(Jt» morphism fF. AF-* BF of X
(preserving the composition of morphisms, and the identity morphisms). For
example, //,: Sat -» Set is the functor with XH, -XxXuidfH, -fxf
[sending (x, y) to ((x\f, (y]f)). The composition of functors F: JT -» 2 and
G:X-*Jt is denoted by F- G- Jt -*JT. For example, X(H, ■ //,) -
{X x X) x {X x X).
Natural transformations are denoted by Greek letters. Given functors
F, G: JT -» St, a natural transformation r: F-» G is a collection of morphisms
TA: AF-* AG in H* (for A in JT°) such that for each morphism /: A -» B in
JT the following square
\
AF =-fcAG
IF IG
■ ■
BF —-—"BC
84
Cluplcr Itl
commutes. (A square is said to commute ir the two passages from the upper
left-hand corner to the lower right-hand one compose as the same morphism.)
A natural isomorphism is a natural transformation r with zA an isomorphism
Tor each A.
For arbitrary objects A and B of a category, the collection or all morphbms
from ,4 to ft denoted by hom(4 B), is a set. A category is small if its
collection of all objects is a set (not a proper class). We list the set-theoretical
conventions we use at the end of this book.
Some or the fundamental concepts or category theory are recalled in the
following exercises. The interested reader can consult one of the following
monographs for further information:
S. Mac Lane: Categories for the Working Mathematician, Springer-Verlag,
Berlin-Heidelberg-New York 1971.
H. Herrlich and C. E. Strecker: Category Theory, 2- Ed., Heldermann
Verlag. Berlin 1979.
J. Adamek: Theory of Mathematical Structures. Reidel Publ. Comp.,
Dordrecht—Boston—Lancaster 1983.
Eaerdaa lll.l
A. CUainatkM of taacton. Recall that a functor F: JT -» X is said to be (a)
faithful if for any two objects A, B of JT, the map (/-. A -»*) ►»
(fF: AF-* BF) is one-to-one; (b) an embedding if F is one-to-one on the class
of all morphisms of JT; (c) full if each morphism g: AF-* BF in if has the
form g- fF for some/: A -» * in JT; and (d) an Isomorphism ofcategories if it
is bijective.
(a) Verify that the "forgetful functor" U: Poa -» Set [which forgets the
ordering, (Xs)f- XF\ is faithful, but neither an embedding, nor full.
(b) Let Lat denote the category of lattices and lattice homomorphisms.
Verify that the "inclusion functor" /: Lat -» Pot (with At - A and fl — f) is an
embedding which is not full.
(c) Verify that the functor F: Sot -» Poa assigning to each set X the
discretely ordered poset (X, —) is a full embedding.
(d) Prove that F: Jtf -» X is an isomorphism of categories iff there is a
functor F->:2 — JT with F- F~' - I, and F-> • F- I,.
B. Compoalat ntaral tranfonurioa*. (a) For natural transformations
r: f-»Cand a: C-» //(where F, G, H: X-+2 are functors), the
composition r- a: F-+ His the natural transformation with (r- o)A — Ia"* For
example, let p://]-» //) (where H, is the cartesian-square functor above) be
defined by pA(x,y) - (y, x). Verify that p-p - I h,, where \r: F-* Fdenotes
the identity transformation.
^Automata 85
(b) Verify that a natural transformation r: F-* Git a natural isomorphism
iff there is a natural transformation r~' with r< r~' - lf and r~' • r- lc.
(c) Let r: f-» C be a natural transformation (F, C:jr-»y). and let
H:!t-*Jt be a functor. Then tH: FH-* GH denotes the natural
transformation with (tH)a - tha. Verify that pH,: H,- H,-* H,- H, is given by the maps
«x„ x,). O,. *)) - ((*. ^x,. x,)).
(d) Let r: F-* G be a natural transformation (F, C:JT -»i»). and let
H: 3t -» JT be a functor. Then Wr: HF-* HG denotes the natural
transformation with (Ht)a - taH. Verify that Hrf>: //, • H, -* H,- H, is given by the
m»P» ((*» *i). (fl. yd) — ((*b *i X*. *))•
(e) A natural transformation r: f-» G is called an tpttnntformaikm if all r,,
are epis: prove that then r-<r- T'<r° implies a- a1. Analogously, for
a monoiranjformailon r(all r,, are monos), <r< r — <r° • rimplies a — <r\
C. Proaocts and cop rodaeta. Recall that a product of objects /4,(i £ /) of a
category is an object X\a, together with morphisnu (called projections)
I c /
*/: II A, -» A/ (/ £ /) having the following universal property: given an object
B and morphisms /}:B-»A,(f€ J), there exists a unique morphism
f:B-* II A, with f„- f.jt, for ally £ J. Then y; are the components of/ A
product of two objects is also denoted by A, x A,,
(a) Verify that in the category Sot, products are the usual cartesian
products, II A, - |(a,),, ,; a, £ A, for each j £ /), and [(a,),.,)», - o>
i ■ '
(b) Verify that in the category Po», products are the usual cartesian
products ordered coordinate-wise.
(c) The concept of coproduei is the dual concept of product (as the prefix
"co-" Indicates), I.e., the direction of all arrows in the above definition is
reversed : a coproduct of objects A,(l e /) is an object LI/4, together with
morphisms (called injections) «,'./*,-* ]_M/(y £ /) with the universal property.
A coproduct of two objects is also denoted by A, + A,.
Verify that in Sat, the coproduct of seta A,(l £ /) is their disjoint union
11/4,- UA,x\l\ with e,:A,— U A, x |f| given by (x)e> - (x, j) for
X £ A).
(d) Verify that in Poa, the coproduct of posets (-4,, £), i £ /, is their
disjoint union ordered in such a way that (x,y) 5 (x°, /) iffy — /, and x £ x' in
A,.
(e) Let A-Mot) denote the category of modules over a given commutative
ring R, and module homomorphisms. Verify that for two modules A, and A,,
86 Chapler III
A\ X A\ ™ A\ + A\
is the cartesian product with coordinate-wise operations. Here the projections
are (x, y)tt, — x and (x, y)x, — y. The injections are (x)e, — (x, 0) and
(y)e, - (0, y).
(0 Let // '■ Aj -» A/ be morphisms (J e J). Veriry that there exists a unique
morphism, denoted by II /, from II A, to IIB, the components of which are
j^'/for the projections it,: Wa,-* A,(i £ J).
i* J
(g) Dually, LI/J'LI^/-* 11*/ denotes the morphism the components of
which are determined by/— formulate properlyl
(h) A coproduct of functors F,: Jtr -» X (I e I) is the functor II F,: Jtr -» X
ii'
given by A( IIF,) - ]1aF, and J{ IIF,) - II JF„ provided that X has copro-
H I I '. I HI it I
ducts. Verify that coproduct injections (bi)a:AFi-» WaF, form a natural
transformation c/. Ft-» \1f,(J e /) with the expected universal property;
For each functor G: Jtf -»X and arbitary natural transformations
r/. F,-» G(J £ /) there is a unique natural transformation r: II F,-» G with
x,- e,-t(j€ 1).
Analogously, the product IIF, of functors is defined "coordinatewise".
111
D. Eqaallzen ami coeqaallzera. Recall that an equalizer of two morphisms/„
f,: A-» Bis a morphism e: £-» A, universal with respect to e-f, — e- f,, i.e.,
any morphism h: H-* A with A-/| - hj, has the form A — A'- r for a
unique A': H-* £.
(a) Verify that in Sat, the equalizer off,,/,: A -» Bit the inclusion map of
the subset E - \a e A: (a\f, - (oV,|.
(b) The dual concept, the coequaiuer of f„ /,: A-* B is a morphism
e: B-*C universal with respect to /, ■ c — f, ■ c Verify that in Sat, the coe-
qualizer is the canonical map c: B-» B/~ of the least equivalence ~ on the
set * with (a)f, ~ (aM for each a € A.
(c) Verify that if a morphism e: £-» A is an equalizer of a pair of
morphisms, then e is a mono. Such morphisms are called regular monos. Prove the
following hierarchy of morphisms:
isomorphism * split mono ^ regular mono ^ mono.
Verify that in Poa, none of these implications can be reversed. Hint: If
e ■ g — I then e is the equalizer of g • e and I.
(d) Verify that in Sat, monos are exactly the one-to-one maps, and they are
all regular. Split monos are exactly the monos with non-empty domain.
^Automata
87
(e) Dually, regular epis are the coequalizers. Formulate and prove the
appropriate hierarchy oCepis. Verity that in Set, epis are exactly the onto maps,
and they are all split epis. In Poa, find a non-regular epi, and a regular epi
that does not split; find a bijective morphism which is not an isomorphism,
and observe that it is both a mono, and an epi.
E. UnrH tmt collnlts. By a diagram D in a category Jtr is meant a scheme,
i.e., a small category 9, together with a functor D:3-»Jtr. A collection of
morphisms ft:A-»dD (d £ 9°) in JT is compatible if each 9-morphiim
6: d-* d~ fulfils St- ff SD. A limit of D is an object L - lim D together
with compatible morphisms *t: L-+ dD (d t »•) universal with respect to
compatibility. That is, for each compatible collection fs-A-* dD there exists
a unique morphism f:A-*Lwith ft -/■ nt(d c 9°). The morphisms ft are
called components of f.
(a) Verify that equalizer is a special case of limit: here 9 is the scheme
consisting of two objects, two parallel morphisms and (necessarily) two identity
morphisms of the given objects.
(b) For discrete categories S, i.e., categories which do not have any
morphism except the identity morphisms, verify that limits are just products.
(c) Verify that the limit of the empty diagram (3 has no object) is the
terminal object 7", i.e., an object such that each object A has exactly one morphism
from A to T. Verify that |0) is terminal in Set, Poa. and R-Mod.
(d) A pullback of morphisms f:A-+ Aandg: C-» £is the name of the limit
of the corresponding diagram (the scheme of which is just the co-span). Verify
that a pullback is a commuting square
T
I * C
« g
a ——- e
such that for any commuting square g, ■ / — /, • g there is a unique morphism /
with g, - /•! and f, - t-f. Verify that a pullback of/and g in Set is
L - |(a, c) € A x C: (a)f- (c)g\. and /and § are the projections.
(e) The concept of colimil of D is dual to that of limit: it is an object
C— cofim/> together with a universal compatible collection tt:dD-*C
(d £ 9"). Example: Coequalizer is the colimit of a parallel pair of
morphisms; coproduct is the colimit of a discrete diagram.
A pushout of morphisms f: A-* B and g: A -» D is the colimit of the
obvious diagram. Verify that it is a universal commuting square
gg Ch«pler III
A »■ B
9 9
D =-*■ C
(0 The colimit or the empty diagram is the initial object J., i.e., an object
such that each object A has exactly one morphism from X to A. Verify that 0
is the initial object or Set and Poa. Find the initial object of Jt-Mod.
(g) A category Jtr is said to be complete if each diagram has a limit A well-
known criterion of completeness: Jtr is complete iff JT has products and
equalizers. The dual concept is cocomplete. Verify that Set is a complete and
cocomplete category.
F. Chain col laird. Each poset (X, £ ) is considered as a small category:
objects are the elements or K, and for Jr, y e A" there is either a unique morphism
x-» y, if x £ y, or no morphism. If x £ y. In particular, each ordinal a is
a small category (the well-ordered poset or all ordinals smaller than a). An
a-ckain in a category JT is a diagram D with the scheme a, i.e., a collection of
objects />,(/ < a) and morphisms />„: D,-» D,{i £ j < a) such that DM — I
and DV' D>» — DA. A category is said to be chain-cocompleie if each chain has
a colimit; this includes the initial object (- colimit of the 0-chain).
Verify that each a-chain D:a-*Jt has the same colimit as the diagram
D,: (X, £) -» JT which is the restriction of D to a cofinal set X c a (i.e., for
each i e a there isy e A" with i £ j). In particular, the colimit of an a-chain is
not changed by leaving out the "start", i.e., all objects D, with i £ % (for some
I, < a).
G. Sibcategary of a category JT is a category 3 with se°s.Jt° and
St" = JT", and with the same composition and unit morphisms as JT. A
subcategory St of JT is /u« iff each JT-morphism f:A-»B with 4 fl € if is an
7-morphism.
Verify that Lat is a non-full subcategory of the category Poa. On the other
hand, Poa is a full subcategory of the category of graphs (— binary relations)
and compatible maps.
\\\X Aatoaiata la a Category
2.1. A sequential ^-automaton (I.I.I) can be depicted by the following
diagram in the category
Set
£Aut«iuu 89
or sets and maps:
1
\
o.i—5_» o —l—*r
Here Q is the set or states, I is the input alphabet, T is the output alphabet
and / - |0| is a singleton set with (0)A € Q the initial state.
Let us define a functor
F: Sat -» Sat
as follows:
XF- Xx I for each set X;
fF - fx 11 for each map /
Then a sequential automaton is a diagram of the following kind:
<•)
OF—$-_ o J— r
Analogously we can represent L-lrce automata. Assume, for simplicity, that
I has just one binary operation. Then a £tree automaton (II.1.2) is a diagram
as follows:
x
oo——«■ o —*-»r
Here, / will be an arbitrary set (of variables). Let us define a functor
F: Sat -» Sat
by
XF- Xx X for each set X;
fF-fxf for each map /
Then a Lxnt automaton is a diagram (<) again.
It is sometimes important to study sequential (or tree) automata with an ad-
90
Chapter III
ditional structure on the sets Q, I and F and with the maps S and y
preserving the structure. For example, Q, I and T are modules and the maps S and y
are linear. Then we get a diagram (<) again, but not in the category Set. These
considerations have led to the following concept
Deflaltloa. Let JT be a category and let F: jr -» jr be a functor. An F-auio-
maton in the category JT is a sintuple
A - (Q. S. r, y, /, A)
consisting of objects of JT
Q (state object):
r (output object):
/ (initialization object)
and morphisms of *
6: QF-» Q (next-state morphism);
y: Q-» r (output morphism):
X: /-» Q (initialization morphism).
Reaurk. We shall often work with less complex concepts: pairs (fl 6) with
6: QF-- Q are called F-algtbras: quadruples (Q, 8. F, y) with (Q, S) an F-il-
gebra and y: Q-* F are called non-initial F-automata.
12. Let us introduce the concept of a morphism. Given two ^algebras
(Q, S) and (Q\ 6'), an F-homomorphism
/•(0.«)-(0'.«)
is a morphism f:Q-*Q' such that the following square
OF !L-»- 0
IF I
CfF -<3
commutes.
Given two f-automata with joint output and initialization objects:
A - (Q, S. r, y, /, A) and A' - «?'. 6~. T, y\ /, A)
a morphism of F-automata
f:A—A-
£Aulonau
91
is a homomorphism /: (ft 5)-» (C, A") with A • /- A' and f.f-y. I.e.,
a morphism for which the following diagram
commutes. If/is an isomorphism (in JT), we say that A and A' are isomorphic
automata. It is easy to check that
(a) given a homomorphism /: (ft S) -»(ft, 6"), such that / is an
isomorphism in JT, then/-': (Q\ o") -»(ft S) is a homomorphism;
(b) the composition of two homomorphisms is a homomorphism, too.
Analogous statements hold Tor morphtsms or ^automata. A more general
concept or morphism (corresponding to 1.1.7) is used in Chapter VI.
13. Exasiple; Seqaeatial £-a*toaita. Assuming that JT has finite products,
we define a functor
St: jr-» jr
(where I it an object of .JT) as follows:
XSi — X x I for each object X:
/S,-/x I,
for each morphism /
Then Sx-automata are called the stqutnttal L-miomata in jr.
(i) JT - S*t Here, sequential .^automata are precisely the concept studied
in Chapter I, except that the initial state is generalized. We have (as in the
case of tree automata, 11.1.2) a set / of variables and an initialization
A: /- ft
If / - |0| is a singleton set, then the morphitms introduced here coincide
with ihote of Chapter I (for theme of a fixed f, see 1.1.7). Indeed, the
condition
A' - A • /
states that / preserves the initial state (0)A.
(ii) jr - Jt-Mod, the category of A-modulet and linear maps (for a fixed
commutative ring R). In case
/-|0|
is the trivial module, a sequential ^automaton consists of
92
Clupler III
a module Q (or states);
a module l~ (of outputs):
a linear (ne«t-step) map S:Qx L-» Q:
a linear (output) map y: Q-* H
These are precisely the linear sequential I-culomala, also called linear,
discrete-time dynamical systems.
Since in Jt-Mod products and coproducts of pairs of objects coincide (see
Exercise III.I.C), the map 6: Q + I-* Q is expressed by • pair of Kneir
maps
S,:I—Qu\<16,.Q—Q
with (q, o)B — (q)6, + (0)6, for each q e Q, a e L. Here 6, represents the
"reaction to time": in each time unit the state is changed from q to (q)S, if no
input (i.e., input 0) arrives; and 6, is the "reaction to input". The addition of
both reactions is the resulting change of stale in one time unit.
Given two linear sequential ^automata
A - (ft «,. 4. r, y) and A' - (Q\ 6\, «, T, y),
a morphism
f-.A — A1
is a linear map/: Q-* Q such that for each q e Q and a e Z.
(a)(.r)6W-(o-)S',;
(b)(q)S,-f-(q\f-Si;
(c) (q)r - (q\f- f-
Thus, / preserves the reaction to inputs and time, as well as the outputs.
(Hi) JT — Poa, the category of posets (i.e., partially ordered sets) and order-
preserving maps. The product of two posets (X, S) and (Y, £) it the set
X x Y ordered coordinate-wise: (x,y) S (*',/) iff both iSi' and y S y.
Thus, a sequential ^automaton in Poa is just a sequential ^automaton in
Sot, with an additional order on each of the sets Q,L,T and / such that 6, y
and A are order-preserving. (For 6 this means that q S 9' and JSa' imply
(<7. it)<5 S (9', a')&| If we think of S as a "preference" relation, then these
conditions mean that (i) if a state q' is preferred to a state q, then after one
step the same relation will hold: (q. 0)8 S (q\ 0)8 for each a e I\ (n) if an
input o-* is preferred to an input <r, then the corresponding changes of state
are in the same relation: (9, o)S£ (<7. <x")o" for each q e Q; (iii) the
preference is shown by the outputs: q£ q' implies (q)y S (fOr; (iv) preference of
variables is preserved by the initialization :iSi' implies (jrH £ (x>L
2v4, The role played by the free monoid of words T'for sequential
automata (and by the free £algebra /'of L-lrm for tree automata) is played by the
free ^algebras for F-automata:
£AutomM«
93
DafteMoa. Let F: Of -» jr be • functor. An object / of jr is said to generate
a free F-algebroU', e>) if there exists a morphism n: /-» /• (called the
injection of generators) with the following universal property:
a
for each F-ilgebri (Q, 5) and each morphism /: /-» Q there exists a unique
homomorphism/*:(/*, *>)->(&£) with/- ij-/*.
If each object of JT generates a free algebra, then F is called a varielor (or
input process in the terminology of M. A. Arbib and E. G. Manes). Equiva-
lentty, F Is a varietor tfT the forgetful functor of the category of ^algebras is
an adjoint (see Exercice. HUB below).
Eiaaaple, The functor
Sx:Sat->Sat
is a varietor. Here
/• - /x T*
and
a>:(/x Z*) x T-»/x Im
is defined by
(t c... a., a)p - (i, it, ... (T.(T)
for each i e /, it, ... it. € T* and a e L Funher,
(i)n - (t 0) for each i £ /.
Indeed, for each Si-algebra (Q, 6) and each map /: /-» Q, the unique
homomorphism/*: (/*, *>) -» (ft S) with/- ij ■ /* is defined as follows:
U W - (')" • /' - Wl
(t a\f - (t •, <r)*> . /• - ((I)/; <r)6i
U otoW - (i, it,, <*)*>•/•- {(i, a,\fm. o\>6:
etc.
See I.I.3.
The following Chapter IV is devoted to an explicit construction of the free
algebra /*, to a characterization of varietors and to related problems.
Rasnrk. Free algebras are determined uniquely up to an isomorphism:
94
Chapter III
(i) For etch isomorphism of Falgebras
A:(.'. *>)-(&, 4).
the algebra (&, 6,) is • free F-ilgebrt generated by / with the injection
n-A:/-0.
Proof. Given an F-ilgebra (Q, S) and • morphism /: /-» Q, there exists
• unique homomorphism /':(!',<p)-* (Q,6) with /—»•/*. Then
A"'•/*:(&,4)-»(&5) is the unique homomorphism with
/-(.j. A). (A-'•/•). D
(ii) If (/*, p) and (/,*, *>,) are both free F-algebras generated by /, then
there exists a unique isomorphism A :(/*,«>) -»(/,*, «»i) with n- A — n,.
Proof. Since (/*, p) is free, the morphism n,: /-» /,* can be extended to
a homomorphism A :(/*,«>) -»(/,*, p,) with n • A - n,. To prove that A it an
isomorphism, we use the fact that (/,*, t>i) is free and hence, n: /-» /* can be
extended to a homomorphism k: (/,*. *»>)-» (/*. p) with n, ■ k- n. Then
A • k - l,« because A ■ k: (/*, p) -»(/*, p) is a homomorphisra extending n
(since n-A-A—n,-A— n) and also !;• is such a homomorphism—but the
extension of any morphism is unique. Analogously, k • A — I ,,•.
We should actually speak about a free F-algebra generated by /. We shall,
nevertheless, disregard the non-uniqueness of free algebras because this leads
to no confusion. For example, let / be a singleton set, then free Sr-algebra /*
is either (I', p) as in 1.1.6, or (/ x I', p) as above.
If /- i. is the initial object (Exercise III.IE), then the free algebra
(i. •, e>) is the Initial F-algebru, i.e., for each F-algebra (ft 5) (here exists a
unique homomorphism from (!.*,*>) to (ft 6°) (extending (he unique
morphism i- -» ft).
Eusaple. The functor
Si \ a .Mod —* a .Mod
is a varietor for each module L.
Let us first describe the initial algebra (i.e., the free algebra generated by
the trivial module 0). This is the module
0- - IM
of all polynomials (i)o — a, + a,z + ... + ov' in indeterminate z and with
coefficients a„.... a. in I (the addition and scalar multiplication are defined
coordinate-wise). The injection n:0-» £[j\ it defined by (0)n — 0 and the
operation by
((r)a, o-)*> - " + (i)o • * - " + <V + "i*' + ■ ■ ■ + V*'.
To verify this, we are to show that for each Si-algebra (ft, S) there is
a unique homomorphism
£Automm 95
A:(r|rJ.«>)-(e.«)-
Put
(a, + <r,z+ ... +iV)A - (etffc + (c,)4 • 6, + ... + «r.)S, • «,".
Then A 1* • homomorphism, i.e., p • A — (A x lx) ■ 6, because for each
(r)a e r(z| and each a € T we have
((r)o, c)*> ■ A - (it + (r)a ■ r)A
- (0)6. + (oi)4 • 6, + ... + (».)£ • 6," '
-«T)S, + HaJ6. + ...(o.)S,-6,-\6,
- (a)S, + |((r)a)A|5,
- ((r)o, »X* x lx) • S.
And A is unique because p • A — (A x lj) • <5 implies that
(oi)A - (0, <*)? • A - (0, Oi)5 - ((*)£.
(<H + c,r)A - (it„(h)*> ■ A - ((o-,)A, Oi)5 - (?,)% • 6, + (e*)*,
etc. Therefore, A is necessarily defined by the rule above.
More in general. Tor each module / we have
/• - l\z\ x I[z\
with ij: /-. I[z] x r|z| defined by (f)ij - (t 0) and
p:l[z\xl[z]x T-/[r| x l[z\
defined by ((z)6, (z)a, a)p - ((z)a, a + (z)o - z). For each Sr-algebra (ft S)
and each linear map /: /-» ft the unique extension to a homomorphism
/•: /[z| x IU|-» 0 '• defined by
■
(<, + *,*+ ...+ ti". a, + <r,z+ ... + of)f - Z VLW+ (».)«.)«,'.
13. The concept of behavior studied in Chapters I and II is generalized as
follows.
DtftaMoa, Let F: jr -»jr be a varietor. For each ^automaton A -
(ft S. r, r. I. A) we denote by
p:(/\ «>)-(ft 6)
the unique homomorphism extending X (i.e., with X — n • p). We call p the
nm map of ,4 and
P-PY-f^r
the btharior of -4.
96 duplet III
Exaatle: £4r*t aartoaiata. Let first I be a type consisting of a single
operation of arity n (where n is a cardinal). Define a functor
W.: Sot-Sat
by forming the n-fold canesian products: for each set X,
XH.- X'-,
for each map /: X-* Y,
where (JCil/1" — ((*ilf)- Then //.-algebras are precisely algebras of type Z.
i.e., pairs (ft S), where 5: Q' -» Q is an n-ary operation. //,-homomorphisms
are also precisely £homomorphisnu.
Now, let I be an arbitrary type. We denote by
Wi:6«t-S*t
the coproduct of functors Hm a € I (where |<r| denotes the arity of it):
Hi — 11 H^
Thus, for each set X we have
XHt- LI X'
and analogously with the maps/Wj. An //i-algebra consists of a set Q and
a map
6: LIO'-O
or, equivalently, a collection of maps (the components of 6),
S.:Q--Q(<T€ i|<r|- «).
This is precisely an algebra of type L. //j-homomorphisms /: (Q, S) -»(C, A")
are also just the usual homomorphisms because
Sf-fHfS ifT S„- f-f"- 6", for each it EX
The functors Ht are varieton: for each set / the free //j-algebra generated
by / is the algebra (/*, *>) of finite-path £trees over /, see II.3.6.
ttree automata are precisely the //i-automata. The run map p: /* -» Q
and the behavior />: /* -» /"have the same meaning as in IIJ.7.
Ressark. More generally, for each category JT with products we define
a functor
FAutmiuu 97
//.-.jr-»jr
on objects X by
XH, - X"
(the it-fold product o( X) and on raorphisms/: X-» Y by
///. - f>: *' -. J",
where/1" denotes the morphism all components or which are equal to/
If jr has also coproducts, then Tor each type I we denne
//,: JT -» JT
by
0(1
2&. Propodrtoa. Let F be a varietor and let
f:A-*A'
be a morphism of automata. The run maps p(of ,4) and p' (at A') fulfil
P/- P-
Proof. The run map p' is the unique homomorphism p' : (/*, «>) -» (Q\ o~)
with ij- p' - A'. Since both p: (/•, *>) — «J fi) and /: (ft S) -» (Q , A") are
homomorphisms, p-/: (/*, «>) -» (ft, 6') is also a homomorphism. We have
>J-(p-/)-A-/=A-.
Therefore, p-/-p'. D
Corollary. Any two ^automata connected by a morphism have the same
behavior.
In fact, for each morphism f:A-»A' we have p-/— p' and hence,
P- p-r- p-f-y' - P'Y -/*'•
2.7. Another concept we want to generalize is reachability. We shall use
image factorizations of morphisms. We begin with two examples.
Ensiles, (i) JT - S*t Each map/: *-» Ycan be factorized as/- e- m
with
e: X-» T epi (— onto)
and
m: 7"-» Y mono (— one-to-one).
96
Ctup4er 111
For example, let T - X/ ~ be the quotient set of X under the kernel
equivalence ~ of f\x ~ x' iff (x)f- tx")fl Let e: *-» Tbt the quotient map,
assigning to each x e X its equivalence class |jr| € 7"; e is clearly onto. Let
m: 7"-» Kbe the map defined by QxDm - (x)ftm each [jr] e 7": m Is dearly
well-defined and one-to-one. We have (x\f- Q*J)m - (x)t- m, and thus,
/- *• m.
This factorization is essentially unique: if/— *' • m' with e': X-* T onto
and m': 7" -» K one-to-one, then the kernel equivalences of/and of e
coincide (because m' is one-to-one) and we have a unique isomorphism i: 7"-» T
such that the following diagram
T
/ I \
\
commutes: Put Q*D < - (*)*' for each |x| £ T.
(ii) JT - Pes. There are two important ways of factorization of a morphiim
/:«S)-.(i;s):
(a) Epis and embedding?. Let 7°- X/~ be as above. Define an ordering
3 • on 7"by
|jc,|3«|*J iff (|*iD»» * d*J) «"•
Then m: (7". 3 *,)-» (K, 3) is an embedding [i.e., an isomorphism of (7°, 3 *)
onto a subposet of (Y, 1)]. And e:{K S)-»(7| 3•) it an order-preserving
map onto, in other words, an epi.
(b) Quotient maps and monos. Define another ordering of 7°by
[jc,1S«Ui1 iff Jt, S Jfj
for some X, ~ x, and *, ~ Xj. Then e:(X, S)-*(T, £•) is a quotient map
(i.e., an order-preserving onto map such that the order of the range is induced
by the order of the domain). And m:(T, £ ") -»(Y, 3) is a one-to-one order-
preserving map, i.e., a mono.
The example of Poa suggests that in order to investigate image
factorizations in a general category, we must specify axiomalically what factorizations
are considered.
DcfteMw. A factorization system in a category .Jt consists of a class * of
epis and a class UT of monos such that
(i) each morphism/: X-» Kcan be factorized as/- e- m with e: X-» Tin
t and m: 7"-» Y in Jl;
£Aulon»M
99
(ii) this factorization is essentially unique: if/- t'■ m' with e' c t and
m € ur, then there exists an iiomorphism Much that the following diagram
\
commutes;
(iii) both t and j* are closed under composition and contain all
isomorphisms.
Remark*, (i) Since factorization systems are fundamental in a number of
considerations throughout the present book, we devote section III.S below to
their properties.
(ii) We call JT an (I, Jt)-caiegory if a factorization system (/, ur) is
specified in jr. Thus, Poa is an
(epi, embedding)-category
(quotient, mono)-category,
according to which factorizations are considered.
(iii) We often work with functors F: jr -» JT preserving i-tpis, i.e. such that
for each e: X-» Kin /, the morphism eF: XF-» YFia in I, too.
LesniM. Each factorization system (/, UT) has the following diagonal fill-in
properly: for each commuting square
with ie( and m e Jl there exists a morphism d: 7"-» S such that the
following diagram
100
Chapter Itt
Proof. Let q- q,- qmbe the image ractorization of q. and p - p,. pm that of
p. The following diagram
T
V
T
y
V T
A
p.\ /
S
commutes. Since t • q, e t and qm e ur, as well as p, e # and p. • m e ur,
there is an isomorphism i: f -» 5 with
ft- '•<!,• I and qm-i-pm-m.
Put
<<- q,-i-p.:T—S.
Then
«• J — f * 4, • '• P. — P, * A- ~ f
and
d- m — g,• »-p«, • w» ™ q,' q* ~ q.
This concludes the proof. D
2JL The reachability of sequential automata (1.2.3) can be generalized as
follows.
Dcfliltloa. Let F be a varietor on an (<r, ur>-categorj jr. An ^automaton is
said to be reachable if its run morphism is an f-epi.
Eaaaplet. (i) Linear ^automata. Let Of - A-Mod with t - all onto
morphisms and .•# — all one-to-one morphisms. This is a (unique, as we prove
below) factorization system in Jt-Mod, since for each linear map /: X-» Y we
have a well-known image factorization
X— X/kaf- Y.
Let A - (Q, 4. S,< /". Y) be a linear automaton. The run map
assigns to each input sequence a,o,... <r„ represented by the polynomial
(z)a - o\ + o~tz+ ... + ey", the state
£Automau
101
(a)p e Q
at which the automaton stops when receiving the given inputs in the initial
state 0.
A linear ^automaton is reachable iff each or its states can be reached from
the stale 0 by a sequence of input symbols.
(ii) Ordered ^automata. For each poset I the functor
Sx: Poe-»Po»
is a varietor: given a poset /, then
I'./kP
where / x I' is ordered coordinate-wise, i.e., (t a, ... a.) £ (J, r,... r.) iff
i S yin /, n - m, and a, S r, in L for / - I a Let / be a singleton poset.
Then Si-automata are just sequential ^-automata with an order on Q and T
such that both 6 and y are order-preserving maps.
Considering Poa as the (epi, embedding>-category, an ordered ^automaton
is reachable iff for each state q e Q there exists a word a,... a. e I' with
q — (c,... o\)p. Thus, reachability is precisely the original concept,
independent of the order.
For the (quotient, mono)-category Pot, an ordered ^-automaton is
reachable ifT for arbitrary two states q. q' e Q with q £ q' there exist words
c,... it. and r,... r.in X*such that a,... a, Z r,... r, and q — (a,... it.)A
17'- (r,... r.)p. For example, if T is discretely ordered (i.e., (TS riff it- r),
then each reachable T-automaton has discretely ordered state set.
Rcasark. By a lubaulomalwi o( m ^automaton A we understand an
^automaton A, together with a morphism m: A, -» A in .41. Two such morphisms
m\At-+A and nt:A'9-+A
are said to represent the same subautomaton if there exists an isomorphism
j: A,-fAi such that; • m - m. (Compare with III.5.2.)
Profochloa. Let.» be an (t, -#)-category and let F be a varietor preserving
/-epia. i.e., e € / implies eF € /. Then each ^automaton hu a unique
reachable subautomaton.
Proof. Let
A - (ft 8, r. y, l A)
be an ^automaton. Its run morphism p: I* -» ft has an image factorization
p - e • m with
e^' — Qmt;
m: Q-»Q in .41.
102
Chapter III
Since «> • p — pF- S and since tF e *, we can use the diagonal Till-in
property:
Then A" is a morphiim such that
*:(/*. «>)-(fi fiand m:(ft, A")-.(ft 6)
are homomorphisms.
Put
A, - (ft, S, r. m ■ r. /. 17 • *).
,4, is an ^automaton. Since * is a homomorphiim, it is clearly the run mor-
phism or Aa. Thus. At is reachable. Since m is a homomorphism, it is a
morphiim or automata
Finally, let m': A', -» A be another reachable subautomaton of A. The run
map p': /* -» ft of A'% is an #-epi with
p' ■ m - p,
by Proposition II 1.2.6. Since pet and m' e ur this is an image
factorization of p and therefore, there is an isomorphism 1: Q-» Q' with
* • 1 — p' and m — i ■ m'.
The following diagram
!•
cF
Of
IF
-♦0.
ar-
-► or
commutes: Since eF is epi, we conclude 8- t — iF- 8' from the following
£Automu
103
tF-(S- .)-•>• *• I- 9. p- - p'F- t - *F' (IF. P).
Thus, i:A.-*A„u a morphuro. Thu proves the unicrty. □
2.9. DsflaMea. Let JT be an (*, ~*>cate|ory and let F: JT -» JT be a varietor.
For each behavior, i.e., a morphlsm
fl-.l' — r (I, r e JT*)
the minimal realization is a reachable ^automaton A, which realizes fi (i.e., its
behavior is fi) and has the following universal property:
Tor each reachable realization A of fi there ezists a morphism
e: A-* Acw\lh (Ef,
Remark. For ttree automata, minimal realizations exist iff Z is finitary
(II.3.6). We devote Chapter V to the general problem which varietors have the
property that each behavior has a minimal realization.
Profosllloa. Minimal realization is unique up to an isomorphism:
(i) l( A, is a minimal realization of fi, then each /^automaton isomorphic to
A, is also a minimal realization,
(ii) Any two minimal realizations of fi are isomorphic
Proof. Let A, and A, be minimal realizations of fi. There exist /-morphism*
e: A,-* A,*n<ii: A,-* A,. Let us check that i- «■-'. Denote by p,: I' -» ft,
and p,: /• -» ft the run moronisms of A, and A,, respectively. Then
p, - p, • e and p, - p, • *
by Proposition 111.2.6. Since A is an epi and p, • (i • e) - p, • e - p» we con-
dude that i■ e- I; analogously e■ i- I.
Conversely, \cli:A,-*A,btm isomorphism of automata. Then A, is a
realization of A* (III-2.6) and its run map is p, • I e t. Given another reachable
realization A of fi, there exists a morphism f.A-* A, with « e *\ Then
t • i: A -» A, is a morphism with «• i e *\ This proves the minimality of A,.
D
1.1*. Aajolat fMcton. The above concepts are much simplified if the
functor F has an adjoint. We recall briefly some of the basic facts concerning
adjoint functors, but a reader not familiar with this theory can skip the rest of
section 111.2, not breaking the continuity of the text.
A functor F: JT -» 2 is said to hare an adjoint functor G: 2 -» JT If there is
a natural transformation n: l.,-» F-G such that each jr-morhpism
/: K-»£G(with Ke JTand L e 2°) has the form/- ih-/*G Tor a unique
f: KF-+ L in 2m. Equivalent condition: There is a natural transformation
c:GF-*\, such that each 2-morphism g:KF--L has the form
g - g*F- cL for a unique g.: K-» LG. The functor F is then called a eoad-
104
OllpUTlll
joint of C (or left adjoint) since this is the dual concept or adjoint (also called
right adjoint).
Exaaates. (i) For each set £ the functor St: Set-* S«t has an adjoint
hom(£ —): Sat -» Sat assigning to each set X the set hom(£ AT) of all maps
from Z to X. and to each map f:X-» Y the map sending p:Z-»X to
p • f: Z-* Y. Here n»: X-* hom(£ Z x X) assigns to each x e X the map
<t— (a, x) in hom(£ Z x X).
(ii) Let It be a subcategory of jr. The inclusion functor G: 3 -» JT k
adjoint iff 3\\ a refledne subcaiegory, i.e., for each JT-object X there is an
3-object X*(the reflection of X in 3) and a JT-morphism r,;K-»K* universal in
the following sense: for each JT-morphism /: X -» L e 3 there is a unique 3-
morphism /*: X*-» L with /- r,-f*. The functor F:J(-*3 given by
KF- X*. and /F- (r, •/)• for all /: X-» X', is the corresponding coad-
joint.
Caaajeuti aai colkaM*. Each coadjolnt F:Jt-*3 preserves colimits. That
is, given a diagram D-.9-* JT with s colimit dB-3. C (tee Eiercise III.IE),
then the diagram D • F: 9-» 3 has a colimit (dD)F^ CF. By Freyd't Adjoint
Functor Theorem, conversely, a functor F:Jt-*3 preserving colimits a
a coadjoint whenever JT is cocomplete, and each 3-object L has (small)
solution tet, i.e., a set of morphisms t,: K,F-» L (i e /) such that any moronism
f: KF-* L factors u|-|.F e, for some g »: X, -» L, j e /.
Dually, an adjoint preserves limits, and the converse holds if solution sets
and limits exist.
2.11. AajeJat aateanta. Let F: JT -» 3 have an adjoint. We then speak about
adjoint automata in JT. Their properties strongly resemble those of sequential
automata in Set. (We prove in 111.4 that the only coadjoints F: Set -» Set
are F — 5r.) We first tum to the construction of free ^algebras—here we only
need the fact that F preserves countable colimits, i.e., colimits of diagrams
with countably many morphisms.
Consider the adjoint pair 5r and hom(£ —) in Sat (2.10). The free Sr-al-
gebra
/• - / x Zm - (/ x |0|) \j (/ x Z)\j(lx Zx Z)yj...
can be re-written as
/• - / + ISt + IS\ + ... - LI M/.
■ < m
where for each F: JT -» JT we put F' - I,, F' - F, F' - F- F, etc.
Analogously, for each coadjoint F: jr -» JT we shall prove that
/• - /+ IF + IP \ ... - LI IF'
FAulomUl I OS
provided that JT has countable coproducts. Since ^preserves colimits we have
then
I'F- U IF"*' - LI IF-
a< m 8 < » < •
and hence,
/• - /+ I'F.
The coproduct injections of the last coproduct are
n:/-»/' and *>:/•>■-»/•.
We prove this slightly more generally:
ProfuMoa. Let JT be a category with countable coproducts and let
F: JT -» JT be a functor preserving countable coproducts. Then each object /
generates a free ^algebra, viz.,
/• - LI IF'
m < m
with n: /-» /* and «>:/*r"-» /* the coproduct injections of /• - /+ I'F.
Proof. For each ^algebra (ft S) and each moronism/: /-» ft define mor-
phiinu/. - IF'-- Qby the following induction:
JS-//-0.
f..,-f.F- S: (IF')F-* ft
Denote by
/V/'-e
the morphism with components f. (n < a>) (Eiercise III.I.C). Since
Fpreserves countable coproducts, the morphism
fF: LI lF'—QF
0 < a < m
has components f.F and thus, f'F-S: I'F-* Q has components /.*i
(ii < at). So does/* -ft:/*/7-* Q and hence,
rF-s-r-v-
We conclude that
/*:(/•.«>) -(0.5)
it t homomorphJtm; moreover,
n-r-k-f-
106
Chapter III
Conversely, let
!:</•■ «>)-(ft «)
be a homomorphiirn with n • g — / Denote by g.: IF' -» Q the n-th
component or g (n < a>). Then g.Fis the n-th component or gF. Since g is a homo-
morphism, we have
p-g-gF-S: LI /F"-0.
0 < *< «
or, by components,
f..i - g.F-8 (n < a).
Since g, — /— Ji, we conclude by induction that f. -/.("< <u), and hence,
*-/ D
2,12, Dmllty ■rwclple. Before continuing with adjoint automata we recall
the duality principle used in category theory.
The dual (or opposite) category or a category jr is obtained from jr by
revelling the direction or all arrows. That is, we define the dual category jr" to
have the same objects as •*?, and the morphisms from A to B in JT ^ to be
precisely the JT-morphiims/: B-+ A. The identity morphisms in Jf and JT" are
the same, and the composition of JT" is inferred from JT as follows
For each concept C concerning categories, the dual concept (often called
co-C) Is obtained by applying Cto the dual categories. For example, the dual
concept of equalizer is coequalizer (see 111.1). For eacb functor F: JT -» 3 we
define the dual Junctor F": Jf -» X" by XF - XF" and fF - fF".
The duality principle states that if a proposition concerning categories and
functors is valid, then so is the dual proposition, i.e., the proposition with all
concepts substituted by their duals.
2.13. Oaati lability. The observability of sequential automata, studied in
1.2.7 and Exercise I.2.B, is captured by duality as follows. Let F: JT -» Jf be
a coadjoint, and let H: JT -» JT be the corresponding adjoint. For each object
Tput
r. - n r//-.
£Antomau 107
Then there it an ^algebra (/"., y) and a morphUm x-.T. -» Twith the
following universal property:
V-
— <i-
for each ^algebra (ft S) and each morphiim /: ft-» rthere exiiti a unique
horoomorphism /, : (ft 6) -»(F., y) with /-/•■*
In Tact, the functor
Jf*»: J"»-»jr^
is a coadjoint (III.2.I0) and hence. Tor each object Twe have a Tree W'-al-
gebra
r. - U rH' Injr".
>< •
in other words,
T. - J! ftf' in jr.
Since H preserves the last product, we have /", — T x f. W (In JT), and the
projections
jr: T. -» Tand *•: T. -» T.H
form the injection (*: T-» r. In Jf) and the operation morphism («/*:
r, W-» /, in JT^) of the free ff^-algebra. The universal piopeily follows
from the bijective correspondence between F-algebras in JT and W^-ilgebras
in JC":
Q-jtQH
Deflaltlea. For each ^automaton A - (ft S, T, y, /, X) the unique £homo-
morphum ym: (ft, 5) -»(r., «/) with
>•-»•■*
is called the observability map of A.
Rtanrk. The components of ym : ft-» \\ VH' are the following mor-
>< •
phlims p.: ft-» fH':
lOg Chapter HI
n - r;
Example. Let JT - S«t and
F- Stand H- hom(£-).
Using the natural bijectlon between hom (A, hom (ft C)) and hom (A x ft C)
and between A and hom (|0|, A), we can write
T. - n r*Y* - T x hom (£ T) x hom (£ hom (Ul)x ...
- hom(|0|, T) x hom(£ T) x hom(X x £ T) x ....
Further, using the natural bijection between hom (A, + A, + A, + ...,B) and
I! hom (A., B), we get
■ < m
r. - hom (|0| + !+!« 1+ ..., D - hom (!•, T).
The observability map
r. ■ 0-»hom(l#. D
Is defined as in Exercise I.2.B: it assigns to each state q e Q its behavior
(»)y. -ft: Z'-rin^.
2.14. Theorta (Mlaiaul rtallzatioa as factsriurlM.) Let jr be an
(/, ut>category with countable products and coproducts, and let F: JT -» JT
be a coadjoint preserving #-epis.
For each behavior fi: /* -» T we can obtain the minimal realization by
forming the image factorization of fi.: (I', «>) -»(/"., y):
Q
More in detail, the unique automaton with state object ft run map i and
observability map m is a minimal realization of B.
Proof, (i) Let us apply the diagonal fill-in:
cF
£AutonulA
109
We obtain an ^algebra (Q,S) such that both e:(l',<p)-*(Q,8) and
m: (& <5)-» (/",, k>) are homomorphisms. It follows that the automaton
4>-(G. ft T, m. x,l,n- *)
has run map e and observability map m. Moreover, such an automaton is
unique, in other words, S is uniquely determined by the Tact that m and e ate
homomorphisnu. (IT 8": QF-* Q also has this property, then 8' • m —
mF- w — S• m, and m is mono, hence, S — <5.)
The behavior of A, is
■0.
■0.
and since (( *, we see that /t» is a reachable realization otp.
(ii) Let A - ({J, 5, F, y, I, X) be another reachable realization of p. The run
morphism p: /• -+Q of A is an l-epi such that
fi-p- f.
We have a unique morphism y. for which the following diagram
commutes. Further,
P. - P' f.
because fi. is the unique £homomorphlim with 0. • n — fi. and we have
P- 9. ■ x- p- y- P-
Hence, we can use the diagonal fill-in:
110
Chapter III
We obtain an /-epi e:Q-»Q |in Tact, let t - e, • m, be a factorization, then
* - ip ■ e,) • m, is a ractorization of t e I and therefore, n, is an
isomorphism, which proves i" e **|. Moreover,
i:A — A,
is a morphism of automata:
(a) I: (Q, 8) -»(ft S) is a homomorphism because pF is an epi (p e
/Implies pF e /), and we have
pF-{IF- 8)- eF- S- «• - e- «•• p- i- p'F(S- e);
(b) X • i — ij . p • i - ij • e:
(c) I ■ (m • *) - y. • x - y.
This proves that A, is a minimal realization of £ D
Corollary. For JT and F as above, an automaton is minimal (i.e., a minimal
realization of its behavior) iff it is
(i) reachable (the run map is an /-epi)
and
(ii) observable (the observability map is an .«Y-mono).
Conversely, \f A has both of these properties, then by p • y - 0 we obtain an
image factorization of fit :
0. - p • y. ipi*; r. e -*)■
Therefore, there exists an isomorphism i with
p — e ■ i and i • v. — m.
It is easy to check that 1:A,-*A is a morphism of automata. Hence, A Is
a minimal realization of 0.
Restart. In case of sequential automata we have /". - hom(X", /") (see
Exercise 1.2.8). Given 0:1'— T. then
l.:X*-»hom(X*. T)
assigns to each word w e Z' the behavior {—w)0:Z*-*r defined by
r~ (rw)fl(v e I"). The kernel equivalence ~ of this map 0, is precisely the
Nerode equivalence o(0 (1.2.6). Thus, our construction of minimal realization
is precisely that considered in Chapter I.
2.15. Exaaiple: Blllaear sesjaearlal £*atoautt. Let A be a commutative ring
with I, and let I be an A-module. A bilinear sequential ^automaton is
defined precisely as the linear one (III.2.3) except that (i) the next-step map
6:Qx Z-Q
£Autonutl III
is not supposed to be linear but bilinear, which means that Tor each state
q e Q and each input a e Z
(a,-)S:Z-Q and (-, a)6:Q^Q
are linear maps, and (ii) the initial state is arbitrary, not necessarily 0.
To show how bilinear automata fit Into our theory, we recall the concept or
tensor product 9. Given A-modules X and Y, their tensor product X 9 Kit
denned as an R-module with a bilinear map t.X x Y-* X 9 Kuniversal in the
following sense: for any bilinear map/: X x Y-* Z there exists a unique
linear map/X® Y-fZw'rthf- x • / The tensor product exists for each X and
y, and it is generated by the elements x 9 y — (x, y )T.
Define the lensor-producl functor
Kr: R-Mod- R-Mod
on objects X by
XVt- X9Z
arid on moronisms f:X-* Y by
fVt-f9 \I:x9a—(xif9 a.
Then bilinear ^automata are precisely ^■automata
* - (0. S, r, r. K A)
where R is considered as a module over itself. In fact,
S:Q9Z-*Q
describes precisely the bilinear next-state map,
v:C-r
is the output map, and
A:R- Q
is fully determined by (l)A, which is the initial state.
The functor Crls a coadjoint. The corresponding adjoint is the horn-functor
hom<£ -): R-Mod — R-Mod
defined as in Sat (III.2.I0) except that for each /(-module X the set hom(£ X)
of all linear maps receives the usual structure of an R-module. Thus, Vt is
a varietor with
/" - II IV\ -1+(19L) + (/« Z9L) + ... .
■ f •
Using the Tact that / z IQR and that the tensor product / 9 — preserves co-
112
Chapter III
products, we can write
/"-(/««) + (19L) + (19 L9L) + ...
-/«(«+ 1+ 19 1+ ...).
Denote
X" - « + 1+ 19 1+ ... .
We have, quite analogously as Tor 5r in Sat:
/• - /« £•.
The analogy goes further: using r~ hom(A,r) and the adjunction of
hom(£, —) and Vt, we get
T. - UjiD(hom(£. -))"
- hom(«, T) x hom(£, T) x hom(£, hom(r, O)...
- hom(« + 2+29Z+..., T)
- hom(X», J~).
For / — A we have /* — X*, and the run map of a bilinear automaton Is
the (unique) linear map
assigning to each
a, 9 a, 9 ...9 a. <= 18 18 ...8 I
the stale obtained from the initial state (l)A by an application of inputs o-,,
a,,..., a,. The observability map
yt: Q-*tmm{£*, T)
assigns to each state q the behavior of the automaton initialized in q.
For each behavior /):£•-»/", the homomorphism fi,:(£•,«>)-»
((hom(£*, D, y) is the unique linear map assigning to each a, 9 ... 9 a. the
map (o-| 9 oj 9 ... 9 o-„ 9 — )0: I* -+ H The kernel equivalence ~ ot0, is
the analogy of the Nerode equivalence: the state algebra of the minimal
realization o(fi is (£•.«>)/~.
CMcMlag mutL The concepts of minimal realization, reachability, and
observability, introduced for sequential automata, are naturally extended to
F-automata with a coadjoint functor F. We find out that observability is the
dual concept to reachability.
This special case does not cover tree automata or linear automata. The
problem of minimal realizations is much more intricate for general functors F.
We shall devote Chapter V to a study of minimal realization.
£Aulomili
113
Exercises 111.2
A. Slaglc-lapat aatonaia are automata of type F- \M.
(i) If JT hu countable coproducts, describe the free algebras for I.,. Do this in
particular for JT — Sot.
(ii) Verify that the minimal realization of any morphism fi: /* -» T is
obtained from the image factorization of the morphism p. : /• -» T x f« T
x ..., the components of which tnP p-P p1 • P ... .
(iii) Let JT - Pot) as the (epi, embedding)-category. Put / = |0) and T = 11, 2|,
ordered by I £ 2. Describe the minimal realization of the behavior
p-.r -/+/+/+ /...-»r
sending the first copy of 0 to I and all other copies to 2.
(iv) Describe the minimal realization of the behavior above in the (quotient,
mono)-category Pot.
B. Forgetful tractor. For each functor F: JT -» JT we denote by F-Alg the
category of F-algebrBs and homomorphisms. Let
l/:F-ANj-»jr
be the forgetful functor, defined by (ft S)U- ft and/l/ - / Prove that Fis
a varietor iff U is an adjoint
Hint. If Fis a varietor, define <P: JT -» F-ANj on objects by I<P - (/*, <f>,) and
on morphisms /: /-» / by ftp - (/• it,)' : (/*, f>() -»(Jm. «v). Then IP is
coadjoint to U. Conversely, if <t> is coadjoint to U, then l<P is a free F-algebra
generated by /.
111J. F-Algebm
In the present section we discuss various types of algebras which can be
expressed as F-algebras for suitable functors F: JT -» jr. We denote by
F-Alg
the category of ^algebras and homomorphisms.
3.1. EpHrusforBntkw. For arbitary two naturally isomorphic (II. I)
functors F, C: Jtf -» JT, the categories F-Alg and G-Alg are also isomorphic: if
p: F-» C is a natural isomorphism, then each F-algebra (ft S) defines a
(/-algebra (ft pg' ■ S) and vice versa. Also, a morphism /: ft-» ft" is a homo-
morphism of F-algebras /:(ft o")-» (ft, 8) iff it is a homomorphism of the
corresponding G-algebras /:(ft Vq'• 5)-* (Q\ fi^'-S). We are going to
identify naturally isomorphic functors bj well as the corresponding categories
of algebras, whenever convenient.
114
Chipter III
More in general, let F, G: Jtf -» Jtf be functors, and let e: F-» G be a
natural transformation. Then we get a functor
<P: C-Alg - F-Alg
assigning to each C-algebra (Q, S) the F-algebra (g, «c ■ 8), and to each horao-
morphism /: (Q, S) -» ({?', S1) in G-Alg the (same) homomoiphism /: (ft
«o-fi)-»(C", £<r-8-):
1 »
OF »-00 »Q
IF 10 f
T
of ►Co——-a
v »
Exanple. Denote by P,: Sat -» Sat the functor assigning to each set X the
set XPt of all non-ordered pairs in AT, i.e., sets |Xi, Xi| £. X, and to each map
/: X-+ fine map//",: |xi, x;| « |(xt^ (x,y|. We have a natural
transformation
*:H,- P,
defined by
Here, H;-Alg is the category ofgroupoids, and Fi-Alg is the category of
commutative groupoids, with <P: PrMg -» WrAlg the full embedding.
As in the example above, if e: F-» G is an epitransformation (i.e., each
Cji XF-* XG is an epimorphism) then G can be considered as a quotient of F,
in the sense made precise in 111.5 below, and the functor <P: C-Alg -» F-Alg is
a full embedding. In fact, <P is one-lo-one on objects since ((?,£<;• <5) - (Q',
ej • 5') implies Q — Q' and eQ- 8 — eg- 8', and the latter implies 5 — 8'. It is
obvious that <t> is one-to-one on morphisms too.
Coareathn. For each epitransformation e: F-» G we consider C-Alg as
a full subcategory of F-Alg by identifying each C-algebra (0, 8) with the
corresponding F-algebra (Q, eQ ■ S).
3J. Varieties. We recall the concept of a variety, i.e., a subcategory of the
category Wi-Alg of ^algebras (in Sat) given by equations. Let /be a set (of
variables), the cardinality of which is infinite, regular and larger than all
antics |o-| for a € I. A pair of £trees (11.3.4)
(!,, /,) € /' X /'
^Aotonutt 115
ii called an equation, and ii uiually denoted by
/, - 4.
An algebra (Q, S) it said to satisfy the equation I, - t, if Tor each map
/: /-» Q the extended homomorphiim/*:(/',«<)-» (C, 7) fulfils
0.1/* - (41/T
For example, let Z consitt of one binary operation, i.e., let ua consider the
category ofgroupoids. A groupoid is commutative I1T it satisfies the following
equation
(x, y € / and x * y).
A variety of talgebru is a full subcategory y of Wi-Alg for which there
exists a set of equations £ c /* x /* such that >-algebras arc precisely those
£algebras which satisfy each of the equations in £ The triple (£ /, E) is
called an taxational presentation of f ■ For example, let £ - |(/,, 4)) for the
trees (, - (x, y)o and 4 - 0>, *)o above. Then (£/,£) is a presentation of
the category of commutative groupoid*. The category of commutative
semigroups is presented by two equations: the commutativity law
and the associativity law
The former example Is the category PrUg. What about the latter? We are
going to characterize varieties of ^algebras which have the form ^Akj for
some set functor F. The variety of commutative semigroups is not of this form.
116 Chapter III
Pupoaltlia. For each epitransformaUon c:Hl-*F, the category F-Hf is
a variety or £algebras, presented by the collection or all equations
where t, f € IHi(c /') are arbltary treei with
and / is an infinite set with card / 2 \a\ for a e L
Proof, (i) Let (ft S) be an F-slgebrs. For each equation
i - f
aa above and each map /: /-» ft we are to prove that (1)/' - ((V-
Put
where c t € land x. € / (n< |<r|), /. € /(m < |r|). Then/* satisfies the
followini:
(t)f -(DfHt-ev'S
and
(/V-(/VHr. £„•«.
The following square
IH,.—^-*-IF
•He
0
►OF
commotes. Thus, if
then
(fjf -(De,-/F-S- (O*/ • /F- 5 - (/V-
(ii) Conversely, let (ft S) be an algebra which satisfies all of the equations
above. We are to prove that given trees t i* € QHt, then
117
(l)eQ - (/')^ Implies (t)S - (0&
Then we can define 5: QF-* Q by «l)Cg)J - (1)6 for each tree / € QH, tni
this proves that (C o*) is an F-ilgebrs (since S - Cq ■ 5).
Put
where a, r € I and a, € Q(n < lol), bm € Q(m < |r|). Since card / is larger
than or equal to \a\ + |r|, there exists a map
which is one-to-one on the set |a.|.<w u |A.|.<^- Choose a map
/: /- Q
with
(.) a,-(a,)g.f and 6.-(».)»•/
Tor each n <\a\ and m < |r|. The following square
commutes. For > - (<)gWrind i' - (Ogr/r, the equation
belongs to the presentation above. Indeed,
(s)st - (DgHt • e, - (l)e, •
grand, analogously,
(j>, - (<■)% ' gF,
thus, (/)£g - (Oeg implies (i)£, - (i>,. Since (ft 6) fulfils this equation, we
have
W - («V.
(il//fr • 5 - (jy/fr • 5.
||g Chapter III
By (•) above clearly
'-('K*/)Hi and /'-(/'K* •/)«!,
thus,
(t)S- (/)»//, •///,• 8
- (s)fHt • S
-(0*«i -fHt.S
- (»•)*
This concludes the proof. □
3J. DefliMoa. A variety of ^algebras is called basic if it has an equational
presentation (£/,£) such that
£ c lHt x IHt,
i.e., each of its equations has the following form:
By the proposition above, each variety F-Alg given by a quotient F of Ht is
basic. We shall prove the converse.
Propottttoa. For each basic variety » of ^algebras there exists an epitrans-
formation e: //r-» F with > — F-Mq.
Proof. Let (Z, I, E) be an equational presentation of > with
£ c /Hr x /Hr. For each set X let ~ > be the least equivalence relation on
XHt such that
holds for each equation /, — /, in £ and each /t: /-» AT. For any map/: X-* Y
and arbitrary a„ d, e JfWj,
(•) o, ~j,a, implies (atfHt ~ y^aitfHt.
To prove (•), it clearly suffices to verify this for o, — (t,)kH[, where A: /-» X
is a map and /, - I; is in £ Put /f - * • /: /-» K, then (/,)*// - ,(IJkH and
we have
(o-WHi - (',)* • /«! - (/,)fHi (i - I, 2).
We can define a quotient functor F of Ht as follows: for each set X
^Aalomata 119
XF- XH,/-,
it the quotient set, I.e., the set or til equivtience classes (() with i € XHt: Tor
etch mtp/: X-» Y define
ff.XF^YF, M-K'MJ.
This it well-denned due to (•). The corresponding nttural Irtnsforratlion
e: //r-» F assigns to etch i € XHttht equivtience class (()£, - (().
(t) Etch y-algebra (ft £) is an F-algebra. More precisely, etch y-tlgebrt
is of the type (ft £,, - S) Tor some F-algebre (ft S). To prove this, we htve to
show that Tor q,, $ € ftWr,
* ~ g <h implies (q,)S - ($)«.
[Then S: ftrV~»-» Q is defined by (\q\)S - (q)S.\ We can clearly assume
that q, - (t,)kHz, where *: /-» g Is a map and (, - t, Is in £
Since (ft S) satlslies the equation d - <,, we have (/,)*• - (/,)*'. Also,
/, € /Wr implies (/,)*• - ((,)*Hr • 5. Thus,
(q,)S - (/,)*//, • S - (/,)«/, • S - («)&
(ii) Each ^algebra it t *-algebra. More precisely. Tor each F-algebra
(ft S), the Hi-algebra (ft £„ - 5) satisfies each equation in £ Let (, - t, be in
£ and let *: /-» Q be a map. Then (/,)*• - (/,)*//, • 5 for S - % • &, and
we have (l,)kHI ~ a (iJ/W/r, therefore,
(/,)*•-(/,)«/,. ^. S
- HMkHtf
- MJkHAB
- (/.)*'. □
Remark. In the next section we shall prove thtt etch set functor F such thtt
F-Mq is t variety mutt be t quotient of Ht for some type £ This will make the
picture complete: varieties of the form F-Aif are precisely the basic ones. This
shows that for example commutative semigroups form a variety distinct from
any F-Alfl.
Enable: />,-algebra*. Define a functor
/",:S»t—Sat
on each set X by
XT,- \M; Af c X, U * 0 finite]
and on each map f:X-* Y by
(MVP, - (U)f for all Af € XT,.
A f, -algebra is a set Q together with an operation 6, assigning to each finite,
120
Chapter III
non-empty set Afc Q an element (A/)<5 e Q. A homomorphism
/:«?■*)-►«?'.*") is a map f:Q—Q' such that (A/)o"-« implies
((Afyi*" - (4l^ An example or a /^-algebra is any join semilattice, where
(M)5 — V Af; for two semilattices, a /^-homomorphism is precisely a semi-
lattice homomorphism. Thus, semilattices form a full subcategory of //-Alg.
Let £ - |<r,|, ,, < . be s type with \a.\ - n for each n - I, 2,3,... . Then
P/'a quotient of Ht: consider the natural transformation
*: //,- P,
assigning to each (*„.., x„ _,) e XH,m the set \x*..., x,_,| € XP,. Thus,
/■/ -Alfl is a basic variety of £algebras. It is presented by the equations
for all n, m - I, 2, 3, ... and x„...,x,_,, *;,...,x'._, € / such that
|x„..,x,_i| - K....,jC.>I-
14. risiali' Aslgebtas. We have seen that quotient functors of the
functors Hi define precisely the basic varieties of universal algebras. But there are
other set functors which are beyond the scope of universal algebra. For
example, the power-sel functor
P: StU — S«t
assigning to each set X the set
XP-npX- |Af; Af c X\
and to each map/: X-* J" the mtp/P with
(M)fP - (M)f for each Af c X.
A f-algebra (Q, S) is given by a map 6: exp Q-* Q. For example, complete
join semilattices and complete homomorphismi form a full subcategory of
/•-Alg: here (U)S - V Af for each Af c Q.
Forming the coproduct functor
/> + />:S«t-»Sa4,
we obtain the category (P + /")-Alg of algebras given by two operations
exp {?-» Q. Thus, for example the category of complete lattices and complete
homomorphisms is a full subcategory of (P + ^)-Alg.
£ Automata 121
3.5. (Mend algebras. An ordered algebra u an algebra defined on a poset
in such a way that all or its operations are order-preserving. Here, for each
poset Q the cartesian power Q' (n a cardinal) is ordered component-wise:
(x,),«. S iy,), <. IfT x, S y, for all / < n.
(This is precisely the product of n copies of the object Q in the category Poa.)
Explicitly, for each type Z, an ordered Enlgebru Is a pair (ft (<5J„, i) which
consists of a poset Q and a collection of operations
«.:t?"-t?(c€ S.)
such that
x, S y,(\ < n) implies (x,),« .5 s (j>,), < .5.
These are precisely //ralgebras for the functor Hz - II H. of Remark
II 1.2.3; a coproduct in the category Poa is just the disjoint union (with the
given order on each summand, and with elements of distinct sununands pairwise
incompatible). An order-preserving map
s-.qh;- II e--e
is precisely a collection of order-preserving maps 8„:Q'-*Q (a € £.).
rYr-homomorphlsms are also precisely the order-preserving homomorphisms.
3.*. (U-uiall—ilia algebras. A poset is said to be a-complele if it has a least
element 0 and each increasing <p.sequence has a join. An order-preserving
map which preserves the least element and joins of increasing <t>-scquenccs is
said to be to-continuous. We denote by
Poa.
the category of <t>-complete posets and o-contlnuous maps. This is the
category in which o>continuous algebras "live".
An ordered £algebra (ft l<5„l) is strict a-conUmiom if Q is a o-complete
poset and each 6: (?'-» Q is <u-continuoua (with respect to the
componentwise order of (?")■ Explicitly, an operation S: g"-» Q Is <t>-continuous iff
(0,0,0....)5-Oind
V(x,. *!.*'.-"J*-(*.*. y,,...)S
t < *
for any o>sequence (xj, x^, xj,...) £ (xj, xj, xj,...) £ (x}, xj, xj,...)... in
O" with joins v. - V xi.
k < m
Now, for each (^-complete poset Q the powers ft" are also o-complete;
|22 Chapter III
hence, we have a functor
W„: Pot.-Poa.
which Is the restriction or Ihe corresponding functor on Poa. And
H.^lg
is the category of <u-continuous (a)-algebras and avcontinuous homomor-
phisms, where Iff I — n.
For more than one operation, we use the coproduct. In the category Poa,,
coproducts are not disjoint unions (because of the least element): we must
Hist form the coproduct in Poa and then we merge all the 0' s. Thus, a
coproduct of objects ft (i e /) of Pot. is the set
lie/-
where ~ is the equivalence, one class of which, denoted by (0), is formed by
all the least elements of all Q's, and all other classes are singletons (denoted
by x rather than [x], for each x € ft—10|). The ordering is given as follows:
x s v ifT x - [0] or x, v e ft, and x s y in ft, for some i, e /.
The injections ft-» LI ft assign |0)to0and xto any x € ft— |0|.
Given a type Lot algebras, we define Hr: Poa.-* Pot. as the coproduct in
Poa.:
Hr- U«..
For each ru-continuous poset Q — (ft,, S) the poset
ftWr-^CIxlo-l
consists, besides the least element |0], of all trees
where a e Z, and if n > 0, there exists i, < n with .r,01* 0. The ordering is
such that [0] is the least element, while
^Automata
123
i(T a - rand i, £ y, Tor each / < |o|. Clearly,
Hx-Alg
is the category or strict <t>-continuous X-algebras.
Reanrfc. Algebras over <t>-complete poseti are investigated in computer
science where, however, the requirement on the operations is usually weaker:
The least element 0 is not supposed to be idempotent. We call the resulting
algebras the (non-strkl) o-contmuous Z-algebrm. These consist of an oi-corn-
plete poset Q and of operations
«.:<?•-<? (c€ I.)
which preserve joins of increasing a»-sequenccs.
Also these algebras are F-algebras. Denote by
Hl:Poa.-»Po«.
the functor given by the disjoint union of all H*, a e Z, with a new element
0* as the least element. Thus, Tor each o-continuous poset Q,
QH1- U 0- x |o-| « |0-1
where the ordering of the basic trees is as above and 0* is the least element
(assumed not to belong to any Q' x |o-|). For each <t>-continuous map
/•'C-» C'the map
equals to/1" on each Q" x |e?|, a e X., and (0«)/W^ - 0*.
An Mj-algcbra (ft S) is given by an <t>-complete poset ft and an <u-continu-
ous map
This means that 0* brings no inroimation: (0*)<5 - 0; and Tor each o- € X. we
have an n-ary operation
S.:Q- x|<t|-C
which clearly preserves joins of <t>-sequences but need not preserve the least
element. We see that
W,-Aig
124
ChapMr 111
is the category or non-strict <»-continuous X-algebras and <u-continuous ho-
momorphiinu.
3.7. Maay-soittsl algebras. Algebras acting on several sets are called many-
sorted or heterogeneous. We discuss 2-sorted algebras. Tor simplicity; the
generalization to more sorts is easy. A 2-sorted algebra consists or two sets Xx
and Xt and or operations or different arities, e.g.,
a: X, x X, -» X,: r: X, x X, x Xt-*XU
etc. The notion or arity or an operation is more difficult than in the one-sorted
case. We must (a) give two exponents: or X\ and or Xi and (b) state whether
the result is in X, or X,. Therefore, a type of 2-sorted algebras is a pair
X — <X,, Xi) or disjoint sets: the elements or X, are called operation symbols
resulting in X, (i - I, 2). For each a e X, \j X,, an arity is given which is
a pair
|o| - (n„ nj
or cardinals.
A 2-sorted X-algebra consists or a pair (X,, X2) or sets and Tor each a e X,
or arity (n,, n,), a map
5.:X? x X\' — Xt.
For example, modules over arbitrary commutative rings can be viewed as
2-sorted algebras with X, the ring and Xt the Jfpmodule. Let ®, 8 and 0 be
the ring operations, and + : Xt x X, -» X, and x : X\ x Xt -» X, the module
operation. Then modules are 2-sorted algebras or type <X„ X,) with
X,- |®, e,0|andX, - | + , x|
where the arity of ® is (2. 0), of + is (0, 2). etc.
Homomorphisms or 2-sorted algebras are pairs or maps (one Tor eacb sort)
preserving the given operations. Thus, let A - ((X,. X,), |5„|) and B - «y„
^i). |o*ol) be two algebras of type <X„ X,). A homomorphism from A to B is
a pair
or maps /: X, -» Y, and fa. Xt -» Y, such that each a e X, of arity (n,, nj
and for each (aj)t <., e X" and (fty), <., € X"1 we have
(a* a, »o, * )«.• / - ((".1/i. (<>>l/i (*.l/i, (Ail/i.. .)*..
In other words, the following square
£ Automata |25
n, •>] %
Y^'lf*—i »Y,
"a
commutes Tor each o £ I^j I,.
The 2-iorted algebras are ^algebras in the category 8*f of pain of sets
and pairs of maps. (The composition of morphisms (/„ fi)-(Xl,Xi)-*(Y,,
r,> and <f„ s,):(Y,, y,>-»<Zi. Z,> is coordinate-wise, i.e., the resulting
moronism is (f, • f i, /, • f ,>.) If X has just one operation of arity (nb nj in X,
the corresponding functor is
defined by
<*,.*,> //,'.,. .„-<*;■ x *;•, e>;
</i./i>W,1.,..,i-<A",,"^"".«>-
Analogously, if X consists of one operation in X,, we define //'.,.,,. sending
<*,, Xj) to <», X," x *,">.
Finally, for each type X — (X,, X]) we use the coproduct (which in 8of is
formed component-wise):
"r- ILni,+ II «£■
ft ti fii]
Thus, on objects <* 1, XJ,
(XuXJHr-i II X," X Xr, II AT,- x *,-■),
analogously on morphisms. Then
Hi-Ato
Is the category of 2-sorted X-algebras.
3JL Attains n ucurte ulifuln. The algebras in Sot, Pot), Poa. and Sat1
have common features which we discuss in general presently.
By a concrete category is meant a category Jt together with a functor
(/:.*-» Sot
which is faithful, i.e., given distinct morphisms f\, ft:A-*B then f,U + f,U
126
Cbipter 111
(for each pair or objects A, B). We can view the objects of JT as sets endowed
with a structure. (Quite formally: given an object A with AU — X then X is
a set with structure A.) Since U is faithful, we can use the same symbol for
a morphism f: A-* B in .X and the corresponding map In Sot Thus, if
AU — X and BU— Y, then morphlsms from A to B are some maps
/: X-* Y—those maps which "preserve" the given structure. The functor U is
called forgetful because it forgets the structure.
For example, Poa is a concrete category with (X, s )U — X. Morphisras are
precisely the structure (— order) preserving maps. Abo 8of can be
considered as a concrete category. The forgetful functor is given by the disjoint
union:
(X„XdU- X, + *„
analogously for morphism.
Given a concrete category JT, a set Mis said to generate a free object W of
•JT if M c M'U and for each object A and each map/: U-* AU there exists
a unique morphism f:U'-*A extending / For example, Poa has free objects
(which means that each set generates a free object): W is the set M endowed
with the discrete order. Also Poa. has free objects: W — U v |0) (where
0( M) with 0 the least element and M discretely ordered.
Assume that JT is a concrete category with concrete products (i.e.. Jt has
products and U preserves them). Then we get a natural concept of an n-ary
algebraic operation on an object Q of .X as a morphism 6: Q"-* Q. The
corresponding functor is the functor
H.: Jt -» JT
of the n-th power. The //.-homomorphisms are the structure-preserving maps
which also preserve the operation. This is the case of JMMod, Pot and Poa.
above, and a lot of other current concrete categories. For example:
Top.
the category of topological spaces and continuous maps. Here Q" is the usual
topological product (of n copies of Q). An //.-algebra is a topological space
Q together with a continuous n-ary operation on Q. An W.-homomorphism is
a continuous homomorphism.
On the other hand. Sef fails to have concrete products: the product of
<*,. Xi> and (Y,. YJ in Sat1 is (X, x Y„ X, x Yj). And. of course, the
equation
(*, x y,) + (at, x r,) = (X, + x,) x <y, + y,)
does not hold in general. This explains why the functors W. are not
"convenient" in Sot1.
Assume that JT has not only concrete products but also (possibly non-con-
^Automiti
127
crate) coproducti. Then Tor each type I or algebras we use the coproduct
functor
Hi - II ««,,
introduced in III.2.5. The category //j-Alg is then the category or JT-itruc-
tured £algebras (with structure-preserving operations) and
structure-preserving X-horaomorphisms.
For each set functor F: Sat -» Sat, the category F-AIq is concrete. It has
Tree objects i(T F is a varietor (see Exercise III.2.B).
Given a functor H: ,x -» 3 between concrete categories, we say that H is
concrete if (/,-//•(/„ i.e., if Tor each object (X, a) of X we have
{X, a)H — {X, a*) Tor some structure a* in 3, and Tor each morphism / we
have fH — / Two concrete categories are concretely isomorphic if there exists
a concrete isomorphism (i.e., a concrete, bijectlve functor) from one to
another. For example, if F and G are two naturally Isomorphic set-functors,
then 5-Alo and G-AJa are concretely isomorphic categories (see III.3.I).
Renarfc, Let (JT, U) be a concrete category which has free objects. For each
set M denote by M<t> - M* a free object generated by M, and for each map
/: Af-» Wlaff: U0-* M'<t> be the unique morphism extending / This
defines a functor
d>:Sat-»Jr
which is coadjoint to the forgetful functor (II 1.2.10): the inclusion maps
n„: *#-» (U0)U define the universal natural transformation
nM^-tK.l/.
(In fact, for each morphism /. Af-» AU in Sat there exists a unique
morphism f* : M<P— A in JT with/- n„. /*.)
For each object A of JT we can extend lAU: AU-* AU to a morphism
tA:(AV)0—A,
and this gives a natural transformation
e-.U-0—i*.
This is an epitransformation: if eA • / - sA • g for two morphisms f, g: A-* B,
then n4 • sAU - I implies
flJ-l4-(.e4.f)U-qA. («4 . g)U- gU
and, since U is faithful, we conclude that/— g.
128
Chipcer 111
XUA. Set Faacton
4.1, Since set functors, i.e., functors
F:S«t-»S«t
play an impoftant role in our book, we devote the present section to their pro-
We have introduced the set functors W, and their coproducts Wrin II 1.2.5,
further the functors Sr(- Ht If each a e I is unary) in III.2J and hom-func-
tors hom(X; —) in III.2.10. Note that hora(L, —) is naturally isomorphic to H.
for n — card £ If X is a singleton set, then Sr and hom(Z, —) are naturally
isomorphic to the identity set functor. Further, recall the functors P, Pi and P/
of IIIJ.3 and III.3.4. We define a subfunctor P. of P for each cardinal n by
XP. - \U c X; 0 < card M S n|.
On morphisms: fPn sends U to (M)f.
For each set U we denote by
CH:S«t-»S«t
the constant functor {XCM - M and JCM - l„). We entend the concept of
constant set functor slightly, by disregarding the empty set and empty map.
Thus, for each map h: U, -» U we define
C£:S«t-»S«t
on objects by
*Ci= M
eci - M, if x ¥■ B:
and on morphisms/: X-* Y by
Ki-
l„ if X ¥■ 9
h \( X-8 + Y
lu, ifX-B-Y.
A set functor Is said to be constant if it is naturally isomorphic to some C£. If
AYo - B we write C0H instead of C£.
4.2. ProaosltloB. Each set functor F *■ C, preserves
(i) non-empty sets (X * B implies XF+ B);
(ii) epis (if e: X-* Y is onto then eF is onto);
(iii) non-empty monos (if m: X-* Y is one-to-one, X * B, then mF is one-
to-one).
Proof, (i) Since F+ C* there exists a set X with XF + B. Let Y* B be ar-
^Automiu
129
bttnuy. There exists a map/: X-» Y; then//7: XF-* YF is a map and hence,
XF+B Implies YF+ 8.
(ii) Each epi e : X -» Y splits: Tor each y e K we can choose 0>V € AT with
(CclO*- y. and/: r'-.Jt'isi map such that/. «- I,. Then//7. «f- l„,
hence, tF is a split epi.
(iii) Each non-empty mono m: JIT-* f splits', we choose x, e X, and we
define j: K-» * by (y)g - * if y e Y- (X)m; (y)g - x if y - (x)m. Then
m • j - lx. Hence, mf- j/7 — l„ and mfis a split mono. D
Reanrfc. The empty mono m: 9 -» X need not be mapped to a mono:
consider the functor ChM above with A a constant map. Then mC^ - k
4J. DefUIHoa. A set functor Fit said to be small if there exists a cardinal y
such that for each set AT we have
XF- |J (MF)fF,
where the union ranges over all maps f:U-*X with cardM < y. If y - K*
then Fit said to be/injury.
r»i|iln (i) W. is small, and rt is finitary iff n is finite. In fact, let y be the
least cardinal larger than it For each set X and each element (Jt,), <. of
XH.-X- put M-\x,: (< n|. Then card U < y and (*,),<. €
W - (AH/.)/*//, for the inclusion map/: U — X.
If n is finite, then r — n + I, hence, we can also choose y — Kfc and we see
that H, is finitary. If n is infinite, choose a set Jfind an iMuple (4)! < . e *W.
such that the elements i, are pairwise distinct. Then for each map f:U-*X
with M finite clearly (*,),< . < (UH.)fH.. Hence, H. Is not finitary.
(ii) The functor P,\% finitary: for each set JT and each element of XF), i.e.,
afiniteset Mc X, we hive M e (MPj)j Pt for the inclusion map j : M -» X.
(ill) The functor P'n not small. For each cardinal r we can choose a set Xof
power y. Then X e eipjf - XP and clearly JT* (MP\fP for any map
/. A/-.* with card U< y.
PisicaHlss. A set functor Fit small iff it is a quotient functor of Ht (i.e.,
there is an epitransformation Wj -» F) for some type L. Fit finitary iff it is
a quotient of Ht for some finitary type £
Proof. I. Let /"be a quotient of Ht and let y be the least infinite cardinal
larger than all arities in X. (Thus, y - K, iff X Is finitary.) The sufficiency of
both of the statements we are proving will be verified when we show that for
each x e JTfthere exists a map/: U -» X with x e (UF)fM and card M < y.
Let c: Hi -» F be an epitransformation. There exists / c -W/j with
x — (/)*r. Let / — (x,)o for <r € X of arity n( < y) and for Xt e X, / < n. Put
A/-|*,; i< n| and let f:M-»X denote the inclusion map. Then
130 Chiptcrlll
card U £ n < g and we have
X - (/)£, - (((*)/»«, - <*,1/«I • €,.
Since the following square
My
,Hi
X
c H—Mf
'
** c ' XF
commutes, we conclude that J e (MF\fF.
II. (a) Let f be a small functor, and let ybe the corresponding cardinal.
Choose a set U of cardinality y. Put
X- UF
and define the arity of any element of Xto be y. We prove that F is a quotient
of//,.
For each set X we have XHC- U.X', and this can be identified with
X" x MF. Then for each map/: X-. Kthemap/Wx: X" x Mf-» 1"« x Aff
is denned by (A, mj/Tir - (A • / m) for all A: U — Xand all m e M5.
Define a natural transformation
by
s:H, — F
(A, m)£* - (m)Af
for each A: U-* X and m € UF. It is easy to verify that this is a well-defined
natural transformation, i.e., that for each map/: X -» fine following square
x"*mf ^ »>
V^MF »-Y
commutes. And the choice of y guarantees that cis an epitransformation: for
each x e XF there exists a map A: M -» X with s e (UF)hF, i.e., J-
(m)Af - (A, m)cx for some m e M£
II. (b) Let Fbc a nnitary functor. For each n < <o put [»| - |l, 2 n|
and define a finitary type X by
X. - ["|5 Tor each a< a.
For each set X we can identify XH, with II AT1"1 x [n\F. We define a natural
transformation
«://x-f
by
(A, «!)«, - (m)Af
for each n< a, A: [n] -» Jfand m € [n|5. Since fit finitary, c Is an epitrans-
formition: for each s e XF there exists a map from a finite set into X, say,
A: [n| -» j; and m € [n|5with x - (m)AF - (A, m)£,. D
Reaurk. A set functor is finitary iff it preserves directed unions (see
Exercise III.4.E below) or directed colimlts (this will be proved in Chapter V).
4.4. DeflaHloa, Let F be t set functor. A point
a € AF,
where A is tn trbltnry set, is said to be diitbtguishtd If for arbitrary two maps /
g: A -» X we have
(a)fF-(a)sF.
Euntlc*. (i) The power-set functor fins 0( e AF for any set ,4) as a
distinguished point.
(ii) No point of W. is distinguished if n > 0.
(iii) Each point of a constant functor is distinguished (and conversely. If
each point of a set functor Fit distinguished, then Fit constant).
Remarks, (i) Etch distinguished point a e AF defines „reltted"
distinguished points a, € XFin all sets X ■> 0: choose any map/: A -» JIT and put
"z - (a\fF (independent of/).
Then
(a,)hF - a,
for each map A: X -» Y. Thus, we obtain a natural transformation
a:C,-f
(where 0C„ - 0 and JTC,, - I - |0| for each X ■> 0) taking the value a, for
each set X ■> 0.
132
Chipin III
(ii) What about a,J In other words, can a be attended to a natural
transformation C, -» Fl Not in general: the point 0 ii diitinguiihed in C„ but there i»
no natural transformation C, -» C,, at all.
(iii) For each set functor F, each point a e BF is diitinguiihed limply
because any two maps / g: B -» X are equal.
DefnUtloa. A distinguished point a e AF is called standard If there ii
a point a0 e Bf with a — (a.^ffor the empty map/: 0 -» A (in other words,
if the natural transformation a can be extended to C,).
4J. Coaveatloa. Let X and y be sets with X c K. Denote by J}:X— Kthe
inclusion map defined by (i\jl — i for each i € X.
DtflalHoB. A set functor ii said to be standard if it preserves inclusion, i.e.,
XcY implies XF<z YF and JJlF-jg,
and each of its distinguished points is standard.
Eaaaaata. (i) The power-set functor P is standard.
(ii) The horn-functor hom(M, —) is non-standard: if X * Y then actually
hom(M, X) >~> hom(M, 10-8 (because a map/carries, by definition, the
information about its codomain). Nevertheless, hom(M, —) is naturally
isomorphic to H. for n - card M, and W. is standard.
(iii) The functor C„ is non-standard because the distinguished point 0 is
non-standard. But C„ differs from the standard functor C, only in the empty
set and empty maps.
(iv) Hs is standard for each type X.
Remark. The reason for introducing the concept of standard functors is to
obtain a class of functors which is -reasonably" representative (this is proved
in the following theorem) and which avoids complicated and not really
interesting examination of the empty set which behaves somewhat irregularly.
For example, standard set functors preserve monoa (also the empty one*)
because the empty maps are actually inclusion maps jl- Further,
85
Is just the set of all distinguished points of F: if a c AF it distinguished, then
a € 9F c AF because there exists a, c BF with
a - (a.V,'f,
and jjF is the inclusion map.
Theorem. (Each set functor is almost standard). For each set functor F there
exists a standard set functor F' such that the restriction of Fand F' to all
nonempty sets and non-empty maps are naturally isomorphic
F-AVtomiu 133
Proof, (a) First, assume that F preserves (empty) monos, and that each
distinguished point or F is standard.
On the class or all pairs
<*.*)
where JIT is a set and x e XF, we define the following relation:
{X,x)~{Y,y) iff MI-'F-WF.
This is an equivalence relation. The reflenivity and symmetry are obvious. For
the transitivity, let
(X, x) ~ (y, y) „ (Z, r)
and consider the following commutative diagram of inclusion maps!
Since (.X,x) ~ (Y, y) means that (x\j,F- (vlA'f, we get
ixy,F ■ itF- (jr)/,f • itF - (v)/if • I,F.
Also, since (Y,y) ~ (Z, r) means that (v^F- (rl/,F, we get
(*Kf. J,F- (*y,F. i,F- O-lAf • J,F- (v)/if • J.F
Thus, (,x\/,F- i,F- (itf, • i, F and since F preserves monos, it follows that
(jr)/,F- (iMJF, i.e., that (**) ~ (Z, i). For each ji e *F denote by
1**1
the equivalence class of (X, *)■ Note that
( + ) (AT, *) ~ (X, x) implies x-t (for each x, i 6 XF)
simply because>/"' - I,.
Let us define a set functor F' on objects X by
W-l'JtxKxc *F|.
and on morphisms /: X-» Y by
/F': [AT, ji| — [K, (j,yF| for each x 6 *F.
134
Chipcer III
The lait map ii well-denned |>et (+) above), and fill functor since F is.
Moreover, F and F' are naturally Itomorphic: consider the natural
transformation
«,: XF— XF'
denned by
(*)*, - \X, x\ (x € XF).
Each cx is a bijection by (+). Let us verify that the functor F' is standard. It
preserves inclusion because given X c Y, then
[X, x\ - [K. (xy/f | for each x 6 XF.
(This follows from y/-r->; and >fur- I,.) Therefore XF' c YF'uuijIF'
is the inclusion map:
Each distinguished point of F' is standard because the naturally isomorphic
functor F has this property.
(b) Let F be an arbitrary set functor. Using (a), it is sufficient to exhibit
a functor F such that F — F on the full subcategory of all non-empty sets, and
F preserves empty monos and has only standard distinguished points. Define
9r to be the set of all natural transformations r: C, -» F. This Is a set (not
a proper class) because each such transformation is fully determined by
(0)ri € If: given r". r": C,, -» F, then
(») if rj - x'i for any X * 9, then r' - r".
(To prove (•), consider any set Y. If Y - 9, then rj - r; because »C„ - 0. If
r * «, choose a map g: X-* Y and then r"r - r?(: |0| -» W) because
(OK - (0)»C., • r'r - (0)ri • tF- (0)rj • tF- (0)rM
For each empty map /: 9 -» AT define fF:9F-* XF by /f- I, if AT -8 and
(rl// - (0)r, for each r: C;, -» F
if X + 9. By (•), fF is one-to-one. Thus, we obtain a functor F with XF - XF
if X * 9 and /f — /f if the domain of/ is non-empty, and this functor
preserves monos. Each distinguished point of F is standard because any
transformation r: C„ -» F is also a transformation r: C„ -» F, thus, r e f £ We can
extend r to a transformation f: C, -» f by (0) f, - r. D
4.*. PisfusHlea. Each sundard set functor F preserves finite intersections.
Reaark. In the category Sat, finite intersections are just pullbacks of
monos:
135
(where m, art the given monos and m, art the corraponding monos, definding
A, r\ A, as a iubobject of A,). Thus, the proposition above states that each
standard set functor preserves pullbacks of monos.
On the other hand, the statement can be understood purely
set-theoretically:
AtFr>A,F-(At r>A,)F
Tor arbitrary two sets A,, A,. Fortunately, this is equivalent to the formulation
above, since F preserves inclusion and we can use A — At\j At and the
inclusion maps m, and m,.
Proof. Denote the inclusion maps as follows:
*1n*J-
-*A,
M
-*A,uA,
I. Let/4, r\A, + 9.
We prove that there exist maps
r: A\ -» Ax r\ Ait s: Ay\j At-* At
such that
(I) J,- r- I:/, • j- r-y, and f, • i- I.
In fact, choose jct e Ay r\ At and define rby
■u
(x)r.
Further, define j by
I jr0
Then (I) is obvious.
If * € A, r\ A,
if jr € A, — A,.
it ye A,
if y e /4, — >,.
136
Clupler III
To prove that F preiervei the pullback above, comider arbitrary mapt pi
and p, with p, ■ i,F — p, ■ l,F.
The map
/>-/>.- rF
fulflla />i — p ■ J, F and p, ■
p-jjF-
p • JjF. The Utter follows from (I) above:
' Pi • (' • h)F
- />i • ('I • ')F
- Pi- itF- iF
- Pi-
The former followi from the Tact that i,F It a mono:
(J>-JiF) .itF-pJ,F. i,F
- Pi • >iF
- P< • hF.
Finally, if p' also fulfils p, — p' ■ j,F and p, — p' • JjF, then
p- Pl. rF- />' • j,F- rF- p.
II. Let A, r> A, - 9.
Since F it standard, it it sufficient to prove that each point
a € A,FnA,Fc(A, w At)F
It distinguished, i.e, an ekmeni o(8F. Indeed, Ihen AtFr\ AiFc. 9F, and the
reverse inclusion it dear, since 0 c A, implies 9Fc AtF(l - 1,2).
Let
/ $:A,\j A,-»X
FAHoan 137
be an arbitrary pair of map*. To prove that
(aifF-(a)fF,
let h:A,vA,— Y
be the map defined by
(J°* IW* lf*iil..
Theo>i • » - j\ ■ fmij, < h-j,< g. Since a € >,f lmplla a - (a)/|f, we
have
(a)hF- (ay,F- hF- (a]l,F-fF- {a)fF.
Analogously,
(a)Af-(«)•/.
The proof it concluded. D
4.7, Pisa—Msa. Let F be a non-connant aet functor. For arbitrary seta
X * 0 and Y,
card *S card r implies card XF S card YF.
Morevoer, there is a cardinal y such that for each set X,
card X ay Implies card Xf 2 card X
Proof. By Theorem 111.4.5 it b clearly sufficient to work with standard
functors F. The first statement Is obvious: card X S card Y means that there
exists a mono X-» Y and hence, a mono XF-» YF.
For the latter statement, we use the obvious fact that each non-constant
functor F has a point a € AF which b not distinguished. Put
Y — max (card A, KJ.
Given a set AT of power 2 y, we can assume A c X Since, moreover, X is
infinite, it has a decomposition
x- Ux
I ■ I
into pairwiae disjoint sets with
card / - card X - card X (<€/)■
For each ( € / we choose a bijection
/:X-.X,
138 Chapter III
and we prove that
(aW * (alff for t J e /; i * J.
Since (a)f,F e X,F c XF, this will prove that
card XFz. card / - card X.
Since/Is a bisection, it It dear that (atf/F u not a distinguished point Id + j,
then X, n. X, - 9, thus (by the preceding proposition), Xfn. X/F -9F and
each point of 9F is distinguished. Therefore,
(aW t Xf
uxihtna, (a]/,F * (a)^£ The proof is concluded. D
Remark. Each standard set functor F has further pleasant properties.
(I) F preserves images. That is, given a map/: X-* Y with (X)f- M, then
(XF)fF- hlF. Let/-: X— hi denote the restriction of/andy: hi— X the
inclusion map, then/— f • yand hence, /f — fF- jF. Sinceyf is the inclusion
map and fF it onto (because/ is onto), we conclude that hlF is the image
of/f.
(Ii) F preserves Drainages for one-to-one maps. That is, given a one-to-one
map/:*-* Y then for each A c Yve have M)-'/)f - (AF )(/F)-'. ThU M-
lows from the preservation of finite intenectiona: for/— / . jas above,/ is
a bljection and A r\ hi is the image of (A)/-' under/
4.8. We are now going to characterize set functors preserving coUmits and
unions. The latter means, for a standard set functor F, that
U«,-V implies U hl,F- hlF
it t itf
for arbitrary sets U„ i e I.
Exasaate. Given sets I, and L*, define
Sr,vS«t-»S«t
on objects X by
XSt,u - (X x X,) + I.
and on morphisms /: X— Y by
Ar,A-(/x lr,)+ ■*•
In other words,
Sz,b - St, + Cfc.
£Aotomau 139
The functor Sz,t, preserves unions: if UM-M, then
(l),*.) X X, - l^Af, x £„
and hence,
||JJtu) x IA + £.- L)((Af, x X, + 2^.
The functor
Si* ~ Si,
preserve! coUmlu because it it a coadjoint (III.2.I0).
PrapoaMoa. Let F be a standard let functor. F preserve) colimlu iff it ii
naturally isomorphic to S, with I - IF, and F preserves onions iff it is
naturally isomorphic to 5fiA with I, - IF and L% - 9F.
Proof. (I) Let F preserve unions. For each set AT we have
x- U ui
MIX
and hence,
XF- U|x|f.
m ■ jr
By 111.4.6, for two distinct points *, y e X,
|x| /-. Lk| - 0 Implies |*| f« \y\F - X*
We define • natural transformation r: 5*6-» Fas follows. For each set X
and each ie X let J,: |0| -» Jf denote the map with (0)/, — x; the map
r,:(ATx X,) + X,-. Jff
U defined by
(jr. <r)rr - (oljrF for each (Jt, e») € X x X,:
(tfjr, - 9 for each * € X»
It is easy to check that r is well-defined, and it remains to verify that each r, is
a bljection. The inverse map
U ijr|f-(Arxr,) + r.
I ■ I
sends each d € £, (- 0f c Jt/*) to 6* (in the second sumand); to each
140
duplet III
o-e [x)F-£, |ie X)
H assigns the pair (x, a)—note that a ( \y\F for any y * jr.
(ii) If F preserves colimiu, it also preserves unions. In fact, if X — U M,
j ■ i
then the canonical map
/: II U,— X
HI
the components of which are the inclusion maps U, -» X, is onto. Hence, the
map
fF: II M,F- XF
• « f
is onto, and its components are inclusion maps, again. This proves that
XF- U M,F.
M I
Therefore, F is naturally isomorphic to St<u.
It remains to prove that if Stlt, preserves colimiu, then £, — 8. Indeed, the
initial object 0 is the colimit of the empty diagram and hence, 9Sitt, — 9. We
have
9 - »St,u -(»xI,) + A-2;
This concludes the proof. D
Century. A standard set functor is an adjoint iff it is naturally isomorphic
to H, for some cardinal «, and a coadjoint iff it is naturally isomorphic to St
for some set £
The second statement follows from the preceding proposition, the former
from the unlcityof idjolnti (for a given coadjoint): honHi —)and St form an
adjoint pair, and hom(.£ —) is naturally isomorphic to H, with n — card £
4.9. We conclude this section by returning to set functors defining varieties
of universal algebras (see II 1.3-2). Recall the concept of concrete isomorphism
(IIIJ.8).
Theanev Let F be a set functor such that f-Alg is concretely isomorphic to
a variety of ^algebras. Then F is small, and if £ is Unitary, then F is Unitary.
Proof. We can assume that F is standard. Let y be the least infinite
cardinal larger than all arities in £ (thus, y - H, iff £ is (injury). For each set AT we
shall prove that XF is the union of all MF with U c X of cardinality smaller
than Y-
If AT is finite, there is nothing to prove. Assume X infinite, and choose
distinct points a, 6 e X. Define an operation
£Antoouu Ml
S: XF— X
by
. .„ fa if jt € MF for tome hlc X with card 1/ < v
W*"!* else.
Let ui prove that the set
Y-X-\b\
it a tobalgebra o((X, 6), more precisely, that (YF)S c Y and therefore (Y, o~)
is a subalgebra of (X, 8\ where 5' is the restriction of £ Let
V: F-Alg - t
be a concrete isomorphism with a variety ► of £algebras. Each variety is
obviously doted under subalgebras and thus, it U fuflicient to show that Y is
a subalgebra of the £algebra
(AT. S) - (X, S)V.
In Tact, we then have a t algebra (Y, S") which (as a subalgebra oft
r-algebra) is i I-algebra, and (r, 8")V-' is i subalgebra of (X, 5). For each a e lot
arity n and for arbitrary y, e f, i < it, we are to show that (yL)S. € Y. Put
Af-|»|„.u|«| cX.
Since card U S n + I < y, we have (M)6 - a and thus, U Is a subalgebra of
(AT, 5). Consequently, Mbi subalgebra o((X,S); thus, (U)6 c 14 c Y and
this proves that 0>,)5, s r.
Since f is a subalgebra of (AT, 5) and 6 « f, we have (jr)5 - a for any
ie YF. In other words, for every x e YF there exists hi c X with ji € MF
and card Af < y[hence x e (Kn A/)f. by III-4.6L Since Y and AT are
isomorphic seta, X also hat the same property. □
Cerolbuy. Varieties concretely Isomorphic to f-Alg for set functors F are
precisely those concretely isomorphic to basic varieties.
Each banc variety it concretely isomorphic to f-Alg by Proposition III.3J.
Conversely, if F-Mg it concretely isomorphic to a variety r, then fit a
quotient of some Ht, and then Y is a basic variety of ^algebras by Proposition
111.3.2.
EierdsallM
A. Vector laaclwa. Let A be a commutative field,
(i) Prove that each epi and each (0 mono in Jt-Vaet split [Hint: If
142
Chapter III
e: JT-» Y'n onto, choose abase B c Y and for each b e B choose (6)m « AT
with ((6)m)e — 6; extend m to a linear map m: Y-* X.\
(ii) Prove that each functor
F. A-V«ct - A-V*ot
is naturally isomorphic to a functor preserving inclusion—such functors will
be called standard. (Hint: Proceed as in II 1.4.5, using bases.)
(ill) Prove thai each standard vector functor preserves finite intersections.
(Hint: Proceed as in 111.4.6, using bases.)
(iv) Prove the analogue of 111.4.7 for vector functors, using dimension
instead of cardinality.
B. Coarodocta aid comaoaeata. (i) A set functor F is said to be connected if
there exist no functors Fu F, distinct from C, such that F is naturally
isomorphic to F, + F,. Prove that this is the case iff F preserves singletons, i.e.,
card X - I implies card XF- I. [Hint: Given a € XF with card X - I,
denote for each set f by (r: Y-* X the unique map and define F, on objects Y
by YFi - I* € YF: (a)t,F - a): on maps f,fF, is a restriction of//7. Then put
F,-F-F,.\
(ii) Prove that each set functor is a coproduct of its maximal connected
subfunctors. [Hint: Choose X of power I and for each a € XF define F, as in
the hint to (i) above.)
C Uaear '■actors. Let A be a commutative ring. A functor F: Jt-Mod -»
A-Mod is Kntar if for arbitrary linear maps f.f.X-* Y and each t € A,
V+i)F-fF+$F «"■ (rf)F-r{/F).
(i) Prove that any product and coproduct of linear functors is linear.
Conclude that for each type £ the functor /fr (III.2.S) is linear.
(ii) When is the constant functor C„ linear? When is the functor £{(111.2.4)
linear?
(iii) Prove that a functor F: A-Mod -» A-Mod is a quotient functor of some
Ht iff F is linear and small The latter means that there is a cardinal y such
that for each module X and each x e XF there is a linear map f: hi-* X with
x € (MFtfF and with M having less than y generators. Hint: The proof is
analogous to that in III.4.3.
D. FmHary feacton tm A-Mod. A functor F: A-Mod-• A-Mod afinltaryit
for each x e XF there exisu a morphUm /: Af-» X with x e (MF)fF and
such that M is finitely generated.
(i) For each module U prove that SMand V„(Mt III-2.l5)are finiury func-
ton. For any cardinal n put
V. - V„.
£Aoloaau
143
where hi Is the free module on n generaton; verify that V. it the coproduct of
n copies of the identity functor.
(ii) Prove that Ht is finitary iff £ is a Unitary type, in which case Ht is
naturally isomorphic to Kfor h equal to the sum of all iritieM Hint: //„ — C, for
n < <o because finite products coincide with finite coproducts.)
(iii) Let A be a field. Prove that each linear, finitary functor F: A-Vact -»
A-Vactis naturally isomorphic to V. for some cardinal n. (Hint: As in 111.4.3,
prove that F is a quotient of some Ht, £ finitary. Prove that each quotient of
Hz- V.'m naturally isomorphic to some IV)
E. Piuenattoa of directed raioaa. A collection of subobjects m,: hi,-* X
(is I) a directed if for arbitrary i,J e / there exists a k e / with m, c m,
and tHj c nit-
(i) Prove that a standard set functor F is Unitary iff it preserves directed
unions, i.e., I U Af IF- U hl,F for each directed collection hi, c X.
(ii) Prove that a functor F: A-Mod -» A-Mod is finitary iff it preserves
directed unions, i.e., if U m, — m is a directed union, then U lm( m,f) —
HI It I
im(mF) (where im means the image). [Hint: Given x e im(mF), there exists
/: Af-» AT with x € (sYFJ/FandAY finitely generated, say, with generaton yh
..., yt. Each {y„\fbc\ot\gt to some im m,. ((. € /) and there exists i € /with
m,, c m, for all n. Then x e im(m,F). The converse inclusion
U im(m,f) c im(mF) is dear.)
F. Preserratloi of coutable colimits. Prove the following statements.
(i) Let Fbe a standard set functor with 0f - 0. If Fpreserves coequaluen,
then F preserves the countable coproduct
r-X+X+X+...tor each set X.
[Hint: Since 9F- 0, no point of Fis distinguished and hence, the copies of
Aff in YF are pairwise disjoint. It remains to prove that each y e YF lies in
some of these copies. Coding Km Y— X x Z (where Z is the set of all inte-
aen), tet g: Y-* Ybe the isomorphism with g(x, z) — (x, z + I). The coequa-
lizer of g and I, is the projection *: Y- X x Z-» X and hence, xF — co-
eq(»f. !»)• Thus, for each y e rT there is n < m and / e (Af x |z|)Fwlth
0')*"''- 00*"fand hence, j> e (* x [r|)f.|
(ii) Any set functor preserving finite colimits preserves countable colimits.
[Hint: If F preserves Unite coproducts, then 9F- 0 and F has no
distinguished point—we can assume that F is standard. To prove that F preserves
countable coproducts Y - X, + X, + X, + ..., find a set AT with Af. c Af
((< a>) and use (i): Since Fpreserves the coproduct X + X + X + ... and
also F preserves finite intersections, any point y e YF lies in some X,F.\
144 Chapter Ml
(iii) Any functor F: A-Mod-» A-Mod preserving finite colimits preserves
countable colimits.
G. PreserratloB of colhnlts. Vector functors, i.e., functors F: A-Vact-»
K-Vort, have properties analogous to set functors if they are linear:
(I) Prove that each linear vector functor preserving coproducts is naturally
isomorphic to some Vt. (Hint: Put £- RF. For each space X with base B we
have X — II R, with injections j,: R -» X defined by (r])M — rx. Then
XF- U<£= £® AT with a natural isomorphism r:X® X-* XF defined by
(o9x)r-(oy,F.\
(ii) Conclude that the only linear co-adjoints in A-Voct are Vt (up to a
natural isomorphism).
Ill j. Factorization Systems
5.1. We have introduced factorizatinn systems in III.2.7. In the present
section, we study some of the basic facts about them needed below.
Recall the hierarchy nf morphisms from Eierdse III.ID. In particular,
each regular (or split) mono which is an epi is an isomorphism.
PrefoalrkM. Let
(#.UT)
be an arbitrary factnrizatinn system,
(i) U* is right cancellative, i.e., if m, • m, e U* then m, e J*;
(ii) jK contains all regular mnnos, hence, all split monos;
(iii) pullbacks carry ur-mnnos, i.e., in each pullback
rrt
f I
m e jK implies m' e jK.
Proof. All this is a simple application of the the diagonal fill-in property
(III.2.7).
(i) Let m, - e. m be an image factorizatinn. We use the diagonal fill-in:
145
Since t a in epi as well as ■ split mono (id- I), we condude that e is an
isomorphism. Hence,
(li) Let m: X-* Kbe the equalizer of/ g: K-» £ and let m - <a ■ m, be its
Image factorization:
Then m, •/- m, ((because <a is an epi and t, m, /- f, • m, g) and thus,
there exists A with
m, — A- m.
Since m, is a mono and nig — A • e, • mfc we have A • «0 — I: since m is a mono
and m — t, • m, — c, • A • m, we have «a ■ A — I. Thus. <o — *"' is an
isomorphism which proves that m e jr.
(iii) Let «'-<(• ntg be the image factorization In the pullback above:
Using the diagonal fill-In we And a morphism d with
f' — tt-d and m„-f-d m.
The latter equation leads to a unique morphism d, such that the following
diagram
|46 Chipur III
commutes. Then e, • d, — I (because the Tact that m it mono implies that m is
mono and we have m — e„- m, — e,-d„-m). Thus, e, is an isomorphism
and we conclude that m' e JT. □
Reaark. We shall actually use the dual properties mnre often:
(i) / is left cancellative;
(li) / contains all regular epis:
(111) pushouts carry /-epis.
These are proved by the duality principle: if Jf is an (/, .#)-category, then
jr°» (III-2.I2) is an (ur. #)-category.
CsnUary. Each of the following categories:
S«t;
Jt-Mod (R a commutative ring):
ff,-Alfl(X any type)
has a unique factorizaltion system with t the class of all epis (- regular epis
— onto morphisms) and Jl the class or all monos (— regular monos — one-
to-one morphlsms).
This follows from (ii) above.
5J. The aim or introducing factorization systems is tn obtain a variety or
concepts or subobject and quotient object. Let JT be an (t, .JQ-category.
A subobject (more orecisely, .^-subobject) or an object A is represented by an
•4r-mono
m: B-* A.
Two ur-monos m:B-+ A and m': B' -» A represent the same subobject of A
ifT they are equivalent.
m — m'
which means that there is an isomorphism l:B-»B'tor which the following
triangle
■^AntomiU
147
B !— tf
n)\ At
A
commutes.
Thus, the exact definition of a subobject of A is: an equivalence class of
some JT-mono m: B -» A. (We usually identify the equivalence class with m
itself, as an abuse of language.)
Given two subobjects, represented by ur-monos m,: B, -»A and
m, :Bj -» A, we write
if there is a morphism /: B, -» B, with
m, — /• m|.
Note that, by the preceding proposition, this implies/e Jf and hence,
/represents a subobject of B,. The fact that we work with equivalence classes
implies that whenever
iw( c nt] and nij c n\u
then m, is the same subobject as m,. (Proof. We have m, - /• m, as well as
m, - g • m,. Then / is an isomorphism because m, - /• g ■ m, implies
/• ( — I and ni| — (•/• ni| implies f •/- I.)
For each object -4 we obtain an ordered class of all subobjects of -4 Its
meets are called intersections and are denoted by R m, (where / can possibly
be a large class); Its joins are called unions and are denoted by U m,.
Given a collection of subobjects
m,: B,-» A (i e /)
we can consider it as a diagram and we can (possibly) form its limit C with
projections
u,:C-.«, (If /)
and
u - u, • m,: C-» -4 (independent of /)'■
148
ClUptM III
(•)
If card / - 2, this is a pullback; generally, this is called a multiple pvBback.
The following extends (iii) of Proposition III.5.1:
Propoalihn. (Intersections are multiple pullbacks.) Let m,: B, -» A (I e /)
be a collection or Jf-subobjects. If (•) is a multiple pullback, then u, € Jt for
each / € /, and
u- fl m,.
Conversely, if u - D m„ then for each i € / there is a unique u, E ur with
u — u, • m,, and then (•) is a multiple pullback.
Proof, (i) Let (•) be a multiple pullback. We prove first that
Hi, « -*
for any <o e /. To do this, let u,, — i ■ m be an image factorization. We use
the diagonal fill-in for each i e I:
Since d, m, is independent of i, by the deflnition of multiple pullbacks there
esists a unique morphism
d.C-*C
with
d,-du, (i € /).
Then i d - \c because
(< ■ d) ■ u, - i ■ d, - u, (i e /).
£Aulomiu
149
Hence, e is a split mono as well as an epi, i.e., an isomoiphism. This proves
that u„ — i ■ m e jr.
Nent, we prove that u - D m,. First, u c m, because u - u, • m, (i e /)■
Furthermore, let u': C -+ A be an JT mono with u' c m, (i € /) and let
u',:C -* B, be the (unique) moronism with
u' - u] ■ m, (/? /)■
Again, there is a unique moronism
v:C-*C
with
u,' - v • ii, (i e /).
We have u' — v • u because, Tor any j e /,
u' — u,' • m, — v • u, • m, — v • n
Hence, u' c u, which concludes the proof that u — [1m,.
(ii) Let u - Urn,. For each i e / we have u c m„ thus,
/ < r
u- «,• m,
Tor some 14: C-» A, (which is unique because m, Is mono, and is in Jt because
ur Is right cancellative by II1.5.I).
To prove that (•) Is a multiple pullback, let/: D-» A and/: D-» B,(i e /)
be arbitrary moronisms with
/-/■ m, «€ /)■
We are to exhibit a moronism J:D-*C with /— /• u and
/-/.«, (/€/)■
(Then / is unique because u is a mono.)
Let/— «• mbean image factorization. Using the diagonal Till-in:
150
Chipter III
v
we conclude that m c m, (i e 0. hence
men
Thus, ifi - /o ■ u for some morphism /0. Put
Then
f-lm-l- /„•«-/.u.
Moreover, Tor each * 6 / we have/ — /■ u, because m, Is a mono and
/. m, -/-/• u-J- u, ■ m,.
This concludes the proof that (•) is a multiple pullback. □
SJ. Deflarttoa. An (#, ~*>eategory JT is said to have interjections if each
(possibly Urge) collection of ur-subobjects of any object A has an
intersection. In other words, if all ur-subobjects of A form a large-complete lattice.
JT is said to be Jt-well-powered if each object has only a (small) set of.M-
subobjects.
Propoaltloa. Let JT be an ur-well-powered (*, .^-category. If JT is either
complete or cocomplete, then X has intersections.
Proof, (i) Let JT be complete. Then it has small intersections, since these
are multiple pullbacks by the preceding theorem. And each large intersection
can be "reduced" to a small one by finding a small set of representatives.
(ii) Let JT be cocomplete. We prove that for each object A the (small) poset
of subobjects is a complete lattice. It is sufficient to prove that any (small)
collection of subobjects m,: B,■-» A (I e /) has a union. We form the coproduct
with injections v,: B, -» B (/ e 0,andwc define
f.B—A
by
». •/- i". (ie /)•
£Aulomiti
Let /- * • * be in image factorization. We prove that
m — Urn,.
First, m, c if> for each / c / by the diagonal (lll-ln.
B,—!—.b,
131
Nent, let *: B -» A be a subobject with m, c * for each / e Ale.,
m, — ii/ • ffi
for some u,: B, -» B. Then the moronism u: B-» B with components u, (i e /)
fulfils
»/•/-<"< -"/•*-»/•«• * (iff),
hence,
/- u- *
Using the diagonal fill in once more.
we conclude that ifi c m. This proves that m- [} m,. □
Rratarfc. Let us spell out the dual concepts which will be needed eitensively
in the subsequent chapters. Epis t.A-* B\nl represent quotient! of A; we
write
«£ «'
if the following triangle
A
152
Chapter III
commutes Tor some /(which is in if since * is left cancellative). If * £ «' and
«' £ e, then t and t represent the same quotient of A.
Joins in the ordered class of all quotients are called cointenections. The
cointenection of a collection e,: A -» B, (I 6 /) of quotients of A is given by
their multiple pushout
•iv
B,
\//
C
as the #-epi e - t,-f, (independent of /). If •* is *-co well-powered, i.e., if each
object has only a (small) set of quotients, then it hu cointenections whenever
It is either complete or cocomplete.
Exasiflem, (i) Quotients in Sat We can represent each quotient of a set A by
the canonical map
e:^-»^/£- \[x\:x e A).
where £ is an equivalence relation on A (and e assigns to each x e A its
equivalence class [x] under £). Then
<S «'i(T£c f:
thus, the least quotient is I., and the largest one has just one equivalence doss.
Given equivalences £ on A (i e /)• their cointenection is the equivalence £
denned as follows: given x, y e A then x E y iff there eiist elements io, z,.
.... r„ e A and indices / i, e / with x — i* y — z. and
*i- i£,*i for * — I n.
(ii) Quotients in fi-Mod. We can represent each quotient of a module A as
the canonical map
t:A-»A/B- |i+I;ie A\
where A is a submodule (and e assigns to each x e A the class x + B). Then
(S tiff Be B ,
thus, the least quotient corresponds to B — 0 and the largest to B — A. The
cointenection of quotients corresponds to union: given quotients
e,:A — A/B, (i € /)
£Automus
153
let B be the tubmodule generated by U '/; then
/ f i
C.A—A/B
Is the cointeraection or t, (i 6 /).
SA. Qaotkat hectors aid saWeecten. Let Jf be a category with a given
factorization system (/, ur). For each rnnctor F: JT -» JT, quotient functor* or F
are introduced analogously to quotients of an objects. Every /-tpitransforma-
tion e: F-* G(i.e., natural transformation with c,E/ Tor all K 6 JT*)
represents a quotient functor of F. Two /-epitransformations c: F-* G and
c : F-* G' represent the same quotient i(T there Is a natural isomorphism
r: C-» C with e-er. For example, the functor P, :S«t-» Sat (III.4.I) is
a quotient of H, because we have an epitransformation e: Ht-» P, given by
(*>•)- i*.yl
Dually, svbfuiKton of F are represented by ur-monotransformations
H:G-*F
3.5. We know that uT-monos are well-behaved with respect to equalizers
and (multiple) pullbacks. We continue with other types of limits. Lei D,
D':9-*X be two diagrams with limits L- lim Dand «>:L-» dD(A e 9°);
V - HmD and nt: V -» dD\d e 9°), respectively. Given a natural
transformation
It: D-D,
there esists a unique morphism
lim n: L -» L
with
lim n ■ av - *i for c*ch d e D''
(because the morphisms *,■ n,. L-* dD' form a compatible collection of D").
Piapaaltlua. Let JT be an (#, u»>cetegory. Let D' and D be two diagrams
which have a limit in JT, and let n: D' -» D be a natural transformation
formed by ur-monos. Then lim /i is also an ur-mono.
Proof. Let lim fi — e- m be an image factorization. Using the noution above,
we apply the diagonal fill-in
, y^
\/ h
dO' ;r—»-dD
(d«ei
154 Chapter III
The resulting collection pt: /.'„-» dD' (d e D'°) is compatible with D
because Tor each S: d, -» d2 in D'm we have
'•Pi, - *'«, - »i,• *D' - '■ Ov,■ SD\
and t is epi. Therefore, there eiists a unique morphism
p:L\ — V
with
Pt- P- x\ (<* e D").
Then <•p - I because
(t-p)-xd- tp4~ *„ (deD").
Since « is a split mono, it is an isomorphism and thus, lim fi is in Jt. □
Corollary. Given .#-monos m1:A',-»Al (i e /), then the product
morphism
rim,: ru,-»ru
is also an ur-mono.
Reaurk. Let D be a diagram with
A — colimD,
let et: dD-* A denote the injections (d e <F). IT e< — et- mt are image
factorizations, then
U m4- I,.
d « 9"
Indeed, given an ur-mono m: B -» A with mt c m(d e 9°), we prove that m
is an isomorphism. For each J E 9' «e have ft:dD-* B with mt — ft<m
Since m Is a mono, it is easy to check that the family et ■ ft(d e 9°) is
compatible. Hence, there exists f:A-*B with et-ft — t,- f. Then /• m — \A (because
et-fm - tjfj-m- t,-m,- c, Tor each d). Thus, m is a split epi and
a mono, hence, m is an isomorphism.
Dually, given a natural /-transformation or two diagrams, the colimit
morphism is in <f, too. In particular, if t, e «"(/ e /), then
For directed diagrams, more can be said. Recall that a directed diagram is
a diagram D: 1 -» JT such that 9 is a directed poset [<7 -(/,£) such that Tor
all i,j € /there eiists * € /with i 5 A and/ £ AL Then 0 consists of objects
D,(i € /) and morphisms d„: D,-» D^j 5 yj.We say that Dis a diagram of/-
epis if d,j € / whenever i < j.
£ADtomau |55
PrapoaJrJea. Let D be a directed diagram of /-epis. If D has a colimit, then
colimit injections are /-epis, too.
Proof. Denote by (/, £ ) the scheme of D and let A - colim D with the
injections
p.:D,-*A (le I)-
For any L e / we choose an image factorization
p„- t-m.
To prove that m:A'-»A is an isomorphism, it is dearly sufficient to verify
that any p, (i e 0 factors through m.
For each i € / choose * e / with (0i * and / £ t, and use the diagonal
fill-in.
Then i 5 * implies
A ~ ^i *' A ~ ^t *' r»' m-
Hence, m is an isomorphism, consequently, p„ e /. □
5.4. Leaiau. In each factorization system, the dass Jl determines the dass
/. a mnrphism /: A -» B is in / ifT for each commuting triangle
f
with q e U>, q is an isomorphism.
Proof. Let/e 4. Then we use the diagonal Till-in:
-►B
156
Chapter III
Since q is a split epi and a mono, it is an isomorphism.
Let/1 /■ The image factorization of/forms a triangle as above, with pet
and q i A. Then qis not an isomorphism (because else/— p-qi /). □
Ressarks. (i) If Jf is an (/,^(-category with -M - all monos, then / Is the
class of all extremal epii, i.e., morphisms/such that If/- p q and q is a
mono, then q is an isomorphism.
(II) If •» is either complete and well-powered or, dually, cocomplete and
cowell-powered, then it is an (eitremal epi, mono)-category. The proof can be
found in Herrlich and Strecker [19791.
If, moreover, regular epis are closed under composition, then
eitremal - regular. (This is usually fulfilled, for eiample in Sot, Poa, Top, A-Mod.)
Then we say that Jf has regular faaorltahont, which means that it Is a (regular
epi, mono)-category. The category of semigroups does not have regular
factorizations, though it is complete and well-powered and hence, is an (eitremal
epi, mono)-category.
(iii) Dually, the class M is determined by the class /. For eiample, if Jf is
an (epi, .JT>category, then ur is the class of all extremal monos. i.e., mor-
phisms/such that if/— p ■ qmi pi* an epi, then pit an isomorphism.
Each complete and well-powered (or cocomplete and cowell-powered)
category is an (epi, eitremal mono)-category.
Exercises III J
A. Moaos aid epis. Even without factorization of morphisms, the class of all
monos hu a lot of properties proved above for the class ur of an (/, ur>cate-
gory. We spell out the dual properties.
(i) Prove that epis are left cancellative, i.e., if a moronism e, • e, is an epi,
then 4 Is an epi.
(ii) Prove that a coproduct LI *.: II *i -* II ^ of eP'» '• always an epi.
(iii) Prove that, more generally, for each epitransformation e: D-* D" of
two diagrams, the colimit morphism eolim e: colim D-» colim D' is an epi.
B. Dincttd dlagrassa «f eats, (i) Generalizing II 1.5.5, prove that for each
directed diagram D of /-epis, a morphism/: colim D-» Kis in / iff each
component of/is in/.
(ii) Prove the same statement about the class / of all epis not assuming any
factorization of morphisms.
^Automate
157
Nous 10 Chspier 111
111.2
Algebras of a "finctoriaT type were investigated la lha category of sets by O. Wylcr 1196*1
V. Tmkova and P. OoraJUk [19*91 V. Koobek and V. Korkova-Pohlova |1974). (Id iHom papers,
iwo Kt fundon F and G arc given, and algebras arc pain (Q, 5), where Q h a tct aad
6: QF-* QC H a map: the cormpondiog categories are called genci allied algebraic categorie>.)
The mvestigatlofl of ut functon (see Note* for 111.4 below) was stimulated by time papen.
^algebras over a general category were tint Introdaced by M. Ban [19701.
M. A. AiMb aad E.G. Manes presented their model of automata based on a functor
F: M -• M in a Mfies of papers (Jl974a, b: 1973a, bD. All renin In 111.2 can be found in some
form in dme papers,
111.3
The fact that bask varieties are categories of ^algebras, and the corresponding eiamples of
set functors, have been a folklore on our seminar. The general problem of characterizing
categories of ^algebras over an arbitrary category has been attacked by J. Reiicrmen [1974).
111.4
Properties of set functors are investigated In a series of papen of V. Koubek, J. Reitennai and
V. Tmkovi. This section presents a selection of those papers. In particular, 111.4.2—6 are from
V. Tmkovi [1969,1971L eiccpt for Theorem 111.4.3 proved by J. Adamek, V. Koobek and V. Pa-
hlovi [19721. For 111.4.7. sec V. Koobek [1971). and for Eierdse III AF. see V. Tmkovi |1971).
111.3
Automatizations of subobjects and quotients appear since the very start of the category theory.
The present form is due to J. R. Isbdl |I937|: further historical references appear In M. Ban*
[1971). A theory of factorization systems Is developed by H Herrlkh and G. E. Strecker [1979).
Chapter IV: Construction of Free Algebras
IV.l. MrodacthM
Free univenal algebras are constructed "iteratively": the sets W, of all trees of
depth S n are defined by induction, and then the free algebra is W» for a
sufficiently large ordinal k (see 11.3.6). In the present chapter we study an iterative
constniction of free algebras in a category: objects W, are defined by
induction, and if the constniction stops, then Wk is the free algebra for a sufUciently
large ordinal k. The categorical constniction is simple and natural, and it can
be applied to a number of situations beyond universal algebra.
We work first with initial algebras, i.e., Tree algebras on 0 generators. In
universal algebra, given a type L, the free ^algebra on n generators is precisely
the initial algebra of the type £"" obtained from L by adjoining n miliary
operation symboli. AUo generally, free and initial algebras are closely related. If
(ft 5) is the initial algebra of type f: JT -» JT, then 8: QF-* Q is an
isomorphism and thus, ft is a fixed point of F (i.e., an object isomorphic to its
£image). Moreover, ft is the least fixed point in the sense defined below. The
initial-algebra constniction we study below is a natural generalization of the
well-known constniction of the least fixed point of an order-preserving map
due to Knaster and Tarski. We recall it below.
All constructions studied in the present chapter are transfinite. We define
a chain of objects and morphisms in a category .X, indexed by all ordinals:
i.e., a functor
W: Ord -► JT
(where Ord is the ordered class of all ordinals). A constniction W is said to
slop after k steps if wt»t, is an isomorphism: then all wL. turn out to be
isomorphisms for kS h. The object If, is then an underlying object of the free
algebra.
Free algebras need not exist, in general. A type-functor Ffor which free
algebras exist is called a tahiior. If F is a varietor preserving monos, we prove
Construction of Fret Algebra
139
that the free-algebra construction must stop eventually (under mild additional
hypothesis on the base category JT). It follows, e.g., that a non-constant set
functor is a varietor iff it has arbitarily large fixed points. If the free-algebra
construction stops after o> steps, we call fa finltary varietor. Whereas in the
category of sets finitary varietors are essentially just the Unitary functors, in
"suitably" ordered categories a surprising number of functors ere finltary
varietors. We present a lot of examples illustrating the way in which the
free-algebra construction works in the category of seta and in other concrete
categories. We also apply our construction to obtain free completions of partial
algebras and, more generally, of span algebras. We conclude the chapter by
a criterion on a functor F to be a (possibly not "constructive") varietor, in
terms of generation of f-algebras.
We are using the iransfmile Induction: in order to define W, for each ordinal
n, it is sufficient to define
(a) W.;
(b) W, t, for any ordinal n for which W, has been defined;
(c) W, for any limit ordinal i for which W.,n < I have been defined.
Also, to prove a statement concerning W, for all ordinals n, it is sufficient to
prove this sutement (a) for W* (b) for W, t, If It holds for W, and (c) for W„ i
a limit ordinal, if it holds for each VY„ with n < L
IVJ. IaMal-Aifefrra Omtractioa
2.1, Knaster-TaraU cnaatnctloa. We recall the construction of the least filed
point of an order-preserving map/: (X, S) -»(X, S ), where (Jf, S ) is a
complete lattice. The first step is the least element J. of X. The next steps are
(J. 1/1(1 )P The ostep Is
(J.)/'- V(J-)/"
and (J.)/'*' - [(J. )/•]/ etc. In general,
(J. )/•♦'-[( J. )/•]/ for each ordinal n;
(J.)/' - V (J-)/" for each limit ordinal (.
■ < i
This construction obviously stops, i.e., there exists an ordinal k with
(J. )/•-(!)/'*'.
Then (J.)/' is the least fixed point of/
Complete lattices are special cases of categories; order-preserving maps are
then precisely functors. What follows Is a natural generalization of Knaster-
Tarski construction.
160 duplet IV
12. Tba lalrlal-alfebra CMStracttoa. Let JT be a chain-cocomplete category
(Exercise III.I.F) and let X denote its initial object (the colimit of the empty
chain).
For each functor f: JT -» JT we define a transfinite chain of objects
J.F" (he Ord)
and morphisms
w..:l F"-» J.F" (n, m e Ord, n £ m)
by the following transfinite induction:
lJiilf^ilfi^...lf.. coltailf-S^^lF"1... .
»< »
(a) First step:
J.F*- 1;
IF' - IF;
wt i: X -» X f is the unique morphism.
(b) Isolated step:
If"*1 .(1F')F;
*.♦.....- »...F:(lF")F-.(iF')F
for arbitratry ordinals n and m with n S m.
(c) Limit step:
IF1- colim(J.F"; m.„).,„, ,
for each limit ordinal i, with the colimit injections
»„.,: 1F" -» 1F' for each n< i
Rtaurk. The fact that the morphisms w. m are supposed to form a chain fills
in all the "missing" morphisms. For example, we need not define explicitly
■»,.,: iF-flF1
because
»i.j - »»i.i-*i.j - >»o.iF-»'..iF1.
Also, w... — I if. Analogously, we need not define
■»...■: Hi-collmIF"-» hV
• < •
becauic it is uniquely determined by the fact that for each n < to.
Contraction of Fret Algebras 161
Therefore, w. - 4, is the (unique) morphism from IF' - colim If'*1 with
components »..mF. Further, »...♦ i - »y. •!».,•♦ n and »v.*i -
*V • +1 * *• +1. • +11 dc,
IS. DeflaltJoa. We say that the initial-algebra construction slops after
k steps if »v i ♦ i is an isomorphism.
1A. PrapaaMoa. If the Initial-algebra construction stops after Ac steps, then
the initial f-algebra is
(lf','u.,|.
Ofeacrmtloa. Even if the initial-algebra construction does not stop, it has the
following universal property: for each algebra (Q. 6) there exists a unique
compatible collection
/.: lf-»t? (n e Ord)
with f. f • S — f, ♦ i for each n e Ord.
Proof. For each f-algebra (Q. S) we define morphisma/.: J. F• -► Q by the
following transfinite induction:
(a) /,: J. -► Q is the unique morphism;
0>) f. * i - f.F- 6, for each ordinal h ;
(c) /: colim lf->ghu components /.(n < 0 for each limit ordinal L
We must prove that this collection is compatible, i.e.,
/. - >»..-•/- (»< i"),
and this will prove both that (c) is well-defined, and that the observation
above is true. We proceed by transfinite induction on m: assume that m, is the
least ordinal such that the equation above fails (for some <i). We prove that (a)
m, > I and (b) m, is not isolated and (c) m, is not a limit ordinal. Thus, m,
does not exist.
(a) For m, - I we hive/, - w,,, •/,: J. -► Q, since X is the initial object.
(b) We prove two auxiliary statements.
(bi)lf/. - »...-/., then/,,, - w., ,..,,•/.,,. We have
/.♦, -f.F-6- »..mF-(fmF-6)- w„,..,,-/..,.
(bj If n, is a limit ordinal with /. - «»._•/., for all n< no, then
^, - »»,-/«• This follows easily from J.f"» - colim If*.
• < *
Now assume that m, is isolated, and let n, be the least ordinal for which
162 ClupterlV
/, *!».,.,■,•/«,. Then <i, cannot be isolated by (b,), and it cannot be a limit
ordinal by (bj).
(c) If m, is a limit ordinal with /. - w, m-fm for all n S m< m* then
/. — >».. -,/-, by the definition of f^
Let the initial-algebra construction stop after k steps. Since
fk ~ *V» + i */» + i ~ *».» + i •./» f * o\
we have
•i:'...-/.-/.^*.
and thus
/,:(If, <...)-«?.*)
is a homomorphisra. To prove the uniqueness, we verify that each homo-
morphisro
g:(J.f.»r.'.*,)-(a«)
fulfil w,. > - f - /.. by induction on <i S *.
(») *•.»• I - /•: -L -» 0 because X is initial.
(t>) >»..»•»-/. implies
*■ ♦ I, I * # ™ ***■ • 1,1 + I ' *"*. ■ + I * f
~ Wn * I. k + I * jf* ^
-<«V.-I)F'«
-/.♦,.
(c) For each limit ordinal i with w.. • ■ (- /. (n < 0 we have
If- colim X F• and for each i < n,
• < *
Thus, w,, • g - /. This concludes the proof. D
Rcsnrk. In the above proof we used a type of transfinite induction which
will be often encountered below: we want to prove a statement S,,m for all
pairs of ordinals with n < m, and we know that
S... and S... imply S..t
for arbitrary n < m < k. Then it is sufficient to prove the following:
(•) S..ii
(b,) S„.. implies S,«,..« i (for each n< m);
Comtractloa of Free Algebra
163
(bj If n, is a limit ordinal and m > n, is an ordinal with S... for all n< n*
then SH..:
(c) If iit»limit ordinal with S.„ for all n < in < i. then S.., for all n< i
The verification of (bj and (c) will usually be elementary.
Examples, (i) The number k of steps necessary for the stopping of the
initial-algebra construction can be arbitrary. Let
JT - Ord
be the category of ordinals. Define a functor
f:jr-»jr
by
_ f fl + I if fl< *
"' " \ » if « S *.
The the initial-algebra construction proceeds as follows:
1,2 *,*,*....
and it stops alter k steps,
(ii) For the functor
f:jr-»jr
defined by
nF- n + I (he Ord)
the construction never stops. There exists no ^algebra, let alone an initial
£algebra.
(iii) Let JT - Ord <-> |oo| denote the category obtained from the ordered
class of all ordinals by adding the largest element eo. For the functor
G:jr-»jr defined by
nG-n+l (n e Ord) and ooG-oo,
the initial-algebra construction never stops: iu i-th step is k. Nevertheless. G
has a unique (hence. Initial) algebra (•», I.).
IS. Proaesttiotj. (i) If the initial-algebra construction stops after k steps,
then each wt, (n 2 k) it an isomorphism.
(ii) Let w, . be an isomorphitm for a pair of ordinal! with n < m. Then the
initial-algebra construction stops after m steps.
(iii) For each limit ordinal k the initial-algebra construction stops after k
steps iff F preserves the colimit
if- colim J. Fm.
164 Chapter IV
Proof, (i) If »>,,», is an isomorphism, then wtt,,.) — wk kt ,f is also an
isomorphism and so ia w».,,, - w».,,, • w(♦i., ♦ > Analogously further. For
the limit step * + a> we have
If'*'- colimIf'"
(see Exercise III.I.F) and • colimit of • chain of isomorphisms is obviously
formed by isomorphisms. Etc
(il) If w, . is an isomorphism (n < m), then we prove that »m.mt ,!• inverse
to
(iii) If the construction stops after k steps, then F preserves the colimit
X F' because colimits are unique up to isomorphism and so
J. F' *' - cplim (± F-)F - cpHm if", eplirn^ J. F'
with injections »„UII — >».»11 • wt. i,,. Conversely, if F preserves the
colimit If, then If" - coHm If*1 - colim If with injections
w. tF— »,U,,|- w,_,, i ■ w, lt i and hence, w».»*, is an isomorphism. D
Enaple: hklal aalrnial algebras. Let
JT - Set and F - Ht
(111.2.5) for a type £ The initial-algebra construction suns as follows:
J. -B; lHt- Z,; J.//}- 2;//,; etc
If we represent the elements of XHL by trees of the following kind
li<n)
Construction of Free Algebras 165
(keJ; and x, c X), then the elements of X /// are the following trees
J.
X/7]
±W
0 »i4
(Kn|
oel.,1,"!^
etc
Since Hi preserves inclusion (111.4.5) and since w„, is the Inclusion map of
0, it follows that *>,, — wt,HL is the inclusion map too and hence, also
"i, i - "i :Wr, etc Therefore, we have X c 1H, c i.H\... and the colimit
X Hf is just the union
x//;- Uih;.
■ < •
Again, iv . ♦ i is the inclusion map (because its restrictions to X HI are
inclusion maps), etc. On each isolated step we have XHI c IKJ*1, and on
each limit step, XH|- U //;.
■ < i
When does this construction stop? If E has no miliary operation, then after
0 steps, since X - X Ht. Assume £ »» 0. For £ finitary, the functor Ht pre-
166
Chapter IV
serves directed unions (111.4.3 and Exercise III.4.E) and hence, it preserves
the colimit J. Hf — colim X H}. It follows by the preceding proposition that
the construction stops after <u steps. And this corresponds to the results of
11.1.5: we see that X Hf is the set of all finite £trees over the empty set
For E infiniUry, the number of steps is larger: it is obvious that the
construction does not stop after k steps unless k is larger than all arities. On the
other hand, if * is » regular cardinal larger than all arities, then Hr obviously
preserves unions of fc-chains, and the constructions stops after k steps.
2.6. Recall that a fixed point of a functor F: JT -► JT is an object Q
isomorphic to QF. More precisely, a fixed point is an object Q together with an
isomorphism 6: FQ-* ft
Definition. The least fixed point of a functor f: JT -» JT is a fixed point
(Co. °o) such that for each fixed point (ft 6) there exists a unique raorphism
/:&- ft with fF- «„/«-'.
Profoshioa. The initial f-algebra, whenever it exists, is the least fixed point
off.
Proof. Let (Co, $t>) be the initial algebra of F. It is clearly sufficient to prove
that 8, is an isomorphism. Then (Co. 8,) is the least fixed point because
for each fixed point (Q,S) there exists a unique homomorphism
/:(Ct. *o) -»(ft *")• The condition fF- «, • /• «-' is equivalent to the fact
that/is a homomorphism, i.e., fF- 6— 6%'f.
For the F-algebra (ft,f, o\F) there exisu a unique homomorphism
/:(&.«.)-(ft *«.'•)• Then
/■«.: (Co, «.)-(©>,«,,)
is a homomorphism, too, because Sff—fF' &\F implies
S,-(f-S,)-/F-S,F-S,-(f- o\)F- oV
By the definition of initial object there exists only one homomorphism of
(Co. Oo) into itself. Since I Bo is a homomorphism, we conclude that
/• «,-■„..
Coiutnicllon of Free Algebras 167
Now, Sq • f — fF • 61F implies
60 •/— IqiF— Iffo/"-
Hence,
/- V
which proves that (Co, $>) is a fixed point D
Emanate*, (i) The power-set functor
/>: S«t-» S«t
(111.3.4) does not have an initial algebra. Indeed, P has no fixed point since
for each set X,
card X < card PX.
(ii) For the functor
//, + C,: S«i —Sot
each infinite set X a a fixed point since card X — card (X x X + [0|). The
least fixed point is the free groupoid on one generator.
Bataark. Interesting problems arise concerning the interrelationship of the
notions above:
(i) If a functor has a fixed point, does it have the least one?
(ii) If a functor has the least fixed point, does it have the initial algebra?
(iii) If a functor has the initial algebra, can it be obtained by the
initial-algebra construction?
The answers are negative, in general (see the exercises below). But under
mild restrictive conditions on the category JT, we shall show in Section IV.4
that the answers are affirmative for all monos-preserving functors.
2.7. If the Initial-algebra construction stops for F, what does thii mean for
related functors? We prove that for quotient functors it also stops; see
Exercise. IV.2.D below for the analogous result about subfunctors. First, we prove
a technical lemma which will be needed on several occasions.
Lesuaa. Let t be a class of epis in a category JT, which is closed under
composition with isomorphisms, and let JT be 4-cowell -powered. Given transfinite
chains U, V: Ord -» JT such that V stops (i.e., starting from some ordinal, V
consists entirely of isomorphisms) and given a compatible collection of/-epis
t.: (/,-» K,(n € Ord), then Valso stops.
168 Clupiwiv
Proof.
Let p be an ordinal such that each u^ m with p 2 n < m is an Isomorphism.
Then each
is an <f-epi. Since V, has only a set of /-quotients, there exists an ordinal q
such that all u, , • e, with 9 £ n represent the same quotient of (/,. Then each
f, . with 9 £ n S m is an isomorphism: since u, , • *„ and u, m- em represent
the same quotient, there exists an isomorphism
i: V,— r.
with
We have u, . • *_ - u, , • u. . • tm - u, , ■(,■*., and therefore.
Since u,. • *. is an epi, it follows that 1 — v,m, thus v... is an isomorphism. D
PropoaHloo. Let JT be a cowell-powered category. If the initial-algebra
construction stops for F: jr -» JT, then it stops for each quotient functor off
preserving epis.
Resaark. More in general, if JT is an /-cowell-powered (/, ur>category, the
same result holds for /-quotients of F preserving /-epis.
Proof. Let e: f-» C be an epitransformation. We present a collection of
epis
*.: J.F"-» J.C" (n € Ord)
which is compatible, i.e., fulfils
(•) wn.m •'*"'■• *..■ (1 <m)
(where »,.:lf"-»lf" and »,.:1C"-»1C" denote the morphisms of
Comtniedon of Five AJfcbres
169
the respective initial-algebra constructions). This will prove the proposition
by the preceding lemma.
(a) *„- I,: J.- J.;
0>) *.♦)- e1F.e.G- t.Fs1B. : ±F"* '-► J.C* ';
UF'IF
t„F
■I1.FTG
UO"IF-
■IKflG
(c) For each limit ordinal I the componenu or
*,: colim J. F' -* colim J. G"
are t, • *,., (n < 0- We must prove the compatibility (in order to verify that t,
Is well-defined). We use Induction in'the sense of Remark IV.2.4.
(a) *>i, ■ '< - t, ■ *>n because 1 is the Initial object.
(b,) If (•) holds, then the following diagram
iG-
- I1F"IF -
I-
I1OTF
!■
•S-F
UGTB •
-llFlF.
-I
UG*IF
1F-
-uono -io*
commutes,
(bi) If (•) holds for all n < n* where n0 is a limit ordinal, then it holds for
n.because if- colim If".
■ < ■•
(c) If (•) holds for all n 3 m < i, where I Is a limit ordinal, then it holds for
/ by the definition of
till remains to prove that each t, it an epi.
(a) n — 0: this is dear.
(b) If t, is an epi, then e.C is an epi and hence, *,., - eir. ■ e,C is an epi.
(c) For the limit step see Exercise lll.].B(ii). D
EufdtesIVJ
A. Least find aelat which ta aot aa laMal algebra. Let JT be the category of
partial groupoidi (JT, ■) (where ■ is a partial map from X x X to JO and
170
Chapter IV
homomorphitms f:(X. -)-*(Y,• ) (which are maps such that f(x, • jrj ~
/(*i) •/(']) whenever x, ■ x, is defined]. Denote by T the singleton (total)
groupoid.
Define a functor F: jr -» Jt on objects by (Jt -JF — T whenever • is
nonempty and (X,8)F- (PX,t) (where P is the power-set functor). On mor-
phisms/: (X, )-»()',») put/F-//"if • and* are empty, else fF is constant.
Prove that T is the least fixed point of F Using the fact that P has no initial
algebra, prove that F also has none.
B. Fixed aorats exist bat mtmt of then ta the least oae. Find such an example,
using posets as categories.
C. Ususpected start of the coastracfioa. Let us redefine the power set
functor (III.3.4) to obtain the following functor P* : Sat-» Sot
For each set X * 0, XP* - \U c X: Af infinite or U - 0|, »P* - a -
|0, 1,2... .|. For each map/: JT-» yeither Ufl" - UfP [ir(X}f\t infinite] or
MfP* - 0 (if (Wis finite and Y * 0] or fP* - l.(if/- I.).
Prove that the initial-algebra construction stops after a) steps, with
canKKf)-) - I. Yet,
card!/** - h„: cardJ.(/,•), - 2-; card J. (P*)1 - 2",....
D. Qaotkat faactan aad sabfaacten. (i) Verify that the functor
F: Ord -» Ord defined by
nF- n + I
is a quotient of the identity functor lM and yet, the initial-algebra
construction does not stop for F Why does it not contradict to Proposition IV.2.77
(ii) Let JT be well-powered. If the initial-algebra construction stops for
F: jr -» jr, prove that it also stops for each subfunctor of F preserving monos.
Hint: Find a compatible collection of monos analogously to the proof of
Proposition IV.2.7.
IVJ. Fto-Algebra Coastnctloa
3.1. Let JT be a category with finite coproducts. We are going to show that the
free F-algebra over an object /of JT is precisely the initial algebra of the
functor
F+ C,: jt-»jt.
Here C, denotes the constant functor of value / and thus,
X(F+ C,)- XF+ 1;
fiF+O-fF+U.
Construction or Free Algebras 171
Each (F+ C,)-algebra (ft 6) is given by a morphism
S.QF+ 1-Q
or, equivalently, by a pair or morphisms
8,:QF-Q and 6,-l—Q-
Conversely, given an /^algebra (ft S,) and a morphism 6",: /-► ft then we
obtain a unique (F + O-ilgebra (ft S) where $> and S, are components or &
Prfualtloa. An /^algebra (ft, &>) is freely generated by the object / with the
injection morphism 8,: /-» gifTthe corresponding (F + C,)-algebra(ft, £)is
initial.
Proof. Denote by jx: XF-* XF+ I and /,:/-» XF + I the coproduct
injections.
I. Ut (ft 5) be the initial (f + C,)-algebra. Then for each F-algcbra (ft 8,)
and each morphism S,: /-» (3 we have the corresponding (f + C,)-algebra
(6 6). The unique (F+ C,)-homomorphism
*,•:«?■ «)-(&<*)
is an F-homoraorphisra 5* : (ft $>) -»((J <5») extending 5,, because the
following diagram
OF 1
^.\
OF'I 0
,, \x
bf»i —r—* a
\ X
Of-. 1
commutes. Conversely, any F-homoraorphijrrj extending 5, defines an
(F+ C,)-horaomorphUm from (ft 6) and thus, it equals to S*.
II. Let (ft S,) be the free algebra with the injection 6,: /-» ft For each
(F+ C,)-algebra (0, 5) we have an F-algcbra £: &F-» (2 and a morphism
6,: I-* Q. Let (5* :(ft s»)-»(ft 4)be the unique F-homomorphism
extending 6,. Then, again, the diagram above commutes and thus
*,'•■( ft «)-((?.«)
BTf
172
diaper IV
is an (F + C,)-homomorphijm. Conversely, any homomorphism from (Q, 6)
to (ft S) is an F-homomorphism extending 6,; hence, it equals to S'. O
Reaurk. The free algebra /* can be constructed by an application of the
initial-algebra construction to F + C,. We present a simpler construction
(which coincides with the previous one on all infinite steps, as we shall
prove): instead or starting with ±(F + C,) — IF + /, we start with / alone.
Since we need both finite coproducts (for the "translation" from F to
F+ C, above) and colimits or chains (for the initial-algebra construction), we
shall assume that the base category JT is cocomplete. It would be sufHcient to
assume that JT is chain-cocomplete and has coproducts. (The existence of
finite coproducts implies the existence of all coproducts in any
chain-cocomplete category.)
XI. The free-algefcra CMtrracttoa. Let JT be a cocomplete category and let
F: .*-»jr be a functor. For each object /we define objects W,(n € Ord) and
morphisms h>, .(n 2 m) which form a functor rf: Ord-» JC:
1-^* I + IF "»"*''. / + (/ + /F)F-» ... -* W. — *'►
l,+ W.F* ... -► fV,-^m± K^i - /+ W.F^... .
We proceed by transfinite induction.
(a) First step:
W, - /;
W,-l+ IF;
»„.,:/-►/ + IF
is the first coproduct injection.
(b) Isolated step:
W ™ / + W F
w.*i.«!-Ii+ h>'.-V:I,+ W.F*\,+ W.F
for all n, m € Ord with n S m (see Exercise III.I.C for the concept of a co-
product like I, + w, mF).
(c) Limit step:
W, - colim W,
w< t
for each limit ordinal / for which the chain W,(n< I) and »,,(»i m< I)
has been defined:
are the colimit injections.
Reaurks. (i) As in the case of the initial-algebra construction, all the "miss-
Construction or Free Algebra* 173
ing" morphisms can be easily Tilled in. For example,
W|.J - *»l.l- »\l - (l|+ ">.!?)• Or + Wl.l'7).
and wm mt, is the unique morphism with
i»»+ !,•• •»•.•♦ i - I; + *>..mF for each n < oj,
etc
(ii) Denote the coproduct injections of W,+ , - I + tV.Fby
n.:/-H'.+ , and <p.: W. F- W. t,.
Each W.n "almost" an * algebra: p. leads from W. Flo W.+, (Instead to W.).
If "j. i +1: "^ -* ►•»+1 is an ismorphism for some t, we obtain an F-algebra:
We are going to prove that this is the free algebra (with the injection 17,).
DefMrtoo. The free-algebra construction Is said to slop after k steps if
m. i +1 is an isomorphism.
The functor Fit called a constructive varletor if tht free-algebra construction
stops for each /; Fis a finltary varletor if it always stops after <u steps.
ExasaaJca. (i) Sr: 8«t -» 8«t is a Unitary varletor (see 111.2.4):
yy,-i.
Wt- 1+ 1 x £- 1 x (|0| + £).
i
Wt-l + (l+lx£)x£-l+lx£+lxP-lx U £'.
*-•
In general,
ry. - 1 x U £' (n< 0)
and
W. - collm w- [j w.- I x £'.
(ii) More in general, each coadjoint is a finitaiy varietor (see IIIJ.I I):
Hi- /,
W, - I + IF.
rVt - I + (/ + IF)F- 1+ IF+ IF',
W. - U IF".
174
Chapter IV
In particular, the functor Vl: /t-Mod-» /t-Mod is a finitary varietor.
(iii) The functor St: /t-Mod-» R-Mod is a finitary varietor (see III.2.4):
Wo- /,
W{ - 1 + ISC - I + I + £,
rfi -/+(/+/ + £)SZ - 1+ 1+ 1+ £+ Z,
in general, W„., is the set of all pairs of polynomials (i. + I, i + ... + Ci",
<t0 + <T|i + ... + a,. ,i" -').
(iv) The functor Ht: Sat -» Sat is a varietor, and it is finitary Iff the type L
is finitary. This can be derived from Exercise IV.2.S and the following
proposition.
33. Proaoslttoa. The free-algebra construction over an object / coincides on
all infinite steps with the initial-algebra construction of the functor F + C,.
Reaurka. (i) The individual steps of the free-algebra construction are
defined as colimits (coproducts for isolated steps and chain-colimits for limit
steps). Since colimits are determined only up to isomorphism, the proposition
just slates that there exist isomorphisms
a.: J.(F+ C,)'— W, (n € Ord, n i a)
which are compatible with the constnictions. [That is, denoting by
*„„: ±(F+ C,)"-» ±(F+ C;)~ the connecting morphUms, then for all
sSiSnmt have *,.. • a. — a. • »,.«.]
(il) The two constructions can differ dramatically on finite steps. For
example, let / + 0 be a finite set and let F be the functor f* of Exercise IV.2.C.
Then
card !(/>• + C,)" - V ' (n< oi)
and yet,
tV, - 1+ IP'- 1 + |0|,
W, - I + (/ + |0|)P* - / + |0|
etc., and hence, the free-algebra construction stops after I step.
Proof. We write C, + F rather than F + C,, and we denote by
the objects and morphisms of the initial-algebra construction of C, + F. Thus
W- ±;
#•.♦,-/ + W,F;
\Vt — colim &. (/limit ordinal).
Construction of Free Algebras
We are going to define compatible morphismt
a.:*.-. W. (n € Ord)
and
A: «'.-*'.♦, (iKa.),
and then we prove that a. are isomorphums Tor ill n 2 in
175
W:l
W:l
-*■ WF
MHFIF-*—-"-WL.
»HHFlF— "Wu
There is a unique morphism
a,: J. -► /;
given a., put
a., , - I, + a,F: 1 + W.F-* 1 + W,F;
Tor each limit ordinal i let
a,: colim Ir7. -» colim W.
have the components a, • w,, (n < /). We prove that these morphisnu are
compatible, i.e., that the following square*
1, ► w«
I I"
commute for all a < m, by induction. See Remark IV 2.4.
(a) "m - I: this is dear, since l&, - ±.
(b,) If the square above commutes, then the following one
VN.F
«L, - I«w„F -
- 1-wlf - w«
\'«*F ViF
'—1
w^ - |.W„F -
-•• 1*<*LF - w—
also commutes.
176 Ck«|H« IV
(bj) Kthe squares above commute for all n < n0 where n, is a limit ordinal,
then they commute Tor n„ because &n - colim &,.
(c) If the squares above commute for all n 2 m< i, where i is a limit
ordinal, then they commute for i by the definition of a,.
Further, let us define A: tV, -» tVn t, (n < oj) by the following induction:
is the first coproduct injection, and
A.i-I/ + Af ("< <»)•
It is easy to prove by induction that
a. -A- *...♦. («<<»)■
P.- a., i- ».,.», (■< a>),
and
*>...■ P. -P.- *.♦!... i (hSffkoj).
Hence, the morphisnu
A-»-i..:W.-»*'. (n< a»)
are compatible, living rise to the unique morphiim
P.: W.— W.
with
*>...■ P. -P. ■ *.♦!.. (■<»).
We claim that a. is an isomorphism with the inverse morphism pm: firstly,
pm • a. — I because for each n < a),
w... • (P. ■ a.) - A • *» • i.. • a.
- A • a.,, • w.,,..
• •"..
Secondly, a. • pm — I because for eacb n < to,
*...(<».• A)- a.- »...- P.
a.- p.- ■»,♦!.,
It follows by transfinite induction that each a., n 2 at, is an isomorphism.
For example, a.., — 1; + a. F is an isomorphism (inverse to I; + pm F) and
".♦ j - 11 + am,\F is an isomorphism, etc. Also alm — colim a.*, is an
Construction of Frc Alfcbru
177
isomorphism because each a.», is an isomorphism, etc. This completes the
proof. D
14, Corollary. If the Tree-algebra construction stops after k steps, then
/• - Wt
with 9 - 9, ■ »£',. ,: I'F-* /' and n - n,: /-► /*.
For a limit ordinal k, tbe free-algebra construction stops after k steps iff F
preserves the colimit Wt — coMm Wm,
For k £ a) this follows from the fact that the initial-algebra construction of
tbe functor F + C, stops after k steps, see Propositions IV.2.4 and IV.3.1 (and
for the latter statement also Proposition IV.2.5<c)]. If the free-algebra
construction stops after k < oi steps, then it also stops after oi steps and
Remark. Even if the free-algebra construction does not stop, it has the
following universal property: For each /^algebra (ft S) and each morphism
there exists a unique compatible collection /,:n',->l?(»f Ord) such that
the components of
/.♦,:/ + rK.F-ft
are/:/-» ft and/.F- 6: W,F-» ft In fact, the first step Is/. -/the isolated
step is given and the limit step is determined by compatibility (the
components of/: colim tV, -» ft must be /„ n < /).
Let the free-algebra construction stop after k steps. Then
/'-/.:(»'..* -H-ri*,)-((?.«).
3.3. Corollary. Each functor preserving colimits of it-chains for some infinite
cardinal till constructive varietor. Eacb functor preserving colimits of o>-
chalns is a finltary varietor.
Raaark. Let JT be a category with finite coproducu and colimits of
it-chains for all k s *» Then we can define the first k, + 2 members of the
free-algebra construction as above. Again, if h^ ,,, is an isomorphism for
some t S *,, then /* - Wt.
Thus, for example, in the category .* of countable sets and maps we can
investigate finitary varietors.
Example: Frce-naay aartH algebras. Let £ be a type of many-sorted
algebras (III.3.7). Say, two-sorted, for simplicity:
r-<r", r»).
178
ClupterlV
Let us apply the free-algebra construction to the functor Ht: S«f-» Sat1 in
order to obtain the free algebra generated by an object / - </*, /i). Recall that
for each (X,, X{> we have
(X„XdHt-( LI X? x X?. II X? x XT )
V^r^J.*! »#rw,. ■! /
Let us represent the elements in the sMh summand of the first sort by the
following trees:
(i<m,l
lj<m,l
where a e £"> has arity |cr| — (m,, mj and x, e X, for i < m„ yt € X, for
j < m,. Analogously for the elements of the second sort The elements of
W» - </„ />)
are represented by singleton trees with two labels:
where x e /, and y € /,.
Given W, - <»".". «"."), then
W.«. - /+ ^.Wf-<»"."♦,. »".*♦,).
The elements of
»".".,-/,+ II (»".")-* en")-
..rfi;..,
are represented (a) by the (singleton) trees of /, and (b) by the following
trees:
(«l
IK ni,)
()<">»>
Construction or Free Algebra
179
where I, e rf"„" for i < m, and j, € W? lor J < m,. (Analogously with »"„".)
We tee tbat the elements of each W. are labelled tree* such that
(i) the label of each leaf is (x, k) with k- I or 2 and ie /, or x € XJ'0;
(ii) the other nodes hive labels (cr, *) where k - I, 2 and cr € X1^,1..,
(m, + m, > 0) and they have m, successon or sort I (i.e., or label (—, I) on
the root) and m, successon or sort 2 (label (—, 2)). The successon or the Tint
sort are depicted left-hand to those or the second sort.
If ris a finltary type, then Wr preserves colimits or axhainj and hence, it is
a Unitary varietor:
/• - Wm.
Here, Wm is the algebra of all finite labelled trees satisfying (i) and (ii) above.
For an infinitary type L, let k be a regular infinite cardinal such that given
a e L with |cr| - (n„ nj, then n, < k and n, < k. Then Hz preserves colimits
of t-chains and hence,
/• - Wt.
Analogously to the one-sorted case (11.3.6) it can be proved that Wt is the
algebra or all finite-path labelled trees satisfying (I) and (ii) above.
X6. EMuptt: Free rniaiiHllii groyoldi. We have seen in III.3.1 that
commutative groupoids are just rYalgebras. Let us apply the free-algebra
construction to a set / assuming, for simplicity, that / does not contain any
element of the type \x, y\ (I.e., / r\ XP, - 9 for each set X). Then
If* - Iv IP, - \x; x e l\ u \\x. y\: x, y e l\:
W, - lu(lu IPJP, - \x; x e /| u ||* y\: x. y e Wt\.
etc.
The elements of
*.- U W.
•re (i) the elements of /, (ii) the sets |x, y\ with x. y e /, (iii) the sets |x, y\
where x and y are elements of type (i) or (ii), etc. Since P, preserves ru-coli-
mits, we have /* — Wm. The operation is defined by *• y — \x, y\.
EurcbalVJ
A. Noa-coHtnicthe varietor. Denote by Gia the category of graphs. I.e., pain
(X, p) where X Is a set and p c X x X; the morphlsnu are compatible maps
f: (X, p)-» (Y. cr), i.e., maps such that Xipx, implies (x,\fa(xjf.
180
Chapter IV
(i) For each cardinal n denote by
C-(«.p.)
the complete graph of power n: here n is the set or all ordinals i < n and ip.j
ifT i + J(i,j < n). The chromatic number of a graph (Jt p) is the least cardinal
n Tor which there exists a morphism from (Jf, p) to C.; we denote it by
*(*, p). Verify that each graph (X, p) without loops (i.e., without points x e *
with xpx) has a chromatic number and that x(X, p) £ ^(J", o~) whenever
a compatible map/: (Jf, p)-» (K a) exists.
(ii) We define a functor F: Gia-» Gra which rums out to be a
non-constructive varietor. Let
t- (io, ie, oi)
denote the graph which consists of a singleton loop. Put
(Xp)F-\T if*-« or (Jtp) has loops
lQ- ifz(*P)-n>0.
For each morphism /: (X, p)-» (Y, a) let fF be the constant map to ( if
(Y.a)F- T; else, we have(X, p)F - C,.and(r. a)F- Q.with2" S 2"and
/Fit the inclusion map.
Verify that Fis well-defined and that it is a varietor with /" - / + Tfor
each graph /.(Hint: For each F-algebri(g, S) the graph Q has a loop. Thus,
6: 7"-» Q is only a choice of a loop.]
(iii) Let / be a graph without loops. Prove that the free-algebra construction
never stops by verifying that £(rf„) < *(lf„,,) for each'a
B. Free ordered £>rgebru, see 111.3.5, are just the free ^algebras (of
labelled trees) with an apropriate ordering. Describe the ordering, using the
free-algebra construction.
C- Free algebras la coacrete categoric*. Let (JT. (/) be a concrete category
(111.3.8) with products and colimits preserved by U. Generalize the preceding
example to prove that free ^algebras in JT are just "appropriately structured"
algebras of £trees.
Compare this with unary linear algebras (II 1.2.4).
D. Faactorlal varieties. Each of the equations below describes a variety of
algebras which coincides with some F-Mq, see IIIJ.3. Find F, and describe
the free algebras (applying the free-algebra construction).
(i) I-It -||;xx-y-y.
(ii) I- |-.0| with |-| - 2,|0|- 0;x-x-0.
(iii) Z- Z, - (-, +|; x-x- x + x.
Construction of Free Algebnu
181
IW4. CbaracteiizatiM Theoren
4.1. Dcflaltio*. A class .M of monoi in a category Jt Is said to be chain-cocom-
pkie if JT is ^•well-powered, Jt contains all isomorphisnu, and each o-chain
of ur-monos in Jf
P*.'-f.-*f. (nSnKa)
has a colimit />„: /"„-» P(n < a) with the folloving propertiei:
(a) p„ e 4r for each n < a:
(b) given a compatible collection q,: P.-» Q(n < a) In Jt, then the unique
factorization morphism q: P-» Q is in Jt, too.
Remark. It follows that, furthermore:
(c) j* is closed under composition. (Given p: f>0-» P, and p': P\-* P, in Ut,
we obtain a 2-chain the colimit of which is Pt with injections p-p', p\ If,.
Thus, by (a) above, p-p' e jr\]
(d) JT has an initial object X and the (unique) morphlsms q: J. -» Q are all
In j*. (Indeed, apply (b) above to a - 0.]
We are going to show that the questions asked In Remark IV.2.6 have
affirmative answers provided that Fpreserves uT-monos, I.e., given m: A-* B in
Jtx then mF: ^4F-* ifFis also in Jt.
Theortta. Let Jf be a category with a chain-cocomplete daas ■■*■ For each
functor F: jr -» jr preserving Uf-monos, the following are equivalent:
(i) Fhas a fixed point;
(ii) Fhas a least fixed point;
(iii) Fhas an initial algebra:
(iv) the Initial-algebra construction stops.
Proof. By Propositions IV.2.6 and IV.2.4, the implications
(iv)-» (iii)-» (ii)-» (i) are clear. We prove (i)-» (iv).
We show first that the morphisms ►»,,. in the initial-algebra construction
are ur-monos: it follows that the colimits defining X F for limit ordinals i
really exist. We proceed by transfinite Induction on m using Remark IV.2.4.
The first step is dear: w0. i e jH by (d) above, (b,) Let n, m be ordinals with
w.m € J*. Then
w.n..n - »,..f£ Ut
because the functor F preserves uT-monos.
(>>i), (c) These steps follow from (a) and (b) In the definition above.
Let J be a fixed point of F, and let
J-.JF^J
182 duplet IV
be an isomorphism. We define compatible uf-monos
p.: 1.F-—J (n e Ord)
by the following transfinite induction:
P.:±-*J
is the unique morphism (In -M, by (d) above].
Given p„ put
P..i -p.Fj:(±F-)F-*J.
Then p,» , e J* by (c) above.
For each limit ordinal >' let
p,: colim ±F"-» J
have components
*>..,■ Pi -P. ("< 0-
Then p, e J* by (b) above. Let us prove that the morphisms p. are compatible,
i.e.,
P.- *...• /».
Tor all n < m, by induction. See Remark IV.2.4.
(a) m - I: Clearly, p, - w0, • p,.
(b) If p.- w... p., then
- V...F-P.FJ
~ *»+ l.« + | * Pm* I'
The limit steps (bj and (c) are clear.
Since JT is uT-well-powered, there exists an ordinal * such that p, represents
the same subobject o(J as any p„, n2i. In particular, as p4» ,. Thus, there is
an isomorphism u: If1-. IF"1 with p, - u • p,4 ,. Since also
Pi - Wi.i,! • Pi»i and p,., is a mono, we conclude that u — w,»♦ i. Hence,'
the initial-algebra construction stops after * steps. □
4J. DeflaHloL A class jM of memos is called constructive If It is chain-co-
complete and "additive", i.e., given p: P-* fi and p': l*'-» ff in -*, then the
morphism p + p': P + P' -» Q + ff is also in Uf.
CbaracterliithMi Theorem. Let JT be a cocomplete category with a
constructive class Jt. For each functor f: JT -» JT preserving uT-monos and each
object /, equivalent are:
(i) F has a free-algebra over /:
Commotion of Fret Alfebm
183
(ii) the free-algebra construction over / stops;
(iii) there exists an object J isomorphic to / + JF.
Proof Apply the preceding theorem to F + C, (see IV.3.1). Since .M Is
"additive" and both F and d preserve uT-monos, F + C, also preserves uT-mo-
nos. □
riif In (I) jr - Sat has a (unique) constructive dau, viz, all monos. The
colimit of a chain of inclusions p.... P.-* P. (nS m < a) is the union
P - UP.. The condition (b) above states that each map q: f>-» Q which is
■ < •
one-to-one on any P., is one-to-one on all of P.
(ii) In a lot of current cateiories. all monos form a constructive dau. For
example, in jr - posets, topological spaces, groups, lattices, etc.
Regular monos also often form a constructive class—see Exerdse IV.4.A
below.
(iii) The category jr of rings and ring homomorphisms fails to have any
constructive dan of monos. Indeed, J. is the ring of integers and there are
lots of rings Q such that the unique homomorphism J. -» Q Is not one-to-one
(— mono).
Corollary. A functor F: Jf -► JT preserving monos of a constructive dau is
a varietor iff for each object / there exists an object J s / + JF.
Resaarfca, (i) In the proof of Theorem IV.4.1 we have seen that
»«,„ e Jt for each n s m.
The same holds for the free-algebra construction (under the hypotheses of the
Characterization Theorem). This relates well to our intuition that If. Is the
"n-th approximation" of the free algebra /*. Consequently, oeuV.
(ii) The functor C: Ord -» Ord of Exerdse IV.2.4(iil) Is a non-constructive
varietor though it (trivially) preserves monos. This shows that the hypothesis
that JT be uT-well-powered is essential.
(iii) The functor of Exercise IV.3.A is a non-constructive varietor (though
all monos are constructive in Qra). This snows that the hypothesis that F
preserve ^aT-Rionos is essential.
4.3. The Characterization Theorem makes it possible to give a simple full
characterization of varietors In Sat (see below) and in categories of vector
spsces (see the next section).
Each constant functor
C»:Sat->Sat
is a Unitary varietor. Here
lf„- /:
184
Chapter IV
W, - I + M;
If, - / + M;
etc.
The free-algebra construction stops liter I step with /• - / + M. Also the
consunt functor Ci(III 4.1) is a rinltiry virietor Tor uiy map h: U, -► M. For
/ * 0, the construction stops after I step, ind for / - 0 we hive
lf| — 0CW ™ Mi,
ind we sec that the construction stops after 2 steps.
TtMortn. A non-constant functor
F:S«t-S«t
is i (constructive) varietor iff it has arbitrarily large fixed points, I.e.. for each
cardinal a there Is a set X with card X - card XFi. a.
Proof. Since F is non-constant, there is a cardinal y such that
ariXFZ card X whenever card X2 r(»ee III.4.7).
(i) Let F be a varietor. For each cardinal a choose a set / of power
max (a, r, K0). The free algebra /' is a fixed point of F + C, (IV.3.1), thus,
card/" - card /• F+ card/- card l'F
(since card I'Fit infinite and larger or equal to card IP2 card /). Hence, /*
Is a fixed point of F of cardinality 2 a.
(ii) Let F have arbitrarily large fixed points. Since F need not preserve mo-
nos (because of the empty maps), let us redefine F on the empty sets and
empty maps—the resulting functor f" is defined by XF" - XF'ttX + 9; 9F' - 9
and for each non-empty map / fF.' — fF.
Then f" preserves monos and has arbitrarily large fixed points. Hence, for
each set / there exists an infinite fixed point J of power 2 max()', card /).
Then
J = I + JF-
because card JF 2 card J 2 card / implies card / -I- JF' - card JF' -
card J. By Corollary IV.4.2, F" is an constructive varietor.
It follows immediately that for each non-empty set / the free-algebra
construction for F stops, too. Let us verify that the free-algebra construction over
9 also stops. This is clear if 0F- 0; let us assume 0F> 0 ind hence XF+ 9
for iny set Jf(see III.4 2). We hive W, - 9F: Let us choose i fixed point J of
Cofutrooton of Free Algtbm
185
Fwith
card J 2 card OF
and let
J.JF^J
be a bljcction. As in the proof or Theorem IV.4.1. it It lufllcient to exhibit
a compatible family of monos p.: OF" -» J (for all ordinal! n).
(a) First two steps:
p,: 0 -► J a the (unique) empty map:
p,:0F-» J is an arbitrary mono
(we use the fact that card J 2 card OF).
(b) Isolated step:
P..>-p.F-j:(0F-)F-*J
for each ordinal n > 0. The veriflcation ofcompatibility is the same induction
as in the proof of Theorem IV.4.1. Since p,: OF'-* J It a non-empty map. the
assumption that p. is mono implies that p. F it mono and hence, so is p. ♦ ,.
(c) Limit step it trivial. □
4A. In universal algebra the number of steps after which the free-algebra
construction stops is independent of the generating set /. In general, the
number of steps can increase with increasing / without any bound. Let us exhibit
such an example.
Euaaate. Given a class C of cardinals, define a functor Pc: Sat -» Sat as
follows: for each set X put
XPC- |Mc *;cardJt#e CorM-0|;
for each map f:X-+Y put
(Aft/P - I '"^ if ^" one-,0_one on M
u c ™ \ 0 else.
Whether Pc is a varietor or not depends on C: for example, if C - all
cardinals, then Pe obviously has no (lied point, hence no free algebra. On the other
hand, Pc is a varietor for each class Cwhh the following property:
(•) There exist arbitrarily large cardinals k
such that *" - * for any n e C, n S *.
In fact, any Infinite set X of power k as above is a fixed point of Pc because
cardWt-cardZ*-- Zk'Sk-k-k- card*.
* • c ■ • c
186
Chapter IV
It is easy to construct a class C or cardinals which fulfils (•) and has arbi-
tratrily large elements. (For example, assuming the Generalized Continuum
Hypothesis, we can choose C— C„ the class of all ri. where n is an even
ordinal.) Then the number of steps necessary for the free-algebra construction
over ^increases over all bounds: if card/ — m e C, then the construction
requires more that m steps. In fact, for each n s m we can find a set A c If. of
cardinality m such that A i. Wm for any n' < a Then A is an element of tV.Pc
with (A )e>, «, (If,) if..., i and hence, w.,« , is not surjective.
ExMik: A cupradacf of two rarletora wblck b aot a rarletor. Let C be
a class of cardinals such that both C and C (the class of all cardinals not
belonging to C) satisfy (•) and contain arbitrarily large cardinals. Then Pc and
Pc are varietors but Pc + Pc is not a varietor, in fact, Pc + Pc has no fixed
point Such a class C can be easily constructed (for example, C, has this
property under the Generalized Continuum Hypothesis).
This example is rather surprising in view of the role which coproducu of
type functors play (see II 1.2.5).
A subfunctor of a varietor need not be a varietor (Exercise IV.4.C below)
and, dually, a quotient of a varietor need not be a varietor, see IV.2.D.
Exercbu IV.4
A. Cafntractrn clatsft of maos. (i) Prove that in every concrete, cocomplete
and well-powered category Jf the class
j* — all monos
is constructive if (I) monos are just the one-to-one morphiims, (2) they are
"additive" and (3) colimits of chains of monos are (suitably structured)
unions.
Verify that all this holds in the categories of posets, graphs, topological
spaces and modules.
(ii) Verify that all regular monos in Poa (— embeddings of subposets) form
a constructive class.
In contrast, regular monos in Top (— embeddings of subspaces) are not
constructive: consider the oi-chain of discrete spaces on n — |0, I
n — I |(n < <»); its colimit is the discrete space on to. Let Q be the topological
space on a in which a set M c a> is closed iff Mis finite or 0 e U. Then the
embeddings n -► Q are regular monos though the induced map id.: o> -» C is
not regular.
(iii) Verify that the category of (^complete lattices and ^complete homo-
morphisms has no constructive class of monos. Consider the i>>-chain of
lattices A, <_/ |T) (n < a) where T is the largest element and A. is the set of all
Construction of Free Algebra!
187
subsets of |l, 2 ..., n| ordered by inclusion. Its colimit Pis uncountable and
there exist ^complete homomorphisms q\ P-+ Q which are not one-to-one
though each restriction to A, <_/ |T) is one-to-one.
B. Qaorleibi of a varietur, (i) Let Jf be a cocomplete, cowell-powered
category. Prove that for each constructive varietor F: Jf -» Jf, all epis-preserving
quotients of Fare also constructive varietors. (Hint: IV.2.7.)
(ii) Verify that the hypothesis that Jf be cowell-powered is essential. (Hint:
Exercise IV.2.D.)
C. Sabfmctors of a varietur, (i) Let Jf satisfy the hypothesis of the
Characterization Theorem. Prove that for each constructive varietor F: Jf -» Jf
preserving J* -monos, all Uf-subfunctors of F preserving Uf-monos are also
constructive varietors. (Hint: Let /<: C-» Fbe a natural transformation with all
/j,In j*. It is sufficient to find compatible Uf-monos p. from If,, the free C-al-
gebra-construction over /, to #., the free F-algcbra-construction. Put po - I;.
Given p.: If.-* ^.putp.,, - I, + p.On»..)
(ii) Consider the varietor F: Gra -» Gia of Exercise. IV.3.1. Prove that its
subfunctor G, defined as F except that
(Jt p)G - («, B) if (Jl£,p) has loops or*- «
is no varietor: it yields no non-empty algebra.
D. CacMaaJetsaeai la the CharacterhatlM Theorem, (i) Verify that the
Characterization Theorem would not be true if instead of cocompleteness of Jf we
would assume only chain-cocompleteness. (Hint: Use a finite poset as Jf.)
(ii) Prove that, however, the Characterization Theorem remains true if co-
completeness is weakened to chain-cocompleteness and the existence of finite
coproducts. Remark: from this, the existence of all coproducts follows
anyway.
IVJ. Algebras la Ceacrete Categories
S.I. Let (jr. V) be a concrete category (see III.3.8). We prove a powerful
criterion for a functor to be a constructive varietor.
DeflaJttoa. A functor F: Jf -► Jf is said to be non-iitertaslitg if there exist
arbitrarily large cardinals n such that
auiAUSn implies card (AF)U S n for all objects A in. «f.
Example. A set functor is non-increasing iff it is a (constructive) varietor.
In fact, each varietor Fis either constant (and then it is clearly
non-increasing) or Fhas arbitrarily large fixed points (IV.4.3). Let n 2 card OF be the
188
Chapter IV
cardinality or a fixed point or F. Then
card A S n implies card AF S n
by Proposition 111.4.7. (If B is a fixed point of cardinality n, then
card A s card B implies card AF s card BF - n for A •> 0. and we have
cardflFS n).
Conversely, let F be a non-increasing set functor. If F is constant, then F is
a Unitary varietor. If Fis non-constant, we choose y such that card AFi.
card A for any set A of cardinality 2 y (II 1.4.7). Then F is a varietor because
each cardinal n 2 y with the property above is a cardinality of some fixed
point of F: if card A - n, then card AF S n and, via n 2 y. card AF 2
card A - n, therefore, card AF- n - card A. □
SJ. Deflahtoa. Let JT be a concrete category which has a free object M* for
each set M of generators (111.3.8). We say that JT has bounded free objects If
there is a cardinal a such that card M — card M* (/ for any set M of
cardinality 2 a
Example*, (i) Each variety of algebras, considered as a concrete category,
has bounded free objects. It is sufficient to choose a regular infinite cardinal a
larger than all arlties and larger than the number of operations.
(ii) The categories Top, Poa, Qra. etc. have bounded free (— discrete)
objects; here M* V — M for each set M and thus, we can choose a — 0.
(iii) The category Comp of compact Hausdorff spaces and continuous
maps has free objects, but not bounded. The free object generated by an
infinite set M is the Cech-Stone compactification BM of the-discrete topology on
M: it is well-known that card BM > card M.
3-J. Tfccore*. Let .JT be a cocomplete and cowell-powered concrete category
with bounded free objects. Each non-increasing functor F: JT -» JT which
preserves epis is a constructive varietor.
Proof. Denote by <P:S»t-»jr the free-object functor (Remark 111.3.8).
I. The functor
F- <f>. F- (/:S«t->S«t
is a constructive varietor.
To prove this, let a be a cardinal with card M — card (M)0 • U whenever
card M 2 a. There exist arbitrarily large cardinals n 2 a such that
card All s n implies card (AF)U S n. For each of these cardinals and each
set*,
card Jf- n implies cardJff- cani(X0)F- US n.
Thus, F is a non-increasing functor, in other words, a constructive varietor.
Comtruction of Free Algebras
189
II. The free-ilgebra construction stops for eich free object / — X0.
We shall use the following functor
0- F- U- 0:Jt — Jt.
It is sufTicient to prove that the free-algebra construction of C stops for each
X. In fact, f is « quotient of C: the epltransformatlons e: U • 0-* \* (see
Remark 111.3.8) yields an epitransformation Fe:F- U • 0-* F. Therefore,
F + C, is a quotient functor of C + C, (because a coproduct of epis is an epi,
Exercise III.S.A). Moreover, since F preserves epis, F+ C/also preserves
epis. Thus, by Proposition IV.2.7, if the intial-algcbra construction stops for
C -I- C,, then it stops for F+ C,. Consequently, by Proposition IV.3.3, if the
free-algebra construction over / — X0 stops for C, then it (tops' for F.
Denote by
>P:ORl-»S«t
the free-algebra construction over X for the functor F. Since 0 preserves coli-
mlts (as any coadjolnt, III.2.I0), the chain
«■ #:Ord-»jr
is the free-algebra construction over X0 for the functor G: JT -»JT. In fact
(a) (W-0\- W,0- X0:
(b) Assuming (W- 0), is the n-th step in the free-algebra construction of
X0, we have
(IP-*).*, -(* + W.F)0-X0 + (#- 0).G
because
F. 0- 0. F- U- 0- 0- G;
(c) Assuming (IP • 0), is the n-th step for each n < i where * is a limit
ordinal, then
(If. 0), -W,0- (colim #A0- colim (IP• 0)..
(Analogously with the morphtsms *,..) Since W stops, there is an ordinal k
such that *,.,» , is an isomorphism; hence *».»♦ ,0 is an isomorphism, too.
III. The free-algebra construction stops for each object /.
We shall use the fact that the construction stops for (IU)0: let
IP:Ord-» jr and lP:Ord-»jr
denote the free-algebra construction for / and (IU)0. respectively. By
Lemma IV.2.7, it is sufTicient to present compatible epis
«„:#.-► W. (he Ord).
190
Ouptcr IV
We proceed by translinite induction.
(a) e0-£,:(/t/)4>-/;
(b) *..,-«,+ e.F: (IU)<t> + tf.F-. / + W.F.
(c) e,: colim IV. -» colim (V, has components f. • w,, (n < i) Tor each limit
ordinal i.
We verify the compatibility, i.e., that the following squares
|n<m)
commute, by induction using Remark IV.2.4.
(a) For m — I we have *o. i ■ tt — e, • w0., — et • w^, because e,
s, + e,F.
(b,) If the square above commutes, then the following diagrmm
W„., - 1*W„F
W».i - 1+W„F
»I + W„F-W.«
» *W„F-W^,
also commutes.
(b,) If the squares above commute for all n < nfc where n, is a limit
ordinal, then they commute for n„ too, because IV,. — colim W..
■ < «
(c) The limit step in m follows from the definition of e,.
It remains to prove that each f. is an epi.
(a) e, - e, is an epi.
(b) If e. is an epi, then e.F is an epi and hence, by Exercise III.}.A, also
t. ♦ i — Ci + tnF is an epi.
(c) The limit step follows from Exercise III.5.B.
This concludes the proof that the free-algebra construction W stops. D
Construction of Free Algcbrai
191
5.4. Example. For each type X, the functor
/ft:JT-»jr (111.2.3)
is a constructive varietor, assuming that JT is a concrete category as above
and, moreover, JT has concrete products and U preserves epis.
Proof. I. For each cardinal k the "*-th power functor" H,: JT -» JT is non-
increasing. This follows from the fact that V preserves products. For each
infinite regular cardinal n > * we have:
card AV - n implies card (AHk)V - card (AU)' - n' - n.
Next, Hi preserves epis: given an epi e: A-+ B, then eU.AU-* BU is onto,
hence
*"'t/ - (*i/y": (au? -» (Bi/y
is onto and this implies that f"' — eH, is epi.
II. It follows immediately that the coproduct
Hz- II Hi, where*- |<r|
fii
preserves epis (a coproduct of epis is an epi, see Exercise III.3.A). Let us
verify that Hi is non-increasing. Let a be the cardinal of Definition I V.5.2, and let
p be an infinite cardinal larger than card X, a and the arity of any a 6 X. We
shall prove that each infinite regular cardinal n i 0 has the property that
cattiAU-n implies card (AHt)UZ n.
We have card A'U £ n for any a e X with |o~| — fc Since also card X £ n, it
follows that the coproduct X — II (A'U) has power £ n. Then n s a im-
plies card X0V£ n. We have JTd>- ]l (^*(/)d>, and there is an obvious
epimorphism t: X0 -» ^Hj. Since eU is an epi in Sot, we conclude that card
(MJl/S » D
5J. Exaaple: A fliltary rarletor wklck b awl ni lacraaalag. Let Ab be the
category of Abelian groups and homomorphisms. We define a functor
F: Ab -» Ab as a composition of several "naturally defined" functors.
Let AW denote the full subcategory of torsion-free groups. For each
Abelian group A the subgroup of all torsion elements (i.e., elements a e A such
that n-a-a+a+... + ah zero for some n > 0) is denoted by Tor (A).
Let
A:Ab-»AM
192 Chlptrr IV
be the reflector, assigning to each Abelian group A its quotient group
AR- A/Tor (A)
(and analogously on morphisms). Denote by
U: Abf - Sat
the forgetful functor and by
P. Sat -» Sat
the power-set functor (III.3.4). Finally, let
#,:S«t-»Ab
be the functor assigning to each set M the free Zrmodule generated by U
(i.e., the elements of M0l are all maps I: M -»|0,11 of finite support and the
addition is defined by (mX'i + <i) - 0 iff (m)f, - (m)lj for each
f „ f] e M0, and me M) and to each map /: M -» AT the unique homo-
morphism emending/|if each m 6 M is considered as i: M-» |0,1) where
(m)r - I and (m')f - 0 for all m i» m].
The functor
F- R U- P <P, :Ab-»Ab
is a finitary varietor. Indeed, starting the free-algebra construction, we have
W,- 1,
W,- 1+ IF
and since IF a a torsion group (hence, (IF)R - 0), clearly IfiF- /F;
W, - 1 + IF:
W,-l+ IF:
etc. The construction stops after one step.
Nevertheless, F fails to be non-increasing: let / be the free group on n
generators, i2K, Then
card / — n.
Since / is torsion-free, we have IR - /, thus,
card/F- 2-.
Remark. In the preceding example we had .* - Ab, the category of
modules over the ring of integers. Nevertheless, in categories of modules over
fields, non-increasing functors are precisely the varietors, as we prove now.
Hence, the situation is analogous to JT - Set for Ji-Vect (but not for Ji-Mod,
in general).
Construction of Free Algebras
193
Theorem. Let A be a commutative Held. The following conditions are
equivalent for each functor
F: A-Vect -» A-V*ct.
(i) Fis a varietor;
(ii) Fis a constructive varietor;
(iii) Fis non-increasing;
(iv) Fhas arbitrarily large filed points or it is a constant functor.
Proof. In the category A-Vact all monos and all epis split Thus, F trivially
preserves monos and epis.
(iv) -»(Hi) This is clear.
(iii) -»(ii) This follows from Theorem IV.5.3, all assumptions of which are
fulfilled by A-Vact.
(ii) -»(i) This is clear.
(i) -»(iv) Let us apply Characterization Theorem 1V.4.2. Here -M - all
monos. If F is non-constant, then there exists a cardinal y such that
dimXF2 dim Xwherever dim X £ y(sce Exercise II 1.4.A(iv)L For each
cardinal a choose a vector space / of dimension max (a, y, Ke). The free algebra
/• is a fined point of F+ C,(IV.3.I), thus
dim /* - dim /'F + dim / - dim IT.
Hence, /* is a Hied point of Fand dim /• £ a. D
Exercises IV J
A- Varieton and fixed potata. The notions varietor, non-increasing functor and
arbitrarily large fixed points are relatively independent. We illustrate this on
the category Qra (IV.4.A); we denote by T- (|f). |(f, 1)1) the terminal object.
In each case, verify that Fis a well-defined functor and that it has the
properties claimed.
(i) A non-increasing varietor without fixed points (except, of course, the in-
itial algebra): on objects (X, A) put (X, A)F - T if A * 8 and (X, 6) F - (Jf, 0)
+ T, on morphisms f:(X, A)-»(J", S) let (l)fF- I (in T) and in case
A- S-0,/F-/on X.
(ii) An increasing varietor without fixed points: See IVJ.A.
(iii) An increasing varietor with arbitrarily large fixed points: define
Fanalogously to IV.3.A except that (Jf, 0)F - (X 0) »nd for morphisms /: (X.
A) -»(K, S),/F - / if S - 0 and /Fis constant if A - 0 * S.
B. Orient types. Let I be an ordered type, i.e., a type of algebras with an
194
Chapter IV
order on each or the sets X,. An ordered X-algebra is then a X-algebra (Q, 5),
ordered in the usual sense (III 3.5) and such that, moreover, if a, t e X, and
as r.then
(jc,)o S (jc,)r for all (*,) £ Q'.
Define a functor F: Poa -» Poa by appropriately enriching the order of Hz:
if Q- (X. £), then QF- U Xk where (jc,)(tS 0-,)r itT |er| - |r| (- *),
0* &
as r in X, and x, £ y, for each i
Verify that Fis a constructive varietor and the free algebras are
appropriately ordered ilgebras of finite-path X-lrees (see 11.3.6).
C. Concrete categories with coacrete coproaacta. (i) Verify that the categories
Pot, Top, Matr, Qra fulfil the assumptions of Exercise IV.5.4 and, moreover,
U preserves coproducts.
(ii) Generalize functors Ht:Jt -»jr, where X has all the properties
mentioned in (i), to obtain algebras of "structured types" as follows. For each
cardinal it with X, * 0 choose an object A, with AkU - X,. Define F: JT -» JT
by
XF- U AtxX*.
&»•
Note that Ht- V - F- (/(and HL - F if A, are discrete objects). Prove that F
is a varietor and that the free algebras are the X-lree algebras with an apropri-
ate structure.
(iii) If JT — Pol we described F-algebras in Exercise B above. Describe
them if X — Top.
D. Varleton la Vect. (i) Prove that each of the functors F in Exercise C (ii)
above is a varietor in Ji-Vect.
(ii) For each Unitary type £ define
A,: Ji-Vect-»Ji-Vect
using the tensor product ® instead of product: fl, is defined by Jffl. — X ®
X 8 ... » X («times) and flr - U #«■ Prove that flr is a finiury varietor.
a t I.
(Hint: Prove that each fl. preserves <u-colimits—then so does each flr. To
prove that, say, fl, preserves the colimit of any chain/. . :X. -» Jf_(n £ m<
o>) choose a basis fl. c X. such that/, .(fl.) c fl. ^ |0| for each n £ m < m.
Then fl. 9 fl. is a basis of X, ® X. and, again,/. . ® £ .(fl. 8 fl.) c fl. ®
fl„^|0|.]
(iii) Find two varietor: in Ji-Vect the coproduct (- product) of which is
not a varietor. (Hint: For each functor F: Set-* Set we have a functor
F- U- F- 0: Ji-Vect -» Ji-Vect which is a varietor iff F is. Use Example
IV.4.4).
Comtructiofi of Free Algebra!
19}
(iv) Biduals do not form a varietor. The hom-functor
hom (-, R): fl-Vact — fl-Vacf
defined on object Jtby hom (X, R) (with the usual addition and scalar
multiplication of linear maps) is a well-known duality functor. Composing it with
itself we obtain a functor F: Jt-Vact -» Jt-Vact. Verify that Fis not a varietor:
indeed, it has no free algebra except the (trivial) initial algebra. (Hint: If
dim Jtis infinite, then dim XF> dim X. Use Theorem IV.5.5.)
IV 6. Flaltary Vaiteton
6.1. In the present section we study finitary varieton, i.e., functors for which
the free-algebra construction stops after a steps. In the category of sets, these
are essentially just the finitary functors and this "essentially" is a question of
the axioms of set theory. In contrast, we sball prove that in suitably ordered
categories the dass of finitary varietors is extremely large, including a lot of
infinitary functors.
*A Recall that each set functor is "almost" standard (111.4.5). A standard
set functor Fis said to preserve unions ofa-chatns ofsvbstts, provided that
X- U X. implies XF- U X.F
■ < m a < m
for each ai-chain X, c X, c X,....
Theorem. A standard set functor is a finitary varietor iff it preserves unions
of ai-chains of subsets.
Proof. I. Let F preserve unions of o>-chalns. Since Fpreserves monos (see
111.4.7), and the coproduct injection w,,: /-• / + /Fis a mono, it is easy to
verify by induction that w,.. is a mono for each n £ m < a. Therefore we
can assume that W, c W, c W, ... and that wK. are the inclusion maps.
Then the colimil Wm - collm W. it just the union rf. - u W.. Since F
preserves this union, and since w. . F are inclusion maps too, it follows that F
preserves the colimit Wm. This means that the free-algebra construction stops
after a steps.
II. Let Fbe a finitary varietor. We can assume that Fis non-constant. Given
sets A, c X, c X, c ..., we put X - U X. and we prove XF - U (X.F).
■ < ■ • < m
By 111.4.7, there exists a cardinal y such that card YF 2 card Y for any set Y
with card Ys y. Let / be an infinite set with X c /and card / £ y. We use
the fact tbat the free-algebra construction for / stops after o> steps. We are go-
196 CtapteMV
ing to present one-to-one maps
f.:jr„-» If. (n< a)
which fulfil
(*„.,-*.)'~,c W..,-(W.)w.,.., (n<a>)
and which are compatible, i.e.,
'.• w....i - j.- I.* i (" < »),
where j.: X, -» X.»i denotes the inclusion map.
Let
la : Xa -» /
be the inclusion map (we have X, c X c /). Then
card (JT, - X,) £ card (If, - (If,,)!**,)
because If, — (If,,)*!, - IF and card /F 2 card / £ card JT £ card X,.
Thererore, we can extend the map I, • wt,,: X, -» W, to a one-to-one map
r,: Jt, -» If, satisfying(X, — X,)i, c If, — (Ifi)w«,,. Analogously,since
card (X, - Jf.) S card (If, - (If,)*,.,),
we can extend r, • h>, , to r,, etc. Denote by
f.:JT-»lf.
the (unique) map extending each I. • w, m: X. -» tf_(n < o>). This map is one-
to-one and fulfils
Klf.)*-...]';'-Jf. (n<a».
Since Fpreserves preimages for one-to-one maps (111.4.7), this implies
l(lf,.FK..F](».F)-1 - X.F (n < a).
Finally, Fpreserves the colimit If.- colim tf„(IV.3.4) and hence, by Remark
lll.5.4weget
If.F- U (lf».F)w...F
Thus,
XF- (If.FX'.F)-1 - #yJ(lf.F)^^•K'.F)-, - ,U/.F.
This concludes the proof. D
Construction of Free Al-fcbm
197
63. Recall that a set iunctor Fis Unitary iff Tor each set J and each point
a e JTFthere exists a finite set Kand a map/: K-»Jrwitha e (YF]fF What is
the relation between the properties "Unitary functor", equivalent to the
preservation of directed unions (Exercise IIM.E) and "Unitary varietor",
equivalent to the preservation of amnions? The answer depends on the axioms of
set theory.
An infinite cardinal n is said to be measurable if on each set X of power n
there exists a non-trivial o-idditive measure /j:X->|0, I) (i.e., a map with
(X)u - I, (M)ji - 0 for each finite Mc X, and ( U M.)ji - £ (M.)ji if
M. c X are pairwise disjoint]. We use a formulation based on the concept of
filter, i.e., a collection 9 of non-empty subsets of X closed under finite
intersections and super-sets (i.e., M,, M, « 9 implies M, n M, e 9 and M, e 9
for any M, d Mi). Recall that maximal filters are called ultra/liters; they are
characterized by the property that for each Mc X either Me/ or
J-Mt J\ For example, the collection J, of all subsets containing a given
element i! X is an ultralilter. A cardinal n is measurable iff for each set X of
power n there exists an ultrafilter / which is non-trivial, i.e., 9*9, for each
jc e X, and is closed under countable intersections. In fact, each such
ultrafilter yields a non-trivial measure /i defined by f<(M) — I iff M e 9 (and vice
versa).
The assumption "there exists no measurable cardinal'* is well-known to be
consistent with the theory of sets.
Tkeorea. Assume that no cardinal is measurable. A standard set functor is
a Dnitary varietor iff it is a finitary functor.
Proof. Each finitary set functor preserves o>-unions (Exercise IIM.E) and
hence, it is a finitary varietor (IV.6.2). Conversely, let Fbe a finitary varietor.
Then F preserves oi-unions: for each set Jf and each point a e JfFwe prove
that there exists a finite set Y c Jtwith a e YF Put
r* - n {Y:Y<z JTando <= YF\.
(i) Lei a € Y'F. If K* is finite, the proof is concluded. If it is infinite, we
choose pairwise distinct elements y*. y,. y,, ... in Y* and put Z,, — Y* —
[y.*i.y.n. ...|.Then Z, c Z, c Z, ...and U Z. - K*; we have
oe r*F-(_U_Z.)F
Since F preserves unions of ai-chalns, there exisu n with a e Z.F. This
contradicts to the definition of Y* because Y* £ Z..
(li) Let a t Y'F Put X' - X - Y' and define a collection of subsets of r.
9- |Zc X'.ae (Zv Y')F).
196
Ch.plet IV
Since Fpreserves inclusion and Unite intersections (111.4.6), S is a niter on the
set X'. By Zorn's Lemma (applied to the set or all filters on X, ordered by
inclusion), there exists an ultralilter V on X' with 9 c 8. By definition of Y*.
clearly PI Z - 8 and hence, fl Z - 0. It follows that each set in V is infi-
*«» in
nite (because any ultrafilter V containing finite sets equals f, for some x).
Since card X" is not measurable, the ultrafilter V is not closed under countable
intersections, thus, we can choose sets K, <= S with fl Y, t S. Put
I < m
z.- n n
I < m
and define sets Z. c Jt" by induction:
z... -z.u(Jr ->".)■
Then clearly Zo c Z, c Z,... and U Z, — Jt" Since Fpreserves unions of
o>-chains and
IE XF-( U (Z.^ Y*))F,
■ < a
there exists n with ie|Z,u K*)F, i.e., with Z. <= y. Let n, be the least
number with Z„ e J cS. Then n, * 0, hence Z„ - Z„_, \j (X" — K,_ ,). This
is a contradiction: any ultrafilter V has the property that ^u<E I implies
either A e » or fl € t. Yet, neither Z, _, nor X" — K, _ , is an element of t.
D
Corollary, The following statements are equivalent:
(i) no cardinal is measurable;
(ii) each standard set functor which is a Unitary varietor is a finitary
functor.
The proof of(i) -»(ii) was presented above. For the converse assume that
there exist measurable cardinals and define a set functor M as follows. For
each set X let XM be the set of all o-addilive measures on X. For each map
/: X-+ Kand each measure \i: Jt-» |0, I) define the measure {p\fM — fl by
(A)fl - (Ml/1) /I for each A c Y.
It is easy to check that fl is a o-additive measure and that Af is a well-defined
functor. Moreover, the existence of measurable cardinals clearly implies that
Mis not a finitary functor. On the other hand, Mpreserves countable unions:
for each o--additive measure fi: U X. -»|0,1) there exists n, with (JTJii - I,
and then the restriction y.' of fi to X„ fulfils
P-(MV„F
Conttniction of Frw Algcbru
199
where (,„: Jt«, -» U X, is the inclusion map. Thus, Mis a finiury varietor. By
111.4.}, there exists a standard functor F naturally isomorphic to M. Then F is
a counterexample to (ii).
M. In contrast to Sot, in the full subcategory
Set.
of all countable sets, each functor is a Unitary varietor. In fact, a finitary
functor, which is defined as in Set (III.4J).
Theorem. Each functor
F: Set.-* Set.
is Unitary and hence, a finitary varietor.
Proof. I. Let us first observe that for each infinite set X there exists an
uncountable collection (M,),,j (i.e., card J> Ko) of infinite subsets M,c X
such that M, n M, is finite for each j, j e J with j * f.
We can assume that X contains the set of all rational numbers. Let J be the
set of all irrational numbers. For each j £ J choose a sequence x. of rational
numbers with lim x„ - j and put M, - |x,; n < to).
II. Let F: Sat, -» Sat. be an arbitrary functor. We can assume that F is
a standard functor—this is quite analogous to the category Sat, see III.4.5.
Let us extend F to a standard functor
G:Set-»Set
as follows. For each set X let
XC- U*"F
where the union ranges over all countable subsets X" of X (and hence,
XC - XF if X is countable); for each map f:X-*Y define /C: XC — YC as
follows: given a E XC, there is a countable set X" c X with a E X'C — X'F,
and we denote by f: X' -»(X^f the restriction of / and put
(a\fG-(a)fF:
Since F is standard, C is obviously a well-defined extension of F. It Is
sufficient to prove that C is a finitary functor. Then G is a finitary varietor, and
since F coincides with C on the category Sat., it follows that F is also both
a finitary functor and a finitary varietor.
For each set X and each point a e XC we present a finite set Y c X with
a e YC. Let X* c X be a countable set with a E X'G. If X" is finite, the proof
is concluded. If X" is infinite, we have a collection M, c X {J E J) as in I.
above. For each> there exists a one-to-one map^: X" -» X" with
M,-(ri/;.
200 Chapter IV
The set of all
(a)/F(e Jf'G) j e J,
is countable simply because JTG - XT is countable. Since the let J it
uncountable, there exist distinct J,ftJ with
(atffi - (a\f,C - b.
Put ?- M,r\ M,, Since (rGXffi) - M,G (see 111.4.7) and analogously
with j', and since G preserves finite intersections (III.4.6), we have
6 <= M/Gn M,C- fC.
The set Y - (rV/"' is finite, since f, is one-to-one, and
a <= KG
because the fact that f, is one-io-one implies thai YC - (KGX/JG)-' by III.4.7.
This proves that G, and hence F, is a Unitary functor. D
&S. For a certain type of ordered categories we shall eihibit a mild criterion
Tor a functor to be a flnltary varietor.
By an ordered allegory is meant a category together with a partial ordering
^ 11 (or just £) on each set hom {A, A) of morphisms from A to B,
compatible with the composition in the tcntc that
/£,!,/* and |ilt| imply /■ g*ACf-t-
Recall that a poset (X, £) is said to be oxompleu if it has a least element 0
and each Increasing (u-sequence has a join. Maps preserving the least element
and joins of increasing o-sequences are said to be to-continuous.
DefurUea. An co-category is an ordered category in which
(i) each hom (A, B) is an (u-complete poset;
(ii) composition is (u-continuous, i.e., given {,<. fx <. f^...: A-+B and
g,s g, £ «,...:«-»£;then
(y/-)-(v«-)-y/-—*
and for the least elements,
Exaaiak*. (i) Pos., the category of (u-complete posets and m-contlnuous
maps, is an oxitegory. Here, hom (A, B) is naturally ordered by f<. g IfT
(x)/£ (x)g for each x e A.
(il) Pfn, the category of sets and partial functions, is an ©-category. The
ordering of hom(Af, K) is defined "by extension": given / g: X -» K, then
fsg Iff (x\f-(x)g for all x with (x)/defined.
Construction of Free Algebra
201
The least map is the empty (nowhere defined) map. The join of a sequence
/„ £ / £ / £ ...: JT-. Y is the map/: JT-. Y defined by (x)/- (x)/.
whenever (x)/ is defined.
(iii) The category Jt-Mod becomes trivially an (u-category when we put
/£ f iff either /- g or / is the zero map.
64. DeflaHkM. A diagram D: 1 -»JT in an ordered category jr is said to
have an isotone limit if it has a limit x,:X-» dD(d <= »•) such that for
arbitrary p, f: K-» Jf we have
p £ 9 Iff p- *> £ q- nt for each d e 9°.
Remark*, (i) If JT is an (u-category, then each itotone limit it in fact m-con-
tinuous in the sense that (I) given p,?.: Y-+X with « £ q, £ % £ ....then
P - V q. iff /> • *> - V «. - *i for each d e 0°,
ll « a • < •
and (2)
/>-0r.r iff p-x,-0,,D for each J e 9°.
This follows easily from the o>continuity of the composition map
- . xt: honKr, X) — hom( K, dD).
(ii) In an ordered category JT, all limits are isotone iff
(a) products are isotone, i.e., II / £ II fi whenever/ £ g,for each i e /:
HI lit
(b) equalizers are isotone, i.e., JT has equalizers and for each regular mono
m: X-* X' and for arbitrary p, g: K-» X
p- m £ q> m implies p £ q.
The proof that (a) and (b) imply that each limit is isotone it analogous to the
non-ordered variant (Exercise III.I.E).
(iii) Isotone colimits are defined dually. An ordered category has isotone
colimits iff it has isotone coproducts and isotone coequalizers.
•5.7. Dtfnkioa. Let JT be an (u-category. By an co-functor we mean a functor
F: JT -»JT which preserves the Join of any m-sequencc p, £ p, £ pi £
...:A-*B, i.e., it fulfils
V/UF- V p.F:AF^BF.
■<■ I »<m
Example. For each type 1 the functor
//r:jr-»jr
is an tu-functor, assuming that Jf has isotone products and coproducts.
202 Clwpiw IV
Rcnirk. Each tv-functor is clearly "locally isotone", i.e, if p £ q in
hom(4 B) then pF £ qF in hom(/4F, *"F).
Note that, however, F is not supposed to preserve the least element of
hom(4 B)
Timiii Let.» be an o-category with isotone (u-colimits. For each <v-func-
tor F: JT -» jr, the initial-algebra construction stops after o> steps.
Proof. Let us define morpnisms
(,: XF"*'-» XF' (n<<»)
by the following induction:
«0: IF— X
is the leut element of hom(IF, 1):
t..,-t.F: {1F-")F-(1F")F.
Then
(1) i»»..i • '. - I if and »,-»,.,,, s ltr.» i (n<<»).
This is obvious If n - 0: »,., ■ (, - I because hom(X, X) - (IJ, and
I, ■ to, s llf because <o is the least element of hom(XF, X) and hence,
>i ■ w,, i is the leut element of hom(If, If) (because the composition
— ■ Wn i is (u-continuous). Since F is "locally isotone", the induction step is
obvious, too. Given n < m, put
I..- I.-,- !.-,■■■■■ ».:XF-- if.
Then (I) clearly implies
(2) »,.l,.-lif and »»..»,. s lif. (n < m < <»).
For a fined t- 0, I, 2 define a family of morpnisms from if
(n < a) to X F' by
w„,.XF"-» XF' foralln-0,1 k;
»„,: XF"-. XF' forall n-*+ l,*+2,... .
Using (2), it is euy to check that this family is compatible with the
initial-algebra construction. Hence, there exists a unique morphism
s,: IF-— if
with
(J) w J.-("■' (BSk)
Let us verify that the morpnisms st- wt .: XF"-» XF* form an (u-chain
Construction of Free Algebras 203
with
(«) VV w...- I lf..
On the one hand. Tor each * < a> we have
4- H4..S lif
because the colimit if- colim X f ia laotone, and Tor each n — k + I,
<•< *
k + 2,... vie have
»V.-(4- »V.) - '».»■ •»»..
S w...-
Analogously with the inequality
4- "i..S «»i ■ "Wi. (*<•»)•
On the other hand, let /: J. F" -► J. F" be a morphlam with
/2 4 ■ N't.. Tor each k < to.
For each Jk < a> we have m . • sk — »y» — I, hence
•»»..■ /* •»».. ■ 4 ■ •»»..- •»»..•
This Implies that/2 I ir., and the proof of (4) Is concluded.
We shall prove that wmmt., Is an Isomorphism with the Inverse
j- V stF ■ n,l.:lf,l-»lP.
First, to show that s is well-defined we must check that 4F- "i + i..£
4»iF- »,»,.. for each * < <w. We hive
4 - 4 ♦ 1 ■ 4
(because for each n > * + I clearly My,. - s, - 4.. - «y.. ■ 4 ♦ 1" 4). ■na'
we conclude that
«F- »t.t..- 4*|F- '«F- Wi«i.»«i ■ Ws + t.
- 4*|F- ('»■ •»».»♦ i)F- Wstt.
- 4*|F- "itj..
(by (i) above]. Next
w...*i • »- lif
beacuse for each n < <v we have
204
CluplcrlV
Finally.
s ■
because F
Therefore,
wm
ia
..♦
an
- "..J-
- x<-
1-0
- •».♦!..•
, - K,...
(u-funclor and hence,
V'.'-
.',)F
1. i 4 1 " '
■.?.<*■
"•♦I.,
■ m ♦ i.
*Wi..
■ w...)J
Vt(*- «v.)F
Thia concludes the proof. D
Corollary. Let jr be an o-category with iaotone countable colimits. Then
each <D-functor F: jr -» jr is i finitiry varietor.
Indeed, since finite coproducts are iaotone (hence, (u-continuoiu, aee
Remark IV.6.6) and since both F and each constant functor C, are (u-functors,
F+ C, is clearly an tv-functor, too. It follows from Proposition I V.J.J and the
preceding theorem that F ia a finiury varietor.
Ensile*, (i) The (u-category Pos. haa iaotone lirnita and colimits, aa we
verify presently. Thus, for etch type I, the functors
f, n[. rOS)a-* rOS)a
(aee 111.J.6) are Unitary varieton. And thia holda even for innnitaiy typea £
The Inner reason will be seen below.
(a) Limits. The product Tlx, in Poa. is the cartesian product, ordered
coordinate-wise. Given morphisms p, q: F-» 11X, such that each projection x,
fulfils p ■ x, s q ■ x„ then p £ q (because the ordering is coordinate-wise).
The equalizer e: X-* r of two morphisms/,^: K-» Z is the embedding of
Conilruction or Free Algebru
20S
the tubpoaet of til y e Y with (y\f, - (y\f,. Given p, q: P-» X with
p- e S q- e, then, obvioualy, p £ q
(b) Colimita. The coproduct II AT, in Poi. ia the disjoint union with the
leut element! merged. Given morphismt p,q:\lX,-»P such that
p/X, s q/X, Tor each i £ I, then p £ $
The coequalizen in Poa. are not ao eaay to describe. It is dear, however,
that each eoequtlizer e: X-* K hu the rollowing property: if Y' ia a subposet
of Y containing (AT )c and doted under joint of incretsing m-sequences, then
Y - Y. Given morphiama p, q: Y-* f with t ■ p £ c ■ q, let y" be the subpot-
et of Y of til y e K with (y)p £ (y)q. Then F hat the properrjet mentioned
tbove and hence, V - Y. Thus p £ q.
(ii) The ai-category Pfn haa itotonc limitt tnd colimltt—tee Exerrite
IV.6.B below. However, the product in Pfn (which we denote by * tnd II) it
not the ctrteiitn product. We htve
X ft Y-(X x Y) + X+ Y
and, in general,
fix,- II Ux,.
[Given ptrtial mtpa /: T-* X„ i e /, then the
/: r- fi X, It defined by («)/- \W,\„, where y
(f)/ii undefined iff each (fl/Iia undefined.)
That, the functors
/ff i Pfn —* Pfn
tre Dnitary varietors for each (even inlinitary) type £ but there teema to be no
intuition whtt the /fi-tlgebru are like.
On the other hand, the functort defined by the cartetitn product tre not
o-functora, in general. For etch cardinal n let ut denote by
Hm'. Pfn —* Pfn
the functor of the n-th ctrtetitn power:
XH: - X- and ///„• - f.
Then W* U an o-functor iff n it finite. At tn eiample, let X, fi X, & X,... be
arbitrary tett and put X — U Xk. Let
unique factorizing map
- I'e ':('!/! is defined);
/.:*-* (*<«»
206 Chiptcr IV
be defined by
(x\ft — x if x € Xt, else undefined.
Then
but. Tor any infinite n,
V/V" * I,..
am 0
Indeed, let (x,), <. e X" be an element such that Xg e X* x, € Af, — X*
x, € AC, — Xh ...; then If. is defined in (x,)(<, but V/\" is not.
(iii) The category X-Mod, with its trivial order, has neither products nor
coproducts isotone. For eumple, consider
f:Xx Y—Xx Y
defined by
/- Hi — Hi and /- Xf — 0.
Though fi. Ir. r. we have
/■»,SltIf», and /•»,slI>r-»r.
&S. Free (u-coatlaaon algebras. For each type I we are going to describe
the Tree o-continuous ^algebras, i.e., the Tree algebras or the functor
ffi:Po».-»Poi..
(See Eiereise IV.6.A below Tor Ht.) We use the description or £trees as maps
r: n«-» /w X(n - V N) introduced in 11.3.
9 a f
Let / be an tv-complete poset (with / n I — 8, for convenience). In the
lint step or the Tree-algebra construction we have
W, - 1+ HJ.
Here, + is the disjoint union with the least element 0 e / merged with the
(formalI) least element of IH\. Thus, as a set, W, - /w /W°r, where the
elements of IH\ are represented (as usual) by the following trees:
li<kl
Construction of Free Alaebm
207
The ordering is such that 0 is smaller then each such tree, while any
x e / — |0) is Incompatible with each auch tree.
In general,
W.., - 1+ W.ffl
is (aa a set) the disjoint union of / and of W. H%. The elements of the latter set
are represented by trees
(a e X, and (, e Wm). Hence, Wmtl is the set of all trees I: it*-» /ulof
depth £ in + I. The ordering of trees (, I': n*-» / >_/ X In W. la defined as
follows:
(•) »£ (ifT for each z e n*
(i)(j)« € XImplies (z)» - (i)f;
(ii) (i)« e / - |0) implies (i)« £ (*)«■ € / - |0).
This is easy to verify by induction on m. Example:
©
Thin
U w.
is the poset or all £<trec* or Unite depth, ordered by (•). This is not Wm;
indeed, the poset U Wm is not (incomplete, as indicated by the example above.
Obsciratloa. Let /• denote the poset of all (finite and Infinite) X-trees over /
with the ordering (•) above. Then /' — collm Wm with respect to the inclusion
208 Chapter IV
maps
w...: W.-*l* (m<m).
Proof, (i) The poset /'is to-complete. Its least element is 0 e / c /*. The
join of a sequence US I, S I, ... of ttrees is the following £4ree
i:i'-<iu I: for each i e n*.
(z)l - x e / iff (z)i. e /for each m< tu, and x - V (z)(. in /-.
m < m
(j)» - a € I iff (*)». - <r for all but finitely many m < <u.
(ii) The inclusion maps are clearly tu-continuous.
(iii) Each tree I e I is a join of an tu-sequence »m £ r1" £ r111 £ ... with
?•> e If. defined by
j(rf, ...;,)< if r < m and (i,... i,)< is defined;
'■■■""' ■» iff - m and (/,.,. i,)( is defined
and undefined else. It is easy to prove by induction that i"' e Wm; using the
description of oi-joins in (i), we see that
l _ V I"1 for each I e /*.
N < ■
(Iv) Let Pbe an tu-complete poset and let pm: Wm-* P(m < to) be a
compatible family. i.e., a family tuch that pm.i extends pm(m < to). Define
/,:/*-l>by
(Dp - V («"')/>..
m < m
Then p clearly emends each pm, and it is sufficient to show that pit tu-contin-
uous [the uniqueness follows immediately from (iii)L For each m < owe have
/"•' - V l't" — this is easy to check using the description of tu-joins pre-
* < m
sented in (i) above. Hence,
(Dp - VmW)P.
- !v! .y.w*-
-'y.'.yy-'^
Conllary. The free tu-continuous £algebra generated by an tu-complete
poset /is the algebra /' of all £treesover / ordered as in (•) above and with
the operations e>„: (/*)* -» /* (o e Ik) defined by
Ci)i<kP. -I if (B)»-ff and fy-t, (j < k).
Construction of Free Algebras
209
This follows from the fact that H\ is a Unitary varietor (hence, /• - Wm)
and from the preceding observation. The definition of f>„ above is correct if all
the trees t,,j < k, are from one Wm for some m < a>: then f>„is the coproduct
injection of W. into Wm ♦ i: In general, it follows from the (u-continuity of «>„,
since
('/),<»»>.- .V.C'")/ <'♦>•■
Excreta.) IV.*
A. Fim strictly ai-coathmow r-algebm. These are algebras for the functor
H[\ Poa.-» Poa.: they differ from the (non-strict) (u-continuous algebras by
the requirement that the operations preserve the least element, i.e., by the
equations
(0,0,..., 0,.. .)?„ - 0 for each a e I — Z+
Verify that the free //{-algebra is obtained from the free HJ-algebra by the
least congruence - such that (0,0 0,.. .)«»„ - 0 for each a e I — I,. Its
elements can be represented by all trees (such that under each node there lies
a leaf not labelled by 0. (Formally: for each />,.../>,€ n* in the domain of (
there exists />,.../>,/>,.,.../>,€ n* with (/>,... />,)» € (/ — |0|) w £*)
B. LtatUi aad calharta la Pfn. (i) Verify that coproducts in Pfn are those in
Sat, I.e., the disjoint unions. Verify that each coequalizer in Pfn is a partial
map onto.
Conclude that Pfn has isotone colimits.
(ii) Verify that the products in Pfn (described in Example IV.6.7) are
isotone. Describe equalizers in Pfn. Conclude that Pfn has isotone limits.
C. Free algebras la Pfn. Denote by Wf: Pfn -» Pfn the coproduct of the
functors WJ,, a e I (IV.6.7). Verify that the free-algebra construction
coincides with that in Sat. Hence, Hf is a finitary varietor iff Xls Unitary.
//I-algebru are precisely partial ^algebras but the homomorphisms here
are not "natural". Describe Wf-homomorphisms in Pfn and explain why free
algebras are just the free universal ^algebras.
D. Flaftary vaiieton oa X-Vact (i) Assuming that no cardinal is
measurable, prove that a standard functor F: X-Vact -» X-Vact is a finitary varietor
iff it is a finiury functor in the sense of 111.4.3. [Hint: The proof is
completely analogous to that of I V.6.3: use the properties of vector functors, indicated
in Exercises III.4.A, D, E.)
(ii) Denote by X-Vact. the full subcategory of X-Vact over counubly-di-
mensional spaces. Prove that each functor F: X-Vact. -» X-Vact. is finitary.
(Hint: Proceed as in IV.6.4.)
210
Chapter IV
IV.7. Free-Coraalerloa Coastractloa
7.1. Partial algebras. Throughout this section, JT denotes a category with
a fined factorization system («°, of). By a partial morphism rrom an object A to
an object fl in jr is meant a morphism from a subobject or A into B. We
denote partial morphisms by —». Thus, a partial morphism 6: A —» B is
represented by a span
A B
where m e .«*. (For each isomorphism I: A,-* A, the span I• 6,: A'e -» Band
/■ m: A', -* A represents the same partial morphism.)
Let F: JT -► JT be a functor. A partial F-algebra is a pair (Q, S) consisting or
an object Q and a partial morphism 6: QF-- Q.
Example. A partial groupoid (i.e., a partial /fi-algebra) consists of a set Q
and a partial binary operation, i.e., a map
O.D—Q
where
Dc Q x Q
denotes the domain or D.
Given partial groupoids (Q, D) and (Q, »), a map/: Q-* Q is a homo-
morphism Iff
(•) (« Q qtf- («,)/• (*)/
holds for arbitrary q,. q, e Q for which q, D q, is defined.
Remark. There are several natural concepts of homomorphism of partial
groupoids (and partial J>algebras in general). All are characterized by (•), and
the difference! are only in the question which side is to be defined. In
Chapters VII and VIII, devoted to partial and nondeterministic automata, we use
so-called state morphisms (characterized, in case of groupoids, by (•)
whenever (fi)/» iqilf'u defined).
Natarloa. A partial f algebra can be represented by a quadruple (Q, D, cV
m), where
m:D— QF
is an #-mono (the domain of the operation) and
fi,:D-C
Construction of Free AlfcbfM
211
it an arbitrary morphism. All other such lepieicumJoiu of the tame partial
alfebra are then
(ft 6. i- *./•"!).
where i; /5-» D it an arbitrary isomorphism. Given partial algebras A - (ft
D, 8+ m) and A' - (ft, D\ S„ m"), a morphism/; Q-» Q" is a homomorphism
Iff there exists a (unique) .£-. D-+ D' such that the fotlowhig diagram
OF-" 0 —«-0
IF \, (
T
ffF- ; 01 p—-0'
commute*. This if clearly Independent of the choice of reprnenutive* of A
and/4'.
7J. One extreme cate of partial f algebras are the dltcreu ^algebras. La*
thote where S u nowhere defined. Formally, let J. be the initial object. A dit-
crete Falgebn on an object Q a represented by
(ftJ.,cVm)
where 6,: ± -* Q and m: J. -► QF are the unique morphisms. But here we
must assume that Jl contains all the morphisms from X.
If a partial ^algebra (ft 8) is discrete, each morphism from Q Is a homo-
morphism. More precisely. Tor each partial Falgebra (ft1,5"), all morphisms
/: Q-» Q" are homomorphismt/:(ft 8) -► (ft-, S").
The opposite extreme are the (lout) F-algtbrtu, represented by those
quadruples (ft D, 6\. m) Tor which m is an isomorphism. (One or the
representatives of an ^algebra (ft S) it (ft QF, B, I „,). of course.]
7J. The free completion of a partial /^algebra (ft S) it a (total) ^algebra
(Q',6') together with a homomorphism
';:(ft«)-(e•.«•)
which has the following universal property:
For each (total) Falgebra (&.F) and each homomorphism
/: (ft S) -»(ft1,5~), there exists a unique homomorphism
212
Chaplar tv
/•:(Q',6',)-(e\A~) «uch that/- »■/"■
Examples. If (Q, S) is the discrete algebra, then (Q',S')'n precisely the
Tree algebra generated by Q. (Indeed, here/is simply a morphiam/: Q-* ff.)
On the other hand, if (ft S) is a total ^algebra then (0\ 6"1) - (ft 6).
7A. We are going to present a construction or Tree completion, generalizing
the free-algebra construction. Before that, we extend the concept of a partial
algebra, no more insisting that the morphism m: D-* Q be a mono. On the
one hand, this will simplify some considerations (for example we shall be able
to work with discrete algebras without unnecessary assumptions on .JO; on
the other hand, in the construction of free completion we study below, there is
no advantage in restricting ourselves to partial algebras.
Let F: JT -» jr be i functor. By a span F-algebw is meant a diagram of the
following type in JT:
A ipan-algtbra morphism from a span algebra (Q, D,6+ S,) to a span algebra
iff. D\ S'v 6\) is a pair (//,) of jr-morphiama such that the following diagram
IF
0"F-
commutes.
F-.-2 0 3U.Q
•o
Comtntctton of Fn< Algebra
213
Raeeark. By the above notation, each partial algebra it represented by
a span algebra with 6, e Jl, and we shall simply identify partial algebni
with (any of the) representing (pan algebras. In this sense homomoiphlsms of
partial algebras are exactly the span-algebra morphisms.
On the other hand, span algebras are ranch more general than partial
algebras—we return to this after Introducing relations in a category (see V.2.S).
Each ^algebra (ft*) will be identified with the span algebra
(ft QF, 6,1 ar) and each horaoraorphism / with the span-algebra morphism
(JJF). We often write simply /:(ft D, 6\. £,)-» (ft-, 6") instead of
W S, /F):<ft D. 6+ «,)- ((T. <TF, o~. \fft).
Deflatttoa, The frtt completion of a span Falgebra A is a (total) ^algebra
A • together with a span-algebra morphism n: A -» A • which has the
following universal property:
For each Falgebra B and each span-algebra morphism/: A -» A there
exists a unique homomorphism f':A'-»B with / — n • / *.
13. Fine t—plill»a naeUnlluat Let Jf be a cocomplete category and let
F: Jf -» Jf be a functor. For each span F■algebra
A - (ft D. 5+ 8,)
we define two traiufinhe chains
V. lf:Ord->jr
and a natural transformation
p:V— W
by the following translinite induction.
I.
(a) First step:
V, - D; V, - ftFand v.., - «,;
W. - Q. A> - «►
2|4 Oupwr IV
(b) Isolated step. For each ordinal n put
V..,- W.F.
v.,,....- w....,F:W.F*W„xF.
and let the following be a pushout (defining wK,., and p., ,):
-V~
*^M
(c) Limit step. For each limit ordinal i:
K(-colim (K„: v.. „)„, . <,:
W,-colim(»f.: *...).,.<,;
p, - colim p..
■taark. The above definition is "complete". In the first step, p, and »,., are
given. By (b), their pushout defines
Pi, w, ,andrL1 - wa,F.
Next, the pushout of p, and v, i defines
Pi, w,.iand »,., - w,,F,
etc. Moreover v0.i - vol • »,.,, etc Hence, we obtain all p., r.„ and w...
with n £ m < o). This yields, by colimit,
V., If. and p.: K.-» W..
Next, to obtain
•v..i: y.— *y.F.
we use the fact that V. - colim V., and for each n< a, »..,..
»...♦ i - ».♦!... i - *>,..F: W.F-* W.F. Then the pushout of p. and v.* i
defines
P..I.W...*! and r.,i..,,-»,.,|f,
etc.
Comtnictiofi of Ficc AJ|tbm
215
7j6. Enmak. Let ((?, ±, 6,, m) be the discrete algebra (IV.7.2). The linl
pushout is a coproduct of Q and QF:
where ifc and a are the coproduct injectioni. see Remark IV.3.2. (Proof: Any
square with X in the upper left-hand corner commutes, and hence the
universal property of pushouts coincides with that of coproducu.) Also the next
pushouts are obtained from the free-algebra construction, since the following
square
. "fc-LnF
■W„F
W„-Q«WnJF ►WL.-Q^F
is a pushout. (Proof: Let p: W.-»Pm4 q:W.F-» Pbt moiphisms with
P.-i-P - <*.-i..F-q. The unique morphism k:W,.,-*P with
P ~ Co + wn-i..F)- k and q- e>.• * has components
*b.. P-Q—P and q:W.F—P.\
Finally, the limit step is obtained by a colimit, analogously as in the
free-algebra construction.
Thus, the chain W in the free-completion construction of a discrete algebra
is just the free-algebra construction.
DefliHhM. The free-completion construction is said to slop after k slept if
both »t,, i and wt,,, are isomorphisms.
Remark, (i) If Vi.,., is an isomorphism, then the construction stops after
Jr. steps because the pushout of pk and »,,», is then formed by
Pun - »»"'»♦ i -P»»nd »,.»,, - l,^
If "i. i ♦ i is an isomorphism, then the construction stops after k + I steps
because »., 1.1. i - »i. i,, fis an isomorphism. This is in particular the case
216
Chapter IV
whenever till limit ordinal such that F preserves the colimit Wk — colim W,.
• < k
(ii) We are going to prove that in case the free-completion construction
stops after k steps, the free completion of the given span algebra is {Wk,
T.'t ♦ i • Pi)- This can °c proved directly by induction. We are going to prove
this by translating the present construction as the initial-algebra construction.
7.7. Free coaakttoa a* the least that ■oiat. Let A - (ft D, &. S,) be a span
^algebra. We denne a functor G whose leut fixed point is the free
completion of A. Denote by BA the following category:
Objects are pairs (*, /) where B - (X, Y, jc* x,) is a span Filgebra (i.e.,
x,: Y-» X and x,: f-» XF) and /- (/o, /,) is a spin-algebra morphism
f:A-*B, i.e., the following diagram
commutes:
Morphlsms from (£, f)lo(B'.f) are such morphisms f - (fk $,): * -» **
of span algebras which fulfil f — /• $.
The formation of pushouts which is used in the free-completion
construction gives rise to the following functor
G-.aA-*xA.
For each object (A,/) - (X, r,*c *,,/,,/,) we form the puihout of x,»nd x,:
and we put
(B, f)G - (Z, XF, z* z,F,/, • z„ f, ■ x,).
For each morphism
CoiMlfvcttaa of FlM AlftbiM
217
there eiiiti • anique morphittn k: Z-» X In Jf for which the following
diagram
TV 5 .. XT
X
,/V
\
commutes (where 4 and 1,' are morphitmt forming the puthout of j£ and x,-).
Put
AG - (t. A.F).
It U euy to verify that Gill well-defined functor.
PiepaaKI—■ Let (B, f) be the leait fixed point of the functor G. Then B it
a (total) falgebra and the free f completion of A U
f:A-+B.
Proof, (i) We prove that Ait an ^algebra. Let
a:(*,/)G-(ft/)
be the Isomorphism for which ((B, /), a) It the leatt fixed point of G. Put
(B,f)-(X, Y, *_*„/../,)
and define
k - (r, • o^, x, ■ a,).
218 CluplerlV
We are |oin| to prove that
A :<*,/) -<*./)
is a moiphism of Bt such that
(1) ah-hGa.
By lite definition of the least fixed point, such A is unique—since also l,t/)
has these properties, we shall conclude that
A — liasi-
This means that r, • a, — I, and x, ■ a, — 11. Since a, and a, are morphisnu,
we shall have
(2) z, - ai' and x, - or'-
Thus, we shall conclude that x, is an isomorphism and A is a total falgebra
(by Remark IV.7.4).
To prove that
A :<*,/)-<*,/)
is a moiphism in 3tA. it is sufficient to inspect the following diagram in
JT (which commutes, since a is a moiphism in XA):
z,F
ZF-« ! XF-
-Y-
pushout
Further, by the definition of G we have
AG - (A, h,F)
where A: Z-» Zis defined by
2o • * - *if- *o - *if- Oof- *• - »o • {<*» ■ z,)
and
z,- A- Aa-z, - z, -(oo■ z,),
which implies
A- o,-2,.
Coiutroctlofi of Fr«« Algcbrai 219
Thus, AG - (a,- z,, i,F- a,F), and hence (I) meant that
a,■ h, — a,- *, • a* and a, - A, — z,F- a»F- a,,
both of which are eaiy to check.
(ii) For each Falgebra 8 and each span-Falgebra morphijm g :A-» 8, we
prove that there Is a unique Fhomomorphlsm g' : B-* 4 with g — /■ g'.
Representing 8 at
8-&Q.B, Iff)
and considerini the following pushout
-A, Of-
-»0f-
pucheut g
-»0F
o »a
-*8
we conclude that the object (ft g) of »,, fulfils
<ft»)G-<4»).
Thus, (4 g) is a fixed point of G with the corresponding morphitm !,»,,.
Therefore, there exittt a unique (r-homomorphitm »*:((*./), a) -»((4 »). I),
I.e., a unique Fhomofnorphlun
such that
g-f-g' and a-f'-f'G.
To conclude the proof (of the unlcity of »), it it sufficient to show that the latt
equation is superfluous: each Fhomomorphism gm : B-» 8 fulfils
ag'-g'G.
By remark IV.7.4, we have g• - (j•, x,-giF). Then f "G - (*, gbf).
where * is defined by the commutativity of the following diagram:
Y-^XF-^l-OF
f
X j-—Z
220 Clupter IV
Using (2), we aee that
k-tv'-gi - <>k-gi «nd gtF- a, ■ x, • f.'F,
which implies
»"C-(o," -g+a, -x, -g^F)- «•»•. Q
IX The initial-algebra construction over G it precisely the free-completion
construction for A over F. In fact, the initial object of BA is clearly
■L -WW
The next step X C is given by the puthout of 6% and 6°,
D 3—»0F-\^ —»! «-W,F
•oj «,
*frO
X C-(W„ K..P,. »,.,: w^,. >v,)
with the connecting morphism
(•"•.i. »l).i):-l- -» XG.
Analogously, X C is obtained from the following pushout
OF-
—=-»-W,F —2—
»W,F
-W,
to get
(»,.,, r,.,): XG-» 1C - (R/„ Vt,p„ »1>: w0, rt J,
etc In order to verify that X G* also represents the o-step in the
free-completion construction (and, more generally, X G" the n-th step for any ordinal n),
we need a characterization of chain-colimits in 9A:
ObMinU—■ »,, is a chain-cocomplete category with coordinate-wise
formation of o-collmits (for any limit ordinal a). That is, given an a-chaln
*..-:(*../.)-►(*-./-) (n S m < o) with *. - (*., Y„ x,.., *,..). then the
Coiulnictloe of Frc« AlgcbrM 221
colimit In Ma ii
B - (eolim X.. collm Y.,x0,x,;f+ /,)
where the morphisms in A ire determined by the fact that the following
diagram
(colimXjF
•y
■ IcollmYJ -
-» X.
\<U.
"IcollmXJ
"i -o
commutet for each m < a. Here A. and A» denote the rcipective collmit
Injection! in JT, and the colimit injection! in 9t are
(A.,*.):*-- B(m<a).
Corallary. If the free-completion constructions stop* alter k steps, then the
f*lgebra/4* - (W,,p, • wj;',» ,) is the free completion of A with respect to
wt t:A-¥ A'.
In fact, if the free-completion construction stops after k steps, so does the
Initial-algebra construction over G and hence. J. C* - {A ', »y,) is the initial
G-algebra.
7.9. We say that a functor F has amtwctirtfttt completions if the
free-completion construction stops for each span Falgebra.
Thaorto. Let JT be a cocomplete, /-cowell-powered (*, .^-category.
A functor F: JT ■ JT preserving /-epis hu constructive free completions iff F
is a constructive varietor.
Proof. By Example IV.7.6, if F hu constructive free completions, then F Is
a coiutnictive varietor. Conversely, let F be a constructive varietor preserving
/-epis. For each span Falgebra (Q. D, 6+ 6,) denote by
p: V—W
the free-completion construction and, for distinction, by
#
the free-algebra construction over Q. We define a compatible collection of I-
epis
222 Chipwr IV
since If stops, If also stops by Lemma IV.2.7.
(a) First step: e, - \Q: Q-* Q.
(b) Isolated step: the components of
«.♦.•■(? + rP.F-»:*i
are
*»..i:8->»'.,i and e.F- p., ,: rK.F-» W,, ,.
(Hmp.^-.V.,,- W.F-W.*,)
(c) Limit step: the components of
e,:lim *.-► lim If.
are*, • »,,(*< n).
We prove the compatibility. Using Remark IV.2.4, we prove that the
following squares
W„-
-w.
commute for all n < m.
(a) m — I: clearly wtx • e, — wt,.
(b|) If the square above commutes, then the following diagram
also commutes. This shows ihat ihe moiphisms
*.♦!.-,i • („*■; «..i • •».,,...,: Q+ rK.F-» Wmt,
Coratrvctloa of Free Atgtbrai
223
have identical second components. The first components of these two mor-
phisms are also identical (viz, wtmt,).
(bt) If the squares above commute for all n < it* where n, is a limit
ordinal, then they commute for no too. because PP„ - collm W,.
(c) The limit step in m follows from the definition of *,.
It remains to prove that each *. is in /:
(a) <0- le.
(b) Let t. € 4. and let
«„♦, - i- *
be an image factorization, i: (P.»i -» Z in 4 and iB: Z-* W,„, in Ut. We
have
where e\: lf.f-» (P.», - C + &.F is the coproduct injection. Since e. and
e.f are tt-epls, we can use the diagonal fill-in twice:
% ''»*(,
V< I / «M
V
Thus, both w.., , and p.♦, factor through the subobject A Since these two
morphisms form a pushout (of »...*i *nd p.), we have im*,,,,^
Imp.,, - I by Remark 111.5.4. Therefore, A Is an isomorphism, and this
proves e.„ , € *.
(c) The limit step follows from Exercise I11.5.B. This concludes the proof.
a
7,1ft. We prove now an important criterion for a functor to have
constructive free completions: the preservation of colimits of o-chains of subobjecu
(for some infinite cardinal a). We know that the preservation of all a-colimiU
is sufficient for the stopping of the initial-algebra construction (I V.3S), and it
can be easily seen that this is sufficient for the free-completion construction
too. Nevertheless, the preservation of colimits of o-chalns of UT-monos is
a considerably milder condition which Is often rather euy to verify (because
colimits of chains of monos are usually unions).
Defralttsa. Let a be an infinite cardinal. A functor has rank a iff it preserves
colimits of o-chsins of UT-monos.
224
Chapter IV
Euaiak*. (i) The functor H.: Sat -» Sat has rank a iff the cofinility of a
Is larger than <t In fact, if cof (o) > n, then for each union
tr-Utr,
> < ■
of an o-chain M, c II, c ... and for each element |i,|i< . € IIH. - II'
there exists I, < a such that j,e M, for all i < n. Thus, |x,) € M; and this
proves
JUTf. - U AW..
Conversely, if cof (a) s n and if the union above is strictly increasing, we
can find elemenu x, € M for i < n, such that for each > < a there existi ■
with x, t U,. Then \x,) € W — U II' and hence, H. does not preserve the
union.
(ii) For each finiury type £, the rank of Ht: Sat -» Sat is a. If 27 is infini-
tary, the rank of Ht is any infinite regular cardinal larger than all arities.
(iii) Let .* be a concrete category (I1I.3.8) with both chaln-colimits and
products preserved by the forgetful functor (/and with Ut — \m\mV\t one-
to-one|. (These hypotheses on jr are rather mild, e.g., all varieties of finitary
algebras and Poa, Top, Qra fulfil them.) Then H.: jr -» Jf has rank a IIT
cof (a) > n. This follows from (i) above.
7,11. Taurus Let JT be a cocomplete, /-cowell-powered (/, ur>cuegory.
Each functor F: Jf -» jr with a rank has constructive free completions.
Proof. I. For each span algebra A we form the free-completion
construction p \ K-» W. Let us consider the image factorizations
with «„.„: W.-* J,,m'mt Ktij..m: J.,m-* W.in.*.Since.* Is/-cowell-pow-
ered, for each ordinal n there exists an ordinal n * such that tm .. represents the
same quotient of W. as any e, m with m a n*. Thus, there are isomorphism
V- -J... —»/..« with
«...-«...••*..« (man*).
Define a map (: Ord -» Ord by transfinite induction as follows:
(0)«- 0:
(n+ l)i-<»)»•;
(/)l _ V (n)( for a limit ordinal L
Conftnioion of Fm Algttbm 225
We shall prove that Fpreserves the collmlt of the chain
defined by
"m ~ *M*)I *n*' *Va ~ Wtn)tAmti -
Then f preserves the colimit W,,v- colim Wm: theset of ill (n)l whh n < aU
«< t«>f
cofinal in (a)( and hence, by Exercise III.I.F,
^•n ™ colim H^a)) ™ colim W
Then the free-completion construction stops after (a)( + I steps by Remark
IV.7.6.
II. To prove that Fpreserves colim W, we define an o-chain of ur-monos /
as follows. For each ordinal n put
and put, for short,
'• ~ *Mf.|a)f* '• "• -* *m '•
By the diagonal fill-in, for each n s m there is a (unique)
such that the following diagram
t
1
'
«,-
1
^
-^» J
«. "J
„-
a
commutes. To prove that
/... « •*
it is sufTiciem to
/..-•
/-■
show that
" *<»». la
>■••
-^—11
l"
U-t«
^nlj.lalf*
(us m).
(the right-hand side morphism is clearly in Jt, and Jt is right cancellarive by
III.5.I). This equation follows from the fact that i, is an epi, since we have
226 Clupief IV
»■ * J*, m ' Jm ™ "V m * *m ' 3m
™ *<>>f.<M>f* *./t*>M»»*
~ '<• * St»)t.lW 'JfU.tmH* •
Therefore, /Is an a-chain of .4r-monos and hence, f preserves the collmlt of/.
The morphisms £„ form a natural transformation
«:lf-/
(this follows from the definition of 7...). Also, if we define If* :a-»JT by
>f.* - >f.*< »nd *;.„-*.♦,.„♦,,
then the morphisms j, from a natural transformation
/:/-lf\
It follows that If and /have the same compatible collections (and therefore,
the same colimits): if
/.:lf.-* (n<a)
b compatible for If, then
J.-f.*<:J.—-X (n< a)
is compatible for /: conversely, if
g.:J,—-X (n< a)
is compatible for /, then
«.•».: If. -» X ("<<>)
Is compatible for If It follows that
(colim lf)f - (colim J)F- colim /• f.
Alto the diagrams If- find /• fare in the same interrelationship: we have
natural transformations
IF: If- F — /• F
and
/f:/. f-»lf*-f- (lf-rT.
Therefore, /• find If- f have the same colimit, and we conclude that
(colim *)f - colim /• f - colim If • f. Q
CoraUary. For JT as above, each functor with a rank is a constructive varie-
tor.
Coratfudton of Fre« Alaeonu
227
T.12. Returning to the partial algebras, we are interested to know whether
the free-completion n: A -► A ' of a partial F-algebra A is an "extension", i.e.,
n € A. We say that the pushout axiom holds if in each pushout
t r
i,
m € A implies in € UT.
Propealtloa. Let jr be an («T, UT (-category such that A is a chain-cocom-
plete class and the pushout axiom holds. Let F: JT -► JT have constructive free
completions and preserve Ur-monos. Then for each partial f-algebra A the
free completion n: A -► A ' fulfils n € A.
Proof. It is sufficient to prove that in the free-completion construction of A
all w, .and »..« »•* Uf-monos (which also implies that the colimits defining V,
and W, for limit ordinals i exist). Since A is a partial algebra, we have
Vi E Jf. By the pushout axiom, also ny, € A, hence, »,.i — w0. if € UT,
etc. For each ordinal n, assuming if,.,»i E JT, we get »,♦,.. +, -
»"...♦ if e UT and hence »■,,,.,, € UT. Using the chaln-cocompleteness of
Ur, we can easily check that h>„ . € A. Since f has constructive free
completions, the chain Wstops, say, after * steps. Then n - ivy, € A. □
Exerdaa IV.T
A. Free coaplrrlea of partial grapoMa. (i) Let (X, ♦) be a partial groupoid. Put
Wt - X; tVt - X + X'/~ where ~ is the least equivalence with (X|, x,) ~ *
whenever x, « x, - x: etc. Verify that U W, is the free completion of (X, •).
Compare this with the free-completion construction.
(ii) Do the same with a relational groupoid, i.e. a pair (X, •) where • Is a
ternary relation on X.
B. Free coaialeHoa of maiy-sortea' algebras. For each type Zo( many-sorted
algebras verify that Hi has a rank, and conclude that each partial ^algebra
has a free completion which is its extension.
C. Free completion la Sat itl A-Vect. Characterize functors f: Sat -» Sat
and F: A-Vact-» A-Vect which have constructive free completions. (Hint:
IV.7.9.)
228
Ch.pttr IV
D. F—tt»n whb a nak. (i) Prove that if a functor F: JT -► JT is a coproduct
of functors with rank a, then Fhas rank a, too.
(il) Prove that each Hc has rank assuming that JT is a concrete category with
both chain-colimits and product! preserved by the forgetful functor. (Hint:
See IV.7.I0(III).|
rv.8. Categories *f Algebras
8.1. In the present section we investigate the basic properties of the category
F-AJg
of ^algebras. Recall that
(/:£Akj-»jr
denotes the forgetful functor (III.2.B) defined by (ft S)U- QmifV-f.
Limits of ^algebras are always formed on the level of JT-objects. More
precisely, if JT has a certain type of limits, then F-Alg also has these limit! and
the forgetful functor f preserves them. For example, let JT have products.
Then for an arbitrary collection of F-algebras
(ft. «,). 1 € /,
we can form the product
e-n,e
In JT with projections «,: Q-+ ft,. By definition of product, there exists
a unique morphism
6:QF-*Q
whh components n,F- S„ i.e.. with
8- it, - K,F- S, for each I € /.
The last equation states that
",AQ,S)-{Q„SI) (fe 1)
are homomorphisms. It follows that we obtain the product
<e *) - n<e. s,)
in the category F-Alfl. More generally:
PrepoarrUHi. Let DQ-+ F-Alg be a diagram of algebras and let ft -
lim D- U be a limit in JT with projections *,: ft-» d(D- UXd € «°). There
CoimnKtJon oTFnc Algtbns
229
exiau a unique motphism 6: QF-+ Qiuch that (Q, 5) — Hm D In F-Mq with
the same projectioiu.
Proof. For each d € 9° put dD - (Qj, ft). The family
XtF-By.QF^Q, (</€»•)
is compatible with the diagram D ■ U: for each /: d-+ d In » we know that
fD: (fa, Sj) -»(Qit S'd) U a homomorphism, i.e,
SdfD-(/D- F)- ft,
and that *v - jr,■ /flit follows that
»>f • ft - X,f • (/"D • f) • 5/ - <V" ft) • /A
Therefore, there exists a unique morphism
S-.QF-.Q
with
SXj-XjFS, (</£»")•
Thus,
*: (ft «)-<&. ft)
are homomorphisms.
Let
A,:(*,o-)-(&.ft) <</£«■)
be a compatible family for D. Then the morphiinu h<: R-+ Q,form a
compatible family for D ■ U. and hence, there is a unique
A:/l—C
with
A • n4 - A, (</ € 9»).
230 Chapter IV
It remains to prove that A Is a homomorphism. I.e..
a- h- hF- &
This follows from the fact that each h4 is a homomorphism:
(ff • A) • Kt - a ■ h4 - h4F■ S4 - hF■ (K„f■ S4) - (hF- S) ■ x4.
This concludes the proof. □
Corollary. If JT is complete, then f-Alfl is complete, and the fortgeful
functor preserves limits.
8.2. Colimits of algebras are closely related to free completions.
For example, let.» have coproducts. Given a collection of algebras
<G. S.) (I € /).
we form the coproducts II Q, (with injections p,) and LI fif (with injections
r,) in jr. We have canonical morphisms:
s,- u t?,f- u e.
^UG^-dlG)*
i.e., morphisms such that the following diagrams
i 6,
0,F-« 0,F <—- 0.
IU0,)F*—0,F T*110'
commute for all j e /. Then
(LI, G.JL^fiF. «,.*.)
is a span f-algebra (IV.7.4).
PrafoaltkM. Let
'^:(LIft•LIG':«^«t)-(G^«•)
be the free completion of the above span algebra. Then
(G".«")-LI,(G.«,)
is a coproduct in f-Alg with injections
P.- 7:(G-«.)-(G",«') O'E /)■
Contraction of Fm Algebras 231
Proof. The above diagrams show that
0>/.',): <<>/•«/)-•• <II ft. U ft*** «.)
are morphisms of span algebras. It follows that pt ■ n are also morphlsma
U e J).
Let
/: (ft. «,)-«?.*) «e /)
be a family of homomorphhms. There exists a unique morphism
*vlie-o
with
Prl>-f) for each./ € /,
and a unique morphism
4V ftf- QF
with
')' S\ ~ P)F' g»F t»t ««eh j € /.
Then
(Jo,*.):(IIft. II ft *«*«.)-«?.£)
is a span-algebra morphism because each of the following diagrams (J € J)
0,F«
lilO.IF-
Of
1
-0,F >—«-0,
5
-HQ^F
r
Of -
no,
i - T—u
commutes. There exists a unique homomorphism
g,:<e,.o-)-«?.A')
with
(*o,*i)- "*••
232 Cliaput IV
Then
f,-Pf »•-(»)■ l)-l' for each; € /,
and iuch g ' ii obviously unique. g
Restart. The aame can be easily proved for each diagram D in F-Alo,: we
obtain a natural ipan algebra
(colim D ■ U, colim D- V- F.St.S,)
and its free completion, if it ezitta, it the colimit of D in the category f-Alg.
Corollary. Let jr be a cocomplete category. For each functor F: JT -. jr
with conatructive free completion! the category F-Alg ii alto cocomplete.
Corollary. Let JT be a cocomplete, /-cowell-powered (/, -O-category. Then
F-Alg it cocomplete whenever F ia
(I) a functor with a rank, or
(ii) a conatructive varietor preserving /-epis.
Sec IV.7.11 for (i) and IV.7.9 for (ii).
8J. The construction of a colimit of ^algebras becomes eaay in case the
functor F preserves the corresponding type of colimita. For example, let f
preserve coproducu. Then the coproduct of ^algebras
(a, 6,) o € o
is the algebra (II Q„ S) where S is defined by
t • f
6- lift:(IIfi)f-lift
[which is meaningful since (]} Q,)F~ ]} Q,F\ More generally:
PrepaalHom. Let 9 be a diagram scheme such that JT has colimita of
diagrams 9 -» JT, and F preserves these colimita. Then the category F-Alg haa
colimita of all diagrams 9 -» F-Alo,, and they are preserved by the forgetful
functor.
Proof. For each diagram D:9—-F-Alg with objects dD- (Qj,6,) for
d c 9° we form the colimit Q- colim D- (/in JT with injections «,: Qj-*Q
(d c 9'). The collection
it clearly compatible for D • V • F and hence, there exists a unique morphism
5: QF- colim D- U ■ F-* Q with
6>«v- CjF- 6 (</€ »•),
Coiutiudloo of Fn< Algebras
233
i.e., luch that et: (Qj, &,) -* (Q. 8) are homomorphismi. Then (g, S) -
coital D in the category F-Aig with injection* «<. In fact, given a compatible
collection
/<: (ft. «,)-(e\6") (<*€«■),
there exists a unique morphiim/: g-» C in JT with components .£. Then/ii
a homomorphiim, i.e.,
6-f-fF-S':QF—ff
became QF - colim Q^F and for each J c 9° we have
«|F-(«■/)-*■*,■/
-eSifF-F). O
CaroUirr. Let jr be cocomplete and let F be a co-adjoint. Then F-Alg ii
cocomplete, with collmita preserved by U.
Eusapk. Unary algebras have coHmits preierved by the forgetful functor:
this ii the case of JT - Sat and of the co-adjoint F - St- In Exercise D below
we show that no other algebras in Sat have coliiniti preserved by U. In fact,
not even finite colimita.
M. CsiatamaiaU. We now present a (Injury varietor
f:Poa-»Poa
for which F-Alg is not cocomplete. In fact, we will find an algebra (Q, 6) such
that the coproduct (Q, 6) + (Q, 6) fails to exist.
We denote by P the power-set functor (111.3.4).
For each poset A denote by A'" the set of ail 3-chaina in A, plus an
additional point i (which is not any 3-chain). That is,
A°> - Hx, y, 1) e A': x < y < i\ yj |fl.
On the set A°'Po( all subsets o(Am we consider the following (trivial) order:
Af^Y iff X-YotX-t forallJT, Yc A">.
This defines a functor F: Poa -» Poa on objects:
AF- A'»P.
Define it on morphiim* f:A-*Bby
fF-fnP
(x, y, 2)P>< - i
234 Chapter IV
where the map/"1: A'" — B»< is defined by
(*V) if (*)/< W< (*1A
else.
It is easy to check that f is a well-denned functor.
fis a finiury varietor: indeed, the free-algebra construction stops after one
step. We have
Wt- I:
rK, - / + P'P,
and thus, W, is a disjoint union of / and 1"'P. Since the latter poset hu no
3-chains, clearly If'" - I"\ hence,
Wt - I + W?P - I + /"'I" - W,
with w, ] — li^, etc. Here, W, is the free ^algebra.
We exhibit an ^algebra (ft 5) such that the coproduct (ft 5) + (ft 5)
does not exist in F-Mq. Let Qbe a 3-chain ft - \x, y, r| with x < y < t, thus,
0"> - (I, {I where f - (x. >•, r).
Let
*:|f,flJ»-»|*,jw|
be the constant map with value z.
Lean. There does not exist the coproduct
(ft S) + (ft «)
in the category F-Alg.
Proof. Assuming that an j^algebra (R, <r) is the coproduct
(* <r) - (ft, S) + (ft «)
with injections v,, v,: (ft, 6) -»(ft, <r), we shall derive a contradiction.
We have a pair of homomorphismi I,, 10: (ft 5) -»(ft 6), and by the
definition of coproduct, we get a homomorphism </:(R, 5)-»(ft 5) with
l0 - »,-</- v, • J. It follows that », and v, are one-to-one maps.
Put
2* - (0)<r c X.
Then
(2)V, - (2)V, - J*
because », (i — I, 2) is a homomorphism, and we have
(*)v, - (0)«- v, - ((0)v,f)<r - (0)<r - r*.
ConunictMn or Free Algebm 235
It follows that
(*)»i < O0»i < **
is a 3-chain in X (because r, is one-to-one), and we put
I, - ((*)»„ 0>)»„ *•) € R'».
Analogously,
h - «*K 0-K «•) e *'"•
Let us prove that
I, + I,.
Let ft, be the following poset:
and let a,: R,F-* ft, be the constant nap with value z. The two obvious em-
beddings w,, w,: Q-* R, are homomorphisms w,, w, :(ft 6)-» (R*, "„). "There
exists a homomorphism w:(R, cr)-.(flfc 5,) with w, - v, - w and
wt — »i • w. Then
(*)», * (*)»,
because ((x)v,)it> * ((x)vt)N>, and hence, (, * i2.
Let us prove that for distinct sets X, X" € X'"J>,
(•) X t [<„ {\Pu \h, {\P implies (X)a * (*>.
Assuming (X)a - (^)tj -re ft, we denote by A the poset obtained from X
by splitting r to two points. That is
*_(K-|r|) w|r„ r,|,
where r, and r] are incompatible points, the ordering of ft — |r| is as in ft, and
for each x e R — |r| we have r, s jt iff r s jt (analogously with rtSi and
r, 2 x, r, 2 x). We define order-preserving maps
A:A-»X and k:R-*R
by
(x)A - (*)* - x for each ie X - |r|;
(r)* - r, and (r,)A - (r,)* - '•
Note that
*•*- I..
236 Chapter IV
Define an operation a: R"'P-* R by
\(Y)h°>P-a-k else.
Then
»i-*.»i-*:(a«)-»(*<?)
are homomorphiuns: for each Z c Q"' clearly (Z)r?*P c |(„ f|, thua
AT i» (ZK'J> - [(ZK'J'- ft^'Pl*™!*.
Therefore, if r- (Z)»',,»l>. Jf'!", then
(Y)o-(Y)h<»P-o-k
- (Z)rf'P-Hk'»P- h°>P)■ a- k [*•*- l|
-(Z)»P»I'.<t-*
- (Z)6 ■ »| • * [»i a horaomorphUra).
Thh prova that (*,- ky"P-o- 6-(»,•*), i.e., that », •* Is a homomor-
phiirn; analogously with "i ■ k.
By the definition of coproduct, there exists a homomorphitm
£:(*,<x)-(*.<?)
with r, • £ - r,. k and n • * - v, • k~. Alio, A: (A, <r) -»(A, <r) is a
homomorphum, i.e., ah- h'»P- a: given Yc R"\ then (Y)k<»P- AT implies
(J>'*-(l)A- r-(X)a- i.Y)h°<P.o
u\<HY)h<»P + AT implies
(!>• * - (K)*»'J>. <r. *• * - (Y)h°'P- a.
Thus,
£A:(*,<x)-(*■")
is an endomorphism with
»,•(£•*)- »,•*•*- », fori- 1,2,
hence,
£.*-!,.
Therefore, ■?"!>- A"'!* - I and hence, ftX)P»P]h'»P - X. It follows that
[(Jf)/P"flfj - r,. Since (is a homomorpbism, i.e, a-H- f"'P- a, we get
'i - ((AOf'^ff
- (Af)<x- £
-(f)*
ConuroaJon of Fi» Alftbru 237
Thi! impliei that Y-W&'P fulfill (r)*"ip-Af [elie (r)«F -
(r)n0>J,o-*,» fj. Thua,
X - (r)A<»J> - (XycmP- h°>P - r,
which prove* (*).
The required contradiction will be obtained by proving that the let
JC- |r c R.l' S r)
admin a one-to-one map from KP — |0| into JC, and yet JC hu more than one
point (Thii ii obvioiuly impouible: for any let JC with card JC > I we have
card (KP— |0|) - 2™* *— I > card JC.] For each non-empty act M c JC put
<
/
m
/
' ,*M )
WSJ
•
*\
"I*
Note that U t {<„ flPw |!„ f]J» and Af i» Af Implia A? * A? for all M,
W c JC. By (*) we conclude that (St)o* (Aif")o-, and lince 0 3 U in Xu<l>
impliei x* - (0)o- £ (AY)o-, alio
(A?)ct c JC for each M c K, H + B.
Thai, A/>-» (A?)o- definei a one to-one map u required. Finally, to prove that
JC hu more than one point, put
Then *i € JC became H |f„ (,| in X'"l>, and by (*) we have (0)o- * i,. Ana-
logoualy, for
h - (U. 'i. 'ii)"
we have t, € JC and by (*) again, r, * t,. Thii conclude! the proof. D
238 ChipWf IV
■J. Nut, let us consider image factorizations (II 1.5) of homomoiphiama of
^algebras. Let F: JT -► jr be an arbitrary functor. Let (/, UT) be a
factorization system in JT such that F preserves /-epis, i.e.,
e e I implies eF e t.
Then (i, .M) is also a factorization system in the category
F-Alg
of algebras. More precisely, each homomorphism
/:(tt«)-(t7.«")
factors as a homomorphism in 4 followed by a homomorphism in Ur". To
prove this, let/— e • mbe an image factorization of/
e:Q-+R'mt and m: R-+ Q" in ur.
We use diagonal fill-in:
OF —»-RF
t / mF
0 / tfF
« / y
B j^-*- Q'
Then (R, a) is an ^algebra such that
i{Q. S)-*(R, a) and m:(R, <x)-»«?', 6")
are homomorphisms.
ur-subobjects in F-Alj are called subalgebras. Thus, a subalgebra of an 5-al-
gebra (Q,S) is represented by a homomorphism m:(R,o)-*(Q,6) with
m € ur. Let m,: rt0 -» C be an ur-subobject of g. We say that a subalgebra
m: (ft, cr) -» (ft. 6) is generated by the subobject m, if m is the least subalgebra
with m, c m. We say that m, generates the algebra (ft 5) if no proper
subalgebra contains m,. I.e., for each m: (ft cr) -»(ft, 6) in ur,
m, c m implies m is an isomorphism.
/-quotients in f-Alg are called quotient algebras. A quotient algebra of
(ft, 5) is represented by a homomorphism e: (ft, 5) -»(ft, <r) with e e /.
Lrauaa. Let JT be an (t, Ur>category with intersections of uf-subobjects.
CoratnKtIon of Fret Algebra 239
and let F: JT -. jr preserve /-epti. Then each .#-subobject of each ^algebra
(Q, S) generates a subalgebra of (Q, 6).
Proof. Let in: S-► Q be an Jtr-mono. Let
m,-(R„ «>i)-»(ftei) (i'€ /)
be the (possibly large) collection of all subalgebras of (ft 6) containing ift. Let
m'\ R'—Q
by the intersection of all m„ I e /. For each i c / we have a morphism
/: X*-» X,with m*-/- m,. Since *c m,(* € /)implies m c m*,it is
sufficient to exhibit an operation morphism
a': R'F-» R'
such that m':(R', a') -» <Q, a) is a subalgebra. Then m* is clearly generated
by m.
Let
m'F- 6- I- ift
be an image factorization, t: R'F-* 7" in « / and irt: 7"-» Q in ur. For each
( £ / we have
* • in- f,F- m,F ■ 6- ftF- a,- m,,
and we can use the diagonal fill-in:
f.F-o,
m.
♦ 0
We see that * c m, (i e /) and hence, Ac m'. Let /; 7"-» X* fulfil
ih — /• m", and put a* — t • f. Then
<7* • m* - * • /• m* - * • rt - mV- 6",
i.e., m * is a homomorphism. This concludes the proof. D
&6. We conclude this chapter by an important criterion for varletors which
is expressed by generation. Let us say that a functor F: jr -» jr has bounded
generation if each object X in •* generates only a (small) set of ^algebras.
That is, there exists a set (ft, 6,), I e /, of Falgebras such that
(i) each (ft, 6,) is generated by some UT-mono X -► ©;
240
Chapter IV
(ii) If an algebra (Q, 6) is generated by some ur-mono X-» Q, then (£6°) Is
isomorphic to (fi, 6,) for some ( c /.
Theoma. Let jr be a complete (/, ^0-category which is /-cowell-powered
and ur-well-powered. A functor F: JT -» JT preserving /-epis is a varietor iff
F has bounded generation.
Proof, (i) Let F have bounded generation. We shall prove that the forgetful
functor U: F-Alpj -» JT is an adjoint (Exercise III.2.B) by verifying the
hypotheses of the Adjoint Functor Theorem (II 1.2.10). We know that F-Alg is
complete and U preserves limits. It remains to show that (i) X has only a set of
/-quotients X', (ii) each X' generates only a set of /^algebras (ft 6°), and (iii)
for each (ft 6) there is only a set of morphisms from X to ft Therefore, we
can find a (small) representative set of morphisms
/:*-(&«)
where (ft, 6) is an algebra generated by a quotient of X, and /: X-» ft is an
arbitrary morphism. This is a solution set: each morphism
»:X-(f?,5)U-(J
factors as
g-fhU
where A: (ft 6")-»(g, 8) is a homomorphism and (ft, £) is generated by
a quotient of ft. To prove this, let g - e, ■ m, be an image factorization,
•V X-» X' in * and m,: X' -» (J in jK.
The subobjects m„ generates a subalgebra m:(Q, 5)-►((?. 8); then «?, 5>is
generated by the quotient X' of X, and we have m„ c rfi, i.e., m„ - p ■ m for
some p: X' -► ft. Thus,
t - (*o • p) ■ mU.
(ii) Let F be a varietor, and let X be an object of jr. We shall prove that
whenever an algebra (ft 5) is generated by ft, then ft is an /-quotient of X*.
Since X * has only a set of /-quotients, and since for each of these quotients ft
we have only a set of morphisms 5: QF-* ft this will prove that X generates
only a set of algebras.
Let m:X-»ft be an urmono generating (ft, £). The homomorphism
m*:(X\«>)-»(g, S) can be factored as m' - e- m, where e:(X*,«>)-►
(ft, 6) ia a quotient algebra and m:(Q, 8)-*(Q, 6) a a subalgebra. Then
mem [because m - n - m* - (n • e) • m c m] and (ft 6) is generated by
m; hence, m is an isomorphism. Therefore, m' e / and ft is an /-quotient of
X'. D
Construction or Free Algebra*
241
Remark. Let JT be a concrete category (111.3.6) such that for each cardinal n
there is, up to isomorphism, only a set of objects X with card (RU) S n. Then
bounded generation can be expressed more concisely as follows: For each
cardinal n there is a cardinal n* such that any F-algebra on n generators [i.e.,
generated by an object X with card (RU) - n] has at most n* points [i.e., it is
an algebra (ft 5) with card(QU) & n'\
Excretes IV.S
A. CoIlaiMi wlrhoat free esaspletJosa. Verify that the following functor
F: Ord -. Ord
Of- 0: nF- n + I if n e» 0
does not have free completions of partial algebras and yet, F-Alg is cocom-
plete.
B. Cotqoallzers aftea exist, (i) Let JT be /-cowell-powered and let F
preserve /-epis- Prove that the free-completion construction stops for each span
algebra (ft D, 8* 6,) with S, c /. (Hint: Prove that Hy. c /and v. e "or
each n by induction, and use the fact thai ft and D have only a set of
quotients.)
(li) Prove that for each /-epis preserving functor F in a cocomplete, /-co-
well-powered category, F-Ahj has coequalizen. (Hint: The span algebra of
Remark IV.8J fulfill «,€/.)
C Flalte colltarts •rcMrred by the forgetfal faacter. For each standard set-
functor F, prove the equivalence of the following statements:
(a) F-Ahj has finite colimits preserved by U\
(b) f-Alg has countable colimits preserved by U;
(c) F preserves finite colimits.
[Hint: (c) implies that Fpreserves countable colimits (see Exercise III.4.F)
and hence (b) follows from IV.8.3. It is sufficient to prove that (a) implies (c).
Since BF-B [for F-Akj has an initial object (0,5)1, we only have to prove that
Fpreserves the pushout of arbitrary maps/: X -+ Yu\d f.X-» Z By 111.4.6.
Fpreserves finite intersection and hence, it is clearly sufficient to prove that F
preserves the pushout of the extended maps
f:Xw\4-*Yw [ajandf- : *w |a|-. Zw |a|
where a is a new element and (a)f - a - (o)f'. Define an operation
6t:(X\j |o|)f-» X\j [a| as the constant to a, analogously with Sr and <V
Then f and g' become homomorphisms. Since (/preserves the pushout of/'
and g\ it is easy to show thai Fpreserves the pushout in Sat.]
D, CollmHs aitstntd hy the fergetfal fnctw. Let F be a standard set
functor.
242
Chapter IV
(i) If F-Alg has colimits preserved by U, then prove that F-Alg is the
category of unary algebras. [Hint: By III.4.8, it is sufficient to prove that Fpreserves
colimits. For finite colimits see Exercise C above, for coproducts II X,
proceed analogously: find a new element a and consider the coproduot of the
algebras (X, \j |a|, 5,), where 6, is constant to a)
(ii) If F-Alg has finite colimits preserved by U and if no cardinal is
measurable (IV. 6.3), prove that F-Alg h the category of unary algebras.
[Hint: By Exercise C above, Fpreserves counlable colimita. To prove that
F preserves any coproduot X — llX,, it is sufficient to show that each
i < i
x € XF lies in some X,F, i e / (since the sets X,F c XFare pairwise disjoint
because Fhas no distinguished point). The set 3 - \Tc X;xe TF] is an ul-
trafilter closed under countable intersections because F preserves finite
unions and countable intersections. Hence, 3 is trivial, & — f, for some y e X
(say, y € X„). Then x e X<,F.)
Moles lo Chipler IV
IVJ
The Initial-algebra comtmction It s special case of Ihe free.alaebra comtniclioii of Stc-
lioil IVJ which wh fiftl investigated for let fbiKton by V. Pohlova|l973|and V. KArkovi.PoMo-
ve and V. Koubek 11974). ind for general functors by J. Adamek |I974i) A muiber of authors
study Ihe restriction of Ihe Initial-algebra construction lo Ihe first e steps. Me M. A. Arbib 11977),
M. B Smyth 11976), M Wind 11971] end references there. The leafl.flied-polnl conitrvctloa n
from B. Knuler |I92»| end A. Terskl 119551
Proposition IV.3.oh due lo M.Barr|l970] and Proposition lv.2.7duelo J. Reheman |l977b|.
IVJ
The term varietor hu been introduced by Ihe preient lulhon: M. A. Arbib and E. G. Manet
uselhelerm Input process or recursive process. Corollary IVJ.4 it from J. Adanck 11974a) Eier
ciH IVJ.A wai suggested by J. Reherman a V. Rodl.
IV.4
The Characterization Theorem hu been proved by V. Tmkova, J. Adamek, V. Koubek and
J. Reilennan 11973). V. KurkovaPohlova and. V. Koubek |I974| described varieton in lot Their
proof was much more complicated than the present one. based on Ihe Characterization Theorem,
but they covered Ihe more general sitaation of F-G-algebras (see the notes lo II 1.2 above).
IV.3
Theorem IV.SJ and Eiample IV.3.3 are due lo J. Reilennan 1197Tb), and Theorem IV.3.3 due
lo V. Tmkova. J. Adamek. V. Koubek and J. Reiterman 119751
Construction of Free Algebras
243
1V.6
J. Adamek ind V. Koubek |I979| characterized flnltary varietors In Set. They abo proved that
i category JT which hu the flied-polnt property (i.e., each rmctor F: jr -» JT has a fixed point)
can be netthcr complete dot cocomplete. An example of a category wkh the flxed-poiat property
b the category Set.: this result, in the form of Theorem IV.6.4, bdwto V.Tmkov*|l974|.
We uk the term 0-category for the enriched categories over the cartesian closed category
Poa«. A number of authon study the flnrtary initial-algebra construction to an of-category, not*
ably M. Wand |I979) whose technique was used hi the proof of Theorem IV.6.7. The Botion of
tsotone coilmlls and the general form of IV.6.7 are new: they were announced in J. Adamek
(1978). The surprising fad that even for L inflnitary the tuactor Wj is a finrtary varicior In Poa»
was established by G. Janembski (1982). Free o-contlnBOos algebras were described by J. A. Go-
goen •* at. f 1977) and E. Nelson (1981). free strictly sKonttnuoas algebras by J. Adamek, E.
Nelson and J. Refterman (1982).
IV.7
Free completion of span algebras was Investigated by V. Koubek and J. Rclterman |I979) who
proved Theoremi IV.7.9 and IV.7.11. The interpretation of the free completion as the least Hied
point (see IV.7.7) Is due to G. M. Kelly's survey |19o2| of Iransflnhe constructions.
The fact that a functor with a rank is a varietor has been eatabHshed already by M. Ban [1970).
Hb proof b existential, and hb additional hypotheses are somewhat snore restrictive than those
of Corollary IV.7.11.
IV.8
CoHmlti of F-algebru were studied by J. Adamek and V. Koubek (1977b. 1978). The earlier
paper ii the source of the results In IV.8 J, or Proposition IV.8.3 and Theorem IV.g.3. the latter of
Counterexample IV.8.4 (which is a modification of an example of J. Adamek 11977b)). Theorem
IV.8.3. Is from J. Adamek |l974b). The Exercises C and D are new.
Chapter V: Minimal Realization and Redoctloa
V.l. Mlalaul Rtdactkw
l.t. The present chapter is devoted to the problem which varietors have
minimal realization (III 2.9) for all behavior morphisms b: /* -» T, and to
consequences of this property. We consider first non-initial /^automata and their
minimal reduction. This can be rormulated without the hypothesis that F be
a varietor. It turns out that, in suitable categories, functors with minimal
reduction are Unitary varietors anyway.
12. Nw-blrlal aatoanta. Let F: •*-».* be an arbitrary functor in an
(#, UO-category jr (see 111.2.7). A non-initial Fautomaton is a quadruple
(C. s. r, y)
consisting of a F-algebra (Q,5) and a morphism y: Q-+ r. A morphism
f'A.Q,S,r, y)-* Q'.S'.r.y') of non-initial /^automata is a morphism
f:Q-+Q'ofj( ch that the following diagram
OF -—»-0
!F
V
ffF —"Of
0
commutes (i.e.,/is a homomorphism commuting with the outputs).
Deflnltlea. Let A be a non-initial fautomaton. A reduction of A is a
non-initial /^automaton A' together with a morphism f:A-+ A' such that/e /.
A reduction r.A-* Aa is minimal if for each reduction f.A-* A' there
exists a unique morphism g: A'-* A„ with
r-/S-
Reaurk. Since /• g - r e t, we conclude that g € * (III.5.I). Hence, the
minimal reduction A, is characterized by the property that any reduction of A
can be further reduced to A„.
Minimal Reallaliofi and Reducttoo
245
Puporitlic Let JT be an (**, ur>category. For each varietor F, equivalent
are:
(i) every behavior has a minimal realization;
(ii) every non-initial automaton has a minimal reduction.
Proof. (ii)-»(i). Let
fi: /* -► T
be a behavior morphism. Put
A - (/*, «\ T, fi).
This is a non-inilial /^automaton. Let
r:A-A, - (Q» 6* T, y>)
be its minimal reduction.
ft-
rF
v-
— I"
%
■Volt
Then the following (Initial) /^automaton
Is the minimal realization of fi. Indeed, the run morphism of A, is r [because
r: (/*, a?) -»(Q, S) Is a homomorphism and n • r is the initialization of A&.
Hence, the behavior of A, is
r-n-fi
and A, is reachable, since r 6 **. Further, for each reachable realization of fi:
A' - (C\ «\ T, r\ /, A),
the run morphism
p':(/', r)-»((?'. «)
is a reduction of ^:
p:^-(C-, «'. T, y).
246 Chapter V
because P—p'-y' (for A realizes />) and p° € t. Thus, there exists a mor*
phism of non*initial automata
*:(C. «'. T, r')-4>
with
r - p' • g.
The last implies ij • r — A" • g, hence,
is a morphism of initial automata as well.
(i)-(ii). Let
A - (ft 8, r, y)
be a non-initial automaton. Consider the initial automaton A' — (Q, S, /", y,
Q, \Q). The run map of A' is the unique homomorphism
p: ((?■.*•)-» (ft*)
with
ij-p- l„.
The behavior of A\
P-pyQ'^r
has a minimal realization
a, - (ft, fifc r, r„ e. A.).
We prove that
i«:A-*A = (ft, ft, T, r.)
is a minimal reduction of A. First, the initial automaton A' is a reachable reali*
zaiion of 0 (for 17 ■ p — I implies p £ toy III.5.1). Thus, there exists a mor*
phism
r: A'-* At,
Then r — h, (since r preserves the initialization) and
r.A-*Aa
is a reduction of A. (Indeed, p • r is the ran morphism of A„ by III.2.5, and
p • f e t implies r i toy III.5.I.) Next, given a reduction
f:A*(Q\S, r,f)
Minimal Realization ind Reduction
247
of A, we form the initial automaton
a -(ff.s-.r, r; /,/)■
Its run morphism is p-f, because this is a homomorphism with
1' (P • f) ~ /• Hence, A' is reachable and it realizes p ■ /■ y" - p • r - fi-
Therefore, there exists a morphism
g:A-*A„.
Then
«:((?•.«•. r,f)^A.
is a morphism with
r-fg
(because r - \, and g preserves the initialization). This concludes the
proof. D
U. Cobttenecthwa, Recall the concept of intersection (111.5.2); the dual
concept is cointenection. All /-quotients e: X-+ Y (€ /) of an object X are
ordered as follows: f& t' iff there exists a commuting mingle
-»V
!
The meets in this ordering are called /-cointersectiona. Each /-cowell-pow-
ered category which is either complete or cocomplete has (possibly large)
cointersections—this is the dual of 111.5.3. Also, if t: X-* Y is a
cointenection of /-quotients t,\ X-* Y, (J e J) and f,:Y/-»Y an moronisms with
' — 'r f>* then the following diagram
/A
is a multiple pushout. This is dual to II 1.5.2.
248
ChifHtr V
A functor F: Jf -»JT preserving <r*epis (i.e., such that e e t implies
eF e f) is said to preserve coinlerseclions if for each coinlenection e:A-*B
of ^quotients e,:A-*Bj(je J) eF'a a coinlenection of the ^-quotients ef
(j 6 I). This is a central concept of the present chapter. There is a close
interrelationship between preservation of cointersections and the existence of
minimal realizations. We present below various characterizations of functors
preserving cointersections. For example if jr - Set or jr - R-Vact, this
characterizes the finitary functors.
Let jr be an (#, ur>category with cointersections. Each functor
F: jr -» or preserving cointersections has minimal reductions.
Reaiark. We prove a slightly more general result. Let us say that F weakly
preserves cointersections if it preserves the coinlenection of any collection of
^-quotients, e/.A-» B,(j € J) for which there exist "operation" morphisms
and
6.AF—A
8,: B,F— B,
(j 6 J)
turning each e, into a homomorphism e,:(A, S) -»(B,, 5,). We prove that also
this weaker condition is sufficient for minimal reductions.
Proof. Let
A - (Q, S, T, y)
be a non-initial ^automaton and let
tl:A*Al-(Ql,8,.r,r,) (;«•/)
be a collection of all reductions of A.
We form the cointersection
*C-<?
Minimal Retliullon ind Reduction
249
of the collection t, (J 6 J), and we obtain a multiple puthout
e Ot • • •
HI
I ► B
Since each et preserves the initializations, we have
'/ • Yi - y f°r eac'1 Je ^
and hence, there exists a unique ?:Q-*r with
(1) Y,-fr? 0« 1)
Furthermore, if F (weakly) preserves cointertectiona, then iF is the coinler-
section of ef and hence, the following diagram
| OF
eF Q,F • • •
1 *■ Of
Is a multiple pushout. Since each e, is a homomorphiim, we have
*/•(«;•/;)- S-erfk- S-e.
Thus, there exists 6: QF-* Q with
(2) Srt-ff-S (Jt J).
We claim that
i;A^A-(Q, S.T, f)
Is the minimal reduction of A.
First, e is a morphlsm because (for any j e J)
S.i-6-erf,
-ef-Brf, by(2)
-ef-f/S
- iF-S
250
Chapter V
and
'•?-',-/;•? by(l)
- Y-
Given an arbitrary reduction of A,
e^.A-A,.,
then (I) and (2) imply that
fh:Am^A
is a morphism, and
'- <>.■/>.■
This concludes the proof. D
1.4. For the converse of the preceding result we need a certain (mild)
additional condition of the (t, ur)-category jr: we say that jr has ngular finite co-
products if it has finite coproducts and the coproduct injections
A — A+ B
are ur-monos (for arbitrary objects A and B).
Tfccoren. Let Jt be an (/, ~4Q-category with cointersections and regular
finite coproducts. An /-epi preserving functor F: * -» * has minimal
reductions iff F weakly preserves cointersections.
Reaurk- For further reference, we denote by (•) the (single) argument in the
following proof in which the regularity of finite coproducts is needed.
Proof. By Remark V. 1.3, it is sufficient to prove that F weakly preserves
cointersections assuming the existence of minimal reductions.
(i) Let ', (Q.S)-*(QrS,) (j e J) be homomorphisms with et e t and
let i: Q-+ 0 be the cointersection of this collection in jr. We are going to
prove that then the l-epis etF(j 6 J) have the cointersection tF. Denote by
the morphisms with
»-*,-/, Ue •/)•
To prove that tF is the cointersection of c,F (j e J), let
p: CF- Y
Minima! Utilization and Reduction 251
be an arbitrary **-epi with (/S p, i.e., for suitable %f. Qjf-* Y,
'/• ft - P U « J)
We are going to prove that
tFZp.
i.e., that there exists g: QF-» Y with
(ii) For each F-algebra (^, a) we define an F-algebra (A, d) as follows. Put
A - A + AF
with injections iA: A -* A and wA: AF-* A. Define
6V A + AF-» A
by
►,<•*>- 14 and wA • d, - a.
Finally, put
d — d)F • wA: AF-* A.
For each homomorphism
f:(A, a) -(*,«,
also
is a homomorphism, i.e., the following diagram
IA»AFIF —- AF * »■ A.AF
(MFIf
IB'BFIF -
V
commutes. In fact
*. •/- (/+ /F) • A: << + ^F- *
because both
^ • (do •/)-/-/• v» • A - v,I(/+ /F) • A]
252
and
Clupur V
»A-«l,'f)-a-f-fF-P-fF- w,.p\- M(/+/f)'Al-
(iii) To find g as above, we use the following automaton
A - (ft S, (t + Y, i + p).
the output morphism of which is
t + p: QF— Q + Y.
Let
r:A—Am-(Q*6\(} + Y, r")
be the minimal reduction of A. For each J 6 J we have f,F € # (since F
preserves #-epis), hence, et + «yF: Q-+ Q, is in *, see III.5.5. Then
e, + tjF-.A^A, - (C/, A';, (J + YJ, + »)
is a reduction of A: it is a homomorphism by (ii), and it preserves the outputs,
since
(«/ + ',F) ■(/, + ft) - (*, • /) + (*,f • ft) - ' + r-
Therefore, for each j t J there exists a morphism
h,:A.-*A'
!•-(*, + */)•*,.
Since
»o • ' - »e * (*/ + */) * */ - '/ * yQi • */•
and since t, ■ f, — i (j' e J) is a multiple pushout, there exists I: £-» g* with
"a • */ ~ J! * '• Hence,
"0• r- erfr I- (• t.
Since r is a morphism of automata, the following diagram
OF
IO0FIF
Minimal Reiliiition and Reduction
253
commutes, where w: Y-* Q + Y denotes the coproduct injection. We
conclude that
p. *-(v„- r)F- «•• y
- IF(IF-B'- y').
Moreover
(•) * is an ur-mono because of the regularity of finite coproducts.
Hence, the morphism g we are looking for is obtained by the diagonal fill-in
(Lemma III.2.7):
IF-5V
»
This concludes the proof. D
13. A category it said to be connected if from each object there leads a mor-
phism into any non-initial object, i.e.,
hom(/«, B) * 0 whenever B * ±.
In a connected category, a more satisfactory result holds, with preservation of
cointertections, not the weak preservation. Lots of categories are connected:
Sat, Jt-Mod (because of the zero maps). Pot and Top (because of the
constant maps), etc. But there are natural categories which are non-connected
(graphs, semigroups, etc.).
Theorem. Let JT be a connected, finitely cocomplete (/, ur>category with
cointersections. An #*epi preserving functor F:Jt-+Jt has minimal
reductions iff F preserves cointersections.
Remark. We are going to use the terminal object of Jf; under the present
hypotheses, JT hat one. Indeed, let A be an arbitrary object, A * J.. Let
e: A -► T denote the cointersection of all quotients of A. Then
(a) for each object X there exists a morphism t,: X-* T (because
A * ± implies that there exists a morphism f:X-*A\ put
(b) thlt morphism is unique (given (,: X-* T, we form the coequali-
zer ea: 7°-» T„ of I, and i'r, since *„ € * (III.5.I), we have
e ■ *0 € * and e ■ ea: A -► Ta is a quotient of A—hence, (• (, S (
and this proves that e, is an isomorphism, thus, I, — t',\.
254
Chipur V
Thus, ris a terminal object. If JT has only one object 1, then 1 is terminal.
Proof. Assuming the existence of minimal reductions, we prove first the
weak preservation and then the preservation of cointersections. The convene
implication has been proved above.
(i) Weak preservation. We distinguish two cases.
(A) For some object A, * ± we have hom(A>, 1) * 0. It follows
immediately that hom(4 B) + B for arbitrary objects A, B. (Indeed, if B * 1, this is
the connectedness, and if B — 1, then we use the fact that hom(^, A,) * B]
Then Jf has regular finite coproducts, in fact, the coproduct injections
i-.A—A + B
are all split monos. Itii sufficient to choose a morphism/': B-» 4 then l^and
/ determine a morphism J:A+ B-*A with »'■/ — l< Thus, i 6 Jt by
III.5.1. Hence, we can apply the preceding theorem.
(B) For all objects Aa * ± we have hornet, 1) - B. In this case, the co-
product injections are split monos, too, with the exception of
X -t X + B- B for 0*1.
Let us inspect the proof of the preceding theorem. The only application of the
regularity of coproducts is denoted by (•) (see the remark preceding the
proof). It concerns the injection
Y-*Q+ Y.
Thus, we only have to check that the proof becomes trivial if Y - X. Since we
have morphisms p: QF-* Y and g,: Q,F-* Y, we conclude that
QF- X and Q,F- X (; <= J).
Assuming Q * X, F is, necessarily, the constant functor C\ of value X
(in which case the preservation of cointersections is obvious). Indeed, for
each object A we have a morphism /: A -* Q, hence, a morphism
fF: AF-* QF— X, and we conclude AF— 1. Analogously, assuming
Qi* X for any/ € J, we have F— CL. Thus, we can assume
Q - X and Q,~ X (j t J)
and the proof is trivial because each e, is I t (J e J).
(ii) Preservation. Let t,\ Q-* g (j e J) be a collection of f-epis. If
Q* X. then we exhibit morphisms 5: QF-+ Q and 5,'. Qf-+ Q> such that
f,: ((>, 5)-»((?,. 5,) are homomorphisms: if Q— 1, then we show that the
proof is trivial. Then clearly (i) implies (ii). We denote by T the terminal
object of JT (see the preceding remark).
Assuming Q * 1, we choose an arbitrary morphism/: 7"-» Q. Put
S-tgr/QF^Q
Minimal Reilinlioii and Reduction 255
and
Then each e, is a homomorphism since the following diagram
commutes.
If g — J., the situation is trivial. We can clearly assume thai no e,,j e J. is
an isomorphism (since isomorphisms do not influence the resulting cointer-
section). Then all e, represent the same quotient of Q: given J,feJ, then
Qt+ i- + Qr implies that there are morphisms
fQj-*Q, »nd t-Qi-*Qi-
The the fact that Q - ± implies
e, ■/- «y and er- g- *,,
hence,
*f(fl)-ei »"<' <■(«■/)-<■
Since both tt and t, are epis, we conclude that f— g-' and hence, t, and
', • /— tj represent the same quotient. The cointersection of a single quotient
is the quotient itself; each functor preserves such a cointersection. □
Example. The functor
Hi: Sat-» Sat
(III.2.5) preserves cointersections iff X Is a finltary type.
Indeed, Ht is a varietor and hence, it has minimal reductions iff it has
minimal realizations. This holds iff I is finltary (11.3.8). On the other hand. Sat is
an (epi. mono)-category which is cocomplete, connected and has
cointersections (because equivalence lattices are complete). Hence, Ht has minimal
reductions iff it preserves cointersections.
We prove below that a set functor preserves cointersections iff it is finitary,
i.e., a quotient of some Ht with L finitary.
Rtaurk. We characterize functors preserving cointersections in Section V.4.
But first we prove certain consequences of the theorems above in V.3, using
relations which we introduce in V.2.
256
Ctupter V
Enerdaet V.I
A. Preservation of cotateraectloas la not necessary. We present a finitary varie-
tor F: Gra -» Gra (the category of graphs, see Exercise IV.3.A) which does
not preserve cointersections and yet, has minimal reductions. We consider the
factorization system (epi, embedding) in Gra.
(i) Verify that Gra fulfils the hypotheses or Theorem V.I.4.
(ii) Denote by T the terminal graph T- (|r|, U (|). Define a functor
F:Gra-»Gra
on objects by
(X,R)F-T if R + 9, (X,9)F-(X; X- x X-);
on morphisms f:(X,R)-*(Y,S) by
/F-consW itS + B, /F-f'-fH. ifS-8.
Verify that F is a well-defined functor preserving epis.
(iii) Since //.: Sat-» Sat fails to preserve cointersections (see Example
V.I.5), conclude that F:Qra -► Gra fails, too. (Hint: Oiven epis e,:A-* B,in
Sat, consider the epis e,: (A, 0) -► (S„ 8) in Gra.)
(iv) Verify that F is a finitary varietor: for each graph / we have
/• - wt - I + T
with <p: T-* /* and n: !-• I* the coproduct injections.
(v) Prove that each behavior 0:1 + T— T has a minimal realization A,
defined by the image factorization of 0 — * • m, with t: I + T-* Q and
m:f2-r:
A - (ft 6, r. m, /, j; • t)
where 6: QF- T-t- ft sends I to (i)e € ft.
(iv) Conclude that F weakly preserves cointersections. Prove this also
directly.
B. Scqaeallal topological atrtoaMta. (i) Verify that if I is a compact Haus-
dorff space, the functor St: Top -» Top preserves cointeraection (with (f, Jt)
either (regular epi, mono) or (epi, regular mono)] and hence, every sequential
^.automaton has a minimal reduction (V.I.3). (Hint: A cointeraection of epis
*,: X— Y, in Top is created on the level of sets: if/: K,-» Y form the cointer-
section in Sat, then a set M c K is open iff (Mtf~' is open for each i Prove
that if Z is a compact Hausdorff space, then again a set U c X x Z is open
iff (MX/ x I;)-1 is open for each i\
(ii) For non-compact £, the functor 5r need not have minimal reductions.
Let Zbe the set of all rational numbers with the usual topology. Prove that the
following ^-automaton (ft, 5, T, v) has no minimal reduction.
Minimal Realization and Reduction
257
Let ff be the subspace of the real plane R x R consisting of the points
(jc, y) with x an integer and y — 0 or y — - (n — I, 2, 3,...). put
n
Q - ff + (ff x Z) + \a\ (a t ff. a t ff x I)
with the topology of topological sum (disjoint union). Derine 6: Q x S -► Q
by
(q\ a)6 - (q\ a) for q' € ff, (q, a)6 - a for q € g— g\
Denote by T the quotient space of Q under the least equivalence ~ with
(jc, 0) ~ (i, 0) for all (jc, 0), (i, 0) € C and (jc, 0. a) ~ (i, 0. cr) for all (jc, 0, a).
(x,0, it) € ff x £ Finally, y is the quotient map. (Hint: For each pair
p — (jc', jc") of integers we have a reduction A, obtained by merging (jc', 0)
with (jc", 0) as well as (jc', 0, a) with (jc~, 0, a). If A is a minimal reduction,
then its state object Is a quotient Q/x with aj larger or equal to ~, In fact,
equal to ~ because of y. Use the fact that the topology of (ff/~ ) x Tis
distinct from that of(Q' x l)/~.\
C. FlaUai} varietora la Saf*. The category Saf*. which is well-known to be
equivalent to that of complete atomic Boolean algebras, has the following
property: Wi(III.2.5) is a finitary varietor for each, possibly infinitary, type L
Prove it. (Hint: In Sat, prove that coproducts commute with limits of
co-chains. Hence, in 8at°>, each H. preserves colimits of ca-chains, and then so
does each H,.)
VJ. Rdallons la a Category
We introduce here the concept of relation in an (/, .* (-category, and the basic
theory concerning relations. The reader can skip this section without breaking
the continuity of the tent; the only concepts needed for Chapter V below are
that of relation, and of equivalence relation, We shall use relations in Chap-
ten VI and VII.
A relation from an object AT to an object risasubobject of X x Y. Thus we
assume throughout the section that a finitely complete (**. ~4/)-category JT is
given.
2.1. A relation
i-:*— Y
from X to Yi% a subobject rofXx Y. This can be represented by an „#-mono
r: R - X x Y,
258 Ctapler V
or by the pair
f,„; R -» X and r„,: R -► Y
of components or r. We also say that a pair or morphisms
J,;R-*X and fr.R-Y
represents the relation r if the induced morphism R -*■ X x Y has Image r (i.e.,
if the morphism /: R-» X x fwith components /, and /J has an image
factorization/- e-r). We write
r-U,.Al
In particular,
'" [/Willi-
For each e: K— R in f,
r- ('•'cii.'-'ciil
(and conversely, any pair [/,,/i] representing r has the form f, - e- r,„ and
ft — e' f,n with t € #).
Each morphism /: Jf-» J"is considered as a special case of relation:
[lr./):Jf-K
A relation r: X—* Kis called a partial morphism if r„,: /?-* Jf is in Jt. Then A
is a subobject of AT (the domain of r) and hence, r is a morphism from a sub-
object or X into Y. (See IV.7.1) A relation
is a morphism /iff/, € t and /i — /, •/: it is a partial morphism g: A— Y
(for a subobject m: R -► X) iff/, -em and /, - *- g for some * € #.
Examples, (i) Set, A relation AT— Kis a subset R <z X x Y It is represented
by any pair /,:&-» X and /,: R-» X of maps with
« - l((x)/,. (x)/,): * e «l-
In particular, by the pair of projections r,„: R — X and r(II: R -* Y.
(ii) Pot, In the (epi, embedding)-category Pot, a relation from (X, S ) to
(Y, 3) is any subset R c Jf x K, ordered component-wise:
(x, >•) E • (x', /) ifT x s x' and >> 3 /
for all x, x' € X and j>, / 6 Y.
In the (quotient, mono)-category Poa, a relation (A, E) from (AT, S) to
(Y, 3) carries any ordering E, contained in E *. For example, R can be
discretely ordered (no matter how X and Y are ordered).
Minimal Reallnlion and Reduction 259
2.2. We are going to define the composition of relations. In Sat, given
r-.X^Y and s: Y^Z
then
r» s; X— Z
is the relation or all (x, z) € X x Z for which there exists y € J" with
(x,y)i R and 0-, z) € S.
This can be expressed by the pullback of the projections r„,and sm(i- 1,2),
representing r and s, as follows. Let us form the pullback of r,3, and s,„;
T
V \r
n s
by \ti> y*n Nfta
x' \' \
Here
r-|(a,6)€ «x S; (a)rin-(6)j,„|
- |(a„ a,, 6,, 6,) € R x S; a, - 6,|
and s, r are the projections,
(a,, ah 6„ 6»)i - (a,, a,); (a„ a„ 6„ 6,)r - (6„ 6,),
The pair of maps
J- r,„: 7"-» Jf and r■ sllt: T-» Y
dearly represents R • S. We use this for the general definition.
Deflartioa). The composition of relations
r:Jf— Y and s:Y~ Z
is the relation
fs-{3TmF-S,n):X~ Z,
where Jand rare denned by the following pullback:
T
R S
260
OupterV
Reanrks. (i) Thii definition ia independent of the representatives: if ~*-mo-
nos r and r' represent the tame relation Jf — Y and if s and s' represent the
tame relation Y— Z, then also r» j and r • 5' represent the same relation —
this is easy to verify.
Note, however, that we formed the pullback above using r,„ and j(0, not
arbitrary pairs r - (/,, /,] and 3 - (g,, g,]l We return to this problem below
when discussing the pullback axiom.
(ii) The composition of morphisnu agrees with that of relations. Indeed,
given morphisnu /: X-* Y and g: Y-* Z, the diagram above defining /• g
has the following form:
x
/\
X Y
X Y Z
(iii) If r: Jf — Y and 3: Y— Z are partial morphisms and i, rare as above,
then ! t Jt, so that i • r,i, € Jl, consequently
(r • s)m - i • r,„ and (r. j),„ - f • j,„.
It follows that partial morphisnu are closed under composition.
13. There is another way of defining the composition of relations:
Leasts. Given relations, represented by Uf-monos
r-.R—XxY and s:S-*Yx Z,
let us form the pullback of r x I z and I, x j:
V —»X.S
I 1-s
R»z—r»- XpY>z
r»l
Put » - i • (r x I) - r • (I x j) and denote by xl% n,, x, the projections of
XxYxZ Then
r • 3 — [r • Xi, r • xt]: X-» Z
Minimi Rotation uul ItahKtKMi 261
Proof. Denote by
jtf: S x Z-* R and *,': R x Z-» Z
the projectioiu: analogoualy,
x?:XxS-*X and *;:XxS-*S.
Obvioualy,
»• «i - /• (f x I) • J, - /• m", • r,D
and
r- *, - f-(l xj).»,-r<' J,],.
To prove that r • s - [»• «,, r • *, J, it it lufTlcient to check that the rollowing
square
v
!•*;/ \r.«ej
Y
it a pullback. Thit aquare obvioualy commutea. Let
p:P-+R and q:P-»S
be morphunu with
p. rf„- q- sw.
Let
?:P—RxZ
have component! p and q - j„)t and let
4: P-*Xx S
have componenta p • rnt and 5. Then the morphunu
P~-(rx l2), 4 • (I, x *): F-» X x J- x Z
both have componenta
P • 'in! P ' tn ~ 9 • 'tit- 9 • *(»•
Hence, the two morphiama above are equal and there exiita a unique A Tor
262 Chtpler V
which the following diagram
commutes. This is the unique morphism with
p — A • s • x[ and q — A • r • nJ'.
This concludes the proof. □
1A. Relations from X to Y are naturally ordered, as subobjects of X x Y
(III.5.2): given
r. s: Jf— Y
represented by ^-monos r: R-» X x Y and s: S-» X x Y. then
rcj iff r- /• s
for some morphism /: R-» S. Note that for each relation r - I/,./,], where
/,: R-» X and /t: A-* f are morphisms, and for each morphism A: S-» R,
we have
[A-/„A-/Jcr.
Moreover,
[*•/,.*• /J - r iff * € <f.
And for the canonical representation r — (rIIH r()J also conversely:
if (A ■ (•<,„ A ■ r„J - r. then A € *.
(Proof: if [A • r„B A • r„J - r, then A • r: S-t- X-x Y has the image r. i.e..
there exists est with A • r — t ■ r and since r is a mono, this implies
A - t e t.)
Reaurk. We shall often use the following consequence of the definition of
the order of relations: if r — [g,. gj c j, then there exists A such that
g, - A • i„, and g, - A • j,,,.
(Indeed, if/: *-► S fulfils r- /• s. then/- *,» - r,uand/-
^i2i ~ ^(i)l since
Minimil Rulizatiofi and Reduction 263
If i- «J is a representation of r, there exists est with
* • In - g) and * • r„, - g,.
Hence, A — * •/ fulfils the equations.)
ProaosltkM. Composition of relations is order-preserving, i.e.
r c r and icj' imply rue r • s'
for arbitrary relations r. r'\ X-* Y and a, s': K-» Z
Proof. Let r-/• r and j - g • *'. then r x lz - (/x Iz) • (r* x lz),
analogously with 11 x j, and we form the corresponding pullbacks as in
Lemma V.2.3:
There exists a unique A: K-» V tuch that the diagram above commutes. The
morphisms
then fulfil
r(l«i| and v' - F ■ (I x s")
A . ,'.
Hence,
r • s - (r • «,, r • jtj c [r' • *,, r' • *,) - r* • s'.
2J. The intent relation to r: JK —» K it the relation
'"' - I'm. 1ij): ^-* *■
For any representation r - I/,,/;) obviously
[/i./.J-'-lA/.l
To express this by ur-monos, denote by
(:Xx Y-*Yx X
2ft4 Ckipwt V
the canonical isomorphism, defined by
£•»! — *! and f • *, — at,.
Then Tor each JT-mono r: fl -» Jf x K we have
r-'-r-i
. The operation or inverse is an order-isomorphism on the dais
of all relations (i.e., a bijective map such that r c s iff r-1 c s~') which
inverts the composition (i.e., (/• s)-' - *-' • r-'] and is an involution
Proof, (i) The isomorphism £: X x Y-» ¥ x X above fulfils f • f - lx. r
and hence, for each relation r,
(i-')-1 - (/•#)• I- '•
Thus, the operation of inverse is onto; it is also one-to-one, since
r * s Implies r~' — r • { * s • { — s~'.
(ii) Let r, j: AT-* K be two relations. If r c J, then r - /■ s for some /and
this implies
i-' - (rati 'oil - I/' '<»• /• 'ml c I*ii). *ml - *"'•
If i-1 c i-', then r - (/->)-' c (*-')-' - ».
(iii) The composition r • j is defined by the following pullback of r(1,
and*,!,
jy/ ^
-%>
UMj-|j>f,i],f. i,,,]. Hence,
(/•*)-' -[r- *„,,/• r„J.
Since the composition of s~' and r-1 is defined by the pullback of s-,,, and rII|t
which is f and i we have
*-'• *-' - If- s,„,s- r„J. □
Remarks, (i) A relation
r. X — *
Minimal Rnlinltofl and Redaction 265
it uid to be symmetric if
r- i-1.
Symmetric relations ire doted under nnioiu and Intersections—thli rollowt
from the preceding proposition,
(ii) For each object X we define the diagonal relation
4t-{\t,\,):X-X.
A relation r'.X-'X is said to be reflexive if &t c r, lx., if there.eiiiti
/: X— R with
f-rm -f.rm- Ijf.
(iii) Each /-epi *: Jf-» K"preserves" reflexive relations: If r: X-' X is
reflexive, to is [r,i, • e, r(ll ■ t): Y-» Y. Indeed, if
[I j» Ij-1 c (r(l> rm),
then
l* '1 <= [r,„ • «, r,D • *)
and since * € * implies (e, r] - |Ir, Irl. we conclude
Art [r,ir*. '(D-'l-
(iv) A relation
r-.X^X
is said to be transitive if
r • r c r.
A reflexive, symmetric and transitive relation is called an equivalence.-
Z.*. Prapasltlea. For each morpbism /: X-» Kiel us form the pullback of/
and/:
R fo— X
111
Then [r(i„ rm): X— Xis an equivalence, called the kernel equivalence of f
266
Ch.plet V
Proof, (i) Since lx-/-
following diagram
lx-/there exists a unique h. X-* A for which the
commutes. Hence,
[I*. I llC ['(», '(1,1
which proves the reflexiviiy.
(ii) Since '»> • /— rm ■ f, there exists a unique A: R-» R for which the
following diagram
commutes. Since, obviously, A • A — I,, A is an isomorphism and we see that
I'll), 'oil — I*' '<»• *• 'ml — ['in. 'oil-
Thus, the symmetry is proved,
(iii) To prove the transitivity, we first verify that the morphism
r:R — X x X
with components rm and r(II is an ^-mono (which then represents the kernel
equivalence). Indeed, let r — e m be its image factorization. Since the
projections *( and *i of X x X fulfil
e-m-Ks-f- !•„>•/- ',]>•/- fm-Kt-f
and since t is an epi, we have
m» if, •/— m- ftff
Minimal Realization and Reduction
and there is a unique A Tor which the following diagram
267
commutes. Then * • h — I because both
(*• A)t0) - em> x, - fx( - rw
and, analogously,
(e-A)T(„- r,,,.
Since * Is a split mono and an epi, it is an isomorphism, therefore, r € -M.
It follows that r • r b defined by the pullback of rnl and r(ll:
" R
y \ y \
r.r- [r(l)• r(>H On• Hnl-
To prove r-rc r, it is sufficient to verify that/merges r01- r(ll and fo, T(«.
And this is clear:
'«>• 'in'/- 'nr'tn-/- '(Vtir/- '<«•''(»•/•
This proves the transitivity. □
Examples, (i) Sot: Equivalence relations have their usual meaning. Each
equivalence relation R c X x X is the kernel equivalence of some morphism
(e.g., of the canonical morphism /: X-» X/R, assigning to each element its
equivalence class).
(ii) Poo: In the (epi, embeddlng)-category Poo, an equivalence relation
Ac X x Xlt ordered component-wise. This need not be a kernel equivalence
268 Ckiptti V
or any morphism: conaider, aa an example, the three-element chain
X — (0,1,2] and the equivalence relation R with two classes-.
(0,2] and (I).
This ia no kernel equivalence (note that the quotient act X/R - QO], (l)| ia not
ordered, tince 0 S I implies [0] S (I), but I S 2 implies (I) S (0D.
2.7. DcfmMoa. An (*. UT>«ategory ia said to satisfy the puBback axiom if in
each pullback
i
i I
with * € t we have * e t.
Rtsnrk. The pullback axiom (which is the dual of the puihont axiom used
in IV.7.12) makes the work with relations much simpler. For example, the
composition of two relations
can be defined (for arbitrary representing pairs) by the pullback of /j and g,:
R S
/\/\
X T Z
as the relation [ j", •/>, /, • g,).
Proof If(/„/i] - r: R,-t-X x Y then, by definition, r is the image of the
morphism R -► X x Y with the components /, and /,. Thus, there is * € t
with
/, - *• f,„ and /, - *• r,„.
Analogously, if Id, gi] - s:S-* Yx Z, then there is an #-epi i:S-t-S,wi»h
g, - i-sm and g, - i-s0).
Minimal Realtution and Reduction
We form the following four pullbaclu:
y\
y \x\
V V
Y
By definition,
r . s - [I• r(ly. F- sm\.
Since adjacent pullbacki Com a new pullbick, the pullback or
/, -e-rm and g, -«•*,„
is roimed by i, • /and r, • 7 above. Thus, what we want to prove is that r «
represented by
U,-i-A.;-r-g,).
We use the fact that
/./, - f. *.f,„- «,•/•»•„,
and
Thus, denoting < - *, • r, - *( ■ it, we have
(«i • #•/» 'i • '• til -('•'• rui. *• ?• *a\\-
Finally, the pullback axiom guarantees that
e, € I and i, € #
and, applied again, yields
*■( e * and «, € i;
consequently,
* - «, - r € *.
270 Clwpler V
Hence, [s ■ rUh r-sol) represents the same relation (which is /■•*) as
I' ■ * • '(i). ' • '■ *pj- Hence,
i-.»-[#,.i/„#, -r- j,). O
ProaoaMoi. The pullback axiom guarantees that the composition or
relations is associative:
/■•(»• 0 -(/■•»)• I
(for arbitrary relations r: X-* Y, s: Y-* Z and I: Z-* V).
Proof. Let us form the following three pullbacks:
y \y \
"ST
y' >i y* vn? y**'n?
z
By definition,
!■• »- [i, • /■„„ f- »,„).
Since adjacent pullbacks form a pullback, the pullback of f • >„, and („> is I
and rs,. Hence, by the preceding remark,
(r. »). i-If. i, ■ /■,„,?• i, • f,„).
Analogously,
»•'-['• «m.*i- '(«)
and, by the preceding remark,
r • (5 • r) - I'• *i • '(I* ' • h • '»>)• D
Example*, (i) Sat fulfils the pullback axiom: the pullback
t—5—z
i i
X »-Y
Minimal Realtettlon and Reduction
271
in Sat can be described as the set
T-Ux, 1)6 X x Z; (*)# - (»)/]
with the projections i and / If t is onto, then so is i because Tor each isZ
the point (i)/€ Y- (.Y)<'canbeexpressedas(zl/'- (*»)«, *o e ^andthen
(x* i) « T
fulHI. i - (x,, z)f.
(ii) Let JT be a concrete (III.3.8) (*, ur>category with * - all morphisms
which are surjective maps. Assume that finite limits arc preserved by the
forgetful functor (which they are in all current categories). Then Jf satisfies the
pullback axiom. This applies to
R-Mod,
in fact, to any variety of universal algebras, as well as to
Poo, Top, Gra, etc.
considered as (epi, embedding)-categories.
(iii) Alas', for other factorization systems the pullback axiom can fail. For
example, the (quotient, mono)-category Top does not satisfy it, see Exercise A
below.
Therefore, we try to work without the pullback axiom, whenever possible.
We must be careful with the composition, however, because it can fall to be
associative.
Rtsaark. Composition of partial morphisms is always associative (even if
the pullback axiom fails). In the above proof, assume sol e Ul and lm € Jl.
Then i„ I (and hence i) are all .4f-mono». Therefore,
r • s - [I, • r,,,. r • j(IJ and j. I - [I ■ s0„ J,„ • f„J
and we obtain (/■• s)» I — /■• (*• f).
2.8. Remark. The span algebras introduced in IV.7.4 can be considered as
representations of "relational" ^algebras. By a relational F-algebra is meant
a pair (ft S) consisting of • relation 5: FQ-* ft. In this sense, the span
algebra morphisms (/,/,): (Q, D, 6* 6,) -* (Q, D\ S„ S\) correspond exactly to
morphisms/: Q-*Q' satisfying
/•/Fc/F'S-.QF^ Q
[where 8 is represented by (6,, <5,> and 6" is represented by (r5J. 5,")). More in
detail, for each span algebra morphism (/.ft)- the first component / satisfies
the inclusion above. Conversely, representing 6: QF-* Q by (b\, 5,) such that
the induced morphism D-* ft x QF is in Ul, and analogously with
6": Q'F-* ft', then for each / satisfying the above inclusion there exists
272
Chspur V
a unique f, such that (//«):(ft A A* £,)-►((?', D', r5J, 5,") U s span algebra
morphism.
The free-completion construction IV.7.6 can also be performed on relations
rather than spans: it is easy to verify that the result or this construction is
independent of the choice of the representing span.
2.9. Fmctora affiled to reUttoaa. For each functor F: JT -* JT and each
relation r: X-* Y we define the relation
rF: XF^ YF
by
rF-lr,„F, rmFl
Eaamplea. (i) Ht: Sat -» Sat Each relation r: X-- Y is represented by the
inclusion map of s set R c X x Y; then rm and ra) are the projections. The
relation rH1:X'^ Y1 is then the inclusion map of the set Rm c X1 x 1" of all
pairs ((*,, X]), Cvi. yd) Tor which there exists (a, b) € R x R with (x,, xj -
((a)r„ (6)r,„) and 0-„ >i) - ((a)r0h (6)r„0, I.e., with a-(x„>,) and »-
(x„>J. Thus,
(x„ x>)*"\y,. >i) i<T x,*>, and x,Ry,.
As a concrete example, consider the relation r: [x, y\ -*[x, >, z], given by the
following graph
K » K
** Z
Then r//, is the following relation
Minimal RnHzafioii and Rjdudton
273
(ii) />:S*)t-*8«t, the power tet functor (III.3.4). Let r be the relation
above. Then rP it the following relation
I
{•>
e
m
*>■
^
\^
V
t
»
w
®
w
w
M
to
■—■lit 0) If Fprmrrts t-tpb (i.e., if #f is an *-epi for each *-epl e\
a more natural definition is the following:
If r-[/„/,! then rF-lf,F,f,F).
Indeed, r- [/,,/:] means that there exists an «*-epi #wlth
»•/■„,-/, and t-ito-fi.
This implies
tF • r„,F -f,F and tF • r,„F - /,f;
since tF e *.
I'd/, 'n)*"] - [«*• 'in*". *F' 'mFl
(ii) If F fmtrra Jt-monot (i.e., mF it an UT-mono for each UT-mono m),
then F preserves partial morphismt, and for each partial morphism
r — [rt, ri), rt c JK, we have
rf-Ir.f.r.F).
(Hi) Each functor F preserve* the ordering of relations:
res implies rF c sF
for arbitrary relations r,s: X-* Y. F also preserves the inverses,
(i-')f-(rf)-'.
Both are easy to verify.
274
Chapter V
ProaoaMoa. L*t F: •* -»•* be a functor preserving #-epis. For arbitrary
relations
r.X^Y and s.Y^Z
we have
(Mt)fc rF'sF.XF^ YF
Proof. We form the pullback or rm and j,i,:
T
y \y'~
to get
(r.i)F-[sFT,nF,rFi,nF).
Ut r": 4-» Jff x JTbe an UT-mono representing rF, and let e,: RF-* A be
the *-epi with
r,F-#,•?„, and r,F-#,•?,„.
Analogously, define {: S-* YF x ZF in Jt and t,:SF-* S in *. Now we
form the pullback or fm and Sm:
y \^ y' ^
There exists a unique morphism d: TF-t-1for which the diagram above
commutes. We bave
rF-sF- f'S-[if{,„fim\.
Minimal Realization and Reduction 275
Therefore,
(r. s)F- [d. J. f„„ </•!• io,] c If- f0f. ?■ Im\ - rF. sF.
This condudea the proof. □
Reaaerfc. If F: JT -► JT preserves UT-monos (but not necessarily f-epis), then
for arbitrary partial morpbitnu r:X-~ Y and t: Y--Z we have, again,
(r • s)Fc rF' sF. The proof la the tame.
Even reasonable functors In reasonable categories can fall to preserve the
composition of relations:
Exaasate. The functor P,: S«t-» Sat (III.4.I) does not preserve
composition of relations. For example, let
f:l*.y,i)-*lx,y)
be the map defined by
(x)f-x.{y)f-x. (z)f-y,
and let r: [x, y\ -»[x, y, z) be the relation of Example V.2.8. Then
Inspecting the graph of rP above, we see that rP, Is the restriction of rP to all
non-empty sets, and that the graph of//", • rP, is a subset of exp |x, y, z] x
exp |x, y, z] containing for example the pair (|x, y, z), [x, y, i|). On the other
hand, the relation/* rhas the following graph
l.r
There is no three-point subset of/* r which is mapped onto \x> y, z\
simultaneously by both projections. Hence, the pair (|x, y, z], [x, y, i|) is not
contained in the graph of (/• r)P,.
2.H. We are going to characterize functors preserving composition of
relations.
Given a pullback P in the category JT: f •. z
J 9
276
Chapter V
the image or this square factors through the pullback PotfFiad gFby a
canonical morphism p: tF-* t, i.e., the unique morphism such that the
following diagram
commutes. (Then Fpreserves the given pullback iff/; Is in Isomorphism.)
DcfhtrlM. A functor F: Jt -* Jt is said to cover pullbacks if the canonical
morphism of each pullback is an *-epi.
Let JT satisfy the pullback axiom, and let F: jr -► JT preserve
/-epit Then F preserves the composition of relations iff F covers pullbacks.
Proof, (i) Let Fcover pullbacks. To prove that
(r. *)F- rF'SF.
we form the pullback of ra) and »„,:
\>y \^ v/ \?n
Then
(i-.»)F-[»Ft,„F, rT-i,„F|.
By Remark V.2.8, the composition of rF and »Fis defined by the pullback of
rreF and »„,F ^
luf/
Sjjf
YF
Minioul Reitizatloa and Reduction 277
u
rf • IF- [i-rmF, r-imf).
By hypothesis, there is an /-epi * with
IF — t • s and fF — # • r.
Then [JF- r^F, fF- »mF] b the same relation as [/• r(llF, f • satF], i.e.,
(/■ • j)F — /F • jF
(il) Let F preserve the composition of relations. Given moronisms
f:X-*Y and g:Z-*Y,
we use the Tact that Fpreserves the composition or
f-Wx.fYX-Y and ,-■ - \g. \t\: Y-* Z.
This composition/* g-' is defined by the pullback of/and g:
I
*/ \<l
1/ \ / ,
.1
/• *-' - [A 4l-
We have
(f'g-')F-fF .(gF)->
where/F. (*F)-' b defined by the pullback of/Fend jF:
p
»/ \n
XF
Thus,
y\s\
[pF.qF\-[p,q\.XF-*ZF
27B Chiplet V
Let * be the canonical morphism with pF— i-pmi qF— i-q. Since
ltp,t-g)-lp.g\,
we conclude that t i i. □
Einilea. (i) The functors //,: JT -» JT preserve composition of relations
because they preserve limits. For JT — Sot (and for a number of current
categories), coproducts of functors covering pullbacks also cover them. Hence,
each Ht: Sot -» Sot preserves composition of relations.
(ii) The power-set functor P: Sot -» Sot preserves composition of
relations—it is easy to verify that /"covers pullbacks. But the subfunctor P, of P
does not cover pullbacks.
Remark. If JC satisfies the pullback axiom and if F:Jt-»Jt preserves
UT.monos, then F preserves the composition of partial morphisms iff F prt-
strves prelmages (\.c, preserves the pullback of/and gwhenever/E Jl). This
can be proved precisely as the preceding theorem, since the preservation of
prelmages is equivalent to the covering of prelmages. [In fact, for each pre-
unage the canonical morphism p: PF-* P is an Jl-mono: / e Ul implies
/e j* and therefore ^ - p-J E UT; hence,/? e Ufby III.3.l(i). Thus, pis an
isomorphism iff p is an 4-epi.)
Eaaasfks. (iii) The functor P, preserves prelmages: given a map g: Z-+ Y
and a subset X c Y, then
(ZP,XgP>)-' - «Z)»-')/>,.
(iv) The following functor D,: Sot -» Sot does not preserves preimages.
For each set JT put
XD, - \(x, y) E X x X: x * y\ u |.)
where • is any element outside of X x X; for each map/: X-* Y,
U>in if (*!/> (>!/";
^™d'-[. if (*!/■-0-1/;
This functor does not preserve the composition of the map/: [x, y, z) -» [x, y)
denned by
(xV- x; (y)f- x;(z)f- y
with the partial map g: [x, y[ —- y, defined by
00* - y-
The relation/- g is defined only in z and hence, (/• g)D, is defined only In •.
On the other hand, fDt • gD, is denned in (x, y) and (y, x).
Minimal ReiMzaliofi and Reduction
279
Exercises V,2
A. 11m pallhack ailoa hi Top. Verify that the (regular epi, mono)-category
Top does not satisfy the pultback axiom (a regular epi is a surjcctive
continuous map f: A-* B such that each open set in A has the form ((/)/*' for
V c B open). Use the following pullback
0 0
inclusion
(^3> G[3
B
• K
1-
*y
incluiion
• n
•1
•Y
• z
where * is the map merging y, and y, to y, and the topology on each set is
indicated In the picture: A is discrete (each set is open), B and D are indiscrete
(only 9 and the whole set are open) and C has open sets I, [x, y,], Lvi, i]
andC
& PmerratMB «f coia—IHaa. (i) Verify that the set functors P, P, and />,
cover pullbacks and thus, preserve composition of relations (in contrast to /",)•
Verify that P. does not preserve composition of relations if 3 S n < a.
(11) Verify that the quotient of H, given by the equation (x, x, y)a —
(x, x, i)o does not preserve preimages.
C Partial ■nana—, For each partial moronism [/,,/i]: X— Y, /, € Jt,
prove that a pair {g„ f J with g, € Ul represents the same relation IfT there is
an isomorphism i with f i - ' • /, and g, - I • /,.
V.3.
FlaHaiy Flatters
3.1. The existence of minimal reductions Is characterized by the preservation
of colntcncctloiu. But this In itself Is a condition difficult to verify. We prove
that under additional hypotheses, a functor preserves cointersections iff it is
finitary (i.e., preserves directed unions). The latter condition Is much easier to
check in a concrete situation, and has a dear Intuitive meaning. For the
implication
Finitary ■* preserves cointersections
we have to restrict the factorization systems to t — regular epis and .M —
mono*, and then we obtain quite a general result. For the convene implication,
some further requirements are needed. All these are fulfilled by every set
280
Chapter V
functor and every functor on Jt-V«ot (R any commutative field). Hence, in
these categories, particularly satisfactory results are obtained.
Definition. Let ■» be an (/, ulQ-citegory. A functor F: JT -► JT is said to be
finitary if it preserves directed unions.
Remarks, (i) Explicitly, F is finitary iff for each union
m — U ffi,
I"
with J directed (i.e., given /„ j, e J there exists j E J such that m„ c m, and
mh c mt) we have
im(mf) - U im(m,f).
> * ^
(ii) For the categories Sot and A-Mod, the definition above is equivalent to
that given in Chapter III: a functor F is finitary iff for each set (module) X
and each point x E XF there exists a morphism f-.Y-t- X with Y finite (finite-
dimensional) and x E (YFyF.
[Proof. If F is finitary in the present sense, we can use the fact that each
object X it * directed union of its finite (or finite-dimensional) subobjects.
Conversely, if F is finitary in the sense of Chapter III and if X — U Xt is
a directed union, then for each x 6 XFwt find /: /*-► X with x e (YF\fF
and Y finite (or finite-dimensional). Since the union is directed, there
exists jt i J with (flfc^ This proves that XFc U(V)"i/f, where
m,: Xt-+ X are the inclusion maps, and the converse inclusion is dear.)
(iii) Some authors define finitary functors as those preserving directed coli-
mits. For our purposes, this does not make much difTerence—see the
Characterization Theorem below.
Lemma. Let jr have pullbacks. A functor F is finitary iff for each directed
family mt {J E J) of UT-subobjects of an object A,
U "»/ - \t implies U im(m>f) — \Ar.
Proof. Let m: A,-* B (J 6 J) be a directed family of Jt-mmm with union
iH:A-* B. We have .^r-monos m^.A,-* A with m, - mt- m(j e J), and then
Um- i,.
(In fact, if a subobject m of A contains each m,, then m • m contains each
mt' m — m; and hence, m > m contains m. It follows that m is an
isomorphism.) Therefore,
yim(m/)- \„.
Minimal Realhatlon and Redoaloa
281
Let m* be an UT-subobJect or BF containing each im(/fl,F). This means that
for each j e J we have
fhjF — if if »i*i
with e", € # and ii, € Uf. Let
be the image factoruation. Then we can use the diagonal fill-In:
Let p and q form the pullbtck of m* and rfif, then for each J e J there exists
a unique r, such that the following diagram
^
0-
r-
■■ A
q
»»B
F
(BF
F
commutes. Thus, 9 is an UT-mono (opposite to m* € Jl In t pullbtck, sec
III.5.1) containing etch u, tnd hence, q is tn isomorphism. Therefore,
rftf-(?-' • /;)• m*.
which proves thtt im(rfiF) cm*.
3.2. Let us assume that ■* Is a finitely complete category with ngularfaetori-
lotions, i.e., an (1*, »40-category where
* ™ regular epis and Jl — monos.
282 Chipier V
For each morphism e: X-* Y we can form the pullback of t with itself:
The pair (r,, rj represents an equivalence relation r: X-- X called the kernel
equivalence or e, see V.2.6.
Kernel equivalences and regular epis are closely related:
(a) If e: X-* Yh a regular epi and (r,, r2): X-- Xi> its kernel equivalence,
then t is the coequalizer or r, and rt.
Proof. Let />,, />]: i>-» * be morphisms such that * is the coequalizer or p,
and />].
Since p,-1 - Pi-e, there exists a unique morphism /: P-* R with />, - /■ r,
and />2 — /■ iy Given a morphism i: X-» f with r, • e — r2 • r, we have also
Pi • * - /• r, • i - /■ r, • i - />, • i
and hence, ? factors uniquely through e. Thererore, tis a coequalizer of r, and
(b) Let * and *' be regular quotients of an object X, and let r c Jf x Jf be
the kernel equivalence of t and r' the kernel equivalence of t'. Then
re r iff f£ t.
Proof. If r c r', then r'„, • i' — r^, • i' implies r,,, • «' — r„, • *'. Since i is
the coequalizer of r,,, and r,,„ it follows that *' factorizes through e, i.eH
* £ «'. Conversely, if t <, t' then r,,, • * - r(1| • t implies rm • t — rm • t'.
Since r'„, and r',;i form the pullback of *' and *', there exists a unique
morphism/with r,„ — /• r'mand r0l — /• r'in,i.e., re r'. □
(c) Let e,: X-» Y, (J € .0 be quotients of an object X. and let r, c X x Jf be
the kernel equivalence of t,{j e J). Put
r - \J r, c X x X.
Minimal RMltaalion ind Redaction
283
The coequalizer of rnl and rm is the cointenection of e,,J e J. Hence, if JT has
unions and coequalizers, it has cointersections. This follows immediately
from (b).
3J. Resnrfc. We want to characterize functors preserving cointersections.
We first consider finite cointersections, i.e., pushouts of regular epis.
Let us say that a pair of morphisms />,, pt: X-* Kis reflexive if it represents
a reflexive relation (V.2.5) (/>,, pt]: Y-* Y. A functor Is said to prtserrt rtflex-
ire coequalizers if it preserves the coequalizer of any reflexive pair.
CwutracHoa of the least equivalence containing a given relation r: X-* X.
Let .X be a complete, well-powered category with regular factorizations. We
define relations
r,:X^X (n € Ord)
by tnnsfinite induction,
(a) Denote by r„ the least reflexive and symmetric relation containing r, i.e.,
r,-(rv i,)u(rud,)-'.
(b)Oiven r„ denote by A. the least set of relations X-- JT containing r, and
closed under composition and the formation of inverses. Put
r„<.i - U »•
(c) Given a limit ordinal { put
r,- Ur,
a < I
The unions In (b) and (c) exist because JT Is complete and well-powered, and
hence, it has intersections, which implies that the posct of all subobjects of
any object is a complete lattice. Put
r« - r.
where kIs an ordinal with r, - r, for all n a k; such an ordinal exists because
JT is well-powered. Then
(i) r* is the least equivalence containing r;
(ii) each of the sets A, above is directed:
(iii) rand r* have the same coequalizer (I.e., a morpbism is a coequalizer of
r„, and r(I) iff it is a coequalizer of rJJ, and r^,).
Proof, (i) The relation r* is
—reflexive: A c r, c r:
—symmetric: for each n we have
r,, i — U Jul"1
284
Chipnr v
because A. is closed under the formation or inverses. Since a union or
symmetric relations is obviously symetric, it can be easily proved by Induction that
each r„ is symmetric;
—transitive: since r, • rt € A,, we have
r* • r* — r, • rt c rtt, — r» — r*.
Let J be an arbitrary equivalence relation containing r. Let B be the set of
all subrelations of s— note that B is clearly closed under composition. To
prove r* € B, we verify that r. € B by induction in n. First step:
r(-(ruil)i(ru 4)~' c j • j-' - j e A Isolated step: if r. € B then
.4. c fl, hence, r,,, c j. Limit step is clear.
(ii) Since each r, is reflexive, all relations in A. are, obviously, reflexive.
Given su 3, € .4, then s, • j, € 4, and
j, - J, -/lc J, •),; j, — A • i] c J, • s,.
(iii) For each morphism /: X-* Kthe statement r(„ •/- ru) •/means that ris
contained in the kernel equivalence ker /; by (i) this is equivalent to r* c
ker/ I.e.. to r,*,, • /- rji, • / Hence, rand r* have the same coequalizer. □
3.4. Deflalttoa. A functor is said to be right exact if it preserves coequalizers
of equivalence relations.
Remarks. (I) This is a much weaker condition than the preservation of
reflexive coequalizers. For example, we shall prove below that each functor on
the category Sat or Jl-Vact is right exact.
(ii) The terminology here comes from homologies! algebra: right exact
functors are those which preserve short right-exact sequences (which are just
the coequalizers of equivalence relations in those categories).
(iii) A functor preserving finite cointersections is right exact. In fact, for
each equivalence relation r(:Jl-» X x Xt mono) there exists d: X-* Jlwith
d- r,„ - d-r(1) - l»,
because ris reflexive. Forming the pushout of rIM and rm
fa.
,1
^
p.
we have
Pi - d- rrp, - d- r2-Pi - ft
and hence, P\ — pt is the coequalizer of r„, and r„,. Since r,„ and rm are split
Minimal Realization and Reduction
285
epis, the pushout above is a cointersection. The preservation of this cointer-
section is equivalent to the preservation or the coequalizer or rm and rm.
3.5. Theorem. Let JT be a complete, well-powered category with regular
factorizations. Each right exact, flnitary functor F: jr -» JT preserves cointenec-
tions.
Obeemtia*. Slightly weaker hypotheses will be needed in the proof below:
(i) JT be finitely complete and well-powered;
(ii) JT have unions and cointersections;
(iii) JT have coequalizers.
Note that the present hypotheses imply that JT has the properties (i)—(iii): JT
has intersections and hence also unions. The existence of cointersections
follows from HI.5,3: JT is regularly cowell-powered because it is well-powered
and we can apply V.3,2,b, therefore, jr has cointersections, This implies that
for each object Y, all regular quotients form a (small) complete lattice.
Consequently, each pair of morphisms/, /,: X-» Khas a coequalizer, viz,, the least
regular quotient t: Y-* Y of Ksuch that / • t — / • *.
Proof. I. Fpreserves the coequalizer of any pair/, /: X-* Ywhich
represents a reflexive relation r: Y-" Y
To prove this, it is sufficient to show that the least equivalence r*
containing r fulfils
rFc r'Fc{rF)'
(where rF is deflned as [rmF, r(1)5], tee V,2,9), Since rf and (rF)* have the
same coequalizer by V,3 J(iii), it is obvious that also rF and r'Fhave the same
coequalizer. And f is right exact, therefore, it preserves the coequalizer of r*
and hence, also of r. Finally, r — (/,/] means that there exists a regular epri t
with/ — f r,i, and/i — t< rm: it follows that the coequalizers of/,/i and
r<if rin coincide, too, and hence, Fpreserves the coequalizer of/ and /,
The first inclusion follows from III,2.9(iii), since rcr'. To prove
r'Fc (rF)', we proceed by induction: let r. denote the steps of the
Construction V.3.3 applied to r, and r. the steps for rF; we prove that
rj'c r, (n € Ord),
(a) Since rls a reflexive relation, we have r, - r- r~' and hence, by V.2,9,
r,F- (r. r-')Fc rF- (rF)-1 c r,.
(b) F Is finiury, i.e. it preserves the directed unions and A, is directed,
hence
r..,F- U sF.
«« A.
286 Chapter V
Also, we have
where A. is the least set of relations containig r. and closed under composition
and inverses. The set
B - \s: X-* X; sFc i for some J € A,\
is obviously closed under composition and inverses. Therefore, A, c B, and
we get
r.,,5- U sFc U sFc U /- f..,.
i« a, a i ti jr,
(c) The limit step is dear, since F preserves unions of chains:
r,F- U r.Fc U K - f,.
• < i *<t
II. F preserves finite cointersections, i.e., pushouts
of regular epis.
To prove this, let r„ rf. R-* A be the kernel equivalence of e. The relation
' — l'i. rJ is reflexive and hence, also (r, • / ri • /): C-* C is a reflexive
relation: we have 4, c r, thus I//] c |r, • / r, • /] and since /is a regular epi,
l//l-[lr.lrl-4c-
The coequalizer of r, • /and rt ■ /is i. To verify this, consider a morphism
k:C—X with
r,-f-k-r,fk.
Since lis a coequalizer of r, and r, (V.3.2(a)|, there is a unique h: B-* X with
/■ k- e- h.
Using the universal property of the pushout above, we conclude that k factors
through t and hence, t is a coequalizer of r, • / and r, ■ /
By I, the functor F preserves this coequalizer: *F is the coequalizer of
(r, •/)Find(r! •/)f. We are prepared to prove that F preserves the pushout
above. Let p and q be morphisms with fF'• p — iF- q:
Minimal Realization and Reduction
287
(r,/)F/>- r,FtFq- r,FiF- q-(r,f)F- p,
and because IF is the coequalizer of (r, • f)F and (r, ■ f)F, there is a mor-
phism I: DF-» Z with p - iF- I. Then also q - JF• I because e-fis a
(regular) epi, and
tF- q-fF- p-fFeF- I- iF-jF- I.
This proves that iF and JF form the pushout or tF and fF.
III. F preserves cointersections. It is sufficient to prove that F preserves
directed cointersections because each colntersection of quotients ',(je J) can
be obtained as a directed cointersections of finite "subcointenections". That
is, consider the collection M„ i e I, of all finite subsets of J, and for each j let
e, be the (finite) cointenection of all i,,j € M,. The collection e„ I € I, is
directed because for arbitrary /,, /, 6 / we have a finite subset A/„<j W, c J,
tbus, A/,,<j A/„ — Af, for some J, € /, and then lh S l^ and J4 S *,,. It is
obvious that the collections c,(j e J) and i, (J € /) have the same cointersection.
Let
;:X-r, <>€ J)
be a directed collection of regular quotients. For each j € J, let r, be the kernel
equivalence of tr Then rt {j e J) is a directed collection of subobjects of
X x X (see V.3.2). The coequalizer t of the relation
is the colntenectlon of e, (J e J), and the relation ris reflexive (because each
r, is reflexive). By I above, F preserves tbe coequalizer of r. Hence, tF is the
coequalizer of
rF- U r,F
Hi
Let us prove that ef is the cointersection of e^F (> € J). For each regular epi
i: XF-t Z
288 Clupttr V
with e,F£ i (j € J) the kernel equivalence f fulfils
r,Fc f.
(Indeed, if r, — (p„ p2] then p, ■ it — pj • tt implies p,F- itF — p^F- tf and
thus, p, F ■ i - ptF ■ i. We conclude that r,F - (p, F, p,F) c ker I - f.) Thus,
rFc f.
Since eF is the coequalizer of rF and i the coequalizer of f, this implies
tF S i. Thus, eF a the cointersection of tf (y € J). □
3.6. Next, we tum to the reverse implication:
F preserves cointersections ■• F is Unitary.
Here, we work with an arbitrary factorization system (if, jK) but we need
rather extensive additional hypotheses. They include the following:
F preserves finite intersections
(i.e., pullbacks of .xT-monos). This is no restriction if ■* — Set (III.4.6) or
JT — Vact (III.4.A.(iii)] but generally, this is a burden, unlike the right
exactness in the preceding theorem (of which we know that it follows from the
preservation of cointersections).
Let us discuss the hypotheses on .*, First, assume that a dirttled coUntion
of pullbacks is given:
r,
D, —»-C,
5, 9,
n
u«j)
This means that {J, S) is a directed poset and that A, B, C and D are
diagrams from (/ S) into .» {A has objects A,, J e J, and morphisms a^,j s k,
analogously B, C and D) and f.f.g and g are natural transformations. Let us
form the colimits of the diagram above:
At — colim A
with injections aK: A,-* A, (j € J), analogously Bo, C, and £>► Here we
assume 0 t J for simplicity. The four transformations above yield four
morphisms forming a commuting square:
Minimal Realfullon and Radidion
289
Bo—r— *o
To
There is, in general, no reason why this colimit square should be a pullback
again. We shall postulate tbis as a condition on JT.
Dcflalrloa. A category with pullbacks and directed collmlts Is said to have
stable pullbacks if Tor each directed collection of pullbacks also the colimit
square is a pullback.
Remark*, (i) Given a directed poset (J, S), denote by ■*"■*' the category of
all diagrams over (/ £) In JT (as objects) and all natural transformations (as
morphlsms), The formation of colimit defines a functor
colim: .*"•*'-» jr.
Then X has suble pullbacks Iff colim preserves pullbacks for each directed
poset.
(ii) It Is easy to check that in each category pushouts are stable (i.e., the co-
limit square of a directed family of pushouts is a pushout). This alto follows
from the general principle that colimits commute with colimits.
Example*, (i) Sat has suble pullbacks. Indeed, tbe functor
colim: Sot" *'-► Set
above preserves all finite limits. This means that colim preserves both finite
products and equalizers, and both are easily verified.
(ii) A-Mod has stable pullbacks for any commuutive ring R. This follows
from the fact that Sot has this property and that both pullbacks and directed
colimits are "created" by the corresponding constructs In Sot (I.e., a
commuting square of linear maps is a pullback in Jl-Mod iff it is a pullback in
Sot, analogously with the directed colimits.)
Further examples are discussed in the Exercises below.
3.7. Another condition we need concerns the amalgams of subobjecls
m:A-*B, i.e., the objects obtained from tbe coproduct B + B by the
identification of the two copies of A. They are expressed by the pushout of m with
itself.
290 Chipttr V
DeflaMoa. An (if, ur)-category jr is said to have the amalgamation properly
ir each pushout
m
A -B
1
B~irc
with m € .M is also a pullback or monos />,, »j € .<#.
Example*, (i) Set has the amalgamation property. Given Ac B then
C-B+B/~-Bx |l,2|/~.
where the equivalence - has the following classes: [a] - ((a, I), (a, 2)) Tor
each a € ,4; |M| - |(6, 1)1 and |6, 2] - |(6, 2)| for each be B - A.
Here, p,: B-» Cis the natural injection defined by (o)/>, - [a] for a e A
and (*)/>,- |6, 11 for 6 e fl—A. Analogously with />,. Then
(fl)B, r.(B)«l-(il)ill-*l,
thus, the square above is a pullback.
(li) A-Mod has the amalgamation property. Given a module B and its sub-
module A, then
C - B + B/^ - A x B/^
is the quotient module of fl x fl under the subspace
^ - |(a, -o): ae A)
[because the equation (o. 0) - (0, a) is equivalent to (o, —a) - (u, 0)].
The two natural embedding* p,, />,: l-»Jx B/A fulfil (fl)/>, o (B)p,
— {A)m- pi, thus, the square above is a pullback.
3.8. Thcoreta. Let Jf be a cocomplete (#, UT)-category with stable pullbackt
and the amalgamation property. If an f-epis preserving functor F: X -* 3t
preserves directed cointersections and finite intersections, then F is finiury.
Proof, (i) Let m,: Xt-*X (j € J) be a directed family of .xT-monos.
Assuming U m; ~ I». we are to prove that U im(m,F) — lIr(see Lemma VJ.I).
For each j. k € J with j £ k we denote by
mi. k '■ Xt ~~* Xt
the .xr-mono with m, - 17^, • m,. This defines a directed diagram in Jr. Put
Y-cohmX, and f-colimXF
i*i i*i
Minimal Realization and Redaction 291
with the colimit injections yt: Xt-» Y and y/.Xf-*? {j € J). Since
U m, - I, the morphiitn
defined by y,-e~ mAJ £ J) a *n **-epi (because eacb m, factors through
im e). To prove that U iro(m,F) - I, it is sufficient to verify that the mor-
phlsm
defined by yt- A - yf{j € J) is an isomorphism. Indeed, then the fact that
U y, - >r(>ec HI.5.4) implies
U \m{ytF) - im A - \„.
Since F preserves **-epis, we have then
Uim(m/) - u im(yre)F- im(«F) - \„.
Without lots of generality, (J, S) is supposed to have a least element j*.
(ii) For each J € J we form the following pushout
Since y,-1 - m, € Jt implies yt € Jl (see III.J.I), this is a pullback of Jl-
mono*, too, by the amalgamation property. We define a directed diagram Jl
over (/ £) with the objects R, above and the moronisms rtt: R,-* Ri(j £ k),
given by the commutativity of the following diagram:
292
Chapter V
This gives rise to ■ directed ramily or pushouts. The colimit or these pushouts
is the following square
This is a pushout (see Remark V.3.6), hence,
colim R - Y and p - q - I r.
Moreover, the given pushouts are pullbacks or .xT-monos, i.e., finite
intersections, and thererore, by the hypotheses on F, also the following squares
X,F—1J—«-YF
»IF
YF-
1|F
are pullbacks. Since pullbacks are stable, the colimit square
•YF
1
»coliinRF
is a pullbick, too. To prove tbat A is an isomorphism, it is sulTicient to prove
that Fpreserves the colimit or R. Then, obviously, p— q — lTrand the pull-
back or I and I is formed by an isomorphism, or course.
(iii) F preserves colim Jl. Indeed, each rA» (j, k € / js k) is an '-epi,
because It Is a coequalizer or
yt-pr.yk- it :*«-» 1-
Thererore, the colimit or Jl is precisely the cointereection of rhi (k € J),
where y„ is the least element of J. Since F preserves cointersections, it preserves
the colimit of R, too. □
Minimal Realization and Redaction
293
Corollary. Let JT be a connected, cocomplete (A*, UT)-category with cointer-
section*, stable pullbadu and the amalgamation property. Let F: jr -► jr pre-
serve f-epis and finite intersections.
If Fhas minimal reductions, then Fit finitary.
This follows from VI.3.
3.9. CharacterttttJM Tfcteres*. Let JT be a cocomplete, finitely complete
and well-powered category with regular factorizations, stable pullbadu, and
the amalgamation property.
For each right exact functor F: JT -► JT preserving finite intersections,
equivalent are:
(I) F preserves cointersections:
(ii) F preserves directed cointersections;
(iii) F preserves directed colimits;
(iv) F is finitary.
If JT is connected, further equivalent conditions are
(v) fhas minimal reductions;
(vi) Fit a finitary varietor with minimal realizations.
Proof, (a) We prove below
(ii)ft(iv)-(iii).
All the rest follows from the results above—let us first explain how. The
hypotheses on JT and F Imply (see Observation V.3.5): JT Is cowell-powered and
has unions and cointersections, and F preserves regular epis.
Thus, we can use Theorem V.3.5 to derive that
(Iv)-(D-(ii).
By Theorem V.3.8, also
(li)-(iv).
Hence, the conditions (i), (ii) and (iv) are equivalent. After tbe Implication
above has been proved, it will be clear that (iii) is also an equivalent condition
[since it evidently implies (ii)].
Let JT be connected. Then (v) is equivalent to (i) by Theorem V.I.6. And
since (iii) implies that Fis a finitary varietor (by Corollary IV.3.5), also (vi) is
equivalent to (i) by Proposition V.I.2.
(b) Assuming that Fpreserves directed cointersections and directed unions,
we are going to prove that it preserves directed colimits.
Let us first remark that given two directed diagrams JTand Kand a mono-
transformation
m.X— Y,
294 CMpter V
then the colimit morphism
colim m: colim JT-» colim Y
is also a monomorphism. Indeed, let (J, S) be the (joint) scheme of * and Y.
Foreachye /the morphism mt: Xt -» >y is a mono, i.e., the following square
is a pullback. Since pullbacks are stable, the colimit square:
colim X ^ colim X
coltm X »-ci>llmY
colim m
is also a pullback. Hence, colim m is a mono.
(c) Let X be a directed diagram with a scheme (/ £): denote by Xt(j € J)
its objects and by xt, (_/ £ fc) its morphisnu. Let us form the image
factorizations
xt.k ~ *>.* • "■>.*
<y.*e Ays*)
where
■ Xt € Jt.
In particular, 7], — X, and f,., — mu — I.
For each J e J wt form a directed diagram 7°' of regular epis as follows.
The objects of T> are all 7)., with /> € J.ji. p. If y S /> S «, then the
morphism f J , of 7"' is the regular epi obtained from the following diagonal fill-in;
Minimi) Rulization ind Redaction
295
Then colim T> is the cointeraection of the quotients eh1:X)-+ 7), (q e J,
J £ q). More precisely, let
*,:*,-►*/
denote this cointeraection. Then for each q £ ./'we have i, — *,., • /,, and
colim P - Xt
with colimit injections/ ,: 7J.,-» JT;.
Since I7 preserves directed cointerseodona, also if a the cointersection of
«,7(«E -US 4), and
colim T*F- Xf.
(d) Given y S /It S fv we use the diagonal fill-in again:
We obtain monos
(>s *s/>)
which form a natural transformation from T> (restricted to objects 7}., with
pi. k) into T'. Since 7' is directed, the restriction does not change the colimit
(Exercise III. IF) thus, we have a colimit morphiim
By (b) above, this Is a mono, again.
The following square
commutes. Indeed, consider the object 7}.» of the diagram T>: we have
//. k ' *t.k ~ ^.4.4 ' Jk.k>
29« ClupKt V
Since/,, - ek as well as x;, »,» - mA»(because in the square above, m,, - I),
we get
ft '*/.*" 'a* ' f/.k' *j.i
™ ft*' *>.».» '/*.»
™ ft.»* m>. *' ft
- */.i • ft-
Hence, the regular epis ft {j E J) define a natural transformation
i: X— X.
(e) The diagrams X and X have the same compatible families. More
precisely, to each compatible family of X,
l-.X^Z IJtJ)
we can assign a compatible family of X,
ft.ft:*,-Z IJeJ),
and we claim that this assignment is bijective. It is obviously one-to-one, since
ft are epis. Now, consider an arbitrary compatible family of X,
g,:X,^Z (jeJ).
Let ft - e' • m'be an image factorization (J E J), then for each p e J with
p £ J we have ft - xt,f ■ gf, thus
ft, * '*•
In fact, consider the diagonal fill-in:
Therefore, ft £ e', i.e., e' - ft • ft. Put ft - ft • m*: .?>-► Z, then
ft - ft • #/
and the family gt (j € J) is compatible since given JSt w have
ft- */»•»» Hence,
ft • ft - */.» • ft • g» - ft • (*/.> ■ it)
and ft is an epi.
Minimal Reiliutioii ind Reduction
297
Since X and X have tbe tame compatible families, they have the tame coli-
mita, too.
(0 The diagrams X • F and X • F are related in tbe same way as the
diagrams X and X. Indeed, F preserves regular epis [see part (a) above) and mo-
nos (since it preserves finite intersections and since monos are characterized
by their pullbaclu) and hence, F preserves image factorizations. Further, F
preserves the colimit of each T(j s J). We conclude that also X • F has the
same colimit as X • F. Therefore, it is sufficient to prove that F preserves the
colimit of X And X is a directed diagram of monos.
Here we use (for the first time) the preservation of directed unions. Let
V-<x>\imX and W-eolim^F
with colimit injections
*I:X,— V and w,.X,F—W (J <■ J).
Then eacb *, is a mono. Indeed, let v, — I • Hi be an Image factorization, then
for each ki. jut have
ei.SeW
(because v, — */,» • v» — *,, ■ my, • »,). Since e^ia tbe cointersecrion of all *,,»
(k £/), we conclude
in other words, i\» an isomorphism. By Remark III.5.4,
U^-i,
and we conclude (since this union is directed) that
Denote by
r:lV— IT
the morpbism defined by
»,.»-»/ ()eJ).
We are to show that »is an Isomorphism. Since U'f- I n< '• i» obvious that
»Is a regular epi (each yfftaon through the Image of v, hence, this must be
all of YF).
298
Chapter V
It remains to prove that v is a mono. Since each v,f is a mono, we have a
directed family of pullbacks
x,f—!—x,f
1 »,F
X,F «-VF
"if
with j 6 J. The colimit square
i
w «- w
t v
W «-VF
v
is a pullback, too. Hence, v is a mono (as well as a regular epi) which proves
that Fpreserves the colimit of JE D
3.1*. Exaeailea. We discuss the hypotheses of the Characterization Theorem
first for JT and then for F.
(i) 8«t and Jt-Mod: The hypotheses are fulfilled. These categories are
complete, cocomplete and well-powered. The amalgamation property has been
discussed in V.3.7. and the stability of pullbacks in V.3.6.
(ii) Varieties of finitary algebras: The hypotheses are fulfilled except,
conceivably, the amalgamation property which is a non-trivial problem of
universal algebra. Some varieties are known to have this property (e.g., groups,
A-modula. and lattices) and some are known not to have it (e.g. commutative
semigroups).
(iii) Po* has the amalgamation property as an (epi, embedding>category
but, unfortunately, not as a (quotient, mono)-category, as required by tbe
Characterization Theorem. For example, let A — |0,11 be the discrete poset
and B- |0,l| the chain 0 £ I. Then m:A-*B defined by (0)m - 0,
(I )m — I is a mono such that the pushout of m with itself is
A ► B
m 1
B p-» B
Minimal Realization and Reduction
299
This square is not a pullback.
All other hypotheses are fulfilled by Pot. Thus, each right exact, flnitary
functor on tbe (quotient, mono)-category Pot preserve* colntenectioru. And
each functor on the (epi, embedding>category Pot which pmervei epis.
finite intersections, and cointenectlons, is flnitary. But "flnitary" In two
factorization systems means two different colndidons, of course.
(iv) Top and Gra: The situation is the same as in Poa, sec Exercises VJ.
below.
Prafostttoa. Let JT be a category in wbich
(i) every regular epi splits:
(ii) every equivalence is a kernel equivalence of some morphism.
Then each functor F: JT -».«" is right exact
Proof. Let e:X-* Y be tbe coequalizer of an equivalence relation
[r„ rj: X-- X. Since [r„ rj la the kernel equivalence of some morphism /, it
is, in fact, the kernel equivalence of e {r,-f- r,./Implies that /factors
through «, say, /- *•/; then each pair p,, p, with p,-e- p,-e fulfils
P\-f- Pi '/"id hence, {p„ p,\ c [r,, rj).
Since t spills, we can choose a morphism i: Y-* X
with
i-e-l,.
The pair I, and (•/ fulfils
therefore 1U. *• fj c [r„ rj. This means that there exists./: X-» R with
}• r, — I, and )• rx — *• /.
All thla implies that for each functor f: JT -».r the coequalizer of r,Fajid r,F
is eF. Indeed, let A: XF-* Z be a morphism with r,f• A - r2F- k Then the
300
Chapter V
morphism H — if. h fulfils
eF■ K-(e- i)f • h-(J- r,)F- ft - jF- r,F- A - ft.
Since eF is a (split) epi. such (is unique. D
Corollary. For each set functor the conditions (i)—(vi) of the
Characterization Theorem are all equivalent to
(vii) F is a quotient functor of Ht for some Unitary type 21
Indeed, f is right exact by Proposition above. Assuming that f is standard
(III 4.5), then it preserves finite intersections, and so all tbe conditions
(i)—(vi) are equivalent: sec III.4.3 for the equivalence of (vii). If f is arbitrary
then, by III.4.3, there is a functor F' with F - F' on non-empty sets and maps
such that F is naturally isomorphic to a standard functor. Obviously,
(i)—(vii) are equivalent for F". And the empty set does not influence any of
these conditions except, possibly, (vi) (because of tbe initial F-algebra) and (v)
(because of difficulties with the empty ^automaton). But, in fact, there are no
problems because (iii) and (i) clearly imply (v) and (vi); conversely,
(vl) -» (v) -» (i) has been proved above. D
Remark. We conclude that the only ^automata in Sot which have minimal
realizations are Unitary tree automata and their basic varieties (III.3.2).
Cordlary. Let A be a commutative Held. For each functor F: K-Voct-*
A-Vact, the conditions (i)—(vi) of the Characterization Theorem are all
equivalent.
Indeed, f is right exact by the Proposition above. And fpreserves finite
intersections by Ex. III.4.A.
3.11. The category Sat. of countable sets and maps has a special property
(shared by A-Vact.. see Exercise D below):
Theorem. Each functor f:8at„-» Sat. is a Unitary varietor with minimal
realizations.
Proof. We proved in IV.6.4 that fis a Unitary varietor. In that proof we
have exhibited a Unitary functor G: Sat -> Sat extending F. Since G has
minimal realizations by tbe Corollary above, so does F. Indeed, each reachable F
automaton is countable, and f coincides with G on countable sets. O
Exercise. V J
A. Stability of aalraacka. (i) Verify that the following categories
Poa, Gra, any variety of Unitary algebras
have stable pullbacks. (Hint: The functor colim: JTU-J,-» JT preserves finite
Minimal Reilinlrati and Reduction
301
products and equalizers.)
(ii) The category
JT - er-Lat
of <j-complete lattices and ^complete homomorphisms fails to have stable
pullbacks. Indeed, consider the <u-chain of pullbacks
i
n »> n
n »■ Ci>»l
v„
fn<cj)
where f.: n -» a> + I is the inclusion of n - (0, I..... n — 11 (linearly
ordered) to a> + I - |0, I,.. | w |a>|. Prove that the colimit square is no pull-
back. (Hint: The colimit of the chain |ii|.« „is the free ^complete lattice X
over a>. The canonical map v.: X-* a> + I Is not one-to-one, hence, the pull-
back of v. and ». is not I,, I,.)
B. FtaHary faacton. (i) Prove that In Gra, Poa, Top with t - epi, UT - em-
beddings, a functor Fpreserving embedding* is Unitary iff for every object X
and every point x e XFthen exists a finite object fand a morphism/: Y-* X
with x 6 (YF*fF).
(ii) Consider Top with regular factorization*. Define a functor
F: Top -» Top as follows: for any space X, let XF be the space on the same
set, the open base of which is precisely the set of all closed-and-open subsets
o( X; on morphisms./F-/. Prove that Fis not flnitary. (Hint: Let A be the
space of real numbers, then XFhas only two open sets, 8 and A; consider the
directed set of all subspaces Yo( X, vhich have only a finite number of
non-isolated points; then Y- IT and hence X- [}Y- {}YF+ XF).
C. Aiaalaanatloa property, (i) Let JT be a concrete (f, ur>category. Assume
there Is m e Jl which is not an isomorphism though its underlying map is
a bljection. Prove that X fails to have the amalgamation property. (Hint: The
pusbout of m with itself is no pullback. In fact, if m-p — m• q is this
pushout, then for the forgetful functor U, pU - (m(/)-|[(m(/)(j>(/)| =
(mU)-'l(mU)(qU)] - qU implies p - q. If m-p » m-p is a pullback, then
I • p — I • p implies that m is a split epi.)
(ii) Deduce that Ora, Poa, Top with regular factorizations fall to have the
amalgamation property.
(iii) Verify that Gra, Poa and Top with (epi, regular mono)-factorizations
have the amalgamation property. (Hint: The pushout is created on the level
of sets and all morphisms in it are regular mono*, hence, it is a pullback.)
302
Chapter V
(iv) Verify that the full subcategory of Top formed by all Hausdorff spaces
fails to have the amalgamation property with respect to (epi, regular mo-
no)-factorizations as well as (regular epi, mono)-factorizations; but it has the
amalgamation property with respect to (*, .^factorizations with t —
continuous maps onto dense subspaces and ur — embedding! of closed subspaces.
(Hint: Consider the pushout of m with itself, where m is the embedding of
the space of rational numbers into the space of real numbers—the resulting
space is the space of real numbers again.)
D. Mkttaal realUatto* la R-Vect.. Prove that on the category R-Vect. of
countably-dimenslonal vector spaces, each functor is a Unitary vanetor with
minimal realizations.
V.4. Conaequma of Mlalmal RedocHoa
4.1. Each functor with minimal reductions is a Unitary vanetor. We have
proved this (V.3.9) under very restrictive additional hypotheses. In the present
section, we prove this more generally. (In V.3.9 we have proved that even the
functor itself is Unitary which is much stronger—see for example IV.6.7.) We
also prove that a functor with minimal reductions preserves epis, thus getting
rid of another additional hypothesis.
A pullback in a category JT is said to be absolute if each functor from jr to
any category preserves it.
Leaasaa. Each pushout
B—j—C
of split monos mand m' is an absolute pullback, and/and (are split monos.
Proof. Choose morphism m: fl-» A and m: B' -» A with
ffi • in ™ in 'in ™ I^.
There exists a unique morphism/: C-» B such that the following diagram
Minimal Rtallmlon and Redaction 303
commutes. Analogously define g: C-» B'. Then we tee that/and (are split
monoi, and we have a diagram
nV
*1 -*
i m-
m
1
9
•
f
such that
(•) m • m - m' • ifi' - \A; m-f-m'-g; f-J-\,\ g-g-\r
and g • / — m • m; /• f — m • m*.
It is sufficient to prove that (•) implies that the pullbaek of/ and f is formed
by in and m: for each functor F the ftmage of the diagram above has the
property analogous to (•) and hence, JF and gF are then proved to have the
pullbaek mF and m'F.
Let p and q be morphinns with
The moronism p • ifi fulfils
p—{p-m)-m and q — (p- m) • m'.
Indeed, the latter follows from (•):
» - V ft- P-f- I- P- * • "•':
the former Is now a consequence of (•) and q - p • m • m'\
p-p.f.f-q.g.f-p.m-m'-gf-p-ifi-iH-f-f-
p ■ ifi ■ m.
304 Ouper V
It is clear that p- mis unique with this property since m is a mono. Thus, (•)
implies that the pushout above is an (absolute) pullback. D
4J Theorem Let jr be a countably cocornplete (f,uir)-category which has
cointersections, stable pullbacks and regular finite coproducts. Let F: JT -» JT
preserve f-epis.
If F has minimal reductions, then the free-algebra construction stops after
a> steps for any object / with hom(/f, I) * B.
Remark. Instead of the stability of pullbacks it would be sufficient to
assume the (i>-stability of split intersections (i.e., of pullbacks of split monos).
Here, <w-stability refers to <v-colimiu of pullbacks (whereas stability concerns
all directed collmlts). The proof of the theorem above uses the same technique
as that of V.3.8.
Proof, (i) We prove that in the free-algebra construction, each
*V •: If. -* If. (" < o>) is a split mono. Let us choose an arbitrary morphism
d: IF-* I.
and define a chain of morphisms
4..: W.— K (nS m< o»)
by the following Induction:
d,.,:l+ IF-* I
has components I / and d:
d..,...,-h+<k.F:l+ lf.f-/+ W.F.
For each n<itt define a collection of morphisms
/,:lf,-lf. (*<«.)
by
I h>, . if tS n:
Ji~\ dt.. if*> n.
It is easy to verify that this collection is compatible with the free-algebra
construction. Hence, there exists
4..' If.-* If.
with ft — wt . • d. . (* < <u), particularly with w. . • d, . — f. — »,. — I.
(ii) To prove that the free-algebra construction stops after a> steps, we are
to verify that F preserves the colimit If. — colim W,. We use the following
Minimal Realiurion wd Reduction
305
a>-chain of puihouu
«^o
Wu"
(n < a>). More precisely, for each n < a we define R. by the pushout above,
and for each n < m we define
v.: «.-► K.
by the commutativity of the following diagram
».)•
(using the fact that w,m • pm -
The colimit square:
1 ' '1,
is a pushout (see Remark V.3.6) and hence,
R. - W. and p.- q.-\,..
Moreover, since w, . are split monos, the following squares
-*J
Wj:-
9„F
P,F
306
Chapter V
are pullbacks of split monos, by the preceding lemma. Since split intersections
are a-stable, the colimit square
h
colimW„F fc-V^F
n<tj
h „
<■
»t,F »■ colim R„F
is a pullback, too. We are to prove that A is an isomorphism. By the preceding
remark, it is sufficient to prove that F preserves the colimit of A, i.e., that
colim A F- W.F
from which we readily conclude that p.— q.— \- since A, A is the pullback of
1,1, clearly, A is an isomorphism.
(iii) Fpreserves colim A. Here we use the fact that Fweakly preserves eoin-
tersections (by Remark V.I.3). First for each n £ m we have
r... E t.
In fact, r. , is a regular epi because it is the coequalizer of wm „■ p. and
"••• 9.. [Proof: Let /: Rm -» S be an arbitrary morphum with
"...•P.f- •»■,..«.•/•
Then, since p. and q. form the pushout, there exists /: R. -» S with
pm-f- p.</and ?_•/- ?.•/. It follows that/- r,.-/, because both
/>.•/-/>-•/-/>.•('...•/)
and
«.•/-«./- «.•('..-•/)
The uniqueness of /is easily seen.)
Thus, the colimit of R is given by the cointenection of r, . (m < ■»). More
precisely, if r, .: Ag -» R. denotes this cointenection, then for each m < a>
we have v.: R„-» A with r, . - r^_< v., and these are the colimit
injections of R. — colim A.. Analogously, each r. „Fis an f-epi, thus, colim A- F
m < m
Is the cointenection of r, ,F(m < <u). It Is sufficient to prove that F preserves
the cointenection of r, . (m < <u). This will be clear when we exhibit
moronism
Sm: A.f-» A. (in < a>)
Minimal Realization and Redaction 307
such that r, .: (Jl* 6,) -»(R,., 6.) are homomorphiinu. I.e.
S, • r,,. - r, ,.F • S. (m < m).
RF JL» w^5^*IF —'—*WF-^S— Vt-?=— R
1
V »»»t/ ►IF ►MF » "t, > B.
tf d^F 1 <«« P-
For each m < <t> there exists (by the property of pushouts) a unique mor-
phiim r.: A. -> If. for which the following diagram
commutes. Clearly,
'•-'•.-•'. (m< »).
Next, there exists a morphlsm 6 from W.F to If, [for example, compote <t, .5
of put (I) of the present proof with the coproduct Injection j: IF-* If, and
»i..|. Put
Sm — FmF- S-pm (m < a).
These morphisms have the required property because the squares above clear
ly commute. □
Corollary. Let JT fulfil the hypotheses above and be connected. Let
F: jr -» jr preserve /-epis and fulfil hom( IF, 1) * 0. Iff has minimal
reductions, then Fis a Unitary varietor.
4J. Tbeorea. Let jr be a connected («", ur>category with finite regular co-
products. If a functor F:Jt-*jt has minimal reduction then
x < implies rFlsanepl.
. Since JT Is connected, the coproduct injections A-* A + A are
split (hence, regular) monos whenever A * 1. Thus, the regularity of finite
308
Ctup)er V
coproducts in the theorem above only means that the canonical morphanu
i. -* B are ~*.monos. Equivalently, that 1 is simple, i.e. has no proper
* -quotients. In Exercise C below we show that this assumption is essential.
Proof. Let e: A-* Abe an 4-epi. Given », A: BF-* Cwith
tF- g - tF- h.
we are going to prove that g - h. This is dear if A - i. since (by the
regularity of finite coproducts) then t is an isomorphism. Assuming A * 1, there
exists a morphism
t:C-*A.
Define a non initial ^automaton:
M-(A+C, S,B+Qe + lc)
where
S:(A+ OF—A+ C
is the following morphism. We use the following notation for the coproduct
injections
A c 8
\/v
A»C &Q
and we define
p:A+C-»B and q:B+C-»B
by
r-p - w-q- l-e: C-» B;
r • p - t and J • q - I,.
Note that p — Pft, where p,: A + C-+ A has the components I „ and t Thus,
pF- g - pF- h. Put
8- pFg-v- pF-h. r: (A + C)F— A + C.
To prove that g — A, we use the minimal reduction of M
r,: *#-»*#,-(ft. oVf+Cn).
We define a reduction of M:
e+ ic:M-*M,-(B+C8„B+C,i)
Minimi] Re*liiallon and Rcducsloo 309
where
S,:(B+ C)F-»B+ C
is deflned by
«,- qF-g-v.
Sincere f,alsor+ lc e t (111.5.5). Moreover, * + I c is a morphism of
automata, since the following diagram
0
lA^IF •
(••yF
X.
-=*—.
pF ^ a
BF »C
sf
IWIF
commutes. Thus, M, is really a reduction or M. Hence, there exists a
morphism of automata
Sm l M- -** M%
with
'•-(*+ lc)-l,.
Quite analogously, we define a reduction
f+ lc: U-* Mk
(always substituting A for »), and we obtain
with
'•-(* + lc)-»»-
Since J, preserves the outputs, we have
lf*c- V)V
Thus, j, is a split mono as well as an f-epi, i.e., j, is an isomorphism.
Analogously,
li-r- 't-Yt,
hence.
«»- * - y.
310 OuplcrV
Both J, and J, are homoroorphisms, hence.
Thus
qF-f t- qF-h-1.
By the definition of q we have j- q - \, and thus, by multiplying the last
equation by jF we get
g. t- h- v.
And v is a mono (since finite coproducu are regular), thus,
g- A. □
4.4. Recall that (epi, extremal mono)-ractorizations exist very often (III.5.6).
Corollary. Let ,jr be a countably incomplete, connected (epi, extremal mo-
no>category with stable pullbaclu and cointenectioiu, in which finite
coproducu are regular.
For each functor F: JT -» jrwith horn (IF, 1) * B, equivalent are;
(i) Fis a Unitary varietor with minimal realizations:
(ii) Fhas minimal reductions;
(iii) F preserves cointersections.
ir Tact, (iii) -»(ii) is Theorem V.I.3; (ii) -»(i) follows from Corollary V.4.2,
the hypothesis of which is fulfilled by Theorem V.4.3, and from Proposition
V.I.2; (i)-» (iii) follows from Theorem V.I.S (using V.4.3 again).
Exaaple. A functor F: A-Mod -» A-Mod has minimal reductions iff F is
Unitary. Moreover, F then preserves epis and is a flnltary varietor. In fact,
A-Mod fulfils all hypotheses of the preceding corollary and, moreover,
homUF, J.) * 0 is always fulfilled.
Exercise* V.4
A. A aM-varieior wtth ■lalsaal redactioa*. Let .* - Sat* be tbe dual to the
category of sets (111.2.12). The power-set functor (111.3.4) defines a functor
P": S«t°» -► 8«t°».
(i) Verify that P" preserves cointersections by proving that P in 8«t
preserves intersections.
Minimal Realiution and Reduction
311
(ii) Prove that no object generate! a free /"•'-algebra. (Hint: uie 1V.2.6 and
IV J.I),
(iii) Explain why thii does not contradict Corollary V.4.2.
B. A ■«■ tuMlmtlw rarktar with ariaianl lallzatJaa*. Prove that the
functor F: Gra -» Gra of IV.3.A hai minimal reductions. Explain why this does
not contradict Corollary V.4.2.
C Praemtloa of eats Ii mat amiary. We eihibit a flnitary varletor on
a connected category which has minimal realizations and yet does not
preserve epis.
(i) Define a category Ab* by enlarging Ab, the category of abelian groups
and homomorphisms, by a new object, the "empty group" 0 and by empty
maps f„: 0 -► A for each A in Ab*. Verify that Ab* is an (epi, mono)-category
with cointersections and coproducu. Verify that fa: 0 -» |0j is an epi in Ab*:
conclude that Ab* does not have regular finite coproducu.
(Ii) Define a functor
F: Ab* -► Ab*
by choosing an arbitrary non-trivial abelian group A and putting
XF-A for each X in Ab*:
given/: X-* Xthen
_ f I,, if X + 8 or X- r-0;
' {zero map if X-i * Y.
Verify that F is a finitary varietor with
/• - /+ A if /^0; 0* - |0].
(Hint: In the free-algebra construction over 0 we have If. — A and w» _ the
zero map (n S m< a) and hence. If. - |0|.)
(iii) Verify that each behavior fi: /• -► r has a minimal reduction obtained
by the image factorization fi — e • m, e: /* -► Q as follows: Q is the state
object, m the output morphism and, if / * 0, the components ofe:/+ A-* Q
are A and S.
(iv) Observe that F does not preserve epis: consider fa I .
V.J, Fbdte Aotoanta
5.1. We are going to prove that each finite automaton has a minimal
reduction. The hypotheses under which this holds are quite mild—for example, all
functors on Sat or A-Vact are included. Throughout this section, JT is an
(•*, ur (-category.
312
Chipler V
DeftnlHoi. An object Q is said tobe/faiYeifhom(C —): jr-» Sat is a fini-
tary functor. Explicitly, if for each directed collection of ur-monos
mt: R)-» R (j E /) with U m, - m.S-* R and for each morphism
there existsy» e / such that/- m factors through «v
ExaBaiea. (i) Sat: this is the usual concepL Indeed, let Q be a set with
finitely many points. Then Q is a finite object since for each
f-.Q^S- U«,
there exists /,! J with (q\fe Rh for all q e Q (because the union is
directed).
Conversely, if Q has infinitely many points, the condition above fails even
for
/■-i^e-e- U/,.
where R,(j E J) is the collection of all finite subsets of Q.
(ii) Poa with / - epis and -M - em beddings, finite objects are jusi finite
posets. the proof is as for Sat. The same is true for 4 — quotients and
ur — monos, but here we must be more catious. Let us consider a directed
union u m, — m. We can assume that R,z. S and m, is the inclusion map
(j E J) but the order of R, can be weaker than that induced by £
Nevertheless, given x, y e R with x £ y, then there is j E / with x, y E Rt and x<, y
also in Rt. Indeed, since / is directed, the relation :S formed by all pairs x, y
for which such j exists, is transitive (as well as reflexive and antisymmetric).
Hence, U m; is the poset 5 with the order i —consequently, the latter coin-
dices with £.
Now, given a finite posei Q and order-preserving map f.Q-* S— U m,,
for each pair x, y e Q with riywt have (x)/£ ly)/ in 5 and we choose
j,,, E / with (x)/S tv)/ in R;, t. There exists 7, E J with mA r c 1% for all
x.y-
The converse is proved as in (i).
(iii) A-Mod: finite means finitely generated. Indeed, let Q be generated by
91 q. E (?. For each f-Q—S- [} R, there exists ;', e J with
(«.)/:.. -.(«.)/'E *„. Hence, (fil/c «„.
Conversely, if (j is not finitely generated, the condition fails even for
f- \„: Q-* Q- U R,, where R, (j e /) is the collection or all finitely
generated submodules.
Mlntaal Rcalizilion tnd Reduction
313
(iv) More generally, in each variety or Unitary algebras, finite means
finitely generated.
(v) ^complete lattices (and ^complete homomorphisnu): no non-empty
object is finite. Let R be the fixe (^completion of at and, for each n < o>, let
m.: (i-► R be the embedding. Then (J m. - I,. Consider any constant map
/: fi-» R — ».
Ltmma. Finite objects are closed under finite coproducts and quotients.
Proof, (i) Let Qt, Q, be finite objects, let/: d + Q,-* S be a morphism
and let m — Urn.: S-* R be a directed union. There exists /■ such that the
/•j '
first component of/- m factors through m,,: analogously, the second
component factors through some mh. \{J e /is larger than Jt and jlt ihen /• m
factors through mt.
(li) Let Q be a finite object, and let e: Q-* Q be a quotient of Q. For each
directed union U m/ ~ m: S-» Jt and each morphism/: C-» S there exists/,
such that e • /• m factors through m^, tay, e • /• m — /• m^ Now use the
diagonal fill-in:
0—^—8
■I/I-
Ri: •" R
Since/- m factors through m„, the object Q is finite. □
iX Remark. An F-automaton A - (Q,6, r, y. I, A) is said to be finite if fi
and / are finite objects. Let F: of -» of be a Unitary varietor preserving finite
objects. Then for each finite object / also the steps of the free-algebra
construction:
/: 1+ IF: / + (/+ IF)F;...
are finite. Given an automaton A, its run morphism /i: /• -» Q is the colimlt
morphism of the following "approximations" (see IV J.I):
ft-A:/-C:
p,:l + IF-*Q
has components A and AF- 4: etc.
We say that an automaton A is reachable In n slept if p. is in t.
Each automaton A with / finite, which is reachable in n steps, is finite
(because C is a quotient of W.) and reachable (because p. — "...- P, hence
314
Oupla V
pit). Conversely, each finite reachable automaton is reachable in n steps
for some n < o. Indeed,
Q- U im p.
m < m
and Tor/— \Q: Q-+ Q there exists n, < a> and f such that l0 — f • im p„.
This implies that im p„ — 10.
For each functor F: Jf -► of we define its flnilary pari Fm as follows. For
each object Jf put
XFm - U im(mF)
where the union ranges over all subobjects m: Y-* Jf of Jf with X finite. Let
ii,:JfF.-»JfF
be a mono representing the union above. For each morphism
f:X— Y
we define/F. as the restriction of/F. i.e., as the (unique) morphism Tor which
the following square
commutes. We must verify that such /F. exists—we do this in the following
proposition. Then /F. is unique because ur is a mono. And the preservation or
composition and unit morphisms is an easy consequence. Note that
u:F.— F
is then a natural transrormation. Thus, F. is a subfubctor or F—the least sub-
functor which coincides with F on the full subcategory or all finite objects.
Pnausltlua. Let Jf be a complete and well-powered. For each functor
F: jr -» jr the flnitary part is well-defined, and it is a finitary sobfunctor or F
Proof, (i) For each morphism /: Jf-» Y we are to exhibit a morphism
fF.: XF.— YF.with
fF..ur-u,.fF.
Minimal Realization ami Redaction 315
Let us form the pullback or ur and fF:
u u,
XF »-YF
IF
Since urlsin ur. so is 0(111.5.1). It suffice* to check that for each finite subob-
ject
m:Q-*X
of X we have
im(mF) c u.
Indeed, then ut c u, i.e., there exists 1: XF.-* T with u, - I • u and we put
JF.-fl
Consider the image factorization of m • /:
m •/■— i- m
where I: Q-» Q is in **, and m: Q-» Y is in ur. Then (? is finite, by Lemma
V.S.I, and hence.
im(mF) c ur.
Thus there exists a morphism p: QF-* YFm with
iflF — p • »j.
Consequently, there is a unique morphism ^such that the following diagram
commutes. Thus, im(mF) c S.
(ii) F. Is finitary: let mt: R,-» R(j € /) be a directed collection of subob-
jccts with
316
CKiptnV
(sec Lemma V.3.1). For each finite subobject m. Q-+ R there enist jt E / and
m'\ Q-+ Rj, with m — m' • m„; in other words.
HI C ITIy0.
Hence,
RFm - Uim(mF) c Uimfm/).
Since the opposite inclusion is obvious, we conclude
UintC"/.) - I,,.. □
Corollary. Let jr be a complete, well-powered (regular epi. mono>category.
Let F: JT -» JT be a functor, the finitary part of which is right exact. Then
each finite F-automaton has a minimal reduction.
Indeed, the finitary part F. preserves cointerseclions by Theorem V.3.S and
hence, each F.-automaton has a minimal reduction by Theorem V.I.4 (since
jr has cointerseclions by Observation V.3.S). Further. F coincides with F.on
flnite objects, and hence, each finite F-automaton has a minimal reduction,
too. □
EiubsIc For each functor
F:Sat-»S«t
every finite F-automaton has a minimal reduction. For each commutative
field R and each functor
F: «-V«ct -► fl-Vect,
every finite-dimensional F-automaton has a minimal reduction.
Indeed, all these functors have right exact finitary parts (Proposition
V.3.10).
Reaurk. In automata theory, a behavior
fi: lm — r
is called recognizable if there exists a finite automaton the behavior of which
is fi.
For .JT — Sat or JT — A-Vsct, each recognizable behavior has a minimal
realization. This is the minimal reduction of (any) finite realization of fi.
EmtcIsmV.S
The aim of the following exercises is to present a generalization of F-automa-
ta to automata over a monad. We explain first the concept of monad, and then
we hint some results on minimal realization.
Minimal Rcallatfoa and Redaction
317
A. MmoM Boaad, For each set X, denote by XT the free monoid (of all
words) generated by X; for each map/:*-* Y, let/T: XT-* YT be the free
extension of /to a homomorphism [defined by (x,... x,)fT - y,... y, where
*-(*)£ and («)/T-9).
(i) Verify that
7°: Sat -» S«t
is a functor, and the injection of generators defines a natural transformation
V- !■«-» T.
(ii) For each set X denote by
Ml:(XT)T*XT
the natural map, assigning to each word *■,... w,, where w, — i\... x'^ e
XT, the concatenated word
(»,«-,... ».)ti, - x\... x'„xi... x'„ ... xM,... x^ € Jf7
Verify that
li:T- T—T
is a natural tranformstion such that the following diagram
HI
commutes.
(Ill) Prove that for each monoid (g, •, e), the map
S: QT-* Q
defined by
BS- e;
(*••• «.)*- «i* 9i 4.
satisfies the following equations:
(2) nB-fi-l„ and 8T- S- fig. 6.
318
Chapter V
(iv) Prove that each T-algebra satisfying (2) corresponds to a unique
monoid on Q. Conclude that the category of monoids and monoid-homomor-
phism is concretely isomorphic (III.3.8) to the full subcategory of the category
7"-Alo("I.3.l) consisting of all 7*-algebras saiisfying (2).
B. Monads. A monad T - (71ij,^)or i category JT consists of a functor
T:Jt-*jt and natural transformations r;: l,-» T and /i:T- T-+ T for
which the diagram (I) commutes. The full subcategory of the category T-Alg
consisting of all T-algebras which satisfy (2) is called the Eilenbrrg-Moore
category of T. and it is denoted by JT'.
(i) For each monad T in Sat, verify that any set X generates a free object
(XT.fj,) of Sat' (if the map r/r: X-» XT is considered to be the inclusion
map).
(ii) Verify that each variety » of algebras, considered as a concrete
category (with homomorphisms as morphisms) is concretely isomorphic to 8atT' for
the following monad T,. For each set X, let XT be the (underlying set of) free
I -algebra generated by X, r/r: X-» XT the injection of generators and
Ii,: (XT)T-* XT the unique homomorphism extending the map Irr- We call
T, the y -frtt algebra monad
(iii) Denote by P - (P. n, n) the following monad on Sat: P is the power-
set functor (II1.3.4), r; is the injection of singleton subsets and
)1,:{XP)P-* XPauiint to each collection Jfc XP of aubaets of X ita union
Verify that P is the »-algebra monad for the variety v of complete join-
semilattices and complete homomorphisms.
(iv) Generalizing (i), verify that for each monad in JT the pair (TT.ii,) a
a T-algebra with the following universal property: for each T-algebra (ft 5)
and each morphism/: /-» ft there exists a unique homomorphism
r:(TT,n,)*(Q,6)
with/- v< •/•■ IHint:/* -fT. S.\
C. Monads and Tarletora. (i) For each varietor F: Jt -► Jt define a monad
T, - (Tf, n, ii) on or as follows. Given / in JT, then IT, - I' and r/, has the
usual meaning: the map lfa has a unique extenaion to an F-homomorphism
Ii,:(!')' -» /*. Verify that T,ij a well defined monad, and that the categories
F-Alg and .JT1'
are isomorphic,
(ii) Prove that the morphisms
r/,F-«>,:/F-» /• - TT,
define a natural transformation r: F-» T, with the following universal
property: For each monad T' — (7", r/', p) and each natural transformation
Mioimal Realization and Reduction
319
r': F-* 7" there exists a unique monad morphum or: T,-> T' (i.e., a natural
traiufbnnation o:T,-*T with 17'- n-cr and n-t — crT-fi) >uch that
r' - r- <r.
D, Moaad aatoanta. A 7"-automaton (Q, S, /", y, I, A) la (aid to be a T-autc-
roaton If (ft 6) is a T-algebra [i.e., (2) ii fulfilled). The T-run morphism ii
defined as p - XT- 8: IT-* ft and the behavior is fi - p- y: IT-* /".
If of is an (**, ur)-cstegory, then the 1-minimal naliiallon of a behavior
fi: IT-* Tis a realization A which is reachable (pet) and such that any
other reachable realization of fi can be reduced to A.
(i) Let rpreserve tT-epis. Prove that each T-automaton has a unique
reachable subautomaton.
(ii) Let rpreserve tT-epis, and let JT have eointersections. Prove that each
behavior has a minimal realization iff r preserves eointersections. [Hint:
Sufficiency is proved as in V.I.3. For the necessity, let e — t,-Pi'- Q-* R be the
cointenection of •"-quotients *,: Q -* ft (I € I). Given morphisnu r,: QJ-* r
with e,T- r, - r(i € /), use the T-automaton
* - (QT. Ih. T, r, ft ij0):
each e, defines a reduction (QT, fig,, /", r,, ft, i)e,) and using the minimal
reduction, it is dear that r factors through tT. Hence, «Tis the cointenection of
'JUe /)•]
(.iii) Prove that in Set, monads with minimal realization are precisely the
•'-free algebra monads of varieties » of Dnitary algebras. [Hint: For each r,
the functor 7"of B(i) above is dearly dnitary and hence preserves
eointersections (V.3.5). Conversely, if T preserves eointersections, then it is finilary
(V.3.8) and hence, it is a quotient or Hs with S Dnitary (111.4.3). Verify that
Sat' is concretely isomorphic to a variety of ^algebras.)
(iv) For each monad T in Sat, prove that any behavior with a finite
realization has a minimal one. [Hint: The Unitary part ofa monad is a monad:
proceed as in V.S.2.]
Nolei 10 Chepler V
V.I
V. Tm kova| 1974| proved that • eel functor adnlte minimal realization IfTk preiervee colnter.
tcctJont, and J. Adamce |l974a| aantralted thai 10 an arbhrsry catesory fnndcr ruber restrictive
additional hrpotheies). The eeneral tcauh V.I J appeared in J. Adiaiek |l977a|.
V.2
A nice eipotition of rcleliofH In e (rafular epi, monoHateaory waa preeenled by P. A. Grille!
11971L where awn of the rraalrj of lection V.11 — 7 can be found. Rdarjona in eo (#,»•* Hatefo-
ry appear io V. Tmkova 119801 which h Ihe louree of VJ.B—10.
320
Chapter V
VJ
The fact that a right exact, finttaiy functor preserve* colntenectiofu was established by
M. Ban-1I974|. His hypotheses were much stronger: lha present form of Theorem V J.4 Ii baud
on the multi of J. Adaraek |l976b| and J. Adamek and v. Koubek |I9BI). The former paper ii the
source of the convene implication (Theorem! V.3.8 and VJ.9).
V.4
All reiuhs In this section were proved by J. Adamek |!974a, 1977a).
V.5
The existence of minimal reductions for finite automata was csttblbhed by J. Adamek {I977a|
lo case jr Ii S«t or AVact. The general mult (Corollary V.5.2) Ii new.
More Information on monads can be found In the monograph of E. Q. Manes 11976). Each var*
letor defines a "free" monad, i.e.. a monad with the unlvenal property of d. V.5.C (ii). tt was
proved by M. Barr {I970| thai conversely, if a functor F generates a free monad, then f is a varie*
tor. Thos, F«ulomaia present just the case of monad automata for the free monads.
Minimal realization for monad automata has been Investigated by J. Adamak 11976b, 1979b).
Chapter VI: Uarfenal Reallzatloa
V1.1. The Caaceat rf UihtralHy
1.1. We »ay that minimal realization it universal if it has "(tinctorial" nature
or, equivalcntly, if reduced automata form a full, reflective lubotegory or the
category of ^automata (with minimal reduction ai reflection). Whereas
sequential automata have this property (II.3.9), tree automata do not: we shall
prove that universality of realization Implies that the type functor Fpreserves
unions.
Throughout this section we work with an (/, ur)-category jr. We use
a more general concept of automata morphiim than before (corresponding to
that of II.I.8). A morphiim from an ^automaton A — (Q, 8, T, y, I, A) into an
^automaton A' - (Q\ S", /", f, /*, A*) is a triple
of morphisms /: Q-+ Q', f^,: /~-» I™ and JJ.: /-» /' such that the following
diagram
commutes. Analogously, a morphiim of non-initial automata is a pair (f,f^).
In case /"- /"' and /^ - idras well as / - /' indjl. - id,, we write
/instead of (/, id, id) (as before).
We formulate the concept of universality first for reduction and later for
realization.
IX DefliMoa. Let F: JT -► jr be a functor such that each non-initial f-au-
tomaton A has a minimal reduction
t^.A-tAr
322
Chapter VI
Then Fi* uid to have universal nducllon provided that Tor each morphum of
automata (/,£*)■ A-+ A' there exiiti a morphism or the minimal reductions
(/../~): A,-* A\ such that the following square
commute*.
Reasarks. (a) Since e4 abbreviates (e4, idr) and e> abbreviates (ev, idr), it is
clear that the morphism A, -* A\ above must have the output-pan equal tof„.
(b) A simple categorical formulation or the universality can be stated by
means of the category
AirKf)
or non-initial /^automata and their morphisrm:
Reduction is universal iff reduced automata form a full reflective
subcategory of Aut(f), the reflections of which are the minimal
reductions.
Eunplo. (i) Sequential automata: reduction is universal. For each
sequential ^automaton A — (ft 6, r, y), the minimal reduction is A, — A/~„ where
q, ~„ q, holds iff $ and q, have the same behavior, and t„ is the canonical map
(1.2.5).
For each morphism
(//«):(ft e, r. r)-(ft-, s: r. n
we know that
q,~4q,inA implies (qM~r(q,)f In A,
see 1.1.8. Hence, we can define
by e„•/ - /• e„ (i.e., \q\f, - \(q)fi>. This defines </,/..):-<- A; with
«.•(/./«)-(/./-)<. ■
1 J. Recall that a subauiomalon oft non-initial ^automaton A — (ft, S, /",
Unlverul Utilization 323
y) is an automaton A' - (Q\ 6", /", y") together with a morphism m: A' -* A
such that m € Jt.
Prapoaltloa. Let f: JT -► JT preserve /-epis and have minimal reductions.
Then f has universal reduction ifT each subautomaton of any reduced f-iuto-
raaton is reduced.
Proof, (i) Assume that subautomata of reduced ^automata are reduced.
Consider a morphism of automata and the minimal reductions of these
automata:
"■Li'
A — -A
•» V
A, --X- A",
Put A - (ft 6\ r, y) and A' - (Q\ 6", /", f): let the subscript r denote the
corresponding data in the minimal reductions.
Since F preserves /-epis, also F-Alg is an (*, ur>category, see I V.8.3. The
homomorphism
can be factored as/- t* • m'with
«•:(&«)-(Co-*), fe t
and
!"••• ((?•.«•) -»((?;.«;). m«€UT.
Define an automaton
A'-W.S'.r.m'.f,).
Then
m':A'-*A\
is clearly a morphism of automata. Since m' t Jt and A\ Is reduced, A • is
also reduced. Define another automaton
A-(Q.6,r,y.f„).
Then
t':A-*Am
324 Clnpttr VI
U a morphlsm because the following diagram
commutes. Since e* € /, we see that A' is a reduction of A. This is, in Tact,
the minimal reduction (because A • is reduced and hence. It cannot be further
reduced to a minimal reduction of A).
Redefining the outputs in 4, we get a new automaton
A,-(Q..6,.r,Y,.f„).
Then, obviously,
t,:A-tA,
Is a reduction. Thererore, A, can be further reduced to the minimal reduction,
i.e., there exists
t:A,-*A'
with
Put
f.-f m«:(ft, 6,)-((?;.«;).
This is a homomorphcsms such that the following diagram
o :—► or
Univciul Rcalbatton
325
commuter This impliei (since e, is an epi) that
/ -f, -r.-f~-
Hence,
</./..):4- A]
if the desired morphiam of reduced automata.
(ii) Let reduction be universal. Let m: A' -* A be a subautomaton or a
reduced automaton A. Let e„- :A' -* A\ be the minimal reduction or A'; note
that \A: A-+ A is the minimal redaction of A. Hence, there exists a morphiam
m, such that the following square
*,-
™r
commutes. Since t4- m, — m z Jt implies e„ € .M (III.5.1) and since
tA- € *, we conclude that t„ is an isomorphism. This proves that A' is
reduced. O
M. Functors with universal reduction can be characterized in a way analo-
goui to that for minimal reduction in Theorem V.I.S.
Recall thaia/mnnagcoranibobject m:Q'-» Q(e -*) under a morphism
/: F-* Q is the subobject * of F defined by the following pullback:
E>ually, a eo-prtimage is any pushout
with e € /. A functor F is said to pnserve co-prrlmagti if it preserves each
pushout of a morphism and an /-epi.
326
ChapKiVI
Theorem. Let JT be a connected, finitely cocomplete (*, Jl )-eategory with
cointersections. Let F-..X-+ ■% preserve /-epis. Then F has universal
reduction ilT F preserves both cointersections and co-preimages.
Remark. For the sufficiency, i.e.. Tor the proof that preservation of
cointersections and co-preimages implies universal reduction, we do not need the
hypothesis that JT be connected. This will be dear Tram the proof.
Proof, (i) Let F preserve cointersections and co-preimages. Then F has
minimal reductions by Theorem V.I.3. By Proposition VI. I J, ft is enough to
prove that each subautomiton m: A -* A' of a reduced automaton A' Is
reduced. Put
* - (ft «. r, r) and A1 - iff, 6". T, r").
For each reduction
e:A^A,-(Q0,St,r, y,)
of A we are to show that t is an isomorphism. Consider the co-preimage of e
under m, i.e., the following pushout
0 ^-» 0'
I I
°>—-m*^
It suffices to find an automaton A\ on ff, such that i: A'-* A't is a mor-
phism. Then I is a reduction of the reduced automaton A' and hence, eis an
isomorphism, and therefore,
e • ifi • I-' — m € .M implies t e A.
Thus, e € * PI -* i> an isomorphism.
The output morphism ft of A't is defined by the universal property of the
above pushout:
Univerul Hesitation
327
Since t ■ Yt - Y - m ■ y', there exists a unique v"0 making the above diagram
commuutive.
The next-state morphism 8', of A' is defined by the universal property of the
f-image of the above pushout (which is a pushout, too, since F preserves co-
preimages):
-» 0
\ mF—
•1
X
-CfF
K
Since both the squares commute, and since m and t are homomorpbiinu,
there exists a unique 8', making the diagram above commutative.
Clearly, t:A'-* (Q"„8i, /", vy is a morphism, which concludes the proof.
(ii) Let F have universal reduction. Then F preserves colntenections by
Theorem V.I.S. Let us prove that F preserves any pushout
V
"
with e € /.
The category JT has a terminal object 7"(by Remark V.I.S). For each object
X denote the unique morphism into T by
»,: JT-» T.
(a) Let Q — X. Then the pushout above is trivially preserved:
(a,) If Q' a also Initial, then/is an isomorphism and the pushout is the
following square
328
Clupttr VI
(»i) If C is non-initial, then there exists • morphiim j: Q, -* Q". Since Q it
initial, we have < • J- f, and the pushout ii the following square
t ■
(b) Let Q * X. Since JT it connected, there exists a morphiim r: T-» g.
We are to prove that F preserves the considered pushout. Thus, let p and p,
be arbitrary morpbisnu with eF- p, — fF- p':
We shall prove that there is a morphiim p: /T-» V with
p- IF. p.
Then (i) p is unique since iF is epi, (« € * implies i € * and hence, eFz f)
and (Ii) />, — /f • p because cr7 Is epi and
*F • p, - fF- p- -fF- iF- p - tF. (fF- p).
To find the morphiim p, we define automata A (on the state-object
Q + QF), A' (on Q' + Q"F), and A, (on Q, + Q,F) in such a way that both
/+ fF: A-* A' and t + tF:A-* A, become automata-morphlsms. Using the
universality or reduction on the moronism f+fF,me shall be able to produce
p as required. The joint output object or all these automata will be T + V.
Denote the various coproduct injections as follows:
8-5* Q + QF*-2- QF
(analogously iq-.Ja and hm'Jo*) ond
r-Ur+ v*J-v.
To define the automaton A, first consider the morphiim
B:Q+ QF-+ Q
Univeital Ralindon 329
with componenu I g «nd („, • r: QF-+ Q, and put
S- SF-jB:(Q+ QF)F—Q+ QF.
Next, the output map will be
r - (/+ fF)-d + p) - (* + rf></+ p,).Q + C- r+ v.
Thill, we obtain an automaton
A-(Q + QF,S,r+ V,y).
I*|JFIF
Analoioinly, define
*' - (C + QF, F.r+V.i + p-)
where f - S"F- ja with 5':Q' + Q"?-* Q' having componenu \a and
Vf "-f- VF— C-Clearly,
f+fF-.A — A1
it a morphiim or automata. Denote the minimal reductions by
e4:A-*A, -(&,«„ T+ V, y,)
and
*A:A-^A\-(Q„S;,r+ V,Y,Y
By hypothesis, reduction is universal. Therefore, there exists a morphiim
/,: A,-* Ar- such that the following square
-"■*.
commutes.
330 OupMr VI
Finally, define another automaton analogously to A and A':
M-(Q, + Q,F,S,,r+ Kf+P.)
where 6, - S,F- jt with S,:Q, + Q,F-+ Q, having coniponenu la and
«■ OF S-
IO»0FIF-
(eeFlF
-<W)F
f»F
'♦P.
■ r«v
Clearly,
e + ef: /4 -► /4,
is a morphlsm. This is a reduction of A. since e € * Implies eF e t and hence,
by III.S.S, e + eF e *. Since -4, is the minimal reduction of 4 there exists
a reduction
A: At-+ A,
with
«, - (« + «f) • A.
We have
<(,•(/+ fF)-f-ii ™<* ig-ie+eFy-cit
and therefore,
-<<,•«,•/■
-^■(«+«F)-*./,
We use the universal properly or the given pushout:
UnJveiul Rcalialion 331
We obtain a unique d Tor which the above diagram commute*, in panicular.
Tor which
I • d - ^ • e>.
Alto the following diagram
1 P'
tfF f OT » V
fOdFIF " » 0>dF —»■ IW
commute*. Indeed, the lower pan commute* became ey it a morphiim of
automata. In the upper part, we hiv«y0 - (t + p") - p' • j, which it trivial, and
J, - iffF-6-.
Hie last Tollowi from the definition of 5' - B'F*./g, since iff • S" - \a.
We conclude that
P' ■ j - Co- • '*)F- S-.-y.-lF.dF- S\ ■ r'r
If honXr, V) + 0, choose a morphiim
ft: T-» V;
we denote by f: T + K-» Kthe morphiim with oomponenti ft and I ■>. Then
p-p.j.t-eF.dF. 6-,.f,.£
and to conclude the proof, it luffiees io put
p- dF- S\ ■ v"r. £
If
hom<r, V) - 0,
then V - X ii the initial object; moreover,-fbr each non-initial object X we
have hom(X, J.) — 0 (for. there is iome morphiim A: /~-» X and illuming
the eiiitence of g: X -► X, we obtain /• g: T-» X, a contradiction). Since
p' • fF € homfgf, X), it followi that QF - X. By our hypothecs, we have
332
duplet VI
t morphlim rF: TF-* QF- J., thui tlio 77°- X. It follows immedittely
thtt F is the constant functor to X: for each object X we have the morphiun
t,F: XF-* TF - J., thus, XF - J.. Then F prewrvei all colimitt. The proof is
concluded. D
13. The above theorem u rather abstract—it is usually hard to decide
whether a given functor preserves co-preimages or not In the neit section, we
prove a more concrete criterion. But first we formulate the universality In
terms of realization.
Let F: JT -► jr be a varietor. Denote by
Autrff)
the category of all reachable (I) initial ^automata and their homomorphistns.
Denote by
B»h(f)
the category of behaviors: objects are triples (/, a, /"), where / and T are
r-objects and fr: /* -» T is a morphism; moronisms are pairs
(/../-)•(/. b.r)*v\b\r)
of moronisms in jr, /.: /-» /' and /„ : T-» /", such that the following
square
f—!>— r
in"—j-r
commutes. It is easy to check that this defines a category.
Assigning to each reachable automaton A its behavior b„: /* -» T, we get
a functor
S:Auti(f)-»Beh(F).
On objects,
AB - (/, bA, r).
Given a morphism
then
(//../«,,)*-(/../<»):(/. b„ D-»(/■, bA, D.
We call B the behavior Junctor.
Univmal RcaHzaltofl
333
It turm out that, even In case that Fhas minimal realizations, there need not
be any way how to define a functor
M:B«h(F)-»Aut,(F),
assigning to each behavior Its minimal realization. In fact, the existence of
such a functor is equivalent to the universality of reduction, as we shall prove
presently.
1.C DeflsMoa. A varietor F is said to have universal nalualUm if there
exists a functor
AT. B«h(F)-»Aut,(F)
assigning to each behavior its minimal realization and such that M-B —
Explicilly, the condition M- B — \<\ means the following. For each
moronism of behaviors
we can find the minimal realization of 6 (with run morphism p: I' -* Qt and
with output v: &-» /") and that of fr'(with p\ /) and we can fill-In the
above diagram by sn/: g»-> g» In such a way that the following diagram
commutes. Then
(/../-)M-(//../-)•
If the functor U exists, we call it the minimal naUiatUm functor. The reason
why we have restricted ourselves to reachable automata when defining
Aut,(F) Is that this fill-in is uniquely determined, hence, canonical.
334 Oupicr vi
Oastrratkn. The functors Mind A are adjoint. I.e., for each automaton A,
with behavior ^, :/*-» /"j> and for each behavior 6: / * -» Twe have a natural
bijection between behavior morphisms and automata morphisms:
(/t,ft..r.)-(/,6,r)
A„-*(l,b,r)M
This bijection assi|ns to each morphism of behaviors
a,/.):('Ar,)-»(ur)
the unique morphism of the form
(//.,/-)• ><.-(/■ »,OM.
1.7. Proaosltloi. A varietor has universal reduction ifT it has universal
realization.
Proof, (i) Let Fhive universal reduction.
Given a morphism of behaviors:
I"—5-^r
"
we form non-initial F-automaU
A-il', v,r,b) and X'- ((f)', », T, »').
Then
iK. f^y-A^A-
is clearly a morphism of automata. Let
t,:A*A, -iQ»S*r,r,)
and
t, :A*A;-(Q;»S»r,Yj
denote the minimal reductions of A and A\ respectively. Since reduction is
unlveml, there exists a morphism
with
Univmal Realization
335
i.e., with
The minimal realization of b a
Al-lQt»S*r,r»l.')-'4)
with the run morphism eA. This is proved in V. 1.2 (the first pan of the proof of
the proposition). Analogously, the minimal realization of b' a A'' with the
run morphism e4. The morphism of minimal realizations "filling-in" the
given morphism of behaviors is (/",, /„, /J :AJ -» A',* :
(II) Let Fhave universal realization. Let (/ fjb: A -* A' be a morphism of
non-lnltlal ^automata, where
A - (ft 6, r, y) and A' - (ft, «', r, r").
Define corresponding reachable Initial automata
<* - (ft 6. r, y, ft l„) and X - (ft, S\ r, Y, ft, l„).
Then put /M — /to obtain a morphism
(//.,A-).^-^'
in Aut,(F). Denote by p: (0", •>)-► (ft S) the run morphism of A We have
r;.p - l„and hence, behavior of A is p• y: Q' -* r. Let
«:-«-►-4, -(C 6Vr, yj
be the minimal reduction of A, then
At - (ft> *. T, yfc ft «)
is the minimal realization of p • y. In fact, the run morphism of A J is p • e
(since rj-p-e-e) and hence, A( is a reachable realization of
p- f yt — p- y. Consequently, the minimal realization A of p- y is a
reduction of Ag. But A, Is reduced and hence, Aj is isomorphic to A, in other
words, AI is minimal realization of p • y.
336 Cluplcr VI
Anilogouily, denote by p' the run morphism if A' and by
e: A'- A; - (Q„ 6"* P* pi)
the minimal reduction of A'. The minimal realization of p' • Y '• A'f '
(ft. £» r\ r'„ Q„ e"). The morphism of behaviort
(j!/-):(fl("r,n-(fi'.p''r,,n
Q -»• Q
can be "filled-in" to a morphiim of the minimal realizations:
U~f.f~)At -~a;:
Then
is a morphism of the minimal reduction with
ff, - f(P- «■/)- l(.f P-f)-f-n-p-f -fe\
i.e., with
<(/,/„)•(//«)•<•. □
IA Eianple. Sequential witonata vita Ran, Recall the functors
Sj,.z.-Sj, + Cr,:S«t-»3»t
from 111.4.8. An Stl j,-sutomaton can be considered as a special case of a
sequential X-automaton, where
I > Ii u Zi
(assuming I, n Z, — 0). In fact, the next-state map
S.Q x X, + Zi-»fi
yields a map from g x rto Q which for pairs (9, a), a e £■>, is independent
off: Thus Sj, j.-automata are just sequential ^-automata with resets in I„ see
Exercise II.I.E.
Univerttl Rcalbstton
337
The functors SIlf t, have univenil realization (11.3.10) ind we ihtll prove In
the next section thit these are the only set functors with universal realization,
1J. Euaik Caaajonta. Let & be an (/, uT)-category with countable
products and coproducts, and let F: JT -► jr be a coadjoint preserving /-epis. By
111.2,14, F has minimal realization, obulned by image rictorization. We shill
prove that F has universal realization.
Let
-»r
(fl*-
be a behavior morphism. Consider
b. : (/",«•)- (r„ v) and b; : (/", *>)- <r.. V).
Then the following square
»«,, I.
commutes too, where (/"J • denotes the unique homomorphism
(/-).: (r.,v)-(r;. *0
with
(see 111.2.13).
The minimal realizations of b and b' are obtained by the image factorizations
of b, and 6',, respectively:
338
Chapter VI
Then the morphism /0 which "fills-in" the behavior morphiim is obtained by
the diagonal Till-in property:
. e
f -%
<■„•*
"«U".
— C
Eseidscs VI. I
A. Weak smsemrloa of co-arebnage*. A functor F is said to preserve cc-pre-
i roa|es weakly iff it preserves each co-preimage
for which there e>lst morphlsms 8: QF-+ Q: 6": QF-+ ff and A>: Q.F-+ Q,
turning both / and e into homomorphisms.
Prove the following generalization of Theorem VI. 1.4. Let JT be a finitely
oocomplete (/, .^-category with cointenections and finite regular copra-
ducts. Then an *-epis preserving functor F has universal reduction l(T it
weakly preserves both cointersecrjons and co-preimages.
[Hint: The proof is quite analogous to that in VI.1.4, based on Theorem
V. 1.4. with two exceptions, (i) The operation S:(Q + QF)F-* Q + QF is
defined by the given operation on ft say 6: QF-+ ft via S — SF- jQ, where
S: Q + QF-+ Q has components l„ and S, analogously with 6" and &- (II) In
the end,y is not a split mono but only; e jM\ the diagonal fill-in must be used
for ye UtuidlFe *.]
B. SeajaeaUal aaliiasata ta a category, (i) A category JT with finite products is
said to be canciian doted if for each object I the functor St - — x I is
a coadjoint. This implies that sequential ^automata In -M have universal
realisation.
Verify that Sat, Poa and Gra are cartesian closed categories.
(ii) Verify that linear sequential automata have universal realization
Univenal Rctllulion
339
(though R-Mod is not cirtesiin closed). [Hint: Prove thit Sx preserves
co-preimages.)
(iii) Verify thit sequentiil ^automata in Top hive univenil realization
whenever Hi i compact HasdorfT spice, both for (regular epi, mono)-fictorl-
zatlons and for (epi, regular monoHactorizations. [Hint: Prove that
Sx:Top-»Top preserves co-preimages and use Exercise V.I.BJ
(Iv) Prove that Top is not cartesian closed. [Hint: Exercise V.I.B(ii).l
C OiiliaUloa of fnctan. Let JT fulfil the hypotheses of Theorem VI. 1.4.
(i) Verify that given functors F,, F, preserving /-epis and having universal
reduction, then Fi + F, has the same properties.
(II) Conclude that F + Cu (where Cu is the constant functor with value £,)
has universal reduction for each /-epis preserving functor F with universal
reduction.
(iii) Can (i) be generalized to arbitrary coproducts? If St, a denotes the
coprodud C6 + II F„ where F, - I., is it clear that SC] u has univenal re-
ductlon?
VIA. Uartersal ReaacHea Tbema.
2.1. The aim of the present section is to prove that any functor with universal
reduction preserves unions. This shows, of course, that universal reduction Is
quite nre. The proof is rather complicated and it requires additional
hypotheses that might look discouraging at first sight Fortunately, we are able to
prove that a concrete category JT" fulfils these hypotheses whenever Its
forgetful functor preserves finite colimlu (which includes Sat, Poa. Gra, Top, etc),
or whenever .V is additive (like R-Mod).
Recall that a functor F: & -* & on an (/, .^-category JT" prtserva unions If
for each collection m,: A, -* B (i e /) of ur-monos
U»i-«i implies U im(m,f) — ira(mF).
11 i it'
12. Cosmatioaa. (i) For each object X we denote by X, (/ a set) the
coprodud X, - II X, where X, - X for all i e /.
<f /
(ii) Given a coprodud II X, where / is a union / ■ U /„ we have a canon-
HI i % T
teal morphism
J40 Ckapur VI
with componenti rf, where r,: II Xt -* II X, li given by the inclusion /, c /
(r E T). We are going to use the term canonical morphism quite freely—in
each caae it will be clear which union / - U A i» meant For example, the caae
/ - U 10 leads to a canonical morphism
it i
s:\1xiF^[\1x\f.
it i yt i I
PiapatlHoa. Let jr be a cocomplete (/, ^r>category, and let F: jr -► jr pre-
Krve /-epU. Then F preserves unions iff for each coproduct IIX,, the
canonical morphism
s:Ux,F-*(Ux\f
it i yt t I
Is an *-epi.
Proof, (i) Let F preserve unions. For each coproduct X - IIX, we denote
11 /
the Image factorization of the injectiona t, by v, - e, • m, (/ £ /), then
U »ii - 11 by Remark 11M.5 and hence,
a i
UlmdnF)- \„.
111
Since ?,f — e,f • m,F and e,F £ /. clearly im(v,F) — im(m,F). Thus,
Uimc.v.F) - I,,.
f« /
Each v,F factors through £. consequently, im c - \n- This is equivalent to
IE/.
(U) Let c £ * for each coproduct. Given subobjectt m,:A,-*B (/ £ /)
with the union m: A -* B, we denote by u,: A, -* A the morphlsms with
m, — u; • m, lei.
Unlverul Rnfattlon 341
Let A - II A, be i coproduct with injection! *,: A, -* A. Then the morphiim
u: A -* A deTined by t, • u — u, (i E /) it in /• In (let, if u — u, • u. is in
image factorization of u, then ua • m is i subobject of B conUining ill m, ind
hence, conUining m. Then u. U in Isomorphism.
Consider the Image factorizations
mF-i'-m' ind m,F- «,*• mf (I e /).
For each subobject d: D-* BF such thit mf c d (I.e., m," - d, ■ d) for ill
/ £ /, we ire to show that also m' c d.
AF » Do
By hypothesis, the canonical morphiim
s: U.A,F-*AF
i «i
is in /. Hence, so is
s. uF• t*:\[A,F-t D*.
For eich / e / we have r,F — w, ■ e (where w, are the Injections of 1] ^if) and
hence, m, - r, • u • m implies
(if • d,) • d - mf - (t, ■ u ■ m)F - w, ■ f uF ■ «• • m*.
Define r:\\AtF-* D by
w..r-1'.d, (le /),
then
w,-(r. </)-», ■(!• uF- «•• m«) (/€ /)
and this implies
r-d-e- uF- i' ■ m'.
142
We ipply the diagonal fill-in
ChspKrVl
mF«e*
-U.A.F »-0b
-»-BF
to conclude thit m*c d. D
U. An object S of i category & is a generaior if for arbitrary distinct mor-
phiinu / f: C-» A there exists morphism s: S-* C with t-f+t-%. In
other words. If the functor
U- hom(S, -): jr -► Sat
U faithful.
Given a generator S in Jf, we consider & as a concrete category (see
111.3.8) with the forgetful functor U.
If S is a generator in an (1, UO-categoiy .*, then S Is said to be projective if
the following holds for any morphism f:C-* B:
ftl iff for each morphism s: S-* B there exists
a morphism 3: S-+ C with » — I ■ f.
A
C —»-B
Equivalently, S is a projective generator ifT the forgetful functor U •
homi.S. -) fulfils
' - I /; /f '• onto).
. (i) All current concrete categories have their forgetful functor of
the form hom(S, —) for some generaior £ Thus, the assumption "S be a
projective generator" does not exclude, essentially, any important category—but
we prove that it does pick up the factorization system,
(il) An embedding in a concrete category & a a mono m: B% -* B such that
Untvnul Rnlhttlon 343
for any morph'um/>: C-» Bind uiy mip a: CU-* B,U with pU - a'("■(/)
A: C-» B, is ilio i motphlim.
Prsfosltloi. Let S be i projective generator of i complete (/, ur)-categoiy
jr. Then
/- onto morphUmi and jM— embeddinga,
and each object ii a quotient of lome coproduct S, (/a ut).
Proof, (i) We start with the last statement. For each object A denote by /
the set hom (S,A)o( all morphisms from S to A; let S, be the coproduct with
the Injections
s,:S—S, (f:S-*A).
Define a moronism
e: S,-*A
by
Sft-f for tick f: S-* A.
Then (£/ because S is a projective generator and for each moronism
f:S-* A we have /- j,: S-> S, with /-/•«. Hence, A is a quotient of S,.
(II) The fad that / - onto morphisms is actually the definition of projecdv-
Ity.
(iii) To prove that .M contains all embeddinga, let
m: A-* B
be an embedding. Let m — «• p be an image factorization,
e: A-+ Ami; p:A-+ Bin**.
We present a map p,: All-* AUwith pU - n, • (mil).
S
344
Chapter VI
Then p,: A -» A is i morphiim (since m is in embedding) with p- p,.m ind
hence, m - «• n, • m. Since m is a mono, the but implies * ■ p, - I ind
therefore, e a in isomorphism, which proves m £ ..#. The mip p, is defined is
follows: for eich "point"
t e AU- hom(S, i)
there exists s: S-* A with
» — »• e
(bcciuK « e * uid S is projective); put
(»)/>• - »•
Then pU - n, • (ml/) because for eich s £ <f (/,
(s)pU — s- p - !• e- p - !• m - l(s)p,]mU.
(iv) Let in: A -+ B be in uT-mono. To prove thit m is in embeding, consider
in irbitruy morphiim p: C-» B. By (i), there exists in *-epi
«:$,-► C
for some set /; let »,: S-» S, (/ £ /) denote the coproduct injections.
S-^S,
<V«lp,
* =—*"B
Assuming thit pU - p,(mlf) for some mip n,: hom(S, C) -» hom(S, ^),
we define
f:S,*A
to hive components (j, • e)n»: S, -► A (i £ /). Then
/•mmfp:Si-*B
because the /-th component of each of these morphisms is
MS
((»/ • *)A)«V - (», • t)pV m s, • e • p. The moronism obtained from the
diagonal fill-in:
-►B
has the underlying map /y This concludes the proof. □
Careflarv. Let JT be a cocoraplete (/, UT)-category with a projective
generator £ A functor F: JT -» jr preserving /-epis preserves unions iff for each set
K, the canonical morphism
e.:{Sf).-S.F
is an /-epi.
In fact, by Proposition VI.2.2 it suffices to prove that each canonical map
*:U.V~(Ufi)'
is in /, assuming e, c / for all sets K. For each i c / we have an /-epi
tt: SM,-* X,: put K — U.K,. The morphism
e- LU:S.-m
iii 11/
is an /-epi (III.5.3). The components of
£, • eF: UlSFU, - (W)» - ( II, XA F
it t \itti
are «t- e,f • f,F (where r, is the <-th Injection of TJAT,) and hence,
e,eF- LI((Ci,-rlf)-c.
Since f preserve* /-epis, clearly e„-eF e /, and this prove* « € /. D
1A. DcflattVsa. A projective generator S Is said to be ptiftel If for each
functor F: JT -» JT preserving /-epis, the following holds: if the canonical
morphism
*-S*nF+ S^F- S*.,.VF
346 Chapter VI
is an 4-epi, then also the canonical morphism
e: SF + SF-» (S + S)F
is an /-epi.
Resaark. We prove below that in quite a number of concrete categories each
projective generator is perfect.
!■»■■■ Let JT be a cocomplete (I, uf)-category with a perfect generator S.
A functor f: JT -» JT preserving /-epis preserves unions iff for each collection
V of sets with fl K + 0, the canonical morphism
l-.Uj.F^-iS^F
is an /-epi.
Proof, (i) Let Fpreserve unions. Then the canonical morphism
£:(SF),-S,f («-UV)
is an /-epi. Denote by /.the disjoint union of the sets in V = |K,; i e /],
Z. - II K.
Then (SF)L - II (SF),,, and the morphism
/:(W)t-(W),
with components (SF),, -»(Sf), given by ihe inclusion X, c A is a split epi.
Hence,
/.«€/.
Further, for each i € / we have a canonical morphism
*:(W)«,-(S«,)f in*
and hence, lie, € / by III.5.5. The following square
ISFIL ^--LLISuFI
t e
i
ls% J-"" V commutes. Thus «£/.
IMivmil RerituHon 347
(ii) Asume that Fdoes not preserves unions. By VI.2.2., there exists a set
0*0 such that the canonical morphism
£.(Sf)»-V
is not an /-epi. We choose such a set A with the smallest cardinality possible;
B has at least two elements, of course.
(a) Let card B - 2. Then the fact that
e:SF + W-»(S+ S)F
is not an /-epi implies that neither is the canonical morphism
(since S is a perfect generator). For K, - |0, I] and K, = |0, 2|, Fdoes not
fulfil the condition above.
(b) Let card B > 2. Choose an element k, e B and let
K,. I e A
be the collection of all subsets of B with
k) e K, and card K, < card B.
By the choice of B, each of the canonical morphisms
«,:(Sf),.-S«,f ('« /)
is an /-epi. Hence, in the square above,
lit; e /.
Since « « / implies/- « « /, we have
(LI *,).*</.
Then JJs, E / implies f ( /. Again, f does not fulfil the condition above. D
15. DtflaMoa. An (/, UT)-catcgory is said to have txacl co-prrimagts If each
ptuhout
A—i-~ C
ml ffl
with e € / and m € u* is also a pull back.
MB
Cbipler Vt
Example*, (i) Sat hu exact co-prelmages. In fact, assuming that A c B
(and m ia the inclusion map), the pusnout above can be described as follows:
D - C + (B — A), where m is the lint injection and (a)i — (a)r for a e A,
(b)i - b for b e B — A. If (6)r - (f)m, then 4 E /4 is the unique element
with b - (fr)m and c - (b)e— thus, the square above is a pullback.
(ii) Jt-Mod has exact cc-preimages. In fact, assuming that A, c A c B are
submodules with m the inclusion map and e:A-*C— A/A, the quotient
map, the pushout can be described as follows: D — B/A, with *the quotient
map and r» — m/l*: /4/^« -» B/A* It is easy to see that this square is a pull-
back, too.
lJt. Uahcraal Rtshcthm Theorem. Let JT be a cocomplete (/, .^category
with a perfect generator S and with exact co-preimages. Let F: JT -» JT
preserve /-epis and fulfil hom(SF, S) * 9.
If F has universal reduction, then F preserves unions.
Proof, (i) Plan of the proof. We are going to verify the condition of
Lemma VU.4: for each collection ji of sets with, say.
we are going to prove that canonical morphism
I: II S,F-tS,F
K c V
is an /-epi.
Denote by
»«:««-«» (He.*)
the injection given by the Inclusion K c B, and by
w,:S,f- II SLF (Ke J)
L • .4
the coproduct injections. Further, the 0-th coproduct injection will be denoted
by
««:«-«« («s *)■
Note that the injection ra: S-» S, of the 0-th coproduct injection fulfils
(1) v, - u, - v, for each (Ei.
Finally, denote by
V<:Si-»S (Ici) and V,:S,-»S
the co-diagonal morphisms (all components of which are lj); note that
(2) ««•?«- I j for all fEi
UnlverMI Rnllutloo 349
and
(3) ?« - »« • V, for all K E V.
Define a morphiam
t: II SKF— W
it I V
by
(4) wK • I - V,f: S,f- W (K e irf).
We can factor the morphiam I a I — e • m with e: II SgF-* D in / and
m: D -» S,F in ur\ To prove I € /, we are golni to verify that met.
Let ua form the puahout of t and I:
(5) t T
SF —"-B
Note that ( E / (indeed, r la a apllt epi aince uKF- w, • t- I), hence, i E /.
Further, let ua form the puahout of m and (":
D—=^V
(6) H If
B »B
n
Then f e / and m e Jl imply that
(6) ia a pullback
(aince co-prrimaiej an lupposed to be exact).
To prove me /, we uae the fact that S la projective: It aufflcea to show that
for each g: S-» S,F there exlats f: S-» D with g - g ■ m:
° sr-^V
350
Chapter VI
We are going to verify that
(7) / - * • m Tor some A: S,f-» 6.
Then we use the universal property or the pullback (6):
Thua, the proor will be concluded when we exhibit h auch that (7) holda. Thia
we do by defining automata A„on the objects St + S„F (K e .if) and an
automaton A, on the object S, + S,F In such a way that
(a) vt + v„F become morphisms from A„ to A, and
(P) the output of A, is V, + i: S, + S,F-» S + 0.
Uaing the universality of reduction, we present then the required morphism A.
(ii) The definition of automata. By hypothesis, there exists a
morphism
f: SF— S.
For each (Ei«t define an automaton
-<«-(«« + S,F, S„S+ D,r,)
as follows. Denote by i„ and j„ the coproduct injections of S„ + S„F, and
define a morphism Si by the commutativity of the following diagram
s.
W
— s.
Put
S, - 8,F- U ■ (S, + S,F)f- S, + S,F
Univtrul Realinllon 351
and uaing I • m: SF-* 6 [aee (5), (6)], put
Yn - V, + (V,f. *. in): S» + S,f- S+ 0.
Without loaa or generality we can assume
10] € J.
(In Tact, Lemma VI.2.4 remains true if only such collections V are
considered.) Then we have an automaton A, (we write 0 instead or |0| in the
indices),
A, - (S + SF, S„, S + B, I, + i ■ *).
Further, define an automaton
A, - (S, + S,F, 6,, J+ftv,+ i),
(the outputs of which are defined in a different way than in A* but the next-
state morphism is analogous):
6,- S,F-j,
where /, and J, are coproduct injections and S,:S,+ S»f-» S, is defined by
I.-S.- I„ and J.S.- V,f{- v
Note that
(B) IS-S.-(I..8.)FJ.-J..
We daim that for each K E V,
»«+ »«'':'<«-»'<»
is a morphism of automata, i.e., that the following diagram
commutes. The verification of the two squares is routine. For the triangle, use
(3) on the first summand: for the second one, we compute (using the fad that
w,,- l- v„F, by definition of I):
v,F. i.
wK» e • m • i
(i- *• m)
3J2 Chtpur VI
-w,-e-f-A (by (6))
-w,-l-i- m (by (5)]
-V.f.f.rS (by (4)).
Denote the minimal reduction of A, (K E .^) by
e,.A,^At- (&,«;, s + A ri)
and the minimal reduction of A, by
«»•• -<»- *i - (a, *;. s + A rt)-
Since reduction ia universal, there exiata a unique morphiam of automata rf,
for each fEi, such that the following square
(»)
*.^-A.
V-T7*S*
commutes.
It ia euy to check that, for each (Ei, another morphiam of automata ia
Since V, ia a aplit epi by (2), so is V, + v,f: hence, /4, is a reduction of ^,.
Therefore, there exiata a unique morphiam
i,.A,^Ai
with
(10) e, - (V, + V,f). *,-
. V"«F __ .
%«M,f
Univma] Amltzalloa
Then i, • vl:At-»Afit independent or K, I.e.,
(II) 'i-'.-rt-'t* for each K e J.
Indeed, by (2), («, + vtF) ■ (V, + V„F) - I, hence
*« ■ 'I - («« + ««f) • (v, + v,f). #,. v;
(«, + n,f) •*,•»;
(■« + ««f) • (»«+ »«f) • *»
(f, + v,F) • r.
«.-».*
(by (10)]
(by (9)]
(by (1)]
[by (»)]•
3S3
(ili) The proof or (7). For each K e jf, the following diagram
w
VI*
commutet—combine (9) and (II). Hence,
(12) /,-*,- V,. t, .(e, ■ f,«): S, - (J,.
Indeed, aince IJ K - B, to prove (12) it aufTicea to ahow that the two mor-
phiama are equal when preceeded by any r,: S, -► S,. We have by (3),
'« • ('» • *») '
V, •<,•(«, • f,«)
»« • (V, • (. • e, • v.*).
Further, denote by /: /J-» S + /(the coproduct injection. Since
354 Oupur VI
is a morphism or automata, the following diagram
commutes: see (8) Tor the upper left square, and use (12) to get
* - I.F• («. • f,V• 6; • rt- SF— S+ D.
(a) Assume hom(S, 0) * 0. Choose a morphism j*-.S + D-» 0 with the
first component arbitrary and the second one ids. Then /• J* - Id, therefore
(13) T-T.J.j'- v,f. (*.;•).
Further by (5),
»,f — wt — w, • e • m
and since (». • V,)f - id;,, we conclude
(14) w, • e- m- V,f- idw.
Thus,
t- v.f •(*•>•) (by(13))
- V,f .(»•„. r. m . V,f). (t. ;«)[by (14))
- V,f. m-,. e.in- f (by (13))
- V,f. w, • *• 1- m (by (6)1.
In (7), it suffices to put
* - V,f • w, i e. I
Unlvenal Rcaliarion
355
(b) Asaume hom(S, 6) - 0. Since (": S,f-» Din morphism, it follows
that hom(S, S,F) - 0. Now, S is a projective generator, hence, the latter
implies that any morphism into S,F is in t. In particular, let. This concludes
the proof. □
2.7. Let us turn to a discussion which categories fulfil the hypotheses of the
Universal Reduction Theorem. By VI.2.3 we know that they are cocomplete,
concrete (onto, embedding)-categories with the forgetful functor hom(S, —);
we prove now that it is sufficient to assume that the forgetful functor
preserves finite colimits. This includes a large number of current categories. But
the important case of A-Mod is not included. Therefore, we prove that addi-
tivity is also sufficient. Let us briefly present some of the basic facts about
additive categories we need below.
By definition, an additive category is a category JT such that
(i) hom(4 B) is endowed with the structure of an abclian group for
arbitrary objects A and B.
(ii) Composition preserves this structure, i.e., given A,A'-A-*B then
* • ifi + A) - * • A + * • ft Tor each h:A->-A
and
(/i + /i) • * - A • k + /, • * for each *: B— B\
(iii) JT has a zero 0. i.e., an object which is both initial and terminal.
From this definition we can easily derive further properties:
(iv) Each finite coproduct is also a product: let A,,A,he two objects and let
«{:A{ + A,-»A, have components I,, and 0:A,-*A„ analogously
jr;: A, + A,-* At. Then
At + Aj ™ At x A}
with the projections jr, and «,. [In fact, given /: X-» A„i- 1,2, and
denoting by y,:A,-*A, + A, the coproduct injections, then/, •»,+/,• v,:X->-
A, + A, is the unique morphism with (f, • t, + /, • f,) • x, — /,.)
(v) The operation + can be derived from the compositions: given
fufi- A -» B, let /: A + A -» B he the morphism with components /, and /,
and let A,: A-* A x A (- A + A) he the "diagonal" morphism with the
components \A and I,. Then
/, + A - A„ • /
(This follows from bA — v, + v,.)
(vi) The zero element of the group hom(<4, B) is obtained as the
composition of the unique morphism A -» 0 and the unique morphism 0 -» B.
(vii) Let m: A -» B he a regular mono. If c: B -» C is the cokemel of m, i.e.,
the coequallzer of m and 0: A -» B, then m is the kernel of c, i.e., the equalizer
of rand 0: B-» C
3S6
Chapter VI
Dually, if c: B -» C is a regular epi and m: A -» B is a kernel of c, then c is
a cokemel of m.
(viii) For each object S of JT we obtain a functor
hom(S, —): jr -» Ab (- abclian groups)
assigning to A € JT" the abclian group hom(5. A) and tof:A-*B the homo-
morphism hom(S,/): p~p- /(for each p: S-» A). This functor preserves all
limits which exist in JT.
U. Tbeores*. Let JT be a cocomplete, concrete (t, Ur>category wilh a
projective generator £ Assume that
either the forgetful functor preserves finite colimits,
or JT is additive and jH — regular monos.
Then S is a perfect generator, and jr has exacts co-preimages.
Remark. Since S is a projective generator, we know that jH - embeddings.
Therefore, the hypothesis (in the additive case) that jH — regular monos is
rather weak; it is equivalent to assuming that a composition of two regular
monos is a regular mono.
Proof, (i) Denote by U either the horn- functor
U- hom(S,-):JT —Set
in case it preserves finite colimits. or
U - hom(£ -): JT — Ab.
see (viii) above, if JT is additive and A - regular monos. We prove first that
also in the additive case, U preserves finite colimits. i.e., finite coproducts and
coequalizers. Note first that since S is a projective generator, and since in Ab
the epis (and the regular epis) are precisely the homomorphisms onto, Ihe
functor U preserves epis.
(a) U preserves finite coproducts. Since U preserves limits (see (viii)
above), it preserves the terminal object, i.e..
01/-0.
And U preserves binary coproducts because they coincide with products |(iv)
above):
(A + B)U - (A x B)U- AU x BU - AU + BU.
(b) U preserves coequalizers. First, U is additive, i.e.,
V,+A)U-f,U + /.£/
for arbitrary /„ f,:A-*B.\n fact, we have
IMtvmal Rnltatiofi
357
/ + A - 4. •/
(tee (vi) above]. Since (/preserve! finite product*. A4U- &AV. Since f
prcservet finite coproducU, the componenti offll: All + All-* A(/are/(/and
/,(/. Hence,
/£/ + /£/- A,vfU- (4, •/)£/-(/ + /)£/.
Let
/./:.*-«
be morphiun* with a cocqualizer
c:fl-C
Since/ • e - f, • fit equivalent to (/ — ft • e - 0 • c - 0, we tee that fit the
cokemel of/ — /. Let
/—/ - e-m
be an image factorization (e: A -* A, ui epi, and n:^->li regular mono).
Then c i* a cokemel of m hence by (vii), mill kernel of c Since (/preserves
limit* by (viii), also mil a a kernel of ell. Since (/preserves epis, and each epi
in Ab is regular, we conclude from (vii) that rf/is a cokemel of mil. Since also
ill is an epi, ell is also a cokemel of
eU-mU -(/-/)£/ _/£/_/£/.
Equivalently, ft/it the coequalizer of/(/and/(/.
(ii) JT has exact co-preimages. This follows easily from the fact that both
Sat and Ab(- Z-Mod) have this property—tee Examples VI.2.S. Let
"1 lS
be a pushout with e e t and m E -M. Then *£/is epi and mil it mono (in Sat
or Ab) because /— onto morphisms and Jt — embedding*, by Proposition
Vl.2.3. Hence, the following square
tu
358
Chipler VI
is a pullback: we know that it is a pushout, since U preserves pushouts and
hence, it is also a pullback (in Sat or Ab). To verify that the original square is
a pullback, let p, q be morphisms in JT with
p • e — q • m.
In Sat or Ab there exists a unique morphum ft Tor which the following
diagram
commules. Since m is an embedding, pU - ft • (ml/) Implies that ft carries
■ morphism in jr. Then p — p,- mand q— p,-e(because Uis faithful) and
ft is unique because m is mono. This proves that JT has exact co-pretmages.
(iii) S is perfect. Consider the following square of coproduct injections:
s»s ■
\x
"■S>S-5
where the indices show which injections are meant. It is easy to see that
(i) this square is a pushout and (ii) v, and v, are split monos. By Lemma V.4.1,
this square is an absolute pullback. We use this three times, forming the
following diagram of coproduct injections:
s
s*s
\
y\
<2
Unlvnul Rnlluiltni 359
Suppose that F: JT -» JT is an t-epis-preserving functor such that the
canonical raorphism
*: (S + S)F + (S + S)F-* (S+ S + S)F,
with components
H,f and \,F,
is an t-epi. We are going to prove that then the canonical moronism
e:SF + SF—(S+ S)F,
with components
y,F and v,F,
is an #-«pi, too. Since (/ preserves finite coproducts, the components of the
onto map {(/are n,f • (/and njf - (/. It is sufficient to prove that eUit onto
(then e e /): its components are »,f • (/and Vjf • V.
(a) (/: JT -» 8«t The fact that «/is onto means that
(S + S + S)f • (/ - im(i»,f • (/) w im(nof • (/)■
To prove that ell is onto, consider any point
* € (S + S)f • (/
and put
.y - (*)»,if • (/ € (S + S + S)f. (/.
Then for / - I or / - 2 we have y € lm(*iF• V)—say, i - I. Choose any
* € (S+ S)F-U
with
(I) 0-,H1f-l/-.v-(*)p„f-(/.
Since the diagram above consists of absolute pullbacks, the following square
SRJ — fc IS-SIF-U
V,F-U
<tfV
IS<SIF-U K-G«5lr-U
Is a pullback in Sat. Hence, (I) implies that there exists r, e Sf ■ U with
*-(i,)v,f.(/ and y, -(i,)*F-U.
360
Ckaput vt
Since »,f - (/is the first component of £(/, this proves that * € im sU. Hence,
eV is onto.
(b) V: JT -» Ab. We define a "dual" diagram, using the zero moronisms
(see Vl.2.7 (iv)]:
s»s«s
Here,
d„ d,: S + S— S
are the projections or the biproduct, i.e., d, has the components I j and 0 and
di has the components 0 and I j. Analogously,
d,,: S + S + S-- S + S
has the Mh andy-th components equal to lj while the remaining component
is 0. It is easy to check that
(2)
and
•rf« - Ij»j
(ty-0.1,2;/#»
*, • J„ - 4, • v, and \, • d„ - d, • *,.
Since f(/is onto, the group (S + S + S)F- (/is generated by im(*,f • U) u
im(«of • (/), i.e., each element y € (S + S + S)f • (/ has the form
(4) J-- CKi)H»f ■ V+ MHiF- V
for some y,, y, € (S + S)f • (/.
To prove that eU a onto, consider any point
* € (S + S)f • (/
and put
y-W^F-U.
UnivmtJ Hesitation
361
There exist y,, y, with the property (4). Then
jr-(*)(v,1.J„)f.l/ (see(2)]
- OO daF ■ V
- (y.) (ib, ■ d„)F• U + («) (*, • d„)F■ U [see(4)]
-0'1)(4-»i)f-l/+0i)(4-H)f- V [see(3)l
This proves that each element * € (S + 5)f lies in the subgroup generated
by im(»,f • IS) u im(v,F- If). Hence, the homomorphism eU, which has
components v,F■ (/and v,f - (/, is onto.
The proof is concluded. □
Exaaiales. Each of the following (onto, embedding)-categories JT fulfils the
hypotheses of the Universal Reduction Theorem.
(i) 8«t, Poa, Gra, Top. The forgetful functor of each of these categories is
(/- hom(S, —) for the object S on a singleton set. Since (/preserves finite (in
fact, all) collmits, 5 is a prefect generator and jr hu exact co-preimages.
(II) The category of unary ^algebras. Here the forgetful functor is hom(r*,
—), where I' is the free algebra on one generator (1.1.6). This functor
preserves colimits. Thus, I' is a perfect generator of Sr-Alg and Sr-Alg has
exact co-preimages.
(iii) A-Mod is a cocomplete additive category in which each mono is
regular. The ring R, considered as a module over itself, is a projective (and hence,
perfect) generator.
(iv) TAb, the category of topological abelian groups and continuous homo-
morphisms. This category is cocomplete: colimits are constructed as in Ab,
and then endowed with the finest possible topology. Further, TAb Is additive
and each embedding m: A -» B (i.e., a mono such that the topology of A is
induced by that of B) is regular. This is again proved as in Ab: if m is an
equalizer in Ab of/, /: B-» C, then we endow C with the indiscrete topology to
let/,/: B-» Cin TAb. Finally, the discrete group (Z, +) of integers is a
projective generator. Hence, (Z, +) is a perfect generator, and TAb has exact co-
preimages.
Corollary. In the category of sets, reduction (or realization) is universal
precisely for the sequential automata with resets (VI.1.8).
Indeed, the sequential automata with resets have universal reduction, see
11.3.10. On the other hand, if ^automata have universal reduction for some
F:8«t-»Set,
then F preserves unions. [This follows from the Universal Reduction Theorem
because F preserves epis and hom(Sf, S) # 0.] Then F Is naturally equivalent
to some S^.t, (see 111.4.8) and, by convention III.3.1, we identify /^algebras
with SJ. ^-algebras. Therefore, ^automata are then Ss. ^-automata, i.e. the
sequential (£, \j ^-automata with resets in Z&
362
Chapter Vt
Remark. There are, or course, important concrete categories which are not
additive and the forgetful functor of which does not preserve finite colimits.
These often fail to have exact co-preimages. See Exercise D below.
Exercises VI.2
A. Uarrenalltf wtrbmt aaloo araemrloa. Define the following functor
F: Gra -» Gra: for each discrete graph (X, 0) let (X, 0)f be the complete graph
on the set X x X: all other graphs are mapped by Fto the singleton loop
([0|, ((0, 0)]). Analogously on morphisms.
(i) Verify that Fis a Unitary varietor with universal realization.
(ii) Prove that Fpreserves epis (— onto morphismms) but does not preserve
unions. Why does it not contradict to the Universal Reduction Theorem?
(Hint: Fdoes not preserve unions because the set functor H, does not.)
B. Uaheraalltf for linear raactora. Prove that a linear (Exercise. III.4.C)
functor F: fl-Voct -» Vaet has universal realization iff F is naturally
isomorphic to some Sr(Hint: Each linear functor preserves finite colimits; if
Fpreserves unions, it preserves all colimits and hence, it has an adjoint.)
C. UaberaalHy for aoa-llaear fnacton. Prove that for arbitrary modules £,
27, the functor
Si..t, - Vt, + C4: S-Mod- «-Mod
has universal reduction. Is it linear?
D. Non-exact co-arelnaga. (i) Let B be a simple group (i.e., a group without
nontrivial quotients) and let A * 0 be its proper subgroup. Verify that the
following square
0
A — 0
inclusion 0
"
B ► 0
0
is a pushout but not a pullback.
Conclude that the category of groups does not have exact co-preimages.
(ii) Generalize the above to any category jr which has a simple object B
with a proper non-singleton subobject: then JT does not have exact
co-preimages.
This includes semigroups, lattices, rings, etc. And also various categories of
Univenal Realization
363
metric spaces, and the category of HausdorfT topological spaces (consider
B - real line and A - the rationals).
VI J. Nerode Eqalraleaca
3.1. Since universal reduction implies the preservation of unions, we are
interested in the converse: does each unions-preserving functor have universal
reduction? We are going to present a construction of minimal realizations
which has the property that (i) if it works, realization is universal and (ii) if the
functor preserves unions, the construction works. Hence, this gives an
affirmative answer to our question.
There is a basic catch, however, analogous 10 that of V 3.10. In the
preceding section we worked with "weak" epis: the class t consisted of all surjective
morphisms of a concrete category. Here, we shall need "strong" epis: the
class *" will be that of all regular epis. Thus, a necessary and sufficient
condition will be obtained, e.g. in the categories Sat, A-Mod and unary algebras,
(having just one factorization system) but not in Top, Poa. etc., where the two
factorization systems differ. Throughout this section we assume that JT is a
finitely complete category with regular factorizations.
3.2. Recall (1.2.6) that for sequential ^-automata, the minimal realization of
a behavior
b:I'-r
has been obtained by factoring the free algebra I' through the Nerode
equivalence E This is the equivalence £ defined by u,£i/] iff (u, w)t — (u,w)b for
each word w € I', i.e.. iff
(i) (u,)o - (u,)o,
(ii) (u,o-)o - (u, a)b for all a € Z,
(iii) (u,oo")b — (u,aa')b for all a, & e I, etc
These conditions (i), (ii), (iii),... can be expressed by arrows, considering the
equivalence £ as a relation [e,, «J: I' —»£* where we denote the projections
of £ c r« x r« by
*„ e,: £-» I:
Then (i) says
*, -b- e,-b:E— Y,
i.e., for each x e £ with x — (u„ u,) we have
(u,)b - (x)e, ■ b - (*)«i • b - (u,)6.
For the condition (ii), consider the concatenation
364 Oupur VI
«>: I' x T-» I' (^ o)v - ua.
Then (ii) says for f, x lr - «,5r(HI.2.3) that
dSz ■ p • b - e,Sz ■ «> ■ b: E x T-» r,
i.e., for each (*, a) € £ x 27 with x — (u„ u,) we have
(u,a)b - (ii,, <r)«> • 6 - (*, o-)*,Sj. «>. 6
- U e)ti ■ St ■ ? • 6 - (U]0-)6.
E-E-I E>I E
*&[[•£ «,S.||'IS, «, «,
♦* -»S, ** <P »» b
►£*.£.£ U-E». I •.£* ».r
Analogously, (iii) says that
e,Si • (ipS. <p-b)- *,# • (ipSt • «• • 6),
etc.
The Nerode equivalence is clearly the largest relation satisfying these
conditions (i), (ii), (iii), This desription can be used for a generalization of the
Nerode equivalence. We shall work with relations in a category, tee V.2.
3J. DefliMoo. Let jr be a finitely complete category with regular
factorizations, and let Fbe a varietor preserving regular epit. Let b: /' -» /"be a
behavior. A relation [*,, ej: /• — 1* is said to be externally b-equiralent if Tor
each n < o> it fulfils
e,F-<.(pF-
■ <pF-
. pF'<p) ■ b
(n)
| *,f-' .(a»f-'.f»f-»....-ajf. •»)•*.
The largest externally fr-equivalent relation is called the external Nerode
equivalence of the behavior 6.
EF'
V, *r' V. *F V t »* b
l*F' »• PF1 PF »■ I* >•
Renarka. (a) The external *.equivalence of [*„ ej means that
(i) *, • b - e, ■ b
Univeiul RMltolion 365
(ii) e,F• v b — «jf ■ p- b
(iii) e,F' ■ (VF. <p) ■ b - e,F> ■ (VF- <p) ■ b
etc. It Is easy to check that these conditions are independent of the concrete
representation or the relation: given a regular epi e: £" -» £ then [*,, *J fulfils
(i), (ii), (iii), etc. iff [e • *,, c ■ «J does. Here we use the hypothesis that F
(hence F', F\ etc) preserves regular epii.
(b) In the sequential case, the state object of the minimal realization is
£•/£, i.e., the coequalizer of t„t,: £-» I'. We generalize this:
3.4. Coaatrectiaa. Let F be a varietor preserving regular epis. Let
6:/"-»r
be a behavior. Assume that b has an external Nerode equivalence
fo.ej: /"-I".
Assume, moreover, that the coequalizer of *, and «i,
c:/•-»(?
is a congrutnct, i.e., there is a 5: QF-+ Q with
c: (/•,*)-.(£«)
a homomorphism.
ff-
* /
OF »■ 0
s
Since by the condition (i), e, •
v: fi-» Twith
b — c • y.
Then the /^automaton
^ - (ft 4 T. r, /. n • c)
is the minimal realization of b.
b— «j ■ b, there exists a unique morphism
366
ChipMrVt
Proof. First, the homomorphism e: (/*./»)-» (ft 6°) extends <] • c and
hence, ris the run morphism of A. This implies both that A is reachable (since
c is a coequalizer) and that it realizes b — e • y.
Next, let
A-(Q,s;r.y.i.x-)
be a reachable realization of b, i.e.,
b-c-y
for the run morphism c°: /* -» Q' of A' which is a regular epi. Let
*;.*;.£•-/•
be the kernel equivalence of e°. Then C is a coequalizer of e'„ e{, see V.3.2. The
relation [*,'. ej] is externally fr-equivalent because the following diagram
ET
.f1 kf1 «;F <v < '
°'F-frffF—r
commutes.
By the definition of the external Nerode equivalence, we get
[*,',*,'] c [*„*,].
Then *, • c - «, • c implies
*; ■ e - tj • e
and, since e' is a coequalizer of t\ and «j. there exists
r.ff-Q
with
c - c" • r.
Unlvenal Realizulon
367
rF
OF—=—»-0
Then r is a regular epi, since e' • r is a regular epi, and we claim that
r:A—A
is a reduction. To prove
S-r- rF-S,
we use the Tact that c'F is a regular epi (since F preserves regular epis), and
c'F- (6" • r) - p ■ c' ■ r — <p • c- cF- S - c'F- (rF- S).
To prove
'• y-Y.
we use the Tact that c' is a regular epi and the behavior c' • y" or A' is b:
C • (r • y) - c • » - * - c' • y\
Finally, to prove
A" • r - n • c,
we use the fact that X - n • c' and thus. A' • r - n • c' • r - n • c. This
proves th at A is the minimal realization of 4. □
Remrk. We say that F has external Nerode realization if (a) each beahvior
has an external Nerode equivalence and (b) its coequallzer is a congruence. It
will be shown that (b) holds quite generally: whenever F has minimal
realizations, then (a) implies (b). Thus, it is the existence of Nerode equivalences
which plays the basic role.
We prove that the existence of Nerode equivalences is trivial if F preserves
unions, i.e., given a union of monos
u
368 Chipur VI
then
im(mf) — U im(ni,f).
/• j '
Recall from IV.7.11 that the preservation of unions implies that F isa varietor
(in reasonable categories).
3.5. Obaemrhw. Let jr have unions and let F be a varietor preserving
regular epis. If F preserves unions, then each behavior b: /• -» rhas in external
Nerode equivalence. Namely, the union of all 6-equivalent relations on /*.
In fact, let e„ I e T, be the collection of all 6-equivalent relations on /*. It
clearly sulTices to verify that the relation
C - [}c,
is also fr-equivalent. Put e, — [e„. ctl\.
(i) For each r we have e„ • b — e,, - b. i.e.. e, is contained in the kernel
equivalence of b. Therefore, also e' is contained in this equivalence, which
proves that
«,'■*- et ■ b.
(ii) For each I we have c„F- (p • b) - e„F- (p ■ b). Since F preserves
regular epis. [e„F. e„F] - e,F, sec V.2.8. Thus, the relation im(e,f) is contained
in the kernel equivalence of p • b. Therefore, also the relation
Uim(e,f) - im( U e,\F- ime'F
is contained in this equivalence. This proves that
sfF-ip- b)-e,'F-b>-b).
Etc.
3.6. Lenan. Each external Nerode equivalence [*„ «J: E— /'is indeed an
equivalence relation on /*.
Proof. Let e: 1* — /• be the Nerode equivalence of a behavior b: /• -» r.
pull, - 4;„and«, - $.,
I. Reflexivity. The diagonal relation
4-[I,.. I, .]:/'-/•
is evidently fr-equivalent and hence.
4 c e.
Univmal Realization 369
II. Symmetry. The inverse relation
«-' -l«i.ft]:/*-l'
is evidently ^-equivalent and hence,
«"' C E.
III. Transitivity. The relation £• eis defined by the following pullback
r
y ^\
E E
y *\ x \,
'" f ,.
as the relation
£• e- (t, ■ *„ f, ■ «J.
It suffice* to prove that «• cis externally (^equivalent,
(i) *, ■ b - «i ■ 6 implies
(i, • *,) ■ b - f, ■ e, • b - e, • e, ■ b - (* • *,) ■ b:
(ii) e,F ■ («> ■ b) - tjF• («> • b) implies
(e*, ■ *,)f • («•• 6) - e*,f • e,f ■ («•• 6) - i>F■ e,F- («•• 6) - (ev ejf • «>• b.
etc. Hence, c is an equivalence relation. □
3.7. Thiaif. Let JT be a finitely complete category with regular
factorizations, which has colnletsectlons and regular finite coproducts. Let F be
a varietor preserving regular epis.
If F has minimal realizations, then the coequallzer of any external Nerode
equivalence is a congruence.
Corollary. If F has minimal realizations and each behavior has an external
Nerode equivalence, then F has external Nerode realization.
Proof. Let b: /' -► /" be a behavior which has a Nerode equivalence,
represented by a pair e„ ey. E— I'.
I. There exists ip: EF-* E such that both e, and e, are homomorphisms.
370 Chipitr VI
To prove this, it is sulTicient to observe that the relation
EF E
«,F «,F e, «,
" * <P » b
I"F «■ i" «-r
[e,F- v, e,F- <p] is externally o-equivalent. Indeed, the condition (ii) Tor
[*,, *,] is just the condition
(i) ie,F-?)-b-ie,F-f)-b
Tor [e,F ■ <p. t.F ■ <p\. Analogously, (iii) Tor [«,. *,] is
(ii) (e,f ■ <p)F ■ (<p . b) - (e,F ■ <p)F ■ (<p ■ b).
etc.
Therefore, [e,F • v, e2F ■ <p\ c |«,, *J, which means that there exists y with
tiF-v—yi-e, and tjF-v — V *i-
II. f preserves the pushout or e, and e::
E—5—,.
"
r——-0
First, note that *, and e, are regular epis—indeed, split epis. since A c [«,. *j]
by Lemma Vl.3.6. Thus, their pushout is a cointersection.
By Theorem V. 1.6, F weakly preserves cointersections. Since *, and t, are
homomorphisms, it follows that F preserves their cointersection.
III. F preserves the coequalizer of e, and et. Indeed, we prove that r, — c,
is the coequalizer c of e, and et: analogously, c,F — c,F is then the coequaliz-
er of e,F and etF. The relation A is contained in [*,, *■] and hence, there exists
a morphism j: /* -» E with
I- *i -/• <i - '/••
This implies
<•> - > • <i • «1 - j • *i - fi - <•]•
UMtenil RraHmJoa
371
Put c - c, - c,. Then t, ■ e - e, ■ c If c' is another moronism with e, ■ c -
e, • c' then e' factors through c because of ihe universal property of pushouu:
IV. The coequalizer cis a congruence. By III above,
• ,F t?F •, • ,
" T » t '
rr »■ p
CF C
OF »0
s
cf is the coequalizer of e,F and e,F. By I, we have
*if■ (t> • c) - yr. *, ■ c - yr. *, • c - *,F ■ (f> • c).
Therefore, c> • c factors through cf. □
Hrisrfc. In ihe preceding proof, Ihe hypothesis lhal F have minimal
realizations was needed only lo prove thai F preserves Ihe coequalizer of Ihe
Nerode equivalence. This can be concluded also whenever F is righl exact, i.e.,
preserves Ihe coequalizers of equivalences (VJ.4).
Thus, if JT is a finitely complete category with regular factorizations and co-
equalizers, and if F is a righl exact vanetor, then F has external Nerode
realization iff each behavior has an external Nerode equivalence.
3A Theoreav Each varietor with Ihe exlemal Nerode realization has
universal realization.
Proof. For each moronism of behaviors (/.,/_): (/, b, T)->(/', b\ /"')
we are lo present Ihe corresponding moronism of minimal realizations.
372
Chapter VI
Lei [*,, «i] be Ihe external Nerode equivalence of b. By hypolhesis, b has
a minimal realization
A - (ft * r, r, /, 17 ■ f).
where c: I' -* Q is Ihe coequliazer of e, and e, (which is also Ihe run mor-
phisin of A). Analogously, let [e\, ej] be Ihe euemal Nerode equivalence of b'
and A' - (Q\ 8", /"', v', 1", n' ■ c') Ihe corresponding minimal realization.
u
The relation [e, ■ /', e, ■ f*\ is externally ^'-equivalent:
(«) (*, -L')F■ (t> ■ 6) - e,F• (t> ■ /„') • 6'
- *,F-(«>■»)■/-
- *,F-(«>■»)■/-
- ',F' («>■/;)■ 6'
-(*i-/.V ■(*>■*■);
Therefore, this relation is contained in [*;, fj]. Consequently,
Since c is the coequalizer of *, and e,, this implies thai there exists f:Q-+ Q
with
To conclude Ihe proof, it is sufficient to show that
UnWenal Reillmlon 373
Is a morphism of automata.
First, it commutes with the initializations:
(17. c)-f- i\-fZ ■ C -f„ . (n-- c').
For the outputs, we use the Tact that c is an epi:
t-u- f) - /.' ■ <' ■ y
-/;•»'
and this implies
Finally, / is a homomorphism, since cF is an epi and
cF.(fF- S^-tiF-cF.S'
-/•F-V-c-
-PL' -c-
- »>• cf
-cF(Sf).
This concludes the proof that (//.,/„), n a morphism. O
Corollary. Let JT be a finitely complete category with regular factorizations,
coequalizers and unions-
Each right exact varietor preserving unions has universal realizations.
(Every behavior has an external Nerode equivalence by Observation Vl.3.5
and thus, F has external Nerode realization by Remark VI.3.7.)
3,9, Theorem. The following are equivalent for any functor
F:8«t—8«t,
and any right exact functor
F: A-Mod -* A-Mod (R commutative ring):
(i) F has universal reduction;
(ii) F has external Nerode realization;
(iii) F Is a varietor with universal realization:
(iv) F preserves unions.
Proof. This is just a combination of the preceding results with Theorem
VI.2.6. The categories S«t and X-Mod fulfil the hypotheses of both.
Moreover, each set functor is right exact (V.3.10). O
374
Chapter VI
Renark. In the theorem above, we have restricted ourselves to Sat and
X-Mod because in these categories we have a unique factorization system and
hence. Theorem VI.2.6 can be combined with the preceding Corollary. (Also
the category or unary algebras fulfils the hypotheses or both results.) The
difference between onto morphisms, used In VI.2.6, and regular epis makes it
impossible to combine these two results in categories like Pot, Top, etc
3.10- We conclude this section by an observation, not related to the
universal realization. Since the external Ncrode equivalences exist only rarely, we
ask whether there exists a general construction or minimal realizations by
means of equivalences? The answer is amrmative Tor all finitary varietors
(which is a small restriction only, in view or V.4.2).
We start with the observation that the conditions Tor £ in the sequential
case can be reformulated as follows:
(i) (u,)6 - (ujft;
(i'O (u,)6 - (u,)6 and (u,a)b - (u,a)b forallo-e 27;
(HO (u,w)r> — (U]W)i Tor all words w e 27* or length s 2;
etc.
These conditions differ only in considering all words of length 3 it rather
than of length - n. And they correspond to the free-algebra construction over
£: W, - £; W{ - £ + £ x 27; W, - £ + W,S, Indeed, (i) states that
t, • b - e, • b: W„ -* /": (i'O »'»'« that (e, + ttSrf■ b - fa + e,^ • b:
IV, — r, etc.
In the following definition, we use the symbols IV* W„ Wb ... as functors
from Jf to Jf: on objects X
XW,-X and XWm t, - X + XW, ■ F;
on morphisms/: X-+ Y
fW„-f and fW,tl-f+fW..F.
In other words, we define functors W„: Jf -» JT as follows:
W, -\,\ Wt - U + F; (f,- I, + (U + F)-F,....
3.11. Deflilrloa. Lei JT be a finitely complete, finitely cocomplete category
with regular factorizations, and let F be a varietor, preserving regular epis.
Given a behavior b: /• -» /", a relation |f,, e2]: /* —* /" is said to be Miner
b-tquitalent if it satisfies the following conditions (with f: /' + l'F-+ /•
having components l,« and e>):
CO e,'b-e,>b:
(i'O e,rK,.(^.6)-e1»f,.(#.6);
(iiOe,rK1.(^rK,.^.6)-e1»f1.(^rK,.^.6);
Universal Reiltzalion
375
in general:
(n") t,Wm.,.(^W..1 tW._,.....f).b
-t1K-,-(*K-1'*'V..,-.--*)-b.
«?'V«.FIF
tjlftp v«,F
HI-fFIF
-•. imivfif
W
f t
-»• r*rr
11
-»• p-
The largest reflexive, inner i-equivalent relation on /* is the Inner Nemdt
equivalence of b.
Reaark. The conditions (0, (10, ("0,... are again Independent of the
representing pair, since Fpreserves regular epis. Note that the definition or the
inner equivalence differs from that or the external one not only in these
conditions but also in considering only reflexive relations.
We say that F has Inner Nemdt realization If each behavior has an inner
Nerode equivalence and its coequalizer is a congruence. (This is completely
analogous to VI.3.4.) And if this is the case, than the minimal realizations are
again easily seen to be constructed as quotients under the inner Nerode
equivalence.
We shall prove now that, roughly speaking, minimal realizations are always
Inner Nerode realizations.
3.12. Tkeorcsa. Let jr be a finitely complete and finitely cocomplete
category with regular factorizations, cointersections and finite regular coproducts.
Let Fbe a finitary varietor, preserving regular epis. Then Fhas minimal
realizations iff F has inner Nerode realization.
Proof. Let Fhave minimal realizations. For each behavior
b:l'-r
we have a minimal realization
a, - (&. s„ r. r„ i. U)
with a run map c,:/*-»&. We shall prove that the kernel equivalence
le'„ *?]: /• - /•
of c0 is the inner Nerode equivalence of b. This will clearly prove that Fhas
inner Nerode realizations.
376
Oupter VI
(a) \t°„ e]] is a reflexive relation (indeed, an equivalence) and is inner
^equivalent:
E*(E*CF)F
E«EF
-»► MMFIF
V'W"7
•W^SF
o) *•• b - e',-c,- ro - «;• <■•• n - <;• *■
(ii) Let 6„: go + Q*F-+ Q, have components I ft and S* then clearly
p- Co — c,F• fig implies $• Cj — c,W,. oV Thus
'\W> •(#•»)- tfK', ••>•«<>•»
— r?(P, • c„(f| • 6g
— r$(f( • Co(f( • 60
-e;»f,.(#.6)
(b) Let |e„ f;l be a reflexive, inner ^-equivalent relation of /*. To prove
that it is contained in \t°„ «JL it is sufTicient to show that
«i • <o - «i • Co-
Extending f 1, t, to homomorphlsms
«,". «," : (£". •»,)-►(/•. •»,).
we have
*,• • b - tf ■ b.
In Tact F is a finitary varietor, hence,
£• - colim£»P..
■ < m
thererore, it suffices to prove that t* • b and t' • b coincide on each of EW„
it< ei For it — 0 this a ("f) e, • b — e, • b: for it - I this is (II') (*, +
t,F-?)- b- ttW,-#-b- t,W,-$-b- (*, + t,F-9)- b; etc.
Unhmul Reilintion 377
Moreover, the relation ((,*, (*] is reflexive. Indeed, since |f,, t,] is reflex-
ive, there exists d: £-» /* with
J.t, - </• f, - l£.
Then d% : (£•, «»)-►(/•, ♦>) fulfils
</••€,' -</••«,• - If.
Thus, the pushout of e' and t*
«,'
has the propeny that c, - c, (- c) is the cocqualizer of e' and e* (because
c, - </• • »? • c, - </■ • e,' • c, - c;).
Since f has minimal realizations, F weakly preserves cointersections by
Theorem V.I.4. Thus, Fpreserves the pushout above (since both e' and e'
are split epis) and consequently, cFis cocqualizer of e'Fand e'F.
<r
-lj,,
OF »-0
a
Since
tfF'(9-c)-p,.t?-c- »>,•«,••«- e,»F-(ye),
there exists 8: QF-* Q such that
(>• c — cF- o\
i.e., such that «:(/*, p)-» (ft o*) is a homomorphisin. Further, since
t' • b- t' • b, there exists y: Q-* Twith
b-c-y-
378 Chapter VI
Then we get an automaton
A-{Q,S,r,r. /, n-c)
with the run morphism c Since c is a coequalizer and the behavior of A is
c- y — b, this automaton is a reachable realization or b.
Therefore, A, is a reduction of A: we have a morphism r:A-+ A* satisfying
c, - c- r.
Then
fi • c0 — fi • c* r - n- f • • c- r — n- r* • c- r — fj* c« r — fj* c0.
This concludes the proof that |t„ f,| is contained in the kernel equivalence
ofc,. O
Corollary. Let Jf be as above. Each finitary. right exact functor has inner
Nerode realization.
Exercises VIJ
A. Each external equivalence b liner equivalence. Prove that every externally
^equivalent relation is inner i-equivalent. Conclude that ihe external Nerode
equivalence of any behavior is its inner Nerode equivalence.
B. The non-existence of the external equivalence. Prove that for each
behavior b with the external Nerode equivalence the minimal realization A, is
"hereditarily reduced", i.e., each subautomaton of A, is reduced.
Use this to find a behavior for F- H,: Sat-*Sat with no external
Nerode equivalence. Find the inner Nerode equivalence. (Hint: The kernel
equivalence of the run morphism of A*.)
Nolei lo Chapter VI
VII-I
We have been inspired lo study ihe universality by Ihe paper of J. A. Gojuen |I973). Results of
Ihe first iwo sections were annouccd by V. Trnhova [19751 (who proved lhal for set functors, Ihe
characleritlni condition is preservation of unions) and V. Trnhova and J. Adameh |I977). The
proofs appear In Ihe present booh for Ihe first lime.
A generaliialion of these reaulls was presented by J. Adameh. H. Ehrigand V. Trnhova |I9R0).
where an abstract category 9 (for eiample of automata) is considered together with a faithful
functor from S to an («*, .«>category jr. The concept of minimal reduction can be presented in
this generality: il is universal iff Ihe faithful functor preserves coinlersecltoits and copreimages.
Universal Reallxailon 379
V1.3
External Nerode equivalence was Introduced by M. A. ArWb and E. O. Manes |l974a| who
proved thai In caw thli equivalence exbts and Its coeqaallter ta a confraence, then h comtnicti
Ihc minimal realization (Vl.3.4). They found out later thai external Nerode equivalence need not
exist Tor tree automata, and they Introduced several related concepts of Nerode equivalence, sec
P. O. Anderson, M. A. ArMb and E. G. Manes |I976). The Inner Nerode equivalence was defined
by J. Adamek (I97<bL who proved Tneorenu VU.7. V1J.S and VtJ.ll
Chapter VII: Nondeterministic Automata tad Kleene Theorem
VIM. NoaaXenxInlstk Behavior
I.I. In the present chapter we investigate the behavior or finite ^automata in
the category of sets, and nondeterministic ^automata in a general category.
Recall from Chapters I and 11 that nondeterministic automata are introduced
because some operations on them are easier to perform than on the
deterministic ones and, fortunately, finite nondeterministic and deterministic automata
have the same behaviors. It turns out that in the category Set, the functors F
for which finite nondeterministic and deterministic ^automata have the same
behaviors are rather special. (This will be proved in VI1.2.) And these special
functors are the only ones for which an analogy of Kleene Theorem holds.
(This will be proved in VI 1.3.)
The first section is devoted to the introduction of nondeterministic
^automata In a general caiegory. We investigate the concept of behavior which is
natural, though not entirely obvious.
I J. Staadlag kypotheab: Throughout the present section, JT denotes a
finitely complete («\ UT)-category.
We work with relations in JT in the sense of V.2.
Dtflaltloa. For each functor F: JT -* jr. a nondeierminislic F-auiomaim is
a sixtuple
A-(Q,S,r,r,l,k)
consisting of objects Q, T and /, and of relations
6: QF- Q:
Y-.Q-T:
I
Noodeterminiuic Aulomui ind Klcenc Theorem 381
If 8, X and y are all partial morphism. then A is called a partial automaton.
ttamrk. Assuming that (i) JT is well-powered and fulfils the pullback
axiom (V.2.7) and (ii) F covers pullbacks (V.2.10), then we can extend F to
FtH«4Jr —H«4Jr,
see V.2.10. Then a nondeterministic /^automaton is simply an /^automaton in
the category Ral Jr. We shall not impose these (rather severe) restrictions on
JT and F. As a consequence, we have to present a new definition of the run
morphism and behavior for nondeterministic automata. We first recall the
example of the first two chapters.
Exasaplea. (i) Nondeterministic sequential automata. Here JT -
8«t and F- St. A relation
S.QxE^Q
assigns to each state a and each input a the set
(a, 0)8 c 0
of all possible next states. For a singleton set / - |i), the relation
X-.I^Q
assigns to ( the set (f)A c Q of all initial states. And the output relation
r-Q-r
generalizes the output map considered in Chapter I.
The run relation
P-.Z—Q
assigns to each sequence of inputs a, ...a. the set (d ... o,)p c Q of all
states that can be possibly reached from one of the initial states when inputs
d, 0j a. are successively applied.
The behavior of this automaton is the relation
fi: L'^ r
assigning to each string a,... a, the set (o\... o.)f) c T of all possible
outputs resulting from an application of <J„..., a. to any of the initial states.
Thus,
(c,... a,)P- U (q)Y for each a,... a. e I'-
f< lot... «mtp
In other words,
P-p.y.l— r.
382
Clupur Vtt
(ii) Nondeterministic tree automata. Consider, for simplicity, the
type I- \a\ with |o-| - 2. A nondeterministic tree ^automaton consists of
a set C a nondeterministic binary operation
0:6* Q-Q,
an output relation
r- Q- r,
and an initialization relation
k-.l-Q.
For each variable x e /, we have a set (x)A c Q of possible interpretations.
Thus, given a binary tree
I e /■,
we have several ways how to interpret the labels on the leaves and then
several ways how to compute the tree using all the possible values of q, O ft
to compute the subtree
The run relation
assigns to each tree re /'the set (i)p of all possible results of computation
of I (with all possible interpretations of the leaves). The behavior relation is
again
p.p.y.f-r.
I J. We want to define behavior of nondeterministic automata for each va-
rietor F. The problem is to generalize the concept of the free extension
A •:(/•,«>)-*(g,o") to the case that both A and S are relations. We cannot
define A * by the condition that the following diagram
t commutes because
A'F
OF
Nondctefminiftic Automata and Kkafte Thaoran
383
(i) such A * need not exist (even in the case or linear sequential automata, see
Exercise VI I. IB below) and
(il) such A * need not be unique (even Tor a finitary varietor in Sat, see
Exercise VII.I.A below).
The concept or A* we define now has the following important features which
are proved below:
(a) If 6 and A are moronisms, A' is the previously studied concept,
(b) A' exists and is unique for arbitrary relations A and 8;
(c) if F is a constructive varietor, A • Is obtained by a construction which
naturally generalizes the case of morph'ums;
(d) for sequential automata and tree automata, the concept agrees with the
examples above.
Coavearloa. Let (Q. 8) and (Q\ 6) be relational ^algebras (i.e., 8: QF-* Q
and 8": Q'F-' Q are relations). A relation /: Q-* Q Is called a stale rtlalion
If
This is the opposite inclusion to homomorphism (V.2.8).
Deflaitfoa. Let F be a varietor and let ((?. 8) be a relational ^algebra. For
each relation A: I-* Q we define ihe free extension as the least state relation
A':(/•, «)-(e5)extending A. Explicitly, A•: /• ^Q is the least relation
with
Ac n. A' and A'F-Btz t> • A».
Reaurk. For each nondetermlnlstlc /^automaton A - (Q, 8, T, y. I, A), we
call p — A * the run relation of A, and
p-p.r.r-r
the behavior of A.
Eiaaipie: Seajanrlal llacar aiteatata. Consider the functor
S,: It-Mod-It-Mod
and put / — |0|. For each nondetermlnlstlc sequential linear ^-automaton
A-(Q.8, r, r, 101. A)
we describe the run relation
(where /* - Z[i] is the module of polynomials, see 111.2.4). First, let us
consider the polynomial
0 - 0 + Or + 0r! + ... .
384 Chapter VII
We have a subspace
(0)A c Q
and for each Hate <fe e (0)/L on receiving the input 0 we can transfer to any
state q, 6 (*. 0)5, and from q, to ft 6 (<?„ 0)5, etc. Therefore,
(1) (0)p-ft- U (?,■'
• a 0
where
and for each n < ai,
C;*''-(C<-',0)«,
here the union meant the union ofiubobjects in the category A-Mod, i.e., the
linear envelope of the let-theoretical union. Given a polynomial
(t)w - oj + a,t + ... + ev\ a. •» 0,
then
(2) (<7+ r. w)p- (0 + <7+ i- w)P-Hw)p,o)Sv ft.
To prove that (I) and (2) define the run relation of A. we must fine check
that p it linear (i.e., a subspace of I\z\ x Q) and that it satisfies
Icij-p and pS[• 6c f>• p.
Both statements are easy. Let p'\ E\i\ —* Q also satisfy
Ac n • p\ i.e., (0)A c (0)p',
and
p'Si* fie «>• />'.
Then we prove that
(h>)P c (w)p' for each w e Z[i]
by induction in the degree of w. For w - 0, we have Qf' - (0)A c (0)p' and
by p'SfSc vp\ we prove that C," c (0)p' implies fil" * " c (0)p'.
Hence,
<s»p - 0 er1 c (0)P:
am 0
Let (w)p c (H')p', then
(v + z •«>)/> - ((w)ft o)8 «-> ft c ((H>)p\ <7)fi -j ft
- (h>, oyifi'Sf S)xj ft c (w, oXvp") <-» Qi
-(0-+ r. w)p'<->ft.
Nondcteminutk Aulootalft ind KJ««M Tkeonrn 3gj
It remains to verify that
Q, c (w)p' Tor each * e £|tl
In fact, 0 + * - * implies (0)p' + (w)p' c (w)p', and Q, c (f>)p' c (0)p' +
(*)*>'.
1.4. In order to prove the basic properties of X •, we need the following
results concerning composition of relations.
Propmhloa. Let / X-+ Y be a morphism, and let g: X-* Z be a relation
represented by an ur-mono m: R-* Y x Z. Let us form the pullback of/x Iz
and m:
A
m/ \?
X.Z R
f«lj\^ Sm
Y.Z
Then *: J?-» AT x Z is an ur-mono representing/* g.
Proof. It is easy to verify that the following square
X.Z
'h
x Y.Z
is a pullback (where *„ and *, are the projections). Consequently, in the
following diagram
X"Z R
X \
y \ a
Y«Z
\
386 Ch»pter Vtl
the outward square is the pullback of/ and m • *,. The relation g is
represented by m and hence,
Id) - m • *r »"<! fin -<»•**.
where
x't:Xx Z-+Z and «i:rxZ-»Z
are the projections. By the definition of composition, we have
/• g - (m . x, • lr, /• "• • *zl
— (m • *r, m • (/■ x 11) ■ xz\
— (m • »,, m • j^L
Since, moreover m is an UT-mono (see lll.5.l(iii)],it follows that/* gIs
represented by m. □
Corollary. For arbitrary morphisms /: X-» Y and g: Y-* Z, and for each
relation A: Z-* T, we have
(/•!)• A-/•(«•• A).
In fact, in the following diagram
R"
Y.T
Z«T
with pullbacks as both of the inner squares, also the outward square is a pull-
back. Let m be an ur-raono representing A. Then m" represents (f'g)'K and
since m' represents f • A, it follows that m" alto representi/> (g • A).
Reaaark. The proposition above can be formulated in terms of the pullback
of/ and f,,,:
Nondctcflnhuitte Auuanu ind Kleene TImotob 387
It states that for each morphism f:X-*Y and each relation g: Y-* Z we have
(/• t\n - i and (/• g\„ - /■ «,„.
I J. Ltma. Let /: X-+ Y be a morphism. For arbitrary relations g: X-" Z
and A: Z-" T. we have
(/•I)'»c/.(|.»).
Proof. Let m:R-*Yx Z be an ur-mono representing g, and
n: 5-» Z x 7° and .^T-mono representing A. In the following pullback
/\
Y x
X PB R
X Y Z
we have, by the preceding Remark,
(/• I*» - An and (/■» «),„ - /• g,„.
The relation (/• g) • A is given by the pullback of/- g,,, with A,,,; this is
obtained by "joining" the pullbackt of gm with A,„ and then of / with H:
-/\T
PB
y\
PB
x'
Thus
(/•«■)**-!*•#./•*• *,»!
On the other hand,
g. A-(A~.g,n. J- A,,,],
and this means that there exists an /-epi t: 5-» 5 such that the canonical
representing pair (g • AX„: 5-* Y and (g» AX„: S-* T fulfils
388 Chapur VII
Let us form the pullback of/ with (g • A),,,:
0
h/ I vl
/ !- \
' » ^
s A \
Then
/•(*•*)-(*•./••(*• *W-
We have (A" ■ g) ■/-(/■ e) • (g • A),,, because
-/•*"• Sin
-/• < • (g • *X,>-
Thus, there exists a unique k: Q-* ft' for which the diagram above
commutes. Hence,
(/•«) •*-(*"•#./• I•*,.,!
-l*-t/-«-(«-*X.,]
-I***.* /••(! •*),.,]
Reaark. Composition of relations with a morphism preserves intersections.
More precisely, for each morphism f:X-*Y and arbitrary relations
I,: Y-- Z (/ e /), we have
C\/-g,-f- r\g,-X^Z
(the intersection of subobjects of X x Z on the left-hand side, and of subob-
jects of Y x Z on the right-hand side). This follows easily from the
Proposition VI 1.1.4. Let m, be an .^r-mono representing g, (i € /). Then/«
misrepresented by the pullback of/x I; with m,. fullbacks commute with limits, in
particular with intersections (which are multiple pullbaclu, see 111.5.2). Thus,
Nondetenniniftic Aulomm ind Klecne Theorem 389
the pullback of/x Iz with f| g; is obtained by the intersection of the pull-
111
backs with g„ 1 € /.
The formula above holds also for empty collections: here It g; is the largest
i < •
relation lr. ;and it is easy lo verify that/* lr, 2 — \„, i - \]f' g,.
We can prove now that A ■ exists quite generally.
Proaotttloa. If .X has intersections, and F is a varietor, then for each
relational algebra (Q, S) and each relation A: /-* Q. the relation A* exists.
Proof. LetA* - fl * where the intersection is taken over all state relations
*'• C.V)-"(C. *) extending A. It is sufficient to prove that also A ■ is a state
relation extending A. For each A we have A c r/ • A and hence, by the
preceding remark,
Ac nr/'A-TnA-TA*.
And each A is a state relation, i.e., AF • S c 9 • A, and hence, by the same
remark, and since A ■ F • S • c AF • S for each A, we get
a*f.«c n *f»«c n «>•*-«>• n *-«>• a*. □
1.6. Next we prove that the present concept of A* coincides with that
studied previously in case both S and A are rnorphisnu.
Proaotttloa. Let Fbe a varietor, and let (Q. S) be an F-algebra. For each
moronism A: /-* Q, the homomorphism A •:(/,«•)-* (Q. S) is the least state
relation extending A.
Proof. The only statement lobe proved is that A * is the least one. Thus, for
each state relation A: /* —* Qextending A, we shall prove that
A' c A.
Let m: R-» /• x Qbt an or-mono representing A, i.e., with
Af|t ™ m. jf| and A(j) ™ m • jrj,
where x, and *, are the projections of /* x Q. Since A* is represented as
(l,a, A*L we have to find a morphism p: I' -» K with
p- A,,, - I,, and p- A„, - A*.
I. We present a morphism
6: UF-» R
for which both Am: (R, S) -* (/*, <>) and A,„: (R, S) -* (Q. S) become homo-
morphisms. We use the fact that A is a state relation, i.e..
390 Chapter Vlt
AF» fie p • A.
Since AF — [hmF, A,„F] (by definition), and since 5 - (I of. 51, clearly
AF.«-|A,„F.A(1)F.«].
Furthermore, by Proposition VII.1.4, in the following pullback
V
IT.Q
*"V\ /™
IMJ
the ur-mono A:R~-+I'F x Q represents «>• A. Thus, denoting by s\
and *", the projections of I'F x ft we have (e>>A)(ll- «•*; and
(♦* • A),], — m- »;. Since AF> £ c «> • A, there exists a mophism d: RI-+ R
with
A,hF—d-m-*', and A,„F-5 - d-m-*;.
Put
5- </■«>.
Then A(l, becomes a homomorphism because the following diagram
commutes. And A(ll becomes a homomorphism because the folowing one
Nondcterninistic Aulomrti anil Ktecne Thtornn
391
commutes too.
II. We use the condition
Ac n» A.
The composition n • A is represented in the following pullback
-0 I
by * (see VII.1.4). Thus, denoting by x" and *',' the projections of / x Q.
then (n • A)„, - *• x", and (n • A)„, m A'X'7. Since n • A contains A, there
exists a morphism
q:l — A
with
I, — 4- #A - j»7 and A™ q-m-x^.
We can extend q- f): I-* R to a homomorphism (</• 4)* '• ('*. «>)-► (". A"),
Then
(«- «"-*.., - If
because (/*,«>) is the free algebra and (q- /))* ■ A„, Is its endomorphism with
q-(q-ffi'-hv, -q.i).hm
- q-if-m-x,
- q'ta-Hn x i0)-*>i
392 Chipler VII
- fl. *•(»"• r/|
- n-
Furthermore,
(«•(?)••*,.,- A'
because (4 ■ r)) * ■ htn is a homomorphism extending A:
r/(«tf)**ii. - «-r)mjc,
- qm-x',
- A.
Thus.f — (q- if)' is themorphism we needed. □
1.7. For constructive varietors (IV.3.2). the free extension A* can be
obtained constructively. Recall first that in case of morphisms, we have
/• - Wt and A- -A'"
for a sufficiently large ordinal, where A101 — A, the components of
A" ♦ '•: I + If.F— Q
are A and A'"F- S, and for each limit ordinal i, the components of
A'":colim>f.-»e
are A1" for n < /. In case A: /-• Q is a relation, we expect that A<": W, -* Q
will be relations defined by an analogous induction. For this, we have to
specify what it means for a relation r: A' + A" —"B to have components
r : A —* B and r": A" —- B. It turns out that the folowing condition
v' . r— r' and v" • r — r" (v', v" injections)
is not satisfactory: Such rneed not exist, and it need not be unique (see
Exercise VIII C below).
Defkiitloa. Let A' + A'btt coproduct with injections v' and v". Given
relations f: A' -* B and r~: A'-* B. we say that a relation r:A' + A"-*Bhas
components r' and r* provided that
(•) r c v' • r and r" c v" • r.
and r is the least relation satisfying (•).
Nondeterminiftic Automau and Kletne Theorem
The relations r* and r" are represented by pairs of rnorphisms:
R*
393
and these form a pair consisting of r'(ll + /■",„ and the morphism r with
components r'„, and r~tl:
i. The relation r — [r'„, + r",,, f): A' + A"-* Bhas components r'
and /•".
Proof. Denote by v', v", w' and w" the coproduct injections as in the
diagram above. We prove first that
r' c v' • r.
Let us form the pullback of •>' and /•;,, + r("„:
r. *ff,
A\A"
394
Ouptr Vlt
Then (»' • r)m - rand (v' • r)ltt - i- rby Remark VII.1.4. Since /•;,,• »' -
w' ■ ('In + r"ii)< there exists a unique morphism *: R' -* P for which the
following diagram
*.A"
commutes. Then r,'n — w' • r implies
'' - M,'ill - I*• '.*• <»• 'H c [f. }.f)-v-.r.
Analogously,
r" c v" • r.
Next, we prove that r contains any relation s:A' + A~-*B with
r" c v' • j and r" c v" • i
Let us form the pullback of »' and s,„:
S
\/i»<\
* A\A"
By Remark VII.1.4, the condition /•' c »' • J means thai there exists
»■:*'-••£•
with
r,'„ - p- - r and r,"„ - p' - r ■ j,,,.
Analogously, the condition r" c v" • j means that there is
p": R~-* Sm
Nondctrnnlniitlc Automata and Klaane Tbtorra 395
with
'<"> - P" • r •nd '(i) - P" • r ■ *a*
The morphism
p:R' + R"-»S
with components p' ■ f and p" • f" fulfill
'.'» + 'i"i - P • ■'m »i>d ' - P ■ h»
In fact
*' • (P- «c») - (P' • »") • *n - P' •*■•»" - 'i'd • »'
and analogously "*■"•(/>• j,,,) - r,7, • v"—this proves the first equation.
Further,
*>'' (P ■ tod - P' ■ F ■ sm - r;„
and analogously, w~ ■ (p ■ j(ll) - r"„—this proves the latter. Consequently,
' - I'l'n + '111. f)-[p- *■». p • >&) c ut,» j,i,1 - s. a
Rcsaark. The concept of components can be generalized to other types of
colimits. For example let
W-.a-tX
be an a-chain with a colimit »,:l*;-»^(iE a). A collection of relations
r'\ W,^B (/e o)
Is said to be compatible if
IS J implies r'c w,,j» r< (!,} e o).
We say that r:A-*B has components r' if r is the least relation with
r' c w, • r (I e a).
We can express r as
r— (collm rj,, r]
where f is the morphism with components r,'„:
396
Ch.pler VII
The proof is analogous to the preceding one.
Comtrartloa. Let Fbe a constructive varietor in a cocomplete, finitely
complete and ur-well-powered (/. .^category.
For each relational algebra (Q, S) and each relation A: I—- Q, we define
a compatible collection of relations
X-i.lV.^Q (ne Ord)
by the following induction.
(a) A™ - A:/— Q:
(b) given A"', then A'"* ": / + WmF^ Q has components A and A'-'F. 8;
(c) given a limit ordinal land A1'* for each n < i, then A">: colim Wm—- Q
has components A1"1 for n < t
We must verify lhat the relations A"1 (n e Ord) form a compatible family
and hence, A"1 is well-defined: to prove
A1"1 c »..„• A'"1 (n< m)
we proceed by induction as in Remark IV.2.4-.
(a) A(m c w„, • A<" because A(m - A is the first component or A<":
(b,) if A'"c W...-A'-1, then A""Fc h-„ „F • A<-'F: hence A"'F««c
w...F» A(-'f. S and thus, A"* " (with components A and A<"F. S) is
contained in »,4|,.4i •A1"* " (with components A and w. _F» A'"'F» 6);
(bj) if A1" c w, „ • A1"1 for all n < Bo, where n0 <> ■ limit ordinal, then
w^.-A'"' is a relation with A(" c w, „ • | w^„ • A'"1] (see Corollary
VII.1.4) and hence, w^ m • A<-' contains A<"»\
(c) if A1" c w, „ • A'"1 for all n < m < i, where i is a limit ordinal, then we
have
A'-'c »..,• A'" (n< i)
by definition of A1".
I J. Propaajthw. There eitists and ordinal * with A" - A1".
Remark. Since F is a constructive varietor, there exists an ordinal n with
/* - If.. It follows that for each morphism A we have A* - A1".
Nevertheless, given a relation A, the ordinal k with A* — A1" can be much larger than
n. In Exercise VII.I.E below we show a case with n — I and k arbitrarily
large.
Proof. Let n be an ordinal for which the free-algebra construction stops,
i.e., such that w,, is an isomorphism for each kin (see IV.2.5). The relations
■»..,. A'": W.^ Q (kin)
form an increasing chain of subobjects of W, x Q. Since •* is uf-well-pow-
ered, there eitists an ordinal * S n with
Nondetemtinbtte Aulomau ind Klecne Theorem 397
»..,• A"'- w,,,tl .A<"».
We shall prove that then
A" - A'".
Here, /• - W, (because kin) with p - p, ■ wi',.,: WtF-* Wt, where
an: WtF-+ / + W,F\t the coproduct injection. Since A'"F» S is the second
component of A" * ", we have
A'"F.«C p,.X>'*".
Further, by Corollary VI1.1.4,
w.,.'V»- ■»„.,♦,• A"*''- *„..• (*,.,♦, .A"*"),
which implies
A1"- w,.i.i •A"*1'
because w,,, is an isomorphism. This proves that A"':(Wi,«>)-*(C, S) is
a state relation:
A"'F.<5c n • A" ♦ " - n . H>;!lt,.A"'-*».A"'.
Furthermore, A"> emends A because
A- A">c m.,.*'"- n» A">.
Finally, let f:(Wk, p)-+(Q, S) be a state relation extending A; we prove
that A<" c / We verify by induction on n that
A'-'c ■»..,•/
(I) n - 0: since /extendi A, we have Ac m>0. i • /
(ii) Assume A"' c *>..,'/■ Recall that n, - w^.* , and «>. are the
coproduct injections or If,,, - / + W.F (Remark IV.3.2 (ii)|. We prove that
w.. 1.1 • /has the following property:
Ac n, •(«>.. )..•/) and A"'F •« c *»„ •(»,,♦,., • /).
Since A"*" is the least relation with this property, this will prove that
A"* " c w.t,., •/ We use Corollary VII.1.4 Tor the Ant inequality:
Ac !)•/- n, •/- (n.t i-«-.»,.,) •/.
For the latter, we apply the induction hypothesis and the fact /is a state
relation, and we use Lemma VI.1.4:
A""f. «c (w..,./)F.«
c(w..,F./F).<5
c w...F-(fF-6)
CW...F-(«••/)•
398
OupurVtt
Nent, «• - p, ■ »T.i ♦ i. and since w.4 ,,„ , - I, + w..,F, clearly
Hence, applying Corollary VII.1.4, we get
W...F- (e> •/) - (w.,,F • «•) •/
- (♦».•«■.♦ i.i* i-i»o*i)»/
-(*•>».♦ !.•)•/
- •>.•(»'.♦ (.I*/)-
(Hi) Let < be a limit ordinal with A1"1 c w.,, • / for each n < i. Then using
Corollary VI1.1.4, we have
A1"1 c h>... •/- w... • (m../) (» < ')•
Since A1" is the least relation with A1*1 c v.., •A1", it follows that
A1" c *>,.,'/■ This concludes the proof. □
1.*. For partial automata, it is important that behavior is also a partial mor-
phism. This we are able to prove for constructive varietors preserving monos
of a constructive class (see IV.4.2):
PuswHIua, Let Jf be a cocomplete, finitely complete and UT-well-powered
(/. -iO-category with jH a constructive class. Let Fbe a varietor preserving JK-
monos. Then the run relation of each partial F-automaton is a partial mor-
phism.
Proof. By IV.4.2, the varietor Fis constructive. Hence, the run relation pis
A"1 for some ordinal * (by the preceding proposition). We prove that A"' is
a partial morphism by induction in n.
(i) A — Ain is a partial morphism in each partial automaton.
(ii) Let A1" be a partial morphism. Since Fpreserves UT-monos, also A""Fis
a partial morphism (V.2.9), and since £ is a partial morphism, we conclude
that A'"F> Sis a partial morphism too (V.2.2). By Lemma VII. 1.7, we have
A"'»-|II+(A'"'F. «),„,fl
We know that (A"'F> £)IM e Jl and since .M is constructive, we conclude
that li+ (A'"'//• S\„ « Jl.
(iii) Let i be a limit ordinal such that each A1"1, n < i, is a partial morphism.
Then (A%, - colim(A""Xn, by Remark Vll.1.7. Since all the moronisms
(A'"V *re in jH and J* is constructive, (V'%, is also in Jt, La, A1" is a partial
morphism. □
1.18. Proaorirloa. In the category Bat, each varietor has the property that
given a relational algebra (Q, S) and a relation A: /-- ft then
(•) A-rj.A* and A'F> 6°-*•• A*.
Nondmnniniftic Automila ind Klcene Theorem 399
Proof. It it easy to verify that for arbitrary relation! rt:A,—-B and
r,:A1-' B in Set, the least relation r.A, + ^i-" B with r, c v, • r and
r, c r, • r actually fulfils
r, — v, • r and rt — »i • r.
Since each varletor in Sat is constructive (IV.4.3), we have
A* - A'"
for some ordinal * with
in* 11 _ ■>?■ . . A">
It is easy to verify by induction that since n, is a coproduct injection, we
have
n„ • X1" — X for each ordinal n.
Hence,
n> A* - A.
And since *>i is the other coproduct injection, we get
...a" -(«>,.<,,,). A'"
- A'"f. s. a
Reatark. Even in Sat we cannot dtfituX' by the equations (•) because such
A * need not be unique (even if A and S are partial maps and f Is a finitary var-
ietor, see Exercise VI 1.1 .A below). For partial maps A and S, we prove that (•)
defines A* at least among partial maps:
1.11. Proaoslthw. Let Fbe a standard varletor in S«t For each partial
/^algebra (Q, S) and each partial map X: 1-* Qthere exists a unique partial map
A * satisfying (•) above.
Proof. I. Fpreserves the compositions of a mono m:X-* Kfollowed by
a partial map /: X—' Z - In fact, the composition is given by the following
puUback
P
y x
X R
1/ m\ A>
400
as
Chapter Vtl
m •/-I/* /ill-
Since both m nad fm are monos, this pullback is an intersection and hence, F
preserves the pullback by 111.4.6. It follows that
(Bf/JF-l/y, if>F-A„F\- mF.fF.
II. Let (C S) be a partial F-algebra, and let A: I—- Qbt a partial map. For
each partial map h: I' —• Q satisfying
A — r/ • A and <p • * — hF • S,
we prove that * — A '. Let * be an ordinal with
A* - A<"
(see VII.1.8). We prove that
A'"' — w,. i • * for each nS k
by induction in n.
(a)A1"- A- ij. A - m, • A.
(b) Let A'"' - w., . A. By I. above,
A<"<F- w.,F- hF.
We prove that ihe components of w.,,, • A are the same as those of A" * ",
viz. AandA'"'F.&
Kf
I«W„F
W.
k-F
I-V^F
W„F
First, since r/. — hv . * i and r/ — r/, ■
1. • (w.*i.i • A) - ij. A - A.
»,,,i,*t have
Nondeterminituc Automm ind Klc«ne Thramn 401
Second, since f • A - AF • 6 and f - f> • wf', 4,, we have
P. ■ (*.»!.»• A) - (f>.-H'.4.,.,<,.i»r.,.*i) • *
- 0..»f- *>»-»Ti.i)* *
-(hv.F. AF)-5.
By I. again,
9. • (».» i.. • *) - (*..t • A)F- « - A'■»/?• 6.
(c) The limit step is clear: A"1 - h>4, • A because the components are
A'"1 — w,, • {w,, • A) by induction hypothesis. D
Raaurfc. For relations A and 5, the solution of (•) is unique provided that
the virietor F preserves preimiges (V.2.10). The proofis the same: in part I we
prove that Fpreserves the composition of i mono mind a relation/since the
pullback defining m • / is a preimage.
EnrdMS V1I.I
A. Free eitrasloas hi Set. Define a set functor F as follows:
XF- |Zc Af;cardZ-2orZ-B|:
fF:Z~(Z)f ifcard(Z)/-2, else, Z.-.B.
(i) Verify that F is a fmitary varietor.
(ii) Define a (deterministicI) automaton
^-(|l. 2|, « |l.2|. y, |l|. A)
as follows:
(Il.2|)5-2 and (0)fi- I;
(Or-I;
<I)A- I.
Verify that the run map p: 111 ■ -♦ 11, 2| is the constam map to 111.
(iii) Prove thai the rein Ion r: |l|* —|t,2| defined by (I)r- I, (x)r -
|l.2|irx# I also fulfils
p • r — fF • S and 17 • p — A,
although r * p by (ii).
[Hint: The relation r is represented by the projections of R - |(l, l)| w
|(jt,(); ** Ml" — Ml and 1 - l,2|. To check (9)f r-(t)rF-8, use z-
|(i, I), (jc 2)| € RF to get |l,2| - (z)r,„F € (9)rF and hence, (0)rF. S-
|0, |l.2||«-(B)f>.r,etc.|
402
CtupierVtl
B. Fret extratoas la R-Vact Let F be the identity functor of R-Voct
(i) Define a relational algebra (X, 5) by 6 - R x R. Prove that Tor
A - \,: R-+ R, we have
A* n. A',
(ii) Conclude that no relation r: Rm —• R fulfils
A — n • /• and p • r— rf • 6.
(iii) Define a partial algebra (R x R, S) as follows:
(*, 0)5 - (jr, 0) and else undefined.
Prove that for A — 8: R'—' R' there exist two distinct partial morphisms ru
rt.W — K'with
A — 17 • r, and p • r, — r,F • fi ((—1,2).
[Hint: (X1)' - R1z| and we put for each (z)w- (a„. b.) + (a,,b,)i +
Wi - I Z J,, 01 if 6, - ... - b. - 0, else undefined;
(H>)r, . j Z j,,o) if 0 - 6, + ... + fc„ else undefined.|
C. Categories of relittoas. Let .t be an (/, .#)-category for which relations
form a category HofJT (see Remark VI1.1.2). Then jr is a subcategory of
Ho) jr.
(i) Prove that Sat is closed in Hal Sat under colimits (Hint: See Lemma
VII.1.7. Let D: »-»8ert be a diagram. For each compatible family of
relations rt;dD-* X, consider the corresponding family of maps f4:dD-+ exp X.)
(ii) Prove that R-Vact is not closed in Hal K-Vact under finite coproducts:
there even exists a partial map p:A-*B and iwo partial maps rlt r,:
A + A —• B with p — v,'rt for i,j — 1,2 (where »,, *t are the injections).
(Hint: Define fiR'-R'by (*>■)/>- (* v) if y- 0, and else undefined;
define r,, r,: K4 — fl1 by
(x, 0, >>, 0)r, - (x, v) and (x; >>, z, -y)r, - (x, r),
else undefined.)
(ili) Let jr be a concrete category with limits and colimits preserved by the
forgetful functor U. Prove that jr is closed under colimits in He4 jr.
(iv) Prove that if jr is closed under colimits in He4 jr, then for every
constructive varietor f: jr-» jr, any relational algebra (ft S) and any relation
A: /— ft the free extension A': (/', «>) — (ft S) fulfils
Nofxlflennmiuk Aulonuu and Klenie Thtona
403
(.) n.X'-X and p-X' -X'F- 8.
If, moreover, j* Is constrnctive and F preserves -#-mono« and preimages,
then A" Is the unique relation which fulfils the equations (•). (Hint: See the
proof of Proposition VII.1.10 and RemarkVIM.il.)
D. Partial algebra*, (i) For each varietor F: R-V»ct -♦ Jt-Vs)Ct and each
partial f-algebra (Q, 6) verify that the free extension of each partial map
X: /-» Q fulfill (•) above. (Hint: Use the fact that F is a constructive
varietor.)
(ii) Can (•) be used to define A'7 (Hint: Exercise VI I. IB.)
(iii) Under what conditions on a category jr Is it true that for each
constructive varietor F: jr -♦ .* the equations (•) hold for all partial moronisms
S and XI
E. Steps reqalrcd bjr X'. (i) Denote by G the set functor defined on sets X
by
XG - \M c X; M is uncountable! w |0|
and on maps /: X-+ Y by
(M)fS-(U\f if card M - card(M)/; (*Q/G - 9 else.
Verify that G is a constructive varietor, and for each countable set /, the free-
algebra construction stops after I step with
/• - / + |0|.
(ii) Describe the functor G acting on relations. In particular, prove that for
each relation f: A-* B, the set (01/C contains any uncountable set M c B
with U - (a)/ for some a e A. (Hint: Representing/by projections of a set
R,c A x B, consider |a| x U e RfG.)
(iii) Define a relational C-aJgebra (Q, S) as follows:
Q- \x\ w(A/x (a>+ I)),
where Af° is an uncountable set and tt> + I - |0, 1,2,.. .| w |oi|, and S is
defined by
(0)5 - M x |0|,
(U x |0|)5- U x |0, l|,
(A/x |0,11)5- Mx |0, l,2|,
(A/x <o)6- A/x (<B+ I)
and (Z)S — 0 for each remaining Z € gG.
Prove that for the inclusion map X:\x\-* Q,vt have
X' -X<-"> but X' +X<->.
404 Clupttr VII
[Hint: For . - (0)f> € [x|*. we have X"> - (8)XmF. S - M x [0| and by
(ii), (.)X»> - (g)X<«F. S - M x |0,11, etc, thus (.)A'«» - M x a but, by (ii)
again (.)A'-"»- M x (<o + I).]
(iv) For each ordinal * find a relational G-algebra and a map X with
X' - X<"» but X' +X<".
VII J. Nwsteertalabtlc LaagM«cs •■ Sat
2.1. We are going to characterize varietors in the category or sets Tor which
languages recognized by nondeterministic acceptors coincide with those
recognized by (deterministic) acceptors. As in case of tree automata (see 11.4.2)
we define an F-acctpior as a quadruple
A - (ft S, T, I)
where (ft S) is a finite /'-algebra and 7 and /are subsets of ft (of terminal and
initial states, respectively). The inclusion map X: /-* ftis extended to the run
map p: (/*, p) -» (ft S). Then the language recognized by A a the set
L,-\wi C;(.|pf r|-(7>-'.
In general, sets
tc /• (/a finite set)
are called languages; a language is recognizable i(il is recognized by an f-ac
ceptor.
Again in an analogy to II.4.5, a nondeterministic F-acctptor is a quintuple
A - (ft 6\ T, I, X)
where (ft S) is a finite relational f-algebra, fc ftis the set of terminal states
and A:/—'ft is a relation. We extend X freely to the run relation
p:(/*, *>) — (ft, 5) (VII.1.3) and the language recognized by A is the set
LA- \w e /\(H>)pr, 7>i|.
If both S and X are partial maps, we call A a partial F-aaeptor.
We say that a language is
N-rtcognizable
if it is recognized by a nondeterministic ^-acceptor; and
P-recognizable
if it is recognized by a partial ^-acceptor.
For tree automata we know that the classes of recognizable, /^recognizable
Nondetermintelic Automata and Klaane Theornn
405
and ^recognizable languages coincide (11.4.6). This, as we prove below, is
caused by the fact that the functors Hi cover pullbacks.
Remark. A deterministic ^acceptor is a special case of a deterministic
^automaton with r - |0,11 as far as (i) the set T c Q'a expressed by the charact-
eristicfunction y. (>-»|0.11 [with (?)x - I tttq e 7"|and(ii)X: I-+ fiisthe
inclusion map of / c Q.
For the nondeterministic acceptors, we have X arbitrary (as in the case of
tree automata in Chapter II) in order to allow a nondeterministic
interpretation of variables. The special choice of X for deterministic automata does not
loose generality because the following proposition can be proved for each var-
letor F: Sot -» Sot analogously as U.4.4.:
ProaosMoa. A behavior
/>:/•-♦/" (/finite)
has a realization by a finite ^automaton iff
(1) the language (y)0~' Is recognizable for each y e /":
(2) the set (/')/) c /"is finite.
IX The main result of the present section is that for a certain class of
"sufficiently small" set functors F
(I) each /^recognizable language is recognizable iff F covers pullbacks
(V.2.10);
(ii) each /"-recognizable language is recognizable iff F preserves preimages
(V.2.10).
The sufficiency of these conditions is eaay, and we present the proof now
(without restrictions on F, in fact). The necessity is quite difficult to prove,
and we devote the rest of the present section to this proof.
Proawltloa. Let F be a varietor in Sot which covers pullbacks. Then each
/^recognizable language is recognizable.
Proof. For each set Xdenote by
e:expX-' X
the "membership relation", i.e., the set e c [up X] x X of all pairs (A, a),
where A c X and a e A. Then for each relation /: P-- X we have
where J\P-* exp* denotes the corresponding map (1.3.4). Since F preserves
the composition of relations (V.2.10), it follows that
fF - fF* eF
406
Chapter Vtl
Let A - (ft ft T, I, A) be a nondeterministic /^acceptor. Define a
deterministic ^-automaton
A-(apQ.S,\0. 11, y, U)
as follows:
S - A : (exp Q)F-+ up ft where A - sF ■ S
v:expft-H0, l|; (AOr-l ifT Mr^T+9
and X: /-» expftcorresponds to the relation A. We prove that A and
j{recognize the same languages (which will conclude the proorby Remark VII.2.1).
If p: /• — ft is the run relation of A, then we prove that /):/•-» exp ft is
the run map of A. The following diagram
(up OIF
-*■ «KpQ
commutes (VII.1.10). Therefore.
/>:(/", «>)-<e*pft£)
is a homomorphism. Furthermore,
X-n-fi
The language recognized by A is
|we I,;(i»W-)' - l| ■
\w e /a;(w)0ri T* 0|,
and this is just the language recognized by A. D
Praaoattkm. Let f be a varietor in Sat which preserves preimages. Then
each /^recognizable language is recognizable.
Reaurk. For partial maps, we follow the usual conventions: we write
(xtf- y[nol(i\f- b | land we say that (Jt^is undefined if (xtf - 8.
Proof. For each set Xdenote by
e:Xw\a\^X
Nonddcmiiniflic AutOflMU and Kleeitt Theorem
407
the partial map with (o)s undefined (a ii any element not in X) and (x)s - x
for each x * X. Then Tor each partial map /: P-* X we have
where/: /"-► JKw \a\ is the eztension of/wich (p)f— a ift(p\fa undefined.
Since F preserves the composition or partial maps (V.2.10), It follows that
/F-fF' eF.
The rest of the proof is completely analogous to that of the preceding
proposition. D
13. Example: A ■oa-recogalxaMe uufuge wblck It ArtcafalzaMe. Let A he
the functor defined on sets Xby XD, - |(x, y); x, y e X, x * y\ w |«,| and
on maps f:X-,X by (x, y)fD,-«x)f, (y)f) it (x)f+ (y)f and
UjO/A - *r - («»)/A if (*!/■- OO/tsee VJ.IO). Consider the free IVal-
gebra on one generator |x|". Denoting by • the element (•„,•)*> € |x|", we
can describe the algebra |x|* by the following trees:
0 ©
The singleton language
M c {x\-
is ^recognizable. For example, the following partial ^-acceptor recognizes
it:
A.-W,o\,\y\,\x\.V)
where Q - |x, y\ (x * y), (•,)& - y and (x, y)6* (y, x)S, are undefined,
and (x)A, — x In fact, the run relation is the following partial map
p:|*r-|*.>|:
(x)p - x, (•) - y, else undefined.
This language |«| is not recognizable, however. For each deterministic
Di-acceptor
A-IQ.S. r,|x|)
with • € LA, we prove that LA is infinite. Since Q'n finite, there exists an infi-
408 Clupnr Vtl
niteset£c |Jt|* on which the run map pis constant. Since • € LA, we have
(•)P - (•ui»)l»- P - (•ui'V'Di • S - (.„)« e T.
Then Tor arbitrary distinct v, w e L. the following tree
AA
is in LA because
(OP - (», »■)«•• p - (», w)pD2. S - (.„)« e T.
14. For the rest of the present section we restrict ourselves to super-Unitary
set functors. Recall the concept of standard functor (111.4.5).
DcftaMlon. A standard set functor F is said to be super-finitary \( it preserves
finite sets, and there exists a natural number n with
XF- U TF
T'_ X. od T ■ ■
for each set X.
Empta. (i) The functor Wris super-finitary iff the type X is super-Unitary,
i.e., consists of finitely many Unitary operations. In particular, Sjis
super-Unitary Iff L is nnite.
(ii) The functor ^(111.3.3) assigning to each set X the set ^of all finite
subsets of X is not super-Unitary (though it is Unitary and preserves finite
sets). For each natural number n and each set X of power n + I clearly
X € XP, - U TP,.
Cooreattoa. For each natural number n we put
[n | — |l.2 n\
(in contrast to n considered as an ordinal, i.e., n — |0, I n — l|). This will
simplify notation below. Elements ofjf" can be identiried with maps from [n\
to X. Given a type £, an element »!l, and a set X. we write
fe X--XH,
to indicate that / € XHC is an element in the p-summand X" of XHi.
Remark. For each super-finitary functor Fthere exists a super-finitary type
Nonddemrinbtic Automata and Kkana Theorem
409
X and an epitransfonnation s:H[-*F. The proor is analogous to that or
Proposition 111.4.3. We call e a presentation of F.
A presentation is often given in the form of equations
(* *.)o- 0"i y.)r
where je £., r e X, and x,,y,*n elements of some set X (of variables). It is
then understood that e is the least congruence on Hz such that the element
(i, x.) € X' - XH, is congruent with the element 0>, ym) e
.*" — JKW,. For example, the functor D, can be presented as a quotient of
H, + HB by the following equation
(x,X)<7-0
(where a denotes the binary operation and 0 the nullary operation).
IS. Each presentation
c:Ht-*F
of a super Unitary functor can be "minimized" as follows. First, choose a set
£ c X such that
(1) for each a e X there exists r e £ with (W„)« c (//,)« and
(ii) if a. r € X, c * r, then neither (//„)« c (#,)« nor (//,)*■ c (H„)£ [The
inclusion (H„)c c (//,)« means that for each set X we have
(XH.)e, c (JfH,)fj-l Since^T b finite, such a choice of £ is clearly possible.
Next, define the arity (<r)ar for each a £ £ as the smallest number n for
which there Is a natural transformation t: H,-+ F with
(//.)« - (H.)t.
Then £ and ir is a new type for which there clearly exists an
^(transformation
*: Ht-~ F.
We call I a minimal [mentation of F. Thus, a presentation f is minimal iff
(i) a* r Implies (//„)*<t (//,)*
and
(ii) If (//„)£is a quotient of H., then |<r| (the arity of a) is at most n.
Another characterization:
PnipoaHlw. A presentation
czHt—F
is minimal iff the following two conditions hold:
410 Chapter VII
(1) For each set X, each one-to-one /€ XH, (a E Z.,n> 0) and each
a E XH,(n £)with
(/)«x - (*)«x,
we have a — r and
*-/>-/■
for some permutation p: [n| -» [n\ such that
(/>)«t-l - 0l.l)«(.r
(2) For distinct a, r E H we have (W„)« * (//,)£
Reaurka. (i) In the language of equations in ihe variety F-A)g (see III.3.2),
the condition above can be reformulated as follows:
(1) Let an equation
(■»i *.)<r - 0"i y.)T
hold in F-Alg, and let n > 0 and i„..., x, be pairwlsc distinct. Then cr - r
and there is a permutation p with y, — *„„ y. - jr,.„. for which the
following equation
(1.2 /i)<T-((l)p.(2)ft...,(/i)p)<T
holds in FnAkj.
(2) For no pair of distinct nullary symbols cr, r E X does
a - t
hold in F-Alg.
(ii) For unary operations cr, condition (I) states that
(/)*» - (»)«* implies /- g.
because / is one-to-one and p — id.
Proof. I. Let ebe a minimal presentation. Then (2) is obvious; let us prove
(I). Since/is one-to-one, there exists a map
with/-/- I,.,. Then
0(.i)«t.i-(»-/)«t.i
because
(l|.|)«t.|- (/•/)«!.!
-(/l/^x-«t„
-(/)e,-/F
Nondetcraimiitic Aulomaia and Klcvne Theorem 411
-H)C-fF
-<*)l/«x-«(.i
- <*• • /)«(.l-
This implies that (H,)e c (H,)e because Tor each A e YHm we have
(*)«,-(!,„. h)eT
-<lw)*«x-*>
-<!«)*>■ AF
-(*-/)*«x-er
-(*■ f-l>)tTi (YH,)e,.
By the minimality, a — r.
Next, we prove that if
Ci.i)«i.i-0»)«i.i (ps !"]«.),
then pis a permutation. Indeed, if not, then pis not onto, say, n t (In])p. Let
/: [n — l|-> [<i] be the Inclusion map, then
p — Pi • j for some p,: [n)-» [n — I].
Define a natural transformation I: H._,-* H.by
(AX, - p, ■ A tot each A € *■ -'.
Then for each A e X' we have
(*)«x-(l(.i)-AHx-*x
-Oi.i)'«|.i- *f
-(Pi'»«m-*>t
-<P,'./)A«x«x
-(P,->-*)«x
-C/-A).(f.t)x.
Hence the natural transformation I • e: //._,-♦ F has the same image as
c: H. -* F—a contradiction with the minimality off.
Returning to p — f - / we see that for my map / with /• /- I, the map
j • / Is a permutation. This clearly implies that g is one-to-one and has the
same image as / Then there exists a permuution p with /- p • g. And
(li.i)« - (p)t follows from the fact that gF Is one-to-one:
«l|.i)«(.i)*r"- (Ih)*Hx- «x - <*)«x
and
((P)*!.!)**"- (P)*Wx • s, - (p • g)cx - (f)s„
and hence, (g)«x -(/)*> implies (I,.,)*,., - (p)«j.h
412 Chapter VII
II. Let «fulfil the condition above.
(a) For a e X. and r € £_. we prove that
(W„)£ c (H,)c implies a - r.
If n - 0, then BH. - B and hence, (BW„)«, c (»«,)«. Implies »//. * B, i.e.,
m — 0. Thus, a — r by (2).
Assume n > 0. For/- I,., we get
(/)«i.i e (|nlH.)«i., c (l/il//,)^.,
and hence, there exists g £ [n]//, with
(/)«i.i - (*)«|.|-
This implies a - rby (I).
(b) Let I ://,-♦ F be a natural transformation with
(//„)* - (//,)* (cr e £.),
then we prove n s *. We can suppose n > 0 (since 0s* anyhow).
For 11„ £ [n]H„ we can choose A € [n]//, with
("i.iXt.i-(*W.h
Let g: ln]-*[n] be a map with
a«D* - <I*D* »nd * • g - h.
Then
('i.j)«t-i — (* • #W-i
- (*)*«. • $4
- <*)$., • *f
- OhM., • *f
- (*)«i.h
Thus, there exists a permutation p with g — p • I,., - p. Hence, gis a
permutation, and ([*1)A - (|n])g - [n]. This implies n £ k. O
Z.6. CMTtarkm. Let
t:Hr-f
be a minimal presentation. For each a e X of arity n > 0 put
/>. - |pe |nl";(p)«i.,-(I,.,)«i.il.
Then P„ is a group or permutations.
Indeed, by the preceding Proposition each p e P„ is a permutation. Since
I,., e />„ and [n] is a finite set, it suffices to show that P, is closed under com-
Nondcumlnistic Automata and Kl«mc Theorem 4|3
position. If Pi.Pi E /", then
(P. • Pi)«t.i - (Pi)Pi«r • *w
- (Pi)«t-i • PiF
-OuO*M'PiF
~ OniPiHf «(.,
- (Pi)«t.i
-(li.i)«w-
Hence, p, • p, e /"„.
Reaurka. (i) For each nitural isomorphism
a:H,-*Hm («, m finite)
we hive
ii — m
end there exists i permutation p on [n] such that
(f)<*x - p • f Tor each set X ind each / € X:
In fact, pulp— lj„ E [n)W„. Since/W. • o, - a,,, •/H», we have (/)o,-
p • / Proceeding analogously with a-', we find out that p is invertible.
(il) More In general, let I ind £ be two super-finltary types for which
i natural isomorphism
o:Hx-Hf
exists. Then for each a e Z. there exists 6* e £ with
(H.)a - H,
[i.e., with (XH,)ax - X/fe Tor each set X} This esublishes a bljection c>-> «
from X. to 11, (for each n). Hence, Z is essentially the same type as £.
Thus, a is determined by permutations p„ on [|cr|l (for ieI| in the sense
that
(f)<>i -p.-feXH, for each / e XH..
(iil) We prove now that minimal presentation Is unique up to a
(non-essential) permutation of variables.
PuipoatUsa. (Uniqueness of minimal presentation.) For arbitrary two
minimal presentations c; Hz-* F and I, Hj-* F there exists a natural
isomorphism a: Hz-* H/tot which the following triangle
«-=—H,
commutes.
F
K/
414 CtiplerVU
Proof. For etch a € I. consider l|a| € [n]H„. Then (lt.|)«t„i e [n]F, tnd
there exists O € X„andp„ € (n)Hjwith
(■[.|)C|.I — (P0>^.h
It follows thtt
(//.)£ C (H;)l
because for etch / s X" - AW, we htve ///r • ti — *w fF and /7/j • {, -
^.i • fF: applying this to I |Ih we get
</)«, - «ii«)«(.a/F
- «p.)«i.a/F
- (p. • /)«»•
Since sIs minimal, we conclude that n £ m.
Analogously, for I,., € ]m]/f„ we can find u" € X,andp^with(l|n,^)<ja,l —
(p'.)«(.i »nd hence,
(H,)t c (//„)£.
Since e is minimal,
(W.)s c (W„ )s implies <r - <r',
and since £ is minimal, we conclude that m£ ri — n. Thus,
n — m.
Moreover pi • p„ is a permutation, because c is minimal and
(P'„ • P.)«w - (p'Jp.Wi • «t-i
- (Pi)«n • P*F
-0M.,-PS
-0\.dP*Hf $.1
- <P.)*m
- Ci.i)«i.|-
Consequently, p, - (/>'„)"' is a permutation.
Define a natural isomorphism
by
(/)<»x-P.-/
for each set X, each <r s £ and each/€ XH.. Then (I „)*)., - (/>„)*[.] clearly
implies that
((/>x)*x - (f)e, for each/€ */fc
Nomleteniiiiiiltic AvIMlurtB *»d KktiM Theorem 4| 5
i.e.,
a • I - e. □
2.7. Deflaittea. Let F be a super-nnitary functor with a minimal
presentation c: Hi-* F.
We say that F is perfect if for each a, r € £ each / € XH„ (not necessarily
one-to-one I) and each g € HX„
(fUi- (*)«i implies o- - r and g - p-f for some p € /"„.
We say that f is regular If for each a € I., r € I,, each / € JK7/„ and
g € *//„
(/>»-(*)*» implies <I«u/- G>Dg;
In other words. If (/)«, — (g)t>, then there exist maps pand p' with *-/>•/
and/-/> •».
(This definition is obviously independent of the concrete choice of minimal
presentation.)
Exaatpka. (i) P, is perfect A minimal presentation is given by the
transformation e:H,-» P, with
(*. r)«x - I* y),
i.e., by the equation
(x, r)c - (r, *)o\
If (f)e - (»)«; then either f- got f- (x, y) and » - (y, *) in which case
g — I'ftot the transposition /: 121 —»■ |2L Here
f.-Mn.'l-
(ii) fj is regular but not perfect. A minimal presentation is given by
e: //,-» fjwith
(x, r, z)s, - )K y, 1).
The regularity is obvious. But tot f- (x, x, y) and g- (x, y, y) which fulfil
(/)« - (g)cthere is no permutationpwith g— p-f.
(iii) The functor A is not regular. A minima) presentation Is given by
e: H, + H,-» D,with
(0)s, - .,.
l», if* - r
416 CtapMrVII
i.e., by the equation
(x.*)o--0.
If/- (x, *) and g - 0>, y) with x + y, then (f)s - (g)ebut the images of/
and g are disjoint,
(iv) Let Pbc a permutation group on the Mt (n). Denote by
the quotient of H. given by the equations
(*i. *J Jt.) c - (i,,,,, n,„ x,.w) (/> € P).
That is, JW/. , - X"/~ where
/~ * <ff t-P-f for some ;t P (/««*•)■
It is clear that H» , is perfect.
Proaostttoi, A super-Unitary functor F is perfect iff
f-LIw,.,
for some permutation groups P, P,.
Proof. Each W.,,is perfect, and a finite coproduct of perfect functors is
obviously perfect. Thus, we only have to prove that each perfect functor Fhas
the form above. Let c: Hz-» Fbe a minimal presentation. Since f is perfect,
a* r implies (W„)s n (H,)c - 8
and hence
F- II (W„)s.
And, clearly, (Ha)e with a € X, is naturally isomorphic to
Ltisma. A functor Fwith a minimal presentation «: Hr-> f is regular iff for
each <j € X. and r s X. with n S m S 2 we have
(/)«i.i - (*)«w implies a»H^- <I»>D*
for any/ € In)//, and $ € WW,.
Proof. If F fulfils the condition above, we prove that Fis regular, l.e, for
each a a X., r € £„ and arbitrary / € XH, and f € XH„
(/)«>-<«)«j implies (l"D/- a»"D*.
Without loss of generality, assume nam.
Nondcteiminbtic Automata and Klaenf Theorem
417
(A) Let m — 0. We prove that is I. Assuming the contrary, we ean choose
maps p, q: X-* [n] which have disjoint images, and we apply the condition
above to a and a, with
f-J-p and g-Jq.
Since f (: B -► X) is the empty map, we have
«•/»- i-1
and hence,
(.0*1.1 - (*)*|.r
(In fact.
(/•P)£w - (/)/>>V*t.i - 0)ex-pF- (i)ex-pF- (*"•/>)«,.,
and analogously, (/• ?)«j.| - (i-?)«j.|.l This is a contradiction, since
(InD/^ Q>Dg - ■•
Ifn — I, then /is one-to-one and hence a — rand J— p-Jfor some
permutation p(sec (I) in VI 1.2.51. Hence,/and f have the same image.
If n - 0, then / - J (see (2) In VI 1.2.5].
(B) Let m — I. Then g is one-to-one and hence r - <j and / — p • g for
some permutation p (see (I) in VII.2.5L hence, /and f have the same image.
(C)Let m S 2. Assuming Q«D/i» QmD#, there exists a map p: X-»C1such
that the maps
f-J-p and t-iP
also have distinct images. This contradicts to the condition above, since
(Z)*H - 0)p»z- *t.i - tf)*,-pF
and analogously, (*)«m - (#)«*' pf, and this proves thst (/)£,.,- (#;)«„. D
Resaarka, (i) There is no descriptive characterization of regular functors, in
contrast to the perfect ones.
(ii) An analogous lemma holds for perfectness; Fit perfect iff for (J € I„
r € Z. with n £ m £ 2 and for arbitrary/ € \n\H„ and g € ]n]H„
(/) <M - (>)<)•> <mP'i*» c-r and g - p-ftorp € P..
(Ill) The lemma above can be formulated more symmetrically If no
restrictions on the size of the sets AT are required: FIs regular UT for each <j, r € Xof
arity £ 2 and any/e XH.and g € XH„
(/)«x - (»)*•«• implies image /- image g.
1A. Piuyuallloa. Each regular functor preserves preimages, and each perfect
functor covers pullbacks.
418 Chapter VII
Proof. Let c: H -* foe a minimal presentation of a regular functor F and
9 g
i
A—p»C
be a pullback. If either g is one-to-one or Fis perfect, we shall prove that F
covers this pullback. That is, for arbitrary a € AFand b € BFwith
(oVF-(b)gF,
we shall present a d s Df such that
a - (</)jf and ft - (</)/f.
(If gis one-to-one, then so are gand j"f, see Remark III.4.5, and hence, such d
is then unique. Thus, factually preserves the pullback.) There exist a, € AHz
with (note, - a and *o € *"i with (6g)ef - ft. Say o( € AH. where (J € X.
and At> £ AW, where r € X.. We have
(o.-/)«c - (Oo^Wr- «c - (a,)eA-fF- (a\fF.
analogously with b, • g Therefore,
(«o-/)«c-(*.g)«c.
Since e is regular, ihe images of a0 -/and 6g • g are equal. Hence, there exists
a mapp:|n]-»|m] with
0,-f-p- b,- g.
Let 4> be the unique map, for which the following diagram
a„\ D —- B
\l' !•
A—j-^C
commutes. We claim that
d - (</„)«„ € Df
is the element we are looking for. First,
a - (flo)^ - («• • >)«< - («•)*«! • Ca - («•)«» • iF
Nondderminuiic Automata and KJaane Tbeoran
419
For b, we most consider the two cases separately.
(i) If e is perfect, then (a„ • f)ec - (A,. g)^ implies a - r and p € P„,
thus,
b - (*,)«, -(p.b,)s.- (</, • /)s, - (ditto• JF
(ii) If g is one-to-one, then so is gF and we have
(b)tF- (a\fF- (d,)eB.gF./F- (4)4 • JF• gF,
thus, again
* - (4)4 ■ JF. D
Rtaurfc. We see that for each regular functor, the ^recognizable and
recognizable languages coincide. For perfect functors, the ^recognizable and
recognizable languages coincide. We are going to prove that the convene holds,
too. First, we prove a technical result concerning epitransformatlons |whlch
actually holds in general (*\ .-#>categories as well].
2.9. Lemma. Let e: H-* F be an epitfansformation. For each relation
r: A —" B in the domain category of Fwe have
rF — eA' • tH• c,
and therefore,
tH • c, c eA • rF
1
BH . -BF
s
Proof. Put r - |r„ rj with r,: R-* A and r,: X-» A Since sj' - [eA, \AH],
it have
AH-
r,H
RH-
','
■ RF
''"I ',F
420 Chapter VII
«;' • rH - {sA, \AH) . {r,H, r,H] - [r,H • eA. r,H\.
Therefore,
eA' • rH• t, — [r,W• cA. r,H■ e,]
- {£, • r,F. £, • r,F].
Since c, is an epi, the last pair represents the same relation as [r,F, r,F], Thus,
eA' ' rH • c, - rF.
Since \AH c cA • sj', this implies
rH' c, c eA • t^1 • rW • c, - eA • rf. D
Remark. The equation
rH • £,- eA' rF
does not hold for relations rin general, see Exercise VII.2.C below.
2.10. Theorem. For each super-linitary functor f. the following are
equivalent:
(i) Every /"-recognizable language is recognizable:
(ii) F preserves preimages;
(iii) F is regular.
Proof. It suffices to prove that a functor F which fulfils (i) is regular]since
(iii)-»(ii) is proved in VI 1.2.8 and (ii)-»(i) in VI 1.2.2). We first construct
/"-recognizable languages with special properties for an arbitrary
super-linitary functor F. Then we prove that the fact that these languages are
recognizable implies that F is regular.
I. Let e: Hz-+ F be a minimal presentation of an arbitrary super-finittry
functor F. For each us £„ n a 2, we shall find a partial f-acceplor A,
recognizing a language
/,c/«
with the following properties:
(a) For each one-to-one n-tuple w € /•//„, the element (*■)«/■ • p s /■
fulfill
(w)t,. ■ pe U iff w, w. € /,.
(b) For each constant m-tuple we I' H„ I € Im, m > 0,
(w)e,m .as I, provided that w, € /,.
(c) Both Z, and /* — i„ are infinite sets.
The partial acceptor A, - (Q, S. T, /, X) has only two states I, 2 with I
Noodctcnntnlitic Automata and Kkcna Theotaa 421
terminal. The partial map
is denned In q s \l\F Iff there exists r € £,, m > 0, and a consUnt m-tuple
a € (2]Hrwith
1 - <«)•«:
in this case,
(«)« - I
(and otherwise (q)6 is undefined]. The object / is |2n + 4), and the partial
map
X:{2n + 4]-[2]
is deHned by (I )X - (2)X - ... - (n + 2)X - I, else undefined.
Since both 6 and X have only one value I, alio the run relation p', /* —" Q
is a partial map which has only value I, It follows that the language Z, or A.
consists or those u € /* Tor which (u)p is defined.
(a) Let » be a one-to-one tuple in (/*)' — /"//„, Then (>»■)«,• • e> is in Z,
iff
I - (w)e,a .p.p- ((w),a . pf). 6",
and this holds iff there is a constant m-tuple a € (2]W„ r £ X., m > 0, Tor
which
(w)s,a .pf-taje,,.
By VII.2,9,
(w)S,a • pf - (»v)t,a • eS- pHz • £,„.
Since e is minimal and h> — (h>, h>.) is one-to-one, we have
(w)t,a . sji - |p . w; ;e />„!,
by Proposition VII.2.5,
Thus.
Hence,(»)«,• • pf is equal to |((h>„)a. ..,(«vfc)p);p s Z*.]^provided that
all (H>y)p are defined {J- I n) and It is undefined else. Therefore,
(H>)C,a • C> S Z» iff
(ivf)p are defined for all j— I n and there exists a constant
tuple a € (2)//, and />€/>„ with (/> • w • p)c^ - (a)^
If this condition is fulfilled, then wt € Z» for j — I n [because (H>,)p
422
Chapter vtl
are delined]. Conversely, if wt € Z, for /- I,.. , n, then (w,)p-\,
w p - (\ I) € [2]//„and we simply put p - I,., e />„and a - h>> p to
conclude that the condition is fulfilled.
(b) Let w - (h> w,) € (/•)" - /•//„ / € £„, m > 0, be a constant
tuple with h>, € /,. Then (w)pHI - (1 I) e [2]H„ and therefore
(w)p//r. £j„. 5- I,
By VII.2.9,
(w)pHt • egg • £ c (H>)t,» • pF' S c. (*■)£;• •♦>•/».
Hence, pis defined in (h>)£,> • p. I.e., (*)«,• • e> € /,,
(c) To prove that Z, is infinite, we observe Pint that it contains 1,2
n + 2 because
(i)o-(iM-I for 1-1.2 n+2.
Since n S 2, it is sufficient to exhibit a one-to-one map from the set exp.Z, of
all n-point subsets of L„ into L,'. we know that Z, has at least n+2 elements,
and therefore it cannot be a finite set.
For each set | h> w.] € exp,/,, we choose an arbitrary ordering and we
obtain a one-to-one n-tuple w € Z»W„. By (a), (>»■)«,• . p € /», and the map
assigning (h>)c> • pio |w, h>.| is one-to-one [because e,t is "essentially"
one-to-one by the minimality of e, and also p is one-to-one, see IV.4.2,
Remark (i)].
Analogously with the complement /* — /*,. It has at least ■ + 2 elements:
n + 3, » + 4 2n + 4. And for each set | h>, w,] of n elements In
/• — Z» we have, by (a), (»)«,• -t? s /• — /,.
11. Let f be a super-fini'tary functor for which the above languages Z, are
recognizable. We prove that then Fis regular. Let Jfbe a set and let/ e XHcmA
g € JCW, be elements with
(f)Sx - <*)«>•
It suffices to prove that im/(the image off) is a subset of im g, i.e.,
if b s im / then b € im g
(by symmetry, then im/— img). Let nbethearity of o~and m be the arity of
r. We can suppose that n, m are at least 2 (see VI1.2.7. Remark (iii)l; we use
the language U. Let
(Q.S.T.I)
be /^acceptor recognizing L,. Since Q is finite and Z, is infinite, there exists
an infinite set L c Con which the run map pis constant, say, with value qa'.
(u)p - qa for each u € L\
Nondeteraitniftic Automata and Kleenc Theortm 423
analogously, there exists an infinite set L c /* — U, and q, € Q with
(u)p — q', Tor each u € L.
Let h> € /* //„ be a one-to-one n-tuple such that
h>, € L if (/)/> ft; w, € L if (0/- ft-
Then (w,)p - q, if (0/- ft and (w,)p - q, if(i)/> ft. Therefore, the
map e: X-* Q defined by
(ft)r - q', and (x)r - q, for all x € * — 1*1
clearly fulfils
f-e- wp: («)-►(?.
By (a)
(w)s,. • e> « /.,
since w, « X, for at least one i € [n]. Thus,
(h>)s,. • q> • p t T.
And we have
(w)e,m . q>.p - (w)e,m ■ pF- S
- (*>)pHf ««• 6
-(/)fWi-*0-«
-(f)cx-cF-6
-(K)s,-cF-6
-(*'C)«(,-fi.
Hence
(4--c)*V,-6-< r.
This implies that ft € im g: otherwise •>• c is the constant m-tuple (f0, q>< ■ ■ ■•
ft) E 0Hr. But
(«o, ?• «i)«e°" e r
by (b) in I: choose a constant m-tuple w € /*//, with *, € L, then
(*)£,• • •> € X,, hence,
(*)s,. . e>.p - (w)pHi- %• 6" - (ft, «. «,0«9' 6" € T.
This concludes the proof. D
2-11. Lemma. Let Fbe a super-finiury functor with a minimal presentation
424 Chapter VII
c. //r-» F. Let a s I., n i. 2, and let y be an equivalence relation or (nL
Then there exists an iV-recognizable language
Lc /*, /a finite set
and subsets L L, of /" with the following properties.
(a) Let w s /*//, be a one-to-one it-tuple with *>, el,,,..., w. € L,.
(r„ ..., r, € (iiD. Then (*)£,• • e> e L iff there exist permutations p, p' € P,
with
f(/»r(Op' fori-I n.
(b) For each r € X of arity m £ n, r * c the restriction * - (h>„ ...,
W.) € /•//,0fH>ruinis(H»)C(.'«7< L
(c) The sets L„ ...,£. are infinite and i, - L, i(T f r7 (4./€ [n]).
Proof. I. First suppose that the given equivalence relation y is non-trivial,
i.e., y + [n] x (fi). We define a nondeterministic /^acceptor on the state set
ft - [n] x [n] v |z|.
where z is an arbitrary element outside of in] x [11]. Put
^ - (ft ft \i\. /, AX
where
/ - in] x (n + 2]
and the relations 6 and A are defined as follows. Put
ft - \(Kj) € In] x [■]: kyi\ for i - I n
and define
U7)A - ft for all (A,) € in] x (n + 2].
Define a map / s ft/ii (i.e., /: |n] -► g) by
</)f-(tl) </- I n),
and for each q € Of put
(ft if f - (a)gg for a one-to-one a € QH,
with a, o. s ft (is M):
1*1 if «-</)*„;
0 else.
This relation is well-defined because c is minimal:
(i) (i)Cq + (a)t0 for any a € Q' because there exists./ € (n] not equivalent
to i under y. and then a i» p • / for any permutation p [because (/, I) is in the
image of / but not of a]:
Nondclennlntftic Automata and Klcenc Tntorcin 425
(ii) (a)gg i» (fr)fg for any one-to-one a € Q' c (?W„ and ft € g; c £//„
with Q,+ Q, because, again, b * /»• a for any permutation p (here a and ft
have disjoint images).
Let L be the language recognized by A, and let
L,- |u e /•;(«)?- 6|. /-I n,
where p: /• -" Q is the run relation of -4.
(a) Since z is the only terminal state, we have (*)«,• • «» € L iff
t € (»>)£,• • e> • p — (■/)£;• ' pF • 6
(see VILLI2) and this holds iff
(/)«•„ € (w)s,. • pF
- (■»)*> • t;*1 • p//r • «j
by VI1.2.9. Since £ is minimal and h» is one-to-one, we have
(W)t,a . tfl - |(H>lly »„„); p € />.|.
Therefore, (>»)«,• • p € L iff
(0«o « U ((>»„i,)p k ... x (H-„„)p)«j,
(because w, € A,) or equlvalently,
(0«e - C>9
for some (" € Qvif x ... x ftw. By Proposition V1I.2.5. this equation holds
iff there exists p' e /", with
f-p'/.
We have (", - r(n,- € g,w, in other words,
(l)p'rr,n, tor I- I n.
<b) Aaaurne that re Im (#n £ «) is such that the restrioion tr € lm H,ot w
fulfils (*)«,• • <? s i. By an argument similar to (a) above, we verify that
(0«e « U ((H>(1„)p x ... x (i»(.„)p)«9.
Since r is one-to-one and e is minimal, this implies <j - r.
(c) To prove that i, is infinite, we observe first that (t I) U"+ 2) s i,
because (tV)P - (>./W - 6- Since n s 2, it is sufficient to exhibit a one-to-
one map from the set exp, L, of all »-point subsets of L, into L,. For each set
|h>, h>,] € exp, L, we choose an arbitrary ordering and we obtain a one-
426 duplet vii
to-one n-tuple » € L' c /•//„; we prove that (h>)£;« • t> E L,. By Lemma
VII.2.9.
(»)«,• • e> • p - (w)t,» ' pF' 6
— (■>»■)£,• • tjij • pHr • gg • 6
- r\)^lw'<»)P * ■■■* (»W>P)«o
- (c;)«„ • «•
By the dennition of S, it is clear that the last set is Q,. Since <? is one-to-one
(IV.4.2. Remark (i)] and e is minimal, the passage from |w, w.] to
(w)e:* • p is clearly one-to-one. Hence. L, is infinite.
Gearly 1,-1, ilT if/.
II. Let y — (n) x (n). Then we are to present an ^recognizable language
L c /* and set L, c /* such that
(a) for each one-to-one n-tuple h> e L; c /•//„.
(w)C(a -pEL:
(b) given r* crofaritymS n and denoting by * E /*W, the restriction of
w, then
(*)«,• 'fit;
(c) L, is inflnite.
Define a nondeterministic acceptor
A-U2.S. [n], |n + 21 -I)
as follows: Q - [nl for l,„ E {n]H„ put ((l,„)«i„)fi - {n\ and else («)« - B.
and (i)A — |»1 for all i — I n + 2. Let L — L, be the language recognized
by A.
(a) Each state in A is terminal and hence,
(w)t,. .fti iff (l[„)«o e U ((wn^Jpx ... x (w„„)p)«g.
The argument is as in I above. Since w, € L, - L implies (w,)p - Q for
f - I n, we get
Ii.i « (»dP x ... x (w,)p - <?".
The proofs of (b) and (c) are analogous to I above. D
2.12. TkaoitsL For each super-finitary functor F, the following are
equivalent:
(i) Every Mrecognizable language is recognizable;
(ii) F covers pullbacks:
(ili) F is perfect.
Nondetenntnlitfc Automata and Klctna TlMoreni
«27
Proof. It is sufficient to prove that each functor with (i) is perfect, since
(lii)-»(il) is proved in VIU.8 and (ii)-»(i) in VII.2.2. Let e: Ht— F be
a minimal presentation. We use the fact that the language L in the preceding
lemma is recognizable.
We first prove that for a € I. and r € Zm.
(/)*>-(()•> implies <j-r (f € XH„and g s XH,).
We can suppose n S m S 2 (see VII.2.7). We use Lemma VI 1.2.11 for the
trivial equivalence f — (n| x (n|. Let (ft S, T, I) be an F-acceptor, recognizing L
Since L,(- Lj — ... — L.) is in infinite set and Q is finite, there exists an
infinite subset £| c L, on which the run map p is constant, say, with value
q, € ft Choose distinct h>„.., w, € £,. This yields w € /'//.such that, by
(a), (»)«(• •«'€/. Thus, the following state
«l - (•»)«;' • V P- (■»)«";• • pf • S
-(»)pHf£q-6
- (*>. «0. •--. «a)«fl • 6"
is terminal.
Denote by e: X-* Q the constant map with value ft, then
(«o.ft.• • •.«a) - f- c and thus, ?, - (/• c)«v S
-(/)f«i«o-«
-(f)s,-cF.6
-(K)sx-cF-6
- (g• f)«e • &
Let * - (w h>.) e /• //, be the restriction of if, then clearly (*)pWr -
(«o. «•.•••. «a) - «• f»nd hence
«, - (w)p//r • «e • 6"
- (*)*;a • f> • p.
This implies (*)«,• • e> e L. By (b), this proves r - <j.
II. We prove that given c s X, with n S 2 and / g € *//„, then
(/)«>-(g)«V implies %-p-f for some ;E />,.
We apply Lemma VI 1.2.11 to the kernel equivalence r of / (i.e., iyj Iff
('V- VIA Let ^ - (ft ft T, 0_be an /^acceptor recognizing the language L.
For each i € (/iL the set L, s /* is Infinite and hence. It has an infinite subset
L, on which the run map p is constant. By (c) in VII J.I I, we can choose these
sets L, so that £, - L, whenever W- U)f Denote by qt € Q the value of p
on L,, I € (n|.
Let w € /*//„be a one-to-one n-tuple with w, € £,. By VII.2.11 (a) (with
'- P-P' - 1)
(H>)S,a .ftl.
426 Chapter VII
Thus, the state
q. - (w)e,m -vp
- (*)£,. • pF• S
- (*>)pHt ■ «« • S
is terminal. Since (w,)p - q„i € (n), and since (i)f- (/Vimplies q, - q,, we
can find a map
c:X-> Q
such that
<(Q/V-ft. >'-! ".
I.e.
/. c - (w)pHt.
Thus,
«.-(/• 0«b- «
-(/)fWi-<0-«
-(«)«,• ff-fi
- (* • 0«tJ • *•
Since F is regular (by Theorem VII.2.10) and (/)«t - (j)£r. the images of/
and f are the same and hence,
g — r • / for some r s |n)".
Choose a one-to-one n-tuple * e /• H„ with
*i s £ *. s £..
Then clearly
(*)P«i - (* iJ - r • /• c -g • c,
therefore
«.-(*• c)«« • «
- (*)pHt • «e • fi
-(*)«•,. -pf.fi
- ((*)«,• • 9) • p.
Hence, q. s T implies that
(*)«•,• • e> s L,
which, by VII J.I 1(a), means that there exist p, p' s /"„ with
'^fOp' (' « I"D
Nondctennmiitlc Automata and Klccnc Theorem 429
i.e., with
p. r.f-p-.f.
Then
1-r-f-(p-'p)f
and, since
P~' • P « K.
this concludes the proof. D
Exercises VI 1.2
A. Minimal prcseatatloas of super-flaltary foactera. (i) Let e: Ht-* F be
a minimal presentation. Prove that for each presentation c'\ Hr-* F there
exists a monotransformation fi: Ht-* Ht with
e - n • e'.
(ii) Why is the epitransfonnation e: H,-+ F, given by
(x, x)e - 0-, y)e
not a minimal presentation of a superfinitary functor? (Hint: F is not
standard.)
(iii) Change 9F of the above functor F to obtain a standard functor and
find its minimal presentation. Compare with Example (iii) in VII.2.7.
nVFancion f.iKellM.I).
(i) Prove that for each natural number n, the functor P, is regular: for
which n is P, perfect?
(ii) Write down a system of equations for a minimal presentation of Ps.
(iii) Define a nondeterministic P,-acceptor
A-W\),S.W\.\x.y\,X)
by (I3I)« - (3| and (M)« - |3| if Af * (3|: (*)A - (3| and (y)A - |3|. Prove
that the language LA recognized by A is not recognizable. (Hint: Verify that
LA and /* — LA are infinite sets and for »,, („ (3 € /■ pairwise distinct, (|r„ (,,
(j|)«,« • e> € LA iff at least two of the elements (,, (3, (3 are in LA.\
C. Relatioaa aad eplrraasfonaatkw*. ft) Prove that the minimal presentation
s:Ht-»Fo( a perfect functor F has the property that for each relation
r: A —- B we have
eA» rF~ rHt» e9.
430 Ctwpttr Vti
(ii) Verify that the minimal presentation of D, (VII.2.7 (iii)| does not have
this property. (Hint: Consider r: |x, y\ -* |x| with (x)t — x and (y)r
undefined!
D. RecognlzaMIHy. Let I - I, w I, with Z, - |0| and I, - |<r, r|. The
quotient f of Ht, given by the equations
(x, x)a - 0 and (x. x)r - 0
has the property that the recognizable, /^recognizable and ^recognizable
languages form three distinct classes:
(i) Proceeding analogously as in Example VII.2.2, find a ^-recognizable
language which is not recognizable.
(ii) Define a nondeterministic acceptor
A-U2lS.[2].\x,y\.X)
by (x)A - (y)A - (2|; for lra € (2|W„ put ((!„) e„)S - (2| and else S
undefined. Verify that the language LA recognized by A is not /*> recognizable by
proving the following properties: LA is infinite and for arbitrary (i, (; € LA
with r, i» I;
((«„ «i)o-)e,. ■ «• € LA and ((»,, l,)r)e,. ■ <> t LA.
(Hint: To prove that a partial acceptor cannot recognize such a language,
consider an infinite subset of LA on which the run relation is constant)
VII J. KImm Tfceoren
3.1. For sequential and tree automata, Kleene theorem characterizes the
languages recognizable by finite automata as the rational languages (i.e., those
obtained from finite languages by union, concatenation and iteration). In the
present section, we define concatenation and iteration for each super finitary
varietor fin Sal We prove that Kleene theorem holds iff F is perfect
This shows that there is a deep interrelationship of the concepts of recog-
nizability and nondeterminism: rational languages coincide with recognizable
languages iff these coincide wiih ^recognizable ones.
3.2. DeflatthM of coacateaarloa. Recall from 11.4.8 that for two L-lm
languages L, K c /* (where / is a finite set of variables) and for each x € /, the
x-concatenation is the language
L-,K<z /•
of all trees obtained from Af-trees by substituting some /.-tree for each leaf
labelled by x. This can be described algebraically as follows. Let us form the
free algebra over the disjoint union of / — |x| and L:
NondcteminMc Automata and Klcem Theorem
431
(/ - |x| + /.)•.
Its elements arc finite trees with leaves labelled by variables other than x, or
by elements of L. (If L contains a variable y € L, we distinguish it from the
element in /by writing/.) Example: L - \x, l\ with
0©
then >„ >, e (/ — |jc| + L)' for the following trees
For each s € (/ — |i| + /.)• denote by
(r)a € /'
the tree obtained from s by substituting each leaf I e L by the actual subtree
i:
0 © 0 0
Thus, we obtain a map
a:(/-|*| + /.)■-./'
which is the homomorphism freely extending the map
o,:(/^|jr|)+ /.-./■
both components of which are the inclusion maps.
432 Chapter Vtl
Each tree in L-, K has the form (j)a for some s € (/ — |i| + L)'. More in
detail, for every tree s € (/ — | jc| + L)' denote by
(J)ft € /'
the tree obtained from s by substituting each leaf I € L by x.
Thus, we obtain a map
6:(/-|x| + /.)■-./■
which is the homomorphism freely extending the map
V(/-|*| + /.)'-./■
the first component of which is the inclusion map and the second is the
constant map with value x Then
L-.K- |(j)a; s € (/ - |i| + /.)• fulfils (s)b € K\
or. shortly,
L-.K- |(j)a: J€ (K)b-'\.
3 J. More generally, let Fbe a varietor in Sat, let /be a finite set and let K,
L c /■ be languages. For each x € /we denote by
Ou. fto=(/- |*|) + /--» /"
the following maps: the first component of a, and bt is the restriction of
n: /-• /*'. the second component of a, is the inclusion map, and that of fro is
the constant map with value (x)n. These maps can be extended freely to F-
homomorphisms
a,b:(l-\*\ + /.)•-./'.
Oeflaltlo*. The language
L-.K- |(j)a: J € (AT)ft-'l c /'
is called the x-concaienaiion of L and AT in /.
This definition turns out to agree well with the concatenation of tree
languages: if e: Ht-* F is a presentation of f-algebras as JT-algebras (II 1.3J).
Nondclenninitlk AuKmau ud Ktome Theorem 433
then we prove that concatenation can be performed on the corresponding tree
language! with the lame result.
Cooreation. For each presentation s: Hz-* F we denote by
(/•,«>) and »:/-»/■
the free ^algebra, and by
(/••,?•) and if:/-./••
the free JT-algebra. Recall from III.3.I that each ^algebra (ft 5) defines
naturally the /fx-algebra (ft £j ■ 6). We denote by
*;:(/'•,»*)-(/■.«;■•»>)
the unique £homomorphism extending 17: /-» /*.
For each L c /■ put
/• - (L)£J< c /••.
For each tree / € /■• put
</>-|j€ /■•;(!)£,-(I)f,|,
and given /. c /■*, then
</.> - u^o.
Remit. For each x € / we have
<*> - 1*1 •
In fact, I'-I+I'F and /••-/+/••//, (sec IV.3.1) and *, -
I, + (l,Ht) ■ «,.. Hence, ((x)n)*,-1 - |(jr)if| and since if: /-. /■• is the
inclusion map, (1) — |i|.
}A. PropMirJoe. For arbitrary languages K.L<zl' and each x € /, we have
L.,K-{L»;K^il.
Proof. Denote by
a, *:(/ — |x| + /.)'-./•
the homomorphisnu from the definition of concatenation of Slanguages, and
let
a* *•:(/- |jc| + /.)••-. /••
by the corresponding Wj-homomorphisms. Denote by
<%:(/ — |x|) + /.• — (/— |x|) + Z.
Analogously,
e- b-
Therefore
b*
- *»•
-«?
•ft.
•ft
434 Chapttr Vlt
the coproduct of I, _,,, and the restriction of ft to L*. Then clearly
4 - a, - af ■ I, and 4 • K - bf ■ ft.
We have a unique /fi-homomorphism
e:(/-|x| + /.•)■•-.(/-|*| + /.)«
with n* - e - 4 • 17. Then t is easily seen to be onto. We have
e ■ a - a* ■ ft:((/ - |x| + /.)■•. *>•)-. (/', s,. • e>)
because e • a and a* • ft are £homomorphisms with
ft).
(/.• -. K*)i, - |(j)a« - ft; * € (AT'XftVl
-!(')«• a: (!)»••«,€ K|
-1((j)«)o :((»)«)»€ AT|.
Since e is surjective, we get
(/.• •, AT*)*/ - l(«)a: (0* e K\- L;K. D
ResnriUL (i) For each standard Unitary varietor F we can assume that
/ c J implies /■ c Jm
and for the inclusion map v: /-» J, v*: /* -> J' is also the inclusion map. In
fact, recall that the free algebra is determined only up to an isomorphism, and
the same is true about coproducts. Assuming a standard choice of copreducti
in Set, we can guarantee that
X<z X- and Kc ¥' imply X+ Kc X + T.
Then /* c Jm follows from the fact that /■ - U W, with
ft < m
W, - I and »",.,-/ + W.F,
analogously with J'. We have
W, - I c J - WJ,
NoMfatefminblJc AstMnsta and Kkcnc Thcornn 435
and if W, c W'„ then l^fc W,F (see III.4.5) and hence,
*"..,-' + »".F<zJ+ I*".- 1^,,.
It u eaiy to verify that v* u the inclusion map.
It follow! that for/: I-* Q and for g: ]-» Q extending/ and for each
^algebra (Q.8), alio/•:(/•, •>)-»«& 6) is extended by g':(J', f) — (Q.S).
(il) Concatenation can depend on the set of variables: given / c J and
x € /, then for K, Ic /' (c J*) the language*
L;K (in /) and L-,K (in J)
can be diatinct. We prove bdow that this cannot happen for a regular
functor F.
£3. DcflaMoa. The x-lleratlon of a language Z. c /• in / Is defined for each
x € / with (jr)n e L as the following language
L"-L w (L-.L) w {L-.L) -, L) w {{(L-.D-.L) -, L)...
Analogously to the concatenation, the iteration agrees well with that for
tree languages:
PnpaaWaa: For each language L c /• with (x)n c L, we have
L" - ((/•«)*,.
Proof. I. We prove first that given languages L, K c /• and a tree
language £c /••with (£)*,- L, then
/..,*-(£,*•)*,.
For this, It ia sufficient to prove that
/.• -, K* c (£., *•>
because then by Proposition VII.3.4 we get L -, K c (£ •, /f*)<„ and the
reverse Inclusion is dear.
Let r E I? -.K*. Then we have a tree t E JC* and for each i-labelled leaf
e e (*)«-■
a tret s, € L* such that ris obtained from I by substituting each c e (jr)f-1 by
i,. Since
mi'- ((£)fi)*r',
we can chooae s't E £ with (j,) — (*,'). Let r" be the tree obtained from f by
substituing each c E (!)("' by s',. Since the equivalence i"r • lj' is a
congruence on the free algebra /**, dearly
(.<■) - <0-
436 Chapter VU
Further,
r- € L .. AT*
which proves that
r € <£ •, K*).
II. By Proposition VII J.4, we have
L ; L - (I? : /.*)«,
and using I above, we conclude that
(/.,/.) .,/.-((/• ,/.•)• .f)l,
and we use I again, etc. Thus.
L" - L w (L.. L) w ((/. •. L) ; L) w ...
- {If w (/.• •, /•) w ((/.• -, /•) -. tf) w . .)*,- ((/•)-)*,. Q
3.6. By VII.2.5. if e: Ht-» F is a minimal presentation, then for each basic
tree s — (x„..., x,)o* with i, pairwise distinct, we have
W- lOW *«.i,)c;/»€ J>.|.
We generalize this to more complex trees, and then we use this generalization
In order to prove that Kleene theorem does not hold for functors which are
not perfect.
Lemma. Let e: Ht -» F be a minimal presentation of a super-finltary
functor, and let
s - {s, s.)a € /•• (c e I., n > 0)
be a £tree with (*,),..., (*,) pairwise disjoint. Then
<*> - 1(4 l.)<r; 4 € <*,„) (i - I,.. , n) for some p € P.\.
Proof. For each tree I € /** we have
I e (s) iff {1)1, - {s)i„
and if this is the case, then 11 I by Remark VIIJ.3. Thus t - (4... , l.)rfor
some r € r,.
Since i, is a homomorphlsm, we have
(*)*/ - (' •».)** • «/ - ((*.)«"< (J.)<i)fi* • «•
and analogously.
(»)*,-((4)*, («.)£,)*,.•«..
Nonddermlnlftic Automata and Klecnc Tbeomn 437
The map e> is one-to-one (Remark IV.4.2) and hence. I € (j) iff
((*.)*, Ml,)*. - ((»,)*, («.)*,)«,..
By hypothesis, (*,)£, are pairwise distinct elements of /■ and hence by VII.2.3.
the last equation is equivalent to the existence of p € P. with
r-c and ((,)£/-(J|,„)ff, for/- I n.
This was to be proved. D
Bask rufli Let e: W,-» f be a minimal presentation, and let a € £
with n> 0. Consider the following trees in variables I, 2,.... n:
Hr©
etc Thus, Vo — I and u, — (I, 2,..., n)a and
■l. i - iHll ■]»,.
By the preceding lemma and Remark VIIJ.3. <u,> is the set of all trees
438
Oupttr Vll
with f e P„. None of these trees belongs to (2),.., <n) and hence, by the
same lemma, (u,) is the set of all trees
with/ME f.and i-(I)?-'.
Analogously, u, is the set of all trees
with p, q, r E J>„and i- (Of1 and;- (l)r-1. etc. Note that
<«!> - <»,) •, <»■>
and <u,> - <u,> -, <u,> -, <u,>.
In general
(a) <u.) - <u,>., (u,) •,...., <«,) (*-umes)
and hence, for U, - |l. n.|,
(b) U?-(Ut)v<.Uu)v<U>t)v... .
Further, since u, has just one leaf labelled by I, clearly
(c) |u.| - | u, | -,111,1 .,...., |u,| (t-times)
Nondctcnnioutic Automata and Kiama HMonm 439
and hence,
(d) u;<-jjmu«.
Further, for
Vt .(l/*ic|»l'
we have
(e> <i/,r - (Kr')«.
In fact, for each it, k' € tv we have by Proposition VII.3.4,
Vt -, V, - (l/,)4., -, (l/,)jj„
Therefore,
- Hu(K..,H)u...
->T;
since by (b) clearly
this proves (e).
Finally,
(o vr -, vr - vr
because by Proposition VII.3.4
Since clearly <l/,>" •, <l/,>" - <£/',>•', this proves (/).
For each map
/:(n|-<»
we put
(g) s, - (U(,„, u,,,, u^a E |n|,#.
If/is one-to-one, then <u(ll/> are pairwise disjoint and hence.
440 Ctapttr VII
(h) (*/) - |(J(,..., s,)o; there exists p € P„ with s, € ("<(„./) for
■- I "I-
It is clear that the depth |>| (II.I.S) of each tree I € (u») is equal to the depth
of u, which is *. Thus,
(k) I € <u») implies |(| - t; ( € (t/»> implies |r| € l/*l7-o-
3.7. Theoreai. Let F be a super finitary functor such that the languages
|v,(x)n|--. Mc /'
are recognizable (for each finite set /, each x € / and f, h> € /*). Then F a
perfect.
Proof. By VII.2.7, it is sufficient to prove that given /e (n|/f, and g €
[n)H„ where
a € I,, r i Im and n S. mi. 2,
then (/)«t„ - (»)«•„, implies
(•) a - t and g - p • / for some p e P„.
Define a one-to -one map/*: |n|-» <uby
('IT -(V+C- I) • n fori- I n.
To prove (•), we use the recognizability of the language
L,- V:'-,\w\
with
w - (*/-)*M.
in the notation of the Basic Example above. Note that by (e) above and
Proposition VII.3.4 we have
/.?-(•':|y,-i i »r-««/.>•'•.<*■»•
(A) For each one-to-one map r: (n| -» <v with
s, € Lf
we prove that there exists a permutation p € P, such that
(f)r - (i)p • /(mod n) for I - I n,
i.e., that (i)r — (Op ■ /is a multiple of n. Since
I,€ «l/. >•'•,<*,»,
there exists » € (*,) n ((l/.)" -( (*/-». By (h) above, there exists p € P, and
Nondewraiinittic Automata and Kleem Thmem 441
'. 6 <"„».,) With
I - (»., ., i.)a.
Since
i € <l/„>" -, <.sr),
the tree Iis obtained from a tree
S E (Sr)
by substitution of trees in ((/,)*' for leaves labelled by I. Applying (h) to/*,
we see that there exist q € f.and s, € (u(l>,./-) with
' - (s, s,)<r.
Each tree in <(/.)*' has depth m 0 (mod n), see (k) above. Thus, the branches
in I and s bave the same depths modulo n:
|(,| m \s,\ (mod n) for / - I,..., n.
By (k) applied to («m,.,) and (u,,,,./-), we conclude that
(Op ■ r a (/)f • f (mod n) for / - I,..., n.
Thererore, the permutation
/>-'•«€ r.
fuinis
(Or - (00»-' •«)•/■ (mod n) for / - I n.
(B) For each one-to-one map r: \m\ -» a and each r € I_, m > 0,
we prove that
("hi u{mV)t s Lj implies r - o-.
In fact, (k) implies that («,,„),..., (u,.,,) are all disjoint, hence by Lemma
VI 1.3.6 there exist />€/>„ and (, € («,,„.,) with
0 Ore <«,)•'•,<*,■>.
Each tree in ((/.)*' ■■ {sr) has its root labelled by a. Therefore, r — o*.
(C) For each r:\n\-* a> such that
('V <(')r-('V (modn) for/- I n
we bave
*- (»«l "l.|r)C€ L.J.
442 Chapcor Vt!
To prove this, put (i)d - (i)r — (i\f'. Since (0^ is a positive multiple of n,
clearly
■W 6 W fori- I n.
The tree
* - (»('* «W)o-
- ("on v >W «(.«■■ "W)o-
is obtained from sr by substituing u,,M for the I-libelled leaf in u,lir, u,,w for
that in u,lir, etc.:
Thus, s, e Z.f.
(D) The proof of (•). We use the fact that Lf is recognized by an ^acceptor
A — (Q.S, 7°, (n|). Clearly, ^.| is one-to-one on the set |u^ u,, u,,.. .|, and
hence, the set
|(u,)^.h(i'...W.i.(''..i.)^.h--l c W
is innnite for each i e (n|. On the other hand, Q is a finite set. Thus, there
exists an infinite set
B,<zUI+ n,l+2n,...\
such that the run map p: [n|* -► Q is constant on the set of all (u,)^,, with
k E A,. More precisely, there are states
(l)ft...,(n),E C
such that
k € B, implies (u.)^.i ■ p - (t)q ('-I n).
This defines a map <j: [n| —► g.
NondetcnnmiBtic Automata and Kltana Thforam 443
In the final part of the present proof we shall verify that the map q fulfils
OX«t.i -qF-S)€T.
Then we conclude the proof as follows. Since
(/Xi - <»)«t.|.
we have
(g■ «)»<, • S- (g)qHt-CffS- (»)«i., -qF-Si T.
Cboose a one-to-one map r: (m| -► ai sucb that
ID'S B„„ (m)r£ ««„,
and put
'-(»(». «W)r.
Then ( E Lf, i.e. (>)^,, ■ p E T because p is a homomorphism and hence,
(0«H • P - («|(K »(->-)•»• ■ «M ■ P
- (*W "(.i.)*S.ir/i ■ pHt- s0- S
- ((K(ii,)5.]' P. • • •. («|.>,)$.| • P)«b ■ *
-((Of ft..(m)j- q)^- S
- IS ■ «)«„ • S E T.
Inl*^,-
inl'*
Then by (B), r - c; consequently, < - J,. By (A), there exists a pennuution
/>€/>„ with rap- /(mod n). Since (Or E fl,,„ implies (Or > (Of (mod n),
we conclude that
(')»-(0/>-/(modn), I- I n.
Since f and /have just the values I,..., n, this implies
t-P-f.
444
Chapter VII
(E) The proof of (/X«t.i • aF- *) 6 T. Choose a map r:[n]-» a with
(Ore B„v and (i)r >(/)/" for r- I n. We have (i)r - (V- (0T
(mod n) for each i and hence, by (C), J, € L*. Thus,
(*,)$., -per.
Finally,
(*,)$„ • P - ("di "Wto* • $.] • P
- (("m,)$.| • P, ■ ■ ■• (lW)*t„| • P)«a • «
- Wif- *,(")/• 9)efl-«
- (/•• «)*o • *
- (/>t.i • «f- «.
This concludes the proof. D
3JL Deflaltloa. Let F be a super-Unitary varietor. The class of rational
languages is the least class of languages containing each finite language and
closed under union, concatenation and iteration.
Thus, a language Lc /'is rational iff there exists a rational expression for
L, i.e., an expression using languages |w| for w e J' and operations
U (union),
•, (^concatenation in J for some finite set J),
and
•'('-iteration in J for some finite set J),
finitely many times. For example, the Isnguages |v, (x)n|*T •, |w| of the
preceding theorem are rational.
Mala Theoren. For each super-finitary functor F, the following statements
are equivalent:
(i) Kleene theorem holds, i.e., an f-language is recognizable iff it is
rational;
(ii) F is perfect.
Proof. Since perfectness is necessary by the preceding theorem, it remains
to prove that it is sumcient. Thus, let Z be a type, and for each a e Z. let F,
be a permutation group on [n|. We prove that the functor
F-]ltH.ur,
(see Proposition Vll.2.7) satisfies the Kleene theorem. We know that Kleene
theorem holds for Hi (11.4.11). Thus, it is sufficient to prove that a language
NofldetenninUlk Asunuu ud Klcinc Theorem 445
tc/'ii rational ifT the tree language L* c /'* is rational, and L is
recognizable Iff L* is recognizable.
I. The minimal presentation
e: «!-► F
of F is given by the canonical maps
e,: II *■-» II*V~
0 « & rl&
where
(*i *.)»~ (y >".)c
holds ifT there exists a permutation p e P, with
n- •*!/» f«f •'- i »•
We can describe the homomorphisms I, analogously as follows.
Denote by ft, the following relation on the set /** of all £trees over
lift,!', (1,1' e /*•). ifT I' is obtained from r by a ^•permutation of
branches of a ^-labelled node (a e I). More precisely, recall that I and I' are
partial maps from m'to/u T (see II. 1.4). Then rXof'ifT there exists a e m*
such that
(a)r - a e T.
and for some p e /"„, the tree r' is defined in each ft E m* as follows:
.... J (*)r if * * ae for each c E m*. e * 8;
1 ' " \ (*>c)f if ft - ate for some c 6 m\ and 7 - (/)/»•
This relation X0 is obviously reflexive and symmetric. Let X be the transitive
closure of Xo [i.e., X - X,, w (X,, • X,,) w (X, • X0 • X«) w .. J. It is easy to
verify that X is a congruence on /** and that
l,:/••-►/• - /'Vx
ia ihe canonical map.
II. For arbitrary tree languages K, L c /**, we prove that
<t> -. <*> - <t., K).
First, consider a tree
I E <t> ., <*>•
It is obtained from a tree
5 6 </f>
446
Ck^xn VII
by substitutions of x-labelled leaves by trees in (£.). For each leaf d e (x)j-1
we have rd e (Z.) such that I is obtained from s by substituting rd for x We
can choose r'd e L congruent to rd. The tree ( obtained from s by substituting
r'd for x in d [d e (x)j-'] is obviously congruent with r:
r/cf: r' e L ■, <JC).
Further, we can choose s' e K congruent to x Without loss of generality, we
assume that
s R, s\
i.e.. there is a node a with (a)s — a and ihere is f e /"„ such that j' is
obtained from s by the p-pcrmutation of the branches of a Then also (o)r' — a.
Let r" be the tree obtained from f by the p-permutation of the branches of a
Then
i r f R r.
Moreover, l" can also be obtained from s by substitions of x-labelled leaves
by trees in L. In fact, if a leaf d € (x)s~x has the form
d — aic (c e m\ i e m),
then for./ - (i)p we have a leaf aj c of s which we substitute by r'd; if d does
not have this form, then d is a leaf of s which we substitute by r'd. Therefore,
r" E L; K, and we have
I e <0 c <t.. *>,
so <t>.. <K> c <t -, K>.
To prove the converse implication, consider a tree
I E <t •, JO-
We can choose a tree I' E L ■, K congruent to t Without loss of generality,
we can assume
tRot',
Nondelcrniinbuc Aulomati and Ktorat Thtoram
447
I.e., there exists a node a e m*with(a)r- a and a permutation p E />„such
that f is obtained from r by the p-permuution of the branches of a.
Let
re*
be a tree such that (is obtained from s' by substitutions of x-labelled leaves
by trees in L. For each d e (xXO~' we denote by u e L the tree used in this
substitution,
(i) Let (a)J' - a
Denote by s the tree obtained from j'by thep-'-permutation of the branches
of a Then
JE <K>
Is a tree from which s' is obtained by the ^permutation of the branches of a
Then I can be obtained from s by substitutions of x-labelled leaves by trees in
L: for each d - alee (jrX')~' we use the tree ofor the leaf ajc{j- (0/»"'l
of s; for each d e (*XO~ ' "°l under a, we use rt for the leaf d of s. Hence,
ret-, <JC).
(ii) Let (a)j' be undefined or equal to x
448 Ckiptcr VII
There exists an x-labelled leaf d of s' such that a - dc for some c e m'.
Then clearly (c)rt — a: let rj be the tree obtained from r^bythep-permutation
of the branches of c. Then
U € <t).
The tree I can be obMined from s' by substituting the leaf d by u, and all
other x-labelled leaves as before. Therefore.
f e <L>., JC.
III. For each tree language L c /** with x e L we have
</.)•' - </.•">.
This is a direct coiueouence of II.
IV. An Slanguage L c /• is rational iff the tree language L* c /•• is
rational.
First, let us observe that concatenation and iteration are independent of the
set of variables: if K, L c /* c J', then for each x e /the language X •, L
is the same when computed in / or J, and the same holds for L". (This
follows from the fact that (/*)£;' - /**.|
For each rational language Lc I', the language L* it rational because the
operation (—)• preserves
(a) finite languages: for each tree I e /**, the class (f) is finite and hence,
if L Is finite, then so is L*:
(b) union;
(c) concatenation: by II above and by VIIJ.4, we have
(Z. -, Kf - [(/• -, *•)£,]•
- </.» •■ *«>
- /•• •, *•;
(d) iteration: by III above and by VIIJ.5, we have
Conversely, for each language Lc I' with L* rational, the language
L - (/•)*!
Is rational because the operation (—)£, preserves
(a) finite languages:
(b) union;
(c) concatenation: by II above and by VII.3.4,
(/.., K)i, - «L-, K))l,
- «t> -, (K))c,
NondetemiifiHIic Automata and Klaene Thtorcm 449
(d) iteration (analogously by III and VII.3.3).
V. An Slanguage Lc /'is recognizable iff the tree language /.• c /** is
recognizable,
(i) First, assume that L* is accepted by an //f-acceptor
A - (ft 6, /. T).
We can suppose that A is minimal (11.2.4), i.e., the run map p: /■• -» ft is
onto and A has no non-trivial congruence. We prove that
(.) (q)S -(p-q)S
(breach?- («„..,«„) e ft//„(where a e r.)and/»- q- («„„ «(.») e
ft//,, where p e rV
Since the run map p: /**-» ft is onto, there exists I: [n] -» /** such that
I e /*•//„ fulfils q - (t)pH,. Then p ■ q - (j> ■ l)pH, and hence both
(,)« - (t)pH. ■ S - M ■ p
and
{p. q)S-(p- i)pH.S-(p- t)pp.
The following trees
are congruent under R. Hence, it is sufficient to prove that
s, Rs, implies (s,)p - (jjp (*„*,€/••).
Let S be the least equivalence on the set ft such that
SiRsj implies (s,)pS(sdp.
We arc to prove that S la trivial. Obviously, S la the transitive hull of
%-l((*i)A(*>fc>):*i A'il-
Ca) S is a congruence on the algebra (ft, 6). To verify this, it is sufficient
to prove that for q, q' e QH„ with q, S, q] (for all / - I,.. ,\a\) we have
iq)SS, (q')S. Let s, i e /'*//, be n-tuples of trees with q - (s)pH„ and
4'.- ('~)pH„. and with s,Ri; for all i Then also (s)q> Jt(*')a since R is
a congruence, and hence,
((s)p)p SW)<p)p.
i.e.. («)« «,(«•)&
450 duplet VII
(b) S is a congruence on the automaton A, i.e, if qSq', then q e T iff
4' E 7: In fact, let s R i be trees with q - (*)pand fa-) - (j>. Then 4 £ 7
iff j € Z*, and L* is closed under R, thus. 4 £ 7iff j' e L*. i.e., 4' E 7!
Since A is minimal, the congurence S is trivial, and this proves (<). It
follows that
(4)<9 - (9>b implies (4)* - (q-)S (4, q' e QHt).
Define
by
«4)£g)o'- (4)f for each 4 E fttfr.
Then
A - (ft & 7. /)
is an ^acceptor, the run map fi: /• -» Q of which fulfils
[because £,■£:(/*•, *>*)-» (ft Eg- 6°) is a homomorphism). The acceptor /J
recognizes the language
which is equal to L because lt is onto and
/• - (7>-' - <rx«, ^)-' - «ry-'j»
Therefore, i is recognizable,
(ii) Let L be accepted by an ^acceptor
A - (ft S, I. 7).
It is sufficient to prove that L* is accepted by the corresponding £tree
acceptor
A - (ft 6, /, T)
with
S- Sq-S.QHi-Q.
In fact, let fi: I ' -» C denote the run map of /J. Since both
*,:</••.«>•)-(/•.«,..•>)
and
/i: (/•,£,.«.)- re. «b-«>
Nomktcnnifilttic Automata and Klecne Theorem 451
are X-homomorphtsms, also S, ■ p is a i-homomorphism. For each i € / we
have
(x)e,-p-- (x)p- i
and hence, t, • p'u the run map of A Therefore, the language accepted by A is
(rx*,-p)-'-((7>-')- z».
This concludes the proof. D
Reanrk. In the course of the preceding proof we saw that if F is perfect,
then the concatenation of tree languages fulfils
This property actually characterizes perfect functors: by Proposition VII.3.4,
the concatenation of Slanguages is clearly associative whenever F has the
above property (see Remark 11.6.9). We prove now that associativity of
concatenation implies that F is perfect.
(We devote the rest of the present section to some of the basic properties of
concatenation.)
J.9, Proyosltlem. A supcr-finitary functor is perfect iff concatenation in each
finite set / is associative, i.e.,
L;{K;H)-{L;K);H (in/)
for each ii /and all L, K. H c /'.
Proof. I. Let F be perfect Concatenation of tree languages is associative
by Remark 11.4.9, and hence,
L*; (K* .,«•)- (/.•., *•) •, H*.
By part II of the proof of the Main Theorem, it follows that
[L.AK;H)f- L»-AK.,H)»
- /.•-, (*•.,«*)
-(/.•.,«•>.,«•
-[(L.,K).,Hf.
This proves the equation above.
II. Let concatenation be associative. We prove that FIs perfect, analogously
to the proof of Theorem Vll.3.7. Using the notation of that proof, we use the
language
l,- i >".r •, m.
452 Chapter Vtl
The associativity of concatenation implies
[see (f) in Vll.3.6]. We now generalize (C) of the proof of VII J.7 as follows:
(C) For each r e Zm and all maps r, q: \m\ -» a with
(Of < (<> - (Of (mod n) for/- I m
if
("hw «(.>,)re *•/.
then
(«(C)r «(.>r)r€ tf.
The proof is completely analogous to (C): since (i)d — (i')r — (1)4 is a positive
multiple of n, we have «,,w 6 (u,)". The tree r — («,,„,..., ii(a<),)ris obtained
from r — (ull|(,..., u,.„)rby substituting ii,,^ for the I-labelled leaf in um.
Consequently, by (e) in Vll.3.6.
'« TO"', 1*1 c (»';')••, Lf c <(»T)»., t?).
and by Proposition VII J.4,
, e (V?-, L,)* - L*.
which proves (C).
We are to prove that for/e [n|//, and j € [n\H, with n - |o| 2 |r| 2 2
and
(/)*M - (»)«!.►
we have a — r and f - />•/ for some p € /"„. We use the fact that
(»di/» u,„„, „.)o-e Zj
by (C). We have »>• • «j„ - ^.,Hr- «j.,. • v
and hence,
l(«CII/t .■.-•■, »(.!/. .0^.1 _ ((»"!/* .>)$.► • • •. (»W* .>)$.|)«t.l« • »>
- (>W. .> <W» .>)«H* ' V 6 £/■
The n-tuple (»„„, , v,.,,, ,1) in \n]'H, can be expressed as/- A, where
/; [n| -»[n| is the given n-tuple and
is deHned by
(0*- »..-> ('- I »)•
Noodelennmiitic Automiia uti Klcane Thmcn 453
Thus,
(/• *)««•• tJ>-(/)AWr-«i.,«-tJ>-(/)«to'AF'*e L,.
Since (»)«j„, - (/)«» we get
(»)«<.l-AF-«>€ I,
■nd, inilogously u for /above, this nwans that
(("nit* Ki.k* •>)rK.i e L,.
Thus,
(»(■>,. ■ ■ - ■<-*)* « *•/
for the map q: [m| -» ai defined by
(09 - <0» + »'•
Let r: [m| -» to be an arbitrary one-to-one map with
(Of < (Or > (04 (mod m) for/- I m.
Then by (C) above,
(»(■>. "l»l'e £*•
By (B) in VII.3.7, this implies a - rand hence.
By (A) in VII.3.7, there exists p e P. with (/)r _ (/)/>-/(mod n). Since
(0r-(0«-(0» (modn),
this implies (Of a (0/>'/(mod n). The values of find/lie between I and n,
therefore, (Of - (0/> '/■ This concludes the proof. D
3.10. The last properly of concatenation we are going to study is its
independence of the concrete set of variables:
DeflaMoa. A super-finitary functor F is said to have absolute concatenation
if for arbitrary languages K, L c / and each >i /.the concatenation
L;K (in I)
is the same language as this concatenation in J for each (finite) set J o I.
Example*, (i) Concatenation of tree languages is obviously absolute,
(ii) The functor D, (Vll.2.3.) does not have absolute concatenation. Put
/- |nr„ r,| and J- \y\ w /.
454 ChaplcrVI]
The concatenation
in / is a language in /* which clearly does not contain the following tree
(because It /•). But the tree
is an element of (>|* — (•)£;', and I is obtained from f by substituting x by
elements of I - I*. Hence, re /*-,M* and this implies that
t-M, € l:\'\(mJ).
3.11. PiaaoaWoi. A super-fmitary functor Fhas absolute concatenation Iff
F is regular.
Proof. I. Assume that Fis a regular functor.
Let ii IcJ and K, Lc I' be given. We denote by d,
b':(l — \x\ + /.)*-» /* the homomorphisms from the definition of L; Kin
I, and analogously a\ b'. Denote by
and
u:/-|*| + L — J -\x\ + L
the inclusion maps. (Then v* and u* are also the inclusion maps, see Remark
Nondetermlntftic Automata and Klecm Theom 455
VI 1.3.3.) Then we prove that
(i) a'.*' - u' -a'
and
(ii) the following square
[|.(„).L|! •.(J-W.L)'
b" bJ
is a pullback. This will conclude the proof: by (i), a'is an extension of a', and
by (ii).
(/•X*')-'-(/-|*l + /.)".
Therefore,
|(j)«': a e (K)b')-'\ - |(j)o': a e (W)-<\.
(i) Since a' ■ r* and ■■ • a' are homomorphisnu, it is sufficient to prove
that they are equal on the set
I- I -\x\ + L
ofgeneraton. Since u* and v* are the inclusion maps, a1- »• is an exteiuion
of a. and u * ■ a' is an extension of a't (restricted to /); for each y e /we have
0-)o, - 0-)«i- Thus, «'.»•- ■• . a'.
(ii) Put also
J-J-\x\ + L
Since Fis a finiury varietor, we have
/• - U rV'.
with the inclusion maps w'.-.tV'.^. /•; analogously with W'„ W, and w\.
Define
b'm: w[-» W>. (n < o>)
by the following induction:
*{:/-►/
4J6 Chapm VII
is the given map:
»!♦ i - »} + l>'.F: I + WIF-* I + W'J.
Analogously,
b{: W\-* W'm.
We prove that for each n < to, the following square
i inclusion ,
b1 bJ
n n
W1 — WJ
n inclusion n
is a pullback. This is clear if n - 0. Assuming this holds for n, then it holds
for n + I because (a) Fpreserves this pullback (in fact, the inclusion maps are
monos and hence, the pullback is a preimage, see VI 1.2.8) and (b) the copro-
duct square of two pull backs in Sat is a pullback.
Pullbacks in Sat commute with colimiu of o>sequences and hence, the co-
limit of the sequence of squares above is a pullback. This is the following
square
b1 L
i* » j*
which proves (ii).
II. Assume that concatenation is absolute. To prove that F is regular, let
e:HL-* Fbe a minimal presentation, and let
(/)** - (»)«,
hold for some <r e S„ r e T. and/ E Jf//„ g e XH„ We prove that for each
re X.
r 6 Qnft/ implies r E dm\)g;
by symmetry, it follows that QfiD/- QmDf. We can suppose that n 2 2
(Vll.2.7). Moreover, without loss of generality, we assume that
Nondeterminhilc Automata and Klctne Theorem 457
W-'-l'.J *l<=[n)
for some (2 I.
Put
/- Ur„ i, r.|
and
J- I^ \yt, • ■ -yX
where the variables x, « and yt are pairwise distinct. Let s - (x, x,..., x)a e
/**, and define languages K, L c /'by
K - |(J)*,|
and
L- I.
Since concatenation is absolute, the language
L;K {in J)
is a subset of /* (because it is equal to L-. K in /). We are going to present
a tree
IE J"
such that
(t)tj * /"
and if r t ([m])f, then (f)i, e /■•, X. This will prove that r e ([m])g
[because we know that (1)1, t L; K\.
III. Let r be the following tree
That is,
l- (s *,. *,♦,..., r.)c
458 Chipur VII
where
'i - (*,. yi y.)°-
By VII.2.5, the class <J,) contains only trees obtained from s, by a permutation
of branches. Each of these trees uses the variable z„ Consequently, the classes
<j,) are pairwise distinct (i — I,.. , k) and distinct from <r;) — |r;|
(/-*+! n). By Lemma vll.3.6, we conclude that also each tree in the
class (r) is obtained from I by permutations of branches. Consequently, none
of these trees belongs to /**. It follows that
0)1, * /'
because else there would exist t e /** with (f)i, - (1)1,, and the last clearly
implies that f e <f>.
Denote
J-(.f-|*|)+ L-\z i.,yi,..^y,\v\x;i\ *;|
where primes are used to distinguish the elements of the second summand
L - I from those of J — |x|.
Let
a,b:Jm—J*
be the f-homomorphisms from (be dennition of
L;K- 1; |(5)£,| (in A
and let
«•.»•:/■•-»y'»
be the corresponding £homomorphisms with respect to / •, |j|. Then
«••*,- £j- o:(/'», •>•)-(./•. «j. • «•)
because these two homomorphisms agree on the set J; analogously,
b* ■ I, - «j • b.
For each tree in J'*, the map a* "forgeu" (he primes and the map b*
changes each i\ to x Therefore,
r-(0«».
where
f e /••
is the tree obtained from I by adding a prime to each t,, I — I,.... n. Thus,
(f)*, - «0*7)a.
Nonddenninlttic Automata and ICIeoni Theorem 459
To conclude the proof, we ihow that if r « ([m])& then
((OOj,.(»)f,;
it follows that
«f)*7)6 - ((f)6V, e K
and hence.
«0&)« - (Oft e L..K.
We have
«0«r)6 - (C')*VJ.
and (06* is the following tree
That is, for
*»-(*-*. >■> *.)»* ■''•
we have
('■)** -(A*\..,*\x,x.., *)ff.
where /> is repeated Ac-times [with (r)/~' - |l, 2,.., kfl. Define maps
ce-.X^J*
as follows: c Is the constant map with value x and
(r)c' - (P)ft
and on X— [r|, also c' is the constant map with value x Then for /• c,
f- e': [n] -» J', written as n-tuples, we have
(X X ...,*)-/■• c
and
(00*,. 00ft <*>)«. X X .... *) - /• c:
460
Chapter VII
Since r e ([m])g, we have
g • e - g • c\
Therefore, uiing Ihe fact thai I, u a homomorphiim (I.e., •>••*/-
i,H, ■ s,. . e>), we get
«f>V, - (A A • • -. A * * •••,*)«••• ft
- (a. p..... a. x, x,.... x)(,H, • e,. ■ p
- ((»)*> (/>W>. *,.••, *)«;• • «•
- (/• c)c,i • p
- ificH, •«,..«•
-if)e,-cF-p
-(«)*> -cF.p,
and alio
(*)**, - (i)*,
- (x, i,.... *)«.• • ft
- (x, x,..., x)l,H, • s,. • p
- (x, x,.... x)s,t • p
- (/• <•>;• • p
-WCfcF-p.
Since g • c - f • e\ we have
(g)t>. cF- (g- e)e,« - (g. 0*>. - (g)t>. cF
and hence,
((r-)Oft - (»)*,.
Thli condudei the proof. □
3.12. Saa—rlntlaa For each super-Unitary Kt functor F, equivalent are:
(i) Each partially recognizable language li recognizable;
(II) concatenation u absolute;
(III) F preserves the composition of partial maps;
(Iv) F preserves preimages;
(v) F Is regular.
For each super-Unitary set functor F equivalent are:
(a) Each nondeterminlstically recognizable language is recognizable;
(b) Kteene theorem holds;
(c) each language |(*)n, *!**•, |»| is recognizable;
(d) concatenation is associative;
(e) F preserves the composition of relations;
(0 F coven pullbacks;
(g) F Is perfect.
Noadetemrialtflc Aulomati and Klwoc ThMfffli
461
The proofs hive been exhibited ibove: the equivalence of (i), (iv) snd (v) is
Theorem V11.2.10, for (ii) see Proposition V11.3.11 snd for (iii) Remark V.2.10.
The equivalence of (a), (f) and (g) is Theorem VII.2.12. for (b) see Theorem
VII.3.8, for (c) Theorem VI 1.3.9, for (d) Proposition VI 1.3.10, and for (e).
Theorem V.2.10.
Enrcbea VIIJ
A. Eacfe recogalnMe laagaage b ratloaal. This statement holds for each super-
rinitary functor F (whereas the convene implication holds Iff F is perfect).
Prove this, using the following steps.
(i) Given Slanguages K, L c /• and x e / with L c (/ — |x|)*, prove
that L-, Kc (/-|jc|)V [Hint: The map a.: /- |x| + L-» /* factors
through (/-|x|)'.|
01) Let L be a language recognized by an ^acceptor A - (ft, 6, T, /).
Prove that for the minimal presentation e: Ht-» F, the Z-titt acceptor
A* - (C. *o • 4 T, /) recognizes L*. Prove that for each U c ft if
p*: M* -» ft is the run map of A* - (ft 6, T, U), then p* - in • P* is the
run map of At- (Hint: VILLI.)
(Ill) Recall that the proof of the rationality of L* in 11.4. It was performed
by finding languages L^j c W' (M c ft j - I,.. , m and * - 0,.... m,
where ft - If qm\) such that
/.•- Ultj
«• r
and (a) Ij,, is finite, (b) Lj,, - Li,-,' •„ (tSri)•« •„ L)f)
for AT - M yj |f,| and (c) (Li,.jV>t c |«|.
(iv) Define analogous f-languages £i.; c A#* : L\, - (L'mj)eK and
£*.;- £*:»' .K^lrT/)*"- £1,7/1 for the operations •„ and •• In AT. Verify
that each Li,,, c A#* Is rational. (Hint: use (1) by Induction on k.)
(v) Prove (LJ, ,)p c [q,\. [Hint: use induction on k. For two languages H,
K c (AT)' with H c hi' and (#/)<?„ - Iftl prove that (H •„ Jt>„ - (JOp„
by verifying that the bomomorphisins a, b defining H „K fulfil
' • PH — * • Pll\
(vi) Prove the rationality of L by verifying that
l- UM,.
«t r
The inclusion D follows from (v): for the inclusion c, prove that
{L\,,)t* c L\,by induction on k. [Hint: by Propositions VII.3.4, VII.3.3 If
H c If and K c P, then H ■, K c (/?• •, *•)• and «•« c (/?•«')•.)
462
duplet VII
B. Deflarag the Itcfattoa. We hive defined the iteration by
L" - Lkj (L.L) kj UL-.L); L)kj (((/.-, L).. D-.L)....
If concatenation is not associative (VI1.3.9), then mother natural delinition
would be
"l- L<J^L■,L)<J^L■.^L■,L))<J^L■.^L■,^L■,Lm....
^i) Prove that whenever'"/. «» L", then the new definition doej not
correspond well with the iteration of tree languages, i.e.. "L *■ ('•(/.•))*>. [Hint:
VIIJ.5 and (/.•)•' - "L*.]
(ii) The two definitions need not agree even for regular functors: let F be
the quotient of Hz with Z — L, — \a, r|, given by the equation (x, x)a —
(x, x)t. Define Fproperly, and verify that Fa regular.
Consider the following trees over I — \x, y):
For L - \x, y. t]i, prove that (*)£, €'•/.- L".
Nolei 10 Chapter VII
VIM
All notions and results of this section appeared in V. Tmkovt |IMO).
VIIJ
Mrecogniiablc languages in Sot were Inverigaled by V. Trnkovi |I9T7. I980J. Theorem
VIIJ.I2 was eniwanced la the former paper, end • proof of e more general retort (unite] ulng
Muzzy ^automata) appeared in V. Tmkovt 11979»J. ^recognizable languages were studied by
V. Tmkovt II9I1L where Theorem VI 1.2.10 was announced: Ihe proof appears here for the first
rime. In all those papers, perfect functors were called Irccgroup functors, and regular functors
were called saturated.
VII.]
Concatenation and iteration of Slanguages was introduced by V. Tmkovt and J. Adtmek
ilVTVL where the Main Theorem VII J.S was announced: the proof appears here for the first rime.
The discussion of properties of concatenation ia VII J.9-II ia new.
Appeadlx
Set-Theoretical CoareMloa*
I. We expect the reader to be acquainted with sets and thus, we do not
Introduce any axiomatic set theory. Nevertheless, we were careful to have all our
constructions well-defined within the framework of Bemays-G&del theory of
sets.
Collections which are "too large" to form a set are called dosses. Thus,
classes are more general than sets: each set is a class, but not vice versa. (For
example, the class of all sets is not a set.) A class is said to be large if it is not
a set, and small otherwise. That is, small class is a synonym to set.
2. The empty set is denoted by 0, the set with elements Jr., ..., x. by |x„...,
x„|. For example, |x| is a one-element set. The set of all elements with a
property P is denoted by
|x: achas property P\.
3. By a palr(x, y) we always mean an ordered pair. More generally, an n-tu-
ple means an ordered n-tuple; we denote it by (*,),<. or (for finite n) by
(**, *!« • • •» *• - l).
Each ordinal a considered to be the well-ordered set of all smaller ordinals.
In particular,
I - |0| - |0|
and 2 - |0. I) - |0,|0||, etc: the set of all natural numbers is the ordinal
o>- |0, I, 2, ...| - |n: n< at].
Ordinals are also used to label domains of trees: here they are just labels (but
this double use does not lead to any confusion).
The cardinality of a set AT is denoted by card X.
4. A mapping (or map) f:X-+ Y\% a triple consisting of a set AT (the
domain), a set y (the adomain) and a subset fc X x Y such that for each
x € X there is a unique y e Y with (x, y) € /[which we write as y — (x)f\.
For example, given a set AT and its subset Zc X, the Inclusion map
»:Z-»Af
is the map defined by (z)v — i for i € Z In case Z — X, this is the idenlily
464
Appendix
map
\4X:X-+X or \X:X-*X.
In cue Z — 0, v is called the empty map.
We also work with class maps allowing the domain and codomain to be
classes.
5. Composition of maps is writen from the left, i.e, the composition of
/: Af-» Kand g: y-» Zyields the map/- g: Af-» Z defined by
("If-1 - «*)/)f•
Iff: Af-» yis a bijection (i.e., both one-to-one and onto), then /-■: Y-* X
denotes the Invent mapping, defined by/-/-1 — I, and f-'.f— lr.
6. For each equivalence relation ~ on a set X, we denote by
X/~ - \[x];x € Af|
the quotient set of all equivalence classes
[x] -\yeX-.x~ y).
The canonical map c: Af-» X/~ is defined by (x)c — [x] (x e X).
7. Each mapping/: Af-» Ydefines the kernel equivalence ~ on Af by
*i ~ Xt iff (Xt)f- (xt)f (x„ x, € Af)
and the (mage, i.e.. the subset
im/- (Afy- \{x\f; x e Af|
or Y. Then /is composed of the canonical map e:Af-»Af/~ the bijection
b:X/~ -»(AfV defined by (M)* - (*M and the inclusion map ?:(Afy-» K
8. The set of all maps from a set Ttoaset Afis denoted by Afr. If r— nisan
ordinal, this is the n-fold cartesian product of X. For example, Af1 — Af,
Af1 — AT x Af, etc. The set X* has just one element, and we use the following
convention:
X* - |0| - I for each set X.
For each map/: Af-» Y, we denote by
f'-.X'-t Y'
the map defined by
9. A collection or family with the index set, or class. / is a map with domain /
(that is, to each / e / we asiign an element x, from the codomain). We write
(x,|,, (or |x,; i € /). In case / is an ordinal, the collection is an n-tuple, and
ordinary parentheses are used.
Reftraces
ADAaaa, J. | I974a|: Frac algebras Mid aafoaiafa reanzanons la Ik* laagaage of categories.
Common, mm*. «/«r>. Cmvmmt IS. 5*9-102.
ADAMta. J. |l974b|: Categorical theory of ulamMi and eahrenal algebra (Cadi). Doctoral Db-
aeflatioa. Charles Uoivenity PragiK.
AdAmeh, J. 119751: Aatoeaata and categories: fiultuiess contra arirJeaalrty, Ltct. Wafer Camp. Set
U Sprlngrr'Veriag. hrfla-Heldeiberg-Nev York, IM-IM.
AdAuer, J. |l97ta|: Limits and collmlu In genenHied algebraic categories, Cue*. Math. J. M,
35-44.
Adaheb, J. |l976b|: Cogmerttion of algebras in regular categories, M Amtnt. Malk. Set. It,
133-170.
AoAwn, J. |l977a|: Rcahnnon theory for •ulomata hi categories, / Pun Appi Algeem 9,
211-29*.
AoAim, J. 11977*1'. ColMtl of algebras nmtrled, M. Aojlml aM Sot. 17,451-430.
AoAuii, J. |I97I|: Flnhary varieurs, Ratchanasberrcht 74, Unitetstry Donraand.
AdAmo, J. |l979a|: Caiegorial retJrratioe theory 1*11, Algebrahcae ModaHa, Kategoricn uad
Orspoiosa, Aaaoaaae-Vcrlag Mm. 111 -13*.
Adaiur, J. 11979b): 0» iha coeaacretlon of algebras. Mar*. MaMm H. 171-1M.
AoAvaR, J. |l9t2|: Conaanjction of fret caattnaoas algebras. Alttma IMreraani KIW-ltl
AdAmer, J. |I9I]|: Theory of malkenallcal uracram. D. Retdel PeN. Coop.. Dordrecht-
Rotten— Lancaster, 1911.
AdAmc r, J, Ehrio, H. and Trnrova, V. |l9t0|: On an rqorvaJnce of ayvKtiMlieorarkaJ and cate>
gorkal concepts. Kytrmnma It, 199-410.
AdAmer, J., and Kouaet, V. |1972): CoeqaaJizeri In generalised algebraic categories. Conrmnir.
Mart. Unit. Cerarata* fj. III -124.
AdAmer, J., Rnd Kouers, V. (I977r|: Remarks on nRed points of fuacton, Lett. Nam Camp. Set.
H. Spriager-Verteg. tkrtla-Heidelberg-New York, 199-203.
AdAmer. J, Rnd Kousir, V. |l977b|: Funclorial algebras and aaumara, Kybtntntm IS. 243-2M.
AdAuo, J . and Koukr, V. |I979|: Least filed point of a functor, / Camp. Snl. ScOarai If.
ltl-171.
AdAhes, J, and Kouan, V. |I9*0): Are coHmits of alfabraa ilmple lo construct? J Alftbn U.
224-250.
Adahul, J, Kouaea, V„ and Pdhlova, V. 11972|: Cohosh* In lac gcacraHccd afasbraic categories.
Arm IM>. Cerarata* It. II1-124.
Aoamu, J, and Mebumcv, W. |I9M|: need points aa equation and eolations, Casual J. Malk.
H, 493-519.
AdAmer* J, Nelson, E. and RcrrERMA* J. |l9t2|: Tree coeatraatoas of free coatinaoai algebras, /
Coma Smt. Sri. 14, 114- 144.
AdAhes, J., and Trnrova, V. |I977|: Recogaiablc and Regular Languages in a Category. Lett.
Nam Cows. StL 54. Spitngrr-Veriag. rMia-Heidelberg-Near Yon, 204-211.
ArMatR. J^ and Trnrova, V. |I9II1: Varietors and machines in a category, Alg. Vmmnam It,
19-112.
Anderson, B. D. O., Arms, M. A. and Manes, E. G. (19761: Foundations of system theory: finiury
466
References
■nd infinitary conditions. Lett, Notes Economics and Math. Systems US, Springer Verieg, Ber-
lln-Heldelberg-Ncw York.
Asms, M. A. |I969|: Theories of Abstract Automata, Prenike<HalL Princeton, New Jersey.
Aaaa, M. A, |I9TT): Free dynamics end algebraic temantics, Lea. Notts Camp. Sci. 5% Springer-
Verlag, Berlin-Heidelberg-New York, 2I2-22T.
Aaaia, M. A. and Gtveon. Y. |I967|: Algebra eatomata I: parallel programming at a prolegomena
to the caiegorial approach, Inf. Control 12, 111-145-
Aaaia, M. A. and Mahu. E. G. 11974a): MacMnes In a category: an expository htfrodocdaa,
SIAM Rewtrw In, lei-192.
Aaaia, M. A. and Mans, E. O. |l974b|: Foandations of system Ibeory: decomposable systems.
Automatic It, 215-302.
Aaaia, M. A. and Manes, E. G. |l97Sa|; Adjoint machines, state-behavior nucUaa and daaHty,
/ Aire Atm4.AH}ebm a. 111-344.
Aaaia. M. A. and Manes, E. O |I975b|: Fuzzy machines in a category. BwO. AmstrvL Math. Sac. IS,
169-210.
Aaaia, M. A. and Manes. E. O. |I9S0): Partially.addllive caiegorles and flow'dtagram semantics,
J. Algebra 42,203-227.
Bai*. M. |I970|: Coequalicen and free Iriples. Math. Z. Ilm, 307-123.
Baa*, M. |I97||: Factorizations, generaton and rank, unpublfahed preprint
Bark, M. |I974|: Right eitct functors, J. Fme AeplAlgebra S. 1-7.
Birrhofp. O. and LinoN. J. D. |I970): Heterogeneous algebras, / Combinatorial Theory t,
IIS-131.
BaAiNtao. W. 5. |I9AS|: The miaimization of iree aulomala. Inf. Control II, 484-491.
Budach. L and Hoehnke. H.J. |I97J|: Auiomaten und Funktoren, Akaderaie-Verlag. Beriia.
Donnoi. J. E. 11970): Tree acceptors and some of their applications, / Cony. Syst. Sciences 4,
406-451
Emio. H., KuaMEiEa. K D. Kreowsri. H.J and KOhmi. W. |I974|: Universal iheory ofaiitoma-
ta. Teubner. Siaiigan.
EiLCNtcac. S. 11974): Auiomata, langugaes and machines. Vol. A, Academic Press, New York and
London.
Ejlewbuo. S. and WatcHT. J. B. |I967): Automata in general algebras. Inf. Control II, 52-7a
Gecseo. F. and Stunit, M. |I9M|: Tree aotoraaia. Akedemial Klado. Budapest.
GocuEN, J. A.|I972|: Minimal realization of machines in dosed categories, BwBAmer. Main. Soc.
71 771-783.
Goquen. J. A. |I971|: Realize Hon is universal. Mart. Syst. Theory 4, 359—374.
Goolen. J. A., Tchatches. J. W, Waoner. E. G. and WaiOHT. J. B. |1977|: Initial algebra semen.
tics and continuous algebras. J. Astoc. Coma. Machinery 24, 61—95.
GaATZca. G. |19o7|: Universal algebn. Van Nonsirand. Princeton. New Jeney.
GaiLLti. P. A. |I97I|: Regular categories. Lett. Notes Mathematics Hs\ Springer-Verlag. Berlin—
Heidelberg-New York. 121-222.
Hesslich, H. and Stiecrci, G. E. 1I979J: Category ibeory, 2nd Ed., HMdersaann-Verlag, Beriia.
IsaiLL, J. R. |I95T): Some remarks concerning categories and mbspacea, Cmnad. J. Mam. t,
563-5T7.
Jam/imshm, G. |l*82|: Tree at-compkle algebras. Alg. ummaki 14. 2JI-234.
Kjuv. G. M. 119*01: A unified treaiment oftransflniie constructions.. , Buff. Avstrat Math, Sac.
U 1-85.
Knastir, B. 119281: Un iheoreme sur les fonctions d'ensembles. Aim. Soc. Fohm. Math. s\
133-134.
KoustR. V. |I97I|: Set functors. Comment. Math. Unit. Carobnae 12, 175- 195.
Kouier. V. |I971|: Set functors II. con I ravsris m case, Commrnt. Math. Univ. Carolina* 14,
47-59.
Rcftrvncm
4<7
Koum, V., ind Riiteiman, J. |I973|: Scl lanctora HI— monomorphmn*. cpimorphiuM. iaofltor.
phlim. Comrnml. Mart. Unit. Canlmat 74,441-455.
Kourcr, V., ind RerrtaMAN, J. |1973|: Aotonala ind cncgoriaa. Input proccnc*. Lttt. Horn
Com/,. Set. It. Sprlnger.Vcrlag, Berlin-Heidelberg-New York, 2W-2M.
Kouaca, V., ind RlmiMAN, J. |l979):Categoriai coiialnicdom of free algebru. coltnlti ind con*
pletioni of partial algebras, J. hut Apft Altthn 14, 195—231.
KoeaovA'PDHUivA, V. and Kouau, V. |I975): When a gtntmllzcd algebraic category is monadic,
Commtm. Hath. t/»r>. CmHaat II, 177-517.
KOaacM.PmuivA, V. |I97)|: On itnaa hi ginaiallnd algebraic catagorlo. Cree*. Man. / II.
DJ-MI.
MACiOoa, M. and Moran, O. |1969|: Finite automata ovtr flame ineea. ftrMaanri itrp. -**• Hebrew
Univenity. Jcraaakn.
Mu.ii, E. O. |197»): Algebraic Theories, S-xiiiger. Verba, New York-HeiddbeTg-lcriln.
Mezu, J. and WarcHT, J. B. |IM7|: AJgtbrmlc autonau and cornell-free sen. In/ Ctmml II,
3-29.
Neuon, E. |IMI|: Z-continuou algebras. I/O. Wow* MalhmaHa 171, SprlrrgrtVerlag, Berlin-
Heidelberg-New York, 115—334.
REmaMAN, J. |I97I|: An CRanple concerning art functors, Commtnt. Hath. Unit. Canlmae II,
227-2JJ.
RErnaMAN, J. |l9T7a|: A more categorical model of universal algebra, Lttt. Notts Coma. Sri. M,
Spriagcr.Verlag. Bcriln-Heidelberg-New York, J0t-)I3.
Rcitqman, J. |l977b|: A left edjoml ccmmucrlon relalcd to free triplet, / hut Apmi Algebra 10.
51-71.
RcntaitAN, J. |l97)a|: One more categorical model of anivenal algebra. Maw. 2. Ill, 1)7-146.
RlfrtaMAN. J. |l97gb): Large algebraic (hemic* with nnall algebras, /iumnawgiMitial 74, Unrrer.
shy Dortmund.
RcmaMAH, J. |I979|: A note to AOTt nibaet systems. Proc "Foal Cr*npr#tstioo Theory', Ma-
Mm roor*wn» 1. Akadenie-Vcrlaa, Berlin. 317-390.
Smtth, M. B. |1976|: Power ooourra. 1 Comm. Sysi Srltmm H 23-24.
STAaaa, P. H. |I972|: Abaract automata. Ehcvier, Aemerdam.
Tassri, A. |1933|: A latiice>lheoreticBl flRpoim iheorem and ita aprjticuioos. Hclflc J. Hath. J,
215-309.
TcKATCHEa. J. B. |I973|: Tree automata, an Informal survey. Current! In Ihe Ihcory of
computation, PreMlee-Hall. Princeton. New Jersey. 143—17],
TcHATTHta, J. B. and Wrmiht, J. B. |196l|: Generalized flnile aulomala ihcory wilh an appllealion
lo a dedalon problem of seoond-ordcr logic. Hath. Sytt, Tmtary 2, 57—II.
TaNROvA. V. 11969): Sonc properties of let functors, Commtnt. Math. Vmtr. Cambnat 19,
323-352.
TrnsovA, V. |l97l|:On deacriptive daiaificatlon of set funaon. I., II. Canwftfltr. Math, Umr. Ca-
rolbm /;. 143-175 led 345-357.
Ta*»«,o*/4, V. (1974): On tnlnjiiial rcalizalioiu oT behavior maps In categorlal aatomata theory.
Commrml. Math. (Mr. Carohmat IS, 555-546.
TaMtovA, V. |l975a|: Automata and categories. Lttt. Nam Comb. Set J2, Springer*Verlag. Bar*
lin - Heidelberg- New York, IM-152.
Tinvova, V. 11973b|: Minimal realizations for finite aett in caxegorial a*rJometa mcory. Cottarjettr.
Hath. Voir. CareUur /*. 21-35.
TamovA. V. 11977): p^lational automau hi a category and theory of language*. Ltct. Notts Comm.
Sri. U, Springer-Verba. Berlin- Heidelberg- New York, 340-355.
TaNtovA. V. |l97*a|: Behaviour of nachlnca in calcgoriaa. Ctnimeiil. Hath. (Mir. Carohmat 29),
267-212.
Trnrova, V. |l979b|: L-fuzzy funclorial aulomau, Lerf. A*HrrComp. Sri. 74. Springer.Vcrtag, Ber.
468
Referenca
lln-Heidelberg-New York, 463-471.
Trniova, V. |l979c|: Machines and ihelr behaviour In ■ category, Proc "Fund. CcaDputattoa
Theory", Mornem. Fondiung I Akaderme-Verlsg. Berlin, 450-4*1
Tbnrova, V. |19«0J: General iheory of relatioaal automata, /fane l^/wmmtkm* I 119—233.
TiniovA, V. 119811: Partial and noDdetermiarsiic automaia In ■ category. Proc. 7* Nat. School
"Mathematical methods in Informatic", Vsrna 1911 (Centre of Appl. Math- Sofia). 71-93,
Tiniova, V. |I9S4|: Kleene type theorems for fundorial automata m categories, Proc 9* NaL
School "Mathematical methods in Informatic", Verne 1983 (Centre of Appl. Math., Sofia),
5-24.
Tkokova v. and Adamh J. (If77aj: On baauaaes accepted by machines In the category of acta,
Utt. Mam Cam?. Sti. St, Sfninger-Verlag. Berlin-Hcidelbcrg-New York, 523-331.
TaNSOvA, V., and AdAmer, J. (I977b|: Realization b not universal, Vortrtge tar Aatomatentheorie,
Weftcrbildungtzeatrum Rlr meJhemaltsche Kybemetlk and Rechentedurik, Heft 21, Tecaat-
schc Univenklt Dresden, 38—55.
TaNcovA, V. and AdAmer, J. ||979|: Tree>gn>up automata, Proc "Fund. Computation Theory',
Mwatm. fonrrtiMf J, Akadcmle.Vcrlag, Berlin. 462-468.
TaNaovA, V. and Adamcr. J. 11*921: Analyses of languages acceptad by varlelor machines ia a
category, Banach Centre Publications 9, Polish Scientific Publishers, Warsaw, 257-272.
TanrovA, V, Aoamer, J., Kouber, V. and RerrraMAN, J. 119751: Free algebras, input processes and
free monads, Commrni. Math. Unit. CaroHna* /a, 339—351.
Trnrova, V. and GoralOr, p. |I969|: On products in generalized algebraic categories, Coavnrar.
Mara. Unlr. Carototot /«, 49-89.
Wand, M. |I979|: Fued point constructions In order>enriched categories, 7a. Com*. Satmr f,
II-30.
Wvlu, O. |I96*|: Operational categories, Proc Conference on categorical algebra.
Springer-Verba. Berlin-Heidelberg-New York, 293-314.
Lbt of Cairat Symbol*
0 behavior 2, 19,36. 95, 103
a branch 33,55
5 next-state map I
e epi-tnmfonnatlon 85
t dau of epii 99
n injection of generator! 93, 238
F functor 83
fm from automata morphiimi 39
Ji. from automata morphiimi 4,39
I/,.A) relation 257
f free-algebra operation 93
Y output map I, 29
r output object (alphabet) 1,29,90
horn Ml of morphiimi 83
/ Initialization object 29, 90
/* free algebra 93
jr category 82
JT* clau of morphiimi 83
JT* daii of objccti 83
JT* dual category 85
X Initialization morphiim 29,90
«# dau of monos 99
* projection 85, 107
Q Hate object (set of Hates) 1, 29,90
p run morphiim (run map) 2, 36, 95
1 type 29, 52
I[i) module of polynomial! 94
T terminal object 87
U forgetful functor 126
Wt itepi in the free algebra construction 34, 172
[ ] equivalence clan 469
|c| arity of a 29, 52
/* free externum of/ 93
J. initial object 87
111.1:1 projection! of a relation 257
47t>
List of Current Symboli
-» arrow (morphum) 83
-* relation 21, 257
• composition 259
1,4, id,, Identity moiphitm 83
[7 product 85
x product of a pair 85
1] coproduct 85
+ coproduct of a pair 85
Sabject M«x
AtaolaU lolrWk M2
_ coaataM»Ml 411
AAtttlw cattfoqr 111
Adjoint 101
- automata 104
- fanctot Uwoim 104
Aixapt 19,16
Aota|Horl«,4«,«M
AIt.bt.4D
Aiphabal LB
AattlfaaMlfcM property 290
«■*<?) 322
«■*,<?) 112
M,(i)U
BnblncU
-Tartar 111
■*»■<?) 112
BitaviorL H.2&M. IM.31)
- fancm «3,332
MJMMHI4M
Bilinear til
BhiaiyH
■Mndcd IVr objeck 1U
- tcnaiatloa 213
BranckJii!
C, US
C. CI 111
Caaomcalaupi&oM
- aoroUuiUI
Cntaiaa doatd 111
CatoforyU
- 0fmaonau62.222.U2
bnavion M. U2
Chain U
- cpwplata jj. HI
Cfcaracurbatkn theorem for varieton 112
mlaiaul nalnatioej HI
Cnroaaatk Bomber 110
Cun4U
- mapoM
CoedjoiM 101
CocomputeU
CodomainI2.4U
Cooqaallaer 86
Cotnaralo iJ
Colaumctloo 112
Catena) 111
CoMnkU
CoHtcrion 4*4
Commote 84
Coaqmtibtle coUxtloa U
of relation. 142
— OMp III
CompoaeMa of ■ morphiam 15. 11
relation 3S2. 311
CoaepoahJoii of map. «M
— of Mtml traaafuraaanoae 14
RMtiOM2iS
CowMtwrtow of words 2
manmtw21.22.432
Concrete category 121
- Armor L22
Coiicitlrly Momorphk 122
Coaaraence S. 44
CoooocMd caeeaery 213
-reactor 142
QienM reactor 121
Comtnidiv« daai UU
- frae aeepMca 22J
— variolar 123
ContimKW. 121.111
Co-prefmaejc 321
Cooreema 11
Cover paflbocfcs 224
Cowdl-poowwl U2
Depth Jilt
Dufonii mi-IB »
- nutioa2ftS
DuireaU
Directed 143. U4
Diecretc aleefcre HJ
— category u
Dntlnjtritticd point 111
Donatio (1,46J
Dul&Utt
DoaHry principle U*
/»
f-omnll-poMnd 112
(«,.#MMe»ory8S
EabxkHoi M, 342
- MRl I
Epill
Epanaslomutiofi U
Eqaaltanr H
Equrioi LLJ
t^oatjoaal prueotMioo 111
Eqernkoce relation 2*1
Equivalent nonoi 146
Bud eo-pntRMfc* 341
entful Ncrodc equivalence 364
realization 367
Batemally equivalent 164
EitremaJoM" lit
FalgrtuM
FaOIOmOlOa gl
oca-InitialM
FactorlsalioB cyalcia SB
FaltWU haoor 14
Family 464
• 117
FMdba* 15,11
Fill-la 19
Filter m
Fataary22
- reactor M, 142, 2*0
-nut 114
-nrieut I59.I7J
Rate ottoaealoa 111
-depth 16
-object 111
-par* tree 34
Fort petal 111
IfenjelMfliactor 126
FreeeKefcraU
luaalntlloo HI
_ ogaa^enon 111
imi—lualoet 213
-object IK
— ruination 42
Fill functor 14
— aibiatcgoiy M
Functor U
— applied to reletlont 222
Oencfate 9i 2U
Generator 9i. 342
OnUS
Graph 129
H. 84
H.,416
H[9t
Have umiwninll 3J2, HI
— Inunecoam US
HocaU
randof 111
HonworarpMun 29, 90, 2J L 319
Id 13,464
Identity functor U
-ramp 443
— morphbm 13
— iranafomacloti 14
Ha 464
Imaae4e4
Inchuloa map 463
Initial algebra 36, 94
coaatnaaioa U9
-object 13
-KateLta
luktaHzauon nwrpMua 25. M
— object 22. M
Injection of generator! 9J. 211
Inner equivalent 114
— Nerode ttailvelinct 173
realleatioe 373
Input |
Interchanaeabk 41
Intenection L42
Invcrie map4M
— movpluani u
— relatioo 261
lionorphk automata 4, 41
liunwrphbni 6,19
liotona coHait 201
Iteration oaliadl 201
Iteration of a language 26,74,411
Kernel 111
— equivalence 263,4M
Kleene theorem 26,76,410
I 19, U, tO*
Lofl Hud pofatf U*
Left cucellMte lit
LbaMtZ
r AiMsr Ii2
112
jr-rabobjea lit
^•wdl-pomrcd ISO
Many-med •Ifebra in
MtmnMc cudbul IS]
Minimal pRtemtfloii 409.
i LLlfll
- Kiiaclloa IA46.144
■WU
MonaDI!
- DMHMlll
MoaoU
MoaotnmfMmatioa U
MotphlmU
- of umn 4, J?, SB, HI
•«uct Ut
U.U.1K
; 19,46, 404
(IS. 66, 70, 404
Ion?
Miction 12,46,314
Rdlcilve pur 3B3
- relation 261
ItetaiarepJIl
- f«aooo«on [J4, 211
- ftnto arproouctt 230
- ranctor 111
- norm 86
- quotient 16
- lobobieclU
»2L212
ial •bjebra 211
relation 231
Ran 12
Riant cencellalive \M
- CUCI2M
Root II
Run nap 2,36,43
iM.lal
SjSl
Sti,l3«
Satbly equation 113
■ 12
uloauaoa 1,91
Sana connection 24, 7J
•MIS
•ot'121
•M.ra
SO functor I2>
^oMooMron L
automaton 22
Small category M
- riiKtor 129,112
-Ml 41]
Spaa-alatbrB 212
SptftrpiU
SUbta pal***'219
Standarr) ranctor U2,112
Stale L_2U9
- relatioalal
Stop after »tttpa 14L 173,211
Stria avGoaUnaoui 121
i23J
■ 7,42, HPL122
Sobfunclor 111
Symatetric itvauoa 262
Tenior prouau 111
Tarailiial object 12
- Data 19,61
Top lit
Treraflnhx laoaaloa 96, LS9
Treneltlve relation 261
Tree 12
— acceptor (6.
— BUtoajatoa 29, 32
Type & 32
Uttranilar 111
Unary 21
Union HZ
- of aataeaala 24,70.
12,122
r-jlll
Variable 21
Varietor 9J
Variety 113
Vector functor 111
Weakly preetrve coua
Wdl-poweml Ufl
Word I
■km 72,112
a-Ueratloa 74, 111
Printed in the United Slates
543.12LVS0O0OIB/I5.1