Автор: Левит М.Е.
Теги: детали машин передачи (механические) подъемно-транспортное оборудование крепежные средства смазка отдельные машиностроительные и металлообрабатывающие процессы и производства инженерия машиностроение справочник детали механизмов балансировка двигателя металлообработка
ISBN: 5-217-00399-5
Год: 1992
СЛИВОЧНИК £
ПО
Б4ГИНСИРСЖКЕ
Под редакцией
канд. техн, наук проф. М.Е. Левита
Москва
• Машиностроение-
1992
ББК 34.686я2
СУД-
УДК 621.828.3 (035)
Авторы:
М. Е. Левит, канд техн наук (предисловие,
гл. I, и. 1-1, 13. 1.4, гл 5, п 5 1, 5.4, 5.6,
гл. 7, п 7.3; гл. 14, п. 14.5), К). В. Агафонов,
канд. техн, наук (гл 8, п, 8.2), Л. Д, Вайнгор-
тин, канд, техн наук (гл 5, и. 5.5). Л. 3. Варта-
нян, канд. техн наук (гл. 8, п. 8 7);
А. А. Гусаров, канд. техн, наук (гл. 8,
и. 8.1 8.4); А. И. Ильянков, канд. техн, наук
(гл. 8, и 8,6; гл 11, п, 11.1 ИЗ; гл 14,
п. 14.2; 14.7); Р. А, Йонушас, канд техн, наук
(гл. 6, п. 6 5); И. А. Ковалев, канд техн, наук
(гл. 5, п 5 3), П- В. Коротков, инж (гл 4,
в 4.6; гл. 7, п 7.1- 7.4); В. М. Коршунов,
канд. техн, наук (гл 3, и 3.4, гл 4, п. 4.5);
Л. Э. Кранцберг, канд. техн, наук (гл. 4, п, 4.7,
4.8; гл. 7, п. 7.3 7.6, гл 8, п 8.7- 8 8, гл 14,
п. 14 3, 14.6); С. Г, Кубланов, канд техн, наук
(гл. 1, п 1-2); А. и. Максименко, д-р техн,
наук (гл. 1, и. 1.5, 1.6; гл. 4, л. 4.1—4.4;
гл 11, и. 11 4); В. И. Петрович, д-р техн,
наук (гл. 9), О. А. Полушкин, д-р техн, даун
(гл 14, п. 14.4); К- М. Рагульскис, д-р техн,
наук (гл. 6. п. 6 5), В- П, Ройзман, д-р техн
наук (гл. 1, п. 1.7, гл. 5, п. 5.2, 5.4); В. М. Ры-
женков, канд. техн, наук (гл. 1, п 1.8, гл 3,
п. 3.1, 3.2, 3.3, гл 10-гл. II, л- 11.1 1L3. гл 12.
гл. 13, гл. 14, п. 14.1); А. В. Салимон, канд. техн.
Наук (гл. 6, п. 6 1—6.4); А. К. Скворчевскнн,
канд. техн, наук (гл. 8, п. 8.6); И. Н. Стельнан,
йнж. (гл. 8, и. 8.7, 8.8, гл. 14, п. 14.3);
В. А. Суетин, канд. техн, наук (гл. 7, п. 7.3),
В. И. Сусанин, канд. техн, наук (гл. 8, п. 83);
В. В. Тихомиров, канд. техн, наук (Основные
термины и определения, принятые обозначения,
гл. 4, н. 4 4. Приложения, список стандартов,
список литературы);Л. Н. Шаталов, инж. (гл, 8,
п. 8.4, 8,5) ; В. А. Щепетильников, Д-р тан.
наук (гл. 2)
Рецензенты:
д-р техн наук Э. А. Горов, канд техн наук
Н, Г. Самаров
С74 Справочник по
Л. Д. Вайнгортин и
строение, 1992.-464
ISBN 5-217-00399-5
Левит, Ю. А.
балансировке/М Е.
др.; Под общ. ред. М. Е. Левита. — М,: №щ^но-
С.. И.П
Изложены основные сведения по балансировочной технике, необходимые в провесе
конструирования роторов машин и механизмов, выбора методов, средств и 'гехнодЬГии
уравновешивания.
Освещены вопросы проектирования оснонцых устройств балансировочной
механизаций и автоматизации процессов определения дисбалансов и корректировки ласс
Справочник предназначен для конструкторов, технологов и эксплуатационников раз„
личных отраслей машине- и приборостроения.
2704090000-621
С ~*О38(01)—92~ КЬ-21-23-90
ISBN 5-217-000399-5
ББК
© М. Е. Левит, Ю. А. АгафоцОВг
Л. Д. Вайнгортин и ДР., 1992
Оглавление
к Этапы многоплоскостной
балансировки валопро-
вода ................. 179
> Метод точной баланси-
ровки изделий с жестки-
ми роторами в собран-
ном состоя нии . 180
’ЕД СТ В А БАЛАНСИ-
ВКИ .................. 188
ьлансировочные станки 188
I Классификация 188
2. Станки общего и специа-
лизированного назначе-
ния .................. 197
3 Специальные баланси-
ровочные ’ станки 209
4 Центровальные бал а ней
ровочные станки . . 224
5. Проектирование основ-
ных систем балансире
вечных станков . . . 228
6. Нормы точности и испы-
тания балансировочных
станков . . 234
зтобалансирующие устрой-
ва .................... 239
1. Основы автобалансиро-
вания роторов . . 239
2. Устройства со свобод-
ным перемещением кор-
ректирующих масс . . 243
3. Автобалансирующие ус-
тройства с принудитель-
ным перемещением кор
ректирующих масс . . 257
.4. Автобалансирующие
устройства для шлифо-
вальных кругов . . . 265
l5. Импульсные автобалан-
сирующие устройства 270
.6. Автоматические балан-
сировочные устройства,
реализующие лазерный
метод корректировки
масс . . . .273
.^Автоматические и полу-
автоматические стан-
ки ... . 285
,.8. Автоматические линии,
участки и гибкие произ-
водственные системы 295
1ортативная балансировоч-
ная аппаратура . 298
1.1. Классификация и об-
ласти применения . 298
1.2. Частотно-избирательные
устройства . 300
).3. Конструкции и основные
характеристики порта-
тивной балансировочной
аппаратуры . . . .316
9.4. Перспективы развития
портативной балансиро-
вочной аппаратуры
Часть III. ТЕХНОЛОГИЯ БАЛАН-
СИРОВКИ РОТОРОВ
Глава 10. Точность балансировки
10.1. Основные понятия
10.2. Расчет требуемой точ
ности балансировки
10.3. Расчет допусков на ба
лансировку деталей и
узлов роторов
10.4. Расчет ожидаемой точ-
ности балансировки
10.5. Определение элемен-
тарных погрешностей
балансировки . .
10.6. Статистический метод
анализа точности ба-
лансировки . . . .
Глава 11. Проектирование технологи-
ческих процессов ....
11.1. Общие сведения о тех-
нологической подго-
товке производства .
11.2. Обеспечение техноло-
гичности конструкций
балансируемых изде-
лий ... . .
11.3. Проектирование тех-
нологического процес-
са балансировки, . .
11.4. Автоматизированное
проектирование техно-
логических процессов
балансировки рото
ров ...................
Глава 12. Основы проектирования ба-
лансировочных приспособ-
лений
12.1. Назначение и типы ба-
лансировочных при-
способлений . . .
12.2. Технологические опо-
ры .. . . . .
12.3. Балансировочные оп-
равки и технологичес-
кие валы .
12.4. Балансировочные рам-
ки . . .
12.5. Приводные валы и
шкивы , . . .
12.6. Защитные кожухи
12.7 Контрольные и тари-
ровочные роторы . .
Глава 13. Способы корректировки
масс . . . - -
13.1. Общие сведения . .
13.2. Способы корректиров-
ки перемещением масс
326
328
328
328
329
331
335
337
338
342
342
343
345
350
358
358
358
365
367
369
372
372
374
374
376
Оглавление
5
13.3. Способы корректиров-
ки добавлением массы 378
13.4. Корректировка масс
механической обработ-
кой . ... 381
13.5. Корректировка масс
электрообработкой 383
Глава 14. Балансировка типовых изде-
лий машине- и приборо-
строения ... . . 384
14.1. Типовые технологичес-
кие процессы баланси-
ровки . . . 384
14.2. Балансировка роторов
гироскопических при-
боров .... 395
14.3. Балансировка кардан-
ных валов . 404
14.4. Балансировка роторов
сельскохозяйственных
машин> . . . . 405
14.5. Балансировка воздуш-
ных винтов . . 410
14.6. Балансировка колес-
ных пар . . .414
14.7. Балансировка узлов
текстильных машин 416
ПРИЛОЖЕНИЯ
ПРИЛОЖЕНИЕ П.1. Описание програм-
мы «Статическая
балансировка ра-
бочего колеса ло-
паточной машины
распределением
лопаток по пазам
диска» . . . 422
ПРИЛОЖЕНИЕ П.2. Программа МК1-
«Расчет дисбалан-
сов детали на оп-
равке» .... 424
ПРИЛОЖЕНИЕ П.З. Программа МК2-
«Балансировка ме-
тодом амплитуд и
фаз» . . . 426
ПРИЛОЖЕНИЕ П.4. Программа МКЗ
«Балансировка в
трех плоскостях» . 428
ПРИЛОЖЕНИЕ П.5. Программы МК4 и
МК5. «Многоплос-
костная баланси-
г ровка» . . . 430
ПРИЛОЖЕНИЕ П.6. Программа МК6
«Расчет главного
вектора и главного
момента дисбалан-
сов» .............................436
ПРИЛОЖЕНИЕ П.7. Описание програм
мы ЕХС1- «Балан-
сировка с примене-
нием системы проб
ных дисбалан-
сов» . . . . 438
ПРИЛОЖЕНИЕ П.8. Описание програм-
мы ЕХСЗ «Опреде-
ление эксцентриси
тетов гибкого рото
ра по известным
значениям его про
гибов» .... 440
ПРИЛОЖЕНИЕ П.9. Описание програм
мы ЕХС4-«Опреде-
ление эксцентриси-
тетов гибкого рото-
ра по его прогибам
и нормальным на-
пряжениям» . . 442
ПРИЛОЖЕНИЕ П.10. Описание програм-
мы ЕХС5. «Опреде-
ление изгибных
жесткостей гибко
го ротора по его от-
носительным де-
формациям и про-
гибам оси» . . 443
ПРИЛОЖЕНИЕ П.11. Описание програм-
мы ДИСБАЛ.
«Расчет удельных
дисбалансов рото-
ра в корпусе» 444
ПРИЛОЖЕНИЕ П.12. Описание програм-
мы «Технология
балансировки ро
торов» .... 446
ПРИЛОЖЕНИЕ ПЛЗ. Описание програм-
мы «Сборочная
технологичность» 448
ПРИЛОЖЕНИЕ П.14. Описание програм
мы «Балансиро-
вочная технологич-
ность» . 450
Список Международных стандартов и
ГОСТов по балансировочной технике . 452
Список литературы . . 454
Предметный указатель .... 452
Одним из важнейших критериев ка-
чества и надежности работы машин явля-
ется уровень их вибраций.
С повышением мощности и быстроход-
ности современных машин обеспечение
допустимого уровня их вибрации пред-
ставляет проблему первостепенной важ-
ности, так как вибрации снижают надеж-
ность и долговечность машин. Статистика
показывает, что более 40% аварий турбо-
машин происходит по причине вибрацион-
ного разрушения деталей. Вибрации также
вредно влияют на организм человека, вы-
зывая физиологические расстройства.
Динамические нагрузки в машинах и
вызываемые ими вибрации создаются в
первую очередь неуравновешенными инер-
ционными силами вращающихся и воз-
вратно-поступательно движущихся масс.
Эти силы вызывают значительные пере-
менные нагрузки в материале, в опорах,
преждевременный износ деталей машины,
а иногда и их разрушение, приводящее
к аварийной ситуации.
Вибрации являются неизбежным спут-
ником работы всех машин, независимо
от их класса, разновидностей и размеров.
Причина вибраций — неуравновешенные
силы. Поэтому главный технологический
путь устранения вибраций машин — при-
менение эффективных методов баланси-
ровки, чему и посвящен справочник.
Если в прошлом вопросы уравновеши-
вания машин решались расчетным путем
в процессе их проектирования, то с появ-
лением быстроходных и гибких роторов
в ряде отраслей техники для снижения
инерционных сил вращающихся и воз-
вратно-поступательно движущихся масс
понадобились новые методы и средства
уравновешивания. Поэтому от уровня раз-
вития балансировочной техники во многом
зависит не только общий уровень вибра-
ций машин и приборов, но также ресурс,
надежность и точность их работы.
Однако не все вибрации вызываются
только неуравновешенными инерционными
силами неравномерно распределенных
масс движущихся или вращающихся час-
тей машин. Исследования показали, что
лишь 50% случаев вибрации вызываются
этими причинами; около 30% вибраций
вызываются плохой центровкой сопряга-
емых валов, примерно 17% — различными
механическими дефектами и 3% - элек-
трическими неисправностями
Все это подтверждает, что борьбу
с вибрацией машин следует начинать с
балансировки, а при высоких частотах
вращения она превращается в первооче-
редную техническую проблему.
Основным технологическим фактором
снижения уровня вибраций машин, как
известно, является выбор оптимального
метода балансировки роторной системы.
Он должен быть осуществлен в результате
выявления (идентификации) динамичес-
ких свойств системы ротор—статор— фун-
дамент и многих факторов, влияющих в
эксплуатации на точность балансировки
ротора, а также методов нахождения и
устранения дисбалансов.
Авторы справочника не ставили своей
целью охватить все существующие методы
балансировки роторных систем и способы
уравновешивания механизмов. В него
включены только основые вопросы балан-
сировочной техники, наиболее часто встре-
чающиеся в практике. В справочнике даны
основные сведения по балансировочной
технике, необходимые в процессе констру-
ирования роторных машин и механизмов,
выбора метода уравновешивания.
При проектировании роторных систем
справочник поможет конструктуру и тех-
нологу в выборе метода, средств и тех-
нологии балансировки. При этом необхо-
димо ознакомиться с классами роторов,
методами и точностью их балансировки;
определить критические частоты вращения
Предисловие
7
проектируемого ротора; выбрать метод
его балансировки, число и положение
плоскостей коррекции, подобрать для него
типовой пример балансировки и. наконец,
определить оптимальное оборудование,
аппаратуру и приспособления.
Справочник состоит их трех частей.
В первой части приводятся теоретические
сведения, необходимые при разработке ме-
тодов балансировки роторов основных
типов, а также излагаются положения
по уравновешиванию плоских механизмов
с симметричными и несимметричными
звеньями.
Поскольку балансировка роторов не
самоцель, а средство снижения уровня
вибрации машин, в первой части справоч-
ника уделено внимание причинам, источ-
никам и видам вибраций, а также мето-
дам их снижения. Показана связь вибра-
ции с балансировкой роторов, дана их
классификация. Приводятся критерии
уравновешенности роторов и выбора ме-
тода их балансировки.
Вторая часть справочника касается
средств балансировки. Сюда входит опи-
сание балансировочных станков и комп-
лектов, приспособлений для балансировки
роторов и разные способы корректиров-
ки неуравновешенных масс, включая об-
работку цапф и центров.
Получение достоверной информации о
дисбалансе, его фазе и значении осущест-
вляется на балансировочном станке, сос-
тоящем из механической и измерительной
систем. Этапы определения и устранения
дисбаланса у ряда станков-автоматов сов-
мещены. Приводятся основные техничес-
кие характеристики универсальных, спе-
циальных и специализированных станков,
широко применяемых в отечественной
практике.
Если остановка машины для баланси-
ровки ротора недопустима, то наиболее
перспективным является применение авто-
балансирующих устройств.
Третья часть справочника посвя-
щена технологическим вопросам баланси-
ровки роторов. Рациональное проектиро-
вание технологических процессов и балан-
сировочной техники является определяю-
щим фактором высокой точности ротор-
ных систем в машине- и приборострое-
нии.
При создании справочника авторы
стремились:
изложить основные сведения по балан-
сировочной технике, необходимые в про-
цессе конструирования роторных машин
и механизмов;
помочь конструкторам и технологам
в осмысленном выборе оптимальных ме-
тодов, средств и технологии балансиров
ки роторных систем машин и механизмов;
указать пути достижения требуемой
точности и производительности при балан-
сировке роторов и уравновешивании меха-
низмов.
Авторы будут признательны читателям
за все замечания и предложения, направ-
ленные на улучшение справочника, и про-
сят направлять их по адресу: 107076,
Москва, Стромынский пер., 4, издатель-
ство «Машиностроение».
ОСНОВНЫЕ ТЕРМИНЫ И ОПРЕДЕЛЕНИЯ
Амплитудно-частотная характеристи-
ка (АЧХ) — зависимость амплитуды пер-
вой гармоники вынужденных колебаний
системы от частоты гармонического воз
буждения с постоянной амплитудой.
Антирезонансные колебания — режим
вынужденных колебаний системы, соот-
ветствующий одному из минимумов ампли
тудно-частотной характеристики.
Балансировка ротора — процесс опре-
деления значений и углов дисбалансов
ротора и уменьшение их корректировкой
его масс. Это технологический процесс
совмещения оси вращения ротора и его
гцои.
Вибрация — колебательное движение
точки или системы.
Виброперемещение — перемещение
при вибрации.
Виброскорость скорость при вибра-
ции.
Виброускорение — ускорение при виб-
рации.
Вынужденные колебания — колебания
системы, вызванные и поддерживаемые
силовым или (и) кинематическим возбуж-
дением.
Вынуждающая сила (момент) пере-
менная во времени внешняя сила (мо-
мент), не зависящая от движения системы
и вызывающая ее колебания.
Динамическая жесткость — отноше-
ние амплитуды гармонической вынужден-
ной силы к комплексной амплитуде
перемещения при гармонических вынуж-
денных колебаниях линейной системы.
Динамическая податливость — вели-
чина, обратная динамической жесткости.
Дисбаланс — векторная величина,
равная произведению неуравновешенной
массы на ее эксцентриситет.
Затухающие колебания - колебания
с уменьшающимся размахом колеблющей-
ся величины.
Значение дисбаланса — числовое
значение, равное произведению неуравно-
вешенной массы на модуль ее эксцентри-
ситета.
Интенсивность вибрации системы —
максимум среднеквадратичных значений
виброскоростей характерных точек систе-
мы.
Колебания — процесс изменения ска-
лярной величины, характеризующийся ее
поочередным возрастанием и убыванием
во времени.
Колебательное движение точки — дви-
жение точки, при котором по крайней
мере одна из ее координат является ко-
леблющейся величиной. Колебание систе-
мы это движение системы, точки которой
колеблются.
Колебательная система — система,
способная совершать свободные колеба-
ния.
Корректирующая масса — масса, ис-
пользуемая для уменьшения дисбалансов
ротора.
Коэффициент податливости — величи-
на, обратная коэффициенту жесткости.
Неуравновешенность ротора — состоя-
ние ротора, характеризующееся таким рас-
пределением масс, которое во время вра-
щения вызывает переменные нагрузки на
опорах ротора и его изгиб.
Период — изменение во времени / ка-
кой-либо координаты х, которое можно
представить функцией х — x(t). В общем
случае такое изменение силовой, линейной
или угловой координаты х может быть про-
извольным. Если же это изменение полно-
стью повторяется по истечении равных
интервалов времени, называемых перио-
дом, то такое изменение является периоди-
ческим колебанием.
Резонансные колебания (резонанс) —
режим вынужденных колебаний системы,
соответствующий одному из минимумов
амплитудно-частотной характеристики.
Резонансная частота — частота, при
которой осуществляется резонанс.
Ротор — тело, которое при вращении
удерживается своими несущими поверх-
ностями в опорах.
Свободные колебания — колебания
системы, совершающиеся без переменного
внешнего воздействия и без поступления
энергии извне и происходящее за счет
первоначально накопленной энергии вслед-
ствие начального возмущения.
Собственная форма колебаний систе-
мы - форма гармонических колебаний ли-
нейной системы, колеблющейся с одной
из собственных частот.
Собственная частота колебаний —
частота свободных колебаний линейной
системы при отсутствии рассеяния энергий.
Угол дисбаланса — угол, определя-
ющий положение вектора дисбаланса в
ПРИНЯТЫЕ ОБОЗНАЧЕНИЯ, СОКРАЩЕНИЯ И ИНДЕКСЫ
9
системе координат, связанной с осью ро-
тора.
Уровень колебаний — характеристика
колебаний, основанная на сравнении зна-
чения параметра колеблющейся величины
Условные обозначения для части I
А — амплитуда, м;
аА — амплитуда ускорения,
м с-2;
а — коэффициент влияния дис-
баланса, ММ • С-,/(г'Мм)
A J— вектор вибраций опоры I
ротора, мкм '• с_|;
а — коэффициент балансиро-
вочной ч увствител ьности,
влияния' мкм/(г • мм);
ар, рр, ур — координаты ротора;
Р — угол между векторами,...0;
b — коэффициент пропорцио-
нальности;
с — коэффициент жесткости,
Н/М:
D— дисбаланс, г мм...°;
6 — радиальный зазор, биение,
мм; коэффициент демпфи-
рования;
DtT — главный вектор дисбалан-
сов, Г’ММ,...а;
d — диаметр, мм;
е — угловое ускорение, с-2;
е—эксцентриситет, мкм;
ест —удельный дисбаланс, мкм;
F, Р-— неуравновешенная сила,
Н:
Ф — вектор инерции;
f — частота периодического
колебания, с-1, Гц;
<р — фаза колебаний, угол,
радиан,...0;
G — вектор силы тяжести звена
Н:
g — ускорение силы тяжести.
—2
м - с :
G\ Н* — коэффициенты, зависящие
от параметров возмуще-
ния;
0- угловое положение кон-
тактной группы,
с заданным отсчетным значением этого
же параметра.
Эксцентриситет массы - радиус-век-
тор центра рассматриваемой массы отно-
сительно оси ротора.
J— момент инерции тела,
2
кг • м ;
k - номер собственной формы,
число (1, 2, ... ,п);
А—целое неотрицательное
число;
L — расстояние между середи-
нами опор ротора, мм;
I- расстояние от центра
^гасс до опоры, длина зве-
на, мм;
W—коэффициенты кинемати-
ческого возмущения;
А4О— главный момент дисбалан-
сов ротора, г мм2,...°;
М— крутящий момент, Н м;
т— -масса, кг или г;
р. — распределенная масса,
кг/м;
f—частота вращения, с-1;
N— мощность, кВт;
р, q, s, t — коэффициенты при балан-
сировке;
-главный вектор неуравно-
вешенных сил;
Q,ip корр — вектор пробной, корректи-
рующей массы, г мм2;
Q,— вектор дисбаланса, г-мм2;
R,(fT) — вектор равнодействующей
силы;
Ri — реакция на опоре рото-
ра;
г - радиус окружности, мм;
S— перемещение, мм, стати-
ческий момент, г - мм;
Snp к—пробная. корректирую-
щая масса, т;
Т — период, с_|;
t — время, с;
U— динамическое перемеще-
ние, мкм;
V А — амплитуда скорости
м - с~ ’;
10
Принятые обозначения
to — угловая скорость ротора,
с
х, у, z— координаты;
у — прогиб ротора, мкм;
Условные обозначения для части II
aG прогиб ротора в АБУ, мкм;
0о — коэффициент дисковых по-
терь, kVA;
0 —угол,...°,
с - коэффициент жесткости
опоры;
ь .., Ci — пол ож ител ьные де йств и-
тельные числа:
EJ—изгибная жесткость рото-
ра, Нм/рад;
| механический импеданс,
кг/см;
Е— экцентриситет беговой до-
рожки, мкм:
F—неуравновешенная сила,
Н;
Гср—частота среза ФНЧ, Гц;
Ft — частота входного сигнала,
Гц;
<ро — сдвиг фазы,___° (ра-
диан)
И — отношение сигнала к
шуму;
/' — параметр «информатив-
ность»;
/ — момент инерции ротора.
2
КГ’М ;
k -- отношение дисбалансов
начального к корректиру-
':i‘ ющему;
kg — коэффициент преобразо-
вания датчика, mV/
(м • с“’);
М — масса ротора, кг;
' 1’ М,— погонная масса ротора,
г/м;
Л4Т— момент трения, Н • м;
N- мощность, kVA,
Акм— количество корректиру-
ющих масс в устройстве;
Аш— число шаров ШП;
Р — частотный спад фильтра,
дБ/октава;
Q — механические и электри-
ческие помехи;
R — радиус обоймы подшипни-
ка, мм;
RIU— радиус шара, мм;
/?к — корректируют ие сопро-
тивления;
г — радиус, мм;
р — плотность, кг м~3;
— статический момент шара,
кт • м;
SK — статический момент ШП,
кг - м;
Т — точность балансировочно-
го станка, г - мм/кг
То — период входных импуль-
сов разряда, с,
г — выходное напряжение, В;
1] — коэффициент демпфирова-
ния опоры, с-1;
tji—КПД механизма, %;
Uo—амплитуда переменного
напряжения, мкм
Условные обозначения для части III
А вектор вибрации,
мкм • с“',
а—жесткость, Н/м;
а.1 -разность температур, °C;
<Х| - коэффициент чувстви-
тельности ротора, мкм/
(г • мм);
Ь — ширина полосы, мм;
£)доп — допустимый дисбаланс
детали, г - мм;
£>wtp — остаточный дисбаланс
оправки, г • мм;
d — диаметр вкладыша, мм;
dp—диаметр поверхности ро-
тора под ремень, мм;
du— диаметр цапфы, мм;
£>нач — начальный дисбаланс.
г • мм;
^р.т — радиальное биение, мм;
Агюя— радиальный зазор под-
шипника, мкм;
V, Арад— радиально? и угловое от-
клонение от соосности,
мм,°;
Принятые обозначения
II
ЛТО|,Ц — торцевое биение, мкм;
- суммарная погрешность,
мкм,
Е — модуль упругости, Н/м2;
81.2 — радиус-вектор, мкм;
ё|.2 — колебания датчиков опор
ротора, мкм;
e=u>,max/u>lKp — отношение max эксплуат.
угловой скорости враще-
ния к первой критичес-
кой;
F — вектор динамического
воздействия, Н;
f6— частота балансировки,
с-1;
частота вращения наруж-
ного кольца подшипни-
ка, с“';
h— глубина сверления, мм;
1—экваториальный момент
2
инерции, кг - м
Кс6 — коэффициент сборности;
Квз—коэффициент взаимозаме-
няемости;
Ку — коэффициент унификации;
Кст — коэффициент стандарти-
зации;
Ki — коэффициент рассеяния;
Кт — коэффициент точности;
LAS — расстояние от опоры А до
ц. м. диска S, м;
I — длина вкладыша, мм;
/ЙОП—допустимая длина балан-
сировочного груза, мм;
М, С, К - матрицы масс, коэффи-
циенты сопротивлений,
жесткостей;
т - масса, г;
Л4Ш— крутящий момент шпин-
деля, Нм;
то — масса ротора, кг;
mOit — масса оправки, кг:
—масса детали, кг;
Мп—главный момент,
г • мм2,...°;
тк — корректирующая масса, г;
тнач—начальная неуравнове-
шенная масса, г;
/пяО1|— допустимая масса ба-
лансировочного груза, г;
JV — угловое положение экс-
центриситета, рад,...°;
Ке число сборочных единиц,
шт.;
7Va—число деталей, шт.;
A'CT— число стандартных дета-
лей, шт.;
Ney — число унифицированных
сборочных единиц, шт.;
Nrv число унифицированных
деталей, шт.;
—число стандартных сбо-
рочных единиц, шт.;
Кя ст - - ч ис л о стан д артн ых дета -
лей, шт.;
п — число деталей, шт.;
NM№~..допустимое число бала-
нсировочных грузов, шт.;
Р — гарантированная надеж-
ность;
р — давление, МПа;
Рпрур— пробные уравновешиваю-
щие грузы, г;
р -плотность материала,
г/мм3;
Ro, Кац — внутренний и внешний ра-
диусы детали, мм;
R. г — радиусы наружной и внут-
ренней беговых дорожек
подшипника, мм;
гк — радиус коррекции, мм;
S - - условная площадь контак-
9
та, мм ;
Smax- максимальный зазор дета-
ли оправки, мкм;
S4 — усилйя на опорах ротора;
7~вз— трудоемкость сборки, мин;
Та~ общая трудоемкость
сборки изделий, мин;
Тб — время на балансировку,
мин;
основное (машинное)
время, мин;
tti — вспомогател ьное время,
мин;
/о6 — время обслуживания ра-
бочего места, мин;
iOT- время на отдых и личные
надобности, мин;
12
Принятые обозначения
UAB— амплитуды вибраций под-
шипника, мкм;
V, — виброскорость, мм - с 1;
V — скорость скольжения,
М -с-1;
УдиН. Уст — динамический и статичес-
кий прогиб, мм;
<р — угол дисбаланса,. . .°;
<рнач — угол начального дисба-
ланса, . ..°;
ц>б — угловая скорость бал анси-
ровки, с_|;
wmax—максимальная угловая
эксплуатационная ско-
рость, с”1;
(о|кр— первая критическая угло-
вая скорость, с_|
АБУ—автоматическое баланси-
ровочное устройство:
АВМ — аналоговая вычислитель-
ная машина;
АЛБМ - автоматическая лазерная
балансировочная маши-
на;
АЧХ—амплитудно-частотная ха-
рактеристика;
БУ — балансировочное устрой-
ство;
ВГС — взрыв горючей смеси;
ГТД — газотурбинный двигатель;
ГЦОИ — главная центральная ось
инерции ротора;
ДКВ—динамический коэффици-
ент влияния,
ЕСКД — единая система конструк
торской документации;
ЕСТД — единая система техноло-
гической документации:
ИМП — импульсное магнитное по
ле;
ИМ—исполнительный меха-
низм ;
ИО— исполнительный орган,
КМ — корректирующие массы;
МСЭ— магнито-стрикционный
эффект;
ОКГ—оптический квантовый ге-
нератор;
ПОН -предварительный осевой
натяг;
ПУ — поверхность уровня функ-
ционала;
РБС разгонный балансиро-
вочный стенд;
ТВД— турбовинтовой двигатель;
ТПП — технологическая подготов-
ка производства;
ФВЧ— фильтр высокой частоты;
ФНЧ—фильтр низкой частоты;
ЦМ — центр масс;
ЧЭ —чувствительный элемент;
ШП — шариковый подшипник;
ЭВМ —- электронная вычисли
тельная машина,
ЭГЭ — электрогидравлический
эффект;
ЭФБ — электрофизическая ба-
лансировка.
Сокращения в индексах
доп —допустимый;
верх — верхний;
к— корректирующая;
кр— критический;
нижн — нижний;
ост- остаточный;
он —опора:
рез — резонансный;
табл — табличный;
i— порядковый;
/ — порядковый;
нач — начальный;
рот— ротор;
с — собственный;
ст —статический;
т — технологический;
ф — функциональный;
э — эксплуатационный:
п — нормальная составляю-
щая;
t -тангенциальная состав-
ляющая
часть!, основы балансировки
К основным вопросам балансировки
относятся технологические методы и
средства, позволяющие уравновесить ро-
торную систему машины и тем самым
снизить вредные динамические нагрузки
на ее элементы
Ниже кратко излагаются некоторые
сведения из теории и практики различных
методов балансировки основных типов ро-
торов и механизмов.
Рассматриваются вопросы повышения
точности балансировки с учетом влияния
технологических и эксплуатационных дис-
балансов, возникающих в процессе сборки
и нормальной работы изделий, а также
выбора допустимого значения неуравно-
вешенности вращающихся элементов ма-
шин и механизмов.
Глава 1
ОСНОВНЫЕ ПОНЯТИЯ
1.1. ВИБРАЦИЯ МАШИН
И БАЛАНСИРОВКА
В природе и технике наблюдаются са-
мые разнообразные повторяющиеся коле-
бательные явления и процессы.
Динамические нагрузки на подшипни-
ки роторных сиетем вызывают повышен-
ный уровень механических колебаний ма-
шин, часто называемых вибрациями.
Вибрация — это периодические коле-
бания, появляющиеся в результате вра-
щения неуравновешенного тела с опреде-
ленными частотой и амплитудой.
Виброизмерительную аппаратуру под-
разделяют на аппаратуру с контактными
и неконтактными виброизмерительными'
преобразователями. К контактным вибро-
измерительным преобразователям относят,
например, сейсмические, тензометричес-
кие, пьезоэлектрические и др., которые ус-
танавливают на колеблющейся системе, а к
неконтактным — фотоэлектрические, оп-
тические, лазерные и др., не имеющие
механического контакта с колеблющейся
системой.
Причины и источники вибраций. 1. Виб-
рацию в машине с частотой вращения
ротора могут вызвать не только дисба-
лансы вращающихся роторов, но и силы,
возникающие в опорах из-за их несоос-
ности или перекосов наружных колец под-
шипников качения. Влияние неп арал л ель-
нос ти и перекоса осей соединенных роторов
невозможно устранить с помощью ба-
лансировки.
Вибрация с удвоенной частотой враще-
ния ротора 2п может возникнуть из-за
овальности внутреннего кольца подшипни-
ка качения, неравножесткости ротора по
окружности, а также вследствие пере-
менного прогиба.
2. Турбулентные явления в жидком
или газовом слое смазочного материала
подшипников скольжения могут вызвать
вибрацию с частотой, примерно равной
0,5 частоты вращения. Суммарное дей-
ствие этой вибрации с вибрацией частоты
вращения ротора п создает так назы-
ваемые «резонансные биения».
!4
Основные понятия
3. Подшипники качения являются
источниками целой гаммы частот вибра-
ций. Вследствие периодически повторяю-
щейся ассимметрии расположения тел
качения в подшипниках качения возни
кают радиальные силы с периодом, рав-
ным половине времени прохождения цап-
фой расстояния между телами качения.
4. Зазоры между телами качения и
кольцами подшипника приводят к ударам,
в результате чего возникают свободные
затухающие колебания различной часто-
ты.
5. Неуравновешенность сепаратора
подшипников качения вызывает вибрацию
с частотой, зависящей от числа тел ка-
чения,
6. Аэродинамические, гидравлические
и газодинамические силы в турбомаши-
нах и в высокооборотных электрических
машинах могут возбудить вибрацию при
трении ротора об окружающую среду,
от ударов потока в лопатки турбин или
вентиляторов из-за кавитации, колебания
давления в маслопроводящих и охлаж-
дающих трубопроводах, малых рессиверах
и турбулизации потока.
7. Резонанс в неподвижных частях
машин при эксплуатационной частоте вра-
щения роторов даже в том случае, когда
они имеют дисбалансы ниже допустимых.
Тогда для достижения удовлетворитель-
ных вибрационных характеристик машины
может потребоваться исключительно точ-
ная балансировка роторов, а иногда и
изменение в конструкции машины для
сдвига ее резонансной частоты.
Методы снижения вибраций и их связь
с балансировкой. Повышенный уровень
вибраций устраняют конструктивным и
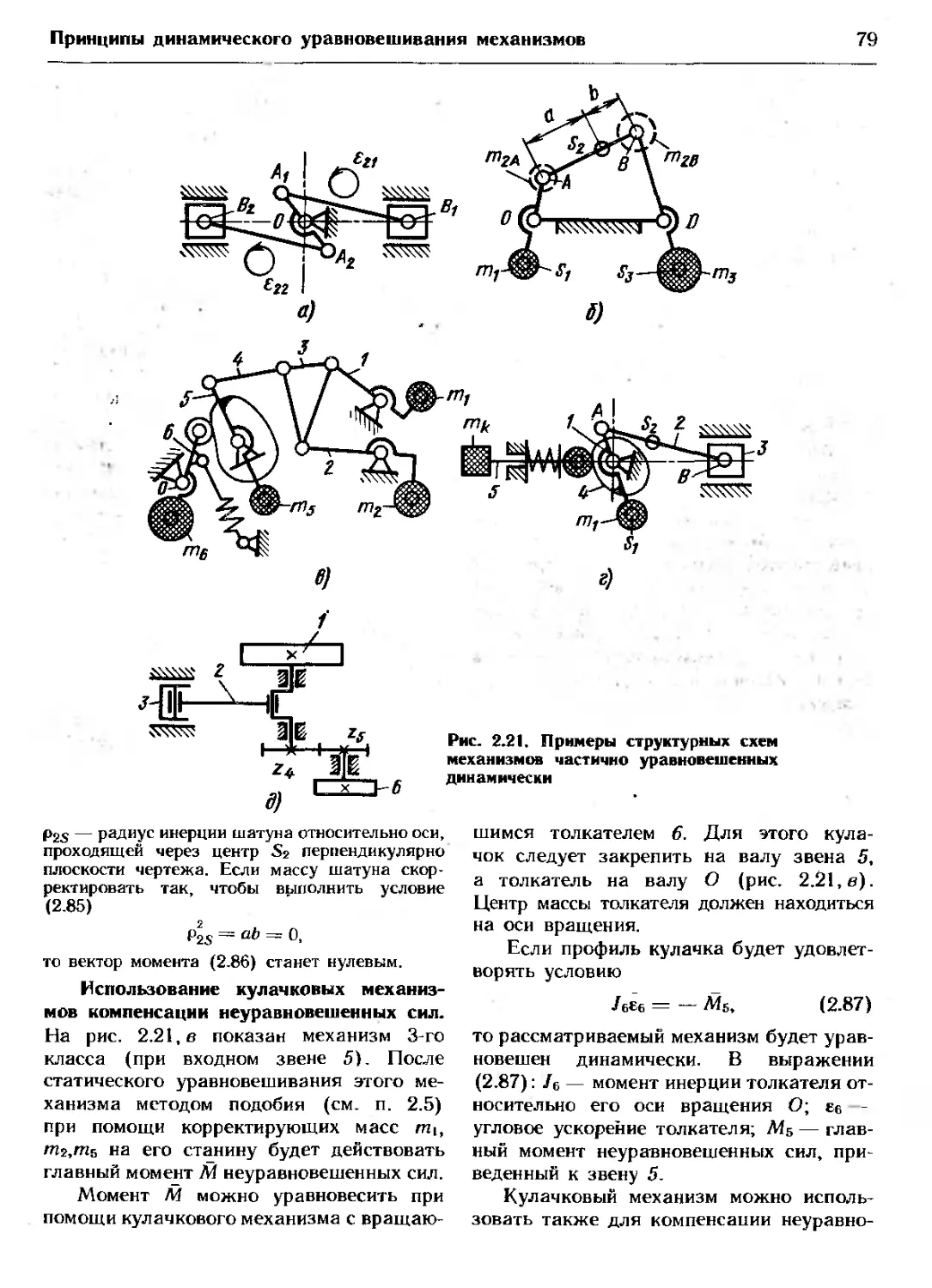
технологическим путем (рис. 1.1). Не рас-
сматривая конструктивные методы, ука-
жем лишь, что среди технологических наи-
более предпочтительным является высоко-
качественная (многоплоскостная) балан-
сировка роторных систем, она состоит из
Рис. 1.1. Структурная схема методов снижения вибрации машин
Необходимые сведения их теории колебаний и балансировки
15
выбора метода нахождения эксцентрисите-
та и его устранения.
К причинам возникновения неуравно-
вешенности ротора можно отнести нека-
чественное изготовление деталей ротора,
ето сборку и балансировку. Например,
при изготовлении дисков ротора возможны
некойцентричность их поверхностей отно-
сительно геометрической оси вращения,
биение посадочных мест, несимметричное
расположение пазов и отверстий, ослаб-
ление натягов сопрягаемых деталей вслед-
ствие температурных влияний, длитель-
ности работы и центробежных сил.
Под балансировкой понимают улучше-
ние общего динамического состояния
машины. Балансировка включает в себя
снижение уровня вибраций не только
опор ротора, но и корпуса изделия,
а также уменьшение прогибов ротора в
различных сечениях и ограничивает напря-
жение по его длине. Выбор метода
и средств балансировки осуществляют на
основе требований, предъявляемых к урав-
новешенности ротора и его конструк-
тивно-технологических особенностей. При
балансировке на первом этапе осу-
ществляют поиск корректирующих масс
или действительных эксцентриситетов, а на
втором этапе находят способы их устра-
нения.
1.2. НЕОБХОДИМЫЕ СВЕДЕНИЯ ИЗ
ТЕОРИИ КОЛЕБАНИЙ И БАЛАНСИРОВКИ
Прямая синхронная прецессия. В об-
щем случае движение вращающегося ро-
тора имеет сложный характер — вращение
относительно оси ротора суммируется с
вращением этой оси относительно оси
подшипников. Если частоты вращений
совпадают, то вал не испытывает пере-
менных напряжений. Такое движение на-
зывают прямой синхронной прецессией.
Кроме этого может быть и вращение
изогнутой оси вала вокруг оси под-
шипников в направлении, обратном вра-
щению вала и с равной частотой. Такой
вид вращения называют обратной син-
хронной прецессией. Возможны и другие
видь; прецессионных движений.
Наглядное представление вращения
изогнутого вала показано на модели ро-
торной системы (рис. 1.2) Пусть имеется
изогнутая металлическая труба 2, лежа-
щая в направляющих стойках 3. Если
внутрь этой трубы ввести шланг 1, то
он изогнется и примет форму трубы.
Труба и шланг имеют на своих торцах
рычаги, через которые можно вращать
трубу и шланг отдельно друг от друга
или вместе, скрепив жестко рычаги. Изо-
гнутая труба будет имитировать враще-
ние изогнутой оси вала, а гибкий шланг —
вращение самого вала.
Пусть (Oi частота вращения шланга-ва-
ла, а и>2 — частота вращения трубы.
При <oi #= 0, <02 — 0 движение можно
осуществить, вращая рычаг шланга и сто-
поря рычаг трубы. При этом вал вращается
вокруг своей изогнутой установившейся
оси. При (oi — «г движение можно осу-
ществить, соединяя жестко оба рычага и
вращая их. Тогда относительная скорость
равна нулю Указанное вращение имити-
рует прямую синхронную прецессию.
При (о> = — (02 движение осуществляется
путем вращения рычагов в разные сто-
роны, но с одной частотой. Оно имитирует
обратную синхронную прецессию.
При обратной синхронной прецессии за
один оборот знак напряжений волокон ва-
ла изменяется дважды. Если движение
ротора представить в проекциях на две
взаимно перпендикулярные плоскости, то в
Рис. 1.2. Модель роторной системы
16
Основные понятия
них будут происходить гармонические
колебания.
Для изучения представленного в таком
виде движения ротора применяют теорию
малых колебаний, являющуюся прибли-
женной теорией движения механических
систем около положения устойчивого рав-
новесия. Одним из наиболее важных при-
ложений теории колебаний систем с одной
степенью свободы является вопрос о кри
тической частоте невесомого вала, несуще-
го один диск массой т (рис. 1.3).
Рис. 1.3. Схема одномассовой роторной
системы
Пусть а — податливость вала в месте
крепления диска, т. е. величина деформа-
ции вала под диском от единичной
вертикальной силы, приложенной в этом
же месте. Величина, обратная податли
вости, с — 1/а есть жесткость вала. Пусть
диск посажен на вал с некоторым смеще-
нием центра масс относительно оси враще-
ния, равным е. Тогда при вращении вала
возникает его прогиб у. Из равенства силы
инерции диска и силы упругости вала
ягеы2а ею2
У = т-----— = -7------
1—тм а с 9
---------------w
т
Если <ос — собственная частота коле-
баний невращающегося невесомого вала с
диском массой т(<о2 = с/т), то прогиб
можно записать в виде функции
У =---------?е. (1.1)
1 —(w/wj
При со —<ос —► <окр, т. е. при стремле-
нии угловой частоты вращения вала к соб-
ственной частоте колебаний невращающе-
гося вала с диском, прогиб у бесконечно
возрастает. Такую частоту вращения, при
которой наступает описанное явление, и
называют критической частотой. Отмечен-
ное свойство распространяется на любые
сложные вращающиеся системы, что осо-
бенно важно, так как позволяет применить
хорошо разработанный аппарат теории
колебаний к вопросу нахождения крити-
ческих частот. Практика показала, что на
критических частотах валы действительно
теряют устойчивость, растут их прогибы и
резко увеличиваются вибрации корпусов.
Работа машины на критических частотах
приводит к многочисленным вибрационным
поломкам, к задеванию ротора о статор,
к выходу из строя подшипников и т. п. Поэ-
тому по возможности необходимо избегать
работы на критических частотах.
Явление критических частот вращения
очень сложно, так как связано не только
с вращением ротора, но и с колебаниями
присоединенных к нему масс машины с их
упруго-инерционными характеристиками и
величинами рассеяния энергии при коле-
баниях. Для простоты будем рассматри-
вать явление критической частоты в чистом
виде без учета указанных факторов. Одна-
ко и такое рассмотрение дает ответы на
важные’для практики вопросы.
Критические частоты наступают не
только у неотбалансированного ротора, но
даже и у идеально отбалансированного.
Дело в том, что воздействие внешних
случайных нагрузок не нарушает устой-
чивой работы вала, вращающегося не на
критических частотах, но если вал достиг
<окр, то при любом случайном отклонении
от оси вращения он уже не возвра-
тится к исходному состоянию, а его про-
гиб начнет расти. Ясно, что такие слу-
чайные воздействия-толчки неизбежны, а в
реальном случае почти всегда существу-
ет воздействие от силы тяжести, так как
большинство роторов вращаются в гори-
зонтальном положении.
Проанализируем, как изменяется про-
гиб вала при переходе через критическую
частоту вращения График функции (1.1)
зависимости прогиба ротора от частот вра-
щения имеет вид, показанный на рис. 1.4.
При возрастании частоты вращения про-
Необходимые сведения из теории колебаний и балансировки
17
Рис. 1.4. График зависимости прогиба ротора
от частот вращения
гиб вала вначале растет от нуля до бес-
конечности (на критической частоте). При
этом от центра вращения вала точки О
гося вала. В этом случае вал враща-
ется вокруг своего центра тяжести.
На критических частотах вращения си-
ла инерции равна силе упругости и вал
находится в безразличном положении, т. е.
он вращается, имея любой прогиб, и на-
личие или отсутствие эксцентриситета
здесь не имеет значения. В практике
расчетов на критические частоты враще-
ния их считают опасными, если они менее
чем на 30% отличаются от диапазона
рабочих частот вращения.
До сих пор предполагалось, что движе-
ние диска происходит в его плоскости.
Если тот же диск поместить на валу вбли-
зи одной из опор на конце вала, находя-
щегося вне опорного пролета, то сущест-
венное влияние на движение диска начина-
ют оказывать повороты вокруг его попе-
речных осей. Тогда несмотря на то, что
жесткость вала и масса диска остаются
прежними, выражение критической часто-
ты системы будет иным. Это происходит
потому, что силы инерции различных ча-
стиц диска не лежат в одной плоскости
и, таким образом, будучи приложенными к
валу, образуют пары сил, стремящихся
выпрямить последний. Следовательно, вал
становится более жестким, что приводит
к повышению критической частоты вра-
щения.
<°кр ~
0,5 (а, ।т — а22-0 + V 0,25( а( । т — ос^/)2 + Щ । «22—
— 1/2
отходит «тяжелая» часть диска и прогиб
вала О А складывается с исходным экс
центриситетом AAt, увеличивая силу инер
ции.
После прохождения критической ча-
стоты вращения знаки у прогиба и экс-
центриситета становятся противополож-
ными, бывшие растянутые волокна стано-
вятся сжатыми. Теперь от центра вра-
щения отходит «легкая» часть диска, про-
гиб уменьшается и при бесконечно боль-
ших частотах вращения становится рав-
ным —е, т. е. наступает эффект, назы-
ваемый самоцентрированием вращающе-
где осц и aj 2—прогиб и угол поворота
от действия единичной силы; а-22 и а щ—
прогиб и угол поворота от действия
единичного момента по теореме Максвел-
ла; т — масса; I — момент инерции диска
относительно оси диска.
Такое явление называют гироскопичес-
ким эффектом. Если положить J = 0, то
(окр ~ 1/^/а.цт = \с/т.
Кроме указанного эффекта, существен-
ное влияние на движение ротора могут
оказывать трение в материале, соединени-
ях, сопротивление внешней среды. Эти
18
Основные понятия
факторы тормозят движения, и энергия
колеблющейся системы переходит в тепло
и рассеивается. Реальный процесс коле-
баний - это не чисто механический про-
цесс. Он требует учета состояния окру-
жающей среды и характеристик самого
тела.
Для ряда конкретных случаев уда-
ется приближенно описать такие колеба-
ния путем введения в систему сил трения,
зависящих только от скорости, с коэффи-
циентом пропорциональности Ь. Тогда кри-
тическая частота вращения ротора
Если с/т > fe2/(4m)2, то при дости-
жении критической частоты вращения ро-
тора амплитуда колебаний остается конеч-
ной, что и наблюдается в реальных слу-
чаях.
Пусть ротор произвольной конфигура-
ции вращается как твердое тело с угло-
вой скоростью о и угловым ускорением е
вокруг оси OZ, проходящей через гео-
метрические центры его жестких опор
А и В (рис. 1.5). Если к динамическим
Рис. 1.5. Схема ротора произвольной кон-
фигурации на жестких опорах
реакциям опор ротора N\ и /Va, представ-
ленным соответственно в виде двух состав-
ляющих Л'|*, N\y н #2*. Nzy, присоединить
силы инерции всех частиц, то, согласно
принципу Даламбера, полученная система
сил будет удовлетворять уравнениям ста-
тики. Относительно координатных осей
X, Y, Z есть три уравнения момен-
тов сил:
Мх == Л — zFY; zFx — xFz;
Mz = xFy — yFx,
на основании которых составлены шесть
уравнений равновесия
/Vi* + 4- ^Fix 4- тхсыг 4- тусг = 0;
Л% 4" /V2y 4- YLFiy 4- tnyc(j)2 4- mxc& = 0;
/V.z 4- Л/2г 4- = 0.
- £/V2a4- - W 4“ 0;
LNzx 4- YLMiy 4" •/ 4* /xzE — 0;
—Je = 0,
где L— расстояние между опорами рото-
ра; /V — сила давления на опоры; Лх, Fiy,
F(t — проекции сил на координатные оси;
Mix, Miy, Mtz -- проекции моментов на ко-
ординатные оси; хс, 'ус — координаты цен-
тра масс; /*2, Jуг — центробежные момен-
ты инерции; J — момент инерции отно-
сительно оси вращения; со, е — соответ-
ственно угловая скорость и ускорение.
Часто в практических решениях ставят
узкую задачу при уравновешиваний рото-
ров — уравновесить силы инерции. Тогда
ЛГ| и Nz зависят только от хс, ус, Jxz, Jyz.
Чтобы /V» —0, N-2—0, должно быть
хс(02 4 усе — 0; — Jxxia2 4- Jyzb =« 0;
ус(о2 4" х<$ ~ 0: Jyz<a2 4- /х2е = 0.
Ротор уравновешен, если динамичес-
кие реакции его опор будут нулевыми.
Это условие из уравнений статики эквива-
лентно равенствам
Хс — Ус ~zr- 0; Jxz J yz == 0.
Иными словами, ротор уравновешен
тогда и только тогда, когда ось его
вращения является главной центральной
осью инерции ротора В этом случае дина-
мические реакции ротора не отличаются
от его статических реакций. Однако в ре-
зультате различных причин, приведенных
выше, возникает неуравновешенность ро-
тора, означающая отклонение главной
центральной оси инерции от оси его враще-
ния. В зависимости от вида, к кото-
рому приводятся силы инерции частиц,
различают три типа неуравновешенности
ротора.
Статическая, моментная и динамичес-
кая неуравновешенности. Статическая не-
Необходимые сведения из теории колебаний и балансировки
19
уравновешенность возникает, если момент
инерционной пары равен нулю. Тогда
ixz = ]yz — 0. т. е. ось вращения является
главной осью инерции и параллельна
главной центральной оси инерции ротора.
В этом случае NiX — Niy~ О, Ni* =
= —Ф„ Nty = —Фу, т. е. динамические ре-
акции уравновешиваются (кинетостати-
чески) главным вектором инерции Ф. Ве-
личины реакций зависят как от кине-
матических характеристик <о и г, так и
от геометрии масс ротора. Для удобства
оценки последней вводится массово-
геометрическая характеристика — дисба-
ланс D массы ротора относительно оси вра-
щения D = те, где ё — радиальное откло-
нение центра масс ротора от оси вращения,
называемое эксцентриситетом массы рото-
ра. Можно показать, что Nt = ejD — a>zD.
Таким образом, статическая неуравно-
вешенность ротора количественно характе-
ризуется наличием дисбаланса или экс-
центриситета массы ротора.
Моментная неуравновешенность воз-
никает, если главный вектор сил инерции
равен нулю. Тогда А'|Л = — Nix, Nty —
— — Niy, хс — ус = О.
Отсюда следует, что Л’| = — ZV2, т. с.
динамические реакции ротора образуют
пару сил. а центр масс ротора лежит на
оси вращения. Значит, ось ротора,
не являясь главной осью инерции, пере-
секается с ней в центре масс ротора.
Следовательно, динамические реакции
опор ротора уравновешиваются (кинето-
статически) инерционной парой.
Можно показать, что_главный момент
сил __инерции _ ротора М = ы2/Ог — ]гё—
— (8^ог)» где Jo?— центробежный момент
инерции массы относительно точки С) на
оси вращения. Второе слагаемое представ-
ляет собой вектор, направленный по оси
вращения ротора, поэтому пара сил с та-
ким моментом не может вызвать дина-
мических воздействий на опоры
Таким образом, моментная неуравно-
вешенность ротора количественно характе-
ризуется центробежным моментом инерции
массы относительно точки на оси враще-
ния.
Динамическая неуравновешенность
представляет собой самый общий случай
неуравновешенности жесткого ротора, так
как в этом случае главный вектор сил
инерции и момент инерционной пары — не-
нулевые векторы, образующие между со-
бой некоторый угол. Следовательно, ось
ротора и его главная центральная ось
инерции либо пересекаются не в центре
масс ротора, либо скрещиваются.
В каждом из трех рассмотренных слу-
чаев устранить неуравновешенность мож-
но путем добавления или удаления масс
в двух плоскостях коррекции, перпенди-
кулярных к оси вращения. С этой целью
вектор дисбаланса массы ротора D за-
меняют двумя векторами дисбалансов Ь\\
и Du, лежащими в плоскостях коррекции
так, чтобы геометрическая сумма этих дис-
балансов была равна D, а сумма их
моментов относительно точки приложения
D была равна нулю. Если 1\ и 12 —
расстояния плоскостей коррекции от цен-
Tjpa массы (рис. 1.6), то, учитывая, что
jDji. &2\ и D лежат в одной осевой
плоскости, эти условия выполняются, если
Du - - liD/(i' - li), Diy = /,£/(/, -
-Ъ).
В этих же плоскостях коррекции рас-
сматривают два других вектора дисбалан-
сов: Du и Da, эквивалентные паре сил
с моментом, равным центробежному мо-
менту ротора относительно точки на его
оси. Рассматриваемые векторы образуют
Рис. 1.6. Приведение неуравновешенности
ротора к системе дисбалансов в двух плос-
костях коррекции
20
Основные понятия
пару, поэтому Di? — —D22. |Д12 j — j D221 =
/Ог/|/1 — Аг|» которая вращает ротор про-
тив хода часовой стрелки при наблю
дении за ней со стороны конца вектора
ОZ'
Таким образом, в каждой плоскости
коррекции получено по два, приложенных
в одной точке, вектора дисбаланса, ко-
торые представляют их геометрическими
суммами D। = jDu + Dw, Ьч = D21 + D22
Векторы jDi и £>2 заменяют совокуп-
ностью вектора D и пары векторов с
моментом JОг, определяющих количествен-
но неуравновешенность ротора. Если вве-
дением корректирующих масс векторы D и
7Ог удается обратить в ноль, то неуравно-
вешенность ротора устраняется.
Однако приведенное утверждение оста-
ется в силе только для ротора, вращаю-
щегося на частотах, меньших первой кри-
тической, когда деформациями ротора в
силу их малости можно пренебречь и рас-
сматривать ротор как твердое тело, кото-
рое можно сбалансировать на любой ча-
стоте вращения в двух произвольных плос-
костях коррекции. Такую балансировку на-
зывают низкочастотной. Как правило, она
проводится на частоте вращения, значи-
тельно меньшей эксплуатационной.
Если дисбалансы ротора, прошедшего
низкочастотную балансировку на частоте
вращения, меньшей первой критической,
могут превышать допустимые дисбалансы
на иных частотах вращения вплоть до
наибольшей эксплуатационной, то такой
ротор называют гибким.
Устранение дисбаланса гибкого рото-
ра. Для устранения неуравновешенности
гибкого ротора низкочастотной баланси-
ровки недостаточно. В большинстве случа-
ев применяют высокочастотную баланси-
ровку, т. е. балансировку на такой часто-
те вращения, при которой ротор уже
нельзя рассматривать как жесткий, а сле-
довательно, необходимо учитывать де-
формации ротора. При высокочастотной
балансировке, проводимой на частоте вра-
щения ротора, близкой к эксплуатацион-
ной, применяют не менее двух плоскостей
коррекции.
В силу деформируемости гибкого рото-
ра при его вращении существует конечное
или бесконечное множество собственных
частот изгибных колебаний системы ро-
тор — опоры в зависимости от распреде-
ления масс ротора. Форму упругой линии
ротора при п-й собственной частоте изгиб-
ных колебаний системы ротор опоры
называют n-й собственной формой изгиба
ротора. Если распределение масс гибкого
ротора таково, что во время его вращения
возникают деформации упругой линии,
характерные для n-й формы изгиба, то
такое состояние ротора называют неурав-
новешенностью по n-й форме изгиба.
Неуравновешенность по п-й форме
изгиба. Такая неуравновешенность вызы-
вает наибольший прогиб ротора по п-й
форме изгиба, превышающий деформацию
его опор, на определенной частоте, назы-
ваемой п-й критической частотой враще-
ния гибкого ротора.
Для устранения переменных нагрузок
на опорах, вызванных неуравновешен
ностью по п-й форме изгиба, применяют
балансировку по п-й форме изгиба.
При этом наименьший теоретически воз-
можный дисбаланс, который следует ском-
пенсировать, называют дисбалансом по п-й
форме изгиба, а наибольший приемлемый
дисбаланс — допустимым дисбалансом по
п-й форме изгиба.
В ряде методов балансировки, опи-
санных в последующих параграфах, пред-
полагается компенсация неуравновешен-
ности по всем формам изгиба на крити-
ческих частотах вращения, попадающих в
диапазон эксплуатационных. При некото-
рых допущениях такие методы правомерны
и получили распространение в практике
отечественных и зарубежных заводов для
балансировки гибких роторов определен-
ных классов, уравновешенность которых
достигается, как правило, обеспечением
заданного уровня реакций или вибраций
опор.
Однако балансировка по формам изги-
ба может вызвать появление прогибов и
внутренних изгибающих моментов, не до-
пустимых при работе многих видов рото-
Неуравновешенность и балансировка ротора
21
ров. В последующих параграфах будут
отмечены и другие недостатки такой балан-
сировки гибких роторов. Поэтому не все
приведенные выше термины, касающиеся
гибких роторов, включая и само их опреде-
ление, приемлемы для тех методов ба-
лансировки, в которых контролю и устране-
нию подлежат не только вибрации или
реакции опор, но и прогибы, внутренние
изгибающие моменты и другие факторы.
В таких случаях гибким следует назы-
вать ротор, у которого после низкочастот-
ной балансировки на частоте вращения,
меньшей первой критической, контролируе-
мые параметры (вибрации или реакции
опор, прогибы, изгибающие моменты, на-
пряжения ит. п.) на иных частотах враще-
ния вплоть до наибольшей эксплуатацион-
ной, могут превышать допустимые значе-
ния.
Таким образом, вместо неизмеряемого
значения дисбаланса, в определение вво-
дят допустимые значения тех параметров,
которые подлежат непосредственному из-
мерению и контролю при обеспечении
нормального функционирования машины.
1.3. НЕУРАВНОВЕШЕННОСТЬ
И БАЛАНСИРОВКА РОТОРА
О критериях уравновешенности и выбо-
ра метода балансировки. Всякий ротор
обладает некоторой податливостью в попе-
речном направлении, что совместно с его
массой определяет критические частоты
его поперечных колебаний. В зависимости
от соотношений между критическими час-
тотами и скоростями вращения роторов
в эксплуатационном диапазоне их разде-
ляют на классы.
Жесткими роторами считают роторы,
рабочая скорость которых не превышает
первой критической скорости вращения. В
отношении количественной оценки соотно-
шения между рабочей скоростью вращения
tip и критической сокр необходим в каждом
конкретном случае индивидуальный подход
для определения класса ротора с учетом
требуемой точности балансировки, кон-
структивных особенностей и других факто-
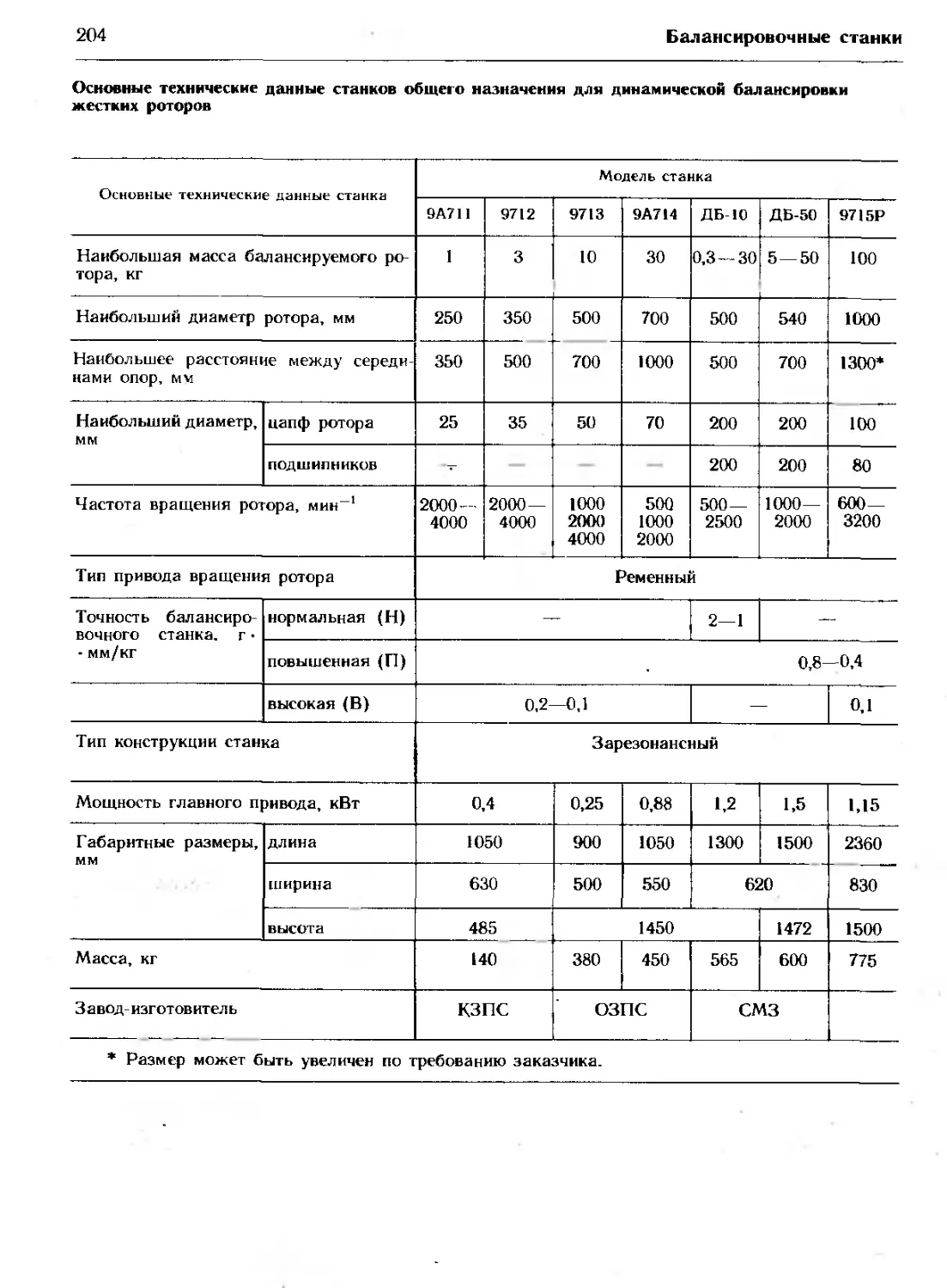
ров, приведенных в табл. 1.1.
Таблица 1.1
Деление роторов на классы
Типы роторов и роторных систем Классы точ- ности балан- сировки по ГОСТ 22061 — 75 тех’ мм • рад/с, не более
Коленчатый вал низ- кооборотного судово- го дизеля с нечетным числом цилиндров 11 4000
Коленчатый вал двух- тактного двигателя большой мощности 10 1600
Коленчатый вал четы- рехтактного двигате- ля большой мощнос- ти. Коленчатый вал судового дизеля, уста- новленного на вибро- изоляторах 9 630
Коленчатый вал жест- ко установленного вы- сокооборотного четы- рехцилиндрового ди- зеля 8 250
Коленчатый вал высо- кооборотного дизеля с шестью и более ци- линдрами. Двигатели в сборе (бензиновые или дизельные) для легковых и грузовых автомобилей и локо- мотивов 7 100
Колеса легковых ав- томобилей, ободы ко- лес, бандажи, привод- ные валы, тормозные барабаны автомоби- ля, колесные пары. Коленчатый вал, уста- новленный на вибро- изоляторах высоко- оборотного четырех- тактного двигателя (бензинового или ди- зельного) с шестью и более цилиндрами. Коленчатый вал дви- гателя для легкового и грузового автомо- билей и локомотива 6 40
22
Основные понятия
Типы роторов и роторных систем Классы точ- ности балан- сировки но ГОСТ 22061 75 мм • рад /с, не более
Приводные валы (ва- лы судовых винтов, карданные валы) со специальными требо- ваниями. Части дро- билок Части сельско- хозяйственных ма- шин. Отдельные части двигателей (бензино- вых или дизельных) легковых автомоби- лей, грузовиков и ло- комотивов. Коленча- тый вал двигателя с шестью и более ци- линдрами со специ- альными требовани- ями 5 16
Части технологичес- кого оборудования: главные редукторы турбин торговых су- дов, барабаны цент- рифуг, вентиляторы, роторы авиационных газотурбинных двига- телей в .сборе, махо- вики, крыльчатки це- нтробежных насосов, части станков и ма- шин общего назначе- ния, роторы обычных электродвигателей, от- дельные детали дви- гателей со специаль- ными требованиями 4 6,3 * Р {
Газовые и паровые турбины, включая главные турбины тор- говых судов. Турбоге- нераторы с жесткими роторами. Турбокомп- рессоры. Приводы мета ллорбрабатыва to- щи х станков. Роторы средних и крупных электродвигателей со специальными требо- ваниями. Роторы не- больших электродви- гателей. Турбонасосы 3 2.5
Типы роторов и роторных систем Классы точ- ности балан- сировки по ГОСТ 22061 -- 75 injx- мм - рал/с. нс более
Приводы магнитофо- нов и проигрывателей. Приводы шлифоваль- ных станков Роторы небольших электро- двигателей специаль- ного назначения 2 1.0
Шпиндели, шлифо- вальные круги и ро- торы электродвигате- лей прецизионных шлифовальных стан- ков. Гироскопы 1 0.4
С изменением частот вращения ротора
в зоне упругих деформаций происходят
не только количественные, но и качествен-
ные изменения вибраций ротора.
С ростом угловых частот вращения,
особенно при прохождении критических
частот, изменяются соотношения между
деформациями и неуравновешенными си-
лами, действующими на ротор в различ-
ных его сечениях, т. е. меняется спектр
сил и жесткостей. Действие одних сил
ослабевает, других — усиливается, сдви-
гаются места узлов и максимальных ам-
плитуд, появляются параметрические
резонансы, претерпевают изменения реак-
ции опор и т. д.
Если при балансировке тихоход ного-
жесткого ротора (при <ор < 0,3о)кр| либо
еы2<^_ 1g) основной задачей является
устранение или сведение к минимуму
реакций опор вне зависимости от частоты
его вращения, то при уравновешивании
быстроходного ротора (при <о > 0.3ц)кр!
либо ею2 1g) необходимо, применяя спе-
циальные методы, сведение к минимуму
не только реакций опор, но и деформа-
ции гибкого ротора во всем диапазоне
эксплуатационных частот вращения.
Таким образом, при решении задач
о балансировке быстроходных роторов
необходимо удовлетворить требования
уравновешенности ротора как гибкого
Неуравновешенность и балансировка ротора
23
(квазигибкого), так и жесткого. Существу-
ет ряд критериев балансировки, но наи-
более общими являются следующие: сведе-
ние к минимуму реакций опор, неурав-
новешенных сил и моментов, действующих
на ротор; сведение к минимуму прогибов
ротора и кинетической энергии при колеба-
ниях системы [24]'.
Можно потребовать удовлетворения
этих критериев на всех частотах враще-
ния. Однако следует выбрать лишь ту зону
частот, где удовлетворение выдвинутых
критериев достаточно из условий вибро-
прочности данной конкретной машины.
Существуют и другие критерии, тре-
бующие, например, ограничения прогиба
ротора в каких-то определенных сечениях,
где имеется опасность касания о статор
либо устранения вибраций некоторой пло-
щадки на корпусе, где установлен агре-
гат или прибор, требующий неподвижного
основания, и т. д. Выполнение этих тре-
бований в отличие от полного уравновеши-
вания иногда может быть осуществлено
быстрее и с меньшими экономическими за-
тратами, но при этом возможно ухудшение
вибрационного состояния машины в других
местах. Исследуя критерии сбалансиро-
ванности ротора, из всех встречающихся
на практике случаев рассмотрим полное
уравновешивание, которое теоретически
исключает передачу возбуждающих сил с
ротора на корпус и деформации самого
ротора на всей его длине.
Задачу по уравновешиванию роторной
системы следует разделить на две части.
К первой части задачи можно отнести
метод определения дисбаланса ротора, а
ко второй — способ его устранения, хотя
то и другое входит в метод уравно-
вешивания.
При определении дисбаланса в основ-
ном выявляют связи между эксцентриси-
тетами ротора и экспериментально найден-
ными прогибами, реакциями опор, вибра-
циями корпусов. При этом, как правило,
эксцентриситеты являются неизвестными
1 Список литературы см. в конце книги
аргументами функции прогибов, реакций
опор, вибраций корпусов.
Балансировкой ротора предусматри
вается компенсация найденной неуравно-
вешенности с учетом возможностей маши-
ны, ротора или балансировочного устрой-
ства. Устанавливается связь между дис-
балансами и уравновешивающими мас-
сами, которая обеспечивает выполнение
требований, предъявляемых к машине с от-
балансированным ротором.
В отдельных случаях связь между дис-
балансом и колебаниями не рассматрива-
ется. В этих случаях для уравновешивания
используют ограниченное число пробных
масс и запусков ротора, с помощью кото-
рых устанавливают зависимость между
дисбалансами и вибрациями и производят
расчет уравновешивающих масс.
Качество балансировки гибких роторов *
определяется уровнем вибрации шеек или
шения центра массы от оси вращения
в функции скорости. За исключением не-
которых (небольшого числа) случаев, этот
метод в настоящее время нельзя приме-
нить к гибким и квазигибким роторам.
Качество балансироки гибких роторов
определяется уровнем вибрации шеек или
подшипников, а также уровнем вибрации,
допустимой в установленных измеритель-
ных точках, или остаточных дисбалансом
в определенных балансировочных плоскос-
тях.
Максимально допустимые уровни ви-
браций роторов и машин обычно приводят
в технических условиях на их испытания.
Метод балансировки выбирают в зави-
симости от класса ротора, а для опреде-
ления класса необходимо знать значение
top/<DKpi, т. е. степень гибкости ротора.
Принято условно считать, что при юр/
/<%j 0,3 ротор балансируют как жест-
кий, при Ыр/сокр! = 0,3 ~ 0,7 — как ква-
зигибкий и при <ор/(окр! > 0,7 — как гиб-
кий.
Если за параметр динамического со-
стояния принять один из известных фак-
торов (вибрации корпусов, прогибы рото-
ров, реакции опор, относительные дефор-
24
Основные понятия
мации и т. п.), то критерий гибкости и сба-
лансированность можно видоизменить, т. е.
представить его в виде отношения макси-
мального значения выбранного параметра,
найденного в диапазоне эксплуатационных
частот вращения или во всем диапазоне
от нуля до максимальных эксплуатацион-
ных частот вращения, к его допустимому
значению. Если это отношение меньше
единицы для несбалансированного ротора,
то он не нуждается в балансировке, в
противном случае его следует балансиро-
вать. Когда это отношение меньше еди-
ницы после балансировки ротора как
жесткого, т. е. в двух произвольных плос-
костях коррекции, то учет гибкости не ну-
жен, в противном случае ротор следу-
ет балансировать как гибкий.
Если после балансировки ротора как
гибкого в трех плоскостях коррекции рас-
сматриваемое отношение не стало меньше
единицы, ротор можно балансировать в
четырех, пяти и более плоскостях до тех
пор, пока отношение максимального зна-
чения измеренного параметра после бала-
нсировки к его допустимому значению не
станет меньше единицы.
На практике до решения вопроса о
критерии гибкости и сбалансированности
необходимо начальное распределение дис-
балансов. Если оно неизвестно, то находят
эксцентриситеты масс (например, вдали от
критических частот вращения), а затем
перерассчитывают контрольный параметр
для всех резонансных, критических и мак-
симальных частот вращения. После этого
сравнивают найденное максимальное зна-
чение контрольного параметра с допусти-
мым и принимают решение о небходимой
балансировке. Для этого расчетом опре-
деляют максимальное значение контроль-
ного параметра после компенсации найден-
ных дисбалансов в двух, трех и более
плоскостях коррекции и. сравнивая это
значение с допустимым, решают вопрос
об учете гибкости и минимально не-
обходимом числе плоскостей коррекции
[20]. С этой точки зрения решение
вопроса о допустимости балансировки
ротора как жесткого представляет со-
бой частный случай решения более об-
щего вопроса о минимально необходимом
числе плоскостей коррекции для выполне-
ния критерия сбалансированности.
Точность балансировки характеризует-
ся двумя составляющими: точностью полу-
чения заданного значения дисбаланса для
жесткого ротора на балансировочном стан-
ке-, точностью балансировки ротора любой
жесткости (в том числе и гибкого)
оцениваемой вибрацией машины по задан-
ному техническими условиями критерию
(перемещение, скорость, ускорение).
Для жесткого ротора точность ба-
лансировки характеризуется ГОСТом
[Г 9]* как произведение удельного дис-
баланса на наибольшую частоту вращения
ротора в эксплуатационных условиях, а
класс точности балансировки определяется
по нормированным предельным значениям
произведения удельного дисбаланса на на-
ибольшую частоту вращения ротора также
Таблица 1.2
Классы точности балансировки
Класс точности Значения произведения удельного дисбаланса (etT) на максимальную экспяуа тационную угловую ско- рость вращения (w,„,a4). мм рад,’с
наименьшее** наибольшее**
(0)* (0,064) (0,16)
1 0,16 0,40
2 0,40 1.00
3 1.1X1 2,50
4 2,50 6,30
5 6.30 16,00
6 16.30 40.00
7 40 IX) 100,00
8 100,00 250,00
9 250.00 630.00
10 630,00 1600.00
11 1600,00 4000,00
(12) (4000.00) —
* Применять факультативно.
** Наибольшие и наименьшие значения
произведений естыЭП1ах, определяющие границы
классов, образуют геометрическую прогрессию
со знаменателем 2,5.
* См список ГОСТов в конце книги
Неуравновешенность и балансировка ротора
25
в эксплуатационных условиях. В табл. 1.2
приведены классы точности балансировки,
а расположение полей классов точности
показано на рис. 1.7.
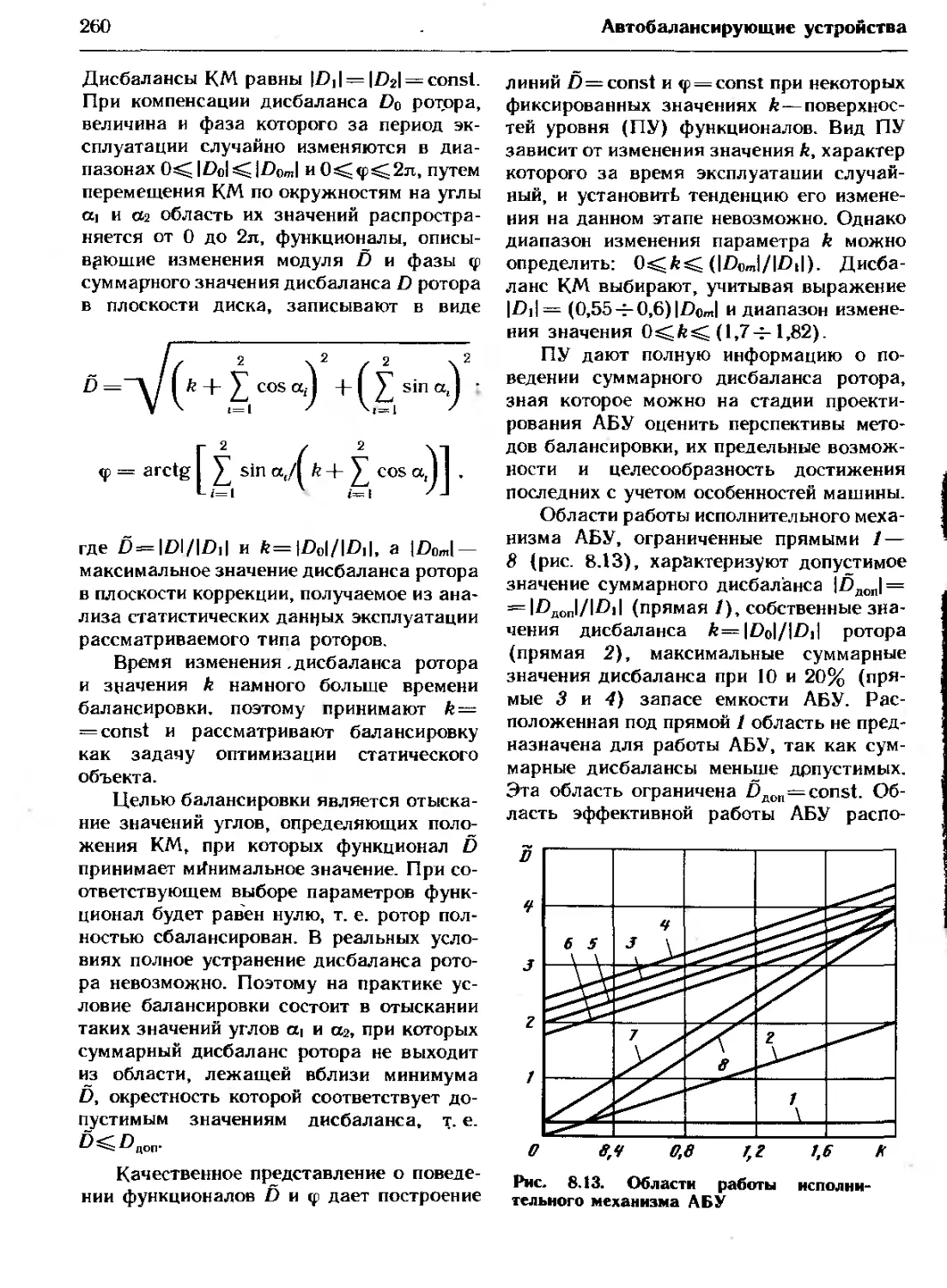
Роторы в изделиях с горизонтальной
осью вращения, попадающие в область
ниже линии НН, где eCT<o^l?iax < g, созда-
ют в опорах динамические нагрузки от дис-
балансов меньшие, чем статистические на-
грузки от веса ротора.
Роторы в изделиях с горизонтальной
осью вращения, попадающие в область вы-
ше линии НН, где тах >« g, создают
в опорах динамические нагрузки боль-
шие, чем статические нагрузки от веса
ротора (в этом случае, если нет других,
кроме веса статических нагрузок, при
выборе класса точности балансировки сле-
дует учитывать радиальные зазоры в под-
шипниках).
ГОСТом устанавливается верхнее зна-
чение главного вектора допустимых дис-
балансов по формулам:
Для ротора, балансируемого в изделии
в сборе,
^стдоп верх = рогаст табл ^ст э>
для ротора, балансируемого в виде отдель-
ной детали,
^ст доп верх ^рот^ст табл ^ст т ^ст э»
где /прот — масса ротора, состоящая из
всех деталей, которые вращаются в соб-
ранном изделии как одно целое (например,
собственно ротор, шкивы, шестерни, вра-
щающиеся вместе с реторсии кольца под-
шипников качения и т. д.); ест табя — таб-
личное значение удельного дисбаланса,
определяемое для данного собранного из-
делия по верхней границе установленного
класса точности балансировки и макси-
мальной эксплуатационной частоте вра-
щения его ротора; DCT т — значение глав-
ного вектора технологических дисбалансов
изделия, ротор которого балансировался
не в сборе; DCT э — значение главного
вектора эксплуатационных дисбалансов
изделия.
Технологические дисбалансы ротора
возникают, если его балансировали до
монтажа деталей (шкивов, полумуфт,
подшипников, вентиляторов и т. д), кото-
рые имеют собственные дисбалансы, вслед-
ствие отклонения формы и расположения
поверхностей и посадочных мест, радиаль-
ных зазоров и т. д.
Эксплуатационные дисбалансы возни-
кают из-за неравномерности износа, релак-
сации, выжигания, кавитации деталей
ротора (например, рабочих колес насо-
сов, вентиляторов, турбин), деформации
деталей ротора под влиянием рабочей
температуры ротора, неравномерности рас-
пределения материала на рабочей поверх-
ности центрифуги, действия шатунных и
поступательно движущихся масс
в поршневых машинах, за заданный
технический ресурс или до ремонта, пре-
дусматривающего балансировку.
Нижнее значение главного вектора
допустимых дисбалансов, приложенного
к центру масс ротора, устанавливают по
формулам
^ст доп нижи (^рот^ст табл/2,5) Dcy э,
для ротора, балансируемого в виде отдель-
ной детали или сборочной единицы,
/^СТ ДОП НИЖН == (^рот^ст табл/2,5) ^ст т
^ст э-
На основании опыта проектирования,
изготовления, эксплуатации роторных сис-
тем и стандарта [Г 1J в табл. 1.1
приведены рекомендации, связывающие
различные типы роторов роторных систем,
машин и механизмов, с классами точности
их балансировки [Г 9].
Более точное определение допустимых
удельных дисбалансов может быть прове-
дено на основании расчетов по определяю-
щим критериям, результатов испытаний
и опытной эксплуатации партии машин.
Расчет допустимых удельных дисба-
лансов. Допустимое значение удельного
дисбаланса eCTi (г • мм/кг) можно полу-
чить по одному из указанных выше кри-
териев, используя следующие соотноше-
ния:
Основные понятия
90000
70000
50000
ЧОООО
30000
20000
16000
12000
9000
7000
5000
9000
3000
2000
1800
1200
900
700
500
ЧОО
300
200
ISO
120
90
70
50
90
30
20
IS
12
250
о,ч
МГН!
ЧОООнм-рад/с
KOO
Г/Е
7,г
0,9
0,7
0,5
0,9
0,3
о, г
0,16
0,12
0,09
0,07
0.05
0,09
0,03
0,02
0,016
0,012
0,01
?.5мн-райк
0,1Бнн-раО/с
6,3мн-pail/с
П~ ID (t>
рзтах г_
Si S. ISSfWa'bS» <5i ^lOO'MUH 1
sb Ma цчСь c>> CsM
Рис. 1.7. Система классов точности балансировки и их полей
Неуравновешенность и балансировка ротора
27
с учетом физиологического воздей-
ствия вибрации на человека
ест1О- I03 • 10Ро/20/(лэ^)» (1-2)
где пэ—эксплуатационная частота враще-
ния, рот. об/мин; Кт=-----—-------------
"»₽<.» + «ст + ^фу.!Л
коэффициент массы; Ро — 2 IgV/V© — ин-
тенсивность колебаний (здесь V = 3,16 X
X Ю_| мм /с — пороговая виброскорость;
У© — виброскорость в центре масс ротора,
мм/с).
При интенсивности колебаний (в дБ)
после ряда преобразований получим
Ро = V - 76;
с учетом общей долговечности деталей
и узлов
ест2С2 • Юе/п2; (1.3)
с учетом долговечности подшипников
качения опор
естзСКт' Ю7«2. (1-4)
где Кг == | (] ДТ/Т)“1/3 — 11— коэффи-
циент снижения долговечности (здесь
ДТ = Т — Т\ —снижение долговечности
подшипников; Т — номинальная долго-
вечность подшипников; 7\ допустимая
долговечность подшипников; Кт = 0,2 при
ЬТ/Т < 0,96);
с учетом резонансных явлений в диа-
пазоне рабочих частот
«„„<2 • 107(<?п|). (1.5)
где Q — nnj/ln (Ло/Л|) —добротность
механической системы (здесь «| — число
периодов свободных колебаний механи
ческой системы при уменьшении ампли-
туды от Ао до значения Я»).
Определяющим для конкретной кон-
струкции критерием нормирования дис-
баланса является тот, при котором
получено наименьшее расчетное значение
допустимого удельного дисбаланса еСТ|-.
На основе результатов исследований
относительной значимости критериев мож-
но предложить следующие рекоменда-
ции (4|:
физиологический критерий необходимо
учитывать при расчете допустимых значе-
ний дисбаланса устройств, работающих
в непосредственном контакте с человеком;
критерий общей долговечности следует
принимать во внимание при расчете до-
пустимых значений дисбаланса деталей
и узлов машин, к которым не предъявляют-
ся никакие дополнительные требования и
рабочие частоты которых значительно
меньше резонансных;
критерий долговечности подшипников
необходимо учитывать во всех случаях,
за исключением тех, когда подшипники
на опорах ротора установлены с большим
запасом по долговечности;
резонансный критерий оказывает су-
щественное влияние на оценку допусти-
мого значения дисбаланса роторных сис-
тем, работающих в области резонансных
частот при пэ>3000 мин*'1.
Дисбаланс роторного узла является ге-
ометрической суммой дисбалансов соб-
ственно ротора и входящих в узел де-
талей, вращающихся вместе с ротором.
Дисбаланс, вносимый монтируемыми на
роторе деталями, является суммой дисба-
ланса самой детали и дисбаланса, вызван-
ного несовпадением геометрического цен-
тра посадочных поверхностей с осью вра-
щений ротора. Высокое качество баланси-
ровки роторных узлов в сборе можно
обеспечить только при достаточно высоком
качестве изготовления и балансировки
всех входящих в узел деталей.
При нормировании значения дисбалан-
са следует учитывать возможность ухуд-
шения динамического состояния роторных
узлов в течение срока их службы, напри-
мер вследствие износа, деформаций или
других причин. С этой целью в расчет
вводит коэффициент запаса Кэ; допуск
(eCTJ на удельный дисбаланс назначают
с его учетом, т. е.
кст<] = ест*/К3. (1.6)
Из опытных данных КЛ~ 1,2.
Нормирование удельного дисбаланса
роторов проводят, используя формулы
(1.5) - (1.8), с учетом установки рото-
ров на реальные опоры. При нормиро-
вании дисбаланса по критериям - физи-
ологическому (еСт1) и долговечности под-
шипника (ест 3) — следует учитывать усло-
вия монтажа ротора и реальную жест-
кость опор.
Расчет допустимых значений удельно-
го дисбаланса ротора по физиологическо-
му критерию с учетом реальной жесткости
опор ротора массой и жесткости соеди-
нения корпуса роторного узла массой
т с фундаментом осуществляют по форму-
ле (1.2) и уточняют с помощью следую-
щей зависимости:
Кт J = ^eCT)m/(m0(l - gf) (1 - ^)J
(1.7)
где £| — отношение рабочей частоты вра-
щения ротора к частоте собственных
колебаний ротора в опорах относительно
корпуса; 1-2 — отношение рабочей частоты
вращения ротора к частоте собствен-
ных колебаний роторного узла относи-
тельно фундамента
Расчет допустимых значений удельного
дисбаланса ротора по долговечности под-
шипниковых опор, проведенный по форму-
ле (1.4), уточняют с помощью следующе-
го выражения:
Ктз] =еет3(1 -£?). (1-8)
Последовательность нормирования
удельного дисбаланса роторов следую-
щая. По конструкции роторной систе-
мы выбирают необходимые расчетные
критерии, определяющие безвибраци-
онную работу машины. На основании
этих критериев формул (1-2) — (1.5)
вычисляют значения ест/ и выбирают
наименьшее из них. После этого уточняют
вычисленное значение с учетом коэффи-
циента запаса Кл и реальной жесткости
опор: для физиологического критерия —
по формуле (1.7); для критерия долго-
вечности подшипников — по формуле
(1-8).
По полученному уточненному значению
[ест J и наибольшей эксплуатационной
частоте вращения пэ (Г9) (рис. 1.7)
определяют класс точности балансировки и
назначают допустимый удельный дис-
баланс (ест) как среднее геометрическое
между верхней и нижней границей зна-
чений ест для данного класса точности,
т. е.
I^ctI == Vl^cTil max min- ( 1 *9)
По результатам исследований, испыта-
ний или опытно-промышленной эксплуата-
ции роторных систем с ротором, отбалан-
сированным с точностью, определяемой
формулой (1.9), окончательно устанавли-
вают нормированную величину удельного
дисбаланса [есТ].
Выбору допустимого значения неурав-
новешенности вращающихся элементов
машин посвящено много работ. Все они
касаются жестких роторов тихоходных ма-
шин. Для них этот дисбаланс считают
неизменным в процессе работы и основной
причиной вибрации машин. Для роторов
2-го и 3-го классов (квазигибких и гибких)
на эксплуатационных частотах вращения
возникает скрытый дисбаланс —- ротор из-
гибается. Последнее имеет не менее важ-
ное значение для величины вибраций,
чем остаточный дисбаланс.
Известны случаи, когда причиной по-
вышенных вибраций авиационных двига-
телей был остаточный дисбаланс роторов,
но вместе с тем многие двигатели с по-
вышенными дисбалансами работали при
меньших уровнях вибраций, чем двигатели,
у которых остаточный дисбаланс лежал
в пределах, оговоренных техническими
условиями.
В промышленности качество баланси-
ровки роторов 2-го класса, производимой
на серийных низкочастотных балансиро-
вочных станках, принято оценивать оста-
точным дисбалансом, пренебрегая упруги-
ми деформациями ротора. В этом случае
выбор допуска на дисбаланс является
сложной задачей, так как для его правиль-
ного назначения необходимо уточнить по-
следствия, которые вызывает любая вели-
чина неуравновешенной силы. При этом не-
Неуравновешенность и балансировка ротора
29
обходимо учитывать динамические, терми-
ческие и другие особенности условия ра-
боты конструкции, а также экономичность
процесса балансировки, так как с умень-
шением допуска на величину дисбаланса
возрастают затраты и время баланси-
ровки.
Если подойти к выбору допуска на
величину дисбаланса с позиций уравнове-
шивания роторов на высоких частотах
вращения с учетом их упругоинерционных
свойств, то эти величины следует назна-
чать не вообще для дисбаланса, а для
каждой из его нормальных составляющих,
так как эти составляющие определяют ре-
зонансы в зоне эксплуатационных частот
вращения и являются опасными.
Допуск на дисбаланс можно также на-
ходить, учитывая величины допустимого
прогиба и угла поворота сечения ротора
или величины допустимого изгибающего
момента и перерезывающей силы для од-
ной или нескольких форм колебаний.
Оценка качества балансировки. Ка-
чество балансировки роторов 2 и 3-го клас-
сов оценивают по предельно допустимому
значению виброскорости опор станка в ра-
бочем диапазоне частот вращений. Этот
балансировочный критерий определяют по
формуле
КБ = С0С1С2С3Кэ,
где V, — допустимое среднее квадратичес-
кое значение виброскорости опор агрега-
та прн его эксплуатации; Со — отношение
допустимого значения средней квадрати-
ческой составляющей виброскорости с час-
тотой, равной частоте вращения, к до-
пустимому значению средней квадратичес-
кой виброскорости полисармонической ви-
брации опор подшипников; С| — коэффи-
циент, устанавливается в случае, когда
характеристики опор на станке отличаются
от последних в эксплуатационных услови-
ях; С2 коэффициент, используемый при
измерении колебаний цапф ротора вместо
вибрации опор подшипников, равный отно-
шению значения вибраций цапф ротора
к значению вибрации его опор; С3 — коэф-
фициент, используемый при измерении ко-
лебаний ротора в местах его макси-
мального динамического прогиба, равный
отношению значений вибрации ротора, из-
меренной в местах его максимального про-
гиба. к значению вибрации цапф ротора.
Допустимое среднее квадратическое
значение виброскорости опор агрегата при
его эксплуатации V3 устанавливается тех-
ническими условиями.
Значение коэффициентов Со должно
быть выбрано на основании статистических
данных обследования спектрального соста-
ва вибрации конкретных типов роторов.
Значение коэффициента С| устанавли-
вают экспериментально. Значение коэф-
фициентов Сг и Сз выбирают на основа-
нии результатов специальных вибрацион-
ных исследований на стендах и на месте
установки для каждого типа ротора, плос-
кости измерения и формы изгиба в за-
висимости от частоты вращения, динами-
ческой жесткости ротора, жесткости опор,
жесткости и демпфирования подшипников.
При балансировке ротора методом из-
мерения вибрации опор принимают коэф-
фициенты С2 = Сз = 1.
В табл. 1.3 даны ориентировочные зна-
чения коэффициентов Q для некоторых
типов машин.
Балансировка роторов машины счита-
ется удовлетворительной, если максималь-
ное среднее квадратическое значение со-
ставляющей гармоники виброскорости
подшипниковых опор не превышает У3.
Результаты балансировки изолирован-
ного ротора или системы роторов (вало-
провода) на месте оценивают по макси-
мальному значению составляющих основ-
ной гармоники колебаний, полученной при
измерении у всех подшипников машины
в вертикальном, горизонтально-попереч-
ном и горизонтально-осевом (по отношению
к оси валопровода) направлениях во
всем возможном диапазоне частот вра-
щения роторов и при работе в режиме
холостого хода.
Основные понятия
Таблица 1.3
Значения коэффициентов С, и V, при высокочастотной балансировке роторов на станках (стендах)
Класс машин Типы машин Значения коэффициентов С, мм - с
Со Ci с2 I Сз
I — отдельные части двигателей и машин, собираемые с ма- шиной в нормальных экс- плуатационных условиях Г ироскопы Небольшие электродви- гатели до 15 кВА 1,0 1,0 1,12
II — машины средних размеров без специальных фунда- ментов и жестко установ- ленные двигатели или ма- шины (до 3000 кВА) Бумагоделательные ма- шины Электрические машины средней величины от 15 до 75 кВА. Электромаши- ны до 3000 кВА на спец- фундаментах Компрессоры Малые турбины 0,7—1,0 0.7 -1.0 0,7—1,0 0.7—1.0 1,0 2 — 6 2— 6 2,6 2 — 6 2 — 6 1.8
III — крупные первичные двига- тели и другие крупные ма- шины с вращающимися массами на жестких и тя- желых фундаментах, ко- торые относительно жест- ки в направлении изме- рений вибрации Крупные электродвига- тели Насосы Двухполюсные генерато- ры Турбины и многополюс- ные генераторы 0,7 1,0 0,7—1.0 0.6—1,0 0.6—1,0 ' 1 Ц 1 1,8
IV — крупные двигатели и дру- гие крупные машины с вращающимися массами на фундаментах, которые относительно податливы в направлении измерений вибрации Газовые турбины специ- ального назначения Двухполюсные генерато- ры Турбины и многополюс- ные генераторы 1,0 0,6—1,0 0,6 -1,0 2 — 6 2 — 6 2 — 10 1 2.8 2,8
Примечания; 1. Значения V. для машин Ш и IV класса соответствуют оценке «хо-
рошо» по СТ СЭВ 1368 — 78.
2. Значения коэффициентов Со, С2 приведены на основании стандарта ИСО 5343 с учетом
опыта СССР.
3. Значения Ct и Сз определяются экспериментально.
1.4. КЛАССЫ РОТОРОВ
Особенности роторов. В зависимости от
расположения опор роторы делят на
межопорные (рис. 1.8), консольные
(рис. 1.9), смешанные (рис. 1.10) и двух-
консольные (рис. 1.11). На схемах показа-
ны возможные варианты расположения в
роторах центров масс (ц- м) и плоскостей
коррекции (/, //).
Из этих схем видно, что при одном
и том же дисбалансе (D) ротора и соот-
ветствующей ему центробежной силе
(Dw2) реакции опор А к В существенно
зависят от типа ротора (межопорный,
консольный, двухконсольный, смешан
ный), положения плоскости коррекции (/,
/7) относительно опор, расстояния между
опорами и плоскостями коррекции
На рис. 1.12 показаны схемы сложных
многоопорных роторных систем. Все схемы
характеризуются конструктивно-техноло-
гическими признаками. К ним относятся
конструкции одно- и многорежимных рото-
ров, разбираемых (неразбираемых) после
балансировки, работающих вблизи резо-
Классы роторов
31
Рис. 1.8. Межопорные роторы с плоскостями
коррекции I, II и реакциями в опорах:
а) Д ?= f fr/a —|——|—/)/>«0^; В ~ > а 4- 1/а 4- b -|- /)/)<о2;
б) А = (Ь 4- 1/о + Ь 4- В — {а/аА-ЬД-1№<*>2
Рис. 1.9. Консольные роторы с плоскостями
коррекции /, II и реакциями в опорах:
a) A :=(b/a + l-~b)Da2, В =(а+l;a +b - 1)йы2\
б) A = (b-l/a + b В = {а/а -b + h^2
Рис. 1.10. Смешанные роторы с плоскостями
коррекции I, II и реакциями в опорах:
а) Д = (Ь/о —*4-/)Р<о2; В==(а4- 1/а 4-1 -
6) Л »- (L - b/a - b 4- /)£><ой; В = (а/а - b 4- /)£><о2
Рис. 1.11. Двухконсольные роторы с плос-
костями коррекции I. II и реакциями в
опорах:
a) A = (b/L)Du>2-, B^iL + b/LWio2,
б) Д = (L 4- а /L)Dw2. В = {ajL)йы2
32
Основные понятия
Рис. 1.12. Схемы сложных многоопорных роторных систем:
а—энергетических; б—летательных аппаратов
нансных режимов системы ротор — статор,
а также роторы с изменяющимся дисба-
лансом в процессе эксплуатации. Харак-
терным для высокоскоростных роторов
являются особенности посадки их деталей
на вал и технология сборки узла. Натяг
сопрягаемых деталей связан с длитель-
ностью работы машины, температурными
условиями и величиной центробежных сил,
возникающих в деталях ротора. Если на-
тяг в процессе работы ослабевает, то про-
исходит ослабление стыка, смещение эле-
ментов относительно друг друга, что при-
водит к появлению дисбаланса и росту
уровня вибраций машины [23].
Признаки деления роторов и структура
их балансировки. Основные конструктив-
но-технологические признаки роторов при-
ведены на рис. 1.13.
Учитывая динамические свойства и
особенности корректировки дисбаланса,
роторы делят на классы (табл. 1.4), для
балансировки которых используют соот-
ветствующие методы [С 4].
Из табл. 1.4 видно, что все роторы
машин разделены на 5 классов и 14 под-
классов с учетом их динамических свойств
и частотного диапазона балансировки.
Роторы класса 1 балансируют по мето-
дикам применительно к жестким роторам,
например в одной и двух плоскостях
коррекции 1а по главному вектору и глав-
ному моменту дисбаланса 1b и много-
плоскостными методами 1с. Выбор метода
Рис. 1.13. Основные конструктивно-технологические признаки роторов
Классы роторов
33
Таблица 1.4
Классификация роторов и особенности корректировки дисбаланса
Класс Плоскости коррекции дисбалансов ротора Пример
Класс 1 Жесткие роторы: Роторы, дисбалансы которых корректируются в двух произвольно выбранных плоскостях Колесо привода
класс 1а класс 1b класс 1с Роторы, балансирую- щиеся в одной и двух плоскос- тях коррекции но главному вектору и главному моменту многоплоскостными мето- дами Диски, колеса, барабаны, компрессоры
Класс 2 Квазигибкие рото- ры: класс 2а класс 2Ь класс 2с класс 2d класс 2е класс 21 класс 2g класс 2h Роторы, которые нельзя пускающие балансиров! измененной методики ба/ Роторы с известным р вдо считать жесткими, но до- су с использованием видо- ансировки роторов класса 1 определением дисбаланса ЛЬ оси в одной плоскости кор- рекции в двух плоскостях кор- рекции в нескольких плоскостях коррекции аспределенными дисбалан- цвух жестких масс значи- оси, находящиеся по се- ным распределением а вдоль оси двумя плоскостями. кор- м начальным дисбалансом тремя плоскостями коррек- одна в середине ротора) зчальным дисбалансом с контролируемым началь- нных плоскостях, в осталь- класса 2 Одномассовый ротор с легким валом, двухмас- совый ротор, многомас- совый ротор, печатный пресс-вал, барабаны па- мяти, компьютера
Роторы, балансирую- щиеся Роторы с равномерно р сами Роторы, состоящие из тельного протяжения пс редине Роторы с неизвест дисбаланс Роторы симметричные с рекции и контролируемы Роторы симметричные с ции (две на концах и и с контролируемым н< Роторы несимметричные ным дисбалансом в зада ном аналогично роторам Многоступенчатый насос центрифуги Высокоскоростной насос центрифуги, ротор турби- ны
Класс 3 Гибкие роторы: класс За класс ЗЬ класс Зс Роторы, требующие применения высокочастотных методов балансировки, их нельзя уравновесить с помощью модифицированных методов классов 1 и 2 Роторы, балансирующиеся (компенсирующие дис- баланс) по первой форме изгиба Роторы, балансирующиеся по первой и второй фор- мам изгиба Роторы, балансирующиеся по более высоким фор- мам изгиба Четырехполюсный ротор генератора, ротор турби- ны, небольшой ротор ге- нератора, крупный ротор генератора
Класс 4 Роторы, относящиеся к имеющие дополнительно соединенных гибких или динение элементов классам 1, 2 или 3, но один или несколько при- имеющих гибкое присое- Ротор с центробежным переключателем
Класс 5 Роторы, относящиеся к классу 3, но по опреде- ленным причинам (например, экономическим) ба- лансируются только для одной рабочей скорости Высокооборотный ротор
2 Зак 1641
34
Основные понятия
зависит от конструктивно-технологичес-
ких факторов ротора и требуемой точности.
Роторы класса 2 балансируют с исполь-
зованием видоизмененных методик жест-
ких роторов. Роторы класса 2 подразде-
ляют на следующие.
Роторы с известным распределением
дисбаланса- в одном поперечном сечении
(класс 2а); в двух поперечных сечениях
(класс 2Ь); в нескольких поперечных
сечениях (класс 2с); с равномерным рас-
пределением или линейно изменяющимся
дисбалансом (класс 2d); с жестким сред-
ним участком (класс 2е).
Роторы с неизвестным распределением
дисбаланса вдоль оси: симметричные ро-
торы с двумя плоскостями коррекции
(класс 2f) и с тремя плоскостями кор-
рекции (класс 2g), начальный дисбаланс
составных частей которых контролируется;
несимметричные роторы с контролируемым
начальным дисбалансом в заданных плос-
костях (класс 2Ь)
Если исходные дисбалансы полностью
собранных роторов класса 2 не превос-
ходят определенных пределов, то для та-
ких роторов допустимы методы низко-
частотной балансировки; в других случаях
требуются методы высокочастотной ба-
лансировки [С1, С4].
Класс 3 — роторы, требующие высоко-
частотной балансировки. Роторы этого
класса подразделяются на роторы, требую-
щие компенсации дисбаланса:
только по 1-й форме изгиба их оси
(класс За);
по 1-й и 2-й формам изгиба их оси
(класс ЗЬ);
по более высоким формам изгиба их
оси (класс Зс).
Класс 4 — роторы, относящиеся к
классам 1, 2 или 3, но имеющие до-
полнительна присоединенные элементы
(гибкие элементы или имеющие гибкое
присоединение).
Класс 5 — роторы, которые могут быть
отнесены к классу 3, но по экономи-
ческим или другим причинам балансируют-
ся только для одной рабочей скорости.
При оценке допустимого остаточного
дисбаланса в заданных плоскостях коррек-
ции гибких роторов вводят понятие экви-
валентного жесткого ротора. Это ротор той
же массы, размеров, скорости вращения и
классов точности балансировки, как и
жесткий ротор, но с таким соотношением
жесткостей вала и подшипников, когда
жесткость ротора вдвое больше жесткости
каждого подшипника в отдельности. При
этом первая критическая скорость в 1,25
раза выше рабочей скорости Допустимый
остаточный дисбаланс для всех классов
гибких роторов устанавливают с учетом
требований к остаточному дисбалансу эк-
вивалентного жесткого ротора в соответ-
ствии со стандартом ИСО 1940 (С1] *.
Остаточный дисбаланс полностью соб-
ранных гибких роторов классов 1 и 2 не
должен превышать остаточного дисбалан-
са для эквивалентного жесткого ротора
в соответствии со стандартом ИСО 1940.
Для роторов подклассов 2f — 2Ь
остаточный дисбаланс йаждой детали (или
составной части) не должен превышать
меньшего из следующих параметров:
предельно допустимого дисбаланса
сборки, деленного на утроенное значение
числа составных элементов;
допустимого остаточного дисбаланса
собранного ротора.
Для роторов класса За с распреде-
лением дисбаланса только по 1-й форме
изгиба остаточный дисбаланс не должен
превышать определенных пределов, вы-
раженных в процентах от общего остаточ-
ного дисбаланса:
эквивалентная 1-я форма дисбалан-
са — 60%;
при условии проведения низкоскорост-
ной балансировки — 100%
Для роторов классов ЗЬ и Зс оценку
остаточного дисбаланса проводят в балан-
сировочном устройстве с жесткими опо-
рами.
Для роторов класса ЗЬ с распреде-
лением дисбаланса только по 1-й и 2-й
Список стандартов см. в копие книги
Жесткий ротор
35
формам остаточный дисбаланс не должен
превышать следующих пределов, рекомен-
дованных для эквивалентного жесткого
ротора:
дисбаланс по эквивалентной 1-й форме
не должен превышать 100%;
дисбаланс по эквивалентной 2-й форме
не должен превышать 60%;
если проводится низкоскоростная ба-
лансировка, то общий остаточный дис-
баланс ротора как жесткого не должен
превышать 100%.
Для роторов класса Зс, у которых
дисбаланс распределен по более высоким,
чем 1-я и 2-я, формам, -рекомендации
могут быть даны по мере накопления
информации и экспериментальных данных.
В заключение следует подчеркнуть, что
приведенные .ориентировочные значения
допустимых остаточных дисбалансов в
плоскостях коррекции гибких роторов от-
носятся к диапазону рабочих частот вра-
щения, отстроенному от любой крити-
ческой частоты вращения на ± Ю%.
При нахождении рабочей частоты враще-
ния в области какой-либо критической
частоты ротора данные допуски не будут
верны, и для устранения дисбаланса в*
этом случае необходима балансировка по
формам колебаний.
1.5. ЖЕСТКИЙ РОТОР
Характерные особенности. Жестким
называют ротор, сбалансированный на
частоте вращения, меньшей первой крити-
ческой в двух произвольных плоскостях
коррекции, у которого значения остаточ-
ных дисбалансов не будут превышать до-
пустимые на всех частотах вращения
вплоть до наибольшей эксплуатационной.
Жестким иногда называют ротор, крити-
ческая частота вращения которого намно-
го выше его эксплуатационной частоты
вращения, т. е. <о<Сшкр|. Оба эти опре-
деления отражают одну из особенностей
в динамике ротора — возможность практи-
чески пренебрегать деформациями при
данных условиях Абсолютно твердые ма-
териалы в природе не существуют. Усло-
2*
вия, при которых ротор является жестким,
неоднозначны в различных отраслях ма-
шиностроения и даже в одной отрасли.
При сохранении общего определения к по-
нятию «жесткий ротор» конструктор имеет
относительно широкие возможности варьи-
ровать этим понятием.
Формально одинаковые по динамичес-
ким характеристикам роторы в различных
изделиях считаются жесткими или гиб-
кими. Пользуясь определенными соотно-
шениями. конструктор самостоятельно ре-
шает, к какой группе отнести проектируе-
мый ротор.
Для ротора на жестких опорах, когда
пренебрегают влиянием деформации кор-
пусных звеньев изделия центробежная
сила F инерции ротора и прогиб у от этой
силы соответственно равны:
F — ты\ё + у)-,
у=^е
. . 2
( IIJ кр |)
1 — («/«крУ
ИЫ2
У = е----
с-тш
. ИЛИ
По количественному соотношению |е| и
|£| конструктор принимает решение.
Пример 1. Рабочая частота вращения
ротора равна 0,2 от критической. Обосновать,
к какой группе относится ротор
Для решения не требуется массодо-геоме-
трических параметров. Находят только соотно-
шение прогиба и эксцентриситета по заданному
условию (о/<йКр j = 0,2:
0 22
у = е--------у » 0,041 е.
1-0,2*
Следовательно, на рабочей частоте враще-
ния центробежная сила только на 4% отли-
чается от силы на абсолютно жестком роторе.
Поэтому такой ротор принимают жестким.
Пример 2. Рабочая частота вращения ро-
тора равна 0,7 от критической. Аналогично
предыдущему решению устанавливают
у = е (0,7) -у « 0.96е
I—-(0,7)
Такой ротор должен относиться к категории
квазигибких, так как на рабочей частоте вра-
щения центробежная сила увеличивается почти
в два раза по сравнению с силой на
абсолютно жестком роторе.
В общем случае принято считать жест-
кими роторы с <о/<окр । <2 0,2 для изделий
36
Основные понятия
с высокими требованиями к уровню вибра-
ций. Для изделий конструктивно сложных,
многозвенных принято считать жесткими
роторы с <л)/<окр । «С 0,6 (например, роторы
авиационных двигателей).
Для ротора на податливых опорах,
когда влияние деформации их существенно
и жесткость опор соизмерима с жесткостью
самого ротора (на жестких опорах), ис-
пользуют более сложную зависимость:
F = т<о1 2(ё + у + ус).
т. е. в рабочих условиях силы инерции только
на 4,21% отличаются от сил жесткого ротора
на жестких опорах. Можно считать ротор жест-
ким. Из сравнения с результатами примера
1, где также w/<i>pae = 0,2 видно, что уменьше-
ние жесткости опор мало повлияло на при-
ращение силы инерции.
Пример 4. Рабочая частота вращения рото-
ра равна 0,7 от критической (ы/сок„ , — 0,7).
Жесткость опор и коэффициент демпфирования
такие же, как в примере 3 (w/<i)Kp, = 0,5;
2п/юос = 0,5). Определить, можно ли считать
ротор жестким.
Аналогично предыдущему примеру полу-
чаем:
-----------------* 0,72
у е----------- -----------------------------------.
1 - 0,72 1 4- 0,52 t - —
V(1 -0,352)2 4- 0,о2 - 0.352 -
1,31 Зе
Здесь к прогибу ротора у — F/cp добавля-
ется прогиб опор:
F 1
Уо — -----г --------—'---'
° Л I ( / V2] 2 4n2uj2
“vL i -(“/«J 1 + —г-
V
где <вос — собственная частота колебаний
опор; п — коэффициент, учитывающий
демпфирование, когда сопротивление дви-
жению пропорционально скорости;
Такой ротор должен относиться к квазигибким,
так как в рабочих условиях сила инерции
более чем в 2 раза превышает силу на жестком
роторе. Из сравнения с результатами примера 2
(со/сйкр j = 0,7 в обоих примерах) можно заклю-
чить, что снижение жесткости опор. влияет
на сбалансированность ротора тем значитель-
нее, чем ближе к <DKp ].
Если учитывать не только конструк-
торские, то и технологические условия
производства, к определению «жесткий ро-
тор» следует подходить с другим крите-
рием: Fpa6<Faon; Мраб<МДО11. Состоя-
Для оценки соотношения у и е необхо-
димо знать п и в>ос.
Пример 3. Рабочая частота вращения ро-
тора равна 0,2 от критической (о>/<окр । — 0,2),
жесткость опор выше жесткости ротора (<й (/
“ос = 0,5), отношение коэффициента демпфиро-
вания к собственной частоте колебаний опор
равно 0,5 (2п/п)ос — 0,5). Установить, можно ли
такой ротор считать жестким.
После подстановки всех данных в формулу
прогиба ротора получаем:
ние сбалансированности, полученное на
балансировочном станке, изменяется при
увеличении частоты вращения. Это явле-
ние обусловлено изменением взаимного
расположения масс относительно оси рото-
ра вследствие податливости. После ба-
лансировки многомассового ротора в
двух произвольных плоскостях коррекции
сбалансированность зависит как от вели-
У = е
1 — 0.22
0,042е,
0,22
1 +0.52 ••.............. -
V (1 -0,12)24-0,52- 0,12.
Жесткий ротор
37
чины рабочей частоты вращения, так и от
величины эксцентриситетов отдельных
масс. Чем меньше эксцентриситеты, тем
больше частота вращения, на которой
сохраняется сбалансированность
Для многомассового ротора в зависи-
мости
п
Р = £ mtb>2(e, + y)
<=1
количественную взаимосвязь у, и ё, можно
установить с помощью численного или фи-
зического эксперимента; но есть другой
путь — приближенный. С точностью, до-
статочной для практических целей, счита-
ется, что
У,/У1 *= У!С./У( ст = У, =
где индекс «ст» означает статический.
п
У/ст~ Е бйа/А, (б,,— вес отдельной
k=i
массы ротора).
На этом основании получена зависи-
мость
п
ml etat,
1 - £
/=|
из которой следует, что прогибы и эксцент-
риситеты связаны линейно. Также линей-
но зависит F и М от е,-. Поэтому при
одних значениях е( и двухплоскостной
низкочастотной балансировке Fpa6 <2 Гдоп,
МРаб«С Мдоп. При других значениях ещу >
>• е,- может быть
Р Р М М
' раб 1 доп» *мраб /Г4доп"
Пример 5. По статистическим данным про-
изводства роторов установлено, что е^етах.
При низкочастотной балансировке в двух плос-
костях коррекции во время работы (о)раб <
<“кр |)
^раб max ~ ®»®^доп-
После изменений в процессе изготовления сни-
зилась стоимость обработки, но снизилась я
точность размеров деталей так. что етах =
= 1,5етах. Вследствие этого
Граб (I) раб» раб max ~ 1 »^Гдоц-
Такой ротор не может считаться жестким,
так как для выполнения условия FpaC гпах
Гщъи необходимо выполнять низкочастотную
балансировку более чем в двух плоскостях
коррекции, либо применить высокочастотную
балансировку.
На рис. 1.14 показана схема проги-
бов балки равномерного сечения в
Рис. 1.14. Схема прогибов балки
зависимости от положения по длине дей-
ствующей последовательно единичной си-
лы F. При этом видно, что наибольший
прогиб у'з возникает от действия силы F$
в среднем сечении. Вообще yti — F^,
а так как аз > аг,, то t/з > уц. Если
приложенные в каждом сечении (1 — 5)
единичные силы уравновесить двумя сила-
ми в сечениях / и 5, то суммарный
прогиб совпадает с направлением силы
в среднем сечении.
Аналогичное состояние возникает на
рабочих частотах вращения после ба-
лансировки ротора в двух крайних плос-
костях коррекции на балансировочном
станке. Но чем меньше |ef|, тем меньше
|у,-| и, соотвегственно, |А|, гем меньше
могут быть частоты вращения, при которых
Граб Гдоп. Определить значения экс-
центриситетов, при которых ротор со-
храняет статус жесткости, можно экспе-
риментально или расчетом:
F — F' — /ntw2e, +
<= (=i
П П
4- Y, Е
i=l /=]
38
Основные понятия
М = 4~
1=1 (=i
п п
+ Е Е р<а‘г
i=l /=1
Роторы такого типа являются проме-
жуточным звеном между жесткими и гиб-
кими роторами
Неуравновешенности ротора. Много-
массовый ротор является сложной систе-
мой, в которой при вращении взаимо-
действуют все виды сил и связей, в
результате чего устанавливается равновес-
ное состояние на установившихся режи-
мах работы В системе ротор — корпус
равновесное состояние обусловлено связя-
ми в местах контакта ротора со статором,
т. е. реакциями опор. Для надежной ра-
боты изделия в общем случае требует-
ся уравновесить ротор.
При вращении ротора возникают силы
инерции вращательного движения, вызы-
вающие давление на подшипники и, в
результате, вибрации всего изделия. Для
уравновешивания нужно определить дав-
ление, оказываемое цапфами на поверх-
ности подшипников и рассчитать на осно-
вании полученных данных компенсирую-
щие массы, так как силы, приложенные к
ротору, уравновешиваются силами инер-
ции всех частиц. Решение этой задачи на-
зывают балансировкой, в отличие от более
общей, когда уравновешиваются и силы
инерции поступательного движения. Усло-
вие сбалансированности по физической
сущности состоит в том, чтобы ось ро-
тора совместилась с главной центральной
осью инерции (ГЦОИ).
В реальных производственных услови-
ях вероятность совмещения оси вращения
с ГЦОИ является событием практически
недостоверным. Слишком большое число
случайных факторов (погрешности обра
ботки, сборки, плотности материала и др.)
влияют на взаимное расположение осей.
Наиболее вероятное состояние, при кото-
ром оси — перекрещивающиеся прямые,
показано на рис. 1.15, а.
Суммы всех сил и моментов отно-
сительно центра масс выражаются зави-
симостями
^рот W ^СТ ,
п п
Е 7Й{= mJo2eI/(=^0.
<»i <=i
Ротор динамически неуравновешен.
Общий случай положения прямых в про-
странстве состоит из двух частных слу-
чаев:
а) оси лежат в одной плоскости и
параллельны (рис. 1.15,6):
Л п
Е Fz#=0, — ротор стати-
<=1 »=]
чески неуравновешен;
б) оси лежат в одной плоскости и
пересекаются в центре масс (рис. 1.15,в):
Жесткий ротор
39
п п
М( 0 — ротор имеет мо-
«=| <=1
ментную неуравновешенность.
В практических расчетах удобнее
пользоваться не понятиями главного век-
тора и главного момента сил. т. е.
п п
F-'LF>-
1=1 <=|
а главным вектором дисбалансов ротора:
п п
— (где DCT — Ь,= wfiCT=
i=i
= трот ест)
и главным моментом дисбалансов ротора:
_ / п
= (где
П \
— S 4 == &М I* ) »
1=1 /
L — плечо результирующей пары сил Ьм.
Динамическая неуравновешенность.
Отрицательное влияние ротора, приводя-
щее к увеличению вибраций в системе
работающего изделия, обусловлено тем,
что жесткие опоры корпуса, как внеш-
ний фактор, ограничивают движение цапф
так, что ротор вращается около оси,
смещенной от Г11ОИ. В результате на
опоры А и В корпуса действуют врашаю
щиеся векторы ЬА и Ьв, в общем случае
разные по величине и угловому положе-
нию. _
Векторы ЬА И D в есть суммарное
проявление статического и моментного
дисбалансов на опоры (рис. 1.16):
Da — DCT А -f- ЬМА, DB — DCT B -f- DMB
и полностью эквивалентны динамической
неуравновешенности ротора. Для абсолют-
но жестких опор строго соблюдаются усло-
вия, при которых статические составляю-
щие сил обратно пропорциональны рас-
стояниям от соответствующей опоры до
центра масс:
^ст a bCTLB/L. Dcr в Dc.rL,A/L,.
Векторы DCT А и Ост в параллельны,
лежат в одной плоскости с DCT и, в общем
случае, разные по величине. Направление
векторов DcjA и ЬстВ для межопорного
ротора (центр масс расположен между
опорами) одинаковое с вектором DCT
(рис 1.16, а), для консольного ротора
(центр масс вне опор) направление векто-
ра на опоре, ближней к центру масс,
совпадает с вектором £>ст, на дальней
опоре—противоположно (рис. 1.16,6).
Моментные^ составляющие пары сил
дисбалансов DMA и DMB равны по ве-
личине и противоположны по направле-
нию, независимо от положения центра масс
относительно опор:
Рис. 1.16. Схема сил на опорах ротора:
а- межопорного: б—консольного
40
Основные понятия
&МА + ^МВ — О’»
I ®ма I — I Ьмв | — DM = М/L\
&МЛ — В МВ — 0
Векторы ЬМА и DMB лежат в плос-
кости пары сил главного момента
дисбалансов ротора
Главный вектор £>ст и главный момент
Л1Д дисбалансов имеют началом точку
центра масс ротора и находятся в плос-
кости, перпендикулярной оси вращения.
Угол <р между векторами £)ст и 7ЙЯ является
величиной случайной, соответственно это-
му_находят углы между £>ст А и DMA, Dcr в
и DMB, учитывая, что плоскость пары сил
перпендикулярна MR.
При решении задач по динамической
неуравновешенности применяют различ-
ные математические методы с использо-
ванием векторных и алгебраических зави-
симостей.
В специализированных аналоговых вы-
числительных устройствах применяют в ос-
новном векторную форму. В универсаль-
ных АВМ и цифровых ЭВМ — алгебра-
ическую, представляя векторные зависи-
мости в координатной форме.
По известным параметрам DA, DB и
углу а между ними определяют DfT, DMA в
и их составляющие в заданных плос-
костях коррекции. Координатные оси при-
вязывают к Da или Db.
Для решения удобно использовать тео-
рему косинусов, тогда
Полученные в результате решения зна-
чения и углы главного вектора дисбалан-
сов и пары сил главного момента дают
возможность определять составляющие
дисбаланса в заданных плоскостях коррек-
ции (две или более).
Статическая неуравновешенность. В
частном случае динамической неуравнове-
шенности, когда ось ротора и ГЦОИ па-
раллельны,- проявляется силовая (стати-
ческая) неуравновешенность. Физически
это означает, что каждый дискретный
элемент ротора смещен от ГЦОИ на
Рис. 1.17. Векторная схема статических дис-
балансов
одинаковую величину. Векторы центро-
бежных сил (дисбалансов) отдельных де-
талей или участков ротора пропорциональ-
ны их массе (рис. 1.17):
FcU — т.{Ь)2еС1, FCT —
2О^Двсоь( 180 —ос! ,
^СТ1 ^рот ^ст»
ОСт« 7)ст X Dcrt гПрОТест.
Статический дисбаланс полностью
эквивалентен одному вектору £>ст. Устра-
нить статическую неуравновешенность
можно одним корректирующим вектором
Ост к ~ “^ст» т- е- ^ст к приложен в
той же точке, центре масс, но направ-
лен противоположно (Дстк = /пкгк. где
Жесткий ротор
41
и гк — корректирующая масса и радиус
коррекции). При любых вариантах распре-
деления корректирующих масс должно
п
соблюдаться условие J' DC1K,
сумма корректирующих дисбалансов рав-
на DCT_K в центре масс, а сумма момен-
тов DCTK<- относительно центра масс
равна нулю.
Статическая неуравновешенность не
влияет на моментную неуравновешенность.
Это обстоятельство используют в тех уст-
ройствах, где по условиям работы необхо-
димо создавать на опорах ротора опреде-
ленно ориентированные нагрузки.
Моментная неуравновешенность. Она
является частным случаем динамической
неуравновешенности, когда ГЦОИ и ось
ротора пересекаются в центре масс, так
что между осями есть некоторый малый
угол -у. В общем случае на роторе возни-
кает момент, называемый моментной неу-
равновешенностью, вызывающей нагрузки
на опорах в виде пары сил.
Особенностью моментной неуравнове-
шенности является неоднозначность связи
между направлением отклонения ГЦОИ от
оси ротора и направлением момента. В
зависимости от конфигурации ротора пара
сил момента может совпадать с направле-
нием отклонения ГЦОИ от оси ротора или
быть противоположным (рис. 1.18). Это
связано с величинами моментов инерции
относительно трех главных центральных
осей инерции ротора: X, У, Z. Для сим-
метричного ротора с равномерным рас-
пределением масс моменты инерции равны
между собой и описываются относительно
осей X и Y зависимостью
/г2 12\
ь-h->«р(т+4) • 1110)
относительно оси Z
(1.11)
Момент, возникающий из-за отклоне-
ния ГЦОИ от оси ротора на малый
угол у, связан с моментами инерции Jх и
J z зависимостью
M = (Jx-/z)<d27. (1.12)
В предельном варианте, когда г с /
(рис. 1.18, а):
2
М (" VZA
6)
Рис. 1.18. Действие моментной неуравнове-
шенности:
а—на цилиндрическом роторе; б на дисковом
роторе
когда г I (рис. 1.18,6):
Следовательно, в роторах дисковой
конструкции моментная неуравновешен-
ность действует в направлении совмеще-
ния ГЦОИ с осью ротора; в роторах
цилиндрической конструкции моментная
неуравновешенность действует в направле-
нии увеличения угла у между осями.
Для жестких роторов эти тенденции не
влияют на решения задач по устранению
моментной неуравновешенности. Момент-
42
Основные понятия
ный дисбаланс полностью эквивалентен
двум векторам: DMA и DMB—на опорах
ротора.
Наиболее специфическим является ва-
риант решения, возникающий при условии
/А — JY = Jъ тогда Л! — 0.
В этом случае любая ось ротора,
проходящая через центр масс, тождествен-
на с главной центральной осью инерции
.Это совершенно очевидно для ротора ша-
ровой. конструкции. Для цилиндрического
ротора такое состояние возможно на ос-
новании формул (1.10) — (112) при усло-
вии I = г уЗ. В таком роторе может быть
только статическая неуравновешенность.
Балансировка ротора. Сбалансирован-
ность ротора можно получить двумя ва-
риантами перемещения осей:
совмещением оси ротора с главной
центральной осью инерции (ГЦОИ);
совмещением ГЦОИ с осью ротора.
Первый вариант имеет ограниченное
число решений. Одно из них — цапфы ро-
тора обрабатывают до совмещения осей.
Второе решение связано со специальным
эксцентриковым устройством между внут-
ренней обоймой подшипника и поверх-
ностью цапфы. Устройство может состоять
из относительно неподвижных деталей, по-
ложение которых (совмещение осей) уста-
навливают при балансировке, или под-
вижных деталей, позволяющих совмещать
оси во время работы с помощью спе-
циальной системы управления — авто-
балансирующего устройства.
Первый вариант балансировки не полу-
чил распространения, хотя и создает на-
илучшие условия по распределению оста-
точных дисбалансов — пропорционально
смещениям между осями ротора и ГЦОИ.
Основной недостаток его состоит в том, что
размер каждой цапфы ротора индивиду-
ален. Невозможно применять стандартные
подшипники и детали. Более того, при
повторной балансировке необходима заме-
на ранее установленных подшипников.
Второй вариант имеет большое число
решений, т. е. столько, сколько плоскостей
коррекции принято на роторе. Чтобы урав-
новесить жесткий ротор, достаточно двух
плоскостей коррекции, но по техническим
условиям иногда устанавливают большее
число плоскостей.
Связь дисбалансов в плоскостях изме-
рения и коррекции. При решении задач
по балансировке роторов возникают ситуа-
ции, когда плоскости коррекции по каким-
либо причинам нельзя совместить с плос-
костями измерения дисбалансов на ба-
лансировочном оборудовании. Тогда вна-
чале определяют дисбалансы DA и DB в
плоскостях измерения Л и В, а затем
на основании полученных данных рас-
считывают дисбалансы DA[ и DB{ в плос-
костях коррекции и В\ (рис. 1.19).
Рис. 1.19. Связь дисбалансов в плоскостях
измерения и коррекции
Достаточно простые зависимости для
перехода от одних плоскостей к другим
дает теорема косинусов. По заданным
величинам £, LA, LB и L, Lai, LBl и
получаемым параметрам DA, DB и а пере-
ход к Da । и DB ] выполняют в следующем
порядке:
определяют £>ст и DMA и углы (Dc^?DA),
{ЬМА\ ЬА) по зависимостям параграфа 1.4;
рассчитывают
Жесткий ротор
43
ОЛ1„=ОСТ-^; DBl„=DCT-^
®МА\ ~ ®МА ~ '> &МВ1 ~ — ®МА15
находят искомые DAl, DBl и углы
(Da~Da) h(Db^Da) :
D2fy\ = ^Л|ст+^М41 —
— Al ст МА I cos ( &А\ст« &МА J ,
где
(^Л»ст5 & МА 1) =
= 180° -[(гл?Лст) +(£и?£мд)] ;
(^лГ> ®а) = {®аГ, ^/Я ст) — (^Д^ст) •
где
/ П 'У'П \ — DAt^ + DAi — DMAl
СО8(£/Л|, DА\ ст/ nr-. r-. »
£L/A] CT ^Al
&B\ — ^BIct + ^MBI
— 2DBl€TDMBi eos(£)filcT; Z5Mei),
где
(OBl ст* ^MBl) —
= (ОЛ; DAq^ |-(£>л; Dma) ,
(Двь ®a) ={Da; Dc^ 4-
+ (^вь DlilC() ,
где
cos(DB1; DBi CT)
^1 + D'et ст ^Л!Л1
DBl DBt (T
Режимы нагружения подшипников ро-
тора. В общем случае на работающем
роторе действуют неоднородные силы, соз-
дающие радиальные нагрузки на опоры.
Они составляют две группы:
силы инерции вращающегося ротора,
которые определяют в виде составляющих
главного вектора F и главного момента
М;
силы тяжести и силы, возникающие от
вида связей ротора (зубчатые и ремен-
ные передачи и др.). _
Первая группа DA вм)2 — постоянная
по величине и направлению относительно
ротора и поэтому переменная по направле-
нию относительно корпуса.
Вторая группа QA в — постоянная по
величине и направлению относительно
корпуса и поэтому переменная по направ-
лению относительно ротора.
Результирующая сила на подшипниках
Ra.B — ^A.B®2 + Qa, В»
переменная по величине и направлению,
а степень изменения К зависит от со-
отношения
К А, В — DА вы2/Qa, в
называемого коэффициентом дисбаланса
для опор А и В.
Под действием RA в в рабочих условиях
ротор колеблется в подшипниках. В за-
висимости* от граничных значений К_А.в су-
ществует три схемы действия RAB и
соответственно три режима работы под-
шипников.
При первом режиме в_< 1, пре-
валирует вектор Qa.b* тогда RAB 8 то^'
ках окружности / — 4 имеет вид, пока-
занный на рис. 1.20, а. Рабочая поверх-
ность внутренней обоймы подшипника из-
нашивается равномерно, а наружной — на
ограниченном участке.
При втором режиме КА в = L в одном
из положений RAB—0 (рис. 1.20,6).
Происходит разрыв контакта между рабо-
чими поверхностями подшипников, нагруз-
ка изменяется скачкообразно, возникает
удар. Это недопустимый режим работы,
способствующий разрушению подшип-
ника.
Третий режим устанавливается при
К>1. Превалирует вектор ЬАВа>2, при
44
Основные понятия
Рис. 1.20. Схема сил на
опорах ротора:
а при первом режиме нагру-
жения, б'—при втором режиме
нагружения; в — при третьем
режиме нагружения
этом Ra в получает вид, приведенный на
рис. 1.20, в. Такое состояние возникает
не только при больших значениях DA вы2,
но и при отсутствии силы тяжести (неве-
сомость, вертикальная ось ротора). Рабо-
чая поверхность наружной обоймы изна-
шивается равномерно, внутренней — на
ограниченном участке.
Колебания ротора в подшипниках при
режимах работы Лд в > 1 и е < 1
подчиняются закономерностям математи-
ческого маятника. Для жестких опор
расстояние между центрами рабочих по-
верхностей внутренней и наружной обойм
подшипников 6—главный параметр. Час-
тота маятниковых колебаний при малых
углах отклонения (практически до 20°)
зависит только от 6 и ускорения силы
тяжести g, т. е.
Когда частота вращения ротора совпадает
с частотой маятниковых колебаний, возни-
кает маятниковый резонанс. Амплитуда ко-
лебаний ротора в подшипниках достига-
ет наибольшей величины. Это сопровож-
дается увеличением амплитуд колебаний
изделия и ускоренным износом подшипни-
ков. Чтобы сдвинуть режим от рабо-
чих частот вращения ротора, нужно из-
менить 6.
t.6. КВАЗИГИБКНЙ РОТОР
Характерные особенности. Квази гиб-
ким называется ротор, который не удовле-
творяет условиям жесткого ротора, но
рабочий диапазон частот его ниже первой
критической частоты вращения. При ба-
лансировке такого ротора необходимо учи-
тывать упругие деформации в рабочем
диапазоне (см. пример 2). Наиболее часто
квазигибким считают ротор с рабочим
диапазоном 0,6 wKp j < < о)кр }. Опреде-
лить, является ли ротор квазигибким, дол-
жен разработчик изделия и на этом ос-
новании установить число и расположе-
ние плоскостей для постановки корректи-
рующих масс. Плоскости коррекции долж-
ны быть увязаны с методом баланси-
ровки так, чтобы выполнялись соотно-
шения
F С Г М СМ
1 раб доп’ 2 'раб 2Г'лои-
Расчет Fpa6, Мраб можно вести при
условии, что опоры абсолютно жесткие,
так как при прочих равных условиях
с уменьшением жесткости опор составляю-
щая прогиба ротора ур в зависимости
F = т«й2(ё + ур + уо)
уменьшается. Этим создается некоторый,
«запас» по точности расчета.
Неуравновешенность ротора. Равнове-
сное состояние сил инерции квазигибкого
и гибкого роторов определяется общими
физическими свойствами. В аналитических
зависимостях есть параметры, учитываю-
щие деформацию ротора. Условие, ха-
рактеризующее состояние неуравнове-
шенности, является общим для всех типов
роторов и состоит в том. что ось вращения
и главная центральная ось инерции не
совпадают. Влияние деформации ротора
проявляется в том, что в общем случае
неуравновешенность изменяется с измене-
нием частоты вращения. Поэтому не-
уравновешенность квазигибкого ротора на
низкой частоте вращения и в рабочем
диапазоне может резко различаться.
Квазигибкий ротор
45
Состояние неуравновешенности пол-
ностью характеризуется относительным
положением оси ротора и ГЦОИ, которое
в общем случае представляется перекре-
щивающимися прямыми, как и для жестко-
го ротора (рис. 1.16). Дополнительной
характеристикой является форма геомет-
рической оси ротора. Эта ось совпадает
с осью ротора, когда нет вращения,
и определяет форму изгиба ротора при
высоких частотах вращения.
Главный вектор сил инерции и главный
момент определяют (без учета гироско-
пических моментов) с использованием за-
висимостей
Рис. 1.21. Влияние моментной неуравнове-
шенности на прогиб:
а — многом ассового ротора: б—одномассового
дискового ротора
п п п
F — т^е^- znf<o2^ Fja^;
<=1 »=1 ;=1
П П г П
т4(й2[ef/J 4- 2 т,(1)21 1(
i=I <-=[ L J=[
Для квазигибдого ротора эти зависи-
мости дают достаточную для практических
целей точность при определении состояния
неуравновешенности. Динамическая не-
уравновешенность характеризуется усло-
виями F О,. М 0; моментная неурав-
новешенность — условиями F = б, М ф 0
и силовая неуравновешенность — условия-
ми F =/= 0, М = 0.
На многомассовом межопорном сим-
метричном роторе силовая неуравновешен-
ность является наиболее опасной, пос-
кольку вызывает первую форму изгиба
и значительное увеличение сил инерции.
Особенность моментной неуравновешен-
ности состоит в том, что под ее вли-
янием изгиб ротора и величина неуравно-
вешенности от силовой составляющей мо-
гут возрастать (рис. 1.21. а) или умень-
шаться (рис. 1.21,6).
Балансировка ротора. В зависимости
от требований к сбалансированности в ра-
бочем диапазоне частот вращения для
квазигибких роторов применяют низко-
частотную или высокочастотную балан-
сировку. В подавляющем большинстве
конструкций используют низкочастотную
балансировку. Сбалансированность дости-
гают совмещением ГЦОИ с осью ротора,
т. е. за счет коррекции отдельных масс.
При оценке экономичности учитывают
не только стоимость процесса баланси-
ровки, но и последствия его — надежность
работы и ресурс изделия, которые зави-
сят от нагрузок на опорах ротора.
Точность низкочастотной балансиров-
ки квазигибких роторов (степень соответ-
ствия действительных и расчетных значе-
ний F и М) зависит от примененного
метода. Точность нельзя определить не-
посредственно в процессе такой баланси-
ровки, так как средства балансировки
дают возможность установить только точ-
ность совмещения оси ротора и ГЦОИ.
Сбалансированность ротора в рабочих
условиях зависит от соотношения зна-
чений начальных и остаточных эксцентри-
ситетов отдельных масс. Чтобы снизить
их уровень, применяют многоплоскостную
низкочастотную балансировку собранного
ротора, раздельную балансировку в цикле
сборка — балансировка, ориентированную
сборку перед балансировкой и другие
приемы, снижающие значения начальных
эксцентриситетов.
Режимы нагружения подшипников и
колебания ротора. Радиальные нагрузки
на опорах квазигибкого ротора определяют
с помощью тех же зависимостей, что и
для жесткого ротора. Аналогично можно
отметить три режима нагружения под-
46
Основные понятия
шинников: первый — Qa.b < Ra в» вто-
рой — Qab^ Ra в и третий -- Qa в >
> Ra. в-
Маятниковые колебания обусловлены
величиной общего радиального зазора в
подшипниках 6К. Они подчиняются законо-
мерностям математического маятника:
Но величина 6К — переменная и зави-
сит от радиального зазора в подшип-
нике 6 и прогиба ротора, т. е.
6 — Д.
Для роликовых подшипников Д —
— 0,5 L tg 0, где L — длина ролика; 0 —
угол наклона геометрической оси ротора
на подшипнике. Для шариковых подшип-
ников Д пренебрежимо мала.
Частота маятниковых колебаний зави-
сит от сбалансированности квазигибкого
ротора. Поэтому необходимо учитывать,
что уровень вибраций изделия может из-
меняться не только из-за дисбалансов,
но .и в результате изменения частоты
маятниковых колебаний и попадать в диа-
пазон рабочих частот вращения.
Изгибные колебания возникают под
влиянием внешних возбуждающих сил.
Угловую частоту собственных изгибных
колебаний вращающегося ротора опреде-
ляют по формуле
где сокр ( — критическая угловая скорость;
со — угловая скорость. Если в системе
связей ротора есть периодические силы,
например от зубчатых зацеплений, то при
совпадении их угловых частот с ьос насту-
пает резонанс. Увеличиваются силы инер-
ции ротора и амплитуды вибраций изделия.
Режим таких колебаний совпадает с
роторной частотой, но амплитуда не
связана непосредственно с точностью
балансировки. При выявлении резонан-
сных изгибных колебаний необходимо по-
высить точность балансировки ротора,
чтобы уменьшить амплитуду, и принять
меры по сдвигу угловой частоты воз-
буждающей силы и сос.
1.7. ГИБКИЙ РОТОР
Интегральное уравнение движения ро-
тора, При анализе движения гибкого рото
ра с произвольным распределением вра-
щающихся масс приходится решать зада-
чу нахождения прогибов и углов по-
воротов сеченнй по длине ротора. При
этом речь будет идти о малых коле-
баниях с применением теории малых ко-
лебаний. Для решения этой задачи
используют различные подходы. Напри-
мер, составляют уравнения, в которых
прогиб и угол поворота выражают с по-
мощью коэффициентов влияния (в случае
сосредоточенных масс) н функций влия-
ния (в случае распределенных).
Используют также закон Тука, со-
_ гласно которому обобщенные координаты
<ri, qi,... ,qn, определяющие положение
упругого тела прн равновесии, являются
линейными функциями внешних нагрузок,
т. е.
Е г=1’ 2. •••’«•
Л=1
Таким образом принимают линейную
зависимость между деформациями рото-
ров и нагрузками.
Величины а. стоящие при внешних
нагрузках, и есть коэффициенты влияния.
Их механическое значение легко обнару-
жить, полагая все внешние силы, кроме
одной, равными нулю, а эту одну — рав-
ной единице. Например, если Qj — 1, а
все остальные равны нулю, то из предыду-
щих уравнений имеем
q\ ~ <Хв, <?2 = сиг,. . . ,qn ~ «in,
т. е. ос,* — значение координаты <д, когда
= 1, а все остальные Q = 0.
В нашем случае обобщенными коорди-
натами будут прогибы и углы поворо-
тов сечений вала, а внешними нагруз-
ками — неуравновешенные центробежные
Гибкий ротор
47
силы и моменты. Будем пользоваться дву-
мя типами статических коэффициентов
влияния: прогиба и поворота. При этом
примем cttk — прогиб под диском I от
действия единичной силы, приложенной
в месте посадки диска k\ — прогиб
под диском i от единичного момента,
приложенного в месте посадки диска k\
у,— угол поворота сечения в месте по-
садки диска i от единичной силы, при
ложен ной в месте посадки диска k;
fit* — угол поворота сечения в месте по-
садки диска i от единичного момента,
приложенного в месте посадки диска k.
По теореме Максвелла а,* = а*(.
Коэффициенты влияния, определяемые
экспериментально или расчетным путем,
зависят от геометрических размеров рото-
ров, их масс, жесткостей, характера и
количества опор.
Функции влияния, или функции Гри-
на,— те же коэффициенты влияния, но
распространенные на случай непрерывно
распределенных масс, т. е когда число
дисков п -> оо. Обозначения у
функций влияния будут те же, что и
у коэффициентов влияния, но точки места
деформаций и приложения нагрузок будут
взяты в скобки. Статические коэффициен-
ты и функции влияния определяют ха-
рактеристику статической упругости систе-
мы без учета инерционного влияния масс.
При рассмотрении колебательных процес-
сов коэффициенты влияния применяют к
динамической системе, а статические силы
заменяют инерционными возбуждающими
силами.
Полное отклонение какой-либо точки
системы есть сумма произведений инерци-
онных сил на соответствующие коэффи-
циенты влияния.
В нашем случае
/
y(z) ~ a(z,s) mis) 4-e(s)l ds,
о
(1.13)
или
I
ylz) = f(z)-f-^ m\s)a(z, s)yls)(.a2ds
о
уравнение Фредгольма 2-го рода отно-
сительно y(z).
Ниже будут использованы и динами-
ческие коэффициенты и функции влияния,
которые рассматриваются, например, как
вектор прогиба в сечении вала I, вызван-
ного центробежной силой от единичного
дисбаланса, приложенного в сечении k,
при данных частотах вращения. Их можно
определить, если последовательно во всех
сечениях ротора прикладывать единичный
дисбаланс и измерять или подсчитывать
прогибы и углы поворота всех сечений
при постоянной частоте вращения. С изме-
нением частоты вращения изменяются и
величины динамических коэффициентов
влияния. Отыскание последних — процесс
более сложный и трудоемкий, но он встре-
чается в некоторых методах уравновеши-
вания, когда используются пробные пуски
с пробными грузами.
Из теории интегральных уравнений из-
вестно, что решение уравнений Фред-
гольма можно получить с помошью трех
различных методов и в различных
формах. Первый метод, принадлежащий
Фредгольму, дает у [г) в виде отношения
2
двух степенных рядов относительно со ,
каждый из которых имеет бесконечный
радиус сходимости. Решение получается
в результате того, что интегральное
уравнение рассматривается как предель-
ный случай системы линейных алгебра-
ических уравнений с п неизвестными
при п —>• ОО.
Таким образом, уравнение Фредгольма
2-го рода может быть с любой наперед
заданной точностью аппроксимировано
системой линейных уравнений, что озна-
чает возможность аппроксимации ротора
с любым распределением параметров, ро-
тором, состоящим из невесомого вала,
несущего п дисков с массами т\, mt,т„
(рис. 1.22. а) и экваториальными момен-
тами инерции Ji,/2, - - -, Каждый из дис-
48
Основные понятия
ков в силу погрешностей изготовления
имеет радиальные эксцентриситеты е>,
е2,.. -, еп и угловые эксцентриситеты, т. е.
отклонения оси диска от оси. проходя-
щей через центры инерции, еь е2, - -, е„.
При вращении вал получает прогибы ylt
У2,...,уп и углы поворота уi,y^...,y'n
(рис. 1.22,6).
Вращение вала при прямой синхрон-
ной прецессии может быть представлено
как колебания в двух взаимно перпенди-
кулярных плоскостях.
Для колебаний в каждой из плоскостей
п
Уь = £ mka.iku)2{yk-ye^ —
k=\
п
— X е*);
k=i
S(1.14)
п
у’.= £ mk ytk о/(yk 4- —
л
— X <1Г •
*=|
Эти уравнения имеют общий характер
и отражают наличие гироскопического
эффекта, упругости опор и могут учи-
тывать колебания присоединенных масс.
Коэффициенты влияния будут изменяться
в зависимости от числа и характера
опор (простая опора, заделка, упругая
опора и т. д.).
Уравнения (1.14) могут описывать
движение не только одиночного ротора,
но и систем соединенных роторов с учетом
дополнительных условий, отражающих
специфику всей системы.
Как следует из этих уравнений, для
гибкого ротора прогиб и угол поворо-
та каждого диска зависят не только
от своих эксцентриситетов- но и от экс-
центриситетов. углов поворота и проги-
бов всех других дисков, входящих в систе-
му. Решение системы уравнений (1.14) от-
носительно у и у' по формуле Кремера
имеет вид
2п
fe=l
2п
fe.-l
Гибкий ротор
49
( 1 —/П।at]ио2) —/и2а12<о2 .. — Щ„а1яы2 /|0ц<»>2 /2Pi2«>2 A(Pin<*>2
— 1 — 1П2а22^') — ^4<X2„6)2 /|P21<02 /2P22<1)2 . ^Ир2л°»2
— гИ|ая|(й2 ~/n2a„2w2 ... ( 1 — ш0а„„бГ) /1Р«1<л>2 /2Р-.2°'2 ЛРдпЮ2
9
— miYub)2 —m2Yi2<o2 . — тпуь^2 !61,со24-1) /2Л12»«»2 -•- /^61н<о2 ;
— WjV2|W2 — m2y22<o2 . — тпу2пы2 /,62lw2 (J2622w2-r 1) ... Jnb2nb)2
-m^fti)2 —т2уп2<^ -~~тпУпп^2 JlSnl™2 ^2^^^ (Jn^n«W2+l)
XffcZ)*, определитель, полученный путем
замены fc-ro столбца в определителе D
столбцом из правых частей системы. Здесь
fk.— свободный член в fe-й строке, Dki—
минор элемента, находящегося на пере-
сечении k-м строки и /-го столбца.
Если приравнять Определитель D нулю,
то из полученного уравнения можно най-
ти все критические частоты вращения
системы: ioi, <jj2, • • •, н>2л.
Если теперь эти значения по очереди
подставить в уравнения (1.14), но опи-
сывающие свободные колебания, то полу-
чим собственную форму изгиба ротора,
соответствующую частоте вращения ыт:
п и
У; — V ^к^чк^тУк к&к^тУк*
к— 1 к«=-- 1
п п
У,= W-к Vik ьутУк X k^tk^/nUk'
I *= ।
i —1, 2, и.
Полученные такйм образом уравнения
характеризуют собственные формы изгиба
ротора.
Если при вращении ротора имеет место
первая форма изгиба, то в неподвижной
системе координат все точки вдоль оси
ротора колеблются с одной частотой
и в одних фазах. При второй собствен-
ной форме изгиба ротора, соответствую-
щей частоте вращения (о2кр, ротор будет
разделен на две в общем случае неодина-
ковых половины, имеющие перемещения,
обратные по знаку. При третьей и чет-
вертой формах изгиба ротор делится на
3 и 4 участка с, чередующимися направле-
ниями движения и т. д.
На некритических частотах вращения
система с 2п степенями свободы (п-дис-
ками) изгибается таким образом, что сме-
щения каждой массы в общем случае
происходит по кривой полигармонического
колебания с гармониками от первой до
2п-й, т. е. прогиб на любых частотах
вращения можно представить как сумму
прогибов на критических частотах враще-
ния, умноженных на некоторую констан-
ту. В этом случае можно ввести понятие
характеристики собственной формы изги-
ба, как отношения амплитуд прогибов
двух различных точек на рассматриваемых
критических частотах вращения, т. е.
р.ь = yik/y\k.
Знание прогиба в какой-либо одной
точке на критических частотах вращения
дает возможность через характеристику
50
Основные понятия
формы определить прогиб в любой другой
точке ротора. В 5том случае движение
системы с п степенями свободы можно
рассматривать как движение системы
с одной степенью свободы.
Условие ортогональности для рас-
сматриваемого случая получают из уравне-
ния взаимности работ, совершаемых дис-
балансами одной собственной формы изги-
ба на прогибах по другой форме, кото-
рое имеет вид
D7п&пУт п&пУт — О*
Ротор с распределенными парамет-
рами. Рассмотрим решение уравнения
со
(1.13) в виде y(z} — У'а„уп\г), где
Л=1
yn(z) составляет в интервале (0;/) пол-
ную ортогональную систему функций,
каждая из которых удовлетворяет гра-
ничным условиям для ylz). За такую
систему принимают систему фундамен-
тальных функций ядра rn(.s)a(z, х), т. е.
решений однородного интегрального урав-
нения
i
y{z) — ы2 m(x)a(z, х)1Д$) ds. 1.1.15)
о
Уравнение (1.13) разрешимо при част-
ных значениях ю2, которые являются фун-
даментальными числами ядра m(s)a(z, х),
а так как фундаментальные числа есть не
что иное, как квадраты собственных частот
изгибных колебаний, то и соответствующие
им фундаментальные функции совпадают
с собственными формами изгиба ротора.
Характерной особенностью собствен-
ных форм изгиба ротора является то со-
отношение, которое имеется у них между
силами и перемещениями. К любой из
масс m(s) приложена сила инерции
Таким образом, каждая соб-
ственная форма изгиба представляет собой
статическую упругую линию, отвечающую
специально подобранной нагрузке, при
которой сила в любой из точек пропорци-
ональна произведению соответствующей
массы на перемещение этой же точки.
Статические нагрузки, отвечающие
различным собственным формам изгиба
ротора, как было указано ранее, взаимно
ортогональны, т. е. работа сил, отвечаю-
щих одной форме на перемещениях по
другой форме, равна нулю.
Если к ротору приложена сложная сис-
тема сил (от соответствующего распре-
деления вдоль ротора дисбалансов), то ра-
бота этой системы сил на возможном пе-
ремещении, совпадающем с к-й соб-
ственной формой изгиба, равна работе
составляющих этих сил по к-й форме
изгиба на указанном перемещении. Работа
всех остальных составляющих разложения
сил по формам изгиба на перемещении
равна нулю.
Для преобразования /(г) воспользуем-
ся известной из теории интегральных урав-
нений теоремой Гильберта - Шмидта, что
всякая непрерывная функция, представ-
ленная «истокообразно» при помощи ядра
m(s)a[z,s) [например, наша функция
f is) = m(s)a(z, s)e{s)ds , разлагается
о
в абсолютно и равномерно сходящийся
ряд Фурье по фундаментальным функциям
ядра Функция f(z) есть кривая прогибов
от действия системы начальных дисбалан-
сов, а теорема Гильберта — Шмидта ха-
рактеризует возможность разложения этой
кривой эксцентриситетов в ряд по собст-
венным формам изгиба рассматриваемого
ротора.
С математической точки зрения «исто-
кообразность» функции эквивалентна воз-
можности использования принципа супер-
позиции. т. е. принципа независимости
действия сил и далее способа наложения.
Примем
e(s) = £ bnyn(s). (1.16)
I
Тогда после преобразований уравне-
ние Фредгольма можно записать в виде
y[zi — у bnyn[z) 2 . —.
rt = l
Гибкий ротор
51
где bn = e{ziyniz)m(z)dz,
о
или у(z) == blyl(z) —- +
til |/со — 1
+ • • + b„yn(z) , (1.17;
<Ы<» — 1 -
где yt,y2,... ,уп и й>1.«2, • • • - собствен-
ные формы изгиба (1,2,... ,п — крити-
ческие частоты вращения).
Из уравнения (1.17) видно, что с при-
ближением к какой-либо из критических
частот вращения преобладающим ста-
новится влияние той составляющей дисба-
ланса, которая соответствует этой соб-
ственной форме изгиба, и на самих
критических частотах вращения в ос-
новном эта составляющая и определя-
ет прогиб, так как влияние осталь-
ных собственных форм изгиба ротора по
сравнению с ней мало. Это позволяет
балансировать отдельно по каждой из
собственных форм изгиба оси ротора.
Сбалансировав ротор на первой крити-
ческой частоте вращения, можно произ-
вести балансировку на второй, затем на
третьей и т. д. Корректирующие массы,
которые установлены на какой-либо одной
критической частоте вращения, в силу
условий ортогональности не могут повли-
ять на сбалансированность ротора при
других критических частотах вращения.
Так как прогибы ротора на любых
частотах вращения могут быть представле-
ны как сумма прогибов на критических
частотах вращения, умноженных на неко-
торую константу, то ротор, сбалансиро-
ванный на всех критических частотах вра-
щения, будет уравновешен для всех час-
тот вращения. Практически же достаточ-
но произвести балансировку на тех
Критических частотах вращения, которые
лежат ниже максимальных эксплуатацион-
ных, ибо, как показала практика, оставши-
еся дисбалансы от неучтенных форм не
опасны, и могут быть скомпенсированы
балансировкой в двух крайних, располо-
женных у опор, плоскостях коррекции
О количестве корректирующих масс.
Зачастую приходится устранять влияние
первых двух собственных форм изгиба
для многомассовых роторов, так как выс-
шие критические частоты вращения у со-
временных машин редко попадают*в диапа-
зон эксплуатационных частот вращения.
С то«ки зрения изгиба группа масс,
совершающих перемещение в одном и том
же направлении, в известной степени
эквивалентна одной массе, перемещаю-
щейся в том же направлении (рис. 1.23).
Форма изгиба вала с двумя смещенными
в противоположных направлениях дисками
будет та. же, что и для вала, нагру-
женного двумя группами дисков, имеющи-
ми обратные по знаку смещения, т. е.
в соответствии со второй собственной
формой изгиба. Таким образом, много-
массовую систему в диапазоне частот
вращения от нуля до примерно 1,2<о2кр
можно представить как двухмассовую,
приняв вместо групп масс по одной массе,
расположенной в центре масс группы,
смещенной в одном направлении. Такое
Рис. 1.23. Эквивалентность перемещения:
а — одной массы, б — группы масс
52
Основные понятия
представление потребует в диапазоне двух
критических частот вращения уравнове-
шивания прогиба в двух точках, где
помешены заменяющие массы и, следо-
вательно, устранения двух прогибов.
При учете прогибов от многих масс
по третьей, четвертой и высшим собствен-
ным формам изгиба ротора эти массы
можно разбить на три. четыре и т. д.
группы масс. Такое представление потре-
бует балансировки в диапазоне трех,
четырех и т. д. критических частот враще-
ния и устранения прогиба в трех, четы-
рех и т. д. точках.
Таким образом, для балансировки
по п формам изгиба можно разбивать
вал на н групп масс и использовать
только п корректирующих масс.
Если исходить из такого представле-
ния, то совершенно очевидно, что для ба-
лансировки гибкого ротора по первой соб-
ственной форме изгиба можно обойтись
одной корректирующей массой, для ба-
лансировки по второй форме — двумя, по
третьей форме — тремя и т. д., т. е. ми-
нимальное число корректирующих масс
равно номеру собственной формы изгиба
ротора.
Изложенные соображения верны не
только для ротора на жестких, но и на
очень податливых опорах, при этом не-
обходимо помнить, что первая собствен-
ная форма изгиба ротора на жестких опо-
рах может быть третьей на податливых
опорах, и тогда первая устраняется одной
корректирующей массой (статическая ба-
лансировка), вторая — двумя (динами-
ческая балансировка), третья, четвертая
ит. д. — тремя, четырьмя и т. д., т. е. в этом
случае к числу корректирующих масс,
балансирующих гибкий ротор на жестких
опорах, добавляются еще два груза, учи-
тывающие его первые две формы пере-
мещения на податливых опорах, т. е. ба-
лансировку ротора как жесткого.
Более строгое доказательство необхо
димого числа корректирующих масс при-
ведено в работе [24]. Для многомас-
совых систем всегда можно найти соот-
ношение между прогибами и дисбалан-
сами по той или иной собственной форме
изгиба.
Уже указывалось, что при балансиров-
ке на критических частотах вращения мы
можем устранить лишь ту часть общего
дисбаланса, эксцентриситет которого по
форме подобен упругой линии на данных
w Причем очевидно, что на критических
частотах вращения нет необходимости из-
мерять прогибы во многих точках. Если
система исследована, известна ее харак-
теристика формы р^, то можно по
значению прогиба в одной точке опреде-
лить прогиб в любой точке.
О представлении составляющих экс-
центриситетов ротора в производных от
прогиба. У гибкого ротора возрастание
прогибов сопровождается ростом неурав-
новешенных сил, а следовательно, реак-
ций опор, вибраций, внутренних изгиба
ющих моментов, углов перекоса сечений
и сидящих на валу дисков, относительных
деформаций и направлений.
Каждый из перечисленных параметров
связан с начальным дисбалансом и про-
гибом. Поэтому, если имеется возможность
измерения или аналитического перехода
к другим параметрам, то они могут быть
использованы для балансировки. В связи
с этим рассмотрим, как проявляется
неуравновешенность в производных от из-
гиба по абсциссе сечения, первая из кото-
рых — угол поворота сечений, вторая -
пропоциональна кривизне ротора, его отно-
сительной деформации и изгибающему мо-
менту, третья — неуравновешенным си-
лам, четвертая — интенсивности распре-
деленной нагрузки от локальных дис-
балансов. Для этого' в общем случае
необходимо дифференцировать выражение
(МЛ 7). Результат будет зависеть от вида
самих функций y(z), описывающих собст-
венные формы изгиба ротора.
Для наглядности рассмотрим часто
употребляемый исследователями однород-
ный вал, опирающийся на две жесткие
шарнирные опоры, у которого собственные
формы изгиба являются синусоидами воз-
растающей кратности аргументов, а крити-
Ротор с изменяющейся геометрией масс
53
ческие частоты вращения определяются из
соотношения to2 —к4л4 EJ/
где п — номер собственной частоты; I —
длина вала; EJ — const — линейная жест-
кость вала при изгибе; т == const — ли-
нейная масса вала.
Тогда формула (1.17) может быть за-
писана для произвольных угловых частот
to в виде
оо
у (z) ~ b„A„sm (nnz/l), (1.18)
Л=1
где Ап =
( 1 — Ь>2)/<1)2
Ьп — коэффициенты разложения эксцент-
риситета по собственным формам изгиба
рассматриваемого ротора
Для рассматриваемого случая
со
6„Tlrtn2sin (nnz//); (1.20)
со
Ь„А,
Ul
ndcos (nnz//);
(1.21)
,v(z) =
оо
bnAntt*sin In.nz/1).
ns=l
(1.22)
Сравнивая формулы (1.22) — (1.25) с
выражением (1.21), заметим, что высшие
(т.е. вторая, третья и т. д.) составляю-
щие разложения экцентриситетов в ряд по
собственным формам изгиба сильнее в п
раз, чем в прогибах, проявляются в углах
поворота сечений, в л2 раз — в деформа*
циях, изгибающих моментах, кривизне уп-
ругой оси ротора, в п3 раз — в попе-
речных (сосредоточенных) неуравнове-
шенных силах, а следовательно, и в реак-
ции опор, наконец, еще сильнее - в л4
раз — в интенсивности распределенной не-
уравновешенной нагрузки, где л — номер
члена разложения параметра на состав-
ляющие.
Для других собственных форм изгиба
эта зависимость будет носить иной коли-
чественный характер. Последнее необходи-
мо всегда иметь в виду при выборе пара-
метров в разрабатываемых методах ба-
лансировки гибких роторов.
1.8. РОТОР С ИЗМЕНЯЮЩЕЙСЯ
ГЕОМЕТРИЕЙ МАСС
Роторы, у которых при вращении из-
меняется масса, момент инерции или поло-
жение центра массы, называют роторами
с изменяющейся геометрией масс или, про-
ще, тело с переменной массой. Такие
тела образуют четвертый класс роторов.
Типовыми роторами этого класса являются
тела вращения, взаимодействующие с ши-
роким и узким гибкими элементами, а так-
же с телами, масса которых описывается
функцией, зависящей от времени. К ним
относятся роторы канатовьющих машин,
барабаны рулонно-ротационных печатных
машин, моталки прокатных станов холод-
ной прокатки, роторы центрифуг, ис-
кусственные спутники Земли и звенья
многих машин и механизмов. Увеличение,
уменьшение, перераспределение массы, из-
менение геометрии —детерминированная
функция времени, положения, скорости
или случайная функция, не зависящая от
характера движения.
Динамика ротора переменной массы.
Используя принцип «затвердевания», ос-
новные уравнения и теоремы для тела пе-
ременной массы получают путем сумми-
рования различных величин для точек пе-
ременной массы таким же образом, как для
систем с постоянной массой (15] Урав-
нения для определения динамических ре-
акций вращающегося ротора с перемен-
ной массой по форме аналогичны урав-
нениям для ротора с постоянной массой.
Сами реакции, даже при постоянной
частоте вращения, будут переменными ве-
54
Основные понятия
Рис. 1.24. Схема ротора с переменной мас-
сой 1-го типа:
01- центр массы сектора листа t-ro слоя на
угле <р, 02 — центр массы ротора с намотан-
ным материалом
Рис. 1.25. Схема ротора с переменной массой
2-го типа:
О—координата ЦМ барабана с полным числом
витков в слое, Oni — координата ЦМ р — ])-го
витка.
О, — координата ЦМ t-го витка
личинами, так как меняются параметры
ротора.
Параметры ротора с переменной мас-
сой могут быть определены расчетным или
экспериментальным путем в процессе
движения тела.
Для ротора 1-го типа в виде бара-
бана массой т® (рис. 1.24), радиусом
Ro, на который наматывается полоса ма-
териала плотностью р шириной L, равной
длине барабана, и толщиной h, эксцентри-
ситет центра массы зависит от угла по-
ворота барабана <р и номера слоя п:
e» = -o+75,n4,/2’
где Rn радиус n-го слоя; v„ — (m0 |
+ m„) /iiRn — условный угол намотки; р—
=h$L — масса полосы на единицу длины;
тп — масса п слоев материала.
Положение центра массы по оси Z
неизменно, а масса ротора
т = то 4- 2л р/?о(п -|- хп2),
где х = h/2Ro.
Эксцентриситет центра массы ротора
2-го типа (рис. 1.25), отличающегося от
предыдущего ротора тем, что на барабан
наматывается узкая полоса шириной /, для
и-го слоя и t-го витка
2/?
е“=ё№Пф/2-
Координата центра массы по оси
Z переменная и выражается дробно-ли-
нейной функцией [5]. Масса ротора 2-го
типа меняется линейно в функции угла
его поворота, пока наматываются витки
одного слоя:
mni = то + 2лц/?„ | (i — 1) + <р/2л].
Параметры ротора 3-го типа, представ-
ляющего собой тонкостенный цилиндр мас-
сой то (рис. 1.26, а) длиной L, радиусом
Ro, внутри которого находится масса т,
убывающая вдоль оси 2 по линейному
закону в функции времени m(Z).
Для всех типов роторов с перемен-
ной массой моменты инерции изменяются
по закону параболы высоких степеней
Основы уравновешивания роторов с
переменной массой. Условие полного урав-
новешивания динамических реакций сво-
дится к тому, чтобы ось вращения ротора
все время была главной центральной осью
Обеспечить это условие с помощью двух
постоянных корректирующих масс невоз-
Ротор с изменяющейся геометрией масс
55
Рис. 1.26. Параметры ротора с переменной массой 3-го типа:
а—схема ротора; б — кривая изменения относительного момента инерции; в — относительные координаты
ЦМ ротора по оси Z
можно. Роторы с переменной массой ос-
нащают автобалансирующими устройства-
ми или уравновешивают приближенно,
обеспечивая сбалансированность их в од-
ном или нескольких фиксированных поло-
жениях Каждая корректирующая масса
представляет собой сумму масс постоян-
ной и переменной частей. Одна из них
уравновешивает неизменную массу ротора,
а другая - переменную массу. Процесс
уравновешивания делится на два этапа:
балансировка тела с постоянной массой;
балансировка тела с переменной массой.
На первом этапе применяют методы и
средства балансировки жестких роторов.
Автобалансирующие устройства с пе-
ременными по массе и направлению кор-
ректирующими грузами обеспечивают пол-
ную сбалансированность переменной мас-
сы тела при условии периодичности де-
терминированных функций параметров ро-
тора.
Приближенное уравновешивание рото-
ров 1-го и 2-го типов ограничивается
постановкой определенных масс на соот-
ветствующих радиусах коррекции, создаю-
щих «корректирующие» дисбалансы. Под-
бор этих дисбалансов выполняют из усло-
вия квадратичного или наилучшего равно-
мерного приближения функций. За время
изменения параметров конец вектора дис-
баланса О(<р) в плоскости коррекции
описывает годограф Г (рис. 1.27). Ана-
Рис. 1.27. Годограф конца вектора дисба-
ланса в плоскости коррекции ротора с пе-
ременной массой
логично строят годограф для другой плос-
кости.
В технических требованиях на ба-
лансировку указываются допустимые дис-
балансы £)доп, поэтому корректирующий
дисбаланс находят из условия наилучше-
го равномерного приближения «в смысле
Чебышева», обеспечивая максимальную
величину max [D(<p) + mKrK) — maxD0CT
минимальной.
Максимальное значение вектора Doct
будет минимальным, если точка С —
центр описанной окружности вокруг годо-
графа Г. Из рис. 1.27 находят значение
(длина отрезка ОС) и угол р постоян-
ной корректирующего дисбаланса ткгк.
Две постоянные корректирующие массы,
определенные таким образом и установлен-
ные в плоскостях коррекции, дадут наи-
Уравновешивание механизмов
лучшее уравновешивание ротора с пере-
менной массой из всех возможных.
Уравновешивание роторов 3~го типа.
У роторов, масса которых изменяется
в функции времени, дисбалансы могут
меняться непрерывно или скачкообразно.
В этих случаях можно установить наиболее
вероятные законы изменения неуравно-
вешенности и сбалансировать роторы так-
же, как роторы 1-го и 2-го типов.
Глава 2
УРАВНОВЕШИВАНИЕ МЕХАНИЗМОВ
2.1. ОСНОВНЫЕ ПОНЯТИЯ
И ОПРЕДЕЛЕНИЯ
Механизм. Механизмом называют
замкнутую или разомкнутую кинемати-
ческую цепь, предназначенную для преоб-
разования движения одного или несколь-
ких звеньев в заданные движения других
звеньев. Механизмы делят на шарнирные
и рычажные. В шарнирных механизмах
звенья образуют только вращательные
кинематические пары. Если механизм со-
держит не только вращательные, но так-
же поступательные, цилиндрические и
сферические кинематические пары, то он
относится к категории рычажных механиз-
мов. Неподвижное звено механизма назы-
вают станиной.
Статические и динамические модели шатуна
57
Главные точки звеньев. Главные точки
Ht (t=l, 2, 3) звеньев шарнирного
четырехзвенного механизма (рис. 2.1, а)
определяют при помощи призмы. Для
этого кинематическую цепь О А ВС меха-
низма отсоединяют со станины и кладут
на ребро призмы П последовательно каж-
дым ее звеном так, чтобы вся цепь нахо-
дилась в равновесии (рис. 2.1,6—г).
Точка В, i-ro звена, расположенная над
ребром призмы, будет главной точкой это-
го звена.
В соответствии с рис. 2.1,6—г
точки Ht (i=l, 2, 3) можно опре-
делить теоретическими векторами
m, OS,-(-(mj + m,) ОА
т,, BS.
J, (2.3)
которые называют векторами главных то-
чек звеньев 1, 2, 3.
В теории механизмов доказывается,
что центр S масс подвижных звеньев ме-
ханизма произвольной структуры опреде-
ляется вектором
OS = £ h„ (2.4)
где hi— вектор главной точки t-го звена;
п — число подвижных звеньев механизма.
Для рассматриьаемого механизма получим
(рис. 2.1,д):
ОХ = й,+Л2 + Й3. (2.5)
2.2. СТАТИЧЕСКИЕ И ДИНАМИЧЕСКИЕ
МОДЕЛИ ШАТУНА
Шатуном называют звено, н£ входя-
щее в кинематические пары со станиной
механизма, поэтому шатун совершает
в общем случае плоскопараллельное дви-
жение. Примером шатуна является звено
Рис. 2.2. Модели шатуна:
и — кривощипно ползунный механизм ОАВ с шату-
ном АВ; б шатун, я, г — статические модели;
<?, е — динамические модели
АВ кривошип но-ползунного механизма
ОАВ (рис. 2.2, а). На этом же рисунке
показаны планы скоростей OAs^bO и ус-
корений OAszb'O этого механизма, сов-
мещенные с его схемой.
Из механики известно, что масса т?
шатуна действует на соединенные с ним
звенья механизма с силой
P2S=m2fi2s. (2.6)
приложенной в центре S? массы шатуна,
и парой сил с моментом (рис. 2.2, 6)
— — J (2-7)
58
Уравновешивание механизмов
Статическая модель шатуна представ-
ляет собой невесомый стержень с двумя
точечными массами:
= (2.8)
а
m9/i = ^9----Г .
2Й 2 а + Ь
расположенными в центрах вращательных
пар А и В (рис. 2.2, в). Из формул
(2.8) следует, что у шатуна и у его
статической модели массы и координаты
их центров одинаковы.
Точечные массы (2.8) действуют на
невесомый стержень АВ с силами
^2А~ — т2А^2А\
(2.9)
^2в — —
где а2А, а^в—векторы ускорений точек А и
В шатуна (рис. 2.2, е).
Если -силы (2.9) привести к центру
S2. то получим также статическую
модель шатуна (рис. 2.2, г), на которую
будут действовать сила
Р 2S~ ^2А~^~ Р2В (2.10)
и пара сил с моментом
М2— — abm2E2. (2.11)
Сила (2.10) равна силе (2.6), а мо-
мент (2.11) отличается от момента (2.7)
на величину
&М2 = М2-М'2. (2.12)
Отсюда следует, что динамическая мо-
дель шатуна (рис. 2.2, д) будет пред-
ствлять собой невесомый стержень с то-
чечными массами (2.8), нагруженный ди-
намическим моментом (2.12)
ДМ2 = — — ab)e2. (2.13)
Таким образом, на динамическую модель
шатуна (рис. 2.2. д) будут действовать
силы (2.9) и пара сил с моментом
(2.13).
В частном случае, при
p'is^^, (2.14)
момент (2.13) будет равен нулю, поэ-
тому при условии (2.14) динамическая
модель шатуна будет представлять собой
невесомый стержень АВ с двумя то-
чечными массами т2А, т2В (рис. 2.2, е), на
который действуют только силы (2.9).
Если эти силы привести к центру S2,
то получим схему сил, показанную на
рис. 2.2, б.
Заметим, что момент (2.11) действует
в статической модели шатуна на стер-
жень АВ (рис. 2,2, г) всегда в направ-
лении, противоположном угловому ускоре-
нию шатуна. Что касается направления
момента (2.13). приложенного к динами-
ческой модели шатуна, то оно зависит от
знака разности (p2s— ub) и поэтому может
как совпадать, так и не совпадать с напра-
влением углового ускорения шатуна.
Очевидно, при условии
момент (2.13) и угловое ускорение е2
шатуна имеют одинаковые направления,
а в случае
направление момента (2.13) будет проти-
воположно направлению углового уско-
рения е2.
2.3. СИЛЫ И МОМЕНТЫ, ВЫЗЫВАЮЩИЕ
КОЛЕБАНИЯ СТАНИНЫ
Входное звено О|А механизма произ-
вольной структуры (рис. 2.3. а) нагружено
движущим моментом А1дв, а выходное зве-
но OjAj силой Рс полезного сопротивле-
ния. В общем случае, механизм имеет h
подвижных звеньев, из которых k звеньев
образуют со станиной кинематические
пары.
Если звенья механизма отсоединить
от станины, а их действия на ста-
нину заменить силами реакций, то получим
систему сил Rt (/= 1, 2, ...,/?)• как
показано на рис. 2.3, б. Силы R,
(j— 1, 2,.... k) можно привести к точке
О|. В результате получим силу
Силы и моменты, вызывающие колебания станины
59
Л / л \
Q = Рс 4- £ G,— J mJ as, <2.15)
носительно оси, проходящей через точку
S, перпендикулярно плоскости Охху, tn,,
ast —-масса /-го звена и вектор ускорения
действующую на подшипник входного
звена, и момент
ее центра; у— вектор ускорения центра
( V
массы I > m
подвижных звеньев ме-
«
М = Мяв4-М0(Рс) 4- £ Мо( G,) -
ханизма; qso — плечо неуравновешенной
силы m(a&t относительно центра 0ь
п п
— £ £ m(aS(^SO| = 0,(2J6j
«=i <=1
воспринимаемый станиной (рис. 2.3,в).
В выражениях (2.15) и (2.16) Al0( Pf) и
п
M()fGf) обозначают моменты отно-
«=|
сительно центра Oi силы Рс и сил тя-
жести G, (/=1,2,. . , и) подвижных
звеньев механизма; е, и /st — угловое ус-
корение и момент инерции /-го звена от-
Формулы (2.15), (2.16) определяют
главный вектор и главный момент неурав-
новешенных сил, действующих на станину
плоского механизма произвольной струк-
туры.
Таким образом, в самом общем слу-
чае, неуравновешенная сила, действую-
щая на станину плоского механизма, рав-
на геометрической сумме внешних сил,
приложенных к звеньям механизма, и
произведения со знаком минус общей
массы
подвижных звеньев меха-
Рис. 2.3. Силы и моменты, действующие на
станину механизма
низма на ускорение as центра этой массы.
Сила (2.15) и момент (2.16) явля-
ются в общем случае переменными по ве-
личине и направлению и поэтому .вызы-
вают вынужденные колебания станины.
Такой механизм является неуравновешен-
ным.
Полное уравновешивание механизма
представляет сложную теоретическую и
инженерную задачу. На практике, при
упрощенном решении этой задачи, не
учитывают воздействия на станину внеш-
/ п \
них сил I Рс4- £ GJ и движущего мо-
\ »=1 '
мента Мдв, а также принимают частоту
вращения входного звена постоянной. В
этом случае вектор силы
(2.17)
являющийся одним из слагаемых формулы
(2.15), и момент
БО
Уравновешивание механизмов
~ £ Л<е,— £ inta„qsini, (2.18)
i-i /_ t
входящий в выражение (2.16), называют
соответственно главным вектором и глав-
ным моментом неуравновешенных сил
механизма.
Механизм, для которого модуль силы
(2.17) равен нулю
Р = 0, (2.19)
называют статически уравновешенным
механизмом. У такого механизма центр
массы I > tn, 1 всех его подвижных звень-
ев остается неподвижным при работе
механизма.
Если на станину не действует момент
(2.18), т.е.
М = 0, (2.20)
то механизм будет иметь моментную урав-
новешенность
Если условия (2.19) и (2.20) выполня-
ются одновременно, то механизм будет
уравновешен динамически.
Отметим, что точное динамическое и
даже статическое уравновешивание ме-
ханизмов весьма затруднительно выпол-
нить простыми конструктивными средства-
ми. Поэтому на практике механизмы
обычно уравновешивают приближенно пу-
тем уравновешивания, например, только
первых гармоник главного вектора (2.17)
и главного момента (2.18) неуравнове-
шенных сил, а также другими спо-
собами.
Заметим также, что после уравнове-
шивания механизма давления в неко-
торых кинематических парах могут увели-
чиваться. Поэтому конструктивный расчет
кинематических пар механизма должен
производиться обязательно после уравно-
вешивания механизма, т. е. после обра-
щения в нули модулей главного вектора
и главного момента неуравновешенных
сил.
2.4. МЕТОДЫ СТАТИЧЕСКОГО
УРАВНОВЕШИВАНИЯ МЕХАНИЗМОВ
Метод нуль-векторов. Этот метод по-
зволяет точно .уравновешивать механиз-
мы произвольной структуры. Рассмотрим
шарнирный четырехзвенный механизм
ОАВС (см. рис. 2.1, а). Положение
центра масс подвижных звеньев механиз-
ма определим, как показано на рис.
2.1,5, в соответствии с формулой (2.5)
вектором
OS = h । /12
Если выполнить условия
ft3 = 0; (2.21)
ft2 = 0; (2.22)
Л! = 0, (2.23)
то центр S общей массы всех под-
вижных звеньев механизма всегда будет
совпадать с его неподвижной точкой О.
Поэтому в соответствии с формулой (2.17)
механизм О АВС сделается статически
уравновешенным.
Условия (2.21) — (2.23) полностью
определяют координаты центров масс
звеньев механизма ОАВС, необходимые
для его уравновешивания. Из условий
(2.21) и (2.3) следует, что центр S3 мас-
сы звена ВС должен совпасть с точкой В;
из условия (2.22) и формулы (2.2) по-
лучим. что с точкой S3 будет совпа-
дать центр Хг.з масс двух звеньев:
АВ и ВС; из условия (2.23) и формулы
(2.1) становится очевидным, что в точке
О должен находиться центр S 1/2.3 масс
подвижных звеньев шарнирного четырех-
звенного механизма ОАВС (рис. 2.4, а).
Метод подобия. Для статического
уравновешивания шарнирного четырех-
звенного механизма ОАВС не обяза-
тельно требовать обращения в нули век-
торов ht (i — 1, 2, 3) главных точек звень-
ев. Тот же результат получится, если
воспользоваться методом подобия. Для
этого необходимо потребовать, чтобы мно-
гоугольник OabS, построенный из векто-
ров hi (i=l, 2, 3) главных точек
звеньев, был подобен кинематической це-
Методы статического уравновешивания механизмов
61
Рис. 2.4. Уравновешивание шарнирного че-
тырехзвенного механизма методом нуль-век-
торов и методом подобия
пи механизма (рис. 2.4,6). В этом слу-
чае вектор OS, определенный формулой
(2.4), сделается постоянным по модулю
и направлению, а механизм статически
уравновешенным.
Из подобия многоугольников OabS и
ОАВС можно, учитывая формулы (2.1)
(2.3), определить дисбалансы звеньев
ОА и ВС:
Di = miOSi = — т2А1г,
Дз= тзС8з — — т2в13.
(2.24)
необходимые для уравновешивания ме-
ханизма. В равенствах (2.24) mi, тз
обозначают массы кривошипа / (рис.
2.4, в) и коромысла 3, a OSi и О5з -мо-
дули эксцентриситетов этих масс; /1, /3—
длины звеньев /, 3.
После реализации (2.24) центр масс
подвижных звеньев механизма будет на-
ходиться на линии ОС на расстоянии
OS = ОС
™3+W2B
от точки О, что непосредственно следует
из рис. 2.4, в.
Метод точечных масс. Уравнения
(2.24) можно интерпретировать по дру-
гому. Если шатун АВ механизма ОАВС
(рис. 2.4, в) заменить статической мо-
делью, показанной на рис. 2.2, в, и пере-
нести точечные массы т2А, т2в соот-
ветственно в точку А кривошипа
ОА и в точку В коромысла ВС, а за-
тем уравновесить эти массы массами
mi, тз звеньев / и 3, то условия
уравновешенности вращающихся звеньев
1 и 3 можно записать в форме урав-
нений (2.24). Такая интерпретация урав-
нений (2.24), называемая обычно мето-
дом уравновешивания механизмов точеч-
ными массами, может быть полезной
в некоторых случаях при уравновеши-
вании механизмов с симметричными
звеньями.
Метод уравновешивания механизмов
с несимметричными звеньями. Несиммет-
ричным звеном (рис. 2.5, а) называют
звено, у которого центр массы не лежит
на оси АВ и имеет в общем случае
координаты
a^AS'- b=S'S.
Параметр b принято называть отрезком
несимметричного звена АВ.
Долгое время отсутствовали методы
уравновешивания механизмов с несим-
метричными звеньями, и только в работах
15. 41] было показано, что такие меха-
низмы произвольной структуры могут быть
уравновешены методом подобия. Пока-
жем это на примере.
На рис. 2.5, б приведена структурная
схема шарнирного четырехзвенного ме-
62
Уравновешивание механизмов
Рис. 2.5. Уравновешивание шарнирного че-
тырехзвенного механизма с несимметричными
звеньями методом подобия
ханизма ОАВС, уравновешенного методом
подобия. Известно [5], что центр обшей
массы подвижных несимметричных звень-
ев механизма определяется вектором
OS = £ А44~ £ ft,, <2.25)
i= I »= 1
где hi, hi—векторы главных точек t-ro
звена и его отрезка; п — число под-
вижных звеньев механизма.
Если многоугольники Oabc и catbyS
(рис. 2.5, б), построенные соответственно
из векторов ht (i— 1, 2, 3) и h' (i— 1, 2, 3),
будут подобны кинематической цели ме-
ханизма ОАВС, то механизм сделается
статически уравновешенным, так как в
этом случае вектор (2.25) будет постояв
ным по величине и направлению, а ускоре-
ние центра S будет равно нулю при работе
механизма. Из сказанного следует, что
для статического уравновешивания мето-
дом подобия произвольного механизма
с несимметричными звеньями необходимо
и достаточно выполнить условия:
hi/OA = h2/AB = hs/BC\ (2.26)
h\/OA = h2/AB == h's/ВС, (2.27)
представляющие отношения сходственных
сторон -многоугольников ОАВС,
Oabc и cai&|S (рис. 2.5,6).
Если принять во внимание, что ра-
венство (2.26) справедливо как при
bi=^0; i= 1, 2, 3, (2.28)
так и при
bi=Q; i= 1, 2, 3, (2.29)
то для решения задачи достаточно вос-
пользоваться формулами (2.24), получен-
ными при условии (2.29). Применитель-
но к шарнирному четырехзвеннику форму-
лы (2.24), при условии (2.28), примут
вид
m\a\—m2(l2 — (2.30)
m3a3= mid&i/lz- (2.31)
Модули hi (Z—1, 2, 3) определяются
так же, как и модули hit при помощи
призмы П по формулам
h। — т।b।/ (tn। 4- т2 4- ш3);
h2 = тгЬч! (т i 4- т2 4- т3);
hs= m^b-il (mi 4- т24- тз),
‘(2.32)
очевидность которых непосредственно сле-
дует из рис. 2.5, в, где показана схема
определения модуля вектора h'для отрезка
S|S( звена О А.
Равенство (2.27) распадается на два
уравнения, которые, с учетом (2.32),
имеют вид
Методы статического уравновешивания механизмов
63
m{b{/l{ = m2b2/l2; (2.33)
«363/(3 =«262/(2. (2.34)
Уравнения (2.30), (2.31) и (2.33),
(2.34) являются расчетными для кон-
структора. Они содержат 12 параметров:
/П| (Ь»1, 2, 3)—массы звеньев; а, и 6,—
координаты центров масс; k—длины
звеньев. Поэтому при проектировании
уравновешенного шарнирного четырех -
звенного механизма конструктор может
выбрать произвольно 8 параметров, а
оставшиеся 4-е параметра определить
из уравнений (2.30). (2.31), (2.33) и
(2.34).
Рассмотрим пример (см. рис. 2.5.6).
Конструктору заданы 1\, 12, 13 (см. рис.
2.5, в)—длины звеньев; т2—масса шату-
на АВ; «2, Ь2—координаты центра массы
«2. Следовательно, конструктор может до-
полнительно выбрать еще два параметра,
например абсциссы аз центров масс
«ь т3, а оставшиеся параметры 6Ь Ьз
и mi, гпз найти из уравнений (2.30),
(2.31), (2.33) и (2.34). Очевидно, из
уравнений (2.30), (2.31) получим
гп} = т2{12 — a2)lt/(а^); (2.35)
— «202/3/ (вз/2), (2.36)
а из уравнений (2.33) и (2.34) найдем
bt = «262/j/ (/2«j)i (2.37)
Ьз = «262(3/ (/г«з). (2.38)
Заметим, что при других исходных
данных получится другое решение, однако
оно по-прежнему будет определяться
уравнениями (2.30), (2.31) и (2.33),
(2.34).
Метод расчленения механизма. Во
многих случаях многозвенный механизм
а целесообразно расчленить иа k меха-
низмов ос; (fe= 1, 2, .. , k) более простой
структуры в отношении их урав-
новешивания. Это может быть достигнуто,
например, расчленением некоторого звена
/ на два или больше число звеньев;
/ь /2, .. -, /к, эквивалентных вместе звену
/ по своим механическим характеристикам.
Возможны и другие способы решения
этой задачи.
Доказано, что статическая уравнове-
шенность каждого из механизмов сч
является необходимым и достаточным ус-
ловием для статической уравновешеннос-
ти механизма а Такой метод уравно-
вешивания сложного механизма а назван,
для краткости, методом расчленения (41].
Пример расчленения механизма. На
рис. 2,6, а показаны структурные схемы
шарнирного восьмизвенного механизма а
с несимметричными звеньями до (рис.
2,6, а) и после (рис. 2.6,6) уравновеши-
вания их методом расчленения в сочета-
нии с методом подобия. Изложим основы
этого метода.
Рис. 2.6. Уравновешивание восьмизвенного
механизма методом расчленения в сочетании
с методом подобия
64
Уравновешивание механизмов
Расчленим механизм а на три шар-
нирных четырехзвенных механизма а,
(1^1, 2, 3),' как показано на «рис.
2.6, б. Для этого расчленим произвольно
звено 3 на два звена 3' и 3", но так,
чтобы выполнялись условия
тз = ктз\
? (2.39)
тз=(1—к)тз. I
где тз—масса звена 3 до его рас-
членения, а тз, т"—массы звеньев
3', 3"; k — постоянная, назначаемая кон-
структором из интервала
0<fe<l. (2.40)
Аналогично делим звено 5 на два звена:
5' и 5".
Механизмы a, (i— 1, 2. 3) уравновеши-
вают статически методом подобия, как
изложено выше, а затем соединяют
вместе. В результате получают исходный
механизм а, уравновешенный статически
(рис. 2.6, в).
Параметры механизма а. Методика
определения масс т, звеньев механизма
а и координат a,, fcj (/=1, 3, 5, 7) их
центров зависит от исходных данных за-
дачи. Для примера, будем считать ис-
ходными данными массы т2, ша-
тунов и координаты ah bt (j —2, 4, 6)
их центров, а также длины I, (j—\,
2, .... 7) всех звеньев механизма (рис.
2.6, а). Из конструктивных соображений
выберем абсциссы а, центров масс т,
(/=1, 3, 5, 7) и примем, что у
механизмов а, (<=1, 2, 3)
аз—аз = аз;
05=05 —а&,
где аз, а" и а&, as обозначают соот-
ветственно абсциссы центров масс т'з,
т'з и ms, т& (рис. 2.6, б).
На основании исходных данных опре-
делим значения масс т, (/«I, 3, 5, 7)
и ординаты Ь, их центров, необходимые
для статического уравновешивания меха-
низма а (рис. 2.6, а).
По формулам (2.35), (2.36) получим
значения масс
т. = т2-------;-----• {2.41!
а,/2
а6/7
т 1 ~ . (2.42)
a?'с
Ординаты центров масс (2.41), (2.42)
вычислим по формулам (2.37) и (2.38):
Ь| = т2Ы1/(^1^);
— гщЬь1т! (lent?).
(2.43)
При определении масс звеньев 3', 3"
примем коэффициент (2.40) равным 0,5.
Тогда в соответствии с условиями (2.39)
получим
тз~ тз = °‘5/пз (2.44)
и, аналогично,
т'ь = mg — 0,5ms. (2.45)
При условии (2.44), (2.45) ма<;сы 3
и 5-го звеньев будут в соответствии
с уравнениями (2.35) и (2.36) опреде-
ляться формулами
1 / «2*3 .
'пз= — /и2 — 4
°3 \ *2
(2.46)
I ( .
* *4
(/f) as) 1Н.
L
12 47)
4”
Ординаты масс (2.46), (2.47), соглас-
но формулам (2.37) и (2.38), будут
равны:
Ьз = Ь'з — 2т^ч1з1 ( ;
Ь% = 2m4,b4 (т&Ц); (2.48)
bs— 2m^b^lEF/
Далее, в соответствии с рис. 2.6, г
и при условии (2.44). получим
Ь3 = (Ы+Ь%)/2. (2.49)
Методы статического уравновешивания механизмов
65
Аналогично, при условии (2.45), имеем
66 = (^4-^')/2. (2.50)
Формулы (2.41) — (2.43), (2.46),
(2.47) и (2.48) — (2.50) полностью опре-
деляют все параметры механизма а
(рис. 2.6, а) после его уравновешивания
методом расчленения в сочетании с ме-
тодом подобия (рис. 2.6. в) при принятых
выше исходных данных.
Заметим, что при других исходных
данных параметры механизмов a, (i=l,
2, 3) и а будут другими, однако их
нужно определять по-прежнему на осно-
вании приведенных выше уравнений
(2.30), (2.31), (2.33), (2.34), которые
являются основными при уравновешива-
нии шарнирных четырехзвенников с не-
симметричными звеньями.
Рассмотренный метод уравновешива-
ния сложных механизмов позволит кон-
структорам решать практические задачи
по статическому уравновешиванию меха-
низмов различных классов и порядков
с несимметричными звеньями.
Метод функциональных цепей. Дока-
зано [41], что для статического урав-
новешивания сложного механизма а, нап-
ример механизма дробилки (рис. 2.7, с),
необходимо и достаточно статически урав-
новесить его функциональную цепь (рис.
2.7.6). Последняя получается из меха-
низма а путем отделения от него в об-'
щем случае одного или нескольких не-
весомых звеньев. В данном примере за
невесомое звено следует принять звено 4.
Чтобы сделать шатун BD невесомым, его
нужно сначала заменить статической мо-
делью (рис. 2.7,г), представляющей не-
весомый стержень BD с двумя точечными
массами (см. гл. .2, п. 2):
DS.
miB--- m4 ’
BS.
^4 fit) ’
(2-5!)
затем перенести массы (2.51) co звена
4 на смежные звенья 3 и 5 и отсоеди-
нить от механизма невесомый стержень
3 Зак 1641
Рис. 2.7. Структурная схема механизма дро-
билки до и после уравновешивания его
методом функциональных цепей в сочетании
с методом подобия
4. В результате получим функциональную
цепь (рис. 2.7, б) для механизма дро-
билки (рис. 2.7, а).
Для уравновешивания функциональ-
ной цепи нужно, пользуясь методом по-
добия, придать звеньям 5, 3 и 1 такие
формы, чтобы центры их масс оказались
соответственно в точках £, S3 и S|. После
восстановления звена 4 в схеме урав-
новешенной функциональной цепи полу-
чим структурную схему исходного меха-
низма дробилки, уравновешенного стати-
чески методом функциональных цепей в
сочетании с методом подобия (рис. 2.7, в).
Метод функциональных цепей являет-
ся универсальным для статического урав-
новешивания сложных механизмов любо-
го класса и порядка как с симметрич-
ными, так и с несимметричными звеньями.
66
Уравновешивание механизмов
2.5. ПРИМЕРЫ УРАВНОВЕШИВАНИЯ
МЕХАНИЗМОВ
Шарнирно-зубчатый механизм. Пяти-
звенный шарнирно-зубчатый механизм с
ведущим солнечным колесом показан на
рис. 2.8, а и б соответственно до и после
уравновешивания его методом нуль-век-
торов.
В соответствии с условиями (2.21) —
(2.23) корректирующие массы т2, пг3, тл
должны быть такой величины, чтобы
центр S2 массы звена 2 совпадал с
точкой В, а центр S2.3 масс звеньев 2, 3
оказался в точке С. Масса пц должна
обеспечить совпадение с неподвижной
точкой D центра масс подвижных звень-
ев 2, 3 и 4 механизма ABCD (рис. 2.8, б)
Рычажно-зубчатый механизм. На
рис. 2.8, в показан механизм ОАВС, с
зубчатым сектором 3 и рейкой 4, урав-
новешенный статически методом нуль-век-
Рис. 2.8. Уравновешивание шарнирно-зубча-
тых механизмов'
торов. Другими методами, например подо-
бия или точечных масс, этот механизм
нельзя уравновесить, так как при враще-
нии кривошипа ОА изменяется его гео-
метрия.
Рис. 2.9. Статическое уравновешивание кри-
вошипно-ползунных механизмов:
а—в- центрального, г дезаксиально! о, д —
центрального с несимметричным шатуном
Примеры уравновешивания механизмов
67
Для решения задачи методом нуль-век-
торов нужно было, в соответствии с ус-
ловиями (2.30) — (2.32), придать звеньям
механизма такие формы (рис. 2.8, в), что-
бы с точками В, А и О совпали соот-
ветственно центры масс m3 (/n3J-zn2) и
(m3 + m2 + mi).
Кривошипно-ползунные механизмы.
Центральные (рис. 2.9, а) и дезаксиаль-
ные (рис. 2.9, г) кривошипно-ползунные
механизмы одноцилиндровых насосов,
компрессоров, двигателей и др. с сим-
метричными шатунами уравновешивают
обычно методом подобия или методом
точечных масс, несмотря на то что этими
методами не устраняется полностью дей-
ствие силы (2.17) по оси цилиндра.
Центральный механизм. Чтобы урав-
новесить статически механизм О АВ
(рис. 2.9, а) методом подобия или мето-
дом точечных масс, необходимо шатун
АВ заменить его статической моделью
(см. п. 2.2 гл. 2), представляющей не-
весомый стержень с двумя точечными
массами: пг2А, т2В (рис. 2.9,6), которые,
согласно (2.8), равны
BS2
т2А = ;
Л52
™2В =
(2.52)
Затем массу т2А следует перенести на
кривошип /, а массу т2В на ползун 5,
и уравновесить массу т2Д массой гп\ кри-
вошипа. Для этого кривошипу нужно при-
дать такую форму (рис. 2.9, в), чтобы
его дисбаланс
D\ = tn\OS\ = — т2АОА. (2.53)
После уравновешивания вращающих-
ся масс гп\ и т2А на станину механизма
будет действовать неуравновешенная сила
Р=— (тз + т2в)&в, (2-54)
где ав — вектор ускорения ползуна <?, рав-
ный по модулю
ав— ОАм2 cos ф + ОАм2А2 cos 2<р +
+ ОЛсо2Л4 cos 4<р -4-. . . (2.55)
Коэффициенты ряда (2.55), зависящие
от геометрического параметра Z= ОА/АВ,
приведены в табл. 2.1,
Таким образом, модуль силы (2.54)
определяется тригонометрическим рядом
Рв= 0Аы2т cos ф + 0Аы2тА2 cos 2<р 4-
+ ОЛ(о2лпЛ4 cos 4ф= .... (2.56)
Здесь
т = т34-т2Л (2-57)
представляет поступательно движущуюся
массу, состоящую из массы звена 3
и одной из точечных масс (2.52).
Слагаемые ряда (2.56)
Р! = ОАы2т cos ср; Y
Pn=04<o2m42cos2«p; (2.58)
P,v= ОАа>2тА, cos 4<p;
называются соответственно силами 1-го,
2-го и более высокого порядка, в за-
висимости от коэффициента при ф.
Силы (2.58) можно рассматривать
как проекции на направление движения
ползуна некоторых вспомогательных век-
Таблица 2.1
Коэффициенты ряда
Коэффициенты ряда Геометрический параметр к
1/3,5 1/4 1/4,5 1/5 1/6 1/7
л2 0,2918 0,2540 0,2250 0,2020 0,1678 0,1436
-л4 0,0062 0,0041 0,0028 0,0020 0,0012 0,0007
Лб 0,000126 0,000069 0,000038 0,000022 0,000009 0,000004
3*
68
Уравновешивание механизмов
торов [5, 41], равных по
(рис. 2.9, а}
оЛ<й2т;
Р^— OAufmAz, »
Г14)— OAtD2mA4,
модулю
(2.59)
и образующих с осью направляющей
углы,
Ф— <»>/;
2<p=2fa)Z; >
4<р — 4u>t,
(2.60)
Из равенств (2.60) следует, что век-
торы (2.59) вращаются с угловыми ско-
ростями со, 2о), 4<л, .... Поэтому силы
(2.58) 2-го, 4-го и более высокого
четного порядка нельзя уравновесить в
одноцилиндровой машине путем прикреп-
ления корректирующих масс к кривошипу.
Точно так же нельзя уравновесить и силу
1-го порядка Р\ но можно, при необхо-
димости, только,повернуть на 90° линию
действия ее составляющей kP\ где
OcfeCI. (2.61)
Для этого достаточно увеличить дис-
баланс кривошипа от значения (2.53)
до значения
£>н = Г?! + OAmk, (2.62)
где ОА—длина кривошипа; т—поступа-
тельно движущаяся масса (2.57).
После реализации дисбаланса (2.62)
на станину кривошипно-ползунного меха-
низма будет действовать остаточная неу-
равновешенная сила
Рвх=( 1-^Р1 -| Pl, + PIV= . ..(2.63)
в направлении оси направляющей и сила
P^kP1' (2.64)
в перпендикулярном направлении.
Очевидно, при k=l сила (2.63)
^bx=^I, + />IV+-..,
а сила (2.64)
Рву= Р1.
Заметим, что коэффициент (2.61) вы-
бирает конструктор в зависимости от
упругих свойств фундамента одноцилин-
дровой машины в горизонтальном и в
вертикальном направлениях.
Дезаксиальный механизм. Чтобы урав-
новесить статически дезаксиальный меха-
низм (рис. 2.9, г), шатун АВ также за-
меняют невесомым стержнем с двумя то-
чечными массами (2.52), из которых мас-
су т2Л переносят на кривошип /, а
массу т2В на ползун 3. Если кривошипу 1
придать такую форму, чтобы центр его
массы Ш| оказался в точке Si, а дис-
баланс был равен (2.53), то кривошип-
но-ползунный дезаксиальный механизм
сделается статически уравновешенным
(рис. 2.9, г).
После уравновешивания механизма
его станина будет воспринимать неурав-
новешенную силу (2.54). Однако в этом
случае ускорение поршня должно опре-
деляться выражением
ав — ОАы2 cos <р -|- ОЛ<й2Лг cos 2<р ±
±xXsin<p. (2.65)
В последнее слагаемое многочлена
(2.65) входит величина
х=е/ОЛ,
а его знак должен быть одноименным
со знаком дезаксиала в системе от-
счета хоу (рис. 2.9, а).
Заметим, что при уравновешивании
кривошипно-ползунных механизмов мето-
дом нуль-векторов можно полностью
компенсировать силу (2.54), но при этом
шатуны получатся консольными, что
усложнит конструкцию механизма и уве-
личит его габаритные размеры. Поэтому
такое уравновешивание редко применяют
на практике.
Центральный механизм с несиммет-
ричным шатуном. При уравновешивании
методом подобия произвольного механиз-
ма с несимметричными звеньями исход-
ными являются выражения (2.1) — (2.3).
Примеры уравновешивания механизмов
69
(2.26), (2.27) и (2.32). Применительно
к кривошипно-ползунному механизму
с несимметричным шатуном (рис. 2.9, д)
запишем расчетные уравнения в виде
mtail2= тч (1ч— (2.66)
m\b {1ч = т 262Z|. (2.67)
В уравнения (2.66), (2.67) входят
8 параметров, поэтому при проектирова-
нии статически уравновешенного механиз-
ма конструктор может выбрать 6 пара-
метров. Если, например, заданы длины
звеньев /], /2 и их массы mi, m2,
а также координаты а2, 62 центра массы
т2, то координаты alt bi центра массы
mi кривошипа можно определить по фор-
мулам (рис. 2.9,6):
fli —m2(/2 —а2)/ (т62);
fel = m2d2/1/(ml/2).
Шарнирный механизм третьего класса
и порядка. На рис. 2.10 показана струк-
турная схема пятизвенного механизма
до (рис. 2.10, а) и после (рис. 2.10,6)
его уравновешивания. Так как шатун 3
несимметричный, то механизм можнс
уравновесить методом подобия в сочета-
нии с методом функциональных цепей.
Для этого выполняют следующие опе-
рации:
1. Звено 2 заменяют статической
моделью согласно рис. 2.2, в и затем
отсоединяют от механизма. При этом то-
чечные массы т2Л, т2й остаются при-
соединенными к звеньям / и 3 соотве-
ственно в точках А и В.
2. Звену / придают такую форму
(рис. 2.10,6), при которой дисбаланс его
массы т{ относительно оси вращения
Dt~ т2АОА. После этой операции центр
вращающихся масс т, и т2А совпадает
с неподвижной точкой О.
3. Шарнирный четырехзвенник BCDEF
с несимметричным шатуном и звеньями
4 и 5 уравновешивают методом подобия
в соответствии с рис. 2.5,6 (см. п. 2.4).
4. Невесомое звено 2 возвращают
на место. В результате получается ста-
Рис. 2.10. Уравновешивание шарнирных и
рычажных механизмов 3-го класса (при на-
чальном звене /)
тически уравновешенный механизм (рис.
2.10, 6)'.
Рычажный механизм третьего класса
и порядка. Уравновесим механизм штам-
повочного пресса с несимметричным ша-
туном 3 (рис. 2.10, в) методом подобия
в сочетании с методом функциональных
цепей. Для этого выполняют следующие
операции:
1. Шатун АВ заменяют статической
моделью согласно рис. 2.2, в и после
переноса точечных масс т2Л, т2е на смеж-»
ные звенья 1 и 3 отсоединяют его
от механизма. В результате получают
70
Уравновешивание механизмов
функциональную цепь, состоящую из
звена / и кривошипно-ползунного меха-
низма с несимметричным шатуном BDE.
2. Звено / проектируют такой формы
(рис. 2.Ю, а), чтобы его дисбаланс от-
носительно оси вращения Dt — т2АОА.
3. Кривошипно-ползунный механизм с
несимметричным шатуном BDE (к кото-
рому присоединена масса т2в) уравно-
вешивают статически методом подобия
в соответствии с рис. 2.9, д.
4. После восстановления невесомого
звена АВ получают статически уравно-
вешенный механизм штамповочного прес-
са (рис. 2.10, в).
2.6. УРАВНОВЕШИВАНИЕ
МАНИПУЛЯТОРОВ
ПРОМЫШЛЕННЫХ РОБОТОВ
Основной механизм манипулятора ПР
представляет в общем случае простран-
ственный механизм с несколькими степе-
нями свободы, содержащий разомкнутые
и замкнутые кинематические цепи. По-
следние образуются, в частности, звенья-
ми приводных устройств, механизмов пе-
редвижения, захвата и других. Отсюда
следует, что кинематические цепи мани-
пуляторов должны уравновешиваться ста-
тически или только методом нуль-век-
торов, или методом нуль-векторов в со-
четании с методами подобия, функцио-
нальных цепей и другими—в зависи-
мости от структуры этих цепей. Покажем
это на примерах.
Манипулятор ПР ЛПИ-2- Манипу-
лятор ЛПИ-2 Лениградского политехни-
ческого института [28] представляет со-
бой шарнирную кинематическую цепь
ABCDEF с шестью степенями свободы
(рис. 2.11, а). Такая кинематическая цепь,
как было указано выше, может быть
точно уравновешена статически методом
нуль-векторов. Для этого достаточно уста-
новить на звеньях 2, 4 и 5 манипу-
лятора корректирующие массы mi 2
и /«1-5 такой величины, чтобы центры
масс
—mi -Г ~Н mi—?» 1
т& Т тз Т т। — 4,/ (2.68)
tn tn -1- m j gj J
совпали соответственно с точками В.
D и Е (рис. 2.11. 6).
Рис. 2.11. Манипулятор ЛПИ-2 до и после
уравновешивания его методом нуль-векторов
Рис. 2.12. Манипулятор ПР фирмы АСЕА
до и после его уравновешивания
Уравновешивание манипуляторов промышленных роботов
71
В выражениях (2.68) mt (i—1, 2,
. . . , 5) обозначает массу i-ro подвижного
звена манипулятора.
Манипулятор ПР фирмы АСЕА
(ASEA, Швеция). На рис. 2.12, а показана
структурная схема манипулятора ПР с
шестью степенями свободы, предназначен-
ного для обрезания заготовок водяной
струей высокого давления [30]. Заметим,
что аналогичную структурную схему име-
ет и манипулятор ПР типа VI5 фирмы
Райс (Reis, ФРГ), служащий для пере-
мещения груза массой до 15 кг в
любую точку сферического пространства,
диаметром 3 м [31].
Так как в данном случае манипуля-
торы имеют шарнирные кинетические це-
пи, они могут быть точно уравновешены
методом нуль-векторов при помощи четы-
рех корректирующих масс. Очевидно, пос-
ле уравновешивания манипулятора (рис.
2.12,6) точки А, В, С, D кинематичес-
кой цепи должны совпадать соответствен-
но с центрами масс
— Ч- m2-|- т(_2;
гав = т а + + пи _3;
тс— тв 4 + mj-4;
тс~1~ T mi 5»
где nii (t= 1, 2,.... 5) — масса i-ro звена;
mt—। — корректирующая масса, установ-
ленная на z-м звене.
Манипулятор ПР УПР-11. На рис.
2.13 показана структурная схема манипу-
лятора ПО НПО Оргстанкинпрома [19],
который может обслуживать загрузочно-
разгрузочными операциями станки с ЧПУ
патронного типа в мелкосерийном произ-
водстве. Манипулятор имеет девять степе-
ней свободы и содержит два замкнутых
контура.
Рассмотрим процесс уравновешивания
манипулятора при его конструировании.
Если пренебречь массой каретки и
захвата с изделием производства, то
манипулятор можно точно уравновесить
семью корректирующими массами мето-
дом нуль-векторов в сочетании с мето-
дом подобия (рис. 2.14).
Очевидно, после уравновешивания
манипулятора центр массы
тА—т} -J-mo-i, (2.69)
состоящей из массы гп\ первого звена
и его корректирующей массы то—ь ока-
жется на оси вращательной кинемати-
ческой пары А, а центры масс
га^— тА -}- га2 -Г гао2;
тс= Що-з; ‘
тd== —|— m4 -f- mo—4
(2.70)
будут совпадать соответственно с точками
В, С и D.
После реализации равенств (2.69),
(2.70) кинематическая цепь A BCD будет
Рис. 2.13. Структурная
схема манипулятора
ПР УПР-11
72
Уравновешивание механизмов
Рис. 2.14. Структурная схема статически уравновешенного манипулятора
ПР УПР-11
уравновешена статически, и центр масс
всех ее подвижных звеньев будет нахо-
диться в точке D (рис. 2.14). Для полного
уравновешивания манипулятора необ-
ходимо уравновесить также два шар-
нирных четырехзвенника: EFGH и IKLM
(рис. 2.14). Так как шатуны EF и IE
этих четырехзвенников являются несим-
метричными, то уравновешивание их мож-
но выполнить только методом подобия
[41 [. Для решения задачи определяют сна-
чала массу mEF несимметричного шатуна
EF и массы звеньев 7 и 8. На основании
рис. 2.14 можно записать
mEF— mD Ч- (2.71)
tn 7 -— tn FF
(Ju- h
lFFa7
(2.72)
aEF^e,
tn&^mEF——,
l£Fue
(2.73)
где m5, —массы звеньев 5, 6; lEF—рас-
стояние между точками Е и F; 1у=ЕН и
Iz—FG—длины звеньев 7 и в; a.EF—
— ES'ef—абсцисса центра SEF массы
(2.71), показанная на рис. 2.15, а; С7 =
= НН’ и as—GG' — абсциссы центров
Рис. 2.15. Уравновешивание фрагмен-
тов кинематической цепи манипуля-
тора ПР УПР-11
Уравновешивание механизмов многоцилиндровых машин
73
масс (2.72) и (2.73), отмеченные на
рис. 2.15, а.
Аналогично находят массу т1К не-
симметричного шатуна /К и массы mt0,
тц звеньев 10, 11 (рис. 2.15,6):
/n/K=/n£f+m74-me4-m9; (2.74)
(//д- а/Л) /10
т ю — /?г/Л'
(2.75)
/Иц — miK~i—7 • (2.761
11Ки\А
где m]0, тц—массы звеньев 10 и //;
—расстояние _ между точками /, /(;
lio—lMHlw — KL — длины звеньев /би //;
aIK—ISIK~~абсцисса центра массы
(2.74); £Х|о=Л/Л/х и an = LL'—абсциссы
центров масс (2.75), (2.76), обозначае-
мые на рис. 2.15, б.
Абсциссы центров масс т7, тъ и
fWto, т\\ конструктор может выбрать при
проектировании манипулятора, а их орди-
наты найти по формулам
fnEf,btfl7
о? — —7------;
lEftn7
610 = I т '
11 “ liKmu
гДе — SefSef; — SfK SfK.
В заключение заметим, что в случае,
когда массой каретки и захвата вместе
с изделием пренебрегать нельзя, то про-
цесс уравновешивания манипулятора
ПР УПР-11 и написанные выше формулы
(2.69) - (2.77) будут также справедливы,
если только формулу (2.69) записать
в виде
тл = тс4~т1+то-1 (2.78)
и считать, что масса то, входящая в
формулу (2.78), имеет относительно оси
вращательной кинематической пары А
эксцентриситет (рис. 2.14)
*4)4" в’о
е°=~2 ’
где еб, во—эксцентриситеты массы mv
при крайних положениях каретки на зве-
не /.
2.7. УРАВНОВЕШИВАНИЕ
МЕХАНИЗМОВ МНОГОЦИЛИНДРОВЫХ
МАШИН
Для отдельно взятого кривошипно-
ползунного механизма силу (2.56) нельзя
уравновесить путем прикрепления коррек
тирующей массы к кривошипу (см. п.2.5).
Но в многоцилиндровых машинах, со-
стоящих из одинаковых центральных кри-
вошипно-ползунных механизмов с сим-
метричными шатунами, уравновешенных
каждый в отдельности методом подобия
или методом точечных масс (см п. 2.5),
вполне возможно достигнуть взаимного
уравновешивания сил 1-го, 2-го, а в не-
которых случаях и более высокого по-
рядка при помощи простейших конструк-
тивных средств, к которым относится,
например, выбор относительного располо-
жения кривошипов. Рассмотрим примеры.
Двухцилиндровая машина с кривоши-
пами, расположенными под углом 180°
(рис. 2.16, а). Для определения сил 1-го
порядка направим по соответствующим
кривошипам вспомогательные векторы
Р?’, Рг\ равные по модулю (см. п.2.5):
Pin= 0Аы2т',
Pf2n=Pf1,\
где ОА—длина кривошипа; т—поступа-
тельно движущаяся масса, определяемая
формулой (2.57), ш—угловая скорость
коленчатого вала. Проекций векторов
Р?*, РУ1 на геометрические оси цилиндров
определяют силы 1-го порядка Д”,
Рг по величине и направлению. Из рис.
2.16, б видно, что неуравновешенные силы
1-го порядка приводятся в двухцилиндро-
74
Уравновешивание механизмов
Рис. 2.16. Неуравновешенные силы
в двухцилиндровой машине
вой машине к паре сил с моментом,
модуль которого изменяется по гармо-
ническому закону:
М’2— OA(i)?ml cos <pi,
где I—расстояние между геометричес-
кими осями цилиндров.
Силы 2-го порядка определяются про-
екциями на геометрические оси цилиндров
вспомогательных векторов Р*2*, Р^2’, кото-
рые равны по модулю, т. е.
Pi2'— ОА(а2тА2;
и совпадают по фазе, так как образуют
Рис. 2.17. Неуравновешенные силы в четы-
рехцилиндровой машине с кривошипами, рас-
положенными под углом 180°
с геометрическими осями цилиндров углы
2<pj и 2(ф|-|-180). Из рис. 2.16,в сле-
дует, что главный вектор сил 2-го по-
рядка равен по модулю
pJJ2 = р« -J- р» = 20АМ2 cos 2ф,,
где коэффициент А2, зависящий от гео-
метрического параметра X = ОА ।/А i В,,
дан в табл. 2.1. Силы более высоких
порядков также приводятся к равно-
действующей.
Четырехцилиндровая машина с криво-
шипами, расположенными под углом 180°
(рис. 2.17, о). Для определения неурав-
новешенных сил 1-го порядка возьмем
вспомогательные векторы (i=l, 2.
3. 4), равные по модулю:
р£11= 0Аи>2т,
и направим их по соответствующим
кривошипам (рис. 2.17, б).
Проекции векторов PJ-" на геометри-
Уравновешивание механизмов многоцилиндровых машин
75
Рис. 2.18. Неуравнове-
шенные силы в шести-
цилиндровой машине с
кривошипами, располо-
женными под углом 120°
ческие оси цилиндров будут равны силам
1-го порядка:
Р| = Р\— 0Аы2т cos <pi;
pj=p‘=_p}.
Отсюда следует, что главный вектор
и главный момент неуравновешенных сил
1-го порядка, действующих в четырех-
цилиндровой машине, представляют ну-
левые векторы (рис. 2.17,6).
Неуравновешенные силы порядка 2п,
где п—произвольное число, приводятся к
равнодействующим, линии действия кото-
рых проходят через среднюю точку ко
ленчатого вала параллельно осям ци
линдров (рис. 2.17, в).
Шестицилиндровая машина с криво-
шипами, расположенными под углом 120'
(рис. 2.18, а). Вспомогательные векторы
Я1) (*= 1, 2,.. . ,6), где
Pf5)= 0Аы2т.
направим по соответствующим кривоши-
пам и спроектируем их на геометрические
оси цилиндров (рис. 2.18, б) В резуль-
тате получим неуравновешенные силы 1-го
порядка:
Р{ = Pf,= 0Аы2т cos
Р|= 0Аы2т cos (<р, 4-120°);
Р13 = = Р\= 0Аы2т cos (<pt 4- 240°).
Так как равенства
Р{ + Н+^=0;
р'+^+рЬ-о.
удовлетворяются тождественно при лю-
бом значении угла <рч, то неуравнове-
шенные силы 1-го порядка Р* (/=1,2,3)
и Р’ (/ = 4,5,6) приводятся соответствен-
76
Уравновешивание механизмов
но к парам сил с моментами Л?’,г.з,
^4,5,6» которые одинаковы по модулю, но
противоположны по направлению:
М 1,2,3= ^4,5,6»
где
М\ 2>3= -д/3 О А со2 ml cos (<pi -f- 30°).
Аналогично силы 2-го порядка
Р,п (<=1. 2, 3) и Р(п (I = 4, 5, 6) также
приводятся к парам сил с моментами /Й5’2,з
и /Ид15 6, одинаковыми по модулю, но
противоположными по направлению
(рис. 2.18, в):
^И2,3= —^4.5.6,
где
М}12 3= -д/3 ОАч2тА21 cos (2<р। — 30°).
Такое же действие будут производить
неуравновешенные силы 4-го (рис. 2.18, г)
и более высоких четных порядков, если
только порядок силы не является кратным
числу 3.
Силы, порядок которых равен ЗКо
(Ко=2, 4, 6,...), приводятся к равно-
действующей:
= cos •
Например, при ka = 2 получим (рис.
2.18, 5)
/?У16= 60Л<о2/пЛ6 cos 6<рь
В общем случае линия действия
силы jR|_63*g проходит через среднюю
точку коленчатого вала параллельно гео-
метрическим осям цилиндров.
Заметим, что моменты неуравновешен-
ных сил, порядок которых не является
кратным числу 3, являются внешне урав-
новешенными, но вызывают изгибные ко-
лебания коленчатого вала в плоскости,
проходящей через геометрические оси ци-
линдров [41].
Технологические втулки коленчатых
валов. Если для коленчатого вала много-
цилиндровой машины справедливы усло-
вия:
а) центр массы коленчатого вала ле-
жит на оси вращения;
б) коленчатый вал является сим-
метричным относительно его средней плос-
кости (левая половина вала является
зеркальным отображением правой полови-
ны), то его можно балансировать дина-
мически на балансировочном станке без
технологических втулок.
Если эти условия не выполняются,
то балансировку коленчатого вала необ-
ходимо производить обязательно с тех-
нологическими втулками. Последние де-
лают разъемными; они имеют такую мас-
су, чтобы их действие на коленчатый
вал во время балансировочного процесса
заменяло действие шатун но-порш невой
группы. Поэтому масса одной техноло-
гической втулки должна быть [см.
формулы (2.8)]
т т = ш2Л — т2 —Ау, (2.79)
где т.2—масса шатуна; а, b — расстоя-
ния от центра массы шатуна до осей
вращения вращательных кинематических
пар (рис. 2.2,6).
В качестве примеров укажем, что
коленчатые валы четырехцнлиндровой
(рис. 2.17) и шестицилиндровой (рис. 2.18)
машин можно динамически балансиро-
вать на балансировочном станке без тех-
нологических втулок. Напротив, балан-
сировку коленчатого вала двухцилиндро-
вой машины (рис. 2.16) необходимо произ-
водить обязательно с технологическими
втулками.
В некоторых случаях, например при
балансировке коленчатого вала двухци-
линдровой V-образной машины с углом
развала цилиндров, равным 90° (рис.
2.19), масса т’т каждой технологической
втулки должна учитывать не только ша-
тунные массы т2А, тЗА шатунов 2 и 3, но
и действие в машине неуравновешенных
сил 1-го порядка, поэтому ее определяют
по формуле [41]
М'Т—тТ + (тз+т4).
Принципы динамического уравновешивания механизмов
77
Рис. 2.19. Неуравновешенные силы в двух-
цилиндровой V-образной машине с углом
развала цилиндров, равным 90°
где (щ3+т4)—масса шатунно-поршне-
вой группы, состоящей из шатуна 3 и
поршня 4\ тт—масса, определяемая по
формуле (2.79).
2.8. ПРИНЦИПЫ ДИНАМИЧЕСКОГО
УРАВНОВЕШИВАНИЯ
МЕХАНИЗМОВ
Выше было показано, что при выпол-
нении условий (2.19) и (2.20) механизм
имеет соответственно статическую или
моментную уравновешенность. Динами-
ческая уравновешенность механизма до-
стигается при одновременном выполнении
условий (2.29), (2.20). Точное решение
этой задачи весьма затруднительно по-
лучить в общем виде простыми кон-
структивными средствами.
В настоящее время разработан лишь
обший метод статического уравновешива-
ния механизмов произвольной структуры
с симметричными и с несимметричными
звеньями и общий метод уравновеши-
вания в механизмах произвольной струк-
туры 1-й гармоники главного момента
неуравновешенных сил [41]. Известны
также решения частных задач моментного
уравновешивания механизмов. Ниже бу-
дут рассмотрены принципы этих мето-
дов.
Компенсация главного вектора и 1-й
гармоники главного момента неуравно-
вешенных сил. Этот метод основан на
принципе независимости статической урав-
новешенности механизма от координат оси
вращения какой-либо вращающейся массы
статически уравновешенного механизма
[1]. Рассмотрим следующий пример.
На рис. 2.20. а показана схема ста-
тически уравновешенного механизма
ОАВС массосмесильной машины. Перено-
сим ось вращения массы kmi кривоши-
па /, где
Аг<1, (2.80)
из положения О в положение Oi
(рис. 2.20,6). От этой операции не
изменится статическая уравновешенность
механизма в силу указанного выше прин-
ципа, но появится пара сил с моментом
Рис. 2.20. Компенсация главного вектора и 1-й гармоники главного момента
неуравновешенных сил
78
Уравновешивание механизмов
Mp=kmibOiA"to2s\r\ (<р4-6 — у), (2.81)
который скомпенсирует момент
AJ( = X sin (<р 4- б). (2.82)
представляющий 1-ю гармонику главного
момента М неуравновешенных сил. В
формуле (2.81) b — расстояние между
осями вращения кривошипа и корректи-
рующей массы ftmu mi — масса кривоши-
па О А статически уравновешенного ме-
ханизма ОАВС (рис. 2.20, а); <о~ угло-
вая координата кривошипа OiA" — экс-
центрисистет массы kmc, — угловая ко-
ордината кривошипа О А относительно
линии ОС; б — угол между линиями
центров ОС и OOi; у — угол между
линиями ОА и OSi. Амплитуду М?
и фазовый угол б| момента (2.82) опре-
делим на основании гармонического ана-
лиза главного момента
М — Л104- £ Af^sin(n<jp4-6,J
n=i
неуравновешенных сил, действующих в ме-
ханизме.
После нахождения значений Л4® и б|
конструктор может выбрать параметр b
и определить коэффициент k из интерва-
ла (2.80) по формуле
Заметим, что для шарнирных меха-
низмов изложенный метод позволяет точ-
но уравновесить главный вектор и 1-ю
гармонику главного момента неуравнове-
шенных сил, при произвольном значении
параметра Ь. В случае рычажных меха-
низмов, которые, как известно, уравно-
вешивают статически приближенно, метод
позволяет, не изменяя качество стати-
ческой уравновешенности механизма, до-
полнительно уравновесить 2-ю гармонику
главного момента неуравновешенных сил
также при произвольном значении пара-
метра Ь. Таким образом, рассмотренный
метод является универсальным и может
быть использован для механизмов про-
извольной структуры.
Принцип симметрии. В некоторых
случаях, при симметричном расположении
одинаковых механизмов, достигается ча-
стичная компенсация неуравновешенных
сил и моментов. Например, у централь-
ных кривошипно-ползунных механизмов
OAiBi и ОАъВъ (рис. 2.21,а), расположен-
ных симметрично относительно точки О,
главные векторы и главные моменты
неуравновешенных сил Р\ Рп. Р™,. .. [см.
уравнение (2.58)] различных порядков
становятся нулевыми векторами. Враща-
ющиеся массы кривошипов также будут
уравновешены. Станина этого механизма
будет воспринимать только действие не-
уравновешенного момента
Мю — —- (J21E21 4- /22822) (2.84)
от масс шатунов AiBi и А2В2- В
выражении (2.84): J2i, /22—моменты
инерции шатунов относительно осей, про-
ходящих через центры их масс пер-
пендикулярно плоскости чертежа; 821,822 —
угловые ускорения шатунов, одинаковые
по величине и направлению.
Компенсация неуравновешенных сил,
создаваемых шатунными массами. Мо-
мент типа (2.84) является переменным
по величине и направлению и поэтому
может быть одной из причин вибрации
станины механизма. Чтобы устранить не-
уравновешенные моменты от N шатунных
масс, достаточно выполнить условия
pL = aA (* = 1,2,....,А), (2.85)
где p2s, — радиус инерции t-ro шатуна
относительно оси, проходящей через
центр S2l- его массы, перпендикулярно
плоскости чертежа; а,, Ь, — расстояние
от центра массы m2j t-го шатуна до осей
вращения кинематических пар.
Пример. После статического уравновешива-
ния четырехзвенного шарнирного механизма
(рис. 2.21,6) методом подобия (см. п 2.4)
главный вектор неуравновешенных сил будет
нулевым, но на станину механизма будет
действовать неуравновешенный момент
AfUI = m^($s — аЬ)ъ (2.86)
от шатунной массы тц. В формуле (2.86):
Е2 — угловое ускорение шатуна; а,Ь рассто-
яния от центра S2 до центров А и В;
Принципы динамического уравновешивания механизмов
79
P2S — радиус инерции шатуна относительно оси,
проходящей через центр S? перпендикулярно
плоскости чертежа. Если массу шатуна скор-
ректировать так, чтобы выполнить условие
(2.85)
2
Р25 —~ =~
то вектор момента (2.86) станет нулевым.
Использование кулачковых механиз-
мов компенсации неуравновешенных сил.
На рис. 2.21, в показан механизм 3-го
класса (при входном звене 5). После
статического уравновешивания этого ме-
ханизма методом подобия (см. п. 2.5)
при помощи корректирующих масс mi,
тъ,ть на его станину будет действовать
главный момент М неуравновешенных сил.
Момент М можно уравновесить при
помощи кулачкового механизма с вращаю-
Рис. 2.21. Примеры структурных схем
механизмов частично уравновешенных
динамически
шимся толкателем 6. Для этого кула-
чок следует закрепить на валу звена 5,
а толкатель на валу О (рис. 2.21, в).
Центр массы толкателя должен находиться
на оси вращения.
Если профиль кулачка будет удовлет-
ворять условию
/6С6 = — (2.87)
то рассматриваемый механизм будет урав-
новешен динамически. В выражении
(2.87): J6 — момент инерции толкателя от-
носительно его оси вращения О; ее -
угловое ускорение толкателя; М5 — глав-
ный момент неуравновешенных сил, при-
веденный к звену 5.
Кулачковый механизм можно исполь-
зовать также для компенсации неуравно-
80
Уравновешивание механизмов
вешенных сил различных порядков,
создаваемых поступательно-движущейся
массой (рис. 2.21,г):
т — т3 4- т2В, (2.88)
где тз — масса звена 3\ miB — nuAS^/
АВ—часть массы т% шатуна 2, при-
веденная к точке В. Для этого про-
филь кулачка 4 должен обеспечить
движение толкателя 5 с ускорением
т ~
ak~~~kaB’
где т — поступательно-движущаяся мас-
са (2.88); тк — корректирующая масса,
установленная на толкателе 5; ав —
ускорение точки В звена 3.
Компенсация действия на станину
момента — Двь При статическом и ди-
намическом уравновешивании механизмов
обычно считают, что угловая скорость
кривошипа <й| — const. В действительности
(0| является переменной величиной даже
при установившемся движении механизма
и изменяется с заранее заданным коэф-
фициентом неравномерности в. Поэтому на
станину механизма передается неуравно-
вешенный момент
Alfi ~ — /|8ь
(2.89)
где J\ — момент инерции вращающихся
масс, приведенных к кривошипу; £ —
угловое ускорение кривошипа. В неко-
торых случаях момент Mt может во мно-
го раз превышать момент от сил полез-
ных сопротивлений и оказывать нежела-
тельное воздействие на станину Момент
Mt можно компенсировать при помощи
маховой уравновешивающей массы, вра-
щающейся с угловым ускорением еур м =
— Е|.
На рис. 2.21, д показана схема механиз-
ма одноцилиндровой машины, состоящей
из маховика Д коленчатого вала и ма-
ховой уравновешивающей массы 6, соеди-
ненной с коленчатым валом зубчатой пере-
дачей. Для устранения действия на ста-
нину механизма неуравновешенного мо-
мента (2.87), вызванного неравномер-
ностью вращения коленчатого вала, мо-
мент инерции уравновешивающего махо-
вика 6 должен быть
J® = / 1Z5/Z4.
Принцип приближенного уравновеши-
вания механизмов методом оптимизации
неуравновешенных сил. В ряде случаев
в механизмах можно полностью устра-
нить моментную неуравновешенность и ми-
нимизировать главный вектор неуравнове-
шенных сил, используя для этого теорию
приближения функций. Покажем это на
примере простейшего рычажного механиз-
ма (рис. 2.22, о).
Будем считать, что станина механиз-
ма О АВ воспринимает, в общем случае,
главный вектор (2.17) и главный момент
(2.18) неуравновешенных сил. Если при-
нять, что угловая скорость кривошипа
G>i = const, то для уравновешивания вра-
щающихся масс и компенсации неуравно-
Рис. 2.22. Уравновешивание механизма ме-
тодом оптимизации неуравновешенных сил
Принципы динамического уравновешивания механизмов
81
вешенного момента, создаваемого массой
шатуна, достаточно выполнить условия
(см. п. 2.5 и 2.8)
miQi — — m2b2lt(l2\ (2.90)
J2S~ tn2<p2s\ (2.91)
pis — a2b2\ (2.92)
(2 = <*2 + 62, (2.93)
где mi,m2 — массы кривошипа и шату-
на; агА — расстояния от точек А и В
шатуна до центра S2 его массы; /2®>р2® —
момент инерции и радиус инерции шату-
на относительно оси, проходящей через
центр S2 перпендикулярно плоскости чер-
тежа; at — абсцисса центра Si массы
кривошипа; /| длина кривошипа ОА;
12— длина шатуна АВ (рис. 2.22,а).
В равенства (2.90)—(2.93) входят де-
вять параметров, из которых пять можно
выбрать на основании технологических и
конструктивных условий. Пусть, например,
выбраны размеры звеньев /],/2 и масса
т2 шатуна, а также абсциссы aita2 центров
масс кривошипа и шатуна. По этим
данным из равенства (2.93) находим
bi — I? — а2,
а из уравнения (2.90) определим массу
кривошипа:
ОТ| — — /П2Ы|/(С|4).
где знак минус показывает, что эксцен-
триситеты массы mt кривошипа и шатун-
ной массы противоположны по зна-
ку. Далее из выражения (2.92) получим
радиус инерции шатуна
P2S = •
и вычислим по формуле (2.91) необхо-
димый момент инерции шатуна;
1 2
“2s — tf&2P2s.
После реализации условий (2.90) —
(2.93) дисбаланс кривошипа
D\ — miai, (2.94)
а станина механизма будет воспринимать
действие только неуравновешенной силы
(2.56);
Рд — /|<о?т cos <р + /|(й|тЛг cos 2<р +
4- /|й)?лгЛ4 cos 4ф 4- ...,
гдет — поступательно движущаяся масса
механизма, определяемая формулой
(2.57); А2,А* ,. —коэффициенты ряда,
приведенные в табл. 2.1.
В тех случаях, когда действие силы
Рд в механизме является нежелатель-
ным, ее можно уменьшить путем увели-
чения дисбаланса кривошипа от значе-
ния (2.94) до значения
£>2 — (mi + m't)ai, (2.95)
где mt — величина дополнительной кор-
ректирующей массы, закрепленной на кри-
вошипе так, чтобы ее центр совпадал
с точкой Si кривошипа.
После реализации (2.95) в механизме
будет действовать неуравновешенная сила
Л>ст=Лв + А, (2.96)
где сила Р(, равная по модулю
Pt — /niniof, (2.97)
будет создаваться дополнительной кор-
ректирующей массой т\.
Для решения задачи о том, какой
должна быть величина силы Р'}, чтобы
максимум модуля остаточной неуравнове-
шенной силы (2.96), воспринимаемой ста-
ниной механизма, был бы наименьшим
(в соответствии с теорией равномерного
наилучшего приближения функций Чебы-
шева), необходимо выполнить следующие
графоаналитические вычисления [5, 18}:
1. По формуле (2.56) определить зна-
чение неуравновешенной силы Рв для
различных положений кривошипа (напри-
мер, для положений 1,2,. . ,12, указанных
на рис. 2.22,а).
2. Построить годограф Г вектора Рв в
системе отсчета., неподвижной относитель-
но кривошипа, в соответствии с принци-
пом обращения движения. За начало годо-
графа Г следует принять точку О кри-
вошипа (рис 2.22,6), а векторы Рв изо-
бразить в масштабе:
kp~ Н/мм,
«2
Статическая балансировка роторов
где (ОГ) — длина произвольно выбранно-
го отрезка (мм), изображающего модуль
силы Ре при ф = 0; т — поступательно
движущаяся масса (кг), вычисляемая по
формуле (2.57); ng—-модуль ускорения
точки В звена 3 (м/с2) при (р = 0
3. Вокруг годографа Г описать окруж-
ность К наименьшего радиуса из тако-
го центра О|, чтобы она не пересекала
годограф Г, но касалась его в нес-
кольких точках (например, в трех точках,
как показано на рис. 2.22,6).
4. Измерить длину отрезка ОО^ (мм) и
определить пропорционвльную ему в мас-
штабе Кр силу (2.97):
Pi = kp(OOi), Н. (2.98)
Из формулы (2.97) и (2.98) найти
величину дополнительной корректирующей
массы
1 =-------7,—
0,0);
кг
и вычислить по формуле (2.95) значение
искомого дисбаланса кривошипа:
/ , К (00()х
т{ + — I , г • мм. (2.99)
у at (а1 )
обеспечивающего уравновешивание в ме-
ханизме вращаюшихся масс и минимиза-
цию главного вектора (2.56) неуравно-
вешенных сил по методу наилучшего при-
ближения функций.
Заметим, что рассмотренную задачу
можно решить также методом квадрати-
ческого приближения функций. В этом
случае точка 0\ должна совпадать не с
центром окружности К, как было указано
выше, а с центром массы годографа Г,
если представить его выполненным из
проволоки с равномерно распределенной
массой [5, 18].
С учетом этого замечания значение
дисбаланса при уравновешивании ме-
ханизма методом квадратического при-
ближения функций также будет опреде-
ляться формулой (2.99).
Замечание о разгрузке кинематических
пар механизма от действия неуравнове-
шенных сил. В инженерной практике
разгрузка кинематических пар от дей-
ствия неуравновешенных сил имеет само-
стоятельное значение, так как уменьшает
силы трения в кинематических парах и по-
вышает ресурс, надежность, КПД и даже
производительность машин. Это достига-
ется путем введения в механизм пружин
или пневматических, гидравлических и
электромагнитных устройств, работающих
по специальной программе. Следует, одна-
ко, иметь в виду, что последние создают
силы, являющиеся внутренними do отно-
шению ко всему механизму, и поэтому
не изменяют главного вектора и главного
момента неуравновешенных сил, действу-
ющих на станину механизма [41].
и
Глава 3
___________ СТАТИЧЕСКАЯ БАЛАНСИРОВКА РОТОРОВ
3. 1. ОСНОВНЫЕ понятия
Неуравновешенность ротора, при кото-
рой его главная центральная ось инер
ции параллельна геометрической оси, на-
зывается статической. Она полностью
определяется главным вектором дисбалан-
сов, или эксцентриситетом центра массы
ротора, или относительным смещением
главной центральной оси инерции и геоме-
трической оси ротора. При статической
балансировке определяется и уменьшается
Основы статической балансировки при помощи сил тяжести
83
главный вектор дисбалансов. С помощью
станка для статической балансировки
определяют £\г, используя силы тяжести
на невращающемся или на вращающемся
роторе (в динамическом режиме) или
вибрацию основания на неврашающемся
роторе. Главный вектор начальных дис-
балансов может быть уменьшен путем
подбора по массе и статических моментов
конструктивных элементов при сборке ро-
тора.
Наиболее распространена статическая
балансировка дискообразных роторов с от-
ношением длины ротора к его диаметру
не более 0,2—0,25. Допустимость стати-
ческой балансировки детали оценивают по
соотношению
Дет ост^А, В “1“ D вач
(^дет “1“ ^вал)^ст доп^-'Л.В-
Статически балансируют следующие
детали: шкивы, зубчатые колеса, соеди-
нительные муфты, рабочие колеса центро-
бежных вентиляторов и насосов, винто-
вых вентиляторов, маховики и диски сцеп
ления автотракторных двигателей, колеса,
фланцы катушек текстильных машин, вил-
ки карданных валов, часовые балансы,
коромысла, рамки карданных подвесов ги-
роскопов и т. п. Статическую балансировку
широко применяют в качестве проме-
жуточной операции технологического про-
цесса, а также при ремонте машин и
приборов в неспециализированных усло-
виях.
3.2. ОСНОВЫ СТАТИЧЕСКОЙ
БАЛАНСИРОВКИ ПРИ ПОМОЩИ СИЛ
ТЯЖЕСТИ
Движение ротора (рис. 3.1, а) на го-
ризонтальной плоскости происходит под
действием момента сил тяжести Ме —
— ecxmg cos ф до тех пор, пока точка
Oi (рис. 3.1,6) не переместится вниз
В этом положении Mg относительно оси
ротора равен нулю, а нижняя точка —
тяжелое место, т. е. угол главного вектора
дисбалансов в системе координат, связан-
ной с ротором. Чтобы определить значе-
ние главного вектора дисбалансов, необхо-
димо повернуть ротор на 90° и в точке
Oz — противоположной тяжелому месту
(рис. 3.1,в), на радиусе ОО2 = гк уста-
новить корректирующую массу тк, создаю-
щую момент силы тяжести Mg. Подбор
массы тк ведется до тех пор, пока
ротор не придет в состояние безраз-
личного равновесия. Значение главного
Рис. 3.1. Статическая балансировка
при помощи сил тяжести
84
Статическая балансировка роторов
вектора дисбалансов ротора £)ст = те„ —
= т*гк. Для определения ОС7 можно ис-
пользовать и другие движения ротора:
поворот вокруг неподвижной оси ротора,
перемещение оси ротора относительно не-
подвижной оси или точки, перемещения
оси ротора в пространстве.
Методы определения корректирующей
массы при статической балансировке.
Значение корректирующей массы или глав-
ного вектора дисбалансов определяют по
показаниям индикатора дисбаланса стан-
ка, предварительно настроенного на ста-
тическую балансировку ротора заданной
массы и геометрии или эксперименталь-
ными методами подбора.
Метод подбора без пробной массы
состоит в последовательной установке раз-
личных корректирующих масс в легком
месте ротора, пока не будет достигнуто
положение безразличного равновесия.
Метод подбора с пробной массой со-
стоит в установке ча несбалансированный
ротор пробной массы m на радиусе
гпр под углом 90° к тяжелому месту
и нахождении нового устойчивого поло-
жения равновесия (рис. 3.2). Значение
главного вектора дисбалансов определяют
по формуле
DCT = wnprnp ctg ф.
Пробную массу выбирают при баланси-
ровке первых роторов из партии, так
чтобы она вызывала поворот несбаланси-
рованного ротора на угол 30.. .40°.
Рис. 3.2. Устойчивое рав-
новесие ротора
Метод кругового обхода состоит в по-
следовательном подборе неуравновешен-
ных масс в каждой из восьми точек, равно
расположенных по окружности радиусом
гпр (рис. 3.3, а), которые поворачивают
ротор на один и тот же угол, напри-
мер 45°. Графическим (рис. 3.3,6) спо-
собом находят легкое (точка Л) и тя-
желое (точка В) места на роторе и
соответствующие им минимальные (mmin)
и максимальные (щтах) значения неурав-
новешенных масс. Значение главного век-
тора дисбалансов определяют по формуле
0,5(/ZZmax ^min)f"iip*
Погрешности статической балансиров-
ки. Элементарными погрешностями стати-
ческой балансировки с использованием сил
тяжести являются: Д> — отклонение фор-
мы несущих и опорных поверхностей рото-
ра и станка; Д2 — деформация этих по-
верхностей; Д3 — трение между ними;
Д4 — отклонение расположения поверх-
ностей балансировочной оправки; наличие
зазора в посадке детали на оправку
Рис. 3.3. Графическое опреде-
ление неуравновешенной массы
Основы статической балансировки при помощи силы тяжести
85
(погрешность базирования); дополнитель-
ный главный момент дисбалансов,
вози икающий при корректировке масс
в одной плоскости, не проходящей
через центр массы детали (погрешность
метода Дм). Сумма погрешностей Д},Дг,Дз
определяет порог чувствительности ба-
лансировочного станка — Дст; комплекс
погрешностей Дст, Д< — точность техноло-
гической системы «станок — приспособле-
ние — деталь». Элементарные погрешнос-
ти статической балансировки определяют
и компенсируют следующим способом.
Погрешность отклонения формы не-
сущих и опорных поверхностей ротора
и балансировочного станка (Д|) находят
путем установки в тяжелое и легкое
-место сбалансированного ротора таких
неуравновешенных масс mi, ms, которые
вызывают его поворот на один и тот
же угол, например на 20°. Причем перед
подбором неуравновешенной массы в лег-
ком месте ротор поворачивают на 180°.
Погрешность Д| определяют по формуле
Aj ==, 0,5fmi — ms)rnp. При этом массой
груза 0,5(mi — m2), установленной в тя-
желом месте, компенсируют эту погреш-
ность.
Погрешности от деформации и трения
между несущими и опорными поверхнос-
тями ротора и станка определяют ме-
тодом кругового обхода. Компенсирующая
погрешности Д2 и Дз масса равна полу-
разнице максимальной и минимальной
пробных масс.
Погрешность базирования находят
способом компенсирующих грузов. Внача-
ле определяют корректирующую массу
тк1 детали на оправке одним из методов.
Затем оправку поворачивают относитель-
но детали на 180° и определяют новую
корректирующую массу тк2. Затем снима-
ют с детали массы тк| и и проводят
окончательную балансировку и контроль
главного вектора остаточных дисбалансов,
после чего снимают компенсирующий
груз тк2/2.
Погрешность метода, возникающая
при корректировке масс в одной плос-
кости, не проходящей через центр массы
Рис. 3.4. Моментная неуравновешенность, воз-
никающая при статической балансировке
детали (рис. 3.4), создает дополнитель-
ный главный момент дисбалансов Дм =
= mKrHh. Он не возникает, если кор-
ректировку масс при статической балан-
сировке проводят в двух плоскостях.
Значения корректирующих масс в них
находят по формулам:
mK I = нач^2/ [ (Л Ч~ il •
^к2 === ^ст I (^1 Ч~ ^2)ГИ g] .
Контроль остаточных дисбалансов.
Значение главного вектора остаточных
дисбалансов после статической баланси-
ровки при помощи силы тяжести опре-
деляют тремя способами: по показаниям
индикатора дисбаланса станка; с исполь-
зованием контрольного груза; с приме-
нением кругового обхода. Выбор спо-
соба контроля зависит от допустимого
дисбаланса, порога чувствительности и ви-
да балансировочного станка.
Первый способ применяют при балан-
сировке деталей на станках 2-й и 3-й
группы (СБС-2, СБС-3) с порогом чув-
ствительности более чем в 2,5 раза выше
допустимых дисбалансов. Значение глав-
ного вектора остаточных дисбалансов
рассчитывают по формуле
^ст ост АЦ zfc Аст,
где А — число делений шкалы индика-
тора; Ц — цена одного деления.
Второй способ пригоден для всех
групп станков с порогом чувствительности
86
Статическая балансировка роторов
в 1.. .2,5 раза выше, чем допустимый
дисбаланс. Контрольный груз массой mi —
— (2,5.. .5) £)стд<)Л/г1 последовательно
устанавливают на радиусе rt в легкое
и тяжелое места и фиксируют числа де-
лений шкалы индикатора дисбаланса стан-
ка Л) и Л2. Значение главного вектора
остаточных дисбалансов рассчитывают по
формуле
^стост — (А—Л2)/(А 4~ ^2). '
При контроле,остаточных дисбалансов
на станках СБС-1, СБС-4 массы контроль-
ных грузов подбирают в легком (mi) и тя-
желом (m2) местах такой величины, чтобы
ротор поворачивался на один и тот же угол,
например 20°, а расчет проводят по фор-
муле
£>сто„= 0,5(ш! ~
По третьему способу контролируют ос-
таточные дисбалансы роторов на станках
с порогом чувствительности, близким к
допустимым дисбалансам. Для станков
СБС-1, СБС-4 контроль Дстост проводят
способом кругового обхода с подбором
контрольных грузов в восьми точках.
Другой вариант метода кругового обхо-
да (для станков СБС-2, СБС-3) заклю-
чается в последовательной установке в
каждой из восьми точек окружности кон-
трольного груза постоянной массы nil и
нахождении показаний индикатора дисба-
ланса. По результатам измерений опре-
деляют максимальные Дтах и минимальные
Д1Т1т показания индикатора и рассчиты-
вают главный вектор остаточных дисба-
лансов:
^ст ост tfllH (-^гпах •
Станки для статической балансировки
при помощи сил тяжести. В зависимости
от характера движения оси ротора при
балансировке станки делят на пять ос-
новных групп (табл. 3.1). Станки 1-й
и 4-й группы имеют простейшее устрой-
ство и могут быть изготовлены из уни-
версальных сборочных приспособлений.
Станки СБС-2, СБС-3 называют также
балансировочными весами. Выбор станка
для статической балансировки определяют
типом производства, конструкцией ротора,
его допустимым дисбалансом. Балансиров-
ку деталей с собственными или техноло-
гическими опорными поверхностями в еди-
ничном и мелкосерийном производствах
целесообразнее проводить на станках
СБС-1, СБС-4. В серийном производстве
выгоднее станки СБС-2 и СБС-3. Тела
вращения типа поплавковых гироскопов
уравновешивают, регулируют их диффе-
Таблица 3.1
Станки для статической балансировки при помощи силы тяжести
Условное обозначение станка Номер группы станка Характер перемещения оси ротора Опоры станка Порог чувствитель- ности станка, мм
СБС-1 а СБС-1 б СБС-1 в 1 Не перемещается Роликовые Дисковые Г азовые 15 — 30 7 — 15 1—5
СБС-2а СБС-26 2 Перемещается относитель- но неподвижной точки Сферическая Упругая 10—20
СБС-За СБС-Зб 3 Перемещается относитель- но неподвижной оси Весы с вертикальной и горизонтальной осью 5—10
СБС-4 4 Перемещаете'’ в непо- движной ПЛОСКОСТИ Г тоскопараллельные 2—5
СБС-5 5 Перемещается в прост- ранстве Жидкостные —
Статическая балансировка комплектов деталей распределением
87
рент и плавучесть в ванне, наполненной
жидкостью (СБС-5), в которой плавает
это тело.
3.3. СТАТИЧЕСКАЯ БАЛАНСИРОВКА
ПРИ ПОМОЩИ ВИБРАЦИЙ
Для повышения точности балансиров-
ки жестких роторов применяют уравнове-
шивание без вращения ротора на вибри-
рующем основании. Изменяя частоту и ам-
плитуду вибраций основания станка, умень-
шают трение в опорах за счет снижения
времени контактирования и увеличивают
порог чувствительности станка до 0,4 мкм
для роторов массой порядка 1 кг.
Статическую балансировку при помо-
щи вибраций применяют для уравнове-
шивания гибких роторов дисковой кон-
струкции. При колебаниях основания стан-
ка каждый диск представляет собой ма-
ятник с разной жесткостью подвески вдоль
оси. Во время колебаний положение масс
эксцентрично расположенных дисков по
отношению к оси вала в любой момент
времени определяется углом Р 4~ ф
(рис. 3.5). Диски будут поворачиваться
тяжелым местом вниз, совершая при этом
вынужденные колебаний, что сопровожда-
ется перекатыванием ротора по приз-
мам в ту или иную сторону. Коррек-
тирующие массы подбирают в каждом
диске до тех пор, пока перекатывание
не прекратится и ротор не займет
устойчивого положения, что соответствует
статической уравновешенности. Дальней-
Рис. 3.5. Статическая балансировка при по-
мощи вибраций
шее уравновешивание ротора производят
как твердого тела.
Условие применимости такого способа
балансировки — динамический крутящий
момент от неуравновешенных масс должен
быть больше момента силы трения ка-
чения. При этом допустимый прогиб диска
определяют по формуле
yt = 0.01g/ (е«о)2].
3.4. СТАТИЧЕСКАЯ БАЛАНСИРОВКА
КОМПЛЕКТОВ ДЕТАЛЕЙ
распределением
При изготовлении роторных машин не-
редко необходимо уравновешивание ро-
торов с равномерно расположенными
по окружности конструктивными эле-
ментами. При этом комплект деталей
должен обеспечивать заданное значе-
ние дисбаланса и равномерную нагрузку
на обод диска при вращении рото-
ра. Указанные требования не выпол-
няются при случайном распределении де-
талей, поэтому их распределение произ-
водят по специальной методике с уче-
том весовой характеристики. Наиболее ха-
рактерным примером таких элементов яв-
ляются рабочие лопатки лопаточных ма-
шин, поэтому рассмотрение статической
балансировки деталей распределением
проведем на примере уравновешивания ло-
паточного венца рабочего колеса ротора
лопаточной машины.
Уравновешивание комплекта рабочих
лопаток путем их распределения по пазам
диска осуществляют при сборке колеса,
и обычно этот процесс называют комплек-
товкой лопаток. Комплектовка рабочих ло-
паток по весовой характеристике занимает
важное место в технологическом процессе
сборки рабочих колес в отношении
снижения дисбаланса и трудоемкости.
Обычно технологический процесс статичес-
кой балансировки комплекта" лопаток со-
стоит из измерения весовой характеристики
каждой лопатки и их кругового распре-
деления по пазам диска. Величина оста-
точного дисбаланса комплекта лопаток при
88
Статическая балансировка роторов
этом зависит от весовой характеристики
лопатки, используемой для уравно-
вешивания, и от методики уравновеши-
вания.
Выбор весовой характеристики для
распределении лопаток. СиЛу, действую-
щую на рабочую лопатку при враще-
нии ротора, определяют по формуле
F — mW,
т. е. величина центробежной силы, дей-
ствующей на обод диска от лопатки,
определяется тремя независимыми пара-
метрами: массой т лопатки, радиусом R
расположения ее центра масс относительно
оси вращения и частотой вращения w ро-
тора. Частота вращения со одинакова для
всех лопаток и характеризует режим
работы ротора.
Масса и радиус расположения центра
масс лопатки относительно оси вращения
характеризуют ее размещение на роторе.
Произведение массы лопатки на радиус
расположения ее центра масс относительно
оси вращения называют статическим (ве-
совым) моментом S лопатки, т. е.
S = mR.
Статический момент — теоретически
наиболее точная весовая характеристика
лопатки, так как он учитывает не толь-
ко массу, но и смещение центра масс
каждой лопатки относительно требуемого
положения.
Номинальное значение измеренных
статических моментов лопаток не влияет
на величину дисбаланса комплекта, так
как геометрическая сумма одинаковых
равнорасположенных по окружности век-
торов равна нулю. Поэтому при распре-
делении лопаток по пазам диска допуска-
ется использовать вместо полного зна-
чения статического момента его откло-
нение от выбранного номинального значе-
ния, одинакового для всех лопаток этого
типа. Предельный с вероятностью 99,5%
дисбаланс комплекта рабочих лопаток рас-
считывают по формуле
D — 2,41од5д/л, *
где оЛ5 — среднее квадратическое откло-
нение ошибки измерения статических мо-
ментов лопаток; п — число лопаток в комп-
лекте.
Другой, менее точной, но широко
распространенной в практике характерис-
тикой для комплектовки лопаток явля-
ется ее масса (предполагается отсутствие
смешения центров масс рабочих лопаток
от номинального положения). Однако та-
кие смещения имеют место и вызывают
изменение статического момента каждой
лопатки:
AS, -= пгД,
где 6 — радиальное смещение центра масс
i-й лопатки от номинального положения;
i — порядковый номер лопатки, приводят к
появлению дополнительной составляющей
в остаточном дисбалансе. Предельная ве-
личина этой составляющей остаточного
дисбаланса комплекта может быть опре-
делена по формуле
D = 2,41Vn [/? + /ср] + тсро/.
где п — число лопаток в колесе; R — за-
данный установочный радиус для лопат-
ки; /ср — среднее из экспериментов или
расчетное расстояние от центра массы
лопатки до ее собственной установочной
базы; тср средняя масса лопатки; о„ —
среднее квадратическое отклонение массы
лопатки; <т/ — среднее квадратическое от-
клонение величины; I—расстояние от цен-
тра масс лопатки до ее собственной уста-
новочной базы.
Если погрешность измерения статичес-
кого момента лопатки велика и превы-
шает величину изменения статического мо-
мента от смещения центра масс, то при-
менение комплектовки лопаток по изме-
ренным значениям статического момента
нецелесообразно, и более эффективно
уравновешивание лопаточного венца по
массе.
Способы измерения статических мо-
ментов рабочих лопаток. Измерение стати-
ческих моментов рабочих лопаток осу-
ществляют либо непосредственно на ры-
чажных моментных весах, либо расчетным
Статическая балансировка комплектов деталей распределением
89
Рис. 3.6. Схема измерения статических моментов лопаток на рычажных
моментных весах
путем с измерением составляющих веса
для каждой рабочей лопатки.
Для непосредственного измерения
статических моментов рабочих лопаток
используют рычажные моментные весы,
устройство которых показано на рис. 3.6.
На неподвижном горизонтально располо-
женном основании 6 размещают корпус
опор, с которым взаимодействует опорная
призма 5 коромысла 4, имеющего демпфер
7. На коромысле 4 размешен фланец
3 для крепления технологического пере-
ходника 2, предназначенного для установ-
ки рабочей лопатки 1. При этом рас-
стояние от замка лопатки в технологи-
ческом переходнике 2 до оси призмы 5
должно быть равно радиусу диска /?.
Масса рабочей лопатки создает момент
относительно опорной призмы 5. равный
статическому моменту лопатки в диске.
Этот момент компенсируется суммой двух
моментов: от уравновешивающего груза
11, размещенного на специальной плат-
форме 10, на плече Rr относительно
призмы, и момента, создаваемого электро-
силовым преобразователем 9, величина ко-
торого высвечивается на индикаторной па-
нели цифрового вольтметра 8. Датчик по-
ложения коромысла 12 обеспечивает про-
ведение измерения статического момента
лопатки при одном и том же поло-
жении коромысла относительно горизон-
тальной плоскости.
Расчетный метод измерения статичес-
кого момента используется для массив-
Рис. 3.7. Схема определения координаты ЦМ
лопасти на весах
ных лопаток (лопастей). Устройство для
определения положения центра масс, обес-
печивающее реализацию этого метода, по-
казано на рис. 3.7. Сущность этого
метода заключается в том, что измеряют
составляющие веса лопатки, по которым
-определяют координату ее центра масс
относительно базового сечения и вес
лопатки, после чего рассчитывают значе-
ние статического момента лопатки в ро-
торе.
Определение координаты центра масс
лопасти осуществляют следующим обра-
зом. На ложементы 2 устанавливают ло-
пасть 5 так, чтобы базовая точка замка,
определяющая ее положение в диске,
лежала в плоскости опоры Положение
лопасти на ложементе регулируют упорами
3. Затем лопасть 5 снимается с плат-
формы 1 и выполняют тарировку устрой-
90
Статическая балансировка роторов
ства. Для этого платформу 1 с ложе-
ментами 2 устанавливают на силоизмери-
тельное устройство 4 (весы) и взвеши-
вают платформу /, определяя тар и
7?Втар. На платформу устанавливают рабо-
чую лопатку и измеряют реакции Rj;.
Составляющие силы тяжести лопатки бу-
ДУТ лоп = тар’ ^Лоп=^В-
— Кв тар- Массу лопатки определяют по
формуле
. тлои ~ К А лоп + Кв тп,
а статический момент лопатки находят с
помощью выражения
К^Лоч 4~ К а лоп^*
Для определения второй координаты
центра масс лопасти платформу устанав-
ливают на три силоизмерительных устрой-
ства.
Статическое уравновешивание ком-
плекта лопаток распределением по пазам
диска. Дисбаланс комплекта рабочих лопа-
ток определяют по формуле
1=1
п — число лопаток в комплекте; S, — ста-
тический момент i-й лопатки в комплек-
те.
Комплект лопаток распределяют по па-
зам диска с помощью круговых диаграмм,
обеспечивающих равномерность нагрузки
по ободу и снижающих начальный дис-
баланс колеса.
Уравновешивание комплекта лопаток
по круговой диаграмме производят следу-
ющим образом. Определяют для всех
лопаток весовую характеристику. Лопатки
распределяют в упорядочивающий ряд
по убыванию или возрастанию их весо-
вых характеристик. Любая круговая диа-
грамма определяет порядок распределе-
ния лопаток по пазам диска из этого
ряда.
В настоящее время известно более
десяти видов различных круговых диа-
грамм. Эти диаграммы применяют для
рабочих колес компрессоров и турбин
Рис. 3.8. Универсальная круговая диаграмма
с различным числом лопаток в комплек-
те.
Индивидуальная особенность колеса,
которая определяет выбор диаграммы,—
число лопаток в комплекте. Каждая ди-
аграмма предназначена для уравновеши-
вания комплектов с четным (нечетным)
числом лопаток, а также для комплектов
с числом лопаток, кратным каким-либо
числам, например трем или четырем.
Однако, как показывает их сравнительный
анализ, выполненный по результатам моде-
лирования, существует универсальная кру-
говая диаграмма, обспечивающая получе-
ние минимального дисбаланса комплекта
с любым числом рабочих лопаток. Ок-
ружность диска (рис. 3.8) разбивают на
две равные части. При наличии четно-
го числа пазов в диске — с первого паза
до паза с номером п/2 и с паза с номером
1 п/2 до п. При наличии нечетного
числа пазов в диске — с первого паза
до паза с номером (п 4- 1)/2 и с паза
с номером (п 3) /2 до п. Пары лопаток
из ряда устанавливают в противолежа-
щие пазы половин диска. Указанные па-
ры лопаток берут поочередно с обоих
концов ряда.
При использовании любой круговой ди-
аграммы подбирают один полный ком-
Классификация методов
91
плект лопаток без запаса. Это связано
с тем, что вначале используют лопатки
с концов ряда, а затем уже из его
середины. Поэтому при наличии запаса
лопаток в исходном массиве сверх ком-
плекта в него войдут лопатки с большей
разностью статических моментов, что вы
зовет увеличение его остаточной неуравно-
вешенности. Если же из одного ряда
набирать сразу два комплекта, разбивая
ряд на две равные части, то у рас-
сматриваемых комплектов суммарная мас-
са будет существенно отличаться, так
как в один комплект попадут все лег-
кие лопатки, в другой — все тяжелые и,
как следствие, резко возрастет нагрузка
на обод диска.
Величина среднего остаточного дис-
баланса комплекта, распределенного по
универсальной круговой диаграмме, может
быть рассчитана по эмпирической формуле
D = (81—0^4д)а,/о|.
где п — число лопаток в комплекте,
oi.o, — средние квадратические отклоне-
ния.
Для более точного статического урав-
новешивания комплектов распределением
используют ЭВМ При этом программа
комплектовки лопаток предусматривает
распределение комплекта по круговой
диаграмме, расчет значения остаточного
дисбаланса комплекта, а также миними-
зацию расчетного дисбаланса комплекта
путем минимального числа парных пере-
становок относительно круговой диаграм-
мы. Текст программы статического уравно-
вешивания комплектов приведен в прило-
жении.
Глава 4
НИЗКОЧАСТОТНАЯ БАЛАНСИРОВКА РОТОРОВ
4.1. КЛАССИФИКАЦИЯ МЕТОДОВ
Особенности статической моментной и
динамической балансировкн. Процесс оп-
ределения значений и углов дисбалансов
и уменьшение их корректировкой масс
может выполняться при различных состо-
яниях ротора и различными способами.
Если не рассматривать роторы с изме-
няющейся геометрией, у которых при вра-
щении перераспределяется относительное
расположение масс, то можно выделить
два способа балансировки.
Первый способ, когда прогибы от
неуравновешенных сил инерции F и мо-
ментов М пренебрежимо малы, так что
величины их зависят, при прочих равных
условиях, только от эксцентриситетов
отдельных масс
п п
F — m,w2 еп М= £ m(u)2[ ё(/(] .
«=> i=i
Это низкочастотная балансировка.
Второй способ, когда прогибы стано-
вятся значительными и в расчетные зави-
симости кроме величины е, включают про-
гиб ротора у. Это высокочастотная балан-
сировка.
В гл. 3 была рассмотрена статичес-
кая балансировка, осуществляемая без
вращения ротора. С ее помощью решают
ограниченную задачу определения стати-
ческого дисбаланса, т. е. находят и устра-
няют смещение центра масс ротора. При
динамической балансировке предусматри-
вают принудительное вращение ротора для
определения неуравновешенных сил инер-
ции и моментов.
Низкочастотная балансировка роторов
В настоя шее время в машинострое-
нии широко распространена балансировка
коррекцией масс, при которой главная цен-
тральная ось инерции приводится к оси
ротора. Все возможные сочетания уравно-
вешивающих масс сводят к трем способам
их распределения: балансировка в одной
плоскости коррекции, балансировка в двух
плоскостях коррекции, многоплоскостная
"балансировка. Реализуются эти способы
в двух условиях:
балансировка в собранном изделии,
когда для определения дисбалансов при-
меняют специализированную и уни
нереальную аппаратуру и методику рас-
чета;
балансировка с использованием
средств, при которой ротор устанавлива-
ют на специальное оборудование (станок,
стенд), оснащенное специальной аппара-
турой для определения дисбалансов; обо-
рудование и-аппаратуру выпускают серий-
но; для многоплоскостной балансировки
используют методику расчета с помощью
ЭВМ.
4.2. БАЛАНСИРОВКА В ОДНОЙ
ПЛОСКОСТИ КОРРЕКЦИИ
В общем случае этот способ не поз-
воляет полностью сбалансировать ротор,
так как для уравновешивания моментно-
го дисбаланса требуется не менее двух
плоскостей коррекции. В одной плоскости
можно уравновесить только смещение цен-
тра массы Как окончательный процесс
балансировки этот способ применяют для
одномассовых роторов при условии, что
большая часть массы сосредоточена на
одном участке малой протяженности (тон-
кий диск, отношение диаметра d к ширине
h 10. рис. 4.1). Для роторов с рас-
пределенной массой балансировку в одной
плоскости допускается применять как
предварительный этап.
Положение плоскостей коррекции на
роторе влияет на точность балансировки.
Из рис. 4.2 видно, что если плоскость
коррекции В — В не проходит через центр
масс ротора, то после балансировки воз-
Рис. 4.1. Одномассовый ротор с тонким
диском
Рис. 4.2. Зависимость точности балансировки
от положения плоскости коррекции
никает дополнительный моментный дисба-
ланс MD~ £>tTJL.
Балансировка в собранном изделии
(обходным грузом). Ее применяют для
одноразовых процессов уравновешивания
роторов или в тех случаях, когда дис-
баланс существенно изменяется при уста-
новке его в изделие. Предполагается, что
величина дисбаланса пропорциональна
амплитуде колебаний.
Способ балансировки обходным гру-
зом. Если по техническим причинам нель-
зя получить отметку фазы неуравнове-
шенности на роторе, то используют аппа-
ратуру с вибродатчиками, устанавливае-
мыми на корпус по возможности ближе
к плоскости коррекции на роторе, либо
применяют бесконтактные датчики, уста-
навливаемые над поверхностью ротора.
Окружность плоскости, в которой уста-
навливают корректирующую массу, делят
равномерно на 8—12 частей. Пробную
массу тп последовательно устанавливают
на все точки и записывают величины
амплитуд вибраций После этого строят
график, как показано на рис 4.3.
При линейной зависимости между ам-
плитудой вибрации А и дисбалансом, а
также при условии, что наибольшая ам-
Балансировка в одной плоскости коррекции
93
плитуда вибраций не превышает удвоен-
ную начальную амплитуду (Дтах<2До),
величину корректирующей массы тк опре-
деляют по зависимостям
тк —-
А -4- А
max * min
—Л-------А------ т
д _______д
max min
ИЛИ
2А0
тк Л _________ Д ,ПП1
max гпт
где величина у(Дтах — Д™,) пропорцио-
нальна пробной массе, а 2 С^тах 4“ ^min)
корректирующей массе.
Положение корректирующей массы, ес-
ли ее добавляют на ротор, соответству-
ет точке Дт1п, если снимают с рото-
ра,— точке Дтах. При нелинейной зави-
симости между амплитудой вибраций и
дисбалансом величину т6 уточняют до
получения допустимых значений А. Для
этого требуется еще несколько запусков.
Пример 1. Необходимо уравновесить ротор,
состоящий из вала и массивного тонкого диска.
Последовательность действий:
на поверхности диска выбирают окружность
и делят ее на 8 равных частей;
в точке 1 на окружности установим проб-
ную массу тп = 20 г;
запустим изделие и определим величину Л»;
последовательно устанавливаем массу тЛ в
точки 2.. .8 и измеряем величины Дг.. ,Дв;
строим график распределения амплитуд
(аналогично рис. 4.3); в результате получим
А'л = ^тах — 30 ед., Aj = = Ю ед.»
рассчитываем корректирующую массу
м _ <30 4-10)20^2.20^40 г:
30- 10
уравновешиваем ротор постановкой массы
40 г в точке Дт^;
осуществляем контрольный запуск изделия
и определяем амплитуды вибраций.
Если величина амплитуды колебаний на-
столько мала, что находится в пределах
точности измерения (например, менее единицы),
то процесс уравновешивания закончен. Если
же она снизилась, но еще недопустимо
большая (например, 5 единиц), то, следователь-
но, зависимость А — Д/пб) нелинейная и уравно-
вешивание продолжают, т. е. увеличивают кор-
ректирующую массу и повторяют контрольные
запуски до тех пор, пока амплитуда колебаний
не достигнет допустимого значения.
Способ трех пусков с пробными
массами, как и первый способ, применяют
в тех случаях, когда отметку фазы полу-
чить нельзя. При этом используют вибро-
измерительную аппаратуру для определе-
ния амплитуды-колебаний корпуса или бес-
контактные датчики, измеряющие переме-
щения ротора. При первом запуске опре-
деляют амплитуду До вибрации с началь-
ным (исходным) дисбалансом ротора. За-
тем в плоскости коррекции устанавливают
пробную массу тя, запускают ротор и
определяют новую амплитуду колебаний
корпуса. Эту операцию повторяют еще
2 раза, устанавливая тп на одном и том
же радиусе, но под различными углами.
Полученным трем амплитудам присваива-
ют номера в следующей зависимости:
Ai > Az, At > Аз и строят диаграмму, как
показано на рис. 4.4. Получают систему
Рис. 4-4. Векторная диаграмма дисбалансов
при способе трех пусков
12 3 4 5 6 7 8 1
Рис. 4.3. График неуравно-
вешенности
треугольников, в каждом из которых
неизвестна одна сторона Ап, но стороны
равны между собой и пропорциональны тп.
На основании теоремы косинусов
Aj = Др 4" Ап — 2ДОДЯ cos -у;
Дг — До 4~ Д« — 2ДоДв cos (у — а);
Дз = До 4“ Д« — 2ДоД« cos(p — у),
94
Низкочастотная балансировка роторов
где а — угол между первым и вторым
положением пробной массы, р — угол меж-
ду первым и третьим положением проб-
ной массы.
Угловое положение у для постановки
корректирующей массы относительно по-
ложения первой пробной массы (в том же
направлении, по которому отмечают аир)
определяют по зависимости
— (1 —cos Р) —
** (Л2 — sin р —
— (Л2 —Л2) (1 — cos а)
— (Л, — Л2) sin а
полученной из первых трех выражений.
Величину Ап находят после подстановки
значения у в одно из тех же выражений,
или из их разности:
А А‘~А*
п 2ЛДсо£ (у— а) — cos у| ’
на основании чего находят и величину
корректирующей массы из соотношения
Ло
"4 =
Если балансировку выполняют удале-
нием массы тк, то место коррекции нахо-
дят под углом у 4- 180°.
Расчет величин у, Ап и тс с помощью
микрокалькулятора достаточно простой,
поэтому нецелесообразно применять менее
точные графические методы решения.
Пример 2. Необходимо уравновесить ро-
тор, состоящий из вала и тонкого массив-
ного, диска. Последовательность действий:
первый запуск; определим величину ампли-
туды Ло вибраций при исходном состоянии
ротора, Ло — 29 ед.;
на поверхности диска установим пробную
массу тп = 20 г на радиусе
первый запуск с пробной массой; опре-
делим величину амплитуды вибраций.
Л| = 20 ед.;
переставим пробную массу в другую точку
поверхности диска под углом 120° к первому
положению, радиус R тот же;
второй запуск с пробной массой; определим
величину амплитуды вибраций. Л2 = 32 ед.;
переставим пробную массу в третью точку
поверхности диска под углом 240° к первому
положению, радиус R тот же;
третий запуск; вибрация Л3 = 42 ед.;
установим порядковые номера амплитуд
вибраций с пробными массами и угловые
положения второго и третьего номеров отно-
сительно первого; согласно требованию Л । > Л2,
Л, >Л3, тогда А) — 42 ед., Л2 = 20 ед.,
Л3 = 32 ед. (можно Л2 = 32 ед., Л3 = 20 ед.),
соответственно а — (Л|;Л2) = 120°, ₽ =
— (Л(;Лз) = 240°; '
рассчитываем угол у
И22 —202) (1 — cos 240°) -
(422— 20й) sin 240° —
— (422 — 322) (1 — cos 120°)
— (,422—322) sin 120°
у = 180° — 27.19° = 152,81°,
и амплитуду колебаний от пробной массы тп;
________422—202
2 -291cos(152.81° — 120о,» — со£ 152,81°) “
= 13,6 ед., >
а также корректирующую массу:
2У
т = 20 — - — 42.64 г,
13,6
которую установим на выбранном радиусе R
под углом 152,8° от места постановки проб
ной массы с присвоенным номером один (Л|),
по направлению к месту пробйой массы с
присвоенным номером два (Л2), т. е. угол у
находим между углами аир,
Контрольный запуск; определим уровень
вибраций, при необходимости выполним до-
балансировку.
Примечание: В общем случае углы а и
Р произвольные. Это одно из основных досто-
инств метода, например, в тех случаях, когда
по техническим причинам нельзя устанавливать
пробные массы равномерно по окружности,
под 120°. как в приведенном примере.
Способ с измерением амплитуды и фа-
зы вибрации. Его применяют в тех особых
случаях, когда по техническим причинам
нельзя определять амплитуду колебаний
корпуса, но можно найти фазу неуравно-
вешенности,.например, с помощью стробо-
скопа, магнитной метки или выступа (впа-
дины) на роторе и бесконтактного датчика
Балансировка в одной плоскости коррекции
95
и др. При этом возможны варианты
компоновки средств измерения.
I. Бесконтактный датчик устанавли
вают над цилиндрической поверхностью
ротора, на который нанесена метка; сигна-
лы метки и перемещений ротора регистри-
руются осциллографом.
2. Первый бесконтактный датчик, ко-
торый фиксирует фазу перемещений, уста-
навливают над цилиндрической по-
верхностью ротора, а второй датчик раз-
мещают над цилиндрической поверхностью
или торцом вала и фиксируют метку;
сигналы регистрируются фазометром или
ос цилл ографом.
3. Бесконтактный датчик устанавли-
вают над цилиндрической поверхностью
вала; вибродатчик размещают на корпусе
по возможности ближе к опоре, около
которой находится плоскость коррекции;
сигнал датчика поступает на стробоскоп,
угловое положение регистрируется визу-
ально по лимбу; могут быть и другие
варианты. Во всех схемах аппаратуры
возможен сдвиг фаз в цепи измерения,
поэтому перед работой необходимо про-
верить софазность сигналов.
Последовательность балансировки.
При первом пуске в исходном состоянии
определяют положение неуравновешеннос-
ти относительно метки на роторе (точка Д',
рис. 4.5). Затем в плоскости коррекции
устанавливают пробную массу тп с неко-
торым углом а относительно положения
начальной неуравновешенности и опреде-
Рис. 4.5. Векторная диаграмма дисбалансов
при способе фаз
ля ют угол р фазы новой неуравновешен-
ности (точка В'). В треугольнике ОАВ
все углы известны, сторона АВ пропорци-
ональна величине пробной массы, сторона
О А — неуравновешенной массе. Корректи-
рующую массу определяют по теореме
синусов (на том же радиусе коррекции,
что и пробная масса) по формуле
тк — тп sin (а— p)/sin ₽
и устанавливают противоположно началь-
ной неуравновешенности (точка С').
Пример 3. Необходимо уравновесить ротор,
состоящий из вала и тонкого массивного
диска. Последовательность действий:
первый запуск; определим угловое поло-
жение фа амплитуды перемещений (ротора или
корпуса) относительно метки на роторе,
фа = 130° против часовой стрелки относительно
метки,
в плоскости коррекции диска на радиусе
/? установим пробную массу тп = 20 г под
углом ф1 = 170° против часовой стрелки, отно-
сительно метки;
второй запуск; определим угловое поло-
жение фг амплитуды перемещений с проб-
ной массой на роторе, фг = 142° против часо-
вой стрелки, относительно метки;
находим параметры:
а= <р, _ ф0= 170° — 130° = 40°;
₽ = <р2 — фо == 142°—130°= 12°;
а — р =40°—12°=28°,
корректирующую массу:
sin 28°
т = 20— == 45,16 г
к sin 12°
угловое положение для установки корректирую-
щей массы фк= ф2 Н~ 180° = 142° 4-180° =
=322° по часовой стрелке относительно метки;
если коррекцию выполняют удалением металла,
то фк = ф2— 142°;
выполним коррекцию массы на радиусе
R на роторе;
осуществим контрольный запуск, определим
уровень вибраций, а при необходимости вы-
полним добалансировку.
Способ одновременного измерения ам-
плитуд и фазы вибраций целесообразно
применять для добалансировки ротора при
серийном выпуске изделий, например в тех
случаях, когда вибрации превышают допу-
стимый уровень. Амплитуды вибраций на
основании статистических данных заранее
градуируют. Для балансировки необхо-
96
Низкочастотная балансировка роторов
дим один пуск, при котором определяют
угол и величину дисбаланса по формуле
£> = КА,
где К - коэффициент пропорциональ-
ности; А — амплитуда. Средства, с по-
мощью которых реализуется способ, раз-
личные. В одном варианте на корпус уста-
навливают вибродатчик, а к ротору в том
месте, где есть метка, подводят бес-
контактный датчик. Оба сигнала записыва-
ют на осциллограф и после расшифровки
осциллограммы определяют амплитуду
(сигнал вибродатчика) и фазу вибраций
(сдвиг между max амплитуды и сигна-
лом метки). Более оперативно решают за-
дачу, когда сигналы поступают на вольт-
метр (амплитуда) и фазометр (угол).
В другом варианте используют вибродат-
чик, установленный на корпус,- и стробо-
скоп, освещающий поверхность вяла с мет-
кой. Показания вибродатчика регистри-
руют на осциллографе или вольтметре,
а фазу определяют визуально с помощью
стробоскопа.
Пример 4. Необходимо выполнить баланси-
ровку одномассового ротора. Последователь-
ность действий:
первый запуск; определим величины ампли-
туды вибраций А и угла <рк между отметкой
на роторе и А, <рк = 70°, А — 46 ед.;
выполним расчет корректирующей массы
mK= £//? = KA/R (радиус коррекции R =
— 300 мм; коэффициент пропорциональности,
на основе статистических данных К =
= 128 г • мм/ед)
128 • 46
т»=~збб-=19’в2г;
осуществим балансировку ротора установ-
кой массы тк— 19,62 г на радиусе коррекции
R под углом 70°+180°, или съем металла на
угловой отметке 70°;
контрольный задуск; определим остаточную
амплитуду вибраций; при необходимости выпол-
ним добалансировку ротора.
Примечание. Методы одноплоскостной ба-
лансировки можно применять для балансировки
ротора последовательно в двух плоскостях кор-
рекции (вначале в одной, затем в другой).
При этом неизбежно проявляется влияние плос-
костей, следовательно, требуется добалансиров-
ка. Использовать такой прием при серийном
выпуске нецелесообразно.
Балансировка с использованием специ-
альных средств. В настоящее время вы-
пускаемые серийно балансировочные стан-
ки дают возможность уравновешивать ро-
торы массой от нескольких грамм до нес-
кольких тонн. У станков для одноплос-
костной балансировки ось шпинделя верти-
кальная, рассчитаны они на уравновеши-
вание роторов типа диск Методику балан-
сировки обычно приводят в описании стан-
ка. Роторы типа вал с диском баланси-
руют на станках с горизонтальной осью
шпинделя. Эти.стаики предназначены для
уравновешивания роторов в двух плоскос-
тях коррекции, поэтому балансировку в
одной плоскости выполняют с помощью
специальных приемов.
Наиболее широко распространены
станки с подвижными опорами (люлька-
ми). Ниже рассмотрены варианты ба-
лансировки в одной плоскости для таких
станков.
Первый вариант. На роторе выделяют
две плоскости измерения так, чтобы одна
из них совпадала с плоскостью коррекции.
Отношение расстояния между опорами ро-
тора Lab и плоскостями измерения I долж-
но соответствовать условию
Настройку аппаратуры станка выполняют
по его описанию. Балансируют в плос-
кости коррекции, совпадающей с плос-
костью измерения. При такой балансиров-
ке уравновесить полностью главный вектор
дисбаланса можно только в одном случае:
если плоскость коррекции совпадает с цен-
тром масс ротора. Но могут быть другие
конструктивно-технологические особен-
ности. Например, вал уравновешен до
постановки диска. Тогда показания дис-
балансов относятся только к диску и точ-
ность балансировки связана с положением
центра масс диска и плоскостью коррекции
на нем. Такое же положение и в случае
балансировки какой-либо дискретной мас-
сы на оправке.
Второй вариант. Его применяют на
станках с индивидуальным торможением
люлек. Настройку аппаратуры станка не
делают. При заторможенной люльке, даль-
ней от плоскости коррекции, методом
Балансировка в двух плоскостях коррекции
97
последовательных приближений по пока-
заниям датчика ближайшей работающей
люльки уравновешивают ротор в плоскости
коррекции.
Третий вариант. Он основан на специ-
альной методике настройки балансировоч-
ного станка, которая более детально
описана в разделе 3 (балансировка в двух
плоскостях коррекции). Эта методика сос-
тоит в том, что станок настраивают на
главный вектор и главный момент дис-
балансов относительно центра масс неза-
висимо от конструкции ротора и положения
плоскостей коррекции. Балансировку в од-
ной плоскости отождествляют с уравно-
вешиванием главного вектора дисбалан-
сов. Но если плоскость коррекции не про-
ходит через центр масс, то появляется
дополнительный моментный дисбаланс
Мо == DCTL (рис. 4.2).
Замечание 1. При балансировке в
одной плоскости коррекции только третий
вариант дает возможность определить и
уравновесить статический дисбаланс. Во
всех остальных вариантах, в том числе и
на станках с вертикальной осью, баланси-
ровка в одной плоскости, не проходящей
через центр масс, одновременно с частич-
ным уравновешиванием статического дис-
баланса изменяет начальный моментный
дисбалансов зависимости от соотношения
значений £)ст и после одноплоскостной
балансировки jDct может увеличиться.
В частном случае, когда на роторе в
исходном состоянии jDct — 0, одноплоскос-
тная балансировка приведет к появлению
Дст, как показано на рис. 4.6.
После постановки балансировочной
массы появившийся дисбаланс D6 ком-
пенсирует одну из составляющих пары сил
момента, например Du м, тогда остав-
шийся дисбаланс DfM приводится к
статическому дисбалансу £)ст — [)6и ново-
му моменту, образованному парой векто-
ров DIM и —D6 — DilM.
Замечание 2. Квазигибкие одно-
массовые роторы балансировать в одной
плоскости коррекции не рекомендуется,
так как вероятность удовлетворительной
4 Зак [ ' [
Рис. 4.6. Одноплоскостная балансировка ро-
тора с начальным
эффективности балансировки существенно
зависит от конструкции и технологии
производства. Как следует из замечания 1,
может увеличиться статический дисбаланс,
вызывающий динамическое приращение
неуравновешенности по первой изгибной
форме
4.3. БАЛАНСИРОВКА В ДВУХ
ПЛОСКОСТЯХ КОРРЕКЦИИ
Балансировку в двух плоскостях кор-
рекции применяют при изготовлении жест-
ких и квазигибких роторов. В зависи-
мости от технических условий на изделие
балансировку выполняют в собранном
изделии, на специальном оборудовании.
При этом для получения необходимой
точности балансировки применяют раз-
личные способы. Наиболее широко при-
меняют следующие способы балансировки:
1) в двух произвольных плоскостях
коррекции;
2) в двух произвольных плоскостях
коррекции с регламентацией- остаточных
дисбалансов по величине и направлению;
3) в двух произвольных плоскостях
коррекции с раздельным уравновешивани-
ем статического и моментного дисбалан-
сов:
4) в двух оптимальных плоскостях
коррекции
С помощью первых трех способов ре-
шают практически все задачи по баланси-
ровке жестких роторов с требуемой точ-
ностью. Для квазигибких роторов лучшие
Низкочастотная балансировка роторов
результаты по точности балансировки
обеспечивают третий и четвертый способы.
Балансировка в собранном изделии.
Ее применяют ограниченно, так как доступ
к ротору не всегда возможен, а длитель-
ность и сложность работ выше, чем на сво-
бодном роторе. Практически используют
только первый и третий способы балан-
сировки. Для определения параметров
балансировки на корпус изделия, по воз-
можности ближе к сечениям, проходящим
через подшипники ротора, устанавливают
вибродатчики в плоскостях А и В. На
ротор наносят отметку углового положения
(выступ, впадина, магнитная метка),
для фиксации которой на корпус устанав
лива ют бесконтактный датчик; можно ис-
пользовать стробоскоп с условием, что за-
дающая частота подается от вибродатчика
поочередно. С помощью комплекта уни-
версальной измерительной аппаратуры,
например вольтметра и фазометра или
шлейфового осциллографа, измеряют ве-
личины амплитуд вибрации Аа и Ав и уг-
ловое положение их относительно отметки
на роторе {^-Ад, Л.АВ). При условии
линейной зависимости амплитуд вибрации
корпуса от дисбаланса на роторе в плос-
костях коррекции I и II можно считать,
ЧТО Дъ ^ц—Н}1Ав, —
— (Лл7^в), где Н, и Нп—коэффициенты
пропорциональности.
Следовательно, для определения вели-
чин корректирующих масс и т}1
необходимо прежде всего найти Н{ и Ни.
Для этого запускают изделие, выводят ро-
тор на балансировочную частоту вращения
и определяют амплитуды вибраций в ис-
ходном состоянии Ад0 и Аво и угол между
ними (Л^о; Аво) = Х.ЛЛ0 — ЛАВ0. Рассчи-
тывают величины пробных дисбалансов
D/n и DUn в плоскостях коррекции I и II
по формулам
Li. Г)СтnL[j Ljjf,
где Lt — расстояние от центра масс ротора
до плоскости коррекции /; Lu—расстоя-
ние от центра масс ротора до плос-
кости коррекции //; L, L/ + LH.
Величину статического пробного дис-
баланса 1\1Г! назначают в зависимости от
класса точности балансировки данного ро-
тора (ест ДО11) и его массы (тр), т. е.
^ст п гПрестп, ест я = (5 10)ест ДОГ|.
Пробные массы т1п и тИп находят по
формулам
min ~ Djn/Rh тнп~ DHn/Rlh
где R, и Ru - соответственно радиусы кор-
рекции в плоскостях / и //.
Устанавливают эти массы в плоскостях
коррекции / и II на радиусах Rt и
Rh в одном направлении, т. е. так, чтобы
векторы Din и ЬПп были параллельны
и направлены в одну сторону. Запускают
изделие второй раз и на тех же частотах
вращения, что при первом запуске, опре-
деляют амплитуды вибраций /4Л1, /4et и
угол между ними {АД{\АВ}) = Z. —
—- Z В общем случае направление
коллинеарных векторов Dln и Dlln — про-
извольное относительно отметки на
роторе. Но если необходимо прове-
рить линейность зависимостей DA =
£»в = /(Лд), то векторы Х)|„ и DIJn
должны совпадать по направлению с век-
тором А20 = Aav 4 Аво.. Тогда подтвер-
ждением линейности этих зависимостей
будут условия неравенства углов
ИдоЗво)>Ид1^в1). и совпадение на-
правлений векторов сумм амплитуд виб-
раций в исходном состоянии и с проб-
ными грузами, т. е. векторы Ахо и АГ1 =
= >4д14-4в1 должны быть коллинеарны.
Расчет коэффициентов пропорциональнос-
ти и корректирующих масс выполняют
по зависимостям аналоговой или числовой
схемы решения.
Построение аналоговой схемы решения
состоит из нескольких последовательных
этапов. Вначале определяют амплитуды
вибраций от пробных масс:
^АО ^А | =* А ВО ^В1 —
а затем рассчитывают коэффициенты про-
порциональности:
Ht— Dln/Aln, Нп— Вцп/А11п.
Балансировка в двух плоскостях коррекции
99
Балансировка в двух произвольных
плоскостях коррекции. Вначале по общей
методике определяют величины Hh Н/},
Аао,Аво, а затем рассчитывают начальные
дисбалансы из условий
£>/о — Н/Адо, НАВо-
При этом корректирующие массы будут
соответственно равны
m/K — Dt(i/Rh mflll = Dlf 0/Rn,
угловые положения их связаны с угла-
ми начальных амплитуд вибрации со-
отношениями
(miv) ~ ^- Адо 4- 180°, Л.(тцк) —
— ^во4~ 180°.
Балансировка в двух произвольных
плоскостях коррекции с раздельным урав-
новешиванием статического и моментного
дисбалансов. Вначале по общей методи-
ке определяют величины Нь Нп, Аао,
Аво, затем находят главный вектор дис-
балансов в исходном состоянии:
®ст О = &10 4? ^ПО»
его составляющие в плоскости коррек-
ции:
&СТ 01 — ^ст (Л,,/
^ст ОН = ^ст
и корректирующие массы:
^ст! ^ст.О. |/™ст II ^ст. 0 II/^11-
Корректирующие массы и пгп к
и угловое положение их определяют по тем
же скалярным зависимостям, что и в ана-
логовой схеме решения первого способа
балансировки.
Для балансировки по третьему способу
рассчитывают и AUn, Ht и #п, и
О110 так ,..е, как по первому способу. Затем
определяют Ост0 и по формулам
Составляющие статического и момент-
ного дисбалансов £)ст,, £)ст |( и DM j, DM 1а и
корректирующие массы mCTi, mGTiI, mMi,
tnw и в плоскостях 1 и // и угловые
положения их находят по тем же зависи-
мостям, что и в аналоговой схеме реше-
ния третьего способа балансировки.
Числовая схема решения предпочти-
тельнее аналоговой. Точность вычислений
с помощью ЭВМ выше, а вероятность
ошибки меньше. Как для единичных про-
цессов балансировки, так и для серийных
вполне достаточно использовать микро-
калькулятор.
Пример. Необходимо выполнить уравнове-
шивание многомассового межопорного ротора
в изделии, балансировку в двух плоскостях
коррекции с разделенным уравновешиванием
статического и моментного дисбалансов.
Для нашего примера примем числовую схему
решения. Последовательность действий:
первый запуск — ротор в исходном состоя-
нии; определим амплитуды вибраций в плос-
костях А и В постановки датчиков: Аао =
= 132 ед., АВС)— 168 ед., угловые положения
относительно отметки на роторе: ^-Аао — 117°,
Z_A — 62°. Угловые положения корректи-
рующих масс связаны с положением вектора
статического дисбаланса и равны между собой:
А(/пСт I = ^тст п = ^-°ст о 4- ?80°;
определим составляющие пары сил глав-
ного момента (межопорного ротора)-
— ri 1 ri ’
^м0 = "lO-?---------Ы 110 ~i---
ИII Ъ'((
моментные дисбалансы в плоскостях кор-
рекции:
|= II = 0
и корректирующие массы:
I = l/K|. II = Б)к |i/₽]J.
___—____________________________I
£>ст.о =-Vd?o+Ou(>-2D,oD„1,cos[ 180°-(Ллс?Л^1 ;
// L \2 / L \2 L L - -
^мо~) + (^«07—) —2£>|{)-T-!-£)n()-~-cos(£)1(); £>||{l) .
V \ 1 \ II / LUI Л-[[|
4*
100
Низкочастотная балансировка роторов
Угловые положения корректирующих масс
моментного дисбаланса связаны с вектором
Ом о и отличаются на 180°, т. е.
(тем l) ~ 0 +180°, ц) = о-
Практическое решение задач балансировки
по аналоговой схеме для эпизодической ра-
боты выполняют графически, построением век-
торных диаграмм. Для систематической балан-
сировки применяют ЭВМ.
Числовая схема решения основана на
завйсимостях, исключающих необходимость век-
торных построений. Для балансировки по
первому способу амплитуды колебаний от проб
них масс определим но формулам
/1 (п — А 4 j 4- А 2А л, A w cos ( А Л (; А ю) .
А и„ = л/Ал Ч- Ал> 2ЛВ1 ABOcos( ABI; A ,,0) ,
рассчитываем угол между амплитудами вибра-
ций в исходном состоянии М-Г|;Ля()) = 117° —
— 62° = 55°;
находим величины главного вектора проб-
ного дисбаланса и пробных масс в плоскостях
коррекции
^ст п трест П’
Дст п, предварительно примем, что /\т 0 и
Лст0 линейно зависимы, тогда Z_b,..,. п =
~ Z. Аст относительно метки на роторе
Ат о = Ат о- Азо)» построени-
ем на базе Л40 и Дво определим Ат q и
(Ат 0’ ^во)’ Лля расчета этого угла вначале
находим
Ат1( = VA + A — 2Д4Двсоз(180°-55°) =
= V13224-1682 —2 • 132- 168 (—0,573) —
= 266,62 ед.; (ActW; Дв„) =
— arccos
1322—266,62"— 1684
2.266,62—168 )
= 24°.
А1(> = 62° + 24° = 86°;
под углом 86° относительно метки па роторе
в плоскости I установим 4.68 г, а в плос-
кости // —5,25 г;
второй запуск - ротор с пробными масса-
ми; определим величины амплитуд вибраций
Ад 1 = 180,4 ед, Ав ( = 235,6 ед и их угловые
положения Z-Дл 1 — 108.7° / Ав j = 72°;
находим амплитуды колебаний от пробных
масс
А |„ ~ ^!~А2л[ ф- Д 2 0 — 2Д [ Ancos ( Ал,-г, А,ц) =
= ХЦ80.42 4-1322—2.180.4 - 132 - cos \117° — 108,3°) = 53,3 ед.;
А|«~ V^Ai"ЬАо 2АВ1 ABOcos( Ащ,; ДВ1) =
= V23524- 1682 —2 - 235 - 168 - cos»72° —62°) = 75,4 ед.
для гдр — 120 кг, „ = 10* ест ДО|] (по
ГОСТ 22061-76 <?ст=1,5 мкм, при «
as 8000 об/мин);
£?ст „ = 1800 г - мм;
^ст л|1 ^ст nAj/A lb ^СГ Л II — ^Аг л
А/ Lj n;
для Lj — 560 мм, LH — 400 мм, L{ (| =
— 960 мм,
£>ст „ ( — 750 г ♦ мм, ОгТ ,, Ц = 1050 г • мм;
I ~ ^ст п )/^b mn II ~ А:т п ll/^tb
для Ri = 160 мм, Rj[ == 200 мм, тпп , =
= 4,68 г, пгп п = 5,25 г;
выполним установку пробных масс в плос-
кости коррекции 1 и II по направлению
и коэффициенты пропорциональности
Н} = Dvtt/Ain^ 750/53,3 = 14,072 г - мм/ед.;
ffT1 — Оп П/Ац я — 1050/75= 13,93 г-мм/ед.;
определим начальные дисбалансы (стати-
ческий и моментный) и их составляющие в
плоскостях коррекции, корректирующие массы
и их угловые положения:
l~ffAAQ=^ 14,07 - 132= 1857,2 г - мм;
О||0=ЯпДВ0= 13,925- 168=2339 г • мм;
Балансировка в двух плоскостях коррекции
101
^сто — "Ь ^ii о 2OI0 D{(0 cos [ 180° (А Л0; Aво)| —
= V1857,2*+2339.42— 2 • 1857.2 • 2339.4 cos (180°— 55°) = 3729 г - мм:
Lt
L1(
-----соя(ЛЛ0?ЛЯ0) =
11
1857 2 56(Л 2
1Ь57’ 960/
2339,4
_ 2 • 1857,2 2339,4 cos 55° = 955,2 г . мм
960/ 960 960
£>ст0| = Рст0 £„/£,,, = 3729 - 400/960 = 1553,75 г • мм
011
DK1()Li/Li „ = 3729 • 560/960 = 2175,25 г . мм:
tn„f = P,lUI//?1 = 1553,75/160 = 9.71 г;
щгг1 = ДС1 (t/Kti = 2175,25/200 = 10,87 г
установим в плоскостях коррекции I и II обе
массы под одинаковым углом относительно мет-
ки на роторе Z.DC 04- 180°, т. е. Amcri —
= ZmCT ,, = 86° 4- 180° - 266°; DM , = DM u=
— DM 0 — 955,2 г • мм; тм ] = DM —
= 955,2/160 = 5,97 r, mM u == DM ц/Кц =
= 955,2/200= 4,77 г; установим в плоскости
коррекции I массу тм (под углом Z DM 0- 180°,
где 0 = ADa о + (Р$; Лл 0), в свою
очередь из теоремы косинусов находим
= 5,3°), а угловое положение ц совпадает
с Z-DM 0(тм ц— 185,3°).
После установки корректирующих масс
выполним контрольный запуск изделия для
проверки эффективности результатов баланси-
ровки.
Балансировка с использованием спе-
циального оборудования это наиболее
распространенный вид балансировки рото-
После подстановки всех данных получим
Z.DM 0 = 117° 4-68,3° =185,3°; Атм , =
= 185,5° - 180° = 5,3?,
^-тми — 185,3°.
Таким образом, угловое положение
корректирующей массы тМ1 сдвинуто на 5,3”
относительно метки на роторе, (Лтл11 =
ров. При этом применяют станки до-
резонансные, резонансные, зарезонансные.
Методику работы обычно приводят в
описаниях станков, не делая различия в
балансировке жестких и квазигибких рото-
ров (в технологических приемах и спо-
собах балансировки).
102
Низкочастотная балансировка роторов
Ниже рассматриваются способы ба-
лансировки на зарезонансных станках с
подвижными опорами, получивших широ-
кое распространение. При этом, прежде
чем выбрать способ балансировки, необхо-
димо учесть в технологическом процессе
массово-геометрические особенности рото-
ра. Асимметричные и консольные роторы
устанавливают в специальные рамки, за-
крепленные в люльках станка так, чтобы
центр масс ротора был по возможности
ближе к среднему положению между люль-
ками; масса рамки минимальная; вес дол-
жен равномерно распределяться на люль-
ках (оптимальным является соотношение,
когда вес люльки с приходящимся на нее
весом рамки равен составляющей веса
ротора на эту люльку).
Необходимо также, чтобы расстояние
Lab между опорами ротора не превы-
шало расстояние п между плоскостями
коррекции больше допустимого (LAB{
10). Если отношение расстояний
больше 10, назначают плоскости измере-
ния. для которых это отношение меньше 10,
затем дисбалансы пересчитывают в плос-
кости коррекции. _
Балансировку в двух произвольных
плоскостях коррекции применяют для
большинства жестких роторов. В описании
балансировочного станка обычно дается
методика настройки аппаратуры на дан-
ный тип ротора. Сущность настройки
состоит в том, что дисбаланс в каждой
плоскости коррекции определяют и устра-
няют независимо. Точность балансировки,
обеспечиваемая станком, в среднем соот-
ветствует 1 мкм остаточного смещения
центра массы ротора. Действительное зна-
чение остаточного дисбаланса назначают
в зависимости от вида изделия и условий
эксплуатации по ГОСТу (19). Необхо-
димо помнить, что балансировочные стаики
дают возможность определять дисбалансы
в плоскостях коррекции с указанной в
описании точностью для межопорных
симметричных роторов и при допустимых
отношениях LAB/Lin. Как известно, для
асимметричных и консольных роторов ап-
паратура станка дает различную точность
левой и правой плоскостей. Квазигибкие
роторы балансировать по этой методике
не рекомендуется ввиду ее малой эффек-
тивности.
Балансировку в двух произвольных
плоскостях коррекции с регламентацией
остаточных дисбалансов по величине и на-
правлению применяют для жестких рото-
ров с высокой частотой вращения. Как
видно из рис. 4.7, такие роторы могут
создавать различные по величине нагрузки
на опорах в зависимости от расположе-
ния остаточных дисбалансов по стати-
ческой (рис. 4.7, о) или моментной схеме
(рис. 4.7,6). В первом случае величины
сил будут существенно большими, чем
во втором. Для симметричного ротора
и жестких опор по статической схеме
I), — Оц «0,5/Прб, по моментной схеме
— Dn|«|0,5znpfi/i//|, где 6—полови
на радиального зазора.
Выполнять балансировку на баланси-
ровочном станке можно в собранном из-
делии. Последовательность балансировки
следующая. Сначала определяют обычным
методом начальные дисбалансы D[ и
£>п. Затем, чтобы сформировать схему
работы по моментной нагрузке на опорах
ротора, уравновешивают один из дисба-
лансов, например, (рис. 4.8), до за-
Рнс. 4.7. Балансировка жесткого ротора в
двух плоскостях коррекции с регламентацией
остаточных дисбалансов:
а — статического; б — моментного
Балансировка в двух плоскостях коррекции
103
Рис. 4.8. Векторная диаграмма при баланси-
ровке с остаточным моментным дисбалансом
данных пределов: Dx min < Dx ост </), max,
а после этого рассчитывают £)п в = ^пост
—Йп, где ВПост=-----Аост. и уравнове-
шивают до £>11ост. Для квазигибких
роторов этот способ балансировки эффек-
тивен в том случае, если прогиб настоль-
ко мал, что динамическое приращение
сил инерции не превысит вес ротора.
Балансировку в двух произвольных
плоскостях коррекции с раздельным урав-
новешиванием статической и моментной
составляющих дисбалансов применяют
для жестких и квазигибких роторов в
собранном изделии или на балансировоч-
ном станке. Преимущество этого способа
наиболее заметно на станках с подвиж-
ными опорами при балансировке асиммет-
ричных, консольных роторов с Lab/Li и >
>10, так как точность определения £)ст
и DM не зависит от массово-геометрических
параметров ротора. Для многомассовых
квазигибких и гибких роторов, собираемых
из отдельных деталей, создаются условия
по достижению высшей точности результа-
тов при последовательной балансировке.
Отдельные детали (диски) гибкого ротора
являются практически жесткими во всем
рабочем диапазоне частот вращения; если
уравновешивать в двух плоскостях кор-
рекции каждую деталь с точностью 1 мкм,
то силы инерции и соответственно ре-
акции опор ротора будут минимальными,
т. е. меньшими, чем при высокочастотной
балансировке многомассового ротора.
Важная особенность рассматриваемо-
го способа состоит также в том, что
раздельное определение £)ст (г • мм) и
Л4с(г • мм2) дает возможность более четко
выполнять процесс балансировки. Напри-
мер, одномассовый квазигибкий ротор типа
вал с сосредоточенной массой балансиру-
ют с определенной точностью. Смещение
центра масс, стимулирующее первую из-
гибную форму прогиба, рассчитано из ус-
ловия fpa6 Гдоп При балансировке в
двух плоскостях коррекции Dj п ост со-
ответствуют величине ек. Но £)111оет =
= D\ II ст ост + II м ост. а прогибы от Ост
и MD при одинаковых значениях Оц1ст —
== Dj и м существенно разные. Чтобы уста-
новить Л4Сдоп (г - мм2), необходимо рас-
считать прогиб ротора при £), {| ст— £)1Пост,
затем определить МОост(г • мм2), соответ-
ствующий этому прогибу, и найти
OiiirtocT= Л4оост/£1Н- в общем случае
1II ост > ^1 в ст ост. Если не разделить
jDi1Ict на Дстост и DM ост, может не
хватить «места» для коррекции Ои!нач.
Методика настройки аппаратуры заре-
зонансных балансировочных станков для
определения DCT и Мй состоит в следую-
щем На роторе определяют положение
центра масс и вносят пробную массу
непосредственно в этом или в параллель-
ных сечениях так, чтобы на роторе был
только статический дисбаланс. Один из
каналов аппаратуры отстраивают обыч-
ным путем от показаний jDct, затем на
роторе устанавливают две пробные массы,
создающие моментный дисбаланс и отстра-
ивают показания второго канала. В ре-
зультате по первому каналу будут про-
ходить показания моментного, а по второ-
му — статического дисбаланса. Масштабы
и Нм показаний регистрирующих
приборов по статическому AD и момент-
ному Ам дисбалансам различные. Для их
определения необходимо несколько проб-
ных масс:
HD— ~ ^ст(2)Мо(2) ==
“ ^ст(3)/^О(3)»
М<2) =
.= Мй(3)/Дд(3).
Балансировку в двух оптимальных
плоскостях коррекции применяют для ква-
зигибких роторов и выполняют преимуще-
104
Низкочастотная балансировка роторов
ственно на балансировочных станках. Рас-
чет оптимального положения плоскостей
коррекции основан на следующем из-
вестном свойстве: наибольший прогиб ро-
тора у г находится в зоне наибольшей
податливости и мало изменяет положение
при изменении точки приложения силы.
Если величина прогиба усл от действую-
щих эксцентриситетов ел будет равной ве-
личине прогиба ус |( от корректирующих
масс, то приращение дисбалансов из-за
прогибов будет незначительным. В общем
случае ус д = f(mt, et <о, а,,) и ус к — [(тьеь
о,,).
При условии yC{i~yCK получена зависи-
мость
Определив сумму в правой части,
подбирают по таблице коэффициентов
податливости ротора aCf t и аС1 п и устанав-
ливают по ним положение плоскостей кор-
рекции / и //. Значения LU/LU1 и
представляют собой коэффициенты про-
порциональности распределения масс от-
носительно их центра. Наибольшая подат-
ливость находится в средней части участка
Lj и ротора.
4.4. МНОГОПЛОСКОСТНАЯ
БАЛАНСИРОВКА
Многоплоскоетную балансировку на-
зывают балансировкой в п плоскостях
коррекции. Ее применяют для жестких
и квазигибких роторов, преимущественно с
использованием специального оборудова-
ния, так как балансировка в собранном
изделии сопряжена с необходимостью пре-
дусмотреть в конструкции корпуса специ-
альные люки для доступа к ротору в
плоскостях коррекции. Жесткие роторы
балансируют в п плоскостях коррекции
в тех случаях, когда по техническим при-
чинам невозможно расположить уравнове-
шивающие массы в двух плоскостях. На-
пример, постановка масс в размерах боль-
ше установленных нарушает рабочий про-
цесс, а для балансировки требуется их
увеличить.
Балансировка квазигибких роторов в п
плоскостях коррекции повышает эффек-
тивность результатов,Поскольку косвенно
учитывает прогибы в рабочих условиях.
Сущность многоплоскостной балансировки
состоит в том, что в общем случае
ось ротора и ГЦОИ представлены перекре-
щивающимися прямыми. Если бы была
техническая возможность обрабатывать
цапфы изготовленного ротора до совме-
щения с ГЦОИ, отпала бы надобность
в низкочастотной балансировке с помощью
коррекции масс. Разница между векто-
рами эксцентриситетов отдельных масс от-
носительно ГЦОИ еон и оси ротора
е® обусловлена смещением осей в этом
сечении ё^и, поэтому eoi — eWi, 4- ёои.
Следов ател ьн о
/*01 ==
и п
~ £ mt<*>2eoou + £ ^»<o2e0U,
i = I
М ~ МЖ1 Мм —
п п
— £ £ т{щ2ёоь/{;
»=t i=i
где /«--расстояние от центра масс до try.
Но сумма сил и моментов относи-
тельно ГЦОИ равна нулю, поэтому на
опоры балансировочного станка действует
« п
т(®24„ М = £ П1,ш2ё(ю111г
i= I i= I
Очевидно, на балансировочном станке
уравновешивают не случайную, неизвест-
ную, систему сил и моментов, а вполне
определенную, обусловленную векторами
эксцентриситетов ёооц. При частотах вра-
Многоплоскостная балансировка
105
щения, когда прогибами пренебрегать
нельзя, изменение этой системы создает
наи лучший вариант остаточных эксцентри-
ситетов ёои из возможных при низко-
частотной балансировке. Система оста-
точных эксцентриситетов будет оптималь-
ной. так как вероятность того, что мож-
но подобрать балансировочные массы,
уменьшающие ее влияние в рабочих усло-
виях, является событием недостоверным.
Такое уравновешивание эквивалентно сов-
мещению оси ротора с ГЦОИ.
Задача оптимальной многоплосксстной
низкочастотной балансировки сводится к
определению векторов воои, т. е. взаимного
положения оси ротора и ГЦОИ. Для
решения задачи балансировки используют
векторы дисбалансов Dx и Dlh опреде-
ленные непосредственно на станке. Затем
находят для многомассового межонорного
ротора ©„ааД-^-Рц,
- ^ст - \\\Ц
^ст = ~Т~т' Сл,£ = ~ ’
Z
«=1
£(Ю11 == есг + £>Л1«-
Величины балансировочных масс опре-
деляют по уравнению ты ~ т}е^пм/гы
(r^ — радиус коррекции). Многоплос-
костную балансировку выполняют также
раздельно по статической и моментной
составляющим. Принимая условное число
м$сс ротора равным 3,4,определяют
балансировочные массы для такого же чис-
ла плоскостей. Для вычислений приме-
няют специализированные или универсаль-
ные АВМ и ЭВМ.
Существуют упрошенные методы мно-
гоплоскостной балансировки, являющиеся
частными случаями рассмотренного выше
мегода. Наиболее простая балансировка
в трех плоскостях коррекции, которую
применяют иногда для собранных изде-
лий, чаще на станках.
Г 1олуэм лирический метод состоит из
двух этапов. Вначале определяют дис-
балансы ротора в двух плоскостях кор-
рекции, как при обычной двухплоскостной
балансировке. Затем выполняют графичес-
кое решение, в определенном масштабе
изображают векторы дисбалансов Д, и
Djj, определяют их векторную сумму £)ст,
делят последнюю на три части и устанавли-
вают корректирующие массы
т, = K\D^/rx, т2 —
тл = KiDcJr2
(здесь Г| -з — радиусы коррекции; Ki-з —
коэффициенты пропорциональности) в
трех сечениях, перпендикулярных оси ро-
тора. Обычно это крайние и средние
части ротора Фазовое положение кор
ректирующих масс на 180° развернуто
Относительно направления вектора DCT.
Есть различные варианты деления £>ст на
три части и выбора положения средней
плоскости. Многое зависит от опыта ис-
полнителей Наиболее приемлемы К\ ~
л 0,2—0,25; К2 » 0,64-0,5; Кз »
« 0,2 4- 0,25. Необходимо учитывать,
что Z)CT приложен в центре масс ротора,
поэтому суммарный вектор /5кор = f
4- £>2-|-£)з должен быть также приложен
в той же точке. Коэффициенты Яд
Кз назначают с учетом расстояния
между тремя плоскостями коррекции. Пос-
ле уравновешивания статического дисба-
ланса на роторе вновь включают станок
и определяют оставшийся дисбаланс, ко-
торый корректируют обычным способом
в двух крайних плоскостях
Балансировку в четырех и более плос-
костях коррекции выполняют по такой же
схеме, т. е. статический дисбаланс кор-
ректируют в нескольких плоскостях, мо-
ментный - только в двух.
Балансировка роторов раздельно по си-
ловому и моментному дисбалансам. Обще-
принятое представление о неуравновешен-
ном роторе, в виде двух дисбалансов
в плоскостях коррекции или на опорах
106
Низкочастотная балансировка роторов
недостаточно строгое» Качественные ха-
рактеристики силовой и моментной состав-
ляющих дисбалансов различны по физи-
ческим свойствам и, следовательно, раз-
лично влияют на динамику ротора как
при балансировке, так и в рабочих ус-
ловиях. Например, для жестких и квази-
гибких роторов в тех случаях, когда массо-
во-геометрические параметры затрудняют
получение точных данных о дисбалансах
в плоскостях коррекции, раздельный ана-
лиз составляющих дает более точные
результаты. Такая ситуация может воз-
никнуть при уравновешивании ротора в
собранном изделии, но наиболее часто
она проявляется на зарезонансных ба-
лансировочных станках. Практически все
асимметричные и консольные роторы, даже
при условии отстройки плоскостей кор-
рекции, на таких станках нельзя уравно-
весить с одинаковой точностью Поэтому
применяют балансировку по главному век-
тору и моменту.
Метод основан на известном положе-
нии теоретической механики: движение
твердого тела под действием п сил и мо-
ментов, приложенных к различным точкам
тела, будет таким же, как под действием
одной силы, равной векторной сумме всех
сил, и одного момента, равного вектор-
ной сумме всех моментов, приложенных
к центру масс. Сила и момент, прило-
женные к ротору, создают различные пред-
посылки движения. Под действием момент-
ной нагрузки, независимо от места ее при-
ложения, возможное движение — поворот
относительно центра масс. Имеющиеся
связи изменяют положение оси поворота,
но не вид движения. Под действием
силовой нагрузки вид движения зависит от
места ее приложения. Так, если сила
приложена к центру масс,— движение пос-
тупательное, во всех других случаях при-
ложения силы движение ротора (твердого
тела) будет сложным, состоящим из посту-
пательного движения центра масс и вра-
щательного относительно этого центра.
Размерности величин силовой и моментной
нагрузок различные. Об этом необходимо
помнить при назначении допусков на урав-
новешивание асимметричных и консольных
роторов. Именно в таких случаях более
четко проявляется различие между /5СТ
и DM.
В ГОСТе [Г.9] даны рекомендации по
расчету допустимых значений остаточных
дисбалансов в зависимости от требуемо-
го класс точности на балансировку. Вполне
обоснованно допуск дан на £>ст, так как
этот вид дисбаланса создает наибольшую
нагрузку на опорах ротора. Если на ба-
лансировочном станке после отстройки
плоскостей коррекции в условиях серийно-
го уравновешивания эти допуски относятся
к моментным составляющим, то ухудшения
уравновешенности ротора не произойдет.
Проблема состоит в том, что на асимметри-
чных и консольных роторах при баланси-
ровке на станках (особенно зарезонан-
сного типа) точность определения £)ст и
DM существенно зависит от массово-
геометрических параметров. Проявляется
неоднозначность составляющих (силовой и
моментной) неуравновешенности, заметно
Рис. 4.9. Нагрузки опор консольного ротора
Многоплоскостная балансировка
107
влияющая на точность получаемых ре-
зультатов.
На асимметричном роторе единичная
сила, приложенная в плоскости ^регистри-
руется на опоре А в виде сигнала, пропор-
ционального величине силы или перемеще-
ния. Та же сила, приложенная в плос-
кости П и зарегистрированная на опоре
В, будет иметь другую величину. Поэтому
показания датчиков опор А и В будут
разные при одинаковых дисбалансах в
плоскостях 1 и //.
Еще более сложная схема действия
сил и моментов на консольных одномас-
совых роторах (рис. 4.9)’ при уравно-
вешивании на станках. Для квазигмбких
консольных роторов (диск жесткий, вал
гибкий) точность балансировки сущест-
венно влияет*на уровень сил на опорах
в рабочем диапазоне частот вращения.
В общем случае при балансировке сумма
всех сил и моментов на двухопорном
роторе определяют по формулам
Рис. 4.10. Балансировка ротора в двух плос-
костях коррекции в собранном изделии:
а—схема ротора, б векторное решение
У* D,— DfiA-De— ^ст’
i=i
п
У, мА + Мв = MD.
«=]
Раздельно влияние DCT и MD на воз-
можный прогиб ротора не рассматривают.
Считают, что заданная точность на DAB
(г • мм) заведомо перекрываег влияний1 мо-
ментных составляющих DABM. В действи-
тельности положение иное. От силовой
составляющей дисбаланса на опорах воз-
никают силы (рис. 4.9. о. где £Лст, FBfr
эквивалентны DAct, DBcT)'.
_ А ст АВ>
D В ст ст АВ ~Ь /^АВ'
Наименьшую силу 4ЛВстост, которая
еще регистрируется аппаратурой баланси-
ровочного станка, определяют по выше-
приведенным зависимостям.
Остаточную неуравновешенную силу от
MD (Рис. 4.9,6) на опорах можно опре-
делить с той же точностью, что и FAB ст ост,
но MD — Dabm^ab — Di ufyfd, IlM —
^DABMlAB/d, следовательно, DAB^, ре-
гистрируемое аппаратурой станка, в
LAB/d раз меньше действительной величи-
ны. Для различных конструкций и рабо-
чих условий изделия влияние DABMozx и
Рдест ост будет различным. Поэтому не-
обходимо на ротор задавать допустимые
остаточные значения по главному вектору
(г * мм) и главному моменту (г • мм2)
раздельно непосредственно в плоскостях
коррекции.
В общем виде решение задачи по опре-
делению Дст и DM состоит в следующем:
а) для межопорного ротора (центр
масс между опорами, рис. 4.10,а) нахо-
дят дисбалансы ЬА и DB в плоскостях
измерения вблизи опор А и В или Ь\
и Дп, если позволяет аппаратура станка.
Затем строят векторную диаграмму
(рис. 4.10,6) или аналитически находят.
А=т = Д + Др. BM=DvLi/L^ и —
^ll^ll/^-l lb
Д1 <T = ДлА/^I lb ^11 ст = lb
Dim — DnM— —
108
Низкочастотная балансировка роторов
Рис. 4.11. Векторная диаграмма при балан-
сировке консольного ротора по DM и Mf}
балансируют с заданной точностью по
D(1 (г * мм) и DM (г • мм2), если уве-
личить число плоскостей коррекции, то раз-
дельный способ непосредственно перехо-
дит в многоплоскостную балансировку;
б) для консольного ротора (центр масс
вне опор, рис. 4.11) приведена схема
векторного решения, где £)ст = DA -| Ьв,
MD= DA(LAli 4- Lc} -f- DBLC, =
= Da(Lab ~f- L^/d -|- DBLc/d.
Для квазигибких роторов балансиров-
ка по главному вектору и главному
моменту позволяет повысить эффектив-
ность балансировки за счет более точного
определения /)С1 и DM (особенно для кон-
сольных роторов). Для жестких роторов
появляется возможность более строго наз-
начать остаточные дисбалансы по Ьм,
которые могут быть увеличены без ухудше-
ния результатов балансировки
При назначении более высоких по срав-
нению с Do ДО11 допустимых значений по
моментному дисбалансу можно исходить
из следующих предпосылок. Если задан
ные значения Z)C1 ЯО|| для квази гибкого
ротора обеспечивают удовлетворительный
уровень вибраций изделия, значит про-
гиб ротора от дисбалансов создает ди-
намическое приращение сил im о? у) в
допустимых пределах:
п
FpaC = £ ,П> •
1-г-1
По этой зависимости определяют про
гиб у от Дстд<)11 и решают обратную
задачу: какому моментному дисбалансу
соответствует прогиб Полученное зниче
ние DM уточняют с помощью теории
вероятностей и в зависимости от типа
ротора назначают DM Г11Т доп
Пример. Для квазигибкого консольного ротора
с массой 20 Ki и расстоянием между плос-
костями коррекции на диске 20 мм назначен
допустимый остаточный дисбаланс 100 г - мм.
Расчетным путем было установлено, что ста-
тическому дисбалансу 100 г - мм на рабочих
частотах вращения динамически эквивалентен
момент Мо = 36 000 г мм2. Учитывая вероят-
ность взаимного углового положения векторов
£)ст и Мв, принимаем 18 000 г - мм2,
сл едовател ыто,
ост доп < ~20~“^ 900 г ' мк-
4.5. БАЛАНСИРОВКА МОДУЛЕЙ
РОТОРОВ
Балансировка модулей роторов обеспе-
чивает взаимозаменяемость по дисбалансу
отдельных частей ротора (модулей) при
наличии у них полной взаимозаменяемости
по геометрическим параметрам стыкуемых
поверхностей.
Балансировку модулей выполняют для
составных роторов в процессе специали-
зированного производства модулей, обес-
печивая восстановление работоспособ-
ности ротора в эксплуатации путем замены
модулей. Технологическую оснастку (оп-
равки), предназначенную для балансиров-
ки деталей одного типоразмера по массе,
уравновешивают так же, как и модули
ротора. Разделение составного ротора на
модули и назначение плоскостей коррек
ции. производят, прогнозируя возможные
повреждения ротора в эксплуатации с
учетом особенностей его производства.
Модулями могут быть* как детали, так и
сборочные единицы ротора. Точность их
балансировки и, следовательно, всего сос-
тавного ротора определяется точностью
измерения значений и углов дисбаланса.
Суммарный дисбаланс ротора измеряют на
балансировочном станке в двух плоскостях
коррекции. Он складывается из остаточ-
ных дисбалансов модулей и технологи-
ческого дисбаланса ротора, обусловленпо-
Балансировка модулей роторов
109
го смешением центров масс уравновешен-
ных модулей с оси вращения ротора при
его сборке из-за биения установочно-сты-
ковочных базовых поверхностей. Следова-
тельно, если установочные поверхности
сопрягаемых модулей выполнены идеально
относительно оси вращения ротора, то его
технологический дисбаланс равен нулю,
и обычная раздельнай балансировка моду-
лей обеспечивает их взаимозаменяемость
по дисбалансу. Это условие используют
при балансировке в тех случаях, когда
взаимное расположение установочных (ба-
зовых) поверхностей модулей ротора мож-
но регулировать относительно оси враще-
ния. Предельно допустимые биения уста-
новочных поверхностей модулей в этом
случае определяют с учетом величины
допускаемого остаточного дисбаланса.
Методы балансировки модулей предус-
матривают уравновешивание каждого мо-
дуля в отдельности с учетом биений
его стыковочных поверхностей и оконча-
тельную сборку составного ротора из
уравновешенных относительно оси враще-
ния ротора модулей. Балансировку оконча-
тельно собранного составного ротора не
делают. На балансируемом модуле поми
мо начальных днебалансов устраняют тех-
нологические дисбалансы сопрягаемого
модуля, появление которых обусловлено
наличием биений стыковочных поверхнос-
тей только балансируемого модуля. Поэто-
му окончательно сбалансированный мо-
дуль имеет остаточный дисбаланс, компен-
сирующий технологический дисбаланс
составного ротора, появляющийся при сты-
ковке рассматриваемого модуля с идеаль-
ным сопрягаемым модулем. Идеальный
модуль — сбалансированный модуль, сты-
ковочные поверхности которого не имеют
биений относительно оси вращения ротора.
Для наглядности рассмотрим баланси-
ровку технологической оправки для урав-
новешивания дисков (рис. 4.12). Ее можно
рассматривать как составной консольный
ротор, состоящий из технологического ва
ла (оправки) 1 и балансируемого диска
(детали) 2. При этом суммарный дис-
баланс ротора, измеряемый на опорах
Рис. 4.12. Балансировка составного консоль-
ного ротора методом совместной баланси-
ровки модулей
А и В балансировочного станка, состоит
изначальных дисбалансов модулей вала 1
(DttJDsi), диска 2 (D22, Р32) и техно-
логического дисбаланса, возникающего
при установке диска на вал (/5Т) из-за
наличия радиального биения посадочного
места на валу относительно оси враще-
ния ротора. Этот технологический дис-
баланс
£>т = етя.
где mR — масса диска: е — эксцентриситет
посадочного места вала.
Поэтому имеем
&А ®В = I + D21 + D22 +- ^32 + D.r
Согласно положениям балансировки
модулей, выявленный технологический
дисбаланс ротора должен быть компенси-
рован за счет корректировки массы вала,
так как он вызван эксцентриситетом по-
садочного места диска на валу относи-
тельно оси вращения ротора. Установка
другого диска такой же массы на вал
вызовет появление такого же по вели-
чине и направлению технологического дис-
баланса, как и от первого диска, кото-
рый уже был компенсирован установкой
корректирующих масс на вал. Известны
методы совместной и раздельной баланси-
ровки модулей.
по
Низкочастотная балансировка роторов
сил: £
Метод совместной балансировки моду-
лей (метод двух сборок). Он предусмат-
ривает сборку ротора, измерение его дис-
балансов в двух плоскостях, разборку ро-
тора на модули, разворот одного модуля
относительно другого на угол а, пов-
торную сборку ротора и измерение его
дисбалансов в двух плоскостях. По изме-
нению дисбалансов ротора, варьируя вза-
имным угловым положением модулей, со-
ставляют уравнение равновесия:
п п
F = 0 и моментов У М = О
«=1 (=1
Для наглядности рассмотрим баланси-
ровку этим методом ротора, показанного
на рис. 4.12. Система уравнений
равновесия сил и моментов для состав-
ного ротора при двух взаимных угловых
положениях модулей в исходном (а =0) и
развернутом (а = 180°) имеет вид
Du -|~ Z?2i D22 + D32 — DA । + Db 1,
Du 4- Du — D22 — D32 = DA 2 + DB 2'г
Diilu -|- £>21/21 4- D22I22 4" Д32/32 — DB iion',
Dilin 4~ D21Z21 — D22I22 — £>32^32 = DB 2Гфи»,
где Di, — дисбалансы модулей в их плос-
костях коррекции с учетом геометрических
отклонений стыковочных поверхностей;
1Ч — расстояние i-й плоскости коррекции
от опоры А (задается разработчиком); DAt,
DBt — дисбалансы ротора, измеренные на
станке; /оп — расстояние между опорами
ротора.
В приведенной выше линейной систе-
ме уравнений четыре неизвестных — на-
чальные дисбалансы модулей в плоскостях
коррекции. Попарно складывая и вычитая
уравнение сил и моментов, выделяем дис-
балансы сначала одного, а затем дру-
гого модуля, после чего остается линей-
ная система из двух уравнений с двумя
неизвестными, которую можно решить ме-
тодом подстановки. Из этой системы урав-
нений с четырьмя неизвестными -находим
значения дисбалансов модулей в их
плоскостях коррекции (£>,-,-) Значения дис-
балансов каждого модуля, найденные этим
методом, являются геометрической суммой
его остаточного и технологического дис-
балансов от сопрягаемого модуля. Урав-
новесив найденные значения дисбалансов
в плоскостях коррекции обоих модулей,
собираем ротор.
При больших начальных дисбалансах
обоих модулей балансировку проводят ме-
тодом последовательного приближения в
два этапа.
Сначала производят грубое уравнове-
шивание обоих модулей с помощью техно-
логических грузов, а затем точное, при
котором суммарную корректирующую мас-
су определяют как векторную сумму дис-
балансов, выявленных в данной плоскости
модуля при грубой и точной баланси-
ровках.
В общем случае, если при второй
сборке угол поворота одного модуля от-
носительно другого не равен 180° (0° С
С а<180°), система уравнений имеет вид;
для первой сборки (<р =0)
4
У Dtj cos = DAl cos осл [ 4- £>si cos aB1;
o=i
4
У £>(/sin = DAi sin aAi 4~ DBi sin aBl;
*/=•
4
У l„ D„ cos atj = Zon Da ! cos aA,;
4=1
4
У ltf Dt} sin = lou Da sin ал1;
»r»i
для второй сборки 10 < < 180°)
2 4
У D4 cos aif 4- У Dtj cos (a,, 4- <p) =
17=1 (/=3
- DД2 tos аЛ2 Ar DB2 COS aB2>
2 4
У Dtj sin 4- У D4 sin (alf 4- y) =
0=1 ч=з
^DA2 sin стЛ2 + DB2 sin aB2;
Балансировка модулей роторов
111
2 4
Zj lii Ц/Cos atj Ч- У" ll} Dt, cos(ae/+ <p) =
</=i 4=3
= lOnDA2cos aA2;
2 4
£ l(, D4 sin a4 4- £ lii Di, sin (a,, + q>) =
4=1 q=3
= ^oti^A2 Si*"* a,42-
Уравновешенные методом совместной
балансировки рабочие модули становятся
взаимозаменяемыми по дисбалансу. Они
могут быть развернуты в роторе на лю-
бой угол или заменены* на такой же
модуль, уравновешенный в составе другого
ротора. Очевидно, что дисбаланс составно-
го ротора £)рот, состоящего из двух моду-
лей; одного — отбалансированного мето-
дом двух сборок (£)М1), и другого—не-
уравновешенного (£>aj2). измеренный на
балансировочном станке, будет равен дис-
балансу неуравновешенного модуля, так
как Z)p01 = DM i + &м 2, но DM । = 0,
тогда £>poT = DM 2-
Таким образом, ротор, состоящий из
уравновешенного и неуравновешенного
модулей, после балансировки в сборе так
же обеспечивает взаимозаменяемость мо-
дулей. Это свойство используют при раз-
дельной балансировке модулей. Метод раз-
дельной балансировки модулей состоит в
динамической балансировке каждого из
них с имитатором, уравновешенным мето-
дом двух сборок. Составной ротор,
собранный из уравновешенных модулей,
не балансируют. Точность уравновешива-
ния этим методом составного ротора опре-
деляется точностью измерения дисбалан-
сов уравновешенных модулей и правиль-
ностью изготовления имитатора сопрягае-
мого модуля.
В общем случае имитатор соответ-
ствует массе сопрягаемого модуля, рас-
положению центра масс относительно
опорных поверхностей, главным централь-
ным моментом инерции и геометрическим
параметрам — конструкции, взаимному
расположению и точности выполнения ба-
зовых поверхностей, т. е. по существу
это должен быть сам сопрягаемый мо-
дуль, отбалансированный методом двух
сборок. Все соединения выполняют по без-
зазорной посадке. В частных случаях
допускают упрощение. Например, при ста-
тической балансировке составных роторов
не требуют имитации главных централь-
ных моментов инерции отсутствующих де-
талей.
Метод раздельной балансировки моду-
лей. Рассмотрим метод раздельной балан-
сировки модулей при статической баланси-
ровке составного ротора, ось вращения
которого определяется одним модулем.
Статическую балансировку модуля, опре-
деляющего ось вращения ротора, выполня-
ют с уравновешенным имитатором, уста-
навливаемым на посадочное место отсут-
ствующего модуля. Модуль, не определяю-
щий ось вращения составного ротора,
балансируют статически на оправке, массу
которой в этом случае выбирают про-
извольно. т. е. она может не повторять
сопрягаемый модуль. После соединения
обоих модулей получают сбалансирован-
ный ротор.
Статическая балансировка межопор-
ного составного ротора, ось вращения
которого определяется двумя модулями,
зависит от взаимного положения их осей.
Имитатор каждого модуля выполняют в
виде сосредоточенной массы (фланца) с
присоединенной к нему опорой. При этом
имитатор повторяет геометрию стыка,
расположения стыка относительно опор
112
Низкочастотная балансировка роторов
и реакций связей, накладываемых стыков
на сопрягаемые натурные модули при
сборке ротора. Способ изготовления этого
имитатора целесообразно рассмотреть па
конкретном примере (рис. 4.13). Из урав-
нений статики для каждого модуля опре-
деляются реакции связей в стыке, т. е.
эквивалентный вес, воспринимаемый рас-
сматриваемым модулем. Так, для модулей
/ и 2 уравнения имеют вид
£Fi — RA + /?стЛ — Gi -= 0;
— R„ л Gil(l А — 0
и XF2 = RB 4-/?ст й- G2 = ();
— /?ст BlC f в Glc в,
где RB- реакции опор ротора: G (, С2 —
реакции от весов натурных модулей;
^стл. RCth реакции опор в стыке (экви-
валентная присоединенная масса, действу-
ющая на рассматриваемый модуль при
сборке ротора); /ст л, /стВ — расстояние от
стыка до опор А н В, lGA, lGB—рас-
стояние от центров масс натурных моду-
лей 1 и 2 до опор Л и В.
Тогда эквивалентный вес, присоединен-
ный в стыке, может быть определен
по зависимостям
^1^&’|/4тД'== Gt R.a'i
R^t в ~ Gzl(i 2/4т в — G-2 —- RB-
Таким образом, величина реакции в
стыке каждого модуля определяется как
его весом, так и отношением расстоя-
ний от центра масс модуля до соот-
ветствующей опоры и от нее до плос-
кости стыка. При изготовлении имитатора
заданное значение реакции получают кор-
рекцией эквивалентного веса фланца на
весах. Фланец устанавливают наружным
диаметром на призму, закрепленную на ве-
сах. Второй конец имитатора в плоскос-
ти опоры устанавливают на шарнирную
опору, размещенную рядом с весами Ба-
лансировку каждого имитатора осущест-
вляют методом двух сборок с сопряга-
емым натурным модулем.
Подготовленный таким образом имита-
тор собирают с сопрягаемым модулем
для балансировки последнего. При этом
измеренные на балансировочном станке
дисбалансы ротора корректируют на моду-
ле. После раздельной балансировки моду-
лей с имитаторами их совместную балан-
сировку не проводят.
В практике эксплуатации лопаточных
машин со съемными рабочими лопатками
нередко возникает необходимость их заме-
ны. Замену рабочих лопаток ротора осу-
ществляют как поштучно, так и целыми
комплектами. При поштучной замене лопа-
тки подбирают с такими же значениями
статических моментов, как у заменяемых.
Однако при необходимости замены одной
лопатки в комплекте целесообразнее заме-
нять сразу пару лопаток, подбирая ее с
таким же значением суммарного статичес-
кого момента, при диаметрально противо-
положном расположении заменяемых ло-
паток — с такой же разностью их стати-
ческих моментов.
Наиболее сложным случаем является
замена целого комплекта лопаток. Основ-
ные технические требования, предъявляе-
мые к комплекту рабочих лопаток, следую-
щие: дисбалансы, создаваемые замени
емым и заменяющим комплектами, должны
быть равны по величине и углу, ком-
плект лопаток должен обеспечивать равно-
мерность нагружения обода диска, раз-
ности масс заменяемого и заменяющих
комплектов, а также лопаток в противо-
лежащих пазах диска должны быть мини-
мальными.
Ниже рассмотрены схемы технологи
ческих процессов балансировки рабочих
колес лопаточных машин, при которых
модулями являются диск и комплект ра-
бочих лопаток.
Для балансировки модулей рабочих ко-
лес можно использовать метод совмест-
ной балансировки модулей. Выявленные
при этом дисбалансы устраняют на со-
ответствующих модулях: на модуле дис-
ка — корректированием масс; на модуле
комплекта лопаток — перераспределением
лопаток и (или) корректированием их
Балансировка модулей роторов
113
масс. Однако применение метода ^двух
сборок довольно трудоемко и не' при-
годно для рабочих колес, лопатки которых
имеют бандажные или антивибрационные
полки. Для таких рабочих колес, выпускае-
мых серийно, целесообразнее использовать
метод раздельной балансировки модулей.
Этот метод предусматривает балансировку
модуля диска с комплектом-имитатором
рабочих лопаток и статическую баланси-
ровку комплекта рабочих лопаток. После
установки рабочих лопаток на диск сба-
лансированность сохраняется.
Технологический процесс статической
балансировки комплекта рабочих лопаток
распределением по пазам диска с помощью
ЭВМ Для статической балансировки
комплектов рабочих лопаток до заданного
значения дисбаланса используют автома-
тизированное рабочее место комплектов-
щика комплекса АРМКо-1.
Комплекс АРМКо-1 объединяет элек-
тронные моментные весы, микроЭВМ и
печатающее устройство. Передача резуль-
татов измерения от весов в ЭВМ осуще-
ствляется автоматически. После взвешива-
ния последней лопатки исходного массива
выполняется расчет распределения лопа-
ток по пазам диска с заданным дис-
балансом — комплектовка лопаток.
Время расчета не превышает I мин.
Величина остаточного расчетного дисба-
ланса комплекта не превышает единицы
последней цифры измерительного значе-
ния статического момента. При этом вели-
чина остаточного дисбаланса комплекта
DCCT < .
где /)р — остаточный расчетный дисбаланс
комплекта; Dt\s ~ 2,4о15^/п — остаточный
дисбаланс комплекта из-за погрешности
измерения статических моментов рабочих
лопаток (здесь oys — среднее квадратичес-
кое отклонение ошибки измерения стати-
ческого момента лопатки; п - число лопа-
ток в комплекте).
Математическое обеспечение комплек-
са АРМКо-1 позволяет выполнять уравно-
вешивание комплекта рабочих лопаток до
заданного значения дисбаланса путем
минимального числа перестановок относи-
тельно самоуравяовешивающей круговой
диаграммы, производить замену одного
комплекта другим после взвешивания ло-
паток обоих комплектов на весах при
работе в автоматическом режиме или при
ручном вводе значений статических момен-
тов лопаток с пульта ЭВМ, заменять часть
лопаток комплекта с подбором заменяю-
щих лопаток из дополнительного массива
с таким же значением и методом
дисбаланса. Статическая балансировка
комплекта рабочих лопаток выполняется
за счет подбора их взаимного положе-
ния на диске, а не в результате пере-
бора большого числа лопаток. Обеспе-
чение равномерной нагрузки по ободу
диска, минимальной разности масс лопа-
ток в противолежащих пазах диска дости-
гают распределением комплекта лопаток
по самоураяновешиваюшей круговой ди-
аграмме. Измерение статических моментов
рабочих лопаток выполняют на моментных
весах. При этом радиус крепления лопатки
на весах должен быть равен радиусу
крепления ее на диске с учетом его
температурного и упругого увеличен ин при
работе изделия.
Комплект-имитатор рабочих лопаток,
используемый для динамической баланса
ровки ротора, должен отвечать следукиним
техническим требованиям: лопатки ком-
плекта-имитатора должны устанавли-
ваться в пазы диска и не контакт
ровать между собой, точность балансиров-
ки комплекта-имитатора должна быть вы-
ше на один класс точности по ГОСТ [Г 9]
по сравнению с заданной разработчиком
изделия для рабочего модуля (комплек-
та рабочих лопаток), предварительную
статическую балансировку технологи
ческого комплекта выполняют с помощью
ЭВМ по той же программе, что и рабочие
комплекты. При этом для распределения
лопаток комплекта-имитатора и рабочего
комплекта используют одну и ту же само-
уравновешивающую круговую диаграмму.
Дальнейшее снижение главного векто-
ра дисбаланса технологического комплек-
114
Низкочастотная балансировка роторов
та осуществляют за счет съема метал-
ла с лопаток без нарушения круговой
диаграммы их распределения по статичес-
ким моментам, дисбалансы комплекта-
имитатора и рабочего комплекта должны
быть равны. Для обеспечения полной
взаимозаменяемости их обычно выполняют
минимальными. Масса комплекта-имита-
тора лопаток не должна отличаться от
средней массы комплектов-модулей более
чем на 0,5%. Выполнение данного требова-
ния при использовании обычных лопаток
затрудйительно, так как при доработке
всех лопаток комплекта-имитатора для
обеспечения гарантированного зазора
между ними их масса уменьшается. Эту
задачу решают следующим образом. Опре-
деляют уменьшение массы рабочих лопа-
ток при их доработке. Массив лопаток
для изготовления комплекта-имитатора бе-
рут большим, чем необходимое число
лопаток, входящих в комплект. Взвешива-
ют лопатки и распределяют их в ряд
по возрастанию веса. Из ряда выбирают
все лопатки, масса которых меньше суммы
масс самой легкой лопатки в ряду и той
массы, которую удаляют при доработке
лопатки. Затем такое же число «тяжелых»
лопаток отделяют с другой стороны ряда.
Если при этом оставшийся массив лопа-
ток больше, чем число лопаток в ком-
плекте, то его уменьшают равномерным
удалением лопаток с обоих концов ряда.
4.6. ОСОБЕННОСТИ БАЛАНСИРОВКИ
КОЛЕНЧАТЫХ ВАЛОВ
Состояние уравновешенности коленча-
тых валов двигателей внутреннего сгора-
ния может быть достигнуто за несколько
циклов балансировки. Число циклов ба-
лансировки определяется соотношением
статистического (или расчетного) началь-
ного Он и требуемого остаточного £),
дисбаланса коленчатого вала. При этом
коэффициент кратности балансировки
Ki = DJDO. Автоматическое балансиро-
вочное оборудование за один никл обес-
печивает гарантированное снижение дис-
баланса в 8-12 раз. Следовательно,
ориентировочное число циклов баланси-
ровки коленчатого вала Ц lg DJDO
(Ц = 1,2,...). По статистике, большин-
ство коленчатых валов требует двух-
кратной балансировки (Ц = 2).
Обычно зона удаления дисбаланса,
определяемая формой противовеса колен
чатого вала как сектора круга, ограни
чена углом 90° —140° в зависимости от
типа коленчатого вала. При этом после
первой балансировки необходимо сохра-
нить остаточный вектор дисбаланса в зо-
не противовеса для осуществления второй
балансировки. Сохранение вектора в зоне
противовеса при двухкратной балансиров-
ке обеспечивают введением коррекции по
величине и углу вектора начального дис-
баланса.
На рис. 4.14 показана зона удаления
дисбаланса в противовесе, определяемая
углом ВОЛ'(2уГ1).
Вектор начального дисбаланса Du
(отрезокJJL} компенсируют вектором кор-
рекции DK (отрезок NA), отличающимся
по величине от DH на величину А (отре-
зок О А) и на угол а. Эти отличия
и определяют вводимую коррекцию векто-
ра дисбаланса. Зона удаления дисбаланса
определяется углом 2ут, а зона допусти-
мого расположения вектора Ьн — углом
2(ут — ал) Погрешность измерения и
компенсации вектора дисбаланса опреде-
ляется зоной круга с радиусом Д£)о.
Коррекцию по углу вводят по закону
Рис. 4.14. Коррекция вектора по углу и ве-
личине в зоне противовеса
Особенности балансировки коленчатых валов
115
а= — ат, поэтому она максимальна на
Ут
на краях зоны противовеса и равна нулю
в центре при расположении Он в направле-
нии оси симметрии ОС. Изменение а
происходит по линейному закону в зави-
симости от у. Остаточный дисбаланс проти-
вовеса для проведения второй баланси-
ровки определяют с помощью векторов
б и Вектор 6 может быть найден
из соотношения | б |2 — | Л ]2 4- | £>н |2 sin а2.
Для сохранения остаточного вектора б +
4- Д£>о в зоне противовеса необходимо
соблюдение граничных условий
sin ат ат >тУ-|. I А] > i &ЬС I
I I
при 2ym = л/2
и |Д|1>0,8|ЛРо| при 2тт = 2л/3.
Если ввести понятия коэффициента
кратности балансировки без коррекции
(k[ — |ДН1/|ДДО| и ожидаемого коэффици-
ента кратности балансировки при кор-
рекции (Кк = |Дн|/|б“|), то
К,
Кк = - t!------»
V14-a2Kf
где a= sin а, так как since С 1.
Если принять гарантированный Ki —
— 10, то при а—0 K*=Ki — 10, т. е.
при расположении вектора начального дис-
баланса в центре противовеса кратность
балансировки максимальна. В худшем слу-
чае, когда a—Om^QJ рад. Кк=7. Прак-
тически коррекцию по величине дисбалан-
са осуществляют уменьшением масштаба
измерения относительно истинного значе-
ния вектора начального дисбаланса. Кор-
рекцию по углу дисбаланса осуществляют
введением вспомогательного вектора
опорного сигнала, направленного по оси
симметрии ОС, с которым суммируется
основной вектор опорного сигнала.
Описанный выше метод коррекции по
величине и углу дисбаланса применяют
в случае, когда первый и второй циклы
балансировки осуществляют в разных
противовесах коленчатого вала, а зоны
противовесов совпадают в пространстве
по углу и величине сектора. В случае,
когда оба цикла балансировки осущест-
вляют в одном противовесе, появляется
опасность совпадения вектора остаточного
дисбаланса б 4- с направлением ком-
пенсирующего вектора DKl что может при-
вести к поломке инструмента коррекции
дисбаланса. В 'этом случае применяют
постоянную по величине коррекцию по углу
дисбаланса а = ат = const. Если вектор
начального дисбаланса £)н расположен в
квадранте 1, то угол а направлен против
часовой стрелки. При расположении Ь*
в квадранте 2 угол а направлен по часо-
вой стрелке в сторону увеличения у
При такой коррекции зона погрешности
Д£)о должна находиться в одном квадран-
те с Ьц при у — ут. В этом случае оста-
точный вектор б 4- KDO при любом у оста-
ется в зоне противовеса, определяемой
углом 2ут. Для данного метода коррекции
16 |2 = |Д|2 4- |DHp sin a2;
j А | —= | ДДо Icosec Ъл + I| sina„, ctgym;
____________________К___________.
V(cosecyTO 4- Я, sinaknctgy„1)24* K?sina*
Этот метод коррекции обеспечивает
меньший коэффициент кратности баланси-
ровки, чем предыдущий. Так, при ут~ л/4,
Kt = 10, sincu — 0,1 ожидаемый К* ~ 4.
Описанные методы коррекции применяют
при балансировке коленчатых валов в двух
и в большем числе плоскостей коррек-
ции.
Поскольку коленчатые валы относятся
к жестким роторам, состояние их уравно-
вешенности может быть достигнуто дина-
мической балансировкой в двух плоскостях
коррекции. Однако из-за зональных огра-
ничений, необходимости двухкратной (или
более) балансировки и конструктивных
особенностей большинство коленчатых ва-
лов требуют многоплоскостной баланси-
ровки. При коррекции дисбаланса в разных
116
Низкочастотная балансировка роторов
противовесах коленчатого вала обеспечи
кается высокий коэффициент кратности
балансировки и устраняется вероятность
поломки инструмента. При многой л ос кост-
ной балансировке начальный дисбаланс
измеряют в двух плоскостях коленчатого
вала. Далее этот дисбаланс пересчитыва
ют в л плоскостей вала. При переходе
к п плоскостям выполняют условия ра
венства нулю суммы начальных £)н
и корректирующих DK дисбалансов, а так
же суммы начальных Л4Н и корректирую-
щих Л4К моментов дисбалансов, т. е.
£ «,,+ £Д,,=0;
S= 1 f ==2
£ м,,+ X «,.,==о
s=.п I 2
(4.1)
где
Мк = хОк и Мн = xD„.
Ввиду тою что уравнений для поиска
DKS два, а число плоскостей коррекции
S больше двух, система уравнений явля-
ется неопределенной. Для придания опре-
деленности эту систему дополняют уравне
ниями, отражающими возможности балан-
сировочной техники. Ниже рассмотрены
методы многоплоскостпой балансировки
коленчатых валов типичных конструкций.
На рис. 4.15,а показан коленчатый вал
V-образною восьмицилиндрового двигате-
ля. Коленчатый вал такого двигателя
имеет четыре шатунные шейки (/—4), на
каждой из которых закрепляют по два
шатуна с поршнями. Шатунные шейки
1, 4 находятся под углом л/2 к шейкам
2,3. Видно, что коленчатый вал конструк-
тивно неуравновешен. Поэтому перед ба-
лансировкой на шейках закрепляют техно-
логические грузы с массой, равной при-
веденной массе шатуна и поршня, или
осуществляют на станке противофазное
с коленчатым валом вращение контргру-
зов, компенсирующих центробежные силы
от конструктивного дисбаланса. Выбор
способа компенсации конструктивной не-
уравновешенности определяется точ-
ностью изготовления шеек коленчатого ва-
ла Коррекция сто дисбалансов возможна
только в противовесах /, 11, V и VI.
Секторы противовесов не охватывают 360°
возможного направления вектора началь-
ного дисбаланса. В связи с этим началь-
ный дисбаланс на стадии изготовления
заготовки вала должен быть заложен
в секторы противовесов в левой и правой
плоскостях. При этом зона расположе-
ния начального дисбаланса должна быть
на 5° 10е уменьшена с каждой стороны
противовеса для (цианизации двухкратной
или трехкратной балансировки (метод кор-
рекции вектора начального дисбаланса по
величине и углу для сохранения вектора
остаточного дисбаланса в зоне второй
балансировки описан выше). Балансиров-
ку коленчатого вала осуществляют сверле-
нием материала противовесов в полярной
или прямоугольной, системах координат.
В противовесах 1 и VI выполняют пер-
вую (предварительную) балансировку. Эту
балансировку осуществляют с коррекцией
вектора начального дисбаланса по величи-
не и углу дисбаланса, поэтому вектор
остаточного дисбаланса сохраняется в зо-
не противовесов 11 и I, где производят
вторую (финишную) балансировку. Перед
второй балансировкой осуществляют новое
измерение дисбалансов вала для выявле-
ния параметров векторов начального дис-
баланса в зонах прот ивовесов 11 и V. Эту
балансировку осуществляют без коррек-
ции по величине и углу до значений
На рис. 4.15,6 показан рядный колен-
чатый вал четырех цилиндрового двигате-
ля. Коленчатый вал имеет четыре шатун-
ные шейки, смещенные попарно на угол л,
на каждой из которых закрепляют шатун
с поршнем. Коленчатый вал конструктивно
уравновешен и не требует для баланси-
ровки технологической оснастки. Баланси-
ровку вала осуществляют сверлением ма-
териала противовесов в прямоугольной
системе координат ±Л, ±У. В направле-
Особенности балансировки коленчатых валов
117
8)
Рис. 4.15. Балансировка коленчатых валов типовых конструкций:
а} У-образный коленчатый вал нос ьмицнл кадрового двигателя, б) рядный коленчатый вал четырех-
цилиндрового двигателя; к) трехкоординат иый коленчатый вал тестицилиндрово! о двигателя
нии —X, —Y сверление выполняют в на-
ружных противовесах /, IV, а в нанравле
нии X, У — во внутренних противовесах
11, 111. Балансировка коленчатого вала
однократная, поэтому в заготовке необхо-
димо обеспечить начальный дисбаланс
10|СЯО„|, где |£дс„| допуск на
остаточный дисбаланс вала При опре-
делении массы металла, необходимого для
устранения дисбаланса, следует обращать
внимание на моментную неуравновешен-
ность, требующую больше металла, чем
статическая. Число плоскостей коррекции
вала зависит от направления начальных
дисбалансов, отнесенных к противовесам
/, /V и их суммы или разности. При
этом возможны три основных случая.
Начальные дисбалансы в противо-
весах I, IV находятся в квадрантах
—ХО - Y. Балансировку вала осуществля-
ют сверлением в противовесах / и IV до
допустимых значений остаточного дисба-
ланса.
Начальные дисбалансы в противовесах
I, IV находятся в квадрантах XOY.
Балансировку вала выполняют в двух
средних противовесах (Н, III) и в одном
из крайних противовесов (/ или IV).
В каждом из средних противовесов устра-
няют дисбаланс, равный по величине боль
118
Низкочастотная балансировка роторов
тему из начальных дисбалансов в крайних
противовесах. При такой балансировке
и симметрии коленчатого вала относитсль
но центра масс в одном из крайних
противовесов (/ или IV) полностью устра-
няется больший из начальных дисбалан-
сов. На другом противовесе, имевшем
меньший начальный дисбаланс, появля-
ется дисбаланс, равный разности началь-
ных дисбалансов, но расположенный в
квадранте —ХО —У, который и устраняет-
ся сверлением в этом противовесе.
Начальные дисбалансы в противовесах
I, IV находятся в разных квадрантах
(—ХО —У и XOY). Балансировку вала
осуществляют в двух средних противове-
сах (II, III) и в одном из крайних
противовесов (/ или IV). Дисбаланс, изме-
ренный в плоскости одного из крайних
противовесов (/ или IV) и расположенный
в квадранте XOY, устраняют в двух сред-
них противовесах (II, III), как в предыду-
щем случае. На втором противовесе, век-
тор дисбаланса которого был расположен
в квадранте —ХО — У, появляется дисба-
ланс, равный сумме начальных дисбалан-
сов; суммарный дисбаланс устраняют
сверлением в этом противовесе. Выбор
варианта балансировки в зависимости от
соотношения и направления начальных
дисбалансов обеспечивается логической
схемой станка. Возможны и другие методы
балансировки коленчатого вала.
На рис. 4.15,в показан трехкоординат-
ный коленчатый вал шестицилиндрового
двигателя. Шатунные шейки вала смеще-
ны в пространство под углом 2л/3.
Коленчатый вал конструктивно уравнове-
шен и не требует для балансировки
технологической оснастки. Коррекцию дис-
баланса осуществляют сверлением или
фрезерованием. Сверление наиболее пред-
почтительно для быстроходных коленчатых
валов, требующих высокой точности ба-
лансировки. Измерение и коррекцию дис-
балансов выполняют в косоугольной систе-
ме координат с углом при вершине 2л/3.
При этом можно заметить, что коорди-
наты косоугольной системы X (противо-
весы HI, IV), У (//, V) и Z (/, VI) сме-
щены по длине вала в левой и правой
плоскостях коррекции. Последнее требует
изменения настройки станка по масштабу
и разделению плоскостей коррекции, что
достаточно сложно. Для упрощения зада-
чи действие векторов начального дис-
баланса DH связывают, например, с плос-
костями III и IV (О3 „ и D4fl соответствен-
но). Если предположить, что вектор распо-
ложен в^ плоскости III и направлен вдоль
оси X (£>3 н л), то его устраняют сверлени-
ем в противовесе III. При направлении
вектора вдоль оси Y(D3li у) его устранение
в противовесе III невозможно. В этом
случае начальный вектор D3 н г расклады-
вают на две плоскости (/ и VI). Используя
уравнения (4.1), можно записать выра-
жения для модулей векторов коррекции
дисбаланса: £>1кУ и Д6кУ соответствен-
но в плоскостях I и VI
П П 2а 4* b „ __2а
Если начальный дисбаланс в плоскости
III совпадает с осью Z (D3hZ), то его
раскладывают на плоскости II и V и кор-
ректируют векторами £>2к2 и £>5kZ; имея
для модулей векторов коррекции дисбалан-
са выражения
г) ___ Г) a-f-b . гх ______ п а
Аналогичные выражения для модулей
векторов коррекции дисбаланса могут быть
получены для правой стороны коленчатого
вала при расположении начального дисба-
ланса в плоскостях IV (Ь4 и). При совпаде-
нии начального дисбаланса с осью X
&4 к X — ^4нХ‘
При совпадении с осью У:
D у = О 4 у —-----—
1К r 4a-Vb
гу ___г) 2g -|- ft
Балансировка обработкой цапф или центров
119
При совпадении с осью Z:
Г) ___ Г) & . г) __ Г) Ь
°2kZ L'4hZ 2a + b ' 2a + b '
В промышленности помимо рассмот-
ренных выше случаев осуществляют ба-
лансировку коленчатых валов в сборе с
маховиком и шкивом. Перед монтажом с
маховиком коленчатый вал предваритель-
но балансируют ло одному из описанных
методов. Балансировку коленчатого вала в
сборе с маховиком выполняют, как прави-
ло, в одной плоскости маховика за счет
его сверления в полярной или прямо-
угольной системе координат. Балансиров-
ку коленчатого вала в сборе с махо-
виком и шкивом осуществляют в двух
плоскостях коррекции За счет плоскостей
шкива и маховика производят и дина-
мическую балансировку двигателя в сборе
с учетом влияния шатунне-порш невой
группы и динамики работы двигателя.
4.7. БАЛАНСИРОВКА ОБРАБОТКОЙ
ЦАПФ ИЛИ ЦЕНТРОВ
Балансировку обработкой цапф или
центров достигают приближением геомет-
рической оси ротора к его главной
центральной оси инерции или их совмеще-
нием. Следует учитывать, что при обработ-
ке цапф вокруг нового положения геомет-
рической оси происходит смещение глав-
ной центральной оси инерции вследствие
съема неравномерного припуска материа-
ла обрабатываемых поверхностей. При
этом полагают, что сама неуравновешен-
ная масса т не изменяется ни по величине,
ни по положению.
Пусть в некоторой плоскости
(рис. 4.16) положение центра масс О\ не
совпадает с геометрическим центром О.
Их относительное смещение е определено
дисбалансом D, внесенным неуравнове-
шенной массой т. Дисбаланс массы т
относительно центра инерции компенсиро-
ван массой криволинейного участка (за-
штрихованный участок). При обработке
цапфы до цилиндрической поверхности ра-
Рис. 4.16. Центрирование ротора
диуса rj с переменным припуском вновь
возникает дисбаланс D' = D — /не:
D' = (p + rj cos tty,
о
где у — плотность материала; й — длина
цилиндрической поверхности (на рис. 4.16
оиа не показана); <р — текущий угол меж-
ду радиусом-вектором начальной поверх-
ности, проведенным из точки Oi, и осью Х\
р — модуль радиуса-вектор а начальной
поверхности, проведенного из точки О».
Последний определяют с помощью уравне-
ния
р — е I cos
— sin2
где г — радиус начальной поверхности.
Метод балансировки обработкой напф
или центров применим для роторов, длина
базирующих поверхностей которых много
меньше их общей длины. У таких рото-
ров дисбаланс, вносимый переменным при-
пуском на цапфах при их обработке отно-
сительно новой оси, много меньше началь-
ного дисбаланса. Для определения коорди-
нат новых центровых отверстий, определя-
ющих положение новой геометрической
оси ротора, следует:
измерить дисбаланс ротора;
разложить измеренный дисбаланс на
статическую и моментную составляющие;
рассчитать вектор плоскопараллельно-
го смещения ест центра масс ротора по
120
Низкочастотная балансировка роторов
статическому дисбалансу и известным мас-
сам колебательной системы и ротора;
рассчитать угол поворота ф оси инер-
ции ротора относительно его центра масс
и перевести его в векторы линейных
перемещений ём в горновых плоскостях
ротора по моментному дисбалансу и из-
вестным главным центральным моментам
инерции системы и ротора;
рассчитать координаты f новых центро-
вых отверстий в торцовых плоскостях
как сумму;
F -= ёст +
Все это удобно производить по проек-
циям в прямоугольной системе координат
ротора. Для более точного учета пара-
зитных масс опор первоначальную на-
стройку станка целесообразно производить
с использованием тарировочного ротора.
Точность балансировки и уменьшение
дисбаланса зависят от многих факторов,
например от точностей определения дис-
баланса и его математической обработки,
формирования новых центровых отверстий
и базовых поверхностей цапф, а также от
соотношения между начальным дисбалан-
сом и припуском на их обработку и пр.
Метод применим в основном для пре
дварительной балансировки заготовок с
целью уменьшения их динамического воз-
действия на технологическое оборудование
и начального дисбаланса при оконча-
тельной балансировке. Практически, при
балансировке коленчатых валов двигате
лей внутреннего сгорания, дисбаланс уда-
ется уменьшить в 3 4 раза и довести
его до 200— 300 г • мм/кг.
4.8. КОНТРОЛЬ КАЧЕСТВА
БАЛАНСИРОВКИ РОТОРОВ
Показателем качества балансировки
является значение дисбаланса, оставшего-
ся после проведения корректировки масс
ротора. Критерием оценки качества балан-
сировки служит допустимое значение дис
баланса, а базой отсчета - нулевое или
некоторое расчетное значение, при кото-
ром ротор п а ил уч шим образом взаимодей-
ствует со смежными элементами кон-
струкции. В отдельных случаях может ока
заться важным не только значение, по
и угол остаточного дисбаланса.
Качество балансировки может быть
оценено величиной:
главного вектора и главного момента
остаточных дисбалансов;
остаточного удельного дисбаланса;
остаточного дисбаланса в плоскостях
коррекции.
В общем случае задача контроля
качества балансировки сводится к опре-
делению дисбалансов D в плоскостях
коррекции.
Пусть жесткий ротор имеет N плос-
костей коррекции и столько же связанных
с ними плоское гей измерения. Рассматри-
вая эту совокупность как линейное век-
торное пространство, представим ее систе-
мой N линейных векторных уравнений:
А ~ йп Dy 4- D2 4~ • 4- О[ v D^ ;
Лд = Dy -}- 022^2 4" • 4~a2xD;\; (4.2)
Лv 1 Dy 4 вд 2D<i 4-.. 4-o.w D^ ,
или в матричной форме:
А, — {a,,}D, (j — 1,2,.. . ,A; i =
= 1. 2, . . . ,A),
где A, — вектор реакции системы в плос-
кости измерения / на действие векторов
дисбалансов D, в /V плоскостях кор-
рекции; а,,— коэффициент влияния дис-
баланса в i-й плоскости коррекции на
реакцию системы в j-й плоскости изме-
рения.
Задачей балансировки и контроля ее
качества являются определение с доста-
точной точностью коэффициентов влияния
flji совокупности Лр которое обычно про-
изводят экспериментально, и решение сис-
темы уравнений (4.2) относительно Dt.
Методы оценки значения дисбалансов ро-
тора в плоскостях коррекции во многом
характеризуется способами определения
att и Л,, которые, в свою очередь, зависит
от применяемого оборудования и аппара-
туры.
Контроль качества балансировки роторов
121
Аппаратура, выполняющая измерение
параметров колебаний на частоте враще-
ния ротора в плоскостях измерения и
обеспечивающая при этом разделение
плоскостей коррекции, получила название
балансировочной, а аппаратура, не имею
щая цепей разделения плоскостей коррек
ции, - виброизмерительной. Общим для
балансировочной и виброизмерительной
аппаратуры является возможность измере-
ния параметров колебаний на частоте
вращения ротора.
Балансировочная аппаратура может
входить в состав балансировочного станка,
применяться отдельно в виде комплекта,
или входить в состав виброизмерительной
аппаратуры. Балансировочный комплект
представляет собой, по существу, вы-
числительное устройство, решающее зада-
чу вычисления Д по измеренным А,
в соответствии с введенными коэффициен-
тами влияния afl.
Методы контроля с использованием
балансировочной аппаратуры. Перед нача-
лом работы аппаратура должна быть на-
строена на соответствующий контроли-
руемый ротор, т. е. в измерительную систе-
му должны быть введены коэффициенты
aft Выявление и введение этих коэф-
фициентов в балансировочных станках
зарезонансного типа производят установ-
кой контрольных дисбалансов в плоскости
коррекции контрольного или тарировочно-
го ротора, приведением к нулю показа-
ний индикаторов дисбаланса в плоскостях,
отличных от плоскости установки конт-
рольного дисбаланса, и выявлением мас-
штабного коэффициента между установ-
ленным дисбалансом и показанием инди-
каторов. В балансировочных станках до-
резонансного типа коэффициенты а/(
вводят при настройке измерительной сис-
темы по геометрическим размерам ротора
(расстояние между плоскостями из мере
пия. расстояния от плоскостей коррекции
до плоскостей измерения, радиусы кор
рекции).
Метод непосредственного измерения
дает достаточную точность при измерении
в плоскостях коррекции дисбалансов,
имеющих значительную величину, соответ-
ствующую положению указателя во вто
рой половине шкалы индикатора дисбалан
с а. Масштабный коэффициент влияния
связывающий дисбаланс Dt в i-й плоскос-
ти коррекции и показания Д, индикатора
дисбаланса /й плоскости измерения, уста-
навливают при настройке. В этом случае
Aj/Иц
Усол дисбаланса определяют непосред-
ственно по показаниям соответствующего
индикатора.
Метод контроля пробными грузами
применяют для определения малых вели-
чин остаточного дисбаланса, при которых
отклонение указателя индикатора величи-
ны дисбаланса не превышает 0,2 шкалы.
Он основан на проведении серии изме-
рений с пробными грузами, для чего
в каждой из N плоскостей коррекции
ротора выбирают k (обычно 6 или 8)
точек, расположенных равномерно по ок-
ружности на одном радиусе гир. В каждую
из выбранных точек одной из плос-
костей коррекции i вводят пробный груз
массой тгр, создающий дисбаланс £)гр —
= /4(II/iip. По /-му индикатору дисбаланса,
связанному с проверяемой плоскостью
коррекции /, снимают ряд показаний
Ahlti (h = 1, 2,.. . , k) и Результаты
измерений записывают в форме таблицы.
Номер точки размещения пробного труза в плоек, i. п 1 2 Показания индикаторов
Плоскость 1 Плоскость 2 Плоскость 1
А । t 41 । й Ац * А..,, Ч'мй
Низкочастотная балансировка роторов
Индикаторы дисбаланса, связанные с
другими плоскостями коррекции настроен-
ного балансировочного станка и аппара-
туры, не изменяют своих показаний.
Из полученных величин Atjj, выбирают на-
ибольшее (А.<,л гпах) и наименьшее
(71, и вычисляют значение остаточ-
ного дисбаланса в данной i-й плоскости по
формуле
д _________д
i t Л max i»i л min
~А 4- А
£ max * t i £ mm
(4.3)
постоянство гпр, соответственно изменяют
массу щпр, добиваясь, чтобы
D, Ир = nPG пР = const.
После проведения аналогичных изме-
рений и вычислений во всех плоскостях
коррекции [Г 10] можно найти удельный
дисбаланс, главный вектор и главный мо-
мент дисбалансов.
Вычисленные значения D, и Дст могут
быть получены графически после выявле-
ния масштабного коэффициента
Угол этого остаточного дисбаланса
можно приближенно определить по вектор-
ной диаграмме (рис. 4.17). Для этого
контрольные точки в плоскости коррекции
Dt
___ ^,4f>
Рис. 4.17. Векторная диаграмма контроля дис-
баланса пробными грузами
связывают с координатной системой рото-
ра, на диаграмму наносят k точек, обозна-
чающих в некотором масштабе концы век-
торов Afj'h- В линейной изотропной систе-
ме эти точки образуют окружность, центр
которой (Л является концом вектора D„
соответствующего остаточному дисбалан
су и проведенного из начала координат
диаграммы. Направление этогр вектора в
координатной системе ротора есть угол
остаточного дисбаланса.
Величину т„р выбирают так, чтобы
значения Арм находились во второй поло-
вине шкалы индикатора дисбаланса. В том
случае, когда нет возможности обеспечить
(4.4)
Методы контроля с использованием
виброизмерительной аппаратуры. Метод
контроля с определением амплитуды и фа-
зы колебании. Коэффициенты afl влияния
дисбаланса Д в i-й плоскости коррекции
на показания А, в /-й плоскости измерения
определяют экспериментальным путем.
Для этого последовательно в каждую из /V’
плоскостей коррекции на радиусе г, пр
вводят пробный груз массой т{ создаю-
щий пробный дисбаланс О(пр = mtnpftnp,
и измеряют векторные параметры колеба-
ний в каждой из плоскостей измерения
А{ пр. Коэффициенты влияния определяют
по формуле
О/« | Л/ А{ Пр | /1 Д; Пр |,
а дисбалансы в плоскостях коррекции
Di — решением системы векторных уравне-
ний (4.2).
Для двухопорного жесткого ротора с
двумя плоскостями коррекции систему век-
торных уравнений (4.2) можно заменить
системой алгебраических уравнений в про-
екциях:
71 |Х = Ии Dix -f- ai^D^x,
А\у — a\\Dfy -4-
Aix — O2\D\x -|- a^D^x,
(4.5)
A?y — a?\D\y -f- 022Diyt
Контроль качества балансировки роторов
123
решение которой
г. ^1х°22 °]2^2л
'-'lx — --------------- >
С11С22 Й12а21
ОцЯ2л А иа2|
/-'О* ----- ’
QH «22 — «12^21
& А1уа22 °ЧА2у
!-У апа22 С12й21
__ С|1^2у ~ 1у°21 .
«ЦЯ22— «12«2|
D,=Vbt4-Dt; ^2 = VpL+^.
При необходимости углы дисбалансов
можно вычислить с учетом знаков проек-
ций по формулам
<Pt = arctg —= arctg
^lyfi22 °12^2у
^^а22~а12А-2Х '
, , °ll^2y Alv°2l
®2 — arctg -yr— = arctg-----------------
Метод контроля с определением ампли-
туды колебаний. Коэффициенты влияния
afi можно найти, используя графоаналити-
ческие приемы. В каждую из k точек
каждой из Л; плоскостей коррекции вносят
пробным грузом дисбаланс Dt пр. Необхо-
димо, чтобы пробный дисбаланс, вводимый
в различные точки одной плоскости, был
постоянен и превышав по значению пред-
полагаемый остаточный дисбаланс ротора
в этой плоскости.
Значения амплитуды Арь колебаний,
найденные в каждой из плоскостей изме-
рения. записывают в форме таблицы.
Коэффициенты влияния вычисляют по
формуле
~ (^/ih max “Ь А jih min) / лр)-
Если пробный дисбаланс меньше оста-
точного, то коэффициенты влияния следует
вычислять по формуле
(^/<Л max А jih mm) / пр) -
Эти формулы используют при вычисле-
нии коэффициентов влияния, имеющих
равные (/ = i) и неравные (/ i) индексы.
Применимость указанных формул можно
определить по векторным диаграммам, по-
строенным по таблице.
Дисбалансы, действующие в плос-
костях коррекции ротора, вычисляют, ре
шая систему векторных уравнений (4,2), а
для двухопорного жесткого ротора — по
формулам решения системы уравнении в
проекциях (4.5). Чем больше число k
контрольных точек в каждой из плоскостей
коррекции, тем точнее результат расчета.
Пример. Дан жесткий несимметричный
двухопорный ротор (рис. 4.18) массой т0 —
= 10 кг и размерами /( =- 600 мм и /2 — 400 мм
динамически отбалансированный на станке. В
плоскостях коррекции 1 и 2 выбраны по 8 точек,
расположенных на радиусе гпр = 100 мм через
Рис. 4.18. Пример жесткого несимметричного
ротора:
/. 2— плоскости коррекции
Пробный дисбаланс в плоек. i D, пр, г • мм Номер точки размещения груза в плоек. L h Показания индикаторов
Плоскость 1 Плоскость 2 Плоскость j
An/,. <pbj, A 2i ft, <f2, ft Aji.h
1 2
Пр нмечание. Число таблиц соответствует числу плоскостей коррекции.
124
Низкочастотная балансировка роторов
Рнс. 4.19. Векторные диаграммы к примеру
45° Масса пробного груза = 1 г.
Требуется определить остаточные дисбалансы
Измерительная аппаратура - настроенная
измерительная система балансировочного
станка.
Результаты измерения шачения и угла
дисбаланса ротора в плоскостях коррекции
1 и 2 при перестановке в них пробного
груза приведены ниже.
Номер точки размещения пробною груза в плоскостях / и 2 и Показания индикаторов
Плоскость 1 Плоскость 2
Значение •4 г in 1 и {сле- пнях ) У гол V,.,, Значение A 22k (в деле- ниях) Угол
1 38 13 58 49
о 50 63 52 85
3 64 103 14 124
4 70 139 34 175
5 68 172 32 237
6 58 208 38 293
7 46 252 48 337
8 36 308 56 14
Векторные диаграммы по результатам
измерений приведены на рис. 4.19.
По формуле (4.3) остаточные дисбалансы
в плоскостях коррекции
^UAinax ^ll/irniir
I In max I- ^Н»; пи,!
ПР
70 — 36
70 + 36
1 . 100 = 32 г • MM,
^22пгпих ^22Aintn
= д yj»P —
122*1 max I e 122л nrm
58 — 32 . inn on
= 7n-,-;v 1 • 100 — 29 г • мм.
58 4- 32
Углы дисбалансов
<p, = 152°; q>2 = 43°.
Угол между векторами дисбалансов Dt и £>2
ф = <pj — <j>2 —-109°.
Модуль главного вектора остаточных дис-
балансов
£»ст = /32? -|- 29а 4 2 -32-29- cos 109°=
=35,5 г - мм.
Модуль главного момента дисбаланса
Мп = V(32 - 600)2 4- (29 - 400)2 — 2 - 32 - 29 -
- 600 - 400 cos 109° = 18 870 г - мм2
Удельный остаточный дисбаланс
е= 35,5/10= 3.55 г - мм/кг.
По векторным диаграммам и формуле
(4.4) масштабные коэффициенты по плоскостям
коррекции
пр 1UU о ,
*'1 = о;^ “ ’2в- -3185 г мм/мм;
Г)1ц, 100 . с_ .
’* = «ЛГ - = '•5» г мм/“ •
откуда
Di = 9 - 3,85=34,6 г - мм; Р2 = 7-4,55 =
=31.8 г • мм.
Погрешность графического метода опреде-
ления значения остаточного дисбаланса в каж-
дой из плоскостей коррекции, по сравнению
с графоаналитическим, нс превышает 10%
Методы балансировки гибких роторов с применением пробных дисбалансов
125
Статическую и моментную составляницие
дисбаланса в каждой из плоскостей коррек-
ции можно выделить, пользуясь известными со-
отношениями и рис. 4.19,0. т. е.
D1„=7^/2=-^400=U.2r.MM;
= = «»=2|-3 г-мм-
На_ рис. 4.19, б показаны в масштабе век-
торы D\, ръ, DCT= Г)\На направлении
вектора ©ст отложены ©, ст и ©2 ст в плос-
костях коррекции £ и 2 Моментные состав-
ляющие DiM и ©2Л1 дисбалансов в плос-
костях 1 и 2 получены как
ЛГ ~ ст’
м = ©г — ©2 €г.
что соответствует в масштабе расчетным зна-
чениям.
Глава 5
ВЫСОКОЧАСТОТНАЯ БАЛАНСИРОВКА РОТОРОВ
5.1. КЛАССИФИКАЦИЯ МЕТОДОВ
БАЛАНСИРОВКИ
Деление роторов на классы, приведено
в гл. 1, где к 3-му классу относятся гиб-
кие роторы. Характерным для этого клас-
са роторов является необходимость учета
изгибных деформаций их оси во время
балансировки неособенно в эксплуатации.
Это крайне усложняет процесс баланси-
ровки и затрудняет установление общей
методики балансировки, пригодной для
гибких роторов любой категории.
В классификации, приведенной на
рис. 5.1, охарактеризованы не только су-
ществующие в настоящее время методы
балансировки, но и даны перспективные.
5.2. МЕТОДЫ БАЛАНСИРОВКИ ГИБКИХ
РОТОРОВ С ПРИМЕНЕНИЕМ ПРОБНЫХ
ДИСБАЛАНСОВ
Эти методы вытекают из решения
урацнения Фредгольма, основа иного на
теореме Гильберта - Шмидта.
Балансировка на критических частотах
вращения по измеренным прогибам ро-
тора. Метод балансировки по формам из-
гиба [5] вытекает из общих теоретичес-
ких предпосылок как для роторов с дис-
кретным, так и с любым распределением
масс.
На критических частотах вращения
имеется явная связь между прогибами,
относительными деформациями, реакция-
ми опор и теми составляющими разло-
жения эксцентриситета в ряд по формам
изгиба, которые их вызывают. На этой ос-
нове и можно идентифицировать указан-
ные составляющие эксцентриситетов и
скомпенсировать дисбалансы.
Допустим, что ротор имеет повышен
ные деформации по /г-й форме изгиба,
которые необходимо устранить путем ба-
лансировки. Для этого ротор разгоняют
до k-и критической частоты вращения и
измеряют его прогиб. Если ротор иссле-
дован ранее, то на основании опыта пре-
дыдущих работ, зная характеристику фор-
мы изгиба, измеряют прогиб лишь в одной
точке, а затем подсчитывают его но всей
длине. Разгон ротора осуществляют в спе-
циально приспособленном сооружении или
непосредственно в испытуемой машине.
Предположим, что каждое поперечное
сечение ротора имеет эксцентриситет,
больше того, в каждом сечении содержат-
ся составляющие этого эксцентриситета
по всем п формам изгиба. Тогда теоре-
тически для компенсации всех локальных
дисбалансов, вызывающих k-ю форму из-
гиба, необходимо разместить на валу рас-
пределенную по длине систему корректи-
рующих масс, статические моменты ко-
126
Высокочастотная балансировка роторов
высокочастотная балансировка роторов
Методы балансировки с применением пробных масс без выявления распределения дисбаланса Методы балансировки без применения пробных масс с выявлением распределения дисбаланса (методы идентификации эксцентриситетов)
Рис. 5.1. Классификация методов балансировки
торых равны соответствующим дисбалан-
сам.
Допустим, что имеется система, в ко-
торой корректирующие распределенные
массы р(г) располагаются на радиусах-
векторах вращения r(z), которые зависят
от конструкции изделия и удобства их
установки.
После такой коррекции исходный экс-
центриситет ротора изменится на вели-
чину
e(z) = p(z)r(z)/[m(z) +
где т (z) — распределенная вдоль оси мас-
са ротора.
В этой формуле учтено увеличение мас-
сы ротора за счет корректирующих масс.
Обычно корректирующими массами по
сравнению с массой ротора пренебрегают,
так как балансировку можно производить
не только добавлением или снятием ме-
талла, но и за счет перераспределения
масс, например перестановкой лопаток.
Поэтому в дальнейшем считают массу ро-
тора при балансировке не меняющейся.
Для определения значения и угла рас-
положения корректирующих масс на рото-
ре по его окружности применяют проб-
ные пуски с пробными дисбалансами. При
этом считают, что кривая прогиба на кри-
тических частотах вращения расположена
в одной плоскости, а зависимость между
прогибом и вызывающими его дисбалан-
сами — линейная. Кроме того, считают фа-
Методы балансировки гибких роторов с применением пробных дисбалансов
127
зовые углы между прогибами и дисба-
лансом на данной критической частоте вра-
щения одинаковыми для всех сечений ро-
тора и близкими к 90°.
После измерения прогиба ротора с на-
чальной неуравновешенностью на k-й кри-
тической частоте вращения в любом (по
углу) месте ротора размешают систему
произвольных по значению пробных дис-
балансов, распределенных вдоль вала по
£-й форме изгиба, т. е.
H*(z)r*(z) = bkyk(z)y.(2).
Затем повторяют на fe-x критических
частотах вращения измерения прогиба ро-
тора в прежних сечениях и подсчитывают
векторное изменение прогибов ротора на
Л-й критической частоте вращения, выз-
ванное внесенными пробными дисбалан-
сами. Для этого из вектора у J(z) прогиба
ротора с установленными на нем проб-
ными дисбалансами вычитают вектор ук{г}
прогиба ротора от начальных дисбалансов.
В соответствии с указанными допуще-
ниями отношение прогиба ротора, вызван-
ного пробными массами, к величине ста-
тистического момента этих масс равно от-
ношению прогиба ротора от начальных
дисбалансов к значениям этих дисбалан-
сов при Л-й форме изгиба, т. е.
l£?(z) -£fe(z)|/ [р *(z)r *(z)] =
= 4/*(z)Z (z)eA(z) 1.
Отсюда определяют значение дисба-
ланса m(z)ek(z) и корректирующих масс
p*(z) и их радиус установки rk(z), по-
скольку
т (г) ек (z) = р» (г) гк (г).
Зная место установки пробной массы и
места прогибов ук, у*, Ук~ Уь* которые
ориентированы относительно неподвижно
зафиксированного места на роторе, назы-
ваемого отметчиком угла, находят уточ-
ненный угол между расположением проб-
ной массы по /г-й форме и прогибом ро-
тора, вызванным пробной массой. Это важ-
но, ибо на практике не всегда можно
производить измерения точно на крити-
ческих частотах вращения, а лишь более
или менее к ним приближаясь, и тогда
фазовый угол будет отличен от прямого
Этот угол в дальнейшем принимается за
угол сдвига фаз между расположением
начальных дисбалансов по fe-й форме из-
гиба и прогибом ротора от этих дисба-
лансов.
Так, если на рис. 5.2 ОА — вектор проб-
ной массы, а у* — Уь~- вектор прогиба
ротора, вызванный этой массой, то угол
а* (угол между АО и прямой ОВ, па-
раллельной вектору у*-— уk) определяет
сдвиг фаз между неуравновешенной силой
и прогибом ротора на k-й критической
частоте вращения, причем вектор Qrp опе-
режает вектор У* — Уь в сторону враще-
ния ротора.
Поворачивая вектор прогиба у % на
угол а* в сторону вращения ротора, по-
лучают направление ОС, соответствующее
расположению на роторе плоскости, в кото-
рой расположен искомый дисбаланс.
Систему корректирующих масс уста-
навливают под углом 180° (ОС') к най-
денному таким образом дисбалансу. На
этом заканчивается один из этапов ба-
лансировки. Обычно производят баланси-
ровку не для одной fe-й критической час-
тоты вращения, а для всех критических
частот, попадающих в эксплуатационный
диапазон. В этом случае последовательно
по мере разгона ротора проводят балан-
сировку на первой критической частоте
128
Высокочастотная балансировка роторов
вращения, затем на второй, третьей, на-
конец, на максимально возможной.
Корректирующие массы, установлен-
ные для устранения прогиба (колебаний)
на какой-либо одной критической частоте
вращения, в силу условий ортогональности
не влияют на сбалансированность ротора
при другой критической частоте вращения.
Теоретически ротор, сбалансированный на
всех критических частотах вращения, бу-
дет сбалансирован и на всех других час-
тотах вращения, так как по формуле (1.13)
прогиб на любых частотах вращения скла-
дывается из прогибов на критических час-
тотах, умноженных на некоторое посто-
янное число
Величину корректирующей массы опре-
деляют также графическим путем
(рис. 5.3). Для этого необходимо выбрать
две координатные оси: У и гпг, на ко-
торых в определенном масштабе будут от-
ложены величины прогибов и статичес-
кие моменты масс для рассматриваемого
сечения ротора. На график наносят точки
у =- уп после запуска с исходной неурав-
новешенностью и у ~ тг—т\г\ — с
пробной массой т\, установленной на ра-
диусе ft
Прямая, проведенная через точки с
координатами у=У(ъ mr~Q и г; — у},
mr = miTi. при пересечении с осью абс-
цисс даст величину корректирующих масс,
при которой у — 0.
Балансировка на (вблизи) критичес-
ких частотах вращения по собственным
формам изгиба ротора ио измеренным виб-
Рис. 5.3. Графическое определе-
ние корректирующей массы
рациям или реакциям опор. На практике
применяют метод уравновешивания по
формам колебаний, в котором за основу
принимают вибрации опор. Преимущество
этого метода перед другими заключается
в том. что отпадает необходимость в из-
мерении прогибов ротора — операции, за-
частую более сложной и трудоемкой, чем
измерение вибраций опор.
При уравновешивании ротора по виб-
рациям или реакциям опор допускают, что
они одинаковы, а ротор симметричен. От-
сюда следует, что прогибы в сечениях,
расположенных на одинаковых расстоя-
ниях от центра массы ротора, будут равны
р направлены в одну сторону на первой,
третьей, пятой и остальных нечетных кри-
тических частотах вращения. При этом
они равны по величине и направлены в
противоположные стороны на второй, чет-
вертой, шестой и остальных четных кри-
тических частотах вращения ротора. Все
нечетные формы называют симметричны-
ми. а четные — кососимметричными.
Кроме этих допущений предполагают,
что при измерении реакций опор или их
вибраций на некоторой частоте вращения
существенными являются лишь те состав-
ляющие общей неуравновешенности ро-
тора, которые относятся к формам колеба-
ний, ближайшим к <о, т. е. со * < о < <о л+1.
Влиянием других форм для ш * С со < <n * t г
пренебрегают
Как показала практика, существует оп-
ределенный класс роторов, для которых
эти допущения оправданны и не влияют
на качество уравновешивания. К ним от-
носятся роторы турбогенераторов с длин-
ными, почти цилиндрическими валами,
опирающиеся на опоры большой жест-
кости.
Пусть имеется ротор (рис. 5.4) с рав-
номерно распределенной по длине массой,
опирающийся на одинаковые опоры. Фор-
мы колебаний такого ротора представляют
собой синусоиды, а амплитуды колебаний
динамического прогиба от k-й составля-
ющей неуравновешенности
yk = ак sin (nkz/L).
Методы балансировки гибких роторов с применением пробных дисбалансов
129
Рис. 5.5. Векторные построения при ба-
лансировке
Если на некоторых частотах со* <
С(о<:<|)*+1 измерить амплитуды верти-
кальных вибраций левой А{ и правой Дп
опор, то для симметричного ротора ампли-
туды этих вибраций можно разложить на
составляющие, одни из которых будут ха-
рактеризовать прогиб нечетных форм коле-
баний, а другие — четных. Симметричные
формы колебаний ротора могут образовать
симметричные реакции и вибрации, а ко-
сосимметричные формы — кососимметрич-
ные реакции и вибрации опор Чтобы по-
лучить необходимое разложение, сложим
и вычтем векторы и Дп. Затем, если
разложить амплитуды вибраций опор.Л]
и Л,, но направлениям, параллельным сум-
ме Д(-|-Дп и разности ц — Дь то оба
вектора А{ будут равны ОК— (А,-1-Ап)/2.
Эти векторы и являются симметричными
составляющими и характеризуют ту нечет-
ную форму колебаний, вблизи которой из-
мерялись векторы Aj и Дп.
Векторы Д2 равны вектору КС — (Дп —
— Д>)/2 и характеризуют ту четную форму
колебаний, вблизи которой измерялись
векторы Д| и Л,,. Эти векторы называют
кососимметричными составляющими. Угол
Р между векторами ОК и КС есть угол
между плоскостями симметричных и косо-
симметричных составляющих.
Для уменьшения влияния на вибрации
опор других форм колебаний необходимо
производить измерения вблизи критичес-
ких частот вращения, где преобладает
влияние лишь одной формы неуравнове-
шенности, которую следует сбалансиро-
вать.
Балансировку роторов производят сле-
дующим образом:
5 Зак 1641
1. Разгоняют ротор почти до первой
критической частоты вращения (0,85
0,95) о» и измеряют вертикальные виб-
рации опор Д1 и АИ.
2. На ротор устанавливают систему
пробных масс, вызывающих изгиб вала по
первой форме колебаний, причем эту сис-
тему устанавливают в любом месте по
окружности ротора вдоль одной из его
образующих. Повторяют измерения верти-
кальных вибраций А * и Д * на частотах
вращения, где были измерены вибрации
без пробных грузов.
3. Производят векторные построения и
определяют полусуммы векторов вибраций
при запусках без пробных масс и с проб-
ными массами (рис. 5.5, а, б). Вектор А}
будет равен полусумме векторов вибраций
Ai и Д„ при запуске без пробных масс,
а вектор А*—равен полусумме векторов
вибраций А * и A при запуске с проб-
ными массами, распределенными по пер-
Рис. 5.4. Разложение векторов вибраций на
составляющие
130
Высокочастотная балансировка роторов
вой форме колебаний ротора. Вектор А *_
— Ai (рис. 5.5. в) характеризует прогиб
ротора под действием установленных масс,
а угол между плоскостью расположения
пробных масс и вектором вибрации А *
— Ai в дальнейшем принимают за угол
сдвига фаз между расположенной неурав-
новешенностью и вибрациями опор, соот
ветствующими первой форме колебаний
ротора.
4. Находят величину корректирующей
массы QKop(z) из соотношения, выражаю-
щего линейную зависимость между величи-
нами реакции опор и массы, установленной
в некотором сечении ротора по данной
форме колебаний:
Окор (z)~ Qnp (z) Л1/|Л*—А11,
QkOP~
где Р — вес корректирующей массы: г —
радиус ее установки.
Угол установки корректирующей-массы
находят следующим образом. Пусть на
рис. 5.6 а - угол между вектором установ-
ки пробных грузов <5пр и вектором виб-
рации от пробных масс А*—Ai, который
принимают за угол сдвига фаз между не-
уравновешенностью и вибрациями опор на
первых критических частотах вращения,
причем вектор Qnp опережает вектор А *
— Ai в сторону вращения ротора.
Поворачивая вектор исходных вибра-
ций А1 на угол а в сторону вращения рото-
ра, определяют направление ОС, соответ-
ствующее расположению на окружности
Рис. 5.6. Определение угла ус-
тановки корректирующей массы
ротора плоскости расположения искомой
составляющей неуравновешенности. Кор-
ректирующие массы устанавливают под уг-
лом 180° к найденному направлению.
Получив значение величины массы
в одном сечении, но характеристике форм
колебаний р находят корректирующие мас-
сы вдоль оси ротора.
Аналогичным образом выполняют ба-
лансировку по второй форме.
Пусть В( и Вц (рис. 5.5, г) - ампли-
туды вертикальных вибраций опор I и П
вблизи второй критической частоты вра-
щения с исходной неуравновешенностью,
а В * и В (рис. 5.5, д) —амплитуды вер-
тикальных вибраций на этой же частоте,
но с системой пробных грузов S(z), по-
добной второй форме колебаний ротора
Для нахождения плоскости действия сос-
тавляющей неуравновешенности, которая
вызывает изгиб ротора по второй форме
колебаний, поступают следующим образом
(рис. 5.5, д): находят полуразность вибра-
ций опор при запусках без пробных гру-
зов Вг== (Вц_— Bf)2 и с пробными гру-
зами (В ц — = В* затем определя-
ют разность (BJi--Bf)/2— (Вц — Bt) /2=^
= КМ/2 (рис. 5.5, е). Вектор КМ/2 соот-
ветствует величине вибраций опор нод дей-
ствием пробных грузов
Величины корректирующих масс нахо-
дят но формуле
•Shop = 511РВ2/1В * В21, где S = Рг.
Угол между плоскостью расположения
системы пробных грузов по второй форме и
вектором КМ принимают равным углу
сдвига фаз между вибрациями опор ио
второй форме колебаний. Определение это-
го угла выполняют так же, как и при
балансировке по первой форме колебаний.
Закончив балансировку ротора по вто
рой форме колебаний, переходят к тре-
тьей и далее до тех пор, пока позволяет
прочность ротора, т. е. пока не будет дос
тигнута частота вращения, выше которой
разгон ротора запрещен.
В случае, когда максимальная рабочая
частота вращения лежит между критичес-
кими частотами вращения <о* и wt+i, про-
Методы балансировки гибких роторов с применением пробных дисбалансов
131
изводят балансировку дополнительно и на
этой максимальной частоте вращения для
ближайшей формы колебаний, которая ос-
талась недостигнутой. Например, если мак-
симальная рабочая частота врашения ле-
жит между первой критической и второй,
то после балансировки ротора по первой
критической частоте разгоняют ротор до
максимальной частоты вращения. Исполь-
зуя данные о вибрациях опор на этих
частотах, находят полуразность амплитуд
вибраций опор без пробных грузов и с
пробными грузами, распределенными в со-
ответствии со второй формой колебаний
ротора, и проводят балансировку по второй
форме колебаний.
Аналогично выполняют балансировку
и в тем случае, когда за исходные дан-
ные приняты не амплитуды вибраций опор,
а их реакции, причем погрешности в этом
случае будут меньше, чем при использо-
вании в качестве исходных данных вибра-
ции.
Методика балансировки на критичес
ких частотах вращения по формам изгиба,
реакциям опор и вибрациям может быть
с успехом использована и для других па-
раметров, измеряемых вдоль оси ротора,
в частности по углам поворота сечений
и относительной деформации, при этом
порядок балансировки почти не отличается
от описанного.
Балансировка на критических частотах
вращения по формам изгиба связана со
значительными трудностями и неудобст-
вами. Так, для балансировки ротора по
п формам изгиба необходимо сделать п
запусков с п пробными системами дис-
балансов. Это связано с определенными
трудностями, так как критические частоты
вращения опасны для прочности конструк-
ции, нестабильны для реальных двигате-
лей, что затрудняет точное определение
прогибов. При этом само уточнение данных
получается не за счет повышения точности
прибора, а за счет увеличения деформа-
ций ротора на критических частотах вра-
щения [П2). Из-за различия в жесткос-
тях опор ротора при балансировке на стен-
де и при эксплуатации в реальной кон
сгрукции формы изгиба в обоих случаях
не будут идентичными, и тогда при уста-
новке в собственные опоры ротор, сбалан-
сированный на стенде, может утратить
состояние уравновешенности. Наконец, не
всех критических частот вращения можно
достичь, так как они ограничены разру-
шающими двигатель частотами вращения.
Не следует забывать и то, что иденти
фикация в предположении о распределе-
нии составляющих эксцентриситета по
формам изгиба по всем сечениям длины
ротора далеко не всегда оправдана. Ротор
может принять собственную форму изгиба
и при наличии дисбаланса, но лишь в не-
которых или даже в одном сечении. В этом
случае установка пробных и корректиру-
ющих масс в других сечениях приводит
к внесению дисбаланса и появлению внут-
ренних изгибающих моментов. Данный
способ благодаря своей доступности полу
чил распространение в ряде отраслей про-
мышленности.
Метод последовательной балансировки
по формам изгиба не иа критических час-
тотах вращения. Этот метод заключается
в следующем. В некоторых сечениях по
длине вала измеряют его Ьрогиб на час-
тотах вращения, далеких от критических.
Этот прогиб складывается из составляю-
щих прогибов по собственным формам из-
гиба и представляет собой пространствен-
ную кривую. Предполагается, что формы
изгиба ротора известны и найдены заранее
каким-либо расчетным или эксперимен-
тальным путем.
На валу размешают систему пробных
дисбалансов, распределенных вдоль вала
по fe-й форме изгиба, по которой произ-
водят балансировку, т. е.
P*(z)r*(z) — m(z)yk(z)b*(z),
где b *— коэффициент, характеризующий
масштаб и плоскость расположения проб-
ных дисбалансов.
Систему масс для балансировки вала
по Л-й форме изгиба записывают в виде
Pb(z)rk(z) *= — m(z)yk(z)bk.
5*
132
Высокочастотная балансировка роторов
Производят пуск с пробными дисба-
лансами и повторяют измерения прогибов
в тех же точках и на тех же частотах
вращения, что и при первом пуске. Затем
подсчитывают y*(z) — изменение Л-й сос-
тавляющей прогиба, вызванное нагрузкой
от пробных дисбалансов, распределенных
по k-н форме изгиба.
Расчет корректирующих масс произ-
водят следующим образом. Подсчиты-
i
вают коэффициенты a/i~^yfc(z)y{z)m(z)dz
о
для прогиба от начальной неуравновешен-
ности и а*= ^yk(z)y* m(z)dz для проги-
о
ба от пробной системы дисбалансов.
Если зависимость между прогибом
и дисбалансом данной формы изгиба при-
нять линейной, то можно записать
~ ak/-
Поскольку
bk/b % = — щ(г) * (z) г *(?),
гиба проявились в прогибах, метод, пред-
ложенный В. М. Фридманом, в ряде слу-
чаев удобно применять в несколько изме-
ненном виде.
Измеряют прогибы на некоторых не-
критических частотах вращения и до уста-
новки пробных дисбалансов осуществляют
гармонический анализ полученной кривой
При этом пространственная кривая разла-
гается в ряд по собственным формам из-
гиба рассматриваемого ротора, каждая из
которых лежит в своей плоскости. Из та-
кого анализа видно, по каким формам
изгиба необходимо производить баланси-
ровку.
Для проведения гармонического ана-
лиза пространственной кривой удобно раз-
ложить ее на проекции в вертикальной
и горизонтальной плоскостях, затем произ-
вести гармонический анализ полученных
плоских кривых, после чего сложить про-
екции составляющих для каждой формы
изгиба.
Далее, в произвольном (по углу) мес-
те ротора и по всей его длине устанав-
ливают систему пробных дисбалансов по
I 7
«л/с* = $£/fe(2)^(z)m(z)dz/^A(z)^*(z)m(z)dz,
о о
то
I I
нД2) r*(z) = — p^(z)r^(z) $ yk(z)y{z)m(z) dz/\ yk(z) y*(z)m(z) dz.
о 0
Последнее равенство отображает за-
кон распределения масс при балансиров-
ке вала по /г-н форме изгиба. Если необ-
ходимо отбалансировать вал не только по
Л-й форме изгиба, то последовательно ус-
танавливают пробные дисбалансы по пер-
вой, второй, третьей и следующим формам
изгиба, измеряют прогиб на выбранных
частотах вращения как без пробных масс,
так и с ними, а затем рассмотренным
ранее способом рассчитывают корректиру-
ющие массы для каждой формы изгиба
вала. В связи с тем, что заранее неиз-
вестно, какие из составляющих разложе-
ния эксцентриситета в ряд по формам из-
Л-й форме изгиба и по этой форме произ-
водят балансировку. С этой целью осу-
ществляют запуск с пробными дисбалан-
сами и повторяют операцию разложения
суммарной кривой прогиба на составляю-
щие или принимают следующее теорети-
ческое положение: установленная по Л-й
форме изгиба система дисбалансов влияет
лишь на прогиб по этой форме. Опреде-
ляют векторную разность y*(z) — yk(z)
и по формуле находят величину дисбалан-
са m (z)et(z) и корректирующих масс. Мес-
то установки корректирующих масс опре-
деляют так же, как и при балансировке
на критических частотах вращения, т. е.
Методы балансировки гибких роторов с применением пробных дисбалансов
133
по положению относительно отметки угла
пробных дисбалансов и прогибов, вызван-
ных этими дисбалансами. Угол между
пробными дисбалансами и прогибами при-
нимают за угол сдвига фаз на данных
частотах вращения и считают углом сдвига
фаз между отыскиваемым дисбалансом и
прогибом от него на данных частотах вра-
щения для fe-й формы изгиба.
Аналогично производят балансировку
по любой требуемой форме изгиба, про-
являющейся в измеренных прогибах. При-
веденный способ, в отличие от баланси-
ровки на критических частотах вращения,
позволяет устранить большее число членов
разложения эксцентриситета, естественно
если они проявились в измеренных про-
гибах. В противном случае метод можно
опробовать по какой-либо производной от
прогиба, измеряемой, например, тензомет-
рированием или получаемой дифференци-
рованием исходной функции, так как в про-
изводных от прогиба влияние высших форм
разложения эксцентриситета существен-
нее, чем в самом прогибе.
Метод одновременной балансировки по
форме изгиба с применением специальной
системы пробных дисбалансов. В рассмот-
ренном выше способе используют проб-
ные дисбалансы, устанавливаемые на ро-
тор по каждой из форм изгиба, для ко-
торых проводят балансировку. При этом
выполняют п запусков с пробными дис-
балансами и один без них с измерением
прогибов оси ротора. Используя свойство
ортогональности между прогибом и на-
грузкой, можно уменьшить число запусков
с пробными дисбалансами до одного.
Если при балансировке на частотах
вращения, далеких от критических, уста-
новить на ротор системы пробных дисба-
лансов для всех форм изгиба, по которым
производилось разложение исходного
прогиба, то по условию ортогональности
каждая из систем пробных дисбалансов
будет влиять лишь на прогиб только по
своей форме изгиба.
Все эти системы пробных дисбалан-
сов в сумме образуют одну систему, экс-
центриситеты которой распределены по-
добно кривой изгиба ротора с начальным
дисбалансом. Поэтому можно упростить
процесс балансировки и свести его к сле-
дующим операциям:
1. Измеряют прогибы на некоторых не-
критических частотах вращения ротора.
Полученную пространственную кривую
разлагают в ряд по собственным формам
изгиба ротора в соответствии с вектор-
ным уравнением
y(z) = yi(z) +y2(z) -I- .
где y(z)—упругая линия ротора; yi(z),
yz(z), — , yn(z) — плоские кривые, соот-
ветствующие первой, второй,... , п-й фор-
ме изгиба, каждая из которых лежит
в своей плоскости.
На практике число идентифицируемых
членов разложения эксцентриситета в ряд
по формам изгиба зависит от степени про-
явления этих составляющих в измерен
ных прогибах и должно заканчиваться тем
членом, прогиб по которому соизмерим
с точностью применяемой аппаратуры.
2. На ротор устанавливают систему
пробных дисбалансов, эксцентриситеты ко-
торой распределены подобно упругой ли-
нии ротора от начальных дисбалансов.
Это достигается установкой пробных масс
таких значений и в таком месте, при ко-
торых статические моменты в рассматри-
ваемых сечениях ро» эра совпадают со зна-
чением и местом пробного дисбаланса в
этом сечении, т. е.
М-г« = tn,hi,
где At, — t-я пробная масса; г, — радиус
ее установки; ht — эксцентриситет проб-
ного дисбаланса.
Вдали от критических частот враще-
ния прогиб и дисбалансы практически сов-
падают по направлению. Поэтому пробный
дисбаланс следует располагать так, чтобы
образованная им центробежная сила
уменьшила прогиб, т. е. под углом 180°
к вектору прогиба в рассматриваемом се-
чении. В этом случае корректирующую
массу устанавливают в то же место, что
и пробную.
134
Высокочастотная балансировка роторов
Система эксцентриситетов пробных
дисбалансов также раскладывается в ряд
по формам колебаний ротора. Векторное
уравнение для этого случая
h(z) =hx(z) Ч-Йй(2) 4- . .. 4Ыг),
где fti(z), Лг<2), ftn(z)—плоские кривые
распределения составляющих системы экс-
центриситетов пробных дисбалансов, ле-
жащих соответственно в плоскостях yi(z),
ye(z),... ,yn(z).
3. Осуществляют запуск с пробными
дисбалансами и на прежних частотах вра-
щения измеряют упругую линию ротора.
Новая кривая также разлагается в ряд
по собственным формам изгиба ротора:
У* (z) = 4- y*(z) 4- ... + y*(z).
Звездочкой обозначены прогибы ротора с
пробными дисбалансами.
4. Подсчитывают начальные эксцент-
риситеты для каждой формы изгиба с
использованием линейной зависимости
между прогибами и дисбалансами:
ei(z) = — fti(z)^,(z)/(^*(z) —yi(z));
e2(z) = — h2(z)y2(zM((y*(z) — y2(z));
en(z) = — hn(z)y„(z) I ((y*(z) — yn(z)).
Каждая из идентифицированных таким
образом систем эксцентриситетов еЦх),
e2(z),относится к своей форме
изгиба и лежит в ее плоскости. Произ-
ведя векторное суммирование, находим
полную систему начальных эксцентриси-
тетов, а умножая их на массы соответ-
ствующих участков ротора, — полную сис-
тему дисбалансов, которая и подлежит
компенсации корректирующими массами,
статические моменты которых равны на-
чальным дисбалансам. Отметим, что сис-
тема корректирующих масс не может быть
подобна пробной системе.
В принципе на ротор можно устана-
вливать любую систему пробных дисба-
лансов, рассматривая составляющие ее
эксцентриситетов по нужным формам из-
гиба, но тогда не исключается случай,
когда эта произвольная система может и
не содержать необходимых составляющих,
и, следовательно, не по всем формам из-
гиба удается идентифицировать эксцент-
риситеты.
При достаточном опыте балансировки
роторов одного изделия, когда имеются
данные о зависимости прогибов от системы
пробных и уравновешенных дисбалансов,
можно уже по прогибу, измеренному при
первом пуске, идентифицировать началь-
ные эксцентриситеты и дисбалансы.
Во всяком случае, если найденную та-
ким образом систему дисбалансов принять
за пробную, то она будет мало отличать-
ся от корректирующей и если не сразу
снизит прогибы до допустимых, то облег-
чит условия балансировки.
Метод Одновременной балансировки по
формам изгиба не на критических час-
тотах вращения будет эффективнее при
использовании вместо прогиба углов пово-
рота сечений, относительной деформации
и более высоких производных, так как при
этом можно лучше выявить составляю-
щие эксцентриситетов по высшим формам
изгиба. Однако необходимо иметь в виду
недостаток алгоритма идентификации,
когда само дифференцирование по ограни
ценному числу точек измерения может при-
вести к погрешностям, и поэтому следует
пользоваться либо непосредственно изме-
ряемыми параметрами, например относи-
тельной деформацией, либо находить опти-
мальную по номеру производную, когда
возрастание чувствительности к дисбалан-
сам по высшим формам изгиба сравня-
ется со снижением точности йолучаемых
данных за счет погрешностей дифферен-
цирования по ограниченному числу точек
измерения.
Разложение прогиба по собственным
формам изгиба ротора. Разложение про-
странственной кривой прогиба ротора на
нормальные составляющие для невесомого
вала с сосредоточенными дисками можно
производить с помощью решения вектор-
ных уравнений, представляющих собой за-
висимость полного прогиба диска от его
составляющих по формам колебаний. В ка-
Методы балансировки гибких роторов с применением пробных дисбалансов
135
Рис. 5-7. Разложение прогиба на сос-
тавляющие
честве примера рассмотрим разложение
прогиба на составляющие для трехдис-
кового ротора.
На рис. 5.7, а изображен трехдисковый
ротор, состоящий из невесомого вала, на
который насажены три диска с массами
/Пь т2, т3. Предположим, что на неко-
торых частотах вращения, не равных кри-
тическим, измерены векторы прогибов в
местах посадки дисков уь £п, £1И. Все
прогибы лежат в разных плоскостях и
различны по величине.
Предполагая, что формы колебаний
этого ротора известны и имея характе-
ристики всех трех форм колебаний р, мож-
но измеренные прогибы представить в виде
сумм составляющих прогибов по формам
колебаний:
Ух ~ У\\ 4- У^ 4" ^1з;
Ун == P21£u 4- Р22р12 4- р33^13;
£]|! = р3l£ll 4- Р32^12 4 р33«/13-
В этих уравнениях у^, угЛ—сос-
тавляющие прогибов первого диска по пер-
вой, второй и третьей формам колеба-
ний, р — отношение прогибов второго и
третьего дисков к прогибу первого диска
в зависимости от формы колебаний. Пер-
вый индекс у р обозначает номер диска,
второй индекс — номер формы колебаний.
Например, р31 — отношение прогиба треть-
его диска к прогибу первого диска по
первой форме колебаний; р23— отношение
прогиба второго диска к прогибу первого
диска по третьей форме колебаний.
В этих уравнениях неизвестными яв-
ляются £]Ь ^12, £|з. Решая уравнения от-
носительно неизвестных по теореме Кра-
мера, можно записать
1 Ух 1 1
У'1== D Ун Р22 Ргз
Ут Р32 Рзз
1 1
1 -г-
~D Р21 */11 Ргз
Р31 Уш Рзз
1 1 Ух
- . 1 —
У™~ ~D Р21 Р22 Ун
Рз( Р32 Ут
1 1 1
где D — P2I Р22 Ргз
Рз1 Р32 Рзз
В развернутом виде:
У|(Р22РЗЗ~ Р32Р23)
— — л
*/||(Рз2 Р24) */lIl(P23 Р22)
D ’ D ’
{^1(Р23Р31 Р2|Рзз) ,
»12 =------------В---------- +
Уц(Рзз Рз1) . Уш(р21 Ргз)
;
136
Высокочастотная балансы ровна роторов
4/|(Ра1Рз2 Р31Р22) .
013 _ ------------------------1-
0n(p3t_ Рзц) J 0Jlt(p22~ Рд)
ъ
D
Для удобства перепишем уравнения
в виде
yi 1 = Af/i 4- В1У11 + Cif/np
f/j2 = A^yi 4- ВъУц 4“ СъУпй
013= А3У1 4- Взуц 4-
Здесь А, В и С равны соответству-
ющим коэффициентам уравнений.
На рис. 5.7, б, г показано построение
векторов ун, у 12, у 13. Из точки О
(рис. 5.7, д) проводят след плоскости, пер-
пендикулярной плоскости листа и прохо-
дящей через ось ротора. От этого следа
отсчитывают углы направлений прогибов
дисков на измеряемых частртах вращения.
Из точки О наносят направление проги-
бов у}, у}}, уп}.
Затем в направлении у} откладывают
Aty} — вектор О At, из его конца — вектор
jBi^h в направлении уи, а затем — вектор
BiCi = Ciy}U. Соединив конец вектора
BiCi с точкой О, получают OGt = уп. Ана-
логично строят векторы £12 = ОС2 и у\3 —
= ОС3.
Вектор уц и ось ротора расположены
в плоскости, в которой изгибается ротор
по первой форме колебаний и лежат век-
торы р21^11 и рз1^п- Вектор г/|2 с осью
ротора расположены в плоскости, в ко-
торой происходит изгиб ротора на час-
тотах <о2кр по второй форме колебаний.
В этой же плоскости лежат векторы р22У12
и р 32^12- Вектор £13 и ось ротора распо-
ложены в плоскости, в которой происхо-
дит изгиб ротора на частотах со3кр по тре-
тьей форме колебаний и лежат векторы
р 23^)3, рззу 13-
Прогибы yb уп, yUi измеряют вдали
от критических частот, поэтому разность
фаз между прогибом и дисбалансом, вы-
звавшим его, примерно равна нулю. На
практике находят плоскости расположения
форм колебаний ротора и считают, что
в этих же плоскостях расположены вы-
звавшие их дисбалансы, которые и ио фор-
ме распределены подобно нормальным
кривым.
Метод балансировки с применением
специальной системы пробных дисбалан-
сов, не требующий знания собственных
форм изгиба ротора. Если на ротор ус
тановить систему пробных дисбалансов,
чьи эксцентриситеты h(z)—Cy(z) (где
С — const =# 0) распределены подобно из-
меренной кривой прогибов, и обе кривые
y(z) и h(z) разложить в ряд по формам
изгиба, то по условию ортогональности
каждая составляющая эксцентриситетов
пробных дисбалансов будет влиять лишь
на такую же составляющую прогиба, из-
меняя ее значение. В таком случае вся
система пробных дисбалансов повлияет
лишь на масштаб кривой у (z), не изме-
няя ее формы. Если разложение кривых
y(z\ и h(z) в ряд по формам изгиба
заменить разложением по любой известной
ортонорм и ров а иной системе функций, на-
пример по синусам, то указанное свой
ство сохраняется, так как каждая сину-
соида разложения h(z) будет влиять лишь
на синусоиду такого же порядка разло-
жения y(z).
Для разложения исходной кривой y(z)
или h{z) в ряд по формам изгиба необ-
ходимо знание или определение этих форм.
При разложении же по вышеуказанным
функциям этого не требуется.
Балансировку осуществляют в такой
последовательности. Измеряют прогиб
у (г} на некоторых выбранных некрити-
ческих частотах вращения, после чего
на ротор устанавливают систему пробных
дисбалансов с распределением эксцентри
ситетов по закону h(z) — Cy(z) относи-
тельно кривой у (г), лучше всего под уг-
лом 180° для снижения прогибов; затем
измеряют прогиб у* (г) с установленной
на ротор системой пробных дисбалансов.
После обработки полученных данных под-
считывают систему начальных эксцентри-
ситетов и корректирующих масс. При этом
Методы балансировки тяжелых роторов на заводских стендах
137
выполняют разложение всех кривых и не-
известной функции e(z) в ряд по синусам
Л
y(z) = а(|/2 Ч- £ 4fesin (nkz/L);
*=i
п
h(z) = b(}/2 4- £ Вk sin (sikz/L} \
v*(z) = dfJ/2 4- £ Dksin{nkz/L);
^('г)=/о/24- £ Fk sin (nkz/L).
Л=1
Принимая линейным соотношение
между дисбалансом и прогибом для оди-
наковых членов разложения, можно за-
писать
Fk sin (nkz/L) Ак sin {nkz/L)
Bk sin (nkz/L) (Dk — AA) sin (jtkz/L)
или
F^A.B^D^A^, F^A2B2/(D2-A2)-.
Fn=AnBn/(D„-Aty,
fо — аоЬо/№о col -
Здесь fo/2 — величина, характеризую-
щая положение средней линии корректи-
рующих масс, на которую накладываются
все остальные синусоиды ряда e(z).
Чем больше взято число членов ряда,
тем точнее при прочих равных условиях
будет проведена балансировка.
После нахождения кривых е(г) для
каждой проекции производят их вектор-
ное сложение и определяют пространст-
венную кривую распределения начальных
эксцентриситетов, а затем дисбалансов и
корректирующих масс. В этом случае
также сохраняют силу замечания о ко-
личестве учитываемых на практике членов
разложения, о возможности получения
систем пробных дисбалансов, близких к
корректирующим, а также об использо-
вании для повышения чувствительности
к дисбалансам по формам изгиба произ-
водных от прогиба.
В заключение целесообразно вернуться
к предположению о таком распределении
дисбаланса, когда в каждом сечении ро-
тора содержатся составляющие эксцентри-
ситетов по всем формам изгиба, которые
можно уравновешивать соответствующими
системами корректирующих масс, и к осно-
ванному на этом предположении алгорит-
му идентификации.
В реальном случае измеренный прогиб
ротора может быть следствием дисбалан-
сов, распределенных совершенно иначе,
например сосредоточенных лишь в неко-
торых или даже одном сечении, а тогда
уравновешивающие дисбалансы, распре-
деленные по формам изгиба, есть не что
иное как дисбалансы, внесенные в те места,
в которых они отсутствовали в исходном
состоянии. В этом отношении задачу ба-
лансировки необходимо рассматривать не
как задачу идентификации истинных на-
чальных дисбалансов, а как задачу иденти-
фикации системы корректирующих масс,
распределенных по формам изгиба с целью
сведения к нулю прогибов по баланси-
руемым формам изгиба в выбранных
сечениях. При этом ротор может быть
нагружен изгибающим моментом, и в этом
один из существенных недостатков спосо-
бов, в которых используются пробные
массы.
Следует также заметить, что на выбор
частот вращения для балансировки по ме-
тодам, изложенным в этом и предыдущих
параграфах, накладывалось лишь условие,
чтобы на них проявлялась деформируе-
мость ротора и тогда в частном случае,
когда to = <nKp. получали метод идентифи-
кации и балансировки на критических час-
тотах вращения по формам изгиба ротора.
5.3. МЕТОДЫ БАЛАНСИРОВКИ ТЯЖЕЛЫХ
ГИБКИХ РОТОРОВ ЭНЕРГОМАШИН
ИА ЗАВОДСКИХ СТЕНДАХ
Высокочастотную балансировку тур-
бинных роторов осуществляют на специ-
альных заводских разгонно-балансировоч-
ных стендах (РБС) методом установки
138
Высокочастотная балансировка роторов
корректирующих масс в штатные балан-
сировочные плоскости по данным измере-
ний вибрации опор или вибрационных уча-
стков ротора (цапф, муфт, сечений в про-
лете) на выбранных частотах вращения,
лежащих во всем диапазоне рабочих час-
тот, включая номинальную частоту и час-
тоту разгонных испытаний. Высокочастот-
ную балансировку применяют в основном
для гибких роторов, для которых низко-
частотная балансировка не обеспечивает
нормального вибрационного поведения ро-
тора на номинальной частоте вращения.
Согласно ГОСТ [Г 12] целью высокочас-
тотной балансировки является достиже-
ние на РБС такого значения составля-
ющей вибрации с частотой вращения, при
котором значение любого компонента виб-
рации каждой из опор ротора при его
работе на холостом ходу будет удовлет-
ворять действующим нормативам. Таким
образом исключают либо сводят к мини-
муму дорогостоящую балансировку вало-
провода в собственных подшипниках при
пуске агрегата. При высокочастотной ба-
лансировке выполняют следующие опера-
ции:
а) разгона ротора до частоты, пре-
вышающей на 15— 20% номинальную час-
тоту вращения; при этом обеспечиваются
прочностная проверка элементов ротора и
окончательная насадка дисков, лопаток,
муфт;
б) достижения заданного норматив-
ного значения колебаний опор или участ-
ков ротора на номинальной и промежу-
точных частотах вращения, в том числе на
безопасных частотах и частотах, соответ-
ствующих поведению ротора как жесткого
тела;
в) поэтапной балансировки (по необ
ходимости) в процессе сборки ротора (до
и после насадки полумуфт, межроторных
проставок, набора лопаток иа отдельные
ступени и т. д.);
г) совместной балансировки (по необ-
ходимости) двух соединенных роторов для
приближения условий их балансировки к
условиям работы в валопроводе (либо при
невозможности или нецелесообразности
раздельной балансировки).
Следует учитывать, что в турбоагре-
гате все роторы соединены в единый ва-
лопровод и не имеют консольных участ-
ков. в то время как на РБС каждый от-
дельный ротор имеет две консоли. Кроме
того, податливость опор роторов на РБС
и в турбине не обязательно совпадает.
Следовательно, формы изгиба роторов на
РБС и в валопроводе не совпадают, т. е.
остаточный дисбаланс, ортогональный к
формам изгиба на РБС, может оказаться
неортогональным к таковым в валопрово-
де, что вызовет дополнительные колебания
в валопроводе (рис. 5.8). Для исключения
этого разрабатывают технологию баланси-
ровки так, чтобы распределение устанавли-
ваемых корректирующих масс (грузов)
было максимально приближено к распре-
делению исходного дисбаланса ротора.
Именно это обстоятельство заставляет ис-
пользовать сложные условия сбалансиро-
ванности ротора (ограничение колебаний
при нескольких значениях частот, вклю-
чая резонансные и низкие частоты, огра-
ничение динамического изгиба консолей и
других участков ротора), а также прибе-
Рис. 5.8. Типичные формы изгиба ротора
на разгонно-балансировочном стенде (сплош-
ная кривая) и в валопроводе турбоагрегата
(штриховая кривая):
а—первая, б—вторая, в—третья, г динамичес-
кий прогиб ротора после балансировки на РБС
Методы балансировки тяжелых роторов на заводских стендах
139
гать к поэтапной и совместной баланси-
ровке роторов.
Классификации роторов при высоко-
частотной балансировке. Роторы совре-
менных турбоагрегатов являются гибкими
роторами- Как правило они работают
вблизи 2-й резонансной частоты вращения,
поэтому их балансируют на высокочас-
тотных РБС. Но конструкции роторов мо-
гут быть различными, что приводит к спе-
цифике в технологии их балансировки. Ос-
новные типы роторов следующие:
а) работающие в трехопорных ротор-
ных системах и имеющие общую цапфу
с соседним ротором; такие роторы балан-
сируют с технологической цапфой, при-
соединяемой к полумуфте с биением, не
превышающим 0,02 мм;
б) с меж роторным и цилиндрическими
проставками, присоединяемыми к полу-
муфтам (рис. 5.9); такие роторы целесо-
образно балансировать поэтапно (сначала
высокочастотная балансировка без про-
ставки, а затем низкочастотная или вы-
сокочастотная балансировка с проставкой
с установкой корректирующей массы толь-
ко в плоскости на проставке);
в) с длинными консольными участками
либо с тяжелыми полумуфтами, имеющими
значительный динамический прогиб в диа-
пазоне рабочих частот вращения; такие
роторы также целесообразно балансиро-
вать поэтапно (сначала без полумуфты,
а затем с полумуфтой) либо назначать
условия сбалансированности, обеслечи-
Рис. 5.9. Конструкция соединения роторов в
валопроводе:
1— ротор I. 2 —межроторная цилиндрическая
проставка, 3—ротор 2
вающие ограничение прогиба консольного
участка на РБС;
г) с рабочими лопатками большой мас-
сы; такие роторы иногда целесообразно
балансировать поэтапно (без лопаток и с
лопатками, наружных ступеней) либо
после окончательной моментной развески
проточенных по бандажам лопаток уста-
навливать до балансировки с лопатками
груз, компенсирующий суммарный вектор
дисбаланса, созданного различием в мо-
ментных весах лопаток. В ряде случаев
наличие такого груза может заменить по-
следний этап —- балансировку с наруж-
ными ступенями.
Требования к конструкции и точности
изготовления роторов. Минимальное число
штатных балансировочных плоскостей для
установки корректирующих грузов для ро-
торов паровых турбин должно быть три:
одна посредине и две по краям у опор
внутри пролета (обычно на дисках край-
них ступеней). Однако для обеспечения
более сложных условий сбалансирован-
ности используют дополнительные плос-
кости на полумуфтах и на роторе. Места,
предусмотренные для крепления корректи-
рующих масс, должны быть легко доступ-
ны, их биение относительно цапфы ротора
не должно превышать 0,5 мм. Способ креп-
ления корректирующих масс должен обес-
печивать полное исключение возможности
смещения груза при вращении ротора
(пригонка по лазу, керновка, стопорение
и т. п.). Для установки и крепления кор-
ректирующих масс чаше всего применяют
кольцевые пазы с трапецеидальным профи-
лем «ласточкин хвост» или отверстия с
резьбой (рис. 5.10). Рассмотрим требова-
ния к конструкции и технологии изготов-
ления роторов, обеспечивающие мини-
мальный исходный дисбаланс, снижение
трудоемкости и повышение эффективности
высокочастотной балансировки.
1. Пол у муфты необходимо изготавли-
вать по 2-му классу точности при полном
отсутствии размеров, не закрытых допус-
ками. Радиальное и торцовое биение полу-
муфт не должно превышать 0,02 мм после
140
Высокочастотная балансировка роторов
Рис. 5.10. Типовые конструкции крепления
корректирующих масс к дискам роторов:
с- паз с профилем «Ласточкин хвост»; б глу-
хие отверстия с резьбой
чистовой проточки на роторе. Биение по-
верхностей цапф роторов не должно пре-
вышать 0,01—0,02 мм.
2. Лопатки с длиной рабочей части
от 90 до 240 мм развешивают на весах
и распределяют на диске с максимально
допустимым остаточным дисбалансом
0,01 кг • м. Лопатки с длиной рабочей час-
ти более 240 мм развешивают на мо-
ментных весах и распределяют на диске
с максимально допустимым остаточным
дисбалансом 0,03 кг • м (для длинных ло-
паток). При невозможности распределить
лопатки по моментным весам, например
после проточки бандажей, следует опре-
делить развеской лопаток остаточный дис-
баланс JD и установить на диск этой сту-
пени соответствующий компенсирующий
груз G из расчета G—D/R, где R—
радиус крепления груза
3. Насадные облопаченные диски дол-
жны быть статически отбалансированы;
максимально допустимый статический дис-
баланс—0,015 кг • м. Биение посадочных
мест для дисков на роторе не должно
превышать 0,02 мм. Горячую насадку
дисков и полумуфт на ротор необ-
ходимо выполнять в вертикальном поло-
жении ротора, чтобы не допустить сило-
вого изгиба последнего при насадке. На-
тяги насадок дисков и пол у муфт должны
полностью исключать возможность снятия
натягов на рабочих частотах вращения.
Средние значения натягов 0,002г/, где d —
диаметр насадки.
4. Кардан привода разгонного устрой-
ства присоединяют к торцу ротора с бие-
нием, не превышающим 0,05 мм.
5. Высокочастотная балансировка —
финишный этап процесса изготовления ро-
тора.
Этапы высокочастотной балансировки:
1. Установка ротора в подшипники.
Масляные зазоры в подшипниках РБС не
должны отличаться более чем на 30% от
аналогичных зазоров в турбине. Набор
вакуума в разгонной камере при обяза-
тельном вращении ротора на вал ©пово-
ротном устройстве (ВПУ).
2. Предварительная балансировка ро-
тора на низкой частоте вращения (400—
600 мин~‘)
3. Разгон ротора до частоты на 15—
20% выше номинальной при переключении
опор на максимальную жесткость. Дина-
мические реакции на опорах не должны
превышать 75% весовых (статических) ре-
акций. При невозможности соблюдения
этих условий выполняют предварительную
балансировку на номинальной пном либо
максимально доступной частоте вращения.
4. Балансировка ротора по принятой
методике.
5. Сдача ротора ОТК или заказчику
с повторением разгона ротора до (1,15—
1,2)лном.
В случае поэтапной балансировки осу-
ществляют сборку присоединяемых частей
с последующей балансировкой их на ро-
торе.
Ротор следует вращать исходным дис-
балансом (до первой установки кор-
ректирующих масс) на номинальной или
промежуточной частоте вращения, пока
показания вибрационных приборов не
станут стабильными. Этим достигают
устранения упругого прогиба ротора, по-
лученного во время транспортировки или
хранения в цехе. «Срыв и набор» ваку-
ума должен производиться при обязатель-
ном вращении ротора на ВПУ для исклю-
чения появления теплового прогиба. Воз-
можно добавление еще одного этапа —
окончательной балансировки ротора после
паровых заводских испытаний турбины.
Методы балансировки тяжелых роторов на заводских стендах
141
Измерения во время высокочастотной
балансировки. Все измерения могут вы-
полняться визуально на определенных час-
тотах вращения, непрерывно записываться
с помощью магнитографа или самописца,
регистрироваться ЭВМ через аналого-чис-
ловой преобразователь Измеряют следу-
ющие величины:
вектор вибрации опор — виброско-
рость или виброперемещение; вектор оп-
ределяют либо в тригонометрическом виде
(модуль, фазовый угол), либо в проек-
циях на декартовы оси координат; со-
временные РБС обеспечивают одновремен-
но оба вида измерений;
динамическую нагрузку Q на опору:
Q = р/Х, где у модуль вектора смеще-
ния корпуса опоры; X — динамическая по-
датливость опоры; на рис, 5.11 приведены
графики динамической податливости опор
РБС на различных частотах при двух дис-
кретно переключаемых значениях (макси-
мальная и минимальная жесткость);
векторы виброперемещений опреде-
ленных участков ротора бесконтактными
датчиками относительных перемещений
(в случае включения таких измерений в
методику балансировки),
давление и температуру среды в раз-
гонной камере;
температуру и давление разгонного
электродвигателя.
Для обеспечения стабильности показа-
ний все перечисленные эксплуатационные
параметры должны быть идентичными для
всех балансировочных пусков для каждого
типа ротора.
Методы высокочастотной баланси-
ровки. При балансировке ротора на РБС
в основном применяют следующие методы
[Г12]:
а) балансировки по формам изгиба
(по формам колебаний) ротора;
б) комбинированный;
в) балансировки по динамическим ко-
эффициентам влияния.
Метод балансировки по формам изги-
ба. Суть метода — разложение амплитуды
колебаний любого участка ротора и его
опор на ортогональные составляющие, со-
ответствующие определенным формам
динамического изгиба, и устранение этих
составляющих корректирующими масса-
ми, которые могут представлять собой
взаимно ортогональные системы, т. е.
каждая система может вызывать динами-
ческий прогиб только по одной изгибной
форме, хотя это условие и не обязательно
для описываемого метода. Амплитуду
колебаний A, i-ro сечения ротора на изо-
тропных опорах с числом масс т,, равным
л, на частоте вращения w определяют,
используя выражение
Рис. 5.11. График динамической податливости
опор разгонно-балансировочного стенда фир-
мы «К. Шенк» на стойках ДН-10 при двух
положениях переключения податливости:
/— максимальная податливость. 2 минимальная
податливость
п п
Уп £ У.П £
Л /=1_________1 I-1__________I
Л7,(/7/о>2- 7) 1)
Van 5
-]--------------------и _|_
п
Ун, ^,e,kyik
+ МДР2/<02-1) +’ - =
= Л + Уц 4- Уш4- • • 4-У*4---- (5.1)
142
Высокочастотная балансировка роторов
п
Суммы вида £ mjefl{ylfi представ-
ляют собой разложение исходного дис-
баланса mtej по формам изгиба на ор-
тогональные составляющие для соб-
ственных частот Рь Ри, Рцн ....где М},
M!f, М1П... — соответствующие приве-
денные массы. Величины ytk (прогиб i-ro
сечения по fe-й форме изгиба), At, е,—
векторы; после выражения векторов в
проекциях на декартовы координаты
уравнение (5.1) распадается на два ана-
логичных по структуре уравнения.
На рис. 5.12 приведена типичная ам-
плитудно-частотная характеристика, по-
Рнс. 5.12. Амплитудно-частотная характерис-
тика колебаний опор при разгоне ротора
на разгонно-балансировочном стенде:
/ опора I: 2 — опора 2
называющая характер изменения амп-
литуды колебаний опор при разгоне ро-
тора на РБС. Можно с достаточной точ-
ностью принять, что амплитуда колебаний
вблизи I резонансной частоты (Р^ опре-
деляется / изгибной собственной формой
(У>), а на номинальной частоте сум-
мой II и III форм (Уп и УП1).
При нечетных формах изгиба (I —- III)
колебания опор синфазны, а при четных
(II) — противофазны. Это обстоятельство
позволяет достаточно просто выделить
указанные составляющие в виде суммы и
разности векторов колебаний опор.
На рис. 5.13 приведены такие построе-
ния. где АоП и ЛО]2—амплитуды коле-
баний опор 1 и 2 на I критической час-
тоте, а Лсн1 и Дои2— то же на номиналь-
ной частоте вращения. Векторы Yj —
— А>11 + Ляг и = Лон1 J- Д>н2 соответ-
ствуют колебаниям по I и III формам,
а Уп — ДСН] — Дом2 — колебаниям по II
форме. Точно так же можно разложить
векторы влияния корректирующих масс на
указанные три формы изгиба, установив
последовательно в балансировочные плос-
кости 1,2,3.. . пробные грузы т, и из-
мерив соответствующие амплитуды коле-
баний. При этом получают матрицу ди-
намических коэффициентов влияния a,k
(для наглядности все вычисления даны
только для трех изгибных форм и трех
балансировочных плоскостей):
Методы балансировки тяжелых роторов на заводских стендах
143
«1. О21 а31
^1(1 С2П азп
al III °21П ЙЗШ
(5.2)
где aik амплитуда колебаний по &-й фор-
ме при установке единичной массы в i-ю
плоскость.
В этом случае условия с балансирован-
ное™ можно записать в виде
"iiau 4- m2a2l 4- m3a3I = — Уо(;
™ialn 4- ш2а2|1 4- ™3а3|| — — Уо||;
т1СЦ1( 4- т2С2Ц1 4“ m3U3in =
(5.3)
где mi, т2, т^—искомые корректи-
рующие массы, совместное влияние кото-
рых должно вызвать колебания, равные
по величине и обратные по знаку исходным
колебаниям несбалансированного ротора
(^оН У oil И ^о1|1)"
В данном случае каждая корректиру-
ющая масса вызывает прогиб по всем
трем формам, т. е. не является ортого
нальной ни к одной из форм, тем не ме-
нее можно вести балансировку, решая на
ЭВМ систему из шести (в данном слу-
чае) линейных уравнений, так как каждый
вектор mi, а^, Yok разлагается в проек-
циях на два скляра (т*, mf), (а*л, с^),
(У**, Таким образом, условия (5.3)
в проекциях будут иметь вид
|Г'Л (5.4)
В результате погрешностей измерений
и ограничений по величинам устанавли-
ваемых грузов за один пуск отбаланси-
ровать ротор, как правило, не удается.
Поэтому производят серию балансиро-
вочных пусков, в которых остаточная ам-
плитуда колебаний опор принимается за
«новую» исходную амплитуду, и после по-
следовательных решений системы (5.4) на-
ходят уточненную систему корректирую-
щих масс. т. е.
К*1К»'| = Щ'1*:
1Ц'1* = 1НЯ- 1П"|.
где | — матрица остаточных
литуд.
(5.5)
ами-
Из системы (5.3) или (5.4) можно оп-
ределить ортогональные системы корректи-
рующих масс, т. е. системы, вызывающие
динамический прогиб ротора только по
одной из форм колебаний. Для этого сос-
тавляют условия
(ппап -4- M2la2l + maia3l= а,;
4~ asiasit 4- щ31а311 = 0;
WI1CHH 4- m 21^2111 4" m3IG311l = О‘>
^111° II 4“ ^2Па2| 4“ W3IIC3I ~ О»
WIHCiIU 4" ,n2Ha2II “У ^3ll°3ll ~
^Hiailll 4" ^211^2111 4" m31IC3lll =
WllllCll 4- ^2111^21 4" ^3111^31 ~ О»
т iniCl!l 4" W2HIC2II1 4” ^ЗН^ЗН = О»
(5.6)
"bllAll, 4" ^2111^2111 4“ ^31IIG3ilf------- С|||-
Принимая т1} — ш|П = т(111 = 1, ре-
шают систему относительно /n2h m2lb т2П|,
m3i, w3ii« m3iib сь сп> °i!i- Таким обра-
зом получают три ортогональные незави-
симые системы грузов: тД/Иц, т21, га31),
тп(шп), т2И, m31I). miU(m
ПИ> т2НЬ ШЗЦ|)>
и коэффициенты влияния по формам из-
гиба: аь ап и аш. Теперь условия сба-
лансированности можно выразить более
простой системой уравнений и предста-
вить систему (5.3) в обобщенных коор-
динатах:
mjCi = — Уо1;
тнсн — — ТоН;
— ТоП1.
(5-7)
Системы уравнений (5.6) и (5.7) мож-
но решать либо с помощью ЭВМ, либо
графически — методом построения векто-
ров (рис. 5.13), так как все вычисления
сводятся к построению трех векторов [сис-
тему уравнений (5.6) так же разбивают
на три независимые системы из трех век-
торов каждая]. Окончательные значения
грузов на плоскостях выражаются вектор-
ными суммами: mj = 4-тш 4-т]]1ь
тц — т2] 4- л?;2п 4- ^211]’ mni = m3]4 тзп 4-
4_/пзн1-
На практике часто бывает целесооб-
разно применять методику последователь-
144
Высокочастотная балансировка роторов
ного устранения составляющих дисбалан
са по изгибным формам, т. е. устанав-
ливать систему корректирующих масс, ор-
тогональных только к предыдущим, ранее
отбалансированным формам. Так, вначале
можно любой системой грузов (предпоч-
тительно симметричной по краям ротора)
отбалансировать ротор на I резонансной
частоте, не заботясь об ортогональности
ко II и III формам, рассчитывая грузы
по формуле
(5-8)
Затем новой системой грузов, ортого-
нальной к I форме отбалансировать изгиб
по II форме, «не испортив» балансировку
по I форме, определяя грузы из системы
уравнений
тП1сП + m2iIc2I = (5.9)
т1П°111 + m2!la2II — — >о*1Ь
где У*и — принимаемая здесь еа исходную
остаточная амплитуда колебаний по II
форме после балансировки по I форме.
Далее, используя последние три урав-
нения из системы (5.6), находят систему
грузов тип’ т2ш и лг/зш Для устране-
ния оставшегося прогиба по форме УоШ.
В случае балансировки по большему чис-
лу форм изгиба, включая, например, кон
сольные формы и формы колебаний ротора
как жесткого тела на низких частотах
вращения, изложенная методика практи-
чески не изменится, структура всех систем-
уравнений остается прежней, а увеличи
вается только число уравнений.
Необходимо отметить, что при изме-
рениях колебаний на резонансных часто-
тах вращения целесообразно производить
измерения на частотах примерно на 10%
ниже резонансных для увеличения ста-
бильности результатов.
Комбинированный метод балансиров-
ки — метод, объединяющий низкочастот-
ную и высокочастотную балансировку по
формам изгиба ротора, — является разно-
видностью метода по формам колебаний,
так как первые две прямолинейные формы
колебаний ротора на низкой частоте вра-
щения включаются в общее число форм,
по которым устраняют соответствующие
дисбалансы.
Метод балансировки по динамическим
коэффициентам влияния ' (ДКВ) основан
на допущении, что вибрация контролиру-
емого участка ротора является результа-
том воздействия распределенного дисба-
ланса, который можно рассматривать как
сумму дискретных дисбалансов, располо-
женных в выбранных плоскостях коррек-
ции. На основании этого динамические
реакции или вибрации опор принима-
ют линейно зависимыми от дискретных
дисбалансов |т| и выражают с помощью
матрицы динамических коэффициентов
влияния. |а|:
| А | = | а 11 m |. (5.10)
Чем больше частот вращения, на ко-
торых производят измерения контрольных
сечений ротора и, следовательно, плоскос-
тей коррекции, тем сложнее системы кор-
ректирующих масс и больше эти системы
приближаются к виду распределения ис-
ходного дисбаланса. Для увеличения числа
уравнений в системе (5.10) можно пользо-
ваться измерениями при разных значениях
податливости опор РБС (обычно имеются
два значения). Матрицу ДКВ получают
определением амплитуды и фазы вибрации
при последовательной установке пробного
груза в каждую из плоскостей коррекции
(/, 2, 3,. . ., k). Так, а11К — колебания j-го
участка или опоры на режиме k (k =
— 1,2,.. . , п) при установке единичного
груза в плоскости i (i — 1, 2.. . . , п) Сис-
тема (5.10) принимает вид
(5.11)
Если рассматривать наиболее типич-
ную балансировку паротурбинного ротора
на двух режимах измерения (при гц =
— 1500 мин-1 и п-2 — 3000 мин-1), систе-
ма (5.11) принимает вид
П + r??2a2l I 4“ 1 = А I Ь
ПТ\О] 12 -|- m2^212 4“ ГИэвЗ|2 = Л I2i
Ш1О122 -f- Щ 2^222 4“ Щзв322 “ А 22-
► (5.12)
Методы балансировки тяжелых роторов на заводских стендах
145
Здесь для режима / принято Лн — Л21,
что часто выполняется на практике. Ус-
ловия сбалансированности:
Лц = — ЛОц;
Л>2 = — Ло|2;
Д22 = --- Ло22-
(5.13)
После определения ДКВ из системы
(5.12) с учетом (5.13) определяют mf, т2,
тз и устанавливают их в соответствую-
щие плоскости коррекции. В случае, если
остаточные амплитуды превышает нор-
мальные, их принимают за новые исход-
ные и решают систему (5.12) вновь.
Все величины в системе (5.12) век-
торные, т. е. уравнений в данном случае
шесть. Необходимо следить за хорошей
обусловленностью матрицы коэффициен-
тов влияния и не допускать ее приближе-
ния к нулю путем рационального выбора
плоскостей коррекции контрольных участ-
ков и частот, на которых производят из-
мерения. Никаких других трудностей и
особенностей в вычислительном отношении
данные методы не содержат.
Методы оптимизации процессов балан-
сировки. Все вышеуказанные методы фор-
мального решения полностью определен-
ных систем линейных алгебраических урав-
нений могут быть эффективны при мини-
мальных отклонениях в определении ДКВ,
малых погрешностях всех измерений и хо-
рошей обусловленности матриц, входящих
в расчеты. Однако на практике все эти
условия обычно не выполняются. В случае
применения графических расчетных мето-
дов при построении векторных диаграмм
используют вероятностный подход к за-
даче, применяя неформальные варианты
распределения векторов ДКВ и корректи-
рующих масс. При применении расчетов
на ЭВМ решения полностью определенных
систем не дают устойчивых, а иногда и
реальных результатов (при формальном
решении часто необходима установка не-
приемлемо больших грузов), а осуществле-
ние вероятностного подхода определяет не-
обходимость применения математической
формализации для осуществления пол-
ностью автоматизированных машинных
расчетов. Одним из таких методов мате-
матической оптимизации расчетов являет-
ся метод наименьших квадратов. Данный
метод требует иной системы уравнений,
т. е. число условий сбалансированности
должно быть больше числа неизвестных
(корректирующих масс либо ДКВ при об-
ратном расчете). Таким образом, система
для определения трех корректирующих
масс может быть представлена пятью век-
торными уравнениями. Обычно добавляют
условия сбалансированности ротора как
жесткого тела на малых частотах враще-
ния или любые другие условия (добав-
ление других частот, контролируемых
участков ротора, различных значений
жесткости опор и т.п.). В этом случае
имеем
miCji 4- /«2021 + == Аг,
W|G!|2 “Ь Щ2О22 “Ь ^3^32---- Аъ',
n?iGi3 — Щ2О23 4~ /ЯзДзз— Аз’, '(5.14)
т |«|4 4- Щ2О24 + ™ЗЯ34 = Аг,
Щ|С|5 + ^2025 + ГПЗЙЗЙ = А&.^
В проекциях система (5.14) превра-
щается в систему из десяти уравнений.
Здесь предполагается, что величины Ai,...,
Л 5 содержат невязки, обусловленные по-
грешностями измерения. Согласно методу
наименьших квадратов требуется найти
такие значения т?_, тз, при которых
сумма квадратов невязок была бы наи-
меньшей
А — ай ~ А{)2 min, (5.15)
где п — число корректирующих грузов (в
проекциях п — 6); I — число уравнений (в
проекциях I== 10).
Система производных дА/дт, == 0, i =
= 1,2.....п дает систему линейных урав-
нений для определения n-го числа грузов
вида
146
Высокочастотная балансировка роторов
ml X ачаЧ Н"т2 °2/ а1/ +
/=1 »=1
I I
4-т3 £ a3jah + - - - + тп £ =
/-1 /=|
i
= 14.^,.
.* i i
т1 Gl/fl2/ + m2 S G2/G2j +
J=1 f=)
Л
+ ™3 £ «3^2/ + • +
/=1
I I
+ £ anja2l = £ A!^i>
/=1 ,= 1
I I
т\ Г al/a3f+^2 £ а‘^а^1 +
1=1 /=«
I
4_,тз 2^ аз/йз; 4- • 4-
1=1
I I
+™« £ ^taA, = £ Afa3i
j=i i=i
i i
m\ Г C|A 4“m2 £ «2/ ani 4-
, /=' J-1
i
4*^3 £ °3/% 4- 4-
i=i
t i
+mn X a„fanj = £ Afaaf. (5.16)
<=i /=i
Дальнейшее развитие метода наи-
меньших квадратов - добавление к нему
условий взвешенного приближения. Тог-
да сумма (5.15) преобразуется во «взве-
шенную сумму» вида
i
Ар" X ач ~~ Af Pi min’ (5J71
/=1
где положительное число > 0 весо-
вой множитель, выбираемый так, чтобы
I,
У Pf — 1 (нормативный вес).
j =1
«Вес» Р, назначают для каждого зна-
чения А, больше или меньше 1 в зави-
симости от оцениваемого значения досто-
верности измерений. Разновидностью оп-
тимизации является метод наименьших
квадратов с дисперсией, при котором после
статистической обработки задается дис-
персия ДКВ в виде среднего квадратиче-
ского отклонения, что и определяет «вес»
каждого уравнения. На базе данного мето-
да создана и применяется на практике спе-
циальная программа. Существует еще ряд
методов оптимизации процесса баланси-
ровки [34j, в которых могут быть использо-
ваны условия минимума квадратов значе-
ний корректирующих масс либо остаточ-
ных амплитуд. Кроме этого разработаны
программы «КОРРЕКТ» и «НЕВЯЗКА»
для обеспечения балансировки с уточне-
нием погрешностей ДКВ при установке
сложных систем корректирующих гру-
зов [32].
Все перечисленные выше методы ба-
лансировки в простых случаях эквивалент-
ны и легко приводятся друг к другу не-
сложными математическими преобразова-
ниями. В вычислительном отношении рас-
чет корректирующих масс и ДКВ сводится
к решению систем линейных алгебраичес-
ких уравнений, т. е. к операциям с мат-
рицами, легко программируемым на сов-
ременных микро- и мини-ЭВМ. Применение
методов с привлечением условий оптими-
зации требует более сложного программ-
ного обеспечения, но и здесь возможности
мини-ЭВМ оказываются достаточными.
Обеспечение эквивалентности распределе-
ния корректирующих масс и распределе-
ния исходного дисбаланса зависит не
столько от выбранного вычислительного
метода балансировки, сколько от числа и
вида условий сбалансированности и ра-
ционального выбора расположения плос-
костей коррекции, имеются, однако, и неко-
торые различия.
Методы балансировки тяжелых роторов на заводских стендах
147
Метод по формам колебаний обеспе-
чивает, как правило, более высокую обус-
ловленность матрицы ДКВ, так как сам
характер метода предполагает наиболее
рациональный выбор частот вращения,
участков измерений и расположения плос-
костей коррекции. Особенно облегчается
эта задача для симметричных роторов.
Метод позволяет определить эксперимен-
тально или теоретически «вклад» каждой
формы при работе ротора в валопроводе,
а это облегчает оценку эффективности ба-
лансировки, назначение сдаточных норма-
тивов и опенку опасности отклонений от
них. Кроме того, этот метод, особенно
в описанном виде, легче выполняется без
ЭВМ. Это важно в тех случаях, когда
дисперсия ДКВ очень велика, приходится
отказываться от одновременной установки
сложных систем грузов и когда эффектив-
ность применения ЭВМ резко снижается,
а автоматическая балансировка невоз-
можна.
Метод коэффициентов влияния являет-
ся наиболее формальным методом., легко
программируемым для расчетов на ЭВМ,
легко включает в себя любые новые ус-
ловия сбалансированности и с наибольшим
успехом применяется при условии сохра-
нения стабильности значений ДКВ для од-
нотипных роторов и от пуска к пуску.
Для сугубо несимметричных роторов, ког-
да трудно подобрать ортогональные сис-
темы грузов, метод ДКВ наиболее эффек-
тивен.
Методы балансировки с применением
оптимизационных расчетных методик
должны рекомендоваться в обязательном
порядке для осуществления машинных
расчетов при автоматизированных спосо-
бах балансировки.
Контроль качества балансировки ро-
торов. Для оценки качества балансиров
ки пользуются балансировочным крите-
рием [Г12], определяющим предельно до-
пустимое значение виброскорости опор
станка в рабочем диапазоне частот вра-
щения ротора КБ в виде
УБ= СоСС^СзУэ, (5.18)
где Уэ — допустимое среднее квадратичес-
кое значение виброскорости опор паротур-
бинного агрегата при его эксплуатации.
Коэффициенты Со — Сз назначают сле-
дующим образом: Со — отношение допус-
тимого значения оборотной составляюшей
переднему значению вибрации ([Г13] ре-
комендует Со = 0,64); Ci—соотношение
податливости опор ротора на РБС и опор
в турбоагрегате. На рис. 4 приведены кри-
вые податливости опор РБС ДН-10. Мак-
симальная податливость равна 0.7—
1,0 мкм кН"1, что не ниже податливости
опор всех современных турбоагрегатов, ле-
жащих в диапазоне от 0,2 мкм • кН-1 (для
выносных опор мощных турбоагрегатов)
до 0,8 мкм - кН1 (встроенные в выхлоп-
ные патрубки опоры). Таким образом,
можно принять С| — 1; Сч = 1 при балан-
сировке по колебаниям опор и Сч. — 5 при
балансировке по колебаниям цапф ротора;
С3 — 1 при балансировке по опорам и Сз =
= 2ч-4 при балансировке по сечениям
ротора в пролете.
Таким образом, при балансировке ро-
тора по колебаниям корпусов опор при
Уэ = 2,8 мм • с-1 имеем
уБ = 0,64 • 1 • 1 • 1 • 2,8= 1,8 мм • с-’.
Для составляющей вибрации с часто-
той вращения ротора нормируемая ампли-
туда ЛБ = 8,1 мкм. Это верхняя, предельно
допустимая граница. Следует учитывать,
что при соединении роторов в валопро-
вод турбоагрегата добавляются новые ис-
точники вибрации, основные из которых
связаны с погрешностями соединения ро-
торов, изменением форм их динамического
изгиба в результате замены консольных
участков на жесткие межмуфточные про-
леты. Эту амплитуду надо умножить на
коэффициент, равный 0,6—0,7, и, таким
образом, наибольшая амплитуда колеба-
ний опор ротора на РБС <4Б = 8,1 • 0,6 яе
мкм при максимальной податливости
опор РБС. Для тяжелых роторов, рабо-
тающих на жестких выносных опорах с
вертикальными податливостями порядка
0,2 мкм-кН-1, можно допустить приемку
148
Высокочастотная балансировка роторов
роторов при минимальном значении подат-
ливости опор на РБС (порядка 0,5 ммХ
ХкН') во всем диапазоне частот вра-
щения.
Примеры балансировки. На рис. 5.14
приведены векторы исходной вибрации
Fw, Fon и Уош. построенные, как пока-
зано на рис. 5.13. При наличии значений
Рис. 5.14. Пример балансировки по формам
колебаний (п. 6.1): первый пуск — сплошные
линии; второй пуск—штриховые линии
ДКВ. полученных из предыдущих балан-
сировок однотипных роторов, решаем сис-
тему уравнений (5.3) и устанавливаем на
роторе расчетные грузы — w3. В резуль-
тате изменения вибраций можно предста-
вить векторами Уь Уп и У1П, а остаточ-
ные значения векторами У*= FOi — Fb
У?! = Уоп — Уп, F = У0Н1 — Yfll. Примем
остаточные значения за исходные, под-
ставим их в систему уравнений (5.3) и
рассчитаем новые значения грузов Wi —
— т3, после установки которых вибрация
по всем формам снижается до допусти-
мых значений- (штриховые линии). В про-
тивном случае описанный процесс балан-
сировки следует продолжать.
Пример /. Балансировка по формам коле-
баний. Предварительно введем символическую
запись комплексных чисел, описывающих век-
торы вибрационных величин в виде Л/qj, где
А — амплитуда вибрации (модуль); <р — фаза
(аргумент).
Пусть исходная вибрация неотбалансиро-
ванного ротора по первым формам
У01 — 51 мкм/300°; Уоп = 70 мкм/30°;
УОш ~ 40 мкм/70°.
На рис. 5.14 векторы вибрации изображены
в масштабе 1000: 1, т. е. 1 мм соответствует
1 мкм, фазовый угол отсчитываем от верти-
кальной линии (<р = 0°) против вращения ро-
тора.
Допустим, что коэффициенты влияния по
указанным формам колебаний определены при
балансировке аналогичных роторов и равны
соответственно а01 = 17 мкм • кг-1/200°; сОц =
= 35 мкм кг"'/90°; с0Н! = 10 мкм - кг_,/20°.
Напомним, что в силу ортогональности ба-
лансировочных систем каждая система грузов
влияет только на одну из форм колебаний,
т. е. о01 ц, a0I jH и т. д. равны нулю.
Из’уравнения (5.7) находим величину и
расположение ортогональных систем баланси-
ровочных грузов, устанавливаемых на роторе
(по правилу деления комплексных чисел).
“ Foi _ 51/120°
о0| ~ 17/200°
= 3 кг/280°
Величина тх = 3 кг является частью сис-
темы с известным соотношением грузов /пп
и тш для балансировки ротора по форме I:
Fon
mH=-—
Uu
70/210°
35/90°
= 2 кг/120°;
=
“ ^oiii 40/280°
а1П ~ 10/20°
= 4 кг/230°.
После установки указанной выше системы
вибрация ротора, разложенная по формам ко-
лебаний, будет описываться векторами Yt
(30 мкм/260°); У*( (27 мкм/350°); У?п (12 мкм/
92°). Построив векторные треугольники, как
это показано на рис. 5Л4, j. е. вычислив век-
торные разности У01 — У£ Уои — У* и Уош —
— У*ц. получим векторы У[ (34 мкм/160°);
Уп (50 мкм/235°) и У]ц (28 мкм/238°), ха-
рактеризующие влияния ортогональных систем
балансировочных грузов.
Далее уточним, сохраняя предположение
об ортогональности, динамические коэффициен-
ты влияния по формам колебаний:
3/280° 11,3 мкм'кг“1/240о;
Гц 50/235” „
---2/1ИК/"5:
Гц, 28/238” , _,,оо
0," = ^7 = Т72зо^= к"'кг /8 '
Методы балансировки тяжелых роторов на заводских стендах
149
Вычислим добавочные системы балансиро-
вочных грузов:
= - a, 11,3/240° -Kfi 27/170° = 2,65/200°, _— I
mH — mTn = aI( ~ -25,5/115° — У*п _ 12/272° «in ~ 7/18° = 1,71/254°
Установив эту систему, получим новые зна-
чения вибрации Xf* (6 мкм/135°); Yf* (8 мкм/
325°); У’*1 (7/145°) В случае несоблюдения
ортогональности приходится системы баланси-
ровочных грузов ставить последовательно и кор-
ректировать.
На рис. 5.15 приведен графический при-
мер последовательной балансировки по
Рис. 5.15. Пример последовательной баланси-
ровки по формам колебаний
формам колебаний. В первый балансиро-
вочный пуск установкой системы грузов
Wj (обычно два синфазных равных по
массе груза в крайних плоскостях) устра-
няем вибрацию по форме У0|: влияние сис-
темы Wj изображено вектором Kj оста-
точная вибрация — вектором /. Затем сис-
темой грузов (обычно два противополож-
ных, примерно равных по массе груза)
устраняем вибрацию по форме влия-
ние системы /д1| изображаем вектором ,УП,
а остаточная вибрация— вектором 2. За-
тем системой грузов гищ устраняем виб-
рацию У**], а остальная вибрация — век-
тором 3.
Во всех пусках имеется возможность
уточнить ДКВ, т. е.
— YJmx\ Од = Yxl/tnn\ аш = Yxxx/mxxx.
В случае необходимости процесс ба-
лансировки продолжается с учетом уточ-
ненных значений ДКВ.
Пример 2. Последовательная балансировка
по формам колебаний {рис. 5.15). Пусть ис-
ходная вибрация разложения по первым трем
формам
Уф = 55 мкм/325°; У011 = 54 мкм/28°;
Уош — 24 мкм/80°.
Установим систему балансировочных грузов тх
для устранения только формы Уф, пользуясь
коэффициентом влияния а01 — 20/200°,
n, _ 55/14У
1 аох 20/200*
2,75/305°.
При этом первая форма будет практически от-
балансирована (вектор /), а формы II и III
изменятся до величины Уф) (56 мкм/40°) и
Уош (45 мкм/12°).
Установим систему ти, ортогональную к
форме I, тогда форма I будет по-прежнему
характеризоваться вектором 1, форма II умень-
шится до приемлемой величины (вектор 2), а
форма III изменится до величины У?]*п (45/
130°). Далее установим систему пг1П, ортого-
нальную к формам I и II, что снижает фо-
рму III до вектора 3, оставляя без изменения
формы I и II (векторы / и 2).
На рис. 5.16 приведен пример балан-
сировки по ДКВ; Л011, Лон1, Лон2 — исход-
ные векторы вибрации на гц = 1500 мин-1,
опоры / и опоры 2 на п — 3000 мин-1.
Пуск 1 — установка груза mit вызвав-
шего изменения вибраций, изображенных
векторами Лш, Л1н1, 'Л|н2:
аи = Ац/тг, а12 = Л1«>/ть
С1з = Л1к2/т|.
Пуск 2 — установка груза /тг2:
a2i — Л2|/ту, азз= Л2и1/т2;
аз2 = Л2|1?/^2.
Пуск 3 — установка груза ту
аз! = Аы/ту, азг = Л3н1/ту,
«зз = Л3н3/ m3-
150
Высокочастотная балансировка роторов
Рис. 5.16. Пример балансировки по динами-
ческим коэффициентам влияния
Далее, полученные значения ДКВ под-
ставим в систему (5.12) и с учетом (5.13)
получим значение корректирующих грузов
W|, т2, т3. За исходные значения виб-
рации можем принять начальные значения
Л0(1, ЛОк1, Л0н2 или значения, полученные
после трех пробных пусков (соответствен-
но точки 1—3). В первом случае проб-
ные грузы снимают с ротора и устанав-
ливают новую, полученную расчетом сис-
тему грузов, во втором случае получен-
ную расчетом систему грузов векторно
складывают с уже установленными проб-
ными грузами. Естественно, за исходную
вибрацию целесообразно принять наи-
меньшую.
Балансировка по всем методикам при
наличии ранее определенных ДКВ должна
вестись так, чтобы каждый пробный груз
либо система грузов приводили к сниже-
нию исходного значения вибрации
5.4. МЕТОДЫ ИДЕНТИФИКАЦИИ
ЭКСЦЕНТРИСИТЕТОВ
Изложенные выше методы баланси-
ровки с применением пробных масс, строго
говоря, не используют для отыскания
распределения дисбалансов, но с их по-
мощью определяют возможность переноса
методов балансировки жестких роторов с
низких частот на высокие. Они имеют ряд
недостатков. Работа на критических час-
тотах вращения или вблизи них небезо-
пасна для прочности или долговечности
конструкции, а измеряемые параметры не-
стабильны; не всех критических частот
можно достичь, так как они ограничены
разрушающими, частотами вращения, а
следовательно, не по всем формам можно
вести балансировку; собственные формы
сложных конструкций могут оставаться не-
известными; не все роторы допускают ус-
тановку пробных масс и не всегда при-
емлемы пробные пуски, так как они бы-
вают слишком дорогими. Пробные и кор-
ректирующие массы могут попадать не в
места расположения дисбалансов, тогда
при снижении вибраций корпусов или опор
может возникнуть рост напряжений и из-
гибающих моментов в роторе и нагрузок
на опоры.
Для улучшения общего вибрационного
состояния машины путем ее балансировки
следует исходить из рассмотрения, а зна-
чит. и нахождения начального дисбаланса.
Зная распределение дисбаланса ротора,
можно устранить его полностью или ком-
пенсировать ограниченным числом коррек-
тирующих масс в зависимости от конкрет-
ных условий и требований на остаточный
дисбаланс
Во всех работах, посвященных выбору
допуска на остаточный дисбаланс враща-
ющихся элементов машины, рассматри-
ваются жесткие роторы, вращающиеся с
малой скоростью. Для них этот дисбаланс
можно считать неизменным в процессе экс-
плуатации и основной причиной вибраций.
Для гибких и квазигибких роторов ма-
шин на рабочих частотах вращения про-
является «скрытый дисбаланс» — ротор
изгибается. Это имеет не менее важное
значение для величины вибраций, чем ос-
таточный дисбаланс. Поэтому идентифика-
ция дисбалансов для указанных роторов
является единственным методом, обеспе-
чивающим высокие требования по уровню
вибраций и надежности.
Методы идентификации эксцентриситетов
151
Для отыскания дисбаланса ротора в
заданных сечениях разработаны методы
идентификации эксцентриситетов. Эти ме-
тоды, как показано на рис. 5-1, не тре-
буют применения пробных масс. Их можно
подразделить на два класса: с известными
и неизвестными упруго-инерционными ха-
рактеристиками. В тех случаях, когда уп-
руго-инерционные характеристики ротора
(распределение масс и жесткостей) извест-
ны или могут быть легко и достовер-
но найдены, методы идентификации раз-
бивают на подклассы.
Когда заданы статические коэффици
енты влияния, то в зависимости от на-
личия средств измерения и их возмож-
ности идентификацию эксцентриситетов
осуществляют методами, основанными на
измерении прогибов, реакций опор или виб-
раций. Если есть возможность измерять
относительные деформации участков ро-
тора, то идентификацию эксцентриситетов
производят по относительным деформа-
циям, напряжениям или кривизне ротора.
Для особо сложных и ответственных
конструкций машин достоверные значения
распределения упруго-инерционных ха-
рактеристик получить трудно. Поэтому их
считают неизвестными и применяют ме-
тоды идентификации эксцентриситетов, в
которых предусматривается и отыскание
Самих неизвестных упруго-инерционных
характеристик. Эти методы в зависимости
от применяемых средств измерения дефор-
мационных параметров ротора и необхо-
димой точности определения эксцентриси-
тетов и упруго-инерционных характеристик
подразделяют на методы параметрической
идентификации, параметрической иденти-
фикации с применением обобщенного диф-
ференцирования, позволяющего избежать
погрешностей, связанных с нахождением
производных от функции прогибов, на
группу методов идентификации, основан-
ной на электротензометрических измере-
ниях и на методы, основанные на исполь-
зовании универсального уравнения изог-
нутой оси вала.
Ввиду того, что применение электро-
тензометрии связано с наклейкой на ро-
тор тензорезисторов и прокладкой по ро-
тору выводных проводов, методы иденти-
фикации, основанные на тензоизмерениях,
используют в опытном производстве или
при исследованиях, а та^же в производ-
ственных условиях для крупногабаритных
конструкций, для которых установка тензо-
резисторов и прокладка проводов не вли-
яют на работоспособность ротора.
Идентификация эксцентриситетов по
измеренным прогибам ротора. Условие
идентифицируемости динамической сис-
темы, описываемой уравнением (1.14)гт. е.
возможности однозначного определения
эксцентриситетов е и в, состоит в нера-
венстве нулю определителя, полученного
из членов, стоящих при неизвестных е и в.
Решая уравнение (1.14) относительно
у, у', получим
У] ~ Р\1т1ец1^2^~
'^Рггт2еу2м2~^--- + Р\пт пе уп^2 —
Уп — Рч\ т। е^[ <о" Ч-
Ч-Рп2^2^2^2Н-...Н-^птпемо)2.
—•••
ЯntJ,
y't ~ +
+ 4- 4- sinmneur,ixi2 — (5.19)
t in^n^'yn^
y'n — SnimieyiuY2
4- Sn2fn2ey2U)2 4 . . 4- 5пптпеупы2 —
П^уП^ -
152
Высокочастотная балансировка роторов
Аналогичные уравнения могут быть за-
писаны для другой плоскости. Коэффици-
енты р, q, s, t зависят от геометрических
и физических свойств ротора и могут быть
заранее подсчитаны для выбранной час-
тоты вращения. Для равножестких рото-
ров они одинаковы для горизонтальной и
вертикальной плоскостей.
Уравнения (5.19) решают относитель-
но эксцентриситетов с помощью ЭВМ или
аналоге-вычислител ьных устройств:
подсчитывают коэффициенты р, q, s, t
для выбранной частоты вращения <о;
разгоняют ротор до частоты вращения
<и, на которой проявляется деформация,
и на этой частоте вращения измеряют
прогибы и углы поворотов дисков;
полученную пространственную кривую
изогнутой оси ротора проектируют на две
взаимно перпендикулярные плоскости и
найденные значения yk, хк, y'k, х'к подстав-
ляют в уравнения типа (5.19);
на ЭВМ по стандартной программе
решают уравнения относительно неизвест-
ных €у, 6Х, £у, Ех,
суммируя векторы проекций эксцент-
риситетов, определяют их величину и мес-
то расположения на роторе;
произведя компенсацию найденных
дисбалансов, заканчивают балансировку
ротора.
Для идентификации всех эксцентриси-
тетов, число которых равно 2п (п ради-
альных и п угловых), необходимо, чтобы
число неизвестных было равно числу урав-
нений. Для этого не обязательно произ-
водить 2п измерений прогибов и углов
поворота на одной частоте вращения <<».
Можно уменьшить число мест измерений
или вовсе не измерять прогибы (или углы
поворота), соответственно увеличив число
частот вращения, на которых производится
измерение. Нетрудно заметить, что при
балансировке по этому методу учитыва-
ются сразу все те составляющие разло-
жения эксцентриситета в ряд по формам
изгиба, которые оказались в значениях
измеренных прогибов и углов поворота.
К выбору частот вращения, на кото-
рых измеряется прогиб, следует подходить
особенно внимательно, так как уравнения
(5.19) отражают не только количествен-
ную, но и качественную сторону дефор-
мации гибких роторов. Однако изменение
прогиба в зависимости от частоты вра-
щения, которое способна зафиксировать
измерительная аппаратура, наступает при
определенной разнице между двумя сосед-
ними частотами вращения, на которых про-
изводятся измерения. Так, например, если
частоты вращения сд, <0*4.1, расположен-
ные вдали от критических частот враще-
ния, близки друг к другу и аппаратура
зафиксировала одинаковые прогибы, то
уравнения для этих частот будут тождест-
венны.
Для балансировки роторов необходимо
путем проб и расчетов выбрать частоты
вращения и плоскости коррекции, пригод-
ные для данного ротора. При выборе
частот вращения следует учитывать, что
при приближении к критическим частотам
вращения усиливается действие одной из
составляющих разложения эксцентриси-
тета по формам изгиба, чем можно поль-
зоваться для более полного выявления со-
ответствующих им дисбалансов по изме-
ренным реакциям (или вибрациям) опор.
При колебаниях ротора в одной плоскости
выражения для неуравновешенных сил Р
и моментов М на дисках имеют следую-
щий вид:
Р,— ; М,— 2( £, + #,) -
Используя выражения (5.19) для у и у',
получают
+
-|-P12w2(1)2£>2 + --- + Pinmni3)2en—
~qiiJiu>2£.i — qwJztufzz— . . . —qinJnto2en,
Методы идентификации эксцентриситетов
153
-}-p„2m2<o2e24“-- + рппт„ы2еп—
— — pn2J2w2E2 —
. 2
Qnn ‘п w Ея •
Ml = +
-f-s12m2coze2-|-...^ slnmno)2e„ —
е1 — ^2^20,2е2 —
— zu7,iw2e„,
snlmlb)2el +
+ s„2 m2 <o2 e2 +... 4- snn m „ <o2ert —
— tnjJlti)ZEi — tn2-f24)2E2 — - -
_ . i 2
'nr.r.^ £„
Здесь значения коэффициентов p, p, s, t
находят из уравнений (1.14). Они зависят
от физических и геометрических свойств
ротора и частот вращения.
Имея выражения для неуравновешен-
ных сил и моментов на дисках, нетрудно
составить выражения для реакций опор
Для двухопорного ротора они имеют вид
/?i = A[£i -J- А^е? 4~ • 4~ АпСп
— Bi«i — В2Е2 — - Виви! (5 2qj
R? = GiCi -|~ 4- - 4~ Сп£п
— DlEl — — • • - — Дп8л- t
Коэффициенты А, В, С, D зависят
от геометрических параметров ротора, его
физических свойств, расстояния дисков от
его опор. Их значения можно найти из
предыдущих уравнений для любой частоты-
вращения ротора. Полученные уравнения
(5.20), выражающие линейную зависи-
мость между реакциями опор и эксцентри
ситетами ротора, используют для опреде-
ления неизвестных дисбалансов.
Так как уравнений всего два, а неиз-
вестных 2л, то недостающее число урав-
нений, равное 2п — 2, можно получить,
произведя добавочные измерения для
п — 1 частот вращения ротора.
Для использования уравнений (5.20)
при пространственном положении реакций
опор необходимо спроектировать реакции
на две взаимно перпендикулярные оси X
и Y При этом
Для вертикальной плоскости
Ryl{ ° 1) ~ А 11 еу\ + А 21 еу2+ • 4"
-^Anleyfl—Вцеу| — B2ikj/2 — • •“_BniE«ni
t01) ~ C\leyl + ^21ej/2+---4“
+ Cnieyn^D иву, —D2ley2 —DntEyn,
►
~ ineyi А~А2„ву2А~
4~ An„eyn В——
^2n^t/2 • • Bnn Е^п,
.У
10J — С\eyl 4- ^2,;^,/? Ь-.. 4-
(5.21)
~\~Cnneyn ~~ &1пеу1 Dnn^yn.
Аналогичное выражение проекций ре-
акций записывают для горизонтальной
плоскости.
Здесь еу, еу и ех, ех — проекции век-
торов неизвестных, эксцентриситетов на
вертикальную и горизонтальную плоскос-
ти. Для равножестких роторов коэффи-
циенты при отыскиваемых эксцентрисите-
тах для обеих плоскостей одинаковы.
Последовательность операций при ба-
лансировке следующая:
выбирают п частот, на которых про-
является прогиб ротора, и для этих час-
тот составляют уравнения (5.21); в этих
уравнениях заранее с помощью ЭВМ под-
считывают значения коэффициентов при
неизвестных е и е;
разгоняют ротор до частоты вращения
ы„ и на всех выбранных частотах вра-
щения от од до <02 измеряют векторы
реакций опор;
проекции этих векторов на две взаим-
но перпендикулярные плоскости подстав-
154
Высокочастотная балансировка роторов
ляют в уравнения (5-21). которые решают
относительно проекций эксцентриситетов;
произведя векторное сложение найден-
ных проекций эксцентриситетов, находят
их величину и место расположения на
роторе.
Нетрудно заметить, что при такой иден-
тификации учитываются дисбалансы по
всем формам изгиба, имеющие влияние
в рассматриваемом диапазоне частот вра-
щения как в прогибах, так и в реакциях
опор, что выражается в балансировке ро-
тора и как гибкого, и как жесткого.
По измеренным реакциям опор и най-
денным через них эксцентриситетам можно
подсчитать прогибы ротора на любых час-
тотах вращения Измерение реакций в ра-
ботающем изделии почти всегда доступ-
нее измерения прогибов его ротора.
Если известна зависимость между ре-
акциями опор и их вибрациями, получен-
ная, например, с помощью ненаправлен-
ного вибратора или вибрациями корпусов
в некоторых точках, то можно с достаточ-
ной точностью идентифицировать эксцен-
триситеты и по контролируемым вибра-
циям.
Для решения задач балансировки, в
частности идентификации эксцентрисите-
тов, целесообразно использовать как циф-
ровые, так и аналоговые вычислительные
машины.
Рис. 5.17. Квазианалогоная модель много-
массового ротора
Для решения задачи на аналоговой
вычислительной машине (АВМ) на
рис. 5.17 показана квазианалоговая мо-
дель многомассового ротора. С целью сок-
ращения записи и удобства решения сис-
тему уравнения (5-19) на АВМ представ-
ляют в матричной форме.
Обозначив
2 2
Ср = Рр/Пёсо ; ;
b ц ' У fiJs!= ” tpJrCty .
переписывают систему (5.19) в виде
L«/i| °11й12 С1л^11^|2
1«/2| • 1 с21#22 а‘2п^ 21^22 ^2п 1 1 .
14 дп 1^л1^п2 •• einnbnibn2 b пп
У? i С21 С22 С2л^2|^22 ^2л
Ух — 1^1^12 С1п^И^12 |6ы‘1
Уп ^л1^п2 еппйп\йп2 dnn
или короче:
£== Re,
(5.22)
где у — матрица проекций прогибов*. R —
матрица преобразования; ё— матрица
проекций эксцентриситетов.
Из выражения (5.22) имеем
ё — R~'y.
Модель системы уравнений (5.19) по-
казана на рис. 5.17, где матрица R пред-
ставлена в виде сетки сопротивлений, об-
ратно пропорциональных соответствую-
щим коэффициентам влияния:
R?f= Яц— 1/b,, и т. д.
Схема набора задачи на АВМ для
случая, когда е, — 0, i — I, 2,.... я, пока-
зана на рис. 5.18.
Процесс уравновешивания с использо-
ванием АВМ выполняют в следующем по-
рядке*.
Рис. 5.19. Идентификация эксцентриситетов
пятимассового ротора:
а —расчетная схема ротора, б- графическое реше
ние системы уравнений
Рис. 5.18. Схема набора задачи на АВМ
Методы идентификации эксцентриситетов 155
156
Высокочастотная балансировка роторов
на АВМ набирают схему, показанную
на рис. 5.18, а; проводимости /?*, /?*, . . . ,
R* устанавливают пропорционально соот-
ветствующим коэффициентам влияния;
разгоняют ротор до скорости, на кото-
рой начинает проявляться его деформа-
ция, и измеряют прогибы yt, у2,... , уп, ко-
торые с помощью специальной аппаратуры
преобразуют в унифицированные сигналы,
подаваемые на входы схем рис. 5.18,6;
пускают машину и считывают искомые
величины проекций эксцентриситетов, од-
новременно производят запись на двух-
координатном регистраторе;
по найденным проекциям эксцентри-
ситетов находят величину и положение
неуравновешенности для каждой плоскос-
ти, а затем производят компенсацию най-
денной неуравновешенности.
Пример. Рассмотрим пример использования
АВМ МН-10 для идентификации эксцентриси-
тетов пятимассового ротора осевого компрес-
сора (рис. 5.19, о) Массы, прогибы и стати-
ческие коэффициенты влияния этого ротора при-
ведены ниже.
0,228
0,184
0,143
0,111
0,067
0,203
0,246
0,23
0,195
0,139
0,195
0,284
0,303
0,29
0,243
0,155 0,1299
0,246 0,2457
0,295 0,3472
0,336 0,444
0,316 0,52
«2
еа
103.
Или после преобразований, обеспечиваю-
щих устойчивое решение, получают
1,94
2,86
2,672 =
2,804
2.55
0,507 0,015 0,014 0,02 0,01б'
0,023 0,722 0,035 0,03 0,03
0,018 0,028 0,716 0,036 0,043
0,014 0,024 0,036 0,733 0,055
0,008 0.017 0,03 0,04 0,694
<?1
ел
-10'.
3. Набирают задачу по схеме, показанной
на рис. 5 18, б.
4. Решение задачи на графопостроителе
АВМ МН-10 приведено на рис 5.19,6.
Значения эксцентриситетов:
= 77,4 - КГ 6 м; е2 =? 89,9 • 10~ь м;
ех = 105 106 м; е4 = 73 - 10“6 м:
= 59,5 • 10~6 м.
Время решения задачи не превышает 20 с.
Номер массы Масса т. кг Прогибы у • 10-ъ, м Статические коэффициенты влияния ач • 10" s, м/Н
1 2 3 4 5
1 9,03 7,87 9,2 7,4 6,23 4,8 2,77
2 9.96 11,38 7,45 9,0 8,95 7,3 5,52
3 12,32 11,16 5,3 7,85 9,88 8.5 6,8
4 12,53 11,37 4,2 7,00 8,62 9,7 8,98
5 17,6 10,35 2.62 4,67 7,6 9,43 10,8
Прогибы измеряют при <в2 = 0,274 -10*’! /с2,
причем все они практически лежат в одной
плоскости.
Расчет эксцентриситетов производят в сле-
дующем порядке:
1. Симметрируют матрицу коэффициентов
влияния так, чтобы имело место равенство ац =
= Ctji-
2. Подсчитывают все значения а^пг,со2 и
приводят систему к так называемому машин-
ному виду
’ 7,87
11,37
11,16 =
11,38
10,35
5.5. ИСПОЛЬЗОВАНИЕ
ИНТЕГРОДИФФЕРЕНЦИАЛЬНЫХ
ЗАВИСИМОСТЕЙ ИЗГИБА
ДЛЯ РАЗРАБОТКИ АЛГОРИТМОВ
ПАРАМЕТРИЧЕСКОЙ ИДЕНТИФИКАЦИИ
Параметрическая идентификация гиб-
ких роботов с неизвестными упругоинер-
ционными характеристиками. Изложенные
выше методы требуют определенной под-
готовительной работы,связанной с нахож-
дением коэффициентов влияния. Поэтому
целесообразно иметь алгоритмы идентифи-
кации, не требующие этой операции, что
особенно важно для новых изделий, не
Разработка алгоритмов параметрической идентификации
157
имеющих изученных аналогов, конструк-
ция которых не допускает установку проб-
ных дисбалансов, а пробные пуски неже-
лательны.
В приведенном ниже методе идентифи-
кация эксцентриситетов, а также упруго-
инерционных и диссипативных параметров,
вся необходимая информация о роторе
может быть получена лишь измерением
его прогибов на некотором числе некри-
тических частот вращения, причем эти из-
мерения могут быть осуществлены извест-
ными методами, например, на вакуумных
виброизмерительных балансировочных
(ВИБС) или других разгонных устройст-
вах, а также непосредственно при рабо-
те машины под нагрузкой.
Пространственные кривые динамичес-
кого прогиба ротора можно разложить
на две взаимно перпендикулярные плос-
кости: XOZ и YOZ, линией пересечения
которых является ось OZ, совпадающая
с осью ротора, т. е. их представляют в
параметрическом виде:
X=X(Z,<D), у = у(2,СО),
где <о — частота вращения ротора.
В основу построения алгоритма пара-
метрической идентификации положены
следующие интегродифференциал ьные за
висимости теории -изгиба валов:
проекция прогиба упругой оси ротора
на плоскость YOZ
j/ = j/(zid); (5.23)
угол поворота поперечного сечения ро-
тора в точке z оси OZ
у' = dy/dz; (5.24)
проекция вектора кривизны упругой
линии ротора на плоскость YOZ
Ш,«)=»'7|1 + («')2)3/2: (5.25)
проекция изгибающего момента ротора
в сечении с координатой z на плоскость
YOZ
Му = Му (z, ы) = kEY\ (5.26)
проекция поперечной силы на плос-
кость YOZ
Qy =Qy(z,v)= dMy/dz; (5.27)
проекция интенсивности инерционной
нагрузки на плоскость YOZ
Уу (z, ti>) = dQy/dz—fn<i)2 (у-[-еу). (5.28)
Аналогичные соотношения можно за-
писывать для проекций векторов на плос-
кость XOZ. В дальнейшем все исследо-
вания проводятся для плоскости YOZ.
В соотношениях (5.23) — (5.28) не
учитывается сопротивление, возникающее
при вращении ротора и являющееся след-
ствием влияния самых различных факто-
ров. Для его учета пусть f=^(z, ы)—
суммарный момент всех сил сопротивле-
ния, возникающих при частоте враще-
ния г». При этом без ограничения общ-
ности рассуждений можно предположить,
что все величины, от которых он зависит,
уже выражены через переменные (z, to).
Тогда можно считать, что соотношение
(5.26) принимает вид
f — {z, &)-]-Му (z, w) — k (z, w) EJ (z),(5.29)
где My(z, ы) — проекция только изгибаю-
щего момента инерционных сил.
I d2f
d2k । dk I
2 2
-f-azfc — eij— w У'
(5.30)
m dz2
где aj=a,(z) —
(5.31)
i d[i\EJ)
m dz'
i=C, 1,2.
В дальнейшем первое слагаемое в ле-
вой части соотношения (5.29) представля-
ют разложенным в ряд по степеням ы
с неизвестными коэффициента 6j(z), зави-
сящими от z, а рассматриваемый ряд за-
меняют его (л-}-1)-й конечной суммой.
При этом модуль остатка ряда вносит
в расчет погрешность, не превышающую
заданную точность измерения прогибов.
Для идентификации по известным фун-
кциям y{z, w/), измеренным эксперимен-
тально на различных п некритических час-
тотах вращения ротора <од значений функ-
ций ey(z), a,(z), i = 0, 1, 2, 6,(z), i —0,
158
Высокочастотная балансировка роторов
1»2,.... п, в точке z — а достаточно сос-
тавить и решить систему линейных урав-
нений (п 4- 5)-го порядка:
бДс)
i=0
(Phiz, Id,)
-f-ac(a)----——
dz
, dk(z,<£>)
+ 2^(0)—^ У
4- a2(a)k{a, Wj) — ey(a)ы2 — (5.32j
w,),
/ = I, 2,... ,«4-5.
Решив эту систему уравнений, опре-
деляют неизвестные величины в заданной
точке а.
Поскольку точка z — а бралась произ-
вольно, то, решив систему уравнений
(5.32) с коэффициентами, найденными в
любой другой точке оси 0Z, можно полу-
чить значения неизвестных в этой точке.
Таким образом, можно считать, что иден-
тифицированы функции ey{z}, а также
a,(z), i = 0, 1,2.
Проведя аналогичные выкладки для
ex(z), получают значения векторов дис-
балансов в каждой точке оси ротора:
D(z) = M(z)y4(z) + efa) ,(5.33)
и угол, составленный этими векторами с
осью ОУ,
tg V = «Mz)/lM2)L (5.34)
Во многих практически важных слу-
чаях количество частот вращения, на ко-
торых необходимо измерить прогиб, зна-
чительно сокращается. В этом случае сис-
тема уравнений (5.32) принимает более
простой вид.
Достаточно хорошим приближением
для силы сопротивления при вращении,
определяемой в основном трением, явля-
ется линейное, не зависящее от z при-
ближение, например, когда сила трения
пропорциональна угловой частоте, тогда
d2k(z, о,) dk(z, w-)
СЦ)---^2----b2ai Ь (Z’
— j~ 1, 2, 3, 4,
т. е. для идентификации неизвестных экс-
центриситетов и упругоинерционных ха-
рактеристик достаточно измерить прогиб
ротора на четырех различных некрити-
ческих частотах вращения.
1. Если частоты вращения ротора, на
которых измеряются прогибы, таковы, что
не проявляется действие сил трения, то
система уравнений имеет такой же вид,
что и в предыдущем случае. Тогда изме-
рение прогибов достаточно производить
на четырех различных некритических час-
тотах вращения
2. Если к тому же жесткость EJ ли-
нейна по г, например ротор — однородный
конус, то EJ ~ vz 4- w, и число необхо-
димых Частот снизится до трех, а сис-
тема уравнений примет вид
VZW d2k{z,w) t 2v dk(z,b)£
m dz2 m dz
- o)/2ei/(z) = wfj/(z, w;), j= I, 2, 3.
3. Если ротор цилиндрического посто-
янного сечения, т. е. EJ — const, то
(EJ)'= (EJ)" = O.
В этом случае измерение прогибов про
изводят на двух различных частотах вра-
щения ротора, к система принимает вид
w d2k{z,a>)
т dz2
rfey=rfy(z, со;),
/=1,2.
4. Если упругоинерционные характе-
ристики ротора заданы, то для иденти-
фикации неизвестного эксцентриситета до-
статочно рассмотреть решение лишь од-
ного уравнения, в которое вырождается
система, т. е.
__ I / w d2k
у <в2 dz2
<Уу
Разработка алгоритмов параметрической идентификации
159
Таким образом, если имеется возмож-
ность измерить прогибы ротора непосред-
ственно в работе или, например, на вы-
сокочастотном балансировочном стенде, то
идентификацию его дисбалансов можно
производить в следующей последователь-
ности:
1) измеряют прогибы ротора в ряде
сечений на необходимом для решения чис-
ло некритических частот вращения;
2) проектируют полученную кривую
прогиба ротора на две взаимно перпен-
дикулярные плоскости;
3) по формулам численного дифферен-
цирования находят нужные производные
проекций прогиба;
4) подставляя полученные значения в
систему уравнений (5.32) или в одну из ее
модификаций, решают ее относительно не-
известных;
5) по формулам (5.34) и (5.35) опре-
деляют искомые дисбалансы в выбранных
сечениях ротора.
Рассмотренные частные случаи имеют
немаловажное практическое значение. На-
уравнений. Для этого в определенном мас-
штабе строится кривая прогибов ротора
y(z) и дважды графически дифференциру-
ется, давая у"(г). Путем увеличения мас-
штаба y"(z) в каждом сечении в EJ раз
(где EJ — изгибная жесткость данного се-
чения) получают эпюру изгибающего мо-
мента.
Затем, графически дифференцируя
эпюру M(z), находят эпюру Q(z), а после
второго дифференцирования
q(z) = m(z) [e(z) + f/(z)]<o2.
Откуда уже можно найти e(z), уменьшив
масштаб в т(г)а>2 раз и вычтя у (г).
При решении системы уравнений (5.32)
или одной из ее модификаций идентифи-
цируется не только эксцентриситет, но и
а, (где i=0, 1,2), а также 6,(z). Вели-
чины 6t-(z) позволяют идентифицировать
суммарный момент сопротивления f(z, <о);
величины а, — приведенные массы и жест-
кости ротора. Распределенную массу и из-
гибную жесткость определяют по фор-
мулам
(5.35)
пример, четвертый частный случай, пред-
полагающий знание упругоинерционных
характеристик, как и метод по статичес-
ким коэффициентам влияния, позволяет
идентифицировать эксцентриситеты, но не
путем решения систем линейных уравне-
ний, а из одного уравнения, в которое
входит четвертая производная измеренной
кривой прогиба ротора или вторая произ-
водная кривой относительной деформации.
Изгибную жесткость EJ в рассматрива-
емом сечении легко можно подсчитать по
коэффициентам влияния. Таким образом,
четвертый частный случай позволяет на-
ряду с аналитическим построить и графи-
ческий алгоритм идентификации неурав-
новешенных сил и эксцентриситетов в лю-
бом сечении ротора без решения систем
EJ(z) = rn{z) oc0(z). (5.36)
Таким образом, погонную массу и из-
гибную жесткость ротора идентифицируют
с помощью той же последовательности
операций, что и эксцентриситеты, если
после решения системы уравнений (5.33)
применить выражения (5.36) и (5.37).
Идентифицированные таким способом
значения упругоинерционных характерис-
тик будут более достоверными, чем полу-
чаемые без учета вращения, трения и дру-
гих реальных условий.
Найдя однажды приведенные упруго-
инерционные характеристики и массы ба-
лансируемой серии роторов, можно в даль
нейшем (для массовых производств) уп-
ростить балансировку, сведя ее к пятому
160
Высокочастотная балансировка роторов
частному случаю. При этом необходимо
измерить прогибы лишь на одной частоте
вращения.
Используя алгоритм идентификации
для балансировки каждого из роторов,
выпускаемых крупными сериями и в те-
чение длительного времени, можно одно-
временно с балансировкой проверять уп-
ругоинерционные характеристики роторов
(по заложенной программе), сравнивать
их с эталонными и следить таким образом
за стабильностью производства.
Специализированный алгоритм пара-
метрической идентификации на основе ме-
тода обобщенного дифференцирования.
При ограниченном числе точек измерения
прогиба вычисление производных связано
с определенными ошибками. Повысить точ-
ность искомых производных можно, изме-
ряя не только прогиб, но и угол пово-
рота сечения, т. е. у' и даже у" и, таким
образом, устанавливать точные соотно-
шения между у и у'.
Но можно вообще избежать ошибок,
связанных с отысканием производных, при-
менив способ обобщенного дифференциро-
вания (основанный на интегрировании по
частям), идея которого в том, чтобы за-
менить дифференцирование неизвестной, в
данном случае заданной таблично функ-
ции. дифференцированием известной, за-
данной аналитически гладкой функции, об-
ладающей некоторыми граничными свой-
ствами. Эти свойства заключаются в том,
что гладкая функция обращается в нуль
на границах рассматриваемого участка
вместе с некоторым числом ее произ-
водных.
В большинстве случаев можно заме-
нить нелинейное дифференциальное урав-
нение
d2 г
w)EJ(z)\ =
dz*
^m(z)to2[ to) + Cj/z)]
на линейное, полагая
fe(z. to) — у"(2, to).
Разбивая вал на участки таким об-
разом, чтобы можно было считать в пре-
делах каждого участка EJif т, и е, по-
стоянными величинами, рассмотрим любой
из участков |z,, Zh-i] :
d*\ EJy"\
---—-----= т^\у 4- ej. (»-37)
Используем гладкую функцию f(z).
Пусть при этом она сама и ее первые
три производные обращаются в нуль на
концах участков, на которые разбит вал,
т. е. при 2 = zf и 2 — 2,4-1:
f = f = f" = f'" = 0. (5.38)
Умножим левую и правую части урав
нения (5.37) на /(z) и, последовательно
четырежды интегрируя, приведем его к
виду
2,+! г<+1
— ydz—^e{ fdz=
rri{ J J
(5.39)
= to2 \ fydz.
В полученном уравнении две неизвест-
ные величины: е, и ЕЦ/т,. Для их иден-
тификации можно записать уравнение для
двух различных некритических частот вра-
щения или для двух различных функций
/1 и /г со свойствами (5.38). Класс таких
функций достаточно велик. Примерами мо-
гут служить
= —z,)4(z —г1+1А
4
f2 = (z-2y(exp^-^-- 1) ;
/?л(г — г)
Г - 4
) 3 = sin
При применении метода обобщенного
дифференцирования для исключения из
уравнений производных от прогиба сле-
дует иметь в виду, что наряду с- избав-
лением от погрешностей, которые могли бы
Разработка алгоритмов параметрической идентификации
161
возникнуть в процессе четырехкратного
дифференцирования, мы теряем в чувстви-
тельности у по сравнению с к сос-
тавляющим дисбаланса по высшим фор-
мам изгиба.
Параметрическая идентификация гиб-
ких роторов с использованием электро-
тензометрии. Применение тензорезисторов
для измерения относительных деформаций
в определенной мере удобно и в извест-
ных случаях имеет преимущество перед
другими способами. На показания тензо-
резисторов, наклеенных вдоль ротора в
рассматриваемых сечениях, не влияют пе-
ремещения ротора в зазорах подшипников,
колебаний опор и самих датчиков.
Для крупных относительно тихоходных
роторов прокладка по их поверхности вы-
водных проводов не влияет на работо-
способность машин, но дает возможность
постоянно следить за динамическим сос-
тоянием ротора при эксплуатации, выяв-
лять возникающие дефекты и изменение
дисбаланса.
Таким образом, в тех конструкциях
роторов, где при доводке или контроле
удобно использовать метод электротензо-
метрии. целесообразно иметь основанные
на показаниях тензорезисторов алгоритмы
идентификации дисбаланса как с приме-
нением пробных дисбалансов на критичес-
ких частотах вращения по формам изгиба,
так и другие, не требующие знания этих
форм, применения пробных дисбалансов
и пусков.
В дальнейшем снова используют шесть
зависимостей теории изгиба
Z
1) у = J y'dz+y^
О
2
2) У' = \ y"dz-]-y0;
о
3) ^==:±=й==-^-=2-; (5.40)
р EJ h
1
4) Mz=EJy"-, ।
I* Ц/ у о
6) q, — = ты (t/4-е) =
d2(EJy")
dz2 dz2
Здесь следует заметить, что любые из-
мерения одного из параметров: прогиба,
угла поворота, относительной деформа-
ции дают возможность использовать
различные методы и варианты идентифи-
кации. Конструктор должен предусмотреть
возможность измерения хотя бы одного из
параметров и дальнейшее преобразование
этого параметра в другой применительно
к избранному алгоритму.
Ниже рассмотрены алгоритмы иденти-
фикации. основанные на применении тен-
зорезисторов сопротивления для измере-
ния относительной деформации.
При изгибе ротора тензорезистор, на-
клеенный на его поверхность вдоль оси Z,
измеряет относительную деформацию во-
локон, на которых он закреплен, т. е е —
— h/p, где h — расстояние от нейтраль-
ной оси до рассматриваемых волокон или
тензорезистора, р радиус кривизны при
изгибе.
Идентификация неуравновешенных
сил и эксцентриситетов по изгибающе-
му моменту. Используя четвертое соотно-
шение (5.40), имеем
Мг= EJy" = EJ (5.41)
Для многомассового ротора, которым
с любой степенью точности за счет роста
числа масс может быть аппроксимирован
ротор с произвольным распределением
масс, неуравновешенные силы
Р, = trii (е, 4- у/) <t>2, (5.42)
а момент в рассматриваемом сечении ра-
вен алгебраической сумме моментов всех
сил (включая реакции опор), лежащих
по одну сторону от рассматриваемого се-
чения, т. е.
6 Зак 1641
162
Высокочастотная балансировка роторов
= £ athPk, г=1,2,...,н, (5-43)
k^i
где atk — коэффициенты, зависящие от рас-
стояния, на которых находится масса от
левой опоры до рассматриваемого сече-
ния (могут быть вычислены заранее).
Произведя измерения е на некоторых
некритических частотах вращения в п се-
чениях, по формуле (5.41) находят момент
в этих сечениях, а затем, решая систему
уравнений (5.43), отыскивают неизвестные
неуравновешенные силы, которые можно
компенсировать соответствующими проти-
вовесами, произведя таким образом балан-
сировку для частоты вращения <о. Если
необходимо идентифицировать не силу, а
эксцентриситет при балансировке для все-
го диапазона частот, то его находят из
выражения (5.42), в котором прогиб оп-
ределяют по первой строке (5.40), т. е.
путем двухкратного интегрирования най-
денной в процессе тензометрирования ро-
тора кривизны.
Идентификация эксцентриситетов по
нормальным напряжениям. Для баланси-
ровки можно использовать перевод отно-
сительной деформации в напряжения по
закону Гука, тогда получают систему сле-
дующих уравнений:
п
°i=ikX ai*Pk’1*2’* (544)
k=l
где о, — нормальное напряжение в сече-
нии i; W, — осевой момент сопротивления
в сечении I.
Параметрическая идентификация гиб-
ких роторов по относительным деформа-
циям. Уравнения (5.43) и (5.44) могут
быть использованы и для идентификации
жесткостей E,J,, соответствующих выбран-
ной динамической модели. Представим
(5.43) в виде
е, Е, Jt/ht =
(5.45)
п
= £ mk(ek 4- <о2, i= 1,2,..., п.
*=1
Для нахождения неизвестных et и £,/,
необходимо получить в 2 раза больше
уравнений, чем представлено системой
(5.45), что можно сделать, измерив е во
всех сечениях еще и на других некри
тических частотах вращения.
Можно использовать для идентифика
ции эксцентриситета и изгибных жесткос-
тей и шестую строку дифференциального
ряда (5.28):
d2(£/(z)^(z,tu)) _
dz2
- J/IVU, ») £/(z) +W(z, Ш1 — +
d2(£/(z))
_|_ f/"(z, <o)-==
dz
= m(z) <d2[#(z, w)4-e(z)|
В этом уравнении, записанном для про-
извольного сечения ротора с любым рас-
пределением масс и жесткостей, можно
считать неизвестными изгибную жесткость
£/(z), массу m(z) и эксцентриситет e(z).
Остальные величины, т. е. у, ylu, ylv, мо-
гут быть найдены интегрированием и диф-
ференцированием у", а не у, а осталь-
ные операции в обоих способах идентичны.
В этом случае также можно воспользо-
ваться методом графического дифференци-
рования, превращая сначала эпюру e(z)
путем изменения ее масштаба в EJ(z)/h
раз (А — расстояние от нейтральной оси
до волокон, на которых наклеен тензо-
резистор) в эпюру M(z), а затем, диф-
ференцируя последнюю дважды, получить
d = — f^(z)le(z) + y(z,
dzz
т. е. интенсивность распределенной на-
грузки.
В ряде случаев такой подход при ана-
литическом, а иногда и графическом ре-
шении дает меньшую погрешность, чем ре-
шение систем уравнений.
Если ротор аппроксимировать систе-
мой сосредоточенных масс /И*, то можно
Разработка алгоритмов параметрической идентификации
163
ограничиться вычислением третьей произ-
водной от прогиба (или первой от кри-
визны). Тогда
а\у" -j- аоу'" — e(af= i/w2, (5.46)
где
„ 1 d “(£/(*)] . _ ,
ai — Т?-----, ~ ~ . * = 0,1.
Mk dz’
Далее необходимо измерить у" на трех
некритических частотах вращения и найти
у и у"'. Затем подставить их в систему
и решать ее относительно неизвестных
а и е.
Чтобы избежать ошибок в процессе
дифференцирования при ограниченном
числе точек измерений, можно восполь-
зоваться изложенным выше приемом обоб
щенного дифференцирования, применяя
интегрирование по частям дважды, чтобы
выделить а и е. Найдя а по формулам
(5.33) и (5.34). определяют m(z) и EJ(z).
Так как во всех случаях приходится
дважды интегрировать кривизну для на-
хождения у, целесообразно рассмотреть
вопрос, как по углам поворота и проги-
бам можно отыскать значения эксцентри-
ситетов и жесткостей.
Использование универсального урав-
нения изогнутого вала для идентифика-
ции эксцентриситетов изгибных жесткос-
тей. Воспользуемся углом поворота или
второй строкой интегрального ряда (5.40),
получаемой в результате первого интегри-
рования измеренной кривизны ротора. Рас-
смотрим универсальное уравнение для оп-
ределения углов поворота сечений от всех
видов нагрузок, в которое входит приве-
денный момент инерции Jo для вала пе-
ременного по длине сечения:
«г
у'=^ + 1м^ +
1=1
Л 2
1 = 1 1= 1
Л ' •
i= I
где все нагрузки на данных участках ва-
ла умножены на коэффициент приведения
рп, равный отношению момента инерции
п-го участка вала к приведенному JG:
Р« — J п]Jo,
Mon — $пМп, Р()п = рчР„,
У On = Рл^л!
где а, Ь, с, d — расстояния от точек при
ложения соответственно сил, моментов, на-
чала и конца распределенной нагрузки
до начала координат.
Вал с любым распределением масс,
жесткостей, эксцентриситетов может быть
представлен в виде вала постоянного се-
чения, нагруженного приведенными:
моментами = 7оо)2(/+ е), сосре-
доточенными силами Port-— тоы2(у ф- е) и
распределенными нагрузками qOn = цОп X
Xw2(t/ + e).
Если балансируемый ротор предста-
вить в виде ступенчатого вала с равными
в пределах каждой ступени значениями
масс и жесткостей, то из выражения вы-
падают члены, содержащие Роп и МОп, и
тогда
EJ у' = Е1уо +
, У „ (г-С) _ у . (z-d)
+L4a L4°‘
1=1 1=1
где
= 1*о,<о2(4/( -ь е).
Если у' измерить или найти путем
n-кратного интегрирования (л — число се-
чений, равное числу ступеней ротора), то
получим систему уравнений, решения кото-
рой дадут значение е для ступеней, на
которые разбит ротор.
Аналогичным образом может быть ис-
пользовано универсальное уравнение
У = Уо + У^ +
6*
164
Высокочастотная балансировка роторов
1=1 <=1
«3 . П3 4
I уд (*-*)* у. (г-d)
+ ^j4i 24И„ Zj9i 24£/0 ’
<=1 1=1
где прогиб и угол поворота в начале ко-
ординат могут быть найдены по измерен-
ной в начале координат кривизне ротора.
При неизвестных изгибных жесткостях"
для их нахождения следует измерить про-
гибы или углы поворота еще и на других
частотах вращения так, чтобы число урав-
нений было равно числу неизвестных е
и EJ.
В заключение заметим, что в изложен-
ных выше методах балансировки, основан-
ных на специализированных алгоритмах
идентификации, отыскиваются эксцентри-
ситеты, соответствующие выбранной дина-
мической модели, аппроксимирующей ре-
альный ротор, и чем точнее аппроксима-
ция, тем меньше отличается найденное
распределение эксцентриситетов от истин-
ного.
Описания программ, реализующих ме-
тоды балансировки, изложенные в п. 5.4
и 5.5. приведены в прил. П.7—ПЛО.
5.6. ВЛИЯНИЕ ЖЕСТКОСТИ ОПОР
РОТОРА НА ЕГО БАЛАНСИРОВКУ
Проводя балансировку гибкого или уп-
ругодеформируемого ротора по формам ко-
лебаний с использованием специальных
разгонных стендов, следует учитывать, что
опоры роторов и присоединяемые к ним
массы, участвующие в колебаниях, отли-
чаются от тех, которые имеют место в
реальных машинах. Поэтому высокочас-
тотная балансировка некоторыми мето-
дами, изложенными в гл. 5, в системе
ротор — стенд, может не удовлетворять
требованиям работы ротора в системе ро-
тор — машина
Стенды, у которых динамические пара-
метры опор такие же, как в изделии, соз-
дать трудно. Однако, если это все же
Рис. 5.20. Формы колебаний ротора и сис-
темы уравновешивающих грузов:
а I-я форма, б—11-я форма; в—I-я изгибная
форма, г— П-я изгибная форма
сделано, а также, если балансировку ро-
тора можно производить непосредственно
в статоре машины, то следует иметь в
виду, что формам колебаний ротора, свя-
занным непосредственно с его деформа-
циями, предшествуют две формы колеба-
ний ротора как твердого тела на подат-
ливых опорах. Это имеет место в том слу-
чае, если жесткость опор меньше жесткос-
ти ротора. Такое соотношение жесткостей
опор и ротора характерно для машин спе-
циального класса, но оно будет со вре-
менем распространяться и на другие
классы. Эта тенденция вызвана снижением
металлоемкости статоров и повышением
быстроходности роторов. Формы колеба-
ний ротора в системе будут иметь вид,
показанный на рис. 5.20. При разложении
прогиба и дисбаланса ротора в ряд по фор-
мам колебаний следует учитывать и пер-
вые две формы.
Формы колебаний ротора и его крити-
ческие скорости вращения. Обозначим че-
рез qi u q? смещения левой и правой
опор ротора (рис. 5.20, а, б). Для первой
формы колебаний твердого тела, при кото-
Влияние жесткости опор ротора на его балансировку
165
рой ротор совершает плоскопараллельное
движение, перемещения в любой точке х:
q(x) = q\ 4- <7i) •
Для второй формы колебаний, при
которой ротор поворачивается относи-
тельно центра вращения,
<?(*) = -р(?|+<72) —<71-
Разлагая перемещения ротора и его
эксцентриситет с учетом всех форм коле-
баний, имеем
+Ч
оо
-y(<7i+<72) “$2]
и=3
е(х) = 6,[ q^ +-±(^-4,)] +
00
+ *г[ + “I £ ЬпУп{х).
п=3
Балансировку следует вести с учетом
всех этих форм колебаний, в частности
первые две формы можно отбалансиро-
вать, измеряя перемещения ротора на час-
тоте вращения этих форм и распределяя
уравновешивающие грузы вдоль цилинд-
рической части ротора по линейному за-
кону.
Обе формы могут быть определены и
отбалансированы с учетом данных о виб-
рациях опор, применяя метод балансиров-
ки по, формам колебаний, в основе ко-
торого проводят измерения вибраций или
реакций опор [16].
Уравновешивание по этим формам оз-
начает балансировку ротора как твердого
тела с учетом всех составляющих перво-
начального дисбаланса, которые отрази-
лись в деформациях опор.
Оставшаяся деформация оси ротора
как гибкого тела будет зависеть от уг-
ловой скорости вращения и в общем слу-
чае не может быть найдена по дефор-
мациям опор. Чтобы определить эту дефор-
мацию. необходимо тензометрировать ро-
тор или применять датчики прогиба.
Первые две формы колебаний ротора
как твердого тела на упругих опорах мо-
гут быть воспроизведены и сбалансиро-
ваны на обычном балансировочном станке
при низкой частоте вращения.
Измеряя с помощью пьезодатчиков ре-
акции опор станка, можно найти плоскости
действия симметричных (плоскость первой
формы) и кососимметричных (плоскость
второй формы) составляющих. При этом
силы неуравновешенности по составляю-
щим, связанным с деформацией ротора,
будут незначительным!!, и ими можно пре-
небречь.
Первую форму колебаний жесткого ро-
тора вызывает статическая, а вторую —
моментная неуравновешенности.
Вместо измерения реакций опор мож-
но измерять дисбалансы ротора в двух
крайних плоскостях с помощью методов,
обычно применяемых при работе на серий-
ных низкочастотных балансировочных
станках.
Если Q, — вектор дисбаланса на левой
опоре, a Qi — на правой, то их вектор-
ная сумма характеризует значение и на-
правление главного вектора дисбалансов
£>ст. Каждый из векторов Qi и Q2 имеет
две составляющие: статическую (Ост । и
Ост2) и моментную (равные и противо-
положно направленные векторы Ом, и
Dm2), как показано на рис. 5.21, а, б.
Рис. 5.21. Определение статической и мо-
ментной составляющих:
а—межопорный ротор, б — консольный ротор
166
Высокочастотная балансировка роторов
Можно не считаться с податливостью
опор, если балансировку роторов осущест-
влять на абсолютно жестких опорах. Дей-
ствительно, пусть Pi — вектор усилия, дей-
ствующий на t-ю опору ротора, вращаю-
щегося на абсолютно жестких опорах со
скоростью <о. При обычно принимаемых
допущениях о линейности колебаний сис-
темы и пренебрежения трением по длине
ротора и защемляющим эффектом на опо-
рах можно считать, что сложные вибра-
ции всей системы ротор — статор состоят
из двух слагаемых. Сам ротор находится
под действием сил неуравновешенности и
реакций со стороны опор Р, и соверша-
ет прецессионное движение на скорости <о
как ротор, установленный на абсолютно
жесткие опоры.
От ротора через опоры на статор пе-
редаются усилия Pi в зависимости от дис-
баланса ротора и его изгиба, которые вы-
зывают колебания всей системы. Таким
образом, векторы смещений точек геомет-
рической оси ротора при его вращении
являются результатом сложения двух сос-
тавляющих: первая вызывается колеба-
ниями ротора на абсолютно жестких опо-
рах, а вторая — опорных шеек ротора и
©предел яется инерционно- жесткостным и
характеристиками системы. Поэтому, если
вести балансировку ротора на жестких
опорах, т. е. устранить k форм колебаний
и реакций его опор то с перестанов-
кой ротора на другие опоры уравновешен-
ность системы сохранится, так как устра-
нены силы -Ph возбуждающие колебания
системы через опоры ротора.
Следовательно, целесообразно произ-
водить балансировку ротора на абсолютно
жестких опорах. Однако создание стендов
с опорами такой высокой жесткости явля-
ется достаточно сложным делом и осу-
ществимо не для всех роторов (требую-
щих балансировки, например, до 5-й кри-
тической скорости). Чтобы избежать этой
трудности, ротор можно балансировать не-
посредственно в машине, если имеется тех-
нологическая возможность доступа к по-
верхности ротора.
Основываясь на знании всех форм
колебаний гибкого ротора при его враще-
нии на упругих опорах, необходимо иметь в
виду, если его первая критическая ско-
рость в системе больше критической ско-
рости на жестких опорах, то ротор тре-
бует балансировки по k формам колеба-
ний на жестких опорах. Затем требуется
добалансировка на низкой частоте враще-
ния в двух плоскостях коррекции для ком-
пенсации двух форм колебаний на упру-
гих опорах.
Если две критические скорости ротора
в системе ниже критической скорости ро-
тора на жестких опорах, то его последо-
вательно балансируют по числу всех форм
& 4- 2, и добалансировки не требуется.
В случае, когда первая критическая
скорость ротора в системе лежит ниже
критической скорости ротора на жестких
опорах, то последовательно уравновеши-
вается k 4- 1 форма, и ротор при этом
частично уравновешивается как твердое
тело. Полного уравновешивания можно до-
стичь применением еще одного груза.
Можно также отыскивать деформации
и реакции ротора при его балансировке
на любых опорах с помощью экспери-
ментально-расчетного метода по измере-
нию деформаций ротора, изложенного в
гл. 5. В этом случае ротор балансируют
одновременно как гибкий и жесткий. Кро-
ме того,жесткость опор не имеет значения,
так как хорошо отбалансированный на
любых опорах ротор при установке его на
другие опоры сохраняет состояние сбалан-
сированности. Ротор без дисбалансов не
имеет возбуждающих сил и не вызывает
реакций опор, кроме реакций от веса, какой
бы жесткостью они не обладали.
Многоопорный валопровод как объект балансировки
167
Глава 6
БАЛАНСИРОВКА РОТОРОВ В СБОРЕ С ИЗДЕЛИЕМ
Длительная эксплуатация роторных
машин и агрегатов возможна только при
соответствии уровня колебаний их опорных
устройств (а иногда и некоторых других
конструктивных элементов) действующим
нормам, последние регламентированы раз-
личными стандартами. Необходимость
обеспечения нормального вибрационного
состояния таких агрегатов часто требует
выполнения балансировочных работ не-
посредственно на месте их установки.
Подавляющее большинство типов ро-
торов подвергают балансировке на заво-
дах-изготовителях, однако, несмотря на
это, вибрационное состояние некоторых аг-
регатов после монтажа (сборки) и в про-
цессе эксплуатации оказывается неудов-
летворительным [3]. Это может быть ре-
зультатом следующих причин:
неустраненного на заводе-изготови
теле или возникшего во время эксплуа-
тации или ремонта дисбаланса ротора;
ошибок, допущенных в процессе сбор-
ки;
неудовлетворительной отстройки сис-
темы ротор-опоры агрегата от резонанса
при рабочей частоте вращения;
несоответствия динамических характе-
ристик опор балансировочного станка ха-
рактеристикам опор агрегата;
влияния эксплутационных факторов —
режимов работы агрегата и сопровожда-
ющих их процессов (нагрузки, темпера-
туры, расцентровки опор, их затруднен-
ных перемещений, деформаций статорных
элементов, задеваний ротора о статор и
т. д.);
несовершенства методики станочной
балансировки ротора, заключающегося в
недоучете особенностей его работы в аг-
регате.
Выявление причин недопустимой виб
рации агрегата и их устранение является
задачей служб виброналадки. В тех слу-
чаях, когда такая вибрация вызвана дей-
ствием дисбаланса ротора (роторов), час-
то экономически и технологически оправ-
данным мероприятием по ее снижению ста-
новится балансировка агрегата в сборе,
т. е. балансировка роторов или их систем
в собственных подшипниках.
6.1. МНОГООПОРНЫЙ ВАЛОПРОВОД
КАК ОБЪЕКТ БАЛАНСИРОВКИ
Наиболее сложная задача — баланси-
ровка многоопорных валопроводов, т. е.
систем, связанных между собою муфта-
ми гибких или жестких роторов на под-
шипниках скольжения или качения, смон-
тированных на упругоподатливых опорах,
обладающих в некоторых случаях зна-
чительными массами и сложными дина-
мическими характеристиками. Ниже под
термином валопровод понимаются систе-
мы. включающие два и более роторов,
установленных на упругоподатливых опо-
рах. Валопроводы являются элементами
турбоагрегатов тепловых и атомных элект-
ростанций, турбокомпрессоров, корабель-
ных силовых установок; некоторых авиа-
ционных двигателей и ряда других типов
машин. При всех различиях конструкции,
габаритных размеров, массовых парамет-
ров и назначения таких машин системы
валопровод опоры имеют практически
идентичную или близкую структурную схе-
му, что позволяет в большинстве случаев
использовать единый метод их баланси-
ровки.
Наиболее подробно исследована про-
блема балансировки многоопорных гибких
валопроводов энергетических турбоуста-
новок в связи с повышенными требова-
ниями к их вибрационной надежности и
уровню допустимой вибрации. Применяе-
мые в энергетике методы многоплоскост-
ной балансировки на месте хорошо отра-
ботаны и проверены длительной практи-
кой; опыт показывает, что они могут быть
168
Балансировка роторов в сборе с изделием
распространены на роторные системы, име-
ющие сходные структурные схемы. Поэ-
тому ниже рассмотрены проблемы балан-
сировки валопровода энергетического тур-
боагрегата, как наиболее общие. В изло-
жении опущено описание приемов балан-
сировки в особых случаях, а также ме-
тодов компенсации дисбаланса роторов во
время ремонтов.
При балансировке двухопорных жест-
ких роторов в собственных подшипниках
следует использовать методы, изложенные
в гл. 3, 4, а при балансировке гибких —
в гл. 5. 6.
Валопровод энергетического турбоаг-
регата представляет систему из 5 — 8 гиб-
ких или жестких роторов на подшипни-
ках скольжения, смонтированных в мас-
сивных упругоподатливых опорах вынос-
ного и встроенного типов. Агрегат уста-
навливают на железобетонном фундаменте
рамного или стенового типа, элементы ко-
торого (колонны, продольные и попереч-
ные ригели, стенки) также являются мас-
сивными податливыми звеньями, что опре-
деляет наличие сложных связей и дальних
динамических влияний. Благодаря этому
возбуждение от дисбаланса, локализован-
ного в одной части валопровода, может
оказывать существенное влияние на коле-
бания удаленных опор и затруднять пред-
варительную оценку распределения дисба-
ланса, необходимую для правильного вы-
бора варианта балансировки. Указанные
свойства присущи также и валопроводам
агрегатов других типов, хотя степень их
проявления может быть различной.
На рис. 6.1 показан многоопорный ва-
лопровод мош него турбоагрегата. На каж-
дом роторе предусмотрено конструктивно
несколько плоскостей коррекции дисбалан-
са в виде кольцевых пазов (чаше всего
в форме «ласточкиного хвоста»), в которых
можно устанавливать корректирующие
массы; кроме того, последние можно ус-
танавливать на муфтах, а также в пролете
ротора генератора в специальные резьбо-
вые отверстия. Таким образом, для балан-
сировки валопровода предусмотрено опре-
деленное число плоскостей коррекции дис-
баланса. Однако на практике не все из
этих плоскостей доступны для установки
корректирующих масс без полного вскры-
тия корпусов цилиндров (их используют
при балансировках роторов на разгонных
стендах или станках во время ремонтов).
6.2. ПРАВИЛА ВИБРАЦИОННОГО
ОБСЛЕДОВАНИЯ И МЕТОДИКА
ИЗМЕРЕНИЙ
Вибрационное состояние современных
энергетических турбоагрегатов оценивают
по уровню средней квадратической виб-
роскорости подшипниковых опор их вало-
проводов. Допустимый уровень вибро-
скорости и места ее измерения (контро-
лируемые точки) регламентированы
ГОСТом [Г 12].
Колебания опор турбоагрегатов и дру-
гих роторных машин имеют выраженный
полигармонический характер, однако в
частотных спектрах превалируют состав-
ляйте с частотой вращения, вызванные
главным образом действием дисбалансов
валопроводов. В тех случаях, когда не-
удовлетворительное вибросостояние агре-
гата определяется недопустимым уровнем
именно этих составляющих, чаще всего
Рис. 6.1. Многоопорный валопровод энергетического турбоагрегата
Правила вибрационного обследования и методика измерений
169
принимается решение о балансировке. Так
как стоимость этой операции очень высо-
ка, решение о ней должно быть обосно-
вано. Выбор варианта балансировки оп
ределяют, исходя из оценки распределе-
ния дисбаланса, а также из конкретной
производственной ситуации, необходимос-
ти сокращения до минимума простоя аг-
регата, учета времени, остающегося до
капитального ремонта, и ряда других со-
ображений. В любом случае балансировка
валопровода должна являться заключи-
тельной операцией в комплексе работ по
доведению до нормального вибрационного
состояния установки, что подразумевает
устранение к ее началу всех других при-
чин, определяющих повышенный уровень
вибрации. Решение о балансировке, выпол-
нении работ по устранению причин недо-
пустимой вибрации или о необходимости
проведения специальных исследований
принимают на основании анализа резуль-
татов вибрационного обследования агре-
гата. Оно заключается в определении раз-
личных параметров вибрации опор, а иног-
да и других элементов конструкции, вы-
полнении спектрального анализа колеба-
ний, снятии контурных, частотных (ампли-
тудных и фазовых) характеристик опор;
при необходимости выявляют зависимости
вибрации от различных параметров, ока-
зывающих на нее влияние. Перед обсле-
дованием необходимо: «тщательно подго-
товить измерительную аппаратуру, под-
робно ознакомиться с вибрационной пре-
дысторией агрегата (протоколами преды-
дущих обследований, балансировок, запи-
сями показаний штатной аппаратуры), пе-
речнем последних ремонтных работ, на-
блюдениями обслуживающего персонала,
наконец, оценить объем предстоящих ра-
бот, а также составить программу. Обычно
специалист знаком с типичными для дан-
ного типа агрегатов зависимостями вибра-
ции от нагрузки, теплового состояния (рас-
ширения корпусных элементов), расхода и
температуры масла через подшипники,
времени после пуска из холодного состоя-
ния и т. д., однако в ходе обследования
он должен учитывать возможность их су-
щественного отличия для конкретного аг-
регата. При решении вопроса о балан
сировке необходимо иметь в виду, что ряд
дефектов (например, дефекты соединения
роторов «коленчатость» и излом оси) яв-
ляются источниками кинематического воз-
буждения опор с частотой вращения, т. е.
они проявляются гак же, как и дисба-
ланс валопровода. Поэтому при анализе
результатов обследования необходимо ис-
пользовать известные вибрационные диаг-
ностические признаки различных дефектов
для выявления истинных причин вибра-
ции и принятия правильного решения по
их устранению. Балансировка валопро-
вода, выполняемая в результате ошибоч-
ного диагноза причин повышенной вибра-
ции, не только не устраняет самого де-
фекта, но в большинстве случаев не может
устранить и его вибрационного проявле-
ния.
Выполняя вибрационное обследование,
необходимо учитывать возможность ба-
лансировки, поэтому измерения должны
обязательно включать определение пара-
метров вибрации, использующихся в про-
цессе балансировочных работ. В ряде слу-
чаев это позволяет избежать повторения
измерений
Методика вибрационных измерений.
Главное в измерительных операциях при
балансировке — методически правильное
определение трех параметров колебаний
контролируемых точек: размаха вибро-
перемещения с частотой вращения; фазы
виброперемещения с частотой вращения;
частоты вращения в момент измерения.
Кроме того, на различных этапах конт-
ролируют уровень среднеквадратической
виброскорости опор.
Далее для обозначения размаха и фазы
виброперемещения с частотой вращения
применяется термин вибрация. При балан-
сировках многоопорных роторных систем
уравнение вибраций можно представить
в комплексной форме, позволяющей за-
писать его в удобном векторном виде:
Asin (Ю/ 4- ф|) = А^'=А, (6.1)
170
Балансировка роторов в сборе с изделием
где А, — размах выброперемешения i-к
контролируемой точки; <р» — фаза вибропе-
ремещения, отсчитываемая от произвольно
выбранного единого начала; со — круговая
частота.
Пробные и корректирующие массы, оп-
ределяемые величиной т и углом уста-
новки а в k-к плоскости коррекции дис-
баланса, также можно представить в ком-
плексной форме:
mke‘a^mk, fe=l,2_______К. (6.2)
Фазовый угол вибрации ср, и угол ус-
тановки масс а* определяют следующим
образом. На практике применяют два спо-
соба измерения фазы вибрации — ваттмет-
рический (см. гл. 8) и стробоскопичес-
кий (рис. 6.2).
В первом способе используют перемен-
ное опорное напряжение, жестко «связан-
ное» с вращающимся валопроводом, источ-
ником которого являются специальные им-
пульсные датчики, присоединенные к вало-
проводу генераторы сельсинного илн иного
типа или переменное напряжение, снимае-
мое с генератора балансируемого агрегата.
Как видно из рис. 6.2, фаза вибра-
ции <р — это угол между подвижной (ва-
лопровод) и неподвижной (статор) поляр-
ными системами координат, соответствую-
щий определенному, например максималь-
ному положительному, отклонению точки
измерения в направлении отсчета. Поло-
жение нулевого радиуса-вектора подвиж-
ной системы координат может задаваться
произвольно путем нанесения на ротор
нулевой метки (см. рис. 6.2), но чаше
оно связывается с каким-либо характер-
ным конструктивным элементом валопро-
вода. Отсчет углов а установки коррек-
тирующих масс т* во всех плоскостях
коррекции должен осуществляться от этой
нулевой метки в направлении, противо-
положном вращению валопровода.
Начало неподвижной системы коорди-
нат определяет положение оси импульс-
ного датчика или нулевой отметки на гра-
дусном лимбе статора. Градусную размет-
ку на статоре выполняют в направлении
Рис. 6.2. Фаза вибрации и способы ее измерения:
1—датчик вибрации; 2— статор; 3— ротор; 4 — стробоскоп; 5—импульсный датчик опорного сигнала
Правила вибрационного обследования и методика измерений
171
вращения (ноль должен быть наверху).
Она необходима для измерения фаз стро-
боскопическим методом и облегчения фик-
сации валопровода в необходимом поло-
жении при установке грузов.
Как показано на рис. 6.2. на вало-
провод помимо нулевой метки («минус»)
следует нанести еще и 180-градусную мет-
ку («плюс»), облегчающую измерения фа-
зы при использовании стробоскопа; значе-
ния фаз, отсчитанные от метки «плюс»,
следует привести к нулевому радиусу-век-
тору путем добавления к ниК1 180°.
Измерения в процессе балансировки
включают определение параметров вибра-
ции опор в контрольных точках на про-
межуточных частотах (снятие частотных
характеристик) и на номинальной часто-
те (стабильный вибрационный режим на
холостом ходу или под нагрузкой) Форма
записей результатов (протоколов) может
быть произвольной, но ясной и понятной.
Наряду с результатами измерений вибра-
ции протоколы должны содержать данные
о времени замеров и значениях парамет-
ров, характеризующих состояние агрегата
в период измерений.
Параметры вибрации измеряют осо-
бенно тщательно. В соответствии с
ГОСТом [Г12] их определяют на подшип-
никовых опорах в трех взаимно перпен-
дикулярных направлениях: вертикальном,
горизонтально-поперечном и горизонталь-
но-осевом по отношению к оси валопро-
вода. Поперечные и осевые составляющие
вибрации измеряют на уровне оси вало-
провода (вблизи разъема), по возможнос-
ти против середин вкладышей подшипни-
ков, вертикальные — на верхних частях
крышек подшипников — над серединой
вкладышей; поперечные составляющие
вибрации измеряют с левой стороны опор,
если смотреть со стороны переднего под-
шипника на генератор.
В процессе балансировки измерения
неоднократно повторяют, поэтому конт-
рольные точки следует тщательно поме-
чать и производить измерения строго в
этих точках. Датчики вибрации должны
быть жестко закреплены на опоре либо
надежно прижаты к ней; измерения при
свободно лежащем на опоре датчике. Не-
допустимы.
Измерения на промежуточных часто-
тах осуществляют при разгоне агрегата
и (или) выбеге со снятием амплитудных
и фазовых частотных характеристик. При
номинальной частоте вращения измерения
выполняют на холостом ходу, причем
дважды: через 5 мин после их стабили-
зации и спустя 15—20 мин; сопоставле-
ние результатов измерений позволяет оце-
нить степень стабилизации вибрационного
состояния, так как в балансировочных рас-
четах следует использовать данные, отно-
сящиеся только к стабильным состояниям.
Если последнее не достигается на холос-
том ходу, агрегат включают в сеть, на-
гружают и повторяют измерения. Резуль-
таты записывают в журнал наблюдений
с фиксацией частоты, размаха, фазы, на-
правления измерения вибрации, а также
основных параметров, характеризующих
режим работы агрегата.
Объем измерений зависит от возмож-
ностей используемой аппаратуры и фак-
торов эксплуатационного характера. Од-
нако для успешного проведения баланси-
ровки необходимо располагать результа-
тами измерений вибрации всех опор в трех
направлениях, относящихся к исходному
состоянию (до балансировки) на номи-
нальной и резонансных частотах враще-
ния. В процессе же балансировки изме-
рения можно выполнять на указанных час-
тотах только на тех опорах, которые на-
ходятся в зоне динамического влияния ус-
танавливаемых единичных масс или их
систем. При этом важнейшим требованием
является сохранение идентичности основ-
ных параметров состояния агрегата (тем-
пературы, давления и расхода пара, тем-
пературы металла цилиндров, их расши-
рений и т. д.). В тех случаях, когда имеет
место существенная зависимость вибрации
от одного или от нескольких параметров,
эта зависимость должна быть выявлена.
Так, например, вибрация генератора зави-
сит от его активной нагрузки (точнее.
172
Балансировка роторов в сборе с изделием
от силы тока в обмотке ротора генера-
тора). Поэтому балансировкой по резуль-
татам измерений вибрации на холостом
ходу нельзя обеспечить нормального виб-
рационного состояния такого агрегата под
нагрузкой.
При снятии частотных характеристик
особое внимание следует уделять диапа-
зонам всех резонансных частот валопро-
водов. Удобнее всего применять для опре-
деления этих характеристик многоканаль-
ные магнитографы. Запись сигналов дат-
чиков вибрации при развороте или взбеге
валопровода позволяет одновременно по-
лучить вибрационные характеристики всех
или наиболее важных с точки зрения ба-
лансировки опор При записи вибрации
опор на магнитную ленту одна из дорожек
должна быть отведена для опорного сиг-
нала, вырабатываемого импульсным дат-
чиком (его следует снимать с выхода
виброизмерительного прибора) или специ-
альным генератором опорного напряже-
ния. В отсутствии магнитографа, т. е.
при использовании для измерений одного
или даже 2 — 3-х портативных виброизме-
рительных приборов, этого добиться
нельзя. В результате может возникнуть
необходимость в выполнении дополнитель-
ных разгонов — выбегов агрегата. В этом
случае разгон следует осуществлять с
ускорением 100—150 об/мин, а параметры
вибрации записывать через 50 об/мин, об-
ращая особое внимание на диапазоны
вблизи резонансных частот.
Амплитудные и фазовые частотные ха-
рактеристики, типичные для опор валопро-
вода энергоагрегата, показаны на
рис. 6.5 6.7. В них содержится инфор-
мация о параметрах вибрации вблизи ре-
зонансных частот, используемая при ба-
лансировочных расчетах. Кроме того, эти
характеристики играют важную роль при
предварительных оценках характера рас-
пределения дисбаланса вдоль валопровода
и выборе плоскостей коррекции дисбалан-
са. Частотные характеристики снимают по
параметрам вибрации с частотой враще-
ния— размаху и фазе виброперемещения
(виброскорости).
6.3. МЕТОДЫ И ХАРАКТЕРНЫЕ
ОСОБЕННОСТИ БАЛАНСИРОВКИ МАШИН
И АГРЕГАТОВ В СБОРЕ
Метод балансировки по формам изги-
ба валопровода. Суть метода изложена
в гл. 5 применительно к балансировке
двухопорных гибких роторов на станках,
оснащенных специальными изотопными
опорами. В принципе идея компенсации
ортогональными системами масс дисба-
ланса, распределенного по формам собст-
венных (резонансных) изгибных колеба-
ний и определяющего наличие в динами-
ческом прогибе ротора соответствующих
составляющих, может быть реализована
и при балансировке многоопорных вало-
проводов. Однако существенная анизотро-
пия опор, различие их динамических ха-
рактеристик, сложность организации изме-
рений амплитуд динамического прогиба
роторов внутри пролетов (между опорами)
и ряд других моментов создают трудно
преодолимые препятствия при использо-
вании метода в производственных усло-
виях обусловливая:
сложность методики разложения век-
торов колебаний многих опор на состав-
ляющие по формам резонансных колеба-
ний валопровода, большие погрешности
разложения, особенно в отсутствии более
надежных и соответствующих сути метода
измерений динамических прогибов вало-
провода;
трудность распределения корректирую-
щих масс вдоль валопровода в соответ-
ствии с формами его резонансных коле-
баний из-за ограниченного числа плоскос-
тей коррекции дисбаланса;
сложность подбора необходимых для
установки ортогональных систем масс со-
четаний плоскостей коррекции из ограни-
ченного их числа (грузы, компенсирующие
действие дисбаланса, распределенного по
одной форме, не должны создавать илн
увеличивать дисбаланс по другой форме).
По указанным причинам при балан-
сировках многоопорных валопроводов ме-
тод по формам колебаний практически не
применяют, хотя системы ортогональных
Методы и характерные особенности балансировки машин и агрегатов в сборе
173
корректирующих масс (симметричные и
кососимметричные) широко используют
в методике по коэффициентам влияния.
Метод балансировки по коэффициен-
там динамического влияния. В баланси-
ровочной практике этот метод является
основным. Он позволяет определять сис-
темы, состоящие из некоторого числа кор-
ректирующих масс, динамическое влияние
которых (после установки на валопровод)
наилучшим образом снижает вибрацию
опор до допустимого уровня на резонанс-
ных и номинальной частотах вращения ва-
лопроводов (на холостом ходу и под на-
грузкой), т. е. на небольшом числе (2—5)
фиксированных частот; этого, однако, до-
статочно для обеспечения надежной ра-
боты агрегата в течение длительного вре-
мени.
В рассматриваемом методе использугют
то обстоятельство, что установка в нёко-
торую k-to плоскость коррекции произволь-
ной массы т* вызывает прямо пропор-
циональное ей изменение исходной вибра-
ции в контролируемых точках. Для i-й
точки это изменение можно описать соот-
ношением
А = Л? + (6.3)
где Л® — исходная вибрация; А, — оста-
точная (измененная) вибрация; aib — ко-
эффициент пропорциональности, динами-
ческий коэффициент влияния (ДКВ).
ДКВ aik в выражении (6.3) опреде-
ляет реакцию (чувствительность) системы
в i-й точке на действие массы mbz
aik=(Ai-Af)/mb. (6.4)
ДКВ — это изменение вибрации i-й
точки под действием груза массой 1 кг,
установленного в fc-й плоскости под углом
0° (аь = 0°). В реальных системах-ДКВ —
величины векторные (графические пост-
роения, выполняемые при определении век-
тора разности А,—Л?, показаны на
рис. 6.3). Значения ДКВ определяют в
результате пробных пусков агрегата.
Метод балансировки многоопорного
валопровода сосредоточенными массами
основан на возможности линейной супер-
Рис. 6.3. Графические построения при рас-
чете динамических коэффициентов влияния
(ДКВ):
Л?—вектор исходной вибрации точки i; А—век-
тор остаточной (после установки пробного груза
на валопровод) вибрации
позиции влияний каждой из них на виб-
рацию опор агрегата (в реальных усло-
виях — по меньшей мере на несколько
опор). Таким образом используют то об-
стоятельство, что после установки на ва-
лопровод К масс вибрацию i-й точки оп-
ределяют из соотношения
k=K
А{ = A t -j- aikt^lk' i=l,2............/, (6.5)
a=i
а, следовательно, изменение вибрации всех
J контрольных точек может быть описано
системой связанных между собою урав-
нений:
Л, — А ( + ап /га, 4- .
А == А° ф a,, +
А Л-О-"
4/ = Aj -j- aj; .
.+ аЛлпА-;
+^KmK
(6.6)
В системе (6.6), как и в формулах
(6.1) — (6.5), индекс i (1,2,..,/) при-
своен точкам, в которых измеряют виб-
рацию (контрольным точкам), а индекс k
(1* 2....К) — плоскостям коррекции ди-
174
Балансировка роторов в сборе с изделием
сбаланса. В тех случаях, когда в систе-
му (6.6) включены уравнения, относящи-
еся к одним и тем же точкам, но раз-
личным скоростям вращения, слагаемые
имеют дополнительные индексы (напри-
мер, Л91, Дэ, Й9з — исходная и остаточная
вибрация и ДКВ для первой резонанс-
ной частоты, относящиеся к контрольной
точке 9). При индексации симметричных
и кососимметричных систем масс, уста-
навливаемых одновременно в две плоскос-
ти коррекции симметричного ротора, а так-
же относящихся к ним ДКВ, добавляют
буквы «с» и «кс»; при этом отмечают
только одну, первую по счету плоскость
коррекции из занимаемых этими массами
[например. ^97(^97), m7(m?c) означает
ДКВ на точку 9 от симметричной (косо-
симметричной) системы масс, установлен-
ной в плоскостях 7 и 9 (см. рис. 6.1)].
В системе уравнений (6.6) значения ос-
таточной вибрации поставлены в зави-
симость от неизвестных масс mi,..., тл.
Если все ДКВ, входящие в уравнения
(6.6), известны, а исходные вибрации
4t,.... Л® измерены, то может быть рас-
считана система масс т*, наилучшим об-
разом снижающая исходную вибрацию
опор на тех фиксированных частотах вра-
щения валопровода, на которых проводи-
лись измерения параметров вибрации и
которые представлены соответствующими
уравнениями в системе (6.6). В ней прак-
тически всегда 7 Ж. Наилучшее сниже-
ние вибрации дают системы корректирую-
щих масс, определенные из условия ми-
нимума суммы квадратов остаточных зна-
чений вибрации. Из системы уравнений
(6.6), записанной в матричной форме:
И] = И0] +[от], (6.7)
выводится матричная формула для рас-
чета корректирующих масс:
[т] = -{[а]т[а])-*[аГ[Л0], (6.8)
где [т] — столбец составляющих коррек-
тирующих масс; [4°] — столбец составля-
щих исходной вибрации; [а] — прямо-
угольная матрица ДКВ; [с]т — транспо-
нированная матрица ДКВ.
Структура приведенных элементов име-
ет ВИД
АЧу
Элементы матриц [т], [4°], [с] со-
ставлены из проекций соответствующих
векторов на оси координат X и Y, связь
которых с градусной сеткой для отсчета
углов показана на рис. 6.3 на примере
вектора А®. Таким образом, число урав-
нений в системе (6.8) вдвое больше числа
корректирующих масс.
Надежность результатов расчета по-
вышается, иногда существенным образом,
при введении в формулу (6.8) диагональ-
ной матрицы дисперсий ДКВ:
[т] = -([оГИ Ч |О])-' [«ГИЧ. (6.10)
в которой
[Д] — diag (Дь Д1,— ,Dk, Dk*— , Д/(,
(6.11)
Дисперсии ДКВ можно определить по
формуле
Дй = Х(оа/А)2, (6.12)
где Gaik — среднее квадратическое откло-
нение ДКВ, которое может быть опреде-
Методы и характерные особенности балансировки машин и агрегатов в сборе
175
лено при наличии ряда значений а,к, обыч-
но имеющихся в распоряжении баланси-
ровщика (ДКВ балансируемого и одно-
типных агрегатов); если са,ь неизвестно,
то можно воспользоваться формулой
0^ = 3 4-0.27^. (6.13)
При балансировке необходимо стре-
миться к достижению наилучшего резуль-
тата при помощи наиболее доступных
плоскостей коррекции. Поэтому расчет сис-
темы корректирующих масс по формулам
(6.9) или (6.10) осуществляют не только
для набора из К плоскостей коррекции
дисбаланса, но и для всех возможных
сочетаний по (К—1), (К—2),..., (К —<?)
и т. д. плоскостей в каждом сочетании.
Для каждого (К—q) определяют опти-
мальный набор плоскостей коррекции (оп-
тимальная системам корректирующих
масс).
Располагая набором из нескольких оп
тимальных систем корректирующих масс,
балансировщик выбирает ту из них, ко-
торую в конкретной производственной си-
туации проще установить на валопровод.
Расчеты по формулам (6.10) выпол-
няют на ЭВМ или микрокалькуляторах,
обладающих соответствующими возмож-
ностями.
В тех случаях, когда в систему (6.6)
включены одновременно уравнения для но-
минальной и резонансных частот, правые
части последних должны быть умножены
на коэффициент нормирования, рав-
ный 0,5.
При составлении программы для опре-
деления корректирующих масс необходим
расчет векторов остаточных вибраций по
формуле (6.7), так как их знание может
оказаться необходимым для корректировки
недостоверных ДКВ.
При существенных отклонениях значе-
ний ДКВ, использованных в расчете, от
действительных установка системы коррек-
тирующих масс на валопровод не дает
ожидаемого эффекта. Однако результаты
такого пуска могут быть использованы
для корректировки ДКВ, что может исклю-
чить необходимость выполнения пробных
пусков агрегата с целью их определе-
ния [32] к Для этого необходимо:
Рис. 6.4. Графические построения при опре-
делении вектора невязки:
Л®— исходная вибрация _точки t; Лр расчетная
остаточная вибрация; At—действительная оста-
точная вибрация; Ct—невязка; б,*—расчетные
ДКВ; действительные ДКВ
а) определить в соответствии с гра-
фическим построением .(рис. 6.4) для всех
контролируемых точек векторы невязок С,
между действительными (т. е. измерен-
ными) А„ и расчетными Af, найденными
по формуле (6.7), значениями остаточной
вибрации, т. е.
С, = Д-ЛР; (6.14)
б) определить модули поправок X,* к
ДКВ по формуле
= (6.15)
k
в которой m*, a,k и С, — модули соответ-
ствующих комплексных (векторных) вели-
чин, fe=l, 2,. ..K,i==l, 2,
в) определить углы поправок
yik — yci— ал, (6.16)
где у?—угол вектора невязки; ял— угол
установки груза;
г) определить графическим построе-
нием или при помощи микрокалькулятора
векторы скорректированных ДКВ:
а* aik A-Kk. (6.17)
1/6
Балансировка роторов в сборе с изделием
Корректировка ДКВ, достоверность ко-
торых несомненна, не производится. Скор-
ректированные по формулам (6.14) —
(6.17) и достоверные ДКВ следует исполь-
зовать для расчета новой системы кор-
ректирующих масс. Наилучшие резуль-
таты корректировки, основанной на ис-
пользовании принципа Лежандра, полу-
чают при числе плоскостей коррекции дис-
баланса К 3 и условии, что используе-
мые в балансировочных расчетах ДКВ
являются величинами одного порядка.
Обычно необходимость выполнения до-
полнительных пусков агрегата при исполь-
зовании скорректированных ДКВ не воз-
никает. Но если невязки вновь оказыва-
ются значительными, а степень снижения
исходной вибрации агрегата — недоста-
точной, причины следует искать:
в грубых ошибках, допущенных при
определении ДКВ, т. е. в значительных
отклонениях их величин от действитель-
ных для балансируемого агрегата;
в больших погрешностях измерений па-
раметров вибрации в процессе баланси-
ровки.
При возникновении такой ситуации не-
обходимо выполнить пробные пуски агре-
гата для определения достоверных ДКВ.
Анализ частотных характеристик и
выбор плоскостей коррекции. Между ха-
рактером распределения дисбаланса по
длине двухопорного гибкого ротора и хо-
дом амплитудных и фазовых частотных
характеристик его опор существуют опре-
деленные зависимости, позволяющие до-
статочно достоверно определить локали-
зацию дисбаланса в промежутке между
опорами и правильно выполнить его ба-
лансировку. Наиболее достоверные оценки
получают при анализе частотных харак-
теристик симметричных роторов на иден-
тичных (равноподатливых) опорах. Од-
нако оценка характера распределения дис-
баланса вдоль валопровода (даже в пре-
делах одного ротора из его состава) пред-
ставляет собой гораздо более сложную
задачу, особенно в системах роторов, со-
единенных жесткими или полужесткими
муфтами. Затруднения при анализе воз-
никают в результате следующих причин:
«наложения» друг на друга частотных
характеристик различных участков вало-
провода из-за наличия в системе дина-
мических влияний;
изменения условий на концах ротора
после присоединения его к соседним ро-
торам;
возможных влияний, отсутствующих в
двухбпорных роторных системах (напри-
мер, уменьшения или увеличения стати-
ческой нагрузки на одну из опор, грубых
ошибок при соединении роторов и т. д.).
Действие первой причины в большин-
стве систем наиболее существенно — ведь
при неизменном распределении дисбаланса
на одном из роторов частотные характе-
ристики его опор зависят от изменения
дисбаланса на других участках (роторах)
валопровода. Однако наличие комплекта
частотных характеристик всех или боль-
шей части опор валопровода (они могут
быть получены при помощи магнитографа
одновременно) все-таки позволяет при
внимательном анализе учесть степень и
характер дальних влияний на характерис-
тики исследуемого ротора. Благодаря это-
му с достаточной для практических це-
лей достоверностью можно оценить рас-
пределение дисбалансов по длине вало-
провода, последовательно применяя к его
роторам результаты специальных исследо-
ваний частотных характеристик.
На рис. 6.5—6.7 показаны амплитуд-
ные и фазовые частотные характеристики
вертикальных колебаний опор энергетичес-
кого агрегата, на которых отражены ха-
рактерные особенности для того или иного
варианта распределения дисбаланса вало-
проводов на подшипниках скольжения не-
зависимо от типа и назначения агрегата.
Аналогичные характеристики опор вало-
проводов на подшипниках качения точнее
отображают упомянутые особенности, так
как относительные колебания ротор —
опора отсутствуют.
При определении неуравновешенных
участков валопровода допустимо считать,
Методы м характерные особенности балансировки машин и агрегатов в сборе 177
Рис. 6.5. Частотные характеристики вертикальных колебаний опор ротора в составе вало-
провода при расположении симметричного дисбаланса вблизи его середины:
j4|. Л2— амплитудные характеристики; <р2— фазовые характеристики
А1гАг,мкм
50
00
зо
го
to
о
<?г
Ai
J00
гчо
ПО
160
60
500
юоо
1500
гооо
о
Z5D0 П,мин~1
Рис. 6.6. Частотные характеристики вертикальных колебаний опор ротора в составе вало-
провода при расположении дисбаланса вблизи его опор (внутри пролета):
АI. Л2 — амплитудные характеристики, <р», — фазовые характеристики
178
Балансировка роторов в сборе с изделием
Рис. 6.7. Частотные характеристики вертикальных колебаний опор ротора в составе
валопровода при расположении дисбаланса вблизи опоры 1 (внутри пролета):
Л|. А-2 — амплитудные характеристики, <;2 фазовые характеристики
что дисбаланс сосредоточен или распре-
делен на тех роторах, опоры которых на
резонансных и рабочей (номинальной)
частотах вращения имеют повышенную
вибрацию. Хотя в некоторых роторных сис-
темах это правило на отдельных резонанс-
ных частотах требует существенных уточ-
нений, оно в большинстве случаев сосре-
дотачивает внимание на наиболее неурав-
новешенных участках.
Если на первой резонансной частоте,
а также на номинальной частоте враще-
ния имеют место интенсивные синфазные
колебания, а ход фазочастотных харак-
теристик вертикальных колебаний опор со-
ответствует показанному на рис. 6.5, то
причиной вибрации является симметрич-
ный дисбаланс, сосредоточенный вблизи
середины пролета ротора. Наиболее эф-
фективно колебания этого участка вало-
провода устраняются в широком частотном
диапазоне путем установки корректирую-
щей массы в среднюю плоскость ротора,
если таковая имеется. Использование тор-
цовых плоскостей (плоскостей, располо-
женных вблизи опор) гораздо менее эф-
фективно
Если частотные характеристики имеют
вид, показанный на рис. 6.6, для кото-
рого характерны интенсивные вертикаль-
ные колебания на первой резонансной час-
тоте и сохранение их синфазности вплоть
до номинальной частоты вращения, сопро-
вождающееся отчетливым уменьшением их
значений после прохода резонанса, то речь
идет о симметричном дисбалансе, сосре-
доточенном вблизи опор. Балансировку
следует производить при помощи торцовых
плоскостей коррекции дисбаланса. В неко-
торых случаях эти плоскости могут ока-
заться нечувствительными к симметрич-
ным системам корректирующих масс на
рабочей частоте вращения, поэтому балан-
сировку необходимо выполнять по изме-
рениям на первой резонансной частоте или
используя другие плоскости коррекции.
Если вертикальные резонансные коле-
бания возникают как на первой, так и на
второй резонансной частотах, то дисбаланс
расположен вблизи одной из опор. Ход
фазовых характеристик позволяет опреде-
лить неуравновешенную сторону ротора
по характерному изгибу частотной харак-
теристики ближней к дисбалансу опоры,
Этапы многоплоскостной балансировки валопровода
179
наблюдаемому в зарезонансной зоне час-
тот (рис. 6.7). Корректирующую массу
следует устанавливать на торцовой плос-
кости на неуравновешенной стороне ротора
(на рис. 6.7 со стороны опоры /).
При дисбалансе на муфте резонанс-
ные колебания соединяемых ею роторов
незначительны, а вибрация ближайших к
муфте двух опор остается синфазной в
широком частотном диапазоне и чаще все-
го монотонно возрастает по мере прибли-
жения к рабочей частоте вращения. Ана-
логичным образом изменяется вибрация
этих опор при соединении роторов с пере-
косом торцов муфт. В первом случае ба-
лансировку осуществляют установкой гру-
за на соединительную муфту, во втором,
кроме этого, необходимо использовать
плоскости на роторах.
6.4. ЭТАПЫ МНОГОПЛОСКОСТНОЙ
БАЛАНСИРОВКИ ВАЛОПРОВОДА
1. Пуск агрегата, снятие частотных ха-
рактеристик опор, измерения параметров
вибрации на номинальной (рабочей) час-
тоте вращения на холостом ходу и под
нагрузкой.
2. Останов агрегата.
3. Выбор плоскостей коррекции дисба-
ланса (варианта балансировки) осущест-
вляют на основании результатов предва-
рительного анализа распределения дис-
баланса. В расчеты следует вводить плос-
кости на неуравновешенных роторах, а так-
же плоскости, динамическое влияние кото-
рых на опоры с повышенной вибрацией
достаточно выражено.
Если ДКВ отсутствуют, то для их оп-
ределения выполняют пробные пуски агре-
гата.
4. Балансировочные расчеты выпол-
няют с помощью ЭВМ или для простых
случаев - вручную.
5. Выбор оптимальной системы коррек-
тирующих масс должен учитывать доступ-
ность плоскостей коррекции, затраты вре-
мени и т. д. По возможности предпоч-
тение следует отдавать вариантам, вклю-
чающим также и средние плоскости кор-
рекции дисбаланса роторов.
6. Установка системы корректирую-
щих масс на валопровод осуществляется
в строгом соответствии с результатами
расчета, требованиями к конструкции и
крепежу балансировочных грузов и прави-
лами техники безопасности.
7. Пуск агрегата с системой корректи-
рующих масс. В процессе пуска и по вы-
ходе агрегата на номинальную частоту
следует выполнить вибрационные измере-
ния в полном объеме. Если остаточная
вибрация опор существенно отличается от
расчетной, а снижения вибрации не про-
изошло, выполняют корректировку ДКВ.
Если же в результате балансировки про-
изошло недостаточное снижение вибрации,
рассчитывают и устанавливают новую сис-
тему корректирующих масс, рассматривая
достигнутое состояние как исходное (это
часто бывает при высоком уровне исход-
ной вибрации опор, понизить который за
один пуск, как правило, не удается).
Оценка качества балансировки. Оцен-
ку качества балансировки осуществляют
путем определения соответствия достигну-
того в ее результате вибрационного сос-
тояния агрегата требованиям ГОСТа или
иных нормативных документов. Так, ГОСТ
[П21 допускает эксплуатацию энергети-
ческих турбоагрегатов при вибрации опор,
не превышающей 4,5 мм • с-1 (среднее
квадратическое значение виброскорости).
Этот уровень обычно обеспечивается при
номинальных оборотах 3000 мин-1 сниже-
нием размаха виброперемещения с-часто-
той вращения до 30— 35 мкм.
Показателем качества балансировки
является также достигнутый уровень виб-
рации опор на частотах резонансных из-
гибных колебаний валопровода. В энерге-
тике этот уровень нормирован. В тех слу-
чаях. когда норматив отсутствует, балан-
сировщик обязан учитывать, что на ре-
зонансных частотах возникают интенсив-
ные изгибные колебания роторов, создаю-
щие угрозу возникновения задеваний о
статорные части, разрушения подшипни-
180
Балансировка роторов в сборе с изделием
ков и даже аварий. Поэтому следует стре-
миться к достижению уровня колебаний,
исключающего не только возникновение
аварийных ситуаций при разворотах и вы-
бегах агрегата, но и возможность появ-
ления различных дефектов в результате
повышенной вибрации. Для энергетичес-
ких агрегатов безопасный уровень вибра-
.ции на резонансных частотах находится
в пределах 40— 100 мкм.
6.5. МЕТОД ТОЧНОЙ БАЛАНСИРОВКИ
ИЗДЕЛИЙ С ЖЕСТКИМИ РОТОРАМИ
В СОБРАННОМ СОСТОЯНИИ
Особенности метода. В точном при-
боре- и машиностроении для обеспечения
требуемого уровня виброактивности изде-
лий роторы помимо их раздельной балан-
сировки на балансировочных станках
должны быть уравновешены в собранном
виде в собственном корпусе при условиях,
максимально приближенных к эксплуата-
ционным. Это позволяет исключить влия-
ние так называемых технологических и экс-
плуатационных дисбалансов, возникаю-
щих в процессе сборки и эксплуатации
изделий. Рассматриваемый метод балан-
сировки применяют для роторов, отнесен-
ных к нулевому, 1 и 2-у классам точ-
ности балансировки согласно ГОСТу [ Г9].
К ним относятся роторы гироскопов, не-
больших электродвигателей специального
назначения, приводов шлифовальных стан-
ков, магнитофонов, шпиндели прецизион-
ных станков и др
Динамическая балансировка ротора в
корпусе собранного изделия должна быть
осуществлена при соблюдении всех усло-
вий эксплуатации с использованием собст-
венного привода. В случае отсутствия соб-
ственного привода следует использовать
специальный привод, который не должен
создавать дополнительную неуравнове-
шенность.
Величины дисбалансов ротора опре-
деляют путем измерения вибрации корпу-
са изделия, установленного на специаль-
ном балансировочном оборудовании. Уст-
ранение неуравновешенности осуществля-
ется обычно добавлением или удалением
масс в двух плоскостях коррекции, пер-
пендикулярных к оси вращения ротора.
Техническими условиями на динами-
ческую балансировку ротора, которые
обычно задаются при конструировании из-
делия, должно быть предусмотрено место-
положение плоскостей коррекции, к кото-
рым обеспечен свободный доступ в соб-
ранном изделии, с указанием, каким ме-
тодом должна проводиться корректировка
масс ротора. Должен быть задан класс
точности балансировки и значения допус-
тимых дисбалансов, отнесенных к двум
плоскостям коррекции |Г9].
Эти данные указывают в рабочих чер-
тежах и в балансировочной карте [10],
если последняя предусмотрена техничес-
ким заданием на разработку изделия.
Технологический процесс динамичес-
кой балансировки ротора в собранном из-
делии включает три этапа: измерение дис-
балансов; преобразование результатов из-
мерения в соответствующие параметры
технологического метода и устранение дис-
баланса. Каждый из этих этапов может
выполняться на специальном оборудова-
нии последовательно или параллельно.
Наибольшие трудности возникают при осу-
ществлении первого этапа, так как при
точном уравновешивании изделий в сборе
на скоростях вращения ротора, макси-
мально приближенных к эксплуатацион-
ным, возникают принципиальные труднос-
ти ввиду проявления упругих свойств и
погрешностей шарикоподшипников (ШП).
Вибрации изделий на частоте вращения
ротора вызываются помимо дисбалансов
также и погрешностями ШП При этом
между дисбалансами ротора и вибраций,
зафиксированной на корпусе изделия, не
существует простой связи [12]. Поэтому
при точном уравновешивании роторов'
в корпусе изделия необходимо учитывать
упругие свойства ШП и наличие кинема-
тического возмущения, вызываемого по-
грешностями ШП. В связи с этим дина-
мические модели уравновешиваемых рото-
ров должны быть уточнены введением до-
полнительных степеней свободы, учитыва-
ющих упругие свойства ШП.
Метод точной балансировки изделий с жесткими роторами в собранном состоянии 181
Первый этап технологического процес-
са рассматриваемого метода точной балан-
сировки ротора в свою очередь состоит
из двух подэтапов: измерения величины
дисбалансов и измерения положения дис-
балансов. Если практическая реализация
второго подэтапа, т. е. измерения положе-
ния дисбалансов, не вызывает особенных
затруднений [24], то измерение величины
дисбалансов с учетом отмеченных выше
особенностей ШП осуществить технически
сложнее.
Погрешности шарикоподшипников, вы-
зывающие колебания ротора на частоте
его вращения. Для математического опи-
сания погрешностей ШП рассмотрим сим-
метричный жесткий ротор (рис. 6.8), вра-
щающийся в двух радиально-упорных ШП,
собранных с предварительным осевым на-
тягом (ПОН) и обладающих определен-
ной жесткостью [10]. Предположим, что
ПОН достаточно велик и на всем рабо-
чем диапазоне скоростей вращения ротора
все шарики находятся в контакте с коль-
цами ШП. Примем, что внутреннее кольцо
вращается вместе с ротором, а наруж-
ное — установлено в корпусе изделия не-
подвижно. Дефект в точках соприкосно-
вения i-го шарика с наружным и внут-
ренним кольцами ШП (вместе они сос-
тавляют i-ю контактную группу) опреде-
ляется как разница двух векторов, харак-
теризующих неидеальный (с определен-
ными погрешностями)
[Ю]:
и идеальный ШП
Рис. 6.8. Параметры
ШП жесткого .симмет-
ричного ротора
Pi.
Ар, = Pi — Ро, (6.18)
где Ар, — дефект i-й контактной группы;
Pi — вектор, характеризующий геометрию
и упругие свойства в точках соприкос-
новения t-й контактной группы; р0 — номи-
нальное значение вектора р,, характери-
зующее идеальный (усредненный) ШП, в
силу чего оно от номера контактной груп-
пы не зависит.
Каждый из трех векторов (6.18) име-
ет s компонент [12] Показатель s, таким
образом, является числом, характеризую-
щим вид дефекта. Причем для наружного
кольца s принимают значения 1, 3, 5, 7,
для внутреннего — 2, 4, 6, 8, а для ша-
рика — s — 9.
Компоненты вектора р, = {рГ] имеют
следующий смысл (рис. 6.8) р} и р2—
радиусы желобов колец; 2pf и 2р,4 — диа-
метры по дну желобов колец; рр и pf—
осевые координаты центров кривизны же-
лобов колец в положении отсутствия ПОН
и люфтов; pl и р,8 — величины, учитыва-
ющие изменения коэффициента Герца;
pf — диаметр шарика.
При определении компонентов р,7 и pf
обычно исходят из того, что
р] = Ар,7 = р? = Apf = с (- Кго) Лп;',
где Лг, — текущее значение коэффициента
Герца; Кго — среднее по следу качения
значение коэффициента Кг,; с — постоян-
ная, обычно приравниваемая геометричес-
кому ПОП.
182
Балансировка роторов в сборе с изделием
В реальных условиях обычно имеет
место соотношение Ар* <С po-
ll последующих выкладках одним
штрихом будем обозначать величины, от-
носящиеся к левому ШП, а двумя — к пра-
вому ШП. При это будем считать, что
ротор вращается в двух одинаковых ШП,
для которых, однако, характерны следую-
щие условия:
Ро ~ ро — Ро', /Сто — ^го “ ^го>
то — то — то; Apf =# Ар",
где то — среднее значение угла контакта,
характеризующее идеальный ШП.
В общем случае дефект i-й контакт-
ной группы Др, = {Др;'} является функцией
(угла) определяющего положение i-й
контактной группы в принятой системе
координат, и приближенно может быть
представлен конечным числом членов ря-
да Фурье:
Ар/ = £ ( cos *6» 4" sin , (6.19)
к
где К — любое целое неотрицательное чис-
ло; at, bf — коэффициенты разложения в
ряд Фурье.
В случае компонентов Ар,7 и Ар,® ко-
эффициенты al, bl следует рассматривать
как приведенные [10].
Угол 0, определяется следующими со-
отношениями:
<opi — <р.
(ОШ/
для s=l,3, 5, 7;
для s = 2, 4, 6, 8;
для s = 9,
где <ор, - угловые скорости вращения
ротора и шарика соответственно; t —
время.
Угол <р, определяется следующим об-
разом :
<р, = 4- — 1)4" Фо.
где шс — угловая скорость вращения сепа-
ратора; п — число шариков в ШП; <р0 —
начальная фаза всего комплекта шариков.
В дальнейшем для простоты примем, что
фб = фб'-
Кинем этическое возмущение ШП, вы-
зывающее вибрацию ротора на частоте
его вращения, обусловливается следую-
щими погрешностями внутреннего (враща-
ющегося) кольца: отклонениями развала
желоба (s = 2). эксцентриситетом (s =
= 4), перекосом (s = 6), изменением по
следу качения коэффициента Герца (s =
= 8). Порождаемые этими погрешностями
внутреннего кольца ШП кинематические
возмущения, которые характеризуются ко-
эффициентами разложений af и bl (s —
= 2, 4, 6, 8) в рядах Фурье на первой
гармонике (X, = 1), складываясь между со-
бой, образуют суммарное кинематическое
возмущение. Это кинематическое возмуще-
ние необходимо учитывать при точной ба-
лансировке ротора, так как оно вызы-
вает вибрации на частоте вращения ро-
тора, которые наравне с вибрациями, вы-
зываемыми дисбалансами ротора, прохо-
дят через электрические фильтры балан-
сировочного оборудования и снижают точ-
ность балансировки.
Динамическая модель колебательной
системы. Колебательная система (рис. 6.9)
представляет собой упруго (С*, Су, С2)
подвешенную симметричную платформу
(Мп), на которой жестко закреплено из-
делие, состоящее из жесткого симметрич-
ного ротора и жесткого корпуса Л4К. Ротор
установлен на два радиально-упорных
ШП, собранных с ПОН и нагруженных
усилием FK.
Такая колебательная система соответ-
ствует механической системе балансиро-
вочных станков VII класса [24] , ио только
в ней дополнительно учитывается подвиж-
ность ротора по отношению к корпусу
и платформе. Особенность колебательной
системы состоит в том, что ротор одно-
временно участвует в переносном (сов-
местно с корпусом и платформой) и в от-
носительном (но отношению к корпусу и
платформе) движениях.
Линеаризованные уравнения движения
системы имеют следующий вид f 13]:
a) (I— (ip)i’+pjx — црррххр =
-(•,[*»!<л + «„,(/));
Метод точной балансировки изделий с жесткими роторами в собранном состоянии 183
Рис. 6.9. Динамическая модель колебательной системы
б) (1 — Рр)£--pnlnr-+-p^4-^r—— ^p[wn2(0+Wn2^j];
__ В ) ( 1 р,р) 2 -j- p,n 111 Р -f- Pz^ Pzp Р Р-рРрг^-р — 9»
г) (1~Пх)а+(Ра-рзд)а-ПхРраар=-Чх[Л/п4(С + Л/ц4(0] ;
д) (l“^y)₽ + nniln_,2-p|z2+(p2~-py Р-“ПуРрА =
= »1Лл/й5(/) + М15(0] ;
. ” I i 2 п (6.20)
е) т- Пп2,п ?/4-pwp4-pyy=0;
ж) (1 Р-р) ^р рххЧ-Ppx-^p ~ Nni(C Ч- ^ui(0»
з) (1 Р-р) Ур 4“ Hii If! У РуУ РyyY 4“ РруУр = ‘^пйСО 4“ ч2^ ’
И) (1 Рр) Zp р,г In р Pz2 4“ PzpP 4“Ppz^-p== 0,
к) I I — Пл) ар+ Йр( * “ Пл) ( 0 + Рр) —(Ра—Ра?) а + Рра«р^ N п4,(0 + ^ц4 (О*.
л) (1- Пу)Рр — Пк,1п-12-“*М1~~ЧаДа+'У +
+ Р₽г2 (рр — Ppg) Р4-Рр₽Рр= —^цз\0>
(------------------------------------
где X, у, г, а, Р, у и хр, #р, zp, ар, рр,
Ур координаты, характеризующие пере-
носное и относительное движения системы.
Функции возмущения центробежного
происхождения имеют вид (/ =
= 1, 2, 4, 5)
7УЦ1(/) = ( — d| sin (ор/4-d2cos <ор0;
TVU2(O =<op(d2sin(op/4'rficos(op0;
Лц4(^) =Wp(d3sinwpZ—d4cos(Dp0;
Mis(0 =<op(d4sinwp/4-d3Cos(opO.
В системе уравнений (6.21) исполь-
зованы следующие условные обозначения
(см. рис. 6.9):
= вй1, dz — в| -j- ^22, d$ = ef/i — ej?/?,
в[ =т|Г|Л4”’;
d4 = eSi = e2sin уя, e22 = e2cos уд,
i es =
где mi, ms, Mp — соответственно массы
дисбалансов и ротора.
184
Балансировка роторов в сборе с изделием
Здесь звездочкой обозначены безраз-
мерные выражения соответствующих вели-
чин, которые получаются путем умноже-
ния их, например, на множитель (где
рр ж радиус инерции ротора относительно
координатной оси ОХ).
Функции кинематического возмущения
N„j(t) на частоте вращения ротора имеют
вид (/ ===== 1, 2, 4, 5)
^nJO = Ppjt(Alpsin сор£-|-
4~ A2pcos <лр/) (2 cos т0)-1;
^П2(0 = Рру(Л2р Sin Wp/~
— Alpcos <opZ) (2cos TfJ)-1;
^n<(0 Ррл(^3P sin в)р/
—A4p cos wp/) (2/?0cos tJ -1;
== Pp₽(^4p Sin GJpZ-f“
4* A^p cos (Op/) (2/?ccos тq) ,
где ppv — соответствующие парциальные,
частоты (q —л, у, а, Р);
#о = I Pol — (рп + Pq) tg Aip — В' Ч-Вр;
Д2р= + ^р, Азр =
^Ер-Е'р,^р=вр-в'р-
а?—(а? + а{) cos т0 —
—( а? 4 -|- а?) sin т0;
Вр = b\—(b\ + cos т0 —
Ч- -д- bfj sin т0.
Коэффициенты Д; р (/ — 1,2, 3,4) пред-
определяют величину суммарного кинема-
тического возмущения, создаваемого ле-
вым и правым ШП, на частоте враще-
ния ротора.
Как видно, движения системы в нап-
равлении отдельных координат связаны
между собой достаточно сложным обра-
зом. Благодаря этому ротор и платформа
с корпусом совершают на частоте <ор не
только радиальные и угловые колебания,
но также и осевые [13].
Благодаря симметричности системы
уравнения движения (6.20) распадаются
на три независимые подсистемы уравне-
ний: (6.20, а, ж), (6.20, б, е, з) и (6.20, в,
г, д, и, к, л). Такое разделение уравнений
позволяет получить аналитическим путем
значения амплитуд вынужденных коле-
баний по отдельным координатам в общем
виде, что является весьма ценным в от-
ношении анализа взаимосвязей между па-
раметрами рассматриваемой системы и па-
раметрами колебаний.
Определение значений дисбалансов.
При решении задачи точного уравновеши-
вания ротора с учетом погрешностей ШП
необходимо уточнить, что следует подра-
зумевать под осью вращения ротора. В
дальнейшем будем считать, что ось, кото-
рая проходит через геометрические центры
идеальных ШП, характеризуемых вектор-
ной величиной Ро —{fo}\ является осью
вращения ротора.
Информацию об неуравновешенности
ротора содержат как вибрации ротора,
так и вибрации корпуса с платформой.
В качестве информативных выбирают ко-
лебания корпуса (платформы), так как их
легче и проще измерить, чем колебания
ротора.
Так как вибрации корпуса на частоте
<йр обусловлены не только неуравнове-
шенностью ротора, но и погрешностями
ШП, естественно, возникает вопрос, на-
сколько эти погрешности влияют на точ-
ность определения параметров неуравнове-
шенности ротора.
Информацию об неуравновешенности
ротора содержат колебания корпуса по
всем шести степеням свободы [13]. Однако
для аналитического решения задачи мож-
но использовать лишь два уравнения связи
между амплитудой вибрации корпуса и па-
раметрами неуравновешенности ротора,
которые получают на основе решения сис-
темы уравнений (6.20). В дальнейшем в
качестве информативных колебаний выби-
рают корпуса в направлении обобщенных
координат х и р. При этом уравнения
связи будут иметь следующий вид:
Метод точной балансировки изделий с жесткими роторами в собранном состоянии 185
В?,г + ^?-<4«;) (6.22)
В?32 + В?)2 = лр-р2Л2№./
где Ахр, Лрр — соответствующие амплиту-
ды колебаний на частоте <о ; лхр, лрр —
суммарные коэффициенты динамичности
113].
Коэффициенты (j = 1, 2, 3, 4) свя-
заны с параметрами возмущений следую-
щими соотношениями:
е?, = (2с<кт„)-'д;»-<г,(н‘рв,+1) ’;
В*2 = (2cos т0) ,Д^4-г/2(к1р>_Ь 1)
В*з~cosТу) Л£+с?з( Лрр*-4~ ') .
В*4 = ( 2/?,Г COS Т„) Д4* + J, ( х'Р’ + 1) .
где — соответствующие коэффи
циенты динамичности [13]. Здесь звездоч-
ка также означает приведение соответ-
ствующего параметра к безразмерной
форме.
Коэффициенты #*,(/ = 1. 2,3,4) пред-
ставляют собой составляющие общего воз-
мущения, действующего на частоте вра-
щения ротора, и характеризуют взаимо-
действие между суммарным кинематичес-
ким и центробежным возмущениями. Это
взаимодействие носит определенный ха-
рактер. Если величина суммарного кине-
матического возмущения не зависит от час-
тоты вращения ротора, то величина цент-
робежного возмущения обусловливается
соответствующим коэффициентом дина-
мичности. Поэтому уровень вибрации изде-
лия будет во многом зависеть от режима
его работы. Суммарное кинематическое
возмущение представляет собой как бы
постоянную составляющую общего возму-
щения, а центробежное возмущение играет
роль переменной составляющей в зависи-
мости от режима работы изделия.
В случае отсутствия неуравновешен-
ности ротора амплитуды колебаний кор
пуса будут зависеть только от параметров
кинематического возмущения ШП, т. е.
* и /1рр —> (Арр)к.
Амплитуды колебаний корпуса при на-
личии только кинематического возмущения
ШП характеризуются следующими выра-
жениями:
(Лр)к = (2cosT(,r‘ лхрд/д^4- А|р;
(^Рр)к ~ (2/?0costq) Лррл/Лзр Ч- i\p.
(6.23)
Влияние чисто кинематического возму-
щения (при отсутствии центробежного
возмущения) на точность уравновешива-
ния роторов рассмотрено в работе [10].
Взаимосвязь между параметрами цент-
робежного и кинематического возмущений
можно проиллюстрировать при помощи
круговых диаграмм (рис. 6.10).
Систему уравнений (6.22) можно до-
полнить уравнением, которое дает сдвиг
фаз между колебаниями в направлении
обобщенных координат х и р (рис. 6.11):
cosT<№ - л^ДВ* В* + В* В£) X
X (4*4*)“' (6.24)
Решая совместно системы уравнений
(6.22) и (6.24), определяют величины
удельных дисбалансов ротора, отнесенных
к двум плоскостям коррекции:
е*— V о*
tg Wi = <?*/<•*:
(6.25)
= ( Г*- Wfp) ( G?p + Z? G*)
с2*2=«?Р+| ~«*р<?* +
I (С2*р + '?О(*р)"‘.
где/ft — If -] W7p, U?*p — коэффициенты,
зависящие как от параметров кинемати-
ческого возмущения ШП, так и от пара-
метров колебаний системы [13]; Gfp, Gfp,
Q*p — коэффициенты, зависящие от пара-
метров колебаний системы; /7*,, /7*,, //*р —
коэффициенты, зависящие от параметров
кинематического возмущения ШП.
186
Балансировка роторов в сборе с изделием
Рис. 6.10. Круговые диаграммы, построенные согласно уравнениям (6.22) и (6.23):
/—область кинематического возмущения, //—область совместного действия кинематического и центро-
бежного возмущений
Рис. 6.11. Векторная диаграмма составляю-
щих амплитуд и фаз колебаний корпуса
на частоте вращения ротора:
sxp- ^хр. sPp, И 4хр, составляющие
амплитуд и амплитуды колебаний в направлении
координат х и р, yxp, урр — соответствующие фазы
колебаний, ТЛрр — сдвиг фаз между колебаниями
в направлении координат х и Р
Описание программы расчета удельных
дисбалансов et и е2 на ЭВМ приведены
в приложении П.11.
Как видно из уравнений (6.25), по-
грешности ШП, характеризуемые коэффи-
циентами Д/р (/=1, 2, 3, 4), могут ока-
зать ощутимое влияние на точность оп-
ределения величин дисбалансов. При точ-
ном уравновешивании ротора в корпусе
изделия, когда проявление погрешностей
ШП становится соизмеримым с неуравно-
вешенностью ротора, возможны сущест-
венные ошибки.
Пример. Рассмотрим зависимость, выража-
ющую погрешность при определении дисба-
ланса
-•+к.
(6.26)
где (еТ)о - значение дисбаланса е?, определен-
ного без учета погрешностей ШП, Ке. — коэф-
фициент, учитывающий характер сочетаний по-
грешностей ШП; — параметр, учитывающий
соотношение погрешностей ШП и неуравнове-
шенности ротора.
Коэффициенты К£| и 6С| характеризуются
следующими выражениями:
^ = "TP(G?P+^GTP) 1/2
Как видно (рис. 6.12), с ростом парамет-
ра б£| погрешность ЛеТ увеличивается и в са-
мых неблагоприятных случаях может достигать
100% и более. Однако при определенном со-
четании погрешностей ШП, например в случае
Kej = ± 0,5 и б£| = + (0,01 ~ 0,90), погреш-
ность Aef мало будет зависеть от проявления
погрешностей ШП.
Устранение дисбалансов ротора целе-
сообразно вести пока амплитуды колеба-
ний корпуса Лхр > (Дхр)к и Д₽р> (Дрр)к.
Этот процесс следует прекратить при дос-
тижении ‘ примерного равенства ампли-
туд. Дхр ~ (^хр)к И ~ (^Рр)к-
187
Рис. 6.12. Графическая интерпретация зави-
симости (6.26)
В особых случаях, когда допустимый
уровень вибраций корпуса изделия на
частоте вращения ротора о)р, регламен-
тируемый техническими требованиями,
должен быть меньшим, чем уровень виб-
раций кинематического происхождения,
задача уравновешивания ротора сводится
не к полному устранению неуравновешен
ности. а к доведению параметров неурав-
новешенности ротора до состояния, когда
центробежное возмущение становится при-
мерно равным по величине и противопо-
ложным по направлению к суммарному
кинематическому возмущению И1П.
Перспективы развития балансировки
изделий в сборе. С ростом требований
к качеству выпускаемой продукции значе-
ние и область применения балансировки
изделий в сборе будут повышаться и рас-
ширяться. В ближайшем будущем должно
быть создано более эффективное балан-
сировочное оборудование для точной ба-
лансировки изделий в сборе, оснащенное
специальными устройствами для выделе-
ния сигналов, пропорциональных дисба-
лансам ротора и погрешностям ШП. В свя-
зи с этим имеющееся разнообразие тре-
бований к точности и технологии балан-
сировки различных изделий в сборе долж-
но быть устранено разработкой отрасле-
вых стандартов, регламентирующих клас-
сы точности балансировки роторов различ-
ных изделий, нужны также рекомендации
по выбору плоскостей коррекции, к кото-
рым был бы обеспечен доступ в собран-
ном изделии, и др. Дальнейшее разви-
тие работ по унификации и стандарти-
зации отдельных блоков балансировочных
станков будет содействовать ускорению
решения балансировки изделий в сборе.
ЧАСТЬ II. СРЕДСТВА БАЛАНСИРОВКИ
К основным средствам балансировки
относят станки, балансировочную аппара-
туру и балансирующие устройства От ка-
чества их работы зависят точность и произ-
водительность балансировки роторных
систем.
Широкая номенклатура балансируе-
мых изделий общего и специального при-
боре- и машиностроения определяет не-
обходимость создания к ним большого ти-
пажа станков и приспособлений. Описание
станков, проектирование их основных си-
стем и применяемая балансировочная ап-
паратура — основное содержание части II
справочника.
В отличие от аппаратуры, входящей в
комплект балансировочных станков, су-
ществует портативная балансировочная
аппаратура, широко применяемая во мно-
гих отраслях техники для балансировки
роторов в собранном изделии в эксплуа-
тационных условиях. Она позволяет изме-
рять не модуль и угол дисбаланса, а ам-
плитуду и сдвиг фазы вибрации подшип-
ников с частотой вращения балансируе-
мого изделия. Область ее применения — от
балансировки роторов в приборостроении
до роторов мощных энергоблоков массой
''выше 100 т.
Задачи ускорения научно-техническо-
го прогресса требуют повышения качества
балансировочной техники. Это касается не
только теоретических вопросов, оборудова-
ния и балансировочной аппаратуры, но
и создания надежных автоматических ба-
лансирующих устройств, которые позволят
значительно повысить скорости вращения
роторов машин без появления у них опас-
ных вибраций.
Глава 7
БАЛАНСИРОВОЧНЫЕ СТАНКИ
7.1. КЛАССИФИКАЦИЯ
Балансировке подлежат изделия раз-
личных отраслей машиностроения; колен
чатые н карданные валы, паровые и газо-
вые турбины, роторы электродвигателей,
центрифуги, шпиндели станков, космиче-
ские тела вращения, маховики, диски сцеп-
ления, судовые и воздушные винты и др.
Для балансировки этих изделий разрабо-
таны и создаются универсальные и
специальные, в том числе автоматические,
балансировочные станкй, линии и участки.
Классификация балансировочных станков
показана на рис. 7.1.
Балансировочный станок определяет
дисбалансы ротора для уменьшения их
корректировкой масс. Некоторые баланси-
ровочные станки имеют встроенные меха-
низмы для корректировки масс и различ-
ную степень автоматизации. Процессы оп-
ределения дисбалансов и корректировки
масс могут быть совмещены в пространст-
Классификация
189
Рис. 7.1. Классификация балансировочных станков
ве и времени, т. е. корректировка масс
ротора и измерение его дисбалансов могут
осуществляться одновременно. По харак-
теру динамического режима работы станка
и конструктивному исполнению различают
балансировочные станки зарезонансного
или дорезонансного типа.
Зарезонансный балансировочный ста-
нок обеспечивает частоту вращения ротора
выше наибольшей собственной частоты
колебаний системы, состоящей из ротора
и паразитной массы. При этом последняя
включает часть массы балансировочного
станка без массы ротора, которая колеб-
лется при балансировке неуравновешен-
ными силами ротора.
Дорезонансный балансировочный ста-
нок обеспечивает частоту вращения ротора
ниже наименьшей собственной частоты
колебаний системы, состоящей из ротора
и паразитной массы.
В балансировочных станках вращение
ротора осуществляется вокруг геометри-
ческой оси, образованной опорными по-
верхностями ротора. В результате изме-
рения определяют дисбалансы ротора, вы-
званные отклонением главной центральной
оси инерции от фактической оси вращения.
При корректировке масс ротора осуществ-
ляют совмещение этих осей с требуемой
точностью. Отдельный класс составляют
центровальные балансировочные станки, в
которых ось вращения ротора задается
так, чтобы она совпала с главной цент-
ральной осью инерции. По найденному
в пространстве положению главной цент-
ральной оси инерции, например, образуют
технологические центры в торцах ротора и
обрабатывают относительно этих центров
его опорные поверхности, т. е. совмещают
ось вращения ротора с главной централь-
ной осью инерции.
190
Балансировочные станки
Центровальный балансировочный ста-
нок определяет координаты главной цент-
ральной оси инерции ротора, относительно
которых осуществляется обработка его ба-
зовых поверхностей. Некоторые центро-
вальные балансировочные станки имеют
встроенные механизмы для зацентровки
ротора по найденным координатам главной
центральной оси инерции или механизмы
для обработки базовых поверхностей в
процессе вращения ротора вокруг главной
центральной оси инерции.
В зависимости от характера неуравно-
вешенности и динамических характеристик
балансируемого изделия применяют одно-
плоскостную (статическую), двухплоско-
стную (динамическую) или многоплоско-
стную балансировку, учитывающую гиб-
кость ротора. Для осуществления пере-
численных видов балансировки необходи-
мо соответствующее балансировочное обо-
рудование, которое включает в себя станки
для статической балансировки, станки для
динамической балансировки жестких ро-
торов и станки (стенды) для балансиров-
ки гибких роторов, а также станки для
статической и динамической центровки и
статической децентровки, т. е. для обеспе-
чения заданного несовпадения центра масс
с осью вращения ротора.
Станки для статической и динамиче-
ской балансировки роторов с горизонталь-
ной осью вращения. Станок для стати-
ческой балансировки определяет в стати-
ческом режиме только главный вектор дис-
балансов при помощи силы тяжести на
невращающемся роторе. Станок для ста-
тической балансировки роторов в дина-
мическом режиме определяет главный век-
тор дисбалансов на вращающемся роторе.
На станках для статической балансировки
осуществляют определение дисбаланса и
корректировку масс в одной плоскости ро-
тора.
Станок для статической центровки оп-
ределяет координаты центра масс ротора,
относительно которых выполняется об-
работка его базовых поверхностей. С по-
мощью станков для статической центровки
можно осуществлять, например, расточку
базовых посадочных отверстий судовых и
воздушных винтов по оси, проходящей
через центр масс.
Помимо балансировки и центровки ро-
торов в машиностроении требуется децент-
ровка роторов. Такая задача возникает,
например, при изготовлении противо-
весов сборных коленчатых валов двига-
телей внутреннего сгорания. Противовес
такого коленчатого вала должен иметь
тарированный по модулю и направлению
вектор дисбаланса для компенсации инер
ционных сил от шатунно-поршневой груп-
пы.
Станок для статической децентровки
определяет главный вектор дисбалансов
ротора для его корректировки по модулю и
направлению. Некоторые станки для стати-
ческой децентровки имеют встроенные ме-
ханизмы для корректировки главного век-
тора дисбалансов по модулю и направ-
лению посредством изменения или пере-
распределения масс ротора. В случае осна-
щения балансировочного станка средства-
ми, обеспечивающими введение вектора
дисбаланса, равного по значению, но про-
тивоположно направленного заданному,
статическая децентровка может быть осу-
ществлена на обычном станке для стати-
ческой балансировки.
Станок для динамической балансиров-
ки жестких роторов определяет главный
вектор и главный момент дисбалансов или
их совокупное действие в двух произволь-
ных плоскостях, перпендикулярных оси ро-
тора. На станках для динамической балан-
сировки определяют и уменьшают дис-
балансы в двух плоскостях коррекции ро-
тора, характеризующие его динамическую
неуравновешенность. Некоторые роторы
машиностроения по своим конструктивным
особенностям требуют балансировки более
чем в двух плоскостях коррекции. Так,
например, дисбалансы коленчатых валов
двигателей автомобилей корректируют в
противовесах, которые ограничены секто-
рами так, что в двух плоскостях их ском-
пенсировать невозможно. Балансировку
таких роторов осуществляют на станках
для динамической балансировки поэтап-
Классификация
191
но- каждый раз в двух новых плоскостях
коррекции, или дисбалансы ротора после
их определения в двух плоскостях коррек-
ции распределяют по нескольким плоско-
стям.
Станок для динамической центровки
определяет координаты главной централь-
ной оси инерции ротора по главному век-
тору и главному моменту дисбалансов или
по их совокупности в двух плоскостях
коррекции ротора. На станках для дина-
мической центровки по найденным двум
точкам на главной центральной оси инер-
ции образуют технологические центры ро-
тора. Относительно центров осуществляют
дальнейшую обработку базовых поверх-
ностей. Например, по центрам на заготов-
ке коленчатого вала обтачивают шейки и
другие элементы.
Рассмотренное выше оборудование
предназначено для балансировки жестких
роторов, которые балансируют, как прави-
ло, в двух произвольных плоскостях кор-
рекции на частоте вращения, меньшей пер-
вой критической для данного ротора. При
этом значения их остаточных дисбалансов
не превышают допустимые на всех часто-
тах вращения, вплоть до наибольшей
эксплуатационной. В машиностроении не-
обходима также балансировка гибких ро-
торов, у которых значения остаточных дис-
балансов могут превышать допустимые на
каких-либо частотах вращения, вплоть до
наибольшей эксплуатационной после ба-
лансировки в двух произвольных плоскос-
тях коррекции на частоте вращения, мень-
шей первой критической.
Станок для динамической балансиров-
ки гибких роторов определяет дисбалансы
на вращаемом им гибком роторе. Он может
выдавать информацию о цисбалансах,
приведенных к одной, двум или нескольким
плоскостям, и работать как в зарезонанс-
ном, так и в дорезонансном режимах.
На станках для балансировки гибких ро-
торов осуществляют низкочастотную и
высокочастотную балансировку. Низко-
частотную балансировку проводят на ча-
стоте вращения, при которой балансируе-
мый гибкий ротор еше можно рассмат-
ривать как жесткий. В этом режиме осуще-
ствляют статическую балансировку ротора
в одной плоскости и динамическую балан-
сировку в двух плоскостях. Высоко-
частотную балансировку выполняют на ча-
стотах вращения, близких к критическим
частотам ротора, вплоть до наибольшей
эксплуатационной. В этом режиме произ-
водят балансировку гибкого ротора по соб-
ственным формам изгиба в трех и более
плоскостях коррекции. Для балансировки
гибких роторов можно применять также
станки для динамической балансировки
жестких роторов, снабженные аппарату-
рой и методикой для расчета прогибов
ротора и корректирующих масс, распреде-
ленных по длине ротора на основании
данных измерений дисбалансов в двух пло-
скостях. На станках для балансировки гиб-
ких роторов осуществляют балансировку,
например, таких изделий машиностроения,
как роторы бумагоделательных машин,
скоростные карданные валы автомобилей
и т. д
Разгонно-балансировочный стенд оп-
ределяет нагрузки на опорах ротора и
изгиб его оси при балансировке гибкого
ротора.
Разгонно-балансировочные стенды ос-
нащены средствами транспортирования,
изменения частоты врашения, динамиче-
ской балансировки, защиты и контроля
состояния гибкого ротора. Разгонно-ба-
лансировочные стенды являются наиболее
сложным оборудованием балансировочной
техники и предназначены для балансиров-
ки гибких роторов массой до 300 т и более.
По своей специализации и области при-
менения станки для балансировки жестких
роторов подразделяют на станки общего
назначения, специализированные, спе-
циальные и станки для автоматической
балансировки в процессе вращения рото-
ров.
Станки общего назначения. Станок
общего назначения определяет дисбалан-
сы роторов произвольной конфигурации в
заданном характеристикой станка диапа-
зоне их массово-геометрических парамет-
ров. Техническая характеристика станка
192
Балансировочные станки
общего назначения устанавливает пределы
изменения масс и геометрических размеров
(диаметров и линейных размеров) роторов,
которые могут быть отбалансированы на
данном станке. В соответствии с потреб-
ностью промышленности выпускают стан-
ки общего назначения для статической и
динамической балансировки. Для обеспе-
чения балансировкой всей номенклатуры
роторов машиностроения станки одного
вида балансировки объединяют в гаммы,
которые содержат ряд моделей станка (на-
пример, гамма станков из 11 моделей для
динамической балансировки роторов мас-
сой от 0,01 кг до 100 т). В пределах
одной гаммы станки общего назначения
могут быть как зарезонансного, так и
дорезонансного типа. Для расширения
универсальности на станках осуществляют
только определение дисбалансов ротора,
т. е. данные станки являются чисто изме-
рительными. Они не оснащены механиз-
мами коррекции дисбалансов, которую вы-
полняют на отдельном оборудовании из-
вестными способами (сверлением, фрезе-
рованием. приваркой грузов и т. д.). В свя-
зи с этим станки общего назначения менее
производительны, чем специализирован-
ные и специальные. Поэтому их применяют
в основном в ремонтном, единичном, мелко-
серийном и частично в серийном произ-
водствах.
Специальные и специализированные
станки. Специализированный баланси-
ровочный станок представляет собой ба
лансировочный станок обшего назначения,
предназначенный и оснащенный для ба-
лансировки конкретного ротора или группы
однотипных роторов. Специализированные
балансировочные станки создают на базе
станков общего назначения для повыше-
ния производительности балансировки
конкретного ротора или группы однотип-
ных роторов. Например, станки для стати-
ческой балансировки дискообразных рото-
ров, у которых коррекцию дисбаланса осу-
ществляют в одной плоскости сверлением
материала ротора, оснащают сверлильны-
ми агрегатами. При этом процессы
определения дисбаланса ротора, установки
ротора на требуемый угол дисбаланса под
инструментом сверления (позиционирова-
ние) и сам процесс сверления ротора на
необходимую глубину могут быть частично
автоматизированы, что повышает произ-
водительность процесса балансировки.
Целесообразность специализации станков
может быть вызвана и конструкцией рото-
ра. Так, например, для динамической ба-
лансировки колес вентиляторов воздухо-
дувных машин большого диаметра необхо-
димо выйолнять станину дорезонансного
станка общего назначения разрезной и
оснащать станок соответствующей оправ-
кой При этом колесо вентилятора монти-
руют базовым отверстием на оправке, а
сама оправка базируется на две опоры
специализированного станка. Колесо вен-
тилятора размещают над шахтой, изготов
ленной между опорами разрезной станины.
По сравнению со станками общего назна-
чения специализированные станки более
широко применяют в серийном производст-
ве.
Специальный балансировочный станок
определяет дисбалансы конкретного рото-
ра или группы однотипных роторов для
уменьшения их корректировкой масс. Спе-
циальные балансировочные станки пред-
ставляют собой наиболее широкую и
многообразную группу балансировочных
станков. Большинство роторов машино-
строения в серийном, крупносерийном и
массовом производствах требуют для
своей балансировки создания специальных
станков. Даже некоторые однотипные ро-
торы, как, например, коленчатые валы
автодвигателей в связи с многообразием
их конструкций (рядные, V-образные; 4- и
6-цилиндровые и т. д.) требуют для своей
балансировки отдельных моделей станков.
Для балансировки таких роторов создают
гамму специальных станков, например, из
3-х моделей для балансировки двух- и
трехшарнирных карданных валов авто-
мобилей. Специальные станки могут быть
зарезонансного и дорезонансного типов.
Их подразделяют на станки для стати-
Классификация
193
ческой и динамической балансировки.
Функции специальных станков могут быть
ограничены только процессом измерения
дисбалансов роторов.
Для повышения производительности
балансировки функции специальных стан-
ков помимо измерения дисбалансов могут
дополняться следующими автом атизи
рованными процессами: позиционировани-
ем ротора на измеренный угол дисбаланса,
корректировкой масс ротора на установ-
ленном угле коррекции, маркированием ро-
тора в легком или тяжелом месте, сорти-
ровкой роторов по значению дисбаланса.
Процесс измерения дисбалансов за-
ключается в определении дисбалансов ро-
тора, включая его разгон до рабочей часто-
ты вращения и торможение до полной
остановки.
Позиционирование ротора представля-
ет собой процесс установки ротора в угло-
вое положение, соответствующее измерен-
ному углу дисбаланса. В результате по-
зиционирования ротор устанавливается на
угол коррекции дисбаланса тяжелым (лег-
ким) местом под инструментом корректи-
ровки масс или маркирования.
Корректировка масс ротора заключает-
ся в изменении или перемещении коррек-
тирующих масс для уменьшения дисбалан-
сов ротора. Для корректировки масс ро-
торов в балансировочной технике широко
применяют традиционные методы металло-
обработки (сверление, фрезерование, шли-
фование и т. д.), которые обеспечивают
высокую производительность и возмож-
ность автоматизации процесса. С учетом
особенностей конструкций роторов для
корректировки их.масс применяют привар
ку корректирующих масс, расклепку на
штырях и в пазах ротора, нанесение быст-
ротвердеющих масс и др.
Сортировка роторов заключается в
группировании роторов по заданным уров-
ням значений дисбаланса.
Маркирование роторов, которое заклю-
чается в отметке на роторе угла дис-
баланса, применяют в специальных стан-
ках при селективной сборке балансируе-
7 Зак 1641
мых изделий. Так, например, при балан-
сировке ступиц и тормозных барабанов
колес автомобилей на специальных стан-
ках осуществляют маркирование близ-
ких по значению дисбаланса изделий (од-
ного в тяжелом, а другого в легком месте
ротора), а также их сортировку и от-
браковку по значению дисбаланса (цветом
маркирования). При сборке метки на со-
ответствующих роторах совмещают для
уменьшения результирующей неуравно-
вешенности изделия. Маркирование рото-
ров по значению дисбаланса может осуще-
ствляться на специальных станках и при
контроле качества работы технологической
цепи производства какого-либо ротора, на-
пример автомобильных шин.
Средствами корректировки масс (мар-
кирования, клеймения) могут оснащаться
специальные станки для измерения дис-
балансов ротора. В этом случае процессы
измерения дисбалансов, позиционирова-
ния и корректировки масс ротора совмеще-
ны в пространстве на одной позиции (на
одном и том же роторе), но разнесены
во времени и выполняются последователь-
но. При автоматизации этих процессов
специальный станок делают автоматиче-
ским.
Автоматические станки, линии, участ-
ки. Станок-автомат представляет собой
специальный балансировочный станок, в
котором процессы измерения дисбалансов,
позиционирования и корректировки масс
(маркирования, клеймения, сортировки)
ротора, а также его загрузку и выгрузку,
осуществляют автоматически. Специаль-
ный балансировочный станок, в котором не
автоматизированы только процессы за-
грузки и выгрузки ротора, является полу-
автоматическим. Специальный станок, в
котором не автоматизирован какой-либо из
перечисленных процессов, например кор-
ректировки масс, является автоматизиро-
ванным. Специальные станки для измере-
ния дисбалансов ротора могут быть до-
полнены отдельными обрабатывающими
станками для корректировки масс и транс-
портом для перемещения ротора с позиции
измерения на позицию коррекции дис-
194
Балансировочные станки
баланса. Если требуемая точность балан-
сировки ротора не может быть достигнута
за один цикл балансировки, то позиций
измерения и коррекции дисбаланса может
быть несколько, например, черновая и
чистовая, связанных общим транспортом
непосредственно или через бункер-накопи-
тель.
Оборудование такого типа является
балансировочной линией иди участком.
Специальные балансировочные участки и
линии могут быть дополнены станками
для измерения и контроля остаточного
дисбаланса (позиция контроля дисбалан-
са), средствами сортировки роторов по
значению остаточного дисбаланса, средст-
вами удаления отходов корректировки
масс и др. В балансировочных участках
и линиях процессы измерения дисбалансов
и корректировки масс роторов разнесены
в пространстве на разные позиции, но
совмещены во времени для разных рото-
ров. т. е. одновременно осуществляют
корректировку масс ротора, ранее из-
меренного, и измерение дисбалансов сле-
дующего ротора. Этим обеспечивается вы-
сокая производительность балансировки.
При автоматизации всех процессов спе-
циальные балансировочные участки и ли-
нии являются автоматическими.
Автоматическая линия или участок
представляет собой специальное балан-
сировочное оборудование, в котором про-
цессы измерения дисбалансов, позициони-
рования, корректировки масс (маркирова-
ния, клеймения, сортировки) и транспорти-
рования ротора, включая его загрузку и
выгрузку, осуществляются автоматически.
Специальные балансировочные линии и
участки, в которых не автоматизированы
только процессы загрузки и выгрузки ро-
тора, являются полуавтоматическими. В
случае, если не автоматизирован какой-
либо из процессов, например корректиров-
ки масс, специальные линии и участки
являются автоматизированными. В авто-
матических балансировочных станках и
линиях процессы измерения дисбаланса и
корректировки масс ротора совмещены
либо в пространстве (на одном роторе
последовательно), либо во времени (на
разных роторах одновременно). Отдель-
ную группу составляют станки для авто-
матической балансировки в процессе вра-
щения роторов.
Станок для автоматической баланси-
ровки в процессе вращения ротора пред-
ставляет собой специальный балансиро-
вочный станок, в котором процессы опреде- 1
ления дисбалансов и корректировки масс |
совмещены во времени и в пространстве.
На таком станке в процессе вращения
ротора одновременно осуществляется из- ч
мерение дисбалансов и их уменьшение
либо автоматическим добавлением коррек-
тирующей массы в легком месте ротора,
либо автоматическим удалением избыточ-
ной массы в тяжелом месте ротора.
При этом корректирующие устройства, уп-
равляемые сигналами дисбаланса, осу-
ществляют автоматическую балансировку
в момент прохождения перед ними со-
ответствующего места на вращающемся
роторе. В современных станках применяют
электрофизические и электрохимические
методы коррекции дисбаланса. Электро-
физическая корректировка масс включа-
ет: удаление избыточной массы ротора
с помощью луча лазера, добавление
корректирующей массы с помощью взрыва
проволок в магнитном поле, добавление
корректирующей массы с помощью элект-
рогидравлического удара
Взрыв металлических проволок осуще-
ствляют подачей на них высоковольтного
напряжения, а расплавленные продукты
взрыва фокусируют и направляют на ротор
магнитным полем.
Для формирования электрогидравли-
ческого удара в среде жидкости, замкнутой
в объеме одной из камер, в ней осуществ-
ляют высоковольтный разряд. Возникший
электрогидравлический удар воздействует
через мембрану на корректирующую массу
(например, расплавленный металл), раз-
мещенную в смежной камере. Через сопло
камер корректирующая масса направляет-
ся на ротор.
К л асе иф икац ия
195
Электрохимическая корректировка масс
основана на принципе анодного растворе-
ния избыточного металла при врашении
балансируемого ротора. Над плоскостью
коррекции ротора установлен электрод, а
в зазор между ним и ротором подается
электролит. В момент прохождения под
электродом тяжелого места ротора между
электродом и ротором пропускают импульс
электрического тока, замыкающегося
через электролит. При этом за каждый
оборот ротора под электродом осуществ-
ляют съем металла.
Отдельные задачи балансировки реша-
ют с помощью контрольно-измерительных
устройств, которые включают весы для
определения масс и статических моментов
элементов роторов, вибростолы для опре-
деления моментов инерции масс. Необхо-
димость определения масс и статических
моментов элементов роторов (например,
лопаток паровых и газовых турбин) возни-
кает при сборке турбоагрегатов по миниму-
му дисбаланса, а необходимость измерения
моментов инерции роторов—при не-
посредственном измерении угла отклоне-
ния главной центральной оси инерции ро-
тора от оси его вращения, так как данный
угол связан с моментным дисбалансом ро-
тора через соответствующие моменты
инерции масс.
Выбор средств балансировки опреде-
ляется видом балансировки (статическая,
динамическая или балансировка гибкого
ротора), требованиями производительно-
сти и точности балансировки, массово-гео-
метрическими характеристиками и конст-
руктивными особенностями, способом ба-
зирования в рабочих условиях, точностью
изготовления и технологией производства
ротора.
Требуемый вид балансировки опреде-
ляется динамическим состоянием ротора в
реальных опорах на рабочих частотах вра-
щения. При этом реа. ции на опорах свя-
заны с действующим на роторе статиче-
ским, динамическим дисбалансом и с про-
явлением его изгибных деформаций. В об-
щем случае на ротор воздействуют все
три вида дисбаланса в различном коли-
чественном соотношении в зависимости от
массово-геометрических характеристик ро-
тора и рабочих частот вращения. Таким
образом, выбор требуемого вида баланси-
ровки связан с установлением превали-
рующего воздействия одного из видов дис
баланса ротора на динамическое состояние
машины. Эта задача решается на стадии
проектирования роторов. Практикой уста-
новлено, что для дискообразных роторов
с малыми осевыми размерами весьма слабо
проявляется моментный дисбаланс. Если
приведенные к опорам дисбалансы от не-
уравновешенного момента существенно
меньше допускаемых удельных дисбалан-
сов. то для ротора достаточна стати-
ческая балансировка в одной плоскости
коррекции. В противном случае необходи-
ма динамическая балансировка ротора в
двух плоскостях коррекции. Аналогично
можно сформулировать требования к кри-
терию балансировки жестких и гибких ро-
торов: если первая изгибная форма
колебаний ротора проявляется слабо (ра-
бочая частота вращения ротора значитель-
но ниже первой критической частоты си-
стемы ротор опоры) и приведенные к
опорам дисбалансы по первой форме из-
гиба меньше допускаемых, то можно огра-
ничиться динамической балансировкой
жесткого ротора в двух плоскостях кор-
рекции. В противном случае необходимо
учитывать гибкость ротора и проводить
балансировку в трех или большем числе
плоскостей коррекции на соответствующем
оборудовании. После установления не-
обходимого вида балансировки выбирают
соответствующий тип станка: для стати-
ческой, динамической балансировки или
для балансировки гибкого ротора. Вопросы
выбора требуемого вида балансировки
более подробно рассмотрены в методи-
ческих указаниях [9].
Требуемая производительность балан-
сировки ротора определяется характером
его производства и влияет на выбор балан-
сировочного станка (общего назначения,
специализированный, специальный с раз-
личной степенью автоматизации). Балан-
сировочные станки общего назначения в
7*
196
Балансировочные станки
основном применяют в единичном и мелко-
серийном производствах. Особенно широко
данные станки используют на ремонтных
базах, станциях технического обслужива-
ния и других предприятиях индивидуаль-
ного производства. В зависимости от масс
балансируемых роторов, оснастки станка,
способа коррекции масс, организации про-
изводства и других факторов станки обще-
го назначения могут балансировать один
ротор в пределах от 3 до 15 мин (для
роторов массой до 100 кг). Специализи-
рованные станки, особенно оснащенные
средствами коррекции и частично авто-
матизированные, способны балансировать
один ротор в пределах от 1 до 5 мин.
Такие станки помимо мелкосерийного
производства находят применение в серий-
ном производстве. Специальные станки в
зависимости от степени автоматизации
способны обеспечить продолжительность
балансировки одного ротора менее 1 мин.
Их применяют в крупносерийном и мас-
совом производствах. Следует отметить,
что на производительность балансировки
существенное влияние оказывают: масса
ротора и способ его загрузки и выгрузки,
необходимость монтажа ротора на техно-
логической оправке (плоские диски и т. д.)
или его оснащения технологическими гру-
зами (коленчатые валы и т. п.), допусти-
мый метод корректировки масс и режимы
резания, величина начального дисбаланса,
требуемая кратность снижения дисбаланса
и т. д. Измерение дисбалансов обычно
обеспечивается на станках в течение 5—
20 с. Процесс коррекции дисбалансов
определяется принятым способом кор-
ректировки масс (сверление, наклепка гру-
зов и т. д.) и величиной начального дис-
баланса, а его продолжительность может
меняться в широких пределах.
Требуемая точность балансировки ро-
тора также воздействует на выбор балан-
сировочного оборудования. Балансировоч-
ные станки общего назначения имеют три
класса точности: нормальный класс (Н)
с наибольшей точностью балансировки до
I мкм остаточного смещения центра масс
ротора; повышенный класс (П)—до
0,4 мкм; высокий класс (В)—до 0.1 мкм.
Специализированные станки, которые
создают на базе станков общего назначе-
ния, обеспечивают более высокую про-
изводительность, но имеют ту же точность
балансировки. Для обеспечения более вы-
сокой точности’ балансировки необходимы
специальные станки. Однако следует иметь
в виду, что точности балансировки выше
0,1 мкм часто ограничиваются не возмож-
ностью балансировочного станка, а конст-
рукцией и качеством изготовления самого
балансируемого ротора или роторного узла
в сборе. Предельная точность балансиров-
ки ротора может быть ограничена чистотой
обработки и точностью геометрической
формы базовых поверхностей ротора, на-
пример шеек ротора электродвигателя, или
точностью подшипников качения, с кото-
рыми собирается ротор.
Более высокая точность может быть
получена при балансировке на станках
изделий в сборе, в которых ротор за-
фиксирован в осевом направлении, а его
базовые поверхности при вращении не ме-
няют своих дорожек качения или скольже-
ния в высокоточных подшипниках. Так,
например, при балансировке гиромоторов
в сборе может быть достигнута точность
балансировки до 0,01 мкм остаточного
смещения центра масс ротора.
Целесообразная точность балансиров-
ки ротора на станке ограничивается до-
пусками на обработку его базовых поверх-
ностей. Точность балансировки ротора,
значительно превышающая допуск на его
посадку при базировании в рабочих опо-
рах, нецелесообразна, так как в собран-
ной машине возникнет технологический
дисбаланс, определяемый разницей бази-
рования ротора на станке и в рабочих
опорах. Если требуемое вибросостояние
машины в сборе не может быть обеспечено
только подетальной балансировкой рото-
ров, то необходима балансировка на стан-
ках вращающихся узлов в сборе или ба-
лансировка машин в сборе (в рабочих
условиях) с помощью балансировочной ап-
паратуры.
Массово- геометрические характеристи-
ки и конструктивные особенности роторов
накладывают дополнительные требования
Станки общего и специализированного назначения
197
на выбор балансировочного оборудования.
Требуемую для балансировки ротора мо-
дель станка из гаммы станков общего
назначения выбирают на основании пара-
метров ротора: массы, диаметра бочки ро-
тора, диаметра базовых поверхностей,
длины и т. д. Перечисленные параметры
влияют также и на конструкции специа-
лизированных и специальных станков.
Конструктивные особенности ротора во
многом определяют требуемый тип привода
вращения ротора на станке. Роторы мас-
сой от 1 кг и выше, конструкция которых
предусматривает осевой привод, обычно
вращаются на станках с помощью кар-
данной или иной муфты. Ряд роторов ма-
шиностроения, не имеющих осевого приво-
да, требует привода с помощью накид-
ного ремня. Ременный привод вращения
применяют также для повышения точности
балансировки роторов, имеющих осевой
привод.
Конфигурация ротора влияет на выбор
измерительной системы станка. Такие ро-
торы, как судовые и воздушные винты,
колеса вентиляторов и т. д., требуют из-
мерения дисбалансов в соответствующей
системе координат (полярная, прямоуголь-
ная, косоугольная). Ограничение допусти-
мой зоны корректировки масс ротора, на-
пример, в секторах противовесов колен-
чатого вала определяет необходимость из-
мерения вектора дисбаланса в ограни-
ченной зоне, его удержания в заданной
зоне после корректировки масс, пересчета
в соседние зоны.
Конструкция и условия работы ротора
определяют допустимый способ корректи-
ровки его массы (сверление, приварка гру-
зов и т. д.), а следовательно, и оснащение
станка соответствующими механизмами
коррекции дисбаланса. При выборе стан-
ков для автоматической балансировки в
процессе вращения роторов необходимо
обращать внимание на допустимость об-
работки ротора электролитом, лазером, на-
пылением, на прочность сцепления наноси-
мого материала на рабочих частотах вра-
щения и на достигаемую чистоту поверх-
ности после балансировки.
Условия работы ротора определяют и
способы базирования на балансировочном
станке. Такие роторы, как центрифуги и
сепараторы, работают в вертикальном по-
ложении на опорном подшипнике. Для вос-
создания рабочих условий и сохранения
состояния сбалансированности они требу-
ют для динамической балансировки стан-
ков с вертикальным расположением шпин-
деля. Большинство роторов, не требующих
при балансировке воссоздания рабочих ус-
ловий. балансируются динамически при
горизонтальном положении ротора, а ста-
тически— на станках с вертикальным
шпинделем.
Точность изготовления и технология
производства ротора определяют величину
максимального начального дисбаланса.
Отношение начального к допустимому ос-
таточному дисбалансу называется требуе-
мой кратностью снижения дисбаланса, ко-
торая во многом определяет технические
возможности балансировочного оборудо-
вания. За один цикл балансировки на авто-
матическом станке дисбаланс ротора
может быть снижен в 10—20 раз. При боль-
ших значениях требуемой кратности сни-
жения дисбаланса балансировку необходи-
мо проводить многократно на автомати-
ческих линиях или участках.
Могут быть и другие факторы, опре-
деляющие тип и конструкцию балансиро-
вочного оборудования, которые уточняют в
процессе согласования технических требо-
ваний на создание специальной баланси-
ровочной техники.
7.2 СТАНКИ ОБЩЕГО И
СПЕЦИАЛИЗИРОВАННОГО НАЗНАЧЕНИЯ
В настоящее время серийно выпуска-
ются балансировочные станки общего
назначения для статической и динами-
ческой балансировки роторов. Станки од-
ного вида балансировки объединены в со-
ответствующие гаммы станков. Каждый из
ее станков предназначен для балансировки
роторов с широким диапазоном изменения
масс, а коэффициент перекрытия станков
гаммы по наибольшим массам балансируе-
198
Балансировочные станки
мых роторов равен 3, например, модели
станков для балансировки роторов массой
до 100, 300, 1000 кг и т. д. Большинство
роторов, требующих статической баланси-
ровки, допускает корректировку масс мето-
дом сверления материала ротора. В связи
с этим на базе станков для статической
балансировки общего назначения выпуска-
ются специализированные станки, которые
оснащены сверлильным агрегатом. На базе
станков для динамической балансировки
общего назначения выпускают специали-
зированные станки, которые оснащены и
приспособлены для балансировки конкрет-
ного ротора или группы однотипных рото-
ров.
Станки для статической балансировки
роторов. Гамма станков общего назначе-
ния предназначена для статической балан-
сировки в динамическом режиме плоских
роторов машиностроения типа дисков,
шкивов, маховиков и т. д. массой до 300 кг.
Гамма содержит четыре модели станков
для балансировки роторов массой до 1 кг
(мод. 9763); до 10 кг (мод. 9764); до
100 кг (мод. 9765М); до 300 кг (мод. 9766).
На станках общего назначения осуществ-
ляется только измерение дисбалансов ро-
тора в одной плоскости коррекции. Кор-
ректировка масс ротора выполняется от-
дельно от балансировочного станка на со-
ответствующем оборудовании. Специали
зированные станки для осуществления
коррекции дисбаланса оснащены свер
л ильным агрегатом, который допускает
переналадку на сверление ротора в осе-
Таблица 7.1
Станки общего назначения и специализированные для статической балансировки роторов*
Наименование параметров Модель станка
9763 9764 9765М 9766
Наибольшая масса балансируе- мого ротора, кг 1 10 100 300
Наибольший диаметр ротора, мм 250 500 1000 1300
Частота вращения балансируе- мых роторов, об/мин 2500 1500 600; 900 480; 960
Точность балансировочного станка, г • мм/кг 10; 4: 1** 10; 4. 1 10.4: 1 10: 4: I
Наибольший начальный дисба- ланс при низшей частоте вра- щения, г • мм/кг 300 800 1000 1000
Наибольший диаметр сверления в балансируемом роторе, мм 6 12 X 14 14
Расстояние от оси сверл ильной головки до балансируемого ро- тора, мм Мощность главного привода. кВт 20— 120 30—280 30—280 30—280
0,18 0,55 2,1/3.0 8,5/10,0
Мощность привода сверлильной головки, кВт Габаритные размеры (без шка- фа электрооборудования), мм 0,18 1.1 1,0/1,3 1.0/1,3
650Х700Х 1400 800Х840Х XI650 1540Х1470Х X 1770 I820X1520X X I960
Масса (с электрооборудовани- ем), кг 300 550 2000 2360
3 авод- изготовитель ОЗПС**» ОЗПС МСПО*** МСПО
* Станки общего назначения не оснащены сверлильным агрегатом.
** Точность специализированного станка может быть повышена по техническим требо-
ваниям заказчика.
*** ОЗПС — Одесский завод прецизионных станков; МСПО Минское станкостроительное
производственное объединение им. Октябрьской революции.
Станки общего и специализированного назначения
199
вом и в радиальном направлениях. Вы-
пускаются также станки зарезонансного и
дорезонансного типов. Основные техниче-
ские данные станков для статической ба-
лансировки приведены в табл. 7.1.
Компоновка и конструкция станков в
значительной мере определяются конст-
рукцией балансируемых роторов и услови
ями их базирования в рабочих машинах.
При базировании ротора по внутреннему
отверстию, характерному для плоских де-
талей, более удобно вертикальное располо-
жение шпинделя станка, на котором с
помощью специальных оправок (патронов,
цанг и т. д.) закрепляют балансируемый
ротор.
Схема колебательной системы станка
приведена на рис. 7.2. На шпинделе 4 за-
креплены зажимное устройство 2, отсчет-
ный лимб 3 и генератор (преобразователь)
опорного сигнала 5. Для восприятия дис-
баланса шпиндель консольно закреплен на
двух параллельных плоских пружинах 6.
В станках зарезонансного типа жесткость
пружин в направлении, перпендикулярном
плоскости чертежа, выбирают так, чтобы
резонансная частота колебательной систе-
мы с ротором была ниже рабочей частоты
вращения (в 3 раза и более). В дорезо-
нансных станках жесткость пружин обе-
спечивает обратное соотношение частот.
Шпиндель приводится во вращение от
электродвигателя 7 через ременную пере-
дачу /. Колебания системы с неуравно-
вешенным ротором воспринимаются элект-
ромеханическими датчиками (индукцион-
ными, пьезокристаллическими или други-
ми). Измерительной системой станка сиг-
налы датчиков преобразуются в удобную
для оператора информацию о дисбалансе
ротора (значение и угол дисбаланса или
составляющие проекции вектора дис-
баланса в декартовой системе координат).
Одной из основных задач измерительной
системы является выделение сигнала дис-
баланса из спектра помех, которые соз-
даются как самим станком, гак и внеш
ними источниками. Наиболее эффективным
средством фильтрации помех является
перемножение сигнала датчика дисбалан
са на вспомогательный опорный сигнал,
который формируется в станке специаль-
ным источником (генератором или пре-
образователем) .
На рис. 7.3 приведена структурная схе-
ма измерительной системы к балансиро-
вочным станкам с осевым приводом вра
шения ротора. Для выделения сигнала
дисбаланса из спектра помех в системе
используется известный принцип умноже-
ния сигнала дисбаланса на синусоидаль-
ный (косинусоидальный) опорный сигнал,
т. е. множительный принцип. Поскольку в
данной системе множительный принцип
осуществляется посредством амплитудной
модуляции с применением вращающегося
трансформатора, система получила назва-
ние АМВТ.
Множительный принцип измерения ре-
ализован в системе с помощью функцио-
нального преобразователя типа синусно-
косинусного вращающегося трансформа-
тора (СКВТ), коэффициент передачи кото-
рого изменяется по тригонометрическим
функциям в зависимости от угла поворота
рабочего элемента. Измерительная систе-
ма работает в двух режимах. В положе-
нии 1 переключателя Kt осуществляется
режим измерения и запоминания парамет-
ров дисбаланса ротора при его быстром
вращении. В положении 2 переключателя
К1 обеспечивается отсчетный режим, при
котором вектор дисбаланса автоматически
пересчитывается из стационарной измери-
тельной системы координат XOY в систему
осей коррекции X'OY' на роторе.
200
Балансировочные станки
Рис. 7.3. Структурная схема измерительной системы AM ВТ
В режиме измерения механические
колебания от неуравновешенного ротора
10 при его быстром вращении преобра-
зуются датчиком, 2 дисбаланса в электри-
ческий сигнал U\, который поступает в
блок / настройки станка на ротор. С по-
мощью амплитудных модуляторов 3 сигна-
лом дисбаланса модулируется амплитуда
сигнала несущей частоты {/2, вырабаты-
ваемого генератором 4. Модулированный
сигнал U2 подводится к первичной обмотке
С КВТ 5, ротор которого механически свя-
зан с балансируемым ротором 10 и вра-
щается вместе с ним. При прохождении
через С КВТ сигнал U-г перемножается на
синусоидальную (косинусоидальную) фун-
кцию преобразователя с частотой враще-
ния ротора. В результате умножения (по-
вторной амплитудной модуляции) на вто-
ричной обмотке СКВТ выделяется сигнал
(7з, содержащий в своем спектре несущую
частоту. Амплитуда этой составляющей
пропорциональна модулю вектора дис-
баланса и косинусу (синусу) его фазового
угла. После синхронного детектирования
в демодуляторе 6 выделяется сигнал U4,
постоянная составляющая которого несет
информацию о дисбалансе, так как являет-
ся копией несущей. Помехи, содержащиеся
в спектре сигнала датчика, отличаются по
частоте от полезного сигнала и выделяются
на выходе демодулятора 6 в виде пере-
менных составляющих, которые подав-
ляются фильтром нижних частот 7. По-
лезный сигнал Uz в виде напряжения по-
стоянного тока подводится к запоминаю-
щему устройству 9, обеспечивающему хра-
нение информации по окончании цикла из-
мерения. Благодаря наличию квадратур-
ных обмоток СКВТ измерительное устрой-
ство обеспечивает измерение дисбаланса
в прямоугольной системе координат XOY.'
В режиме отсчета устройство работает
аналогичным образом, но вместо сигнала
датчика ко входам модуляторов подводят-
ся сигналы Ux и Uy из запоминающего
устройства 9, отображающие проекции
вектора дисбаланса в измерительной си-
стеме координат. При этом суммарный век-
тор магнитного поля ротора СКВТ являет-
ся копией измеренного вектора дисбалан-
са. Благодаря механической связи ротора
СКВТ 5 с балансируемым ротором 10 век-
тор дисбаланса может поворачиваться со-
Станки общего и специализированного назначения
201
вместно с последним относительно не-
подвижных обмоток статора С КВТ. Эти об-
мотки образуют отсчетную прямоугольную
систему координат Х'ОУ, неподвижную в
пространстве и выраженную указателями
X', У''. Каждому указателю соответствует
свой индикатор дисбаланса 8. 8'. Для лю-
бого углового положения а ротора 10 ин-
дикаторы 8, 8' показывают координаты
(X', У') вектора дисбаланса G, т. е. зна-
чение дисбаланса в прямоугольной системе
координат Указатели X', У', размешенные
на станке вблизи ротора, являются одно-
временно указателями осей коррекции на
роторе. Поскольку ротор может поворачи-
ваться относительно указателей, его оси
коррекции являются текущими и обеспечи-
вают свободу выбора точек коррекции
на роторе. Система обеспечивает измере-
ние дисбаланса в полярной, прямоуголь-
ной и любых косоугольных системах коор-
динат.
Блок 1 настройки станка на ротор со-
держит элементы условной балансировки
ротора и компенсации влияния эксцентри-
ситета шпинделя.
Эти операции осуществляются путем
электрической компенсации сигнала дат-
чика дисбаланса сигналом генератора ус-
ловного дисбаланса.
Структурная схема условной баланси-
ровки и компенсации эксцентриситета
шпинделя приведена на рис. 7.4. В качестве
генератора в схеме использован синусно-
косинусный вращающийся трансформатор
/, ротор йа я обмотка которого возбуждает-
ся постоянным током от источника 2. При
вращений ротора СКВТ от шпинделя стан-
ка в его статорных обмотках возбуждают-
ся синусоидальные сигналы с относитель-
ным сдвигом фаз 90°. В положении 1 пере-
ключателя 8 осуществляют условную ба-
лансировку суммарного вектора дисбалан-
са, вызванного неуравновешенностью ба-
лансируемого ротора и эксцентриситетом
шпинделя станка. Компенсирующий век-
тор формируется по составляющим проек-
циям с помощью регуляторов 3, 4. Этот
электрический вектор, сформированный
сигналами условной балансировки, являет-
ся копией вектора дисбаланса, но направ-
Рис. 7.4. 'Структурная схема условной балан-
сировки ротора я компенсации влияния экс-
центриситета шпинделя
ление еп> противоположно. Результирую-
щий сигнал условной балансировки от ре-
гуляторов 3, 4 суммируется с сигналом
датчика дисбаланса 10 в сумматоре 9 до
нулевых значений индикатора дисбаланса.
После выполнения операции условной
балансировки переключатель 8 устанавли-
вают в положение 2, а балансируемый
ротор на шпинделе станка разворачивают
на 180°. В этом положении переключателя
к сумматору.9 подводится сигнал датчика
дисбаланса 10, сигналы условной баланси-
ровки от регуляторов 3, 4 и сигналы от
регуляторов 5, 6, компенсирующие состав-
ляющую от эксцентриситета шпинделя
При этом вектор дисбаланса ротора не
изменит своего направления, так как одно-
временно с поворотом ротора группы с и б
переключателя 8 меняют полярность дат-
чика на противоположную. Вектор дис-
баланса от эксцентриситета шпинделя по-
вернется на 180° и сложится с таким же
вектором, содержащимся в сигнале услов
ного дисбаланса. В результате на выходе
сумматора 9 будет действовать сигнал,
равный удвоенному вектору дисбаланса от
эксцентриситета шпинделя. Этот сигнал
компенсируется с помощью регуляторов 5,
6. С помощью делителя напряжения 7
половина компенсирующего сигнала вво-
202
Балансировочные станки
дится в цепь сигнала датчика дисбаланса
в положении 3 переключателя 8. При этом
на выходе сумматора 9 действует сигнал,
содержащий только вектор дисбаланса от
неуравновешенного ротора. В этом поло-
жении переключателя осуществляется ба-
лансировка роторов на станке.
Специализированный станок мод.
9765М для статической балансировки ро-
торов показан на рис. 7.5.
Станок выполняет автоматическое из-
мерение и запоминание параметров дис-
баланса в различных системах координат:
полярной, прямоугольной, косоугольной.
Ротор устанавливают на станок с по-
мощью пневмоподъемника и закрепляют в
оправке шпинделя автоматическим меха-
низмом с пневматическим приводом. Вер-
тикальная сверлильная головка устраняет
дисбаланс без снятия ротора с оправки
благодаря разгрузочному устройству, иск-
лючающему передачу усилий на опоры
шпинделя. Станок оснащен системой
отсоса стружки.
Точность базирования балансируемых
роторов по внутреннему отверстию на
шпинделе станка и в рабочих условиях
может достигать 3—10 мкм. В этих же
пределах обеспечивается точность стати-
ческой балансировки роторов на станках
общего назначения. Станки класса Н обе-
спечивают точность балансировки 10 мкм,
а станки класса П — точность 4 мкм. Точ-
ность балансировочного станка проверяют
по методике, изложенной в параграфе 7.6,
и по ГОСТ 20076—89 Для роторов, конст-
рукция которых обеспечивает более высо-
кую технологическую точность базировки,
точность балансировки на специализиро-
ванных станках может быть повышена по
техническим требованиям заказчика. Пре-
дельная точность статической балансиров-
ки без снятия и перестановки ротора на
шпинделе станка может быть доведена до
1 мкм остаточного смещения центра масс.
Наладку балансировочного станка осу-
ществляют с помощью тарировочного ро-
тора, в качестве которого может быть ис-
пользован один из серийных роторов. На-
ладка включает операции настройки стан-
Рис. 7.5. Специализированный станок мод.
9765М для статической балансировки роторов
ка на балансируемый ротор и регулировки
узлов станка. Настройка станка на балан-
сируемый ротор состоит из следующих
операций: условной балансировки ротора,
тарирования измерительной системы, ком-
пенсации эксцентриситета шпинделя стан-
ка, компенсации моментной составляющей
сигнала дисбаланса, установки требуемого
радиуса корректировки масс. Условная ба-
лансировка ротора позволяет исключить
электрическим путем влияние начального
дисбаланса ротора на процесс тарирова-
ния. При тарировании станка цену деле-
ния индикатора дисбаланса связывают с
единицами коррекции, выбранными для
данного ротора. Операции компенсации
эксцентриситета шпинделя станка и мо-
ментной составляющей дисбаланса по-
зволяют исключить электрическим путем
влияние этих составляющих дисбаланса
на показания станка. Регулировка узлов
станка включает операции монтажа на
шпинделе станка механизма зажима, тре-
буемого для данного ротора, и перемеще-
ние сверлильной головки на заданный
радиус сверления. Перечисленные опера-
ции настройки осуществляют по методике,
изложенной в руководстве по эксплуата-
ции соответствующей модели станка.
После наладки станка по тарировочно-
му ротору производят балансировку пар-
Станки общего и специализированного назначения
203
тии однотипных роторов. При этом ротор
устанавливают на оправке станка, авто-
матически закрепляют и включают враще-
ние шпинделя. По окончании измерения и
запоминания параметров дисбаланса ро-
тор автоматически останавливается. Ротор
поворачивают до получения на одном из
индикаторов дисбаланса нулевых значе-
ний. При этом на втором индикаторе уста-
навливается значение дисбаланса ротора,
а точка коррекции дисбаланса на роторе
размещается против указателя станка
(для станков общего назначения) или
против сверла механизма коррекции (для
специализированных станков). Коррек-
тировку масс осуществляют в соответствии
с показаниями индикатора дисбаланса и
выбранными единицами коррекции. Пу-
ском шпинделя станка производят конт-
рольное измерение остаточного дисбалан-
са. В случае необходимости повторяют
операции для корректировки масс ротора.
Станки для динамическом балансиров-
ки жестких роторов. Гамма станков-общего
назначения предназначена для динамиче-
ской балансировки жестких двухопорных
роторов машиностроения типа тел враще-
ния массой до 100 т. Гамма содержит 15
моделей станков. Станки мод. 9А7П, 9712
выпускает Кироваканский завод преци-
зионных станков (КЗПС). станки мод.
9713,9714 — Одесский завод прецизионных
станков (ОЗПС), станки мод. 9715Р,
9715—9718,9719М, 9719Б— Минское стан-
костроительное производственное объеди-
нение им. Октябрьской революции
(МСПО). Станки серии ДБ выпускает
Савеловский машиностроительный завод
(СМ3).
На станках общего назначения осуще-
ствляют только измерение дисбалансов ро-
тора в двух плоскостях коррекции. Кор-
ректировка масс ротора выполняется на
опорах станка известными методами (свер-
ление. навешивание грузов и т. д.) или
отдельно от станка на соответствующем
оборудовании. Основные технические дан-
ные станков приведены в табл. 7.2
Роторы, требующие динамической ба-
лансировки, в большинстве случаев бази-
руются на двух цапфах (подшипниках).
В связи с этим в станках для динами-
ческой балансировки предусматривается
горизонтальная установка ротора на две
опоры, в которых размещены колебатель-
ные системы с требуемыми подшипниками
(призмами, вкладышами, роликами и
т. д.)
На рис. 7.6 показана схема станка
общего назначения для динамической ба-
лансировки. Ротор 4 базируется на опорах
9, 9', установленных на станине станка.
В зависимости от динамического режима
работы различают станки зарезонансного
или дорезонансного типов. В зарезонанс-
ных станках устанавливаются опоры 5,
в которых колебательная система 7
(люлька) подвешена на лентах. Резонанс-
ная частота колебательной системы вместе
с массой ротора ниже рабочей частоты
вращения. В дорезонансных станках уста-
навливаются опоры 6, в которых коле-
бательная система 7' образована верти-
Рис. 7.6. Схема станка общего назначения для динамическом балансировки роторов
204
Балансировочные станки
Основные технические данные станков общего назначения для динамической балансировки
жестких роторов
Основные технические данные станка Модель станка
9А711 9712 9713 9А714 ДБ-К) ДБ-50 9715Р
Наибольшая масса балансируемого ро- тора, кг 1 3 10 30 0,3—30 5 — 50 100
Наибольший диаметр ротора, мм 250 350 500 700 500 540 1000
Наибольшее расстояние между середи- нами опор, мм 350 500 700 1000 500 700 1300*
Наибольший диаметр, мм цапф ротора 25 35 50 70 200 200 100
подшипников - 200 200 80
Частота вращения ротора, мин-1 2000— 4000 2000 — 4000 1000 2000 4000 500 1000 2000 500 — 2500 1000— 2000 600— 3200
Тип привода вращения ротора Ременный
Точность балансиро- вочного станка, г • - мм/кг нормальная (Н) — 2—1 —
повышенная (П) 0,8—0,4
высокая (В) 0.2—0,1 — 0,1
Тип конструкции станка Зарезонансный
Мощность главного привода, кВт 0,4 0,25 0,88 1,2 1,5 1,15
Габаритные размеры, мм длина 1050 900 1050 1300 1500 2360
ширина 630 500 550 620 830
высота 485 1450 1472 1500
Масса, кг 140 380 450 565 600 775
Завод-изготовитель кзпс озпс СМ3
Размер может быть увеличен по требованию заказчика.
. Станки общего и специализированного назначения
205
Таблица 7.2
9715 9716 ДБ-ЗОЗМ 9717 ДБ-1001 9718 9719М 9719Б ДБ-10 ДБ-50 ДБ-ЗОЗМ ДБ-1001
100 300 100 300 1000 100— 1000 3000 10000 30000 0,3— 30 5—50 100— 300 100— 1000
1000 1300 1500 1800 2000 2300 3000 4000 500 540 1500 2000
1300* 1800* 2300 2300 2800 3000 4000* 5600* 500 700 2300 2500
100 130 250 200 300 250 360 500 200 200 250 300
160 225 250 320 300 450 630 850 100 100 — —
400— 3200 315— 2500 600— 800 250— 2000 450— 600 200— 1600 200— 1250 200— 1000 500— 2500 1000 — 2000 600— 800 450— 600
Осевой Ременный Осевой Ременный
2—1 2—1 2—1 — — —
0,8—» 0,4 0,4 0.4 0,4
— —
Дорезонансный Зарезо- нансный Дорезо- нансный Зарезо- нансный Дорезо- нансный Дорезонанс- ный Зарезонансный
2,2 11 6,3 20 18,5 45 ПО 1.2 1,5 11 20
3200 3270 3140 4030 5900 6300 8000 11500 1300 1500 3140 5900
695 1680 880 1300 1600 1490 2430 620 620 1680 1300
1550 1420 1425 1800 1700 2105 2650 1450 1472 1420 1800
2080 2115 6100 4500 7100 8000 15 500 32360 565 600 6100 7100
МСПО СМ3 МСПО СМ3 МСПО СМ3
206
Балансировочные станки
кальными стойками опоры. При этом резо-
нансная частота колебательной системы с
ротором выше рабочей частоты вращения.
Верхняя часть опоры на которую бази-
руется ротор, выполнена сменной. В гамме
станков предусмотрень Три конструкции
опор: призматическая, роликовая и гидро-
статическая. В призматических опорах
ротор может базироваться на собственных
подшипниках качения. Для обеспечения
крутильных колебаний ротора призмати
ческая опора снабжена цилиндрическими
роликами. Такими опорами комплектуются
станки для балансировки роторов массой
от 1 кг до 3 т (станки мод. 9714— 9718).
В тех случаях, когда опорными поверх-
ностями являются посадочные шейки ро-
тора, применяют призматические опоры
скольжения. Такие опоры изготавливают
(или снабжают вкладышами) из различ-
ных материалов: текстолита, фторопласта,
капролона, агата и др. Материал вклады-
ша выбирают с учетом технических данных
шейки ротора, частоты вращения на станке
и требуемой точности балансировки.
Опоры скольжения поставляются со
станком, а вкладыши из различных ма-
териалов могут быть дополнительно из-
готовлены потребителем по типовому чер-
тежу руководства по эксплуатации станка.
Призматические опоры скольжения, кото-
рые обеспечивают высокую точность ба-
лансировки, применяют в станках классов
точности П и В для балансировки роторов
массой от 0,01 до 30 кг (станки мод.
9А7Н, 9712—9714).
При базировании ротора на станке
посадочными шейками применяют также
роликовые опоры. Точность балансировки
роторов на роликовых опорах ограничи-
вается точностью изготовления образую-
щей поверхности роликов и качеством
подшипников качения, так как осевые и
радиальные биения роликов создают по-
мехи измерению. Достижимая точность
балансировки на роликовых опорах мень-
ше. чем в опорах скольжения. Одна-
ко роликовые опоры применяют в станках
классов точности Н и П для баланси-
ровки роторов массой от 1 кг до 3 т
(станки мод. 9715- 9718).
В станках мод. 9719М и 9719Б лгля
балансировки роторов массой до 30 т при-
меняют гидростатические опоры. Гидро-
подушка опоры обеспечивает всплытие ро-
тора с зазором 0,1 —0,5 мм, что разгружает
привод станка и повышает его надежность.
Балансируемый ротор 4 приводится во
вращение на станке от электродвигателя
12 через шпиндель 11 станка и карданный
вал 3. Применение осевого привода в стан-
ках ограничивает точность балансировки
по ряду причин. Приводной вал ухудшает
параметры колебательной системы станка.
Дисбаланс вала пересчитывают в плоско-
сти коррекции ротора, причем множители
приведения больше единицы. Несоосное
присоединение приводного вала восприни-
мается колебательной системой как дис-
баланс, значение которого пропорциональ-
но эксцентриситету приводной шейки рото-
ра или муфты вала. Повышение точности
балансировки достигается облегчением
карданного вала по отношению к массе
балансируемого ротора и повышением точ-
ности его изготовления В связи с из-
ложенным осевой карданный привод при-
меняют в станках класса точности Н для
балансировки роторов массой от 1 кг до
30 т (станки мод. 9715--9718, 9719М,
9719Б). При этом каждый станок снабжа-
ют комплектом сменных карданных валов
для передачи крутящего момента.
Для повышения точности балансиров-
ки в станках классов точности П и В
применяют ременные приводы различных
типов: привод ротора накидным ремнем
(станок мод. 9715Р), боковой тенгенциаль-
ный привод (мод. 9713, 9714), верхний
тангенциальный привод (мод. 9А711,
9712). Для быстрого торможения ротора
на станке установлен тормоз 10. В станках
для балансировки тяжелых роторов тормо-
жение осуществляют электрическими ме-
тодами В станках с ременным приводом
торможение ротора происходит за счет
трения между приводной поверхностью и
поверхностью ремня. Для отсчета угла
Станки общего и специализированного назначения
207
дисбаланса применен градуированный
лимб 2, закрепленный на шпинделе станка.
Со шпинделем станка кинематически свя-
зан ротор’ генератора 13 или преобразова-
теля опорного сигнала. В измерительный
пульт 1 поступают сигналы от генераторов
13 и датчиков дисбаланса 8 (8'), разме
щенных в опорах станка.
В станках класса Н с осевым при-
водом врашения измерительный пульт 1
выполнен по схеме с ваттметровыми инди-
каторами, которыми обеспечивается филь-
трация помех. Пульт изготовлен по одно-
канальной схеме с поочередным измерени-
ем дисбаланса по левой и правой пло-
скостям ротора. Значения дисбаланса— по
шкале дистанционного индикатора углово-
го положения статора генератора опорного
сигнала.
В станках с осевым приводом враще-
ния для повышенной точности балан-
сировки измерительный пульт выполнен по
системе АМВТ, описанной выше. Пульт
обеспечивает одновременное измерение
дисбалансов по левой и правой плоско-
стям коррекции с цифровой индикацией
значений дисбалансов. Место коррекции
на роторе устанавливают с помощью све-
тового или стрелочного индикатора, а угол
дисбаланса может быть считан со шкалы
шпинделя.
В станках класса Н с ременным при-
водом вращения измерительный пульт вы-
полнен по схеме со строболампой. Филь-
трация помех осуществляется избиратель-
ным усилителем, а угол дисбаланса от-
считывается по меткам на роторе с исполь-
зованием стробоэффекта.
В станках с ременным приводом вра-
щения классов П и В измерительный
пульт выполнен по схеме аналого-цифрово-
го перемножения сигнала датчика на
опорный сигнал, сформированный с по-
мощью фотодатчика и контрастной метки
на роторе. Индикация угла дисбаланса
осуществляется в цифровой форме, а зна-
чения дисбаланса— в цифровой или анало-
говой форме по желанию потребителя.
Угол дисбаланса Отсчитывают по градус-
ной шкале на роторе (от контрастной мет-
ки) или с помощью специального измери-
теля угла.
На станках для динамической балан-
сировки, как и на станках для статической
балансировки, осуществляется операция
условной балансировки ротора. В станках
с осевым приводом вращения в качестве
источника сигнала условной балансировки
применяют отдельный генератор, кинема-
тически связанный со шпинделем. В стан-
ках с ременным приводом вращения в ка-
честве сигнала условной балансировки
используют опорный сигнал, сформирован-
ный от фотодатчика пульта.
Специфической операцией настройки
на ротор станка для динамической балан-
сировки является разделение плоскостей
коррекции, которое имеет целью уменьше-
ние взаимного влияния плоскостей коррек-
ции ротора, т. е. обеспечение независимо-
сти измерения составляющих дисбаланса
по левой и правой плоскостям. В измери-
тельных системах зарезонансных станков
эта операция осуществляется специальной
схемой решающего устройства за счет
алгебраического суммирования сигналов
двух датчиков опор пропорционально
коэффициентам взаимного влияния пло-
скостей коррекции ротора.
В станках зарезонансного типа раз-
деление плоскостей коррекции выполняют
с помощью тарировочного (электрически
или физически отбалансированного) рото-
ра и пробных пусков станка. В одну из
плоскостей коррекции этого ротора вводят
пробный груз, осуществляют измерение и
соответствующим регулятором цепи раз-
деления плоскостей сводят показания ин-
дикатора дисбаланса противоположной
плоскости к нулевому (минимальному)
значению. Аналогичную операцию вы-
полняют для второй плоскости, переставив
пробный груз на роторе.
В станках дорезонансного типа опера-
ции разделения плоскостей коррекции и
тарирования (регулировки масштаба из-
мерения) осуществляют без применения
тарировочного ротора и пробных пусков
208
Балансировочные станки
станка. Это возможно, так как зависи-
мость между динамическими давлениями
на опорах дорезонансного станка и неурав-
новешенными центробежными силами,
действующими в плоскостях коррекции ро-
тора, выражается системой уравнений ста-
тики из условий равновесия сил и момен-
тов. В измерительной системе станка эти
уравнения решаются электронной схемой
решающего устройства, в которую в ка-
честве коэффициентов уравнений вводятся
геометрические параметры ротора. Для та-
рирования масштаба измерения вводят ра-
диусы установки корректирующих масс на
роторе, а для разделения плоскостей кор-
рекции- координаты оп£р станка и пло-
скостей коррекции ротора.
На рис. 7.7, а показан зарезонансный
станок мод. 9717 для динамической балан-
сировки роторов массой до 1 т, а на рис.
7.7, б, в —созданные в ЭНИМСе экспери-
ментальные образцы дорезонансных стан-
ков соответственно мод. МА9715Д для ро-
торов массой до 100 кг и МА97Д16РП
повышенной точности для роторов массой
до 300 кг
Рис. 7.7. Станки для динамической балансировки:
а — зарезонансный для роторов массой до I т — модели 9717; б — дорезонансный для роторов массой
до 100 кг мод МА9715Д; в- дорезонансный для роторов массой до 300 кг повышенной точности
мод. МА97Д16РП
. Специальные балансировочные станки
209
Точность станков для динамической ба-
лансировки определяется величиной оста-
точного дисбаланса в плоскостях коррек-
ции ротора. Остаточный дисбаланс ротора
выражается в единицах удельного дис-
баланса. Станки общего назначения имеют
три класса точности: Н, П и В. Станки
класса Н обеспечивают точность баланси-
ровки 1 мкм, станки класса П — 0,4 мкм,
а станки класса В—0,1 мкм. Точность
станков проверяют с помощью двух конт-
рольных роторов в соответствии с ГОСТом
[Г81.
Наладка станка для динамической
балансировки включает операции регули-
ровки механических узлов и настройки на
ротор. Перед базированием ротора на
станке осуществляют следующие опера-
ции: регулировку расстояния между опора-
ми в соответствии с базовыми поверхностя-
ми ротора, регулировку высоты опор в со-
ответствии с диаметром базовых поверх-
ностей ротора (для станков с осевым при-
водом), соединение муфты карданного ва-
ла с приводной шейкой ротора (для стан-
ков с осевым приводом), регулировку на-
тяжения приводного ремня (для станков с
ременным приводом)
Настройка станка на ротор включает
операции: условную балансировку ротора
(для станков зарезонансного типа), разде-
ление плоскостей коррекции и тарирование
измерительной системы. Перечисленные
операции регулировки и настройки осуще-
ствляют по методике, изложенной в руко-
водстве по эксплуатации станка соответст-
вующей модели.
При балансировке роторов оператор
станка выполняет следующие операции;
выбирает масштаб измерения в соответст-
вии с начальным дисбалансом ротора;
по запомненным значениям углов дисба-
лансов устанавливает места коррекции
в левой и правой плоскостях ротора;
по запомненным значениям дисбалансов
осуществляет корректировку масс в левой
и правой плоскостях ротора; выполняет
контрольное измерение остаточного дис-
баланса ротора.
7.3. СПЕЦИАЛЬНЫЕ БАЛАНСИРОВОЧНЫЕ
СТАНКИ
Классификация. На специальных стан-
ках осуществляется балансировка различ-
ных изделий машиностроения в серийном
и крупносерийном производствах: отдель-
ных роторов (например, электродвигате-
лей), роторных узлов в сборе (шпиндель-
ных узлов металлообрабатывающих стан-
ков), изделий в сборе (двигателей внут-
реннего сгорания). В связи с много-
образием параметров и широкой номенкла-
турой специальные станки могут быть
классифицированы по многим признакам, в
первую очередь по типам балансируемых
роторов.
Классификация специальных станков и
типы балансируемых жестких роторов и
машин в сборе приведены на рис. 7.8.
По конструктивному признаку специ-
альные станки подразделяются на станки
с вертикальной и горизонтальной осью вра-
щения. На станках с вертикальной осью
вращения осуществляют в основном стати-
ческую балансировку, а также динамиче-
скую балансировку роторов, работающих
в вертикальном положении, например
центрифуг, сепараторов и т. д. На специ-
альных станках можно осуществлять вы-
борочную балансировку по статической
или моментной составляющей дисбаланса.
Такая балансировка необходима, на-
пример, для космических тел вращения,
колес автомобилей и других изделий.
По типам балансируемых роторов наи-
более широкую группу представляют
специальные станки для статической и ди-
намической балансировки отдельных рото-
ров. Это вызвано тем, что предварительная
подетальная балансировка роторов требу-
ется независимо от последующей баланси-
ровки узла или машины в сборе.
Специальные станки имеют высокую
степень унификации базовых узлов в раз-
личных моделях станков. Так, в специаль-
ных станках для балансировки различных
роторов могут быть унифицированы: коле-
бательная система, шпиндельный узел,
привод, измерительная система и др.
210
Балансировочные станки
Рис. 7.8. Классификация специальных балансировочных станков
Однако многообразие конструкции и ши-
рокая номенклатура роторов машино-
строения требуют для их балансировки
создания отдельных моделей специальных
станков. Необходимую модель станка и
степень ее унификации с ранее разработан-
ными станками выявляют на основании
анализа технических требований на балан-
сировку конкретного ротора.
Для балансировки группы однотипных
роторов промышленность выпускает гамму
специальных станков В качестве примера
ниже рассмотрены некоторые модели и
гаммы специальных станков.
Станки с вертикальной осью вращения.
Как видно из рис. 7.8. балансировочные
станки с вертикальной осью вращения вы-
пускает отечественная промышленность
для статической, динамической и статико-
моментной балансировки. Станок мод.
МА9747 (рис. 7.9) предназначен для
Рис. 7.9. Станок для низкочастотной динами-
ческой и статико-моментной балансировки мод.
МА9747
Специальные балансировочные станки
211
низкочастотной динамической и статико-
моментной балансировки роторов и изде-
лий в сборе, работающих на частотах вра-
щения менее 100 мин
Внутри литой тумбы расположен шпин-
дельный узел, связанный с неподвижным
основанием упругими элементам и-стерж-
ням и, образующими колебательную меха-
ническую систему дорезонансного типа.
Ось шпинделя вертикальна. Балансируе-
мое изделие крепят к вращающейся план-
шайбе, жестко соединенной с верхним
фланцем шпинделя.
Вращение шпинделя вместе с изделием
осуществляется от тиристорного регули-
руемого привода постоянного тока через
ременную передачу. В качестве преобразо-
вателей механических колебаний в элект-
рические аналоговые сигналы применены
параметрические датчики виброперемеще-
ний трансформаторного типа, соединенные
тягами с корпусом шпинделя в плоскостях
измерения системы шпиндель—изделие.
Генератор опорного напряжения — синус-
но-косинусный вращающийся трансфор-
матор, ротор которого вращается синхрон-
но и синфазно шпинделю.
Станок выполняет измерение дис-
балансов в двух плоскостях коррекции или
их статической и моментной составляю-
щих. На основании данных по моментной
составляющей и известным осевым момен-
там инерции масс изделия измерительная
система станка может быть тарирована в
углах отклонения а главной центральной
оси инерции от оси вращения изделия.
Для линейных систем, при малых значе-
ниях а, пренебрежимой малости уравно-
вешивающих масс по сравнению с массой
изделия и при выполнении условия Jy—
— (И;—1с) tnK угол отклонения а мож-
но с достаточной точностью рассчитать по
формуле
где D - дисбаланс в плоскости коррекции;
Jу— момент инерции изделия относительно
оси, проходящей через его центр масс
перпендикулярно оси вращения; Jz—мо-
мент инерции изделия относительно оси
вращения; /с—расстояние от плоскости
коррекции до центра масс изделия; гк—
радиус коррекции; тк- корректирующая
масса, определенная с учетом того, что
/пкгк=£>.
Настройку измерительной системы
производят по тарировочному изделию.
Наличие в измерительной системе станка
устройства электрического эталонирова-
ния позволяет провести настройку не-
посредственно по серийному балансируе-
мому изделию.
Технические характеристики
станка мод. МА9747
Диапазон масс балансируемых
изделий, кг ... . .
Наибольший диаметр изделий,
мм ..........................
Наибольшая высота изделия, мм
Диаметр посадочного отверстия,
мм ..........................
Наибольшее начальное смеще-
ние центра масс, мм . .
Наибольшее начальное отклоне-
ние главной центральной оси
инерции от оси вращения изде-
лия. °................ . . .
Порог чувствительности по углу
отклонения главной центральной
оси инерции от оси вращения из-
делия, углов, мин............
Погрешность измерения модуля
дисбаланса, %, не более . .
Погрешность измерения угла
дисбаланса, °, не более . . *.
Частота вращения при балан-
сировке, мин-1 . . .
Мощность двигателя привода
вращения, кВт
Габаритные размеры, мм
Масса станка, кг
100—500
1000
2000
500
10
7
2
±5
±3
30—100
1,15
1600Х150ПХ
XI380
1500
В МВТУ им. Н. Э. Баумана разработан
и изготовлен ряд специальных станков.
На этих станках определяют главный век-
тор дисбалансов детали в динамическом
режиме, измеряя амплитуду и фазу колеба-
ний подвижной части станка под действием
неуравновешенных сйл.
Особенность конструкции станков
МВТУ им. Н. Э. Баумана—выполнение
подвижной части колебательной системы
212
Балансировочные станки
Таблица 7.3
Технические характеристики балансировочных станков с вертикальной осью вращения
шпинделя конструкции МВТУ им. Н- Э. Баумана
Технические характеристики Модель станка
МВТУ-0748 МВ ТУ-0758 МВТУ-0768 МВТУ 0770 МВТУ-0782
Масса балансируемой детали, ,К1 6 — 30 0.1 — 1 5 — 25 0,1 — 1 0,5 5
Наибольший момент инерции, кг • м2 1.87 0.01 1.56 0.02 0,11
Наибольший диаметр, мм 50U 200 500 300 300
Частота вращения, мин-1 950 2800 950 1420 1350
Порог чувствительности по зна- чению дисбаланса, г мм/кг 20 10 20 10 15
Мощность привода, кВт 1,5 0,4 1.5 1.0 0,4
Габаритные размеры, мм 1000X710Х X 1250 730X590X XI120 1450Х745Х Х188 1200Х 650Х XI750 1160Х865Х Х1700
Масса станка, кг 750 400 850 700 700
в виде упруго подвешенной платформы,
имеющей 6 степеней свободы и обеспечи-
вающей зарезонансный режим измерения
параметров колебаний. Достоинство коле-
бательной системы — высокая помехоза-
щищенность по отношению к вибрациям
фундамента и основания, что позволяет
применить для измерения колебаний на
рабочей частоте фильтрующие системы с
низкой добротностью. Конструкция станка
требует защиты колебательной системы от
воздействия ударных нагрузок.
Станки имеют шпиндель, ось вращения
которого расположена вертикально, и
могут быть оборудованы специальными
устройствами для коррекции дисбаланса.
Балансируемую деталь устанавливают на
шпиндель. Информация о значении дис-
баланса индицируется на стрелочном при-
боре, а об угле- на поворотном лимбе
поискового устройства. При совмещении
показаний лимба и градусной шкалы
шпинделя «тяжелое место» детали уста-
навливается в заранее заданной плоско-
сти. Станки оснащены устройством элект^
рического эталонирования, компенсирую-
щим дисбаланс шпинделя и сменных оп-
равок и приспособлений. Технические ха-
рактеристики некоторых моделей станков
с вертикальной осью вращения шпинделя
для статической балансировки деталей
приведены в табл. 7.3, а внешний вид
одного из станков—на рис. 7.10.
Станок модели МВТУ-0730 (рис. 7.11)
предназначен для определения значения
и угла статического дисбаланса шин легко-
вых автомобилей при их вращении. За-
крепление шины на приспособлении, раз-
мещенном на верхнем фланце шпинделя
Рис. 7.10. Станок мод. МВТУ-0748 для стати-
ческой балансировки муфты сцепления трак-
тора К-701
Специальные балансировочные станки
213
Рис. 7.11. Станок мод. МВТУ-0730 для изме-
рения статического дисбаланса шин легковых
автомобилей
станка, осуществляется с помощью сжато-
го воздуха. Значение дисбаланса в относи-
тельных единицах индицируется на
стрелочном приборе, а угловое положе-
ние—на автоматически останавливаю-
щейся шкале вращающегося лимба. Время
определения значения и угла дисбаланса
не превышает 15 с. При установке станка
в производственных помещениях не требу-
ется специального фундамента или других
средств виброизоляции.
Технические характеристики
станка мод. МВТУ-0730
Масса балансируемой шины, кг
Диаметр балансируемой шины,
мм ........................
Частота вращения шины при ба-
лансировке, мин-' ....
Порог чувствительности по зна-
чению дисбаланса, г • мм/кг
Порог чувствительности по углу
дисбаланса, ° ....
Мощность привода, кВт .
Габаритные размеры, мм
Масса, кг
10—30
500—800
900
40
5
2,8
1400Х 850Х
Х1300
800
Тот же принцип построения колеба-
тельной системы с шестью степенями сво-
боды использован в конструкции станка
модели МВТУ-0726 (рис. 7.12) для дина-
мической балансировки карданных валов
автомобиля. Станок предназначен для ра-
боты в составе поточных линий и при
установке в производственном помещении
не требует фундамента или других средств
виброизоляции. Определение значения и
угла дисбаланса осуществляется одно-
временно в каждой из двух плоскостей
коррекции. Станок снабжен генераторами
для компенсации дисбаланса привода и
настройки станка без применения эталон-
ного ротора. Значение и угол дисбаланса
одновременно для двух плоскостей коррек-
ции индицируются на двух стрелочных при-
Рис. 7.12. Станок мод. МВТУ-0726 для динамической баланси-
ровки карданных валов
214
Балансировочные станки
Технические характеристики
станка мод. МВТУ-0726
Масса балансируемого вала, кг 5—25
Наибольший диаметр вала, мм 150
Наибольшая длина вала, мм . 1400
Частота вращения вала при ба-
лансировке, мин-' .... 1080
Порог чувствительности по зна-
чению дисбаланса, г - мм/кг . 10
Порог чувствительности по углу
дисбаланса, ° .............5
Мощность привода, кВт . . 1,7
Габаритные размеры, мм 3100Х620Х
XI150
Масса, кг 1500
борах и поворотных градуированных
лимбах.
Станки с горизонтальной осью враще-
ния применяют для динамической баланси-
ровки широкого круга роторов, узлов, из*
делий и машин в сборе. Специфика ба-
лансируемых изделий и характер произ-
водства влияют на конструкцию и техни-
ческие характеристики станков.
Специальные балансировочные станки
мод. МА9707Д и МА9708 (рис. 7.13) пред-
назначены для измерения дисбаланса в
двух плоскостях коррекции солнечных
шестерен и сателлитов больших много-
ступенчатых планетарных редукторов. Ба-
зирование на станках солнечных шестерен
осуществляется по их зубчатому венцу,
а сателлитов — по внутренней расточке на
оправке с гидростатическими опорными по-
верхностями. Различные условия базиро-
вания соответствуют условиям их работы
и взаимодействия в собранных изделиях.
Колебательная система станка пред-
ставляет собой платформу, сейсмически
установленную на основании на четырех
стержнях ступенчатой формы. Вращение
балансируемому ротору передается от ти-
ристорного привода вращения постоянного
тока через ременную передачу.
Индукционные датчики колебаний раз-
мещены на платформе. Величина дис-
баланса индицируется на стрелочных при-
борах измерительного пульта. Для опреде-
ления углов дисбаланса применен стробо-
эффект. Возможна модификация измери-
тельной системы путем использования
фотодатчика в качестве генератора опор-
ного сигнала, что значительно повышает
точностные характеристики станков.
Рис. 7.13. Специальный станок для динамической балансировки
сателлитов и солнечных шестерен мод. МА9708
Специальные балансировочные станки
215
Технические характеристики станков
Наименования Модели станка
параметров МА9707Д МА9708
Масса балансиру- емых деталей, кг * 120 - 650 500 - 2500
Размеры рабочей поверхности плат- формы, мм . . 850X 600 1600Х1200
Частота враще- ния, мин-' . . 400—1000 450—600
Точность измере-
ния дисбаланса,
г • мм/кг: при базирова- нии по зубча- тому венцу . 2 2
при базирова- нии по отвер- стию .. . 1 1
Наибольший на-
чальный удельный
дисбаланс, г ♦ мм/кг . . . 500 500
Мощность приво- да вращения, кВт 5,5 22
Габаритные раз меры, мм . . . 1290Х1200Х 4360Х 3700Х
Х1230 Х1230
Масса, кг 1750 2700
Специальный балансировочный станок
мод. МС991 (рис. 7.14) предназначен для
балансировки колесных пар железно-
дорожного транспорта. Особенность техно-
логической операции балансировки колес-
ных пар состоит в необходимости изме-
рения ее дисбаланса относительно оси,
проходящей через геометрические центры
ободов качения. Этот метод впервые был
сформулирован и обоснован В. А. Щепе-
тильниковым.
Рис. 7.14. Специальный станок для дина-
мической балансировки колесных пар мод.
МС991
Колесную пару цапфами укладывают
на опоры балансировочного станка, со-
единяют приводным валом со шпинде-
лем, размещенным в бабке и приводят
во вращение. Бесконтактные индуктивные
датчики, закрепленные на стойках опоры,
измеряют биение ободов колес по принципу
амплитудной модуляции несущей частоты
По результатам измерения дисбаланса
производят фрезерование внутренних по-
верхностей ободов, для чего на станке
установлены подвижный суппорт с фре-
зерной головкой и силовая бабка для
привода колесной пары во вращение при
фрезеровании. Все узлы станка смонтиро-
ваны на общем основании.
Технические характеристики станка мод. МС991
Наибольшая масса колесной пары,
кг.............................1500
Наибольший диаметр поверхности
катания, мм . . ............950
Диаметры шеек цапф, мм . . 130, 135
Частота вращения при балансиров-
ке, мин-1 ... .......... 350—700
Допустимый остаточный дисбаланс,
кг♦см . . . . . .70
Гамма специальных станков для ба-
лансировки карданных валов автомобилей
состоит из трех моделей и предназначена
для динамической балансировки в ремонт-
ном, мелкосерийном и серийном производ-
ствах (табл. 7.4). Станки мод. М.С9731 и
МС9732 служат для балансировки двух-
опорных валов, а станок мод. МС9734
предназначен для балансировки двух- и
трехопориых валов. На этих станках осу-
ществляют измерение и коррекцию дис-
балансов карданных валов. Измерение
дисбалансов осуществляется автоматиче-
ски в зарезонансном режиме работы опор
станка с индикацией величин и углов дис-
баланса в двух плоскостях коррекции вала.
Коррекцию дисбаланса выполняют полу-
автоматически методом приваривания ура-
вновешивающих масс по результатам
измерения. Гамма станков обеспечивает
балансировку карданных валов массой от
1 до 200 кг, с точностью до 10 мкм услов-
ного остатОчного смещения центра масс.
216
Балансировочные станки
Таблица 7.4
Технические характеристики специальных станков для динамической балансировки
карданных валов
Наименование параметров Модель станка
МС9731 МС9732 МС9734
Тип карданного вала
двухопорный двухопорный двухопорный.
Масса балансируемого вала, кг 1—50 4 — 200 трехопорный 1—50
Наибольший диаметр вала, мм 100 НО 100
Наибольшее расстояние между опо- рами, мм 3500 3500 3500
Пределы частот вращения, мин-" 1200 — 3200 400 — 2500 До 3200
Точность балансировки, г-мм/кг 20 — 10 20 — 10 20—10
Мощность электродвигателя главного привода, кВт 5,3 5,3 5,3
Габариты станка, мм 4300X1300X1900 6340X 1300Х 1900 5350X 1200Х 1650
Масса, кг 4450 5650 5500
На рис. 7.15 показан станок мод
МС9731 для динамической балансировки
двухопорных карданных валов. Две опоры
станка выполнены в виде изотропных коле-
бательных систем, обеспечивающих пере-
мещение вала в вертикальном и горизон-
тальном направлениях. Верхняя часть опор
оснащена пневматическими кулачковыми
патронами для закрепления шарниров кар-
данного вала. Привод вращения вала вы-
полнен осевым от шпинделя станка. По-
следний имеет тиристорный электропривод
с плавной регулировкой частоты враще-
ния. Измерение дисбалансов осуществля-
Рис. 7.15. Специальный станок для динами-
ческой балансировки двухопорных карданных
валов мод. МС9731
ют с помощью индукционных датчиков,
размещенных в опорах.
Измерительный пульт станка выполнен
по системе АМВТ, принцип действия кото-
рой описан в параграфе 7.2. Фильтрацию
помех в системе реализуют на основе пере-
множения сигнала дисбаланса на пара-
метрический опорный сигнал синусно-
косинусного вращающегося трансформа
тора (СКВТ), ротор которого вращается
синхронно с балансируемым валом. Пара-
метры дисбаланса в двух плоскостях кор-
рекции вала определяют автоматически.
Для коррекции дисбаланса станок осна-
щен сварочной машиной с двумя головка-
ми, которые перемещаются вдоль портала
по всей длине карданного вала.
Для предотвращения аварийных ситуа-
ций на станке смонтированы защитные
ограничители амплитуды перемещений
вала.
Сварочная машина станка мод.
МС9734 оснащена тремя перемещаемыми
головками а сам станок имеет три опоры
для базировки карданного вала. В осталь-
ном конструкции трех моделей станков
гаммы аналогичны.
Станки гаммы обеспечивают точность
балансировки карданных валов 20-
10 г-мм/кг остаточного удельного дис-
баланса в зависимости от массы баланси-
Специальные балансировочные станки
217
руемого вала (для наименьшей массы —
большее значение, для наибольшей —
меньшее).
Точность станков проверяют по методи-
ке, изложенной в ГОСТе [Г8]
Наладка станков включает операции
регулировки механических узлов и на-
стройки на ротор. При установке кардан-
ного вала на станок выполняют регулиров-
ку расстояния между опорами в соответст-
вии с длиной вала и закрепление опорных
фланцев вала в пневматических патронах,
управляемых педалями.
Настройка станка включает разделе-
ние плоскостей коррекции и тарирование
масштаба измерения. Перечисленные опе-
рации осуществляют с помощью тариро-
вочного карданного вала по методике, из-
ложенной в руководстве по эксплуатации.
Цикл работы на станках для балан-
сировки карданных валов состоит из
следующих операций: закрепления вала
в патронах станка; автоматического изме-
рения параметров дисбаланса; ручного по-
зиционирования вала на измеренный угол
дисбаланса; коррекции дисбаланса мето-
дом приваривания пластин сварочной го-
ловкой; контрольного измерения остаточ-
ного дисбаланса; съема вала со станка.
При позиционировании карданный вал
поворачивают на станке до появления на
одном из индикаторов пульта нулевых зна-
чений. При этом на втором индикаторе
станка устанавливается значение модуля
дисбаланса, а легкое место вала оказы-
вается под электродом сварочной головки.
Из ячейки кассы оператор станка выби-
рает пластину, эквивалентную по массе
измеренному дисбалансу, и устанавливает
ее в точке коррекции вала под электродом
головки. Сварка осуществляется авто-
матически при плавном нарастании тока
для предотвращения искрообразования
Станки для балансировки автомобиль-
ных колес. Динамическая балансировка
автомобильных колес облегчает управле-
ние автомобилем и значительно уменьшает
износ покрышек. Условия базирования и
работы колес определяют целесообраз-
ность их балйнсировки на станках с гори-
Рнс. 7.16. Станок мод. МА97Д52 для дина-
мической балансировки колес легкового авто-
мобиля
зонтальной осью вращения. Эксперимен-
тальный образец станка для динамической
балансировки колес мод. МА97Д52, раз-
работанный в ЭНИМСе, показан на рис.
7.16. Его используют для балансировки
колес легковых автомобилей всех марок,
а также колес грузовых автомобилей в
пределах технической характеристики
станка.
Технические характеристики
станка мод. МА97Д52
Диапазон масс балансируе-
мых колес, кг .... 10 — 60
Наибольший наружный диа-
метр колеса, мм ... 800
Диапазон ширины ободов ко-
лес, мм . .... 60—320
Диапазон измеряемых значе-
ний неуравновешенной мас-
сы, г . .............0—200
Точность балансировки по ос-
таточной массе в каждой из
плоскостей коррекции, г 5
Время измерения дисбалан-
са, с . . ...........7
Частота вращения при ба-
лансировке, мин -1 . . 450
218
Балансировочные станки
Габаритные размеры, мм . ПООХЮОХ
X 1350
Масса, кг . . . . 250
Инерционная нагрузка от неуравно-
вешенного колеса воспроизводится в виде
аналогового сигнала пьезокварцевых дат-
чиков силы, установленных в жестких опо-
рах шпинделя.
Основные установочные геометриче-
ские,размеры балансируемого колеса (рас-
стояние от базовой плоскости станка до
ближнего края обода колеса, ширина и
диаметр обода) вводят в измерительную
систему с пульта управления с помощью
программных переключателей. Колесо на-
девают консольно на шпиндель и кнопкой
«Пуск» приводят во вращение. Через оп-
ределенное время измерения дисбаланса
колесо автоматически останавливается, а
на измерительном пульте индицируются
значения масс балансировочных грузов,
которые должны быть установлены в левой
и правой плоскостях коррекции по ободу.
Позиционирование колеса производят
вручную по положению световой точки на
пульте. Среднее положение точки между
указателями направления поворота коле-
са при позиционировании соответствует
верхнему положению того места обода, в
которое следует установить балансировоч-
ный груз указанной массы.
Измерительная система станка пред-
усматривает возможность балансировки
колес раздельно по статической и момент-
ной составляющим дисбаланса.
Станок предназначен для оснащения
автотранспортных предприятий и станций
технического обслуживания автомобилей.
Балансировку роторов без их вращения
проводят путем приложения в нескольких
плоскостях ротора гармонической силы,
имеющей частоту, равную частоте враще-
ния, на которой следует вести балансиров-
ку.
Возбуждение ротора осуществляют от
динамика или от вибратора. Ротор уста-
навливают в технологическом корпусе ма-
шины и создают условия, близкие к экс-
плуатационным. Используя виброизме-
рительную и балансировочную аппарату-
ру определяют, а затем устраняют дис-
балансы ротора [16].
Существуют методы и станки, дейст-
вующие на принципе малых угловых
колебаний (34]. В основе этих методов
лежит сообщение балансируемой детали
углового колебательного движения (отно-
сительного или переносного) с малой ам-
плитудой и некоторой частотой. Компенса-
ция дисбаланса выполняется путем авто-
матического нанесения уравновешиваю-
щего материала в жидком или рас-
плавленном виде на поверхность детали
в «легком» месте при ее колебаниях.
В такой автоматической системе пара-
метры неуравновешенности определяются
по амплитуде и фазе вынужденных колеба-
ний детали, процесс компенсации дис-
баланса управляется усиленными сигнала-
ми датчика «текущей» (компенсируемой)
неуравновешенности. Установка детали на
рабочую позицию и ее снятие осущест-
вляются транспортно-пнтающим мани-
пулятором.
На рис. 7.17 приведена схема, поясняю-
щая метод автоматической балансировки
роторов и вентиляторов электрических ма-
шин дозированным нанесением на них
уравновешивающего материала. В качест-
ве последнего может быть использована
композиция на основе эпоксидной смолы
или расплавленный припой при наличии
на детали технологических углублений.
Схема имеет привод угловых колебаний
5, оправку 4 для установки на ней ба-
лансируемого вентилятора 3, базирован-
ную рамку 6 для установки в ней ба-
лансируемого ротора 7, датчик 9, усили-
Рис. 7.17. Схема балансировочной установки
Специальные балансировочные станки
219
тель сигналов датчика 1, дозатор 2 и
механизм 8 поворота детали «легким ме-
стом» под дозатор 2.
Балансируемым деталям сообщается
угловое колебательное движение <р с ам-
плитудой 0,02—0,05 рад и частотой 40—
60 Гц. Этот вид движения выбран для
его получения с помощью обычного асин-
хронного электродвигателя.
При наличии неуравновешенной массы
т возникают также угловые колебания а
детали, которые воспринимаются датчиком
9 и усиливаются усилителем 1, управляю-
щим механизмом 8 для поворота де-
тали «легким местом» под дозатор 2 и ра-
ботой дозатора.
В момент компенсации дисбаланса до-
зирование* прекращается. Отбалансиро-
ванный вентилятор снимается с оправки,
а ротор переустанавливается в рамке для
аналогичной балансировки в нижней пло-
скости.
Станки для динамической балансиров-
ки гибких роторов. Высокочастотную ба-
лансировку гибких роторов выполняют с
помощью специальных станков1. Они отли-
чаются от станков для балансировки жест-
ких роторов тем, что кроме уравновешива-
ния на них осуществляют вибрационное
испытание роторной системы (ротор — опо-
ры), а в некоторых случаях выполняют
балансировку ротора «в сборе» на эксплуа-
тационных частотах вращения [16]. Ос-
новные преимущества этих станков в том,
что они позволяют:
приблизить процесс балансировки ро-
торов к реальным эксплуатационным ус-
ловиям, используя при этом собственные
опоры и корпуса:
на первых опытных образцах машин
или их роторных систем выявить характер
вибрации, определить оптимальные пло-
скости коррекции для балансировки рото-
ра,
использовать вакуум для значительно-
го снижения мощности, необходимой для
вращения ротора при его балансировке.
1 Эти станки называют также установками
или разгонно-балансировочными стендами
(РБС).
а также для оценки влияния дисбаланса
ротора на вибрацию машины при ее экс-
плуатационных частотах вращения.
Принципиальная схема виброизмери-
тельного балансировочного станка2 * *, сос-
тоящего из систем: привода I, вакуумной
II, измерительной III и смазки IV, показана
на рис. 7.18.
Вакуумная система создает и поддер-
живает необходимое разрежение в вакуум-
ной камере. Это достигается .рациональ-
ным выбором рабочего объема вакуумной
камеры, созданием надежных уплотнений
во всех разъемах камеры. Основные эле-
менты системы показаны на рис. 7.18.
Вакуумную камеру и ее элементы рас-
считывают на прочность и проверяют на
потерю устойчивости из условия избыточ-
ного давления снаружи камеры, равного
106 Н/м2. Частота собственных колебаний
камеры не должна находиться вблизи диа-
пазона эксплуатационных частот враще-
ния ротора при условии размещения каме-
ры на жестких опорах.
При конструировании камер учитыва-
ют условия эксплуатации станка: на-
пример, виброизоляцию фундамента и от-
дельных узлов между собой, резонансные
состояния стенда, пригодность специаль-
ной кремнеорганической жидкости для
смазки подшипников балансируемого ро-
тора в условиях вакуума и др.
Опоры ротора на балансировочном
стенде неподвижные; конструктивно они
делятся на изотропные и неравно5кесткие.
Применение изотропных опор вызвано тем,
что резонансные частоты ротора зависят
от жесткости опор.
В случае изотропности опор обеспечи-
вается совпадение критических частот в
вертикальной и горизонтальной плоско-
стях, проходящих через ось ротора. Это в
значительной мере упрощает методику и
технологию балансировки. Необходимость
широкого диапазона частот вращения вы-
звана тем, что уравновешивание гибких
2 Авторское свидетельство № 117925. Бюл-
летень «Открытия, изобретения, промышлен-
ные образцы, товарные знаки», 1959, № 26.
Рис. 7.18. Принципиальная схема стенда:
1 — реостат шунтовой; 2 — реостат пусковой; 3—электродвигатель постоянного тока; 4—мультипликатор; 5—вакуумная камера, 6 — вибро-
датчик вертикальный; 7 вибродатчик горизонтальный, 8 —датчик тахометра; 9— генератор фазоуказателя; 10 — вакуумный насос, // — ем-
костный датчик, 12— предварительный усилитель, 13— фазоуказатель; 14— указатель числа оборотов; 15— шлейфовый осциллограф,
16— осциллограф, /7—указатель вибрации; 18, 19—редукционные клапаны; 20—масляный насос; 21— фильтр; 22. 27, 30- масляные
баки; 23 обратный клапан; 24 — насос, 25. 26—фильтр; 28 — баллон для сжатого воздуха; 29- радиатор
220 Балансировочные станки
Специальные балансировочные станки
221
изделий должно производиться вблизи
каждой критической частоты и на эксплуа-
тационных частотах.
Система привода. Система привода
должна быть автономной, благодаря чему
можно производить разгон различных ро-
торов. По схеме (см. рис. 7.18) разгон
балансируемого ротора осуществляется от
электродвигателя. Плавность выхода на
необходимые частоты вращения ротора до-
стигается пусковым и шунтирующим ре-
остатами. Вал электродвигателя 3 соеди-
нен с мультипликатором 4, установленным
иа одной фундаментной плите с электро-
двигателем Мультипликатор (£=1/11)
может передавать значительную мощ-
ность, при этом потребляемая им мощность
не превышает 10% передаваемой Веду-
щий вал мультипликатора связан с вали-
ком обгонной муфты, которая исключает
влияние привода на балансируемый ротор
Привод отключается после выхода балан-
сируемого ротора на требуемую частоту
вращения.
При уравновешивании ротора вблизи
резонансных режимов для поддержания
постоянства частоты вращения электро-
двигателя постоянного тока используют
дроссели с подмагничиванием и выпрями-
телями, а тйкже тиристорные электропри-
воды.
Мощность N, затрачиваемая на враще-
ние балансируемого ротора, зависит от
конструкции и геометрических размеров
ротора, а также от величины вакуума в
камере. Основная часть этой мощности
расходуется на преодоление потерь трения
ротора о воздух. Мощность сил трения
для колеса с заданным соотношением гео-
метрических параметров является функци-
ей угловой частоты ы, внешнего диаметра
D колеса и плотности р воздуха:
7V=/(e>, D, р).
Расход мощности определяют при-
ближенно, используя следующую зависи-
мость:
N — ₽ры3£)5, где p=po(l 4-56/D), где 0О=
==(84-10) 10-€—коэффициент дисковых
Рис. 7.19. График необходимой мощности на
привод ротора в зависимости от частоты его
вращения и разрежения в вакуумной ка-
мере
потерь; b, D — соответственно ширина и
диамеДр диска ротора; р — плотность воз-
духа в корпусе; о)—угловая скорость ро-
тора.
Значения необходимой мощности для
привода ротора крупной турбомашины в
зависимости от разрежения в камере при-
ведены на рис. 7.19.
Масляная система состоит из двух
автономных циркуляционных систем. Пер-
вая предназначена для смазки подшип-
ников, расположенных в зоне нормаль-
ного атмосферного давления, вторая —для
смазки подшипников, расположенных в зо-
не разрежения (в вакуумной камере).
В первой системе имеется двухступен-
чатый масляный насос/в который масло
поступает из бака 30 (см. рис. 7.18). При-
вод насоса осуществляется от электро-
двигателя. Из нагнетающей ступени насо-
са масло через фильтр 21 подается к под-
шипникам. Для регулирования рабочего
давления смазывающего материала слу-
жит редукционный клапан 19. Откачиваю-
щая ступень насоса соединена своим вхо-
дом со сливными полостями механизмов.
С выхода откачивающей системы смазы-
вающий материал через радиатор 29 по-
ступает в бак.
В вакуумной масляной системе уста-
новлен одноступенчатый насос 24. Подача
смазывающего материала к подшипникам
исследуемого ротора осуществляется по
приведенной выше схеме. Возврат масла
в бак 22 осуществляется по трубопроводу
самотеком. В случае вынужденной оста-
222
Балансировочные станки
новки вакуумной масляной системы пред-
усмотрена аварийная система, в которой
сжатый воздух, устремляясь из баллона
28 в бак 27, выталкивает находящийся
там смазывающий материал через фильтр
26 и обратный клапан к подшипникам.
Измерительная система стенда пред-
назначена для определения усилий и сме-
щений, возникающих в опорах ротора;
формы прогиба упругой линии оси ротора;
колебаний опор, корпусов и агрегатов ма-
шины.
При выборе аппаратуры, как правило,
исходят не из общих ее свойств, а из
требований и условий, в которых аппара
тура должна работать.
Измерение деформаций ротора или ви
браций машины на высокочастотном стен-
де, наряду с аппаратурой, приведенной в
гл. 9, выполняют с помощью лазера. Пре-
имущества этого метода — в измерении
скорости, перемещения или ускорения
тех колеблющихся элементов источника
вибровозбуждений, куда установка датчи-
ка невозможна из-за его габаритных раз-
меров или агрессивности среды. Метод об-
ладает весьма высокой точностью при ши-
роком диапазоне частот измерения.
Нечувствительность устройства к тем-
пературным воздействиям, малый угловой
раствор луча и значительная спектральная
интенсивность светового потока, позволяю-
щие производить измерение в трудно до-
ступных местах и на значительных рас-
стояниях от измеряемой поверхности, обе-
спечивают необходимые условия для широ-
кого применения оптического метода (зер-
кального и интерференционного).
Зеркальный метод основан на измере-
нии амплитуды колебаний пучка лучей
света, отраженного от вибрирующего
объекта, где установлено зеркало, пре-
образующее прямолинейные колебания
объектов в угловые. Отраженные лучи по-
падают на шкалу с делениями или на
вращающийся барабан со светочувстви-
тельной бумагой.
Интерференционные методы широко
применяют для калибровки виброизмери-
тельной аппаратуры при высоких частотах
и весьма малых амплитудах вибраций.
Они основаны на наблюдении интерферен-
ционного явления, получающегося в ре-
зультате взаимодействия двух лучей моно-
хроматического света, прямого и отражен-
ного от зеркала, укрепленного на вибри-
рующем объекте. Основной трудностью
этого метода является подсчет интерферен-
ционных полос.
Приведем пример использования лазе-
ра для измерения колебаний, а также рас-
смотрим метод, позволяющий определить
перемещения элементов роторной машины
с высокой точностью (0,3 мкм). В этом
методе измеряется частота биений, воз-
никающих при сложении опорного и от-
раженного от объекта световых лучей. Бие-
ния, вследствие движения измеряемой по-
верхности, меняют свою частоту пропорци-
онально скорости перемещающегося объ-
екта.
Для измерения колебаний различных
элементов турбомашин с помощью лазера
можно применить установку, схема кото-
рой показана на рис. 7.20, а.
Луч лазера /, попадая на полу-
прозрачное зеркало 2. раздваивается. Од-
на часть луча, частотою vo, направляется
на неподвижное зеркало 3, отражаясь от
которого, попадает на приемник излучения
фотоэлектронного умножителя (ФЭУ).
Вторая часть луча направляется на вал
ротора. Отраженное валом излучение по-
падает на зеркало 2 и также поступает
на приемник излучения ФЭУ. Если вал не
имеет перемещений относительно луча, то
на приемнике складываются два луча с
одинаковой частотой, при этом возникает
интерференция.
Если измеряемая поверхность совер-
шает перемещение вдоль светового потока,
то в соответствии с эффектом Допплера
частота излучения лазера относительно
движущейся поверхности v„ не будет •
совпадать с частотой источника и опре-
деляется по формуле
v« = voc/(c —и),
где с—скорость света; v — скорость дви-
жения поверхности.
Специальные балансировочные станки
223
Рис. 7.20. Схемы применения лазера:
а—принципиальная, б измерения прогиба вала
Считая колеблющуюся поверхность ис-
точником излучения, можно найти частоту
отраженного излучения Vi, принимаемую
ФЭУ:
vl = v„(c + o)/c.
Тогда
V1=(c-|-u)/(c —v)v0.
Разложив последнее выражение в ряд
Маклорена, получим
Поскольку v<^c, можно ограничиться
двумя первыми членами ряда:
Это выражение показывает, что часто-
та принимаемых колебаний получила при-
ращение, обычно называемое частотой
Доплера-.
. 2v
= vo + vc —.
Таким образом, на приемник попадают
два излучения разной частоты, что при-
водит к биению. Частота биений может
быть определена из выражения
Дт —vi — vo= 2v/cv0.
Так как с —const и vQ=const, то Av за-'
висит только от скорости перемещения
— Скорость перемещения поверх-
ности за полупериод колебания изменится
от о = 0 до о = тах и снова до о = 0.
Таким же образом изменится частота бие-
ний снимаемого с ФЭУ сигнала. Регист-
рируя эту частоту на экране осциллографа
или цифрового частотомера, можно перей-
ти к определению перемещения колеблю-
щейся поверхности.
Один период биений сигнала, который
снимается с ФЭУ, соответствует пере-
мещению измеряемой поверхности на вели-
чину, равную половине длины волны Л
применяемого излучения лазера (Z/2--
= 0,3164 мкм).
Таким образом, зная число периодов
биения сигнала, можно с точностью до
половины длины волны подсчитать ампли-
туду колеблющейся поверхности.
Колеблющаяся поверхность может
быть зеркальной и диффузной (матовой)
В первом случае величина отраженного
сигнала значительна, однако необходима
тщательная настройка системы, чтобы от-
раженное излучение попадало на прием-
ную оптическую систему. Во втором слу-
чае индикатриса отраженного излучения
подчиняется закону Ламберта, что при-
водит к значительному уменьшению вели-
чины лучистого потока, приходящего на
224
Балансировочные станки
приемную оптическую систему, но в этом
случае отпадает необходимость тщатель-
ной юстировки.
Функция Av = f(t>) характеризует сину-
соидальное колебание с переменной часто-
той, по которому как аналитически, так и
практически сложно произвести количест-
венную оценку величины перемещения.
Поэтому, аппроксимируя функцию Av==
— f(v) как синусоидальную с постоянной
частотой, можно величину перемещения
определить по формулам, приведенным
выше.
Применение лазера не ограничивается
описанным методом замера линейных пе-
ремещений колеблющейся поверхности.
Применив специальные устройства для
приема сигнала, можно использовать его
для измерения перемещений вала ротора
или колеблющихся стержней в высоко-
температурной среде.
На рис. 7.20, б приведена схема много-
точечного измерения прогиба вала.
7.4. ЦЕНТРОВАЛЬНЫЕ
БАЛАНСИРОВОЧНЫЕ СТАНКИ
Станок для статической децентровки
противовесов коленчатых валов. Станок
мод. МА9А764 предназначен для измере-
ния главного вектора дисбалансов про-
тивовеса и его корректировки по модулю
и направлению. После сборки противове
сов на коленчатом валу введенные в них
векторы дисбалансов компенсируют со-
ответствующие векторы дисбалансов от
шатунно-порш невой группы двигателя
внутреннего сгорания. Станок оснащен
метрологическими средствами, обеспечи-
вающими введение в колебательную систе-
му вектора дисбаланса, равного по значе-
нию, но противоположно направленного
заданному в противовесе.
На рис. 7.21 показана конструктивная
схема компенсации на шпинделе станка
цетробежной силы от дисбаланса противо-
веса 2. Балансируемый противовес 5 уста-
навливают на планшайбе 4, закрепленной
на вертикальном шпинделе станка. Пред-
варительно планшайбу со шпинделем ба-
лансируют. Центровку и крепление про-
тивовеса на шпинделе станка осуществля-
ют с помощью шпонки 7 и зажимного
механизма 3 цангового типа.
Напротив противочеса на планшайбе
станка устанавливают эталонную массу /.
Радиус /? установки эталона и его посадку
на планшайбе обеспечивают с высокой
точностью. Перед установкой эталон тари-
руют по массе и совмещают центр его масс
с геометрической осью с помощью стати-
ческой балансировки и взвешивания Вели-
чина эталонной массы и радиус ее уста-
новки от оси вращения обеспечивают вве-
дение вектора дисбаланса, имеющегося в
противовесе.
Направление вектора дисбаланса к
осевой, линии шпоночного паза в противо-
Рис. 7.21. Схема компенсации на шпинделе
станка центробежной силы от дисбаланса
противовеса
Центровальные балансировочные станки
225
весе определяет угол а. Под этим же углом
к осевой линии шпонки зажимного меха-
низма устанавливают на планшайбе и
эталонную массу. При балансировке на
станке противовеса другого размера эта-
лонная масса перезакрепляется на план-
шайбе в угловом положении и на радиусе,
обеспечивающем компенсацию вектора
дисбаланса этого противовеса. Для по-
вышения точности балансировки станок
оснащают средствами электрической ком-
пенсации моментной составляющей дис-
баланса и эксцентриситета шпинделя стан-
ка. Благодаря описанной оснастке стати-
ческую децентровку противовесов на стан-
ке осуществляют методом обычной стати-
ческой балансировки до допустимой вели-
чины остаточного дисбаланса. Коррекцию
дисбаланса производят сверлением отвер-
стий 6.
Технические характеристики станка мод. 9А764
Масса балансируемых проти-
вовесов, кг ... . . 1 —10
Наибольший устраняемый
дисбаланс, г • см . . . 900
Допустимый остаточный дис-
баланс, г • см . . 25
Частота вращения при ба-
лансировке, мин"1 . . . 1000
Наибольший диаметр сверла,
мм.......................14
Наибольшая глубина сверле-
ния, мм ... 22
Суммарная мощность элект-
родвигателей, кВт . . . 1,42
Габаритные размеры, мм 800X 640X1700
Масса, кг . .... 900
Конструкция станка мод. МА9А764 по-
казана на рис. 7.22. Станок смонтирован
в корпусе /. Колебательная система 4 со-
держит вертикальный шпиндель, смонти-
рованный на двух лентах. Жесткость лент
обеспечивает дорезонансный режим рабо-
ты станка. Привод вращения шпинделя
осуществляется от электродвигателя 2
через карданную муфту 12. На верхней
консоли шпинделя закреплена планшайба
с эталонной массой 9. На планшайбе соос-
но со шпинделем смонтирован зажимной
механизм цангового типа для автомати-
ческого крепления противовеса 5. Зажим
8 Зак J641
Рис. 7.22. Конструкция станка
мод. МА9А764
противовеса управляется механизмом 11, а
разжим -механизмом 3.
Для коррекции дисбаланса станок ос-
нащен сверлильной головкой 8 с пинолью
7 автоматической подачи. Сверлильная го-
ловка имеет возможность автоматического
перемещения по результатам измерения
дисбаланса на черновой или чистовой ра-
диус сверления противовеса. Сверлильная
головка выполнена «плавающей» для раз-
грузки шпинделя и подвесной системы от
усилий резания. Для автоматической кор-
рекции дисбаланса на станке установлен
механизм 6 контроля глубины сверления.
Зона вращения противовеса защищена ко-
жухом 10. Для удаления продуктов свер-
ления станок оснащен стружколомом и
пневмоотсосом. Измерительный пульт
станка выполнен по системе АМВТ,
описанной в п. 7.2 в станках для стати-
ческой балансировки общего назначения.
Электроавтоматика станка размещена в
отдельном шкафу.
Станок обеспечивает точность стати-
ческой балансировки противовесов до
25 мкм остаточного смещения центра масс.
Эта точность оценивается по методике.
226
Балансировочные станки
изложенной в п. 7.6. Точность статической
децентровки противовесов определяется
оснасткой станка и оценивается по следую-
щим параметрам: масса эталона, радиус
его закрепления на планшайбе станка и
угол установки эталона к осевой линии
шпонки зажимного механизма. При этом
на станке должны быть проконтролирова-
ны: точность балансировки планшайбы со
шпинделем без эталона и противовеса,
исключение моментной составляющей дис-
баланса и исключение эксцентриситета
шпинделя.
При наладке станка на новый тип
противовеса выполняют следующие опера-
ции
исключают электрическим путем мо-
ментную составляющую дисбаланса и экс-
центриситет шпинделя;
осуществляют тарирование масштаба
измерения в черновом и чистовом режи-
мах;
производят настройку угла дисбаланса
(совмещение «легкого» места противовеса
со сверлом механизма коррекции);
осуществляют тарирование масштаба
измерения системы контроля глубины
сверления;
производят наладку сверлильной го-
ловки на глубину сверления.
Эти операции выполняют по методике,
изложенной в руководстве по эксплуата-
ции станка.
При эксплуатации цикл балансировки
противовесов проводят следующим обра-
зом. Оператор станка закрепляет эталон в
положении, соответствующем балансиров-
ке данного противовеса. После установки
противовеса на зажимном приспособлении
и запуска станка автоматически выпол-
няется следующая последовательность
операции: зажим детали, включение вра-
щения шпинделя, измерение дисбалансов,
торможение и остановка шпинделя, пере-
мещение сверлильной головки на внешний
или внутренний радиус детали.
Вручную или автоматически вращени
ем шпинделя до нулевых показаний инди-
катора угла (в измерительном пульте)
Рис. 7.23. Комплекс оборудования для ба-
лансировки противовесов коленчатых валов
совмешают «легкое» место противовеса со
сверлом механизма коррекции. Нажатием
ножной педали включают сверление, кото-
рое осуществляется автоматически до за-
данной глубины. После автоматического
отвода сверлильной пиноли вновь произ-
водят измерение дисбаланса для «чисто-
вой» балансировки или контроля остаточ-
ного дисбаланса.
Действующий комплекс оборудования
для балансировки противовесов показан на
рис. 7.23.
Станок для динамической центровки
роторов турбокомпрессоров. Станок мод.
ЭЗ-146 предназначен для предваритель-
ной балансировки турбокомпрессоров ме-
тодом динамической центровки с целью
снижения начальных дисбалансов роторов.
Поскольку плоскости коррекции турбоком-
прессоров выполнены из тугоплавких ма-
териалов, предварительная балансировка
роторов методом центровки обеспечивает
значительное повышение производитель-
ности и точности станков для окончатель-
ной балансировки обычными методами.
При динамической центровке необхо-
димо определение координат главной цент-
ральной оси инерции (ГЦОИ) заготовки
изделия, относительно которых изделие в
дальнейшем обрабатывается. На станке
мод. ЭЗ-146 осуществляется как измере-
ние параметров, так и обработка базовых
поверхностей турбокомпрессоров в автома-
тическом режиме. С этой целью в двух
Центровальные балансировочные станки
227
плоскостях ротора турбокомпрессора из-
меряют смещение ГЦОИ от оси враще-
ния, т. е, от геометрической оси ротора.
Далее, по запомненным результатам из-
мерения, прикладывают механические ко-
лебания к вращающемуся ротору в двух
параллельных плоскостях, перпендикуляр-
ных оси вращения. При этом ГЦОИ оста-
ется неподвижной в пространстве, а вра-
щение ротора осуществляется вокруг нее.
В этом положении выполняют механиче-
скую обработку центровых отверстий рото-
ра. В дальнейшем по центровым отвер-
стиям осуществляют обработку базовых
поверхностей турбокомпрессоров.
Технические характеристики
станка мод. ЭЗ-146
Масса балансируемого рото-
ра, кг ............... . -0,5 —5,0
Наибольший диаметр базо-
вых шеек, мм .... 30
Наименьший диаметр цент-
рового отверстия, мм . . 2,5
Частота измерения смещения
главной центральной оси
инерции, Гц ............
Частота обработки центро-
вых отверстий, Гц . . .
Точность балансировки, мкм
Средняя производительность
при начальном дисбалансе
300 мкм, шт/ч ....
Потребляемая мощность, кВт
Габаритные размеры, мм:
механической части
электрической части
Масса оборудования, кг
10 — 200
15 — 20
2.0
25
1.8
1170Х 620Х
X 1150
570X570X1040
500
Станок состоит из колебательной си-
стемы с осевым и тангенциальным при-
водами, двух резцедержателей со своими
суппортами, двух механических вибрато-
ров, измерительного устройства и шкафа
электроавтоматики с пультом управления.
Кинематическая схема станка ЭЗ-146
приведена на рис. 7.24. Динамическую
центровку турбокомпрессоров в атома-
тическом режиме осуществляют на станке
8*
228
Балансировочные станин
следующим образом. После базирования
ротора 3 на колебательную систему 4
включают тангенциальный привод 13.
В процессе вращения ротора осуществ-
ляется измерение координат ГЦОИ в двух
плоскостях, т. е. измерение амплитуды и
фазы сигналов дисбаланса, пропорцио-
нальных отклонению ГЦОИ ротора от оси
вращения. Эти параметры запоминаются в
измерительном устройстве (измеритель-
ный пулы и датчики дисбаланса, связан-
ные с колебательной системой, на схеме не
показаны). Одновременно включаются
элекромагниты 8 и 10, соединяющие коле-
бательную систему 4 с вибраторами 15 и 20.
Вибраторы сообщают колебательной си-
стеме колебания в соответствии с запом-
ненными значениями координат ГЦОИ.
Настройку вибраторов осуществляют с по-
мощью двигателей с редукторами 14, 17—
18, 21. Настройку фазы производят вра-
щением фазовращателей 7, 11, а настрой-
ку амплитуды—перемещением ползунов
16, 19. Затем включают осевой привод
2, который кинематически жестко связы-
вает колебательную систему 4 с валом 9
привода вибраторов В этот момент осу-
ществляется подача инструментов коррек-
ции 1, 5 в зону обработки центровых
отверстий ротора. Подача выполняется при
помощи суппортов 6, 12. После обработки
центров резцедержатели автоматически
отводятся
Станок обеспечивает точность балан-
сировки до 2 мкм остаточного смещения
центра масс турбокомпрессора. Точность
балансировки роторов определяется на
станке по методике, изложенной в пара-
графе 7.6.
В процессе наладки станок настраива-
ют на балансируемый ротор. При настрой-
ке станка осуществляют следующие опера-
ции: разделение плоскостей коррекции ро-
тора, тарирование масштаба измерения,
настройку амплитуды и фазы вибраторов
по минимуму вибрации ротора (сопряже-
ние измерительной и вибрационной си-
стем). Настройку выполняют по методике,
изложенной в руководстве по эксплуата-
ции станка
При использовании станка ротор тур-
бокомпрессора устанавливают в опорах
колебательной системы и соединяют с осе-
вым и тангенциальным приводами. После
включения вращения процесс баланси-
ровки ротора методом центровки осуществ-
ляется автоматически.
7.5. ПРОЕКТИРОВАНИЕ ОСНОВНЫХ
СИСТЕМ БАЛАНСИРОВОЧНЫХ СТАНКОВ
Балансировочный станок предназначен
для определения дисбалансов ротора с
целью уменьшения их корректировкой
масс. Основные элементы, узлы и системы
конструкции станков для динамической ба-
лансировки роторов следующие (рис.
7.25): основание (станина) 1, опоры 2,
привод (на рисунке не показан); системы
измерения дисбаланса (СИД) 7, дополни-
тельные устройства для зажима опор,
отсоса стружки и пр. Привод включает
в себя приводной вал 4, шпиндель 5 и
электродвигатель, установленные в шпин-
дельной бабке 6.
СИД состоит из механической системы
преобразования (СМП) вибраций,в широ-
ком диапазоне частот, в колебания под-
вижных частей опор 2 на тех же частотах
и электрической системы измерений (СЭИ)
колебаний опор, выделения и индикации
полезных сигналов дисбаланса. СМП со-
держит балансируемый ротор 3 с привод-
ным валом 4, подвижные части опор 2,
упругие элементы связи подвижных и не-
подвижных частей опор. На СМП оказы-
вают влияние масса и характер связей
основания 1 с фундаментом. В станках
с ременным приводом вращения ротора
приводной вал может отсутствовать и не
входить в состав СМП. СЭИ содержит
датчики — преобразователи механических
колебаний в электрические аналоги, узлы
фильтрации, усиления электрических сиг-
налов, разделения плоскостей коррекции,
индикации, памяти и др.
Точность балансировочного’станка за-
висит от общей чувствительности СИД и ее
защищенности от воздействия сигналов —
помех. Характеристика точности — наи-
Проектирование основных систем балансировочных станков
229
Рис. 7.25. Кон-
струкция станка
общего наз-
начения для
динамической
балансировки
меньший удельный дисбаланс ест, который
может быть измерен или достигнут при
балансировке на станке контрольного ро-
тора.
Опоры балансировочного станка. Важ-
нейшей характеристикой балансировочно-
го станка является частота собственных
колебаний системы ротор—подвижные
элементы опор на упругих связях.
В станках для статической баланси-
ровки и для динамической балансировки,
имеющих раздельные опоры, при свобод-
ной, шарнирной установке на них сим-
метричного балансируемого ротора ча-
стота собственных колебаний может быть
определена по формуле
(ос— (7.1)
где k — жесткость системы в направлении
плоскопараллельных перемещений; т —
масса системы, включающая массу ротора,
подвижных элементов опор и эквивалент-
ную массу приводного вала.
В станках для динамической баланси-
ровки со связанными опорами система
имеет две собственные частоты: плоско-
параллельных и поворотных перемещений
[24]. Для их расчета следует:
а) вычислить парциальные частоты
системы:
поступательную
Wnrl = VV^
и поворотную
%=.даЖ
(7.2)
где 6С—жесткость системы в направлении
поворотных перемещений относительно ее
центра жесткости; b—расстояние между
центром жесткости и центром масс систе-
мы ротор—опоры; /—момент инерции
системы относительно оси, проходящей
через ее центр масс и перпендикулярной
плоскости колебаний;
б) выразить парциальную поворот-
ную частоту системы через поступатель-
ную <опк= и вычислить
2 ec/fe + fe2
(7-3)
где i—радиус инерции системы,
в) определить резонансные множители
системы
01,2 —
(7-4)
г) рассчитать собственные частоты
('*с] 2~ЧУ1 2ИП!|- (7-5)
Принято <ис1 обозначать меньшую, а
о>с2—большую из собственных частот.
В табл. 7.5 приведены некоторые зна-
чения резонансных множителей у} 2 в за-
висимости от квадрата отношения пар-
циальных частот О2 и отношения b/i, рас-
считанные по формуле (7.4).
Отношение £ рабочей частоты шр вра-
щения ротора на балансировочном станке
230
Балансировочные станки
Таблица 7.5
Значения резонансных множителей г
fe/i
& 0,05 0,10 0,15 0,20 0,30 0,40 0,50 0,60 0,80 1,00
0,25 1,003 0,247 1,013 0,237 1,029 0,221 1,050 0,200 1,105 0,145 1,173 0,077 1,250 0,000
0,50 1,005 0,495 1,019 0,481 1,042 0,458 1,070 0,430 1,141 0,359 1,222 0,278 1,309 0,191 1,400 0,100
0,75 1,010 0,740 1,035 0,715 1,070 0,680 1,111 0,639 1,200 0,550 1,294 0,456 1,390 0,360 1,488 0,262 1,685 0,065
1.00 1,050 0,950 1,100 0,900 1,150 0,850 1,200 0,800 1,300 0,700 1,400 0,600 1,500 0,500 1,600 0,400 1,800 0,200 2,000 0,000
1,25 1,260 0,990 1,285 0,965 1,320 0,930 1,361 0,889 1,450 0,800 1,544 0,706 1,640 0,610 1,738 0,512 1,935 0,315 2,133 0,117
1,50 1,505 0,995 1,519 0,981 1,541 0,958 1,570 0,930 1,641 0,859 1,721 0,778 1.809 0,691 1,900 0,600 2,088 0,412 2,281 0,219
1,75 1,753 0,997 1,763 0,987 1,779 0,972 1,800 0,950 1,855 0,895 1,923 0,827 2,000 0,750 2,083 0,667 2,259 0,491 2,443 0,307
2,00 2,002 0,998 2,010 0,990 2,022 0,978 2,039 0,962 2,083 0,917 2,140 0,860 2,207 0,793 2,281 0,719 2,443 0,557 2,618 0,382
2,50 2,502 0,998 2,507 0,993 2,515 0,985 2,526 0,974 2,558 0,942 2,600 0,900 2,651 0,849 2,710 0,790 2,847 0,653 3,000 0,500
3,00 3,001 0,999 3,005 0,995 3,011 0,989 3,020 0,980 3,044 0,956 3,077 0,923 3,118 0,882 3,166 0,834 3,281 0,719 3,414 0,586
4,00 4,001 0,999 4,003 0,997 4,007 0,993 4,013 0,987 4,030 0,970 4,052 0,948 4,081 0,919 4,116 0,884 4,200 0,800 4,303 0,687
к частоте собственных колебаний <йс1 2 ха-
рактеризует режим работы станка. При
сор/<ос23> 1 —режим зарезонансный, а
при £=<ор/(ос| С1 — режим дорезонанс-
ный. Устойчивая работа станка обеспечи-
вается: для зарезонансного режима — при
£;>3; для дорезонансного—при £<;0,3.
При 1 —частный случай дорезонансно-
го режима—режим «жестких опор». Если
0,3<£<3, то следует изменить (увеличить
или уменьшить) жесткость опор.
На рис. 7.26 приведена схема алго-
ритма расчета колебательной системы
станка для динамической балансировки,
где в скобках указаны номера расчетных
формул
Опора станка для статической балан-
сировки показана на рис. 7.27. Балан-
сируемый ротор / закрепляют на столе
шпинделя 2, смонтированного в корпусе
3 Корпус соединен со стойкой 5, жестко
связанной с основанием 7 упругими эле-
ментами 4. Такая колебательная система
обладает одной степенью свободы в на-
правлении плоскопараллельных перемеще-
ний корпуса шпинделя 3. Вращение шпин-
деля осуществляется от электродвигателя
с помощью ременной передачи 6.
Опора станка общего назначения для
динамической балансировки, работающего
в зарезонансном режиме, изображена на
рис. 7.28. Ротор / устанавливают на роли-
Рис. 7.26. Схема алгоритма расчета коле-
бательной системы станка для динамической
балансировки
Рис. 7.27. Опора станка для статической балансировки
Рис. 7.28. Опора стайка общего назначения для динамической
балансировки
Проектирование основных систем балансировочных станков
232
Балансировочные станки
ках обоймы 2, жестко закрепленной на
подвижной люльке 3 опоры. Люлька со-
единена с неподвижным корпусом 4 опоры
стержнями 5, нагруженными растягиваю-
щими силами веса ротора, роликов, люльки
и т. д. Корпус 4 опоры жестко соединен
с основанием 6. Опора обладает одной
степенью свободы, однако установка на
основании 6 двух опор (рис. 7.25) обе-
спечивает механической части СИД две
степени свободы—в направлении плоско-
параллельных и поворотных перемещений
ротора вместе с люльками в горизонталь-
ной плоскости. Для уменьшения влияния
опорных роликов на точность балансиров-
ки необходимо обеспечить радиальное бие-
ние их рабочих поверхностей не более
2 мкм, а также выполнение условия: 0,8 >
>d/dp>l,2 (здесь d—диаметр опорной
поверхности балансируемого ротора; dp—
диаметр наружной поверхности опорного
ролика). Рабочую поверхность ролика вы-
полняют в виде сферы диаметром (1—2) dp.
На рис. 7.29 показана опора с общей
плитой станка для динамической баланси-
ровки изделий в сборе или деталей слож-
ной формы (коленчатых валов и др.). Пли-
та 1 соединена с основанием 3 стержнями
2, нагруженными вертикальными сжимаю-
щими силами.
Зарезонансный режим по сравнению с
дорезонансным обладает большей помехо-
защищенностью, допускает меньшую тща-
тельность изготовления отдельных элемен-
тов конструкции и обеспечивает более
высокую точность балансировки. Настрой-
ку таких станков выполняют с примене-
нием пробных пусков тарировочного рото-
ра и введением в СЭИ средств электри-
ческого эталонирования. При коррекции
дисбаланса непосредственно на баланси-
ровочном станке следует предусмотреть
специальные механизмы для зажима опор
н защиты их упругих элементов как от
избыточного силового воздействия, так и
от стружки, пыли и охлаждающей жидко-
сти.
Дорезонансный режим по сравнению с
зарезонансным обладает меньшей помехо-
защищенностью, в особенности к внешним
возбуждениям, требует применения в СЭИ
фильтров не ниже 2-го порядка с более
высокой добротностью, тщательного изго-
товления отдельных элементов конструк-
ции (роликов опор, приводных валов,
шпинделя). Существенным преимущест-
вом дорезонансных станков являются их
высокая надежность и удобство в эксплуа-
тации— настройка по геометрическим раз-
мерам балансируемого ротора. Последнее
свойство обеспечивает станкам дорезо-
нансного типа более высокую производи-
тельность.
Привод вращения ротора имеет при-
водной электродвигатель, шпиндель, при-
водной вал и элементы передачи вращения
от электродвигателя к шпинделю. При-
водной электродвигатель обычно устанав-
ливают на основание. Он должен быть
тщательно отбалансирован, а частота его
вращения при балансировке должна отли-
чаться от рабочей частоты вращения рото-
ра. Это позволит свести к минимуму влия-
ние помех от приводного электродвигателя
на точность балансировки.
Шпиндель станка следует монтировать
на высокоточных подшипниках качения.
Рис. 7.29. Опоры
с общей плитой
станка для ди-
намической ба-
лансировки
Проектирование основных систем балансировочных станков
233
Его радиальное и осевое биения, измерен-
ные в шарнире соединения с приводным
валом, не должны превышать 0,01 мм.
Приводные валы оказывают сущест-
венное влияние на точность балансировоч-
ного станка. Более высокую точность обе-
спечивают приводные валы с упругими
муфтами, несколько меньшую— валы с
шарнирными муфтами. В приводных валах
с упругими муфтами (рис. 7.30, а) упругий
элемент 2 соединяет приводной вал / с
втулкой 3 балансируемого ротора 4 и обе-
спечивает высокую жесткость при передаче
крутящего момента и малую жесткость в
направлении поперечных перемещений.
В приводных валах с шарнирными муфта-
ми (рис. 7.30, б) крутящий момент от вала
I балансируемому ротору 4 передается
через оси 5, подшипники 6, крестовину
2 и втулку 3. Трение в шарнирах вызы-
вает появление зоны нечувствительности,
которая характеризуется потерей чувст-
вительности станка к статической или мо-
ментной составляющим дисбаланса рото-
ра. Оценку наименьших значений стати-
ческого DCT и моментного £)м дисбалансов
в плоскостях коррекции, которые еще вы-
зывают колебания опор станка при враще-
нии ротора с угловой частотой со, можно
выполнить с помощью формул |24]
4Л1 4Л4
D >------Z_- £) >-----—
ла) лю ZB
। де 7WT — момент трения в шарнирах при-
водного вала; /в— длина приводного вала;
/ и li — расстояния от центра масс (ЦМ)
ротора до шарнира, соединяющего ротор с
приводным валом, или до правой плоскости
коррекции дисбаланса соответственно.
Для уменьшения трения в шарнирах
вала и влияния шарниров на точность
измерения дисбаланса роторов шарниры
следует монтировать на подшипниках ка-
чения высоких классов точности.
Шпиндели и приводные валы необходи-
мо тщательно балансировать. Их остаточ-
ный дисбаланс не должен превышать 0,3
допуска на удельный дисбаланс баланси-
руемого ротора [ест]. Радиальное биение
шпинделя может быть частично скомпен-
сировано балансировкой вала. Масса вала
должна быть возможно меньшей, так как
она входит в состав массы колебательной
Рис. 7.30. Приводные валы:
а — с упругой муфтой; б с шарнирной муфтой
234
Балансировочные станки
системы в виде некоторой эквивалентной
массы тэк, вычисляемой по формуле
^вх)/^в*
где тп— масса приводного вала; J вг и
/вх— соответственно экваториальный и по-
лярный моменты инерции массы вала; 1В —
длина вала; с — расстояние от шарнира
шпинделя до центра масс вала.
При необходимости балансировки ро-
торов с точностью. превышающей
0,2 г-мм/кг остаточного удельного дис-
баланса, следует применять ременный при-
вод, который может быть использован для
вращения роторов массой до 1000 кг. Огра-
ничением по применению ременного при-
вода является превышение суммы момента
трения вращения ротора в опорах и момен
та, требуемого для разгона ротора до за-
данной частоты вращения за заданное вре-
мя, над моментом сил трения ремня по
поверхности привода ротора относительно
его оси.
Основание станка. Оно включает в себя
все неподвижные части станка: плиту, ста-
нину, корпуса опор, шпиндельную бабку
и пр. Для ослабления влияния внешних
вибраций на точность измерения дисбалан-
са желательно иметь основание массой,
в 10—15 раз превосходящей массу балан-
сируемого ротора. Это соотношение масс
может быть уменьшено для роторов мас-
сой свыше 1000 кг.
Основания станков дорезонансного ти
па, как правило, жестко крепят к изоли
рованйому фундаменту помещения, а осно-
вания станков зарезонансного типа - уста-
навливают на общей фундаментной плите*
свободно или через виброизолирующие
опоры.
7.6. НОРМЫ ТОЧНОСТИ И ИСПЫТАНИЯ
БАЛАНСИРОВОЧНЫХ СТАНКОВ
Объективным показателем точности
балансировочного станка или комплекта
является наименьшая величина нескомпен-
сированного дисбаланса, которая может
быть достигнута в результате балансиров-
ки ротора по стандартной методике.
Точность балансировочного станка за-
висит от точности измерения дисбаланса и
точности коррекции, включая точность по-
зиционирования ротора. Балансировочные
станки общего назначения, как и комплек-
ты, выполняют только измерение дисбалан-
са, поэтому в дальнейшем под их точ-
ностными показателями будем понимать
совокупность характеристик общей из-
мерительной системы, к которым относят-
ся:
точность балансировочного станка или
минимальный достижимый остаточный
удельный дисбаланс Т:
коэффициент уменьшения дисбаланса
Лу;
коэффициенты взаимного влияния пло-
скостей коррекции КБ| и КВ2;
чувствительность по значению дис-
баланса sD-
погрешность измерения угла дисбалан-
са Д<р;
линейность системы по значению дис-
баланса X.
В зависимости от цели проводят испы-
тания по определению или проверке харак-
теристик точности. В последнем случае
полученные величины характеристик срав-
нивают с заданными (паспортными).
Испытания проводят на настроенном ба-
лансировочном оборудовании с примене-
нием двухопорного контрольного ротора с
симметричным расположением плоскостей
коррекции и плоскостей измерения относи-
тельно его центра масс или по тари-
ровочному ротору.
Испытания на точность. Под точностью
балансировочного станка понимают значе-
ние приведенного к плоскости коррекции
удельного дисбаланса ротора, отбаланси-
рованного на данном станке с наибольшей
возможной точностью. Оценку точности
станка проводят по следующей методике
[Г8|.
В каждой из двух плоскостей коррек-
ции контрольного или тарировочного ро-
тора выделяют k равномерно по окруж-
ности расположенных контрольных точек
(k — 8...12) на радиусе г*. Контрольный
Нормы точности и испытания балансировочных станков
235
ротор балансируют с наибольшей возмож-
ной точностью по стандартной методике
на проверяемом балансировочном станке.
В каждую из контрольных точек одной
из плоскостей коррекции последовательно
вводят контрольный груз массой т*, соз-
дающий контрольный дисбаланс £>*=
и снимают k показаний Ai (1 ~ 1.2....,
k) соответствующего индикатора дисба-
ланса. Массу контрольного груза выбира-
ют такой, чтобы создаваемый контрольный
дисбаланс Dk приблизительно в 5 раз пре-
вышал ожидаемое значение остаточного
дисбаланса контрольного ротора.
Из полученных значений >4(1.2)! находят
наибольшее гитах и наименьшее
>4(i.2}imin и определяют точность станка в
проверяемой плоскости по формуле
rII2i=(n--r)
Ajj^-A, 2)„„,я
Ад 21«1ПихА ^4,1 2. г <11111
г - мм/кг,
где то— масса контрольного ротора; h —
расстояние от центра масс контрольного
ротора до проверяемой плоскости коррек-
ции; 1-2—расстояние от центра масс конт-
рольного ротора до другой плоскости кор-
рекции.
Для симметричного контрольного рото-
ра (/( = /8) эта формула принимает вид
у о А.1 2 «max A. I 2ктй1
U-2)-“ д ( 2imax4-«4 , 2i(ihii) m()
г • мм/кг.
Точность балансировочного станка Т
соответствует большему из вычисленных
значений 7(1,2).
При испытании станков для статиче-
ской балансировки роторов, имеющих одну
плоскость коррекции (/|~0), их точность
определяют по формуле
д _____д
Пмпах г min
----, г-мм/кг
7 =
При испытаниях балансировочного
станка на соответствие его фактической
точности заданному значению 1Л необхо-
Таблица 7.6
Нормы точности горизонтальных
балансировочных станков
общего назначения
Класс точности бал ан
сировочного станка
Наибольшая масса
балансируемого
ротора, кг
нор-
маль- повышен высоки»
ный ный П В
Н
г • мм/кг
1 3 10 30 100 1 0.4 0,1
300
1000
3000
10 000
30 000
димо проверить выполнение условия Т^.
, где [Г] —паспортная точность ба-
лансировочного станка (табл. 7.6). Для
проведения этих испытаний применяют
пробный груз, массу которого выбирают
в соответствии с соотношением
"М л
rk
Для симметричного ротора —------------.
rk
Для ротора с одной плоскостью кор ре-
ляции mk 5---------.
Испытания балансировочного станка
для определения коэффициента уменьше-
ния дисбаланса. Методы проверки балан-
сировочного оборудования зависят от их
типов (измерительные балансировочные
станки общего назначения, специализи-
рованные, специальные со средствами кор-
рекции дисбаланса и др.).
Определение коэффициента у меньше
ния дисбаланса станков общего назначе-
ния [3]. На опоры станка устанавливают
тщательно сбалансированный контроль-
236
Балансировочные станки
ный ротор и настраивают по нему изме-
рительную систему. В правую плоскость
коррекции ротора произвольно вводят
контрольный груз, соответствующий по
значению 25-кратной величине [Т]. В ле-
вую плоскость коррекции /, в точку, со-
впадающую с направлением оси начала
отсчета угла дисбаланса, вводят контроль-
ный груз, соответствующий дисбалансу 5
[Г]. В левую плоскость коррекции, в точку,
ближайшую к контрольному грузу 5 [7*|.
вводят груз, соответствующий дисбалансу
25 [Г], и, зная угол ф[ между этими
контрольными грузами, рассчитывают зна-
чение Dt и угол <р[ полученного суммарного
дисбаланса по формулам
D । — л/д g + £>25 + 2£>r,£>25 cos Ч1 ь (7-8)
• (D*> • ,
<Pi — arcsm I sin ipj I,
где D$— дисбаланс, соответствующий 5
[Г]; £>25- дисбаланс, соответствующий 25
[Г] i Ф1 — известный угол между векторами
Ds и £>25-
Квадрант, в котором находится вычис-
ленный угол <р), определяют по известному
углу ф[ или взаимному положению векто-
ров £>5 и £>25.
Приводят контрольный ротор во вра-
щение и измеряют по индикаторам зна-
чение Di и угол <pf дисбаланса. Рассчиты-
вают модуль разности векторов дисбалан-
сов Di и Di по формуле
£> i.o = VOf + D'f — 2D 1 Di cos ф],
где ф1 = <р|-—(pl.
По вычисленным значениям Di и D\q
определяют коэффициент уменьшения дис-
баланса
£>, о
Ки='-^-
17.7)
Переставляют контрольный груз, со-
ответствующий дисбалансу 25 [Г] в левой
плоскости коррекции, в следующую конт-
рольную точку и повторяют предыдущие
измерения и вычисления. Наименьшее из
полученных значений /(у| принимают в ка-
честве показателя коэффициента уменьше-
ния дисбаланса в левой плоскости кор-
рекции.
Указанные выще действия, измерения
и вычисления повторяют для правой пло-
скости и находят для нее коэффициент
уменьшения дисбаланса Л\.2. Меньшее из
полученных значений /<у| или /<у2 опреде-
ляет коэффициент уменьшения дисбаланса
балансировочного станка общего назначе-
ния в целом.
При заданной в паспорте или техни-
ческих условиях на станок допустимой
величине [Ку] вычисленную величину
Ky(It2) сравнивают с паспортной Станок
считают выдержавшим испытания, если
выполнено условие
Ky(i,2)>[Ky]. (7.8)
Испытание на соответствие коэффици-
ента уменьшения дисбаланса паспортной
величине [Лу] может быть проведено с
использованием векторной диаграммы
(рис. 7.31). Для этого следует предвари-
тельно подготовить лист для построения
диаграммы в полярных координатах.
На листе миллиметровой бумаги на-
носят центр координатной системы О и
Рис. 7.31. Векторная диаграмма проверки
коэффициента уменьшения дисбаланса
Нормы точности и испытания балансировочных станков
237
выбирают масштаб таким образом, чтобы
вектор дисбаланса, соответствующий
35 [7], не выходил за пределы диаграммы.
От центра координат вертикально вверх
откладывают вектор дисбаланса, соответ-
ствующий 5 [7}, и из конца этого вектора
проводят окружность, радиус которой в
выбранном масштабе соответствует дис-
балансу величиной 25 [7J. Эту окружность
делят на 12 (8—для контрольных или та-
рировочных роторов с восемью отверстия-
ми для установки контрольных грузов в
каждой из плоскостей коррекции) равных
частей, нанеся на нее точки через 30°
(45°), начиная от верхней. Исключая из
рассмотрения верхнюю точку, для каждой
из И (7) оставшихся рассчитывают зна-
чения дисбалансов D\ по формуле (7.6).
Для каждой из этих точек рассчитывают
допустимые по технической характеристи-
ке станка значения D\,o по формуле
С центром в каждой из рассматривае-
мых точек проводят в выбранном масштабе
предельные окружности радиусами, соот-
ветствующими вычисленным значениям
Di.o- Из центра координатной системы про-
водят прямые через 15°. начиная от вер-
тикальной, и наносят градусную шкалу,
приняв вертикальное направление вверх
за начальное.
Последовательно переставляя груз, со-
ответствующий дисбалансу 25 [Г] в левой
плоскости коррекции, измеряют значения
Di и углы ff>t дисбаланса ротора и на-
носят на диаграмму серию точек, являю-
щихся, в выбранном масштабе, концами
измеренных векторов Z?f. Эти точки не
должны выходить за пределы проведенных
на рис. 7.31 предельных окружностей.
В противном случае считают, что станок не
прошел испытания. Те же испытания про-
водят для правой плоскости коррекции.
Определение коэффициента уменьше-
ния дисбаланса специальных станков со
средствами коррекции дисбаланса. Станок
настраивают по тарировочному ротору.
Проводят балансировку партии серийных
роторов. Результаты измерения дисбалан-
са до и после балансировки в каждой из
плоскостей коррекции вносят в таблицу,
имеющую форму, приведенную ниже; для
каждой пары значений дисбаланса по
формуле (7.7) вычисляют коэффициент
уменьшения дисбаланса
Величину коэффициента уменьшения
дисбаланса Л'у определяют по ,вычислен-
ным Лу(1,2) так, чтобы не менее 95% зна-
чений |,2> превышали принятое Kv-
Объём партии серийных роторов, на
которых проводят испытания, должен обе-
спечивать достаточную достоверность по-
лученных результатов и, как правило,
содержит не менее 20 роторов.
При заданной в паспортных данных
станка допустимой величине полу-
ченное Ку сравнивают с паспортным. Ста-
нок считают выдержавшим испытания,
если выполнено условие (7.8).
Испытания для определения коэф-
фициентов взаимного влияния плоскостей
коррекции. На настроенный станок уста-
навливают тщательно отбалансированный
контрольный или тарировочный ротор.
В левую плоскость коррекции ротора вво-
дят контрольный груз, соответствующий
дисбалансу 25 IT] Приводят ротор во
Номер серий- ного ротора Левая плоскость коррекции Правая плоскость коррекции
Дисбаланс начальный Pi Дисбаланс остаточный О» о Коэффициент уменьшения дисбаланса Дисбаланс начальный Дисбаланс остаточный 1)г о Коэффициент уменьшении дисбаланса К9г
1
2
238
Балансировочные станки
вращение и с индикаторов дисбаланса
снимают показания по левой ) и пра-
вой (Л21) плоскостям. Переставляют конт-
рольный груз из левой плоскости коррек-
ции в правую и при вращении ротора
снимают с индикаторов дисбаланса по-
казания по левой (Л|,2) и правой (Лг.г)
плоскостям.
Определяют коэффициенты взаимного
влияния плоскостей коррекции но форму-
лам
— А [.г/Л и и Аъд/Аъ.ъ.
При заданном в паспорте или техни-
ческих условиях на станок значении [Лл|
должны быть выполнены условия
Чувствительность к моментному дис-
балансу. Это испытание преследует цель
установить, насколько полно станок для
динамической балансировки воспроизво-
дит на индикаторах статическую и момент-
ную составляющие дисбаланса или же на-
сколько полно станок для статической ба-
лансировки исключает из индикации мо-
ментную составляющую дисбаланса.
В плоскости коррекции тщательно от-
балансированного и установленного на
опоры станка ротора вводят контрольные
грузы, создающие дисбаланс, равный 25
[TJ, таким образом, чтобы они составляли
чистый статический дисбаланс. При вра-
щении ротора снимают показания индика-
торов Л1ст и Л2ст. В одной из плоско-
стей коррекции груз переставляют в проти-
воположное начальному положение так,
чтобы образованная пара грузов создава-
ла чистый моментный дисбаланс. При вра-
щении ротора вновь снимают показания
индикаторов Л1м и Л2м.
Чувствительность измерительной си-
стемы к моментному дисбалансу опре-
деляют в относительных единицах как
коэффициент по плоскостям коррекции
и К2м) по формулам
К|м ^1м/^1сг» ^2м ^2м/^2ст-
В станках для динамической баланси-
ровки, при их правильной настройке,
^(|.2)м= 1- в станках для статической ба-
лансировки
Чувствительность по значению дис-
баланса. Тщательно отбалансированный
контрольный или тарировочный ротор
устанавливают на опоры настроенного
станка. Проверяют показания индикаторов
дисбаланса Zlt>e и Да,© в плоскостях кор-
рекции. В эти плоскости вводят контроль-
ные грузы, создающие дисбалансы £>[,
и D^, соответствующие последовательным
значениям 5 [Г], 25 [Т], 75 [TJ, и снимают
показания индикаторов А и и Д2>1. По каж-
дой из плоскостей вычисляют чувствитель-
ность по значению дисбаланса:
с _______ А>.2)« 1
’ЭЩ1,2)« г) ______ г\
^412)1 1
Меньшая из полученных величин опре-
деляет чувствительность балансировочно-
го станка по значению дисбаланса.
Погрешность измерения угла дис-
баланса. В каждой из плоскостей коррек-
ции контрольного или тарировочного рото-
ра определяют чувствительность станка по
углу дисбаланса £([,2» как отношение пол-
ного числа делений 0(1,2) шкалы прибора-
индикатора угла к соответствующему наи-
большему измеряемому углу дисбаланса
ротора <Р(1,2)тах-
£(1,2)4. — 0.1,2/<р( 1,2) max-
привязывают начало отсчета углов на
роторе к начальному (нулевому) делению
индикатора. В обе плоскости коррекции
тщательно отбалансированного ротора,
установленного на опоры настроенного
станка, вводят произвольно контрольные
грузы, создающие дисбаланс, эквивалент-
ный 25 [7], и измеряют углы дисбалан-
сов «и и аг,| в делениях соответст-
вующих индикаторов, после чего оценива-
ют измеренные углы по формуле
<Р(1.2)1 = су j. 2) [/£([. 2)ч>-
Вычисляют разность
Аф| 1.2)1 = <Р(| .2)1 — Ч>(1.2)|
между оценкой угла <p'i.2)i и истинным уг-
лом <р(i.2)i введенного в ротор дисбаланса.
Основы автобалансирования роторов
239
Переставляя последовательно конт-
рольный груз в одной из плоскостей кор-
рекции в соседние точки, радиусы-векторы
которых образуют с начальным направ-
лением углы <P(i.2>-, при неизменном поло-
жении груза в другой плоскости повторяют
измерения углов дисбалансов 0(1.2), с по-
мощью соответствующих индикаторов, их
оценку ф(1.2)< и вычисляют разности
Аф(1.2)> = ф(1,2У — ф(1.2>.
< = 1, 2, .... k — число контрольных точек
в каждой из плоскостей коррекции.
Наибольшее из k полученных значений
Лф([.2> определяет погрешность измерения
угла дисбаланса и не должно превышать
заданной погрешности [Лф].
Линейности по значению дисбаланса.
Испытания проводят с использованием
тщательно отбалансированного контроль-
ного или тарировочного ротора. Метод
оценки предложен Н. JI. Степановым.
В плоскости коррекции ротора в произ-
вольные точки последовательно вводят п
контрольных грузов mkj (i— 1, 2,. . . , n),
создающих дисбалансы DkJt соответствую-
щие, например, 3 [7’1,5 [7*1,8 [7],20 [Т] и
охватывающие весь диапазон измерения
вплоть до наибольшего возможного дис-
баланса Р*тах.
Производят п последовательных изме-
рений значений дисбаланса ротора на
настроенном балансировочном станке и за-
писывают соответствующие показания ин-
дикаторов Л(|.2>. Для каждой пары Dki
и /1(1.2)«находят «цену деления» 0(1.2)» инди-
катора значения дисбаланса:
ац.2\ = Dki/A(\^.
Относительный коэффициент нелиней-
ности А, вычисляют по формуле
П I 2i max I 2j min
Л(1,2) = '—n “ •
<=l
Глава 8
АВТОБАЛАНСИРУЮЩИЕ УСТРОЙСТВА
8.1. ОСНОВЫ АВТОБАЛАНСИРОВАНИЯ
РОТОРОВ
Уровень развития методов и средств
балансировки позволяет довести дисба-
ланс ротора до величины, соответствую-
щей допустимому по заданному классу
точности балансировки [Г9]. Однако за-
дачи ускорения научно-технического про-
гресса требуют создания техники, способ-
ной многократно повысить производитель-
ность труда, открыть путь к полной ав-
томатизации производства. Этому требо-
ванию отвечают работы по созданию ме-
тодов и средств автоматической баланси-
ровки роторов, обеспечивающих повыше-
ние производительности с помощью спе-
циальных станков и устройств для балан-
сировки на ходу с высокой точностью.
При эксплуатации во многих машинах
может возникать режимное изменение на-
чального дисбаланса, а для ряда машин
изменение дисбаланса является следстви-
ем технологического процесса. Режимное
изменение дисбаланса во времени проис-
ходит с различными скоростями и обычно
имеет случайный характер. Для компен-
сации изменения дисбаланса проводят до-
полнительную балансировку, связанную с
остановкой машины и требующую больших
экономических затрат. Иногда остановка
недопустима по условиям выполнения тех-
нологического процесса или эксплуатации.
Наиболее перспективным является приме-
нение автобал ансиру юших устройств
(АБУ), компенсирующих изменение дис-
баланса ротора в эксплуатационных ус-
ловиях без его остановки.
Автобалансирующие устройства
В перспективе их значимость будет
возрастать, так как повышение произво-
дительности технологического оборудова-
ния невозможно без широкого примене-
ния АБУ.
Основные требования к АБУ вытекают
из свойств вращающейся неуравновешен-
ной системы [7]:
размеры корректирующих масс (КМ)
и самого АБУ должны обеспечивать ком-
пенсацию наибольшего возможного дис
баланса;
на всех режимах работы АБУ не дол-
жно увеличивать дисбаланс; остаточный
дисбаланс не должен превышать допус-
тимый;
АБУ должно эффективно работать как
при разгоне, так и при остановке ротора,
учитывать положение «тяжелой» точки ро-
тора на разных частотах вращения и обес-
печивать безопасный переход машины че-
рез критический режим;
АБУ должно иметь достаточную чув-
ствительность к изменению дисбаланса в
процессе работы и автоматически его ком
пенсировать;
АБУ должно работать при любом по-
ложении оси ротора;
конструкция АБУ должна быть макси-
мально простой, надежной в работе и легко
обсл уж и ваться;
плоскость устранения дисбаланса в
АБУ должна обеспечивать одновременное
снижение реакций в опорах и напряже-
ний в роторе;
при работе АБУ не должно быть вред-
ных выбросов в атмосферу.
В приборостроении на первом месте
стоит повышенная точность балансировки,
что усложняет АБУ и повышает его стои-
мость. Для серийных же машин важным
является снижение стоимости АБУ, упро-
щение его конструкции и облегчение об-
служивания. Для тяжелых машин не име-
ют значения размеры АБУ, а главным
становится требование емкости и произ-
водител ьност и.
Классификация основных видов авто-
балансирующих устройств приведена на
рис. 8.1.
По способу компенсации дисбаланса
различают устройства, балансирующие
ротор путем совмещения его оси вращения
с главной центральной осью инерции
(ГЦОИ) методом принудительного цент
рирования, балансирующие ротор путем
совмещения ГЦОИ с осью вращения и
устройства силового воздействия на ротор.
По характеру слежения и воздействия на
дисбаланс АБУ делят на пассивные—со
свободным перемещением КМ, и актив-
ные— с их принудительным перемещением,
присоединением или удалением.
Пассивные АБУ имеют чувствительный
элемент, который сам создает усилие,
достаточное для балансировки ротора.
Монтируют эти АБУ на балансируемом
роторе. Их питание осуществляется за счет
кинетической энергии ротора, передавае-
мой на чувствительный элемент. Пассив-
ные АБУ работают за счет того, что КМ,
участвующие в колебаниях ротора, зани-
мают «наинизшее» положение. Существен-
ным их недостатком является то, что они
обычно снижают вибрации ротора только
на скоростях, лежащих выше критичес-
кой. Простота конструкции этих АБУ де-
лает целесообразным их применение, когда
рабочая скорость машины выше критичес-
кой, а режимное изменение дисбаланса
связано с наработкой ресурса. Пассивные
АБУ, имеющие малые размеры, достаточ-
ные лишь для управления и не влияющие
на динамику балансируемого ротора,
применяют в качестве чувствительных
элементов (ЧЭ), управляющих рабо-
той исполнительного механизма (ИМ)
в АБУ с принудительным перемеще-
нием КМ.
К активным АБУ относят устройства
с принудительным перемещением или из-
менением масс ротора, а также с при-
нудительным центрированием и силовым
воздействием на ротор. Такие АБУ обыч-
но содержат регулятор перестройки цепи
управления на критической скорости, а ба-
лансировка выполняется ниже и выше ее.
Активные АБУ сложнее пассивных, но они
обеспечивают более точную и всережим-
ную балансировку.
MmoS таксирующие устройства
242
Автобалансирующие устройства
Метод принудительного центрирования
[7] состоит в кинематическом совмещении
оси вращения балансируемого ротора с
его ГЦОИ без перераспределения или
изменения его масс. Такое совмещение
достигают путем размещения между цап-
фой ротора и внутренней обоймой под-
шипника качения, или вкладышем подшип-
ника скольжения и его корпусом, валом
и диском, устройства, обеспечивающего
необходимую концентричность цапфы от-
носительно подшипника или диска отно-
сительно вала.
АБУ принудительного центрирования
с механическим приводом изображено на
рис. 8.2, где эксцентрики 2, 4 размещены
в плоскости опоры 7 ротора 3 между по-
садочными местами подшипника 14 и цап-
фы 6. Каждый эксцентрик имеет кони-
ческое зубчатое колесо 5, связанное че-
строенного на пороговое значение колеба-
ний опоры. Если амплитуды колебаний
опоры превышают допустимую величину,
то виброскоп включает соленоид, который
вводит ударник в зацепление со звездоч-
кой. Вращение звездочки через эксцент-
рики перемещает ось вращения ротора
по спирали, описываемой формулой
г = Г] cos
<0!----«2
<0( + ю2
где г и р—(Ы1+^2)^/2 — радиус и угол
положения оси вращения в плоскости опо-
ры; г, = г2 — эксцентриситеты эксцентри-
ков; ой « Ы2 и (о22>о)]—угловые скорости
эксцентриков.
Точность балансировки зависит от ве-
личины шага спирали
При необходимом для балансировки
, Г 0)1—0)9Т Г О).—(1)о"|
Дг, = 2r( sin л--------------- sin (л + 0)----------;----- .
о), + о>2 L 0), + 0)2J
--------------------------------1
рез другое коническое колесо 8 и червяч-
ную пару 9 с приводной звездочкой 10.
Опора имеет ударник 11, приводимый в
движение соленоидом 12, включенным в
блок управления (БУ), имеющий усили-
тель с релейным выходом и реле 13, пи-
таемое с резонансного виброскопа 1, на-
многократном повороте эксцентриков про-
исходит повторное проявление минимума
и максимума вибраций, что усложняет
контроль за процессом балансировки и
снижает долговечность подшипников. Вы-
сокое передаточное отношение кинемати
ческих цепей поворота эксцентриков ус-
Устройства со свободным перемещением корректирующих масс
243
ложняет опорный узел ротора. АБУ при-
нудительного центрирования применяют
для компенсации дисбаланса в собранной
машине. Их использование целесообразно,
если конструкция ротора не позволяет раз-
мещать КМ с ИМ в требуемом месте и
при допустимости изменения положения
оси вращения ротора, что существенно
ограничивает область применения этих
устройств. Размещенные на неподвижных
частях машины АБУ принудительного цен-
трирования достаточно просты, надежны,
легко управляются автоматически и при-
годны для балансировки как жестких, так
и гибких роторов. Жесткие роторы балан-
сируются полностью, а у гибких реакции
полностью устраняются только в опреде-
ленном диапазоне скоростей вращения, так
как эта балансировка эквивалентна уста-
новке на ротор КМ, распределенных по
закону трапеции, которая имеет ограни-
чения по скоростям применения [7].
Устройства силового воздействия на
ротор не устраняют дисбаланс, а лишь
создают силовое поле, компенсирующее
результат его действия на вращающимся
ротор. В этих АБУ вокруг ротора в соб-
ранной машине монтируют электромаг-
ниты, в которых создают магнитное поле,
вращающееся с частотой вращения рото-
ра. Направление вектора магнитных сил
противоположно направлению вектора
центробежных сил от дисбаланса при ра-
венстве их величин и скоростей вращения.
Таким образом достигают устранения виб-
раций опор, но ротор остается нагружен-
ным. Недостатком АБУ силового воздей-
ствия является их большая энергоемкость,
требующая создания силового магнитного
поля для компенсации больших центро-
бежных сил.
8.2. УСТРОЙСТВА СО СВОБОДНЫМ
ПЕРЕМЕЩЕНИЕМ КОРРЕКТИРУЮЩИХ
МАСС
Жидкостные автобалаисирующие уст-
ройства [7|. АБУ Леблана разработано
для экстракторов с вертикальной осью вра-
щения, имеющих большой изменяющийся
Рис. 8.3. Жидкостное АБУ Леб-
лана
при работе дисбаланс. Избыток отжима-
емой в них жидкости используется в ка-
честве КМ. В коническом корпусе экст-
рактора 1 (рис. 8.3) располагают два ряда
отверстий 2 и 3 для удаления отжимаемой
жидкости. С корпусом жестко скрепляют
две концентричные обоймы 4 м 5 разной
высоты. Угол наклона образующей кор-
пуса и высоту отверстий выбирают так,
чтобы при докритических скоростях отжи-
маемая жидкость поступала во внутрен-
нюю обойму 4 и- удалялась из системы.
Выше критической скорости жидкость вы-
текает через верхний ряд отверстий 2,
попадает во внешнюю обойму 5 и балан-
сирует систему.
Принцип действия АБУ следующий.
При закритической скорости ротор откло-
няется в сторону, противоположную век-
тору дисбаланса. Частично заполняющая
внешнюю обойму жидкость перетекает
в часть, наиболее удаленную от оси вра-
щения, и приводит общий центр масс сис-
темы к оси вращения. Эффективность ра-
боты АБУ. характеризуемая отношением
прогиба ротора при действии АБУ (а6) и
без него (а«), определяют по формуле
2 2
«б/ао-(Т!-!)/[(! +*)?!-II. (8.1)
244
Автобалансирующие устройства
Здесь обозначено
*=мрй/(> + м)(1~р2);
V?= = +|х)<й/с,
где р = Л4ж/Л4р—отношение массы жид-
кости в АБУ к массе ротора с жидкостью;
со — частота вращения ротора; coj—соб-
ственная частота колебаний ротора с жид-
костью в АБУ; <i)i--с/Л4р(1 4~ р); с- ра-
диальная жесткость упругого элемента,
приведенная к плоскости центра масс эк-
страктора; р — г//? — отношение радиусов
свободной. поверхности балансирующей
жидкости и балансировочной обоймы.
На закритических скоростях, особенно
вблизи резонанса, АБУ уменьшает виб-
рацию ротора, но не полностью устраняет
дисбаланс. Балансирующий эффект в этом
АБУ имеет только слой жидкости, толщина
которого не превышает удвоенной вели
чины прогиба. Поэтому большая часть
объема балансировочной обоймы не ис-
пользуется. Для повышения объема участ-
вующей в создании балансировочного эф-
фекта жидкости создают многокамерное
жидкостное АБУ, содержащее несколько
концентрично расположенных друг в друге
цилиндрических обойм, частично заполнен-
ных жидкостью. Емкость многокамерного
АБУ равна сумме емкостей всех камер.
В АБУ с расплавляемым материалом
цилиндрическую обойму частично запол-
няют легкоплавким материалом, располо-
женным симметрично ее оси. На низких
частотах обойма с затвердевшим матери-
алом не меняет дисбаланс ротора. На за-
критической скорости материал с помощью
электронагрева расплавляют, и он дей-
ствует в обойме как жидкость в АБУ Леб-
лана. Устройство можно устанавливать на
роторах с горизонтальной осью вращения.
После окончания рабочего процесса подо-
грев включают, и материал затвердевает
в форме, соответствующей балансировке,
обеспечивая переход через критическую
скорость при остановке машины с урав-
новешенным ротором.
Вместо легкоплавкого материала в
АБУ можно использовать жидкость, твер-
деющую при действии магнитного поля,
создаваемого электромагнитом в оцреде-
ленные периоды работы.
АБУ Сирла [7] является устройством
с направленным перемещением балансиру-
ющей жидкости, учитывающим изменение
угла запаздывания прогиба на разных
частотах вращения. В АБУ (рис. 8.4) ба-
лансировочную обойму радиальными пере-
городками делят на несколько отсеков 5,
в которые отжимаемую жидкость направ-
ляют через распределительный диск 2 и
неподвижную питающую обойму 12, при-
жатую к диску пружинами 8. Систему
впускных отверстий в распределительно^
диске располагают так, что при отсутствии
отклонений корпуса экстрактора отверстия
закрыты. При отклонении корпуса от оси
вращения диск смещается относительно
питающей обоймы и открывает одно или
два отверстия, через которые жидкость
поступает из питающей обоймы в распре-
делительный диск. Впускные отверстия 15
и направляющие лопатки 4 выполняют так,
что жидкость под действием центробежных
сил поступает в отсек на легкой стороне
ротора как при докритических, так и при
закритических скоростях вращения. АБУ
Сирла применяют только на вертикальном
роторе в машинах с избытком жидкости.
Необходимость перекрытия отверстий при
уравновешенном роторе и трение между
частями распределительной системы при-
водят к неустраняемому остаточному дис-
балансу. Во время балансировки скорость
вращения системы уменьшается из-за уве-
личения момента инерции вращающихся
частей за счет поступающей в них жид-
кости.
АБУ с отводными трубками является
устройством с направленным перемец^е
нием балансирующей жидкости. Это АБУ
(рис. 8.5) имеет две распределительные
обоймы, соосные оси ротора, две установ-
ленные в плоскостях коррекции (ПК) ба-
лансировочные камеры, разделенные на от-
секи 4, и два насадка с клапанами 7
для подвода в распределительные обоймы
жидкости от источника ограниченной ем-
кости. В распределительные обоймы вво-
Устройства со свободным перемещением корректирующих масс
245
О)
Рис. 8.4. Жидкосное АБУ Сирла:
а — общий вид; б —сечение по Л — А. / — корпус, 2—распределительный диск. 3, •/ — лопатки;
5 — балансировочный Лэтсек, 6— горизонтальная перегородка; 7 — дно нижних каналов, 8 —пружины,
9— кольцевой канал; 10 — электродвигатель; II —- упругий элемент; /2— питающая обойма; 13 гибкий
шланг; 14 — резервуар; 15 — впускные отверстия; 16 — выпускные отверстия
Рис. 8.5. Жидкостное АБУ с отводными трубками:
а при статической; б при моментной неуравновешенности; 1— распределительная камера; 2—отводные
трубки; 3—ротор; 4 балансировочный отсек; 5, 11 -плоскости измерения; б- конец отводной трубки;
7 — насадок с клапаном; 8, 10~ плоскости коррекции; 9, 13, 14— точечные неуравновешенные массы;
12—упругая опора
246
Автобалансируюшие устройства
дят отводные трубки 2. так что их входы
равно удалены от оси ротора, выходные
концы трубок 6 вводят в соответствующие
балансировочные отсеки 4. Распредели-
тельную обойму в верхней плоскости из-
мерения соединяют с отсеками в нижней
ПК, и наоборот. Насадки устанавливают
вне ротора так, что при открытии их кла-
панов жидкость от источников попадает
в распределительные обоймы через цент-
ральные отверстия При скорости враще-
ния, достаточной для подъема жидкости
из распределительной обоймы в баланси-
ровочные отсеки, жидкость через открытые
клапаны насадков попадает в распреде-
лительные обоймы, в которых она распре-
деляется так, что ее свободная поверх-
ность соосна оси вращения. Наиболее
удаленные от оси концы отводных тру
бок затапливаются, и через трубки жид-
кость отводится в соответствующие отсеки.
При статической неуравновешенности,
расположенной, например, на правой сто-
роне ротора (рис. 8.5, а), при скорости
вращения, большей первой критической,
затопленными будут левые стороны обеих
распределительных обойм; жидкость через
отводные трубки поступает в левые ба-
лансировочные отсеки в обеих ПК, устра-
няя статический дисбаланс При момент-
ной неуравновешенности, созданной, на-
пример, неуравновешенными массами 13
и 14 (рис. 8.5, б), на скорости вращения,
меньшей второй критической, ось ротора
повернута в сторону действия момента дис-
баланса. При этом затопленными будут
правая сторона верхней распределитель-
ной обоймы и левая — нижней; это напра-
вит жидкость в левый отсек в верхней ПК
и в правый отсек в нижннй ПК для уст
ранения моментного дисбаланса.
Рассмотренное АБУ динамически ба-
лансирует ротор в диапазоне между пер-
вой и второй критическими скоростями.
Соответствующим соединением распреде-
лительных обойм с балансировочными
отсеками с помощью отводных трубок по-
лучают устройство для автоматической ба-
лансировки ротора на докритической ско-
рости. Оно выгодно отличается от АБУ
Сирла отсутствием дополнительного пере-
мещения, необходимого для открытия
впускных отверстий, и трения между под-
вижными и неподвижными частями сис-
темы, что обеспечивает большую точность
балансировки.
АБУ Дункан представляет собой поп-
лавок-контейнер с неуравновешенной мас-
сой, помещенной во вращающийся сосуд
с тяжелой жидкостью, имеющий свободу
перемещения по радиусу. Силы всплытия
нет из-за отсутствия жидкости под кон-
тейнером. Принцип действия АБУ следу-
ющий. В заполненном жидкостью враща-
ющемся сосуде на тонкую безмассовую
жесткую стенку, изолирующую объем жид-
кости массы тж, изнутри действуют внут-
реннее давление и центробежные силы с
равнодействующей тжеы2, направленной
по радиусу от оси вращения (в—расстоя-
ние от оси вращения до центра масс объе-
ма). Эти силы уравновешены силами, дей-
ствующими снаружи оболочки, препят-
ствующими ее взрыву и перемещению от
оси вращения. При замене оболочки кон-
тейнером такого же объема с грузом, об-
щая масса которых тк меньше массы вы-
тесненной жидкости, избыточное внешнее
давление воспримет контейнер, а меньшая
равнодействующая центробежных сил
внутри контейнера будет равна т^есо2.
Приложенная к центру масс контейнера
сила F— (тж — тк)е<£?. перемешает его к
оси вращения, пока эксцентриситет не ста-
нет равным нулю. АБУ Дункан работает
при любых скоростях, но в нем дисбаланс
внешнего сосуда не компенсируется. Идея
устройства Дункан использована в меха-
ническом АБУ с легкими телами качения,
описанном ниже.
Видоизменением АБУ Дункан является
устройство для автоматической баланси-
ровки барабанов стиральных машин, в
котором подшипники вала жестко скреп-
лены с корпусом, а барабан соединен с
валом через пружины. На валу закреп-
лено кольцо, охватывающее барабан и вра-
щающееся вместе с валом. Между бара
баном и кольцом расположена заполнен-
Устройства со свободным перемещением корректирующих масс
247
ная жидкостью кольцевая камера. На до-
критической скорости неуравновешенный
барабан отклоняется в сторону дисбалан-
са, зазор между барабаном и кольцом
с этой стороны уменьшается, и жидкость
перетекает в сторону увеличенного зазора
кольцевой камеры, что приводит общий
центр масс системы к оси вращения.
Механические автобалансирующие
устройства [7]. КМ механических АБУ
выполняют в виде маятников (колец) либо
тел качения (шаров, цилиндров). Прин-
цип действия этих АБУ одинаков, но АБУ
с телами качения применяют чаще ввиду
их большей эффективности, технологич-
ности и компактности.
В маятниковом АБУ на валу закреп-
лены два диска с осями, на которых сво-
бодно вращаются маятники, расстояние
от осей которых до центров дисков превы-
шает наибольшее возможное отклонение
вала в месте установки АБУ. Формула
эффективности устройства подобна фор-
муле эффективности АБУ Леблана, т. е.
они схожи по характеристикам. Маятники
увеличивают дисбаланс системы на докри-
тических скоростях, ухудшая условия пе-
рехода через резонанс. При закритичес-
ких скоростях АБУ снижает вибрации, но
не очень эффективно. Уменьшение радиуса
подвеса маятников до нуля превращает
устройство в кольцевое АБУ (рис. 8.6).
Наиболее эффективно АБУ с двумя коль-
цами, свободно висящими на приводном
валу в кожухе, заполненном маслом и вы-
полненном так, что на докритических ско-
ростях центры колец совпадают с центром
вала. Выше критической скорости центро-
бежные силы, приложенные к центрам
масс колец, поворачивают их к легкой
чарти ротора. Центр масс системы при-
ближается к центру ротора, уменьшая дис-
баланс системы.
Шаровое АБУ имеет [7J заполненную
маслом обойму (рис. 8.7) с несколькими
шарами, центр которой совпадает с цент-
ром ротора. Диаметр нижней части обоймы
R' такой, что лежашие в ней при малых
скоростях шары равномерно распределены
Рис. 8.6. Кольцевое АБУ:
R’ *н. RB, — соответственно радиусы обоймы
наружного, внутреннего кольца и оси подвеса
Рис. 8.7. Шаровое АБУ
248
Автобалансирующие устройства
по окружности и не меняют дисбаланс
ротора. При скорости выше критической,
определяемой углом р наклона образую-
щей переходного конуса, шары перекаты-
ваются в верхнюю цилиндрическую часть
большего диаметра /?. Перемещаясь пбд
действием тангенциальных составляющих
центробежных сил, шары занимают поло-
жение, балансирующее систему. Для двух-
шарового АБУ имеются четыре положения
равновесия шаров, из которых только одно
(основное) устойчивое на закритической
скорости положение соответствует балан-
сировке. Для многошаровых АБУ таких
положений множество.
Для исключения ухода шаров из рав-
новесного положения на докритических
скоростях созданы АБУ с фиксаторами
шаров на малых скоростях и освобожде-
нием их на рабочей скорости. Перемеще-
ние фиксатора осуществляется с помощью
пружин или электромагнитного, гидравли-
ческого, пневматического приводов или
центробежным регулятором. Последняя
конструкция наиболее предпочтительна,
так как не требует подвода энергии к
вращающимся частям и работает авто-
матически.
АБУ с фиксацией шаров центробеж-
ным регулятором показано на рис. 8.8.
АБУ содержит коническую обойму с ци-
линдрическими частями, в которой распо-
ложены шары, и механизм фиксации ша-
ров в виде конуса, соосного обойме, с при-
водом от центробежного регулятора. На
докритических скоростях фиксатор удер-
живает шары в равновесном положении
в нужней части обоймы. При достиже-
нии заданной закритической скорости ре-
гулятор сжимает пружину и освобождает
шары, которые поднимаются по коничес-
кой поверхности и занимают в верхней
части положение, соответствующее балан-
сировке системы. При уменьшении скорос-
ти регулятор опускает фиксатор прежде,
чем шары начнут скатываться в нижнюю
часть обоймы. Шары фиксируются в верх-
ней ча£ти обоймы в положении баланси-
ровки, переход через критическую скорость
при торможении происходит при сбалан-
Рис. 8.8. АБУ с фиксацией шаров с помощью
центробежного регулятора:
1 — переходная часть обоймы; 2- дно обоймы,
3—ротор; 4 — шары; 5 — рабочая часть обоймы;
6—пружина; 7—груз; 8—неподвижная опора; 9—
рычаги регулятора; 10 — фиксатор
сированном роторе. Возвращают шары в
нижнюю часть обоймы подъемом фикса-
тора вручную или автоматически при не-
вращающемся роторе.
Учет рассеяния энергии в опорах,
влияния колебаний шаров друг на друга
и на ротор и, наоборот, наличия несколь-
ких резонансных частот ротора определя-
ют необходимость рассматривать устойчи-
вость шарового АБУ в роторной системе,
динамические свойства которой заданы в
виде_ входного механического импеданса
— F/v, равного отношению комплексных
амплитуд приложенной гармонической си-
лы к вызванной действием этой силы виб-
роскорости [59). Для двух шаров в обойме
существуют четыре положения равнове-
сия Критерием устойчивости основного
балансирующего положения является ус-
ловие
Jm{gc}>0. (8.2)
Для ротора массой М с коэффици-
ентами жесткости опор с и демпфирова-
ния т] входной импеданс gc— г]Д /(<Г>Л4 -
Устройства со свободным перемещением корректирующих масс
249
—<7 со), и частотная область устойчивой
работы АБУ будет при
со > too = \с/М.
Частотные области устойчивой работы
АБУ для ряда практически важных слу-
чаев приведены в табл. 8.1, в которой
обозначено: Л4 — масса ротора; Л40—мас-
са единицы длины ротора; / — момент
инерции относительно центра масс 0; EJ —
изгибная жесткость ротора; <оо- собствен-
ная частота.
Для ротора с анизотропными опорами
(импедансы и из четырех возмож-
Т а б л и ц а 8.1
Частотные области устойчивой работы АБУ
Динамическая модель Входной механический импеданс Частотные области устойчивой работы АБУ
t, _ к н Gc = Ч + /(соМ — <7<о) to > <t)o = ус/М
Ь”, _ , 4 Л 5
1 F "г ес=/А2/(оВ2; А2=(<о2Л11 — С1) (<о2Л12 — с2) — w2M2t?2; 62 = <1>2Л12 — Сг <О1 < <0 < <о0 = -yfcz/Mz; <oi С<1)2 — корни уравнения Л2=0
1
Л ^2 ^2 П мп
Г н sc=/<oAf-Ps₽; Ср — произвольный импеданс <uA1-pjm{gp} >0
гТ ь а F В €<= 1А</ыВс А< = (оЛМ - с) [ о)2 - (cb2 + б) - (сё)2]; В. = <д2(/ + Ма2) - [ 6 + с[а + ё)2] tot <ы< (йд ¥=0; <й2<;о>; wi < о)2— корни уравнения А4 = 0; <0д — уравнения В^ — О
) 1 L
> 0 ► С
Б а ’ ". F п ес=jA/wBs; А5 == [ <о2М — (и + с2)] 1 /о2 — {Cid -р -рс2/2)] —(<М. -рс2/2)2; Вб == <д2(/ -р Л1с2) -f- a (ci с2) (С1Л -р -рсг/г) — 2o(Ci/| -j-Culz) oil < о) <С о>« 0; ь)2<(о; <1)1 <0)2 — корни уравнения А5 = 0; о)а — уравнения Вб = 0
— М )-
> 0 >С1
У/2. €с = — №3Е]/ы [tga— th а]; a=fe//2; й4=Л4о<о2/£/;_ <Хл’-/0- - п-й корень уравнения tg a— th а Бесконечное число областей {(2л- i)//|2«2V£77m; < «D<(an//2) лГЕ]/Мй. п= 1. 2. 3, ..
1
250
Автобалансирующие устройства
ных положений равновесия шаров основ-
ное положение является единственно ус-
тойчивым в области частот вращения,
определяемой критерием
Jm (8.3)
для которого критерий (8.2) является
частным случаем при с,х= ^у= gc.
Ротор массой М, опиравшийся на
опоры с коэффициентом жесткости сх и
Су(сх>Су}, импедансы равны Gx = /(coM —
— сх/<о); — су/со). В этом случае
он имеет две области устойчивой рабо
ты АБУ:
(Ох<<о<о)0 и 0),yCd>,
“де <ох=-уЪх/Л7; Ыу=^су/М—резонанс-
ные частоты системы; 0.5(<ох4-<*>«)
При бесконечно жестких в одном на-
правлении (су=со) опорах АБУ устой-
чиво работает в зарезонансной области
частот для другого направления (о>«х).
Частным случаем такой модели является
стиральная машина с горизонтально рас-
положенным барабаном на жестких кат-
ках, для которой автоматическая баланси-
ровка возможна во всем диапазоне частот
вращения со >0. Ряд факторов препятству-
ет полной балансировке шаровым АБУ.
Эксцентриситет в беговой дорожки не ме-
няет условий (8.2) и (8.3) устойчивой
автобалансировки, но смещает положения
равновесия шаров. У двухшарового АБУ
на роторе с изотропными опорами [19]
центр колебаний системы смещается в
центр беговой дорожки, а ось ротора ко-
леблется с амплитудой, равной е. При
анизотропных опорах и дисбалансе D ось
ротора колеблется как если бы на ротор
действовал дисбаланс /Л — 2s/^/ql + <724-
-f-2<7i<72cos(A] — Л2) , где q\, q^ и A2-~
модули и аргументы левых частей выра-
жений
—/w/GK=<7iexp()A|) и — /м/ду =
=q2e*p(fa).
При существенно анизотропных опорах
(<?i^>g2) De — 2e/qi и амплитуды вибра-
ций будут |х| = 2е; |t/l = 2е (q2/qt) -
Если плоскость движения шаров не
совмещена с плоскостью дисбаланса, то
центр колебаний ротора совпадает с
геометрическим центром беговой дорожки,
а ось ротора описывает коническую по-
верхность с вершиной в центре беговой
дорожки. При малом расстоянии а между
плоскостями движения шаров и дисбалан-
са колебания ротора эквивалентны воз-
действию на него неуравновешенного
момента М — Dai»2: чем меньше а, тем
меньше остаточная вибрация.
Трение качения шаров k снижает
чувствительность АБУ, так как возникают
зоны равновесия шаров и при медленном
изменении дисбаланса АБУ начинает ра-
ботать только после достижения эксцен-
триситетом величины [7]
Ae=pft(l —уо)(Я —г)2/ [уоХ
X (г ^4e2 — e2i — kei],
где ц = 2т/Л1; ej = Ale/(7W-|-2m);
e2—m(R~r)/(MA-2m); уо=ы/<йо.
Чувствительность АБУ тем выше, чем
меньше трение качения k, относительные
масса р, дисбаланс ш, скорость у» и гиб-
кость опор, а также чем меньше радиус
обоймы R и больше радиус г шаров и
больше их относительный статический
Момент е2.
Чувствительность АБУ определяют
шары, расположенные вблизи диаметра,
перпендикулярного вектору дисбаланса,
поэтому целесообразно увеличивать их
число. При этом растет вероятность раз-
мещения их в зоне наибольшей чувстви-
тельности, но при ограниченности раз-
меров АБУ увеличение числа шаров умень-
шает его емкость.
Достижение высокой чувствительности
при сохранении достаточной емкости обес-
печивают многорядные АБУ [15], в кото-
рых применяют две или более концентрич-
но расположенные беговые дорожки. Внут-
ренние беговые дорожки заполнены боль-
шим числом шаров, а на внешней на-
ходятся шары, размеры и количество ко-
торых определено из условия требуемой
емкости АБУ. Для снижения трения ша-
ров о беговую дорожку в АБУ создают
с помощью электромагнитного возбуди-
Устройства со свободным перемещением корректирующих масс
251
теля колебания в направлении, перпенди-
кулярном плоскости обоймы. Возбуждать
дополнительное движение шаров можно
также пневматически
Автобалансировку с шарами целесо-
образно проводить, применяя программи-
рование и микроЭВМ.
В качестве примера приводится при-
кладная программа для микроЭВМ «Вы-
числение радиуса (высоты) обоймы АБУ
с цилиндрами».
Исходной информацией для расчетов
являются: D — ожидаемый наибольший
дисбаланс ротора, гем; k3—коэффициент
запаса емкости АБУ (1,2- -1,1); р — при-
веденный удельный вес материала КМ,
гем3, р— r/R — относительный радиус
КМ; N—число КМ в обойме АБУ.
Для вычисления радиуса обоймы с
новыми исходными данными следует вы-
Инструкция пользователю
поднять инструкцию пользователю, на-
чиная с п 7
Замечания: 1. Подпрограммы, начи-
нающиеся с команд 36, 53 и 67, приведены
в подпрограмме 8.2.
2. Значения р рекомендуется прини-
мать с учетом таблицы 8.2.
Пример I. Вычислить радиус обоймы АБУ
с цилиндрами. Исходные данные для расчета:
D= 150 гем; йз=1,2; р = 7 гем'-3; р —0,1443;
N— 11; h — 2 см. Ответ: /? = 3,43 см: г—0.5 см
Расчет параметров механических АБУ.
Качество балансировки определяется пра-
вильностью выбора параметров АБУ: его
емкости, типа, размеров и числа КМ; гео-
метрических параметров, обеспечивающих
вывод шаров на рабочую дорожку после
прохода критической скорости <о(, и т. п.
Исходными для определения параметров
АБУ на стадии проектирования являются
максимально возможный дисбаланс Dm
Содержание Набрать число Выпол- нить команды Резуль- тат Содержание Набрать нить Выпол- нить команды Резуль- тат
1. Включите микрокалькулятор 2. Включите режим програм- мирования 3 Введите программу, 8,1а или 8.16 БПРГ 0 00 6.2. Перейди- те к выводу результатов 6.3. Введите контрольную информацию 6.4. Выведите результаты 150; 1,2 7; 0,1443 10; 3,4 В/О С/П ПД, ПС ПВ, ПА П8, П4 В/О С/П 3,432 . .. 150; 1,2 7; 0,1443 10; 3,4 2,058..
4. Введите под- программу, начи- ная с команд 36, 53 и 67 6.5. Очистите программный счетчик FABF в/о
5. Очистите прог- раммный счетчик FABT в/о 0 7. Вычислите радиус (вы- соту) обоймы АБУ:
6. Проверьте пра- вильность набора программы с под- программами: 6.1. Введите контрольную информацию 150; 1,2 7; 0,1443 11; 2 ПД, ПС ПВ, ПА П8, ПЗ 150; 1,2 7; 0,1443 11 7.1. Введите исходную информацию 7.2. Выведите результат D, k3 Р. Р У,(/?) ПД, ПС ПВ, ПА П8 ПЗ (П4) С/П D, k3 Р, Р *.(*) Значение R, (ft)
252
Автобалансирующие устройства
Программа 8.1 для микроЭВМ «Электроника» БЗ-34, МК-54, МК-56
Адрес Команда Код Адрес Команда 1 Код
00 01 02 03 04 05 06 07 08 09 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 " 26 27 28 29 30 31 32 33 34 35 00 0J 02 03 04 05 06 07 08 09 П 1 рограмма 8.1 ПП 36 ипз ПП 53 Fx—0 16 1 /-/ П7 ПП 67 2 X БП 24 0 П7 ПП 67 2 X 1 ИП2 3 Fl/x S ИПА С/П БП 00 1рограмма 8. ипд ИПА Fx2 1 ИПА X ИПА FBx а 53 36 63 53 53 5Е 16 01 0L 47 53 67 02 12 51 24 00 47 53 67 02 12 01 10 62 14 13 03 23 14 24 6 — 13 50 51 00 16 6Г 6 — 22 01 6 — И 12 6— 0 13 10 и 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 Ре п Г П8 — П П7 Время о Farcsin П1 FO ИПС X Fn ипв ИП4 Bf Fx2 X ПП 53 Fx=0 37 1 /-/ U7 ПП 67 2 X БП 45 0 П7 ПП 67 2 X 1 + ИП2 С/П БП 00 гистры памя' Д-D ПС- IB- р ПА— N ПЗ - Л П 0, П1, П2, П —оперативн ета при /V — ги: Аз Р 4 — 6, ые 11 19 41 25 13 6С 12 20 13 6L 13 64 ОЕ 22 12 53 53 5Е 37 01 0L 47 53 67 02 12 51 45 00 47 53 67 02 12 01 10 62 14 13 50 51 00 R — 44 с.
Устройства со свободным перемещением корректирующих масс
Подпрограммы 8.2
Адрес Команда Код . Адрес, Команда Код , Адрес Команда Код
36 ИПА 6— 53 13 €7 ИП7 67
37 1 01 54 П2 42 68 2 02
38 ИПА 6— 55 0 00 69 + 10
39 11 56 П6 46 70 П7 47
40 13 57 ИП8 68 71 ИП1 61
41 Farcsin 19 58 2 02 72 X 12
42 П1 41 59 — 13 73 Feos 1Г
43 FBx 0 60 П7 47 74 ИП6 66
•44 ипд 6Г 61 КИП7 Г7 75 +• 10
45 X 12 62 14 76 П6 46
46 ипс 6С 63 ИП7 67 77 FLO 5Г
47 X 12 64 ПО 40 78 67 67
48 ипв 6L 65 —- 11 79 В/О 52
49 — 13 66 в/о 52
50 Лг 20
51 — 13
52 в/о 52
Подпрограмма 8.2 содержит 3 подпрограммы, начинающиеся с адресов 36, 53 и 67 и исполь-
зуемые в прикладных программах 8.1 для расчета параметров АБУ с цилиндрами.
ротора, резонансная частота coi и допус-
каемое габаритными размерами конструк-
ции значение радиуса обоймы.
Наибольший статический момент колен
относительно оси их подвеса
$к==ярМ?3(р*—р*) (рв—рп),
где h—суммарная высота колец; p~ps-~
—р*—приведенная плотность КМ, учиты-
вающая плотность материала колец (рт)
и плотность масла (рж), залитого в обой-
му; Рн=Яи//?; рв=/?в/Я; р„ =/?„//? (здесь
/?, R„, RB, Rf,—соответственно радиусы
обоймы, наружного и внутреннего кольца
и оси подвеса).
Наибольшая емкость кольцевого АБУ
при заданных R и Rn
(SJm=nphR*(l +pj (1 -рп)7&
Она обеспечивается кольцами с относи-
тельными размерами
Рн—0,25 (3+рп); рв=О,25(1+Зрп).
Для повышения емкости АБУ радиус
оси подвеса колец должен быть малым,
обеспечивающим только условия прочнос-
ти и жесткости. Предельная емкость коль-
цевого АБУ (рп«0) равна (SK)np=
— О.ЗЭЗрй/?3. Для повышения емкости АБУ
без особого удорожания кольца делают
из латуни, мельхиора или другого тяже-
лого металла, но при большом дисбалансе
кольцевое АБУ становится громоздким.
Для шарового АБУ размеры шаров
гш и их число NU) можно определять дву-
мя способами.
По первому способу число шаров вы-
бирают из расчета заполнения рабочей
части обоймы наполовину, т. е.
ЛГЮ « я (1 — рш) /2рш, (8.4)
где рш=гш//?.
Полагая, что шары представляют тон-
кую по сравнению с R полоску в виде
полукольца, емкость АБУ
Sul^2NUisl/nt
где sj — 4лрг3 (R—гш) /3 — наибольший
статический момент одного шара; р=
= рж+рж—приведенная плотность шара.
Емкость АБУ включает коэффициент
запаса Лэ= 1,14-1,2 к наибольшему воз-
254
Автобалансирующие устройства
можному дисбалансу Dm. Необходимый ра-
диус шара
гш=0,5( Rw —
_-7^-2 л/з^/лр) .
(8.5)
При этом должно выполняться условие
/?^,>2 д/ЗА3Дт/лр, в противном случае
следует увеличить радиус обоймы.
Уточненное число шаров находят по
формуле
Л\п —л/2 arcsin [гш/(/?ш —гш)]-
Число цилиндров определяют по фор-
муле (8.4). их радиус равен
гц-0,5(/?ц —
- л/^ц-4 ,
(8.6)
где Vh—h/rtl—-отношение высоты цилинд-
ра к его радиусу.
Формулы (8.5) и (8.6) дают размеры
шаров или цилиндров, обеспечивающие
устранение ожидаемого дисбаланса, но они
применимы только при р 1. Кроме того,
расположение КМ по полукольцу не опти-
мально для получения максимальной ем-
кости АБУ при заданном размере обоймы.
Во втором способе учитывают коор-
динаты центров масс каждой КМ, а не
приближенное положение центра масс
тел, представленных как сплошное полу-
кольцо малой толщины. Это точнее ре-
шает задачу и позволяет оптимизировать
размеры данного числа КМ.
Наибольший статический момент име-
ют шары, прижатые друг к другу:
‘ ~ ФыУ N ^шУм*
где Уn—сумма координат центров 2VUJ ша-
ров относительно оси, перпендикулярной
вектору дисбаланса; й1Ь = 4лр^,/3; y'N—
РыУк/
В табл. 8.2 приведены оптимальные
значения рш и рассчитанные по ним зна-
чения y'N для разных Аш. По табличным
значениям у'^ для выбранного числа Л',.,
рассчитывают требуемые радиусы обоймы
и шара:
/?ш > \1з^От/4прун; гш = р1М/?,„. (8.7)
Из табл. 8.2 видно, что с увеличением
Лш обеспечение заданной емкости требует
увеличения радиуса обоймы при уменьше-
нии >ее высоты й = 2гш. Наибольшую ем-
кость при заданном Rw имеет АБУ с двумя
шарами.
Таблица 8.2
Оптимальные значения параметров АБУ
с телами качения
Л'ш W АБУ с шарами АБУ с цилиндрами
₽ш уа- ю2 ₽ц
1 0,7500 10,547 0,6667 14,815 j
2 0,4296 5,950 0,4000 14,311
3 0,3636 5,183 0,3333 14,815 1
4 0,3152 *4,389 0,2863 14,536 1
5 0,2778 3,702 0,2510 13,948
6' 0,2482 3,138 0,2235 12,950
7 0,2242 2,681 0,2014 12,552 (
8 0,2044 2,311 0,1833 11,875 !
9 0,1898 2,098 0,1681 11,241 *
10 0,1736 1,759 0,1553 10,655
11 0,1615 1,553 0,1443 10,115
Аналогично рассчитывают радиус
обоймы /?ц, число Ац, радиус гц и высоту
h КМ для АБУ с цилиндрами. Оптималь-
ные значения рц и рассчитанные по ним
величины у'н для разных Мц приведены
в табл. 8.2. С использованием табличных
значений радиусы обоймы и цилиндра
либо его высота
гц=рц/?ц;
h^k^Dm/npRlyN. (8.8)
Цилиндры обеспечивают заданную ем-
кость АБУ при меньших размерах обоймы,
чем шары. Наибольшую емкость имеет
АБУ с тремя цилиндрами, но их исполь-
зование требует специальных мер обеспе-
чения нейтрального положения КМ на
докритических скоростях.
Радиус нижней части обоймы R’ такой,
что на малых скоростях шары в ней при-
жаты друг к другу и расположены по
окружности
Я' = гш [ 1 +1 /sin (л/Л;.,) ].
Устройства со свободным перемещением корректирующих масс
255
Угол наклона образующей переходного
конуса обоймы определяют из условия
равновесия шара на этой поверхности
Р= arctg(/?'ojp/g),
где top—угловая скорость выхода шаров
из нижней части обоймы; g—ускорение
силы тяжести.
В таком АБУ неравны частоты выхода
шаров из нижней части и начала балан-
сировки при разгоне ротора (ыр) и пре-
кращения балансировки и опускания ша-
ров в нижнюю часть при остановке ротора
(wo): mo—<dp-y/R'/R . Переходы шаров из
одной части обоймы в другую происхо-
дят ускоренно с ударами о рабочую часть
беговой дорожки.
Известна переходная поверхность, ка
которой угол наклона касательной к тра-
ектории центра шара изменяется пропор-
ционально его расстоянию от оси враще-
ния. Поверхность является огибаюшей
семейства окружностей радиуса г||р центры
которых расположены на параболоиде
вращения параболы ус=Вх* вокруг оси
(рис. 8.9). Координаты точек образующего
поверхность сечения
х= хс( 1 + 2BrJ^\ +4В2Л?); у=
= Вх%— + 4B2xf,
где B = <$l2g.
При заданной скорости ыр в любой
точке поверхности шар будет в равнове-
сии под действием силы тяжести и цен-
тробежных сил. При увеличении (умень-
шении) скорости шар перекатывается по
поверхности вверх (вниз). В таком АБУ
скорости начала и конца балансировки
совпадают, хотя радиусы нижней и верх-
ней частей различаются. Шары перекаты-
ваются без ударов.
В комбинированном АБУ с легкими
телами обойма имеет наружную и внут-
реннюю цилиндрические части, полость
между которыми содержит КМ из мате-
риала малой плотности или пустотелые,
а вместо масла применена тяжелая жид-
кость, например ртуть, на докритических
скоростях находящаяся в коническом ре-
Рис. 8.9. Переходная поверхность шарового
АБУ:
I ротор; 2—крышка, 3~ рабочая поверхность;
4 шар. 5 -переходная поверхность
Рис. 8.10. Комбинированное АБУ с легкими
телами:
а~ при 6><сок; б при ых»к; 1—ротор, 2—
балансирующая жидкость, 3—конический резер-
вуар; 4 отверстие, 5, 7— легкие цилиндры; б —
крышка; 8—цилиндрическая часть; У — обойма
зервуаре в нижней части обоймы и посту-
пающая при закритической скорости в
верхнюю часть через отверстия во внут-
ренней стенке (рис. 8.10). Действие АБУ
использует эффект АБУ Дункана. Силы,
действующие в АБУ, показаны на рис. 8.11.
На докритической скорости (рис. 8.11, а)
жидкость находится ц резервуаре, а КМ —
в условиях, аналогичных АБУ с тяжелыми
телами: центробежные силы F\ направ-
лены от оси вращения, и под действием
тангенциальных составляющих ft тела
256
Автобалансирующие устройства
Рис. 8.11. Силы, действующие в АБУ:
а—при докрдтической; б —при закритической
частотах вращения. Ot — ось подшипников вра-
щения; О—центр обоймы; С—центр масс ро-
тора
уходят на тяжелую сторону, увеличивая
дисбаланс ротора. Из-за большой раз-
ницы весов тяжелых и легких тел в этом
АБУ увеличение дисбаланса на порядок
меньше, чем в известных. Выше крити-
ческой скорости (рис. 8.11,6) жидкость
из резервуара через отверстия во внут-
ренней стенке заполнит обойму. Легкие
тела оказываются в условиях поплавка
в АБУ Дункан: центробежные силы F2
направлены к оси вращения и прижима-
ют легкие тела к внутренней стенке. Под
действием тангенциальных составляющих
Т2 тела перемещаются на тяжелую сто-
рону, что при тяжелой жидкости в обойме
приводит к уменьшению дисбаланса ро-
тора. Силы Т2 обращаются в ноль при
совмещении точек С, О и О}. При умень-
шении скорости жидкость из обоймы пе-
ретекав! в резервуар, и переход через
резонанс проходит при малом добавочном
дисбалансе.
Расчет размеров легких тел осущест-
вляют по формулам (8.5) — (8.8). При-
веденная плотность тел (р—рж—рт) для
ртути й легкого тела р'^ 13 г/см3, а для
тяжелого тела в масле р"~7 г/смэ. Это
позволит уменьшить размеры АБУ при за-
данной емкости. Добавочный выигрыш в
размерах АБУ дает применение легких
цилиндров вместо шаров.
АБУ используют также для гашеиня
направленных гармонических сил. Обычно
такие силы гасят системой двух постоян-
ных дисбалансов, вращающихся в проти-
воположных направлениях с частотой
действующей силы. Рассматриваемая сис-
тема неэффективна при изменяющихся
амплитуде и направлении действия силы.
В этом случае нужно применять систему
двух меняющихся в соответствии с изме-
нением силы дисбалансов—АБУ со сво-
бодным перемещением КМ.
Исследуя поведение шарового АБУ в
анизотропной роторной системе (входные
импедансы £х при действии под уг-
лом сро направленной силы F==2£)<o2cosX
Х((о/ + т]о) заменяем силу системой двух
дисбвлансов Di D2, вращающихся с
частотой (о в противоположных направ-
лениях симметрично относительно направ-
ления действия силы. Основное баланси-
рующее положение равновесия двух шаров
устойчиво в области, определяемой крите-
рием (8.3). Прн этом обойма АБУ совер-
шает круговые колебания с амплитудой
L — 2qi q^Dil^q^A- ql+2</i ^cos (X, — ,
где qu q2 и Xi, Xs определяют как по-
казано выше.
АБУ с принудительным перемещением корректирующих масс
257
В изотропной системе (^1 = ^2; Х]=Х2)
компенсируется составляющая D\ (эф-
фект гашения в 2 раза) и обойма ко-
леблется под действием составляющей
©2. В анизотропной системе частично га-
сятся обе составляющие, и эффект гаше-
ния тем больше, чем значительнее q\ от-
личается от $2. Если q\ — 0 или q^=0.
например, при установке машины на опоры
скольжения, то вибрации гасятся даже,
если действует лишь составляющая £)г-
При действии силы, направленной вдоль
одной из осей, например х, амплитуда
колебаний системы
Л = L092/V9? 4~ 4~ 2^| 92COS (Х| — Xg),
где Lo=29j£) — амплитуда колебаний в от-
сутствие АБУ.
Если 92 то если qv<^qu
то LxLo(qz/qt). Одно АБУ целесообраз-
но применять при действии силы вдоль
направления с наименьшим по модулю
импедансом. При этом эффект гашения ра-
вен отношению модулей импедансов. При
применении двух шаровых АБУ, приводи-
мых во вращение в противоположных на-
правлениях с частотой действия силы, по-
лучают компенсацию обеих составляющих
дисбалансов. Каждое АБУ компенсирует
часть дисбаланса, вращающегося в ту же
сторону, что и обойма АБУ.
8.3. АВТОБАЛАНСИРУЮЩИЕ
УСТРОЙСТВА С
ПРИНУДИТЕЛЬНЫМ
ПЕРЕМЕЩЕНИЕМ КОРРЕКТИРУЮЩИХ
МАСС
АБУ со случайным поиском содержит
установленные на роторе КМ, положение
которых можно изменять на ходу с по-
мощью исполнительного механизма (ИМ).
Команды на ИМ подают с блока уп-
равления (БУ), размещенного на роторе
или неподвижных частях машины. В пос-
леднем случае команды подают через токо-
съемник. БУ содержит генератор случай-
ных сигналов, вырабатывающий команды
для ИМ с равной вероятностью движения
в каждом направлении. При этом изме-
9 Зак 164»
ряют величины вибрации опор или напря-
жения изгиба ротора. Сигналы вибрации
опор с датчиков через усилители подают
в блок сравнения. При неправильном вы-
боре направления движения КМ и не-
умен ьшении уровня вибраций поиск про-
должают по другому случайному варианту
движения, пока оно не приведет к умень-
шению уровня вибраций. Такой вариант
движения становится предпочтительным
на время уменьшения вибрации. При дос-
тижении допустимого уровня вибраций по-
дачу сигналов прекращают и останавлива-
ют ИМ. Если вибрации становятся неизме-
ненными или начинают возрастать, то БУ
выдает другой случайный вариант движе-
ния, и балансировка продолжается.
Случайность варианта движения КМ
обеспечивает независимость работы АБУ
от частоты вращения и устранение вибра-
ций не только от дисбаланса, но и от
неравномерного нагрева, трения, эксплуа-
тационных факторов и т. п. Система не
требует измерения фаз и работает с ап-
паратурой» показывающей только наличие
и изменение вибраций опор. Но она сложна
и требует каналов передачи энергии и ин-
формации с неподвижных частей на вра-
щающиеся. Из-за случайного поиска вре-
мя балансировки не постоянно, и нет га-
рантии ее обеспечения в практически при-
емлемое время. При балансировке дис-
баланс может розрастать на неопределен-
ную величину.
В АБУ с направленным перемещением
по заданным траекториям КМ, управля-
емых с помощью следящих систем или
систем экстремального регулирования, ба-
лансировка роторов в работающей машине
на всех частотах более надежна и про-
изводительна. Такие АБУ являются замк-
нутой системой автоматического регулиро-
вания непрямого действия, питающейся
от внешнего источника энергии.
АБУ со следящими системами [7] ра-
ботают за счет реагирования на рассогла-
сование между выходными (вектор дис-
баланса) и входными [векторы дисбалан-
сов КМ или чувствительных элементов
(ЧЭ)[ сигналами, что обеспечивает высо-
258
Автобалансирующие устройства
кую точность балансировки и быстродейст-
вие системы. АБУ содержит ЧЭ, определя-
ющий положение вектора дисбаланса с
учетом динамических свойств системы.
Требуемое перемещение КМ обеспечивает
ИМ. Кроме того, АБУ содержит усилитель-
ной реобразующее устройство для усиле-
ния снимаемых с ЧЭ сигналов и регулятор
для учета изменения фазы между векто-
рами дисбаланса и прогиба.
Механический ИМ имеет управля-
емые системой контактов электродвигате-
ли для перемещения КМ через механичес-
кую передачу. Жидкостным ИМ управляют
с помощью клапанов для пропуска жид-
кости, подаваемой с помощью насоса или
под действием центробежных сил. Пере-
ключение контактов или клапанов произ-
водят ЧЭ, в качестве которых применяют
АБУ со свободным перемещением малых
КМ. На докритических скоростях ЧЭ пока-
зывают тяжелую, а на закритических —
легкую стороны балансируемого ротора.
Функциональная зависимость между
частотой вращения, положением и вели-
чиной дисбаланса и прогиба, устойчивое
положение ЧЭ обеспечивают перемещение
КМ в сторону уменьшения дисбаланса на
всех скоростях. АБУ не содержат изме-
рительной аппаратуры, расположены на
балансируемом роторе, не имеют кана-
лов передачи информации с ротора на
неподвижные части и применимы для ба-
лансировки роторов в работающих маши-
нах.
Управлять ИМ можно системой экстре-
мального регулирования [7], содержащей
датчики вибраций и автоматическое управ-
ляющее устройство, сравнивающее сиг-
налы датчиков с допустимыми и выраба-
тывающее программу направленного пере-
мещения КМ в сторону уменьшения дис-
баланса до требуемого уровня. ИМ в АБУ
со следящими системами и с экстремаль-
ным регулированием практически одина-
ковы.
Системы экстремального регулирова-
ния по методу градиента или наискорей-
шего спуска осуществляют одновремен-
ное перемещение КМ в направлении умень-
шения дисбаланса до допустимого значе-
ния, но при этом конструкция АБУ полу-
чается достаточно сложной. В системе уп-
равления по методу Гаусса — Зайделя ми-
нимум колебаний ротора достигают после-
довательными перемещениями КМ с дости-
жением минимума вибраций при каждом
движении» что приводит к относительно
небольшому увеличению продолжитель-
ности балансировки.
В качестве главных конструктивных
признаков, характеризующих ИМ, и вы-
полняемый с его помощью процесс балан-
сировки, принимают реализованную в ИМ
схему компенсации дисбаланса ротора и
алгоритм перемещения КМ. При рассмот-
рении вариантов схем компенсации дис-
баланса решают задачу, каким числом
КМ и по каким алгоритмам их переме-
щения можно обеспечить изменение вели-
чины и фазы суммарного дисбаланса с
учетом того, что при отсутствии дисба-
ланса ротора суммарный дисбаланс от КМ
должен равняться нулю.
Возможные варианты схем компенса-
ции дисбаланса ротора приведены на
рис. 8.12. Компенсация дисбаланса с по-
мощью подвижных КМ может быть реа-
лизована перемещением:
одной КМ по дуге и радиусу окруж-
ности, рис. 8.12, а;
двух КМ по дугам окружностей, рис.
8.12, б;
трех КМ на углы а, 0 и у по дугам
окружностей, концентричных или с цент-
рами на вершинах равностороннего тре-
угольника, рис. 8.12, в, з;
трех КМ по трем пересекающимся
между собой направлениям (в том числе
под углом 120°), рис. 8.12, г, и\
двух КМ по двум взаимопересекаю-
щимся (в том числе—взаимноперпенди*
кулярным) направлениям, рис. 8.12, д, е\
трех КМ по сторонам равностороннего
треугольника, рис. 8.12. ж\
одной КМ по двум взаимно перпендику-
лярным направлениям, рис. 8.12. н:
одной КМ по дуге окружности, центр
АБУ с принудительным перемещением корректирующих масс
259
Рис. 8.12. Возможные варианты схем компенсации дисбаланса ротора
которой перемещают по дуге другой ок-
ружности, рис. 8.12, о;
двух КМ по двум окружностям, центр
одной из которых перемешают по дуге
окружности другой КМ, рис. 8.12, п\
двух КМ по дугам окружностей с не-
совпадающими центрами, рис. 8.12, р\
трех КМ, одна из которых неподвижна,
а две другие перемещают по дугам
окружностей, рис. 8.12, к;
трех КМ, одна из которых неподвижна,
а две другие перемешают по двум взаимно
пересекаемым (в том числе взаимно
перпендикулярным) направлениям, рис.
8.12, м, л.
Наиболее распространенной и удобной
в реализации является схема компенса-
ции дисбаланса Do дискового ротора пе-
ремещением двух КМ mt и т? по дугам
окружностей на углы оц и аг (рис. 8.12, б).
9*
260
Автобалансирующие устройства
Дисбалансы КМ равны 17), | — |Д2| = const.
При компенсации дисбаланса Do ротора,
величина и фаза которого за период эк-
сплуатации случайно изменяются в диа-
пазонах 0^ Юс1 <1 IA)ml и0^<р^2л, путем
перемещения КМ по окружностям на углы
eti и «2 область их значений распростра-
няется от 0 до 2л, функционалы, описы-
вающие изменения модуля D и фазы
суммарного значения дисбаланса D ротора
в плоскости диска, записывают в виде
- /г 7 V fv V
D —~\/ I k 4- / cos af I + I ) sin «г I •
= arctg £ sin a(/(k I £ cos a,^ .
где IDI/IDil и fe=|£»0|/|Dl|, a |Z)Offl|-
максимальное значение дисбаланса ротора
в плоскости коррекции, получаемое из ана-
лиза статистических данных эксплуатации
рассматриваемого типа роторов.
Время изменения .дисбаланса ротора
и значения k намного больше времени
балансировки, поэтому принимают k —
= const и рассматривают балансировку
как задачу оптимизации статического
объекта.
Целью балансировки является отыска-
ние значений углов, определяющих поло-
жения КМ, при которых функционал Ь
принимает мйнимальное значение. При со-
ответствующем выборе параметров функ-
ционал будет равен нулю, т. е. ротор пол-
ностью сбалансирован. В реальных усло-
виях полное устранение дисбаланса рото-
ра невозможно. Поэтому на практике ус-
ловие балансировки состоит в отыскании
таких значений углов cti и а2, при которых
суммарный дисбаланс ротора не выходит
из области, лежащей вблизи минимума
£>, окрестность которой соответствует до-
пустимым значениям дисбаланса, т. е.
ЯСЯдоо-
Качественное представление о поведе-
нии функционалов D и дает построение
линий D — const и <р = const при некоторых
фиксированных значениях k—поверхнос-
тей уровня (ПУ) функционалов. Вид ПУ
зависит от изменения значения k, характер
которого за время эксплуатации случай-
ный, и установить тенденцию его измене-
ния на данном этапе невозможно. Однако
диапазон изменения параметра k можно
определить: 0^/г^ (|DOm|/|£>d). Дисба-
ланс КМ выбирают, учитывая выражение
|£)||= (О,554-О,6)|Дот| и диапазон измене-
ния значения 0^fe<; (1,7ч-1,82).
ПУ дают полную информацию о по-
ведении суммарного дисбаланса ротора,
зная которое можно на стадии проекти-
рования АБУ оценить перспективы мето-
дов балансировки, их предельные возмож-
ности и целесообразность достижения
последних с учетом особенностей машины.
Области работы исполнительного меха-
низма АБУ, ограниченные прямыми 1 —
8 (рис. 8.13), характеризуют допустимое
значение суммарного дисбаланса |£>доп| =
— |£)доп|/|Д11 (прямая /), собственные зна-
чения дисбаланса k= |О0|/|Д11 ротора
(прямая 2), максимальные суммарные
значения дисбаланса при 10 и 20% (пря-
мые 3 и 4) запасе емкости АБУ. Рас-
положенная под прямой / область не пред-
назначена для работы АБУ, так как сум-
марные дисбалансы меньше допустимых.
Эта область ограничена DRon—const. Об-
ласть эффективной работы АБУ распо-
АБУ с принудительным перемещением корректирующих масс
261
ложена между прямыми 1 и 2 и для каж-
дого k находится внутри окрестности Г) =
~k. Балансировку целесообразно вести в
области, ограниченной ПДСГ1—const и £)=
==£. Работа АБУ в области, ограничен-
ной прямыми 2 и 3, 4, неэффективна, так
как работа ИМ при этом минимизирует
суммарный дисбаланс, рост которого на ве-
личину, большую собственного дисбалан-
са k, вызван паразитным влиянием от КМ.
Эту непроизводительную балансировку со-
кращают сверху (прямая 5) отказом от
запаса емкости КМ. Дополнительно непро-
изводительную балансировку сокращают
сверху на величину допускаемого значения
дисбаланса (прямая 6). Существенного
сокращения непроизводительной баланси-
ровки достигают в случае расположения
регулируемых параметров at и а2 перед
каждой балансировкой внутри области, ог-
раниченной прямыми 1 и 2. Для этого:
(1)—подбирают КМ так, чтобы суммар-
ный дисбаланс от них был равен собствен-
ному дисбалансу ротора (прямая 7), если
балансировку ведут до нулевых значе-
ний D, или (2)—суммарный дисбаланс
КМ должен быть меньше собственного
дисбаланса ротора на величину допусти-
мого (прямая 8), когда балансировку ве-
дут к достижению допустимой области.
Для выполнения первого условия нужно
знать заранее значение k, тогда на ПУ
определяют такие сочетания а, и а2, при
которых D<k.
Для выполнения второго условия ис-
пользуют третью подвижную массу т3,
с помощью которой при разведенных в
противоположные стороны массах ггц и
т2 корректируют суммарный дисбаланс
от дополнительной КМ и изменяющейся
в процессе работы неуравновешенной мас-
сы ротора так, чтобы этот суммар-
ный дисбаланс перед каждым этапом ба-
лансировки был постоянен. Это гаран-
тирует, что процесс балансировки всегда
будет происходить с заранее определен-
ным значением параметра k.
В АБУ КМ выполняют в виде сек-
торов, сегментов, шаров, плунжеров,
колец. Известны АБУ с КМ, выполнен-
ными в виде подшипников качения с не-
уравновешенными за счет сверления в них
отверстий наружными кольцами или с не-
равномерно расположенными в сепарато-
рах телами качения. Шары и цилиндры
обычно применяют в АБУ со свободным
их перемещением, поршни и плунжеры —
при использовании для их перемещения
гидравлического или пневматического при-
вода. Наиболее распространенные кон-
структивные формы КМ, применяемые в
АБУ с принудительным их перемещением,
и формулы для определения положения
центров масс и создаваемых ими дисба-
лансов приведены в табл. 8.3.
Наиболее простой и технически удоб-
ной является кольцевая форма КМ. Ос-
новной способ создания дисбаланса коль-
ца— сверление параллельных оси ^ли ра-
диальных отверстий, число и диаметр ко-
торых определяют величиной £)от. Реже
используют фрезерование на торце кольца
эксцентричного кольцевого паза. Кольце-
вые КМ обеспечивают компактность АБУ
с размещением одного кольца в другом,
что исключает появление дополнительного
моментного дисбаланса. Однако при рав-
ных наружных диаметрах кольцевая фор-
ма менее эффективна, чем секторная.
Для проектирования АБУ с принуди-
тельным перемещением КМ нужно знать
характер влияния конструктивных и дина-
мических факторов на точность баланси-
ровки, определяемую в основном погреш-
ностью установки КМ в требуемое для
балансировки положение. Величина этой
погрешности зависит в первую очередь
от схемы перемещения общего центра сис-
темы КМ, определяемой расположением
плоскости коррекции по оси балансируе-
мого ротора, значением дисбалансов КМ
и величиной этих масс, наличием тормо-
зящих устройств и их параметрами, чув-
ствительностью и быстродействием управ-
ляющих устройств и аппаратуры. Конкрет-
ную величину погрешности рассчитывают
применительно к конкретному испол-
нению устройства.
Возможность повышения точности ба-
лансировки за счет снижения массы кор-
ректирующих элементов АБУ позволяет
при недостаточной точности АБУ в ряде
262
Автобалансирующие устройства
Таблица 8.3
Форма корректирующей массы Ордината центра масс Дисбаланс корректирующей массы
s= X w ю 2. ДЭ Л Й 3 “ " Я 1 1 х х X D = г3) sin ahg <5
Ж?
47
зг/2 (jR2 — г2) cos а + > Ус~ п(Я-г) + > -f- 2 (/? + г)2 sin а 4-4a(/?-f-r) X cos а + 2 (R + г) sin а] hg
5b
1/7
— (/? + rising + Ус л(/?-г)+ "• > 4-2r(jR —r)X г 4- 4га / Л \ 1 « (-2— а) cos — г) D = (R-r) ’ -±-(R + г)2 X
ц/ X sin а + r (R—г) cos а X X (v—а)+"ё-(/?”‘г)2] ag
L*/ 4 jRsin3 а Ус 3 2а — sin 2а D = -|-fl3sin3a/ig
\ а
iff
случаев выбирать величину КМ не из усло-
вия компенсации полного дисбаланса, а
только для компенсации его нестационар-
ной части. Это возможно потому, что зна-
чительная часть дисбаланса постоянна и
вызвана некачественным изготовлением
ротора и погрешностями монтажа. По-
скольку эта часть неуравновешенности не-
изменна в период срока службы ротора,
она может быть устранена после его монта-
жа с применением в и броиз мерительной ап-
паратуры АБУ и постоянных КМ, закреп-
ляемых на роторе. Емкость же АБУ рас-
считывают по величине максимального
дисбаланса, возникающего в процессе ра-
боты ротора.
Использование в АБУ различных схем
перемещения общего центра системы КМ
(рис. 8.12), выбора их числа и формы,
конструктивной схемы исполнительного
баланснровочного устройства не позволя-
ют дать общий метод расчета для все-
возможных конструкций АБУ. Можно
лишь привести общие методики расчета
отдельных элементов АБУ. Остальные де-
тали для выбранной конкретной конструк-
ции следует рассчитывать на основе об-
щих методов расчета машин.
Исходными данными для расчета АБУ
являются допустимый и максимальный
дисбалансы ротора и необходимые г аба-
АБУ с принудительным перемещением корректирующих масс
263
ритные размеры устройства. На основа-
нии величины найденного или заданного
максимального дисбаланса определяют
суммарный дисбаланс КМ АБУ:
2т,у1= (1,14- 1.2)ОПга.
где mi—масса i-го корректирующего эле-
мента; у,—максимальный радиус смеще-
ния центра масс этого элемента.
На данном этапе определяют число,
форму и размеры КМ. Большой запас
емкости АБУ принимать не следует, так
как это ведет к увеличению размеров ИМ
и снижению точности балансировки вслед-
ствие увеличения инерционных сил в уст-
ройстве. В АБУ с принудительным пере-
мещением КМ следует учитывать, что дис-
балансы этих элементов обычно делают
равными, поэтому
^,= (1,14-1,2) (DOm/N),
где А—число КМ в устройстве.
В режимах пуска и остановки машины
при неработающем АБУ из-за больших
угловых ускорений вследствие инерцион-
ности конструктивных элементов АБУ воз-
никают большие перегрузки, которые могут
привести к самопроизвольному смещению
КМ и разбалансировке системы. Для обес-
печения неподвижного относительно ро-
тора положения КМ при этих режимах
в АБУ применяют фиксирующие элемен-
ты— подпружиненные фрикционные по-
верхности или прижимные шпильки. Необ-
ходимую силу прижатия фиксатора опре-
деляют по формуле
w
4- 1,2) £ Л-
»=
где «— число оборотов ротора, мин-1,
П — КПД кинематической цепи ИМ; tp_____
время разгона ротора, определяемое экс
периментально; /?пр — радиус окружности,
по которой действуют прижимы; /^ко-
эффициент трения покоя пары трения;
Л—полярный момент инерции вра-
«=1
щающихся элементов кинематической
цепи ИМ, включая моменты инерции КМ.
Общие передаточные отношения кине-
матических цепей относительного движе-
ния КМ, соответствующих схеме по рис.
8.12, б:
(л4-п0)/п; «2=(л —«о)/п,
где п0—число оборотов КМ относитель-
но ротора, мин-1.
Значение по рекомендуют принимать
в пределах 2—5 мин-1. Увеличение по
сверх этих величин снижает точность ба-
лансировки. а понижение частоты враще-
ния уменьшает производительность балан-
сировки, практически не повышая точнос-
ти, так как при этом определяющими ста-
нут погрешности, обусловленные порогом
реагирования системы управления, а не
инерционностью подвижных элементов
АБУ.
Найденные передаточные отношения
разбивают по парам зубчатых колес. По-
лученные числа зубьев для первой цепи
определяют значения межцентровых рас-
стояний валов коробки передач ИМ, ко-
торые следует сохранить для второй ки-
нематической цепи с помощью изменения
модуля, угла наклона зубьев и коррегн-
рования их профиля.
В рабочем режиме АБУ — режиме ав-
томатической балансировки—основную
нагрузку на детали АБУ вызывают КМ,
так как все остальные детали и узлы сба-
лансированы и трение в опорных поверх-
ностях является величиной второго поряд-
ка малости. Определяющий момент тре-
ния, возникающий в корректирующих эле-
ментах
N
мт= ш,-^<оггт/2,
t=i
где <о—угловая скорость ротора; гт—
радиус опорной поверхности КМ; /2—
коэффициент трения покоя пары трения.
Мощность привода для перемещения
КМ (Вт) при стационарном режиме ба-
лансировки
M.rnG • 103/ (973,8т] ,т]2).
где т]1 и т]2—КПД механизма кинемати-
ческого воздействия КМ и кинематичес-
кой цени от электродвигателя к КМ.
264
Автобалансмрующие устройства
Основной режим работы АБУ — его
пуск — рассчитывают на преодоление мо-
мента трения в элементах устройства:
/Ип>/Ит/(ТИТ|2)-
Приближенно пусковой момент элек-
тродвигателя определяют по формуле
Мп«1,8Апр.973,81/пдв,
где i—наибольшее передаточное отноше-
ние кинематической цепи от электродви-
гателя к КМ; пда—частота вращения элек-
тродвигателя в минуту.
Расчет и конструирование остальных
элементов ИМ АБУ осуществляют по
обычным методикам расчета деталей ма-
шин.
Для облегчения расчета параметров
элементов ИМ АБУ удобно использовать
программируемые микроЭВМ типа «Элек-
троника» БЗ-34, МК-54, МК-56, МК-61
и др. В качестве примера приведены про-
грамма 8.2 и инструкция для расчета па-
раметров КМ по формулам, приведенным
в табл. 8.3
Прикладные программы для микро-
ЭВМ: «Вычисление внешнего радиуса кор-
ректирующей массы типа 1 по табл. 8.3»
(прогр. 8.2, с), «Вычисление толщины кор-
ректирующей массы типа 1» (прогр. 8.2,6),
«Вычисление угла корректирующей массы
типа 1» (прогр. 8.2, в).
Исходной информацией для расчетов
являются: D — наибольший ожидаемый
дисбаланс ротора, гем; k3 коэффициент
запаса емкости АБУ (fe»= 1,1 4-1,2); р—
удельный вес материала корректирующей
массы, г<см-3; p=r/R—отношение внут-
реннего диаметра корректирующей массы
к ее внешнему диаметру; h — толщина кор-
ректирующей массы, см (для прогр. 8.1, а,
8.1, в); R— радиус корректирующей мас-
сы, см (для прогр. 8.1, б, 8.1, в); а—
угол корректирующей массы, ° (для прогр.
8.1, а, 8.1, б).
Для вычисления параметров корректи-
рующей массы с новыми исходными дан-
ными необходимо работать по инструк-
ции пользователю, начиная с п. 8.
Программа 8.2 для мнкроЭВМ «Электроника»
БЗ-34, МК-54, МК-56
Адрес Команда Код Адрес Команда Код Адрес Команд»- Код
I рограмма 8. 2,42 05 X 12 Программа 8.2 ,г
00 ПП 53 06 — 13 12 НПО 60
01 12 12 07 ИП6 66 13 ИП1 61
02 ИП4 64 08 F sin 1С 14 X 12
03 — 13 09 -Z_ 13 15 3 03
04 ИП6 66 10 С/П 50 16 X 12
05 F sin 1С Программа 8.2 в 17 2 02
06 — 13 00 ПП 53 18 — 13
07 3 03 01 12 12 19 ИП2 62
08 Fl/x 23 02 ИП4 64 20 — 13
09 Fxy 14 03 13 21 i 01
10 24 04 ИП5 65 22 КПЗ 63
11 С/П 50 05 t ОЕ 23 t ОЕ
Программа 8.2,6 06 Fx2 22 24 Fx2 22
00 ПП 53 07 X 12 25 X 12
01 12 12 08 — 13 26 — 11
02 ИП5 65 09 F arcsin 19 27 — 13
03 t 0Е 10 С/П 50 28 в/о 52
04 Fx2 22 Регистры памяти; ПК ₽ ПП ПО—D, П1 -ft3,J12—р, ПЗ— р, П4—ft
Автобалансирующие устройства для шлифовальных кругов
265
Инструкция пользователю
Содержание Набрать число Выполнить команды Результат
1. Включите микрокалькулятор 2. Включите режим программиро- 0
вання ЕПРГ 00
3. Введите программу 8.2, а (8.2, б, 8.2. в) 4. Введите подпрограмму 8.2, г 5. Очистите программный счетчик 6. Установите переключатель Г/Р/ГРД в положение Г 7. Проверьте правильность набора FABT В/О 0
программы с подпрограммой: 150; 1.2 ПО, П1 150; 1,2
7.1, а. Введите контрольную ин-
формацию для прогр. 8.2, а 7,85; 0,8 П2, ПЗ 7,85; 0,8
1; 60 П4, П6 1; 60
или
7.1,6. Введите контрольную ин- 150; 1,2 ПО, П1 150; 1,2
формацию для прогр. 8.2, б 7,85; 0,8 П2, ПЗ 7,85; 0,8
4,3; 60 П5, П6 4,3; 60 ’
или
7.1, в Введите контрольную ин- 150; 1,2 ПО, П1 150; 1,2
формацию для прогр. 8.2, е 7.85; 0,8 П2, ПЗ 7.85; 0,8
1; 4.3 П4, П5 1; 4,3
7.2. Перейдите к выводу ре- зультатов: для программы 8.2, а В/О С/П 4,3335.
для программы 8.2, 6 В/О С/П 1,0236. .
для программы 8.2, в 7.3. Очистите программный В/О С/П 62.434 ..
счетчик FABT В/О
8. Вычислите значение искомого пара- метра корректирующей массы: ПО. П1 D. к3
8.1. Занесите исходную нн- D. к3
формацию р, Р П2, ПЗ Р. Р
h (R), а П4(П5), П6 h(R), а
или R(h), а П5(П4), П6 R (ft). а
или h. R П4, П5 h, R
8.2. Выведите результат С/П Значение h (R; а)
Замечания: 1 Подпрограмму с
команды 12 брать из прогр. 8.2, г.
2. Угол а рекомендуется принимать
а ^60°.
3. Значение р следует принимать мень-
ше 0,5.
Пример I. Вычислить внешний диаметр
корректирующей массы типа 1 по табл. 7.3.
Исходные данные для расчета: D= 150 гем;
р = 0,8; 1,2; р = 7,85 гем”3; Л=1 см; а =
= 60°. Ответ: ₽ = 4,33 см.
Пример 2. Вычислить толщину корректи-
рующей массы типа 1 при тех же исход-
ных данных и /? = 4,3 см Ответ. ft «= 1,02 см.
Пример 3. Вычислить угол корректирую-
щей массы типа 1 при тех же исходных дан-
ных и Л= 1 см; R=4,3 см. Ответ: а— 62,4°.
8.4. АВТОБАЛАНСИРУЮЩИЕ
УСТРОЙСТВА ДЛЯ ШЛИФОВАЛЬНЫХ
КРУГОВ
Обеспечение высокой точности и ка-
чества поверхностей при шлифовании не-
возможны без тщательной балансировки
абразивного инструмента. Балансировку
осуществляют при изготовлении шлифо-
вальных кругов и в процессе эксплуатации.
"Основными источниками дисбаланса
шлифовального круга в процессе его из-
готовления являются абразивная масса,
формообразование, термическая и меха-
ническая обработка. Для устранения дис-
баланса кругов на абразивных заводах
266
1
Автобалансирующие устройства ]
применяют заливку свинца в канавку, вне-
сение порошка в легкую часть круга и
изменение геометрии круга. Эти методы
непроизводительны, трудоемки и требуют
действий оператора над шлифовальным
кругом. Более перспективным является
устранение дисбаланса нанесением на лег-
кое место с помощью АБУ дискретных
порций КМ (см. разд. 8.5).
Перед установкой на станок шлифо
вальные круги также балансируют. Ста-
тическую балансировку производят на па-
раллелях, дисковых, роликовых устрой-
ствах и весах. Точность балансировки на
этих устройствах ограничивается момен-
том трения. Для уменьшения влияния тре-
ния применяют вибрационное воздействие
на параллели или подшипники на воздуш-
ной подушке. Статическую и моментную
балансировку с большой точностью прово-
дят в динамическом режиме иа баланси-
ровочных станках, на которых определяют
величину и угол дисбаланса. Устранение
дисбаланса осуществляют при остановлен-
ном круге обычными методами. Для сов-
мещения операций измерения и устра-
нения дисбаланса алмазных кругов с ме-
таллическим корпусом в НПО «Армста-
нок» разработан станок модели ЭЗ-28,
работающий по методу электрохимичес-
кого растворения (см. п. 8.7).
Однако балансировка абразивного
круга не на шлифовальном станке непро-
изводительна и неэффективна, так как
вследствие пористости структуры, неравно-
мерного износа, применения смазывающе-
охлаждающих жидкостей и т. д. дисбаланс
круга в процессе работы существенно из-
меняется. Величина его может изменять-
ся в 5 раз, а угловое положение до 150°.
Балансировка КМ непосредственно на
шлифовальном станке вручную приводит
к простоям шлифовального оборудования,
а ее точность зависит от квалификации
оператора и используемой виброизмери-
тельной аппаратуры.
Решение задачи снижения уровня виб
рации и связанного с этим повышения
точности обработки обеспечивают лишь
специальные устройства, устанавливаемые
на шлифовальном станке и позволяющие
балансировать круг без его снятия на хо-
лостом ходу или в процессе шлифования.
Известно значительное число типов подоб-
ных устройств. Конструктивные схемы и
работы ряда устройств достаточно под-
робно описаны в специальной литера-
туре [7].
По степени автоматизации управления
устройства делят на неавтоматические
(ручные), полуавтоматические и автоба-
лансирующие. При работе неавтоматичес-
ких устройств управление перемещением
КМ осуществляет непосредственно опера-
тор с помощью соответствующих руко-
яток, кнопок, кранов и т. п. по показаниям
виброизмерительных приборов, установ-
ленных на опорах станка. Во время ба-
лансировки круга шлифовальный станок
на 1—2 мин выключают. К данному типу
относится устройство «Эльтродин» с ам-
плитудно-фазовым методом балансировки,
предназначенное для балансировки кругов
диаметром свыше 500 мм при 400—6000
об/мин и диаметром до 500 мм при 1500—
6000 об/мин. Дисбаланс устраняют руч-
ным перемещением КМ к положениям,
указываемым шкалой прибора с реша-
ющим устройством.
Устройство модели ШУ-297 крепится к
планшайбе 6 круга 5 (рис. 8.14). Ручное
управление осуществляется с помощью ру-
кояток 15 и 16. При вращающемся вместе
с кругом механизме и остановленной ру-
коятке 16 шестерни 13 и 14 обкатывают-
ся вокруг неподвижной шестерни 17, вра-
щая через червячную пару 8, 9 червяк
10. Червячное колесо 2 жестко связано
с КМ 4, а через шестерни 3, 1 и И
с массой 7. Обе КМ вращаются относи-
тельно круга. В случае останова рукоят-
ки 15 неподвижной становится шестерня
18, по которой обкатывается колесо 12,
что приводит через те же передачи во
вращение КМ 4 и 7 в противоположном
относительно круга направлении. Переда-
точные отношения кинематических цепей
выбраны так, что при остановке рукоят-
ки 16 КМ 4 медленно обгоняет КМ 7,
Автобалансирующие устройства для шлифовальных кругов
267
Рис. 8.14. Устройство модели ШУ-297:
1, 3. 11—14. 17. 18— зубчатые колеса; 2. 9- чер-
вячные колеса; 4. 7 — корректирующие массы;
8. 10—червяки; 5 — шлифовальный круг. 6- план-
шайба; 15, 16—рукоятки
и угол между ними увеличивается, а при
остановке рукоятки 15 этот угол медлен-
но уменьшается. Общий центр КМ пере-
мещается по спирали, что соответствует
схеме компенсации дисбаланса, приведен-
ной на рис. 8.12, б. С уменьшением шага
спирали точность балансировки повыша-
ется, но время балансировки возрастает.
Для контроля уровня вибраций шлифо-
вальной бабки оператор использует при-
бор, установленный на опоре шпинделя.
При каждом обороте КМ их центробеж-
ная сила суммируется с силой от дис-
баланса круга, что вызывает многократ-
ное появление минимума и максимума виб-
раций системы, приводя к дополнитель-
ным нагрузкам на опоры шпинделя и к
усложнению контроля за процессом ба-
лансировки. Точность балансировки соста-
вляет 3— 5 мкм.
Устройство МАИ (рис 8.15) принуди-
тельного центрирования балансирующего
диска 3 имеет три рабочие камеры 11,
образуемые внутренней поверхностью
шпинделя 5 и уплотнениями 4, расположен-
ными под углом 120° друг к другу. Масло
от насоса по каналу 9 через золотник
Рис. 8.15. АБУ МАИ:
/, 2— фланцы. 3 — балансирующий диск; 4 — уп-
лотнения; 5 — шпиндель; 6— трубопроводы; 7—
упругие прокладки, 8 — золотник; 9— питающий
канал; 10—краны слива, 11 — рабочие камеры
8 и трубопроводы 6 подают в рабочие
камеры, давление в которых регулируют
кранами 10. Смещение диска в радиаль-
ном направлении компенсирует дисбаланс
круга по схеме, соответствующей рис. 8-12,
и. Балансировку ведут вручную методом
направленного поиска по приборам, уста-
новленным на опорах станка. В обоих
описанных выше устройствах плоскости
КМ и шлифовального круга не совпадают,
что вызывает неуравновешенный момент.
При полуавтоматическом режиме ба-
лансировка частично выполняется опера-
тором, а частично—автоматически по
программе.
Устройство фирмы Нортон (Norton,
Англия) (рис. 8.16) при нажатии кнопки
перемешает кольцевую КМ 17 по двум
взаимно перпендикулярным направлениям
соответственно схеме компенсации дисба-
ланса по рис. 8.12, и; КМ, опирающуюся
на две пары пружин 15 и 16, располо-
женных под прямым углом, перемещают
по двум координатам в плоскости круга.
Силовое замыкание осуществляется дву-
плечими рычагами 2, с которыми сопри-
касаются концентричные чашки 4 и 3,
перемещаемые вдоль оси шпинделя винто-
рычажными механизмами 5 и 6 Электро-
двигатели 7 и 8 для перемещения чашек
смонтированы на кронштейне 9, закре-
пленном на кожухе / шлифовального кру-
268
Автобалансирующие устройства
Рис. 8.16. Балансировочное устройство фирмы Нортон
га 10. Каждый из электродвигателей ра-
ботает поочередно в течение 15 с. Ам-
плитуду вибрации шпинделя 14 регистри-
руют индукционным датчиком 11, шток
12 которого перемешается от закреплен-
ного на шпинделе кольца 13. Датчик свя-
зан с усилителем и выпрямителем, выход-
ной сигнал которых управляет вращением
электродвигателя.
В АБУ устранение дисбаланса осу-
ществляют без вмешательства оператора.
Они включаются в работу автоматически
в зависимости от уровня вибраций опор
или другого критерия, связанного с ве-
личиной дисбаланса круга.
По способу компенсации дисбаланса
АБУ делят на балансирующие круг пе-
рераспределением масс устройства и ба-
лансирующие круг добавлением к нему
или удалением с него КМ. К первому
типу относят также АБУ принудитель-
ного центрирования. В АБУ с перерас-
пределением масс используют как само-
устанавливающиеся, так и принудительно
перемещаемые КМ.
В первом случае в качестве КМ при
меняют маятник, шары, ролики, легко-
плавкие сплавы, затвердевающую жид-
кость и т. п„ самоустановка которых проис-
ходит при за резонансном режиме работы
(см. разд. 8.2). Для создания этого ре-
жима подвешивают шпиндельный узел на
пружинных опорах либо закрепляют круг
на упругом валу, т. е. существенно переде-
лывают шлифовальный станок.
Для АБУ с телами качения шпиндель
должен иметь опорные шейки строго кон-
центричные рабочим поверхностям обоймы
и механизм фиксации КМ в нужном по-
ложении. Это существенно ограничивает
их применение. В АБУ со свободным пе-
ремещением КМ балансировка осущест-
вляется без применения сложной вибро-
измерительной аппаратуры с точностью,
не зависящей от квалификации оператора,
которая, однако, ниже точности, получа-
емой при применении АБУ с принудитель-
ным перемещением КМ. Для расчета па-
раметров АБУ со свободным перемещени-
ем КМ следует использовать материалы
п. 8.2.
В шаровом АБУ конструкции ЭНИМСа
(рис. 8.17) в шпинделе 8 находятся ра-
бочая обойма 2 для размещения КМ и
отверстие, являющееся полостью гндро-
цилиндра для размещения штока 5. На
штоке, поджатом пружиной 6, закреплен
зажимной грибок 10 В нерабочем со-
Автобалансирующие устройства для шлифовальных кругов
269
Рис. 8.17. Шаровое АБУ ЭНИМС:
1 — шары; 2 — обойма; 3 — крышка; 4 — центр не-
подвижной опоры; 5—шток гидроцилиндра; 6—
пружина; 7—упругая подвеска; 8—шпиндель; 9—
абразивный круг. 10—зажимной грибок
стоянии шары 1 прижаты грибком к торцу
шпинделя и неподвижны относительно
шлифовального круга 9. Переднюю опору
шпинделя можно* переводить с жестких
на упругие 7 опоры, равножесткие во всех
поперечных направлениях. При баланси-
ровке процесс шлифования прекращают,
шпиндель переводят с жесткой на упру-
гую опору. При этом вращающийся с не-
уравновешенным кругом шпиндель совер-
шает круговые колебания с центром в
точке 4 на другой опоре. Через отверс-
тие в шпинделе подают масло в гидро-
цилиндр, шток с зажимным грибком сме-
щается влево и освобождает шары, ко-
торые самоустанавливаются в положении
балансировки круга. После устранения
дисбаланса полость гидроцилиндра соеди-
няют со сливом, и поршень с грибком
под действием пружины 6 зажимает шары
в занятом положении. Шпиндель перево-
дят на жесткие опоры и возобновляют
процесс шлифования. Время установки
шаров в положение балансирования сос-
тавляет 10—15 с, остаточная амплитуда
вибрации 1—3 мкм.
'Действие другого АБУ основано на
применении суспензии (трансформаторное
масло—55%, кварцевый порошок—40%,
глицериновый моноолеат—5%), способ-
ной многократно увеличивать вязкость в
электрическом поле. Выполненная из изо-
лирующего материала обойма частично
заполнена суспензией и содержит коль-
цевые электроды, к которым через токо-
съемник подают напряжение от внешнего
источника. При отсутствии напряжения
на электродах суспензия находится в жид-
ком состоянии и действует как в АБУ
Дункан, т. е. перемещается в наиболее
удаленную от оси вращения часть обой-
мы— в легкое место при закритической
скорости. Затем на электроды подают на-
пряжение, под действием которого сус-
пензия густеет, сохраняя сбалансирован-
ное состояние шпинделя с кругом. При-
менение быстро густеющей в электричес-
ком поле суспензии не требует изменения
конструкции шпинделя, так как для нее
не столь строго требование соосности опор-
ных цапф и обоймы, как для тел качения.
Остается необходимым обеспечение пере-
хода от жесткой опоры шпинделя к уп-
ругой и обратно. Точность балансировки
повышается ввиду замены трения качения
шаров о беговую дорожку значительно
меньшим трением между слоями жидкости.
АБУ с принудительным перемещением
КМ содержит ИМ, датчик вибрации и
автоматическое управляющее устройство.
ИМ . содержит определенное число КМ,
которые с помощью отдельного привода
через систему передач перемещают отно-
сительно вращающегося шлифовального
круга по одному из вариантов, показан-
ных на рис. 8.12. Датчик передает сиг-
налы об уровне вибрации балансируемого
шпинделя в автоматическое управляющее
устройство, которое их сравнивает с до-
пустимым уровнем и вырабатывает коман-
ды на начало, направление и конец переме-
щения КМ.
Все системы управления процессом
балансировки делят на четыре типа: дей-
ствующие по методу случайного поиска,
следящие системы, системы экстремаль-
ного регулирования по методу градиента
и системы экстремального регулирования
по методу Гаусса—Зайделя.
В последнее время предпринимаются*
попытки применения для автоматической
270
Автобалансирующие устройства
балансировки шлифовальных кругов АБУ
с использованием импульсного нанесения
на круг дискретных порций балансирую-
щей жидкости (см. п. 8.5). Применение
таких АБУ исключает необходимость пе-
ределки шлифовального станка, так как
исполнительный орган АБУ имеет малые
размеры и может быть установлен на стан-
ке вблизи балансируемого круга, а управ-
ляющее устройство располагается отдель-
но. С помощью таких АБУ балансиров
ку круга можно выполнять, не прерывая
основной процесс шлифования.
8.5. ИМПУЛЬСНЫЕ
АВТОБАЛАНСИРУЮЩИЕ УСТРОЙСТВА
Группа устройств автоматически ба-
лансирует ротор путем силового нанесения
дискретных порций КМ, находящихся в
жидком состоянии, на легкое место по-
верхности ротора при его вращении (см.
рис. 8.1). Это совмещает во времени и
автоматизирует операции измерения дис-
баланса и его корректирования с высокой
производительностью и точностью неза-
висимо от опыта и квалификации опера-
тора. Эти АБУ можно применять как в
специализированных балансировочных
станках, так и устанавливать вблизи ба-
лансируемого ротора для устранения дис-
баланса, образующегося в процессе рабо-
ты. К этой группе устройств относят элек-
тро импульсные АБУ, в основу действия
которых положено использование управля-
емой энергии взрыва проволочки при ко-
ротком замыкании \(ЭФБ), электрогидрав-
лического эффекта (ЭГЭ). импульсного
магнитного поля (ИМП), магнитострик-
ционного эффекта (МСЭ) или энергии
взрыва горючей смеси (ВГС). К вещест-
вам, используемым в этих АБУ в качестве
балансирующих, предъявляют ряд тре-
бований, главными из которых, с учетом
динамики процесса, являются хорошие
адгезионные свойства и быстрота затвер-
девания. Большое значение имеют состоя-
ние поверхности ротора (гладкая, пори-
стая), ее чистота и подготовка (обезжири-
вание, лужение и т. п.). Учитывают также
эксплуатационные условия.
Разработанные в ИМАШ АН СССР
АБУ основаны на применении управля-
емой энергии ЭГЭ для получения ударных
импульсов, под действием которых на-
носят дискретные порции жидких быстро-
твердеющих КМ на поверхность балан-
сируемого ротора в легком месте. ЭГЭ
является источником большой мощности
с высокой концентрацией энергии (102 —
I03 Дж/сМ3), возникающей при высоко-
вольтном разряде в жидкости. Применение
ЭГЭ характеризуют простота осуществле-
ния процесса и возможность управления
энергетическими параметрами импульса.
Главным действующим фактором в АБУ
с применением ЭГЭ являются ударные
волны, создаваемые в разрядной камере.
При вращении балансируемого ротора
1 (рис. 8.18) вибрации его опор воспри-
нимаются датчиком 2 и преобразуются
в электрические сигналы (пропорциональ-
ные величине дисбаланса), которые пере-
даются в БУ 3. По сигналам от БУ ге-
нератор импульсных токов 4 выдает- на
электроды 5 исполнительного органа (ИО)
7 импульсы высокого напряжения; ИО
представляет собой прочный корпус, раз-
деленный подвижным элементом в виде
мембраны 9 на камеры 6 и 10. Разрядная
камера 6 с размещенными в ней элек-
тродами 5 заполнена рабочей жидкостью
для производства ЭГЭ, а камера 10—
балансирующим веществом. Рабочей жид-
костью является техническая вода, а в
отдельных случаях—вода, специально
подготовленная (конденсат, растворы со-
лей, щелочей и т. д.). В качестве ба-
лансирующих веществ применяют легко-
плавкие сплавы, клеи, смолы, пластмассы
и т. п_, выбор которых определяется быст-
ротой затвердевания вещества, материа-
лом балансируемого изделия и условиями
работы. Камеру 10 снабжают нагрева-
телем 11, обеспечивающим нужную тем-
пературу балансирующего вещества, по-
дачу которого по мере расходования во
время работы осуществляют из питате-
ля 8.
Импульсные автобаланснрующме устройства
271
Р
Рис. 8.18. АБУ И МАШ с применением ЭГЭ
При подаче на электроды импульса
высокого напряжения, пропорционального
величине дисбаланса, в камере 6 проис-
ходит искровой разряд Выделившаяся
энергия направляется на мембрану, что
приводит к ее перемещению и выбросу
порции жидкой балансирующей массы
через сопло 12 на легкую часть поверх-
ности балансируемого ротора, где она
твердеет, компенсируя часть дисбаланса.
Процесс балансировки продолжают авто-
матически, пока величина дисбаланса не
станет меньше или равной заданной ве-
личине. За счет возможности управления
энергией ЭГЭ можно наносить КМ как
постоянные по величине Дгд= const, так
и пропорциональные величине дисбаланса
Дг«со/(£)т). Тогда состояние сбаланси-
рованности ротора можно оценить по фор-
муле
п п
Dt,-Y.ac<D^
I 1
где Do — начальный дисбаланс; Dt—дис-
баланс в момент времени т; D&— допус-
тимый дисбаланс; dCt df(Dj)—дисбаланс,
устраняемый за один выброс соответствен-
но при Дт = const и Днгс«/(РТ).
Использование управляемой энергии
ЭГЭ позволяет создать всережимное ЛБУ,
выполнять балансировку роторов с высо-
кой точностью и производительностью во
время изготовления и на ходу в процессе
эксплуатации при полной автоматизации
балансировки.
. В АБУ с использованием И МП выброс
порций жидкой КМ происходит в резуль-
тате действия ударных волн, генерируемых
импульсными деформациями упругого эле-
.мента [7]. В АБУ с плоским индуктором
4 (рис. 8.19) по сигналам датчика виб-
раций 1, передаваемым в БУ 2, генера-
тор импульсных токов 3 подает на индук-
тор импульсы высокого напряжения. В ин-
дукторе возникает ИМП, взаимодейст-
вующее с током, индуктируемым в уп-
ругодеформируемом элементе 5 рабочей
камеры 7. Величина электромагнитных сил
P=§Tds,
где f=ц[(пЯ)Н—^-Н2п]; Т—плотность
поверхностных сил; п — единичный век-
тор нормали к поверхности проводника;
/?- напряженность магнитного поля; р,—
магнитная проницаемость металла.
272
Автобал ансирующне устройства
Рис. 8.19. АБУ ИМАШ с плоским индук-
тором
Для полной реализации энергии ИМП
глубина его проникновения б должна быть
меньше толщины упругого элемента Л:
б = -\/2i|)o/(o^ h.
где фо= (оор)-1—коэффициент диф-
фузии; оо— электропроводность материала
упругого элемента; to — частота возму-
щения.
Электромагнитные силы осуществля-
ют импульсное перемещение упругого
элемента, генерируя в балансирующем ве-
ществе 8 ударную волну, приводящую к
выбросу порции КМ через сопло 9 на
легкую сторону ротора 11. В процессе
работы камера 7 получает балансирую-
щее вещество из питателя 6. Рабочая ка-
мера и питатель могут быть оборудованы
обогревателем 10.
В разработанном совместно ИМАШ
и НПО «Армстанок» АБУ в ИО исполь-
зуют энергию ВГС для выброса порций
КМ. При вращении балансируемого ро-
тора 1 (рис. 8.20) сигнал с датчика 2
подают на БУ 3, выдающий импульсы
высокого напряжения на запальное уст-
ройство 4. ИО представляет собой кор-
пус 5, разделенный мембраной 9 на ка-
меры 6 и 10. Взрывную камеру 6 запол-
няют энергоносителем, а рабочую 10—
балансирующим веществом. В качестве
энергоносителя применяют газовые смеси
кислорода с водородом или метаном, а в
качестве балансирующих — вещества та-
кие же, как в АБУ с ЭГЭ.
Рис. 8.20. АБУ со взрывом горючей смеси
Автоматические балансировочные устройства, реализующие лазерный метоп
273
Камера 6 снабжена системами подачи
горючей смеси 12 и выпуска 8 с элек-
тромагнитными клапанами 7 и 13. Из бал-
лонов окислитель (кислород) и горючее
поступают в смесительную систему, управ-
ляемую клапаном 13, сигнал на откры-
тие которого выдает БУ 3. После запол
нения камеры 6 горючей смесью ее вос-
пламеняют электрической искрой от по-
дачи импульсов высокого' напряжения с
БУ на запальное устройство 4 (свечу за-
жигания) . При взрыве ударная волна воз-
действует на мембрану 9, что приводит
к ее перемещению и выбросу порций ба-
лансирующего вещества. Импульсы высо-
кого напряжения подают на запальное
устройство в момент прохождения легкого
места ротора перед соплом //. Удаление
продуктов сгорания из камеры 6 проис-
ходит по сигналам с БУ на клапан 7.
АБУ с использованием ВГС в качестве
источника энергии применяют в случаях,
когда требуется нанесение больших пор-
ций КМ с невысокой частотой выбросов
или при устранении дисбаланса на оста-
новленном роторе, т. е. когда АБУ исполь-
зуют как инструмент устранения дисба-
ланса.
8.6. АВТОМАТИЧЕСКИЕ
БАЛАНСИРОВОЧНЫЕ УСТРОЙСТВА,
РЕАЛИЗУЮЩИЕ ЛАЗЕРНЫЙ МЕТОД
КОРРЕКТИРОВКИ МАСС
Автоматические лазерные балансиро-
вочные машины (АЛБМ) применяют для
одновременного решения следующих за-
дач [33]:
определения величины неуравновешен-
ной массы (дисбаланса);
нахождение угла дисбаланса;
размерного съема материала в тре-
буемом (тяжелом) месте. АЛБМ можно
классифицировать по результатам работы
лазера (рис. 8.21).
АЛБМ для уравновешенных шаровых
роторов. Функциональная схема такой ма-
шины показана на рис. 8.22. Балансиру-
емый шаровой ротор 1 устанавливают в
Рис. 8.21. Классификация АЛБМ
Рис. 8.22. Функциональ-
ная схема АЛБМ для
уравновешивания шаро-
вых роторов
274
Автобалансирующие устройства
технологическую камеру 2 и приводят во
вращение, например, при помощи электро-
магнитной системы 3. Когда частота вра-
щения ротора достигнет —200 Гц, осу-
ществляют настройку светового луча из-
мерительного лазера 15 на наибольшую
чувствительность. Для этого лазер и при-
емник 9 перемещают в вертикальной плос-
кости с помощью узлов 10 и 14 до со-
прикосновения светового луча с поверх-
ностью балансируемого ротора.
Измерение величины дисбаланса осно-
вано на сравнении двух световых лучей,
поступающих на индикатор 12 после от-
ражения от зеркал 16 и 8 с использова-
нием фильтра 13. В момент измерения
места дисбаланса происходит модуляция
светового луча с частотой прохождения
тяжелого места через точку касания с
лучом света. Фотоприемник 9 преобразует
световой луч в электрический сигнал. Пос-
ле усиления и преобразования в измери
тельном блоке 11 сигналы поступают на
вход блока синхронизации 7. Последний
в момент прохождения тяжелого места
через оптическую ось фокусирующей сис-
темы 4 включает исполнительный импульс-
ный лазер 6. Блок 5 обеспечивает питание
импульсного лазера.
АЛБМ для уравновешивания одно-
опорных роторов. Особенностями одно-
опорных роторов, например роторов гиро-
моторов. являются следующие:
подвижная система на постоянных
магнитах;
наличие всего одной точки опоры в
системе подвеса;
наличие при вращении ротора глав-
ного вектора и главного момента дисба-
лансов.
Функциональная схема АЛБМ показа-
на на рис 8.23. В конструкцию АЛБМ
включен узел для определения величины
дисбаланса. Этот узел выполнен в виде
экрана с щелями 7—9, расположенными
в фокальной плоскости сферического зер-
кала. Зеркало помещают на уравновеши-
ваемом роторе и 'соединяют с помощью
световодов 4 — 6 с фотоумножителями
1 —3, подключенными через релейный блок
26 к синхронизатору 25.
Ротор 12 при вращении опирается на
сферическую пяту 13 и приводится во вра-
щение кольцевым статором 11. Наиболее
массивная часть ротора представляет
собой постоянный магнит, на одной сто-
роне которого (по стрелке А) выполнены
канавки для устранения неуравновешен-
ности, а на другой стороне, непосредст-
венно на поверхности самого магнита, на-
ходится кольцевое сферическое зеркало.
Рис. 8.23. Схема АЛБМ для уравновешивания одноопорных роторов
Автоматические балансировочные устройства, реализующие лазерный метод
275
Массивная часть ротора имеет оптичес-
кую головку. Узкий луч лазера 10 непре-
рывного действия направляется с помощью
зеркала, поставленного под углом 2<р=
= 45°, на сферическое вогнутое зеркало,
выполненное на поверхности массивной
части ротора 12 Отразившись от поверх-
ности сферического зеркала, луч попадает
через тонкую щель 7, 8 или 9 на вход
одного из световодов: 4, 5 или 6.
Если ротор не уравновешен, то ось
его вращения совпадает со щелью 7 или
со щелью 9. Пройдя одну из этих щелей,
световой луч проникает через световод 4
или 6 на фотоумножитель I или 3. Уси-
ленный им сигнал поступает на релейный
блок 26, который управляет через синхро-
низатор 25 и блоки автоматики 22 -24
работой лазера 21, устраняющего неурав-
новешенную массу ротора. Энергия, излу-
чаемая при этом лазером, пропорциональ-
на величине неуравновешенной массы ро-
тора. Заметим, что релейный блок 26 реа-
гирует только на тот сигнал, который со
ответствует большей величине неуравно-
вешенности.
Если же ротор уравновешен, то све
товой луч попадает в щель 8 и световод
5, расположенные на одной оси с вра-
щающимся ротором. Световод 5 соединен
с фотоумножителем 2, сигнал с которого
попадает на тот же релейный блок 26,
оставляющий в этом случае лазер 21 в без-
действии.
Световодов может быть и больше трех,
что увеличивает чувствительность опти-
ческой системы. Наличие ряда световодов
обеспечивает разделение светового сигна-
ла, поступающего со сферического зер-
кала, на сигналы, пропорциональные ве-
личине статической неуравновешенности
в динамическом режиме и соответствую-
#шие уровням необходимой энергии испол-
нительного лазера 21. а это предопреде-
ляет высокую точность и значительную
производительность процесса устранения
дисбаланса.
Часть схемы -АЛБМ, собранная на
блоках 14—17, 19 и 20, служит для устра-
нения неуравновешенности магнитного
диска ротора 12. Исполнительный лазер
18 работает в режиме свободной гене-
рации.
Частота вращения балансируемого ро-
тора не превышает (6 —12)•103 мин'1.
Применение рассматриваемой АЛБМ
позволяет повысить точность и произво-
дительность балансировки примерно в
10 раз по сравнению с механическим устра-
нением дисбаланса.
АЛБМ для уравновешивания осевых
роторов. Эта машина предназначена для
динамического уравновешивания роторов
электрических машин массой от 20 до 200 г
в процессе их вращения в диапазоне час-
тот от 3600 до 15 000 мин*-’.
Оиа состоит из оптического квантового
генератора на твердом теле, механичес-
ких опор для установки’ и закрепления
уравновешиваемого ротора, пневмбсис-
темы, чувствительной избирательной сис-
темы, синхронизатора, блока инициирую-
щего сигнала, электронного тахометра,
следящей системы и модулятора, управля-
ющих энергией и длительностью излуче-
ния лазера пропорционально частоте вра-
щения ротора и величине остаточной не-
уравновешенности Для привода ротора
во вращение применен транзисторный блок
питания. Надежность и безопасность ра-
боты машины обеспечивают система водя-
ного охлаждения оптической головки ла-
зера и система зашиты от поражения вы-
соким напряжением.
Балансировочная машина автомати-
чески обеспечивает определение величины
и места неуравновешенности и одновре-
менно устранение дисбаланса за счет ис-
парения неуравновешенной массы лучом
лазера.
Полное уравновешивание осуществля-
ется за один уставов и пуск ротора на
механических опорах. Пары факела уда-
ляются пневмосистемой в специальное
приемное устройство.
Продолжительность полного цикла
уравновешивания составляет от 1 до 5 мин
в зависимости от первоначальной неурав-
новешенности и требований к величине
остаточного дисбаланса.
276
Автобалансмрующие устройства
Принцип действия автоматической ла-
зерной балансировочной машины можно
пояснить с помощью функциональной
схемы, показанной на рис'. 8.24. Уравно-
вешенный ротор 3 подключается к блоку
питания 4 привода ротора, а затем раз-
гоняется до заданной частоты вращения.
Контроль последней осуществляется элек-
тронным тахометром, состоящим из эта-
лонного генератора //, регенеративного
фильтра и осциллографической трубки,
экран которой выведен на пульт управ-
ления 10.
В момент достижения заданной балан-
сировочной частоты вращения оператор
включает автоматическую систему управ-
ления. При этом сигнал от датчика виб-
рации 5, расположенного на механичес-
ких опорах, поступает на каскад предва-
рительного усиления блока преобразова-
теля 6, с выхода которого преобразован-
ный сигнал с частотой, равной частоте
вращения ротора, поступает на вход син-
хронизатора 8 и одновременно на вход
электронного тахометра, установленного в
блоке управления 10. В схеме осуществле-
на связь выхода синхронизатора с бло-
ком инициирующего сигнала 9, который
непосредственно управляет лампами опти-
ческой накачки лазерной головки 1. В тот
момент, когда тяжелое место ротора про-
ходит через главную оптическую ось ла-
зера, синхронизатор выдает на блок ини-
циирования 9 сигнал, приводящий в дей-
ствие систему оптической накачки лазера.
Излучение лазера с помощью фокусирую-
щей системы 2 концентрируется на поверх-
ности уравновешиваемого ротора 3 по
одной из плоскостей исправления.
В АЛБМ предусмотрено автоматичес-
кое управление энергией излучения лазе-
ра пропорционально величине остаточной
неуравновешенности ротора. Эта сложная
операция осуществляется следящей сис-
темой 7. Компенсационный принцип дей-
ствия системы позволяет осуществить
сравнение амплитудного значения сигна-
ла от дисбаланса и опорного сигнала.
В зависимости от величины остаточно-
го дисбаланса ротора на блок питания
лазера 12 подается управляющий сигнал,
изменяющий величину входного напря-
жения.
Одновременно с циклом излучения оп-
тической лазерной головки начинает дей-
ствовать пневмосистема, состоящая из
сопла А, баллона сжатого воздуха Б и
приемного всасывающего устройства В.
Струя сжатого воздуха, проходящая в
вертикальной плоскости в непосредствен-
Рис. 8.24_ Схема АЛБМ для уравновешивания осевых роторов
Автоматические балансировочные устройства, реализующие лазерный метод
277
ной близости от ротора, защищает фоку-
сирующую оптику от продуктов эрозии и
удаляет факел испаренного материала из
зоны обработки, способствуя также увели-
чению массы, снимаемой за один импульс.
Водяное охлаждение лазерной головки 1
осуществляется от замкнутой системы 13.
Уравновешивание ротора происходит
за несколько циклов излучения лазера.
При достижении уравновешенного состоя-
ния ротора на пульт управления подается
сигнал, свидетельствующий об окончании
цикла балансировки, после чего автомат
отключается.
Технические характерис-
тики АЛВМ
Масса уравновешиваемого
ротора, г............. 20—200
Диаметр ротора, мм . 20- 40
Ширина ротора, мм . . 5—160
Энергия излучения лазе-
ра, Дж..................30 — 40
Частота повторения им-
пульсов, имп/с . . . от 1 до 2-1(Г2
Длительность импульса из-
лучения, мс . ... 0,5—0,8
Фокусное расстояние фоку-
сирующей системы, мм . 45—60
Охлаждение . . Водяное
Оптимальная частота вра-
щения ротора, мин1 7500—15 000
Точность уравновешивания,
мкм .............. ОД — 0,02
Производител ьность.
шт/ч.................10—20
Потребляемая мощность,
кВт ............ .3
Габаритные размеры,
мм . . . 1115X850X950
Масса, кг 450
АЛБМ для высокочастотной баланси-
ровки роторов. Функциональная схема
этой машины показана на рис. 8.25. Ее
особенностью является применение двух
лазеров, снабженных модуляторами доб-
ротности, выполненными в виде враща-
ющихся зеркал.
Применение двух лазеров, устраня-
ющих неуравновешенную массу по двум
плоскостям исправления, вдвое сокращает
время балансировки. Использование мо-
дуляторов позволяет уравновешивать ро-
торы на высоких частотах—вплоть до
30- 103 мин-1.
АЛБМ работает следующим образом.
Балансируемый ротор 4 устанавливают в
механические опоры и приводят во вра-
щение с заданной частотой. При этом дат-
чики, расположенные в опорах, воспри-
нимают вибрацию дисбаланса и преобра-
зуют ее в электрические сигналы.
Рис. 8.25. Схема АЛБМ для уравновешивания скоростных роторов
278
Автобалансирующие устройства
С датчиков вибрации сигнал, пропор-
циональный величине и соответствующий
фазе дисбаланса, поступает на блок 12,
осуществляющий усилие, фильтрацию и
преобразование сигнала в наиболее удоб-
ную для последующих операций форму.
Блок 1 синхронизирует моменты излуче-
ния оптических лазерных головок 2 и 9
с моментом прохождения тяжелого места
соответствующей плоскости исправления
ротора. Одновременно синхронизируются
вращающиеся зеркала 11 и 5, работаю-
щие от приводов 13 и 10. Для надежной
синхронизации зеркал модуляторов осу-
ществлено управление ими с помощью
датчиков угловой скорости 3 и 6» сигнал
от которых сравнивается с фазой полез-
ного сигнала от дисбаланса в этих бло-
ках Лазеры, устраняющие неуравнове-
шенную массу, срабатывают только в том
случае, если сигналы в этих блоках сов-
падают по фазе. Включение лазеров осу-
ществляется через блок питания 7. С по-
мощью описываемой установки роторы
можно уравновешивать на рабочих час-
тотах. АЛБМ имеет хорошо демпфирован-
ную платформу 8, на которой закреплены
все узлы.
Применение двух лазерных головок
и наличие двух каналов усиления и пре-
образования сигнала, удорожает машину,
но дает ‘ей важное преимущество перед
другими типами АЛБМ—одновременное
устранение дисбаланса по двум плоскос-
тям исправления, позволяет обойтись без
блоков исключения влияния сторон, так
как взаимное влияние неуравновешенных
масс не оказывает воздействия на фазовые
соотношения полезных сигналов. Процесс
уравновешивания заканчивается при дос-
тижении области нечувствительности. Точ-
ность уравновешивания во многом опре-
деляется добротностью преобразующей
схемы.
Автоматическая лазерная балансиро-
вочная установка может быть с успехом
использована для окончательной баланси-
ровки на рабочей частоте вращения.
АЛБМ для уравновешивания универ-
сальных роторов. АЛЬМ-2 предназначена
для уравновешивания открытых роторов
массой до 300 г со значительной перво-
начальной неуравновешенностью в широ-
ком диапазоне частот вращения—от 360
до 50 000 мин”1. АЛБМ является удобной
автоматической лазерной балансировоч-
ной машиной для точного приборострое-
ния.
АЛБМ работает следующим образом
(рис. 8.26). Ротор 9, установленный на
рабочих опорах, приводится во вращение
с помощью блока питания привода 10
с пульта управления 17, а затем выво-
дится на заданную частоту вращения в
соответствии с величиной первоначальной
неуравновешенности. При этом выполня-
ется зависимость: чем больше дисбаланс,
тем ниже частота вращения ротора, но
при всех условиях она будет не менее
3600 мин-1.
Контроль за процессом балансировки
ротора обеспечивается оператором с пуль-
та управления при помощи эталонного
генератора напряжений 16. Сигнал от дис-
баланса ротора поступает на чувствитель-
ный пьезодатчик вибрации 11, а с его
выхода —на вход селективного усилителя
12. Последний преобразует полученный
сигнал в синусоидальное напряжение, про-
порциональное величине неуравновешен-
ной массы ротора. С выхода селективного
усилителя сигнал одновременно подается:
через разделительный трансформатор на
блок следящей системы 13, а через фа-
зовращатель—на -вход синхронизатора
15. Выходные каскады синхронизатора сос-
тоят из четырех тиратронов—по числу
импульсных ламп оптической накачки, при-
мененных в резонаторе лазера. С выхода
тиратронов сигнал поступает на блок 14
инициирования поджига импульсных ламп.
Через систему импульсных трансформа-
торов и высоковольтных разделительных
конденсаторов блок 14 связан с импуль-
сными лампами 1 и с высоковольтным
блоком 18 питания лазера. Последний
электрически связан с модулятором све-
тового луча 13. В момент подачи напря
жения на лампы накачки 1 оптической
лазерной головки 2 автоматически пода-
ется также напряжение и на обмотки 3
Автоматические балансировочные устройства, реализующие лазерный метид
1Б ---------*• 17
Рис. 8.26. Схема АЛБМ для уравновешивания универсальных роторов
соленоида модулятора. При тонкой балан-
сировке, когда процесс устранения неурав-
новешенной массы ведется на рабочей час-
тоте вращения ротора, модулятор вклю-
чен в схему работы лазера.
В момент включения лазера в работу
ток подается в секции модулятора и бла-
годаря сильному электромагнитному полю
смещает плоскость поляризации кварце-
вого стержня 4, что является причиной
создания мощных коротких импульсов из-
лучения длительностью I О’4 мс Время
действия электромагнитного поля, завися-
щее от энергии накачки, может быть раз-
личным, что приводит к изменению дли-
тельности воздействия светового луча че-
рез фокусирующую систему 5 на поверх-
ность ротора. Схема управляется в зави-
симости от скорости балансировки: чем
выше частота вращения, тем короче им-
пульс излучения оптической лазерной го-
ловки, охлаждаемой системой 20.
Отличительной особенностью схемы
включения модулятора в цепь балансиро-
вочной машины является наличие блока
управления работой модулятора 19 про-
порционально частоте вращения ротора.
Этот блок включает в себя трансформа-
тор с поперечным магнитным полем. Для
устранения продуктов эрозии предусмотре-
на пневматическая система 6 и 7, рабо-
тающая от баллона сжатого воздуха 8.
АЛБМ с вращающейся оптической
системой. Особенностью данной машины
является то, что в процессе корректиров-
ки массы частота вращения ротора равна
частоте вращения оптической системы.
Схема АЛБМ (рис. 8.27) включает в себя
лазер 3, вращающуюся оптическую сис-
Рис. 8.27. Схема АЛБМ с вращаю-
щейся оптической системой
280
Автобалансирующие устройства
тему 1, привод системы 2, блок 4 управле-
ния частотой вращения оптической си-
стемы. блок 5 синхронизации положения
вращающейся оптической системы относи-
тельно тяжелого места ротора и момента
генерации лазера, соответствующего дан-
ному совпадению, блок 6 управления энер
гией накачки лазера в соответствии с
величиной неуравновешенности. В этой
схеме могут быть использованы твердо-
тельные лазеры.
Тип лазера выбирают в соответствии
с требуемой точностью уравновешивания,
необходимой производительностью балан-
сировки и первоначальной неуравновешен-
ности балансируемых роторов.
Привод вращающейся оптической схе-
мы может быть осуществлен электричес-
ким или пневматическим методом. В пос-
леднем случае целесообразно применять
устройства на газодинамических опорах,
обеспечивающие высокую частоту враще-
ния (20 4- 60)4О3 мин~‘ при отсутствии
вибраций. Данные устройства, как пра-
вило, малогабаритны, имеют высокую
жесткость и надежны в работе.
Использование электрических приво-
дов связано со сложностью обеспечения
вращающейся оптической системе рабочей
частоты вращения при небольших геомет-
рических параметрах самого привода.
После установки уравновешиваемого
ротора в технологическую рамку баланси-
ровочной машины оптическая система и
ротор приводятся во вращение При вы-
ходе ротора и оптической системы на ра-
бочие частоты включаются датчики не-
уравновешенности, сигнал с которых по-
ступает на вход системы автоматической
регулировки усилителя, где осуществля-
ются процесс усреднения амплитуды сиг-
нала неуравновешенности и сужение его
динамического диапазона. Это позволяет
значительно уменьшить фазовую погреш-
ность, возникающую в случае перегруз-
ки частотно-избирательного устройства
при больших величинах динамической не-
ур а вновеш енности.
В частотно-избирательном усилителе
происходит выделение 1-й гармоники из
спектра сигнала неуравновешенности, фа-
за максимума которой определяет поло-
жение тяжелого места. После выделения
1-й гармоники сигнала неуравновешен-
ности происходит его ограничение в уси-
лителе-ограничителе, затем из сигнала в
пороговом устройстве формируются пря-
моугольные импульсы, фронт которых ха-
рактеризует положение нулевой фазДО
неуравновешенности. Затем сигнал посту-
пает на вход управляемой фазосдвига-
ющей цепи, где осуществляется согласо-
вание фазы прямоугольных импульсов с
положением максимума 1-й гармоники
сигнала неуравновешенности с учетом фа-
зового опережения момента инициирова-
ния лазера, определяемого длительностью
его импульса.
Сдвинутые по фазе импульсы усили-
ваются и формируются в цепи формиро-
вателя импульсов и поступают в блок уп-
равления энергией излучения. Так как
частотно-избирательные усилители имеют
фазовую характеристику, изменяющуюся
в зависимости от частоты 1-й гармоники
поступающего на вход сигнала, то изме-
нение частоты вращения уравновешивае-
мого ротора может вызвать в конечном
итоге изменение фазы выходного сигнала,
а следовательно, и фазовую погрешность.
Для компенсации этой погрешности в рас-
сматриваемом устройстве предусмотрена
зависимая от частоты обратная связь;
амплитуда сигнала с выхода цепи обрат-
ной связи пропорциональна частоте 1-й
гармоники сигнала неуравновешенности.
Полученное таким образом аналоговое
компенсирующее напряжение управляет
длительностью фазовой задержки фазо-
сдвигающей цепи, что позволяет добить-
ся компенсации фазовой погрешности,
вызванной частотно-избирательным усили-
телем. При совпадении тяжелого места
ротора с положением фокуса вращающей-
ся оптической системы сигнал с датчика
неуравновешенности поступает на вход
частотно-избирательного усилителя, в ко-
тором происходит выделение 1-й гармо-
Автоматические балансировочные устройства, реализующие лазерный метод
281
ники из спектра сигнала неуравновешен-
ности. Амплитуда получаемого гармони
ческого напряжения характеризует вели-
чину неуравновешенности.
Гармонический сигнал после прохож-
дения через усилитель выпрямляется и
фильтруется, в результате чего выделя-
ется постоянная составляющая, величина
которой пропорциональна амплитуде не-
уравновешенности. Этот сигнал управляет
частотой следования импульсов, генериру-
емых управляемым генератором. При по-
даче сигнала со схемы разрешения на-
качки первый импульс с управляемого ге-
нератора через схему включения накачки
запускает исполнительный механизм. Кро-
ме того, импульсы поступают на делитель
частоты.
Интервал времени между первым и
последним импульсами соответствует вре-
мени накачки, поэтому последний импульс
через схему включения накачки отключит
исполнительный механизм, тем самым за-
кончив процесс накачки. Полученный ин-
тервал времени зависит от амплитуды
входного сигнала, что в конечном итоге
приводит к амплитудной зависимости энер-
гии, излучаемой лазером, от дисбаланса.
По окончании подготовки всей сис-
темы подается сигнал на блок управле-
ния частотой вращающейся оптической
системы. С помощью этого блока осу-
ществляется некоторое рассогласование в
частоте вращения вращающейся оптичес-
кой системы и ротора.
В момент приближения фокуса фоку-
сирующей линзы вращающейся оптичес-
кой системы к месту положения тяжелого
места ротора подается инициирующий им-
пульс на поджиг ламп накачки лазера.
Световой луч, прошедший через вращаю-
щуюся оптическую систему, взаимодей-
ствует с поверхностью ротора, удаляя оп-
ределенную массу металла Далее про-
цесс повторяется, при этом корректируют-
ся амплитуда и фаза входного сигнала
в соответствии с изменением величины
и места положения неуравновешенной
массы.
АЛБМ с корректировкой масс по двум
плоскостям коррекции. Эта АЛБМ отли-
чается от рассмотренной (рис. 8.25) кон-
струкцией вращающейся оптической сис-
темы, которая содержит поворотное зер-
кало 2 (рис. 8.28). С помощью послед-
него изменяется ход луча лазера. Кор-
ректировка масс осуществляется одним ла-
зером, луч которого сначала направляют
на левую плоскость через оптическую сис-
тему, а затем на правую плоскость через
оптическую систему 3. используя поворот-
ное зеркало 2. Вся система собрана на
вращающемся корпусе /.
АЛБМ с лазером, работающим в ре-
жиме свободной генерации. Отличитель-
ной особенностью данной машины явля-
ется использование лазеров, работающих
в режиме свободной генерации.
Структурная схема машины показана
на рис. 8.29. Световой луч лазера 1 воз-
действует непосредственно на балансируе-
мый ротор 3 при отсутствии его вращения.
Кроме того, структурная схема содержит
Рис. 8.28. Схема АЛБМ с кор-
ректировкой масс по двум плос-
костям
Рис, 8.29. Схема АЛБМ с лазером, рабо-
тающим в режиме свободной генерации
282
Автобалансирующие устройства
фокусирующую оптику 2, датчики 4 из
мерения дисбаланса, блок 5 синхрониза-
ции тяжелого места на роторе и момента
излучения лазера, блок 6 управления мощ-
ностью излучения в зависимости от зна-
чения начального дисбаланса. Съем ма-
териала осуществляется на некотором
участке поверхности балансируемого ро-
тора.
АЛБМ с лазером, работающим в режи-
ме непрерывного излучения. Структурная
схема такой АЛБМ приведена на рис.
8.30. В ней наиболее часто применяют
лазеры на смеси газов с СОа, обладающие
повышенной мощностью излучения в уль-
трафиолетовом диапазоне.
Отличительным элементом схемы явля-
ется преобразователь-прерыватель 2 све-
тового луча, синхронизированный со ско-
ростью прохождения тяжелого места ро-
тора 4 через ось светового луча лазера /.
АЛБМ содержит блоки датчиков дисба-
ланса 5, преобразователь сигналов 6, син-
хронизатор 7 и блок питания лазера 8.
Фокусирующую систему 3 выполняют из
кристаллов поваренной соли.
Очевидно, что плотность излучения
таких лазеров недостаточна для мгновен-
ного испарения материала балансируемого
тела. Это является главным препятстви-
ем применения их для целей балансировки.
Энергетические характеристики не удов-
летворяют требованиям, предъявляемым
к световому лучу как к инструменту для
устранения дисбаланса, Временные харак-
теристики могут быть вполне удовлетво-
Рис. 8.30. Схема АЛБМ с лазером, рабо-
тающим в непрерывном режиме излучения
ригельными благодаря применению преоб-
разователей и прерывателей. Как видно,
в принципе можно создать систему с вы-
сокой частотой следования импульсов,
что обеспечивает важные предпосылки
успешного использования АБМ с лазе-
рами, работающими в режиме непрерыв-
ного излучения, для повышения произво-
дительности и точности процесса баланси-
ровки.
АЛБМ с оптическим исключением вли-
яния плоскостей коррекции. Эта машина
автоматически определяет величину и мес-
то дисбаланса и удаляет неуравновешен-
ную массу лучом лазера. Последний спо-
собен исправлять поверхность роторов,
выполненных из различных материалов,
в том числе и с повышенными физико-
механическими свойствами.
АЛБМ состоит из лазера на твердом
теле, механических опор для установки
и закрепления уравновешиваемого ротора,
чувствительной оптической избирательной
системы, синхронизатора, блока иници-
ирующего сигнала, управляющей оптичес-
кой системы, приводящей энергию излу-
чения лазера в соответствие с величиной
остаточной неуравновешенности ротора.
Для привода ротора во вращение и удер-
живания его на технологической скорости
уравновешивания служит транзисторный
блок питания привода ротора. Полное
уравновешивание осуществляется за один
установ и пуск ротора. Надежность и безо-
пасность работы автомата обеспечиваются
системой водяного охлаждения оптичес-
кой головки лазера и системой защиты
от поражения высоким напряжением.
Лазерная балансировочная машина
работает следующим образом (рис. 8.31).
Уравновешиваемый ротор / устанавли-
вают на опорах, механически связанных
с оптическим датчиком измерений дисба-
ланса с помощью тяг 2. С целью повы-
шения чувствительности измерений опти-
ческие датчики выполнены в виде опти-
ческих резонаторов.Фабри-Перро с охва-
тывающими зеркалами. В качестве по-
следних применены оптические зеркала
Автоматические балансировочные устройства, реализующие .налсрпии
Рис. 8.31. Схема АЛБМ с оптическим исключением плоскостей коррекции
4 с диэлектрическим покрытием. Для уси-
ления генерации выделенных частот дис-
баланса балансируемого ротора служат
блоки питания 3.
Для устранения влияния сторон ис-
правления в оптическом диапазоне при-
меняют систему из поворачивающихся
на 90° полупрозрачных пластин 5 с чет-
вертьволновым диэлектрическим покры-
тием. Через входные фильтры и щелевые
диафрагмы оптический сигнал от полу-
прозрачных пластин поступает на вход
фотоумножителей 6.
Оптический сигнал преобразуется в
электрический, усиливается блоками 7—
9 и подается с блоков 9 на вход синхро-
низатора //. Блок синхронизатора обес-
печивает одновременность срабатывания
исполнительного лазера 18 и модуля-
тора 10. Для этого применяют блок сов-
падения сигналов 12, выполненный по ком
пенсационной схеме. На его входы посту-
пают сигналы от делителя обратной связи
блоков питания 16, 17 импульсного ла-
зера, выпрямителя 15, блока поджига 13
и накопителя 14.
Режим балансировки после включения
осуществляется автоматически. Но воз-
можно и ручное управление — с помощью
пульта оператора, на который вынесены
ручки регулировки частоты вращения ро-
тора и модулятора, а также кнопки и
приборы, управляющие режимом работы
оптических датчиков.
Блок накопителя имеет кнопочное уп-
равление. После установки ротора на ме-
ханических опорах автомат Считается го-
товым к работе.
Уравновешивание роторов, враща-
ющихся на рабочих частотах, осуществля-
ется импульсным лазером, работающим
с частотой от 5 до 20 Гц. При этом неурав-
новешенная масса испаряется малыми
порциями (до 1 мг) с высокой степенью
точности, что позволяет достигать точ-
ности уравновешивания 0,001 мкм на ро-
торах массой до 500 г. Процесс уравно-
вешивания отнимает от 0,5 до 2 мин в
зависимости от величины первоначальной
неуравновешенности.
Настройку АЛБМ на заданный типо-
размер балансируемого ротора выполняют
по эталонному ротору. Режим сохраняется
до окончания балансировки всей партии
роторов.
284
Автобалансирующие устройства
Технические характерис-
тики АЛБМ
Масса уравновешиваемого
ротора, г . . ... 10 — 500
Диаметр ротора, мм . . 10 — 60
Ширина ротора, мм ' . . 5 180
Энергия излучения лазера,
Дж . . . . . 1,5 — 3
Частота повторения импуль-
сов. имп/с............20
Длительность импульса из-
лучения, мс...........02
Фокусное расстояние фоку-
сирующей системы, мм . 20—80
Охлаждение .... Водяное
Оптимальная частота вра-
щения ротора, мин . (24Ч-125)-103
Точность уравновешивания,
мкм ..................0,5 — 0.02
Производит ел ьность,
шт/ч .................30
Потребляемая мощность,
кВт ...................3
Габаритные размеры,
мм . . . .... 1115X760X450
Масса, кг 360
АЛБМ с модулятором добротности.
Структурная схема и принцип работы этой
машины аналогичны приведенной на рис.
8.24.
АЛБМ с электрофизическим улучше-
нием качества поверхности. Отличием дан-
ной машины от рассмотренных выше яв-
ляется совмешение воздействия лазерного
луча и разряда электрической дуги на
поверхность балансируемого ротора. При
этом ударная волна, образованная элек-
трическим пробоем вблизи поверхности ро-
тора, действует в поперечном направлении
относительно направления лазерного луча.
Этим достигается воздействие электричес-
кой искры на продукты эрозии.
Схема электрофизической части АЛБМ
(рис. 8.32), работающая по этому прин-
ципу, состоит из двух электродов 1 и 2,
расположенных под углом к поверхности
балансируемого тела 3 с таким расчетом,
чтобы между ними мог пройти лазерный
луч. Расстояние h от электродов до по-
верхности ротора подбирают эксперимен
тально, добиваясь получения наибольшего
эффекта от применения устройства Элек-
троды соединены с выходными клеммами
разрядного контура 4, состоящего из RC
Рис. 8.32. Схема электро-
физической части устрой-
ства АЛБМ
Рис. 8.33. Схема устройства для улучшения
качества поверхности, применяемого в АЛБМ
цепочки и блока питания 5. В процессе
уравновешивания ротора с применением
этого способа механизм электроразряда
действует автоматически.
Когда продукты эрозии, испаряющиеся
с поверхности ротора под действием ла-
зерного луча, достигают электродов, про-
исходит замыкание электрической цепи.
Электрическая искра, проскакивая между
электродами I и 2, деформирует факел
испаряющегося материала, и он отклоня-
ется от своего первоначального направ-
ления. Возникающая ударная волна воз-
действует также на зону облоя и сбра-
сывает часть образовавшегося облоя с по-
верхности ротора.
АЛБМ с пневматическим улучшением
качества поверхности. В машине совме-
щен процесс испарения материала (лу-
чом лазера) с процессом воздействия струи
сжатого воздуха из сопла / (рис. 8.33)
давлением Р (направляемой перпендику-
лярно лазерному лучу), расположенного
Автоматические и полуавтоматические станки
в непосредственной близости (//, Л) от
поверхности балансируемого тела 2. Опти-
ческую часть данного устройства можно
включать практически во все АЛБМ, рас-
смотренные выше.
8.7. АВТОМАТИЧЕСКИЕ
И ПОЛУАВТОМАТИЧЕСКИЕ СТАНКИ
Автоматические и полуавтоматические
балансировочные станки широко применя-
ют в условиях массового производства,
когда требования к точности и произво-
дительности позволяют сконцентрировать
операции измерения и коррекции дисба-
ланса на одной рабочей позиции при их
последовательном проведении. В полуав-
томатах, как правило, вне цикла остаются
переходы, связанные с загрузкой и раз-
грузкой станка, а иногда и ориентация
балансируемой заготовки относительно ин-
струмента. Эти переходы могут быть ме-
ханизированы или выполняться вручную.
В автоматах весь цикл, включая загрузку
и разгрузку, выполняется без вмеша-
тельства оператора. Автоматические и
полуавтоматические балансировочные
станки МСПО им. Октябрьской революции
классифицируют по следующим при-
знакам:
по массе балансируемых роторов (до
10. 30 и 100’кг);
по положению оси балансируемых ро-
торов: вертикальные, горизонтальные;
по степени автоматизации (полуавто-
маты, автоматы);
по положению осей шпинделей инстру-
ментальных головок (вертикальное, го-
ризонтальное) ;
по виду системы координат коррекции
дисбаланса на балансируемом роторе
(полярная, фиксированная).
Каждый станок создают для баланси-
ровки конкретного ротора. Требования по
производительности, точности, методу кор-
рекции, условиям встраиваемости в тех-
нологический поток и т. д. согласовыва-
ют на стадиях выдачи заявки и разра-
ботки технического задания и предло-
жения.
Автоматы и полуавтоматы с верти-
кальной осью вращения. Эти станки пред-
назначены в основном для статической
балансировки деталей и роторов, имеющих
форму диска с отношением высоты к диа-
метру менее 0,3. К ним относят шкивы,
шестерни, маховики, диски сцепления, по-
лумуфты. тормозные барабаны и пр.
Технические характеристики станков
Модель 1 Модель 2 Модель 3
Наибольшая масса ба- лансируемого ротора,
кг Частота вращения. 10 30 100
мин-1. 1200 900 600
900 600 360
Точность балансиров- ки, г-мм/кг . . . Производител ьность, шт/ч . ... Мощность привода 600 360 10 20—30
вращения, кВт . . Г абаритные размеры (ориентировочно), 3 3 4
мм Масса (ориентировоч- 4500X 4000X 2800
но), кг ... 4000 4000 | 5000
Автоматический станок может иметь
одну из указанных частот вращения шпин-
деля. Ее устанавливают с учетом требуе-
мой точности балансировки и особеннос-
тей конструкции балансируемого ротора;
все параметры и размеры станков уточ-
няют прн заказе оборудования.
На рис. 8.34 и 8.35 показаны полу-
автоматы с вертикально и горизонтально
расположенной сверлильной головкой без
вынесенного электро- и гидрооборудова-
ния. Эти полуавтоматы обеспечивают ав-
томатическое измерение и запоминание
параметров дисбаланса, позиционирова-
ние ротора, коррекцию дисбаланса по ре-
зультатам измерений и контроль ка-
чества балансировки.
Ротор 2 пневмоподъемником 3 уста-
навливают на оправку шпинделя станка,
затем он автоматически зажимается. Пос-
ле этого шпиндель приводится во враще-
ние, измеряется дисбаланс; затем шпин-
286
Автобалансирующие устройства
Рис. 8.34. Полуавтомат для статической ба-
лансировки с вертикальной сверлильной го-
ловкой
Рис. 8.35. Полуавтомат для статической
балансировки с горизонтальной сверлильной
головкой
дель останавливается и ротор ориентиру-
ется тяжелым местом против инстру- '
ментов сверлильной головки 1. Сверлиль- |
ная головка автоматически корректирует
в нужном месте массу ротора без снятия
его с оправки. Это достигается примене-
нием специального разгрузочного устрой-
ства, исключающего передачу усилий ре-
зания на опоры шпинделя. Полуавтоматы
оснащены системой отсоса стружки.
Точность балансировки может дости-
гать 10 г-мм/кг остаточного удельного
дисбаланса ротора. При этом она в боль-
шой степени зависит от точности выпол-
нения базирующих поверхностей как ро-
тора, так и оправки шпинделя.
Наладку производят с помощью специ-
ально изготовленного и поставленного
вместе со станком тарировочного ротора
в последовательности, определяемой ин-
струкциями по наладке и эксплуатации
станка. Дополнительной операцией по на-
ладке является согласование масштабов
автоматического измерения дисбаланса и
его автоматической коррекции.
Балансировочный автомат мод. МС
9294 для дисковых деталей с вертикаль-
ной сверлильной головкой и автоматичес-
ким загрузчиком-манипулятором показан
на рис. 8.36.
Автоматические и полуавтоматические станки
287
Автоматы и полуавтоматы с горизон-
тальной осью вращения. Они предназна
чены для динамической балансировки ши-
рокого круга роторов, охватывающего
практически все отрасли машиностроения
с массовым характером производства
(шпиндели станков и силовых головок,
роторы электродвигателей и генераторов,
коленчатые валы двигателей внутреннего
сгорания и пр.). Многообразие роторов,
особенности их конструкции и требования
к точности не позволяют свести известные
технические решения в единую классифи-
кацию по определяющим признакам. Стан-
ки могут быть только измерительными или
иметь средства для коррекции дисбаланса.
Станки для балансировки коленчатых
валов изготавливают автоматизирован-
ными или полуавтоматическими. Отдель-
ные операции и переходы, например опре-
деление величин и углов дисбалансов в
плокостях коррекции, позиционирование,
коррекция дисбаланса, могут выполняться
автоматически. Для коленчатых валов
V-образных двигателей внутреннего сго-
рания при их балансировке на станках
общего назначения требуется специальная
технологическая оснастка в виде ком-
плекта сменных грузов, имитирующих
шатунно-поршневую группу, которая на
полуавтоматах и автоматах заменена
системой постоянных масс («контрвал»),
вращающихся синхронно и синфазно с
балансируемым валом.
Каждый станок предназначен для ба-
лансировки коленчатого вала конкретного
типоразмера. При заказе оборудования
оговаривают его параметры и характе-
ристики (точность, производительность)
и, при необходимости, обусловливают
встройку в действующий технологический
процесс.
Коленчатый вал уравновешивают за
один, два или несколько пусков с после-
дующим контролем остаточного дисбалан-
са. Число циклов зависит от соотношения
начального и допустимого дисбалансов и
от конструкции самого коленчатого вала.
Последний может балансироваться на спе-
циальных автоматах в сборе с маховиком
и дисками сцепления.
Рис. 8.37. Полуавтомат для динамической
балансировки коленчатых валов
На рис. 8.37 показан автоматизиро-
ванный станок для динамической балан-
сировки коленчатого вала, оснащенный
сверлильными головками для коррекции
дисбаланса в плоскостях противовесов.
Станок обеспечивает автоматическое из-
мерение и запоминание параметров дис-
баланса и коррекцию дисбаланса по ре-
зультатам измерений. Ротор /, установ-
ленный на опорах 4, приводят во вращение
и определяют величины и углы дисбалан
сов в плоскостях коррекции коленчатого
вала по сигналам датчиков, обработанных
в измерительном пульте 5. Результаты из-
мерения запоминают и производят кор-
рекцию дисбаланса левой 2 и правой 3
сверлильными головками без снятия ба-
лансируемого вала со станка. Усилия свер-
ления воспринимают опоры 7 и передают
их непосредственно на станину и основание
станка 6, предохраняя тем самым от сило-
вых перегрузок механическую колебатель-
ную систему. Точность балансировки сос-
тавляет 5—10 г-мм/кг.
Наладку станка проводят с помощью
специально изготовленного и поставляемо-
го вместе со станком тармровочного ро-
тора. Наладка включает установку опор,
привода и силовых головок в позиции, со-
288
Автобалансирующие устройства
ответствую щие геометрическим размерам
коленчатого вала, компенсацию взаимного
влияния плоскостей коррекции, установ-
ление масштабных соотношений между
дисбалансами в каждой из плоскостей
коррекции и выходными сигналами изме-
рительной системы, т. е. те же операции,
что и при наладке специальных станков и
общего назначения. Дополнительно сле-
дует согласовать масштабы автоматичес-
кого измерения дисбаланса и его кор-
рекции.
Технические характеристи-
ки станка
Масса балансируемого ро-
тора, кг...............До 150
Частота вращения, мин-1 250— 600
Точность балансировки,
г-мм/кг . . ... 5- 10
Производится ьность, шт/ч 10—20
Мощность привода враще-
ния ротора, кВт . . . 2,2
Габаритные размеры (ори-
ентировочно), мм . . 2500X1000X 2500
Масса (ориентировочно),
кг..................... 5000
Частоту вращения ротора из указан-
ного диапазона назначают, исходя из тре-
буемой точности балансировки и особен-
ностей конструкции коленчатого вала. Все
данные уточняют при заказе и разработке
конкретного оборудования.
Полуавтомат для динамической балан-
сировки роторов турбокомпрессоров мод.
ЭЗ-145 разработан НПО «Армстанок».
Особенность станка—коррекция дисба-
ланса методом виброударного шлифования
(ВУШ). Сущность метода заключается в
обеспечении кратковременного контакта
абразивного инструмента с тяжелым мес-
том плоскости коррекции ротора путем
вибрационного воздействия на ротор или
инструмент в направлении оси ротора с
частотой его вращения.
Полуавтомат состоит из трех отдель-
но выполненных частей: балансировочного
станка, измерительного устройства и пуль-
та системы автоматического управления.
Конструктивная схема станка приведена
на рис. 8.38. Станок имеет колебательную
систему с тангенциальным ременным при-
водом, две шлифовальные головки 6, осе-
вой привод вращения ротора 5, электро-
динамический вибратор 1 и механизм авто-
матической подачи шлифовальных головок
(не показан). Особенностью конструкции
станка является связь колебательной сис-
темы 3 с электродинамическим вибратором
1 с помощью упругого стержня 2, который
позволяет передавать осевое колебатель-
ное движение, не ограничивая степеней
свободы колебательной системы.
Рис. 8.38. Полуавтомат для динамической балансировки роторов турбокомпрессоров методом
виброударного шлифования мод. ЭЗ-145
Автоматические и полуавтоматические станки
289
Ротор устанавливают на колебатель-
ную систему 3 и приводят во вращение
от тангенциального ременного привода.
После измерения и запоминания величины
и фазы дисбаланса в двух плоскостях
коррекции муфта 4 осевого привода 5
осуществляет зацепление с ротором, обе-
спечивая его вращение при корректировке.
Затем на вибратор / подают синусоидаль-
ный сигнал с постоянной составляющей,
отчего ротор смещается в сторону левой
плоскости коррекции и вступает в вибро-
ударное взаимодействие с левой шлифо-
вальной головкой 7. Длительность БУШ
устанавливают пропорционально величине
дисбаланса. Затем ротор получает осевое
перемещение в сторону правого торца; на
вибратор поступает сигнал синусоидаль-
ной формы, соответствующий по фазе
дисбалансу в правой плоскости кор-
рекции. Цикл измерение—корректировка
повторяют до получения заданного зна-
чения остаточного дисбаланса, после чего
станок автоматически отключается.
В качестве инструмента на станке
можно использовать бесконечную абра-
зивную ленту или абразивные круги Вы-
сокоскоростные шлифовальные головки
расположены у торцов ротора с опреде-
ленным зазором, величина которого (при
использовании абразивных кругов) обес-
печивается устройством для правки кру-
гов и механизмом автоматической подачи
шлифовальных головок. Все выполняемые
операции, кроме загрузки и разгрузки
станка, полностью автоматизированы.
Технические характерис-
тики станка мод. ЭЗ-145
Масса балансируемого ро-
тора, кг..............1,0
Частота вращения при ба-
лансировке, мин-1 . . 1500
Точность балансировки,
г-мм/кг 2,0
Средняя производитель-
ность (при начальном дис-
балансе 200 г-см/кг),
шт/ч . ..........20
Скорость корректировки
дисбаланса, г-мм/(кг-с ’) 4
Скорость резания при
ВУШ, м/с . . 70
10 Зак. 1641
Максимальное усилие воз-
буждения, Н .... 100
Число электродвигателей,
шт.....................5
Потребляемая мощность,
кВт .2,0
Габаритные размеры (без
пульта управления*), мм 1250X700X1200
Масса, кг . 500
Взрывное нанесение балансируемого
расплава. Разработанный в НПО «Арм-
станок» способ взрывного нанесения ба-
лансирующего расплава на детали при
их вращении-—электрофизическая балан-
сировка (ЭФБ) позволяет совместить во
времени и автоматизировать операции
измерения вектора дисбаланса и его кор-
ректировку с высокой точностью незави-
симо от опыта и квалификации баланси-
ровщика.
На рис. 8.39 приведена схема ЭФБ.
Тонкую металлическую проволоку 1 уста-
навливают в зазоре электромагнита 2 меж-
ду контактами А и Б источника тока 4
против балансируемого ротора 5. Накоп-
ленная в батарее конденсаторов источника
4 энергия через ключ 3 н контакты А и Б
подается на проволоку. Когда легкое место
вращающегося ротора находится против
зазора электромагнита, измерительным ус-
тройством подается команда на ключ 3,
который, замыкая емкость источника на
проволоку, вызывает ток разряда /р, под
действием которого участок проволоки
Рис. 8.39. Схема взрывного нанесения
балансирующего расплава
290
Автобалансирующие устройства
между контактами А и Б быстро (за 30—
50 мйс) нагревается до температуры
1400—1500°С. Электродинамические си-
лы, действующие на проволоку с током
в магнитном поле, сообщают ускорение
участку проволоки, и образовавшиеся в
результате взрыва проволоки жидкие час-
тицы со скоростью 70 м/с вылетают из
зазора электромагнита на вращающийся
ротор и сцепляются с его поверхностью
на легком месте. Нанесение корректирую-
щей массы продолжается до достижения
требуемого остаточного дисбаланса.
В реализующих ЭФБ станках-полуав-
томатах механизм корректировки дисба-
ланса выполнен в виде отдельного узла —
монитора (рис. 8.40), представляющего
собой автономное устройство, осуществля-
ющее циклическую подачу проволоки в
зазор электромагнита, ее взрыв и выброс
образовавшихся расплавленных частиц.
Технические характеристики мониторов НПО
«Армстанок»
Тип взрываемой прово-
локи ...............Проволока медная,
голая, тип ММ,
ГОСТ 2112—79*
Диаметр проволоки,
мм . . .... 0,1 —0,3
Длина взрываемого участ
ка, мм . .... 15
Напряжение технологи-
ческого источника, В 80 - 200
Частота нанесения,
мин-1 . . . . 600
П рои'зводител ьн ость,
г-мин-1 ...... 0,6—5,4
Плотность нанесенного
слоя, г/см'* . . . 8,1
Предельная прочность
сцепления, кг/см .
со сталью . . 550
с алюминием . 450
с медью .... 320
Широкий диапазон производитель-
ности позволяет использовать один и тот
же монитор для балансировки роторов
массой 0,2—10 кг.
Для агрегатного построения станков
разработаны отдельные блоки: технологи-
ческого напряжения, измерения дисбалан-
са, управления монитором, зарезонансных
колебаний системы с приводом баланси-
руемого изделия и т. п.
На рис. 8.41 приведена структурная
схема станка для динамической баланси-
ровки взрывными проволочками. Две ав-
тономные системы измерения дисбаланса
и нанесения корректирующей массы поз-
воляют вести балансировку одновременно
в двух плоскостях коррекции. В станках
для статической балансировки применены
одна система измерения и одно устройство
(для крупных изделий с большими началь-
ными дисбалансами—два) нанесения кор-
ректирующей массы.
Для исключения случайного механи-
ческого повреждения корректирующего
Рис. 8.41. Структурная схема станка для динамической балансировки взрывными про-
волочками
Автоматические и полуавтоматические станки
Технические характеристики специализированных
балансировочных полуавтоматов НПО сАрмстаиок»
для динамической и статической балансировки изделий
Наименование параметров -
ЭЗ-105
Параметры ротора:
масса, кг 0,5- 3
диаметр, мм 40- 100
длина, мм Точность балансировки, 100 — 350
мкм Производится ьность. I 10
шт/ч Частота вращения ротора ври балансировке, 30- 60
мин-1 . . 2160
Питание станка от сети переменного тока: 50
частота, Гц’ . .
напряжение, В Потребляемая• мощность. 380
кВ • А 1,0
Габаритные размеры, мм 1400X 800X1400
Масса, кг 500
Модель стайка
ЭЗ-139 ЭЗ-156 ЭЗ-175
0,2—0,8 0,2 -10 0,1— 1
30—60 30 150 40— 120
70—150 70—300 10—40
1 — 10 0,5— 10 4 10
60—150 30- 150 100
2160 2160 1200
50 50 50
380 380 380
0,8 1,0 0,6
1200X700X1250 1250X 700X1200 800Х 700Х
Х1200
400 500 300
слоя расплава и улучшения внешнего ви-
да изделии расплав наносится в специаль-
ные канавки на периферии или торцах
балансируемых изделий. В роторах асин-
хронных электродвигателей они выполнены
в короткозамыкающих кольцах на тор-
цах роторов. Для получения нормальной
сцепляем ости слоя расплава со стенками
канавки онн должны быть чистыми и обез-
жиренными.
Специализированный полуавтомат мо-
дели ЭЗ-105 предназначен для динами-
ческой балансировки роторов асинхронных
электродвигателей массой до 3 кг (рис.
8.42). Область его применения—электро-
техническая и приборостроительная про-
мышленность с крупносерийным и мас-
совым производством Цикл работы станка
автоматический (кроме установки и снятия
ротора). Балансировка до требуемой точ-
ности осуществляется за один пуск.
Станок состоит из зарезонансной ко-
лебательной системы, содержащей плат-
форму с опорами для ротора, установлен-
10*
ными на 4-х вертикальных стержнях, сле-
дящего привода в виде управляемого ду-
гового статора, поддерживающего пос-
тоянную скорость вращения роторов раз-
ных диаметров, мониторов с механизмом
их перемещения и электронной системы,
Рис. 8.42. Станок 33-105
292
Автобалансирующие устройства
содержащей блоки измерения дисбаланса
и управления процессом балансировки,
управляемого привода, технологического
напряжения, а также схему релейно-кон-
тактной автоматики. Для предотвращения
касаний ротора с дуговым статором по-
следний жестко крепится на платформе.
Станок имеет сварную станину, на ко-
торой смонтированы механические узлы:
мойиторы (левого и правого исполнения)
с механизмом их перемещения, колеба-
тельная система с приводом и пульт уп-
равления. Блоки электроники размещены в
станине. Мониторы, кроме связанного с
циклом работы станка предельного пере-
мещения влево и вправо от ротора, имеют
также установочные движения в верти-
кальном направлении и поворота вокруг
оси, которые позволяют установить их от-
носительно ротора в зависимости от его
размеров. Роль оператора сводится к ус-
тановке ротора на станок и его снятию,
что обеспечивает возможность применения
многостаночного обслуживания.
Специализированный полуавтомат мо-
дели ЭЗ-139 предназначен для автома-
тической динамической балансировки ро-
торов массой до 0,8 кг.
Область применения—электротехни-
ческая, приборостроительная, машино-
строительная и другие промышленности с
крупносерийным и массовым производ-
ством. Основные узлы станка и конструк-
тивная компоновка такие же, что и у стан-
ка мод. ЭЗ-105.
специализированный полуавтомат
мод. ЭЗ-156 предназначен для автомати-
ческой динамической балансировки рото-
ров асинхронных и коллекторных элек-
тродвигателей и других изделий массой
0,2—10 кг (рис. 8.43). Область приме-
нения —электротехническая, приборостро-
ительная. машиностроительная, авиаци-
онная промышленности. В этом станке,
как и в первых двух, принята замкнутая
система автоматической балансировки при
вращении ротора. Две автономные систе-
мы автоматической балансировки, рабо-
тающие по сигналам датчиков дисбалан-
сов в двух плоскостях, позволяют вести
Рис. 8.43. Станок ЭЗ-156
балансировку в двух плоскостях коррек-
ции.
В конструкции станка учтен опыт эк-
сплуатации станков моделей ЭЗ-105 и
ЭЗ-139. Расширен вес’овой диапазон балан-
сируемых изделий от 0,2 до 10 кг. Для
изделий массой более 3 кг с целью повы-
шения производительности на отдельных
предприятиях применяют комбинирован-
ный способ балансировки — сверлением
(грубо—до 2—3 допусков) снижают уро-
вень начального дисбаланса, а на станке
производят окончательную балансировку
до требуемой точности.
Станок состоит из зарезонансной плат-
формы с опорами скольжения или каче-
ния для установки ротора, привода балан-
сируемого ротора (тангенциальный ремен-
ный привод, установленный снизу ротора),
мониторов с механизмом их перемещения,
электронной системы, содержащей блоки
технологического напряжения, измерения
дисбаланса и управления процессом, а
также релейно-контактную автоматику.
Как и в предыдущих станках, выбор ко-
лебательной системы и диаметр взрыва-
емой проволоки зависят от конструкции,
размеров деталей и предъявляемых к ним
технических требований.
Станок работает следующим образом.
После установки на опоры колебательной
системы балансируемого ротора нажи-
мают кнопку пуска, отодвинутые в край
Автоматические н полуавтоматические станки
293
ние исходные положения мониторы пере-
мещаются к ротору и останавливаются
на расстоянии 3—4 мм от поверхности
нанесения. Одновременно с вращением де-
тали начинается процесс корректировки
дисбаланса. По достижении требуемой
точности, контролируемой по сигналам
датчиков дисбалансов, процесс корректи-
ровки прекращается, мониторы возвраща-
ются в исходные положения и освобож-
дается зона обслуживания станка. После
установки новой детали цикл повторяется.
Специализированный полуавтомат
мод. ЭЗ-175 предназначен для автомати-
ческой балансировки дисковых деталей,
например маховиков магнитофонов (рис.
8.44). Применение станков позволило ав-
томатизировать ручной труд, повысив про-
изводительность в 3—4 раза, а точность
балансировки в 2 раза.
Станок состоит из зарезонансной ко-
лебательной системы с опорой для уста-
новки балансируемого ротора, ось кото-
рого расположена горизонтально, узла
привода (накидной ремень), монитора и
электронной системы. Движение в вер-
тикальном направлении и поворот мони-
тора определяются вручную. Для уста-
Рис. 8.44. Станок ЭЗ-175
новки и снятия детали колебательная сис-
тема имеет возможность поворота вокруг
вертикальной оси на 90°. Цикл работы
станка автоматический, кроме установки
и снятия детали. Балансировка до тре-
буемой точности осуществляется за один
пуск.
Специальный балансировочный полу-
автомат модели ЭЗ-181 предназначен для
автоматической статической балансировки
дисковых деталей (ограночных дисков)
массой до 10 кг при их вращении (рис.
8.45). Большая масса балансируемых де-
талей обуславливает необходимость на-
несения Значительной массы корректирую-
щего расплава, поэтому в рассматрива-
емом станке, в отличие от станка моде-
ли ЭЗ-175, установлены два монитора.
Ось балансируемого диска вертикальна,
зажим детали на шпинделе—при помощи
конической втулки. Нанесение расплава
осуществляется в канавку, выполненную
на периферии балансируемого изделия.
Электрохимическая балансировка су-
ществует для изделий, при балансировке
которых не допускается ни сверление (тон-
костенность), ни добавление корректирую-
щей массы. Для таких изделий в НПО
«Армстанок» разработан метод электрохи-
мической балансировки (ЭХБ), сущность
которого заключается в управляемом ло-
кальном анодном растворении металла с
«тяжелого места». В плоскостях коррекции
Рис. 8.45. Станок ЭЗ-181
294
Автобалансирующие устройства
вращающегося ротора, подключенного к
отрицательному полюсу источника, с за-
зором 0,3—0,5 мм установлены электроды
Э1—Э4 (рис. 8.46), подключенные к по-
ложительному полюсу источника; через
зазоры непрерывно подается электролит.
Когда при вращении ротора его тяжелое
место находится под электродом, по сигна-
лу от датчиков VD\ и УО2 поочередно
открываются тиристоры VTt и VTS, про-
пуская ток съема через соответствующие
электроды 51 и Э2. Конденсатор связи
Ci при отпирании очередного тиристора
запирает предыдущий. Аналогично рабо-
тают тиристоры УТз и УТ4 в другой плос-
кости коррекции. Между соответствующим
электродом и деталью протекает электри-
ческий ток длительностью менее полуобо-
рота ротора и происходит элементарный
съем материала ротора (анодное раство-
рение) в плоскости коррекции. Этим обес-
печивается локальный съем металла не-
большими порциями за каждый оборот.
В НПО «Армстанок» создан ряд стан-
ков для-электрохимической балансировки
роторов при их вращении.
Специальный полуавтомат модели
ЭЗ-125 предназначен для автоматической
балансировки крышек масляных цент-
рифуг.
Специальная балансировочная уста-
новка модели 33-102 предназначена для
Технические характеристики полуавтоматов
для электрохимической балансировки НПО
«Армстанок»
Наименование параметров Модель станка
ЭЗ-125 ЭЗ-102
Масса ротора, кг Диаметр ротора. 0,3- 0,2 1.1
мм 100—200 110
Длина ротора, мм Точность баланси- 200 200
ровки, мкм . . . Точность измерения 5 1
дисбаланса, мкм . Производится ьность, — 0.3
шт/ч . . Частота вращения ротора при баланси- 15 — 20 —
ровке, мин1 Напряжение тока технологического 2400 —
съема, В Питание станка от сети переменного тока: 20 10; 15
частота, Гц 50 50
напряжение, В Потребляемая мощ- ность суммарная. 380 380
кВА ... Г абаритные разме- 3 15
ры, мм ... . Без бака 1350Х450Х Х1325 С баком 3700Х 160GX XI700
Масса, кг ... 600 5000
Рис. 8.46. Схема электрохимической балан-
сировки
динамической электрохимической баланси-
ровки роторов турбокомпрессора ТКР-11Н.
Балансировочный цикл состоит из двух
раздельных операций—измерения и кор-
ректировки. Поэтому и установка также
имеет две позиции—измерения дисбалан-
са и его корректировки. Для измерения
вектора дисбаланса установленный на опо-
ры платформы колебательной системы ро-
тор разгоняется до рабочих частот. Ко-
лебания платформы через два горизон-
тальных стержня передаются вибродатчи-
кам, сигналы которых, преобразованные в
сигналы дисбаланса, фиксируются и вво-
дятся в запоминающий блок измеритель-
ного прибора. Фазы дисбаланса опреде-
ляются фазодатчиком относительно опор-
ного сигнала—метки на роторе.
Автоматические линии, участки и гибкие производственные системы
295
Корректировка дисбалансов произво-
дится электрохимическим способом в ка-
тодном устройстве одновременно в двух
плоскостях коррекции. Съем металла в
каждой плоскости определяется величиной
тока и временем его пропускания через
электроды в каждой плоскости, контроли-
руемыми автоматически в соответствии со
значением измеренного дисбаланса.
8.8. АВТОМАТИЧЕСКИЕ ЛИНИИ, УЧАСТКИ
И ГИБКИЕ ПРОИЗВОДСТВЕННЫЕ
СИСТЕМЫ
В ряде отраслей народного хозяйства,
характеризующихся крупносерийным и
массовым производствами и большим объ-
емом выпуска продукции, таких, как авто*
мобильная и электротехническая, сельско-
хозяйственное машиностроение, широко
применяют автоматическое оборудование
для статической или динамической балан-
сировки деталей, «як одной из финишных
операций при их изготовлении.
Состав автоматического оборудования,
его компоновочное решение во многом за-
висят от конструкции балансируемых ро-
торов, метода коррекции дисбаланса, зало-
женного в конструкцию и технологический
процесс, требуемой точности, производи-
тельности, соотношений наибольшего воз-
можного начального и допустимого дис-
балансов, условий введения линии в кон-
кретный технологический цикл и т. п.-Каж-
дую автоматическую линию или участок
создают на определенный балансируемый
ротор. При заказе и в начальных стадиях
разработки уточняют его параметры и ус-
ловия встраиваемости в действующий тех-
нологический поток заказчика.
Один из наиболее типичных роторов,
балансируемых на автоматических линиях
н участках в условиях массового произ-
водства,— коленчатые валы двигателей
внутреннего сгорания.
Автоматические линии. На рис. 8.47
показана автоматическая линия для ди-
намической балансировки коленчатого
вала массой 40 кг V-образного двигателя
внутреннего сгорания.
Коленчатый вал транспортером 9 по-
дают на балансировочный станок 8 пер-
вичного цикла уравновешивания. Осу-
ществляется определение величины и угла
дисбаланса в каждой из двух плоскос-
тей коррекции. Полученные данные запо-
минаются, а вал подается на корректи-
рующий станок 7, где механической обра-
боткой уменьшается • дисбаланс в левой
плоскости коррекции, считая по направле-
нию движения линии. Коррекция дисба-
ланса в правой плоскости проводится на
станке 6. Этим завершается первый цикл
уравновешивания. Однако требуемая точ-
ность балансировки коленчатого вала мо-
жет быть еще не достигнута. Тогда про-
водят второй цикл, который начинается
Рис. 8.47. Планировка автоматической линии для динамической балансировки колен-
чатого вала V-образного двигателя внутреннего сгорания
296
Автобалансирующие устройства
с подачи коленчатого вала на баланси-
ровочный станок 5 и измерения на нем
величин и узлов дисбаланса в каждой
из плоскостей коррекции, оставшихся пос-
ле окончания первого цикла. Измерения
выполняют с более высокой точностью,
чем на. нервом цикле. Для коррекции дис-
баланса в каждой из двух плоскостей ко-
ленчатый вал подают последовательно на
станки 4 и 3, а для окончательного кон-
троля качества уравновешивания—на ста-
нок 2. Обработанные коленчатые валы ук-
ладывают на транспортный накопитель /,
обеспечивающий гибкую связь с последую-
щим транспортным и технологическим
потоком.
Технические характерис-
тики
Масса коленчатого вала,
кг...................40
Число станков в линии, шт. 7
Наибольшая величина на-
чального дисбаланса, г-мм 17 000
Допустимый дисбаланс,
г*мм............... 300
Число циклов уравновеши-
вания .............. .2
Производительность при
коэффициенте технического
использования 1, шт/ч 69
Частота вращения по из-
мерении дисбаланса,
мин-1................250
Число инструментальных
шпинделей в первом цикле
коррекции на каждом из
двух станков, шт. . . 3
Число инструментальных
шпинделей во втором цик-
ле коррекции на каждом
из двух станков, шт. .
Габаритные размеры,
мм................... 12000Х 5400Х
Х3700
Масса линии (ориентиро-
вочная), кг . . 34 000
Автоматические участки. Автоматичес-
кие линии могут быть скомпонованы в
автоматический участок с единой системой
управления и транспортом. Пример пла-
нировки автоматического участка для ди-
намической балансировки коленчатого ва-
ла массой 10 кг рядного двигателя вну-
треннего сгорания приведен на рис. 8.48.
Участок состоит из двух автоматичес-
ких линий, установленных параллельно ос-
новному транспортному потоку, и секции
доводки коленчатых валов, сошедших с
участка с повышенным дисбалансом. Опе-
рации перемещения на самой линии и связь
между станками и транспортом осуществ-
ляется при помощи манипуляторов.
Коленчатый вал по транспортеру за-
готовок 1 поступает к портальным мани-
пуляторам 2 и 5 соответственно первой
и второй автоматических линий. Манипу-
лятором 2 коленчатый вал подают на ба-
лансировочный станок /4, где определяют
дисбалансы в двух плоскостях коррекции.
Затем манипулятор переносит коленча-
тый вал на корректирующий станок 13
первого цикла уравновешивания и после
соответствующей механической обработки
(сверления в тяжелом месте каждой* из
плоскостей коррекции) возвращает на ба-
лансировочный станок 14 для контроля
остаточного дисбаланса. Если дисбаланс
превышает допустимое значение, манипу-
лятор переносит балансируемую заготовку
на корректирующий станок 12 для оконча-
тельной балансировки. После повторной
коррекции на балансировочном станке 14
проводят контроль качества выполнения
операций. Обработанный годный колен-
чатый вал тем же манипулятором перекла-
дывается на транспортер готовой продук-
ции 3. В том случае, если остаточный
дисбаланс коленчатого вала после прове-
дения двух циклов балансировки все же
превышает допустимое значение, манипу-
лятор 2 с балансировочного станка 14
переносит его на транспортер 4.
Аналогично организована работа на
второй линии, включающей портальный
манипулятор 5, балансировочный станок
7 и корректирующие станки 9, 11 первого
и второго циклов уравновешивания.. Авто-
матический участок состоит из двух па-
раллельных независимых автоматических
линий, объединенных общей транспортной
системой.
Коленчатые валы с остаточным дисба-
лансом, превышающим допустимое значе-
Автоматические линии, участки и гибкие производственные системы
297
Рис.. 8.48. Планировка автоматического участка для динамической балансировки колен-
чатого вала рядного двигателя внутреннего сгорания
ние, транспортером 4 подаются в зону
действия портального манипулятора 6
секции доводки. Манипулятор передает
коленчатый вал на балансировочный ста-
нок 8, на котором определяют его дис-
балансы, а затем на корректирующий ста-
нок 10, управляемый автоматически или
вручную. После доводки коленчатого вала
до допустимых значений дисбаланса и его
контроля на станке 8 манипулятор переда-
ет окончательно отбалансированный вал
на транспортер 3 готовой продукции.
Технические характерис-
тики участка
Число автоматических ли-
ний, шт..................2
Число секций доводки,
шт. .....................1
Число портальных мани-
пуляторов, шт............3
Общее число станков, шт. 8
Мас коленчатого вала,
кг......................10
Наибольшая величина на-
чального дисбаланса,
г-мм.................. 1800... 2700
Допустимый дисбаланс,
г-мм .... 150
Число циклов уравновеши-
вания .... . . 2
Производительность при
коэффициенте технического
использования 1, шт/ч 77
Габаритные размеры (ори-
ентировочно). мм . . 20 000Х 9200Х
Х3300
Масса участка (ориентиро-
вочно) , кг .35 000
Гибкие производственные системы. По-
вышение качества работы и производи-
тельности оборудования, применяемого в
условиях мелкосерийного и серийного про-
изводств, а также стремление исключить
ручной труд, вызвало появление специа-
298
Портативная балансировочная аппаратура
лизированных переналаживаемых комп-
лексов.
Гибкая производственная система
(ГПС) представляет собой совокупность
оборудования с ЧПУ, роботизированных
технологических комплексов, гибких про-
изводственных модулей, отдельных единиц
технологического оборудования и систем
обеспечения их работы в автоматическом
режиме в течение заданного интервала
времени. ГПС обладает свойством авто-
матизированной переналадки при произ-
водстве изделий произвольной но-
менклатуры в установленных пределах
значений их характеристик.
ГПС по организационным признакам
может представлять собой гибкий авто-
матизированный цех, участок или линию
Составной частью ГПС является гибкий
производственный модуль (ГПМ), пред-
ставляющий собой автономную единицу
технологического оборудования для произ-
водства изделий произвольной номенкла-
туры с установленным пределом значений
технических характеристик и программным
управлением, имеющую возможность
встраивания в ГПС.
Специфические особенности баланси-
ровочных ГПС и ГПМ предусматривают
сочетание систем ЧПУ с микропроцессор-
ной техникой.
Кроме обычных задач управления цик-
лом работы в число ее функций входит:
выделение проекций амплитудных зна-
чений колебаний датчиков на частоте вра-
щения балансируемого ротора из широ-
кого спектра частот;
решение системы линейных уравнений,
связывающих дисбалансы в плоскостях
коррекции с амплитудами колебаний, вос-
принимаемых датчиками на рабочей час-
тоте;
разложение дисбалансов на проекции
в заданной системе координат на роторе;
пересчет дисбалансов в параметры тра-
ектории движения обрабатывающих ин-
струментов;
накопление и анализ данных с целью
диагностики состояния как балансировоч-
ного, так и формообразующего технологи-
ческого оборудования, и т. д.
Глава 9
ПОРТАТИВНАЯ БАЛАНСИРОВОЧНАЯ АППАРАТУРА
9.1. КЛАССИФИКАЦИЯ И ОБЛАСТИ
ПРИМЕНЕНИЯ
Портативную балансировочную аппа-
ратуру применяют при уравновешивании
валов, роторов и других врашаюшихся
частей механизмов в собственных подшип-
никах. В отличие от аппаратуры, входящей
в комплект балансировочных станков и
автоматов, портативная аппаратура позво-
ляет измерять не модуль и угол дис-
баланса, а амплитуду и сдвиг фазы вибра-
ции подшипников с частотой вращения
балансируемого изделия. Так как различ-
ные модели балансировочной аппаратуры
измеряют разные параметры вибрации, то
в дальнейшем принимают: — амплитуда,
размах, среднее или среднее квадратиче-
ское значение виброперемещения, вибро-
скорости или виброускорения; <ро — раз-
ность фаз между искусственной точкой
отсчета (обычно меткой на роторе) и ам-
плитудой вибрации с частотой вращения.
Область применения портативной ба-
лансировочной аппаратуры очень обшир-
на— от балансировки роторов микрома-
шин массой несколько граммов до балан-
сировки многоопорных валопроводов мощ-
ных энергоблоков массой свыше 100 т.
Естественно, что портативная баланси-
ровочная аппаратура, применяемая в раз-
личных отраслях промышленности, разли-
Классификация и области применения
299
чается по составу, конструкции и основ-
ным техническим характеристикам.
Вместе с тем конструкции и харак-
теристики различных моделей современной
балансировочной аппаратуры имеют много
общего. Например, все модели работают
с вибродатчиками инерционного действия,
имеют индикаторы амплитуды и сдвига
фазы. В зависимости от массы баланси-
руемых роторов, частоты вращения, на
которой производится балансировка, и
конструкций механизмов в балансировоч-
ной аппаратуре применяют вибродатчики
с различными способами преобразования
механических колебаний в электрический
сигнал. В балансировочной аппаратуре,
работающей в частотном диапазоне до
200 Гц, применяют в основном электро-
динамические вибродатчики, а выше
200 Гц — пьезоэлект р ические.
Положения вибродатчиков и датчика
(генератора) опорной фазы показаны
на рис. 9.1. При вращении ротора 1 в
опорах 2, 2' с угловой частотой ©о, на
выходах вибродатчиков 4, 4' возникают
переменные напряжения
U(t) — t/osin( <ooi -f- <ро) 4- Q(t),
где С/е=ЛдЛо—амплитуда переменного
напряжения, пропорциональная амплиту-
де Л о вектора составляющей с частотой
вращения ш0; Кя—коэффициент преобра-
Рис. 9.1. Схема балансировки двухопорного
ротора:
1— ротор, 2.2'— первая и вторая плоскости уста-
новки балансировочных грузов; 3.3'—первая и
вторая опоры, 4,4'— вибропреобразователи; 5 —
измерительный блок, 6— генератор опорной фазы
зовання вибродатчика; (?(/)—механиче-
ские и электрические помехи, т. е. перемен-
ные напряжения на выходе вибродатчика
с частотами <Oi=#=<D0.
Все расчеты при балансировках рото-
ров выполняют при условии линейности
колебательной системы, т. е.
б Vo/ (6s) — const при ©о = const.
Наличие в спектре сигнала на выходе
вибродатчика Q (/) нарушает это условие,
особенно при снижении амплитуды виб-
рации с частотой <оо. Если обозначить по-
казания измерительного блока 5 в виде
среднего квадратического значения As, по-
лагая шум в полосе частот Асо стацио-
нарным нормальным процессом, то отноше-
ние сигнала к шуму на выходе измери-
тельного блока
я=л/_±.
V 2Л5Д<и ’
"де Аго—полоса пропускания измеритель-
ного блока, включая вмбродатчик.
Для удобства дальнейшего изложения
можно ввести параметр /—«информатив-
ность», характеризующий отношение изме-
нения амплитуды на выходе измеритель-
ного блока к амплитуде Л о:
/==АД5/(АД0) или /=л/(4//2-|-1)/(2//).
Информативность />1 при Д->со,
т. е. А(о—>-0. Следовательно, для повыше-
ния информативности необходимо сужать
полосу пропускания измерительного блока
До, т. е. применять узкополосные фильтры
Еще более высокие требования к фильтра-
ции устанавливают при измерении сдвига
фазы. Известны случаи, когда даже при
достаточной информативности произво-
дить измерение фазы становится невоз-
можно. Этот парадокс объясняется тем,
что в аппаратуре со стрелочными и циф-
ровыми индикаторами фазы, показания
индикаторов не усредняются в начале и
конце диапазона измерений. Например,
если флуктуация из-за. помех составляет
± 10°, то при сдвиге фазы от 0 до 10° и от
350 до 360° погрешность может достигать
я
зоо
Портативная балансировочная аппаратура
180°. Приведенные примеры показывают,
что системы фильтрации являются одними
из основных узлов современной баланси-
ровочной аппаратуры. В зависимости от
способа фильтрации вся современная пор-
тативная балансировочная аппаратура де-
лится на два класса: с частотно-изби-
рательными фильтрами и с множитель-
ными избирательными устройствами. Су-
ществуют и другие различия в конструк-
циях рассматриваемых моделей баланси-
ровочной аппаратуры, но они не являются
принципиальными. В некоторых моделях с
множительными избирательными устрой-
ствами используют частотно-зависимые
фильтры.
Часто портативная балансировочная
аппаратура комплектуется из отдельных
измерительных приборов общего назначе-
ния. Например, балансировочный комп-
лекс фирмы «Брюль и Къер» (Bruel Kier,
Дания) состоит из универсального вибро-
измернтельного прибора с пьезо датчиком,
узкополосного перестраиваемого фильтра,
индикатора фазы с фотоэлектрическим
датчиком опорного сигнала. Однако боль-
шинство моделей представляет собой еди-
ную конструкцию с определенными функ-
циональными возможностями.
9.2. ЧАСТОТНО-ИЗБИРАТЕЛЬНЫЕ
УСТРОЙСТВА
В большинстве моделей применяют ак-
тивные частотно-зависимые фильтры. Пас-
сивные фильтры в новых моделях почти
не применяют. Практически не известны
случаи использования в портативной ап-
паратуре цифровых фильтров, моделирую-
щих структуру аналоговых активных
фильтров.
Активные фильтры по назначению раз-
деляют на фильтры нижних частот (НЧ),
высших частот (ВЧ), полосовые (ПФ),
узкополосные (УПФ) с полосами про-
пускания AF1>2, режекторные (РФ) и фа-
зовые (ФФ). На рис. 9.2 приведены ти-
пичные амплитудно-частотные характе-
ристики активных фильтров. Фильтры НЧ
и ВЧ применяют в балансировочной ап-
Рис. 9.2. Амплитудно-частотные характерис-
тики активных фильтров:
/- ФНЧ; 2— ПФ, 3 — УПФ; 4- ФВЧ
паратуре для ограничения частотного диа-
пазона измерений. Основными параметра-
ми фильтров НЧ и ВЧ являются неравно-
мерность амплитудно-частотной характе-
ристики (АЧХ) в полосе пропускания, ча-
стота среза и спад (затухание) АЧХ в
полосе задержания. Фильтры ВЧ и НЧ
различаются фазочастотными характери-
стиками (ФЧХ), временем задержки, вре-
менем нарастания и относительной вели-
чиной перерегулирования. ФЧХ является
зависимой от АЧХ, а остальные пара-
метры учитываются при переходных про-
цессах и влияют только иа инерционность
балансировочной аппаратуры. Нерав-
номерность АЧХ в полосе про-
пускания влияет на погрешность из-
мерений параметров вибрации на различ-
ных частотах. Частота среза Fcp—частота,
на которой затухание составляет 3 дБ
(около 30%). Затухание АЧХ в полосе
задержания равно п-6 дБ (где п — по-
рядок фильтра).
Простейшими фильтрами являются
ФНЧ и ФВЧ 1-го порядка. ФНЧ часто
применяют в балансировочной аппаратуре
для преобразования вырабатываемого
вибродатчиком напряжения, пропорцио-
нального виброускорению, — в пропорцио-
нальное виброскорости, или виброскоро-
сти—в пропорциональное вибропереме-
щению. ФВЧ выполняют обратные функ-
ции. ФНЧ и ФВЧ 1 -го порядка, у которых
/(s 1/и и К о соответственно, часто
называют аналоговыми интеграторами и
Частотно-иэбйрательные устройства
301
Рис. 9.3. Схема дифференцирующего
усилителя:
а—идеальный; б— реальный
Рис. 9.4. Схема интегрирующего
усилителя:
с— идеальный; б — реальный
дифференциаторами. Схемы дифференци-
рующих и интегрирующих усилителей
обычно строят на операционных усилите-
лях.
Схема дифференцирующего усилителя
показана на рис. 9.3, а. Если принять
К->оо, то входной ток 11 равен выходному
току 4-
, - с dlJ-
^--С~
— т) ~^7~ ’
где xj — постоянная времени диф-
ференцирующей цепи, т. е. выходное на-
пряжение пропорционально первой произ-
водной от входного.
Если входное напряжение
^вх (0= t/pBxSinto/,
то ^вых(0~—T|<t»l/MCOSwC
или £/Овыя= — СОмТ1Ш, а ф= - л/2.
Упрощенная дифференцирующая цепь
является неустойчивой, так как
Для повышения устойчивости частот-
ный диапазон дифференцирования огра-
ничивается сверху. Для этого вводят до-
полнительно элементы коррекции Сь и
(рис. 9.3, б).
В такой схеме максимальный коэффи-
циент передачи на средних частотах
Kmax~Ri/R^ а при to-юс К+0.
Расчет корректирующих цепей ведут в
каждом конкретном случае с учетом ча-
стотного диапазона дифференцирования,
допустимых погрешностей и частотных ха-
рактеристик операционных усилителей
Схема интегрирующего усилителя по-
казана на рис. 9.4, а. Коэффициент пе-
редачи определяется по формулам
^вых(П = “^’2(0^,
. . ^вх
так как — —t2, a i2 =-, то
^ВЫх(0-------М ^BX(/)d/,
*2 J
где т2 — R1С,,
ИЛИ К— —Tjio-^oo При to—>-оо.
или г/ОвЫх = -
302
Портативная балансировочная аппаратура
при =
К=1Ь'оЮх1/1Ь'о.х1=1/(«>тг).
Для того чтобы ограничить коэффи-
циент передачи на низких частотах
(/(—►«о при ь>—*0), в цепь обратной связи
вводят корректирующее сопротивление Р*
(рис. 9.4,6). Тогда максимальный коэф-
фициент передачи
Ктах=Я*/Я1.
Наиболее распространенными являют-
ся фильтры 2-го порядка, имеющие за-
тухание в полосе задерживания 12 дБ на
октаву Для получения большего затуха-
ния часто используют последовательные
соединения фильтров 1-го и 2-го порядков.
В общем виде передаточная функция
ФНЧ
К (Р) _ ----------;
1+С(Р + сгР^+... + сг(Р«
где К(Р)— коэффициент передачи фильт-
ра на различных частотах; Ко—коэффици-
ент передачи фильтра при Р—0; Fcp—час-
тота среза ФНЧ; с, — положительные
действительные числа. При Р= 1, т. е.
F=/’cp, коэффициент передачи = 0,707.
Обычно в ФНЧ и ФВЧ Ко=1-
В зависимости от методов аппроксима-
ции амплитудно-частотных характеристик
в полосе пропускания и затухания в полосе
задержания различаются пять основных
групп фильтров НЧ и ВЧ: с критическим
затуханием, Бесселя, Баттерворта, Чебы-
шева, Золотарева — Кауэра.
На рис. 9.5 изображены амплитудно-
частотные, фазочастотные и переходные
характеристики различных НЧ фильтров
4-го порядка, из которых видно, что фильтр
с критическим затуханием имеет монотон -
но-спадающую характеристику в полосе
пропускания и пологий спад в полосе за-
держания, но меньший сдвиг фазы и луч-
шую переходную характеристику. Фильтр
Бесселя обладает оптимальной переходной
\А\/\Ао\,дб
О
-ю
-го
-зо
-оо
-50
0.010,03 0,1 0,3 1 3 10 51
О)
Рис. 9.5. Характеристики для НЧ фильтров
4-го порядка:
и — амплитудно-частотные, б— фазочастотные; в —
групповое время задержки; / — с критическим за-
туханием; 2—Бесселя; 3— Баттерворта; 4. 5 - Че-
бышева
характеристикой, что объясняется пропор-
циональностью фазового сдвига, однако
спад амплитудно-частотной характеристи-
ки оказывается более пологим по срав-
нению с фильтрами Чебышева [7] и
Баттерворта. Фильтры Чебышева имеют
наиболее крутой спад для частот Р>1,
но большую неравномерность в полосе
Р<1. При уменьшении неравномерности
фильтры Чебышева переходят в фильтры
Баттерворта. Переходные характеристики
фильтров Баттерворта и Чебышева имеют
большую амплитуду колебаний при пере-
ходном процессе. Нан лучшими парамет-
Частотно-избирательные устройства
303
рами при переходном процессе обладают
фильтры с частотно-независимыми группо-
выми временами задержки. Этим свойст-
вом обладают фильтры Бесселя. Пара-
метры фильтра рассчитывают так, чтобы
при PsSs 1 групповое время задержки как
можно меньше зависело от частоты.
Для этого используют аппроксимацию
Баттерворта [37]. На рис. 9.6, 9.7 при-
ведены примеры электрических схем основ-
ных типов НЧ и ВЧ активных фильтров,
применяемых в современной балансиро-
вочной аппаратуре.
Полосовые и режекторные фильтры
строят путем последовательного или па-
раллельного соединения ВЧ и НЧ фильт-
ров. Примеры таких фильтров показаны
на рис 9.8. На рис. 9.9 показана схема
Рмс. 9.6. Схемы НЧ-фильтров 2-го порядка:
о—без корректирующей цепи; б с корректирую-
щей цепью
Рис. 9.8. Схема фильтров:
а, б—полосовых, в — режекторных
Рис. 9.9. Схема фазового фильтра 1-го
-Рис. 9.7. Схема ВЧ фильтра 2-го порядка порядка
304
Портативная балансировочная аппаратура
фазового фильтра 1-го порядка. Фазовые
фильтры применяют для коррекции фазо-
частотных характеристик измерительных
трактов.
В последнее время большое распрост-
ранение получили фильтры переменных со-
стояний, позволяющие с помощью одной
схемы получить частотные характеристики
фильтров нижних и верхних частот, по-
лосовых, режекторных и фазовых [37].
Коэффициент передачи для произвольного
фильтра 2-го порядка можно записать в
виде
Коэффициенты передачи различных
фильтров могут быть получены при следую-
щих значениях параметров:
ФНЧ di = d2=0; ФВЧ do==rfi = O; ПФ
rfo= 0; РФ do—ds, di — 0; ФФ do—Co,
—C|j di=C2.
Схема фильтра переменных состояний
2-го порядка приведена на рис. 9.10.
В зависимости от требуемых параметров
фильтра выходными напряжениями могут
быть: Ui—для РФ, Ui—для ФВЧ, 1/з—
для ПФ и U—для ФНЧ. Основным пре-
имуществом фильтров переменных состоя-
ний является простота их перестройки.
Частоты среза пропускания для ПФ и
режекции перестраиваются изменением R
или С. Коэффициенты аир определяют
коэффициент передачи и полосу пропуска-
ния. Для перестройки фильтров часто при-
меняют аналоговые умножители, которые
соединяют последовательно с сопротив-
лениями R. В этом случае
т<=т()7}—; то==ЯС,
17 у пр «
где t/ynp,—напря/кение, подаваемое на ум-
ножающий вход аналогового умножителя;
Uo—масштабирующее напряжение, по-
даваемое на вход деления
При этом частота настройки фильтра
зависит от управляющего напряжения:
1
2лт0
Диапазон перестройки такого фильтра
ограничен параметрами аналоговых умно-
жителей [2] и не превышает 20—30
^пйп<20-~30). кроме того, из-за
ограниченного амплитудного диапазона
аналоговых умножителей возникают до-
полнительные погрешности при измере-
ниях малых уровней вибрации.
Расширить амплитудный и частотный
диапазоны измерений позволяет перестра-
еваемый фильтр с коммутируемыми кон-
денсаторами, схема которого показана -на
рис. 9.11. В этой схеме функции аналого-
вых умножителей интегрирующих сопро-
тивлений ВЫПОЛНЯЮТ КЛЮЧИ Л2|, Л22, Д4-1«
Д4.2 и конденсаторы Сь. Ключи переключа-
ются с частотой Fjfc»Fo, а эквивалентное
сопротивление и постоянная времени ин-
R1
Рис. 9.10. Схема фильтра переменных состояний
Частотно-избирательные устройства
Рис. 9.11. Схема многофункционального фильтра с коммутируемыми конден-
саторами
теграторов связаны с частотой коммута-
ции:
/?= 1/(Г*С*); Л = ЛС*/(2лС0).
Следовательно, частота настройки
фильтра регулируется частотой коммута-
ции Fk.
Основным недостатком активных филь-
тров является сильная зависимость по-
грешностей измерений амплитуды и сдвига
фазы от точности их настройки, ста-
бильности параметров и частоты враще-
ния балансируемого ротора. В некоторых
случаях эти погрешности можно умень-
шить путем введения цепи автоподстройки
резонансной частоты узкополосных фильт-
ров.
Структурная схема включения цепи
автоподстройки приведена на рис. 9.12.
Перед узкополосным фильтром 2 устанав-
ливают фильтр нижних частот 1 с
ФНЧ необходим для исклю-
чения влияния на погрешность измерений
составляющих спектра вибрации с часто-
тами, близкими к минимальной частоте
коммутации. Выходы узкополосного.филь-
тра 2 и ФНЧ соединены с входами фазо-
вого детектора, на выходе которого вы-
рабатывается постоянное напряжение
^01 twos <р,
где б'ш, £7о2 — амплитуды переменного на-
пряжения, пропорциональные амплитуде
основной гармоники виброперемещения;
ф—сдвиг фаз между напряжениями на вы-
Рис. 9.12. Структурная схема узкополосного
фильтра на переключаемых конденсаторах с
автоподстройкой
ходе и входе узкополосного фильтра 2;
Кф—коэффициент передачи фазового де-
тектора. Напряжение суммируется с
напряжением управления Uynp в сумма-
торе 4 и поступает на интегрирующий
преобразователь напряжение—частота 5.
С выхода преобразователя напряжение—
частота импульсы с частотой FK пере-
ключают конденсаторы Ск (рис. 9.11) и
управляют частотой резонанса фильтра F,.
При неточной настройке фильтра сдвиг
фазы <р=т^л/2, и на выходе фазового де-
тектора 3 вырабатывается постоянное на-
пряжение, которое изменяет частоту ком-
мутации до тех пор, пока это напряжение
306
Портативная балансировочная аппаратура
не станет равным нулю, т. е. л/2, что
соответствует точной настройке узкополос-
ного фильтра. Система фазовой авто-
подстройки имеет узкую частотную об-
ласть захвата, а точность настройки за-
висит от амплитуды переменного напряже-
ния, подаваемого на вход фильтра.
Перечисленные недостатки активных
фильтров ограничивают области их при-
менения. В последнее время появилось
много публикаций по проектированию ак-
тивных ‘ фильтров на ПК-конденсаторах.
Эти фильтры легко перестраиваются на
различные частоты и имеют высокую из-
бирательность. Однако фильтрам на ПК-
конденсаторах присущи те же характер
ные недостатки, что и всем активным
фильтрам. Поэтому в большинстве моделей
современной балансировочной аппаратуры
применяют множительные избирательные
устройства.
Множительные избирательные устрой-
ства до недавнего времени применялись
в измерительных блоках балансировочных
станков. В качестве множительных и ин-
тегрирующих устройств использовались
ваттметры и векторометры. В последнее
время множительные избирательные уст-
ройства суали применяться в портативной
балансировочной аппаратуре, что объясня-
ется широким внедрением новых элемен-
тов микроэлектроники.
В некоторых образцах балансировоч-
ных приборов в качестве множительных
избирательных устройств применяют син-
хронные детекторы, которые строят на эле-
ментах с параметрическим управлением
или с использованием фазочувствительных
выпрямителей [19]. Основным недостат-
ком этих схем является значительная по-
грешность измерений параметров вектора
вибрании, возникающая из-за наличия в
спектре опорного сигнала прямоугольной
формы всех нечетных гармоник.
Множительные избирательные устрой-
ства с кольцевыми модуляторами на дио-
дах и транзисторах имеют небольшие ам-
плитудные диапазоны и коэффициенты пе-
редачи. Недостатком этих схем является
также наличие симметричных входов и вы-
ходов. С появлением аналоговых интег-
ральных микросхем в новых моделях пор
тативной балансировочной аппаратуры
такие множительные устройства практи-
чески не применяются.
В новых разработках балансировочных
приборов широкое применение нашли мно-
жительные избирательные устройства с ис-
пользованием аналоговых четырехквад-
рантных умножителей. Упрощенная схема
множительного избирательного устройства
показана на рис. 9.13. Если на вибро-
датчик / воздействуют механические ко-
лебания а (/), то он вырабатывает напря-
Частотно-избирательные устройства
307
жение U (t), которое подается на входы
аналоговых умножителей 3 и 5, на вторые
входы которых подаются переменные на-
пряжения с частотой вращения баланси-
руемого ротора, но сдвинутые по фазе на
1/4 периода вращения, вырабатываемые
генератором опорного сигнала. К выходам
аналоговых умножителей подключены ана-
логовые интеграторы 4 и 6. Если генератор
опорного сигнала (ГОС) 2 вырабатывает
синусоидальные напряжения
^oux(0 Е^о1)уSintOif; t^onj/(0—t/onoCOSWif.
а в спектре напряжения, вырабатываемого
вибродатчиком, содержатся кроме ко
лебаний с частотой вращения еще и со-
ставляющие с другими частотами:
ной формы этого сигнала бесконтактным
способом.
В большинстве случаев отсутствует
возможность механического подсоедине-
ния генератора опорного сигнала к ба-
лансируемому ротору. Поэтому исходным
опорным сигналом является короткий им-
пульс, вырабатываемый датчиком импуль-
сов при прохождении под ним отметки
на роторе.
В некоторых моделях переносных ба-
лансировочных приборов применяют схемы
формирования аналогового опорного сиг-
нала, в которых напряжения треугольной
формы преобразовываются в синусоидаль-
ные с помощью нелинейных цепей. На рис.
9.14 изображена структурная схема, а на.
рис. 9.15— временная диаграмма формиро-
= Um sin{(rtl/4-(₽1) 4-
оо
4" Yj Uqi sirl ( + <£,) ,
то на выходах аналоговых интеграторов
4 и 6 вырабатываются постоянные напря-
жения, пропорциональные синфазной и
квадратурной составляющим вектора ви
броперемещения основной гармоники:
Ux=KU0lUw0sin^- Uv= KUm Oonocostp,
где К—коэффициент передачи умножите-
ля и интегратора.
Напряжения Ux и Uv поступают на
блок вычисления модуля 7, на выходе кото-
рого вырабатывается постоянное напряже-
ние, пропорциональное амплитуде основ-
ной гармоники:
£/01 = V^+^
В блоке 8 определяется сдвиг фазы
<4
9i = arcsin -ту—
*4)1
Основными недостатками множитель-
ных избирательных устройств такого типа
являются зависимость погрешностей опре-
деления Uoi и <pi от амплитуды и не-
линейных искажений опорного сигнала, а
также сложность получения синусоидаль-
Рис. 9.15. Временная диаграмма формиро-
вания опорного сигнала
308
Портативная балансировочная аппаратура
вания опорного сигнала. Датчик импуль-
сов 2 вырабатывает короткий импульс при
прохождении под ним метки 1, вращаю-
щейся вместе с балансируемым ротором.
После одновибратора 3 импульс за-
пускает триггер 4, на выходе которого
образуются прямоугольные импульсы «ме-
андр» с частотой следования, в 2 раза
меньшей частоты вращения. На выходе
интегратора 6 образуется однополярное
напряжение треугольной формы. В блоках
5, 7 происходит разделение постоянной
и переменной составляющих напряжения.
В детекторе 8 происходит двухполупериод-
ное выпрямление. При этом на его выходе
вырабатывается однополярное переменное
напряжение треугольной формы с часто-
той, равной частоте вращения. В усили-
теле 9 с автоматической регулировкой
коэффициента усиления происходит стаби-
лизация .амплитуды.
Стабилизированное напряжение тре-
угольной формы в цепи разделения 10
преобразуется в двухполярное, а в функ-
циональном преобразователе 11 -в почти
синусоидальное К недостаткам такого
формирователя опорного сигнала можно
отнести: большую инерционность измере-
ний, вносимую цепями разделения постоян-
ной и переменной составляющих и цепью
автоматической регулировки усиления; на-
личие в спектре опорного сигнала состав-
ляющих с другими частотами, возникаю-
щих из-за неидеальности синусоидальной
формы; большую зависимость формы и
спектрального состава от амплитуды треу
гольного напряжения и температуры, вно-
симую диодным функциональным преобра-
зователем.
Два последних недостатка могут быть
уменьшены при применении многозвенных
транзисторно-диодных функциональных
преобразователей, осуществляющих ку-
сочно-линейную аппроксимацию. Такая
схема применена в формирователе опор-
ного сигнала, используемого в цифровом
балансировочном приборе «Вибропорт»
фирмы «Шенк» (Schenck, ФРГ). Не-
достатками этой схемы являются ее гро-
моздкость, необходимость применения ста-
билизации амплитуды треугольного напря-
жения и большая инерционность.
Формировать напряжение почти сину-
соидальной формы из напряжения тре-
угольной формы можно с помощью схем
с аналоговыми умножителями. Близкой к
синусоидальному сигналу является функ-
ция у = х (л — х) при 0 х <1 л. Струк-
турная схема преобразования функции
т
при изображена на рис. 9.16. На
вход U\ аналогового умножителя подается
напряжение треугольной формы, на вход
{/2 поступает напряжение с сумматора.
Рис. 9.16. Схема реализации функции
У=А'(л-А')
Напряжение на выходе аналогового ум-
ножителя
где К—коэффициент передачи умножите-
ля.
В спектре напряжения вида U (/) [L()—
— U (/)], кроме основной гармоники, при-
сутствуют нечетные гармоники, амплитуды
которых обратно пропорциональны 3-й
степени номера гармоники:
, 1 = 2п -|- 1,
<2п + 1)"
где Uoi — амплитуда г-й гармоники; £?oi —
амплитуда 1-й гармоники; «=1, 2,
3,. .. — целые числа.
Амплитуда ближайшей 3-й гармоники
f/оз ~ 3,7% от основной, а 5-й—
«0,08%.
Ввиду того что для анализа погреш-
ности измерений, вносимой высшими гар-
мониками, важно не эффективное значе-
Частотно-избирательные устройства
309
ние, а амплитудное, коэффициент гармоник
определяют по формуле
.00 £
П=1
Ц>.
(2л ± 1)
У-——%
0^ + 1)
Следовательно, максимальную погреш-
ность измерений и амплитуды основной
гармоники вносит 3-я гармоника:
f/03=3,7.10-2t/0b
При использовании формирователя
опорного напряжения в множительных
избирательных устройствах важным пара-
метром является также зависимость сдви-
га фазы амплитуды от напряжения тре-
угольной формы. В литературе приведены
примеры реализации функций у « sjnx при
помощи полинома у=Ах-[-Вх2.
Схема, реализующая функцию у~
= 1,155х— О.ЗЗх2, показана на рис. 9.17.
Рис. 9.17. Схема реализации функции
^1.155х-О.ЗЗ?
Входное напряжение треугольной формы
поступает на вход аналогового умножите-
ля, работающего в режиме квадратора.
На инвертирующий вход аналогового сум-
матора поступает напряжение с выхода
умножителя через делитель с К — 0,33.
На неинвертирующий вход сумматора по-
дается входное напряжение через усили-
тель с К~ 1,165. Минимальная погреш-
ность аппроксимации при такой схеме реа-
лизации функции ymsinx может быть рав-
на ±2,1%.
Наличие в спектре опорного сигнала
всех нечетных гармоник ограничивает
точность измерений амплитуды и сдвига
фазы основной гармоники. Исключить из
спектра опорного сигнала высшие гармо-
ники с близкими частотами возможно при
применении множительных избирательных
устройств с дискретным изменением
коэффициентов передачи в течение одного
периода. Существуют два основных спосо-
ба формирования дискретного изменения
коэффициентов передачи: с равномерным
квантованием во времени и неравномер-
ным по уровню; с неравномерным во време-
ни и равномерным по уровню.
На рис. 9.18 и 9.19 изображены диа-
граммы изменения коэффициентов переда-
г. 70
чи в течение времени U t .
Лучшие характеристики имеют множи-
тельные избирательные устройства с рав-
номерным квантованием во времени, так
как позволяют исключить из спектра опор-
ного сигнала любые гармоники.
Рис. 9.18. Диаграмма изменений коэффи-
циента передачи при равномерном кванто-
вании по времени
Риг. 9.19. Диаграмма изменений коэффи-
циента передачи при равномерном кванто-
вании по уровню
310
Портативная балансировочная аппаратура
Мгновенное значение коэффициента
передачи для такого устройства
K(a) = sinf 7г «) .
где Р— число разбиений половины периода
основной гармоники; а~ 1 . . 2Р — целое
число.
Если на вход устройства подать по-
стоянное напряжение Uo, то переменное
напряжение на выходе будет содержать
основную гармонику с амплитудой
я
_. S,n 2F .. г 1
-------и частотой F, = —,
п-----' о
2F
а также высшие нечетные гармоники с
амплитудами и частотами:
СЛ
При достаточно большом значении Р
Utn ~ Uо, а высшие нечетные гармоники
могут быть вынесены за пределы частот-
ного диапазона измерений. Например, при
Р — 8 ближайшими высшими гармониками
будут 15-я и 17-я, а их амплитуды не
будут превышать 6% от основной гармони-
ки. Для исключения влияния этих гармо-
ник на точность измерений перед множи-
тельным избирательным устройством ста-
вится ФНЧ с частотой среза Fcp^8Fi,
который практически не вносит амплитуд-
но- и фазочастотных погрешностей. При
расширении частотного диапазона измере-
ний необходимо увеличивать Р. Для рабо-
ты множительных избирательных уст-
ройств с дискретным изменением коэффи-
циента передачи необходимо применять
умножитель частоты.
Умножители частоты являются одним
из основных узлов большинства моделей
современной балансировочной аппарату-
ры. Их используют при измерениях ча-
стоты вращения, сдвига фазы, при фильт-
рации, в схемах аппроксимации и т. д.
Умножители частоты могут быть построе-
ны на аналоговых, цифровых и комби-
нированных схемах.
Простейший аналоговый умножитель
частоты можно построить в виде после-
довательного соединения преобразовате-
лей частота — напряжение (Fi-*-t/|) и на-
пряжение— частота (Ut—^Fz). Напряже-
ние на выходе преобразователя Ft —
т/e.
f>l==K|Fb
где Kt — коэффициент преобразования
Fi^-Ui; Ft—частота входного сигнала, а
частота на выходе преобразователя {Д—>-
-> Fg, т. е.
F2=K2Ut = KFt,
где К=К1К2- общий коэффициент пре-
образования (умножения).
Однако такие умножители имеют низ-
кую стабильность, так как Kt и Л/ зависят
от параметров преобразователей F\ -»-(?!
и t/i-^Fg. Улучшить стабильность рас-
сматриваемых умножителей можно введе-
нием обратной связи ОС по частоте (рис.
9.20). В этом умножителе погрешность пре-
образования определяется только погреш-
ностью второго преобразователя часто-
та— напряжение {F2-^U2). При этом уве-
личивается инерционность всей схемы.
Кроме того, коэффициент умножения ча-
стоты не является настолько стабильным,
чтобы не вносить дополнительные погреш-
ности.
Значительно лучшими характеристи-
ками обладает умножитель частоты с де-
Рис. 9.20. Структурная схема умножителя
частоты
Рис. 9.21, Структурная схема умножителя
частоты с делителем частоты в цепи обрат-
ной связи
Частотно-избирательные устройства
311
лителем частоты в цепи обратной связи.
Схема такого умножителя показана на рис.
9.21. Такие умножители могут применяться
в балансировочной аппаратуре, работаю-
щей в узких частотных диапазонах, так как
они имеют ограниченный диапазон захвата
системы автоподстройки; примерно от
0,7 Л i до l,5Fi. Для полной синхронизации
необходимо значительное время, которое
определяется инерционностью преобразо-
вателя частота—напряжение и фильтра
нижних частот.
В современных моделях балансировоч-
ной аппаратуры применяют умножители
частоты с импульсной обратной связью.
Эти умножители частоты имеют высокое
быстродействие, а их коэффициент умно-
жения не зависит от стабильности эле-
ментов схемы.
Принципиальная схема этого умножи-
теля частоты изображена на рис. 9.22, а
временные диаграммы, поясняющие прин-
цип его работы,—на рис. 9.23. Короткие
импульсы с частотой вращения валопрово-
да, вырабатываемые датчиком импульсов и
формирователем (на схеме не показаны),
поступают на вход 1 -го одновибратора Di ь
выход которого соединен с ключом пере-
записи Д1.з и входом 2-го одновибратора
Dj.2, включающим ключ Л| 2 разряда кон-
денсатора Сз. "Эти одновибраторы выра-
батывают короткие импульсы (£ЛСг),
сдвинуты между собой на длительность
1-го импульса. Конденсатор Сз заряжает-
ся от источника тока ViTR3R4 за один
период напряжения:
Мо + Мз
С| =---~
сз
где ti — время, в течение которого включе-
но сопротивление R3; t3—время, в течение
которого сопротивление Rs закорочено;
й» *2—токи заряда конденсатора Сз при
включенном и закороченном сопротивле-
нии R$; То—период входных импульсов;
ti—длительность входных импульсов раз-
ряда.
Параметры одновибраторов выбраны
таким образом, что и i2==2ii.
Перед приходом импульса разряда (С2)
конденсатор Сз через ключ Ац перезаря-
жает конденсатор С4 до напряжения
itT(2-a)
Ci — г '
где a—tpITo.
Максимальный диапазон автопод-
стройки составляет ±25% при начальной
установке а л 0,5. Для уменьшения разря-
да конденсатора С4 применен операцион-
ный усилитель Аг с малыми входными тока-
ми. Выход усилителя Аг подключен к неин-
вертирующему входу операционного уси-
лителя A3. К инвертирующему входу этого
усилителя подключены конденсатор Сз и
линеаризирующее сопротивление R$. Меж-
ду выходами этого усилителя и его инвер-
тирующим входом включена цепь заряда
конденсатора Сз, состоящая из диодного
моста V3D полевого транзистора У%Т и
сопротивления Rt. Полевой транзистор
УгТ и сопротивление R? образуют источник
тока, который заряжает конденсатор С5.
При увеличении напряжения на конденса-
торе Cg до UC4 напряжение на выходе
операционного усилителя Аз изменяет по-
лярность. При этом ключ Af 4 закорачи-
вает неинвертирующий вход, а конденса-
тор С5 заряжается до нуля При этом
напряжение на выходе Аз опять изменяет
полярность, и конденсатор Cs заряжается
до £/С4. Таким образом на выходе Аз обра-
зуются прямоугольные импульсы типа
«меандр» с периодом
где /з—ток заряда конденсатора С5; Л —
период импульсов на выходе Аз
Емкости конденсаторов Сз и Се вы-
бирают с учетом соотношения
То — пТ,
или
l,5tt t3
откуда
Сз « 1,5пСз.
Рис. 9.22. Принципиальная схема умножителя частоты с им-
пульсной обратной связью
Рис. 9.23. Временные диаграммы ра-
боты умножителя частоты
312 Портативная балансировочная аппаратура
Частотно-избирательные устройства
313
Для работы умножителя в частотном
диапазоне 5- 1000 Гц емкость конденса-
тора Сз выбирают в пределах 1—5 мкф
Импульсы с выхода Лз через преобразова-
тель уровня (Z?eV4 и Vs) поступают на
триггер и делитель частоты О? и Ре, кото-
рый имеет коэффициент деления 90 при
подключении ко входу одновибратора
Ds г выхода 9, или 100. при подключении
выхода 10, Одновибратор вырабатывает
короткие импульсы с частотой следования
Fo, которые устанавливают в нулевое по-
ложение счетчик Di и /?5-триггер Ds ь
На Я-вход триггера D2.i поступают им-
пульсы с одновибратора D\,2. Триггер О2।
управляет ключом Л»», который закорачи-
вает или включает сопротивление /?з, т. е.
регулирует ток заряда конденсатора Сз-
Таким образом происходит автоматиче-
ская подстройка частоты следований вы-
ходных импульсов при изменении частоты
входного сигнала или параметров схемы.
Время полного цикла автоподстройки со-
ставляет 2—3 периода входного сигнала.
На рис. 9.24 изображена структурная
схема множительного избирательного уст-
ройства, работающего с умножителем ча-
стоты. Преобразованное напряжение с вм-
бродатчика f/BX (Z) поступает на два мно-
жительных устройства /, на вторые входы
которых поступают сдвинутые на 90° уп-
равляющие сигналы с распределителя им-
пульсов 2. На вход распределителя им-
пульсов поступают импульсы с частотой
F, в п раз большей частоты вращения
балансируемого ротора Если представить
входное напряжение в виде спектра:
47ВХ(Л = £/Oi sin^wt*4-<Pi) +
оо
+£ t/0<sin(<o/ + <p,)
<=о
(где £#= I; С/0|, w q>j — параметры электри-
ческого сигнала, характеризующие вибра-
ции; 1^, <о, — параметры электрического
сигнала, характеризующие механические
помехи), а управляющие сигналы-принять
в виде sin и cos Ш|/, го на выходах
множительных устройств будут вырабаты-
ваться постоянные напряжения, пропор-
циональные синфазной и квадратурной со-
ставляющим вектора вибрации с частотой
вращения Us= UOj sin фЪ Uc— UOi cos ф(.
Эти постоянные напряжения поступа-
ют на входы множительных устройств 3,
которые управляются сигналами от рас-
пределителя импульсов 4, но с фикси-
рованной частотой Fo. Импульсы на вход
распределителя 4 поступают с импульсного
генератора 5.
Таким образом на выходах умножи-
телей 3 образуются переменные напря-
жения С7& sin 23iFo# и Uc cos 2л/;0/, которые
поступают на вход сумматора 6 На выхо-
де сумматора образуется переменное на-
Рис. 9.24. Структурная схема множительного избирательного устройства
314
Портативная балансировочная аппаратура
пряжение с частотой Fq, амплитудой и
сдвигом фазы, равными амплитуде и
сдвигу фазы оборотной составляющей
спектра, г. е.
^ВЫх(0=М) sin ф|),
где
Z70t = \U2S + U2C; ф, = arcsin .
voi
Назначение фильтра нижних частот 7
и блока вычисления сдвига фазы 8 будет
показано ниже. На рис. 9.25 приведена
структурная схема множительного уст-
ройства, которое состоит из аналогового
инвертора 7, ключа 2, резисторного де-
лителя 3, переключателя 4, фильтра по-
стоянной составляющей 5 и распреде-
Рис. 9.25. Структурная схема множительного
дискретно-аналогового устройства
лителя импульсов 6. Резисторный делитель
состоит из Р-постоянных сопротивлений, а
распределитель импульсов — из счетчика и
дешифратора. На вход счетчика в течение
одного периода поступает 4Р импульсов.
В первой половине периода делитель 3
подключен непосредственно ко входу, а
второй —к выходу инвертора. Переключа-
тель 4 подключает вход фильтра 5 ко всем
точкам делителя за четверть периода.
В данной схеме примерно равномерное
квантование во времени и неравномер-
ное по уровню.
В работе [28] предложена сравни-
тельно простая схема устройства, позволя-
ющая с достаточной точностью вычислять
амплитуду и сдвиг фазы переменного
напряжения, пропорционального пара-
метрам вектора основной гармоники.
Структурная схема этого устройства по-
казана на рис 9.26. Импульсный гене-
ратор, вырабатывающий импульсы с ча-
стотой следования Fr, подключен к дели
телю частоты на 90. С выхода делителя
частоты импульсы поступают на двух-
разрядный двоичный счетчик, к выходам
которого подключены дешифраторы. По-
следние управляют ключами Kis, K?s, К\с,
В состоянии счетчика 00 и 01 вклю-
чается ключ Kis- постоянное напряжение
Us поступает на вход аналогового сум-
матора. В состоянии счетчика 10 и 11
включается ключ на вход сумматора
подается напряжение через инвертор— Us.
Рис. 9.26. Структурная схема измерения амплитуды и сдвига фазы основной (1-й) гармоники
Частотно-избирательные устройства
Ключ К и включен в состояниях счет-
чика 01 и 10, а ключ К2с—00 и 11. Таким
образом на входы сумматора подаются
два переменных напряжения прямоуголь-
ной формы (меандр), сдвинутые друг от-
носительно друга на четверть периода и
имеющие амплитуды ±US и ±UC- Эти пе-
ременные напряжения прямоугольной фор
мы можно представить в виде суммы ос-
новной гармоники с частотой Fq и не-
четных гармоник:
Sin(i)n/ +
со
+ У 9пП 1 Sin(2ffl4-l)<o0/
Д—/ “I 1
4 I
Uc(t) = Uc —I cos coof +
оо -
2^ТГСО5(2га+1)ш<''
»l= I
где со0 = 2л/(!, Fo— /\/360.
В этом случае переменное наряжение
на выходе сумматора можно также пред-
ставить в виде суммы составляющих
спектра:
sin <o0t 4- <р0 +
1
2m 4-1
sin[(2m + l) ю0^ + ф2т+1]
где Uqi= \ U^+ U2C — амплитуда основ-
ной
ной
гармоники;
гармоники;
Фо — сдвиг фазы основ-
^0
“о—;—г* , 4^2/п-п — ампли-
2m -f-1 vz/n+i
туды и сдвиг фазы нечетных гармоник;
— коэффициент передачи сумматора.
К выходу сумматора подключен фильтр
нижних частот, имеющий частоту среза
Fcp=(l,l ... 1,2) Fo Если принять коэф-
фициент передачи фильтра К (Fo) ~ 1 и
K(F,)«1 при F,»F0, то амплитуды
высших гармоник на выходе фильтра резко
уменьшаются и форма напряжения стано-
вится практически синусоидальной Если
же принять затухание фильтра на частотах
F>Fo равным оо, то напряжение на вы-
ходе фильтра
Ui(t) = Ua] sin (а>0/ + <Ро + <Рф),
где фф—сдвиг фазы, вносимый фильтром
на частоте Fo.
Измерение сдвига фазы осуществляет-
ся следующим образом. Синусоидальное
напряжение в одновибраторе преобразует-
ся в короткие импульсы,- возникающие
при переходе синусоидального напряжения
через нуль из отрицательной полярности
в положительную. Эти импульсы подаются
на /?-вход FS-триггера, на S-вход кото-
рого подаются сигналы импульсов, сов-
падающие по времени с включением ключа
Kis; FS-триггер находится в единичном
состоянии с момента прихода импульса
на S-вход до момента прихода импульса
на Я-вход. В единичном состоянии RS-
триггер открывает ключ, на второй вход
которого поступают импульсы с генерато-
ра, имеющие частоту следования Fr~
= 36OFo- Таким образом за один период
через ключ пройдет число импульсов, рав-
ное сдвигу фазы:
Д/=1д™_360,
Т о
где Готк—время открытия ключа; Го—пе-
риод переменного напряжения на* выходе
фильтра.
Дополнительный сдвиг фазы фф, вноси-
мый фильтром нижних частот, может быть
легко скомпенсирован установкой фазы
сигналов, управляющих ключами множи-
тельного избирательного устройства, или
предварительной установки счетчиков ин-
дикации, производящей подсчет импуль-
сов. Ввиду того что на фильтр поступает
переменное, напряжение с постоянной ча-
стотой. фф= const, т. е. фф не вносит по-
<510
ортативная алансировочная аппаратура
грешность при измерении сдвига фазы па
раметров вектора основной гармоники, а
только смещает начало отсчета.
Множительные избирательные устрой-
ства следящего типа применяют не только
в балансировочной, но и в виброизмери-
тельной аппаратуре, предназначенной для
вибродиагностики ротационных механиз-
мов, так как они позволяют измерять ам-
плитуды и фазы высших гармоник и суб-
гармоник. Перестройку для измерения лю-
бых гармоник осуществляют простым из-
менением коэффициента умножения часто-
ты.
9.3. КОНСТРУКЦИИ И ОСНОВНЫЕ
ХАРАКТЕРИСТИКИ ПОРТАТИВНОЙ
БАЛАНСИРОВОЧНОЙ АППАРАТУРЫ
Современный парк портативной балан-
сировочной аппаратуры разделяют на два
основных класса: с активными фильтрами
и с множительными избирательными уст-
ройствами.
К первому классу относят оте-
чественные модели БИП-5, БИП-5А\
БИП-6М, УБП-1, УБП-2, ВБВ-001, а ко
второму классу — новые модели ап-
паратуры типа БИП-7, БИП-8, ВВМ-337
и т. д. [25, 26]
Аппаратура БИП-5, БИП-5М. БИП-
6М, УБП-1, УБП-2 и ВБВ-001 предназ-
начена для балансировки в собственных
подшипниках роторов энергетических ма-
шин и других крупных механизмов. Прин-
цип действия аппаратуры этих моделей
можно пояснить на примере БИП-5,
структурная схема которой изображена
на рис. 9.27. На подшипнике 2 балан-
сируемого ротора 1 устанавливают вибро-
датчик 3, который вырабатывает перемен-
ное напряжение, пропорциональное ско-
рости колебаний подшипника. Если счи-
тать что внешние помехи отсутствуют, то
напряжение Ui(t) на выходе вибродат-
чика можно определить по формуле
f/i (/)= KflAO(osin (to/ -|-<ро),
1Де —коэффициент преобразования
вибродатчика; Ао, too, фо—амплитуда, уг-
ловая частота вращения ротора и сдвиг
фазы колебаний.
Приведенная формула справедлива
для угловых частот too»4op (здесь (ир —
собственная угловая частота сейсмической
системы вибродатчика). Вибродатчик 3 со-
единяют кабелем с измерительным бло-
ком. Временной преобразователь 4 пред-
ставляет собой интегрирующую цепь, на
выходе которой вырабатывается перемен-
ное напряжение t/2 (0, пропорциональное
амплитуде виброперемещения:
U2 (t) — KbAq (costo/ 4- фо),
где Кв — коэффициент передачи времен-
ного преобразователя.
Рис. 9.27. Структурная схема
аппаратуры БИП-5
Конструкции и основные характеристики портативной балансировочной аппаратурыЗ 17
Фильтр нижних частот 5 служит для
уменьшения влияния высокочастотных
помех на погрешность измерений ампли-
туды и сдвига фазы. Аппаратура БИП-5
и БИП-5М снабжена набором фильтров
с частотами среза 25, 50, 100 и 200 Гц.
Усилитель 6 имеет коэффициент передачи
Ку и служит для усиления напряжения
U2 (0 До необходимого для нормальной ра-
боты детектора 7 уровня. Стрелочный ин-
дикатор 8 подключают к детектору 7 через
переключатель П1. Шкала стрелочного ин-
дикатора проградуирована непосредствен-
но в микрометрах, что позволяет произ-
водить отсчет размаха виброперемещения.
Коэффициент передачи усилителя 6 может
дискретно изменяться, что позволяет уста-
навливать пределы измерений 50, 200, 500
и 2000 мкм. К выходу усилителя 6 под-
ключены ограничитель 9 и вертикальные
пластины электронно-лучевой трубки 13.
Ограничитель 9 преобразует синусоидаль-
ную форму напряжения в прямоугольную.
К выходу ограничителя подключены пре-
образователь 10 частоты в постоянное на-
пряжение и стробоскоп 11. Через пере-
ключатель П1 стрелочный индикатор 8 мо-
жет подключаться к преобразователю 10
при измерениях частоты. Шкала имеет два
предела измерений частоты: 55 и 220 Гц.
К блоку стробоскопа подключена через ка-
бель лампа стробоскопа 12, которая осве-
щает торец ротора 1. Перед балансиров-
кой на торец ротора наносится риска, а
на подшипнике закрепляется круговая
шкала, проградуированная в градусах.
Сдвиг фазы определяют по угловому по-
ложению риски на шкале.
Сдвиг фазы можно определить, исполь-
зуя сельсинную схему. В этом случае
балансируемый ротор соединяют с ротором
сельсина-датчика 16, статор которого со-
единяют с помощью кабеля со статором
сельсина-приемника 15, расположенного в
измерительном блоке. Переменное напря-
жение с ротора сельсина-прием ника по-
дается на горизонтальные пластины элект-
ронно-лучевой трубки 13. Отсчет сдвига
фазы осуществляют по круговой шкале,
закрепленной на роторе сельсина-прием-
ника.
При наблюдении формы колебаний и
отсчете размаха виброперемещення на
горизонтальные пластины электронно-лу-
<?)
Рис. 9.28. Вибродатчик ВД-5:
а—конструкция; /- нижняя противонаводочная катушка; 2- верхняя противонаводочная катушка;
3 — арретир, 4— демпфирующая обмотка; 5 — рабочая обмотка, 6 — башмак; 7— пружины. 8—ос-
нование, 9—магнитопровод, 10—магнит; II— полюсный наконечник; 12—подвижная катушка, б —
электрическая схема
318
Портативная балансировочная аппаратура
чевой трубки подастся пилообразное на-
пряжение через переключатель П2 с гене-
ратора развертки 14.
В аппаратуре БИП-5 применен вибро-
датчик электродинамического типа ВД-5,
различные модификации которого при-
меняют в аппаратуре БИП-5М, БИП-6М,
УБП-1. и др. На рис. 9.28 приведены кон-
струкция и электрическая схема этого
вибродатчика.
В аппаратуре БИП-6М, кроме фильт-
ров нижних частот, имеются еще фильтры
высших частот с частотами среза 25, 50 и
100 Гц, что позволяет уменьшать влияние
внешних помех с частотами выше и ниже
частоты вращения балансируемого ротора.
В аппаратуре УБП-1 применен узко-
полосный перестраиваемый фильтр.
Основные технические характеристи-
ки балансировочной аппаратуры данного
класса приведены в табл. 9.1.
Значительно лучшие параметры и боль-
шие функциональные возможности имеет
аппаратура с множительными избиратель
ными устройствами.
В энергомашиностроении широкое при-
менение нашла аппаратура типа БИП-7,
которая обладает высокой избиратель-
ностью, имеет цифровую индикацию раз-
маха виброперемещения, сдвига фазы и
частоты, что позволяет производить точные
измерения при наличии значительного
уровня помех на различных частотах вра-
щения. В комплект аппаратуры входят:
измерительный блок, два электродинами-
ческих вибродатчика типа ВД-5М, фото-
электрический датчик импульсов и соеди-
нительные кабели длиной 10 м. Масса
измерительного блока—около 4 кг. масса
прибора (комплектно) около 8 кг. Пита-
ние от сети переменного тока 220 В,
50 Гц. Потребляемая мощность—около
10 ВА Структурная схема балансировоч-
но-измерительного прибора БИП-7 показа-
на на рис. 9.29.
В приборе БИП-7 применены вибро-
датчики 1 и 2 электродинамического типа
ВД-5 со схемой электрической коррекции
амплитудно-частотной характеристики.
Эти вибродатчики подключаются к анало-
говому интегратору 5 через переключа-
тель П1, ко входу которого может под-
ключаться также блок контрольного сигна-
ла 4. Выход интегратора 5 подключается
к масштабирующему усилителю 7 через
переключатель пределов 6. Прибор БИП-7
имеет два предела измерений размаха виб-
роперемещения 99,9 и 999 мкм.
В режиме измерений размаха вибро-
перемещения полигармонической вибра-
ции масштабирующий усилитель 7 под-
ключают через переключатель ПЗ ко входу
детектора размаха 8. С выхода послед-
него снимается постоянное напряжение,
пропорциональное размаху вибропереме-
щения. Преобразователь напряжение—
частота 9 вырабатывает прямоугольные
импульсы с частотой следования, пропор-
Таблица 9.1
Основные технические характеристики портативном балансировочной аппаратуры
Наименование параметров Тип аппаратуры
БИП-5 БИП-5М БИП-6М УБП-1 ВБВ-1
Измеряемые пара- метры Тип избирательного устройства Способ измерения сдвига фазы Частотный диапа- зон, Гц Основная погреш- ность, % S„ V„ ar <р, F НЧ фильтры Сельсин 15 — 200 ±10 Sr. V„ а, ф. г НЧ фильтры стробоскоп 15—200 ±10 Sr, V., аг Ф F НЧ и ВЧ фильтры 13 -220 ±5 Sr, Vr, а, ф. Г Узкополосный фильтр Стробос 15—150 ± 15 ф, F коп 25 — 250
Конструкции и основные характеристики портативной балансировочной аппаратуры319
Рис. 9.29. Структурная схема балансировочно-измерительного прибора БИ П-7
Циональной входному напряжению. Эти
импульсы через блок управления 10 посту-
пают на цифровой индикатор вибропере-
мещения 11. Блок управления 10 пред-
ставляет собой логические ключи и одно-
вибратор, формирующий импульсы сброса
предыдущих измерений.
Для измерений частоты вращения,
сдвига фазы и размаха основной гармони-
ки в приборе используют датчик импуль-
сов 4, вырабатывающий один импульс
за один оборот балансируемого ротора
Импульсы с датчика импульсов 3 через
переключатель П2 поступают на компа-
ратор 21, на выходе которого выраба-
тываются импульсы логического уровня с
частотой, равной частоте вращения балан-
сируемого ротора. Преобразователи пери-
од-напряжение 22, напряжение—часто-
та 23 и счетчик 17 составляют умножи-
тель частоты с импульсной обратной
связью. Коэффициент умножения умножи-
теля частоты равен 16, т. е. на выходе
преобразователя напряжение—частота 23
вырабатываются импульсы с частотой сле-
дования F= 16FBX. Эти импульсы посту-
пают через блок управления 10 на цифро-
вой индикатор частоты 13. Одновременно
эти импульсы поступают на счетчик 17, ко-
торый управляет коэффициентом передачи
дискретно- а нал огового ум н ожител я-п ре-
образователя синфазной и квадратурной
составляющих вектора вибрации основной
гармоники. Схема преобразователя 14
состоит из двух дискретно-аналоговых ум-
ножителей, управление коэффициентами
передачи которых осуществляется-со сдви-
гом на четверть периода. На выходах
интеграторов образуются постоянные на-
пряжения, пропорциональные синфазной и
квадратурной составляющим вектора виб-
рации оборотной составляющей.
Для уменьшения влияния составляю-
щих спектра вибрации с частотами
Г<=ГВХ (ml6± 1), где т--=1, 2. .
в масштабирующем усилителе 7 имеется
фильтр нижних частот с частотой среза
«200 Гц.
Импульсный генератор 24 вырабатыва-
ет импульсы с частотой следования
Г,.= 28,8 кГц. Распределитель импульсов
18 управляет двумя дискретно-аналоговы-
ми умножителями, которые вместе с сум-
матором составляют блок вычисления мо-
дуля 15. На выходе фильтра нижних ча-
стот 16 Fcp« 100 Гц образуется пере-
менное напряжение с частотой 80 Гц и
амплитудой, пропорциональной амплитуде
оборотной составляющей. Блок измерения
сдвига фазы 19 работает аналогично. Так
как Fr=360«80 Гц, то каждый импульс,
прошедший на цифровой индикатор фа-
зы 12, соответствует 1° сдвига фазы.
При измерении размаха вибропереме-
щения оборотной составляющей преобра-
зователь размаха 8 подключается к выходу
ФНЧ 16.
320
Портативная балансировочная аппаратура
При проведении спектрального анали-
за к компаратору 21 умножителя частоты
подключается перестраиваемый генератор
20. Настройка последнего осуществляется
вручную. При совпадении частоты гене-
ратора 20 с частотой составляющей спект-
ра вибрации на индикаторе 11 индицирует-
ся размах виброперемещения, а на инди-
каторе 13- частота. Частотный диапазон
спектрального анализа 15—200 Гц.
К входу детектора 8 прибора БИП-7
можно подключить внешние приборы (ос-
циллограф, вольтметр и т. д.).
Еще более совершенной моделью яв-
ляется прибор БИП-8, который позволяет
производить автоматический спектраль-
ный анализ вибрации с записью размаха
виброперемешения, сдвига фазы и частоты
(или частоты вращения) на двухкоорди-
натных самописцах или цифропечатающих
устройствах. Аналогичную автоматиче-
скую регистрацию результатов измерений
можно производить при снятии скоростных
и режимных характеристик турбоагрегатов
и другого вращающегося оборудования.
В приборе БИП-8 имеется тахометр с по-
грешностью измерений ±1 об/мин, по-
вышена точность измерения частоты (до
±0.1 Гц), расширен амплитудный диапа-
зон, увеличена избирательность следящего
фильтра, введены регистры хранения ре-
зультатов измерений, а при измерениях
1-й и 2-й гармоник на турбоагрегатах,
находящихся в режиме синхронизации,
можно не устанавливать датчик импуль-
сов.
Структурная схема прибора БИП-8 по-
казана на рис. 9.30. Входной тракт при-
бора БИП-8, включающий два вибродат-
чика типа ВД-5', интегратор, переключа-
тель пределов измерений и масштабирую-
щий усилитель, аналогичен прибору БИП-
7. В приборе БИП-8 применен более со-
вершенный умножитель частоты, имеющий
коэффициент умножения, равный 64, а
резисторные делители дискретно-а налого-
вого умножителя-преобразователя син-
фазной и квадратурной составляющих
Рис. 9.30. Структурная схема балансировочно-измерительного прибора БИП-8
Конструкции и основные характеристики портативной балансировочной аппаратуры321
состоят из 8-и сопротивлений. За счет
этого снижены погрешности модуля и сдви-
га фазы, улучшена помехоустойчивость и
уменьшена фазочастотная погрешность, а
частота среза фильтра нижних частот в
масштабирующем усилителе повышена до
360 Гц.
Для подключения двух координатных
самописцев служат выходы 25—27, по-
стоянные напряжения на которых про-
порциональны размаху виброперемеще-
ния, сдвигу фазы и частоте (или частоте
вращения). Выходы —34 предназначены
для подключения внешних цифропечатаю-
ших устройств (например, Щ68000), ра-
ботающих в коде 1—2—4—8.
Блок вычисления модуля и сдвига фазы
состоит из кварцевого генератора 24,
распределителя 18 импульсов, блока вы-
числения модуля 15, фильтра 16 нижних
частот и преобразователя фазы 19. Квар-
цевый генератор вырабатывает импульсы
с частотой следования 32 768 Гц, а на
выходе ФНЧ 16 образуется переменное
напряжение с частотой 91,02 Гц и ам-
плитудой, пропорциональной размаху виб-
роперемешения выделяемой гармоники.
Стабилизация с помощью кварцевого ге-
нератора частоты переменного напряже-
ния, снимаемого с выхода фильтра ниж-
них частот 16, позволила значительно сни-
зить фазочастотные погрешности блока
преобразования сдвига фазы 19.
При спектральном анализе к компара-
тору 21 умножителя частоты подключают
импульсный генератор 20, частота гене-
рируемых импульсов которого управляется
генератором линейно изменяющегося на-
пряжения 28. Настройка частоты гене-
ратора 20 может производиться автома-
тически или вручную. Имеются два режима
автоматического анализа «медленно» и
«быстро». Остальные блоки прибора ана-
логичны БИП-7 (см. рис 9.29).
Прибор БИП-8, несмотря на значи-
тельное усовершенствование, выполнен в
том же конструктиве, что и БИП-7. Вы-
сокие метрологические параметры и рас-
ширенные функциональные возможности
прибора БИП-8 позволяют использовать
его не только при балансировке, но и при
вибрационной диагностике технического
состояния турбоагрегатов.
С помощью прибора БИП-8, цифро-
печатающего устройства и таймера осу-
ществляют длительные вибрационные ис-
пытания, например исследуют тенденцию
изменения вибрационных параметров тур-
боагрегатов.
Наиболее совершенными моделями
отечественной аппаратуры с множитель-
ными избирательными устройствами яв-
ляются виброанализаторы ВВМ-337 и
АСВ-10. Обе модели имеют практически
одинаковые характеристики и функцио-
нальные возможности.
Основным назначением виброанали
затора ВВМ-337 является вибродиагности-
ка газокомпрессорных установок магист-
ральных газопроводов. Но его функцио-
нальные возможности позволяют приме-
нять виброанализатор ВВМ-337 и в дру-
гих отраслях промышленности для вибро-
диагностики и балансировки ротационных
механизмов (например, в энергетике,
станкостроении, на нефтепроводах и в
авиации). Виброанализатор АСВ-10 ис-
пользуют для вибродиагностики нерота-
ционных механизмов или агрегатов, имею-
щих многочастотные возбудители виб-
рации.
В комплект виброанализаторов входят:
измерительный блок, два вибродатчика и
фотоэлектрический датчик импульсов. Ви-
броанализаторы позволяют измерять в
частотном диапазоне 10 -1000 Гц следую-
щие параметры:
среднее квадратическое значение виб-
роскорости и виброперемещения полигар-
монической вибрации;
среднее квадратическое значение ви-
броскорости, размах виброперемещения и
частоты составляющих спектра вибрации;
среднее квадратическое значение виб-
роскорости, размах виброперемещения,
частоты и сдвиги первых десяти гармоник,
кратных частоте вращения;
частоту вращения исследуемых рото-
ров.
И Зак 1641
322
Портативная балансировочная аппаратура
Измерение среднего квадратического
значения виброскорости и виброперемеше-
ния полигармонической вибрации и спект-
ральный анализ осуществляют как во всем
частотном диапазоне, так и в ограничен-
ных частотных диапазонах с пределами
le^Fi^mlOO Гц,
40<E^ml()0 Гц;
100 Гц,
где т = 1, 2,. .. , 10.
Нижнюю граничную частоту измерений
устанавливают одним постоянным и двумя
переключаемыми фильтрами верхних ча-
стот. Верхнюю граничную частоту изме-
рений устанавливают переключаемым
фильтром нижних частот, в котором часто-
ту среза регулируют дискретно от 100 до
1000 Гн через 100 Гц.
Регулируемые границы частотного диа-
пазона измерений вызваны наличием зна-
чительного уровня неинформативных по-
мех и большим значением виброскорости
высших гармоник, имеющихся в спектре
вибрации газокомпрессорных установок.
При измерениях виброперемещения
большую погрешность могут вносить низ-
кочастотные сейсмоколебания фундамен-
та, которые срезаются фильтром верхних
частот с частотой среза 10 Гц, а в случаях
появления низкочастотных помех с часто-
той выше 10 Гц или при измерениях
виброперемещения высших гармоник, уро-
вень которых значительно ниже уровня
1-й гармоники, включаются дополнитель-
ные ВЧ-фильтры с частотами среза 40 и
150 Ги. Дополнительные ВЧ-фильтры
включают и при использовании вибродат-
чика в качестве виброшупа для того,
чтобы исключить влияние колебаний РУК.
Переключаемые НЧ-фильтры позво-
ляют производить измерения параметров
виброскорости основной гармоники на низ-
ших пределах при наличии высших гармо-
ник, уровни которых превышают эти пре-
делы. Кроме того, НЧ-фильтры позволяют
производить контроль вибрационного со-
стояния агрегатов, имеющих различные
частотные диапазоны нормирования.
С помощью виброанализатора ВВМ-
337 осуществляют гармонический и спект-
ральный анализ вибрации. При гармо-
ническом анализе измеряют параметры
векторов первых десяти гармоник с синх-
ронизацией от фотоэлектрического датчи-
ка импульсов. Измерения модуля, сдвига
фазы и частоты гармоник выполняют пере-
ключателем номера гармоники. Спектраль-
ный анализ осуществляют в ручном и авто-
матическом режимах.
В ручном режиме выполняют настрой-
ку на частоту измеряемой составляющей.
Модуль этой составляющей спектра вибра-
ции отсчитывают по цифровому или
стрелочному индикатору. В приборе имеет-
ся система автоматической подстройки ча-
стоты, и после ее срабатывания по циф-
ровому индикатору частоты (или частоты
вращения) отсчитывается частота состав
ляюшей спектра.
В автоматическом режиме осуществ-
ляется запись модулей и частот состав-
ляющих спектра анализируемой вибрации
на двухкоординатном самописце. Наличие
линейных выходов, постоянные напряже-
ния на которых пропорциональны средне-
му квадратическому значению или разма-
ху, сдвигу фазы, частоте и частоте вра-
щения. позволяет выполнять запись на
двухкоординаткых самописцах скорост-
ных, нагрузочных и других характеристик
исследуемых агрегатов.
Возможность измерения параметров
вибрации основной гармоники и высокая
избирательность следящего фильтра по-
зволяют производить балансировку аг-
регатов в собственных подшипниках на
месте их эксплуатации при наличии зна-
чительного уровня помех.
Структурная схема виброанализатора
ВВМ-337 приведена на рис. 9.31. Для виб
роанализатора разработан специальный
пьезодатчик ПТ-1 со встроенными согласу-
ющими усилителями заряда и напряжения.
Переменное напряжение, пропорциональ-
ное виброускорению, с помощью соеди-
нительного кабеля подается с измеритель-
ного блока на вход фильтра / нижних
Конструкции и основные характеристики портативной балансировочной аппаратуры323
частот четвертого порядка с частотой среза
1200 Гц, предохраняющего входной тракт
от перегрузок.
В аппаратуре ВВМ-337 и АСВ-10 от-
сутствуют традиционные аналоговые инте-
граторы, применяемые обычно для пре-
образования переменного напряжения,
пропорционального виброускорению, в
переменные напряжения, пропорциональ-
ные виброскорости и виброперемещению.
Временные преобразования осуществля-
ются с помощью двух полосовых фильтров
2 и 4 и корректирующих усилителей 3 и 5.
Частота резонанса фильтров 2 и 4 состав-
ляет 7 Гц. Таким образом эти фильтры
с корректирующими усилителями допол-
нительно выполняют функции фильтров
верхних частот с граничной частотой 10 Гц.
Неравномерность амплитудно-частотной
характеристики по виброскорости и вибро-
перемещению не превышает ±2%. Затуха-
ние на частотах ниже 7 Гц составляет
18 и 36 дБ на октаву при измерениях
виброскорости и виброперемещения.
При измерении виброскорости ко входу
масштабирующего усилителя 7 подключа-
ют корректирующий усилитель 3, а при
определении виброперемещения — коррек-
тирующий усилитель 5. Переключение ре-
жимов измерения осуществляют с по-
мощью переключателя П/, с помощью
которого подключают также генератор
контрольного сигнала 6 при проверке ра-
ботоспособности прибора.
К выходу усилителя 7 подключены
фильтры верхних частот 8 (Fcp—40 Гц)
и 9 (Гср= 150 Гц), включение которых
осуществляют переключателем П2. К вы-
II*
324
Портативная балансировочная аппаратура
ходу П2 подключают фильтр 10 нижних
частот, частоту среза которого устанав-
ливают переключателем 11, а включение—
переключателем ПЗ. Последний подклю-
чают к масштабирующему усилителю 12.
Масштабный коэффициент (1:1 или 1:10)
устанавливают переключателем масшта-
ба 13.
Фильтр нижних частот 10 построен
по принципу фильтра с переключаемыми
конденсаторами 3-го порядка. Номиналы
переключаемых конденсаторов выбраны из
условия неравномерности амплитудно-ча-
стотной характеристики ±2% в полосе
пропускания, затухания не менее 30 дБ
на октаву на частотах выше частоты
среза и отношения частоты переключе-
ния к частоте среза 120— 150. Последнее
условие спектра с частотами 10—1000 Гц,
т. е.
F
Р КОММ р
Г tn in —р > Г* П!ах,
1 ср
где и jFmax—граничные частоты из-
меряемого диапазона (jFmin= 10 Гц, Fmax=
= 1000 Гц); FK0HW/jFcp—отношение часто-
ты переключения конденсаторов к частоте
среза фильтра.
Частота переключения конденсаторов,
а следовательно, и частота среза фильтра
изменяются путем перестройки частоты
следования импульсов мультивибратора
11.
При измерении параметров полигармо-
нической вибрации переменное напряже-
ние с усилителя 12 поступает через пере-
ключатель П4 на нормирующий усилитель
14, к выходу которого подключены пре-
образователь среднего квадратического
значения 15 и клемма выхода перемен-
ного тока 16.
Выход преобразователя 15 подключен
к выходу по постоянному току 17 и через
переключатель масштаба 18 к стрелочно-
му указателю 19. Выход по постоянному
току 17 предназначен для подключения
самописцев, внешних вольтметров и других
приборов. Постоянное напряжение на вы-
ходе 17 пропорционально виброскорости
или виброперемещению в зависимости от
положения переключателя П1. Переключа-
тель масштаба 18 изменяет пределы изме-
рений по шкале стрелочного указателя
19 на 10 дБ. Стрелочный указатель удобно
применять при измерениях нестационарной
вибрации и одновременных измерениях мо-
дуля, сдвига фазы и частоты. Постоянное
напряжение с выхода преобразователя 15
поступает на преобразователь напряже-
ние— частота 20.
Импульсы с частотой следования, про-
порциональной виброперемещению или
виброскорости, поступают через блок уп-
равления индикацией 21 на цифровой ин-
дикатор 22. В блоке управления 21 форми-
руются интервалы счета, импульсы сброса
и перезаписи, записываются и запоми-
наются в регистрах результаты измерений,
осуществляется коммутация, необходимая
при динамической индикации. В аппарату-
ре применен восьмиразрядный вакуумный
цифровой индикатор типа ИВ-28.
Четыре левых разряда индикатора ис-
пользуют для измерений виброскорости,
виброперемещения или сдвига фазы, а ос-
тальные четыре разряда 23—для индика-
ции частоты и частоты вращения.
Для измерения частоты вращения,
сдвига фазы и синхронизации следящего
фильтра в приборе ВВМ-337 применены
фотоэлектрический датчик импульсов и
схема умножителя частоты с переменным
коэффициентом умножения, состоящая из
входного компаратора 37, преобразователя
38 периода в напряжение, аналоговой па-
мяти 39, преобразователя напряжение—
частота 40, шести разрядного счетчика 41,
счетчика с регулируемым коэффициентом
пересчета 42, переключателя гармоник 43 и
фазового детектора 44.
При измерении параметров основной
гармоники выход аналоговой памяти 39
подключается с помощью переключателя
П8 к входу преобразователя напряже-
ние— частота, а коэффициент пересчета
счетчика 42 устанавливают равным едини-
це с помощью переключателя гармоник
43. В этом случае частота следования
Конструкции и основные характеристики портативной балансировочной аппаратуры325
импульсов на выходе преобразователя
40 в 64 раза выше частоты импульсов,
поступающих с фотодатчика. В блоке уп-
равления индикацией 21 формируются ин-
тервалы времени счета импульсбв, равные-
15/16 секунды, используемые при измере-
ниях частоты и частоты вращения.
При измерении частоты вращения им-
пульсы с преобразователя 40 поступают
через переключатель П6 на блок управ-
ления 2! и преобразователь 36 частота —
напряжение. В этом случае число импуль-
сов, прошедших за один цикл на счетчики
индикации,
Л/ = 64/гвх7'сч —60F
т. е. один импульс соответствует 1 об/мин.
На выходе 45 вырабатывается постоян-
ное напряжение, пропорциональное часто-
те вращения. При измерении частоты блок
управления 2! и преобразователь 36 под-
ключают к делителю частоты 35, имею-
щему коэффициент деления, равный 6.
В этом случае число импульсов N— 10jF6x,
т. е. один импульс соответствует 0,1 Гц.
При измерении параметров высших гармо-
ник с помощью переключателя 43 уста-
навливают коэффициент деления счетчика
42 от 2 до 10; при этом коэффициент
умножения частоты равен 64я (где п —
= 2... 10), т. е. измеряют параметры от
2-й до 10-й гармоники.
Схема множительного избирательного
устройства состоит из дискретно-а налого-
вых умножителей 24, интеграторов 25,
блоков вычисления модуля 26 и сдвига
фазы 27, схемы управления 28, кварце-
вого генератора 29, преобразователя фа-
за— напряжение 30 и дешифратора 33.
При измерении модуля и сдвига фазы
первой (основной) гармоники дискретно-
аналоговый умножитель управляется де-
шифратором, на вход которого поступай/г
импульсы с частотой, равной 32FBX.
С выхода блока 26 переменное напря-
жение поступает на вход усилителя 14
через переключатель П4. Блок вычисления
фазы 27 вырабатывает число импульсов,
пропорциональное сдвигу фазы между ос-
новной гармоникой и импульсом, выраба-
тываемым датчиком импульсов. Эти им-
пульсы поступают на вход преобразова-
теля фаза—напряжение 30 и через пере-
ключатель П5 на блок управления 21.
На цифровом индикаторе 22 отсчитывается
сдвиг фазы с дискретностью 1 °, а на выходе
31 образуется постоянное напряжение,
пропорциональное этому сдвигу фазы.
При измерении параметров высших
гармоник дискретно-аналоговый умножи-
тель управляется частотой, равной п32Гвх
(где п — номер гармоники, устанавливае-
мый переключателем 43). Измерение пара-
метров высших гармоник осуществляют
так же, как и при измерении основной
гармоники, т. е. по цифровым индикаторам
22 и 23 и стрелочному указателю 19
отсчитываются модуль, сдвиг фазы и ча-
стота соответствующей гармоники.
При спектральном анализе на вход
преобразователя напряжение—частота 40
подается постоянное напряжение с гене-
ратора линейно-изменяющегося напряже-
ния 32 через переключатель П8. Для
уменьшения времени автоматического ана-
лиза и увеличения стабильности при руч-
ном измерении составляющих спектра виб-
рации служит фазовый детектор 34,
вырабатывающий постоянное напряжение,
пропорциональное квадратурной состав-
ляющей вектора вибрации.
Основные технические характеристики
портативной балансировочной аппаратуры
с множительными избирательными устрой-
ствами приведены в табл. 9.2.
Анализ конструкций балансировочной
аппаратуры показывает, что в большин-
стве новых моделей в качестве избира-
тельных узлов применяются только ана-
логовые, аналого-цифровые, или цифровые
множительные избирательные устройства.
Это объясняется тем, что множительные
избирательные устройства позволяют соз-
давать следящие системы с автоподстрой-
кой частоты, имеют узкую полосу про-
пускания, минимальные амплитудно-час-
тотные и фазочастотные погрешности.
Другим преимуществом множительных
326
Портативная балансировочная аппаратура
Таблица 9.2
Технические характеристики портативной балансировочной аппаратуры с множительными
избирательными устройствами
Наименование Тип аппаратуры
параметров БИП-7 БИП-8 ВВМ-337 АСВ-10
Измеряемые параметры: В иброперемещение Частота Частота вращения Сдвиг фазы Виброскорость Спектральный анализ Гармонический анализ + ± + + +++ + + ь + 4- 4- 4- 4-4" 4-4-4—1-
Частотный диапазон измерений Гц(мин“') .15—200 10—300 (600—18 000) 10—1000 (600—60000) 10— 1000 (600—6000)
Основные погрешности, виброперемещения и виброскорости, % частоты колебаний, Гц частоты вращения, мин-1 сдвига фазы.® 1+ I 1+ ел >— ел ±5 ±0,1 ± 1 ±2 ±5 ±0,1 ± 1 ±2 ±5 ±0.1 ± 1 ±2
Масса, кг: измерительного блока вибродатчика 6 0,5 6 0,3 4,5 0,25 4,5 0,25
устройств является возможность получе-
ния информации, пригодной для непосред-
ствённого ввода в ЭВМ, на цифропеча-
тающие устройства и другие вспомогатель-
ные приборы.
В абсолютном большинстве баланси-
ровочных приборов применены электроди-
намические вибродатчики, что объясняется
их небольшим временем установления, вы-
сокой помехозащищенностью, меньшей по-
грешностью измерения сдвига фазы и
виброперемещения и хорошей линей-
ностью. Частотный диапазон большинства
балансировочных приборов ограничен
сверху 2—4 гармониками и лежит в преде-
лах от 10—15 до 200— 300 Гц. Улучшение
уравновешивания валопроводов можно
достичь путем повышения точности балан-
сировочных приборов, автоматизацией
процесса измерения и вычислений урав-
новешивающих грузов.
9.4. ПЕРСПЕКТИВЫ РАЗВИТИЯ
ПОРТАТИВНОЙ
БАЛАНСИРОВОЧНОЙ АППАРАТУРЫ
Развитие балансировочной аппарату-
ры ведется в трех направлениях: повыше-
ния точности измерений параметров виб-.
рации, увеличения функциональных воз-
можностей и автоматизации процессов из-
мерений и вычислений при балансировках.
Использование современной микро-
электроники позволяет проектировать из-
мерительные блоки балансировочной ап-
паратуры, обладающие достаточно высо-
кими метрологическими параметрами. Зна-
чительно сложнее улучшать характери-
стики вибропреобразователей. В отличие
от измерительной аппаратуры баланси-
ровочных станков в портативной баланси-
ровочной аппаратуре в ближайшее время
трудно ожидать появления новых вибро-
преобразователей, обладающих значи-
Перспективы развития портативной балансировочной аппаратуры
327
тельно лучшими характеристиками. Основ-
ными типами вибропреобразователей ос-
танутся электродинамические и пьезоэлек-
трические, Улучшение технических харак-
теристик этих преобразователей возможно
только за счет увеличения надежности,
стабильности и повышения коэффициента
преобразования.
В последнее время появились публика-,
ции об использовании пьезорезисторных
вибропреобразователей, которые имеют
преимущества при измерениях вибрации в
инфранизкочастотном диапазоне, но широ-
кого внедрения они пока не получили.
Характерным недостатком этих вибро-
преобразователей, как и всех парамет-
рических преобразователей (индуктивных,
емкостных, тензорезисторных, холотрон-
ных и т. д.), является необходимость под-
вода к ним напряжения для питания
встроенных электронных узлов.
Появление микромощных интеграль-
ных аналого-цифровых преобразователей
(например, К1ПЗПВ1 и К572ПВ1) и
микропроцессоров (например, серии 1806 и
К588) позволит расширить функциональ-
ные возможности балансировочной аппа-
ратуры при одновременном уменьшении
их габаритных размеров и числа элемен-
тов, так как многие функции аналоговых
схем (интегрирования, умножения и т. д)
смогут выполнять микропроцессоры.
Применение в конструкциях измери-
тельных блоков микропроцессоров уже
сейчас позволяет автоматизировать про-
цессы вычислений при многоплоскостных
балансировках. Вычисление балансиро-
вочных грузов осуществляется по жесткой
программе (например, в аппаратуре
МТА-020 фирмы «Ниппон Стил», Япония)
или на программируемых микрокалькуля-
торах с помощью сменных магнитных мо-
дулей (САВ-178 фирмы «Шенк» ФРГ).
В ближайшее время ожидается появ-
ление многоканальной портативной балан-
сировочной аппаратуры с автоматической
передачей результатов измерений й комп-
лексных коэффициентов влияния в ЭВМ
для расчета систем балансировочных уз-
лов при многоплоскостных балансировках
с квадратной и прямоугольной матрицами
коэффициентов влияния.
ЧАСТЬ III. ТЕХНОЛОГИЯ БАЛАНСИРОВКИ РОТОРОВ
Балансировка ротора начинается с из-
готовления деталей и завершается испыта-
нием машины. Изменение неуравновешен-
ного состояния происходит в процессе об-
работки и соединения деталей. Достиже-
ние заданного неуравновешенного состоя-
ния осуществляется в процессе баланси-
ровки деталей, узлов и роторов в сборе.
При этом находят применение различные
методы и средства балансировки, изложен-
ные в частях 1 и 2 настоящего справочника.
В части III справочника даны методы
их использования для достижения задан-
ного качества уравновешивания роторов
Совокупность методов, обеспечивающая
допустимые дисбалансы ротора, представ-
ляет собой технологический процесс его
балансировки. Технология балансировки,
как и многие другие различные по физи-
ческой сущности процессы изготовления
машин, базируется на учении о точности
машиностроения.
В практической работе к технологи-
ческому процессу балансировки ротора
подходят как к некоторому комплексу тех-
нологических процессов, имеющих разли-
чия в потребном оборудовании, методах
его использования и решаемых технологом
задачах.
Глава 10
ТОЧНОСТЬ БАЛАНСИРОВКИ
10.1. ОСНОВНЫЕ ПОНЯТИЯ
Параметры, характеризующие уравно-
вешенное состояние ротора, -дисбалансы
в его поперечных сечениях в эксплуата-
ционных условиях. К ним относятся: зна-
чение и угол дисбаланса в t-м сечении,
закон распределения дисбалансов вдоль
оси ротора. Исходное неуравновешенное
состояние возникает при изготовлении де-
талей, сборки узлов и ротора. Это состоя-
ние изменяется при балансировке и на
рабочих частотах вращения в эксплуата-
ционных условиях. Качество уравновеши-
вания оценивают в зависимости от класса
ротора точностью балансировки по ГОСТу
[Гб] для жестких и квазигибких роторов,
или вибрациями корпуса, происходящими
с частотой вращения гибкого ротора на
холостом ходу машины.
Допустимый класс точности баланси-
ровки жестких и квазигибких роторов
или допустимые уровни вибраций гибких
роторов устанавливает конструктор, исхо-
дя из требуемой вибропрочности машины,
с учетом условий работы ее деталей и
роторов. Эти требования обеспечиваются
заключительными балансировочными опе-
рациями. Однако важно соблюсти техно-
логический регламент изготовления дета-
лей, узлов и ротора, так как результаты
балансировки ротора существенно зависят
от качества выполнения предшествующих
операций. Поэтому устанавливают допуски
на дисбалансы деталей и узлов, входящих
в балансируемый ротор. Таким образом,
точность балансировки — это степень со-
ответствия действительных дисбалансов
заданным. Под погрешностью балансиров-
ки понимают отклонение действительного
Расчет требуемой точности балансировки
329
дисбаланса от допустимого ^заданного).
Абсолютная погрешность выражается в
единицах рассматриваемого параметра;
относительная погрешность - отклонение
абсолютной погрешности от заданного
значения параметра.
При оценке точности балансировки, в
общем случае, различают три характери-
стики точности:
по значению дисбаланса в плоскости
измерения;
по углу дисбаланса в плоскости из-
мерения;
по взаимному расположению дис-
балансов в заданных плоскостях измере-
ния (закон распределения дисбалансов
вдоль оси ротора или вид неуравновешен-
ности).
Заданная (требуемая) точность регла-
ментируется допустимыми дисбалансами.
Действительная точность характеризуется
действительными (начальными или оста-
точными) дисбалансами. Ожидаемая точ-
ность моЖет быть определена:
при проектировании технологического
процесса балансировки;
при сборке ротора в корпус машины
без йосле дующей балансировки;
на рабочих частотах вращения в экс-
плуатационных условиях, на основании
учета причин, вызывающих погрешности
балансировки.
10.2. РАСЧЕТ ТРЕБУЕМОЙ ТОЧНОСТИ
БАЛАНСИРОВКИ
Виброактивность машин оценивают
виброскоростью, виброускорением, на-
грузками на подшипниковые опоры, вибро-
перемешением ротора относительно корпу-
са, напряжением в роторных узлах.
При проектировании колебания машин
моделируют с помощью ЭВМ, изучая свой-
ства частот и форм собственных колебаний
и влияние на них конструктивных пара-
метров. Анализ вынужденных колебаний
проводят при различных законах распре-
деления дисбалансов ротора.
Модели. Любая роторная машина яв-
ляется динамической системой, состоящей
из множества взаимодействующих эле-
ментов и подсистем. Связь вектора виб-
рационного состояния X (/) с вектором
динамического воздействия на нее F (О
описывается выражением
X(0 = LF(Z),
где L—оператор, определяющий необ-
ходимые линейные или нелинейные пре-
образования. В случае линейных колеба-
ний динамической системы оператор L на-
ходят из дифференциального уравнения
[М]х+[С]х+[А]х-Н0.
где [Ml, [С]. [К] — матрицы масс, коэф-
фициентов сопротивлений, жесткостей.
Для исследования вибрационных про-
цессов обусловливаются модели входных,
выходных и преобразующих параметров.
Входной параметр - n-мерный вектор сил
(моментов), приложенных в сечениях ро-
тора, где под сечением понимают опреде-
ленный участок ротора с эквивалентным
значением масс tn (я), жесткостей k (z, s),
моментов инерции J (s), эксцентриситетов
е (я). В сечении с координатой я приложен
вектор F (я) под углом <р(я) относительно
выбранного начала отсчета, связанного
с ротором F — т (s)e (я)со2. Центр экви-
валентной массы т (я) смещен относитель-
но геометрической оси ротора на ве-
личину эксцентриситета е (я), представ-
ляющего собой геометрическую сумму:
ё(я) = ё(я)нач + ё(я)т+ё (s)9 + e (я)к.
Эксцентриситеты е (я)нач, е (я)т, е (я)э
определяют соответственно начальные,
технологические и эксплуатационные дис-
балансы. Эксцентриситет е (я)к образуется
при наличии корректирующей массы в дан-
ном сечении. В условиях серийного про-
изводства все составляющие эксцентриси-
тета е (я) являются случайными величина-
ми, обусловленными погрешностями изго-
товления деталей, сборки роторов, де-
формациями и износом деталей при ис-
пытаниях и эксплуатации. Следовательно,
сила (момент) в сечении я— векторная
случайная величина, распределенная по
соответствующему закону с определенны-
330
Точность балансировки
ми числовыми характеристиками. На этапе
проектирования машины принимают: дли-
на вектора F распределена по закону
Релея или Гауса, а угол вектора имеет
равномерное распределение.
Выходной параметр—m-мерный век-
тор вибраций с частотой вращения ротора,
измеренный в т точках на корпусе, опо-
рах или роторе. При построении модели
вибрация рассматривается как стационар-
ный эргодический процесс с распределе-
нием амплитуды по закону Релея, а фазы
колебаний — по закону равной вероятно-
сти. При наличии внешних негармониче-
ских сил, действующих в системе, что имеет
место при испытаниях машины под на-
грузкой. вибрация аппроксимируется мо-
делью «синусоида 4-шум» с распределе-
нием амплитуд близко к нормальному.
Преобразующие параметры (матрицы
[Л4], [С], [К]) отражают геометрию и
механические свойства системы: плот-
ность, модуль упругости, модуль Юнга и
т. п. На практике погрешности этих вели-
чин имеют нормальное распределение.
Этапы моделирования колебаний (рис.
10.1). Составление расчетной схемы. При
выполнении практических расчетов целе-
сообразно в качестве расчетной схемы
использовать схему ротора с сосредоточен-
ными массами и безынерционными участ-
ками вала. Машина схематизируется си-
стемой «ротор — подшипниковые опоры—
корпус—подвеска». Ротор и корпус, не-
зависимо друг от друга, разбиваются на
невесомые расчетные участки, на гра-
нице которых находятся расчетные то’чки.
К ним приведены эквивалентные массы,
моменты инерции, усилия и моменты от
упругих связей. Корпус через неосесим-
метричную подвеску крепится к непод-
вижному основанию с линейными упру-
гими связями. Численные значения ли-
нейных упругих связей, аппроксимирую-
щих жесткость подшипников, подвески
корпуса выбирают на основании предва-
рительных расчетов или результатов ис-
пытаний предшествующих и разрабаты-
ваемых машин. Для различных роторных
машин составлены типичные расчетные
схемы (6], отражающие конструктивные
особенности, условия эксплуатации, уро-
вень вибронадежности.
Методы расчета колебаний основаны
на дискретной расчетной схеме, пред-
ставляют собой специальные способы ре-
шения линейных алгебраических урав-
нений с кв аз итрехдиагон альной матрицей
коэффициентов. Распространены методы
матричной прогонки и начальных пара-
метров [6].
Расчет собственных колебаний. В ре-
зультате расчета находят собственные
частоты в диапазоне, превышающем мак-
Рис. 10.1. Этапы моделирования колебаний
Расчет допусков на балансировку деталей и узлов роторов
331
симальную эксплуатационную скорость
вращения в 3 раза, и строят на этих
частотах формы колебаний ротора. Путем
имитационного моделирования исследу-
ют влияние преобразующих параметров на
собственные колебания, задавая их пре-
дельно возможные значения. По предел^
ному частотному отношению *]=<аэтах/
/<°omin, где womin—наименьшее значение
угловой скорости, при которой ротор из-
гибается по 1-й собственной форме, уста-
навливается класс ротора
Частное
отношение
менее 0,3 0,3—0,7 более 0,7
Класс ротора
Расчет вынужденных колебаний. При
расчете вынужденных колебаний опреде-
ляют вибрации корпуса, нагрузки на под-
шипниковые опоры, прогибы и динами-
ческие перемещения ротора и соответст-
вующие им напряжения. В зависимости
от класса ротора расчетная схема машины
может быть упрошена путем уменьшения
числа дискретных масс ротора вплоть до
одной для жесткого ротора Методика рас-
чета состоит в следующем.
Последовательно задавая для каждой
дискретной массы предельно возможные
значения эксцентриситета е (s), вычисляют
значения и фазу выходного параметра,
например виброскорость корпуса в точке
/. По формуле
ais=V,^/e(s)
определяют коэффициенты балансировоч-
ной чувствительности a/s. В результате
п расчетов находят матрицу коэффициен-
тов балансировочных чувствительностей
a/s размерностью п X m для заданных
частот вращения ротора. Анализ a(s поз-
воляет установить менее чувствительные
плоскости на роторе, упростить расчетную
схему ротора, ограничить число входных
параметров.
Расчет функциональных дисбалансов.
Задавая предельно возможные значения
эксцентриситетов для каждой дискретной
массы ротора и принимая N возможных
положений эксцентриситета по углу, /Vй"
раз вычисляют выходные параметры. Про-
ведя расчеты с различными е (s), уста-
навливают функциональные дисбалансы в
каждой плоскости по длине ротора, обе-
спечивающие требуемую виброактивность
машины на всех эксплуатационных часто-
тах вращения.
В результате моделирования колеба-
ний устанавливают:
нормы виброактивности машины
виброскорость корпуса, нагрузки на под-
шипники, прогибы (виброперемещения)
ротора:
допустимые динамические характери
стики машины—собственные частоты,
коэффициенты балансировочных чувстви-
тельностей-,
функциональные дисбалансы — глав-
ный вектор и главный момент дис-
балансов (жесткий ротор), значение и
угол дисбалансов в плоскостях измерения
(квазигибкий ротор), значение дисбалан-
са по п-й форме изгиба (гибкий ротор);
класс точности балансировки в со-
ответствии с принятыми стандартами для
данного типа машин.
10.3. РАСЧЕТ ДОПУСКОВ НА
БАЛАНСИРОВКУ ДЕТАЛЕЙ И
УЗЛОВ РОТОРОВ
Цель расчета — установить допустимые
дисбалансы на детали, узлы и роторы,
балансируемые при изготовлении и ре-
монте изделия. Методика расчета вклю-
чает определение эксплуатационных, тех-
нологических, начальных дисбалансов ро-
тора и его составных частей согласно схеме
сборки машины.
Эксплуатационный дисбаланс е (s)3 об-
условлен:
ослаблением посадок, деформациями и
смещением деталей под действием термо-
механических нагрузок;
радиальными зазорами подшипников
качения;
несоосностью ротора и вала присоеди-
няемой машины,
332
Точность балансировки
неравномерным износом и другими
причинами.
Ослабление посадок от центробежных
сил Af, разницы температур в сопрягаемых
деталях Л/ оценивают с использованием
выражений
Д/г= (/?оЧ~/?вн) / • А*=2о&/?о£.
где р — плотность м ате риала; Е—модул ь
упругости; at— коэффициент линейного
расширения; t—разность температур; /?«,
/?вн—внешний и внутренний радиусы дета-
ли.
При втором и третьем режиме нагру-
жения подшипника с радиальным зазором
эксцентриситет массы устанавливают по
формуле
t?(s) = 0,5Д
Ч---— Ацодв] >
где ДподА<Д|ЮдВ—радиальный зазор под-
шипника А и В в свободном состоянии;
А — коэффициент уменьшения зазора при
запрессовке кольца подшипника на вал
(Д = 0,55-5-0,6) или в корпус (Д = 0,65-=-
0,7).
Эксцентриситет массы от несоосности
ротора и вала присоединяемой машины при
соединении с помощью жестких муфт
(рессор) устанавливают по формуле
е (5) ^рад“Ь Ф^-As»
где Драд, ф—радиальное и угловое от-
клонение от соосности в плоскости опоры
A, LAs—расстояние от опоры А до
центра масс диска S.
Технологический дисбаланс е (s)T обу-
словлен многими факторами, наиболее зна-
чимые из которых:
точность изготовления поверхностей
деталей, монтируемых на ротор;
точность подшипников;
деформации деталей и вала, возникаю-
щие при сборке ротора.
Эксцентриситет диска относительно
геометрической оси ротора устанавливают
по формулам:
для ротора дисковой конструкции
3 2
е (S) “ 0,5 S Арадi + 8^0m(s) 2 Аторцi >
1=1 ,=|
для ротора барабанной конструкции
(роторного пакета)
e(s) = Lks (es + e^).
Здесь эксцентриситет диска роторного
пакета от радиальных биений центрирую-
щих поверхностей
в(х) ^-А s| АрадПП Ч-
И
X- (Арад«“f" J /(2L),
«=i J
где Арад„„, Арад„ — радиальные биения
центрирующих поверхностей 1-й или п-й
концевых деталей относительно их базовых
поверхностей; Драдй- радиальное биение
одной центрирующей поверхности неконце-
вой детали относительно ее второй цент-
рирующей поверхности; Др-ну—поле до-
пуска размера центрирующей поверхности
U+П-й детали в месте ее сопряжения
с i-й деталью.
Эксцентриситет диска от торцовых
отклонений в месте соединения деталей ро-
торного пакета
АТорц(«+ 111
2^1,4-Ц,
где AT<w-(l+1)—торцовое биение t-й детали
в месте ее сопряжения с (* + 1)-й деталью,
измеренное на радиусе Ri (/+d; Аторц(, + n f—-
торцовое биение (* +1) -й детали в месте ее
сопряжения с t-й деталью, измеренное на
радиусе
Эксцентриситет диска S относительно
оси подшипников качения устанавливают
по формуле
e(s) = 0.5 [(АподА-|-Ла) (1----
Ч-(АпадВ-|-Ав) —| , "Ь
Расчет донусков на балансировку деталей и узлов роторов
333
где Дподд<ДподВ—радиальное биение бе-
говых дорожек качения подшипников А и
В относительно посадочных поверхностей
своих колец и поля допусков ДА, Дв их
диаметров в местах посадки на цапфы
ротора.
Эксцентриситеты, возникающие при
затяжке роторного пакета или диска, уста-
навливают по формуле e(s) — ys, где у* -
прогиб вала в сечении s, определяемый
по правилам сопротивления материалов
при изгибе оси от торцовых биений деталей
в месте их сопряжения и осевой нагрузки.
При этом угол касательной к изогнутой
оси вала в месте приложения усилия за-
тяжки
п
О Д-ropm'/ Ri»
«+1
жесткость вала
k^EJ^jLA+AFoJL,
г др. i\ момент инерции сечения стержня
в утоненном месте; <ри—коэффициент фор-
мы стержня при изгибе; А— коэффициент,
равный для валов, работающих после за-
тяжки на растяжение, 4-1,1, а для валов,
работающих на'растяжение, — 1,1; Fw—
продольная сила.
Примечание. У роторов, разбираемых
после- балансировки, имеет место нестабиль-
ность технологического дисбаланса, т е. при
повторной сборке полностью сбалансированного
ротора с сохранением взаимного углового по
дожения деталей может вновь проявиться дис-
баланс, что следует учесть в расчетах.
Начальный дисбаланс конструктивно
уравновешенных деталей обусловлен точ-
ностью обработки и плотностью материа
ла. Дисбалансы тел вращения простой
формы (валы, диски, барабаны), возни-
кающие от отклонений расположения ци-
линдрических поверхностей, образующих
форму детали, относительно геометриче-
ской оси или базовых поверхностей (рис.
10.2), устанавливают по формулам:
при радиальном биении t-й поверхности
£)/ “ 0,5 л р//? вн Драд/,
*7
Рис. 10.2. Элементарные отклонения распо-
ложения поверхностей, образующих форму
детали:
а — поверхность с радиальным биением, б—по-
верхность с торцовым биением; в — изогнутая
поверхность
при торцовом биении i-й поверхности
/л-о,5п|>л,ч.м (№„—«;>/Л0;
при изогнутости t-й поверхности
Di — 0,67л^Ли.
Ориентировочные значения начальных
эксцентриситетов деталей сложной формы
в зависимости от точности обработки при-
ведены в табл. 10-1.
334
Точность балансировки
Таблица 101
Начальные эксцентриситеты масс деталей
Точность летали Значения эксцентри смтета. мкм Типовая деталь
Особо точ- ная Точная Среднеточ- ная Низкоточ- ная 0,4 4 4 . 10 15 — 40 60 — 400 Ротор ультрацент рифуги Шпиндель станка Диск турбины Молотильный бара- бан
Структурная схема балансировки рото-
ра в обшем случае (рис. 10.3) состоит
из технологических процессов низко и
(или) высокочастотной балансировки де-
талей, узлов, роторов, роторов в собст-
венном корпусе на холостом ходу или (и)
в эксплуатационных условиях. Выбор схе-
мы балансировки конкретного ротора уста-
навливают на основании класса и типа
роторов, а также значений начальных,
технологических, эксплуатационных, функ-
циональных дисбалансов.
Допуски на балансировку деталей, уз-
лов и роторов рассчитывают в соответ-
ствии с общим положением теории раз-
мерных цепей. В качестве замыкающего
звена выступает функциональный дисба-
ланс, а в роли составляющих—начальные,
технологические, эксплуатационные и кор-
ректирующие дисбалансы. Рассчитывают
допустимые значения главного вектора
(главного момента) начальных и остаточ-
ных дисбалансов.
Допустимое значение главного вектора
начальных дисбалансов детали рассчиты-
вают вероятностным методом, рассматри-
вая дисбалансы частей детали, возникаю-
щие от отклонения расположения поверх-
ностей, образующих эти части, как слу-
чайные величины. Для большого числа
составляющих предельно возможное зна-
чение главного вектора начальных дис-
балансов с надежностью 0,95
£>стнач = 0,683
Допустимое значение главного вектора
остаточных дисбалансов детали устанав-
ливают из условия обеспечения допусти-
мых начальных дисбалансов ротора, т. е.
сумма остаточных и технологических дис-
балансов деталей не должна превышать
допустимый начальный дисбаланс ротора.
Практически допустимые остаточные дис-
балансы деталей роторов всех классов
назначают по рекомендациям ГОСТ [Г9]
на класс точнее, чем для соответствующе-
го (жесткого, квазигибкого или гибкого)
ротора.
Допустимое значение главного вектора
начальных дисбалансов составных рото-
ров рассчитывают смешанным методом,
принимая, что некоторые дисбалансы от-
носятся к систематическим погрешностям,
например гарантированный зазор в посад-
ке. а другие—к случайным погрешностям.
Суммирование первых выполняют по мето-
ду максимума-минимума, а для учета вто-
рых применяют вероятностное суммирова-
ние. При числе дисков в роторе не более
трех начальный дисбаланс равен ариф-
метической сумме его составляющих, т. е.
3 3
•^стнач == ^Zs-ocT “Ь Ш (S) £?( SjT.
S=1 5=1
где е (s)T— эксцентриситет диска, возника-
ющий при сборке ротора, рассчитанный
вероятностным методом. Для многом ас-
Расчет ожидаемом точности балансировки
335
сового ротора с надежностью 0,95 началь-
ный дисбаланс
{п
[ ^SOCT + mfS)^(s)T] 2
s=I
1/2
где коэффициент А принимают в зависи-
мости от закона распределения дисбалан-
сов и числа слагаемых равным от 1 до
1,73.
Допустимое значение главного вектора
остаточных дисбалансов устанавливают из
условия обеспечения допустимых началь-
ных дисбалансов ротора в собственном
корпусе, т. е. в собранной машине. Пред-
варительно Дстдсп ротора выбирают по
рекомендациям стандартов.
Допустимое значение главного вектора
начальных дисбалансов ротора в соб-
ственном корпусе рассчитывают по
методу максимума-минимума:
п
^стнач ^СТОСТ 4“
5= I
где e(s)T— максимально возможное изме-
нение технологического дисбаланса при
повторной сборке ротора.
Примечание. Если ротор балансиро-
вался на технологических подшипниках, то вели-
чина e(s)T должна включать эксцентриситет
диска относительно оси штатных подшипников
каления. То же относится и к другим дета
лям, впервые монтируемым на ротор при сборке
машины.
Для сборных роторов 2-го класса при
средней точности обработки деталей ре-
комендуется, чтобы начальный дисбаланс
в каждой из двух плоскостей коррекции
не превышал утроенного произведения чис-
ла дисков на их остаточный дисбаланс,
т. е.
•^стнач 3SDSOCT.
Максимально возможное изменение
технологического дисбаланса при повтор-
ной сборке ротора на практике ограни-
чивают двух -трехкратным остаточным дис
балансом.
Допустимое значение главного вектора
остаточных дисбалансов ротора в собст-
венном корпусе устанавливают из условия
обеспечения функциональных дисбалан-
сов. Предварительно £>стост выбирают по
рекомендациям стандартов в зависимости
от класса ротора (табл. 10.2), заменяя
роторы 2-го и 3-го классов эквивалентным
жестким ротором.
Таблица 10.2
Ориентировочные значения главного вектора
остаточных дисбалансов роторов в собственном
корпусе машины
Класс ротора Расчетная формула Форма изгиба
1 tneCT та(; л
2 тесттабл
За «есг табл Первая
36 0,6шесттадГ1
1,0теСТтаб л Вторая
По результатам расчета допусков на
балансировку деталей узлов, роторов уста-
навливают:
схему балансировки -перечень балан-
сируемых деталей, узлов, роторов и после-
довательность их уравновешивания;
допуски на балансировку -допусти-
мые значения начальных и остаточных
дисбалансов для всех .уравновешиваемых
деталей, узлов, роторов относительно их
конструкторских баз;
допустимый вид балансировки — стати-
ческая, низкочастотная, высокочастотная
на холостом ходу или в эксплуатационных
условиях.
10.4. РАСЧЕТ ОЖИДАЕМОЙ ТОЧНОСТИ
БАЛАНСИРОВКИ
Цель расчета:
оценить возможное рассеяние заданно-
го дисбаланса детали, узла, ротора, т. е.
вычислить суммарную погрешность балан-
сировки;
установить долю элементарных по-
грешностей, разработать мероприятия,
снижающие влияние доминирующих по-
грешностей на точность балансировки.
336
Точность балансировки
Методика расчета включает схемати-
зацию реальной операции и ее теоре-
тический анализ, в результате которого
устанавливают зависимости для расчета
элементарных и суммарных погрешностей.
При анализе точности балансировки рас-
сматривают технологическую систему ста-
нок— приспособление—деталь как линей-
ную динамическую систему, процессы в ко-
торой протекают во времени. Внешние воз-
мущения, действующие на входе в систему,
вызывают определенные выходные воз-
действия.
Основные элементарные погрешности
балансировки следующие:
Дм—метода балансировки (наладки
технологической системы);
Ду—установки детали в приспособле-
нии;
Дст—балансировочного станка;
Дд—колебания в технологической си-
стеме под влиянием сил инерции,
Дп—колебания технологической си-
стемы под влиянием внешних сил раз-
личной природы.
Расчет суммарной погрешности балан-
сировки осуществляют путем суммирова-
ния факторов, учитываемых при анализе
данной операции. Закон суммирования оп-
ределяется природой этих погрешностей.
При расчете наихудшего случая элемен-
тарные погрешности суммируют по методу
максимума-МИнимума, что. как правило.
арифметически суммируют системати-
ческие погрешности со случайными:
случайные погрешности суммируют по
формуле
Таблица 10.3
Значения коэффициента относительного
рассеяния
Законы распределения погрешности к.
Гаусса 1.000
Релея 1,097
Максвелла 1,130
Симпсона 1,220
Равной вероятности 1,73
Гаусса и равной 1,2—1,5
вероятности
где Ki—коэффициент относительного рас-
сеяния, характеризующий отношение поля
рассеяния погрешности при нормальном
законе распределения к действительному
полю рассеяния (табл. 10.3); К—коэф-
фициент относительного рассеяния сум-
марной погрешности, корректирует сум-
марную погрешность при заданной гаран-
тированной надежности Р:
Р...
1/К
0,7 0,8 0,9
0.347 0,427 0,548
0,95 0,98 0,9973 0,9999
0,683 0,775 1.000 1,47
дает завышенное (в 1,5—10 раз) значение
погрешности выходного параметра. При
вероятностном методе расчета погрешно-
сти рассматривают как случайные величи-
ны и возможно занижение суммарной
погрешности (в 6 раз).
Смешанный метод расчета представ-
ляет комбинацию метода максимума-мини-
мума и вероятностного суммирования.
Правила сложения погрешностей следую-
щие:
алгебраически суммируют системати-
ческие погрешности;
Методика определения суммарной по-
грешности предусматривает:
исключение грубых и известных систе-
матических погрешностей;
вычисление среднеарифметического ис-
правленных результатов и среднеквадра-
тического отклонения и;
проверку гипотезы о принадлежности
результатов наблюдений нормальному рас-
пределению;
определение доверительных границ
случайной еслуч и неисключенной систе-
матической погрешности есист.
Определение элементарных погрешностей балансировки
337
Доверительная граница суммарной по-
грешности е будет; 1) е=еслуч при
^сяст/®*-^0,8, 2) е—®сист при ErwT/cr5>8,
3) если указанные границы не выпол-
няются, то
/2 2
£ — К~\1 О I О<;ист ’
где Д (®случ Ч- ®сист)/СЧ- ^сист) коэффи-
циент, зависящий от соотношения случай
ной и неисключенной систематической
ап х 1/2
* ®сист« I —
среднеквадратическое отклонение суммы
неисключенных систематических погреш-
ностей.
10.5. ОПРЕДЕЛЕНИЕ ЭЛЕМЕНТАРНЫХ
ПОГРЕШНОСТЕЙ БАЛАНСИРОВКИ
Технологические системы. Балансиров-
ку деталей, узлов и роторов осуществ-
ляют в следующих технологических систе-
мах:
балансировочный станок- приспособ-
ление—деталь (ротор);
балансировочный стенд—приспособ-
ление— ротор;
собствен н ый корпус — бал ансировоч -
ный комплект—ротор.
Допустимые дисбалансы могут быть
обеспечены различными технологическими
методами в зависимости от масштаба
производства. В мелкосерийном произ-
водстве наладку технологической системы
и балансировку осуществляют методом
пробных пусков с тщательной выверкой
каждой детали при установке. В серий-
ном производстве балансировку выполня-
ют в технологической системе, предвари-
тельно настроенной на ротор конкретной
массы и геометрии. В то же время
контроль остаточных дисбалансов осуще-
ствляют для каждого ротора методом
пробных пусков. В крупносерийном произ-
водстве балансировку выполняют в техно-
логических системах с применением уст-
ройств автоматизированного управления и
контроля.
Во всех технологических системах по-
являются дополнительные относительные
смещения и колебания детали, связанные
с действием на систему различных факто-
ров, что вызывает погрешности баланси-
ровки. Элементарные погрешности харак-
теризуют действие одного или нескольких
элементов технологической системы под
действием одного или нескольких факто-
ров.
Погрешности метода балансировки.
Любой метод уравновешивания включает
в себя определение вибрационных пара-
метров некоторых точек балансировочного
устройства технологической системы или
самого ротора, расчет неуравновешенных
масс в соответствии с принятой моделью
ротора, корректировку масс в заданных
плоскостях.
Погрешность определения вибрацион-
ных параметров Ами —отклонение резуль-
тата измерений (значения и угла) от ис-
тинного значения. Пределы допустимых
погрешностей измерения, включающие
случайные и неучтенные систематические
погрешности измерительных средств, оце-
ниваются порогом чувствительности, т. е.
минимальным уровнем сигнала. Порог
чувствительности средств измерения уста-
навливают при метрологической проверке.
Погрешность расчета неуравновешен-
ных масс включает точность вычислитель-
ных операций Амв и отклонение принятой
модели неуравновешенного ротора от ре-
альной Амм. Задавая допустимые дис-
балансы, конструктор полагает, что все
роторы данной массы и геометрии имеют
одинаковый вид неуравновешенности. На
основании этого выбирают метод баланси-
ровки. Каждой модели соответствует свой
метод балансировки (и наоборот).
Например, .принимая, что диск стати-
чески неуравновешен, задают статическую
балансировку в динамическом режиме в
одной плоскости коррекции. После из-
готовления такой диск будет иметь и мо-
ментную неуравновешенность, которая во
время вращения при эксплуатации вызовет
переменные нагрузки на опорах ротора й
его изгиб. Поле рассеяния значений глав-
338
Точность балансировки
кого момента начальных дисбалансов
может быть широким и приводить к не-
допустимым нагрузкам.
При низкочастотной балансировке пар-
тии роторов на настроенном станке по-
грешности Дмм устанавливают по форму-
лам, приведенным в табл. 10.4.
Таблица 10.4
Основные формулы для расчета погрешностей
Балансировка
Одноплоскостная
Статическая
Моментная
Статико-моментная
Двухплоскостная
Многоплоскостная
Л1П/Т; (2~Тл/Т)Мл/£
Л1О/Д Мо(Лст+1/1)
Дст (Лм + La е/L\
КдвРаА’ KtlADHB
^нач<
Примечание. Кст, /См. КАв, KltA-
коэффициенты взаимного влияния плоскостей
коррекции.
Погрешность корректировки масс Дмк
слагается из точности измерения коррек-
тирующей массы Дт, радиуса коррекции
Аг, угла коррекции Д<р, т. е.
. / Ал? Дг , , \
^мк ^кГк| “Ь 4-Дф|.
\ ГПК ’к /
Погрешности, вызываемые баланси-
ровочными приспособлениями Ду. Fix раз-
деляют на две группы:
связанные с установкой детали в при-
способлении;
связанные с установкой приспособле-
ния на станке.
Погрешности первой группы возникают
вследствие того, что конструкторская база
смещается относительно установочной ба-
зы приспособления. Например, диск сме-
щается относительно оси балансировочной
оправки, ось ротора смещается в техно-
логических подшипниках качения, диск
смешается относительно оси планшайбы
вертикального балансировочного станка
Погрешности второй группы возникают
вследствие того, что приспособление само
смещается относительно оси вращения
шпинделя станка. Методы расчета по-
грешностей первой и второй групп при-
ведены в работе [6]
Другие погрешности балансировки.
Погрешности балансировки, возникающие
вследствие неточностей станка,— Дст опре-
деляются классами точности станков. По-
грешности балансировки, возникающие
вследствие колебаний в технологической
системе под влиянием сил инерции, —Дд
обусловлены движением тел качения, из-
менением геометрии ротора, колебаниями
элементов приспособления и ротора, а
также внешних сил Дп, обусловлены ви-
брациями фундамента, электрическими и
магнитными полями, движением воздуха и
другими производственными помехами.
Экспериментальные способы опреде-
ления погрешностей балансировки. В про-
цессе настройки балансировочного станка
определяют элементарные и суммарные
погрешности балансировки. Погрешности
АМ|), Лмм, Амк устанавливают в процессе
тарирования средств измерения, разделе-
ния плоскостей коррекции различными
способами, корректировки масс (по коэф-
фициенту уменьшения дисбаланса). По-
грешности Ду находят путем многократного
съема и установки нескольких деталей
в приспособлении и приспособления на
станке и последующей статистической
обработки дисбалансов, в результате ко-
торого выявляют систематическую и слу-
чайную составляющие. Погрешности Дп
находят путем многократных измерений
дисбалансов тарировочного ротора в тече-
ние суток.
Погрешность балансировки от случай-
ных составляющих равна наименьшему
достижимому дисбалансу ротора в задан-
ных условиях. Суммарная погрешность
Дг- —. Г) I , р
1 0СТ1ТШ1 I ^сист-
10.6. СТАТИСТИЧЕСКИЙ МЕТОД АНАЛИЗА
ТОЧНОСТИ БАЛАНСИРОВКИ
Статистический метод позволяет оце
нить влияние всей совокупности факторов
в реальных условиях на точность балан-
сировки. Он основан на измерении дейст-
вительных дисбалансов и обработки ре-
Статический метод анализа точности балансировки
339
зультатов измерения методами математи-
ческой статистики. Статистический метод
применяют для опенки точности техно-
логических процессов и их стабильности,
а также для определения ожидаемой доли
брака, установления зависимости между
точростными характеристиками смежных
операций и решения других задач.
Построение кривых распределения и
точечных диаграмм. В партии деталей дис-
баланс может изменяться по величине и
углу. При большом числе деталей прояв-
ляются закономерности статистического
распределения дисбаланса.
В полярной системе координат каждой
точке Ai (рис. 10.4) на плоскости со-
ответствует вектор дисбаланса, значение
которого D, равно расстоянию от центра
круга до данной точки; угол у, отсчиты-
вают от нулевой точки. При большом
числе деталей дисбалансы одного значе-
ния равномерно рассеиваются вокруг
центра. Значения дисбалансов вдоль лю-
бого радиуса распределяются по некоторо-
му закону
Для проекций вектора дисбаланса в
прямоугольной или косоугольной системе
координат и для модуля вектора дис-
баланса строят плоские кривые распреде-
ления (рис. 10.5) следующим образом.
Все поле рассеяния результатов изме-
рения дисбалансов партии деталей делят
на ряд интервалов i и для каждого ин-
тервала вычисляют значение частостей h.
т. е. отношение числа деталей, дисбалансы
которых попали в данный интервал, к
числу деталей исследуемой партии. Кро-
ме того, строят кривые распределения уг-
лов дисбалансов.
Для оценки третьей характеристики
точности балансировки (закона распреде-
ления дисбалансов вдоль оси ротора)
строят кривые распределения £>ст/£)м
и угла между главным вектором и глав-
ным моментом дисбалансов.
Практическую кривую распределения
характеризуют следующие основные ста-
тистики:
относительная частота h=nt/n — отно-
шение числа выборочных значений гг,,по-
Рис. 10.5. Гистограмма распре-
деления модуля вектора дисба-
ланса
Рис. 10.6. Точечная диаграмма
дисбалансов партии деталей
павших в г-й интервал, к объему выборки п\
выборочное среднее х значение величи-
ны х;
выборочное среднее квадратическое от-
клонение о;
характеристики асимметрии и эксцес-
са;
размах выборки —аП|£> — хП1^_
Точечную диаграмму строят по ходу
балансировки партии деталей в коорди-
натах номер детали п,—дисбаланс детали
D, (рис. 10.6). Другой вид диаграммы
получают следующим образом. Из боль-
шой партии выбирают несколько групп
деталей, отбалансированных в различное
340
Точность балансировки
Рис. 10.7. Точечная диаграмма
средних дисбалансов групп де-
талей
Рис. 10.8. Плотность вероятности ср(ф) равно-
мерного закона распределения угла ф Дис-
балансов партии деталей
время. Для каждой группы вычисляют
числовые характеристики распределения
и откладывают одну из них, например
£>ср, по оси ординат для соответствующего
промежутка времени t. Полученные точки
соединяют прямыми (рис. 10.7).
Законы распределения дисбалансов.
В серийном производстве встречаются
различные законы распределения дисба-
лансов, характерные для данного типа ро-
тора, точности изготовления деталей и его
сборки.
Распределение по закону равной веро-
ятности часто имеет угол ф дисбаланса
(рис. 10.8). Математическое ожидание и
среднеквадратическое отклонение соответ-
ственно будут = 180°, о(ф) = 104°;
асимметрия равна нулю, эксцесс—1,2. При
сложении двух случайных величин, под-
чиненных закону равной вероятности с оди-
наковой областью возможных значений,
образуется распределение Симпсона.
Распределение Гаусса может иметь
начальный дисбаланс деталей сложной
формы при низкой, и деталей простой фор-
мы при высокой точности изготовления
(рис. 10.9). Математическое ожидание и
среднеквадратическое отклонение равны:
М {D}~ а, о(£)) = о. Медиана и мода сов-
падают с математическим ожиданием,
асимметрия и эксцесс равны нулю.
Распределение по закону Релея наи-
более часто имеют начальные и техно-
логические дисбалансы деталей средней
точности изготовления (рис. 10.10). Для
нормированного закона математическое
ожидание и среднеквадратическое откло-
нение будут: М (£>} = 1,253оо, o(D) =
Рис. 10.9. Плотность вероятности гр(£>) рас-
пределения дисбалансов по закону Гаусса
Рис. 10.10. Плотность вероятности <f(D) рас-
пределения дисбалансов по закону Релея
= 0,655ос; медиана—1,177<то; мода — о0;
асимметрия — 0,631; эксцесс—0,245; где
оо— среднеквадратическое отклонение ис-
ходного двухмерного гауссова распределе-
ния.
Композиция законов распределения
встречается в большинстве случаев на
практике. Таковы распределения главного
вектора и главного момента начальных
Статический метод анализа точности балансировки
341
дисбалансов сборных многомассовых ро-
торов (рис. 10.11), образованные по схеме
суммирования ограниченного числа сла-
гаемых (дисбалансов дисков) или боль-
Рис. 10.11. Кривые распределения начальных
дисбалансов пятимассового ротора:
1— главного вектора, 2—главного момента (в от-
носительных величинах)
того числа слагаемых (дисбалансы ва-
лов) с суммой неслучайных и случайных
величин, число и значение которых сис-
тематически изменяется во времени.
Методика обработки эксперименталь-
ных данных включает следующие этапы.
1. Формирование информационного
массива и составление на его основе
выборок одноименных параметров, опре-
деление граничных значений в каждой
выборке.
2. Построение гистограмм для каждо-
го параметра, разбивая область распреде-
ления на 6—12 интервалов так, чтобы в
каждом интервале содержалось не менее
3-х значений исследуемого параметра.
3. Расчет средних значений, средне-
квадратических отклонений, асимметрии,
эксцессов и других статистических харак-
теристик выборок Построение точечных
диаграмм для этих характеристик по вре
мен и.
4. Аппроксимация теоретическими за
конами распределения гистограмм по ста-
тистическим характеристикам выборок.
Вычисление коэффициентов парной кор-
рекции для заданного уровня доверия и
проверка их достоверности.
Анализ экспериментальных данных.
Основные положения для анализа сле-
дующие.
Распределение значений главного век-
тора и главного момента начальных
дисбалансов партии деталей должно сле-
довать кривой нормального распределе-
ния. Угол между £>ст и углы дис-
балансов <рст, должны быть равномерно
распределены. Все параметры, характери-
зующие начальное неуравновешенное со-
стояние детали, должны быть некоррели-
рованы. Все параметры, характеризующие
остаточное неуравновешенное состояние
детали, должны быть некоррелированы.
Между начальными и остаточными пара-
метрами неуравновешенности должна
иметь место достоверная корреляционная
связь.
Распределение значений главного век-
тора и главного момента начальных дис-
балансов партии роторов дисковой конст-
рукции согласуются с Х'РаспРеделеиием
с параметром т,равным числу дисков плюс
2, а угол между ними— с законом равной
вероятности. Корреляция между МОнач,
*>стнач, д>иач отсутствует.
Значения главного вектора, главного
момента начальных дисбалансов партии
роторов барабанной конструкции также
имеют х-рас,!РеДеление» а между ними
должна быть корреляционная связь. Для
каждого типа ротора и особенностей его
изготовления могут быть расчетным путем
получены законы распределения всех пара-
метров неуравновешенности.
Ротор в собственном корпусе. Рас-
пределение параметров начального не-
уравновешенного состояния и их кор-
реляционная связь для партии роторов
при низкочастотной балансировке анало-
гичны распределениям и корреляционным
связям роторов барабанной конструкции.
Параметры остаточной неуравновешен-
ности партии роторов распределяются по
экспоненциальному закону.
Точность изготовления деталей, сборки
роторов и изделия оценивают по пара-
метрам начальной неуравновешенности.
Точность технологических процессов ба-
лансировки оценивают по параметрам
342
Проектирование технологических процессов балансировки
остаточной неуравновешенности. Точность
технологического процесса считается иде-
альной, если поле рассеяния дисбалансов
совпадает с заданным полем допуска.
В этом случае -доля брака не превышает
0.27%. Если граница поля рассеяния
выходит за пределы поля допуска, то доля
брака увеличивается.
Для сопоставления поля рассеяния
с полем допуска применяют коэффициент
точности р — &/& и настроенности процес-
сов Е, равный коэффициенту относитель-
ной асимметрии при идеальной точности.
Зависимость вероятностного брака q от
коэффициентов точности и настроенности
будет
•
где F?—функция распределения норми-
рованного закона; /? = 6о/Д— коэффици-
ент относительного рассеяния.
По положению в поле допуска кривой
распределения и по ее форме судят о
постоянной и доминирующей переменной
погрешности.
Глава 11
ПРОЕКТИРОВАНИЕ ТЕХНОЛОГИЧЕСКИХ ПРОЦЕССОВ
11.1. ОБЩИЕ СВЕДЕНИЯ
О ТЕХНОЛОГИЧЕСКОЙ ПОДГОТОВКЕ
ПРОИЗВОДСТВА
Согласно ГОСТ 14.004—83 под тех-
нологической подготовкой производства
(ТПП) понимают совокупность мероприя-
тий, обеспечивающих технологическую го-
товность производства. ТПП начинается
с получения исходных документов на раз-
работку и производство новых изделий,
организацию нового и совершенствова-
ние действующего производства. Весь не-
обходимый комплекс работ по ТПП под-
разделяется функционально следующим
образом:
обеспечение технологичности конст-
рукции изделия;
разработка технологических процес-
сов;
проектирование и изготовление средств
технологического оснащения;
организация и управление процессом
ТПП.
На уровне предприятия решают сле-
дующие задачи.
1. При обеспечении технологичности
конструкции изделия: проводят техноло-
гический контроль конструкторской до-
кументации; оценивают уровень техноло-
гичности конструкции изделия; отрабаты-
вают конструкцию изделия на технологич-
ность; вносят необходимые изменения в
конструкцию изделия и в документацию.
2. При разработке технологических
процессов: разрабатывают типовые техно-
логические процессы и технологические
операции на детали и сборочные единицы;
разрабатывают рабочие технологические
процессы на детали и сборочные едини-
цы; организовывают заводские фонды до-
кументации на типовые технологические
процессы и технологические операции.
3. При проектировании и изготовлении
средств технологического оснащения про-
водят унификацию и стандартизацию
средств технического оснащения; органи-
зуют применение средств технического
оснащения; проектируют и изготавливают
специальные средства технического осна-
щения.
Обеспечение технологичности конструкций балансируемых изделий
343
11.2. ОБЕСПЕЧЕНИЕ ТЕХНОЛОГИЧНОСТИ
КОНСТРУКЦИЙ
БАЛАНСИРУЕМЫХ ИЗДЕЛИЙ
Согласно ГОСТ 18 831—73 под тех-
нологичностью конструкции изделия по-
нимают совокупность свойств конструкции,
позволяющих вести ТПП, изготавливать,
эксплуатировать и ремонтировать изделия
при наименьших затратах труда, средств,
времени и материалов по сравнению с
однотипными конструкциями изделий ана-
логичного назначения при обеспечении
установленных показателей качества. От
технологичности конструкции во многом
зависят содержание и технико-экономиче-
ские показатели технологического процес-
са (ТП), так как технологичная конст-
рукция предполагает использование в ТП
прогрессивных методов и средств произ-
водства. Технологичность конструкции
оценивается качественно и количественно.
К качественным характеристикам тех-
нологичности конструкции относятся сле-
дующие: взаимозаменяемость; ‘регулируе-
мость; контролепригодность; инструмен-
тальная доступность; трудоемкость из-
готовления, сборки; технологическая себе-
стоимость; уровень технологичности по
трудоемкости изготовления; уровень техно-
логичности по 'себестоимости изготовле-
ния.
Количественно технологичность конст-
рукции изделия оценивается с помощью
системы показателей, которые включают:
базовые (исходные) значения показа-
телей технологичности, являющиеся пре-
дельными нормативами технологичности,
обязательными для выполнения при раз-
работке изделия, указываемые в техни-
ческом задании на разработку изделия;
достигнутые при разработке изделия
значения показателей технологичности;
показатели уровня технологичности
конструкции разрабатываемого изделия.
Одной из функций ТПП является
обеспечение технологичности конструкции,
которая предусматривает взаимное реше-
ние конструкторских и технологических за-
дач, направленных на повышение произ-
водительности труда. Обеспечение техно-
логичности конструкции изделия вклю-
чает:
отработку конструкции изделий на тех-
нологичность на всех стадиях разработки
изделия и при ТПП;
совершенствование условий выполне-
ния работ при производстве, эксплуатации
и ремонте изделий и фиксацию принятых
решений в технологической документации;
количественную оценку технологично-
сти конструкции изделия;
технологический контроль конструк-
торской документации;
подготовку и внесение изменений в
конструкторскую документацию по резуль
тэтам технологического контроля, обеспе-
чивающих достижение базовых показате-
лей технологичности.
Применительно к процессам сборки и
балансировки говорят о следующих видах
технологичности составных роторов и их
деталей:
сборочная технологичность узлов, не
подвергающихся последующей баланси-
ровке;
балансировочная технологичность де-
талей составных роторов (дисков, валов,
рабочих колес, крыльчаток и др.);
сбороч но-баланс ировоч н ая технологи-
чность составных роторов и узлов, соби-
раемых специально для балансировки, т. е.
балансировочных узлов.
Эти разновидности технологичности
достаточно точно определяют требования,
предъявляемые к деталям и узлам по
обеспечению технологичности.
К количественным показателям, харак-
теризующим сборочную технологичность
конструкции, можно отнести следующие
технико-экономические и технические
коэффициенты:
сборности Ксб — NJ (7Ve Л\ ,
где —число сборочных единиц, включая
покупные; Na—число деталей, не вошед-
ших в состав сборочных единиц Л’(,;
Л\т—число стандартных (крепежных) де-
талей;
344
Проектирование технологических процессов балансировки
эффективности взаимозаменяемости
Квз — ^вз/^и» гДе ^вз—трудоемкость сборки
изделия, осуществляемой по принципу пол-
ной взаимозаменяемости; Ти—общая тру-
доемкость сборки изделия;
унификации изделия Ky=(Nvy+NRy)/
/(^е+^д —Л/дк). где Ney — число унифи-
цированных сборочных единиц; N—чис-
ло унифицированных деталей, не вошед-
ших в состав унифицированных сбороч-
ных единиц;
стандартизации изделия /Сст—(Л'ест +
+ Лдст)/(Л'е + Л'п— Адк), где NecT— число
стандартных сборочных единиц изделия;
Л\сг—число стандартных изделий, не во-
шедших в число стандартных сборочных
единиц.
Балансировочную и сборочно-баланси-
ровочную технологичность изделия можно
оценить по следующим показателям
Класс ротора, точности балансировки
ротора.
Значения начального, остаточного, до-
пустимого, технологического, эксплуатаци-
онного дисбалансов
Число плоскостей коррекции, метод
корректировки масс конструкции изделия.
Метод балансировки, применимый для
данной конструкции изделия
Объем выпуска изделий.
Параметры 1-й и 2-й характеристик
точности деталей составного ротора.
Усилия завинчивания крепежных дета-
лей.
Зазоры в подшипниковых опорах ро-
тора и т. д.
Обеспечение технологичности конст-
рукции изделия производится на этапе
ТПП и включают следующие виды работ.
Отработка конструкции изделия на
технологичность на всех стадиях раз-
работки изделия.
Совершенствование условий вы-
полнения работ при производстве, экс--
плуатации и ремонте изделий и фиксация
принятых решений в технологической до-
кументации.
Количественная оценка технологично-
сти конструкции изделия.
Технологический контроль конструк-
торской документации.
Внесение изменений в конструкторскую
документацию.
После отработки на технологичность
составные роторы и их летали должны
отвечать следующим основным требова-
ниям.
1. По возможности большее расчлене-
ние конструкции изделия на технологи-
ческие узлы, допускающие независимую
сборку, балансировку и контроль без
последующей их переборки.
2, Возможность компоновки балан-
сируемых изделий из стандартных и уни-
фицированных деталей и узлов.
3. Возможность применения механи-
зированной и автоматизированной балан-
сировки, а если надо, то и робото-
технических комплексов.
I 4. Обеспечение возможности общей
сборки изделия без разборки ранее от-
балансированных составных частей.
5. Уменьшение числа деталей в сос-
тавных роторах, подвергающихся баланси-
ровке.
6. Возможность применения типовых
технологических процессов балансировки и
типовых средств технологического оснаще-
ния.
7. Возможность использования про-
грессивных методов балансировки и кор-
ректировки масс.
8. Устранение из процесса баланси-
ровки механического съема материала в
случае требований по стерильности сборки
изделий.
9. Обеспечение балансировки изделия
на месте и во время эксплуатационного
обслуживания.
10. Применение рациональных методов
обеспечения точности балансировки с
учетом физического состояния ротора.
11. Наличие мест захвата баланси-
руемого изделия подъемным механизмом,
если его масса превышает 20 кг.
Проектирование технологического процесса балансировки
345
11.3. ПРОЕКТИРОВАНИЕ
ТЕХНОЛОГИЧЕСКОГО ПРОЦЕССА
БАЛАНСИРОВКИ
Под технологическим процессом балан-
сировки деталей и составных роторов
понимают последовательное изменение
исходного состояния балансируемой дета-
ли или узла в заданное состояние путем
добавления, уменьшения или перемещения
(корректировки) масс.
Балансировочная операция —это часть
технологического процесса, выполняемая
на одном рабочем месте до перехода к
балансировке следующей детали или узла.
Балансировка может быть выполнена за
одну или несколько операций. Поэтому
балансировочные операции подразделяют
на предварительные и окончательные.
Считается приемлемым, если за одну ба-
лансировочную операцию достигают сни-
жения дисбаланса в 15- 20 раз. Чем боль-
ше значение начального дисбаланса, тем
больше нужно балансировочных операций.
Число балансировочных операций воз-
растает и с увеличением точности балан-
сировки.
Нормы на балансировочные работы ус-
танавливают путем хронометрирования от-
дельных операций при балансировке ус-
тановочной партии деталей или роторов
с последующей статистической обработкой
результатов хронометрирования.
Время на балансироку Гб такой детали
или ротора на заранее настроенном станке
складывается из основного (машинного)
времени t0, вспомогательного времени
/в, времени на обслуживание рабочего
места /о6, времени на отдых и личные
надобности torn:
^ОТД"
Основное время — это время, в течение
которого достигается цель балансировоч-
ной операции. На операции определения
дисбалансов балансируемого изделия ос-
новное время составляет продолжитель-
ность измерительного цикла, а на операции
корректировки масс — время на съем необ-
ходимого количества материала (напри-
мер. сверлением или фрезерованием).
Вспомогательное время равно времени
на установку, закрепление и снятие ба-
лансируемого изделия, управление стан-
ком и других действий, сопровождающих
выполнение основной работы.
Основное время и вспомогательное вре-
мя в сумме составляют время оператив-
ной работы, называемое продолжитель-
ностью балансировки.
Время обслуживания рабочего места,
затрачиваемое балансировщиком в тече-
ние рабочего дня на уход за рабочим
местом, техническое обслуживание станка,
подготовку к работе балансировочных при-
способлений, инструмента, документации.
Время перерывов на отдых баланси-
ровщика принимают 2—7% от основного
времени.
Балансировочные работы выполняют
операторы-балансировщики деталей и уз-
лов, квалификация которых должна соот-
ветствовать выполняемым работам (табл.
11.1).
Этапы проектирования ТП балансиров-
ки следующие:
выбор типового технологического про-
цесса;
определение последовательности и со-
держания технологических операций;
определение, выбор и разработка ТЗ на
проектирование средств технологического
оснащения;
выбор режимов работы балансировоч-
ных станков;
выбор средств механизации и авто
матизации ТП;
выбор организационной структуры на
балансировочном участке;
оформление технологической докумен-
тации.
Для решения перечисленных выше
задач необходимо знать: класс ротора,
классификатор балансируемых изделий,
виды балансировки, правила выбора мето-
да балансировки, виды технологической
документации.
Определение класса ротора. Основным
параметром, определяющим класс ротора.
346
Проектирование технологических процессов балансировки
Таблица 11.1
Классификационная характеристика профессии «Балансировщик деталей и узлов:
Разряд балан- сиров- щика Объем знаний, которыми должен владеть баланси- ровщик Характеристика и примеры выполняемых работ Разряд бал ан сиров- щика Объем знаний, которыми должен владеть баланси- ровщик . Характеристика и примеры выполняемых работ
2 Способы опреде- ления значения и .угла главного век- тора дисбалансов на станках для статической ба- лансировки на ножах. Способы опреде- ления центра масс, массы груза и ста- тических момен- тов. Способы коррек- тировки масс сня- тием материала и приемы их реали- зации. Устройство и тех- ческое обслужива- ние станков для статической ба- лансировки на ножах. Пользование прос- тыми балансиро- вочными средст- вами. Типовой тех- нологический про- цесс статической балансировки на ножах Подготовка дета- лей к балансиров- ке на ножах. Ста- тическая баланси- ровка деталей на ножах. Простые слесарные опера- ции (разметка, рубка, сверление, опиливание). На- стройка станка для статической балансировки на ножах под руко- водством мастера. Балансировка на ножах барабанов,- маховиков, крыль- чаток, вентилято- торов и др. дета- лей общего назна- чения. । балансировки де- талей |тродвигателей, '[крыльчатки цен- тробежных насо- 1сов, части станков I и машин, диски, вентиляторы. ,
4 Методы низкочас- тотной баланси- ровки жестких ро- торов сложной конструкции. Способы расчета корректирующих масс. Устройство и тех- ническое обслужи- вание сложных станков для дина- мической баланси- ровки. Методика наст- ройки балансиро- вочных станков. Типовые техноло- гические процессы низкочастотной балансировки жестких роторов сложной конструк- ции. Подготовка дета- лей и роторов с повышенными тре- бованиями к точ- ности балансиров- ки и их баланси- ровка на сложных, заранее настроен- ных станках. Нас- тройка простых станков для дина- мической баланси- ровки самостоя- тельно, а слож ных — под руко- водством мастера. Расчет корректи- рующих масс. Сложные работы по корректировке масс при баланси- ровке. Баланси- ровка роторов тур- богенераторов, крупных электро- двигателей, турбо- насосов.
3 Методы динами- ческой баланси- ровки деталей и жестких роторов. Способы коррек- тировки масс пере- мещением грузов. Устройство и тех- ническое обслу- живание станков для динамической балансировки. Методика наст- ройки станков для статической ба- лансировки на ножах. Типовой техноло- гический процесс Подготовка дета- лей к динамичес кой балансировке. Динамическая балансировка де- талей на станках Настройка стан- ков для статичес- кой балансировки самостоятельно, а для динамической балансировки под наблюдением мас- тера. Основные ви- ды работ по кор- ректировке масс. Балансировать на станках роторы асинхронных элек-
5 Методы низкочас- тотной баланси- ровки квазнгибких роторов. Особенности ба- лансировки рото- ров в собственных подшипниках и корпусах. Способы расчета дисбалан- сов при многоплос- костной баланси- ровке и высокочас- тотной баланси- ровке жестких ро- торов на месте ус- Подготовка жест- ких роторов в соб- ственных подшип- никах и в соб- ственных корпусах к балансировке. Балансировка во многих плоскос- тях квазнгибких роторов. Баланси- ровка на высоких частотах враще- ния жестких рото- ров на месте уста- новки. Настройка сложных станков
Проектирование технологического процесса балансировки
347
Продолжение табл. 11.1
Разряд балан- сиров- щика Объем знаний, которыми должен владеть баланси- ровщик .. Характеристика н примеры выполняемых работ Разряд балан- сиров- щика j Объем знаний, которыми должен владеть баланси ровщик Характеристика и примеры выполняемых работ
5 тановки. Устройст- во и техническое обслуживание станков для высо- кочастотной ба- лансировки. Методика наст- ройки сложных станков для дина- мической балан- сировки. Типовые техноло- гические процессы высокочастотной балансировки. для динамической балансировки. Все виды расчетных работ при балан сировке Баланей ровка роторов компрессоров, многоступенч аты х паровых и газе вых турбин, при- водов станков, ги роскопов. 6 лансировочных стендах. Правила выбора рабочих техноло- гических процес- сов балансировки. Методика расчета допустимых дис- балансов. Методика наст- ройки станков для высокочастотной балансировки. лансировать гиб- кие роторы. Наст- раивать разгон- но-балансировоч- ные стенды под ру- ководством мас- тера Составлять технологические процессы низко- частотной балан- сировки жестких и квазигибких рото- ров простой кон- фигурации. Балансировать ро- торы крупных тур- богенераторов, гибкие валы, уни- кальные роторы с особо высокими требованиями к точности баланси- ровки.
6 Методы низкочас- тотной баланси- ровки гибких рото- ров. Способы рас- чета дисбалансов при высокочастот- ной балансировке на . разгонно-ба- Балансировать особо ответствен- ные роторы раз- личных типов на •станках для дина мической баланси- ровки и на месте их установки. Ба-
"является отношение максимальной экс-
плуатационной угловой скорости <1)ЭП]ах ро-
тора к 1-й критической угловой скорости
<"1 кр-
Класс ротора
Отношение w3rnax/wll(p
Жесткий
Квазигибкий
Гибкий
Не более 0,3
0,3—0,7
Более 0,7
Значение <о1кр определяют расчетным
или экспериментальным путем.
Классификация балансируемых рото-
ров приведена в табл. 11.2.
Выбор вида балансировки (низко-
частотной или высокочастотной) зависит
от класса ротора, начальных, технологи-
ческих и эксплуатационных дисбалансов,
конструкции ротора и точности его ба-
лансировки. Роторы 1-го и 2-го классов
балансируют на низких или высоких ча-
стотах вращения в зависимости от точно-
сти балансировки и значения эксплуата-
ционных дисбалансов. Условия выбора ви-
да балансировки:
Dnon>DT — низкочастотная баланси-
ровка;
£>ДО11<£)Т- высокочастотная баланси-
ровка.
Роторы 3-го класса балансируют
на высоких частотах вращения независимо
от дисбалансов, конструкции и других
факторов.
Выбор метода низкочастотной балан-
сировки. Одноплоскостную балансировку
применяют для консольных и двухкон-
сольных роторов 1-го класса (жестких),
а также 2а и 2Ь классов (квазигибких),
дисбалансы которых сосредоточены на
консолях. Допустимость одноплоскостной
балансировки зависит от значения момент-
ной неуравновешенности.
Двухплоскостную балансировку при-
меняют для балансировки роторов 1-го
класса (жестких), а также классов 2Ь и 2е
(квазигибких), у которых отношение j рас-
348
Проектирование технологических процессов балансировки
Классификация балансируемых роторов
Таблица 11.2
Класс ротора Тип ротора Примеры
1-й класс (жесткие) Межопорный Консольный Двухконсольный Ротор электродвигателя, барабан, приводной вал, шпиндель, гироскоп Вентилятор, маховик, центрифуга, шлифовальный круг Турбокомпрессор, турбогенератор, ко- лесная пара
2-й класс (квазнгибкие) 2а 2Ь 2с 2d 2е 2Д 2g 2h 3-й класс (гибкие) За 36 Зс Роторы с известным распреде. Консольный с одной или двумя плоскостями коррекции на консолях Двухконсольный с двумя плоскостями коррекции на консолях Межопорный с более чем двумя плоскостями коррекции Межопорный симметричный ротор с равномерно распределенными мас- сой и дисбалансами вдоль оси Межопорный симметричный ротор с жесткой средней частью Роторы с неизвестным pacnpedt Межопорный симметричный ротор с дискретными массами на гибком валу Межопорный несимметричный ротор Роторы с дисбалансом по 1-й форме изгиба Роторы с дисбалансами по 1-й и 2-й формам изгиба Роторы с дисбалансами более чем по 2-м формам изгиба пением дисбалансов вдоль оси Ротор турбонасоса Ротор турбонасоса Ротор компрессора Вал прокатного стана, приводной вал Барабан печатной машины, ротор турбомолекул яркого насоса глением дисбалансов вдоль оси Многоступенчатый ротор насоса, тур- бонасос Роторы паровых и газовых турбин Четырехполюсный ротор генератора Малые двухполюсные роторы гене- раторов Большие двухполюсные роторы гене- раторов
4-й класс (изменяемой гео- метрией) Роторы 1, 2, 3-го классов, изменяющие свою геометрию на эксплуатационных частотах вращения
5-й класс эоторы 3-го класса, которые по техническим или экономическим причинам балансируют в двух плоскостях коррекции на максимальной эксплуатационной частоте вращения
стояния между плоскостями коррекции / к
расстоянию между опорами L лежит в
пределах /=0,94-4-0,05. Дополнительным
условием выбора метода двухплоскостной
балансировки для роторов класса 26 яв-
ляется отсутствие моментной неуравно-
вешенности у консолей. Если /^0,05 —
0,94, то для жестких роторов назначают
статико-моментную балансировку. Если
роторы классов 2Ь и 2а имеют большую
моментную неуравновешенность, то для
них назначают статико-моментную балан-
сировку.
Если конструкция роторов 2-го класса
позволяет проводить поэлементную балан-
сировку каждой дискретной массы по мере
его сборки, то для таких роторов назнача-
ют статико-моментную балансировку.
Многоплоскостную балансировку наз-
начают для роторов классов 2с, 2/, 2g с
равномерным распределением начальных
дисбалансов, т. е. когда при сборке конт
Проектирование технологического процесса балансировки
349
ролируют начальный дисбаланс каждой
массы. При этом корректирующие массы
распределяют вдоль оси ротора пропорцио-
нально смешению главной центральной оси
инерции относительно оси ротора. Рас-
пределение же корректирующйх масс
вдоль осн ротора пропорционально форме
изгиба вала применяют для роторов клас
са 2d.
Выбор операций ТП зависит от метода
балансировки, способа корректировки
масс, начальных и остаточных дисбалансов
и др. Однако типовыми операциями для
всех методов балансировки 'являются:
определение значения и угла дис-
балансов в плоскостях измерения;
расчет корректирующих масс;
корректировка масс;
контроль остаточных дисбалансов.
Считают, что за один балансировочный
цикл дисбаланс должен снизиться в 15—
20 раз. Поэтому число таких циклов
n = Dlia4/(154-20)DOCT.
Выбор балансировочной частоты вра-
щения производят с учетом возможностей
балансировочного оборудования (диапа-
зон частот вращения, мощность привода).
Выбор балансировочного оборудова-
ния. Согласно ГОСТ 14.304- 73 выбор
технологического балансировочного обору-
дования должен начинаться с анализа
методов балансировки деталей и сбороч-
ных единиц с целью определения наи-
более эффективных методов балансировки,
исходя из параметров балансируемого из-
делия. Выбор осуществляют по главному
параметру, т. е. по точности балансировки.
При этом должна быть установлена
взаимосвязь параметров выбираемого обо-
рудования (диапазон частот вращения,
точность балансировки, мощность привода
и др.) с параметрами балансируемого
на нем изделия (масса, диаметр цапф
и максимальный диаметр ротора, его длина
и др.).
Порядок выбора следующий.
1. Выбирают из числа станков те, кото-
рые допускают балансировку роторов
массой, соответствующей массе баланси-
руемого изделия. Причем в массу баланси-
руемого изделия включается также масса
опор, балансировочного приспособления,
подшипников и др деталей, входящих в
колебательную систему.
2. Выбирают станки, допускающие
балансировку ротора данных габаритных
размеров и других параметров (длина ро-
тора, максимальный диаметр, диаметр
шейки под ремень привода, диаметр шейки
под осевое соединение и др.).
3. Выбирают частоту вращения ротора
при балансировке из диапазона частот
вращения станка и мощности привода.
Выбор балансировочного оборудования,
характеризующегося степенью механиза-
ции и автоматизации, производят исходя
из следующего:
затраты на выполнение технологиче-
ского процесса и период окупаемости
оборудования должны быть минимальны-
ми.
Годовая потребность в балансировоч
ном оборудовании определяется из годо-
вого объема работ, устанавливаемого ста-
тистическим анализом затрат средств и
времени на балансировку типовых изделий.
Годовые затраты на использование
оборудования определяются размерами за-
трат на его эксплуатацию и изготовле-
ние. Производительность балансировоч-
ного оборудования устанавливают на осно-
вании анализа времени балансировки из-
делия до заданной точности.
Выбор балансировочного оборудова-
ния по производительности зависит от объ-
ема выпуска изделий и их габаритных
размеров, т. е. типа производства. В еди-
ничном производстве используют в основ-
ном дорезонансные балансировочные стан-
ки с измерительным устройством по схемам
а, Ь, с. В серийном производстве выбор
станка определяется подготовительно-за-
ключительным временем на баланси-
ровочную операцию. При малом времени
Гпз преимущество дорезонансных станков
перед зарезонансными незначительное.
Выбор балансировочной оснастки. Со-
гласно ГОСТ 14.305—73 выбор баланси-
350
Проектирование технологических процессов балансировки
ровочной оснастки основывается на анали-
зе затрат на реализацию технологического
процесса в установленный промежуток
времени с заданной точностью.
К балансировочной оснастке относят-
ся: балансировочные оцравки (разборные
и •неразборные); балансировочные рамки;
вкладыши под подшипники; сменные
шкивы для ремня привода; технологи-
ческие подшипники (качения или скольже-
ния); приспособления для металлорежу-
щих станков.
Тип балансировочной оправки и ее ос-
новные размеры зависят от типа баланси-
руемой детали и ее основных характер-
ных размеров (табл. 12.2).
Балансировочные рамки необходимы
для установки: консольных роторов на
зарезонансный балансировочный станок,
меж опорных роторов, наружные диаметры
которых превышают размеры опор выбран-
ного типа балансировочного станка; ро-
торов в собственных корпусах на баланси-
ровочный станок; роторов на зарезонанс-
ные балансировочные станки, опоры кото-
рых имеют одну степень свободы. Кроме
этого балансировочные рамки необходимы
для регулирования режима работы станка
при балансировке консольных и двухкон--
сольных роторов и роторов в сборе с
большой паразитной массой, а также для
обеспечения максимальной точности ба-
лансировки. Конструкция балансировоч-
ных рамок определяется балансируемым
ротором и необходимостью регулирования
режима работы станка.
Технологические подшипники качения
выбирают по точности и фактическим
диаметрам внутреннего кольца. Точность
изготовления технологического подшипни-
ка должна быть на 1—2 класса выше точ-
ности штатного подшипника. Погрешность
балансировки может быть уменьшена под-
бором подшипников из имеющихся с наи-
меньшими зазорами, биениями и др. Выбор
подшипников качения производят следую-
щим образом. Замеряют действительное
значение диаметра цапфы балансируемого
ротора Затем рассчитывают необходи-
мый внутренний диаметр подшипника
^вн” <*«4-0,005 и подбирают подшипник,
соблюдая условие <*гтах ><*««> <*п mm* где
dnnlm, <*п max ' СООТВеТСТВСННО МИНИМЗЛЬ-
ный и максимальный диаметры внутрен-
него кольца подшипника.
Приспособления для металлорежущих
станков и слесарно-сборочный инструмент
выбирают в зависимости от способа
корректировки масс, типа производства
И др.
Согласно ЕС ТПП на балансировочные
работы оформляют маршрутную и опера-
ционную карты технологического процес-
са, карты эскизов, а также ведомости ос-
настки и материалов, аналогичные доку-
ментам на сборочные и электромонтаж-
ные работы.
11.4, АВТОМАТИЗИРОВАННОЕ
ПРОЕКТИРОВАНИЕ
ТЕХНОЛОГИЧЕСКИХ ПРОЦЕССОВ
БАЛАНСИРОВКИ РОТОРОВ
Балансировка роторов различных изде-
лий требует комплексного решения ряда
задач, по-разному влияющих на конечный
результат — эффективность балансировки.
Можно выделить четыре группы этих
^адач, определяющих метод, аппаратуру,
оборудование и оснастку для балансиров
ки.
Прежде чем перейти к разбору главной
задачи, выбору метода балансировки, не-
обходимо выработать общий подход к ре-
шению, установить общие критерии, по-
зволяющие сравнивать результаты ба-
лансировки с одинаковых позиций. Необхо-
димо знать возможности реализации мето-
дов с тем, чтобы выбранный метод бази-
ровался в основном на существующем
оборудовании, но в то же время был пер-
спективным, мог применяться длительное
время.
При таком решении учитывается боль-
шое количество факторов, сравниваются
все варианты, чтобы выбрать оптималь-
ный. Очевидно, применение ЭВМ авто-
матизирует решение задачи, дает объек-
тивные рекомендации выбора метода, ап-
351
Автоматизированное проектирование технологических процессов балансировки роторов
паратуры, оборудования и оснастки для
балансировки.
Выбор параметров и разработка ма-
тематической модели ротора. Наиболее об-
щим подходом к решению задачи выбора
метода балансировки целесообразно при-
нять известные положения теоретической
механики, по которым сбалансированность
ротора оценивается по величинам глав
ного вектора F и главного момента М цен-
тробежных сил относительно центра массы
ротора. Но в теоретической механике рас-
сматривается ротор нед сформируем ый, в
то время как реальный ротор в рабочих
условиях изгибается. Поэтому аналити-
ческие зависимости и физическое состоя-
ние реального ротора существенно отли-
чаются от идеального. Определить дейст-
вительные значения F и М на рабочих
оборотах, используя существующее балан-
сировочное оборудование с низкой часто-
той вращения, невозможно. Но можно
определить F и М для ротора как твер-
дого тела и в зависимости от того,
как будут сбалансированы эти векторы
(метода балансировки), величина остав-
шихся векторов и Мост во время ра-
боты будет различная.
Если задать допустимые значения
Fa(W и Л1доп на рабочих оборотах, то ус-
ловия удовлетворительной сбалансирован-
ности запишутся в следующем виде:
F IF <1
OCT f 1 ДОП ’
(11.1)
Это и есть критерий оценки метода
балансировки, который сохраняет свою
значимость при любых условиях.
Практическую проверку условия (1 k 1)
представить не сложно: ротор последо
вательно балансировать различными мето-
дами, определять и 7ИОСТ, а затем
после проверки по (11.1) решить, какой из
методов выбрать. Реализовать же эту
схему весьма сложно. Необходим специ-
альный стенд, на котором ротор можно вы-
водить на рабочие частоты вращения, и
испытания группы роторов, чтобы получить
достоверные данные но каждому из мето-
дов.
Значительно проще, с достаточной сте-
пенью надежности, условие (11.1) можно
проверить аналитически. Для этого не
обходимо разработать математическую мо-
дель ротора.
Величины F и М для ротора опреде-
ляются по известным зависимостям:
М = £ Mi>
<=i
где F, и М,— векторы центробежных сил и
моментов дискретных масс.
Если учитывать только главные фак-
торы, пренебрегая второстепенными, таки-
ми, как гироскопический момент и демп-
фирование, то
F, = (ё, Ц- у,), М = F,I,, (11.3)
где т,—величина дискретной массы; со -
угловая скорость вращения; е, — эксцент-
риситет дискретной массы; у, —прогиб в Z-M
сечении; k—расстояние от центра массы
ротора до i-й массы.
Величина прогиба
п
У,— £ (11-4)
k=\
где а,*—податливость ротора. После под-
становки (11.4) в (П.З) получим си-
стемы линейных уравнений:
п
F(~ rn,<o2et+m,w2 Fkalk;
k^i
(11.5)
п
— etli + /, Гka[k;
Ь=± I
решив которые получим и решение зави-
симостей (11-2).
По сути зависимости (11.2) и (11.5)
являются математической моделью ротора,
позволяющей определить величины F и М.
Чтобы решить задачу выбора метода ба-
лансировки, нужно знать параметры в
уравнениях (11.5). Из них только вектор
эксцентриситета ё, необходимо дополни-
тельно обосновать по значению и углу.
352
Проектирование технологических процессов балансировки
Остальные параметры практически всегда
получают при проектировании ротора.
Для проверки условия (ИЛ) опреде-
ляем FOCT и М0С1 по зависимостям:
^ост иск Л- ^бал» исх 4~Мбал, где
FI1CX, Мнсх— главный вектор и главный
момент от сил, обусловленных исходными
эксцентриситетами; F6aJ1, М6ал— главный
вектор и главный момент от балансиро-
вочных сил; эти векторы можно найти
по уравнениям (11.5) и (11.2), если пред
ставить векторы эксцентриситетов диск-
ретных масс ёг.
Значение эксцентриситетов [ё4] опре-
деляем как математическое ожидание слу-
чайной величины, распределенной по нор-
мальному закону. Такой подход правоме-
рен потому, что значение [ёг] зависит от
большого числа производственных факто-
ров, оказывающих примерно одинаковое
влияние.
Более сложный вопрос — обоснование
угловых положений эксцентриситетов. Ре-
шение может быть общим или частным
в зависимости от принятого технологи-
ческого процесса сборки Например, если
в процессе сборки ротора дискретные мас-
сы взаимно ориентируются относительно
векторов эксцентриситетов, то схема угло-
вых положений эксцентриситетов с уче-
том дисперсии будет определенной. Так,
сборка по принципу взаимной компенса-
ции предусматривает постановку элемен-
тов ротора в положение, при котором
рядом расположенные эксцентриситеты
направлены под углом 180°. Это частное
решение. В общем случае угол дисбаланса
дискретной массы ротора—случайная ве-
личина. Выбор углов эксцентриситетов—
задача более сложная. Необходимо найти
наиболее вероятное положение их на ро-
торе. Один из путей решения состоит в
следующем.
Угол эксцентриситета дискретной мас-
сы— независимая случайная величина с
равновероятностным законом распределе-
ния. Принимаем /V возможных положений
эксцентриситета по углу для каждой диск-
ретной массы. Тогда, например, для
двухмассового ротора будет N вариантов
взаимных положений эксцентриситетов;
для трехмассового на каждое из /V поло-
жений третьей массы, т. е. количество
возможных положений /<=№. Вообще,
для «-массового ротора К=ДМ—п. Под-
ставив в уравнения Ц1.5) и (11.2) значе-
ния эксцентриситетов и последовательно
решая их К раз, по числу возможных
угловых положений эксцентриситета полу-
чим соответственные числа F и М для
ротора. Выделим [FMHH], [Fmax] и [Ммин],
[Мтах], разделим на несколько групп с
интервалом' AF и ДМ, затем построим
гистограмму (в координатах «частота зна-
чений— номер группы»), по которой опре-
делим группу с наибольшим числом зна-
чений [Л и [М]. Это и будет наиболее
вероятное расположение углов эксцентри-
ситетов на роторе.
Описанная последовательность яв-
ляется логическим алгоритмом для. реше-
ния задачи на ЭВМ. Можно изменять
отдельные звенья алгоритма, например,
вместо полного перебора К вариантов ре-
шений применить метод случайного по-
иска. Определив угловые положения экс-
центриситетов дискретных масс, можно
решать задачу выбора метода балансиров-
ки ротора.
Для этого определяем по уравнениям
(11.2) и (11.5), при частоте вращения
ротора на балансировочном станке, век-
торы дисбалансов и Мд, которые поз
, *
воляют наити балансировочные векторы
п
F6j и,Мб( так, чтобы Ри-± У F6l = 0 и
<=1
п
Мд + S Мб( = 0. Затем определяем е,б и
i=i
новые значения эксцентриситетов eiy в
местах постановки ебад как сумму elX—
=ё,4-ё,б.
После этого находим FOCT и MotT и
проверяем зависимости (11.1) Решение
повторяется с различными методами' ба-
лансировки до тех пор, пока не будет
353
Автоматизированное проектирование технологических процессов балансировки роторов
получен положительный ответ на зави-
симость (11.1).
Идентификация методов балансиров-
ки. Рассмотренная выше схема матема-
тической модели балансировки ротора не
имеет ограничений по применению методов
балансировки. Можно было проанализи-
ровать все известные методы и ввести их
в схему определения е|б в какой-то, не-
скол ько п роизвол ьной, п оследовател ьн о-
сти, т. к. нет четкого критерия по пре-
имущественному характеру различных ме-
тодов. Например, нельзя предварительно
утверждать, что метод балансировки по
коэффициентам влияния более (или менее)
эффективен, чем метод балансировки по
формам колебаний.
При подобном подходе нужно прове-
рить все методы балансировки по за-
висимости (11.1), и лишь после этого
оператор на основании субъективных оце-
нок выбирает один из соответствующих
методов.
Необходимо идентифицировать методы
балансировки с тем, чтобы при одинаковых
входных параметрах обеспечить совпаде-
ние выходных результатов для всех -рото-
ров, т. е. выбрать математическую модель,
общую для всех методов балансировки.
Моделью являются зависимости (11.2)
и (11.5), используемые в обратной по-
следовательности. Если в модели ротора
задаемся параметрами_ эксцентриситета
для определения F и М, то для модели
метода балансировки задаем F и М и
определяем ё,.
Основанные на этой модели методы
балансировки имеют строгое соподчине-
ние: каждый последующий метод более
эффективен, чем предыдущий.
Последовательность методов определя-
ется последовательным представлением
ротора системой двух, трех и более масс.
В соответствии с этим первый метод ба-
лансировки заключается в том, что по
известным значениям F и М определяются
взаимное положение оси вращения и глав-
ной центральной оси инерции ротора и экс-
центриситеты условных дискретных масс
Например, считаем эти условные массы
12 Зак 1641
на первом и последнем дисках. После
балансировки на этих дисках появятся
дополнительные эксцентриситеты ё|б и ёп6.
Затем по зависимости (11.5) опреде-
ляем на рабочих частотах вращения F^ и
Л10ст и проверяем результат по зависимости
(11.1). При неудовлетворительном ответе
ротор рассматривается как трех массовый,
и т. д.
Очевидно, первая схема -наиболее
грубое приближение. Все последующие
схемы дают более точное представление
о роторе и, следовательно, более эффек-
тивные результаты балансировки.
Принципиально эта схема сохраняется
при использовании как низкочастотного,
так и высочастотного балансировочного
оборудования.
Если применять низкочастотное балан-
сировочное оборудование, то дисбалансы
и балансировочные эксцентриситеты опре-
деляются по зависимостям:
Д=т1-ё1-, ё,б= —
«= । i
где /=1—п — количество условных диск-
ретных масс (плоскостей коррекции);
I—расстояние от дискретной массы до
центра массы ротора.
Для многомассового ротора наилуч-
шая эффективность балансировки, когда п
равно числу дискретных масс ротора.
Используя эту методику, необходимо по-
мнить, что F и М рассчитаны и могут
быть определены на низкочастотном ба-
лансировочном оборудовании и, следова-
тельно, дают представление о силах и
моментах, обусловленных смещением глав-
ной центральной оси инерции относитель-
но оси вращения. Силы и моменты от
носительно главной центральной оси инер-
ции при этом взаимно уравновешены и
проявляются с появлением прогиба ротора.
Следующий шаг предусматривает при-
менение 'Высокочастотного балансировоч-
ного оборудования.
354
Проектирование технологических процессов балансировки
Как и в зависимости (11.6), экс-
центриситеты е<б определяются по сме-
щению геометрической оси ротора (линии
прогиба) и главной центральной оси инер-
ции. Для устранения составляющей глав-
ного вектора эксцентриситеты ё, опреде-
ляем по зависимостям
/= 1
п п
(11.7)
п п
Ук^™^ m<aWC< + t°2 т‘ак.У^
i= I «= I
п
где k—l— п, /= 1 —п, mfe{—0.
Главный вектор сил — известная вели-
чина; определяем ё|=—ё|б и,следователь-
но, балансировочную систему сил. Такое
решение дает удовлетворительные резуль-
таты, если динамическое приращение
центробежных сил в основном обусловлено
составляющей первой критической часто-
ты вращения.
Аналогичные зависимости можно сос-
тавить и для условий, когда главное влия-
ние оказывает вторая критическая частота
вращения.
Как видно из зависимостей (11.7),
решение построено на предположении,
что форма линии прогиба ротора плоская,
хотя из уравнений (11.5) и (11.2) можно
заключить, что эта линия пространствен-
ная. Так как уравнения (11.5) и (11.2)
общеизвестны, возникает сомнение в пра-
вомерности использования зависимостей
(11-7).
Чтобы установить действительное сос-
тояние, были тщательно проанализирова-
ны уравнения (11.2), (11.5) с помощью
расчетов и экспериментально Получен-
ные результаты показали хорошее совпаде-
ние экспериментальных и расчетных дан-
ных и могут быть сформулированы в сле-
дующем виде: форма линии прогиба много-
массового ротора практически плоская
На модельных роторах с пятью и
семью массами пространственность формы
линии прогиба обнаружить не удалось
в диапазоне частот вращения 0,5ыкр1<:
<(й<1.5ш|ф|. Индуктивные датчики были
установлены в трех сечениях по длине
ротора в горизонтальной и вертикальной
плоскостях.
Расчетные работы по уравнениям
(11.2) и (11.5) были выполнены на ЭВМ
по специальной программе.
Рассматривалась плоскость, проходя-
щая через плоскость вращения и наи-
больший прогиб ротора: Пространствен-
ность оценивалась как отношение их
проекций на эту плоскость к прогибам.
При различных сочетаниях положений
эксцентриситетов отношения проекции к
прогибам составляли 0,97—0,99, т. е. про-
екции отличаются от прогибов на 1—3%.
Следует отметить, что к составным
роторам применение методов и оборудова-
ния для балансировки на высоких частотах
вращения, позволяющих измерить динами-
ческое приращение центробежных сил или
прогиб ротора, необязательно. Такую же
эффективность балансировки, и даже
более высокую, можно получить с по-
мощью обычного низкочастотного обору-
дования, применяя специальный метод
сборки и балансировки. Например, делим
ротор на 2, 3 или более технологических
частей (модулей). Каждую из них балан-
сируем в двух или нескольких плоскостях
коррекции, используя зависимость (11.6).
Затем последовательно собираем и до-
балансируем каждую часть, если возника-
ет необходимость.
В пределе, при делении на п частей,
такой метод более эффективен, чем балан-
сировка на высокочастотном оборудова-
нии, так как эксцентриситеты дискретных
масс могут быть близкими к 1 мкм, до-
стижимому на низкочастотном оборудова-
нии. Ротор сохранит сбалансированность
на любых частотах вращения.
Разработка алгоритма выбора метода
балансировки. После того как разработа-
Автоматизированное проектирование технологических процессов балансировки роторов 35!
на математическая модель ротора и идеи
тифииированы методы балансировки, сос-
тавление алгоритма выбора метода балан-
сировки не вызывает затруднений. Остает-
ся лишь выявить логические связи. Прежде
всего устанавливаем исходные данные,
необходимые для решения задач. Это уже
известные нам параметры зависимостей
(11.1), (11.2), (11.5): mit lh а.„ шраб,
«бал. МДС1Р е, Как уже отмечалось,
значения всех параметров могут быть по-
лучены еще на стадии разработки ротора
изделия. Неизвестным остается лишь угол
вектора эксцентриситета.
Первым шагом после ввода исходных
данных, в которых содержится и [ё,], яв-
ляется расчет углов а,. Затем по зависи-
мостям (11.7) определяются эксцентриси
теты ei6 балансировочных сил и по зависи-
мостям (11.2) и (11.5) главный вектор и
главный момент сил дисбалансов на ро-
торе при рабочих условиях.
Сравнив значения £ост и Л4ОСТ с задан-
ными £доп и получим ответ, со-
ответствует данный метод балансировки
поставленным требованиям или нет. При
отрицательном ответе решение повторяют,
но со следующим методом балансировки.
И так до тех пор, пока не будет получен
положительный ответ. Описание такой
программы дано в прил. П.12.
Целесообразно построить схему с диа-
логом. Например, не включать в решение
все методы балансировки сразу. На первом
этапе оставить группу методов низкоча-
стотной балансировки. Тогда при отри-
цательном ответе по всей группе методов
на печать вынести предложение оператору
перейти к проверке второй группы методов
балансировки или уменьшить значение ё,_
Оператор может запросить результаты ре-
шения последнего метода балансировки и
составить предварительное мнение о даль-
нейшем пути. Вполне вероятно, что можно
ограничиться более простой группой мето-
дов, так как значения ё, уменьшают за счет
повышения точности размеров деталей, их
балансировки и ориентированной сборки
ротора как это описано в программе
П.14. Если не будут достигнуты •при-
емлемые результаты, можно применить
высокочастотную балансировку, необходи-
мость которой следует обосновать рас-
четом значений сил и моментов на роторе
в рабочих условиях. Описание программы
расчета дано в прил. ПЛЗ.
Структурная схема алгоритма опреде-
ления метода балансировки представлена
на рис. 11.1.
В блок Аг вводятся все исходные Дан-
ные, необходимые для решения задачи.
В блоке Б2 определяются углы векторов
дисбалансов. В блоке В 2 формируется
команда для варианта S,, определяющего
аналитическую зависимость для определе-
ния ё(б. В блоке Г2 решается задача
по определению ё1б. В блоке Д2 решается
система уравнений, дающая значения
главного вектора и главного момента сил.
В блоке £2 сравнивается результат реше-
ния с контрольными параметрами £яоп и
Л4ДОГ. В блоке Mi формируется команда
S = t+1 для перехода к следующему вари-
анту определения ё[б. В блоке Жз форми-
руются команды для печати выбранного
Рис. 11.1. Структурная схема алгоритма оп-
ределения метода балансировки
12*
356
Проектирование технологических процессов балансировки
метода балансировки, управляющие кома-
нды для выбора оборудования, аппаратуры
и оснастки. В блоке 3| проверяется, все
ли параметры исчерпаны. В блок И2 пере-
дается команда на печатание рекоменда-
ций в связи с отрицательным решением.
В целом структурна^ схема достаточно
гибкая и может применяться к роторам
любых конструкций.
Разработка общего алгоритма проек-
тирования технологии балансировки. Про-
ектирование технологического процесса
балансировки, основанного на конкретном
методе, содержит ряд разделов, требую-
щих предварительной проработки. Необхо-
димо выбрать по оптимальным условиям
оборудование, аппаратуру и оснастку и
лишь после этого составлять последова-
тельность операций балансировки.
Структурная схема алгоритма выбора
балансировочной аппаратуры. Для балан-
сировки роторов применяют аппаратуру
двух типов: высокочастотную и низко-
частотную (в зависимости от метода ба-
лансировки). Есть различные варианты
каждого из типов, но существуют общие
критерии выбора оптимального варианта.
Рассмотрим схему выбора низкочастот-
ной балансировочной аппаратуры, которую
можно разделить на три варианта;
1. Серийная аппаратура. 2. Серийная
аппаратура в сочетании с ЭВМ. 3. Се-
рийная аппаратура в сочетании с анало-
говым вычислительным устройством.
Использование того или иного вариан-
та аппаратуры зависит от типа ротора
(симметричный, асимметричный), отноше-
ния L/l (L — расстояние между опорами
ротора, I—расстояние между плоскостя-
ми коррекции), вида производства (опыт-
ное, серийное) и метода балансировки
(двухплоскостная, многоплоскостная).
На рис. 11.2 изображена структурная
схема выбора аппаратуры. Блок про-
веряет, симметричный ли ротор. Если ротор
асимметричный, то сигнал поступает в блок
/ц, где проверяется тип производства,
опытное или серийное. В опытном про-
изводстве можно применять вариант 2
(блок В]), учитывая частую переналадку
Рис. 11.2. Структурная схема выбора ап-
паратуры
программы для различных роторов. В се-
рийном производстве рекомендуется вари-
ант 3 (блок В2), как более производи-
тельный.
Если ротор симметричный, то сигнал
поступает в блок Б2 и после проверки
отношения L/1 найравляется в блок В3
либо Вь-
В первом случае сигнал поступает на
проверку метода балансировки В3. При
двух плоскостях коррекции применяют ва-
риант 1 аппаратуры (Г8) независимо от
вида производства. При многоплоскостной
балансировке, в зависимости от вида про-
изводства (Г3), применяют второй (Д3)
или третий (Д4) вариант аппаратуры.
Во втором случае первый вариант
аппаратуры не применим, так как при
L/l>5 нельзя отстроить плоскости кор-
рекции. Сигнал направляется в блок Be для
проверки вида производства. Для серий-
ного— рекомендуется вариант 3 (Г6). для
опытного—вариант 2 (/\) аппаратуры.
Выбор балансировочного оборудова-
ния и оснастки. Разработка алгоритмов
выбора оборудования может быть сведена
к задаче подбора балансировочного станка
под данный тип ротора, подлежащего
балансировке. При этом соответствие стан-
ка и ротора может основываться на учете
различных критериев: как массово-геомет-
рических, так и физических, качественных.
Однако с целью упрощения задачи вы-
бора оборудования при одновременном со-
хранении общности методического подхода
в качестве критериев выбраны такие,
среди которых преобладают массово-гео-
Автоматизированное проектирование технологических процессов балансировки роторов 357
метрические. Таким образом, алгоритмы
выбора оборудования учитывают длину ро-
тора, его диаметр, массу, диаметр опорных
шеек, а также ограничения по типу приво-
да (ременного или осевого).
Использование указанных параметров
позволяет иметь определенные решения
для задачи выбора балансировочного обо-
рудования в зависимости от заданного
ротора.
Алгоритм выбора балансировочного
станка относительно каждого из пере-
численных параметров достаточно про-
стой.
Например, составляем программный
массив чисел Л, характеризующих длины
балансировочных станков. Последова-
тельно сравнивая эти числа с длиной
ротора, отбираем соответствующие типы
станков и посылаем их индексы iL в блок
памяти.
Аналогично отбираем станки по диа-
метру ротора (£д), массе (1т), диаметру
опорных шеек (id) и типу привода (хпр).
На рис. IL3 показана обобщенная
структурная схема алгоритма выбора ба-
лансировочного станка.
Сигналы iL, 1д, im, ia, inp из блоков
памяти поступают в блок сравнения А!, где
проверяется условие iL= La—i„—id—inp.
При положительном решении сигнал по-
ступает в блок Б1 программного массива
типов станков и оттуда в блок В1 печати
типа станков.
Алгоритм выбора оснастки также не-
сложный. Это ряд последовательных логи-
ческих операций, определяющих необходи-
мость вкладышей к подшипникам ротора,
балансировочной рамки, защитного кожу-
ха, приводной муфты. Результаты выбора
сообщаются в виде названий и чертежей
с основными размерами (если есть графо-
построитель).
Выбор технологии балансировки. Тех
нологический процесс балансировки за-
висит от метода балансировки, аппарату-
ры, оборудования и оснастки. Если все эти
факторы известны, то последователь-
ность действий очевидна. Поэтому можно
разработать ряд типовых технологических
процессов, соответствующих всем возмож-
ным вариантам балансировки роторов.
Тогда основным блоком алгоритма выбора
технологического процесса будет блок
сравнения, куда из блока памяти после-
довательно поступают номера типовых тех-
нологий, методов балансировки, аппара-
туры, оборудования и оснастки, получен-
ные при решении ранее. В результате
логических операций в блоке сравнения
выбирается номер технологического про-
цесса с адресом ячейки, содержание кото-
рой и печатается.
358
Основы проектирования балансировочных приспособленки
Глава 12
ОСНОВЫ ПРОЕКТИРОВАНИЯ БАЛАНСИРОВОЧНЫХ
ПРИСПОСОБЛЕНИЙ
12.1. НАЗНАЧЕНИЕ И ТИПЫ БАЛАНСИРО-
ВОЧНЫХ ПРИСПОСОБЛЕНИЙ
Приспособлениями называют дополни-
тельное оборудование к балансировочным
станкам, предназначенное для соединения
со станком балансируемых деталей и уз-
лов. Приспособления делят на две группы:
общего назначения и специальные. Глав-
ным признаком приспособлений общего
назначения является широкая универсаль-
ность. Специальные приспособления при-
годны только для детали определенной
конструкции или определенной операции.
Балансировочные приспособления общего
назначения, такие как приводные валы,
роликовые опоры, ленточные ремни, кон-
трольные роторы и т. д.,обычно прилагают
в качестве принадлежностей к станкам
заводы-изготовители. Специальные при-
способления проектируют и изготавливают
по мере необходимости при эксплуатации
станков.
Балансировочные приспособления про-
ектируют так же, как станочные и
сборочные, обеспечивая прежде всего об-
щие требования к приспособлениям: кон-
струкция приспособлений должна надежно
связывать деталь (узел) со станком, обес-
печивать заданную точность, производи-
тельность и безопасность балансировки.
По своему назначению приспособления де-
лят на четыре типа. Приспособления пер-
вого типа предназначены для установки
детали, узла в балансировочном устрой-
стве. К этому типу относят:
технологические опоры;
балансировочные оправки и техноло-
гические валы;
балансировочные рамки;
технологические корпуса.
Второй тип приспособлений служит для
соединения балансируемого ротора с при-
водным устройством станка:
приводные валы;
шкивы;
ленточные ремни.
Для обеспечения безопасности при ба-
лансировке применяют третий тип приспо-
соблений — защитные кожухи для враща-
ющихся роторов, частей станка и других
приспособлений. Контрольные и тариро-
вочные роторы, другие вспомогательные
приспособления, используемые для повер-
ки и настройки станка, выделяют в
четвертый тип приспособлений. Все
типы приспособлений и их конструк-
тивные разновидности имеют одноимен-
ные элементы, выполняющие сходные
функции (установочная, зажимная, нап-
равляющая и т. д.), допускают общий
подход к их проектированию.
12.2. ТЕХНОЛОГИЧЕСКИЕ ОПОРЫ
Установочные элементы, связывающие
цапфы или собственные подшипники рото-
ра с балансировочным устройством станка,
называют технологическими опорами. По-
верхность цапф или поверхности, их за-
меняющие, устанавливают в подшипники
трения скольжения, качения, ролико-
ковые опоры, призмы. Для установ-
ки собственных подшипников применя-
ют установочные призмы, полуиилиндри-
ческие гнезда, косые ролики (рис. 12.1).
В качестве технологических опор для
балансировки применяют подшипники тре-
ния скольжения, базирующиеся на сухом,
граничном, жидкостном трении, газоста-
тические опоры. Их эксплуатационные ха-
рактеристики определяются коэффициен-
том трения, моментом страгивания и рядом
других показателей. Основное преиму-
щество подшипников скольжения перед
другими типами опор заключается в про-
стоте обслуживания Они удобнее, ком-
Технологические опоры
359
Рис. 12.1. Технологические опоры:
а—роликовая оцора. б— призма; в—подшипник
скольжения. г пол у цилиндрическое гнездо,
д— подшипник качения
пактнее и надежнее для миниатюрных
и крупных цапф роторов Качественные
критерии выбора вида трения в подшип-
нике приведены в табл. 12.1.
Таблица 12.1
Критерии выбора вида трения
в технологической опоре для балансировки
Вид трения в подшип - нике Масса баланси- руемого ротора Частота баланси- ровки Вид про- изводства
Сухое Малая Низкая Единичное
Граничное Средняя Мелкосе- рийное
Жидкостное Большая Высокая Крупносе- рийное
Газовое Средняя Любая Массовое
Подшипники трения скольжения в ос-
новном состоят из ’корпуса и вкладыша,
на которой опирается цапфа. Наиболее
часто при балансировке применяют разъ-
емные подшипники. Они удобны при сборке
и позволяют регулировать зазор между
цапфой и вкладышем, возрастающий из-за
износа в процессе балансировки. Для этого
между верхним и нижним вкладышами
размещают прокладки из тонких пласти-
нок. после удаления которых при ре-
монте можно с помощью болтов подтянуть
вкладыш и уменьшить зазор. На рабочей
поверхности вкладыша подшипника гра-
ничного трения делают смазочные канав-
ки (рис. 12.2). При обильной подаче
смазочного материала для увеличения теп-
лоотвода применяют сквозные канавки
(рис. 12.2, tz), а при его недостатке
канавки делают глухими (рис. 12.2,6). В
подшипниках, смазываемых консистент-
ными мазями, возле торцов проделывают
кольцевые канавки (риё. 12.2,в). Нор-
мальная работа подшипника скольжения
возможна при условии равномерного рас-
пределения нагрузки по длине вкладыша.
В противном случае возникает заедание
вкладыша и цапфы. Для предотвращения
этого вредного явления тщательно выве-
ряют соосность опор или применяют само-
устанавливающиеся подшипники с внут-
ренним сферическим кольцом и желобом.
а)
в)
8)
Рис. 12.2. Смазочные канавки в подшип-
никах пол у жидкостного трения
360
Основы проектирования балансировочных приспособлений
Расчет подшипников скольжения сухо-
го и граничного трения основан на
критериях прочности и теплостойкости:
р — F/S [р]; pv = pndn/SQ^ [ро].
где р — удельное давление; F сила, дей-
ствующая на опору; S — условная пло-
щадь контакта: [р] — допускаемое удель-
ное давление; v — скорость скольжения;
[ри] — допускаемое значение критерия
теплостойкости.
Предварительно выбирают материал
вкладыша и назначают размеры под-
шипника. Рассчитывают скорость сколь-
жения цапфы, а затем проверяют расчет
по критёриям р и pv. При необходи-
мости уточняют размеры подшипников,
определяют температуру, зазор и затраты
энергии на трение в подшипнике. Рас-
чет технологических подшипников для ба-
лансировки имеет ряд особенностей
1. В качестве материала вкладыша
рекомендуются синтетические материалы,
алькусип, графит, металлокерамика, обла-
дающие хорошими антифрикционными
свойствами и надежно работающие без
дополнительного смазывающего матери-
ала.
2. Сила, действующая на опору, равна
сумме сил тяжести ротора, силы натя-
жения ремня, центробежной силы от
начальных дисбалансов, приходящихся на
эту опору.
3. Условная площадь контакта опреде-
ляется углом контакта цапфы в под-
шипнике. Значение этого угла зависит от
относительного диаметрального зазора,
модуля упругости материала и нагрузки.
Так как относительный радиальный зазор
в технологическом подшипнике для партии
балансируемых роторов переменный, в рас-
чете следует принимать его наихудшее
(наибольшее) значение, которому соответ-
ствует центральный угол контакта 2<р
50°. Для этого случая удельное давле-
ние рассчитывают по формуле
Ртах = I ’3 — ( | 4- ctg 1,4<р0) ,
где d и I — диаметр и длина вкладыша,
затраты энергии (мощность) на трение
А'тр = 0.65/Дб/, где f — приведенный коэф-
фициент трения цапфы.
4. В зависимости от поля допуска
цапфы выбирают фактический
диаметр вкладыша, обеспечивающий ми-
нимальный зазор для всей партии балан-
сируемых роторов. Минимальный и мак-
симальный зазоры должны соответство-
вать предельным отклонениям по СТ
СЭВ 144—75. Технологические опоры жид-
костного трения полностью соответствуют
подшипникам скольжения, применимым в
изделии
Газостатические опоры — наиболее
перспективный тип технологических опор
для статической и динамической баланси-
ровки роторов. Исключительные преиму-
щества газовой смазки отсутствие изна-
шивания и контактных напряжений — оп-
ределяют их высокую работоспособность,
а низкий уровень шума — высокую точ-
ность и производительность балансировки.
Принцип действия газостатических под-
шипников заключается в подаче газа под
давлением в зазор между цапфой и вкла-
дышем через отверстия малого диаметра,
расположенные на разных расстояниях по
окружности в один или несколько рядов.
Проходящий через подшипники газ, при
эксцентричном положении цапфы во вкла-
дыше, создает «подъемную силу» — не-
сущую способность газостатического под-
шипника. Удельные нагрузки в газоста-
тических подшипниках при небольших
давлениях наддува достигают 35 Н/см2.
Основной тип такого подшипника —
циркулярный (рис. 12.3). Для него харак-
терны значительная несущая способность,
удовлетворительная устойчивость, просто-
та конструкции. Наличие малых канавок
(карманов) повышает его характеристики
на 20— 30%. Отсутствие контакта между
цапфой и вкладышем определяет возмож-
ность произвольного выбора материала
вкладыша. Однако, учитывая аварийные
режимы работы и коррозионную стойкость
подшипника, рекомендуется изготавливать
вкладыши из более мягкого и хорошо
Технологические опоры
зол
Рис. 12.3. Газостатнческнй циркулярный под-
шипник:
/— вкладыш, 2 - цапфа. 3- питатель, 4- корпус
прирабатываемого антифрикционного ма-
териала, чем цапфа (бронзографита, же-
лезографита, графита с пропиткой бабитом
и др.), а также из пористых материа-
лов типа алькусипа.
Особенность проектирования техноло-
гического газостатического подшипника в
том, что размеры вкладыша: диаметр d,
длина подшипника L, диаметральный за-
зор 2С предопределяются цапфой балан-
сируемого ротора. Поэтому его коэффици-
ент несущей способности и массовый рас-
ход газа получаются не оптимальными.
При выборе параметров вкладыша можно
рекомендовать следующие значения:
отношение длины к диаметру £/d=(),5~?
1.5;
относительное расстояние сопел от краев
подшипника //£ = 0,254-0,375;
число сопел в ряду п = 4; 6; 8;
средний диаметральный зазор 2С = (0,001 —
-0,003) d;
коэффициент несущей способности С'. =
= 0.25—0,5.
Давление подачи газа в подшипни-
ке определяется возможностями производ-
ства. При использовании в качестве сма-
зочного материала воздуха, чтобы избе-
жать перер асш прения (запирание отвер-
стия), отношение давления окружающей
среды к давлению наддува при нормаль-
ной температуре не должно превышать
0,528.
Для восприятия осевых сил, действую-
щих на балансируемый ротор, применяют
плоские подпятники, конические и сфери-
ческие опоры.
При балансировке установочной пар-
тии или опытных образцов роторов уточ-
няют параметры и производят регулиров-
ку режима работы подшипников скольже-
ния. В результате устанавливают вид, рас-
ход. температуру и давление подачи сма-
зочного материала в подшипник, назнача-
ют параметры, подлежащие контролю при
эксплуатации, оформляют технологиче-
ский паспорт.
В качестве технологических опор тре-
ния качения применяют шариковые и ро-
ликовые радиальные и радиально-упорные
шариковые подшипники. Правила выбора
подшипников, типовые конструкции под-
шипниковых узлов, систем смазки изложе-
ны в справочниках. Государственных и от-
раслевых стандартах. При балансировке
роторов все подшипники качения нару-
шают расчетный режим работы станка,
создают помехи, обусловленные движени-
ем тел качения и неточностью изготовле-
ния деталей подшипника. Влияние этих
недостатков на точность и производитель-
ность процессов уравновешивания умень-
шают специальными методами уравнове-
шивания (см. гл. 3 и 4) и повышенными
требованиями к параметрам подшипника.
Основные технические требования к
технологическим подшипникам качения
следующие:
I. Класс точности технологического
подшипника по ГОСТ 520 — 71 и груп-
па зазоров по ГОСТ 24810—81 должны
быть выше, чем у рабочего (товарного)
подшипника.
2. Посадку подшипника на вал произ-
водят с зазором, а при отсутствии осе-
вой фиксации'внутреннего кольца — с на-
тягом.
3. Посадку подшипника в корпус осу-
ществляют с натягом.
4. Упругие радиальные смещения цен-
тров тяжести одного кольца относительно
другого при максимальной силе, действую-
щей на опору, не должны превышать
40% от допустимого удельного дисбалан-
са, приведенного к этой опоре.
362
Основы проектирования балансировочных приспособлений
5. Перед эксплуатацией подшипник
должен пройти обкатку на испытательной
машине.
6. В эксплуатации периодически конт-
ролируют геометрические параметры, мо-
мент трения, плавность хода, уровень
вибраций, чистоту рабочих поверхностей.
Конструкция подшипникового узла
должна обеспечивать:
фиксацию вала в осевом направлении;
.смазку, предохранение от пыли;
удобство монтажа и демонтажа.
Основным способом крепления под-
шипников на валу является затяжка
внутреннего кольца гайкой. При этом при-
меняют те же элементы крепления, что и
в изделии. В концевых установках под-
шипников 2 (рис. 12.4, о) на балансиро-
вочной оправе или технологическом валу
силовую затяжку осуществляют шайбами
3, притягиваемыми к торцу вала /
центральным болтом 4. С целью умень-
шения разбалансировки оправки при пере-
монтаже подшипника шайбу центрируют и
фиксируют в определенном положении
относительно оправки, а для повышения
производительности ее делают быстро-
съемной. Для установки подшипника на
гладком валу при необходимости регули-
ровки осевого положения используют уста-
новочные кольца 5 (рис. 12.4,6). Техно-
логический подшипник часто крепят в про-
межуточном целом корпусе (рис. 12.5),
предохраняющем его от пыли и грязи,
а также обеспечивающем смазку
Рис. 12.4. Крепление технологического
гет±Н
шипника качения на валу
под-
। 1Н~Т7~11 $
1
Рис. 12.5. Крепление тех-
нологического подшип-
ника качения в корпусе:
1 корпус, 2 подшипник.
3—цапфа вала; 4—крышка
Установка технологических подшипни-
ков на валу может быть раздельная
и парная. При раздельной установке один
из подшипников радиально-упорный или
двухрядный шариковый, а другой — ради-
альный или роликовый. Такое сочетание
подшипников создает меньшие погреш-
ности балансировки. Самоустанавливаю-
щийся подшипник применяют при баланси-
ровке длинных гибких валов. Парная
установка шарикоподшипников, особенно
радиально-упорных с пружинным натягом,
обеспечивает достижение высоких классов
точности балансировки.
При проектировании технологических
опор качения- рассчитывают погрешность
балансировки от неточности изготовления
и сборки. Исходными данными для расче-
та служат геометрические параметры под-
шипников и цапф ротора: несоосность
цапф, радиальное смещение оси дорожек
качения подшипника относительно оси по-
садочной поверхности внутреннего кольца,
неперпендикулярность упорных заплечи-
ков относительно оси посадочной поверх
ности цапф, осевое биение дорожки ка-
чения кольца относительно его базового
торца, радиальный зазор между цапфой
и посадочной поверхностью внутреннего
кольца. Расчет радиального смещения оси
вращения в плоскостях цапф относи-
тельно геометрической оси балансируемого
ротора проводится по методике, изложен-
ной в гл. 10. По результатам расчета
устанавливают технологический дисба-
ланс, вносимый посадкой подшипника, и
Технологические опоры
363
допустимый перекос оси внутреннего коль-
ца относительно геометрической оси. С
целью уменьшения технологического дис-
баланса применяют ориентированную по
меткам групповую сборку, дорабатывают
внутреннее кольцо подшипника, баланси-
руют методами двух сборок.
Основной особенностью сборки техно-
логического подшипника является конт-
роль качества монтажа подшипника,
осуществляемый по следующим пар а мет
рам: легкость вращения в опоре, зна-
чение посадочного радиального зазора,
перекос колец (измеряют торцовые бие-
ния колец), усиление затяжки. Подшипни-
ки хранят во влагонепроницаемой бумаге,
пропитанной ингибитором, периодически
контролирующих геометрические размеры,
которые заносят в технологический пас-
порт.
Роликовые опоры обладают большой
универсальностью, так как на одной и
той же паре роликов возможна установ-
ка роторов с широким диапазоном диа
метров цапф; имеют малый коэффициент
трения, не создают погрешностей баланси-
ровки, ведь ротор вращается вокруг сво-
ей геометрической оси. К недостаткам
относятся помехи, возникающие из-за ра-
диального и торцового биений роликов,
и большие контактные напряжения. Ос-
новные технические требования к ро-
ликовым опорам следующие:
1. Отклонение формы рабочей по-
верхности ролика (до диаметра 260 мм)
не должно превышать 0,004 мм.
2. Отклонения расположения роликов
в сборе на опоре, такие, как радиальные
и торцовые биения, непараллельность,
должны соответствовать III — IV степени
точности.
3. Значение параметра шероховатости
рабочих поверхностей Ра не должно пре-
вышать 0,16 мкм, твердость НрС 60 — 62.
Роликовая опора (рис. 12.6) состоит
из основания 1 с двумя опорными роли-
ками 4, откидной (съемной) крышки 5 с
прижимным роликом. Основание может
перемешаться по вертикальным направ-
Рис. 12.6. Роликовая опора
Рис. 12.7. Схема для расчета роли-
ковой опоры
ляющим. Опорные и прижимной ролики
фиксируют в одном из многих возмож-
ных положений. Ось 2 с подшипником ка-
чения 3 и роликом, имеющим сферичес-
кую или цилиндрическую наружную по-
верхность, закрепляют на основании /.
Основные геометрические параметры
роликовой опоры (рис. J2.7) определяют
в результате расчета сферических или
цилиндрических сочленений. Для сфери-
ческих роликов отношение диаметров i
вычисляется по формуле
о+о3 1о]а <
Е- F ~
Аф.
(12.1)
364
Основы проектирования балансировочных приспособлений
где [с] — циклическая контактная проч-
ность; Е модуль упругости материала;
t/ц — диаметр цапфы, мм; F—сила тя-
жести ротора, приведенная к роликовой
опоре, кгс, или номограмме (рис. 12.8,
кривая /)
Размеры цилиндрических роликов вы-
числяют по формуле
i ТГф 2i * i
(12.2)
или номограмме (рис. 12.8, кривая 2).
Здесь обозначения те же, что и в
формуле (12.2), а / — длина ролика, мм
Нагружаемость цилиндрических роликов
превосходит нагружаемость сферических
роликов при малых значениях [о] =
= (0,5 — 2)10~4Н/м2, с повышением (с]
несущая способность роликов уменьшает-
ся. Нагружаемость цилиндрических роли-
ков можно повысить увеличением длины.
Однако из-за неточностей изготовления
возникает неравномерность распределения
нагрузки по длине.
После определения основных размеров
ролика находят геометрические параметры
подшипника из условия снижения по-
Рис. 12.8. Номограмма для определения от-
ношения диаметров ролика и цапфы балан-
сируемого ротора
мех с частотой, близкой к частоте баланси-
ровки Вычисляют частоту вращения на-
ружного кольца подшипника по формуле
L =
где — частота балансировки: частоту
вращения сепаратора подшипника по фор-
муле
(«+<•);
частоту вращения шарика или ролика
в подшипнике по формуле
fw = №/(#-'),
где /?, г радиусы наружной и внутрен
ней беговых дорожек подшипника.
Для удовлетворительной фильтрации
помех необходимо, чтобы эти частоты от-
личались от частоты балансировки не
менее чем на 15—20%.
При наличии комплекта роликовых
опор проводят проверочные расчеты на
контактную прочность и уровень помех
по приведенным выше формулам. Роли-
ки изготавливают из высокопрочных ста-
лей (содержание углерода ~1%, твер-
дость не ниже HRC 60—62). Ролики
небольших диаметров выполняют из угле-
родистых сталей УП, У12, или легиро-
ванных инструментальных сталей, а роли-
ки больших диаметров — из цементируе-
мых сталей 20Х, ЗОХГТ, 18Х2Н4В, причем
глубина цементации 1—1,5 мм.
Сборка роликовых опор, контроль ка-
чества монтажа, условия эксплуатации и
хранения должны соответствовать требо-
ваниям, предъявляемым к технологичес-
ким подшипникам качения.
Все типы технологических опор в
процессе эксплуатации подлежат смазке.
При выборе смазочного материала учиты-
вают конструктивные особенности опоры,
удельную нагрузку, относительную ско-
рость движения соприкасающихся поверх
ностей, допустимую температуру нагрева.
Система смазки технологических опор
при низкочастотной балансироке, как пра-
вило, периодическая или непрерывная без
принудительного давления. Консистентные
смазочные материалы периодически пода-
ются колпачковой или поршневой маслен-
Балансировочные оправки и технологические валы
365
кой в трущиеся пары в определенном
количестве (не превышающем 1/3 внут-
реннего свободного пространства). Жид
кие смазочные материалы подают в зону
трения шприцами, мембранными и фитиль-
ными масленками. При высокочастотной
балансировке преимущественно применя-
ют циркуляционную систему смазки жид-
ким маслом. В технических требовани-
ях на балансировку указывают вид,
количество и способ подачи смазочного
материала в технологическую опору.
Установочные призмы (рис. 12.9) име-
ют две рабочие поверхности, расположен-
ные под углом 90°, иногда применяют
призмы и с другими углами. Силу закреп-
ления подшипника в призме рассчиты-
вают по формуле
Л = kM/ [</пад(Л + h) /sin 0.5а],
где k — коэффициент запаса: ft, f? — ко-
эффициенты трения;— диаметр под-
шипника; а — угол призмы; М — крутя-
щий момент, приложенный к наружному
кольцу подшипника.
Расстояние от центра призмы до осно-
вания должно быть таким, чтобы ось
призмы совпадала с осью опор станка.
Призмы изготавливают из стали 20Х с
цементацией рабочей поверхности и термо-
обработкой на твердость HRC 56- 61.
В отличие от призм по ГОСТ 12195—66
призмы для балансировки имеют упорный
штифт, фиксирующий подшипник в осе-
вом направлении. К опоре станка приз-
му крепят винтами, а после выставления
соосности опор фиксируют контрольными
штифтами. Если призма служит опорой
для вращающейся цапфы, то материал
для нее выбирают как для подшипни-
ка скольжения. В призмы из графита и
фторопласта устанавливают легкие роторы
при низкочастотной балансировке.
Полуцилиндрическое гнездо применя-
ют для роторов большой массы. Уста-
новочную функцию выполняет только
гнездо — нижнее полуотверстие. Съемоч-
ная или откидная крышка служит лишь
для приложения силы закрепления к под-
шипнику.
Косые ролики — разновидность приз-
мы, у которой рабочими поверхностями
служат цилиндрические ролики. Они име-
ют точечный контакт с наружным коль-
цом подшипника, что обеспечивает высо-
кую стабильность его положения при мно-
гократных установках.
12.3. БАЛАНСИРОВОЧНЫЕ ОПРАВКИ
И ТЕХНОЛОГИЧЕСКИЕ ВАЛЫ
Технологические оправки являются
промежуточными установочными элемен-
тами, связывающими балансируемые дета-
ли и узлы, не имеющие собственных
несущих поверхностей, с технологическими
опорами. За устанавливаемую поверхность
(установочную базу) принимают ту по-
верхность детали, на которой она сопря-
гается с другими деталями ротора.
Основные технические требования к ба-
лансировочным оправкам следующие:
1. Обеспечивать заданную точность
и производительность балансировки дета-
ли.
2. Соответствовать по массе и гео-
метрии балансируемой детали и баланси-
ровочному станку.
3. Надежно связывать балансируемую
деталь со станком.
Основными факторами, понижающими
точность балансировки, являются оста-
точные дисбалансы и прогиб оправки,
погрешность, связанная с установкой
детали на базовой поверхности от-
носительно геометрической оси оправки.
366
Основы проектирования балансировочных приспособлений
Масса и моменты инерции оправки
также понижают порог 'Чувствительности
балансировочного станка, что может при-
вести к потере точности балансировки.
Производительность процесса балан-
сировки зависит от применяемого метода
уравновешивания, геометрических разме
ров оправки и погрешности установки
детали.
Проектирование оправок ведут на ос-
новании рабочего чертежа детали и тех-
нических данных балансировочного стан-
ка Выбирают схему установки детали на
оправке, ее геометрические размеры. Дли-
на оправки не должна превышать мак-
симального и быть больше минимального
расстояния между опорами станка. Если
деталь балансируется в двух плоскостях
коррекции, то длина оправки ограничена
5—20 расстояниями между плоскостями.
Меньшее значение относится к зарезо-
нансным балансировочным станкам, а
большее — к дорезонансным станкам с
цепью разделения плоскостей кор-
рекции по схеме а, Ь, с.
Массу оправки топ выбирают из усло-
вия
— тл,
где та — масса детали; £)доп — допусти-
мый дисбаланс детали; Де — паспортный
порог чувствительности станка по удельно-
му дисбалансу в плоскостях опор. Сум-
марная масса оправки с деталью долж-
на находиться в диапазоне допустимых
масс балансировочного станка.
Требуемое положение центра массы уз-
ла (деталь с оправкой) определяют из
уравнения, выражающего принцип инер-
ционного регулирования режима работы
зарезонансного балансировочного станка
ь.=± + /' ‘
L 2 у -1 Z.2(mOT+mJ '
Ожидаемую погрешность балансиров-
ки детали на оправке рассчитывают по
формуле
^ОСТ Ч- ЛМдй/д>|И 4“ !/ст 4“ 5 4- 6) ,
где /)<чт — остаточный дисбаланс оправки
в заданной плоскости; удин, г/ст — дина-
мический и статический прогиб; S —
максимальный зазор в посадке детали на
оправку; б — максимальное радиальное
биение посадочной поверхности оправки
относительно геометрической оси.
При D <1 D&vn оправка обеспечивает
заданную точность балансировки.
Основными элементами оправок явля-
ются: установочные поверхности для дета-
ли (плоские, цилиндрические, конические
и др.), цапфы, зажимные элементы,
элементы, соединяющие оправку с при-
водом (приводная муфта или поверхность
под ремень). В тех случаях, когда тре-
буются повышенные точность и произво-
дительность балансировки деталей, приме-
няют гидропластовые оправки, с разрез-
ной цапфой и мембранные. В качестве
зажимных элементов используют простые
винтовые зажимы с подвижной гайкой.
Рис. 12.10. Балансировочные оправки:
а — межопорная: б консольная, в — сборная
Балансировочные рамки
367
Характеристики типовых оправок
Таблица 12.2
Оправка Диаметр базовой поверх НОСТИ. ММ Точность обработки базовой поверхнос- ти. квали теты Точность установки в осевом направ- лении, мкм Допуск на биение степени точности ГОСТ 24643 — 81
радиальное торцовое
Цилиндричес- кая для уста- новки детали с зазором 3- 100 4 — 6 10-40 3-4 6—7
Прессовая Коническая 30—60 3 100 5—7 5 7 10 -80 4-5 4 5 —
С разрезной цангой Гидропласто- вая 10-100 30—150 Свободные 6—9 10—40 4—5 3-6 6-7
Балансировочные оправки (табл. 12.2,
рис. 12.10) делят на межопорные, кон-
сольные; сборные. Межопорные оправки
применяют для балансировки деталей с
центральным отверстием преимущественно
на зарезонансных балансировочных стан-
ках. Область применения консольных опра-
вок — детали без сквозного центрального
отверстия. Эти оправки чаще бывают с раз-
резной цангой и гидропластовые. Консоль-
ные оправки используют на дорезонансных
балансировочных станках. Допускается их
установка на зарезонансном станке с по-
мощью балансировочной рамки. Сборные
оправки предназначены для балансировки
узлов, не имеющих собственных опорных
поверхностей.
Оправки изготавливают из легирован-
ных конструкционных сталей, рабочие по-
верхности тщательно обрабатывают, обе-
спечивая высокие твердость и износостой-
кость. Динамическую балансировку опра-
вок проводят обязательно со всеми деталя-
ми в двух плоскостях коррекции. Перед
эксплуатацией статистическими методами
определяют действительную точность ба-
лансировки деталей на оправке, ее геомет-
рические размеры и дисбалансы. В процес-
се эксплуатации периодически контролиру-
ют параметры оправки, хранят их в верти-
кальном положении, оберегая от повреж-
дения, загрязнений, коррозии.
Технологические валы являются разно-
видностью балансировочных оправок; они
предназначены как для балансировки,
так и для различных испытаний .(разгон-
ные, гидравлические и т. п.) деталей и уз-
лов ротора. Установочные и зажимные.эле-
менты должны соответствовать реальной
конструкции. При этом конструкция цап-
фы, технологических опор, соединительных
элементов должна выполнять функции
балансировочной оправки и быть пригод-
ной для испытательного стенда. Технологи-
ческие валы проектируют жесткими. Кор-
ректировку масс детали проводят в плос-
костях, расположенных на валу,’ поста-
новкой балансировочных грузов. Условия
эксплуатации и хранения технологических
валов те же, что и для оправок, но
с учетом специфики испытаний.
12.4. БАЛАНСИРОВОЧНЫЕ РАМКИ
Балансировочные рамки предназна-
чены:
для установки роторов на опорах стан-
ка при балансировке в собственных под-
шипниках и в собственном корпусе;
для установки консольных роторов на
опорах зарезонансных балансировочных
станков;
для регулирования режима работы
станков.
Основными элементами балансировоч-
ной рамки (рис. 12.11) являются техно-
логические опоры 1 для установки ба-
лансируемого ротора, опорные узлы 2 для
установки рамки на опорах станка,
корпус или направляющие 3. В качестве
технологических опор ротора используют
установочные призмы, полуцилиндриче-
ские гнезда, подшипники трения скольже-
ния. Корпуса роторов устанавливают в
рамке на плоской поверхности и зажимают
винтовым зажимом или металлической
лентой. В специальных рамках (рис.
12.11, б) технологические опоры неподвиж-
но закреплены на корпусе. Технологиче-
ские опоры универсальных рамок (рис.
12.11, а) могут передвигаться по направля-
ющим и фиксироваться в заданном по-
ложении.
Конструкция опорных узлов рамки оп-
ределяется конструкцией опор станков.
Они могут иметь цилиндрическую или
плоскую поверхность. На станках, опоры
которых имеют две степени свободы, рам-
ку устанавливают с помощью шарниров,
обеспечивающих ей малые угловые переме-
щения. Роль шарниров выполняют упор-
ные подшипники скольжения или качения.
Рис. 12.11. Балансировочная рамка:
а—универсальная: б—специальная
внутреннее кольцо которых связано с рам-
кой. а внешнее — с опорой станка. На кор-
пусе рамки (направляющих) фиксируются
все элементы конструкции.
Конструкция рамки должна отвечать
следующим требованиям:
обладать высокой жесткостью во всех
направлениях;
центр массы рамки с ротором должен
находиться на оси станка между его
опорами;
не нарушать расчетный режим работы
станка.
Расчет основных параметров рамки,
обеспечивающих заданную точность ба-
лансировки ротора, производят в следую-
щей последовательности.
1. Выбирают типовую схему балан-
сировочной рамки по рис. 12.11.
2. Составляют расчетную схему рамки,
заменяя распределенные массы сосредо-
точенными на невесомых жестких стерж-
нях.
3. Вычисляют массу рамки, положение
ее центра масс относительно датчиков
станка и порог чувствительности балан-
сировочного станка к статической не-
уравновешенности по формуле
Дест=ДС/(1 — т/гпо),
где ДС'—паспортный порог чувствитель-
ности балансировочного станка; тп — масса
балансировочной рамки с учетом массы
опор стайка, корпуса и других паразит-
ных масс; то—-масса ротора; а также
порог чувствительности балансировочного
станка к моментной неуравновешенности
по формуле
KMD— AUmlo,
где /о—расстояние между центрами масс
ротора и рамки.
4. Сравнивают расчетные значения
Дест, ДЛ4С с допустимыми дисбалансами.
Если &ecrcDcraon/m0, &MD<zMDao„, to
балансировочная рамка обеспечивает за-
данную точность уравновешивания ротора.
Приводные валы и шкивы
369
В противном случае повторяют расчет,
задаваясь другими исходными данными.
5. Вычисляют собственные частоты ко-
лебаний рамки и проводят расчет рамки
на прочность
Регулирование режима работы про-
водят также экспериментальными спосо-
бами.
По первому, способу необходимый ре-
жим устанавливают путем изменения па-
разитной массы К опорным узлам рамки
прикрепляют такие дополнительные мас-
сы, которые увеличивают чувствительность
станка. Это происходит, когда центр масс
балансировочного устройства с ротором,
рамкой и дополнительными массами будет
находиться в середине между опорами.
По второму способу регулирования ре-
жима работы стайка осуществляют изме-
нением геометрии рамки (ее длины) и
положения балансируемого ротора. После-
довательно перемещая технологические
опоры с, ротором и опорные узлы рамки
по направляющим, находят их оптималь-
ное положение, при котором порог чув-
ствительности станка выше допустимого
значения дисбаланса. Это наблюдается
при условии mLALB - J-+0, где m
вся паразитная масса вместе с массой
ротора, La, Lb—расстояние от центра
масс балансировочного устройства до опо-
ры станка А(В), J—экваториальный мо-
мент инерции балансировочного устройст-
ва.
Балансировочная рамка должна отве-
чать тем же техническим требованиям,
что и механическая часть станка. Откло-
нения от параллельности направляющих,
осей технологических опор, вертикальной
и горизонтальной плоскостей, а также
отклонения от соосности опор должны
соответствовать VIII IX классам точ-
ности.
В процессе эксплуатации балансиро-
вочные рамки периодически контролируют
на соответствие заданным техническим
требованиям, оберегают от повреждений,
загрязнений и коррозии.
12.5. ПРИВОДНЫЕ ВАЛЫ И ШКИВЫ
Приводной вал является основным эле-
ментом осевого соединения. В балансиро-
вочной практике применяют двухшарнир-
ные приводные валы, приводные валы с
упругими или зубчатыми муфтами для
роторов массой от 1 кг до 100 т и выше.
Двухшарнирные приводные валы име-
ют жесткую и прочную конструкцию, обес-
печивающую передачу больших крутящих
моментов. Такой приводной вал (рис.
12.12) состоит из вала 4 и двух шар-
нирных муфт 3 на его концах. Шар-
нирные муфты передают крутящий мо-
мент и допускают перемещение самого
вала в двух перпендикулярных плос-
костях.
Шарниры муфт выполняют на под-
шипниках качения или скольжения. Оси
шарниров расположены под углом 90°
друг относительно друга. Полумуфту 1
жестко соединяют винтами 2 со шпинде-
лем балансировочного станка. Другая
часть муфты приварена к валу. Полу-
муфту 5 через переходную втулку со-
единяют с валом. Переходную втулку
изготавливают индивидуально для каж-
дого типа балансируемого ротора. Более
высокую точность балансировки роторов
от 1 до 50 кг обеспечивают приводные
валы с одинаковыми моментами инер-
ции относительно главных центральных
осей, т. е. эллипсоид инерции которых —
шар.
Приводные валы с упругими муфтами
применяют при балансировке роторов мас-
сой до 100 кг. Они обеспечивают более
высокую точность балансировки, чем дру-
370
Основы проектирования балансировочных приспособлений
гие конструкции приводных валов. По-
датливость муфты обеспечивается за счет
деформации упругости кольца. В кольце
расположены четыре отверстия под углом
90° друг относительно друга. В эти
отверстия входят два пальца полумуфты,
закрепленной на шпинделе (роторе), и два
пальца, установленные в полумуфте, свя-
занной с валом. Большую податливость
муфты обеспечивают кольца из резины.
Высокую жесткость соединения имеют
приводные валы с зубчатыми муфтами
Полумуфты соединяют сферическим шар-
ниром и зубчатым зацеплением. На вен-
це одной полумуфты нарезают наружные,
а иа венце другой полумуфты — внутрен-
ние зубья со специальным профилем.
К недостаткам приводных валов, соз-
дающим погрешность балансировки, отно-
сят: трение в шарнирах; дисбаланс вала;
радиальные биения шпинделя, полумуфт
и промежуточной втулки.
Трение в шарнирах приводного вала
снижает чувствительность балансировоч-
ного станка по значению и углу дис-
баланса. Приводной вал имеет собствен-
ный дисбаланс, который воспринимается
измерительным устройством станка как
дисбаланс ротора. Поэтому приводные ва-
лы тщательно балансируют с помощью
контрольного ротора. Большое значение
имеет центровка приводного вала относи-
тельно оси ротора. В соединениях вала со
шпинделем, промежуточной втулкой и ва-
лом за счет радиальных биений поса-
дочных поверхностей, наличием зазоров в
соединениях происходит смещение оси при-
водного вала, приводящее к дисбалансам.
Значение и угол этих дисбалансов из-
меняются от ротора к ротору при
балансировке партии.
Уменьшение погрешности балансиров-
ки за счет радиальных биений дости-
гается высокой точностью изотовления
посадочных поверхностей и правильным
выбором приводного вала. Конструкция
приводных валов должна отвечать сле-
дующим требованиям:
иметь минимальную массу, габаритные
размеры и главные моменты инерции;
обладать достаточной прочностью -
крутильной и изгибной, жескостью. изо-
тропностью;
обеспечивать заданную точность ба-
лансировки.
Масса приводного вала обусловлена
его прочностью, зависит от массы рото-
ра и точности балансировки (табл. 12.3).
При этом погрешность балансировки, вно-
симая приводным валом, дана без учета
его остаточного дисбаланса, радиальных и
осевых биений шпинделя станка, про
межуточной втулки и т. п., но с учетом
смещения оси приводной шейки ротора
до 0,01 мм относительно его цапф.
Поэтому необходимо, чтобы эта погреш-
ность не превышала 20% от заданной
точности балансировки. Длина и диа-
метр приводного вала зависят от ампли-
туды колебаний опо'р станка, т. е. от на-
чальных дисбалансов ротора, балансиро-
вочной и критической частот вращения
вала.
Для сохранения расчетного режима ра-
боты балансировочного станка (обеспече-
ние малых колебаний) промежуточный вал
должен поворачиваться на угол до 2°, а
амплитуда колебаний опор не превышать
0,2 —0,5 мм. Следовательно, минимальная
длина вала 10—15 мм. Конструктивно дли-
на всегда получается больше этого значе-
ния. Верхний предел длины промежуточно-
го вала определяет его диаметр и крити-
ческую частоту вращения, которая должна
превышать частоту балансировки в 4 раза.
Максимально допустимую длину полого
стального вала £в (см) наружным диа-
метром cl" (см) прн угловой скорости
балансировки находят по формуле
£в « 630ydH/w6.
Крутильную жесткость определяет
крутящий момент, достигающий наиболь-
шего значения при разгоне и остановке
ротора. Наибольшее значение крутящего
момента (без учета трения в опорах) на
приводном валу при разгоне
О/(7О -К /п),
Таблица 12.3
Зависимость погрешности измерения удельных дисбалансов от массы балансируемого изделия и приводного вала
Масса бал а нс и- Масса приводного вала тв, кг
руемого изде- лия ти, кг 0.25 0,5 1,0 2,0 4.0 8.0 16 32 64 128
Погрешность измерения, мкм •
1—10 5-40 20-100 50 - 400 200—1000 500 - 4000 2000—10000 5000 — 40 000 20000—100 000 5—0,5 1—0.2 5 2 — 0,3 0.5—0,1 5-0,5 1—0,2 0,5—0,1 2-0.5 0,7—0,1 0,2-0,1 5 — 0,7 2-0,2 0,5—0,1 0,2—0,1 5—0,5 0,7 0,3- 0,1 0,1 2—0,3 0,5 -0,1 0,2 —0,1 0,1 6—0,6 1,0-0,1 0,3-0,1 0,2—0,1 0,1 2,0-0,3 0,6—0,2 0,3—0,1 0,1 1,5—0,3 0,5—0,1 0,2—0,1
Приводные валы и шкивы
372
Основы проектирования балансировочных приспособлений
где /Ии, — максимальный крутящий момент
шпинделя; J„ — момент инерции ротора
и привода (якорь электродвигателя, пере-
дача, шпиндель), пересчитанный на шпин-
дель.
Расчеты на прочность выполняют из-
вестными методами сопротивления матери-
алов.
Балансировочные станки оснащают
комплектом приводных валов, рассчитан-
ных для передачи различных крутящих мо-
ментов и привода роторов заданного диа-
пазона масс. В этом случае при выборе
вала выполняют поверочный расчет.
При эксплуатации приводных валов
контролируют геометрические размеры по-
садочных поверхностей полумуфт, дисба-
лансы валов, трение в шарнирах, пери-
одически заменяют смазочный материал в
шарнирах.
Шкивы и ленточные ремни используют
в ленточных и тангенциальных соедине-
ниях для передачи вращения от привод-
ного устройства к ротору.
Шкив устанавливают на выходной вал
приводного электродвигателя или коробки
передач. Внутренний диаметр шкива дол-
жен соответствовать диаметру выходного
вала. Наружный диаметр шкива выби-
рают в зависимости от заданной частоты
вращения ротора при балансировке по
формуле
<< = dpct>6/<on,
где — диаметр поверхности ротора под
ремень; соб — угловая скорость ротора при
балансировке: <оп — угловая скорость вы-
ходного вала приводного устройства
Радиальное и торцовое биения шкива
должны быть минимальными для того,
чтобы не оказывать влияния на баланси-
руемый ротор.
В приводных устройствах применяют
плоские бесконечные ремни на синтети-
ческой основе. Они обладают малым растя
жением под действием усилия натяжения,
покрыты маслоотталкивающим лаком,
имеют хорошее сцепление с приводными
поверхностями. При вращении ротора
практически отсутствует скольжение рем-
ня, что обеспечивает высокую стабиль-
ность балансировки. Для уменьшения
погрешностей, вносимых ремнем при ба-
лансировке, его длину делают более трех
окружностей приводной поверхности рото-
ра.
При балансировке легких роторов ре-
мень заменяют капроновой нитью.
12.6. ЗАЩИТНЫЕ КОЖУХИ
Защитные кожухи устанавливают на
балансировочных станках для ограждения
вращающихся частей и ротора, а также
уменьшения потерь на трение о воздух
роторов с лопатками. При высокочастот-
ной балансировке кожухи защищают рабо-
чее место балансировщика при разрыве
балансируемого ротора.
Кожухи изготавливают из тонколис-
товой стали и оргстекла. Их закреп
ляют на станине станка или опорных
стойках. Кожух для ротора должен иметь
горизонтальный разъем, верхнюю крышку
укрепляют на петлях и снабжают упорами.
Перед балансировкой крышку опускают и
закрывают на замки.
Защитные кожухи изготавливают из
толстолистовой стали сварной конструк-
ции. В нижней части кожух имеет ро-
лики, с помощью которых его надвига-
ют на балансировочное устройство станка.
12.7. КОНТРОЛЬНЫЕ И ТАРМРОВОЧНЫЕ
РОТОРЫ
Контрольные роторы применяют для
проверки балансировочных станков. Раз-
меры, масса и другие параметры этих
роторов определены ГОСТом [Г9] и при-
ведены в табл. 12.4, 12,5. Контрольные
роторы (рис. 12.13) для станков с го-
ризонтальной осью вращения имеют сим-
метричную цилиндрическую форму посто-
янного диаметра с двумя одинаковыми
цапфами. Обработку всех поверхностей
проводят при одной установке относитель-
но центров. В крайних плоскостях бочки
ротора выполнено по восемь радиальных
резьбовых отверстий через 45°. Кроме того,
Контрольные н тарировочные роторы
373
Таблица 12.4
Конструктивные параметры контрольных роторов для балансировочных станков
с горизонтальной осью вращения
Обозначение параметра Значение параметра
Номер контрольного ротора
1 2 3 4 5 6 7
т, кг 0,5 1,6 5 16 50 160 500
J, кг • м Ю4 6-10~4 4-10-3 0,03 0,2 1.3 9
0D, мм 38 56 82 120 176 260 380
L, мм 95 140 205 300 440 650 950
0d, мм 8 12 17 25 35 50 75
С, мм 19 28 41 60 88 130 190
Е, мм 6 9,5 11,5 15 27 40 60
F, мм 45 65 100 150 210 310 450
G, мм 19 28 41 60 88 130 190
О, мм М2 М2 М3 М3 Мб Мб М12
лкр • Ю3 МИН1 200 140 95 65 45 30 20
пдоп ’ Ю3, мин-1 20 14 9,5 6,5 4,5 3 2
М, мм М3 М3 Мб Мб М12 М12 М20
Таблица 12.5
Конструктивные параметры контрольных
роторов для вертикальных балансировочных
станков
Обозначение параметра и его размер- ность Значение параметра
Номер контрольного ротора
1 2 3 4 5
т, кг /, кг-м 0D > 0d Н А В = С F N 2 мм 1.1 0,0025 НО 99 55 8 20 6,5 М3 3,5 0,017 160 144 80 12 30 9,5 М3 11 0,12 230 206 127 19 45 13 Мб 35 0,8 345 310 170 25 60 20 мю НО 5,5 510 460 255 38 90 30 МЮ
через каждые 10° нанесены осевые линии
с указанием углов через каждые 90°. Мас-
су и моменты инерции контрольного ро-
тора устанавливает изготовитель станков.
Для проверки станка необходимы два
контрольных ротора. Один ротор имеет
массу и моменты инерции, соответствую-
щие нижнему, а другой — верхнему диа-
пазону масс балансируемых роторов. Кон-
трольный ротор полностью сбалансирован.
имеет высокую точность изготовления всех
рабочих поверхностей. Отклонения формы
и расположения поверхностей соответству-
ют III- IV степени точности.
Для проверки станков с вертикальной
осью вращения контрольные роторы пред-
ставляют собой диск (рис. 12.14) с отно-
шением D/H = 2/1. В нижней части диска
имеется центрирующий поясок и отверстия
для его установки и крепления на шпин-
деле станка. В трех сечениях ротора вы-
полнены радиальные резьбовые отверстия
через каждые 15°. Причем средняя плос-
кость проходит через центр масс кон-
Рис. 12.13. Контрольный ротор для горизон-
тального балансировочного станка
374
Способы корректировки масс
Рис. 12.14. Контрольный ротор для верти-
кального балансировочного станка
трольного ротора, а крайние плоскости на-
ходятся от средней плоскости на одина-
ковых расстояниях. Технические тре-
бования, предъявляемые к контрольным
роторам для станков с вертикальной
осью вращения, те же, что и для
контрольных роторов для станков с гори-
зонтальной осью. К контрольным роторам
прилагается набор контрольных грузов,
масса которых охватывает весь диапазон
показаний станка.
Тарировочный ротор используют для
настройки станка на балансировку ротора
определенной геометрии и массы. Его соби-
рают из тех же деталей и с учетом
тех же требований, что и серийный
ротор. Для каждого типа балансируемых
роторов изготавливают свой тарировочный
ротор. Такой ротор должен быть сбалан-
сирован по крайней мере на класс
точнее серийного ротора.
На каждый тип тарировочного и кон-
трольного ротора оформляют технологи-
ческий паспорт. В паспорте указывают все
технические данные ротора, фактические
значения остаточных дисбалансов и ре-
зультаты периодических проверок. Кон-
трольные и тарировочные роторы хранят
в вертикальном положении в специальной
таре, предотвращающей его от поврежде-
ний и загрязнений.
Глава 13
СПОСОБЫ КОРРЕКТИРОВКИ МАСС
13.1. ОБЩИЕ СВЕДЕНИЯ
Корректировкой масс называют про-
цесс изменения или перемещения коррек-
тирующих масс для уменьшения дисбалан-
сов ротора (рис. 13.1). Изменение кор-
ректирующих масс достигают добавлением
или уменьшением материала, а переме-
щение — изменением углового положения
или массы деталей ротора, перемещением
материала ротора, изменением положения
постоянных по значению специальных гру-
зов.
Возможности способов корректировки
масс характеризуются прежде всего при
пуском, точностью балансировки, проч
костью соединения корректирующей массы
с поверхностью ротора и производитель-
ностью. Под припуском понимают не толь-
ко слой материала^ снимаемый с поверх-
ности во время корректировки, но и то
количество массы, которое необходимо до-
бавить к массе детали (ротора), чтобы
сформировать плоскость коррекции, отве-
чающей конструктивно-технологическим
особенностям изделия Так, например, при
съеме металла по круговому кольцу при
максимально допустимой неуравновешен-
ной массе в 100 г на дуге 120° масса
этого кольца дожна быть 300 г. Величина
припуска зависит от точности изотовле-
ния деталей и достигает 0,4- 1% массы
ротора для различных отраслей машино-
строения. Меньшее значение относится к
изделиям точного машиностроения (гиро-
скопы, приводы и т.п.), а большое к из-
делиям низкоточного машиностроения
Общие сведения
375
Рис. 13.1. Способы корректировки масс
(части сельскохозяйственных машин, тех-
нологического оборудования и т. п.).
Под точностью способа корректировки
понимают степень соответствия ее дис-
балансу в плоскости коррекции. Так как
дисбаланс £)нач определяется неуравнове
шейной массой тк, радиусом коррекции
гк и углом ф, то, сопоставляя действи-
тельные параметры с расчетными,, полу-
чают точность способа по каждому пара-
метру (рис. 13.2). Совокупность результа-
тов сопоставления по трем параметрам
представляет собой точность способа кор-
ректировки масс ротора. В данном слу-
чае точность определения значения и угла
дисбаланса, а, если надо, то и точность
пересчета дисбалансов из плоскостей из-
мерения в плоскость коррекции, не учиты-
вается. Понятие о точности составляющих
параметров аналогичны основным поняти-
ям точности обработки деталей машин.
Точность способа считается удовлетвори-
тельной, если за один цикл корректи-
ровки масс на 95% снижается начальный
дисбаланс в плоскости коррекции.
Прочность соединения корректирую-
щей массы с поверхностью ротора зави-
сит от ее конструкции, вида поверхности
и метода соединения. Конструкция груза
и стопорение должны отвечать требо-
ваниям, предъявляемым роторам в экс-
плуатации. При установке корректирую-
щей массы на наружную, торцовую или
внутреннюю поверхность ротора соответ-
ственно возрастает прочность соединения.
Рис. 13.2. Схема коррек-
тировки масс
Она существенно зависит от метода сое-
динения и качества его выполнения. К ним
относятся: склепывание, сваривание, пая-
ние, склеивание, запрессовка, резьбовое
соединение. Прочность соединения при
наклеивании определяется физико-меха-
ническими свойствами материала ротора
и корректирующей массы.
Производительность способа коррек-
тировки зависит от производительности
корректирующего устройства, значения
начального и допустимого дисбалансов.
Способ корректировки масс определя-
ют на этапе проектирования изделия. Ис-
376
Способы корректировки масс
ходными данными для проектирования
служат:
расчетные значения максимальных на-
чальных дисбалансов деталей;
расчетные значения максимальных тех-
нологических дисбалансов узлов, ротора в
сборе;
число плоскостей коррекции, причем
в него входят все плоскости на деталях,
узлах, роторе;
допустимые дисбалансы в плоскостях
коррекции.
В результате проектировщик создает
конструкцию плоскости коррекции и уста-
навливает технические требования к кор-
ректировке масс. На последующих эта-
пах жизненного цикла изделия уточняют
возможности выбранного способа коррек-
тировки, определяют корректирующее уст-
ройство, разрабатывают технологический
процесс корректировки.
К средствам корректировки масс отно-
сят: металлорежущие станки-и инструмен-
ты, механизированный слесарно-сбороч-
ный инструмент, станочные и сборочные
приспособления. В зависимости от вида
обработки применяют токарные, сверлиль-
ные, шлифовальные станки, электрофизи-
ческие и электрохимические методы, а так-
же сверлильные машины, рубильные и кле-
пальные молотки и гайковерты. В оди-
ночном и мелкосерийном производстве ис-
пользуют ручной инструмент. Металлоре-
жущие станки, механизированный инстру-
мент оснащают соответствующим лезвий-
ным или абразивном инструментом. В про-
цессе выполнения операций корректировки
масс применяют станочные и сборочные
приспособления. Выбор рациональных ре-
жимов резания зависит от характера об-
работки, типа и размеров инструмента,
материала и используемого оборудования.
13.2. СПОСОБЫ КОРРЕКТИРОВКИ
ПЕРЕМЕЩЕНИЕМ МАСС
Корректировку масс перемещением
деталей или узлов осуществляют:
перестановкой деталей по окружности
в плоскости коррекции;
изменением взаимного углового поло-
жения узлов ротора.
Перестановка деталей. Этот способ
уменьшает дисбаланс за счет; разности
масс деталей, распологаемых в легком и
тяжелом месте плоскости коррекции. Мето-
дика перестановки деталей следующая.
Вычисляют корректирующую массу тк =
— £нач/Гк- Симметрично линии действия
начального дисбаланса на дуге окружнос-
ти в 30—60° снимают равное число
деталей п в легком и тяжелом месте.
Определяют действительную массу каждой
снятой детали и комплект деталей, сня-
тый в легком (л) и тяжелом (т) месте.
Вычисляют начальную разницу масс
комплектов
п Г- fl
Атнач= £ (т,)т- £ (т,)л.
i=i /=i
Если Атнач >0, то в легком комплекте
заменяют детали меньшей массы на де-
тали большей массы из тяжелого ком-
плекта так, чтобы разница масс комплек-
тов стала Ат = Атнач — тк. В противном
случае (Атнач <0) в легком комплекте
заменяют детали большей массы на де-
тали меньшей массы из тяжелого ком-
плекта, обеспечивая разницу масс ком-
плектов Ат = Аткач + тк.
В технических требованиях на кор-
ректировку масс перестановкой деталей
указывают: наименование, позицию черте-
жа, число и чертежный номер'детали;
последовательность и допустимое число
одновременно снимаемых деталей; допус-
тимость замены детали ротора на деталь
другой массы из запасного комплекта;
радиус коррекции. Для этих целей исполь-
зуются гайки, болты, шпильки, проставки,
шайбы, съемные лопасти и лопатки ра-
бочих колес. Рассматриваемый способ кор-
ректировки масс не требует припуска,
обеспечивает высокую прочность соедине-
ния. Низкая производительность и точ-
ность способа, обусловленные методом
подбора и малыми отклонениями масс
деталей от номинальных значений, огра-
ничивают его область применения предва-
рительными балансировочными операция-
ми: индивидуальной балансировкой уз-
Способы корректировки перемещением масс
377
лов, корректировкой масс в дополнитель-
ных плоскостях при больших начальных
дисбалансах.
Способ корректировки масс измене-
нием взаимного углового положения
деталей. Его применяют для уменьшения
начальных дисбалансов ротора дисковой
или барабанной конструкции, допускаю-
щей такие изменения. Первая конструкция
состоит из вала, на посадочные поверх-
ности которого насаживаются детали. Его
начальные дисбалансы будут равны сумме
независимых дисбалансов деталей, каж-
дый из которых есть сумма остаточного
и технологического дисбалансов. В рото-
рах барабанной конструкции детали цент-
рируются друг на друге, а цапфы явля-
ются элементами крайних деталей. В этом
случае дисбалансы деталей — зависимые
величины, т. е. дисбаланс каждой после-
дующей детали зависит от векторной
суммы эксцентриситетов предыдущих де-
талей, которые определяются накопленной
радиальной и торцовой погрешностями
изготовления стыков всех деталей ротора.
Методика выбора взаимного углового
положения деталей при сборке ротора
состоит в следующем. Определяют глав-
ный вектор и главный момент остаточ-
ных дисбалансов каждой детали отно-
сительно ее посадочных поверхностей.
Измеряют действительные значения и фа-
зы радиальных 6р и торцовых 6Т
биений посадочных поверхностей вала
относительно оси цапф и заданного
начала отсчета фаз. Вычисляют главный
вектор и главный момент начальных дис-
балансов ротора по формулам
п
^СТ у1, ^1 ( ^ОСТ» ’
i=l
п
~ + 6р1) + ,
где J — экваториальный момент инерции
детали; /? — радиус измерения торцового
биения; — расстояния от центра масс
t-го диска до центра масс ротора с
учетом его знака. Вычисления ведут по
прикладной программе до тех пор, пока
не получат допустимые дисбалансы ротора.
В простейшем случае на вал последо-
вательно устанавливают детали, выдержи-
вая направления дисбаланса каждой пос-
ледующей детали в противофазе отно-
сительно предыдущей. Методика сборки
ротора барабанной конструкции обеспечи-
вает как допустимые начальные дисбалан-
сы, так и допустимые биения контроль-
ных поверхностей ротора.
Методика корректировки масс измене-
нием взаимного углового положения дета-
лей при балансировке ротора составлена
в соответствии с правилами планируемого
эксперимента. При постоянном значении
технологического дисбаланса корректи-
ровку масс проводят методом амплитуд и
фаз. Определяют начальный дисбаланс
(Z)Ha,J в плоскости коррекции при произ-
вольном угловом положении детали в рото-
ре. Поворачивают одну или несколько де-
талей на угол 180° относительно перво-
начального положения и определяют дис-
баланс £>'ач графически или по прикладной
программе (см. прил. П.2). Кроме того,
вычисляют значения полуразности Д£>] ~
— 0,5 (£>нач — D'„24) и угол а также по-
лусуммы Д£>2 = 0,5(£>„ач 4- ^нач) И УГОЛ ф2
этих дисбалансов. Если |Д£>11<|Д£>2|,
то деталь устанавливают под углом
<р2 — 180°, в противном случае — под уг-
лом (pi — 180°.
Способ корректировки масс пере-
мещением материала ротора применяют
в точном приборостроении. На поверхности
ротора (обычно внутренней) размещают
специальные материалы или устройства.
Премещение этого материала осу-
ществляют электролитическим способом
(рис. 13.3, а), перемещением расплавлен-
ного материала гравитационными силами
(рис. 13.3, б) или объемным расширением
(рис. 13.3, в).
Способ корректировки масс переме-
щением балансировочных грузов обладает
высокой точностью и производитель-
ностью. Для реализации этого способа
необходимо иметь в плоскости коррекции
378
Способы корректировки масс
Рис. 13.3. Схемы уст-
ройств для корректировки
масс перемещением ма-
териала ротора:
а — электролитическим раст-
ворением, переносом и
осаждением: б - легкоплав-
кого материала силами гра-
витации; в — легкоплавкого
материала объемным рас-
ширением; 5| 2 — ЦМ до и
после балансировки
2тг* /Df/ay
Рис. 13.4. Номограмма для опре-
деления угла между баланси-
ровочными грузами
кольцевой паз и два постоянных и равных
по массе балансировочных груза, которые
можно перемещать по окружности ра-
диусом гк и стопорить в любом угловом
положении. Методика корректировки масс
проста: рассчитывают отношение начали
кого к допустимому начальному дисбалан-
су; по номограмме (рис. 13.4) находят угол
между балансировочными грузами. Уста-
навливают эти грузы симметрично относи-
тельно линии действия начального дис-
баланса (легкого места) и стопорят. До-
пустимый начальный дисбаланс ограничен
неравенством £>нач доп < 2/пкгк.
13.3. СПОСОБЫ КОРРЕКТИРОВКИ
С ДОБАВЛЕНИЕМ МАССЫ
Добавление материала, ротора при
корректировке масс осуществляют ба-
лансировочными грузами и наплавкой ма-
териала Способ корректировки масс ба-
лансировочными грузами имеет более вы-
сокую точность, чем при корректировке
перемещением массы, но ниже, чем при
корректировке уменьшением массы. Поэто-
му добавление массы рекомендуется для
роторов, точность балансировки которых
соответствует 3—5-му классам по ГОСТ
1Г 91 Возможности данного способа, в
основном, зависят от конструкции ба-
лансировочных грузов и плоскости кор-
рекции.
Балансировочные грузы выполняют в
виде распределенной или точечной массы
К первому виду относятся полосы (плас-
тины), прутки, сегменты; ко второму ви-
ду — болты, гайки, шайбы и др. крепеж-
ные детали, а также детали специаль-
ной формы, размеры которых пренебре-
жимо малы по сравнению с размерами
плоскости коррекции. Их устанавливают
на наружной, торцовой или внутренней
поверхности ротора. Балансировочные гру-
зы стопорят индивидуальными или груп-
повыми методами контровки. Примерами
индивидуальной контровки являются плас-
тинчатые замки (рис. 13.5, а и б),
контровочная проволока и упругие кольца
(рис. 13.5. д, ж, к), детали ротора
(рис. 13.5, в, е, з). Групповые методы кон-
тровки обеспечивают элементами ротора
(рис. 13.5, в, и, л), специальными контро-
вочными элементами (рис. 13.5, г, е).
В технических требованиях на кор-
ректировку масс балансировочными гру-
зами указывают: наименование, позицию и
номер чертежа балансировочных грузов;
Способы корректировки с добавлением массы 379
380
Способы корректировки масс
допустимое число и места установки
балансировочных грузов; требования к
стопорению грузов. Для кольцевых грузов
дополнительно указывают размеры заго-
товки и допустимые размеры баланси-
ровочного груза.
При корректировке масс ротора вы-
числяют значение неуравновешенной мас-
сы, ее размеры, число и угловое поло-
жение балансировочных грузов. Распреде-
ленные массы устанавливают в плоскости
коррекции на наружную, внутреннюю или
торцовую поверхность по дуге окружности
(рис. 13.6, tz) или вдоль оси ротора
(рис. 13.6, б). Исходные данные для расче-
та: R — радиус окружности, мм; h — тол-
щина полосы, мм; Ь — ширина полосы, мм;
р — плотность материала, г/мм3; I — до-
пустимая длина балансировочного груза,
мм; £)нач, <рнач - значение и угол началь-
ного дисбаланса в плоскости коррекции.
Размер корректирующей массы (в данном
случае только ее длина) вычисляют по
формуле
/=2 • 103£>нач/(2/? + h)phb.
Если />/доп, то нужно изменить раз-
меры полосы или изготовить две массы.
При необходимости следует учесть массу
материала (деталей), соединяющих кор-
ректирующую массу с ротором.
Точечные массы устанавливают в про-
извольной (рис. 13,7, а) или определенных
(рис. 13.7, б, в) местах плоскости кор-
рекции. Исходные данные для расчета:
R- радиус окружности, мм; mt(i =
= 1,2,...,/) — масса t-ro балансировоч-
ного груза в наборе (здесь / — число
грузов в наборе); тДО11 — допустимая мас-
са балансировочных грузов; h'nou — до-
пустимое число балансировочных грузов;
1,2,.. . , п — число мест установки балан-
сировочных грузов; £>на11, <риач — значение и
угол начального дисбаланса в плоскости
коррекции.
Массу одного балансировочного груза,
устанавливаемого в произвольном месте
плоскости, вычисляют по формуле =
= D"S4/R, а число балансировочных гру-
зов определяют с помощью выражения
Рис. 13.7. Схема установки точечной массы:
а—в произвольном месте, б— в двух опреде-
ленных местах, в — во многих определенных
местах, /- балансировочные грузы. 2—места
установки грузов
Л' = (£)нач — moR)/(mR), где то — масса
крепеж.ных деталей; т — масса одного ба-
лансировочного груза в наборе. При
установке балансировочных грузов в два
определенных места плоскости коррекции
их массы вычисляют по прикладной прог-
рамме.
Способ корректировки наплавкой мас-
сы применяют при балансировке роторов
из неметаллических или композитных ма-
териалов, а также в ряде других обосно-
ванных случаях.
Точности и производительность этого
способа низки, так как трудно придать
определенную форму расплавленному ма-
териалу. Прочность соединения при разно-
родных материалах также невелика. При
использовании данного способа корректи-
ровки масс конструкция ротора должна
обеспечивать наплавку материала на его
внутреннюю поверхность.
Корректировка масс механической обработкой
381
13.4 КОРРЕКТИРОВКА МАСС
МЕХАНИЧЕСКОЙ ОБРАБОТКОЙ
Корректировка масс механической об-
работкой рекомендуется для роторов, точ-
ность балансировки которых соответствует
2- -4-му классам точности по ГОСТ [Г9].
При этом съем материала выполняют лез-
вийным или абразивным инструментом по
различным поверхностям ротора: ци-
линдрической. сферической, конической,
тороидальной и т. п. Данный способ кор-
ректировки масс требует большого при-
пуска в плоскости коррекции, но обеспе-
чивает высокую точность и производи-
тельность корректировки масс, максималь-
ную прочность соединения корректирую-
щей массы с поверхностью ротора, так
как они образуют единое целое. Плос-
кости коррекции представляют собой либо
поверхность ротора, либо дополнительную
поверхность (выступ, прилив), в которой
производят съем распределенной или дис-
кретной массы.
Съем материала по окружности
(рис. 13.8) производят точением на стан-
ках токарного типа. В технических тре-
бованиях на корректировку масс ука-
зывают: начальным радиус (или диаметр)
окружности; допустимое радиальное е,
а при необходимости и торцовое биение
поверхности относительно установочных
баз ротора на токарном станке; допусти-
мую ширину b и глубину резания или
допустимый остаточный радиус /?ост (диа-
метр) окружности; класс шероховатости’
поверхности после корректировки масс.
Исходными данными для расчета парамет-
ров резания являются: значение и угол
начального дисбаланса; действительные
размеры поверхности (начальный радиус
или диаметр окружности), значение и угол
радиального биения; плотность материала,
ширина резания По прикладной програм-
ме вычисляют значение и угол биения
поверхности относительно установочных
баз, остаточный радиус (диаметр) окруж-
ности. Если результаты расчета превыша-
ют допустимые значения, то увеличивают
ширину резания и повторяют расчет. По
расчетным данным выставляют деталь на
токарном.станке и обтачивают поверхность
до расчетного диаметра.
Невысокая точность измерения биений
поверхности и ориентированной установки
детали на токарном станке снижает точ-
ность корректировки масс, поэтому данный
способ рекомендуется для предваритель-
ных балансировочных операций.
Съем материала по сегменту
(рис. 13.9) производят на фрезерных,
шлифовальных, строгальных и протяжных
станках, а также ручным инструментом.
В технических требованиях на корректи-
ровку масс указывают: допустимую глуби-
ну h и ширину b резания; классы шеро-
ховатости поверхностей после корректи-
ровки масс; диаметр (радиус /?) окруж
ности. Исходными данными для расчета
глубины (ширины) резания являются:
значение и угол начального дисбаланса;
действительный радиус окружности, шири-
на (глубина) резания; плотность материа-
ла. По номограмме (рис. 13.10) нахо-
дят высоту сегмента, т. е. Глубину резания.
Производят разметку и обработку поверх-
ности на соответствующем станке или
вручную.
Рис. 13.8. Съем материала по окруж-
ности
Рис. 13.9. Съем
материала по сегменту
382
Способы корректировки масс
Рис. 13.10. Номограмма для определения
размеров сегмента при корректировке масс
Рис. 13.11. Съем материала по дуге
окружности:
/ — место съема материала, 2 ротор
Достаточная точность измерения дей-
ствительных размере^, простота геометри-
ческой фигуры (сегмента), малое число
исходных данных для расчета, возмож-
ность тарированного съема материала на
станке или вручную позволяют применять
этот способ для окончательных балансиро-
вочных операций.
Съем материала по дуге окружности
(рис. 13.11) производят на фрезерных
и шлифовальных станках, а также руч-
ным инструментом. В технических тре-
бованиях на корректировку масс указы-
вают: диаметр (радиус) окружности; до-
пустимую глубину и ширину резания;
допустимую длину дуги окружности или
центральный угол; классы шероховатости
поверхностей после корректировки масс.
Исходными данными для расчета цент-
рального угла 2<р являются: значение и
угол начального дисбаланса; действи-
тельный диаметр окружности; глубина и
ширина резания; плотность материала. По
номограмме (рис. 13.12) находят цент-
ральный угол 2<р, полностью определя-
ющий корректирующую массу при задан--
ных параметрах резания. Данный способ
применяют для окончательных балансиро-
вочных операций.
Съем материала сверлением отверстий
(рис. 13.13, 13.14) производят на сверлиль-
ных станках или ручными сверлильными
машинками, В технических требованиях на
корректировку масс указывают: диаметр
(радиус) окружности; допустимые диа-
метры отверстий; допустимое число и рас-
стояние между отверстиями; класс шеро-
ховатости поверхности после корректиров-
Рис. 13.12. Номограмма для определения дуги
окружности при корректировке масс
Рис. 13.13. Съем материала сверлением
осевых отверстий
Рис. 13.14. Съем материала сверлением
радиальных отверстий
Корректировка масс электрообработкой
383
ки масс. Исходными данными для расчета
являются: значение и угол начального
дисбаланса; действительный диаметр ок-
ружности (радиус); принятый диаметр и
угол в плане сверла; плотность матери-
ала. Число осевых отверстий находят по
формуле
* = 4£>нач/лс?2р/? (haon - 0,19d),
округляя N в большую сторону до це-
лого числа; глубину сверления определя-
ют пи формуле
h = 0,19d J- 4£>Ha4/nd2p/?A?.
Число и глубину сверления радиальных
отверстий находят, задаваясь диаметром
отверстий с помощью номограммы
(рис. 13.15), где mh =» nd2p/?/40. Если
^начЛЯ^й) < 5, то достаточно одного от
верстия, в противном случае числа отвер-
стий находят по формуле N = £>нач/
(5/?/п*), округляя его в большую сторону до
целого числа, а глубину сверления вновь
определяют по номограмме. Сверление
отверстий — широко распространенный
способ корректировки масс при предвари-
тельных и окончательных операциях на
универсальных и автоматических балан
сировочных станках.
Съем материала обработкой пазов
производят на фрезерных станках или
вручную рубкой и опиливанием. В техни-
ческих требованиях на корректировку масс
указывают: диаметр (радиус) окружности;
Рис. 13.15. Номограмма для определения
параметров радиального отверстия
допустимые размеры пазов; допустимое
число и расстояние между пазами;
класс шероховатости поверхностей после
корректировки масс. Исходные данные
для расчета и расчетные зависимости ана-
логичны тем, которые используют при
съеме материала сверлением осевых или
радиальных отверстий.
13.5. КОРРЕКТИРОВКА МАСС
ЭЛЕКТРООБРАБОТКОЙ
Корректировку масс электрообработ-
кой осуществляют: 1) электроэрозионным,
2) электронно-лучевым, 3) электрохими-
ческим способами и 4) с помощью взрыва-
ющихся проволочек. Способы 1—3
уменьшают, а способ 4 увеличивает массу
ротора, первые — требуют значительно-
го припуска на корректировку масс.
Они обладают высокой точностью, про-
изводительностью, прочностью соедине-
ния, позволяют полностью автоматизи-
ровать процесс балансировки. В то же
время их можно применять при балан-
сировке роторов из различных материалов,
на универсальных станках. К недостаткам
способов корректировки масс электро-
обработкой относятся сложность корректи-
рующих устройств и относительно невы-
сокий класс шероховатости поверхности
после обработки. Корректировка масс
электрообработкой рекомендуется для ро-
торов малой массы, точность балансировки
которых соответствует 1 -3-му классам по
ГОСТ [Г 10).
Электроэрозионный способ основан на
эрозии металла с поверхности баланси-
руемого ротора в искровом разряде, об-
разующемся между ним и электродом.
Основные характеристики способа: масса
балансируемых роторов 60 -400 г; диаметр
20—50 мм; производительность съема ме-
талла 20 мг/мин; остаточный удельный
дисбаланс 1-5 мкм; напряжение на
электродах 300 В.
Электронно-лучевой способ состоит в
испарении материала электронным пучком
в глубоком вакууме. Основные характерис-
384
Балансировка типовых изделий машине- и приборостроения
тики способа; масса балансируемых рото-
ров 20—50 г; диаметр 15-20 мм;
порог чувствительности способа (мини-
мальная масса, снимаемая при обработке)
0,2 мг; остаточный удельный дисбаланс
0,01 мкм; анодное напряжение до 100 кВ.
Электрохимический способ основан на
анодном растворении металла в тяжелом
месте ротора. Его основные характеристи-
ки: масса балансируемого ротора
0.5—40 кг; производительность обработки
от 0,5 до 15 г/мин при плотности тока
от 100 до 500 А/мин; остаточный удель-
ный дисбаланс 1—2 мкм.
Лазерный способ основан на расплав-
лении и испарении любого материала
мощным световым лучом лазера. При энер-
гии излучения лазера 10—100 Дж
достигают высокой точности балансировки
(0,02—0,5 мкм) роторов массой от 10 до
50 г.
Способ корректировки масс с помощью
взрывающихся проволочек состоит в напы-
лении металла в легкое место ротора.
В магнитной системе корректирующего
устройства происходит микровзрыв прово-
лочки при воздействии на нее высокого
напряжения. Проволочка мгновенно рас-
плавляется, а магнитное поле с боль-
шой скоростью выбрасывает расплавлен-
ный металл в сторону ротора. Основ-
ные характеристики способа: масса балан-
сируемых роторов 0,03—10 кг; остаточный
удельный дисбаланс 0,03—20 мкм; порог
чувствительности способа 0,01—I мг;
производительность корректировки масс
до 1 г/мин; диаметр проволочки 0,1—
0,3 мм.
Глава 14
балансировка типовых изделии маш ин о-
и приборостроения
14.1. ТИПОВЫЕ ТЕХНОЛОГИЧЕСКИЕ
ПРОЦЕССЫ БАЛАНСИРОВКИ
Типизация технологических процессов
базируется на классификации по различ-
ным признакам объектов производства:
конструкции, классу точности, типу обо-
рудования. виду производства и т. п.
Наиболее общими процессами баланси-
ровки являются: статическая при помощи
сил тяжести, в динамическом режиме;
низкочастотная в одной или в двух
плоскостях коррекции; статйко-момент-
ная; многоплоскостная; высокочастотная.
Типовой технологический маршрут балан-
сировки партии роторов состоит из следую-
щих операций:
Номер операции Наименование операции
05 Подготовка балан-
сировочного станка
10 Входной контроль
ротора
15 Подготовка балан-
сируемого узла
20 Определение значе-
ния и углов дисба-
лансов в плоскости
измерения
25 Р а с.ч е т к о р р е к т и-
р у ю щ и х масс
30 Корректировка масс
ротора
35 Контроль рстаточ
и ы х дисбалансов
Кроме того и операций по настройке
(наладке) станка на балансировку партии
роторов определенной массы и геометрии:
подготовки тарировочного ротора, подго-
товки балансировочного станка, контроля
остаточных дисбалансов тарировочного
ротора, разделения плоскостей коррекции
и тарирования станка.
Настройка балансировочного станка.
Подготовка тарировочного ротора заклю-
чается во входном контроле деталей и его
г
^Типовые технологические процессы балансировки
385
СбОрки, измерении массы, положения цент-
ра масс, геометрических размеров и дру-
гих параметров, необходимых для настрой-
ки станка. Подготовка балансировочного
станка к настройке состоит в механичес-
кой регулировке привода, установке при-
способлений, элементов крепления, провер-
ке функционирования устройств и их тех-
ническом обслуживании, предварительной
настройке измерительного устройства.
Контроль остаточных дисбалансов тари-
ровочного ротора проводится способом
кругового обхода. Их значения должны
быть в 2,5 раза меньше допустимых
дисбалансов ротора, заданных технически-
ми требованиями. В противном случае
тарировочный ротор добалансируют. Раз-
деление плоскостей коррекции зависит от
типа требуемой точности метода баланси-
ровки. Плоскости коррекции на зарезо-
нансном станке разделяют двумя спо-
собами.
Первый способ. В 1-й плоскости
тарировочного ротора на радиусе п
(рис. 14.1. а) прикрепляют точечную не-
уравновешенную массу mlt создающую до-
пустимый начальный дисбаланс. Настраи-
вают частотно-избирательные фильтры из-
мерительного устройства (пульта станка)
на частоту вращения ротора. Переклю-
чатель, указывающий плоскость измере-
ния, переводят в положение измерения по-
казаний индикатора дисбалансов 2-й плос-
кости и записывают их (Л2иач). Вращая
ручку настройки, находят такое ее поло-
жение (не крайнее), при котором наблю-
даются минимальные показания индикато-
ра (Л2т|П). Снимают неуравновешенную
массу mi и во 2-й плоскости на радиусе
г2 прикрепляют массу m2, создающую до-
пустимый начальный дисбаланс в этой
плоскости. Переключатель, указывающий
плоскость измерения, переводят в 1-ю
плоскость. Вновь определяют начальные
иач) и минимальные (Л( min) показания
индикатора дисбалансов, так же как для
2-й плоскости.
Для повышения точности разделения
плоскостей коррекции в двухканальных из-
мерительных устройствах регулируют фа-
13 Зак 1641
Рис. 14.1. Расположение точечных неурав-
новешенных масс на межопорном роторе при
разделении плоскостей коррекция зарезонанс-
ного балансировочного станка
зы датчиков таким же образом. Операцию
повторяют несколько раз для различных
значений mj и т2, если процесс
балансировки будет происходить за не-
сколько циклов. Рассчитывают коэффици-
енты уменьшения взаимного влияния плос-
костей коррекции по формулам
Ал2 нач/^1 min» ^21 -^2 нач/^2 mirr
Значения и /С21 считаются прием-
лемыми для роторов простой формы,
если они более 15—20, для роторов
сложной формы — более 7—10.
Второй способ. В двух плоскос-
тях тарироврчного ротора прикрепляют
точечные неуравновешенные массы т\ и т2
на радиусах г,, г2 (рис. 14.1,6), создаю-
щие неуравновешенность
Мр нач = т1г>А +
386
Балансировка типовых изделий машине- и приборостроения
Переключатель плоскостей измерения
последовательно переводят из одного по-
ложения в другое и записывают по-
казания индикатора дисбаланса станка
для каждого положения. По показаниям
в этих плоскостях выбирают плоскости
измерения главного вектора и главного
момента дисбалансов. Переводят переклю-
чатель плоскостей на плоскость измерения
главного вектора дисбалансов, например
1-ю, и, вращая ручку настройки данной
плоскости, уменьшают влияние главного
момента на показания по 1-й плоскости.
Для исключения влияния главного
вектора на показания по плоскости глав-
ного момента дисбалансов (в нашем при-
мере 2-я плоскость) на тарировочном ро-
торе создают статическую неуравновешен-
ность:
на межопорном роторе — одной точеч-
ной массой mcr на радиусе гст в плос-
кости, проходящей через его центр масс;
на консольном роторе — двумя точеч-
ными антнпараллельными массами mt и т?
на радиусах rt и г2 в двух плос-
костях (рис. 14.2,0!), значения которых
рассчитывают по формулам
nil = ^стиачМЦА +
m2 — Dn мч1\/ [ (/2 -I- Л) г2];
на двухконсольном роторе — двумя то-
чечными массами тщ и т2 на радиу-
сах и и г2 в двух плоскостях парал-
лельно друг другу (рис. 14.2,6), значения
которых рассчитывают по формулам
— Д€Т на-А/ 1 (Л -4" ^)г11 ,
— DCT KSJ-i/1 (А “I- Л?)г2J.
Действия балансировщика при исклю
ченим влияния главного вектора анало-
гичны рассмотренным выше.
При статической балансировке в дина-
мическом режиме достаточно выполнить
первую часть операции исключить вли-
яние главного момента на показания
индикатора дисбаланса в плоскости изме-
рения главного вектора дисбалансов рото-
ра.
Рис. 14.2. Расположение точечных неуравно-
вешенных масс при разделении плоскостей
коррекции зарезонансного балансировочного
станка по второму способу
На дорезонансных станках предусмот-
рено разделение плоскостей коррекции
для двухплоскостной и раздельной стати-
ко-моментной балансировки. Разделение
плоскостей в цепи, выполненной во схеме
abc, проводится по геометрическим разме-
рам ротора (рис. 14.3) без его вращения.
Двухплоскостная балансировка. Кног
почный переключатель ставят в положе-
ние на двухплоскостную балансировку.
Нажимают кнопки, указывающие место-
нахождение плоскостей коррекции в за-
висимости от типа ротора:
для меж опорного — от опор к плос-
костям, т. е. к середине ротора;
для консольного - от опор в направле-
нии к консольной части нажимают обе
левые или обе правые кнопки переклю-
чателя;
для двухконсольного — от середины к
консолям (нажимают левую и правую
Типовые технологические процессы балансировки
387
Рис. 14.3. Геометрические размеры ротора,
необходимые для настройки пульта дорезо-
нансного балансировочного станка
кнопки переключателей) Ручками потен-
циометров набирают числовые значения
радиусов коррекции п и г 2, расстояние
между плоскостями Ь и от опор до
плоскостей а и с. Числа a,b,c должны
быть выражены в мм, см или м. Уста-
навливают переключатель диапазонов час-
тот вращения в положение, соответству-
ющее частоте вращения балансируемого
ротора.
Статико-моментная балансировка. На-
жимают-кнопку, указывающую на стати-
ко-моментную балансировку. В зависи-
мости от типа ротора кнопки местона-
хождения плоскостей коррекции ставят
в следующее положение:
для меж опорного или двухконсольного
ротора—от опор к середине;
для контрольного ротора — от опор в
направлении консольной части. Если плос-
кость измерения моментной неуравнове-
шенности совпадает с плоскостью опоры,
то кнопки соответствующего переключа-
теля не нажимают.
Ручкой потенциометра г\ набирают
число, равное радиусу коррекции глав-
ного вектора дисбалансов Потенциомет-
рами а и с набирают числа, равные рас-
стояниям от плоскости коррекции DCT
до опор ротора, причем сумма чисел а + с
равна расстоянию между опорами. Если
плоскость расположена на консоли, то
а — с равно расстоянию между опорами.
Первый индикатор будет показывать зна-
чение mt и угол корректирующей массы
13*
<рст по главному вектору. На потенцио-
метре b набирают число, равное рас-
стоянию между плоскостями коррекции
главного момента дисбалансов, а на г2 —
радиус коррекции. Втброй индикатор будет
указывать значение т2 и угол корректи-
рующей массы ф2 по главному моменту
только для одной плоскости. Чтобы найти
«з во второй плоскости на радиусе Гз,
нужно выполнить расчет:
т3 — m2r2/r3,
<рз = <рг -4- 180°.
Для измерения главного момента дис-
балансов на потенциометрах г2 и b
набирают фиктивные числа, чаще г2 = Ь —
— 100 мм, тогда
МD = показания индикатора X цена
делениях 10000 (г-мм2).
Тарирование балансировочного стан-
ка. При тарировании зарезонансного стан-
ка проводят регулировку индикатора угла
дисбаланса и определяют:
порог чувствительности по значению и
углу дисбаланса;
цену деления индикаторов дисбаланса;
линейность шкалы индикатора;
диапазон показаний станка.
Регулировку индикатора угла дисба-
ланса выполняют на станках, в измери-
тельном устройстве которых имеется фазо-
вращатель. В плоскости коррекции тари-
ровочного ротора прикрепляют максималь-
но допустимую точечную неуравновешен1
ную массу против нулевой отметки,
нанесенной на роторе. Включают привод
станка и на постоянной частоте враще-
ния ротора находят цифры меток, совпа-
дающие с индикатором угла дисбаланса.
Поворачивая ручку фазовращателя, при-
водят его к нулевой отметке. При опре-
делении угла дисбаланса с помощью
вращающейся шкалы находят деления
подвижной шкалы и после остановки ро-
тора поворачивают внешнюю шкалу (не-
подвижную) до совмещения с подвижной
шкалой.
В измерительных устройствах с гене-
ратором опорного сигнала опорные точки
смещены на 90°. Соответствие между
388
Балансировка типовых изделий машино- и приборостроения
фазами опорных токов и определенным
угловым положением на роторе при не-
обходимости может быть восстановлено
поворотом статора генератора. В плос-
кости коррекции тарировочного ротора
прикрепляют точечную неуравновешенную
массу в угловом положении 0°. Вклю-
чают привод станка и находят угол дис-
баланса. Если он не равен 0°, то
отпускают винты зажимного кольца, пово-
рачивают статор генератора на этот
угол и снова зажимают винты. Точность
регулировки индикатора дисбаланса про-
веряют перестановкой массы на 90°.
Для определения порога чувствитель-
ности станка по значению дисбаланса
в плоскости коррекции в тяжелом месте
на радиусе гк прикрепляют такую точеч-
ную неуравновешенную массу тмин, кото-
рая при вращении ротора вызывает наи-
меньшее изменение показаний индикатора
дисбаланса. Эту массу подбирают при
нескольких пробных пусках ротора. За
наименьшее изменение показаний индика-
тора дисбаланса принимают одно деление
шкалы. Порог чувствительности по дис-
балансу рассчитывают по формуле ДД =
“ ^мин^к-
Порог чувствительности станка по уг-
лу дисбаланса находят с помощью такой
точечной неуравновешенной массы, кото-
рая вызывает устойчивые показания инди-
катора угла. В тяжелом месте в плос-
кости коррекции прикрепляют на радиусе
гк массу т, включают привод станка
и фиксируют показания индикатора угла.
Последовательно перемещают массу т по
окружности радиусом гк и находят такое
ее положение, при котором наблюдаются
минимальные изменения угла дисбалан-
са Д^.
Цену деления индикатора дисбаланса
определяют как отношение изменения из-
меряемого значения дисбалансов к изме-
нению показаний индикатора. Обратную
величину цены деления называют чувстви-
тельностью по дисбалансу. В тяжелом
месте плоскости коррекции на радиусе
гк прикрепляют точечную неуравновешен-
ную массу т, вызывающую допустимый
начальный дисбаланс ротора в данной
плоскости коррекции. Включают привод
станка и фиксируют показания индикатора
дисбаланса. Подсчитывают изменение зна-
чения дисбаланса как -разность между
допустимым начальным и остаточным дис-
балансами и изменение показаний инди-
катора при остаточном и допустимом на-
чальном дисбалансах.
Цена деления =
изменение значения дисбаланса
изменение показаний индикатора
Диапазоном показаний станка называ-
ют наибольший и наименьший дисбалансы,
измеряемые станком в заданных условиях.
Наибольший дисбаланс определяют по
предельному отклонению показаний инди-
катора дисбаланса. Наименьший дисба-
ланс соответствует минимально достижи-
мому остаточному дисбалансу.
Линейность шкалы индикатора дисба-
ланса находят опытным путем. В тяже-
лом месте в плоскости коррекции после-
довательно прикрепляют 5—7 различных
точечных неуравновешенных масс и фикси-
руют показания индикатора дисбаланса
при вращении ротора. Дисбалансы, соз-
даваемые этими массами, должны охваты-
вать весь диапазон показаний станка.
Рассчитывают цену деления индикатора
для каждой неуравновешенной массы;
ДьДг,...,Цп и среднюю цену деления
в диапазоне показаний по формуле
п
(=1
Находят отклонение от среднего значе-
ния в процентах для каждой неуравно-
вешенной массы:
Если отклонение от среднего зна-
чения во всех точках не превышает
5%, то шкалу индикатора дисбаланса
считают линейной. В противном случае
диапазон показаний станка делят на
Типовые технологические процессы балансировки
389
поддиапазоны, где сохраняется линейность
шкалы.
Тарирование станка при статико-мо-
ментной балансировке проводят по главно-
му вектору и главному моменту дис-
балансов. В плоскостях коррекции или
измерения прикрепляют точечные неурав-
новешенные массы, создающие соответст-
венно статическую и моментную неуравно-
вешенность. Значения неуравновешенных
масс рассчитывают по тем же формулам,
что и при разделении плоскостей кор-
рекции. Сам процесс тарирования станка
аналогичен рассмотренному выше.
Тарирование балансировочного станка
выполняют для каждой плоскости кор-
рекции. Полученные результаты заносят в
карту настройки балансировочного станка.
Тарирование дорезонансного баланси-
ровочного станка состоит в выборе цены
деления индикатора дисбаланса. В станках
данного типа цену деления индикатора
указывает переключатель диапазонов час-
тот вращения. Однако она может быть
неудобной для балансировки ротора дан-
ной массы и геометрии. Поэтому на пульте
измерительного устройства имеется пере-
ключатель чувствительности.
В плоскости коррекции тарировочного
ротора в тяжелом месте прикрепляют на
радиусе г точечную неуравновешенную
массу т, создающую допустимый на-
чальный дисбаланс. Включают привод
станка и фиксируют показания индика-
тора дисбаланса. Переключатель чувстви-
тельности устанавливают в необходимое
положение, дающее наибольшее численное
значение показаний в пределах шкалы.
, При балансировке на низкой часто-
те вращения легких роторов чувствитель-
ность станка может быть недостаточной
для осуществления высокоточной балан-
сировки. Для повышения чувствитель-
ности станка действительные радиусы кор-
рекции заменяют фиктивными, уменьшен-
ными в произвольно выбранном масшта-
бе. Цена деления снижается пропорцио-
нально уменьшению радиусов коррекции.
Новая цена деления = цена деления X
фиктивный радиус коррекции
действительный радиус коррекции
Контроль качества настройки дорезо-
нансного балансировочного станка прово-
дят с помощью тарировочного ротора.
В плоскости коррекции в тяжелом месте
прикрепляют точечную неуравновешенную
массу. Включают привод станка и фикси-
руют показания индикатора дисбаланса.
Сравнение показаний индикатора с учетом
цены деления и внесенной массы с уче-
том остаточного дисбаланса в данной
плоскости показывает качество настройки.
В процессе настройки станка находят
продолжительность измерительного цикла,
который включает в себя: настройку
балансировочного станка; подготовку ро-
тора к балансировке; разгон; считывание
показаний; торможение; преобразование
показаний балансировочного станка к ви-
ду, удобному для уменьшения дисбалансов
и др.
Для исключения субъективных ошибок
настройку станка выполняют несколько
раз.
Технологический процесс статической
балансировки диска на станке СБС-4.
Технические требования. Диск (рис. 14.4)
необходимо балансировать статически от-
носительно базы А. Допустимое значение
главного вектора остаточных дисбалансов
£)ст (г • мм); значение главного вектора на-
чальных дисбалансов Ма (г*мм2). Кор-
ректировку масс выполнять в плоскости
17 сверлением осевых отверстий диамет-
ром не более d (мм), глубиной до h (мм),
на радиусе /? (мм). Допускается сверление
ие более N отверстий.
Содержание операций. Опера-
ция 05. Произвести внешний осмотр
балансировочного станка. Протереть рабо-
чие поверхности опор станка хлопчато-
бумажной салфеткой, смоченной обезжи-
ривающей жидкостью. Установить кон-
трольный ротор на опоры станка. Ротор
должен сохранять состояние безразлично-
го равновесия. В противном случае от-
регулировать станок. Ввернуть контроль-
390
Балансировка типовых изделий машина- и приборостроения
Рис. 14.4. Диск
ный груз в одно из отверстий кон
трольного ротора до упора. Повернуть
контрольный ротор с контрольным грузом
в горизонтальное положение и освободить
его. Освобожденный ротор должен выйти
из равновесия, повернуться вокруг оси.
В противном случае проверить порог
чувствительности станка согласно техноло-
гической инструкции на статическую ба-
лансировку диска.
Операция 10. Проверить комплек-
тность и правильность оформления сопро-
водительной документации чна диск. Про-
извести внешний осмотр диска. Корро-
зия, забоины, вмятины и другие повреж-
дения на поверхностях детали не допуска-
ются. Измерить диаметр отверстия А.
Операция 15. Установить диск
диаметром А на балансировочную оправ-
ку, предварительно смазав ее посадочную
поверхность жидким маслом. Завернуть
гайку от руки до упора. Затянуть гай-
ку динамометрическим ключом, обеспе-
чив момент затяжки Л1(Н - м).
Операция 20. Установить диск с
оправкой (сборочную единицу) на опоры
станка. Определить тяжелое место диска
и отметить его нанесением риски каранда-
шом. Уменьшить начальный дисбаланс,
прикрепляя в противоположном месте
(легком месте) на радиусе R в плоскости
П восковые грузы. Подобрать массу груза
такой, чтобы диск не проворачивался
(находился в равновесии), когда тяжелое
место расположено в горизонтальной плос-
кости. Снять воск с диска. Взвесить груз
и записать его массу в рабочий блок-
нот. Определить значение главного вектора
начальных дисбалансов диска по формуле
£>ст — mR
и записать в технологический паспорт
балансировки.
Операция 25. Определить число от-
верстий, диаметр и глубину сверления по
номограмме, приведенной на карте эскизов
к операции. Записать параметры сверле-
ния в рабочий блокнот.
Операция 30. Установить и закре-
пить диск с оправкой в приспособление.
Закрыть цапфы оправки защитными чех-
лами. Совместить кондукторную втулку
с риской на диске, указывающей тяжелое
место. Установить и закрепить на столе
сверлильного станка приспособление с дис-
ком. Настроить сверлильный станок. Про-
сверлить рассчитанное число отверстий на
заданную глубину. Глубину сверления кон-
тролировать по шкале лимба и нониуса
станка. Снять приспособление со стола
сверлильного станка, очистить от стружки,
вынуть диск с оправкой, снять защитные
чехлы.
Операция 35. Установить диск с
оправкой на опоры станка и повторить
выполнение переходов операции 20.
Технологический процесс динамичес-
кой балансировки ротора и а дорезо-
нансном станке с осевым приводом. Тех-
нические требования. Ротор (рис. 14.5)
необходимо балансировать динамически
в двух плоскостях коррекции относительно
поверхностей А и Б на частоте вращения
я (с~1). Допустимый дисбаланс в плоскос-
тях коррекции не более /Д д0!1 и Д2доп.
Корректировку масс выполнять установкой
балансировочных грузов в кольцевые пазы
плоскостей коррекции I и //. Крайние
балансировочные грузы закрепить.
Содержание операций. Опера-
ция 05. Проверить внешним осмотром
Типовые технологические процессы балансировки
391
отсутствие механических повреждений ста-
нины, балансировочного устройства, пуль-
та управления и электрокабелей станка.
Проверить легкость вращения роликов
роликовых опор. Протереть их поверхность
хлопчатобумажной салфеткой и смазать
2—3-мя каплями жидкого масла. Прове-
рить положение органов управления изме-
рительным пультом станка по карте на-
стройки. На диске приводного угломера
установить заданный шарнир (приводной
вал). Включить питание пульта станка.
Отрегулировать яркость световых точек
векторметров.
Операция 10. Проверить комплект-
ность и правильность оформления сопро-
водительной документации на балансируе-
мый ротор. Произвести внешний осмотр
ротора. Коррозия, забоины, вмятины и дру-
гие механические повреждения цапф и
поверхностей ротора не допускаются.
Операция 15. Установить на
ротор переходную втулку, соединяю-
щую приводной вал с балансируе-
мым ротором. Закрепить на роторе
приспособление для подъема. Проте-
реть цапфы хлопчатобумажной сал-
феткой.
Операция 20. Снять ротор с
транспортной тележки и плавно опус-
тить цапфами на ролики станка. Снять
с ротора приспособление для подъема.
Опустить зажимные ролики роликовой
опоры. Между зажимным роликом и
цапфой должен быть зазор до I мм.
Закрепить шарнир приводного вала в
переходной втулке винтом. Проверить
надежность крепления защитного
кольца приводного вала. Провести
два-три кратковременных пуска рото-
ра. Убедиться в надежности крепления
вращающихся частей и правильности
установки балансируемого ротора.
Включить привод станка. Выждать не-
обходимое время (1—2 мин) для дости-
жения постоянной частоты вращения
балансируемого ротора и включить
индикаторы дисбалансов нажатием
клавиши, фиксирующей показания.
Выключить привод станка. Занести по-
казания векторметров в рабочий блок-
нот и в технологический паспорт балан-
сировки ротора.
Операция 25. Рассчитать число
балансировочных грузов. Максимальное
число балансировочных грузов не
должно превышать N шт.
Операция 30. Набрать рассчи-
танное число балансировочных грузов
для 7-й и П-н плоскостей коррекции.
Установить в пазу Z-й плоскости кор-
рекции под углом, соответствующим
углам, полученным в операции 20,
рассчитанное число балансировочных
грузов. Закрепить балансировочные
грузы стопорными винтами. Грузы
располагать симметрично отно-
сительно линии действия дисбаланса.
Повторить то же для /7-й плоскости
коррекции.
Операция 35. Повторить пере-
ходы операции 20. Если остаточные
дисбалансы в плоскостях коррекции
7 и И меньше допустимых дисбалансов,
то балансировка выполнена полностью. В
противном случае повторить операции 25
и 30. Значение остаточных дисбалансов в
плоскостях коррекции занести в техно-
логический паспорт балансировки.
Технологический процесс стати ко-мо~
ментной балансировки ротора на заре-
зонансном станке с ленточным приводом.
Технические требования. Ротор (рис. 14.6)
необходимо балансировать динамически в
392
Балансировка типовых изделий машнно- и приборостроения
Рис. 14.6. Консольный ротор
собственных подшипниках на частоте вра-
щения п (с-1). Допустимое значение глав-
ного вектора остаточных дисбалансов
Пстдоп(г -мм). Допустимое значение глав-
ного момента остаточных дисбалансов
МГдОц (г • мм2). Корректировку масс вы-
полнять в /-й и 2-й плоскостях свер-
лением осевых отверстий диаметром не
более d (мм), глубиной до h (мм), на
радиусе (мм). Допускается сверление не
более Л/ отверстий в каждой плоскости
коррекции. Уменьшение значения глав-
ного вектора начальных дисбалансов про-
изводить во 2-й плоскости коррекции.
Уменьшение значения главного момента
начальных дисбалансов производить в 1 и
2-й плоскостях.
Содержание операций. Опера-
ция 05. Внешним осмотром проверить
отсутствие механических повреждений ста-
нины, балансировочного устройства пульта
управления и электрокабелей станка. Уста-
новить на опоры станка балансировочную
рамку. Проверить плавность перемещения
опор балансировочного устройства. Пере-
мещение должно быть свободным, без
заеданий. Проверить положение органов
управления измерительным пультом стан-
ка п.о карте настройки пульта. Проте-
реть рабочие поверхности шкива, направ-
ляющих роликов и ленточного ремня хлоп-
чатобумажной салфеткой, смоченной обез-
жиривающей жидкостью. Включить пита-
ние пульта станка.
Операция 10. Проверить ком-
плектность и правильность оформления
сопроводительной документации на ротор.
Произвести внешний осмотр балансируе-
мого узла. Коррозия, забоины, вмятины
и другие механические повреждения по-
верхностей не допускаются.
Опера цчи я 15. Установить на вал
балансируемого узла подшипники в соот-
ветствии с инструкцией по монтажу. Про-
тереть поверхность ротора хлопчатобу-
мажной салфеткой, смоченной обезжири-
вающей жидкостью.
Операция 20. Установить баланси-
руемый узел на балансировочную рамку
и закрепить винтами. Надеть ленточный
ремень на поверхность балансируемого уз-
ла, ролики и шкив электродвигателя.
Натянуть ремень и установить натяжные
ролики так, чтобы ветви ремня были
вертикальны и лежали в одной плос-
кости. Нанести на левом торце ротора
метку. Отрегулировать положение стробо-
скопа, установив его против левого торца.
Произвести два-три кратковременных пус-
ка балансируемого узла. Убедиться в на
дежности крепления подвижных и вра-
щающихся частей и правильности установ-
ки балансируемого узла. Включить при
вод станка, выждать в течение 2—3 мин
до достижения ротором устойчивой балан-
сировочной частоты вращения. Растор
мозить опоры станка. Установить переклю-
чатель плоскостей измерения в положение
измерения главного вектора дисбалансов.
Записать показания индикатора дисбалан
са (число делений) в рабочий блокнот.
Установить переключатель «Значение —
Угол» в положение «Угол» и сделать
отметку углового положения дисбаланса.
Затормозить рычагом опоры станка. Вы-
ключить привод станка.
Вычислить значение главного вектора
начальных дисбалансов по формуле
Пст нач = число делений X цена деле-
ния по главному вектору.
Типовые технологические процессы балансировки
393
Вычислить значение неуравновешен-
ной массы по формуле
= ^ст нач/^к*
Отвесить пластилиновый груз массой
т. Прикрепить пластилиновый груз в лег-
ком месте ротора во 2-й плоскости на
радиусе /? (мм). Определить значение и
угол главного момента начальных дисба-
лансов, повторив переходы для другой
плоскости измерения.
Вычислить значение главного момента
начальных дисбалансов по формуле
Л4С нач =•- число делений X цена деления по
главному моменту.
Вычислить значения неуравновешен-
ных масс в / и 2-й плоскостях измерения
по формуле
mi = m2 == MD нач/ (г J).
Отвесить пластилиновые грузы массой
Ш} и т2 и сформировать из них параллеле-
пипеды толщиной 10 мм. Прикрепить
пластилиновый груз mt в легком месте
в /-й плоскости на радиусе /?(мм).
Пластилиновый груз т2 прикрепить под
углом 180° относительно первого груза
во 2~й плоскости на радиусе (мм).
Повторить переходы для определения оста-
• точных значений главного вектора и глав-
ного момента дисбалансов. Если остаточ-
ные значения меньше допустимых, то за-
нести начальные значение DCT „дч и MD иач в
технологический паспорт на балансировку
и перейти к следующей операции.
Операция 25. По номограммам
определить число, диаметр и глубину
сверления отверстий в / и 2-й плос-
костях коррекции. Результаты расчета за-
писать в рабочий блокнот.
Операция 30. Снять балансируе-
мый узел со станка, надеть защитные
чехлы на подшипники. Разметить на ро-
торе линии действия главного вектора и
главного момента дисбалансов. Подгото-
вить к работе сверлильный станок. Уста-
новить ротор в приспособление для свер-
ления и просверлить отверстия в / и 2-й
плоскостях. Снять балансируемый узел со
сверлильного станка. Зачистить отверстия
от заусенцев. Волосяной щеткой удалить
опилки и стружку. Снять защитные чехлы.
Операция 35. Повторить переходы
операции 20. Установить переключатель
плоскостей измерения в положение измере-
ния главного момента дисбалансов. Запи-
сать показания индикатора дисбаланса
(число делений) в рабочий блокнот.
Затормозить опоры станка. Выключить
привод станка. Вычислить значение глав-
ного момента остаточных дисбалансов
по формуле
M D ос,. — число делений X цена деления.
Разделить окружность ротора на 8 рав-
ных частей нанесением меловых отметок.
Отвесить пластилиновый груз массой
т(г). Прикрепить груз массой m на пра-
вом торце ротора на радиусе R, мм, в
точке 1. Повторить переходы операции
20 для каждого из восьми положений
груза массой m (г).
Рассчитать значение главного вектора
остаточных дисбалансов ротора по форму-
ле
стост = (^rnax ^min)^^/ (^max “Ь ^min)*
Сравнить полученное значение DCT ост с
допустимым. Значения остаточных дис-
балансов занести в технологический пас-
порт балансировки. Снять балансируемый
узел со станка.
Технологический процесс низкочастот-
ной миогсялоскостиой балансировки рото-
ра на зарезонансном станке. Технические
требования. Ротор (рис. 14.7) необходимо
балансировать динамически относительно
поверхностей А и Б на частоте враще-
ния п (с“‘). Допустимое значение глав-
ного вектора остаточных дисбалансов
йстдоп (г-мм). Допустимое значение
главного момента остаточных дисбалансов
/ИСдоп (г - мм2). Корректировку масс вы-
полнять в 1—5-й плоскостях съемом ме-
талла по кольцу шириной I (мм), глубиной
не более h (мм). Места съема металла
заполировать Расчет корректирующих
масс в 1—5-й плоскостях осуществить по
394
Балансировка типовых изделий машине- и приборостроения
Рис. 14.7. Многомассовый ротор
технологической инструкции на баланси-
ровку ротора.
Содержание операций. Опера-
ция 05. Проверить внешним осмотром
отсутствие механических повреждений ста-
нины, балансировочного и приводного ус-
тройств измерительного пульта и электро-
кабелей станка. Протереть салфеткой,
смоченной обезжиривающей жидкостью,
установочные поверхности опор станка,
шкив, направляющие ролики, ленточный
ремень. Установить и закрепить на опо-
рах станка роликовые опоры, а на валу
электродвигателя — шкив. Проверить
плавность перемещения опор балансиро-
вочного устройства. Перемещения должны
быть свободными, без заеданий. Про-
верить положение органов управления
измерительным пультом по карте настрой-
ки пульта станка. Подготовить к работе
микроЭВМ, введя прикладные программы
расчетов дисбалансов в 1—5-й плоскостях.
Включить питание измерительного пульта
станка.
Операция 10. Проверить комплект-
ность и правильность оформления сопро-
водительной документации на ротор. Про-
вести внешний осмотр ротора. Коррозия,
забоины, царапины, вмятины и другие
механические повреждения не допускают-
ся.
Операция 15. Закрепить на роторе
приспособление для подъема. Снять ротор
с транспортной тележки и установить его
на опоры станка, предварительно накинув
на ротор ремень. Снять приспособление
для подъема. Протереть поверхность рото-
ра салфеткой, смоченной обезжиривающей
жидкостью, надеть ремень. Натянуть ре-
мень и установить натяжные ролики так,
чтобы ветви ремня были вертикальны
и лежали в одной плоскости. Смазать
цапфы ротора маслом (2—3 г). Нанести
на левом торце ротора меловую от-
метку. Отрегулировать положение стробо-
скопа, установив его против левого тор-
ца ротора. Закрыть балансируемый ротор
защитным кожухом Осуществить два-
три кратковременных пуска ротора. Убе-
диться в надежности крепления подвиж-
ных и вращающихся частей и правиль-
ности установки балансируемого ротора.
Операция 20. Включить привод
станка, выждать несколько минут до
достижения ротором устойчивой баланси-
ровочной частоты вращения, растормозить
опоры станка. Установить переключатель
плоскостей измерения в положение изме-
рения главного вектора дисбалансов. За-
писать показания индикатора дисбаланса
(число делений) в рабочий блокнот.
Установить переключатель «Значение —
Угол» в положение «Угол» и сделать
отметку углового положения главного век-
тора дисбалансов. Повторить предыдущие
переходы для другой плоскости измерения,
в которых измеряется главный .момент
дисбалансов. Затормозить опоры станка.
Выключить привод станка. Вычислить
значение главного вектора и главного
момента начальных дисбалансов по фор-
мулам Z)CT нач — число делений X цена де-
ления по главному вектору;
MD нач = число делений X цена деления
по главному моменту.
Результаты расчета занести в рабочий
блокнот.
Операция 25 Согласно технологи-
ческой инструкции на балансировку ротора
по прикладной номограмме рассчитать
значения и углы дисбалансов в /—5-й
плоскостях, а также рассчитать значения
неуравновешенных масс для каждой из
пяти плоскостей. Отвесить пластилиновые
грузы массой т,. Открыть защитный ко-
жух. Прикрепить в /—5-й плоскостях
соответствующие пластилиновые грузы
под расчетным углом к метке, нанесен-
ной на левом торце ротора на радиусе
Балансировка роторов гироскопических приборов
395
Защитный кожух закрыть. Повторить
переходы операции 20 Согласно техно-
логической инструкции на балансировку
ротора по номограммам определить цен-
тральные углы, в пределах которых не-
обходимо провести съем металла с круго-
вого кольца для каждой из пяти «плос-
костей коррекции. Занести результаты в
рабочий блокнот.
Операция 30. Открыть защитный
кожух. Закрепить на роторе приспособле-
ние для подъема. Снять со станка,
установить его на транспортную тележку.
Надеть на цапфы защитные чехлы. От-
вести тележку с ротором в зону, где
производится съем металла. Съем ме-
талла осуществить в трех плоскостях.
Снять пластилиновый груз в 3-й плос-
кости. Произвести съем металла по раз-
метке, заполировать место съема металла.
Очистить ротор от опилок. Отвести те-
лежку с ротором на балансировочный
участок
Операция 35. Повторить перехо
ды операции 20. Если значения оста-
точных дисбалансов меньше допустимых,
то перейти к следующей операции. В
противном случае произвести балансиров-
ку ротора постановкой пластилинового
груза только в 3-й плоскости, после
чего повторить операции 30 и 35 для
этой плоскости.
Операции 30, 35 повторяют после
довательно для 2, 4. / и 5-й плос-
костей коррекции. После корректировки
масс в 5 й плоскости контроль остаточ-
ных дисбалансов ротора осуществить с по-
мощью контрольного груза. В 3-й плос-
кости на радиусе /?3 (мм), прикрепить
неуравновешенную массу пластилина и
повторить переходы операции 20. Открыть
защитный кожух, снять неуравновешенную
массу пластилина в 3-й плоскости. В / и
5-й плоскостях прикрепить под углом
180° неуравновешенные массы пластилина
в (г), на радиусе К|15 (ммк Повто-
рить переходы операции 20, после чего
снять обе массы. Вычислить главный
---------------------------------------
вектор и главный .момент остаточных дис-
балансов.
Значения остаточных дисбалансов не
должны превышать допустимые значения,
указанные в технических требованиях.
14.2. БАЛАНСИРОВКА РОТОРОВ
ГИРОСКОПИЧЕСКИХ ПРИБОРОВ
Гироскопические приборы нашли ши-
рокое применение в инерциальных систе-
мах навигации, предназначенных для
точного выдерживания заданной траекто-
рии полета или заданного курса ле-
тательного аппарата. К гироскопическим
приборам предъявляют ряд требований по
точности, так как инерциальная система
работает автономно и должна быть на-
дежной и нечувствительной к много-
численным внешним помехам..Г1редъявля-
емые требования обеспечивают наряду
с рациональным выбором конструктивных
решений технологий изготовления, сборки,
балансировки и испытаний роторов гиро-
скопов, гироскопических узлов и гиро-
скопических устройств в целом.
Среди возмущающих факторов особое
место занимает вибрация, создаваемая
вращающимся ротором гироприбора. В
условиях вибрации создаются дополни-
тельные динамические нагрузки на детали,
что может служить причиной поломок и
быстрого износа подшипников. Гироско-
пический прибор с зазорами в подшип-
никах не может работать в системе
управления, так как уходы гироскопов
будут особенно велики. Поэтому необходи-
ма тщательная балансировка роторов и
узлов гироскопических приборов.
Допустимые дисбалансы. Статический
и динамический дисбалансы гиромотора
влияют на скорость дрейфа гироскопа
Под влиянием момента
Л4 = (/ ~J3)cg
пары неуравновешенных сил, действующих
на рамку вокруг оси XX для абсо-
лютно жесткого двухстепенного гироскопа
(рис. 14.8) с кинематическим моментом
396
Балансировка типовых изделий машине- и приборостроение
Рис. 14.8. Схема абсолютно жесткого двух-
степенного неуравновешенного гироскопа;
У1У1 главная центральная ось инерции ротора
гиромотора, УУ — ось собственного вращения ро-
тора; XX — ось вращения рамки кожуха, ZZ
прямая, перпендикулярная к плоскости XOY
Н — /Q, угловую скорость систематическо-
го дрейфа определяют по формуле
где р0 — угловая скорость систематическо-
го дрейфа; / — осевой момент инерции
ротора; /э — экваториальный момент инер-
ции ротора; момент инерции кожуха
гиромотора вместе с рамкой относительно
оси XX; Q — угловая скорость вращения
ротора гиромотора; е — угол между осью
вращения и главной центральной осью
инерции ротора; щ2 — вертикальная со-
ставляющая угловой скорости суточного
вращения Земли; — коэффициент вяз-
кого трения между кожухом гироскопа
и жидкостью.
Статически неуравновешенный ротор
гиромотора {а, а2, а0) приводит к по-
явлению угловой скорости систематическо-
го дрейфа трехстепенного гироскопа (рис.
14.9) вокруг оси карданова подвеса, ко-
торая может быть определена по формуле
' _ 6a(J^+^Px+/npa,aoctg р„) sin
2Q2cos 30[ /в/с— (J cos
где G — вес ротора гиромотора; а -- рас-
стояние между точками О\ и Ор, пред-
Рис. 14.9. Схема трехстепенного гироскопа
со статически неуравновешенным ротором
гиромотора:
XX— ось симметрии внутренней рамки карданного
подвеса; Х|Х| — главная центральная ось инерции
гиромотора; Х2Х?— ось собственного вращения ро-
тора гиромотора; У У — ось симметрии наружной
рамки карданного подвеса, У|Уь ZZ — оси вра-
щения внутренней и наружной рамок кардан-
ного подвеса соответственно; О — центр кардан-
ного подвеса; Ов—точка пересечения оси вра-
щения внутренней рамки карданного подвеса с ее
осью симметрии XX, (Д — точка пересечения оси
Х2Х2 собственного вращения ротора гиромотора
с осью симметрии наружной рамы карданного
подвеса; Ор—точка пересечения главной централь-
ной инерции ротора с его плоскостью, нрохо
дящей через центр масс
ставляюшее собой смещение центра масс
ротора с оси вращения; /н z — момент
инерции наружной рамы карданного под-
веса относительно оси ZZ; /вх, /В2—
моменты инерции внутренней рамки кар-
данного подвеса относительно осей XX, YY,
ZZ; /в = /э + /ву^с — ^нг+(^э+/вг)Х
X cos 2ро + JB х sin 2р; тр — масса гиромо-
тора; аг — расстояние между осью враще-
ния ротора и осью симметрии внутрен
ней рамки; aD—расстояние между точ-
ками О и Ов, представляющее собой
смещение центра масс гироузла по оси
ОХ; р0 — угол между плоскостью внутрен-
ней рамки и перпендикуляром к плос-
кости наружной рамки.
Динамически неуравновешенный ро-
тор гиродвигателя трехстепенного гиро-
скопа (рис. 14.10), например гироверти
кали, приведет к появлению системати
Балансировка роторов гироскопических приборов
397
Рис. 14.10. Схема трехстепенного гироскопа
с динамически неуравновешенным ротором ги-
родвигателя:
/ — ротор гиродвигателя; 2, 3 — соответственно
внутренняя и наружная рамки карданного подвеса
ческой составляющей угловой скорости
дрейфа наружной рамы карда нова под-
веса, определяемый по формуле
Рис. 14.11. Схема расположения двух
трехстепенных • гироскопов со стати-
чески неуравновешенными роторами
на платформе
относительно осей х или у; oil, ш2—собст-
венная частота платформы по оси х и у;
со—частота вращения ротора гиродвига-
теля.
Основным элементом современных ги-
роскопических устройств является гиро-
двигатель. Ротор последнего, вращаясь
2 (Лх4-Лг4-/)(/-Л)2(/-Л)281'п₽о
а — — е со
2J(/s/r-J2coS'2p0)2
где /н х — момент инерции наружной рам-
ки карданного подвеса относительно оси
XX;
h — JВх + *) s*n 2Р» + (Лх 4~
4- /э) cos 2₽о.
h = J? + Jbx-
Взаимное влияние двух трехстепенных
гироскопов 2 и 3 (рис. 14.11) со ста-
тически неуравновешенными роторами 1 и
4, установленными на одной платформе,
приведут к возникновению дрейфа. Систе-
матическая составляющая угловой скорос-
ти определяется по формуле
mpSrL2V^r (<o?-<o*)q
2Я/ш! [g 1- —~ |.
где г — смещение центров масс роторов
в радиальном направлении, 2L — расстоя-
ние между осями вращения роторов;
Н—кинетический момент гироскопа; /пл—
полярный момент инерции платформы
с большой угловой скоростью, создает ки-
нетический момерт, необходимый для со-
хранения неизменным положения главной
оси гироскопа в инерциальном простран-
стве.
Ротор гиродвигателя должен иметь на-
ибольший момент инерции при наимень-
ших габаритных размерах, постоянное
положение центра тяжести и надежность в
эксплуатации. Для уменьшения угловой
скорости систематического ухода (дрей-
фа) гироскопа необходимо добиваться
максимальной точности балансировки ро-
тора, т. е. более точно совмещать ось
собственного вращения ротора с глав-
ной центральной осью инерции ротора.
Гиродвигатель, помещенный в корпус
(кожух, поплавок) с деталями, называют
гироузлом. Ось вращения корпуса (внут-
ренней рамки карда нова подвеса) являют-
ся осью прецессии гироскопа. Гироузел
должен быть статически сбалансирован
398
Балансировка типовых изделий машине- и приборостроения
относительно оси вращения внутренней
рамки.
Карданов подвес включает гироузел,
узел наружной рамы с осями, токо-
подводы и др. Карданов узел является
основным и необходимым узлом всякого
трехстепенного гироскопа. Точность стати-
ческой балансировки карданова узла от-
носительно осей подвеса является необхо-
димым условием получения заданной точ-
ности работы гироскопических приборов
с трехстепенным гироскопом.
Пример. Определить систематическую со
ставляющую угловой скорости дрейфа абсолют-
но жесткого двухстепенного гироскопа, ротор
которого динамически неуравновешен. Двух-
степенный поплавковый гироскоп имеет следую-
щие параметры:
1 = 9,8 - КГ5 Н • м • с2;
/э = 9,8 - 0,4 • К)-5 Н • м • с2;
dK = 200 • 9,8 - Н) ь Н • м • с;
е = 3 • 10-4 рад;
ф = 55°36';
<о2 = <«»з sin ф = 12,45°/ч;
Q = 3 - 103 с"';
JB у = 2,6 • 9, 8 - 10-5 Н • м . с2
Пользуясь формулой (14.1), учитывая, что
А) А у Т" I
определим систематическую составляющую уг-
ловой скорости дрейфа двухстепенного гиро-
скопа вокруг оси гироскопа
0 = 2,24- 10—° °/ч = 11,2- 10-12 с 1
Балансируемыми узлами гироскопических
приборов являются ротор гироскопа,
внутренняя рамка карданного подвеса,
гироузел, наружная рамка карданного
подвеса и поплавковый узел.
Особенности балансировки роторов ги-
роскопов. В настоящее время имеется
большое число конструкций гироскопов,
отличающихся системами подвеса. Так,
например, есть роторы с внешним и вну-
тренним кардановыми подвесами, с упру-
гим и воздушным подвесами, с электро-
статическим и электромагнитным подве-
сами и др. Требования к точности ак-
сиального уравновешивания для всех ро-
торов, независимо от системы его под-
веса, примерно одинаковы, как и для
роторов традиционной конструкции с
внешним кардановым подвесом. Различие
состоит в выборе способов уравновеши-
вания, определения величины и места дис-
баланса, способов корректировки масс.
Балансировка роторов гироскопов с
внутренним карданным подвесом. Ротор 4
гироскопа с внутренним карданным под-
весом 3 (рис. 14.12) отличается просто-
той конструкции, компактностью и надеж-
ностью в работе. Обе рамки карданного
подвеса размещены внутри ротора. Ротор
такой конструкции имеет три плоскости
коррекции (/ — III). Плоскости коррекции
I и II расположены по обе стороны
от центра масс ротора, а плоскость
III проходит через центр масс ротора.
Главные опоры 2 расположены между
плоскостями I и III асимметрично от-
носительно центра масс ротора. Рас-
стояние между опорами равно ширине
подшипника.
Дисбаланс задается в виде главного
.вектора и главного момента. Моментную
неуравновешенность (по плоскостям / и II)
определяют или по биению конца нако-
нечника 1 ротора в плоскости, перпенди-
кулярной оси вращения ротора, или по
углу пятна контакта на параболической
поверхности ротора, расположенной в
плоскости коррекции /. Моментная неу-
равновешенность таких роторов имеет пре-
валирующее значение над силовой не-
уравновешенностью.
Схема балансировки ротора показана
на рис. 14.13, когда балансируемому ро-
тору I обеспечивается одна степень сво-
боды. Измерение неуравновешенности по
Рис. 14.12. Схема расположения опор и плос-
костей коррекции неуравновешенного ротора
гироскопа с внутренним кардановым подвесом
Балансировка роторов гироскопических приборов
399
Рис. 14.13. Схема балансировки ротора, обес-
печивающая одну степень свободы:
Ос — центр карданова нодвеса
плоскости коррекции / осуществляют при
неподвижной (заарретированной) рамке 3
способом масляного пятна контакта. Ро-
тор считается сбалансированным, если
след мазка вписывается в угол, боль-
ший 180 °. Измерение неуравновешен-
ности по плоскости коррекции // про-
изводится при подвижной (разарретиро-
ванной) рамке 3 и совмещенной плос-
костью / с осью 2 колебаний этой
рамки. Точность балансировки роторов по
данной схеме по плоскости коррекции
II не превышает 5 мкм по условному
смещению центра масс ротора.
Схема балансировки ротора /, обеспе-
чивающая две степени свободы баланси-
руемому изделию (без учета собственного
вращения ротора), приведена на
рис. 14.14. Остаточная моментная не-
уравновешенность ротора определяется
биением конца наконечника рамки 4 балан-
сировочного станка. Силовую неуравнове-
шенность в плоскости коррекции III из-
меряют одним электрическим датчиком 3.
Точность балансировки роторов составля-
ет 1,5 мкм по условному смешению
центра масс ротора. Моментная неуравно-
вешенность определяется оптическим дат-
чиком 2 с точностью до 0,8 мм Точность
балансировки можно достичь 0,4 мкм по
условному смешению центра масс ротора,
если ротор предварительно балансировать
статически относительно осей карданного
Рис. 14.14. Схема балансировки ротора, обес-
печивающая две степени свободы
Рис. 14.15. Схема неуравновешенного сфери-
ческого ротора гироскопа
подвеса (плоскость коррекции III), а затем
применить схему балансировки с двумя
степенями свободы. Электрические датчи-
ки необходимо экранировать.
Балансировка сферических гироско-
пов. Сферический ротор выполняет основ-
ную функцию носителя кинетического мо-
мента и является одним из основных
элементов подвеса, обеспечивающим рото-
ру угловую подвижность. К нему предъ-
являют высокие требования по точности
и качеству изготовления наружной сфе-
рической поверхности с одновременным
обеспечением требований по остаточной
неуравн свешен ности.
Неуравновешенность сферического ро-
тора (рис. 14.15) гироскопа определяется
лишь одной величиной — статическим мо-
ментом массы ротора, вызванным сме-
щением 6 центра масс (ЦМ) ротора
от геометрического центра О наружной
сферической поверхности (несущей по-
>и.л изделии машино- и приборостроен
Т
верхности). Наличие трех угловых сте-
пеней свободы позволяет ротору при
вращении устанавливаться таким образом,
чтобы ось собственного вращения совпала
с одной из главных осей инерции. Это
означает, что сферический ротор прин-
ципиально не может иметь динамической
неуравновешенности. Расчетная ось OZ
вращения, задаваемая системой отсчета
углового положения ротора, в силу дейст-
вия технологических погрешностей при из-
готовлении ротора может оказаться не
главной осью инерции. Угловое расхож-
дение этих осей не скажется на дина-
мическом состоянии системы, как это
случилось бы у обычных двухопорных рото-
ров, так как главный момент неурав-
новешенных сил при установившемся дви-
жении сферического ротора всегда равен
нулю. Термин «динамическая неуравнове-
шенность» применительно к сферическим
роторам лишен физического основания.
Величина угловой ошибки у связана с
величиной центробежного момента инер-
ции, подлежащего устранению при ба-
лансировке, к которому и относится
термин «динамическая неуравновешен-
ность», следующим отношением:
tg2T = 2/xz/(/-/9),
где / и J3 — соответственно полярный
и экваториальный моменты инерции ро-
тора, определенные для расчетной оси
вращения; Jxz — mrh — центробежный мо-
мент инерции, подлежащий исправлению;
тг — динамический дисбаланс; h — пле-
чо дисбалансной пары; у — угловая
ошибка расположения расчетной оси
вращения относительно главной оси
инерции ротора.
Динамической баланейровки как про-
цесса устранения угловой ошибки у можно
избежать вовсе, если выбор расчетной
оси вращения (нанесение на ротор элемен-
тов системы съема информации об угло-
вом положении) производить после опре-
деления главной центральной оси инер-
ции статически уравновешенного ротора.
Динамическая неуравновешенность сфери-
ческого ротора не оказывает влияния на
главную характеристику прибора — ско-J
рость его дрейфа, поэтому основное вни-|
мание при балансировке уделяется ста-1'
тическому уравновешиванию ротора.
Статическая неуравновешенность сфе-
рического ротора может быть представ-
лена в виде суммы радиальной и осе-
вой составляющих статической неуравно-
вешенности, характеризуемых соответ-
ствующими смешениями 6С и б0 центра
масс и называемых в дальнейшем, для
краткости, радиальной и осевой неуравно-
вешенностями.
Радиальная неуравновешенность при-
водит к цилиндрическому движению оси
ротора, амплитуда и фаза которых опре-
деляется величиной бс радиального сме-
щения центра масс, соотношением частоты
вращения ротора и резонансной частоты
подвеса, а также демпфированием под-
веса. Действительная ось вращения ротора
практически приближается к главной
центральной оси инерции, а наружная
поверхность ротора испытывает биение,
равное удвоенному радиальному смеще-
нию бс центра масс ротора от гео-
метрической оси ротора. При этом на
корпус подвеса действует циклическая ре-
акция
R =
где k — радиальная жесткость подвеса.
Определение величины и углового по-
ложения радиальной неуравновешенности
осуществляется путем фиксации биения
наружной поверхности и выделения гармо-
ники, соответствующей дисбалансу.
Осевая неуравновешенность бо сфери-
ческого ротора приводит к уводу гиро-
скопа, находящегося в поле ускорения, и
требует нового вида балансировки отдель-
но взятого ротора. Скорость системати-
ческого дрейфа неуравновешенного в осе-
вом направлении сферического ротора
определяют по формул?
фе=Сах/(Л2). (14.2)
Величину осевой неуравновешенности
сферического ротора можно определить на
рабочей частоте вращения по скорости
Балансировка роторов гироскопических приборов
401
Рис. 14.16. Виды траектории движения центра
масс неуравновешенного сферического ротора
увода оси ротора, определяемой формулой
(14.2), или используя маятниковый способ
измерения неуравновешенности сферичес-
кого ротора. Если ротор вывести из
положения равновесия путем поворота от-
носительно некоторой произвольной гори-
зонтальной оси, то он будет совершать
сложное колебательное движение. Траек-
тория движения центра масс, записан-
ная в угловых координатах, представляет
собой фигуру Лиссажу в виде эллипса.
Пример такой траектории приведен на
рис. 14.16, а для начальных углов ко-
лебаний 0 и ф, равных 10°. Колебания в
направлениях 0 и ф происходят с раз
ними частотами. При этом центр масс
практически не проходит через положение
равновесия (точку О). Осью выведения ро-
тора из положения равновесия должна
быть одна из экваториальных осей, перпен-
дикулярная к меридианной плоскости, в
которой расположен центр масс ротора.
Тогда траектория движения центра масс
будет значительно сужена (рис. 14.16,6).
Подсчет дисбаланса тах осуществляют по
формуле
тах
Л / 4л2 х2 \
где Т — период демпфированных угловых
колебаний ротора; -к — угловой коэффи-
циент сопротивления.
Чувствительность майтникового спо-
соба определяется величиной минимальной
неуравновешенности
— x2/(4g/).
При меньших значениях статической не-
уравновешенности колебания ротора будут
хаотическими.
Балансировка поплавковых гироско-
пов. Поплавковые гироскопы подвергают-
ся статической балансировке в специаль-
ной (рабочей) жидкости. На поплавковый
узел / (рис. 14.17), помещенный в жид-
кость, будут действовать сила тяжести
поплавкового узла, приложенная в центре
масс Oq, сила Р, выталкивающая попла-
вок из жидкости, приложенная в центре
давления Ор. Эти силы передают свое
воздействие через цапфы, определяющие
ось подвеса X — X. на подшипниковые
узлы.
Степень сбалансированности узла ха-
рактеризуется плавучестью, дифферентом
и статической неуравновешенностью отно-
сительно оси цапф (ось поворота по-
плавка X — X). Плавучесть поплавкового
узла
П **
р=с„+£<3|.
1=1
где Qi — уравновешивающий груз.
Дифферент поплавкового узла опреде-
ляют из следующей зависимости;
X2Q2 = хг(Сз + Qt) 4- XqQ„ — хрР.
Статическая сбалансированность по-
плавкового узла относительно оси подве-
Рис. 14.17. Схема статической балансировки
поплавкового узла
402
Балансировка типовых изделий машине- и приборостроения
са определяется с помощью следующих
уравнений:
!0<2з = уРР — yQQn;
Z2Q4 — zpP — zqQip
где Qa, Q4, Qi — сила тяжести соответ
ственно грузиков 3, 4 и 2; xit уt — коорди-
наты центра масс грузиков 3; z?—коорди-
ната центра масс грузиков 4, хз—ко-
ордината центра масс грузика 2; xQ, «/q,
Zq — координаты центра масс поплавково-
го узла; хр, ур, zp — координаты центра
давления поплавкового узла.
Регулировка плавучести поплавкового
узла в жидкости производится изменением
силы тяжести Qi подвижного грузика 2 с
точностью до 0,1% от его силы тяжести.
Допуск на плавучесть AG может быть
положительным и отрицательным. Он опре-
деляет наибольшую допустимую разность
силы тяжести Qn и силы Р.
Регулировку дифферента осуществля-
ют перемещением в жидкости грузика 3
вдоль оси XX без изменения его массы.
Допуск на дифферент AZ) поплавко-
вого узла задается в виде приведенной
к цапфам допустимой реакции. Он опре-
деляет наибольший допустимый момент,
действующий вокруг поперечной оси по-
плавкового узла, который вызван несовпа-
дением его центра масс с центром пла-
вучести.
Статическую балансировку поплавко-
вого узла в жидкости относительно оси
подвеса производят грузиками 3 и 4.
Допуск на статическую неуравнове-
шенность АЛ4 поплавкового узла отно-
сительно оси его цапф определяет наи-
больший допустимый момент, действу-
ющий на узел из-за несовпадения его
центра масс с осью подвеса.
Типовой технологический процесс ба-
лансировки поплавкового узла содержит
следующие операции', подготовку по-
плавкового узла к балансировке, подго-
товку ванны и жидкости к балансировке,
регулирование плавучести, устранение
дифферента, статическую балансировку,
контроль качества балансировки.
При выполнении всех операций важно,
чтобы при погружении всех деталей
поплавкового узла в ванну с жидкостью
на поверхностях деталей не возникли бы
пузырьки воздуха. Поэтому необходимо
тщательное вакуумирование всех деталей
и узлов, а также их хранение в ванне
с рабочей жидкостью при определенной
температуре.
Качество регулирования плавучести
поплавкового узла проверяют контроль-
ными грузиками, силу тяжести Gr которых
определяют по формуле
Gr = AGp,./ (р, рж),
где рг и рж массовая плотность матери-
алов грузиков и жидкости (г/см3) при
определенной температуре; AG — допуск
на плавучесть.
Если при прикреплении контрольного
грузика к поплавку поплавковый узел
не тонет и не всплывает, то его пла-
вучесть находится в пределах допуска
AG.
Дифферент поплавкового узла устра-
няется в рабочей жидкости перестанов-
кой специальных грузов (винтов, гаек,
шайб) вдоль оси цапф по специальным
резьбовым направляющим, не вынимая их
из жидкости. Точность устранения опре-
деляют с помощью контрольного грузика,
силу тяжести Сд которого рассчитывают
до формуле
Gn = Д/)р2/(рг — рж),
где А£) — допуск на дифферент.
Если дифферент находится в преде
лах допуска, то под действием контроль
него грузика, прикрепленного на воз-
вышающуюся цапфу поплавкового узла,
этот узел начнет поворачиваться в дру-
гую сторону. Ванна при этом должна
быть изготовлена из прозрачного мате-
риала, а на ее стенах нанесены линии
под определенным углом.
Точность статической балансировки
относительно оси подвеса проверяют
контрольными грузиками в виде винтов:
их завинчивают в радиальном направле-
Балансировка роторов гироскопических приборов
403
нии, поворачивая на угол <р, который
определяют по формуле
<р = 360 * ДМ (рг — рж) / (sprQ^),
где Q<f сила тяжести винта на воздухе;
s — шаг резьбы.
Остаточный статический дисбаланс ДМ
поплавкового узла относительно оси X — X
проверяется навешиванием контрольных
грузиков (в виде гаек) на выступаю-
щие концы винтов, расположенных на ра-
диусе R. Сила тяжести контрольного груза
Gr = ДМрг/(Я{Рг - рж)].
Пути повышения статической баланси-
ровки поплавковых гироскопов. Суммар-
ный дрейф интегрирующих поплавковых
гироскопов определяют по формуле
<»др = МтР/Н>
где Л!тр — момент трения в опорах поп-
лавкового гироскопа; Н - кинетический
момент гироскопа.
Минимальное трение в опорах обеспе-
чивается нулевой плавучестью. Поэтому
балансировку поплавковых узлов выполня-
ют в три приема:
статическая балансирока на воздухе,
при которой совмещают центр масс поп-
лавка с осью подвеса;
балансировка в жидкости, при кото-
рой устраняют ДМ, ДО и Дб;
балансировка поплавкового узла в соб-
ранном приборе.
В ряде конструкций компенсационные
устройства в виде резьбовых пар за-
меняют балансировочными ампулами, час-
тично заполненными легкоплавким спла-
вом с индивидуальным нагревом. Эти ам-
пулы размещают во внутренней полости
поплавкового узла. Температура
плавления такого сплава строго регла-
ментирована; ее выбирают из следую-
щего соотношения:
^-пл (^раб ^пср) ’
где /пл — температура плавления сплава
внутри балансировочной ампулы; /ДО1, —
максимально допустимая температура ра-
зогрева гироприбора; /раб — температура
рабочей жидкости в приборе, поддержи-
ваемая системой терморегулирования;
^иер — допустимая температура перегрева
внутренней полости поплавкового узла
при работающем двигателе.
С помощью балансировочных ампул
балансируют поплавковый узел относи-
тельно оси вращения путем перемещения
от центра масс в заданном направле-
нии, которое осуществляется одновремен-
но по двум взаимно перпендикулярным
осям. Для этого предварительно опре-
деляют угловое положение плоскости, в
которой должен производиться наклон
поплавка, по следующей зависимости:
tg а. - содр у/с)др г,
где (Одр s, (Одр z — дрейф от неуравнове-
шенных масс» измеренный при горизон-
тальном положении оси У У и ZZ соответ-
ственно.
После определения углового положе-
ния плоскости наклона ампулы нагрева-
ют, сплав в них расплавляется, прибор
наклоняется на угол а. после чего обо-
грев ампул отключают, и металл засты-
вает.
Контроль точности статической ба-
лансировки поплавковых гироскопов. Кон-
троль статической неуравновешенности
поплавкового гироузла осуществляют в
технологической ванне в собранном гнро-
приборе. Для этого применяют различные
устройства, например электромеханичес-
кие граммометры. Для контроля поплавок
помешают в ванну с жидкостью. Цапфы
поплавка вводят в отверстия тяг Двух
граммометров двустороннего действия.
При контроле плавучести и дифферента
поплавка измеряют давление на тягу,
что выражается в повороте стрелки грам-
мометра. Допуск на плавучесть AG опре-
деляют с помощью следующего выра-
жения:
KG > |gi + g2|,
где gi, g2 — показатели граммометров.
Допуск на дифферент ДО находят,
используя выражение
АО>
^i-^2
2
404
Балансировка типовых изделий машино- и приборостроения
Контроль статической сбалансирован-
ности поплавкового узла в собранном гиро-
приборе выполняют путем определения
суммарного момента на выходной оси
при вертикальном и горизонтальном по-
ложениях оси ротора гиродвигателя, когда
питание обмоток статора гиродвигателя
отключено. При этом по датчику мо-
мента гироприбора определяют зави-
симость
/=/(Л1о),
где / — величина тока в датчике мо-
мента гироприбора от действия суммар-
ного момента Л40, приложенного к выход-
ной оси
Сигнал с датчика угла гироприбора
подается на его датчик момента и по
величине тока в датчике момента оцени-
вают величину суммарного момента на вы-
ходной оси при различных угловых
положениях ротора. Измерение повторяют
многократно. Момент статической не-
уравновешенности определяют по формуле
Mo = (^tnax-Afxmin)/2,
гдеМх= £ MJn.
1= 1
14.3. БАЛАНСИРОВКА КАРДАННЫХ ВАЛОВ
Особенности балансировки карданных
валов определяются их гибкостью и на-
личием шарнирных соединений. Статисти-
ческий анализ конструкций карданных ва-
лов автомобильного транспорта показал,
что из всего объема их выпуска ~15%
составляют одношарнирные, ~65%—
двухшарнирные и ~20%—трехшарнир-
ные. Почти для 30% выпускаемых кардан-
ных валов при их балансировке необходи-
мо учитывать упругую деформируемость
при вращении на наибольших рабочих
частотах или гибкость. Возможность ба-
лансировки различных типов валов на
одном станке обеспечивается оснащением
его унифицированной измерительной си-
стемой и комплектом из трех изотропных
опор.
Во избежание возникновения больших
осевых усилий в эксплуатационных усло-
виях, требующих специальных методов их
компенсации, необходимо при балансиров-
ке обратить особое внимание на совпаде
ние рабочего положения карданного вала и
его положения на балансировочном станке
При балансировке гибких карданных ва-
лов следует иметь в виду, что допустимая
стрела их прогиба не должна превышать
0,2—0,3 мм. При больших значениях про-
гиба валы предварительно следует рихто-
вать.
Следует также учитывать, что дости-
жимая точность балансировки карданных
валов во многом зависит от качества из-
готовления шарнирных сочленений. Увели-
ченные зазоры в подшипниках и шарнирах
приводят к отсутствию стабильности
взаимного расположения составных частей
валов и, как следствие, к нестабильности
показаний индикаторов дисбаланса. Слиш-
ком большой натяг в шарнирах и по-
вышенный момент трения в них, а также
трение в шлицевом соединении вызывают
уменьшение чувствительности измеритель-
ной системы, особенно к моментной состав-
ляющей дисбаланса.
Наиболее известными методами кор-
рекции дисбаланса являются приварка
пластин к трубе вала и установка уравно-
вешивающих грузов под фланцы кардан-
ных сочленений. Места приварки пластин
и установки грузов и их массу определяют
по показаниям индикаторов дисбаланса
измерительной системы. Малые величины
радиусов коррекции в сочетании с больши-
ми начальными дисбалансами вызывают
необходимость установки балансировоч-
ных грузов большой массы. В этих услови-
ях грузы следует устанавливать по углу
как можно точнее, так как даже незначи-
тельные угловые ошибки вызывают появ-
ление остаточных дисбалансов, превышаю-
щих допустимые величины.
Станки для балансировки карданных
валов в условиях крупносерийного и мас-
сового производств оснащены электро-
сварочными аппаратами для закрепления
балансировочных грузов, которые выпол-
Балансировка роторов сельскохозяйственных машин
405
йены в виде пластин различной ширины
или длины. Сварочное оборудование раз-
мещено непосредственна на станке и со-
ставляет с ним единое технологическое и
конструктивное целое.
Современное балансировочное обо-
рудование и применяемые методы коррек-
ции дисбаланса позволяют за один ба-
лансировочный цикл уменьшить началь-
ный дисбаланс вала в 8—10 раз. В произ-
водственных условиях обычным является
превышение начального дисбаланса над
допустимым в 30—40 раз. В этом случае
качественная балансировка может быть
осуществлена за два цикла. Конструкции
карданного вала и балансировочного стан-
ка должны обеспечивать возможность при-
варки рядом двух пластин—баланси-
ровочных грузов, размеры и место крепле-
ния которых определяют последовательно
по результатам измерения дисбаланса.
14.4. БАЛАНСИРОВКА РОТОРОВ
СЕЛЬСКОХОЗЯЙСТВЕННЫХ МАШИН
Роторы машин сельскохозяйственного
назначения имеют следующие конструк-
тивные, технологические и эксплуатацион-
ные особенности:
большое разнообразие конструкций,
типоразмеров и, как следствие, широкий
диапазон масс (1—500 кг и выше) и частот
вращения (10—10 000 мин-1);
преимущественно представляют собой
жесткие двухопорные роторы на подшип-
никах качения;
привод осуществляется в основном
ременными передачами с литыми чугун-
ными или алюминиевыми шкивами, со-
измеримыми по массе приводимого ротора;
широко распространены роторы, представ-
ляющие собой контрприводы трансмиссий;
преобладает сборно-сварной тип конст-
рукции с окончательной сборкой на маши-
не;
преимущественно имеют крупносерий-
ное и массовое производство;
низкий класс точности исполнения де-
талей, значительные уровни погрешностей
сборки и монтажа ротора на машине;
интенсивное изнашивание элементов
конструкции роторов, представляющих
собой рабочие органы; необходимость час-
той замены таких элементов в эксплуа-
тации;
возможность частого засорения рото-
ров обрабатываемым материалом, пылью,
почвой и технологическими отходами.
Эти особенности предопределяют сле-
дующую специфику балансировки роторов
сельскохозяйственных машин:
невозможность унификации нормати-
вов балансировки роторов (необходимость
использования и способ балансировки,
класс точности и пр.) с помощью универ-
сальных таблиц и критериев и небходи*
мость обоснования этих нормативов рас-
четными методами, дифференцированно
учитывающими все конструктивные, кине-
матические, динамические, технологиче-
ские и эксплуатационные особенности каж-
дого ротора;
преимущественное использование по-
детальной балансировки, когда отдельно
балансируют основные сборочные единицы
(шкивы, барабаны) ротора, из которых его
собирают на машине без дополнительной
балансировки на месте в сборе;
высокий уровень и большой разброс
значений начальных дисбалансов изделий
до их балансировки ограничивает приме-
нение станков с определением дисбалансов
в динамическом режиме;
значительные уровни технологических
дисбалансов я эксплуатационных раз-
балансировок роторов;
отсутствие надежных, эффективных и
быстродействующих балансировочных ко-
мплектов для использования их как в про-
изводстве, так и в эксплуатации; балан-
сировку роторов при ремонте машин (даже
на специализированных предприятиях) не
производят; сборочные единицы роторов
поставляют отбалансированными.
Классификация роторов сельхозма-
шин. Для классификации всего много-
образия роторов машин сельскохозяйст-
венного назначения целесообразно исполь-
зовать признак стабильности характери-
стик и уравновешенности в эксплуатации.
406
Балансировка типовых изделий машино- и приборостроения
Для жестких роторов эта стабильность
определяется следующими факторам#;
постоянством геометрии, характеризую-
щимся отсутствием возможности относи-
тельных функциональных перемещений де-
талей и сборочных единиц ротора, и сте-
пенью изнашиваемости элементов конст-
рукции ротора. Введенному классифика
ционному признаку отвечает деление жест-
ких роторов сельхозмашин на четыре типа
(рис. 14.18). Гибкие роторы практически
не используют в конструкциях машин сель-
скохозяйственного назначения.
К роторам типа 1 относят, например,
контрприводы машин сельскохозяйствен-
ного назначения, молотильные барабаны
зерноуборочных комбайнов, вентиляторы,
шнеки; примерами роторов типа 2 служат
блоки вариаторов хода зерноуборочных
комбайнов, роторы сепараторов и центри-
фуг для обезвоживания суспензий; к рото-
рам типа 3 относят различного рода из-
мельчающие барабаны с шарнирными ра-
бочими элементами (ножами, молотками);
примерами роторов типа 4 являются из-
мельчающие барабаны с неподвижными
рабочими элементами, фрезбарабаны фу-
ражиров.
Характерным для роторов типа 3, 4
является необходимость частой замены в
эксплуатации сменных элементов
конструкций, претерпевающих значитель-
ный износ. При этом для устранения зна-
чительных эксплуатационных разбалан-
сировок пары элементов, устанавливаемых
в диаметрально противоположных точках
ротора при его изготовлении и ремонте,
Рис. 14.18. Типы роторов сельхозмашин
должны быть подобраны по массе с опре-
деленными допусками.
Способы организации технологиче-
ского процесса балансировки роторов
сельхозмашин. Способ организации техно-
логического процесса балансировки пред-
усматривает. последовательность и содер-
жание этапов обеспечения уравновешен-
ности ротора в производстве. Для роторов
сельхозмашин используют:
подетальную балансировку, когда все
или некоторые сборочные единицы ротора
балансируют отдельно, ротор собирают из
сбалансированных и несбалансированных
сборочных единиц;
балансировку в сборе, когда ротор со-
бирают из несбалансированных деталей и
балансируют как отдельную сборочную
единицу;
комплексную балансировку, совме-
щающую предварительную подетальную
балансировку с последующей балансиров
кой в сборе;
последовательную балансировку, когда
ротор балансируют после установки каж-
дой его сборочной единицы.
Ротор балансируют подетально, если:
сборочные единицы ротора связаны с
валом и между собой разъемными соеди-
нениями, а окончательную сборку ротора
осуществляют непосредственно в машине;
в процессе эксплуатации и ремонта
необходима разборка ротора с целью
замены изношенных деталей и сборочных
единиц;
в запчасти поставляют не ротор в сбо-
ре, а отдельные его сборочные единицы,
сбалансированные в производственных ус-
ловиях.
При подетальной балансировке вал
ротора отдельно не балансируют; динами-
ческую балансировку сборочных единиц
проводят вместе с рабочим валом на
собственных подшипниках; статическую
балансировку сборочных единиц роторов
осуществляют на балансировочной оправ-
ке
Балансировка роторов сельскохозяйственных машин
407
Ротор балансируют в сборе, если:
сборочные единицы ротора связаны с
валом между собой неразъемными соеди-
нениями, а ротор устанавливают на ма-
шине в собранном состоянии;
ротор не подлежит разборке и ремонту
в течение всего срока службы машины;
в запчасти ротор поставляют сбаланси-
рованным в сборе.
При использовании балансировки в
сборе необходимо учитывать следующее:
динамическую балансировку в сборе вы-
полняют на рабочем валу, рекомендуется
осуществлять такую балансировку не на
технологических, а на собственных под-
шипниках; статическую балансировку в
динамическом режиме проводят с рабочим
валом на собственных подшипниках, до-
пускается статическая балансировка в ди-
намическом режиме ротора в сборе на
балансировочной оправке; статическая ба-
лансировка ротора в сборе при помощи
силы тяжести на невращающемся роторе
производится с рабочим валом без под-
шипников.
Ротор балансируют комплексно, если:
сборочные единицы ротора связаны с
валом и между собой разъемными соеди-
нениями, а установку ротора на машине
выполняют в собранном состоянии без
предварительной разборки;
при сборке ротора из сбалансирован-
ных сборочных единиц возникают значи-
тельные технологические дисбалансы, со-
измеримые с допустимым значением глав-
ного вектора функциональных дисбалан-
сов ротора;
в запчасти поставляют отдельно сба-
лансированные сборочные единицы ротора,
но при ремонте имеется возможность кор-
ректировки дисбалансов ротора в сборе.
При использовании комплексной ба-
лансировки необходимо учитывать те же
требования, что и при проведении по-
детальной балансировки и балансировки
в сборе.
Ротор или отдельную его сборочную
единицу балансируют последовательно,
если:
детали ротора и (или) его сборочной
единицы связаны с валом и между собой
разъемными соединениями, допускающи-
ми при работе относительную осевую
подвижность, а установку ротора на
машине осуществляют в собранном состоя-
нии или ротор собирают на машине по
меткам;
ротор не подлежит разборке и ремонту
в течение всего срока службы машины;
в запчасти ротор поставляют в сборе,
сбалансированным последовательно.
При использовании последовательной
балансировки необходимо учитывать сле-
дующее: на каждой ступени последова-
тельной балансировки корректировку масс
необходимо вести на вновь установ-
ленной сборочной единице ротора; все
ступени последовательной балансировки
необходимо осуществлять на рабочем валу
ротора и в собственных его подшипниках,
если выполняется последовательная ди-
намическая балансировка ротора; при ди-
намической балансировке последовательно
балансируемого ротора рекомендуется осу-
ществлять предварительную статическую
балансировку основных его сборочных
единиц; все ступени последовательной ба-
лансировки рекомендуется выполнять на
одном общем балансировочном оборудо-
вании.
В сельхозмашинах наиболее широко
применяют подетальную балансировку
всех типов роторов, реже—балансировку
в сборе и комплексную балансировку
(типы 2, 3) и крайне редко- последова-
тельную балансировку (тип 2).
Нормативы балансировки роторов.
Нормативы устанавливаются конструкто-
ром на проектной стадии создания маши-
ны; они призваны обеспечить нормальное
функционирование ротора, характеризую-
щееся отсутствием возможности возникно-
вения недопустимо высокого уровня вибра-
ций от неуравновешенности ротора при ра-
боте машины, и минимум затрат на его
изготовление и ремонт. Эти нормативы
должны содержать обоснование:
целесообразности балансировки рото-
ра каждой конкретной конструкции;
408
Балансировка типовых изделий машино- и приборостроения
метода балансировки (статический,
динамический) ротора и (или) его сбороч-
ных единиц при принятом способе органи-
зации технологического процесса баланси-
ровки;
класса точности балансировки ротора
по ГОСТ [Г9] и допустимого значения
главного вектора его функциональных
дисбалансов;
допустимых дисбалансов ротора и от-
дельно балансируемых его сборочных еди-
ниц.
Для роторов типов 3, 4 приведенный
выше перечень дополняется обоснованием
допуска на разность- масс сменных элемен-
тов.
Решающим фактором вредного прояв-
ления неуравновешенности роторов сель-
хозмашин является снижение надежности
их опор. Если весь комплекс нормативов
балансировки этих роторов решается ис-
ходя из указанного фактора, то вибрации
от неуравновешенности не только не при-
ведут к недопустимому снижению надеж-
ности подшипников роторов, но и не вызо-
вут ухудшения качества технологического
процесса машины, не будут генерировать
вибрации рабочего места оператора, пре-
вышающие допустимый санитарными нор-
мами уровень.
Ротор с изменяющейся геометрией.
Неуравновешенность цилин-
дрических винтовых пружин.
Функционирование отдельных роторов тре-
бует относительных перемещений их дета-
лей вдоль оси ротора с обеспечением
нормированного по осевому усилию кон-
такта между этими деталями. Для этого
в конструкции ротора обычно используют
цилиндрические винтовые пружины (рис.
14.19).
Уравновешенность роторов обеспечи-
вается подетальной или комплексной их
балансировкой, при которой отдельная ба-
лансировка пружины не производится
из-за отсутствия возможности корректи
ровки ее масс. Это требует оценки не-
уравновешенности, вносимой пружиной в
конструкцию ротора, и обоснования рацио-
Рис. 14.19. Цилиндричес-
кая винтовая пружина
нальных параметров пружины, обеспечи-
вающих минимальное значение этой не-
уравновешенности с учетом изменения ге-
ометрии ротора и принятого способа
организации технологического процесса
его балансировки.
Значения главного вектора DCT, глав-
ного момента MD дисбалансов пружины и
угол а между ними функционально опре-
деляются основным конструктивным пара-
метром пружины—углом ф навивки ее
спирали, т. е.
Рст = 2у/?-д /R2 + ~ Isin -|J ,
V 4л2 I 2 I
г-м; (14.3)
ф ф I 2
“ 2 C0S 2|’ Г*М ’ <14-4)
“ = т[ 1 ~ Sign( sin ’f) sign( sin “
Ф
-f COS
(14.5)
где у—линейная цлотность материала
(проволока, пруток) пружины, г/м; R —
радиус среднего цилиндра спирали пружи-
ны, м; t—шаг спирали пружины в рабочем
Балансировка роторов сельскохозяйственных машин
409
ее состоянии, м; sign(4)=l, если расчет
выражения в скобках за символом sign
дает Д^О, и sign(4) =—1, если Д<0.
Исключая тривиальное ф = 0, не су-
ществует значений ф, одновременно обра-
щающих в нуль Ост и MD. DCT=0, если
ф— 2Лл, 1,2,...; Л)о=0 при ф, при-
нимающем значения (в рад): 8,987; 15,450;
21,808; 28,132: 34.441: 40.743: 47.039;
53,332; 59,623. При числе витков пру-
жины п>10 MD~0 для ф«59,6234-
4-2 (я —10) л.
Значения дисбалансов пружины в пло-
скостях ее торцов равны между собой.
Установка и работа пружины в агрега-
те связаны с ее осевыми упругими де-
формациями, в результате которых нри
неизменной длине I спирали нружины мо-
гут меняться остальные параметры (/, R,
ф), определяющие ее неуравновешенность.
У свободной (недеформированной)
пружины
I = ф«• <14 61
где фо, Ro, to - параметры конструкции в
свободном ее состоянии.
Если установка пружины выполняется
с фиксацией концов ее спирали или если
относительному провороту этих концов
препятствует значительное сопротивление
трения (поверхности ротора, на которые
опирается пружина, не допускают свобод-
ного относительного проворота, такой про-
ворот возможен, если хотя бы одна из
этих поверхностей опирается на подшип-
ник), то деформация (осадка) пружины
происходит при неизменном ф = фо; осталь-
ные параметры конструкции нружины оп-
ределяются при этом как функции осадки
Л пружины уравнениями
Если установка пружины обеспечивает
свободную относительную проворачивае-
мость концов ее спирали, то деформация
Л пружины происходит при неизменном
= остальные параметры конструкции
пружины в деформированном ее состоянии
определяются как
4=
(14.8)
Пример. Для пружины ведомого блока
вариатора хода СК-5М «Нива» (рис. 14.19),
имеющей 0,074 м, Ro~ 0,085 м, у== 1200 г/м.
необходимо найти характеристики неуравно-
вешенности при предельных скоростях вращения
блока и различных значениях <(.-< При расчетах
учитывают, что концы пружины в блоке не
допускают относительного проворота, поэтому
в рабочем состоянии пружины <р= остальные1
параметры находим, используя формулы (14.7).
Результаты расчетов по уравнениям
(14.3) — (14.5). (14.7), характеристики н сура в-
вешенности нружины блока вариатора хода
комбайна СК-5М «Нива» при различных фр
сведены в таблицу по форме
ф=фо. рад А. м п, мин 1 t, м R, м Дст- г’м Мд, г-м2 а,°
43.982 (7 витков) 0,335 912 0,0261 0,0879 0 1,696 0
0,371 2100 0,0210 0,0882 0 1,374 0
40,743 (6,484 витка) 0.335 912 0,0223 0,0881 18.627 0 0
0,371 2100 0.0168 0,0884 18,743 0 0
410
Балансировка типовых изделий машине- и приборостроения
Конструкция пружины блока с <ро =
= 40,743 рад является рациональной, так как
обладает лишь главным вектором дисбалансов,
устраняемым при статической балансировке
блока в сборе с пружиной.
14.5. БАЛАНСИРОВКА ВОЗДУШНЫХ
ВИНТОВ
Одним из источников вибраций на са-
молете является воздушный тяговый винт
турбовинтового двигателя (ТВД). Причи-
ной возбуждения вибраций является сила,
возникающая с частотой вращения от
статического, динамического и аэродина-
мического дисбалансов винта. Статический
дисбаланс винта возникает из-за несовпа-
дения центра массы винта с осью враще-
ния. Так как воздушный винт можно рас-
сматривать почти как диск, то этот вид
дисбаланса является определяющим.
Динамический дисбаланс возникает
из-за несовпадения главной центральной
оси инерции винта с осью вращения ТВД.
Его можно представить, если рассмат-
ривать воздушный винт не как плоский
диск, а как объемное тело, отдельные части
которого вдоль оси вращения имеют свои
статические дисбалансы. Так, если центры
масс лопастей винта не лежат в одной
плоскости из-за погрешностей изготовле-
ния, сборки и разницы в жесткостях, а
следовательно, и в деформациях во время
работы ТВД, то имеет место динамический
дисбаланс.
Статический и динамический дисбалан-
сы при достаточно жесткой конструкции
лопастей не зависят от скорости полета
самолета, его высоты и режима работы
ТВД. Но при недостаточной жесткости они
зависят от указанных факторов.
Аэродинамический дисбаланс выра-
жается в том, что равнодействующие силы
тяги отдельных лопастей винта приложены
на разных расстояниях от оси вращения,
и поэтому равнодействующая силы тяги
всех лопастей может не совпадать с осью
винта. В результате этого создается из-
гибный момент, действующий в плоскости,
перпендикулярной плоскости вращения
винта.
На практике такой вид неуравновешен-
ности создается из-за наличия допусков
на геометрическое совпадение плоскостей
лопастей и на различие их угла установки
на собранном винте.
С увеличением высоты полета самолета
и уменьшением скорости снижается раз-
ность между силами тяги отдельных лопа-
стей и, следовательно, уменьшается вели
чина аэродинамической неуравновешен-
ности.
Все три перечисленных вида неурав-
новешенности создают силу и моменты,
вращающиеся с частотой вращения воз-
душного винта в направлении, совпадаю
щем с вращением винта, и вызывают
круговое (точнее, по замкнутой кривой)
движение установки двигатель — стенд
(или двигатель) - мотогондола, причем
наиболее серьезное возбуждение создается
в тяге лопастей.
Все перечисленные виды неуравно-
вешенности вызывают колебания с часто-
той вращения винта или с частотой первой
винтовой гармоники. Их воздействия могут
складываться или сводиться к минимуму
при помощи, например, балансировочного
груза.
Балансировка воздушных винтов на
самолетах и испытательных стендах при
наличии отметчика места. Для баланси-
ровки воздушных винтов на самолетах и
испытательных стендах применимы спосо-
бы, изложенные в гл 5. п. 5.4, причем в
данном случае эффективность всех мето-
дов повышается в связи с тем. что воздуш-
ный винт можно рассматривать почти как
плоский диск, для которого возможна ста-
тическая балансировка в динамическом
режиме
До начала уравновешивания осущест-
вляют дооборудование ТВД (рис. 14.20):
устанавливают вибродатчики-.?, 4 в конт-
рольных точках двигателя и на носке
редуктора, на втулке винта закрепляют по-
движную пластину отметчика места Д а на
ближайшем торце редуктора — неподвиж-
ную пластину 2, выбирают места для креп-
ления пробных грузов.
Балансировка воздушных винтов
411
Места установки пробных грузов опре-
деляются конструкцией воздушного винта,
точнее его втулкой и способом соедине-
ния с валом винта Пробными и балансиро-
вочными грузами могут быть крепежные
гайки различной высоты, с помощью ко-
торых соединяют втулки винта с валом,
металлические цилиндры, закрепляемые на
шпильках втулки, и т. д.
Неподвижную пластину 2 емкостного
датчика крепят в плоскости, совпадаю-
щей с плоскостью установки контрольного
вибродатчика для облегчения расшифров-
ки записей колебаний.
Предварительно для конкретного воз-
душного винта и ТВД выбирают место
на корпусе двигателя, для которого зависи-
мость вибраций от величины установлен-
ного на воздушный винт груза наиболее
близка к линейной. В это место устанав
ливают вибродатчик и ио его показаниям
осуществляют балансировку.
Для проверки линейности внешней виб-
рации двигателя от величины установлен-
ного груза проводят опыт на нескольских
экземплярах ТВД одной конструкции и
строят зависимости 2А и гр от G (рис.
14.21, а, б).
Несмотря на то, что углы наклона
прямых 2A = f((G) различны для каждой
конкретной машины, прямые <р = Д (G), па-
Рис. 14.21. Зависимость амплитуд и фаз виб-
раций от величины груза G:
1 4 номера JRiidJlBui dTe.ieii
рал дельные оси G, расположены на разных
расстояниях от этой оси, препятствий для
использования линейных соотношений при
балансировке нет.
Аппаратура для записи вибраций
должна содержать фильтры для выделе-
ния лишь колебаний с частотой ш рвой вин-
товой гармоники. Процесс балансировки,
основанный на линейных соотношениях,
проводят в следующей последсзательно-
сти:
запускают двигатель, на рабочих обо
ротах записывают вибрации Ai и сигнал от
отметчика места <р(;
в произвольном по углу месте устанав-
ливают пробный груз и повторяют выше-
указанные измерения, определяя А?, <р?;
обрабатывают результаты.
412
Балансировка типовых изделий машино- и приборостроения
Рис. 14.22. Векторные построения при опре-
делении уравновешивающего груза
Из вектора вибрации Д2 (рис. 14.22)
вычитают вектор Ль полученный при запи-
си вибраций с исходной неуравновешен
ностью. Вектор А2— Л[ дает величину виб-
рации от установленного груза
Р^Р^^/А.-А,).
Место установки уравновешивающего
груза находят по разности фаз между
положением Р и вектором вибраций
Л2—Л[ от Рпр, как и при балансировке
роторов
Учет нелинейности при уравновешива-
нии воздушных винтив.
В случае, когда снятые зависимости
амплитуд и фаз вибраций двигателя под
действием установленного на винт груза
нельзя считать линейными,этот способ не
дает требуемого снижения вибраций
по первой винтовой гармонике. Поэтому
операцию балансировки следует повто-
рить, приняв пуск с пробным грузом за
исходный, а пуск с уравновешивающим
грузом за пуск с пробным, т. е. необходимо
воспользоваться рекомендациями, изло-
женными в гл. 1, п. 1.6, о балансировке
при нелинейных соотношениях.
Для повышения точности и сокращения
времени, затрачиваемого на балансировку
[16], предложен следующий способ: проб-
ный груз крепят не в произвольном месте,
а в таком, где вибрации ТВД становятся
линейными в такой же степени, как и
вибрации двигателя от собственной не-
уравновешенности винта. Чтобы отыскать
это место, измеряют вибрации при обыч-
ных запусках двигателя без пробного груза
и с пробным грузом, установленным в
любом месте по окружности винта На
основании данных, полученных при этих
двух запусках, определяют угол, на кото-
рый следует сместить данный пробный
груз, чтобы при новом запуске двигателя
с этим грузом его вибрации были равны
вибрациям двигателя от собственной не-
уравновешенности винта. На рис. 14.23
показано построение векторных треуголь-
ников, из которых ДОД[Д2 построен по
известным векторам вибраций A i и Д2. Этот
треугольник перестраивают в треугольник
ОД3Д1, у которого Аз~А[.
Для определения положения вершины
Аз достаточно найти точку пересечения
двух окружностей, проведенных радиусами
Аз—• А. из точки О и Д3 —Д| = Д2—Д, из
точки Д[. Чтобы положение пробного груза
соответствовало построению треугольника
ОД3Д1, необходимо .пробный груз Рц по
вернуть на угол Д3Д1Д2. т. е. на угол по-
ворота вектора вибраций Д2 — А1 до совпа-
дения с вектором А3—Д|. Новое положе-
ние пробного груза обозначено буквой
Р12- Затем записывают вибрации двигателя
с пробным грузом Р12 и но данным за-
пуска без пробных грузов и с пробным
грузом Рц окончательно определяют из
векторного треугольника место располо-
жения неуравновешенности на воздуш-
ном винте.
При подсчете величины уравновеши-
вающего груза пренебрегают изменением
степени затухания при почти равных ви-
Рис. 14.23. Построение векторных тре-
угольников
Балансировка воздушных винтов
413
брациях Л| и Дз и считают, что изме-
нение амплитуды колебаний по амплитуд-
ной характеристике линейно.
Балансировка без отметчика места.
Этот метод, основанный на предположении
о линейности системы, позволяет опреде-
лить положение и величину уравновеши-
вающего груза только по значениям ампли-
туд колебаний носка редуктора. При этом
требуются два пробных пуска двигателя.
Пусть амплитуда колебаний корпуса
ТВД (носка редуктора) при запуске
с исходной неуравновешенностью и ампли-
туда Аг при запуске с пробным грузом,
установленным в место Рц. Переставим
этот груз в другое место Р|2 (на прежнем
радиусе), как это было ранее в методе
трех пусков, но лучше под углом 90° к
своему первоначальному положению. При
этом получают новую величину вибраций
Аз. Полученных данных достаточно, чтобы
с помощью несложных построений опре-
делить необходимую величину и место
установки уравновешивающего груза (рис.
14.24).
Пусть известны направления векторов
ДЬЛ2, Аз. Строим вектор A i в горизонталь-
ном направлении и относительно него от-
мечаем место установки пробных грузов
Рис. 14.24. Векторные построения при урав-
новешивании без отметчика места
Ри, Р\г- Далее проводят окружности с
центром в точке О, радиусы которых в
определенном масштабе равны величинам
Аг и Аз, откладывают из центра окруж-
ности О векторы Аг и Аз, концы которых
соединяют с концом вектора А|. Векторы
Аг — Ai и Аз — А1 равны по величине, так
как выражают приращение вибраций, по-
лученное под действием одного и того же
груза и, кроме того, они перпендикулярны
друг к другу вследствие того, что положе-
ние пробного груза изменилось на 90°
Для нахождения места установки
уравновешивающего груза нужно найти
угол, на который следует повернуть груз
Р12 так, чтобы вектор вибраций от него
был направлен противоположно вектору
Д(. Как это видно из рис. 14.24, вектор
Аз — Ai, а следовательно, и груз Рю
необходимо повернуть на угол А3А1О в
сторону вращения винта, а вектор Аг— Ai,
а значит и груз Рц,— на угол Д2Д1О также
в сторону его вращения.
Величину уравновешивающего груза
находим по формуле
р — р _ о
*УР — ^лр~~ — Pnv ~~----=- .
Аг-At 1 Л, — А,
Процесс балансировки осуществляют в
следующей последовательности: сначала
(при первом запуске) выполняют вибро-
графирование ТВД на рабочей частоте
вращения с исходной неуравновешен-
ностью, затем (при втором запуске) с
пробным грузом Рц и далее (при третьем
запуске) с пробным грузом Р|2, смещен-
ным на 90° по отношению первого положе-
ния в сторону вращения винта.
На основании этого строят векторные
треугольники для определения величины и
места установки уравновешивающего гру-«
за. Для этого выбирают масштаб и прово-
дят окружности радиуса А2 и Аз- Далее
откладывают вектор вибраций с исходной
неуравновешенностью от конца кото-
рого (рис. 14.24) под прямым углом строят
треугольник. Поворачивая треугольник
вокруг конца вектора А| (вокруг вер-
шины прямого угла), находят такое поло-
414
Балансировка типовых изделий машино- и приборостроения
жение, при котором оба катета пересекают
окружности А? и А3, причем расстояние
от вершины треугольника до точек пере-
сечения с окружностями А? и Аз должны
быть одинаковы; соединяя точку О с А% и
А3 и точку Л| с и А3, получают тре-
угольники, из которых находят искомые ве-
личины.
На рис. 14.24 показаны два возможных
построения относительно вектора Л|, кото-
рые являются зеркальными отображения-
ми друг друга. Для исключения ошибки в
определении места уравновешивающего
груза следует обращать внимание на ход
перестановки пробного груза в со-
ответствии с вибрацией ТВД.
Из рис. 14.24 видно, что перестановка
пробного груза Ри в положение Рц против
хода часовых стрелок приводит к умень-
шению вибраций ЛзСД! и повороту
Лг — Л] (для построений, выполненных
сплошными и штриховыми линиями) в
таком направлении, чтобы при дальнейшем
его повороте в том же направлении на
угол A3AtO= он оказался противо-
положно направленным вектору исходных
вибраций Ль
Следовательно, поворот пробного гру-
за Р]2 против хода часовых стрелок на
угол A3AiO=<^.a даст положение урав-
новешивающего груза.
Если же произошла ошибка в опреде-
лении места установки уравновешивающе-
го груза и вибрации возросли, то груз
перемещают на 180°.
14.6. БАЛАНСИРОВКА КОЛЕСНЫХ ПАР
Особенности технологии балансиров
ки колесных пар впервые обоснованы
В. А. Щепетильниковым. Эти особенности
определяются тем, что центром скоростей
колесной пары является точка ее касания
с рельсом, а центром ускорения - геомет-
рический центр обода колеса. Несмотря на
то, что балансировочные станки определя-
ют дисбаланс как несовпадение главной
центральной оси инерции ротора с осью
его вращения (геометрической'осью цапф),
балансировка колесных пар может произ-
водиться на обычных станках общего на-
значения с горизонтальной осью вращения,
оснащенных дополнительными бесконтакт-
ными датчиками, регистрирующими бие-
ния ободов колес.
Теоретические и экспериментальные
исследования показали {411, что при урав-
новешивании ротора относительно оси его
цапф инерционные параметры колебатель-
ной системы балансировочного станка
(массы и моменты инерции приводного ва-
ла, подвижных элементов опор) не оказы-
вают существенного влияния на точность
балансировки, а только уменьшают чувст-
вительность, что легко компенсируют по-
вышением коэффициента усиления и до-
бротности фильтров измерительной систе-
мы. При балансировке колесных пар имеет
место обязательное несовпадение геомет-
рической оси, проходящей через центры
ободов качения и геометрические оси цапф.
В этом случае даже при идеальном урав-
новешивании колесной пары относительно
обода качения на колебательную систему
балансировочного станка действуют силы
дисбаланса, пропорциональные относи-
тельному смещению указанных выше осей.
Эти силы вызывают колебания опор с ам-
плитудами, зависящими не только от си
ловой нагрузки, но и от инерционных ха-
рактеристик балансировочного станка, ко-
торые должны соответствовать аналогич-
ным характеристикам вагонной буксы.
Если такого соответствия нет, то опреде-
ление корректирующей массы и места ее
установки на колесной паре следует про-
изводить с введением постоянной для дан-
ного станка и данного типа колесной
пары поправки
Схема установки колесной пары на
балансировочном станке показана на рис.
14.25. Колесную пару 2 цапфами устанав-
ливают в опоры / и 4 станка. Для изме-
рения биения ободов колес станок оснащен
бесконтактными датчиками 5 и 6 Враще-
ние осуществляется от приводного вала
3, масса которого пренебрежимо мала по
сравнению с массой колебательной систе-
мы ротор—опоры.
Балансировка колесных пар
415
Рис. 14.25. Схема установки колесной пары
на опоры балансировочного станка
На малой частоте вращения (в 5—
10 раз ниже частоты собственных колеба-
ний системы ротор —опоры) датчиками 5
и 6 измеряют биение ободов колес от-
носительно оси цапф О и определяют век-
торы ё| 2 (рис. 14.26) смещения геометри-
ческих центров ободов О2 относительно
геометрических центров цапф. На рабочей
частоте вращения по колебаниям датчиков
опор определяют векторы ё^2 смещения
геометрических центров цапф О относи-
тельно центра инерции О(. Тогда искомый
радиус-вектор ё12 центра качения по отно-
шению к центру инерции вычисляют как
сумму векторов, т. е.
81.2= «1.2 + ^1 «2
Это равенство справедливо, если инер-
ционные характеристики каждой из опор
станка равны инерционным характеристи-
кам вагонной буксы. В противном случае
при слагаемом ё\,2 должен быть введен
коэффициент, учитывающий различия в
массовых и инерционных характеристиках
установки колесной пары на опоры станка
и в вагонных буксах.
Для измерения биения ободов колес
применяют бесконтактные датчики, на-
пример индуктивные, емкостные, токових-
ревые. Так, в станке мод. МС991 при-
менен индуктивный датчик, основой кото-
рого является трансформатор с замыка-
нием магнитного силового потока через
обод балансируемого колеса Первичная
обмотка трансформатора питается от спе-
рме. 14.26. Векторная
диаграмма расчета дис-
балансов колесных пар:
О геометрические центры
цапф; ()i- центр инерции.
Oj — геом етри ческис центры
ободов
циального генератора переменным током
частотой 1800 Гц. Изменение зазора между
ободом колеса и трансформатором вызыва-
ет амплитудную модуляцию несущей час-
тоты во вторичной обмотке Детектиро-
ванием на выходе выделяют переменный
сигнал, пропорциональный амплитуде ра-
диального биения обода с частотой вра-
щения колесной пары, который поступает
в измерительную систему балансировочно-
го станка.
Использование современных измери-
тельных систем позволяет предварительно
запомнить векторы ё\2 и получить искомые
векторы ё),2 непосредственно на индикато-
рах станка. Другой метод учета векторов
ё),2 заключается в использовании системы
электрического эталонирования, при кото-
ром во время медленного вращения колес-
ной пары специальными органами настрой-
ки сводят к нулю показания индикаторов
станка. Тогда при вращении на рабочей
частоте измерение дисбаланса осуществ-
ляют относительно О2, т. е. индикаторы
дисбаланса показывают непосредственно
смещение геометрического центра О2 обо-
да колеса относительно центра инерции
Oi. Следует иметь в виду, что применение
описанного приема возможно только в
станках, имеющих системы эталонирова-
ния.
Колесные пары возможно также балан-
сировать, используя в качестве датчиков
дисбаланса бесконтактные датчики коле-
баний обода. В этом случае успокоение
обода характеризует совмещение оси инер-
ции колесной пары с геометрической осью
поверхностей качения.
Техническая характеристика станка
для балансировки колесных пар мод.
МС991 приведена в гл. 7.
Опыт эксплуатации таких станков по-
казал, что для получения достаточной
точности балансировки следует обеспечить
равенство между собой масс подвижных
деталей опор балансировочного станка и
букс. Влиянием массы и моментов инерции
приводного вала станка можно пренебречь,
при этом погрешность балансировки не
превысит 3% наблюдаемого значения.
416
Балансировка типовых изделий машино- и приборостроения
14.7. БАЛАНСИРОВКА УЗЛОВ
ТЕКСТИЛЬНЫХ МАШИН
В текстильных машинах применяют
ряд узлов и механизмов, балансировка
которых имеет существенные отличия
от балансировки деталей общего машино-
строения. На рис. 14.27 приведена класси-
фикация балансируемых узлов текстиль-
ных машин, отличающихся друг от друга
по массе подвижных частей, по скоростным
режимам, по конструктивному признаку
и т. п. Все балансируемые механизмы раз-
деляют на две группы: роторные (стержне-
вые) и кулачковые.
Роторные узлы (или системы) различа-
ют быстроходные (частота вращения выше
20-103 мин-1) и тихоходные (частота
вращения ниже 2- 10 3 мин ’).
Балансировка быстроходных узлов.
Характерными представителями быстро-
ходных узлов являются вьюрковые меха-
низмы, крутильно-формирующие механиз-
мы, веретена с различными приводами.
Вьюрковый механизм представляет
собой рабочий орган машины, производя-
щей эластичную пряжу. Вьюрок 3-^-полая
трубка (рис. 14.28, с), в средней части
которой имеются утолщения. Такой вью-
рок магнитной системой 4 (рис. 14.28, б)
прижимается к фрикционным дискам 2,
которые и приводят его во вращение.
Диски приводятся во вращение с помощью
ремня /. Частота вращения вьюрка до-
ходит до 10-105 мин-1. Режим работы
вьюрка непрерывный, габаритные размеры
и масса незначительные. Число вьюрков на
одной машине доходит до 200 шт. На-
личие остаточной неуравновешенности у
вьюрка приводит к росту износа упругого
покрытия приводных фрикционных дисков,
резкому возрастанию шума, увеличению
потребляемой мощности привода, а также
приводит к вылету вьюрка из магнитной
системы. Вьюрки балансируют на специ-
альных малоразмерных станках, которые
рассчитаны на роторы с массой 0,001 —
0,1 кг. Частота вращения вьюрка при
балансировке (3—60) Ю3 мин"1. Точность
балансировки составляет 0,5—1 мкм. Кор-
ректировку массы выполняют удалением
материала с торцов
Крутильне-формирующий механизм
п невмопрядильных машин является их
основным рабочим органом. Диаметр чаш-
ки механизма достигает 68 мм, а ее масса
55 г (рис. 14.29). Масса всего узла в
сборе 200 г. Эксплуатационная частота
вращения достигает (30—60)1О3 мин-1.
Конструктивной особенностью такого узла
является отсутствие амортизационных уст-
ройств и внутреннего кольца шарико-
подшипника. Беговая дорожка для шари-
ков выполнена непосредственно на валу
шпинделя. Балансировка может осуществ-
ляться лишь в сборе всего узла, включая
и корпус. Точность балансировки 0,2 мкм.
Корректировка масс выполняется удале-
нием материала в плоскостях коррекции
А—А и Б- Б. Применяют специальные
балансировочные станки. На каждой пря-
дильной машине имеется до 200 шт. таких
механизмов.
Веретена с механическим и электри-
ческим приводами, центрифуги. Одним из
наиболее массовых быстровращающихся
узлов текстильных машин является вере-
тено с механическим приводом, число кото-
рых на одной прядильной машине может
достигать 360. Выпуск т^аких веретен носит
массовый характер. Йосадочная часть
шпинделя веретена зависит от типа пря-
женосителя (шпуля, катушка, металличе-
ский патрон, колоколообразная насадка,
металлическая насадка). Посадочная
часть веретена расположена консольно
(рис. 14.30). Массы, которые крепятся
на шпинделе веретена, достигают 5 кг,
есть тенденция к их увеличению. Частоты
вращения веретен во время работы на-
ходятся в пределах (3.5 —18) 103 мин"1.
На эти длинные, тонкие двухопорные кон-
сольные шпиндели, работающие в верти-
кальном положении, многократно надева-
ют новые плохо сбалансированные шпули,
катушки или бобины. Посадку шпуль стро-
го не фиксируют. На вал действует усилие
оператора-ткача при зажиме шпули. Рабо-
та таких станков — непрерывная трехсмен-
14 Зак 1641
Рис. 14.28. Вьюрковый механизм
Балансировка узлов текстильных машин
418
Балансировка типовых изделий машине- и приборостроения
Рис. 14.30. Посадочные части веретен с механическим приводом:
1— посадочная часть шпинделя; 2 — шпуля, 3 — катушка, 4- копе; 5 — бобина, 6—бумажный патрон
ная. Поэтому точность балансировки таких
узлов должна быть высокой. В конструк-
ции узлов предусмотрены демпфирующие
устройства, а также использован эффект
самоцентрирования. Уровень колебаний
веретен стремятся снизить и конструктив-
ными мероприятиями.
Веретена с электрическим приводом
применяют при производстве химических
волокон. Рабочие частоты вращения вере-
тен лежат в пределах (8—9) 103 мин-1.
В таких веретенах съемную чашку насажи-
вают на насадок, жестко закрепленный
на гибком консольном шпинделе, вращаю-
щемся на двух подшипниках. Для огра-
ничения колебаний при разгоне веретена
в верхней части шпинделя предусмотрен
демпфер-ограничитель.
Массивный корпус электроверетена
устанавливают на резиновых амортизато-
рах. Масса чашки без волокна 1,9—2,2 кг,
а с намотанным волокном — 2,5—3,5 кг.
Балансировка узлов текстильных машин
419
Втулку и ротор балансируют на станках
типа ДБ-10. Однако зазор при посадке
чашки снижает эффект балансировки.
Поэтому применяют и конструктивные ме-
тоды для снижения вибрации Имеются
веретена с невращаюшимся шпинделем.
Патрон с волокном насаживают на длин-
ную металлическую насадку, которая вра-
щается на двух шарикоподшипниках. Сни-
жение вибрации в данном случае дости-
гается за счет точной динамической ба-
лансировки насадки на станках типа
ДБ-10, а также конструктивными способа-
ми.
Исследование показало, что в рабочем
диапазоне частот вращения может быть
до трех критинеских скоростей. Для сниже-
ния вибрации осуществляют контроль
съемных деталей в статических и динами-
ческих условиях. В статических условиях
контролируют геометрические параметры
(биение поверхностей намотки, посадоч-
ных мест), а в динамических условиях —
динамическую неуравновешенность на
специальных устройствах с отбраковкой
шпуль с повышенным дисбалансом. Конт-
роль ведут путем сравнения с эталоном.
При этом используют найденные связи
между геометрическими параметрами и ви-
брацией веретена. Практика показала, что
у веретен, работающих с чашками, имею-
щими остаточный дисбаланс до 50 г-см,
вибрация увеличивается более интенсивно.
Считают приемлемым остаточный дис-
баланс чашек 50 г - см.
Балансировка тихоходных вращаю-
щихся узлов. Рогульки являются ОДНИМ из
основных рабочих органов ровничных ма-
шин хлопчатобумажного производства и
для лубяных волокон. Размеры рогулек
стандартизованы. Длина рогулек в пре-
делах 230—360 мм (см. рис. 14.31), шири-
на вилки в пределах 75—160 мм, масса
400—900 г, частота вращения 950—
1700 мин1. Рогулька приводится во вра-
щение с помощью длинного двухопорного
консольного веретена, на котором она
свободно фиксируется. К динамической ба-
лансировке рогулек предъявляют доста-
точно жесткие требования. Балансировоч-
Рис. 14.31. Ро-
гулька
ная технологичность рогулек невысокая,
так как на ней имеется подвижная лапка,
имеющая свое положение относительно оси
вращения, что изменяет геометрию масс.
Балансировку осуществляют при среднем
положении лапки. Кроме* того, наличие
лапки и асимметрии ветвей располагает
неуравновешенные силы инерции и их мо
менты не в одной плоскости. Поэтому ком-
пенсация дисбаланса в каждой из пло-
скостей коррекции (/- / и II—II) может
быть только частичной, когда уравно-
вешиваются силы и моменты, действующие
в средней плоскости. Сама рогулька—не
жесткое тело, поэтому при балансировке
и работе наблюдается деформация вет-
вей. Во время работы рогулька изменяет
свое положение относительно оси враще-
ния шпинделя при каждом съеме и уста-
новке (что дрлается довольно часто), а
это нарушает начальный дисбаланс. Кор-
ректировку масс осуществлять при балан-
сировке рогулек практически негде. Это
определяет весьма низкую балансировоч-
ную технологичность рогульки, которую
балансируют лишь статически. Корректи-
ровку мйсс производят удалением ма-
териала с балансовой ветви или ее от-
гибанием. Контроль остаточных дисбалан-
сов и отработку рогулек по указанному
параметру осуществляют на станке ДПР-1
путем сравнения с эталонной рогулькой.
Забракованные рогульки проходят повтор-
ную балансировку
Практика показала, что конструкция
рогулек позволяет лишь частично снизить
дисбаланс до 8—10 г-см. В общем случае
14*
420
Балансировка типовых изделии машино- и приборостроения
Рис. 14.32. Схема неуравнове-
шенных сил рогульки
вектор остаточного дисбаланса С (рис.
14.32) расположен под некоторым углом
<р к плоскости 1—I ветвей рогульки. Этот
вектор С можно разложить на две со-
ставляющие: одну Сп, лежащую в плоско-
сти ветвей рогульки, другую Ct, находя-
щуюся в плоскости, перпендикулярной к
средней плоскости ветвей. Корректировкой
масс можно компенсировать составляю-
щую за счет чего удается снизить
величину дисбаланса в 3—5 раз. Положе-
ние лапки А влияет на величину дис-
баланса рогульки. Балансировка рогульки
при среднем положении лапки обеспечи-
вает изменение дисбаланса ±(7—8) г • см
при изменении положения лапки
Барабаны чесальных машин являются
ответственными узлами машин текстиль-
ного производства. К их изготовлению и
балансировке предъявляют повышенные
требования. На одной машине обычно
имеются четыре барабана Для баланси-
ровки применяют станки типа 9А734-4 и
МС-901-27, на которых балансируют дета-
ли массой от 10'до 100 кг. Балансировку
барабанов осуществляют при частоте вра-
щения 800 мин-1. В процессе эксплуатации
возможно изменение остаточного дис-
баланса в случае замены обечайки бараба-
на. Качество балансировки влияет на чис-
ло обрывов на прядильных машинах. При-
меняют также специальные устройства,
позволяющие осуществлять динамическую
балансировку непосредственно на месте в
производственных условиях (в собствен-
ных подшипниках). В этом случае пло-
скости коррекции близко расположены к
опорам, поэтому взаимным влиянием дис-
балансов плоскостей пренебрегают. Тяже-
лое место определяют стробоскопом, а ве-
личину дисбаланса, например, методом
трех пусков.
Приводные валы прядильных машин.
Такие валы собирают из отдельных секций
длиной до 1 м. Общая длина приводных
валов достигает 15—18 м. На каждой сек-
ции имеются шкивы диаметром 200—
250 мм и массой 1—1,5 кг. Частота враще-
ния такого вала (10—18) 102 мии~’. Балан-
сируют валы различными методами. Вна-
чале шкивы балансируют статически, а
затем балансируют секции в сборе на стан-
дартных балансировочных станках. Осо-
бенностью является балансировка длин-
ных многоопорных валов, соединенных
жесткими муфтами непосредственно иа ма-
шине.
Стержневые и кулачковые механизмы
в текстильных машинах находят широкое
применение. Например, батанные механиз-
мы ткацких станков с частотой вращения
Рис. 14.33. Схема стайка ДПР-1
Балансировка узлов текстильных машин
421
главного вала 250—400 мин~', многозвен-
ные механизмы гребнечесальных машин,
основовязальные машины с частотой вра-
щения главного вала (8—20) 102 мин-1,
эксцентриковые механизмы уплотнения
ровницы, работающие при частоте враще-
ния главного вала (3—5)102 мин-1 и др.
Масса батана может составлять 100 кг.
Точная балансировка по главному вектору
и главному моменту данных механизмов
является сложной задачей и сопровож-
дается введением дополнительных меха-
низмов в масс. В ряде случаев ограни-
чиваются балансировкой главных валов
и частичной балансировкой по главному
вектору механизмов. Поэтому широко при-
меняют виброизмеряющие устройства раз-
личного типа.
Рассмотрим для примера работу стан-
ка ДПР-1 для проверки дисбаланса ро-
гулек ровничных машин и их отбраковки,
если остаточный дисбаланс выше допусти-
мого.
От электродвигателя / (рис. 14.33)
через фрикционную передачу вращение пе-
редается на контрпривод 2. Основной
частью станка является жесткий вращаю-
щийся вертикально расположенный шпин-
дель 4, опирающийся на шарик 3, уста-
новленный на торце вала контрпривода и
получающий от него вращение с помощью
эластичной муфты. В верхней части шпин-
деля имеется шарикоподшипник 5, смон-
тированный в ползуне, в который с обеих
сторон упираются цилиндрические пружи-
ны. С движущимся ползуном связан ме-
ханизм оптического индикатора, с по-
мощью которого определяют колебания
шпинделя. Проверяемую рогульку 6 уста-
навливают на верхней части шпинделя,
который вместе с ней вращается с рабо-
чей скоростью.
Шпиндель совершает вынужденные
колебания с амплитудой, пропорциональ-
ной моменту от неуравновешенных сил от-
носительно точки качания шпинделя. Ре-
жим работы станка выбирают близким к
критическому, что повышает его чувст-
вительность. Перед проверкой на ста-
нок устанавливают эталонную рогульку с
жестко закрепленной лапкой, предвари-
тельно сбалансированную и имеющую
строго заданный остаточный дисбаланс,
не превышающий допустимый. Произво-
дительность проверки на станке состав-
ляет 600—700 шт. деталей в смену.
422
Описания и тексты программ
ПРИЛОЖЕНИЯ
ПРИЛОЖЕНИЕ П.1
ОПИСАНИЕ ПРОГРАММЫ «СТАТИЧЕСКАЯ БАЛАНСИРОВКА РАБОЧЕГО КОЛЕСА
ЛОПАТОЧНОЙ МАШИНЫ РАСПРЕДЕЛЕНИЕМ ЛОПАТОК ПО ПАЗАМ ДИСКА»
Программа предназначена для расчета
на ЭВМ типа ЕС распределения комп-
лекта рабочих лопаток по пазам диска
с заданным значением дисбаланса.
Программа предусматривает следую-
щие возможности: распределение комплек-
та лопаток по круговой диаграмме; подбор
лопаток с обеспечением заданного значе-
ния дисбаланса каждого комплекта; ком-
пенсация исходного статического дис-
баланса ротора распределением лопаток.
Ограничением максимальное число за-
даваемых лопаток, шт... 300.
В колоду исходных данных включа-
ются следующие перфокарты (ПК):
Карта № 1 содержит информацию:
1—3 Шифры изделия (произвольная
символьная информация, печатает-
ся в заготовке таблицы распределе-
ния лопаток);
4—5 Номер ступени (например, 01);
6—8 Число лопаток комплекта (на-
пример, 099);
9—13 Наименьшее допустимое -значение
статического момента (или массы в
десятых долях грамма),
19—23 Номинальный радиус положения
центра масс лопаток относитсяfa-
но оси колеса в мм. При подборе
по статическим моментам данную
величину не указывать.
Карта № 2 содержит информацию
1—3 Код расчета (любое число, кроме
ООО и 009, где 000—расчет дис-
баланса порции лопаток, 009—за-
мена одного комплекта другим);
4—6 Число заданных лопаток;
7— 11 Исходный дисбаланс диска в г • мм
(допускается указывать вес урав-
новешивающего груза в десятых
долях грамма; например, 00325,
если вес груза 32,5 г);
12—14 Номер кода легкого места;
15—19 Радиус установки уравновеши-
вающего груза в мм.
Если исходный дисбаланс указан
в г-мм, то данную величину ука-
зывать нельзя.
Набор ПК с характеристиками комп-
лектуемых лопаток перфорируется, начи-
ная с первой колонии ПК следующим
образом: три колонки ПК — номер лопатки;
пять колонок—статический момент в г-мм
(или масса в десятых долях грамма).
На каждой ПК перфорируются харак-
теристики 10 лопаток. Последняя ПК
может быть неполной.
При замене одного комплекта другим
в массив исходных данных (после карт
№ 1 и № 2) вкладывается сначала набор
ПК с характеристиками заменяемого комп-
лекта, затем перфокарты с характери-
стиками заменяющего комплекта, в этом
случае число задаваемых лопаток должно
быть равно числу лопаток в комплекте.
Характеристики лопаток каждого ком-
плекта перфорируются с начала новой ПК-
Спецификация идентификаторов вы-
ходных параметров программы дана в
табл. П.1.1.
Программа <Статическая балансировка колеса лопаточной машины>
423
Таблица П.1.1
Спецификация идентификаторов выходных параметров
Идентификатор мас- сива с указанием размерности Инженерное обозначение параметра Размерность физической величины Содержательное наименование параметра (входного)
KI — — Шифр изделия
КС — Номер ступени
к — — Номер комплекта
т — “— Номер паза лопатки
МН (300) — — Массив номеров лопаток
С(300) 1 г*мм Массив статических моментов лопаток
S2 > , D г-мм Дисбаланс позиции лопаток
м — — Номер паза легкого места
СК (100) — — Массив номеров лопаток в комплекте
R1 I Г’ММ Наименьшее допустимое значение статмомента
R2 1 Г'мм Наибольшее допустимое значение статмомента
R . г ММ Номинальный радиус положения центра масс лопаток относительно оси колеса
FM — — Код расчета v
В рассмотренном примере расчета комплект лопаток состоит из 40 шт., наибольшее допус-
тимое значение статмомента 99999.
Таблица П.1.2
Пример расчета тестовой задачи
Ступень 4 Комплект 25
Номер паза Номер лопатки Статический момент лопатки Номер паза Номер лопатки Статический момент лопатки
1 10 2565.0 20 33 2556.0
2 19 2483-0 21 4 2483.0
3 27 2554.0 22 37 2548.0
4 13 2494.0 23 1 2502.0
5 6 2503.0 24 30 2544.0
6 17 2544.0 25 7 2504.0
7 8 2543.0 26 29 2542.0
8 34 2507.0 27 32 2512.0
9 2542.0 28 23 2540.0
10 11 2516.0 29 24 2517.0
11 14 2540.0 30 5 2540.0
12 20 2518.0 31 2 2519.0
13 21 2536.0 32 31 2535.0
14 15 2523.0 33 18 2525.0
15 35 2533.0 34 16 2532.0
16 28 2527.0 35 12 2529.0
17 25 2533,0 36 3 2532.0
18 19 22 36 2529.0 2531.0 37 26 2531.0
Дисбаланс равен 0,2 г «мм. Легкое место—паз 26
Комплект проверен(подпись)
424
Описания и тексты программ
Дополнительные возможности. Пакет
исходных данных может содержать произ-
вольное число вариантов исходных данных.
Никаких разграничений одного варианта
от другого не требуется.
Допускается подготовка перфокарт с
характеристиками лопаток другим спосо-
бом. В этом случае на ПК1, начиная с
колонки 24, должен быть указан формат
подготовки исходных данных в виде К (IN,
FM,L), где:
К—целое число без знака, равное числу
лопаток, характеристики которых пер-
форируются на ПК1;
N—целое число без знака, равное числу
колонок, отведенных для перфорации
номера лопатки;
М—целое число без знака, равное числу
колонок, отведенных для перфорации
массы или статического момента ло-
паток;
L—целое число без знака, равное числу
колонок (последние из колонок), в
которых перфорируется дробная часть
массы или статического момента; L
может быть равно 0, если статический
момент—целое число.
Например: 4 (13, F5,2)
При этом на каждую перфокарту массива
характеристик лопаток перфорируются ха-
рактеристики 4 лопаток, номер занимает
3 колонки, масса—5 колонок, из них 2
последние—дробная часть числа (десятые
и сотые доли грамма).
Ресурсы, необходимые для решения
тестовой задачи: Объем оперативной па-
мяти—5К, время работы программы—
30 с.
Пример расчета тестовой задачи про-
граммы приведен в табл. П.1.2.
ПРИЛОЖЕНИЕ П.2
ПРОГРАММА МК1. <РАСЧЕТ ДИСБАЛАНСОВ ДЕТАЛИ НА ОПРАВКЕ»
/. Общие сведения.
1.1. Программа предназначена для ав-
томатизации вычисления значения и угла
суммы нескольких дисбалансов (или эк-
вивалентной массы нескольких корректи-
рующих грузов), вычисления дисбаланса
детали, балансируемой на оправке с уче-
том дисбаланса оправки, биения посадоч-
ных поверхностей оправки относительно
балансировочных баз, а также дисбаланса
самой оправки.
1.2. Программа разработана для
микроЭВМ «Электроника» МК-56, БЗ-
34, МК-52, МК-61.
1.3. Исходные данные для вычислений:
Dt, ., Di,. . ,Dn [г • мм] —сумми-
руемые дис-
балансы;
или
т],...,ть...,тп [г]—массы корректиру-
ющих грузов, экви-
валентную массу
которых нужно вы-
числить;
(°]—углы расположения
дисбалансов или кор-
ректирующих масс (от-
, считываются против ча-
совой стрелки);
£)0о(т0<«1, фо<>—дисбаланс (корректи-
рующая масса) и его
угол при установке де-
тали на оправке в пер-
воначальном положе-
нии;
£>)8О‘>(т180°)>Ф)8О°—дисбаланс и угол
при установке дета-
ли ца оправке под
180° к первоначаль-
ному положению.
1.4. Результатами расчета по програм-
ме являются*.
£Мтх)« ФХ —суммарный дисбаланс
(эквивалентная масса) и
его угловое положение;
£)д(твд), фд—собственный дисбаланс
(корректирующая масса) де-
тали, балансируемой на оп-
Программа МК1 «Расчет дисбалансов детали на оправке»
425
равке,и его угловое положе-
ние;
Don, фоп—дисбаланс, вносимый оп-
равкой, и его угловое поло-
жение
2. Инструкция
2.1. Включить машину, установить
переключатель «Г-Р-ГРД» в положение
«Г», нажать клавиши F, ПРГ, ввести про-
грамму (см. п. 2.4), нажать клавиши
F, АВТ, В/О, Сх, С/П.
2.2. Контрольный пример. Нажимая
клавиши, выполнять расчет контрольного
примера 3, С/П («3»), О, С/П («О»),
4, С/П («4»), 90, С/П («0»), С/П («5»),
С/П («53,1301»), С/П («2,5»), С/П
(«126,8699»), С/П («2,5»), С/П («53,
1301»).
Если контрольный пример не решается,
проверить правильность введения про-
граммы.
Примечание. Здесь («...») число,
появляющееся на индикаторе машины в
результате счета по программе.
2.3. Работа.
2.3.1. Нажать клавиши В/О, Сх, С/П.
2.3.2. Вычислить сумму нескольких
дисбалансов Dj, ф£, вводя их значения и
углы:
£)j, С/П («Di»). <рь С/П («0»),...
Dn, С/П («£)„»), <рп. С/П («0»).
Введя последний дисбаланс, выпол-
нить: С/П («£>£»), С/П(«<р£»).
2.3.3. Дисбаланс детали фд
вычисляется при выполнении и. 2,3.1 и
2.3.2. Вместо Di, ф| вводится Do<=, фоъ а
вместо £)й, Ф2 вводится £)!80», ф18о°-
2.3.4. Дисбаланс оправки. Выполнить
п.2.3.1 и 2.3.3, затем С/П («Доп»), С/П
(«Фон»)-
2.4. Текст программы МК1 1
Адрес Команда Код
00 Сх ог
I хПЗ 43
2 хП4 44
3 х115 45
4 хП6 46
Продолжение табл. 2.4
Адрес Команда Код
5 С/П 50
6 хП1 41
7 С/П 50
8 хП2 42
9 F sin 1С
10 FBx 0
1 F cos 1Г
2 Пх1 61
3 X 12
4 ч-> 14
5 Пх| 61
6 X 12
7 В| ОЕ
8 ПхЗ 63
9 + 10
20 хПЗ 43
1 F’ 25
2 Пх5 65
3 .— 11
4 хП5 45
5 14
6 В| ОЕ
7 Пх4 64
8 + 10
9 хП4 44
30 14
1 Пхб 66
2 — 11
3 хПб 46
4 Сх ОГ
5 С/П 50
6 Fx = 0 5Е
7 06 06
8 ПхЗ 63
9 Пх4 64
40 ПП 53
1 78 78
2 хП7 47
3 С/П 50
4 ПхЗ 63
5 Пх4 64
6 Пх7 67
7 ПП 53
8 84 84
9 хП8 48
50 С/П 50
1 Пх5 65
2 Пхб 66
3 ПП 53
4 78 78
5 хП9 49
6 Пх5 65
7 Пхб 66
8 Пх9 69
9 ПП 53
60 84 84
1 хПа 4-
426
Описания и тексты программ
Адрес Команда Код
2 Пх9 69
3 2 02
4 13
5 хП9 49
6 С/П 50
7 Пха 6—
8 С/П 50
9 Пх7 67
70 2 02
1 — 13
2 хП7 47
3 С/П 50
4 Пх8 68
5 С/П 50
6 БП 51
7 00 00
8 Fx2 22
9 14
Продолжение табл. 2.4
Адрес Команда Код
80 Fx2 22
1 Ь 10
2 F< 21
3 В/О 52
4 — 13
5 F cos~* 1-
6 -ч-*- 14
7 Fx<0 5С
8 96 96
9 F’ 25
90 3 03
1 6 06
2 0 00
3 /-/ 0L
4 4- 10
5 14
6 14
7 В/О 52
ПРИЛОЖЕНИЕ П.З
ПРОГРАММА МК2. <БАЛАНСИРОВКА МЕТОДОМ АМПЛИТУД И ФАЗ»
1. Общие сведения
1.1. Назначение—автоматизация вы-
числений корректирующих масс и их уг-
ловых положений при динамической ба-
ланс ировке симметричных роторов на ме-
сте установки с помощью балансировоч-
ных комплектов УБП-1, ИВП-1, ПКВ-1,
БИП-7 и других, имеющих отметчик фазы.
1.2: МикроЭВМ—«Электроника» БЗ-
34, МК-56, МК-54, МК-52, МК-61.
1.3. Исходная информация—амплиту-
ды вибрации опор А п В балансируемого
ротора и их угловые положения относи-
тельно метки 0° на роторе.
2. Обозначения
А, В, VOCT, 1/доп, Упроб [мм-с_,| — векто-
ры вибрации: опор А. В, остаточной, до-
пустимой. от пробных грузов;
£ [мм-с”1 2]—сумма векторов вибра-
ций, характеризующая
статический дисбаланс;
Д [мМ’С-’] —разность векторов виб-
раций, характеризую-
щая моментный дис-
баланс;
<р[°] угловое положение век-
тора (груза);
п [мин“'[ —обороты балансировки;
mn Н —масса пробного груза;
М [т] — масса ротора;
г [мм]—радиус коррекции.
Индексы при £ и А: 0—исходное со-
стояние; 1—с парой пробных грузов; 2—
состояние после корректировки масс.
3. Подготовка к работе
3.1. Включить МК, нажать В/О, F ПРГ,
ввести программу, F АВТ, В/О, устано-
вить переключатель «Г-Р-ГРД» в положе-
ние «Г».
3.2. Решить контрольный пример:
ввести 0 П1, 90 ПЗ, 3 П2, 4 П4.
Выполнить: С/П («306.8699»), С/П
(«53.1301»), С/П («180»), («5»).
Примечание. Здесь («...») —ре-
зультат на индикаторе.
Программа МК2 «Балансировка методом амплитуд и фаз»
427
4. Работа
4.1. Ввести ф/, П1, фв ПЗ, П2, Во П4.
4.2. Выполнить: В/О, С/П, («...»), С/П,
(«...»), С/П, («...») «Угловое положение
пробных грузов» («О» — грузы софазны,
«180» — грузы в противофазе), «До» (или
«Хо»)- Записать До (или £о).
Примечание. До нового счета ре-
зультаты хранятся: ИП2, До ИП4,
Фе0 ИП1, фдо ИПЗ.
4.3. При необходимости рассчитать
пробные грузы.
4.3.1. Вычислить (или заранее вычис-
лить и набрать) коэффициент
К,
= / 3000 \ 2
“ 20г П )
для чего выполнить М, В|,20, ~ г, ,3000,
В|, п,4-, Fx2, X, («Кп»)-
4.3.2. Вычислить массу пробного груза.
Выполнить: набрать К„, В], ИП2 (для Хо),
или ИП4 (для \(i), X, («тп»).
4.4. Установить пробные грузы под
углом а к вектору Хо(До) начальной виб-
рации (а—определить экспериментально
по критерию лучшей сходимости из ряда
0°, 90°, 180°, 270°), измерить и записать
А» ,ФлР <Рвг А
4.5. Выполнить п.4.1 для Ai и Bi.
4.6. Если при выполнении п.4.4 были
поставлены софазные грузы, то выполнить
п.4.6.1, если грузы в противофазе, выпол-
нить п.4.6.2.
4.6.1. Выполнить: В/О, С/П («...»),
С/П, j»,-»-*,(«£t»), записать результа-
ты и перейти к выполнению п.4.7.1.
4.6.2. Выполнить: В/О, С/П («фд^»),
(«Д|»), записать результаты и перейти
к выполнению п.4.7.2.
Примечание. Результаты вычис-
лений по п.4.6.1 и 4.6.2 до нового счета
хранятся; Xj ИП2, Д( ИП4, ф2 ИП1,
Фд. ИПЗ. '
4.7.1. Если выполнен п.4.6.1, то ввести:
Фх1 П1, ПЗ, £[П2, ^о114.
4.7.2. Если выполнен п.4.6.2, ю ввести:
фд^Н, Ф^ПЗ, Л|П2, AJI4.
4.8. Выполнить: В/О, С/П («фсф»)
(угол сдвига фазы вибрации),**, («Vn»)
(вибрация от пробного груза). Записать
Fn и Фсф-
4.8.1. Вычислить фк—угол установки
корректирующих грузов от метки 0* (ф2о и
<рд0 из п.4.2 здесь обозначены фо, a—
из п.4.4, фсф—из п.4.8): фк— фо + а-|-
+фсф;
если а=0, то фк= фо + фсф-
Для этого выполнить: набрать фо, Bf,
а,В|, Фсф,-|-,+, («Фк»)
4.8.2. Вычислить массы корректирую-
щих грузов тк по формуле (20 и До из п.4.2
здесь обозначены Vo):
[г] ;
* II
для этого выполнить: набрать Vo, В|, /ип,
X, Vn, («тк»).
4.8.3. Установить корректирующие мас-
сы на ротор и произвести измерения
А» фд2» А, Фй2-
4.9. Для уравновешивания по другой
составляющей дисбаланса перейти к п.4.1,
приняв за исходные данные, полученные в
п.4.8.3.
4.10. Текст программы МК2
Адрес Команда Код
00 5 05
1 ПО 40
2 П5 45
3 кипо Г0
4 Fx=#0 57
5 19 19
6 В| 0E
7 кипо ГО
8 Fsin 1С
9 FBx 0
10 F cos 1Г
1 F’ 25
2 X 12
3 КП5 L5
4 P 25
5 X 12
6 КП5 L5
7 БП 51
8 03 03
9 5 05
20 no 40
1 ИП8 68
2 ИП6 66
3 — 11
4 КП5 L5
5 ИП9 69
6 ИП7 67
428
Описания и тексты программ
Адрес Команда Код
7 — 11
8 КП5 L5
9 ПП 53
30 67 67
1 ИПА 6-
2 ИПВ 6L
3 ИП4 64
4 ПП 53
5 74 74
6 С/П 50
7 ИП8 68
8 ИП6 66
9 + 10
40 КП5 L5
1 ИП9 69
2 ИП7 67
3 + 10
4 КП5 L5
5 ПП 53
6 67 67
7 ИПС 6С
8 ипд 6Г
9 ИП2 62
50 ПП 53
1 74 74
2 С/П 50
3 ИП4 64
4 ИП2 62
5 — И
6 Fx>0 59
7 64 64
Продолжение табл. 4.10
Адрес Команда Код
8 ИП4 64
9 1 01
60 8 08
1 0 00
2 БП 51
3 66 66
4 ИП2 62
5 0 00
6 С/П 50
7 Fx2 22
8 14
9 Fx2 22
70 + 10
1 F< 21
2 кпо L0
3 В/О 52
4 — 13
5 F cos"1 1
6 14
7 Fx<0 5С
8 86 86
9 F’ 25
80 3 03
1 6 06
2 0 00
3 — 11
4 /-/ 0L
5 14
6 ч—► 14
7 кпо L0
8 В/О 52
ПРИЛОЖЕНИЕ П.4
ПРОГРАММА МКЗ. < БАЛА НС МРОВКА В ТРЕХ ПЛОСКОСТЯХ»
/. Общие сведения
1.1, Программа предназначена для
автоматизации вычисления значений и уг-
лов установки корректирующих масс при
балансировке квазигибких роторов в трех
плоскостях коррекции на серийных балан-
сировочных станках.
1.2. Программа может быть реализова-
на на микроЭВМ «Электроника» МК-52,
МК-61.
1.3. Для работы с программой по каж-
дому типу ротора рассчитать коэффициен-
ты:
Кг>,. КВз. К
т,- т I
где тр, гп\, т2, т3 [г]—масса ротора
и условные дискретные массы ротора
в плоскостях коррекций;
Гь г2, г3 ' [мм | - радиусы коррек-
ции в соответствующей плоскости;
/ц 4, /з [мм] —расстояния от центра
масс (ЦМ) ротора до соответствующей
плоскости коррекции (/ отсчитывать от
координаты «0» в ЦМ влево со знаком
« + », вправо со знаком «—»). Массу рото-
ра условно разделить на три точечные
дискретные массы, расположенные в пло-
скостях коррекции так, чтобы
Программа МКЗ «Балансировка в трех плоскостях»
429
т 1 4 m2 4 тз = тр;
mill + т?12 + тз1з~ 0.
1.4. Исходные данные, используемые
при балансировке:
£)ст [г-мм], <рс [°]—главный вектор
дисбалансов ротора и его угловое поло-
жение;
MD [г - мм2], [°] главный момент
дисбалансов ротора и угловое положение
плоскости его действия.
Примечания. 1. Углы отсчитывать
против Часовой стрелки.
2. Вместо £)ст и MD можно использовать
—число делений индикатора при
измерении D„ и MD, а вместо коэффи-
циентов К, по п.1.3 рассчитать коэффици-
енты K'i—CKi, где C—D^JN^ См~
=^Md/Nm определяются при тарировании
станка по £)ст и
1.5. Результатами расчета являются:
mKl, ф1, тк2, фг, фз—корректирующие
массы в плоскостях коррекции и углы их
установки на роторе (против часовой
стрелки).
2. Подготовка к работе
2.1. Выполнить: Вкл, F, ПРГ, ввести
программу, F, АВТ, В/О, переключить
«Р-ГРД-Г» в положение «Г».
2.2. Контрольный пример
Ввести: 1 хП1, хП4, хПв, хПй, 0 хПс,
270, хПе.
Выполнить: В/О, 1, С/П («1,41»),
С/П («315»), здесь («...»)—резуль-
таты расчета на индикаторе).
2.3. Ввод данных в ППЗУ МК-52 про-
изводить согласно руководству по экс-
плуатации МК. Адреса для очистки памя-
ти, записи и считывания из ППЗУ:
программы 1000063;
коэффициентов К, 1012849.
Занесение в оперативную память и
запись в ППЗУ коэффициентов Ki произ-
водить после записи программы.
2.4. Ввод данных балансируемого рото-
ра
Ввести Кщ хП1, К mi хП4, хП2,
хП5, Кр3 хПЗ, КМз хПб.
3. Работа
3.1. При необходимости считать из
ППЗУ программу и коэффициенты К со-
гласно п.2.3, проверить их по кодам и
значениям.
3.2. Ввести £)ст хПв, MD хПй, фп хПс,
Фл) хПе (или вместо £)ст и MD ввести
Nd> Nm по п.1.4).
3.3. Выполнить: В/О. набрать I (но-
мер плоскости 1,2,3... в любой последо-
вательности), С/П («т,-»), С/П («ф,-»).
3.4. Для расчета по следующей пло-
скости коррекции выполнить п.3.3.
Примечание. До расчета по сле-
дующей плоскости результаты хранятся в
памяти
mi Пх7, ф,- Пх8.
3 Текст программы МКЗ
Адрес Команда Код
00 хПа 4—
1 Сх ОГ
2 хПО 40
3 хП9 49
4 КПха Г-
5 Пхб 6L
6 X 12
7 В| 0Е
8 Пхс 6С
9 ПП 53
10 46 46
1 Пха 6-
2 3 03
3 4- 10
4 хПа 4-
5 КПха Г—
6 Пхб 6Г
7 X 12
8 Bf 0Е
.9 Пхе 6Е
20 ПП 53
1 46 46
2 Bf 0Е
3 Fx2 22
4 ПхО 60
5 Fx2 22
6 10
7 21
8 хП7 47
9 С/П 50
30 13
1 F cos"' 1
2 хП8 48
3 ПхО 60
430
Описания и тексты программ
Адрес Команда Код
4 Fx<0 5С
5 42 42
6 3 03
7 6 06
8 0 00
9 Пх8 68
40 — 11
1 хП8 48
2 Пх8 68
3 С/П 50
4 БП 51
5 00 00
I. . .. 6 F sin 1С
Продолжение табл. 3.5
Адрес Команда Код 1
7 FBx 0 1
8 Feos 1Г
9 F> 25
50 X 12
1 ПхО 60
2 + 10
3 хПО 40
4 Р 25
5 X 12
6 Пх9 69
7 + 10
8 хП9 49
9 В/О 52
ПРИЛОЖЕНИЕ П.5
ПРОГРАММЫ МК4 И МК5. «МНОГОПЛОСКОСТНАЯ БАЛАНСИРОВКА»
/. Общие сведения
1.1. Программы предназначены для
автоматизации вычисления значений и уг-
лов постановки корректирующих масс при
балансировке упругодеформируемых (ква-
зигибких) роторов в нескольких плоско-
стях коррекции на серийных низкочастот-
ных балансировочных станках.
1.2. Программы разработаны для
микроЭВМ «Электроника» МК-56, БЗ-34,
МК-54, МК-52.
1.3. Для вычислений по каждому типу
ротора следует подготовить исходные дан-
ные (см. рис. П.5.1):
[кг] — масса ротора;
п — количество плоскостей коррекции
(ПК), 2<«<9;
/п[кг] —дискретные массы
ротора; ротор условно разделяется на от-
дельные массы, число которых равно п,
так, чтобы плоскости коррекции находи-
лись приблизительно в центрах этих масс,
п
£ тг= Мр;
.......[мм] —расстояния от плос-
костей коррекции до центра масс (ЦМ),
который определяется на любом серийном
роторе вывешиванием, установкой на
призму и т. п.;
[мм] —радиусы коррекции
в соответствующих плоскостях;
а, Ь [мм] —расстояния от плоскостей
измерения (ПИ) до ЦМ (ПИ—техно-
логические плоскости коррекции, в кото-
рых ротор уравновешивается пластилином,
могут совпадать со штатными плоскостями
коррекции).
1.4. При балансировке ротор уравно-
вешивается в ПИ технологическими гру-
зами и определяется:
Db [г - см]- дисбалансы, создава-
емые грузами;
<р [°] —угол между грузами.
I
Программа MK4 я МК5 <Многоплоскостная балансировка»
431
Отчет целой Ч> и ы
Вид А
у ® -yg*
-Jzg* 270°
Й0°
Рис. П.5.2
1.5. В результате расчета по програм-
ме получаются:
mki..ты,...,ткп [г] — корректирующие
массы в соответствующих плоскостях;
ф1....,фь—,фп [°]—их угловые положе-
ния относительно £)| против часовой стрел-
ки (см. рис. П.5.2).
2. Алгоритм вычислений
2.1. Вычисления производятся по сле-
дующим формулам.:
К, — mi J < 1 а/, \ _1_ j •
h Г, 1 <М? ' X mtl* ) ’
Ко — mi / f I ч у
Г. \ ч X mJ?) '
— DjK^-j-Dycos фК2<;
Dn sin фК2г;
mki — S^;
ф/ =
S(x
arccos----, (S > 0), [ 0°, 180°];
“arccos7^7’ (Sw<0), [0°,—180°].
2.2. Вычисление коэффициентов К» и
Ктл по формулам из п.2.1 и размещение
их в ячейках памяти ЭВМ производится
для каждого типа ротора один раз с по-
мощью программы МК4 (или вручную).
2.3. Вычисления по формулам из п.2.1
производятся при балансировке с по-
мощью программы МК5.
3. Пример балансировки.
Пятимассовый ротор с пятью
плоскостями коррекции
Схема ротора представлена на рис
П.5.1, П.5.2, а исходные данные и резуль-
таты расчетов по программе в табл, П.5.1
и П.5.2.
4. Программа МК4. «Вычисление ти-
повых коэффициентов Ки> Къ». Инструк-
ция.
4.1. Для вычисления используются
следующие данные о балансируемом ро-
торе:
Л1Р [кг] — масса ротора;
п [шт.] —количество
плоскостей кор-
рекции (ПК);
mi,.... mn [кг] —д и е кр ет н ы е
массы, на кото-
рые разбит ро-
тор;
Л,[мм] — расстояния от
ЦМ до ПК;
И,...., г„...., гп [мм] — радиусы кор-
рекции в соот-
*’ ветствующих
ПК;
а, Ь [мм] расстояния от
ЦМ до, плос-
костей изме-
рения.
4.2. Подготовка к работе.
4.2.1. Выполнить: Вкл., F, ПРГ, ввести
программу (см. п.4.6), F, АВТ, В/О,
перекл. «Г-Р-ГРД» в полож. «Г».
4.2.2. Контрольный пример.
Ввести: 6 хПО, —200.1 хП5, 200.1
хП1, 200 хПа, 100.1 хП2, 200 хПв, 0.1
хПЗ, 5000 хПс,—100.1 хП4, 0 хПй.
Выполнить: В/О, С/П («2.—06»),
1, С/П («1000»), 1, С/П («600,12»),
2, С/П («1000»), 1, С/П («400»),
3. С/П («1000»), 1, С/П, («200,02»),
4, С/П, («1000»), 1, С/П («4.—02»),
5, С/П, («1000»), 1,С/П, («1200,06»).
Вывести: Пх1 («600.12»), Пх4 («4.—
02»), Пх2 («400»), Пх5 («1200.06»),
ПхЗ («200.02»)
Примечание. Здесь («...»)—ре-
зультат вычислений на индикаторе.
432
Описания и тексты программ
Таблица П.5.1
Вычисление коэффициентов К и и К2< (Программа МЦ4)
Типовые данные ротора (рис. П5.1)
Плоскость коррекции 1 2 3 4 5 п — 5 Л4р=500 кг с = 200 мм 6 = 200 мм £ = 400 мм
т,, кг г<, мм li, мм Ki. К» 100 100 200 0,6 —0,2 100 100 100 0,4 0 100 100 0 0,2 0,2 100 100 -100 0 0,4 100 100 -200 -0,2 0,6
В памяти ЭВМ 600,12 400 200,02 4_02 1200,06
Таблица П.5.2
Балансировка (Программа МК5)
Ва- ри ант Дисбалансы Корректи- рующие массы Плоскости коррекции
1 2 3 4 5
1 D 1 = 500 г-мм DI( = 500 г-мм <р=60° т*/(г ч><° 2.645 -19,1 2,0 0 1,732 30 2,002 59,88 2,645 79.1
2 D1 = 300 г-мм Dn = 400 г-мм <р = 90° ГПн,Г ч>° 1,97 —24 1,2 ‘0 1 53,1 1,6 89,9 2,47 104
3 Dj=300 г-мм £>ii = 400 г-мм q>= 180° Щц, г 2,6 0 1.2 0 0,2 180 1,6 180 3 180
4 Di— 1670 г-мм £)ц= 1120 г-мм q>=257° (—103°) т^, г 10,75 11,7 6,68 0 3,58 —37,6 4,48 -102,8 8,15 — 126,5
4.3. Ввод данных балансируемого ро-
тора.
4. 3.1. Данные вводятся в следующие
регистры памяти:
(n-f-1) хПО, а хПа, гщ хП1, b хПв.
...»Л4р хПс, 1п, mn хПп, 0 хПб.
4. 3.2. Примечания:
I) 2<л<9, вводится (п-J-l), напри-
мер п — 7, вводится 8 хПО;
2) /, и т, вводить совместно, в один
регистр памяти;
- 3) h [мм] для плоскостей справа от
ЦМ вводить со знаком «—» (см. п.З);
li вводить целым числом; /п,- [кг] вводить
после/,-, отделив запятой, четырьмя цифра-
ми: первая—сотнн кг, четвертая—деся-
тые доли кг, например, /2= 325 мм справа
от ЦМ, /Иг =32,7 кг;
ввести: —325,0327 хП2;
4) а и b [мм] можно вводить с долями
мм,
например, b = 675,5 мм, ввести
675,5 хПв;
5) Мр [кг] вводить не более чем че-
тырьмя цифрами, без запятой: первая циф-
ра—сотни кг, четвертая—десятые доли
кг, например Л4р=241,5; ввести: 2415 хПс,
Программа МК4 и МК5 «Многоплоскостная балансировка»
433
или Л4р==41,5 кг, ввести: 0415 хПс или
415 хПс;
6) масштабы h, а, 5, а также т, и Мр
можно пропорционально изменить, на-
пример, увеличить или уменьшить в 10
раз;
7) данные для контрольного примера
соответствуют ротору из п.З.
4.4. Работа.
4.4.1. Ввести данные ротора согласно
п.4.3.1, 4.3.2.
4.4.2. Выполнить В/О, С/П («1/2т, X
4.4.3. Ввести I (номер плоскости в про-
извольном порядке), С/П («/nf«lO»),
ввести л/100, С/П («Ки, К»»).
4.4.4. Повторить п.4.4.3 для всех других
плоскостей.
4.4.5. Вывести и записать: Пх1 («Кп,
К21»),...» Пх, («Ku-, К21»),.... Пхп («Кщ,
Л2»>).
4.4.6. Примечания:
1) радиусы коррекции вводятся в мас-
штабе г,-/100;
2) если в результате счета по про-
грамме МК5 нужно получить значения
корректирующих дисбалансов Dm [г«мм],
то вместо г,/100 следует вводить 1;
3) размещение коэффициентов в реги-
страх памяти ЭВМ после счета следующее:
(знак Ки), (модуль Кн- -три разряда\
(запятая), (знак Кг,), модуль Ка—три
разряда).
Знаки коэффициентов обозначены циф-
рами: 0 — соответствует «-]-», 1 — соответ-
ствует «—».
4) Для контрольного примера (п.4.2.2)
и ротора (рис. 5.1):
Регистр В памяти ЭВМ Значения
Кч, Кг. Ki. Кг.
Пх1 600.12 0,6 —0,2
Пх2 400. 0,4 0
ПхЗ 200.02 0,2 0,2
Пх4 4-02 0 0,4
Пх5 1200.06 -0,2 0,6
Модули коэффициентов записываются
не более чем 3-мя цифрами и /Ки.2«/<:1,
поэтому в первом и пятом разрядах ин-
дикатора не должно быть цифр, кроме О
или 1 (при сомнениях проверить ручным
расчетом).
Если это условие не соблюдается, то
Г( вводить в масштабе г,/10 [см], а
программу МК5 изменить согласно п.5.4.3,
или перейти к расчету £)*, вместо т*,.
4.5. Время счета Т\ — 40и с.
4.6. Текст программы МК4
Адрес Команда Код
00 КПхО ГО
1 ПП 53
2 70 70
3 14
4 Fx2 22
5 X 12
6 nxd 6Г
7 + 10
8 хП<1 4Г
9 ПхО 60
10 Fx—0 5Е
1 00 00
2 Пха 6—
3 nxd 6Г
4 -А- 13
5 хПа 4—
6 Пхв 6L
7 nxd 6Г
8 —А- 13
9 хПв 4L
20 С/П 50
1 xnd 4Г
2 KHxd ГГ
3 ПП 53
4 70 70
5 С/П 50
6 — 13
7 хПО 40
8 F* 25
9 Bf 0Е
30 Пха 6—
1 X 12
2 Пхс 6С
3 Fl/x 23
4 1 10
5 ПхО 60
6 X 12
7 14
8 Пхв 6L
9 X 12
40 /-/ 0L
1 Пхс 6С
2 F!/x 23
3 10
4 ПхО 60
.5. 12
434
Описания и тексты программ
Продолжение табл. 4.6
Адрес Команда r 1 । Код
6 Fx<0 J 5C
7 51 51
8 I 01
9 — 11
50 /_../ 0L „
1 1 01
2 0 00
3 13
4 14
5 Fx<0 5C
6 60 60
7 1 01
8 — 11
9 /-/ 0L
60 1 01
1 вп ОС
2 3 03
3 X 12
4 ПП 53
5 91 91
6 + 1 10
7 KxHd Lr
8 БП 51
9 20 20
70 Bj 0E
1 Bj 0E
2 Fx>0 59
3 79 79
4 1 01
5 0-
6 8 08
7 FI/x 23
8 — 11
9 ПП 53
80 91 91
1 — 11
2 FBx 0
3 14
4 Fx2 22
5 F< 21
6 F’ 25
7 FBx 0
8 ВП ОС
9 4 04
90 B/0 52
1 I 01
2 ВП ОС
3 7 07
4 + 10
о FBx 0
6 — 11
7 B/O 52
Продолжение табл. 4.6
Регистры памяти
R0 (n-j-l) R1 (А, «и) опер. (Ku, K21)
R5 (/$, m5) (K15. Kss)
R9 (Z9, (Kl9, K29)
Ra a опер.
Rb b опер.
Rc
Rd опер. опер.
5. Программа МК5. Вычисление
корректирующих масс. Инструкция
5.1. Для вычисления используются сле-
дующие данные о роторе:
Ки, Кг< — вычисленные в п.4 и разме-
щенные в памяти ЭВМ, согласно п.4.4.6;
£>1, Вц [г-мм) - корректирующие дис-
балансы, установленные на роторе в двух
плоскостях ПИ:
<р(°]—угол от О, к £)п, замеренный
против часовой стрелки со знаком «+»
(или по стрелке со знаком «—»), глядя с
левого торца ротора (см. п.З и рис. П.5.2).
5.2. Подготовка к работе.
5.2.1. Выполнить: Вкл., F, ПРГ, ввести
программу (см. п.5.6), F, АВТ, В/О, пе-
рекл. «Г-Р-ГРД» в полож. «Г».
5.2.2. Контрольный пример (см. рис.
П.5.1)
Ввести: 600.12 хП 1, 50 хПа, 0,04 хП4,
400 хП2, 50 хПв, 1200,06 хП5,
200,02 хПЗ, 60 хПс
Выполнить: В/О, С/П(«0»), 1,
С/П («2,645»), С/П («—19.1»)
Вывести: Пх<1 («2,645»), Пхс
(«—19.1»), 2, С/П(«2.0»),С/П(«0.0»),
3, С/П («1,732»), С/П («30»), 4,
С/П («2,002»), С/П («59,876»), 5, С/П
(«2,645»), С/П («79,1»).
5.3. Ввод данных балансируемого рото-
ра.
5.3.1. Данные вводятся в следующие
регистры памяти: Кц, К2! хЩ, Di хПа,... ;
Kii, Ка хПг, D2 хПв,... ; К)я, К2п хПп,
хПс.
5.3.2. Примечания:
Программа МК4 и МК5 «Многоплоскостная балансировка»
435
I) Di (г- мм] —дисбаланс в левой пло-
скости; Ds (г-мм] —дисбаланс в правой
плоскости;
2) <р [°] —угол от D) к D^ — 360°<
’Сф’С +360°; «J-»—против часовой
стрелки (см. п.З);
3) коэффициенты Кн, Ка размещаются
в регистрах памяти хП1 .. . хП9 в том же
виде и порядке, что получены в п.4;
4) данные для контрольного примера
соответствуют ротору на рис. П.5.1.
5.4. Работа.
5.4.1. Ввести данные ротора согласно
п.5.3.1 и 5.3.2.
5.4.2. Выполнить и записать: В/О,
С/П («0»), 1, С/П(«т*1»), С/П(«ф|>»), 2,
С/П(«т*2»)' С/П(««pi»)С/П(«т*п»),
С/П(«<р^»).
5.4.3. Примечания:
1) Wjh,. . [г]—корректирующие
массы, устанавливаемые на роторе (про-
верку остаточных дисбалансов произво-
дить после установки Мы во всех плоско-
стях коррекции);
2) [°] — углы установки кор-
ректирующих масс от Dt,«+»-- против ча-
совой стрелки (см. п.З);
3) вычисления для плоскостей можно
производить в любой последовательности,
любое число раз, при этом коэффициенты
Ки, Ка сохраняются в памяти ЭВМ;
4) результаты вычислений сохраняют-
ся в памяти (ты Пхб, <р( Пхс) до начала
вычислений по следующей плоскости кор-
рекции;
5) если при вычислении коэффициен-
тов Ки, Къ в программе МК4 вместо г,/100
введены 1, то для -получения D, в про-
грамме МК5 следует набрать вместо
команд с адресами 34, 35, 36 команды
КНОП;
6) если в программе МК4 получены
коэффициенты для расчета Dkt (см.
п.4.4.6), то для вычисления корректирую-
щих масс дисбалансы следует разделить
на радиусы коррекции ты—Оы/гр,
7) данные для контрольного примера
соответствуют ротору из п.З;
8) ошибка вычислений 6<С0,2%.
5.5. Время счета Т— (10-|-26п) с.
5.6. Текст программы МК5
Адрес Команда Код
00 Пхв 6L
1 Пхс 6С
2 F sin IC
3 X 12
4 хПО 40
5 Пхв 6L
6 Пхс 6С
7 F cos 1Г
8 X 12
9 хПв 4L
10 Сх ОГ
1 С/П 50
2 xlld 4Г
3 КПх ГГ
4 ПП 53
5 53 53
6 В| 0Е
7 ПхО 60
8 X 12
9 хПс 4С
20 F- 25
1 Пхв 6L
2 X 12
3 Ч-к 14
4 Пха 6—
5 X 12
6 + 10
7 ч ОЕ
8 Fx2 22,
9 Пхс 6С
30 Fx2 22
1 10
2 21
3 В| 0Е
4 вп ОС
5 1 01
6 /-/ 0L
7 xnd 4Г
8 С/П 50
9 F’ 25
40 — 13
1 F cos-' 1 —
2 Пхс 6С
3 Fx<0 5С
4 48 48
5 F’ 25
6 /-/ 0L
7 Bt 0Е
8 F’ 25
9 хПс 4С
50 С/П 50
1 БП 51
2 12 12
3 Bf 0Е
4 Bt 0Е
5 1 01
6 0
436
Описания и тексты программ
Продолжение табл. 5.6
Адрес Команда Код
8 08
8 Fl/x 23
9 — 11
60 1. 01
1 ВП ОС
2 7 07
3 + 10
4 FBx 0
5 —~ и
6 — 11
7 FBx 0
8 ВП ОС
9 3 03
70 /-/ 0L
1 Bf 0Е
2 1 01
3 14
4 — 11
5 FBx 0
6 14
7 Fx<0 5С
8 80 80
9 14
80 F« 25
Продолжение табл. 5.6.
Адрес Команда Код
1 2 3 4 5 6 7 8 9 90 1 2 3 4 5 6 0 1 FBx Fx<0 92 F- 1 0 X В/О 14 00 0- 01 04 11 0 14 5C 92 14 25 01 00 12 52
Регистры памяти
R0—опер. ! Rl-K.i, Ki2 R5—>25 '] R9—К19, К29 Ra- jDj Rb— Rc — q>, (р. Rd— mu
ПРИЛОЖЕНИЕ П.6
ПРОГРАММА МК6. «РАСЧЕТ ГЛАВНОГО ВЕКТОРА И ГЛАВНОГО
МОМЕНТА ДИСБАЛАНСОВ»
/. Общие сведения
1.1. Назначение—вычисление значе-
ний и углового положения главного век-
тора Dcr и главного момента MD дисбалан-
сов ротора.
1.2. Исходная информация:
значения и угловое положение дис-
балансов в двух плоскостях измерения;
массово-геометрические параметры ро-
тора.
1.3. МикроЭВМ — «Электроника» БЗ-
34, МК-52, МК-54, МК-56.
2. Алгоритмы вычислений
2.1. Условные обозначения:
mi, т2 [г]—корректирующие массы
в плоскостях коррекции;
ipt, [°] —угловое положение коррек-
тирующих масс;
И, г2 (мм]—радиусы коррекции;
а, b (мм] — расстояния от первой и
второй плоскостей коррекции до центра
масс ротора;
DCT [г-мм] — главный вектор дис-
балансов;
MD [г-мм2]—главный момент дис-
балансов.
2.2. Исходный "алгоритм
DCT=Di + D2=(/niFl) +(mlr2);
MD— —Di ‘d-{-D2'b= —{т\Гуг) 4-(т2Г2^Х
2.3 Машинный алгоритм
1) |= |£hx 4-=
— т\Гу (cos «pi 4- sin ф|);
| D21 = | D2x -J- D2y j=
— m2r2(cos <p2 -f- sin <p2);
Программа МК6 «Расчет главного вектора и главного момента дисбалансов»
437
2) I DCT|= | £>стх+Ост{/| =
= {mvrx cos q>j /n2r2cos Фг) +
4~ (/n(rj sin <Pj 4"/ft2r2s*n Ф?)»
3) |d„|=VidLi + IO^I;
Фо =
l£>CTXI
arccos —,
I
360 — arccos _L£zd
I fled
I I > 0;
PcTJ<0;
4) — ^1G, DM2— ^2^i
5) \MD\~\DMx+DMy\ =
= ( cos<p!G4-/n2r2cos<p26) 4-
+ ( т(г(8т ЦР1С4-m2r2sinq)2fe);
— / _О __ 9
l^ol= VjOMJ4-in^|;
Пха(«4»), Пхв(«3»), Пхс(«1»), Пхб
(«1»),
Примечания:
1) здесь («...»)—результат на инди-
каторе;
2) при случайном нажатии клавиши
В/О повторить п.3.2.
3.3. Работа.
Ввести: т\ хП1, ф| хП2, а хПа,
Г| хПс,т2 хПЗ, ф2 хП4, b хПв, г2 хПб.
Выполнить: С/П («Дсг»), С/П
(«Фо»), С/П («2ИО»), С/П(«<рм»).
Для дальнейших расчетов по ротору
ввести:
mi хП1, epi хП2, т2 хПЗ, фг хП4.
3.3.1. Примечания:
1) угловое положение корректирую-
щих масс отсчитывать против часовой
стрелки;
2) координаты а и 6, если они слева
от центра масс ротора, вводить со знаком
«—»;
3) значения DCT, <pD, MD, фЛ при рас-
четах хранятся в регистрах RG6, RG7
(см. распределение памяти);
4) для контрольного примера
Ш| = 3, ф| = 90°, т2=4, <р2—160°, а—
= 4, * = 3, r, = r2=l.
4>м =*
arccos
|MW| ’
360°-arccos
|MD|
I DMy I > 0;
I ® My I < 0.
3. Инструкция
3.1 Выполнить: Вкл, В/О» F, ПРГ,
ввести программу (см. п.3.4), F, АВТ, В/О,
переключатель «Г-Р-ГРД» в положение
«Г».
3.2 Контрольный пример.
Ввести: 3 хП1 хПв, 90 хП2, 4 хПЗ
хПа, 180 хП4, I хПс хПб.
Выполнить:
В/О, С/П («5»), С/П («143,1301»),
С/П («16,97»), С/П («135»).
Вывести:
Пх1(«12»), Пх2(«90»), ПхЗ(«12»),
Пх4(«180»), Пхб («16.97»), Пх7
(«135»), Пх8(«—12»), Пх9(«12»),
3.4. Текст программы МК6
Адрес Команда Код
00 2 02
1 хПО 40
2 Сх ОГ
3 хП8 48
4 хП9 49
5 FL0 5Г
6 17 17
7 Пх1 61
8 Пха 6—
9 X 12
10 хГП 41
1 ПхЗ 63
2 Пхв 6L
3 X 12
4 хПЗ 43
5 БП 51
6 25 25
7 Пх1 61
8 Пхс 6С
9 X 12
20 хП1 41
438
Описания и тексты программ
Адрес Команда Код
1 ПхЗ 63
2 Hxd 6Г
3 X 12
4 хПЗ 43
5 Пх4 64
6 ПП 53
7 59 59
8 Пх1 61
9 Пх2 62
30 ПП 53
I 59 59
2 Fx2 22
3 14
4 Fx2 22
5 р 10
6 21
7 хП6 46
8 С/П 50
9 Пх8 68
40 Пхб 66
1 13
2 F cos1 1 —
3 хП7 47
4 Пх9 69
5 Fx<0 5С
6 53 53
7 3 03
8 6 06
9 0 00
50 Пх7 67
1 — 11
2 хП7 47
3 Пх7 67
4 С/П 50
5 FL0 5Г
6 00 00
7 БП 51
8 02 02
Продолжение табл. 3.4
Адрес Команда Код
9 В| 0Е
60 F sin 1С
1 F’ 25
2 F cos 1Г
3 -<-> 14
4 X 12
5 FBx 0
6 -«-> 14
7 F* 25
8 ч—►- 14
9 F* 25
70 X 12
1 Пх9 69
2 -p 10
3 хП9 49
4 14
5 Пх8 68
6 -ь 10
7 хП8 48
8 В/О 52
Распределение памяти
RG1 RG2 RG3 RG4 RGa RGb RGc RGd 4>i ф2 a b ri Г2
RG6 RG7 ^ст» 4>D* 4>M
RGO, RG8, RG9 — оперативные
ПРИЛОЖЕНИЕ П.7
ОПИСАНИЕ ПРОГРАММЫ ЕХС1. «БАЛАНСИРОВКА С ПРИМЕНЕНИЕМ СИСТЕМЫ
ПРОБНЫХ ДИСБАЛАНСОВ»
Программа реализует алгоритмы ме-
тодов одновременной балансировки с при-
менением специальной системы пробных
дисбалансов как по собственным формам
изгиба ротора, так и с применением
ортогональной системы синусов кратных
аргументов.
Программа ЕХС1 «Балансировка с применением системы пробных дисбалансов» 439
Спецификация идентификаторов входных и выходных параметров
Идентификатор массива с указа- нием размерности Инженерное обозначение параметра Размерность физической величины Содержательное наименование параметра
N N1 — Количество точек измерения прогиба ротора Количество функций в ортонормиро- ванной системе
ZIN] Zi м Осевые координаты точек измерения прогиба
Y1[N] XI [N] yi Xl м м Проекции прогиба ротора с началь- ной неуравновешенностью на оси У и X
HY[N] HX[NJ hx м м Проекции эксцентриситетов пробных масс на оси Y и X
Y2[NJ X2[N] У? Xz м м Проекции прогиба ротора, вызван- ного совместным действием начальной неуравновешенности и пробных масс на оси Y и X
L L м Длина ротора
EY[N] ey м Проекции идентифицируемых экс- центриситетов на оси Y и X
E[N] . O[N] e D м кг-м Величины идентифицируемых эксцен- триситетов Величины идентифицируемых дис- балансов
Таблица П.7.1
Параметр Номера сечений
0 1 2 3 4 5 6 7 8 9 10 11
х(-106, м 0 0 0 0 42 173 173 163 163 156 175 0
м 0 0 0 43 42 50 50 163 163 90 47 0
Л*-106, м 0 0 0 0 4,2 17,3 17,3 16,3 16,3 15,6 17,5 0
Л„-106, м 0 0 0 4,3 4,2 5 5 16,3 16,3 9 4,7 0
Х2- 10®, М 0 0 0 0 105 519 519 570,5 652 624 612,5 0
у2-106, м 0 0 0 86 105 150 150 570,5 652 360 164,5 0
z-Ю8, м 0 68 153 232 307 384 462 534 601 667 730 840
£.1О"6, м £Ы0-6, кгм 0 0,74 0 36 1,15 3,71 3,04 4,48 2,94 4,41 3,88 0
440
Описания и тексты программ
В тестовой задаче программы про-
изводится идентификация эксцентрисите-
тов ротора, описываемого десятимассовой
расчетной моделью, путем измерения его
прогиба на частоте вращения ы =
= 1047,2 с”1, соответствующей 104 мин-1,
и разложения функций по системе функ-
ций, содержащей 10 синусов кратных аргу-
ментов.
В задаче приняты следующие значения
исходных данных; N= 12, Nl = 10, L =
= 840-10-3 м. Значения проекций прогиба
ротора с начальной неуравновешенностью
Xi и yi, эксцентриситетов пробных масс,
распределенных подобно упругой линии
оси ротора от действия начальных дис-
балансов hy и hx, прогиба ротора от сов-
местного действия начальных и пробных
дисбалансов х2 и у%, а также координат
точек измерения и результаты расчета
приведены в табл. П.7.1.
ПРИЛОЖЕНИЕ П.8
ОПИСАНИЕ ПРОГРАММЫ ЕХСЗ. «ОПРЕДЕЛЕНИЕ ЭКСЦЕНТРИСИТЕТОВ
ГИБКОГО РОТОРА ПО ИЗВЕСТНЫМ ЗНАЧЕНИЯМ ЕГО ПРОГИБОВ»
Программа реализует алгоритмы пара-
метрической идентификации гибких рото-
ров с неизвестными упруго-инерционными
характеристиками по известным значени-
ям прогибов на четырех некритических
частотах вращения ротора.
В тестовой задаче программы произ-
водится идентификация эксцентриситетов,
дисбалансов, значений погонной массы,
изгибной жесткости ротора, а также углов,
составленных векторами дисбалансов с
осью У, по измеренным в 20 точках на оси
Спецификация идентификаторов входных и выходных параметров
Идентификатор массива с указа- нием размерности Инженерное обозначение параметра Размерность физической величины Содержательное наименование параметра
N — — Количество точек измерения на оси .ротора
Z[N] z м Осевые координаты точек измерения
W[4] co с-1 Некритические частоты вращения ро- тора, на которых проводятся из- мерения
Y[NX4] X[NX4] У X м Проекции црогибй упругой оси ротора на оси X и У
M м кг Масса ротора
D[N] D кг*м Дисбалансы
GAM[N] У Углы, составленные дисбалансами С Х)СЬЮ
E[N] e м Идентифицируемые эксцентриситеты
Таблица П8.
Значения координат точек измерения и проекций прогиба ротора и вычисленные
программой эксцентриситеты
Z (N) 10-3, м 0 20 35 46 60 80 95 110 120 135 150 184 210 230 250 292 300 310
х(wi) • I06. м 7 6,5 6 5 4,6 4 3 2 0 -4 -6 -10 -9 -8 -6 0 1 2
у (<1>! ) • 106, м -17 -16,5 — 16 -15 -13,5 -10,9 -8 -3,7 0 4,5 6 8 8,5 8,6 8 0 -10 -22
х(«2) -106, М 8 7,3 7 6 5,6 4,2 4 2,5 0 -4,5 —9 -15 -14 -12 -10 0 1,5 3
у(шг) -106, м -15 -14,5 14 -13 -11,9 -10,5 -8,5 —4 0 5 8 12 12 11,5 10,5 0 -13 -25
х(соз) • Ю6, м 10 9,4 9 8 7 6 4,5 2,5 0 —5 -9 -12 - И -9 -8 0 2 2.5
y(w3) *Ю6, м -18 -17,5 -17 -16 -14,5 -12 -9 -4,5 0 5,2 8,3 12 12,3 11,5 10,7 0 -14 -26
х(<о4) *!06, м 4 3,6 3 2 1,7 1,5 1,5 1 0 -0,5 -1 -2 -2 -1,5 -1 0 2 3
у(<о4) • Ю6, м -24 -23,5 -23 -22 -19- -14 -10 -4 0 7 14 22 21 19 16 0 -13 -26
E(N)«!0“5, м 2,63 2,99 1.28 3,0 2,56 1,46 0,62 0,26 0 0,41 0,36 4,83 2,31 1,3! 1,43 0 0,38 2,80
GAM(N) 0,69 1.95 59,5 -0,23 3,84 -22,9 -38,1 —44,6 0 -26,0 -51,1 3.14 3,16 26,7 24,4 0 57,3 29.2
Описания и тексты программ
442
Описания и тексты программ
7. на четырех некритических частотах вра-
щения ротора значениям проекций про-
гиба на оси X и У,
В задаче приняты следующие исходные
данные. Частоты вращения, на которых
производятся измерения прогибов, <В) =
= 1476,6 с-*, €о2=1570,8 с"'. €о3=
= 1633,6 с1, €о4— 1675,5 с-1 Масса ротора
составляет Л4=17,8 кг
Значения координат точек измерения
Zj, а также проекций прогиба ротора на
оси координат %(€of), f/(€o,) указываются в
табл. П.8.1, после которой приводится рас-
печатка результатов решения.
Ресурсы, необходимые для решения
тестовой задачи: объем оперативной памя-
ти—21 К, время работы программы—
4 мин 25 с.
ПРИЛОЖЕНИЕ П.9
ОПИСАНИЕ ПРОГРАММЫ ЕХ.С4. «ОПРЕДЕЛЕНИЕ ЭКСЦЕНТРИСИТЕТОВ
ГИБКОГО РОТОРА ПО ЕГО ПРОГИБАМ И НОРМАЛЬНЫМ НАПРЯЖЕНИЯМ»
Программа реализует идентификацию
эксцентриситетов по значениям нормаль-
ных напряжений и прогибов, измеренных
на частоте вращения го.
Время работы центрального процессо-
ра 2 мин 54 с, объем оперативной памяти
составляет 14К-
Спецификация идентификаторов входных и выходных параметров
Идентиф икатор массива с указа- нием размерности Инженерное обозначение параметра Размерность физической величины Содержательное наименование параметра
OMEG €1) С-1 Частота вращения, на которой про- изводятся измерения
N — — Число точек измерения
SIGM[N] О Н/м2 Нормальные напряжения
PIN] Р Н Неуравновешенные силы
W[N] м3 Осевой момент сопротивления
A[NXN] — — Коэффициенты системы уравнений относительно неизвестных эксцентри- ситетов
M[NJ tn кг Массы
Y[N] У м Прогиб ротора
E|N] е м Идентифицируемые эксцентриситеты
443
Программа ЕХС5 «Определение изгибных жесткостей гибкого ротора по прогибам оси»
Таблица П.9.1
Параметр Номер сечения
I 2 3 4 5
о., Н/м2 20013 20890 13792 7324 3102
Wf- 104. м3 27 64 125 216 343
у, • fO*, м 7,87 11,38 11,16 11,37 10,35
mir кг 9,03 9,96 12,32 12,53 17,6
Gii-103 63,42 50,08 37,3 24,9 13,25
ся-Ю3 52,92 152,64 112,36 76,32 40,28
Сз<-103 38,68 114,56 184,44 125,28 66,12
- Ю3 26,80 77,6 122,40 172,80 91,20
аы - I03 15,64 42,88 64,12 94,44 114,76
Р(А), Н 217,8 268,9 395,4 312,7 318,8
Е, мкм 81,3 88,5 107,5 80,9 56,6
В тестовой задаче программы произ-
водится идентификация эксцентриситетов
на основе пятимассовой расчетной модели
ротора по измеренным на частоте враще-
ния (о = 0,52-103 1/с в N = 5 точках оси
ротора значениям напряжений.
Значения напряжений о», осевых мо-
ментов сопротивления Wit прогибов yh
масс а также матрица коэффициентов
системы линейных уравнений и результаты
выполнения программы приводятся в
табл. П.9.1.
ПРИЛОЖЕНИЕ П.10
ОПИСАНИЕ ПРОГРАММЫ ЕХС5 «ОПРЕДЕЛЕНИЕ ИЗГИБНЫХ ЖЕСТКОСТЕЙ ГИБКОГО
РОТОРА ПО ЕГО ОТНОСИТЕЛЬНЫМ ДЕФОРМАЦИЯМ И ПРОГИБАМ ОСИ>
Программа реализует алгоритм иден-
тификации эксцентриситетов и изгибных
жесткостей по измеренным на двух раз-
личных частотах вращения относительным
деформациям и прогибам оси ротора.
Время работы центрального процессо-
ра 3 мин 8 с, объем оперативной
памяти составляет 15К-
В тестовой задаче программы произ-
водится идентификация значений эксцент-
Спецификация идентификаторов входных и выходных параметров
И дентифик атор массива с указа- нием размерности Инженерное обозначение параметра Размерность физической величины Содержательное наименование параметра
N — Число точек измерения
W1 ТС-1 Частоты вращения, на которых про-
W2 (02 с“‘ изводятся измерения
EPS 1JN] 8| — Относительные деформации оси ро-
EPS2fN] «52 тора, измеренные на частотах вра-
щения с»| и (о2
H{N] h м Расстояния от нейтральной оси ро-
тора до деформированных волокон
M[N] m кг Массы
Y1|N] У\ м Прогибь! ротора на частотах вра-
Y2[N] У2 м щения <0|, <ог
GIN] EJ Н-м2 Изгибные жесткости
E[N] e м Эксцентриситеты
444
Описания и тексты программ
риситетов ротора, описываемого пятимас-
совой моделью, по измеренным на часто-
тах вращения = 0,52*103 с 1 и а>2—
= 0,73*103 с-1 относительным деформаци-
ям е, и прогибам оси ротора у,.
Значения коэффициентов системы ли-
нейных уравнений относительно эксцент-
риситетов и изгибных жесткостей а,, и
масс ш, приведены в табл. П.9.1. Значения
прогибов у,, относительных деформаций
е, и расстояний от нейтральной оси до
деформированных волокон hi, а также
результаты решения приведены в табл.
П.10.1.
Таблица Г1.10.1
— Номер сечения Параметр 1 2 3 4 5
У1(Ы|) • Ю6, м 7,87 11,38 11,16 11,37 10,35
Ю6, М 11,8 17,0 16,7 16,9 15,5
еД<О|)*10" 10006,5 10445 6896 3662 1551
М<92)*10и 20843,3 21805 14418 7697 3291
hr 10, м 3 4 5 6 7
G(/V)-108, Нм2 1,50 4,72 11,28 22,57 38,65
E(N), мкм 75,8 89,4 101,8 73,5 25,4
ПРИЛОЖЕНИЕ П.11
пПгИ«^ННЕ ПР0Г₽АММЫ ДИСБАЛ <РАСЧЕТ УДЕЛЬНЫХ ДИСБАЛАНСОВ РОТОРА
D 1 I Д' П>
1. Программа ДИСБАЛ предназначена
для расчета удельных дисбалансов ротора,
установленного в корпусе изделия, с уче-
том погрешностей шарикоподшипников.
Она написана на программном языке
VS-FORTRAN и может быть реализована
на ЭВМ, обеспеченных трансляторами
Фортрана.
2. Идентификаторы программы при-
ведены с указанием размерностей физи-
ческих величин.
Время работы ЭВМ типа ЕС-1045 при
проведении расчетов удельных дисбалан-
сов по программе ДИСБАЛ составляет
0,5 мин, занимаемая оперативная память
4,484 КБ.
3 Тестовая задача программы
ДИСБАЛ составлена для изделия типа
симметричного гиромотора массой 0,1 кг.
Масса ротора 0,028 кг. Тип радиально-
упорных шарикоподшипников—6023Е. Ве-
личина геометрического осевого предвари-
тельного натяга 3 мкм. Амплитуды вибра-
ции корпуса изделия Ахр, Арр и сдвиг фаз
Ухрр определяются экспериментально. Ос-
тальные исходные данные определяются
на основе технических характеристик и
паспортных данных как всего изделия в
целом, так и шарикоподшипников в от-
дельности.
Программа ДИСБАЛ «Расчет удельных дисбалансов ротора в корпусе
Спецификация идентификаторов программы ДИСБАЛ и данные для тестовой задачи
Иденти- фикатор параметра Инженерное обозначение параметра Размерность физической величины Содержательное наименование параметра Данные тестовой задачи
WP flip рад/с Угловая скорость вращения ротора 314,16
МР мР КГ Масса ротора 0,028
МР1 кг Масса платформы 0,2
м М кг Масса всей колебательной системы 0,328
IPX кгм2 Момент инерции ротора относительно оси Z 2,8-11)”
IPY Jpy кгм2 Момент инерции ротора относительно оси У 2,8-10”
[PZ Jpz кгм4 Момент инерции ротора относительно оси Z 4,2-1 (У6
РОРХ ^рх м Радиус инерции ротора относительно оси X 10'2
их hz м Момент инерции всей колебательной системы относительно оси Z Кб-10"4
ПУ hy м Момент инерции всей колебательной системы относительно оси У 10 4
I1Z hz м Момент инерции всей колебательной системы относительно оси Z 10~4
LMH In м Расстояние между началом системы координатных осей и центром масс платформы 2-10”2
LM1 It м Расстояние от начала системы коор- динатных осей до I плоскости кор- рекции 0,8 -10”2
LM2 c м Расстояние от начала системы коор- динатных осей до II плоскости кор- рекции 0,8-10 v
XI A м 2,2-КГ2
Y1 yi м Координаты точек крепления упругих 2,5- I0”2
Z1 Z1 м элементов к платформе 2,5-10”
СХ Cx Н/м Жесткость упругого элемента в нап- равлении оси X 4-Ю”3
CY Cy Н/м Жесткость упругого элемента в нап- равлении оси У 2-103
CZ cz Н/м Жесткость упругого элемента в нап- равлении оси Z 2-103
АХР AXp м Амплитуда радиальных колебаний корпуса изделия — 5,13-Ю”8
АВР A ftp рад Амплитуда угловых колебаний кор- пуса изделия 0,784 -И)”
GM g м/с2 Ускорение свободного падения 9,81
А12 a?' м 9- Ю”4
А14 ai' м 3-I0”5
А16 ai' м 2-10”5
А18 ai' м Ю”5
В12 Ы' м Коэффициенты разложений в ряды 0
В14 b\’ м 0
В16 Ы' м Фурье погрешностей шарикоподшип- ников 0
В18 bi' м 0
А1211 ai" м 2,6-10”5
446
Описания и тексты программ
Продолжение табл.
Иденти- фикатор параметра Инженерное обозначение параметра Размерность физической величины Содержательное наименование параметра Данные тестовой задачи
AI411 О| М 1,2-10 у
А16П Gl м 3-10“5
А1811 BI211 „8// di м Коэффициенты разложений в ряды 1(Г5 0
B141I bl" м Фурье погрешностей шарикоподшип- ников 0
В1611 b4" м 0
BI8I1 b\" м 0
Р02 Ро м Номинальное значение радиуса же- .лоба внутреннего кольца шарикопод- шипника 8,6- Ю 2
Р04 Ро м Номинальное значение радиуса по дну желоба внутреннего кольца ша- рикоподшипника 2,5-10 3 9,7-10-3
АР06 IpSI м Абсолютное номинальное значение осевой координаты центра кривизны желоба внутреннего кольца шарико- подшипника
TAU0 То рад Номинальное значение угла контакта шарикоподшипника 0,314
NM п — Число шариков в шарикоподшипнике 6
DH вн мм Геометрический предварительный осе- вой натяг 3-103
KGO Рез Кго ультаты расч Н/мм3/2 ета Номинальное значение коэффициента Герца 8-Ю4
Е1 ei мкм Удельный дисбаланс ротора в I плос- кости коррекции 1.67-10-2
Е2 es MJKM Удельный дисбаланс ротора в II плос- кости коррекции 0,583
GAMG Ъ рад. Угол между дисбалансами — 0,828
ПРИЛОЖЕНИЕ ПЛ2
ОПИСАНИЕ ПРОГРАММЫ «ТЕХНОЛОГИЯ БАЛАНСИРОВКИ РОТОРОВ>
Программный модуль предназначен
для проектирования технологических про-
цессов балансировки роторов ВРД и ре-
шает следующие задачи:
проектирование метода балансировки
ротора ВРД;
выбор оборудования для технологиче-
ского процесса балансировки;
выбор аппаратуры для технологиче-
ского процесса балансировки.
Описание используемого алгоритма.
Порядок решения задач: сначала решает-
ся задача балансировки ротора. Если най-
дены балансировочные параметры, удов-
летворяющие заданным критериям, то
далее решаются задачи выбора аппарату-
ры и оборудования. В противном случае
последние задачи не решаются и програм-
ма завершает работу.
Пакет состоит из 7 программ, исполь-
зующих стандартные функции языка
ФОРТРАН ОС ЕС и стандартную про-
грамму DGELG из пакета стандартных
программ на языке ФОРТРАН (библио-
Программа «Технология балансировки роторов»
447
тека SYS1, SSPLIB). Главная программа
MAIN и подпрограммы R, Z, DGELG и
ARCTAN реализуют алгоритм выбора ба-
лансировочных параметров; программа
GOVBO и VBO реализует алгоритм выбора
балансировочнрго оборудования. Про
грамма APPAR — выбор аппаратуры. Про
граммный модуль инициируется как обыч-
ная задача ОС ЕС, использующая язык
ФОРТРАН. Спецификация идентификато-
ров входных параметров модуля приведе-
на в табл. П.12.1.
Описание тестовой задачи. В качестве
примера принят пятимассовый ротор,
имеющий все необходимые параметры для
получения промежуточных результатов и
обеспечивающий проверку правильности
алгоритма решения задачи в процессе
отладки программы.
Исходные данные тестовой задачи:
масса ротора т = 6,6 кг;
дискретные массы ротора m> = m%—
= тз—гп4 — т&=^ 1,32 кг;
номера методов балансировки S— 1, 2, 3
(принимаем три способа балансировки:
в 2-х, 3-х и 5-ти плоскостях коррекции);
условные дискретные массы:
при 5 = 1 ти = 3,3 кг, туг— /П1з==гП14 = 0,
mis=3,3 кг;
при S — 2 m2j —2,2 кг, гк22=0, т23=
= 2,2 кг, т24== 0, т25 = 2,2 кг:
при 5 = 3 т3| = т32=т33=т34=т35 =
= 1,32 кг.
Расстояние от центра массы до услов-
ной дискретной массы:
при 5=1 /и”130-10 3, /!2=/|3=/и=
= 0. 115=”13010-3 м:
Спецификация идентификаторов входных параметров модуля
Таблица П.12.1
Идентифи катор массива с указа- нием размерности Инженерное обоз- начение параметра Размерность физи- ческой величины Содержательное наименование входного параметра
Е е м Начальные эксцентриситеты
М пг кг Дискретные массы
L 1 м Расстояния от опорных плоскостей
W (й рад/с Угловая скорость
ALF а — Коэффициенты взаимного влияния
SFC — н Значения критериев по суммарной F
SMC — Нм Значения критериев по суммарному М
NPLOSK п шт. Число плоскостей балансировки для различных методов
TIPP Тип производства может принимать значения: 1 — серийное, 0—опытное
TIPROT — Тип ротора (может принимать значения 1 — асимметричный, 0— симметричный) Отношение 1/L
LKL IFI Тип станка (может принимать зна- чения: <0- - осевой, >0 — ременный, = 0—любого типа)
DR DP м Диаметр ротора
DAB Dfi& м Диаметр опорных шеек
AM m кг Масса ротора
AL L м Расстояние между опорами
Примечание. Последние пять чисел вводятся по формату: 12, 5Х, F6.2, 5Х. F6.2,
5Х, F6.2, 5Х, F6.2.
448
Описания и тексты программ
ПрИ 5— 2 /2]— 130-10 3 М, /22={23~^24 =
— о, Z25——130-10~3 м;
при 5 = 3 /31= 130- 1О“3 м, Z32=65-10~3 м,
?:« = О; Z34 = — 655 10“3 м, Z35 -- - 130 X
X К)-1 м. ‘
Угловая скорость при работе w —
= 380 рад/с.
Угловая скорость при балансировке
(об=60 рад/с.
Эксцентриситеты дискретных масс:
Z1 = Z2==Z3=Z4 = Z5=25.10-6 м.
Угол эксцентриситета дискретной мас-
сы ротора:
<Р1 = 0°, <р2=0°, <р3=0°, <р4=0°, <р5=0°.
Расстояние от центра массы ротора до
дискретной массы:
Zi= 130-10~3 м, Z2=65-10‘ 3 м, Z3 = 0. Z4 =
==—65-1()3 м, Z5=—130-10-3 м.
Коэффициент, зависящий от метода
балансировки:
при 5=1 <?ц = 1, <712 = <?1з—<?14 —О,
<?i5= 1;
ПрИ 5 = 2 <721=1, 022 = 0, <723= 1, <724 = 0,
<725= 1;
При 5 = 3 <?3| = <?32= <?33= <734= <735= 1:
коэффициент влияния а,, - 10~7 м/ГК
Номер массы i j — номер точки приложения нагрузки
1 2 3 4 5
1 3,35 7,20 6,32 5,66 2.57
2 5,65 9,50 11,00 9,30 4,70
3 5,20 11,00 13,40 11,60 6,27
4 4,76 9,48 11,93 11,20 6,53
5 1,78 4,60 6,73 6,98 4,76
Допустимое значение главного вектора
Гдсп=100 Н.
Допустимое значение главного момен-
та МДО11=52 Н м.
Результаты применения тестовой зада-
чи. Результаты выводятся на печать в виде
протокола балансировки с помощью трех
методов по трем критериям, затем, если
найдена удовлетворительная балансиров-
ка, печатается решение задачи выбора
аппаратуры и выбора оборудования.
Ресурсы, необходимые для решения
тестовой задачи:
объем оперативной памяти—ЗЗК,‘
время работы программы—48 с.
Результаты расчетов печатаются в следую-
щем виде:
----Выбор метода балансировки -------
Результат проверки по первому критерию:
Метод № 2 обеспечивает балансировку,
удовлетворяющую 1-му критерию.
-------— Метод выбран------------
---------Выбор аппаратуры —----------
Рекомендуется серийная аппаратура 4~
4-АРУ
----— Аппаратура выбрана-------------
- ----Выбор оборудования ------------
Подходит станок № 3
Выбрано станков
— ----Оборудование выбрано-----------
ПРИЛОЖЕНИЕ П.13
ОПИСАНИЕ ПРОГРАММЫ «СБОРОЧНАЯ ТЕХНОЛОГИЧНОСТЬ»
Программный модуль предназначен
для количественной оценки технологиче-
ских процессов балансировки роторов
ДЛА путем исследования зависимостей
величин главного вектора и главного мо-
мента центробежных сил неуравновешен-
ного ротора от угловой скорости его вра-
щения.
При разработке технологии баланси-
ровки роторов ДЛА ставится задача сни-
жения сил инерции на опорах ротора.
В процессе балансиров-ки управляют этими
Программа «Сборочная технологичность»
449
величинами путем изменения значений
эксцентриситетов дискретных масс ротора
Сравнивая ожидаемые значения сил на
опорах ротора при различных баланси-
ровочных параметрах, можно оценить ба-
лансировочную технологичность конкрет-
ных процессов.
Программный модуль представляет
собой пакет прикладных программ (ППП),
состоящий из двух программ, использую-
щих стандартные функции языка
ФОРТРАН и стандартной подпрограммы
решения системы линейных уравнений
SIMQ из библиотеки стандартных про-
грамм на языке ФОРТРАН.
Программный модуль инициируется как
обычная задача ОС ЕС, использующая
язык ФОРТРАН.
Спецификация идентификаторов вход-
ных параметров модуля приведена в табл.
П.13.1.
Таблица П.13.1
Спецификация идентификаторов входных
параметров
Идентифика тор массива с указанием размерности Инженер- ное обоз- начение пара- метра Размер- ность фи- зической величины Содержа- тельное наименова- ние вход него пара- метра
N п ШТ. Число масс
М(10) rtli кг Массы
Ц10) 1, м Расстояния
Е(10) et м Эксцентри- ситеты
Fi(10) <Pi о Углы
ALFA (10,10) м/Н Коэффи циенты влияния
W 6) рад/с Угловая скорость
Результаты расчетов печатаются в следую-
щем виде;
Главный вектор сил равен 31,070 Н;
Главный момент равен 1,902 Н-м.
Описание тестовой задачи: в качестве
примера принят пятимассовый ротор,
имеющий все необходимые параметры для
получения промежуточных результатов и
обеспечивающий проверку правильности
алгоритма решения задачи в процессе
отладки модуля.
Описание исходных данных для тесто-
вой задачи:
число масс ротора zf=5;
дискретные массы ротора: г?ц —
= ш»= 1,32 кг;
Расстояния от центра массы ротора до
условной дискретной массы:
/1 = 0,13 м; /г— 0. 065 м; /з—0; /4 =
= —0,065 м; /5=—0,13 м.
Эксцентриситеты дискретных масс:
е]=е2=?з-е^е5-0,3-10~4 м.
Углы эксцентриситета дискретных
масс:
<р( = 0, <р2==72°, <р3= 144°, ф4 = 216°, <р5 =
= 288°.
Коэффициенты влияния cty’10-7 м/Н.‘
Номер массы i j — номер точки приложения нагрузки
1 2 3 4 5
1 3,з 7,2 6,3 5,7 2,6
2 5,6 9,5 111 9,3 4,7
3 5,2 11 313 12 6,3
4 4,8 9,5 212 11 6,5
5 1,7 4,6 6,7 7 4,8
Ресурсы, необходимые для решения те-
стовой задачи.
Время работы центрального про-
цессора—8,3 с.
Объем оперативной памяти, необходи-
мой для решения тестовой задачи,—35К.
•5 15 Зак 1641
450
Описания и тексты программ
ПРИЛОЖЕНИЕ П.14
ОПИСАНИЕ ПРОГРАММЫ «БАЛАНСИРОВОЧНАЯ ТЕХНОЛОГИЧНОСТЬ»
Программный модуль предназначен
для выбора оптимальных угловых поло-
жений эксцентриситетов дискретных масс,
обеспечивающих минимальную величину
главного вектора центробежных сил
неуравновешенного ротора.
Реализация модуля позволяет скомпен-
сировать погрешности изготовления дета-
лей роторов ДЛА определенным взаим-
ным положением деталей ротора при его
сборке.
Программный модуль представляет
собой пакет 3-х прикладных программ,
использующих стандартные функции язы-
ка ФОРТРАН и стандартной программы
решения системы линейных уравнений из
библиотеки стандартных программ на язы-
ке ФОРТРАН (библиотека SYS1,
SSPLJB).
Программный модуль инициируется
как обычная задача ОС ЕС, использую-
щая язык ФОРТРАН.
Спецификация идентификаторов вход-
ных параметров модуля «Балансировоч-
ная технологичность» приведена в табл.
П.14.1.
В колоду исходных данных включаются
• следующие перфокарты (ПК):
а) число п по формату (12),
например, для n = 7t_,7;
б) число ш по формату (F 8.1),
например, для <д=300:,_3000.0;
в) число L по формату (F 8.5),
например, для 1,56: t, 1.56000;
г) число Н по формату (12),
например, при //=10:10;
д) п чисел |ет(-| по 10 на одной ПК по
формату (10 F 8.6),
например, при «==3 |ёт|] =0,00001,
|ёт|2= 0.000002, |ет|3= 0,00003:
, , • 0,000 , • 000002^ • 000030,
если л >10, то значения |eT|f для
г >10 заносятся на следующую карту,
если nsClO, то достаточно одной карты;
е) п чисел |ер|,- по 10 на одной ПК по
формату (10 F 8.6);
ж) п чисел ур( по 10 на одной ГТК по
формату (10 F 8.3) в радианах:
з) п чисел Di по 10 на одной ПК по
формату (10 F. 8.5);
з) п чисел Di по 10 на одной ПК по
формату (10 F 8.5);
к) матрица размером пХ« построчно
по п чисел на одной карте (если n<J10).
если «>10, то остаток строки поме-
щается на следующей дополнительной
карте, формат (10 F 8.2).
Например, если л==11, а все ац =
= 1,Ы0“10, то ПК будут следующими:
1 ПК: _1.Ю Е—8 ^1.10 Е—
8....1.10 Е—8;
2 ПК: . . 1.10 Е-—8;
3 ПК ^1.10 Е—8 1.10 Е—8 .....
^1.10Е—8;
4 ПК: _1.Ю Е—8;
22 ПК: U-10 Е—8.
Таким образом, при п=Н(п>10) по-
лучаем 22 ПК для записи массива а;
л) матрица / размером по-
строчно по п чисел на одной карте (если
nsgZIO). Если л>10, то. остаток строки
помещается на дополнительной карте, фор-
мат (10 F 8.5).
При этом первая строка матрицы / за-
полняется числами /<о, последующие стро-
ки— элементами Например, для случая
п = 5 матрица будет следующей:
Ао ^20 /зо Ао /50
Al 0 0 0 0
/з1 /32 0 0 0
^41 /42 /43 0 0
^51 /52 Аз 1st 0
Начиная со второй строки матрицы,
на главной диагонали и выше не следует
ставить нули, так как эти значения не
определены из физической сущности зада-
чи.
Программа «Балансировочная технологичность»
451
Примечание. При вводе десятичных
вещественных чисел (всех кроме п и Н) поло-
жение десятичной точки может быть произ-
вольным при ее наличии, однако под каждое
число всегда отводится 8 позиций.
Спецификация идентификаторов выходных
параметров модуля
На печать в случае нормального за-
вершения программы выводится значение
модуля главного вектора центробежных
сил ротора F и значения углов ут, при
которых получен этот минимальный вектор.
Режимы работы модуля
В головной программе с помощью ло-
гической переменной ДВС устанавливает-
ся режим .отладки (ДВС—TRUE.) или рис цд4д
рабочий режим (ДВС = . FALSE.). В ре-
жиме отладки в процессе счета на печать
выводятся промежуточные результаты,
необходимые для контроля правильности
выполнения программы.
Ограничения на использование опре-
деляются ограничениями, накладываемы-
ми на допустимые значения входных пара-
метров.
В случае ввода недопустимых исходных
данных программа распечатывает их зна-
чения, их допустимые границы и прекраща-
ет работу.
Описание тестовой задачи
В качестве примера принят пятимассо-
вый ротор, имеющий все необходимые
параметры для получения промежуточных
результатов и обеспечивающий проверку
правильности алгоритма решения задачи
в процессе отладки модуля (рис. П.14.1).
Исходные данные для тестовой задачи:'
число масс ротора п — 5;
угловая частота вращения ротора
<й=340 рад/с;
расстояние между опорами ротора
£ — 0.39 м;
модули эксцентриситетов торцового
биения-
ми = |ёг|2 = |ёт1з== |ёг|<= |ёт|6 = 0;
.г . Тт] =-- =Тт5=0;
модули эксцентриситетов радиально-
го биения:
|ёр| । = |ёр|2 = |ер|3 = 1ёр|4 = |ёрIs = 0,00002 м;
?р = 0°—360°;
диаметр соединения массы
D\ — D2'== Оз = 0,016 м;
дискретные массы:
пц = m2 —тц —т^— 1,32 кг.
Коэффициенты влияния а,,*10-7 м/Н:
Номер массы i f - номер точки приложения нагрузки
1 2 3 4 5
1 3,3 7,2 6,3 5,7 2,6
2 5,6 9,5 Н 9,3 4,7
3 5,2 11 13 12 6,3
4 4,8 9,5 12 11 6,5
5 1,8 4,6 6,7 7 4,8
Расстояния от ЦМ до вспомогатель-
ной поверхности 1ц (м):
Номер массы i / — номер точки приложения нагрузки
1 2 3 4 5
1 0,065 0,13 0,195 0,16 0,325
2 0,055 0,0 0,0 0,0 0,0
3 0,12 0,055 0,0 0,0 0,0
4 0,135 0,12 0,055 0,0 0,0
5 0,250 0,185 0,12 0,055 0,0
13*
452
Описания и тексты программ
Число анализируемых начальных по-
ложений при их переборе /7—6.
Ресурсы, необходимые для решения
тестовой задачи Время работы централь-
ного процессора—6 мин 40 с. Объем
оперативной памяти, необходимый для ре-
шения тестовой задачи, — 50 К байт.
Результаты расчетов печатаются в
следующем виде:
Тр1 = 0°. V₽2=180°, Vp3=0°, ур4—180°,
7Р5=о°;
Тя=о°, Тт2=о°, ут3 —0°, тт4=0°, тт5=0°.
Спецификация идентификаторов входных параметров
Таблица П.14.1
Идентификатор массива с указа- нием размерности Инженерное обозначение параметров Размерность фи- зической величины Содержательное наименование входного параметра
N W L ET(N) GAMT(N) n co L |eT| Тт» шт. рад/с м м рад Число масс Углов, част. Расстояние между опорами ротора Модуль и угол эксцентриситета торцового биения
ER(N) GAMR(N) |ёр| Tpi м рад Модуль и угол эксцентриситета ра- диального биения
D(N) M(N) D m м кг Диаметр соединения массы Масса
ALF(N, N) a Коэффициент влияния
LIJ(N, N) I м Расстояние от ЦМ до вспомогатель- ной поверхности
H H шт Число анализируемых начальных по- ложений при их переборе
СПИСОК МЕЖДУНАРОДНЫХ СТАНДАРТОВ И
ТЕХНИКЕ
1. МС ИСО 1940—73. Качество баланси-
ровки вращающих-
ся жестких тел.
2. МС ИСО 1925—74. Терминология ба-
лансировки.
3. МС ИСО 2953—75. Балансировочные
машины — описа-
ние и опенка.
•*. МС ИСО 5406—80. Балансировка гиб-
ких роторов.
ГОСТов ПО БАЛАНСИРОВОЧНОЙ
5. Единая система технологической под-
готовки производства.
ГОСТ 14-001—73...
ГОСТ 14.416—83.
6. ГОСТ 19534—74. Балансировка враща-
ющихся тел. Термины.
7. ГОСТ 20075—74. Станки балансиро-
вочные. Основные па-
раметры и размеры.
Список Международных стандартов и ГОСТов по балансировочной технике 453
8. ГОСТ 20076—89.
е ГОСТ 22061—76.
10. ГОСТ 12327—79.
Станки балансире- сы роторов. Нормы и
вечные. Нормы том- методы измерений,
ности. И. ГОСТ24346—80. Вибрация. Термины и
Система классов точ- определения.
ности балансировки. 12. ГОСТ 25466—82. Вибрация. Роторы гиб-
Основные положения. кие паротурбинных
Машины электриче- агрегатов. Требова-
ские вращающиеся. ния к балансировке.
Остаточные дисбалан-
СПИСОК ЛИТЕРАТУРЫ
1. Агафонов Ю. В., Базыкнн Ю. В. Ис-
следование устойчивости шарикового авто-
балансира роторной системы на анизотропных
упругих опорах//Машиноведение. 1985. № 5.
С. 111 113.
2. Агаханян Т. М. Интегральные микро-
схемы. М.: Энергоатомиздат, 1983. 464 с.
3. Балансировка машин н приборов/Под
ред. В А. Щепетильникова. М.: Машинострое-
ние, 1979. 294 с.
4. Барке В. Н., Кранцберг Л. Э. Ба-
лансировка шпиндельных узлов. Методические
рекомендация. М.: ЭНИМС, 1983. 20 с.
5. Бессонов А. П. Динамика механизмов //
Кинематика, динамика и точность механизмов:
Справочник./Под ред. Г. В. Крейн ина. М.: Ма-
шиностроение, 1984. С. 75- 110.
6. Вибрация в. технике: Справочник: в 6-ти
т./Ред. совет В. Н. Челомей (пред.) М.: Ма-
шиностроение, 1978 1983.
7. Гусаров А. А., Сусанин В. И., Шата-
лов Л. Н., Грушин Б. М. Автоматическая балан-
сировка роторов машин. М.. Наука, 1979. 152 с.
8. Динамика и балансировка роторов:
Библиогр. указатель литературы/Под ред.
А. А. Гусарова, Л. Н. Шаталова. М.:
ИМАШ АН СССР, 1986. 166 с.
9. Епанечников В. А., Цветков А. Н. Спра-
вочник по прикладным программам для микро-
калькуляторов. М.: Финансы и статистика,
1988. 320 с.
10. Журавлев В. Бальмонт В. Б. Меха-
ника шарикоподшипников гироскопов/Под ред.
Д. М. Климова. М.: Машиностроение. 1986.
272 с.
II. Захаров В. А. Технология сборки и
контроля подшипниковых опор ГТД. М.:
Машиностроение, 1985. С. 38—45.
12. Йоиушас Р. А. Расчет спектра вибра-
ций ротора, обусловленных неуравновешен
ностью ротора и несовершенствами подшип-
ников качения/КПИ Каунас, 1984. 46 с. Деп.
вЛитНИИНТИ 16.08.1984, Я? 1286.
13. Йоиушас Р. А. Вынужденные колебания
ротора, установленного в амортизированный
корпус и вращающегося в неидеальных под-
шипниках качения/КПИ Каунас, 1985.36 с. Деп.
в ЛитНИИНТИ 0.9.10.1985, № 1503.
14. Ковалев И. А., Бородулин М. В. Иссле-
дование вибрационного состояния валопровода,
состоящего из роторов, отбалансированных на
разгонном стенде//Энергомашиностроение.
1976. № 3. С. 10.
15. Кравченко В. И., Ромащенко В. А.
О равновесии шаров относительно ротора в
шаровом автобалансирующем устройстве спе-
циальной конструкции//Технология заготови-
тельного и механосборочного производства.
Краматорск: НИИПТМАШ. .1982. С. 190—195.
16. Левит М. Е., Ройзман В. П. Вибрация
и уравновешивание роторов авиадвигателей.
М_: Машиностроение, 1970. 171 с.
17. Левит М. Рыженков В. М. Балан-
сировка деталей и узлов. М.: Машиностроение,
1986. 247 с.
18. Левнтская О. Н., Левитский Н. И.
Курс теории механизмов и машин. М.: Высшая
школа, 1985, 279 с.
19. Макс Ш. Методы и техника обработки
сигналов при физических измерениях. М.: Мир,
1983. Т. 1. 312 с.
20. Максименко А. И. Особенности балан-
сировки роторных систем турбомашнн//Балан-
сировка машин и приборов.: Машиностроение,
1979. С. 119—129.
21. Никитин А. И. Технология сборки дви-
гателей летательных аппаратов. М.: Машино-
строение. 1982. 269 с.
22. Опоры осей и валов машин и приборов/
Под ред. Н. А. Спицина, М. М. Машнева.
Л.: Машиностроение, 1970. 519 с.
23. Орлов П. И. Основы конструирования:
Справочно-метод. пособие: в 3-х кн. М..- Маши-
ностроение. 1977. Кн." 1—623 с. Кн. 2 - 574 с’
Кн. 3—360 с.
24. Основы балансировочной техники: В 2-х
т./Под ред. В. А. Щепетильникова. М.: Маши-
ностроение, 1975. Т. 1—527. с. Т. 2—679 с.
25. Петрович В. И. Переносные баланси-
ровочные приборы//Измерения, контроль, авто-
матизация. 1981. № 6. С. 27—33.
26. Петрович В. И. Виброиэмерительные и
балансировочные приборы, применяемые в энер-
гетике/ /Энергетическое машиностроен не.
*(НИИЭ Инфорэнергомаш). 1982. № 4. 35 с.
Список литературы
455
27. Подшипники качения: Справочник/
Р. Д. Бейзельман, Б. В. Цыпкин, Л. Я. Перель.
М.: Машиностроение, 1975. 572 с.
28. Приборы и системы для измерения ви-
брации, шума и удара//Под ред. В. В Клюева.
М.: Машиностроение. 1978. Т. 2. С. 112—136.
29. Промышленные роботы и манипуляторы:
Каталог. М.: НИИ информации по машино-
строению, 1982. С 53—54.
30 Робототехника: Экспресс-информ М.:
ВИНИТИ. 1985, Кв 32. С. 1- 24.
31. Робототехника: Экспресс-информ. М.:
ВИНИТИ. 1985. Ке 33. С. 1—20.
32. Салимом А. В., Тараканов В. М.,
Рузский В. А. Особенности балансировки рото-
ров энергетических турбоагрегатов//Соврёмён-'
ные методы и средства балансировки машин
и приборов. М.: Машиностроение, 1985. 73 с.
33. Скшфчевский А. К., Промыслов Е. В.
Уравновешивание вращающихся масс гиро-
приборов. М.: Машиностроение, 1977. 248 с.
34. Современные методы и средства
балансировки машин и приборов/Под ред.
В. А. Щепетильникова М.: Машиностроение,
1985. 232 с.
35. Теория и практика уравновешивания
машин и приборов/Под ред. В. А. Щепетиль-
никова. М.: Машиностроение, 1970 440 с.
36. Теория и практика балансировочной
техники/Под ред. В. А. Щепетильникова. М.:
Машиностроение. 1973. 457 с.
37. Титце У., Шенк К. Полупроводниковая
схемотехйика. М.: Мир, 1982. 512 с.
38. Управление роботами от ЭВМ/Под ред.
Е. И. Юревича. Л: Энергия, Ленингр. отд-ние,
1980. С. 80—89.
39. Урашювешняанне роторов и механиз-
мов/Под ред. В. А. Щепетильникова. М.: Маши-
ностроение, 1978. 320 с.
40. Харрис С. М., Крвд Ч. И. Справочник
по ударным нагрузкам..Л.: Судостроение, 1980.
259 с.
41. Щелетильников В. А. Уравновешивание
механизмов. М.: Машиностроение, 1982. 256 с.
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
А
Автобалансирующее устройство (АБУ) 55,
239
---для шлифовальных кругов 265
---импульсное 270
---с использованием импульсного маг-
нитного поля (ИМП) 271
---с направленным перемещением 257
---со следящей системой 257
---со случайным поиском 257
---с принудительным перемещением
масс 257, 269
Автоматическая балансировка жестких ро-
торов 191
Автоматические лазерные балансировоч-
ные машины (АЛБМ) 273
□ * для высокочастотной балансировки
277
□ — уравновешивания одноопорных ро-
торов 274
□ осевых роторов’275
□ унифицированных роторов 278
□ шаровых роторов 278
□ с корректировкой масс по двум плоско-
стям коррекции 281
□ с лазером, работающим в режиме не-
прерывного излучения 282
□ □ свободной генерации 281
□ .с оптическим исключением влияния
плоскостей коррекции 282
□ с пневматическим улучшением качества
поверхности 284
□ с электрофизическим улучшением ка-
чества поверхности 284
Алгоритм выбора метода балансировки 354
Анализ частотных характеристик симмет-
ричных роторов 176
Анизотропия опор 172
Б
Балансировка 15
— агрегатов в сборе, метод 172
— в 2-х плоскостях коррекции 97, 103, 189
—т-----произвольных плоскостях кор-
рекции 99, 102
------------— с регламентацией оста-
точных дисбалансов 102
— в одной плоскости коррекции 92, 189
— воздушных винтов 410
— , выбор оснастки 349
— ,— режимов 349
* Знак, символизирующий понятие, состоящее
из трех и более слов.
— , — технологического балансировочно-
го оборудования 349
- в собранном изделии 92, 98
— высокочастотная 125
— гибкого ротора по формам колебаний
164
— изделий в сборе, перспективы развития
187
— карданных валов 404
— , классы точности 25
— колесных пар 414
— коррекцией масс 92
— многоплоскостная 104, 189
— модулей роторов 108
— , метод 109
- - на критических частотах 131
— обработкой цапф или центров 119
— обходным грузом 92
— , оценка качества 29
— по коэффициентам динамического вли-
яния, метод 173
— по формам колебаний 149
— ротора 7, 8, 42
— без вращения 218
---в сборе с изделием 167
---, контроль качества 120, 147
— раздельно по силовому н моментному
дисбалансам 105
— роторов гироскопических приборов 395
— сельскохозяйственных машин 405
---с использованием специальных
средств 96, 101
— узлов в сборе 196
---текстильных машин 416
Балансировочная линия (участок) 194
Балансировочные автоматы и полуавтома-
ты с вертикальной осью вращения 285
□ с горизонтальной осью вращения 287
приспособления, типы 358
---, назначения 358
Балансировочный станок дорезонансного
типа 189
□ , тарирование 389
---зарезонансного типа 189
---, класс точности 196
— — , повышение чувствительности 389
— , тарирование 387
В
Валопровод турбоагрегата 168
—, вибрационное обследование 168, 169
— , частотные характеристики 172
Валы технологические 365
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
457
Взаимозаменяемость рабочих модулей 111
Вибрационные измерения, методика 169
Вибрация 8, 13
— , виды 7
— , источники 7, 13
— машин 13
— системы 8
—, параметры 171
Виброизмер ител ьн ые преобразов ател и
контактные 13
---- неконтактные 13
Виброперемещения 8
Виброскорость 8
Виброускорение 8
Влияние жесткости опор ротора на ба-
лансировку 164
Выбор весовой характеристики лопаток 88
— плоскостей коррекции дисбаланса двух-
опорного гибкого ротора 176
— метода балансировки 350
— технологии балансировки 357
Вынужденные колебания 8
----станины 59
Высокочастотная балансировка 91, 140
----турбинных роторов 137
----, классификация роторов 139
----, сравнительный анализ 146
Г
Газостатические опоры 360
Геометрическая ось ротора 45
Гибкий ротор 20, 21, 46, 52
---- двухопорный 176
----, качество балансировки 23
Гироскопические приборы, балансировка
роторов 395
Гироскопический эффект 17, 48
Главная центральная ось инерции
(ГЦОИ) 38
Главные точки звеньев 57
Главный вектор 77
----дисбалансов роторов 39
----, компенсация 77
— момент дисбалансов роторов 39, 40
----неуравновешенных сил 77
Д
Двухплоскостная балансировка 386
Дезаксиальный механизм 68
Деформация ротора, измерение 222
---- при балансировке 166
Децентровка ротора 190
Динамическая балансировка жесткого
двухопорного ротора 203
------ ротора, технологический процесс 390
— жесткость 8
— неуравновешенность 38
— податливость 8
Динамический коэффициент влияния
(ДКВ), метод 145
Дисбаланс 8
, выбор допуска 28
— , значение 8, 184
— кривошипа 68
— критерий нормирования 25
— начальный 197
— остаточный 34
— скрытый 28
— технологический 25
— удельный 28
Допустимый удельный дисбаланс 25
□ , расчет 25
Ж
Жесткие опоры 39
Жесткий ротор 21, 35
---, качество балансировки 23
---эквивалентный 34.
Жидкостное автобалансирующее устрой-
ство (АБУ) 243
□ Дункан 246
□ Леблана 243
□ Сирла 244
□ с отводными трубками 244
□ с расплавляемым материалом 244
3
Закон распределения дисбалансов 340
Затухающие колебания 8
Звенья невесомые 65
- .........Й
Идентификация эксцентриситетов, метод
150
---по изгибным жесткостям изогнутого
вала 163
---по нормальным напряжениям 162
— гибких роторов по относительным де-
формациям 162
— кососимметричных масс 174
— неуравновешенных сил и эксцентриси-
тетов по из гибкому моменту 161
— симметричных Масс 174
Изгибные колебания вращающегося рото-
ра 46
Измерение деформаций ротора 222
— величины дисбаланса 274
Импульсные автобалансирующие устрой-
ства 270
458
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Интенсивность вибраций системы 8
Испытание на точность балансировочного
станка 234
— балансировочного станка для оценки
линейности по значению дисбаланса 239
Источник вибраций 13
К
Калибровка виброизмерительной аппара-
туры, интерференционный метод 222
Карданный вал, балансировка 404
Качество балансировки, оценка 179
Квазигибкий ротор 44
Квалификационные характеристики про-
фессии балансировщика 346
Классификация балансировочных станков
188
— балансируемых роторов 350
— специальных балансировочных станков
209, 210
Классы роторов 21, 30, 32—34
— точности балансировки 24, 25
---- балансировочных станков 196
Колебания 8
— вынужденные 59
— корпуса 184, 185
— резонансные 8
— ротора 184
Колебательная система 8, 182
----, динамическая модель 182
— станка 199
Колебательное движение точки 8
Коленчатый вал 76
— — особенности балансировки 114
Комбинированное АБУ 255
Комбинированный метод балансировки 144
Компенсация неуравновешенности 20
— неуравновешенных сил 79
— эксцентриситета шпинделя 201
Корректировка масс ротора 193, 374
— — , способы 375
Корректирующая масса 8, 41, 51, 68, 128
----, методы определения 84
Коэффициент балансировочной чувст-
вительности 331
— дисбаланса 43
— кратности балансировки 114
— уменьшения дисбаланса 234
— податливости 8
'Коэффициенты взаимного влияния плоско-
стей коррекции 234
Кривошипа дисбаланс 68
Критическая частота вращения 16, 22, 35,
49- 52
----— невесомого вала 16
Кулачковые механизмы для компенсации
неуравновешенности 79
Л
Линейность системы по значению дис-
баланса 234
М
Манипулятор, структурная схема 71
Масса корректирующая 41
Математическая модель ротора 351
Машина с кривошипами 73—75
Маятниковое АБУ 247
Маятниковый резонанс 44
Метод балансировки 44, 125
---, выбор 6
--- гибких роторов 125
---оптимальный 6
---по форме изгиба 125, 133, 141
----------- не на критических частотах
131
---пробными грузами 121
— динамического уравновешивания ме-
ханизма 60
— контроля качества балансировки 121 —
123
— определения корректирующей массы 84
— подбора пробной массы 84
— подобия 60, 65, 67
— принудительного центрирования 240
— раздельной балансировки модулей
111—112
— расчленения механизма 63, 65
— снижения вибраций 14
— совместной балансировки^ модулей 110
— статического уравновешивания меха-
низма 60
— уравновешивания по формам колеба-
ний 128
— функциональных цепей 65
Методы коррекции дисбаланса 194
Механизм 56
— дезаксиальный 68
— динамически уравновешенный 60
— кривошипно-ползунный 57, 65
---дезаксиальный 68
— манипулятора 70
— , моментная уравновешенность 60
— неуравновешенный 59
— рычажно-зубчатый 66
— рычажный 3-го класса 69
— с несимметричными звеньями, метод
уравновешивания 61
— статически уравновешенный 60
— центральный 67
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
459
— шарнирно-зубчатый 66
— шарнирный 3-го класса 69
Механические автобалансирующие уст-
ройства 247
Многомассовый симметричный ротор 45
Многоопорный валопровод, балансировка
167
Многоплоскостная балансировка 92, 116
---- валопровода 179
Многорядные АБУ 250
Множительный принцип измерения 199
Модуль неуравновешенный 111
— уравновешенный 111
Момент инерции 41
Моментная неуравновешенность 41
Н
Наладка балансировочного станка 202,209
Начальный дисбаланс 50, 117, 118, 150.
197, 333
Неуравновешенная сила остаточная 68
Неуравновешенность динамическая 19, 45
— моментная 19, 39, 165
— по п-й форме изгиба 20
— ротора 8, 44, 82
— статическая 18, 38, 40, 165
Низкочастотная балансировка 20, 45, 91
— многоплоскостная балансировка, тех-
нологический процесс 393
0
Обратная синхронная прецессия 15
Объем измерений 171
Опоры трения качения 361
Оправки балансировочные 365
----межопорные 367
----, основные элементы 366
----, проектирование 366
----уборные 367
----, | технические требования 365
----, характеристики 367
Определение коэффициента уменьшения
дисбаланса 235
□ специальных станков 237
----взаимного влияния плоскостей кор-
рекции 237
Оптимизация неуравновешенных сил 80
— балансировки, метод 145
Основные виды автобалансирующих уст-
ройств, классификация 240
Основы автобалансировки роторов 239
Остаточная неуравновешенная сила 68
Остаточный дисбаланс 150, 191
----главного вектора и главного момен-
та 120
П
Паразитная масса 189
Параметрическая идентификация гибких
роторов 156, 161
Параметры возмущений 185
Переходная поверхность 255
Плоскость коррекции 19, 42
Повышение чувствительности баланси-
ровочных станков 389
Погрешности статической балансировки 84
Погрешность измерения удельных дисба-
лансов 371
----угла дисбаланса 234. 238
Податливость опор 166
Подетальная балансировка 196
Подшипники качения, конструкции 362
----, технические требования 361
Приводные валы 369
----двухшарнирные 369
----с зубчатыми муфтами 370
----с упругими муфтами 369
Принудительное центрирование, метод 240
Принцип динамического уравновешивания
механизмов 77
— симметрии 78
Пробная масса 93
Пробные дисбалансы 134
----, метод балансировки 136
Проектирование балансировочных при-
способлений 358
— основных систем балансировочных
станков 228
Производительность балансировки 195
Р
Разгонно-балансировочный стенд 191
Разгрузка кинематических пар от дейст-
вия неуравновешенных сил 82
Разделение плоскостей коррекции 207
Рамки балансировочные 367
Расчет корректирующих масс 132
Резонансная частота 8
Резонансные колебания 8
Ременный привод 206
Роликовые опоры 363
----, технические* требования 363
Ротор 8
— двухконсольный 30
— консольный 30
— контрольный 372
----, конструктивные параметры 373
— межопорный 30
— многомассовый 38
— переменной массы 54
-------, динамика 53 1
460
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
— с изменяющейся геометрией масс 53,
408
— смешанный 30
— тарировочный 374
— шаровой конструкции 42
С
Самоцентрирование вала 17
Свободные колебания 8
Синхронная прецессия 15
обратная 15
---- прямая 15
Система корректирующих масс 175
— экстремального регулирования 258
Снижение вибраций, методы 14
Собственная форма колебаний система 8
----изгиба ротора 49, 50, 51
— частота колебаний 8
------- опор 36
Средства балансировки 7, 188
Специализированные балансировочные
станки 191—193
Специальные балансировочные станки 210,
214
Средства балансировки, выбор 195
Станина, вынужденные колебания 59
Станок для автоматической балансировки
194
---- балансировки гибких роторов 189,
219
------- коленчатых валов 287
----динамической балансировки 189
----------жестких роторов 190
------- центровки 191
----— — роторов турбокомпрессоров
226
----статической балансировки 86, 189,
198
------- децентровки 190
------- центровки 190
— модели МА 9747 211
----МА 9707Д 214, 215
----МА 9708 214, 215
----МА 97Д52 217
----МА 9А764 224, 225
----МВТУ-0726 214
----МВТУ-0730 211. 213
----МС9731 216
----МС991 215
----ЭЗ-125 294
----*- ЭЗ-145 289
----ЭЗ-146 226, 227
----ЭЗ-175 293
Станки специальные балансировочные
192, 193
— универсальные балансировочные 188
Статико-моментная балансировка 387
— — , технологический процесс 391
Статическая балансировка 87, 113
----дисков, технологический процесс 389
----при помощи сил тяжести 83
вибраций 87
— неуравновешенность 38, 40
Статический коэффициент влияния 47
Т
Тарирование балансировочного станка 387
— дорезонансного балансировочного
станка 389
Технологические дисбалансы 25
— требования к подшипникам качения 361
Технологический процесс балансировки де-
талей 345
□ , балансировочные операции 345
□ , — работы 345
Технологичность конструкций балансиру-
емых изделий 343
□ , сборочная 343
Типовые изделия машино- и приборострое-
ния, балансировка 384
— технологические процессы балансиров-
ки 384
Типы роторов 21
Точечная масса 58
Точная балансировка изделий с жесткими
роторами в собранном состоянии 180
Точность балансировки 328
---- действительная 329
---- заданная 329
----«- ожидаемая 329
— балансировочного станка 234
— измерения дисбаланса 234
— уравновешивания 111
У
Угол дисбаланса 8
Удельный дисбаланс 25, 27
----, нормирование 28 . >>?.
Упругость опор 48
Уравнение Фредгольма 47
Уравновешенность моментная 60, 77
Уравновешивание в собранном виде 180
— ротора вблизи резонансных режимов
221
— роторной системы 23
-------приближенное 55
— функциональной цепи 66
Уровень вибраций 6
— колебаний 9
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
461
Условия балансировки 351
----, структурная схема 201
Устройства со свободным перемещением
корректирующих масс 243
Ф
Фредгольма уравнение 47
Функциональная цепь 66
Функциональные цепи, метод уравновеши-
вания 65
Функция влияния (функция Грина) 47
Ц
Центр масс, ординаты 64
Центральный механизм с несимметричным
шатуном 68
Центровальные балансировочные станки
189
Цикл балансировки 194
Ч
Частота вращения критическая 49
— маятниковых колебаний 44
Чувствительность АБУ 250
— к моментному дисбалансу 238
— по значению дисбаланса 234, 238
Ш
Шарнирный механизм 3-го класса 69
Шаровое АБУ 247
Шатун 57
—, Модель динамическая 57, 58
— , — статическая 57
Шкив приводной 372
Шпиндель, компенсация эксцентриситета
201
Э
Эквивалентный жесткий ротор 34
Эксплуатационный дисбаланс 331
Эксцентриситет массы 9
Электроимпульсное АБУ 270
Электрохимическая балансировка 294
ГРУППА ИССЛЕДОВАНИЙ ВИБРАЦИЙ (ГИВ)
МОСКОВСКОГО АВИАЦИОННОГО ИНСТИТУТА,
ИМЕЮЩАЯ МНОГОЛЕТНИЙ ОПЫТ РАБОТЫ
В ОБЛАСТИ БАЛАНСИРОВОЧНОЙ ТЕХНИКИ
И ВИБРАЦИЙ ПРОВОДИТ:
консультации и обучение специалистов промышленности в об-
ласти балансировки и сборки роторов;
конструкторско-технологический анализ, балансировку и сниже-
ние вибраций серийных и опытных образцов роторов и роторных
машин;
разработку методов, оборудования, аппаратуры, проектирова-
ние технологий и оснастки для балансировки роторов;
внедрение прогрессивных высокопроизводительных методов ба-
лансировки иа предприятиях с применением ПМК и ПЭВМ;
настройку и ремонт балансировочного оборудования;
разработку автоматизированных балансировочных участков
иа базе ПЭВМ, серийного и специального балансировочного обо-
рудования;
изготовление многоканальной балансировочной и виброизмери-
тельиой аппаратуры с бесконтактными индуктивными и емкостными
датчиками;
изготовление лазерных измерителей вибрации;
разработку АСНИ для балансировки и исследования вибрации;
другие виды работ по требованию заказчика.
Для проведения исследований группа располагает современной ап-
паратурой и балансировочным оборудованием, в том числе высоко-
качественным вакуумным разгоино-балансировочиым стендом.
Наш адрес:
125871, Москва, ГСП, Волоколамское шоссе, 4
Для телеграмм:
Москва—Шарнир, телетайп 113088,
тел. 158-58-70, 158-43-33, 158-43-91
УВАЖАЕМЫЙ ЧИТАТЕЛЬ!
Если Вы занимаетесь вопросами
конструирования,
расчета,
изготовления,
уравновешивания
гибких роторов;
если Вы знакомы с ПЭВМ типа ДВК или уже используете их’в своей работе,
то поспешите направить нам заказ на книгу
«УРАВНОВЕШИВАНИЕ ГИБКИХ БЫСТРОХОДНЫХ РОТОРОВ»,
которую издательство «Машиностроение» вместе с авторами М. Е. Левитом
(МАИ), В. М. Рыженковым (МАИ), В. А. Петушковым (ИМАШ), С. П. Аксе-
новым (КБ «Химавтоматика») и А. М. Кашкаровым (НПО «Энергомаш»),
предполагает подготовить и выпустить в свет в ближайшее время.
В книге будут рассмотрены:
методы, средства и технология низко- и высокочастотной балансировки
гибких быстроходных роторов повышенной надежности и длительного ресурса,
правила конструирования роторных узлов и их основных элементов, оп-
ределяющих сбалансированность в эксплуатационных условиях;
методы расчета колебаний и прочности роторной конструкции.
В книге будут приведены:
типовые методики расчетов;
схемы и примеры конструктивных решений роторных узлов;
типовые технологические процессы контроля, испытаний и балансировки
деталей, узлов и быстроходных роторов в сборе на рабочих частотах вращения.
Используемый в книге материал взят из теории и практики создания
высоконагруженных роторных систем повышенной надежности и длительного
ресурса маршевых двигателей ракетоносителя «Энергия» и отражает передовой
опыт турбостроения.
Особенностью книги являе ся прилагаемый к ней гибкий магнитный диск
(ГМД) с записью комплекта прикладных программ для ПЭВМ типа ДВК,
иллюстрирующих предлагаемые методики расчетов.
Качество записи программ и их работоспособность гарантируются!
Ориентировочная цена книги без ГМД 3—5 руб., с ГМД 15—18 руб.
Наше решение о целесообразности издания книги будет зависеть от коли*
чества поступивших заказов.
464
Предварительные заказы на открытках, вложенных в конверт, следует на-
правлять по адресу: 107076, Москва, Стромынский пер., 4, издательство «Машино-
строение», отдел распространения.
На лицевой стороне открытки в графах «Куда», «Кому» нужно написать
свой адрес (не забудьте указать свой почтовый индекс!); в графе «Индекс
предприятия связи и адрес отправителя» нами будет указан адрес книжного
магазина, в котором Вы сможете приобрести данную книгу.
На обороте открытки следует указать:
а) издательство «Машиностроение»;
б) название книги;
в) с ГМД или без Г'МД;
г) количество экземпляров.
ЖДЕМ ВАШИХ ЗАКАЗОВ!
СПРАВОЧНОЕ ИЗДАНИЕ
ЛЕВИТ Михаил Ефимович, АГАФОНОВ Юрий Викторович, ВАЙНГОРТИН Лев Давидович и др.
СПРАВОЧНИК ПО БАЛАНСИРОВКЕ
Редактор Л П. Строганов
Переплет художника А. Д. Андреева
Художественный редактор С. Н. Голубев
Технический редактор О. В. Куперман
Корректоры Т. В- Багдасарян, И. М. Борешиа
ИБ № 5287
Сдано в набор 17.05.89.
Бумага офсетная № I.
Усл. печ. л. 37,7.
Тираж 1000 экз.
Подписано в печать 09.08.90.
Гарнитура литературная.
Усл. кр.-отт. 37,7.
Заказ 7641.
Формат 70X100*/i6-
Печать офсетная.
Уч.-изд. л. 47,0.
Ордена Трудового Красного Знамени издательство «Машиностроение», 107076, Москва, Стро-
мынский пер., 4
Отпечатано в московской типографии № 4 Министерства печати и массовой информации РФ
129041. Москва, Б. Переяславская, 46, с оригинал—макета, изготовленного в типографии ЦАГН.