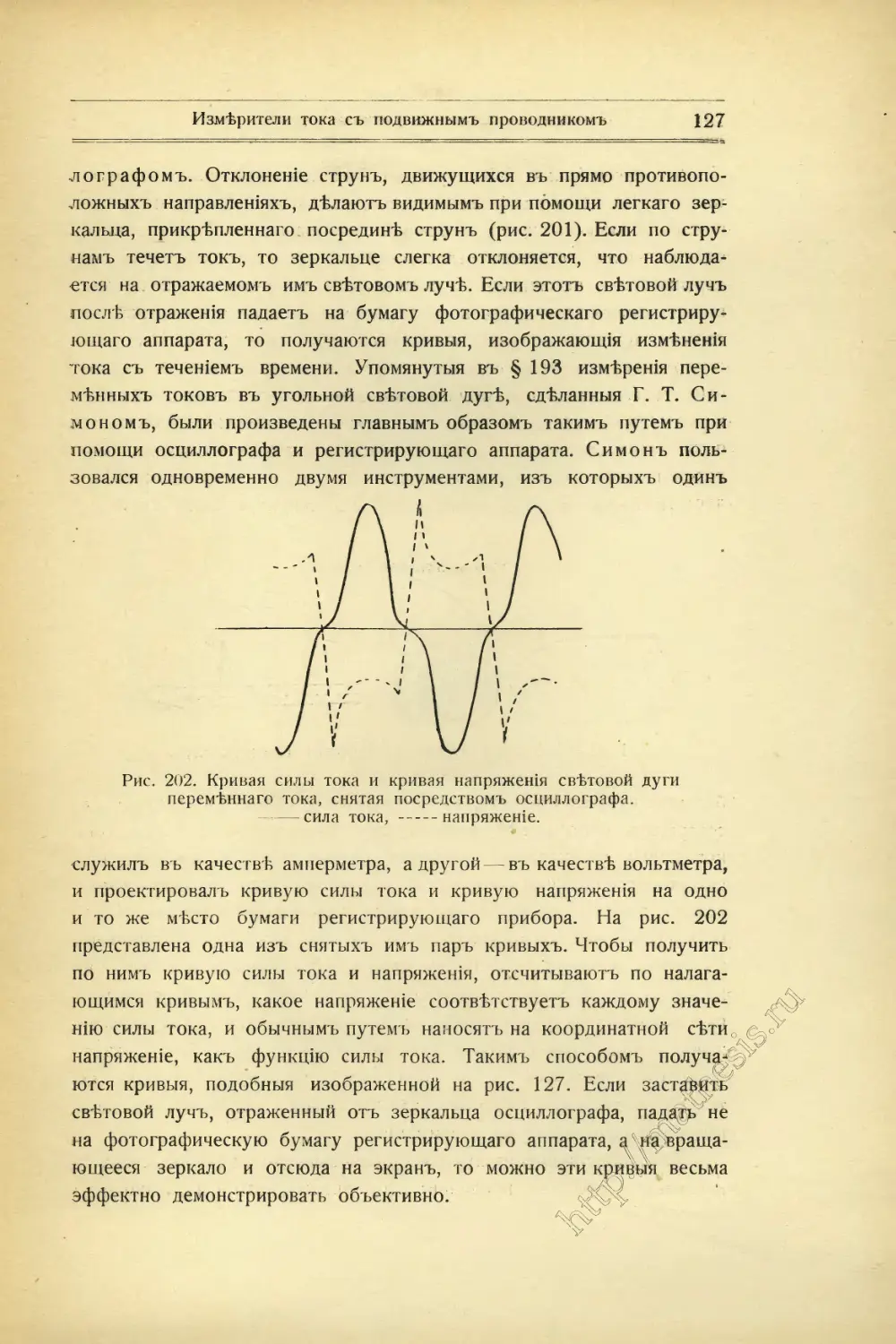
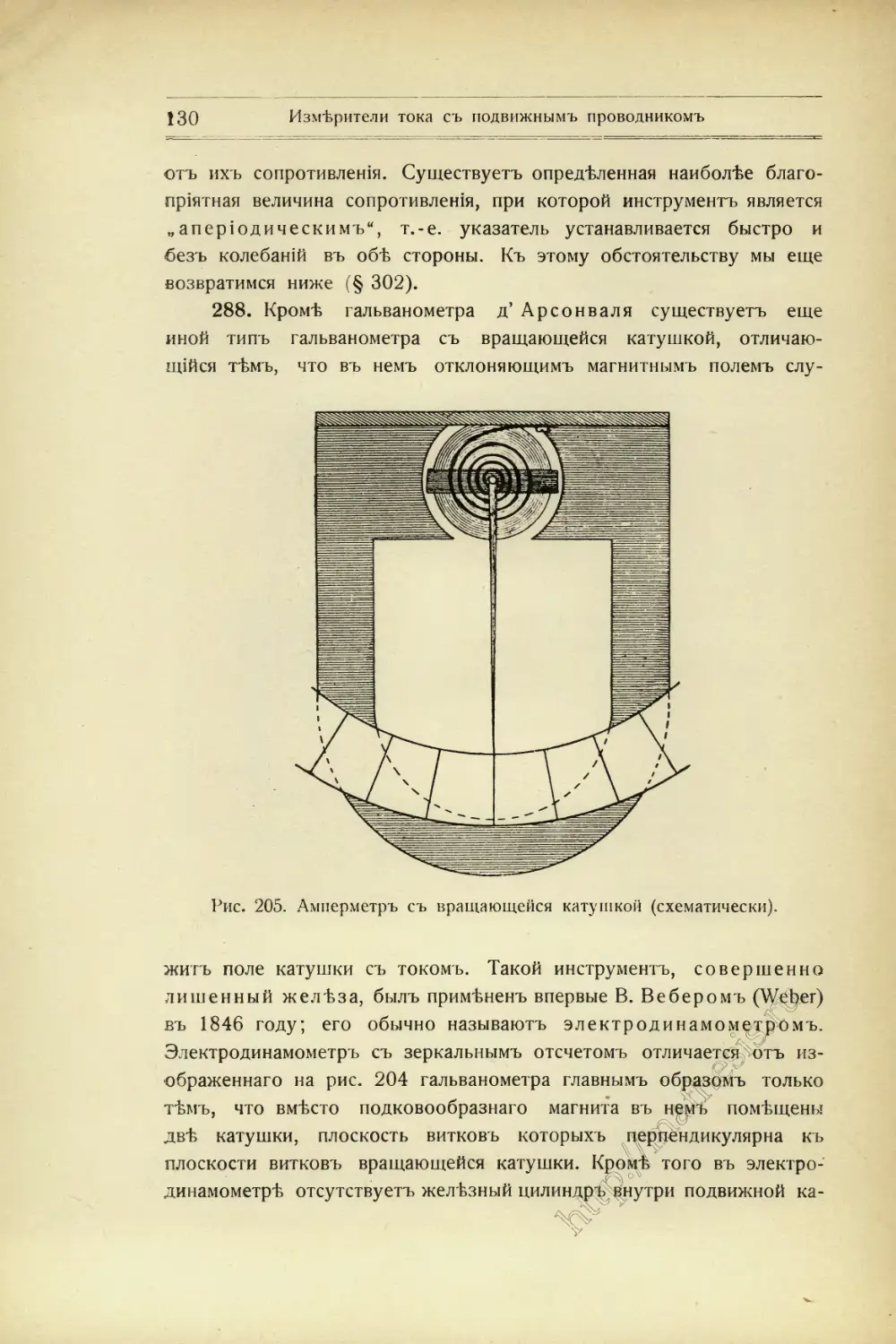
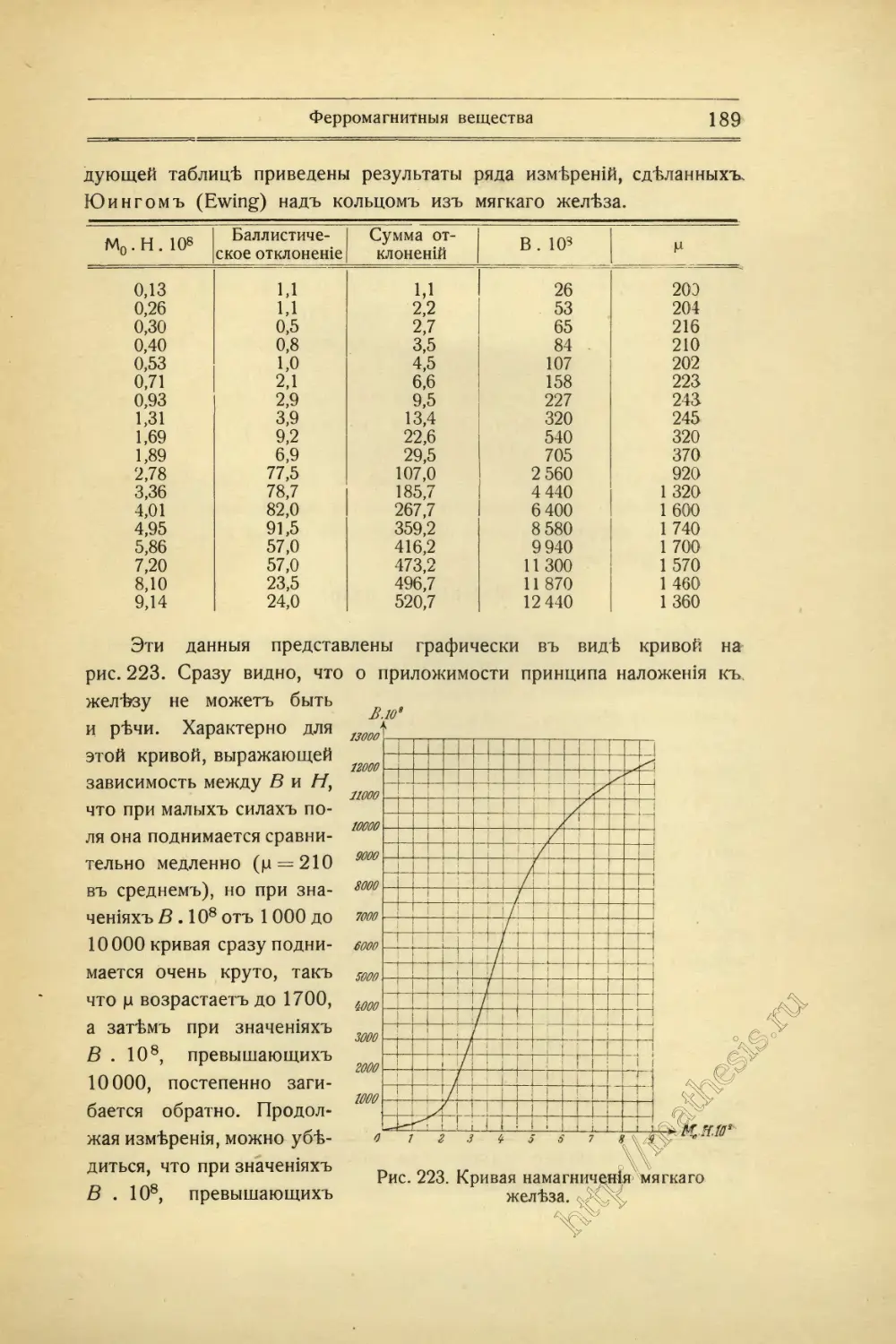
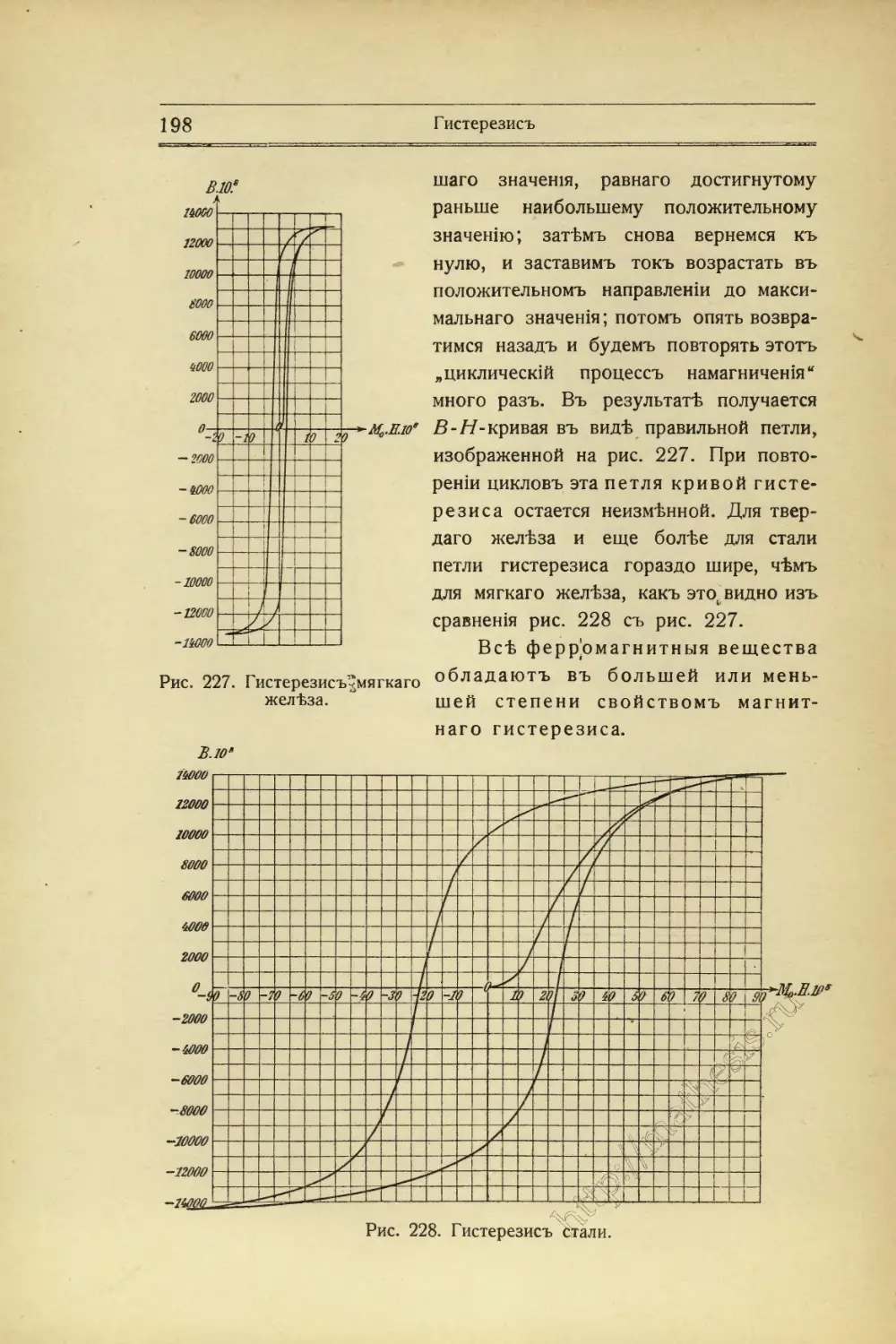
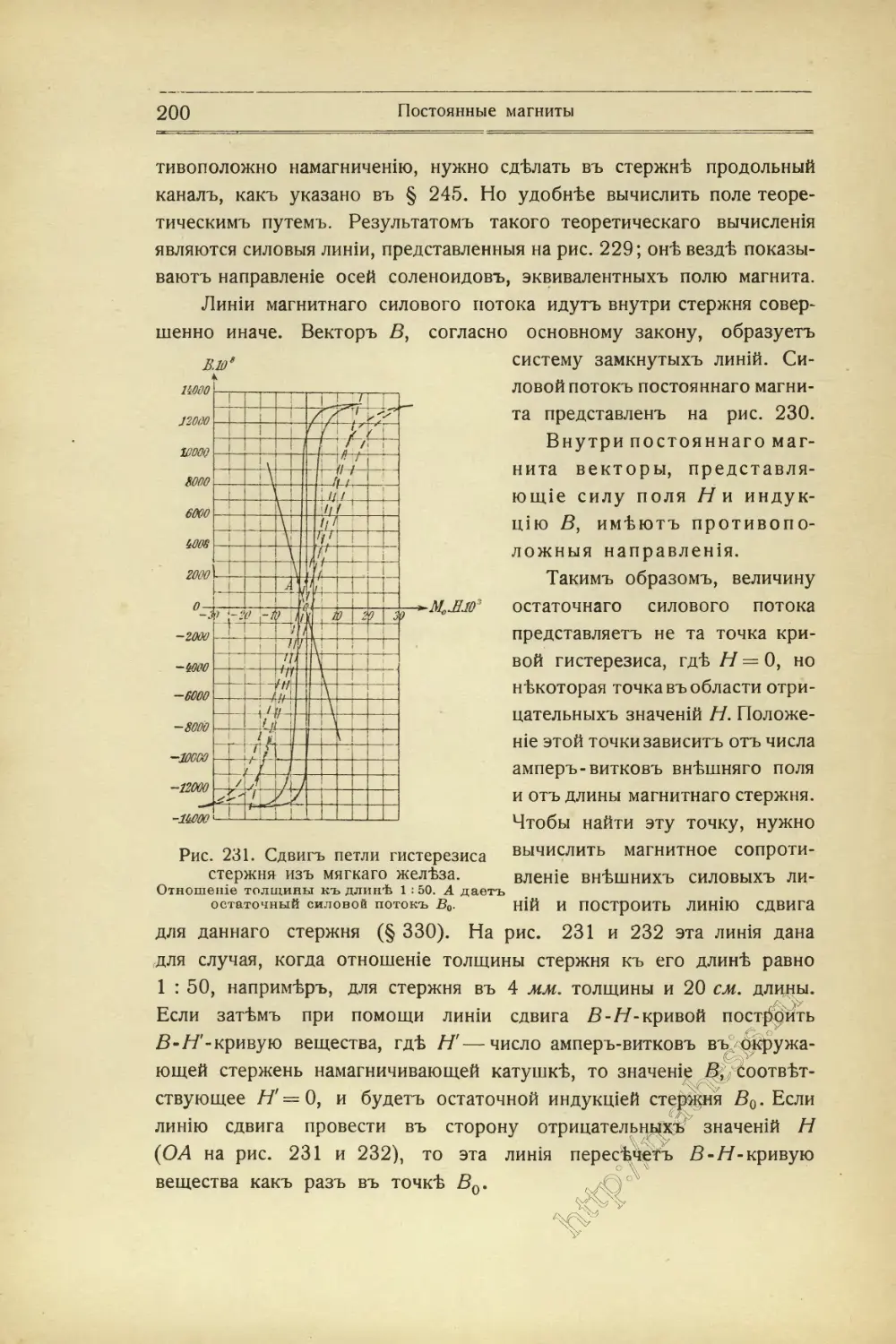
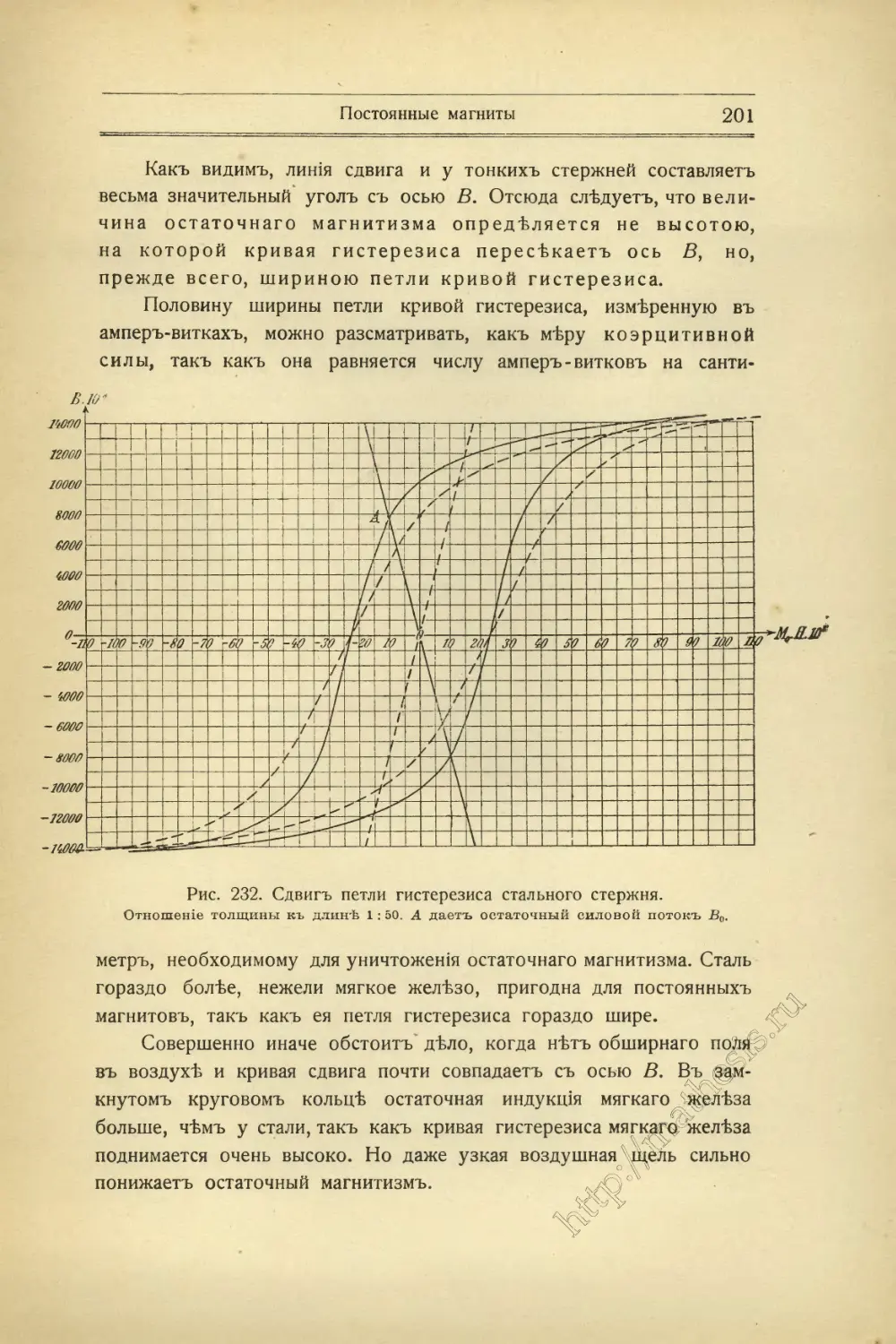
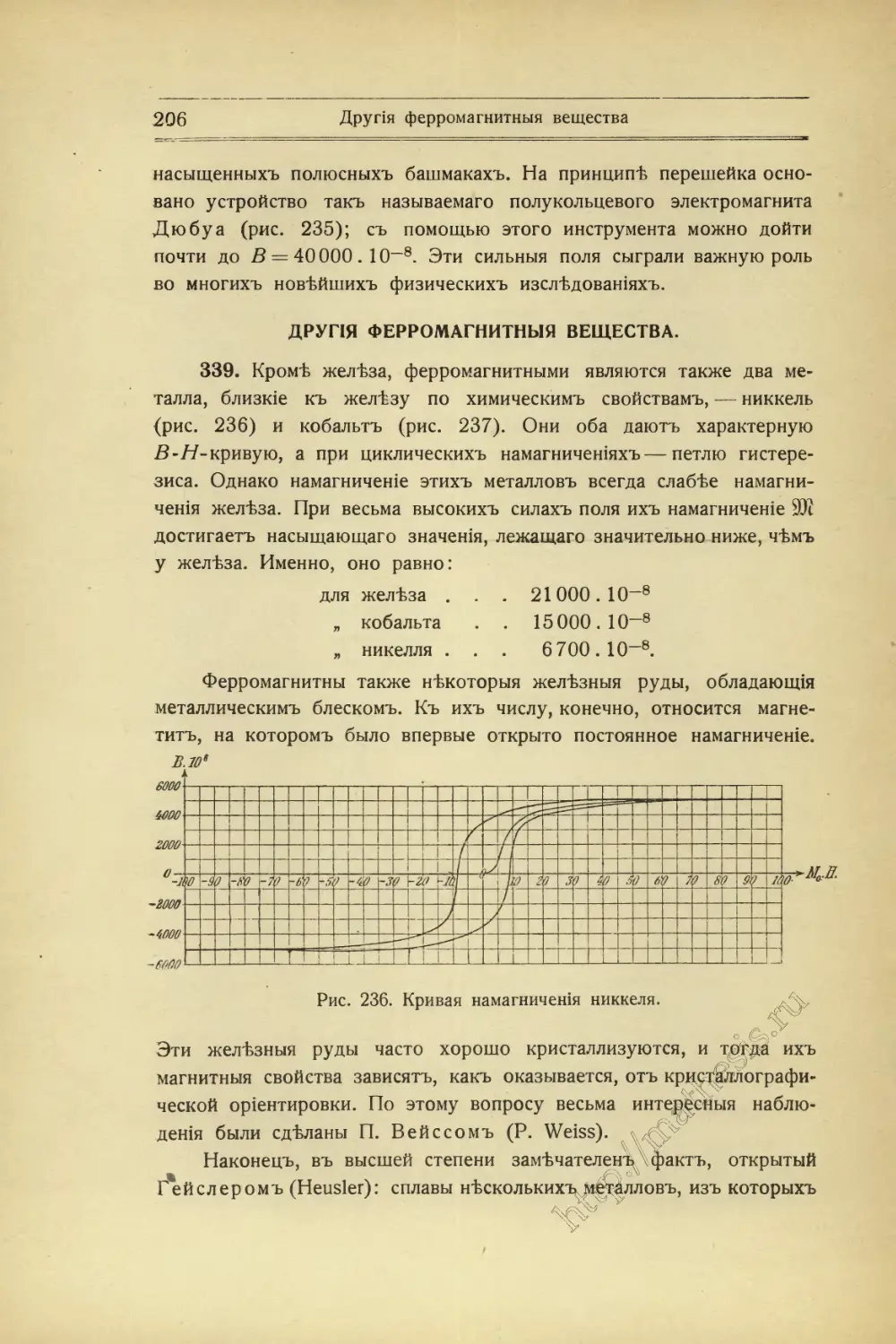
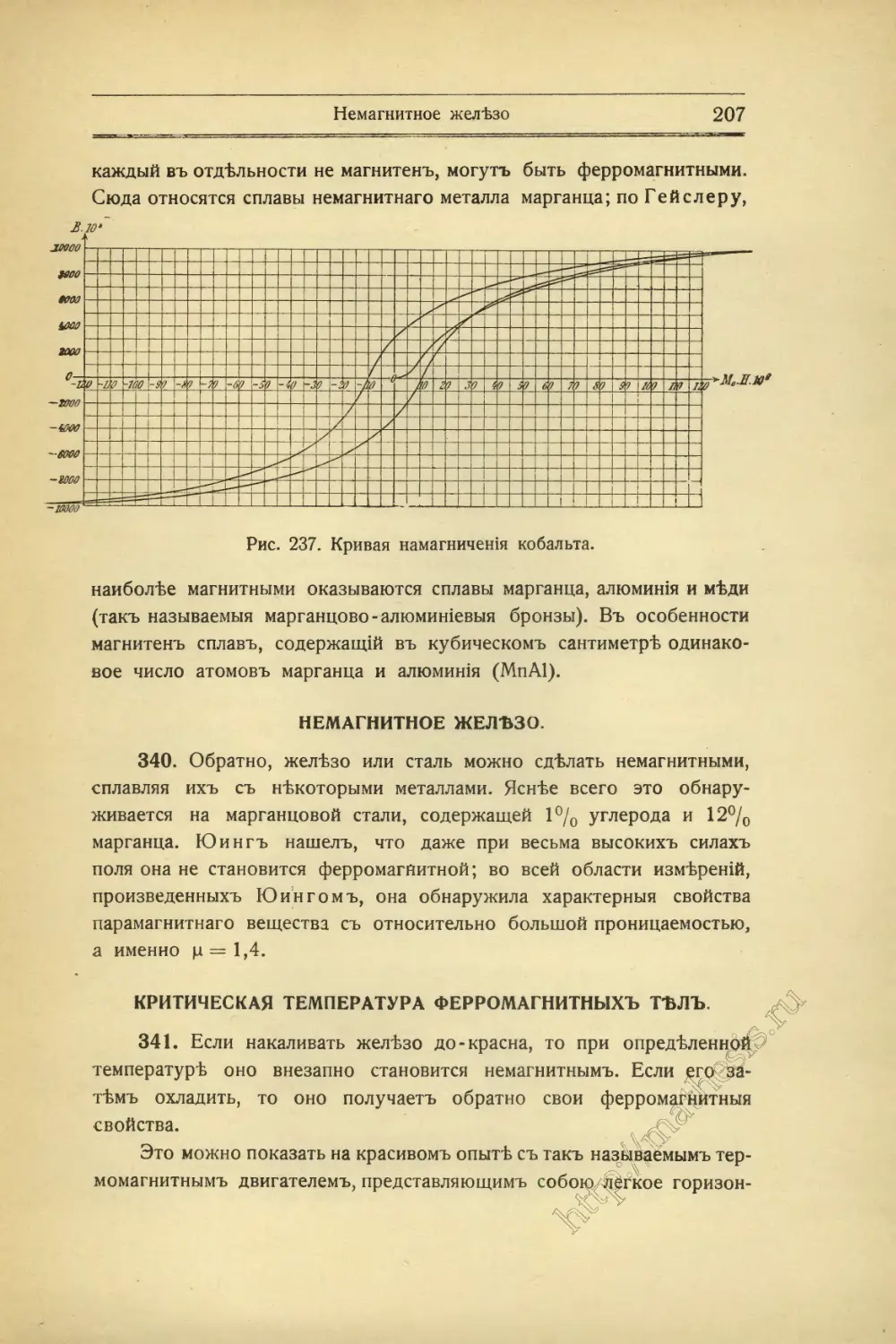
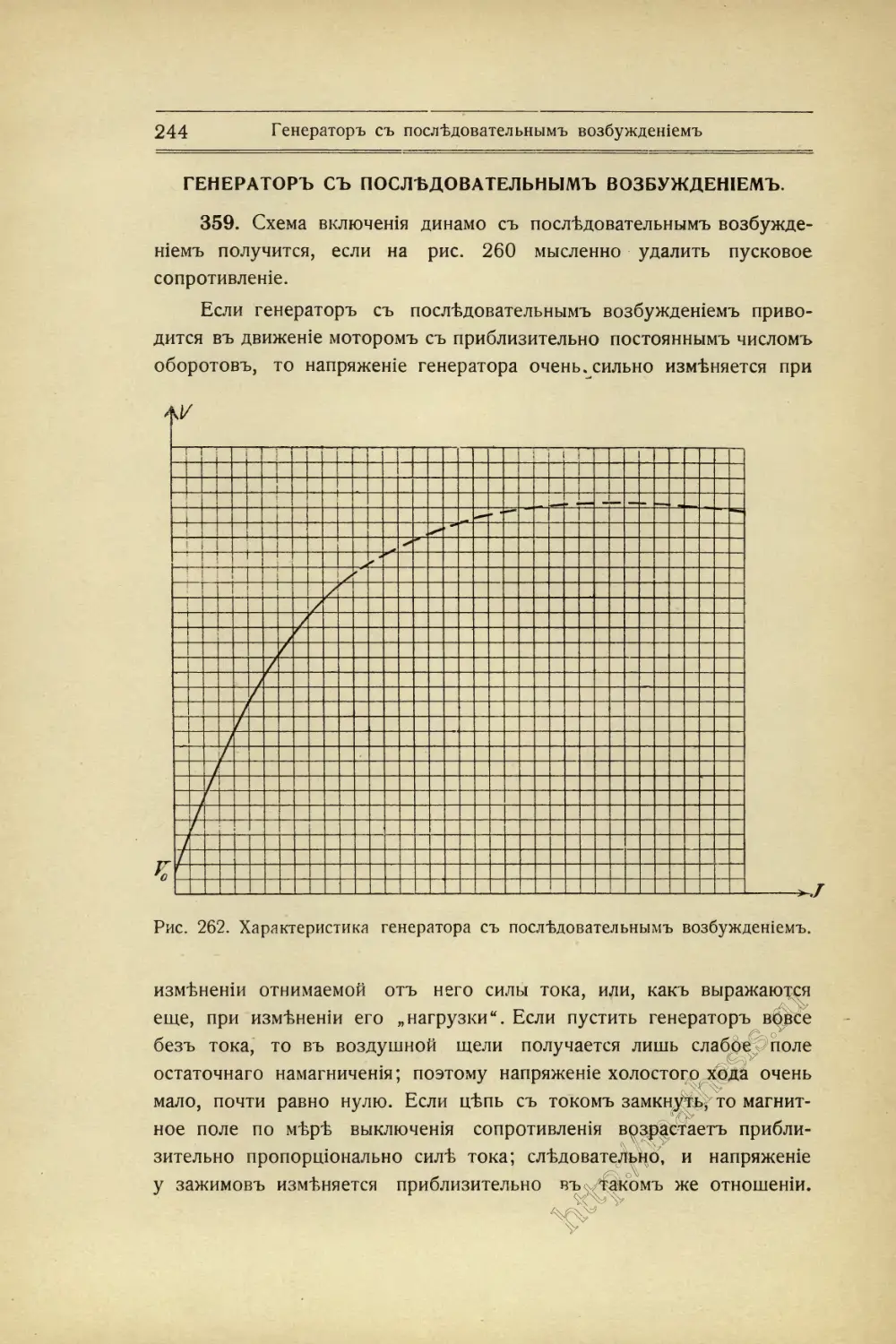
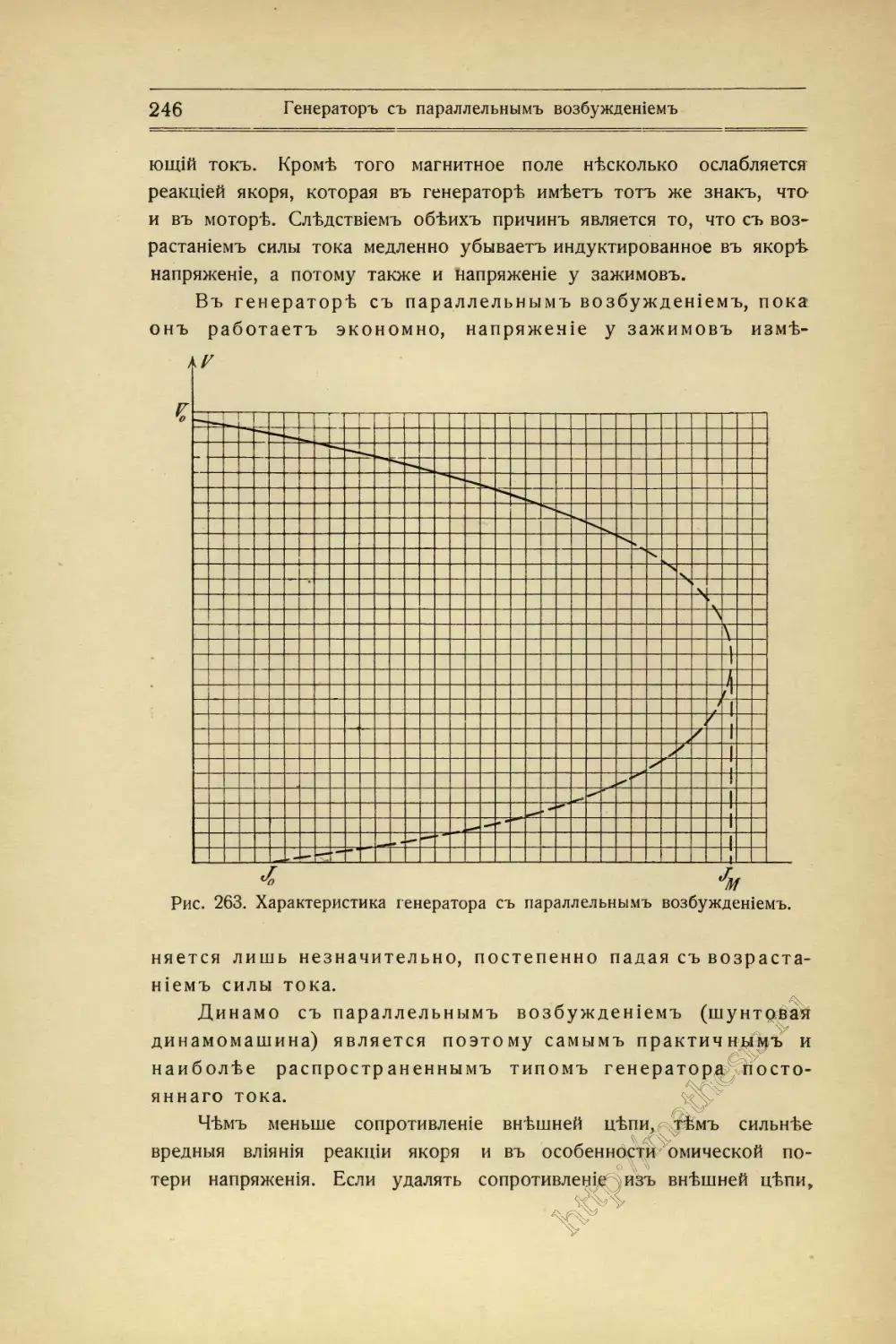
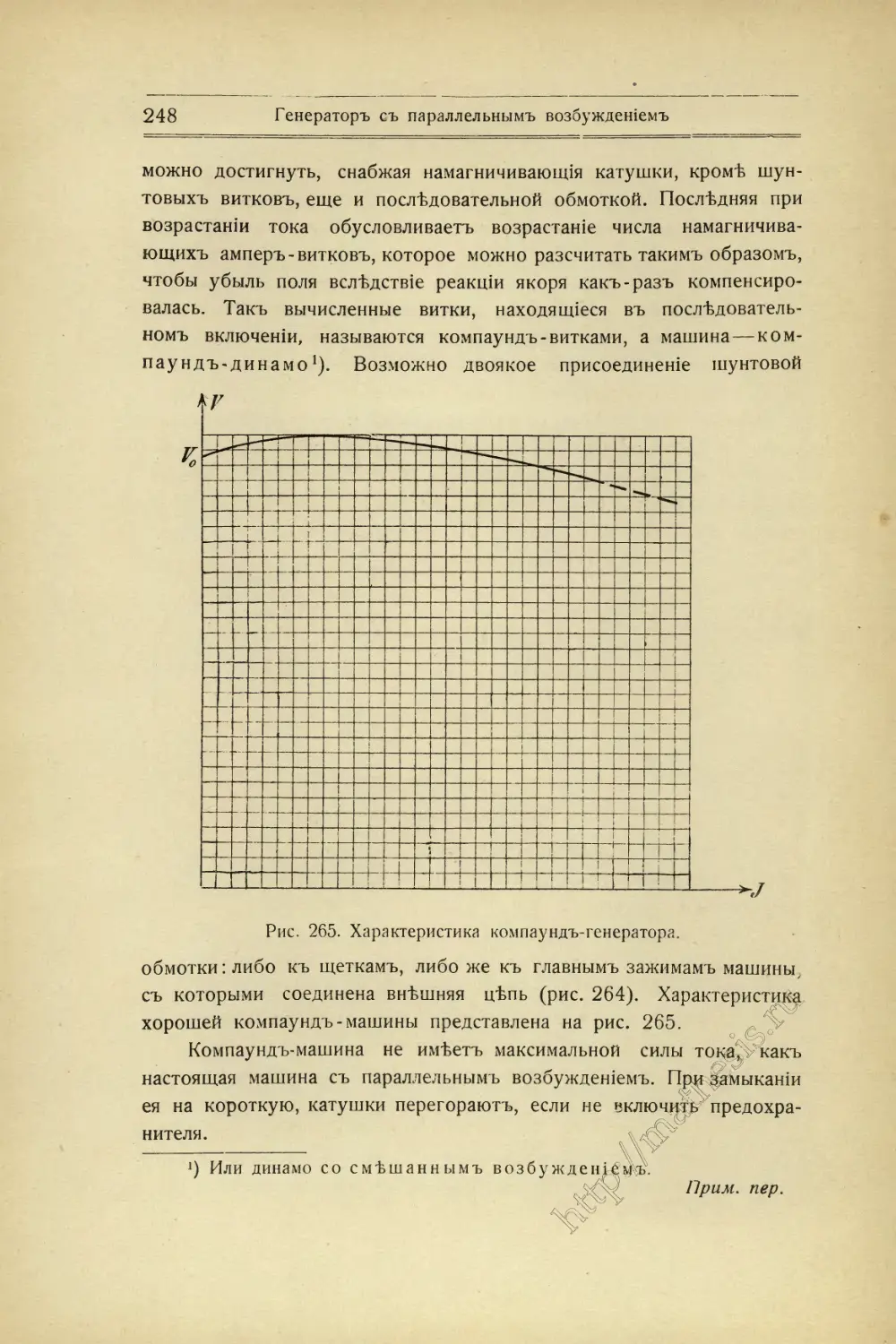
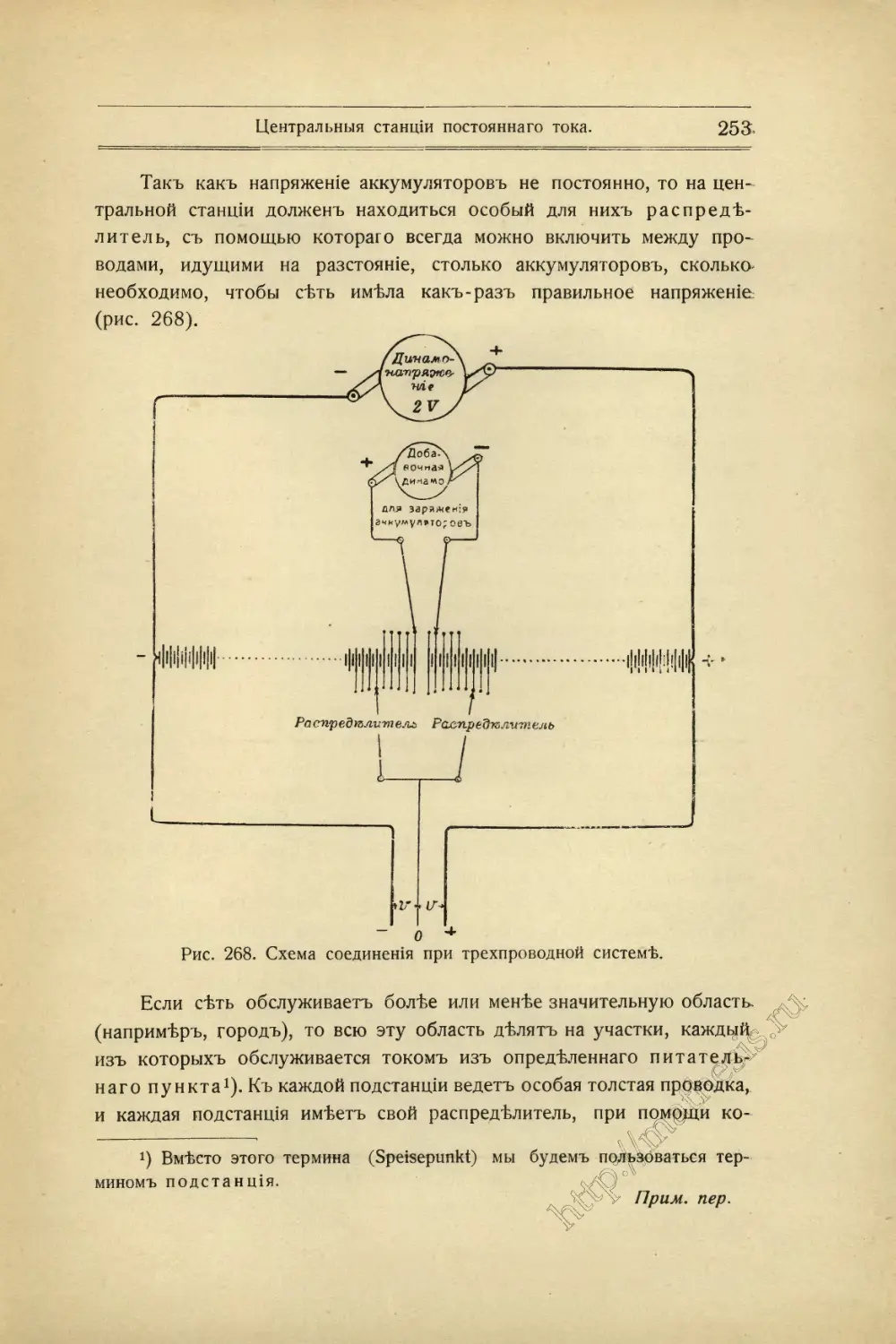
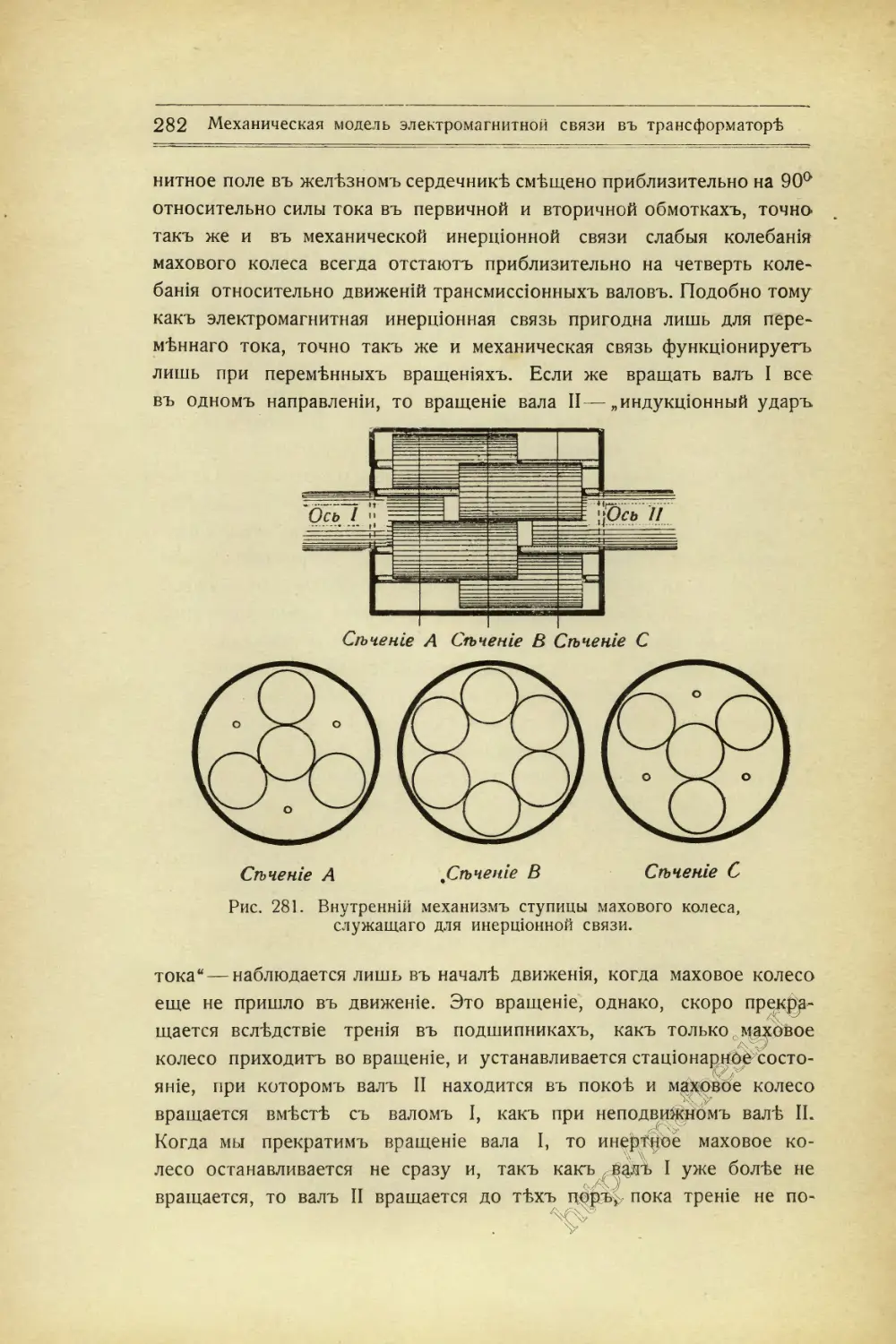
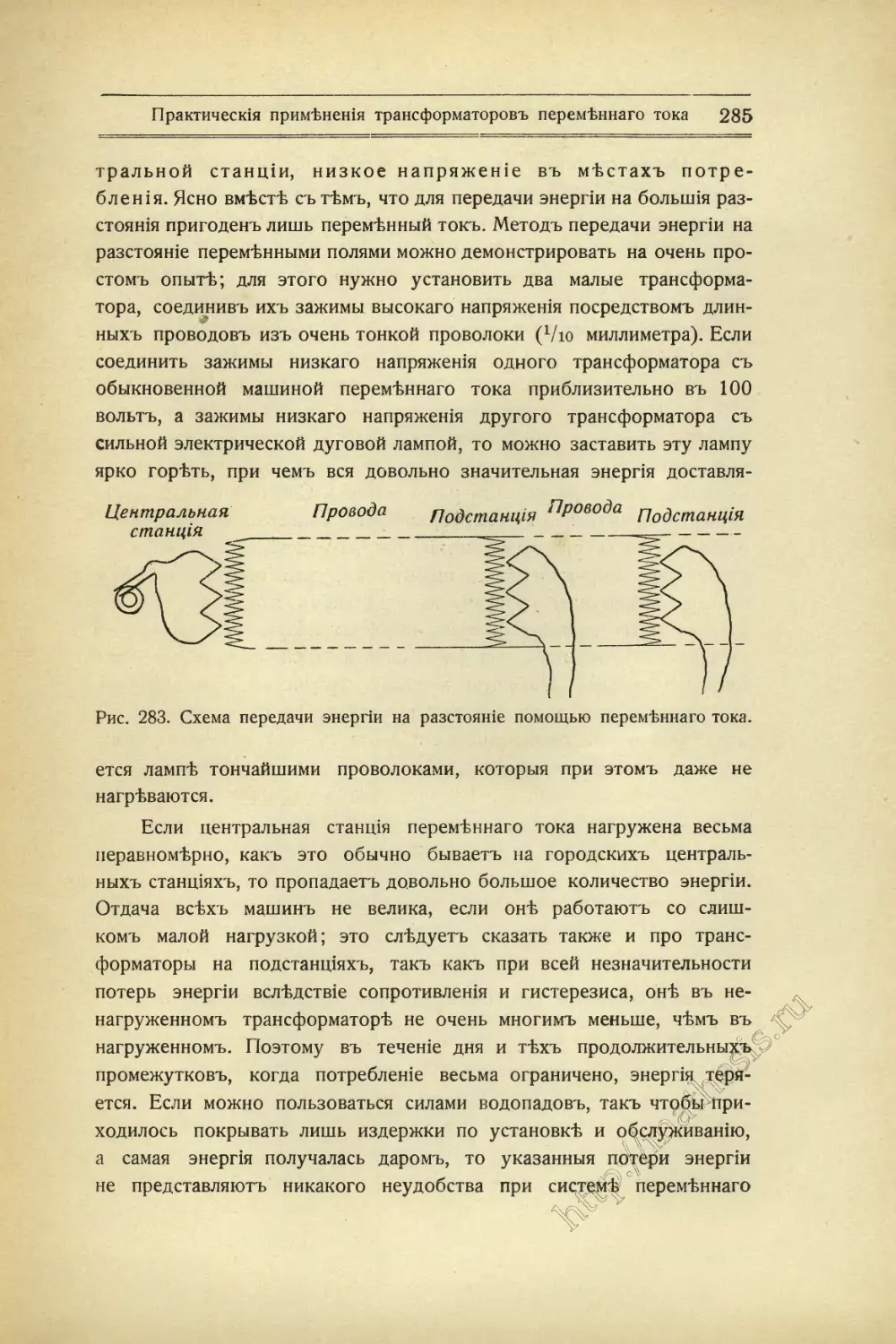
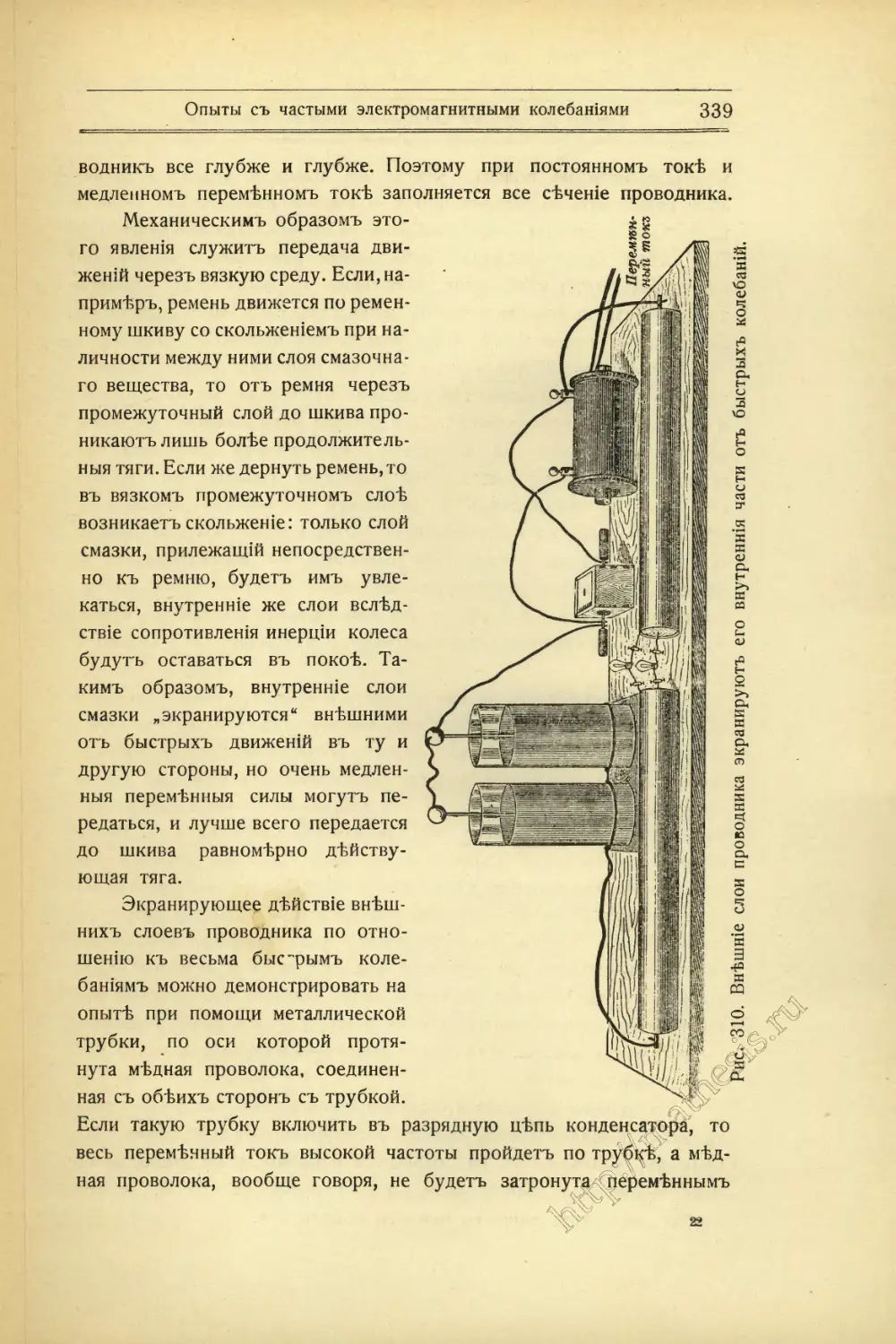
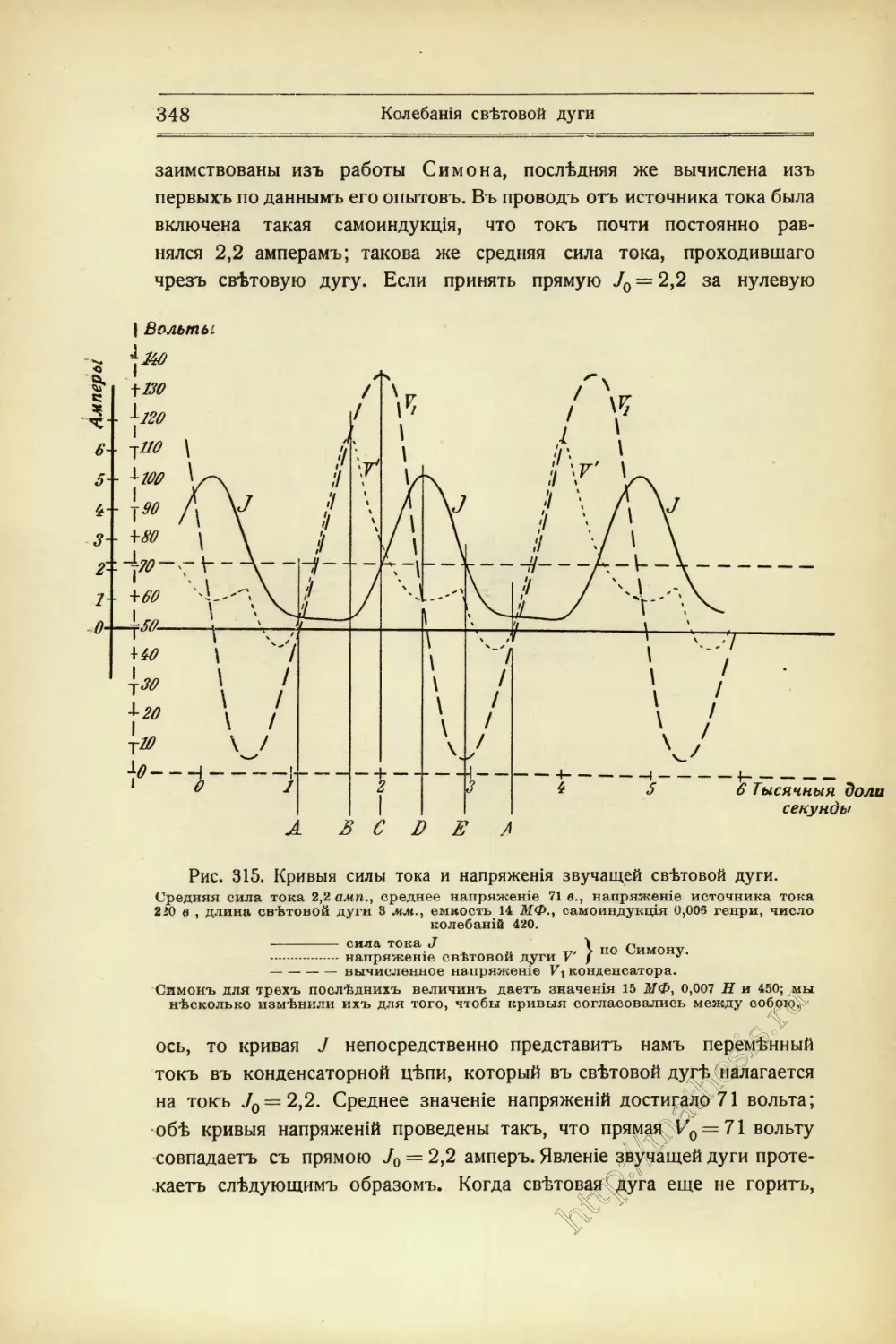
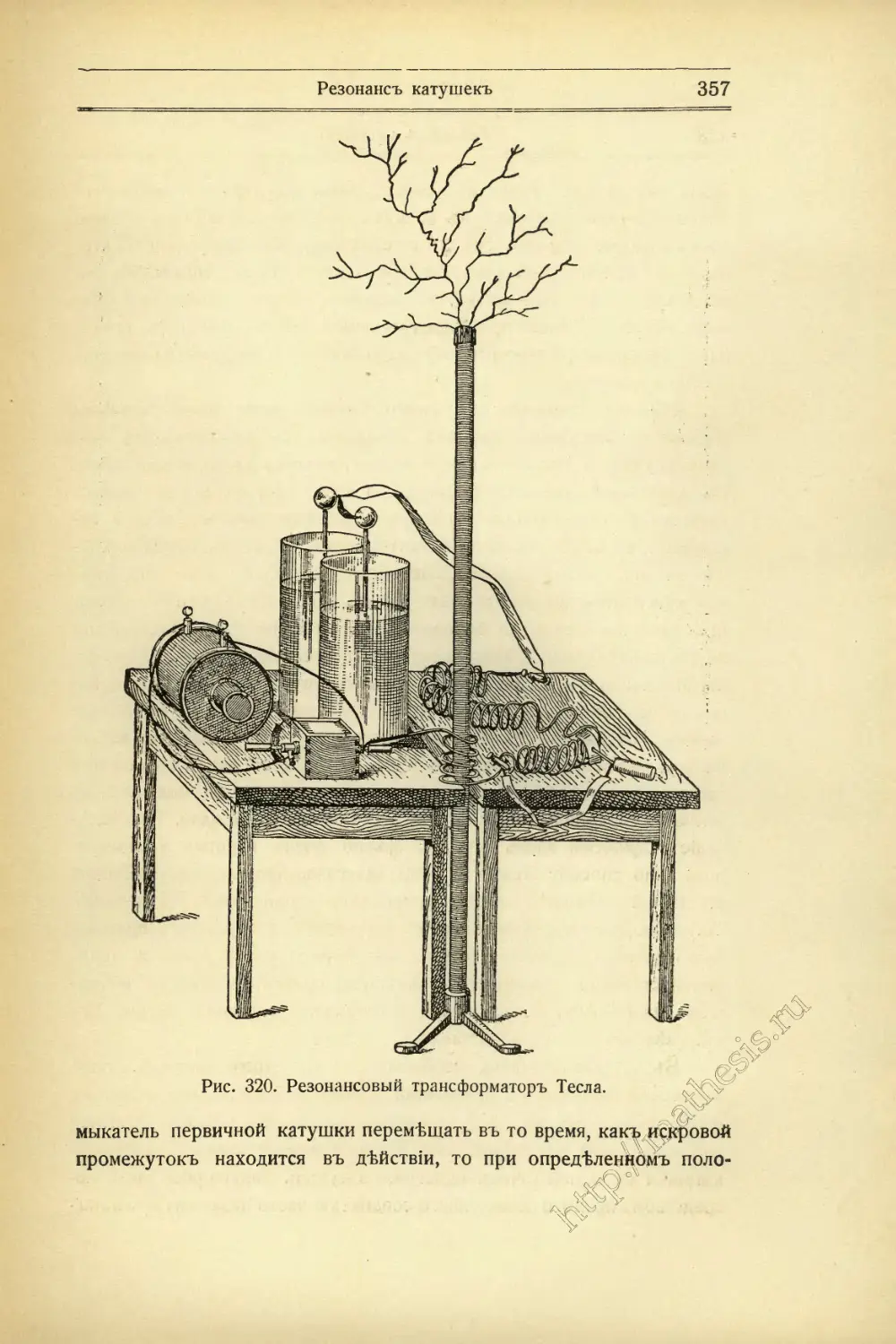
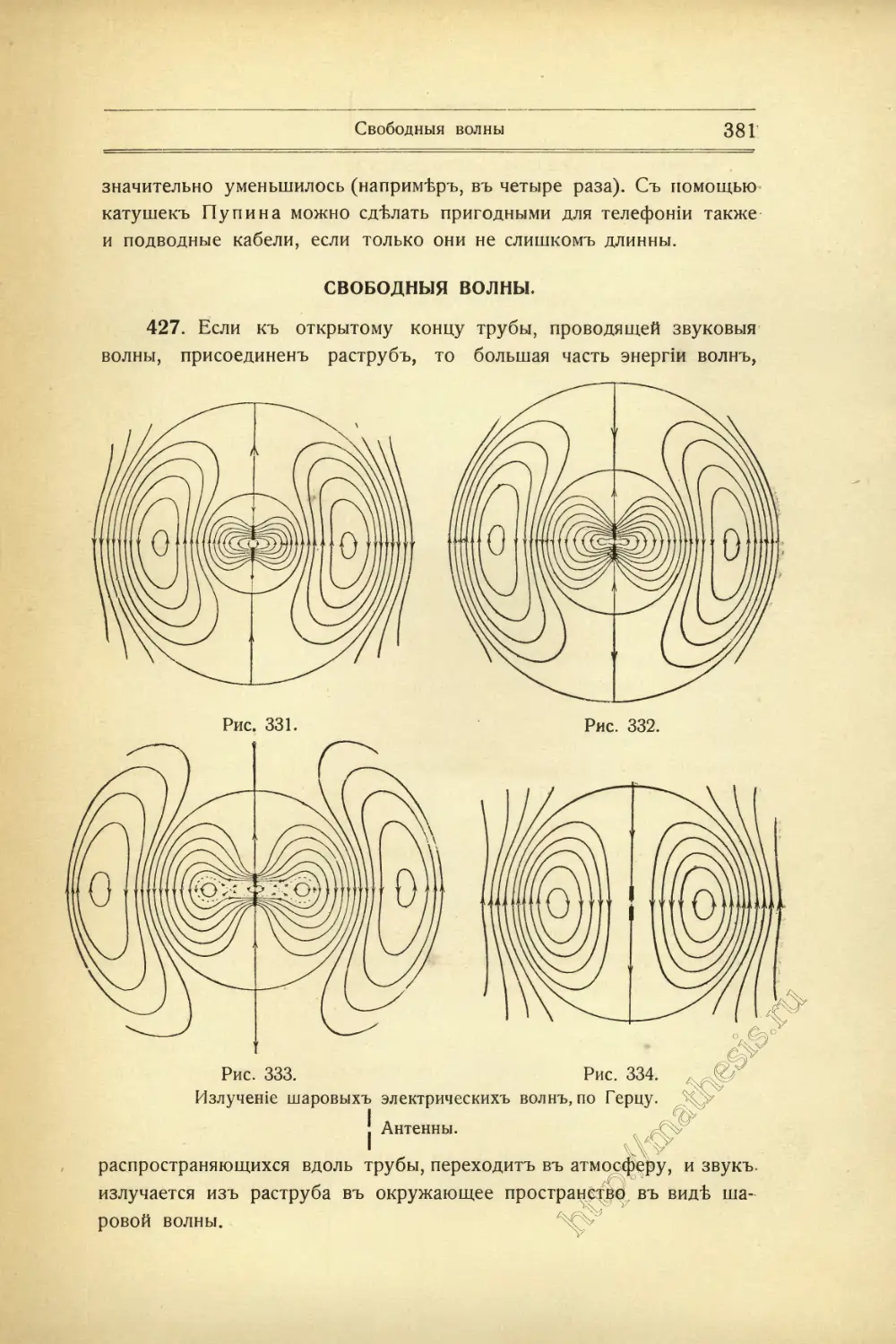
Текст
г, ми
Профессоръ Грейфсвальдскаго Университета
*—.-----ИТ" '
КУРСЪ
ЭЛЕКТРИЧЕСТВН
И МНГНИТИЗМН
Переводъ съ нѣмецкаго Ѳ. Ѳ. Соколова
подъ редакціей заслуженнаго профессора
О. Д. ^Свольсона
ЧИСТЬ II. ЭЛЕКТРОДИНАМИКИ.
зизтлѵ міе
ЬеНгЬисН сіег ЕІекігЫіаі ипсі дез Мадпеіізшиз
ГУСТАВЪ МИ
профессоръ и директоръ Физическаго Института Грейфсвальдскаго Университета
‘==і ===асг=—
КУРСЪ
ЭЛЕКТРИЧЕСТВА
И МАГНИТИЗМА
Экспериментальная физика мірового эѳира
для физиковъ, химиковъ и электротехниковъ
Разрѣшенный авторомъ переводъ съ нѣмецкаго
Ѳ. Ѳ. СОКОЛОВА
подъ редакціей заслуженнаго профессора
о. Д. ХВОЛЬСОНА
Часть II. ЭЛЕКТРОДИНАМИКА
ОДЕССА 1914.
ЧАСТЬ ВТОРАЯ
Электродинамика
Ми. Электричество и магнитизмъ.
ГЛАВА ПЕРВАЯ
ОБЩІЯ СВОЙСТВА МАГНИТНАГО ПОЛЯ
ПРИЗНАКИ МАГНИТНАГО ПОЛЯ.
223. Помимо электрическаго состоянія, пустота можетъ нахо-
диться еще въ иномъ состояніи, называемомъ магнитным[ъ. Впервые
это состояніе было замѣчено около минерала магнетита,
состоящаго' изъ химическаго соединенія Ре2О3 . ЕеО-
Магнетитъ представляетъ собою весьма распространен- 4 М
ную желѣзную руду, встрѣчающуюся во многихъ гор- {Ь
ныхъ породахъ въ видѣ толстыхъ жилъ или отдѣльныхъ I
включеній. Если вблизи куска магнетита находятся не- |
большіе кусочки желѣза, напримѣръ, желѣзные опилки
или проволочные обрѣзки, то они испытываютъ опредѣ-
ленныя силовыя дѣйствія, при чемъ направленіе дѣйству-
ющей на нихъ силы по большей части оказывается обра-
щеннымъ къ магнетиту. Эти особыя силовыя дѣйствія, на-
блюдаемыя только на желѣзѣ и веществахъ, содержащихъ
желѣзо, указываютъ на существованіе въ пространствѣ, |Н I
окружающемъ магнетитъ, особаго состоянія — магнит- Ц
наго состоянія. Часть пространства, въ которой это Ц'
состояніе отчетливо замѣчается, называется магнитнымъ Ц
полемъ. Такимъ образомъ, магнетитъ окруженъ магнит- >
нымъ полемъ.
Рис. 138.
Висмутовая
спираль для
измѣрены^
Магнитное поле рѣзко отличается отъ электрическаго
поля прежде всего тѣмъ, что обнаруживающіяся въ немъ
силовыя дѣйствія распространяются только на вещества,
содержащія желѣзо. Но существуетъ кромѣ того цѣлый магнитнаго
рядъ иныхъ признаковъ, вполнѣ опредѣленно характери- г/у
зующихъ магнитное поле. Если внести кусокъ стекла (или^ѣбе про-
зрачное тѣло) въ магнитное поле, то это тѣло пріобрѣтаетъ» свойство
вращать плоскость поляризаціи свѣта, подобно распору сахара;
і.
Носители магнитнаго поля
электрическое же поле вызываетъ, какъ мы видѣли выше (§ 2), свой-
ство двойного лучепреломленія. Другой особенностью магнитнаго
поля является способность вліять на электрическое сопротивленіе
металловъ. Чрезвычайно сильно это вліяніе обнаруживается на вис-
мутѣ, почему весьма часто для констатированія и измѣренія магнит-
наго состоянія употребляютъ небольшую спирально свернутую вис-
мутовую проволоку. Такія висмутовыя спирали имѣются въ продажѣ
(рис. 138). Спираль включаютъ въ цѣпь, состоящую изъ гальвани-
ческой батареи и измѣрителя тока. Если затѣмъ помѣстить спираль
въ сильное магнитное поле, то сопротивленіе возрастаетъ, и вслѣд-
ствіе этого замѣчается уменьшеніе силы тока, тѣмъ болѣе значи-
тельное, чѣмъ сильнѣе магнитное состояніе въ томъ мѣстѣ, гдѣ
спираль находится.
Вышеупомянутыя дѣйствія магнитнаго состоянія, а также еще
нѣкоторыя, менѣе важныя, могутъ быть использованы для построенія
магнетоскоповъ и магнетометровъ, т. е. инструментовъ, при
помощи которыхъ констатируется и измѣряется магнитное состояніе.
Для нашихъ цѣлей наиболѣе удобнымъ магнетоскопомъ является
пока подвижная частичка желѣза.
НОСИТЕЛИ МАГНИТНАГО ПОЛЯ.
по от-
всѣхъ_
и въ
224. Если изслѣдовать, въ какихъ тѣлахъ можетъ возникать
магнитное поле, подобно тому, какъ мы это дѣлали въ § 2
ношенію къ электрическому полю, то отвѣтъ получается: во
Кромѣ того, магнитное поле можетъ существовать также
пустотѣ—магнитное состояніе есть состояніе эѳира.
Легко установить рѣзкое отличіе магнитнаго поля отъ поля элек-
трическаго. Тогда какъ послѣднее въ нѣкоторыхъ тѣлахъ—въ ме-
таллахъ и иныхъ проводникахъ—прерывается, магнитное поле про-
низываетъ металлы такъ же хорошо, какъ стекло или бумагу, и не
существуетъ вообще такихъ тѣлъ, въ которыхъ оно не могло бы
существовать продолжительное время. „Магнитныхъ проводни-
ковъ“ не существуетъ. д>
Точныя изслѣдованія выяснили, что присутствіе моле^удъ вообще
не оказываетъ замѣтнаго вліянія на магнитное поле.^рДинственное
исключеніе представляютъ собою атомы желѣзадзначительно измѣ-
няющіе магнитныя свойства пространства, въ которомъ они нахо-
дятся. Этимъ объясняются тѣ силовыя дѣйдвій^ которыя испытыва-
Намагниченіе
5
ютъ тѣла, содержащія желѣзо, подъ вліяніемъ эѳира, находящагося
въ магнитномъ состояніи.
НАМАГНИЧЕНІЕ.
225. Тѣло, обладающее особой способностью возбу-
ждать въ окружающемъ его эѳирѣ магнитное состояніе,
называется магнитомъ.
Такимъ образомъ, магнетитъ является примѣромъ магнита. О ве-
ществѣ, изъ котораго состоитъ магнитъ, говорятъ, что оно намаг-
ничено; иногда его называютъ магнитнымъ (что менѣе удобно).
Способность вещества вызывать магнитное состояніе называютъ маг-
нитизмомъ или намагниченіемъ.
Желѣзо обладаетъ, по сравненію со всѣми прочими веществами,
тѣмъ особеннымъ свойствомъ, что оно, будучи помѣщено въ маг-
нитномъ полѣ, намагничивается, т. е. само становится возбудителемъ
новаго магнитнаго поля. Это легко показать, приложивъ желѣзный стер-
жень однимъ концомъ къ куску магнетита. Если при этомъ погрузить
другой конецъ стержня въ кучу желѣзныхъ опилокъ, то на немъ пови-
саетъ цѣлая кисть этихъ опилокъ (рис. 139) ; это доказываетъ, что около
конца стержня образуется магнитное поле. Этотъ фактъ обычно выража-
ютъ слѣдующей фразой: магнитное поле магнетита индуктируетъ
въ желѣзномъ стержнѣ магнитизмъ. Если вывести желѣзный стержень
изъ магнитнаго поля, то опилки
отъ него отпадаютъ—онъ сно-
ва становится немагнитнымъ.
Такимъ образомъ, индуктирован-
ное въ желѣзѣ намагниченіе
Рис. 139. Индуктированное
намагниченіе.
является лишь временнымъ и су-
ществуетъ лишь до тѣхъ поръ,
пока желѣзо находится въ маг-
нитномъ полѣ.
Если вмѣсто желѣзнаго стер-
жня сдѣлать описанный опытъ
съ небольшой стальной иглой,
то оказывается, что она и послѣ удаленія ея изъ магнитнаго поля^со-
храняетъ индуктированный магнитизмъ. Магнитизмъ, остающійся въ
тѣлахъ на продолжительное время, называютъ постоянномъ. Впро-
чемъ, если воспользоваться достаточно тонкими методами изслѣдова-
6
Полюсы магнита
нія, то удается обнаружить, что и желѣзо при его удаленіи изъ маг-
нитнаго поля не вполнѣ теряетъ индуктированный магнитизмъ. Не-
большой остатокъ намагниченія обнаруживается и въ желѣзѣ—этотъ
остатокъ такъ и называютъ остаточнымъ намагниченіемъ. Спо-
собность удерживать индуктированный магнитизмъ называютъ коэр-
цитивной силой. Сталь обладаетъ большой коэрцитивной силой,
кованое желѣзо—малой.
Коэрцитивной силой стали пользуются для изготовленія искус-
ственныхъ постоянныхъ магнитовъ, которымъ можно придавать
простыя формы, удобныя для изученія законовъ магнитнаго поля.
Прямой магнитъ лучше всего получается, если вдоль стального стер-
жня (напримѣръ, вязальной иглы) по всей его длинѣ нѣсколько разъ
провести въ одномъ направленіи уже готовымъ магнитомъ; при этомъ
намагничиваемаго предмета должно касаться все время одно и то же
мѣсто магнита и лучше всего такое мѣсто, около котораго магнит-
ное поле всего сильнѣе.
ПОЛЮСЫ МАГНИТА.
226. Если погрузить приготовленный вышеописаннымъ образомъ
прямой магнитъ въ желѣзныя опилки, то оказывается, что на обо-
ихъ его концахъ остаются висѣть кисти опилокъ; къ остальнымъ же
частямъ магнита опилки не пристаютъ. Слѣдовательно, только у обоихъ
концовъ прямого магнита образуются магнитныя поля, достаточно-
сильныя для того, чтобы они могли быть обнаружены при помощи
нашего примитивнаго метода. Во всякомъ случаѣ, оба эти конца явля-
Рис. 140. Магнитная стрѣлка.
ются центрами, изъ которыхъ ис-
ходятъ поля. Чтобы отмѣтить это
свойство, ихъ называютъ магнит-
ными полюсами намагниченнаго
тѣла.
Мы убѣдились выше (§ 6)въ
томъ, что эѳиръ, находящійся? въ
состояніи электрическаго йацряже-
нія, оказываетъ силовьіЯ^Дѣйствія
только на электрически заряженныя
тѣла, т. е. на тѣла, являющіяся центрами или узловымищунктами элек-
трическихъ полей. Аналогичному принципу подчиняются и тѣ сило-
выя дѣйствія, которыя матеріальныя тѣла испытываютъ со стороны
Полюсы магнита
7
эѳира, находящагося въ магнитномъ состояніи. Такія дѣйствія испы-
тываютъ только частички желѣза, такъ какъ только на нихъ обра-
зуются въ магнитномъ полѣ магнитные полюсы. Чтобы ближе изучить
эти силовыя дѣйствія, возьмемъ легко вращающійся прямой постоян-
ный магнитъ—такъ называемую магнитную стрѣлку (рис. 140). При-
близивъ къ ней другой прямой магнитъ, полюсы котораго обозначимъ
черезъ I и II. Приближая полюсъ I по очереди къ обоимъ полю-
самъ магнитной стрѣлки, мы замѣчаемъ, что они относятся къ ней
различно. На одинъ полюсъ эѳиръ оказываетъ силовое дѣйствіе,
стремящееся удалить его изъ поля — полюсъ I его „отталкиваетъ".
Другой полюсъ подъ вліяніемъ эѳира, находящагося въ состояніи
магнитнаго возбужденія, стремится, наоборотъ, продвинуться ближе
къ центру поля — полюсъ I его „притягиваетъ". Чтобы удобнѣе
было различать полюсы стрѣлки, отмѣтимъ первый красной мѣткой,
а второй зеленой. Затѣмъ повторимъ тотъ же опытъ, приближая къ
обоимъ полюсамъ магнитной стрѣлки поле полюса II. Въ этомъ слу-
чаѣ получаются явленія, какъ разъ обратныя: красный полюсъ при-
тягивается, зеленый отталкивается.
Оба полюса магнитнаго стержня обладаютъ во всѣхъ
отношеніяхъ прямо противоположными свойствами: вызы-
ваемыя ими магнитныя поля взаимно противоположны; си-
лы, испытываемыя ими въ одномъ и томъ же магнитномъ
полѣ, также имѣютъ взаимно-противоположныя направленія.
Слѣдовательно, оба полюса относятся другъ къ другу, какъ по-
ложительныя и отрицательныя числа въ алгебрѣ. Поэтому мы бу-
демъ называть одинъ полюсъ магнитнаго стержня положи-
тельнымъ, а другой отрицательнымъ.
Для того, чтобы установить разъ навсегда опредѣленные знаки
полюсовъ, нужно исходить изъ какого-либо нормальнаго полюса,
напримѣръ, полюса I выше употреблявшагося стержня. При помощи
его мы испытываемъ всякій иной магнитъ и называемъ отталкива-
емый имъ полюсъ (съ красной мѣткой) положительнымъ, а притяги-
ваемый (съ зеленой мѣткой)—отрицательнымъ. Если мы стержень с^
полюсами I и II также сдѣлаемъ подвижнымъ, подвѣсивъ его зд^сре?-
дину, и сравнимъ силовыя дѣйствія, испытываемыя полюсами Г и II
въ полѣ третьяго къ нимъ приближеннаго магнитнаго (^т^кня, съ
тѣми дѣйствіями, которыя въ томъ же полѣ испытываетъ? красный
и зеленый полюсы, то найдемъ, что полюсъ I ведетъА:ебя такъ же,
8
Полюсы магнита
какъ красный (положительный) полюсъ, а полюсъ II—какъ зеленый
(отрицательный).
Силовыя дѣйствія, испытываемыя магнитными полюсами
въ магнитныхъ поляхъ, направлены такъ, что одноименные
полюсы всегда отодвигаются ими другъ отъ друга, разно-
именные же другъ къ другу придвигаются.
Другого рода магнитныхъ полюсовъ, кромѣ положительныхъ
и отрицательныхъ, не существуетъ. И въ естественныхъ магнитахъ,
на поверхностяхъ которыхъ магнитныя поля обычно распредѣлены
весьма неправильно, можно съ точностью различить участки, соста-
вленные изъ положительныхъ полюсовъ, и участки, составленные изъ
отрицательныхъ полюсовъ.
227. Если изслѣдовать всѣ возможные магниты, спеціально об-
ращая вниманіе на наличность у нихъ положительныхъ или отрица-
тельныхъ полюсовъ, то выясняется чрезвычайно важный фактъ: не
существуетъ магнитовъ, имѣющихъ только положительные или только
отрицательные полюсы.
Положительные и отрицательные полюсы ни въ ка-
комъ магнитѣ не встрѣчаются раздѣльно; всякій магнитъ
содержитъ въ одинаковой мѣрѣ полюсы обоихъ родовъ.
Это съ особенною отчетливостью можно видѣть на прямомъ
магнитѣ; у него всегда на каждомъ концѣ находится по полюсу, на
одномъ концѣ—положительный, на другомъ отрицательный. Поля
обоихъ полюсовъ равны, что можно заключить уже по одинаковой вели-
чинѣ тѣхъ пучковъ желѣзныхъ опилокъ, которые пристаютъ къ обо-
Рис. 141. Разломанный магнитный
стержень.
имъ полюсамъ. Можно было бы предположить, что положительный^
отрицательный полюсы получатся отдѣльно, если переломить ^маг-
нитный стержень посрединѣ. Однако, на дѣлѣ получается не^тб. На
обѣихъ поверхностяхъ излома образуются новые полюсы,одной
положительный, на другой отрицательный (рис. 141), т^ь что каж-
дая половина стержня представляетъ собою обыкновенный магнит-
ный стержень съ двумя полюсами. Если обѣ половины сложить такъ,
чтобы снова получился одинъ цѣлый стержень^тб окружающія ихъ
Направленіе магнитнаго поля
9
поля налагаются одно на другое и снова получается одинъ магнит-
ный стержень съ полюсомъ на каждомъ концѣ.
228. Если стержень изъ мягкаго желѣза внести въ магнитное
поле, то онъ становится магнитомъ. При этомъ въ той его части,
которая обращена къ возбуждающему поле полюсу, индуктируется
магнитный полюсъ противоположнаго знака, на удаленной сторонѣ
получается, слѣдовательно, полюсъ, одноименный съ возбуждающимъ
поле. Въ этомъ легко убѣдиться при помощи небольшой магнитной
•стрѣлки.
Такъ какъ два разноименные полюса подъ вліяніемъ силового
дѣйствія эѳира взаимно притягиваются, то кусокъ желѣза подъ влі-
яніемъ индуктируемаго въ немъ магнитизма стремится приблизиться
къ поднесенному къ нему магниту. Такимъ образомъ мы получаемъ
точное объясненіе того факта, на основаніи котораго мы впервые
убѣдились въ существованіи магнитнаго состоянія.
НАПРАВЛЕНІЕ МАГНИТНАГО ПОЛЯ.
229. Всѣ описанные выше факты приводятъ насъ къ нижеслѣ-
дующему заключенію:
Магнитное состояніе эѳира можетъ быть вполнѣ оха-
рактеризовано векторіальной величиной.
Это свойство является общимъ у магнитнаго состоянія и у элек-
трическаго состоянія, описаннаго въ I части этой книги. Направле-
ніемъ магнитнаго поля въ нѣкоторомъ мѣстѣ эѳира мы будемъ счи-
тать направленіе силы, съ которой дѣйствуетъ въ этомъ мѣстѣ
эѳиръ на положительный магнитный полюсъ. Удобнѣе всего опре-
дѣляется направленіе магнитнаго поля при помощи магнитной стрѣлки.
Направленіе, въ которомъ устанавливается магнитная
стрѣлка, если, кромѣ силы магнитнаго поля, никакія другія
силы на нее не дѣйствуютъ, представляетъ собою направле-
ніе магнитнаго поля; при этомъ положительный полюсъ
стрѣлки указываетъ положительное направленіе поля.
Если изслѣдовать поле помощью магнитной стрѣлки, отмѣти^ьгЬ
повсюду его направленіе и затѣмъ провести рядъ кривыхъ такимъ
образомъ, чтобы каждая изъ нихъ въ любомъ мѣстѣ совпадала съ
направленіемъ магнитнаго поля въ этомъ мѣстѣ, то получаются маг-
нитныя линіи поля или магнитныя силовыя ли^і|ѣ предста-
вляющія собою прекрасное графическое изображеніе^ роля. Эти линіи
10
Изображенія магнитныхъ полей
можно получить тѣмъ же способомъ, что и линіи электрическаго поля
(ср. рис. 7, стр. 21 первой части).
Магнитныя силовыя линіи выходятъ изъ положительнаго полюса
магнита и втекаютъ въ отрицательный полюсъ. Положительные полю-
сы являются „источниками" поля, отрицательные полюсы—„стоками*.
ИЗОБРАЖЕНІЯ МАГНИТНЫХЪ ПОЛЕЙ.
230. Тотъ же пріемъ, помощью котораго мы запечатлѣвали элек-
трическія силовыя линіи (§ 20), мы можемъ примѣнить и къ маг-
нитному полю. Вмѣсто рутиловаго порошка мы въ этомъ случаѣ
воспользуемся мелкими желѣзными опилками. Подъ вліяніемъ индук-
ціи каждая частичка желѣза превращается въ маленькій магнитъ и
устанавливается въ направленіи поля; примыкая другъ къ другу,
опилки образуютъ цѣпи, которыя приблизительно имѣютъ видъ си-
ловыхъ линій. Но, конечно, такая картина прямо не даетъ указаній
на положительное направленіе этихъ кривыхъ.
Сравнивая полученныя такимъ образомъ изображенія магнит-
ныхъ полей, воспроизведенныя на рисункахъ 142—145, съ изобра-
женіями электрическихъ полей на рис. 8, нельзя не замѣтить, что
магнитныя силовыя линіи получаются гораздо болѣе отчетливыми,,
чѣмъ электрическія. Это обстоятельство не является случайнымъ;
оно зависитъ отъ того, что не существуетъ никакой магнитной „про-
водимости". Полученіе изображеній электрическихъ полей требуетъ
большаго вниманія и удается только при слабыхъ поляхъ, хотя и
въ этихъ случаяхъ часто невозможно избѣжать искаженій, происхо-
дящихъ отъ переноса электрическихъ зарядовъ благодаря проводи-
мости. Такихъ искаженій въ изображеніяхъ магнитныхъ полей со-
вершенно не бываетъ.
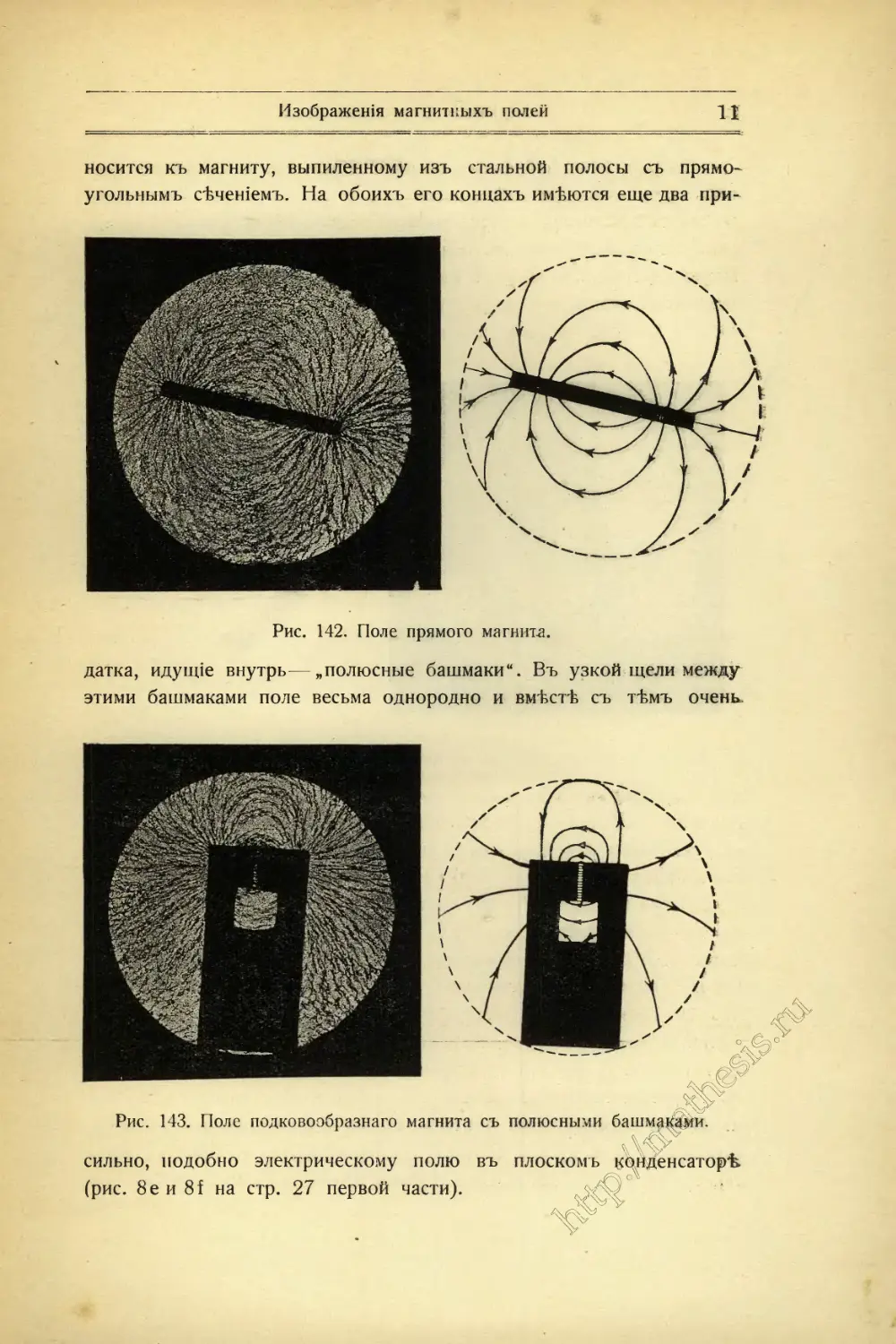
На рис. 142 мы видимъ распредѣленіе силовыхъ линій вокругъ
прямого магнита. Онѣ исходятъ изъ части магнита, примыкающей
къ положительному полюсу, изгибаются въ сторону отрицательнаго
полюса и, наконецъ, снова входятъ въ магнить у отрицательнаго
полюса. Вблизи обоихъ полюсовъ силовыя линіи располож^д^осо-
бенно густо; какъ разъ въ этихъ мѣстахъ поле особенно сильно (§ 226).
Весьма часто искусственнымъ магнитамъ придают^также под-
ковообразную форму. Такая форма обладаетъ^ тѣмъ преимуще-
ствомъ, что поле между обоими полюсами пол^ча^тся почти одно-
родное, при чемъ оно можетъ быть весьма сц^ьрымъ. Рис. 143 от-
Изображенія магнитныхъ полей
11
носится къ магниту, выпиленному изъ стальной полосы съ прямо-
угольнымъ сѣченіемъ. На обоихъ его концахъ имѣются еще два при-
Рис. 142. Поле прямого магнита.
датка, идущіе внутрь—„полюсные башмаки“. Въ узкой щели между
этими башмаками поле весьма однородно и вмѣстѣ съ тѣмъ очень
Я
Рис. 143. Поле подковообразнаго магнита съ полюсныгии башма^йіи.
сильно, подобно электрическому полю въ плоскомъ конденсаторѣ
(рис. 8е и 8! на стр. 27 первой части). ИХО
12
Изображенія магнитныхъ полей
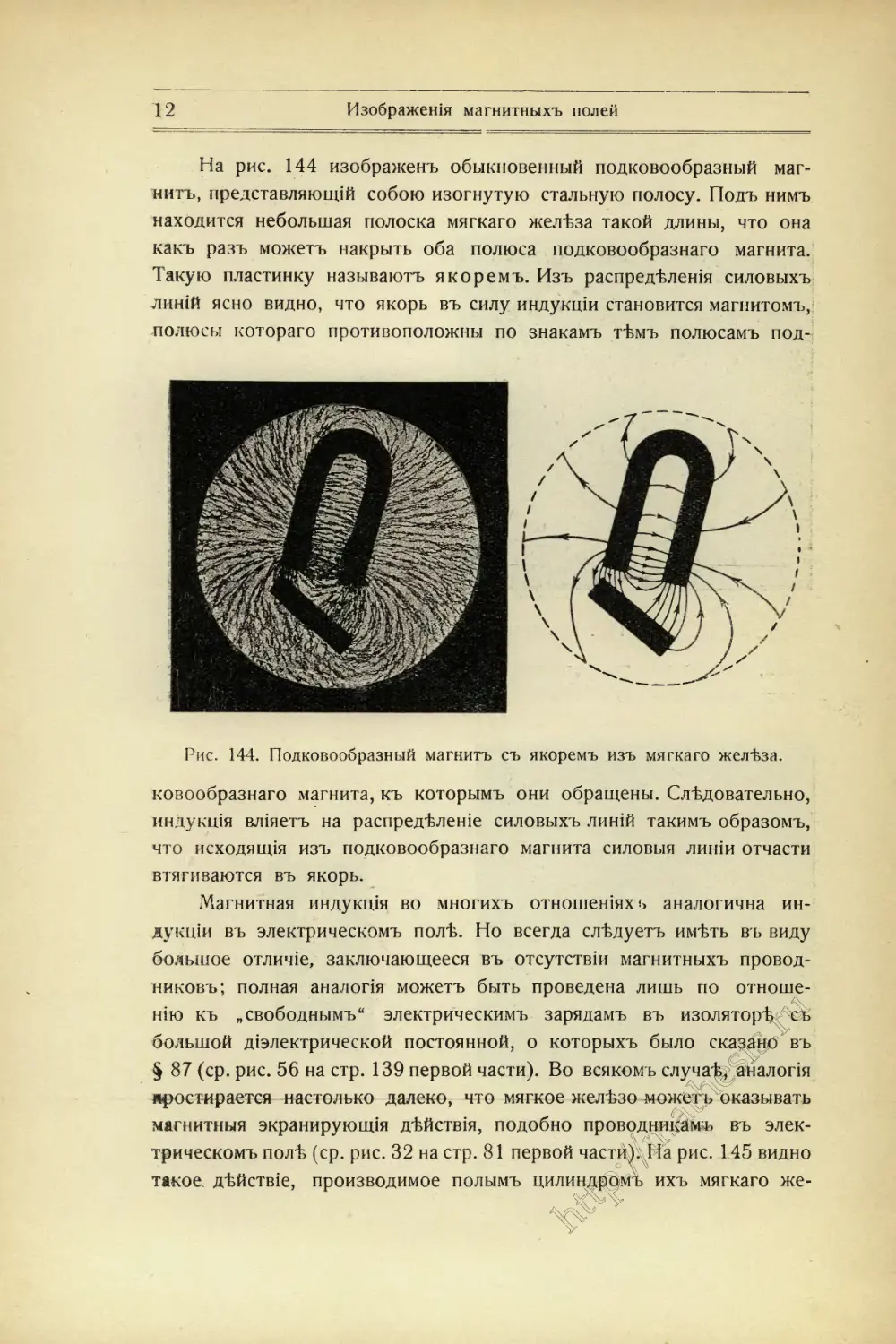
На рис. 144 изображенъ обыкновенный подковообразный маг-
нитъ, представляющій собою изогнутую стальную полосу. Подъ нимъ
находится небольшая полоска мягкаго желѣза такой длины, что она
какъ разъ можетъ накрыть оба полюса подковообразнаго магнита.
Такую пластинку называютъ якоремъ. Изъ распредѣленія силовыхъ
линій ясно видно, что якорь въ силу индукціи становится магнитомъ,
полюсы котораго противоположны по знакамъ тѣмъ полюсамъ под-
Рис. 144. Подковообразный магнитъ съ якоремъ изъ мягкаго желѣза,
ковообразнаго магнита, къ которымъ они обращены. Слѣдовательно,
индукція вліяетъ на распредѣленіе силовыхъ линій такимъ образомъ,
что исходящія изъ подковообразнаго магнита силовыя линіи отчасти
втягиваются въ якорь.
Магнитная индукція во многихъ отношеніяхъ аналогична ин-
дукціи въ электрическомъ полѣ. Но всегда слѣдуетъ имѣть въ виду
большое отличіе, заключающееся въ отсутствіи магнитныхъ провод-
никовъ; полная аналогія можетъ быть проведена лишь по отноше-
нію къ „свободнымъ" электрическимъ зарядамъ въ изолятор^сѣ
большой діэлектрической постоянной, о которыхъ было ска^ано? въ
§ 87 (ср. рис. 56 на стр. 139 первой части). Во всякомъ случа^іналогія
простирается настолько далеко, что мягкое желѣзо можетъ оказывать
магнитныя экранирующія дѣйствія, подобно проводникамъ въ элек-
трическомъ полѣ (ср. рис. 32 на стр. 81 первой частй^&а рис. 145 видно
такое дѣйствіе, производимое полымъ цилиндромъ ихъ мягкаго же-
Изображенія магнитныхъ полей
13
лѣза въ полѣ между двумя магнитными полюсами. Слѣдуетъ отмѣ-
тить, что экранирующее дѣйствіе проводниковъ электричества замѣ-
чается уже у тончайшихъ металлическихъ слоевъ, магнитное же экра-
нирующее дѣйствіе можетъ быть замѣчено только въ томъ случаѣ,
Рис. 145. Магнитное экранирующее дѣйствіе полаго желѣзнаго цилиндра.
когда часть пространства защищена толстыми желѣзными стѣнками;
кромѣ того, даже въ лучшемъ случаѣ, пользуясь весьма чувствитель-
ными индикаторами, всегда еще можно замѣтить слабое поле внутри
экранированнаго пространства. Это вновь служитъ доказательствомъ
того, что желѣзо не представляетъ собою „магнитнаго проводникаи,
внутри котораго поле уничтожается. Однако, все же и это не совер-
шенное экранирующее дѣйствіе желѣза на магнитное поле играетъ
важную роль при построеніи магнитныхъ измѣрительныхъ грибо-
ровъ (такъ называемыхъ гальванометровъ); помощью желѣзной обо-
лочки (панцыря) можно почти совершенно устранить вліяніе всѣхъ
постороннихъ магнитныхъ полей.
МАГНИТНОЕ ПОЛЕ ЗЕМЛИ.
231. Если гдѣ-либо внѣ дѣйствія другихъ магнитовъ укрЩл
пить на вертикальной оси легкоподвижную магнитную строку,
то оказывается, что она всегда устанавливается по вп^лр^ опре-
дѣленному направленію, мало отличающемуся отъ направленія сѣ-
веръ-югъ. Какъ извѣстно, такою вращающеюся въ горизонтальной.
- ’ V
14
Магнитное поле земли
плоскости магнитной стрѣлкою, снабженною раздѣленнымъ кругомъ,
пользуются подъ именемъ компаса или буссоли для опредѣленія
направленія сѣверъ-югъ (рис. 146). Если желательно получать при
помощи компаса точныя указанія,
то необходимо знать, насколько
отклоняется его стрѣлка отъ напра-
вленія сѣверъ-югъ. Уголъ, соста-
вляемый магнитной стрѣлкой ком-
паса съ географическимъ мериді-
аномъ, носитъ названіе склоненія.
Такъ какъ величины склоненій раз-
личны въ разныхъ мѣстахъ земли,
то для практическихъ цѣлей поль-
зуются картами, на которыхъ нане-
сены величины склоненія. Мѣста
Рис. 146. Буссоль одинаковаго склоненія соединяются
на такихъ картахъ кривыми—такъ
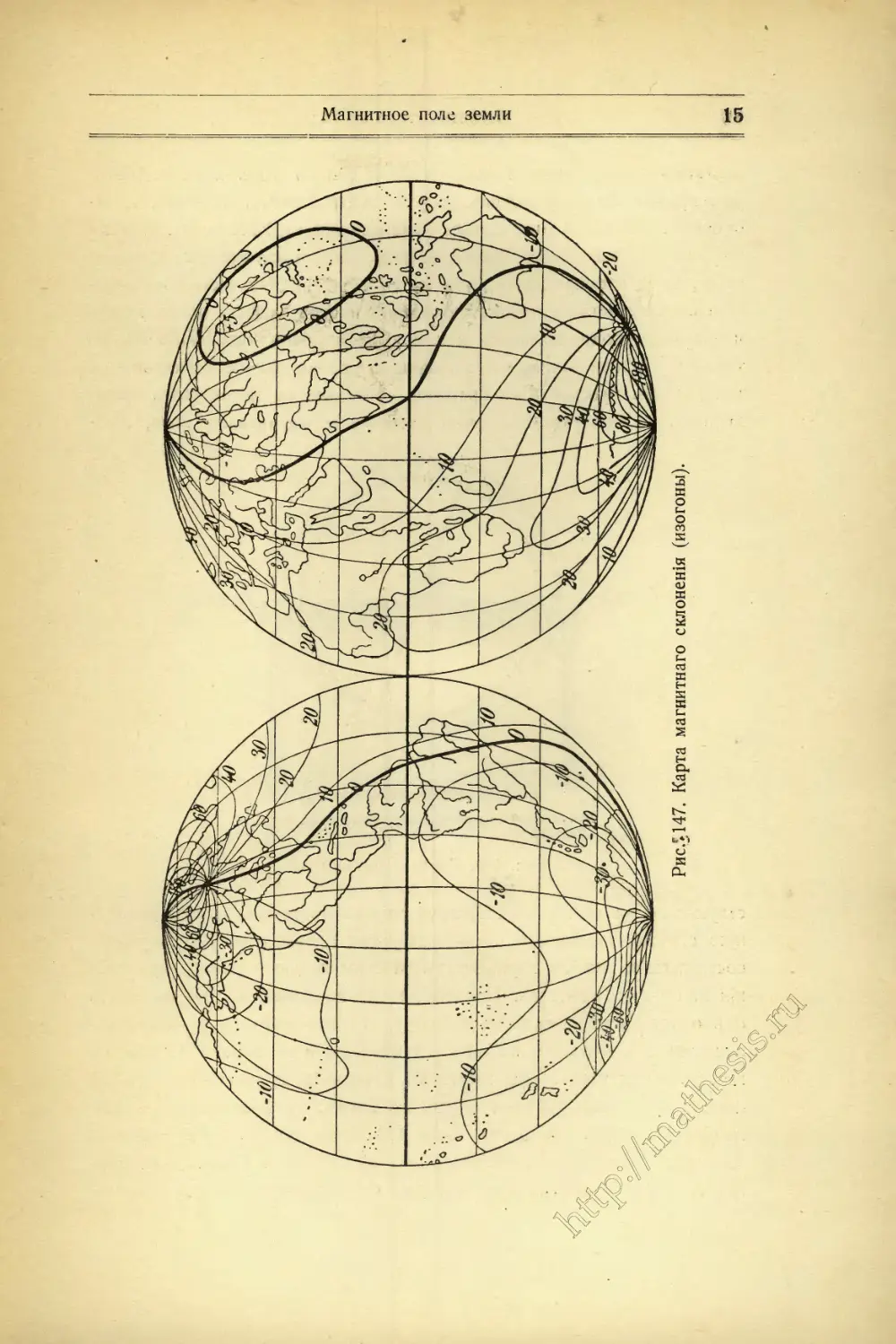
называемыми изогонами. Изогоны обычно проводятся для скло-
неній, выражающихся цѣлымъ числомъ градусовъ (0°, 1°, 2° и т. д.);
иногда употребляются и иные интервалы. По такой картѣ можно
опредѣлить величину склоненія для любого мѣста земли. На рис. 147
дана такая карта, содержащая изогоны для интерваловъ въ 10°. Въ
Германіи склоненіе колеблется между 6° и 13°, при чемъ стрѣлка
отклоняется къ сѣверо-западу (или юго-востоку). Направленіе стрѣлки
компаса часто называютъ магнитнымъ меридіаномъ даннаго
мѣста.
Если подвѣсить магнитную стрѣлку такъ, чтобы она могла вра-
щаться вокругъ горизонтальной оси, проходящей точно черезъ ея
центръ тяжести, то стрѣлка опять устанавливается во вполнѣ опре-
дѣленномъ положеніи равновѣсія. Если бы стрѣлка не была намаг-
ничена, то, будучи подвѣшена такимъ образомъ, она, конечно, нахо-
дилась бы въ состояніи безразличнаго равновѣсія. Чтобы убѣдиться въ
томъ, что стрѣлка подвѣшена точно въ центрѣ тяжести, примагни-
тимъ такую стрѣлку1), натирая ее сильнымъ магнитом^^ёсли это
условіе выполнено, то стрѣлка устанавливается совершенно такъ
Ч Т. е. намагнитимъ ее такъ, 'чтобы сѣверный крнецъ сталъ южнымъ
и наоборотъ. Прим. пер.
Рис5147. Карта магнитнаго склоненія (изогоны).
сл
Магнитное поле земли
16
Магнитное поле земли
же, какъ и при первомъ намагниченіи; только тотъ конецъ, кото-
рый прежде былъ обращенъ вверхъ, теперь смотритъ внизъ, и на-
оборотъ. Если при вторичномъ намагниченіи стрѣлка не составляетъ
съ горизонталью точно такого же угла, какъ и при первомъ намагни-
ченіи, то это показываетъ, что на ея оріентировку оказываетъ влі-
яніе сила тяжести, и потому положеніе центра тяжести должно быть
исправлено (подпиливаніемъ и т. п.). Если послѣ того, какъ центръ
тяжести стрѣлки приведенъ въ надлежащее положеніе, установить ее
такъ, чтобы плоскость ея вращенія совпадала съ магнитнымъ мери-
діаномъ, то она укажетъ точно направленіе магнитнаго поля, дѣй-
Рис. 148. Стрѣлка наклоненія.
ствующаго на ея полюсы. Такимъ способомъ установленную магнит-
ную стрѣлку называютъ стрѣлкой наклоненія (рис. 148), а уголъ,
составляемый ею съ горизонтальной плоскостью—угломъ наклоне-
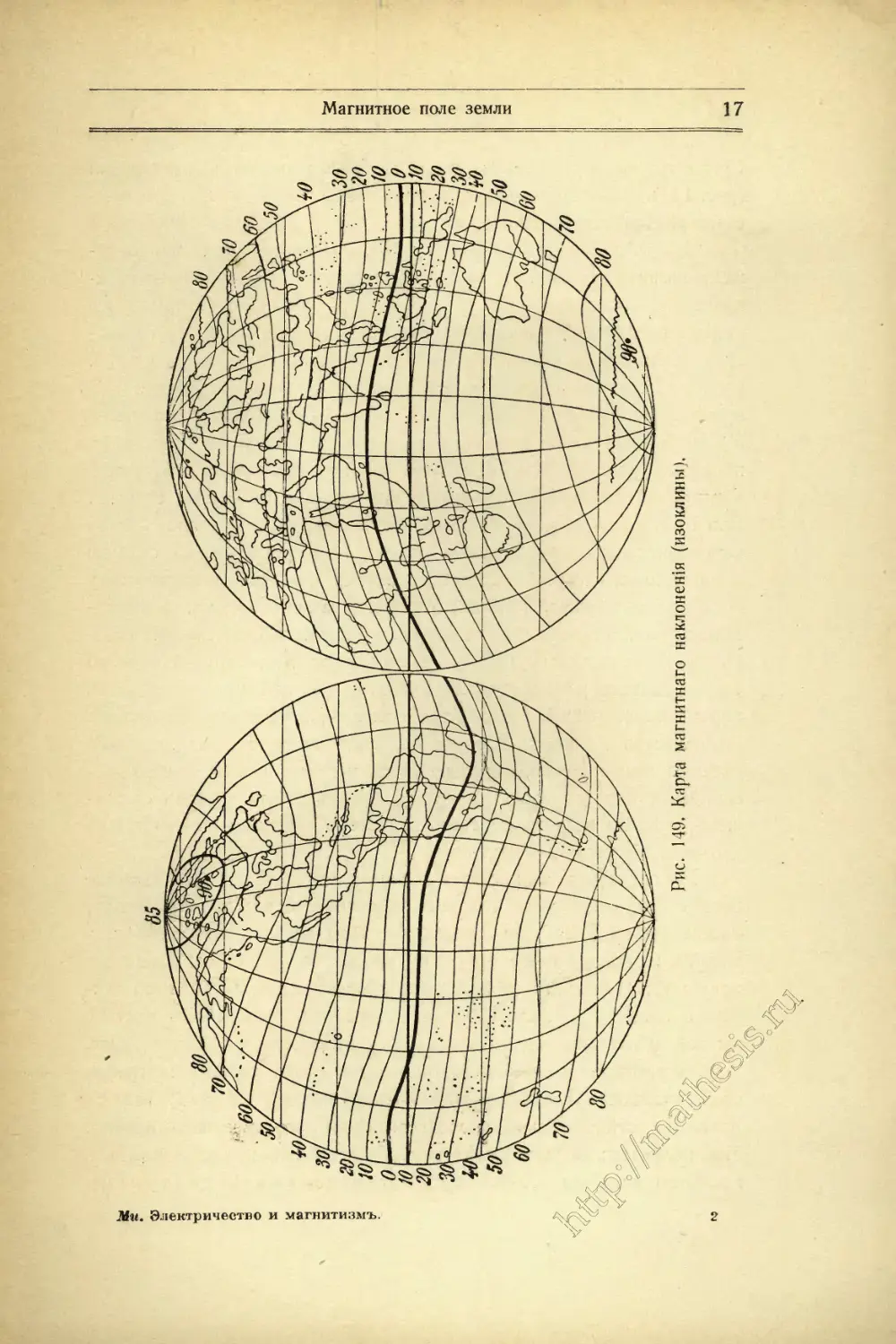
нія или наклоненіемъ. Наклоненіе сильно мѣняется при переходѣ
отъ одного мѣста земли къ другому. Вблизи экватора оно мало^ от-
личается отъ нуля, но по мѣрѣ приближенія къ полюсамъ,^вдобще
говоря, возрастаетъ. При этомъ въ сѣверномъ полушарі^^ѣверный
конецъ магнитной стрѣлки обращенъ внизъ; въ южндмъ полушаріи,
наоборотъ, внизъ обращенъ южный конецъ стрѣлки^ Въ Германіи
величина наклоненія колеблется отъ 64° до 68 Кривыя, соединя-
ющія мѣста одинаковаго наклоненія, на^ф^фтся изоклинами.
Ми. Электричество и магнитизмъ.
Магнитное поле земли
18
Магнитное поле земли
Существуютъ карты земли съ нанесенными на нихъ изоклинами
(рис. 149). Понятно, что эти кривыя не имѣютъ такого практиче-
скаго значенія, какъ изогоны.
Изъ всего вышеизложеннаго ясно, что земля постоянно окру-
жена магнитнымъ полемъ, т. е. представляетъ собою магнитъ; на-
правленіе силовыхъ линій у поверхности земли, о которыхъ мы
судимъ по стрѣлкѣ наклоненія, показываетъ, что полюсы этого маг-
нита расположены вблизи географическихъ полюсовъ земного шара.
Существованіе этого земного поля можетъ быть иногда замѣчено и въ
практической жизни. Если мы будемъ держать стальной стержень
въ направленіи поля, указываемомъ стрѣлкой наклоненія, и ударимъ
нѣсколько разъ по нему молоткомъ, то онъ превратится въ прямой
магнитъ, въ чемъ легко убѣдиться при помощи магнитной стрѣлки.
При этомъ тотъ конецъ стержня, который во время ударовъ былъ
направленъ внизъ, отталкиваетъ отъ себя сѣверный полюсъ стрѣлки
и притягиваетъ къ себѣ южный; обратныя свойства оказываются у
того конца стержня, который былъ направленъ вверхъ. Слѣдова-
тельно, намагниченіе, дѣйствительно, принимаетъ направленіе, соот-
вѣтствующее индуктирующему дѣйствію поля земли. Стержень легко
„ перемагнитить “, если помѣстить его въ магнитное поле земли въ
обратномъ направленіи и снова нѣсколько разъ ударить молоткомъ.
Большинство стальныхъ предметовъ, подъ вліяніемъ индукціоннаго
дѣйствія земного поля, обращаются въ магниты, и человѣчество, не-
сомнѣнно, познакомилось бы этимъ путемъ съ магнитнымъ состоя-
ніемъ, если бы магнитъ не сталъ извѣстенъ раньше, чѣмъ вошли въ
употребленіе стальныя издѣлія.
Мы воспользуемся магнитнымъ полемъ земли, чтобы разъ навсегда
опредѣлить знаки обоихъ родовъ магнитныхъ полюсовъ. Методъ,
описанный въ § 226, не давалъ бы возможности легко избѣгать
ошибки и потому былъ бы мало пригоденъ, если бы всякій не
могъ имѣть всегда въ своемъ распоряженіи магнитъ, полюсы ко-
тораго повсюду считались бы за „нормальные полюсыКъ счасуью,
мы всѣ обладаемъ такимъ магнитомъ—имъ является самая^Гземля.
Тотъ магнитный полюсъ который лежитъ около южнагд^^ѣёографи-
ческаго полюса, условились принимать за полюсъ I § 226; полюсъ
II лежитъ, слѣдовательно, около географическаго езернаго полюса.
Мы получаемъ отсюда слѣдующее опредѣленЦ^'тотъ
прямого магнита, который въ магнитном:%и°лѣ земли указы-
полюсъ
Магнитное поле земли
19
ваетъ на сѣверъ, представляетъ собою положительный
магнитный полюсъ, а тотъ полюсъ, который указываетъ на
югъ, —отрицательный.
Поэтому часто обозначаютъ положительный магнитный полюсъ
буквою IV, и отрицательный—буквою 6*. Земной магнитъ имѣетъ
положительный полюсъ (/V) около географическаго южнаго полюса,
а отрицательный полюсъ (5) —вблизи географическаго сѣвернаго
полюса.
232. О точномъ опредѣленіи и о способахъ измѣренія силы
магнитныхъ полей мы подробно будемъ говорить послѣ того, какъ
нами будутъ изложены закономѣрныя зависимости, существующія
между магнитными и электрическими явленіями. Для измѣренія силы
поля земли методы были разработаны еще Гауссомъ (Оаизз). Про-
стѣйшій изъ этихъ методовъ заключается въ непосредственномъ
сравненіи поля земли съ другимъ постояннымъ извѣстнымъ полемъ.
Для магнитнаго состоянія (какъ и для электрическаго) имѣетъ силу
законъ, по которому, если къ одному уже существовавшему полю
присоединяется новое, вызываемое другими причинами, то эти поля
налагаются одно на другое аддитивно, не оказывая вліянія другъ
на друга. Такимъ образомъ, напримѣръ, поле, исходящее изъ маг-
нитнаго стержня, не мѣняется подъ вліяніемъ окружающаго его по-
всюду поля земли, но просто складывается съ нимъ. (Здѣсь имѣется
въ виду сложеніе векторовъ, происходящее по такъ называемому за-
кону параллелограмма векторовъ; см. § 245). Если взятое для срав-
ненія постоянное поле, которое можно было бы принять за единицу,
но которое мы для общности обозначимъ черезъ 771, расположить
такимъ образомъ, чтобы оно оказалось перпендикулярнымъ къ
полю земли Н, то оба поля вмѣстѣ образуютъ новое поле, соста-
вляющее нѣкоторый уголъ а съ первоначальнымъ полемъ земли.
Этотъ уголъ а, т. е. уголъ, на который поворачивается стрѣлка изъ
ея первоначальнаго положенія подъ вліяніемъ поля можетъ
быть измѣренъ. По принципу наложенія мы затѣмъ получаемъ
Н — Нг. соі^ а.
Остается еще выяснить, какимъ образомъ получается поле срав-
ненія для этого крайне удобнаго метода. Если нужно произвести
только относительныя измѣренія, то удобнѣе всего воспользоваться
постояннымъ прямымъ магнитомъ, устанавливая его на ^опредѣлен-
номъ разстояніи отъ магнитной стрѣлки. О том^^Сакъ цѣлесо-
Яг 2
20
Магнитное поле земли
образнѣе всего опредѣлить единицу поля для абсолютныхъ измѣ-
реній, будетъ рѣчь въ слѣдующей главѣ.
233. Такъ какъ магнитное поле опредѣлено по величинѣ и по
Рис. 150. Магнитное поле земли.
направленію во многихъ мѣстахъ у поверхности земли/то при по-
мощи математическихъ вычисленій можно построить и все поле въ
пространствѣ, окружающемъ землю. Получается^при этомъ прибли-
зительно картина, воспроизведенная на рис.\1^0.
Магнитное поле земли
21
Совершенно сходное распредѣленіе силовыхъ линій получается
вокругъ стального шара, по возможности равномѣрно намагничен-
наго помощью сильнаго однороднаго магнитнаго поля (рис. 151).
Однако, намагниченіе земли не является вполнѣ равномѣрнымъ. Ея
оба магнитные полюса, подъ которыми мы разумѣемъ тѣ точки, гдѣ
поле направлено строго перпендикулярно къ поверхности земли,
лежатъ вблизи географическихъ полюсовъ, но они не лежатъ точно
другъ противъ друга, какъ въ случаѣ равномѣрно намагниченнаго
шара, изображеннаго на рис. 151. Именно,
полюсъ I лежитъ подъ?2° 35'южн. шир. и 152° 30' вост. долг. отъ Гринвича,
полюсъ II — подъ 73°35' сѣв. шир.и 95°39'зап. долг.отъ Гринвича.
Рис. 151. Поле намагниченнаго шара.
Надъ магнитнымъ полемъ земли производятся систематическія
наблюденія во многихъ обсерваторіяхъ. Эти наблюденія показываютъ,
что оно не является постояннымъ. Оно подвергается медленнымъ измѣ-
неніямъ (вѣковыя варіаціи), которыя, накопляясь въ теченіе столѣтій,
могутъ достигнуть значительной величины. Ясно, что намагничені^^ З
земли и положеніе магнитныхъ полюсовъ медленно, но непрерывйй^
измѣняются; лучше всего это замѣтно по измѣненію склоненідМ^
Кромѣ этихъ медленныхъ измѣненій происходятъ также періодиче-
скія суточныя варіаціи, которыя связаны съ солнечнымъ^лучеиспу-
сканіемъ и потому оказываются болѣе значительными и ф>^ѣе продолжи-
22
Существенное различіе между состояніями эѳира
тельными лѣтомъ, нежели зимою. Замѣчаются также и періодическія
годичныя варіаціи, указывающія на существованіе вліянія относи-
тельнаго положенія солнца и земли на магнитное поле послѣдней.
Наконецъ, случаются еще неправильныя, часто весьма значитель-
ныя, магнитныя возмущенія, всегда сопровождающіяся сѣверными сія-
ніями и, во всякомъ случаѣ, отличающіяся силой вблизи сѣверныхъ сія-
ній (магнитныя бури); во время такихъ возмущеній компасомъ
совершенно нельзя пользоваться.
СУЩЕСТВЕННОЕ РАЗЛИЧІЕ МЕЖДУ ЭЛЕКТРИЧЕСКИМЪ И
МАГНИТНЫМЪ СОСТОЯНІЯМИ ЭѲИРА.
234. Какъ электрическое, такъ и магнитное состояніе эѳира пред-
ставляются векторіальными величинами; оба эти состоянія мы одина-
ково узнаемъ по силовымъ дѣйствіямъ на матеріальныя тѣла, и оба
они обладаютъ двумя родами исходныхъ мѣстъ, которыя мы различаемъ,
какъ положительныя и отрицательныя. Подъ вліяніемъ этой аналогіи
оба эти состоянія, несмотря на ихъ существенное различіе, часто
смѣшиваются начинающими, откуда проистекаютъ многочисленныя
неясности и затрудненія. Поэтому мы съ самаго начала рѣзко под-
черкивали различіе обоихъ состояній эѳира. Но мы можемъ пойти
теперь еще дальше: кажущееся совпаденіе физическаго характера
обоихъ состояній, выражающееся въ томъ, что оба состоянія изобра-
жаются при помощи векторіальныхъ величинъ, при ближайшемъ раз-
смотрѣніи оказывается недоразумѣніемъ. Въ случаѣ электрическаго
состоянія дѣйствительно существуетъ физическая разница между на-
чаломъ и концомъ силовыхъ линій, между стекляннымъ и смолянымъ
электричествомъ, между недостаткомъ и избыткомъ электроновъ. Мы
имѣли поэтому полное право уподобить электрическое состояніе
вѣтру или же перемѣщенію жидкости въ студнеобразной модели, гдѣ
начало и конецъ являются, дѣйствительно, физически различными;
такой векторъ мы обозначали стрѣлкою. ^0*
Совершенно иное мы имѣемъ въ магнитномъ полѣ. По^о^йтель-
ный и отрицательный магнитные полюсы не отличаются (^физически
одинъ отъ другого ничѣмъ, кромѣ знаковъ ихъ дѣйствій. Поэтому,
во избѣжаніе недоразумѣній, мы должны были сравнивъ всѣ магниты съ
какимъ-нибудь однимъ, который всегда имѣетсялицо и которымъ
всегда можно воспользоваться; такимъ магнитомъ является земной маг-
Существенное различіе между состояніями эѳира
23
нить; по знаку той силы, которая въ полѣ этого магнита дѣйствуетъ на
нѣкоторый полюсъ, мы должны были рѣшать, является ли этотъ полюсъ
положительнымъ или отрицательнымъ. Типичнымъ примѣромъ такого
вектора, обѣ стороны котораго обладаютъ прямо противоположными
свойствами, является ось вращенія. Она также имѣетъ опредѣленное
направленіе и въ ней также можно различить двѣ стороны. Если
разсматривать ее съ одной стороны, то движеніе будетъ казаться
правымъ, если же разсматривать ее съ другой стороны, движеніе бу-
детъ казаться лѣвымъ. Въ теоретической физикѣ условились всегда
считать положительнымъ направленіе отъ первой изъ упомянутыхъ
сторонъ ко второй. Это условіе, какъ и условіе относительно на-
правленія магнитнаго поля, основывается на чисто геометрическомъ
признакѣ. Въ одномъ случаѣ за норму берется земной магнитъ (сѣ-
веръ и югъ), въ другомъ — человѣческое тѣло (правая сторона и лѣ-
вая сторона). Векторы такого типа, подобные оси вращенія, назы-
ваются аксіальными векторами или роторами. Символомъ такого
вектора слѣдовало бы взять не стрѣлку, а ось вращенія. Векторы
другого рода, типичнымъ примѣромъ которыхъ служитъ смѣщеніе
и символомъ которыхъ является стрѣлка, называются полярными
векторами.
Электрическое состояніе есть полярный векторъ, а маг-
нитное состояніе аксіальный.
Въ дальнѣйшемъ, по мѣрѣ того какъ мы будемъ все глубже
проникать въ природу магнитнаго поля, мы все яснѣе будемъ ви-
дѣть, что здѣсь нами установлено существенное свойство магнитнаго
поля. То обстоятельство, что каждый магнитъ долженъ обладать
двумя полюсами различныхъ знаковъ и что никакихъ „магнитныхъ
проводниковъ" не существуетъ, оказывается тѣснѣйшимъ образомъ
связаннымъ съ аксіальной природой магнитнаго состоянія. Уже раз-
личіе въ видѣ электрическаго и магнитнаго полей земли (рис. 29 и 150)
является доказательствомъ существеннаго различія между обоими со- /
стояніями эѳира. Въ связи съ этимъ слѣдуетъ еще разъ упомянуть
про пироэлектрическіе кристаллы (§ 90), которые, подобно посто^%
нымъ магнитамъ, обнаруживаютъ положительный и отрицат^і^іЙ
полюсы. Хотя можно провести довольно широкую аналогіи) Міежду
пироэлектрической поляризаціей и намагниченіемъ, одн^фЧи здѣсь
проявляется характерное различіе между этими двумя рядами явле-
ній. Оба конца пироэлектрическаго (гемиморфнаго) жристалла всегда
24
Существенное различіе между состояніями эѳира
различаются по своимъ физическимъ свойствамъ, что можно замѣ-
тить уже, напримѣръ, по формѣ кристалла турмалина (рис. 58).
Между тѣмъ полюсы магнита различными являются, такъ сказать,
только математически, какъ положительный и отрицательный.
Нѣкоторые теоретики желали сгладить это различіе и вводили по-
нятія положительнаго и отрицательнаго магнитныхъ „зарядовъ". Та-
кого рода теоріи можно заранѣе считать безплодными и неудачными.
Въ слѣдующихъ главахъ мы самыми фактами будемъ приведены къ
общепринятой нынѣ теоріи магнитизма, которая совмѣстима только
съ аксіальнымъ характеромъ магнитнаго состоянія.
ГЛАВА ВТОРАЯ
МАГНИТНОЕ СОСТОЯНІЕ И ЭЛЕКТРИЧЕСКІЙ ТОКЪ
МАГНИТНОЕ ПОЛЕ, ОКРУЖАЮЩЕЕ ЭЛЕКТРИЧЕСКІЙ ТОКЪ.
235. Поднесемъ магнитную стрѣлку къ проволокѣ, которая соеди-
нена съ полюсами мощнаго источника электричества и по которой, слѣ-
довательно, идетъ постоянный электрическій разрядъ. Мы замѣтимъ при
этомъ, что на стрѣлку дѣйствуютъ силы, стремящіяся расположить
ее поперекъ проволоки. Это „электромагнитное дѣйствіеи было впер-
вые замѣчено въ 1820 году датскимъ физикомъ Эрстедомъ (Оегзіесі).
Это была первая связь между электрическими и магнитными явле-
ніями, которую удалось открыть.
Проводникъ электричества, по которому течетъ элек-
трическій токъ, всегда окруженъ магнитнымъ полемъ.
Изслѣдуемъ теперь подробнѣе это поле. Какъ указано выше,
магнитная стрѣлка устанавливается въ этомъ полѣ всегда поперекъ
проводника, несущаго токъ. Удобнѣе всего это наблюдается, если
проволока, по которой течетъ токъ, расположена вертикально. Если
обойти вокругъ такой проволоки съ магнитною стрѣлкою и въ каж-
домъ мѣстѣ отмѣтить направленіе, въ которомъ устанавливается
стрѣлка, то получающіяся такимъ образомъ силовыя линіи имѣютъ
видъ окружностей, охватывающихъ проволоку. Если помощью ком-
мутатора перемѣнить направленіе тока въ проволокѣ, то магнитная
стрѣлка поворачивается на 180°, т. е. силовыя линіи остаются тѣми
же, и только направленіе ихъ мѣняется на обратное. Если установить,
въ какую сторону обращенъ положительный полюсъ магнитной
стрѣлки, то получается слѣдующее правило, дающее направленіе ра§^?°
сматриваемаго поля.
Силовыя линіи магнитнаго поля, окружающаго приво-
локу, по которой течетъ электрическій токъ, им^^гъгвидъ
колецъ, охватывающихъ проволоку. Направленій этихъ ли-
ній положительное или правое, если смотр'|тъщо направле-
26
Магнитное поле, окружающее электрическій токъ
нію, въ которомъ переносится по проволокѣ положитель-
ное электричество.
Положительнымъ или правымъ направленіемъ на окружности
Рис. 152. Магнитное поле, окружающее прямолинейный проводникъ съ токомъ
(Проводникъ расположенъ перпендикулярно къ плоскости рисунка, и токъ,
идетъ сверху внизъ).
(или вообще на замкнутой кривой), называется то направленіе, кото-
рое совпадаетъ съ направленіемъ движенія часовой стрѣлки.
Рис. 153. Модель магнитныхъ силовыхъ линій, окружающихъ
прямолинейный проводникъ съ токомъ. /
Магнитное поле, окружающее проволоку, полДОторой течетъ
электрическій токъ, легко можно зафиксировать ц^іощью желѣзныхъ
опилокъ. Для этого проволоку пропускаютъ^дерезъ отверстіе, про-
-
Вращательныя движенія въ полѣ тока 27*
сверленное въ стеклянной пластинкѣ, такъ чтобы проволока была
перпендикулярна къ плоскости пластинки. На стекло насыпаютъ же-
лѣзныхъ опилокъ и пропускаютъ по проволокѣ токъ, потряхивая
слегка пластинку. При этомъ опилки располагаются, какъ показыва-
етъ рис. 152, по окружностямъ, охватывающимъ проволоку.
Изображенная на рис. 153 модель показываетъ намъ харак-
теръ поля, окружающаго токъ. Прямой стержень представляетъ здѣсь
отрѣзокъ проводника съ токомъ. Резиновыя кольца укрѣплены по-
мощью тонкихъ проволочекъ такимъ образомъ, что они концентри-
чески окружаютъ стержень; эти кольца изображаютъ отдѣльныя си-
ловыя линіи.
ВРАЩАТЕЛЬНЫЯ ДВИЖЕНІЯ ВЪ ПОЛЪ ТОКА.
236. Та особенность магнитнаго поля тока, что его линіи обра-
зуютъ вокругъ провода замкнутыя кривыя безъ начала и безъ концаъ
влечетъ за собою одно замѣчательное
слѣдствіе. Именно, если бы какъ-нибудь
возможно было обвести вокругъ про-
вода, несущаго токъ, отдѣльный маг-
нитный полюсъ, то по возвращеніи
полюса въ исходную точку должно
было бы оказаться, или что затрачена
работа, или же что выиграна работа.
Если бы полюсъ двигался въ такомъ
направленіи, что работа выигрывается,
то сила магнитнаго поля поддержи-
вала бы его движеніе, и при доста-
точно маломъ треніи вращеніе полю-
са совершалось бы непрерывно. Такой
опытъ можно произвести въ дѣйстви-
тельности, хотя, какъ мы знаемъ, изо-
лированные магнитные полюсы не су-
Рис. 154. Вращеніе
кругъ проводника
магнита во-,
съ токомъ.
ществуютъ. Расположеніе опыта ука-
зано на рис. 154. Токъ подводится
черезъ кольцеобразный желобъ, наполненный ртутью и снабжецпый
винтовымъ зажимомъ; черезъ центръ желоба проходитъ прямолиней-
ный толстый латунный проводъ, соединенный внизу со^гррымъ вин-
товымъ зажимомъ. На верхній конецъ этого латуньфф ‘Сѣержня опи-
28
Вращательныя движенія въ полѣ тока
рается ось вращенія, составляющая его продолженіе. Къ оси при-
крѣплена короткая горизонтальная металлическая проволока, конецъ
которой загнутъ внизъ и слегка погруженъ во ртуть. Такимъ обра-
разомъ, при всякомъ положеніи оси эта проволока образуетъ соеди-
неніе между стержнемъ и желобомъ со ртутью. Кромѣ того, съ осью
•скрѣплены два параллельные ей прямые магнита, имѣющіе внизу оди-
наковые полюсы. Если оба винтовые зажима соединить съ батареей,
то по латунному стержню потечетъ токъ, и вокругъ него образуются
замкнутыя магнитныя силовыя линіи; по вращающейся же оси токъ не
будетъ проходить, и вокругъ нея магнитнаго поля не будетъ. На
оба нижніе одноименные магнитные полюса дѣйствуетъ при этомъ
сила поля, окружающаго проводъ, верхніе же полюсы лежатъ внѣ
поля и не испытываютъ никакого силового дѣйствія. Поэтому ось вра-
щенія, съ которой скрѣплены оба магнита, приходитъ во вращатель-
ное движеніе и вращается непрерывно съ опредѣленной скоростью,
при чемъ дѣйствующая на магниты сила какъ разъ преодолѣваетъ
треніе.
Это явленіе замѣчательно тѣмъ, что здѣсь эѳиръ доставля-
етъ энергію въ формѣ работы, хотя магнитные полюсы описываютъ
замкнутые пути, и потому магнитное поле не испытываетъ никакихъ дли-
тельныхъ измѣненій. Магнитное поле тока этимъ существенно отличается
отъ стаціонарнаго электрическаго поля, изъ котораго никакъ нельзя из-
влечь работу посредствомъ движенія электрически заряженныхъ тѣлъ
по замкнутымъ путямъ (§ 25). Однако и въ магнитномъ полѣ
~такое полученіе работы возможно лишь въ томъ случаѣ, когда по-
люсъ передвигается вокругъ провода, несущаго токъ. Это слѣдуетъ
себѣ представлять такъ, что небольшая доля потока энергіи, пере-
носимаго эѳиромъ изъ источника электричества въ проводъ и превра-
щающагося въ немъ въ теплоту, захватывается магнитнымъ полю-
сомъ прежде, чѣмъ она достигаетъ провода и переводится въ меха-
ническую работу. Отчетливѣе понять это явленіе можно, только
познакомившись съ такъ называемой индукціей. Кромѣ того слѣду-
етъ замѣтить, что изображенный на рис. 154 простой моторъ -дол-
женъ имѣть подвижной контактъ или, какъ обычно говорятъ, сколь-
зящій контактъ, именно—ртутный желобъ съ погруженной въ него
проволочкой. Моторы постояннаго тока, т. е. так^ф>торы, которые
работаютъ при помощи силовыхъ дѣйствій магнитнаго поля стаціо-
нарнаго тока, невозможно строить безъ к^ки^ъ-либо подвижныхъ
Примѣры магнитныхъ полей тока
29
контактовъ, такъ какъ невозможно пользоваться отдѣльнымъ маг-
нитнымъ полюсомъ.
ПРИМЪРЫ МАГНИТНЫХЪ ПОЛЕЙ ТОКА.
237, Мы разсмотримъ теперь для нѣсколькихъ важныхъ случа-
евъ все магнитное поле, возбуждаемое цѣпью электрическаго тока.
Какъ первый примѣръ, возьмемъ параллельные провода, помощью,
которыхъ производится электрическая передача энергіи на большое
разстояніе. Мы имѣемъ въ этомъ случаѣ двѣ параллельныя проволоки;
одна изъ нихъ несетъ опредѣленный токъ въ положительномъ на-
правленіи, другая—тотъ же токъ въ отрицательномъ направленіи.
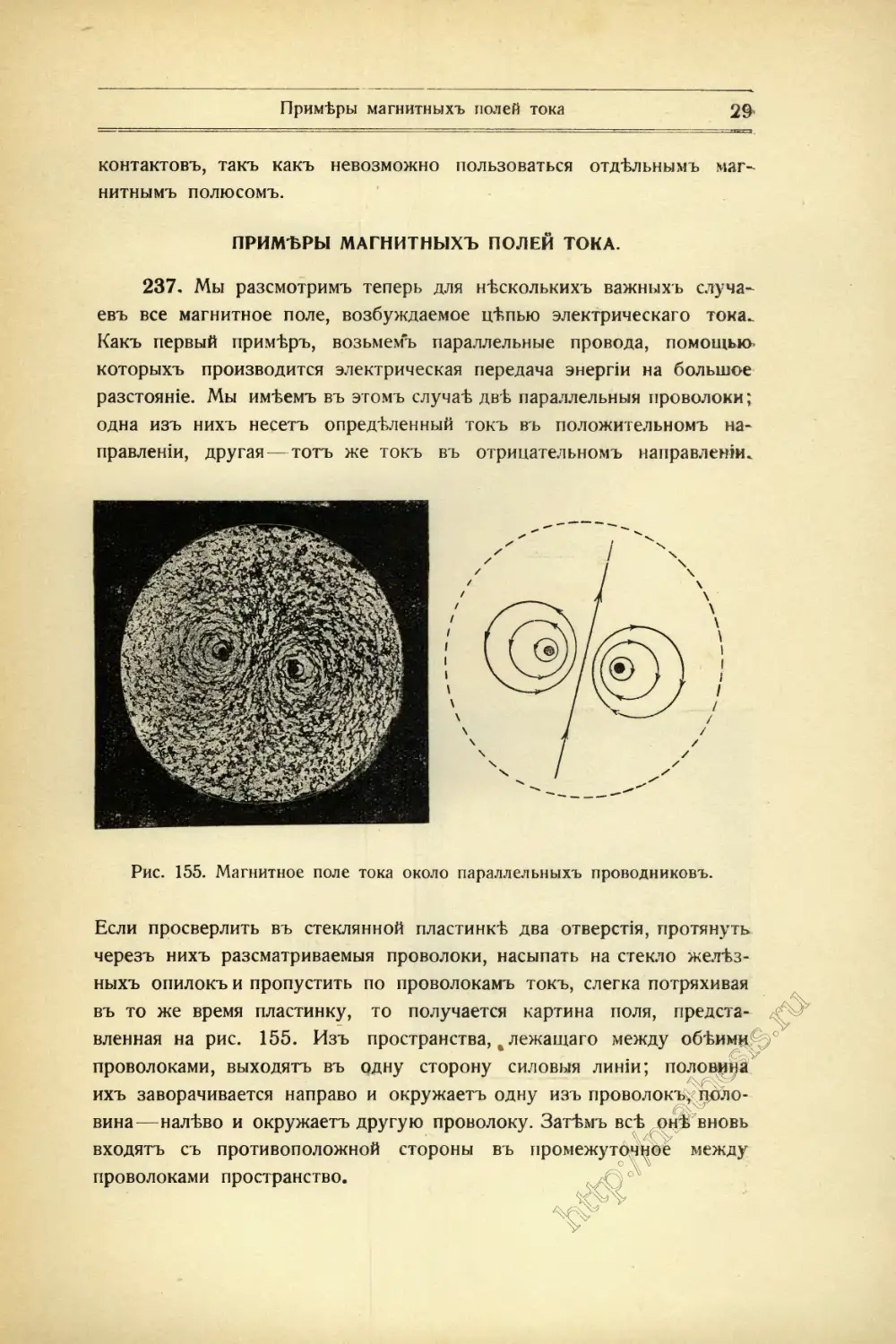
Рис. 155. Магнитное поле тока около параллельныхъ проводниковъ.
Если просверлить въ стеклянной пластинкѣ два отверстія, протянуть
черезъ нихъ разсматриваемыя проволоки, насыпать на стекло желѣз-
ныхъ опилокъ и пропустить по проволокамъ токъ, слегка потряхивая
въ то же время пластинку, то получается картина поля, предста-
вленная на рис. 155. Изъ пространства, лежащаго между обѣимц^0
проволоками, выходятъ въ одну сторону силовыя линіи; половила
ихъ заворачивается направо и окружаетъ одну изъ проволокъ^гціло-
вина—налѣво и окружаетъ другую проволоку. Затѣмъ всѣ^онѣвновь
входятъ съ противоположной стороны въ промежуточное между
проволоками пространство. /0 :Л И
30 Примѣры магнитныхъ полей тока
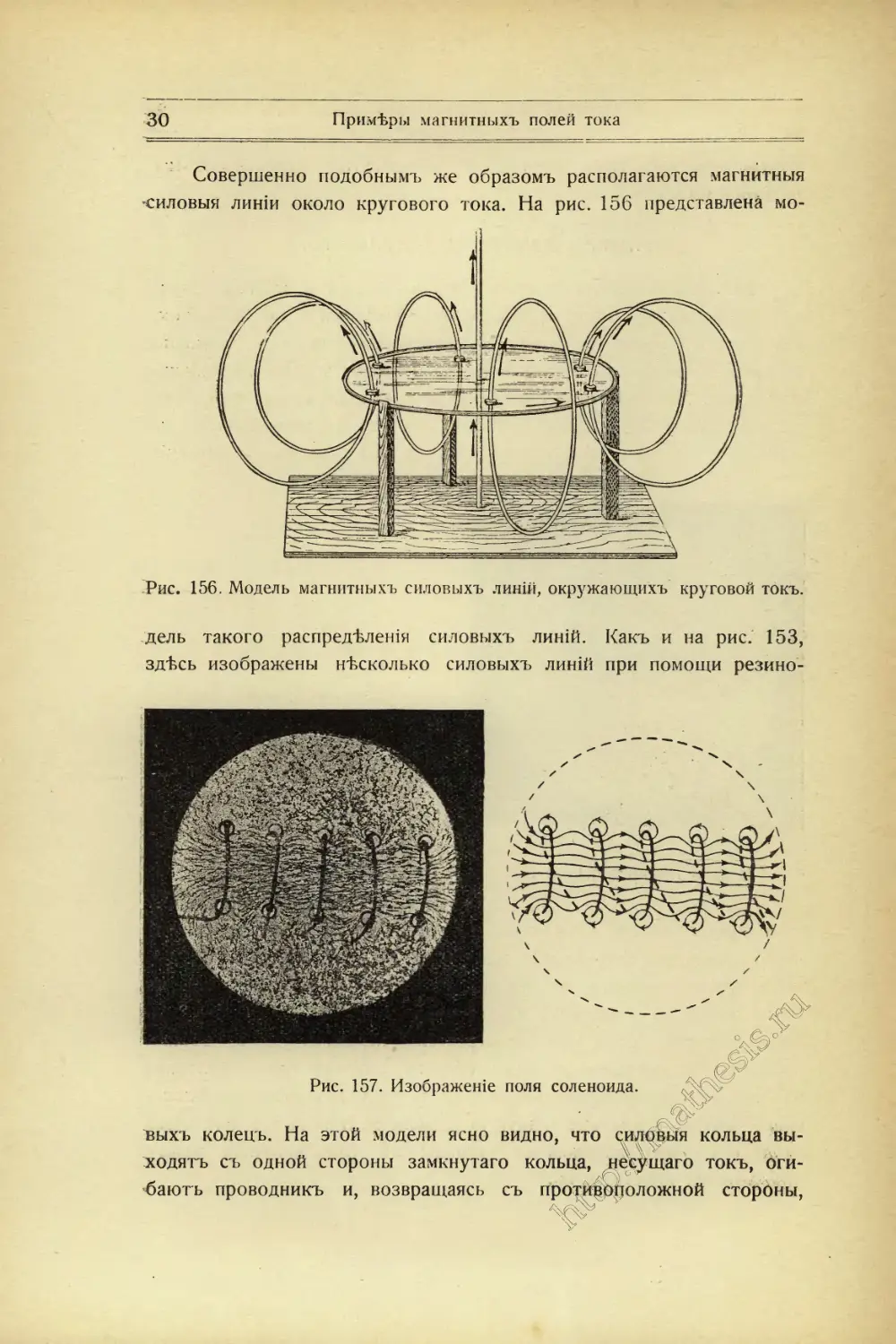
Совершенно подобнымъ же образомъ располагаются магнитныя
•силовыя линіи около кругового тока. На рис. 156 представлена мо-
Рис. 156. Модель магнитныхъ силовыхъ линій, окружающихъ круговой токъ.
дель такого распредѣленія силовыхъ линій. Какъ и на рис. 153,
здѣсь изображены нѣсколько силовыхъ линій при помощи резино-
Рис. 157. Изображеніе
поля соленоида.
ъыхъ колецъ. На этой модели ясно видно, что силовыя кольца вы-
ходятъ съ одной стороны замкнутаго кольца, несущаго токъ, оги-
баютъ проводникъ и, возвращаясь съ проти^рроложной стороны,
Примѣры магнитныхъ полей тока
31
смыкаются. Распредѣленіе силовыхъ линій въ полѣ кругового тока
совершенно тождественно съ ихъ распредѣленіемъ вокругъ намагни-
ченнаго круга, имѣющаго съ одной стороны положительный магни-
тизмъ, съ другой отрицательный.
Такъ называемый соленоидъ, т. е. катушку, имѣющую круговое
сѣченіе, можно разсматривать, какъ состоящую изъ ряда круговыхъ
колецъ, надвинутыхъ на поверхность ци-
линдра. Если черезъ соленоидъ пропу-
стить токъ, то возникаетъ магнитное поле,
изображенное на рис. 157. Внутри соле-
ноида силовыя линіи идутъ почти пря-
молинейно и параллельно оси соленоида.
Выходя съ одного конца соленоида, онѣ
круто загибаются назадъ и снова вхо-
дятъ въ него съ другого конца. Видъ
магнитнаго поля внѣ соленоида тожде-
ственъ съ видомъ поля прямого магнита.
Распредѣленіе силовыхъ линій въ про-
странствѣ для этого случая представлено
на модели, изображенной на рис. 158.
Внутри соленоида силовыя линіи тѣмъ
ближе къ прямымъ линіямъ, чѣмъ тоньше
и тѣснѣе расположены витки соленоида,
т. е. чѣмъ равномѣрнѣе распредѣляется
токъ по поверхности цилиндра. Внутри
Рис. 158. Модель внѣшняго
поля соленоида.
очень длиннаго и тонкаго цилиндра, на
поверхности котораго электрическій токъ распредѣляется съ совер-
шенно равномѣрной плотностью, магнитное поле вполнѣ параллельно
оси соленоида и вполнѣ равномѣрно по силѣ (однородно). Это
обстоятельство будетъ имѣть важное значеніе въ послѣдующемъ.
ЭЛЕКТРОМАГНИТЪ.
238. Мы видѣли въ § 225, что кусокъ мягкаго желѣза, внесец-<
ный въ магнитное поле, самъ становится магнитомъ. Для
чиванія желѣза можно воспользоваться также магнитнымъ полемъ
тока. Удобнѣе всего примѣнить съ этой цѣлью поле цилиндрической
катушки, вставляя въ нее брусокъ желѣза. Намагниченій^сёлѣзнаго
бруска внутри катушки легко демонстрировать на слѣдующемъ про-
32
Электромагнитъ
стомъ опытѣ. Помѣстимъ магнитную стрѣлку на такомъ разстояніи
отъ катушки съ токомъ, чтобы она подвергалась лишь незначитель-
ному силовому дѣйствію магнитнаго поля тока. Если затѣмъ ввести
внутрь 'катушки брусокъ мягкаго желѣза, то по движеніямъ стрѣлки
мы тотчасъ замѣтимъ, что появилось сильное магнитное поле. Срав-
нительно слабое поле внутри катушки сдѣлало желѣзный брусокъ
чрезвычайно сильнымъ магнитомъ. Если токъ въ катушкѣ прекратить*
Рис. 159. Электромагнитъ и большія тяжелыя булавки.
то по магнитной стрѣлкѣ видно, что и поле тотчасъ же исчеза-
етъ. Какъ мы уже знаемъ (§ 225), намагниченіе въ желѣзѣ не со-
храняется.
Желѣзный брусокъ, окруженный катушкой съ токамъ
и намагничиваемый магнитнымъ полемъ тока, называю^^ъ^лек-
тромагнитомъ.
Электромагнитъ обладаетъ двумя свойствами, дѣлаю-
щими его крайне удобнымъ для многихъ примѣненій. Во-
первыхъ, замыкая и размыкая токъ, идущі^гіо намагничи-
вающей катушкѣ, можно произвольно возбуждать и пре-
Электромагнитъ
33
кращать его магнитное состояніе. Во-вторыхъ, электромаг-
нитъ гораздо сильнѣе стального магнита, имѣющаго одина-
ковые съ нимъ размѣры.
На рис. 159 изображенъ большой электромагнитъ, поле кото-
раго поддерживаетъ въ воздухѣ дугу изъ большихъ тяжелыхъ гвоз-
дей. Такихъ силовыхъ дѣйствій никоимъ образомъ нельзя получить
при помощи стальныхъ магнитовъ. Если къ полюсамъ такого электромаг-
нита приложить желѣзную полосу, то ее удается оторвать отъ нихъ
только съ большимъ усиліемъ. Кромѣ того, поле такого большого
Къ батареѣ
Рис. 160. Магнитная индукція въ полѣ большого электромагнита.
электромагнита весьма далеко распространяется въ окружающемъ
пространствѣ. Если держать въ нѣкоторомъ отдаленіи отъ электро-
магнита желѣзную полосу, располагая ее въ направленіи силовыхъ
линій, то она такъ сильно намагничивается, что къ ея полюсамъ
можно подвѣсить по нѣскольку гвоздей (рис. 160). Наиболѣе удобны-й ^
способъ полученія постоянныхъ магнитовъ состоитъ въ томъ^Н'О
стальную полосу, которую хотятъ намагнитить, помѣщаютъ в'|рйілі>-
ное поле электромагнита. Здѣсь она тотчасъ же намаш^Йвается
и подъ дѣйствіемъ коэрцитивной силы сохраняетъ магнитныя свой-
ства и по удаленіи изъ поля.
Ми. Электричество и магнитизмъ.
з
34
Безъ магнитнаго поля электрическій токъ невозможенъ
Еще большія силовыя дѣйствія можно получить, если поста-
раться сосредоточить поле электромагнита въ тѣхъ мѣстахъ, гдѣ имъ
нужно воспользоваться. Иногда къ цѣпямъ подъемныхъ крановъ въ
тѣхъ случаяхъ, когда приходится поднимать желѣзныя тяжести (балки,
рельсы и т. п.), вмѣсто крюка подвѣшиваютъ электромагнитъ. При-
близивъ его къ тяжести, которую нужно поднять, замыкаютъ токъ;
тогда грузъ, даже весьма тяжелый, прочно пристаетъ къ электро-
магниту и можетъ быть поднятъ. Чтобы отцѣпить грузъ, достаточно
прервать намагничивающій токъ.
На колоссальныхъ силовыхъ дѣйствіяхъ электромагнитовъ осно-
вываются всѣ механическія примѣненія электрической энергіи, о ко-
торыхъ мы будемъ подробнѣе говорить въ главахъ VII и VIII. Мы
можемъ даже сказать, что безъ электромагнитовъ не была бы воз-
можна электротехника вообще: помощью слабыхъ силовыхъ дѣй-
ствій электрическихъ полей, магнитныхъ полей тока безъ желѣза
или полей стальныхъ магнитовъ невозможно было бы достигнуть
тѣхъ грандіозныхъ дѣйствій и преобразованій энергіи, которыя именно
и дѣлаютъ выгоднымъ примѣненіе электротехническихъ механизмовъ.
БЕЗЪ МАГНИТНАГО ПОЛЯ ЭЛЕКТРИЧЕСКІЙ ТОКЪ НЕВОЗМОЖЕНЪ.
239. Безчисленными опытами установлено съ полной достовѣр-
ностью, что электрическіе токи не могутъ существовать безъ окру-
жающаго ихъ магнитнаго поля. Существуетъ тѣснѣйшая связь между
токомъ и магнитнымъ полемъ. Чѣмъ сильнѣе токъ, тѣмъ сильнѣе и
магнитное поле. Доказано, кромѣ того, что вокругъ проводника
Опредѣленной формы при опредѣленной силѣ тока всегда возника-
етъ совершенно опредѣленное магнитное поле, независимо отъ того,
изъ какого матеріала сдѣланъ проводникъ, т.-е. независимо отъ его
сопротивленія и отъ величины напряженія, вызывающаго токъ.
Сила магнитнаго поля, окружающаго токъ, является
мѣрою силы электрическаго разряда въ проводникѣ.
Мы видѣли, что электрическій токъ представляетъ собою не что
илое, какъ непрерывное разрушеніе электрическаго поля|въ провод-
никѣ, при чемъ поле одновременно возстанавливается посредствомъ нѣ-
которыхъ процессовъ въ эѳирѣ, о которыхъ мы до с^сьпоръ еще ничего
не знали. Установленная нами только-что закономѣрная зависимость
между магнитнымъ полемъ и элекгрическимъ разрядомъ дѣлаетъ не-
Измѣрители тока съ подвижнымъ магнитомъ
35
?
сомнѣннымъ, что указанное дѣйствіе вызывается именно магнитнымъ
состояніемъ эѳира.
Въ магнитномъ полѣ тока имѣютъ мѣсто тѣ процессы,
которые непрерывно возстанавливаютъ разрушающіяся въ
проводникѣ электрическія напряженія.
Мы можемъ съ полнымъ правомъ сказать, что электрическій
токъ безъ магнитнаго поля невозможенъ. Совсѣмъ другой вопросъ,
можетъ ли существовать магнитное поле, не связанное съ электри-
ческимъ токомъ. Существованіе постоянныхъ магнитовъ даетъ какъ
будто положительный отвѣтъ на этотъ вопросъ. Однако, какъ мы уви-
димъ ниже, существуютъ вѣскія основанія предполагать, что магнитъ въ
сущности представляетъ собой скрытые молекулярные токи, которые
и обнаруживаются магнитными дѣйствіями. Если это справедливо, то
мы можемъ сказать, что не существуетъ также и магнитнаго поля
безъ электрическаго тока. Иными словами, магнитное поле и элек-
трическій токъ представляютъ собою лишь различныя про-
явленія одного и того же процесса въ эѳирѣ.
ИЗМЪРИТЕЛИ ТОКА СЪ ПОДВИЖНЫМЪ МАГНИТОМЪ.
240. Изъ вышеизложеннаго слѣдуетъ, что въ магнитномъ полѣ
мы имѣемъ средство, позволяющее намъ непосредственно измѣрять
силу тока. Для этой цѣли нужно магнитное поле тока ввести внутрь
инструмента, дающаго возможность судить объ его силѣ по тому
дѣйствію, которое испытываетъ въ немъ магнитъ.
Всякій такой инструментъ, служащій для измѣренія силы тока,
состоитъ изъ двухъ существенныхъ частей—катушки, обмотанной
проволокой, концы которой соединены съ двумя зажимами, и по-
движного магнита, отклоняющагося отъ своего положенія равновѣсія
подъ дѣйствіемъ поля тока, проходящаго по обмоткѣ катушки. Эта
сила тока уравновѣшиваетъ непрерывно дѣйствующую на магнитъ
направляющую силу, которая стремится возвратить его въ первона-
чальное положеніе. Чтобы измѣрить силу тока, разъединяютъ въ ка-г
комъ-нибудь мѣстѣ цѣпь, по которой проходитъ токъ, и вводятъ
нее катушку измѣрителя силы тока такъ, чтобы по ея обмоткѣ про-
ходилъ тотъ же токъ, что и по всей остальной цѣпи. Пш0этомъ
опредѣленной силѣ тока соотвѣтствуетъ опредѣленное^ отклоненіе
магнита; послѣднее тѣмъ больше, чѣмъ сильнѣе токъГ^С
36
Измѣрители тока съ подвижнымъ магнитомъ
На рис. 161 изображенъ весьма простой типъ такого измѣри-
теля силы тока. Катушка этого прибора раздѣлена на двѣ части, и
онъ снабженъ поэтому четырьмя винтовыми зажимами, соединен-
ными съ концами обѣихъ обмотокъ. Обѣ катушки можно соединять,
Рис. 161. Гальванометръ со стрѣл-
кою.
смотря по надобности, послѣдова-
тельно или параллельно. Если черезъ
катушки идетъ токъ, то въ узкомъ
пространствѣ, окруженномъ оборо-
тами проволоки, образуется почти
однородное поле, силовыя линіи ко-
тораго направлены перпендикуляр-
но къ плоскости оборотовъ. Въ
этомъ пространствѣ помѣщается
магнитная стрѣлка, на рис. 161, по-
нятно, не видимая. Ее подвѣшива-
ютъ на тонкой нити такъ, чтобы она
могла легко вращаться. Эта магнит-
ная стрѣлка скрѣплена помощью
проволочнаго стерженька, выступа-
ющаго черезъ небольшое отверстіе
изъ катушки, съ указателемъ, пока-
зывающимъ на раздѣленномъ кругѣ
величину отклоненія стрѣлки отъ
ея нулевого положенія. На рис. 161
видно, какъ неизмѣняемая система
(стрѣлка и указатель) при помощи
крючечка подвѣшивается къ упомя-
нутой тонкой нити. Направляющей
силой въ этомъ простомъ приборѣ является магнитное поле земли,
въ нашихъ странахъ достаточно постоянное. Катушка прибора должна
быть установлена такимъ образомъ, чтобы поле тока было перпен-
дикулярно къ полю земли, т.-е. такъ, чтобы при отсутствіи дока въ
катушкѣ магнитная стрѣлка располагалась въ плоскости оборо-
товъ. Поэтому катушка такого прибора помѣщается нахтоликѣ, ко-
торый можно поворачивать.
241. Только случайности, которой мы вообще.^обязаны многими
курьезами въ номенклатурѣ, нужно приписать тр обстоятельство, что
описанный измѣритель силы тока получилщназваніе гальванометра.
Измѣрители тока съ подвижнымъ магнитомъ
37
Гальвани самъ и не подозрѣвалъ о существованіи магнитнаго поля
тока, и конструкція этого прибора совершенно не находится въ ка-
кой-либо связи съ открытымъ Гальвани явленіемъ, если не считать -
того, что при помощи открытыхъ вслѣдъ затѣмъ Вольта гальвани-
ческихъ цѣпей впервые стало возможнымъ экспериментированіе съ
длительными электрическими токами. Болѣе умѣстно было бы назы-
вать этотъ инструментъ по имени Эрстеда или же „магнитоме-
тромъ" по аналогіи съ „электрометромъ"; тѣмъ не менѣе этотъ при-
боръ обычно называется гальванометромъ. Гальванометръ, градуиро-
ванный, какъ ниже будетъ описано, называется амперметромъ (отъ
единицы силы тока—амперъ).
Въ частностяхъ отдѣльные типы гальванометровъ могутъ значи-
тельно различаться между собою. Чтобы имѣть по возможности не-
большой и все же чувствительный индикаторъ для магнитнаго поля,
вмѣсто стрѣлки, встрѣчающейся у старыхъ приборовъ, теперь упо-
требляютъ либо намагниченную круглую пластинку или кольцо, при
чемъ полюсы лежатъ на противоположныхъ концахъ одного діаметра,
либо же небольшой подковообразный магнитъ съ сильно сближенными
полюсами, которому придаютъ видъ маленькаго колокола. Если нужно
построить магнитъ возможно малой массы для особо чувствительнаго
инструмента, который позволялъ бы обнаруживать весьма слабыя си-
ловыя дѣйствія, то къ легкому стерженьку прикрѣпляютъ рядомъ,
какъ это видно на рис. 162, нѣсколько маленькихъ кусочковъ тон-
кой часовой пружины и намагничиваютъ ихъ въ направленіи, пер-
пендикулярномъ къ стерженьку, который служитъ осью вращенія.
Отклоненіе магнита тоже можно наблюдать разными способами.
Въ нѣкоторыхъ приборахъ, какъ, напримѣръ, въ томъ, который из-
ображенъ на рис. 161, и во всѣхъ градуированныхъ инструментахъ—
амперметрахъ — пользуются стрѣлкой-указателемъ. Въ другихъ прибо-
рахъ къ магниту прикрѣплено, какъ это изображено на рис. 162, неболь-
шое зеркальце, отклоненія котораго наблюдаютъ въ трубу, пользуясь
отражающейся въ немъ миллиметровой шкалой. Такіе инструменты у по-
требляются только въ лабораторіяхъ, гдѣ ихъ можно въ любо^х
время вновь проградуировать. Большая чувствительность достим^гі
только при употребленіи зеркальныхъ инструментовъ.
Въ различныхъ приборахъ пользуются разнообразной^напра-
вляющей силой, стремящейся удержать магнитъ въ опредѣленномъ
. нулевомъ положеніи. Съ этой цѣлью въ старыхъ инструментахъ, въ
38
Измѣрители тока съ подвижнымъ магнитомъ
родѣ изображеннаго на рис. 161, примѣнялось магнитное поле земли,
на это сопряжено съ нѣкоторыми неудобствами. Инструменты со стрѣл-
кою, для того чтобы ими удобно было пользоваться, должны быть
годны къ употребленію во всякомъ положеніи безъ предварительной
Рис. 162. Гальванометръ Томсона съ четырьмя катушками.
оріентировки относительно поля земли, какъ того требуетъ гальвано-
метръ, изображенный на рис. 161. Кромѣ того, сила земшжГгіоля въ раз-
личныхъ мѣстахъ весьма различна и даже въ одномъ томъ же мѣстѣ
измѣняется, какъ мы знаемъ, съ теченіемъ времени^ Но самое большое
неудобство происходитъ отъ того, что на магнитное поле земли ока-
зываютъ сильное вліяніе большія массы желѣза, которыя входятъ въ
Измѣрители тока съ подвижнымъ магнитомъ
39
составъ машинъ и аппаратовъ на заводахъ и въ лабораторіяхъ, и
не всегда установлены неподвижно.
По этимъ причинамъ инструментъ, въ которомъ направляющей
силой служитъ сила земного магнитизма, невозможно проградуиро-
вать такъ, чтобы онъ всегда давалъ вѣрныя показанія; такой инстру-
ментъ не можетъ, слѣдовательно, служить амперметромъ. Въ нѣко-
торыхъ инструментахъ вмѣсто поля земли пользуются искусственнымъ
магнитнымъ полемъ, напримѣръ, полемъ сильнаго подковообразнаго
магнита, по сравненію съ которымъ земное поле является исчезающе
слабымъ. Въ другихъ инструментахъ магнитъ удерживается въ своемъ
начальномъ положеніи помощью пружины, упругая сила которой на-
столько превосходитъ направляющую силу земного поля, что по-
слѣднюю по сравненію съ ней можно принять равной нулю. Въ тѣхъ
инструментахъ, которые при употребленіи находятся всегда въ верти-
кальномъ положеніи, какъ, напримѣръ, въ инструментахъ распредѣли-
тельныхъ досокъ, удобно въ качествѣ направляющей силы использо-
вать силу тяжести. Съ этой цѣлью магнитъ подвѣшивается на горизон-
тальной оси, при чемъ его центръ тяжести лежитъ ниже этой оси,
какъ въ вѣсахъ.
Съ другой стО| іы, и въ весьма чувствительныхъ гальвано-
метрахъ, предназначаемыхъ для лабораторій, также стараются изба-
виться отъ дѣйствія направляющей силы земного поля. Причиной
этого является то обстоятельство, что инструменты, на магниты ко-
торыхъ дѣйствуетъ земное поле, могутъ обладать лишь относительно
малой чувствительностью. Для достиженія весьма высокой чувстви-
тельности, нужно пользоваться гораздо болѣе слабыми направляю-
щими силами. Можно, напримѣръ, уменьшить силу земного поля до
нѣкоторой малой ея доли при помощи прямого магнита, укрѣплен-
наго на гальванометрѣ въ опредѣленномъ разстояніи отъ подвижного
магнита. Чрезвычайно чувствительные инструменты получаются, если
при помощи толстой желѣзной оболочки („панцырной защиты") от-
городить заключенное въ ней пространство отъ земного поля и воз-
будить въ этомъ пространствѣ при помощи особыхъ магнитовъ искус-
ственное направляющее поле, которое можно сдѣлать сколь угодно
слабымъ. Удобнѣе всего, какъ оказалось на практикѣ, придаватъ'же-
лѣзнымъ оболочкамъ форму полыхъ шаровъ. Снабженньі^^акими
оболочками инструменты носятъ названіе шаровыхъ панцырныхъ
гальванометровъ. Панцырные гальванометры, подобно электри-
40
Измѣрители тока съ подвижнымъ магнитомъ
чески защищеннымъ электрометрамъ, описаннымъ на стр. 79 первой
части, имѣютъ то преимущество, что на нихъ не оказываютъ вліянія
внѣшнія поля; въ нихъ почти совершенно не проникаютъ поля боль-
шихъ желѣзныхъ массъ, электрическихъ дорогъ и вообще установокъ
сильнаго тока. Наконецъ, весьма важнымъ типомъ инструмента съ чрез-
вычайно малой направляющей силой являются еще такъ называемые
астатическіе гальванометры; особенно точные инструменты такого
типа были построены В. Томсономъ (лордомъ Кельвиномъ). Въ
этихъ инструментахъ къ твердому стерженьку прикрѣплены одинъ надъ
другимъ два магнита. Оба магнита дѣлаются по возможности одина-
ковыми и располагаются такъ, что надъ сѣвернымъ полюсомъ одного
приходится южный полюсъ другого, благодаря чему почти совершен-
но уничтожается вліяніе земного поля. Такую систему магнитовъ назы-
ваютъ а ста зирован ной. Небольшую разницу въ силѣ обоихъ магни-
товъ компенсируютъ при помощи двухъ магнитовъ, укрѣпленныхъ
надъ гальванометромъ на вертикальной штангѣ такъ, что ихъ можно
передвигать внизъ и вверхъ и поворачивать (рис. 162). Помощью
этихъ магнитовъ можно достигнуть того, чтобы поля, окружа-
ющія оба магнитика гальванометра, немного разнились между собой и
чтобы эта разница въ силахъ полей была какъ разъ противоположна
разности силъ полюсовъ самихъ магнитиковъ, такъ что направляющая
сила станетъ ничтожно малой. Когда такое состояніе достигнуто, то
это обнаруживается по тому, что колебанія, совершаемыя аста-
тической системой магнитиковъ около вертикальной оси, стано-
вятся весьма медленными. Чѣмъ больше періодъ этихъ колебаній,
тѣмъ чувствительнѣе инструментъ. Въ гальванометрѣ Томсона каж-
дый изъ астазированныхъ магнитиковъ находится внутри пары ка-
тушекъ. Такимъ образомъ инструментъ имѣетъ всего четыре катушки
и, соотвѣтственно этому, восемь зажимовъ. Включеніе этого гальва-
нометра должно производиться, конечно, такимъ образомъ, чтобы
оба магнитика отклонялись въ одну и ту же сторону подъ дѣй-
ствіемъ полей тока въ соотвѣтствующихъ катушкахъ. Слѣдовательно,
эти поля должны имѣть взаимно противоположныя направленія въ
верхней и нижней парахъ катушекъ. Во всѣхъ гальванометрахъ съ
высокой чувствительностью для подвѣшиванія магнитикоѣ^? употребля-
ются тончайшія кварцевыя нити, у которыхъ сопротивленіе закру-
чиванію ничтожно мало. гѴѵ"
Измѣрители тока съ подвижнымъ магнитомъ
41
Въ нѣкоторыхъ амперметрахъ вмѣсто постояннаго магнита внутри
катушки употребляютъ тѣло изъ мягкаго желѣза. Поле тока дѣла-
етъ желѣзо магнитомъ и затѣмъ вызываетъ его отклоненіе. Очень
легко понять устройство подоб-
наго инструмента, изображеннаго на
рис. 163. Внутри вертикальной ци-
линдрической катушки подвѣшенъ
тонкій цилиндрическій желѣзный
стержень, прикрѣпленный къ ниж-
нему концу спиральной пружины
изъ тонкой проволоки. Упругая
сила пружины является здѣсь на-
правляющей силой, удерживающей
желѣзный стержень на опредѣлен-
ной высотѣ. Если по катушкѣ про-
ходитъ токъ, то стержень намагни-
чивается и подъ дѣйствіемъ поля
тока втягивается внизъ, при чемъ
пружина слегка растягивается. Чѣмъ
сильнѣе токъ, тѣмъ больше сила,
тянущая стержень внизъ и тѣмъ
Рис. 163. Амперметръ съ мягкимъ
желѣзомъ.
глубже входитъ онъ внутрь катушки. Помощью небольшого рычаж-
наго механизма движеніе стержня передается стрѣлкѣ, показывающей
на шкалѣ силу тока. Инструменты съ мягкимъ желѣзомъ обладаютъ
двумя характерными особенностями. Во-первыхъ, они всегда даютъ
отклоненія въ одну и ту же сторону, такъ какъ при перемѣнѣ направле-
нія тока желѣзо также перемагничивается. Во-вторыхъ, они чувстви-
тельнѣе при большихъ силахъ тока, нежели при малыхъ, такъ какъ
при значительной силѣ тока мягкое желѣзо сильнѣе намагничивается.
Это видно по шкалѣ изображеннаго на рис. 163 инструмента, на
которой дѣленія, соотвѣтствующія слабымъ силамъ тока, расположены
чаще, чѣмъ тѣ дѣленія, которыя соотвѣтствуютъ большимъ силамъ
тока. На концѣ шкалы чувствительность инструмента опять умень-
шается, такъ какъ съ погруженіемъ стержня внутрь катушки маг-г"
нитная втягивающая сила уменьшается.
42 Градуированіе измѣрителей тока
ГРАДУИРОВАНІЕ ИЗМѢРИТЕЛЕЙ ТОКА.
242. Выбравъ единицу электрическаго заряда —кулонъ (§ 100),
мы тѣмъ самымъ предрѣшили, что мы должны принять за единицу
силы электрическаго разряда вмѣстѣ съ сопровождающимъ его маг-
нитнымъ полемъ, т.-е. мы опредѣлили единицу силы тока.
Сила такого электрическаго тока, при которомъ въ
каждую секунду разряжается 1 кулонъ электричества, при-
нимается за единицу силы тока и называется амперомъ.
Рис. 164. Градуированіе амперметра.
Это опредѣленіе непосредственно даетъ и методъ градуированія
амперметра. Составляютъ цѣпь, въ которую включаютъ послѣдова-
тельно кулонметръ и амперметръ, и регулируютъ сопротивленіе такъ,
чтобы токъ въ теченіе нѣкотораго промежутка времени оставался
постояннымъ, т.-е. чтобы стрѣлка амперметра все это времях стояла
точно на одномъ и томъ же мѣстѣ. Это мѣсто отмѣчают$Ьѵизмѣ-
ряютъ время, въ теченіе котораго проходилъ токъ, и < наблюдаютъ,
какое количество электричества т прошло въ теченіеэтого проме-
жутка времени і черезъ кулонметръ. Если время ^в^іражено въ секун-
дахъ и т—въ кулонахъ, то сила тока, соотвѣтствующая отмѣченному
Градуированіе измѣрителей тока
43
положенію стрѣлки, равняется ,1^= — амперъ. Измѣняя сопроти-
вленіе и тѣмъ измѣняя силу тока, можно такимъ образомъ програ-
дуировать постепенно всю шкалу инструмента на амперы. Если тре-
буется весьма точная градуировка, то нужно пользоваться серебря-
нымъ кулонметромъ (§ 100); болѣе грубую градуировку удобнѣе
всего производить при помощи кулонметра съ гремучимъ газомъ
(рис. 164).
Если указаннымъ путемъ точно проградуировать шкалу одного
какого-либо ампермет-
ра, то этимъ инструмен-
томъ можно пользовать-
ся въ качествѣ нормаль-
наго и при его помо-
щи градуировать любой
другой измѣритель силы
тока. Съ этой цѣлью оба
амперметра — градуиру-
емый и нормальный —
включаются въ одну и
ту же цѣпь; пропуска-
ется токъ и отмѣчает-
ся отклоненіе, даваемое
градуируемымъ инстру-
ментомъ ; нормальный
амперметръ показыва-
етъ силу тока, соотвѣт-
ствующую этому откло-
ненію. Такимъ путемъ
градуированіе произво-
дится очень быстро.
Рис. 165. Градуированіе гидродинамическаго
измѣрителя скорости тока.
Градуированіе из-
мѣрителя силы тока по-
мощью кулонметра является одной изъ основъ всѣхъ измѣреній над|>
магнитными полями. Оно вполнѣ аналогично градуированію ^гидро-
динамическаго измѣрителя скорости теченія жидкости. Простѣйшій
измѣритель этой скорости представляетъ собою планку,<^ѳдвѣшен-
ную перпендикулярно къ направленію тока жидкости, АДодъ давле-
ніемъ текущей жидкости эта планка отклоняется от^сѣоего положенія
44
Магнитное поле соленоидовъ
равновѣсія, и это отклоненіе тѣмъ значительнѣе, чѣмъ больше ско-
рость теченія. Если установить такой измѣритель въ трубѣ, изъ ко-
торой жидкость вытекаетъ въ градуированный сосудъ (рис. 165) и
измѣрить по часамъ въ секундахъ промежутокъ времени і, въ тече-
ніе котораго вытекаетъ опредѣленный объемъ жидкости г>, то полу-
т ѵ литръ
чится величина силы тока У = —-------— • Такимъ путемъ можно по-
і сек. '
градуировать шкалу для соединенной съ планкой стрѣлки, не зная
законовъ гидравлическихъ силъ. Здѣсь измѣритель скорости теченія
жидкости является вполнѣ аналогичнымъ амперметру, а градуирован-
ный пріемникъ жидкости аналогиченъ кулонметру.
МАГНИТНОЕ ПОЛЕ СОЛЕНОИДОВЪ.
243. Разсматривая расположеніе силовыхъ линій на рис. 157,
мы видимъ, что внѣ соленоида поле безконечно слабо по сравненію
съ полемъ внутри соленоида. Въ этомъ можно еще нагляднѣе убѣ-
диться при помощи соленоида, снабженнаго особенно тонкой и равно-
мѣрной обмоткой и настолько длиннаго, что его длину можно при-
нять безконечно большою по сравненію съ его толщиной. Если
пропустить токъ черезъ такой соленоидъ, то по силовымъ дѣйствіямъ,
испытываемымъ магнитной стрѣлкой, можно заключить, что вблизи
обоихъ „полюсовъ" соленоида образуются очень сильныя магнитныя
поля; въ этихъ мѣстахъ сильное внутреннее магнитное поле выхо-
дитъ во внѣшнее пространство. Наоборотъ, около середины соле-
ноида стрѣлка никакого поля не обнаруживаетъ, даже при прибли-
женіи ея къ самымъ виткамъ. Витки, по которымъ проходитъ токъ,
рѣзко отграничиваютъ сильное внутреннее поле отъ внѣшняго про-
странства, гдѣ интенсивность поля нужно принять равной нулю.
Внутри безконечно длиннаго соленоида, по цилиндри-
ческой поверхности котораго проходитъ электрическій,
токъ равномѣрной плотности, заключается сильное магнит-
ное поле, рѣзко ограниченное этой поверхностью^ Внѣ
этой границы интенсивность поля равна нулю.
Вмѣсто „безконечно длиннаго" соленоида можн<йлгакже взять
„безграничный соленоидъ", именно соленоидъД^имѣющій форму
кольца. .фѴ
Магнитное поле соленоидовъ
45
Кольцеобразный, замкнутый соленоидъ съ постоян-
нымъ поперечнымъ сѣченіемъ, по поверхности котораго
течетъ равномѣрно плотный электрическій токъ, не даетъ
совершенно внѣшняго магнитнаго поля, тогда какъ во вну-
треннемъ кольцеобразномъ пространствѣ образуется силь-
ное магнитое поле.
Этимъ свойствомъ обладаютъ не только соленоиды постояннаго
поперечнаго сѣченія. Въ двухъ соленоидахъ, имѣющихъ различныя по-
Рис. 166. Картина поля кольцеобразнаго соленоида.
перечныя сѣченія, можно всегда урегулировать силы токовъ такъ, чтобы
оба соленоида имѣли полюсы одинаковой силы, т. е. чтобы эти по-
люсы какъ разъ компенсировали другъ друга, если приложить положи-
тельный полюсъ одного соленоида къ отрицательному полюсу другого.
Для этого нужно плотность тока, идущаго по болѣе тонкому солено-
иду, увеличить въ опредѣленномъ отношеніи сравнительно съ плот-
ностью тока, идущаго по болѣе толстому соленоиду. Соленоидъ
непостояннаго сѣченія можно представить себѣ состоящимъ изъ
ряда маленькихъ соленоидовъ, сѣченія которыхъ различны. Если
витки тока распредѣлить по поверхности соленоида такимъ образомъ,
чтобы полюсы каждыхъ двухъ соприкасающихся маленькихъ ^ленои-
довъ взаимно компенсировались, то внѣшнее поле такогосоленои-
да непостояннаго сѣченія также будетъ равно нулю. О^тобы этого
достигнуть, нужно витки тока располагать въ болѣеузкихъ частяхъ
46
Сила магнитнаго поля
соленоида въ опредѣленномъ отношеніи плотнѣе, нежели въ широ-
кихъ его частяхъ. Это ясно видно на рис. 166, представляющемъ
картину поля кольцеобразнаго соленоида непостояннаго попереч-
наго сѣченія. Такъ какъ обмотка на немъ сдѣлана правильно, то,
дѣйствительно, все поле находится только въ кольцеобразной по-
лости; снаружи опилки расположились совершенно безпорядочно.
Для кольцеобразнаго тѣла съ произвольнымъ пере-
мѣннымъ сѣченіемъ можно всегда подобрать такую обмот-
ку перемѣнной плотности, чтобы при прохожденіи тока
все магнитное поле тока сосредоточивалось во внутренней
кольцеобразной полости, а сила внѣшняго поля была равна
нулю.
СИЛА МАГНИТНАГО ПОЛЯ.
244. Сила поля внутри безконечно длиннаго соленоида не
зависитъ отъ величины сѣченія, но лишь отъ плотности тока, т.-е.
ютъ силы тока, приходящейся на каждый сантиметръ цилиндрической
поверхности обмотки или же, какъ говорятъ, отъ числа амперъ-
витковъ, приходящагося на сантиметръ. Въ этомъ можно убѣдиться
экспериментальнымъ путемъ, но можно это вывести также и теорети-
чески изъ вышеописанныхъ фактовъ. Представимъ себѣ два соленоида
одинаковой длины съ одинаковымъ прямоугольнымъ сѣченіемъ и съ
•одинаковой плотностью тока на призматическихъ поверхностяхъ.
Предположимъ, что эти соленоиды приложены одинъ къ друго-
му равными боковыми гранями такъ, чго сѣверный полюсъ одного
расположенъ рядомъ съ сѣвернымъ полюсомъ другого и южный
полюсъ—рядомъ съ южнымъ. При этомъ поля внутри соленоидовъ
не измѣнятся, но получится вдвое большее призматическое полое
пространство, раздѣленное посрединѣ поперечной стѣнкой, при чемъ
въ каждой изъ обѣихъ половинъ будетъ поле одной и той же . ин-
тенсивности. Въ поперечной стѣнкѣ получатся два тока, равные и
взаимно противоположные. Слѣдовательно, результирующій' токъ
въ поперечной стѣнкѣ равенъ нулю, и можно его исключить изъ
разсмотрѣнія, не измѣняя этимъ поля. Такимъ образомъ получается
соленоидъ съ поперечнымъ сѣченіемъ двойныхъ ^размѣровъ, но съ
тѣмъ же числомъ амперъ-витковъ, что и у каждагоизъ первоначально
взятыхъ соленоидовъ. Поле въ призматический,полости этого со-
Сила магнитнаго поля
47
леноида повсюду тождественно съ полемъ каждаго изъ соленоидовъ
половиннаго поперечнаго сѣченія. Но можно пойти еще дальше;
соленоидъ совершенно произвольнаго сѣченія можно мысленно раз-
ложить на совокупность произвольно большого числа одинаковыхъ
прямоуголь-
Рис. 167. Разложеніе со-
леноида съ большимъ по-
перечнымъ сѣченіемъ на
элементарные соленоиды.
между собою ,,элементарныхъ соленоидовъ
нымъ сѣченіемъ (рис. 167). Если каждый изъ
этихъ элементарныхъ соленоидовъ окруженъ
тѣмъ же числомъ амперъ-витковъ, что и боль-
шой соленоидъ, то во всѣхъ поперечныхъ
стѣнкахъ токи взаимно уничтожаются. Поэто-
му эти стѣнки можно совершенно исключить
изъ разсмотрѣнія, не измѣняя этимъ поля;
отсюда слѣдуетъ, что по всему сѣченію боль-
шого соленоида поле постоянно, и именно рав-
но въ точности полю элементарнаго соленои-
да съ тѣмъ же числомъ амперъ-витковъ.
Пользуясь этимъ свойствомъ магнитнаго
поля въ соленоидѣ, можно дать опредѣленіе силы магнитнаго поля. Дѣло
въ томъ, что любую часть силовой трубки можно воспроизвести от-
дѣльно, независимо отъ остального поля, при помощи безконечно
тонкаго соленоида. И подобно тому, какъ въ § 242 мы приняли электри-
ческій токъ за мѣру полной величины его магнитнаго поля, такъ же
и теперъ мы примемъ его за мѣру „удѣльной силы" или напря-
женія поля. Плотность тока или число амперъ-витковъ на сантиметръ
изолированной силовой трубки является однозначной мѣрой ея силы;
направленіе оси соленоида мы будемъ принимать за направленіе поля.
Мы его будемъ считать положительнымъ въ томъ случаѣ, если,
глядя по этому направленію, наблюдатель видитъ окружающій сило-
выя трубки токъ текущимъ по направленію часовой стрѣлки. Это
направленіе совпадаетъ съ выше указаннымъ направленіемъ силы,
дѣйствующей на положительный магнитный полюсъ въ полѣ.
Сила магнитнаго поля въ произвольномъ мѣстѣ измѣ-
ряется числомъ амперъ-витковъ, приходящимся на санти^Л
метръ, у соленоида, поле котораго тождественно съпол^мі
въ изслѣдуемомъ мѣстѣ. Если оба сравниваемыя пол^Ѵди-
наково оріентированы въ пространствѣ, то поло^цт-ельное
направленіе оси соленоида опредѣляетъ направленіе поля.
Тождественность обоихъ полей можно констатировать по
48
Сложеніе магнитныхъ полей
ихъ силовому дѣйствію на магнитный полюсъ или же по-
мощью какого-либо иного магнитоскопа.
За единицу силы магнитнаго поля мы примемъ силу
такого поля, въ которомъ число амперъ-витковъ, приходя-
щееся на длину одного сантиметра, равно единицѣ.
Ниже мы увидимъ, какимъ образомъ практически производятся
измѣренія поля на основаніи этого опредѣленія. Измѣряемую въ
этихъ единицахъ силу поля мы будемъ всегда обозначать буквою Н,
Согласно опредѣленію, сила магнитнаго поля Н пред-
ставляетъ собою роторъ.
СЛОЖЕНІЕ МАГНИТНЫХЪ ПОЛЕЙ.
245. Если въ магнитное поле силы внести параллельно на-
правленію его силовыхъ линій соленоидъ, по обмоткѣ котораго
течетъ токъ, при чемъ на 1 сантиметръ приходится 772 амперъ-вит-
ковъ, то сила поля внутри соленоида въ общей сложности соста-
вляетъ Н1-\-Н2 амперъ-витковъ на сантиметръ. Въ этомъ можно убѣ-
диться экспериментально, но это слѣдуетъ уже а ргіогі изъ даннаго
выше
опредѣленія силы
поля.
Такъ какъ соединенное дѣйствіе полей
Нг и Н2 имѣетъ мѣсто лишь внутри
соленоида, то поле, находящееся внѣ
пространства, ограниченнаго витками
соленоида, не оказываетъ никакого
вліянія на результатъ ихъ наложенія.
Поэтому мы можемъ принять, что и
поле подобно полю Н2, распо-
ложено лишь внутри соленоида. Это
предположеніе соотвѣтствуетъ тому
случаю, когда поле Нг вызывается
Рис. 168. Сумма двухъ векторовъ. ВТ0Р0Й обмоткой того же соленоида,
по которой проходитъ токъ, имѣющій
плотность Нг амперовъ на сантиметръ. Въ общемъ плотности ^г(Жа на
соленоидѣ при этомъ равняется Нх + ^4» откуда ясно, чт^^/1 и Н2
вмѣстѣ эквивалентны полю съ числомъ амперъ-вит^рѣъ^ равнымъ
+ Н2. Если Н1 и Н2 направлены прямо противоположно, то, ко-
нечно, получается величина Нг ~ Н2. Въ обще^^случаѣ, когда Н1
и Н2 имѣютъ произвольныя направленія, сло^еціе производится по
правилу сложенія векторовъ. Пользуясь этимъ правиломъ, легко найти
Сложеніе магнитныхъ полей
49
сумму двухъ векторовъ Нх и 772, если ихъ представить графически
отрѣзками прямыхъ, направленія которыхъ совпадаютъ съ напра-
вленіями векторовъ и длины которыхъ пропорціональны величинамъ
векторовъ. Если начало вектора Н2, представленнаго отрѣзкомъ
ВС (рис. 168), совмѣстить съ концомъ отрѣзка АВ, представляю-
щаго векторъ то отрѣзокъ АС отъ начала перваго вектора
до конца второго представитъ собою по величинѣ и по направленію
векторъ, равный суммѣ + Н2. Что два магнитныхъ поля Нг и Н2,
измѣренныя ихъ числами амперъ-витковъ, всегда слагаются по этому
правилу, можно убѣдиться такимъ же образомъ, какъ для только-что
разсмотрѣннаго частнаго случая параллельнаго расположенія. Конечно,
это положеніе легко провѣрить также и экспериментально.
Два магнитныя поля, числа амперъ-витковъ которыхъ
извѣстны и равняются Нг и Н2, образуютъ при любомъ
косомъ наложеніи поле, число амперъ-витковъ котораго
равняется векторіальной суммѣ Н1-\-'Н2.
На этомъ предложеніи можно основать удобный методъ измѣ-
ренія поля. Внесемъ въ неизвѣстное магнитное поле очень длинную
и очень тонкую катушку и пропустимъ черезъ нее электрическій токъ
такой силы, чтобы слагающая силы поля въ направленіи оси катушки
стала равной нулю. Если катушка параллельна измѣряемому полю, то
поле будетъ при этомъ равно нулю, если же она наклонена къ
направленію измѣряемаго поля, то останется еще поле, перпендику-
лярное къ оси катушки. Это можно распознать при помощи неболь-
шого желѣзнаго стержня, который вводятъ внутрь катушки. Въ
зависимости отъ того, какой изъ двухъ случаевъ имѣетъ мѣсто,,
стержень либо устанавливается перпендикулярно къ оси катушки,
либо вовсе не принимаетъ опредѣленнаго направленія. Плотность
тока въ обмоткѣ соленоида равна слагающей магнитнаго поля въ на-
правленіи оси соленоида, а въ частномъ случаѣ, когда поле и со-
леноидъ одинаково направлены, она равна самому измѣряемому
магнитному полю, но имѣетъ противоположный знакъ.
Такой методъ измѣренія магнитнаго поля можно примѣнять также^-1
и къ внутреннимъ частямъ твердыхъ тѣлъ; для этого нужно лишь сдѣ^У
лать въ тѣлѣ длинные тонкіе каналы, въ которые можно было бькѣ^-
дить соленоидъ. Вообще же, какъ и при электрическихъ измѣненіяхъ,
довольствуются опредѣленіемъ полной величины числа амперъ-витковъ,
поля и вычисленіемъ распредѣленія поля въ прострашгтвф-
іУм. Электричество и магнитизмъ, ч. II.
50
Сила магнитнаго поля земли
Другой весьма удобный методъ измѣренія магнитнаго поля былъ
уже упомянутъ нами выше (§ 232): на неизвѣстное поле Нх мы
налагаемъ перпендикулярное къ нему поле Н2, число амперъ-вит-
ковъ котораго извѣстно, и измѣряемъ уголъ а, на который при та-
комъ наложеніи поворачиваются силовыя линіи относительно своего
первоначальнаго положенія. Тогда = Н2 со! а, какъ это непо-
средственно слѣдуетъ изъ рис. 168. Поле Н2 можно получить по-
мощью соленоида съ достаточно большимъ сѣченіемъ, позволяю-
щимъ ввести внутрь соленоида буссоль для измѣренія угла а. Если
извѣстны длина соленоида Л и число витковъ Ы, то для опредѣле-
нія Н2 остается только измѣрить помощью градуированнаго ампер-
метра силу тока Именно,
ь см.
Съ болѣе удобнымъ инструментомъ мы познакомимся въ слѣ-
дующемъ параграфѣ.
СИЛА МАГНИТНАГО ПОЛЯ ЗЕМЛИ.
246. На основаніи всего
разрѣшить поставленную въ §
Рис. 169. Тангенсъ-гальванометръ.
вышесказаннаго мы можемъ теперь
232 задачу полученія поля опредѣ-
ленной величины для сравнительнаго
измѣренія поля земли. Для большаго
удобства съ этой цѣлью пользуются
не длинной катушкой, какъ это было
сказано выше, но просто проволоч-
нымъ кругомъ (рис. 169). Теорети-
ческія и экспериментальныя изслѣдо-
ванія поля, образующагося около кру-
Нг
гового проводника съ токомъ, уста-
новили съ достовѣрностью, что въ
центрѣ кругового проводника радіуса
/?, при силѣ тока У, сила магнитнаго по-
ля тока Н’ (расположеннаго перпенди-
кулярно къ плоскости Круга) выража-
ется слѣдующею простою формулою:
У а.-в.
2 /? см
Сила магнитнаго поля земли
51
Если установить проволочный кругъ такъ, чтобы его плоскость
была параллельна магнитному меридіану, т.-е. чтобы при отсутствіи
тока магнитная стрѣлка помѣщенной въ центрѣ круга буссоли уста-
навливалась въ плоскости круга, то по отклоненію стрѣлки а, со-
отвѣтствующему силѣ тока У, можно опредѣлить горизонтальную
составляющую земного поля. Она равняется
Нк = = Н' сі§ а.
Такъ какъ пропорціоналенъ Н' и, слѣдовательно, также У, то этотъ
инструментъ (часто употреблявшійся прежде въ качествѣ гальвано-
метра, для чего онъ, однако, мало пригоденъ) называется тангенсъ-
гальванометромъ.
При измѣреніи помощью тангенсъ-гальванометра горизонталь-
ной составляющей земного поля въ различныхъ мѣстностяхъ Гер-
маніи были получены числа отъ 0,139 до 0,164. Въ Грейфсвальдѣ,
напримѣръ, 77^=0,146 При этомъ, конечно, предполагается,
что измѣренія были произведены въ такихъ пунктахъ, гдѣ земное поле
не возмущается вліяніемъ большихъ массъ желѣза. Какъ показы-
ваетъ положеніе, принимаемое стрѣлкой наклоненія, кромѣ гори-
зонтальной составляющей, существуетъ еще вертикальная составля-
ющая Н земного поля. Если уголъ наклоненія равенъ ср, то, по
закону сложенія магнитныхъ полей, Нѵ = /У^і^ср, а самая сила поля Н,
ни
дѣйствующая въ направленіи стрѣлки наклоненія, равна Н = •
Такъ какъ въ Грейфсвальдѣ (§231) ср = 67,7°, то здѣсь для невоз-
мущеннаго поля земли Нѵ = 0,356, Н = 0,385
247. Какъ выше уже было указано (§ 233), магнитное поле
земли подвержено правильнымъ суточнымъ колебаніямъ, величины
которыхъ налагаются на нѣкоторую, въ достаточной степени посто-
янную, среднюю величину. Это перемѣнное магнитное поле съ пе-
ріодомъ въ однѣ сутки представляетъ собою, какъ впервые пока-
залъ Фарадэй, поле четырехъ большихъ круговыхъ атмосферныхъ
токовъ, изъ которыхъ два приходятся на сѣверное полушаріе и дв^ф
на южное; каждый изъ нихъ, такимъ образомъ, покрываетъ прибли-
зительно четверть земной поверхности. Эти токи циркулируі^р/въ
атмосферѣ параллельно земной поверхности, такъ что т^ердая^ земля
не является проводникомъ этихъ токовъ. Центрами этихъкруговыхъ
токовъ являются четыре точки, находящіяся въ одной плоскости,
4
52
Сила магнитнаго поля земли
т.-е. расположенныя подъ двумя меридіанами, различающимися на 180°,
и притомъ такъ, что каждая изъ этихъ точекъ удалена отъ ближай-
шаго географическаго полюса приблизительно на 45°. Эти центры
вмѣстѣ съ круговыми токами движутся вслѣдъ за солнцемъ, совер-
шая полный оборотъ вокругъ земной оси въ 24 часа, чѣмъ и вызы-
ваютъ періодическія колебанія земного поля. Несомнѣнно, что эти
атмосферные токи находятся въ нѣкоторой связи съ прохожденіемъ
солнечныхъ лучей черезъ атмосферу. Быть можетъ, они связаны съ
іонизаціей воздуха ультрафіолетовыми лучами; во всякомъ случаѣ,
ничего болѣе опредѣленнаго относительно причинъ ихъ возникно-
венія сказать нельзя.
Также и сильныя магнитныя возмущенія („магнитныя бури"),
которыми всегда сопровождаются сѣверныя сіянія, объясняются дѣй-
ствіемъ магнитныхъ полей атмосферныхъ электрическихъ токовъ.
Сѣверныя сіянія представляютъ собою не что иное, какъ непрерыв-
ные тлѣющіе электрическіе разряды въ верхнихъ слояхъ атмосферы;
поле этихъ (конечно, непостоянныхъ) тлѣющихъ токовъ и наблюда-
ется при „магнитныхъ буряхъ“.
Наоборотъ, постоянная или, вѣрнѣе, подверженная медленнымъ
(вѣковымъ) измѣненіямъ главная часть магнитнаго поля земли свя-
зана съ твердою землею. Вопросъ о томъ, въ какой мѣрѣ эта глав-
ная часть должна считаться полемъ циркулирующихъ въ земной ко-
рѣ электрическихъ токовъ (земныхъ токовъ) и въ какой мѣрѣ по-
лемъ постояннаго магнитнаго ядра, находящагося, можетъ быть,
внутри земли, остается до сихъ поръ открытымъ.
ПЕРВЫЙ ОСНОВНОЙ ЗАКОНЪ ЭЛЕКТРОДИНАМИКИ МАКСВЕЛЛА.
248. Поле, окружающее проводникъ съ токомъ У, можно пред-
ставить себѣ разложеннымъ на кольцевыя силовыя трубки. Каждую
такую трубку можно, согласно § 244, разсматривать въ отдѣльности,
какъ кольцеобразный соленоидъ. Изъ такихъ соленоидовъ можно
построить поле, вполнѣ тождественное съ полемъ тока, но с$ётМ-
щее изъ отдѣльныхъ, физически не связанныхъ между собофШило-
выхъ трубокъ. Такимъ путемъ искусственно построенн^^ область
оказывается раздѣленной многочисленными поперечными" стѣнками,
составленными изъ частей поверхностей окружающихъ каждую пару
смежныхъ соленоидовъ. Только внутренняя драница внутренняго
кольца не представляетъ собою двойной ст^нк^ если пространство,
Первый основной законъ электродинамики Максвелла
53
занимаемое проводникомъ тока, считать пустымъ. Ядромъ пространства,
заполненнаго клѣтками, является въ такомъ случаѣ нитеобразная по-
лость / (рис. 170), имѣющая форму проводника тока и состоящая
только изъ одиночныхъ частей поверхностей, окружающихъ соле-
ноиды. Если поле тока дѣйствительно тождественно съ такъ постро-
еннымъ искусственнымъ полемъ, то въ области, заполненной клѣт-
Рис. 170а
Рис. 170. Разложеніе поля тока на отдѣльныя силовыя трубки.
а) Сѣченіе параллельно силовымъ линіямъ.
Ь) Сѣченіе перпендикулярно къ силовымъ линіямъ,/—нить тока.
ками, вообще долженъ происходить такой же переносъ электри^х%
чества, какъ и въ токѣ, такъ - какъ магнитное поле и переносъ*
электрическихъ зарядовъ, согласно § 239, представляютъ собоюдвѣ
стороны одного и того же явленія. Отсюда слѣдуетъ,дчто, во-
первыхъ, въ двойныхъ стѣнкахъ искусственной области^эаполнен-
ной клѣтками, повсюду токъ долженъ быть въ ^р^зультатѣ ра-
венъ нулю, т.-е. токи обѣихъ соприкасающихся ^обмрТбкъ соленой-
54
Первый основной законъ электродинамики Максвелла
довъ должны быть всегда взаимно противоположны и равны и, во-
вторыхъ, въ нитеобразной полости /, которую окружаютъ внутрен-
нія трубки, токъ долженъ быть равенъ У, т.-е. долженъ быть такимъ
же, какъ и токъ въ проводникѣ, окруженномъ полемъ тока.
Разсмотримъ теперь кольцевые соленоиды въ отдѣльности.
Токъ, окружающій соленоидъ, съ наружной стороны кольца имѣ-
етъ точно такую же силу, что и съ внутренней стороны. Дли-
на же соленоида оказывается различной съ внутренней стороны
и съ наружной: вслѣдствіе различія въ кривизнѣ наружная длина
немного превосходитъ внутреннюю. Въ силу этого плотность тока
или число амперъ-витковъ, приходящееся на сантиметръ, для наруж-
ной части соленоида немного меньше, чѣмъ для внутренней его
части. Такъ какъ токи взаимно уничтожаются въ общей части по-
верхностей соприкасающихся соленоидовъ, то слѣдующее внѣшнее
кольцо должно съ внутренней стороны имѣть ту же плотность тока,
что и первое кольцо съ наружной стороны. Отсюда слѣдуетъ, что
общее число амперъ-витковъ внѣшняго кольца въ точности равно
числу амперъ-витковъ внутренняго кольца. Напротивъ, сила поля,
измѣряющаяся числомъ амперъ-витковъ, приходящимся на 1 санти-
метръ оси соленоида, во внѣшнемъ кольцѣ нѣсколько меньше, чѣмъ
во внутреннемъ, такъ какъ длина оси внѣшняго соленоида немного
больше длины оси внутренняго. По мѣрѣ перехода къ болѣе внѣш-
нимъ кольцамъ плотность тока или сила поля въ кольцахъ убываетъ,
но полное число амперъ-витковъ остается всегда постояннымъ. По
мѣрѣ перехода къ болѣе внутреннимъ кольцамъ сила поля возра-
стаетъ, но полное число амперъ-витковъ остается неизмѣннымъ. Когда
мы подойдемъ такимъ образомъ къ нитеобразной полости /, то ока-
жется, что постоянная полная величина силы поля въ кольцахъ пред-
ставляетъ собою не что иное, какъ полную величину силы тока въ
нити / или, иначе говоря, силу тока У.
Полная величина силы магнитнаго поля на силово^^й-
ніи, окружающей проводникъ съ токомъ, выраженнд^нол-
нымъ числомъ амперъ-витковъ мысленно изолированной си-
товой трубки, на всѣхъ разстояніяхъ отъ про^бдника оди-
накова и равна току, проходящему по про^рдмику.
Если вдоль отрѣзка силовой линіи длины сила поля, вычис-
о’П гг
ленная въ амперъ-виткахъ на сантиметръ, рашіяется Н, то число
всѣхъ амперъ-витковъ на отрѣзкѣ I равняется Если вдоль боль-
Первый основной законъ электродинамики Максвелла
55
шого отрѣзка силовой линіи сила поля непрерывно измѣняется и
на маленькихъ отрѣзкахъ /2, /3,..., дающихъ въ общей сложности
длину /, имѣетъ соотвѣтственно значенія Нѵ Н2, Н3,... , то число
всѣхъ амперъ-витковъ V вдоль отрѣзка I равняется линейной сум-
мѣ силъ И:
и=н1і1+н2і2+н.іі3+-...
Если отрѣзокъ I имѣетъ направленіе, не совпадающее съ на-
правленіемъ Н, то для вычисленія 1} нужно принять во вниманіе
слагающія Н въ направленіяхъ малыхъ отрѣзковъ /(, /2, /3 ,... Если
углы между Нѵ Н2, Н.3,.... и отрѣзками 12,13 ,.. . равняются
Фі,Ф2> Фз>---> то
V = СО8фх 4" Н2 12 СО8ф2 4- Н3 13 СО8ф3 4-. • • •
Полная величина силы магнитнаго поля вдоль опредѣленнаго
отрѣзка вычисляется, слѣдовательно, въ видѣ линейной суммы, со-
вершенно такъ же, какъ и полная величина силы электрическаго по-
ля (§ 24). Только-что формулированное основное положеніе можетъ
быть высказано еще такъ:
Вычисленная въ амперъ-виткахъ линейная сумма маг-
нитнаго поля тока, взятая вдоль опредѣленной замкнутой
линіи, одинъ разъ обвивающей проводникъ съ токомъ, все-
гда равняется силѣ электрическаго тока, вычисленной въ
амперахъ.
Линейная сумма поля вдоль замкнутой кривой, окру-
жающей пространство, черезъ которое токъ вовсе не про-
ходитъ, равняется нулю.
Слѣдовательно, линейная сумма поля вдоль замкнутой кривой
всегда указываетъ намъ, проходятъ ли черезъ ограничиваемую
этой кривой поверхность электрическіе заряды, и какой они силы.
Здѣсь мы имѣемъ причинную связь между магнитнымъ полемъ и
переносомъ электрическихъ зарядовъ, установленную въ формѣ про-
стого закона.
249. Особенно простымъ оказывается распредѣленіе силовыхъ
линій въ случаѣ прямолинейнаго проводника. Въ этомъ случаѣ
ловыя линіи представляютъ собою окружности, центры котоцыхъ
лежатъ на оси съ токомъ. Во всѣхъ точкахъ, отстоящихъ на оди-
наковомъ разстояніи г отъ оси проводника съ токомъ, сшіа^поля Н
одинакова; это вытекаетъ уже изъ симметріи поля. Слѣдовательно,
линейная сумма силы поля вдоль окружности радаус^ г равняется
56
Первый основной законъ электродинамики Максвелла
просто амперъ-виткамъ. Если сила тока въ прямолинейномъ
проводникѣ равняется амперамъ, то
2тгг Н = У
и, слѣдовательно,
„ .1 а.-в.
гі — х------•
2ітг см.
Сила магнитнаго поля, окружающаго прямолинейный
проводникъ съ токомъ, обратно пропорціональна разстоя-
нію отъ проводника.
Въ этомъ простомъ случаѣ совершенно ясно выступаетъ свой-
ство поля тока, которое выражается закономъ, изложеннымъ въ § 248.
Но и въ болѣе сложныхъ случаяхъ (напримѣръ, въ случаѣ круго-
вого проводника съ токомъ) вычисленіе силы поля основывается на
этомъ же законѣ, при чемъ пользуются тѣмъ (установленнымъ ниже)
фактомъ, что магнитныя силовыя линіи не могутъ заканчиваться или
начинаться въ свободномъ эѳирѣ.
250. Болѣе глубокое значеніе установленнаго въ § 248 основ-
ного закона магнитнаго поля тока было впервые выяснено Макс-
велломъ. Какъ мы видѣли, электрическій токъ представляетъ
собою постоянное возстановленіе электрическаго поля, непрерыв-
но стремящагося исчезнуть въ проводникѣ вслѣдствіе переноса
іоновъ. Какъ было уже указано въ § 239, магнитное поле слѣду-
етъ разсматривать, какъ процессъ въ эѳирѣ, непрерывно возстана-
вливающій напряженіе въ проводникѣ. Если мы представимъ себѣ
магнитное поле въ родѣ поля тока, но не съ проводникомъ, а съ
изоляторомъ въ центрѣ, то такое поле должно было бы быть не-
прерывно возрастающимъ электрическимъ полемъ, такъ какъ въ
этомъ случаѣ дѣйствіе магнитнаго процесса уже не компенсируется
разрывами напряженій. Поэтому мы должны въ магнитномъ полѣ
видѣть прежде всего эѳирные процессы, которые порождаютъ и
измѣняютъ электрическія напряженія.
Роль магнитнаго поля въ физикѣ эѳира, такимъ образомъ, совер-
шенно аналогична роли движеній въ механикѣ вѣсомыхъ тѣлѣХНа-
пряженіе въ упругомъ тѣлѣ никакъ не можетъ возникну^Фили из-
мѣниться, если не вызваны растяженіе, сжатіе, изгибъ или Накручиваніе
тѣла опредѣленными движеніями, которыя бываютъ иногда весьма малы,
ѵгѴі
но никогда не могутъ вполнѣ отсутствовать. Если'^тѣло пластично,
, ° \ Ѵ
какъ, напримѣръ, свинцовая проволока или вязкая жидкость, то напря-
женіе, соотвѣтствующее опредѣленной де^брмаціи, самопроизвольно^
Первый основной законъ электродинамики Максвелла
57
уменьшается вслѣдствіе внутреннихъ перемѣщеній молекулъ подобно
тому, какъ въ электрическомъ проводникѣ само по себѣ разрыва-
ется электрическое напряженіе. Въ такомъ случаѣ можетъ возник-
нуть непрерывное движеніе, длительная деформація, „теченіе" тѣла
безъ того, чтобы упругое напряженіе повышалось. Кромѣ того, встрѣ-
чаются также стаціонарныя движенія, длящіяся продолжительное
время и не вызывающія вообще деформацій. Примѣромъ являются
движенія въ системѣ зубчатыхъ колесъ, которыя равномѣрно вра-
щаются, при чемъ не возникаютъ возрастающія внутреннія напряженія.
Въ физикѣ эѳира стаціонарнымъ движеніямъ аналогичны стаціо-
нарныя магнитныя поля, имѣющія длительное существованіе и не
возбуждающія опредѣленныхъ электрическихъ полей. При какомъ
именно условіи магнитное поле стаціонарно, мы уже выяснили въ
§ 249. Это условіе заключается въ слѣдующемъ: полная величина
силы поля для замкнутой кривой должна равняться нулю. Примѣ-
ромъ является магнитное поле внѣ проводника, по которому течетъ
постоянный электрическій токъ; полная величина силы этого поля
вдоль кривыхъ, не обвивающихъ проводника, всегда равняется нулю.
И, дѣйствительно, въ этомъ случаѣ въ окружающемъ проводникъ
изоляторѣ поле не вызываетъ никакихъ возрастающихъ напря-
женій. Наоборотъ, внутри проводника поле не удовлетворяетъ ука-
занному условію, и потому здѣсь происходитъ постоянное образо-
ваніе электрическихъ напряженій, которыя тотчасъ же вновь исчеза-
ютъ. Прекрасную механическую аналогію магнитнаго поля тока
представляетъ зубчатая система часового механизма, который вра-
щаетъ мѣшалку, находящуюся въ какой-либо жидкости. Источ-
никъ силы — гиря или пружина часового механизма — соотвѣтству-
етъ гальванической цѣпи или батареѣ. Движущіеся колеса и валы,
передающіе силовыя дѣйствія на разстояніе, при чемъ движенія не
возбуждаютъ въ нихъ самихъ непрерывно возрастающихъ напряже-
ній, соотвѣтствуютъ внѣшнему магнитному полю. Движущаяся мѣ-
шалка, которая вызывала бы въ размѣшиваемой жидкости напряже-^р^
нія, если бы они постоянно не разрушались вслѣдствіе скольже^у^
частицъ жидкости, и которая, въ силу этого непрерывнаго уничтоже-
нія напряженій, характеризуемаго словомъ „треніе", непрерывно
поглощаетъ энергію, соотвѣтствуетъ проводнику съ токбмѣ^къ ко-
торому точно такъ же непрерывно подводится внѣшнимъ полемъ
энергія, превращающаяся въ немъ въ теплоту.
Ъ8
Первый основной законъ электродинамики Максвелла
Изложенный въ § 248 основной законъ устанавливаетъ, въ
какой мѣрѣ магнитное поле вызываетъ электрическое состояніе эѳи-
ра. Если въ проводникѣ протекаетъ въ секунду электрическій разрядъ
въ У кулоновъ, то это соотвѣтствуетъ уничтоженію поля, ч полное
возбужденіе котораго на поперечномъ сѣченіи проводника иначе
увеличивалось бы на У кулоновъ въ секунду. Это увеличеніе воз-
бужденія является дѣйствіемъ магнитнаго поля, полная величина ко-
тораго вдоль замкнутыхъ кривыхъ равняется У амперъ-виткамъ; это
дѣйствіе компенсируется въ проводникѣ уничтоженіемъ поля, но въ
изоляторѣ оно дѣйствительно проявляется. Что слѣдуетъ здѣсь по-
нимать подъ „электрическимъ возбужденіемъ“, было подробно разъ-
яснено въ §§ 56 и слѣдующихъ. Теперь мы можемъ основной за-
конъ магнитнаго поля тока высказать въ слѣдующей формЬ?
Магнитное поле, для котораго линейная сумма вдоль
замкнутой кривой не равняется нулю, вызываетъ измѣненіе
электрическаго состоянія въ окружаемомъ кривой про-
странствѣ. При этомъ полное электрическое возбужденіе
эѳира измѣняется на поверхности, ограничиваемой кривою,
со скоростью кулоновъ въ секунду, въ точности равною
полному числу амперъ-витковъ магнитнаго поля, прихо-
дящемуся на замкнутую кривую. Если окружаемое про-
странство частью заполнено проводникомъ, то возрастаніе
электрическаго поля можетъ быть въ немъ отчасти или
вполнѣ парализовано распадомъ поля. Въ послѣднемъ слу-
чаѣ линейная сумма магнитнаго поля даетъ также скорость,
съ которою непрерывно распадающееся поле непрерывно
вновь возстанавливается.
Если линейная сумма магнитнаго поля вдоль замкну-
равняется нулю, то магнитный процессъ въ эѳи-
стаціонарнымъ и не вызываетъ никакихъ элек-
полей.
нѣтъ никакой необходимости подчеркивать, что, х со-
закону, не только возникновеніе, но
а также исчезновеніе электрическихъ полей, вызывается маг-
и всякое<измѣ-
- лЬ
той кривой
рѣ является
трическихъ
Конечно,
гласно этому
неніе,
нитными процессами. Этотъ законъ носитъ названіе перваго зако-
на электродинамики Максвелла. Ту величину,/^оторую мы на-
звали электрическимъ возбужденіемъ (/)), Максвеллъ называетъ
„электрическимъ смѣщеніемъ", а измѣненіе^полнаго возбужде-
Первый основной законъ электродинамики Максвелла 59'
элек-
огра-
тока
нія на нѣкоторой поверхности за секунду—„токомъ смѣщенія,,
проходящимъ черезъ поверхность“. Эти термины легко уяснить се-
бѣ, если обратиться къ студнеобразной модели эѳира (§ 58). Поль-
зуясь ими, можно весьма кратко выразить первый законъ электроди-
намики Максвелла въ слѣдующей формѣ:
Линейная сумма магнитнаго поля вдоль замкнутой кри-
вой, вычисленная въ амперъ-виткахъ, равняется всему
трическому току, проходящему сквозь поверхность,
ниченную кривою, т.-е. суммѣ тока проводимости и
смѣщенія, вычисленныхъ въ кулонахъ на секунду.
Хотя теорія Максвелла совершенно не утверждаетъ, что электри-
ческія и магнитныя явленія могутъ быть сведены на механическіе
процессы въ эѳирѣ, и хотя въ послѣднее время преобладаетъ
взглядъ, согласно которому никакихъ дѣйствительныхъ движеній и
деформацій въ эѳирѣ не происходитъ, все же весьма замѣчательно,
насколько полно можетъ быть проведена аналогія между явленіями
въ эѳирѣ и механическими матеріальными явленіями. Движеніями
прежде всего вызываются деформаціи, вмѣстѣ съ которыми по-
являются тотчасъ упругія напряженія. Точно такъ же и въ физикѣ эѳира
магнитное поле прежде всего является мѣриломъ измѣненій электри-
ческаго возбужденія или смѣщенія, механической аналогіей котораго
является деформація; электрическое же смѣщеніе, конечно, сопро-
вождается соотвѣтствующимъ напряженіемъ въ эѳирѣ. Въ матеріаль-
номъ тѣлѣ, обладающимъ не слишкомъ малымъ модулемъ упругости,,
большія напряженія возбуждаются даже весьма малымъ толчкомъ,
такъ какъ небольшимъ деформаціямъ здѣсь соотвѣтствуютъ боль-
шія напряженія. То же самое имѣетъ мѣсто и въ эѳирѣ. Мы знаемъ,
что единица возбужденія — кулонъ чрезвычайно велика (§ 74), и
что даже сильнѣйшія напряженія соотвѣтствуютъ лишь крайне ма-
лымъ величинамъ возбужденія. Поэтому для образованія электриче-
скихъ напряженій въ изоляторѣ требуется лишь ничтожно малый
и короткій магнитный толчокъ. При этомъ необходимо, однако^^
имѣть въ виду, что безъ такого ничтожно слабаго магнитнаго толч-^
ка все же никакое электрическое поле не можетъ возникнут^Дз-
мѣниться или исчезнуть. Въ механикѣ значительными и продолжи-
тельными являются только такія движенія, которыя не вызываетъ воз-
растающихъ напряженій, напримѣръ, движенія пластичн^ы^Хѣлъ, или
стаціонарныя движенія, не порождающія никакихъ деформацій, напри-
'60
Первый основной законъ электродинамики Максвелла
мѣръ, движенія зубчатыхъ системъ. Совершенную аналогію этому мы
имѣемъ и въ физикѣ эѳира. Сильными и длительными являются
только такія магнитныя поля, которыя не сопровождаются возра-
стающими электрическими напряженіями, т.-е. поля проводниковъ
постояннаго электрическаго тока или же чисто стаціонарныя поля,
•окружающія постоянные магниты.
251. Новый взглядъ на сущность магнитнаго поля тока полу-
чается, если приложить идеи Максвелла къ іонной теоріи прово-
димости. Согласно этой теоріи, разрывы электрическаго поля въ
проводникѣ обусловливаются передвиженіями электрическихъ ча-
стицъ іоновъ, къ числу которыхъ мы относимъ также и электроны.
Согласно изложенному въ §211, мы разсматриваемъ іонъ, какъ уз-
ловую точку въ эѳирѣ, изъ которой по всѣмъ направленіямъ исхо-
дятъ электрическія напряженія. Если іонъ движется въ эѳирѣ, то
съ нимъ движется и все его электрическое поле; поэтому оно осла-
бляется въ частяхъ пространства за іономъ и усиливается передъ
іономъ; кромѣ того, оно измѣняетъ повсюду свое направленіе.
Всѣ эти измѣненія могутъ возникнуть лишь въ силу дѣйствія
гвъ эѳирѣ магнитныхъ процессовъ. Движущійся іонъ долженъ быть
окруженъ со всѣхъ сторонъ магнитнымъ полемъ, которымъ обу-
словливается постоянное смѣщеніе электрическаго поля и безъ ко-
тораго движеніе было бы невозможно. Въ силу симметріи линіи
этого поля должны представлять собою окружности, центры кото-
рыхъ лежатъ на тѣхъ прямыхъ, вдоль которыхъ движется центръ
іона. Такъ какъ, въ силу этого, каждый отдѣльный движущійся іонъ
окруженъ силовыми линіями, то картина магнитнаго поля внутри
проводника тока, которую намъ даетъ іонная теорія, оказывается
весьма сложной. Направленіе и сила поля въ проводникѣ сильно и
ъесьма замѣтно измѣняются уже на небольшихъ интервалахъ, и то,
что мы вообще называемъ магнитнымъ полемъ внутри проводника,
является лишь среднею величиною силы поля. Если бы это среднее
значеніе равнялось нулю, то каждое магнитное поле іона вдувало
бы такое измѣненіе электрическаго поля, слѣдствіемъ кото{^го^въ об-
щемъ являлось бы уничтоженіе поля. Во избѣжаніе такого уничтоженія
поля необходимо, чтобы среднее значеніе силы поля при стаціо-
нарныхъ движеніяхъ іоновъ оставалось отличнымъ^отъ нуля и под-
чинялось по величинѣ и силѣ основному зац^у} изложенному въ
§ 248. Какъ извѣстно, магнитное поле^ возникаетъ также и внѣ
Первый основной законъ электродинамики Максвелла
61
проводника; при этомъ всѣ магнитные процессы дѣйствуютъ со-
вмѣстно такимъ образомъ, что средняя величина электрическаго поля,
внутри и внѣ проводника остается постоянной, хотя въ простран-
ствѣ, непосредственно окружающемъ каждый іонъ, и происходятъ,
измѣненія электрическаго поля, которыя должны быть безусловно,
связаны съ его перемѣщеніемъ.
Почти такія же точно явленія происходятъ въ тѣхъ случаяхъ,,
когда механическими средствами приводятся въ движеніе электри-
чески заряженныя тѣла. Представимъ себѣ, напримѣръ, плоскій кон-
денсаторъ, одна пластинка котораго представляетъ собою кругъ,.
могущій вращаться вокругъ оси, проходящей черезъ его центръ пер-
пендикулярно къ плоскости пластинки. Зарядъ на поверхности пла-
стинки состоитъ изъ отдѣльныхъ электрическихъ частицъ, іоновъ
или электроновъ, движущихся вмѣстѣ съ нею и потому окружен-
ныхъ малыми магнитными полями. Все сложное магнитное явленіе,
сопровождающее движеніе пластинки, и здѣсь можетъ быть стаціо-
нарнымъ лишь въ томъ случаѣ, когда въ пространствѣ, окружаю-
щемъ пластинку, имѣется магнитное поле, подчиняющееся тѣмъ же
законамъ, какъ и поле тока; сила тока здѣсь опредѣляется числомъ
іонныхъ зарядовъ, проходящихъ вмѣстѣ съ движущейся пластинкой
за одну секунду черезъ сѣченіе, перпендикулярное къ направленію
движенія. Это большое магнитное поле дѣйствуетъ, какъ и въ случаѣ
тока проводимости, вмѣстѣ съ малыми магнитными полями іоновъ
такимъ образомъ, что электрическія поля отдѣльныхъ іоновъ пере-
носятся въ эѳирѣ впередъ въ направленіи движенія, при чемъ,
однако, среднія величины электрическихъ напряженій, единственно до-
ступныя измѣренію, остаются въ общемъ неизмѣнными. Магнитное
поле въ пространствѣ, окружающемъ вращающуюся заряженную
круглую пластинку, было наблюдаемо впервые Ролэндомъ (Кохѵіапсі),
при чемъ экспериментальное изслѣдованіе всесторонне подтвердило
теоретическія предсказанія.
Увлеченіе электрическихъ зарядовъ движущимися заряженными
тѣлами часто называютъ конвекціоннымъ электрическимъ т^^°
комъ. По іонной теоріи, обычный токъ проводимости является срб-^
ственно лишь частнымъ видомъ конвекціоннаго тока, характеризуе-
мымъ тѣмъ, что при немъ заряженныя тѣла, именно іоны^цбддер-
живаются въ движеніи силовыми дѣйствіями электрическаго поля,
несмотря на противодѣйствующее этому движенію треніе. Поэтомук
62
Механическая модель эѳира
іонная теорія приводитъ насъ къ слѣдующему выраженію закона
Максвелла, болѣе общему, нежели всѣ предыдущія, такъ какъ оно
охватываетъ также и конвекціонные токи, съ которыми мы встрѣчаемся
въ опытѣ Ролэнда и еще часто будемъ встрѣчаться:
Линейная сумма магнитнаго поля вдоль замкнутой кривой
равняется все му электрическому току, которы й проходитъ че-
резъ ограниченную кривой часть поверхности, и въ общемъ
случаѣ состоитъ изъ тока конвекціоннаго и тока смѣщенія.
МЕХАНИЧЕСКАЯ МОДЕЛЬ ЭѲИРА.
252. Простая модель, описанная въ §§ 23 и 58, не даетъ намъ
никакого представленія о магнитныхъ явленіяхъ и объ особенностяхъ
возникновенія электрическихъ напряженій; она, слѣдовательно, весьма
неполно иллюстрируетъ физическія свойства эѳира. Однако, мы мо-
жемъ значительно улучшить эту модель небольшимъ измѣненіемъ.
Если электрическій токъ мы въ модели представляемъ поступатель-
нымъ движеніемъ, то магнитная силовая линія, которую мы характе-
ризуемъ и измѣряемъ, какъ нѣкоторый окруженный токомъ соле-
ноидъ, должна, несомнѣнно, быть представляема вращательнымъ дви-
женіемъ. Но такія вращательныя движенія невозможны, если упругія
клѣтки, изъ которыхъ мы строимъ нашу модель, всѣ прочно соеди-
нены между собою. Поэтому мы будемъ представлять себѣ, что
каждая упругая клѣтка соединяется съ сосѣдней при посредствѣ
шариковъ, которые могутъ кататься по границѣ клѣтокъ, соста-
вляя все-таки достаточно прочное соединеніе между ними; эти
шарики, слѣдовательно, не могутъ соскальзывать или отрываться отъ
клѣточной стѣнки. Для удобства мы будемъ принимать эти соеди-
нительные шарики за твердые. Такъ какъ студнеобразный эѳиръ не
сжимаемъ, какъ мы это видѣли въ § 58, то мы должны предполо-
жить, что какимъ-либо способомъ разстояніе между центрами твер-
дыхъ шариковъ поддерживается постояннымъ, напримѣръ, при по-
мощи особой твердой сѣтки, находящейся между клѣтками С/йе
препятствующей ихъ деформаціямъ. Эта твердая сѣтка должнаудер-
живать шарики такимъ образомъ, чтобы они могли свободно вра-
щаться вокругъ любой оси, какъ, напримѣръ, шарикцЧѣ?шаровыхъ
сочлененіяхъ. Усложненный такимъ образомъ студнеобразный эѳиръ
становится похожимъ на весьма сложную системуЧубчатыхъ колесъ,
съ движеніями которой мы уже сравнивалаСвыше явленіе магнит-
Механическая модель эѳира
63
наго поля. Когда твердые шарики вращаются въ опредѣленномъ
направленіи, а упругія клѣтки — въ противоположномъ, можетъ
имѣть мѣсто стаціонарное вращательное движеніе, не вызывающее
въ упругихъ клѣткахъ никакихъ деформацій, связанныхъ съ напря-
женіями. Это вращательное движеніе представляетъ процессы, совер-
шающіеся въ эѳирѣ въ магнитномъ полѣ; средняя вращательная
скорость шариковъ представляетъ силу магнитнаго поля въ соотвѣт-
ственномъ мѣстѣ, а то направленіе ихъ осей вращенія, въ которомъ
слѣдуетъ смотрѣть, чтобы вращеніе казалось правымъ, представляетъ
направленіе магнитнаго поля. Въ кольцеобразной магнитной сило-
вой линіи шарики движутся подобно частицамъ жидкости въ вих-
ревомъ кольцѣ (рис. 171). Такъ
какъ скольженіе здѣсь невоз-
можно, то въ пространствѣ,
окруженномъ вихревымъ коль-
цомъ, должно происходить смѣ-
щеніе клѣтокъ въ опредѣлен-
номъ направленіи. При этомъ
клѣтки будутъ продвигаться впе-
редъ и протискиваться меж-
ду окружающими ихъ шариками,
такъ какъ послѣдніе, по наше-
му предположенію, удержива-
ются твердою сѣткою. Все ко-
Рис. 171. Движеніе въ вихревомъ
кольцѣ.
личество вещества, продвигающееся за секунду, пропорціонально ско-
рости вращенія и числу вращающихся на кольцѣ шариковъ, т.-е.
„линейной суммѣ магнитнаго поля“ вдоль кольца. Смѣщеніе и про-
тискиваніе упругихъ клѣтокъ между твердыми шариками не должно
происходить непремѣнно во всемъ пространствѣ, ограниченномъ коль-
цомъ. Если, напримѣръ, полная сумма вращеній на кольцѣ меньшаго
радіуса, лежащемъ цѣликомъ внутри перваго кольца, равняется суммѣ
вращеній на первомъ кольцѣ, то въ пространствѣ между обоими коль-
цами шарики и клѣтки вращаются стаціонарно, т.-е. такъ, что клѣтки хр
не протискиваются въ ту или иную сторону. Въ этомъ случаѣ
поступательное передвиженіе происходитъ лишь въ пространствѣ,
ограниченномъ меньшимъ кольцомъ. Если мы при этомъ держимъ
предположеніе, высказанное нами уже, какъ необходимбецпри вве-
деніи студнеобразной модели эѳира (§ 23), именц^.^Дго упругія
64
Механическая модель эѳира
напряженія въ этой модели вызываются исключительно смѣщеніями
клѣтокъ, т.-е. ихъ протискиваніемъ между твердыми шариками, такъ
что всѣ прочія деформаціи, въ силу особыхъ свойствъ клѣтокъ, не
вызываютъ никакихъ силовыхъ дѣйствій, то, дѣйствительно, въ на-
шей улучшенной модели вращенія шариковъ, смѣщенія клѣтокъ и
напряженія будутъ происходить по тѣмъ самымъ законамъ, по ко-
торымъ магнитныя явленія въ эѳирѣ вызываютъ и измѣняютъ элек-
трическія смѣщенія и напряженія.
Въ качествѣ проводника мы представляемъ себѣ на нашей модели
такую часть пространства, въ которой смѣщеніе клѣтокъ само со-
бою снова уничтожается. Въ примитивной модели мы могли предста-
влять себѣ это, просто считая стѣнки клѣтокъ въ проводникѣ не
сплошными. Въ усложненной модели мы вмѣсто этого должны при-
нять, что въ проводникѣ связь клѣтокъ съ шариками не является
совершенно прочной, такъ что они могутъ слегка скользить другъ
относительно друга. Поэтому, если клѣтки проводника испытываютъ
смѣщеніе, то они тотчасъ же соскальзываютъ обратно въ свое нор-
мальное положеніе, если только смѣщеніе не возбуждается непре-
рывно вновь длительными вращательными движеніями. На рис. 172
представлена механическая модель электрическаго тока въ проволокѣ
въ продольномъ ея сѣченіи. Внѣ проволоки сверху и снизу видны
сѣченія кольцевыхъ магнитныхъ силовыхъ линій. Вращенія происходятъ
такимъ образомъ, что внутри колецъ происходитъ непрерывное пере-
мѣщеніе впередъ въ направленіи прямыхъ стрѣлокъ. Внѣ проводника
вращенія стаціонарны, какъ у колесъ часового механизма. Внутри
проволоки также находятся „вращательныя кольца", но здѣсь вра-
щенія постепенно ослабѣваютъ по мѣрѣ перехода къ центральнымъ
частямъ и, вслѣдствіе существованія разностей въ скоростяхъ вра-
щеній, упругія клѣтки непрерывно протискиваются. Перемѣщеніе
клѣтокъ впередъ компенсируется скольженіемъ ихъ около шари-
ковъ, и напряженіе все время сохраняетъ постоянную величину,
при которой оно уравновѣшивается сопротивленіемъ тренія,^вя-
заннымъ со скольженіемъ. Это напряженіе, представленной на
рис. 172 деформаціями клѣтокъ, соотвѣтствуетъ внутрен^іу элек-
трическому полю проводника. Если явленіе стаціонардс^у то и внѣ
проводника должно быть постоянное электрическд^?тіоле, находя-
щееся въ равновѣсіи съ внутреннимъ полемъ. Г^овтбму внѣ прово-
локи должна существовать параллельная ей сжигающая поля, къ ко-
Механическая модель эѳира
65
торой можетъ присоединиться еще слагающая, перпендикулярная
къ поверхности проволоки. На рис. 172 для простоты послѣдняя
принята равной нулю, и потому здѣсь видны лишь искривленія
въ направленіи тока. Если сила тренія скользящихъ частицъ воз-
растаетъ вмѣстѣ со скоростью скольженія, то сила электрическаго
поля возрастаетъ съ силою тока.
Такимъ путемъ можно въ грубыхъ чертахъ построить механи-
ческую аналогію явленій электрическаго тока, если пока не имѣть
Рис. 172. Механическая модель электрическаго тока.
въ виду атомнаго строенія электрическихъ зарядовъ и іонной теоріи
проводимости. Если бы мы желали выразить на модели и эти теоріи,,
то ее пришлось бы значительно усложнить. Но мы намѣреваемся лишь <
уяснить себѣ общій характеръ явленій, происходящихъ въ эѳирѣ°^|ро
фг Ч
посредствомъ сравненія ихъ съ привычными намъ механическими7
явленіями въ вѣсомыхъ тѣлахъ, и отнюдь не стремимся къ уИдао-
вленію теорій, которыя ввели бы насъ глубже въ сущнос^хМѳира.
Поэтому развивать эту модель дальше для насъ представляется со-
вершенно безцѣльнымъ. °
Ми. Электричество и магнитизмъ, ч. II.
66
Механическая модель эѳира
253. Опишемъ вкратцѣ еще одну весьма интересную механиче-
скую аналогію, объясняющую фактъ установки магнитной стрѣлки
въ направленіи магнитныхъ силовыхъ линій. Маленькій магнитный
стержень, какъ мы знаемъ, весьма сходенъ съ маленькимъ солено-
идомъ, и мы увидимъ, когда познакомимся съ магнитными свой-
ствами желѣза, что это сходство имѣется и по существу. Поэтому мы
можемъ разсматривать магнитный стержень какъ небольшую часть
сильной магнитной силовой трубки; на модели ей соотвѣтствуетъ
небольшое цилиндрическое пространство, въ которомъ происходятъ
сильныя вращенія шариковъ вокругъ осей, параллельныхъ оси стержня.
Рис. 173. Модель изъ волчковъ, представляющая магнитную силовую линію.
Если это небольшое цилиндрическое пространство расположено внутри
большей области, въ которой имѣется общее состояніе вращенія —
большое магнитое поле,—то оно стремится установиться такимъ об-
разомъ, чтобы его собственныя вращенія были параллельны вращеніямъ
общаго большого поля. Механически это можно хорошо представить
при помощи модели, изображенной на рис. 173. Длинная ось, которая
можетъ быть приведена во вращеніе при помощи рукоятки, изобра-
жаетъ магнитную силовую линію; на ней расположены три кольца,
представляющія собою какъ бы части оси. Въ этихъ трехъ кольцахъ
на особыхъ кардановскихъ подвѣсахъ помѣщены три волчка, оси кото-
рыхъ поэтому могутъ быть наклонены подъ любымъ угломъкъдлин-
ной оси модели. Эти три волчка предварительно приводятся въ быстрое
вращеніе. Они представляютъ собою три маленькихъдмагнитныхъ
стерженька. На рис. 173 „сѣверный14 и „южный14 рр$бса отмѣчены
остріями и опереніями на осяхъ волчковъ. Сначала оси волчковъ
могутъ быть установлены подъ любыми угламг^кь главной оси при-
Механическая модель эѳира
67
бора. Но если „возбудить магнитное поле", т.-е. начать медленно
вращать большую ось, то всѣ три „магнитика" тотчасъ же устана-
вливаются параллельно „силовой линіи", т.-е. такимъ образомъ, что
ихъ оси вращенія совпадаютъ съ главной осью, и направленіе ихъ
вращеній совпадаетъ съ направленіемъ вращенія большой оси. Если
мы обернемъ „магнитное поле", т.-е. направленіе вращенія большой
оси, то и всѣ три волчка повернутся на 180° и послѣ нѣсколькихъ
колебаній въ ту и другую сторону установятся, подобно магнит-
нымъ стрѣлкамъ, въ новомъ направленіи большой „силовой линіи".
5
ГЛАВА III
НАПРЯЖЕНІЕ И СИЛА ТОКА
ЗАКОНЪ ОМА.
254. Въ пространствѣ, окружающемъ проводникъ съ токомъ,
эѳиръ находится въ состояніи какъ электрическаго, такъ и магнитна-
го возбужденія. Полная величина магнитнаго поля постоянна вдоль
всего проводника. Она измѣряется при помощи гальванометра; гра-
дуированный гальванометръ чаще называется амперметромъ. Вклю-
чается амперметръ такимъ образомъ, что въ проводникѣ съ токомъ
дѣлается въ нѣкоторомъ мѣстѣ разрывъ и въ него вводится катуш-
ка инструмента. Такимъ образомъ въ инструментъ вводится магнит-
ное поле, и оно можетъ быть имъ измѣрено. Какъ мы видѣли, маг-
нитное поле показываетъ силу тока іоновъ (или электроновъ) въ
проводникѣ. Поэтому амперметръ градуируется при помощи кулон-
метра, и слово „сила тока" часто употребляется въ смыслѣ: „пол-
ная величина магнитнаго поля тока". О полной величинѣ элек-
трическаго поля можно говорить лишь по отношенію къ проме-
жутку между какими-либо двумя опредѣленными точками проводника.
Ее измѣряютъ помощью электрометра; градуированный электро-
метръ называется также вольтметромъ. Включеніе вольтметра про-
изводится такимъ образомъ, что его оба зажима соединяются по-
средствомъ металлическихъ проволокъ съ двумя точками, между ко-
торыми измѣряется напряженіе эѳира. Такимъ образомъ электрическое
поле вводится въ инструментъ и можетъ быть имъ измѣрено.
Соединимъ концы металлической проволоки съ полюсами^) не-
большой батареи и введемъ амперметръ въ одинъ изъ проѣздовъ,
подводящихъ токъ. Затѣмъ къ обоимъ концамъ проводки присо-
единимъ зажимы электрометра. Такимъ образомъ мьі^^ожемъ одно-
временно измѣрять силу тока въ проволокѣ и напряженіе между ея
концами (рис. 174). Если, включая проволоку различныхъ длинъ
Законъ Ома
69
(реостаты, § 257) или измѣняя число элементовъ въ батареѣ, мѣнять
показываемую амперметромъ силу тока, то параллельно будетъ мѣ-
няться также и величина напряженія между концами проволоки. При
этомъ легко установить нижеслѣдующую простую зависимость, ко-
торая называется закономъ Ома:
Электрическое напряженіе между концами однород-
наго проводника всегда пропорціонально силѣ тока въ
проводникѣ.
Рис. 174. Повѣрка закона Ома.
силѣ тока назы-
Постоянное отношеніе напряженія къ
ваютъ сопротивленіемъ проводника.
Если V—напряженіе, У—сила тока, /? — сопротивленіе, то
Ѵ=/?.У; 7 = ^.
к
Если сила тока равна нулю, то и V — 0, т.-е. потенціалъ по-
стояненъ вдоль всей проволоки; въ этомъ заключается условіе рав-
новѣсія электрическаго поля, указанное нами въ § 26. -о
Если проводникъ не однороденъ, но состоитъ изъ проволрйѣ
различныхъ металловъ, соединенныхъ между собою (мѣдной* ^кёлѣз-
иой, никкелиновой и т. д.), то, въ случаѣ не вполнѣ одинаковой
температуры вдоль всего проводника, наблюдается и при^ртсутствіи
тока нѣкоторое напряженіе между концами проволокир^г термоэлек-
трическое напряженіе (§ 214). Если термоэлектри^Мкре напряженіе
70
Легальная единица сопротивленія
равняется І/о, а напряженіе, получаемое при прохожденіи черезъ всю
систему проводниковъ тока силы У, равняется У, то, по закону Ома*
V — У0 = /?.У,
гдѣ /? — сопротивленіе всѣхъ проводовъ.
ЛЕГАЛЬНАЯ ЕДИНИЦА СОПРОТИВЛЕНІЯ.
255. Законъ Ома настолько строго приложимъ къ металламъ*
что даже при тончайшихъ измѣреніяхъ не замѣчается отклоненій
отъ него. Поэтому сопротивленіе проводника ^является величиной*
опредѣлимой съ большой точностью; при этомъ, какъ мы увидимъ
ниже, и сравненія сопротивленій легко производятся съ большою
точностью. Такъ какъ, кромѣ того, проводникъ—при неизмѣнности
всѣхъ вообще его физическихъ свойствъ—обладаетъ также неиз-
мѣннымъ сопротивленіемъ, то нормальныя сопротивленія изготовля-
ются весьма легко. По международному соглашенію въ основу ихъ
устройства положена единица сопротивленія, опредѣляемая слѣду-
ющимъ образомъ:
Единицей электрическаго сопротивленія обладаетъ
столбъ ртути въ стеклянной трубкѣ постояннаго сѣченія*
имѣющій длину, равную 106,3 см., при вѣсѣ ртути, равномъ
14,4521 гр., и при температурѣ, равной 0°. Сопротивленіе
этого столба ртути называютъ 1 омомъ.
Въ опредѣленіи ома указывается вѣсъ столба ртути, а не его
поперечное сѣченіе, такъ какъ вѣсъ опредѣляется легче и точнѣе.
Это сѣченіе равняется въ точности 1 кв. мм., такъ какъ удѣльный
вѣсъ ртути при 0° равенъ 13,5956.
Такъ опредѣленная единица сопротивленія является собственно
излишней единицей, такъ какъ сопротивленіе опредѣляется численно
изъ уравненія V — 3. Я, если установлены единицы V и У. При опре-
дѣленіи легальнаго ома было обращено вниманіе на то, чтобы оста-
вались въ силѣ какъ опредѣленія, приведенныя въ § 37, § 10ф и
здѣсь, такъ и законъ Ома. '
Когда черезъ проводникъ, имѣющій сопротивленіе /?
.„ г кулонъ
омовъ, течетъ электрическій токъ въ У —-------> /голнапряже-
г секунда г
ніе между концами проводника равняется V У вольтамъ.
То обстоятельство, что для единицы сопротивленія было уста-
новлено, независимо отъ закона Ома, еще осоШ^опредѣленіе, осно-
Легальная единица сопротивленія
71
вывается на томъ, что электрическія сопротивленія особенно легко»
воспроизводить. Быть можетъ, было бы удобнѣе упразднить еди-
ницу напряженія или единицу заряда, такъ какъ эти единицы труднѣе
воспроизводить, и замѣнить ее уравненіемъ Ома. Однако, до сихъ
поръ не могли рѣшиться на непрямое опредѣленіе этихъ величинъ,
являющихся основными во всей области электрическихъ измѣреній
Во всякомъ случаѣ, всѣ три единицы опредѣлены настолько точно, что
при самыхъ тонкихъ современныхъ измѣреніяхъ не оказывается ни-
какого отступленія отъ зависимости V = 7?.Ѵ. Если когда-нибудь
будутъ найдены еще болѣе точные измѣрительные методы, нежели
современные, то все же можно будетъ оставить въ силѣ нынѣ
узаконенныя опредѣленія единицъ вольтъ, кулонъ и омъ и просто
ввести въ уравненіе Ома поправочный множитель С. Уравненіе
Ома тогда приметъ видъ V — С. 7?. У; множитель С, во всякомъ’
случаѣ, настолько мало будетъ отличаться отъ единицы (навѣрное,
меньше, чѣмъ на одну десятитысячную), что его обычно можно бу-
детъ опускать. Нѣчто аналогичное мы имѣемъ въ нашемъ опредѣленіи
единицы вѣса: мы имѣемъ, во-первыхъ, спеціальный эталонъ пла-
тиновый килограммъ, хранящійся въ парижскомъ Бюро Мѣръ и
Вѣсовъ, и, во-вторыхъ, непрямое опредѣленіе, согласно которому, вѣсъ
единицы объема воды при 4° равняется единицѣ. Оба опредѣленія,
конечно, не могутъ математически точно совпасть между собою, но
они отличаются другъ отъ друга столь незначительно, что на раз-
ницу практически никогда не обращаютъ вниманія.
Уравненіе Ома прямо даетъ намъ простой и точный способъ
измѣренія сопротивленія, если въ нашемъ распоряженіи имѣются гра-
дуированные измѣрители тока и напряженія. Пропустимъ черезъ из-
слѣдуемый проводникъ токъ, измѣримъ его силу У амперметромъ и
одновременно измѣримъ напряженіе V между концами проводника
вольтметромъ. Въ такомъ случаѣ сопротивленіе 7? вычислится по
формулѣ
7? = -г- омовъ.
г) Согласно постановленію международнаго конгресса въЛондонѣ
1908 года, омъ опредѣляется, какъ здѣсь указано, амперъ опре^л^тся, какъ
указано въ § 100, а вольтъ является производною единицею^Цопредѣляемою
на основаніи первыхъ двухъ изъ закона Ома. Л^^Прим. пер.
72
Соединеніе нѣсколькихъ проводниковъ
СОЕДИНЕНІЕ НЪСКОЛЬКИХЪ ПРОВОДНИКОВЪ.
256. Если мы соединимъ послѣдовательно нѣсколько провод-
никовъ и включимъ источникъ тока, то по всѣмъ проводникамъ
будетъ проходить одинъ и тотъ же токъ У. Если сопротивленія от-
дѣльныхъ проводниковъ суть /?2,...,/?п, то напряженіе между
концами перваго проводника равняется . 7, между концами
второго Ѵ2 = /?2.7,....., между концами послѣдняго Ѵп = /?п.7. Напря-
женіе между началомъ и концомъ всей системы проводовъ, по за-
кону равновѣсія напряженій, равняется
уг+ѵ2 + ....+ ип-(/?і + /?2 + .... + /?п).л
Назовемъ, какъ обычно, отношеніе напряженія V къ силѣ тока 7
•сопротивленіемъ /? всей системы проводовъ; въ такомъ случаѣ
/? — /?1 + /?2 4"-----------Ь
При послѣдовательномъ соединеніи нѣсколькихъ про-
водниковъ ихъ сопротивленія слагаются.
Если же всѣ п проводниковъ соединены параллельно между
точками А и В, между которыми электрическое напряженіе равня-
ется V, то черезъ всѣ проводники идутъ токи вообще различ-
ной силы. Если въ первомъ проводникѣ сила тока равняется 7Г,
во второмъ 72 ..., въ послѣднемъ 7П, то, по закону Ома и согласно
закону равновѣсія напряженій,
1/ = /?2.72,.... Ѵ = Кп.1п.
Въ общемъ черезъ А и В проходитъ токъ силы 7=71 +ЛЧ----------
и, слѣдовательно,
Сопротивленіе А? всей системы проводниковъ въ этомъ случаѣ
вычисляется изъ уравненія
1
7?п
1
Обратную величину сопротивленія — часто называютъ прово-
димостью проводника. Слѣдовательно, при параллельномъ со-
единеніи нѣсколькихъ проводниковъ слагаются обратныя
величины ихъ сопротивленій — ихъ пррѣбдимости.
Реостаты
73
РЕОСТАТЫ.
257. На вышеизложенныхъ правилахъ соединенія проводниковъ
основывается устройство перемѣнныхъ сопротивленій—реостатовъ.
Весьма простую форму перемѣннаго сопротивленія представляетъ
собою реостатъ со скользящимъ контактомъ (рис. 175). Про-
волока съ довольно большимъ сопротивленіемъ -намотана на хорошо
изолирующемъ цилиндрѣ (напримѣръ, фарфоровомъ). Оба конца ея со-
Рис. 175. Реостатъ со скользящимъ контактомъ.
единены съ двумя зажимами, изъ которыхъ одинъ хорошо изолиро-
ванъ отъ металлической рамы реостата, а другой соединенъ съ нею
проводящимъ образомъ. По обмоткѣ цилиндра перемѣщается ла-
тунная пружина, соединенная проводникомъ съ латуннымъ стержнемъ,
служащимъ для ея передвиженій. Этотъ стержень находится въ
хорошо проводящемъ соединеніи съ металлической рамой, а потому
также со вторымъ зажимомъ. Сопротивленіе толстаго латуннаго
Рис. 176. Схема реостата со скользящимъ контактомъ.
стержня весьма мало сравнительно съ сопротивленіемъ обмотки.
Поэтому между обоими зажимами существенную роль играетъ лишь
сопротивленіе части проволочной обмотки, заключенной между пер^
вымъ зажимомъ и передвижнымъ контактомъ (рис. 176). Чѣмъ больше^
количество оборотовъ проволоки мы введемъ, тѣмъ больше^о-
противленіе.
Съ описаннымъ реостатомъ весьма сходенъ по устройству рео-
статъ съ вращающейся рукояткой (рис. 177)^Нѵдоскѣ изъ
хорошо изолирующаго матеріала (шифера) расположенія дугообразно
74
Реостаты
на равныхъ разстояніяхъ другъ отъ друга нѣсколько латунныхъ кно-
покъ; каждая пара этихъ кнопокъ соединена проволокой, имѣю-
щей значительное сопротивленіе (рис. 178). Вокругъ центра дуги,,
образуемой кнопками, перемѣщается при помощи рукоятки тугая ла-
тунная пружина, конецъ которой скользитъ какъ разъ по кнопкамъ.
Реостатъ снабженъ двумя зажимами, изъ которыхъ одинъ сообщенъ
съ осью латунной пружины, а другой съ одной изъ крайнихъ ла-
Рис. 177. Реостатъ съ вращающейся рукояткой.
тунныхъ кнопокъ. Вращеніемъ рукоятки можно произвольно измѣ-
нять число введенныхъ между обоими зажимами проволокъ бол^-
шого сопротивленія. .
Обычно пользуются при измѣреніяхъ штепсельнымъ^^бста-
томъ (рис. 179). Въ немъ проволоки, вводимыя въ качествѣ сопро-
тивленій, смотаны въ катушки и помѣщены въ дердвя>ный ящикъ,
снабженный эбонитовой крышкой. На этой крышкѣ расположены въ
опредѣленномъ порядкѣ толстыя латунныя планкйД тщательно изо-
лированныя одна отъ другой. Каждыя двѣ послѣдовательныя планки
Реостаты
75.
соединены между собою внутри ящика черезъ посредство одной изъ
катушекъ (рис. 180). Величина сопротивленія каждой изъ катушекъ
Рис. 178. Схема реостата съ вращающейся рукояткой.
указывается числомъ, стоящимъ на эбонитовой крышкѣ у соотвѣт-
ственнаго промежутка между планками. Каждый изъ этихъ ироме-
Рис. 179. Штепсельный реостатъ.
жутковъ снабженъ посрединѣ круглымъ отверстіемъ, оѴръ эти от-
верстія плотно вставляются слегка коническіе латунные штепсели.
76
Электрометръ, какъ измѣритель тока
Подобнымъ штепселемъ можно коротко замкнуть сопротивленіе, со-
единяющее двѣ послѣдовательныя планки. Сопротивленія планокъ и
штепселей практически являются ничтожно малыми по сравненію съ
сопротивленіями катушекъ, помѣщенныхъ въ ящикѣ. Если штепсель
Рис. 180. Схема штепсельнаго реостата.
вставленъ въ отверстіе между двумя планками, то сопротивленіе въ
этомъ мѣстѣ практически становится равнымъ нулю; если же штеп-
сель вынутъ, то этимъ включено сопротивленіе, величина котораго
дается написаннымъ около отверстія числомъ.
ЭЛЕКТРОМЕТРЪ, КАКЪ ИЗМЪРИТЕЛЬ ТОКА.
258. По закону Ома напряженіе между концами неизмѣннаго
•сопротивленія находится въ опредѣленной связи съ силою тока въ
сопротивленіи. Поэтому иногда возможно, пользуясь неизмѣннымъ
сопротивленіемъ, измѣрять силы тока электрометромъ, а напряженія
гальванометромъ.
Измѣренія перваго рода удобны въ тѣхъ случаяхъ, когда при-
ходится измѣрять малыя силы тока въ цѣпи съ большимъ сопро-
тивленіемъ. Примѣромъ можетъ служить случай, описанный выше
въ § 126. Для измѣренія силы тока помощью электрометра вводятъ
въ цѣпь неизмѣнное сопротивленіе, малое по сравненію съ имѣю-
щимся уже въ цѣпи сопротивленіями и потому не вліяющее замѣтно
на силу тока; концы этого сопротивленія соединяютъ съэлектро-
метромъ (рис. 181). Если электрометръ показываетъ V ^вольтъ, а
сопротивленіе, къ которому приключенъ электрометръ;<равняется /?
у
омамъ, то искомая сила тока въ цѣпи равняется У -^ амперамъ. Въ
случаѣ, разсмотрѣнномъ въ § 126, сопротивленіе въ іонизируемомъ во^
духѣ было настолько велико, что можно былфівъ качествѣ отно-
Гальванометръ, какъ измѣритель напряженія
77'
сительно малаго сопротивленія, включить параллельно электрометру
описанное тамъ амилъ-алкогольное сопротивленіе, подчиняющееся*
закону Ома. Такимъ об-
разомъ можно пользо-
ваться совершенно опре-
дѣленными сопротивленія-
ми въ нѣсколько милліар-
довъ омовъ и измѣрять си-
лы тока, на которыя не
реагируетъ даже чувстви-
тельнѣйшій гальванометръ.
Бронзонъ (Вгопзоп) не-
давно предложилъ поль-
Рис. 181. Электрометръ въ качествѣ
измѣрителя тока.
зоваться при такихъ измѣреніяхъ чрезвычайно большимъ сопроти
вленіемъ изъ воздуха, іонизированнаго лучами радія.
ГАЛЬВАНОМЕТРЪ, КАКЪ ИЗМѢРИТЕЛЬ НАПРЯЖЕНІЯ.
259. Обратно, часто оказывается удобнымъ измѣрять напряже-
нія при помощи гальванометра, если сопротивленіе самаго источни-
ка электричества и сопротивленіе проводовъ отъ источника до тѣхъ
двухъ точекъ, между которыми измѣряется напряженіе, весьма ма-
лы. Примѣръ такого рода мы имѣли уже въ § 214, гдѣ приходи-
лось измѣрять весьма малое напряженіе между зажимами термоэле-
мента. Методъ измѣренія въ этомъ случаѣ заключается въ слѣдую-
щемъ: обѣ точки А и В, между которыми должно быть измѣрено
напряженіе (рис. 182), мы соединяемъ съ зажимами гальванометра, имѣ-
къ нему
катушкѣ
большое
сопроти-
ющаго въ самыхъ сво-
ихъ катушкахъ или въ
приключенной
проволочной
относительно
„внутреннее"
Рис. 182. Гальванометръ въ качествѣ вленіе. Если черезъ галь- Г
измѣрителя напряженій. ванометръ проходит^р)ѵ
токъ въ У амперъ и все сопротивленіе гальванометра равно /? о$й^ъ,
то искомое напряженіе между А и В равняется V = вольтамъ.
Этотъ методъ, благодаря удобству его примѣненія, ктоль часто
употребляется въ электротехникѣ, что подъ словомъ /^о\ьтметръ“
78
Гальванометръ, какъ измѣритель напряженія
Или лучше „техническій вольтметръ обычно понимаютъ гальвано-
метръ съ большимъ сопротивленіемъ. Полезно, однако, имѣть въ ви-
ду, что употребленіе техническаго вольтметра ограничивается опре-
дѣленными рамками. Имъ нельзя пользоваться, если въ источникѣ
электричества содержатся большія сопротивленія, или если напряже-
ніе возникаетъ вслѣдствіе процессовъ, протекающихъ въ изоляторахъ,
Какъ въ электрическихъ машинахъ, или если измѣряются напряженія
конденсаторовъ. Нельзя имъ пользоваться также и въ томъ случаѣ,
<если токъ, проходящій черезъ вольтметръ, какимъ-либо образомъ
вліяетъ на измѣряемое напряженіе, напримѣръ, черезъ электролити-
ческую поляризацію, какъ въ случаѣ нормальныхъ элементовъ, отъ
которыхъ можно брать лишь очень слабые токи (§ 116). Такимъ
образомъ, спеціальнымъ измѣрителемъ напряженія, который можно
употреблять при всевозможныхъ обстоятельствахъ, остается попреж-
нему электрометръ.
Такъ какъ техническій вольтметръ во многомъ сходенъ съ ам-
перметромъ, то мы отмѣтимъ здѣсь еще разъ вкратцѣ различіе
между обоими инструментами.
Въ амперметрѣ внутреннее сопротивленіе дѣлаютъ возможно
меньшимъ; въ вольтметрѣ внутреннее сопротивленіе дѣлается на-
столько большимъ, насколько это возможно безъ замѣтнаго пони-
женія его чувствительности.
Включается амперметръ такимъ образомъ, что его катушка не-
посредственно вводится въ цѣпь; вольтметръ же включается такъ,
что оба его зажима соединяются съ тѣми двумя точками, между
которыми измѣряется напряженіе. Зажимы техническаго вольтметра
поступаютъ, такимъ образомъ, на мѣсто зажимовъ электрометра (§ 254).
ИЗМѢРИТЕЛЬНЫЕ ИНСТРУМЕНТЫ ДЛЯ РАЗЛИЧНЫХЪ
ОБЛАСТЕЙ ИЗМѢРЕНІЙ.
260. Весьма удобнымъ свойствомъ техническаго вольтметра
является чрезвычайная легкость, съ которою можетъ быть из^яена
область измѣреній, для которой приборъ предназначается^ Д|Йпи со-
противленіе вольтметра равняется /?, то включеніемъ предваритель-
наго сопротивленія, равнаго 9/?, чувствительность щі|урумента по-
нижается въ десять разъ. То же отклоненіе, которое безъ предва-
рительнаго сопротивленія, соотвѣтствовало 1 воліту, при введеніи
л/У
Измѣрительные инструменты для различныхъ областей измѣреній 79
указанаго предварительнаго сопротивленія, соотвѣтствуетъ 10 воль-
тамъ. Продажные вольтметры часто имѣютъ нѣсколько предвари-
тельныхъ сопротивленій, которыя могутъ быть вводимы и выводимы-
помощью штепселей. Такимъ инструментомъ можно измѣрять съ
•одинаковою процентною точностью какъ малыя напряженія до нѣ-
сколькихъ милливольтъ, такъ и большія напряженія, равныя многимъ
вольтамъ.
Амперметры также могутъ быть приспособлены для различ-
ныхъ областей измѣреній. Понятно, что этого нельзя достигнуть
включеніемъ предварительныхъ сопротивленій, такъ какъ въ этомъ
случаѣ весь измѣряемый токъ ослаблялся бы до тѣхъ предѣловъ,
.для которыхъ пригоденъ амперметръ. Если желательно измѣрять ам-
перметромъ болѣе сильные токи, нежели тѣ, для измѣренія кото-
рыхъ онъ построенъ, то нужно устроить такъ, чтобы отъ сильнаго
тока отвѣтвлялась небольшая часть его и проходила черезъ ампер-
метръ. Иными словами, область измѣреній для даннаго амперметра
мѣняютъ помощью отвѣтвленій. Если, напримѣръ, сопротивленіе от-
вѣтвленія равно /?, гдѣ /? — сопротивленіе катушки амперметра,
то, согласно правилу развѣтвленія токовъ (§ 256), токъ въ отвѣт-
вленіи относится къ току въ катушкѣ амперметра, какъ 9 къ 1.
9
Иными словами, изъ всего тока въ цѣпи пойдутъ черезъ отвѣт-
вленіе и лишь пойдетъ черезъ катушку амперметра. То же откло-
неніе указателя, которое безъ отвѣтвленія соотвѣтствовало 1 амперу,
при наличности этого отвѣтвленія1) будетъ соотвѣтствовать 10 ам-
перамъ. Многіе продажные амперметры снабжены отвѣтвленіями, ко-
торыя можно приключать и выключать помощью штепселей, такъ
что однимъ и тѣмъ же инструментомъ можно пользоваться для из-
мѣреній въ различныхъ областяхъ.
ПОТЕРИ НАПРЯЖЕНІЯ ВЪ ПРОВОДАХЪ.
261.------При снабженіи электрической энергіей большой областц,
напримѣръ, города, чрезвычайно важно, чтобы въ распоряженіи ка.-^'
ждаго потребителя находилось постоянное электрическое напр^еніе
между двумя проводами, проведенными въ его установку. Электри-
ческія лампы и почти всѣ электротехническіе аппараты^обладаютъ
---------- О дЧ
3) Такое отвѣтвленіе обычно называется шунтомъ. ^^Тірим. пер.
80
Потери напряженія въ проводахъ
свойствомъ правильно функціонировать лишь при вполнѣ опредѣ-
Рис. 183. Демонстрація потери напряженія въ проводахъ.
ленномъ напряженіи. Если
электрическая лампа приклю-
чена къ двумъ точкамъ, на-
пряженіе между которыми
слишкомъ мало, то она го-
ритъ слишкомъ темно и
позволяетъ использовать для
освѣщенія лишь небольшую
долю подводимой энергіи.
Если же напряженіе слиш-
комъ велико для лампы, то
температура ея нити чрез-
мѣрно повышается, нить раз-
мягчается и, наконецъ, раз-
рывается въ какомъ - либо
мѣстѣ, гдѣ она особенно не-
прочна.
Требованію постоянства
напряженія, которое, такимъ
образомъ, является необхо-
димымъ въ электрическихъ
установкахъ, можно удовле-
творить лишь тщательнымъ
расчетомъ сѣти. Чтобы въ
этомъ убѣдиться, полезно
разобрать примѣръ такой
электрической проводки, ко-
торая практически совершен-
но непригодна. Проведемъ
отъ двухъ неподвижныхъ по-
стоянныхъ зажимовъ, соеди-
ненныхъ толстыми мѣдными
проводами съ больуіоЙ бата-
реей ^аккумуляторовъ, двѣ
и Фу
параллельныя^ между собой
тонкія металлическія проволоки къ двумъ другимъ" неподвижнымъ
изолированнымъ постояннымъ зажимамъ (рис. 18^ Эти двѣ проволоки
Потери напряженія въ проводахъ
81
должны представлять собою кабель, отъ котораго отвѣтвл яютсяпрово-
да къ отдѣльнымъ потребителямъ. Для этой цѣли по проволокамъ
передвигаются нѣсколько зажимовъ; каждая пара такихъ зажимовъ
представляетъ собою мѣсто отвода, а двѣ прикрѣпляемыя къ нимъ
мѣдныя проволоки представляютъ собою проводку, ведущую въ
установку потребителя. Предположимъ, что имѣется цѣлый рядъ та-
кихъ проводокъ — одна вблизи начала „кабеля", другая въ самомъ
его концѣ и остальныя посрединѣ. Каждое отвѣтвленіе ведетъ къ ду-
говой лампѣ или же къ одной или къ нѣсколькимъ лампамъ накаливанія,
соединеннымъ параллельно; всѣ эти лампы накаливанія построены
для напряженія, даваемаго батареей аккумуляторовъ. При такой про-
водкѣ наблюдается слѣдующее. Если сначала горитъ свѣтло одна
изъ среднихъ лампъ, то она сразу начинаетъ горѣть темнѣе, какъ
только включается вторая лампа, не находящаяся въ началѣ „кабеля".
Особенно плохо ея горѣніе, если второю включается дуговая лампа,
берущая относительно много тока; при этомъ можетъ случиться даже,
что сначала горѣвшая лампа накаливанія совершенно потухнетъ.
Если же вновь выключить дуговую лампу, то лампа накаливанія на-
чинаетъ горѣть, какъ и прежде. Если включить всѣ установлен-
ныя въ цѣпи лампы, то лампы накаливанія, находящіяся въ кон-
цѣ цѣпи, горятъ наименѣе ярко; болѣе ярко онѣ горятъ по мѣрѣ
приближенія къ началу цѣпи, но нормально и независимо отъ вклю-
ченія и выключенія остальныхъ горятъ только лампы, соединенныя
мѣдной проволокой непосредственно съ начальными зажимами. Эти
наблюденія могутъ быть объяснены на основаніи закона Ома, и
колебанія напряженія, обусловливающія измѣненія яркости лампъ,
могутъ быть точно разсчитаны. Обозначимъ черезъ сопротивленіе
проводовъ отъ начальныхъ зажимовъ до перваго отвѣтвленія, черезъ
— сопротивленіе отъ перваго отвѣтвленія до второго, черезъ /?3—
отъ второго до третьяго и т. д.; силы тока въ отдѣльныхъ частяхъ
цѣпи обозначимъ черезъ 73 и т. д. Положимъ, что постоян-
ное напряженіе между начальными зажимами равняется І/о, а напря-
женія въ точкахъ перваго, второго, третьяго,... отвѣтвленій 060-Г4
значимъ черезъ Ѵ19 Ѵ2, Ѵ3,... По закону Ома,
Ѵо-= Ѵ,= ѵо-^.^
V,-1/2 = /?2.У2; Ѵ2 = Ѵо-^.
ѵ2-к3 = /?3./3; ѵ3= ѵ0-/?2./2-^3
и т. л. ,43^
Ми. Электричество и магнитизмъ, ч. II. 6
82
Потери напряженія въ проводахъ
Потеря напряженія въ произвольномъ участкѣ цѣпи
равняется произведенію сопротивленія этого участка цѣпи
на силу тока, въ немъ проходящаго.
Напряженіе въ произвольномъ мѣстѣ цѣпи равняется
напряженію между начальными зажимами, уменьшенному
на сумму всѣхъ потерь напряженія отъ начала цѣпи до раз-
сматриваемаго мѣста.
Очевидно, тонкая проволока непригодна, такъ какъ при ея
употребленіи сопротивленія/?х, /?2, /?3,... слишкомъ велики, и по-
тому потери напряженія также очень велики; эти потери тѣмъ
больше, чѣмъ сильнѣе токъ, посылаемый въ цѣпь, что особенно
замѣтно при включеніи дуговыхъ лампъ.
Чтобы разсчитать проводку отъ электрической станціи къ по-
требителямъ, слѣдуетъ опредѣлить силы тока, которыя могутъ встрѣ-
титься въ отдѣльныхъ частяхъ цѣпи. Затѣмъ слѣдуетъ сообразно
съ этимъ разсчитать сопротивленія проводовъ, при чемъ ставится
требованіе, чтобы и при максимальныхъ значеніяхъ силы тока вся
потеря напряженія составляла вездѣ лишь нѣсколько процентовъ
начальнаго напряженія Уо. Если при проводкѣ сдѣлана на мѣди
чрезмѣрная экономія, и потому сопротивленіе проводовъ слишкомъ
велико, то потребители замѣчаютъ это весьма непріятнымъ обра-
зомъ: ихъ лампы накаливанія часто внезапно тускнутъ и затѣмъ
вновь ярко разгораются, въ зависимости отъ включеній и выключеній
большого количества тока у сосѣдей.
МОСТЪ ВИТСТОНА.
262. Если какимъ-либо проводомъ соединить двѣ точки А и В,
между которыми поддерживается постоянное напряженіе путемъ со-
единенія ихъ съ обильнымъ источникомъ электричества, то вдоль этого
провода устанавливается непрерывный переходъ потенціала отъ зна-
ченія его въ А до значенія его въ В. Потенціалъ въ нѣкоторой
точкѣ С провода можно вычислить, если извѣстны сопротивленія ча-
стей провода АС и СВ. Обозначимъ эти сопротивленія^нерезъ
и /?,2; силу тока въ проводѣ обозначимъ черезъ У иразиости по-
тенціаловъ между А и С и между С и В черезъ (Лг и (С, В). По
закону Ома,
(А с) = л/?і; (С, =
Мостъ Витстона
83
Мы имѣемъ, слѣдовательно, пропорцію
(А С):(С, В) = /?1:/?2.
Если соединить А и В еще вторымъ проводомъ, то на немъ потен-
ціалъ будетъ имѣть всѣ тѣ же значенія, что и на первомъ. Если
сопротивленія частей этого провода отъ А до нѣкоторой точки О
и отъ В до В суть /?3 и /?4, то
Рис. 184. Мостъ Витстона.
Въ точкахъ Си/) потенціалъ одинъ и тотъ же, и напряженіе
между ними равно нулю, если
/?1 • — ^3 * ^4 •
На этомъ положеніи основанъ весьма важный методъ сравненіи
двухъ сопротивленій. Неизвѣстное сопротивленіе х и извѣстное дСО-^
противленіе /? включаются послѣдовательно между полюсами неболь-
шой батареи А и В. Точку, въ которой соединяются обо-
значимъ черезъ С. Кромѣ того, А и В соединяются еще однимъ
проводомъ; въ качествѣ послѣдняго весьма удобщэВупотреблять
6.
84
Мостъ Витстона
гладкую полированную проволоку съ не слишкомъ малымъ сопро-
тивленіемъ, натянутую вдоль раздѣленной метровой шкалы — такъ
называемую измѣрительную проволоку (рис. 184). Въ началѣ и
въ концѣ шкалы находятся латунныя пластинки, къ которымъ плот-
но прижимается проволока; длина натянутой проволоки въ точности
равняется длинѣ шкалы. Вдоль шкалы передвигается четырехугольная
металлическая пластинка, имѣющая зажимъ и небольшой горизон-
тальный штифтъ, прилегающій къ измѣрительной проволокѣ и обра-
зующій хорошій контактъ. На шкалѣ отсчитывается дѣленіе, указы-
вающее мѣсто, на которомъ передвижной контактъ прилегаетъ къ
проволокѣ. Обозначимъ это мѣсто черезъ О. Отъ С и О прово-
дятся проволоки къ какому-нибудь указателю напряженій; обычно
для этой цѣли употребляется гальванометръ, служащій здѣсь до
нѣкоторой степени вольтметромъ. Контактъ О перемѣщаютъ до тѣхъ
поръ, пока напряженіе между С и О не станетъ равнымъ нулю;
тогда отсчетъ на шкалѣ даетъ длины а и Ь отрѣзковъ, на которые
измѣрительная проволока дѣлится точкой О. Если измѣрительная
проволока имѣетъ повсюду одинаковую толщину и изготовлена изъ
однороднаго матеріала, то электрическое поле тока въ ней постоянно
и напряженія относятся, какъ длины, т.-е. (Л, О) : (О, В) = а :
Слѣдовательно,
а г»
х=т. /г.
Соединительный проводъ между С и О, содержащій гальвано-
метръ, называютъ мостомъ между обѣими вѣтвями или, въ честь
изобрѣтателя этого метода, мостомъ Витстона (ШЬеаЫопе).
УДѢЛЬНАЯ ПРОВОДИМОСТЬ МЕТАЛЛОВЪ.
263. Положимъ, что токъ У течетъ по проволокѣ равномѣрной
толщины, изготовленной изъ однороднаго матеріала и имѣющей
длину /; напряженіе между ея концами пусть будетъ V. Раздѣлимъ
мысленно эту проволоку на п частей; напряженіе меаду" концами
і
каждаго отрѣзка равняется — У. Представимъ себѣ/далѣе, что изъ
проволоки выдѣлена часть, содержащая въ себѣ^т^ такихъ отрѣз-
ковъ; ея длина равняется Іг = • /. Напря^фйе между концами этой
Удѣльная проводимость металловъ
85
части проволоки обозначимъ черезъ Ѵ±, Въ такомъ случаѣ
V! = П! . — = • V
1 1 п I
или же
Ѵ1 : V - : /.
Напряженія относятся между собою, какъ длины. Этимъ обстоятель-
ствомъ мы пользовались только-чтопри описаніи мостаВитстона. Если,
далѣе, сопротивленія всей проволоки и выдѣленной части суть
/? и то
и, слѣдовательно,
/?:/?!= V: ѴГ = 1*.1Г.
Сопротивленіе проволоки постоянной толщины, со-
стоящей изъ однороднаго матеріала, пропорціонально ея
длинѣ.
Если сопротивленіе 1 сантиметра равняется р омамъ, а длина
проволоки равняется I см., то сопротивленіе всей проволоки равно
/? = I. р омамъ.
Условіе равновѣсія электрическаго поля требуетъ, чтобы въ
проволокѣ, по которой течетъ токъ, сила электрическаго поля была
постоянна на всемъ поперечномъ сѣченіи д проволоки. Отсюда слѣ-
дуетъ, что въ случаѣ однородности матеріала проволоки токъ рас-
предѣляется равномѣрно по всему ея поперечному сѣченію, т.-е. что
плотность тока въ проволокѣ постоянна. Представимъ себѣ, что про-
волока 'расщеплена на ѵ волоконъ равномѣрной толщины; попе-
речное сѣченіе каждаго волокна равно , и токъ, проходящій по
каждому изъ нихъ, имѣетъ силу • Проволока, составленная изъ
такихъ волоконъ и имѣющая, слѣдовательно, поперечное сѣченіе
дг = при той же внутренней Гейлѣ поля, будетъ нести токъ
— ^3- Слѣдовательно, силы тока У и въ двухъ прово-о (
локахъ, сдѣланныхъ изъ одного и того же однороднаго матеріа^ар
и имѣющихъ одну и ту же длину, относятся между собою,$0ри
одномъ и томъ же напряженіи V между ихъ концами, какъ ^Попе-
речныя сѣченія этихъ проволокъ: \ >
86
Удѣльная проводимость металловъ
Такъ какъ 7?./=^.^ = V, то отношеніе сопротивленій /? и рав-
няется обратному отношенію поперечныхъ сѣченій:
При данной длинѣ сопротивленіе проволоки изъ одно-
роднаго вещества обратно пропорціонально ея попереч-
ному сѣченію.
Если длина проволоки равняется I см., ея поперечное сѣ-
ченіе — д кв. см., и сопротивленіе отрѣзка проволоки изъ того же
вещества, имѣющаго длину въ 1 см. и поперечное сѣченіе въ
1 кв. см., равняется о омамъ, то /? = омамъ. Величина о называется
удѣльнымъ сопротивленіемъ вещества приволоки. Обратная ве-
личина = ~ носитъ названіе удѣльной проводимости. Слѣдо-
г» 1
вательно, Н— —-•
д.Х
Въ слѣдующей таблицѣ даны удѣльныя сопротивленія и про-
водимости нѣкоторыхъ металловъ при 18°.
а X а X
Серебро . Мѣдь . . Золото Алюминій Цинкъ . . Кадмій . Платина отъ до . . . Никкельотъ до . Желѣзо отъ ДО . . . Если выраженн съ попер 0,016 . іо-* 0,017 . 10-4 0,023 . ІО-4 0,032 . 10~4 0,061 . іо-4 0,076 . 10-4 0,108 10-4 0,14 ІО-4 0,08 . ІО-4 0,11 . 10-4 0,09 . ІО-4 0,15 . ІО"4 въ значені ое въ ома> ечнымъ сѣчі 62,1 . 10* 58,8 . 10* 43,4 . 10* 31,2 . 10* 16,4 . 10* 13,2 . 10* 9,3 . 10* 7,1 . 10* 12,5 . 10* 9,1 . 10* 11,1 . 10* 6,7 . 10* и О отбрс съ сопроті гніемъ въ 1 Сталь отъ . . . до Латунь отъ . . до . - • • Нейзильберъотъ до . • • • Свинецъ . . . 1 Константанъ . | Никкелинъ . . Манганинъ . Ртуть ... Ретортный уголь • . • ' >сить множителі явленіе проволо кв. мм. Если въ хм 0,15 .10-*' 0,5 . 10-* 0,07 . 10-*, 0,09 . 10-* 0,16 . іо—* 0,40 .10-* 0,21 .10—* 0,49 .10’* 0,42 .10-* 0,42 .10~* 0,9563. 10—* 50,0 . 10^ > 1(И1° ки ^длиною 5? величинѣ X 6,7 . ІО4 2,0 . ІО4 14,3 . ІО4 11,1 . ІО4 6,2 . ІО4 2,5 . 104 4,76 . ІО4 2,04 . ІО4 2,38 . ІО1 2,38/хк, ІО4 1,0457. ІО4 рѢ,02 . ІО4 получится въ 1 м. и отбросить
Удѣльная проводимость металловъ
87
множитель ІО4, то получится число, выражающее въ метрахъ длину
проволоки съ сѣченіемъ въ 1 кв. мм., сопротивленіе которой рав-
няется какъ-разъ 1 ому. Послѣ серебра и золота наибольшую про-
водимость имѣютъ мѣдь и алюминій. На практикѣ для электриче-
скихъ проводовъ употребляется почти исключительно мѣдь.
264. Видеманнъ (АѴіедетапп) и Францъ (Ргапх) открыли слѣ-
дующій законъ, относящійся къ проводимости металлическихъ эле-
ментовъ:
ЗаконъВидеманна-Франца. Отношеніе электрической про-
водимости къ теплопроводности при опредѣленной темпе-
ратурѣ является универсальной постоянной для чистыхъ
металлическихъ элементовъ въ твердомъ аггрегатномъ со-
стояніи.
Если мы обозначимъ теплопроводность черезъ к, то
к-С.Х
или
к . о = С.
Здѣсь С есть постоянная закона Видеманна-Франца при
опредѣленной температурѣ.
Если теплопроводность разсчитывать, беря за единицу пере-
носъ 1 малой калоріи тепла въ 1 сек. черезъ сѣченіе въ 1 кв. см.
и за единицу градіента температуры 1° Цельзія па 1 см. и если
удѣльное сопротивленіе выражать въ омахъ и сантиметрахъ, то при
18° постоянная закона Видеманна-Франца С = 1,61. ІО-6. Для
серебра, напримѣръ, при 18° о = 0,016 . ІО-4 и к= 1,005.
Для металлическихъ сплавовъ, металлически проводя-
щихъ рудъ, углей и жидкихъ металловъ (ртуть) законъ Ви-
манна-Франца не имѣетъ силы.
ИЗМЪНЕНІЕ ПРОВОДИМОСТИ СЪ ТЕМПЕРАТУРОЮ.
265. Если полюса небольшой батареи аккумуляторовъ соеди-
нить черезъ свободно подвѣшенную въ воздухѣ желѣзную спираль
и черезъ амперметръ, то можно замѣтить, что сила тока значительно^
падаетъ, когда желѣзную проволоку сильно нагрѣваютъ при п(доЩи
Бунзеновской горѣлки. Если затѣмъ удалить пламя и дать ^дррво-
локѣ охладиться до комнатной температуры, то токъ возрастаетъ
до своей первоначальной величины. При погруженіи проволоки въ
жидкій воздухъ сила тока возрастаетъ весьма замМйб; если въ.
88
Измѣненіе проводимости съ температурою
цѣпи нѣтъ никакого сопротивленія, сравнимаго съ сопротивленіемъ
желѣзной проволоки; именно, въ этомъ случаѣ сила тока болѣе
чѣмъ въ три раза превосходитъ силу тока при комнатной темпера-
турѣ. Слѣдовательно, сопротивленіе желѣзной проволоки тѣмъ боль-
ше, чѣмъ выше температура. То же самое наблюдается для всѣхъ
твердыхъ металлическихъ элементовъ. При этомъ у совершенно чи-
стыхъ твердыхъ металлическихъ элементовъ при нагрѣваніи сопро-
тивленіе возрастаетъ нѣсколько быстрѣе, нежели пропорціонально
абсолютной температурѣ. Довольно точнымъ является слѣдующій за-
конъ, впервые установленный Друде (Эшде):
При различныхъ температурахъ постоянныя закона
Видеманна - Франца относятся между собою, какъ абсолют-
ныя температуры.
Такимъ образомъ,
к . сг = с. Ѳ,
гдѣ г = 5,53.10 9 — независимая отъ температуры универсальная
постоянная. При 18° 0 = 273+ 18-291, С = с. 291 = 1,61 . ІО-6.
Теплопроводность металловъ к измѣняется съ температурою весьма
мало, сг-же возрастаетъ приблизительно пропорціонально Ѳ. Если тем-
пература приближается къ абсолютному нулю, то чистый металличе-
скій элементъ по своей проводимости приближается къ совершен-
ному проводнику, для котораго 0 = 0.
266. Совершенно иначе обстоитъ дѣло съ тѣми металлически-
ми проводниками, для которыхъ законъ Видеманна-Франца не
имѣетъ силы. Если въ опытѣ, описанномъ въ § 265, замѣнить же-
лѣзную проволоку никкелиновою, то при нагрѣваніи ея почти до
бѣлаго каленія показаніе амперметра мѣняется едва замѣтно. То же
наблюдается и для другихъ сплавовъ; по большей части ихъ со-
противленіе возрастаетъ при нагрѣваніи сравнительно весьма мало.
Но существуютъ и такіе сплавы, сопротивленіе которыхъ при^о-
вышеніи температуры нѣсколько убываетъ. Вслѣдствіе этого путемъ
тщательнаго сплавленія можно получить такіе промежуточное сорта
сплавовъ, для которыхъ температурный коэффиціентъ ^противленія
почти точно равенъ нулю. Этому требованію удовлетворяютъ про-
дажные сплавы манганинъ и константанъ.
Ясно, что сплавы такого рода имѣютъ весьма важное значеніе
въ электрической измѣрительной техникѣ+^Ъ^кая проволока при
Измѣненіе проводимости съ температурою
89
прохожденіи черезъ нее электрическаго тока слегка нагрѣвается. По-
этому, чтобы имѣть строго опредѣленное сопротивленіе изъ металла,
проводимость котораго измѣняется съ температурою, пришлось бы
держать это сопротивленіе въ ваннѣ постоянной температуры, что
сопряжено съ неудобствами. Всѣ копіи нормальнаго сопротивленія,
опредѣленнаго въ § 255, и всѣ катушки въ точно градуированныхъ
штепсельныхъ реостатахъ изготовляются изъ манганина или изъ кон-
стантана.
Къ числу металлическихъ проводниковъ, сопротивленіе которыхъ
убываетъ съ возрастаніемъ температуры, относится также уголь, и при-
томъ для угля это убываніе особенно замѣтно. Накаленный уголь про-
водитъ гораздо лучше холоднаго угля; это можно показать при
помощи куска древеснаго угля, имѣющаго не слишкомъ малую,
плоскую площадку. Въ эту плоскость воткнута перпендикулярная къ
ней проволочка, соединенная съ полюсомъ большой батареи аккумуля-
торовъ. Къ другому полюсу батареи присоединяемъ помощью гиб-
каго проводящаго шнура угольный стержень, который держимъ въ
рукѣ. Поднесемъ сначала стержень къ проволокѣ, присоединенной къ
углю, касаясь въ то же время и самаго угля, и такимъ образомъ
замкнемъ токъ. Если токъ достаточно силенъ, то между стержнемъ
и проволокой образуется небольшое пламя. Если теперь медленно
удалять стержень отъ проволоки, то весь путь, описываемый кон-
цомъ стержня по поверхности угля, остается въ видѣ пылающей
черты, такъ какъ почти весь токъ проходитъ черезъ уже накаленный
уголь, который вслѣдствіе этого остается раскаленнымъ, а не черезъ
холодный плохо проводящій уголь. Это становится особенно яс-
но, если угольнымъ стержнемъ описать небольшую дугу и воз-
вратиться въ заключеніе къ точкѣ вблизи проволоки. Если не слиш-
комъ приближаться къ проволокѣ, то токъ предпочитаетъ длинный
путь черезъ раскаленный уголь короткому пути черезъ холодный уголь;
это ясно по виду раскаленной кривой, описанной концомъ стержня.
БОЛОМЕТРЪ.
267. Для измѣренія температуры какого-либо пространства
„ . „ ѵСу ж
сто пользуются проволокой, сопротивленіе которой сильно^ измѣ-
няется въ зависимости отъ температуры. Проволоку * соединяютъ
съ амперметромъ и небольшимъ источникомъ тока и цо^фщаютъ въ
изслѣдуемое пространство. Такіе приборы могутъ быт^употребляемы
90
Теорія проводимости металловъ
для измѣренія весьма высокихъ и весьма низкихъ температуръ съ
такимъ же удобствомъ, какъ и описанные выше термоэлементы (§ 215)..
Если проволоку, служащую для измѣренія температуры, вклю-
чить въ качествѣ вѣтви въ мостъ Витстона, то приборъ можетъ-
быть сдѣланъ весьма чувствительнымъ и пригоднымъ для измѣренія
чрезвычайно малыхъ измѣненій температуры. Такой приборъ обыч-
но называютъ болометромъ. Болометръ употребляется, какъ и
термоэлектрическій столбикъ (§ 215), напримѣръ, для измѣренія
интенсивности лучеиспусканія. Болометръ можетъ быть сдѣланъ бо-
лѣе чувствительнымъ, чѣмъ термоэлектрическій столбикъ, но обра-
щеніе съ нимъ болѣе сложно.
ТЕОРІЯ ПРОВОДИМОСТИ МЕТАЛЛОВЪ.
268. Какъ указано въ § 213, мы должны представлять себѣ-
структуру металла слѣдующимъ образомъ. Атомы образуютъ твер-
дую пористую ткань, въ порахъ которой движутся по всѣмъ на-
правленіямъ чрезвычайно малые электроны, подобно тому, какъ моле-
кулы газа движутся въ порахъ глиняной перегородки. Внутреннее
электрическое поле гонитъ въ одну сторону отрицательно заряжен-
ный электронный газъ черезъ пористую ткань атомовъ. При этомъ
онъ испытываетъ сопротивленіе тренія, которое, по извѣстному изъ
механики закону Пуазейля (Роізеиіііе), пропорціонально скорости
теченія. Такимъ образомъ, законъ Ома не является новымъ закономъ
природы; онъ указываетъ лишь, что электронный газъ, какъ и всякій
другой газъ, подчиняется закону Пуазейля. Изъ ученія о газахъ
извѣстно далѣе, что сопротивленіе тренія, которое испытываетъ
газъ, пропускаемый подъ давленіемъ черезъ пористое вещество или
черезъ капиллярную трубку, при прочихъ одинаковыхъ обстоятель-
ствахъ, увеличивается съ возрастаніемъ температуры. То же мы
имѣемъ и въ случаѣ чистыхъ металлическихъ элементовъ. Почему
сплавы, руды и угли отличаются иными свойствами, пока еще
ясно; быть можетъ, въ нихъ съ измѣненіемъ температуры сй^ѣно
измѣняется число свободныхъ электроновъ или, быть можетъ^?здѣсь
играютъ роль интрамолекулярныя термоэлектрическія напряженія.
Связь между электрической и тепловой проводимостью, уста-
навливаемая закономъ Видеманна - Франца, указываетъ, что пе-
реносъ тепла въ металлахъ совершается преимущественно подъ дѣй-
Проводимость электролитовъ
91
ствіемъ свободныхъ электроновъ. Электронный газъ отнимаетъ отъ,
атомовъ теплоту въ нагрѣтыхъ мѣстахъ и проводитъ ее по тѣмъ же*
законамъ, какъ и всякій иной газъ, къ холоднымъ мѣстамъ, гдѣ
вновь отдаетъ ее атомамъ. Такъ какъ электроны гораздо меньше
молекулъ обыкновенныхъ газовъ, то электронный газъ проводитъ те-
плоту очень хорошо, настолько хорошо, что несравненно превосхо-
дитъ въ этомъ отношеніи твердую атомную субстанцію, которая,
вѣроятно, проводитъ теплоту такимъ же образомъ, какъ и всѣ во-
обще твердые изоляторы. Тѣмъ обстоятельствомъ, что одинъ и тотъ
же электронный газъ осуществляетъ во всѣхъ металлахъ электри-
ческую и тепловую проводимость, объясняется постоянство отноше-
нія этихъ двухъ проводимостей. Въ рудахъ, сплавахъ и угляхъ,
вѣроятно, тѣ же усложненія, которыми вызываются аномальныя из-
мѣненія электрической проводимости съ температурой, маскируютъ,
также и связь между электрической и термической проводимостями,,
выражаемую закономъ Видеманна - Франца.
ПРОВОДИМОСТЬ ЭЛЕКТРОЛИТОВЪ.
269. Законъ Ома прилагается къ электролитамъ, какъ и къ.
металлическимъ проводникамъ. Однако, электролизъ вызываетъ нѣ-
которыя усложненія. Во-первыхъ, какъ мы видѣли въ § 113, онъ.
часто влечетъ за собою весьма значительныя напряженія поляризаціи.
Если напряженіе поляризаціи въ вольтметрѣ есть Ѵо, то, согласно,
закону Ома, V— І/о = /? .7, гдѣ /? — постоянная (сопротивленіе вольта-
метра). Во-вторыхъ, электролизъ вызываетъ непрерывно возраста-
ющее измѣненіе химическаго состава или, по крайней мѣрѣ, концен-
траціи раствора у электродовъ; вслѣдствіе этого непрерывно измѣ-
няется сопротивленіе вольтаметра, такъ что измѣрительный приборъ,
не можетъ дать никакого постояннаго показанія. Для измѣренія со-
противленій электролитовъ, въ силу этого обстоятельства, заставля-
ютъ токъ часто мѣнять направленіе; при этомъ условіи не можетъ
наступить постоянно возрастающаго измѣненія электролита. Чтобы по-
лучить „перемѣнный токъ“, можно было бы между точками развѣт-^)о<
вленія А и В схемы моста Витстона (§ 262) и источникомъ
тричества помѣстить быстро вращающійся коммутаторъ. Но удобнѣе
воспользоваться въ этомъ случаѣ индукціоннымъ аппар^т^мъ, ко-
торый будетъ описанъ ниже. Пока о немъ намъ нужно^знать лишь,
что при соединеніи проводникомъ „вторичныхъ зажимовъ" этого
Проводимость электролитовъ
92
аппарата получается перемѣнный токъ, разряжающій въ обоихъ на-
правленіяхъ одно и то же количество электричества и потому не
разлагающій непрерывно электролита. При этомъ въ мостѣ долженъ
быть установленъ приборъ, реагирующій на періодически измѣня-
ющееся напряженіе. Удобнѣе всего взять въ подобномъ случаѣ теле-
фонъ (рис. 185), который при наличности малѣйшаго перемѣннаго
напряженія между Си/) даетъ слышный тонъ, соотвѣтствующій
время одинъ и тотъ же
при помощи „телефоннаго
напряженій поляризаціи,
Рис. 185. Телефонный мостъ для измѣренія сопротивленія электролитовъ,
періоду колебаній напряженія; звукъ въ телефонѣ исчезаетъ лишь
въ томъ случаѣ, если Си/) имѣютъ все
потенціалъ.
Измѣреніе сопротивленія электролита
моста“ кажется простымъ, но появленіе
котораго нельзя избѣжать и при перемѣнномъ токѣ, влечетъ за собою
нѣкоторое затрудненіе. Возникновеніе напряженій поляризаціи ^всегда
даетъ знать о себѣ тѣмъ, что препятствуетъ полному исчезновеній звука
въ телефонѣ и позволяетъ получить лишь болѣе или м|нѣе заглу-
шенный минимумъ звука. Это обстоятельство зависитъ отъ того,
что напряженія поляризаціи всегда отстаютъ отъ^силы тока, тогда
какъ омическія напряженія, которыя исключительно принимаются во
Проводимость электролитовъ
93
вниманіе въ теоріи моста Витстона, измѣняются одновременно съ
силою тока. Именно, пока токъ идетъ черезъ электролитъ въ одномъ
направленіи, двойные электрическіе слои заряжаются одинаковымъ
образомъ; если продолжительность тока при частыхъ перемѣнахъ
настолько коротка, что напряженіе поляризаціи не можетъ достиг-
нуть своего наибольшаго возможнаго значенія, которое затѣмъ оста-
валось бы постояннымъ, то оно возрастаетъ лишь до тѣхъ поръ,
пока не происходитъ перемѣна направленія тока. Такимъ образомъ,
лишь въ тотъ моментъ, когда токъ равенъ нулю, напряженіе поля-
ризаціи какъ разъ достигаетъ наибольшей величины. Въ теченіе слѣ-
дующаго полуперіода, когда токъ имѣетъ обратное направленіе, по-
ляризація сначала падаетъ и приблизительно посрединѣ полуперіода,
т.-е. какъ разъ когда токъ имѣетъ наибольшую силу, она падаетъ
до нуля; затѣмъ, въ теченіе второй части полуперіода она возра-
стаетъ въ противоположномъ смыслѣ и въ концѣ его, когда токъ
опять равенъ нулю, достигаетъ снова наибольшей величины. По-
этому, хотя въ точкѣ О измѣрительной проволоки моста Витстона
потенціалъ измѣняется параллельно измѣненіямъ тока, въ точкѣ С,
гдѣ присоединяются напряженія поляризаціи, невозможно имѣть въ
теченіе нѣкотораго промежутка времени тотъ же потенціалъ, что и
въ /), какъ бы ни былъ установленъ передвижной контактъ. Для
точныхъ и вѣрныхъ измѣреній нужно прежде всего постараться по
возможности уничтожить напряженія поляризаціи. Пригодный для
всѣхъ случаевъ способъ открылъ Ф. Кольраушъ (Р. КоНІгаизсЬ),
которому мы обязаны разработкой этого метода измѣренія сопро-
тивленія электролитовъ; онъ предложилъ пользоваться платиниро-
ванными платиновыми электродами. Если электролитическимъ путемъ
покрыть платиновыя пластинки, которыя должны служить электро-
дами, слоемъ тонкаго чернаго платиноваго порошка (платиновая
чернь), то площадь соприкосновенія платины съ электролитомъ
увеличится въ громадное число разъ; въ силу этого поверх-
ностная плотность продуктовъ разложенія, обусловливающихъ поля- 4^
ризацію, становится настолько незначительной, что при достаточдо^
быстрыхъ перемѣнахъ направленія тока не образуется никакцх^ра-
мѣтныхъ напряженій поляризаціи. Въ такомъ случаѣ при Давиль-
ной установкѣ передвижного контакта звукъ въ телефонѣ^очти со-
вершенно исчезаетъ. 9
•94
Проводимость электролитовъ
270. Проводимость какого-либо воднаго раствора зависитъ какъ
ютъ химической природы растворенной соли, такъ и отъ концен-
траціи раствора. Концентрація обычно выражается въ процентахъ по
вѣсу или же, что гораздо удобнѣе при сравненіи свойствъ различ-
ныхъ растворовъ, по числу химическихъ граммъ-эквивалентовъ соли г),
приходящихся на единицу объема. Растворъ, въ которомъ прихо-
дится одинъ граммъ-эквивалентъ на литръ, называется нормаль-
нымъ растворомъ; если на литръ приходятся п граммъ-эквивален-
товъ, растворъ называется п - разъ нормальнымъ. Если, какъ обычно,
за единицу объема принять кубическій сантиметръ, то концентра-
ція нормальнаго раствора г) равняется 10—3, а концентрація п-разъ
'нормальнаго раствора ц равняется п. 10~3. Для примѣра укажемъ про-
водимость нѣкоторыхъ хорошо проводящихъ нормальныхъ растворовъ.
Проводимость водныхъ растворовъ при 18° и ц — 10 3.
кон . . . . . 0,184 ИаСІ .... . 0,0743 і2п8О4 . . . . 0,0266
КС1 . . . . . . 0,0983 ИаМО3 . . . . 0,0659 |Сп8О4 . . . . 0,0258
кгю3. . . . . 0,0805 Ша25О4. . . . 0,0508 АеИО3 . . . . 0,0678
КС2Н3О2 . . . 0,0634 ЬІН4С1 . . . . 0,0970 НС1 . . . . . 0,300
ік28о4’: . . . . 0,0718 ЬіСІ .... . 0,0634 1 НІ\Ю3 . . . . . 0,299
|К2СО3 . . . . 0,0707 }СаС1., . . 0,0678 ! ‘ |Н28О4 . . . . 0,197
ИаОН . . . . 0,160 1МёС1, . . . . 0,0615
Изъ этихъ чиселъ видно, что проводимость электролитовъ го-
раздо ниже проводимости металлическихъ проводниковъ. Изъ та-
блицы § 263 видно, что худшій изъ всѣхъ перечисленныхъ въ ней
проводниковъ—уголь все же обладаетъ удѣльной проводимостью
Х = 200, а для мѣди даже Х = 588000.
Для достаточно разбавленныхъ растворовъ имѣетъ силу законъ,
по которому при дальнѣйшемъ убываніи концентраціи проводимость
раствора также непрерывно убываетъ; проводимость совершенно
чистой воды близка къ нулю. Однако, проводимость измѣняется не
пропорціонально концентраціи соли: въ разбавленныхъ раствору»
отношеніе проводимости къ концентраціи всегда больше, нежели;въ
крѣпкихъ. Слѣдовательно, соли въ разбавленномъ состояніі^йрово-
дятъ сравнительно лучше. Отношеніе проводимости къ концентраціи
называютъ эквивалентной проводимостью Л соотвѣтственнаго
О Лл4>
электролита. Эквивалентная проводимость Л -=^- всегда воз-
растаетъ съ разбавленіемъ раствора.
Проводимость электролитовъ
95
Пояснимъ это положеніе двумя примѣрами.
Эквивалентная проводимость растворовъ различной концен-
траціи при 18°.
Ц . 108 = 1 0,5 0,2 0,1 0,05^0,02 1 0,01 0,005 0,002 0,001 0,0005 0,0002 0,0001 1 0 ~
ИаСІ . 74,3 80,9 87,7 92,0 [95,7 99,6 102,0 103,8 105,6 106,5 107,2 107,8 108,1 109,0
ІМ88О4 29 35 44 50 57 68 77 85 94 100 105 109 1,1 117
Ло въ таблицѣ представляетъ предѣльное значеніе Л при ц = 0.
Въ §§ 104—106 мы видѣли, что электрическая проводимость
въ электролитахъ обусловливается двумя родамиЧоновъ — аніонами и
катіонами, движущимися одновременно въ противоположныхъ напра-
вленіяхъ. Числа переноса Па и пк указываютъ, въ какой мѣрѣ оба
рода іоновъ участвуютъ въ токѣ, и весь токъ У можно разложить
на токъ іоновъ За = Па^ и токъ катіоновъ ,Ік = пк-^ Такъ какъ
Па + п% = 1> то /к Соотвѣтственнымъ ^образомъ мы мо-
жемъ разсматривать отдѣльно проводимость аніоновъ и катіоновъ.
Эквивалентныя проводимости Лл и Л# для обоихъ родовъ іоновъ вы-
числяются изъ полной эквивалентной проводимости Л : Лл = Па . Л,
Лк — ПК’Ь и Л = Лл + Л#. Напримѣръ, для весьма разбавленнаго
раствора ИаСІ Яд=0,60, = 0,40. Величина Ло= 109,0 даетъ по-
этому въ качествѣ предѣльныхъ значеній эквивалентной проводи-
мости въ безконечно разбавленномъ растворѣ ИаСІ для іоновъ на-
трія 43,6, для іоновъ хлора 65,4. Для очень хорошо проводящихъ
электролитовъ Кольраушъ нашелъ слѣдующую важную зависимость:
Предѣльная эквивалентная проводимость каждаго іона,
при безконечномъ разбавленіи, имѣетъ во всѣхъ раство-
рахъ одно опредѣленное для іона даннаго рода значе-
ніе, независимо отъ того, съ какимъ другимъ іономъ онъ
-соединенъ. I
Напримѣръ, С1 имѣетъ одинаковыя предѣльныя значенія пров^Й^
димости въ растворахъ КС1, ИаСІ, ЬіСІ, 1/2СаС12, 1/22пС12 ичГуХ
Въ нижеслѣдующей таблицѣ даны предѣльныя значенія эквивалент-
ной проводимости для нѣкоторыхъ важныхъ іоновъ при^ Г8°, со-
Т Г °
гласно даннымъ Кольрауша.
чя
' Чу
96
Теорія электролитической проводимости
Предѣльныя значенія эквивалентной проводимости отдѣльныхъ іоновъ при 18°.
Катіоны Аніоны
К . . . . 64,7 І8г . ... 54 С1 . . . . 65,4 ЛО3 ... 33,9
№ . . . . 43,6 |Са . ... 53 Вг . . . 66 ЛО4 ... 48
Ьі . . . . 33,4 іМ8 ... 47 Л . . . 66 СНО2 . . 46
ЫН4 . . . 64 |7п . ... 47 ГЮ3 . . 61,8 С2Н3О2 . • 34
. . . 56 |Си . ... 48 СЮ3. . . 56 |8О4 . . . 70
|Ва . . . 57 Н . ... 318 С1О4 . . . 64 ОН . . . 174
' Изъ данныхъ этой таблицы можно, суммируя /\А и А#, полу-
чить величины предѣльной электропроводности любого соляного
раствора, аніонъ и катіонъ котораго имѣются въ таблицѣ. Такъ, для
КС1 Л = 64,7 + 65,4= 130,1; для А^Ю3 Л = 56 + 61,8= 117,8 и т. д.
ТЕОРІЯ ЭЛЕКТРОЛИТИЧЕСКОЙ ПРОВОДИМОСТИ.
271. Въ электролитахъ обѣ силы тока и У# пропорціональ-
ны, во-первыхъ, числу заряженныхъ электричествомъ частичекъ,
называемыхъ іонами, въ 1 куб. см., и, во-вторыхъ, скорости, съ
которою онѣ движутся вь жидкости. Законъ Ома указываетъ намъ,
что въ опредѣленномъ электролитѣ скорость частицъ пропорці-
ональна силѣ поля, т.-е. силѣ, дѣйствующей на частицы въ элек-
трическомъ полѣ. Такъ какъ эта сила должна уравновѣшиваться со-
противленіемъ тренія, испытываемымъ движущимися іонами, то за-
конъ Ома и здѣсь является тождественнымъ съ закономъ Пуазейля,
согласно которому сопротивленіе тренія, испытываемое движущимся
въ жидкости тѣломъ, пропорціонально его скорости.
Распаденіе молекулъ соли на іоны слѣдуетъ, вѣроятно, пред-
ставлять себѣ такимъ образомъ, что вода оказываетъ на соль не-
прерывное іонизирующее дѣйствіе, подобно тому какъ эманація іони-
зируетъ газъ, къ которому она примѣшана. Число іоновъ, непре-
рывно образующихся въ каждую секунду, пропорціонально кр^пйче-
ству имѣющихся въ наличности неразложенныхъ молекулъ Г соли.
Этому непрерывному процессу іонизаціи противодѣйствуетъ само-
произвольное соединеніе іоновъ, сталкивающихся между собою и
снова соединяющихся въ молекулы. Эти рекомбинацій происходятъ,
какъ и въ газахъ (§ 127), тѣмъ чаще, чѣм^' больше прихо-
дится іоновъ на 1 куб. см. Если растворъъильно разбавленъ, то
Скорость переноса и величина іоновъ
97
рекомбинація настолько слабо вліяетъ на іонизирующее дѣйствіе во-
ды, что въ растворѣ оказываются почти исключительно іоны и лишь
весьма немногія недиссоціированныя молекулы. Этотъ теоретическій
выводъ вполнѣ подтверждается измѣреніями надъ пониженіемъ точ-
ки замерзанія весьма разбавленныхъ растворовъ, которыя указыва-
ютъ, что число растворенныхъ частичекъ равняется числу іоновъ,
образующихся при расщепленіи молекулъ.
Эта теорія объясняетъ, почему эквивалентная проводимость
растворовъ солей непрерывно возрастаетъ съ разбавленіемъ. Число
іоновъ тѣмъ больше по сравненію со всѣмъ количествомъ раство-
ренной соли, чѣмъ сильнѣе разбавленъ растворъ. Предѣльное зна-
ченіе эквивалентной проводимости соотвѣтствуетъ совершенной дис-
соціаціи всѣхъ молекулъ соли. Предѣльная величина эквивалентной
проводимости для опредѣленнаго рода іоновъ даетъ намъ проводи-
мость одного эквивалента свободныхъ іоновъ этого рода, находя-
щихся въ растворѣ. Этимъ вполнѣ разъясняется законъ Кольрауша.
СКОРОСТЬ ПЕРЕНОСА И ВЕЛИЧИНА ІОНОВЪ.
272. По величинѣ предѣльной проводимости для опредѣленнаго
рода іоновъ можно вычислить скорость, съ которою эти іоны дви-
жутся въ электрическомъ полѣ с ——— • Если мы назовемъ ско-
рости катіона и аніона соотвѣтственно черезъ и ѵА, то токъ У
на квадратный сантиметръ раствора, содержащаго V граммъ-эквива-
лентовъ іонизированныхъ молекулъ на одинъ кубическій сантиметръ,
равняется /д + Зк = (ѵа + ^к) ѵ . 96540, такъ какъ каждый граммъ-
эквивалентъ несетъ зарядъ, равный 96 540 кулонамъ. Въ сильно раз-
бавленныхъ растворахъ концентрація іоновъ равна всей концентра-
ціи раствора, такъ какъ всѣ молекулы диссоціированы, т.-е. ѵ = г).
Отсюда слѣдуетъ, что 3 = ^а) и, слѣдовательно,
Ѵк ~ 96540 Е ’
Здѣсь Кк и ^а сУть предѣльныя
положимъ
Ѵа= 96540 Е'
значенія проводимости. Если мц
ѵк = ик . Е ,
гдѣ ик и иА — скорости іоновъ
мы сокращенно будемъ называть скоростями переноса
_ _ Лд
11 к~ 96540’ 11А ~ 96540
Ми. Электричество и магнитизмъ, ч. ІГ.
ѵА = иА.Е,
, . вольтъ
въ полѣ силы 1 —т-—, которыя
іоновъ, то
см.
98
Скорость переноса и величина іоновъ
Вмѣсто Л# и Л4 сюда слѣдуетъ подставить числа таблицы,
приведенной въ § 270. Такъ напримѣръ, для скорости пере-
носа іона калія находимъ // = 0,000670, для іона натрія
и = 0,000452 ^(ср. § 128).
Какъ мы видѣли, зарядъ одновалентнаго іона е= 1,564 • 10~1а ку-
лона (§ 106); слѣдовательно, силовое дѣйствіе, испытываемое имъ въ
полѣ Е- , равняется Р=е..Е, если пользоваться единицей силы,
указанной въ § 82. Измѣреніе, описанное въ § 102, указываетъ,
что эта единица силы равняется ІО7 динъ. Поэтому сила, дѣйствую-
, г- вольтъ
щая на юнъ въ полѣ Е ———, равняется
Р= 1,564. Е- ІО-12 динъ.
Эта сила должна равняться сопротивленію тренія при движеніи іона
въ водѣ. Если р есть коэффиціентъ тренія въ С.-О.-8 единицахъ и
если мы примемъ, что іонъ имѣетъ форму шара діаметра а, то, какъ
извѣстно изъ механики, при скорости ѵ сопротивленіе Р = Зтт . а р . ѵ
динамъ. Такъ какъ ѵ = и . Е, то, слѣдовательно,
Зпя.р.и = 1,564 - ІО-12,
откуда
Величина р въ результатѣ тщательныхъ измѣреній оказывается рав-
ною 0,01055 С.-С.-8. при 18° Ц. Вставляя это число и замѣняя тг
его значеніемъ 3,1416, получаемъ
15,73 1П 19
а =-----• ІО-12 см.
и
Если это вычисленіе правильно, то діаметръ іона калія составля-
етъ 2,35-10 8 см., а діаметръ іона натрія 3,48-ІО-8 см. Эти ве-
личины оказываются того же порядка, что и діаметры молекулъ ^во-
обще, лежащіе большей частью между 2 . ІО-8 и 3 . ІО-8. Но /фор-
мула, дающая сопротивленіе тренія, предполагаетъ, что діа^гръ а
разсматриваемаго шара великъ по сравненію съ молекулярными раз-
мѣрами; поэтому эти числа слѣдуетъ разсматривать лишы какъ при-
ближенныя. Однако, изъ нихъ можно все же съ увѣренностью за-
ключить, что величины іоновъ въ водныхъ растворахъ не слишкомъ
сильно разнятся отъ величины молекулъ воды.ѵ
Законъ диссоціаціи
99
Было бы ошибочнымъ, однако, предполагать, что въ водномъ рас-
творѣ іонъ обладаетъ простымъ строеніемъ, напримѣръ, представля-
етъ собою заряженный атомъ калія, атомъ натрія, атомъ хлора и т. п.
Цѣлый рядъ фактовъ указываетъ на то, что, какъ и въ газахъ (§ 129),
въ водныхъ растворахъ вокругъ элементарнаго іона скопляются нѣ-
сколько нейтральныхъ молекулъ (молекулъ воды), образуя прочный
комокъ. Одинъ изъ фактовъ, приводящихъ къ такому выводу, за-
ключается въ слѣдующемъ. Если къ водному электролиту подбавить
какого-либо индифферентнаго вещества (напримѣръ, алкоголя), то измѣ-
ненія концентраціи, происходящія при прохожденіи электрическихъ за-
рядовъ, указываютъ, что при переносѣ іоновъ переносятся не толь-
ко К, или Иа, или С1 и т. п., но также и Н2О.
ЗАКОНЪ ДИССОЦІАЦІИ.
273. Если изложенная въ § 271 теорія диссоціаціи вѣрна, то
слѣдуетъ ожидать, что въ электролитахъ дѣйствуетъ законъ диссо-
ціаціи, подобный тому, который мы нашли въ § 127 для іонизиро-
ваннаго газа. Положимъ, что ц есть число граммъ-эквивалентовъ, рас-
творенныхъ въ 1 куб. см., при чемъ изъ нихъ п находятся въ
формѣ молекулъ иѵ — расщеплены на іоны. Очевидно, что г| = лг—ѵ.
Диссоціирующее дѣйствіе воды расщепляетъ въ одну секунду д—рп
молекулъ, гдѣ р — постоянный множитель, величина котораго слу-
житъ мѣрою диссоціирующаго дѣйствія воды на данную соль. Если
далѣе коэффиціентъ рекомбинаціи іоновъ равенъ а, то, согласно
§ 127, въ одну секунду образуются вновь аѵ2 молекулъ. Если
явленіе диссоціаціи стаціонарно, т.-е. отношеніе числа диссоціирован-
ныхъ молекулъ къ числу недиссоціированныхъ постоянно, то долж-
но соблюдаться равенство:
р . п = а. ѵ2.
Положимъ -^- = с, эту величину с обычно называютъ постоянной
диссоціаціи. Въ такомъ случаѣ
V2
-
п
или, такъ какъ п — ц — ѵ,
ѵ2 = с. (г — ѵ).
Были сдѣланы попытки провѣрить это уравненіе цри'помощи
эквивалентной проводимости. Если Ло есть предѣльнб^ ея значеніе
100
Законъ диссоціаціи
для даннаго раствора соли, т.-е. эквивалентная проводимость при
полной диссоціаціи, если, далѣе, X — проводимость и ѵ — концентра-
ція іоновъ, то Х=ѵ . Ло. Если, съ другой стороны, эквивалентная прово-
димость равна и общая концентрація есть ц, т.-е. Лл = , тоХ = т].Л>р
Отсюда слѣдуетъ, что
Ау] _ ѵ
ло ~ п
Отношеніе эквивалентной проводимости при концен-
траціи ц къ предѣльной проводимости равно отношенію
числа распавшихся на іоны молекулъ къ общему числу рас-
творенныхъ молекулъ.
Если мы обозначимъ дробь посредствомъ одной буквы, по-
ложивъ
ѵ
И ~ \ ~ У’
и раздѣлимъ обѣ части уравненія диссоціаціи на г), то получимъ:
г] ._у2 = г. (1 — у).
Эквивалентная проводимость въ силу этого должна зави-
сѣть отъ концентраціи ц по слѣдующему закону
л.Лп2 = с.(Л0-Лп),
гдѣ С — с. Ло.
При повѣркѣ этой формулы обнаруживается ея примѣнимость
ко всѣмъ электролитамъ, содержащимъ относительно мало іоновъ,
напримѣръ, къ органическимъ кислотамъ и вообще къ очень слабо
диссоціированнымъ органическимъ соединеніямъ, имѣющимъ харак-
теръ солей. Иначе обстоитъ дѣло съ сильно диссоціированными
неорганическими солями.
Для всѣхъ хорошо проводящихъ солей, дающихъ бо^ь-
шое число іоновъ, измѣренія не подтверждаютъ теорети-
ческой формулы диссоціаціи.
Для иллюстраціи характера отклоненій отъ теоретической фор-
мулы дана на рис. 186 кривая, выражающая зависимость эквива-
лентной проводимости горькой соли (М^8О4) отр ^фПіентраціи ц, со-
гласно даннымъ таблицы § 270. Здѣсь же штрихами нанесена кривая,
выражающая зависимость, которая получилась^бы по закону диссоціаціи
Законъ диссоціаціи
101
изъ свойствъ весьма разбавленныхъ растворовъ для болѣе концен-
трированныхъ при томъ же значеніи Ло. Мы видимъ, что вторая
кривая, сначала совпадающая съ первою, вскорѣ спускается значи-
тельно ниже ея; слѣдовательно, измѣренная проводимость нѣсколько
концентрированныхъ растворовъ значительно превышаетъ вычи-
сленную по формулѣ диссоціаціи. Для нормальнаго раствора М^8О4
отношеніе обѣихъ проводимостей приблизительно равняется 2,6.
Причина такого отклоненія электролитовъ, богатыхъ іонами,
отъ теоретическаго закона, вѣроятно, связана съ образованіемъ ком-
Рис. 186. Эквивалентная проводимость горькой соли (М§804)
------измѣренная
------вычисленная по формулѣ диссоціаціи.
ковъ, упомянутыхъ въ предыдущемъ параграфѣ. Когда іонъ обра-
зуется изъ молекулы, онъ, вѣроятно, представляетъ собою малень-
кую частичку, которая лишь постепенно нагружается водяными ^мб-
лекулами. Въ растворахъ, весьма богатыхъ іонами, въ весьм^^алый
промежутокъ времени происходятъ какъ расщепленія, так^. и реком-
бинаціи. Поэтому въ нихъ находится чрезвычайно много7 неболь-
шихъ іоновъ, не нагруженныхъ водяными молекулами или слабо
102
Измѣреніе проводимости съ температурою
ими нагруженныхъ. Маленькіе іоны, вѣроятно, имѣютъ меньшую
склонность къ рекомбинаціи, нежели большія скопленія, т.-е. для
нихъ постоянная с имѣетъ большее значеніе. Кромѣ того, они, ко-
нечно, испытываютъ меньшее сопротивленіе тренія, такъ что и Ло для
нихъ больше. Вмѣстѣ съ тѣмъ въ изслѣдуемой формулѣ величина
С= с не является постоянной, но замѣтно возрастаетъ съ увели-
ченіемъ г]. Такимъ образомъ объясняется противорѣчіе между тео-
ріей и опытомъ. Однако, въ настоящее время еще нельзя утвер-
ждать, чтобы этотъ вопросъ былъ окончательно разрѣшенъ.
ИЗМЪНЕНІЕ ПРОВОДИМОСТИ СЪ ТЕМПЕРАТУРОЮ.
274. Разбавленные водные растворы электролитовъ, въ проти-
воположность большинству металлическихъ проводниковъ, обнару-
живаютъ возрастаніе проводимости съ повышеніемъ температуры, и
притомъ очень сильное. Причиной этого является то обстоятельство,
что коэффиціентъ тренія воды, какъ и всѣхъ жидкостей вообще,
сильно убываетъ съ возрастаніемъ температуры, въ противополож-
ность коэффиціенту тренія газовъ, который играетъ роль въ проводи-
мости металловъ и который возрастаетъ съ повышеніемъ температуры.
Уменьшеніе сопротивленія тренія и обусловливаемое имъ возраста-
ніе скоростей переноса іоновъ настолько велики, что по сравненію
съ ними имѣютъ лишь малое значеніе измѣненія степени диссоціа-
ціи въ достаточно разбавленныхъ растворахъ. Для хорошо прово-
дящихъ сильно разбавленныхъ растворовъ солей возрастаніе прово-
димости вблизи температуры 18° достигаетъ приблизительно 2,4 — 2,7%
на каждый градусъ. Уменьшеніе тренія воды достигаетъ 2,5% на 1°.
Температурный коэффиціентъ проводимости электролитовъ нѣсколь-
ко отступаетъ отъ этого числа въ ту или другую сторону; это об-
стоятельство зависитъ, вѣроятно, отъ того, что съ температурой
нѣсколько измѣняется величина тѣхъ молекулярныхъ скопленій, ко-
торыя функціонируютъ въ качествѣ іоновъ.
ТЕОРІЯ ГАЛЬВАНИЧЕСКИХЪ ЦЪПЕЙ.
275. При соприкосновеніи металлической пластиі^ірй электроли-
та, у поверхности соприкосновенія образуется двойной электрическій
слой (рис. 22 на стр. 64 первой части), напряженіеХбтораго равняется
напряженію при соприкосновеніи металла исэлектролита. Нернстъ
Теорія гальваническихъ цѣпей.
103
развилъ нижеслѣдующую теорію образованія этого двойного слоя.
Положительные іоны металла, находящіеся, какъ мы знаемъ, и въ
твердомъ металлѣ, имѣютъ извѣстное стремленіе къ растворенію въ
водѣ, подобно молекуламъ любого растворимаго тѣла. Это стремле-
ніе находится въ зависимости отъ двухъ факторовъ: оно тѣмъ сильнѣе,
чѣмъ больше „упругость растворенія" растворимаго тѣла, и оно
тѣмъ слабѣе, чѣмъ большее количество растворенныхъ частицъ уже
находится въ водѣ, т.-е. чѣмъ выше концентрація раствора. Если,
какъ при обычномъ процессѣ растворенія, незаряженныя молекулы
переходятъ въ воду, то этотъ процессъ длится до тѣхъ поръ, пока
концентрація раствора не придетъ въ равновѣсіе съ упругостью
растворенія. Но иначе обстоитъ дѣло при раствореніи іоновъ, такъ
какъ при этомъ водный растворъ заряжается положительно, а ме-
таллъ отрицательно. Такъ какъ и растворъ и металлъ являются про-
водниками, то при раствореніи іоновъ между ними устанавливается
постоянное напряженіе, и, слѣдовательно, въ мѣстахъ ихъ соприкос-
новенія образуется двойной электрическій слой, толщина котораго
равна разстоянію молекулъ металла отъ молекулъ воды. Такъ какъ ме-
таллъ заряженъ отрицательно, а растворъ положительно, то іоны испы-
тываютъ въ полѣ двойного слоя силовое дѣйствіе, направленное къ
металлу. Вслѣдствіе большой величины заряда іона это силовое
дѣйствіе возрастаетъ, послѣ перехода въ растворъ даже ничтожнаго
по вѣсу количества іоновъ, настолько значительно, что имъ уравно-
вѣшивается стремленіе къ дальнѣйшему растворенію. Напряженіе
двойного слоя, т.-е. напряженіе при соприкосновеніи металла съ
электролитомъ, даетъ, такимъ образомъ, мѣру стремленія металли-
ческихъ іоновъ къ растворенію. Оно тѣмъ больше, чѣмъ меньше
металлическихъ іоновъ растворено въ водѣ; у болѣе концентрирован-
ныхъ растворовъ оно уменьшается и становится равнымъ нулю,
когда степень концентраціи металлическихъ іоновъ въ водѣ какъ
разъ соотвѣтствуетъ упругости растворенія, т.-е. когда стремленіе
металла испускать въ растворъ новые іоны равно нулю. Если сдѣ-
лать растворъ настолько концентрированнымъ, чтобы онъ сталъ пе-
ресыщеннымъ по сравненію съ упругостью растворенія метал^^о
положительные іоны, осаждаются на металлѣ и образуется двойной
слой съ обратнымъ напряженіемъ: металлъ заряженъ положительно,
а растворъ отрицательно. Силовое дѣйствіе поля этогс^ двойного
слоя, послѣ того, какъ осадится небольшое количество Доновъ, ста-
104
Теорія гальваническихъ цѣпей
новится настолько значительнымъ, что оно препятствуетъ дальнѣй-
шему развитію процесса; поэтому напряженіе при соприкосновеніи
является въ этомъ случаѣ мѣрою стремленія іоновъ къ осажденію
изъ раствора. Первый случай (металлъ заряженъ отрицательно, рас-
творъ положительно) имѣетъ мѣсто преимущественно тогда, когда
металлъ обладаетъ очень большой упругостью растворенія. Всѣ не-
благородные, легко окисляющіеся металлы—цинкъ, свинецъ, кадмій
и т. д. отличаются большой упругостью растворенія и заряжаются
даже въ значительно концентрированныхъ растворахъ отрицательно,
т.-е. образуютъ отрицательный полюсъ гальванической цѣпи. На-
оборотъ, благородные металлы — мѣдь, серебро, ртуть — имѣютъ
по большей части столь малую упругость растворенія, что даже въ
разбавленныхъ растворахъ они заряжаются положительно, т.-е. об-
разуютъ положительный полюсъ въ цѣпи. Перекиси также заклю-
чаютъ въ себѣ трудно растворимые положительные іоны. Если мы
беремъ отъ гальванической цѣпи токъ, то мы непрерывно от-
нимаемъ отъ двойныхъ слоевъ ихъ заряды, и вслѣдствіе этого
снова начинаются задержанные ими процессы растворенія и выдѣ-
ленія іоновъ, которые продолжаются все время, пока отъ цѣпи
берутъ токъ. Такимъ образомъ въ элементѣ Даніеля растворяется
цинкъ и выдѣляется мѣдь. Химическія силы, вызывающія раство-
реніе и выдѣленіе, влекутъ іоны по направленію, противополож-
ному силовому дѣйствію электрическаго поля двойныхъ слоевъ, и
такимъ образомъ непрерывно доставляютъ энергію эѳиру, которую
послѣдній переноситъ по цѣпи тока и распредѣляетъ по провод-
никамъ, составляющимъ цѣпь.
Кромѣ напряженій въ мѣстахъ соприкосновенія металла и элек-
тролита, доставляющихъ въ гальваническихъ цѣпяхъ главную часть
всего напряженія между зажимами цѣпи, несомнѣнно образуются
еще болѣе слабые электрическіе двойные слои въ мѣстахъ сопри-
косновенія различныхъ растворовъ, напримѣръ, въ элементѣ Даніеля
на поверхности соприкосновенія растворовъ цинковаго и мѣднаго
купоросовъ внутри стѣнки глинянаго цилиндра. Іоны диффундиру-
ютъ въ воду подобно раствореннымъ молекуламъ; приэтомъ поло-
жительные и отрицательные іоны могутъ обладать различными ско-
ростями диффузіи. Вслѣдствіе этого оба соприкасай>щіеся раствора
получаютъ заряды противоположныхъ знаковъ)^ въ переходномъ
между жидкостями слоѣ возникаетъ электрическое поле. Это поле
Тепловое дѣйствіе тока
105
имѣетъ такое направленіе, что его силовыя дѣйствія противополож-
ны силовымъ дѣйствіямъ, вызваннымъ разностью скоростей диффу-
зіи; вслѣдствіе большой величины заряда іона, это поле весьма ско-
ро вполнѣ компенсируетъ разницу въ скоростяхъ диффузіи. Съ
этого момента диффузія черезъ пограничный слой становится ста-
ціонарнымъ процессомъ, и оба раствора имѣютъ постоянное напря-
женіе при соприкосновеніи.
ТЕПЛОВОЕ ДѢЙСТВІЕ ТОКА.
276. Когда въ проводникѣ происходитъ электрическій разрядъ,
проводникъ нагрѣвается; въ § 102 мы видѣли, какъ можно измѣ-
рить энергію, выдѣляющуюся въ проводникѣ въ видѣ теплоты. Те-
перь мы можемъ дать отвѣтъ на вопросъ о томъ, какимъ путемъ
эта энергія попадаетъ въ проводникъ.
Очевидно, что при этомъ энергія непрерывно почерпается изъ
того источника электричества (напримѣръ, батареи аккумуляторовъ),
отъ котораго мы беремъ токъ. Тѣ части проводника, въ которыхъ
энергія обнаруживается въ видѣ теплоты тока, могутъ находиться
на значительномъ разстояніи отъ источника электричества; такимъ
образомъ, электрическій токъ связанъ съ переносомъ энергіи на
произвольныя разстоянія. Средою, переносящею энергію, можетъ
быть, конечно, лишь эѳиръ, такъ какъ въ немъ происходятъ про-
цессы, поддерживающіе токъ электрически заряженныхъ частицъ въ
проводникѣ. Эти процессы въ эѳирѣ проявляются, какъ электриче-
ское и магнитное поля вокругъ проводника съ токомъ, и перено-
симый эффектъ поэтому опредѣляется вмѣстѣ силою электрическа-
го и магнитнаго полей.
Можно поставить себѣ, напримѣръ, такую задачу: измѣрить
энергію, переносимую въ электрическую лампу накаливанія, за то
время, когда она горитъ. Для этого мы должны сначала измѣрить
электрическое напряженіе между обоими зажимами, ведущими къ уголь-
ной нити лампы; это дѣлается путемъ приключенія вольтметра къ этимъ
двумъ точкамъ. Затѣмъ мы должны измѣрить полную величину магн^рР
наго поля вокругъ проводника съ токомъ, для чего служитъ ампер^^ръ,
введенный въ проводъ. Совершенно такимъ же образомъ мьШизмѣ-
ряли въ § 102 энергію, передаваемую проволокѣ черезъ ?ёѳиръ, и
превращающуюся въ ней въ теплоту; разница лищьрта, что тамъ
106
Тепловое дѣйствіе тока
мы вмѣсто амперметра пользовались кулонметромъ (рис. 69 на стр.
173 первой части). Если напряженіе между концами проводника равня-
ется V вольтамъ и количество электричества, прошедшее черезъ провод-
никъ, равняется М кулонамъ, то энергія равняется У/_ ЛП/ джу-
лямъ (4,19 джулей = 1 малой калоріи). Если промежутокъ времени,
за который перенесена энергія ІГ, равняется I секундамъ, то мощ-
ность или напряженіе потока энергіи равняется о = — джулямъ въ
секунду. Съ другой стороны, полная величина магнитнаго поля во-
т М 'г
кругъ проводника съ токомъ равняется 7 = • амперъ-витковъ. Та-
кимъ образомъ Ѵ — .ѴЗ. Такъ какъ единица мощности (джуль въ
секунду) называется ваттомъ, то содержаніе этого равенства мож-
но выразить слѣдующимъ образомъ:
Потокъ энергіи, или мощность, вызываемый эѳиромъ въ
какомъ-либо электрическомъ аппаратѣ, равенъ произведе-
нію изъ электрическаго напряженія между зажимами аппа-
рата и силы тока, т.-е. полной величины магнитнаго поля во-
кругъ проводника съ токомъ. Если электрическое напря-
женіе измѣряется вольтами, а полная величина магнитнаго
поля (или сила тока) амперами, то мощность выразится
въ ваттахъ; 1 ваттъ равенъ 1 джулю въ секунду.
Если, напримѣръ, напряженіе между зажимами лампы накали-
ванія равняется 110 вольтамъ, а сила тока 0,9 ампера, то лампа
потребляетъ 99 ваттъ, т.-е. около 0,1 киловатта. Такая мощность
соотвѣтствуетъ силѣ свѣта приблизительно въ 32 свѣчи.
Въ электротехникѣ при измѣреніяхъ обычно пользуются киловат-
томъ. Такъ какъ 1 джуль = 0,102 килограммъ-метра, то 1 киловаттъ
равенъ 102 килограммъ-метрамъ въ секунду. Въ механикѣ за еди-
ницу мощности принимается лошадиная сила, сокращенно обо-
значаемая черезъ Р8 г) и равная 75 килограммъ-метрамъ въ секунду.
Такимъ образомъ,
1
1
Производной отъ
киловаттъ = 1,36 Р8\
Р8 =0,736 киловатта.
киловатта является упомянуі^^въ § 102
крупная техническая единица энергіи киловаттъ-чао^/^ киловаттъ-
часъ равенъ 3 600000 джулей (такъ какъ джуль равентГІ ваттъ-секундѣ).
0 Сокращеніе нѣмецкаго Ріегсіезіагке; чаще употребляется обозначеніе
НР — сокращеніе англійскаго Ногзерошег. Прим. пер.
Техническія примѣненія теплового дѣйствія тока
107
ТЕХНИЧЕСКІЯ ПРИМѢНЕНІЯ ТЕПЛОВОГО ДѢЙСТВІЯ ТОКА.
277. Важнѣйшимъ техническимъ примѣненіемъ нагрѣванія, со-
провождающаго прохожденіе тока въ проводникѣ, является электри-
ческое освѣщеніе. Существуютъ два принципіально различныхъ метода
полученія электрическаго свѣта. Первый состоитъ въ использованіи
электрическаго дугового разряда. Для этой цѣли употребляются ду-
говыя лампы, важнѣйшіе типы которыхъ были описаны въ главѣ
IX первойчасти. Всѣ дуговыя лампы имѣютъ очень большую силу свѣта
и потому употребляются только въ тѣхъ случаяхъ, когда приходится
освѣщать большія пространства. Второй методъ полученія электри-
Рис. 187. Лампа съ угольной нитью.
Рис. 188. Танталовая лампа.
ческаго свѣта состоитъ въ томъ, что теплотою тока накаливается
добѣла твердый проводникъ, имѣющій большое сопротивленіе. На
этомъ принципѣ основано устройство лампъ накаливанія, примѣ-
няющихся преимущественно въ тѣхъ случаяхъ, когда нельзя пользо-
ваться чрезмѣрно большой силой свѣта дуговыхъ лампъ, напри-
мѣръ, въ квартирахъ. Старѣйшей лампой накаливанія является
лампа съ угольной нитью, изобрѣтенная Эдисономъ (Есіізоп) 1).‘
Эта лампа обладаетъ многими достоинствами, но имѣетъ тотъ боль-
шой недостатокъ, что расходуемая ею энергія весьма велика срав^?
нительно съ ея свѣтосилою, почему ея свѣтъ весьма дорогъ (рис.х|^7).
Угольная нить не должна нагрѣваться до слишкомъ высоцойЛем-
Э Еще раньше была изобрѣтена основанная на томъ о же принципѣ
лампа Ладыгина. ^Лурим. ред.
108
Техническія примѣненія теплового дѣйствія тока
пературы, такъ какъ иначе она размягчается и легко перегараетъ въ
наименѣе прочномъ мѣстѣ. Но чѣмъ ниже температура раска-
леннаго тѣла, тѣмъ большая часть испускаемыхъ имъ лучей лежитъ
въ инфракрасной области, къ которой нашъ глазъ не чувствите-
ленъ. Процентное содержаніе видимыхъ лучей быстро возрастаетъ
съ повышеніемъ температуры, и поэтому полезная работа источни-
ка свѣта существенно зависитъ отъ его температуры (ср. §181). Вслѣд-
ствіе этого въ послѣднее время стали замѣнять угольныя нити лампъ на-
каливанія такими веществами, которыя выдерживаютъ накаливаніе до
болѣе высокихъ температуръ. Первымъ образцомъ такой лампы является
лампа Нернста, въ которой накаливается стержень изъ магнезіи. Одна-
ко, надежды, сначала возлагавшіяся на лампу Нернста, не оправдались,
такъ какъ она обладаетъ одною весьма непріятною особенностью:
какъ подробно описано въ § 121, она крайне чувствительна къ коле-
баніямъ напряженія. Въ послѣднее время лампы Нернста выдѣлыва-
ются въ весьма маломъ количествѣ. Повидимому, онѣ пригодны пре-
имущественно въ тѣхъ случаяхъ, когда желательно получить очень боль-
шую силу свѣта. Въ новѣйшихъ лампахъ накаливанія примѣняется метал-
лическая нить; таковы осрамовыя лампы, танталовыя лампы (рис. 188)
и т. д. Тонкія металлическія нити, которыя накаливаются въ этихъ
-лампахъ, могутъ выдержать нагрѣваніе до весьма высокихъ темпера-
туръ, не расплавляясь. Поэтому такія лампы горятъ весьма экономно.
Кромѣ того, по сравненію съ лампами съ угольною нитью онѣ
имѣютъ еще то преимущество, что ихъ сопротивленіе возрастаетъ
съ повышеніемъ температуры, тогда какъ сопротивленіе угля убы-
ваетъ при повышеніи температуры. Поэтому, въ противоположйость
лампѣ Нернста, лампы съ металлическою нитью весьма мало чув-
ствительны къ колебаніямъ напряженія — менѣе, чѣмъ лампы съ
угольною нитью. Недостаткомъ ихъ является то обстоятельство,
что весьма тонкія металлическія нити, размягчаясь въ раскаленномъ
состояніи, легко разрываются отъ механическихъ сотрясеній; пр-
этому такія лампы нельзя толкать. Въ особенности это относится къ
осрамовымъ лампамъ. • і
Нижеслѣдующая таблица даетъ понятіе о свѣтовой ^полезности
электрическихъ лампъ. Въ ней дано число ваттъ, расходуемыхъ лам-
пою на 1 свѣчу:
лампа съ угольною нитью . . 2,8 -
лампа Нернста ...... 2,0^
ваттъ
Техническія примѣненія теплового дѣйствія тока
109
танталовая лампа.............1,6 ваттъ
осрамовая лампа ...... 1,1
угольная дуговая лампа . . .1,0—1,4 „
пламенная дуговая лампа . . 0,4 — 0,6 „
За исключеніемъ магнезіеваго стержня лампы Нернста, кото-
рый накаливается, какъ и угли обыкновенныхъ дуговыхъ лампъ,
прямо на воздухѣ, нити лампъ накаливанія помѣщаются въ стеклян-
ный сосудъ, возможно лучше эвакуированный. Благодаря этому отъ.
накаленныхъ нитей отнимается черезъ теплопроводность лишь неболь-
шая доля энергіи, и почти вся мощность затрачивается на лучеиспу-
сканіе. Какъ уже было указано выше, изъ этихъ лучей лишь не-
большая часть приходится на видимый свѣтъ.
278. Многочисленны также и непосредственныя примѣненія те-
плового дѣйствія электрическаго тока. Изъ многихъ примѣровъ упо-
мянемъ здѣсь лишь электрическіе кухонные аппараты, существующіе-
въ продажѣ. Они представляютъ собою сосуды съ двойными стѣн-
ками, между которыми расположены катушки очень хорошо изоли-
рованной тонкой проволоки или вообще какіе-либо металлическіе-
проводники съ большимъ сопротивленіемъ. Само собою разумѣется,
что нагрѣваніе токомъ обходится сравнительно дорого, такъ какъ
электрическая энергія представляетъ собою гораздо болѣе благород-
ную форму энергіи, нежели теплота.
Особенно важнымъ примѣненіемъ нагрѣванія токомъ являются
предохранители, которые при „короткомъ замыканіи" предотвра-
щаютъ возрастаніе силы тока въ проводѣ до опасныхъ размѣровъ.
Подъ короткимъ замыканіемъ понимается вызванное несчастной слу-
чайностью соединеніе двухъ проводовъ, находящихся при постоян-
номъ напряженіи, проводникомъ весьма малаго сопротивленія. Въ.
такомъ случаѣ можетъ получиться настолько сильный токъ, что бу-
дутъ повреждены машины, аккумуляторы или измѣрительные инстру-
менты; иногда теплота такого тока можетъ вызвать даже пожаръ.
Эта опасность и предотвращается включеніемъ предохранителей. Они
представляютъ собою короткія тонкія проволоки съ относительно
большимъ сопротивленіемъ, изготовленныя изъ достаточно діеГйб-
плавкаго металла. Токъ нагрѣваетъ эти проволоки до высок^^ тем-
пературы, при чемъ, вслѣдствіе ихъ незначительныхъ размѣровъ, на
это тратится лишь нѣсколько процентовъ всей переносимой энергіи.
Если происходитъ короткое замыканіе, то сила тока) можетъ воз-
110
Тепловые инструменты
расти лишь до опредѣленнаго максимальнаго значенія, при которомъ
еще нѣтъ опасности, но предохранитель нагрѣвается уже до темпе-
ратуры плавленія. Предохранитель расплавляется, и токъ моментально
прерывается; при этомъ вмѣсто цѣнныхъ электрическихъ аппаратовъ
гибнетъ лишь дешевый предохранитель, который легко замѣнить но-
вымъ, и опасность пожара вполнѣ устраняется.
ТЕПЛОВЫЕ ИНСТРУМЕНТЫ.
279. Тепловымъ дѣйствіемъ тока пользуются также для измѣ-
ренія силъ тока и напряженій. Измѣряемый токъ при этомъ пропу-
скается черезъ тонкую „тепловую проволоку", къ срединѣ которой
Рис. 189. Тепловой инструментъ.
припаяна другая проволока, ко-
торая при помощи часовой пру-
жины оттягиваетъ первую пер-
пендикулярно къ ея длинѣ
(рис. 189). Тепловая проволока,
нагрѣваясь при прохожденіи то-
ка, расширяется; вслѣдствіе этого
часовая пружина сжимается и
тѣмъ сильнѣе, чѣмъ сильнѣе
токъ въ тепловой проволокѣ.
Движеніе пружины передается
стрѣлкѣ, движущейся по шкалѣ.
Тепловые инструменты собствен-
но принадлежатъ къ числу из-
мѣрителей тока, но ихъ можно,
подобно гальванометрамъ, при-
мѣнять также и въ качествѣ вольтметровъ. Изображенный на рис. 189
тепловой инструментъ представляетъ собою тепловой вольтметръ.
Тепловые инструменты, какъ и инструменты съ мягкимъ желѣ-
зомъ (§ 241), даютъ отклоненія всегда въ одну сторону, независимо
отъ направленія тока; при большихъ силахъ тока ихъ отклоненія воз-
растаютъ быстрѣе, нежели при слабыхъ токахъ.
ТЕОРЕМА ПОЙНТИНГА О ПЕРЕНОСѢ ЭНЕРГІИ ВЪ ЭЛЕКТРО-
МАГНИТНОМЪ ПОЛѢ.
280. Мы обратили особое вниманіе на случай^превращенія въ
теплоту энергіи, переносимой черезъ эѳиръ е.эъ источника электри-
чества въ проводники, чтобы имѣть возможность основываться на
Теорема Пойнтинга о переносѣ энергіи
111
указанныхъ въ § 102 измѣреніяхъ. Понятно само собою, что пере-
носъ энергіи обусловливается лишь происходящими въ эѳирѣ про-
цессами, совершенно независимо отъ того, что въ заключеніе изъ
этой энергіи получается. Поэтому въ предложеніи, формулирован-
номъ нами въ § 276, ничего не говорится о конечномъ результатѣ
переноса энергіи. Для большей опредѣленности мы въ послѣдую-
щихъ разсужденіяхъ представимъ себѣ обычную параллельную про-
водку, вдоль которой энергія переносится отъ электрической станціи
къ потребителямъ. Проведемъ мысленно въ какомъ-либо мѣстѣ пло-
скость, перпендикулярную къ проводкѣ. Этимъ мы раздѣлимъ про-
странство на двѣ области: въ области, лежащей передъ сѣченіемъ,,
находится электрическая станція, а въ области за сѣченіемъ нахо-
дятся потребители; энергія, такимъ образомъ, должна проходить
черезъ это сѣченіе. Если электрическое напряженіе между обѣими
проволоками въ томъ мѣстѣ, гдѣ мысленно проводится сѣченіе, рав-
няется V вольтъ, а полная величина магнитнаго поля равна У ампе-
рамъ, то весь потокъ энергіи, проходящій черезъ сѣченіе, равняется
= ваттъ. При помощи этой формулы можно изобразить рас-
предѣленіе потока энергіи по отдѣльнымъ частямъ сѣченія. Прове-
демъ въ нашей плоскости нѣсколько магнитныхъ силовыхъ линій;
онѣ раздѣлятъ плоскость на п кольцевыхъ полосъ. Каждую такую
полосу мы раздѣлимъ на т частей, имѣющихъ по одинаковому
числу амперъ-витковъ • Если при этомъ дѣленіи мы будемъ
въ каждомъ кольцѣ исходить
изъ точекъ той прямой, которая со-
единяетъ центры поперечныхъ сѣченій обѣихъ проволокъ, то всѣ
точки дѣленія будутъ лежать на кривыхъ, идущихъ отъ поверхности
одной проволоки къ поверхности другой и пересѣкающихъ силовыя
линіи магнитнаго поля повсюду подъ прямымъ угломъ (рис. 190).
Эти кривыя мы будемъ называть „магнитными эквипотенціальными
кривыми". Такимъ образомъ вся плоскость раздѣляется на пт кри-
волинейныхъ прямоугольныхъ областей. Изъ нихъ четыре прости-
раются въ безконечность, но, если числа п и т достаточно велики^ (
то можно пренебречь 4 по сравненію съ пт и принимать во вни^
маніе лишь небольшія области, лежащія вблизи проводовъ.
слимъ мощность, проходящую черезъ одну такую, мысленно изоли-
рованную область. Чтобы предварительно выдѣлить кольцевую по-
лосу, къ которой принадлежитъ наша область, нужноѵмысленно
112
Теорема Пойнтинга о переносѣ энергіи
построить кольцеобразный замкнутый соленоидъ (§ 248), витки ко-
тораго проходили бы черезъ плоскость какъ разъ въ точкахъ обѣ-
ихъ кривыхъ, ограничивающихъ кольцевую полосу. По виткамъ со-
леноида идетъ токъ и при томъ такъ, что на каждый небольшой
прямоугольникъ, на которые раздѣлена полоса, приходится амперъ-
Рис.р90. Распредѣленіе потока энергіи по поперечному сѣченію парал-
лельныхъ проводовъ, п = 10, т = 8.
витковъ. Поле соленоида только въ томъслучаѣ переноситъ энергію
черезъ плоскость рисунка, если между обѣими кривыми, ограничи-
вающими кольцевую полосу, имѣется электрическое напряженіе^Р.
Мы можемъ представить себѣ это такимъ образомъ, что ^передъ
плоскостью полосы въ каждый витокъ соленоида включенъ'/источ-
никъ электричества напряженія Р, а позади плоскостный* каждомъ
виткѣ помѣщено сопротивленіе, поглощающее всір^доставляемую
источникомъ энергію послѣ ея прохожденія черезъ^плоскость. Если
мы теперь обратимся къ формулѣ 1} = Ѵ7, тр^найдемъ, что мощ-
ность, переносимая черезъ отдѣльную область,сравняется Р($ ваттамъ.
Теорема Пойнтинга о переносѣ энергіи
113
Величина Р соотвѣтствуетъ только одной слагающей электрическаго
поля, перпендикулярной къ направленію оси соленоида. Мы нахо-
димъ такимъ образомъ, что потокъ энергіи сквозь мысленно изоли-
рованный прямоугольникъ вычисляется по тому же правилу, что и
для всей плоскости сѣченія, и равенъ произведенію полныхъ вели-
чинъ электрическаго и магнитнаго полей въ этомъ прямоугольникѣ.
Такъ какъ переносъ энергіи является функціей эѳирныхъ процессовъ
въ каждомъ отдѣльномъ мѣстѣ, то мощность переносится черезъ
малый прямоугольникъ, согласно этому закону, также и въ томъ
случаѣ, когда этотъ прямоугольникъ является частью болѣе об-
ширнаго поля параллельныхъ проводовъ. Мощность, переносимая
черезъ полосу, ограниченную двумя сосѣдними эквипотенціальными
кривыми, вычисляется слѣдующимъ образомъ. Если электрическія
напряженія въ отдѣльныхъ прямоугольникахъ, составляющихъ эту
полосу, равны Р1, Р2і . . . , Рп, то искомая мощность равняется
О.^ + О.^ + .-. + С* = V, гдѣ Ѵ = р^р^.-. + Р^ т.-е.
представляетъ собою полное электрическое напряженіе между по-
верхностями проволокъ. Такая же самая величина получается для каж-
дой полосы, а такъ какъ число всѣхъ полосъ равно т, то сумма
потоковъ энергіи, переносимыхъ черезъ пт прямоугольниковъ, рав-
няется ш . ф . V .V, т.-е. дѣйствительно равняется всему потоку
энергіи, проходящему черезъ плоскость.
Формула, доказанная нами сейчасъ для малой прямоугольной
области, имѣетъ вполнѣ общее значеніе; мы можемъ поэтому вы-
сказать слѣдующую теорему, впервые найденную Пойнтингомъ
(Роупііпё):
Въ области, гдѣ протекаютъ электромагнитные про-
цессы, благодаря соединенному дѣйствію электрическихъ
напряженій и магнитнаго поля, происходитъ переносъ энер-
гіи въ направленіи, перпендикулярномъ какъ къ магнитно-
му, такъ и къ электрическому полю. Потокъ энергіи 1} че- *
резъ небольшую прямоугольную полосу, границы которой
соотвѣтственно параллельны и перпендикулярны магнит-
нымъ силовымъ линіямъ, равенъ произведенію изъ чи^^ф
амперъ-витковъ полосы и электрическаго напряж^ія' Р
вдоль протяженія полосы, перпендикулярнаго къН^гагнит-
ному полю, т.-е. 11 =Р^. . . І
Потокъ энергіи направленъ въ ту сторону, въ‘^к©|орую нужно
Ми. Электричество и магнитизмъ, ч. II.
8
114
Теорема Пойнтинга о переносѣ энергіи
смотрѣть, чтобы уголъ отъ направленія электрическаго поля къ
направленію магнитнаго,. описываемый слѣва направо (по часовой
стрѣлкѣ), былъ меньше двухъ прямыхъ (рис. 191).
Какъ мы видѣли, потокъ энергіи въ параллельныхъ проводахъ,
подобно ихъ магнитному и электрическому полямъ, ограничивается
ближайшей окрестностью проводовъ, если не принимать во вниманіе
безконечно малыхъ дѣйствій. Потокъ энергіи несется вплотную по
обоимъ проводамъ, какъ по рельсамъ, слѣдуя за всѣми искривле-
ніями и заворотами проволокъ. Представимъ себѣ въ нѣкоторомъ
Потокъ энергіи входитъ въ Потокъ энергіи выходитъ снизу
плоскость рисунка сверху. изъ плоскости рисунка.
Рис. 191. Направленіе переноса энергіи въ эѳирѣ.
мѣстѣ второе сѣченіе, болѣе удаленное отъ электрической станціи,
нежели первое. Пусть напряженіе въ этомъ мѣстѣ будетъ Ѵ1. Вслѣд-
ствіе потери напряженія, нѣсколько меньше, чѣмъ 1/, и, слѣдова-
тельно, переносимая черезъ это сѣченіе мощность Ц = . У также нѣ-
сколько меньше, чѣмъ 17. Потерянная мощность V — 17г = ( V — Ѵг) . 7
осталась на пути въ проводахъ въ формѣ теплоты тока. Эта потеря
соотвѣтствуетъ слагающей электрическаго поля, параллельной прово-
дамъ, которая вслѣдствіе омическаго сопротивленія проводовъ слагается
съ нормальнымъ полемъ между обѣими проволоками (при хорошихъ
проводникахъ послѣднее поле значительно превосходитъ первое). Если
сопротивленіе проводки между обоими сѣченіями равно /? омамъ,
то потеря напряженія, согласно § 261, равняется V — Л^и
потеря мощности будетъ I) - - Ц = 7? . У2. о 4
- . ’• • - *
ПРИМѢРЫ ПЕРЕНОСА ЭНЕРГІИ. 3 .
281. Въ проводникѣ съ большимъ сопротивленіемъ; напримѣръ,
въ нити лампы накаливанія, преобладаетъ слагающая"электрическаго
поля, параллельная направленію проводника. Изъ теоремы Пойнтинга
слѣдуетъ, что въ. такихъ проводникахъ энергія переносится почти
Примѣры переноса энергіи
115
перпендикулярно къ ихъ длинѣ,
электрическое поле и магнитное
пающую энергію равномѣрно по
она расходуется и превращается
Внутри проводника также имѣются
поле, которое распредѣляетъ посту-
всей внутренности проводника, гдѣ
въ теплоту.
Если электрическій токъ проходитъ черезъ двойной электриче-
скій слой въ направленіи поля этого слоя, то, по теоремѣ Пойн-
тинга, энергія вступаетъ снаружи въ узкій слой, какъ въ щель, и
распредѣляется здѣсь, распространяясь по линіямъ, идущимъ въ пло-
скости двойного слоя. Если этотъ двойной слой образованъ между ме-
талломъ и электролитомъ, то энергія тратится на происходящія въ слоѣ
химическія превращенія. Если электрическій токъ идетъ въ обратномъ
направленіи, то химическія превращенія доставляютъ энергію; эта по-
слѣдняя вытекаетъ изъ узкой щели двойного слоя въ свободное
пространство и затѣмъ переносится къ болѣе отдаленнымъ частямъ
проводки. Первый случай мы имѣемъ при зарядѣ аккумуляторовъ,
второй — при ихъ разрядѣ. Если напряженіе двойного слоя равня-
ется Ѵ1 и сила тока равна У, то мощность, вступающая въ двойной
слой или изъ него выходящая, равняется Ѵ1 . У. Если имѣется нѣ-
сколько двойныхъ слоевъ, включенныхъ послѣдовательно одинъ за
другимъ, и сумма всѣхъ напряженій равна V, то вся вступающая въ
нихъ или изъ нихъ выходящая мощность равняется V. У.
Третьимъ примѣромъ можетъ служить электрическій двигатель,
съ которымъ обстоятельнѣе мы познакомимся въ главѣ VII. На об-
моткѣ вращающейся части— „якоря" -электрическое поле слагается
изъ омическаго напряженія V и такъ называемыхъ индуктирован-
ныхъ напряженій V"; эти послѣднія преобладаютъ и располагаются
параллельно
поверхности проводника. Энергія втекаетъ, какъ и въ
лампѣ накаливанія, извнѣ въ обмотку якоря приблизительно перпен-
дикулярно къ проволокѣ, при чемъ лишь малая ея часть (ІУ' — Ѵ'.У)
превращается въ теплоту. Большая часть мощности (ІУ" = V”. У) про-
является снова въ видѣ работы, которая можетъ быть снята съ вала
мотора.
Переносимая электромагнитными процессами энергія можетъ таки^л
скопиться и въ самомъ эѳирѣ въ формѣ электрической (или магНйт-
ной) энергіи. Представимъ себѣ, напримѣръ, конденсаторъ с^/річень
высокой емкостью, пластины котораго соединены
сопротивленіе съ полюсами гальванической батареи.
торъ заряжается, въ подводящихъ проводахъ течетъ^электрическій
черезъ/ большое
ПокаоКонденса-
8
116
Примѣры переноса энергіи
токъ, и вдоль нихъ, по теоремѣ Пойнтинга, переносится энергія,
проникающая въ діэлектрикъ конденсатора (подобно тому, какъ она
проникаетъ въ двойные слои заряжаемаго аккумулятора). Здѣсь
энергія распредѣляется равномѣрно по всему электрическому полю.
Если сила заряжающаго тока (непрерывно убывающая) въ очень ко-
роткій промежутокъ времени т составляетъ въ среднемъ и напря-
женіе конденсатора (непрерывно возрастающее) въ это время равно
въ среднемъ V", то за промежутокъ времени т въ діэлектрикъ всту-
паетъ энергія Ѵ'.У.т. Если напряженіе батареи равняется V, то доста-
вляемая ею за это время энергія равняется V. У. т; разность ( V— V'). У. т
превращается въ теплоту тока въ проводахъ. Для полнаго заряженія
конденсатора до напряженія V, онъ долженъ, какъ доказано въ § 83,
получить энергію, равную Ѵг V .М джулямъ, если М- его зарядъ. Но
батарея доставила V. М джулей; слѣдовательно, половина этого ко-
личества, т.-е. Ѵ2 Ѵ.М джулей, превращается въ теплоту тока въ
проводахъ. Такъ обстоитъ дѣло, если включено большое сопроти-
вленіе. Если же его нѣтъ, то энергія Ѵ2 М.Ѵ отчасти тратится на
образованіе электрическихъ колебаній въ эѳирѣ, о которыхъ мы по-
говоримъ подробнѣе въ главѣ VIII.
Движущееся электрически заряженное тѣло, какъ мы видѣли въ
§ 251, окружено магнитнымъ полемъ. Это послѣднее вмѣстѣ съ
электрическимъ полемъ, которое возбуждено тѣломъ, производитъ
переносъ энергіи, при чемъ въ этомъ случаѣ переносится изъ одного
мѣста пространства въ другое энергія самаго электрическаго поля,
движущагося вмѣстѣ съ тѣломъ.
МЕХАНИЧЕСКАЯ АНАЛОГІЯ ПЕРЕНОСА МОЩНОСТИ ВЪ ЭѲИРЪ.
282. Механическимъ способомъ можно переносить мощность
только въ томъ случаѣ, если въ механизмѣ, обслуживающемъ
этотъ переносъ, процессъ движенія связанъ съ силами, т.-е. съ
упругими напряженіями. Величина мощности въ этомъ ^дучаѣ
равна произведенію изъ полнаго напряженія на скоростВ^ движенія.
Простымъ примѣромъ является переносъ энергіи, происходящій
при перемѣщеніи вагона лошадью или моторомъ.^рнергія пере-
носится лишь при томъ условіи, если канату® прикрѣпленный
къ вагону, испытываетъ опредѣленное натяж^^чзъ Р кгр. и если
его тянутъ съ опредѣленной скоростью ѵ . Въ такомъ случаѣ
Механическая аналогія переноса мощности въ эѳирѣ
117
лошадь или моторъ отдаютъ и вагонъ поглощаетъ мощность, равную
кгр.-м. ~ .
Р.ѵ——-----То же самое происходитъ и въ томъ случаѣ, если ва-
сск*
гонъ скрѣпленъ съ локомотивомъ ^и мощность передаетъ поршне-
вая штанга паровой машины локомотива, поперемѣнно двигаясь взадъ
и впередъ.
Другимъ примѣромъ можетъ служить переносъ мощности при по-
мощи трансмиссіоннаго вала. Мощность можетъ быть имъ передана
лишь при томъ условіи, чтобы, во-первыхъ, къ его шкиву были при-
ложены силы, вызывающія въ валѣ напряженіе крученія, и, во-вто-
рыхъ, чтобы онъ находился во вращательномъ движеніи. Полная вели-
чина напряженія крученія выражается приложеннымъ къ шкиву враща-
ющимъ моментомъ который мы можемъ выразить въ килограммъ-
метрахъ; мѣрою движенія служитъ угловая скорость гдѣ
М — число полныхъ оборотовъ въ секунду. Въ такомъ случаѣ пере-
даваемая валомъ мощность равняется (2. ш ' Связанный съ
напряженіями процессъ движенія, переносящій энергію, ограничива-
ется поверхностью вала, гдѣ постоянно происходитъ скольженіе по
окружающей средѣ — воздуху или подшипнику. Слой, въ которомъ
происходитъ это скольженіе, мы можемъ считать проводникомъ по-
тока энергіи, такъ какъ направленіе послѣдняго зависитъ отъ оріен-
тировки этого слоя. Напримѣръ, потокъ энергіи при гибкомъ валѣ
можно направлять по произволу; онъ всегда идетъ параллельно по-
верхности вала, т.-е. слою скольженія. Такъ какъ скольженіе всегда
соединено съ треніемъ, то напряженіе вала отъ шкива, соединеннаго
съ моторомъ, до шкива, на который накидывается ремень потре-
бляющей мощность машины, испытываетъ небольшія потери, особенно
въ твердыхъ подшипникахъ, и вращающій моментъ второго шкива
нѣсколько меньше момента, съ которымъ моторъ вращаетъ свой ре-
менный шкивъ. Параллельно съ потерей напряженія происходитъ и
небольшая потеря мощности: небольшая часть передаваемой валомъ
энергіи превращается въ теплоту тренія.
Также и въ модели эѳира, описанной въ § 252, энергія пере- о
носится только въ томъ случаѣ, если, во-первыхъ, происходятъ вра-^>
щательныя движенія шариковъ, представляющія магнитное по^^и^
если, во-вторыхъ, вмѣстѣ съ тѣмъ въ упругихъ клѣткахъ, крторыя
соединяются между собою шариками, дѣйствуютъ напряженія; пред-
ставляющія электрическое поле. Переносимая мощность ; пропорціо-
118
Механическая аналогія переноса мощности въ эѳирѣ
нальна произведенію изъ силы напряженія и скорости вращательнаго
движенія, т.-е. и эта модель подчиняется теоремѣ Пойнтинга. На-
правленіе, въ которомъ переносится энергія, въ этой модели пер-
пендикулярно какъ къ направленію напряженія (электрическихъ си-
ловыхъ линій), такъ и къ направленію осей вращенія (магнитныхъ
силовыхъ линій). Если, напримѣръ, напряженіе распространяется па-
раллельно поверхности „ проводника“, какъ на рис. 172, то мощ-
ность со всѣхъ сторонъ вносится въ „проводникъ" совершенно такъ
же, какъ и у настоящихъ проводниковъ большого сопротивленія
(напримѣръ, у лампъ накаливанія). Но если бы направленіе напря-
женія было приблизительно перпендикулярно къ поверхности про-
водника, какъ въ случаѣ кабеля малаго сопротивленія, то и на мо-
дели энергія распространялась бы вдоль проводника, и лишь малая
ея часть терялась бы въ проводникѣ, который является передатчикомъ
потока энергіи и въ которомъ должны происходить скольженія упру-
гихъ клѣтокъ о шарики.
Такимъ образомъ, существуетъ полная аналогія между механи-
ческими процессами въ передающемъ энергію трансмиссіономъ валѣ,
съ одной стороны, и электромагнитными процессами въ кабелѣ, съ
другой. Поэтому въ послѣдующемъ, когда намъ желательно будетъ
прибѣгать къ сравненію съ механическими процессами, мы чаще
всего будемъ пользоваться не сложной моделью эѳира, описанной
въ § 252, но трансмиссіоннымъ валомъ.
ГЛАВА ЧЕТВЕРТАЯ
СИЛОВЫЯ (ПОНДЕРОМОТОРНЫЯ) ДѢЙСТВІЯ
МАГНИТНАГО ПОЛЯ.
СИЛОВОЕ ДѢЙСТВІЕ МАГНИТНАГО ПОЛЯ НА ПРОВОДНИКЪ
СЪ ТОКОМЪ.
283. Формулированный въ электростатикѣ (§ 63) принципъ про-
тиводѣйствія примѣнимъ также и къ стаціонарнымъ магнитнымъ
Къ батареѣ
Рис. 193. Вращеніе проводника съ
токомъ вокругъ магнитнагойолюса.
полямъ. Если мы соединимъ нѣсколько постоянныхъ магнитовъ не-
подвижнымъ образомъ другъ съ другомъ или же неподвижный провод-
120 Силовое дѣйствіе магнитнаго поля на проводникъ съ токомъ
никъ съ токомъ соединимъ неподвижно съ постояннымъ магнитомъ,
то внутреннія силовыя дѣйствія не смогутъ вызвать никакого движе-
которой идетъ токъ, об-
магнитнаго стержня.
Къ батареѣ
Рис. 194. Проволока, по
вивается вокругъ
волоку, погруженную
нія, ни поступательнаго,
ни вращательнаго. Если,
напримѣръ, подвѣсить
на тонкой легко враща-
ющейся нити (рис. 192)
магнитъ, неподвижно
соединенный съ про-
водникомъ съ токомъ,
то не произойдетъ ни-
какого вращенія, хотя
на магнитъ въ полѣ то-
ка дѣйствуетъ большой
вращающій моментъ.
Отсюда слѣдуетъ, что
проводникъ съ токомъ
въ полѣ магнита испы-
тываетъ такое силовое
дѣйствіе, которое въ
точности уравновѣши-
вается дѣйствіемъ про-
водника на магнитъ.
Это силовое дѣйствіе
можно легко демон-
стрировать непосред-
ственно, если въ опытѣ,
описанномъ въ § 236,
магнитъ закрѣпить не-
подвижно, а прямоли-
нейный проводникъ^ съ
токомъ расположить
такъ, чтобы Дну могъ
вращаться^ вокругъ од-
ного изъ полюсовъ маг-
нита.у^Ми черезъ ко-
роткую мѣдную про-
въ ртуть, окружающут^Одинъ изъ полюсовъ
Силовое дѣйствіе магнитнаго поля на проводникъ съ токомъ 121
магнита (рис. 193), пустить токъ, то она начинаетъ тотчасъ вращаться
въ направленіи, которое указывается принципомъ противодѣйствія.
То же самое можно показать на весьма интересномъ опытѣ,
если воспользоваться болѣе интенсивнымъ силовымъ дѣйствіемъ
электромагнита. На рис. 194 представлена намагничивающая катуш-
ка, изъ которой выдается вверхъ на большое разстояніе ея желѣз-
ный сердечникъ. Рядомъ съ этимъ послѣднимъ подвѣшена мягкая
проволока, нижній конецъ которой укрѣпленъ въ зажимѣ; вначалѣ
проволока свободно спускается внизъ. Отъ зажима идетъ проводъ
къ одному полюсу батареи; другой ея
полюсъ соединенъ съ верхнимъ кон-
цомъ подвѣшенной проволоки. Какъ толь-
ко мы замкнемъ токъ батареи, проволока
начинаетъ вращаться вокругъ электро-
магнита; такъ какъ она снизу закрѣпле-
на, то она наматывается на выступающій
изъ катушки сердечникъ. Если измѣнить
направленіе тока, то проволока сначала
разматывается, а затѣмъ наматывается на
сердечникъ въ обратномъ направленіи.
Замѣтивъ, въ какомъ направленіи наматы-
вается проволока, мы убѣдимся, что ея
витки съ токомъ усиливаютъ магнитное
поле, намагничивающее сердечникъ. От-
сюда мы должны заключить, что энер-
гія магнитнаго поля увеличивается при
этомъ движеніи проволоки съ токомъ.
Слѣдовательно, батарея должна давать
Рис. 195. Магнитный стержень
въ качествѣ мотора.
энергію не только для движенія проволоки, но и для усиленія маг-
нитнаго поля. То же самое можно замѣтить и во всѣхъ нижеопи-
санныхъ опытахъ, въ которыхъ проводникъ съ токомъ движется въ
магнитномъ полѣ къ положенію равновѣсія. 4^
Изъ одного магнитнаго стержня можно, какъ замѣтилъ впер-^у М
вые Фарадэй, сдѣлать моторъ, если черезъ одну его половину
пускать электрическій токъ вдоль его длины. Для этого нужно приблизи-
тельно посрединѣ магнита помѣстить скользящій контакрз/^соеди-
ненный съ однимъ полюсомъ источника электричества. оДругой по-
люсъ соединяется съ концомъ магнита. Если послѣднійіможетъ вра-
122 Силовое дѣйствіе магнитнаго поля на проводникъ съ токомъ
щаться вокругъ своей длинной оси (рис. 195), то при замыканіи
тока онъ/начинаетъ вращаться. Исходящее извнутри магнитное поле,
пересѣкай наружныя части магнита, дѣйствуетъ на нихъ, когда онѣ
проводятъ токъ, совершенно такъ же, какъ въ опытѣ съ враще-
ніемъ мѣдной проволоки (рис. 193).
284. Чтобы точнѣе изучить сило-
вое дѣйствіе, испытываемое проводни-
комъ съ токомъ въ магнитномъ полѣ,
подвѣсимъ проволочный прямоугольникъ
на нити, прикрѣпленной посрединѣ верх-
ней горизонтальной стороны. Нижняя
сторона посрединѣ имѣетъ разрывъ, и
оба конца проволоки погружены въ
чашки со ртутью, изъ которыхъ одна
окружаетъ кольцеобразно другую. Эти
двѣ чашки соединяются съ полюсами ба-
тареи, такъ что прямоугольникъ можетъ
вращаться вокругъ своей вертикальной
средней линіи безъ перерыва тока. Та-
кой приборъ былъ построенъ впервые
Амперомъ (Ашрёге) и называется стан-
комъ Ампера (рис. 196). Если прибли-
зить къ одной изъ вертикальныхъ сто-
ронъ прямоугольника магнитный полюсъ,
то оказывается слѣдующее:
Проволока, несущая токъ, ис-
пытываетъ въ магнитномъ полѣ
дѣйствіе силы, направленіе кото-
Рис. 196. Станокъ Ампера, рой перпендикулярно къ силовымъ
линіямъ и къ направленію тока;
эта сила тѣмъ больше, чѣмъ сильнѣе, во-первыхъ, магнит-
ное поле и, во-вторыхъ, токъ.
Направленіе дѣйствія силы можно опредѣлить и помимо ; опыта
на основаніи принципа противодѣйствія. Она дѣйствуетъ {рѣдкомъ на-
правленіи, въ которомъ слѣдуетъ смотрѣть, чтобы уголъ^оѣъ направле-
нія тока къ направленію магнитнаго поля, описываемъ#^слѣва направо,
былъ меньше двухъ прямыхъ. (Ср. рис. 191, гдѣ слѣдуетъ замѣнить Е
„электрическимъ токомъи и потокъ энергіи—^ейіовымъ дѣйствіемъ").
Силовое дѣйствіе магнитнаго поля на проводникъ съ токомъ 123
Если прямоугольникъ съ токомъ малъ по сравненію съ размѣ-
рами поля, то онъ стремится установиться такимъ образомъ, чтобы
его поверхность была перпендикулярна къ направленію поля и чтобы
собственное магнитное поле внутри его имѣло одинаковое
направленіе съ большимъ магнитнымъ полемъ. То же прави-
ло справедливо и для небольшого плоскаго замкнутаго тока любой
формы. Если цѣлый рядъ одинаковыхъ круговыхъ токовъ соединенъ
въ видѣ соленоида, то длинная ось соленоида стремится устано-
виться въ направленіи силовыхъ линій. Мы видѣли въ § 237,. что*
собственное магнитное поле соленоида съ токомъ вполнѣ аналогич-
Рис. 197. Соленоидъ въ качествѣ магнитнаго стержня.
но полю прямого магнита. Соленоидъ имѣетъ „сѣверный полюсъ",,
изъ котораго выходятъ силовыя линіи его поля, и „южный полюсъ",
въ который онѣ входятъ. Въ большомъ магнитномъ полѣ соленоидъ
устанавливается такъ, что его сѣверный полюсъ обращенъ въ по-
ложительную сторону силовыхъ линій, такъ какъ поле тока внутри со-
леноида имѣетъ тогда такое же направленіе, какъ и дѣйствующее поле.
Такимъ образомъ соленоидъ во всѣхъ отношеніяхъ подобенъ,
прямому магниту (рис. 197). Если взять два соленоида съ токами,
то съ ними возможно производить совершенно такіе же опыты,
какъ съ двумя прямыми магнитами. Одноименные полюса соленои-
довъ взаимно отталкиваются, разноименные - притягиваются.
285. Если два соленоида обращены другъ къ другу разноимен-
ными полюсами, то въ обоихъ виткахъ соленоидовъ, расположенныхъ
непосредственно другъ противъ друга, токъ идетъ въ одномъ и
томъ же направленіи. Такъ какъ эти полюса взаимно притягиваются^)
то, слѣдовательно, два проводника, въ которыхъ токъ имѣетъ
наковое направленіе, стремятся приблизиться другъ къ другуХоб-
ратно, разноименные полюса двухъ соленоидовъ отталкиваются,,
изъ чего мы заключаемъ, что проводники съ токами противополож-
ныхъ направленій стремятся удалиться другъ отъ друта5
124 Силовое дѣйствіе магнитнаго поля на проводникъ съ токомъ
Параллельные проводники взаимно притягиваются, если
токи въ нихъ имѣютъ одинаковыя направленія, и взаимно
отталкиваются, если токи въ нихъ имѣютъ
противоположныя направленія.
Если свободно подвѣсить соленоидъ изъ упру-
гой проволоки, то, при прохожденіи черезъ него
тока, онъ стягивается, такъ какъ всѣ его витки
взаимно притягиваются. Это легко показать, под-
водя токъ къ нижнему концу соленоида черезъ
стаканчикъ со ртутью (рис. 198). Если токъ доста-
точно силенъ, то соленоидъ стягивается настолько,
что его нижній конецъ выскакиваетъ изъ ртути.
Вслѣдствіе этого токъ прерывается, соленоидъ вновь
подъ дѣйствіемъ силы тяжести растягивается, и
токъ опять замыкается. Такимъ образомъ нижній
конецъ соленоида непрерывно движется вверхъ и
внизъ („танцующая спираль*).
Взаимное отталкиваніе проводниковъ съ про-
тивоположно направленными токами приводитъ къ
интересному слѣдствію: замкнутый плоскій токъ
стремится расшириться такъ, чтобы ограничиваемая
проводникомъ площадь была возможно большей.
Это явленіе можно демонстрировать при помощи
горизонтальнаго прямоугольника съ токомъ, имѣю-
Рис 198 Танцую- щаго ТРИ неподвижныя стороны изъ толстой про-
щая спираль, волоки; четвертая его сторона представляетъ собой
цилиндрическій стержень, который можетъ катиться
по двумъ пересѣкаемымъ имъ сторонамъ, какъ по рельсамъ. Если
эту подвижную сторону мы помѣстимъ вблизи противоположной не-
подвижной стороны прямоугольника такъ, чтобы остальныя двѣ сто-
роны были весьма короткими, и замкнемъ токъ, то подвижная
•сторона откатится отъ неподвижной.
ИЗМѢРИТЕЛИ ТОКА съ подвижнымъ проводникомъ:
286. Если между полюсами сильнаго электромагнита пропустить
длинную гибкую проволоку (рис. 199) и концы ея при помощи ком-
мутатора соединить съ батареей, то въ моментъ замыканія тока про-
волока изогнется въ направленіи, перпендикулярномъ къ магнитнымъ
Измѣрители тока съ подвижнымъ проводникомъ
125
силовымъ линіямъ. Если измѣнить направленіе тока, то проволока
выгибается въ противоположную сторону.
Это явленіе, согласующееся съ изложенными въ § 284 зако-
нами, было использовано физіологомъ Эйнтховеномъ (Еіпйіоѵеп)
для построенія весьма важнаго измѣрителя тока — струннаго галь-
Къ батареѣ
Къ батареѣ
Рис. 199. Прямой гибкій проводникъ съ токомъ между двумя магнитными
полюсами.
ванометра. Въ полѣ сильнаго подковообразнаго магнита (рис. 200),
башмаки котораго отдѣлены одинъ отъ другого лишь узкой щелью^°
ХА
натянута „струна"—чрезвычайно тонкая платиновая нить (прово-
лока Вульстена) или же кварцевая нить, покрытая слоемъ раскален-
ной (ср. § 175) платины и потому обладающая проводимостью.
Нить наблюдается при помощи микроскопа, который Остановленъ
передъ отверстіемъ, проходящимъ черезъ оба полюсные башмака.
Если по нити проходитъ токъ, то она отклоняетсАвъ сторону и
126
Измѣрители тока съ подвижнымъ проводникомъ
тѣмъ больше, чѣмъ сильнѣе токъ. Отклоненіе измѣряется при по-
мощи окулярнаго микрометра микроскопа. Такъ какъ нить отклоня-
ется тѣмъ сильнѣе, чѣмъ свободнѣе она виситъ, то инструментъ
можно употреблять для различныхъ областей измѣреній, измѣняя
лишь натяженіе нити. На рис. 200 виденъ сверху микрометрическій
винтъ, который служитъ для регулировки напряженія нити. Струн-
ный гальванометръ имѣетъ передъ прочими измѣрителями тока то
преимущество, что, вслѣдствіе малой инерціи струны, онъ чрезвы-
Къ генератору тока
Рис. 200. Струнный
гальванометръ.
Рис. 201. Осциллографъ
(схематически).
майно быстро реагируетъ на всякое колебаніе тока. Поэтому струн-
ный гальванометръ часто употребляется въ соединеніи съ фото-
графическимъ регистрирующимъ аппаратомъ, воспринимающцмрна
быстро движущейся полосѣ фотографической бумаги изображеніе
малой части струны. Если полоса движется перпендикулярно къ на-
правленію перемѣщеній струны, то получается крива$^йзображаю-
щая измѣненіе силы тока съ теченіемъ времени.
Струнный гальванометръ съ двумя струнада, изъ которыхъ
одна подводитъ токъ, а другая отводитъ его>4называется осцил-
Измѣрители тока съ подвижнымъ проводникомъ
127
біографомъ. Отклоненіе струнъ, движущихся въ прямо противопо-
ложныхъ направленіяхъ, дѣлаютъ видимымъ при помощи легкаго зер-
кальца, прикрѣпленнаго посрединѣ струнъ (рис. 201). Если по стру-
намъ течетъ токъ, то зеркальце слегка отклоняется, что наблюдай
ется на отражаемомъ имъ свѣтовомъ лучѣ. Если этотъ свѣтовой лучъ
послѣ отраженія падаетъ на бумагу фотографическаго регистриру-
ющаго аппарата, то получаются кривыя, изображающія измѣненія
тока съ теченіемъ времени. Упомянутыя въ § 193 измѣренія пере-
мѣнныхъ токовъ въ угольной свѣтовой дугѣ, сдѣланныя Г. Т. Си-
мономъ, были произведены главнымъ образомъ такимъ путемъ при
помощи осциллографа и регистрирующаго аппарата. Симонъ поль-
зовался одновременно двумя инструментами, изъ которыхъ одинъ
Рис. 202. Кривая силы тока и кривая напряженія свѣтовой дуги
перемѣннаго тока, снятая посредствомъ осциллографа.
- - сила тока,----напряженіе.
служилъ въ качествѣ амперметра, а другой—въ качествѣ вольтметра,
и проектировалъ кривую силы тока и кривую напряженія на одно
и то же мѣсто бумаги регистрирующаго прибора. На рис. 202
представлена одна изъ снятыхъ имъ паръ кривыхъ. Чтобы получить
по нимъ кривую силы тока и напряженія, отсчитываютъ по налага-
ющимся кривымъ, какое напряженіе соотвѣтствуетъ каждому значе-
нію силы тока, и обычнымъ путемъ наносятъ на координатной сѣтис
напряженіе, какъ функцію силы тока. Такимъ способомъ получа^
ются кривыя, подобныя изображенной на рис. 127. Если заставятъ
свѣтовой лучъ, отраженный отъ зеркальца осциллографа, пада^ь^ не
на фотографическую бумагу регистрирующаго аппарата, ^йфвраща-
ющееся зеркало и отсюда на экранъ, то можно эти кривыя весьма
эффектно демонстрировать объективно.
128
Измѣрители тока съ подвижнымъ проводникомъ
Въ качествѣ какъ бы струннаго гальванометра можетъ служить
также трубка Брауна. Роль „струны“ въ этомъ случаѣ исполняетъ
пучекъ катодныхъ лучей, выходящій изъ діафрагмы. Но, въ отличіе
отъ настоящаго струннаго гальванометра, токъ катоднаго луча под-
держивается постояннымъ, а измѣряемый токъ пропускается, какъ
въ обыкновенномъ гальванометрѣ, черезъ двѣ катушки, между ко-
торыми проходитъ пучекъ катодныхъ лучей (рис. 203). Поле тока
отклоняетъ его тѣмъ сильнѣе, чѣмъ больше сила тока; это откло-
неніе наблюдается при помощи свѣтового пятна на флуоресцирую-
щемъ экранѣ трубки. Въ этомъ инструментѣ отклоненіе происходитъ
почти моментально, и его можно примѣнять также къ изслѣдованію
перемѣнныхъ токовъ весьма высокой частоты, съ числомъ перемѣнъ,
достигающимъ многихъ милліоновъ въ секунду. Если требуется
Рис. 203. Трубка Брауна въ качествѣ гальванометра.
большая чувствительность, то пользуются трубкой Венельта съ ея
совершенно мягкими катодными лучами. Если трубку Брауна, уста-
новленную въ качествѣ электрометра (см. рис. 99), снабдить еще
гальванометрическими катушками, магнитное поле которыхъ парал-
лельно электрическому полю между пластинами электрометра, то
пятно подъ вліяніемъ обоихъ полей будетъ испытывать отклоненія
въ двухъ взаимно перпендикулярныхъ направленіяхъ и будетъ по-
казывать одновременно напряженіе и силу тока. Такимъ образамъ,
при помощи этой трубки можно, напримѣръ, прямо снять кривую напря-
женія и силы тока свѣтовой дуги перемѣннаго
тоже былъ примѣненъ Г. Т. Симономъ. Онъ
такихъ чрезвычайно быстрыхъ электрическихъ
рымъ осциллографъ уже непримѣнимъ.
287. Важнѣйшій инструментъ, основанны^на дѣйствіи сильнаго
* сЛ
магнитнаго поля на проводникъ съ токоір>/ это — гальванометръ
тока. Этотъ хметодъ
пригоденъ даже для
колебаній, къ кото-
Измѣрители тока съ подвижнымъ проводникомъ
129
подво-
Рис. 204. Старая форма галь-
ванометра д' Арсонваля»
д’ Арсонваля (В’ Агзопѵаі). Въ этомъ инструментѣ (рис. 204)
проводникъ, по которому проходитъ токъ, представляетъ собою
тонкую проволоку, намотанную на весьма легкую прямоугольную
рамку, подвѣшенную на тонкой нити между полюсами сильнаго
стального магнита. Чтобы возможно лучше сконцентрировать поле
магнита, внутри прямоугольной катушки помѣщается еще цилиндри-
ческій желѣзный сердечникъ, прикрѣпленный къ штативу гальвано-
метра. Въ инструментѣ, изображенномъ на рис. 204, токъ
дится при посредствѣ металлической ни-
ти подвѣсами другой тонкой нити, спу-
скающейся внизъ совершенно свободно и
при вращеніи катушки не получающей
никакихъ замѣтныхъ напряженій. Въ по-
слѣднее время весьма часто строятся
также и градуированные амперметры со
вращающимся катушками (рис. 205).
Въ этихъ инструментахъ катушка вра-
щается на оси, снабженной двумя за-
остренными подшипниками, а напра-
вляющую силу ей сообщаютъ двѣ тон-
кія часовыя пружины, изъ которыхъ на
рис. 205 изображена лишь одна. Эти
часовыя пружины служатъ также для
того, чтобы подводить токъ. Конечно,
такіе инструменты можно строить лишь
для слабыхъ токовъ, но, пользуясь
надлежащими параллельными отвѣтвле-
ніями (§ 260), ихъ можно употре-
блять для любой области измѣреній.
Инструменты съ вращающейся катушкой имѣютъ, по сравненію съ
инструментами съ подвижнымъ магнитомъ, то важное преимуще-
ство, что ихъ показанія независимы отъ внѣшнихъ магнитныхъ 4^
полей. Въ этомъ отношеніи они превосходятъ даже панцырные галь--ф4
ванометры. Въ тѣхъ мѣстахъ, гдѣ происходятъ сильныя магни^Ш§г
возмущенія отъ электрическихъ дорогъ и т. п., работать в^лЬж-
но почти исключительно съ инструментами съ гюдвижн}>імпжагуш-
ками. Особенностью инструментовъ съ вращающейс^Ѵ^катушкой
является то ихъ свойство, что ихъ затуханіе существенно зависитъ
Ми. Электричество и магнитизмъ, ч. II. а
130
Измѣрители тока съ подвижнымъ проводникомъ
отъ ихъ сопротивленія. Существуетъ опредѣленная наиболѣе благо-
пріятная величина сопротивленія, при которой инструментъ является
„аперіодическимъ", т.-е. указатель устанавливается быстро и
безъ колебаній въ обѣ стороны. Къ этому обстоятельству мы еще
возвратимся ниже (§ 302).
288. Кромѣ гальванометра д’ Арсонваля существуетъ еще
иной типъ гальванометра съ вращающейся катушкой, отличаю-
щійся тѣмъ, что въ немъ отклоняющимъ магнитнымъ полемъ слу-
Рис. 205. Амперметръ съ вращающейся катушкой (схематически).
житъ поле катушки съ токомъ. Такой инструментъ, совершенно
лишенный желѣза, былъ примѣненъ впервые В. Веберомъ (Ѵ^фег)
въ 1846 году; его обычно называютъ электродинамометромъ.
Электродинамометръ съ зеркальнымъ отсчетомъ отличается^отъ из-
ображеннаго на рис. 204 гальванометра главнымъ образомъ только
тѣмъ, что вмѣсто подковообразнаго магнита въ нфѣ помѣщены
двѣ катушки, плоскость витковъ которыхъ ^перпендикулярна къ
плоскости витковъ вращающейся катушки. Кромѣ того въ электро-
динамометрѣ отсутствуетъ желѣзный цилиндру внутри подвижной ка-
Измѣрители тока съ подвижнымъ проводникомъ
131
тушки. Въ инструментѣ, изображенномъ на рис. 206, неподвижная
катушка находится цѣликомъ внутри подвижной. Отсчетъ на такомъ
инструментѣ дѣлается по особому методу, изобрѣтенному Симен-
сомъ (Зіешепз). Подвижная катушка виситъ на нити и кромѣ того
соединена со спиральною пружиною, которую можно натянуть до
желаемой степени при помощи крутильной головки. Эту головку
закручиваютъ настолько, чтобы подвижная катушка находилась во
вполнѣ опредѣленномъ положеніи, при которомъ соединенный съ
нею стерженекъ устанавливается на опредѣленной мѣткѣ. Если въ
катушкахъ тока нѣтъ, то
пружина не натянута, и ука-
затель, соединенный съ кру-
тильной головкой, показы-
ваетъ нуль. Когда же че-
резъ катушки проходитъ токъ,
то пружину нужно закрутить
настолько, чтобы ея упругая
сила въ точности уравновѣ-
шивала силовое дѣйствіе,
испытываемое подвижной ка-
тушкой въ полѣ неподвиж-
ной. Уголъ закручиванія от-
считывается на раздѣленномъ
кругѣ, по которому движется
указатель вращающейся го-
ловки ; этотъ уголъ и является
мѣрою силового дѣйствія маг-
Рис. 206. Крутильный электродинамометръ.
нитнаго поля.
Если обѣ катушки электродинамометра включить въ цѣпь по-
то имъ, какъ и всякимъ гальванометромъ, можно
въ качествѣ амперметра и въ качествѣ вольтметра.
слѣдовательно,
пользоваться и
Съ инструментами, содержащими мягкое желѣзо, и съ тепловыми
инструментами электродинамометръ имѣетъ то сходство, что его от-
клоненіе не измѣняется при измѣненіи направленія тока,
чувствительность при большихъ силахъ тока выше, чѣмъ при ^ма-
лыхъ. Это обстоятельство зависитъ отъ того, что какъ ^о^доняю-
щее поле, такъ и токъ въ подвижномъ проводникѣ всегда измѣ-
няются въ одномъ и томъ же смыслѣ. чДГ I
9
132
Дѣйствіе магнитнаго поля на движущіеся іоны-
Весьма часто электродинамометромъ пользуются, какъ измѣрите-
лемъ мощности,’ т.-е. въ качествѣ ваттметра. Въ этомъ случаѣ не-
подвижная катушка включается въ цѣпь, какъ катушка амперметра,
а подвижная катушка черезъ достаточное предварительное сопро-
тивленіе соединяется, подобно катушкѣ вольтметра, съ зажимами,
между которыми переносится энергія. По отклоненію мы нахо-
димъ произведеніе изъ силы тока и напряженія, т.-е. измѣряемую
мощность.
Полное отсутствіе желѣзныхъ частей дѣлаетъ электродинамо-
метръ особенно пригоднымъ для измѣреній перемѣнныхъ токовъ.
ДѢЙСТВІЕ МАГНИТНАГО ПОЛЯ НА ДВИЖУЩІЕСЯ ЮНЫ.
289. Электрическій токъ въ проводникѣ есть не что иное, какъ
движеніе электрически заряженныхъ частицъ. Эти частицы и испы-
Кь батареѣ
Къ батареѣ
тываютъ силовое дѣйствіе магнит-
наго поля. Поэтому положеніе,
высказанное въ § 284, мы можемъ
выразить еще въ такой формѣ:
Вслѣдствіе магнитнаго со-
стоянія мірового эѳира элек-
трически заряженныя частицы
при своемъ движеніи въ маг-
нитномъ полѣ
силовое дѣйствіе,
перпендикулярна
вленію движенія и
вленію силовыхъ
тѣмъ больше, 1) чѣмъ силь-
нѣе поле, 2) чѣмъ больше сла-
гающая движенія, перпенди-
кулярная къ направленію^пр-
ля, и 3) чѣмъ больше зарядъ
частицы. &&
испытываютъ
Эта сила
къ напра-
къ напра-
линій; она
Рис. 207. Вращеніе раствора соли въ
магнитномъ полѣ при прохожденіи
тока.
Силовое дѣйствіе магнитнаго поля на движущіяся ^электрически
заряженныя частицы обнаруживается съ особенной^тчетливостью
въ описанныхъ выше явленіяхъ отклоненія катоднымъ и Качаловыхъ
лучей (§§ 148 и 161). Но и кромѣ этого многочисленными опытами
Дѣйствіе магнитнаго поля на движущіеся іоны
133
можно показать, что въ проводникѣ съ токомъ силовое дѣйствіе въ
дѣйствительности испытываютъ лишь движущіеся іоны.
Кольцеобразный каналъ, дно котораго сдѣлано изъ стекла или
иного изолятора, а стѣнки — изъ тонкихъ мѣдныхъ полосъ, напол-
нимъ какимъ-либо электролитомъ, напримѣръ, растворомъ мѣднаго
купороса, и пропустимъ черезъ него токъ, пользуясь въ качествѣ
электродовъ мѣдными стѣнками канала. Если внутренній электродъ
служитъ анодомъ, то положительные іоны идутъ наружу радіально, а
отрицательные — внутрь, также радіально. Если переключить токъ,
то измѣнятся и направленія движенія обоихъ родовъ іоновъ. По-
мѣстимъ этотъ каналъ надъ полюсомъ сильнаго электромагнита
(рис. 207) такъ, чтобы магнитныя силовыя линіи проходили черезъ
него снизу вверхъ. Оба рода іоновъ будутъ испытывать силовое
дѣйствіе, перпендикулярное къ ихъ радіальному направленію движе-
нія и обращенное въ одну и ту же сторону, такъ какъ они
имѣютъ противоположные заряды и противоположныя направленія
движенія. Двигаясь подъ вліяніемъ этого импульса, іоны, благодаря
тренію, увлекаютъ съ собою жидкость. Вслѣдствіе этого жидкость
приходитъ въ движеніе и совершаетъ круговоротъ по каналу. Быстрое
движеніе жидкости можно сдѣлать видимымъ издалека, помѣстивъ на
нее маленькій деревянный поплавокъ, который будетъ кружиться
по каналу.
Подобнымъ образомъ магнитное поле отклоняетъ также и
іоны электрическихъ токовъ въ газахъ. Оно дѣйствуетъ совершенно
такъ же, какъ токъ воздуха, продуваемаго перпендикулярно къ пу-
ти разряда и къ силовымъ линіямъ поля. Въ этомъ можно убѣ-
диться, если, напримѣръ, держать подковообразный магнитъ надъ
положительной свѣтовой колонной тлѣющаго разряда, или если по-
мѣстить между полюсами магнита свѣтовую дугу. Если магнитъ очень
силенъ, то такимъ „магнитнымъ способомъ" можно „потушить" дугу.
Это дѣйствіе магнитнаго поля примѣняется въ пламенныхъ дуговыхъ
лампахъ. Какъ изображено на рис. 119, оба угля въ такой лампѣ
поставлены наклонно внизъ, и можно было бы думать, что свѣтовд^Ѵ
дуга здѣсь будетъ непрерывно увлекаться вверхъ подъ вліяніемъ,вос-
ходящаго тока горячаго воздуха, какъ въ рогообразномъ громоотводѣ
(рис. 118). Этого не происходитъ именно вслѣдствіе дѣйствія магнит-
наго поля сильнаго тока, питающаго дугу; какъ мы видѣли въ опытѣ со
скользящей шиной, это поле стремится отдалить ч^сТй, проводника
134
Дѣйствіе магнитнаго поля на движущіеся іоны
съ токомъ но возможности наружу. И въ рогообразномъ громоот-
водѣ магнитное поле оказываетъ свое вліяніе, но здѣсь оно тол-
каетъ свѣтовую дугу въ томъ же направленіи, какъ и воздушное
теченіе, т.-е. вверхъ. Въ пламенныхъ лампахъ это дѣйствіе поля тока
часто еще усиливаютъ помощью небольшого магнита, полюса ко-
тораго обращены къ обѣимъ сторонамъ свѣтовой дуги, а силовыя
линіи направлены въ ту же сторону, какъ и силовыя линіи тока дуги.
Весьма интересное явленіе наблюдается при образованіи свѣто-
вой дуги въ радіальномъ направленіи между кольцеобразнымъ уголь-
Къ батареѣ
Къ батареѣ
Рис. 208. Колесо Барлоу.
нымъ электродомъ и находящимся въ центрѣ этого кольца уголь-
нымъ стержнемъ, если при этомъ черезъ плоскость кольца про-
ходитъ перпендикулярное къ дугѣ не очень сильное магнитное поле.
При возбужденіи этого магнитнаго поля свѣтовая дуга начинаетъ
вращаться съ возрастающею скоростью и кажется огненнымъ ди-
скомъ. Это явленіе объясняется такъ же, какъ и описанное выше
вращеніе раствора мѣднаго купороса.
Давленіемъ электроновъ, находящихся въ магнитном;ь> полѣ,,
можно привести во вращеніе металлическій дискъ. Это\ явленіе мож-
но показать на такъ называемомъ колесѣ Барлоу (Вагіохѵ)— мѣд-
номъ дискѣ, который можетъ вращаться между полисами сильнаго элек-
тромагнита (рис. 208). По оси диска скользитъ пружинный кон-
тактъ, который подводитъ токъ. Край диска; внизу погруженъ въ
Явленіе Голла ч
135
ртутную ванну, съ которою соединенъ второй проводъ. Если замк-
нуть батарею, то отъ центра диска въ радіальномъ направленіи
къ краю пойдетъ токъ, и дискъ тотчасъ же начнетъ вращаться въ
магнитномъ полѣ, подобно раствору мѣдного купороса и свѣтовой
дугѣ въ описанныхъ выше опытахъ. Это вращательное движеніе
можетъ быть объяснено только тѣмъ, что и въ металлѣ электри-
ческій токъ представляетъ собою движеніе заряженныхъ матеріаль-
ныхъ частицъ, испытывающихъ силовое дѣйствіе отъ магнитнаго
поля. Эти частицы (электроны) очень скоро сталкиваются съ густо
распредѣленными атомами твердой мѣди, при чемъ токъ не можетъ
замѣтно отклониться отъ своего пути, а самый дискъ, подъ вліяніемъ
непрерывныхъ ударовъ, приходитъ въ движеніе.
ЯВЛЕНІЕ ГОЛЛА.
290. Если черезъ прямоугольную полосу однороднаго металла
равномѣрной толщины проходитъ электрическій токъ въ ея продоль-
номъ направленіи, то, въ силу симметріи, двѣ взаимно противоположныя
точки на краяхъ полосы должны имѣть одинаковые потенціалы. По-
этому, если приключить къ двумъ такимъ точкамъ измѣритель напря-
женій, то его отклоненіе будетъ нуль. Но если помѣстить полосу
съ токомъ между полюсными башмаками сильнаго электромагнита
такъ, чтобы магнитныя силовыя линіи проходили перпендикулярно
черезъ плоскость полосы, то при возбужденіи поля измѣритель на-
пряженій тотчасъ даетъ отклоненіе. При этомъ величина отклоненія,
вообще, пропорціональна произведенію изъ силы магнитнаго поля и
силы тока въ полосѣ. Это такъ называемое явленіе Голла (Наіі)
тоже обнаруживаетъ намъ дѣйствія магнитнаго поля на электроны, пе-
реносящіеся въ проводникѣ съ токомъ. Вслѣдствіе отклоненія элек-
троновъ въ одномъ направленіи, одна сторона полосы заряжается
положительно, а другая —отрицательно, и такимъ образомъ въ измѣри-
телѣ напряженій возникаетъ наблюдаемое отклоненіе.
Это объясненіе явленія Голла представляется крайне простымъ,
если ограничиться такими указаніями общаго характера; но крайне^
трудно разъяснить детали этого явленія. Если бы отрицательно ^за-
ряженные электроны двигались въ металлѣ, черезъ который ^прохо-
дитъ токъ, среди твердыхъ атомовъ, подобно газу, диффундирую-
щему въ пористомъ тѣлѣ, то они должны были бы рф\Йсѣхъ ме-
таллахъ отклоняться одинаковымъ образомъ, и при одинаковыхъ усло-
136
Явленіе Голла
віяхъ наблюдаемое напряженіе должно было бы имѣть для всѣхъ
металловъ одинаковые знакъ и величину. Въ дѣйствительности ока-
зывается, однако, не такъ, и металлы дѣлятся на двѣ группы, въ за-
висимости отъ знака явленія Голла. Для одной группы знакъ явленія
совпадаетъ съ тѣмъ, котораго слѣдовало бы ожидать, согласно простой
теоріи, но если бы электроны были заряжены не отрицательно, но
положительно. Такъ какъ это невозможно, то мы должны заключить,
что между положительными атомами металла и электронами суще-
ствуютъ разнообразныя взаимодѣйствія, которыя оказываютъ рѣшаю-
щее вліяніе на результатъ явленія Голла.
Особенно сильно обнаруживается явленіе Голла въ висмутѣ.
Въ связи съ явленіемь Голла находятся еще нѣкоторыя другія
•сходныя явленія. Такъ, напримѣръ, если тщательно поддерживать въ
металлической полосѣ постоянный токъ, то при возбужденіи магнитнаго
поля измѣняется также напряженіе между зажимами, подводящими къ
полосѣ токъ. Это явленіе часто называютъ „продольнымъ" явле-
.леніемъ Голла въ отличіе отъ вышеописаннаго „поперечнаго"
•явленія Голла. Такъ какъ отношеніе напряженія къ силѣ тока на-
зывается „сопротивленіемъ" проводника, то это явленіе называютъ
также „измѣненіемъ электрическаго сопротивленія въ магнитномъ
полѣ". Оно зависитъ несомнѣнно отъ какихъ-то вихревыхъ движе-
ній, совершаемыхъ электронами подъ дѣйствіемъ магнитнаго поля.
Это явленіе тоже наблюдается особенно рѣзко въ висмутѣ; какъ мы
упоминали выше (§ 223), оно часто примѣняется для измѣренія маг-
нитнаго поля.
ТЕОРІЯ МОЛЕКУЛЯРНЫХЪ МАГНИТОВЪ.
въ § 284, что съ соленоидомъ можно произ-
что и съ прямымъ магнитомъ. Однако, суще-
291. Мы видѣли
водить тѣ же опыты,
ствуетъ одно различіе между ними, котораго не слѣдуетъ упускать
изъ виду: соленоидъ является магнитомъ лишь какъ цѣлое, тогда
какъ магнитный стержень является магнитомъ въ любой своей части.
Если магнитный стержень разломать, то, какъ указано в^р227,
каждый его кусокъ, въ свою очередь, представитъ собою^діагнитъ.
Такимъ образомъ, мы приходимъ къ выводу, что каждая моле-
кула желѣза представляетъ собою маленькій магниту а весь магнит-
ный стержень состоитъ изъ безчисленнаго множества маленькихъ оди-
наково оріентированныхъ молекулярныхъ магнидрвъ. Возможно, что
Теорія молекулярныхъ магнитовъ
137
намагниченное и ненамагниченное желѣзо различаются только тѣмъ,
что въ первомъ молекулы оріентированы въ извѣстномъ порядкѣ,
тогда какъ во второмъ онѣ расположены совершенно безпорядочно.
Это предположеніе можно обосновать небольшимъ опытомъ. Если
стеклянную трубку, закрытую съ обѣихъ сторонъ пробками, набить
(не плотно) стальными опилками, предварительно намагниченными въ
полѣ сильнаго электромагнита, и встряхнуть эту трубку, то отдѣль-
ные магнитики расположатся совершенно безпорядочнымъ образомъ,
и стеклянная трубка поэтому не будетъ окружена снаружи магнит-
нымъ полемъ, какъ легко убѣдиться, поднося къ ней буссоль.
Если мы теперь проведемъ вдоль трубки магнитный полюсъ, то ма-
ленькіе магнитики, по крайней мѣрѣ,-частью, расположатся въ опре-
дѣленномъ направленіи, и теперь буссоль покажетъ, что трубка на-
магничена. При этомъ она оказывается вполнѣ сходной съ обыкно-
веннымъ стальнымъ стержнемъ, который также можно намагнитить,
натирая его магнитомъ. В. Веберъ разработалъ теорію, по которой
маленькіе молекулярные магниты въ желѣзѣ и въ стали имѣ-
ютъ постоянную силу. Въ желѣзѣ по прекращеніи дѣйствій намагни-
чивающей силы эти магниты сами по себѣ снова располагаются въ
безпорядкѣ; въ стали же они менѣе подвижны и, по крайней мѣрѣ
отчасти, сохраняютъ направленіе, данное имъ намагничивающимъ по-
лемъ. Эта теорія простѣйшимъ образомъ объясняетъ также и другія
свойства ферромагнитныхъ тѣлъ, о которыхъ мы будемъ говорить ниже.
Но если каждая отдѣльная молекула желѣза въ цѣломъ пред-
ставляетъ собою магнитъ постоянной силы, то естественно заклю-
чить, что каждая отдѣльная молекула желѣза представляетъ
собою соленоидъ, по которому проходитъ постоянный элек-
трическій круговой токъ. Такой взглядъ на магниты, впервые
высказанный Амперомъ, становится болѣе понятнымъ въ свѣтѣ элек-
тронной теоріи. Согласно этой теоріи, мы должны представлять себѣ,
что молекула желѣза содержитъ нѣкоторое число электроновъ, ко-
торые вращаются всѣ вокругъ общей оси въ одномъ и томъ же на-
правленіи. Такъ какъ при этомъ вращательномъ движеніи не про^/
исходитъ траты энергіи, совершенно такъ же, какъ при вращеніи
планетъ вокругъ солнца, то „ намагниченіе“ молекулы желѣза^оста-
ется неизмѣннымъ. Въ молекулахъ же другихъ тѣлъ электроны не
совершаютъ такого простого вращательнаго движенія вокругъ одной
общей оси; и этимъ объясняется особенность желѣза.^
138
Индуктированная электродвижущая сила въ проводникахъ
Въ теоріи Ампера передъ нами опять весьма явственно выступаетъ
аксіальная природа магнитныхъ величинъ, такъ какъ направленіе намаг-
ниченія есть направленіе оси вращенія. Согласно этой теоріи, помимо
электрическаго заряда не существуетъ никакой другой дѣйствующей
связи между эѳиромъ и матеріей, которую можно было бы назвать
„магнитизмомъ". Магнитное поле всегда представляетъ собою
лишь одну сторону явленія, которое мы называемъ „элек-
трическимъ токомъ“, и всѣ дѣйствія,магнитнаго состоянія
эѳира на вѣсомую матерію происходятъ лишь черезъ по-
средство движущихся электрическихъ зарядовъ.
ИНДУКТИРОВАННАЯ ЭЛЕКТРОДВИЖУЩАЯ СИЛА ВЪ ДВИЖУ-
ЩИХСЯ ПРОВОДНИКАХЪ.
292. Силовое дѣйствіе магнитнаго поля на движущіеся электри-
ческіе заряды обнаруживается не только въ тѣхъ случаяхъ, когда
іоны поддерживаются въ движеніи помощью электрическаго поля въ
проводникѣ, но и тогда, когда движеніе вызывается какими-либо ме-
ханическими силами. Когда мы на полюсѣ большого магнита помѣ-
щаемъ описанный въ § 289 круговой каналъ, наполненный раство-
ромъ мѣднаго купороса, или когда мы удаляемъ каналъ отъ полюса,
то вмѣстѣ съ каналомъ мы двигаемъ черезъ магнитныя силовыя линіи
также и находящіеся въ растворѣ іоны. Но, тогда какъ въ электри-
ческомъ токѣ, въ которомъ при описанномъ опытѣ двигались іоны,
положительные и отрицательные іоны двигались въ прямо противо-
положныя стороны, при перемѣщеніи всего сосуда оба рода іоновъ
увлекаются въ одномъ и томъ же направленіи. Поэтому въ первомъ
случаѣ магнитное поле толкаетъ движущіеся іоны всѣ въ одну сто-
должны
возник-
въ маг-
й токъ.
рону, такъ что получается механическое теченіе всей жидкости, во
второмъ же случаѣ положительные и отрицательные іоны
перемѣщаться въ противоположныя стороны, т.-е. долженъ
нуть электрическій токъ.
При движеніи замкнутаго проводящаго кольца
нитн.омъ полѣ, въ кольцѣ возникаетъ электрическі^
293. Для этого явленія характерно то обстоятельство^что элек-
трическій токъ возникаетъ безъ электрическаго поля, ^Еила, которая
гонитъ іоны, представляетъ собою не электрическое'^напряженіе, но
„электродвижущую силу“ иного рода,— а именноусилу, съ которой
Индуктированная электродвижущая сила въ проводникахъ 139
магнитное поле дѣйствуетъ на движущіеся іоны. Для измѣренія этой
электродвижущей силы лучше всего сравнить ея дѣйствіе съ дѣй-
ствіемъ какого-либо электрическаго напряженія. Съ этой цѣлью пред-
ставимъ себѣ, что кольцо въ одномъ мѣстѣ разрѣзано и къ обѣимъ
поверхностямъ разрѣза приложено электрическое напряженіе; мы ре-
гулируемъ послѣднее такимъ образомъ, чтобы оно вызывало такой
же токъ, какой возникалъ при движеніи кольца въ магнитномъ полѣ.
Такое напряженіе мы назовемъ равнымъ или эквивалентнымъ элек-
тродвижущей силѣ магнитнаго поля въ движущемся кольцѣ.
Электрическое напряженіе, эквивалентное электродвижущей силѣ
магнитнаго поля, мы можемъ измѣрить непосредственно, если пере-
рѣжемъ въ опредѣленномъ мѣстѣ движущееся проводящее кольцо и
поверхности разрѣза соединимъ съ зажимами электрометра. Въ пе-
рерѣзанномъ кольцѣ подъ дѣйствіемъ магнитнаго поля перемѣщается
лишь неизмѣримо малое число іоновъ или электроновъ, такъ какъ
вслѣдствіе большой величины заряда іоновъ на концахъ кольца тотчасъ
возникаютъ сильные заряды, электрическое поле которыхъ противо-
дѣйствуетъ силѣ магнитнаго поля. Если электрическое напряженіе
между концами кольца эквивалентно электродвижущей силѣ магнит-
наго поля, то оба дѣйствія на іоны взаимно уничтожаются, и іоны
остаются въ покоѣ. Такимъ образомъ весьма скоро само собой уста-
навливается напряженіе, эквивалентное электродвижущей силѣ маг-
нитнаго поля, и мы можемъ его прямо измѣрить электрометромъ.
Характерно при этомъ то обстоятельство, что электрическое поле въ
кольцеобразномъ проводникѣ существуетъ при отсутствіи электри-
ческаго тока, такъ какъ сила магнитнаго поля компенсируетъ силу
электрическаго поля. Подобныя же соотношенія мы встрѣчали въ
термоэлектрическихъ и гальваническихъ цѣпяхъ (§ 220 и § 275;
ср. также § 29).
Напряженіе, наблюдаемое между двумя концами не-
замкнутаго проводника, движущагося въ магнитномъ полѣ,
называется индуктированной въ проводникѣ электродви- %
жущей силой. '
Чтобы удобнѣе было наблюдать то напряженіе, о ковромъ
здѣсь идетъ рѣчь, полезно взять не одно отдѣльное разогнутое
кольцо, но разомкнутую катушку изъ многихъ, скажемъ^ ^.^витковъ.
Эти п витковъ представляютъ собою какъ бы п послѣдовательно
соединенныхъ колецъ, и индуктированныя въ этихъ кольцахъ напря-
140
Индуктированная электродвижущая сила въ проводникахъ
женія суммируются совершенно такъ же, какъ напряженія элементовъ
гальванической батареи.
Напряженіе, индуктируемое въ катушкѣ съ п оборо-
тами при ея движеніи въ магнитномъ полѣ, въ п разъ больше
электродвижущей силы, индуктируемой въ одномъ един-
ственномъ оборотѣ.
Рис. 209. Индуктированное напряженіе въ катушкѣ, движущейся въ
магнитномъ полѣ.
Если производить наблюденіе съ помощью электрометра Ган-
келя, устанавливающагося моментально (рис. 209), то можно замѣтитъ,
что индуктируемое напряженіе за короткое время движенія зависитъ
отъ скорости движенія и силы магнитнаго поля. Чѣмъ быстрѣе дви-
женіе, тѣмъ сильнѣе отклоненіе электрометра; отклонені^достигаетъ
наибольшей величины, когда катушка передвигается черезъ сильное
поле непосредственно у магнитнаго полюса. Прих удаленіи катушки
отъ полюса отклоненія электрометра противоположны отклоненіямъ,
которыя наблюдаются, когда катушку приближаетъ къ полюсу. Ин-
Индуктированная электродвижущая сила въ проводникахъ 141
дуктированныя электродвижущія силы были открыты Фарадэемъ и
имъ же впервые были точно изучены.
294. Если зажимы катушки мы соединимъ проводникомъ, то при
движеніи катушки возникаетъ токъ, сила котораго равна, согласно
закону Ома, частному отъ дѣленія индуктированнаго напряженія на
сопротивленіе всего проводника. Обозначимъ сопротивленіе катушки
черезъ 7?', сопротивленіе приключеннаго къ зажимамъ проводника
черезъ 7?" и индуктированную электродвижущую силу черезъ V; сила
тока, слѣдовательно, равна 3= V : (/?' 4-7?"). Величину V можно раз-
ложить на два слагаемыя V и V", при чемъ V' — З.К представитъ
собою „потерю напряженія" въ катушкѣ, а V" = V — V' = У. 7?" -— на-
пряженіе между зажимами. Направленіе электрическаго тока У въ
катушкѣ таково, что ея магнитное поле ослабляетъ индуктирующее
поле, если она движется въ сторону возрастающей силы поля, иг
обратно, усиливаетъ его при движеніи въ сторону убыванія силы
поля. Итакъ, всѣ случаи подчиняются правилу: „индуктированный
токъ" стремится препятствовать измѣненію того магнитнаго
поля, которое онъ окружаетъ. Изъ закона, найденнаго въ § 284г
слѣдуетъ теперь, что сила, дѣйствующая на катушку съ токомъ въ
магнитномъ полѣ, всегда направлена противоположно движенію. Слѣ-
довательно, для движенія катушки должна быть затрачена работа.
Мощность, сообщаемая при этомъ катушкѣ въ видѣ работы, равня-
ется V = V. У ваттамъ; она поглощается катушкою и соединеннымъ
съ нею проводомъ. Въ катушкѣ поглощается мощность V = V . У, а
въ проводъ поступаетъ мощность I]" — V" . У, при чемъ 77' 4" 77" — 77.
Если во внѣшнемъ проводѣ дѣйствуетъ электродвижущая сила
Ѵаі то напряженіе V" у зажимовъ должно уравновѣшивать сумму Ѵа
и омическаго напряженія 7?". У, т.-е. Ѵ" = Ѵа 4- 7?". У. Сила тока У вы-
числяется изъ условія равновѣсія Ѵ= І/' + Ѵ" = 7?'. 7+ 7?". У-|- Ѵа\ слѣ-
довательно, /=(І7—І7Й):(7?'4-Т?"). Знакъ электродвижущей силы
Ѵа можетъ быть положительнымъ и отрицательнымъ. Если онъ отри-
цательный, то разсматриваемыя электродвижущія силы даютъ мощ-
ность, слагающуюся съ мощностью 77 = V. 7 и вмѣстѣ съ нею доста-^р0
вляющую въ катушку и въ проводъ теплоту тока (7?'4-7?") ./2. Если
же этотъ знакъ положительный, то электродвижущія силы потЛОща-
ютъ, какъ описано въ § 281, мощность 17^.7= 77а, а ругающаяся
мощность Ѵ—1}а превращается въ теплоту тока. Цорто вѣрно
лишь въ томъ случаѣ, если Ѵа < V. Если же напряженіе Ѵа больше
77
142
Законы индукціи въ магнитномъ полѣ
индуктированной въ катушкѣ электродвижущей силы V, то токъ
мѣняетъ знакъ, и внѣшняя электродвижущая сила доставляетъ мощ-
ность 17а = Ѵа , часть этой мощности, именно 17 = I/. У, получаетъ
катушка, а остальная часть 17а —17 обращается въ теплоту тока.
Легко понять, что дѣлается съ мощностью 17, если вспомнить, что
при томъ направленіи тока, которое онъ имѣетъ въ этомъ случаѣ,
сила магнитнаго поля дѣйствуетъ на катушку въ направленіи ея дви-
женія. Такимъ образомъ, при движеніи катушки мощность 17 = Ѵ .3
будетъ получена въ формѣ работы.
Когда катушка съ токомъ У движется въ магнитномъ
полѣ, то въ зависимости отъ направленія тока либо въ ней
работа переходитъ въ форму электрической энергіи, либо
же. наоборотъ, электрическая энергія переходитъ въ работу.
Если индуктированное напряженіе равно V, то количество
превращаемой мощности равняется 17= Ѵ^.
Это можно выразить еще такъ: движущаяся въ магнитномъ
полѣ катушка, по которой течетъ токъ, дѣйствуетъ, въ зависимости
отъ направленія тока, либо какъ генераторъ, либо какъ моторъ.
ЗАКОНЫ ИНДУКЦІИ ВЪ МАГНИТНОМЪ полъ.
295. Соединимъ концы проволоки съ чувствительнымъ струй-
нымъ электрометромъ или же со струннымъ гальванометромъ, имѣю-
щимъ большое сопротивленіе (вольтметромъ). Туго натянувъ прово-
локу, будемъ ее перемѣщать въ щели между полюсными башмаками
сильнаго электромагнита, перпендикулярно къ длинѣ проволоки и
къ магнитнымъ силовымъ линіямъ. При помощи этого простого при-
бора мы можемъ установить слѣдующіе два закона, найденные уже
Фарадэемъ.
Первый законъ индукціи: электрическое напряженіе, индук-
тируемое въ проволокѣ при ея движеніи черезъ маг-
нитное поле, при прочихъ неизмѣнныхъ условіяхъ (дліфа
проволоки, скорость, сила поля) не зависитъ отъ матеріала
и толщины проволоки.
Второй законъ индукціи: при прочихъ равныхъ^ сл о віяхъ
индуктированное напряженіе пропорціона^^сг^скорости,
съ которою проволока движется перпендикулярно къ своей
длинѣ и къ магнитнымъ силовымъ линія^ѣ?.0
Индукція или магнитный силовой потокъ
143
При движеніи проволоки параллельно силовымъ линіямъ на-
пряженіе не индуктируется вовсе; электроны испытываютъ въ маг-
нитномъ полѣ силовое дѣйствіе только въ томъ случаѣ, если они
движутся перпендикулярно къ силовымъ линіямъ. Индуктированнаго
напряженія не получается, если двигать проволоку въ направленіи
ея длины; въ самомъ дѣлѣ, такъ какъ электродвижущая сила, съ
которой на электроны дѣйствуетъ магнитное поле, перпендику-
лярна къ направленію движенія, то она не даетъ слагающей, парал-
лельной проволокѣ. Такимъ образомъ, величина индуктированнаго
напряженія зависитъ лишь отъ той слагающей скорости, которая
перпендикулярна къ направленію поля и къ направленію проволоки.
Второй законъ короче выражается такъ: индуктированное на-
пряженіе пропорціонально скорости, съ которою проволо-
ка пересѣкаетъ магнитныя силовыя линіи.
ИНДУКЦІЯ ИЛИ МАГНИТНЫЙ силовой потокъ.
296. Если при только-что описанномъ опытѣ мы будемъ пере-
двигать проволоку черезъ магнитное поле сначала медленно, а за-
тѣмъ быстро, то въ первомъ случаѣ струнный гальванометръ пока-
жетъ малое, но продолжительное напряженіе, во второмъ же слу-
чаѣ индуктированное напряженіе велико, но длится короткое время.
Если индуктированное напряженіе за все время движенія постоянно,
то по второму закону индукціи произведеніе изъ напряженія на
промежутокъ времени, въ теченіе котораго оно длится, имѣетъ въ
обоихъ случаяхъ одинаковую величину. Вообще говоря, индукти-
рованное напряженіе не остается постояннымъ за все время движе-
нія. Но если мы весь этотъ промежутокъ времени разобьемъ на
множество маленькихъ частей, такъ чтобы въ каждый маленькій
промежутокъ напряженіе можно было считать постояннымъ, то из-
ложенное нами правило можно будетъ приложить и къ общему
случаю. Если умножимъ величину каждаго элемента времени на
соотвѣтствующее значеніе напряженія и возьмемъ сумму всѣхъ такихъ
произведеній, то полученная „сумма напряженій по времени" не^
будетъ зависѣть отъ скорости, если только проволока движется^
„
каждый разъ черезъ одну и ту же часть одного и того жеуйрЛя.
Понятіе суммы по времени играетъ важную роль такжуи въ
механикѣ; когда, мы, напримѣръ, приводимъ въ движеніе^егельный
шаръ, то скорость, которой онъ достигаетъ въ концѣХ движенія,
144
Индукція или магнитный силовой потокъ
пропорціональна произведенію изъ силы на продолжительность дѣй-
ствія силы или же, если сила, дѣйствующая во время бросанія, не
остается постоянной, пропорціональна суммѣ силъ по времени. Въ
механикѣ сумма силъ по времени называется „ударомъ" или „силой
удара"; скорость, пріобрѣтаемая шаромъ, пропорціональна удару.
Силы удара удобно измѣрять при помощи баллистическаго маятника.
Это —маятникъ, періодъ качаній котораго значительно превышаетъ
продолжительность измѣряемаго удара. Ударъ, который желаютъ из-
мѣрить, напримѣръ, ударъ ружейной пули, направляютъ на маятникъ.
Первое его отклоненіе пропорціонально удару.
Такъ какъ индуктированное въ проволокѣ напряженіе пропор-
ціонально силѣ, которая дѣйствуетъ на электроны при движеніи въ
магнитномъ полѣ, то сумма напряженій по времени пропорціональна
удару, дѣйствующему на электроны, и потому мы ее будемъ назы-
вать просто „ударомъ напряженія". Этотъ ударъ измѣряется при
помощи баллистическаго электрометра или вольтметра. Это — инстру-
ментъ съ относительно тяжелою подвижною системою, періодъ ко-
лебаній которой, во всякомъ случаѣ, великъ по сравненію съ про-
должительностью измѣряемаго удара напряженія. Подвижная система
приводится ударомъ въ движеніе, подобно баллистическому маятни-
ку, и первое ея отклоненіе пропорціонально измѣряемому удару
напряженія. Если передвигать проволоку по опредѣленному сѣченію
опредѣленнаго магнитнаго поля, то соединенный съ ней баллистиче-
скій вольтметръ даетъ всегда одно и тоже первое отклоненіе; этимъ
доказывается законъ постоянства суммы напряженій по времени.
При передвиженіи проволоки по поверхности, пересѣ-
кающей магнитное поле, индуктированный ударъ напряже-
нія не зависитъ ни отъ скорости движенія, ни отъ вещества
проволоки.
Ударъ напряженія зависитъ исключительно отъ величины маг-
нитнаго поля, пересѣкаемаго поверхностью, которую описываетъ про-
волока. Онъ даетъ намъ простѣйшій способъ измѣренія магнитнаго
поля по его силовымъ дѣйствіямъ.
Магнитная индукція. Ударъ напряженія,наблюд^Мйй между
концами проволоки при ея движеніи по нѣкоторой поверх-
ности, служитъ мѣрою магнитнаго поля, пронизывающаго
всю эту поверхность. Такъ измѣренную ов^дичину называ-
ютъ полною магнитною индукціею че^.^ь данную поверх-
Индукція или магнитный силовой потокъ
145
ность или же полнымъ магнитнымъ силовымъ потокомъ.
Единицей магнитной индукціи или магнитнаго сило-
вого потока въ узаконенной системѣ мѣръ служитъ вольтъ-
секунда.
Чтобы найти удѣльную величину магнитнаго поля, или удѣль-
ную индукцію, нужно измѣрить полную индукцію черезъ малую по-
верхность и раздѣлить ее на величину этой поверхности. Единицей
удѣльной магнитной индукціи, которую часто называютъ также
просто магнитной индукціей, является вольтъ-секунда на ква-
дратный сантиметръ.
Какъ для измѣренія электрическихъ полей мы имѣемъ два неза-
висимые другъ отъ друга метода—методъ напряженія (въ вольтахъ)
и методъ возбужденія (въ кулонахъ), точно такъ же и для магнит-
наго поля, кромѣ силы поля, измѣряемой въ амперъ-виткахъ, мы
имѣемъ еще второе независимое опредѣленіе; при этомъ ясно, что
магнитная индукція также есть векторіальная величина.
Если двигать проволоку по поверхности, параллельной силовымъ
линіямъ, то индукція оказывается равной нулю; въ перпендикуляр-
ной поверхности величина индукціи на одинъ квадратный сантиметръ
будетъ наибольшей; въ наклонномъ же направленіи ударъ напряже-
нія на квадратный сантиметръ оказывается меньше.
Направленіе магнитнаго силового потока совпадаетъ съ
направленіемъ нормали къ той поверхности,
вдоль которой нужно перемѣщать прово-
локу, чтобы получить въ разсматриваемомъ
мѣстѣ максимальный ударъ напряженія на
Рис. 210. Направле-
ніе магнитнаго си-
лового потока.
Стрѣлка указываетъ,
направленіе тока, ин-
дуктируемаго въ про-
квадратный сантиметръ.
Положительнымъ направленіемъ нормали счи-
тается то направленіе, въ которомъ нужно смо-
трѣть, чтобы индуктированная электродвижущая
сила казалась направленной слѣва направо при дви- угодьникѣ'при пово
женіи проволоки сверху внизъ. Если повернуть р°тѢ ег0 въ п°ложѳ-
г г г ; ніе, перпендикуляра
замкнутую катушку изъ положенія, парал- ~ ное къ полю.
» г Силовой потокъ про-
лельнаго СИЛОВЫМЪ ЛИНІЯМЪ, ВЪ положеніе, Х°ДИТЪ черезъ #Ло-
’ ’ скость рисунка
перпендикулярное къ нимъ, то индуктиро- сверху. >
ванный токъ въ ней идетъ справа налѣво, еслусмотрѣть
на него по положительному направленію силоцсфо потока
(рис. 210). При такомъ опредѣленіи направленіе силовогрпотока Совпа-
ли. Электричество и магнитизмъ, ч. И.
146
«Линіи магнитнаго силового потока
даетъ съ направленіемъ силы поля (§ 244) и съ направленіемъ, указы-
ваемымъ положительнымъ полюсомъ магнитной стрѣлки, такъ какъ
магнитное поле тока, индуктированнаго въ замкнутой катушкѣ, стре-
мится препятствовать измѣненію окружаемаго катушкой поля. Изъ опре-
дѣленія этого направленія можно видѣть, что магнитный силовой
потокъ, подобно силѣ магнитнаго поля, имѣетъ характеръ
ротора.
Удѣльную индукцію магнитнаго поля, измѣренную въ вольтъ-
секундахъ на квадратный сантиметръ, мы въ послѣдующемъ будемъ
всегда обозначать буквою В.
ЛИНІИ МАГНИТНАГО СИЛОВОГО ПОТОКА.
297. Магнитное поле можно представить графически при по-
мощи линій, которыя своимъ направленіемъ даютъ повсюду на-
Рис. 211. Изображеніе магнитнаго силового потока при помощи
силовыхъ линій.
правленіе поля, а своею густотой опредѣляютъ удѣльную индук-
цію въ данномъ мѣстѣ. Если эти линіи проведены такъ, что
черезъ каждый элементъ поверхности, черезъ который прохо-
дитъ силовой потокъ, равный одной вольтъ-секундѣ, проходитъ
въ среднемъ одна линія, то каждую линію мы будемъ разсма-
тривать какъ единицу силовой линіи. Чтобы сдѣлать это изображе-
ніе болѣе точнымъ, нужно проводить линіи гуще, такъ чтрйрьі одна
линія приходилась, напримѣръ, на элементъ поверхности,^ на кото-
і і
ромъ индукція составляетъ или вольт^<екунды. Каж-
дую изъ такихъ линій (рис. 211) мы должны тогда считать соот-
1 1 -° V
вѣтственно замЪгѵ- или за . ААА ААА единичной ^Жніи.
1 ООО 1 ООО ООО л .
Линіи магнитнаго силового потока суть линіи замкнутыя
147
Съ помощью линій силового потока можно формулировать за-
коны индукціи Фарадэя весьма нагляднымъ образомъ:
Напряженіе, индуктированное въ движущемся провод-
никѣ, равняется числу магнитныхъ силовыхъ линій, пере-
сѣкаемыхъ имъ за секунду.
При одинаковой скорости проводникъ пересѣкаетъ большее
число линій, если онъ движется по поверхности, перпендикулярной
къ полю; когда же проводникъ движется по поверхности, параллель-
ной силовымъ линіямъ, то онъ ни одной изъ нихъ не пересѣкаетъ.
ЛИНІИ МАГНИТНАГО СИЛОВОГО ПОТОКА СУТЬ ЛИНІИ
ЗАМКНУТЫЯ.
298. Придавъ проводнику надлежащую форму, можно заставить
его описать замкнутую поверхность. Простымъ примѣромъ можетъ
служить проволока, согнутая въ формѣ прямоугольника безъ одной
стороны или же въ формѣ полуокружности. Если оба конца такой
дуги держать неподвижно и вращать ее вокругъ прямой, соединяющей
эти концы, то дуга опишетъ замкнутую поверхность. Если это дви-
женіе происходитъ въ магнитномъ полѣ, то индуктированное |на-
пряженіе между неподвижными зажимами будетъ то положительнымъ,
то отрицательнымъ. Болѣе подробное экспериментальное изслѣдо-
ваніе показываетъ, что при этомъ положительный ударъ напряже-
нія имѣетъ точно такую же величину, какъ и отрицательный; если
все движеніе происходитъ съ достаточной быстротой, то баллисти-
ческій инструментъ не обнаруживаетъ никакого отклоненія.
Третій законъ индукціи: Если проводникъ описываетъ
въ магнитномъ полѣ замкнутую поверхность, возвращаясь
въ заключеніе въ свое начальное положеніе, то общая
сумма по времени напряженій, индуктированныхъ при этомъ
входящи^ьДвъ
с т о р о с егда
ірвррхности
движеніи, равняется нулю.
Когда проводникъ описываетъ нѣкоторую поверхность, то ударъ
напряженія равняется числу магнитныхъ силовыхъ линій, ^проходя-^
щихъ черезъ эту поверхность; слѣдовательно:
Число магнитныхъ силовыхъ линій,
замкнутую поверхность черезъ одну ея
равно числу силовыхъ линій, выходящихъ изъ п
съ другой ея стороны.
ю
148
Измѣреніе магнитнаго силового потока
Такимъ образомъ, никогда не случается, чтобы линіи магнит-
наго силового потока въ какомъ-либо мѣстѣ пространства заново
начинались или же прекращались.
Основной законъ магнитнаго силового потока. Линіи маг-
нитнаго силового потока не имѣютъ ни начала ни конца:
онѣ представляютъ собою линіи замкнутыя.
ИЗМѢРЕНІЕ МАГНИТНАГО СИЛОВОГО ПОТОКА.
299. Для измѣренія магнитнаго поля лучше всего воспользо-
ваться катушкой, обмотка которой занимаетъ мало мѣста по срав-
ненію сь ограничиваемой ею площадью. Катушка должна легко по-
ворачиваться на 180° вокругъ оси, лежащей въ плоскости витковъ.
При этомъ движеніи каждая изъ силовыхъ линій, проходящихъ черезъ
Рис. 212. Пересѣченіе силовыхъ линій
[при поворотѣ катушки на 180°.
ограничиваемую катушкою поверх-
ность, пересѣкается два раза. Если
мы черезъ ѵ обозначимъ подлежа-
щее измѣренію число силовыхъ ли-
ній, проходящихъ черезъ указанную
поверхность, то число пересѣчен-
ныхъ силовыхъ линій равняется 2ѵ
(рис. 212). Если, далѣе, число вит-
ковъ катушки равняется п, а индуктированный при поворотѣ ударъ
напряженія, измѣренный баллистическимъ вольтметромъ, равенъ <2, то
<2 = 2 и . ѵ,
Обозначимъ, далѣе, черезъ д площадь, ограничиваемую катушкой;
слагающая магнитнаго силового потока, перпендикулярная къ поверх-
ности витковъ, равняется
Остается, слѣдовательно, только проградуировать вт^вбльтъ-се-
кундахъ баллистическій вольтметръ, помощью котораго . ^мѣряется ф.
Какъ это дѣлать, мы покажемъ на конкретномъ^рримѣрѣ измѣре-
нія земного поля.
Силовой потокъ земного поля
149
СИЛОВОЙ ПОТОКЪ ЗЕМНОГО ПОЛЯ.
300. Чтобы измѣрить силовой потокъ земного поля по описан-
ному сейчасъ методу, возьмемъ круглое деревянное кольцо, обмо-
танное многими оборотами тонкой проволоки, какъ на рис. 209.
Оба конца этой катушки соединимъ съ гальванометромъ, который
служитъ здѣсь въ качествѣ вольтметра. При всякомъ движеніи ка-
тушки мы замѣчаемъ отклоненія стрѣлки, такъ какъ при этомъ пе-
Рис. 213. Градуированіе баллистическаго гальванометра въ вольтъ-
секундахъ. (Схема соединеній).
ресѣкаются линіи земного поля. Если быстро повернуть катушку на
180°, то получимъ искомое баллистическое отклоненіе.
Для градуированія гальванометра помѣстимъ катушку на столъ /
и включимъ въ цѣпь, содержащую гальванометръ, небольшое напря- %
женіе V (рис. 213). Для полученія этого напряженія замкнемъ гальт^р
ваническій элементъ извѣстнаго напряженія на большое сопротивленіе
(штепсельный реостатъ) и отведемъ параллельно опредѣленную ^мдлую
часть этого сопротивленія. Такимъ путемъ легко получить напряженіе
V въ нѣсколько милливольтъ, которое можно варіировдѣ^ Напря-
женіе V можно коротко замкнуть толстой мѣдной скобкой. Если эта
150
Силовой потокъ земного поля
скобка включена, то напряженіе у гальванометра равно нулю или, во
всякомъ случаѣ, безконечно мало по сравненію съ V. Для включенія
и выключенія скобки служитъ маятникъ, который при своихъ кача-
ніяхъ послѣдовательно производитъ включеніе и выключеніе. Напря-
женіе V приложено къ гальванометру въ теченіе времени т одного
качанія маятника и вызываетъ баллистическое отклоненіе, которое мы
и отсчитываемъ. Такъ какъ промежутокъ т нетрудно опредѣлить,
то мы можемъ, слѣдовательно, вычислить ударъ напряженія І/.т;
такимъ образомъ, варьируя V, мы можемъ всю шкалу гальванометра
градуировать на вольтъ-секунды.
Подобнаго рода опытъ далъ, напримѣръ, что баллистическія от-
клоненія взятаго гальванометра пропорціональны ударамъ напряженія,
при чемъ отклоненіе, соотвѣтствовавшее 1 милливольтъ-секундѣ, рав-
нялось 6 дѣленіямъ шкалы. Послѣ того какъ мѣдная скобка была
включена окончательно и проволочная катушка повернута на 180°
вокругъ вертикальной оси, при чемъ плоскость витковъ была пер-
пендикулярна къ направленію сѣверъ-югъ, получилось баллистическое
отклоненіе въ 22 дѣленія шкалы = 3, 7 милливольтъ-секундамъ. Такъ
какъ взятая катушка имѣла 1300 оборотовъ, то число силовыхъ
линій, проходившихъ черезъ ограничиваемый ею кругъ, равнялось
3,7.10-з 1 Ип_6
ѵ — о "іоал " ~ Ю ° вольтъ-секундъ.
Л • ІоОѵ
Средній радіусъ катушки былъ равенъ 32 см.; ограничиваемая ею
поверхность равнялась 800 кв. см. Для горизонтальной слагающей
земного поля получилась величина
В11 = . 10-6 = 0,18.10-81^^
800 кв. см.
Подобнымъ образомъ была опредѣлена вертикальная составляю-
щая земного поля. Для этого катушка была положена своимъ осно-
ваніемъ на столъ и повернута на 180°. Измѣреніе показало, что^
Вѵ = 0,44.10-8 о
Кв. см.
Весь Шиловой потокъ равенъ В=Ув^-\-В^=0ДВ . ;
• чій*’’
уголъ наклоненія ф получается изъ уравненія^ ф = —-, которое
даетъ ф = 67,7°. °
Вихревые токи
151
ВИХРЕВЫЕ ТОКИ.
301. При движеніи большого проводника, напримѣръ, металличе-
ской пластинки, въ магнитномъ полѣ, электродвижущая сила поля
дѣйствуетъ на его іоны или электроны такимъ же образомъ, какъ и
въ случаѣ проволоки. При этомъ возникаютъ токи, замкнутые въ
самой проводящей массѣ, т.-е. возникаютъ въ нѣкоторомъ родѣ вих-
ревыя движенія электроновъ. Эти вихревые токи1), въ виду осо-
бенности ихъ расположенія, не могутъ быть открыты амперметромъ;
но ихъ можно ясно обнаружить инымъ путемъ.
Вихревые токи прекрасно обнаруживаются опытомъ Ара го
(Ага^о), опубликованнымъ еще до фундаментальныхъ работъ Фа-
радэя. Надъ срединой крѣпкой круглой мѣдной пластинки, которая
при помощи центробѣжной машины можетъ быть приведена въ
быстрое вращеніе, подвѣшена магнитная стрѣлка. Между мѣднымъ
дискомъ и магнитной стрѣлкой помѣщаютъ толстую стеклянную пла-
стинку, чтобы возникающія при вращеніи воздушныя теченія не дости-
гали магнитной стрѣлки. При вращеніи диска магнитная стрѣлка на-
чинаетъ также вращаться, сначала медленно, а затѣмъ все быстрѣе,
какъ бы увлекаемая движеніемъ вполнѣ изолированнаго отъ нея
мѣднаго диска. Араго назвалъ это явленіе „магнитизмомъ вращенія1';
позже оно было объяснено Фарадэемъ, какъ слѣдствіе индуктиро-
ванныхъ вихревыхъ токовъ. Согласно законамъ, изложеннымъ въ
§ 294, въ тѣхъ частяхъ диска, которыя приближаются къ магнит-
ному полюсу, индуктируются токи, магнитное поле которыхъ оттал-
киваетъ полюсъ, въ частяхъ же, удаляющихся отъ магнитнаго полюса,
индуктируются вихревые токи, поле которыхъ притягиваетъ полюсъ.
Вслѣдствіе этого магнитная стрѣлка и увлекается движеніемъ диска.
Металлическая пластинка, въ которой циркулируютъ вихревые
токи, также испытываетъ силовое дѣйствіе; именно, магнитъ, отъ
котораго исходитъ индуктирующее поле, стремится задержать ея
движеніе. Сильное магнитное поле можетъ производить поразительно
сильное тормозящее дѣйствіе. Когда подвѣшенная въ видѣ маятнику I
толстая мѣдная пластинка (рис. 214) качается между полюсами элек^
тромагнита, то при возбужденіи магнитизма она внезапно застр^р^еть
между его полюсами и чрезвычайно медленно движется къ^вбему
наиболѣе низкому положенію, какъ если бы она находилась;!?въ>весьма
Э Часто ихъ называютъ также токами Фуко.
пер.
152
Вихревые токи
вязкой жидкости. Теряющаяся при этомъ энергія движенія пластинки
переходитъ черезъ вихревые токи въ теплоту. Описанный приборъ на-
зывается „маятникомъ Вальтенгофена" (ХѴаІіепЬоіеп) (рис. 214).
Успокаивающее дѣйствіе вихревыхъ токовъ часто примѣняется
въ измѣрительныхъ инструментахъ для прекращенія нежелательныхъ
качаній стрѣлки (другой способъ успокоенія — посредствомъ воз-
духа или жидкости нерѣдко бываетъ менѣе удобенъ). На оси
указателя укрѣпляется круглая металлическая пластинка, ирядомъ
помѣщается сильный стальной магнитъ, между полюсами^^тораго
оставлена лишь узкая щель (ср. рис. 143) такимъ об^зрмъ, чтобы
край пластинки двигался въ этой щели, не задѣвая ^магнита. При
вращеніи пластинки возникаютъ вихревые токи, которые неизмѣнно
оказываютъ равномѣрное успокаивающее дѣйствіе.
Успокоеніе гальванометра д’Арсонваля
153
УСПОКОЕНІЕ ГАЛЬВАНОМЕТРА Д’ АРСОНВАЛЯ
302. Въ инструментѣ д’Арсонваля магнитное поле должно быть
очень сильно, и потому его индукціонныя дѣйствія также сильны.
Если вращающаяся катушка инструмента замкнута, то она сама собой
успокаивается электромагнитнымъ путемъ, и указатель быстро оста-
навливается. Наоборотъ, если катушка разомкнута, то указатель ко-
леблется, подобно указателю вѣсовъ. Такъ какъ сила индуктирован-
ныхъ токовъ существенно зависитъ отъ сопротивленія катушки, то
отъ него же зависитъ и затуханіе. Если инструментъ обладаетъ
весьма малымъ внутреннимъ сопротивленіемъ, то катушка, послѣ ко-
роткаго замыканія, остается въ томъ мѣстѣ, гдѣ ее застало замы-
каніе, и измѣреніе въ такомъ случаѣ не можетъ быть произведено.
Если же катушка замкнута на очень большое сопротивленіе, то за-
туханіе незначительно, какъ и при разомкнутой катушкѣ. Существуетъ
опредѣленное наилучшее сопротивленіе, при которомъ инструментъ
устанавливается скоро и безъ колебаній—„аперіодически". При по-
строеніи инструментовъ д’Арсонваля необходимо принять это во
вниманіе. Если катушка имѣетъ шунтъ, какъ это бываетъ всегда въ
амперметрахъ для большихъ силъ тока, то изъ катушки и провод-
никовъ, связанныхъ съ шунтомъ, можно составить какъ разъ нужное
сопротивленіе, чтобы получился инструментъ, отличающійся весьма
быстрымъ и постояннымъ затуханіемъ.
Иначе обстоитъ дѣло съ лабораторными инструментами, не имѣю-
щими шунтовъ, при измѣреніи весьма малыхъ токовъ. Ихъ затуханіе
можетъ въ сильной степени зависѣть отъ внѣшняго сопротивленія.
На это слѣдуетъ обращать особенное вниманіе при употребленіи
гальванометра д’Арсонваля въ качествѣ баллистическаго аппарата,
такъ какъ въ послѣднемъ величина перваго отклоненія существенно
зависитъ отъ затуханія колебаній. Поэтому инструментъ слѣдуетъ
градуировать при томъ же внѣшнемъ сопротивленіи, при которомъ
онъ употребляется для измѣренія.
ГЛАВА ПЯТАЯ
ВОЗНИКНОВЕНІЕ И ИСЧЕЗНОВЕНІЕ МАГНИТНЫХЪ ПОЛЕЙ
ЗАКОНЪ ОТНОСИТЕЛЬНОСТИ ИНДУКЦІОННЫХЪ ДѢЙСТВІЙ.
303. Если мы соединимъ неподвижно катушку со стальнымъ
магнитомъ и будемъ ихъ вмѣстѣ двигать, то электрометръ, соеди-
ненный съ концами катушки, не дастъ отклоненія, хотя проволоч-
ные витки при этомъ непрерывно перемѣщаются въ магнитномъ по-
лѣ, и, слѣдовательно, электродвижущія силы поля должны оказывать
дѣйствіе на электроны проволоки. Уже отсутствіемъ эффекта при
спокойномъ положеніи катушки и магнита относительно земной по-
верхности подтверждается законъ относительности индукціонныхъ
дѣйствій, такъ какъ въ этомъ случаѣ катушка и магнитъ оба
участвуютъ въ движеніи земли. Только въ томъ случаѣ, когда ка-
тушка движется относительно магнита, получаются описанныя выше
индукціонныя явленія. Если затѣмъ, обратно, перемѣщать магнитъ
относительно катушки такимъ образомъ, чтобы возстановить ихъ
первоначальное относительное положеніе, то снова наблюдается
ударъ напряженія, и притомъ равный и противоположный наблю-
давшемуся раньше. Когда же магнитъ и катушка движутся вмѣстѣ
такимъ образомъ, что ихъ относительное положеніе остается неиз-
мѣннымъ, то оба дѣйствія взаимно уничтожаются.
Представимъ себѣ, что катушка находится въ абсолютномъ по-
коѣ въ міровомъ эѳирѣ. Если мы къ этой катушкѣ будемъ прибли-
жать стальной магнитъ, то электрометръ, соединенный съ концами
катушки, обнаруживаетъ напряженіе, которое длится все время, пока
движется магнитъ. Чѣмъ объясняется это напряженіе? Магнитное поле
само по себѣ не
" ’° I
можетъ оказывать силового дѣйствія на э/іуіугроны
что магнитное поле, какъ намъ хорощоОізвѣстно,
катушки, потому
дѣйствуетъ лишь на движущіеся электроны,
дѣйствуетъ лишь электрическое поле,
тельно, заключить, что магнитное
въ пространствѣ сопровождается
на покоющіеся же
Мы должны, слѣдова-
поле при^своемъ движеніи
электрическими напряженіями
Законъ относительности индукціонныхъ дѣйствій
155
въ эѳирѣ. Это обстоятельство въ извѣстной мѣрѣ соотвѣтствуетъ
разсмотрѣнному выше (§251) факту, что электрическое поле мо-
жетъ измѣнить свое положеніе въ пространствѣ лишь въ томъ слу-
чаѣ, если къ нему присоединяется магнитное поле.
При движеніи магнитнаго поля въ пространствѣ оно
всегда сопровождается электрическими напряженіями; ве-
личина этихъ напряженій вдоль произвольной замкнутой
кривой равна и противоположна электродвижущей силѣ,
съ которой магнитное поле дѣйствовало бы на электроны
проволоки, имѣющей форму этой кривой, если бы прово-
лока перемѣщалась съ тою же скоростью, какъ и поле.
Дѣйствія, вызываемыя этими электрическими напряженіями, тя-
ковы же, какъ и дѣйствія электродвижущихъ силъ, разсмотрѣнныхъ
выше. Если въ движущемся магнитномъ полѣ помѣстить покоющійся
кольцеобразный проводникъ, то эти напряженія вызовутъ въ немъ
токъ. Если кольцо въ одномъ мѣстѣ перерѣзать, то обѣ поверх-
ности разрѣза заряжаются до напряженія, которое равно и проти-
воположно напряженію вдоль проводящаго кольца, связанному съ
магнитнымъ полемъ; поэтому эти напряженія внутри проводника
взаимно уничтожаются. Но въ изолирующемъ сѣченіи имѣется элек-
трическое поле того же напряженія, и если мы обѣ поверхности
разрѣза соединимъ двумя очень близкими между собой проволоками
съ зажимами электрометра, то послѣдній обнаруживаетъ наличность
напряженія.
Невозможно отличать силовыя дѣйствія этихъ электрическихъ
полей на іоны и электроны проводника отъ электродвижущихъ силъ
магнитныхъ полей. Поэтому напряженія, наблюдаемыя между кон-
цами перерѣзаннаго въ одномъ мѣстѣ проводящаго кольца, назы-
ваются индуктированными напряженіями, независимо отъ того,
вызваны ли они электродвижущими силами магнитнаго поля или же
электрическимъ полемъ, которое связано съ перемѣннымъ полемъ.
Мы можемъ теперь формулировать законъ относительности ин- 4^
дукціонныхъ дѣйствій:
Посредствомъ наблюденія индукціонныхъ дѣйств^^ъ
""........ ...........— въ магнитномъ полѣ ничего
абсолютнаго движец/фгэтихъ
зависятъ лишь иженія
замкнутыхъ проводникахъ
нельзя узнать относительно
проводниковъ; эти дѣйствія
проводниковъ относительно
поля.
156
Электродинамическія поля
ЭЛЕКТРОДИНАМИЧЕСКІЯ ПОЛЯ.
304. Хотя непосредственными наблюденіями по большей части
невозможно отличить электродвижущія силы магнитнаго поля отъ
электрическихъ напряженій, однако безусловно необходимо строго
различать ихъ другъ отъ друга. Электродвижущія силы не имѣютъ
самостоятельнаго существованія помимо магнитнаго поля: онѣ
являются лишь дѣйствіями, по которымъ узнается магнитное поле.
Электрическое поле, соединенное съ движущимся магнитнымъ по-
лемъ, наоборотъ, представляетъ собою самостоятельное состояніе
эѳира; оно существуетъ и тогда, когда мы не наблюдаемъ его по-
средствомъ проводящаго кольца, введеннаго въ поле; для его воз-
никновенія эѳиру должна быть сообщена энергія хотя бы въ очень
маломъ количествѣ. Далѣе, послѣ того какъ магнитный стержень
приведенъ въ движеніе, необходимъ нѣкоторый промежутокъ (хотя
бы и очень малый), чтобы вокругъ стержня образовалось электри-
ческое поле и установилось стаціонарное состояніе. Роль этого
электрическаго поля состоитъ въ перенесеніи магнитнаго состоянія
въ эѳирѣ; дѣйствительно, такъ какъ магнитное поле также требуетъ
извѣстнаго количества энергіи, то, по теоремѣ Пойнтинга, для
переноса энергіи въ другія части эѳира необходима совмѣстная ра-
бота электрическаго поля съ магнитнымъ.
Для начинающихъ нѣсколько трудно представить себѣ суще-
ствованіе этихъ особенныхъ электрическихъ полей при отсутствіи
электрическихъ зарядовъ, изъ которыхъ они могли бы исходить.
Весьма важно, однако, освоиться со своеобразной природой этихъ
полей; безъ этого вся физика эѳира остается непонятной.
Представимъ себѣ, что цилиндрическій магнитный стержень
движется съ постоянной скоростью по направленію своей оси. Пред-
ставимъ себѣ въ полѣ движущагося стержня проволочное кольцо,
плоскость котораго перпендикулярна къ оси стержня, а центръ ле-
вкитъ на продолженіи этой оси. Въ этомъ кольцѣ возникаетъ элей^
трическій токъ; направленіе его мы можемъ предсказать налбено-
ваніи закона относительности, и вмѣстѣ съ тѣмъ мы увидимъ, какъ
устроено электрическое поле, соединенное съ движущимся магнит-
нымъ полемъ. Изъ симметріи слѣдуетъ, что сило^г линіи этого
поля представляютъ собою окружности, центрьДкоторыхъ лежатъ
на оси стержня. Если смотрѣть въ направлеціи движенія, то вблизи
Электродинамическія поля
157
положительнаго полюса (7Ѵ) магнита силовыя линіи идутъ справа
налѣво, а вблизи отрицательнаго полюса (5) слѣва направо; въ
плоскости симметріи магнита поле равно нулю. Электрическое поле
вокругъ движущагося магнитнаго стержня представлено на рис. 215.
Напряженія, возникающія при измѣненіи магнитныхъ
полей, могутъ существовать безъ электрическихъ зарядовъ;
они въ этомъ случаѣ образуютъ замкнутыя кривыя.
Эти напряженія не удовлетворяютъ условію равновѣсія электри-
ческихъ полей, такъ какъ линейная сумма поля по замкнутой кри-
вой отлична отъ нуля. Какимъ образомъ можно непосредственна
измѣрить линейную сумму поля вдоль замкнутой кривой, мы пока-
зали въ § 303.
Рис. 215. Электрическое поле вокругъ магнитнаго стержня, движущагося
въ направленіи своей длины.
Если въ электрическое поле, связанное съ движущимся-
магнитнымъ полемъ, ввести проволочное кольцо, перерѣ-
занное въ одномъ мѣстѣ, и соединить поверхности разрѣ-
за посредствомъ двухъ проволокъ, идущихъ весьма близко \
одна рядомъ съ другой, со струннымъ электрометромъ или
инымъ моментально устанавливающимся вольтметромъ, • то
этотъ инструментъ покажетъ линейную сумму, которую. ,
имѣло бы электрическое поле вдоль кривой, образуемой 4^
проволокою, если бы самой проволоки не было.
Дѣйствіе проволочнаго кольца состоитъ вь томъ, что всц^Йю-
мая линейная сумма поля концентрируется между повер^^етями
разрѣза кольца. Если вмѣсто кольца взять катушку съ к витками,
то между концами обмотки получится въ п - разъ о большая ли-
нейная сумма. сДЗІ
158
Возникновеніе и исчезновеніе магнитныхъ полей
Электрическія поля, не удовлетворяющія условію рав-
новѣсія, называются электродинамическими, а поля, на-
пряженія которыхъ находятся въ равновѣсіи, называются
электростатическими. .
Съ этими двумя названіями не слѣдуетъ связывать какой-либо
разницы по существу, такъ какъ дѣйствія, по которымъ обнаружи-
ваются электрическія напряженія, одинаковы для статическихъ и
динамическихъ напряженій. Напримѣръ, поле конденсатора на рис. 10
мы можемъ назвать динамическимъ при первыхъ двухъ распредѣле-
ніяхъ и статическимъ — при третьемъ. Въ механикѣ также разли-
чаются статическія и динамическія давленія. Статическимъ является,
напримѣръ, постоянное давленіе газа, сжатаго въ замкнутомъ со
всѣхъ сторонъ сосудѣ, динамическимъ — давленіе въ волнѣ сжатія,
распространяющейся въ газѣ.
ВОЗНИКНОВЕНІЕ И ИСЧЕЗНОВЕНІЕ МАГНИТНЫХЪ ПОЛЕЙ.
305. Перемѣщеніе магнитнаго поля заключается въ томъ, что
магнитное состояніе эѳира исчезаетъ въ одномъ мѣстѣ и появляется
въ другомъ. Такимъ образомъ, электрическія напряженія, о кото-
рыхъ была рѣчь въ предыдущей главѣ, въ однихъ мѣстахъ возбу-
ждаютъ магнитное поле, а въ другихъ мѣстахъ уничтожаютъ его.
Всякое возникающее, какъ и всякое исчезающее магнитное поле
связано съ электрическими напряженіями. Если мы наложимъ на
полюсь электромагнита (рис. 216) круглую катушку съ п проволоч-
ными витками и концы обмотки соединимъ съ зажимами электро-
метра Ганкеля, то электрометръ покажетъ существованіе напряже-
нія сейчасъ же, какъ только мы замкнемъ намагничивающій токъ.
Это напряженіе длится до тѣхъ поръ, пока магнитное поле не до-
стигнетъ стаціонарнаго значенія. Дѣля это напряженіе на л, мы по-
лучаемъ линейную сумму электрическаго поля, связаннаго съ воз-
никновеніемъ магнитнаго поля, вдоль окружности, образуемой ка-
тушкой. Если разомкнуть намагничивающій токъ, то электрометръ
даетъ во время исчезновенія магнитнаго поля отклоненіе про-
тивоположную сторону. (І
Для возбужденія магнитнаго поля необходй^о возни-
кновеніе электрическихъ напряженій, которыддіе уравновѣ-
шиваются взаимно; чтобы магнитное поле^вновь исчезло,
требуются электрическія напряженія противоположнаго на-
правленія.
Возникновеніе и исчезновеніе магнитныхъ полей
159
Если пользоваться аналогіей между магнитнымъ полемъ и дви-
женіями и между электрическимъ полемъ и упругими силами (срав.§ 252),
то это предложеніе выражаетъ, что магнитныя явленія въ эѳирѣ
обладаютъ инерціей, которая можетъ быть преодолѣна лишь элек-
трическими силами напряженій при измѣненіи поля. Это становится
вполнѣ яснымъ,
если мы для сравненія будемъ разсматривать вра-
щеніе оси, какъ въ § 282;
инерціи болѣе наглядными,
мы представимъ себѣ, что
на ось насажено маховое
колесо. Чтобы привести
во вращеніе ось съ махо-
вымъ колесомъ, нужно
приложить силу, вызываю-
щую въ оси упругія си-
лы. Эти послѣднія не урав-
новѣшиваются другими,
пока онѣ еще должны пре-
одолѣвать сопротивленія
инерціи; это продолжа-
ется до тѣхъ поръ, пока не
установится стаціонарная
скорость вращенія. Только
при постоянной скорости
(какъ въ магнитномъ по-
лѣ постояннаго тока) всѣ
дѣйствующія силы нахо-
дятся въ статическомъ рав-
новѣсіи. Чтобы ось и ма-
при этомъ, чтобы сдѣлать дѣйствія
Къ батарею
Рис. 216. Измѣреніе электрическихъ напря-
женій въ возникающемъ и исчезающемъ маг-
нитномъ полѣ при помощи проволочной ка-
тушки и электрометра.
ховое колесо привести
обратно въ состояніе покоя, нужно прило-
жить силы, направленныя противоположно тѣмъ, которыя требова-
лись для возбужденія движенія. . х
Если электрическія напряженія не находятся въ равновѣсіи, то л^)
они всегда должны либо возбуждать магнитное поле, либо же, ес^^Ч
таковое уже имѣется, измѣнять его. Электрическое поле, которое,
подобно представленному на рис. 10, не находится въ равновѣсіи,
л.
возбуждаетъ, слѣдовательно, магнитное поле, вызывающее, какъ мы
видѣли въ § 250, перемѣщеніе электрическихъ силовухъ-диній. Из-
160
Второй основной законъ электродинамики Максвелла
мѣненіе электрическаго поля идетъ въ такомъ направленіи, что поле
приближается къ состоянію равновѣсія. Но поле не можетъ оста-
ваться въ состояніи равновѣсія, если магнитный процессъ не закон-
чился. Благодаря этому сперва возникаютъ электромагнитныя коле-
банія, которыя затухаютъ вслѣдствіе поглощенія энергіи въ провод-
никахъ и, наконецъ, приводятъ къ электрическому равновѣсію. Этотъ
процессъ аналогиченъ механическому процессу, наблюдаемому нами
при внезапномъ отпусканіи согнутой пружины. Такъ какъ сейчасъ
послѣ того, какъ мы отпустимъ пружину, упругія силы не находятся
въ равновѣсіи, то возникаетъ движеніе, направленное къ положенію
равновѣсія; но пружина не можетъ остаться въ равновѣсіи, такъ
какъ движеніе еще не прекращается. Такимъ образомъ возникаютъ
колебанія, при которыхъ вслѣдствіе тренія теряется энергія до тѣхъ
поръ, пока, наконецъ, не установится равновѣсіе.
ВТОРОЙ ОСНОВНОЙ ЗАКОНЪ ЭЛЕКТРОДИНАМИКИ МАКСВЕЛЛА.
306. Изъ закона относительности непосредственно видно, на-
сколько велики электрическія напряженія, которыми сопровождаются
измѣненія магнитнаго поля. Для того, чтобы внезапно вызвать маг-
нитное поле въ опытѣ, описанномъ въ § 305, можно было бы, вмѣсто
того, чтобы замыкать намагничивающій токъ, быстро передвинуть
подъ неподвижную катушку постоянный магнитъ, находившійся на
большомъ разстояніи отъ катушки. Изъ закона относительности слѣ-
дуетъ, что ударъ напряженія, наблюдаемый при внезапномъ возник-
новеніи поля столь же великъ, какъ и ударъ, вызываемый электро-
движущими силами магнитнаго поля, если катушку, весьма уда-
ленную отъ постояннаго магнита, приблизить и положить на магнитъ.
Ударъ напряженія, сопровождающій исчезновеніе магнитнаго поля,
таковъ же, какъ и толчекъ, получаемый при удаленіи катушки изъ
постояннаго магнитнаго поля, т.-е. онъ равенъ первому толчку по
величинѣ, но противоположенъ по направленію. Эти теоретическія
слѣдствія изъ закона относительности могутъ быть легко провѣрены
экспериментально.
Если мы будемъ переводить катушку изъ весьм^уДаленной
области, гдѣ сила магнитнаго поля равна нулю или бе^онечно мала,
въ область, гдѣ сила поля больше, то каждая сиговая линія, входя-
щая въ ограничиваемое катушкой пространство,Должна однажды пе-
ресѣчь кольцо катушки. Поэтому витки ^іушки пересѣкаютъ то»
Второй основной законъ электродинамики Максвелла
161
самое число силовыхъ линій, которое проходитъ по окончаніи опы-
та черезъ ограничиваемый катушкой кругъ. Отсюда получается слѣ-
дующій законъ:
Полный электрическій ударъ напряженія вдоль замкну-
той кривой, сопровождающій возникновеніе магнитнаго
поля, равенъ магнитному силовому потоку, пронизываю-
щему послѣ окончательнаго образованія поля поверхность,
ограничиваемую этою кривою.
Электрическій ударъ напряженія при исчезновеніи маг-
нитнаго поля равенъ по величинѣ удару при возникновеніи
того же поля и противоположенъ ему по направленію.
307. Этотъ законъ даетъ намъ возможность найти механическую
аналогію той величины, которая называется „магнитнымъ силовымъ
потокомъ". Если въ модели эѳира, описанной въ § 252, существу-
етъ напряженіе упругихъ частицъ вдоль замкнутой кривой, то внутри
этой кривой должно происходить вращеніе шариковъ, такъ какъ кри-
вую, составленную изъ упругихъ частичекъ, можно разсматривать, какъ
охватывающій шарики канатъ, къ которому приложены силы, стремя-
щіяся повернуть его въ одну’сторону. Если силы, тянущія этотъ „ка-
натъ" въ его собственномъ направленіи, взаимно уничтожаются, какъ
въ электростатикѣ, то имѣетъ мѣсто равновѣсіе. Изъ механики извѣст-
но, что ударъ, дѣйствующій .на тѣло, равенъ возникающему при этомъ
количеству движенія, т.-е. произведенію изъ массы на скорость.
Этотъ законъ имѣетъ силу не только для брошеннаго по прямой
линіи тѣла, для котораго количество движенія равняется т. ѵ, гдѣ
т—масса, ѵ—скорость, но также и для вращательныхъ движе-
ній, напримѣръ, маховаго колеса. Если К—моментъ инерціи враща-
ющагося тѣла, ш = 2 и. 7Ѵ—его угловая скорость (М—число оборо-
товъ въ секунду), то количество движенія при вращеніи равно /Сш.
Оно равняется суммѣ по времени силъ вращенія, т.-е. моментовъ вра-
щенія, приведшихъ тѣло во вращеніе. Въ механической модели эѳира
эта сумма напряженій по времени вдоль замкнутой кривой рав-
няется количеству движенія вызываемыхъ ею эѳирныхъ вращеній.
Если въ механической модели эѳира аналогіей силькмдг-
нитнаго поля служитъ угловая скорость, то аналогіетД^маг-
нитнаго силового потока будетъ связанное съ врѣЛцёніями
количество движенія частицъ. глоѴ
Ми. Электричество и магнитизмъ, ч. II.
П
162
Второй основной законъ электродинамики Максвелла
308. Такъ какъ въ перемѣнномъ магнитномъ полѣ вся сумма по
времени напряженія вдоль замкнутой кривой отъ возникновенія поля
до любого момента равняется числу магнитныхъ линій индукціи, охва-
тываемыхъ кривою, то произведеніе изъ напряженія V, наблюдаемаго
на струнномъ электрометрѣ въ малый промежутокъ времени т, на
величину т, т.-е. V. т, должно равняться происшедшему за время т
измѣненію числа охватываемыхъ линій индукціи. Если мы назовемъ
это измѣненіе черезъ ѵ, то V. т = ѵ, или V = ~ Частное предста-
вляетъ собою скорость измѣненія силового потока, или его измѣненіе,
разсчитанное на секунду.
Второй основной законъ электродинамики Максвелла. Если
въ эѳирѣ имѣются электрическія напряженія, не находя-
щіяся въ равновѣсіи, то происходитъ измѣненіе магнитнаго
состоянія; при этомъ приращеніе за одну секунду силового
потока, пронизывающаго нѣкоторую площадь, равняется
Измѣненіе силового потока предста- Измѣненіе силового потока предста-
влено слагающей, вступающей въ пло- влено слагающей, выходящей изъ пло-
скость рисунка. скости рисунка.
Рис. 217. Направленіе электрическихъ напряженій, вызывающихъ
измѣненіе магнитнаго силового потока.
линейной суммѣ электрическаго поля вдоль кривой, огра-
ничивающей эту площадь.
Силовой потокъ возрастаетъ въ томъ направленіи, по которому
нужно смотрѣть, чтобы получить положительную линейную сумму
(рис. 217), идя вдоль кривой справа налѣво, т.-е. въ направленіи,
обратномъ движенію часовой стрѣлки. Если поверхность окру-
жить замкнутой проволочной катушкой, то напряженіе на-
зоветъ въ ней электрическій токъ, магнитное поле котораго
стремится уменьшить измѣненія силового потока.
Второй основной законъ Максвелла вполнѣ аналогиченъ урав-
ненію механики „сила равняется массѣ, умноженной^/ускореніе",
которое можно выразитъ еще такъ: „сила равняется^риращенію коли-
чества движенія во времени". Электрическому напряженію вдоль зам-
кнутой кривой въ механической модели эѳира соотвѣтствуетъ сила упру-
Законъ индукціи
163
гихъ напряженій, не уравновѣшиваемыхъ другими силами, а возрастанію
силового потока во времени соотвѣтствуетъ приращеніе количества
движенія вращающихся эѳирныхъ шариковъ.
ЗАКОНЪ ИНДУКЦІИ.
309. Какъ было уже указано въ § 303, полное напряженіе
между концами катушки при ея движеніи въ магнитномъ полѣ или
же при измѣненіи магнитнаго поля называется индуктированнымъ
въ катушкѣ напряженіемъ. Законъ Максвелла вмѣстѣ съ за-
кономъ относительности приводитъ къ слѣдующему общему закону:
Индуктированное въ катушкѣ напряженіе равняется
произведенію изъ разсчитаннаго на секунду измѣненія маг-
нитнаго силового потока, проходящаго черезъ плоскость ея
витковъ, на число витковъ.
Часто оказывается болѣе удобнымъ формулировать этотъ законъ
при помощи примѣненнаго въ § 297 представленія о пересѣченіи
силовыхъ линій. Чтобы обнять также и общій случай измѣненія маг-
нитнаго поля, напримѣръ, въ опытѣ, изображенномъ на рис. 216,
нужно вообразить, что силовыя линіи магнитнаго поля при его воз-
никновеніи приходятъ изъ безконечности и при его исчезновеніи
удаляются въ безконечность. Чтобы проникнуть въ окруженное ка-
тушкой пространство или чтобы выйти изъ него, силовыя линіи
должны пересѣчь витки катушки. Полное напряженіе между концами
катушки получается по слѣдующему правилу:
Напряженіе, индуктированное въ какой-либо части про-
водника, по абсолютной величинѣ равняется числу магнит-
ныхъ индукціонныхъ линій, пересѣкаемыхъ ею въ одну
секунду.
Напряженіе между концами катушки получается посредствомъ
суммированія напряженій, индуктированныхъ вдоль всего проводника.
При этомъ слѣдуетъ, конечно, имѣть въ виду, что, смотря по
направленію магнитныхъ силовыхъ линій, ивъ зависимости отъ того,о
выходятъ ли силовыя линіи или входятъ, напряженіе должно сч^&^
таться то положительнымъ, то отрицательнымъ. Направленіе индуктиро-
ваннаго напряженія проще всего опредѣляется по слѣдующему/пра-
вилу: магнитное поле индукціоннаго тока, получаемаго соеди-
ДѴ
неніи концовъ катушки проводникомъ, стремится препятствовать измѣ-
ненію поля, пронизывающаго плоскость витковъ,
164
Самоиндукція
САМОИНДУКЦІЯ.
310. Въ опытѣ, описанномъ въ § 305, можно замѣтить, что
при замыканіи намагничивающаго тока напряженіе возрастаетъ не
очень сильно, но держится довольно долго; наоборотъ, при размы-
каніи тока напряженіе повышается очень сильно, но длится весьма
короткое время. Произведеніе изъ напряженія на время, т.-е. ударъ
напряженія, конечно, одинаковъ въ обоихъ случаяхъ.
Чтобы объяснить это различіе явленій при замыканіи и размы-
каніи намагничивающаго тока, мы воспользуемся сравненіемъ съ осью,
снабженной маховымъ колесомъ. Предположимъ, что мы вращаемъ
колесо съ помощью постоянной не очень большой силы и желаемъ
сообщить ему опредѣленную скорость; для этого требуется нѣкото-
рое время, въ теченіе котораго скорость вращенія постепенно на-
растаетъ до желаемой величины. При этомъ въ оси не возникаетъ
напряженій, превосходящихъ тѣ, которыя соотвѣтствуютъ приложен-
ной силѣ. Съ другой стороны, при помощи тормаза мы можемъ,
напротивъ, чрезвычайно скоро остановить вращающееся колесо, при
чемъ возникаютъ очень большія силы реакціи.
Ясно, что и въ случаѣ магнитнаго поля причиной медленнаго
возрастанія, наблюдаемаго въ опытѣ, является его инерція. Постоян-
ное напряженіе V батареи, соединенной съ зажимами катушки, должно
уравновѣшивать двѣ противодѣйствующія силы: во-первыхъ, омиче-
ское напряженіе, имѣющее, при силѣ тока У и при сопротивленіи
намагничиваемой катушки /?, величину /? . У и, во-вторыхъ, линейную
сумму V' электрическаго поля, возбуждаемаго магнитнымъ полемъ,
вдоль витковъ катушки. Слѣдовательно, Ѵ = Ѵ'-|-/?../. Чѣмъ боль-
ше I/', тѣмъ быстрѣе, согласно закону Максвелла, возрастаетъ
магнитное поле. Сначала, когдаѴ'=У, т.-е. все приложен-
ное напряженіе можетъ идти на преодолѣніе инерціи магнитнаго
поля; поле и вмѣстѣ съ нимъ токъ возрастаютъ съ наибольшей
скоростью. Но когда токъ У достигаетъ замѣтной величины, то на-
пряженіе Ѵ'=Ѵ—/?./ убываетъ, и потому дальнѣйшее возрастаніе
магнитнаго поля (и тока) идетъ все медленнѣе и медл^щѣе^ и» на-
конецъ, когда будемъ имѣть /? . У = V, V' = О, поле Дѣлается ста-
ціонарнымъ. Промежутокъ времени, потребный для достиженія стаціо-
нарнаго состоянія, зависитъ отъ инерціи магнитнаго поля и сопро-
тивленія катушки. Его можно было бы сократить, заставляя при
Самоиндукція
165
образованіи поля на нѣкоторое время дѣйствовать напряженіе, ббль-
шее, чѣмъ V. Зато магнитное поле катушки можно уничтожить
съ произвольной быстротой посредствомъ размыканія тока. При
этомъ въ эѳирѣ возникаютъ весьма высокія напряженія, и витки ка-
тушки должны быть хорошо изолированы, чтобы между ними при
этомъ не происходило разрядовъ. Сильныя напряженія, значительно
превосходящія напряженіе I/, при помощи котораго вызывается маг-
нитное поле, возникаютъ въ особенности между концами проводовъ
въ мѣстѣ ихъ размыканія. Вслѣдствіе этого между ними происхо-
дитъ дуговой разрядъ, такъ называемая искра размыканія, быстро
истощающая энергію магнитнаго поля. Аналогія съ маховымъ коле-
сомъ вполнѣ ясна. Инерціи магнитнаго поля соотвѣтствуетъ моментъ
инерціи махового колеса, омическому сопротивленію соотвѣтствуютъ
различныя сопротивленія тренія, напряженію V—сила, приводящая
колесо во вращеніе, и, наконецъ, искрѣ размыканія соотвѣтствуетъ тор-
мазъ, въ которомъ поглощается кинетическая энергія махового колеса.
Напряженія между концами намагничивающейся катушки, урав-
новѣшивающія инерцію магнитнаго поля, называются напряже-
ніями самоиндукціи, такъ какъ они индуктируются въ катушкѣ
ея собственнымъ магнитнымъ полемъ. Явленія, зависящія отъ напря-
женій самоиндукціи, называются явленіями самоиндукціи, а свой-
ство катушки обнаруживать ихъ называется самоиндукціей. Тер-
минъ „самоиндукція" можно было бы вполнѣ замѣнить болѣе на-
гляднымъ выраженіемъ „инерція магнитнаго поля катушки".
Нижеслѣдующимъ опытомъ можно показать, какія большія на-
пряженія получаются при быстромъ исчезновеніи сильнаго магнит-
наго поля. Приключимъ къ двумъ зажимамъ большого электромаг-
нита лампу накаливанія, горящую нормально при напряженіи I/, взя-
томъ для намагничивающаго тока. Въ моментъ замыканія тока лампа
горитъ съ нормальной яркостью. Если не введено никакого предвари-
тельнаго сопротивленія, то яркость остается постоянной; если же вве-
дено предварительное сопротивленіе, то яркость нѣсколько падаетъ съ
развитіемъ магнитнаго поля и намагничивающаго тока, вслѣдствіе^
потери напряженія. Если затѣмъ, когда магнитное поле станетъ ста-
ціонарнымъ, быстро разомкнуть токъ, то лампа, прежде чѣм^Ѵйо-
тухнуть, вспыхиваетъ на подобіе молніи съ чрезвычайноі^ркбстью,
во много разъ превышающей нормальную; если размыканіе произ-
водится очень быстро, то нить перегораетъ (рис. 218)Л
166
Самоиндукція
Какъ мы видѣли, энергія магнитнаго поля поглощается искрой
размыканія, и послѣдняя поэтому тѣмъ сильнѣе, чѣмъ больше
энергія магнитнаго поля. Эта энергія зависитъ, однако, не только
отъ силы тока, но также и отъ другихъ особенностей поля, глав-
нымъ образомъ, отъ присутствія желѣза. Приключимъ къ одному
полюсу маленькой батареи аккумуляторовъ мѣдный штифтъ, а къ
другому—обыкновенный напилокъ; кромѣ того, гдѣ-либо въ цѣпь
введемъ катушку съ не слишкомъ малымъ числомъ витковъ. Если
провести штифтомъ вдоль по напилку, то токъ будетъ то замы-
Рис. 218. Демонстрація напряженій самоиндукціи въ большомъ
электромагнитѣ.
каться, то размыкаться; при этомъ ^будутъ замѣтны небольшія
искорки, появляющіяся при размыканіи тока. Если теперь, оставляя
все прочее безъ измѣненія, введемъ въ катушку желѣзный сер-
дечникъ, то искорки тотчасъ же станутъ значительно болѣе силь-
ными, такъ какъ при той же силѣ тока присутствіе желѣза значи-
тельно увеличиваетъ энергію поля.
311. Юиттъ (Недѵііі) предложилъ примѣнять высокія °яйряже-
нія самоиндукціи, возникающія при размыканіи тока, длд (зажиганія
ртутной дуговой лампы. Мы видѣли въ § 184, что хъфтовую дугу
можно зажигать двумя способами: чтобы довести^ электроды до
требуемой высокой температуры, либо сближаютъ ихъ до сопри-
косновенія и затѣмъ разъединяютъ, либо же/короткое время до-
Самоиндукція
167
водятъ напряженіе до максимальной величины напряженія при раз-
рядѣ и тѣмъ возбуждаютъ искры, быстро переходящія въ свѣтовую
дугу. Юиттъ пользуется въ своихъ ртутныхъ дуговыхъ лампахъ
вторымъ пріемомъ, такъ какъ при первомъ способѣ приходится
передвигать всю лампу. Въ качествѣ самоиндукціи передъ ртутной
дуговой лампой включается катушка съ желѣзнымъ сердечникомъ
(рис. 219), лампа же сперва коротко замыкается мѣдной дугой. Если
Рис. 219. Зажиганіе ртутной дуговой лампы посредствомъ напряженія
самоиндукціи.
затѣмъ приложить напряженіе, то токъ проходитъ черезъ самоин-
дукцію и черезъ короткій замыкатель. Затѣмъ послѣдній вынимается,
и тогда, вслѣдствіе сильнаго магнитнаго поля, въ катушкѣ въ точ-
кахъ разрыва, т.-е. у зажимовъ ртутной лампы, возникаетъ столь
сильное напряженіе, что происходитъ разрядъ, который быстро раз-
вивается въ свѣтовую дугу и въ этой формѣ сохраняется и при
постоянномъ болѣе низкомъ напряженіи освѣтительнаго провода.
Ку
У'
ГЛАВА ШЕСТАЯ
МАГНИТНЫЯ СВОЙСТВА ТѢЛЪ
ПУСТОТА.
312. Мы можемъ сравнить два опредѣленія магнитнаго поля съ
двумя опредѣленіями электрическаго поля. Оба состоянія эѳира, во-
первыхъ, опредѣляются чисто количественнымъ образомъ: электри-
ческое возбужденіе — количествомъ электрическихъ зарядовъ (§ 51),
сила магнитнаго поля — числомъ амперъ-витковъ (§ 244). Во-вто-
рыхъ, оба состоянія эѳира опредѣляются путемъ измѣренія силъ:
электрическое напряженіе — опредѣляется силой, дѣйствующей на
покоющуюся электрически заряженную частичку (§ 19), магнитный
словой потокъ — силой, дѣйствующей на движущіеся электроны и
іоны (§ 296). Механическими аналогіями являются: въ первомъ слу-
чаѣ — геометрически измѣряемыя величины деформаціи модели эѳира
и угловой скорости ея вращающихся частицъ, во второмъ случаѣ
— величины, опредѣляемыя силами: напряженіе въ модели эѳира и
количество движенія вращающихся частицъ.
Какъ обѣ величины, характеризующія электрическое поле, такъ
и обѣ величины, характеризующія магнитное поле, опредѣляются
совершенно независимо одна отъ другой, и а ргіогі нельзя ничего
сказать объ ихъ взаимномъ отношеніи. Ясно, во всякомъ случаѣ,
только то, что, разъ обѣ величины измѣряютъ одно и то же со-
стояніе эѳира, онѣ должны быть связаны однозначной зависимостью.
Практическія измѣренія показали, что для пустоты эта зависимость
простѣйшая, т.-е. имѣетъ форму пропорціональности.
Сила магнитнаго поля и магнитный силовой потравъ
пустотѣ направлены всегда одинаково и пропорціональны
между собою: ЗС?
В = М . Н.
Величина М, т.-е. коэффиціентъ пропорціональности между си-
ловымъ потокомъ и силой поля, носитъ назваді^°йроницаемости
Проницаемость эѳира
169
мірового эѳира. Механическою аналогіею проницаемости является
удѣльная инерція, т. е. плотность.
Соотвѣтственный законъ электростатики мы изложили въ § 62
подъ именемъ закона Кулона. Такимъ образомъ, какъ діэлектрическая
постоянная, такъ и проницаемость мірового эѳира не измѣняются въ
зависимости отъ силы электрическаго или магнитнаго поля. Опыты
показываютъ, что это обобщеніе можетъ быть проведено и дальше.
Діэлектрическая постоянная эѳира не мѣняется отъ присутствія магнит-
наго поля, а проницаемость — отъ присутствія электрическаго поля.
Оба свойства эѳира являются абсолютными универсальными постоян-
ными. Мы приходимъ такимъ образомъ къ всеобщему принципу на-
ложенія (суперпозиціи):
Физическія свойства мірового эѳира нисколько не мѣ-
няются въ зависимости отъ его электрическаго или маг-
нитнаго состоянія. Если къ имѣющимся уже полямъ присо-
единяются новыя поля, то они налагаются другъ на друга
такъ, какъ если бы эѳиръ былъ лишенъ поля.
Этимъ весьма замѣчательнымъ закономъ эѳиръ рѣзко отлича-
ется отъ всякой вѣсомой матеріи. Физическія свойства вѣсомаго ве-
щества измѣняются всѣ вмѣстѣ, какъ только физическое состояніе
вещества измѣняется въ какомъ-нибудь одномъ отношеніи (напри-
мѣръ, когда измѣняется температура или давленіе и т. д.), и по измѣ-
неніямъ свойствъ можно наблюдать измѣненія состоянія вещества.
Состоянія же эѳира въ силу принципа наложенія не могутъ быть по-
знаваемы по его собственнымъ свойствамъ, и мы должны поэтому
изучать ихъ по дѣйствіямъ полей на вѣсомыя тѣла (электроскопы
и магнитоскопы).
ПРОНИЦАЕМОСТЬ ЭѲИРА.
313. Для отличія отъ проницаемостей вѣсомыхъ веществъ мы
въ дальнѣйшемъ изложеніи будемъ обозначать проницаемость пусто-
ты черезъ Мо. Какъ найти Мо, ясно изъ самаго опредѣленія этой
величины. Одно и то же поле измѣряется по методу, описанному^
въ § 245, въ амперъ - виткахъ на сантиметръ, а затѣмъ
описаннымъ въ § 299 и сл., въ вольтъ-секундахъ на
сантиметръ. Такъ, напримѣръ, для земнаго поля мы нашли246
у г р. о о г; йМП.'ВШи. ~ о г\г\ о л л о 1 л я
Н = 0,385--------->а въ § 300 В = 0,48. ІО-8 -------• Отсю-
да получается: Мо = В : 77 — 1,25 . ІО-8. Производятся ли измѣре-
способс^гь;
квадратный
170
Такъ называемыя абсолютныя электромагнитныя единицы
нія въ пустотѣ или въ воздухѣ, результатъ получается одинъ и
тотъ же.
Чрезвычайно точныя измѣренія абсолютной проницаемости чи-
стаго мірового эѳира дали:
Мо = 1,256.10-8
у амп.-см.
ТАКЪ НАЗЫВАЕМЫЯ АБСОЛЮТНЫЯ ЭЛЕКТРОМАГНИТНЫЯ
ЕДИНИЦЫ.
314. Въ литературѣ мы часто встрѣчаемъ единицы, получа-
ющіяся отъ умноженія легальныхъ единицъ на нѣкоторую степень-
числа 10, т.-е. принадлежащія къ той же десятичной системѣ. По
причинѣ, съ которой мы сейчасъ познакомимся, эти единицы на-
зываются абсолютными электромагнитными и обозначаются симво-
ломъ ет. За ет единицу напряженія принимаютъ сантимикро-
вольтъ: 1 ет = ІО-8 вольтъ; ет единицей заряда считается дека-
кулонъ: 1 е А77 = 10 кулонамъ. Единица силы магнитнаго поля по
1 п амп.-витк.
этой системѣ, именно 10----------, никогда не употребляется; ве-
см.
личину поля всегда выражаютъ лишь силовымъ потокомъ, при чемъ
1 я вольтъ-сек. „
единицей служитъ Ю~8 ------------- . Эта единица настолько рас-
кв. см. г
пространена, что въ большинствѣ случаевъ, если не дѣлаютъ оговор-
ки, предполагается именно эта единица. Такъ, напримѣръ, принято
говорить, что горизонтальная слагающая земного поля равняется 0,18,
х м 1 о і я вольтъ-сек. ,
вмѣсто 0,18. ІО-8 —---------, или что въ сильномъ полѣ элек-
кв. см.
тромагнита число силовыхъ линій равняется 10000 на кв. см.,
. 1 л . вольтъ-сек. ,
вмѣсто 10-1-----------. Въ виду того, что магнитное поле измѣ-
кв. см. д
ряется только этой единицей, она то называется силой магнитнаго
поля и обозначается буквой /7, то называется магнитной индукціей
и обозначается черезъ В. Такое смѣшеніе двухъ совершенно раз-
личныхъ понятій недопустимо, хотя оно исторически, можетъ быть,
и оправдывается. Поэтому мы будемъ строго различать сийуЭполя
тт декаамп.-в. . „ сантимикровольтъ-сек. о
гі----------- отъ индукціи В------------------------Въ ет едини-
см. кв. см.
цахъ абсолютная проницаемость эѳира въ ІО9 разъ^Ълыпе, нежели
въ легальныхъ единицахъ, т.-е. Мо = 12,56. Это число, въ предѣлахъ
погрѣшностей наблюденій, равно 4и. Единицей!Энергіи въ ет-си-
Такъ называемыя абсолютныя электромагнитныя единицы
171
стемѣ служитъ произведеніе изъ 10 кулоновъ на 10~8 вольтъ,,
т.-е. 10“7 джулей — 1 эргъ.
Такъ называемая абсолютная электромагнитная систе-
ма мѣръ характеризуется тѣмъ, что единицей энергіи въ.
ней служитъ 1 эргъ, а абсолютная проницаемость эѳира
равняется 4п= 12,56.
315. Чтобы понять эту странную систему мѣръ, необходимо
обратиться къ историческому развитію измѣрительной техники. Пер-
вый опытъ установленія системы мѣръ былъ сдѣланъ Гауссомъ и Ве-
беромъ въ ту эпоху, когда современные весьма удобные и тонкіе из-
мѣрительные методы еще не были извѣстны. Поэтому Гауссъ и
Веберъ въ своемъ стремленіи установить постоянныя единицы
должны были идти совершенно инымъ путемъ, чѣмъ мы теперь.
Они исходили изъ измѣренія силъ, такъ какъ въ ихъ время, когда
между всѣми отдѣлами измѣрительной физики наиболѣе развита
была измѣрительная механика, измѣреніе силъ относительно отлича-
лось точностью. Два совершенно тождественные магнитные полюса,
дѣйствующіе другъ на друга на разстояніи 1 см. съ силою
въ 1 дину, они приняли за полюсы-единицы, а единицей поля они
считали поле на разстояніи 1 см, отъ полюса-единицы (В = 1).
Единица электрическаго тока опредѣлялась помощью длиннаго
соленоида съ поверхностью витковъ въ 1 кв. см. Когда че-
резъ этотъ соленоидъ проходилъ токъ, поле котораго на нѣкото-
ромъ разстояніи было повсюду тождественно съ полемъ магнит-
наго стержня, имѣвшаго ту же длину и силу полюсовъ 1, то чи-
сломъ витковъ съ токомъ должно было точно выражаться значеніе
1 ет на сантиметръ. Такимъ путемъ, дѣйствительно, были получены еди-
ницы, которыя можно было воспроизводить съ нѣкоторою точностью,
именно ет-единицы. Слѣдуетъ упомянуть, что была сдѣлана по-
пытка построить вторую систему единицъ, подобную ///-системѣ,
именно, описанную въ § 78 ^-систему. Въ послѣдней вмѣсто
двухъ полюсовъ-единицъ въ основу положены два электрическіе
заряда-единицы, дѣйствующіе другъ на друга на разстояніи 1 слі^
съ силою, равною 1 динѣ. Но такъ какъ мѣры ^///-системы все-та^
легче реализовать, нежели мѣры ^-системы, то она и предцочи-
талась послѣдней до тѣхъ поръ, пока обѣ онѣ не уступил|Сйіѣста.
единицамъ „ практической “ системы мѣръ, опредѣленныіф^посред-
ствомъ современныхъ измѣрительныхъ методовъ. о\Л
172
Такъ называемыя абсолютныя электромагнитныя единицы
Современная система мѣръ не есть ни электрическая,
ни „электромагнитная", такъ какъ она не основана на из-
мѣреніи механическихъ силъ.
Замѣчательно, однако, что нерѣдко все-таки высказывается непра-
вильный взглядъ, будто наша система мѣръ есть „электромагнитная".
По понятнымъ соображеніямъ (чтобы облегчить переходъ отъ одной
системы къ другой), единицы вольтъ и кулонъ опредѣлены были
такъ, чтобы онѣ различались отъ единицъ старой системы Гаусса
лишь множителями, представляющими степени 10. Но фактически
нельзя отрицать, что опредѣленіе самыхъ единицъ помощью нор-
мальнаго элемента и серебрянаго кулонметра совершенно иное.
Большимъ недостаткомъ старыхъ системъ единицъ является то,
что ихъ опредѣленія страдаютъ вреднымъ смѣшеніемъ двухъ совер-
шенно различныхъ научныхъ задачъ.
Для развитія количественной, измѣрительной науки
прежде всего необходимо опредѣлять единицы такъ, чтобы
ихъ можно было воспроизводить легко и съ точностью.
Эта задача весьма несовершенно разрѣшалась сложными и очень
трудными операціями такъ называемой электромагнитной системы
мѣръ. Наоборотъ, при помощи нормальнаго элемента, серебрянаго
кулонметра и нормальнаго ома она разрѣшается наилучшимъ образомъ.
Вторая задача, которая не имѣетъ съ первой ничего
общаго и при всей своей важности далеко не имѣетъ та-
кого фундаментальнаго значенія, какъ первая, заключается
въ возможно болѣе точномъ нахожденіи обѣихъ универ-
сальныхъ постоянныхъ/Со и Мо, діэлектрической постоя нной
я проницаемости мірового эѳира, въ установленныхъ еди-
ницахъ.
Эта вторая задача связываетъ электромагнитную систему мѣръ
съ первой задачей, такъ какъ эта система полагаетъ М0 = 4п. Но
несомнѣнно, что научный путь существуетъ только одинъ: къ рѣ-
шенію второй задачи слѣдуетъ приступить лишь по разрѣшеніи
первой. Она имѣетъ для физики такое же значеніе, какъ опредѣле-
ніе механическаго эквивалента теплоты, ускоренія силы^тяжести,
скорости свѣта, газовой константы.
Поэтому, нисколько не умаляя заслугъ Гаусса и Вебера,
создавшихъ первую удовлетворительную систему мѣръ, нужно,
однако, признать, что было бы желател^ш^ совершенно изъ-
Коэффиціентъ самоиндукціи
173-
ять, наконецъ, изъ употребленія старыя, т. н. абсолютныя, еди-
ницы. И прежде всего слѣдуетъ разстаться съ ошибочнымъ мнѣ-
ніемъ, будто желательно слить обѣ указанныя задачи и при всякомъ
усовершенствованіи въ измѣреніи Мо пересматривать установленныя
единицы и исправлять ихъ, дабы онѣ съ достигнутой точностью со-
отвѣтствовали равенству Мо=4п.109. Наоборотъ, для прогресса
науки необходимо, чтобы единицы были по возможности прочно
установлены и никогда болѣе не мѣнялись. Подобнымъ образомъ
единица длины —метръ—теперь опредѣляется, какъ длина платиновой
линейки, находящейся въ Парижѣ, и уже никто не собирается послѣ
новаго измѣренія земли мѣнять единицу длины такъ, чтобы она
1
снова равнялась части меридіана, съ которой она не совпа-
даетъ, какъ уже давно извѣстно.
КОЭФФИЦІЕНТЪ САМОИНДУКЦІИ.
316. Если катушку или другой проводникъ тока внезапно со-
единить съ источникомъ электричества, то напряженіе между обоими
подводящими токъ зажимами проводника слагается изъ двухъ вели-
чинъ— напряженія, уравновѣшивающаго, по закону Ома, сопроти-
вленіе проводника (/?/), и напряженія самоиндукціи, необходимаго,
для преодолѣнія инерціи магнитнаго поля. По второму основному
закону Максвелла (§ 308), самоиндукція пропорціональна прира-
щенію магнитнаго силового потока за секунду и, согласно принципу
наложенія, пропорціональна также приращенію силы тока въ секунду.
Опредѣленіе коэффиціента самоиндукціи: Коэффиціентъ
пропорціональности, на который слѣдуетъ помножить при-
ращеніе силы тока за секунду, чтобы получить напряженіе
самоиндукціи между подводящими токъ зажимами провод-
ника, называется коэффиціентомъ самоиндукціи этого про-
водника.
Единица коэффиціента самоиндукціи въ легальной си-
стемѣ мѣръ называется 1 генри:
. . вольтъ-сек. г
1 генри == 1 -------- •
г амперъ
Коэффиціенты самоиндукціи обозначаются обычно буквою А.
Законъ наложенія мы можемъ теперь формулировать ец^е такъ:
Коэффиціентъ самоиндукціи опредѣленной^іѣпи въ
пустотѣ есть величина постоянная для всякой^Вйлы тока.
174
Коэффиціентъ самоиндукціи
Чтобы составить приблизительное представленіе о величинѣ
одного генри, вообразимъ катушку, которая можетъ имѣть нѣсколько
слоевъ обмотки, но такихъ, что толщина обмотки мала въ сравне-
ніи съ діаметромъ катушки. Предположимъ, что средняя поверх-
ность витка равняется д и на каждый сантиметръ приходятся п
витковъ. Положимъ, что длина катушки I весьма велика въ срав-
неніи съ ея толщиной и что общее число витковъ Ы=1.п весьма
велико. Какъ мы знаемъ, поле внутри весьма длинной катушки почти
. т тт гамп.-витк.
однородно и при силѣ тока л сила поля равняется гі = п .Л-------
см.
Далѣе, индукція равняется В = М п.1, и полное число силовыхъ ли-
ній, окруженныхъ катушкой, равняется М . п . У. д волътъ-сек. Сумма
по времени всего напряженія вдоль М витковъ катушки, измѣряю-
щая ударъ напряженія между подводящими зажимами, составляетъ
до момента, когда токъ возрастаетъ до своей конечной силы У,
ѴА . п.}. д . Ы волътъ-сек. Слѣдовательно, коэффиціентъ самоинду-
кціи равняется
Ь = М ,Ы,п.д = М .гР.І.д генри.
Если мы здѣсь, вмѣсто М, подставимъ величину 1,256. ІО-8,
то посредствомъ простого вычисленія найдемъ, что катушка облада-
етъ коэффиціентомъ самоиндукціи въ 1 генри, если ея витки имѣ-
ютъ средній діаметръ въ 10 см. (д = 78,54 кв. см.), на 1 см. при-
ходится п= 100 витковъ (напримѣръ, толщина проволоки 0,5 мм.\
5 слоевъ) и длина катушки немного больше 1 метра (точнѣе
^= 10140 витковъ). Изъ этого примѣра видно, что генри предста-
вляетъ практически пригодную единицу. Въ продажѣ имѣются нор-
мальныя катушки съ самоиндукціею въ 1 генри, съ которыми можно
сравнивать неизвѣстныя катушки самоиндукціи.
Коэффиціентъ самоиндукціи А катушки можно нѣкоторымъ обра-
зомъ разсматривать, какъ полную величину инерціи магнитнаго
поля катушки. Онъ зависитъ поэтому какъ отъ величины М (усиль-
ной инерціи), такъ и отъ размѣровъ катушки. Коэффиціентъ^дмо-
индукціи находится приблизительно въ такомъ отношеніиЖѣ про-
ницаемости, какъ емкость къ діэлектрической постоянфіГ (§ 68).
ЭНЕРГІЯ МАГНИТНАГО ПОЛяДкО ‘ \
317. Если катушку внезапно соединить съ источникомъ электри-
чества, то въ теченіе нѣкотораго начальнагр|^ріода токъ возраста-
Энергія магнитнаго поля
175
етъ отъ нуля до конечнаго значенія У. Предположимъ, что за весьма
короткую часть т этого періода токъ возрастаетъ на Д/, при
чемъ его среднее значеніе за время т есть /т, а напряженіе между
зажимами равно Ѵт. По теоремѣ Пойнтинга, за время т перено-
сится между зажимами энергія Ѵт . /т ваттъ, т.-е. въ общемъ пере-
носится ІГТ = Ут . Ѵт. т джулей. Если /? есть сопротивленіе катушки,
то линейная сумма электрическаго напряженія вдоль витковъ катушки
равняется Ут. /?. Поэтому энергія, вступающая чрезъ поверхность
проволоки въ металлъ и превращающаяся здѣсь въ теплоту, равня-
ется /?.УТ./Т.т джулямъ. Но это не вся энергія, такъ какъ напря-
женіе между зажимами больше: Ѵт = Ѵт' 4" гд^ — напря-
женіе самоиндукціи; соотвѣтственно этому М7Т = І/т' . /т. т т.
Первое слагаемое этой суммы Ѵт'. /т. т = М7Т' представляетъ собою
количество энергіи, которое проходитъ между зажимами, но не дости-
гаетъ витковъ катушки, т.-е. остается въ окружающемъ катушку
пространствѣ. Эту энергію поглощаетъ возрастающее магнитное поле
за короткій промежутокъ времени т. Если коэффиціентъ самоин-
дукціи катушки равенъ ѣ генри, то Ѵт = Ь. —, и потому прира-
щеніе энергіи магнитнаго поля за малый промежутокъ времени
т равно = Ѵт'./т. т — 7 ./т. Д У. Положимъ теперь, что Д/
представляетъ собою л-ую часть конечнаго значенія силы тока, т.-е.
что = и обозначимъ черезъ , т2, т3,..., тп соотвѣтствен-
ные малые промежутки времени, за которые токъ возрастаетъ отъ О
до Д У, отъ У до 2 Д У, отъ 2 Д У до 3 Д У.... отъ (п—1) . Д У
до п. Д У = У, считая отъ момента соединенія съ источникомъ элек-
тричества. Обозначимъ черезъ /2,..., среднія значенія силы
тока за малые промежутки времени тх, т2,..., тп; они образуютъ
непрерывно возрастающій рядъ отъ 0 до У, и ихъ среднее значеніе
равняется Ѵ2Л Полное количество энергіи, пріобрѣтаемой магнит-
нымъ полемъ, когда сила тока возрастаетъ до У, представится въ
видѣ слѣдующей суммы: 4
^=^'+^2'4--------Ь^п'=А./1.Д/4-Л.Л.Д/4-------
= 7. Д у. 4-4-------НЛО-
Р 4, • Л 7 -7
Если сюда подставить вмѣсто приращенія Д/ его значеніе то
получимъ:
ІГ=а . у 4 • (Л+Л + • • • + 4) = • Ѵ2 гР"
п V
176
Энергія магнитнаго поля
Такимъ образомъ, полная энергія магнитнаго поля равняется
Ѵ7 = Ь . У2 джулей.
Если черезъ катушку, имѣющую коэффиціентъ самоин-
дукціи въ Ь генри, проходитъ токъ въ У амперъ, то энергія
магнитнаго поля въ катушкѣ равняется половинѣ произве-
денія изъ коэффиціента самоиндукціи на квадратъ силы
тока т.-е. Ѵ7 — У2 джулямъ.
318. Предположимъ, что В есть удѣльный силовой потокъ маг-
нитнаго поля въ катушкѣ и А В — его приращеніе потока при воз-
растаніи тока на А/. Если сѣченіе катушки равняется д кв. см.,
то число всѣхъ силовыхъ линій равно д. В и его приращеніе
равняется д. А В. Если, далѣе, полное число витковъ на ка-
тушкѣ есть Ы, то напряженіе самоиндукціи за малое время т, въ
д
теченіе котораго В возрастаетъ на А В, равно У'т = 7Ѵ. д . -у- • Если
сила магнитнаго поля, выраженная въ амперъ-виткахъ на сантиметръ,
равняется Н и вся длина катушки есть /, то I .Н есть полное число
амперъ-витковъ; слѣдовательно, когда сила тока равняется 7Т ампе-
рамъ, то I. Н = М. и 7Т = /. 77: 7Ѵ. Отсюда слѣдуетъ, что энергія^
получаемая магнитнымъ полемъ за малое время т, равняется
Ѵт' ..1хл = 1.д.Н.АВ = ѵ.Н.&В джулей,
гдѣ ѵ — объемъ катушки. На каждый кубическій сантиметръ (у — 1)
поля приходится поэтому Н. А В джулей.
_ г гамп.-вшпк.
Если магнитное поле силы Н------—— возрастаетъ, такъ что
см.
. л о вольтъ-сек.
его удѣльный силовой потокъ увеличивается на АВ —
д куб. см.
то оно получаетъ энергію въ количествѣ Н.&В джулей на
одинъ кубическій сантиметръ.
Это положеніе справедливо и въ тѣхъ случаяхъ, къ которымъ
непримѣнимъ принципъ наложенія (какъ въ ферромагнитныхъ сре-
дахъ, съ которыми мы ниже познакомимся подробнѣе).
Но въ тѣхъ случаяхъ, которые подчиняются принципу наложенія^
мы можемъ для каждаго кубическаго сантиметра сдѣлатьтакое же
вычисленіе, которое мы въ § 317 произвели для поля всей катушки.
Такимъ путемъ мы получаемъ для плотности энергіи магнитнаго поля
выраженіе
Силовыя (пондеромоторныя) дѣйствія поля на магнитные полюсы 177
Эту формулу можно написать еще и такъ:
Въ тѣхъ случаяхъ, когда принципъ наложенія имѣетъ
силу, плотность энергіи магнитнаго поля возрастаетъ про-
порціонально квадрату силы поля.
Когда тѣло, моментъ инерціи котораго равенъ К> вращается
съ угловою скоростью ш, то энергія вращательнаго движенія равня-
ется К. щ2. Эта формула вполнѣ аналогична формулѣ о =
Въ модели эѳира М есть инерція шариковъ, содержащихся въ од-
номъ кубическомъ сантиметрѣ, Н—ихъ угловая скорость.
Полная энергія поля въ катушкѣ длины I и сѣченія д рав-
няется ІГ= у I. д. Н. В джулямъ. Если/V—число всѣхъ витковъ ка-
тушки, Л— ея самоиндукція, У—сила тока, то I.Н=Ы.3 д
и, слѣдовательно, у Л. У2.
СИЛОВЫЯ (ПОНДЕРОМОТОРНЫЯ) ДѢЙСТВІЯ ПОЛЯ НА МАГНИТНЫЕ
ПОЛЮСЫ.
319. Весьма часто по энергіи магнитнаго поля можно вычис-
лить тѣ механическія силовыя дѣйствія, которыя испытываютъ въ.
немъ постоянные магниты; мы можемъ это сдѣлать во всѣхъ тѣхъ
случаяхъ, когда возможно пренебречь тѣми (мало извѣстными)-
измѣненіями, которыя испытываетъ внутреннее поле магнита при его
перемѣщеніяхъ. Примѣромъ могутъ служить весьма тонкіе магнит-
ные стержни, находящіеся въ обширномъ и сравнительно слабомъ
полѣ. Въ этихъ случаяхъ нужно вычислить то измѣненіе энергіи
ДІЕ, которое испытываетъ все внѣшнее поле при маломъ пере-
мѣщеніи магнита. Отнимаемая отъ эѳира энергія Д ІЕ должна быть .
равна полученной при этомъ перемѣщеніи механической работѣ^ Я
отсюда можно опредѣлить силовое дѣйствіе, испытываемое магни^Х
томъ, такъ какъ работа равна произведенію изъ силы на^цупк
Если два магнитные стержня одинаковаго сѣченія съ
основаніями расположены другъ противъ друга таким^'^^бразомъ,
что между гладкими разноименными полюсными поверхностями оста-
ется лишь узкая щель равномѣрной ширины, то поливъ этой щели,
Ми. Электричество и магнитизмъ, ч. II.
12
178 Силовыя (пондеромоторныя) дѣйствія поляна магнитные полюсы
какъ показываетъ рис. 143, можно считать однороднымъ. Пусть
* о волыпъ-сек.
удѣльный силовой потокъ въ щели будетъ равенъ В
кв.-см.
сѣченіе магнитовъ равно и разстояніе между полюсными поверх-
ностями равно 5. Въ такомъ случаѣ энергія поля, находящагося въ
щели, равняется
Ц7 = 1 .В2.д.8 джулямъ.
2 /Ѵ\о
Если полюсныя поверхности сблизить на разстояніе Д$, то энергія
уменьшается на величину
Д М7 = - * • В2 . д . Д 5 джулямъ.
Никакихъ другихъ измѣненій ни внутри магнитовъ ни внѣ ихъ
не происходитъ. Мы имѣемъ такимъ образомъ случай, когда лег-
ко можно вычислить силу, дѣйствующую на магниты. Только-что
вычисленное количество энергіи, теряемое магнитнымъ полемъ, прі-
обрѣтается въ формѣ работы при перемѣщеніи магнита. Эта
работа равняется РД 5, гдѣ Р — сила притяженія между магнитами;
слѣдовательно,
За единицу силы мы беремъ величину, соотвѣтствующую энергіи въ
1 джуль, т.-е. ІО7 диновъ = 10,2 кгр.\ эта единица не имѣетъ осо-
баго наименованія. Если же за единицу силы принять килограммъ, то
П 10’2 02
-ч кгр-
Если за единицу силы принять динъ, то
о 107 П2
Р 2 М -В -Я диновъ.
Эта формула выражаетъ также силу притяженія между полюс-
ными поверхностями двухъ электромагнитовъ. Если, напримѣръ,
В=10-4 (т.-е. 10000 епі), то на каждый квадратный сантиметръ
полюсной поверхности приходится сила, превышающая 4 килограмма.
СИЛОВЫЯ (ПОНДЕРОМОТОРНЫЯ) дѣйствія магнитнаго поля
НА ПРОВОДНИКЪ съ токомъ. Лу
А X '
320. Если черезъ однородное магнитное полеРсъ силовымъ по-
о волыпъ-сек. * см.
токомъ въ В-------------движется со скоростью ѵ-----длинный пря-
кв. см. Г "кѴѵ сек- н
у'
Силовыя (пондеромоторныя) дѣйствія магнитнаго поля на проводникъ 179
мой проводъ, по которому течетъ токъ въ У амперъ, то въ каждомъ
сантиметрѣ проволоки возникаетъ индуктированная электродвижущая
сила, равная В. ѵ вольтъ. Такъ какъ энергія поля при этомъ движеніи
не измѣняется, то получаемая при перемѣщеніи работа доставляется
всецѣло источникомъ тока въ видѣ энергіи З.В.ѵ. За время і проволока
перемѣщается на разстояніе 5 — ѵ. /, и въ каждомъ сантиметрѣ про-
волоки энергія У. В .ѵ .і = . В .8 доставляется эѳиромъ на произ-
водство работы. Отсюда непосредственно слѣдуетъ, что на каждый
сантиметръ проволоки дѣйствуетъ сила Р = }.В.
Прямолинейный проводникъ съ токомъ въ амперъ
испытываетъ вь магнитномъ полѣ съ силовымъ потокомъ
~ вольтъ-сек.
В ---------, силовыя линіи котораго перпендикулярны къ
кв. см.
проводнику, силовое дѣйствіе, направленное перпендику-
лярно какъ къ У, такъ и къ В, и равное В./^на сантиметръ.
За единицу силы при этомъ берется ІО7 диновъ=10,2 кгр.
Это предложеніе даетъ намъ дѣйствіе магнитнаго поля на дви-
жущіеся іоны и электроны въ формѣ механической силы, тогда
какъ раньше (§ 296) мы измѣряли его чисто электрически, какъ
индуктированную электродвижущую силу. При вычисленіяхъ, отно-
сящихся къ катоднымъ и Качаловымъ лучамъ (§ 150), мы уже поль-
зовались приведенной здѣсь формулой.
Нужно, однако, замѣтить, что сила, дѣйствующая на проволоку
съ токомъ въ магнитномъ полѣ, пропорціональна силѣ тока лишь
въ тѣхъ случаяхъ, которые подчиняются принципу наложенія. На-
примѣръ, для желѣзной проволоки при большихъ силахъ тока эта
пропорціональность не имѣетъ мѣста, такъ какъ поле тока вызы-
ваетъ въ магнитномъ полѣ измѣненія, которыя оказываютъ вліяніе на
силовое дѣйствіе. Лишь въ тѣхъ случаяхъ, когда имѣетъ мѣсто прин-
ципъ наложенія, эти дѣйствія поля тока уничтожаются, и сила про-
порціональна У. На этомъ основана возможность измѣрять энергію
при помощи электродинамометра, какъ описано въ § 288.
321. Изъ только-что доказаннаго предложенія мы видимъ, чт^ф^
магнитный силовой потокъ В можетъ быть измѣряемъ также
мощью механическихъ силовыхъ дѣйствій. Для этой цѣли^роще
всего пользоваться соленоидомъ. Если небольшой проволочный прямо-
угольникъ, стороны котораго равны а и Ь и по которрму прохо-
дитъ токъ въ амперъ, помѣстить такъ, чтобы одна его сторона
180 Силовыя (пондеромоторныя) дѣйствія магнитнаго поля на проводникъ
была параллельна линіямъ магнитнаго поля В, то онъ получаетъ
моментъ вращенія С? вокругъ оси, перпендикулярной къ В, при чемъ
ф = В.,І.а.Ь = В.,І.ді гдѣ д — площадь прямоугольника. Эта же
формула вѣрна и для малаго замкнутаго тока любой формы, если
его поверхность д параллельна направленію В. Поэтому соленоидъ,
который состоитъ изъ М малыхъ круговыхъ токовъ и ось котораго
перпендикулярна къ направленію поля, получаетъ моментъ вращенія
С} = Ы.д..!.В.
Величина . д . 3 = М часто называется магнитнымъ моментомъ
соленоида; такимъ образомъ,
($ — В.М.
Магнитный моментъ соленоида имѣетъ еще и другое значеніе:
имъ опредѣляется величина собственнаго магнитнаго поля соленоида
на большихъ разстояніяхъ. Поэтому можно, не опредѣляя величинъ
д, въ отдѣльности, опредѣлить Л4, измѣривъ поле на боль-
шомъ разстояніи отъ соленоида.
Это обстоятельство имѣетъ особенно важное значеніе потому,
что оно позволяетъ намъ замѣнять соленоидъ магнитнымъ стерж-
немъ. Магнитный стержень, имѣющій на большомъ разстояніи во-
кругъ себя точно такое же поле, какъ и соленоидъ съ магнит-
нымъ моментомъ 7И, согласно принципу равенства дѣйствія и про-
тиводѣйствія, испытываетъ въ данномъ магнитномъ полѣ В такое же
самое силовое дѣйствіе, какъ и этотъ соленоидъ, т.-е. получаетъ
моментъ вращенія С? — В .М. М называется тогда магнитнымъ мо-
ментомъ магнитнаго стержня.
ИЗМЪРЕНІЕ ЗЕМНОГО ПОЛЯ ПО МЕТОДУ ГАУССА.
322. Намѣченный сейчасъ способъ измѣренія поля по его ме-
ханическимъ силовымъ дѣйствіямъ является не самымъ простымъ,
хотя и наиболѣе старымъ. Онъ былъ разработанъ еще Гауссомъ,
который примѣнилъ его къ измѣренію земного поля. <іПо^методу
Гаусса сначала измѣряется моментъ вращенія <2, получаемый посто-
яннымъ магнитнымъ стержнемъ, когда его ось наловлена перпен-
дикулярно къ земному полю. Если неизвѣстны^ ^гнитный моментъ
стержня есть М, то С? = В . М. Чтобы найтио\Й, помѣщаютъ стер-
4, •
жень на опредѣленномъ разстояніи отъ буссоли и располагаютъ его
Измѣреніе земного поля по методу Гаусса
181
такъ, чтобы поле магнитнаго стержня въ томъ мѣстѣ, гдѣ находится
буссоль, было перпендикулярно, къ земному полю. Если при этомъ
на буссоли наблюдается отклоненіе а, то отношеніе поля В' стержня
къ земному полю В вычисляется изъ уравненія В = В'. соі^ а
(§ 232). Но значеніе В’ пропорціонально Л4, а именно В' = Во М,
гдѣ Во — значеніе поля магнитнаго стержня на такомъ же точно
разстояніи отъ стержня, когда его магнитный моментъ равенъ еди-
ницѣ. Слѣдовательно, В — М. Во соі а. Величину Во нѣтъ необхо-
димости опредѣлять эмпирически; принимая для Мо опредѣленное
значеніе, можно найти Во чисто математическимъ путемъ, такъ какъ
все магнитное поле, окружающее магнитный стержень, можетъ быть
выражено простыми математическими формулами. Такимъ образомъ
можно вычислить отношеніе В : М = Во соі^ а; мы обозначимъ его
черезъ С. Зная = М. В и С = В : /И, мы найдемъ и В — ]/ . С.
Этотъ методъ совершенно не требуетъ градуированныхъ измѣ-
рительныхъ инструментовъ или эталоновъ, установленныхъ между-
народными соглашеніями. Въ эпоху Гаусса это былъ, дѣйствитечьно,
единственный возможный способъ для измѣренія величины земного
поля въ строго опредѣленныхъ единицахъ.
ПАРАМАГНИТНЫЯ И ДІАМАГНИТНЫЯ ВЕЩЕСТВА.
323. Проницаемость большинства веществъ почти не отличается
отъ проницаемости пустоты. Катушка можетъ быть внутри пустою
или заполнена воздухомъ, водою, масломъ, деревомъ или инымъ
веществомъ, не содержащимъ желѣза и другихъ ферромагнитныхъ
тѣлъ (съ ними мы познакомимся ниже), — самоиндукція отъ этого
не измѣняется сколько-нибудь замѣтнымъ образомъ.
Однако, нѣкоторое весьма малое различіе въ проницаемости
этихъ тѣлъ все-таки существуетъ; это можно замѣтить по малымъ
механическимъ силамъ, дѣйствіе которыхъ испытываютъ почти всѣ
тѣла въ очень сильныхъ магнитныхъ поляхъ. Если въ поле магнита,
изъ полюсовъ котораго исходитъ постоянный силовой потокъ, внести о
тѣло, проницаемость котораго больше проницаемости окружающе||Эѵ
среды, то энергія поля нѣсколько уменьшится, какъ это слѣдуетътйъ
1 • <
формулы о = В2 для плотности энергіи (§ 318). Отдаваемдяполемъ
энергія можетъ быть получена въ формѣ работы, и увлека-
ется силовымъ дѣйствіемъ поля въ область наибольшей ѵ плотности
182
Парамагнитныя и діамагнитныя вещества
силового потока. Если, наоборотъ, проницаемость тѣла меньше про-
ницаемости среды, то оно выталкивается изъ поля. Если тѣлу при-
дать форму стерженька и подвѣсить его въ сильномъ однородномъ
полѣ, то въ случаѣ, если его проницаемость больше проницаемости
окружающей среды, оно установится параллельно направленію сило-
выхъ линій и получитъ слабое индуктированное намагниченіе, на-
правленіе котораго совпадаетъ съ направленіемъ поля. Если прони-
цаемость тѣла меньше, чѣмъ проницаемость окружающей среды, то
оно получаетъ индуктированное намагниченіе, противоположное на-
правленію поля, и стерженекъ устанавливается перпендикулярно къ
силовымъ линіямъ (рис. 220 и 221).
Парамагнитный стержень.
Рис. 220. Силовой потокъ
Діамагнитный стержень,
въ стержнѣ.
Подобнаго рода опыты въ пустотѣ показали, что существуютъ
какъ тѣла съ проницаемостью, немного большей, нежели проница-
емость чистаго эѳира, такъ и тѣла съ проницаемостью, немного
меньшей, чѣмъ проницаемость эѳира.
Парамагнитный стерженекъ. Діамагнитный стерженекъ.
Рис. 221. Положеніе стерженька въ магнитномъ полѣ.
Тѣла, проницаемость которыхъ больше, нежели прони-
цаемость пустоты, называются парамагнитными, а тѣла, цро-
е (6^°
ницаемость которыхъ меньше, чѣмъ проницаемость^пусто-
ты, называются діамагнитными. I
Діамагнитнымъ въ сильной степени является вцсМутъ; парамаг-
нитны платина, палладій, желѣзныя соли (напрцмфф>, хлористое же-
лѣзо, силикаты желѣза и др.)
Отношеніе М:М0=ц абсолютнойСпроницаемости ве-
Измѣренія воспріимчивости
183
щества къ проницаемости эѳира носитъ названіе удѣльной
проницаемости этого вещества.
Если рѣчь идетъ просто о проницаемости, то всегда под-
разумѣвается именно удѣльная проницаемость.
Разность между удѣльной проницаемостью вещества и
единицей, т.-е. величина ц—1, называется магнитной воспрі-
имчивостью этого вещества.
Такъ какъ проницаемость парамагнитнаго вещества больше 1,
то воспріимчивость такого вещества есть величина положительная;
напротивъ, проницаемость діамагнитнаго вещества меньше 1, и вос-
пріимчивость его поэтому выражается отрицательнымъ числомъ. Въ
литературѣ обычно, безъ особыхъ для того основаній, воспріимчи-
востью называютъ менѣе удобную величину —• Многочисленныя
точныя измѣренія доказали, что съ большою точностью можно счи-
тать справедливымъ слѣдующій законъ:
Проницаемость парамагнитныхъ и діамагнитныхъ тѣлъ
не измѣняется съ силой поля.
Слѣдовательно, въ парамагнитныхъ и діамагнитныхъ средахъ
принципъ наложенія имѣетъ такую же силу, какъ и въ чистомъ эѳирѣ.
ИЗМѢРЕНІЯ ВОСПРІИМЧИВОСТИ.
324. Воспріимчивость жидкости опредѣляется сравнительно про-
сто по силовымъ дѣйствіямъ, испытываемымъ жидкостью въ магнит-
номъ полѣ. Жидкость наливается въ двѣ сообщающіяся трубки, изъ
которыхъ одна помѣщается въ магнитномъ полѣ такъ, чтобы вер-
шина жидкости находилась въ возможно болѣе однородной ча-
сти магнитнаго поля; другая трубка помѣщается вдали внѣ маг-
нитнаго поля. Какъ только мы возбудимъ поле, между высотами
уровней жидкости въ обоихъ колѣнахъ обнаруживается разность.
Парамагнитная жидкость въ магнитномъ полѣ слегка поднимается,
діамагнитная—слегка опускается. Если В—сила магнитнаго силового
потока въ вольтъ-секундахъ на квадратный сантиметръ, М'— проница-
емость воздуха, М — проницаемость жидкости, то энергія поля, приэ@-Ѵ
дящаяся на кубическій сантиметръ, въ воздухѣ составляетъ В2 : 2№>йъ
жидкости —В2: 2М. Если малую высоту поднятія жидкости обо^йчимъ
черезъ б, а сѣченіе трубки черезъ а. то магнитное поле отдаетт^энергію
184
Измѣренія воспріимчивости
Отсюда видно, что на менискъ жидкости дѣйствуетъ сила
Какъ мы увидимъ ниже, М и М' отличаются отъ Мо менѣе,
чѣмъ на одну промилле; поэтому мы можемъ съ вполнѣ достаточною
точностью замѣнить въ знаменателѣ М . М' черезъ М^. Такимъ
образомъ мы получимъ
В2
гдѣ р и ц' суть удѣльныя проницаемости жидкости и воздуха. Если
за единицу силы мы примемъ вѣсъ 1 грамма, то
Р = —Дд— • (ц—ц') . 7.10,2 . ІО3 = 0,406 . ІО12. В2. (р —ц'). д граммъ
Эта магнитная сила Р должна уравновѣшиваться давленіемъ, ко-
торое соотвѣтствуетъ разности уровней жидкости, вызванной маг-
нитнымъ полемъ. Если эта разность уровней равняется И см. и
удѣльный вѣсъ жидкости есть 5, то давленіе, дѣйствующее на менискъ
жидкости, равняется Р = И . 8 . д. Слѣдовательно,
/г. 5 = 0,406. ІО12. Б2.(ц-цЭ-
Измѣривъ В, А, 5, можно найти р — р'. Если удалить воздухъ, на-
ходящійся надъ жидкостью въ обѣихъ трубкахъ, то устанавливается
нѣсколько иная разность уровней А', при чемъ:
к' .5 = 0,406 . ІО12.В2.(р-1);
(Л'-Л) . 5 = 0,406 . ІО12 . В2 . (р-1).
Такимъ образомъ опредѣляются воспріимчивости воздуха и жидко-
сти. Если же пространство надъ жидкостью наполнить вмѣсто воз-
духа инымъ газомъ, то, сравнивая соотвѣтственную разность уровней
съ величиной к', можно опредѣлить воспріимчивость этого газа.
Описанный методъ былъ впервые разработанъ и примѣненъ
Г. Квинке (С. Оиіпске).
Нѣсколько труднѣе опредѣлить воспріимчивости твердыхъ ^тѣлъ;
удобнѣе всего пользоваться для этой цѣли непрямымъ методомъ.
Если ввести въ магнитное поле стерженекъ такъ, чтобц^рнъ соста-
влялъ острый уголъ съ направленіемъ силовыхъ линій^то онъ по-
лучитъ моментъ вращенія, пропорціональный р-^^^гдѣ ц —прони-
цаемость вещества стерженька, р'— проницаемость той жидкой или
Измѣренія воспріимчивости
185
газообразной среды, въ которой подвѣшенъ стерженекъ. Послѣдо-
вательно вводя въ поле различныя жидкости, проницаемость кото-
рыхъ извѣстна, и подвѣшивая стерженекъ всякій разъ въ совершенно
одинаковомъ положеніи относительно поля, мы измѣряемъ моментъ вра-
щенія. Посредствомъ интерполированія, а въ случаѣ необходимости
и экстрополированія, мы теперь легко опредѣлимъ, какова должна
быть проницаемость жидкости, чтобы моментъ вращенія былъ ра-
венъ нулю. Это значеніе проницаемости и есть искомая проница-
емость вещества стерженька. Въ слѣдующей таблицѣ даны нѣкото-
рыя изъ полученныхъ такимъ способомъ чиселъ.
Парамагнитныя тѣла , 1 ц- 1 Діамагнитныя тѣла и- 1
Азотъ + 0,01.10-6 Алкоголь - 8,2 . 10—6
Воздухъ + 0,32.10-6 Вода - 9,8 . 10-6
Кислородъ + 1,26.10-6 Каменная соль . . - 13 . 10-6
Олово + 3,8 .ІО-6
Алюминій + 23 .ІО”6 Мѣдь - 10 . 10-6
Платина ... + 365 .ІО-6 Цинкъ - 13 . 10-6
Палладій ... + 700 .ІО”6 Серебро - 19 . 10—6
28°/о растворъ хлор- Ртуть - 25 . 10—6
наго желѣза (уд. Золото - 38 . 10—6
вѣсъ 1,27) .... + 384 . ІО-6
48% растворъ хлор- Висмутъ -176 . ІО-6
наго желѣза (уд.
вѣсъ 1,51) .... + 805 .ІО-6
Парамагнитны не только растворы всѣхъ желѣзныхъ солей, но
также и всѣ растворы марганцовыхъ, кобальтовыхъ, никкелевыхъ и
хромовыхъ солей. Замѣчательно, что и растворы мѣдныхъ соединеній
ясно парамагнитны, хотя сама мѣдь діамагнитна.
ИЗМѢРЕНІЕ ПОЛЯ ПО ВЫСОТѢ ПОДНЯТІЯ ЖИДКОСТИ.
325. Если мы наполнимъ двѣ сообщающіяся трубки жидкостью,
воспріимчивость которой извѣстна, и одинъ менискъ жидкости пом^^
стимъ въ магнитномъ полѣ, то по вызываемой дѣйствіемъ^іоля
разности уровней И мы можемъ опредѣлить силу поля въ томъмѣстѣ,
гдѣ находится менискъ. Именно,
в = с.уй, /Лг
486
Теорія парамагнетизма и діамагнетизма
гдѣ
Здѣсь 5 обозначаетъ удѣльный вѣсъ жидкости, ц и ц'— удѣльныя
проницаемости жидкости и воздуха.
Для измѣреній особенно удобны растворы хлорнаго желѣза.
По изслѣдованіямъ I. Кенигсбергера (Л. Кбпі^зЬег^ег) величина
—ц для любой концентраціи такого раствора весьма точно опре-
дѣляется по формулѣ
. ІО6 - 1101 .р- 9,8.(1- р),
гдѣ р есть количество соли (РеСІ3) на одну вѣсовую единицу рас-
твора, а 1 — р соотвѣтственное количество воды.
ТЕОРІЯ ПАРЛМАГНИТИЗМА И ДІАМАГНИТИЗМА.
326. Явленія, обнаруживаемыя парамагнитными тѣлами въ маг-
нитномъ полѣ, вполнѣ аналогичны явленіямъ, обнаруживаемымъ
діэлектрикомъ въ электрическомъ полѣ. Мы можемъ поэтому объяс-
нить себѣ парамагнитизмъ такимъ же образомъ, какъ діэлектрическія
свойства матеріальныхъ тѣлъ. Мы принимаемъ, что въ парамагнит-
номъ тѣлѣ содержится большое число маленькихъ молекулярныхъ
магнитовъ (§ 291), которые удерживаются молекулярными силами
въ опредѣленныхъ положеніяхъ такимъ образомъ, что въ полѣ, сила
котораго равна нулю, они имѣютъ всевозможныя направленія безъ
преобладанія одного какого - либо направленія. Если такое тѣло
внести въ поле, то всѣ магнитики слегка отклоняются, такъ что
направленіе, соотвѣтствующее направленію поля, становится преобла-
дающимъ; отклоненія пропорціональны силѣ поля. Если удалимъ
поле, то магнитики возвращаются въ свои первоначальныя положенія.
Дѣйствіе магнитнаго поля, вызывающее діамагнитизм^Ь^Совер-
шенно отличается отъ дѣйствія, вызывающаго парамагц^ірмъ. Оба
эти дѣйствія, вѣроятно, всегда одновременны, но преобладаетъ то
одно изъ нихъ, то другое. Согласно теоріи, разви^Й^въ § 291, мо-
лекулярный магнитъ представляетъ собой молейу^ съ вращающи-
мися электронами. Но магнитное поле само шшетъ вызвать вращеніе
Теорія парамагнитизма и діамагнитизма
187
электроновъ, содержащихся въ молекулѣ, такъ какъ при возникновеніи
магнитнаго поля и при всѣхъ его измѣненіяхъ появляются электри-
ческія силы, линейная сумма которыхъ вдоль замкнутыхъ кривыхъ от-
лична отъ нуля. Эти интрамолекулярныя движенія электроновъ, вызы-
ваемыя возникновеніемъ магнитнаго поля, совершаются въ противопо-
ложность „индуктированнымъ ударамъ напряженія" въ обыкновенныхъ
проводникахъ все время, пока поле остается постояннымъ, такъ
какъ эти движенія не требуютъ никакой затраты энергіи. При исчезнове-
ніи же магнитнаго поля, вызываемыя этимъ силы противоположнаго на-
правленія вновь возвращаютъ электроны въ состояніе покоя. Скорость
вращенія, т.-е. намагниченіе молекулярныхъ магнитовъ, вызванное
самымъ полемъ, всегда пропорціональна суммѣ индуктированныхъ
напряженій по времени, или, что то же, силовому потоку магнит-
наго поля. Индуктированные въ молекулахъ замкнутые токи, со-
гласно законамъ индукціи, направлены такимъ образомъ, что они
ослабляютъ индуктирующее поле; поэтому молекулярные магнитики
располагаются въ направленіи, противоположномъ полю. Эти именно
молекулярные магнитики, возбужденные самымъ магнитнымъ по-
лемъ, и вызываютъ діамагнитизмъ.
Что индуктированныя электродвижущія силы дѣйствительно
могутъ вызвать діамагнитныя дѣйствія, можно показать при помощи
очень красиваго опыта съ пламенемъ свѣчи; какъ только мы вне-
семъ снизу въ междуполюсное пространство сильнаго электромаг-
нита пламя, оно тотчасъ раздувается въ обѣ стороны и та-
кимъ образомъ увлекается отъ сильныхъ частей поля къ слабымъ,
какъ если бы оно было діамагнитнымъ. Это явленіе легко объяс-
няется тѣмъ, что магнитное поле дѣйствуетъ на іоны поднимаю-
щихся вверхъ проводящихъ газовъ пламени съ силами, которыя го-
нятъ іоны изъ поля въ обѣ стороны. Движущіеся іоны увлекаютъ
съ собою остальные газы, вслѣдствіе чего и самое пламя выталки-
вается изъ магнитнаго поля.
ФЕРРОМАГНИТНЫЯ ВЕЩЕСТВА.
327. Если въ проволочную катушку вставленъ желѣзный сер-
дечникъ, то этимъ ея самоиндукція замѣтно повышается (§^310).
Это значитъ, что проницаемость желѣза несравненно больш^прони-
цаемости чистаго эѳира. Измѣреніемъ самоиндукціи ЦО^но непо-
средственно опредѣлить проницаемость желѣза. Съ дтрй цѣлью бе-
188
Ферромагнитныя вещества
рется желѣзное кольцо равномѣрной толщины, снабженное равно-
мѣрной обмоткой изъ изолированной проволоки. Черезъ обмотку
будемъ пропускать токъ и измѣримъ, съ одной стороны, число
амперъ-витковъ амперметромъ, а, съ другой стороны, посредствомъ
баллистическаго инструмента, приключеннаго къ зажимамъ обмотки,
измѣримъ ударъ напряженія, сопровождающій измѣренное измѣненіе
числа амперъ-витковъ. Отсюда можно опредѣлить самоиндукцію
замкнутаго соленоида и проницаемость желѣзнаго сердечника. Это
вычисленіе весьма простое, такъ какъ все магнитное поле прохо-
дитъ внутри желѣза и кромѣ того почти однородно. Произведеніе
Рис. 222. Измѣреніе проницаемости желѣзнаго кольца.
измѣренной силы тока У на число витковъ, приходящееся на 1 санти-
метръ, непосредственно даетъ намъ силу магнитнаго поля Н въ же-
лѣзѣ. Сумма всѣхъ наблюдаемыхъ ударовъ напряженія при возрастаніи
тока отъ 0 до У, раздѣленная на число всѣхъ витковъ катушки и
сѣченіе желѣзнаго сердечника, дастъ намъ величину В. Мы мо-
жетъ поэтому сейчасъ же вычислить также М = В: Я и ц - ГИ: М (.
Такъ какъ обычно ищутъ только величину удѣльной проницаемости ц,
то вмѣсто Н вычисляютъ прямо Мо ц, и затѣмъ находятъ ц Мо//.
Въ большинствѣ случаевъ удобнѣе для опредѣленія В измѣ-
рить ударъ напряженія между зажимами небольшой^)вторичной ка-
тушкии, изолированной отъ намагничивающей обмотки, какъ пока-
зано на рис. 222, изображающемъ схему соединеній. Въ нижеслѣ-
Ферромагнитныя вещества
189
дующей таблицѣ приведены результаты ряда измѣреній, сдѣланныхъ.
Юингомъ (Е\ѵіп^) надъ кольцомъ изъ мягкаго желѣза.
Мо. Н . 108 Баллистиче- ское отклоненіе Сумма от- клоненій В. 10? М
0,13 1,1 1,1 26 20Э
0,26 1,1 2,2 53 204
0,30 0,5 2,7 65 216
0,40 0,8 3,5 84 210
0,53 1,0 4,5 107 202
0,71 2,1 6,6 158 223
0,93 2,9 9,5 227 243
1,31 3,9 13,4 320 245
1,69 9,2 22,6 540 320
1,89 6,9 29,5 705 370
2,78 77,5 107,0 2 560 920
3,36 78,7 185,7 4 440 1320
4,01 82,0 267,7 6 400 1600
4,95 91,5 359,2 8 580 1 740
5,86 57,0 416,2 9 940 1 700
7,20 57,0 473,2 11300 1 570
8,10 23,5 496,7 11 870 1 460
9,14 24,0 520,7 12 440 1360
Эти данныя представлены графически въ видѣ кривой на
рис. 223. Сразу видно, что о приложимости принципа наложенія къ
желѣзу не можетъ быть
и рѣчи. Характерно для
этой кривой, выражающей
зависимость между В и Ну
что при малыхъ силахъ по-
ля она поднимается сравни-
тельно медленно (ц = 210
въ среднемъ), но при зна-
ченіяхъ В . ІО8 отъ 1 000 до
10000 кривая сразу подни-
мается очень круто, такъ
что ц возрастаетъ до 1700,
а затѣмъ при значеніяхъ
В . ІО8, превышающихъ
10 000, постепенно заги-
бается обратно. Продол-
жая измѣренія, можно убѣ-
диться, что при значеніяхъ
В . ІО8, превышающихъ
190
Магнитныя цѣпи
13000, кривая становится, наконецъ, почти горизонтальной. При
этомъ желѣзо находится, какъ говорятъ, въ состояніи „магнитнаго
насыщенія".
Ферромагнитныя вещества характеризуются тѣмъ, что
ихъ проницаемость, во-первыхъ, весьма велика и, во-вто-
рыхъ, зависитъ отъ силы поля. Для слабыхъ полей ихъ про-
ницаемость меньше, чѣмъ для болѣе сильныхъ, а въ весьма
сильныхъ поляхъ они приближаются къ состоянію магнит-
наго насыщенія. Такимъ образомъ, существуетъ опредѣ-
ленная сила поля, при которой проницаемость ферромаг-
нитнаго вещества имѣетъ максимумъ.
Разность В— Мо/У = называютъ намагниченіемъ. Для
парамагнитныхъ и діамагнитныхъ веществъ намагниченіе близко къ
нулю; для ферромагнитныхъ же тѣлъ оно весьма велико и почти
не отличается отъ В.
МАГНИТНЫЯ ЦѢПИ.
328. Магнитными цѣпями называются магнитныя силовыя трубки,
проходящія частью черезъ ферромагнитныя, частью же черезъ не-ферро-
магнитныя вещества; таковы, напримѣръ, силовыя линіи катушки съ же-
лѣзнымъ сердечникомъ. Для всѣхъ магнитныхъ цѣпей сохраняетъ силу
основное положеніе, по которому число всѣхъ амперъ-витковъ вдоль
какой-либо изъ замкнутыхъ силовыхъ линій всегда равняется числу
амперъ-витковъ намагничивающей катушки, внутри которой прохо-
дитъ эта линія. Мы можемъ поэтому узнать число всѣхъ амперъ-
витковъ силовой линіи, измѣривъ токъ въ намагничивающей катушкѣ.
Но трудно сказать, сколько изъ этого числа амперъ-витковъ при-
ходится на внутреннее поле въ желѣзѣ и сколько — на внѣшнее
поле, такъ какъ присутствіе желѣза оказываетъ сильное вліяніе на
внѣшнее поле, а именно усиливаетъ его, вслѣдствіе чего внутрен-
нее число амперъ-витковъ меньше, чѣмъ въ катушкѣ безъ желѣза.
Основной законъ, согласно которому магнитный силовой потокъ
идетъ лишь по замкнутымъ путямъ, остается справедливы^^ѣакже
для сложныхъ магнитныхъ цѣпей. Согласно этому изъ^рюлюса на-
магниченнаго желѣзнаго стержня выходитъ столько же линій индукціи,
сколько ихъ внутри желѣза идетъ къ полюсу. Число этихъ индук-
ціонныхъ линій можно измѣрить при помощи прр^Одочной окружно-
сти, охватывающей стержень вблизи полюсной прверхности; ударъ на-
Магнитныя цѣпи
191
пряженія при какомъ-либо измѣненіи поля всегда равенъ измѣненію
числа индукціонныхъ линій, которыя пронизываютъ поверхность,
ограниченную проволочной окружностью. Но черезъ эту окружность
можно провести много поверхностей, какъ проходящихъ снаружи, т.-е.
огибающихъ полюсъ, такъ и пересѣкающихъ желѣзо. На всѣхъ
этихъ поверхностяхъ измѣненіе силового потока одинаково; такъ
какъ это справедливо, вообще, съ момента возникновенія поля, то въ
дѣйствительности общее число индукціонныхъ линій внутри и сна-
ружи одинаково.
Оба основные закона магнитнаго поля очень сходны съ зако-
нами электрическаго тока. Если мы замкнемъ проводящей цѣпью
гальваническую батарею, то, во-первыхъ, полное напряженіе вдоль
каждой линіи тока будетъ одинаково и равно электродвижущей си-
лѣ батареи и, во-вторыхъ, электрическій токъ будетъ протекать по
замкнутымъ линіямъ.
Линіи магнитнаго силового потока въ какомъ-либо зам-
кнутомъ кольцѣ идутъ совершенно такъ же, какъ распростра-
нялись бы линіи электрическаго тока въ кольцѣ такой же
формы, если бы проводимость кольца, черезъ которое
•идетъ токъ, была повсюду равна проницаемости кольца,
пронизываемаго магнитнымъ силовымъ потокомъ, а элек-
тродвижущая сила въ цѣпи съ токомъ была равна числу
амперъ-витковъ магнитной цѣпи.
Терминъ „магнитный силовой потокъ" былъ введенъ вмѣсто
стараго термина „индукція" именно для того, чтобы указать на
аналогію съ электрическимъ токомъ. Число амперъ - витковъ маг-
нитной цѣпи часто называютъ „намагничивающей силой" или „магни-
тодвижущей силой". По тѣмъ же соображеніямъ было введено поня-
тіе „магнитнаго сопротивленія". Если сѣченіе отрѣзка силовой
трубки есть его длина равна I и абсолютное значеніе проницае-
мости въ разсматриваемомъ мѣстѣ есть М, то „магнитное сопроти-
вленіе" этого отрѣзка силовой трубки вычисляется, подобно электри-
ческому сопротивленію (§ 263), по формулѣ С ч
1
П д. М ’
Если полный силовой потокъ въ отрѣзкѣ силовоЦСтрубки
^стѣТ-=В.д и число амперъ-витковъ равно 4=//./,\бѵ
А А /ЧЧ
р = а М • - = -. чЛ
Я I В
192
Магнитныя цѣпи
Эта формула выражаетъ „законъ Ома" для магнитнаго силового
потока. Слѣдуетъ, однако, замѣтить, что въ ферромагнитныхъ тѣлахъ
величина не есть постоянная.
Говоря языкомъ этой аналогіи, ферромагнитныя вещества от-
личаются отъ всѣхъ другихъ своей несравненно большей проводи-
мостью для магнитнаго силового потока. По сравненію съ ними
прочія вещества являются какъ бы полупроводниками. Вслѣдствіе
этого кусокъ желѣза, находящійся въ магнитномъ полѣ, втягиваетъ
въ себя магнитныя силовыя линіи (рис. 144), а желѣзный цилиндръ,
не пропускаетъ поля въ свою полость (рис. 145).
329. Очень просто вычисляется магнитное поле, находящееся
большей частью въ желѣзѣ и встрѣчающее лишь узкій воздушный
путь. Практически мы имѣемъ подобный случай въ электромагни-
тахъ съ полюсными башмаками, между которыми оставлена лишь
узкая воздушная щель. Сюда же относятся электромагниты динамо-
машинъ и электромоторовъ, „магнитно замыкаемые" желѣзными
якорями такъ, что съ обѣихъ сторонъ якоря остается лишь узкое
промежуточное пространство. Покажемъ на небольшомъ числен-
номъ примѣрѣ вліяніе воздушнаго промежутка, представляющаго со-
бою тонкій плохо проводящій слой даже въ весьма хорошемъ маг-
нитномъ проводникѣ. Желѣзное кольцо постояннаго сѣченія <?, сред-
няя линія котораго имѣетъ длину /, разрѣзано въ одномъ мѣстѣ
такъ, что получилась воздушная щель ширины Ь. Удѣльная индук-
ція равна В; въ такомъ случаѣ силовой потокъ равенъ Р = В .
Если число оборотовъ катушки обозначимъ черезъ Ы, а намагничи-
вающій токъ черезъ У, то число амперъ-витковъ Д = /.7Ѵ. Имѣемъ:.
А = Р.
-4г')=? • —ѵ • (-+-’м • с1+м • *>)
?.М0/ ^.Мо \М ) д.М у 1 г 7
или
В~ 1 + м.Ь‘
Напримѣръ, при силовомъ потокѣ В— 12000.10~8 проницаейрСть
ц— 1400. Если желаемъ получить такую силу поля, то нес^^одимая
для этого сила тока У вычисляется по формулѣ
/ѵ. м
Такимъ образомъ, на 1 мм. воздуха требуется5 ^только же амперъ-
витковъ, сколько на 1,4 м. желѣза.
Катушка съ желѣзнымъ сердечникомъ
193
КАТУШКА СЪ ЖЕЛѢЗНЫМЪ СЕРДЕЧНИКОМЪ.
330. Теоретически столь изящный и безупречный методъ измѣ-
ренія проницаемости ферромагнитныхъ веществъ при помощи коль-
цевого соленоида на практикѣ употребляется лишь въ исключитель-
ныхъ случаяхъ. Для быстраго и точнаго измѣренія необходимо по-
мѣстить изслѣдуемое вещество въ готовой намагничивающей катушкѣ,
составляющей часть готоваго аппарата. Это возможно лишь при усло-
віи, если катушка имѣетъ цилиндрическую форму, а изслѣдуемое
вещество имѣетъ форму стержня.
При измѣненіи силы тока, проходящаго по катушкѣ съ желѣз-
нымъ сердечникомъ, форма магнитныхъ силовыхъ линій, тожествен-
ная съ формой силовыхъ линій въ случаѣ соленоида съ токомъ
(рис. 138), измѣняется очень мало. Вслѣдствіе этого магнитное
сопротивленіе внѣшняго поля почти не измѣняется. Обозначимъ его
черезъ /?0; число амперъ-витковъ катушки Л = связано съ
магнитнымъ силовымъ потокомъ Л соотношеніемъ
\ 0 1 #. М/
здѣсь I—длина желѣзнаго сердечника, д — его сѣченіе, М—его
абсолютная проницаемость. Если мы можемъ какимъ-либо спосо-
бомъ вычислить /?0, то для опредѣленія проницаемости М (а также,
слѣдовательно, и ц) остается лишь извѣстнымъ способомъ измѣ-
рить А и Р.
Внѣшнія силовыя линіи совершенно не измѣняются только въ
томъ случаѣ, если желѣзный сердечникъ имѣетъ форму эллипсоида.
Въ этомъ случаѣ, сверхъ того, внутреннее поле будетъ дѣйстви-
тельно вполнѣ однороднымъ, если только эллипсоидъ находится
весь внутри катушки. Величину 7?0 можно точно вычислить по простымъ
формуламъ, а съ помощью величины ГИ можно также опредѣлить и
магнитное сопротивленіе эллипсоида. Если мы желаемъ при помощи
катушки и сердечника точно измѣрить ГИ, то нужно предварительно
изготовить изъ изслѣдуемаго матеріала удлиненный эллипсоидъ вра<О^
щенія.
„В-Н-кривая“ изслѣдуемаго ферромагнитнаго вещества^мо-
жетъ быть получена слѣдующимъ графическимъ способомъ.^ Пусть
И' будетъ число амперъ-витковъ самой катушки, приходящееся на
сантиметръ, т. е. Н' — Ы.3 \ Ц гдѣ /—длина катуіцки.^ Сначала мы
Ми. Электричество и магнитизмъ, ч. II. V 1.3
194
Методъ замкнутаго кольца (методъ Гопкинсона)
представляемъ величину В (измѣряемую суммою ударовъ напряже-
ній) въ видѣ кривой, какъ функцію величины Н'. Затѣмъ мы че-
резъ нулевую точку проводимъ косо вверхъ линію, разстояніе кото-
рой отъ оси ординатъ вездѣ указываетъ, какую величину нужно
вычесть изъ Н’ при соотвѣтственномъ значеніи В, чтобы получить
силу поля Н внутри желѣзнаго стержня; въ нашемъ случаѣ это
будетъ величина/7^ : I. Эта такъ называемая „линія сдвига" предста-
вляетъ собою прямую, если магнитное сопротивленіе внѣшняго поля
постоянно. Если затѣмъ каждую точку В-Н'-кривой передви-
нуть на отрѣзокъ, указываемый линіей сдвига для соотвѣтствую-
щаго значенія В, то сдвинутая такимъ образомъ кривая и будетъ
искомая В-Н-кривая изслѣдуемаго вещества. Это графическое по-
строеніе представлено на рисункахъ 231 и 232.
. МЕТОДЪ ЗАМКНУТАГО КОЛЬЦА (МЕТОДЪ ГОПКИНСОНА).
331. Вліяніе внѣшняго поля на измѣренія можно исключить
весьма простымъ способомъ: для этого достаточно сдѣлать число
Рис. 224. Магнитное „ярмо“ Гопкинсона (схематически).
его амперъ-витковъ очень малымъ. Съ этой цѣлью изслѣдуемый
стержень вставляется въ толстое кольцо („ярмо") изъ мягкаго кованаго
желѣза такимъ образомъ, чтобы оба его конца были соединены
между собою желѣзомъ и магнитно замкнуты „на-коротку^>%° Самый
стержень имѣетъ точную цилиндрическую форму и о^прёдѣленную
толщину (нѣсколько миллиметровъ) и какъ разъ вхрдитъ въ ярмо.
Концы стержня прочно прижимаются винтами^ё^ желѣзу ярма
такъ, чтобы не оставалось промежуточнаго воздушнаго простран-
ства. Намагничивающая катушка и маленькая^ катушка, служащая
Измѣреніе магнитной индукціи силовыми (пондеромоторными) дѣйствіями 195
для измѣренія ударовъ напряженій, прочно соединены съ ярмомъ;
въ нихъ вставляется стержень, когда на этотъ послѣдній надѣваютъ
ярмо. Такъ какъ поперечное сѣченіе ярма весьма велико, то плот-
ность магнитнаго силового потока (удѣльная индукція) въ ярмѣ В$
гораздо меньше, чѣмъ удѣльная индукція въ стержнѣ В. Если сѣченіе
ярма въ 200 разъ больше сѣченія стержня, то 2^ = 0,005 В. Далѣе, такъ
какъ проницаемость ярма весьма велика, то ясно, что приходящееся на
ярмо число амперъ - витковъ не превосходитъ 1°/0 общаго числа.
Такимъ образомъ, безъ большой погрѣшности можно число амперъ -
витковъ намагничивающей катушки считать равнымъ числу амперъ -
витковъ строго однороднаго поля въ изслѣдуемомъ тонкомъ стержнѣ.
Если же требуется очень большая точность, то слѣдуетъ опредѣлить
„линію сдвига* аппарата, которая, конечно, не представляетъ собою
прямой, такъ какъ внѣшнее поле проходитъ въ желѣзо.
Методъ замкнутаго кольца (рис. 224) изобрѣтенъ Топки нео-
номъ (Норкіпзоп), который впервые примѣнилъ его къ изслѣдова-
нію ферромагнитныхъ веществъ.
ИЗМѢРЕНІЕ МАГНИТНОЙ ИНДУКЦІИ СИЛОВЫМИ (ПОНДЕРОМО-
ТОРНЫМИ) ДѢЙСТВІЯМИ.
332. Во всѣхъ описанныхъ до сихъ поръ методахъ измѣреніе
силового потока имѣетъ тотъ недостатокъ, что искомая величина
получается лишь путемъ суммированія многихъ ударовъ напряженій,
измѣряемыхъ при отдѣльныхъ внезапныхъ измѣненіяхъ тока. Конеч-
но, несравненно лучше опредѣлять искомую величину сразу, при
помощи одного только измѣренія. Чтобы измѣрить въ одинъ пріемъ
магнитную индукцію, удобнѣе всего пользоваться механическими
силовыми дѣйствіями поля.
Если ферромагнитный стержень не замкнутъ на-короткую ярмомъ,
то можно просто измѣрить поле на большомъ разстояніи отъ стержня ,
и отсюда вычислить его магнитный моментъ (§321). Силовой по-
токъ внутри стержня въ этомъ случаѣ въ точности равенъ силоЦ
вому потоку въ пустомъ соленоидѣ, имѣющемъ форму стер^сня^Вй
его магнитный моментъ, и поэтому можетъ быть сейчасъ ж^Увычи-
сленъ. Если желательно произвести такимъ методомъ точйгё^измѣ- I
реніе, то стержню слѣдуетъ придать форму удлиненнаго эллипсоида
вращенія (ср. § 330). ° 9
13
196 Измѣреніе магнитной индукціи силовыми (пондеромоторными) дѣйствіями
333. Обыкновенно при измѣреніи поля механическими силами
тоже предпочитаютъ замкнуть концы стержня на-короткую при по-
Рис. 225. Аппаратъ Кёпселя (схематически).
мощи магнитнаго ярма, такъ какъ при этомъ можно пользоваться
цилиндрическими стержнями, которые легче вытачиваются съ точ-
ностью. Въ ярмѣ должна находиться гдѣ-нибудь узкая воздушная щель,
въ которой измѣряется силовое дѣйствіе поля. Очень^добенъ аппа-
ратъ Кёпселя (Кбрзеі) съ вращающейся катушксэ^;^здѣсь магнитный
индукторъ замѣненъ намагничивающей катушкой- съ изслѣдуемымъ
стержнемъ, а полюсные башмаки — сильнымъ^магнитнымъ ярмомъ
Гистерезисъ
197
(рис. 225). Электрическій токъ во вращающейся катушкѣ регули-
руется при помощи реостата до извѣстной предписанной силы,
отсчитываемой по включенному въ цѣпь точному амперметру. Сила,
съ которой магнитное поле ярма дѣйствуетъ на катушку, а, слѣдо-
вательно, и отклоненіе стрѣлки прямо пропорціональны силовому
потоку Вд въ ярмѣ, а также, слѣдовательно, и силовому потоку В
въ стержнѣ. Поэтому шкалу инструмента можно градуировать такимъ
образомъ, чтобы непосредственно отсчитывать на ней значеніе В. При
вычисленіи намагничивающей силы Н слѣдуетъ принять во вниманіе,
что цилиндрическая щель, въ которой движется вращающаяся катушка,
обладаетъ магнитнымъ сопротивленіемъ, которымъ нельзя совершенно
пренебречь и которое должно быть исключено посредствомъ не-
большой поправки на число витковъ намагничивающей катушки.
Другой инструментъ съ ярмомъ и со щелями для измѣреній силы
поля называется магнитными вѣсами Дюбуа (ПиЬоіз) (рис. 226).
Посредствомъ передвижного груза можно опредѣлить, съ какой
силой взаимно притягиваются двѣ полюсныя поверхности, ограни-
чивающія щель. Посредствомъ формулы, выведенной въ § 319, по
величинѣ этой силы можно опредѣлить величину В.
ГИСТЕРЕЗИСЪ.
334. Если силу намагничивающаго тока сперва увеличить на*
столько, чтобы желѣзный сердечникъ сильно намагнитился, а затѣмъ
постепенно уменьшать силу тока, то для каждаго числа амперъ-
витковъ убывающаго въ силѣ тока получается большая магнитная
индукція, нежели для тока возрастающаго. Это явленіе предста-
вляетъ собою не что иное, какъ уже упомянутое въ § 225 оста-
точное намагниченіе. Оно относится къ числу тѣхъ свойствъ
матеріи, которыя носятъ названіе послѣдѣйствій или гистерезиса,
и потому обычно называется теперь магнитнымъ гистерезисомъ
желѣза. Если уменьшать силу тока до тѣхъ поръ, пока число амперъ-
витковъ въ желѣзѣ не станетъ равнымъ нулю, то магнитная индук-
ція при этомъ сохранитъ весьма замѣтное значеніе, какъ показы^Ь
ваетъ В-Н-кривая желѣзной проволоки на рис. 227. Только при
перемѣнѣ знака числа амперъ-витковъ значеніе В становится,н&ко-
нецъ, равнымъ нулю. Будемъ увеличивать далѣе намагі^^вающій
токъ въ отрицательномъ направленіи до отрицательнагоуйаибѳль-
198
Гистерезисъ
шаго значенія, равнаго достигнутому
раньше наибольшему положительному
значенію; затѣмъ снова вернемся къ
нулю, и заставимъ токъ возрастать въ
положительномъ направленіи до макси-
мальнаго значенія; потомъ опять возвра-
тимся назадъ и будемъ повторять этотъ
„циклическій процессъ намагниченія"
много разъ. Въ результатѣ получается
м^е.іо* В-Н-кривая въ видѣ правильной петли,
изображенной на рис. 227. При повто-
реніи цикловъ эта петля кривой гисте-
резиса остается неизмѣнной. Для твер-
даго желѣза и еще болѣе для стали
петли гистерезиса гораздо шире, чѣмъ
для мягкаго желѣза, какъ это видно изъ
сравненія рис. 228 съ рис. 227.
Всѣ ферромагнитныя вещества
Рис. 227. Гистерезисъ^мягкаго обладаютъ въ большей или мень-
желѣза. шей степени свойствомъ магнит-
наго гистерезиса.
Постоянные магниты
199
Если механически встряхивать намагничиваемый стержень, то
гистерезисъ уменьшается и можетъ даже почти исчезнуть. Вмѣсто
петли тогда получается одна кривая посрединѣ между восходящей
и нисходящей вѣтвями петли. Остаточное намагниченіе желѣзнаго
стержня исчезаетъ отъ сильныхъ ударовъ. Намагниченіе, возбужда-
емое въ такомъ стержнѣ слабымъ полемъ, гораздо сильнѣе, если
стержень при этомъ ударяютъ, чѣмъ если онъ находится въ покоѣ.
Этимъ объясняется упомянутое въ § 231 намагниченіе стальныхъ
инструментовъ земнымъ полемъ.
Подобно механическому встряхиванію дѣйствуетъ перемѣнное
магнитное поле, вызывающее колебательное движеніе молекулярныхъ
магнитовъ. Можно размагнитить магнитъ, подвергая его дѣйствію
постепенно ослабѣвающаго перемѣннаго поля. Этимъ способомъ
часовые мастера исправляютъ часыѴвъ тѣхъ случаяхъ, когда пру-
жина подъ дѣйствіемъ сильнаго магнитнаго поля становится магнит-
ной, и часы потому идутъ неправильно.
ПОСТОЯННЫЕ МАГНИТЫ.
335. Остаточнымъ магнитизмомъ, или гистерезисомъ, объяс-
няется существованіе постоянныхъ магнитовъ. Внутри постояннаго
магнитнаго стержня, не окруженнаго катушкой съ токомъ, поле, измѣ-
ренное въ амперъ-виткахъ, отлично отъ нуля. Если мы будемъ считать
Рис. 229. Силовыя линіи посто-
яннаго магнита
Рис. 230. Линіи силового потока
постояннаго магнита. в
амперъ-витки внѣшняго поля положительными, то внутри стержня
будетъ находиться поле отрицательныхъ амперъ-витковъ: въ сомомъ
дѣлѣ, сумма всѣхъ амперъ-витковъ вдоль замкнутой кривойдолжна
равняться нулю, потому что намагничивающій токъ равенъ нулю.
Чтобы наблюдать и измѣрить поле внутри стержня, нзррайленное про-
200
Постоянные магниты
тивоположно намагниченію, нужно сдѣлать въ стержнѣ продольный
каналъ, какъ указано въ § 245. Но удобнѣе вычислить поле теоре-
тическимъ путемъ. Результатомъ такого теоретическаго вычисленія
являются силовыя линіи, представленныя на рис. 229; онѣ вездѣ показы-
ваютъ направленіе осей соленоидовъ, эквивалентныхъ полю магнита.
Линіи магнитнаго силового потока идутъ внутри стержня совер-
шенно иначе. Векторъ В, согласно основному закону, образуетъ
стержня изъ мягкаго желѣза.
Отношеніе толщины къ длинѣ 1 : 50. А даетъ
остаточный силовой потокъ Во.
систему замкнутыхъ линій. Си-
ловой потокъ постояннаго магни-
та представленъ на рис. 230.
Внутри постояннаго маг-
нита векторы, представля-
ющіе силу поля Ни индук-
цію В, имѣютъ противопо-
ложныя направленія.
Такимъ образомъ, величину
остаточнаго силового потока
представляетъ не та точка кри-
вой гистерезиса, гдѣ Н = 0, но
нѣкоторая точка въ области отри-
цательныхъ значеній Н. Положе-
ніе этой точки зависитъ отъ числа
амперъ-витковъ внѣшняго поля
и отъ длины магнитнаго стержня.
Чтобы найти эту точку, нужно
вычислить магнитное сопроти-
вленіе внѣшнихъ силовыхъ ли-
ній и построить линію сдвига
для даннаго стержня (§ 330). На рис. 231 и 232 эта линія дана
для случая, когда отношеніе толщины стержня къ его длинѣ равно
1 : 50, напримѣръ, для стержня въ 4 мм. толщины и 20 см. длины.
Если затѣмъ при помощи линіи сдвига В-Н-кривой построить
В-/7'-кривую вещества, гдѣ Н'—число амперъ-витковъ въокружа-
ющей стержень намагничивающей катушкѣ, то значеніе ^/Соотвѣт-
ствующее Н — 0, и будетъ остаточной индукціей стержня Если
-о Г Т
линію сдвига провести въ сторону отрицательныхъ значеній Н
(ОА на рис. 231 и 232), то эта линія пересѣчетъ В-Н-кривую
вещества какъ разъ въ точкѣ Во.
Постоянные магниты
201
Какъ видимъ, линія сдвига и у тонкихъ стержней составляетъ
весьма значительный уголъ съ осью В. Отсюда слѣдуетъ, что вели-
чина остаточнаго магнитизма опредѣляется не высотою,
на которой кривая гистерезиса пересѣкаетъ ось В, но,
прежде всего, шириною петли кривой гистерезиса.
Половину ширины петли кривой гистерезиса, измѣренную въ
амперъ-виткахъ, можно разсматривать, какъ мѣру коэрцитивной
Рис. 232. Сдвигъ петли гистерезиса стального стержня.
Отношеніе толщины къ длинѣ 1 : 50. А даетъ остаточный силовой потокъ Во.
метръ, необходимому для уничтоженія остаточнаго магнитизма. Сталь
гораздо болѣе, нежели мягкое желѣзо, пригодна для постоянныхъ
магнитовъ, такъ какъ ея петля гистерезиса гораздо шире. /
Совершенно иначе обстоитъ дѣло, когда нѣтъ обширнаго поля;
въ воздухѣ и кривая сдвига почти совпадаетъ съ осью В. Въ^^й-
кнутомъ круговомъ кольцѣ остаточная индукція мягкаго ^з^елѣза
больше, чѣмъ у стали, такъ какъ кривая гистерезиса мягка^ желѣза
поднимается очень высоко. Но даже узкая воздушная \щель сильно
понижаетъ остаточный магнитизмъ.
202 Энергія намагниченія
Какъ показываетъ рис. 229, линіи силъ въ постоянныхъ магни-
тахъ сходны съ линіями электростатическаго поля: онѣ имѣютъ
начало и конецъ. По аналогіи съ обозначеніями, принятыми въ уче-
ніи объ электричествѣ, мѣста, гдѣ линіи начинаются и гдѣ онѣ
кончаются, называются соотвѣтственно положительнымъ и отрица-
тельнымъ свободнымъ магнитизмомъ. Этому соотвѣтствуютъ
свободные электрическіе заряды у двухъ концовъ турмалиноваго
стержня (§ 90). Дѣйствительныхъ же магнитныхъ зарядовъ, которые
могли бы переноситься черезъ проводники, не существуетъ, какъ
мы уже неоднократно указывали выше.
ЭНЕРГІЯ НАМАГНИЧЕНІЯ.
336. Обозначимъ силу поля въ амперъ-виткахъ черезъ Н и
индукцію въ вольтъ - секундахъ черезъ В. Чтобы увеличить индук-
цію на малую величину ДВ, нужно, согласно формулѣ, выве-
денной въ § 318, сообщить желѣзу черезъ посредство эѳира коли-
В
Рис. 233. Энергія намагниченія желѣза.
чество энергіи, равное Н.&В джулямъ на кубическій сантиметръ.
Отсюда легко вычислить энергію, поглощаемую электромагнитомъ.
На рис. 233, представляющемъ //-23-кривую, величі^йЙ/У. ДВ
равна четыреугольнику А ВС О, образуемому отрѣзковъ Д В оси
ординатъ, двумя горизонтальными прямыми, проведенными изъ его кон-
цовъ, и отрѣзкомъ 77-В-кривой, соотвѣтствующимъ\іриращенію ДВ.
Отсюда легко вывести слѣдующее: <х
Энергія намагниченія
203
Энергія, поглощаемая каждымъ кубическимъ санти-
метромъ желѣзнаго стержня, когда магнитная индукція
возрастаетъ въ немъ отъ значенія до В2, графически
представляется площадью, ограниченной осью В, двумя
прямыми, параллельными оси Н и проходящими черезъ
точки Вг и В2, и соотвѣтствующимъ отрѣзкомъ В-/7-кривой.
При убываніи намагничивающаго тока магнитъ обратно отдаетъ
энергію; расчетъ при этомъ точно такой же, какъ и въ случаѣ
поглощенія энергіи. Но такъ какъ при убываніи поля Н-В-кривая,
вслѣдствіе гистерезиса, лежитъ повсюду выше, нежели при возра-
станіи поля, то при возвращеніи къ начальному значенію намагни-
чивающаго тока отдаваемая магнитомъ энергія меньше того количе-
ства, которое раньше было доставлено магниту. Если мы выпол-
нимъ полный магнитный циклъ, то повсюду будемъ имѣть эту раз-
ницу: магнитъ поглощаетъ энергію, которой онъ не отдаетъ обратно.
При каждомъ магнитномъ циклѣ часть доставляемой
энергіи поглощается желѣзомъ, и эта потеря энергіи соста-
вляетъ на 1 кубическій сантиметръ количество, равное
площади, ограниченной петлею гистерезиса.
Такимъ образомъ магнитный гистерезисъ, какъ и всякое послѣ-
дѣйствіе, сопровождается потерей энергіи. Конечно, въ этомъ случаѣ,
какъ и всегда, затраченная энергія проявляется въ желѣзѣ въ фор-
мѣ теплоты.
Въ виду потери энергіи черезъ гистерезисъ, въ электромагнит-
ныхъ машинахъ части желѣзныхъ сердечниковъ, подвергаемыя пере-
мѣнному намагниченію, изготовляются изъ такихъ сортовъ мягкаго
желѣза, которые обладаютъ наиболѣе узкой петлей гистерезиса.
ФЕРРОМАГНИТНЫЯ ТЪЛА ВЪ ОЧЕНЬ СИЛЬНЫХЪ МАГНИТНЫХЪ
ПОЛЯХЪ.
337. Вопросъ объ измѣненіи величины В при весьма боль-
шихъ значеніяхъ Н разрѣшенъ Юингомъ при помощи весьма инте-
ресныхъ опытовъ. Онъ изготовлялъ изъ изслѣдуемаго матеріала тѣлр^
имѣвшее форму катушки для нитокъ. Какъ показываетъ рис. 234,
изслѣдуемое тѣло состояло изъ двухъ конусовъ съ угломъ^ при
вершинѣ, нѣсколько большимъ 120°. Эти конусы соединены между
собою при помощи тонкаго цилиндрическаго „перешей*'. Осно-
ванія конусовъ точно пригонялись къ полюснымъДцоверхностямъ
204 Ферромагнитныя тѣла въ очень сильныхъ магнитныхъ поляхъ
Рис. 234. Магнитный
перешеекъ.
сильнаго электромагнита. Перешеекъ нужно
представлять себѣ окруженнымъ индукціон-
ной катушкой, помощью которой измѣряется
величина В. Для этой цѣли либо изслѣдуе-
мое тѣло внезапно выводилось изъ поля,
либо же основанія конусовъ дѣлались въ
видѣ цилиндрическихъ отрѣзковъ, которые
плотно входили въ полый цилиндръ, обра-
зуемый полюсными башмаками, и для измѣ-
ренія удара напряженія тѣло поворачивалось
на 180°. Большой электромагнитъ легко
было возбудить до такой силы, чтобы по-
ле между полюсными башмаками достигало
1ЛЛЛА амп.-витк. „
величины Н = 10000 ------—-----(гІ0.// =
12500.10-8). При такой установкѣ сила поля Н въ перешейкѣ
почти такая же, какъ и въ непосредственно окружающемъ его
Рис. 235. Полукольцевой электромагнитъ Дюбуа.
пространствѣ. Такимъ образомъ, сконцентировавъ при помрщй кону-
совъ силовыя линіи съ широкой полюсной поверхнор^ въ узкій
перешеекъ, можно получить такое число амперъ-витковъ на санти-
метръ, какого нельзя было бы достигнуть непосредственно при помощи
намагничивающей катушки, такъ какъ при оч^еі^ большой плотности
Полукольцевой электромагнитъ
205»
тока проволоки раскалились бы до-бѣла. Чтобы найти силу поля//
въ перешейкѣ, измѣряютъ поле непосредственно вблизи него при
помощи индукціонной катушки. Для этой цѣли перешеекъ снабжа-
ютъ, кромѣ плотно прилегающей къ нему катушки, еще второю
катушкою, отдѣленною отъ перешейка слоемъ воздуха. Разность
между числами силовыхъ линій въ этихъ двухъ катушкахъ даетъ
число силовыхъ линій въ этомъ воздушномъ промежуткѣ. Если
индукція въ воздухѣ равна В, то Н — В : Мо; это и есть значеніе Н
въ перешейкѣ.
Помощью „метода перешейка" Юингъ нашелъ слѣдующій важ-
ный результатъ:
При весьма большихъ числахъ амперъ-витковъ (для мяг-
. г-, амп.-витк.\
каго желѣза приблизительно отъ /7=2000------------ намаг-
г см. )
ниченіе ЗК = В—Мо/7 въ ферромагнитныхъ веществахъ со-
храняетъ постоянное значеніе.
Состояніе, соотвѣтствующее максимальному намагни-
ченію, которое достигается при высокихъ силахъ поля и
остается затѣмъ постояннымъ, называется „состояніемъ на-
сыщенія".
Когда намагниченіе достигло насыщающей величины, поле далѣе
налагается совершенно такъ же, какъ и въ чистомъ эѳирѣ, гдѣ
В= Мо/7.
Намагниченіе, соотвѣтствующее состоянію насыщенія, для мяг-
каго желѣза равняется приблизительно 21000.10~8 60Льтъ сек'. Для
кв. см.
стали и другихъ сортовъ желѣза получаются весьма сходныя между
собою величины. Главное различіе между отдѣльными сортами
желѣза заключается въ томъ, что нѣкоторые сорта съ воз-
растаніемъ числа амперъ-витковъ быстрѣе достигаютъ со-
стоянія насыщенія, другіе же сорта — медленнѣе. Самыя же
величины намагниченія, соотвѣтствующія состоянію насы-
щенія, различаются между собою лишь незначительно.
ПОЛУКОЛЬЦЕВОЙ ЭЛЕКТРОМАГНИТЪ. ^7
338. Методъ перешейка позволяетъ получать магнитны^поля
чрезвычайно высокой силы. Если перешеекъ перерѣзать ^.образовать
небольшую воздушную щель, то въ ней можно получатьсилы по#як
значительно превосходящія тѣ, которыя получаются^ црр обычныхъ
206
Другія ферромагнитныя вещества
насыщенныхъ полюсныхъ башмакахъ. На принципѣ перешейка осно-
вано устройство такъ называемаго полукольцевого электромагнита
Дюбуа (рис. 235); съ помощью этого инструмента можно дойти
почти до В = 40000.10~8. Эти сильныя поля сыграли важную роль
во многихъ новѣйшихъ физическихъ изслѣдованіяхъ.
ДРУГІЯ ФЕРРОМАГНИТНЫЯ ВЕЩЕСТВА.
339. Кромѣ желѣза, ферромагнитными являются также два ме-
талла, близкіе къ желѣзу по химическимъ свойствамъ, — никкель
(рис. 236) и кобальтъ (рис. 237). Они оба даютъ характерную
В-Н-кривую, а при циклическихъ намагниченіяхъ—петлю гистере-
зиса. Однако намагниченіе этихъ металловъ всегда слабѣе намагни-
ченія желѣза. При весьма высокихъ силахъ поля ихъ намагниченіе 9)1
достигаетъ насыщающаго значенія, лежащаго значительно ниже, чѣмъ
у желѣза. Именно, оно равно:
для желѣза . . . 21000. ІО-8
„ кобальта . . 15000. ІО-8
„ никелля . . . 6 700.10~8.
Ферромагнитны также нѣкоторыя желѣзныя руды, обладающія
металлическимъ блескомъ. Къ ихъ числу, конечно, относится магне-
титъ, на которомъ было впервые открыто постоянное намагниченіе.
Рис. 236. Кривая намагниченія никкеля.
Эти желѣзныя руды часто хорошо кристаллизуются, и т^гда ихъ
магнитныя свойства зависятъ, какъ оказывается, отъ крц^Білографи-
ческой оріентировки. По этому вопросу весьма интересныя наблю-
денія были сдѣланы П. Вейссомъ (Р. ^Ѵеізз).
Наконецъ, въ высшей степени замѣчателент^Ч фактъ, открытый
Г*ейслеромъ (Неизіег): сплавы нѣсколькихтуіе^лловъ, изъ которыхъ
Немагнитное желѣзо
207
каждый въ отдѣльности не магнитенъ, могутъ быть ферромагнитными.
Сюда относятся сплавы немагнитнаго металла марганца; поГейслеру,
наиболѣе магнитными оказываются сплавы марганца, алюминія и мѣди
(такъ называемыя марганцово-алюминіевыя бронзы). Въ особенности
магнитенъ сплавъ, содержащій въ кубическомъ сантиметрѣ одинако-
вое число атомовъ марганца и алюминія (МпАІ).
НЕМАГНИТНОЕ ЖЕЛЪЗО.
340. Обратно, желѣзо или сталь можно сдѣлать немагнитными,
сплавляя ихъ съ нѣкоторыми металлами. Яснѣе всего это обнару-
живается на марганцовой стали, содержащей 1°/0 углерода и 12°/0
марганца. Юингъ нашелъ, что даже при весьма высокихъ силахъ
поля она не становится ферромагнитной; во всей области измѣреній,
произведенныхъ Юингомъ, она обнаружила характерныя свойства
парамагнитнаго вещества съ относительно большой проницаемостью,
а именно ц = 1,4.
КРИТИЧЕСКАЯ ТЕМПЕРАТУРА ФЕРРОМАГНИТНЫХЪ ТЪЛЪ.
341. Если накаливать желѣзо до-красна, то при опредѣленно^
температурѣ оно внезапно становится немагнитнымъ. Если егр/за-
тѣмъ охладить, то оно получаетъ обратно свои ферромагнитныя
свойства.
Это можно показать на красивомъ опытѣ съ такъ называемымъ тер-
момагнитнымъ двигателемъ, представляющимъ собою/Огкое горизон-
208
Критическая температура ферромагнитныхъ тѣлъ
тальное колесо, свободно вращающееся на остріѣ. Ободъ колеса сдѣ-
ланъ изъ тонкаго листового желѣза и проходитъ между полюсами силь-
наго подковообразнаго магнита. Съ одной стороны магнита устана-
вливаютъ пламя бунзеновской горѣлки, которое накаливаетъ ободъ
колеса до-красна. Такъ какъ магнитное поле совершенно не дѣйству-
етъ на накаленную до-красна часть обода, то магнитъ всегда притя-
гиваетъ къ себѣ холодную половину колеса, которое вслѣдствіе этого
получаетъ вращательное движеніе.
Температура, при которой ферромагнитное вещество внезапно
становится немагнитнымъ, называется его критической темпера-
турой. Каждому сорту желѣза соотвѣтствуетъ вполнѣ опредѣлен-
ная критическая температура; она колеблется для различныхъ сор-
товъ въ довольно широкихъ предѣлахъ—отъ 690° до 870°. Кри-
тическая температура никкеля значительно ниже, а именно, равня-
ется 310°. Вещество испытываетъ при критической температурѣ вне-
запное измѣненіе не только магнитныхъ, но и всѣхъ своихъ другихъ
физическихъ свойствъ: плотности, проводимости и т. д. Очевидно,,
что при этой температурѣ происходитъ полное измѣненіе структуры.
Если нагрѣть желѣзо выше критической температуры и медленно
его охлаждать, то наблюдается небольшое переохлажденіе, которымъ
часто сопровождаются измѣненія структуры и аггрегатнаго состоянія..
Вещество становится вновь ферромагнитнымъ лишь при температурѣ
ниже критической на два-три градуса.
У многихъ тѣлъ наблюдается и большее переохлажденіе, такъ
что точка превращенія можетъ быть значительно удалена отъ точки
обратнаго превращенія. Особенно замѣчательно это явленіе въ ник-
келевой стали. Гопкинсонъ изслѣдовалъ весьма интересный сплавъ
желѣза съ 25°/0 никкеля. Этотъ сплавъ сначала былъ немагнитнымъ,
подобно марганцовой стали, но послѣ охлажденія ниже 0° сталъ маг-
нитнымъ. При нагрѣваніи способность къ намагниченію сохранялась
до 580°. Эта температура оказалась точкой превращенія, при которо^
никкелевая сталь становилась немагнитной. Если перейти критиче-
скую точку и затѣмъ обратно понижать температуру, то никелевая
сталь остается немагнитной вплоть до температуры 0°, при которой
происходитъ обратное превращеніе. Такимъ образомъ,^ѣо вещество
можно сохранять въ двухъ разновидностяхъ -^способной и не-
способной къ намагниченію. Обѣ разновидн^гиЛ явственно отли-
чаются одна отъ другой также и своими^другими физическими;
Вліяніе возраста
209
свойствами - электрической проводимостью, модулемъ растяженія и т. д.
Сплавы Гейслера также имѣютъ точку превращенія, въ кото-
рой они становятся немагнитными и внезапно измѣняютъ свою плот-
ность. У большинства этихъ сплавовъ критическая точка лежитъ
около 200° но иногда и ниже. При охлажденіи прежнія свойства,
послѣ небольшой задержки, появляются вновь. Но при нагрѣваніи
выше 500° сплавъ испытываетъ глубокое превращеніе: онъ стано-
вится немагнитнымъ, и его способность намагничиваться больше уже
не возвращается.
ВЛІЯНІЕ ВОЗРАСТА.
342. Въ свѣже приготовленномъ веществѣ магнитныя свойства,
подобно всѣмъ вообще свойствамъ матеріи, еще не имѣютъ постоян-
наго характера. Только черезъ много дней, или недѣль, или даже
мѣсяцевъ проницаемость, гистерезисъ и коэрцитивная сила становятся
постоянными. Это обстоятельство необходимо имѣть въ виду при
изготовленіи постоянныхъ магнитовъ съ вполнѣ установившимися
свойствами, напримѣръ, для измѣрительныхъ инструментовъ. „Созрѣ-
ваніе" магнитнаго вещества можно искусственно ускорить, держа его
въ теченіе достаточно долгаго времени при постоянной высокой тем-
пературѣ (около 100°).
ТЕОРІЯ ФЕРРОМАГНИТИЗМА.
343. Какъ показываетъ кривая на рис. 223, при весьма малыхъ
силахъ поля проницаемость ферромагнитнаго вещества относительно
мала и мало измѣнчива. Лордъ Рэлей (Кауіеі^ѣ) изслѣдовалъ же-
лѣзо при чрезвычайно малыхъ силахъ поля (между 0,00003 и 0,03
амп.-витк^ нашелъ, что при этихъ условіяхъ желѣзо совершенно
см.
сходно съ парамагнитными тѣлами: проницаемость постоянна и ве-
лика по сравненію съ другими парамагнитными веществами (ц = 81);
соотвѣтственно этому не наблюдается никакихъ слѣдовъ гистерезиса. і
Только когда сила поля перейдетъ извѣстный предѣлъ (0,03), про- бИ
ницаемость начинаетъ возрастать, сперва медленно, затѣмъ все б^^гі
стрѣе, и одновременно появляется также гистерезисъ. Мы видѣли
уже, что при значительныхъ силахъ поля 2?-//-кривая вновь^аги-
бается, и намагниченіе = В — Мо/7 при очень высокойѴЙМ поля
достигаетъ, наконецъ, „насыщающаго значенія", которое ди сохра-
няется постояннымъ. "
Ми. Электричество и магнитизмъ, ч. II.
14
210
Теорія ферромагнетизма
Эти факты могутъ быть объяснены теоретически, если допу-
стить, что молекулярные магниты, изъ которыхъ, по теоріи Вебера,
состоитъ магнитное вещество, настолько сильны, что они сильно дѣй-
ствуютъ другъ на друга своими полями. Если намагниченіе равно
нулю, то молекулярные магниты не могутъ располагаться совершенно
безъ всякаго порядка, но образуютъ множество небольшихъ зам-
кнутыхъ магнитныхъ цѣпей, напримѣръ, какъ четыре магнитика на
рис. 2381. Если возбудить
слегка поворачиваются изъ
слабое поле, то молекулярные магнитики
своего положенія покоя въ направленіи
Рис. 238. Цѣпи молекулярныхъ магнитовъ.
поля и прибавляютъ къ
полю небольшую, пропор-
ціональную ему слагаю-
щую. Если поле удалить,
то всѣ магнитики возвра-
щаются въ свои прежнія
положенія покоя; никакого
гистерезиса при этомъ не
оказывается. Парамагнит-
ныя тѣла, молекулярные
магниты которыхъ испытываютъ всегда лишь малыя отклоненія, оста-
ются въ этой первой стадіи. Наоборотъ, ферромагнитныя тѣла, въ
которыхъ молекулярные магниты отклоняются гораздо значительнѣе,
при извѣстной силѣ поля переходятъ въ новую стадію: молекуляр-
ныя магнитныя цѣпи разрываются, и группы молекулъ образуютъ
новыя, менѣе устойчивыя системы равновѣсія (рис. 238II). При пе-
реходѣ въ новое положеніе равновѣсія цѣпь сразу весьма сильно
увеличиваетъ поле; чтобы объяснить постепенно все болѣе усили-
вающееся возрастаніе В-Н-кривой, мы должны представлять себѣ,
что въ новое положеніе равновѣсія переходятъ сначала лишь немногія
исчезновеніи поля вещество остается намагниченнымъ,
противоположнаго направленія заставляетъ цѣпи воз-
прежнему болѣе устойчивому распредѣленію. Мы ви-
легко разрывающіяся цѣпи, а за ними все больше и больше другихъ.
Если теперь ослаблять магнитное поле, то цѣпи сохраняютъ свое
новое положеніе, или только немногія возвращаются къ своему
прежнему кольцеобразному распредѣленію. Такимъ образо^Я даже
при полномъ ---------------------------- -------- ------~--------
и лишь поле
вратиться къ
димъ такимъ образомъ, что описанная сейчасъ вторая стадія должна
быть связана съ гистерезисомъ. Наконецъ, еслщвсѣ имѣвшіяся первона-
Теорія ферромагнетизма
211
чально магнитныя молекулярныя цѣпи разорваны, то всѣ молеку-
лярные магниты имѣютъ направленіе, близкое къ направленію поля, и,
во всякомъ случаѣ, всѣ образуютъ съ нимъ острый уголъ; при даль-
нѣйшемъ усиленіи поля намагниченіе вещества увеличивается лишь
оттого, что углы молекулярныхъ магнитовъ съ направленіемъ поля
все болѣе и болѣе уменьшаются. Мы подходимъ, такимъ образомъ,
къ третьей стадіи, которой соотвѣтствуетъ третья часть В-Н-кривой,
гдѣ послѣдняя послѣ второго изгиба поднимается лишь очень медленно.
Пока мы остаемся въ этой третьей части кривой и не переходимъ
обратно во вторую, гистерезисъ отсутствуетъ. Наконецъ, когда при
весьма большой силѣ поля всѣ молекулярные магниты становятся почти
вполнѣ параллельными направленію магнитнаго поля (рис. 238 III),
достигается состояніе насыщенія. При этомъ вступаетъ въ силу такой
же законъ наложенія, какъ въ чистомъ эѳирѣ; поле молекулярныхъ
магнитовъ достигло предѣльнаго значенія и болѣе уже не усиливаетъ
внѣшняго намагничивающаго поля.
Это объясненіе ферромагнитныхъ явленій было дано I. А.
Юингомъ (Ехѵіп^).
ГЛАВА СЕДЬМАЯ
ТЕХНИЧЕСКІЯ ПРИМѢНЕНІЯ ЭЛЕКТРОМАГНИТНЫХЪ
СИЛОВЫХЪ ДѢЙСТВІЙ
СИГНАЛЬНЫЕ АППАРАТЫ.
344. Первымъ по времени техническимъ примѣненіемъ электро-
магнита является передача сигналовъ. Станція отправленія и станція
назначенія соединяются двойнымъ проводомъ, въ который включена
гальваническая батарея. На станціи отправленія устанавливается пре-
рыватель, помощью котораго можно замыкать и размыкать токъ; на
станціи назначенія устанавливается электромагнитъ, катушка котораго
включена въ двойной проводъ. У полюсовъ электромагнита нахо-
дится либо якорь изъ мягкаго желѣза либо магнитная стрѣлка, дви-
жущіеся при замыканіи и размыканіи тока. Пользуясь этими движе-
ніями, можно передавать условные знаки со станціи отправленія на
станцію назначенія.
Такой принципъ передачи знаковъ былъ впервые использованъ,
съ полнымъ .сознаніемъ его общаго значенія, Гауссомъ и Вебе-
Рис. 239. Телеграфная клавиша.
ромъ въ Геттингенѣ1) при одномъ изъ
изслѣдованій. Въ настоящее время элект
ловъ на разстояніе примѣняется въ весы
которые здѣсь невозможно перечислить.
г) Русскій изобрѣтатель баронъ Шилли
ными учеными, построилъ приборъ для пере;
жущейся магнитной стрѣлки.
Прим. ред.
ихъ совмѣстныхъ научныхъ
юмагнитная передача сигна-
а разнообразныхъ случаяхъ,
гъ, одновременно съ назван-
ьи извѣстій'при помощи дви-
Сигнальные аппараты
213
Важнѣйшимъ примѣненіемъ указаннаго принципа является теле-
графъ — одно изъ тѣхъ техническихъ изобрѣтеній, которыя даютъ
современной жизни ея характерный обликъ. Прерыватель, помощью
котораго передаются знаки, — „клавиша", представленъ на рис. 239.
При нажатіи на кнопку клавиши проводъ, идущій на далекое раз-
стояніе и постоянно соединенный съ металлическимъ рычагомъ кла-
виши, соединяется съ полюсомъ гальванической батареи (см. схему
соединенія на рис. 240). Этотъ проводъ идетъ на станцію назначенія,
гдѣ онъ соединяется съ однимъ изъ зажимовъ пріемнаго аппарата.
Другой зажимъ аппарата и другой полюсъ гальванической батареи
соединены проводниками съ землею; соединеніе черезъ землю все
Рис. 240. Соединеніе двухъ телеграфныхъ станцій (схема).
время не прерывается и замѣняетъ собой второй проводъ. Если от-
пустить кнопку клавиши, то подъ дѣйствіемъ пружины контактъ съ
полюсомъ батареи прерывается, а съ другой стороны замыкается со-
единеніе рычага клавиши, а, слѣдовательно, и провода, идущаго на да-
лекое разстояніе, съ пріемнымъ аппаратомъ станціи. Когда клавиша
находится въ покоѣ, здѣсь прямо принимаются телеграммы, передачѣ
ваемыя другой станціей. При такомъ соединеніи для телеграфиро-
ванія въ обоихъ направленіяхъ нуженъ только одинъ проводѣ.
Пріемный аппаратъ, изображенный на рис. 241 нѣск^^ко схе-
матически, представляетъ собою электромагнитъ, надъ которымъ рас-
положенъ рычагъ съ якоремъ, въ обычномъ положеніи прижатый
214
Сигнальные аппараты
пружиной къ нижнему концу винта, который изображенъ съ правой
стороны рис. 241. Когда на станціи отправленія включается бата-
рея, сила притяженія электромагнита преодолѣваетъ силу пружины, и ры-
Рис. 241. Телеграфный пишущій аппаратъ (нѣсколько схематично).
чагъ съ якоремъ опускается; когда же соединеніе прерывается, рычагъ
поднимается обратно. Когда рычагъ опускается, то соединенный съ нимъ
стержень, снабженный колесикомъ съ краскою, нажимаетъ на бумаж-
и
ную ленту; при подъемѣ
рычага надавливаніе нален-
ту прекращается. Если при
помощи часового механиз-
ма заставить бумажную
ленту передвигаться мимо
колесика съ краской, то*
сигналы будутъ отмѣщэггься
на ней въ видѣ длйнныхъ
или короткихъХчерточекъ
(точекъ). ДѴр?рзе (Могзе)>
изобрѣтатель телеграфа та-
точекъ^ алфавитъ, которымъ
Рис. 242. Схема включенія релэ.
кой системы, составилъ изъ черточекъ
и пользуются для телеграфной передачи словъ?.
Сигнальные аппараты
215
Для полученія отчетливо отпечатанныхъ знаковъ на бумажной по-
лосѣ необходимо» чтобы электромагнитъ пріемнаго аппарата намагни-
чивался не слишкомъ слабыми токами. Съ другой стороны, по тон-
кимъ телеграфнымъ проводамъ должны течь лишь весьма слабые токи,
такъ какъ иначе потеря энергіи въ нихъ была бы слишкомъ велика.
Чтобы удовлетворить этимъ обоимъ требованіямъ вмѣстѣ, включаютъ
въ качествѣ пріемника не прямо пишущій аппаратъ Морзе, но пред-
варительно особый аппаратъ, требующій весьма слабаго тока, — релэ.
Послѣдній представляетъ собою не что иное, какъ электромагнитный
выключатель, какъ показано на рис. 242. Если чрезъ намагничиваю-
щую катушку релэ проходитъ даже весьма слабый токъ, то рычагъ,
поддерживаемый пружиной очень малой силы, притягивается внизъ
и прижимается къ контактному штифту, соединенному съ однимъ полю-
сомъ особой,такъ называемой мѣстной батареи. Такимъ образомъ за-
мыкается цѣпь, въ которую включенъ пишущій аппаратъ Морзе и
въ которой сила тока можетъ быть доведена до требуемой величины.
Ясно, что къ одному проводу можно присоединить не только
двѣ, но и большее число станцій. При телеграфированіи съ одной
изъ этихъ станцій телеграмма тотчасъ же получается на всѣхъ стан-
ціяхъ, присоединенныхъ къ проводу, но только на той станціи, куда
предназначена телеграмма, чиновникъ пускаетъ въ ходъ часовой ме-
ханизмъ, передвигающій бумажную ленту подъ пишущимъ рычагомъ.
Съ передачей телеграммы приходится всегда ждать до тѣхъ
поръ, пока не освободится нужный проводъ. Представляется чрез-
вычайно важнымъ сократить по возможности время, требуемое для
передачи телеграммы. Для этой цѣли на сильно перегруженныхъ
телеграфныхъ линіяхъ старая система Морзе замѣняется болѣе но-
выми системами, требующими болѣе сложныхъ аппаратовъ, но за-
то работающими несравненно быстрѣе. При помощи остроумныхъ
приспособленій удалось добиться также и того, что по одному
проводу можно одновременно передавать нѣсколько телеграммъ
(до шести).
Особая отрасль техники посвящена подводнымъ кабельнымъ те-^
леграфамъ, соединяющимъ между собою части свѣта. По дводныйка-
бель имѣетъ не только сопротивленіе, но также и большую^^кость,
тогда какъ его самоиндукція ничтожно мала. Такъ какъ4-Й|зъ внѣш-
няго электрическаго поля не можетъ быть тока, а пол^ невозможно
безъ электрическихъ зарядовъ въ проводѣ, то преждевсего долженъ
216
Сигнальные аппараты
зарядиться кабель. Если онъ очень длиненъ, то токъ, посылаемый
при нажатіи клавиши, заряжаетъ сначала лишь ближайшую часть
кабеля. Такимъ образомъ возникаетъ паденіе потенціала между на-
чаломъ кабеля и болѣе удаленной его частью, и вслѣдствіе этого
возникаетъ токъ, переносящій часть заряда въ болѣе удаленныя части
кабеля. Такъ зарядъ передвигается все дальше и дальше, вплоть до
станціи назначенія, гдѣ онъ порождаетъ паденіе потенціала и токъ,
который и приводитъ въ дѣйствіе пріемный аппаратъ. Если при этомъ
напряженія самоиндукціи весьма малы по сравненію съ напряженіями,
преодолѣвающими омическое сопротивленіе, то переносъ электриче-
скихъ зарядовъ въ кабелѣ происходитъ по тѣмъ же законамъ, какъ
и переносъ теплоты въ хорошо проводящемъ стержнѣ. Если держать
одинъ конецъ стержня въ пламени, то, благодаря теплоемкости ве-
щества стержня, притекающая тецлота сначала нагрѣваетъ лишь часть
стержня, ближайшую къ этому концу. Вслѣдствіе этого возникаютъ
разность температуръ и тепловой токъ, распространяющійся посте-
пенно все дальше и дальше къ другому концу стержня. Подобнымъ
же образомъ распространяется электрическій токъ въ подводномъ
кабелѣ; вслѣдствіе этого сигналы перестаютъ быть кратковремен-
ными и какъ бы расплываются. Когда на станціи отправленія токъ
сперва быстро замыкаютъ и сейчасъ послѣ этого быстро размыкаютъ,
то на пріемномъ аппаратѣ нѣкоторое время спустя замѣчается по-
степенно усиливающійся токъ, достигающій длительнаго максимума
и затѣмъ снова постепенно падающій до нуля. Поэтому въ кабель-
ной телеграфіи нельзя посылать сигналы быстро одинъ за другимъ,
такъ какъ они въ этомъ случаѣ, расплываясь, налагаются другъ на
друга. Кромѣ того, здѣсь невозможно употребленіе пишущаго аппа-
рата Морзе, такъ какъ черточекъ нельзя было бы отличить отъ
точекъ. Сэръ В. Томсонъ (лордъ Кельвинъ) первый показалъ, что
кабельная телеграфія возможна, если въ качествѣ пріемника восполь-
зоваться чувствительнымъ гальванометромъ, отклоненія котораго ре-
гистрируются на движущейся лентѣ. Черточки и точки замѣняются
въ этомъ случаѣ отклоненіями вправо и отклоненіями влѣво ;^г^рЭтому
клавиша должна служить одновременно и переключателемъ7. Теле-
грамма получается на движущейся бумажной лентѣ въ/видѣ линіи
съ выступами вправо и влѣво; изъ такихъ выступовъ составляется
алфавитъ, подобный алфавиту Морзе. Какъ мыоувидимъ въ § 426, въ
послѣднее время передачу сигналовъ удалось усовершенствовать.
Телефонъ
217
345. Чтобы привести хотя бы одинъ примѣръ изъ безчислен-
наго множества другихъ электрическихъ сигнальныхъ аппаратовъ,
укажемъ на установленные почти во всѣхъ городахъ электромагнит-
ные часы, автоматически передающіе показаніе нормальныхъ вокзаль-
ныхъ часовъ. Здѣсь прерывателемъ, дающимъ сигналы, является ко-
лесо нормальныхъ часовъ, совершающее полный оборотъ въ теченіе
минуты и послѣ каждаго оборота замыкающее на короткое время
токъ. Въ городскихъ часахъ, соединенныхъ съ этими часами, нахо-
дится небольшой электромагнитъ, который при каждомъ замыканіи
тока притягиваетъ рычагъ. На концѣ рычага имѣется небольшой
крючекъ, который упирается въ зубчатое колесо и каждый разъ по-
ворачиваетъ его на одинъ зубецъ. Это колесо имѣетъ 60 зубцовъ
и снаружи соединено съ минутной стрѣлкой. Такимъ образомъ, че-
резъ каждую минуту минутная стрѣлка передвигается впередъ на
одно дѣленіе циферблата. Кромѣ того, какъ и во всякихъ часахъ,
съ минутнымъ колесомъ связано другое колесо, передвигающее соот-
вѣтствующимъ образомъ часовую стрѣлку. Такимъ путемъ элек-
тромагнитные часы въ точности воспроизводятъ показаніе нормаль-
ныхъ часовъ, находящихся на вокзалѣ.
ТЕЛЕФОНЪ.
346. Телефонъ также можно разсматривать какъ электромаг-
нитный сигнальный аппаратъ. Воспринимающій приборъ, въ кото-
рый говорятъ, представляетъ собою родъ выключателя тока съ уголь-
нымъ контактомъ. Такой контактъ обладаетъ тѣмъ свойствомъ, что
его сопротивленіе непрерывно мѣняется
вмѣстѣ съ давленіемъ, подъ которымъ
прижимаются другъ къ другу уголь-
ныя поверхности. Это легко демонстри-
ровать, соединивъ полюсы аккумулятора
съ двумя изолированными горизонталь-
ными угольными стержнями, расположен-
ными рядомъ, и замыкая гокъ при по-
мощи третьяго угольнаго стержня, по-
ложеннаго сверху поперекъ первыхъ
двухъ. Если между аккумуляторомъ и
угольнымъ стержнемъ включенъ ампер-
метръ, то сначала онъ обнаруживаетъ который
Рис. 243. Микрофонъ из^ уголь-
ныхъ зерець^И
(Посрединѣ угольной мембраны
приклеенъ станіолевый кружокъ,
можи^нр отсутствовать).
218
Телефонъ
весьма слабый токъ. Но если надавить на поперечный стержень, то
токъ усиливается, и чѣмъ больше давленіе, тѣмъ сильнѣе становится
токъ. Если надавливаніе ослабить, токъ соотвѣтственно ослабѣваетъ.
На рис. 243 видно, какъ устроенъ угольный контактъ въ теле-
фонномъ разговорномъ аппаратѣ, такъ называемомъ микрофонѣ. Въ
металлической капсюлѣ микрофона укрѣплена хорошо отъ нея изолиро-
ванная круглая угольная пластинка, въ которой сдѣланы круглые желоб-
ки. Гибкая тонкая угольная мембрана закрываетъ капсюлю. Внутри по-
слѣдней мембрана и угольная пластинка соединяются при помощи круп-
Рис. 244. Воспринимающій телефонный
аппаратъ съ микрофонной капсюлей.
видно, какъ производится соединеніе.
ныхъ угольныхъ зеренъ (ми-
крофонъ съ зернами); въ
лучшихъ микрофонахъ вмѣсто
угольныхъ зеренъ для этой
цѣли служатъ правильные
угольные шарики. Микрофон-
ная капсюля включается въ
воспринимающій звуки аппа-
ратъ такимъ образомъ, что
одинъ конецъ проволоки со-
единяется съ капсюлей и
угольной мембраной, а дру-
гой—съ угольной пластинкой,
находящейся внутри капсюли,
откуда хорошо изолирован-
ныя металлическія соединенія
черезъ дно капсюли прохо-
дятъ ко внѣшней металли-
ческой пружинѣ. На рис. 244
Передъ мембраной помѣща-
ется еще раструбъ. Изображенный на рис. 244 аппаратъ для воспри-
ниманія звуковъ снабженъ деревянной ручкой, за которую его можно
держать передъ ртомъ; въ телефонныхъ же учрежденіяхъ он^обыч-
но укрѣпляется на шкафикѣ, въ которомъ помѣщены вс^вспомо-
гательные приборы (звонокъ, переключатель и т. д.). 3
Сигналы, подлежащіе передачѣ, даются въ микрофонъ самыми
звуковыми волнами. Когда говорятъ въ раструбъ.угольная мем-
брана подъ вліяніемъ звуковыхъ волнъ начинает^^олебаться, вслѣд-
ствіе чего контакты угольныхъ зеренъ или шариковъ испытываютъ
Телефонъ
219
перемѣнное давленіе. Благодаря этому, токъ отъ батареи, замкнутой
черезъ микрофонную капсюлю, въ точности воспроизводитъ воздуш-
ныя колебанія, которыя вызываетъ падающій на мембрану звукъ.
Телефонный токъ подводится при помощи провода къ слухо-
вому аппарату. Пріемникъ и здѣсь, какъ во всѣхъ электромагнит-
ныхъ сигнальныхъ аппаратахъ, представляетъ электромагнитъ съ
якоремъ. Въ телефонѣ якоремъ служитъ тонкая гибкая желѣзная
пластинка. Эта пластинка точно воспроизводитъ всѣ колебанія тока,
Рис. 245. Слуховой телефонъ.
т.-е. колебанія воздушнаго давленія, которыя вызываетъ падающій
на мембрану микрофона звукъ, и передаетъ ихъ вновь воздуху въ
звукахъ.
Проводящее соединеніе обѣихъ телефонныхъ станцій, между
которыми происходитъ разговоръ, должно быть устроено такимъ
образомъ, чтобы цѣпи, заключающія въ себѣ микрофоны, были совер-
шенно отдѣлены одна отъ другой. При этомъ все-таки звукъ дол-
женъ передаваться въ обоихъ направленіяхъ при помощи одной пары
проводовъ. Это достигается тѣмъ, что микрофонъ не включается прямо
въ цѣпь проводовъ, идущихъ на далекое разстояніе. Цѣпь, заклю-
чающая въ себѣ микрофонъ, замыкается катушкой, навитой на же-
лѣзный сердечникъ (5Х на рис. 246) и находящейся въ телефон-
номъ шкафикѣ. Вокругъ этой катушки наматывается вторая катушШ
(5*2 на рис. 246), которая хорошо изолирована отъ первой и Уеди-
няется черезъ слуховой телефонъ съ проводами, идущиминдддлекое
разстояніе. Колебанія магнитнаго поля въ вызываютъ^индуктиро-
ванныя напряженія того же темпа, а послѣднія возбуждаютъ въ
220
Телефонъ
перемѣнный токъ, проходящій черезъ оба слуховые телефона. Но
тогда какъ въ токъ всегда идетъ въ одномъ и томъ же напра-
вленіи и сила его колеблется между максимумомъ и минимумомъ,
индуктированное напряженіе и, слѣдовательно, также токъ въ 52
мѣняютъ свои знаки. Поэтому въ слуховомъ телефонѣ токъ коле-
блется между положительнымъ максимумомъ и отрицательнымъ
максимумомъ. Если бы въ слуховомъ телефонѣ находился обычный
электромагнитъ, то его желѣзная мембрана совершала бы всегда
вдвое большее число колебаній, нежели мембрана микрофона, и вся-
кій слышимый въ телефонѣ тонъ былъ бы октавой выше произ-
носимаго. Это неудобство устраняется очень просто тѣмъ, что обѣ
катушки электромагнита пріемника насаживаются на полюсы посто-
яннаго магнита (рис. 245). Поэтому желѣзная мембрана всегда нахо-
дится въ магнитномъ полѣ, и это поле усиливается при одномъ на-
правленіи тока и ослабляется при противоположномъ. Колебанія
Микро-
фонъ
&
ШМ ЦІ Телефонъ
|і 8‘
ЧШІІН
8г
Телефонъ
Микро
фонъ
Рис. 246. Схема телефонной проводки.
этого поля, подобно колебаніямъ тока въ микрофонной цѣпи, за-
ключаются между максимумомъ и минимумомъ, и тонъ правильно
воспроизводится слуховымъ телефономъ.
Въ дѣйствительности соединеніе въ телефонныхъ проводкахъ
нѣсколько сложнѣе, такъ какъ при каждомъ аппаратѣ долженъ еще на-
ходиться вызывной звонокъ. Пока слуховая трубка виситъ у Теле-
фоннаго шкафика на особомъ крючкѣ, она отклоняетъ соедини-
тельный рычагъ, вслѣдствіе чего микрофонная цѣпь остаетсяразомк-
нутой и слуховой телефонъ — выключеннымъ изъ цѣйц5 проводовъ»
идущихъ на далекое разстояніе. Но при этомъ ^Хцѣпь включенъ
электрическій звонокъ, такъ что съ его помощью^мджетъ быть данъ
вызывной сигналъ. Токъ для звонка обычно доставляется небольшой
Электрическій звонокъ и автоматическій прерыватель
221
магнито-электрической машиной (§ 358), якорь которой при помощи
рукоятки вращается отъ руки. Механизмъ устроенъ такимъ обра-
зомъ, что эта машина автоматически включается въ цѣпь при вра-
щеніи рукоятки и выключается, когда вращеніе прекращается. Когда
слуховая трубка снимается съ крючка, рычагъ отскакиваетъ вверхъ
и выключаетъ звонокъ; одновременно онъ автоматически замыкаетъ
микрофонную цѣпь и включаетъ слуховой телефонъ въ цѣпь про-
водовъ, идущихъ на далекое разстояніе. Схема телефонной проводки
изображена на рис. 246.
ЭЛЕКТРИЧЕСКІЙ ЗВОНОКЪ И АВТОМАТИЧЕСКІЙ ПРЕРЫВАТЕЛЬ.
347. Замкнутый электрическій токъ, проходя черезъ автомати-
ческій прерыватель, возбуждаетъ въ немъ непрерывное движеніе.
Такимъ образомъ автоматическій прерыватель является до нѣкото-
рой степени электромоторомъ весьма простой конструкціи. Прин-
ципъ устройства этого „мотора" слѣдующій. Передъ электромагни-
томъ находится маленькій желѣзный якорь,
ческой пружинящей пластинкой. Якорь
служитъ замыкателемъ тока; онъ по-
стоянно соединенъ съ однимъ полю-
сомъ гальванической батареи и сопри-
касается съ маленькимъ винтомъ либо
непосредственно, либо же, какъ изо-
бражено на рис. 247, при посредствѣ
прочно скрѣпленной съ нимъ металличе-
ской пластинки; винтъ соединенъ про-
водниками съ другимъ полюсомъ бата-
реи. Когда якорь притягивается электро-
магнитомъ, то его соприкосновеніе съ
винтомъ прекращается, и токъ прерыва-
ется. Въ этомъ отношеніи автоматиче-
скій прерыватель похожъ на релэ для
прерыванія мѣстнаго тока. Отличіе авто-
матическаго прерывателя отъ релэ заклю-
чается въ томъ, что обмотка его элек-
тромагнита включена въ ту самую цѣпь,
которая имъ размыкается; это ясно видно
на рис. 247. Такимъ образомъ, когда
удерживаемый металли-
Рис. 247. Электрическій
токъ зам]
222
Электрическій звонокъ и автоматическій прерыватель
магнитъ тотчасъ же -автоматически его прерываетъ; вслѣдствіе пре-
кращенія намагниченія якорь отскакиваетъ обратно и снова замы-
каетъ токъ; электромагнитъ вновь начинаетъ дѣйствовать, и весь
процессъ, такимъ образомъ, правильно повторяется. Металлическая
пружина съ якоремъ колеблется въ обѣ стороны, пока включена
батарея, при чемъ число колебаній въ единицу времени зависитъ,
главнымъ образомъ, отъ инерціи якоря и упругой силы пружины.
Описанный автоматическій прерыватель называется, по имени его
изобрѣтателей, Вагнеровскимъ (ХѴа^пег) или Нефовымъ (Иее!)
молоточкомъ. Электрическій звонокъ представляетъ собою Вагне-
Рис. 248. Домашняя звонковая проводка.
ровскій молоточекъ, къ якорю котораго прикрѣпленъ язычекъ, уда-
ряющій при колебаніяхъ якоря по металлическому колоколу. Въ
домашней звонковой проводкѣ соединеніе батареи со звонками, какъ
показываетъ рис. 248, обычно прервано и замыкается лишь при
нажатіи на контактную кнопку. Поэтому звонъ раздается только въ
то время, пока нажата одна изъ кнопокъ.
Автоматическій прерыватель часто употребляется таки^Якогда
нужно получить пульсирующіе токи при помощи источника посто-
яннаго тока. Въ этомъ случаѣ онъ служитъ какъ бы „умформеромъи
(преобразователемъ) постояннаго тока въ перемѣнный. Мы встрѣ-
тимся съ нимъ еще разъ при описаніи индукці^іуяхъ аппаратовъ.
Если желательно получить постоянное числфУ періодовъ преры-
Электромоторы для постояннаго тока
223
ваній, то берутъ, вмѣсто пружинящей металлической полосы, камер-
тонъ, вѣтви котораго служатъ „якоремъ". Прерывающійся контактъ
образуется при помощи металлическаго штифта, соединеннаго съ
одной изъ вѣтвей и погруженнаго въ стаканчикъ со ртутью. При
помощи такого электромагнитнаго камертона получаются весьма
чистые и продолжительные тоны, вслѣдствіе чего онъ играетъ важ-
ную роль также и во многихъ акустическихъ опытахъ.
ЭЛЕКТРОМОТОРЫ ДЛЯ ПОСТОЯННАГО ТОКА.
348. Каждый моторъ постояннаго тока состоитъ изъ сильнаго
неподвижнаго магнита, называемаго магнитнымъ индукторомъ,
и вращающагося магнита,.расположеннаго между полюсами неподвиж-
наго магнита и называемаго якоремъ или арматурой. На ста-
рыхъ моделяхъ въ качествѣ магнитныхъ индукторовъ часто можно
встрѣтить стальные магниты; такія машины однако никогда не упо-
Рис. 249. Старинный электромоторъ.
требляются въ современной техникѣ, гдѣ пользуются исключительно
электромагнитами,- дающими гораздо болѣе сильное поле.
Во время движенія мотора магнитный индукторъ непрерывно на-
магничивается. Якорь, наоборотъ, снабженъ приспособленіемъ—такъ
называемымъ коммутаторомъ, благодаря которому онъ при враще-
ніи правильно перемагничивается; проще всего можно уяснить себѣ
принципъ коммутаціи на старомъ двойномъ-Т-якорѣ, который пред-
ставленъ, напримѣръ, на рис. 249, изображающемъ старинный мо-^|Ь
торъ. Якорь этого мотора представляетъ собою короткій прямой"
магнитъ съ двумя полюсными наконечниками (башмаками),Дсрто-
рые имѣютъ форму цилиндрическихъ сегментовъ и проходятъ при
вращеніи якоря башмаками индуктора, отдѣляясь отъ снихъ очень
узкими промежутками. Оба конца проволоки, обмотанной вокругъ
224
Электромоторы для постояннаго тока
стержня якоря, идутъ къ двумъ изолированнымъ одна отъ другой
половинамъ латуннаго кольца, окружающаго ось и представляю-
щаго собою коммутаторъ. По коммутатору скользятъ двѣ щетки—
хорошо прилегающія пружинящія латунныя полоски, расположенныя
одна противъ другой и соединенныя съ полюсами источника электриче-
ства. Благодаря коммутатору, намагниченіе якоря мѣняетъ свой знакъ
послѣ каждаго полуоборота; щетки же установлены такимъ обра-
Рис. 250. Схема стараго двойного-Т-якооя.
зомъ, что перемагниченіе полюсовъ якоря происходитъ какъ разъ
въ тотъ моментъ, когда они проходятъ мимо полюсовъ магнитнаго
индуктора. Пока полюсъ якоря еще приближается къ полюсу индук-
тора, онъ притягивается послѣднимъ; въ моментъ, когда полюсъ
якоря находится какъ разъ противъ полюса индуктора и начина-
етъ отъ послѣдняго удаляться, онъ получаетъ обратный знакъ и
начинаетъ поэтому отталкиваться полюсомъ индуктора, и въ то же
время другой полюсъ индуктора начинаетъ его притягивать. Такимъ
образомъ движеніе якоря непрерывно поддерживается и въ томъ
случаѣ, когда онъ производитъ работу (рис. 250).
349. Описанный старинный моторъ обладаетъ многими недо-
статками. Онъ имѣетъ весьма неравномѣрный ходъ, такъ какъ вра-
щающій моментъ, поддерживающій движеніе его якоря, дѣйствуетъ
толчками. Этотъ моментъ очень великъ, когда башмаки якоря
наютъ двигаться къ башмакамъ индуктора или начинаютъ отъ нихъ
удаляться. Но въ моментъ перемѣны направленія тока, когд^> якор-
ный стержень какъ разъ соединяетъ оба полюса индуктррй, вращаю-
щій моментъ равенъ нулю. Такимъ образомъ, стары^ моторъ дви-
жется толчками и, чтобы получить достаточно равномѣрное вра-
\ 'ХУ та
щеніе, моторъ нужно снабдить тяжелымъ маховымъ колесомъ. Изъ
прочихъ его недостатковъ упомянемъ лишд^іце одинъ: въ мо-
Электромоторы для постояннаго тока
225
ментъ обращенія поля въ якорѣ, на коммутаторѣ неизбѣжно появля-
ются сильныя искры вслѣдствіе большой самоиндукціи якоря; онѣ по-
глощаютъ много энергіи и разрушаютъ вещество щетокъ и комму-
татора. Эти и другіе недостатки устранены въ современныхъ элек-
тромоторахъ. Однимъ изъ общеизвѣстныхъ большихъ преимуществъ
этихъ машинъ является ихъ движеніе подъ совершенно равномѣр-
нымъ силовымъ дѣйствіемъ, вслѣдствіе чего онѣ вращаются безъ
всякаго махового колеса съ удивительной равномѣрностью. Это до-
стигается улучшеніемъ формы якоря и метода коммутаціи. Желѣз-
ный сердечникъ якоря въ современномъ электромоторѣ имѣетъ форму
тѣла вращенія (желѣзное кольцо
или желѣзный цилиндръ), вслѣд-
ствіе чего его вращеніе не оказы-
ваетъ вліянія на поле магнитнаго
индуктора. Коммутаторъ раздѣленъ
не на два только, а на большое
число сегментовъ, 'соединенныхъ
съ небольшими частями якорной
обмотки. Вслѣдствіе этого токъ,
намагничивающій якорь, никогда
не коммутируется во всей обмот-
кѣ сразу, но всегда лишь въ ма-
лой ея части и при томъ такимъ
образомъ, что вращающіеся вмѣстѣ
Рис. 251. Схема кольцевого якоря.
съ якоремъ полюсы въ моментъ, когда щетка переходитъ на слѣду-
ющій сегментъ коммутатора, снова отскакиваютъ на свое старое
мѣсто. Такимъ образомъ, полюсы якорнаго магнита непрерывно оста-
ются приблизительно въ однихъ и тѣхъ же мѣстахъ поля, лишь не-
много качаясь въ обѣ стороны отъ своего средняго положенія. Какъ
это достигается, проще всего можно уяснить себѣ путемъ разсмотрѣ-
нія представленной на рис. 251 схемы кольцевого якоря (изобрѣтенъ
Пачинотти (Расіпоііі) въ 1860 г. и позже независимо Граммомъ
(Сгашше) въ 1868 г.). Такой якорь вращается подъ равномѣрнымъ^^
силовымъ дѣйствіемъ. Кромѣ того, образованіе искръ вслѣдствіе^
самоиндукціи здѣсь весьма ослаблено, такъ какъ токъ комМухй-
руется всегда лишь въ малой части всей обмотки. На рис.^ 252Жред-
ставленъ небольшой моторъ съ кольцевымъ якоремъ. Мы ^видимъ
здѣсь коммутаторъ со многими сегментами, по которой^скользятъ
Ми. Электричество и магнитизмъ, ч. II.
15
226
Электромоторы для постояннаго тока
щетки, затѣмъ соединительные провода между сегментами комму-
татора и частями обмотки якоря и самое кольцо, густо обмотанное
изолированной проволокой и точно пригнанное въ цилиндрическое
пространство между башмаками магнитнаго индуктора. Каждая щетка
состоитъ изъ толстой пружинящей латунной полосы, которая спе-
реди несетъ въ оправѣ четырехугольный кусокъ угля, прижимаемый
латунной пружиной къ коммутатору. На большинствѣ новѣйшихъ
машинъ можно видѣть подобнаго рода угольныя щетки, оказав-
шіяся весьма практичными.
Моторъ, представленный на рис. 252, самъ по себѣ имѣетъ
уже довольно хорошую форму, но все-таки не является еще совре-
Рис. 252. Маленькій электромоторъ съ кольцевымъ якоремъ.
менной машиной. За послѣднія десятилѣтія кольцевой якорь совер-
шенно вытѣсненъ барабаннымъ якоремъ (изобрѣтенъ Гефнер^-
Альтенекомъ (Неіпег-АІіепеск) въ 1872 г.), который отличается
отъ кольцевого якоря главнымъ образомъ тѣмъ, что въ немѣ отсут-
ствуютъ части проволочной обмотки внутри кольца, которыяне спо-
собствуютъ увеличенію намагничивающаго числа амперъ-витковъ
якорной обмотки. Напримѣръ, намагничивающее амперъ-вит-
ковъ кольца, представленнаго на рис. 251, опредѣляется полною
силою тока въ проводахъ на внѣшней сторонѣ^который вправо отъ
Электромоторы для постояннаго тока
227
линіи выступаетъ изъ плоскости рисунка, а влѣво отъ нея вхо-
дитъ въ плоскость рисунка. Такимъ образомъ, проволоки, располо-
женныя на внутренней поверхности кольца, не приносятъ никакой
пользы, и съ ними, напротивъ, связанъ рядъ значительныхъ неудобствъ:
1) излишній расходъ мѣди, повышающій стоимость машины; 2) услож-
Рис. 253. Схема барабаннаго якоря.
Рис. 254. Небольшой закрытый
электромоторъ.
неніе работы наматыванія проволоки на якорь; 3) увеличеніе
сопротивленія якорной обмотки. Какимъ образомъ можно упразд-
нить внутренніе витки проволоки и получить барабанную якор-
ную обмотку, расположенную' только на поверхности цилиндри-
ческаго желѣзнаго сердечника, показываетъ схема такой обмотки на
рис. 253. Каждая изъ штриховыхъ линій съ двумя маленькими
кружками на концахъ представляетъ тонкую проволочную катушку,
якорь.
Рис. 255. Барабанный
намотанную на желѣзный сердечникъ; плоскость витковъ ея п^р^
лельна оси барабана. Два маленькіе кружка представляютъ^Іче-
нія пучка проволокъ, идущаго по поверхности барабана параллельно
оси. Въ пучкахъ проволокъ, отмѣченныхъ знакомъ е, т^цр^йдетъ по
направленію отъ зрителя къ плоскости чертежа, а вт^йу^кахъ, отмѣ-
ченныхъ знакомъ Ѳ, — въ обратномъ направленіи. Йрнцы каждой ка-
228
Магнитное поле мотора
тушки представлены сплошными линіями; они соединены съ концами
каждой пары другихъ катушекъ, такъ что всѣ катушки якорной обмотки
(на рис. 253 только шесть, въ дѣйствительности ихъ всегда гораздо
больше) соединены послѣдовательно. Какъ показываетъ рис. 253,
каждая проволока, соединяющая двѣ катушки, присоединена при по-
средствѣ короткой проволоки къ сегменту такъ называемаго коллек-
тора (коммутатора). Когда два взаимно противоположные сегмента
соединены черезъ посредство щетокъ съ полюсами источника тока,,
то желѣзный барабанъ становится электромагнитомъ, магнитная ось
котораго перпендикулярна къ оси барабана и къ линіи, соединя-
ющей оба сегмента, къ которымъ прижимаются щетки. При враще-
ніи якоря направленіе магнитной оси колеблется лишь немного.
На рис. 255 представленъ барабанный якорь, вынутый изъ неболь-
шого мотора, изображеннаго на рис. 254. Мы видимъ здѣсь тонкія
проволочныя обмотки, вложенныя вдоль якоря въ небольшіе каналы,
заливаемые изолирующей массой. Съ перваго взгляда ясно видно,
что обмотать барабанный якорь гораздо легче, чѣмъ кольцевой якорь.
Впрочемъ, кромѣ схемы, представленной на рис. 253, существуетъ
еще множество другихъ схемъ обмотки.
МАГНИТНОЕ ПОЛЕ МОТОРА.
350. Чтобы получить въ катушкахъ магнитнаго индуктора силь-
ное поле при возможно малой затратѣ тока, нужно позаботиться
Рис. 256. Магнитный поставъ двупо-
люснаго мотора (съ указаніемъ хода
силового потока).
о томъ, чтобы по возможности
все поле находилось въ желѣзѣ,
обладающемъ большою прони-
цаемостью. Кромѣ того, сило-
выя линіи должны быть возможно
болѣе короткими. Поэтому двумъ
половинамъ магнита придаютъ
компактную форму, и концы е|х>,
удаленные отъ кольца, сочи-
няютъ посредствомъ крѣпкаго
короткаго желѣзнаго Йрма. Весь-
ма выгодна фордіа> магнитнаго
постава, проявленная на
рис. 256. Здѣсь ярмо образуетъ
замкнутое^ ° желѣзное кольцо,
Магнитное поле мотора
229
поддерживающее внутри себя въ двухъ противоположныхъ мѣстахъ
магнита два короткихъ толстыхъ цилиндрическихъ стержня. Вокругъ
этихъ двухъ стержней обмотаны намагничивающія катушки; внутри
они несутъ полюсные башмаки, образующіе цилиндрическую полость,
въ которую какъ-разъ входитъ барабанный якорь. Обѣ части ци-
линдрической полости должны быть весьма точно центрированы, такъ
какъ, чѣмъ меньше толщина воздушнаго промежутка Ь, тѣмъ меньше
можетъ быть число намагничивающихъ амперъ-витковъ. Правильные
размѣры намагничивающей катушки разсчитываются слѣдующимъ
образомъ. Пусть В будетъ требуемая величина магнитнаго силового
потока въ воздушномъ промежуткѣ и/—вся поверхность, заполнен-
ная полемъ, т.-е. отрѣзокъ цилиндрической поверхности, образуемый
однимъ изъ башмаковъ; тогда полное число линій сглового потока
въ воздушномъ промежуткѣ будетъ ВДалѣе, число амперъ-
витковъ поля въ воздухѣ равняется (Мо = 1,256 . ІО-8). Въ арма-
турѣ силовыя линіи раздваиваются; если поперечное сѣченіе одной
изъ двухъ вѣтвей силового потока равняется /а, то въ среднемъ сила
поля въ якорѣ равняется Ва = В.~-- По В-Н кривой матеріала,
а
изъ котораго сдѣланъ якорь, мы можемъ опредѣлить значеніе ца,
соотвѣтствующее величинѣ Ва. Средняя длина силовыхъ линій въ
якорѣ пусть будетъ Іа\
въ такомъ случаѣ число амперъ-витковъ
поля въ якорѣ равняется
В 1а
М0'7’мо.2/а
Подобнымъ же образомъ вычисляется поле въ вѣтвяхъ магнита и въ
толстомъ желѣзномъ ярмѣ, соединяющемъ вѣтви магнита. Обозна-
чимъ среднія длины силовыхъ линій, сѣченія силовыхъ потоковъ,
величины магнитной индукціи и соотвѣтствующія значенія прони-
цаемости черезъ Іт и /у, и /7-, Вт и В;, и Тогда
Вт=В.^; В^В-уВ’
Вп &
и число амперъ-витковъ легко вычислить. Сумма ихъ равняется
ѵ у — __•/(2 — -I______і_ 2 . ——_I___/
Здѣсь ѵ и У обознача ъ число всѣхъ витковъ обѣихъ намагни-
230
Магнитное поле мотора
чивающихъ катушекъ и пропущенный черезъ нихъ намагничивающій:
токъ, который требуется для того, чтобы въ воздушномъ проме-
, о вольтъ-сек. . . - .
жуткѣ получилось поле В-------------Сѣченія /а, Л должны быть
кв. см.
таковы, чтобы значенія Ва, Вт, В^ лежали около изгиба В-Н кри-
(г> іолпл 1П а вольтъ-сек.\
т. е. В — 12 000 . I О-8------- • При такихъ условіяхъ маг-
Кв. СМ. /
нитное свойство желѣза будетъ использовано наилучшимъ образомъ,
и въ воздушной щели будетъ достигнуто сильное поле4 при отно-
сительно малой массѣ желѣза и маломъ числѣ амперъ-витковъ.
Слѣдуетъ еще замѣтить, что мы произвели наше вычисленіе
такимъ образомъ, какъ будто силовыя линіи оставались цѣликомъ
въ желѣзѣ машины. Если бы это имѣло мѣсто, то, несмотря на силь-
ное магнитное поле въ воздушной щели, вокругъ машины не на-
блюдалось бы ни малѣйшихъ магнитныхъ дѣйствій. Въ этомъ слу-
чаѣ желѣзныя массы были бы использованы самымъ выгоднымъ
образомъ. Въ дѣйствительности же всегда небольшая часть сило-
выхъ линій мѣстами проходитъ черезъ воздухъ. Линіи, образующія
въ воздухѣ, на ряду съ силовымъ потокомъ въ желѣзѣ, какъ бы
побочный магнитный потокъ, называются разсѣянными линіями.
Отношеніе силового потока, проходящаго черезъ желѣзо, ко всему
силовому потоку, которое должно быть возможно болѣе близкимъ
къ единицѣ, называется коэффиціентомъ разсѣянія. Чтобы внести
поправки, при точномъ вычисленіи въ качествѣ множителей вводятся
эмпирически найденные приближенные коэффиціенты разсѣянія для-
отдѣльныхъ частей магнитной цѣпи.
Поставъ для магнита изготовляется изъ сталеватаго чугуна.
Этотъ матеріалъ при правильной выработкѣ обладаетъ почти столь
же большой проницаемостью, какъ и лучшее мягкое желѣзо, и по
сравненію съ послѣднимъ обладаетъ тѣмъ важнымъ свойствомъ, что
поддается отливкѣ. Сердечникъ якоря, наоборотъ, дѣлается изъ
полосового мягкаго желѣза; причина этого выяснится нш^е
(§ 353)- -ЗІ51
РЕАКЦІЯ ЯКОРЯ.
351. Поверхность якоря распадается на двѣ областт^бдинаковой
величины: черезъ одну магнитныя силовыя линіи входяті, черезъ дру-
гую онѣ выходятъ. Линія раздѣла этихъ двухъ областей .носитъ на-
званіе нейтральной зоны. Полный враща -моментъ, дѣйствую-
И Г
Реакція якоря
231
щій на якорь въ полѣ, равняется суммѣ отдѣльныхъ вращающихъ
силъ, которыя дѣйствуютъ на отдѣльныя проволоки съ токомъ и легко
могутъ быть вычислены, согласно § 320. Наилучшее дѣйствіе полу-
чается въ томъ случаѣ, если направленіе тока одинаково во
всѣхъ проволокахъ .одной изъ двухъ
областей и противоположно во всѣхъ
проволокахъ другой области, иными
словами, если коммутація тока въ якор-
ной проволокѣ происходитъ всегда въ
тотъ моментъ, когда онъ проходитъ
черезъ нейтральную зону. Но нейтраль-
ная зона должна быть наклонной къ
линіи, соединяющей полюсы (рис. 257),
такъ какъ якорный токъ не можетъ
итти такимъ образомъ, чтобы его маг-
нитное поле было параллельно полю
магнитнаго индуктора. Такимъ обра-
зомъ, для полученія наилучшей комму-
таціи, щетки не должны быть симмет-
ричны относительно магнитнаго индук-
тора, но должны быть отклонены изъ
положенія симметріи на извѣстный
Рис. 257. Реакція якоря.
уголъ, противоположный направленію вращенія якоря. Этотъ уголъ
называется угломъ сдвига щетокъ.
Сдвигъ щетокъ необходимъ не только для достиженія воз-
можно большаго силового дѣйствія. Коммутація должна происходить
въ области нейтральной зоны главнымъ образомъ уже потому, что
только въ этомъ случаѣ она почти не сопровождается образованіемъ
искръ на щеткахъ. Въ этомъ отношеніи лучше всего, если комму-
тація происходитъ не какъ-разъ въ нейтральной зонѣ, но немного
раньше, какъ это ясно видно изъ расположенія щетокъ на рис. 257.
Вслѣдствіе сдвига щетокъ часть якорныхъ витковъ даетъ нѣ-
которое число амперъ-витковъ параллельно линіи соединенія обоимъ
полюсовъ магнитнаго индуктора, какъ это видно на рис. 2Д7^эти
амперъ-витки якоря противоположны полю индуктора.
Вслѣдствіе сдвига щетокъ часть арматурн^Д^обмотки
получаетъ размагничивающее дѣйствіе, тѣмъ большее, чѣмъ
сильнѣе арматурный токъ.
232
Оборотъ энергіи въ моторѣ
Это размагничивающее дѣйствіе называютъ также реакціей
якоря. Ее необходимо учитывать при вычисленіи числа амперъ-витковъ
магнитнаго индуктора, прибавляя такое число амперъ-витковъ, какое
составляетъ реакція якоря при нормальномъ арматурномъ токѣ. Попе-
речное намагничивающее дѣйствіе остальной якорной обмотки не имѣ-
етъ большого вліянія на разсчетъ машины.
ОБОРОТЪ ЭНЕРГІИ ВЪ МОТОРЪ.
352. То количество энергіи, которое моторъ, находящійся въ
дѣйствіи, отдаетъ непрерывно въ видѣ работы, должно быть, конечно,
сообщено ему другимъ источникомъ въ видѣ электрической энергіи.
Можно уяснить себѣ это путемъ простого измѣренія. На рис. 258
Рис. 258. Измѣреніе энергіи на маломъ моторѣ.
представленъ небольшой электромоторъ, съ оси котораго
снимается при помощи тормоза — такъ называемаго нажима
(Ргопу). Пользуясь этимъ тормозомъ, можно измѣрить энергію^отда-
ваемую моторомъ въ видѣ работы. Нажимъ Прони состоитъ изъ
двухъ деревянныхъ обхватокъ, между которыми какть-разъ прихо-
дится шкивъ мотора; при помощи винтовъ эти обх^дтки?могутъ быть
болѣе или менѣе сильно прижаты къ шкиву. Одна/изъ обхватокъ
снабжена небольшимъ рычагомъ, при помоп^С^сотораго ее можно
энергія
гт
Прони
Оборотъ энергіи въ моторѣ
233
удерживать неподвижной въ то время, какъ шкивъ вращается съ тре-
ніемъ между обхватками. Силу тренія можно измѣрить, привѣсивъ
къ рычагу такой грузъ въ Р килограммовъ (въ нашемъ примѣрѣ
Р=\ кгр.\ который при вращеніи мотора какъ-разъ удерживается
треніемъ въ горизонтальномъ положеніи. Тогда моторъ увлекаетъ
его съ силой, которая уравновѣшивается вращающимъ моментомъ,
равнымъ а.Р кгр.-м., гдѣ а есть горизонтальное разстояніе груза
отъ центра шкива, измѣренное въ метрахъ. Если моторъ дѣлаетъ
въ секунду п оборотовъ, то онъ отдаетъ энергію
2п.П.а.Рк-^^ = 2-^^-^Р8.
сек. /5
Эта работа совершенно уничтожается въ тормозѣ, и тамъ образу-
ется эквивалентное количество теплоты тренія.
Съ другой стороны, можно измѣрить энергію, сообщаемую мо-
тору электрическимъ путемъ. Для этого нужно включить въ подво-
дящіе токъ провода амперметръ и соединить оба подводящіе зажима
мотора съ измѣрителемъ напряженій. Положимъ, что измѣренная сила
тока равняется 3 амперамъ, а напряженіе у зажимовъ I/ вольтамъ;
въ такомъ случаѣ, по теоремѣ Пойнтинга, сообщаемая мотору
энергія составляетъ
V .3 ваттъ.
Для маленькаго мотора, изображеннаго на рис. 258 (такъ на-
зываемаго мотора съ послѣдовательнымъ возбужденіемъ), измѣреніе
дало, напримѣръ, 7—9 амперъ, V = 100 вольтъ; слѣдовательно, до-
ставлено 900 ваттъ =1,22 лош. силы. Доставляемая мотору энергія
распадается на двѣ части; одна часть идетъ на теплоту тока, другая
на производство работы. Соотвѣтственно этому, количество V со-
стоитъ изъ двухъ слагаемыхъ: Ѵ=Ѵ^-\- V, гдѣ Ѵ$ = Р.З есть на-
пряженіе, необходимое для преодолѣнія омическаго сопротивленія, а
напряженіе V уравновѣшиваетъ электродвижущую силу магнитнаго
поля въ воздушной щели мотора, черезъ которую движутся витки
якорной обмотки. Ѵ0.7 есть теплота тока, Ѵ'.7—энергія, превра- г
щаемая въ работу. Чтобы отдѣлить одно отъ другого эти два сла-
гаемыя, можно произвести слѣдующій опытъ. Нажимъ Пронина?
жимаютъ столь сильно, чтобы скольженіе шкива было невозможно,
и какимъ-либо образомъ закрѣпляютъ рычагъ. Въ такомъТЬіучаѣ
моторъ вращаться не можетъ; если теперь при помощи.включеннаго
сопротивленія урегулировать силу тока такъ, чтобы въ моторъ снова
234
Оборотъ энергіи въ моторѣ
вступали У амперъ, то вольтметръ покажетъ напряженіе Ѵо, которое
уравновѣшиваетъ омическое сопротивленіе. Для маленькаго упомя-
нутаго выше мотора было такимъ путемъ найдено, что Ѵо = 12 вольтъ,,
если сила тока =9 амперамъ. Мы имѣемъ, слѣдовательно:
100 вольтъ = 88 вольтъ+12 вольтъ;
900 ваттъ = 792 ватта + 108 ваттъ.
Изъ всей доставляемой мотору электрической энергіи 88°/0 идутъ на
работу (792 ватта =1,07 Р5), а 12% —на нагрѣваніе проволоки
въ моторѣ.
Одновременно произведенное измѣреніе работы при помощи
нажима Про ни дало 0,91 Р5, т.-е. на 15% меньше, нежели элек-
трическое измѣреніе. Отсюда слѣдуетъ, что при переходѣ электри-
ческой энергіи въ работу происходятъ еще нѣкоторыя другія не-
большія потери. Къ этому вопросу мы возвратимся въ слѣдующемъ
параграфѣ.
Ясно, во всякомъ случаѣ, что, если моторъ работаетъ экономно,
то теплота тока должна быть незначительной по сравненію съ работой.
Напряженіе между подводящими зажимами электромо-
тора состоитъ изъ двухъ частей: во-первыхъ, изъ напряже-
нія, индуктируемаго въ проволокахъ якоря при ихъ движе-
ніи въ магнитномъ полѣ, во-вторыхъ, изъ потери напряже-
нія вслѣдствіе омическаго сопротивленія. Если моторъ по-
строенъ правильно, то первая величина должна быть во
много разъ больше второй.
Отсюда вытекаетъ практически важное слѣдствіе. Если бы сооб-
щить мотору, прежде чѣмъ онъ придетъ въ движеніе, сразу полное
напряженіе И, то вслѣдствіе отсутствія индуктированнаго напряженія
въ якорь вошелъ бы токъ, который, согласно закону Ома, во много
разъ больше тока У, при которомъ моторъ правильно идетъ. А такъ
какъ проволока якорной обмотки и намагничивающихъ катушекъ,
конечно, берется лишь такой толщины, какая необходима ^ля|тока
нормальной силы или немного болѣе сильнаго, то вслѣдствіе огром
ной начальной силы тока проволока при этомъ раскалилась бы, спаи
расплавились бы, и изоляція витковъ перегорѣла бы% послѣ чего
моторъ потребовалъ бы довольно сложной починки.?
ѵС'ѵ
Чтобы не испортить обмотки электромотора, онъ не-
премѣнно долженъ имѣть „пусковое%сопротивленіе. При
Потери энергіи въ якорномъ желѣзѣ
235
пусканіи въ ходъ мотора слѣдуетъ выключать это сопроти-
вленіе лишь постепенно и выключить вовсе только послѣ
того, какъ моторъ достигнетъ полнаго числа оборотовъ.
Обмотка можетъ перегорѣть также и въ томъ случаѣ, когда мо-
торъ перегруженъ и потому вращается послѣ выключенія всего со-
противленія слишкомъ медленно. Чтобы предотвратить поврежденіе
вслѣдствіе небрежности при включеніи или вслѣдствіе перегрузки,
слѣдуетъ включать въ подводящіе провода предохранители, кото-
рые перегораютъ ранѣе, нежели сила тока становится опасной.
ПОТЕРИ ЭНЕРГІИ ВЪ ЯКОРНОМЪ ЖЕЛѢЗѢ.
353. Какъ уже было упомянуто, энергія, измѣренная нажимомъ
Прони, нѣсколько меньше, нежели электрически доставляемая энергія
за вычетомъ теплоты тока. Нѣкоторая малая часть энергіи теряется
вслѣдствіе тренія осей въ подшипникахъ, но и кромѣ этого якорное
желѣзо поглощаетъ еще небольшое количество энергіи.
Такъ какъ желѣзо является проводникомъ, то при вращеніи
въ сильномъ магнитномъ полѣ оно испытываетъ дѣйствіе тормо-
зящей силы, вслѣдствіе возбужденія вихревыхъ токовъ. Какъ слѣ-
дуетъ изъ опытовъ, описанныхъ въ § 301, эта тормозящая сила
была бы чрезвычайно велика и вызывала бы огромнѣйшую потерю
энергіи, если бы желѣзный сердечникъ былъ массивнымъ металличе-
скимъ тѣломъ. Практическая пригодность электромоторовъ была бы
тогда весьма сомнительна. Къ счастью, вихревые токи можно почти
совершенно уничтожить, составляя желѣзный сердечникъ арматуры
изъ тонкихъ желѣзныхъ полосъ, изолированныхъ одна отъ другой
бумажными прокладками. Изъ желѣзныхъ полосъ, оклеенныхъ съ
одной стороны бумагой, вырѣзаютъ круглыя пластинки, размѣры ко-
торыхъ опредѣляются поперечнымъ сѣченіемъ устраиваемаго якоря,
и иногда снабжаютъ ихъ углубленіями на краю для образованія ка-
наловъ на поверхности якоря. Затѣмъ эти пластинки накладываются
одна на другую и сжимаются винтами такимъ образомъ, что онѣ
образуютъ цилиндръ надлежащей формы и величины. На рис. 2^5^'
видно, какъ желѣзный сердечникъ якоря составленъ изъ пластиі^кѣі
Такъ какъ плоскость каждой полосы расположена параллельносило-
вымъ линіямъ тока, то въ ней могутъ образоваться лишь крайне сла-
бые вихревые токи, и вызываемая ими потеря энергіи^ достигаетъ
лишь нѣсколькихъ процентовъ.
236
Скорость вращенія мотора
Точно такъ же во всѣхъ электромагнитныхъ аппаратахъ (маши-
нахъ и трансформаторахъ) тѣ желѣзныя части, которыя при работѣ
все время болѣе или менѣе перемагничиваются, изготовляются изъ
полосэгого желѣза или изъ пучковъ изолированной желѣзной про-
волоки.
Кромѣ вихревыхъ токовъ, существуетъ еще другая причина по-
тери энергіи въ якорномъ желѣзѣ, именно магнитный гистерезисъ,
вслѣдствіе чего слѣдуетъ употреблять для арматурныхъ полосъ ма-
теріалъ съ крайне узкой петлей гистерезиза. Поэтому важно обла-
дать инструментами въ родѣ прибора Кепселя, съ помощью кото-
рыхъ можно быстро изслѣдовать магнитныя свойства даннаго сорта
желѣза.
СКОРОСТЬ ВРАЩЕНІЯ МОТОРА.
354 Скорость вращенія мотора постояннаго тока зависитъ не-
посредственно отъ двухъ величинъ: во-первыхъ, отъ силы магнит-
наго поля въ воздушной щели и, во-вторыхъ, отъ напряженія между •
щетками, уменьшеннаго на омическую потерю напряженія. Можно
экспериментально изслѣдовать вліяніе каждой изъ этихъ двухъ вели-
чинъ въ отдѣльности, если пустить моторъ при помощи независи-
маго возбужденія, т.-е. если соединить намагничивающія катушки
и щетки мотора съ двумя отдѣльными источниками электричества.
Если сначала поддерживать постоянное напряженіе между щет-
ками и измѣнять намагничивающій токъ при помощи включеннаго
въ цѣпь реостата, то оказывается, что моторъ вращается тѣмъ мед-
леннѣе, чѣмъ сильнѣе магнитное поле. Если увеличивать сопротивле-
ніе, то моторъ вращается все быстрѣе и быстрѣе, и наибольшее число
оборотовъ получается, когда намагничивающій токъ совершенно вы-
ключается и поле поддерживается лишь остаточнымъ намагниченіемъ.
Это обстоятельство легко понять, если вспомнить, что за вычетомъ
относительно малой омической потери напряженія, напряженіе у ще-
токъ должно равняться напряженію, индуктированному въ якорѣ,
должно быть пропорціонально произведенію изъ скорости враіценія
на силу магнитнаго поля. При неизмѣнномъ напряженіи на/щеткахъ
это произведеніе имѣетъ поэтому приблизительно постоянную ве-
личину.
При постоянномъ напряженіи у щетокъ^скорость вра-
щенія мотора тѣмъ больше, чѣмъ слабѣомагнитное поле
хч
Моторъ съ параллельнымъ возбужденіемъ
237
въ воздушной щели, и почти въ точности обратно пропор-
ціональна силѣ поля.
Если поддерживать постояннымъ намагничивающій токъ и измѣ-
нять напряженіе у щетокъ, то оказывается, что число оборотовъ уве-
личивается тѣмъ болѣе, чѣмъ больше напряженіе. Это обстоятельство
также легко понять послѣ вышеприведенныхъ разсужденій.
При постоянной силѣ магнитнаго поля скорость вра-
щенія мотора возрастаетъ почти въ точности пропорціо-
нально напряженію у щетокъ.
МОТОРЪ СЪ ПАРАЛЛЕЛЬНЫМЪ ВОЗБУЖДЕНІЕМЪ.
Ксім&г нини а аю щъя
катушки
Рис. 259. Схема включенія мотора
съ параллельнымъ возбужденіемъ,
снабженнаго пусковымъ сопроти-
вленіемъ.
355. Обычно пользуются однимъ и тѣмъ же источникомъ тока
какъ для возбужденія магнитнаго индуктора, такъ и для арматурнаго
тока; при этомъ нужно различать два существенно различные типа
моторовъ постояннаго тока, въ зависимости отъ того, включаются ли
арматура и катушки индуктора параллельно или же послѣдовательно.
Способъ включенія мотора перваго типа — мотора съ парал-
лельнымъ возбужденіемъ—представленъ схематически на рис.259.
Въ этомъ случаѣ все потребляемое
напряженіе V приложено къ намаг-
ничивающимъ катушкамъ, и намаг-
ничивающій токъ / долженъ быть
весьма малъ по сравненію съ ар-
матурнымъ токомъ 7, такъ какъ
теплота тока въ катушкахъ V. 7'
должна быть весьма мала по срав-
ненію съ энергіей V. дающей
работу. Поэтому для полученія до-
статочнаго числа амперъ-витковъ
при маломъ значеніи 7', катушки
должны имѣть очень большое число
витковъ.
Намагничивающія катушки мотора съ параллельнымъ.^
возбужденіемъ должны имѣть гораздо большее сопроти-
вленіе, нежели цѣпь арматурнаго тока; онѣ должны соМЬ^ть
изъ очень большого числа оборотовъ тонкой п^рдѣб'локи.
Положимъ теперь, что къ щеткамъ и къ намагничивающимъ ка-
тушкамъ приложено нормальное напряженіе V, при ксйгоромъ моторъ
238
Моторъ съ параллельнымъ возбужденіемъ
работаетъ наилучшимъ образомъ. Если нѣсколько увеличимъ нагрузку
мотора, то число его оборотовъ, вообще, немного уменьшится. По-
этому и индуктированное напряженіе V' уменьшится, а арматурный
токъ нѣсколько возрастетъ, пока сумма не станетъ снова
равной V (здѣсь 7?— сопротивленіе якорной обмотки); напротивъ,
токъ въ намагничивающихъ катушкахъ остается совершенно неиз-
мѣннымъ. Поэтому вслѣдствіе увеличенія реакціи якоря сила поля въ
воздушной щели нѣсколько понижается, благодаря чему происходитъ
дальнѣйшее убываніе И, т.-е. снова возрастаетъ арматурный токъ,
и т. д. Если машина вѣрно разсчитана, то можно достигнуть того,
что ослабленіе магнитнаго поля вслѣдствіе реакціи якоря,, при малѣй-
шемъ измѣненіи скорости, тотчасъ будетъ вызывать большое возра-
станіе силы тока. Но такъ какъ токъ возрастаетъ лишь до тѣхъ
поръ, пока сила, дѣйствіе которой испытываетъ якорная обмотка въ
магнитномъ полѣ, не станетъ вновь равна приложенной извнѣ силѣ,
то измѣненіе нагрузки, какъ мы видимъ, имѣетъ довольно большое
вліяніе на силу якорнаго тока, но весьма малое на число оборотовъ.
Правильно построенный моторъ съ параллельнымъ воз-
бужденіемъ имѣетъ при всѣхъ нагрузкахъ почти одинаковое
число оборотовъ.
Въ этомъ заключается характерное свойство мотора съ парал-
лельнымъ возбужденіемъ, обусловливающее его чрезвычайную при-
годность для многихъ цѣлей, напримѣръ, для приведенія въ дѣйствіе
станковъ и другихъ подобныхъ машинъ. Если же постоянство числа
оборотовъ не является необходимымъ условіемъ, то моторъ съ па-
раллельнымъ возбужденіемъ представляется мало практичнымъ по
слѣдующей причинѣ:
Моторъ съ параллельнымъ возбужденіемъ не развива-
етъ при пускѣ въ ходъ большой двигательной силы.
Это обстоятельство зависитъ отъ того, что магнитное поле мо-
тора съ параллельнымъ возбужденіямъ никогда не бываетъ оченьѵ
сильнымъ. Понятно само собою, что у мотора съ параллельнымъ^в'рз-
бужденіемъ пусковое сопротивленіе помѣщается лишь передту^ѣпью
арматурнаго тока, и намагничивающимъ катушкамъ сразу ^о^бщается
полное напряженіе. Поэтому моторъ сразу дѣйствуетъ с^нЙрмальной
двигательной силой. Часто его включаютъ такъ,. какъ показано на
схемѣ рис. 259: пуская моторъ въ ходъ, выключаетъ сопротивленіе
изъ арматурной цѣпи и одновременно съ тѣмъвкрючаютъ добавочное
’ Г; Чу 1
Моторъ съ послѣдовательнымъ возбужденіемъ
239
-сопротивленіе въ цѣпь намагничивающаго тока. Въ такомъ случаѣ
при пускѣ магнитное поле, а слѣдовательно, и двигательная сила мо-
тора нѣсколько больше, чѣмъ во время самаго хода. Но ясно, что
и тогда увеличеніе силы не слишкомъ значительно. Во всѣхъ слу-
чаяхъ, когда необходимо, чтобы при пускѣ моторъ развивалъ осо-
бенно большую тягу, слѣдуетъ пользоваться другимъ типомъ мотора
— моторомъ съ послѣдовательнымъ возбужденіемъ.
МОТОРЪ СЪ ПОСЛЪДОВАТЕЛЬНЫМЪ ВОЗБУЖДЕНІЕМЪ.
356. Устройство мотора съ послѣдовательнымъ возбу-
жденіемъ представлено схематически на рис. 260. Арматура и маг-
нитная обмотка образуютъ одну цѣпь. Чтобы потери напряженія и
энергіи въ намагничивающихъ катушкахъ были возможно меньше,
ихъ сопротивленіе должно быть мало.
гІамагниѵива'ЮѴ{ія Главные
катушки шеймы
Рис. 260. Схема соединенія мотора съ послѣдовательнымъ возбужденіемъ,
снабженнаго пусковымъ сопротивленіемъ.
Въ моторѣ съ послѣдовательнымъ возбужденіемъ со-
противленіе намагничивающихъ катушекъ должно быть воз-
можно мало, т.-е. онѣ должны состоять изъ относительно
малаго числа витковъ толстой проволоки.
Небольшого числа витковъ достаточно, такъ какъ черезъ нихъ
проходитъ весь арматурный токъ.
Когда къ подводящимъ зажимамъ приложено постоянное напря-
женіе, то при возрастаніи нагрузки происходитъ уменьшеніе ско-
рости, влекущее за собою возрастаніе арматурнаго тока. Обратно
тому, что имѣетъ мѣсто въ моторѣ съ параллельнымъ возбужденіемъ^
въ моторѣ съ послѣдовательнымъ возбужденіемъ возрастаніе арма-
турнаго тока, являющагося одновременно и намагничивающаго то-
комъ, связано съ возрастаніемъ магнитнаго поля; ясно п^эубму, что
возрастаніе нагрузки влечетъ за собою сильное уменьшеніе числа
240
Моторъ съ послѣдовательнымъ возбужденіемъ
оборотовъ. Но такъ какъ при возрастаніи силы тока одновременно
увеличивается количество преобразуемой энергіи, т.-е. произведеніе
изъ двигательной силы на скорость вращенія, то двигательная сила
мотора съ уменьшеніемъ числа оборотовъ чрезвычайно сильно возра-
стаетъ ; такъ какъ и магнитное поле, и якорный токъ возрастаютъ одно-
временно, то она возрастаетъ, приблизительно, пропорціонально У2.
Вслѣдствіе этого моторъ съ послѣдовательнымъ возбужденіемъ вы-
носитъ весьма большія колебанія нагрузки, во всякомъ случаѣ, боль-
шія, нежели моторъ съ параллельнымъ возбужденіемъ, который при
слишкомъ большой нагрузкѣ легко можетъ остановиться. Когда
нагрузка убываетъ, то моторъ съ послѣдовательнымъ возбужденіемъ
вращается все быстрѣе и быстрѣе. Ненагруженный онъ развиваетъ
громадную скорость, такъ какъ вслѣдствіе чрезвычайно малой силы
тока магнитное поле при этомъ очень слабо. Этотъ „выбѣгъ" мотора
можетъ оказаться опаснымъ; поэтому необходимо слѣдить за тѣмъ,
чтобы моторъ съ послѣдовательнымъ возбужденіемъ никогда не
пускался въ ходъ не нагруженнымъ.
Моторъ съ послѣдовательнымъ возбужденіемъ можетъ
переносить большія колебанія нагрузки, но при этомъ его
число оборотовъ испытываетъ значительныя измѣненія.
Сильно нагруженный онъ вращается медленно, менѣе на-
груженный— быстро, ненагруженный — чрезмѣрно быстро.
Въ особенности при пускѣ въ ходъ моторъ съ послѣдова-
тельнымъ возбужденіемъ, при выключеніи значительнаго сопроти-
вленія, можетъ временно развить очень большое силовое дѣйствіе.
Поэтому его употребляютъ обычно въ тѣхъ случаяхъ, когда тре-
буется сильная тяга и когда нагрузки сильно измѣняются. Для элек-
трическихъ желѣзныхъ дорогъ, подъемныхъ машинъ, крановъ и т. д.
всегда пользуются моторами съ послѣдовательнымъ возбужденіемъ.
Если желательно избѣжать „выбѣга" мотора при недостаточной
нагрузкѣ, то его магнитный поставъ снабжается еще вторичной
обмоткой изъ тонкой проволоки, параллельно присоединенной къ
арматурной цѣпи. Въ этомъ случаѣ магнитное пспе никакъл^ё’ мо-
жетъ упасть ниже опредѣленной величины, и скорость^ цёи можетъ
превысить опредѣленный максимумъ. Въ всемъ остальномъ4 такой ком-
паундъ-моторъ1), какъ называютъ этотъ типъ, промежуточный между
:-------------- ДѴ
Или моторъ со смѣшаннымъ возбужденіемъ.
Прим. пер.
Генераторы постояннаго тока
241
моторомъ съ послѣдовательнымъ возбужденіемъ и моторомъ съ па-
раллельнымъ возбужденіемъ, имѣетъ такія же свойства, какъ и мо-
торъ съ послѣдовательнымъ возбужденіемъ, но менѣе рѣзко выра-
женныя.
ГЕНЕРАТОРЫ ПОСТОЯННАГО ТОКА.
357. Въ электромоторѣ электродвижущія силы, индуктирован-
ныя въ якорныхъ проволокахъ, дѣйствуютъ противъ электрическаго
тока. Проволоки поглощаютъ поэтому энергію отъ эѳира; онѣ
испытываютъ въ магнитномъ полѣ силу, которая дѣйствуетъ въ напра-
вленіи движенія и преодолѣваетъ противодѣйствіе нагрузки, вслѣд-
ствіе чего якорь отдаетъ энергію въ видѣ работы. Если при
томъ же арматурномъ токѣ вращать якорь въ обратномъ направленіи,
то сила магнитнаго поля дѣйствуетъ противоположно движенію, и,
чтобы поддерживать вращеніе якоря, необходимо расходовать рабо-
ту. Одновременно индуктированныя электродвижущія силы дѣйству-
ютъ въ направленіи тока, и проволоки отдаютъ энергію эѳиру,
который переноситъ ее къ другимъ частямъ проводки. Такимъ обра-
зомъ, одна и та же машина при первомъ направленіи вращенія пре-
вращаетъ электрическую энергію въ работу, при второмъ — превра-
щаетъ работу въ электрическую энергію. Въ первомъ случаѣ ма-
шину называютъ моторомъ, во второмъ — генераторомъ. Генераторъ
постояннаго тока отличается отъ мотора постояннаго тока не кон-
струкціей, но лишь способомъ употребленія. Якорь генератора вра-
щается двигателемъ, и онъ поэтому становится источникомъ элек-
тричества, доставляющимъ электрическую энергію въ соединенную
съ нимъ цѣпь; наоборотъ, обмотка мотора снабжается токомъ отъ
посторонняго источника, поддерживающимъ вращеніе его якоря.
Если въ качествѣ якоря генератора взять двойной Т-якорь,
то онъ будетъ давать электрическія напряженія толчками подобно
тому, какъ моторъ, представленный на рис. 249, толчками даетъ дви-
женіе. Хотя эти напряженія, благодаря коммутатору, имѣютъ одно и е
то же направленіе, но отъ источника постояннаго тока требует^Ѵ
большее. Чтобы получить непрерывное, постоянное напряженіе, нужно
взять кольцевой или барабанный якорь съ коммутаторами, раздѣлен-
ными на большое число сегментовъ. Хотя и при этомъ^усдрвіи при
каждомъ переходѣ щетокъ на новый сегментъ происходитъ незначи-
тельное колебаніе напряженія, но, чѣмъ больше сегмец^эдѣ заключаетъ
Ми. Электричество и магнитизмъ, ч. II.
16
242
Генераторы постояннаго тока
въ себѣ коммутаторъ, т.-е. чѣмъ больше отдѣловъ имѣетъ якорная
обмотка, тѣмъ менѣе замѣтны эти весьма слабыя колебанія напря-
женія. Такъ какъ щетки вбираютъ электрическіе заряды изъ комму-
татора и уводятъ ихъ въ цѣпь, то коммутаторъ генератора называ-
ютъ также коллекторомъ или собирателемъ.
358. Особыя затрудненія для изобрѣтателей представляло маг-
нитное поле генератора. Чтобы обойтись безъ особаго источника по-
стояннаго тока для полученія намагничивающаго тока, сперва строили
генераторы со стальными магнитами. Машины съ постоянными маг-
Рис. 261. Старый магнито-электрическій генераторъ постояннаго тока.
нитными индукторами называются магнито-электрическими ^ма-
шинами. Рис. 261 представляетъ такой старый генераторъ съ^бара-
баннымъ якоремъ. Магнито-электрическія машины не имѣ^гРуспѣха,
такъ какъ поле постояннаго стального магнита слишкомъ^ слабо для
того, чтобы можно было съ его помощью преобразовать большія
количества энергіи. Чтобы быть сколько-нибуд^прбизводительной,
такая машина должна имѣть колоссальные размѣры, и потому она
Генераторы постояннаго тока
243
не выгодна. Въ настоящее время магнито-электрическія машины при-
мѣняются лишь для нѣкоторыхъ цѣлей въ техникѣ слабыхъ токовъ,
напримѣръ, для телефонныхъ вызововъ и т. п.
Въ практически пригодныхъ, мощныхъ генераторахъ постоян-
наго тока магнитное поле возбуждается электромагнитами. Первая
такая машина была построена въ 1862 году Вильде (ХѴіШе) въ Ман-
честерѣ. Вильде просто соединилъ свою машину съ небольшимъ
магнито-электрическимъ генераторомъ, доставляющимъ намагничиваю-
щій токъ. Такимъ образомъ онъ построилъ генераторъ съ посторон-
нимъ (независимымъ) возбужденіемъ. Нѣсколько лѣтъ спустя,
въ декабрѣ 1866 года, Вернеру Сименсу (ХѴегпег Зіешепз) уда-
лось построить генераторъ, который самъ доставлялъ намагничиваю-
щій токъ. Это изобрѣтеніе самовозбуждающагося генератора
положило начало развитію техники сильныхъ токовъ.
Изобрѣтеніе Сименса основывается на томъ фактѣ, что элект-
ромагнитъ машины, будучи лишь одинъ разъ возбужденъ, удержи-
ваетъ столь значительное количество остаточнаго магнитизма, что
при вращеніи якоря между щетками тотчасъ же появляется небольшое
напряженіе. Посредствомъ этого напряженія получаютъ въ намагни-
чивающихъ катушкахъ токъ такого направленія, чтобы имѣющееся
уже намагниченіе усиливалось. Напряженіе вслѣдствіе этого повыша-
ется, и вмѣстѣ съ тѣмъ усиливается также намагничивающій токъ;
магнитное поле и напряженіе въ теченіе нѣкотораго времени взаимно
усиливаютъ другъ друга, пока не будетъ достигнута опредѣленная
граница, зависящая отъ сопротивленія катушекъ, числа витковъ, маг-
нитныхъ свойствъ желѣза и вообще отъ конструкціи машины. Про-
межутокъ времени, въ теченіе котораго машина возбуждается до по-
стоянной нормальной силы поля, длится около одной минуты,самое
большее нѣсколько минутъ, послѣ чего машина работаетъ съ по-
стояннымъ напряженіемъ. Сименсъ назвалъ описанный методъ само-
возбужденія динамо-принципомъ, а самовозбуждающіеся генера-^ѵ
торы—динамомашинами. Позже названіе динамо было перенесенф^7
также и на генераторы съ постороннимъ возбужденіемъ.
Подобно моторамъ съ самовозбужденіемъ, динамо бываютъдвухъ
типовъ: 1) машины съ послѣдовательнымъ возбужденіемъ^ 2) ма-
шины съ параллельнымъ возбужденіемъ. °
к»
244 Генераторъ съ послѣдовательнымъ возбужденіемъ
ГЕНЕРАТОРЪ СЪ ПОСЛѢДОВАТЕЛЬНЫМЪ ВОЗБУЖДЕНІЕМЪ.
359. Схема включенія динамо съ послѣдовательнымъ возбужде-
ніемъ получится, если на рис. 260 мысленно удалить пусковое
сопротивленіе.
Если генераторъ съ послѣдовательнымъ возбужденіемъ приво-
дится въ движеніе моторомъ съ приблизительно постояннымъ числомъ
оборотовъ, то напряженіе генератора очень, сильно измѣняется при
измѣненіи отнимаемой отъ него силы тока, или, какъ выражаются
еще, при измѣненіи его „нагрузки". Если пустить генераторъ врівсе
безъ тока, то въ воздушной щели получается лишь слаб^рполе
остаточнаго намагниченія; поэтому напряженіе холостого^йда очень
мало, почти равно нулю. Если цѣпь съ токомъ замкнуѣь>то магнит-
ное поле по мѣрѣ выключенія сопротивленія возрастаетъ прибли-
зительно пропорціонально силѣ тока; слѣдовательно, и напряженіе
у зажимовъ измѣняется приблизительно въ рѣдкомъ же отношеніи.
Генераторъ съ параллельнымъ возбужденіемъ
245
Напряженіе у зажимовъ динамо съ послѣдовательнымъ
возбужденіемъ измѣняется при постоянномъ числѣ оборо-
товъ и при экономной работѣ приблизительно пропорціо-
нально отнимаемой силѣ тока. Лишь если дать силѣ тока воз-
расти настолько, что желѣзо индуктора почти достигнетъ магнитнаго на-
сыщенія, то напряженіе у зажимовъ будетъ возрастать лишь медленно,
достигнетъ максимума, а при дальнѣйшемъ возрастаніи тока будетъ
даже убывать вслѣдствіе потери напряженія въ проволочной обмоткѣ
машины и вслѣдствіе реакціи якоря. Кривая, представляющая зави-
симость напряженія у зажимовъ отъ силы тока при постоянномъ
числѣ оборотовъ, такъ называемая характеристика, имѣетъ по-
этому для динамо съ послѣдовательнымъ возбужденіемъ форму,
представленную на рис. 262. При большихъ силахъ тока въ области
максимума, гдѣ величина напряженія (мало измѣняется въ зависи-
мости отъ силы тока, динамо работаетъ неэкономно. На практикѣ
значеніе имѣетъ лишь первая, круто поднимающаяся часть характери-
стики, которая на рис. 262 представлена сплошной линіей. Штрихо-
ванное продолженіе кривой имѣетъ лишь теоретическій интересъ.
Вслѣдствіе непостоянства напряженія динамо съ послѣдователь-
нымъ возбужденіемъ можно употреблять лишь при нѣкоторыхъ со-
вершенно особенныхъ условіяхъ. Поэтому такія динамо строятся
рѣдко и только для спеціальныхъ цѣлей.
ГЕНЕРАТОРЪ СЪ ПАРАЛЛЕЛЬНЫМЪ ВОЗБУЖДЕНІЕМЪ.
360. Схема соединенія динамо съ параллельнымъ возбужденіемъ
изображается рисункомъ 259, если на немъ мысленно удалено
пусковое сопротивленіе.
Въ динамо съ параллельнымъ возбужденіемъ, какъ и въ моторѣ
съ параллельнымъ возбужденіемъ, большія измѣненія силы тока и дви-
гательной силы при почти постоянномъ числѣ оборотовъ сопрово-
ждаются лишь незначительными измѣненіями магнитнаго поля. Если
отъ динамо не брать вовсе тока, то обѣ щетки все-таки будутъ
замкнуты черезъ намагничивающія катушки и поэтому, согласйЪ^
принципу динамо, развиваются опредѣленный намагничивающій^г^ъ
и опредѣленное постоянное напряженіе между зажимами—напря-
женіе холостого хода Ѵо. Если присоединить внѣшннэюцѣпь,
то вслѣдствіе потери напряженія въ якорѣ напряженіе \^ѵзажимовъ
нѣсколько понижается; понижается, слѣдовательно,./іГГнамагничива-
246
Генераторъ съ параллельнымъ возбужденіемъ
ющій токъ. Кромѣ того магнитное поле нѣсколько ослабляется
реакціей якоря, которая въ генераторѣ имѣетъ тотъ же знакъ, что-
и въ моторѣ. Слѣдствіемъ обѣихъ причинъ является то, что съ воз-
растаніемъ силы тока медленно убываетъ индуктированное въ якорѣ
напряженіе, а потому также и напряженіе у зажимовъ.
Въ генераторѣ съ параллельнымъ возбужденіемъ, пока
онъ работаетъ экономно, напряженіе у зажимовъ измѣ-
Рис. 263. Характеристика генератора съ параллельнымъ возбужденіемъ.
няется лишь незначительно, постепенно падая съ возраста-
ніемъ силы тока.
Динамо съ параллельнымъ возбужденіемъ (шунтовая
динамомашина) является поэтому самымъ практичномъ и
г' X
наиболѣе распространеннымъ типомъ генератор^посто-
яннаго тока.
Чѣмъ меньше сопротивленіе внѣшней цѣпи, хтѣмъ сильнѣе
вредныя вліянія реакціи якоря и въ особенности' омической по-
тери напряженія. Если удалять сопротивленій изъ внѣшней цѣпи,
Генераторъ съ параллельнымъ возбужденіемъ
247
то напряженіе у зажимовъ падаетъ и, наконецъ, столь быстро, что
сила тока уже болѣе не возрастаетъ. Слѣдовательно, сила тока ди-
намо съ параллельнымъ возбужденіемъ можетъ быть повышена лишь
до опредѣленнаго максимума 7М—такъ называемой критической
силы тока. Если затѣмъ продолжать еще выключать сопротивле-
ніе, то напряженіе у зажимовъ понижается такъ сильно, что сила
тока уменьшается. Если зажимы замкнуть коротко, чтобы внѣшнее
сопротивленіе было безконечно мало по сравненію съ сопротивле-
ніемъ арматуры, то напряженіе между зажимами будетъ равно нулю,
намагничивающій токъ будетъ также равенъ нулю и останется лишь
слабое поле остаточнаго магнитизма, индуктированное же напряже-
ніе, какъ и токъ, будутъ весьма малы, почти равны нулю. Конечно,
во всѣхъ случаяхъ, когда потеря напряженія въ якорѣ играетъ за-
мѣтную роль, машина работаетъ
Обмотка нимагн ичиьающеи
кату алки
весьма неэкономно, и потому прак-
гически важной является лишь первая, сплошная, часть характе-
ристки, изображенной на рис. 263; штрихованная часть имѣетъ лишь
теоретическій интересъ.
Токъ динамо съ параллельнымъ возбужденіемъ не мо-
жетъ превысить опредѣленной максимальной величины—
критической силы тока. При короткомъ замыканіи токъ
падаетъ почти до нуля; поэтому короткое замыканіе
вредитъ машинѣ.
361. Для многихъ цѣлей желательно, чтобы напряженіе, @6-
ставляемое динамо при постоянномъ числѣ оборотовъ, по возмож-
ности не измѣнялось въ зависимости отъ силы тока, чтобы
было устранено также незначительное паденіе напряженія машины
съ параллельнымъ возбужденіемъ при возрастаніи силы0 тока. Этого
248 Генераторъ съ параллельнымъ возбужденіемъ
можно достигнуть, снабжая намагничивающія катушки, кромѣ шун-
товыхъ витковъ, еще и послѣдовательной обмоткой. Послѣдняя при
возрастаніи тока обусловливаетъ возрастаніе числа намагничива-
ющихъ амперъ-витковъ, которое можно разсчитать такимъ образомъ,
чтобы убыль поля вслѣдствіе реакціи якоря какъ-разъ компенсиро-
валась. Такъ вычисленные витки, находящіеся въ послѣдователь-
номъ включеніи, называются компаундъ-витками, а машина—ком-
паундъ-динамо1). Возможно двоякое присоединеніе шунтовой
Рис. 265. Характеристика компаундъ-генератора,
обмотки: либо къ щеткамъ, либо же къ главнымъ зажимамъ машины
съ которыми соединена внѣшняя цѣпь (рис. 264). Характеристику
хорошей компаундъ-машины представлена на рис. 265.
Компаундъ-машина не имѣетъ максимальной силы тока<>какъ
настоящая машина съ параллельнымъ возбужденіемъ. Пр^г^амыканіи
ея на короткую, катушки перегораютъ, если не »зключитыхпредохра-
нителя.
!) Или динамо со смѣшаннымъ возбужденій
Прим. пер.
Многополюсныя машины
249
Рис. 266. Схема барабаннаго якоря
четырехполюсной машины.
МНОГОПОЛЮСНЫЯ МАШИНЫ.
362. Большія машины, въ особенности генераторы, часто стро-
ятся болѣе чѣмъ съ двумя магнитными полюсами. По существу
многополюсныя машины предста-
вляютъ мало новаго.
На рис. 266 дана схема ба-
рабаннаго якоря многополюсной
машины. Обмотка якоря предста-
вляетъ собою лишь многократное
повтореніе обмотки двуполюснаго
якоря. Между каждыми двумя по-
люсами помѣщается щетка; въ
общемъ, слѣдовательно, щетокъ
столько же, сколько полюсовъ.
Щетки соединены между собой въ
двѣ группы—первая съ третьей,
пятой и т. д., вторая съ четвертой,
шестой
лельно.
сяти и
включены парал-
доходитъ до де-
и т. д., такъ что части якорной обмотки
На большихъ машинахъ число полюсовъ
болѣе.
^іаіійишій
м
Рис. 267. Шестиполюсная шунтовая динамомашина^д^^
На рис. 267 представлена шестиполюсная динамо съ^параллель-
нымъ возбужденіемъ.
250
Электрическая передача силы
ЭЛЕКТРИЧЕСКАЯ ПЕРЕДАЧА СИЛЫ.
363. Часто приходится слышать, что вѣкъ пара уже вытѣсненъ
вѣкомъ электричества. Такое утвержденіе, однако, весьма невѣрно;
въ дѣйствительности, электротехника открыла для паровыхъ машинъ,,
какъ и для другихъ двигателей (газовыхъ моторовъ,’ турбинъ) но-
вую обширную область примѣненія. Не-электрическіе двигатели,
прежде всего, приводятъ количества энергіи, которыя безъ нихъ
оставались бы неиспользованными, въ пригодную для употребленія
форму и доставляютъ ихъ въ видѣ работы. Они являются, такъ ска-
зать, источниками годной къ потребленію энергіи. Электрическія же
машины имѣютъ совершенно другое назначеніе: онѣ служатъ, соб-
ственно, лишь мощной связью между эѳиромъ и настоящими маши-
нами. Электрическій генераторъ связываетъ эѳиръ съ какимъ-либо
двигателемъ—турбиной, паровой машиной или газовымъ моторомъ,—
и совершаемую имъ работу переноситъ на эѳиръ. Выходящіе изъ ди-
намо-машины провода ограничиваютъ собой эѳирную полосу—транс-
миссію, посредствомъ которой энергія переносится отъ источника
силы къ мѣстамъ потребленія. Моторъ связываетъ эксплуатируемыя
рабочія машины съ этой эѳирной трансмиссіей.
На старыхъ фабрикахъ можно видѣть длинные трансмиссіонные
валы, проходящіе по всему фабричному зданію. Съ одной стороны
фабрики находится большая паровая машина — источникъ силы, на
которой имѣется большой шкивъ, соединенный толстымъ ремнемъ со
шкивомъ на валу. Вдоль вала размѣщены многочисленные меньшіе
шкивы; на каждомъ токарномъ станкѣ, машинѣ для сверленія или.
другомъ механизмѣ имѣется свой шкивъ, который можетъ быть со-
единенъ со шкивомъ вала посредствомъ ремня.
Въ новыхъ фабрикахъ большая ременная трансмиссія къ источ-
нику силы замѣнена большой динамо-машиной, трансмиссіонный
валъ — идущими отъ нея двумя проводами, а малыя ременныя трансмис-
сіи къ рабочимъ механизмамъ—небольшими электромоторами, кото-
рые часто монтируются прямо на осяхъ машинъ.
Такимъ образомъ, трансмиссіонному валу соотвѣтствуетъ/йблоса
эѳира между двумя проводами, скорости вращенія вала—^агнитное
поле въ эѳирной полосѣ, упругимъ напряженіямъ въ^аду; безъ ко-
торыхъ невозможенъ никакой переносъ энергіи, соотвѣтствуетъ элек-
трическое напряженіе, потерямъ энергіи отъ трелій въ подшипни-
кахъ и объ окружающій валъ воздухъ—потерд Лнергіи и напряже-
Центральныя станціи постояннаго тока
2511
нія въ проводахъ, которые ограничиваютъ полосу эѳира, перено-
сящую энергію.
Электрическая передача энергіи и распредѣленіе силы во всѣхъ
отношеніяхъ гораздо болѣе выгодны, чѣмъ передача механическая. ,
Во-первыхъ, проводка можетъ быть повсюду простѣйшимъ образомъ
введена въ тѣ мѣста, гдѣ желательно потреблять энергію, и, что-
особенно важно, ее можно провести на произвольно большое раз-
стояніе, на цѣлые километры, чего невозможно достигнуть при меха-
нической трансмиссіи. Во-вторыхъ, если не пользоваться слишкомъ,
высокими напряженіями, то не требуется никакихъ охранительныхъ
приспособленій, такъ какъ энергія переносится безъ движенія ка-
кихъ-либо вѣсомыхъ тѣлъ. Въ-третьихъ, потери энергіи при элек-
трической передачѣ гораздо менѣе значительны, чѣмъ при механической.
Въ-четвертыхъ, электрической энергіей можно также пользоваться
для освѣщенія, и притомъ безопаснаго въ пожарномъ отношеніи.
ЦЕНТРАЛЬНЫЯ СТАНЦІИ ПОСТОЯННАГО ТОКА.
364. Самымъ замѣчательнымъ свойствомъ электрической пере-
дачи энергіи является то, что разстоянія и прочія мѣстныя условія
не играютъ для нея почти никакой роли.
Поэтому благодаря электротехникѣ стала возможной необыкно-
венная централизація источниковъ силы. Мелкія механическія ма-
стерскія требовали прежде множества отдѣльныхъ малыхъ источни-
ковъ силы (небольшихъ паровыхъ машинъ и т. п.). Эти небольшіе-
двигатели совершенно вытѣснены изъ употребленія электротехникой,
такъ какъ они работаютъ весьма неэкономно. Вмѣсто этого сильно
развилась постройка большихъ двигателей, которые работаютъ го-
раздо болѣе экономно, чѣмъ малые. Многочисленныя мелкія фабрики,
напримѣръ, всѣ фабрики одного города, могутъ снабжаться необхо-
димой энергіей и вмѣстѣ съ тѣмъ свѣтомъ отъ одной единственной
центральной станціи. Возможны двѣ существенно различныя системы
такого снабженія силой: постоянный токъ и перемѣнный
токъ. До сихъ поръ мы говорили только о постоянномъ токѣ;. Л
перемѣннымъ токомъ мы займемся въ слѣдующей главѣ. Мы
димъ (§378), что онъ представляетъ особыя удобства при передачѣ
энергіи изъ одной центральной станціи на весьма большій^разсто-
яіня, напримѣръ, во всѣ города цѣлой провинціи. Прй^^алыхъ же
252
Центральныя станціи постояннаго тока
разстояніяхъ, напримѣръ, при постройкѣ центральной станціи для
одного города, чаще всего пользуются постояннымъ токомъ.
Система постояннаго тока имѣетъ то большое преимущество,
что она легко допускаетъ сильныя временныя колебанія въ потре-
бленіи энергіи. Какъ показываетъ опытъ, въ городахъ потребленіе
энергіи различно въ различное время дня; вообще говоря, оно рѣзко
повышается вечеромъ, когда зажигаются лампы, и падаетъ днемъ, когда
лампы тушатся. Было бы, конечно, неэкономно днемъ и ночью пу-
скать въ ходъ динамо-машину, чтобы поддерживать провода сѣти
при предписанномъ постоянномъ напряженіи, такъ какъ ббльшую
часть времени машина работала бы съ нагрузкой, гораздо меньшей,
чѣмъ нормальная, а въ теченіе нѣкоторыхъ промежутковъ времени
была бы перегружена. Экономно же она работаетъ, какъ мы знаемъ,
лишь при силѣ тока, близкой къ нормальной. Въ случаѣ постояннаго
тока можно между источникомъ силы и сѣтью включить батарею
аккумуляторовъ въ качествѣ эластичнаго резервуара энергіи. Токъ
отъ аккумуляторной батареи можетъ колебаться въ весьма широкихъ
предѣлахъ безъ существеннаго измѣненія полезной работы батареи.
Поэтому на центральной станціи постояннаго тока всегда имѣется
кромѣ одного или нѣсколькихъ генераторовъ еще большая батарея
аккумуляторовъ, при чемъ провода, идущіе на разстояніе, соединя-
ются съ полюсами этой батареи. Машины служатъ прежде всего для
заряженія батареи. Поэтому онѣ не должны находиться въ ходу весь
день, но лишь столько, сколько необходимо, чтобы каждый разъ
заряжать батарею, для чего требуется постоянный токъ. Кромѣ того
машины пускаются въ ходъ еще тогда, когда потребленіе тока въ
городѣ настолько велико, что аккумуляторы могутъ получить по-
врежденіе. Машины включаются параллельно батареѣ, такъ что часть
потребляемаго тока доставляется машинами, а другая часть батареей.
Напряженіе сѣти обыкновенно бываетъ кратнымъ 55-ти вольтъ,
потому что таково напряженіе обычной дуговой лампы. Если напря-
женіе равно 110 вольтамъ, то желающій пользоваться дуговой лампой
долженъ включить двѣ лампы послѣдовательно; иначе ему придется
устранить 55 вольтъ добавочнымъ сопротивленіемъ, и онъ бул^рймѣть
одну лампу съ такимъ же расходомъ энергіи, котораго бы^субы доста-
точно для двухъ лампъ. Если напряженіе равно 22^'вольтамъ, то
для избѣжанія потери нужно включать послѣдовательно по четыре
.дуговыя лампы. , д
Центральныя станціи постояннаго тока.
25&
Такъ какъ напряженіе аккумуляторовъ не постоянно, то на цен-
тральной станціи долженъ находиться особый для нихъ распредѣ-
литель, съ помощью котораго всегда можно включить между про-
водами, идущими на разстояніе, столько аккумуляторовъ, сколько,
необходимо, чтобы сѣть имѣла какъ-разъ правильное напряженіе.
Рис. 268. Схема соединенія при трехпроводной системѣ.
Если сѣть обслуживаетъ болѣе или менѣе значительную область,
(напримѣръ, городъ), то всю эту область дѣлятъ на участки, каждый^
изъ которыхъ обслуживается токомъ изъ опредѣленнаго питат|ль-
наго пункта1)- Къ каждой подстанціи ведетъ особая толстая проводка,
и каждая подстанція имѣетъ свой распредѣлитель, при помрщи ко-
і) Вмѣсто этого термина (Зреізерппкі) мы будемъ прльзоваться тер-
миномъ подстанція.
Прим. пер.
254
Центральныя станціи постояннаго тока.
тораго и поддерживается постоянство напряженія. Благодаря такому
устройству, потребители, удаленные отъ электрической станціи, имѣ-
ютъ, несмотря на потерю напряженія въ проводахъ, то же напря-
женіе между подводящими проводами, что и потребители, живущіе
близко отъ станціи.
365. При расчетѣ проводки приходится примирять двѣ взаимно
противоположныя цѣли. Съ одной стороны, потери энергіи и на-
пряженія тѣмъ меньше, чѣмъ толще провода, а съ другой — про-
водка обходится тѣмъ дешевле, чѣмъ тоньше провода. Потеря энер-
гіи въ данной проводкѣ зависитъ исключительно отъ силы тока (У?/2),
тогда какъ переносимая энергія равна произведенію изъ напряженія
между проводящими проволоками на силу тока. Чѣмъ выше напря-
женіе на электрической станціи, тѣмъ меньше сила тока при одина-
ковомъ количествѣ переносимой энергіи и тѣмъ меньше, слѣдова-
тельно, потеря энергіи въ проводахъ. Поэтому, чѣмъ выше напря-
женіе на электрической станціи, тѣмъ тоньше могутъ быть провода
безъ слишкомъ большой потери энергіи и тѣмъ дешевле, слѣдова-
тельно, обходится проводка. Съ другой стороны, однако, слишкомъ
высокое напряженіе оказывается невыгоднымъ для потребителей. Кому
нуженъ свѣтъ дуги, тотъ долженъ каждый разъ зажигать одновре-
менно много лампъ; лампы накаливанія для высокихъ напряже-
ній должны имѣть весьма тонкія нити, которыя легче разрушаются,
нежели толстыя; поэтому для напряженія, подъ которымъ горятъ
лампы накаливанія, всегда существуетъ верхняя граница; къ тому же
рабочее напряженіе для моторовъ не можетъ быть произвольно по-
вышаемо вслѣдствіе трудностей изоляціи и т. п. Къ тому же
присоединяется еще опасность высокихъ напряженій для жизни.
Поэтому желательно, чтобы напряженіе на электрической станціи и
на выходящихъ изъ нея проводахъ было возможно болѣе высокимъ,
а въ домашнихъ проводкахъ — возможно болѣе низкимъ. Какъ мы
увидимъ въ слѣдующей главѣ, преимущество перемѣннаго токй івъ
томъ и состоитъ, что онъ весьма просто удовлетворяетъ этимъобоимъ
требованіямъ. При постоянномъ токѣ дѣло не столь просто^ но и
здѣсь есть средство повысить напряженіе на электричЦ&ой станціи
вдвое по сравненію съ напряженіемъ въ домашш^ѵ проводкахъ.
Этимъ средствомъ является трехпроводная сис^ма, схематически
представленная на рис. 268. Если напряжені^|ѣ домашнихъ про-
водкахъ должно равняться V вольтамъ (нар^імѣръ, 110 вольтамъ),
Центральныя станціи постояннаго тока
255
то аккумуляторной батареѣ центральной станціи даютъ напряженіе
въ 2Ѵ вольтъ (220 вольтъ), при чемъ, кромѣ двухъ проводовъ,
соединяемыхъ съ концами батареи, присоединяютъ еще посрединѣ
тонкую проволоку — „средній проводъ", соединенный провод-
никомъ съ землею, и такимъ образомъ одновременно утилизи-
руютъ проводимость влажной земли. Между среднимъ проводомъ и
хорошо изолированными отъ земли внѣшними проводами напря-
женіе равняется V вольтамъ (110 вольтамъ). Домашнія проводки
присоединяются къ среднему проводу и одному изъ внѣшнихъ. При
этомъ слѣдуетъ заботиться, чтобы повсюду обѣ половины проводки
были по возможности одинаково нагружены. Если бы отъ нихъ по-
всюду, дѣйствительно, брался совершенно одинаковый токъ, то по-
всюду оба напряженія V были бы просто послѣдовательно вклю-
чены, и токъ въ среднемъ проводѣ равнялся бы нулю. Если же
сила тока въ обѣихъ половинахъ проводки различна, то сила тока
въ среднемъ проводѣ равна разности токовъ во внѣшнихъ прово-
дахъ. На практикѣ всегда можно достигнуть того, чтобы эта раз-
ность оставалось малой, почему и можно брать очень тонкій сред-
ній проводъ. Стоимость проводки при этомъ лишь немногимъ пре-
вышаетъ издержки на простую двойную проводку для 2Ѵ вольтъ
и, во всякомъ случаѣ, значительно ниже издержекъ на простую двой-
ную проводку, которая могла бы передавать ту же энергію при напря-
женіи V.
ГЛАВА ВОСЬМАЯ
ЭЛЕКТРОМАГНИТНЫЯ КОЛЕБАНІЯ
ПЕРЕМѢННЫЯ ПОЛЯ.
366. Электромагнитными колебаніями или перемѣнными полями
называются правильно и періодически измѣняющіяся состоянія эѳира.
Въ этой главѣ мы познакомимся съ нѣсколькими совершенно различ-
ными методами возбужденія электромагнитныхъ колебаній. Простѣйшій
изъ нихъ заключается въ томъ, что проволочную катушку заставля-
ютъ вращаться съ постоянной скоростью вокругъ оси, лежащей
въ плоскости ея оборотовъ, въ магнитномъ полѣ, перпендику-
лярномъ къ этой оси. При этомъ магнитное поле дѣйствуетъ на
электроны проволочныхъ витковъ съ правильно и періодически из-
мѣняющейся электродвижущей'силой, и если катушку замкнуть про-
волокой, то въ ней возникаетъ перемѣнный токъ, а вокругъ про-
вода появляется перемѣнное магнитное поле. Если же соединить
концы катушки съ двумя обкладками конденсатора то въ немъ воз-
никаетъ перемѣнное электрическое поле.
Электродинамика учитъ насъ, что перемѣнныя магнитныя поля
не могутъ существовать сами по себѣ, какъ не мыслимы и перемѣн-
ныя электрическія поля сами по себѣ. Въ самомъ дѣлѣ, измѣненія
магнитнаго состоянія обязательно вызываютъ перемѣнныя электриче-
скія напряженія "въ эѳирѣ (правда, слабыя), и обратно. Ниже мы
будемъ говорить, вообще, только объ электромагнитныхъ колебаніемъ
хотя въ однихъ случаяхъ можетъ преобладать энергія перемѣннаго
магнитнаго поля, а въ другихъ—энергія перемѣннаго электриче-
скаго поля.
Нѣчто подобное мы имѣемъ и въ механических^ Колебаніяхъ.
Мы можемъ сообщить медленныя колебанія воздуху^ заключенному
въ цилиндрической трубѣ, если будемъ двигать^въ трубѣ взадъ и
впередъ плотно входящій въ нее поршень, труба открыта, то
Перемѣнныя поля
257
колебаніе заключается преимущественно въ перемѣнномъ движеніи
воздуха; если труба закрыта, то оно заключается преимущественно
въ измѣненіи давленія. Но въ первомъ случаѣ перемѣнное движеніе
воздуха возможно лишь благодаря вызывающимъ его небольшимъ
правильно измѣняющимся давленіямъ; точно такъ же во второмъ
случаѣ перемѣнное давленіе воздуха невозможно безъ малыхъ движеній.
367. Для теоретической разработки вопроса о колебаніяхъ су-
ществуетъ весьма удобный графическій методъ, общепринятый въ
техникѣ перемѣнныхъ токовъ. Проведемъ отрѣзокъ, длина котораго
а служитъ мѣрою амплитуды перемѣннаго поля, т.-е. того макси-
мальнаго значенія, которое поле получаетъ дважды въ теченіе каж-
даго періода, одинъ разъ съ положительнымъ знакомъ и одинъ
разъ съ отрицательнымъ. Представимъ себѣ, что этотъ отрѣзокъ
Рис. 269. Часовая діаграмма.
вращается съ постоянной угловой скоростью вокругъ одного изъ
своихъ концовъ. Если проектировать вращающійся отрѣзокъ на пря-
мую линію, то величина проекціи будетъ правильно и періодически
мѣняться отъ значенія — «до значенія -4- а. Если вращающійся отрѣ-
зокъ совершаетъ п оборотовъ въ секунду, то п есть также число
колебаній проекціи въ секунду. Пусть п будетъ равно числу періо-
довъ перемѣннаго поля; тогда проекція точно воспроизводитъ періо-
, дическія измѣненія поля. Вращающійся отрѣзокъ, мысленно проек-
тируемый указаннымъ образомъ, будетъ представлять намъ изобра-
женіе перемѣннаго поля. Это графическое изображеніе мы будемъ|ро
называть часовой діаграммой перемѣннаго поля. При каждомъ
полномъ оборотѣ стрѣлка діаграммы описываетъ уголъ, равный Ѵ^60о
. 1 о Г?
или 2 и; скорость вращенія равняется, слѣдовательно, 2 п /г.^ли отсчи-
тывать время і отъ момента, когда проекція х стрѣліЦг^ равняется
нѵлю, то въ каждый моментъ х = а. зіп 2 и п /, такъ какъ0 2 п п і есть
Ми. Электричество и магнитизмъ, ч. II.
258
Перемѣнныя поля
уголъ, описанный за время і. Уголъ 2пл/ называютъ фазой
колебанія. Фазу часто выражаютъ не въ дуговой мѣрѣ, но въ
градусахъ ^- — 90°, -^- — 45° и т. д.^. На рис. 269, кромѣ часовой
діаграммы, представлена еще кривая, изображающая зависимость вели-
чины поля х отъ времени і. Колебаніе, происходящее по пред-
ставляемому кривой простому закону, называютъ синусоидаль-
нымъ или простымъ колебаніемъ. Если представить себѣ, что
стрѣлка діаграммы вращается съ перемѣнной скоростью, но такъ, что
при каждомъ новомъ оборотѣ скорость проходитъ черезъ тѣ же
значенія, то въ проекціи получатся правильныя колебанія, слѣду-
ющія иному закону. Такія колебанія, согласно математической тео-
ремѣ Фурье (Ропгіег), могутъ быть всегда представлены какъ ре-
зультатъ сложенія многихъ синусоидальныхъ колебаній съ числомъ
періодовъ п, 2п, Зп, . (основное колебаніе и верхнія доба-
вочныя колебанія), почему ихъ и называютъ сложными коле-
баніями. При объясненіи явленій перемѣннаго тока мы будемъ
часто предполагать, что имѣемъ дѣло лишь съ простыми синусо-
идальными колебаніями. Даже въ тѣхъ случаяхъ, когда это пред-
положеніе не вполнѣ соотвѣтствуетъ дѣйствительности, упрощен-
ная теорія въ существенномъ правильно воспроизводитъ факты,
и лишь при количественныхъ изслѣдованіяхъ представляется необ-
ходимость въ болѣе точномъ вычисленіи.
Когда нѣсколько перемѣнныхъ полей одинаковаго рода нала-
гаются одно на другое, то сложеніе ихъ совершается по принципу
наложенія, и если всѣ' они имѣютъ одно
и то же число періодовъ п, то въ резуль-
татѣ сложенія получается одно перемѣнное
поле того же періода. Такъ, какъ въ физи-
кѣ эѳира всѣ величины, характеризующія
состояніе, представляются векторами, то мы
должны строго различать два случ^хі)
слагающіяся поля направлены параллельно;
2) направленія слагающихся полей обра-
зуютъ нѣкоторый уголъ. Разсмотримъ по-
Рис. 270. Сложеніе двухъ
перемѣнныхъ полей.
слѣдовательно оба случая. Сперва мы разсмотримъ^^оженіе парал-
лельно направленныхъ перемѣнныхъ полей. Этотъ случай
имѣетъ мѣсто, напримѣръ, когда нѣсколько^ Генераторовъ пере-
XX-
- ѵ
Перемѣнныя поля
259
мѣннаго тока съ одинаковымъ числомъ періодовъ одновременно
снабжаютъ токомъ одну проводку. Поля тока слагаются въ этомъ слу-
чаѣ, какъ алгебраическія величины. Положимъ, что два поля предста-
влены на часовой діаграммѣ (рис. 270) вращающимися отрѣзками ОА
и ОВ, образующими уголъ <р, равный разности фазъ двухъ соот-
вѣтственныхъ колебаній. Результирующее поле получается въ этомъ
случаѣ, если отъ конца А' проекціи О'А' отложить отрѣзокъ
А’С = О'В'', О'С и есть искомая величина. Очевидно, что О’С
представляетъ собою проекцію отрѣзка ОСІ который получается
изъ векторовъ ОА и ОВ по правилу сложенія векторовъ. Это спра-
ведливо для всякой фазы колебанія.
Сложеніе двухъ параллельно направленныхъ перемѣн-
ныхъ полей съ одинаковымъ числомъ періодовъ можно про-
извести графически при помощи часовой діаграммы; для это-
го слѣдуетъ обѣ стрѣлки, представляющія два складыва-
емыя перемѣнныя поля, сложить, какъ два вектора.
Благодаря этому свойству, часовая діаграмма часто называется
также „діаграммой векторовъ".
Средняя энергія результирующаго перемѣннаго поля, вообще,
не равняется суммѣ среднихъ энергій обоихъ слагаемыхъ полей.
Въ простѣйшемъ случаѣ, когда оба поля имѣютъ одну и ту же
амплитуду, получается слѣдующее: 1) если разность фазъ полей
равняется нулю, то амплитуда удваивается, энергія же, пропорціо-
нальная квадрату силы поля, увеличивается вчетверо; [2) если раз-
ность фазъ равна 90°, то квадратъ результирующей амплитуды ра-
венъ суммѣ квадратовъ слагаемыхъ амплитудъ, и энергія результи-
рующаго поля равняется суммѣ энергій слагаемыхъ полей; 3) если
разность фазъ равна 180°, то результирующая амплитуда равняется
нулю, и энергія также равна нулю. Явленія, основывающіяся на томъ,
что сумма двухъ колебаній зависитъ отъ разности ихъ фазъ, назы-
ваются
говорить,
дитъ ихъ
интерференціонными явленіями, и поэтому принято
что при наложеніи двухъ перемѣнныхъ полей происхо-
интерференція.
ИЗМѢРЕНІЯ ПЕРЕМѢННЫХЪ ПОЛЕЙ.
368.
Инструменты, въ которыхъ сила, дѣйствующая неподвиж-
ную систему, пропорціональна измѣряемой величинѣ, характеризу-
. °
ющей поле (электрометръ съ заряженнымъ индикаторомъ1/ гальвано-
17
260
Измѣренія перемѣнныхъ полей
метръ съ постояннымъ магнитомъ, инструменты д’Арсонваля) не-
пригодны для перемѣнныхъ полей. Дѣйствительно, такъ какъ инер-
ція отклоняемой системы всегда настолько велика, что система не
можетъ слѣдовать за быстрыми измѣненіями поля и устанавливается
спокойно, то показаніе упомянутыхъ инструментовъ даетъ среднее
значеніе поля, т.-е. всегда нуль.
Для измѣренія перемѣнныхъ полей требуются инструменты,
отклоненіе въ которыхъ совершается въ одну и ту же сторону при
обоихъ знакахъ поля. Таковы: 1) электрометръ, индикаторъ кото-
раго не имѣетъ собственнаго заряда, но соединенъ съ однимъ изъ
зажимовъ; 2) гальванометръ изъ мягкаго желѣза; 3) электродина-
мометръ съ послѣдовательно включенными катушками; 4) тепловые
инструменты. Въ инструментахъ трехъ первыхъ классовъ откло-
няющая сила въ каждый моментъ пропорціональна второй степени
измѣряемой величины, характеризующей поле (напряженія въ электро-
метрахъ, силы тока въ инструментахъ изъ мягкаго желѣза и въ дина-
мометрахъ). Для инструментовъ изъ мягкаго желѣза это, конечно,
было бы вполнѣ справедливо лишь въ томъ случаѣ, если бы проница-
емость магнита изъ мягкаго желѣза была постоянна; однако, можно
строить инструменты такимъ образомъ, чтобы измѣнчивость проница-
емости не повлекла за собою большой ошибки. Въ четвертой ка-
тегоріи—въ тепловыхъ инструментахъ — теплота тока въ каждый
моментъ также пропорціональна квадрату мгновенной силы тока Л
Дѣйствительно, если 7? есть сопротивленіе нагрѣваемой проволоки,
то напряженіе между ея концами есть V = Н .3 и, слѣдовательно,
доставленная энергія равняется V = V. У = 7?. У2. Такимъ обра-
зомъ, когда подвижная система слишкомъ тяжела, чтобы слѣдо-
вать за быстрыми колебаніями, въ инструментахъ всѣхъ четырехъ
классовъ отклоненіе зависитъ отъ средняго значенія второй сте-
пени величины, опредѣляющей поле. Если инструментъ прокалибри-
рованъ при помощи источника постояннаго тока, т.-е. при постоян-
номъ напряженіи или при постоянной силѣ тока, то числа еі^иГкалы
даютъ первую степень величины, опредѣляющей полег/или, соб-
ственно говоря, квадратный корень изъ квадрата величины, опре-
дѣляющей поле, т.-е. V2 или У2. При измѣреніи перемѣн-
ныхъ полей, вмѣсто V2 и У2, нужно подставитьу среднія значенія
этихъ величинъ, которыя мы обозначимъ черезъ V2 и У2. Такимъ
образомъ, величина, отсчитываемая ца^щкалѣ инструмента, есть
Измѣренія перемѣнныхъ полей
261
V V2 или V У2—квадратичная средняя соотвѣтственной вели-
чины, опредѣляющей поле.
На инструментахъ для перемѣннаго тока отсчитывается
всегда квадратичная* средняя измѣряемой величины, опре-
дѣляющей поле (напряженія или силы тока). Это отсчи-
тываемое значеніе называютъ эффективнымъ значеніемъ
напряженія или силы тока. Такимъ образомъ,
ѴеГГ=У^-
Если перемѣнное поле представляетъ собою правильное сину-
соидальное колебаніе, то значеніе силы тока } въ нѣкоторый опре-
дѣленный моментъ і равняется Лі . 8іп2пя^, гдѣ обозначаетъ ам-
плитуду тока (максимумъ тока). Отсюда получается среднее значе-
ніе У2 = Зм2 5Іп2 2тиіі, если $іп2 2ъпі есть среднее значеніе величины
5іп22пя^ за одинъ періодъ. Но величина $іп22пя^ колеблется между
О и 1 и притомъ такъ, что ея значенія группируются симметрично
около какъ это видно изъ формулы 8Іп2ф = ^-(1— соз2ф), если
принять во вниманіе, что среднее значеніе соз2ф равняется нулю.
Слѣдовательно, 8Іп22п/г^‘=~ и У2 — ^УдА Для правильныхъ си-
нусоидальныхъ колебаній можно по измѣренному эффек-
тивному значенію легко вычислить амплитуду колебанія.
Такъ какъ ]/2= 1,414, то получается
1,414 ЗеГГ и Ѵм= 1,414 ѴеГГ.
ГЕНЕРАТОРЫ ПЕРЕМѢННАГО ТОКА.
369. Если въ кольцевомъ или барабанномъ якорѣ двуполюснаго
генератора постояннаго тока уменьшить число соединеній катушки съ
коллекторомъ, оставивъ только два соединенія, прямо противополож-
ныя и идущія къ двумъ расположеннымъ вокругъ оси изолиро-
ваннымъ металлическимъ кольцамъ, по которымъ скользятъ щетки
(рис. 271), то при вращеніи якоря въ магнитномъ полѣ между щетками^
получается перемѣнное напряженіе. Дѣйствительно, въ каждой прово-
локѣ якоря при вращеніи въ магнитномъ полѣ дѣйствуетъ п^^мійная
электродвижущая сила, и перемѣнныя напряженія отдѣльныхъ* прово-
локъ слагаются въ результирующее перемѣнное напряженіе между ме-
262
Генераторы перемѣннаго тока
таллическими кольцами. Якорь машины перемѣннаго тока, подобна
якорю генератора постояннаго
Рис. 271. Схема якоря двуполюс-
ной машины перемѣннаго тока.
тока, можно заставить вращаться и
въ многополюсномъ магнитномъ полѣ,
если только надлежащимъ образомъ
включить проволоки якоря; въ машинѣ
перемѣннаго тока это даже особенно
удобно. Число оборотовъ якоря дву-
полюсной машины должно быть очень
велико, для того, чтобы получить
число періодовъ, употребительное въ
техникѣ, а именно, оно должно рав-
няться 50 въ секунду, т.-е. 3000 въ
минуту. Машина съ 2ѵ полюсами
имѣетъ болѣе удобную скорость вра-
1 «
щенія, равную— -ой части выше ука-
занной. Такъ, напримѣръ, десятиполюсная машина дѣлаетъ только*
600 оборотовъ въ минуту, а двадцатиполюсная всего лишь 300.
Поэтому въ машинахъ перемѣннаго тока обыкновенно имѣется
большое число магнитовъ. Въ силу относительности индукціоннаго*
дѣйствія, въ машинѣ перемѣннаго тока можно сдѣлать неподвиж-
нымъ якорь и заставить вращаться магниты. Въ такомъ случаѣ
якорю даютъ форму очень широкаго кольца, въ которомъ вращается
большое маховое колесо, несущее на ободѣ магниты. Якорныя про-
волоки идутъ, конечно, по внутренней сторонѣ неподвижнаго
кольца, соединяются же онѣ между собою по тѣмъ же правиламъ,
какъ и проволоки у многополюснаго якоря перемѣннаго тока, несу*
щаго ихъ снаружи. Машина перемѣннаго тока съ внутрен-
ними полюсами представлена на рис. 272. На оси большого
магнитнаго колеса видны два контактныхъ кольца со щетками, ко-
торыя подводятъ намагничивающій токъ. Главные зажимы машцны,,
отъ которыхъ берется перемѣнный токъ, на рисункѣ не видны; они
соединены неподвижно съ проволоками неподвижнаго ^бря. Ма-
шина перемѣннаго тока съ внѣшними по людьми изобра-
жена ниже на рис. 298. Она имѣетъ два неподвижные подводя-
щіе зажима для намагничивающаго тока и отличается отъ динамо^
% \ ѵ
постояннаго тока, главнымъ образомъ, лишь тѣ^гь, что якорь несетъ,,
вмѣсто пластинчатаго коллектора, контактныя кольца; этихъ колецъ
Генераторы перемѣннаго тока
263
на обычномъ генераторѣ перемѣннаго тока имѣется два, на машинѣ же,
изображенной на рис. 298, ихъ три, по причинѣ, которая выяснится ниже.
Важнѣйшее отличіе генератора перемѣннаго тока отъ генера-
тора постояннаго тока заключается въ томъ, что въ генераторѣ
перемѣннаго тока намагничивающій токъ не можетъ быть взятъ отъ
самой машины. Всѣ генераторы перемѣннаго тока имѣютъ
постороннее возбужденіе. Хотя машины перемѣннаго тока
могутъ имѣть самыя разнообразныя формы — мы назвали лишь двѣ
важнѣйшія, именно машину съ внѣшними полюсами и машину съ
Рис. 272. Машина перемѣннаго тока съ внутренними полюсами.
внутренними полюсами, — однако, ихъ конструкція и расчетъ оди-
наковы для всѣхъ типовъ и гораздо проще, чѣмъ для машинъ по-
стояннаго тока, характерныя свойства которыхъ зависятъ отъ метода
самовозбужденія. Съ другой стороны, постороннее возбужденіе
требуетъ, чтобы къ генератору перемѣннаго тока всегда присоед.й\і
нялся отдѣльный источникъ постояннаго тока для намагниченья;
Если не имѣется для этой цѣли аккумуляторной батареи, т^: при-
ходится вмѣстѣ съ машиной перемѣннаго тока пускать небольшую
динамо постояннаго тока, которая часто монтируется п^ямо на оси
генератора перемѣннаго тока.
264 Индуктированныя напряженія въ перемѣнномъ магнитномъ полѣ
Генераторы перемѣннаго тока, примѣняемые въ Европѣ въ тех-
никѣ сильныхъ токовъ, имѣютъ при нормальномъ числѣ оборотовъ
обыкновенно 50 періодовъ въ секунду. Такимъ образомъ, продолжитель-
ность колебанія обыкновеннаго перемѣннаго тока равна 0.02 секунды.
Въ послѣднее время въ особыхъ случаяхъ берутъ также и меньшія
числа періодовъ, напримѣръ, 25 въ секунду. Въ Сѣверной Америкѣ
употребительны нѣсколько большія числа періодовъ, соотвѣтству-
ющія меньшей продолжительности колебаній.
ИНДУКТИРОВАННЫЯ НАПРЯЖЕНІЯ ВЪ ПЕРЕМЪННОМЪ
МАГНИТНОМЪ ПОЛЪ.
370. Перемѣнное магнитное поле невозможно безъ дѣйствія
электрическихъ напряженій,
приводящихъ магнитное поле въ состо-
яніе покоя и вновь его возбуждающихъ. Эти ^^пряженія могутъ
быть очень сильными, если въ магнитномъ по^ находится желѣзо,
Индуктированныя напряженія въ перемѣнномъ магнитномъ полѣ 265
т.-е. тѣло съ большой проницаемостью, въ которомъ удѣльная инер-
ція эѳира весьма сильно увеличена благодаря содѣйствію молеку-
лярныхъ магнитовъ. Желѣзо дѣйствуетъ подобно тому, какъ тяжелое
маховое колесо дѣйствуетъ на валъ, который при помощи рукоятки
вращаютъ правильно періодически въ ту и въ другую сторону. Дви-
женіе маховаго колеса вызываетъ въ валѣ высокія перемѣнныя
упругія напряженія.
Если пропускать перемѣнный токъ черезъ катушку, имѣющую
внутри себя сердечникъ изъ мягкаго желѣза, который во избѣжаніе
вихревыхъ токовъ долженъ быть составленъ изъ полосъ или изъ
изолированныхъ желѣзныхъ проволокъ, то упомянутыя электрическія
напряженія проявляются въ формѣ приблизительно круговыхъ сило-
выхъ линій, обвивающихъ желѣзный сердечникъ. Можно легко обна-
ружить эти напряженія, если на катушку съ сердечникомъ надви-
нуть болѣе широкую катушку, концы которой соединены съ лампой
накаливанія. Если эта вторичная катушка имѣетъ достаточное
число оборотовъ, то подъ дѣйствіемъ индуктированныхъ напряженій
лампа накаливанія вспыхиваетъ яркимъ свѣтомъ.
Можно, по крайней мѣрѣ отчасти, воспрепятствовать образова-
нію измѣняющихъ магнитное поле напряженій, если надвинуть на
электромагнитъ перемѣннаго тока металлическій цилиндръ съ не
очень тонкими стѣнками (рис. 273). Лампа накаливанія, присоеди-
ненная къ вторичной катушкѣ, тухнетъ, какъ только мы достаточно
низко надвинемъ этотъ цилиндръ. Дѣло въ томъ, что въ метал-
лическомъ цилиндрѣ напряженія весьма быстро распадаются, и,
благодаря его присутствію, кругомъ не можетъ образоваться элек-
трическое поле. Если мы обратимся къ нашей прежней механической
аналогіи съ маховымъ колесомъ, то явленіе происходитъ такимъ об-
разомъ, какъ если бы колесо было не прочно скрѣплено съ осью,
но между нимъ и осью находился скользящій слой. Въ такомъ слу-
чаѣ колесо лишь отчасти слѣдовало бы за осью въ ея движеніяхъ
въ ту и другую сторону, и упругія напряженія оси были бы лишь
незначительны. Тяжелому маховому колесу соотвѣтствуетъ желѣзный
сердечникъ, скользящему слою — металлическій цилиндръ, оси — изол^З1
рующее окружающее пространство. Конечно, металлическій цилйндръ
одновременно въ значительной степени препятствуетъ обра^рцанію
какъ напряженій, такъ и магнитнаго поля, измѣненіе котораго безъ
этихъ напряженій невозможно; индуктированные въ
металлическомъ
266 Индуктированныя напряженія въ перемѣнномъ магнитномъ полѣ
цилиндрѣ токи, соотвѣтствующіе распаду электродинамическаго поля,,
направлены противоположно токамъ намагничивающей катушки и
потому уменьшаютъ число амперъ-витковъ поля, хотя при надвиганіи
цилиндра токъ въ катушкѣ не только не убываетъ, но, наоборотъ,
даже нѣсколько возрастаетъ, какъ легко убѣдиться при помощи
амперметра перемѣннаго тока. Металлическій цилиндръ, надѣтый на
намагничивающую катушку, дѣйствуетъ до нѣкоторой степени такъ,
какъ будто его присутствіе при перемѣнныхъ токахъ понижало про-
ницаемость желѣзнаго сердечника или какъ если бы онъ самъ былъ
діамагнитенъ. Дѣйствительно, какъ мы видѣли въ § 326, истинный
діамагнитизмъ тоже, вѣроятно, объясняется малыми круговыми токами,
индуктированными въ молекулахъ.
371. Подобно тому, какъ при вращеніи оси съ маховымъ ко-
лесомъ въ ту и другую сторону движущія силы должны преодолѣть
Рис. 274. Индуктивное сопротивленіе.
Перемѣнный токъ
колеса, точно такъ же для существованія магни'^Ді'о пере-
поля напряженіе генератора перемѣннаго тока должно пре-
индуктированныя напряженія, представляі^ія'собою ни что
инерцію
мѣннаго
одолѣть
иное, какъ дѣйствія инерціи магнитнаго поля, ^сли мы сообщимъ
полю большую инерцію (напримѣръ, вводя вд> желѣзныя массы)*
Индуктированныя напряженія въ перемѣнномъ магнитномъ полѣ 267
то при томъ же перемѣнномъ напряженіи будетъ развиваться меньшая
сила тока, подобно тому какъ вращающееся въ ту и другую сторону
маховое колесо при одной и той же движущей періодической силѣ
получаетъ тѣмъ меньшія отклоненіе и угловую скорость, чѣмъ
больше его моментъ инерціи. Можно легко демонстрировать пони-
жающее токъ дѣйствіе самоиндукціи, если соединить лампу нака-
ливанія съ источникомъ перемѣннаго тока и ввести въ цѣпь длин-
ную катушку. Ярко горящую лампу можно довести до потуханія,
ничего не измѣняя въ проводкѣ, а только вводя въ катушку пла-
стинчатый желѣзный сердечникъ (рис. 274).
Такимъ образомъ, включеніе самоиндукціи въ цѣпь перемѣн-
наго тока дѣйствуетъ подобно включенію сопротивленія. Перемѣнный
токъ не можетъ достигнуть большой силы даже при омическомъ
сопротивленіи цѣпи, близкомъ къ нулю, если въ цѣпи находится боль-
шая самоиндукція. Кажущееся сопротивленіе самоиндукціонной ка-
тушки перемѣнному току, называемое иногда также индуктивнымъ
сопротивленіемъ, тѣмъ больше, 1) чѣмъ больше „магнитная инер-
ція", т.-е. коэффиціентъ самоиндукціи катушки, и 2) чѣмъ больше
періодовъ въ секунду имѣетъ перемѣнный токъ. Болѣе точное вы-
численіе даетъ слѣдующее:
Если коэффиціентъ самоиндукціи катушки равенъ Ь
генри и число періодовъ перемѣннаго тока въ секунду
равно п, то индуктивное сопротивленіе катушки перемѣн-
ному току при синусоидальныхъ колебаніяхъ /?/ равняется
2тгя.7 омамъ. Если омическое сопротивленіе катушки без-
конечно мало по сравненію съ индуктивнымъ сопротивле-
ніемъ /?/ и эффективное напряженіе между зажимами ка-
тушки равняется а эффективная сила тока равняется
то имѣетъ мѣсто соотношеніе: = 2 п п 7.
Однако, аналогія между ослабляющимъ токъ дѣйствіемъ самоин-
дукціи и дѣйствіемъ истиннаго сопротивленія лишь весьма поверхно-
стная. Тогда какъ напряженіе между концами сопротивленія въ каждый 1
моментъ, по закону Ома, пропорціонально силѣ тока, такъ что сила7
тока и напряженіе всегда имѣютъ одинаковыя фазы, напряженіе
между зажимами самоиндукціонной катушки всегда идетъѣпереди
силы тока, которую оно вызываетъ лишь съ преодолѣн^іемт> магнит-
ной инерціи. Пока напряженіе дѣйствуетъ въ одну сторону, оно вы-
зываетъ возрастаніе магнитнаго поля въ постоянномъ направленіи*.
268 Индуктированныя напряженія въ перемѣнномъ магнитномъ полѣ
и магнитное поле достигаетъ максимума, лишь когда напряженіе ста-
новится равнымъ нулю. Когда же напряженіе мѣняетъ знакъ, то и
измѣненіе магнитнаго поля также мѣняетъ знакъ. Образовавшееся
ранѣе поле сперва уменьшается, и за первую часть новаго полупе-
ріода оно понижается до нуля, а въ теченіе второй части оно раз-
вивается въ противоположномъ направленіи и возрастаетъ до новаго
максимума, когда напряженіе снова становится равнымъ нулю, и такъ
далѣе. Напряженіе всегда идетъ впереди вызываемаго имъ
перемѣннаго магнитнаго поля на четверть періода, и потому
напряженіе между конечными зажимами самоиндукціонной
катушки, свободной отъ сопротивленія, и сила тока имѣютъ
разность фазъ или 90°. Эту разность фазъ легко демонстри-
Рис. 275. Осциллограмма напряженія и
силы тока въ сопротивленіи.
-------Кривая силы тока.
...... Кривая напряженія между конеч-
ными зажимами сопротивленія.
Рис. 276. Осциллограмма напряженія и
силы тока въ самоиндукціонной ка-
тушкѣ.
------ Кривая силы тока.
...... Кривая напряженія между конеч-
ными зажимами самоиндукціон-
ной катушки.
двойныхъ осциллограммъ (§ 286),
ровать, напримѣръ, при помощи
представленныхъ на- рис. 275 и 276.
Совершенно такую же разность фазъ мы можемъ обнаружить
и въ нашей механической модели — маховомъ колесѣ на валу —
между силою и движеніемъ, если правильно и періодически вращать
валъ при помощи рукоятки въ ту и въ другую сторону. Маховое
колесо достигаетъ максимальной скорости лишь тогда, когда сила •
дѣлается равной нулю, чтобы затѣмъ перемѣнить свой знакъ. ЛЕ
Мы найдемъ теперь связь между напряженіемъ и силой^ока
для случая простого синусоидальнаго колебанія, когда въ пе-
ремѣннаго тока, кромѣ самоиндукціи, введено еще истинціо^сопроти-
вленіе, включенное между зажимами, между которьімц>йзмѣряется
напряженіе; таковъ, напримѣръ, случай, когда исѣфшое сопроти-
вленіе проволоки самоиндукціонной катушки не° Дёзконечно мало.
Индуктированныя напряженія въ перемѣнномъ магнитномъ полѣ 269
сопротивленіе /?, пред-
Рис. 277. Часовая діаграмма
соединеннаго дѣйствія сопро-
тивленія и самоиндукціи.
Удобнѣе всего для этой цѣли воспользоваться часовой діаграммой.
Пусть на рис. 277 стрѣлка ОА=]у представляетъ силу тока У;
напряженіе, уравновѣшивающее омичесі
ставлено стрѣлкой ОВ, совпадающей по
направленію съ О А и равной ./?; на-
пряженіе, соотвѣтствующее самоиндукціи
Ь и имѣющее разность фазъ въ 90°
относительно У, представлено стрѣлкой
ОС, перпендикулярной къ ОА и равной
2тг«7.Л/. Если мы сложим^ ОВ и ОС
по правилу сложенія векторовъ, то полу-
чимъ стрѣлку ОО, представляющую полное напряженіе V между
зажимами; длина этой стрѣлки ОО равняется Ѵм, а уголъ 7)ОД = ф
представляетъ разность фазъ между V и 7. Для вычисленія этой;
разности фазъ имѣемъ непосредственно изъ чертежа:
ОС _ 2 7Т/2І
ОВ~~7Г~
и
Ѵм = Уос2 + ОВ2 = . ]//?2 + 4 тт2 и2 А2.
Слѣдовательно,
ѴеГГ = ^гг. ]//?2-|-4тг2и2/.2.
Кажущееся сопротивленіе /? между обоими зажимами рав-
няется ]Л?2 + 4 тх2п2Ь2. Найденныя формулы имѣютъ силу какъ въ
томъ случаѣ, когда сопротивленіе /? и самоиндукція 7 включены по-
слѣдовательно, такъ и въ томъ случаѣ, когда одна катушка одно-
временно обладаетъ сопротивленіемъ /? и самоиндукціей 7.
ЭНЕРГІЯ, ПЕРЕНОСИМАЯ ПЕРЕМѢННЫМЪ ТОКОМЪ.
372. Если V и 7 суть величины напряженія и силы тока въ
данный моментъ, т.-е. полныя величины электрическаго и магнит-
наго полей на подводящихъ токъ зажимахъ аппарата, питаемаго
перемѣннымъ токомъ, то энергія, переносимая эѳиромъ, имѣетъ есь^
данный моментъ величину
Л 17 1
= V. 7 ваттъ.
Если разность фазъ величинъ V и А равняется нулдерто при
синусоидальныхъ колебаніяхъ < о\Ѵ I
У = . Лг • 8ІП2 2пп/.
270
Энергія, переносимая перемѣннымъ токомъ
Такъ какъ среднее значеніе 8Іп22тгя/ равняется-^, то среднее
значеніе ^7, т.-е. количество энергіи, переносимое за одну
секунду, V равняется Ѵм • 1м , или, согласно § 368,
1} = Ѵе#. 7е/Г ваттъ.
Такимъ образомъ вычисляется, напримѣръ, средняя энергія, по-
глощаемая электрической лампой накаливанія, питаемой перемѣннымъ
токомъ. Если же разность фазъ между 7 и V равна 90°, какъ въ
случаѣ самоиндукціонной катушки безъ замѣтнаго омическаго сопро-
тивленія, т.-е. если 7= 7м. зіп 2пп/, V = Ѵм • соз 2тт/?7, то ' энергія,
.поступающая между зажимами въ данный моментъ, равняется
I] = Ѵм . . СО8 2тш/. 8ІП 2ппі.
Но зіп 2тгя^. соз 2ття/ =зіп 4п/г^, и среднее значеніе этой вели-
чины равняется нулю; слѣдовательно,
77=0.
Итакъ, хотя значеніе 13 въ каждый моментъ отлично отъ нуля, однако,
за время цѣлаго колебанія между зажимами вовсе не проходитъ энер-
гіи. Это нужно понимать такъ: энергія въ данный моментъ то входитъ
въ аппаратъ (самоиндукціонную катушку), то выходитъ изъ него
обратно въ провода. Въ теченіе первой четверти періода отъ і = 0
тг Т
до (т.-е. до 1=-^, гдѣ Т— продолжительность одного ко-
лебанія) сила тока возрастаетъ отъ 0 до 7м, напряженіе же падаетъ
отъ Ѵм до 0; входящая энергія въ теченіе этого времени поло-
жительна, и самоиндукціонная катушка поэтому получаетъ энер-
гію сперва медленно, затѣмъ быстрѣе и, наконецъ, опять медленно;
до 2тгл/ = ти 7т.-е.
2
) Vмѣняетъ свой знакъ, измѣняясь отъ 0 др— Ѵм,
2 / лсѵ
эта энергія служитъ для образованія сильнаго магнитнаго поля. Въ
теченіе второй четверти періода отъ 2ппі =
Т
отъ і = — до і =
и въ то же время значеніе 7 падаетъ отъ 7м до 0, ^энергія отри-
цательна, т.-е. самоиндукціонная катушка отдае^і?обратно энер-
гію, полученную за первую четверть періода,^сначала медленно,
затѣмъ быстрѣе, наконецъ, опять медленноч4^онечно, въ теченіе
Энергія, переносимая перемѣннымъ токомъ.
271
второй четверти періода изъ катушки уходитъ то же количество
энергіи, которое было ей сообщено въ теченіе первой четверти
періода. Такимъ образомъ, за первую половину періода энергія вовсе
не поступаетъ въ аппаратъ. То же самое имѣетъ мѣсто и въ теченіе
второго полуперіода: за первую его часть—третью четверть пері-
ода—отъ 2п/г/=тт до 2тт«/ = ^ V измѣняется отъ —Ѵм ДО О,
У измѣняется отъ 0 до —/у, энергія положительна, и снова обра-
зуется магнитное поле; за вторую часть полу періода, отъ —
до 2тт/7^= 2тт, V имѣетъ положительное значеніе и измѣняется
отъ 0 до Ѵм, а значеніе У отрицательно и измѣняется отъ —Л/
до 0, энергія отрицательна, т.-е. энергія магнитнаго поля вновь
отдается обратно.
Когда электрическое и магнитное поля электромаг-
нитнаго колебанія имѣютъ разность фазъ, равную 90°, то
не происходитъ переноса энергіи; аппаратъ, въ который
вступаютъ колебанія, поперемѣнно получаетъ и отдаетъ
энергію, ничего^изъ нея не удерживая.
Если разность фазъ между напряженіемъ на зажимахъ V и силой
тока У равна <р, такъ что 7= Л/. зіп 2тглг^, V = Ѵм- зіп (2тгл^ + ср),
то V можно разложить на два слагаемыя:
V = Ѵм- СО8 ф . 8ІП 2ття^4- Ѵм-8ІП ф . СО8 2тгп/,
изъ которыхъ первое имѣетъ одинаковую фазу съ У, а второе от-
личается по фазѣ отъ У на 90°. Соотвѣтственно и величина энергіи
въ данный моментъ распадается на два слагаемыя, изъ которыхъ
первое имѣетъ среднее значеніе, отличное отъ нуля, второе же въ
среднемъ даетъ нуль. Именно,
V — V.3= Ѵм- -Ім- со8ф.8іп2 2тгя/-|-Ѵл/. -/м- зіпф . 8іп 2ття^ . соз 2пя/
Такъ какъ среднее значеніе 8іп22тгя/, какъ извѣстно, равното
энергія, переносимая перемѣннымъ полемъ за секунду, равняется
I/ = ѴеГГ. . соз ф ваттъ. Й
Чтобы найти энергію, переносимую въ эѳирѣ син^<ри-
дальнымъ колебаніемъ, нужно умножить произде^ніе
эффективныхъ значеній силы тока и напряженіями^7коси-
нусъ разности фазъ между ними. Ерл
272
Энергія, переносимая перемѣннымъ токомъ
Если между двумя мѣстами проводки перемѣннаго тока сопро-
тивленіе проводки равняется 7? омамъ, то потеря напряженія между
этими двумя мѣстами равняется V — Я. У, ея эффективное значеніе
равняется Ѵ'е^ = /?. и разность фазъ между V' и У равна нулю.
Потеря энергіи въ проводкѣ между обоими мѣстами равняется
V е/т- 1віт= Я. она зависитъ лишь отъ силы тока, но не отъ
величины напряженія между двумя проволоками проводки и не отъ
разности фазъ между напряженіемъ и силой тока. Такъ какъ пере-
носимая энергія пропорціональна созср, т.-е. при данномъ напряже-
ніи генератора перемѣннаго тока тѣмъ больше, чѣмъ меньше <р, то от-
ношеніе потерянной энергіи ко всей переносимой энергіи тѣмъ меньше,
чѣмъ меньше разность фазъ ф между напряженіемъ и силой тока,
и тѣмъ лучше, слѣдовательно, использована проводка. Если значе-
ніе ф близко къ 90°, то и при большой силѣ тока переносится
лишь небольшое количество энергіи, а провода все-таки нагрѣва-
ются не меньше, чѣмъ при переносѣ большого количества энергіи.
Поэтому при передачѣ энергіи выгодно, чтобы значеніе ф было по
возможности мало.
Энергію перемѣннаго тока можно, подобно энергіи постояннаго
тока, измѣрять при помощи ваттметра, описаннаго въ § 288. Если
съ помощью этого аппарата найти величину & и, кромѣ того, при
помощи спеціальныхъ инструментовъ для перемѣннаго тока опредѣ-
лить величины Ѵер и то при синусоидальныхъ колебаніяхъ
можно по тремъ измѣреннымъ величинамъ опредѣлить разность фазъ ф
между напряженіемъ и силою тока, пользуясь уравненіемъ
V
СО8 ф = - -V— •
ДРОССЕЛЬНЫЯ (РЕАКТИВНЫЯ) КАТУШКИ.
373. Какъ мы видѣли, индуктивныя сопротивленія не погло-
щаютъ энергіи; на этомъ основано устройство дроссельныхФйли
реактивныхъ катушекъ, помощью которыхъ напряженідйремѣн-
наго тока, слишкомъ высокое для опредѣленной цѣлил (^понижается
до желательной величины.
При описаніи установокъ постояннаго токд^ъ/§ 364, мы упо-
минали, что дуговыя лампы всегда горятъ при ^пряженіи, равномъ
55 вольтамъ. Если станція даетъ 110 вольуѣ^то нужно или брать
Сравненіе коэффиціентовъ самоиндукціи
273
Рис. 278. Часовая діа-
грамма дроссельной
катушки.
сила тока У и число
двѣ лампы, включенныя послѣдовательно, или же, если желаютъ
пользоваться только одной лампой, слѣдуетъ включить сопротивле-
ніе, которое понизило бы напряженіе до 55 вольтъ. Послѣдній спо-
собъ, однако, весьма убыточенъ, такъ какъ предварительное сопро-
тивленіе, какъ мы видѣли, поглощаетъ ровно столько же энергіи,
какъ и лампа.
Гораздо удобнѣе имѣть дѣло съ перемѣн-
нымъ токомъ, такъ какъ здѣсь для пониженія
напряженія, вмѣсто сопротивленія, можно вклю-
чить самоиндукціонную катушку —дроссельную
катушку. Діаграмма (рис. 278) показываетъ,
какъ можно графически вычислить напряже-
ніе Ѵ2, которое должно быть поглощено
самоиндукціонной катушкой, по данному
напряженію V станціи и требуемому напря-
женію 1^]. Если, далѣе, извѣстны нормальная
періодовъ щ то можно вычислить самоиндукцію Л, которую нужно
дать дроссельной катушкѣ: Ь = Дроссельная катушка, ко-
нечно, должна имѣть желѣзный сердечникъ, составленный изъ полосъ,
во избѣжаніе вихревыхъ токовъ. Но и при такомъ устройствѣ сер-
дечникъ поглощаетъ нѣкоторое количество энергіи вслѣдствіе гисте-
резиса; однако, потеря энергіи въ дроссельной катушкѣ чрезвычайно
мала въ сравненіи съ потерей энергіи въ дроссельномъ сопротивленіи.
СРАВНЕНІЕ КОЭФФИЦІЕНТОВЪ САМОИНДУКЦІИ.
374. Въ продажѣ имѣются точно калибрированныя катушки
опредѣленной постоянной самоиндукціи, напримѣръ, въ 1 генри.
Эти катушки, понятно, совершенно лишены желѣза, такъ какъ иначе
ихъ самоиндукція не могла бы быть вполнѣ постоянной. Простѣй-
шій методъ измѣренія коэффиціентовъ самоиндукціи другихъ кату-
шекъ заключается въ томъ, что ихъ сравниваютъ съ точно калибри-
рованными катушками. Это легко сдѣлать въ случаѣ перемѣннаго'^?'
тока, пользуясь особымъ видомъ моста Витстона съ телефонрм^
(§ 269). Слѣдуетъ лишь въ одной вѣтви замѣнить оба сопротивленія
самоиндукціонными катушками, коэффиціенты которыхъ
желаютъ сравнить; въ другой вѣтви остается измѣрительная^прово-
лока. Если истинное сопротивленіе самоиндукціонцыхтАкатушекъ
Ми. Электричество и магвитизмъ, ч. II.
18
274
Сравненіе коэффиціентовъ самоиндукціи
безконечно мало по сравненію съ ихъ индуктивнымъ сопротивле-
ніемъ, то въ самоиндукціонной вѣтви идетъ токъ У, имѣющій раз-
ность фазъ въ 90° относительно напряженія V, приложеннаго къ точ-
камъ развѣтвленія А и В. Напряженія и Ѵ2 между концами двухъ
самоиндукцій, т.-е. между точками А и С, С и В (С—точка, въ кото-
рой обѣ катушки присоединены одна къ другой), имѣютъ одну и ту
же разность фазъ относительно т.-е. они имѣютъ одинаковыя
фазы съ V; по величинѣ они относятся между собою, какъ индук-
тивныя сопротивленія 2плгЛ1 и 2ігпЛ2, т.-е. Ѵг : Ѵ2 — : Ц. Если
мы на измѣрительной проволокѣ перемѣстимъ подвижной контактъ
въ точку О, раздѣляющую проволоку на двѣ части съ сопроти-
вленіями и /?2, которыя относятся между собой, какъ къ Л2,
то напряженія (Л, Л) и (7), В) будутъ имѣть такія же точно зна-
ченія и І/2, какъ и напряженія (Д, С) и (С, В), и притомъ какъ
по величинѣ, такъ и по фазѣ; телефонъ въ мостѣ въ такомъ слу-
чаѣ совершенно замолкаетъ. По этому признаку можно весьма точно
опредѣлить точку Л, раздѣляющую проволоку на такія двѣ части,
что ихъ сопротивленія и /?2 относятся между собою, какъ срав-
ниваемые коэффиціенты самоиндукціи и 72.
Если бы напряженія (А, С) и (С, В) не были постоянно въ
одинаковой фазѣ между собою и съ напряженіемъ (Д, В), то между
С и Л никакъ нельзя было бы достигнуть постояннаго напряженія,
равнаго нулю. Въ такомъ случаѣ звукъ телефона можно было бы,
пожалуй, свести къ минимуму, но онъ не прекратился бы совершенно.
Это бываетъ, напримѣръ, когда самоиндукціонныя катушки имѣютъ
омическія сопротивленія и /?2', которыя не безконечно малы въ
сравненіи съ индуктивными сопротивленіями 2'ппѣ1 и 2пяА2. Лишь
въ томъ частномъ случаѣ, когда /?/ : /?2' = Ц : В2, разность фазъ ф
напряженій (Д, С) и (С, В} относительно тока въ самоиндукціонной
вѣтви У одинакова, а именно равна разности фазъ напряженія (Д, В) и
тока У, потому что тогда
. _2ъп _2ттп Ь2 _2ттп (7^ + Л).
ёФ = = +#>'
Въ этомъ случаѣ телефонъ тоже совершенно замолкае^эрёсли пе-
редвижной контактъ дѣлитъ мостъ на двѣ части, соцр^тивленія ко-
торыхъ относятся, какъ къ А2. Итакъ, если прил^Мѣреніи наблю-
дается неясный минимумъ звучанія, то можнадюмочь дѣлу, вклю-
чивъ въ одну изъ двухъ самоиндукціонныхъ вѣтвей (въ ту, омическое
Безъиндукціонныя сопротивленія
275
сопротивленіе которой сравнительно слишкомъ мало) еще неболь-
шое, свободное отъ индукціи сопротивленіе, которое измѣняютъ
до тѣхъ поръ, пока не будетъ достигнутъ рѣзкій минимумъ зву-
чанія или же полное молчаніе.
Особое преимущество этого метода заключается въ томъ, что
при пользованіи имъ мы совершенно не зависимъ отъ числа коле-
баній и, котораго можно поэтому не знать. Перемѣнный токъ можетъ
также быть составленъ любымъ образомъ изъ множества синусоидаль-
ныхъ колебаній, и можно въ качествѣ источника тока взять, какъ
на рис. 185, небольшой индукторій, который вовсе не даетъ сину-
соидальнаго колебанія.
Катушки съ желѣзнымъ сердечникомъ, какъ неоднократно уже
было упомянуто, не имѣютъ строго опредѣленнаго коэффиціента само-
индукціи и потому, если ихъ измѣряютъ описаннымъ методомъ, онѣ
не позволяютъ достигнуть полнаго молчанія телефона. Однако,
можно все-таки наблюдать минимумъ звучанія и, основываясь на
немъ, опредѣлять и для этихъ катушекъ нѣкоторый коэффиціентъ,
характеризующій въ общемъ ихъ свойства и пригодный для болѣе
грубыхъ вычисленій.
БЕЗЪИНДУКЦІОННЫЯ СОПРОТИВЛЕНІЯ.
375. Чтобы сопротийленія штепсельныхъ реостатовъ были при-
годны и для измѣреній надъ перемѣннымъ токомъ, они должны
быть навиты такъ, чтобы ихъ самоиндукція была возможно ближе
къ нулю. Это достигается, если токъ проходитъ каждые два смеж-
ные витка катушки во взаимно противоположныхъ направленіяхъ.
Въ такомъ случаѣ магнитное поле, поскольку оно имѣетъ замѣт-
ную силу, ограничено лишь непосредственной окрестностью витковъ,
и одновременно съ малымъ пространственнымъ протяженіемъ оно
обладаетъ относительно очень малой энергіей и инерціей. Суще-
ствуютъ два метода обмотки безъиндукціонныхъ катушекъ сопро-
тивленія: либо навиваютъ одну на другую двѣ проволоки и спаи-^3
ваютъ ихъ концы такимъ образомъ, что одна проволока проводитъ
токъ въ одномъ направленіи, а другая — въ обратномъ (бифи^рная
обмотка), либо же наматываютъ одну проволоку такъ, чт^&і по-
лучилось большое число слоевъ, въ которыхъ поперемѣцйр' мѣня-
ютъ направленіе навивки. Второй методъ лучше перваг@°
18
ѵ
276
Трансформаторъ перемѣннаго тока
ТРАНСФОРМАТОРЪ ПЕРЕМѢННАГО ТОКА.
376. Если на электромагнитъ перемѣннаго тока надвинуть вто-
рую катушку, какъ івъ опытахъ, описанныхъ въ § 370, то между
ея концами наблюдается перемѣнное напряженіе. Въ дальнѣйшемъ
изложеніи мы всегда будемъ называть катушку для намагничиваю-
щаго тока первичной катушкой, а вторую, надвинутую катушку
— вторичной катушкой. Чтобы легче было оріентироваться, мы
примемъ, во-первыхъ, что мы можемъ пренебречь поте-
рями напряженія вслѣдствіе омическаго сопротивленія въ
первичной и вторичной катушкахъ по сравненію съ напря-
женіями, связанными съ перемѣннымъ магнитнымъ полемъ,
и, во-вторыхъ, что первичная и вторичная катушки такъ
тѣсно пригнаны одна къ другой, что обѣ всегда охваты-
ваютъ одинъ и тотъ же магнитный силовой потокъ. При
такихъ условіяхъ, очевидно, имѣетъ мѣсто слѣдующее предложеніе:
Если первичная и вторичная катушка имѣютъ одинако-
вое число проволочныхъ витковъ, то напряженіе между
зажимами вторичной катушки всегда въ точности равно
перемѣнному напряженію между зажимами первичной ка-
тушки.
Дѣйствительно, оба напряженія равняются скорости измѣненія
магнитнаго силового потока, умноженной на число витковъ. Если-же
катушки имѣютъ неодинаковое число витковъ, то имѣетъ силу слѣ-
дующее предложеніе:
Напряженія Ѵ1 и Ѵ2 между зажимами первичной и вто-
ричной катушекъ всегда относятся между собою, какъ числа
витковъ и ТѴ2 катушекъ, т.-е. Ѵ1:Ѵ2 = ^:^.
называется трансформирующимъ
Напряженіе первичной катушки, такимъ образомъ, преобра-
зуется или трансформируется во вторичной катушкѣ въ напря-
женіе Ѵ2=Ѵ1^- Описанный аппаратъ поэтому называютъ траріс-
форматоромъ, а дробь
/Ѵі
коэффиціентомъ.
Оба формулированныя предложенія при вышеуказанныхъ двухъ
условіяхъ всегда остаются вѣрными, независимости величины силы
тока въ первичной и вторичной катушкахъ и о независимо отъ того,
примѣнимъ ли принципъ наложенія или нфИЭ
Трансформаторъ перемѣннаго тока
277
Если вторичные зажимы оставить разомкнутыми такъ, чтобы
черезъ вторичную катушку вовсе не шелъ токъ, то первичная катушка
будетъ совершенно подобна обычной самоиндукціонной катушкѣ:
ея токъ всегда отстаетъ относительно напряженія между зажимами
на разность фазъ тг/2, и его величина вычисляется по формулѣ
Ѵе1Г
2ъпЬ’ ГД^ —эффективное значеніе напряженія между за-
жимами, Ь — коэффиціентъ самоиндукціи первичной катушки. Въ
этомъ случаѣ энергія не поступаетъ въ трансформаторъ и изъ него
не выступаетъ.
Если-же вторичная катушка замкнута, то возникаетъ токъ /2,
который легко можно вычислить, зная напряженіе между зажимами и
включенныя въ цѣпь сопротивленія и самоиндукціи. Этотъ вторич-
ный токъ дѣйствуетъ обратно на первичный токъ /1, такъ какъ они
должны вмѣстѣ дать число амперъ-витковъ, соотвѣтствующее пере-
мѣнному магнитному полю въ желѣзномъ сердечникѣ, а это пере-
мѣнное поле, по второму основному закону Максвелла, однозначно
опредѣляется напряженіемъ на зажимахъ. Для случая синусоидаль-
ныхъ колебаній можно разсчитать первичный токъ, измѣненный реак-
ціей вторичнаго тока, пользуясь часовой діаграммой. На діаграммахъ
а и б рис. 279 напряженіе между
зажимами первичной катушки
представлено векторомъ ОА; пер-
пендикулярный къ нему векторъ
ОВ представляетъ число амперъ-
витковъ 7 перемѣннаго поля
въ желѣзномъ сердечникѣ, вы-
званнаго напряженіемъ и всегда
отстающаго отъ на четверть
періода колебанія. Число №2 /2
амперъ-витковъ тока во вторичной катушкѣ, сила и фаза котораго
предполагаются извѣстными, представится векторомъ ОС. Въ такомъ
случаѣ векторъ ОО, имѣющій одинаковую длину и направленіе су^р?°
отрѣзкомъ СВ, представитъ намъ число амперъ-витковъ
маго первичнаго тока, такъ какъ лишь такимъ образомъ можетъМ^ійъ
соблюдено условіе, чтобы числа и ІУ2 /2 вмѣстѣ давали истинное
число амперъ-витковъ 7. Если разложить векторы и каждый
на два слагающихъ, изъ которыхъ V/ и одинаковы по фазѣ
Рис. 279 а. Часовая діаграмма транс-
форматора перемѣннаго тока.
278
Трансформаторъ перемѣннаго тока
съ напряженіемъ V, а и смѣщены относительно V на
четверть періода, то непосредственно получается:
*
Если силы тока въ первичной и вторичной катушкахъ
трансформатора и /2 разложить каждую на двѣ слагающія
У/, Л" и изъ которыхъ первая совпадаетъ по фазѣ
съ перемѣннымъ напряженіемъ, а вторая смѣщена на чет-
верть періода, то числа амперъ-витковъ второй слагающей
вмѣстѣ составляютъ число амперъ-витковъ перемѣннаго маг-
нитнаго поля, вызываемаго въ желѣзномъ сердечникѣ транс-
форматора перемѣннымъ напряженіемъ; числа же амперъ-
витковъ слагающихъ, одинаковыхъ по фазѣ съ напряже-
ніемъ, равны и противоположны.
Если обѣ катушки трансформатора имѣютъ одинаковое
число витковъ, то слагающая первичнаго тока, имѣющая
одинаковую фазу съ напряженіемъ, равна соотвѣтствую-
щей слагающей вторичнаго тока и противоположно напра-
влена; если числа витковъ и №2
тока, имѣющія одинаковыя фазы съ
пропорціональны числамъ витковъ,
Изъ соображеній, изложенныхъ въ
вычисленія энергіи имѣютъ значеніе лишь слагающія 4^
какъ . /1" и Ѵ2 . У2" въ среднемъ даютъ нуль.
Слагающая тока, которая совпадаетъ п^^азѣ съ напря-
женіемъ и одна только имѣетъ значеніеоддя электрически
различны, то слагающія
напряженіемъ, обратно
т.-е. Л =
§ 372, слѣдуетъ^мто для
У2', такъ
Трансформаторъ перемѣннаго тока
279
переносимой энергіи, преобразуется въ трансформаторѣ
обратно пропорціонально напряженіямъ.
Такимъ образомъ, всегда . У/ = — Ѵ2. иначе говоря, энер-
гія, вступающая въ первичную обмотку трансформатора, выходитъ
изъ вторичной обмотки. Ясно, что это имѣетъ мѣсто, лишь если
пренебречь омическимъ сопротивленіемъ въ обѣихъ катушкахъ. Если-же
при вычисленіи принять во вниманіе потери напряженія въ катуш-
кахъ, то получится небольшая разница между величинами и
Ѵ2. У2', соотвѣтствующая теплотѣ тока, поглощенной въ катушкахъ.
Кромѣ того, еще играетъ роль гистерезисъ желѣзнаго сердечника; если
его принять во вниманіе, то вычисленіе нѣсколько усложняется; во вся-
комъ случаѣ, гистерезисъ также даетъ нѣкоторую малую потерю энергіи.
На практикѣ, однако, удается строить трансформаторы такимъ обра-
зомъ, что ихъ отдача, т.-е. отношеніе Ѵ2 32 : ^7/ лишь весьма
немного отличается отъ единицы. Производительность трансформа-
тора дѣйствительно использована лишь въ томъ случаѣ, если онъ
выполняетъ требованія, характеризуемыя діаграммой б рис. 279, гдѣ
стрѣлка Д т.-е. намагничивающее число амперъ-витковъ, мала по
сравненію съ и ТѴ2./2, а разности фазъ силъ токовъ относи-
тельно напряженій между зажимами ср, и ср2 незначительны.
Если генераторъ соединенъ по возможности непосредственно
съ первичными зажимами трансформатора безъ промежуточныхъ
сопротивленій или дроссельныхъ катушекъ, то напряженіе между
зажимами тождественно съ напряженіемъ, которое порождается
генераторомъ, и измѣняется лишь незначительно съ измѣненіемъ
силы отнимаемаго отъ трансформатора тока. Поэтому магнитное
поле въ сердечникѣ трансформатора должно всегда развиться до
своего нормальнаго значенія независимо отъ того, силенъ или малъ
токъ во вторичной катушкѣ. Представленный на рис. 273 опытъ,
проводку перемѣннаго тока включедаг
усиленіемъ первичнаго тока связано'сйль-
между зажимами Ѵ1 вслѣдствіе пбтери
первичную
такъ что съ
напряженія
проводкѣ.
въ которомъ возникновеніе магнитнаго поля въ желѣзномъ сердеч-
никѣ трансформатора замѣтно парализовалось надвинутымъ метал-
лическимъ цилиндромъ, удается, слѣдовательно, лишь въ томъ слу^
чаѣ, если въ
сопротивленія,
ное пониженіе
напряженія въ
280 Механическая модель электромагнитной связи въ трансформаторѣ
МЕХАНИЧЕСКАЯ МОДЕЛЬ ЭЛЕКТРОМАГНИТНОЙ СВЯЗИ ВЪ
ТРАНСФОРМАТОРЪ.
377. Въ качествѣ механической модели обѣихъ электрическихъ
трансмиссій—двойной проводки, связанной черезъ трансформаторъ,
мы возьмемъ два трансмиссіонные вала. Желѣзному сердечнику
трансформатора будетъ соотвѣтствовать маховое колесо (рис. 280),
соединенное съ обоими валами такимъ образомъ, что каждый мо-
жетъ вращаться независимо отъ другого подобно тому, какъ каждая
изъ двухъ трансформаторныхъ проводокъ можетъ нести токъ неза-
висимо отъ другой. При этомъ нужно, однако, чтобы они могли
быть связаны между собою дѣйствіемъ инерціи колеса, которое
вполнѣ аналогично дѣйствію инерціи магнитнаго поля. Какъ можетъ
Рис. 280. Два трансмиссіонные вала, связанные между собою
инерціей махового колеса.
быть произведено соединеніе валовъ съ маховымъ колесомъ для
полученія инерціонной связи, показываютъ представленныя на
рис. 281 сѣченія черезъ ступицу связывающаго махового колеса.
Ступица представляетъ собою широкую цилиндрическую капсюлю, ѣъ
которую съ обѣихъ сторонъ входятъ своими концами связываемые
валы I и II. Концы валовъ внутри ступицы сдѣланы въ видф^короткихъ
зубчатыхъ валиковъ. Ихъ зубцы зацѣпляютъ по три зубчатыхъ валика,
которые расположены вокругъ нихъ симметричными подшипники
Д. •
которыхъ находятся въ боковыхъ стѣнкахъ капсюли, т.-е. непо-
движно соединены съ маховымъ колесомъ. л шести валиковъ три
Механическая модель электромагнитной связи въ трансформаторѣ 281
(1, 3 и 5) соединены съ валомъ I, и три (2, 4, 6) соединены съ
валомъ II. Всѣ шесть валиковъ нѣсколько длиннѣе концовъ транс-
миссіонныхъ валовъ и въ средней части капсюли, куда не дохо-
дятъ концы валовъ, каждый валикъ сцѣпляется съ двумя сосѣдними.
Если мы теперь будемъ держать валъ II неподвижно и вра-
щать валъ I за рукоятку, то мы приведемъ во вращеніе маховое колесо.
Это соотвѣтствуетъ процессу въ трансформаторѣ, когда мы при
разомкнутой вторичной обмоткѣ прилагаемъ къ первичной обмоткѣ
нѣкоторое напряженіе; при этомъ развивается электрическій токъ и
вмѣстѣ съ нимъ магнитное поле въ желѣзномъ сердечникѣ. Когда
мы приводимъ во вращеніе валъ I, то намъ приходится главнымъ
образомъ преодолѣвать сопротивленіе инерціи махового колеса („само-
индукцію"); когда же мы достигнемъ постоянной скорости вращенія,
то вращающая сила должна будетъ уравновѣшивать лишь сопро-
тивленіе тренія въ подшипникахъ („омическое сопротивленіе про-
водовъ"). Если желаютъ быстро прекратить вращеніе, то для прео-
долѣнія инерціи махового колеса нужно приложить тормозящую силу,
которою уничтожается накопленная въ колесѣ энергія движенія.
Если, наоборотъ, держать неподвижнымъ маховое колесо, то валъ I
можно будетъ вращать, лишь если оставить свободнымъ валъ II, кото-
рый при этомъ неподвижно связанъ съ валомъ I и вращается вмѣстѣ
съ нимъ. Соотвѣтственное явленіе мы можемъ получить въ транс-
форматорѣ, лишь если включимъ параллельно первичную и вторичную
обмотки такимъ образомъ, чтобы при соединеніи съ источникомъ
тока онѣ обѣ получали токъ одновременно и въ противополож-
ныхъ направленіяхъ. Если затѣмъ соотвѣтствующей регулировкой
сопротивленій уравнять числа амперъ-'витковъ обѣихъ катушекъ, то
въ трансформаторѣ не можетъ вовсе возникнуть магнитное поле;
вмѣстѣ съ тѣмъ совершенно такъ же, какъ въ механической мо-
дели, обѣ трансмиссіи будутъ тогда неподвижно соединены между
собою.
Если мы оставимъ свободными колесо и оба вала и будемъ
быстро вращать рукоятку вала I періодически въ ту и другую ст^^р
рону, то инерція колеса дѣйствуетъ совершенно такъ же, ^акъ
если бы оно было закрѣплено. Колесо совершаетъ лишь слабыя^кбле-
банія, между тѣмъ какъ большія колебанія вала I переносятся:^фликомъ
на валъ II, соотвѣтственно діаграммѣ трансформаціи бой^?рис. 279.
Подобно тому, какъ при электромагнитной инерщо|Щ^й связи маг-
282 Механическая модель электромагнитной связи въ трансформаторѣ
нитное поле въ желѣзномъ сердечникѣ смѣщено приблизительно на 900,
относительно силы тока въ первичной и вторичной обмоткахъ, точно-
такъ же и въ механической инерціонной связи слабыя колебанія
махового колеса всегда отстаютъ приблизительно на четверть коле-
банія относительно движеній трансмиссіонныхъ валовъ. Подобно тому
какъ электромагнитная инерціонная связь пригодна лишь для пере-
мѣннаго тока, точно такъ же и механическая связь функціонируетъ
лишь при перемѣнныхъ вращеніяхъ. Если же вращать валъ I все
въ одномъ направленіи, то вращеніе вала II—„индукціонный ударъ
Сѣченіе А ^Сѣченіе 3 Сѣченіе С
Рис. 281. Внутренній механизмъ ступицы махового колеса,
служащаго для инерціонной связи.
тока“ — наблюдается лишь въ началѣ движенія, когда маховое колесо
еще не пришло въ движеніе. Это вращеніе, однако, скоро прекра-
щается вслѣдствіе тренія въ подшипникахъ, какъ только о пу^согвое
колесо приходитъ во вращеніе, и устанавливается стаціона^бе состо-
яніе, при которомъ валъ II находится въ покоѣ и маховое колесо
вращается вмѣстѣ съ валомъ I, какъ при неподвижномъ валѣ II.
Когда мы прекратимъ вращеніе вала I, то инертное маховое ко-
лесо останавливается не сразу и, такъ какъвалъ I уже болѣе не
вращается, то валъ II вращается до тѣхъ црръ^ пока треніе не по-
Практическія примѣненія трансформаторовъ перемѣннаго тока 283
глотитъ энергіи движенія колеса. Это явленіе соотвѣтствуетъ индук-
ціонному удару тока при размыканіи первичной цѣпи.
Связь, представленная на рис. 281, соотвѣтствуетъ электромаг-
нитной связи въ трансформаторѣ, у котораго вторичная обмотка
имѣетъ такое же число витковъ, какъ и первичная, и коэффиціентъ
трансформаціи поэтому равняется единицѣ. Примѣняя валики различ-
ныхъ діаметровъ, можно получить механическія инерціонныя связи
со всевозможными коэффиціентами трансформаціи; такъ какъ энер-
гія, доставляемая связи валомъ I, должна равняться энергіи, переда-
ваемой связью валу II (потери вслѣдствіе тренія не принимаются
въ расчетъ), то коэффиціентъ трансформаціи для скоростей вращенія
является обратной величиной коэффиціента трансформаціи для вра-
щающихъ силъ. Мы имѣемъ здѣсь механическую аналогію предло-
женія, изложеннаго въ § 376.
ПРАКТИЧЕСКІЯ ПРИМѢНЕНІЯ ТРАНСФОРМАТОРОВЪ ПЕРЕМѢН-
НАГО ТОКА.
378. Какъ мы видѣли, напряженіе станціи перемѣннаго тока
возможно трансформировать по желанію въ болѣе высокое или болѣе
низкое напряженіе при помощи весьма простыхъ аппаратовъ, каковы
трансформаторы, въ которыхъ къ тому же происходятъ лишь незна-
чительныя потери энергіи. Благодаря этому, при электромагнитной
передачѣ энергіи на разстояніе, перемѣнный токъ въ весьма мно-
гихъ случаяхъ имѣетъ большое преимущество передъ постояннымъ
токомъ.
На рис. 282 представленъ обыкновенный типъ трансформатора
перемѣннаго тока. Чѣмъ большія количества энергіи желательно
передать, тѣмъ больше долженъ быть силовой потокъ магнитнаго
поля, осуществляющаго связь. Чтобы достигнуть этого съ возможно
меньшимъ количествомъ желѣза, „магнитное сопротивленіе" сердеч-
ника трансформатора (§ 328) дѣлаютъ возможно меньшимъ. Въ
трансформаторѣ, изображенномъ на рисункѣ, сердечникъ предста-€
вляетъ собой замкнутый прямоугольникъ, составленный изъ четы{х^0>
прочно свинченныхъ между собою желѣзныхъ стержней, без^ воз-
душныхъ щелей. Желѣзо, конечно, берется полосовое и «ірлосы,
изъ которыхъ составлены стержни, стягиваются вмѣстѣ ^деревянными
обхватами. Около каждаго изъ двухъ вертикальных^^ержней же-
лѣзнаго прямоугольника укрѣплена цилиндрическа^цф^ювая насадка,
284 Практическія примѣненія трансформаторовъ перемѣннаго тока
на которую намотана катушка низкаго напряженія. Она состоитъ
изъ относительно малаго числа витковъ толстой проволоки. На
рис. 282 она не видна, такъ какъ на нее надвинута катушка высо-
каго напряженія, состоящая изъ весьма большого числа оборотовъ
тонкой проволоки и навитая по секціямъ для достиженія лучшей
изоляціи.
Важнѣйшее приложеніе трансформаторовъ состоитъ въ пере-
дачѣ энергіи на разстояніе. На центральной станціи устанавли-
ваются генераторы перемѣннаго тока; они либо даютъ очень вы-
сокія напряженія непосредственно, либо же напряженіе ихъ повы-
Рис. 282. Трансформаторъ перемѣннаго тока.
шается до нѣсколькихъ тысячъ вольтъ при помощи большого транс-
форматора. Въ силу этого можно переносить на разстоянія весьма
большія количества энергіи при относительно малыхъ силахъ тока.
Если, напримѣръ, эффективное значеніе напряженія равно 10000
вольтъ, то при той же энергіи сила тока составляетъ сотую долю
силы тока, соотвѣтствующей напряженію въ 100 вольтъ. Поэтому
при такомъ напряженіи можно брать тонкія проволоки и, несмотря,
на то, имѣть лишь малыя потери энергіи. На подстанціяхъ устанавлй-
ваются меньшіе трансформаторы, понижающіе напряженіе доД^дьшей
величины, удобной для потребителей (напримѣръ, 100 в^лйъ), и от-
туда идутъ домашнія проводки. На рис. 283 дана С-^ема передачи
энергіи при помощи перемѣннаго тока.
Таково весьма простое и весьма совершенное рѣшеніе технической
проблемы, формулированной въ §365: высокоё^напряженіе на цен-
Практическія примѣненія трансформаторовъ перемѣннаго тока 285
тральной станціи, низкое напряженіе въ мѣстахъ потре-
бленія. Ясно вмѣстѣ съ тѣмъ, что для передачи энергіи на большія раз-
стоянія пригоденъ лишь перемѣнный токъ. Методъ передачи энергіи на
разстояніе перемѣнными полями можно демонстрировать на очень про-
стомъ опытѣ; для этого нужно установить два малые трансформа-
тора, соединивъ ихъ зажимы высокаго напряженія посредствомъ длин-
ныхъ проводовъ изъ очень тонкой проволоки (Ѵю миллиметра). Если
соединить зажимы низкаго напряженія одного трансформатора съ
обыкновенной машиной перемѣннаго тока приблизительно въ 100
вольтъ, а зажимы низкаго напряженія другого трансформатора съ
сильной электрической дуговой лампой, то можно заставить эту лампу
ярко горѣть, при чемъ вся довольно значительная энергія доставля-
Центральная Провода Подстанція пРовода Подстанція
Рис. 283. Схема передачи энергіи на разстояніе помощью перемѣннаго тока.
ется лампѣ тончайшими проволоками, которыя при этомъ даже не
нагрѣваются.
Если центральная станція перемѣннаго тока нагружена весьма
неравномѣрно, какъ это обычно бываетъ на городскихъ централь-
ныхъ станціяхъ, то пропадаетъ довольно большое количество энергіи.
Отдача всѣхъ машинъ не велика, если онѣ работаютъ со слиш-
комъ малой нагрузкой; это слѣдуетъ сказать также и про транс-
форматоры на подстанціяхъ, такъ какъ при всей незначительности
потерь энергіи вслѣдствіе сопротивленія и гистерезиса, онѣ въ не-
нагруженномъ трансформаторѣ не очень многимъ меньше, чѣмъ въ
нагруженномъ. Поэтому въ теченіе дня и тѣхъ продолжительны^^0
промежутковъ, когда потребленіе весьма ограничено, энергіігітеря-
ется. Если можно пользоваться силами водопадовъ, такъ что&гпри-
ходилось покрывать лишь издержки по установкѣ и обслуживанію,
а самая энергія получалась даромъ, то указанныя потери энергіи
не представляютъ никакого неудобства при сис^мф перемѣннаго
286 Практическія примѣненія трансформаторовъ перемѣннаго тока
тока. Иначе обстоитъ дѣло, когда энергія доставляется тепловыми
машинами, такъ какъ въ этомъ случаѣ перерасходъ горючаго мате-
ріала сильно повышаетъ издержки эксплоатаціи. При такихъ обстоятель-
ствахъ перемѣнный токъ, несмотря на всѣ свои преимущества, можетъ
оказаться гораздо менѣе выгоднымъ, нежели постоянный токъ съ его
гибкимъ резервуаромъ энергіи-—аккумуляторной батареей. Поэтому
на городскихъ электрическихъ станціяхъ часто отдаютъ предпочтеніе
постоянному току, какъ было уже объяснено въ § 364.
379. Трансформація перемѣннаго тока играетъ важную роль
еще въ нѣкоторыхъ совершенно спеціальныхъ техническихъ прило-
женіяхъ, именно во всѣхъ тѣхъ случаяхъ, когда необходимо имѣть
чрезвычайно высокія напряженія (при малой силѣ тока) или же громад-
ной силы токи (при низкихъ напряженіяхъ). Собственно говоря, ста-
рѣйшимъ примѣненіемъ трансформаторовъ является именно возбу-
жденіе весьма высокихъ напряженій, для чего спеціально и былъ изоб-
рѣтенъ трансформаторъ подъ именемъ индукціоннаго аппарата.
Мы еще возвратимся къ этому въ отдѣльномъ параграфѣ. Въ по-
слѣднее время перемѣнный токъ высокаго напряженія примѣняется
въ широкомъ масштабѣ для фабрикаціи азотной кислоты изъ атмо-
сфернаго воздуха. Помощью высокаго напряженія получаются ги-
гантскія свѣтовыя дуги, которыя вызываютъ въ продуваемомъ воз-
духѣ химическое соединеніе части азота съ кислородомъ въ окись
азота; изъ этой послѣдней уже легко получается азотная кислота.
Задачей, обратной возбужденію высокихъ напряженій, является
возбужденіе чрезвычайно сильныхъ токовъ низкаго напряженія. Для
этой цѣли строятся особые трансформаторы, вторичная обмотка ко-
торыхъ состоитъ изъ весьма небольшого числа витковъ очень тол-
стой мѣдной проволоки. Такіе трансформаторы часто употребляются
на большихъ фабрикахъ для сварки желѣза, раскаляемаго помощью
сильнаго перемѣннаго тока (сварочные трансформаторы).
ВОЗМОЖНЫ ЛИ ТРАНСФОРМАТОРЫ ПОСТОЯННАГО ТОКА?
380. Если бы существовалъ столь же простой методъ трансфор-
маціи постояннаго тока, какой существуетъ для перемѣннагрЗубка, то,
конечно, постоянный токъ слѣдовало бы предпочитать во всѣхъ случа-
яхъ; это была бы вполнѣ идеальная система передачи энергіи. Къ сожа-
X • д-
лѣнію, не существуетъ простыхъ трансформаторовъ гюстояннаго тока.
Существуютъ лишь вращающіеся конверторы (преобразователи)
Возможны ли трансформаторы постояннаго тока?
287
постояннаго тока. Такой конверторъ представляетъ собою двѣ меха-
нически связанныя машины постояннаго тока, изъ которыхъ одна
служитъ моторомъ, а другая —динамо. Если эти двѣ машины имѣютъ
различныя напряженія между зажимами то электрическая энергія
опредѣленнаго напряженія, введенная въ такую двойную машину
съ одной стороны, будетъ получаться съ другой стороны съ инымъ
напряженіемъ. Но такой „трансформаторъ", конечно, никоимъ обра-
зомъ не можетъ быть сравниваемъ съ трансформаторомъ перемѣн-
наго тока. Уже съ чисто практической точки зрѣнія онъ пред-
ставляетъ собой нѣчто совершенно иное. Это — сложная машина,
которая, во-первыхъ, дорого стоитъ, во-вторыхъ, не можетъ быть
просто помѣщена въ трансформаторной будкѣ, но требуетъ непре-
рывнаго присмотра, въ-третьихъ, даетъ несравненно большую потерю
энергіи, нежели простой трансформаторъ перемѣннаго тока. Понятно
само собою, что проводка постояннаго тока съ такими „трансфор-
маторами", аналогичная проводкѣ перемѣннаго тока, представлен-
ной схематически на рис. 283, практически совершенно невозможна.
Было бы чрезвычайно интересно разрѣшить окончательно во-
просъ, возможны ли трансформаторы для постояннаго тока безъ
подвижныхъ машинныхъ частей, которые поэтому были бы
столь же удобны, какъ и трансформаторы для перемѣннаго тока.
Этотъ вопросъ можетъ быть сведенъ къ другому, болѣе глубокому
вопросу: возможно ли получить положительный и отрицательный
магнитные полюсы отдѣльно другъ отъ друга, подобно положи-
тельнымъ и отрицательнымъ электрическимъ зарядамъ, иными сло-
вами, существуютъ ли магнитные іоны, подобно электрическимъ?
Если бы магнитные іоны существовали, то можно было бы полу-
чить магнитный проводникъ, въ которомъ магнитные іоны могли бы
свободно двигаться, какъ электрическіе іоны въ электрическомъ
проводникѣ. Если бы при этомъ замкнутая магнитная цѣпь въ транс-
форматорѣ, изображенномъ на рис. 282, была замѣнена замкнутой
цѣпью изъ магнитнаго проводника, то получился бы настоящій
трансформаторъ постояннаго тока. При прохожденіи постояннаго^
тока черезъ первичную обмотку магнитное поле внутри катушкйу
дѣйствовало бы, какъ настоящая „магнитодвижущая сила" и вызы-
вало бы въ проводящемъ магнитизмъ сердечникѣ постоянныйОгокъ
магнитныхъ іоновъ. Но, какъ мы видѣли въ § 304, движущійся маг-
288
Возможны ли трансформаторы постояннаго тока?
нитный полюсъ всегда сопровождается электрическими силовыми
линіями, кольцеобразно его обвивающими. Поэтому магнитный токъ
долженъ былъ бы быть окруженъ постояннымъ электрическимъ
полемъ, вполнѣ сходнымъ съ магнитнымъ полемъ, окружающимъ
электрическій токъ (рис. 152). При этомъ, если пренебречь омиче-
ской потерей напряженія, напряженіе между зажимами первичной
обмотки было бы равно полной величинѣ электрическаго поля, окру-
жающаго магнитный проводникъ, умноженной на число витковъ
катушки. Такимъ образомъ, сила магнитнаго тока вполнѣ опредѣ-
лялась бы напряженіемъ между зажимами первичной обмотки. На-
пряженіе между зажимами вторичной обмотки относилось бы къ на-
пряженію между зажимами первичной обмотки, какъ соотвѣтственныя
числа витковъ (трансформирующій коэффиціентъ). Если бы мы брали
токъ отъ вторичной катушки, то онъ дѣйствовалъ бы обратно на
первичный токъ такимъ образомъ, чтобы числа амперъ-витковъ
обоихъ токовъ вмѣстѣ всегда давали магнитный токъ въ сердечникѣ
трансформатора, вполнѣ опредѣляемый напряженіемъ между зажи-
мами первичной обмотки. Словомъ, мы получили бы трансформа-
торъ постояннаго тока, функціонирующій совершенно такимъ же
образомъ, какъ обыкновенный трансформаторъ перемѣннаго тока.
Однако, къ сожалѣнію, наше предположеніе о существованіи магнит-
ныхъ іоновъ ложно.
Невозможно построить правильный трансформаторъ
постояннаго тока безъ движущихся машинныхъ частей, такъ
какъ не существуетъ магнитныхъ зарядовъ и магнитныхъ
проводниковъ.
Мы видимъ, такимъ образомъ, что важный для техники вопросъ
о возможности трансформатора постояннаго тока тѣснѣйшимъ обра-
зомъ связанъ съ основными принципами физики эѳира. Дѣйстви-
тельно, то обстоятельство, что не существуетъ магнитныхъ заря-
довъ, зависитъ отъ того, что между эѳиромъ и матеріей существу-
етъ лишь одна дѣйствительная связь, именно, электрическій^ за-
рядъ; этотъ послѣдній вызываетъ какъ электрическое, та^Ѣ^и (при
своемъ движеніи) магнитное состояніе въ эѳирѣ (ср. §^2І-Г).
Съ вопросомъ о возможности трансформатора п^тояннаго тока
тѣсно связанъ также вопросъ о генераторахъ и ^моторахъ постоян-
наго тока безъ скользящихъ контактовъ. Генераторы перемѣннаго
тока возможны безъ скользящихъ контактрв^О таковы, напримѣръ.
Индукціонный аппаратъ
289
машины съ внутренними полюсами (§ 369), которыя можно было бы
строить и съ постоянными магнитами. Ниже мы познакомимся и съ
моторами перемѣннаго тока, не имѣющими скользящихъ контактовъ.
Но машины постояннаго тока безъ скользящихъ контактовъ невоз-
можны (ср. § 236). Причина та же, по которой невозможны транс-
форматоры постояннаго тока.
ИНДУКЦІОННЫЙ АППАРАТЪ.
381. Трансформаторы, служащіе спеціально для возбужденія
высокихъ напряженій, давно' уже употребляются въ физикѣ подъ
названіемъ индукціонныхъ аппаратовъ или индукторовъ. По
сравненію съ индуктивными машинами (электростатическими), которыя,
вообще, даже превосходятъ ихъ по высотѣ напряженія, они имѣютъ
то преимущество, что доставляютъ токи гораздо большей силы,
Рис. 284. Индукціонный аппаратъ для высокихъ напряженій съ
молоткомъ - преры вател емъ.
или, что сводится къ тому же, гораздо большія количества энергіи.
Такъ, напримѣръ, опыты надъ разрядами въ разрѣженныхъ газахъг
прежде, когда еще не умѣли строить аккумуляторныхъ батарей
машинъ постояннаго тока, дающихъ высокое напряженіе, произво-
дились почти исключительно при помощи индукціонныхъ^^уйара-
товъ, такъ какъ энергія, доставляемая индуктивными ^машинами,
слишкомъ незначительна.
Ъіи. Электричество и магнитизмъ, ч. II.
19
290
Индукціонный аппаратъ
Такъ какъ въ индукціонномъ аппаратѣ экономія не играетъ
такой большой роли, какъ въ трансформаторахъ, употребляемыхъ
въ техникѣ, то его строятъ, почти исключительно для боль-
шей простоты, съ незамкнутымъ желѣзнымъ сердечникомъ. Берутъ
прямой цилиндрическій желѣзный стержень, составленный, во избѣжа-
ніе вихревыхъ токовъ, изъ тонкихъ, изолированныхъ одна отъ дру-
гой желѣзныхъ проволокъ, надвигаютъ на него первичную обмотку,
состоящую изъ небольшого числа оборотовъ толстой мѣдной про-
волоки, и на первичную обмотку надвигаютъ вторичную обмотку;
послѣдняя должна выдерживать высокія напряженія и потому она
изготовляется съ особою тщательностью. Вторичная обмотка дѣлается
изъ тонкой мѣдной проволоки и имѣетъ весьма большое число оборо-
товъ, тщательно другъ отъ друга изолированныхъ и разложенныхъ
(какъ на рис. 282) на многочисленныя небольшія изолированныя
секціи. Снаружи она заливается хорошо изолирующей массой и, по
большей части, окружается цилиндрической твердой каучуковой обо-
лочкой, какъ показываетъ рис. 284.
382. Индукціонные аппараты обычно питаются не перемѣннымъ
токомъ, но правильно пульсирующимъ выпрямленнымъ токомъ, кото-
рый можно брать отъ обыкновеннаго источника постояннаго тока.
Необходимо только въ проводъ, идущій отъ источника постояннаго
тока къ первичной катушкѣ, включить періодически дѣйствующій
прерыватель. Для измѣреній перемѣннаго тока весьма часто поль-
зуются, какъ мы уже видѣли въ § 269, небольшимъ индукторомъ
съ періодическимъ прерывателемъ, въ качествѣ преобразователя по-
стояннаго тока въ перемѣнный. Перемѣнное напряженіе между за-
жимами вторичной обмотки изображеннаго тамъ очень маленькаго
индуктора гораздо выше напряженія аккумулятора, служащаго источ-
никомъ постояннаго тока; именно, оно близко къ 100 вольтамъ,
что удобно для измѣреній. Оно не представляетъ собою синусо-
идальнаго колебанія: измѣненіе напряженія въ первую половину
періода, когда первичный токъ возрастаетъ, иное, нежели в^ѣто-
рую половину, въ теченіе которой первичный токъ понижается до
нуля. Однако, по законамъ индукціи положительные^ неотрицатель-
ные удары напряженія въ общей сложности равны между собою, и
этого свойства вполнѣ достаточно для весьма многихъ измѣреній.
Старѣйшимъ и теперь еще наиболѣе употребительнымъ прерыва-
телемъ для индукціонныхъ аппаратовъ являетс^С^блоточекъ Вагнера;
Индукціонный аппаратъ
291
въ § 347 мы уже познакомились съ его дѣйствіемъ въ качествѣ
аппарата для возбужденія пульсирующихъ токовъ. Прерыватель
по большей части приводится въ движеніе желѣзнымъ сердечникомъ
самаго индуктора; это видно на рисункѣ 284, гдѣ представленъ аппа-
ратъ, снабженный молоточкомъ. Если желательно получать между
зажимами вторичной обмотки очень высокія напряженія, то для этой
цѣли пользуются ударомъ напряженія при размыканіи первичнаго
тока. Мы видѣли уже въ § 310, что при размыканіи тока можно
получать гораздо болѣе высокія напряженія, нежели при замыканіи,
и притомъ тѣмъ болѣе высокія, чѣмъ быстрѣе прекращаютъ токъ.
Поэтому слѣдуетъ заботиться о возможно болѣе скоромъ потуханіи
свѣтовой дуги, всегда возникающей въ мѣстѣ размыканія первич-
наго тока. Для этого, по предложенію Физо (Рігеаи, 1853), слу-
житъ конденсаторъ высокой емкости (отъ 0,1 до 1 М. Ф.), непосред-
$ \ \ \ Сила тока
Рис. 285. Кривыя силы тока и напряженія индуктора, питаемаго преры-
вистымъ постояннымъ токомъ.
Напряженіе
ственно присоединяемый параллельно’ мѣсту размыканія. Въ качествѣ
діэлектрика для этого конденсатора берутъ по большей части пропитан-
ные параффиномъ бумажные листы. Вслѣдствіе малой толщины діэлек-
трика такой конденсаторъ занимаетъ мало мѣста и помѣщается въ пло-
скомъ деревянномъ ящикѣ, на которомъ устанавливается индукторъ. На
рис. 284 видны соединенія мѣста размыканія съ обкладками конден-
сатора. Вслѣдствіе большой емкости конденсатора токъ, заряжа-
ющій его до напряженія самоиндукціи, возникающаго въ мѣстѣ
перерыва, довольно силенъ; образуя отвѣтвленіе, параллельной
свѣтовой дугѣ размыканія, онъ отнимаетъ отъ послѣдней боль-
шую долю тока. Но ослабленіе тока оказываетъ вліяніе нац|вѣто-
вую дугу—она гораздо легче тухнетъ; такимъ образомъ, .благодаря
присоединенію конденсатора, свѣтовая дуга размыканія^ становится
гораздо болѣе кратковременной, чѣмъ при отсутствій^конденсатора,
292
Индукціонный аппаратъ
такъ что перерывъ первичнаго тока совершается гораздо быстрѣе.
Кривыя рис. 285 показываютъ, какъ періодически измѣняются, во-
первыхъ, амперъ-витки магнитнаго поля и, во-вторыхъ, напряженіе
между зажимами индуктора. Кривая напряженія весьма не симмет-
рична: при замыканіи она пологая и широкая, а при размыканіи—
крутая и узкая. Какъ мы видѣли выше, включеніе конденсатора дѣ-
лаетъ ударъ напряженія при размыканіи особенно рѣзкимъ. Если
зажимы вторичной обмотки такого индукціоннаго аппарата соеди-
нить съ электродами Гейсслеровой трубки, то обычно лишь напря-
женіе размыканія вызываетъ разрядъ, такъ какъ напряженіе при
замыканіи первичнаго тока далеко не достигаетъ величины разряд-
наго потенціала. Такимъ образомъ, можно съ извѣстнымъ правомъ
различать зажимы вторичной обмотки, какъ положительный и отри-
цательный, такъ какъ разрядный токъ идетъ лишь въ одномъ на-
правленіи. Но напряженіе будетъ, конечно, все время перемѣннымъ.
Первые индукціонные аппараты были построены въ сороко-
выхъ годахъ XIX вѣка. Первый аппаратъ, пригодный для медицин-
Рис. 286. Ртутный
струйный прерыватель
(турбинный прерыва-
тель).
ватель, приводимый въ движеніе особымъ небольшимъ электромото-
скихъ цѣлей, которыя требуютъ лишь полу-
ченія быстро слѣдующихъ другъ за другомъ
ударовъ напряженія довольно незначительной
величины, именно въ нѣсколько сотъ вольтъ,
построилъ Э. Дюбуа-Реймонъ (Е. ПиЬоіз-
Кеуиюпсі) въ 1848 году. Большіе индукторы
для высокихъ напряженій впервые началъ
строить Румкорфъ (КиНшкогіГ) въ Парижѣ
(съ 1850 года).
383. За послѣднее время выяснилась необ-
ходимость въ прерывателѣ, который работалъ
бы быстрѣе молоточнаго, такъ чтобы можно
было брать отъ индуктора большія количества
энергіи въ секунду, напримѣръ, для питанія
Рентгеновыхъ лампъ. Чаще всего съ этой цѣлью
употребляется быстро вращающійся преры-
. . -Мі-
ромъ. Одинъ изъ типовъ вращающагося прерывателѣ —струйный
ртутный прерыватель — представленъ на рис. 2^Д^Вѣ довольно ши-
рокомъ сосудѣ вращается вертикальная ось, накоторую снизу наса-
жена круглая желѣзная пластинка. Радіальный^ каналъ въ этой ила-
Индукціонный аппаратъ
293
стинкѣ соединяется при посредствѣ канала, идущаго внутри оси внизъ,
со ртутью, покрывающею дно сосуда. Вслѣдствіе возникающей центро-
бѣжной силы ртуть всасывается вверхъ и выбрасывается тонкой струей
изъ радіальнаго канала. Эта ртутная струя образуетъ хорошо проводя-
щее соединеніе съ желѣзнымъ цилиндромъ, окружающимъ желѣзную
пластинку. Желѣзный цилиндръ имѣетъ въ нѣсколькихъ мѣстахъ
вырѣзы, и въ каждомъ вырѣзѣ контрактъ прерывается. Ось соеди-
нена съ однимъ зажимомъ, а желѣзный цилиндръ съ другимъ, и
такимъ образомъ они могутъ быть включены въ первичную цѣпь
индуктора. Чтобы избѣжать вредныхъ паровъ ртути и по возмож-
ности уменьшить продолжительность искры размыканія, сосудъ боль-
ше чѣмъ наполовину заполняется алкоголемъ и герметически заку-
поривается. Съ помощью этого аппарата можно легко получить
много сотенъ прерываній въ секунду.
При всѣхъ быстро дѣйствующихъ прерывателяхъ слѣдуетъ
брать болѣе высокое первичное напряженіе, нежели при медленныхъ,
такъ какъ магнитное поле въ индукторѣ при пользованіи скорыми
прерывателями должно гораздо скорѣе достигать максимальнаго
значенія, съ котораго оно внезапно низводится при перерывѣ тока до
нуля. Но нельзя пускать прерыватель медленно, когда къ нему при-
ложено высокое напряженіе, такъ
какъ въ этомъ случаѣ первичный
токъ можетъ слишкомъ сильно воз-
расти и обмотка можетъ перего-
рѣть. Кромѣ того, высокое напря-
женіе слѣдуетъ прилагать, лишь
когда прерыватель уже пущенъ въ
ходъ и дѣлаетъ нормальное число
оборотовъ.
Прерыватель Венельта, при-
надлежащій къ числу быстро дѣй-
ствующихъ, основанъ на совер-
шенно иномъ принципѣ, чѣмъ до
сихъ поръ описанные прерыватели.
Онъ состоитъ изъ большого стек-
ляннаго сосуда съ разведенной сѣр-
ной кислотой, въ которую погру-
жены два электрода, весьма неодинаковые по величицѣсвоей поверх-
Рис. 287. Прерыватель Веѣельта.
..
294
Индукціонный аппаратъ
ности. Одинъ электродъ представляетъ собою большую полосу свинца,
тогда какъ другимъ служитъ тонкое остріе платиновой проволоки,
которое выдается изъ окружающей проводъ стеклянной или фарфо-
ровой трубки. Когда этотъ элементъ включаютъ въ первичную цѣпь
индуктора такъ, чтобы платиновое остріе было анодомъ, то на
остріѣ возникаютъ очень быстро, но равномѣрно (нѣсколько сотъ
разъ въ секунду), пузыри пара; каждымъ изъ нихъ токъ на корот-
кое время прерывается. Эти пузыри пара образуются вслѣдствіе
большой плотности тока на маленькомъ остріѣ, вызывающей очень
сильное нагрѣваніе. Для возникновенія каждаго пузыря требуется
вполнѣ опредѣленный промежутокъ времени, въ теченіе котораго
электрическій токъ и нагрѣваніе острія возрастаютъ до надлежащей
высоты. Величина этого промежутка времени зависитъ отъ прило-
женнаго напряженія, самоиндукціи первичной обмотки, величины
острія и температуры разбавленной сѣрной кислоты. Вслѣдствіе того,
что всегда имѣетъ мѣсто перегрѣваніе, пузырь образуется почти
моментально, и токъ поэтому прерывается очень быстро. Вслѣдствіе
хорошей теплопроводности окружающей среды, температура тотчасъ
же падаетъ, пузырь пара конденсируется, сѣрная кислота вновь
приходитъ въ соприкосновеніе съ платиновымъ остріемъ, токъ
замыкается, и процессъ начинается снова. Пока указанные четыре
фактора остаются постоянными, число перерывовъ также постоянно.
Если же одинъ изъ этихъ факторовъ измѣняется, то измѣняется
тотчасъ же и число перерывовъ, чтб можно замѣтить по измѣненію
громкаго звука, непрерывно испускаемаго прерывателемъ. Плати-
новое остріе должно служить анодомъ, такъ какъ между
металлическимъ анодомъ и воднымъ катодомъ не образуется свѣто-
вой дуги вслѣдствіе того, что для образованія послѣдней катодъ
долженъ быть раскаленъ. Наоборотъ, между платиновымъ катодомъ
и электролитическимъ анодомъ образуется свѣтовая дуга, и пузы-
рекъ пара не вызываетъ тогда перерыва тока. Такъ какъ искра рДз-
мыканія при платиновомъ анодѣ тотчасъ же тухнетъ сама со^оір, то
при прерывателѣ Венельта нѣтъ надобности включа/гь кон-
денсаторъ, какъ при прерывателяхъ описанныхъ выше/С^'
Съ прерывателемъ Венельта весьма сходенъ прерыватель Си-
мона (прерыватель съ малымъ отверстіемъ); онъ срстойтъ изъ сосуда
съ разбавленной сѣрной кислотой, въ которую погружены два большіе
свинцовые пластинчатые электрода, раздѣленныеТтеклянной перегород-
Синхронные моторы
295
кой съ маленькимъ отверстіемъ. Такъ какъ весь токъ долженъ пройти
черезъ это отверстіе, то плотность тока и нагрѣваніе около него уси-
ливаются настолько, что наступаетъ парообразованіе и, вообще, тѣ же
процессы, что и въ прерывателѣ Венельта. Въ качествѣ стеклянной
перегородки лучше всего воспользоваться пробиркой, погруженной
нижнею частью въ сѣрную кислоту, съ маленькимъ отверстіемъ на
днѣ; внутри пробирки помѣщается одинъ электродъ. Въ преры-
вателѣ Симона оба электрода могутъ быть замѣнены одинъ другимъ.
СИНХРОННЫЕ МОТОРЫ.
384. Подобно машинамъ постояннаго тока, машины перемѣн-
наго тока, служащія генераторами, могутъ быть употребляемы также
въ качествѣ моторовъ. Такой моторъ перемѣннаго тока предста-
вляетъ, однако, то неудобство, что, помимо перемѣннаго тока для
кольца, доставляющаго энергію, преобразуемую въ работу, онъ тре-
буетъ еще особаго тока постояннаго напряженія для намагничива-
ющихъ катушекъ; послѣднія поглощаютъ, впрочемъ, очень мало энер-
гіи. Безъ спеціальнаго источника постояннаго тока моторъ не мо-
жетъ дѣйствовать.
Но этого еще недостаточно. Пока подвижная часть мотора на-
ходится въ покоѣ, на нее въ каждый періодъ перемѣннаго тока дѣй-
ствуютъ двѣ равныя и прямо противоположныя силы, которыя по-
этому взаимно уничтожаются. Вслѣдствіе этого, моторъ перемѣн-
наго тока, въ противоположность моторамъ постояннаго тока, не на-
чинаетъ вращаться самостоятельно, но долженъ быть приведенъ въ
движеніе ^внѣшней движущей силой. Въ этомъ отношеніи онъ сходенъ
со многими двигателями, а именно съ газомоторами, бензиновыми мо-
торами, моторами Дизеля: всѣ они должны быть пускаемы въ ходъ
внѣшней силой. Но моторъ перемѣннаго тока отличается отъ назван-
ныхъ машинъ, которыя продолжаютъ идти сами, послѣ того какъ /
ихъ надлежащимъ образомъ приводятъ въ движеніе, тѣмъ, что онъ
идетъ самъ только тогда, когда доведенъ до вполнѣ опредѣленнаго^^7
свойственнаго ему числа оборотовъ, именно такого, которое
долженъ былъ бы имѣть, чтобы возбуждать въ качествѣ генератора
перемѣнное напряженіе того же числа періодовъ, какое имѣетъ пита-
ющій его перемѣнный токъ. Вообще, при иномъ чи<^|^ Оборотовъ
моторъ перемѣннаго тока не можетъ идти самостоятельно. Дѣйстви-
296
Синхронные моторы
тельно, необходимо, чтобы обращеніе тока въ проволокахъ якоря совер-
шалось все время въ тактъ съ обращеніемъ поля, пересѣкающаго прово-
локи якоря и образуемаго вращающимися относительно нихъ магнит-
ными полюсами: только при этомъ условіи магнитное притяженіе, дѣй-
ствующее на подвижную часть машины, можетъ все время быть напра-
влено въ одну сторону. Если же темпъ обращеній тока отличается отъ
темпа обращеній магнитнаго поля, то магнитная сила дѣйствуетъ то въ
направленіи движенія, то въ противоположномъ направленіи, такъ что
въ среднемъ она равняется нулю, какъ и въ случаѣ, когда моторъ
находится въ состояніи покоя. Величина энергіи, превращаемой въ
работу въ синхронно идущемъ моторѣ перемѣннаго тока, зависитъ
отъ величины постоянной разности фазъ между перемѣннымъ
токомъ въ якорѣ и магнитнымъ полемъ, образуемымъ вращающимися
относительно якоря полюсами. Количество преобразуемой энергіи
наиболѣе велико, когда перемѣнное напряженіе, индуктируемое пе-
ремѣннымъ магнитнымъ полемъ въ проволокахъ якоря, совпадаетъ
по фазѣ съ якорнымъ токомъ; если мы обозначимъ все напряженіе,
индуктируемое въ обмоткѣ якоря, чрезъ V и якорный токъ — чрезъ
У, то въ этомъ случаѣ преобразуемая энергія будетъ равна 17 = 7е^. Ѵе$
ваттъ. Если вращающаяся часть идетъ нѣсколько впереди, такъ что
токъ отстаетъ отъ напряженія на постоянную разность фазъ ф, то
превращаемая энергія равняется 17 = Л//'. Ѵе^. соз ф ваттъ. Съ умень-
шеніемъ соз ф соотвѣтственно уменьшается и движущая сила мотора.
Какъ только мы уменьшимъ нагрузку мотора, подвижная часть смѣ-
стится нѣсколько впередъ и установится подъ большей разностью
фазъ ф, при которой дѣйствующая на эту часть магнитная сила
вновь будетъ равна нагрузкѣ. Если пустить моторъ ненагружен-
нымъ, то уголъ ф будетъ близокъ къ 90°, и преобразуемая энергія
. Л/т • соз ф будетъ почти равна нулю. Такъ какъ при этомъ
фаза магнитнаго поля полюсовъ также смѣщена на 90° относительно
якорнаго тока, то магнитная движущая сила въ теченіе одной^чет-
верти періода дѣйствуетъ постоянно въ направленіи движещй?°а въ
слѣдующую четверть періода — въ противоположномъ направленіи,
т.-е. въ среднемъ она, дѣйствительно, равна нулю. Еслибы уголъ ф
возрасталъ далѣе, то машина шла бы, какъ генераторъ, потребляя
работу и давая электрическую энергію. При увеличеніи нагрузки
она нѣсколько оттягиваетъ назадъ вращающуюсячасть мотора, и ф
уменьшается, пока снова не установится^ равновѣсіе. При этомъ слѣ-
Синхронные моторы
297
дуетъ имѣть въ виду, что существуетъ опредѣленный конечный
максимумъ преобразуемой энергіи; именно, Ѵтах = Ѵе#при
ср — 0. Если нагрузка превышаетъ среднюю магнитную движущую
силу, дѣйствующую при ф — 0, то моторъ перестаетъ быть синхрон-
нымъ и тотчасъ же останавливается.
Если заставить обыкновенный генераторъ перемѣннаго
тока идти въ качествѣ мотора, то онъ идетъ, какъ син-
хронный моторъ, т.-е. число его оборотовъ при всякой на-
грузкѣ автоматически регулируется такъ, что оно равняется
какъ разъ тому числу оборотовъ, съ которымъ должна
была бы идти машина въ качествѣ генератора, чтобы воз-
буждать перемѣнное напряженіе съ такимъ же числомъ пе-
ріодовъ, какъ и подводимый къ ней перемѣнный токъ.
Синхронный моторъ допускаетъ лишь опредѣленную
максимальную нагрузку; какъ только нагрузка превышаетъ
этотъ предѣлъ, моторъ тотчасъ останавливается.
По принципу синхроннаго мотора можно неподвижно соединить
черезъ большое разстояніе двѣ машины, генераторъ и моторъ, та-
кимъ образомъ, что одна будетъ всегда вращаться такъ же, какъ и
другая. Это свойство, конечно, можетъ имѣть громадное значеніе
для извѣстныхъ спеціальныхъ случаевъ, но для обычнаго употре-
бленія синхронные моторы не пригодны. Недостатки ихъ заклю-
чаются въ слѣдующемъ. Во-первыхъ, они требуютъ особаго источ-
ника постояннаго тока для магнитовъ; во-вторыхъ, они сами собою
не начинаютъ идти, но необходимо посредствомъ внѣшней силы
доводить ихъ до нормальнаго, довольно высокаго числа оборотовъ;
въ-третьихъ, при случайной перегрузкѣ они тотчасъ же остана-
вливаются. Техника перемѣннаго тока требуетъ такихъ машинъ, кото-
рыя были бы свободны отъ этихъ недостатковъ; необходимо, прежде
всего, чтобы машина начинала идти сама и съ возможно большей
двигательной силой. Такія машины должны быть, слѣдовательно, асин-
хронными моторами. Устройство этихъ асинхронныхъ моторовъ^
конечно, должно быть совершенно отлично отъ устройства генерато-
ровъ. Въ этомъ заключается отличіе передачи работы при р^лощи
перемѣннаго тока отъ передачи, которая пользуется токомфпосто-
яннымъ: генераторы и моторы постояннаго тока строятся одинаково.
А
298
Асинхронные моторы перемѣннаго тока
АСИНХРОННЫЕ МОТОРЫ ПЕРЕМЪННАГО ТОКА.
Перемѣнный.
токъ
Рис. 288. Опытъ съ отталкива-
ніемъ по Э. Томсону.
385. Моторъ постояннаго тока можно питать также пере-
мѣннымъ токомъ. Такъ какъ при перемѣнѣ направленія тока обра-
щаются намагниченіе якоря и полюсы магнитнаго индуктора, то
направленіе двигательной силы, дѣйствующей на якорь, остается
одинаковымъ въ теченіе обоихъ полуперіодовъ перемѣннаго тока, а
именно такимъ же, какъ и при пользованіи постояннымъ токомъ. Для
того, чтобы моторъ могъ быть питаемъ перемѣннымъ токомъ, же-
лѣзные сердечники электромагнитовъ должны быть сдѣ-
ланы изъ полосового желѣза, во из-
бѣжаніе вихревыхъ токовъ. Нѣкоторыя
затрудненія причиняетъ самоиндукція маг-
нитныхъ катушекъ и якорной обмотки.
Поэтому для перемѣннаго тока строятъ,
лишь моторы съ послѣдовательнымъ
возбужденіемъ, въ которыхъ невоз-
можны смѣщенія фазъ между магнитнымъ,
полемъ и якорнымъ токомъ, какъ въ мо-
торахъ съ параллельнымъ возбужденіемъ.
При питаніи мотора перемѣннымъ токомъ
самоиндукція якорной обмотки весьма
легко вызываетъ образованіе искръ на
коллекторѣ; необходимо прилагать осо-
быя старанія, чтобы этихъ искръ не было.
386. Особый моторъ перемѣннаго
тока, питаемый не постояннымъ токомъ и
все же идущій асинхронно, представляетъ
собою изобрѣтенный Э. Томсономъ (ЕІіЬи ТНотзоп) репульсіон-
ный моторъ. Дѣйствіе его основано на своеобразномъ отталкиваніи,
которое электромагнитъ перемѣннаго тока оказываетъ на замкнутыя
металлическія кольца. Если металлическое кольцо для салфеткщндйви-
нуть на вертикальную катушку съ желѣзнымъ сердечникомъ (рис'. 288)
и положить на деревянное кольцо, находящееся на катушкѣ нѣ-
сколько выше ея середины, то оно испытываетъ при<прохожденіи
перемѣннаго тока чрезъ катушку весьма сильное Дѣйствіе, которое
стремится вытолкнуть его вверхъ за предѣлы ^для. Если кольцо
не слишкомъ тяжело, то оно поднимается иСцстается висѣть въ
Асинхронные моторы перемѣннаго тока
299^
воздухѣ подъ дѣйствіемъ силы перемѣннаго поля. Если внезапно
замкнуть цѣпь перемѣннаго тока, то кольцо высоко подскакиваетъ.
Это дѣйствіе вызывается индуктируемыми въ кольцѣ токами, кото*
рые противодѣйствуютъ намагничивающимъ токамъ въ катушкѣ, какъ
мы видѣли въ § 370, и стремятся уничтожить магнитное поле. Кольцо
для салфетки представляетъ собою соленоидъ, магнитная ось кото-
раго—по крайней мѣрѣ, въ теченіе большей части періода перемѣн-
наго тока—направлена противоположно оси магнита перемѣннаго тока,
и вслѣдствіе этого оно выталкивается изъ поля (ср. § 285). Если
держать надъ магнитомъ перемѣннаго тока металлическое кольцо,
которое можетъ вращаться вокругъ горизонтальной оси, то оно по-
варачивается такимъ образомъ, что плоскость его становится па-
раллельной магнитнымъ силовымъ линіямъ. Вращающій моментъ, дѣй-
ствующій на кольцо, имѣетъ максимумъ, когда плоскость кольца на-
клонена на 45° къ направленію поля. Этотъ вращающій моментъ
примѣняется въ репульсіонномъ моторѣ для производства работы..
Съ внѣшней стороны репульсіонный моторъ почти вполнѣ схо-
денъ съ моторомъ постояннаго тока съ барабаннымъ якоремъ, маг-
нитный остовъ котораго сдѣланъ изъ полосового желѣза. Но въ ре-
пульсіонномъ моторѣ магнитныя катушки и якорная цѣпь совершенно
отдѣлены другъ отъ друга. Въ намагничивающія катушки пускаютъ
перемѣнный токъ. Наоборотъ, скользящія по коммутатору щетки
коротко соединяются между собою и устанавливаются такъ, чтобы
магнитная ось арматуры, при прохожденіи тока по ея обмоткѣ, со-
ставляла уголъ въ 45° съ полемъ магнитныхъ индукторовъ. Поэтому
арматура получаетъ въ перемѣнномъ полѣ подъ вліяніемъ индукти-
руемыхъ въ ней токовъ сильный вращающій моментъ. При вращеніи
якоря уголъ, составляемый замкнутой на себя арматурной обмоткой
съ магнитнымъ полемъ, остается неизмѣннымъ, что достигается съ-
помощью коммутатора; такимъ образомъ, якорь вращается подъ дѣй-
ствіемъ постоянной силы. Описанный моторъ асинхрониченъ и идетъ,
съ большой движущей силой.
ВРАЩАЮЩІЯСЯ ПОЛЯ.
387. Въ общемъ ученіи о волнахъ такое колебаніе, которое
имѣетъ, подобно обыкновенному перемѣнному полю, одцохаракте-
ристическое направленіе — именно, направленіе вектора поля, — назы-
ваютъ прямолинейно поляризованнымъ. При сложеніи нѣсколь-
зоо
Вращающіяся поля
кихъ колебаній одинаковаго числа періодовъ получается результи-
рующее колебаніе того же числа періодовъ; если при этомъ всѣ
•слагающіяся колебанія поляризованы параллельно между собой, то
результирующее колебаніе также будетъ прямолинейно поляризован-
нымъ и имѣетъ то же самое направленіе поляризаціи. До сихъ поръ мы
разсматривали исключительно такой случай, при чемъ сложеніе коле-
баній мы выполняли при помощи часовой діаграммы (§ 367).
Мы перейдемъ теперь къ разсмотрѣнію болѣе общаго случая,
когда взаимно налагающіяся перемѣнныя поля поляризованы различ-
нымъ образомъ. Предположимъ сначала, что векторы полей соста-
вляютъ уголъ, равный 90°. Этотъ случай можно легко реализовать
съ помощью двухъ катушекъ, расположенныхъ подъ прямымъ угломъ
одна къ другой. Результирующее поле можно изслѣдовать съ по-
мощью трубки Брауна, проходящей черезъ пространство въ углу,
Перемѣнный токъ съ включенной
Перемѣнный токъ съ включеннымъ
гопротивленіемъ
Рис. 289. Трубка Брауна во вращающемся полѣ.
образуемомъ катушками (рис. 289). Отклоненіе свѣтового пятна отъ
нулевого положенія представляетъ собою векторъ, который въ точ-
ности перпендикуляренъ къ магнитному полю и по величинѣ про-
порціоналенъ силѣ поля. Фигура, описываемая свѣтовымъ пятномъ
при прохожденіи пучка катодныхъ лучей трубки Брауна черезъ
перемѣнное магнитное поле, ясно указываетъ, какъ поляризовано
перемѣнное поле. Если пропустить черезъ одну изъ двухъ ^ату-
шекъ перемѣнный токъ, то на экранѣ покажется прямая линія,обпи-
сываемая быстро колеблющимся въ обѣ стороны свѣтовымъ пятномъ;
поле, слѣдовательно, прямолинейно поляризовано, и длина неболь-
шого свѣтящагося отрѣзка на экранѣ пропорціональна амплитудѣ
перемѣннаго поля. Если пропустимъ перемѣнный ^гокъ лишь черезъ
другую катушку, то на экранѣ опять появляется прямая линія, но
перпендикулярная къ первой; въ этомъ случаѣ поле тоже поляри-
Вращающіяся поля
301
зовано прямолинейно, но перпендикулярно къ полю первой катушки..
Теперь пропустимъ токъ одновременно черезъ обѣ катушки и
устранимъ самоиндукцію въ вѣтвяхъ для того, чтобы оба тока совпа-
дали по фазѣ; на экранѣ появляется прямая линія, расположенная
наклонно къ двумъ первымъ. Наши два поля слагаются въ пере-
мѣнное поле, наклонное къ нимъ и прямолинейно поляризованное..
Если слагающіяся поля Нг и Н2 всегда находятся въ одинаковой фазѣ,
т.-е. если = а .$іп2тіпіг Л/2 — . зіп 2п/г^, то уголъ а, образуе-
мый результирующимъ полемъ Н съ полемъ , будетъ постояннымъ,
такъ какъ /^а = : Н2 — а: Ь есть величина постоянная. Поэтому
результирующее поле имѣетъ постоянное направленіе, т.-е. прямоли-
нейно поляризовано. Если амплитуды обоихъ перемѣнныхъ полей
равны между собою, т.-е. а = Ь, то а = 45°. Но если существуетъ
разность фазъ между Н± и Н2, то отношеніе НГ\Н2 перестаетъ быть
Рис. 290. Поляризація колебаній, образующихся при наложеніи двухъ
взаимно перпендикулярно поляризованныхъ перемѣнныхъ полей одинаковой
амплитуды.
постояннымъ, а измѣняется втеченіе періода, и результирующее поле уже
не будетъ прямолинейно поляризованнымъ. Если мы вызовемъ разность
фазъ между магнитными полями, включивъ въ проводъ одной изъ
катушекъ самоиндукцію, то на экранѣ трубки Брауна, вмѣсто пря-
мой линіи, получается въ общемъ случаѣ эллипсъ. Если амплитуды
обоихъ полей будутъ оставаться равными, а разность фазъ повысимъ
до 90° (для этого въ цѣпь одной катушки нужно ввести лишь ин-
дуктивныя сопротивленія, а въ цѣпь другой — безъ-индукціонныя на-
стоящія сопротивленія), то кривая на экранѣ будетъ окружностью. Дѣй-
ствительно, по закону сложенія векторовъ векторъ = а . соз 2п/г7,
съ перпендикулярнымъ къ нему векторомъ Н2 = а . зіп 2тг/г/ даютъл*
въ суммѣ векторъ, величина котораго во всякой фазѣ будетъ
Н—а, и который составляетъ съ уголъ 2ъпі. Результирующее
магнитное поле остается постояннымъ по величинѣ, и лиі^ьу^б на-
правленіе измѣняется періодически, при чемъ числр^оборотовъ
равняется п. Подобное магнитное поле называется вращающимся
302 Генераторы съ вращающимся полемъ и проводка къ нимъ
п|олемъ или же кругово поляризованнымъ колебаніемъ. Проме-
жуточное положеніе между колебаніями, поляризованными прямо-
линейно и поляризованными по окружности, занимаютъ колебанія,
поляризованныя по эллипсу. Послѣднія наблюдаются при выше-
описанномъ опытѣ, когда амплитуды не равны между собою, или
когда разность фазъ не равняется въ точности 90° (рис. 290).
При наложеніи двухъ перемѣнныхъ полей, поляризо-
ванныхъ по взаимно перпендикулярнымъ направленіямъ и
имѣющихъ одинаковыя амплитуды и разность фазъ, рав-
ную тг/2, возникаетъ вращающееся поле, т.-е. колебаніе,
поляризованное по окружности. При иныхъ разностяхъ фазъ
и неодинаковыхъ амплитудахъ возникаетъ, вообще, коле-
баніе, поляризованное по эллипсу.
Перемѣнныя поля, наклоненныя другъ къ другу подъ острымъ
угломъ, въ общемъ случаѣ также даютъ въ суммѣ эллиптически по-
ляризованныя колебанія, а въ частныхъ случаяхъ — вращающіяся поля.
ГЕНЕРАТОРЫ СЪ ВРАЩАЮЩИМСЯ ПОЛЕМЪ И ПРОВОДКА
КЪ НИМЪ.
388. Всякую машину перемѣннаго тока можно построить такъ,
ятобы она давала нѣсколько перемѣнныхъ токовъ съ различными фа-
Рис. 291. Схема кольцевого якоря
для двуфазнаго тока.
Рис. 292. Схема кольцевргр^коря
для трехфазнаго тока (теірсоеди-
неніе треугольникомъ).
зами. Напримѣръ, если обмотку кольцевого якоря двуполюсной машины
снабдить (рис. 291) четырьмя отводящими проволоками на разстояніи
90° одна отъ другой, идущими къ четыремъ скользящимъ кольцамъ,
ЛЧ
Генераторы съ вращающимся полемъ и проводка къ нимъ 303
то между первой и третьей щетками получится обыкновенное пере-
мѣнное напряженіе, какъ и между второй и четвертой, но напряженія
обѣихъ паръ щетокъ будутъ взаимно смѣщены на четверть періода
колебанія (разность фазъ тт/2). Такой генераторъ, доставляющій два
перемѣнныя напряженія съ разностью фазъ п/2, называютъ двуфаз-
нымъ генераторомъ. Если будемъ брать отъ него при помощи раз-
дѣльныхъ проводовъ два перемѣнные тока, то съ помощью по-
слѣднихъ можно прямо получить вращающееся поле. Двуфазный пе-
ремѣнный токъ называютъ поэтому также вращающимъ токомъ
или, точнѣе, двуфазнымъ вращающимъ токомъ; отдѣльные два
перемѣнные тока, составляющіе вмѣстѣ двуфазный токъ, называются
двумя фазами вращающаго тока.
. Рис. 293. Вращающееся поле въ трехфазномъ кольцевомъ
магнитѣ.
На практикѣ болѣе важное значеніе имѣетъ трехфазный вра-
щающій токъ. Если обмотку кольцевого якоря снабдить тремя от-
водящими проволоками, отстоящими одна отъ другой на 120° и иду-
щими къ тремъ скользящимъ кольцамъ (рис. 292), то на каждой
щеткѣ получится перемѣнное напряженіе относительно земли, при
чемъ три перемѣнныя напряженія будутъ имѣть разности фазъ, равныя
2 п . °
каждая 120° = Если три зажима трехфазнаго генератора соеди^ ѵ
нить посредствомъ проволокъ съ тремя точками обмотки ^непо-
движнаго желѣзнаго кольца, отстоящими одна отъ другой 'Лна^120°
(рис. 293), то внутри этого кольца возникаетъ вращающееся поле,
изображеніе магнитнаго поля, вращающагося въ ^г^іёраторѣ от-
304 Генераторы съ вращающимся полемъ и проводка къ нимъ
носительно якоря. Если въ серединѣ кольца помѣстить магнитную-
стрѣлку, то вращающееся поле увлекаетъ ее за собою, и она вра-
щается съ большой скоростью въ ту же сторону, какъ и поле.
Описанная трехфазная система характеризуется тѣмъ, что три:
катушки, къ которымъ присоединены три провода, образуютъ зам-
кнутую фигуру. Такое соединеніе можно изобразить схематически*
какъ на рис. 294; его называютъ „соединеніе треугольникомъ".
Рис. 295. Схема соединенія
звѣздой.
Рис. 294. Схема соединенія
треугольникомъ.
Но можно также всѣ три катушки соединить съ одной стороны св-
одной точкой, а три свободныхъ конца ихъ соединить съ тремя
проводами, какъ схематически намѣчено на рис. 295. Такое соеди-
неніе, представленное схематически также на рис. 296, называется
„соединеніемъ звѣздой". Послѣднее оказалось для генераторовъ,
болѣе пригоднымъ, нежели соединеніе треугольникомъ, и въ послѣднее
время почти исключительно оно одно и употребляется. Во многихъ,
случаяхъ полезно присоединить еще къ средней точкѣ звѣзды выравни-
вающій проводъ, соединенный
Рис. 296. Схема кольцевого якоря
для мотора трехфазнаго тока (т. н.
соединеніе звѣздой).
проводникомъ съ землею (рис. 297).
Онъ играетъ точно такую же роль,
какъ выравнивающій проводъ въ
трехпроводной системѣ постояннаго
тока (§ 365). Какъ тамъ имѣются
двѣ независимыя половины, кото-
рыя должны быть нагружены по
возможности равномѣрно, такъ и
въ трехфазной системѣ ^^вырав-
нивающимъ проводомъ^имѣютоі
три независимые участка перемѣн-
наго тока; въ кда^йй въ отдѣль-
ности можно ^Цлючить лампы, нэ
они должндъбыть нагружены по
Генераторы съ вращающимся полемъ и проводка къ нимъ 305
возможности равномѣрно, чтобы выравнивающій проводъ несъ лишь
незначительный токъ. Кромѣ того, можно конечно, присоединить къ
проводкѣ моторы какъ треугольникомъ, такъ и звѣздой. Эффектив-
Рис. 297. Трехфазная система съ выравнивающимъ проводомъ.
ное напряженіе между двумя внѣшними проводами въ 1,73 раза
больше напряженія между внѣшнимъ и выравнивающимъ проводами;
такимъ образомъ, потребитель получаетъ напряженіе болѣе низкое
Вращающій токъ
Рис. 298. Генераторъ трехфазнаго тока (машина съ внѣшними полюсами).
по сравненію съ тѣмъ, которое служитъ для переноса энергіи, какъ
и при трехпроводной системѣ постояннаго тока. ДС?"
Генераторы вращающаго тока представляютъ с^^&^гене-
раторы перемѣннаго тока, и относительно нихъ ничегоДсуществен-
наго нельзя прибавить къ тому, что было сказано въ Только
Намагничива-
ющій токъ
Ми. Электричество и магнитизмъ, ч. II.
20
306
Моторы вращающаго тока
включеніе якорныхъ проволокъ должно быть произведено такимъ
образомъ, чтобы получить три различныя фазы. На рис. 298 пред-
ставленъ трехфазный генераторъ съ вращающимся якоремъ (слѣдо-
вательно, машина съ внѣшними полюсами). Наружно онъ отличается
отъ обыкновенной машины перемѣннаго тока лишь тѣмъ, что имѣетъ
три скользящія кольца, три щетки и три главные зажима.
Точно также и трансформаторы вращающаго тока ни-
чѣмъ существенно не отличаются отъ трансформаторовъ перемѣннаго
тока, описанныхъ въ § 378. Только вмѣсто двухъ магнитныхъ поста-
вовъ, видимыхъ на рис. 282, они должны имѣть три — по одному для
каждой фазы. Катушки могутъ быть соединены между собою какъ
треугольникомъ, такъ и звѣздой.
МОТОРЫ ВРАЩАЮЩАГО ТОКА.
389. Многофазный перемѣнный токъ цѣнится въ техникѣ осо-
бенно потому, что магнитными вращающимися полями можно при-
водить въ дѣйствіе простѣйшіе асинхронные моторы и, вообще, про-
стѣйшіе изъ существующихъ электромоторовъ. Если изъ представлен-
наго на рис. 293 кольцевого магнита съ вращающимся полемъ уда-
лить столикъ съ магнитной стрѣлкой и вмѣсто него ввести во вра-
щающееся поле замкнутый проволочный прямоугольникъ, подвѣшен-
ный отвѣсно на нити, или, еще лучше, барабанообразную клѣтку,
составленную изъ нѣсколькихъ проволочныхъ прямоугольниковъ, то
этотъ проводникъ начинаетъ быстро вращаться подобно магнитной
стрѣлкѣ. Этотъ опытъ представляетъ собою не что иное, какъ обра-
щеніе опыта Арато, описаннаго въ § 301. Въ коротко замкнутой
клѣткѣ индуктируются электрическіе токи, стремящіеся задержать
вращающееся поле. Магнитное поле этихъ индуктированныхъ токовъ
во всякій моментъ перпендикулярно къ направленію вращающагося
поля; вслѣдствіе этого результирующее поле все время отстаетъ отъ
начальнаго вращающагося поля на постоянный уголъ. Такимъ^бра-
зомъ, клѣтка представляетъ собою до нѣкоторой степени магнитъ,
все время перпендикулярный къ вращающемуся полю и увдрекаемый
имъ съ постоянной силой во вращеніе въ одну съ цийъ сторону.
На рис. 299 представленъ моторъ вращающаго ^хкаГсъ коротко
замкнутымъ якоремъ въ видѣ бѣличьяго колеса.Якорь, называемый
роторомъ, имѣетъ барабаннообразный желѣзнЬ^ сердечникъ, вхо-
дящій въ неподвижное магнитное кольцо ^Стращающимся полемъ
Моторы вращающаго тока.
307
—стойку, или статоръ, такъ что между ними остается лишь
весьма узкое пространство; такимъ образомъ небольшимъ числомъ
амперъ-витковъ вызывается сильное поле. Для большей ясности обѣ
части мотора представлены на рисункѣ отдѣльно. Къ обмоткѣ ста-
тора ведутъ три провода для вращающаго тока; мѣдные стержни
въ пазахъ ротора припаяны своими концами къ двумъ замкнутымъ
мѣднымъ кольцамъ и, такимъ образомъ, являются коротко замкнутыми.
Конечно, всѣ желѣзныя части какъ въ статорѣ, такъ и въ роторѣ,
должны быть пластинчатыми.
Моторъ вращающаго тока съ коротко замкнутымъ якоремъ
можно разсматривать, какъ особаго рода трансформаторъ. Обмотка
Рис. 299. Моторъ вращающаго тока съ коротко замкнутымъ якоремъ,
представленнымъ отдѣльно. (Подшипники на рисункѣ не изображены).
статора представляетъ собою его первичную обмотку, обмотка
ротора—вторичную. Амперъ-витки вращающагося магнитнаго поля
слагаются изъ амперъ-витковъ статора и ротора. Но, если можно
пренебречь потерями напряженія вслѣдствіе омическаго сопротивле-
нія въ моторѣ, амплитуда поля, какъ въ трансформаторѣ, одно-
значно опредѣляется напряженіемъ между подводящими зажимами,
которое при сдѣланнномъ предположеніи одно должно преодолѣ-
вать сопротивленіе инерціи магнитнаго поля его непрерывному и^^
мѣненію. Величина Н для вращающагося поля, опредѣляемая наря-
женіемъ между зажимами, представлена на часовой діаграмму (рис/300)
стрѣлкой О А. Если стрѣлка О А будетъ вращаться со ско^рью вра-
щающагося поля, то она сама (а не ея проекція на осц^какъ въ случаѣ
20
308
Моторы вращающаго тока
прямолинейно поляризованнаго перемѣннаго поля) будетъ представлять
вращающееся поле. По законамъ индукціи токи /д, индуктированные
въ коротко замкнутомъ якорѣ, должны идти такимъ образомъ, что-
бы ихъ поле Н2 было перпендикулярно къ полю /7, представлен-
ному на рис. 300 векторомъ ОВ. Якорные токи дѣйствуютъ, по-
добно вторичному току въ трансформаторѣ, на силу тока въ обмоткѣ
статора такимъ образомъ, что поле Н1У которое вызывали бы сами
по себѣ амперъ-витки статора, вмѣстѣ съ Н2 даетъ по правилу
сложенія векторовъ имѣющееся въ дѣйствительности вращающееся
поле /7, опредѣляемое напряженіемъ между зажимами. На рис. 300
поле Нг представлено векторомъ ОС.
Легко показать, что количество преобразующейся въ моторѣ
энергіи пропорціонально полю Н2. Поле Нх можно разложить на
двѣ взаимно перпендикулярныя слагающія, изъ которыхъ одна то-
ждественна съ Ні а другая равна и противоположна полю Н2. Соот-
Рис. 300. Часовая діаграмма мотора вращающаго тока съ коротко
замкнутымъ якоремъ.
вѣтственно этому можно каждый изъ трехъ перемѣнныхъ токовъ
въ обмоткѣ статора разложить на двѣ слагающія съ разностью
фазъ у; одна изъ нихъ / вызываетъ поле Н1, другая поле—Н2.
Если бы въ якорѣ не было вовсе тока, т.-е. если бы /72=0, то
слагающей 7" не существовало бы. Въ этомъ случаѣ вращающая
сила, дѣйствующая на якорь, равнялась бы нулю, и моторъ не отда-
валъ бы вовсе энергіи въ формѣ работы, а, слѣдовательно, и не
поглощалъ бы электрической энергіи. Поэтому разность фазъ ^е$ду
токомъ У въ каждомъ изъ трехъ проводовъ и напряжені^мъМіро-
вода относительно земли равна у, такъ что переносимая энергія
является то положительной, то отрицательной, а длявсѣхъ трехъ
проводовъ вмѣстѣ всегда равна нулю. Такъ какъ^окъ 7" въ каж-
домъ проводѣ смѣщенъ по фазѣ на 90° относительно 7', то 7"
совпадаетъ по фазѣ съ напряженіемъ, и^Жнергія, вступающая въ
Моторы вращающаго тока
309
моторъ, равняется утроенному произведенію изъ эффективной вели-
чины силы тока въ проводѣ У" на эффективную величину напря-
женія этого провода относительно земли. Но значеніе У пропор-
ціонально полю Н2, и напряженіе между зажимами постоянно; слѣ-
довательно, величина преобразуемой энергіи пропорціональна вели-
чинѣ ТУ2.
Съ другой стороны сила тока въ коротко замкнутой обмоткѣ
ротора, число амперъ - витковъ которой мы обозначили черезъ /72,
равняется частному отъ дѣленія электродвижущей силы на сопро-
тивленіе. Индуктированная электродвижущая сила въ каждомъ отдѣль-
номъ стержнѣ якорной обмотки состоитъ изъ двухъ слагающихъ—
напряженія во вращающемся магнитномъ полѣ, обусловливающаго
непрерывное измѣненіе поля, и электродвижущей силы магнитнаго
поля, силовыя линіи котораго пересѣкаются стержнемъ вслѣдствіе
вращенія якоря. Эти двѣ электродвижущія силы направлены въ про-
тивоположныя стороны; мы обозначимъ ихъ соотвѣтственно черезъ
Ѵо и — Ѵ1. По закону относительности индукціонныхъ дѣйствій
результирующая электродвижущая сила (V = Ѵо— Ѵх) имѣетъ такую
величину, какъ если бы роторъ оставался неподвижнымъ и поле
вращалось съ относительной скоростью и0—и19 гдѣ и0—скорость
вращенія поля, их —скорость вращенія якоря, и и0 = 2пп(п—число
періодовъ перемѣннаго тока). Мы имѣемъ, слѣдовательно,
Ѵ=І/0*
Мр-Кі
«о
При этомъ электродвижущая сила Ѵо опредѣляется напряженіемъ
между зажимами, а величина V, а, слѣдовательно, и якорный токъ,
і_г • н0— щ
т.-е. /72, пропорціональны частному —--•
п0
Частное отъ дѣленія скорости и0—вращенія поля
относительно ротора на абсолютную скорость вращенія
. —щ
поля т.-е. отношеніе —------называется скольженіемъ мо-
0 «о
тора вращающаго тока. Л
Скольженіе обычно выражаютъ въ процентахъ. Если, налри-
и___и
мѣръ, —--- = 0,02, то говорятъ, что скольженіе составляете 2%.
"° ; я
Изъ вышеприведенныхъ соображеній слѣдуетъ, чт^оэлектри-
ческая энергія, преобразуемая въ моторѣ, при постоянномъ
«о
310
Моторъ вращающаго тока
напряженіи между зажимами пропорціональна скольженію.
Напримѣръ, если скольженіе равняется нулю, то и0 = иг, поле нахо-
дится въ покоѣ относительно ротора, никакихъ токовъ, слѣдователь"
но, вовсе не индуктируется, и преобразуемая энергія равняется нулю.
Величина скольженія вліяетъ также и на потерю энергіи въ
моторѣ. Если сила тока въ якорной проволокѣ равна величина
напряженія вдоль нея равняется І/о и электродвижущая сила пере-
сѣкаемаго ею магнитнаго поля есть Ѵ\,то, по теоремѣ Пойнтинга,
вся доставляемая ей энергія равняется І/о. /д ваттъ. Согласно ска-
занному въ § 294, изъ этого количества лишь часть пере-
дается далѣе въ видѣ работы, величина же (Ѵо— предста-
вляетъ собою теплоту тока. Отношеніе потери энергіи ко всей энергіи
равняется, слѣдовательно, (Ѵо— V!): 1^0 = (и0 — и^) : иОі т.-е. сколь-
женію. Величина скольженія непосредственно даетъ въ про-
центахъ ту часть доставляемой энергіи, которая теряется
въ роторѣ въ видѣ теплоты тока. Подобную же величину имѣетъ
и потеря энергіи въ статорѣ. Если желательно хорошо использо-
вать моторъ, то полезный токъ 7" долженъ быть, какъ и въ транс-
форматорѣ, великъ по сравненію съ намагничивающимъ токомъ 7'.
Потеря энергіи въ обмоткѣ статора вслѣдствіе образованія теплоты
тока, пропорціональная количеству 7<?//2 = 7'^/у2 + 7"<?//2, можетъ
быть съ большимъ приближеніемъ принята пропорціональной коли-
честву 7"е#2, а вся доставляемая мотору энергія—пропорціональ-
ной У'е#, какъ мы видѣли выше. Отношеніе этихъ двухъ величинъ,
т.-е. процентное количество теряемой энергіи, будетъ поэтому при-
близительно пропорціонально У'е// или, что то же, пропорціонально
скольженію. Въ общемъ, слѣдовательно, потеря энергіи въ моторѣ,
вычисленная въ процентахъ подводимой энергіи, является кратной
скольженія. Для того, чтобы моторъ работалъ экономно, сколь-
женіе не должно прерывать небольшого числа процентовъ.
Скольженіе зависитъ всецѣло отъ нагрузки, т.-е. отъ движу-
щей силы, дѣйствующей на роторъ. Дѣйствительно, вр^іщрбщее
поле /7, вызываемое напряженіемъ между зажимами, дѣйствуетъ на
роторъ съ силой, пропорціональной силѣ тока въ коротко замкну-
той обмоткѣ, т.-е. пропорціональной скольженію.Если увеличить
нагрузку мотора, то число оборотовъ немног^\^>геньшится, пока
скольженіе не возрастетъ настолько, что магнитная движущая сила
будетъ вновь уравновѣшивать нагрузку. Энергій, отдаваемая въ видѣ
Моторы вращающаго тока
311
работы, равняется произведенію изъ вращающаго момента, дѣйству-
ющаго на роторъ, на скорость вращенія. Такъ какъ послѣдняя при-
близительно постоянна, именно, равна приблизительно скорости вра-
щающагося поля, то энергія, отдаваемая въ видѣ работы, прибли-
зительно пропорціональна вращающему моменту, т.-е. скольженію.
Мы выше доказали, что преобразуемая въ моторѣ энергія въ точ-
ности пропорціональна скольженію. Получаемая работа нѣсколько
меньше, такъ какъ скорость вращенія якоря вслѣдствіе скольженія
нѣсколько меньше скорости вращенія магнитнаго поля. Разность
между этими скоростями въ точности соотвѣтствуетъ потерѣ энергіи
въ коротко замкнутомъ якорѣ. Къ этому присоединяется еще потеря
энергіи въ обмрткѣ статора, связанная съ потерей напряженія и,
слѣдовательно, съ уменьшеніемъ вращающагося поля Н, вслѣдствіе
чего движущая сила ротора и энергія, отдаваемая въ видѣ работы,
нѣсколько уменьшаются.
Пока моторъ вращающаго тока съ коротко замкну-
ъ работаетъ экономно, скольженіе мало, т.-е.
съ почти постояннымъ числомъ оборотовъ;
бразующаяся въ моторѣ, и движущая сила
Пока
тымъ якорем
моторъ идетъ
энергія, прес
пропорціональны скольженію; процентное количество энер-
гіи, теряющейся въ видѣ теплоты тока, является кратнымъ
скольженія.
Мы разсмотримъ теперь вопросъ о пускѣ мотора въ ходъ.
Моторъ начинаетъ идти, конечно, съ весьма большимъ скольженіемъ,
достигающимъ въ первый моментъ 100°/о. Для движущей силы это
обстоятельство весьма неблагопріятно. Дѣйствительно, когда сколь-
женіе превышаетъ нѣсколько процентовъ, то въ правильно конструиро-
ванномъ моторѣ сила тока въ коротко замкнутомъ якорѣ и потому
также въ обмоткѣ магнита становится столь большой, что вызы-
ваетъ очень сильныя потери напряженія. Чтобы получить величину
напряженія, идущаго на образованіе вращающаго поля, эту потерю
нужно вычесть изъ напряженія между зажимами. Но если напря-
женіе убываетъ, то вращающееся поле ослабѣваетъ, и вслѣдствіе^
этого при увеличеніи скольженія движущая сила перестаетъ^о^
растать, несмотря на увеличеніе силы тока въ якорныхъ проволокахъ.
При опредѣленной большой величинѣ скольженія движ^ая" сила
достигаетъ максимума и затѣмъ понижается. Такимъ образомъ, при
пускѣ мотора имѣется движущая сила, но лишь маласОвь малыхъ
312
Моторы вращающаго тока
моторахъ съ этимъ обстоятельствомъ мирятся, чтобы сохранить ихъ
крайне простую конструкцію. Такъ какъ малый моторъ не имѣетъ
вовсе скользящихъ контактовъ, то его можно цѣликомъ заключить
въ футляръ, изъ котораго выдается лишь ось съ ременнымъ шкивомъ, и
на которомъ находятся три зажима для вращающаго тока статора.
Въ большихъ моторахъ, строющихся для полученія очень большой
отдачи при нормальномъ числѣ оборотовъ, съ этимъ обстоятельствомъ
мириться невозможно. Дѣйствительно, въ нихъ токи при пускѣ мотора
въ ходъ могутъ стать настолько большими, что обмоткѣ будетъ грозить
опасность перегорѣть, и при этомъ, вслѣдствіе колоссальной по-
тери напряженія, магнитное поле становится настолько слабымъ, что
движущая сила очень мала. Поэтому приходится пользоваться пуско-
вымъ сопротивленіемъ. Послѣднее не слѣдуетъ включать передъ на-
магничивающими катушками статора, потому что это вызывало бы
такое повышеніе потери напряженія, что движущая сила въ концѣ кон-
цовъ почти уничтожилась бы. Чтобы имѣть возможность ввести пу-
сковое сопротивленіе въ обмотку ротора, нужно рѣшиться пожер-
твовать преимуществомъ простого коротко замкнутаго якоря малыхъ
моторовъ. Якорные стержни соединяютъ, какъ и въ генераторѣ вра-
щающаго тока, „звѣздою" въ три группы, каждая изъ которыхъ
соединяется со скользящимъ кольцомъ. Отъ трехъ щетокъ идутъ
провода къ тремъ сопротивленіямъ, концы которыхъ соединены
между собою по способу звѣзды и такимъ образомъ замыкаютъ
якорную обмотку. Сопротивленіе вычисляется такъ, чтобы якорный
токъ, въ который оно при пускѣ вначалѣ включено полностью, воз-
расталъ лишь до благопріятной величины, при которой потери напря-
женія въ катушкахъ статора не слишкомъ велика. Такимъ образомъ
возбуждается сильное вращающее поле, и моторъ идетъ съ весьма
большой движущей силой. По мѣрѣ того, какъ онъ приходитъ въ
ха-
движеніе, сопротивленіе постепенно выключается помощью рукоятки,
такъ чтобы съ достиженіемъ нормальнаго числа оборотовъ якррныя
проволоки были коротко замкнуты. Тогда хорошія экономныя свой-
ства мотора проявляются во всей своей силѣ.
Моторъ вращающаго тока близокъ къ идеалу мртора; онъ
рактеризуется слѣдующими свойствами. ,
1. Онъ выноситъ очень сильныя колебаніяѴв^ нагрузкѣ;
движущая сила и продуктивность легко могутно превысить въ
сколько разъ нормальную величину (наибол^ Экономную).
его
нѣ-
Моторы вращающаго тока
313
2. Число оборотовъ его измѣняется едва замѣтно, всего на
нѣсколько процентовъ, такъ какъ движущая сила и продуктивность
возрастаютъ приблизительно пропорціонально скольженію.
3. Онъ пускается въ ходъ съ большой движущей силой, если
имѣетъ пусковое сопротивленіе для ротора.
4. Уходъ за нимъ чрезвычайно простъ, и онъ имѣетъ очень
простую конструкцію.
5. По сравненію со своей продуктивностью онъ очень малъ —
меньше всякаго другого мотора.
390. Нѣкоторое затрудненіе можно было бы усмотрѣть въ томъ,
что мы связаны опредѣленной скоростью вращенія. Такъ какъ при-
нятое повсемѣстно въ Европѣ число періодовъ перемѣннаго тока
равняется 50 въ секунду, то роторъ мотора вращающаго тока съ
простымъ вращающимся полемъ долженъ дѣлать приблизительно 50
оборотовъ въ секунду. Это число слишкомъ велико, и его необхо-
димо было бы перевести на практически удобныя скорости. Но дѣлу
можно помочь, увеличивъ число полюсовъ статора. Простое враща-
ющееся поле получается съ тремя полюсами, фазы которыхъ отли-
чаются одна отъ другой на 120°. Моторъ, изображенный на рис. 299,
вмѣсто этого имѣетъ 4.3=12 полюсовъ. Подобно тому, какъ гене-
раторъ перемѣннаго тока съ ѵ парами полюсовъ долженъ дѣлать
лишь 50: ѵ оборотовъ въ секунду, чтобы число періодовъ равнялось
50, точно такъ-же и моторъ вращающаго тока съ ѵ тройками полю-
совъ долженъ дѣлать нормально 50: ѵ оборотовъ въ секунду, если не
принимать въ расчетъ скольженія (напримѣръ, для мотора на рис. 299
50:4 = 12Ѵ2 оборотовъ). Это можно себѣ представлять такимъ обра-
зомъ, какъ будто вращающееся поле въ теченіе одного періода
всегда передвигается на одну тройку полюсовъ. Хотя поле много-
полюснаго статора уже не является такимъ простымъ вращающимся
полемъ, какъ поле одной тройки полюсовъ, однако теорія много-
полюсныхъ моторовъ вращающаго тока ни въ чемъ существенномъ
не отличается отъ теоріи простого трехполюснаго мотора, и резуль-
таты, полученные нами для этого простого мотора, вѣрны для вей-;
каго мотора вращающаго тока съ коротко-замкнутымъ якоре^Д^ѵ |
391. Превосходныя свойства моторовъ вращающаго тода^-много
способствовали распространенію передачи энергіи помоп^юперемѣн-
ныхъ токовъ, въ частности многофазныхъ перемѣнныхъ^тЪковъ. Воз-
можность такихъ установокъ перемѣннаго тока былаЦйеі>вые показана
314
Однофазный моторъ съ вращающимся полемъ
въ 1891 году на франкфуртской электротехнической выставкѣ. На этой
выставкѣ фирма АП^етеіпе ЕІекігігіШз^езеІІзсЬай вмѣстѣ съ машинной
фабрикой Оегіікоп устроила знаменитую первую передачу энергіи —
изъ Лауффена на Неккарѣ во Франкфуртъ на Майнѣ. Трехфазный
генераторъ приводился въ движеніе турбиной въ Лауффенѣ. Напря-
женіе сейчасъ же повышалось трансформаторомъ до 8000 .вольтъ
(напряженіе между проводомъ и землею). Такимъ образомъ можно
было мощность приблизительно въ 150 Р5 переносить во Франк-
фуртъ, на разстояніе 175 километровъ, при помощи трехъ тонкихъ
мѣдныхъ проволокъ (4 мм. толщины каждая). Отдача установки была
равна приблизительно 75°/0, такъ какъ въ Лауффенѣ турбина да-
вала около 200 Р8. Эта первая, сравнительно небольшая установка
вращающаго тока вызвала громадное распространеніе электрической
передачи силы. Въ горныхъ мѣстностяхъ, богатыхъ водостоками,
каковы, напримѣръ, Альпы, цѣлыя провинціи съ деревнями, городами
и фабриками снабжаются энергіей при помощи перемѣннаго тока
отъ одной или немногихъ водопадныхъ центральныхъ станцій;
мощность при этомъ часто достигаетъ многихъ тысячъ лошади-
ныхъ силъ.
ОДНОФАЗНЫЙ МОТОРЪ СЪ ВРАЩАЮЩИМСЯ ПОЛЕМЪ.
392. Принципомъ мотора вращающаго тока пользуются также
для построенія однофазныхъ моторовъ перемѣннаго тока. Вообще
говоря, коротко замкнутый якорь не можетъ придти во вращеніе
въ прямолинейно поляризованномъ перемѣнномъ полѣ: это противо-
рѣчило бы симметріи поля. Если же привести его во вращеніе по-
сторонней силой и довести число оборотовъ приблизительно до 50
въ секунду, то перемѣнное поле будетъ поддерживать его движеніе,
и моторъ будетъ имѣть очень большую движущую силу, какъ на-
стоящій моторъ вращающаго тока.
Изъ законовъ индукціи слѣдуетъ, что въ обмоткѣ вращающагося
коротко замкнутаго якоря индуктируются токи, стремящіеся, пр°воз-
можности препятствовать измѣненіямъ магнитнаго поля возвраща-
ющемся якорѣ. Если якорь вращается въ тактъ съ /перемѣннымъ
токомъ, т.-е. если число его оборотовъ точно равночислу періодовъ
перемѣннаго тока, то возникаетъ почти совершенное вращающееся
поле, неизмѣнно вращающееся съ якоремъ. Въ^томъ случаѣ въ об-
моткѣ якоря индуктируются токи, которые^сміщены относительно
Однофазный моторъ съ вращающимся полемъ
315
перемѣннаго магнитнаго поля статора на фазу у и магнитное поле
которыхъ всегда перпендикулярно къ полю статора и имѣетъ оди-
наковую съ нимъ силу. Такимъ образомъ получается поле двуфаз-
наго тока, гдѣ якорь играетъ роль одной пары полюсовъ. Электро-
движущія силы, дѣйствующія въ проволочныхъ виткахъ якоря при
ихъ вращеніи въ перемѣнномъ магнитномъ полѣ статора, какъ разъ
уравновѣшиваютъ напряженія, необходимыя для возбужденія въ якорѣ
поперечнаго перемѣннаго поля. Потеря напряженія вслѣдствіе сопро-
тивленія коротко замкнутой якорной обмотки безконечно мала въ
сравненіи съ дѣйствіями инерціи магнитнаго поля, и ею можно пре-
небречь: она влечетъ за собою лишь безконечно малое смѣщеніе
фазъ и такое же ослабленіе поперечнаго магнитнаго поля. Точно
такъ же напряженія, вызываемыя измѣненіями магнитнаго поля статора,
уравновѣшиваются электродвижущими силами, которыя поперечное
магнитное поле индуктируетъ въ якорныхъ проволокахъ при ихъ
движеніи въ немъ. Вслѣдствіе упомянутаго выше безконечно малаго
вліянія потерь напряженія въ якорныхъ проволокахъ на поперечное
поле получается небольшая разница между обѣими силами. Но вызы-
ваемый вслѣдствіе этого небольшой токъ, поле котораго должно быть
параллельно полю статора, компенсируется совершенно такъ же, какъ
въ трансформаторѣ перемѣннаго тока, слагающей перемѣннаго тока,
въ обмоткѣ статора имѣющей то же число амперъ-витковъ, но
противоположное направленіе. Такимъ образомъ, этотъ токъ ника-
кого вліянія на поле не оказываетъ. Если пренебречь неболь-
шими потерями энергіи въ проволокахъ, происходящими вслѣдствіе
образованія теплоты тока, то въ моторѣ, идущемъ строго въ тактъ,
совершенно не происходитъ преобразованія энергіи. Но если скорость,
вращенія якоря нѣсколько меньше скорости вращающагося поля
п0— щ
иначе говоря, когда скольженіе якоря равняется —---> то электро-
по ,
движущая сила, дѣйствующая на проволоки якоря вслѣдствіе ихъ дви-
женія въ перемѣнномъ полѣ статора, а, слѣдовательно, и поперечное^0
магнитное поле якоря, въ конечномъ счетѣ вызываемое этой электро-
движущей силой, будетъ меньше перемѣннаго поля статора въртно-
шеніи : и0. Напряженія, вызываемыя измѣненіями поля статора, уже
не уравновѣшиваются электродвижущими силами, дѣйствующими въ
якорныхъ проволокахъ вслѣдствіе ихъ движенія ^въ^ тіоперечномъ
магнитномъ полѣ. Послѣднія слишкомъ малы пд Дѣуйіѣ причинамъ г
316
Однофазный моторъ съ вращающимся полемъ
во-первыхъ, поперечное поле уменьшено въ отношеніи — , во-вто-
«о
рыхъ, скорость уменьшена въ отношеніи —. Электродвижущая сила
ио
поперечнаго поля, слѣдовательно, относится къ перемѣнному
электрическому напряженію Ѵо, какъ къ и02. Поэтому въ коротко
замкнутыхъ якорныхъ виткахъ, сопротивленіе которыхъ ничтожно
мало, долженъ возникнуть сильный перемѣнный токъ, сила котораго,
по закону Ома, пропорціональна разности между электрическимъ
напряженіемъ и электродвижущей силой поперечнаго поля, т.-е.
пропорціональна величинѣ
Ѵо- V, = Ѵо. (1-^) = ѵо . ''о2—2^= у . '^±21.
0 1 0 \ «о2/ 0 «о2 0 «о «о
Если скольженіе очень мало, то величина Ѵо — Ѵг приблизи-
тельно равняется
у 2-^Д
т.-е. при данномъ перемѣнномъ напряженіи токъ почти пропорціо-
наленъ скольженію. Этотъ токъ, поле котораго параллельно статору,
не оказываетъ никакого вліянія на вращающееся поле, такъ какъ
одновременно въ обмоткѣ статора должна возникать компенсиру-
ющая его слагающая перемѣннаго тока. Легко видѣть, что эта ком-
пенсирующая слагающая имѣетъ относительно намагничивающаго
тока статора разность фазъ, равную и совпадаетъ по фазѣ
съ перемѣннымъ напряженіемъ между подводящими токъ зажимами.
Слѣдовательно, преобразуемая въ моторѣ энергія пропорціональна
ей. Такъ какъ соотвѣтствующій перемѣнный токъ въ якорѣ также
совпадаетъ по фазѣ съ поперечнымъ магнитнымъ полемъ якоря, то
движущая сила, съ которою дѣйствуетъ на якорь магнитное поле
также пропорціональна полю. Отсюда вытекаетъ слѣдующее пред-
ложеніе: . ѵ
I
Энергія, преобразуемая въ однофазномъ моторѣ/съ вра-
щающимся полемъ, и движущая сила его якор^пропорці-
ональны скольженію якоря при условіи, чтр^рпослѣднее
мало.
Еще въ другомъ отношеніи теорія такогр^однофазнаго мотора
.весьма сходна съ теоріей настоящаго мотора вращающаго тока.
Однофазный моторъ съ вращающимся полемъ
317
Процентная потеря энергіи въ якорныхъ проволокахъ равняется
удвоенному скольженію, а потеря во всемъ моторѣ больше сколь-
женія въ нѣсколько разъ. Однофазный моторъ съ вращающимся
полемъ только тогда работаетъ экономно, когда скольже-
ніе не превышаетъ нѣсколькихъ процентовъ.
Существенное различіе между однофазнымъ моторомъ съ вра-
щающимся полемъ и моторомъ вращающаго тока заключается въ
томъ, что въ первомъ одна фаза вращающагося поля, именно попе-
речное поле якоря, развивается тѣмъ слабѣе, чѣмъ меньше скорость
вращенія якоря. При уменьшеніи числа оборотовъ поле становится по-
ляризованнымъ по все болѣе и болѣе вытянутому эллипсу и, наконецъ,
при неподвижномъ якорѣ становится поляризованнымъ прямолинейно.
Вслѣдствіе этого движущая сила, имѣющая максимумъ, какъ при
опредѣленномъ числѣ оборотовъ въ моторѣ вращающаго тока,
съ уменьшеніемъ скорости вращенія падаетъ значительно быстрѣе,
чѣмъ въ моторѣ вращающаго тока, и при неподвижномъ якорѣ
равняется нулю. Однофазный моторъ не начинаетъ идти са-
мостоятельно и при нагрузкѣ, превосходящей максимумъ
его движущей силы, окончательно останавливается. Однако,
онъ менѣе неудобенъ, чѣмъ синхронный моторъ, такъ какъ, во-пер-
выхъ, число оборотовъ, съ которымъ его пускаютъ въ ходъ, не
должно быть точно опредѣленнымъ, какъ въ синхронномъ моторѣ,
и, во-вторыхъ, съ помощью небольшого вспомогательнаго приспо-
собленія его можно пускать въ ходъ и безъ посторонней силы. Это
приспособленіе состоитъ во вспомогательныхъ полюсахъ, которые вво-
дятся между перемѣнными полюсами статора; чтобы пустить моторъ въ
ходъ, въ катушки вспомогательныхъ полюсовъ пускаютъ перемѣнный
по фазѣ на -у • Такимъ образомъ сначала возни-
вращающееся поле, въ которомъ якорь самосто-
токъ, смѣщенный
каетъ двуфазное
ятельно начинаетъ вращаться. Токъ для вспомогательныхъ полюсовъ
отвѣтвляютъ отъ основной цѣпи перемѣннаго тока, при чемъ необ- /
ходимая разность фазъ вызывается включеніемъ соотвѣтственнымъ^
самоиндукцій, конденсаторовъ (см. слѣдующіе параграфы), а иногда
также сопротивленій. Когда моторъ начнетъ идти, токъ вспомога-
тельныхъ полюсовъ выключается, послѣ чего моторъ идетъ, какъ
однофазный.
318
Перемѣнный токъ и емкость
ПЕРЕМЪННЫЙ ТОКЪ И ЕМКОСТЬ.
393. Если мы присоединимъ къ главнымъ зажимамъ машины
перемѣннаго тока зажимы конденсатора емкостью въ нѣсколько
микрофарадъ и включимъ въ эту цѣпь подходящую лампу накали-
ванія, то лампа будетъ ярко горѣть (рис. 301). Если умень-
шать емкость, свѣтъ лампы будетъ тускнѣть. Съ источникомъ элек-
тричества постояннаго напряженія такой опытъ невозможенъ. Если
мы его присоединимъ къ конденсатору, то въ первый моментъ мы
получимъ ударъ тока, равный Ѵ.С (V—напряженіе источника элек-
тричества, С—емкость). Но когда конденсаторъ будетъ заряженъ
до напряженія V, электрическое поле придетъ въ равновѣсіе, и не
будетъ ни тока, ни магнитнаго поля, ни передачи энергіи; лампа
не горитъ совершенно. Наоборотъ, перемѣнное напряженіе за-
ряжаетъ конденсаторъ поперемѣнно то положительно, то отрицательно,
и такимъ образомъ возбуждаетъ въ проводахъ правильный перемѣн-
ный токъ, который можетъ довести лампу до каленія.
Очень легко подыскать механическія аналогіи этому явленію.
Какъ и выше, мы возьмемъ въ качествѣ механической модели
электрической проводки трансмиссіонный валъ. Скорость вращенія
вала соотвѣтствуетъ силѣ тока (магнитному полю), его напряженіе
при закручиваніи—электрическому напряженію. Если мы соединимъ
валъ со спиральной пружиной такъ, чтобы онъ болѣе^н^могъ не-
прерывно вращаться, то пружина будетъ соотвѣтственъ включен-
ному въ цѣпь конденсатору; податливость пружиы|ѴТ.-е. уголъ, на
который долженъ повернуться валъ, чтобы въ^пружинѣ получилась
сила напряженія, равная единицѣ, будетъ ^^Дѣтствовать емкости.
Перемѣнный токъ и” емкость
319
Если мы будемъ вращать валъ съ силою V, и податливость пру-
жины равна С, то ось совершитъ вращеніе на уголъ, равный СѴ,
послѣ чего установится равновѣсіе силъ. Это вращеніе соотвѣт-
ствуетъ удару тока. Если же мы будемъ вращать валъ при помощи
періодически измѣняющейся силы, то ось будетъ непрерывно дви-
Рис. 302. Осциллограмма напряженія и силы тока въ конденсаторѣ.
-------------кривая силы тока, .....кривая напряженія.
гаться въ ту и другую сторону, — мы имѣемъ здѣсь „перемѣнный
токъ", при чемъ „сила тока", соотвѣтствующая опредѣленному „пе-
ремѣнному напряженію", пропорціональна податливости пружины и
числу перемѣнъ.
394. Если при помощи двойного осциллографа получить одно-
временно кривыя силы тока и напряженія у зажимовъ конденсатора
(рис. 302), то оказывается, что онѣ смѣщены одна относительно
другой и разность фазъ между ними равняется у • Согласно
§371, включеніе самоиндукціи даетъ такую же разность фазъ, но
въ этомъ случаѣ сила тока развивается послѣ напряженія, тогда
какъ въ конденсаторѣ, наоборотъ, сперва образуется токъ (или маг-
нитное поле), а затѣмъ уже вызываемое имъ электрическое поле
въ конденсаторѣ.
Передача энергіи совершается такимъ же образомъ, какъ было
описано въ § 372 для случая самоиндукціи. Въ первую четверть
періода, когда конденсаторъ заряжается, напряженіе повышается отъ
максимума; сила тока въ это время падаетъ отъ максимума
Энергія въ это время переносится эѳиромъ въ конденса-
нуля до
до нуля,
торъ, сначала медленно, потомъ быстрѣе и, наконецъ, опять медленно;
здѣсь она накопляется въ видѣ электрической энергіи
ѵ 2 Ъсу і
вторую четверть сила тока имѣетъ обратный знакъ и измѣняется
отъ нуля до отрицательнаго максимума, знакъ же напряженія оста-
ется прежнимъ, и оно падаетъ отъ положительнаго мф^Мума до
нуля. Конденсаторъ въ это время разряжается и охаетъ энергію?
320
Перемѣнный токъ и емкость
скопившуюся въ немъ за первую четверть періода, сначала медленно,
затѣмъ быстрѣе и въ заключеніе снова медленно. Такой же про-
цессъ повторяется и въ обѣ послѣднія четверти періода, только на-
пряженіе въ это время имѣетъ обратный знакъ. Такимъ образомъ,
переносимая энергія въ общей сложности равняется нулю, что можно
было предвидѣть по разности фазъ, равной ~
395. Эффективная величина силы тока /е// въ цѣпи перемѣн-
наго тока, содержащей емкость, должна быть пропорціональна слѣ-
дующимъ тремъ величинамъ: 1) эффективному напряженію Ѵе//
между зажимами конденсатора; 2) емкости С конденсатора; 3) числу
періодовъ п перемѣннаго напряженія. Какъ показываетъ болѣе точ-
ное вычисленіе, сюда нужно еще присоединить численный множи-
тель 2п, т.-е.
Луу = 2тт. п . С. Ѵе//.
Кажущееся сопротивленіе конденсатора перемѣнному
току равняется
о __ 1
Кс~ 2тспС’
Если между главными зажимами генератора и конденсаторомъ
нѣтъ сопротивленія, то Ѵе// есть эффективное напряженіе самаго
генератора. Если же между генераторомъ и конденсаторомъ вклю-
чить сопротивленіе /?, то напряженіе понизится, и помощью часо-
вой діаграммы легко опредѣлить, насколько именно. Сила тока въ
проволокѣ, образующей сопротивленіе, столь же велика, какъ и сила
тока смѣщенія въ конденсаторѣ; мы обозначимъ ее черезъ У; пусть,
на діаграммѣ рис. 303 она изображается стрѣлкой ОА. Напряже-
ніе Ѵ} между зажимами конденсатора имѣетъ величину и от-
стаетъ отъ У на четверть періода; на діаграммѣ оно представляется
стрѣлкой ОВ. Напряженіе между зажимами сопротивленія Ѵ2 V
имѣетъ всегда одинаковую фазу съ 7; оно представлиіосстрѣл-
кой ОС. Если можно пренебречь самоиндукціей, т.-е. если можно-
принять, что напряженія электродинамическаго поля, которымъ вы-
зывается образованіе магнитнаго поля тока, бе^ОНёчно малы въ.
сравненіи съ Ѵг и Ѵ2 (и если пренебречь безконечно малыми откло-
неніями), то въ электрическомъ полѣ цѣпиуіфіжно господствовать
Перемѣнный токъ и емкость
321
статическое равновѣсіе, т.-е. линейная сумма поля вдоль всей про
водки ѴІ 1/2 должна быть равна
напряженію V между зажимами ----------------
генератора. Векторъ ОО, пред-
ставляющій на діаграммѣ рис. 303
напряженіе V у зажимовъ генера-
тора, долженъ быть поэтому ра-
венъ геометрической суммѣ векто-
ровъ ОВ и ОС. Отсюда вытекаетъ
соотношеніе между Л# и Ѵе/у:
2лпС
Рис. 393. Часовая діаграмма цѣпи
перемѣннаго тока съ сопротивле-
ніемъ и емкостью.
Кажущееся сопротивленіе перемѣнному току цѣпи,
имѣющей омическое сопротивленіе 7? омовъ и емкость С
фарадъ, равняется
7?, = 1/ Д—.
5 г 1 4ТТ-И-С2
Разность фазъ ср между напряженіемъ у главныхъ зажимовъ
генератора и силой тока У вычисляется, какъ видно изъ рис. 303,
по формулѣ
^ = 2^7?-
Энергія ІУ, выходящая между главными зажимами изъ машины,
равняется энергіи, поглощаемой сопротивленіемъ /?, такъ какъ кон-
денсаторъ ничего не поглощаетъ.
Слѣдовательно, О = Ѵе/7 • Л/т • соз ср (ср. § 372).
Если перемѣнное напряженіе Ѵе^ между зажимами имѣ-
етъ разность фазъ ф относительно силы тока, то энергія,
переносимая эѳиромъ между зажимами, равняется произ-
веденію изъ эффективныхъ величинъ напряженія и силы
тока на косинусъ разности фазъ: ІУ = Ѵе^. Уе^. соз ср.
СРАВНЕНІЕ ЕМКОСТЕЙ.
396.
Если соединить послѣдовательно двѣ емкости Сх и^С^и
къ конечнымъ зажимамъ А и В приложить перемѣнное напряженіе У,
то напряженія конденсаторовъ Ѵі и Ѵ2 всегда будутъ сор^адать по
Ми. Электричество и магнитизмъ, ч. II. 21
322
Сравненіе емкостей
фазѣ между собою и
какъ токъ смѣщенія
одинаковымъ, то
съ Ѵ\ кромѣ того, + 1/2 = V. Далѣе,
въ обоихъ конденсаторахъ долженъ
такъ
быть
с,.ѵ, = с2.ѵ2.
Слѣдовательно,
'2_ 17- ѵ — V
~С2 ѵ с;4-с2
Если, кромѣ того, точки А и В соединить измѣрительной
волокой, какъ въ мостикѣ Витстона (§ 262), то напряженія V/ и 1/2'
между какой либо точкой Р этой проволоки и точками развѣтвле-
нія Л и В будутъ всегда совпадать по фазѣ съ I/; кромѣ того,
ВР равны
у,=
про-
ру-|-2'ІЛ Если сопротивленія отрѣзковъ АР и
и /?2, то
V ' = —— у • у' =у
Если точку Р выбрать такимъ образомъ, чтобы
/?, -.х2=с2-.су = р. ,
то все время будутъ имѣть мѣсто уравненія Ѵх' —
Поэтому двѣ емкости С{ и С2 можно съ большимъ
и очень точно сравнивать между собою при помощи телефоннаго
моста, подобно электролитическимъ сопротивленіямъ (§ 269) или
самоиндукціямъ (§ 374). Такъ какъ правильность колебаній не игра-
етъ при этомъ никакой роли, то перемѣнный токъ можно возбу-
ждать небольшимъ индукціоннымъ аппаратомъ. Если въ воспользо-
ваться калибрированнымъ нормальнымъ микрофарадомъ, то можно лю-
бую емкость измѣрить въ легальныхъ единицахъ.
Методъ моста Витстона является безусловно удобнѣйшимъ и
лучшимъ способомъ измѣренія емкостей; большинство діэлектриче-
скихъ постоянныхъ были измѣрены этимъ способомъ. Если въ вѣтви
съ емкостью находятся, кромѣ того, сопротивленія или самоиндукціи,
замѣтно вліяющія на смѣщеніе фазы перемѣннаго тока, то |і>?теле-
фонѣ звукъ не прекращается полностью, но получается минимумъ.
Однако, примѣняя компенсирующія сопротивленія самоиндукціи или
емкости, какъ описано въ § 374, можно напряженія^ на обоихъ кон-
цахъ моста заставить совпадать по фазѣ и добитѣся рѣзкаго мини-
мума и даже полнаго исчезновенія звука. ХоѴ
Ѵ2.
удобствомъ
Цѣпь перемѣннаго тока, содержащая емкость и самоиндукцію 323
ЦѢПЬ ПЕРЕМѢННАГО ТОКА, СОДЕРЖАЩАЯ ЕМКОСТЬ
И САМОИНДУКЦІЮ.
397. Если два главные зажима машины перемѣннаго тока соеди-
нить съ включенными послѣдовательно емкостью и самоиндукціей,
то оказывается, что при неизмѣнномъ напряженіи между зажимами
токъ въ цѣпи гораздо сильнѣе, нежели при включеніи только само-
индукціи или только емкости. Это легко продемонстрировать, если
включить въ цѣпь лампу накаливанія, а зажимы емкости и зажимы само-
индукціи соединить отдѣльно съ двумя парами наполненныхъ ртутью
чашечекъ, которыя можно замыкать на короткую мѣдною дугою.
Выбравъ надлежащимъ образомъ самоиндукцію и емкость, можно
достигнуть того, что лампа будетъ оставаться темной при короткомъ
замыканіи одной изъ паръ чашекъ и будетъ ярко горѣть при по-
слѣдовательномъ прохожденіи тока черезъ самоиндукцію и емкость.
Если при помощи вольтметра перемѣннаго тока измѣрить эффек-
тивную величину напряженія между зажимами емкости и между за-
жимами самоиндукціи, когда онѣ обѣ включены одновременно, то она
оказывается значительно выше напряженія между зажимами машины.
Эти на первый взглядъ изумительные факты легко объясняются
при помощи часовой діаграммы. Пусть У будетъ сила тока въ цѣпи,
Ѵ1 — напряженіе между зажимами лампы накаливанія, І/2 и У3 — на-
пряженія между зажимами самоиндукціонной катушки и конденса-
тора. Тогда какъ Ѵ1 всегда совпадаетъ по фазѣ съ У, напряженія
и І/3, наоборотъ, смѣщены соотвѣтственно па -ф и —(рис. 304).
Напряженіе вдоль всей цѣпи, т.-е. сумма Ѵ} ф Ѵ2 -ф Ѵ3 равняется
напряженію V между главными зажимами генератора. Если соста-
вить эту сумму, то оказывается, что Ѵ2 и Ѵ3 отчасти взаимно
уничтожаются. Если же выбрать самоиндукцію и емкость такимъ
образомъ, чтобы количество 2тгяА незначительно отличалось отъ
и чтобы /? было мало по сравненію съ этими величинами, то
напряженія І/2 и Ѵ3, каждое въ отдѣльности, будутъ велики въ срав^
неніи съ V. Если мы самоиндукцію или емкость замкнемъ на к^рсйф
кую, то въ діаграммѣ отпадетъ Ѵ2 или Ѵ3, и для напряженія^ V
должна получиться при томъ же токѣ гораздо большая ітеличина.
Но такъ какъ количество V, какъ напряженіе у зажимовъ^машины,
постоянно, то сила тока должна замѣтно понизиться,^Ярка резуль-
21
324 Цѣпь перемѣннаго тока, содержащая емкость и самоиндукцію
тирующее изъ напряженій Ѵ\ и или напряженій и Ѵ3 не ста-
нетъ снова равнымъ данной величинѣ V.
Легко построить механическую модель описываемыхъ явленій.
Представимъ себѣ, что на ось съ рукояткой насажено маховое ко-
лесо, и что ось неподвижно соединена со спиральной пружиной.
Если вращать рукоятку поперемѣнно въ ту и другую сторону, при-
лагая одинаковую силу при вращеніяхъ въ обѣ стороны, то макси-
мальная скорость будетъ получаться всякій разъ при прохожденіи
колеса черезъ положеніе равновѣсія, когда сила напряженія пружи-
ны равняется нулю. Когда маховое колесо перейдетъ черезъ поло-
женіе равновѣсія, движеніе колеса будетъ постепенно замедляться; такъ
какъ въ то же время натяженіе пружины все болѣе и болѣе про-
тиводѣйствуетъ движенію, то приложенной на рукоятку силѣ при-
ходится уравновѣшивать лишь разность между сопротивленіемъ
инерціи махового колеса и натяженіемъ пружины. Послѣ того какъ
маховое колесо, наконецъ, остановится, оно начинаетъ двигаться въ
Рис. 304. Часовая діа-
грамма для цѣпи пере-
мѣннаго тока съ емко-
стью, самоиндукціей и
сопротивленіемъ.
махового колеса,
числа періодовъ
обратную сторону съ возрастающею ско-
ростью; при этомъ натяженіе пружины дѣй-
ствуетъ въ сторону движенія, и сила, при-
ложенная къ рукояткѣ, опять должна урав-
новѣшивать лишь разность между сопро-
тивленіемъ инерціи и натяженіемъ пружины.
На какой сторонѣ будетъ перевѣсъ, зави-
ситъ отъ величины
крѣпости пружины и
перемѣннаго движенія. Во всякомъ слу-
чаѣ, можно достигнуть того, чтобы при-
ложенная къ рукояткѣ сила была меньше
натяженія пружины и меньше сопротивле-
нія инерціи. Тогда движеніе колеса будетъ
происходить, главнымъ образомъ, подъ
дѣйствіемъ натяженія пружины, щобрат-
но, пружина будетъ приводитьс^іГсосто-
яніе напряженія, главнымъ образомъ, дви-
женіемъ колеса. Энергія колебанія будетъ
скопляться поперемѣнно то въ пружинѣ, въ формѣ энергіи напряженія,
то въ маховомъ колесѣ, въ формѣ энергіи движенія; энергія же, пере-
ходящая въ ту и другую сторону черезъ^^укоятку, весьма мала.
Резонансъ
325
Съ описанной моделью совершенно аналогичны явленія въ раз-
сматриваемой цѣпи перемѣннаго тока. Напряженіе конденсатора воз-
буждаетъ, главнымъ образомъ, магнитное поле самоиндукціонной
катушки, а магнитное поле при исчезновеніи обратно отдаетъ боль-
шую часть напряженія, необходимую для заряженія конденсатора;
источникъ перемѣннаго тока лишь выравниваетъ разности. Энергія
переходитъ изъ конденсатора въ самоиндукціонную катушку и
обратно; энергія же, выходящая изъ генератора и доставляемая ему,
при правильно выбранныхъ отношеніяхъ мала.
398. То обстоятельство, что въ цѣпи перемѣннаго тока, содер-
жащей емкость и самоиндукцію, могутъ возникать напряженія, зна-
чительно ббльшія, нежели возбуждаемыя между главными зажимами
генератора, не лишено значенія для техники перемѣнныхъ токовъ.
Длинный кабель вмѣстѣ съ діэлектрикомъ между обоими проводами
представляетъ емкость и, кромѣ того, онъ имѣетъ довольно боль-
шую самоиндукцію. Поэтому въ длинномъ кабелѣ на большомъ раз-
стояніи отъ генератора перемѣннаго тока могутъ возникать при бла-
гопріятныхъ условіяхъ высокія „перенапряженія “, и можетъ про-
изойти поврежденіе изоляціи. Въ виду этого при проводкахъ перемѣн-
наго тока на большія разстоянія необходимо спеціальными мѣрами пред-
отвратить или обезвредить подобныя перенапряженія.
РЕЗОНАНСЪ.
399. Если емкость и самоиндукція выбраны такимъ образомъ,
что на діаграммѣ векторы и Ѵ3 равны между собою, то гене-
раторъ перемѣннаго тока вообще уже не играетъ роли въ движе-
ніи энергіи въ ту и въ другую сторону. Онъ только доставляетъ ту
энергію, которая поглощается сопротивленіемъ цѣпи. Возбужденіе
магнитнаго поля самоиндукціи совершается всецѣло за счетъ напря-
женія конденсатора; и обратно, конденсаторъ вновь заряжается исклю-
чительно дѣйствіями самоиндукціи. Энергія колеблется между кон-
денсаторомъ и самоиндукціонной катушкой въ ту и другую сто- ~
рону. Въ этомъ случаѣ говорятъ, что цѣпь перемѣннаго тока находитс^||
въ резонансѣ съ электромагнитными колебаніями генератора. Урлэ-
віе возникновенія резонанса вытекаетъ равет^рѣва
У2=У3; оно гласитъ:
2тг/гА — о —~ ,
2ъпС
326
Электромагнитныя колебанія при разрядѣ конденсатора
или
4тг2. п2 = ь
Изъ принципа сохраненія энергіи слѣдуетъ, что въ случаѣ
резонанса энергія, отнимаемая конденсаторомъ въ макси-
мумѣ, равняется энергіи, которая находится въ магнитномъ
полѣ самоипдукціонной катушки на четверть періода до
и послѣ того.
ЭЛЕКТРОМАГНИТНЫЯ КОЛЕБАНІЯ ПРИ РАЗРЯДЪ КОНДЕНСАТОРА
400. Когда заряженный до высокаго напряженія конденсаторъ
внезапно разряжаютъ черезъ проволоку, обладающую опредѣлен-
ной самоиндукціей, но лишь весьма малымъ сопротивленіемъ, то
электрическое напряженіе конденсатора возбуждаетъ магнитное поле
тока разряда и доводитъ его, наконецъ, до нѣкотораго максималь-
наго значенія, когда вся энергія электрическаго поля въ конденса-
торѣ превратится въ магнитную энергію поля тока. Но процессъ
этимъ еще не кончается. Дѣйствительно, пока существуетъ магнит-
ное поле, оно должно, какъ было указано въ §§ 250 и 251, сопро-
вождаться перемѣщеніями электрическихъ зарядовъ, а именно элек-
трическимъ токомъ въ проводѣ; этотъ токъ, отнявшій сперва зарядъ
отъ конденсатора, за время существованія магнитнаго поля даетъ
конденсатору противоположный зарядъ. Вслѣдствіе этого возникаютъ,
однако, электрическія напряженія, противоположныя тѣмъ, которыя воз-
будили магнитное поле, и благодаря имъ поле затѣмъ уничтожается. Вся
энергія магнитнаго поля вновь вступаетъ въ діэлектрикъ конденса-
тора въ видѣ электрической энергіи. Если же магнитное поле или
токъ становятся равными нулю, то напряженіе между пластинами
конденсатора вызываетъ въ цѣпи обратный токъ, который разря-
жаетъ конденсаторъ и затѣмъ заряжаетъ его вновь въ первоначаль-
номъ направленіи. Иными словами, возникаютъ правильныя электри-
ческія колебанія, при которыхъ энергія колеблется между элеД/ри-
ческимъ полемъ въ конденсаторѣ и магнитнымъ полемъ р&уй Эти
колебанія отличаются отъ явленій, описанныхъ выше, лишь тѣмъ,
что энергія, поглощаемая въ сопротивленіяхъ, не вводится въ цѣпь
внѣшнимъ источникомъ тока. Сейчасъ мы не прири^іали въ расчетъ
сопротивленія разрядной цѣпи. Въ дѣйствительности же оно, ко-
нечно, не можетъ равняться нулю, и часть напряженія должна идти
Электромагнитныя колебанія при разрядѣ конденсатора
327
на преодолѣніе сопротивленія, потому пропадая для магнитнаго
поля. Потеря напряженія составляетъ, можетъ быть, ничтожную часть
общаго напряженія, но все-же, благодаря ей, магнитное поле не мо-
жетъ достигнуть той величины, которую оно имѣло бы въ случаѣ
совершеннаго отсутствія сопротивленія. Вслѣдствіе этого и электри-
ческое поле конденсатора при своихъ правильно совершающихся
повтореніяхъ постепенно ослабѣваетъ. При каждомъ колебаніи нѣ-
которая часть энергіи переходитъ въ теплоту тока, пока весь
запасъ энергіи, заключавшійся сначала въ конденсаторѣ, не будетъ
постепенно исчерпанъ; тогда колебанія затухаютъ. Если сопро-
тивленіе мало въ сравненіи съ самоиндукціей, то выведенное въ
предыдущемъ параграфѣ условіе, при которомъ напряженіе конден-
сатора постоянно находится въ равновѣсіи съ напряженіемъ само-
индукціи, почти не измѣняется. Такимъ образомъ, число п періодовъ
колебаній, возникающихъ при разрядѣ конденсатора, опредѣляется
уравненіемъ
Если мы обозначимъ черезъ Т продолжительность одного пол-
наго колебанія, то будемъ имѣть: п. Т = 1 секундѣ, Т = се-
кунды., Изъ вышеприведенной формулы слѣдуетъ, что
Т=2п.уТГС.
Такъ какъ емкость С, измѣренная въ фарадахъ, равна а
г вольтъ
т . вольтъ-сек.
самоиндукція А, измѣренная въ генри, равна——» то размѣр-
т „ кулонъ . вольтъ . секунда о
ность произведенія Ь.С будетъ —--------------------= сек, слѣ-
г амперъ. вольтъ
довательно, размѣрность Т, дѣйствительно, есть секунда.
Описанныя сейчасъ электрическія колебанія цѣпи, содержащей
емкость и самоиндукцію, называются собственными колебаніями
цѣпи, въ отличіе отъ вынужденныхъ колебаній, вызываемыхъ
постороннимъ генераторомъ перемѣннаго тока и имѣющихъ про-
извольную частоту.
Продолжительность колебанія собственныхъ колебан^І
цѣпи, содержащей емкость и самоиндукцію, равняется
Т— 2тг.)/С.Ь секундамъ, если емкость С измѣрена въ^фара-
дахъ, а самоиндукція Л — въ генри.
Формула для продолжительности колебанія была^Дана сэромъ
В. Томсономъ (лордомъ Кельвиномъ), почему ѵі называется
328
Электромагнитныя колебанія при разрядѣ конденсатора
формулой Томсона. Слѣдующее предложеніе является теперь
очевиднымъ.
Цѣпь, заключающая емкость и самоиндукцію, находится
въ резонансѣ съ генераторомъ перемѣннаго тока, если
число періодовъ ея собственныхъ колебаній совпадаетъ съ
числомъ періодовъ генератора перемѣннаго тока.
Легко найти соотвѣтствующую механическую аналогію. Пред-
ставимъ себѣ ось съ маховымъ колесомъ, неподвижно соеди-
ненную со спиральной пружиной, напримѣръ, съ балансиромъ
карманныхъ часовъ. Если мы повернемъ колесо такъ, чтобы пру-
жина пришла въ состояніе напряженія, и затѣмъ внезапно его
отпустимъ, то возникнутъ правильныя колебанія. Упругія силы
пружины приводятъ колесо въ движеніе, и его скорость до-
стигнетъ наибольшей величины, когда пружина придетъ въ нормаль-
ное состояніе. Вслѣдствіе движенія колеса, пружина начнетъ затѣмъ
закручиваться въ противоположную сторону и при этомъ будетъ про-
тиводѣйствовать движенію колеса, пока, наконецъ, не приведетъ его въ
состояніе покоя. Послѣ этого пружина начинаетъ двигать колесо въ
противоположномъ направленіи, закручивается имъ вновь въ ту же сто-
рону, что и первоначально, и весь процессъ повторяется снова. Энергія
колеблется между пружиной, гдѣ она является въ видѣ энергіи на-
пряженія, и колесомъ, которое получаетъ ее въ видѣ энергіи дви-
женія. Такъ какъ упругія силы пружины должны преодолѣвать, кромѣ
инерціи колеса, еще сопротивленія тренія, то колебанія будутъ за-
тухающими, при чемъ все время часть энергіи будетъ переходить въ те-
плоту тренія. Самоиндукціи Ь здѣсь соотвѣтствуетъ моментъ инерціи
колеса, который мы обозначимъ черезъ /С; емкости С соотвѣтству-
етъ податливость пружины Р по отношенію къ вращеніямъ колеса,
т.-е. отношеніе угла, на который поворачивается колесо изъ своего
положенія равновѣсія, къ моменту вращенія, съ которымъ натя-
нутая пружина стремится повернуть колесо въ обратную сторону.
Величину, обратную податливости, т.-е. отношеніе момента враще-
. °л
нія къ углу вращенія, называютъ направляющей силой пру-
1 ,
жины; если мы обозначимъ ее черезъ Е>, то О = -р • Періодъ колебанія
балансира опредѣляется извѣстной формулой маятника
Электромагнитныя колебанія при разрядѣ конденсатора
329
Если вмѣсто В ввести сюда Г = , то получимъ
Т=2пУк.Р.
Очевидна аналогія между этой формулой и формулой Томсона,
которая поэтому и представляетъ собою не что иное, какъ фор-
мулу маятника для электромагнитныхъ колебаній.
Если колеблющійся часовой балансиръ мы предоставимъ самому
себѣ, то черезъ нѣкоторое время онъ остановится вслѣдствіе зату-
ханія колебаній. Поддерживать его въ движеніи въ теченіе продол-
жительнаго времени можно лишь путемъ вынужденныхъ колебаній.
Если число періодовъ вынужденныхъ колебаній равняется числу
періодовъ собственныхъ колебаній, то, примѣняя перемѣнную враща-
ющую силу опредѣленной величины, мы получимъ относительно наи-
большія отклоненія. Въ этомъ случаѣ имѣетъ мѣсто резонансъ.
401 Если для наблюденія электрическихъ колебаній разрядить
большую емкость черезъ довольно большую самоиндукціонную
катушку, то накопленная энергія уже при малыхъ напряженіяхъ
достаточно велика, чтобы дать сильныя колебанія. При малыхъ
напряженіяхъ замыканіе тока въ разрядной цѣпи можно произво-
дить обыкновеннымъ замыкателемъ. Такія колебанія, конечно, явля-
ются относительно медленными; напримѣръ, при С = 1Л4 Ф и
Т = 0,0063, т.-е. число колебаній въ секунду равняется 156.
Если желаютъ получить большія числа колебаній, возбуждая
послѣднія при помощи малыхъ емкостей и малыхъ самоиндукцій,
напримѣръ, при помощи лейденской банки и короткаго замыкателя
между ея обкладками, то емкость заряжаютъ до высокаго напря-
женія для того, чтобы энергія колебанія не была слишкомъ мала, и
Рис. 305. С >ема включенія искррвого
Къ источ
ни/ку длек
~тричества
въ качествѣ замыкателя тока пользуются искрой разряда. Такимъ
образомъ, опытъ сводится просто
къ тому, что обѣ обкладки лей-
денской банки соединяются корот-
кими толстыми проволоками съ не-
большимъ искровымъ перерывомъ,
къ электродамъ котораго присо-
единяются провода отъ индукціон-
наго аппарата или электростати-
ческой индуктивной машины (рис.
гается разрядное напряженіе, проскакиваетъ искра^Сііринимающая,
305). Всякій разъ °^а^ъ дости-
330
Электромагнитныя колебанія при разрядѣ конденсатора
какъ мы знаемъ (§ 194), весьма скоро форму хорошо проводящей
дуговой искры. Пока возникающій при этомъ перемѣнный токъ
большой частоты имѣетъ большую силу, искра проводитъ хорошо.
Но когда сила тока вслѣдствіе затуханія слишкомъ понизится, искра
слабѣетъ и колебанія довольно быстро прекращаются.
Емкость лейденской банки вообще близка къ микрофарада,
самоиндукція проволочной дуги длиною около метра близка къ
ГобООбѳ генРи* При С= 10~9, Л=10- формула Томсона даетъ
Т— 2.10~7, т.-е. частота колебаній составляетъ круглымъ счетомъ
5 милліоновъ въ секунду. Обычно при разрядахъ лейденскихъ ба-
нокъ или батарей такихъ банокъ черезъ длинныя и короткія прово-
локи частота колебаній составляетъ милліоны или сотни тысячъ
въ секунду.
Что разрядъ конденсатора имѣетъ колебательный характеръ,
впервые было доказано теоретически сэромъ В. Томсономъ, а позже
(1862) это было экспериментально установлено Феддерсеномъ
(Ребсіегзеп). Дуговая искра, подобно непрерывной свѣтовой дугѣ, отли-
чается тѣмъ большей яркостью, чѣмъ больше сила тока. Поэтому, если
черезъ искровой промежутокъ проходитъ перемѣнный токъ высокой
частоты, то искра имѣетъ поперемѣнно то яркій, то слабый свѣтъ.
Феддерсенъ при помощи весьма быстро вращающагося вогнутаго
зеркала направлялъ изображеніе разрядной искры на фотографи-
ческую пластинку и такимъ образомъ получалъ рядомъ одно за
другимъ фотографическія изображенія послѣдовательныхъ стадій раз-
витія искры. Когда скорость вращенія была достаточно велика, то
получался рядъ свѣтлыхъ изображеній искры, раздѣленныхъ темными
промежутками. Такъ какъ скорость вращенія зеркала и разстоянія
зеркала отъ искры и отъ пластинки были извѣстны, то путемъ измѣ-
ренія разстояній между изображеніями искры можно было опредѣ-
лить продолжительность электрическаго колебанія. Результатъ под-
твердилъ формулу Томсона.
402. Возникновеніе быстрыхъ электрическихъ колебаній при
разрядахъ имѣетъ особенно важное значеніе потому,^что при по-
мощи машинъ перемѣннаго тока можно достигнуть)Члишь сравни-
тельно небольшого числа періодовъ. Тесла (Тезіа) однажды при
помощи спеціально построенной машины достигъ числа періодовъ,
Электромагнитныя колебанія при разрядѣ конденсатора
331
равнаго 30000 въ секунду. Для всѣхъ большихъ чиселъ періодовъ
приходится пользоваться собственными колебаніями конденсаторныхъ
цѣпей. Здѣсь мы имѣемъ то же самое, что и въ механикѣ. Аппа-
раты, совершающіе колебанія въ ту и другую сторону съ неболь-
шимъ числомъ періодовъ, можно приводить въ движеніе при по-
мощи мотора. Чтобы получитъ большія частоты, разсматриваемыя
въ той части механики, которая называется акустикой, пользуются
собственными колебаніями механическихъ осцилляторовъ — струнъ»
воздушныхъ столбовъ, колоколовъ и т. д.
Чтобы по возможности уменьшить затуханіе колебаній конден-
сатора, слѣдуетъ сдѣлать возможно меньшимъ сопротивленіе цѣпи.
Главное сопротивленіе всегда заключается въ искрѣ и обычно со-
ставляетъ нѣсколько омовъ. Прежде всего, слѣдовательно, нужно
сдѣлать искру весьма сильной, а для этой цѣли необходимъ разряд-
ный токъ большой силы. Поэтому емкость конденсатора должна
быть не слишкомъ малой и искровой промежутокъ не слишкомъ
короткимъ, такъ какъ сила разряднаго тока падаетъ пропорціонально
разрядному напряженію. Съ другой стороны, искра не должна быть
также и слишкомъ длинной, такъ какъ сопротивленіе искры сильно
возрастаетъ съ длиною. Для каждой емкости существуетъ наивыгоднѣй-
шая длина искры, при которой колебанія наименѣе затухаютъ; ее
слѣдуетъ опредѣлять эмпирически. Когда искра даетъ хорошія коле-
банія, ея трескъ отличается особенной рѣзкостью. Поэтому слѣду-
етъ заботиться о томъ, чтобы, кромѣ искры, въ цѣпи не было ника-
кихъ сопротивленій, которыя могли бы оказывать вліяніе. Дѣйстви-
тельно, сила разряднаго тока уменьшается этими сопротивленіями,
вслѣдствіе чего искра тотчасъ же ослабляется и затуханіе возраста-
етъ чрезвычайно сильно. Во многихъ случаяхъ оказывается прак-
тичнымъ пускать искру не въ воздухѣ, но въ изолирующей жид-
кости, лучше всего въ керосинѣ. При этомъ уже при короткихъ
искровыхъ промежуткахъ получаются очень высокія разрядныя на-
пряженія, т.-е. большія силы тока, и сопротивленіе искры становится
поэтому очень малымъ.
ВОЗНИКНОВЕНІЕ КОЛЕБАНІЙ ВСЛѢДСТВІЕ РЕЗОНАНСА.
403. Если замкнутую разрядную цѣпь конденсато^ ^внести въ
перемѣнное электромагнитное поле, то въ ней возникаемъ индукти-
рованный перемѣнный токъ. Онъ имѣетъ весьма значительную ампли-
332
Возникновеніе колебаній вслѣдствіе резонанса
туду, если цѣпь конденсатора находится въ резонансѣ съ перемѣн-
нымъ полемъ. Дѣло въ томъ, что каждый электрическій ударъ на-
пряженія вызываетъ въ цѣпи собственныя колебанія. Если перемѣны
возбуждающаго поля совершаются въ томъ же темпѣ, какъ и соб-
ственныя колебанія, то каждое слѣдующее колебаніе будетъ усили-
ваться полемъ, и амплитуда будетъ все возрастать, пока, наконецъ,
возрастающія одновременно потери энергіи вслѣдствіе омическаго
сопротивленія и т. д. не станутъ равны количеству энергіи, доста-
вляемому перемѣннымъ полемъ; тогда дальнѣйшее возрастаніе ампли-
туды прекратится. Такимъ образомъ, послѣ ряда колебаній ампли-
туда достигаетъ максимума; затѣмъ, когда первичныя колебанія зату-
хаютъ, она постепенно падаетъ вмѣстѣ съ ними. Если же собствен-
ныя колебанія цѣпи имѣютъ иной періодъ, то они не поддержива-
ются долго перемѣннымъ полемъ и не развиваются до большой
амплитуды. Въ этомъ случаѣ мы получаемъ, главнымъ образомъ,
вынужденное колебаніе съ числомъ періодовъ перемѣннаго поля,
налагающееся на слабое собственное колебаніе конденсаторной цѣпи.
Вынужденное колебаніе также сравнительно очень слабо, такъ какъ
въ теченіе большого числа послѣдовательныхъ періодовъ не проис-
ходитъ его усиленія черезъ резонансъ.
Получаемыя посредствомъ резонанса сильныя колебанія можно
демонстрировать съ помощью весьма простого опыта, впервые про-
изведеннаго Лоджемъ (Ьосі^е). Около электрическаго осциллятора
(искровой промежутокъ котораго нужно представлять себѣ соеди-
неннымъ съ индукторомъ) помѣщаютъ цѣпь колебаній, поддающуюся
настраиванію, а именно лейденскую банку, которая должна быть
возможно точнѣе равна банкѣ осциллятора (рис. 306). Съ обклад-
ками этой банки соединяютъ двѣ параллельныя проволоки, которыя
между собой соединены третьей, передвижной проволокой. Если
этотъ проволочный мостъ передвинуть въ такое положеніе, чтобы
замкнутая имъ цѣпь проводниковъ была равна цѣпи осциллятора, то
въ ней вслѣдствіе резонанса возникаютъ очень сильныя колебанія.
Эти послѣднія можно наблюдать при помощи небольшого искрового
промежутка, включаемаго, какъ показываетъ рис. 306, ^еждувнѣш-
ней и внутренней обкладками лейденской банки безъ/промежуточ-
ныхъ длинныхъ проволокъ. Въ случаѣ резонанса, перемѣнное на-
пряженіе между обкладками повышается настолько, что проска-
киваетъ искра. Каждая искра осциллятора сопровождается тогда
Возникновеніе колебаній вслѣдствіе резонанса
333
искрой въ небольшомъ искровомъ промежуткѣ резонансной цѣпи.
Если резонансъ разстроить, для чего достаточно перемѣстить пере-
движную проволоку изъ ея положенія, дающаго резонансъ, то со-
провождающія искры тотчасъ же прекращаются, такъ какъ ампли-
туда напряженія уже не достигаетъ величины, необходимой для
искрового разряда.
Врядъ ли нужно указывать на полную аналогію между этими
резонансными явленіями и резонансомъ механическихъ колебаній,
Рис. 306. Опытъ Лоджа, показывающій резонансъ электрическихъ колебаній.
Искровой промежутокъ осциллятора долженъ быть соединенъ съ полюсами
индуктора.
извѣстнымъ изъ акустики. Если ударить по одному изъ двухъ со-
вершенно одинаково настроенныхъ камертоновъ, то, спустя короткое
время, второй камертонъ также начинаетъ совершать колебанія и
звучать. Если же первый камертонъ слегка разстроить, напримѣръ,
приклеивъ къ его вѣтви шарикъ, то исходящія отъ него воздушныя
колебанія уже не будутъ возбуждать второго камертона.
404. На возбужденіи колебаній посредствомъ резонанса основанъ
важный методъ экспериментальнаго опредѣленія числа періодовъ элек-
тромагнитнаго колебанія. Для этой цѣли употребляютъ измѣрителѣ
частоты, принципъ устройства котораго легко понять изъ рис.
Важнѣйшей частью этого инструмента является передвижно^кон-
денсаторъ; обѣ системы его пластинокъ составлены изъ листовъ въ
~ Ху
формѣ полукруговъ. Одна система пластинокъ закрѣплена^подвижно,
а другая можетъ вращаться вокругъ оси, такъ что въ, промежуточныя
334
Возникновеніе колебаній вслѣдствіе резонанса
пространства неподвижной системы входятъ большій или меньшій
секторъ. Чѣмъ глубже вдвинуть подвижную систему въ неподвиж-
ную, тѣмъ больше будетъ емкость. На оси вращенія наверху помѣ-
щенъ указатель, скользящій по круговой шкалѣ. Обѣ системы пла-
стинъ соединены между собою проволочной окружностью, состоящей
изъ не очень широкихъ витковъ; числа на круговой шкалѣ вмѣсто
емкости даютъ прямо соотвѣтствующее ей число періодовъ цѣпи,
содержащей конденсаторъ и самоиндукцію. Къ аппарату присоеди-
няютъ нѣсколько проволочныхъ окружностей съ различными само-
индукціями; имъ соотвѣтствуютъ нѣсколько чиселъ, нанесенныхъ у
каждаго дѣленія круговой шкалы. Такимъ путемъ при помощи одно-
го инструмента можно получить большую область частотъ. Чтобы
Рис. 307. Измѣритель частоты.
измѣрить число періодовъ электромагнитнаго колебанія, въ пере-
мѣнное поле вводятъ проволочную окружность измѣрителя частотъ та-
кимъ образомъ, чтобы индуктировались возможно болѣе сильные
токи. Послѣ этого устанавливаютъ вращающійся конденсаторъ и
наблюдаютъ, какому дѣленію шкалы соотвѣтствуютъ наиболѣе ин-
тенсивныя индуктированныя колебанія. Интенсивность ихъ опредѣ-
ляется при помощи теплового инструмента, связаннаго индуктивно
при помощи изолированной катушки съ другой небольшой сватуш-
кой, включенной въ цѣпь измѣрителя частотъ. Этотъ ^епловой
инструментъ виденъ на рис. 307 съ лѣвой стороны; нарывающаяся
проволока пропущена черезъ сосудъ небольшого в озду111 наго тер-
мометра, и перемѣщеніе жидкаго столба, сжимаемаго воздухомъ,
служитъ мѣрою нагрѣванія проволоки. Вращающійся конденсанторъ
Возникновеніе колебаній вслѣдствіе резонанса
335
устанавливается такимъ образомъ, чтобы при прочихъ равныхъ усло-
віяхъ воздушный термометръ давалъ максимальную температуру на-
грѣванія. Число колебаній, указываемое при этомъ стрѣлкой, и яв-
ляется искомымъ, такъ какъ измѣритель частотъ на него резонируетъ.
405. Если первичную колебательную цѣпь приблизить къ на-
строенной одинаково съ ней вторичной цѣпи настолько, чтобы обѣ
цѣпи (какъ въ трансформаторѣ) были очень сильно между собою свя-
заны, то наблюдается своеобразное явленіе. Сильное перемѣнное поле
вызываетъ при этихъ условіяхъ во вторичной цѣпи настолько силь-
ные токи, что энергія колебанія послѣдней вскорѣ становится столь
же большой, какъ и у первичнаго осциллятора. Первичный осцилля-
торъ долженъ, конечно, сообщать энергію вторичной цѣпи, и энер-
гія, такимъ образомъ, переходитъ изъ первичной цѣпи во вторич-
Рис. 308. Біенія вслѣдствіе сильной связи двухъ резонирующихъ цѣпей.
ную. Если связь очень сильна, то первичная цѣпь въ концѣ концовъ
отдаетъ всю энергію еще прежде, чѣмъ значительная ея часть истра-
тится въ силу неизбѣжныхъ потерь; тогда во вторичной цѣпи будутъ
господствовать сильныя колебанія, а въ первичной цѣпи они совер-
шенно затухаютъ. Въ этотъ моментъ осцилляторы мѣняются ролями;
второй осцилляторъ отдаетъ энергію первому до тѣхъ поръ, пока
изъ него не выйдетъ вся энергія, и колебанія сохранятся лишь въ
первомъ. Затѣмъ весь процессъ начинается снова. Если при помощи
приспособленнаго для этой цѣли осциллографа снять кривыя коле^
баній, то получаются кривыя, изображенныя на рис. 308. -/4В?
При сильной связи двухъ одинаково настроенныхъ
осцилляторовъ въ нихъ возникаютъ біенія: энергія^оле-
банія поперемѣнно переходитъ отъ одного осциллятора
къ другому. Ч 42/
336 Опыты съ частыми электромагнитными колебаніями
Это явленіе давно уже извѣстно изъ механики. Его можно наблю-
дать, напримѣръ, если два маятника, имѣющіе совершенно одина-
ковые періоды колебаній, подвѣсить рядомъ на упругомъ горизон-
тальномъ стержнѣ, такъ что, благодаря колебанію стержня, энергія
можетъ передаваться отъ одного маятника къ другому. Біенія можно
получить также путемъ сложенія двухъ колебаній, числа пе-
ріодовъ которыхъ немного различаются между собой. Поэтому най-
денный нами выше результатъ можно выразить еще такъ: при проч-
ной связи двухъ одинаково настроенныхъ осцилляторовъ
возникаютъ два налагающіяся одно на другое колебанія,
числа періодовъ которыхъ нѣсколько различаются между
собой. Одно колебаніе нѣсколько медленнѣе, а другое
— быстрѣе по сравненію съ числомъ періодовъ соб-
ственнаго колебанія обоихъ осцилляторовъ, когда они ко-
леблются отдѣльно. Вмѣстѣ они даютъ біенія.
ОПЫТЫ СЪ ЧАСТЫМИ ЭЛЕКТРОМАГНИТНЫМИ КОЛЕБАНІЯМИ.
406. Много поучительныхъ опытовъ съ колебаніями, число пері-
одовъ которыхъ близко къ ІО6, описалъ Тесла; иногда ихъ назы-
ваютъ въ его честь „колебаніями Тесла", хотя вовсе не онъ ихъ
открылъ. Мы опишемъ сейчасъ нѣкоторые опыты Тесла.
Въ противоположность тому, что имѣетъ мѣсто при стаціонар-
ныхъ токахъ, омическое сопротивленіе при конденсаторныхъ ко-
лебаніяхъ играетъ второстепенную роль. Какъ непосредственно
можно предсказать на основаніи теоріи, развитой въ § 400,
главной функціей электрическихъ напряженій перемѣннаго тока вы-
сокой частоты является возбужденіе и прекращеніе быстро мѣ-
няющагося магнитнаго поля. Для преодолѣнія омическаго сопроти-
вленія достаточно чрезвычайно малой доли напряженій, и несравненно
ббльшая часть ихъ идетъ на преодолѣніе самоиндукціи. Если мы соеди-
нимъ обкладки большихъ лейденскихъ банокъ (рис. 309) черезъ искро-
вой промежутокъ и широкую спираль изъ толстой мѣдной прово-
локи и параллельно искровому промежутку приключимъ о мощный
индукторъ, разряды котораго вызываютъ сильныя электромагнитныя
колебанія, то между отдѣльными витками мѣднаго соленоида воз-
никнутъ столь сильныя напряженія, служащія для возбужденія измѣ-
неній магнитнаго поля въ соленоидѣ, чуо при^нфкоторомъ сбли-
женіи двухъ витковъ будутъ проскакивать между ними искры. Полезно
Опыты съ частыми электромагнитными колебаніями
337
заключить искровой промежутокъ осциллятора въ деревянный ящикъ,
какъ показываетъ рис. 309, чтобы рѣзкій свѣтъ искры не мѣшалъ
наблюденіямъ. Если къ двумъ не слишкомъ удаленнымъ другъ отъ
друга виткамъ приложить провода, ведущіе къ лампѣ накаливанія,
то она ярко вспыхиваетъ. Этотъ опытъ долженъ казаться поразитель-
нымъ для незнакомыхъ съ явленіями электрическихъ колебаній, такъ
какъ выходитъ какъ будто, что лампа накаливанія, сопротивленіе ко-
торой составляетъ, можетъ быть, 50 омовъ, замкнута на короткую
Рис. 309. Демонстрація сильныхъ напряженій самоиндукціи въ электри-
ческомъ осциляторѣ.
мѣдной проволокой, сопротивленіе которой меньше ома. Въ дѣй-
ствительности, если бы мы пожелали включенную такимъ образомъ
лампу заставить горѣть помощью постояннаго тока, то мѣдная про-
волока расплавилась бы гораздо раньше, чѣмъ мы могли бы достиг-
нуть нашей цѣли.
407. Съ большими напряженіями въ перемѣнныхъ поляхъ высо-
кой частоты можно хорошо познакомиться на явленіяхъ индукціи.
Если въ разрядную цѣпь лейденскихъ банокъ включить катушку,,
состоящую изъ небольшого числа витковъ съ діаметромъ приб.0?
зительно въ 20 сантиметровъ, и приближать къ ней другую ^кую
катушку съ нѣсколько большимъ числомъ витковъ, въ которую
включена лампа накаливанія, то послѣдняя начинаетъ <^рѣть уже
на довольно большомъ разстояніи отъ первой цѣпи. При надлежа-
Ми. Электричество и магнитизмъ, ч. II. 22
338
Опыты съ частыми электромагнитными колебаніями
щемъ выборѣ катушекъ легко такимъ путемъ заставить горѣть
лампу на 100 и больше вольтъ. Лампа меньшаго напряженія горитъ
уже въ томъ случаѣ, когда вторичная цѣпь состоитъ только изъ
одной мѣдной проволоки, имѣющей форму окружности.
Линіи электрическаго поля, которое должно вызывать измѣне-
нія магнитнаго поля внутри круговой катушки, имѣютъ приблизи-
тельно форму окружностей, концентричныхъ съ катушкой. Это
своеобразное электрическое поле съ замкнутыми силовыми линіями
можно демонстрировать при помощи полаго стекляннаго шара, въ
которомъ воздухъ разрѣженъ настолько, что легко образуются
тихіе разряды. Если ввести этотъ шаръ въ катушку, то мы уви-
димъ въ немъ разрядъ, представляющій собою свѣтящееся кольцо.
Наиболѣе силенъ разрядъ во внѣшней части; сила свѣта слабѣетъ
по мѣрѣ приближенія къ центру шара, гдѣ воздухъ оста-
ется темнымъ. Путь разряда показываетъ намъ здѣсь приблизи-
тельно ходъ силовыхъ линій перемѣннаго электрическаго поля. На
этомъ опытѣ мы можемъ съ особой наглядностью познакомиться съ
сущностью электродинамическихъ полей, а именно съ тѣмъ обсто-
ятельствомъ, что въ нихъ линейная сумма напряженія вдоль замкну-
той кривой не равняется нулю.
408. При всякомъ электрическомъ токѣ напряженіе, приводя-
щее въ движеніе электроны или іоны внутри проводника, и уничто-
жающееся вслѣдствіе передвиженія іоновъ, всегда возстановляется
извнѣ. Какъ мы видѣли въ § 239, функція магнитнаго поля тока
состоитъ въ безпрестанномъ возбужденіи переноса напряженій извнѣ
внутрь проводника. Въ проводникѣ эти напряженія тотчасъ исчеза-
ютъ и съ тѣмъ большей скоростью, чѣмъ больше проводимость.
Поэтому, если внѣшнее поле измѣняется очень быстро, какъ, напри-
мѣръ, при электрическомъ колебаніи, то электрическое напряженіе
въ очень хорошихъ проводникахъ не проникаетъ вовсе вглубь про-
волоки, такъ какъ напряженіе уничтожается въ ея внѣшнихъ слряхъ,
прежде чѣмъ оно вызоветъ достаточно сильное магнитное состояніе
для переноса напряженій вглубь. Внѣшніе слои проводника
экранируютъ его внутреннія части отъ быстрых(ѣ7Электри-
ческихъ колебаній. Только въ томъ случаѣ, есл^фнѣшнее напря-
женіе поддерживается въ теченіе продолжителі^го^времени, поле,
несмотря на непрерывный распадъ, постепенно проникаетъ въ про-
Опыты съ частыми электромагнитными колебаніями
339
водникъ все глубже и глубже. Поэтому при постоянномъ токѣ и
медленномъ перемѣнномъ токѣ заполняется все сѣченіе проводника.
Механическимъ образомъ это-
го явленія служитъ передача дви-
женій черезъ вязкую среду. Если, на-
примѣръ, ремень движется по ремен-
ному шкиву со скольженіемъ при на-
личности между ними слоя смазочна-
го вещества, то отъ ремня черезъ
промежуточный слой до шкива про-
никаютъ лишь болѣе продолжитель-
ныя тяги. Если же дернуть ремень, то
въ вязкомъ промежуточномъ слоѣ
возникаетъ скольженіе: только слой
смазки, прилежащій непосредствен-
но къ ремню, будетъ имъ увле-
каться, внутренніе же слои вслѣд-
ствіе сопротивленія инерціи колеса
будутъ оставаться въ покоѣ. Та-
кимъ образомъ, внутренніе слои
смазки „экранируются" внѣшними
отъ быстрыхъ движеній въ ту и
другую стороны, но очень медлен-
ныя перемѣнныя силы могутъ пе-
редаться, и лучше всего передается
до шкива равномѣрно дѣйству-
ющая тяга.
Экранирующее дѣйствіе внѣш-
нихъ слоевъ проводника по отно-
шенію къ весьма быстрымъ коле-
баніямъ можно демонстрировать на
опытѣ при помощи металлической
трубки, по оси которой протя-
нута мѣдная проволока, соединен-
ная съ обѣихъ сторонъ съ трубкой.
Если такую трубку включить въ разрядную цѣпь конденсатора, то
весь перемѣнный токъ высокой частоты пройдетъ по труф^ѣ, а мѣд-
ная проволока, вообще говоря, не будетъ затронут^/^еремѣннымъ
8 ©
22
340
Опыты съ частыми электромагнитными колебаніями
электромагнитнымъ полемъ. Чтобы это показать, трубку и прово-
локу разрѣзаютъ посрединѣ и обѣ половины какъ трубки, такъ и
проволоки соединяютъ черезъ небольшую лампу накаливанія (рис. 310).
При этомъ будетъ горѣть лишь лампа накаливанія, включенная
въ трубку, тогда какъ лампа, включенная въ проволоку, останется
темной. Если къ концамъ трубки приложить постоянное напряженіе
надлежащей величины, то обѣ лампы горятъ одинаково ярко.
Изъ теоріи экранирующаго дѣйствія непосредственно слѣдуетъ,
что оно будетъ выражено тѣмъ сильнѣе, чѣмъ выше число періодовъ
и чѣмъ больше проводимость. При обычно примѣняемомъ въ техни-
кѣ числѣ періодовъ—50 въ секунду —даже мѣдная проволока тол-
щиною въ 1 — 2 см. даетъ едва замѣтную разницу въ плотно-
сти тока во внутреннихъ и внѣшнихъ ея слояхъ; по оси плот-
ность тока лишь на нѣсколько процентовъ меньше, чѣмъ на поверх-
ности. Но если число періодовъ достигаетъ ІО6 въ секунду, то въ
мѣди токъ ограничивается преимущественно поверхностнымъ слоемъ
толщиною въ 0,1—0,2 мм., а при еще большихъ частотахъ прово-
дящій слой сокращается до нѣсколькихъ микроновъ (1 микронъ =
0,001 мм.).
Отсюда вытекаетъ весьма важное въ практическомъ отношеніи
слѣдствіе: во первыхъ, при быстрыхъ электрическихъ колебаніяхъ оми-
ческое сопротивленіе проволоки гораздо больше, нежели при постоян-
номъ токѣ; во-вторыхъ, у быстрыхъ электрическихъ колебаній омиче-
ское сопротивленіе зависитъ не отъ поперечнаго сѣченія проводника,
какъ въ случаѣ постояннаго тока, но отъ его поверхности. Тонко-
стѣнная трубка представляетъ для колебаній такое же сопротивленіе,
какъ и массивная проволока изъ того же матеріала и одинаковаго внѣш-
няго діаметра. Поэтому брать толстыя проволоки съ цѣлью уменьшить
сопротивленіе значило бы понапрасну терять матеріалъ. Весьма вы-
годными проводами для колебаній высокой частоты являются широ-
кія полосы изъ тонкихъ металлическихъ листовъ. Въ техникѣ без-
проволочной телеграфіи пользуются тонко подраздѣленными довода-
ми, составленными изъ отдѣльныхъ изолированныхъ чрезвычайно тон-
кихъ мѣдныхъ нитей.
Проводники съ незначительной проводимостью, ^примѣръ, элек-
тролиты, обладаютъ лишь малымъ экранирующи^і^Дѣйствіемъ. На-
примѣръ, колебаніе въ ІО6 періодовъ проникаетъ въ наиболѣе хо-
рошо проводящіе водные растворы на глубину, въ 10 см. и еще
глубже, ослабѣвая лишь на немного процентовъ.
Трансформаторъ Тесла
341
ТРАНСФОРМАТОРЪ ТЕСЛА.
409. Перемѣнный токъ высокой частоты въ разрядной цѣпи
лейденской банки можно трансформировать на болѣе высокія напря-
женія совершенно такимъ же образомъ, какъ и перемѣнный токъ
малаго числа періодовъ. Однако, трансформаторы для высокихъ
частотъ, трансформаторы Тесла, въ одномъ пунктѣ существенно
отличаются отъ трансформаторовъ для меньшихъ частотъ: они не
имѣютъ желѣзнаго сердечника. Желѣзный сердечникъ въ обыкновен-
ныхъ трансформаторахъ перемѣннаго тока имѣютъ цѣлью увеличи-
вать индуктивныя напряженія настолько, чтобы омическія потери на-
Рис. 311. Трансформаторъ Тесла.
пряженія сравнительно съ ними были ничтожно малы, и чтобы индук-
тивная связь вслѣдствіе этого сопровождалась весьма малыми поте-
рями энергіи. При весьма большихъ частотахъ индуктивныя напря-
женія, какъ можно заключить изъ фактовъ, описанныхъ въ § § 406
и 407, и безъ желѣзнаго сердечника преобладаютъ настолько, что въ -
немъ нѣтъ никакой необходимости. Если бы такой трансформаторъ^
снабдить желѣзнымъ сердечникомъ, то это оказалось бы скорѣе^^?
нымъ, нежели полезнымъ. Даже если бы сердечникъ былъ изготовленъ
изъ тонкихъ изолированныхъ желѣзныхъ проволокъ, то вЪх ОТдѣль-
ныхъ проволокахъ возникали бы столь сильные вихревые\токи, что,
во-первыхъ, не происходило бы никакого существеннаго усиленія
342
Трансформаторъ Тесла
магнитнаго поля и его индуктивныхъ напряженій вслѣдствіе того, что
проволоки экранируются вихревыми токами отъ поля, и, во-вторыхъ, на-
грѣваніе вихревыми токами вызывало бы значительную потерю энергіи.
Весьма употребительная форма трансформатора Тесла пред-
ставлена на рис. 311. Емкостью служитъ лейденская банка; искро-
вой промежутокъ заключаютъ въ деревянный ящикъ, чтобы при
опытахъ не мѣшалъ его рѣзкій свѣтъ. Самоиндукція колебательной
цѣпи, служащая также первичной катушкой трансформатора, состоитъ
изъ небольшого числа витковъ весьма толстой негибкой мѣдной про-
волоки. Вторичная обмотка, окруженная первичной обмоткой, состо-
итъ изъ весьма большого числа витковъ тонкой изолированной прово-
локи, намотанной на стеклянный цилиндръ. Весь трансформаторъ по-
мѣщается въ параффиновое масло для достиженія хорошей изоля-
ціи. Если бы вторичная катушка пэмѣщячась въ воздухѣ, то невоз
можно было бы избѣжать разрядовъ между ея тонкими, густо на-
витыми проволоками. Въ установкѣ, изображенной ниже на рис. 326,
виденъ подобный трансформаторъ Тесла безъ сосуда съ параффи-
новымъ масломъ. Зато здѣсь вся вторичная катушка залита твердымъ
параффиномъ, такъ что она имѣетъ видъ толстаго параффино-
ваго стержня.
Если присоединить въ воздухѣ ко вторичнымъ зажимамъ транс-
форматора Тесла тонкія проволоки, то онѣ цѣликомъ покрываются
сѣтью тонкихъ свѣтящихся линій и получаютъ видъ тонкихъ вѣтокъ,
покрытыхъ инеемъ. Эту нѣжную свѣтящуюся паутину образуютъ пу-
ти разряда. Какъ высоки напряженія около провода трансформа-
тора, можно видѣть, если приблизить къ нему эвакуированную
стеклянную трубку безъ электродовъ. Она вспыхиваетъ тлѣющимъ
свѣтомъ, совершенно ее заполняющимъ.
Интересно, что эти высокія перемѣнныя напряженія производятъ
лишь слабыя физіологическія дѣйствія. Можно дотрагиваться рукой
до полюсовъ трансформатора Тесла, можно пропускать черезъ рурсу
искры длиною въ нѣсколько сантиметровъ, не испытывая принтомъ
электрическаго толчка. Что при этомъ черезъ тѣло дѣйствительно
проходятъ электрическіе токи, видно изъ гого, что, есл^въ одной
рукѣ держать эвакуированную трубку, а другою казаться полюса
трансформатора Тесла, то трубка ярко вспыхиваетъ^ Отсутствіе фи-
зіологическаго дѣйствія, вѣроятно, объясняется отфмъ, что при малой
силѣ тока во вторичной катушкѣ количествѣ электричества, про-
Колебанія при исчезновеніи магнитнаго поля
343
ходящее за весьма короткое время одного полуперіода въ одномъ
направленіи, настолько ничтожно, что вызываемое имъ въ нашемъ
тѣлѣ электролитическое разложеніе меньше того, которое необхо-
димо для возбужденія нервовъ. Отсутствіе физіологическаго дѣй-
ствія, во всякомъ случаѣ, связано съ высокой частотой колебаній.
Часто пользуются, вмѣсто обычнаго трансформатора или индук-
тора, трансформаторомъ Тесла, чтобы при помощи его разря-
довъ получать электрическія колебанія чрезвычайно высокой частоты
(ІО8 и болѣе періодовъ въ секунду). Онъ даетъ, во-первыхъ, весьма
высокія разрядныя напряженія и потому весьма дѣятельныя искры
небольшого сопротивленія. Во-вторыхъ, число искръ въ секунду въ
этомъ случаѣ очень велико, а именно, равняется числу колебаній; такъ
какъ каждая искра сопровождается рядомъ требуемыхъ колебаній
высокой частоты, то энергія этихъ колебаній, приходящаяся на секунду,
весьма велика. Во всѣхъ случаяхъ, когда нужно измѣрить колебанія
весьма высокаго числа періодовъ при помощи термоэлемента или
нагрѣвающейся проволоки, по указаннымъ причинамъ удобно вызы-
вать колебанія при помощи разрядовъ аппарата Тесла, имѣющихъ
нѣсколько милліоновъ періодовъ въ секунду.
КОЛЕБАНІЯ ПРИ ИСЧЕЗНОВЕНІИ МАГНИТНАГО ПОЛЯ.
410. Подобно тому, какъ при внезапномъ короткомъ замыка-
ніи электрическая энергія конденсатора прежде всего преобразуется
въ магнитную энергію и возникаютъ электрическія колебанія, точно
такъ же, если внезапно прервать электрическій токъ, изъ энергіи
магнитнаго поля тока получается электрическая энергія, такъ какъ
въ мѣстѣ перерыва вслѣдствіе самоиндукціи образуется сильное
электрическое поле и могутъ возникнуть также электрическія коле-
банія. Для ихъ возбужденія нужно при помощи емкости, присоеди-
ненной параллельно мѣсту перерыва, воспрепятствовать тому, чтобы
чрезмѣрно возростали напряженія и энергія поля тотчасъ же /
уничтожалась черезъ процессы разряда. Въ § 382 мы видѣли,^»
что въ индукціонныхъ аппаратахъ по большей части параллельно
мѣсту перерыва первичной катушки присоединяется конденсаторъ
достаточно большой емкости. Поэтому разрывъ первичьіД^о тока
сопровождается электрическими колебаніями, при чемъ' конден-
саторъ вслѣдствіе самоиндукціи сначала заряжается^^затѣмъ разря-
344
Колебанія при исчезновеніи магнитнаго поля
жается, вновь заряжается и т. д. Эти колебанія, конечно, весьма
сильно затухаютъ, и напряженіе индукціоннаго аппарата возраста-
етъ особенно высоко лишь въ теченіе перваго полуперіода, когда пер-
вичный токъ падаетъ до нуля и затѣмъ обращается; однако, и послѣ-
дующія перемѣнныя напряженія часто бываютъ замѣтны. Въ гейс-
слеровыхъ трубкахъ, соединенныхъ съ индукціоннымъ аппаратомъ,
въ тѣхъ случаяхъ, когда ихъ разрядное напряженіе не слишкомъ
высоко, часто наблюдается не желаемый односторонній разрядъ, но
перемѣнный токъ. Въ этихъ случаяхъ оба электрода одновременно
Рис. 312. Демонстрація колебаній, возникающихъ при исчезновеніи магнит-
наго поля, по Кенигу.
обнаруживаютъ признаки анода и катода, но всегда, однако, разрядъ
обладаетъ большей интенсивностью въ одномъ направленіи, а
именно, въ направленіи перваго полуколебанія.
Колебанія, возникающія при внезапномъ исчезновеніи магнит-
наго поля, въ случаѣ, когда имѣется параллельно присоединенная
емкость, могутъ быть легко демонстрированы на интересномъ опытѣ,
описанномъ Кенигомъ (\Ѵ. Кбпі^). Какъ показываетъ рис. Д12,
вторичные зажимы индуктора соединяются съ обкладками лейден-
ской банки. Въ первичную цѣпь не включаютъ автоматическаго пре-
рывателя, а лишь ртутную чашку для того, чтобы одиііъ^азъ пре-
рвать токъ. Когда прекращается токъ первичной цѣ^пи,^возникаетъ
токъ во вторичной цѣпи, такъ какъ магнитное полене можетъ ис-
чезнуть само по себѣ; лейденская банка заряжается, и только возни-
кающее при этомъ электрическое напряженк/ приводитъ магнитное
Гудокъ (Зуммеръ)
345
поле въ состояніе покоя. Послѣ этого лейденская банка вновь раз-
ряжается и такимъ образомъ возникаетъ рядъ колебаній. Если вну-
треннюю обкладку банки соединить съ остріемъ, подъ которымъ при
помощи вращающаго аппарата быстро вращается эбонитовый дискъ,
то на него при каждомъ колебаніи переходитъ небольшой разрядъ,
и на дискѣ получаются въ правильной послѣдовательности продолго-
ватыя пятна то съ положительными, то съ отрицательными зарядами.
Чтобы сдѣлать ихъ видимыми, посыпаютъ пластинку изобрѣтен-
нымъ Лихтенбергомъ порошкомъ изъ сѣры и сурика. Этотъ поро-
шокъ обладаетъ тѣмъ свойствомъ, что при контактѣ частички сѣры
заряжаются отрицательнымъ электричествомъ, а частички сурика —
положительнымъ электричествомъ. На эбонитовомъ дискѣ положи-
тельно заряженныя полосы получаютъ отъ сѣры желтый цвѣтъ, а
отрицательно заряженныя—красный отъ сурика.
ГУДОКЪ (ЗУММЕРЪ).
411. Зуммеръ представляетъ собою небольшой инструментъ,
помощью котораго можно получить равномѣрный звукъ; иногда
зуммеръ употребляется въ телефонѣ, вмѣсто сигнальнаго звонка.
Дѣйствіе зуммера основано на возбужденіи электрическихъ колебаній
перемѣннымъ магнитнымъ полемъ. Какъ показываетъ рис. 313, зуммеръ
въ извѣстной степени представляетъ собой одновременно микрофонъ
и телефонъ. Въ микрофонную цѣпь включена первичная катушка не-
большого трансформатора; его вторичная катушка соединена черезъ
телефонную катушку съ обоими рядами пластинъ конденсатора.
Когда первичная цѣпь замыкается, то во вторичной цѣпи возника-
ютъ электрическія колебанія, такъ какъ конденсаторъ заряжается
вслѣдствіе индукціоннаго дѣйствія при замыканіи тока. Число періо-
довъ этихъ колебаній опредѣляется самоиндукціей вторичной катушки
и емкостью включеннаго конденсатора. Такъ какъ токъ вторичной
катушки проходитъ черезъ телефонъ инструмента, то электрическія
колебанія приводятъ желѣзную телефонную мембрану въ колебанія
съ одинаковымъ числомъ періодовъ. Телефонная мембрана имѣет^
снизу посрединѣ небольшую угольную пластинку и одновременно
служитъ также и микрофонной мембраной; телефонный магнитъ
имѣетъ форму полаго цилиндра, внутри котораго вдѣлан;]^? микро-
фонный угольный контактъ. Такъ какъ микрофонъ вьюченъ въ
первичную цѣпь и колебанія микрофона имѣютъ т^ое же число
346
Гудокъ (Зуммеръ)
періодовъ, какъ и собственныя колебанія вторичной цѣпи, то оба
колебанія взаимно усиливаются вслѣдствіе резонанса, и инструментъ
звучитъ все время, пока первичный токъ остается замкнутымъ. Зум-
меръ часто примѣняется при измѣреніяхъ, когда требуются весьма чи-
стыя синусоидальныя колебанія, такъ какъ его колебанія отличаются
чистотой. Кромѣ того, число его періодовъ можно съ удобствомъ
мѣнять въ широкихъ предѣлахъ, измѣняя включенную во вторичную
цѣпь емкость.
о Ог^А)0
КОЛЕБАНІЯ СВѢТОВОЙ ДУГИ.
412. Какъ мы видѣли въ § 190, свѣтовая дуга^ должна стать
прерывающейся, если параллельно ей включена^<фльшая емкость.
Если въ параллельное дугѣ отвѣтвленіе включить емкость въ
нѣсколько микрофарадъ и, кромѣ того, самоиндукцію въ нѣсколько.
Колебанія свѣтовой дуги
347
миллигенри, то возникаютъ сравнительно медленныя колебанія, кото-
рыя тотчасъ проявляются въ томъ, что свѣтовая дуга начинаетъ изда-
вать соотвѣтственный тонъ (ср. § 189). Для удачи опыта необходимо,
чтобы самоиндукціонная катушка не поглощала много энергіи, т.-е.
чтобы она состояла изъ витковъ довольно толстой мѣдной про-
волоки и не имѣла желѣзнаго сердечника. Кромѣ того, свѣтовая
дуга должна быть довольно неустойчивой. Если берутъ угольные
электроды, то они должны быть сдѣланы не изъ „угля съ фити-
лемъ", обычно употребляемаго для анода въ лампахъ, но изъ такъ
называемаго гомогеннаго угля, на которомъ свѣтовая дуга не дер-
жится такъ прочно, какъ на мягкомъ углѣ съ фитилемъ. Источникъ
электричества долженъ имѣть достаточно высокое напряженіе, во
Рис. 314. Схема включенія звучащей свѣтовой дуги.
всякомъ случаѣ, въ нѣсколько сотъ вольтъ, и въ провода должно
быть включено большое сопротивленіе. Благодаря этому свѣтовая
дуга можетъ горѣть при слабомь токѣ и не тухнетъ легко, какъ это
имѣло бы мѣсто про низкомъ напряженіи. Слабый токъ благопріятенъ
для колебаній, такъ какъ онъ лишь незначительно нагрѣваетъ уголь-
ныя острія, и потому дуга весьма неустойчива. Кромѣ того, полезно
еще включить въ проводы дроссельную катушку (рис. 314), чтобы
колебанія по возможности хорошо поглощались и не отнимались
отъ конденсаторной цѣпи. Такимъ путемъ Дуддель (Оіккіеіі) впер-
вые получилъ и наблюдалъ колебанія.
Болѣе тщательное изслѣдованіе колеблющейся свѣтовой дуги
было произведено впервые Г. Т. Симономъ. Кривыя, представле-
ныя на рис. 315, были сняты имъ при помощи двойного осцилло-
графа (ср. § 286) со звучащей угольной свѣтовой дуги. ^Кривая,
обозначенная буквой У, даетъ дуговой токъ; кривая Ѵ'д^электри-
ческое напряженіе между электродами свѣтовой дуги, а кривая Ѵг—
тт х
напряженіе между пластинами конденсатора. Дв^первыя кривыя
348
Колебанія свѣтовой дуги
заимствованы изъ работы Симона, послѣдняя же вычислена изъ
первыхъ по даннымъ его опытовъ. Въ проводъ отъ источника тока была
включена такая самоиндукція, что токъ почти постоянно рав-
нялся 2,2 амперамъ; такова же средняя сила тока, проходившаго
чрезъ свѣтовую дугу. Если принять прямую /0 = 2,2 за нулевую
| Вольты
Рис. 315. Кривыя силы тока и напряженія звучащей свѣтовой дуги.
Средняя сила тока 2,2 ялш., среднее напряженіе 71 е., напряженіе источника тока
220 в , длина свѣтовой дуги 3 мм., емкость 14 МФ., самоиндукція 0,006 генри, число
колебаній 420.
-------- сила тока \
-------- напряженіе свѣтовой дуги V / У’
--------вычисленное напряженіе Ѵ\ конденсатора.
Симонъ для трехъ послѣднихъ величинъ даетъ значенія 15 ЛФ, 0,007 Н и 450; ,мы
нѣсколько измѣнили ихъ для того, чтобы кривыя согласовались между собрк^
О
ось, то кривая У непосредственно представитъ намъ перемѣнный
токъ въ конденсаторной цѣпи, который въ свѣтовой дугѣ/налагается
на токъ /0 = 2,2. Среднее значеніе напряженій достига^> 71 вольта;
обѣ кривыя напряженій проведены такъ, что пря^^/ѵ0 = 71 вольту
совпадаетъ съ прямою = 2,2 амперъ. Явленіе двучащей дуги проте-
каетъ слѣдующимъ образомъ. Когда свѣтоваяСдуга еще не горитъ,
Амперы
Колебанія свѣтовой дуги
349
въ пластины конденсатора проходитъ постоянный токъ /0, который
его и заряжаетъ. При этомъ напряженія находятся въ статическомъ
равновѣсіи, такъ какъ магнитное поле не измѣняется; такимъ обра-
зомъ, если пренебречь небольшой потерей напряженія вслѣдствіе
омическаго сопротивленія, то имѣетъ мѣсто равенство Ѵг = V'. Это
продолжается до тѣхъ поръ, пока конденсаторъ не зарядится до
напряженія, вызывающаго воспламененіе свѣтовой дуги; въ этотъ
моментъ начинается разрядъ черезъ свѣтовую дугу и вмѣстѣ съ тѣмъ
новая стадія явленія. Если свѣтовая дуга уже горѣла раньше, то,
какъ мы знаемъ (§ 193), напряженіе, необходимое для воспламененія,
довольно низко; кривая V на рис. 315 даетъ 113 вольтъ. Часть
АВ на рис. 315 соотвѣтствуетъ описанному сейчасъ процессу заря-
женія. При опытѣ, которому соотвѣтствуетъ рис. 315, дуговой
промежутокъ не былъ вполнѣ лишенъ тока — онъ слегка прово-
дилъ, такъ какъ электроды были еще накалены отъ предыду-
щаго разряда; поэтому все время черезъ него шелъ слабый и
почти постоянный токъ (около 0,4 амперъ). Этотъ токъ лишь слегка по-
нижалъ зарядный токъ, но, кромѣ этого, никакого вліянія на процессъ не
имѣлъ. Продолжительность этого періода заряженія зависитъ отъ
силы тока /0 — /, емкости конденсатора и величины напряженія, необ-
ходимой для воспламененія дуги. Когда это напряженіе достигнуто,
устанавливается настоящая свѣтовая дуга, и, пока въ ней возраста-
етъ токъ, разрядное напряженіе значительно понижается. Вслѣдствіе
этого между конденсаторомъ и электродами возникаетъ разность
напряженій — И, поддерживающая магнитное поле тока въ само-
индукціонной катушкѣ и такимъ образомъ вызывающая паденіе заряд-
наго тока конденсатора въ такой мѣрѣ, въ какой возрастаетъ токъ
въ свѣтовой дугѣ. Сумма обоихъ токовъ постоянна и равна Ѵо.
Вскорѣ (С на рис. 315) токъ въ конденсаторной цѣпи совершенно
исчезаетъ, а токъ въ свѣтовой дугѣ достигаетъ величины /0. Въ
этотъ моментъ зарядъ конденсатора достигаетъ максимума, и конденса-
торъ начинаетъ разряжаться, вслѣдствіе чего токъ въ свѣтовой дугѣ пре-
выситъ значеніе /0. Разрядный токъ возрастаетъ и достигаетъ максИ|Э
мума, когда конденсаторъ разрядится до напряженія свѣтовой дуги
(О на.рис. 315). Съ этого момента токъ убываетъ, такъ какъ^ежду
конденсаторомъ и электродами образуется противоположу ^напра-
вленная разность напряженій — V. Когда токъ упадетъ до /0,
разрядъ конденсатора прекращается, и его напряженіе достигаетъ мини-
350
Колебанія свѣтовой дуги
мума (Е на рис. 315, 5 вольтъ). Въ теченіе разряда (отъ С до Е)
напряженіе свѣтовой дуги колеблется лишь незначительно въ срав-
неніи съ сильнымъ измѣненіемъ напряженія конденсатора, и весь
процессъ поэтому протекаетъ совершенно такъ же, какъ полъ-пе-
ріода колеблющейся искры. Продолжительность процесса между С и Е
поэтому можетъ быть вычислена по формулѣ у = тт. ]//, . С, что даетъ
въ нашемъ случаѣ 0,91 . 10~3 секунды, величину, согласующуюся съ
длиною отрѣзка СЕ на рис. 315. Во вторую половину процесса раз-
ряда {ЕЕ) напряженіе свѣтовой дуги вновь возрастаетъ вслѣдствіе
уменьшенія дугового тока, но не достигаетъ той высоты, которую
оно имѣло вначалѣ, въ точкѣ С, такъ какъ тѣмъ временемъ элек-
троды успѣли сильнѣе накалиться подъ дѣйствіемъ свѣтовой дуги, и
потому іонизація сильнѣе, нежели въ С. Это явленіе послѣдѣйствія,
о которомъ мы уже упоминали въ § 193, Симонъ называетъ гисте-
резисомъ свѣтовой дуги. Гораздо сильнѣе еще оно обнаружи-
вается въ слѣдующій, послѣдній процессъ колебанія ЕА, когда кон-
денсаторъ начинаетъ вновь заряжаться и дуговой токъ поэтому
Рис. 316. Кривая напряженія и
силы тока свѣтовой дуги при
колебаніи, представленномъ на
рис. 315.
параллельно включенному зарядному
току. Изъ рис. 315 видно, что тамъ,
гдѣ дуговой токъ У падаетъ очень
быстро — около точки Е—кривая на-
пряженія вообще перестаетъ поды-
маться. По достиженіи максимума она
внезапно падаетъ вмѣстѣ съ кривою
тока совершенно такъ, какъ если бы
свѣтовая дуга подчинялась закону Ома.
Это является слѣдствіемъ имѣющейся
еще іонизаціи газоваго участка и вы-
сокой температуры электродовъ, ко-
торыя не исчезаютъ сейчасъ же съ
уменьшеніемъ дугового тока. Но такъ
какъ при слабомъ токѣ и слабомъ
напряженіи дуговому промежутку до-
ставляется мало энергіи, за про-
межутокъ времени ЕДлтёмпература
и іонизація въ концѣ все же очень
і. К V
падаютъ, свѣтовая дуі а почти тухнетъ,
и остается лишь небольшой остаточный то^ѣ^ъ нашемъ примѣрѣ
Колебанія свѣтовой дуги
351
равный 0,4 ампера. Такъ въ промежутокъ ЕА подготовляется фаза
заряженія ЛВ, которой мы начали описаніе. Гистерезисъ свѣто-
вой дуги при электрическомъ колебаніи выступаетъ особенно
отчетливо, если построить кривую напряженій и силъ тока, какъ
на рис. 316. Очевидно ея сходство съ кривой рис. 127, если при-
нять во вниманіе различіе масштабовъ. Заряженіе конденсатора, про-
исходящее цѣликомъ между Е и С, въ противоположность разряду (СЕ)
не слѣдуетъ закону искровыхъ колебаній. Напримѣръ, продолжи-
тельность процесса ЛВ, какъ мы уже указали, зависитъ отъ вели-
чины постоянной силы тока /0 — т.-е. между прочимъ и отъ сопро-
тивленій въ проводахъ, идущихъ отъ источника тока, но не отъ само-
индукціи конденсаторной цѣпи. Кромѣ того, продолжительность про-
межутка АВ зависитъ также отъ напряженія, необходимаго для
возникновенія свѣтовой дуги, а такъ какъ это напряженіе зависитъ
отъ природы электродовъ, длины дугового промежутка и силы ду-
гового разряда въ предыдущее колебаніе, то трудно достигнуть, что-
бы полная продолжительность колебанія звучащей свѣтовой дуги была
совершенно постоянной. При каждомъ измѣненіи и перемѣщеніи свѣто-
вой дуги немного измѣняется также и продолжительность колебанія. Она
всегда нѣсколько больше количества, вычисленнаго по формулѣ Томсо-
на т = 2п. рТГс, такъ какъ при заряженіи неизбѣжно протекаетъ
промежутокъ ЛВ, въ теченіе котораго токъ приблизительно посто-
яненъ. Поэтому кривая тока при заряженіи, т.-е. отъ Е до С, должна
быть болѣе плоской и широкой, нежели при разряженіи отъ С до Е,
гдѣ она имѣетъ правильную синусоидальную форму. Такъ какъ промежу-
токъ времени СЕ равняется п . ]/С. 7, то промежутокъ ЕС долженъ
быть больше, чѣмъ тг ,уЬ. С, и весь процессъ поэтому долженъ
длиться болѣе, нежели 2тг.]ЛЬ.С секундъ. Въ случаѣ, предста-
вленномъ на рис. 315, 2тг. . С — 1,83.10—3 сек., а продолжитель-
ность колебанія равна 2,83.10—3 сек.
413. Описаннымъ сейчасъ образомъ происходятъ электрическія
колебанія въ конденсаторной цѣпи, присоединенной параллельно къ
свѣтовой дугѣ; они продолжаются все время, пока свѣтовая ду.Ц
горитъ, подобно тому, какъ механическія колебанія въ воздушномъ
столбѣ органной трубы длятся все время, пока производится вдуваніе.
Подобно тому, какъ въ органной трубѣ сила вдуваемаго\тбка имѣ-
етъ рѣшающее значеніе для возникновенія колебаній, т^ъ въ случаѣ
352
Колебанія свѣтовой дуги
Свѣтильный
газъ
Рис. 317. Лампа Поульсена для
лабораторныхъ опытовъ.
колеблющейся свѣтовой дуги эту роль играетъ сила тока дуги. Если
токъ слишкомъ слабъ, то во время заряда конденсатора электроды
охлаждаются столь значительно, что напряженіе, необходимое для
воспламененія дуги, превышаетъ наличное напряженіе, вслѣдствіе чего
свѣтовая дуга окончательно тухнетъ. Если же сила тока слишкомъ
велика, то электроды нагрѣваются столь сильно, что быстрыя коле-
банія тока не могутъ вызвать охлажденія, необходимаго для возник-
новенія длительныхъ колебаній, и дуга горитъ тогда непрерывно,
безъ колебаній. Легче всего получаются сравнительно медленныя коле-
банія, въ особенности если пользоваться
весьма большими емкостями и сравни-
тельно малыми самоиндукціями.
Если желательно получить быстрыя
колебанія, то прежде всего слѣдуетъ
позаботиться объ очень хорошемъ охла-
жденіи электродовъ для того, чтобы
температура ихъ могла точно слѣдо-
вать за колебаніями тока. Это было
впервые достигнуто на практикѣ Поуль-
сеномъ (Роиізеп). На рис. 317 изобра-
жена лампа Поульсена въ формѣ
весьма удобной для демонстрацій. Одинъ
электродъ представляетъ собою тол-
стый мѣдный стержень, на которомъ
сдѣлана винтовая нарѣзка, такъ что вращеніемъ въ гайкѣ его можно
очень медленно передвигать впередъ или назадъ. Другой элек-
тродъ представляетъ собою угольный стержень, имѣющій каналъ
вдоль оси, и одновременно служитъ подводящей трубкой для
свѣтильнаго газа или водорода, которымъ наполняется сосудъ, гдѣ
горитъ свѣтовая дуга. Благодаря примѣненію мѣднаго стержня и
легкаго газа, т.-е. веществъ, хорошо проводящихъ теплоту, электроды
при пониженіи силы тока тотчасъ же охлаждаются. Для того, ^ѣобы
вся лампа съ теченіемъ времени не накалялась, въ ней имѣйся еще
приспособленіе для охлажденія водой. Свѣтовая дуга ^ульсена
должна быть очень коротка и горѣть при высокомъ^напряженіи;
важно также тщательно регулировать силу тока. Если желательно
достигнуть очень быстрыхъ колебаній, то слѣдуетъ, какъ указано
на рис. 317, мѣдный стержень дѣлать катодомъ, такъ какъ катодъ
Вода для
охлажденія
Колебанія свѣтовой дуги
353
свѣтовой дуги особенно чувствителенъ къ колебаніямъ температуры
(§ 185). Если переключить электроды, то нельзя уже достигнуть
столь высокаго числа колебаній, но зато въ этомъ случаѣ дуга го-
ритъ спокойнѣе и не такъ легко тухнетъ.
Съ помощью лампы Поульсена легко получаются колебанія
такой частоты, какъ колебанія Тесла (около ІО6 въ секунду). Кри-
выя колебаній лампы Поульсена отличаются отъ кривыхъ рис. 315,
соотвѣтствующихъ колебаніямъ угольной свѣтовой дуги, прежде
всего тѣмъ, что измѣненія напряженія на нихъ значительно больше
вслѣдствіе повышенной величины напряженія, необходимаго для за-
жиганія дуги. Конденсаторъ не только разряжается, но еще и за-
ряжается противоположно; точно также и напряженіе у электродовъ на
мгновеніе становится отрицательнымъ. Кромѣ того, когда напря-
женіе падаетъ до нуля и мѣняетъ знакъ, свѣтовая дуга почти со-
вершенно тухнетъ вслѣдствіе хорошаго охлажденія электродовъ;
во всякомъ случаѣ, остающаяся въ дугѣ сила тока значительно
меньше, нежели въ колебаніяхъ, представленныхъ на рис. 315. Ко-
лебанія, при которыхъ напряженіе на электродахъ никогда не дости-
гаютъ нуля и токъ свѣтовой дуги не затухаетъ совершенно, назы-
ваются колебаніями перваго рода, а колебанія, при которыхъ
напряженіе у электродовъ переходитъ черезъ нуль и становится
отрицательнымъ, при чемъ дуговой токъ почти совершенно прекра-
щается, называются колебаніями второго рода.
414. Нѣчто совершенно отличное отъ описанныхъ колебаній
представляютъ собою такъ называемыя колебанія третьяго рода;
они получаются, если пользоваться весьма высокимъ напряженіемъ и
весьма большимъ добавочнымъ сопротивленіемъ. Въ этомъ слу-
чаѣ происходитъ обычный прерывистый разрядъ, описанный въ § 169.
Если емкость не слишкомъ мала, то тлѣющій разрядъ каждый разъ
переходитъ въ свѣтовую дугу, и получается прерывистая свѣтовая
дуга, состоящая изъ безчисленнаго множества быстро слѣдующихъ
другъ за другомъ „частичныхъ разрядовъ". Легче всего это удаетс^?
при металлическихъ электродахъ (ср. §190), но особенной кра<^угой
и правильностью явленіе отличается при хорошо охлаждаемой ртутной
лампѣ съ двумя ртутными электродами и короткой свѣтспюй/дугой.
Впрочемъ, прерывистый характеръ свѣтовой дуги легкоЗ^бнаружить
по звучанію телефона, включеннаго въ проводъ, а^мъ^случаѣ сво-
бодной дуги—по издаваемому ею шуму наподобіе^цййпінія. Каждый
Ми. Электричество и магнитизмъ, ч. II. 23
ё
х
'О
к
и?
О
2
и1
У
и
354
Возбужденіе электромагнитныхъ колебаній толчками
малый частичный разрядъ представляетъ собою настоящую, хотя и
слабую, электрическую искру и сопровождается небольшимъ числомъ
сильно затухающихъ колебаній, продолжительность которыхъ можетъ
быть вычислена посредствомъ формулы Томсона по даннымъ емкости
и самоиндукціи отвѣтвленія. Хотя каждая отдѣльная искра разви-
ваетъ лишь весьма малую энергію колебанія, однако, вслѣдствіе
чрезвычайно большого числа искръ энергія колебаній, приходящаяся
на секунду, можетъ оказаться достаточно большой, чтобы съ нею
удобно было экспериментировать. Такимъ образомъ, колебанія свѣ-
товой дуги третьяго рода въ дѣйствительности являются лишь видо-
измѣненіемъ искровыхъ колебаній, хотя чрезвычайно малая, слабо
свѣтящая, слегка лишь шумящая прерывистая свѣтовая дуга внѣш-
нимъ образомъ совершенно отличается отъ яркой, громко и рѣзко
трещащей искры, которою обычно возбуждаются искровыя колеба-
нія. Въ послѣднее время особенно важное значеніе пріобрѣли сла-
быя шипящія искры съ очень быстро затухающими колебаніями.
ВОЗБУЖДЕНІЕ ЭЛЕКТРОМАГНИТНЫХЪ КОЛЕБАНІЙ ТОЛЧКАМИ.
415. Мы видѣли въ § 405, что посредствомъ тѣсной связи съ
резонирующей колебательной цѣпью можно очень быстро отнять
отъ электрическаго осциллятора его энергію колебанія. Въ томъ
случаѣ, который представленъ кривыми въ § 405, примѣрно уже
послѣ четырехъ полныхъ колебаній вся энергія переходитъ изъ пер-
вичной цѣпи во вторичную. Если первичная искра очень сильна, то
искровой промежутокъ еще. долгое время остается проводящимъ,
хотя его сопротивленіе съ убываніемъ средней силы тока постепенно
возрастаетъ; энергія колебанія много разъ переходитъ отъ первич-
ной цѣпи во вторичную и обратно. Явленіе совершенно мѣняется,
когда первичная искра представляетъ собою небольшую, слабую
шипящую искру, которая производитъ у электродовъ весьма
лишь незначительныя количества теплоты. Въ этомъ случаѣ легко
достигнуть того, чтобы въ теченіе того времени, за котовое
энерги^ переходи т па вторичную цѣпь, электроды совершенно ^хла-
мсдались г так чтобы искровой промежутокъ при токѣ, равно^т?нулю,
Затѵхал, т.-е. совер шенно терялъ проводимость и преграждалъ путь
То Ну утон энергія не можетъ уже вернуться въ первичную цѣпь
и поэтому остдется цѣликомъ во вторичной цѣпи/йакъ показываетъ
дилгрАМмА 318). Вторичная цѣпь является теперь осцилля-
Возбужденіе электромагнитныхъ колебаній толчками
355
торомъ, послѣ того какъ колебанія въ ней вызваны небольшимъ
числомъ колебательныхъ толчковъ цѣпи съ затухающимъ искро-
вымъ промежуткомъ. Здѣсь мы встрѣчаемся съ новымъ методомъ
Вторичная система
Рис. 318. Возбужденіе колебаній толчками. Осциллограмма.
возбужденія электрическихъ колебаній — методомъ возбужденія
толчками. ф
Возбужденіе толчками было изобрѣтено М. Виномъ (М. \Ѵіеп)
въ 1906 году. Осцилляторъ Вина представленъ схематически на
Рис. 319. Осцилляторъ съ возбужденіемъ толчками. Схема включенія.
рис. 319. Этотъ методъ имѣетъ особое значеніе, такъ какъ самый о
осцилляторъ не содержитъ искрового промежутка. Поэтому сопроД^
тивленіе въ колебательной цѣпи можно дѣлать произвольно ма^ьшѣ^
и тѣмъ сильно уменьшать затуханіе. Такимъ образомъ, при помощи
осциллятора Вина можно получать особенно длинные^праівильные
ряды колебаній. Связь лучше всего устроить такъ, чтрбы цѣпь съ
. 23
V
356
Резонансъ катушекъ
затухающей искрой возможно скорѣе отдавала свою энергію коле-
банія. Тогда потери въ ней и во всемъ аппаратѣ будутъ вообще
очень малы, и можно будетъ, несмотря на низкое разрядное напря-
женіе короткаго искрового промежутка, получать большія количе-
ства энергіи для опытовъ.
Вмѣсто того, чтобы пользоваться въ возбуждающей цѣпи зату-
ханіемъ самой искры, можно въ качествѣ задерживающаго клапана
ввести въ цѣпь достаточно широкую гейсслерову трубку, которая
имѣетъ весьма малое сопротивленіе при прохожденіи черезъ нее
сильныхъ токовъ, но, по прекращеніи тока, тотчасъ становится со-
вершеннымъ изоляторомъ. Въ качествѣ искры возбудителя можно
въ этомъ случаѣ взять сильную длинную искру, чтобы получить
большія амплитуды, но при этомъ связь должна быть нѣсколько
свободнѣе, нежели въ случаѣ возбудителя съ затухающей искрой,
такъ чтобы большое количество энергіи болѣе постепенно перехо-
дило на. осцилляторъ и чтобы это время было достаточно для пол-
наго затуханія гейсслеровой трубки.
РЕЗОНАНСЪ КАТУШЕКЪ.
416. Если катушки трансформатора Тесла правильно подо-
браны, то можно достигнуть того, чтобы разомкнутая вторичная
катушка безъ привключеннаго конденсатора резонировала на пер-
вичную цѣпь. Въ этомъ случаѣ свободные концы вторичной ка-
тушки образуютъ емкость. Но такъ какъ эта емкость очень мала,
то самоиндукція катушки должна быть очень большой, т.-е. нужно
взять очень большое число витковъ тонкой проволоки. Уже при
очень слабыхъ токахъ въ этихъ виткахъ напряженія, до которыхъ заря-
жаются концы катушки, становятся вслѣдствіе ея малой емкости чрезвы-
чайно высокими, и отъ катушки тогда исходятъ въ воздухъ искрящіеся
разряды. На рис. 320 представленъ резонансовый трансформаторъ.
Лишь небольшое число витковъ первичной катушки охватываетъ
вторичную катушку, плотно обмотанную вокругъ стержня^^йьшую
часть первичной цѣпи составляетъ лежащая на столѣ спираль изъ не
изолированной мѣдной проволоки. Помощью гибкаго провода можно
коротко замыкать произвольное число ея витковъ^ итакимъ образомъ
произвольно измѣнять самоиндукцію и, слѣдовательно, также число пе-
ріодовъ колебаній. Нижній конецъ вторичц$^4атушки соединенъ съ
водопроводомъ, верхній, наоборотъ, изолированъ. Если теперь за-
Резонансъ катушекъ
357
Рис. 320. Резонансовыи трансформаторъ Тесла.
мыкатель первичной катушки перемѣщать въ то время, какъискровой
промежутокъ находится въ дѣйствіи, то при опредѣленномъ поло-
358
Резонансъ катушекъ
женіи его можно видѣть въ темнотѣ, какъ изъ верхняго конца вто-
ричной обмотки выходятъ въ воздухъ большіе, свѣтящіеся, сильно
развѣтвленные разряды. Это явленіе на рис. 320 представлено чер-
нымъ по бѣлому, т.-е. какъ бы „негативно". Если перемѣстить за-
мыкатель вправо или влѣво, то разрядъ быстро прекратится. Та-
кимъ образомъ, лишь при опредѣленномъ числѣ періодовъ возни-
каетъ резонансъ, которымъ обусловливаются громадныя напряженія
у конца обмотки.
417. По сравненію съ разсмотрѣнными выше колебательными
цѣпями резонирующая катушка обладаетъ той особенностью, что
самоиндукція и емкость въ ней не разграничены рѣзко между собой.
Въ настоящей конденсаторной цѣпи сила тока во всѣхъ частяхъ
катушки въ опредѣленный моментъ одинакова такъ же, какъ и на-
пряженіе во всѣхъ мѣстахъ діэлектрика конденсатора. Въ разомкну-
той катушкѣ внизу, гдѣ она соединена съ землей, сила тока имѣ-
етъ максимумъ, по направленію вверхъ токъ постепенно убыва-
етъ, такъ какъ сильный боковой токъ смѣщенія, соотвѣтствующій
возрастающему или убывающему электрическому полю, образуетъ
параллельную вѣтвь. На изолированномъ концѣ катушки токъ, ко-
нечно, всегда равенъ нулю, и здѣсь, главнымъ образомъ, скопляется
зарядъ. Напряженіе проводника относительно земли имѣетъ макси-
мальную величину наверху; по мѣрѣ перемѣщенія внизъ по катушкѣ
зарядъ ея и напряженіе ея поля слабѣютъ, а внизу у соединенія съ
землею напряженіе, конечно, все время безконечно мало. Распредѣ-
леніе напряженія вдоль катушки можно очень хорошо демонстри-
ровать по способу Зейбта (8еіЬі), натягивая параллельно описанной
вторичной катушкѣ тонкую проволоку, соединенную съ землею.
Тогда разряды переходятъ на эту проволоку и образуютъ правиль-
ную свѣтовую полосу. Наверху эта полоса очень ярка, а книзу
она постепенно становится все блѣднѣе, соотвѣтственно съ убыва-
ніемъ напряженія, и, наконецъ, совершенно исчезаетъ. На рис? 321
эта свѣтовая полоса представлена „негативно". : °^Ь°
Въ установкѣ опыта, изображенной на этомъ рисункѣ, связь
вторичной катушки съ первичной цѣпью осуществлена? нѣсколько
иначе, нежели на рис. 320, а именно просто при^прмощи короткой
соединительной проволоки, связывающей нижній ^конецъ вторичной
катушки съ одной точкой первичной катушкд^Т&кого рода связь по-
средствомъ прямого проводящаго соединенія часто называютъ гальва-
Резонансъ катушекъ
359
нической связью, тогда какъ связь, изображенную на рис. 320,
называютъ индуктивной. Принципіально оба рода связи собственно
ничѣмъ не различаются. Перемѣнное электрическое напряженіе, воз-
Рис. 321. Распредѣленіе напряженія вдоль резонирующей катушки, поЗейбту..
буждающее въ отвѣтвленіи гальванической связи перемѣнный токъ,,
который затѣмъ продолжается во вторичной катушѣі,^ предста-
вляетъ собою часть индуктивныхъ напряженій, выздщ|еМыхъ измѣ-
неніями первичнаго магнитнаго поля, потому что^дкъ^ мы видѣли въ
360
Резонансъ катушекъ
§ 406, по сравненію съ ними могутъ быть оставлены безъ вниманія
напряженія, соотвѣтствующія сопротивленію проводника. Тѣ же са-
мыя индуктивныя напряженія дѣйствуютъ также на часть вторичной
катушки и въ установкѣ, изображенной на рис. 320. Но при поль-
зованіи индуктивной связью можно лучше использовать перемѣнное
электрическое поле первичной цѣпи и заставить его дѣйствовать на
большую часть вторичной катушки, нежели при пользованіи гальва-
нической связью. Иными словами, индуктивная связь легко можетъ
быть сдѣлана гораздо болѣе сильной, нежели гальваническая связь,
всегда лишь слабая.
Если электрическіе осцилляторы, имѣющіе раздѣльныя емкость
и самоиндукцію, можно сравнивать съ механическими осцилляторами,
въ которыхъ, какъ въ пружинѣ хронометра, пружинящая сила и
инерція принадлежатъ различнымъ частямъ—спиральной пружинѣ и
качающемуся колесу,—то спираль Зейбта мы можемъ сравнить съ
колеблющимся воздушнымъ столбомъ, гдѣ нѣтъ возможности про-
вести рѣзкое различіе между частью, обладающей инерціей, и частью,
обладающей упругой податливостью. Но и въ колеблющемся воз-
душномъ столбѣ есть мѣста, гдѣ развивается преимущественно дви-
женіе безъ упругихъ напряженій, и мѣста, гдѣ развиваются лишь
упругія напряженія безъ движеній. Эти особыя мѣста называются
пучностями и узлами. Въ закрытой органной трубѣ воздухъ внизу
у амбушюра имѣетъ пучность, а у верхняго закрытаго конца—узелъ.
Части, находящіяся между пучностью и узломъ, подвергаются какъ
движеніямъ, такъ и напряженіямъ, и черезъ нихъ происходитъ пере-
мѣщеніе энергіи поперемѣнно отъ узла къ пучности и отъ пучности
къ узлу. Если мы изъ двухъ состояній эѳира будемъ магнитное состоя-
ніе считать аналогичнымъ съ движеніями, а электрическое — съ напря-
женіями, то мы должны будемъ нижній конецъ изображенной на
рис. 321 катушки назвать пучностью, а верхній — узломъ. Эѳирная
полоса близъ катушки колеблется аналогично воздушному столбу
въ закрытой органной трубѣ. Энергія будетъ поперемѣнно магнит-
ной около пучности и электрической около узла. Въ каждый/пе-
ріодъ она дважды перемѣіцается въ ту и другую сторону^р
418. Относительно колеблющихся воздушныхъ столбовъ мы
знаемъ, что въ нихъ очень легко возникаютъ болѣе ЛаСгыя, доба-
вочныя колебанія, при чемъ они раздѣляются на равныя части. Напри-
мѣръ, закрытая органная труба очень легко даетъ тонъ, число колебаній
Резонансъ катушекъ
361
котораго въ три раза больше числа колебаній основного тона. Въ такомъ
случаѣ воздушный столбъ колеблется тремя
рается отъ нижней пучности до -у высоты,
о
гдѣ образуется узелъ, вторая — отъ этого
2 ж
узла до высоты, гдѣ находится пучность,
о
третья — отъ этой пучности до закрытаго
конца, гдѣ всегда находится узелъ. Про-
должительность колебанія пропорціональна
длинѣ колеблющейся части; въ силу этого
простого правила въ приведенномъ при-
мѣрѣ продолжительность колебанія равня-
ется одной трети продолжительности основ-
ного колебанія.
Совершенно аналогичное явленіе пред-
ставляютъ собой и электрическія колебанія
въ эѳирной полосѣ у катушки. Если умень-
шать емкость первичной цѣпи, понижая
также и самоиндукцію, до тѣхъ поръ,
пока не будетъ достигнута треть началь-
ной продолжительности колебанія, то вто-
ричная катушка'внезапно начинаетъ вновь
резонировать, что обнаруживается по воз-
никновенію искрящихся разрядовъ. При
этомъ въ установкѣ Зейбта получается
картина, представленная „негативно" на
рис. 322. Совершенно такъ же, какъ и въ
органной трубѣ, мы здѣсь имѣемъ, кромѣ
узла у верхняго конца катушки, еще одинъ
1
узелъ на -у высоты, и, кромѣ пучности у
частями; первая прости-
нижняго конца катушки, образуется еще
2
одна пучность на -у высоты. Легко полу-
чить на катушкѣ также пять и больше колеблющихся част^Йр
если соотвѣтственнымъ образомъ понизить число колебаній первич-
ной цѣпи.
Рис. 322. Добавочныя коле-
банія катушки Зейбта
362
Опыты Лехера
ОПЫТЫ ЛЕХЕРА.
419. Если посредствомъ уменьшенія емкости и самоиндукціи
сдѣлать число періодовъ весьма высокимъ, то можно наблюдать,
явленія резонанса на обыкновенныхъ прямыхъ проволокахъ, вмѣсто
катушекъ, какъ въ описанныхъ выше опытахъ. Такіе опыты впер-
вые были произведены Г. Герцемъ, а затѣмъ въ лучшей уста-
новкѣ Лехеромъ (Е. Ьесѣег). Въ опытахъ Лехера пользуются
двумя одинаковыми воздушными конденсаторами, включенными по-
слѣдовательно; эти конденсаторы состоятъ изъ четырехугольныхъ
или круглыхъ пластинъ, которыя имѣютъ поверхность въ нѣсколько
сотъ квадратныхъ сантиметровъ и находятся на разстояніи нѣсколь-
кихъ сантиметровъ одна отъ другой; они имѣютъ, слѣдовательно,
весьма малую емкость. Обѣ переднія пластины соединяются искро-
вымъ промежуткомъ (рис. 323), а къ другой парѣ пластинъ при-
соединяются двѣ длинныя параллельныя проволоки, которыя между
I
Рис. 323. Опытъ Лехера.
собой сообщаются мостомъ — поперечной проволокой. Образующееся
такимъ образомъ проволочное соединеніе заднихъ пластинъ конден-
саторовъ имѣетъ весьма малую самоиндукцію. Послѣдняя измѣняется
приблизительно пропорціонально длинѣ проволокъ; поэтому пере-
мѣщеніемъ моста можно очень просто измѣнять самоиндукцію, а
вмѣстѣ съ ней и число колебаній. При указанныхъ размѣрахъ кон-
денсаторовъ получаются по формулѣ Томсона числа колебаній,
близкія къ ІО8 (сто милліоновъ). Параллельныя проволоки за мостомъ
гальванически связаны съ осцилляторомъ, и потому въ нихъ^воз-
буждаются колебанія. Первичную цѣпь можно настроить такъ^чтобы
проволочная цѣпь была съ ней въ резонансѣ. Для этой^Йіи вклю-
чаютъ между обоими концами параллельныхъ проволокъ гейссле-
рову трубку и во время дѣйствія искрового промежутка передви-
гаютъ мостъ до тѣхъ поръ, пока трубка не вспыхнетъ очень ярко;
тогда проволока находится въ резонансѣ съ^сцилляторомъ. Если
теперь передвигать гейсслерову трубку^даолы параллельныхъ про-
Опыты Лехера
363.
волокъ и если послѣднія достаточно длинны, то можно обнаружить
на нихъ еще рядъ узловъ на равныхъ разстояніяхъ одинъ отъ дру-
гого: въ этихъ мѣстахъ гейсслерова трубка ярко вспыхиваетъ, такъ
какъ въ узлахъ электрическое напряженіе имѣетъ максимальную
величину. По срединѣ между каждой парой узловъ находится пуч-
ность, въ которой трубка остается темной и напряженіе равно нулю.
Между узломъ и пучностью яркость разряда постепенно падаетъ,
какъ и въ опытѣ Зейбта. Если разстояніе между параллельными
проволоками очень мало въ сравненіи съ разстояніемъ между двумя
узлами, то можно въ пучностяхъ соединять проволоки поперечными
проволоками, не разстраивая резонанса; но если мостъ слегка лишь
передвинуть изъ пучности, то разрядъ въ гейсслеровой трубкѣ, ука-
зывающій на присутствіе колебаній, затухаетъ. Такимъ образомъ
можно очень точно опредѣлить положенія пучностей и длину коле-
блющагося участка.
Столь же хорошій резонансъ получается, если коротко замкнуть
концы параллельныхъ проволокъ при помощи толстой проволоки.
На этомъ концѣ тогда получается пучность, а ближайшій узелъ,,
гдѣ гейсслерова трубка вспыхиваетъ, лежитъ между концевымъ
мостомъ и осцилляторомъ; число колебаній, при которомъ въ этомъ
случаѣ получается резонансъ, конечно, иное, нежели при открытомъ
концѣ. Параллельныя проволоки съ открытымъ концомъ можно
уподобить закрытой трубѣ; проволоки съ короткозамкнутымъ кон-
цомъ можно уподобить открытой трубѣ. Въ закрытой трубѣ у за-
крытаго конца образуется узелъ, такъ какъ здѣсь невозможны коле-
банія воздуха въ ту и другую стороны; на концѣ же открытой
трубы вслѣдствіе сообщенія съ внѣшней атмосферой не могутъ воз-
никнуть колебанія давленія, и потому здѣсь образуется пучность.
Аналогія съ электрическими колебаніями у параллельныхъ прово-
локъ очевидна.
420. Вмѣсто того, чтобы связывать параллельныя проволоки I
съ осцилляторомъ гальванически, можно также воспользовасься инду^й/
тивной связью. Такимъ именно образомъ установка Лехера была
видоизмѣнена Блондло (Віопсііоі). Возбудитель Блондло (рцс|324)
состоитъ изъ двухъ согнутыхъ толстыхъ проволокъ, образующихъ
вмѣстѣ окружность. Съ одной стороны концы этихъ проволбкъ обра-
зуютъ небольшой искровой промежутокъ, а другіе^ва конца со-
единены съ двумя пластинами конденсатора. Если^елательно полу-
'364
Опыты Лехера
чить очень быстрыя колебанія, то конденсаторныя пластины уда-
ляютъ, такъ что остается лишь емкость свободныхъ концовъ про-
волокъ. Весь осцилляторъ чаще всего помѣщается въ керосинъ, гдѣ
искры особенно сильны. Параллельно съ первой проволочной окруж-
ностью идетъ вторая проволочная цѣпь, которая съ одной стороны
открыта и переходитъ въ двѣ параллельныя проволоки. Соединяя
надлежащимъ образомъ параллельныя проволоки поперечными мо-
стами, легко получить участки, находящіеся въ резонансѣ съ осцил-
ляторомъ. Конечно, число колебаній осциллятора Блондло нельзя измѣ-
нять съ такимъ удобствомъ, какъ число колебаній осциллятора Лехера.
На установкахъ Лехера и Блондло легко уяснить себѣ раз-
ницу между гальванической и индуктивной связью. Если мостъ въ
Рис. 325. Гальваническая и индуктивная связи, по существу тожественныя.
установкѣ Лехера замѣнимъ двумя очень близкими и изолированными
одна отъ другой проволоками и между ними перерѣжемъ^обѣ па-
раллельныя проволоки, то получимъ индуктивную связь^по суще-
ству совершенно тожественную съ гальванической (рц^325). Если
же послѣ раздѣленія перемѣстить осцилляторъ т^^^чтобы полоса
между параллельными проволоками была, какъ въ установкѣ Блондло,
Опыты Лехера
365
частью покрыта поверхностью,
ограниченной цѣпью осциллятора,
то связь, конечно, станетъ гораздо
болѣе сильной, такъ какъ боль-
шая часть магнитныхъ силовыхъ
линій осциллятора пересѣкаетъ при
этомъ поверхность вторичной цѣпи,
тогда какъ въ установкѣ рис. 325
обѣ проводки связываются отно-
сительно малымъ числомъ общихъ
силовыхъ линій. Такимъ образомъ,
установка Блондло существенно
отличается отъ установки Лехера
лишь болѣе сильной связью, обу-
словливающей болѣе быстрый пе-
реходъ энергіи колебаній изъ
осциллятора во вторичную цѣпь.
Впрочемъ, путемъ измѣненія раз-
стоянія между двумя цѣпями ин-
дуктивная связь очень легко можетъ
быть сдѣлана болѣе сильной или
болѣе слабой, смотря по требова-
ніямъ опыта.
421. Какъ и въ спирали Зейбта,
можно на короткихъ колебаніяхъ
опытовъ Лехера сдѣлать види-
мымъ распредѣленіе напряже-
нія, пользуясь явленіями разряда
между параллельными проволоками.
Для этой цѣли нужно получить
колебанія съ весьма высокими на-
пряженіями. Лучше всего возбу-
ждать искру осциллятора, погружен-
наго въ керосинъ, при помощи
высокихъ напряженій вторичной
обмотки трансформатора Тесла,
какъ показываетъ рис. 326. Парал-
лельныя проволоки ограничены мо-
стомъ изъ толстой проволоки, при
366
Элекромагнитныя волны
помощи котораго ихъ можно очень удобно настроить на колебанія
осциллятора. На мѣстѣ первой пучности помѣщается мостъ, соеди-
ненный посредствомъ толстаго провода съ землею, чтобы такимъ
путемъ удалить колебанія Тесла отъ параллельныхъ проволокъ.
Если обѣ параллельныя проволоки тонки и достаточно близки между
•собой, то, какъ и въ опытѣ Зейбта, между ними видны широкія
полосы свѣта, которыя отличаются особенной яркостью въ узлахъ
и отсутствуютъ' въ пучностяхъ. Легче это явленіе получается по
способу Аронса (Агопз), если помѣстить параллельныя проволоки
въ широкой и длинной стеклянной трубкѣ, которую разрѣжаютъ
настолько, чтобы облегчить возникновеніе разрядовъ. Явленіе пред-
ставлено „негативно" на рис. 326.
ЭЛЕКТРОМАГНИТНЫЯ ВОЛНЫ.
422. Если держать камертонъ около отверстія широкой сте-
клянной трубки, закрытой съ противоположнаго конца подвижнымъ
поршнемъ, который установленъ такъ, что воздушный столбъ въ
трубѣ находится какъ разъ въ резонансѣ съ камертономъ, то въ
этомъ воздушномъ столбѣ возникаетъ правильное колебаніе съ уз-
лами и пучностями, которое продолжается все время, пока звучитъ
камертонъ. Въ этомъ опытѣ мы имѣемъ точную механическую ана-
логію опыта Лехера: первичному осциллятору соотвѣтствуетъ ка-
мертонъ, параллельнымъ проволокамъ — стеклянная труба, а эѳирной
полосѣ, поле которой ограничено параллельными проволоками, —
воздушный столбъ, ограниченный стеклянной трубой. Иныя явленія
наблюдаются, если въ акустическомъ опытѣ замѣнить стеклянную
трубу весьма длиннымъ трубопроводомъ. Колебанія воздуха, вызы-
ваемыя звучащимъ камертономъ, возбуждаютъ въ началѣ трубо-
провода колебанія, распространяющіяся въ немъ въ видѣ посту-
пательно движущагося ряда волнъ. Такъ какъ камертонъ звучитъ
лишь въ теченіе опредѣленнаго промежутка времени, то и этотъ
рядъ волнъ имѣетъ лишь опредѣленную длину. Мы примемъ,^Счто
трубопроводъ гораздо длиннѣе этого ряда волнъ; въ такомъ слу-
чаѣ требуется замѣтный промежутокъ времени для ^^-ого, чтобы
эти волны достигли конца трубы. Если труба закрыта, то волны
испытываютъ полное отраженіе и двигаются обратно съ тою же
скоростью, съ какою онѣ двигались впередъ. ^Подобное же явле-
Электромагнитныя волны
367
ніе происходитъ и въ томъ случаѣ, когда труба открыта, но при
этомъ отщепляется малая часть энергіи волнъ и выходитъ во внѣшнее
пространство въ видѣ слабой шаровой волны; остальная же несрав-
ненно ббльшая часть энергіи отражается и остается въ трубѣ. Въ
обоихъ случаяхъ крайняя часть трубы въ теченіе нѣкотораго про-
межутка времени заполняется волнами, идущими въ ту и другую
стороны; оба ряда волнъ имѣютъ почти одинаковую интенсивность
и взаимно налагаются. Такъ какъ переносъ энергіи, совершаемый
однимъ рядомъ волнъ, компенсируется переносомъ энергіи, соверша-
емымъ другимъ рядомъ, то въ дѣйствительности не происходитъ
переноса энергіи ни въ ту, ни въ другую сторону; все это явленіе
называютъ стоячей волной. Стоячая волна имѣетъ такой же видъ,
какъ и колебаніе въ короткой трубѣ; подобно ему она состоитъ изъ
опредѣленныхъ участковъ, ограничиваемыхъ узлами и пучностями. Дѣй-
ствительно, возникновеніе колебаній въ короткой трубѣ можно пред-
ставлять себѣ такимъ образомъ: волна, вступающая въ отверстіе
трубы, отражается отъ конца трубы обратно; отброшенная волна
у начала трубы вновь отражается и т. д. Вслѣдствіе наложенія
большого числа волнъ, идущихъ въ ту и другую сторону, въ трубѣ
извѣстной длины получается стоячая волна, такъ какъ ни одно изъ
двухъ направленій распространенія не преобладаетъ надъ другимъ
Разница между процессами протекающими въ длинной и короткой
трубахъ, заключается, слѣдовательно, въ томъ, что вторую всю за-
нимаетъ стоячая волна, а въ первой стоячая волна занимаетъ лишь
относительно малую часть, которая, однако, можетъ быть гораздо .
длиннѣе короткой трубы.
Совершенно аналогичныя явленія мы получимъ, присоединяя къ
осциллятору Лехера параллельныя проволоки длиною въ нѣсколько
километровъ. Мы замѣтимъ узлы и пучности лишь въ послѣднемъ
участкѣ проводовъ. Въ остадьной проводкѣ можно, правда, обнару-
жить перемѣнныя электрическія напряженія по индукціоннымъ дѣй-
ствіямъ или даже по явленіямъ резонанса въ небольшихъ настраи-
ваемыхъ цѣпяхъ, помѣщенныхъ вблизи проводки, но узловъ и пуч-
ностей здѣсь не получается. Въ этихъ частяхъ проводки мы им^р
емъ ряды электрическихъ волнъ, послѣдовательно движущіеся в^т^Й
другую стороны. Здѣсь передъ нами совершенно новое явленіе^рас-
пространяющаяся электрическая волна,
:мы ниже изучимъ подробнѣе.
природу^ ^котораго
368
Электромагнитныя волны
423. Чтобы понять, какимъ образомъ электрическія волны мо-
гутъ распространяться черезъ эѳиръ, намъ полезно будетъ руковод-
ствоваться механическимъ образомъ воздушныхъ волнъ, который
непосредственно является для насъ болѣе нагляднымъ. Представимъ
себѣ весьма длинную наполненную воздухомъ трубку, въ которую
съ одного конца короткимъ ударомъ немного вдвигаютъ поршень.
Сначала непосредственно у поршня образуется небольшое сгущеніе,
которое сейчасъ же передается къ слѣдующимъ частямъ воздушнаго
столба, тогда какъ у поршня вновь возстанавливается нормальная
плотность воздуха; толчокъ и сгущеніе передаются, такимъ образомъ,
вдоль всей трубы. Отдѣльные моменты этого явленія можно видѣть
на рис. 327. Здѣсь штриховкой представлено сгущеніе, только-что
достигшее части АЕ. Паденіе давленія съ передней стороны А
Рис. 327. Распространеніе волны сгущенія въ воздушномъ столбѣ.
сгущенія вызываетъ движеніе частицъ воздуха, до этого момента
находившихся въ покоѣ, въ направленіи маленькой стрѣлки. Все
время, пока происходитъ паденіе давленія, скорость этого движенія
возрастаетъ все болѣе и болѣе. Поэтому частицы, находящіяся въ Вг
нѣсколько дальше внутри сгущенія, движутся скорѣе, такъ какъ здѣсь
паденіе давленія дѣйствуетъ уже съ того момента, когда передняя по-
верхность волны прошла черезъ В. Максимумъ скорости находится въ
С, гдѣ находится также и максимумъ сгущенія. Дѣйствительно, по
другую сторону этого максимума сгущенія, въ I), съ того момента,
когда максимумъ прошелъ чрезъ I), имѣло мѣсто отрицательное
паденіе давленія, вслѣдствіе чего движеніе здѣсь замедлялось.^ГІо-
этому въ О скорость меньше, нежели въ С, и при томъ тѣмъ мейыпе,
чѣмъ ближе точка 7) находится къ тылу сгущенія Е. І||рточкахъ
же сзади отъ Е, черезъ которыя волна сгущенія^уже прошла
совершенно, движеніе прекратилось. Такимъ образомъ, всѣ воз-
душныя частицы въ области ЕА послѣдовательно начинаютъ и
-заканчиваютъ краткое поступательное движ^е; послѣднее и явля
ется причиной распространенія сгущенія, вмѣстѣ съ которымъ одно-
Электромагнитныя волны
369
временно происходитъ вышеописаннымъ образомъ также и распро-
страненіе движенія, которымъ вызывается сгущеніе. Изъ этой тео-
ріи слѣдуетъ, что скорость передачи толчка зависитъ отъ двухъ
свойствъ газа. Во-первыхъ, чѣмъ тяжелѣе среда, тѣмъ медленнѣе
движенія, вызываемыя опредѣленнымъ паденіемъ давленія, и тѣмъ
медленнѣе также сгущеніе передается впередъ. Во-вторыхъ, чѣмъ
податливѣе среда, тѣмъ меньше будутъ силы давленія, возника-
ющія при опредѣленномъ сгущеніи, и тѣмъ медленнѣе вызываемыя
имъ движенія, тѣмъ медленнѣе поэтому передается сгущеніе. Если
удѣльная плотность среды равняется 5, коэффиціентъ упругости, или
сжимаемость, т.-е. отношеніе сжатія къ связанному съ нимъ измѣ-
ненію давленія, равняется у, то скорость распространенія волны сжа-
тія с или, что то же, скорость распространенія энергіи тѣмъ меньше,
чѣмъ больше произведеніе 5. у. Болѣе точное математическое вы-
численіе даетъ формулу
1
с = - г__•
.у
Если плотность 5 выражена въ граммахъ на кубическій санти-
метръ, а давленіе въ выраженіи сжимаемости дано въ динахъ на
квадратный сантиметръ, то формула даетъ количество с въ • Съ
такой же самой скоростью распространяется, конечно, и правильная
смѣна сгущеній и разрѣженій, т.-е. рядъ волнъ. Для воздуха при 0°С.
по этой формулѣ получается скорость 33 100 такую же вели-
чину даютъ и измѣренія.
Тѣмъ же способомъ можно развить и теорію распространенія
энергіи въ эѳирѣ. Представимъ себѣ, что въ началѣ длинной про-
водки, состоящей изъ двухъ параллельныхъ проволокъ, какимъ-либо
Въ первый моментъ электрическое поле будетъ
образомъ вызвано кратковременное электрическое напряженіе между
обѣими проволоками.
находиться лишь въ началѣ проводки, но сейчасъ же оно перене-о
сется въ сосѣднюю
изъ перваго мѣста; ............................ г----
далѣе по всей проводкѣ. На рис. 328 представленъ моментъ^когда
импульсъ напряженія дошелъ до мѣстаЛЕпроводки. На фронтѣволны А
имѣетъ мѣсто убыль напряженія, и потому условіе равновѣсія электри-
ческаго поля здѣсь нарушено. Напримѣръ, если напряженіе вдоль
часть проводки и въ то же время исчезне^§)
такимъ образомъ поле будетъ перемѣщаться
ЛІп. Электричество и магнитизмъ, ч. II.
24
370
Электромагнитныя волны
АА' меньше, чѣмъ вдоль ВВ’, то вся линейная сумма поля вдоль
АА'В'ВА отлична отъ нуля. Отсюда слѣдуетъ, что эѳирныя напря-
женія на фронтѣ волны вызываютъ магнитное поле, которое возра-
стаетъ тѣмъ болѣе, чѣмъ дольше продолжаются возбужденныя на-
пряженія. Такимъ образомъ, магнитное поле въ области В, лежа-
щей уже дальше внутри волны, сильнѣе, нежели на фронтѣ, такъ
какъ тамъ напряженія дѣйствовали все время въ одномъ и томъ же
направленіи съ момента, когда фронтъ волны прошелъ черезъ В.
Магнитное поле достигаетъ максимума въ тотъ же моментъ, какъ
и электрическое напряженіе, а именно въ С на рис. 328. Дѣйстви-
тельно, по другую сторону максимума электрическаго поля, въ об-
ласти 7), электрическое поле дѣйствовало въ обратномъ направле-
Рис 328. Распространеніе электрическаго толчка напряженія въ полосѣ
эѳира, ограниченной двумя параллельными проволоками.
ніи съ того момента, когда максимумъ прошелъ черезъ такъ какъ
напряженіе вдоль ВО' меньше, нежели вдоль СС, и линейная сумма
вдоль СС О' ОС имѣетъ потому знакъ, противоположный тому,
который имѣетъ сумма вдоль ВВ' С' СВ. Въ области О электриче-
ское поле постепенно уменьшаетъ поэтому магнитное поле, кото-
рое, наконецъ, въ тылу Е импульса напряженія равняется нулю. Линіи
описаннаго магнитнаго поля перпендикулярны къ электрическимъ
силовымъ линіямъ и на рис. 328 представлены въ сѣченіи, какъ
линіи ротора, посредствомъ кружковъ со стрѣлками. Дѣйствіемъ
этого магнитнаго поля все электрическое поле перемѣщается въ
эѳирѣ впередъ, какъ легко понять изъ того, что изложено нами4 въ
§§ 250 и 251. Но волна импульса напряженія, распространяясь подъ
дѣйствіемъ вызываемаго ею магнитнаго поля вдоль проволокѣ, увле-
каетъ съ собою магнитное поле; поэтому распространеніе энергіи
въ эѳирѣ вполнѣ аналогично распространенію энер|іиТвъ упругой
матеріальной средѣ. Подобно тому, какъ скоростьюраспространенія
энергіи въ матеріальной средѣ зависитъ отъ плотности и упругости
Электромагнитныя волны
371
среды, такъ въ эѳирѣ она опредѣляется соотвѣтственными величи-
нами проницаемости и діэлектрической постоянной и вычисляется
по той же формулѣ, приведенной нами выше.
424. Эту формулу не трудно, впрочемъ, вывести, и мы дока-
жемъ ее вкратцѣ. Пусть с будетъ скорость распространенія волны,
Е — сила поля въ нѣкоторомъ мѣстѣ РР' (рис. 328) и В — магнит-
ная индукція въ этомъ мѣстѣ. Положимъ далѣе, что (№' есть линія
передъ фронтомъ волны, куда импульсъ, слѣдовательно, еще не
пришелъ. Обозначимъ черезъ т тотъ безконечно малый промежу-
токъ времени, въ теченіе котораго импульсъ перемѣщается на без-
конечно малый отрѣзокъ б — РгР такъ что Ь = с . т. Въ теченіе
малаго промежутка времени т магнитный силовой потокъ, прони-
зывающій узкую полосу РР' РА'РА, вступаетъ въ четырехугольникъ
(№' Р' Р. Если длину РР' обозначимъ черезъ а, то полное прира-
щеніе магнитныхъ силовыхъ линій, получаемое четырехугольникомъ
(№' Р' Р за безконечно малый промежутокъ времени т, равняется
В . а .Ъ = В. а. с .ѵ, слѣдовательно, скорость, съ которой возрастаетъ
въ это время полный силовой потокъ, пронизывающій четырехуголь-
никъ, равняется В . а . с. По второму закону Максвелла эта скорость
возрастанія магнитнаго поля должна равняться линейной суммѣ
электрическаго поля вдоль границы четырехугольника. Такъ какъ
только вдоль стороны РР’ имѣется слагающая Е, отличная отъ нуля,
то линейная сумма равняется Е.аь и мы имѣемъ поэтому:
Е . а = В . а. с ; слѣдовательно, Е = В.с.
Электрическое напряженіе вдоль нѣкоторой линіи
равняется числу магнитныхъ силовыхъ линій, проходящихъ
черезъ нее въ теченіе секунды.
Первый законъ Максвелла также даетъ нѣкоторое соотно-
шеніе между электрическимъ полемъ и магнитнымъ. Чтобы убѣдиться
въ этомъ, разсмотримъ прямоугольникъ, двѣ стороны котораго Пересѣ- ,
каютъ перпендикулярно плоскость рисунка, т.-е. направлены парал-
лельно магнитнымъ силовымъ линіямъ. Положимъ, что длина этихъ
сторонъ равна 6, и что онѣ проходятъ черезъ точки Р" и С?" діряСР
мыхъ РР' и С<5'. Назовемъ черезъ 7) электрическое возбужденіе
и черезъ Н силу магнитнаго поля въ мѣстѣ Р". Скорость, съ которою
возрастаетъ пронизывающее прямоугольникъ электрическое^фзбужде-
ніе, т.-е. проходящій черезъ прямоугольникъ электр^феск ій токъ
24
372
Электромагнитныя волны
смѣщенія, вычисляется совершенно такимъ же способомъ, какимъ мы
выше нашли скорость возрастанія магнитнаго силового потока; она
равняется В.Ь.с, а линейная сумма силы магнитнаго поля вдоль
границы прямоугольника равняется Н.Ь. По первому закону Макс-
велла Н .Ь = О . Ь . с, или Н = О .с. Полная величина силы маг-
нитнаго поля вдоль нѣкотораго отрѣзка равняется числу
электрическихъ линій возбужденія, проходящихъ черезъ
него въ теченіе секунды. Оба результата мы переписываемъ
еще разъ:
Е = В.с = М ,Н.с,
Н=О.с = К.Е.с.
Изъ этихъ уравненій тотчасъ же получается очень интересное
слѣдствіе относительно энергіи въ волнѣ. Оказывается, что количе-
ства электрической и магнитной энергіи въ кубическомъ сантиметрѣ
равняются соотвѣтственно
4 о.е=4 к-Е2=і-к-м -с-н-е’
и 111
±-В.Н=-Е м . К.с.Е.Н.
Энергія магнитнаго поля, вызывающаго перемѣщеніе
электрическаго импульса въ эѳирѣ, въ точности равняется
энергіи самого перемѣщаемаго электрическаго поля. Обозна-
чимъ черезъ р плотность всей энергіи, т.-е. сумму электрической и
магнитной энергіи, приходящуюся на кубическій сантиметръ; тогда
потокъ энергіи черевъ одинъ квадратный сантиметръ равенъ
Е=р.с\ съ другой стороны, по теоремѣ Пойнтинга (§ 280),
17 = Е .Н. Такимъ образомъ мы получаемъ уравненіе
Е. Н — р . с.
Величина р можетъ быть вычислена слѣдующимъ образомъ:
р = 1 О.Е^В.Н^-К. М.с.Е.
Поэтому потокъ энергіи равенъ
и=Е.Н = К. М.&.Е.Н,
откуда получаемъ
Электромагнитныя волны
373
Это и есть искомая формула, аналогичная формулѣ, приве-
кулонъ
денной въ § 423. Если мы К вычислимъ въ
л вольтъ. сантим.
IV, вольтъ. сек. сантим.
гі — въ ----------------, то получимъ с въ -------
амперъ. сантим. сек.
эѳира 7С0 = 0,8842.10 18, Мо = 1,256.10 8. Эти числа
Для чистаго
даютъ:
с0 = 3000.1010 санггги—.
и сек.
Правильно слѣдующія одна за другой пульсаціи напряженія,
направленныя поперемѣнно то въ положительную, то въ отрица-
тельную сторону, образуютъ рядъ волнъ (рис. 329). Ясно, что ско-
рость распространенія электромагнитныхъ волнъ въ пустотѣ также
равна с0. Въ каждой точкѣ Р, черезъ которую проходитъ рядъ
волнъ, электрическое напряженіе, а вмѣстѣ съ нимъ и магнитное
поле получаютъ правильно и періодически измѣняющіяся значенія.
Рис. 329. Электромагнитныя волны.
Иными словами, въ точкѣ Р есть перемѣнное электромагнитное поле.
Обозначимъ черезъ Т продолжительность одного періода, т.-е. про-
должительность колебанія. Разстояніе X между двумя точ-
ками Р и <2, въ которыхъ электромагнитное колебаніе
всегда имѣетъ одинаковую фазу, называется длиной волны.
Въ теченіе періода Т въ точкѣ Р смѣняются послѣдовательно всѣ
фазы, вначалѣ соотвѣтствовавшія точкамъ между Р и такимъ
образомъ, за это время черезъ Р проходитъ какъ разъ часть волны,
заключавшаяся вначалѣ между Р и т.-е. рядъ волнъ передви-
гается впередъ на X. Отсюда слѣдуетъ, что скорость распростра-
X
ненія волнъ равняется -у, т.-е.
ео ~ ’ X = с0 . Т.
Такимъ образомъ, опредѣленному періоду
соотвѣтствуетъ также опредѣленная длина волны
порціональная періоду.
колебанІ50'всегда
въ эѳирѣ, про-
374:
Электромагнитныя волны
Распространяющаяся электромагнитная волна образу-
етъ въ каждой точкѣ, чрезъ которую она проходитъ, пере-
мѣнное электромагнитное поле, въ которомъ электриче-
ское и магнитное поля всегда имѣютъ одинаковую фазу и
одинаковую энергію. Оба поля взаимно перпендикулярны,
и волна распространяется въ направленіи, перпендикуляр-
номъ къ обоимъ полямъ, согласно теоремѣ Пойнтинга. Въ
точкахъ, расположенныхъ по направленію распространенія
волны, перемѣнное поле имѣетъ различныя фазы, при чемъ
опредѣленная фаза правильно и періодически повторяется
черезъ разстояніе, называемое длиною волны. Длина волны X
равняется произведенію изъ скорости распространенія
волны с на продолжительность колебанія перемѣннаго
поля Т, т.-е \ = с.Т. Скорость распространенія с вычи-
, ж 1
сляется по формулѣ с = ; для чистаго эѳира полу-
чается с0 = 3 . ІО10 т.-е. 300 000 километровъ въ секунду.
Для другихъ средъ имѣетъ мѣсто формула:
у ц.к
гдѣ ц обозначаетъ удѣльную проницаемость, а к — діэлектри-
ческую постоянную. Такъ какъ для всѣхъ изоляторовъ можно поло-
жить ц = 1 , то
с
^о_
V ь
Обозначимъ длину волны перемѣннаго поля опредѣленнаго пе-
ріода Т въ чистомъ эѳирѣ черезъ Хо, а въ матеріальномъ діэлек-
трикѣ — черезъ X.
Тогда Хо = с0 . Т, \ = с.Т\ слѣдовательно,
Эта формула
даетъ методъ опредѣленія діэлектрцческихъ по-
стоянныхъ, такъ какъ существуетъ, какъ мы сейчасъ уѣдимъ, удоо-
ный методъ измѣренія длинъ
Такъ какъ скорость с0
исключительно высокихъ
чтобы можно было въ
при
мала,
ВОЛНЪ. АЧг
„ ’ЗЙЖ I
весьма велика, то^длина волны лишь
числахъ колебаній бываетъ настолько
. А
лабораторіи наблюдать разности фазъ
Электромагнитныя волны
375
въ различныхъ мѣстахъ двухъ параллельныхъ проволокъ. Такъ, напри-
мѣръ, перемѣнное поле съ числомъ колебаній, равнымъ 1000 въ
секунду, имѣетъ длину волны, равную 300 километрамъ.
425. Если навстрѣчу волнамъ, представленнымъ на рис. 329,
распространяется другой рядъ волнъ, параллельно поляризованный,
то въ тѣхъ мѣстахъ, гдѣ электрическое поле второго ряда совпа-
даетъ съ электрическимъ полемъ перваго, его магнитное поле про-
тивоположно магнитному полю перваго; наоборотъ, тамъ, гдѣ элект-
рическія поля взаимно противоположны, магнитныя поля имѣютъ
одинаковое направленіе. Если періодъ колебаній для обѣихъ волнъ
одинаковъ, то въ рядѣ равноотстоящихъ точекъ ихъ электрическія
поля совпадаютъ по фазѣ. Дѣйствительно, если въ нѣкоторомъ мѣстѣ
фазы въ опредѣленный моментъ совпадаютъ, то онѣ будутъ совпа-
дать все время, такъ какъ оба колебанія имѣютъ одинаковый пе-
ріодъ. Кромѣ того, фазы совпадаютъ также въ двухъ точкахъ, ко-
торыя удалены отъ данной точки на разстояніе, равное половинѣ
длины волны, такъ какъ въ этихъ точкахъ одна волна смѣщена
на полъ-колебанія назадъ, а другая на столько же впередъ, т.-е.
онѣ имѣютъ разность, равную цѣлому колебанію. Такимъ образомъ,
существуетъ рядъ точекъ, которыя отстоятъ одна отъ другой на по-
ловину длины волны и въ которыхъ электрическія поля обѣихъ волнъ
всегда направлены одинаково и потому слагаются. Магнитныя поля
обѣихъ волнъ, согласно вышесказанному, въ этихъ мѣстахъ всегда
взаимно противоположны и, если обѣ волны одинаково сильны, то
они взаимно уничтожаются, такъ что остается только перемѣнное
электрическое поле. Такимъ образомъ, эти мѣста имѣютъ характеръ
узловыхъ точекъ. Посрединѣ между двумя узловыми точками электри-
ческія поля обѣихъ волнъ направлены взаимно противоположно, такъ
какъ одно поле здѣсь смѣщено на четверть колебанія назадъ, а
другое на столько же впередъ и въ общемъ они смѣщены одно отно-
сительно другого на половину колебанія, т.-е. они взаимно противо-
положны. Если обѣ волны одинаково сильны, то въ этихъ мѣстахъ^
электрическія поля взаимно уничтожаются, и остается лишь перемѣн-
ное магнитное поле, такъ какъ, согласно вышесказанному, ^ійѣнит-
ныя поля обѣихъ волнъ одинаково направлены, когда элегическія
поля взаимно противоположны. Такимъ образомъ, между каждыми
двумя узлами мы имѣемъ пучность. Распредѣленіе^состояній эѳира,
представленное на рис. 330, соотвѣтствуетъ, слѣ^ф^Ѣейьно, стоячему
376
Электромагнитныя волны
колебанію съ узлами и пучностями. При этомъ слѣдуетъ замѣтить,
что электрическое и магнитное состоянія измѣняются такимъ обра-
зомъ, что, когда электрическое достигаетъ максимума, магнитное ста-
новится нулемъ, и обратно. Энергія въ теченіе каждаго колебанія
перемѣщается дважды отъ узла къ пучности и обратно.
Эти соображенія даютъ теоретическое объясненіе факта, опи-
саннаго въ § 420: рядъ волнъ даетъ послѣ отраженія стоячее коле-
баніе. Кромѣ того, изъ нихъ вытекаетъ еще слѣдующее важное пред-
ложеніе.
Разстояніе между двумя сосѣдними узлами стоячаго
колебанія на параллельныхъ проволокахъ равняется поло-
винѣ длины волны распространяющагося колебанія того
же періода.
Прямыя стрѣлки обозначаютъ направленіе .распространенія энергіи, въ данный
моментъ совершающагося отъ узловъ къ пучностямъ, такъ что электрическая энер
гія превращается въ магнитную.
Мы видѣли въ § 419, что съ помощью опыта Лехера можно
очень точно опредѣлить положеніе пучностей стоячихъ волнъ въ
параллельныхъ проволокахъ, наблюдая явленія . резонанса посред-
ствомъ перекинутыхъ мостовъ. Такъ какъ разстояніе между двумя
сосѣдними пучностями равняется половинѣ длины волны, то опытъ
Лехера даетъ прекрасный методъ для опредѣленія длины
волны, соотвѣтствующей данному числу колебаній.
Если мы возбудимъ колебанія при помощи осциллятора, про-
должительность колебанія котораго можетъ быть вычислена по фрр?
мулѣ Томсона Т = 2 тг . С,
воздухѣ,
скорость
скорости ихъ въ пустотѣ, с0 — -у- • Измѣренія такого рода под-
и измѣримъ длину волну^Увъ
пользуясь способомъ Лехера, то мы можемъ вычислить
электрическихъ волнъ въ воздухѣ, которая /гфчти равна
Хо .. - •
твердили
теоретически найденное число 3 .
Распространеніе весьма длинныхъ волнъ по проволокамъ 377
Если измѣрить длину волны одного и того же колебанія въ
различныхъ средахъ, то, какъ мы видѣли въ § 424, посредствомъ
этихъ измѣреній можно вычислить діэлектрическія постоянныя.
РАСПРОСТРАНЕНІЕ ВЕСЬМА ДЛИННЫХЪ ВОЛНЪ ПО
ПРОВОЛОКАМЪ.
426. Очень длинныя волны нѣсколько отличаются отъ корот-
кихъ, которыя мы исключительно имѣли въ виду въ послѣднихъ па-
раграфахъ. Въ случаѣ короткихъ волнъ мы могли предполагать, что
самые провода не оказываютъ вліянія на процессъ, такъ какъ волны
почти не входятъ въ проволоку, но лишь скользятъ вдоль по ней,
и, главнымъ образомъ, потому еще, что омическая потеря напряженія
-составляетъ въ этомъ случаѣ лишь безконечно малую часть напря-
женія, такъ что послѣднее идетъ почти исключительно на измѣненія
магнитнаго поля. Дѣйствительно, на короткія волны проволоки дѣйству-
ютъ лишь такъ, какъ звукопроводная труба, съ которою мы ихъ срав-
нивали, дѣйствуетъ на звуковыя волны: онѣ удерживаютъ энергію
волнъ въ эѳирной полосѣ, ими ограниченной. Иначе обстоитъ дѣло въ
случаѣ медленныхъ колебаній. Они не только проникаютъ глубоко
въ проволоки, но при нихъ сравнительно существенную роль играетъ
также омическая потеря напряженія, такъ какъ инерція магнитнаго
поля при медленныхъ колебаніяхъ играетъ меньшую роль.
Совершенно то же самое относится и къ звуковымъ волнамъ.
На короткія волны въ сравнительно широкихъ трубахъ стѣнки
трубъ оказываютъ малое вліяніе. На медленныя же колебанія въ
относительно узкихъ трубахъ замѣтно вліяютъ стѣнки трубъ. Въ
этомъ случаѣ важную роль, между прочимъ, играютъ силы тренія
вблизи стѣнки трубы, тогда какъ при быстрыхъ колебаніяхъ онѣ
почти равны нулю въ сравненіи съ противодѣйствующими силами
инерціи колеблющихся массъ воздуха.
На телефонныхъ и телеграфныхъ проводахъ дѣлались много-
численныя наблюденія надъ распространеніемъ электромагнитныхъ
волнъ, числа колебаній которыхъ того же порядка, какъ у зву-^
новыхъ волнъ. Если между двумя удаленными мѣстами имѣются?
нѣсколько двойныхъ проводовъ, то по одному изъ нихъ посцлаіотъ
волны, а другую пару проволокъ присоединяютъ къ первой для
обратнаго движенія волнъ; волны возвращаются обратно въ4 исходный
пунктъ, пройдя въ ту и другую сторону ДЛИННЫЙ пуж въ нѣсколь-
378
Распространеніе весьма длинныхъ волнъ по проволокамъ
ко сотъ километровъ. Задавая опредѣленный тонъ, при помощи
соотвѣтствующаго инструмента, напримѣръ, осциллографа, наблю-
даютъ разность фазъ волны и отношеніе амплитудъ колебанія въ
началѣ и въ концѣ провода. Отсюда можно вычислить продолжи-
тельность перехода и скорость, а, кромѣ того, и поглощеніе волнъ
на ихъ пути вдоль проводовъ.
Такими измѣреніями было установлено, что длинныя волны
распространяются вдоль параллельныхъ проволокъ съ меньшей ско-
ростью, нежели короткія, и что скорость распространенія такихъ
волнъ въ значительной степени зависитъ какъ отъ числа колебаній,
такъ и отъ размѣровъ и сопротивленія проволокъ. Въ очень узкихъ
кабеляхъ, въ которыхъ самоиндукція мала и потому особенно силь-
но сказываются омическія потери напряженія, скорость распростра-
ненія и длинныхъ волнъ приблизительно слѣдуетъ такому закону:
« = 2.1/
г С.-и/’
здѣсь С обозначаетъ емкость единицы длины кабеля въ фарадахъ,
— сопротивленіе единицы длины въ омахъ, п—число колебаній
и тт=3,14. Какъ мы должны представлять себѣ распространеніе электри-
ческихъ полей въ кабелѣ, лишенномъ самоиндукціи, было уже ука-
зано въ § 344. Для подводнаго кабеля, гдѣ однимъ проводомъ явля-
ется мѣдная проволока въ 2 мм. толщины, окруженная гуттапер-
чевой оболочкой съ діаметромъ въ 12 мм., а другимъ проводомъ
служитъ море, сопротивленіе котораго въ виду его безконечно боль-
шого сѣченія можно считать равнымъ нулю, получаются слѣдующія
числа: ^ — 5,5 омовъ на километръ, С = 0,0771.10—6 фарадъ на
километръ. Слѣдовательно, для такого кабеля и = 5460 1Лп киломі.
г сек.
Для средней высоты тона, п — 500, получается и = 124 000 , т.-е.
скорость, значительно меньшая, чѣмъ с.
Но прежде всего оказывается, что длинныя волны чрезвычайно
сильно поглощаются въ кабеляхъ съ і
есть отрѣзокъ, пройденный волною, то амплитуда е^іконцѢ
отрѣзка уменьшается въ е~кх разъ въ сравне^Ц^съ ампл
въ началѣ отрѣзка; здѣсь к — поглощающая о способность
г. ...
малой самой иду кохіей; Если х
> этого
сравне^и^съ амплитудой
въ началѣ отрѣзка; здѣсь к — поглощающая о способность кабеля
р ... лХГ' о,693
для данной волны. Всякій разъ по прохожденій пути, равнаго —- - >
Распространеніе весьма длинныхъ волнъ по проволокамъ. 379*
амплитуда уменьшается до Ѵ2 своей начальной величины, а по про-
2 303
хожденіи пути въ --------до Ѵю. Поглощающая способность кабеля’
съ весьма малой самоиндукціей приближенно выражается формулой
к = ]/тг. С . іи . п.
Слѣдовательно, поглощеніе будетъ тѣмъ сильнѣе, чѣмъ больше-
емкость, чѣмъ больше сопротивленіе, и чѣмъ быстрѣе колеба-
ніе. Послѣднее обстоятельство вполнѣ согласуется съ тѣмъ, что мы
видѣли въ § 344. Многочисленные слѣдующіе другъ за другомъ
импульсы тѣмъ сильнѣе сливаются въ длинномъ кабелѣ, чѣмъ быстрѣе
они слѣдуютъ одинъ за другимъ. Поэтому перемѣнное поле послѣ
передачи черезъ кабель имѣетъ тѣмъ меньшую амплитуду, чѣмъ,
быстрѣе слѣдуютъ другъ за другомъ его положительные и отри-
цательные импульсы, т.-е. чѣмъ короче его періодъ колебанія. Для
вышеописаннаго кабеля получается к = 0,001 15. при чемъ за
единицу длины принятъ опять километръ. Для п = 500 получается
к = 0,0258; иначе говоря, всякій разъ по прохожденіи пути въ
26,8 километровъ амплитуда колебанія уменьшается до половины,
по прохожденіи 3.26,8 = 80,4 километровъ — до р по прохо-
жденіи 89,5 километровъ — до •
Изъ этихъ чиселъ видно, что невозможно телефонировать по-
длиннымъ подводнымъ проводамъ, такъ какъ тонъ при этомъ слишкомъ
ослабляется. Въ болѣе короткихъ кабеляхъ, которые не слишкомъ силь-
но ослабляютъ тонъ, произносимыя гласныя сильно искажаются, такъ
какъ высокіе тоны поглощаются сильнѣе, нежели низкіе, и тембръ,
звука поэтому становится глухимъ, что сильно вредитъ отчетли-
вости рѣчи.
Кабельная телеграфія на очень большихъ разстояніяхъ также .Д
возможна лишь въ томъ случаѣ, если число п чрезвычайно малр, і
т.-е. знаки слѣдуютъ другъ за другомъ весьма медленно; мы эір
отмѣтили уже въ § 344. Вслѣдствіе этого трансокеанскія телеграммы
требуютъ больше времени для передачи, нежели континец^льныя..
Несравненно болѣе выгодны такіе провода, которые^ имѣютъ
болѣе значительную самоиндукцію, такъ какъ въ нихъ вредное
вліяніе сопротивленія проявляется не столь рѣзкдрДЛри вычисленіи
“380
Распространеніе весьма длинныхъ волнъ по проволокамъ
проводки рѣшающую роль играетъ величина —, гдѣ Ь—само-
индукція единицы длины провода, выраженная въ генри, те/— сопро-
тивленіе единицы длины въ омахъ, п — число колебаній волны и
тг — 3,14. Если эта величина мала въ сравненіи съ единицей, то вычи-
сленіе нужно вести по даннымъ выше формуламъ для кабелей; если же
она велика сравнительно съ единицей, то дѣйствія инерціи магнит-
наго поля, т.-е. напряженія самоиндукціи, берутъ верхъ надо омиче-
скими потерями напряженія. Въ этомъ случаѣ скорость распростра-
ненія волны приближенно выражается формулой с = —• > и по-
глощеніе волнъ въ проводкѣ относительно мало. Оно вычисляется
по формулѣ
Для провода, состоящаго изъ двухъ мѣдныхъ проволокъ, имѣ-
ющихъ каждая толщину въ 2 мм. и подвѣшенныхъ въ воздухѣ на
разстояніи 10 см. одна отъ другой, получается: ^=11 омамъ на
километръ, Ь = 0,00184 генри на километръ, т.-е. к —0,010. По
прохожденіи 69,3* яш. амплитуда падаетъ до послѣ 230 км. — до -
Если колебанія не очень быстры, т.-е. если величина--------не
г 1Н)
очень велика, то формулы для с и к оказываются не вполнѣ точ-
ными. Болѣе точное математическое изслѣдованіе даетъ для выше-
описанныхъ параллельныхъ проводовъ:
при п = 500 с = 236 000 --- ,
сек.
при «= 1000 с = 270 000 —,
сек.
Поглощеніе оказывается, слѣдовательно, еще
нежели вычисленное по вышеприведеннымъ
к - 0,008
к - 0,009.
нѣсколько меньшимъ,
простымъ формуламъ.
Чѣмъ больше самоиндукція провода, тѣмъ слабѣе вредное вліяніе
омическаго сопротивленія. Это обстоятельство нашло чрезвычайно
важное практическое примѣненіе. Пупинъ (А. Риріп) показалъ5*счто
можно значительно уменьшить поглощеніе волнъ въ телефонныхъ
проводахъ, если въ цѣпь ввести нѣсколько катушекъ съукелѣзнымъ
сердечникомъ высокой самоиндукціи. Оказалось, ч^о,^вообще, до-
статочно на каждые 10 километровъ вводить въѣаждую прово-
-локу по одной самоиндукціонной катушкѣ Пуп.ийа^чтобы поглощеніе
Свободныя волны
381
значительно уменьшилось (напримѣръ, въ четыре раза). Съ помощью
катушекъ Пупина можно сдѣлать пригодными для телефоніи также
и подводные кабели, если только они не слишкомъ длинны.
СВОБОДНЫЯ ВОЛНЫ.
427. Если къ открытому концу трубы, проводящей звуковыя
волны, присоединенъ раструбъ, то большая часть энергіи волнъ,
Рис. 331.
Рис. 332.
382
Свободныя волны
Совершенно тоже самое наблюдается и въ случаѣ электромагнит-
ныхъ волнъ, распространяющихся вдоль параллельныхъ проволокъ,
•если обѣ проволоки въ концѣ разогнуть одну отъ другой. Въ этомъ
случаѣ электромагнитное поле распространяется въ окружающемъ
пространствѣ на большее разстояніе, чѣмъ въ случаѣ сближенныхъ
проволокъ, когда поле ограничено лишь ихъ ближайшей окрест-
ностью. Отъ расширившагося поля часть отщепляется и свободно
распространяется въ окружающемъ пространствѣ въ видѣ электро-
магнитной шаровой волны. По рисункамъ 331—334, построеннымъ
теоретически Герцемъ, можно видѣть, какимъ образомъ происхо-
дитъ отдѣленіе электрическихъ силовыхъ линій, распространяющихся
въ видѣ шаровой волны отъ разогнутыхъ концовъ параллельныхъ
проволокъ. Магнитное поле, которое мы должны представлять себѣ
вмѣстѣ съ отшнуровывающимися силовыми линіями и которое вызы-
ваетъ ихъ распространеніе въ отдаленное пространство, имѣетъ
видъ окружностей, центры которыхъ лежатъ на оси симметріи фи-
гуръ силовыхъ линій. Такимъ образомъ, магнитное и электрическое
поля повсюду взаимно перпендикулярны. Переходъ энергіи совер-
шается, по теоремѣ Пойнтинга, въ направленіи, перпендикулярномъ
къ обоимъ полямъ. Вблизи экватора, гдѣ сила поля наибольшая,
электрическія силовыя линіи распространяются почти точно по на-
правленіямъ меридіановъ шара, центръ котораго совпадаетъ съ цен-
тромъ излученія; магнитныя силовыя линіи образуютъ параллельные
круги, и излученіе происходитъ въ направленіи радіуса шара.
Въ другихъ мѣстахъ имѣется, вообще, кромѣ радіальной слага-
ющей, еще и небольшая тангенціальная слагающая потока энергіи;
но эта слагающая, однако, ослабѣваетъ по мѣрѣ удаленія отъ центра
излученія. Такимъ образомъ, на большихъ разстояніяхъ получается
правильная шаровая волна, распространяющаяся въ радіальномъ на-
правленіи совершенно такъ же, какъ звуковая волна. Но тогда какъ
шарообразная звуковая волна распространяется изъ центра ея пр
всѣмъ направленіямъ съ одинаковой напряженностью, напряженность^
электрической волны весьма различна въ различныхъ направжнІяхъ.
Въ направленіи оси симметріи, опредѣляемой двумя отогнутыми
концами проводовъ, энергія вовсе не распространяется ;_^въ эквато-
ріальномъ направленіи, перпендикулярномъ къ преды^щдёму, излуче-
ніе достигаетъ максимума. Если мы напряженность^^лученія на раз-
стояніи единицы отъ центра излученія въ экватрріальномъ напра-
Свободныя волны
383
вленіи назовемъ черезъ 70, то напряженность У излученія въ напра-
вленіи радіуса, составляющаго съ осью симметріи уголъ Ѳ, на раз-
1 Л . 8ІП2 Ѳ т т
•стояніи г отъ центра выразится уравненіемъ / = ----Напра-
вленіе электрическаго вектора, опредѣляющаго поле, перпендику-
лярно къ лучу и почти совпадаетъ съ меридіаномъ шара радіуса г.
Напряженность и направленіе электрическаго вектора представлены
на рис. 335 длиною и направленіемъ небольшихъ черточекъ,
перпендикулярныхъ къ лучамъ. Здѣсь мы имѣемъ типичный примѣръ
поперечной шаровой волны въ противоположность звуковой
волнѣ — продольной.
Величина той доли энергіи колебанія, которая излучается въ про-
странство изъ отогнутыхъ концовъ параллельныхъ проволокъ, зави-
ситъ отъ многихъ обстоятельствъ. Концы проволокъ, отъ которыхъ
исходитъ излученіе, назовемъ, какъ
принято въ послѣднее время, ан-
теннами. Излученіе тѣмъ больше,
чѣмъ длиннѣе антенны. Кромѣ того,
большое вліяніе имѣетъ число ко-
лебаній. Излученіе очень быстро
возрастаетъ съ увеличеніемъ числа
колебаній. Если обѣ антенны вмѣ"
стѣ взятыя меньше, чѣмъ поло-
вина длины волны колебанія, то
величина той части всей наличной
энергіи перемѣннаго поля, кото-
рая излучается за единицу времени,
при данныхъ антеннахъ пропор-
Рис. 335. Распредѣленіе напряжен-
ности въ поперечной шаровой волнѣ
вокругъ центра излученія.
ціональна четвертой степени числа колебаній, или, что то же,
обратно, пропорціональна четвертой степени длины волны.
По этой именно причинѣ свободныя электрическія волны ни-
когда не могли быть обнаружены при опытахъ съ относительно
медленными перемѣнными полями. Но какъ только перешли къ весьма0/^
высокимъ числамъ колебаній, а именно въ нѣсколько сотъ миллі^|р
новъ въ секунду, тотчасъ же были получены и свободныя электри-
ческія шаровыя волны. Герцъ первый (1888 г.) произвелъ опвітй съ
весьма быстрыми колебаніями и при этомъ получилъ свободнЫЯ/волны.
384
Осцилляторъ Герца
ОСЦИЛЛЯТОРЪ ГЕРЦА.
428. Для возбужденія свободныхъ электромагнитныхъ волнъ
Герцъ пользовался приборомъ, который изображенъ на рис. 336.
Онъ состоитъ изъ двухъ толстыхъ стержней — отрѣзковъ латунныхъ
трубокъ, которые оканчиваются шаровыми поверхностями и вмѣстѣ
образуютъ искровой промежутокъ. Провода отъ индуктора подхо-
дятъ возможно ближе къ искрѣ. Такой стержневой осцилляторъ
представляетъ собою колебательную цѣпь съ весьма малой емкостью.
Она образуется обоими наружными концами стержней, которые во
время колебаній заряжаются поперемѣнно: то верхній положительно
и нижній отрицательно, то наоборотъ. Вслѣдствіе большого разсто-
янія между концами
Рис. 336. Осцилляторъ
Герца.
Къ и,Н-
дукціонному
аппарату
стержней емкость, конечно, чрезвычайно мала.
Средняя часть осциллятора Герца съ искро-
вымъ промежуткомъ образуетъ цѣпь замыка-
нія этой емкости; вокругъ нея обвиваются
магнитныя силовыя линіи. Этотъ осцилляторъ
отличается чрезвычайно малымъ коэффиціен-
томъ самоиндукціи. Благодаря этому, при по-
мощи такого осциллятора получаются чрез-
вычайно быстрыя колебанія. Такъ какъ у
концовъ стержней лежатъ узлы, а искра при-
ходится въ пучности, то вся длина I осцил-
лятора приблизительно равняется половинѣ длины волны колебанія,
, X „ . З.юю
т.-е. I — -- Поэтому число періодовъ въ секунду равняется п = ——
Осцилляторъ, которымъ пользовался Герцъ, имѣлъ въ длину 26 см.,
длина волны его колебанія была равна приблизительно 60 см., число
періодовъ было 5.108.
Существенное отличіе такого осциллятора отъ осциллятора съ
плоскимъ конденсаторомъ и цѣпью замыканія заключается въ ^томъ,.
что его электрическое поле охватываетъ большое пространство,
почему онъ самъ излучаетъ: онъ является одновремеі|йОѵосцил-
ляторомъ и антенной.
Осцилляторы съ весьма обширными длежтрическими
полями называются открытыми. Тѣ осцилляторы, электри-
ческія поля которыхъ въ моментъ ^исчезновенія тока
ограничены узкимъ пространствомъ^ді^лектрика конден-
Пріемники для свободныхъ электрическихъ волнъ
385
сатора, называются закрытыми. Открытые осцилляторы
излучаютъ сильно, закрытые же почти не излучаютъ.
Такъ какъ осцилляторъ Герца одновременно играетъ также
роль антенны, то опыты съ нимъ очень просты. Но онъ обладаетъ
тѣмъ свойствомъ, что его колебанія очень сильно затухаютъ вслѣд-
ствіе большого излученія энергіи. Поэтому, если желательно рабо-
тать со слабо затухающими свободными волнами, то нужно поль-
зоваться болѣе сложной установкой, описанной въ § 427. Суще-
ствуетъ возможность строить закрытыя конденсаторныя цѣпи для
весьма короткихъ волнъ.
ПРІЕМНИКИ ДЛЯ СВОБОДНЫХЪ ЭЛЕКТРИЧЕСКИХЪ ВОЛНЪ.
429. Чтобы обнаружить электромагнитныя волны въ простран-
ствѣ, пользуются со времени Герца металлическимъ стержнемъ —
пріемной антенной, въ которую, вмѣсто искрового промежутка,
включенъ аппаратъ, обнаруживающій волны —детек-
торъ. Простѣйшимъ детекторомъ можетъ служить
очень малый искровой промежутокъ; исключительно
такимъ детекторомъ пользовался Герцъ. На рис. 337
представленъ пріемникъ Герца; искровой проме-
жутокъ состоялъ въ немъ изъ шара и острія, кото-
рое при помощи микрометрическаго винта можно
было очень близко подвести къ шару.
Чтобы демонстрировать волны, нужно имѣть воз-
можность обнаружить появленіе искорки посред-
ствомъ какого-нибудь видимаго издалека дѣйствія.
Для этой цѣли изобрѣтены многочисленные мето-
ды; простѣйшій основанъ на примѣненіи когерера
Бранли (Вгапіу). Этотъ приборъ представляетъ со-
бою короткую замкнутую стеклянную трубку, въ
которую съ обѣихъ сторонъ введены металлическіе
провода; къ послѣднимъ внутри прикрѣплены элек-
троды съ нѣсколько большей поверхностью. Трубка
наполнена рыхлымъ и грубымъ металлическимъ по-
рошкомъ,— напримѣръ, мелкими желѣзными стружками. ТакрйСпо-
рошокъ обычно является весьма дурнымъ проводникомъ; ^с^когда
черезъ него проходитъ электрическій разрядъ, изъ зеренъ соста-
вляются какимъ-то въ точности неизвѣстнымъ образовъ ^проводящія
нити, и порошокъ внезапно становится очень хорошимъ проводни-
Рис. 337.
Пріемникъ Герц|. р
Ми. Электричество и магнитизмъ, и. II.
25
386
Пріемники для свободныхъ электрическихъ волнъ
комъ. Это внезапное сильное измѣненіе электропроводности можетъ
быть демонстрировано различными способами. На рис. 344 видно, какъ
когереръ включенъ въ пріемную антенну; кромѣ того, черезъ когереръ
замкнута цѣпь, содержащая небольшой гальваническій элементъ и
звонокъ. Когда волны падаютъ на антенну и въ когерерѣ проскаки-
ваютъ маленькія искорки, онъ становится проводя-
щимъ, и звонокъ начинаетъ дѣйствовать. Когереръ
обладаетъ тѣмъ свойствомъ, что сдѣлавшись разъ хо-
рошимъ проводникомъ, онъ самъ по себѣ не теряетъ
проводимости. Чтобы сдѣлать его вновь дурнымъ
проводникомъ, т.-е. пригоднымъ къ употребленію въ
качествѣ детектора, нужно сначала постукиваніемъ
разрушить образовавшіяся небольшія проводящія нити.
Въ опытѣ, представленномъ на рис. 344, это про-
исходитъ просто вслѣдствіе сотрясенія прибора при
дѣйствіи находящагося вблизи звонка. Но обыкно-
прекращенія волнъ опять становится дур-
производить измѣренія надъ электрическими
всего пользоваться термоэлементами изъ
Къ
гальванометру
Рис. 338.
Пріемная ан. чѵ
теннадля корот-венно пользуются особымъ молоточкомъ, построен-
кихъ волнъ съ нымъ по принципу молотка Вагнера, въ видѣ звонка,
термоэлемен- г > >
томъ. язычокъ котораго ударяетъ по трубочкѣ съ металли-
ческимъ порошкомъ въ теченіи всего времени, пока
когереръ хорошо проводитъ. Благодаря этому приспособленію, коге-
реръ очень скоро послѣ
нымъ проводникомъ.
430. Если желаютъ
колебаніями, то лучше
тонкихъ проволокъ, нагрѣвающихся подъ дѣйствіемъ перемѣннаго
тока высокой частоты. Термоэлементы можно, конечно, включать
также въ качествѣ детекторовъ въ пріемныя антенны для свободныхъ
волнъ; такіе детекторы не только оказываются очень чувствитель-
ными, но позволяютъ также измѣрять интенсивность волнъ. Термо-
элементъ удобнѣе всего дѣлать изъ желѣзной и константановой Про-
волокъ, имѣющихъ толщину волоса (рис. 338); онѣ припаяны однимъ
концомъ къ антеннѣ и посрединѣ перевиты одна вокру^>щругой
въ видѣ креста. Оба свободные конца этихъ проволоюь^припаяны
къ проводамъ очень чувствительнаго гальванометра? Особенной
чувствительности можно достигнуть, помѣщая термоэлементъ въ
очень хорошо эвакуированный стеклянный сосудъ-). При данномъ
*) Это было открыто П. Н. Л ебедевымъ.^^ Прим. ред.
Опыты съ волнами Герца
387
количествѣ энергіи термоэлементъ нагрѣвается гораздо сильнѣе,
если теплота не уходитъ черезъ окружающій воздухъ. Чтобы на-
строить антенну на изслѣдуемое колебаніе, полезно не включать
термоэлементъ въ металлическій стержень, какъ изображено на
рис. 338, но дѣлать антенну изъ цѣльнаго стержня, длина котораго
равна половинѣ длины волны, а термоэлементъ привключить въ видѣ
отвѣтвленія къ пучности. Чѣмъ меньше сопротивленіе стержня, тѣмъ
лучше онъ резонируетъ, и напряженія при этомъ возрастаютъ на-
столько, что параллельно включенное сопротивленіе сильно нагрѣ-
вается, какъ въ опытѣ, представленномъ на рис. 309.
ОПЫТЫ СЪ ВОЛНАМИ ГЕРЦА.
431. Металлы отражаютъ электромагнитныя волны. Если параллель-
ныя проволоки замкнуть очень толстымъ металлическимъ мостомъ, то
волны, идущія вдоль проволокъ,будутъ отражаться отъ него почти пол-
ностью. Точно такъ же металлическая пластинка отражаетъ падающія на
нее свободныя волны. Если между осцилляторомъ и пріемникомъ уста-
новить большую металлическую пластину, то волны вовсе не дойдутъ
до пріемника, такъ какъ металлическая пластина ихъ не пропуститъ.
Но если на нѣкоторомъ разстояніи сбоку помѣстить второй метал-
лическій экранъ такимъ образомъ, чтобы лучъ, идущій отъ осцил-
лятора, могъ, по закону отраженія, попасть въ пріемникъ, минуя
металлическія преграды, то детекторъ обнаруживаетъ излученіе. Мы
видимъ, такимъ образомъ, что металлическая пластина совершенно
не пропускаетъ черезъ себя излученія, ‘но сильно его отражаетъ.
При этомъ часть излученія поглощается металломъ вслѣдствіе оми-
ческаго сопротивленія. Можно производить эти опыты съ очень
тонкими металлическими листками; оказывается, что отраженіе и
сопровождающее его поглощеніе въ случаѣ быстрыхъ колебаній обна-
руживаются во всей полнотѣ уже при чрезвычайно тонкихъ металли-
ческихъ слояхъ, съ поперечникомъ въ нѣсколько сотыхъ миллиметра.
Благодаря этому отражающему дѣйствію металловъ, волны удер-
живаются между двумя проволоками параллельной проводки подобно^Д
тому, какъ звукъ удерживается внутри трубы, благодаря ея от{э^
жающимъ твердымъ стѣнкамъ. Мы видѣли уже. въ § 408, чтобы-
стрыя колебанія при этомъ очень мало проникаютъ въ ^металлъ.
Медленныя волны проникаютъ глубже, но и онѣ отражаются; мы
видѣли, напримѣръ, въ § 370, что металлическій цилиндръ можетъ
25
388
Опыты съ волнами Герца
частью ограждать свое внутреннее пространство отъ весьма медлен-
наго перемѣннаго поля съ числомъ періодовъ, равнымъ пятидесяти,
т.-е. можетъ отражать это поле.
432. Металлическимъ отраженіемъ пользуются для построенія
вогнутыхъ зеркалъ, чтобы при опытахъ со свободными волнами луч-
ше концентрировать ихъ энергію. Обычно пользуются, какъ это дѣ-
лалъ уже Герцъ, цилиндрическимъ зеркаломъ съ параболическимъ по-
перечнымъ сѣченіемъ. Осцилляторъ помѣщаютъ вдоль фокальной ли-
ніи параболическаго цилиндра, изъ котораго излученіе исходитъ тогда,
какъ отъ прожектора. Пріемникъ помѣщаютъ вдоль фокальной линіи
второго параболическаго цилиндра. Если пучокъ лучей, исходящій отъ
Рис. 339. Диффракція волнъ
Герца, идущихъ отъ цилин-
дрическаго вогнутаго
зеркала.
Длина радіуса-вектора даетъ
интенсивность излученія въ
данномъ направленіи Длина
волны излученія X — 40сл(.
Отверстіе зеркала 54 см.
образномъ движеніи, сильное разсѣяніе лучей, н^^Йаемое диффрак-
ціей. При длинныхъ электромагнитныхъ волнамъ всегда наблюдаются
довольно сильныя явленія диффракціи. На^рис. 339 графически
ЧІЯи
„прожектора", перехватить вогнутымъ зер-
каломъ пріемника, то лучи концентируются
на его фокальной линіи, т.-е. на пріемной
антеннѣ, и' въ детекторѣ получаются силь-
ныя дѣйствія. Еще лучше было бы давать
вогнутымъ зеркаламъ форму параболоида
вращенія (какъ это дѣлается при устрой-
ствѣ свѣтовыхъ прожекторовъ), такъ какъ
цилиндрическія зеркала отчасти разсѣива-
ютъ лучи вверхъ и внизъ, вслѣдствіе че-
го концентрація лучей оказывается несо-
вершенной. Однако, по большей части, до-
вольствуются цилиндрическими зеркалами,
такъ какъ ихъ весьма легко изготовлять.
Кромѣ того, въ нихъ происходитъ еще до-
вольно сильное разсѣиваніе лучей въ эква-
торіальныхъ направленіяхъ, такъ какъ за-
конъ отраженія, изъ котораго мы исходи-
ли при построеніи вогнутаго зеркала, спра-
ведливъ лишь въ томъ случаѣ, когда раз-
мѣры зеркала безконечно велики сравни-
тельно съ длиной волны излучен&Асли же
это условіе не удовлетворено^^ происхо-
дитъ, какъ извѣстно изъ „ученія о волно-
Опыты съ волнами Герца
389
представлена для одного опредѣленнаго случая зависимость напря-
женности излученія, идущаго отъ цилиндрическаго вогнутаго зер-
кала, отъ направленія. Длина радіуса, проведеннаго въ опредѣлен-
номъ направленіи, представляетъ соотвѣтственную напряженность.
Кривая получена при помощи пріемника съ термоэлементомъ. Длина
волны излученія была лишь немного меньше отверстія зеркала, и
поэтому диффракція здѣсь весьма значительна. Напряженность пучка
лучей, выходящаго изъ вогнутаго зеркала, мало измѣняется при
отклоненіи въ обѣ стороны до 15° и лишь при большихъ углахъ
быстро падаетъ до очень малыхъ значеній.
433 Такъ какъ выходящее изъ вогнутаго зеркала излученіе
до нѣкоторой степени направлено опредѣленнымъ образомъ, то
Рис 340. Законъ отраженія волнъ Герца.
посредствомъ него можно показать, что законы преломленія и отра-
женія свѣтовыхъ лучей справедливы также и для волнъ Герца.
Если вогнутыя зеркала съ осцилляторомъ и пріемникомъ уста-
о (С^\°
Рис. 341. Преломленіе волнъ Герііа въ парафиновой призмѣ^/'
новлены, какъ показано на рис. 340, такъ чтобы во^рц| не падали
на пріемникъ, то ихъ можно посредствомъ отраженія^отъ жестяного
390
Опыты съ волнами Герца
листа направить на пріемникъ. Вращая листъ, можно убѣдиться, что
максимумъ дѣйствія получается, когда углы, составляемые падаю-
щимъ и отраженнымъ лучами съ нормалью къ поверхности зер-
кала, равны между собою.
Подобнымъ же опытомъ (рис. 341) можно показать, что лучи
Герца преломляются призмой изъ изолирующаго вещества (смола,
параффинъ и т. п). Если по углу отклоненія луча вычислить посред-
ствомъ формулъ оптики показатель преломленія призмы п, то ока-
зывается, что онъ равняется квадратному корню изъ удѣльной діэлек-
трической постоянной к вещества призмы: п = ']/гк. Изъ общаго
ученія о волнахъ извѣстно, что показатель преломленія обратно
пропорціоналенъ скорости распространенія волнъ; слѣдовательно,
п — > гдѣ с0 — скорость волны въ воздухѣ, с — скорость въ пре-
ломляющей средѣ. Такимъ образомъ, соотношеніе п = ]/гк подтвер-
ждаетъ теоретическіе выводы, развитые нами въ § 424.
434. Наконецъ, при помощи установки, изображенной на рис. 342,
Рис. 342. Интерференція волнъ Герца.
можно путемъ интерференціонныхъ опытовъ убѣдиться въ волно-
вой природѣ излученія, выходящаго изъ вогнутаго зеркала. Оба
Рис. 343. Кривая интерференціи волнъ Герца, порученная при помощи
термоэлектрическаго детектора^
вогнутыя зеркала съ отправителемъ и пріемникомъ поставлены ря-
домъ, и противъ нихъ расположены дф плоскіе жестяные листа,
Опыты съ волнами Герца
391
Это возможно лишь
лучи состоятъ изъ
полей, которыя въ
слагаются съ проти-
фазами. Это явленіе
отражающіе излученіе къ пріемнику. Если одно зеркало перемѣ-
щать впередъ или назадъ, держа
гому, то можно наблюдать интер-
ференцію двухъ отраженныхъ лу-
чей. При помощи термоэлемента
получается кривая напряженности,
изображенная на рис. 343. Мѣстамъ
наименьшей напряженности соот-
вѣтствуютъ такія положенія вто-
рого зеркала, при которыхъ оба
отраженные пучка лучей взаимно
уничтожаются полностью или боль-
шей частью,
потому, что
перемѣнныхъ
этомъ случаѣ
воположными
интерференціи служитъ прямымъ
опытнымъ доказательствомъ, что
лучи Герца представляютъ собою
правильныя волны, распространя-
ющіяся въ пространствѣ съ конеч-
ной скоростью. Для того, чтобы отъ
одного максимума перейти къ со-
сѣднему, нужно перемѣстить зер-
кало на половину длины волны,
потому что такое перемѣщеніе
измѣняетъ путь излученія, пада-
ющаго на перемѣщенное зеркало
и отъ него возвращающагося,
какъ разъ на длину волны. Такимъ
образомъ, посредствомъ интерфе-
ренціи можно опредѣлять длину
волны колебанія осциллятора. Если
ее измѣрять, кромѣ того, мето-
домъ Лехера, описаннымъ въ §§ 419 и 425, то^^црлу чаются
точно такія же числа. На рис. 343 видно, что интерференціонная
кривая по мѣрѣ возрастанія смѣщенія становится все менѣе отчетливой;
его все время параллельно дру-
Рис. 344. Поляризація волнъ Герца при помощи рѣшетки.
392
Опыты съ волнами Герца
это обстоятельство зависитъ отъ того, что, вслѣдствіе разсѣяні-
энергіи, волна, отраженная отъ болѣе удаленнаго зеркала, при слоя
женіи съ волной, отраженной отъ передняго зеркала, тѣмъ болѣе
ослаблена, чѣмъ дальше расположено зеркало.
435. Отраженіе совершается не только отъ сплошныхъ металли-
ческихъ поверхностей, но также и отъ проволочныхъ рѣшетокъ,
если отверстія рѣшетокъ малы сравнительно съ длиной волны. Рѣшетка,
составленная изъ параллельныхъ проволокъ, разстоянія между кото-
рыми значительно меньше длины волны, отражаетъ только такія
колебанія, электрическое поле которыхъ параллельно проволокамъ.
Если поставить два зеркала Герца точно одно противъ дру-
гого и между ними помѣстить проволочную рѣшетку такъ, чтобы
проволоки были параллельны осциллятору, то излученіе не будетъ
попадать въ пріемникъ, такъ какъ оно полностью отражается. Если
же повернуть рѣшетку на 90°, то излученіе будетъ проходить че-
резъ нее безпрепятственно, не подвергаясь отраженію. Если рѣ-
шетка повернута подъ какимъ-либо инымъ угломъ, то излученіе
разлагается на два слагающихъ: элетрическое колебаніе, параллель-
ное проволокамъ, отражается, а колебаніе, перпендикулярное къ про-
волокамъ, проходитъ черезъ рѣшетку. Это можно провѣрить на
опытѣ, измѣряя интенсивность термоэлементомъ.
Опыты съ рѣшеткой очень ясно показываютъ, что волны,* исхо-
дящія отъ осциллятора Герца, состоятъ изъ поперечныхъ колеба-
ній, поляризованныхъ прямолинейно, какъ и обыкновенное перемѣн-
ное поле. Если пустить вмѣстѣ двѣ волны, поляризованныя взаимно
перпендикулярно и обладающія нѣкоторою разностью фазъ, то онѣ
вмѣстѣ составятъ вращающееся электромагнитное поле, распростра-
няющееся со скоростью свѣта; въ болѣе общемъ случаѣ получается
эллиптически поляризованное поле. Такое поле можно получить,
напримѣръ, отводя параллельные провода отъ осциллятора Лехера
или Блондло къ двумъ антеннамъ, расположеннымъ взаимно пер-
пендикулярно. Если обѣ антенны находятся въ одной плоскости и
одну изъ подводящихъ проволокъ осциллятора сдѣлать ^длиннѣе
другой, то исходящія отъ антеннъ волны будутъ имфѣь^ нѣкото-
рую разность фазъ. Въ зависимости отъ величины послѣдней, ре-
зультирующія волны будутъ поляризованы по окружности или по
эллипсу. °
Электромагнитная теорія свѣта
393
ЭЛЕКТРОМАГНИТНАЯ ТЕОРІЯ СВЪТА.
436. Свѣтъ состоитъ изъ волнъ. Дѣйствительно, если отразить
свѣтовой лучъ отъ двухъ поверхностей, расположенныхъ одна близко
позади другой, — напримѣръ, отъ обѣихъ поверхностей, ограничи-
вающихъ тонкую прозрачную пластинку, то два отраженные луча
интерферируютъ между собою. Свѣтовыя волны распространяются
въ пустотѣ или въ міровомъ эѳирѣ со скоростью, равной 3 . 1010-^.
сек.
Свѣтовыя волны являются волнами поперечными; помощью такъ
называемаго поляризатора можно выдѣлить прямолинейно поля-
ризованныя волны изъ той неправильной смѣси многочисленныхъ
волнъ, которую представляетъ собою естественный свѣтъ. Въ
качествѣ поляризатора можно воспользоваться полированной по-
верхностью прозрачнаго тѣла, отражая отъ нея свѣтъ подъ такъ на-
зываемымъ „угломъ поляризаціи"; или же можно пропускать свѣтъ
черезъ призму Николя (Місоі) изъ известковаго шпата. Изъ пря-
молинейно поляризованнаго свѣта можно получить свѣтъ, поляризо-
ванный по окружности или по эллипсу, пропуская лучи черезъ про-
зрачную кристаллическую пластинку. Послѣдняя разлагаетъ лучъ на
два взаимно перпендикулярно поляризованные луча, которые при
прохожденіи черезъ пластинку пріобрѣтаютъ нѣкоторую разность
•фазъ. Такимъ образомъ, свѣтъ вообще имѣетъ характеръ электро-
магнитныхъ волнъ; онъ отличается отъ волнъ Герца лишь однимъ
свойствомъ — чрезвычайной малостью длины волны. Каждый одно-
родный цвѣтъ имѣетъ опредѣленную, ему свойственную, длину вол-
ны. Наибольшую длину волны — до 0,79 ц — имѣютъ красные лучи.
Наиболѣе короткими являются фіолетовыя волны; ихъ длина соста-
вляетъ 0,39 ц (1 р. = 0,001 мм.). Но въ излученіи раскаленнаго тѣла
имѣются, кромѣ того, болѣе длинныя волны, инфракрасныя, къ ко-
торымъ глазъ уже не чувствителенъ, и чрезвычайно короткія, уль-
трафіолетовыя, также не ощущаемыя глазомъ; длина первыхъ дохо-
дитъ до 60 ц, длина вторыхъ—до 0,1 ц !). Бѣлый свѣтъ можно счи-
тать смѣсью всевозможныхъ волнъ; онъ состоитъ изъ соверше^^
но неправильнаго, неперіодическаго и весьма быстро мѣняюц|а^ося
электромагнитнаго поля. & । •
і) Согласно новѣйшимъ изслѣдованіямъ, эти предѣльныя о длины волнъ
равняются соотвѣтственно 314 ц и 0,09 р.
394
Электромагнитная теорія свѣта
Лучи Рентгена, какъ уже упомянуто въ § 157, по всей вѣро-
ятности, также представляютъ чрезвычайно быстрыя электромагнит-
ныя колебанія, гораздо болѣе быстрыя, нежели свѣтовыя. Они от-
носятся къ излученію накаленныхъ тѣлъ примѣрно такъ, какъ это
послѣднее къ излученію Герца.
437. Не подлежитъ сомнѣнію, что осцилляторами, испускающими
свѣтъ, являются самые атомы вѣсомой матеріи. Характеръ колебаній
атомовъ можно опредѣлить путемъ наблюденій надъ свѣтящимися
парами металловъ, напримѣръ, ртутной дуговой лампы, или надъ
свѣтомъ Гейсслеровыхъ трубокъ. Съ помощью спектральнаго аппа-
рата можно убѣдиться, что такой свѣтъ состоитъ изъ ряда чистыхъ
синусоидальныхъ волнъ и даетъ такъ называемый линейчатый спектръ;
т.-е. онъ испускается осцилляторами, колеблющимися съ ненару-
шаемой правильной періодичностью, при чемъ различнымъ родамъ
осцилляторовъ соотвѣтствуютъ различныя числа періодовъ. Наобо-
ротъ, въ частицахъ твердаго раскаленнаго тѣла частыя столкнове-
нія и другія вліянія нарушаютъ правильность колебаній, и поэтому
такія частицы даютъ неправильныя колебанія, составляющія бѣлый
свѣтъ. Если помѣстить источникъ свѣта, осцилляторы котораго ис-
пускаютъ правильныя періодическія волны, въ сильное магнитное
поле, то, какъ показываетъ наблюденіе, поле закономѣрно вліяетъ
на колебанія атомовъ. Каждое чистое синусоидальное колеба-
ніе разлагается замедляющими и ускоряющими силами магнитнаго
поля на нѣсколько колебаній съ числами періодовъ, чрезвычайно
мало различающимися между собою. Это явленіе называется по имени
открывшаго его ученаго явленіемъ Зеемана (Хеетапп). Явленіе
Зеемана объясняется очень просто, если принять теорію матеріи,
изложенную нами въ §§ 210 и 211. Согласно этой теоріи, атомы
построены изъ положительно и отрицательно заряженныхъ частицъ.
Когда эти частицы колеблются какимъ-либо образомъ около поло-
женій равновѣсія, то колеблются заряды атомовъ, и отъ ихъ полей
отшнуровываются электромагнитныя волны, какъ и въ стеряшёвыхъ
осцилляторахъ Герца. Магнитное поле дѣйствуетъ съ ^орредѣлен-
ными силами на движущіяся электрическія частицы^ и вліяетъ
поэтому на колебанія атомныхъ осцилляторовъ; этимъ объясняется
въ общихъ чертахъ явленіе Зеемана. Если вычислить силовыя дѣй-
ствія магнитнаго поля, то они оказываются ст^і^ малыми, что лишь
легчайшія частички могутъ замѣтнымъ рбра^омъ подвергаться ихъ
Электромагнитная теорія свѣта
395
вліянію. Именно, если принять, что эти частички обладаютъ массокь
того же порядка, какъ и электроны, то получается порядокъ вели-
чины наблюдаемаго явленія Зеемана. Если, кромѣ того, принять во
вниманіе знакъ силъ, то изъ наблюденій можно заключить, что
колеблющіяся частицы, испускающія свѣтъ линейныхъ спектровъ,
должны быть заряжены отрицательнымъ электричествомъ. Изъ этихъ,
фактовъ слѣдуетъ, что колеблющіяся частички атомовъ, испу-
скающія линейные спектры, тождественны съ электронами,
которые могутъ отъ нихъ отщепляться въ видѣ частичекъ,,
составляющихъ катодные лучи.
При болѣе детальномъ изученіи явленія Зеемана оно оказы-
вается весьма сложнымъ, и обнаруживаются многочисленные его
типы. Отсюда заключаютъ, что атомы имѣютъ весьма сложную струк-
туру, что они содержатъ весьма большое число электроновъ, и что-
колебанія, вообще, сводятся къ довольно сложнымъ движе-
ніямъ многочисленныхъ электроновъ, связанныхъ между
собою силовыми дѣйствіями. Колебанія, совершаемыя одинако-
вымъ числомъ одинаково связанныхъ электроновъ, должны поэтому
давать всегда одинъ и тотъ же типъ явленія Зеемана. Особенное
мѣсто среди всѣхъ химическихъ элементовъ занимаетъ гелій. Мы по-
знакомились съ этимъ веществомъ при описаніи радіоактивныхъ явле-
ній (§ 200): частички, составляющія положительные а - лучи, выбра-
сываемыя при самопроизвольныхъ взрывахъ атомовъ, всегда предста-
вляютъ собою атомы гелія. Гелій имѣетъ довольно сложный спектръ,
состоящій изъ многихъ линій, но всѣ эти линіи обнаруживаютъ явле-
ніе Зеемана одного и того же типа. На каждую линію гелія
магнитное поле вліяетъ такимъ образомъ, какъ если бы
она испускалась колебаніями одной только отрицательной
электрической частички, совершающей свои колебанія око-
ло положенія равновѣсія по закону маятника. Въ этомъ про-
стомъ случаѣ можно посредствомъ несложной формулы опредѣлить^
по величинѣ явленія Зеемана отношеніе заряда колеблющейся ча-
стички къ ея массѣ. По измѣреніямъ Ломана (АѴ. Ьокшапп) для ^всѣхъ
линій гелія получается одна и та же величина, а именно $,77.10я'
кулоновъ на граммъ. Эта величина какъ-разъ ^а^гяется от-
ношенію заряда къ массѣ для электроновъ, ^полученному
изъ новыхъ измѣреній надъ катодными лу^<мй (§ 153). Въ
виду этого результата невозможно сомнѣватьс|^ічтб наиболѣе про-
396
Электромагнитная теорія свѣта
стыя электрическія колебанія въ атомѣ гелія представляютъ собою
колебанія электроновъ въ атомѣ.
438. Когда свѣтовой лучъ переходитъ въ другую прозрачную
среду, онъ преломляется совершенно такъ же, какъ и лучи Герца
(§ 433). Но показатель преломленія для чрезвычайно быстрыхъ элек-
тромагнитныхъ колебаній свѣта вообще отличается отъ показателя
преломленія для болѣе медленныхъ Герцовыхъ колебаній, равнаго
п = '\/гк (§ 433). Именно, показатель преломленія для свѣта значи-
тельно измѣняется въ зависимости отъ длины волны; чѣмъ меньше
длина волны, тѣмъ больше вообще показатель преломленія. Какъ
мы видѣли въ § 88, удѣльная діэлектрическая постоянная к (а слѣ-
довательно, и показатель преломленія для медленныхъ колебаній)
вѣсомыхъ діэлектриковъ отличается отъ единицы потому, что элек-
трическое поле въ матеріальныхъ молекулахъ и атомахъ вызываетъ
перемѣщенія элементарныхъ электрическихъ частицъ, изъ которыхъ
они составлены. Если эти перемѣщенія происходятъ не моментально,
но вслѣдствіе инертности частицъ требуютъ опредѣленнаго проме-
жутка времени того же порядка, что и продолжительность свѣто-
вого колебанія, то показатель преломленія для этихъ быстрыхъ свѣ-
товыхъ колебаній долженъ быть инымъ, нежели для медленныхъ
колебаній, дающихъ частицамъ достаточно времени для перемѣ-
щенія. Для полнаго теоретическаго объясненія оптическихъ свойствъ
прозрачныхъ тѣлъ слѣдуетъ непремѣнно имѣть въ виду, что діэлек-
трическія смѣщенія частицъ въ молекулахъ не происходятъ путемъ
одного единственнаго движенія, такъ сказать аперіодически, но
при этомъ должны происходить затухающія колебанія вокругъ окон-
чательнаго положенія. Особенно замѣчательны оптическія свойства
тѣлъ для такихъ свѣтовыхъ колебаній, числа которыхъ близки къ
числу собственныхъ колебаній молекулярныхъ частицъ, такъ что
становится замѣтнымъ резонансъ. Въ этомъ случаѣ наблюдается
очень сильное поглощеніе и очень сильное отраженіе, связанное^съ'
такъ называемой аномальной дисперсіей.
Особую главу составляютъ оптическія свойства металло^^кото-
рые сильно отражаютъ какъ свѣтовые лучи всѣхъ родовъ, такъ и
волны Герца; этимъ металлы отличаются отъ всѣхъ^пр^чихъ тѣлъ.
Весьма замѣчательно, что электролиты, которые ^вслѣдствіе своей
хорошей проводимости сильно поглощаютъ Отражаютъ лучи
Герца, обладаютъ относительно свѣта такими; свойствами, какъ
Электромагнитная теорія свѣта
397
и всѣ прочія прозрачныя тѣла. Причину этого различія слѣдуетъ
искать въ томъ, что грубые, трудно подвижные іоны электролитовъ
не могутъ или почти не могутъ слѣдовать за быстрыми свѣтовыми
колебаніями, тогда какъ перемѣнныя электрическія поля Герцо-
выхъ волнъ ихъ увлекаютъ съ собой. Въ металлахъ проводящія
частицы представляютъ собою чрезвычайно легкіе электроны, кото-
рые могутъ слѣдовать даже за столь быстрыми колебаніями,
какъ свѣтовыя. Въ видимой части спектра число періодовъ уже
лежитъ въ области, гдѣ и электроны постепенно перестаютъ слѣдо-
вать за колебаніями, и потому при переходѣ къ фіолетовой части
замѣтно уменьшается отражательная способность всѣхъ металловъ..
Для волнъ Герца отражательная способность металла вполнѣ можетъ,
быть вычислена по его проводимости и числу періодовъ волнъ;
чѣмъ больше проводимость, тѣмъ лучше металлъ отражаетъ. Если бы
мы примѣнили формулы, справедливыя для длинныхъ волнъ, къ ви-
димой части спектра, то вообще получили бы слишкомъ большія
значенія для отражательной способности, такъ какъ здѣсь инерція
электроновъ уже играетъ роль, которая не учитывается теоріей. Откло-
ненія вычисленныхъ значеній отъ измѣренныхъ тѣмъ меньше, чѣмъ
больше длина волны. Для волнъ, длина которыхъ превышаетъ 10 ц
(ультракрасные лучи), измѣренія, выполненныя Гагеномъ (На^еп) и
Рубенсомъ (КиЬепз), даютъ почти точно такія же величины, какъ
простая формула, общепризнанная для области волнъ Герца. Если
обозначимъ черезъ 7? отражательную способность металла въ про-
центахъ, то число А = 100 — 7? представитъ процентное количество
излученія, вступающее въ металлическую пластинку и тамъ погло-
щаемое. Нижеслѣдующая таблица даетъ значенія этой величины А
для излученія съ длиной волны Х= 12 ц, какъ измѣренныя Гагеномъ
и Рубенсомъ, такъ и вычисленныя изъ проводимости.
Поглощеніе въ металлическихъ пластинкахъ, X = 12 ц. По Га гену и Рубенсу
< О < 2 Е Патентъ- никкель Р Патентъ- никкель /И Константанъ Сплавъ Розе Сталъ
Измѣренныя вели- чины .... Вычисленныя . . 1,15 1,3 1,6 1,4 2,1 1,6 3,5 3,5 4,1 3,6 17,8 11,5 5,7 5,4 7,0^ 6,0 \\ 7,4 7,1 7,3 4,9 4,6
'398
Телеграфированіе безъ проводовъ
Если не считать висмута, который, повидимому, является исклю-
ченіемъ среди металловъ, то оказывается, что къ излученію съ дли-
ной волны 12 р металлы относятся почти совершенно такъ
.же, какъ къ волнамъ Герца.
Измѣренія Га гена и Рубенса доказываютъ непосредственно,
что шкала свѣтовыхъ лучей представляетъ собою ни что иное, какъ
продолженіе шкалы Герцовыхъ лучей.
ТЕЛЕГРАФИРОВАНІЕ БЕЗЪ ПРОВОДОВЪ.
439. Впервые волны Герца примѣнилъ къ телеграфированію
.Маркони (Магсопі) въ 1895 году. Отправителемъ безпроволоч-
наго телеграфа служитъ осцилляторъ съ передающей антенной; пріем-
никъ представляетъ собою антенну съ детекторомъ. Отправляющая
-станція посылаетъ ряды волнъ черезъ условные промежутки времени,
напримѣръ, по буквенной системѣ Морзе. Принимающая станція пе-
Рис. 345. Длинныя электрическія волны, распространяющіяся отъ антенны.
рехватываетъ эти ряды волнъ, и въ детекторѣ ея получаются понят-
ные сигналы. Изобрѣтеніе Мар ко ни основано, главнымъ образоічъ,
на примѣненіи сильно излучающаго отправителя и очень Чув-
ствительнаго детектора.
Волны, при помощи которыхъ работаетъ безпроволочной теле-
графъ, всегда имѣютъ большую длину, достигающую ^нѣсколькихъ
сотенъ или даже нѣсколькихъ тысячъ метровъ. Тольк^въ такія от-
носительно медленныя колебанія можно преобразовать большія ко-
личества энергіи. Передающая антенна въ своейзпростѣйшей формѣ
Телеграфированіе безъ проводовъ
399
представляетъ вертикальную проволоку, длина которой должна быть
близка къ четверти длины волны, чтобы вверху она имѣла узелъ,
а внизу — пучность. Внизу антенна соединяется либо съ землею, ли-
бо съ проводникомъ большой емкости, такъ называемымъ проти-
вовѣсомъ. Рисунокъ 345, на которомъ изображены силовыя ли-
ніи, показываетъ, какъ распространяются волны, исходящія отъ
антенны. Внизу онѣ должны скользить вдоль пдверхности земли.
Рис. 346. Антенна въ видѣ арфы.
Рис. 347. Клѣточная антенна,
Такимъ образомъ, въ безпроволочномъ телеграфѣ землею пользуются
въ качествѣ проводника, и волны слѣдуютъ за формой земной по-
верхности; онѣ могутъ огибать горы и распространяться вокругъ
земного шара. Такое, участіе земли влечетъ за собой вредное с^ф^-
лтвіе: благодаря своей плохой проводимости земля поглощаетъ^до-
вольно много энергіи. Интенсивность волнъ вслѣдствіе этогх) убы-
ваетъ не обратно пропорціонально квадрату разстоянія^^нѣсколь-
ко быстрѣе. Хорошо проводящая морская вода поглодаетъ гораздо
400
Телеграфированіе безъ проводовъ
меньше энергіи, нежели плохо проводящая влажная земля. Поэтому
на морѣ можно телеграфировать на болѣе далекое разстояніе, неже-
ли на сушѣ.
440. Чтобы увеличить излучающую способность передающей
антенны, ей придаютъ значительные размѣры. Мар ко ни при своихъ
опытахъ на итальянскомъ военномъ кораблѣ Сагіо АІЬегіо пользо-
вался такъ называемой арфовой антенной (рис. 346). Особенно по-
лезнымъ оказалось увеличеніе емкости верхняго конца антенны, какъ,
у изображенной на рис. 347 клѣточной антенны. Такая антенна
вбираетъ больше энергіи, нежели простая проволока, и потому силь-
нѣе излучаетъ. Особенно большая емкость получается, если отъ
верхняго конца вертикальной мачты антенны натянуть широкій про-
волочный зонтъ, конечно, хорошо изолированный отъ земли. Почву
подъ зонтомъ дѣлаютъ хорошо проводящей при помощи вложен-
ныхъ въ нее проволокъ, и такимъ путемъ получаютъ огромный
конденсаторъ большой емкости. На рис. 348 представлена нѣсколь-
ко схематически подобная зонтичная антенна, которою пользуются*
напримѣръ, на опытной станціи Науэнъ (Паиеп) около Берлина.
Зонтичная антенна имѣетъ, собственно, меньшую излучающую спо-
собность, нежели другія, совершенно открытыя антенны; однако, она
вбираетъ гораздо большія количества энергіи, и потому съ ея по-
мощью можно посылать въ пространство гораздо болѣе сильныя
волны, нежели при помощи иныхъ антеннъ.
Пріемная антенна подобна передающей; вообще говоря, одною
антенною можно пользоваться какъ для отправленія, такъ и для
пріема волнъ; въ первомъ случаѣ ее соединяютъ съ осцилляторомъ,
а во второмъ — съ детекторомъ. Чтобы не нарушить резонанса*
детекторъ обычно не вводится въ самую антенну, но связывается
съ нею индуктивно.
441. Детекторъ представляетъ едва ли не важнѣйшую состав-
ную часть всего аппарата; онъ лежитъ въ основѣ какъ изобрѣтенія
Марко ни, такъ и новѣйшаго развитія безпроволочнаго телеграфа.
Существуютъ два рода детекторовъ: во-первыхъ, детекторы^отвѣ-
чающіе только на первую часть ряда волнъ, при чемт^Мльнѣй-
шія волны не играютъ роли; во-вторыхъ, детекторы^суммирующіе
дѣйствіе всѣхъ волнъ, перехваченныхъ антенноіо^Детекторы ка-
ждаго рода, въ свою очередь, распадаются на два' класса. Детекто-
рами перваго рода являются 1) когереръ и 2)•'/магнитные детекторы*
Телеграфированіе безъ проводовъ
401
детекторами второго рода: 3) электрическіе клапаны и 4) термо-
метрическіе детекторы.
Детекторъ, впервые примѣнен-
ный на практикѣ Маркой и, пред-
ставляетъ собою когереръ Бранли;
о принципѣ этого аппарата мы уже
говорили въ § 429. Его чрезвы-
чайно большой чувствительности
Мар ко ни обязанъ своими первыми
удачными опытами, доказавшими
возможность телеграфировать безъ
проводовъ. Вътеченіе многихъ лѣтъ
послѣ этого когереръ былъ наи-
болѣе употребительнымъ детекто-
ромъ. Для правильнаго дѣйствія
когереръ долженъ быть изгото-
вленъ весьма тщательно. Металли-
ческія зерна должны быть изслѣ-
дованы съ помощью лупы каждое
въ отдѣльности; нужно брать лишь
зерна съ острыми ребрами и углами.
Продолговатыя зерна не годятся,
такъ какъ они легко сцѣпляются
и даютъ поэтому длительные кон-
такты. Но больше всего нужно
позаботиться о тщательной про-
сушкѣ зеренъ; ихъ помѣщаютъ
вмѣстѣ съ электродами въ сте-
клянныя трубки, которыя осво-
бождаютъ отъ влаги путемъ эва-
куаціи и запаиваютъ (рис. 349).
Дѣйствительно хорошій когереръ
никогда не долженъ быть подвер-
гаемъ дѣйствію сильныхъ электри-
ческихъ токовъ; поэтому ни въ ка-
комъ случаѣ его нельзя включать
въ цѣпь вызывного звонка или пи-
шущаго телеграфнаго аппарата. Когереръ вклюядекя всегда въ
Рис. 348.Антенна въ видѣ зонтика. (Для отчетливости задняя половина зонтика не изображена).
Ми. Электричество и магнитизмъ, ч. II.
26
402
Телеграфированіе безъ проводовъ
цѣпь слабаго тока релэ, которое замыкаетъ токи для самого сигналь-
наго аппарата и для молотка, „расцѣпляющаго" когереръ. Кромѣ
того, нужно еще примѣнять соотвѣтственныя приспособленія, чтобы
предохранить когереръ отъ высокихъ напряженій, возникающихъ
при перерывахъ тока.
Кромѣ когереровъ съ металлическимъ порошкомъ, было пред-
ложено также много другихъ когереровъ, дѣйствіе которыхъ осно-
Рис. 349. Когереръ.
вано на перемѣнныхъ сопротивленіяхъ при контактѣ, напримѣръ,
ртутный когереръ. Однако, эти когереры не получили такого широ-
каго распространенія, какъ когереръ съ металлическимъ порошкомъ.
Еще болѣе чувствительными, чѣмъ когереръ, являются магнит-
ные детекторы, впервые примѣненные также Маркони. Ихъ дѣй-
Рис. 350. Магнитный детекторъ Маркони.
ствіе основано на свойствѣ перемѣнныхъ магнитныхъ полей ^пони-
жать гистерезисъ (§ 334). Примѣромъ магнитнаго детектораМожетъ,
служить изображенный на рис. 350 магнитный детектор^^Іаркони-
По двумъ колесамъ, непрерывно вращаемымъ небольшимъ моторомъ,
движется безконечный канатъ изъ туго натянутых'ьѵжелѣзныхъ про-
...
волокъ, проходя предъ полюсами сильнаго подковообразнаго магни-
та. Сейчасъ же за магнитомъ проволока проводитъ черезъ катушку,
Телеграфированіе безъ проводовъ
403
приключенную къ пріемной антеннѣ. На эту катушку насажена
другая катушка, замкнутая на чувствительный телефонъ. Пока на
антенну не попадаютъ волны, намагниченіе, которое проволока имѣ-
етъ вслѣдствіе гистерезиса послѣ прохожденія передъ магнитомъ,
остается въ катушкѣ постояннымъ. Но когда на антенну падаютъ
волны, онѣ вызываютъ въ катушкѣ перемѣнное магнитное поле вы-
сокой частоты, вслѣдствіе чего остаточное намагни- ,-и
ченіе желѣзной проволоки понижается. Благодаря этому,
каждый рядъ волнъ вслѣдствіе индукціи сопровождается ІПГІЯК
трескомъ въ телефонѣ. Каждой искрѣ, проскакивающей || ||И
въ осцилляторѣ передатчика, соотвѣтствуетъ отдѣлъ- || I' !||М
ный трескъ, а болѣе длинному ряду искръ соотвѣт-
ствуетъ столь же продолжительный шумъ. Поэтому '+ •
въ телефонѣ можно различать точки и штрихи азбу- рис
ки Морзе и такимъ путемъ принимать телеграмму. Электролита -
Особенно разнообразны детекторы третьяго класса. ческій детек"
Ихъ устройство основано на дѣйствіи электрическихъ Шлёмильха.
клапановъ, и они выдѣляютъ изъ перемѣнныхъ напря-
Рис. 352. Детек-
торъ изъ свинцо-
ваго блеска Брау-
на (для лаборатор-
ныхъ опытовъ).
женій электрической волны одинаково направленные импульсы, дѣй-
ствующіе затѣмъ на релэ или на чувствительный гальванометръ. Въ
качествѣ примѣра такого детектора назовемъ прежде всего весьма
употребительный электролитическій элементъ Шлё-
мильха (ЗсЫбтіІсЪ). Онъ представляетъ собою не-
большой сосудъ (рис. 351) съ разбавленной сѣрной
кислотой, въ которую погружены два платиновые
электрода, соединенные съ гальваническимъ эле-
ментомъ. Напряженіе этого элемента должно быть
выбрано такъ, чтобы оно едва замѣтно превышало
максимальное напряженіе поляризаціи элемента Шлё-
мильха. Поэтому при обычныхъ условіяхъ въ цѣпи
идетъ
чается
даютъ
скихъ колебаній, въ теченіе каждаго полуперіода, когда оно имѣетъ^
одинаковое направленіе съ напряженіемъ элемента, преодолѣвается
напряженіе поляризаціи, въ силу чего каждый разъ происходитъ
толчокъ тока. Въ теченіе времени, пока длится рядъ вол^^на вклю-
ченный гальванометръ дѣйствуетъ толчокъ сильнаго^тока, равный
26
лишь весьма слабый токъ. Детекторъ вклю-
въ пріемный аппаратъ; когда на него па-
волны, то, благодаря напряженію электриче-
404
Телеграфированіе безъ проводовъ
суммѣ многихъ малыхъ толчковъ, соотвѣтствующихъ отдѣльнымъ
полуперіодамъ. Такимъ образомъ, элементъ Шлёмильха принадле-
житъ къ тѣмъ детекторамъ, въ которыхъ всѣ отдѣльныя волны
ряда слагаются для общаго дѣйствія. Практика показала, что на-
дежность и чувствительность этого детектора тѣмъ больше, чѣмъ
меньше поверхность анода. Въ виду этого въ качествѣ анода берутъ
тончайшую Вульстеновскую проволоку, запаянную въ стеклянной
трубочкѣ и возможно короче срѣзанную у мѣста запайки. Вторымъ
практически важнымъ примѣромъ детекторовъ этого класса является
детекторъ Брауна (Вгаип) изъ свинцоваго блеска. На рис. 352 онъ
представленъ въ формѣ, удобной для лабораторныхъ цѣлей. На
маленькую пластинку изъ свинцоваго блеска опирается съ чрезвы-
чайно слабымъ давленіемъ заостренный графитовый штифтикъ. Бла-
годаря этому, возникаетъ контактное сопротивленіе, которое въ
одномъ направленіи гораздо меньше, чѣмъ въ другомъ. Если коле-
банія достигаютъ детектора, то въ первомъ направленіи проходитъ
токъ, во второмъ же онъ либо вовсе не проходитъ, либо чрезвы-
чайно слабъ. Всѣ одинаково направленные импульсы слагаются въ
одинъ толчокъ тока, которымъ приводится въ дѣйствіе релэ. На-
правленіе лучшей проводимости контакта зависитъ отъ давленія
графитоваго острія на пластинку свинцоваго блеска.
Термометрическіе детекторы представляютъ собою либо термо-
элементы, либо болометры (§ 267). Съ ихъ помощью прямо измѣря-
ется полная энергія прибывающаго ряда волнъ, какъ мы видѣли уже въ
§ 430. Такіе детекторы до сихъ поръ не играли большой роли въ
практикѣ безпроволочнаго телеграфа. Возможно, однако, что въ
детекторѣ Брауна дѣйствуютъ также термоэлектрическія силы, такъ
что и онъ, собственно, принадлежитъ къ этому классу.
442. Исторію развитія безпроволочнаго телеграфа можно раздѣ-
лить на два періода по роду детекторовъ, въ немъ примѣнявшихся.
Первый періодъ характеризуется почти исключительнымъ примѣне-
ніемъ введенныхъ Маркони детекторовъ первой группы, т.%.°коге-
рера и магнитнаго детектора. Въ то время техника ставила себѣ
цѣлью, главнымъ образомъ, испускать изъ антенны передатчика медлен-
ный рядъ очень сильныхъ импульсовъ энергіи (отт^1()до20 въ секун-
ду). Для этой цѣли въ осцилляторѣ пользовались^медленнымъ рядомъ
очень мощныхъ искръ при возможно болѣеОвысокомъ напряженіи.
Въ старѣйшемъ и простѣйшемъ передатчикѣ 'Маркони (рис. 353)
Телеграфированіе^безъ проводовъ
405
осцилляторъ есть вмѣстѣ и антенна, какъ въ простомъ осцилляторѣ
Герца; отъ этого послѣдняго онъ 'отличается лишь гораздо большей
длиной волны и еще тѣмъ, что нижняя половина осциллятора замѣ-
нена землею; во многихъ установкахъ этотъ передатчикъ вскорѣ
былъ вытѣсненъ передатчикомъ Брауна (рис. 354). Въ послѣднемъ
осцилляторъ представляетъ отдѣльную замкнутую колебательную цѣпь,
связанную съ антенной индуктивно или гальванически. Этотъ пере-
датчикъ удобнѣе простого передатчика Марко ни потому, что въ
закрытомъ осцилляторѣ, вслѣдствіе его значительно большей емко-
сти, при данномъ искровомъ напряженіи скопляется гораздо больше
энергіи, чѣмъ въ полѣ антенны. Въ цѣпи осциллятора получаются
очень сильные токи, малое искровое сопротивленіе и потому малыя
Рис. 354. Передатчикъ Брауна.
Къ землѣ
Рис. 353. Передатчикъ Маркони.
настроенная на осцилляторъ, играетъ
какъ вторичная катушка въ транс-
потери въ искрѣ. Антенна,
совершенно такую же роль,
форматорѣ Тесла; въ ней напряженія достигаютъ чрезвычайно вы-
сокихъ значеній при малой силѣ тока, что необходимо для излуч^У
нія большихъ количествъ энергіи. Но для напряженія существуетъ
верхній предѣлъ, обусловливаемый искрящимися разрядами, которые
всегда сопровождаютъ высокія напряженія (§ 409) и вызцваюТь значи-
тельныя потери энергіи. Поэтому, для дальнѣйшаго у^ел^ченія излу-
ченія энергіи начали придавать антеннѣ большую еі^кррть (ср. § 440),
406
Телеграфированіе безъ проводовъ
благодаря чему она можетъ вбирать большія количества энергіи
безъ опаснаго повышенія напряженія.
Чтобы возможно лучше использовать энергію, доставляемую
осциллятору электрическими генераторами, и вмѣстѣ съ тѣмъ по
возможности уменьшить потери доставляемой энергіи въ искрѣ и
въ проводахъ, необходимо, чтобы энергія быстро переносилась отъ
осциллятора на антенну. Поэтому антенну тѣсно связываютъ съ ос-
цилляторомъ. Тѣсная связь влечетъ за собою, конечно, ущербъ, съ
которымъ въ передатчикѣ Брауна приходится мириться: какъ мы
видѣли въ § 405, сильная связь вызываетъ біенія. Такъ какъ біенія
мы можемъ разсматривать, какъ результатъ наложенія двухъ рядовъ
волнъ, различающихся немного по числу періодовъ, то можно сказать,
что передатчикъ Брауна излучаетъ одновременно двѣ различныя
волны. Но пріемная антенна должна быть точно настроена, чтобы
возможно было достигнуть наибольшаго максимума амплитуды коле-
баній (ср. § 403), который является рѣшающимъ для дѣйствія детек-
тора перваго рода. Если же антенна настроена невѣрно, то дѣйствіе
детектора будетъ гораздо слабѣе. Когда же имѣются двѣ волны,
какъ въ передатчикѣ Брауна, то антенна можетъ быть настроена
лишь на одну изъ нихъ, и потому около половины излучаемой
энергіи остается неиспользованной.
443. Когда пользуются детекторомъ перваго рода, то осцилля-
торъ передатчика приводятъ въ дѣйствіе медленно слѣдующими одна
за другой искрами, такъ какъ при болѣе быстромъ слѣдованіи искръ
не получается никакого усиленія дѣйствія детектора, и слишкомъ
обильныя искры вызываютъ лишь напрасную трату энергіи. Иначе
обстоитъ дѣло, если примѣняется детекторъ второго рода. Въ этомъ
случаѣ получается одинаковое дѣйствіе, попадаетъ ли на передат-
чикъ большое число слабыхъ волнъ или же малое число сильныхъ
волнъ, ибо рѣшающее значеніе имѣетъ не велич
лишь количество энергіи, получаемой въ теченіе
даже питать осцилляторъ болѣе слабыми, но 6е
одна за другой искрами, такъ какъ тогда невоз
резъ разряды на антеннѣ.
То же самое можно сказать и о длинѣ рядовъ волнъ. Если
на пріемникъ съ детекторомъ перваго рода падаетъ столько волнъ,
что амплитуда пріемника достигаетъ своего ^аксимума, то дальнѣй-
шія волны ряда излишни, такъ какъ дѣйствіе детектора зависитъ
гна амплитуды, но
секунды. ІЗьі^одно
стро слѣдующими
ложны, потери че-
Телеграфированіе безъ проводовъ
407
только отъ амплитуды перемѣннаго напряженія, а не отъ продолжи-
тельности его. При употребленіи детектора перваго рода дѣйстви-
тельно использованной оказывается лишь первая часть ряда волнъ,
и если ряды волнъ, выходящіе отъ передатчика, слишкомъ длин-
ны, т.-е. взятъ осцилляторъ съ очень медленнымъ затуханіемъ ко-
лебаній, то происходитъ напрасная трата энергіи. Детекторъ же вто-
рого рода, напротивъ, дѣйствуетъ тѣмъ лучше, чѣмъ длиннѣе ряды
волнъ; длинные ряды слабыхъ волнъ даютъ такое же дѣйствіе, какъ
короткіе ряды сильныхъ волнъ.
При этомъ слѣдуетъ еще имѣть въ виду, что настраиваніе на
длинные ряды волнъ должно быть гораздо точнѣе, чѣмъ на ко-
роткіе, если желательно вполнѣ использовать ихъ энергію. Если на-
строить не вполнѣ точно, но все же такъ, чтобы при первыхъ вол-
нахъ имѣли мѣсто лишь небольшія разности фазъ между волною и
колебаніемъ пріемника, то разность фазъ возрастаетъ пропорціо-
нально числу волнъ; и если рядъ волнъ очень длиненъ, то доходитъ
даже до того, что колебаніе волны направлено противоположно ко-
лебаніямъ пріемника и ихъ ослабляетъ. Въ этомъ случаѣ болѣе
позднія колебанія, вліяющія на детекторъ, оказываются, такимъ обра-
зомъ, значительно уменьшенными, и въ детекторѣ второго рода по-
лучается значительно меньшее дѣйствіе, чѣмъ въ случаѣ весьма точ-
ной настройки. Въ детекторѣ же перваго рода такая же разница
въ настройкѣ не была бы замѣчена.
Когда пользуются длинными рядами не затухающихъ
волнъ и детекторомъ второго рода, то получается гораздо
болѣе полный резонансъ, чѣмъ при употребленіи детек-
тора перваго рода.
Полный резонансъ обладаетъ многими весьма важными практи-
ческими преимуществами. Можно взять волны столь малой интен-
сивности, чтобы только совершенно точно настроенный пріемникъ
воспроизводилъ сигналы. Если двѣ станціи по взаимному соглаше-
нію пользуются секретнымъ, вполнѣ опредѣленнымъ числомъ коле-
баній, то постороннимъ лицамъ, не знающимъ этого числа коле^днІЙ,
очень трудно перехватить телеграмму, тогда какъ станціимогутъ
сноситься между собою съ большимъ удобствомъ. Вмѣс^фь тѣмъ
пріемная станція, антенна которой сильно резонируетъ? лишь на
вполнѣ опредѣленное число колебаній, не обременится телеграм-
мами другихъ чиселъ колебаній, для нея не предназначенными. Та-
408
Телеграфированіе безъ проводовъ
кимъ образомъ, въ пространствѣ одновременно можетъ идти очень
много телеграммъ, при чемъ каждая станція получаетъ только для
нея предназначенныя телеграммы. Устраненіе возмущеній, со-
ставляющее едва ли не важнѣйшую задачу безпроволоч-
ной телеграфіи, проще всего достигается употребленіемъ
длинныхъ рядовъ волнъ съ малымъ затуханіемъ и малой
амплитуды и примѣненіемъ детекторовъ второго рода.
Такимъ образомъ, пока употреблялись исключительно детекто-
ры перваго рода, необходимо было, чтобы передатчикъ излучалъ
ряды волнъ, медленно слѣдующіе другъ за другомъ и возможно
болѣе интенсивные, но относительно быстро прекращающіеся. Когда
же въ практику были введены детекторы второго рода, очередной
задачей сдѣлалось полученіе рядовъ волнъ, быстро слѣдующихъ
другъ за другомъ и относительно слабыхъ, но очень длинныхъ и съ
медленнымъ затуханіемъ. Лишь съ разрѣшеніемъ этой задачи переходъ
къ детекторамъ второго рода явился крупнымъ успѣхомъ техники.
444. Получить очень длинные ряды волнъ высокой частоты,
пригодные для безпроволочнаго телеграфированія, удалось впервые
въ началѣ 1906 года датскому иженеру Паульсену при помощи
его дуговой лампы (ср. § 413). Однако, болѣе точныя испыта-
нія обнаружили, что дуговая лампа Пауль се на не удовлетворя-
етъ поставленнымъ требованіямъ. Какъ мы видѣли въ § 413, число
періодовъ колебаній свѣтовой дуги зависитъ не только отъ емкости
и самоиндукціи колебательной цѣпи, но также и отъ свойствъ свѣ-
товой дуги. Такъ какъ свѣтовая дуга лампы Паульсена не можетъ
оставаться совершенно постоянной, то и продолжительность ея ко-
лебанія также не остается постоянной. Это обстоятельство весьма
вредитъ полнотѣ резонанса. Но главнымъ недостаткомъ лампы
Паульсена является ея весьма малая отдача. Большая часть затра-
ченной энергіи поглощается въ сопротивленіяхъ и въ свѣтовой дугѣ,
и лишь небольшая часть получается изъ антенны въ видѣ электро-
магнитныхъ волнъ. Поэтому полученіе достаточной энергіи для те-
леграфированія требуетъ большихъ машинъ для возбужденія электри-
ческаго тока, что особенно неудобно для переносныхъ станцій. Кро-
мѣ того, чтобы получить не слишкомъ малую отдачу,^цужно поль-
зоваться возможно болѣе медленными колебаніями^ слѣдствіе чего
антенны должны быть очень велики, м весь аппаратъ становится
крайне неудобнымъ.
Телеграфированіе безъ проводовъ
409
445. Въ 1906 году М. Винъ открылъ методъ возбужденія
толчками весьма мало затухающихъ колебаній. Этотъ методъ послѣ
того былъ технически разработанъ Обществомъ Безпроволочной Те-
леграфіи (ОезеІзсИаіі ійг сІгаМозе ТеІе^гарИіе). На практикѣ въ ка-
чествѣ колебательной цѣпи берутъ прямо антенну, съ которой силь-
но связанъ возбудитель толчковъ. Такимъ образомъ, аппаратъ для
возбужденія толчковъ, примѣняемый въ безпроволочномъ телеграфѣ,
похожъ на передатчикъ Брауна (рис. 354). Отъ послѣдняго онъ
отличается, главнымъ образомъ, лишь искровымъ промежуткомъ, ко-
торый устраивается такъ, чтобы искра быстро затухала. Когда искра
въ возбуждающей цѣпи прекращается, самый осцилляторъ ко-
леблется совершенно такъ же, какъ простой передатчикъ Мар ко ни
безъ искрового промежутка. Поэтому энергія теряется только
въ видѣ теплоты тока въ проволокѣ антенны и на излученіе волнъ.
Главную роль играетъ первая потеря, но и она мала въ сравненіи
съ потерями энергіи у искрового осциллятора, которыя влечетъ за
собой искра, и сообразно съ этимъ затуханіе колебанія незначи-
тельно. Такимъ образомъ, получается продолжительный рядъ волнъ,
амплитуда которыхъ падаетъ лишь медленно и постепенно (рис. 318).
Кромѣ того, возможно еще уменьшить затуханіе, вызываемое излу-
ченіемъ; для этого нужно лишь свернуть часть антенны въ видѣ
широкой катушки, такъ чтобы часть антенны, выдающаяся свободно
въ воздухѣ, сдѣлалась короче. Тогда антенна излучаетъ меньше, и
амплитуда испускаемыхъ волнъ также уменьшается, но вмѣстѣ съ
тѣмъ ряды волнъ будутъ нѣсколько менѣе затухающими. Наивы-
годнѣйшую длину свободной антенны необходимо опредѣлить прак-
тически, путемъ опытовъ.
Важнѣйшею частью прибора, служащаго для возбужденія толч-
ковъ, является искровой промежутокъ. Онъ работаетъ надежно,
лишь если искра никогда не задерживается и накаливаніе электро-
довъ на ея концахъ поэтому не мѣшаетъ быстрому исчезновенію
проводимости искрового промежутка. Наиболѣе практичнымъ ока-
зался искровой промежутокъ съ большими плоскими кольцеобраз-^°
ными металлическими электродами, находящимися на весьма маломъ
разстояніи другъ отъ друга. При проскакиваніи искры, онС^подъ
.дѣйствіемъ магнитнаго поля тока переносится внаружу^р./^ 289),
и потому не можетъ удержаться на мѣстѣ. Особенно^ыгодно дѣ-
лать электроды изъ металла, обладающаго большой^ теплопровод-
410
Телеграфированіе безъ проводовъ
ностью; лучше всего пользоваться мѣдью, покрытою слоемъ серебра..
Чтобы имѣть возможность достигать большихъ разрядныхъ напря-
женій и потому большихъ амплитудъ колебанія, включаютъ послѣ-
довательно рядъ короткихъ кольцевыхъ искровыхъ промежутковъ.
Такой искровой промежутокъ представленъ на рис. 355. Чѣмъ боль-
шія разрядныя напряженія мы желаемъ примѣнять, тѣмъ больше
должно быть число кольцевыхъ искровыхъ промежутковъ. Если же
желательно перейти къ болѣе низкимъ напряженіямъ, то нѣкоторые
изъ нихъ просто замыкаются на короткую.
Мы видѣли, что. при употребленіи детекторовъ второго рода
— только о нихъ, конечно, и можетъ быть рѣчь при затухаемыхъ.
Рис. 355. Искровой промежутокъ передатчика съ возбужденіемъ толчками.,
і—отдѣльный кольцевой искровой промежутокъ.
искрахъ — нужно пользоваться искрами, быстро слѣдующими одна
за другой. Чтобы добиться возможно полнаго постоянства числа
искръ въ секунду, Общество Безпроволочной Телеграфіи употребля-
етъ для возбужденія затухающихъ искръ перемѣнное напряженіе
(между 4000 и 70 000 вольтъ); при тщательномъ выборѣ длины
искрового промежутка, т.-е. числа кольцевыхъ промежутковъ,^^
емкости искровой цѣпи искра проскакиваетъ лишь при каждомъ,
максимумѣ перемѣннаго напряженія. Число періодовъ генератора
перемѣннаго тока выбираютъ между 250 и 1000 въ секунду, такъ
что число искръ составляетъ отъ 500 до 2000. Еслрвъ пріем-
никѣ пользуются телефономъ, соединеннымъ съ детекторомъ, и те-
леграмму принимаютъ на слухъ, то въ телефонѣ получается чистый,
и ясный музыкальный тонъ, число колебаній ^фтораго равняется
числу искръ передатчика. Если каждая станція имѣетъ особое число*
Телеграфированіе безъ проводовъ
411
искръ, то этимъ еще вѣрнѣе предотвращается возможность возму-
щеній. Кромѣ того, для усиленія звука можно еще пользоваться ре-
зонанснымъ релэ, которымъ также уничтожаются всякіе другіе зву-
ки, поступающіе въ пріемникъ. Резонансное релэ можетъ примѣ-
няться также и для пишущаго телеграфа.
Конечно, отсутствіе возмущеній гарантируется, главнымъ обра-
зомъ, свойствомъ передатчика съ затухающей искрой высылать слабо
затухающія волны только одного опредѣленнаго рода. Настройка
на эти волны гораздо точнѣе, чѣмъ на волны передатчиковъ Брауна
и Паульсена, почему телеграмма можетъ получаться съ очень
удаленныхъ станцій безъ возмущеній, даже если совсѣмъ близко
испускаются волны другими передатчиками. Число колебаній отпра-
вителя можно измѣнять простымъ образомъ, включая или выключая
въ антеннѣ и искровой цѣпи нѣсколько витковъ. При этомъ очень
удобно то обстоятельство, что не требуется совершенно точной
настройки. Продолжительность колебаній испускаемыхъ волнъ за-
виситъ только отъ всей длины антенны. Если желательно очень,
сильно измѣнить продолжительность колебанія, то слѣдуетъ перемѣ-
нить конденсаторъ искровой цѣпи и воздушный проводъ антенны.
Вообще говоря, въ телеграфѣ съ описываемымъ передатчикомъ
можно взять на выборъ волны различной длины, а именно — отъ
200 до 5000 метровъ. Это обстоятельство очень важно, такъ какъ,
даетъ возможность избѣгать возмущеній и въ томъ случаѣ, когда
одновременно работаетъ много станцій.
Большимъ преимуществомъ системы затухающихъ искръ явля-
ется большая отдача осциллятора. Такъ какъ колебаніе въ замкну-
той первичной цѣпи длится лишь очень короткое время, и.энергія
очень быстро передается во вторичную цѣпь, то въ первичной цѣ-
пи поглощается лишь немного энергіи, тогда какъ искра передатчи-
ка Брауна, напримѣръ, поглощаетъ значительную часть всей энер-
гіи въ теченіе всего того времени, пока длятся колебанія. Изъ все-с
го количества энергіи, доставляемаго генераторомъ перемѣннаго т^а;)
около 70% поступаютъ въ антенну въ видѣ энергіи колеб^щй и
здѣсь частью тратятся на неизбѣжную теплоту тока, а частью излу-
чаются. Лишь 30% поглощаются въ трансформаторѣ высокаго на-
пряженія и въ искровой цѣпи. Поэтому вся устанорКа^занимаетъ,
очень мало мѣста и весьма удобна.
412
Телеграфированіе безъ проводовъ
Большая отдача передатчика съ затухающей искрой означаетъ
не только экономію энергіи, но также и отсутствіе вредныхъ и не-
желательныхъ побочныхъ дѣйствій, которыя въ другихъ системахъ
вызываются теряемой частью энергіи. Сильныя искры передатчика
Брауна потребляютъ много энергіи на то, чтобы накалять электроды
искрового промежутка и постепенно ихъ разрушать, и на сопрово-
ждающій ихъ оглушительный шумъ. Весьма цѣннымъ преимуще-
ствомъ затухающихъ искръ является, во-первыхъ, то обстоятельство,
что электроды почти не изнашиваются, и потому ихъ лишь рѣдко
приходится мѣнять, и, во-вторыхъ, отсутствіе шума на передающей
•станціи. Благодаря этому высылаемые ряды волнъ могутъ получить
указанное выше полезное свойство—давать чистый музыкальный тонъ.
По существу, описанная система звучащихъ затухающихъ
искръ является, вѣроятно, наиболѣе совершенной системой возбу-
жденія колебаній для безпроволочнаго телеграфа,—подобно тому, какъ
современная форма динамомашины является совершеннымъ типомъ
электрическаго генератора; въ деталяхъ, можетъ быть, она еще бу-
детъ улучшена, но навѣрное не будетъ превзойдена другими систе-
мами. Зато разрѣшеніе другихъ задачъ безпроволочной телеграфіи
и, прежде всего, проблемы посыланія электрическихъ волнъ по опре-
дѣленному направленію, а также разрѣшеніе проблемы безпрово-
лочнаго телефонированія всецѣло принадлежитъ будущему.
ГЛАВА ДЕВЯТАЯ.
ПРИНЦИПЪ ОТНОСИТЕЛЬНОСТИ.
ИНЕРЦІЯ МАТЕРІИ ЗАВИСИТЪ ОТЪ ПРОЦЕССОВЪ, ПРОИСХОДЯ-
ЩИХЪ ВЪ ЭѲИРЪ.
446. Согласно электронной теоріи, невозможно мыслить матерію
отдѣльно отъ единой міровой субстанціи — эѳира. Движенія атомовъ
по существу представляютъ собою лишь извѣстныя измѣненія въ
эѳирѣ, происходящія въ немъ повсюду тамъ, гдѣ его внутреннія силы
не находятся въ равновѣсіи. Такимъ образомъ, движеніе никоимъ обра-
зомъ не является процессомъ, который пространственно ограниченъ
самимъ атомомъ, какъ предполагалось прежде: вмѣстѣ съ перемѣ-
щеніемъ въ эѳирѣ узловъ силовыхъ полей, которые мы называемъ
„электронами", „іонами" или „атомами", измѣняются и окружаю-
щія ихъ поля. Чтобы получить нѣсколько болѣе опредѣленное пред-
ставленіе объ этихъ процессахъ, мы сначала оставимъ безъ вниманія
всѣ недостаточно извѣстныя намъ состоянія эѳира, каковымъ, на-
примѣръ, является тяготѣніе, и займемся исключительно свойствами
электромагнитнаго поля, окружающаго іонъ.
Электронъ или іонъ вмѣстѣ съ окружающимъ его электриче-
скимъ полемъ можетъ перемѣщаться въ эѳирѣ лишь въ томъ случаѣ,
если онъ окруженъ магнитнымъ полемъ въ видѣ окружностей, ко-
торое служитъ для перенесенія электрическихъ напряженій. Это маг-
нитное поле безусловно участвуетъ въ тѣхъ процессахъ, которые
въ своей совокупности образуютъ то, что мы называемъ движеніемъ^
Но магнитное поле содержитъ въ себѣ энергію; поэтому вокругъ
движущагося іона энергія эѳира больше, нежели около неподвижнаго
іона, .и для приведенія іона въ движеніе нужно какимъ-71^60 обра-
зомъ доставить ему то количество энергіи, которо§днеобходимо>
чтобы уравновѣсить эту разность. Это количество ^энергіи мы назы-
ваемъ энергіей движенія юна. Она есть не чтвлинЪе, какъ энергія
414 Инерція матеріи зависитъ отъ процессовъ, происходящихъ въ эѳирѣ
магнитнаго поля, увеличенная, можетъ быть, еще на нѣкоторое ко-
личество энергіи, необходимое для иныхъ, еще неизвѣстныхъ, про-
цессовъ въ эѳирѣ» также связанныхъ съ движеніемъ іона. Сила маг-
нитнаго поля пропорціональна скорости, съ которой движется іонъ;
его энергія, какъ вообще энергія движенія, пропорціональна второй
-степени силы поля, а, слѣдовательно, и второй степени скорости.
Когда іонъ или электронъ приводятся въ движеніе, то должны
возникнуть напряженія, которыя взаимно уравновѣшиваются и воз-
буждаютъ магнитное поле. Эти напряженія возникаютъ вслѣдствіе
того, что электрическія силовыя линіи вокругъ электрона нѣсколько
перемѣщаются изъ своего положенія равновѣсія, когда электронъ
начинаетъ двигаться; при этомъ поле получаетъ нѣкоторую асим-
метричность, связанную съ такимъ дѣйствіемъ на электронъ, которое
противодѣйствуетъ возникающему движенію. Эта асимметричность
около электрона и связанная съ нею сила существуютъ до тѣхъ
поръ, пока движеніе не становится стаціонарнымъ.
Эту силу въ механикѣ называютъ реакціей инертной массы
электрона. Точнѣе говоря, это реакція магнитнаго поля, возника-
ющаго въ окружающемъ электронъ эѳирѣ, или сопротивленіе
инерціи магнитнаго поля. Это сопротивленіе инерціи уравновѣ-
шивается другой силой, дѣйствующей на электронъ въ противопо-
ложномъ направленіи — движущей силой. Черезъ нее электронъ
получаетъ энергію, которую можно вычислить, какъ работу движу-
щей силы; но вслѣдствіе того, что электронъ движется противъ
силы реакціи магнитнаго поля, эта работа тотчасъ же передается
далѣе электромагнитному полю, и здѣсь распредѣляется, согласно
теоремѣ Пойнтинга, въ видѣ энергіи магнитнаго поля, связаннаго
съ движеніемъ. Нѣчто подобное можно было бы, вѣроятно, ска-
зать и о силѣ реакціи, или инерціи, иныхъ, пока еще неизвѣстныхъ
„процессовъ движенія" въ эѳирѣ, которая, можетъ быть, вмѣстѣ съ
магнитной инерціей образуетъ полную инертную массу электрона.
Если движущійся узелъ поля переходитъ въ состояніе покоя/ то
магнитное поле должно исчезнуть, и тогда возникаетъ сила/реМкціи,
направленная въ сторону движенія. Чтобы ее преодолѣть,необхо-
димо употребить силу, противоположную движенію, щтакимъ обра-
зомъ, электронъ отдаетъ обратно въ видѣ работы энергію магнитнаго
поля и, быть можетъ, также другихъ, еще неизвѣстныхъ, процес-
совъ въ эѳирѣ, сопровождающихъ движеніе. ; X
Инерція матеріи зависитъ отъ процессовъ, происходящихъ въ эѳирѣ 415
Согласно электронной теоріи, инерція матеріальной
частицы представляетъ собою не что иное, какъ ин)ерцію
магнитнаго поля и, можетъ быть, еще другихъ, пока неиз-
вѣстныхъ, явленій въ эѳирѣ, составляющихъ существенную
часть всего процесса движенія, но не ограниченныхъ ма-
лымъ объемомъ узловыхъ мѣстъ въ эѳирѣ.
Согласно этому воззрѣнію, механика, всегда разсматривавшая
понятіе инерціи, какъ элементарное, простѣйшее понятіе, должна по-
терять свое положеніе основной науки. Не эѳиръ слѣдуетъ объяс-
нять механически, но матерію — электромагнитизмомъ. Механическія
аналогіи, о которыхъ часто шла рѣчь въ этой книгѣ, не являются
попытками глубже проникнуть въ сущность эѳира, такъ какъ въ
дѣйствительности механическіе процессы могутъ быть поняты лишь
на основѣ электромагнитныхъ. Но какъ это бываетъ и въ другихъ
случаяхъ, въ данной области явленія, логически болѣе сложныя и
болѣе трудныя для пониманія, привычнѣе нашимъ представленіямъ,
нежели явленія, болѣе простыя въ смыслѣ понятій; поэтому мы
и могли пользоваться механическими явленіями въ качествѣ примѣ-
ровъ, облегчающихъ пониманіе.
447. Изъ точки зрѣнія электронной теоріи на инерцію выте-
каетъ весьма замѣчательное слѣдствіе. Магнитное поле вокругъ дви-
жущагося электрона должно двигаться черезъ эѳиръ вмѣстѣ съ элек-
трическимъ полемъ. Но это можетъ происходить только при томъ
условіи, чтобы электрическое поле вокругъ движущагося электрона
вызывало въ тѣхъ мѣстахъ, откуда оно удаляется, исчезновеніе маг-
нитнаго поля, а тамъ, гдѣ оно появляется,—возникновеніе магнитнаго
поля. Это, въ свою очередь, возможно лишь въ томъ случаѣ, если
электрическое поле вокругъ движущагося электрона само по себѣ не
находится въ равновѣсіи, какъ это имѣетъ мѣсто около покоющагося
электрона. Болѣе точный математическій анализъ этого процесса на
основѣ двухъ Максвелловыхъ законовъ электродинамики указы-
ваетъ, что у движущагося электрона радіальныя электрическія сило-
выя линіи нѣсколько удаляются отъ полюсовъ, лежащихъ по линіц^
движенія, и тѣснѣе собираются въ области экватора (рис. 356).
скорость движенія поля мала въ сравненіи со скоростью распростра-
ненія свободныхъ электромагнитныхъ импульсовъ энергіи. Л^*е. съ
см
величиною 3. ІО10 , то различіе въ поляхъ электродовъ движу-
416 Инерція матеріи зависитъ отъ процессовъ, происходящихъ въ эѳирѣ
щагося и покоющагося столь незначительно, что оно не можетъ
быть замѣчено ни при какомъ явленіи, доступномъ наблюденію. Но
чѣмъ больше скорость движенія, тѣмъ сильнѣе становится это раз-
личіе, и, когда скорость приближается къ критической величинѣ
3 . ІО10 С^~, поле становится совершенно отличнымъ отъ статическаго
сек. г
поля. Вслѣдствіе этого энергія электромагнитнаго поля очень быстро
движущагося электрона при измѣненіи скорости измѣняется совершен-
но иначе, чѣмъ та же энергія въ случаѣ медленно движущагося элек-
трона; сообразно съ этимъ сила реакціи, возникающая при опредѣлен-
номъ ускореніи движенія, при большихъ скоростяхъ будетъ не та-
кой, какъ при малыхъ. Короче говоря, инертная масса электрона есть
Рис. 356. Электрическое поле покоющагося и движущагося электроновъ.
функція скорости, съ которою онъ движется. Измѣненію направленія
скорости поле также противодѣйствуетъ съ нѣкоторою силою, вооб-
ще извѣстною подъ именемъ центробѣжной силы. При медленномъ
движеніи инерція поля, или инертная масса электрона, изъ которой
можно по извѣстной формулѣ механики вычислить центробѣжное
сопротивленіе, въ точности равняется инерціи, которая проявляется
при дѣйствительномъ измѣненіи величины скорости, т.-е. при Уско-
реніи. При весьма большихъ скоростяхъ оба инерціонныя свойства
измѣняются различно, и тогда необходимо строго различать про-
дольную инертную массу электрона, проявляющуюся въ проти-
водѣйствіи измѣненію величины скорости при построчномъ направле-
ніи, и поперечную инертную массу, дѣйствіе которой проявля-
ется въ центробѣжной силѣ, когда скорость^ остается постоянной по
величинѣ, а измѣняется направленіе движенія. При опытахъ съ откло-
Инерція матеріи зависитъ отъ процессовъ, происходящихъ въ эѳирѣ 417
неніемъ катодныхъ лучей въ электрическомъ или въ магнитномъ полѣ,
сила отклоняющаго поля уравновѣшиваетъ центробѣжную силу ча-
стицъ. Такимъ образомъ, въ формулахъ §§150-151тобозначаетъ по-
перечную инертную массу электрона, а въ формулахъ § 149 —продоль-
ную массу. Зарядъ е электрона, или элементарное количество элек-
тричества, разсматривается въ физикѣ эѳира, какъ абсолютная кон-
станта. Путемъ измѣренія магнитнаго и электрическаго отклоненій
весьма быстрыхъ электронныхъ лучей можно поэтому обнаружить,
измѣняется ли поперечная инертная масса въ зависимости отъ ско-
рости и насколько. Если Е есть сила отклоняющаго электрическаго
поля въ ———, рг—радіусъ кривизны лучей въ этомъ полѣ, В —
„ вольтъ сек.
силовой потокъ отклоняющаго магнитнаго поля въ--------и ро—
кв. см. г
радіусъ кривизны лучей въ этомъ полѣ, то, согласно §§ 150—151,
мы должны положить
а= ІО7. Е . рх; Ь= ІО7. В . р2;
мы получимъ тогда:
е а а
т Ь2 Ь
Очень быстрыми электронными лучами являются (3-лучи радіо-
активныхъ веществъ, и слѣдуетъ полагать, что на нихъ возможно
наблюдать измѣненіе инертной массы въ зависимости отъ скорости.
Дѣйствительно, Кауфманнъ (Каиітапп), а послѣ него и другіе экспе-
риментаторы подтвердили правильность этого предположенія. Кауф-
манну мы обязаны большимъ рядомъ чрезвычайно тщательныхъ из-
мѣреній, которыя даютъ намъ представленіе о томъ, по какому закону
измѣняется инерція электрона съ возрастаніемъ скорости. Методъ из-
мѣренія заключался въ одновременномъ примѣненіи электрическаго и
магнитнаго полей, одинаково направленныхъ. Вслѣдствіе этого пучокъ
[3-лучей, выдѣленный черезъ узкія діафрагмы, испытывалъ одновре-
менно два отклоненія въ двухъ взаимно-перпендикулярныхъ напра-
вленіяхъ. Затѣмъ онъ падалъ на фотографическую пластинку и да-
валъ здѣсь изображеніе, отклоненія котораго отъ нулевой точки,
т.-е. отъ изображенія неотклоненныхъ у-лучей и почти неотклонен-
ныхъ а-лучей, могли быть измѣрены при помощи точнаго кбмйа-
ратора. Изображеніе отклоненныхъ лучей всегда оказыва^р4^> вытя-
нутымъ въ длинную черту, такъ какъ скорость Р-част^цъѵ имѣетъ
весьма различныя значенія. Во время экспозиціи весьаііпаратъ сильно
Ми. Электричество и магнитизмъ, ч. II
27
418 Инерція матеріи зависитъ отъ процессовъ, происходящихъ въ эѳирѣ
эвакуировался, такъ что не происходило вовсе диффузнаго разсѣ-
янія 0-лучей. Такимъ путемъ были получены рѣзкіе, тонкіе штрихи.
Послѣ достаточно продолжительной экспозиціи электрическое поле
обращалось, при чемъ все прочее оставалось безъ измѣненія, и вто-
рично производилась столь же продолжительная экспозиція. Такимъ
образомъ получились двѣ кривыя, вполнѣ симметричныя относительно
прямой, проходящей черезъ нулевую точку перпендикулярно къ на-
правленію полей; для каждой отдѣльной точки этихъ кривыхъ можно
было измѣрить отклоненія перпендикулярно и параллельно къ сило-
вымъ линіямъ. Отсюда можно было, зная размѣры аппарата, вычислить
оба радіуса кривизны рх и р2 такимъ же путемъ, какъ и въ § 150. Если,
наконецъ, извѣстны величины Е и В, то для каждой точки кривой мо-
гутъ быть вычислены скорость ѵ и отношеніе Хотя Кауфманнъ
произвелъ эти въ высшей степени трудныя измѣренія съ чрезвычай-
ной тщательностью, его числа, повидимому, не совсѣмъ вѣрны, вслѣд-
ствіе погрѣшности, источникъ которой до сихъ поръ еще неиз-
вѣстенъ. Такъ, для скорости наименѣе отклоненныхъ, наименѣе гиб-
кихъ лучей получается величина, превышающая скорость свѣта, что
непріемлемо по теоретическимъ соображеніямъ; но и помимо это-
го, если экстраполировать по надлежащимъ формуламъ въ обрат-
• е
номъ направленіи, то числа даютъ для малыхъ скоростей значеніе —,
гораздо большее, чѣмъ величина 1,75 . ІО8, полученная на основаніи
новѣйшихъ очень точныхъ измѣреній. Разница такова, какъ если
бы мы приписали силѣ электрическаго поля Е слишкомъ большое
значеніе. Поэтому въ нижеслѣдующей таблицѣ, которая составлена
по даннымъ Кауфманна, данное имъ значеніе Е исправлено путемъ
умноженія его на 0,895. При такой поправкѣ измѣренія Кауфманна
наилучшимъ образомъ согласуются съ упомянутыми измѣреніями надъ
катодными лучами.
Измѣренія Кауфманна надъ 0-лучами.
а ь ѵ = а : Ь 0 = т/:3.10Ю в _ . /,2
1146,0.1010 412,6 2,778.1010 0,926 0,673. 10»
749,8.1010 290,3 2,583.1010 0,861 '•0,890.108
561,7.1010 • 232,1 2,420.1010 0,807 о V 1,043. ІО8
437,1 .ІО10 192,7 2,268.1010 0,756 " 1.177.108
347,7.1010 165,8 2,097.1010 0,699Л> 1,264.108
281,7.1010 145,4 1,938.1010 0г64(р 1,333.10»
234,0,1010 129,4 1,808.1010 .<603 1,395.108
200,7.1010 117,6 1,706.1010 КО,569 1,450.108
169,2.1010 106,0 1,599.10Ю г 0,533 1,504.108
Инерція матеріи зависитъ отъ процессовъ, происходящихъ въ эѳирѣ 419
Отсюда видно, что значеніе для большихъ скоростей измѣ-
няется вполнѣ опредѣленнымъ образомъ: оно тѣмъ меньше, чѣмъ
ближе скорость ѵ къ скорости свѣта. Если мы предположимъ, что
количество е постоянно, то отсюда слѣдуетъ, что поперечная
инертная масса электрона возрастаетъ тѣмъ больше, чѣмъ
ближе его скорость къ скорости свѣта.
Теорія позволяетъ предсказать такую зависимость. Такъ какъ
энергія электрическаго поля, какъ мы видѣли въ § 25, имѣетъ наимень-
шее значеніе въ томъ случаѣ, когда его напряженія взаимно уравно-
вѣшиваются, то электрическое поле быстро движущагося электрона
содержитъ больше энергіи, нежели въ случаѣ медленнаго движенія.
Но большему содержанію энергіи всегда соотвѣтствуетъ, какъ можно
доказать математически, и большая инерція. Абрагамъ (АЬгаЪаш)
точно вычислилъ, какъ въ зависимости отъ скорости измѣняются
продольная и поперечная массы электрически заряженнаго шара,
зарядъ и форма котораго постоянны. Такимъ путемъ, дѣйствительно,
получается теоретически такой же законъ измѣненія массы, какой
даютъ экспериментальныя измѣренія Кауфманна. Болѣе точное
количественное изслѣдованіе этого вопроса мы приведемъ въ § 461.
Здѣсь мы упомянемъ только, что сначала физики были склонны за-
ключить изъ совпаденія теоріи съ опытомъ, что вся масса (по край-
ней мѣрѣ, электроновъ) имѣетъ электромагнитную природу, такъ
что центробѣжная сила и сопротивленіе измѣненіямъ скорости у
нихъ должны полностью быть сведены къ силамъ реакціи ихъ элек-
тромагнитнаго поля. Это заключеніе нужно, однако, признать слиш-
комъ поспѣшнымъ. Въ самомъ дѣлѣ, если въ движеніи играютъ роль
еще иные процессы въ эѳирѣ, — напримѣръ, такіе, которые находятся
въ болѣе тѣсной связи съ тяготѣніемъ, — то эти процессы, можетъ
быть, подчиняются такимъ законамъ, что связанное съ ними инерт-
ное сопротивленіе измѣняется въ зависимости отъ скорости совер-
шенно такъ же, какъ и сопротивленіе электромагнитнаго поля. Какъ
мы увидимъ ниже, имѣются серьезныя основанія полагать, что суще- ^
ствуютъ общіе законы, которымъ подчиняются всѣ процессы въ
рѣ, и потому мы не будемъ заходить столь далеко въ развитіи
выводовъ, вытекающихъ изъ измѣреній Кауфманна.
420
Относительность движеній въ механикѣ
ОТНОСИТЕЛЬНОСТЬ ДВИЖЕНІЙ ВЪ МЕХАНИКѢ.
448. Инерція при всѣхъ обстоятельствахъ зависитъ отъ нѣкото-
рыхъ процессовъ въ міровомъ эѳирѣ; это заключеніе вытекаетъ уже
изъ той роли, которую въ механикѣ играетъ эѳиръ или, какъ
говорятъ еще въ этомъ случаѣ, абсолютное пространство.
Въ чистой геометріи принято что всякое движеніе относи-
тельно. Дѣйствительно, если положеніе предмета мы можемъ опре-
дѣлять лишь посредствомъ измѣренія его разстоянія отъ другихъ
матеріальныхъ предметовъ, которые служатъ намъ для оріентиро-
ванія, то и измѣненіе положенія, т.-е. движеніе, мы можемъ опре-
дѣлять лишь относительно извѣстныхъ предметовъ, произвольно при-
нятыхъ за неподвижные. Движеніе должно оказаться весьма различ-
нымъ, въ зависимости отъ выбора предметовъ, которые мы счита-
емъ неподвижными. Напримѣръ, мы обычно производимъ оріенти-
ровку относительно поверхности земли, считая ее неподвижной, и
относительно нея мы описываемъ всѣ движенія на землѣ. Въ древ-
ности эта точка зрѣнія проводилась вполнѣ послѣдовательно, и тогда
утверждали поэтому, что всѣ неподвижныя звѣзды совершаютъ вра-
щательное движеніе вокругъ земного шара съ періодомъ въ 24 часа.
Коперникъ предложилъ обмѣнять роли, и съ тѣхъ поръ мы при-
выкли считать болѣе удобнымъ предположеніе, что въ покоѣ нахо-
дится небо неподвижныхъ звѣздъ; въ такомъ случаѣ мы должны при-
нять, что земля обращается въ 24 часа вокругъ своей оси. На основаніи
чисто геометрическихъ измѣреній невозможно сдѣлать выборъ между
обѣими системами міра — системой Птолемея и системой Копер-
ника— и, дѣйствительно, мы нерѣдко слышимъ, что система Копер-
потому, что она съ точки зрѣнія геометріи
нежели система Птолемея.
немного знакомъ съ механикой, знаетъ, что
предѣлы чистой геометріи и даетъ сред-
ника побѣдила только
гораздо яснѣе и проще,
Однако всякій, кто
эта наука выходитъ за
ства, съ помощью которыхъ можно сдѣлать рѣшительный выборъ
между обѣими системами міра, и что различными способами^можно
убѣдиться въ фактѣ абсолютнаго вращательнаго движеші^земли во-
кругъ ея оси въ 24 часа. Въ видѣ примѣра относящихс/Оюда механи-
ческихъ опытовъ назовемъ здѣсь маятникъ Фу^(Роисаиіі). Отли-
чіе механическихъ методовъ опредѣленія положенія мѣста отъ гео-
метрическихъ можно сдѣлать яснымъ на примѣрѣ того, какъ опредѣ-
Относительность движеній въ механикѣ
421
ляютъ положеніе мѣста мореплаватели. Человѣкъ, находящійся на па-
роходѣ, можетъ опредѣлить свое мѣстонахожденіе чисто геометриче-
скими измѣреніями на звѣздномъ небѣ или же, въ меньшихъ вод-
ныхъ бассейнахъ, путемъ измѣреній по спеціальнымъ береговымъ вѣ-
хамъ. Но вдали отъ берега при облачномъ небѣ геометрическій ме-
тодъ непримѣнимъ. Въ такомъ случаѣ мореплаватель кидаетъ логъ —
небольшой поплавокъ, который остается на водѣ на томъ мѣстѣ, куда
его бросили, и наблюдаетъ, съ какой скоростью скользитъ мимо его
руки или мимо какой-либо иной мѣтки, неподвижно соединенной
съ судномъ, канатъ, прикрѣпленный къ логу. Такъ мореплаватель
опредѣляетъ скорость, съ которою движется корабль по водѣ.
Опредѣливъ затѣмъ направленіе движенія по компасу, онъ можетъ
вычислить путь, пройденный за опредѣленную часть путешествія.
Этотъ методъ, связанный съ употребленіемъ лога, отличается тѣмъ,
что измѣреніе дѣлается посредствомъ наблюденій надъ вѣхами на
самомъ суднѣ безъ помощи какихъ-либо внѣшнихъ вѣхъ. Подоб-
нымъ образомъ механическіе методы наблюденія вращенія земли
представляютъ собою чисто земные методы; они не требуютъ
употребленія какихъ-либо внѣ земли находящихся вѣхъ. Океаномъ,
въ которомъ движется нашъ корабль-земля, является эѳиръ или
абсолютное пространство; логомъ служитъ маятникъ Фуко, ось вра-
щенія котораго обладаетъ свойствомъ сохранять неизмѣннымъ свое
направленіе въ абсолютномъ пространствѣ; вѣхой служитъ неподвиж-
ный раздѣленный кругъ, связанный съ поверхностью земли.
Второй пунктъ теоріи Коперника — что земля въ теченіе года
совершаетъ полный оборотъ вокругъ солнца — до сихъ поръ еще не
доказанъ непосредственно механическими измѣреніями. Однако, нѣтъ
никакихъ принципіальныхъ основаній полагать, что такія измѣренія
невозможны. Они только слишкомъ трудны, и потому до сихъ поръ
не были произведены.
449. Во всякомъ случаѣ, механика знаетъ, слѣдовательно, абсо-
лютныя движенія въ абсолютномъ пространствѣ - — въ міровомъ
эѳирѣ. Однако, это положеніе нуждается въ нѣкоторомъ ограниченіе
ніи. Тогда какъ мореплаватель при помощи лога можетъ на^лю>
дать любое движеніе судна по водѣ, нѣтъ возможности констати-
ровать движеніе въ міровомъ эѳирѣ, если оно совершается Нудномъ
опредѣленномъ направленіи и съ постоянной скоростью. ^Примѣръ,
маятникъ Фуко можетъ обнаружить только вращате^йбе движеніе,
422
Относительность движеній въ механикѣ
Представимъ себѣ, что
закрыты, и никакихъ
не можемъ. Въ такомъ
покоѣ ли вагонъ, въ.
т.-е. отклоненіе отъ прямой линіи. Представимъ себѣ, что мы нахо-
димся въ поѣздѣ желѣзной дороги, движущемся по совершенно ров-
нымъ, гладкимъ рельсамъ, такъ что его движеніе не сопровождается
никакими толчками или колебаніями вагоновъ,
мы находимся въ вагонѣ ночью, что окна
внѣшнихъ предметовъ мы поэтому наблюдать
случаѣ совершенно невозможно рѣшить, въ
которомъ мы находимся, или же онъ движется прямолинейно съ
постоянной скоростью. Зато нами были бы замѣчены всѣ измѣненія:
въ движеніи. Измѣненія направленія пути мы замѣтили бы по центро-
бѣжной силѣ, отклоняющей всѣ предметы и пассажировъ въ ваго-
нѣ къ наружной сторонѣ траекторіи. Измѣривъ силу Р, дѣйству-
ющую на опредѣленное тѣло массы т, можно даже вычислить
произведеніе изъ абсолютной скорости ѵ поѣзда на угловую ско-
рость ш, съ которою онъ вращается вокругъ центра кривой. Дѣй-
ствительно, механика даетъ намъ для центробѣжной силы Р выра-
Р
женіе Р — т . ѵ . ш; слѣдовательно, г/. ш = —. Далѣе, по направ-
ленію силы мы узнаемъ направленіе радіуса кривизны кривой, и мы
можемъ такимъ образомъ установить, въ какомъ направленіи лежитъ
точка, вокругъ которой происходитъ вращеніе. Но не существуетъ
метода для опредѣленія сомножителей ѵ и ш въ отдѣльности или
разстоянія до центра вращенія. Итакъ, хотя здѣсь мы, какъ и для
земли, можемъ съ несомнѣнностью убѣдиться въ наличности вра-
щательнаго движенія безъ помощи какихъ-либо внѣшнихъ объек-
товъ, однако, для его полнаго опредѣленія недостаетъ всегда одной
величины, которой нельзя найти. Аналогично этому, всякое измѣ-
неніе величины скорости поѣзда можно было бы замѣтить по си-
ламъ реакціи инертныхъ массъ въ вагонѣ. При замедленіи хода по-
ѣзда каждое тѣло испытываетъ реакцію, направленную впередъ, при
ускореніи — направленную назадъ. Такимъ образомъ можно было бы
опредѣлить знакъ измѣненія движенія, а величину измѣненія движе-
нія мы найдемъ, измѣряя силу Р, дѣйствующую на тѣло извѣстной
массы т. Но движеніе при этомъ все же остается неизчетнымъ,
если не принять его за данное хотя бы для одного опредѣленнаго
момента. Если положить его равнымъ нулю на одно^; изъ станцій,
то этимъ мы введемъ уже въ область разсмотрѣнія внѣшній міръ.
Относительность движеній въ механикѣ
423
Земля является тѣмъ кораблемъ, на которомъ мы несемся по
міровому пространству. При этомъ путешествіи мы можемъ, какъ и
въ желѣзнодорожномъ вагонѣ, посредствомъ наблюденій на нашемъ
кораблѣ замѣтить всѣ измѣненія скорости движенія и его на-
правленія; но мы никакъ не можемъ опредѣлить самой скорости дви-
женія. Для этой цѣли намъ нужно было бы принять за неподвижное
какое-либо тѣло внѣ земли, по которому мы могли бы оріентиро-
ваться. Пока мы имѣемъ дѣло только съ движеніями внутри нашей пла-
нетной системы, мы принимаемъ за неподвижную точку центръ солнца
или, точнѣе, центръ тяжести планетной системы, и къ нему отно-
симъ всѣ движенія. Но если ввести въ область разсмотрѣнія весь
міръ неподвижныхъ звѣздъ, то мы не имѣемъ никакого права отда-
вать предпочтеніе нашему солнцу, и приходится тогда выбирать
иную основную точку,— напримѣръ, центръ тяжести всей системы
неподвижныхъ звѣздъ. При этомъ мы всегда дѣйствуемъ до нѣко-
торой степени произвольно.
Невозможно опредѣлить движеніе относительно эѳира
съ такой же однозначностью, съ какою опредѣляется, на-
примѣръ, движеніе корабля относительно воды въ морѣ.
Для полнаго опредѣленія движенія необходимо принять
нѣкоторое произвольно выбранное матеріальное тѣло за
основное тѣло для сравненія и считать его въ произвольно
выбранный моментъ покоющимся въ эѳирѣ,
мента движенія всѣхъ другихъ тѣлъ міра
основного тѣла могутъ быть разсматриваемы
нія ихъ въ эѳирѣ. Движенія же ихъ во всѣ
моменты можно будетъ опредѣлить посредствомъ абсолют-
ныхъ измѣреній, такъ какъ каждое измѣненіе движенія въ
эѳирѣ можетъ быть обнаружено и количественно измѣрено
по реакціямъ инерціи.
Это предложеніе называется теоремой относительности въ
механикѣ, такъ какъ, согласно этому предложенію, движеніе мате-
ріи является до извѣстной степени относительнымъ. °^Ь°
Для этого мо-
относительно
и какъ движе-
послѣдующіе
ОТНОСИТЕЛЬНОСТЬ ДВИЖЕНІЙ ВЪ УЧЕНІИ ОБЪ
ЭЛЕКТРИЧЕСТВѢ.
450. Теорема относительности не ограничивается До^іько сило-
выми дѣйствіями эѳира, воспринимаемыми нами, какХ сопротивленія
424
Относительность движеній въ ученіи объ электричествѣ
Въ самомъ дѣ-
неизмѣнно свя-
получается ин-
того, постоян-
инерціи, но имѣетъ совершенно общее значеніе. Мы не можемъ от-
личить дѣйствія магнитнаго поля на движущіяся вмѣстѣ съ проволо-
кою электрическія частички (іоны или электроны) отъ дѣйствія элек-
трическаго поля, возникающаго при движеніи того же магнитнаго
поля, на покоющіяся электрическія частички проволоки, пока мы
ограничиваемся наблюденіемъ индуктированнаго напряженія (§ 303).
Относительность движеній, отъ которыхъ зависитъ индуктированное
напряженіе, имѣетъ столь же общій характеръ, какъ и относитель-
ность движеній въ чисто геометрическомъ смыслѣ,
лѣ, если двигать катушку и магнитный стержень,
занные между собою, то ни въ какомъ случаѣ не
дукціоннаго дѣйствія, совершенно независимо отъ
нымъ или перемѣннымъ, прямолинейнымъ или вращательнымъ явля-
ется абсолютное движеніе тѣлъ, неподвижныхъ другъ относительно
друга. Эта далеко идущая относительность основана, главнымъ об-
разомъ, на томъ, что при индукціонныхъ дѣйствіяхъ мы не наблю-
даемъ поля точку за точкой, но измѣряемъ лишь линейную сумму
его силового дѣйствія на іоны вдоль замкнутой кривой, да и ту не
въ каждый отдѣльный моментъ: въ виду инертности всѣхъ измѣри-
тельныхъ инструментовъ, не исключая и струннаго гальванометра, мы
измѣряемъ лишь суммы по времени для интерваловъ, по крайней мѣ-
рѣ, въ 0,001 секунды или еще большихъ. Если бы возможно было
изслѣдовать поля въ каждый моментъ точку за точкой, то и по
теоріи Максвелла можно было бы предвидѣть относительность, но
только въ томъ объемѣ, въ какомъ ее знаетъ механика.
Это легко выяснить на простомъ примѣрѣ. Представимъ себѣ
магнитный стержень, движущійся въ направленіи своей оси съ по-
стоянной скоростью. На рис. 215 представлены силовыя линіи элек-
трическаго поля, окружающаго такой магнитъ. Эти линіи даютъ ве-
личину и направленіе силы, дѣйствующей на покоющійся въ про-
странствѣ электронъ, мимо котораго движется стержень; онѣ по-
всюду расположены перпендикулярно къ направленію магнитныхъ
силовыхъ линій. Представимъ себѣ, во-вторыхъ, что магнитцьШ стер-
жень находится въ покоѣ, а параллельно его оси движься элек-
тронъ съ такою скоростью, съ какою въ первомъ сл^Ч^Ѣ стержень
двигался мимо электрона. Теперь электрическаго поф^ нѣтъ, но дви-
жущійся электронъ въ магнитномъ полѣ испытываетъ силовое дѣй-
ствіе одинаковаго направленія (перпендикуля^^къ магнитнымъ си-
Относительность движеній въ ученіи объ электричествѣ
425
ловымъ линіямъ) и одинаковой величины съ силовымъ дѣйствіемъ,
испытываемымъ покоющимся электрономъ въ электрическомъ полѣ
движущагося стержня.
Представимъ себѣ теперь, что магнитный стержень и электронъ
движутся другъ относительно друга прямолинейно, но съ перемѣн-
ной скоростью. Если магнитъ находится въ покоѣ, а электронъ
движется, то силовое дѣйствіе вычисляется совершенно такимъ же
образомъ, какъ и въ случаѣ постоянной скорости, а именно оно
равно произведенію изъ скорости въ данный моментъ на слагаю-
щую магнитнаго поля, перпендикулярную къ ея направленію, въ
той точкѣ, черезъ которую проходитъ электронъ, и на зарядъ элек-
трона. Если же электронъ неподвиженъ, а магнитный стержень дви-
жется, то получается нѣсколько иная сила. Электрическое поле во-
кругъ движущагося стержня, вслѣдствіе конечной скорости распро-
страненія всѣхъ электромагнитныхъ дѣйствій, не можетъ развиться
мгновенно во всемъ пространствѣ. Оно возникаетъ сначала непосред-
ственно у поверхности движущагося магнита и отсюда распростра-
няется по всему пространству съ огромной скоростью, такъ какъ
величина с имѣетъ огромное значеніе З.Ю10-^1-- Если магнит-
г сек.
ный стержень движется съ непостоянной скоростью, то въ нѣко-
торомъ разстояніи отъ него сопровождающее его электрическое
поле имѣетъ значеніе, соотвѣтствующее значенію скорости стержня
въ весьма близкій предшествующій моментъ. Вслѣдствіе этого, если
скорость увеличивается, то дѣйствующая на электронъ сила бу-
детъ нѣсколько меньше той, которая соотвѣтствовала бы скорости
въ данный моментъ; если же скорость убываетъ, то сила нѣсколько
больше. Сила, дѣйствующая на покоющійся электронъ въ
полѣ движущагося магнита, относится къ силѣ, дѣйству-
полѣ покоющагося
скорость въ обоихъ случа-
если бы измѣненія скорости
наступали нѣсколько позже^
см.
ющей на движущійся электронъ
магнита, — если относительная
яхъ одна и та же, — такъ, какъ
при движеніи магнита всегда
чѣмъ при движеніи электрона.
Кажущаяся „разность фазъ" между скоростями въ обоих^фуча-
яхъ, понятно, очень мала въ виду очень большого значенія^величины
с = 3 . и не можетъ быть обнаружена обычными измѣритель-
ными инструментами, обладающими относительно большой инерціей.
426 Относительность движеній въ ученіи объ электричествѣ
Если магнитный стержень вращать около оси, перпендикуляр-
ной къ его длинѣ и проходящей черезъ его центръ тяжести, то во-
кругъ стержня образуется электрическое поле, переносящее магнит-
ныя дѣйствія и вращающееся вмѣстѣ со стержнемъ. Распредѣленіе
этого поля въ плоскости, проходящей черезъ магнитный стержень
и ось вращенія, представлено приблизительно на рис. 357. Если
магнитный стержень неподвиженъ, а электроны движутся по окруж-
ностямъ, центры которыхъ лежатъ на прямой, служившей раньше
осью вращенія, то эти электроны испытываютъ силовыя дѣйствія, на-
правленіе и величина которыхъ опредѣляются направленіемъ и тол-
щиной линій, изображенныхъ на рисункѣ 358 спеціально для пло-
скости, проходящей черезъ магнитный стержень и ось вращенія.
Рис. 357. Электрическое поле вокругъ
магнитнаго стержня, вращающагося
около перпедикулярной къ нему оси.
Рис. 358. Силовое дѣйствіе на элек-
троны, движущіеся по окружностямъ
около оси, перпендикулярной къ дли-
нѣ магнита.
Оба силовыя дѣйствія, представленныя на рисункахъ 357 и 358,
связаны между собою однимъ закономъ. Если составить линейную
сумму силы по одной и той же замкнутой кривой, то по рисунку
357 всегда получается та же величина, какъ и по рисунку 358; въ
этомъ заключается теорема относительности индукціонныхъ дѣйствій.
Но закономъ индукціи, который опредѣляетъ только значеніе ли-
нейной суммы электродвижущей силы вдоль замкнутыхъ ^ривыхъ,
еще не вполнѣ опредѣляется распредѣленіе силы въ обѣльныхъ
точкахъ поля. Для болѣе точнаго опредѣленія въ случаѣ^7электриче-
скаго поля движущагося магнита должно быть еще^облюдено усло-
віе: силовыя линіи поля не могутъ возникать о'^Заканчиваться въ
эѳирѣ (§ 57). Силовое же дѣйствіе магнитнаго поля на движу-
Относительность движеній въ ученіи объ электричествѣ
427
щійся электронъ должно быть перпендикулярно къ магнитнымъ си-
ловымъ линіямъ и къ направленію движенія (§ 289). Вообще го-
воря, эти два условія не совмѣстимы. Поэтому электрическое поле
на рис. 357, вообще, не перпендикулярно къ магнйтнымъ силовымъ
линіямъ, а линіи силового дѣйствія, представленнаго на рис. 358,
постепенно исчезаютъ, если идти въ томъ направленіи, въ которомъ
находится ось вращенія.
Оба условія удовлетворяются одновременно въ пред-
ставленномъ на рис. 215 полѣ магнита, движущагося прямолинейно
съ постоянной скоростью. Это имѣетъ мѣсто не только въ томъ
спеціальномъ случаѣ, который представленъ на этомъ рисункѣ, но
во всѣхъ тѣхъ случаяхъ, когда магнитъ или проводникъ съ
токомъ движется въ какомъ-либо направленіи съ постоян-
ной скоростью, и притомъ только въ этихъ случаяхъ.
Если мы перемѣщаемъ въ эѳирѣ въ опредѣленномъ направленіи
матеріальную систему, содержащую магниты, провода съ токомъ и
какія-либо заряженныя частицы, то силы, испытываемыя заряжен-
ными частицами вслѣдствіе постояннаго движенія въ магнитныхъ
поляхъ и съ магнитными полями, всегда вполнѣ уравновѣшиваются
силовымъ дѣйствіемъ электрическаго поля, сопровождающаго посто-
янное движеніе магнитнаго поля; поэтому въ системѣ наблюдаются
только такія силы, которыя можно было бы точно такъ же за-
мѣтить въ ней, если бы она находилась въ абсолютномъ покоѣ въ
эѳирѣ. Но если система движется ускоренно или криволинейно, то
электродвижущія силы магнитнаго поля, дѣйствующія на заряженныя
тѣла, не компенсируются электрическими силами, сопровождающими
движущееся магнитное поле, какъ1 мы видѣли сейчасъ на двухъ
примѣрахъ; въ подобныхъ случаяхъ должны быть возможны опы-
ты, показывающіе, что при неравномѣрномъ движеніи внутреннія
силы въ системѣ будутъ иныя, нежели при равномѣрномъ движеніи
или покоѣ.
Посредствомъ наблюденія внутреннихъ электромагниту
ныхъ силъ въ матеріальной системѣ, состоящей изъ Маг-
нитовъ, проводниковъ съ токомъ и заряженныхъ^Жлъ,
нѣтъ возможности установить, движется ли вся система съ
X л *
какою-либо постоянною скоростью въ эѳирѣ же нахо-
дится въ покоѣ. Зато всякое измѣненіе движенія по на-
428
Относительность движеній въ ученіи объ электричествѣ
правленію или по величинѣ можетъ быть замѣчено по со-
вершенно опредѣленнымъ измѣненіямъ внутреннихъ силъ.
Это положеніе мы называемъ закономъ относительности въ
электродинамикѣ. Онъ утверждаетъ въ области электродинамики
совершенно то же, что предложеніе, изложенное въ § 449, утвержда-
етъ въ области механики. Поскольку инерція является, по крайней
мѣрѣ отчасти, особымъ проявленіемъ электромагнитныхъ силъ, по-
стольку мы можемъ разсматривать механическую теорему относи-
тельности лишь какъ частный случай общаго электромагнитнаго
принципа; реа’кціи инерціи являются лишь примѣромъ такихъ вну-
треннихъ электромагнитныхъ силъ, которыя указываютъ на измѣненіе
движенія въ эѳирѣ. Съ другой стороны, отнюдь нельзя быть увѣ-
реннымъ въ томъ, что инертныя реакціи имѣютъ чисто электромаг-
нитную природу: возможно, что здѣсь играютъ роль еще иные, до
сихъ поръ неизвѣстные процессы въ эѳирѣ. Если это вѣрно, то тео-
рема относительности въ механикѣ указываетъ, что и эти неизвѣст-
ныя силовыя дѣйствія управляются законами, которые, подобно за-
конамъ электродинамики, согласуются съ теоремою относительности.
Общность теоремы относительности основана, главнымъ обра-
зомъ, на томъ, что состоянія эѳира мы можемъ наблюдать лишь по
силовымъ дѣйствіямъ на вѣсомыя тѣла. Какъ мы видѣли въ §312,
это является слѣдствіемъ принципа наложенія, имѣющаго силу
во всѣхъ областяхъ физики эѳира. Если бы мы могли наблюдать
состоянія эѳира, слѣдя за происходящими въ немъ внутренними
измѣненіями, то мы имѣли бы возможность констатировать налич-
ность или отсутствіе электрическаго поля и этимъ могли бы раз-
рѣшить вопросъ о томъ, движется ли магнитное поле въ эѳирѣ или
находится въ покоѣ.
451. Можно было бы возразить, что въ изложенной выше тео-
ремѣ относительности имѣются въ виду только тѣ силы, которыя
дѣйствуютъ на электрически заряженныя тѣла при движеніи въ
магнитныхъ поляхъ, но не тѣ силы, которыя дѣйствуютъ на Маг-
ниты и провода съ токомъ при движеніи ихъ въ электричествѣ по-
ляхъ заряженныхъ тѣлъ. Электрическое поле, движу щеесявъ про-
странствѣ, должно сопровождаться особымъ магнитнымъ полемъ,
которымъ производится передача напряженій, и этоЛйагнитное поле
могло бы дѣйствовать на увлекаемый магнитъ. Л^грб, однако, убѣ-
диться въ томъ, что при постоянной скорост^сціиа магнитнаго поля
Относительность движеній въ ученіи объ электричествѣ
429
должна компенсироваться инымъ дѣйствіемъ, такъ что обнаружить
ее невозможно. При стаціонарныхъ процессахъ, какъ мы видѣли,
всегда имѣетъ силу принципъ равенства дѣйствія и противо-
дѣйствія; поэтому, если электрически заряженныя тѣла въ движу-
щемся магнитномъ полѣ не испытываютъ никакого силового дѣй-
ствія, то и магниты не испытываютъ никакихъ силовыхъ дѣйствій въ
движущемся электрическомъ полѣ.
Если заряженный плоскій конденсаторъ движется съ большою
скоростью въ направленіи, параллельномъ плоскости его пластинъ,
то въ конденсаторѣ непремѣнно должно быть сильное магнитное
поле, линіи котораго параллельны пластинамъ конденсатора и пер-
пендикулярны къ направленію движенія. Силовыя линіи магнитнаго
поля образуютъ внѣ конденсатора замкнутыя кривыя, распростра-
няясь перпендикулярно къ силовымъ линіямъ электрическаго поля
конденсатора; въ каждомъ мѣстѣ сила магнитнаго поля пропорціо-
нальна слагающей силы электрическаго поля, перпендикулярной къ
направленію движенія. Но если бы мы подвѣсили гдѣ-либо въ этомъ
магнитномъ полѣ стрѣлку, движущуюся равномѣрно и прямолинейно и
съ такою же скоростью, какъ и конденсаторъ, то мы не замѣтили бы
никакихъ слѣдовъ поля. Дѣйствительно, согласно принципу равенства
дѣйствія и противодѣйствія, стрѣлка не можетъ испытывать никакого
силового дѣйствія, такъ какъ ея собственное поле не оказываетъ
никакого силового дѣйствія на заряженныя пластины конденсатора
(§ 450). Такимъ образомъ, дѣйствіе несомнѣнно существующаго маг-
нитнаго поля компенсируется другимъ дѣйствіемъ; послѣднее мо-
жетъ состоять только въ дѣйствіи, испытываемомъ полюсами стрѣлки
при ихъ движеніи въ электрическомъ полѣ. Поэтому мы должны
на основаніи принципа равенства дѣйствія и противодѣйствія заклю-
чить, что магнитный полюсъ при движеніи въ электрическомъ полѣ
испытываетъ дѣйствіе силы, совершенно аналогичной той силѣ, съ
которой дѣйствуетъ магнитное поле на движущуюся въ немъ элек-
трическую частичку.
Чтобы произвести соотвѣтственный опытъ, можно восполь^^
ваться движеніемъ земли по ея орбитѣ вокругъ солнца. Эі;о^ви-
женіе совершается съ весьма большою скоростью и, въ виду гро-
мадной величины радіуса земной орбиты, можетъ считать^ равно-
мѣрнымъ и прямолинейнымъ. Можно предвидѣть, чтоДдрсмотря на
большую скорость движенія, нельзя обнаружить на опытѣ никакихъ
430
Опытъ Майкельсона и Морлея
его слѣдовъ. Дѣйствительно, опытъ, произведенный Рентгеномъ,
далъ вполнѣ отрицательный результатъ.
452. Изъ теоремы относительности какъ въ механикѣ, такъ и •
въ электродинамикѣ вытекаетъ своеобразное слѣдствіе: энергія есть
величина относительная. Примемъ, напримѣръ, центръ тяжести сол-
нечной системы за неподвижную точку, къ которой мы относимъ
всѣ движенія. Въ такомъ случаѣ энергія движенія земли въ теченіе
года будетъ измѣняться лишь незначительно, такъ какъ земля опи-
сываетъ вокругъ солнца приблизительно круговую орбиту. Но если
мы будемъ считать неподвижной другую точку мірового простран-
ства, относительно которой центръ тяжести солнечной системы обла-
даетъ равномѣрнымъ движеніемъ въ опредѣленномъ направленіи, то
энергія движенія земли будетъ имѣть максимумъ всякій разъ, когда
направленіе кругового движенія земли вокругъ солнца будетъ совпа-
дать съ направленіемъ движенія центра тяжести солнечной системы,
и будетъ имѣть минимумъ всякій разъ, когда эти направленія про-
тивоположны. Такъ какъ законъ сохраненія энергіи остается въ си-
лѣ во всѣхъ случаяхъ, то отсюда можно заключить, что между зе-
млею и солнцемъ происходитъ періодическій обмѣнъ энергіи, если
центръ тяжести солнечной системы движется, тогда какъ въ случаѣ,
если центръ тяжести солнечной системы находится въ покоѣ, такого
періодическаго обмѣна энергіи не происходитъ. Такимъ образомъ,
распредѣленіе энергіи и обмѣнъ энергіи до нѣкоторой степени оказы-
ваются зависящими отъ нашего произвольнаго допущенія. Точно
такъ же энергія поля въ конденсаторѣ и энергія поля вокругъ маг-
нита зависятъ отъ нашихъ допущеній относительно движенія, такъ
какъ отъ этого зависитъ сопровождающее магнитное или электриче-
ское поле.
ОПЫТЪ майкельсона и морлея.
453. Соображенія, которыя привели насъ къ изложенной деа-^
ремѣ относительности, справедливы лишь при извѣстномъ ^Грани-
ченіи. Теорема относительности въ механикѣ неразрыв^оСсвязана
съ допущеніемъ, что инертныя массы тѣлъ постоянны у не^зависятъ
отъ скорости, а теорема относительности въ электродинамикѣ свя-
зана съ допущеніемъ, что движущіяся въ пространствѣ поля магни-
товъ и заряженныхъ тѣлъ не отличаются отъ ^^іей, которыя наблю-
дались бы въ положеніи покоя, если нерринимать во вниманіе
Опытъ Майкельсона и Морлея
431
что къ нимъ присоединяются добавочныя поля, обусловливающія
ихъ переносъ въ эѳирѣ. Какъ мы видѣли въ § 447, оба эти допущенія
чрезвычайно тѣсно связаны между собою; оба они рушатся, когда
скорости движенія матеріи въ эѳирѣ приближаются къ с = 3 . ІО10"' •
сек.
Лоренцъ (Н. А. Ьогепіх), которому наука обязана точнымъ
обоснованіемъ теоремы относительности въ электродинамикѣ, дока-
залъ, что при большихъ скоростяхъ ѵ можно было бы наблюдать
отклоненія отъ теоремы относительности и такимъ образомъ кон-
статировать абсолютныя движенія въ эѳирѣ, если бы уда-
лось произвести измѣренія съ такой степенью точности,
чтобы можно было съ полной достовѣрностью улавливать
разности, достигающія лишь весьма малой доли (ф2: с2) всей
измѣряемой величины,—такъ называемыя разности второ-
го порядка. Если ф есть весьма малая доля величины с, то дробь
ф2: с2, конечно, гораздо меньше. Поэтому замѣтныхъ отклоненій вто-
рого порядка можно ожидать только при большихъ скоростяхъ.
Разности перваго порядка, которыя приблизительно равны части
{ф: с) измѣряемой величины, и которыя можно было бы замѣтить
при меньшихъ скоростяхъ, всегда уничтожаются тѣми компенсиру-
ющими дѣйствіями, о которыхъ шла рѣчь въ §§ 450 и 451. Поэто-
му при малыхъ скоростяхъ теорема относительности не имѣетъ ис-
ключеній.
454. Положеніе, установленное Лоренцомъ, можно уяснить
себѣ на слѣдующемъ оптическомъ опытѣ. Представимъ себѣ, что
лучъ свѣта проходитъ черезъ діафрагму А до достаточно удален-
наго зеркала В, гдѣ онъ отражается, послѣ чего возвращается по
тому же пути обратнЪ къ А (рис. 359). Обозначимъ длину АВ че-
резъ а. Свѣтовой лучъ проходитъ этотъ путь за время а : с и
обратный путь — за такой же промежутокъ времени, т.-е. на про-
хожденіе луча туда и обратно требуется всего промежутокъ вре-
мени, равный 2 —, при этомъ предполагается, что аппаратъ нахр-
„ с
дится въ абсолютномъ покоѣ относительно эѳира. Если же ^рйа-
ратъ движется по направленію АВ со скоростью ф, то за время^пока
лучъ движется къ зеркалу, аппаратъ передвигается нѣсколько впе-
редъ и занимаетъ положеніе А'В'. Поэтому лучъ достигаетъ зеркала
по истеченіи промежутка времени, который на ВВ' : Дольше проме-
432
Опытъ Майкельсона и Морлея.
жутка а : с. Но, пока лучъ распространяется обратно отъ зеркала
до діафрагмы, аппаратъ перемѣщается въ положеніе Л"В", и лучъ
достигаетъ діафрагмы за время, которое на А'А" : с меньше проме-
жутка времени а : с. Если скорость аппарата ѵ мала въ сравненіи
съ с, то величины ВВ' и А' А? малы въ сравненіи съ а и равны
между собою. Промежутокъ времени, въ теченіе котораго свѣтовой
лучъ распространяется въ ту и другую сторону, равняется проме-
жутку времени, который потребовался бы для этого при неподвиж-
номъ аппаратѣ, такъ какъ измѣненія при движеніи туда и обратно
взаимно компенсируются. Такимъ образомъ, теорема относитель-
ности удовлетворяется.
А А* А” в’ вп
і—і—і-----------------------—। 1
*-------------а---------—----3
Рис. 359. Путь луча, отражающагося по своему перво-
начальному направленію, въ случаѣ движенія въ напра-
вленіи луча.
9
Однако, при этомъ разсужденіи мы допустили нѣкоторую не-
точность. ВВ' есть путь, проходимый точкою В со скоростью ѵ за
промежутокъ времени т', въ теченіе котораго свѣтовой лучъ прохо-
дитъ АВ', т.-е. за время т' = АВ': с. Такимъ образомъ,
ВВ' = ѵ.т' =АВ’~.
С
Точно такъ же, если черезъ т" обозначить промежутокъ времени,
за который свѣтъ проходитъ путь В'Л", то
А'А" = ѵ.т" = В'А" —
С
Слѣдовательно, пути ВВ' и А'А" были бы равны между собою, если бы
длины АВ’ и В'А" были равны между собою. Это не вполнѣ точно,
но вѣрно лишь съ большимъ приближеніемъ, такъ какъ скорость ѵ
мала въ сравненіи съ с и, слѣдовательно, перемѣщенія точекъ
А и В малы по сравненію съ АВ. Пути ВВ' и А'А" различаются, на
величину второго порядка, и слѣдуетъ ожидать, что при наблю-
деніи величинъ второго порядка можно обнаружить„откло-
ненія отъ теоремы относительности.
Очень легко вычислить разность ВВ' — А’А". Мьжимѣемъ:
АВ’ = АВ + ВВ’ = а + ВВ’, Ѵу
В'А" = А'В' - А'А" = а- Й
V
Опытъ Майкельсона и Морлея
433
Внеся эти выраженія въ вышенаписанное равенство, мы путемъ весь-
ма легкаго вычисленія получаемъ:
ВВ' = —— —; А'А" = ——
1—— с 1 +-
С с
с2
Согласно съ этимъ, когда оптическая скамья съ діафрагмой А и
зеркаломъ В движется въ эѳирѣ въ направленіи луча со скоростью ѵ,
то длина пути луча нѣсколько больше, чѣмъ при неподвижной ска-
мейкѣ. Если мы разность длинъ путей при движеніи и при покоѣ
обозначимъ черезъ 6 и положимъ ѵ: с = (3, то
1 —р2*^2 2бХ(і — рг ’
гдѣ 2 а— длина пути луча въ случаѣ покоя.
Это имѣетъ мѣсто и въ томъ случаѣ, когда скамья движется
со скоростью ѵ въ прямо противоположномъ направленіи.
Подобное вычисленіе можно сдѣлать и для случая, когда опти-
ческая скамья движется въ направленіи, перпендикулярномъ къ лучу.
Пусть А будетъ діафрагма и С—зеркало (рис. 360). Пока лучъ дой-
детъ до зеркала, скамья перемѣстится впередъ въ положеніе А'С, и,
Рис. 360. Путь свѣтового луча, отражающагося по
своему первоначальному направленію, въ случаѣ
движенія, перпендикулярнаго къ направленію луча.
пока лучъ возвратится къ діафрагмѣ, скамья перемѣстится дальше о (
на такое же разстояніе въ новое положеніе Л"С". При этомъ сред-ё^
нимъ лучомъ, вокругъ котораго симметрично располагаются^^
лучи, вступающіе въ инструментъ, является не лучъ АС, идущійвъ
направленіи длины оптической скамьи, но нѣсколько наклонённый
къ ней лучъ, описывающій путь АСА". Длина пути не
отличается отъ АС, если принимать во вниманіе ЛИІръ, величины
Ми. Электричество и магнитизмъ, ч. 11 28
434
Опытъ Майкельсона и Морлея
перваго порядка (у : с). Но если принимать во вниманіе и величины
второго порядка, то получается разность между этими длинами, ко-
торую можно вычислить слѣдующимъ образомъ. Мы имѣемъ:
= АА'=АС'^і
АС с с
АС2 АГ'‘2 = ДС'2 - ДТ2 = ЛСЧ (1 - •
Положимъ снова АС = а, = въ такомъ случаѣ
Полная разность путей е между лучомъ АС'А" въ случаѣ движенія
и лучомъ АСА въ случаѣ покоя вычисляется, слѣдовательно, по
формулѣ
Ъ —2а.^ !_р2 —е +
Разность длинъ путей Ь при движеніи въ направленіи луча больше,
нежели разность длинъ путей е при движеніи въ направленіи, пер-
пендикулярномъ къ направленію луча. Именно, легко видѣть, что
€ . е
-г-....................................; 6 — е = _ •
— ₽2 Кі —Р2
Если величина [3 мала въ сравненіи съ 1, то можно воспользоваться
слѣдующими приближенными формулами:
д = 2а.р2; е = ^-і> = а.р‘2; &-е = е = а.р‘2.
455. Майкельсонъ (МісНеІзоп) и Морлей (Могіеу) произвели
въ 1887 году рѣшающій опытъ, чтобы открыть вліяніе движенія
земли въ эѳирѣ на длину пути свѣтового луча, отражающагося по
своему первоначальному направленію. Рис. 361 представляетъ гру-
бую схему опыта. А есть стеклянная пластинка, слегка посеребренная
съ задней стороны, такъ что большая часть лучей, падающиХѣ^на
нее отъ источника свѣта 7, отражается къ зеркалу С, тогда какъ
другая часть лучей проходитъ сквозь пластинку и падае^ на зер-
кало В. Послѣ отраженія лучи вновь падаютъ на посеребренную
поверхность Д, при чемъ свѣтъ, возникающій отъ соединенія обоихъ
лучей, наблюдается при помощи телескопа /^.Л^іучъ, идущій отъ
зеркала С и наблюдаемый черезъ трубу Т7, ^прошелъ сквозь слой
серебра, а лучъ, приходящій въ В отъ зеркала В, отразился отъ
Опыты Майкельсона и Морлея
43 5
этого слоя. Лучи, попадающіе въ трубу Е, оба, слѣдовательно,
прошли по одному разу черезъ слой серебра и одинъ разъ отъ него
отразились, и потому имѣютъ приблизительно одинаковую яркость.
Отражающая поверхность А должна быть тщательно установлена,
чтобы оба пучка лучей въ точности совпали въ телескопѣ. За-
тѣмъ посредствомъ параллельныхъ перемѣщеній одного изъ зер-
калъ В и С при помощи салазокъ и микрометрическаго винта, раз-
стоянія АС и АВ должны быть уравнены съ такой точностью, чтобы
пути обоихъ свѣтовыхъ пучковъ были равны до тысячныхъ долей
миллиметра. Телескопъ устанавливается на поверхность зеркалъ В и С.
Рис. 361. Схема опыта Майкельсона и Морлея.
Такъ какъ оптическія разстоянія зеркалъ В и С отъ А равны между
собою, то амплитуды свѣтовыхъ волнъ, идущихъ отъ обоихъ зер-
калъ, слагаются
равны, то обѣ
рою разностью
ференціи. Если
разстояніе отъ А нѣсколько различно для различныхъ точекъ его
въ телескопѣ1). Если же эти разстоянія не совсѣмъ
свѣтовыя волны въ телескопѣ обладаютъ нѣкото-
фазъ, вслѣдствіе чего возникаютъ явленія интер-
одно изъ зеркалъ расположено наклонно, такъ что
!) Лучъ, отразившійся отъ С, проходитъ черезъ стеклянную пластйнку А
три раза, а лучъ, отразившійся отъ В,—одинъ разъ. Поэтому междуЛиВ
на пути второго луча помѣщалась „компенсирующая пластинка “/^подобная
А и ей параллельная.
Прам. пер.
28
436
Опытъ Майкельсона и Морлея
поверхности, то въ телескопѣ видны интерференціонныя полосы. Эти
полосы перемѣщаются, если одному изъ двухъ зеркалъ сообщить,
не мѣняя его наклонна, небольшое перемѣщеніе вдоль направленія
АС или АВ. Наблюдая это перемѣщеніе полосъ, можно измѣрить
небольшую разность длинъ путей АС — АВ, возникающую вслѣд-
ствіе перемѣщенія зеркала. Если зеркало В установлено въ направле-
ніи движенія земли, такъ что прямая АС перпендикулярна къ этому
направленію, то вслѣдствіе движенія его къ разности длинъ обоихъ
свѣтовыхъ путей присоединяется еще величина б — е = =
— а. (З2. Если затѣмъ произвести поворотъ прибора на 90° вокругъ
оси, перпендикулярной къ плоскости АВС, то разность, соотвѣт-
ствующая движенію, получитъ обратный знакъ, т.-е. будетъ равна
— а.(32. Слѣдуетъ поэтому ожидать, что при вращеніи прибора на
90° въ телескопѣ будетъ наблюдаться смѣщеніе интерференціонныхъ
полосъ, по величинѣ соотвѣтствующее параллельному перемѣщенію
одного изъ зеркалъ на разстояніе 2а. (З2.
Оптическій аппаратъ, которымъ пользовались Майкельсонъ и
М орлей, былъ монтированъ на толстой каменной плитѣ, плававшей
на ртути, такъ что ее очень легко было вращать вокругъ верти-
кальной оси. Легкими толчками плита приводилась въ медленное
движеніе; не прерывая ея вращенія, изслѣдователи наблюдали поло-
женіе интерференціонныхъ полосъ въ 16 мѣстахъ, на одинаковыхъ
угловыхъ разстояніяхъ одно отъ другого. Такимъ путемъ устранялись
всякія измѣненія въ приборѣ при его вращеніи. Если бы можно
было наблюдать движеніе аппарата вмѣстѣ съ землею въ міровомъ
пространствѣ, то слѣдовало бы ожидать, что въ телескопѣ на оку-
лярномъ микрометрѣ при двухъ взаимно перпендикулярныхъ поло-
женіяхъ должны получиться максимумъ и минимумъ для положенія
средней интерференціонной полосы. Точность отсчета была столь
велика, что должны были быть явственно замѣтны измѣненія разно-
сти АВ — АС, меньшія 10~9.а, т. е. одной 1 000000000-рй^части
всего свѣтового пути а. Опытъ Майкельсона и Морлей->повто-
ренный въ различные дни и въ различные моменты дня,
далъ, какъ среднее изъ большого числа набти<?деній, точ-
ное постоянство разности свѣтовыхъ пууеф^'
Трудно было понять этотъ совершенноусхгрицательный резуль-
татъ опыта. Для насъ невозможно отказ^тьс^ отъ предположенія,
что земля вращается вокругъ солнца; мынепремѣнно приписываемъ
Опытъ Майкельсона и Морлея
437
ей абсолютное движеніе въ міровомъ пространствѣ. Если принять,
что солнце находится въ покоѣ, то простое вычисленіе даетъ для
движенія земли по ея приблизительно круговой орбитѣ скорость, рав-
ную 30 2^1, т,-е. Ю"4.с. Если бы предположеніе о неподвижности
солнца было справедливо, то Майкельсонъ и Морлей должны
были бы при вращеніи аппарата получить измѣненія въ разностяхъ
длинъ путей порядка 2а. 10"8, т.-е. въ двадцать разъ большія той
минимальной величины с. ІО-9, которую еще можно было обнару-
жить съ достовѣрностью. Но если солнце движется въ міровомъ
пространствѣ, то, чтобы получить абсолютную скорость земли,
нужно сложить геометрически скорость солнца съ относительной
скоростью движенія земли по ея орбитѣ. Такъ какъ движеніе земли
по ея орбитѣ мѣняетъ съ каждымъ днемъ свое направленіе, то эта
сумма векторовъ не можетъ быть постоянной, не можетъ, въ част-
ности, быть равна постоянна нулю. Нуль получился бы только въ
одномъ опредѣленномъ случаѣ, именно, если бы скорость солнца
по абсолютной величинѣ была равна относительному движенію зем-
ли по ея орбитѣ, и если бы, кромѣ того, земля случайно находи-
лась въ такомъ мѣстѣ своей орбиты, гдѣ направленіе ея движенія
прямо противоположно направленію движенія солнца. Такимъ обра-
зомъ, земля должна двигаться въ міровомъ пространствѣ, и ея ско-
рость должна быть, по крайней мѣрѣ, порядка величины 10~4.с.
Опытъ Майкельсона и Морлея былъ многократно и въ различ-
ныя времена года повторенъ съ еще большей точностью Морлеемъ
и Миллеромъ (Міііег) въ 1905 году, и всякій разъ онъ давалъ
тотъ же результатъ.
Отрицательный результатъ этихъ опытовъ былъ, кромѣ того,
вполнѣ подтвержденъ электрическими и оптическими опытами, ко-
торые были произведены другими изслѣдователями по совершенно
инымъ методамъ. Ни въ одномъ случаѣ нельзя было доказать опы-
томъ вліянія движенія земли въ міровомъ пространствѣ, предусматри-
ваемаго теоріей. Чтобы объяснить эти отрицательные результаты, 1
можно сдѣлать два предположенія. Либо слѣдуетъ принять, что\|^
земля и міровой эѳиръ находятся въ покоѣ другъ относительно
га, либо же нужно допустить, что при движеніи матеріи въ^ѳйрѣ
въ ней совершаются извѣстныя измѣненія, уничтожающ^|еорети-
чески ожидаемый эффектъ. Такъ какъ первое предположеніе въ на-
438
Опытъ Майкельсона и Морлея
стоящее время ни для кого непріемлемо1), то остается лишь вто-
рое предположеніе.
456. Черезъ нѣсколько лѣтъ послѣ опыта Майкельсона и
Морлея, Лоренцъ и Фитцджеральдъ (Рііг^егаісі) независимо
другъ отъ друга дали объясненіе отрицательнаго результата опы-
товъ, произведенныхъ съ цѣлью открыть абсолютное движеніе земли
въ міровомъ пространствѣ. Эти два изслѣдователя высказали пред-
положеніе, что матерія при своемъ движеніи въ эѳирѣ испытываетъ
извѣстныя измѣненія формы. Такъ, оптическая скамья, которая въ
состояніи покоя относительно эѳира имѣетъ длину а, при движеніи
въ эѳирѣ имѣетъ длину, отличную отъ а. Назовемъ черезъ а ея
длину, когда она движется въ направленіи своей длины, и че-
резъ а" — ея длину, когда она движется перпендикулярно къ это-
му направленію. Опытъ Майкельсона и Морлея вполнѣ объ-
ясняется, если *2а б = 2а" + е. Такъ какъ Ь =
1
эѳирѣ должно, слѣдовательно, быть такимъ, чтобы удовлетворялось
1
и
е = 2а".
то измѣненіе матеріи при ея движеніи въ
равенство
а' а" , ,
7---— = или а =а
1 —Р2 ]Л1 — р2
Лоренцъ и Фитцджеральдъ вычислили, что отрицательные
результаты опытовъ -какъ Майкельсона и Морлея, такъ и всѣхъ
другихъ изслѣдователей — объясняются, если принять, что размѣры
матеріи не измѣняются въ направленіи, перпендикулярномъ
къ направленію движенія, а въ направленіи движенія про-
исходитъ равномѣрное сжатіе въ отношеніи — 1
Такимъ образомъ, нужно положить, что
а!' = а, а! = а . V Г->2 = а” )/Т^рГ.
Деформацію матеріи при ея движеніи въ эѳирѣ мы должцьі
приписывать не только большимъ видимымъ ея частямъ, но т^кже
и мельчайшимъ частицамъ — молекуламъ, атомамъ, и даже^йктро-
*) Это предположеніе, которое можно формулировати такъ: „эѳиръ
вполнѣ увлекается движущимися въ немъ тѣлами", противорѣчитъ извѣст-
ному явленію „аберраціи свѣта14 и ряду опытныхъ (данныхъ.
Прим. пер.
Принципъ относительности
439
намъ. Каждому, кто не посвященъ въ электронную теорію, допу-
щеніе такой всеобщей деформаціи должно казаться чудовищнымъ.
Но, основываясь на электронной теоріи, его не трудно понять. Со-
гласно этой теоріи, не только всѣ силы, связывающія между собою
элементарныя частицы матеріи, являются дѣйствіями эѳира, но даже
форма іоновъ и электроновъ опредѣляется равновѣсіемъ между раз-
двигающей силой электрическаго поля и силами молекулярнаго сцѣ-
пленія. Если же матерія движется въ эѳирѣ, то, какъ мы видѣли въ
§ 447, электрическое поле каждой элементарной частицы измѣня-
ется: оно усиливается около экватора и ослабѣваетъ у полюсовъ.
Давленія, вызываемыя сцѣпленіемъ, сплющиваютъ поэтому частицу
такъ, что она становится сжатой у полюсовъ. Относительно этихъ
давленій, вызываемыхъ сцѣпленіемъ, до сихъ поръ извѣстно очень
немного, какъ мы уже неоднократно указывали выше. Изъ теоріи
деформаціи матеріи Лоренца и Фитцджеральда вытекаетъ только
одно положительное свойство этихъ давленій: при движеніи въ
эѳирѣ они должны дѣйствовать такъ, чтобы получалась настоящая
форма элементарныхъ частицъ. Далѣе, на всѣ силовыя дѣйствія,
посредствомъ которыхъ эѳиръ связываетъ элементарныя частицы въ
атомы, молекулы и вѣсомыя матеріальныя тѣла, движеніе должно
вліять совершенно такъ же, какъ и на силы въ отдѣльныхъ элемен-
тарныхъ частицахъ, такъ что все должно деформироваться одина-
ковымъ образомъ.
ПРИНЦИПЪ ОТНОСИТЕЛЬНОСТИ.
457. Теорія Лоренца и Фитцджеральда сначала была пред-
назначена лишь для объясненія отрицательнаго результата произве-
денныхъ до тѣхъ поръ опытовъ, имѣвшихъ цѣлью открыть абсолют-
ную скорость матеріи въ эѳирѣ. Лоренцъ вскорѣ пошелъ дальше
и сдѣлалъ попытку найти, при какихъ условіяхъ всякій опытъ подоб-
наго рода, оптическій или электромагнитный, долженъ оказаться без-
успѣшнымъ. Эйнштейнъ (Еіпзіеіп) выставилъ въ 1905 г. относи-
тельность въ качествѣ общаго принципа, имѣющаго силу для всей
физики. Математикъ Минковскій (Міпкохѵзкі) развилъ этотъ прин^
ципъ въ весьма изящной и удобообозримой математической форкіѣ^
чрезвычайно удобной для дальнѣйшихъ теоретическихъ изы^к^ній.
Физическое содержаніе общаго принципа относительности
можетъ быть передано приблизительно въ двухъ нижеслѣдующихъ
предложеніяхъ. "
440
Принципъ относительности
Всѣ дѣйствія эѳира управляются законами такого рода,
что наблюденія въ матеріальной системѣ, движущейся со
скоростью, постоянной по величинѣ и направленію, произ-
водимыя наблюдателемъ, движущимся вмѣстѣ съ системою,
математически точно согласуются съ наблюденіями, кото-
рыя получились бы въ системѣ, состоящей изъ тѣхъ же
элементарныхъ частицъ, если бы она и наблюдатель нахо-
дились въ абсолютномъ покоѣ.
Вслѣдствіе этого никакими измѣреніями, даже самыми
точными, нельзя опредѣлить абсолютную величину ско-
рости, съ которою тѣло движется въ міровомъ простран-
ствѣ. Абсолютно наблюдаются только измѣненія скорости
или направленія движеній.
Такимъ образомъ, если этотъ принципъ справедливъ, понятіе
абсолютнаго пространства пріобрѣтаетъ нѣкоторую произвольность,
такъ какъ оно зависитъ отъ того, какія тѣла мы условно считаемъ
покоющимися въ тотъ моментъ, который мы принимаемъ за началь-
ный. Это та же произвольность, съ которой связано понятіе положенія
тѣла въ міровомъ пространствѣ или въ міровомъ эѳирѣ: при опре-
дѣленіи положенія остается произвольной та матеріальная точка,
въ которой помѣщается начало координатъ, такъ какъ точки самого
мірового эѳира не могутъ отожествляться и по нимъ невозможно
оріентироваться.
458. Какъ мы видѣли въ § 452, количество энергіи, которое
мы приписываемъ матеріальной системѣ, относительно и зависитъ
отъ выбора системы для сравненія, принимаемой за неподвижную.
Болѣе точное разсмотрѣніе принципа относительности приводитъ
къ заключенію, что и многія другія величины — почти всѣ, съ кото-
рыми имѣетъ дѣло физика, — точно такъ же являются относитель-
ными. Мы убѣдились въ этомъ (§ 456) по отношенію къ длинѣ.
Если масштабъ расположенъ въ направленіи своего абсолютнаго движе-
нія, относительно котораго мы извѣстнымъ образомъ можемъ^дѣлать
произвольныя предположенія, то его длина отличается одѣхбй, ко-
торую онъ имѣетъ, находясь въ направленіи, перпендикулярномъ
къ первому. Для всѣхъ веществъ обѣ эти длины ^а^дятся въ со-
вершенно опредѣленномъ отношеніи 1 — р2 : 1^\поэтому нѣтъ воз-
можности убѣдиться въ этомъ измѣненіи длинъ? прямыми измѣре-
Принципъ относительности
441
ніями масштабовъ. Точно такъ же невозможно убѣдиться въ немъ,
какъ мы уже знаемъ изъ опыта Майкельсона, оптическими или
какими-либо иными методами. Намъ приходится повсюду вводить
измѣненіе длины въ видѣ численной поправки, которая зависитъ
отъ скорости, принимаемой нами за абсолютную.
459. Нѣчто подобное относится и къ другой основной величинѣ
измѣрительной физики — времени. Представимъ себѣ, напримѣръ, что
мы можемъ какимъ-либо образомъ измѣрить время, въ теченіе кото-
раго свѣтъ проходитъ въ аппаратѣ Майкельсона отъ А до В и
обратно къ А. Если оптическая скамья АВ находится въ покоѣ, то
2 а „
этотъ промежутокъ времени равенъ т = —--Если же она движется
въ направленіи своей длины, то путь, проходимый свѣтомъ, равня-
ется = -----р.гдѣя' — а. ]/" 1 — р2, и мы получимъ по-
, 2а 1 с
этому т = — • Если скамья движется по направленію, пер-
пендикулярному къ своей длинѣ, то путь, проходимый свѣтомъ,
о . 2 а ,2а 1
равняется 2а 4- € — , и опять т ----------- —•
V 1 — ра С у 1 _ 32
Если бы мы имѣли возможность механическими средствами по-
строить часы, которые отличались бы абсолютно постояннымъ хо-
домъ, то при помощи ихъ мы могли бы по измѣненіямъ т судить
объ измѣненіяхъ абсолютной скорости, съ которою часы движутся
въ пространствѣ. Такіе часы давали бы, напримѣръ, различныя
значенія т' въ различныя времена года, такъ какъ солнечная си-
стема движется съ опредѣленною скоростью въ пространствѣ и
вслѣдствіе присоединенія кругового движенія земли около солнца
періодически измѣняется ея абсолютная скорость. Если бы движеніе
часовъ относительно солнца принимало всевозможныя направленія, то
наблюдались бы максимумъ и минимумъ значенія т'. Максимумъ
долженъ наблюдаться, когда относительное движеніе часовъ имѣетъ
одинаковое направленіе съ абсолютнымъ движеніемъ солнца въ міро-
вомъ пространствѣ, минимумъ — при противоположномъ направленьи^0
относительнаго движенія. Такимъ образомъ, возможно было бы о^ѣ-7
нымъ путемъ опредѣлить направленіе абсолютнаго движенія^ въ
эѳирѣ. Если бы мы затѣмъ измѣрили максимальную и минимальную
величины т', то изъ отношенія этихъ двухъ величинъ легко можно
было бы вычислить также величину абсолютной скорости. Иными
442
Принципъ относительности
словами, помощью часовъ можно было бы опредѣлять абсолютныя
скорости въ пространствѣ. Но такъ какъ это должно быть невоз-
можно, то ходъ всякихъ часовъ зависитъ, слѣдовательно,
отъ абсолютной скорости, съ которою они движутся въ
міровомъ пространствѣ. Если ₽ = ѵ: с есть отношеніе ея
къ скорости свѣта, то время т, отсчитываемое на часахъ,
. 1
должно быть посредствомъ поправочнаго множителя •• ——
Ѵ1 -
приведено къ времени т', которое давали бы часы, если бы
они въ теченіе наблюдаемаго явленія находились въ абсо-
лютномъ покоѣ: т' =——-—......-.
V і - з2
Такъ какъ, по нашему предположенію, всѣ часы идутъ одина-
ково, то зависимость хода опредѣленнаго экземпляра часовъ отъ
скорости земли не можетъ быть обнаружена путемъ сравненія. Со-
гласно принципу относительности, всѣ иные методы, — напримѣръ,
оптическое измѣреніе времени, за которое свѣтъ проходитъ опре-
дѣленное разстояніе, — тоже не могутъ дать положительныхъ ре-
зультатовъ. Все же измѣненіе хода часовъ въ зависимости отъ ско-
рости, принимаемой нами за абсолютную, должно быть повсюду
вводимо въ видѣ численной поправки.
Относительность измѣреній времени физически объясняется тѣмъ,
что регулирующая часть часовъ — маятникъ или балансиръ - измѣ-
няется вслѣдствіе движенія въ міровомъ пространствѣ. Мы видѣли
уже въ § 447, что инерція матеріи измѣняется въ зависимости отъ
скорости ея движенія въ міровомъ эѳирѣ. Но, кромѣ того, измѣня-
ются также и ея внутреннія силы, т.-е. упругость пружины балан-
сира, и сила тяжести, т.-е. направляющая сила маятника. А отъ
этой послѣдней силы и отъ инерціи зависитъ періодъ колебанія
балансира или маятника, а вмѣстѣ съ тѣмъ и ходъ часовъ.
460. Сравненіе времени въ различныхъ мѣстахъ міра также за-
виситъ отъ того, какое тѣло мы принимаемъ за основное и ^по-
движное. Представимъ себѣ, что на одной изъ главныхъ астроно-
мическихъ обсерваторій земли установлены нормальные час^постро-
енные съ величайшею тщательностью, и что отъ этихъ ^йбрмальныхъ
часовъ передаются во всѣ остальныя астрономическими физическія
обсерваторіи сигналы, отмѣчающіе время. Проінё/всего это можно
было бы сдѣлать при помощи электромагнитныхъ^или оптическихъ
Принципъ относительности
443
сигналовъ. При этомъ каждая обсерваторія вводитъ поправку на
время, необходимое для распространенія сигнала отъ главной обсер-
ваторіи. Длина свѣтового пути отъ нѣкоторой точки А до точки В
зависитъ (§ 454), однако, отъ абсолютнаго движенія, которое мы
приписываемъ землѣ.
Можно было бы передавать эти сигналы и механическими сред-
ствами, — напримѣръ, акустически. Тогда при поправкѣ мѣсто ско-
рости свѣта займетъ скорость звука. Если бы скорость звука въ
матеріальномъ тѣлѣ не зависѣла отъ скорости, съ которою это тѣло
движется въ эфирѣ, то поправка, необходимая при акустической
передачѣ сигналовъ вслѣдствіе измѣненій размѣровъ матеріи при
движеніи въ міровомъ пространствѣ, зависѣла бы также отъ того,
чтб мы принимаемъ за абсолютную скорость земли, но эта зависи-
мость была бы совершенно иной, нежели въ случаѣ электромагнитной
передачи. Отсюда можно было бы сдѣлать опредѣленное заключеніе
относительно абсолютнаго движенія земли: оно должно быть такимъ,
чтобы оба сигнала, по введеніи соотвѣтствующихъ поправокъ, совпа-
дали. Принципъ относительности требуетъ, чтобы это было невоз-
можно. Согласно этому принципу, скорость звука въ матеріаль-
номъ тѣлѣ должна измѣняться при его движеніи въ міро-
вомъ эѳирѣ, а именно, зависимость скорости звука отъ движенія
должна быть такова, чтобы при любомъ предположеніи относитель-
но абсолютнаго движенія земли акустическій сигналъ совпадалъ съ
электромагнитнымъ, послѣ надлежащаго исправленія ихъ обоихъ.
Для измѣреній времени можно воспользоваться также силой
тяжести. Если считать извѣстнымъ поле силы тяжести вокругъ солн-
ца, то можно вычислить для любого момента времени положеніе пла-
неты на ея орбитѣ, а также, слѣдовательно, и обратно — можно опре-
дѣлять моменты времени, соотвѣтствующіе опредѣленнымъ положе-
ніямъ планеты. Если наблюдать планету въ телескопъ, то она даетъ
своего рода хронометрическіе сигналы, которые можно сравнивать
съ показаніями точныхъ астрономическихъ часовъ. Эти данныя должны
быть подвергнуты соотвѣтственнымъ поправкамъ въ виду конечной
величины скорости распространенія свѣта. Величина этихъ понра^
вокъ зависитъ отъ того, принимаемъ ли мы солнечную систему^за
неподвижную или же за движущуюся, а въ этомъ послѣднемъ слу-
чаѣ поправка зависитъ отъ того, каковымъ мы считаеМ^это дви-
женіе. Если бы поле силы тяжести, окружающее солнце, и сообраз-
444
Измѣненіе массы въ зависимости отъ скорости
но съ этимъ ходъ „гравитаціонныхъ часовъ", каковыми являются
планеты, совершенно не зависѣли отъ движенія солнечной системы
въ эѳирѣ, то сравненіе съ астрономическими часами давало бы согла-
сующіеся результаты только при введеніи поправокъ, соотвѣтству-
ющихъ вполнѣ опредѣленному абсолютному движенію. Допущеніе
иного движенія приводило бы къ невѣрнымъ результатамъ, и поэтому
его пришлось бы отвергнуть. Мы имѣли бы такимъ образомъ сред-
ство обнаруживать абсолютныя движенія въ міровомъ пространствѣ,
что противорѣчитъ принципу относительности. Принципъ отно-
сительности требуетъ, чтобы поле силы тяжести въ си-
стемѣ вѣсомыхъ тѣлъ измѣнялось въ зависимости отъ
движенія въ абсолютномъ пространствѣ или, что сво-
дится къ тому же, чтобы это поле, подобно электромаг-
нитному, распространялось въ пространствѣ не момен-
тально. Для обоихъ родовъ полей должны имѣть силу
сходные законы.
ИЗМЪНЕНІЕ МАССЫ ВЪ ЗАВИСИМОСТИ ОТЪ СКОРОСТИ.
461. Принципъ относительности позволяетъ сдѣлать опредѣлен-
ныя заключенія о томъ, какъ въ зависимости отъ движенія матеріи
въ міровомъ эѳирѣ измѣняются продолжительность колебанія коле-
блющейся системы, скорость звука въ упругой средѣ и другія меха-
ническія величины. Можно вычислить въ совершенно общемъ видѣ,
какъ измѣняются въ зависимости отъ абсолютнаго движенія матеріи
ея упругія свойства и масса.
Провѣрить опытомъ до сихъ поръ удалось только одно по-
ложительное утвержденіе, вытекающее изъ принципа относитель-
ности, а именно, что масса зависитъ отъ скорости. Какъ мы ви-
дѣли въ § 447, при большихъ скоростяхъ нужно строго разли-
чать продольную массу пц и поперечную массу Если при весь-
ма малыхъ скоростяхъ масса равняется т0, то математическій ана-
лизъ принципа относительности даетъ, по Лоренцу:
2 . (1 — У1 - Р2) ЗДЯІ
ті = т0------
Здѣсь Р=77:г = 77:3.1О10, и ѵ — абсолютная скорость матеріаль-
наго тѣла.
Измѣненіе массы въ зависимости отъ скорости
445
Формулы, которыя принципъ относительности даетъ для ті и
гпі, отличаются отъ тѣхъ, которыя Абрагамъ вычислилъ для шаро-
образнаго неизмѣняемаго электрона (§ 447). Это легко понять, такъ
какъ, согласно принципу относительности, элементарныя частицы
матеріи не являются неизмѣняемыми, но при своемъ движеніи въ
эѳирѣ деформируются въ болѣе или менѣе сжатые эллипсоиды]),
вслѣдствіе измѣненія ихъ полей въ зависимости отъ скорости. Ока-
зывается, однако, весьма затруднительнымъ рѣшить, чьимъ форму-
ламъ для пц — Абрагама или Лоренца — соотвѣтствуютъ значенія,
получающіяся изъ опытовъ Кауфманна, такъ какъ кривыя, выража-
ющія зависимость между величинами пи и (3, построенныя по обѣимъ
формуламъ, оказываются весьма сходными. Кауфманнъ находитъ,
что его измѣренія согласуются съ формулою Абрагама лучше,
нежели съ формулою Лоренца, но ни съ одной изъ нихъ не со-
гласуются вполнѣ. Какъ мы замѣтили уже въ § 447, весьма вѣ-
роятно, что на результаты измѣреній Кауфманна повліялъ еще ка-
кой-то — пока намъ неизвѣстный — источникъ ошибокъ. Чтобы полу-
чить полное совпаденіе съ формулой Абрагама, слѣдовало бы зна-
ченіе силы электрическаго поля, даваемое Кауфманномъ, умножить
на 0,96. Но въ такомъ случаѣ экстраполированіе даетъ для медлен-
ныхъ лучей значеніе еіт, равное 1,86.108, что не согласуется съ
результатами измѣреній надъ катодными лучами. Если же умножить
силу электрическаго поля на 0.90 (точнѣе на 0,895), какъ это сдѣ-
лано въ таблицѣ § 447, то экстраполируемое число получаетъ истин-
ное значеніе (1,77.108), но зато результаты?измѣреній совершенно
не сходятся съ формулой Абрагама, а очень хорошо сходятся съ
формулой Лоренца, какъ показываетъ нижеслѣдующая таблица.
Сравненіе измѣреній Кауфманна съ формулою Лоренца.
р = г/: 3.1010 0,926 0,861 0,807
о і 00 0,673 0,890 1,043
0,378 0,508 0,591
— • ІО-8: V 1 — ₽2 т 1,78 1,75 1,76
0,756 0,699 0,646 0,603 0,569 0,533
1,177 1,264 1,333 1,395 1,450 1,504
0,655 0,715 0,761 0,798 0,823
1,80 1,77 1,75 1,75 1,76> 1,78
) Если въ состояніи покоя онѣ представляютъ собою сф^ры.
Прим, пер.
446
Верхній предѣлъ скорости
Конечно, эти числа нельзя считать окончательнымъ подтвер-
жденіемъ теоріи относительности. Однако, и новѣйшія измѣренія
Бухерера (ВисИегег) также подтвердили теорію Лоренца. Кромѣ
того, Гупка (Нирка), измѣривъ одновременно катодное напряженіе и
магнитное отклоненіе для весьма быстрыхъ катодныхъ лучей, срав-
нилъ продольную массу съ поперечной и также нашелъ результаты,
подтверждающіе формулы теоріи относительности. Слѣдуетъ замѣ-
тить, однако, что эти двѣ работы встрѣтили возраженія, и поэтому
мы не можемъ еще считать разрѣшенной задачу экспериментальнаго
опредѣленія зависимости массы отъ скорости.
ВЕРХНІЙ ПРЕДѢЛЪ СКОРОСТИ.
462. Если въ формулы теоріи относительности подставлять зна-
ченія р = ѵ : с, превышающія единицу, то вообще получаются мни-
мые результаты, какъ можно убѣдиться по всѣмъ формуламъ, при-
веденнымъ въ послѣднихъ параграфахъ. Эти формулы, слѣдовательно,
не годятся для значеній р, большихъ единицы. Болѣе точное разсмо-
трѣніе этого вопроса приводитъ къ заключенію, что въ природѣ
вообще невозможны значенія р^І, такъ какъ, если скорость мате-
ріальнаго тѣла могла бы достигнуть значенія с == 3 . ІО10, то та-
кое тѣло должно было бы превратиться въ настоящую математи-
ческую плоскость двухъ измѣреній, что, конечно, невозможно.
Согласно теоріи относительности, для скорости ма-
теріальнаго тѣла существуетъ верхній предѣлъ, который
никогда не можетъ быть достигнутъ. Этимъ верхнимъ
предѣломъ является скорость свѣта с = 3. ІО10 с-и- .
с&к.
Если вспомнить, что, согласно теоріи относительности, нельзя
опредѣлить абсолютной скорости тѣлъ въ міровомъ эѳирѣ, то съ
перваго взгляда предыдущее предложеніе кажется абсурднымъ.
Существуютъ тѣла,—напримѣръ, частицы, излучаемыя радіемъ,—ско-
рость которыхъ относительно земли немногимъ лишь меньше, чѣмъ
скорость свѣта. Положимъ, что такая частица движется въ направленіи,
совпадающемъ съ направленіемъ движенія земли въ міровомъ простран-
ствѣ. Принципъ относительности позволяетъ намъ пр^птйать ско-
рости движенія земли сколь угодно большую величину, и можно
было бы подумать, что для этой скорости можно ^выбрать столь
большое значеніе, чтобы скорость частицы была\ораздо больше,
чѣмъ 3.1010. Это заключеніе, однако, основыйётся на невѣрномъ
Общее значеніе принципа относительности
447
предположеніи, что большія скорости складываются такъ же, какъ
и малыя. Это предположеніе невѣрно потому, что всѣ опредѣленія
времени и длинъ, въ случаѣ справедливости принципа относитель-
ности, зависятъ отъ того, какія предположенія мы дѣлаемъ отно-
сительно абсолютныхъ движеній. Если продѣлать вычисленія вполнѣ
согласно съ принципами теоріи относительности, то и въ случаяхъ,
подобныхъ только-что указанному, всегда получаются абсолютныя
скорости, меньшія, чѣмъ скорость свѣта.
ОБЩЕЕ ЗНАЧЕНІЕ ПРИНЦИПА ОТНОСИТЕЛЬНОСТИ.
463. Принципъ относительности замѣчателенъ тѣмъ, что онъ
утверждаетъ существованіе внутренней связи между всѣми свой-
ствами, матеріи и всѣми физическими явленіями. Природа, повиди-
мому, воспроизводитъ все богатство физическаго міра изъ неболь-
шого числа простыхъ процессовъ въ одной міровой субстанціи,
подобно тому какъ математика выводитъ необозримое множество
интересныхъ истинъ изъ немногихъ основныхъ положеній — аксіомъ.
СОДЕРЖАНІЕ II ТОМА
Часть вторая. Электродинамика.
Стр.:
Глава I. Общія свойства магнитнаго поля........................ 3 — 24
Признаки магнитнаго поля ................................... 3
Носители магнитнаго поля..................................... 4
Намагниченіе................................................. 5
Полюсы магнита . . . •....................................... 6
Направленіе магнитнаго поля.................................. 9
Изображеніе магнитныхъ полей....................• . 10
Магнитное поле земли ........................................ 13
Существенное различіе между электрическимъ и магнитнымъ
состояніями эѳира..................................... 22
Глава II. Магнитное состояніе и электрическій токъ .... 25 — 67
Магнитное поле, окружающее электрическій токъ............... 25
Вращательныя движенія въ полѣ тока.......................... 27
Примѣры магнитныхъ полей тока............................... 29
Электромагнитъ.............................................. 31
Безъ магнитнаго поля электрическій токъ невозможенъ . . 34
Измѣрители тока съ подвижнымъ магнитомъ . .... 35
Градуированіе измѣрителей тока.............................. 42
Магнитное поле соленоидовъ................... . . . . 44
Сила магнитнаго поля ....................................... 46
Сложеніе магнитныхъ полей................................... 48
Сила магнитнаго поля земли.................................. 50
Первый основной законъ электродинамики Максвелла ... 52
Механическая модель эѳира . . ................ 62
Глава III. Напряженіе и сила тока....................68—118
Законъ Ома ...
Легальная единица сопротивленія
Соединеніе нѣсколькихъ проводниковъ . . .
Реостаты .................
Электрометръ, какъ измѣритель тока
Гальванометръ, какъ измѣритель напряженія
Измѣрительные инструменты для различныхъ областей измѣ-
реній .............................. . . . . 78
Ми. Электричество и магнитизмъ, ч. II.
29
450
Содержаніе
Стр.:
Потери напряженія въ проводахъ.............................. 79
Мостъ Витстона.............................................. 82
Удѣльная проводимость металловъ............................. 84
Измѣненіе проводимости съ температурою...................... 87
Болометръ................................................. 89
Теорія проводимости металловъ............................... 90
Проводимость электролитовъ.................................. 91
Теорія электрической проводимости........................... 96
Скорость переноса и величина іоновъ......................... 97
Законъ диссоціаціи.................... . . ... 99
Измѣненіе проводимости съ температурой..................... 102
Теорія гальваническихъ цѣпей................................. 102
Тепловое дѣйствіе тока....................................... 105
Техническія примѣненія теплового дѣйствія тока............... 107
Тепловые инструменты ...................•................... ПО
Теорема Пойнтинга о переносѣ энергіи въ электромагнит-
номъ полѣ................................................. 110
Примѣры переноса энергіи................................... 114
Механическая аналогія переноса мощности въ эѳирѣ ... 116
Глава IV. Силовыя (пондеромоторныя) дѣйствія магнитнаго
поля...........................................119—153
Силовое дѣйствіе магнитнаго поля на проводникъ съ токомъ 119
Измѣрители тока съ подвижнымъ проводникомъ ... 124
Дѣйствіе магнитнаго поля на движущіеся іоны............... 132
Явленіе Голла........................................... 135
Теорія молекулярныхъ магнитовъ............................ 136
Индуктированная электродвижущая сила въ движущихся
проводникахъ.............................................. 138
Законы индукціи въ магнитномъ полѣ........................ 142
Индукція или магнитный силовой потокъ..................... 143
Линіи магнитнаго силового потока.......................... 146
Линіи магнитнаго силового потока суть линіи замкнутыя . 147
Измѣреніе магнитнаго силового потока...................... 148
Силовой потокъ земного поля .............................. 149
Вихревые токи.............................................. 151
Успокоеніе гальванометра д’Арсонваля.....................^0>153
Глава V. Возникновеніе и исчезновеніе магнитныхъ полей . 154— 167
Законъ относительности индукціонныхъ дѣйствій . . . 154
Электродинамическія поля.............................• 156
Возникновеніе и исчезновеніе магнитныхъ полей . 158
Второй основной законъ электродинамики Максвелла ... 160
Законъ индукціи........................ и о\\............. 163
Самоиндукція.............................................. 164
Содержаніе
451
Стр.:
Глава VI. Магнитныя свойства тѣлъ...........................168 — 211
Пустота.................................................. 168
Проницаемость эѳира...................................... 169
Такъ называемыя абсолютныя электромагнитныя единицы . 170
Коэффиціентъ самоиндукціи........................ . 173
Энергія магнитнаго поля.................................. 174
Силовыя (пондеромоторныя) дѣйствія поля на магнитные
полюсы ................................................... 177
Силовыя (пондеромоторныя) дѣйствія магнитнаго поля на
проводникъ съ токомъ...................................... 178
Измѣренія земного поля по методу Гаусса.................. 180
Парамагнитныя и діамагнитныя вещества.................... 181
Измѣренія воспріимчивости................................ 183
Измѣреніе поля по высотѣ поднятія жидкости............... 185
Теорія парамагнитизма и діамагнитизма.................... 186
Ферромагнитныя вещества.................................. 187
Магнитныя цѣпи......................................... 190
Катушка съ желѣзнымъ сердечникомъ........................ 193
Методъ замкнутаго кольца (методъ Гопкинсона)............. 194
Измѣреніе магнитной индукціи силовыми (пондеромоторны-
ми) дѣйствіями............................................ 195
Гистерезисъ . ........................................... 197
Постоянные магниты...................................... 199
Энергія намагниченія..................................... 202
Ферромагнитныя тѣла въ очень сильныхъ магнитныхъ по-
ляхъ .......................................... ..... 203
Полукольцевой электромагнитъ ............................ 205
Другія ферромагнитныя вещества........................... 206
Немагнитное желѣзо....................................... 207
Критическая температура ферромагнитныхъ тѣлъ............. 207
Вліяніе возраста......................................... 209
Теорія ферромагнитизма ................................. 209
Глава VII. Техническія примѣненія электромагнитныхъ сило-
выхъ дѣйствій........................................212 — 255
Сигнальные аппараты...................................... 212
Телефонъ ................................................ 217
Электрическій звонокъ и автоматическій прерыватель ... 221
Электромоторы для постояннаго тока....................... 223
Магнитное поле мотора.................................... 228
Реакція якоря ........................................ х ;23О
Оборотъ энергіи въ моторѣ...............................^ѵ232
Потеря энергіи въ якорномъ желѣзѣ....................7(4^ ^35
Скорость вращенія мотора...........................ѵ 236
Моторъ съ параллельнымъ возбужденіемъ.................... 237
29
452
Содержаніе
Стр.:
Моторъ съ послѣдовательнымъ возбужденіемъ................ 239
Генераторы постояннаго тока............................... 241
Генераторъ съ послѣдовательнымъ возбужденіемъ .... 244
Генераторъ съ параллельнымъ возбужденіемъ................. 245
Многополюсныя машины...................................... 249
Электрическая передача силы .............................. 250
Центральныя станціи постояннаго тока...................... 251
Глава VIII. Электромагнитныя колебанія
256 — 412
Перемѣнныя поля......................................... 256
Измѣреніе перемѣнныхъ полей............................. 259
Генераторы перемѣннаго тока............................. 261
Индуктированныя напряженія въ перемѣнномъ магнитномъ
полѣ ... 264
Энергія, переносимая перемѣннымъ токомъ................. 269
Дроссельныя (реактивныя) катушки........................ 272
Сравненіе коэффиціентовъ самоиндукціи................... 273
Безъиндукціонныя сопротивленія.......................... 275
Трансформаторъ перемѣннаго тока......................... 276
Механическая модель электромагнитной связи въ трансфор-
маторѣ ........................................... • 280
Практическія примѣненія трансформаторовъ перемѣннаго
тока ................................................... 283
Возможны ли трансформаторы постояннаго тока • • • 286
Индукціонный аппаратъ.................................... 289
Синхронные моторы............................... .... 295
Асинхронные моторы перемѣннаго тока...................... 298
Вращающіяся поля........................................ 299
Генераторы съ вращающимся полемъ и проводка къ нимъ 302
Моторы вращающаго тока .................................. 306
Однофазный моторъ съ вращающимся полемъ .... 314
Перемѣнный токъ и емкость • ................. 318
Сравненіе емкостей....................................... 321
Цѣпь перемѣннаго тока, содержащая емкость и самоиндук-
цію ................................................ 323
Резонансъ
Электромагнитныя колебанія при разрядѣ конденсатора
Возникновеніе колебаній вслѣдствіе резонанса
Опыты съ частыми электромагнитными колебаніями
Трансформаторъ Тесла .........................
Колебанія при исчезновеніи магнитнаго поля •
Гудокъ (зуммеръ)..............................
Колебанія свѣтовой дуги.....................
Возбужденіе электромагнитныхъ колебаній толчками
Резонансъ катушекъ
325
3?6
341
343
345
346
354
356
Содержаніе
453
Стр.:
Опыты Лехера............................................... 362
Электромагнитныя волны..................................... 366
Распространеніе весьма длинныхъ волнъ по проволокамъ 377
Свободныя волны............................................ 381
Осцилляторъ Герца.......................................... 384
Пріемники для свободныхъ электрическихъ волнъ • • • 385
Опыты съ волнами Герца..................................... 387
Электромагнитная теорія свѣта ............................. 393
Телеграфированіе безъ проводовъ............................ 398
Глава IX. Принципъ относительности..........................413 — 447
Инерція матеріи зависитъ отъ процессовъ, происходящихъ
въ эѳирѣ............................................ 413
Относительность движеній въ механикѣ...................... 420
Относительность движеній въ ученіи объ электричествѣ • 423
Опытъ Майкельсона и Морлея................................. 430
Принципъ относительности .................................. 439
Измѣненіе массы въ зависимости отъ скорости .... 444
Верхній предѣлъ скорости .................................. 446
Общее значеніе принципа относительности.................... 447
АЛФАВИТНЫЙ УКАЗАТЕЛЬ
Римскія цифры указываютъ темы, а арабскія — страницы.
А
Абрагамъ М., вычисленіе измѣненія
инерціи электрона въ зависимости
отъ скорости II, 419
Азотная кислота, добываніе ея изъ
атмосфернаго воздуха II, 286
Айртонъ, г-жа, кривая напряженія
тока свѣтовой дуги I, 313, 314
Аккумуляторъ I, 62, 200
—, емкость I, 203
—, формированіе I, 203
Аксіальный векторъ И, 23
Актиній I, 332
Алхимія, возможна ли она? I, 348
Алюминіевая индустрія I, 303
Алюминіевый анодъ въ электриче-
скомъ выпрямителѣ 1,204
Амперметръ II, 37
—, включеніе II, 69
— для измѣренія перемѣнныхъ по-
лей II, 260
— съ мягкимъ желѣзомъ II, 41
Амперъ (единица силы тока) II, 42
Амплитуда колебаній (перемѣннаго
тока) II, 257
Аніонъ I, 181
Анодъ при дуговомъ разрядѣ I, 308
— при тихомъ разрядѣ 1, 236
— при электролизѣ I, 159
Анодные лучи I, 298
Антенна II, 383
Антикатодъ рентгеновской трубки
1, 264
Аперіодическое успокоеніе инструмен-
та II, 153
Аппаратъ Кепзеля (для измѣренія не-
проницаемости ферромагнитныхъ
веществъ) II, 196
Араго, магнитизмъ вращенія II, 151
Арматура машины II, 223
Арнольдъ и Кеди, свѣтовая дуга съ
холоднымъ анодомъ I, 316
Аронсъ, ртутная лампа I, 306
Асинхронный моторъ II, 297
Астатическіе гальванометры Кельви-
на II, 40
Атомные осцилляторы II, 394
Атмосфера, содержаніе іоновъ I, 230
—, эманація 1, 349
Атомы, число I, 183, 229
—, процессы въ нихъ I, 336
— гелія, какъ а-частицы, I, 335
Аустинъ и Штаркъ, вторичные лучи
I, 263
Б
Баллистическій вольтметръ II, 144
-----, градуированіе II, 149
Барабанный якорь II, 226
-----многополюсной машины II, 249
Батарея высокаго напряженія I, 65
— гальваническая I, 63
— лейденская I, 119
Безъиндукціонныя сопротивленія
II, 275
Беккерель, открытіе радіоактивности
I, 332
Біенія вслѣдствіе сильной связи 2-хъ
резонирующихъ цѣпей II, 335
— въ передатчикѣ Брауна II, 406
Болометръ II, 89
Болтвудъ, іоній 1, 343
—, періодъ распада радія I, 341
Браунъ Ф., безпроволочная телегра-
фія II, 405
Брэггъ и Клееманъ, число частицъ
а-лучей ; авно числу распадающих-
ся атомовъ I, 345
Бунзенъ, элементъ I, 198
Буссоль I, 14
Бухереръ, инерція быстро движущих-
ся электроновъ II, 446
Быстро прекращающійся разрядъ
I, 318, 321. о
В
Вагнеровскій молоточекъ11^222
— прерыватель для индукціонныхъ
аппаратовъ II, 290 \
Варбургъ, электропроводность нака-
леннаго стекла ^ ^05
—, задержка разряда 1, 327
456
Алфавитный указатель
Варбургъ, нормальное катодное на-
пряженіе въ разрядѣ тлѣющаго свѣ-
та I, 240
Варіаціи поля земли II, 21
--------, объясненіе II, 51
Ваттметръ II, 132
Ваттъ (единица мощности) II, 106
Веберъ, теорія молекулярныхъ маг-
нитовъ II, 136
— , электродинамометръ II, 130
Веберъ и Гауссъ, абсолютная систе-
ма мѣръ II, 171
--------, изобрѣтеніе телеграфа
II, 212
Векторы I, 25, 30
— аксіальные и полярные II, 23
— сложеніе II, 48
Величины второго порядка въ теоріи
относительности II, 431
Венельтъ, раскаленный катодъ I, 297
Верхній предѣлъ скорости II, 446
Вильде, изобрѣтеніе генератора съ по-
стороннимъ возбужденіемъ II, 243
Вильсонъ, образованіе тумана въ
газіонахъ I, 228
Винъ В., изслѣдованіе закатодныхъ
лучей I, 274
Винъ М., возбужденіе электрическихъ
колебаній толчками II, 335, 409
Висмутовая спираль для измѣренія
магнитнаго поля II, 3
Висмутъ, діамагнитизмъ II, 185
—, явленіе Голла II, 136
Вихертъ, скорость катодныхъ лучей
I, 262
Вихревые токи II, 151
-----, потеря энергіи II, 235
Віолль, температура въ свѣтовой ду-
гѣ I, 301
Включеніе амперметра I, 69
Внѣшнее темное пространство I, 236,
281
Вогнутыя зеркала для опытовъ съ
волнами Герца II, 388
Водородный электродъ въ газовомъ
элементѣ 1,192
Возбудитель Блондло II, 363
Возбужденіе электромагнитныхъ ко-
лебаній толчками II, 354; примѣне-
ніе въ безпроволочной телеграфіи
II, 409
Волны Герца II, 387
—, земля, какъ проводникъ, II, 399
— , поглощеніе въ кабеляхъ II, 378
— распространяющіяся II, 367
— свободныя II, 381
—, скорость распространенія II, 373
Волны стоячія II, 376
— , электрическая и магнитная энер-
гія въ распространяющейся волнѣ
II, 372
— съ малымъ затуханіемъ II, 408,409
Вольта, напряженіе при соприкосно-
веніи двухъ проводниковъ I, 51
—, открытіе электролитовъ I, 160
Вольтаметръ I, 166
Вольтметръ I, 62
— баллистическій II, 144, 148
—, включеніе II, 68
— для перемѣннаго тока II, 260
— техническій II, 78
Вольтовъ столбъ I, 66
Вольтъ-секунда, единица магнитнаго
силового потока II, 145
Вольтъ (единица напряженія) I, 61
Воспріимчивость магнитная II, 183
— , измѣреніе II, 183
Вращательныя движенія электриче-
скаго тока въ магнитномъ полѣ
II, 27
----проводника съ токомъ въ маг-
нитномъ полѣ II, 120, 132
Вращающій токъ, II, 314
Вращающіяся поля II, 299
Вращеніе свѣтовой дуги въ магнит-
номъ полѣ II, 134
Всеобщій принципъ наложенія (супер-
позиціи) II, 169, 173
Вторичная катушка индуктора II, 290
— — осциллятора съ возбуждені-
емъ колебаній толчками II, 355
----трансформатора II, 284
----трансформатора Тесла II, 342
Вторичные лучи у закатодныхъ лу-
чей 1,278
----у катодныхъ лучей I, 262
----у рентгеновскихъ лучей I, 268
Второй принципъ термодинамики, при-
мѣненіе къ термоэлектрическимъ
явленіямъ I, 363
Выпрямитель перемѣннаго тока 1,205
— , ртутная лампа I, 310
— съ алюминіевыми анодами 1^204
— , трубка Венельта I, 297
— электролитическій I, 203-<^°
Гагенъ и Рубенсъ, отражательная спо-
собность металловъ для ультра-
красныхъ луйейЛі, 397
Газы, проводящіе I, 16, 209
—, іоны I, 213, 220, 275, 289
—, разряда.газовъ I, 138, 300
Алфавитный указатель
457
Гальваксъ, фотоэлектрическое дѣй-
ствіе I, 270
Гальвани, опытъ съ лягушкой I, 57
Гальваническая батарея I, 63
Гальваническія цѣпи 1,57,111; II, 102
----обратимыя I, 200
---- постоянныя и непостоянныя
I, 61,197
Гальванометръ II, 36
— баллистическій II, 149
— д’Арсонваля II, 129
—, какъ измѣритель напряженія II, 77
—, лишенный желѣза II, 130
— струнный II, 125
— съ панцырной защитой И, 39
— со стрѣлчой II, 36
— , успокоеніе II, 153
Гальванопластика I, 161
Гальваностегія I, 161
Гауссъ, измѣреніе силы магнитнаго
поля земли II, 19, 180
Гауссъ и Веберъ, абсолютная систе-
ма мѣръ II, 171
--------, изобрѣтеніе телеграфа
II, 212
Гейгеръ и Рётгерфордъ, счетъ «-ча-
стичекъ I, 335
Гейслеръ, ферромагнитные сплавы
II, 209
Гейсслеровы трубки I, 238
----, какъ задерживающіе клапаны
при возбужденіи электромагнит-
ныхъ колебаній толчками, II, 356
Гейтель и Эльстеръ, проводимость
атмосфернаго воздуха I, 230
----, фотоэлектрическія свой-
ства различныхъ металловъ 1,271
----—, эманація въ атмосферѣ
I, 349
Гельмгольцъ, методъ измѣренія діэ-
лектрической постоянной I, ПО
—, свободная и скрытая энергія 1,188
Генераторъ многополюсный II, 249
— перемѣннаго тока II, 261
— постояннаго тока II, 241
Генераторъ съ вращающимся полемъ
II, 302
— съ параллельнымъ возбуждені-
емъ II, 245
—- съ послѣдовательнымъ возбу-
жденіемъ II, 244
Герке и Рейхенгеймъ, анодные лучи
I, 298
Герцъ А., сила поля въ области поло-
жительной свѣтовой колонны ти-
хаго разряда I, 280
Герцъ,весьма быстрыя колебанія 11,383
Герцъ, волны II, 387
—, прозрачность тонкихъ пласти-
нокъ для катодныхъ лучей I, 248
—, свободныя волны II, 383
-, фотоэлектрическое дѣйствіе I, 271
Гефнеръ-Альтенекъ, барабанный
якорь II, 226
Гистерезисъ магнитный II, 197
— , не существуетъ въ дѣйствитель-
ности никакого діэлектрическаго
гистерезиса I, 149
— діэлектрическій I, 147
—, потеря энергіи II, 203
— . теорія 11,210
— свѣтовой дуги II, 350
Гитторфъ, вліяніе высокой темпера-
туры на катодное напряженіе 1,297
—, открытіе темнаго катоднаго про-
странства I, 239
—, перемѣщеніе іоновъ въ водныхъ
растворахъ I, 179
Гольдштейнъ, закатодные лучи I, 272
Гопкинсонъ, измѣреніе проницаемо-
сти ферромагнитныхъ веществъ
II, 195
—, магнитныя свойства никкелевой
стали II, 208
Гроза I, 232
Громоотводъ I, 18
Гудокъ (зуммеръ) I, 345
Гупка, отношеніе между продольной
и поперечной массой быстро дви-
жущихся электроновъ II, 446
Д
Два рода электрическихъ зарядовъ 1,9
Движеніе эѳира безсмысленно I, 352
—, понятіе по электронной теоріи
I, 352
— , явленія въ эѳирѣ при движеніи
матеріальныхъ частичекъ 11, 413
Движущійся іонъ, магнитное поле
II, 60
Двойной кружокъ для измѣренія элек-
трическаго напряженія I, 90
Двойной Т-якорь II, 223 п
Двуфазный вращающій токъ 11, 30$^
Де-Кудръ, трубка для полученія Лео-
нардовыхъ лучей I, 248
Детекторъ Брауна II, 404
— изъ свинцоваго блеска; ІДЧ04
Детекторы для электрическихъ волнъ
II, 385, 401 ^о\Ѵ
Джуль, единица энергіи въ ученіи
объ электричествѣ 1, 133, 172
458
Алфавитный указатель
Динамомашины II, 243
—, характеристика II, 245
Динамо-принципъ II, 243
Дисперсія свѣта II, 396
Диссоціація въ іонизированныхъ га-
захъ I, 218
— въ электролитахъ I, 184; II, 96,
99, 100
Диффракція волнъ Герца II, 388
Диффузія іоннаго газа I, 220
--------въ сыромъ воздухѣ 1,224
Діаграмма сложенія перемѣнныхъ по-
лей II, 259
Діамагнитныя вещества II, 131
Діэлектрики I, 66
— силовыя дѣйствія въ жидкихъ
діэлектрикахъ I, 109
Діэлектрическая поляризація I, 138
-----постоянная 1,142
Діэлектрическая постоянная,абсолют-
ная и удѣльная I, 111
-----, измѣреніе 1, 111, 114
-----, — посредствомъ скоростей
электрическихъ волнъ II, 374
-----матеріальныхъ тѣлъ I, 106
-----эѳира I, 104, 125, 171
Діэлектрическій гистерезисъ I, 147
Діэлектрическія свойства кристалловъ
I, 141
Діэлектрическое послѣдѣйствіе I, 147
Длина волны И, 373
— — , измѣреніе методомъ Лехера
II, 376
— — , свѣта II, 393
— искръ I, 324
Добавочныя колебанія II, 360
Дроссельныя катушки II, 272
Друде, проводимость чистыхъ твер-
дыхъ металлическихъ элементовъ
II, 88
Дуговая лалпа I, 302
-----говорящая 1,314
Дуговой разрядъ, образованіе I, 300,
316
-----, теорія, I, 312
Дуддель, звучащая свѣтовая дуга
II, 347
Дюбуа, магнитные вѣсы II, 197
Дюбуа-Реймонъ Э., индукціонный ап-
паратъ II, 292
Е
Единица мощности II, 106
— напряженія I, 61
— силы въ ученіи объ электриче-
ствѣ I, 132; II, 179
Единица силы тока II, 42
----электрическаго поля I, 73
— сопротивленія II, 70
— электрическаго заряда 1,120,168,
171
— энергіи I, 132, 171
Единицы практическія, узаконенныя
I, 122, 132,167; II, 70, 171
— электрическія I, 126
— электромагнитныя II, 170
Емкость I, 111
— аккумулятора I, 202
— въ цѣпи перемѣннаго тока II, 318,
323
— единица I, 124, 170
— земли I, 126
- измѣреніе I, 124, 169; II, 321
— телеграфнаго кабеля II, 378
Ж
Желѣзныя руды, магнитныя свойства
I, 206
Желѣзо, гистерезисъ I, 197
— , магнитныя свойства I, 188
— немагнитное I, 207
— полосовое I, 236
3
Задержка разряда I, 327
Зажиганіе ртутной дуговой лампы
посредствомъ напряженія самоин-
дукціи II, 165
Закатодные лучи I, 272
----, вторичные I, 278
----, отношеніе между зарядомъ и
массой I, 274
— — , явленіе Допплера I, 27
Законъ Видеманна-Франца II, 87
----, теорія 11,90
— Кольрауша II, 95
Законъ Кулона I, 104
— напряженій Вольта I, 55
— Ома II, 69, 91
----для магнитныхъ цѣпей 11/191
----, теорія II, 91, 96
— относительности индукціонныхъ
дѣйствій II, 154, 424
— Пашена объ искровомъ напряже-
ніи I, 324
Законы индукціи 11,(142, 163
Замкнутыя электрическія силовыя ли-
ніи II, 156, 338 V
Заряды электрическіе, два рода I, 9
----, единица 1,120,168,172
----, законъ4 сохраненія 1,85^
Алфавитный указатель
459
Заряды электрическіе земли I, 73,232
-----, измѣреніе I, 85, 166
-----, опредѣленіе I, 7
-----отдѣльнаго газіона I, 224
-----свободные I, 136, 143
Затуханіе колебаній конденсатора
II, 331
Звучащія затухающія искры, система
безпроволочнаго телеграфа II, 410
Зейбтъ, опыты съ резонирующими
катушками II, 358
Зейтцъ, опыты съ катодными луча-
ми II, 256
Земля, какъ проводникъ, I, 14
Земля, какъ проводникъ въ безпро-
волочной телеграфіи, II, 399
Земные методы для наблюденія вра-
щенія земли II, 421
Зеркала вогнутыя для опытовъ съ
волнами Герца II, 388
Зеркальные инструменты (гальвано-
метры) II, 37
Зиловъ, методъ измѣренія діэлек-
тричности жидкостей I, 110
И
Излученіе радіоактивныхъ тѣлъ (а, р,
Т-лучи) I, 332
— электрическихъ волнъ II, 381,382
Измѣненіе концентраціи раствора при
электролизѣ I, 178
— размѣровъ матеріи при ея дви-
женіи въ эѳирѣ II, 438
— хода часовъ вслѣдствіе движенія
земли II, 441
Измѣненія направленія движенія, объ-
ясняемыя механикой, II, 422
-------, — электромагнитизмомъ
II, 425
Измѣреніе температуры посредствомъ
термоэлементовъ I, 362
-----посредствомъ болометра II, 89
Измѣрительная проволока въ мостѣ
Витстона I, 84
Измѣрители тока II, 35, 125
-----, градуированіе II, 42
— —, электрометръ II, 76
Измѣритель скорости тока II, 43
— частоты (числа періодовъ элек-
тромагнитнаго колебанія) II, 333
Измѣрительный конденсаторъ I, 113
Измѣрительные инструменты для раз-
личныхъ областей измѣреній И, 78
Изображенія полей магнитныхъ 1,10,
26
-----электрическихъ I, 25
Изогоны II, 14
Изоклины II, 16
Изоляторы электрическіе 1,12,79,185
Индикаторы для магнитнаго поля
II, 3, 4
— въ гальванометрѣ II, 37
— въ электрометрѣ I, 43
— для электрическаго поля I, 3
Индуктивное сопротивленіе II, 267
Индукторъ II, 289
— для измѣреній II, 91, 92, 273,274,
322
— , электромагнитныя колебанія
II, 343
Индуктированное намагниченіе II, 5,
190
Индуктированное напряженіе въ дви-
жущихся проводникахъ II, 139, 143
----въ магнитныхъ поляхъ высо-
кой частоты II, 336, 377
----въ окрестности движущагося
магнитнаго стержня II, 156, 426
----въ перемѣнномъ магнитномъ
полѣ II, 264
----при измѣненіи магнитныхъ по-
лей II, 155, 162
Индуктированный токъ II, 141
Индукціонная машина Гольца I, 100
----Теллера I, 101
----Вимшурста I, 101
Инерціонная связь, какъ аналогія элек-
тромагнитной связи въ трансфор-
маторѣ II, 280
Индукціонное дѣйствіе въ перемѣн-
номъ магнитномъ полѣ II, 264, 337
----, относительность 11,154,244
Индукціонный аппаратъ II, 289
----для измѣренія самоиндукціи и
емкостей II, 273, 274, 322
----для измѣренія сопротивленія
электролитовъ II, 92
----, электромагнитныя колебанія
II, 343
Индукціонныя машины I, 99
Индукція I, 80
Индукція въ движущихся проводни-
кахъ II, 139
Индукція въ перемѣнномъ полѣ II, 264^^
337
—, измѣреніе магнитнаго силовбйх
потока II, 148
— магнитная II, 142
—, механическая аналогія 11,161
— при измѣненіи магнитныхъ по-
лей II, 158 ДѴ
Инертная масса электрона, измѣне-
ніе ея въ зависимости отъ скоро-
сти II, 419, 4Щ>
460
Алфавитный указатель
Инерція магнитнаго поля II, 159
— матеріи и процессы, происходя-
щіе въ эѳирѣ, II, 413
Инструменты для измѣренія напря-
женія, электрометръ I, 42
Интерференція II, 259
— волнъ Герца II, 391
— свѣта II, 393
Искра дугового разряда I, 322
— въ индукціонномъ аппаратѣ II, 290
— размыканія II, 165
— тлѣющаго свѣта I, 323
Искровое напряженіе I, 282, 323
----, законъ Пашена I, 324
Искровой осцилляторъ II, 329
— промежутокъ I, 321
Искры длина I, 324
Искрящіеся разряды при быстрыхъ
колебаніяхъ II, 356; потеря энер-
гіи въ безпроволочномъ телеграфѣ
II, 405
Искусственные драгоцѣнные камни,
изготовленіе I, 303
Исчезновеніе электрическаго поля
I, 79, 151
Іоній I, 343
Іонная теорія діэлектрика I, 140, 184
----матеріи I, 185, 350
—. — проводимости I, 182
Іонизація посредствомъ раскаленна-
го тѣла I, 209, 295
----столкновенія іоновъ 1,234, 278
----------, нижній предѣлъ напря-
женія I, 278
— рентгеновскими лучам и, 1,209, 268
— , свѣтовыя явленія I, 233, 237
—, степень I, 216; II, 99, 100
Іоны въ атмосферѣ I, 230
— въ воздухѣ I, 211, 221
— въ газахъ I, 213, 221, 275, 290
— въ электролитахъ I, 181, 182;
II, 98, 100
—, какъ ядра тумана I, 224, 232
К
Кабель для перемѣннаго тока, пере-
напряженія II, 325
Кабельный телеграфъ II, 215, 379
Капиллярный электрометръ I, 195
Карбиды, примѣненіе въ электриче-
скихъ печахъ I, 303
Карръ, искровое напряженіе при
весьма малыхъ длинахъ искры 1,326
Каскадная батарея I, 129
Кассуто и Штаркъ, дуга загорается
только при раскаленномъ катодѣ
I, 308
Катіоны въ электролитахъ 1,181,182
Катодъ I, 159
— вогнутый сферическій въ Рент-
геновской лампѣ I, 264
- - въ видѣ вогнутаго ’ сферическа-
го зеркала I, 248
— , раскаленность I, 298
— , распыленіе I, 293
— свѣтовой дуги I, 309
— тихаго разряда I, 236
— трубки Венельта I, 298
Катодное напряженіе въ свѣтовой
дугѣ I, 310
----тихаго разряда, нормальное
и анормальное I, 240
— —, значеніе I, 279
— темное пространство I, 239, 242,
279
Катодные лучи I, 247
----жесткіе и мягкіе I, 262
----, отклоненіе I, 252
----, отношеніе заряда къ массѣ
I, 257
----, поглощеніе I, 249, 262
----, скорость I, 261
----, энергія I, 253
Катодный свѣтовой поясъ I, 239, 272
Катушка Пупина въ телефонныхъ
проводахъ II, 380
Кауфманъ, измѣреніе инерціи весьма
быстро движущихся электроновъ
II, 417, 445
Квадрантный электрометръ Томсона
I, 43
Кварцъ піезоэлектрическій I, 145
Квинке Г., измѣреніе воспріимчиво-
сти II, 184
Кельвинъ, астатическій гальвано-
метръ II, 40
—, кабельная телеграфія II, 216
—, квадрантный электрометръ I, 43
—, продолжительность одного коле-
банія электромагнитныхъ колеба-
ній II, 3.7
Кенигъ В., демонстрированіе элек-
тромагнитныхъ колебаній II, 344
Кенигсбергеръ, измѣреніе магнитна-
го поля II, 186 о- Ѵ
Кепзель, аппаратъ для измѣренія по-
ля II, 196
Киловаттъ (единица мощности) II, 106
Киловаттъ-часъ,(/единица энергіи
и, 106 ѴѴ.
Кислородный ^Электродъ въ газовомъ
элементѣ^ 192
Клаузіусъ* теорія діэлектриковъ 1,137
Алфавитный указатель
461
Клееманъ и Брэггъ, число а-частицъ
равно числу распадающихся ато-
мовъ I, 345
Клейстъ, изобрѣтеніе Лейденской бан-
ки I, 117
Кобальтъ, магнитныя свойства II, 206
Когереръ Бранли II, 385, 401
Колебанія II, 256
— весьма быстрыя II, 330
— , возбужденіе толчками II, 354
— въ длинной катушкѣ II, 358, 359,
360
— въ индукціонномъ аппаратѣ 11,343
— на параллельныхъ проволокахъ
II, 362
— при исчезновеніи магнитнаго по-
ля II, 343
— при разрядѣ конденсатора II, 326
—, продолжительность II, 351
— свѣтовой дуги II, 346
— стоячія II, 376
Колебательный характеръ разряда
конденсатора II, 330
Колесо Барлоу II, 134
Количество движенія II, 161
Коллекторъ динамомашины II, 242
— для измѣренія электрическаго по-
ля I, 70
— съ пламенемъ I, 70
Кольраушъ Ф., измѣреніе сопроти-
вленія электролитовъ П, 93
Кольцевой магнитъ въ гальваноме-
трахъ II, 37
— — для вращающаго тока II, 303
— якорь II, 225
-----Пачинотти II, 225
Компасъ II, 14
Компаундъ-динамо II, 247
Компаундъ-моторъ II, 240
Компенсаціонный методъ сравненія
электрическихъ напряженій I, 156
Компенсирующія дѣйствія, дѣлающія
невозможнымъ наблюденіе абсолют-
ныхъ скоростей II, 429
Конвекціонный электрическій токъ
II, 61
Конверторы (преобразователи) посто-
яннаго тока II, 286
Конденсаторъ индуктора II, 291
—, магнитное поле вслѣдствіе дви-
женія земли II, 429
— подвижной II, 333
— , токъ энергіи при заряженіи И, 116
Конденсаторы I, 114, 119
—, параллельное соединеніе 1,119
— , послѣдовательное соединеніе 1,128
Контактное напряженіе металловъ
I, 258, 366, 369
Константанъ II, 88
Короткое замыканіе II, 109
Коротко замкнутый якорь мотора
вращающаго тока II, 307
Коэрцитивная сила постояннаго маг-
нита II, 6, 201
Коэффиціентъ разсѣянія въ магнит-
ныхъ цѣпяхъ II, 230
— распада радіоактивныхъ веществъ
I, 339
— рекомбинаціи іоновъ въ газѣ 1,217
— самоиндукціи II, 173, 273
— электролитовъ II, 102
Крестъ Крукса I, 247
Кривая намагниченія II, 189
— напряженія при тихомъ разрядѣ
I, 283
— силы тока и напряженія для все-
го разряда I, 317
-------------для свѣтовой дуги
перемѣннаго тока I, 320
— — — — — звучащей свѣтовой
дуги II, 350
---------- _ угольной свѣтовой
дуги I, 314
Критическая температура ферромаг-
нитныхъ тѣлъ II, 207
Круговаятіоляризація колебанія II, 302
Крутильные вѣсы Кулона I, 23
Крутильный электродинамометръ
II, 131
Кулонъ, единица заряда I, 123
Кулонметръ I, 166
Кюри, г-жа, открытіе радія I, 332
Кюри П., піезоэлектричество I, 145
Л
Ладенбургъ и Маркау, жесткость ка-
тодныхъ лучей I, 271
Лампа накаливанія II, 106
— Нернста I, 207; II, 108
— съ металлической нитью II, 108
— съ угольной нитью II, 107
Лейденская банка I, 117
-----разборная I, 148
Леманъ, опытъ объясненія возникъ
новенія прерывистаго разряда 1,318
Ленардъ, іонизація газовъ ультрафіо-
летовыми лучами кратчайшихъ
волнъ I, 269
— прозрачность тонкихъ листковъ
для катодныхъ лучей 249
—, фотоэлектрическіе!^электроны
462
Алфавитный указатель
Ленардовы лучи I, 248
Лехеръ, опытъ съ электромагнитны-
ми колебаніями II, 362
Линейная сумма магнитнаго поля
II, 55, 58
-----электрическаго поля I, 36
Линейчатый спектръ I, 237; II, 394
Линіи индукціи II, 146
Логъ мореплавателя для опредѣленія
скорости движенія корабля 11,421
Лоджъ, резонансъ электрическихъ ко-
лебаній II, 332
Ломанъ, явленіе Зеемана въ спектрѣ
гелія II, 395
Лоренцъ, теорія относительности
II, 431, 439
— , теорія сжатія матеріи въ напра-
вленіи ея движенія II, 438
—, формулы зависимости инертной
массы отъ скорости II, 444
Лучи радія іонизируютъ газы I, 209
-Лучи Рентгена I, 264
— — вторичные 1, 268
-----жесткіе и мягкіе I, 266
— —, іонизирующее дѣйствіе 1,209,
268
-----, теорія I, 266; II, 394
М
•
Магнетитъ II, 3
Магнетометръ II, 4
Магнетоскопъ II, 4
Магнитъ II, 5
— въ видѣ колокола II, 37
— постоянный II, 199
Магнитная индукція, или магнитный
силовой потокъ, единица, II, 145
— —, измѣреніе II, 148, 185, 195
— - , линіи- II, 146
-----, механическая аналогія 11,161
-----, направленіе II, 145
-----, полная величина II, 191
— стрѣлка II, 6
Магнитизма настоящаго не суще-
ствуетъ II, 138
Магнитизмъ вращенія II, 151
— свободный II, 202
Магнитное вещество, вліяніе возра-
ста II, 209
— насыщеніе II, 190, 205
— отклоненіе закатодныхъ лучей
I, 273
-----катодныхъ лучей I, 257
— поле II, 3
-----вокругъ движущихся іоновъ
II, 60
Магнитное поле земли II, 12,50,149,180
----постоянныхъ магнитовъ II, 10
---- вокругъ электрическаго тока
II, 25
----, возникновеніе и исчезновеніе
II, 158
----, вычисленіе II, 191
----, механическая аналогія II, 57
мотора II, 228
----, направленіе II, 9, 48, 145
----, силовыя дѣйствія на движу-
щіеся іоны и электроны II, 132
----, силовыя дѣйствія на магнит-
ные полюсы II, 177
----, силовыя дѣйствія на провод-
ники съ токомъ II, 178
----, полученіе весьма сильнаго маг-
нитнаго поля II, 203
----и электрическій токъ II, 35
----, энергія II, 174, 177
— сопротивленіе II, 191
— состоянье эѳира, отличіе отъ
электрическаго II, 22
— экранирующее дѣйствіе II, 13
— ярмо II, 194
Магнитные вѣсы Дюбуа II, 196
— детекторы для свободныхъ элек-
трическихъ волнъ II, 402
— полюсы II, 6
Магнитныхъ зарядовъ не существу-
етъ II, 24
— проводниковъ не существуетъ
II, 4, 288
Магнитный гистерезисъ И, 190
— индукторъ машины 11,223,350
— стержень въ качествѣ мотора
II, 121
— стержень движущійся, электри-
ческое поле вблизи него 11,156,425
Магнитныя бури II, 22
— поля токовъ II, 29, 34, 55
— свойства вѣсомыхъ тѣлъ II, 181,
190
----------, вліяніе на нихъ возра-
ста II, 209
--------— , вліяніе на нихъ темпе-
ратуры II, 208
----------? теорія И, 126,186, 209
— силовыя линіи II, 10
внутри постояннаго маг-
нита-------------------------------II, 199
--------, модель изъ волчковъ II, 66
— цѣпи II, 190 ДХ
Магнито-электричеСкая машина II, 242
Майкельсонъ и Морлей, вліяніе дви-
женія земли на длину пути свѣ-
тового луча II, 434
Алфавитный указатель
463
Максвеллъ, второй законъ электро-
динамики II, 160
—. первый законъ электродинамики
II, 57, 59
Манганинъ II, 88
Марганцевая сталь, немагнитная
II, 207
Маркони, изобрѣтеніе безпроволоч-
наго телеграфа II, 398
Матерія, іонная теорія I, 185
—, электронная теорія I, 350, 413
Машина перемѣннаго тока съ вну-
тренними полюсами II, 262
-----— съ внѣшними полюсами
И, 262
Маятникъ Вальтенгофена II, 152
— Фуко II, 420
Металлическіе проводники I, 356
-----, электронная теорія 1,357; II, 90
Методъ перешейка для полученія вы-
сокихъ силъ магнитнаго поля 11,205
Механика и электромагнитизмъ II, 415
Механическая аналогія электричества
I, 104
-----емкости II, 318
-----магнитной индукціи II, 161
-----непроницаемости II, 169
-----переноса мощности въ эѳирѣ
II, 116
-----самоиндукціи II, 266, 267
-----силы магнитнаго поля II, 57
-----трансформатора II, 280
-----электрическаго возбужденія
I, 95
-----электрическихъ волнъ II, 368
----- электрическихъ колебаній
II, 328
- — электрической силы поля I, 33
— модель эѳира I, 31, 33, 95; II, 62
Микрокулонъ I, 121
Микрофарадъ I, 121, 170
Микрофонъ II, 218
— изъ угольныхъ зеренъ II, 217
ДОиллеръ и Морлей, повтореніе опы-
та Майкельсона и Морлея II, 437
Минковскій, принципъ относитель-
ности II, 439
Многополюсныя машины постояннаго
тока II, 249
Молекулярные магниты II, 136,186,210
-----перемѣннаго тока II, 261
-----мотора вращающаго тока
II, 312
Молнія I, 305
Морлей и Майкельсонъ, вліяніе дви-
женія земли на длину пути свѣ-
тового луча II, 434
Морлей и Миллеръ, повтореніе опы-
та Майкельсона и Морлея II, 437
Мостъ Витстона II, 82
Моторъ съ параллельнымъ возбу-
жденіемъ II, 237
— съ послѣдовательнымъ возбужде-
ніемъ II, 239
Моторы перемѣннаго тока, асинхрон-
ные II, 297
—------синхронные II, 295
----— съ вращающимся полемъ
II, 313
Моторы постояннаго тока безъ под-
вижныхъ контактовъ невозможны
II, 28, 288
Мощность, измѣреніе II, 132
— мотора вращающаго тока II, 309
— перемѣннаго тока II, 269
— , переносъ въ эѳирѣ, механическая
аналогія II, 116
—, потеря въ якорномъ желѣзѣ
II, 235
— трансформатора II, 279
— (энергія), электрическая II, 106,
111, 142
Муассанъ, изготовленіе искусствен-
ныхъ драгоцѣнныхъ камней I, 303
Мушенброкъ, изобрѣтеніе Лейденской
банки I, 117
Мѣстная батарея на телеграфной
станціи II, 215
Мѣстные токи I, 189
Н
Нажимъ Прони II, 232
Наклоненіе магнитное II, 18
Намагниченіе II, 5, 29
— въ весьма сильныхъ поляхъ 11,203
— въ весьма слабыхъ поляхъ 11,210
— діамагнитныхъ и парамагнитныхъ
тѣлъ II, 181
—, теорія II, 136, 186, 209
— ферромагнитныхъ веществъ II, 190
Напряженіе анода въ тихомъ разря-
дѣ I, 281
—, единица I, 61
— , полученіе произвольныхъ напря-
женій I, 154
— поляризаціи I, 191
—, примѣры I, 67
— при соприкосновеніи
57, 67; II, 103
-------металловъ I, 359^366, 369
— свѣтовой дуги I, 302! Vх
— электрическое, опредѣленіе I, 34
— электромагнитное;!!, 158
I, <49, 52,
464
Алфавитный указатель
Настройка антеннъ II, 405
Насыщеніе магнитное, II, 190, 205
— . теорія II, 209
Натрій, электролитическое добыва-
ніе I, 206
Нейтральная зона на якорѣ машины
II, 230
Немагнитная марганцевая сталь II, 207
Неполяризующіеся электроды I, 193
Непостоянныя цѣпи I, 197
Нернстъ, теорія гальваническихъ цѣ-
пей И, 102
Несжимаемость эѳира I, 95
Нефовъ (Вагнеровскій) молоточекъ
II, 222, 290
Никкель, магнитныя свойства II, 206
Никкелевая сталь, магнитныя свой-
ства II, 208
Нормальное катодное напряженіе при
тихомъ разрядѣ I, 240
— сопротивленіе II, 89
Нормальный конденсаторъ I, 121
— растворъ электролита II, 94
— элементъ I, 61, 62, 199
----Кларка I, 62,199
О
Обратимыя цѣпи I, 200
Однофазный моторъ съ вращающимся
полемъ II, 314
Омъ, единица сопротивленія II, 70
Омическое и кажущееся сопротивле-
нія при перемѣнномъ токѣ II, 267
Оптическій аппаратъ Майкельсона
II, 436
Опредѣленіе положенія мѣста геоме-
трическими измѣреніями II, 421
Опытъ Вольта I, 51
— —, объясненіе I, 68
— Лехера для измѣренія діэлектри-
ческихъ постоянныхъ II, 376, 377
— Фарадэя съ ведромъ I, 82
— — съ клѣткой I, 75
Ореолъ свѣтовой дуги I, 301
Основное тѣло для опредѣленія дви-
женія II, 423
Осрамовыя лампы II, 108
Остаточное намагниченіе II, 6, 190
----имѣетъ важное практическое
значеніе въ динамомашинахъ II, 244
Осциллограмма звучащей свѣтовой
дуги II, 348
— осциллятора съ затухающей
искрой II, 355
— электромагнитныхъ колебаній при
сильной связи двухъ осцилляторовъ
II, 335
Осциллограмма свѣтовой дуги пере-
мѣннаго тока II, 127
Осциллографъ II, 126
Осцилляторъ Герца II, 384
— съ возбужденіемъ толчками II, 355
— электрическій II, 329
Осцилляторы открытые и закрытые
II, 384
Отвѣтвленіе амперметра II, 79
Отдѣленіе электрическихъ силовыхъ
линій II, 382
Относительность времени II, 441
— движеній въ геометріи и въ ме-
ханикѣ II, 420
-----въ ученіи объ электричествѣ
II, 154, 423
— длины II, 438, 441
— тяготѣнія II, 441
— индукціонныхъ дѣйствій II, 154,
423
— упругости матеріи II, 442
— энергіи II, 430
Отправитель безпроволочнаго теле-
графа II, 398
Отражательная способность метал-
ловъ для ультракрасныхъ лучей
II, 397
Отраженіе волнъ Герца II, 389
Отрицательный зарядъ I, 10
— магнитный полюсъ II, 7, 19
— тлѣющій свѣтъ I, 236
-----распрэстраніе его I, 239
-------, три слоя его I, 239
Отталкиваніе взаимное проводниковъ
съ противоположными токами II, 124
П
Паденіе потенціала равно силѣ поля
I, 73
Панцырные гальванометры II, 39
Параллельное соединеніе нѣсколь-
кихъ конденсаторовъ I, 119
Параллельные провода, перенесеніе
энергіи II, 113
-----, распространеніе электромаг-
нитныхъ волнъ II, 370, 377
-----, электромагнитныя коле^айія
II, 362 ° А>°ѵ
Парамагнитизмъ, теорія 11/1:86
Парамагнитныя вещества- II/ 181
Первичная катушка 11/276
Передача силы электрическая II, 250,
284, 314
— энергіи на /разстояніе помощью
перемѣннаго дока II, 284
-----, перенапряженія 11,325
Алфавитный указатель
465
Передатчикъ Брауна II, 405
— Маркони II, 404
Перемѣнный токъ и емкость II, 318
— — , измѣреніе II, 261
-----и самоиндукція II, 267
-----, кажущееся сопротивленіе
II, 269, 320
-----, омическое сопротивленіе при
большомъ числѣ періодовъ II, 340
-----, энергія II, 269
Перемѣнныя поля II, 256
-----, измѣреніе II, 259
— —, сложеніе II, 259
Перенапряженія въ проводахъ пере-
мѣннаго тока II, 325
Переносъ энергіи въ электромагнит-
номъ полѣ II, 110
-----на далекія разстоянія II, 285,314
-----, техническое примѣненіе II, 250
Пересѣченіе силовыхъ линій II, 147,
163
Періодъ распада радіоактивныхъ ве-
ществъ I, 339
-----перемѣннаго поля II, 257
Петля гистерезиса II, 198
-----и потеря энергіи II, 203
-----постоянныхъ магнитовъ 11,199
Пироэлектричество I, 142
— ложное I, 146
Питательные пункты въ проводахъ
сѣти II, 252, 253
Піезоэлектрическій кварцъ I, 145
Піезоэлектричество I, 144
Пламенная дуговая лампа I, 306
—-------, тушеніе дуги магнитнымъ
способомъ II, 133
Пламя свѣчи въ магнитномъ полѣ
II, 187
Планте, аккумуляторъ I, 203
Платино-родіевый сплавъ для термо-
элементовъ, пригодныхъ для измѣ-
ренія высокихъ температуръ, I, 362
Поверхностная плотность электри-
ческаго заряда I, 77, 89
Поверхностное натяженіе, измѣненіе
отъ электрическихъ зарядовъ 1,193,
194
Повышеніе точки кипѣнія электро-
литовъ I, 184
Поглощеніе волнъ въ кабеляхъ II, 378
Подковообразный магнитъ, поле его
II, 11
Подвижной конденсаторъ II, 333
Подводный кабель II, 215, 378
Подстанція II, 252, 253
Пойнтингъ,теорема о переносѣ энер-
гіи въ электромагнитномъ полѣ
II, 110
Поле тока магнитное II, 28, 35, 55
----, механическая модель II, 65
----электрическое I, 152
Полезный эффектъ лампы Паульсена
II, 408
----передатчика съ затухающей
искрой II, 412
----при передачѣ на разстояніе
II, 314
----электрическихъ лампъ I, 302;
II, 108
Полное напряженіе I, 34
----, измѣреніе I, 34
— — магнитнаго поля II, 54
— — магнитнаго силового потока
II, 145
— электрическое возбужденіе I, 87
Положительная свѣтовая колонна ти-
хаго разряда I, 236
— — —, сила поля I, 280, 326
Положительные лучи I, 273, 299
Положительный зарядъ I, 10
— кратеръ свѣтовой дуги I, 302
Положительный полюсъ магнита II, 7,
19
Полоній I, 332
Полосатый спектръ I, 237
Полосовое желѣзо II, 236
Полупроводники I, 16, 79
Полукольцевой электромагнитъ 11,205
Поляризація волнъ Герца II, 391
— діэлектрическая I, 138
— поперечной шаровой волны II, 383
— постоянная I, 142
— свѣта II, 393
— электролитическая 1,190
Полярные векторы II, 23
Полюсные башмаки II, 11, 226, 229
Пониженіе точки плавленія электро-
литовъ I, 184; II, 97
Понятіе „движеніе эѳира" безсмы-
сленно I, 352
Поперечная шаровая волна II, 383
— инертная масса II, 416, 444
Порошокъ Лихтенберга II, 345
Поставы магнитной машины II, 230
Постороннее возбужденіе магнитна-
го индуктора машины II, 263
Постоянное намагниченіе II, 5, 199
Постоянныя цѣпи I, 198 -у.
Потенціалъ I, 41
— , аналогія I, 96
— разряда съ острія I, 291^^
Потенціалъ шара I, 106
Потеря напряженія II, 79\Ѵ
— электрическихъ войнѣ’ по прово-
дамъ II, 377
— энергіи черезі> гистерезисъ II, 203
466
Алфавитный указатель
Потокъ энергіи, механическая ана-
логія И, 116
-----по Пойнтингу II, 113
Поульсенъ, лампа для быстрыхъ элек-
трическихъ колебаній II, 352, 408
Пупина катушка въ телефонныхъ
проводахъ II, 380
Пусковое сопротивленіе II, 234
Пучкообразная дуга (по Теплеру)!, 288
Пучкообразный разрядъ I, 291
Пучности II, 360, 363, 375
Практическія единицы въ ученіи объ
электричествѣ 1,122,132, 167; II, 70,
170
Предохранители II, 109
Преломленіе волнъ Герца II, 389
— свѣта II, 396
Преобразованіе перемѣннаго тока въ
постоянный I, 205, 298, 309
Прерыватель II, 291, 294
— индукторовъ II, 290
— Венельта II, 293
— съ малымъ отверстіемъ II, 294
Прерывистый тихій разрядъ I, 286
— свѣтовой дуговой разрядъ 1,315
------------ , связанныя съ нимъ ко-
лебанія II, 353
Принципъ дѣйствія и противодѣй-
ствія I, 105; II, 119
— относительности II, 439
— суперпозиціи II, 169
Пріемная антенна II, 385, 400
Пріемники для свободныхъ электри-
ческихъ волнъ II, 385
— у безпроволочнаго телеграфа
II, 398
Пробный кружокъ I, 89, 91
Проводимость металловъ II, 86
—, непостоянство ея въ газахъ I, 210
— электролитовъ II, 91
Проводники электричества I, 13, 48
— —, газы-проводники I, 16, 209
-----металлическіе I, 355; II, 90
-----, нагрѣтое стекло I, 206
----- перваго и второго классовъ
1,356
-----, проблема электрической про-
водимости I, 157
-----, электролитическая проводи-
мость I, 182; II, 96
Продолжительность колебанія II, 264
-----, формула для осциллятора II, 373
Продольная инертная масса II, 416,
444
Продольныя шаровыя волны II, 383
Продольныя волны въ эѳирѣ невоз-
можны I, 96
Проницаемость абсолютная и удѣль-
ная II, 182
— желѣза II, 189, 204, 209
— , измѣреніе II, 183, 187, 192
— парамагнитныхъ и діамагнитныхъ
тѣлъ II, 185
—, теорія II, 186, 209
— ферромагнитныхъ веществъ 11,206
— эѳира II, 168, 169
Прямолинейный проводникъ съ то-
комъ II, 26, 56
Прямолинейно-поляризованное коле-
баніе II, 299
Прямолинейно - поляризованныя вол-
ны свѣта II, 393
Птолемеева система II, 420
Путь луча, отражающагося по свое-
му первоначальному направленію,
въ случаѣ движенія въ напра-
вленіи луча II, 432
Р
Работа и электрическая энергія II, 142
Равновѣсіе напряженій I, 36
Радій I, 332, 335
—, начало и конецъ I, 342
— , періодъ распада I, 340
— , почва, какъ источникъ, I, 349
— , содержаніе въ уранѣ I, 343
Радій-^^ВгС-А-Д-/7 I, 340, 346
Радіоактивные процессы, энергія 1,347
----, самопроизвольность распада
I, 349
----, сопровождающіе ихъ лучи
(а,-р,-Т-лучи) I, 209, 332, 344
— элементы I, 332
----, періодъ распада I, 339
Радіоактивныя превращенія I, 335
— семейства I, 346
Размагничиваніе магнита II, 199
Разность электрическихъ потенціа-
ловъ равна напряженію I, 42д^
Разность фазъ вдоль волны II, 373
----двухъ колебаній II, 259
----между напряженіемъ ^ силою
тока II, 271 ч (ЯЯ
Разрядное напряженійПЯ282, 323
Разрядъ, быстро прекращающійся,
I, 318, 321
— дуговой и зоо
—, іонизирующее дѣйствіе I, 17
— само^тт^ельный черезъ газы
Алфавитный указатель
467
Разрядъ съ острія I, 289
— темный I, 282
— тихій I, 235
Рамзай и Содди, образованіе гелія
изъ эманаціи I, 336
Распадъ атомовъ радіоактивныхъ
тѣлъ I, 348
Распредѣленіе силы II, 251
Распредѣлитель II, 253
Распространеніе волны сгущенія въ
воздушномъ столбѣ II, 368
Распыленіе катода I, 293
Реакція якоря II, 230
Регенеръ Е., счетъ а-частичекъ 1,334
Резонансъ электромагнитныхъ ко-
лебаній II, 325
-------въ катушкахъ II, 356
-------въ параллельныхъ прово-
дахъ (опыты Лехера) II, 362
-------, демонстрація сильныхъ ко-
лебаній, полученныхъ посредствомъ
резонанса, II, 332
-------при сильной связи II, 335
Резонирующій трансформаторъ Те-
сла II, 356
Рейхенгеймъ и Герке, анодные лучи
I, 298
Релэ II, 215
—, употребленіе въ безпроволочномъ
телеграфѣ II, 411
Рентгеновская лампа I, 264
Рентгенъ, изслѣдованіе вліянія дви-
женія земли на силу поля конден-
сатора II, 430
—, открытіе лучей I, 264
Реостаты II, 73
— съ вращающейся рукояткой 11,74
— со скользящимъ контактомъ II, 73
Репульсіонный моторъ Э. Томсона
II, 298
Рётгерфордъ, законъ распада радіо-
активныхъ атомовъ I, 338
—, измѣреніе степени іонизаціи га-
зовъ I, 217
Рётгерфордъ и Гейгеръ, образованіе
эманаціи изъ радія I, 337
-------, періодъ распада радія I, 341
-------, превращеніе радіоактив-
ныхъ элементовъ I, 339
-----—, счетъ а-частичекъ 1,335
Рике, пироэлектричество I, 144
Ричардсонъ, электроны, вылетающіе
изъ раскаленной платины, I, 357
Рогообразный громоотводъ I, 304;
II, 134
Ролэндъ, магнитное поле конвекціон-
наго электрическаго тока II, 61
ДІй. Электричество и магнитизмъ, ч. II.
Роторъ мотора вращающаго тока
II, 306
—, магнитный силовой потокъ имѣ-
етъ характеръ ротора II, 146
--, опредѣленіе II, 23
—, сила магнитнаго поля есть ро-
торъ II, 48
Ртутная дуговая лампа I, 307
-------для электрическихъ коле-
баній II, 353
-------, зажиганіе II, 166
Рубенсъ и Гагенъ, отражательная
способность металловъ для ультра-
красныхъ лучей II, 397
Румкорфъ, изобрѣтеніе индукціонна-
го аппарата II, 292
Ряды волнъ, длинные или короткіе въ
безпроволочной телеграфіи II, 406,
407
Рядъ металловъ (Вольта) I, 54 •
— напряженій I, 49
Рэлей, лордъ, намагниченіе желѣза
при весьма малыхъ силахъ поля
II, 209
С
Самовозбужденіе динамомашины
II, 243
Самоиндукція II, 164
— въ перемѣнномъ токѣ II, 267
— и емкость въ цѣпи перемѣнна-
го тока II, 323
—, коэффиціентъ II, 173, 273
—, напряженіе, какъ ея слѣдствіе,
II, 165, 336
— телефоннаго провода II, 380
«Самостоятельные» разряды въ га-
захъ I, 235
Сварочный трансформаторъ II, 286
Свинцовое дерево I, 160
Свинцовый аккумуляторъ I, 63, 200
Свободная энергія I, 188, 193
Свободные электрическіе заряды
I, 138, 143
Свободный магнитизмъ II, 202
Свѣтовая дуга I, 300, 303
-----, вліяніе предшествующей исто-
ріи на кривую напряженія I, 319
-----говорящая I, 315
— — звучащая И, 347
-----, кривая напряженія I,
— — между металлическими/элек-
тродами I, 301, 315
-----перемѣннаго трка' Т, 319
-----, потуханіе I, 304ѵ\У
-----прерывистая 3,^315; II, 353
468
Алфавитный указатель
Свѣтовая дуга ртутная I, 307; II, 353
-----съ холоднымъ анодомъ 1,316
-----, температура I, 301
-----, тушеніе магнитнымъ спосо-
бомъ II, 132
-----угольная I, 301
-----шипящая I, 314
-----, электрическое поле I, 310
-----перемѣннаго тока 1,304
-----— — , кривая напряженія 1,320
-----, осциллограмма силы то-
ка и напряженія II, 127
— колонна, объясненіе слоевъ 1,281
-----положительная, I, 236
-----слоистая I, 237
Свѣтовой кратеръ I, 301
Свѣтовыя явленія при іонизаціи 1,233
Свѣтъ, испускаемый закатодными лу-
чами, I, 276
— свѣтовой дуги I, 304
— твердыхъ тѣлъ и паровъ метал-
ловъ II, 394
— тихаго разряда I, 237
Связь гальваническая и индуктивная
двухъ колебательныхъ цѣпей II, 359,
364
— между эѳиромъ и машинами II, 250
— механическая вслѣдствіе инерціи
II, 280
— при возбужденіи колебаній тол-
чками II, 355
— сильная II, 335
— электромагнитная въ трансфор-
маторѣ II, 283
Сдвигъ петли гистерезиса II, 200
Сегментъ коллектора (коммутатора)
машины постояннаго тока II, 225
Сжатіе матеріи въ направленіи ея
движенія въ эѳирѣ II, 438
Сила инерціи эѳира II, 413
— магнитнаго поля, единица II, 48
--------, измѣреніе II, 49
--------, механическая аналогія II, 62,
--------, направленіе II, 47
--------, полная величина II, 34, 54
--------, сложеніе II, 48
— сцѣпленія матеріальныхъ элемен-
тарныхъ частицъ I, 351, 439
— удара, какъ аналогія удара на-
пряженія, II, 144
— электрическаго поля I, 22
--------, единица I, 73
--------, измѣреніе I, 70
-----тока, единица ея II, 42
-----• —, измѣрители II, 35,76, 124
Силовыя дѣйствія въ жидкихъ ді-
электрикахъ I, 109
Силовыя дѣйствія магнитнаго поля
II, 177, 178, 183
— — электромагнита II, 34
— линіи I, 21
----, изображенія I, 25
----постояннаго магнита II, 199
Сименсъ, изобрѣтеніе динамомаши-
ны II, 243
Симонъ, говорящая дуговая лампа
I, 314
—, измѣреніе свѣтовыхъ дугъ пере-
мѣннаго тока I, 319; II, 127
— , изслѣдованіе звучащей свѣтовой
дуги II, 347
— , прерыватель въ индукціонномъ
аппаратѣ II, 294
Синхронные моторы II, 295
Синусоидальное колебаніе II, 258
Система снабженія силой, постоян-
ный токъ II, 251
— Коперника II, 420
— Птолемея II, 420
Скаляръ I, 30
Склоненіе магнитной стрѣлки II, 14
Скольженіе мотора вращающаго то-
ка II, 309
Скользящія искры I, 330
Скорость, верхняя граница II, 446
— относительная и абсолютная
II, 421
— переноса іоновъ въ проводящихъ
газахъ I, 219, 224
—--------въ электролитахъ II, 97
— распространенія энергіи II, 369
— свѣта II, 393
— свѣтовыхъ волнъ II, 393
— электромагнитныхъ волнъ II, 373
Слагающая сила магнитнаго поля
II, 19, 49
---- магнитнаго силового потока
II, 148
----электрическаго поля I, 25, 38
Слагающія перемѣнныхъ полей II, 258,
277
Сложеніе параллельно направлен-
ныхъ перемѣнныхъ полей II, 258
Слои отрицательнаго тлѣющаго свѣ-
та I, 239 V"
— положительной свѣтовой колон-
ны I, 237, 243, 281
Слоистая свѣтовая колонна I, 237
Содди и Рамзай, образованіе гелія изъ
эманаціи I, 337
Сложеніе емкостей 1/119
Соединеніе звѣздой трехфазнаго тока
II, 304
— конденсаторовъ I, 129
г
“*/// -
Алфавитный указатель
469
Соединеніе проводниковъ II, 72
— сопротивленій II, 72
— треугольникомъ при вращающемъ
токѣ II, 304
Созрѣваніе магнитнаго вещества
II, 209
Соленоидъ, изображеніе поля II, 30
— замкнутый II, 45
—, какъ магнитъ II, 123
—, число амперъ-витковъ, какъ мѣ-
ра силы магнитнаго поля, II, 46
Сопротивленіе безъиндукціонное
II, 275
— , единица II, 70
— , измѣненіе электрическаго сопро-
тивленія въ магнитномъ полѣ II, 136
— , измѣреніе II, 82, 83, 91
— индуктивное II, 266
— кажущееся для перемѣннаго то-
ка II, 269, 320
— металловъ II, 86
— омическое для перемѣннаго тока
съ большимъ числомъ періодовъ
II, 340
— , опредѣленіе II, 69
— , соединеніе II, 72
— уюльнаго контакта II, 217
— электролитовъ II, 94
Составныя части атома суть не что
иное, какъ узловыя точки силовыхъ
полей въ эѳирѣ I, 351; II, 413
Состояніе насыщенія при намагниче-
ніи ферромагнитныхъ тѣлъ II, 205
Спектры газовъ въ Гейслеровыхъ
трубкахъ I, 237, 238
— свѣтовой дуги I, 306
— свѣтящихся паровъ металловъ
II, 394
Станокъ Ампера I, 122
Статоръ мотора вращающаго тока
II, 307
Стекло, электризація отъ соприко-
сновенія I, 9
—, электрическая проводимость на-
грѣтаго стекла I, 206
Стержневой осцилляторъ II, 384
Стойка мотора вращающаго тока
II, 307
Столбъ Замбони I, 65
Струнный гальванометръ по Эйнтхо-
вену II, 125
Студнеобразная модель эѳираі, 32,94
-------улучшенная II, 62
Сумма по времени индуктированнгго
напряженія II, 143
Счетъ атомовъ I, 183, 229
Сѣверный полюсъ магнитный II, 18
Сѣверныя сіянія, сопровождающія ихъ
магнитныя возмущенія II, 22
-----, объясненіе II, 52
Сѣть проводовъ II, 252
-----, потеря напряженія II, 79
Т
Тангенсъ-гальванометръ для измѣре-
нія поля земли II, 50
Танталовая лампа II, 107
Танцующая спираль II, 124
Телеграфъ II, 213
Телеграфированіе безъ проводовъ
II, 398
-------, общество безпроволочной
телеграфіи II, 409
-------, устраненіе возмущеній 11,408
Телеграфный пишущій апп< ратъ Мор-
зе II, 214
Телефонъ 11, 217
—, примѣненіе въ безпроволочномъ
телеграфѣ II, 403
Телефонный мостъ для измѣренія ем-
костей II, 322
----------сопротивленія электроли-
товъ II, 92
Телефонныя проводки II, 220
----, поглощеніе тоновъ II, 379
Темное пространство внутреннее, или
Гитторфово I, 239
----внѣшнее, или Фарадэя, I, 236,
243
Темный разрядъ I, 282
Температурный коеффиціентъ прово-
димости металловъ II, 87
Тензоръ I, 30
Теплеръ,тихій разрядъ въ обыкновен-
номъ воздухѣ (пучкообразная дуга)
I, 289
Тепловое дѣйствіе тока I, 172; 11,105
Тепловые инструменты II, 110
----для перемѣннаго тока II, 260
Теплопроводность и электропровод-
ность металловъ II, 87 р ё
Теплота, образующаяся при химиче-^
скомъ процессѣ I, 187
Теорія діамагнитизма II, 186
— магнитизма Ампера I, 138 >
— проводимости іоновъ
— свѣта, электромагнитная II, 393
— ферромагнитизма ДІ,\209
Термомагнитный двигатель II, 207
Термометрическіе детекторы II, 404
470
Алфавитный указатель
Термостолбики I, 361
Термоэлектрическія напряженія 1,358
----, электронная теорія термоэлек-
тричества I, 369
Термоэлементы I, 362
— для измѣренія интенсивности
электромагнитныхъ колебаній 11,387
— изъ платины и сплава платины
съ родіемъ для измѣренія высо-
кихъ температуръ I, 362
Тесла, машина перемѣннаго тока для
весьма большихъ чиселъ періодовъ
И, 330
—, опыты съ колебаніями искрового
осциллятора II, 336
Тихій разрядъ, вліяніе давленія газа
I, 287
----, кривая напряженія I, 283
----«оборванный» I, 289
----прерывистый I, 286
----при давленіи атмосфернаго
воздуха I, 288, 290
----при низкомъ давленіи возду-
ха I, 236
----шарообразный II, 338
Тлѣющій свѣтъ отрицательный 1,236
----, распространеніе, I 239
----, три слоя I, 239
Токъ насыщенія въ проводящемъ га-
зѣ I, 215
— проводимости II, 59
— смѣщенія II, 59
Томсонъ Дж. Дж., изслѣдованіе іоновъ
проводящихъ газовъ I, 220
— ,мягкіе іонизирующіе лучи въ отри-
цательномъ тлѣющемъ свѣтѣ 1,264
— , счетъ іоновъ проводящаго газа
I, 228
Томсонъ, астатическій гальванометръ
II, 40
—, вычисленіе продолжительности ко-
лебанія осциллятора II, 327
— , кабельная телеграфія II, 216
— , квадрантный электрометръ I, 43
— , формула II, 328
— , явленіе I, 369
Торій I, 332
Тормозъ для измѣренія работы II, 232
Тоунсенъ, диффузія газіоновъ II, 221
—, іонизирующая сила движущихся
электроновъ I, 281
Трансмиссіонный валъ, переносъ мощ-
ности при его помощи, какъ ана-
логія переноса электромагнитной
мощности II, 117, 250
Трансформаторъ II, 276
—, механическая модель II, 280
Трансформаторъ перемѣннаго тока
II, 276, 283
— Тесла II, 341
Трансформаторы постояннаго тока
невозможны II, 289
Трансформирующій коэффиціентъ
II, 276
Третичные лучи I, 263
Трехпроводная система II, 254
Трехфазный вращающій токъ II, 303
Трубка Аронса II, 365, 366
— Брауна I, 258
— въ вращающемся полѣ II, 300
— , какъ гальванометръ II, 128
— , какъ электрометръ I, 251
— Венельта I, 297
— Гитторфа I, 244
Турбинный прерыватель II, 292
Турмалинъ, постоянная діэлектриче-
ская поляризація и пироэлектриче-
ство I, 142, 143
Тушеніе свѣтовой дуги магнитнымъ
способомъ II, 133
Тѣла для испытанія магнитнаго по-
ля II, 4
-------электрическаго поля I, 3
Тюдоръ, формированіе пластинокъ ак-
кумулятора I, 203
Тяготѣніе и сила сцѣпленія матеріаль-
ныхъ элементарныхъ частицъ I, 353
—, конечная скорость распростране-
нія II, 443
У
Уголъ сдвига щетокъ II, 231
Угольная дуговая лампа I, 302
Угольныя щетки въ моторахъ и гене-
раторахъ II, 226
Ударъ молніи,холодный и горячій 1,323
— напряженія II, 144, 161
----въ индукціонномъ аппаратѣ
II, 291 *
— —, измѣреніе II, 148
----при размыканіи тока для за-
жиганія ртутной дуговой .лампы
II, 166 о г >
----, распространеніе непараллель-
ной проводкѣ II, 370 •
Узаконенныя единицы Т, 122, 132, 167;
II, 70, 172
Узловыя точки электрическихъ по-
лей въ эѳирѣупредставляютъ со-
бою составныя части атомовъ 1,351;
п, 413 л
Узлы колебаній II, 360, 363, 375
Алфавитный указатель
471
Ультракрасные лучи, длина волнъ
II, 393
-----, отражательная способность
металловъ II, 397
Ультрафіолетовые лучи, длина волнъ
I, 293
-----дѣлаютъ газы проводниками
I, 269
-----, фотоэлектрическій эффектъ
Упругость растворенія II, 103
Уранъ I, 332
Уранъ-Х I, 343
Условіе равновѣсія электрическаго
поля I, 37
Успокаивающее дѣйствіе вихревыхъ
токовъ II, 152
Успокоеніе вращающейся катушки
въ инструментѣ д’Арсонваля II, 153
Устраненіе возмущеній въ безпро-
волочномъ телеграфѣ II, 408
Ф
Фаза вращающаго тока II, 303
— колебанія II, 258
Фарадъ (единица емкости) I, 124, 169
Фарадэй, законы индукціи II, 142
—, законы электролизовъ 1,162, 175
—, опытъ съ ведромъ I, 82
—, опытъ съ клѣткой I, 75
—, сравненіе емкостей I, 124
—, теорія суточныхъ колебаній маг-
нитнаго поля земли II, 51
Фарадэевскій сосудъ I, 83
-----для катодныхъ лучей 1,253
Феддерсенъ, колебательные разряды
II, 330
Ферромагнитныя вещества II, 187, 206,
207
— —, критическая температура II, 207
Фигуры Лихтенберга I, 293
Физо, конденсаторъ въ индукторѣ
II, 291
Фитцджеральдъ, теорія сжатія мате-
ріи въ направленіи ея движенія 11,438
Фихтбауеръ,вторичные лучи 1,263,278
Флемингъ, катодъ и анодъ у свѣто-
вой дуги I, 309
Флуоресценція отъ закатодныхъ лу-
чей I, 246
— , фотоэлектрическое дѣйствіе 1,272
Фогтъ, доказательство постоянной
діэлектрической поляризаціи въ
турмалинѣ I, 142
Формированіе аккумулятора I, 203
Формула маятника для электромаг-
нитныхъ колебаній II, 329
Формы антеннъ II, 400
Фотоэлектрическія явленія I, 269
Франклинова доска I, 118
Фуко, маятникъ II, *420
Фурье, основное колебаніе и верхнія
добавочныя колебанія II, 258
X
Характеристика динамо II, 245
Хронометрическіе сигналы II, 443
Ц
Центральная станція перемѣннаго то-
ка II, 285
Центральныя станціи постояннаго то-
ка II, 251
Центробѣжная сила II, 422
Цѣпи Вольты I, 58
— непостоянныя I, 198
Ч
Часовая діаграмма II, 257
Частички катодныхъ лучей I, 257
— закатодныхъ лучей I, 274
— а-лучей I, 332
—• ₽-лучей I, 333
«Частичные разряды» I, 305; II, 353
Часы, размагниченіе II, 199
— электромагнитные II, 217
Числа переноса іоновъ I, 181
Число амперъ-витковъ II, 46
— атомовъ по Планку I, 185
— колебаній II, 257, 264
-----, измѣреніе съ помощью измѣ-
рителя частоты II, 333
— періодовъ, обыкновенное, для пе-
ремѣннаго тока II, 264
Чэттокъ, электрическое давленіе при
разрядѣ съ острія I, 290
Ш
Шаровыя волны, продольныя и попе??
речныя II, 383
-----электромагнитныя II, 382
Шипящія искры II, 354
Шлёмильхъ, электролитическій детек-
торъ II, 403
Штаркъ и К' ссуто, дуговой разрядъ
возможенъ толькрТбгда, когда ка-
тодъ раскаленъ ^308
472
Алфавитный указатель
Штаркъ, явленіе Допплера въ зака-
тодныхъ лучахъ I, 276
Штарке и Аустинъ, вторичные лучи
I, 263
Шуманъ, ультрафіолетовые лучи съ
весьма малой длиной волны I, 269
Щ
Щелочный металлъ, полученіе въ
большихъ количествахъ путемъ
электролиза I, 206
Э
Эдиссонъ, лампа накаливанія II, 107
Эйнтховенъ,струнный гальванометръ
II, 125
Эйнштейнъ, принципъ относительно-
сти II, 439
Эквивалентная проводимость II, 94
Эквивалентныя количества продук-
товъ разложенія I, 178
Экранирующее дѣйствіе внѣшнихъ
слоевъ проводника на быстрыя
электромагнитныя колебанія II, 338
—----магнитное желѣза II, 13, 39
-----металловъ на перемѣнные то-
ки II, 265
-----электрическое, металловъ I, 78
Электрическая искра I, 285, 321
-----, вліяніе на электромагнитныя
колебанія II, 331
— — въ жидкостяхъ и твердыхъ
тѣлахъ I, 329
-----въ керосинѣ II, 331
-----, два рода электрическихъ
искръ I, 322
-----колебательная II, 330
— лампа, полезный эффектъ 1,302;
II, 108
— машина I, 18, 99
-----съ треніемъ I, 18
— мощность 11,106,111, 142
-----, измѣреніе ея II, 132
-----, механическая аналогія II, 116
-----и работа II, 142
— передача силы II, 250
--------на большія разстоянія II, 285,
314
—- станція II, 82
— стрѣлка I, 11
— штора I, 114
Электрическій вѣтеръ I, 289
— двойной слой I, 48, 193; II, 102
--------, энергія тока 11,115
Электрическій диполь I, 138
— звонокъ II, 221
— зарядъ, I, 7
-----, два рода I, 9
-----, единица I, 110, 168, 171
-----, законъ сохраненія I, 85
-----земли I, 74, 231
-----, измѣреніе его I, 84, 166
-----отдѣльнаго газіона I, 224
-----, свободные заряды I, 138, 143,
-----, элементарное количество!, 183
335
— изоляторъ I, 13, 79, 185
— колебатель II, 330
— остатокъ I, 146
— потенціалъ I, 41
-----, механическая аналогія I, 96
-----разряда съ острія I, 289
— — шара I, 106
— скатъ I, 67
— токъ I, 150
-----и магнитное поле II, 34
-----, механическая модель II, 65
— угорь I, 67
— ударъ напряженія II, 144, 161
--------, измѣреніе II, 148
--------, распространеніе вдоль про-
водки, состоящей изъ паоаллель-
ныхъ проволокъ II, 369
— фонтанъ I, 194
Электрическіе проводники I, 13, 79
-----, газы, I, 16, 209
-----металлическіе I, 355; II, 90
-----, нагрѣтое стекло I, 206
----- перваго и второго классовъ
I, 356
-----, проблема электрической про-
водимости I, 157
-----электролитическіе 1,182; II, 96
Электрическія линіи поля, или сило-
выя линіи I, 21
-----замкнутыя II, 156, 338
-----, изображеніе поля I, 25
-----отшнурованныя II, 382
— печи I, 303
Электрическое возбужденіе I, 88, 90
-----, законъ постоянства I, 92^ 95
-----, измѣреніе I, 90 о
— напряженіе, опредѣленіе 36
-----, единица I, 60
-----, измѣреніе I, 42; ІІ, 77
-----неуравновѣшенное II, 158
-----, полученіе произвольныхъ на-
пряженій I, 94Ѵу>
-----, примѣры Д 67
----- при соприкосновеніи метал-
ловъ I, 360, 366, 367
Алфавитный указатель
473
Электрическое напряженіе у поверх-
ности соприкосновенія тѣлъ I, 49,
52, 58, 67, 359
-----, условіе равновѣсія I, 37
— паденіе потенціала равно силѣ по-
ля I, 73
— поле I, 3
----- вокругъ магнитнаго стержня
II, 156, 426
-----вокругъ проводника тока 1,152
-----въ свѣтовой дугѣ I, 310
-----земли I, 73, 231
-----, исчезновеніе 1,79,151,182
-----, направленіе I, 20
-----, не удовлетворяющее условію
равновѣсія, II, 158
-----при тихомъ разрядѣ I, 241
-----, условіе равновѣсія I, 37
-----, энергія I, 132, 135
— реактивное колесо I, 289
— смѣщеніе I, 92
Электрическое состояніе, различіе его
отъ магнитнаго состоянія II, 22
Электричество отъ тренія есть элек-
тричество отъ соприкосновенія
I, 47, 59
Электродвижущая сила при соприко-
сновеніи I, 49; II, 102
-----магнитнаго поля на движущіеся
іоны II, 139
Электродинамическія поля II, 156
Электродинамометръ II, 130
— , какъ инструментъ для измѣренія
перемѣнныхъ полей, II, 260, 272
Электроды I, 159
— неполяризующіеся I, 193
Электролизъ I, 159
—, законы Фарадэя I, 162, 178
—, измѣненіе концентраціи 1,179
—, перенесеніе іоновъ I, 182
Электролитическая поляризація I, 190
Электролитическій выпрямитель съ
алюминіевымъ анодомъ I, 204
-----, детекторъ II, 401
— детекторъ Шлёмильха II, 403
Электролиты, богатые іонами, II, 101
—, проводимость II, 91
—, теорія электролитической прово-
димое! и II, 96
Электромагнитъ II, 301
Электромагнитная инерція электрона
II, 414
— теорія свѣта II, 393
Электромагнитизмъ, какъ основная
наука физики, II, 415
Электромагнитные часы 11, 217
Электр магнитныя волны II, 366
Электромагнитныя волны свободныя
II, 381
-----шаровыя II, 381
— единицы II, 170
— колебанія II, 256
-----, возбужденіе толчками II, 354
-----, возникновеніе вслѣдствіе ре-
зонанса II, 331
-----, опыты съ частыми электро-
магнитными колебаніями II, 336
-----въ индукторѣ II, 343
-----при длинной катушкѣ II, 358
----- при исчезновеніи магнитнаго
поля II, 343
-----при параллельныхъ проволо-
кахъ II, 362
----- при разрядѣ конденсатора
II, 326
-----стоячія II, 376
Электрометръ I, 42
— Ганкеля I, 43
—, какъ измѣритель тока II, 76
— капиллярный I, 195
— квадрантный I, 43
— Экснера съ золотыми листочками
I, 45
Электромоторы II, 223
—, превращеніе энергіи II, 115, 232
—, перегруженіе II, 235
—, скорость вращенія II, 236
Электронная теорія металлическихъ
проводниковъ I, 357
-----матеріи I, 350
-----термоэлектричества I, 369
Электроны I, 258
—, атомный вѣсъ I, 260
— весьма быстрые II, 417, 446
— , зарядъ I, 260
— раскаленныхъ тѣлъ I, 296
— фотоэлектрическіе, I, 270
Электропроводность расплавленныхъ
щелочныхъ солей I, 206
Электроскопъ I, 4
Электростатическая и электродина-
мическая точки зрѣнія I, 371
Электростатическія единицы I, 126
Электрофорная машина I, 98
Электрофоръ I, 96 0
Элементарное количество электричер
ства I, 183, 335
Элементъ Бунзена I, 198 ДѴ"
— Вестона 1, 62, 199
— Даніеля I, 61, 186, 188098; II, 104
— Лекланше I, 199 О\Ѵ
-- Мейдингера I,
Элементы гальваническіе I, 58, 188;
II, 102
474
Алфавитный указатель
Элементы обратимые I, 200
— постоянные и непостоянные I, 60,
197
Эльстеръ и Гейтель, проводимость
атмосфернаго воздуха I, 230
--------, расположеніе металловъ въ
рядъ по ихъ фотоэлектрическому
дѣйствію I, 271
--------,эманація въ атмосферѣ 1,349
Эманація I, 332, 336
— въ атмосферѣ I, 349
— радія 1, 336
Энергія движенія, объясняемая элек-
тромагнитизмомъ, II, 413
— магнитнаго поля II, 174
— намагниченія II, 202
—, передача на большія разстоянія
II, 285, 314
—, плотность I, 136
—?, плотность энергіи магнитнаго по-
ля II, 176
— свободная и скрытая I, 187, 193
— электрическаго поля I, 134
— , электрическая единица I, 132, 171
— электрическихъ волнъ II, 373
Эффективное значеніе перемѣнныхъ
полей II, 261
Эѳирныя ^константы 1,125, 183
Ю
Южный полюсъ, магнитный II, 19
Юиттъ, ртутная дуговая лампа I, 306
—, зажиганіе посредствомъ напря-
женія самоиндукціи И, 166
Юнгъ, кривая намагниченія желѣза
II, 189
—, методъ перешейка при весьма
сильныхъ поляхъ II, 203
— , теорія ферромагнитизма И, 209
Я
Явленіе Голла II, 135
— Допплера въ закатодныхъ лучахъ
I, 276
— Зеемана II, 394
— Пельтье I, 363
Ядра тумана I, 224, 232
Якорное желѣзо, потеря энергіи II, 235
Якорь машины II, 223
— мотора вращающаго тока, въ видѣ
бѣличьяго колеса, II, 306
— подковообразнаго магнита II, 12
— съ проволочными обмотками
II, 228
Ярмо Гопкинсона II, 194
ЧИСТАЯ и ПРИКЛАДНАЯ МАТЕМАТИКА
АДЛЕРЪ, А. Теорія геометрическихъ построеній. Переводъ съ нѣмецкаго
подъ ред. прив.-доц. С. О. Шатуновскаго. ХХІѴ+325 стр. 8°. Съ 177 рис. 1910.
Ц. 2 р. 25 к.
Предлагаемая вниманію читателей книга А. Адлера представляетъ крупнѣйшій
интересъ во многихъ отношеніяхъ... Педагогическій Сборникъ.
АППЕЛЬ, П. проф. и ДОТЕВИЛЛЬ, С. проф. Курсъ теоретической меха-
ники. Введеніе въ изученіе физики и прикладной механики. Пер. съ фр. I. Ле-
винтова подъ ред. прив.-доц. С. О. Шатуновскаго.
Вып. 1 (механика точки и геометрія массъ). ХѴ-}-385 стр. 8°. Съ 136 черт. 1912.
Ц. 2 р. 50 к.
Вып. II (механика системы). ХѴЧ-359 стр. 8°. Съ 87 черт. 1912. Ц. 2 р. 50 к.
Книга по содержащемуся въ ней матеріалу соотвѣтствуетъ университетскому курсу
теоретической механики и представляетъ собой сокращенную переработку обшир-
наго трѳхтомнаго трактата П. Аппеля по теоретической механикѣ.
АРХИМЕДЪ, ГЮЙГЕНСЪ, ЛЕЖАНДРЪ, ЛАМБЕРТЪ. О квадратурѣ
круга. Съ приложеніемъ исторіи вопроса, составл. проф. Ф. РУДІО. (Библ.
класс.). Пер. съ нѣм. подъ ред. прив.-доц. С. Бернштейна. ѴІЩ-155 стр. 8°
Съ 21 черт. 1911. Ц. 1 р. 20 к.
... является едва ли не единственной, столь полно разсматривающей задачу о ква-
дратурѣ круга. Природа и Люди.
БОЛЬЦАНО, Б. Парадоксы безконечнаго. (Библ клас.). Перев. съ нѣм.
подъ ред. проф. И.В. Слешинскаго. ѴПЦ-120 стр. 8°. Съ 12 черт. 1911. Ц. 80 к.
... представляетъ собой одну изъ первыхъ попытокъ строго математическаго обо-
снованія понятія о безконечности и его разновидностяхъ. Педагогическій Сборникъ
БОРЕЛЬ, Э. проф. Элементарная математика. Въ обработкѣ проф. В. Штёк-
келя. Пер. съ нѣм. подъ ред. и съ дополненіями прив.-доц. В. Ф. Кагана.
Ч. I. Ариѳметика и Алгебра. ЕХІѴ-Н34 стр. 8°. 1911. Ц. 3 р.
Ч. II. Геометрія. ѴІІІ+332 стр. 8°. Съ 403 черт. 1912. Ц. 2 р.
Переводъ сочиненія Бореля является весьма цѣннымъ вкладомъ въ нашу влемен-
тарную математическую литературу. Педагогическій Сборникъ.
^ѴЕВЕК Н., проф. и АѴЕЬЬЗТЕІМ Л., проф. Энциклопедія элементарной
математики. Руководство для преподающихъ и изучающихъ элементарную
математику. Пер. съ нѣм. подъ ред. и съ прим. прив.-доц. В. Кагана.
Томъ I. Элементарная алгебра и анализъ,* обраб. проф. Веберомъ
ХХІѴ+666 стр. больш. 8°. Съ 38 черт. 2-е изд. 1911 г. Ц. 4 р.
Вы все время видите передъ собой мастера своего дѣла, который съ любовью по*хѴ
называетъ великія творенія человѣческой мысли, извѣстныя ему до тончайшихъ
подробностей. Педагогическій Сборникъ. ^)°Ѵ
Томъ II. Элементарная геометрія, составленная Веберомъ, Велыитейномъ
и Якобсталемъ.
Книга I. Основанія геометріи.* Состав. /. Велыитейнъ. ХІЦ-360, стрбольш.
8°. Съ 142 черт. и 5 рис. Изд. 2-е. 1913. Ц. 3 р.
Особый интересъ представляетъ въ книгѣ г. В< .штейна своеобразное изложеиіо
нс-свклидовой геометріи, а также изложеніе проективной геометріи. ЯСур.Мин. Н.Пр
*) Изданія, отмѣченныя звѣздочкой, признаны Учен. Ком. Мин. Нар. Просі.
подлежащими внесенію въ списокъ книгъ, заслуживающихъ вниманія при по-
полненіи ученическихъ библіотекъ среди, учебн. заведеній.
1
КНИГОИЗДАТЕЛЬСТВО „МАТЕЗИСЪ*.
Книга II и III. Тригонометрія, аналитическая геометрія и стереометрія.
Составили Г. Веберъ и В. Якобсталь. ѴІІІ+321 стр. больш. 8°. Съ 109 черт.
1910. Ц. 2 р. 50 к.
ГЕЙБЕРГЪ, I. проф. Новое сочиненіе Архимеда*. Посланіе Архимеда къ
Эратосѳену о нѣкоторыхъ вопросахъ механики. (Библ. класс). Перев. съ нѣм.
подъ ред. и съ предисл. прив.-доц. И. Ю Тимченко. XV 4-27 стр. 8°. Съ 15
рис. 1909. Ц. 40 к.
Математикамъ... будетъ весьма интересно познакомиться съ новой драгоцѣнно*
научной находкой... Образованіе.
ДЕДЕКИНДЪ, Р. проф. Непрерывность и ирраціональныя числа.*
(Библ. класс.). Пер. съ нѣм. прив.-доц. С. О. Шатуновскаго, съ присоед. его
статьи: «Доказательство существованія трансцендентныхъ чиселъ*. 2-е изд. 40
стр. 8°. 1909. Ц. 40 к.
Небольшой по объему, но, такъ сказать, законодательный по содержанію трудъ...
Русская Школа.
ДЗЮБЕКЪ, О. проф. Курсъ аналитической геометріи. Пер. съ нѣм. подъ
ред. и съ примѣч. проф. СПБ. высш. женск. курсовъ Вѣры Шиффъ.
Часть 1. Аналитическая геометрія на плоскости. ѴІІІ+390 стр.8°.
Съ 87 черт. 1912. Ц. 2 р. 50 к.
Часть II. Аналитическая геометрія въ п ростра не твѣ. ѴІІІ4-356
стр. 8°. 36 черт. 1912. Ц. 2 р. 50 к.
Много задачъ, много упражненій, бездна матеріала и—научность изложенія. Твхнич.
и Коммерч. Образованіе.
КАГАНЪ, В. прив.-доц. Задача обоснованія геометріи въ современ-
ной постановкѣ. Рѣчь, произнесенная при защитѣ диссертаціи на степень
магистра чистой математики. 35 стр. 8°. Съ 11 черт. 1908. Ц. 35 к.
КАГАНЪ, В. прив.-доц. О преобразованіи многогранниковъ. Докладъ, про-
читанный въ Общемъ Собраніи Перваго Всероссійскаго Съѣзда преподавателей
математики. 27 стр. 8°. Съ 10 фиг. 1913. Ц. 35 к.
КАГАНЪ, В. прив.-доц. Что такое алгебра?* 72 стр. 16°. 1910. Ц. 40 к.
Книжка написана яснымъ простымъ языкомъ н, несомнѣнно, вызоветъ къ себѣ
интересъ. Русская Мысль.
КЛЕЙНЪ, Ф. проф. Вопросы элементарной и высшей математики.
Лекціи, читанныя для учителей. Пер. съ нѣм. подъ ред. и съ дополн. прив.-доц.
В. Ф. Кагана. ѴШ+480 стр. 8°. 1912. Ц. 3 р.
Книги, подобныя труду Клейна, должны быть настольными: снѣ появляются рѣдко.
Технич. и Коммерч. Образованіе.
КОВАЛЕВСКІЙ, Г. проф. Введеніе въ исчисленіе безконечно-малыхъ. •
Пер. съ нѣм. подъ ред. и съ прим. прив. доц. С. О. Шатуновскаго. ѴІІІ+140
стр. 8°. Съ 18 черт. 1909. Ц. 1 р.
Книга проф. Ковалевскаго, несомнѣнно, прекрасное введеніе въ высшій анализъ.
Русская Школа.
КОВАЛЕВСКІЙ, Г. проф. Основы дифференціальнаго и интегральнаго
исчисленій. Пер. съ нѣм. подъ ред. прив.-доц. С. О. Шатуновскаго. Ѵ’Ш+496
стр. 8°. 1911. Ц. 3 р. 50 к.
Курсъ профессора бонскаго университета, нееомнѣнно, является однимъ изъ луч-
шихъ по ясности и чрезвычайной строгости обоснованія одного изъ могуществен-
ныхъ методовъ современнаго анализа. Современный Міръ. /Г ѵ
КУТЮРА, Л. Алгебра логики. Пер. съ фр. съ прибавленіями проф. 1. Сле-
минскаго. ІѴ+Ю7+ХІІІ стр. 8°. 1909. Ц. 90 к.
КЭДЖОРИ, Ф. проф. Исторія элементарной математикамъ указаніями
на методы преподаванія)*. Пер. съ англ, подъ ред. и,съ прим. прив.-доц.
И. Ю. Тимченко. ѴПІ+368 стр. 8°. Съ рис. 1910. Ц. 2 р. 50 к.
Книга читается съ большимъ интересомъ и весьма полёзѣа... Мы настоятельно
рекомендуемъ «Исторію влем. мат.“ Кѳджори. Вѣстни^^оспитанія.
ЛИТЦМАННЪ, В. Теорема Пиѳагора съ приложеніемъ нѣкоторыхъ свѣдѣній
о теоремѣ Ферма. (Библ. элем. мат. I). Пер. съ нѣм. подъ общей ред. прив.-
доц. С. О. Шатуновскаго. ІѴ+80 стр. 16°. Съ 44 рис. 1912. Ц. 40 к. к
я
КНИГОИЗДАТЕЛЬСТВО „МАТЕЗИСЪ“.
>
МАРКОВЪ, А. акад. Исчисленіе конечныхъ разностей. Въ 2 частяхъ
Изданіе 2-е, исправленное и дополненное. ѴІ1І+274 стр. 8°. 1911. Ц. 2 р. 25 к.
НЕТТО, Е. проф. Начала теоріи опредѣлителей. Пер. съ нѣм. подъ ред.
и съ прим. прив.-доц. С О. Шатуновскаго. ѴІІІ+156 стр. 8°. 1912. Ц. 1 р. 20 к.
ПУАНКАРЕ, Г. проф. Наука и методъ. Пер. съ франц. И. Брусиловскаго
подъ ред. прив.-доц. В. Кагана. ѴІІІ+384 стр. 16°. 1910. Ц. 1 р. 50 к.
... книгу Пуанкаре можно рекомендовать особому вниманію преподавателей мате*
матики и естествознанія. Вѣстникъ Воспитанія.
РОУ, С. Геометрическія упражненія съ кускомъ бумаги. Пер. съ англ.
ХѴЦ-173 стр. 16°. Съ 87 рис. 1910. Ц. 90 к.
Производитъ впечатлѣніе гармоничнаго цѣлаго и читается въ большимъ интере-
сомъ. Русская Школа.
Русская математическая библіографія. Списокъ сочиненій по чистой и при-
кладн. математикѣ, напечатанныхъ въ Россіи. Подъ ред. проф.Д. М. Синцова.
Вып. I. За 1908 годъ. 76 стр. 8°. Ц. 60 коп.
Вып. II. За 1909 годъ. ХѴІ+92 стр. 8°. Ц. 75 к.
ФИЛИППОВЪ, А .О. Четыре ариѳметическія дѣйствія. Числа натураль-
ныя. ѴІІЦ-88 стр. 8°. 1912. Ц. 70 к.
ФУРРЕ, Е. Очеркъ исторіи элементарной геометріи. (Библ. элем мат II).
Пер. съ фр. подъ ред. прив.-доц. С. Шатуновскаго. 52 стр. 16°. Съ 5 рис.
- 1912. Ц. 30 к.
ФУРРЕ, Е. Геометрическіе головоломки и паралогизмы. (Библ. элем.
мат. III). Пер. съ фр. подъ ред. прив.-доц. С. Шатуновскаго. 52 стр. 16°.
Съ 83 рис. 1912. Ц. 30 к.
ЦИММЕРМАНЪ, В. проф. Объемъ шара, шарового сегмента и шаро-
вого СЛОЯ. 34 стр. 16°. Съ 6 черт. 1908. Ц. 25 к.
Распространеніе подобнаго рода элементарныхъ монографій среди учащихся весь-
ма желательно. Русская Школа.
ЧЕЗАРО, Э. Элементарный учебникъ алгебраическаго анализа и исчи-
сленія безконечно малыхъ. Пер. съ нѣм. подъ ред. проф. С.-П.-Б. универс.
К. А. Поссе. Ч. I. ХѴІІІ+632 стр. 8°. Съ 26 черт. 1913. Ц. 5 р.
ШУБЕРТЪ, Г. проф. Математическія развлеченія и игры. Пер. съ нѣм.
I. Левинтова, подъ ред., съ прим. и доб. ЛВ. О. Ф. и Эл. Мат.” XIV+358 стр.
16°. Со мног. табл. 1911. Ц. 1 р. 40 к.
Неутомимая идейная издательская фирма „Матезисъ"*.. выпустила въ свѣтъ пре-
восходный переводъ превосходной книги... Русская Школа.
ФИЗИКА
АВРАГАМЪ, Г. проф. Сборникъ элементарныхъ опытовъ по физикѣ. •
Пер. съ франц. подъ ред. проф. Б. П. Вейнберга.
Часть I: ХѴЦ272 стр. 8°. Свыше 300 рис. 2-е изд. 1909. Ц. 1 р. 50 к.
Систематически составленный сводъ наиболѣе удачныхъ, типичныхъ и поучительА
ныхъ опытовъ. Вѣстникъ и Библіотека Самообразованія >
Часть II: 434+ЬХХѴ стр. 8°. Свыше 400 рис. 2-е изд. 1910 г. Ц. 2 р. 75 к. ^)°
Мы надѣемся, что разбираемый трудъ станетъ настольной книгой каждой фшіж-
ческой лабораторіи въ Россіи. Русская Мысль.
АУЭРБАХЪ, Ф. проф. Царица міра и ея тѣнь. * Общедост. изложеніе основ.
ученія объ энергіи и энтропіи. Пер. съ нѣм. ѴІП+50 стр. 8°. 6-е изд. 1913. Ц. 40 к.
Слѣдуетъ признать брошюру Ауѳрбаха чрезвычайно интересной. К. Пр.
БРАУНЪ, Ф. проф. Мои работы по безпроволочной телеграфіи и по
электрооптикѣ. Рѣчь, произн. по случаю полученія Нобелевской преміи, съ
дополн. автора. Пер. съ рукоп. Л. Мандельштама и Н. Цапалекси, со вступі
тельной статьей переводч. ХІѴ+92 стр. 16°. Съ 25 рис. и портр. авт. 1911. Ц. 70 к.
Проф. Браунъ излагаетъ свои работы, заключающіяся въ изобрѣтеніи и усовер-
шенствованіи очень важныхъ для телеграфіи приборовъ...Естествозн. и Географія.
іи-
8
КНИГОИЗДАТЕЛЬСТВО „МАТЕЗИСЪ-.
БРУНИ, К. проф. Твердые растворы*. Пер. съ итал. подъ ред. 9Вѣстн.
Оп. Физ. и Эл. Мат* 37 стр. 16°. 1909. Ц. 25 к.
Изъ брошюры К. Бруни читатель выноситъ много цѣнныхъ свѣдѣній въ сферѣ за-
тронутыхъ вопросовъ. Физикъ-Любитель
ВЕТГЭМЪ, В. проф. Современное развитіе физики *. Пер. съ англ, подъ
ред. проф. Б. П. Вейнберга и прив -доц. А. Р. Орбинскаго. Съ Прилож. рѣчи
А. Бальфура. Нѣсколько мыслей о новой теоріи вещества. ѴІП+277 стр. 8°.
Съ 5 порт. и 39 рис. 2-е изд. 1912. Ц. 2 р.
...рисуетъ читателю дѣйствительно захватывающую картину грандіозныхъ завое-
ваній человѣческаго генія. Современный Міръ.
ВЕЙНБЕРГЪ, Б. П. проф. Снѣгъ, иней, градъ, ледъ и ледники*.
ІѴЦ-127 стр. 8°. Съ 137 рис. и 2 фототип. таб. 1909. Ц. 1 р.
„МаѣЬезіз" можетъ гордиться ѳтимъ изданіемъ. Ж. М. Н. Пр.
НЭИНЕРЪ, О. проф. О цвѣтной фотографіи и родственныхъ ей есте-
ственно-научныхъ вопросахъ*. Пер. съ нѣм. подъ ред. проф. Н. П. Ка-
стерина. ѴІ+69 стр. 8°. Съ 3 цвѣт. табл. 1911. Ц. 60 к.
Все это дѣлаетъ книгу интересной какъ для лицъ, желающихъ только ознако-
миться съ явленіями цвѣтной фотографіи, такъ и для лицъ, серьезно заинтересо-
ванныхъ этимъ вопросомъ. Естествознаніе и Географія.
ГЕРНЕТЪ, В. А. Объ единствѣ вещества. 46 стр. 16°. Ц. 25 к.
ЗЕЕМАНЪ, П. проф. Происхожденіе цвѣтовъ спектра Съ прил. статьи
В. Ритца „Линейные спектры и строеніе атомовъ“. Пер. съ нѣм. 50 стр. 16°.
Ц. .30 к.
... Книжка, принадлежащая перу одного изъ извѣстныхъ ученыхъ нашей эпохи...
Русская Мысль.
КАЙЗЕРЪ Г. проф. Развитіе современной спектроскопіи *. Пер. съ
нѣм. подъ ред. „Вѣстн. Оп. Ф. и Эл. М* 45 стр. 16°. 1910. Ц. 25 к.
Одинъ изъ лучшихъ обзоровъ... Онъ содержитъ, въ сжатомъ видѣ, исторію от-
крытія спектральнаго анализа и дальнѣйшаго ея развитія до нашихъ дней.
Журн. Мин. Н. Пр.
КЛОССОВСКІЙ, А. заслуж. проф. Основы метеорологіи. * ХѴІ+527 стр.
больш. 8°. Съ 199 рис., 2 цвѣтн. и 3 черн. табл. 1910. Ц. 4 р.
Честь и слава „МаѣЬѳзів* за изданіе этой прекрасной книги, которою можетъ гор-
диться русская наука. Ж. М. Н. Пр.
КЛОССОВСКІЙ, А. заслуж. проф. Современное состояніе вопроса о
предсказаніи погоды. 52 стр. 8°. Съ 4 черт. 1913. Ц. 49 к.
КЛОССОВСКІЙ А. заслуж. проф. Физическая жизнь нашей планеты на
основаніи современныхъ воззрѣній. * 46 стр. 8°. 2-е изданіе, испр. и
дополн. 1908. Ц. 40 к.
Рѣдко можно встрѣтить изложеніе, въ которомъ въ такой степени соединялась бы
высокая научная эрудиція съ картинностью и увлекательностью рѣчи. Педагоги-
ческій Сборникъ.
" КОНЪ, Э. проф. и ПУАНКАРЕ, Г., акад. Пространство и ьремя съ
точки зрѣнія физики. Пер. подъ ред. „Вѣстн. Оп. Физ. и Эл. Мат.\
81 стр. 16°. Съ 11 рис. 1912. Ц. 40 к.
Авторы сдѣлали все возможное, чтобы разъяснить не спеціалисту сущность прин-
ципа относительности и новой механики. Природа.
ЛАКУРЪ П. и АППЕЛЬ Я. Историческая физика. * Пер. съ нф^мЛподъ
ред. „Вѣстн. Оп. Физики и Эл. Мат*. Въ 2-хъ томахъ больш. формата 892
стр. Съ 799 рис. и 6 отд. цвѣтн. табл. 1908. Ц. 7 р. 50 к.
Нельзя не привѣтствовать этого интереснаго изданія... Книга читается легко; содер-
житъ весьма удачно подобранный матеріалъ и обильно снабжена хорошо выпол-
ненными рисунками. Переводъ никакихъ замѣчаній не вызываетъ.^. М. И. Пр.
^ДИНДЕМАНЪ, Ф. проф. Спектръ и форма атомовъ.РѢчь ректора Мюн-
хенскаго университета 23 стр. 16°. 2-е изд. Ц. 15 к. /' '
ЛОДЖЪ О., проф. Міровой эѳиръ. Пер. съ англ* ° подъ ред. прив.-доц.
Д. Д. Хмырова. ІѴЧ-216 стр. 16°. Съ 12 рис. 1911. Ц. 80 к.
Въ этой, чрезвычайно интересной книжкѣ, проводится мысль, что „міровой эѳиръ
есть непрерывное, несжимаемое, недвижимое основное вещество или совершен-
ная жидкость...* Природа.
КНИГОИЗДАТЕЛЬСТВО „МАТЕЗИСЪ*.
ЛОРЕНЦЪ, Г. проф. Курсъ физики. * Пер. съ нѣм. подъ ред. проф. Н. П.
Кастерина. Съ добавленіями автора къ русскому изданію.
Т. I. Ѵ1П+356 стр. бол. 8°. Съ 236 рис. 2-е изд. 1912. Ц. 2 р. 75 к.
Т. П. ѴПІ-И66 стр. болын. 8°. Съ 257 рис. 1910. Ц. 3 р. 75 к.
Съ появленіемъ этого перевода русская литература обогатилась превосходнымъ
курсомъ физики. Ж. М. Н. Пр.
МАЙКЕЛЬСОНЪ, А. проф. Свѣтовыя волны и ихъ примѣненія.
Перевела съ англ. В. О. Хволъсонъ подъ ред. заслуж. проф. О. Д. Хвольсона
съ дополн. статьями и примѣч. редактора. ѴПІ+192 стр. Съ 108 рис. и 3 цвѣти,
табл. 1912. Ц. 1 р. 50 к.
Завлекательна простота и конкретность мысли и живость изложенія. Журн.
Р. Ф.-Х. О-ва.
МИ, Г. проф. Курсъ электричества и магнитизма. Пер. съ нѣм. подъ ред.
засл. проф. О. Д. Хвольсона. Въ 2-хъ частяхъ. Около 50 печ. листовъ. Со
многими рис. Выходитъ въ свѣтъ выпусками. Цѣна по подпискѣ 5 р.
МОРЕНЪ, Ш. Физическія состоянія вещества. Пер. съ франц. подъ ред
проф. Л. В. Писаржевскаго. VII1+224 стр. 8°. Съ 21 рис. 1912. Ц. 1 р. 40 к.
ПЕРРИ, Дж. проф. Вращающійся волчокъ*. Публ. лекція. Съ до-
бавл. статьи проф. Б. Доната-. „Волчекъ и его будущее въ техникѣ*. Пер. съ
англ, и нѣм. ѴПІ+116 стр. 8°. Съ 73 рис. 3-е изданіе. 1912. Ц. 60 к.
Книжка, воочію показывающая, какъ люди истиннаго знанія, не цеховой только
науки, умѣютъ распоряжаться научнымъ матеріаломъ при его популяризаціи.
Русская Школа.
ПЛАНКЪ, М. проф. Отношеніе новѣйшей физики къ механистиче-
скому міровоззрѣнію. Пер. съ нѣм. I Левинтова, подъ ред. 9Вѣст.
Оп. Ф. и Эл. М.и 42 стр. 16°. 1911. Ц. 25 к.
... Планкъ разъясняетъ теорію относительности, указываетъ, что ея методы удобны
о и универсальны... Естествознаніе и Географія
ПОЙНТИНГЪ, Дж. проф. Давленіе свѣта. Пер. съ англ, подъ ред. 9Вѣстн.
Оп. Физ. и Эл. Мата. 128+П стр. 16°. Съ 42 рис. 1912. Ц. 50 к.
Наглядность изложенія теоретической стороны вопроса, иллюстрація его черте-
жами, аналогіями и со авненія ми ивъ повседневной жизни не оставляетъ желать
большаго. Природа.
РАМЗАЙ, В. проф. Благородные и радіоактивные газы. Пер. подъ
ред. яВѣстн. О. Ф. и Э. М.л. 37 стр. 16°. Съ 16 рис. 1909. Ц. 25 к.
РИГИ, А. проф. Современная теорія физическихъ явленій*. (Іоны,
электроны, радіоактивность). Пер. съ 3-го итальян. изданія. Ѵ1ІІ+146стр. 8°. Съ
21 рис. 1910. 2-е изд. Ц. 90 к.
Книгу Риги можно смѣло рекомендовать образованному человѣку, какъ лучшее
имѣющееся у насъ изложеніе новѣйшихъ взглядовъ на обширную область физи-
ческихъ явленій. Педагогическій Сборникъ.
РИГИ, А. проф. Электрическая природа матеріи. * Вступительная лекція.
Пер. съ итальян. подъ ред. „Вѣст. Оп. Ф. и Эл. Мат.л. 28 стр. 8°. 2-е изд.
1911. Ц. 30 к.
Эта прекрасная рѣчь обладаетъ всѣми преимуществами многочисленныхъ популяр-
ныхъ сочиненій знаменитаго профессора Болоньскаго университета. Ж. М. Н. И а.
СЛАБИ, А. проф. Безпроволочный телефонъ. Пер. съ нѣм. подъ ред.
9Вѣст. Оп. Физ. и Эл. Мат.л. 28 стр. 8°. Съ 23 рис. 1909. Ц. 30 к.
'СЛАБИ, А. проф. Резонансъ и затуханіе электрическихъ волнъ. Пер. съ
нѣм. подъ ред. 9Вѣст. Оп. Физ. и Эл. Мат.“. 41 стр. 8°. Съ 36 рис. Ц. 40 к?
Обѣ брошюры принадлежатъ перу большого знатока предмета и выдающагося
самостоятельнаго работника въ области практическаго примѣненія электрический ь
волнъ. Педагогическій Сборникъ. /
СОДДИ, Ф. проф. Радій и его разгадка.* Пер. съ англ, подъ ред.
прив.-доц. Д. Хмырова. ХѴЦ185 стр. 8°. Съ 31 рис. 1910. Ц. 1 р.-^Ж.
... авторъ въ увлекательномъ изложеніи вводитъ читателя въ необыкновенно за-
манчивую область... Педагогическій Сборникъ.
ТОМСОНЪ Дж. Дж. проф. Корпускулярная теорія вещества. Пер. съ
англ. I. Левинтова, подъ ред. 9Вѣст. О. Ф. и Э. М.л. У5НІ+162 стр. 8°. Съ
29 рис. 1910. Ц. 1 р. 20 к.
Воя книга, а въ особенности части, содержащія личныя изслѣдованіяа втора,
чжтаются оъ жеоолабѣвающимъ интересомъ. Физическое Обозрѣніе,
КНИГОИЗДАТЕЛЬСТВО «МАТЕЗИСЪ*.
3
ТОМПСОНЪ, СИЛЬВАНУСЪ, проф. Добываніе свѣта*. Общедоступная
лекція для рабочихъ, прочитанная на собраніи Британской Ассоціаціи 1906. Пер.
съ англ. ѴПІ+88 стр. 16°. Съ 28 рис. 1909. Ц. 50 к.
Въ ѳтой весьма интересно составленной рѣчи собранъ богатый матеріалъ по во*
просу добыванія свѣта. Ж. М. Н. Пр.
ФУРНЬЕ ДАЛЬБЪ. Два новыхъ міра. 1 Инфра міръ. 2. Супра-міръ. Пер.
съ англ. ѴІІІ+119 стр. 8°. Съ 1 рис. и 1 табл. 1911. Ц. 80 к.
... содержаніемъ своимъ она способна увлечь мыслящаго человѣка. Прав. Вѣсти.
УСПѢХИ ФИЗИКИ. Сборникъ статей подъ ред. „Вѣстника Опытной Физики и
Элементарной Математики*.
Выпускъ I.* ѴШ+148 стр. 8°. Съ 41 рис. и 2 табл. 3-е изд. 1909. Ц. 75 к.
Изящно изданный и недорогой сборникъ прочтется каждымъ интересующимся съ
большимъ интересомъ. Вѣстникъ Знанія.
Выпускъ II. ІѴ+204 стр. съ 50 рис. 1911. Ц. 1 р. 20 к.
Второй выпускъ сборника обладаетъ тѣми же положительными сторонами, что и
первый: т. е. содержательностью, ясностью изложенія и полной научностью статей.
Природа.
ХИМІЯ.
ГРОТЪ, П. проф. Введеніе въ химическую кристаллографію. Пер. съ
нѣм. I. Левинтова подъ ред. проф. М. Д. Сидоренко. VI11+104 стр. 8°. Съ 6
черт. 1912. Ц. 80 к.
МАМЛОКЪ, Л. д-ръ. Стереохимія. (Ученіе о пространственномъ расположеніи
атомовъ въ молекулѣ). Пер. съ нѣмецк. подъ ред. проф. П. Г. Меликова.
ѴІІІ+164 стр. 8°. Съ 58 рис. 1911. Ц. 1 р. 20 к.
Въ книгѣ описывается стереохимія углерода, азота, сѣры, селена, олова и неорга-
ническихъ соединеній. Естествознаніе и Географія.
ПЕШЛЬ, В. проф. Введеніе въ коллоидную химію. Очеркъ коллоидной
химіи для учителей, врачей и студентовъ. Пер. съ нѣмецкаго А. С. Комаров-
скаго. Съ пред. проф. /7. Г. Меликова. ѴІІІ+86 стр. 8° 1912. Ц. 75 к.
РАМЗАЙ, В. проф. Введеніе въ изученіе физической химіи, пер. съ
англ, подъ ред. проф. П. Г. Меликова. VII1+76 стр. 16°. 1910. Ц. 40 к.
Главный интересъ обзора конечно въ томъ, что онъ сдѣланъ крупнымъ самосто-
ятельнымъ изслѣдователемъ въ згой области. Педагогическій Сборника.
СМИТЪ, А. проф. Введеніе въ неорганическую химію. Пер. съ англ, подъ
ред. проф. 77. Г. Меликова. ХѴЦ-840 стр. 8°. Съ 107 рис. 1911. Ц. 3 р. 50 к.
Такіе первокласныѳ ученые, какъ Лёбъ, Оствальдъ и др. признали, что „Введеніе въ
неорганическую химію* Смита обогащаетъ учебную литературу и въ ряду много-
численныхъ руководствъ по химіи должно занять особое значительное мѣсто. Рѣчь.
Успѣхи химіи. Сборникъ статей о важнѣйшихъ изслѣдованіяхъ послѣдняго
времени въ общедоступномъ изложеніи подъ ред. „Вѣстн. Оп. Физ. и Элем
Мат.*. Вып. I. ѴІП+240 стр. 8°. Съ 83 рис. 1912 г. Ц. 1 р. 50 к.
ЦЕНТНЕРШВЕРЪ, М. Г. Очерки по исторіи химіи. Популярно-научныя
лекціи. ХѴІ+318 стр. 8°. Съ 83 рис. 1912 г. Ц. 2 р. 20 к.
ШТОКЪ, А. проф. и ШТЕЛЕРЪ, прив.-доц. Практическое руковод-
ство по количественному анализу. Пер. съ нѣм. лабор. Новор. Унив.
Л. 7. Коншина подъ ред. проф. П. Г. Меликова. Пер. съ нѣм. Ѵ1ІІ+172 стр. 8°.
Съ 37 рис. 1911. Ц. 1 р. 20 к.
Руководство написано ясно и понятно и можетъ быть очень полезно при самостоя-
тельномъ прохожденіи анализа. Естествознаніе и Географія.
АСТРОНОМІЯ Ж\
- 1 ' ’
АРРЕНІУСЪ, Св. проф. Образованіе міровъ *. Пер. ^нѣм. подъ ред.
проф. К. Д. Покровскаго. ѴІІІ4-200 стр. 8°. Съ 60 рис. 2-«озд.1912. Ц. 1 р. 75к.
Книга чрезвычайно интересна и богата содержаніемъ. Педагогическій Сборникъ
БОЛЛЪ, Р. С. проф. Вѣка и приливы. Пер. съ англ) подъ ред. прив.-доц.
А. Р. Орбинскаго. ІѴ+104 стр. 8°. Съ 4 рис. и 1 75 к.
... настоящее изданіе „МаіЪѳзіз* слѣдуетъ привѣтствовать наравнѣ съ прочими,
какъ почтенный, заслуживающій распространенія'и серьезнаго вниманія, вкладъ
въ русскую науку. Русская Школа.
в
КНИГОИЗДАТЕЛЬСТВО „МАТЕЗИСЪ*.
ВИХЕРТЪ, Э. проф. Введеніе въ геодезію * Пер. съ нѣм. ІѴЧ-95 стр. 16®.
Съ 41 рис. 2-е изд. 1912. Ц. 35 к.
Излагаетъ основы низшей геодезіи, имѣя въ виду пользованіе ею въ школѣ въ
качествѣ практическаго пособія... Изложеніе очень сжато, но иолно и послѣдова-
тельно. Вопросы Физики.
ГРАФФЪ, К. Комета Галлея *. Пер. съ нѣм. Х4-71 стр. 16°. Съ 13 рис. и
2 отд. табл. Изд. второе испр. и доп. 1910. Ц. 30 к.
Брошюра Граффа хорошо выполняетъ свое назначеніе. Педагогическій Сборникъ.
Галлеева комета въ 1910 году. Общедоступное изданіе. Содержаніе:
О вселенной—О кометахъ—О кометѣ Галлея. 32 стр. 8°. Съ 12 иллюстраціями.
1910. Ц. 12 к.
КЛАРКЪ, А. Исторія астрономіи XIX столѣтія. Пер. съ англ, прив.-доц.
СПБ. университета В. В. Серафимова. ѴІІІ+648 стр. 8°. Съ рис. 1913. Ц. 4 р.
ЛОВЕЛЛЪ, П. проф. Марсъ и жизнь на немъ. Пер. съ англ, подъ ред. и
съ предисл. прив.-доц. А. Р. Орбинскаго. ХХІ+272 стр. 8°. Со многими рис. и
1 цвѣтн. табл. 1912. Ц. 2 р.
Книгу эту можно рекомендовать всякому, кто хочетъ знать состояніе науки о Марсѣ
въ настоящее время; читается опа легко и вполнѣ доступна для средняго, знако-
маго съ астрономіей, читателя. Извѣстія Р. О-ва Любителей Міровіъдюнія.
НЬЮКОМЪ, С. проф. Астрономія для всѣхъ *. Пер. съ англ, подъ ред.
и съ предисл. прив.-доц. А. Р. Орбинскаго. ХХ4-288 стр. 8°. Съ порт. автора,
64 рис. и 1 табл. 2-е изд. 1911. Ц. 1 р. 50 к.
Вполнѣ научно, и совершенно доступно, и изящно написанная книга... переведена
и издана очень хорошо. Вѣстникъ Воспитанія.
БІОЛОГІЯ.
ВЕРИГО, Б. проф. Единство жизненныхъ явленій. (Основы общей біо-
логіи /.). ѴП1+276 стр. 8®. Съ 81 рис. 1912. Ц. 2 р.
... книгу нельзя не признать очень интересной и заслуживающей полнаго внима-
нія. Она написана просто и потому доступна большому кругу читателей. Русская
Школа»
ВЕРИГО, Б. проф. Біологія клѣтки, какъ основа ученій о зароды-
шевомъ развитіи и размноженіи. (Основы оощ. біологіи II) ІѴ+336
стр. 8°. Съ 60 рис. 1913. Ц. 2 р. 50 к.
ЛЁБЪ, Ж. проф. Динамика живого вещества. Пер. съ нѣм. подъ ред. проф.
В. В. Завьялова. ѴПЦ-352 стр. 8°. Съ 64 рис. 1910. Ц. 2 р. 50 к.
Классическая книга Лёба, отъ чтенія которой трудно оторваться, устанавливаетъ
вѣхи достигнутаго въ познаніи динамики живого вещества. Русское Богатство.
ЛЁБЪ, Ж. проф. Жизнь. Пер. съ нѣм. 30 стр. 8®. 1912. Ц. 30 к.
Докладъ этотъ прекрасно резюмируетъ взгляды Лёба и его школы на сущность
жизненыхъ явленій и потому является въ высшей степени интереснымъ. Русская
Школа.
УШИНСКІЙ, Н. проф. Лекціи по бактеріологіи ѴІП+135 стр. 8°. Съ 34
черн. и цвѣтн. рис. на отдѣльн. табл. 1908. Ц. 1 р. 50 к.'
Успѣхи біологіи. Сборникъ статей о важнѣйшихъ изслѣдованіяхъ послѣдняго
времени. Вып. і. Подъ ред. проф. В. В. Завьялова. IV-} 244 стр. 8°і Съ 24 рис.
V Д К I А.
ГАМПСОНЪ-ШЕФЕРЪ. Парадоксы природы. ♦. Книга для ^ юношества
объясняющая явленія, которыя находятся въ противорѣчіи съ повседневнымъ
опытомъ. Пер. съ нѣм. ѴПІ+193 стр. 8°. Съ 67 рис. Ц. 1 р. 2фй.
Матеріалъ подобранъ интересный. Жур. Мин. Н. Пр.
ГАССЕРТЪ, К. проф. Изслѣдованіе полярныхъ страі,ъ.^ Исторія
шествій къ сѣверному и южному полюсамъ съ древнѣфійхъ временъ
путе-
до на-
КНИГОИЗДАТЕЛЬСТВО „МАТЕЗИСЪ*.
стоящаго времени. Пер. съ нѣм. подъ ред. и съ дополн. проф. Г. И. Танфилъ*
ева. ХП4-216 стр. 8°. Съ двумя цвѣтн. картами. 1912. Ц. 1 р. 50 к.
... видно, какъ широко охваченъ въ книгѣ предметъ и какъ много даетъ она для
интересующихся полярными изслѣдованіями. Естествознаніе и Географія.
ДАННЕМАННЪ, Ф. Исторія естествознанія. Пер. съ нѣм. подъ ред. засл.
проф. СПБ. унив. И. И. Боргмана. ІѴЦ-486 стр. 8°. Съ 87 рис. и портр. Гали-
лея. 1913. Ц. 3 р.
НИМФЮРЪ, Р. Воздухоплаваніе. • Научныя основы и техническое раз
витіе. Пер. съ нѣм. ѴТІІ4-161 стр. 8°. Съ 52 рис. 1910. Ц. 90 к.
Въ книгѣ собранъ весьма обширный описательный матеріалъ. Ж. ЛІ Н. Пр.
СНАЙДЕРЪ, К. проф. Картина міра въ свѣтѣ современнаго естество-
знанія. Пер. съ нѣм. подъ ред. проф. В. В. Завьялова. ѴІП+193 стр. 8°.
Съ 16 отд. порт. 1909. Ц. 1 р. 50 к.
Книга касается интереснѣйшихъ вопросовъ о природѣ. Педагогическій, Сборникъ.
ТРЁЛЬС-ЛУНДЪ, проф. Небо и міровоззрѣніе въ круговоротѣ вре-
менъ. Пер. съ нѣм. ІѴЧ-233 стр. 8°. 1912. Ц. 1 р. 50 к.
... астрологія и астрономія, богословскія и этическія системы и спекуляціи раз-
смотрѣны (въ сжатомъ, но увлекательномъ ивложѳніи) на протяженіи трехъ съ
половиною тысячелѣтій... Русская Мысль.
ТРОМГОЛЬТЪ, С. Игры со спичками. Задачи и рззвлеченія Пер. съ нѣм
146 стр. 16°. Свыше 250 рис. и черт. 2-е изд. 1912 Ц. 50 к.
ШМИДЪ, Б. проф. Философская хрестоматія. Пер. съ нѣм. Ю. А. Гов-
сѣева, под. ред. и съ пред. проф. И. Н. Ланге. ѴІІІ+172 стр. 8°. 1907. Ц. 1 р.
, ... Для человѣка, занятаго самообразованіемъ и немного знакомаго съ философіей
и наукой, она (книга) даетъ разнообрааный и интересный матеріалъ. Вопросы
философіи и психологіи.
ЩУКАРЕВЪ, А. проф. Проблемы теоріи познанія въ ихъ приложеніяхъ
къ вопросамъ естествознанія и въ разработкѣ его методами. ІѴ4-137 стр. 8°
Ц 1 р.
Имѣется на складѣ:
БИЛЬТЦЪ, Г. и В. Упражненія по неорганической химіи. Пер. съ нѣм.
А. С. Комаровскаго, съ предисл. проф. Л. В. Писаржевскаго. ХѴІ-| 272 стр. 8°.
Съ 24 рис. Ц- 1 р. 60 к.
СЪ ТРЕБОВАНІЯМИ ОБРАЩАТЬСЯ
въ главный складъ изданій „МАТЕЗИСЪ**.
Одесса, Стурдзобскій пер., д. За.
ПОДРОБНЫЙ КАТАЛОГЪ ИЗДАНІЙ ПО ТРЕБОВАНІЮ.
Выписывающіе изъ главнаго склада „МАТЕЗИСЪ" на сумму 5 р.
и болѣе за пересылку не платятъ.
Отдѣленія главного склада изданій „МДТЕЗИСѴг
Въ Москвѣ—Книжный магазинъ „Образованіе" (Кузнецкій мостъ, 11);
въ Кіевѣ—Книжный магазинъ В. А. Просяниченко (Фундуклеевская).
Складъ изданій „МАТЕЗИСЪ" въ С.-Петербургѣ — Книжный мага-
зинъ Г. С. Цукермана (Александровская площадь, 5).
КНИГОИЗДАТЕЛЬСТВО „МАТЕЗИСЪ“
Проф. Ф, КОЛЬРНУШЪ
Краткое руководство къ практическимъ
занятіямъ по Физикѣ.
Пер. съ нѣм. прив.-доц. Д. Хмырова и лаборанта Е. Кириллова подъ
редакціей проф. Н. Кастерина.
VIII+ 288 стр. 8°. Съ 125 рис. 1914. Ц. 2 р. 25 к.
Содержаніе: Изъ предисловія автора — Введеніе—Взвѣшиваніе и опре-
дѣленіе плотности — Измѣреніе пространства и времени — Давленіе — Теплота
—Упругость и звукъ—Капиллярность и треніе—Свѣтъ — Магнитизмъ — Элек-
тричество—Таблицы — Алфавитный указатель.
Изъ предисловія автора'. „Настоящая книга предназначена для начи-
нающихъ и притомъ въ особенности для тѣхъ, кто предполагаетъ въ обла-
сти практической физики ограничиться первоначальными работами... Научное
познаніе... не есть единственный носитель культуры; однако, оно принадле-
житъ къ числу носителей, наиболѣе широко распространенныхъ... И къ числу
вспомогательныхъ средствъ, приготовляющихъ къ работѣ вмѣстѣ съ другими
въ этой области, принадлежитъ, играя роль важной составной части, физи-
ческій практикумъ... Элементарный практикумъ вообще не долженъ дѣлать
слишкомъ рѣзкихъ индивидуальныхъ разграниченій при выборѣ задачъ для
студентовъ различныхъ категорій. На этомъ-то и основывается универсаль-
ное значеніе упражненій по физикѣ.
Таблицы заключаютъ въ себѣ то, что требуетъ намѣченная цѣль, а, кромѣ
того, кое-что полезное для домашней работы по физикѣ11.
Н. Н. МНЙКЕЛЬСОНЪ
СВѢТОВЫЯ ВОЛНЫ И ИХЪ ПРИМѢНЕНІЯ
Подъ редакціей, съ дополненіями и примѣчаніями
засл. проф. О. Д. ХВОЛЬСОНА
перевела съ англійскаго В. О. Хвольсонъ.
VIII +192 стр. 8°. Съ 109 рисунками и тремя цвѣтными таблицами.
Цѣна 1 р. 50 к.
Уч. Ком. Мин, Нар. Пр. признана заслуживающей вниманія при пополненіи учени-
ческихъ библіотекъ средн. учебн. заведеній.
Содержаніе. Лекція I. Волновое движеніе и интерференція. Лек-
ція II. Сравненіе микроскопа и телескопа съ интерферометромъ. Лекція
III. Примѣненіе методовъ интерференціи для измѣренія разстояній и угловъ.
Лекція IV. Примѣненіе методовъ интерференціи въ спектроскопіи. Л е к-
ц і я V. Свѣтовыя волны, какъ единицы длины. Лекція VI. Изслѣдованіе
вліянія магнитизма на свѣтовыя волны при помощи интерферометра и стуЧ
пеньчатой рѣшетки (эшелона). Лекція VII. Приложенія интерференціон-
наго метода въ астрономіи. Лекція VIII. Эѳиръ. /+І?
Дополнительныя статьи проф. О. Д. ХВОЛЬСОНА.
1. О диффракціи.
2. Объ интерференціонныхъ полосахъ.
8. Нѣсколько словъ о спектральномъ анализѣ. Ѵѵ
4. Современное положеніе вопроса объ эѳирѣ. -^оѴ
5. Другой интерференціонный способъ изслѣдованій строенія спек-
тральныхъ ЛИНІЙ.
КНИГОИЗДАТЕЛЬСТВО „МАТЕЗИСЪ"
ГО^ОВ~-ІТОЯ КЪ ПЕ-ЧЛТИ
Проф. Ф, СОДДИ
Радій и его разгадка
Второе изданіе.
Переводъ съ 3-го англійскаго изданія подъ ред. прив.-доц. Новороссійскаго
Университета Д. Д. Хмырова.
Предисловіе автора къ послѣднему изданію:
Пересматривая вновь эту книгу и освѣжая ея данныя, я старался пи-
сать такъ, какъ если бы я читалъ тѣ лекціи, изъ которыхъ она составилась,
теперь, а не четыре года тому назадъ. Сказанное въ первоначальномъ изда-
ніи осталось почти безъ серьезныхъ измѣненій,—быть можетъ, наилучшій
отвѣтъ на вызванныя книгой замѣчанія, что не пришло еще время прини-
мать сполна новые взгляды на атомный распадъ и безусловную формули-
ровку всѣхъ логическихъ слѣдствій, къ которымъ неизбѣжно приходитъ
наука о явленіяхъ радіоактивности. Я не упустилъ, конечно, случая внести
послѣднія и болѣе полныя данныя, какія были получены, новыя открытія и
выводы, поскольку мнѣнія работниковъ въ этой области сходятся въ оцѣнкѣ
этого новаго.
Первоначальныя лекціи касались почти исключительно радія и дру-
гихъ членовъ семейства урана. Но и семейство торія, послѣ того, какъ тех-
ника стала получать новыя радіоактивныя вещества, мезоторій и радіоторій,
пріобрѣло теперь большое значеніе, притомъ все растущее. Поэтому я при-
бавилъ еще одну главу въ концѣ книги, посвященную группамъ торія и
актинія, и я надѣюсь, что желающіе заняться этимъ предметомъ глубже най-
дутъ здѣсь общій обзоръ всей области радіоактивности. Ф. С.
Августъ 1912.
Проф. Ш. МОРЕНЪ
ФИЗИЧЕСКІЯ СОСТОЯНІЯ ВЕШЕСТВН
Перев. съ французскаго I. Л. Левинтова подъ редакціей проф. Л. В. Писар-
жевскаго. ѴШ-|-224 стр. 8°. Съ 12 рис. 1912 г. Ц. 1 р. 40 к.
Содержаніе: Введеніе. Газообразное состояніе. Іоны. Жидкое со-
стояніе. Кристаллы и кристаллическое состояніе. Строеніе твердыхъ ве-
ществъ. Измѣненія состоянія твердыхъ веществъ. Отвердѣваніе. Анизотроп-
ность, вызванная внѣшними дѣйствіями. Мягкіе кристаллы. Жидкіе кристал-
лы. Кристаллическія жидкости. Свойства поверхностныхъ слоевъ и тонкихъ
пластинокъ твердыхъ веществъ. Переходные слои. Однородныя смѣси. Ге-
терогенныя смѣси. Коллоидальное состояніе.
Учен. Ком. М Н. Пр. признана заслуживающей вниманія при пополненіи учени-
ческихъ библіотекъ среднихъ учебныхъ заведеній
ИЗЪ ОТЗЫВОВЪ: Изученіе основныхъ свойствъ тѣлъ приводитъ насъ къ утвер-
жденію, что внутреннее строеніе тѣлъ представляетъ всегда сложную систему, ставшую
болѣе ясной только въ послѣднее время, благодаря тщательному изученію окружающихъ
явленій. Это же ученіе приводитъ насъ и къ другому заключенію о невозможности да-
вать въ каждомъ отдѣльномъ случаѣ точную формулировку даннаго физическаго^ состо-
янія тѣла. Изученіе кристалловъ, жидкостей и газовъ даетъ возможность'построенія
общихъ теорій; этимъ-то теоріямъ и посвященъ трудъ Морена. Свойства кристалловъ,
жидкихъ кристалловъ и коллоидовъ—вотъ тѣ тѣла, изученіе которыхъ составляетъ сущ-
ность данной книги... Книга представляетъ несомнѣнный интересъ. Изданіе не оставляетъ
желать ничего лучшаго. В. Лѣтникъ (Русская Мысль, май 1912г.).
--..наиболѣе интересно и подробно изложены главы о кристаллахъ, кристалличе-
скомъ состояніи и кристаллической жидкости.
Не менѣе обстоятельно написана глава и о неоднородныхѣ^смѣсяхъ, въ которой
затронутъ вопросъ о сплавахъ металловъ, закалкѣ и отжигѣ.
Заключается эта интересная книга разсмотрѣніемъ коллоидальнаго состоянія
Переведена книга Ш. Морена хорошо, издана изящнрГй Снабжена недурными ри-
сунками въ текстѣ44. В. Д - цевъ (Голосъ Москвы, 9 мая 191^ !>)•
Цѣна за обѣ части 6 руй.
Типографія .ТЕХНИКУ,
Одесса, Екатерининская, 58.