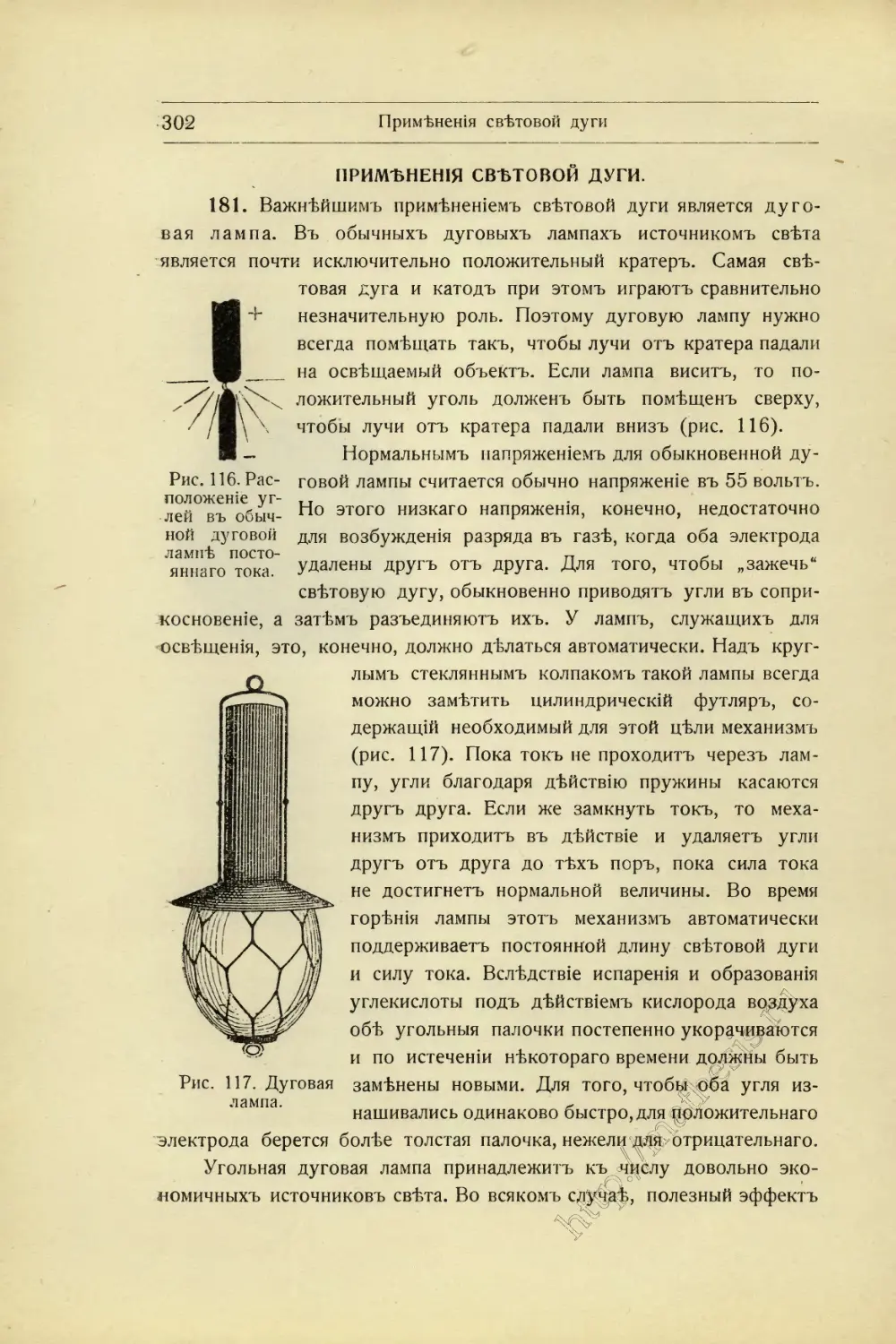
Текст
г. ми
Профессоръ Грейфсвальдскаго Университета
' цЩ ..........’
КУРСЪ
ЭЛЕКТРИЧЕСТВЯ
И МЯГНИТИЗМЯ
Переводъ съ нѣмецкаго Ѳ. Ѳ. Соколова
подъ редакціей заслуженнаго профессора
О. Д. ^вольсона
ЧИСТЬ I. ЭЛЕКТРОСТАТИКИ.
.. : ,л.'^77'-:-=тгг77- ..............: 17........................................................................................................................................................- 0
КНИГОИЗДАТЕЛЬСТВО „МАТЕЗИСЪ*.
Г. А. ЛОРЕНЦЪ, проф. КУРСЪ ФИЗИКИ.
Разрѣшенный авторомъ переводъ съ нѣмецкаго подъ редакціей проф.
И. П. Кастерина. Съ добавленіями автора къ русскому изданію
Томъ I. VIII+ 356 стр. большого 8°. Съ 236 рис. Изд. 2-е, исправлен-
ное и дополненное. 1912 г. Ц. 2 р. 75 к.
Томъ II. VIII+ 466 стр. больш. 8°. Съ 257 рис. 1910 г. Ц. 3 р. 75 к.
Содержаніе тома I. Математическое введеніе. Главы I—VIII: Дви-
женіе и силы. - Работа и энергія.—Твердыя тѣла неизмѣнной формы.—Равно-
вѣсіе и движеніе жидкостей и газовъ.—Свойства газовъ.- Принципы термо-
динамики.— Свойства твердыхъ тѣлъ.—Свойства жидкостей и паровъ.—Имен-
ной и предметный указатели.
Содержаніе тома II. Главы IX—XVIII: Колебательное движеніе
тѣлъ.—Распространеніе колебаній.—Отраженіе и преломленіе свѣта.—Природа
свѣта.—Поляризованный свѣтъ.—Электростатика.—Электрическіе токи.—Дѣй-
ствіе магнитнаго поля.—Электрическія колебанія.—Распространеніе электро-
магнитныхъ нарушеній равновѣсія,—Явленія, объясняемыя при помощи те-
оріи электроновъ.—Задачи,—Таблицы.—Именной и предметный указатель.
Учен. Ком. М. Н. ІІр. признана заслуживающей вниманія при пополненіи
ученическихъ библіотекъ среднихъ учебныхъ заведеній.
ИЗЪ ОТЗЫВОВЪ. Авторъ этой книги, Г. А. Лоренцъ (Н. А. Ьогепіг),
знаменитый основатель электронной теоріи, занимаетъ нынѣ, послѣ смерти
лорда Кельвина и Больцмана, первое мѣсто среди физиковъ всѣхъ странъ...
Распредѣленіе матеріала необычайное, но въ то же время весьма цѣле-
сообразное и интересное. Достаточно отмѣтить, что отдѣльнаго ученія о те-
плотѣ вовсе пѣтъ. Тепловыя явленія изучаются попутно при разсмотрѣніи
свойствъ твердыхъ, жидкихъ и газообразныхъ тѣлъ.
Переводъ, подъ редакціей столь компѳнтентнаго лица, какъ проф. Н. П.
Кастеринъ, никакихъ замѣчаній не вызываетъ.
Съ появленіемъ этого перевода русская литература обогатиласьпревос-
ходнымъ курсомъ физики. Проф. О. Хвольсонъ {Журналъ М. Н. Пр.,
іюнь 1910).
„Уже по поводу перевода нѣмецкаго изданія спеціальные журналы от-
мѣтили своеобразное достоинство книги Лоренца. Оригинальная система
распредѣленія мтеріала, точность и строгость выводовъ и современность
взглядовъ автора дѣлаютъ эту книгу въ равной степени важной какъ при
самостоятельномъ изученіи физики, такъ и въ качествѣ пособія при уни-
верситетскихъ запятіяхъ. Пользованіе книгой едва ли вызоветъ у начина-
ющихъ изучать физику какія-либо затрудненія, такъ какъ математическіе
выводы достаточно элементарны, и высшій анализъ примѣняется только
мѣстами... Переводъ, выполненный подъ редакціей проф. Н. П. Кастерина,
представляется вполнѣ хорошимъ, и книгу можно смѣло рекомендовать вся-
кому, кто желалъ бы приступить къ серьезному изученію физики". П. Ла-
за р е в ъ (іЖ. Р. Физ.-Хим. Общ. за 1909, вып. 7).
Дж. Дж. ТОМСОНЪ, проф. КОРПУСКУЛЯРНАЯ ТЕОРІЯ
ВЕЩЕСТВА.
Переводъ съ англійскаго /. Л. Левинтова подъ редакціей „Вѣстника
Опытной Физики и Элементарной Математики". VIII + 162 стр. 8°. Съ 29 черт.
1910 г. Ц. 1 р. 20 к.
Оглавленіе: Введеніе. Корпускулы въ пустыхъ трубкахъ.—Проис-
хожденіе массы корпускулы.—Свойства корпускулы.—Корпускулярная теорія
проводимости.—Вторая теорія электропроводности.—Расположеніе корпускулъ
въ атомѣ.—Число корпускулъ въ асомѣ.—Указатель.
ИЗЪ ОТЗЫВА: „Вся книга, въ особенности части, содержащія личныя
изслѣдованія автора, читаются съ неослабѣвающимѣ интересомъ. Пере-
водъ въ общемъ вполнѣ удовлетворителенъ... Для желающихъ позна-
комиться съ началами электронной теоріи проводимости металловъ на рус-
скомъ языкѣ переводъ можетъ быть рекомендовацъ+С. Поповъ. {Физиче-
ское Обозрѣніе. 1911 г., т. 12, № 6).
«Э05ТМѴ МІЕ
1_еНгЬисН сіег ЕІекігі/ііаі ипд скз Мадпеіізтиз
ГУСТАВЪ МИ
профессоръ и директоръ Физическаго Института Грейфсвальдскаго Университета
ТО
КУРСЪ
ЭЛЕКТРИЧЕСТВО
И МОГНИТИЗМН
Экспериментальная физика мірового эѳира
для физиковъ, химиковъ и электротехниковъ
Разрѣшенный авторомъ переводъ съ нѣмецкаго
Ѳ. Ѳ. СОКОЛОВА
подъ редакціей заслуженнаго профессора
О. Д. ХВОЛЬСОНА
Часть I. ЭЛЕКТРОСТАТИКА
Типографія
ОДЕССН.
,Техникъ“, Екатерининская^}^ 58.
1912.
ПРЕДИСЛОВІЕ РЕДАКТОРА
Ученіе объ электрическихъ и магнитныхъ явленіяхъ подверглось
за послѣднее десятилѣтіе коренному преобразованію. Не только были
открыты новыя явленія, между которыми явленія радіоактивности
занимаютъ первое мѣсто, но и основы теоріи, взглядъ на сущность,
и міровое значеніе электромагнитныхъ явленій совершенно измѣни-
лись. Развилась и, повидимому, твердо установилась электронная
теорія, разсматривающая электричество, какъ особаго рода вещество,
обладающее атомнымъ строеніемъ. Въ связи съ этой теоріей под-
вергся глубокой эволюціи взглядъ на химическій атомъ обыкновен-
ной матеріи и совершенно измѣнилась роль, приписываемая міро-
вому эѳиру г). Наконецъ, возникло новое, поразительное ученіе о реля-
тивности, совершившее такой переломъ въ научномъ міровоззрѣніи,
какого еще не было въ исторіи наукъ о природѣ, не исключая даже
перехода отъ геоцентрическаго міровоззрѣнія къ геліоцентрическому.
Замѣчательная книга проф. Ми даетъ ясную и стройно закон-
ченную картину новаго ученія. Изложеніе, вездѣ оригинальное, можно
назвать образцовымъ въ дидактическомъ отношеніи; оно безусловно-
популярное, ибо авторъ нигдѣ не пользуется серьезною математи-
кою. Исходя изъ самаго элементарнаго, онъ, шагъ за шагомъ, до-
ходитъ до изложенія новѣйшихъ завоеваній науки. Онъ не остана-
вливается и передъ такимъ труднымъ, съ перваго взгляда, вопро-
сомъ, какъ принципъ релятивности, не вошедшій еще ни въ одинъ
изъ учебниковъ, появившихся въ Россіи, и посвящаетъ ему обшир-
ную главу. Даже весьма мало знакомый съ физикою безъ труда по-
черпнетъ изъ этой книги ясное представленіе о современномъ со-
стояніи ученія объ электромагнитныхъ явленіяхъ, а спеціалисты, на-
примѣръ, учителя физики, увидятъ передъ собою образецъ строго^
научнаго и все-таки популярнаго изложенія.
Этой книгѣ нельзя не пожелать самаго широкаго распростраХ
ненія.
О. Хвольсонъ. |
Э См. статью проф. О. Д. Хвольс о на, приложенную къпсреводу книги
Майкел ьсона „Свѣтовыя волны и ихъ примѣненія", „МаШе$гё'“, Одесса, 1912^
ПРЕДИСЛОВІЕ АВТОРА
Не можетъ быть ни малѣйшаго сомнѣнія въ томъ, что основой
звсей современной физики является ученіе объ электричествѣ. Это
лученіе занимаетъ теперь то положеніе, которое сто лѣтъ тому на-
задъ приписывалось механикѣ, а механика, подобно оптикѣ, все бо-
^лѣе и болѣе превращается въ обширный отдѣлъ ученія объ элек-
тричествѣ. Несомнѣнно далѣе, что въ настоящее время существуетъ
только одна научно разработанная точка зрѣнія на электромагнитныя
явленія, именно - точка зрѣнія Максвелла (МахАѵеІІ), развитая далѣе
•съ большею отчетливостью и строгостью въ теоріи Лоренца (Н. А.
Еогепіх). Всѣмъ извѣстно, однако, что эта теорія, несмотря на ея
•основное значеніе для основной науки естествознанія — физики, не
проникла еще за предѣлы узкаго круга ученыхъ. Она остается почти
•совершенно чуждой не только естествоиспытателямъ вообще, но
даже многимъ лицамъ, весьма усердно занимающимся физикой, какъ,
шапримѣръ, преподавателямъ или техникамъ.
Причину этого, по моему мнѣнію, слѣдуетъ искать въ томъ,
"что до сихъ поръ никто еще не сдѣлалъ серьезной попытки раз-
’вить теорію Максвелла индуктивнымъ путемъ, исходя изъ экспери-
ментальнаго фактическаго матеріала. И хотя существуютъ прекрасные
теоретическіе труды, въ которыхъ послѣдовательно проведена точка
зрѣнія Максвелла, экспериментальные курсы стоятъ, собственно
товоря, все еще на старой точкѣ зрѣнія такъ называемаго дѣйствія
на разстояніи, а взгляды Фарадэя и Максвелла, въ качествѣ ^Чи-
стой теоріи только упоминаются въ нихъ въ видѣ дополнен^ж
Въ этой книгѣ я сдѣлалъ попытку развить ученіе элек-
тромагнитизмѣ постепенно, подвигаясь впередъ шаг^за шагомъ
и основываясь все время на фактическихъ данныхъ.^ При этомъ
х) Оригиналъ посвященъ авторомъ профессорамъ Энгельберту
-Арнольду и Отто Леману. Прим. пер, лЧЧІ
Предисловіе автора
ІХГ
нельзя было, конечно, избѣжать нѣкоторой „предвзятости", которая?
выражается въ группировкѣ фактовъ по опредѣленному плану и въ.
пользованіи опредѣленной терминологіей. Моя терминологія характе-
ризуется тѣмъ, что я не боюсь употребленія словъ эѳиръ или мі-
ровой эѳиръ, и опредѣляю ученіе объ электричествѣ, какъ физику
эѳира или, сшп ^гапо заііз, даже какъ механику эѳира. Врядъ лщ
нужно говорить о томъ, что соотвѣтственно естественно-научному-
характеру этого учебника, свойства эѳира предполагаются сна-
чала совершенно неизвѣстными и постепенно выясняются читателю-
изъ экспериментальныхъ данныхъ. Такимъ образомъ, изложенію при-
дана форма экспериментальнаго изученія физическихъ свойствъ эѳира.
Прежде всего слѣдуетъ обратить особенное вниманіе на то
обстоятельство, что понятія механики, если исключить весьма поучи-
тельныя, по моему мнѣнію, „аналогіи", не должны быть прилагаемы,,
къ эѳиру; какъ это слѣдуетъ изъ опытныхъ данныхъ, эти понятія,
и не могутъ вообще къ нему прилагаться. Это — альфа и омега?
современныхъ взглядовъ на электромагнитныя явленія въ той формѣ,.,
которую этимъ взглядамъ придалъ Лоренцъ. Постепенное развитіе-
нашего знанія постоянно все болѣе и болѣе стремится къ тому^
чтобы разсматривать атомы и молекулы, какъ особенныя области^
эѳира, а не эѳиръ, какъ особый родъ матеріи. Иными словами —на-
шей цѣлью является сведеніе механики къ электромагнитнымъ явле-
ніямъ и законамъ, а не сведеніе электромагнитизма къ механиче-
скимъ явленіямъ. Это я считаю труднѣйшимъ пунктомъ физики,
эѳира. Ибо, во-первыхъ, насколько механическія явленія и законьь
намъ близки изъ ежедневнаго опыта, настолько же чужды всякому
не-физику электромагнитныя явленія и ихъ законы, и, во-вторыхъ,.,
становясь на эту точку зрѣнія, приходится ломать многовѣковую тра-
дицію физики, согласно которой всѣ явленія могутъ быть сведены
къ явленіямъ механическимъ. Но эта ломка неизбѣжна; не наше
усмотрѣніе, но факты, которые нынѣ даютъ экспериментальныя изслѣ-
дованія, указываютъ намъ этотъ путь, а онъ рѣзко удаляетъ насъ,
отъ механистическаго міровоззрѣнія.
Еще одно обстоятельство сильно затрудняетъ общее пониманіе
теоріи эѳира. Эѳиръ не матеріаленъ, такъ какъ подвижность, ^про-
ницаемость, — короче, все то, на чемъ основывается изу^ем^л мате-
ріальныхъ тѣлъ,—теряютъ для него'всякій смыслъ. Онъ4 шГ только,
совершенно не осязаемъ, но вообще самъ по себѣ не воспринимаемъ..
Предисловіе автора
Измѣненія состоянія матеріальныхъ тѣлъ мы воспринимаемъ потому,
что вмѣстѣ съ ихъ состояніемъ измѣняются одновременно и всѣ ихъ
физическія свойства; мы наблюдаемъ, напримѣръ, измѣненіе темпе-
ратуры по связанному съ нимъ измѣненію плотности и т. д. Для
эѳира это не имѣетъ мѣста. Его физическія свойства абсолютно
неизмѣнны и, въ силу этого, мы никогда не можемъ воспринять
какого-либо измѣненія его состоянія. Я называю этотъ замѣчатель-
ный законъ „принципомъ наложенія (суперпозиціи)". Изъ него слѣ-
дуетъ, что всѣ явленія въ эѳирѣ могутъ быть изучаемы лишь по ихъ
дѣйствіямъ на матеріальныя тѣла.
Эти особенности физики эѳира въ недавнее время дали поводъ
многимъ физикамъ высказаться за упраздненіе самаго термина „эѳиръ",
такъ какъ слишкомъ уже вошло въ привычку соединять съ этимъ
словомъ представленіе о чемъ-то матеріальномъ. Удобнѣе было бы
вмѣсто термина „эѳиръ" употреблять слова вакуумъ или пустота.
Нельзя отрицать того, что такая терминологія до нѣкоторой сте-
пени оказывается подходящею и, во всякомъ случаѣ, исключаетъ вся-
кія недоразумѣнія механическаго характера. Однако, она заставляетъ
насъ думать, что мы имѣемъ дѣло съ чѣмъ-то совершенно лишен-
нымъ положительнаго содержанія, въ то время какъ относительно
нематеріальной міровой субстанціи все-таки можно высказать нѣ-
сколько весьма общихъ положительныхъ сужденій. Вся эта субстан-
ція совершенно однообразна и неизмѣнна; ея поведеніе подчиняется
весьма простымъ и яснымъ закономѣрнымъ зависимостямъ, которыя,
повидимому, совершенно точно выражаются простыми математиче-
скими формулами — уравненіями Максвелла. Въ этомъ заключается
рѣзкое различіе между этой субстанціей и ощутимой матеріей, слож-
ная и запутанная природа которой не можетъ быть точно матема-
тически описана. Но очевидная простота физическихъ свойствъ пу-
стоты, я думаю, никакимъ словомъ не выражается такъ кратко и
полно, какъ стариннымъ греческимъ названіемъ „эѳиръ"; и, если,
изъ-за механистическихъ злоупотребленій послѣдняго времен^,4^то
названіе обезцѣнилось, то не слѣдуетъ его отвергать совдцденно,
но нужно попытаться вернуть ему его прежнее значеніе. Подобнымъ
образомъ развѣ то, что мы въ электронной теоріи мыслимъ подъ
словомъ „атомъ", не является рѣзко отличнымъ отъ^упругихъ бил-
ліардныхъ шаровъ механистическаго періода?... ор
Теорія относительности въ той формѣ^^оторую ей придалъ
Предисловіе автора
XI
Минковскій (Міпкохѵзкі), приводитъ къ заключенію, что физиче-
скій міръ собственно является четырехмѣрнымъ, и что существуетъ
одна только форма воспріятія четырехъ измѣреній,—именно простран-
ство - время. Но отсюда нельзя заключать, что понятіе пустого про-
странства само по себѣ, безъ четвертаго измѣренія — времени, не
будетъ имѣть никакого смысла. Наоборотъ, намъ часто приходится
попрежнему пользоваться понятіемъ о трехмѣрныхъ тѣлахъ. До сихъ
поръ, по крайней мѣрѣ, никто еще не пошелъ такъ далеко, чтобы
утверждать, что понятіе объ атомѣ, по этой теоріи, лишено всякаго
смысла. Но если мы должны мыслить атомы, то мы должны также
мыслить и „пустоту" между ними, принимающую участіе во всѣхъ
физическихъ процессахъ въ мірѣ атомовъ, и въ которой атомы пред-
ставляютъ лишь особенныя ея области. Если попытаться уяснить
себѣ процессы, происходящіе въ электромагнитной волнѣ (съ ними
читатель этой книги встрѣчается, напримѣръ, въ §423) безъ пред-
ставленія о пустотѣ или эѳирѣ, то становится очевиднымъ, что безъ
этого представленія обойтись нельзя.
Къ послѣдовательному изложенію современнаго ученія объ элек-
тричествѣ должно относиться также чисто электрическое опредѣленіе
единицъ мѣръ. Отъ старой механистической эпохи мы унаслѣдовали
тяжелый балластъ въ видѣ двухъ такъ называемыхъ абсолютныхъ
системъ мѣръ, которыя пригодны только для затемненія существен-
наго и затрудняютъ переходъ къ новой электромагнитной точкѣ
зрѣнія. Притомъ въ практикѣ онѣ давно уже вышли изъ употребле-
нія. Мы знаемъ^ это электромагнитныя измѣренія мы не должны
сводить на массу, длину и время, но что мы безусловно должны,
кромѣ длины и времени, пользоваться двумя независимо другъ отъ
друга опредѣляемыми электрическими основными единицами. Проще
всего за эти единицы взять электрическій зарядъ и электрическое
напряженіе. Естественной единицей заряда является эквивалентный
зарядъ, къ измѣренію котораго сводится опредѣленіе кулона. Еди-
ница напряженія можетъ быть естественно связана съ тѣмъ свой-
ствомъ іоновъ, что они обладаютъ опредѣленною упругостью рас-^
творенія въ водѣ. На этомъ основывается построеніе нормальнаго
элемента и опредѣленіе вольта. Магнитныя измѣренія чрезвычайно
просто могутъ быть приведены къ измѣреніямъ электрическимъ;
при этомъ получаются обѣ магнитныя единицы—чис^ о амперъ-вит-
ковъ и вольтъ-секунда. Практическая система единицъ не только
XII
Предисловіе автора
оказывается наиболѣе подходящей къ употребляемымъ въ дѣйствитель-
ности измѣрительнымъ методамъ, но она также прекрасно выясняетъ
и теоретическія зависимости между измѣряемыми величинами. На-
сколько она превосходитъ искусственныя старыя системы мѣръ, вы-
ясняется, напримѣръ, при установленіи формулъ измѣреній производ-
ныхъ единицъ. Насколько эти формулы запутаны, непонятны и потому
трудны для пользованія въ такъ называемыхъ абсолютныхъ систе-
махъ мѣръ, настолько же ясны и просты онѣ въ практической
системѣ, которую можно было бы также назвать естественной си-
стемой мѣръ. Чтобы установить связь съ единицами механики, до-
статочно замѣтить, что произведеніе вольтъ X кулонъ имѣетъ измѣ-
реніе энергіи.
Такъ какъ предлагаемая книга имѣетъ характеръ элементарнаго
введенія въ ученіе объ электричествѣ, то я мало вниманія обращалъ
на то, какихъ авторовъ я цитировалъ. Главное вниманіе я обращалъ
на то, чтобы возможно глубже ввести читателя въ область фактовъ,
а имена авторовъ приводятся мною, до нѣкоторой степени, въ видѣ
случайныхъ примѣровъ. Во многихъ случаяхъ авторы названы по
ничтожнымъ поводамъ, тогда какъ въ нѣкоторыхъ болѣе важныхъ
случаяхъ авторъ не упоминается. Вопросовъ о пріоритетѣ я старался
не касаться.
Густавъ Ми.
Грейфс вальдъ, 1910 г.
ЧИСТЬ ПЕРВАЯ
Электростатика
1
ГЛАВА ПЕРВАЯ
ОБЩІЯ СВОЙСТВА ЭЛЕКТРИЧЕСКАГО ПОЛЯ
ПРИЗНАКИ ЭЛЕКТРИЧЕСКАГО ПОЛЯ.
1. Если мы приложимъ другъ къ другу два разнородныя тѣла
(напримѣръ, руку и стеклянную пластинку) и потремъ ихъ одно о дру-
гое, чтобы получить возможно лучшее соприкосновеніе ихъ поверх-
ностей, то, разъединивъ снова оба тѣла, мы, вообще говоря, обна-
ружимъ, что они пріобрѣли свойство въ любомъ положеніи приво-
дить окружающее ихъ пространство въ особое, опредѣленное со-
стояніе. Если мы приблизимъ потертую рукою стеклянную пластинку
къ легкимъ бумажнымъ обрѣзкамъ, кусочкамъ пробки и тому подоб-
нымъ легкимъ предметамъ, лежащимъ на столѣ, то окажется, что эти
легкія тѣла стремятся передвинуться къ стеклу, преодолѣвая инерцію
и силу тяжести. Мы видимъ, такимъ образомъ, что пространство,
окружающее стеклянную пластинку, пріобрѣло особое свойство, за-
ключающееся въ томъ, что находящееся въ этомъ пространствѣ лег-
кое тѣло испытываетъ какое-то вліяніе, побуждающее его двигаться
въ опредѣленномъ направленіи (къ стеклянной пластинкѣ). Такое
вліяніе мы называемъ, какъ извѣстно, силою.
Нѣчто подобное каждый, конечно, наблюдалъ въ дѣтствѣ, когда
на его глазахъ кусочки бумаги или нитки притягивались, какъ бы
влекомые какой-то таинственной силой, къ потертой о куртку эбонито-
вой ручкѣ для перьевъ или сургучной палочкѣ. Еще лучше удается
такой опытъ, если эбонитовую палочку потереть о кошачій мѣхъ.
Мы видимъ, такимъ образомъ, что натертая мѣхомъ эбонитовая^?
палочка приводитъ окружающее пространство въ особое состоящіе
о наличности котораго мы судимъ по сопровождающему егс^М-
ствію особыхъ силъ на расположенныя въ этомъ пространстві^малыя
тѣла. Мы можемъ назвать такія тѣла индикаторами для эт^го состоя-
нія пространства. Я не могу не упомянуть о томъ, чт^уществуютъ
4
Признаки электрическаго поля
еще и другіе весьма разнообразные индикаторы, и всѣ они употре-
бляются при различныхъ обстоятельствахъ для научныхъ изслѣдова-
ній этого состоянія. Такъ, напримѣръ, кусокъ стекла или иного про-
зрачнаго тѣла, будучи помѣщенъ въ пространство, находящееся въ
этомъ состояніи, становится въ незначительной степени двупреломляю-
щимъ; кусокъ кварца (или другого кристалла) подвергается въ та-
комъ пространствѣ весьма малой деформаціи. Наблюденія этихъ явле-
ній, конечно, гораздо болѣе затруднительны, чѣмъ всѣмъ извѣстныя
наблюденія надъ силовымъ дѣйствіемъ на легкія тѣла. На индикато-
рахъ послѣдняго рода мы поэтому и остановимся при дальнѣйшихъ,
болѣе тщательныхъ изслѣдованіяхъ.
Методы изслѣдованія пространства, находящагося въ особенномъ
состояніи, которое мы, какъ это общепринято, будемъ называть
электрическимъ состояніемъ, можно для наглядности сравнить
съ методами, помощью которыхъ изслѣдуется тепловое состояніе
какой-либо части пространства. При этомъ также помѣщаются въ
изслѣдуемое мѣсто извѣстные индикаторы, называемые термоскопами
или термометрами. На одномъ термоскопѣ наблюдаются измѣненія
объема (какъ, напримѣръ, на обычномъ ртутномъ термометрѣ), на
другомъ—измѣненія цвѣта, на третьемъ- -измѣненія электрическаго
сопротивленія и т. д. Всѣ наблюдаемыя измѣненія характеризуютъ
вполнѣ опредѣленно изслѣдуемое тепловое состояніе.
Индикаторы для электрическаго состоянія носятъ названіе элек-
троскоповъ. Существуютъ, напримѣръ, электроскопы оптическіе,
электроскопы, дѣйствіе которыхъ основано на деформаціи кристалла;
мы будемъ въ послѣдующемъ пользоваться исключительно только
легкимъ тѣломъ, наблюдая дѣйствіе на него нѣкоторой силы. Это и
есть обычный электроскопъ. Можно воспользоваться, напримѣръ, шари-
комъ изъ бузинной сердцевины или листочкомъ алюминія, подвѣ-
шеннымъ на нити, и т. п.
Ту часть пространства, въ которой электроскопъ любого {рода
указываетъ на наличность электрическаго состоянія, называют^Элек-
трическимъ полемъ.
НОСИТЕЛИ ЭЛЕКТРИЧЕСКАГО ПОЛЯ-ЛСР
2. Прежде всего естественно является вопросъ;о томъ, можетъ
ли электрическое состояніе имѣть мѣсто во всякой части простран-
ства, независимо отъ того, какого рода ^вещество ее заполняетъ,
Носители электрическаго поля
5
или же необходимымъ условіемъ для возникновенія электрическаго
состоянія является присутствіе воздуха. Если, поднося натертую эбо-
нитовую палочку къ подвѣшенному бузинному шарику, мы наблю-
даемъ, что шарикъ къ ней притягивается, то отсюда мы можемъ за-
ключить, что шарикъ находится въ электрическомъ полѣ эбонитовой
палочки. Чѣмъ ближе мы поднесемъ эту палочку, тѣмъ больше бу-
детъ сила поля въ томъ мѣстѣ, гдѣ находится шарикъ, и тѣмъ
дальше онъ отклонится отъ своего начальнаго положенія равновѣсія.
Если мы теперь помѣстимъ между эбонитовой палочкой и шарикомъ
большую стеклянную или эбонитовую пластинку, то мы убѣдимся,
что никакого измѣненія вслѣдствіе этого не произойдетъ: шарикъ
укажетъ на такую же интенсивность электрическаго состоянія, какъ
и раньше. Слѣдовательно, такого рода плотная преграда не задер-
живаетъ возбуждаемаго эбонитовой палочкой электрическаго поля, и
электрическое состояніе проникаетъ черезъ нее насквозь. Отсюда мы
можемъ заключить, что и самая пластинка, составляющая преграду,
заполнена электрическимъ полемъ, такъ какъ иначе двѣ части поля,
на которыя оно дѣлится этой пластинкой, не могли бы находиться
въ закономѣрной связи между собою; а наличность такой связи мы
можемъ установить, если будемъ эбонитовую палочку передвигать
въ различныхъ направленіяхъ съ одной стороны преграды и наблю-
дать соотвѣтствующія измѣненія положенія бузиннаго шарика съ
другой стороны ея.
Но совершенно иное окажется, если мы вмѣсто стеклянной или
эбонитовой пластинки помѣстимъ между натертой эбонитовой палоч-
кой и шарикомъ большой металлическій листъ. Въ этомъ случаѣ
шарикъ остается въ своемъ обычномъ положеніи равновѣсія, т. е.
уже не находится въ электрическомъ полѣ. Ниже мы будемъ еще
имѣть случаи убѣдиться, что стекло, эбонитъ и многія другія твер-
дыя тѣла могутъ въ теченіе продолжительнаго времени заключать въ
себѣ электрическое поле; металлы же такимъ свойствомъ не обла-
даютъ.
Жидкія тѣла также могутъ быть заполнены электрическимъ пр|
лемъ. Если погрузить подвѣшенный алюминіевый листокъ въ сосуМ
съ керосиномъ, то натертая эбонитовая палочка будетъ его также
хорошо притягивать, какъ если бы онъ висѣлъ въ воздух^.^<
Мы можемъ отсюда вывести слѣдующее заключеніеДчтобы въ
опредѣленной части пространства могло возникнуть^лектрическое
6
Пустота или эѳиръ
состояніе, не представляется необходимымъ, чтобы въ ней находился
только воздухъ или иной газъ; могутъ въ ней находиться также
многія твердыя и жидкія тѣла. Но существуютъ и такія опредѣлен-
ныя тѣла — къ ихъ числу прежде всего принадлежатъ металлы,—въ
которыхъ мы не можемъ, по крайней мѣрѣ, съ помощью современ-
ныхъ средствъ, получить электрическаго поля.
ПУСТОТА ИЛИ ЭѲИРЪ.
3. Для изученія электрическаго состоянія имѣетъ особенное зна-
ченіе опытъ съ безвоздушнымъ пространствомъ (пустотою). Помѣ-
стимъ подвѣшенный бузинный шарикъ подъ колоколъ воздушнаго
насоса (рис. 1) и будемъ наблю-
дать его отклоненія при приближе-
ніи къ нему натертой эбонитовой
палочки. Если затѣмъ эвакуировать
пространство подъ колоколомъ, то
можно замѣтить, что наблюдавшія-
ся до эвакуаціи отклоненія при этомъ
совершенно не измѣнились. Налич-
ность- воздуха или его отсутствіе
являются, какъ можно отсюда за-
ключить, обстоятельствами совер-
шенно безразличными для возник-
новенія электрическаго поля. Даже
при наиболѣе совершенной эвакуа-
ціи, какая въ настоящее время только
достижима при помощи лучшихъ
насосовъ, это заключеніе вполнѣ
сохраняетъ силу. Слѣдовательно,
электрическое состояніе принадле-
_ , ~ житъ къ числу такихъ явленііѣ ко-
Рис. 1. Электрическое поле въ пустотѣ.
торыя, подобно свѣтовымъ, ^могутъ
имѣть мѣсто въ частяхъ пространства, совершенно лишенныя^ рѣсомой
матеріи, въ пустотѣ. Позже мы изучимъ еще одно подофо^ Состояніе,
тѣсно связанное съ электрическимъ, именно—магнитное" со стоя н іе.
Ученіе объ электрическомъ и магнитномъ состояніяхъ пустоты
до нѣкоторой степени аналогично ученію о состояніяхъ натяженія и
движенія упругой и вѣсомой матеріи, однцмт»^ словомъ, аналогично
Пустота или эѳиръ
7
механикѣ. Въ настоящей книгѣ мы именно ставимъ себѣ цѣлью изло-
жить ученіе объ электромагнитизмѣ, какъ „ механику“ пространства,
лишеннаго матеріи, пустоты.
Мы не будемъ, поэтому, со словомъ „ пустотаи или „ простран-
ство “ связывать того представленія, которое связывается съ нимъ
въ геометріи — представленія математической области, или же пред-
ставленія о формѣ познанія, основаннаго на воспріятіяхъ нашихъ
внѣшнихъ органовъ чувствъ. Подъ „пространствомъ" мы будемъ по-
нимать нѣчто физическое, принимающее извѣстныя состоянія, какъ и
ощутимая нашими чувствами матерія, нѣчто такое, чему нужно при-
писать извѣстныя физическія свойства, которыя до нѣкоторой сте-
пени поддаются числовымъ измѣреніямъ. Чтобы различить оба зна-
ченія слова „пространство", приходится ввести новый терминъ: пу-
стое пространство, разсматриваемое, какъ объектъ физики, называ-
ютъ „эѳиромъ" или же „міровымъ эѳиромъ". Ученіе объ электро-
магнитизмѣ будетъ для насъ механикой эѳира; ученіе о свѣтѣ соот-
вѣтственно можно назвать „акустикой эѳира".
4. Что электрическое поле можетъ вообще существовать также
и въ вѣсомыхъ тѣлахъ, должно вытекать изъ того, что всѣ эти
тѣла состоятъ изъ молекулъ и „пустыхъ" промежутковъ между ними.
Эѳиръ представляетъ собою среду, въ которой расположены моле-
кулы, и въ этой средѣ можетъ возникать электрическое состояніе.
Можно думать, конечно, что присутствіе молекулъ вліяетъ на воз-
никающее между ними электрическое поле. Мы уже имѣли примѣръ
такого вліянія: въ металлахъ какія то явленія, происходящія въ мо-
лекулахъ, совершенно не допускаютъ возникновенія электрическаго
поля. Но, если молекулы раздѣлены другъ отъ друга болѣе значи-
тельными промежутками, какъ въ газахъ, то онѣ имѣютъ лишь
крайне незначительное вліяніе на электрическое поле, какъ это слѣ-
дуетъ и изъ соотвѣтственныхъ опытовъ. Слѣдовательно, когда мы
въ дальнѣйшемъ будемъ производить наши опыты въ воздухѣ, то
при этомъ мы будемъ имѣть условія, почти столь же благопріятныя, \
какъ если бы мы производили наши наблюденія въ
ЭЛЕКТРИЧЕСКІЙ ЗАРЯДЪ, КАКЪ СВЯЗЬ МЕЖДУ
МАТЕРІЕЮ.
5. Мы видѣли, что электрическое поле можетъ
тамъ, гдѣ нѣтъ никакой вѣсомой матеріи. Это положрйіе ^нуждается,
однако, въ немедленномъ дополненіи. Электрическое^ поле не мо-
пустотѣ.
существовать и
8 Электрическій зарядъ, какъ связь между эѳиромъ и матеріею
жетъ возникнуть безъ всякаго участія матеріальныхъ тѣлъ, такъ
какъ всегда должно быть тѣло, возбуждающее его, подобное на-
тертой эбонитовой палочкѣ въ вышеописанныхъ опытахъ. Возбуди-
телемъ электрическаго поля, согласно даннымъ всѣхъ нашихъ опы-
товъ, должно быть обязательно матеріальное тѣло.
Тѣло, обладающее особымъ свойствомъ возбуждать въ эѳирѣ
электрическое поле, мы называемъ заряженнымъ электричествомъ.
Подъ электрическимъ зарядомъ мы понимаемъ ту связь
между матеріальнымъ тѣломъ и эѳиромъ, дѣйствіе которой даетъ
возможность тѣлу вызвать въ эѳирѣ электрическое поле.
Электрическій зарядъ можно до нѣкоторой степени уподобить
клейкому веществу, связывающему два тѣла настолько, что одно
можетъ вызвать въ другомъ натяженіе. Но понятіе электрическаго
заряда должно быть не только качественнымъ, но и количествен-
нымъ: чѣмъ больше зарядъ тѣла, тѣмъ сильнѣе возбуждаемое имъ
поле. Зарядъ тѣла и электрическое возбужденіе въ эѳирѣ предста-
вляютъ собою, такъ сказать, двѣ стороны одного и того же явленія.
Подчеркивая то обстоятельство, что электрическое поле можетъ
быть возбуждено только дѣйствіемъ вѣсомой матеріи, мы можемъ
выразиться еще такъ:
Носителемъ электрическаго заряда можетъ быть только
матеріальное тѣло и ни въ какомъ случаѣ не эѳиръ.
6. Мы должны поставить себѣ теперь обратный вопросъ: дѣй-
ствуетъ ли эѳиръ, находящійся въ электрическомъ состояніи, на вся-
кое матеріальное тѣло или же и для этого дѣйствія между эѳиромъ
и матеріальнымъ тѣломъ должна существовать особая связь?
Для разрѣшенія этого вопроса воспользуемся стеклянной палоч-
кой, горизонтально подвѣшенной на длинной нити и могущей, та-
кимъ образомъ, легко вращаться вокругъ точки подвѣса. Если мы
внесемъ эту палочку въ электрическое поле, образованное другой
стеклянной палочкой, натертой предварительно шелковой матеріей,
то никакого ея движенія не обнаружимъ. Слѣдовательно, эѳиръ^не
вызываетъ никакой силы притяженія или никакого давленія. Но если
мы подвѣшенную вращающуюся палочку натремъ шелковоЦ матеріей
и сообщимъ ей такимъ образомъ электрическій зарядъ?до мы замѣ-
тимъ, что въ этомъ случаѣ она подвергается опредѣленному дѣй-
ствію электрическаго поля: она отталкивается съ-нѢкоторою силою
отъ палочки, возбуждающей поле.
Два рода электрическихъ зарядовъ
9
Такимъ образомъ, мы видимъ, что электрическій зарядъ
представляетъ собою не только связь, подъ вліяніемъ ко-
торой матеріальное тѣло дѣйствуетъ на эѳиръ, возбуждая
въ немъ электрическое поле, но одновременно представля-
етъ собою и такую связь, въ силу которой эѳиръ, нахо-
дящійся въ состояніи электрическаго напряженія, обратно
дѣйствуетъ съ опредѣленною силою на матеріальное тѣло.
Слѣдовательно, электрическій зарядъ представляетъ собою взаимную
связь между матеріей и эѳиромъ.
Слѣдуетъ здѣсь же отмѣтить, что до сихъ поръ неизвѣстно
никакого способа убѣдиться въ дѣйствіи находящагося въ состо-
яніи электрическаго напряженія эѳира на матеріальныя тѣла, безъ
посредства электрическихъ зарядовъ. Тотъ фактъ, что въ электри-
ческомъ полѣ легкія тѣла приходятъ въ движеніе, т. е. испытываютъ
дѣйствіе какихъ то силъ, станетъ понятнымъ, когда мы впослѣдствіи
убѣдимся, что электрическое поле само возбуждаетъ въ этихъ тѣ-
лахъ заряды, какъ говорятъ, посредствомъ индукціи.
ДВА РОДА ЭЛЕКТРИЧЕСКИХЪ ЗАРЯДОВЪ.
7. Если упомянутую выше подвѣшенную на нити и могущую
вращаться наэлектризованную стеклянную палочку мы внесемъ въ
электрическое поле, возбуждаемое натертой эбонитовой пластинкой,
то, какъ этого и слѣдовало ожидать, замѣтимъ дѣйствіе на нее
опредѣленной силы. Но, между тѣмъ, какъ въ полѣ, образованномъ
натертой стеклянной пластинкой, вращающаяся палочка, какъ мы ви-
дѣли, отталкивается отъ возбуждающаго поле тѣла, тутъ мы замѣ-
тимъ, наоборотъ, что она притягивается къ эбонитовой пластинкѣ.
Такимъ образомъ, хотя стекло и эбонитъ оба возбуждаютъ электри-
ческое поле, однако, производятъ они это различнымъ образомъ; по-
веденіе подвѣшенной палочки указываетъ намъ, что одно изъ этихъ
тѣлъ возбуждаетъ поле, такъ сказать, обратное полю другого.
Отсюда слѣдуетъ заключить, что и дѣйствіе электрическаго поля
на натертую эбонитовую палочку будетъ инымъ, нежели дѣйствѣ^
его на стеклянную палочку. Если мы дѣйствительно подвѣеймѣ
вмѣсто стеклянной палочки натертую эбонитовую, то замѣти^^слѣ-
дующее: она притягивается натертой стеклянной пластикой, но
отталкивается другой натертой эбонитовой пластинкой. Всѣ эти опыт-
ныя данныя мы можемъ объединить въ слѣдую чрезвычайно
10
Два рода электрическихъ зарядовъ
важномъ заключеніи: существуютъ два различные рода элек-
трическихъ зарядовъ, отличающіеся діаметрально проти-
воположными дѣйствіями; это различіе до нѣкоторой сте-
пени сходно съ различіемъ положительныхъ и отрицатель-
ныхъ чиселъ въ чистой математикѣ.
Поэтому оба рода электрическихъ зарядовъ мы будемъ отмѣчать
слѣдующимъ образомъ: заряды, обладающіе свойствами заряда на-
тертаго стекла, будемъ называть положительными, а заряды того
же рода, что и зарядъ натертаго эбонита отрицательными.
Слѣдуетъ считать твердо установленнымъ, что кромѣ
положительныхъ и отрицательныхъ зарядовъ не суще-
ствуетъ никакихъ другихъ видовъ электрическаго заряда.
8. Если двѣ матеріальныя частички заряжены, одна положи-
тельно, другая отрицательно, но обѣ одинаково сильно, то въ со-
отвѣтственныхъ точкахъ два возбуждаемыя ими поля равны по силѣ,
но взаимно противоположны по свойствамъ. Если эти двѣ матеріаль-
ныя частички привести въ соприкосновеніе, то ихъ дѣйствія на
эѳиръ взаимно уничтожатся (если не принимать во вниманіе точекъ,
прилежащихъ къ самымъ частичкамъ), и вызванное ими возбужденіе
будетъ равно нулю.
Если эти двѣ частички помѣстить одну рядомъ съ другой и
внести ихъ въ электрическое поле, то дѣйствія эѳира на нихъ вза-
имно уничтожаются, такъ какъ они равны и взаимно противоположны,
и эѳиръ дѣйствуетъ на совокупность этихъ частичекъ съ силой, рав-
ной нулю.
Такимъ образомъ, какъ и въ алгебрѣ, сумма равныхъ
положительныхъ и отрицательныхъ зарядовъ равна нулю.
Поэтому легко понять, что электрическое поле во многихъ тѣ-
лахъ можетъ вызывать, какъ мы уже упоминали, оптическія измѣне-
нія и деформаціи. Дѣйствительно, согласно общепринятому въ физикѣ
взгляду, каждая молекула составлена изъ электрическихъ частццъи
притомъ такимъ образомъ, что въ ней содержится одинаковоеъоли-
чество положительныхъ и отрицательныхъ зарядовъ. Въ сйлу этого
всякое тѣло, какъ цѣлое, оказывается не заряженнымъ^ йр, если оно
помѣщается въ электрическое поле, то послѣднееможетъ вызвать
перемѣщенія заряженныхъ частичекъ внутри молекулъ, слѣдствіемъ
которыхъ и являются наблюдаемыя измѣненія физическихъ свойствъ
тѣла.
Электрическая стрѣлка
11
Всѣ индикаторы электрическаго состоянія, въ сущности, пред-
ставляютъ собою заряженныя малыя тѣла; зарядъ можетъ распола-
гаться на тѣлѣ замѣтныхъ размѣровъ, какъ въ обычномъ электро-
скопѣ, или же лишь внутри молекулъ, какъ въ оптическомъ и де-
формаціонномъ электроскопахъ. Эѳиръ дѣйствуетъ на матерію именно
черезъ посредство этихъ зарядовъ.
ЭЛЕКТРИЧЕСКАЯ СТРЪЛКА.
9. Чрезвычайно удобный электроскопъ представляетъ собою
такъ называемая электрическая стрѣлка. Два пробковыхъ ша-
рика закрѣпляются на концахъ легкой палочки, которая при помощи
стеклянной шляпки насажена на стальную ось, на которой можетъ,
легко вращаться (рис. 2). Чтобы шарики
можно было сразу отличать одинъ отъ А
другого, они отмѣчены — одинъ бумаж- '
ной стрѣлкой, другой— бумажнымъ пе-
ромъ. Шарикъ со стрѣлкой наэлектризо-
ванъ положительно, шарикъ съ перомъ—
отрицательно, но оба, приблизительно,
съ одинаковою силою. Концы палочки,
на которую насажены шарики, сдѣланы
изъ янтаря. Это очень важно для „ изо-
ляціи “ зарядовъ на шарикахъ; понять
это очень легко на основаніи опытовъ,
которые будутъ описаны ниже. п п _
г і Рис. 2. Электрическая стрѣлка.
Помощью этой электрической стрѣл-
ки мы можемъ легко убѣждаться въ наличности электрическаго поля.
Такъ какъ положительный шарикъ перемѣщается въ немъ въ опредѣ-
ленномъ направленіи, а отрицательный — въ противоположномъ, то
вся стрѣлка принимаетъ въ электрическомъ полѣ совершенно опре-
дѣленное положеніе. Въ тѣхъ же мѣстахъ, гдѣ нѣтъ электрическагос
поля, стрѣлка можетъ оставаться въ любомъ положеніи, которое ей
Оу
придано.
Если приблизить стрѣлку къ положительно заряженному^ тѣлу»
го она установится по направленію отъ него, если же приблизить ее
къ отрицательно заряженному тѣлу, она установится пр направленію
къ
нему.
12
Проводники и изоляторы
ПРОВОДНИКИ И ИЗОЛЯТОРЫ.
10. Прежде, чѣмъ перейти къ болѣе подробному изученію
свойствъ и законовъ электрическаго поля, намъ слѣдуетъ ознако-
миться еще съ однимъ весьма важнымъ различіемъ въ электрическихъ
свойствахъ различныхъ матеріальныхъ тѣлъ. Расположимъ на столѣ
въ нѣкоторомъ отдаленіи одно отъ другого нѣсколько металлическихъ
тѣлъ, укрѣпленныхъ на стеклянныхъ ножкахъ. Если мы коснемся
одного изъ этихъ тѣлъ натертой стеклянной палочкой, то замѣтимъ,
что она сообщила тѣлу, съ которымъ пришла въ соприкосновеніе,
способность возбуждать электрическое поле. Дѣйствительно, если
къ этому тѣлу приблизить электрическую стрѣлку, то она укажетъ
на наличность электрическаго поля; при этомъ металлическое тѣло
оказывается заряженнымъ положительно (какъ и стеклянная палочка),
такъ какъ стрѣлка устанавливается по направленію отъ него. Если,
по прошествіи нѣкотораго промежутка времени, мы снова поднесемъ
стрѣлку къ этому тѣлу, то замѣтимъ то же самое. Слѣдовательно,
металлическое тѣло остается наэлектризованнымъ.
Тѣло, которое сохраняетъ электрическій зарядъ неизмѣннымъ
въ теченіе продолжительнаго промежутка времени, мы называемъ
электрически изолированнымъ.
Такимъ образомъ, стеклянная и эбонитовая палочки, такъ часто
употребляющіяся при нашихъ опытахъ, представляютъ собою также
изолированныя тѣла.
Если мы будемъ подносить нашу электрическую стрѣлку къ
прочимъ металлическимъ тѣламъ, расположеннымъ на столѣ, то во-
кругъ нихъ не обнаружимъ никакихъ слѣдовъ электрическаго со-
стоянія. Слѣдовательно, тѣло заряженное при помощи стеклянной
Рис. 3. Винтовые зажимы.
палочки, не передало имъ ничего отъ своего
заряда; иначе говоря, прочія тѣла отъ него
изолированы.
Укрѣпимъ теперь на каждомъ метал-^
лическомъ тѣлѣ по короткой проволокѣ;
имѣющей на другомъ концѣ винтовой7 за-
жимъ (рис. 3), и черезъ всѣ этрушнтовые
зажимы протянемъ длиннук}^ проволоку.
Если мы теперь повтори^Пррежній опытъ
и проведемъ наэлектризованной стеклянной палочной вдоль одного
изъ металлическихъ тѣлъ, то электрическая стрѣлка укажетъ на на-
Проводники и изоляторы
13
личность электрическаго поля не только вблизи этого тѣла, но и
вблизи каждаго изъ металлическихъ тѣлъ, связанныхъ съ этимъ про-
волокой. Всѣ тѣла, соединенныя между собою проволокой, прини-
маютъ положительный зарядъ.
Этотъ переносъ способности вызывать электрическое напряженіе
въ эѳирѣ съ одного тѣла на другое называютъ электрическою
проводимостью. Проволока, вызывающая переносъ заряда, назы-
вается электрическимъ проводникомъ. Всѣ металлы являются
электрическими проводниками.
Точно такъ же и переносъ заряда съ натертой стеклянной палочки
на металлическое тѣло есть, конечно, явленіе электрической прово-
димости. Онъ проходитъ въ этомъ случаѣ черезъ тонкій слой воз-
духа между стекломъ и металломъ. Отсюда мы заключаемъ, что при
извѣстныхъ обстоятельствахъ воздухъ также является проводникомъ;
это свойство воздуха мы ниже тщательно изучимъ.
Вообще говоря, воздухъ, конечно, не представляетъ собою
проводника; иначе невозможно было бы получать какіе бы то ни
было изолированные заряды. Точно такъ же не представляетъ собою
проводника, напримѣръ, стекло, изъ котораго сдѣланы Подставки вы-
шеописанныхъ металлическихъ тѣлъ, такъ какѣ электрическій зарядъ
съ этихъ тѣлъ, какъ въ этомъ легко убѣдиться, на столъ не пере-
ходитъ.
Такія тѣла, которыя не являются проводниками, называютъ
электрическими изоляторами. Воздухъ и стекло представляютъ
собою примѣры изоляторовъ.
Кромѣ проводниковъ и изоляторовъ можно различить еще одинъ—
третій классъ тѣлъ. Если проволоку вынуть изъ винтовыхъ зажимовъ
и замѣнить ее обыкновенной веревкой, то окажется, что, при заря-
женіи одного изъ металлическихъ тѣлъ помощью стеклянной палочки,
вблизи остальныхъ не обнаруживается электрическаго поля, т. е. ве-
ревка является какъ бы изоляторомъ. Но по истеченіи нѣкотораго
промежутка времени поле можетъ быть обнаружено уже вблизи^
всѣхъ тѣлъ, соединенныхъ веревкой съ заряженнымъ тѣломъ, ррір
чемъ всѣ они получаютъ положительный зарядъ. Такимъ обрдзймъ,
веревка проводитъ электричество, но только медленно.
Тѣла, которыя переносятъ электрическіе заряды ^лифь очень
медленно, называютъ полупроводниками. Пеньковый^шнуръ пред-
ставляетъ собою полупроводникъ.
14
Проводники и изоляторы
Строго говоря, нельзя провести рѣзкихъ границъ между этими
тремя классами тѣлъ. Не существуетъ вполнѣ совершенныхъ изоля-
торовъ, которые не переносили бы мало-по-малу незначительной части
заряда; не существуетъ также и совершенныхъ проводниковъ, въ
которыхъ переносъ электричества совершался бы мгновенно. Изоля-
торы и проводники представляютъ собою лишь крайніе случаи осо-
бенно плохо и особенно хорошо проводящихъ тѣлъ. Поэтому при
нѣкоторыхъ обстоятельствахъ понятія изолятора и проводника мо-
гутъ оказаться лишь относительными. Если мы, напримѣръ, поль-
зуемся источникомъ электричества, дающимъ громадныя количества
электрическихъ зарядовъ (мы вскорѣ познакомимся съ такими источ-
никами электричества и ихъ употребленіемъ), то при этомъ весьма
часто мы можемъ употреблять такой полупроводникъ, какъ дерево,
бъ качествѣ изолятора, такъ какъ ничтожные заряды, имъ перено-
симые, являются совершенно исчезающими въ сравненіи съ тѣми,
которые возбуждаются въ источникѣ электричества. Но если мы
имѣемъ лишь малые заряды, напримѣръ, такіе, какіе получаются на
металлическихъ тѣлахъ отъ стеклянной палочки въ вышеописанномъ
опытѣ, то не слишкомъ сухое дерево проводитъ ихъ такъ же хо-
рошо, какъ и металлическая проволока.
Послѣ этихъ предварительныхъ замѣчаній я перечислю главныхъ
представителей всѣхъ трехъ классовъ тѣлъ, даваемыхъ опытами. При
этомъ здѣсь я ограничиваюсь твердыми тѣлами.
Изоляторы: сѣра, смолы, янтарь, каучукъ, эбонитъ, гуттаперча,
•слюда, кварцъ, фарфоръ, нѣкоторые сорта стекла, шелкъ, параффинъ.
Полупроводники: обыкновенное стекло, гипсъ, известь, мно-
гіе минералы, дерево, бумага, шерсть, хлопчатая бумага, ткани, ко-
нопля, кожи, волоса.
Проводники: всѣ металлы, уголь, графитъ, всѣ минералы,
«обладающіе металлическимъ блескомъ.
11. Прежде,
газовъ, слѣдуетъ
изложено выше.
Укрѣпимъ на
ЗЕМЛЯ, КАКЪ ПРОВОДНИКЪ. 1
чѣмъ перейти къ изученію свойствъ жидкостей и
вывести еще одно важное слѣдствіе изъято, что
одномъ изъ вышеописанныхъ метаболическихъ тѣлъ
{стоящемъ на стеклянной подставкѣ) проволоку с^\приведемъ эту
проволоку въ соприкосновеніе съ деревянной /фоской стола. Если
Земля, какъ проводникъ
15
теперь провести по этому тѣлу натертой стеклянной палочкой и за-
тѣмъ воспользоваться нашей электрической стрѣлкой, то окажется,
что она не указываетъ уже на наличность поля, какъ это было въ
предыдущемъ опытѣ. Почему же это? Можетъ быть, зарядъ со сте-
клянной палочки не перешелъ на металлическое тѣло такъ хорошо,
какъ въ предыдущемъ опытѣ? Конечно, онъ перешелъ такъ же,
какъ и прежде, но съ металлическаго тѣла по проволокѣ онъ пе-
решелъ также на деревянный столъ, на которомъ производится опытъ,
оттуда на полъ, на газопроводныя, и водопроводныя трубы, на всю
поверхность земли, занятую нашимъ городомъ, и далѣе на весь зем-
ной шаръ. При такомъ распространеніи зарядъ, понятно, сталъ на-
столько разрѣженнымъ, и электрическое поле стало настолько сла-
бымъ, что его нельзя обнаружить даже чувствительнѣйшими инстру-
ментами, не говоря уже о нашей простой электрической стрѣлкѣ.
Мы говоримъ въ такомъ случаѣ, что зарядъ металлическаго тѣла
отведенъ въ землю. Если снова удалить проволоку, но положить
на металлическое тѣло руку и теперь перенести на него зарядъ
натертой стеклянной палочки, то опять никакого поля не окажется.
Почему? Кожа, волосы, ткани принадлежатъ, какъ мы знаемъ, къ
числу полупроводниковъ. Слѣдовательно, въ этомъ случаѣ зарядъ
переходитъ черезъ тѣло, черезъ подошвы на полъ, оттуда же че-
резъ газопроводныя и водопроводныя трубы на всю землю. Но если
держать металлическое тѣло рукою снизу за его стеклянную под-
ставку, то возможно снова, какъ и прежде, перенести на него за-
рядъ, такъ какъ оно въ такомъ случаѣ опять изолировано отъ земли.
Поэтому при всѣхъ опытахъ съ электричествомъ мы должны
заботиться о томъ, чтобы тѣла, которымъ сообщаются заряды, были
изолированы отъ земли. Поэтому, напримѣръ, для опытовъ съ тре-
ніемъ, съ которыхъ мы начали, такъ удобна стеклянная или эбони-
товая палочка; такую палочку можно держать въ рукѣ и зарядъ ея
при этомъ не уйдетъ въ землю.
ЖИДКІЕ ПРОВОДНИКИ. *
12. Возьмемъ изолированное металлическое тѣло, заряженроё
настолько сильно, что возбуждаемое имъ поле можетъ быть^тчет-
ливо замѣчено при помощи электрической стрѣлки. Соедфимъ съ
водопроводомъ одинъ конецъ веревки, смоченной въ водѣ, а другой
ея конецъ наложимъ на заряженное металлическо^тѣлр, при чемъ
16
Жидкіе проводники. Проводящіе газы
для предосторожности дотрагиваться до веревки будемъ лишь изо-
ляторомъ (напримѣръ, палочкой сургуча). Тогда металлическое тѣло
потеряетъ мгновенно весь свой зарядъ. Слѣдовательно, вода дѣлаетъ
веревку, въ сухомъ состояніи представляющую собою только полу-
проводникъ, хорошимъ проводникомъ.
Мы заключаемъ отсюда, что ключевая вода представляетъ со-
бою проводникъ. Еще лучше она проводитъ, какъ мы это увидимъ
ниже, если распустить въ ней какую-либо соль. Человѣческое тѣло
является проводникомъ, такъ какъ содержитъ въ себѣ воду и соли.
Большинство остальныхъ жидкостей представляютъ собою по-
лупроводники или изоляторы. Къ ихъ числу принадлежатъ керосинъ,
сѣрнистый углеродъ, бензолъ, сѣрнистый эѳиръ, алкоголь. Очень
хорошимъ изоляторомъ является параффиновое масло.
ПРОВОДЯЩІЕ ГАЗЫ.
13. Мы уже убѣдились, что газы (какъ, напримѣръ, воздухъ)
представляютъ собою вообще прекрасные изоляторы. Но при нѣ-
которыхъ особенныхъ условіяхъ они могутъ также становиться про-
Рис. 4. Проводимость газоваго
пламени.
водниками или, по крайней мѣрѣ,
полупроводниками.
Уже съ давнихъ поръ извѣстно,
что химическіе процессы сгоранія газа
дѣлаютъ его проводникомъ; прово-
дящими являются какъ самое пламя,
такъ и свѣжіе газообразные продукты
горѣнія. Если, напримѣръ, установить
двѣ изолированныя металлическія пла-
стинки одну противъ другой и между
ними помѣстить пламя бунзеновской
горѣлки (рис.4), затѣмъ зарядить одну
изъ пластинокъ и сейчасъ же послѣ
этого удалить другую отъ пламени,
то вблизи послѣдней можно при по-
мощи электрической стрѣлки оонару-
жить наличность поля. ^Зарядъ этой
оказывается при этомъ того же знака, чт^ и-зарядъ, нане-
первую пластинку. Слѣдовательно, въ^эѣойъ случаѣ дѣй-
часть заряда перешла черезъ газы п^мени съ первой пла-
вторую.
пластинки
сенный на
ствительно
стинки на
Проводящіе газы
17
Другое извѣстное средство сдѣлать газъ проводящимъ заклю-
чается въ примѣненіи весьма сильныхъ электрическихъ полей. Если
между двумя тѣлами возникаетъ очень сильное поле, то появляется
искра, соединяющая эти тѣла. Электрическая искра представляетъ
собою слой воздуха, очень хорошо проводящій. Тѣ слои воздуха,
черезъ которые прошла искра, также остаются въ теченіе короткаго
времени послѣ этого проводящими, подобно газамъ, выдѣляющимся
изъ пламени.
Этотъ методъ примѣненія сильныхъ электрическихъ полей можно
сдѣлать дѣйствующимъ непрерывно, если воспользоваться металличе-
скимъ остріемъ. Укрѣпимъ на изолированной металлической пластинкѣ
тонкую швейную иглу такъ, чтобы между нею и пластинкою не на-
ходилось изоляторовъ. Если теперь зарядить электричествомъ пла-
стинку, то въ непосредственной близости къ иглѣ образуется поле,
какъ показываютъ опыты, исключительной силы. При достаточно
сильномъ зарядѣ на остріѣ образуется крошечное свѣтлое пятно; въ
этомъ именно мѣстѣ воздухъ и пріобрѣтаетъ свойство проводимости.
Проводящій воздухъ устремляется прочь съ острія и растекается во всѣ
стороны. Если мы приблизимъ къ заряженной пластинкѣ съ остріемъ
другую изолированную металлическую пластинку, то черезъ короткій
промежутокъ времени при помощи электрической стрѣлки можно
будетъ убѣдиться въ томъ, что на нее перешла часть заряда.
Мы можемъ послѣдній опытъ произвести также въ обратномъ
порядкѣ, оставляя пластинку съ остріемъ незаряженной и прибли-
жая къ ней другую заряженную пластинку. И въ этомъ случаѣ обра-
зующееся поле концентрируется вблизи острія и сообщаетъ въ этомъ
мѣстѣ воздуху проводимость. Если черезъ нѣкоторое время мы удалимъ
иглу и къ пластинкѣ, на которой она была укрѣплена и которая не
была наэлектризована, приблизимъ электрическую стрѣлку, то опять
окажется, что электрическій зарядъ перешелъ на нее черезъ воздухъ.
При послѣднемъ опытѣ необходимо, прежде чѣмъ испытывать
поле электрической стрѣлкой, удалить остріе, т. е. иголку. Это не-
обходимо потому, что, если на заряженномъ металлическомъ тѣлѣ,
имѣется остріе, то черезъ окружающій это остріе воздухъ, в^|йлу
его проводимости, зарядъ уносится въ окружающее пространство-—
на стѣны, полъ и т. д. Все происходитъ такъ, какъ ес^Щфьі метал-
лическое тѣло было соединено проводникомъ съ землею; и такое
исчезновеніе заряда продолжается до тѣхъ поръ, цоѣі\поле у острія
Ми. Электричество и магнитизмъ. 2
18
Проводящіе газы
не станетъ настолько слабымъ, что уже не будетъ въ состояніи дѣ-
лать воздухъ у острія проводящимъ. Укрѣпимъ при помощи про-
водниковъ на изолированной металлической пластинкѣ пучекъ бу-
мажныхъ полосъ и зарядимъ пластинку. Такъ какъ при этомъ всѣ
бумажныя полосы зарядятся электричествомъ одного знака, то онѣ
будутъ, какъ мы уже знаемъ, другъ отъ друга отталкиваться, и пу-
чекъ, спускавшійся прежде безформенно внизъ, раздувается, такъ
какъ полосы стремятся удалиться одна отъ другой возможно дальше.
Если теперь укрѣпить на металлической пластинкѣ острую иглу, то
полосы бумажнаго пучка начинаютъ снова спадать внизъ и черезъ
нѣкоторое время принимаютъ прежній безформенный видъ.
Этотъ опытъ можно произвести
и иначе’ именно, можно поднести
иглу, соединенную проводникомъ
съ В°ДОПРОВОД°МЪ> къ бумажному
пучку, развернувшемуся отъ нане-
О сеннаго на металлическую пластин-
ку заряда (рис. 5). Бумажныя поло-
1 । сы въ такомъ случаѣ опять медлен-
но спадаютъ; отсюда слѣдуетъ, что
V зарядъ черезъ воздухъ и остріе
\ проникаетъ въ землю.
•і \ 14. Такого рода остріе, соеди-
•і \ ненное съ землею, представляетъ
' \ собою громоотводъ; этотъ при-
боръ является, такимъ образомъ,
Рис. 5. Остріе сообщаетъ проводи- важнымъ практическимъ примѣне-
мость окружающему воздуху.
ніемъ опытовъ, съ которыми мы
сейчасъ познакомились. Остріе громоотвода медленно удаляетъ за-
ряды съ заряженныхъ грозовыхъ тучъ, проходящихъ мимо него, и
отводитъ ихъ въ землю. Въ силу этого поле, возбуждаемое тучеіо
надъ защищеннымъ громоотводомъ зданіемъ, непрерывно ослабляется
и не можетъ при сліяніи нѣсколькихъ грозовыхъ тучъ достигать той
опасной силы, которая необходима для возникновенія молніи.
XV
ЭЛЕКТРИЧЕСКАЯ МАШИНА СЪ ТРЕНІЕМЪ:
15. Другое важное примѣненіе дѣйствія осѣрй представляетъ
собою „гребень" электрической машины. Электрическая машина ста-
раго типа состоитъ въ существѣ изъ круглой ^стеклянной пластинки,
Электрическая машина съ треніемъ
19
сидящей на оси, которую можно вращать при помощи колѣнчатой
рукоятки (рис. 6). При ея вращеніи край стекляннаго круга прохо-
дитъ между двумя кожанными подушками. Кожа этихъ подушекъ
покрыта цинковой амальгамой, такъ какъ оказывается, что стекло
при соприкосновеніи съ этой амальгамой пріобрѣтаетъ особенно силь-
ный положительный зарядъ. Такимъ образомъ, стеклянный кругъ,
проходя между подушками, очень сильно заряжается. Послѣ этого
онъ проходитъ между двумя металлическими гребенками, острія ко-
торыхъ обращены къ кругу, но его не касаются. Какъ мы знаемъ,
Рис. 6. Электрическая машина съ треніемъ.
острія, подъ вліяніемъ сильнаго электрическаго поля, дѣлаютъ воз-
духъ проводящимъ; проводящій же слой воздуха, черезъ который
кругъ проходитъ, такъ сказать, стираетъ съ него зарядъ и перено-
ситъ его на металлическія гребенки. Обѣ гребенки неподвижно за-
крѣпляются на большомъ цилиндрическомъ или шарообразномъ ме-
таллическомъ тѣлѣ—кондукторѣ, а послѣдній устанавливается съ°^
помощью хорошо изолирующей стеклянной подставки на стойкѣ
шины. Такимъ образомъ, на кондукторѣ накопляются положитель-
ные заряды, которые снимаются со стекляннаго круга при вращеніи,
а съ кондуктора ихъ можно удобно отвести въ любое время.
ГЛАВА ВТОРАЯ
ЭЛЕКТРИЧЕСКОЕ НАПРЯЖЕНІЕ
НАПРАВЛЕНІЕ ЭЛЕКТРИЧЕСКАГО ПОЛЯ.
16. Приступая теперь къ болѣе тщательному изученію особен-
ностей электрическаго состоянія эѳира и относящихся къ нему зако-
новъ, мы условимся во всѣхъ случаяхъ для достиженія большей
отчетливости и большей легкости въ обобщеніяхъ сравнивать это
состояніе съ состояніями напряженія вѣсомой матеріи. Мы будемъ*
слѣдовательно, представлять себѣ, что электрически заряженное тѣло
вызываетъ въ окружающемъ его эѳирѣ электрическія напряженія, до
нѣкоторой степени подобно тому, какъ инородное тѣло, попавшее
въ расплавленное стекло, вызываетъ послѣ охлажденія (вслѣдствіе
разницы въ коэффиціентахъ расширенія) упругія напряженія въ окру-
жающемъ стеклѣ.
Если мы станемъ изслѣдовать эти напряженія при помощи
электрической стрѣлки, то прежде всего обнаружимъ, что напряже-
ніе эѳира въ каждомъ мѣстѣ связано съ совершенно опредѣленнымъ
направленіемъ. Какъ мы знаемъ, положительно заряженная частичка
въ силу напряженія въ эѳирѣ увлекается въ нѣкоторомъ опредѣлен-
номъ направленіи, а заряженная отрицательно увлекается въ напра-
вленіи діаметрально противоположномъ. Мы примемъ направленіе
силы, дѣйствующей на положительную частичку, за положительное
направленіе электрическаго поля. Слѣдовательно, отрицательная^ча-
стичка испытываетъ дѣйствіе силы, направленной по
направленію поля. Отсюда ясно, что наша электрическая
прямо указываетъ направленіе электрическаго поля, такъ какъ она
всегда устанавливается именно по этому направленію.^
Мы разсмотримъ теперь поле, возникающее л между двумя изо-
лированными металлическими тѣлами, когда одною заряжается поло-
жительно, другое — отрицательно. Если внесщС|ъ это поле электри-
Аггрѣлка
Направленіе электрическаго поля
21
ческую стрѣлку, то она установится неизмѣнно въ одномъ направле-
ніи, идущемъ отъ положительно заряженнаго тѣла къ отрицательно
заряженному тѣлу. Опредѣлимъ въ нѣсколькихъ мѣстахъ направленіе
поля и отмѣтимъ его мѣломъ черточками на столѣ. Легко видѣть,
что съ помощью этихъ опытныхъ данныхъ мы можемъ построить рядъ
линій (рис. 7), которыя всѣ опредѣляютъ направленіе поля. При
Рис. 7. Зарисовываніе электрическихъ силовыхъ линій.
помощи этихъ линій, начинающихся у положительно заряженнаго
тѣла и кончающихся у отрицательно заряженнаго тѣла, мы можемъ
составить себѣ отчетливое представленіе о распространеніи изучае-
маго поля. Мы назовемъ эти линіи линіями напряженій или ли-
ніями поля ]).
СИЛА ИЛИ НАПРЯЖЕНІЕ ПОЛЯ,
о (
17. Кромѣ направленія у электрическаго состоянія эѳира должна^?
конечно, во всѣхъ мѣстахъ обнаруживаться и опредѣленная
Подвѣсимъ на шелковой нити, закрѣпленной на штативѣ, легкій іпа-
]) Въ русскомъ научномъ языкѣ общеупотребителенъ терминъ линіи
силъ, которымъ мы и будемъ пользоваться. Прим. пер.
22
Сила или напряженіе поля
рикъ и сообщимъ ему нѣкоторый зарядъ. Вслѣдствіе хорошей изо-
ляціи этотъ зарядъ останется неизмѣннымъ во все время опыта.
Кромѣ того на штативѣ укрѣпимъ раздѣленный кругъ, центръ ко-
тораго совпадаетъ съ точкой привѣса нити. Этотъ маленькій при-
боръ мы будемъ называть „электрическимъ маятникомъ". Первона-
чально шарикъ этого маятника виситъ вертикально и указываетъ на
нулевое дѣленіе раздѣленнаго круга. Если мы станемъ дѣйствовать
на шарикъ нѣкоторой силой, направленной горизонтально, то онъ
передвинется до нѣкотораго другого дѣленія; при этомъ отклоненіе
будетъ тѣмъ больше, чѣмъ больше приложенная къ шарику сила*.
Съ помощью этого простого аппаратика мы можемъ измѣрить такое
электрическое поле, въ которомъ линіи силъ горизонтальны. Для
этой цѣли мы совмѣщаемъ направленіе отдѣльной силовой линіи
(опредѣленное, приблизительно, съ помощью электрической стрѣлки)
съ плоскостью раздѣленнаго круга и отсчитываемъ то его дѣленіе,
до котораго отклоняется шарикъ. Мы получаемъ такимъ образомъ
величину силы Р, съ которой находящійся въ электрическомъ состоя-
ніи эѳиръ въ изслѣдуемомъ мѣстѣ дѣйствуетъ на заряженный ша-
рикъ. Если мы измѣримъ величину Р во многихъ мѣстахъ, то полу-
чимъ такимъ образомъ картину распредѣленія электрическаго состоя-
нія въ эѳирѣ. Очевидно, чѣмъ больше оказывается Р, тѣмъ сильнѣе
электрическое напряженіе эѳира.
Такъ, напримѣръ, мы найдемъ такимъ путемъ, что поле, силовыя
линіи котораго мы только-что изслѣдовали при помощи электриче-
ской стрѣлки, тѣмъ сильнѣе, чѣмъ ближе изслѣдуемое мѣсто къ
одному изъ заряженныхъ тѣлъ. Если мы теперь обратимъ вниманіе
на полученную выше картину расположенія силовыхъ линій въ этомъ
полѣ, то увидимъ, что вблизи заряженнаго тѣла, гдѣ сила поля
больше, линіи силъ располагаются гуще, нежели на большомъ раз-
стояніи отъ заряженнаго тѣла, гдѣ поле слабѣе. Этотъ результатъ,
который мы здѣсь установили для одного частнаго случая, подтвер-
ждается также и для всякаго другого электрическаго поля.
Графическое изображеніе электрическаго подопри по-
мощи его силовыхъ линій даетъ намъ понятіе не только о
распредѣленіи его направленія, но также и о распредѣленіи
его силы; сила поля тѣмъ больше, чѣмъх гѴще располага-
ются зарисованныя линіи силъ. :
Мы будемъ поэтому часто употреблятѣСвыраженіе „плотность
Сила или напряженіе поля
23
силовыхъ линій" для обозначенія того же понятія, что и „сила элек-
трическаго поля".
18. Вмѣсто того, чтобы сравнивать силу, съ которою дѣйствуетъ
эѳиръ на заряженный шарикъ, съ силою тяжести, мы можемъ, под-
вѣсивъ шарикъ инымъ способомъ, удерживать его въ положеніи рав-
новѣсія при помощи какой-либо упругой силы безъ всякаго участія
силы тяжести.
Такого рода пріемъ былъ примѣненъ Кулономъ для измѣреній
силы поля. Его инструментъ носитъ названіе крутильныхъ вѣ-
совъ. Въ немъ заряженный шарикъ укрѣпленъ на одномъ концѣ
стерженька, сдѣланнаго изъ изолирующаго вещества; на другомъ
концѣ этого стерженька имѣется соотвѣтствующій легкій противо-
вѣсъ. Стерженекъ подвѣшенъ въ центрѣ тяжести на тонкой нити и
находится въ горизонтальномъ положеніи. Проволока сверху закрѣ-
плена въ шляпкѣ, позволяющей ее закручивать. При такомъ устрой-
ствѣ прибора стерженекъ съ заряженнымъ шарикомъ подъ дѣйствіемъ
силы упругости при крученіи нити, на которой онъ виситъ, устанавли-
вается въ опредѣленномъ положеніи равновѣсія. Вращеніемъ шляпки
можно произвольнымъ образомъ измѣнить это положеніе равновѣсія
и перенести такимъ образомъ заряженный шарикъ въ другое мѣсто
измѣряемаго поля. Если приборъ окажется въ электрическомъ полѣ,
то шарикъ будетъ отклоняться отъ своего положенія равновѣсія,
пока упругая сила крученія нити, которая при этомъ начинаетъ дѣй-
ствовать, не уравновѣситъ силы, съ которою дѣйствуетъ на шарикъ
измѣряемое поле. Если при этомъ опредѣлить при помощи раздѣ-
леннаго круга, которымъ снабженъ приборъ, величину отклоненія
шарика отъ его положенія равновѣсія, то отсюда можно вычислить
величину силы крученія нити, а, слѣдовательно, также и величину
силы, дѣйствіе которой испытываетъ шарикъ въ томъ мѣстѣ поля,
гдѣ онъ при этомъ находится.
Этотъ приборъ, вѣроятно, можно было бы построить въ болѣе
удобномъ видѣ такъ, чтобы равновѣсіе стерженька съ шарикомъ^
достигалось не съ помощью закручивающейся нити, а, напримѣръ,У
при помощи тонкой часовой пружины, употребляемой въ карман-
ныхъ часахъ для ихъ регулированія. Такимъ образомъ можг^сгоыло
бы во всякомъ случаѣ, построить инструментъ, пригодный^нё только
для измѣренія горизонтально направленныхъ полей, кдъ^ крутильные
вѣсы Кулона и электрическій маятникъ, которымъпользовались
24
Сила или напряженіе поля
выше, но и для измѣреній во всевозможныхъ иныхъ направленіяхъ.
19. Такихъ приборовъ въ продажѣ, конечно, не существуетъ;
однако, мы представимъ себѣ на нѣкоторое время, что какой-либо
механикъ устроилъ намъ два прибора, изъ которыхъ одинъ, анало-
гичный электрической стрѣлкѣ, указываетъ повсюду направленіе элек-
трическаго состоянія, другой же, аналогичный электрическому маят-
нику, позволяетъ измѣрять силу, съ которой эѳиръ дѣйствуетъ на
опредѣленную заряженную частичку.
Пользуясь этого рода измѣреніями, мы будемъ получать, однако,
лишь относительныя значенія величины электрическаго состоянія.
Точно мы можемъ сказать лишь слѣдующее: напряженія въ эѳирѣ
тѣмъ сильнѣе, чѣмъ значительнѣе тѣ силовыя дѣйствія, которыя мы
измѣряемъ. Однако, для величинъ силы поля введена совершенно
опредѣленная числовая шкала, такъ какъ въ наукѣ считается безу-
словно правильнымъ нижеслѣдующее положеніе: сила электриче-
скаго поля пропорціональна тому силовому дѣйствію, ко-
торое испытываетъ въ этомъ полѣ опредѣленная употре-
бляемая для измѣреній электрически заряженная частичка.
Въ силу этого необходимо только выбрать за поле, предста-
вляющее собою единицу, какое-либо легко получаемое поле и измѣ-
рить ту силу Рг, дѣйствіе которой испытываетъ въ немъ упомянутая
частичка. Если затѣмъ въ нѣкоторомъ измѣряемомъ полѣ на эту
частичку дѣйствуетъ сила Р, то, согласно нашему опредѣленію, сила
измѣряемаго поля Е выразится такъ:
Е = Р : Рх.
Слѣдовательно, возможность производить электрическія измѣре-
нія вполнѣ зависитъ отъ возможности найти методъ, съ помощью
котораго можно было бы въ любой моментъ легко получить опредѣ-
ленное электрическое поле. Здѣсь уже слѣдуетъ отмѣтить, что эта
задача, какъ мы ниже въ этомъ убѣдимся, дѣйствительно
чески разрѣшена. Такимъ образомъ, мы всегда можемъ для
поля найти посредствомъ измѣренія число, вполнѣ опредѣленной ха-
рактеризующее силу этого поля. -
Электрическое напряженіе эѳира представ^дедъ собою
величину, характеризующуюся одновременноС^ѣкоторымъ
опредѣленнымъ числомъ и нѣкоторымъ опредѣленнымъ на-
правленіемъ.
* * ? *•
практи-
любого
Сила или напряженіе поля. — Изображенія поля.
25
Всякая величина такого рода въ физикѣ вообще называется
векторомъ. Сила электрическаго поля, слѣдовательно, есть векторъ.
Хотя измѣреніе поля въ жидкой или газообразной средѣ опи-
саннымъ методомъ весьма затруднительно и непрактично, однако
во многихъ случаяхъ оно все же выполнимо. Хуже обстоитъ дѣло
въ тѣхъ случаяхъ, когда поле возбуждается внутри твердаго тѣла. Въ
подобномъ случаѣ слѣдовало бы просверлить въ тѣлѣ узкіе каналы,
въ которые можно было бы вводить заряженную электричествомъ
частичку, соединенную съ динамометромъ. Силу Р8, дѣйствующую на
эту частичку въ направленіи 5 узкаго канала, слѣдовало бы
принять за величину составляющей силы поля въ направле-
ніи 5. Направленіе же силы поля Е въ этомъ случаѣ будетъ совпа-
дать съ направленіемъ того канала, въ которомъ вводимая частичка
испытываетъ вдоль его длины дѣйствіе болѣе сильное, чѣмъ въ
любомъ другомъ каналѣ. Такого рода измѣренія на практикѣ, ко-
нечно, производить невозможно. Но ниже мы познакомимся съ весьма
употребительнымъ на практикѣ инымъ методомъ, который въ суще-
ствѣ основывается на тѣхъ же соображеніяхъ, что и выше описан-
ный способъ измѣренія.
ИЗОБРАЖЕНІЯ ПОЛЯ.
20. Если, не производя точныхъ измѣреній, мы желаемъ лишь
получить общую картину распредѣленія электрическаго поля, то до-
статочно, какъ мы это видѣли въ § 17, прослѣдить за направленіями
силовыхъ линій. Для этой цѣли существуетъ методъ, еще болѣе про-
стой, чѣмъ употребленіе электрической стрѣлки. Если мы возьмемъ
просто слегка влажный плохо проводящій стерженекъ, могущій, по-
добно нашей электрической стрѣлкѣ, легко вращаться на остріѣ, и при-
близимъ его къ заряженному тѣлу, то мы замѣтимъ, что стерженекъ
установится въ опредѣленномъ направленіи, въ томъ же самомъ, въ
которомъ устанавливается и электрическая стрѣлка, т. е. въ направле-
ніи силовой линіи. Это происходитъ потому, что стерженекъ, пред-
ставляя собою полупроводникъ, въ электрическомъ полѣ оказываете^
заряженнымъ; при этомъ онъ заряжается положительно на ко^ійЬ,
соотвѣтствующемъ передней части силовой линіи, и отрицательн©
на концѣ, соотвѣтствующемъ задней части силовой линіи.^Это явле-
ніе—такъ называемую индукцію- мы ниже изучимъ болѣе-подробно.
Пока намъ достаточно знать,- что вслѣдствіе индуДда^ стерженекъ
26
Изображенія поля
превращается въ электрическую стрѣлку, и мы при его помощи мо-
жемъ изслѣдовать все поле такъ же хорошо, какъ и настоящею
Рис. 8 а и 8Ь. Поле заряженнаго шара.
стрѣлкою. Если стерженекъ повернуть на 180°, то и индуктирован-
ные заряды, очевидно, взаимно перемѣщаются, и стерженекъ уста-
Рис. 8 с и 8сі. Поле между двумя заряженными шарами.
навливается въ направленіи, противоположномъ прежнему. Слѣдова-
тельно, употребляя стерженекъ, мы уже не можемъ различить, какъ
при употребленіи электрической стрѣлки, порржительнаго и отрица-
Изображенія поля
27
тельнаго направленій въ указываемой имъ линіи силъ. Для ихъ раз-
личенія можно, однако, воспользоваться извѣстнымъ намъ свойствомъ,
Рис. 8е и 8і. Поле плоскаго конденсатора.
въ силу котораго силовыя линіи исходятъ изъ положительно за-
ряженнаго тѣла и заканчиваются на заряженномъ отрицательно.
Рис. 8^ и 8й. Поле между остріемъ и пластинкой.
Если мы возьмемъ большое число маленькихъ ^стерженьковъ,
вещество которыхъ представляетъ собою полупроводни|<ъ, и внесемъ
ихъ въ электрическое поле, то они всѣ сами собою ^установятся въ
28
Изображенія поля
направленіяхъ силовыхъ линій. Такимъ образомъ, полупроводящій
крупный порошекъ, частицы котораго замѣняютъ собою маленькіе
стерженьки, будучи внесенъ въ электрическое поле, даетъ возможность
прямо видѣть силовыя линіи. Очень удобный порошекъ такого рода
получается раскалываніемъ минерала рутила, который обладаетъ приз-
матической спайностью и потому расщепляется на мельчайшія полоски.
Рутилъ обладаетъ еще нѣкоторыми свойствами, дѣлающими его осо-
бенно пригоднымъ для такихъ опытовъ, и, во всякомъ случаѣ, даетъ
прекрасныя изображенія силовыхъ линій; но и кромѣ рутила можно
найти еще много тѣлъ, могущихъ служить для той же цѣли.
Чтобы получить электрическое поле, мы беремъ стеклянныя пла-
стинки, съ которыми скрѣплены мѣдныя части, имѣющія формы тѣхъ
проводниковъ, поля которыхъ мы желаемъ изучить. Стеклянныя пла-
стинки мы подбираемъ такой величины, чтобы можно было при помощи
нашего проекціоннаго аппарата отбросить изображеніе поля на экранъ.
Возьмемъ сперва пластинку, къ которой прикрѣпленъ посрединѣ
мѣдный кругъ, а съ краевъ—узкое концентрическое кольцо. Къ кругу
и къ кольцу припаяны мѣдныя проволоки, которыя, кромѣ того, при-
крѣплены сургучомъ къ краямъ стеклянной пластинки. Съ этими
проволоками соединяются длинные провода, ведущіе къ двумъ по-
люсамъ такъ называемой индуктивной электрической машины. Какъ
мы ниже увидимъ, эта машина даетъ одновременно и въ равныхъ
количествахъ положительное и отрицательное электричество. Мы мо-
жемъ зарядить, напримѣръ, кружокъ положительно, а внѣшнее кольцо
отрицательно. Если мы теперь нанесемъ на стеклянную пластинку
рутиловый порошекъ и приведемъ его въ сотрясеніе, постукивая по
пластинкѣ палочкой, то частицы порошка расположатся по прямымъ
линіямъ, расходящимся лучеобразно отъ центральнаго кружка. Это и
будутъ линіи силъ въ полѣ круглой пластинки или также шара.
Рисунокъ, помѣщенный рядомъ съ фотографіей этой картины (рис. 8),
полученъ слѣдующимъ путемъ: на фотографію былъ наложенъ ку-
сокъ прозрачной бумаги и на немъ были нанесены линіи, образо-
ванныя расположеніемъ частицъ порошка.
Вторую картину мы получимъ для поля, образующагосінмежду
двумя круглыми пластинками, сидящими на двухъ стержняхъ и за-
ряженными соотвѣтственно положительнымъ и отрицательнымъ элек-
тричествомъ. Приблизительно такое же поле получй^ся между двумя
шариками на стержняхъ, представляющими собрку обычную форму
Изображенія поля
29>
такъ называемаго „искромѣра". Здѣсь, какъ и въ слѣдующихъ слу-
чаяхъ, на рисункѣ рядомъ съ фотографіей помѣщено изображеніе
силовыхъ линій, нанесенныхъ на прозрачную бумагу.
Третью картину мы получимъ для случая двухъ параллельныхъ,
близко расположенныхъ мѣдныхъ полосъ, имѣющихъ заряды проти-
воположнаго знака. Здѣсь мы получаемъ приблизительную картину
поля, образующагося въ такъ называемомъ „плоскомъ конденсаторѣ\
состоящемъ изъ двухъ расположенныхъ другъ противъ друга метал-
лическихъ пластинокъ, по возможности плоско отшлифованныхъ и
взаимно параллельныхъ. Здѣсь характерна сила поля между обѣими
пластинками; силовыя линіи всѣ расположены нормально къ обѣимъ,
пластинкамъ и съ равномѣрною плотностью. Такое поле называется
„однороднымъ". На краю поля силовыя линіи сперва слегка искри-
вляются во внѣшнюю сторону, а затѣмъ, все болѣе и болѣе выпя-
чиваясь, превращаются въ дуги окружностей, идущихъ отъ одной
пластинки къ другой. Это „краевое поле" чрезвычайно слабо по срав-
ненію съ сильнымъ полемъ между пластинками.
Четвертую картину даетъ поле между заряженнымъ стержнемъ
и мѣдной пластинкой, отведенной къ землѣ. Тутъ ясно видно, какъ
сильно сгущается поле у острія стержня. Отъ этого острія расхо-
дится цѣлый пучокъ силовыхъ линій.
ФИЗИЧЕСКОЕ РАЗЛИЧІЕ МЕЖДУ МАТЕРІЕЙ И ЭѲИРОМЪ.
21. Мы теперь сдѣлаемъ попытку сопоставить понятія эѳира ц
вѣсомой матеріи, имѣя въ виду, что мы отчетливо установили при-
роду электрическаго напряженія, какъ векторіальной величины. Прежде
всего весьма замѣчательно то обстоятельство, что упругія напряже-
нія вѣсомыхъ тѣлъ ни въ какомъ случаѣ не могутъ выражаться век-
торіальными величинами, подобно электрическимъ напряженіямъ въ
эѳирѣ. Разсмотримъ, напримѣръ, упруго растянутую проволоку; въ
ней, конечно, имѣются напряженія, направленныя по ея оси, а попе- /
речныхъ напряженій нѣтъ. Напряженіе проволоки представляетъ со-
бою, слѣдовательно, геометрически оріентированную величину. Но х-
не въ состояніи указать, натянута ли проволока сверху внизъ ил^с^Йу
вверхъ, такъ какъ растяженіе ея вызывается двумя силамиЛірило-
женными къ обоимъ концамъ проволоки и направленными^ проти-
воположныя стороны. Дѣйствительно, механика учитъ, чѣо Дапраженіе
въ твердыхъ тѣлахъ вполнѣ опредѣляется величиною., рѣющій харак-
30
Физическое различіе между матеріей и эѳиромъ.
теръ такъ называемаго тензора. Это есть величина, пространственную
оріентировку которой можно символически представить эллипсоидомъ;
хотя у этого э ллипсоида можно различить продольную, поперечныя
и наклонныя оси, однако, ни одна изъ этихъ осей не имѣетъ напра-
вленія „ впередъ“ или „назадъ". Наоборотъ, символомъ векторіальной
величины является стрѣлка (рис. 9).
Въ жидкостяхъ же и въ газахъ, какъ
дйШ извѣстно, упругое напряженіе можетъ
/ч быть вполнѣ опредѣлено даже про-
™ стой численной величиной величи-
Рис. 9. Тензоръ, скаларъ и векторъ. ной давленія, лишенной всякой про-
странственной оріентировки. Дѣйствительно, согласно основному по-
ложенію гидростатики, это давленіе направлено строго перпендику-
лярно къ площадкѣ жидкости (или газа) и дѣйствуетъ съ силою,
одинаковою для всякаго положенія площадки. Величина, не имѣю-
щая пространственной оріентировки, называется въ физикѣ скала-
ромъ. Такую величину символически можно представить сферою, по-
лучающеюся изъ эллипсоида, если всѣ различно направленныя оси
его становятся равными между собой.
Векторіальный характеръ электрическаго состоянія является основ-
ною причиною, въ силу которой мы должны разсматривать два рода
активной связи между матеріей и эѳиромъ, различаемые нами, какъ
положительный и отрицательный заряды. Въ зависимости отъ этой
же причины, линія, имѣющая опредѣленное направленіе, должна имѣть
начало и конецъ. Положительный зарядъ является началомъ электри-
ческаго поля, отрицательный — его концомъ. Никакихъ другихъ ро-
довъ электрическаго заряда нельзя себѣ представить. Оба заряда —
положительный и отрицательный - представляютъ собою границы
электрическаго поля; эти границы лежатъ, слѣдовательно, всегда на
двухъ удаленныхъ другъ отъ друга частяхъ пространства, которыя
могутъ быть даже безконечно малыми, и съ ними сопряжены силы^
которыя и даютъ намъ свидѣтельство о существованіи напряженій
въ эѳирѣ.
Наоборотъ, въ вѣсомыхъ тѣлахъ граница „поля напряженій"
представляетъ собою непремѣнно вполнѣ замкнутую поверхность безъ
начала и безъ конца; она охватываетъ все тѣло, ^находящееся въ
состояніи упругаго напряженія; въ точкахъ этой Спрверхности при-
ложены силы, соотвѣтствующія состоянію напряженія въ этомъ мѣстѣ.
Нѣкоторыя уподобленія
31
При сопоставленіи процессовъ, совершающихся въ эѳирѣ, съ
процессами, совершающимися въ матеріальныхъ тѣлахъ, важно всегда
имѣть это различіе въ виду.
НЪКОТОРЫЯ УПОДОБЛЕНІЯ.
22. Изъ вышеизложеннаго ясно, что простое механическое тол-
кованіе процессовъ, совершающихся въ эѳирѣ, совершенно невоз-
можно. А такъ какъ, съ другой стороны, мы чувствуемъ потребность
уяснить себѣ явленія, совершающіяся въ области недоступной на-
шимъ чувственнымъ воспріятіямъ субстанціи при помощи ежедневно
наблюдаемыхъ явленій, происходящихъ въ матеріальныхъ тѣлахъ, то
приходится пойти на компромиссъ съ природой. Мы представимъ
себѣ механическую модель, которая дастъ намъ вѣрное подобіе
наиболѣе интересующихъ насъ сторонъ явленій, происходящихъ въ
эѳирѣ, хотя въ нѣкоторыхъ отношеніяхъ она необходимо будетъ
отличаться отъ того, что дѣйствительно имѣетъ мѣсто въ эѳирѣ.
Поставимъ себѣ, напримѣръ, такой вопросъ: существуютъ ли
механическія состоянія, которыя, подобно электрическимъ состояніямъ,
удобно можно представить векторіальными величинами? Легко привести
примѣръ такого состоянія — теченіе жидкости или газа. Вѣтеръ въ на-
шей атмосферѣ всегда имѣетъ опредѣленное направленіе, устанавлива-
емое при помощи флюгера, который играетъ здѣсь, такимъ образомъ,
роль электрической стрѣлки. Если направленія вѣтра, наблюденныя
на различныхъ метеорологическихъ станціяхъ, нанести стрѣлками на
карту, то по нимъ можно построить линіи тока воздуха, соотвѣт-
ствующія, такимъ образомъ, нашимъ силовымъ линіямъ. Въ тѣхъ
мѣстахъ, гдѣ эти линіи тока располагаются плотнѣе, вѣтеръ имѣетъ
большую силу, нежели въ тѣхъ мѣстахъ, гдѣ линіи тока распола-
гаются рѣже. Силу вѣтра можно измѣрить при помощи лопасти, ви-
сящей при отсутствіи вѣтра отвѣсно и отклоняемой вѣтромъ изъ
положенія равновѣсія, которое она принимаетъ подъ дѣйствіемъ силы
тяжести. Величина отклоненія ея служитъ мѣрой силы вѣтра. Такая
лопасть соотвѣтствуетъ электрическому маятнику. Однако, если мі^
будемъ изучать кривыя вѣтровъ на картѣ, то убѣдимся, что^ѳнѣ
распространяются по совершенно инымъ законамъ, чѣмъ кривця$лек-
трическаго поля. Онѣ могутъ, напримѣръ, представлять с^бдю зам-
кнутыя линіи (вихрь). Но, вообще говоря, онѣ возникаютъ; въ опре-
дѣленныхъ мѣстахъ (гдѣ увлекаемый воздухъ замѣщаемся опускаю-
32
Нѣкоторыя уподобленія
щимися верхними слоями) и въ другихъ опредѣленныхъ же мѣстахъ
оканчиваются (гдѣ избытокъ воздуха устремляется обратно вверхъ).
Эти точки, представляющія собою начала и концы воздушныхъ то-
ковъ, соотвѣтствуютъ положительнымъ и отрицательнымъ зарядамъ
въ электрическомъ полѣ.
23. Хотя такое сравненіе электрическаго состоянія съ вѣтромъ
можно провести достаточно далеко, однако, полнаго уподобленія оно
дать не можетъ. Если бы провести это уподобленіе до конца, то
намъ пришлось бы разсматривать положительно заряженную частичку,
какъ источникъ постояннаго тока жидкости, въ которомъ изъ ни-
чего жидкость непрерывно вновь создается въ постоянномъ количе-
ствѣ, а отрицательно заряженную частичку — какъ пучину, поглощаю-
щую постоянно жидкость въ опредѣленномъ количествѣ. Можно
избѣгнуть этого ненагляднаго представленія, если сравнить электри-
ческое поле съ потокомъ жидкости, слегка отвердѣвшимъ. Мы бу-
демъ представлять себѣ, слѣдовательно, что жидкость, съ которой
мы сравниваемъ эѳиръ, заключается въ ткани, имѣющей клѣтчатое
строеніе, подобно клѣтчаткѣ живыхъ организмовъ. Въ обычномъ со-
стояніи клѣтки такого „ студня “ не деформированы, и потому ника-
кихъ силъ напряженій не существуетъ. Но если мы какимъ-либо
способомъ увеличимъ, сравнительно съ нормальнымъ, содержаніе жид-
кости въ одной изъ клѣтокъ, то отъ этой клѣтки во всѣ стороны
распространится смѣщеніе окружающихъ ее клѣтокъ съ заполняющей
ихъ жидкостью, и это смѣщеніе будетъ длиться въ теченіе нѣкото-
раго времени. Это смѣщеніе мы можемъ, какъ и токъ жидкости,
охарактеризовать нѣкоторымъ векторомъ. Одновременно со смѣще-
ніемъ въ стѣнкахъ клѣтокъ должны возникать упругія силы, которыя
стремятся измѣнить направленіе смѣщенія на обратное. Направленіе
вектора, изображающаго смѣщеніе, совпадаетъ съ направленіемъ па-
денія давленій въ жидкости, уравновѣшивающагося съ силами напря-
женій, т. е. совпадаетъ съ направленіемъ самаго смѣщенія. Это уде-
ніе давленій или, какъ можно выразиться иначе, сила смѣщенія/раз-
считанная на единицу объема, можетъ быть уподоблена электриче-
скому напряженію въ эѳирѣ. Какъ и электрическое нацряженіе, эта
сила есть величина векторіальная.
Мы исходили изъ предположенія, что въ одной изъ клѣтокъ
появляется избытокъ содержанія жидкости по сравненію съ нормаль-
нымъ. Но совершенно подобнымъ образомт^Щц можемъ предполо-
Нѣкоторыя уподобленія
33
жить и недостатокъ жидкости въ клѣткѣ. Въ послѣднемъ случаѣ также
возникнетъ смѣщеніе жидкости вокругъ этой клѣтки, но направлено
оно будетъ къ этой клѣткѣ. Мы видимъ такимъ образомъ, что избы-
токъ и недостатокъ жидкости вполнѣ аналогичны положительному
и отрицательному заряду.
Въ этомъ уподобленіи наиболѣе удивительнымъ является то
обстоятельство, что студень, какъ мы его понимаемъ, по своимъ
механическимъ свойствамъ долженъ быть отнесенъ къ числу твер-
дыхъ тѣлъ. А между тѣмъ непосредственно передъ этимъ мы ука-
зали, что уподобленіе эѳира твердому тѣлу недопустимо. Это кажу-
щееся противорѣчіе разрѣшается, если вспомнить, что, разсматривая
студень, какъ модель эѳира, мы не обратили достаточнаго вниманія
на физическое состояніе упругихъ клѣтокъ, — а это состояніе мо-
жетъ быть точно опредѣлено лишь при помощи тензоровъ, но огра-
ничились разсмотрѣніемъ паденія давленій заключенной въ клѣткахъ
жидкости. Иными словами: пользуясь этимъ уподобленіемъ, мы прини-
маемъ, что внутренняя структура эѳира и ея измѣненія при всѣхъ
наблюденіяхъ остаются отчасти скрытыми, и что при наблюдаемыхъ
явленіяхъ играютъ роль не самыя деформаціи, но только общія смѣ-
щенія клѣтокъ и сопровождающее ихъ паденіе давленій.
Но и это уподобленіе имѣетъ свою слабую сторону. Оказывается
затруднительнымъ представить себѣ, какимъ образомъ вѣсомыя тѣла
могутъ двигаться въ студнеобразномъ эѳирѣ. Эѳиръ и вѣсомая мате-
рія не должны быть непроницаемыми другъ для друга, напротивъ, вѣ-
сомыя тѣла должны, подобно тѣнямъ, проникать черезъ студень. Но
даже если мы остановимся на такомъ предположеніи, оказывается еще
затруднительнымъ представить себѣ, какимъ образомъ электрическіе
заряды, которые все же связаны съ матеріей, могутъ вмѣстѣ съ ней
мѣнять свое мѣсто. При такомъ движеніи положительно заряженнаго
тѣла избытокъ жидкости долженъ пропадать въ одной клѣткѣ и
появляться въ другой. Поэтому на нашей модели движеніе положи-
тельнаго заряда нужно представлять себѣ, какъ мгновенное разру;
шеніе хрупкихъ стѣнокъ клѣтки и проникновеніе черезъ нихъ избытка^
жидкости безъ затраты энергіи. Совершенно подобнымъ ^обра-
зомъ слѣдуетъ представлять себѣ и движеніе отрицательно завялен-
наго тѣла. Но простого механизма такихъ явленій предъявить себѣ
мы не въ состояніи и потому приходится принять, что наша модель
не разъясняетъ отчетливо движенія матеріальныхъ гМф^и силъ, дѣй-
Ми. Электричество и магнитизмъ. 3
34
Полное напряженіе
ствующихъ между заряженными тѣлами. Но если мы ограничимся
разсмотрѣніемъ электрическаго поля неподвижныхъ тѣлъ, то наша
модель оказывается вполнѣ пригодной и можетъ намъ помочь легче
и отчетливѣе представить себѣ многіе нижеописанные факты, нежели
мы это смогли бы сдѣлать, не пользуясь никакой моделью.
Но и при указанныхъ ограниченіяхъ все же не слѣдуетъ слиш-
комъ сильно настаивать на представленіи эѳира въ видѣ студня. Въ
электродинамикѣ мы увидимъ, что структуру этого студня мы должны
представлять себѣ еще нѣсколько болѣе сложной, сравнительно съ
указанной здѣсь ради простоты, если только потребуемъ отъ нея,
чтобы она дѣйствительно передавала намъ свойства механизма явле-
ній въ эѳирѣ.
ПОЛНОЕ НАПРЯЖЕНІЕ.
24. При изученіи упругихъ напряженій въ деформированномъ
тѣлѣ, вообще говоря, крайне затруднительнымъ оказывается опре-
дѣлить состояніе напряженія въ каждой отдѣльной точкѣ. Иногда,
правда, удавалось производить такія точныя изслѣдованія, напри-
мѣръ, надъ деформированнымъ стекломъ; въ этомъ случаѣ наблю-
дали для каждой точки двойное лучепреломленіе, связанное съ упру-
гой деформаціей, и отсюда уже дѣлали общее заключеніе о степени
напряженія и объ его пространственной оріентировкѣ. Подобное же
обстоятельное изслѣдованіе предстояло бы намъ, если бы мы стали,
какъ это до сихъ поръ предполагалось, измѣрять электрическое поле
какимъ-нибудь электроскопомъ во всѣхъ его точкахъ.
Но при механическихъ изслѣдованіяхъ обычно съ полнымъ пра-
вомъ ограничиваются опредѣленіемъ величины, которая можетъ быть
названа „полнымъ напряженіемъ" или „интегральной величиной" упру-
гихъ напряженій. Въ случаяхъ, когда потребуется большая точность
въ терминологіи, намъ придется отличать „величину напряженія въ
отдѣльной точкѣ" отъ „полнаго напряженія". Полное напряженіе
относятъ не къ какой-либо отдѣльной точкѣ, но къ цѣлой поверх-
ности, проходящей черезъ упругое тѣло. Напримѣръ, полное напряже-
ніе на нѣкоторомъ сѣченіи проволоки, растянутой по напі^ленію ея
длины, равняется величинѣ удѣльнаго напряженія, которое^ можно вы-
разить въ атмосферахъ на единицу поверхности, умноженной на ве-
личину поперечнаго сѣченія, выраженную въ квадратныхъ сантимет-
рахъ. Это полное напряженіе равняется растягивающей проволоку
силѣ, выраженной въ килограммахъ. Подобнымъ образомъ полное
Полное напряженіе
35
напряженіе сжимаемой въ гидравлическомъ прессѣ жидкости на по-
верхность поршня равняется удѣльному напряженію жидкости, т. е.
ея давленію на единицу поверхности, умноженному на площадь
сѣченія поршня. И въ этомъ случаѣ полное напряженіе равняется
величинѣ той силы, которая дѣйствуетъ на поршень. Если же имѣетъ
мѣсто болѣе сложный случай неоднородной деформаціи, какъ, на-
примѣръ, изгибъ стержня, то напряженія въ различныхъ точкахъ
имѣютъ различныя значенія; въ такомъ случаѣ нужно для каждаго
мѣста опредѣлить произведеніе изъ величины удѣльнаго напряженія
(точнѣе — одной слагающей этого напряженія) въ этомъ мѣстѣ и
величины элемента поверхности въ томъ же мѣстѣ, и затѣмъ про-
суммировать такія произведенія для всѣхъ элементовъ, на которые раз-
лагается вся поверхность. Такимъ образомъ получается величина, со-
впадающая съ величиною приложенныхъ извнѣ силъ.
При такомъ опредѣленіи нужно еще имѣть въ виду, что каж-
дый элементъ поверхности имѣетъ двѣ стороны. Если для какого-
либо элемента мы замѣнимъ направленія, которыя мы называемъ
„внутрь" и „наружу", одно другимъ, то сила давленія на этотъ эле-
ментъ останется неизмѣнной по величинѣ и лишь измѣнитъ свое на-
правленіе на обратное. Такъ, напримѣръ, вертикально висящая на-
тянутая проволока дѣйствуетъ съ нѣкоторою силою на ограничиваю-
щую ее сверху поверхность, и эта сила направлена внизъ; на поверх-
ность же, ограничивающую проволоку снизу, дѣйствуетъ такая же
по величинѣ сила, но направленная вверхъ. Если столбъ жидкости
снизу ограниченъ перегородкой, то онъ производитъ на эту перего-
родку давленіе, направленное внизъ; если—при той же высотѣ стол-
ба— перегородка находится сверху, то на нее дѣйствуетъ давленіе
той же величины, но направленное вверхъ. Итакъ, если мы замѣнимъ
для всей поверх-
или сила давленія,
одно другимъ направленія „внутрь" и „наружу"
ности, на которую вычисляется полное давленіе
то отъ этого измѣнится знакъ этой величины.
Соотношеніе между напряженіемъ въ данной точкѣ и полнымъ ,
напряженіемъ въ эѳирѣ совершенно аналогично такому же соотно^
шенію для вѣсомой матеріи. Но въ виду векторіальнаго характера^лек-
трическаго напряженія полную величину его относятъ къ нѣк^орой
линіи, проведенной въ электрическомъ полѣ. Если уголъ ме^фу напра-
вленіемъ поля, сила котораго есть Е, и направленіемъ дикаго отрѣзка
длины 5, вдоль котораго мы желаемъ вычислить полную величину
з
36
Полное напряженіе
силы поля, есть </, то прежде всего мы опредѣляемъ слагающую ве-
личины Е по направленію 5; она равняется Е8 = Есо$с[. Полное
напряженіе эѳира вдоль отрѣзка 5 представляется произведеніемъ этой
слагающей на длину отрѣзка Е8 . 8 — Е . $ . соз (р. Въ случаѣ отрѣзка
большей длины прямолинейнаго или криволинейнаго, мы разбиваемъ
его на элементы , $.2, и т. д., которые можно считать всѣ прямоли-
нейными и которые настолько малы, что на протяженіи каждаго изъ
нихъ сила поля не измѣняется на замѣтную величину и можетъ счи-
таться соотвѣтственно постоянной, равной Ег, Е2, и т. д. Затѣмъ
мы опредѣляемъ полное напряженіе вдоль отдѣльныхъ элементовъ и
составляемъ изъ нихъ сумму
V = Ех . . СО8 (рі + Е.г . 82 . СО8 (р2 -]-•••= ЕЕ8 . 8,
Эту величину сумму величинъ силы поля вдоль данной линіи
мы и примемъ за полное напряженіе по этой линіи.
При этомъ слѣдуетъ замѣтить, что величина слагающей Е8, въ
зависимости отъ направленія, по которому отсчитывается длина 8,
будетъ либо положительной, либо отрицательной. Слѣдовательно,
полное напряженіе V мѣняетъ знакъ при измѣненіи направленія ли-
нейнаго отрѣзка. Если А и В суть концы этого отрѣзка, то указанное
свойство можно выразить такъ:
Весьма полезно эти крайне важныя опредѣленія запомнить въ
формѣ слѣдующаго положенія: полное напряженіе эѳира вдоль
линейнаго отрѣзка АВ равно „линейной суммѣ" силъ поля,
указаннымъ образомъ разсчитанной на этотъ отрѣзокъ; его
величина мѣняетъ знакъ съ измѣненіемъ направленія, при-
писываемаго отрѣзку.
Слѣдуетъ замѣтить, что такое опредѣленіе полнаго напряженія
электрическаго поля вдоль нѣкотораго линейнаго отрѣзка вполнѣ
сохраняетъ силу и для полей, образующихся внутри твердыхъ зфлъ;
это становится яснымъ, если принять во вниманіе данное въконцѣ
§19 опредѣленіе
силы такого поля.
РАВНОВѢСІЕ НАПРЯЖЕНІЙ.
интегральныхъ величинъ для измѣреній выясняется
вопроса о равновѣсіи. Внутри дѣсомаго тѣла рав-
25. Значеніе
при разсмотрѣніи
новѣсіе имѣетъ мѣсто въ томъ и только въ случаѣ, если полныя
Равновѣсіе напряженій
37
напряженія на любыя двѣ поверхности, лежащія цѣликомъ внутри тѣла и
имѣющія общую линейную границу, равны между собой. Дѣй-
ствительно, если мы разсмотримъ двѣ такія поверхности съ общей
линейной границей, то мы замѣтимъ, что онѣ вмѣстѣ образуютъ
одну замкнутую поверхность, заключающую въ себѣ нѣкоторый
> объемъ подвергнутаго напряженіямъ тѣла. Ясно, что направленія
„внутрьи и „наружу" измѣняются на обратныя при переходѣ отъ од-
ной изъ нашихъ двухъ поверхностей къ другой. Если теперь выше-
указанное условіе равновѣсія выполнено, то силы, дѣйствующія на обѣ
части этой поверхности, равны между собой и противоположны по
знаку. Слѣдовательно, на весь этотъ объемъ тѣла дѣйствуетъ сила, рав-
ная нулю, и потому внутреннія силы находятся въ равновѣсіи. Но если
указанное условіе не соблюдено, то отдѣльныя части тѣла испыты-
ваютъ дѣйствія силъ, вызывающія ихъ передвиженія. Получается, та-
кимъ образомъ, внутреннее движеніе, необходимая для котораго энер-
гія получается, конечно, отъ энергіи напряженій. При этомъ движе-
ніи энергія будетъ непрерывно тратиться на треніе и т. п., пока тѣло
не придетъ снова въ состояніе покоя. Если же это состояніе достиг-
нуто, то въ тѣлѣ устанавливается такое распредѣленіе напряженій,
которое удовлетворяетъ условію равновѣсія. Отсюда слѣдуетъ, что
при одинаковыхъ прочихъ обстоятельствахъ внутренняя энергія тѣла
имѣетъ при равновѣсіи напряженій меньшую величину, чѣмъ при
любомъ иномъ распредѣленіи ихъ.
Въ частномъ случаѣ жидкости или газа слѣдствіемъ указаннаго
условія равновѣсія является нижеслѣдующее простое положеніе: при
равновѣсіи давленіе въ жидкости или въ газѣ имѣетъ повсюду одно
и то же значеніе. Если, напримѣръ, въ нѣкоторой части газа, за-
ключеннаго въ замкнутый сосудъ, имѣетъ мѣсто большая плотность
(т. е. большее давленіе), чѣмъ въ остальныхъ частяхъ его объема,
то прежде всего возникаютъ болѣе или менѣе неравномѣрныя волны
давленій, распространяющіяся во всѣ стороны; затѣмъ внутреннее
и внѣшнее треніе совершенно поглощаютъ избытокъ свободной энер-
гіи, и газъ принимаетъ спокойное состояніе, наполняя весь объемъ со-^'
суда съ равномѣрной повсюду плотностью.
Совершенно такъ же обстоитъ дѣло и для случая электриче-
скаго поля. Для него условіе равновѣсія заключается въ^гижеслѣ-
дующемъ положеніи: электрическія напряженія эѳира нахо-
дятся въ равновѣсіи въ томъ и только въ томъ^случаѣ, когда
38
Равновѣсіе напряженій
полныя напряженія на всѣ кривыя съ общими конечными
точками равны между собой.
Представимъ себѣ двѣ кривыя, имѣющія общія конечныя точки
А и В. Ясно, что онѣ обѣ вмѣстѣ образуютъ замкнутую линію. Ко-
нечно, при этомъ направленіе одной изъ кривыхъ нужно измѣнить
на обратное. Если напряженія на эти двѣ кривыя суть соотвѣтственно
V и У", то напряженіе вдоль всей замкнутой линіи равняется
У'ав+^ВА=^ЛВ У"лл=^.^).
Если условіе равновѣсія соблюдено, то эта сумма, взятая вдоль замк-
нутой линіи, должна равняться нулю. Чтобы уяснить себѣ значеніе
этого условія, вообразимъ въ нѣкоторой точкѣ замкнутой кривой,
напримѣръ, въ точкѣ Л, заряженную частичку, которую особый ме-
ханизмъ передвигаетъ вдоль всей замкнутой кривой, пока она не
окажется снова въ точкѣ А. Послѣ совершенія этого процесса поло-
женія всѣхъ тѣлъ, возбуждающихъ поле, и самой маленькой заряжен-
ной частички оказываются неизмѣнившимися. Но осталось ли послѣ
этой операціи и самое поле также неизмѣннымъ? На это отвѣтъ
намъ даетъ величина суммы, взятой вдоль замкнутой линіи. Дѣй-
ствительно, если величина силового дѣйствія, которое испытываетъ
частичка въ полѣ, равномъ единицѣ, равняется Р1, то, согласно дан-
ному въ § 19 опредѣленію силы поля Е, сила, дѣйствующая въ на-
шемъ полѣ на частичку, равняется Р = Е . Рх. Поэтому каждый членъ
нашей суммы равенъ
Е . 8 . СО8 ср = . Р . 5 . соз .Ц,
гдѣ Ь8 означаетъ энергію, поглощаемую механизмомъ, движущимъ
частичку при передвиженіи ея вдоль линейнаго отрѣзка 5. Слѣдо-
вател ьно,
2Е, . 5 ± =
о о
гдѣ А—-энергія, поглощаемая движущимъ механизмомъ отъ электри-
ческаго поля эѳира при передвиженіи частички вдоль всей замкнутой
линіи. Если условіе равновѣсія не соблюдено, то величиц^Уотлична
отъ нуля и, слѣдовательно, послѣ указанной операці^эійргія эѳира
и самое поле измѣняются, хотя обстоятельства, возбуждающія поле,
9 Знакъ 5 указываетъ символически на то, чтодинейные элементы, по ко
торымъ производится суммированіе, образуютъ <яДмкнутую литію. Поим п? р
ч Равновѣсіе напряженій
39
остаются безъ измѣненія. При этомъ Л представляетъ собою величину
положительную или отрицательную, въ зависимости отъ выбраннаго
нами направленія движенія по замкнутой кривой. Положимъ, это на-
правленіе выбрано такъ, что А является величиною положительною.
Въ такомъ случаѣ при нашемъ процессѣ мы получаемъ энергію отъ
эѳира. Если мы нѣсколько разъ этотъ процессъ повторимъ, то коли-
чество энергіи въ эѳирѣ будетъ становиться все меньше и меньше,
и вмѣстѣ съ тѣмъ силовыя линіи будутъ располагаться все иначе и
иначе. Запасъ энергіи будетъ, слѣдовательно, постепенно исчерпы-
ваться, т. е. силовыя линіи будутъ располагаться такъ, что погло-
щаемая при передвиженіи вдоль замкнутой кривой энергія Ь будетъ
становиться все меньше и меньше, и, наконецъ, даже станетъ без-
конечно малой, иначе говоря, нулемъ. Когда это достигнуто, въ
дальнѣйшемъ поле уже остается неизмѣннымъ; его энергія при этомъ
имѣетъ наименьшее значеніе, какое только она можетъ имѣть при
заданномъ распредѣленіи возбуждающихъ поле тѣлъ. Условіемъ для
этого является равенство Ь = 0, т. е. %Е8 .5 = 0 или же V . о = V" лѵ
Все это разсужденіе имѣетъ силу не только для полей въ газо-
образныхъ и жидкихъ средахъ, но также и для полей, лежащихъ
отчасти или вполнѣ внутри твердыхъ тѣлъ. Въ послѣднихъ только
приходится вообразить (какъ это было замѣчено уже въ концѣ §19)
пробуравленные каналы, по которымъ электрически заряженная ча-
стичка можетъ двигаться.
Условіе равновѣсія электрическаго поля тождественно
съ условіемъ, чтобы энергія поля при данномъ распредѣ-
леніи возбуждающихъ поле тѣлъ имѣла величину меньшую,
чѣмъ при всякомъ иномъ распредѣленіи силовыхъ линій.
Но какъ это возможно, чтобы поле, не находящееся въ равно-
вѣсіи, измѣнялось вслѣдствіе перемѣщенія электрической частички по
замкнутой кривой? Конечно, это возможно только въ томъ случаѣ,
если перемѣщеніе частички вызываетъ въ эѳирѣ состояніе, соотвѣт-
ствующее тому, которое для вѣсомой матеріи называется „движеніемъ“5х
и которое можетъ переносить напряженія съ одного мѣста на другре.
Это „состояніе движенія“ эѳира мы изучимъ въ электродинамической
части нашего курса. Здѣсь мы укажемъ только, что это ^Стояніе
можетъ возникать также и само собою безъ внесенія электрической
частички, пока условіе равновѣсія не соблюдено.Обстоятельства»
имѣющія мѣсто въ эѳирѣ, слѣдовательно, вполнѣ ацздогичны обстоя-
40
Равновѣсіе напряженій
тельствамъ, имѣющимъ мѣсто въ области вѣсомой матеріи. Предста-
вимъ себѣ, напримѣръ, плоскій конденсаторъ и въ немъ электриче-
ское поле, въ которомъ линіи силъ въ одномъ мѣстѣ расположены
плотнѣе, чѣмъ въ остальныхъ частяхъ объема, заключеннаго между
пластинками. Легко понять, что въ этомъ случаѣ мы можемъ провести
такія замкнутыя линіи, что взятая вдоль нихъ сумма 2Е8.8 отлична
отъ нуля. Слѣдовательно, часть электрической энергіи должна отдѣ-
литься и произвести въ эѳирѣ нѣкоторый процессъ, вызывающій
переносъ сильно сконцентрированнаго въ этомъ мѣстѣ напряженія
въ иныя мѣста. Такимъ образомъ въ пространствѣ между двумя
пластинками конденсатора возникаютъ болѣе или менѣе неправильныя
„электрическія волны"; мѣста уплотненія силовыхъ линій передви-
Рис. 10. Поле плоскаго конден-
сатора.
гаются то къ краямъ, то къ серединѣ
пространства, лежащаго между пла-
стинками. Но, какъ мы увидимъ ниже,
электрическія волны всегда связаны съ
поглощеніемъ энергіи тѣлами, ограни-
чивающими поле (въ данномъ случаѣ
пластинками конденсатора). Въ силу
этого избытокъ энергіи будетъ посте-
пенно уничтожаться, пока, наконецъ,
не установится такое распредѣленіе
силовыхъ линій, которое соотвѣтствуетъ условію равновѣсія (рис. 10).
Въ этомъ случаѣ мы будемъ имѣть картину поля, съ которой мы
уже познакомились въ § 20.
Такъ какъ въ статическомъ электрическомъ полѣ величина пол-
наго напряженія зависитъ только отъ выбора конечныхъ точекъ
(А и В), но не отъ вида соединяющей ихъ кривой, то ее называютъ
просто электрическимъ напряженіемъ между А и В или, если
желательно подчеркнуть направленіе, — напряженіемъ отъ А къ В.
26. Къ условію равновѣсія для статическаго поля слѣдуетъ при-
соединить еще одинъ весьма важный законъ: Ч
Полное напряженіе между двумя точками въ р^овод-
никѣ равняется нулю. I
Изъ этого закона слѣдуетъ:
Полное напряженіе между любыми дву^^роводниками
есть величина постоянная, не зависящая отъ вида кривой,
проведенной между этими проводниками^
Потенціалъ
41
Изъ него же можно вывести, что электрическое поле на по-
верхности проводника направлено всегда нормально къ ней-
Въ справедливости этихъ законовъ можно убѣдиться, разсма-
тривая тѣ поля, изображенія которыхъ приведены въ § 20. Чрезвы-
чайно наглядной въ этомъ смыслѣ является третья картина (плоскій
конденсаторъ). Ясно видно, что между обѣими пластинами, гдѣ длина
силовыхъ линій постоянна, плотность ихъ, т. е. сила поля, также по-
стоянна. На краяхъ, гдѣ силовыя линіи удлиняются, сила поля осла-
бляется; при томъ она становится тѣмъ меньше, чѣмъ длиннѣе ста-
новятся линіи силъ. Нашъ законъ указываетъ, что средняя величина
силы поля вдоль силовой линіи обратно пропорціональна длинѣ этой
линіи.
ПОТЕНЦІАЛЪ.
27. Для описанія электрическаго поля очень удобно выбрать въ
немъ постоянную точку В и напряженіе во всякой другой точкѣ А
опредѣлять, какъ полное напряженіе по линіи, соединяющей А съ В.
Поле будетъ вполнѣ изучено, если въ каждой его точкѣ мы будемъ
знать напряженіе, опредѣленное такимъ образомъ. Раньше для озна-
комленія съ электрическимъ полемъ, мы старались изучить силу поля
во всѣхъ его точкахъ; мы должны отмѣтить преимущество новаго
способа, къ которому мы прибѣгаемъ теперь: тогда какъ сила поля
есть векторъ, напряженіе представляется простымъ числомъ. Со-
гласно сказанному въ § 26, мы можемъ вмѣсто неподвижной точки В
выбрать опредѣленный проводникъ; конечно, этотъ проводникъ во
всякое время долженъ находиться въ нашемъ распоряженіи. Ясно,
что наиболѣе удобнымъ такимъ проводникомъ является для насъ
земная поверхность; мы знаемъ, что она является проводникомъ,
такъ какъ заключаетъ въ себѣ воду.
Электрическое напряженіе между нѣкоторой точкой А
и земной поверхностью называютъ электрическимъ потен-
ціаломъ точки А.
Потенціалъ земли, слѣдовательно, равенъ нулю.
На этомъ основаніи мы можемъ указанное въ § 26 свойство'
проводниковъ выразить иначе такъ: если электрическое^<оле
находится въ состояніи равновѣсія, то проводникъ имѣетъ
во всѣхъ точкахъ одинаковый потенціалъ.
Если мы имѣем ъ два удаленные другъ отъ друга полированные
проводника, изъ которыхъ одинъ имѣетъ потенціалъ^ равный нулю,
42
Потенціалъ
т. е. не возбуждаетъ въ окружающемъ его пространствѣ никакого поля,
а другой заряженъ до опредѣленнаго потенціала I/, и соединяемъ
ихъ проводящей проволокой, то распредѣленіе возбуждающихъ поле
зарядовъ и силовыхъ линій станетъ послѣ этого соединенія измѣ-
няться, пока, наконецъ, оба проводника не примутъ одинъ и тотъ
же потенціалъ. Слѣдовательно, послѣ такого соединенія электриче-
ское поле возникаетъ также вокругъ тѣла, не бывшаго заряженнымъ.
Отсюда мы заключаемъ, что указанное въ § 26 свойство проводни-
ковъ имѣетъ важнѣйшее значеніе въ дѣлѣ распредѣленія зарядовъ;
въ силу этого свойства, тѣла, имъ обладающія, и называются про-
водниками.
Когда мы, пользуясь даннымъ въ §§ 24 и 25 опредѣленіемъ
полнаго напряженія между точками А и В, соединяемъ эти точки
нѣкоторой линіей, то мы, конечно, можемъ провести эту лині^
такъ, что она въ нѣкоторой точкѣ С коснется земли. Въ такомъ
случаѣ
^ав = V ас + Ѵсв-
Но ѴАС представляетъ собою потенціалъ въ точкѣ Л, который мы
сокращенно обозначимъ чрезъ ѴА; Ѵсв = — Ѵвс = Ѵв предста-
вляетъ собою взятый со знакомъ минусъ потенціалъ Ѵв въ точкѣ В.
Слѣдовательно,
ѴАВ=ѴА ѴВ-
Напряженіе между двумя точками равняется разности
ихъ потенціаловъ.
ЭЛЕКТРОМЕТРЪ.
28. Какъ уже было указано при введеніи понятія о полномъ
напряженіи, оно особенно важно потому, что почти всѣ электриче-
скія измѣренія практически ограничиваются опредѣленіемъ полнаго
напряженія между тѣлами, возбуждающими поле.
Приборы, предназначаемые для измѣренія напряженія менаду
двумя точками, называются электрометрами.
Всякій электрометръ состоитъ изъ индикатора (казеннаго въ
§ 1 электроскопомъ), помѣщеннаго между двумя изолированными
другъ отъ друга металлическими тѣлами. Эти два тѣла ^соединяются
при помощи проводящихъ проволокъ съ тѣми днуМя точками, пол-
ное напряженіе между которыми мы желаемъ ^изучить. Благодаря
этому они заряжаются, и напряженіе ме^му^ ними равняется на-
Электрометръ
43
пряженію между изслѣдуемыми точками; сила поля, которую ука-
зываетъ индикаторъ, тѣмъ значительнѣе, чѣмъ больше это напряже-
ніе. По показанію индикатора мы можемъ поэтому прямо сдѣлать
заключеніе о силѣ изучаемаго поля.
При примѣненіи такого способа мы вносимъ измѣряемое поле
внутрь небольшого инструмента, такъ какъ послѣдній не слѣдуетъ
переносить съ его мѣста, гдѣ онъ разъ навсегда прочно установленъ
и хорошо вывѣренъ. Понятно, что это крайне важно для точныхъ
измѣреній.
При выборѣ индикатора можно, какъ это уже было оговорено»
въ § 1, пользоваться разнообразными дѣйствіями электрическаго поля
на вѣсомую матерію. Наиболѣе употребительные инструменты осно-
ваны на простѣйшемъ изъ этихъ дѣйствій— силовомъ дѣйствіи, испы-
тываемомъ заряженнымъ тѣломъ въ электрическомъ полѣ.
Простѣйшимъ типомъ электрометра является электрометръ Ган-
келя (рис. 11). Онъ состоитъ изъ двухъ изолированныхъ металли-
ческихъ пластинокъ, расположенныхъ другъ противъ друга, какъ въ
плоскомъ конденсаторѣ. Посрединѣ между ними подвѣшена тонкая
металлическая нить (или же золотой листочекъ), которой сообщается
нѣкоторый зарядъ; она представляетъ собою, такимъ образомъ, чув-
ствительный электрическій маятникъ.
Вмѣсто этого въ квадрантномъ электрометрѣ Томсона (лорда
Кельвина) для достиженія большей чувствительности примѣненъ
родъ крутильныхъ вѣсовъ. Здѣсь индикаторомъ служитъ очень тон-
кій легкій листочекъ жести, вырѣзанный въ формѣ бисквита и под-
вѣшенный горизонтально на тончайшей металлической нити, которому
сообщается опредѣленный зарядъ. Подъ этимъ „ бисквитомъ“ нахо-
дится горизонтально расположенная плоская металлическая пластинка
(обычно круглой формы), раздѣленная на четыре квадранта. Каждые
два взаимно противолежащіе квадранта соединены между собою ме-
таллически ; съ этими парами квадрантовъ соединяются проводя-
щими проволоками точки, между которыми опредѣляется полное наЛх
пряженіе (рис. 12). Бисквитообразный индикаторъ виситъ непосред-
ственно надъ квадрантами и притомъ симметрично надъ^оДйимъ
изъ разрѣзовъ. Поле, возникающее между парами квадрантовъ,
выводитъ бисквитъ изъ его положенія равновѣсія, и отклоненіе бис-
квита тѣмъ значительнѣе, чѣмъ сильнѣе это поле. ЙноѴда употре-
бляются вмѣсто одной двѣ раздѣленныя на квадраты круглыя пла-
44
Электрометръ
стинки; одна изъ нихъ помѣщается, какъ сейчасъ описано, подъ
бисквитомъ, другая же надъ нимъ. Каждые два другъ надъ другомъ
расположенные квадранта соединяются своими краями при помощи
пригнанной къ нимъ металлической полосы. Въ этомъ случаѣ обѣ
Рис. 11. Электрометръ
Ганкеля.
Рис. 12. Квадрантный электро-
метръ.
полую металлическую коробку, .внутри
пластинки образуютъ собою
которой виситъ индикаторъ.
Иную форму квадрантнаго электрометра представляетъ собою
цилиндрическій квандрантный электрометръ; въ немѵйіеталлическая
коробка замѣнена разрѣзаннымъ на четыре части^металлическимъ
цилиндромъ, квадранты котораго опять попарн(Деоединены металли-
Электрометръ
45
листочками. Электрометръ Экснера"отли-
въ немъ симметрично
Рис. 13. Электрометръ
Экснера.
напряженіяхъ; они,
возможности опре-
Если одинъ изъ за-
соединимъ съ зем-
чески. Индикаторомъ здѣсь служитъ подвѣшенный внутри цилиндра
металлическій барабанъ.
Процессъ измѣренія часто упрощаютъ, не прибѣгая къ особому
источнику электричества для электризаціи индикатора. При такомъ
упрощеніи электрометръ Ганкеля обращается въ обыкновенный элек-
трометръ съ золотыми
чается отъ послѣдняго только тѣмъ, что
подвѣшены два золотые листочка (рис. 13).
Электроскопы съ золотыми листочками ста-
ринной формы, въ которыхъ между листоч-
ками нѣтъ твердой пластинки, для измѣреній
мало пригодны.
Инструменты, въ которыхъ индикатору
сообщается особый зарядъ, отличаются не толь-
ко высокой чувствительностью, но еще и тѣмъ,
что при обращеніи напряженія ихъ отклоне-
ніе также измѣняется на обратное. Инстру-
менты, въ которыхъ индикатору не сообщается
особаго заряда, даютъ отклоненіе въ одну и
ту же сторону при всѣхъ
слѣдовательно, не даютъ
дѣлить знакъ напряженія,
жимовъ электрометра мы
лею, а другой съ заряженнымъ тѣломъ Л, то
мы измѣримъ непосредственно потенціалъ Л.
Чтобы ознакомиться съ употребленіемъ электрометра, мы провѣ-
римъ съ помощью электрометра Экснера законъ постоянства потен-
ціала во всѣхъ точкахъ проводника. Въ качествѣ источника электри-
чества здѣсь удобнѣе всего воспользоваться такъ называемой галь-
ванической батареей; подробнѣе съ нею мы ознакомимся ниже, а
здѣсь лишь замѣтимъ, что съ ея помощью получаются поля постоян-
наго напряженія. Соединимъ одинъ полюсъ этой батареи и одинъ<^
изъ зажимовъ электрометра Экснера съ водопроводомъ (т. е^бсъ
землею). Другой зажимъ электрометра, сообщающійся съ пластинкой„
расположенной между листочками, соединимъ съ помощью, изолиро-
ванной проволоки г) съ вторымъ полюсомъ батареи. Если^теперь спро-
Э Т. е. проволоки, обмотанной шелкомъ. Прим. пер..
46
Электрометръ
'ектировать электрометръ на экранъ, гдѣ имѣется масштабъ какъ
разъ въ томъ мѣстѣ, гдѣ получаются изображенія концовъ листоч-
ковъ, то можно будетъ легко отсчитывать величины отклоненій, даю-
щія напряженіе батареи. Разъединимъ сперва листочки электроскопа
и полюсъ батареи и соединимъ послѣдній проволокою съ нѣсколь-
кими металлическими тѣлами, расположенными на стеклянныхъ под-
ставкахъ (какъ въ § 10). Если мы затѣмъ будемъ соединять свобод-
ный конецъ ведущей къ электроскопу проволоки съ различными
точками этой системы проводящихъ тѣлъ, то всегда будемъ полу-
Рис. 14. Въ системѣ соединенныхъ между собою проводни-
ковъ потенціалъ постояненъ.
мать одно и то же отклоненіе - то самое, которые мы получаемъ и
при прямомъ соединеніи электроскопа съ батареей. Это и служитъ
доказательствомъ, что каждое изъ металлическихъ тѣлъ, соединен-
ныхъ проводникомъ съ полюсомъ батареи, возбуждаетъ въ окру-
жающемъ его пространствѣ поле, полное напряженіе въ которомъто
же, что и въ полѣ гальванической батареи (рис. 14).
ДВОЙНЫЕ СЛОИ НА ИЗОЛЯТОРАХЪ.
29. Возвратимся теперь къ нашему исходному вопросу о воз-
никновеніи электрическаго возбужденія при соприкосновеніи двухъ
тѣлъ. До сихъ поръ мы обращали вниманіе только на зарядъ одного
изъ двухъ приводимыхъ въ соприкосновеніе тѣлъ,> напримѣръ, стек-
Двойные слои на изоляторахъ
47
лянной или эбонитовой палочки, но не задавали себѣ вопроса, не
пріобрѣтаетъ ли при соприкосновеніи способности создавать электриче-
ское возбужденіе эѳира также и то тѣло, которое играетъ роль терки.
Если мы пожелаемъ заняться этимъ вопросомъ, то мы должны,
конечно, позаботиться о хорошей изоляціи. Изслѣдуемыя тѣла должны
быть скрѣплены съ деревянными пластинками, снабженными хорошо
изолирующими стеклянными ручками. Возьмемъ, напримѣръ, деревян-
ную пластинку, покрытую кожею, на которую нанесена цинковая
амальгама, и деревянную пластинку, на которую наклеено оконное
стекло. Прежде, чѣмъ привести въ соприкосновеніе стекло и цинко-
вую амальгаму, поднесемъ ихъ къ пламени бунзеновской горѣлки,
чтобы удалить съ нихъ случайные заряды. Послѣ этого мы можемъ
при помощи электрической стрѣлки убѣдиться въ томъ, что эти тѣла
въ окружающемъ ихъ пространствѣ не возбуждаютъ никакого поля.
Приложимъ теперь обѣ пластинки другъ къ другу и, слегка нажавъ,
сейчасъ же вновь разнимемъ. Если послѣ этого вновь приблизить къ
нимъ электрическую стрѣлку, то она укажетъ на наличность заря-
довъ, положительнаго на стеклѣ и отрицательнаго на цинковой амаль-
гамѣ. При этомъ оба тѣла возбуждаютъ поля приблизительно оди-
наковой силы.
Слѣдовательно, на поверхности соприкосновенія двухъ тѣлъ про-
исходитъ, такъ сказать, раздѣленіе двухъ количествъ электричества,
дающихъ вмѣстѣ нуль, такъ какъ одно тѣло заряжается положи-
тельно, другое — отрицательно.
Этотъ процессъ мы можемъ уяснить себѣ, пользуясь предста-
вленіемъ, уже упомянутымъ въ § 8, согласно которому молекулы
матеріальныхъ тѣлъ являются носительницами положительныхъ и
отрицательныхъ зарядовъ; въ незаряженномъ тѣлѣ эти заряды со-
вмѣстно даютъ нуль. Мы представимъ себѣ далѣе, что молекулы
каждаго опредѣленнаго рода обладаютъ способностью въ опредѣ-
ленной мѣрѣ присоединять въ избыткѣ одинъ изъ двухъ родовъ
зарядовъ. Такъ, напримѣръ, молекулы стекла имѣютъ большую спо- г
собность заряжаться положительно, а молекулы цинковой амалі^®
гамы — наоборотъ, отрицательно. Если 'два тѣла, обладающія эгида
противоположными способностями, привести въ соприкосновеніе, то
молекулы одного рода отнимаютъ отъ молекулъ другого^ рода при-
тягиваемый ими зарядъ (стекло — положительный, цинковая амаль-
гама — отрицательный). Такимъ образомъ, на грани^Ъбоихъ сопри-
48
Двойные слои на изоляторахъ
касающихся тѣлъ образуется „электрическій двойной слой“, возбу-
ждающій электрическое поле въ интра-молекулярныхъ промежуткахъ
соприкасающихся тѣлъ. Это поле стремится вызвать движеніе заря-
довъ въ направленіи, обратномъ тому, въ которомъ ихъ заставляетъ
двигаться притяженіе молекулъ; такъ, въ нашемъ примѣрѣ это поле
направлено отъ стекла къ цинковой амальгамѣ и стремится удалить
Рис. 15. Электризація при соприкосновеніи изоляторовъ.
положительные заряды отъ стекла, отрицательные заряды — отъ цин-
ковой амальгамы. Это поле дѣлается, наконецъ, настолько сильнымъ,
что стремленіе молекулъ къ дальнѣйшему заряженію уже не можетъ
превозмочь его дѣйствія. Если теперь разнять соприкасающіясях^ѣла,
то они, понятно, окажутся заряженными зарядами одинаковой Гвели-
чины, такъ какъ никакихъ электрическихъ зарядовъ вновь при со-
прикосновеніи не создалось; образовался только двоййой^электриче-
скій слой изъ зарядовъ, существовавшихъ и рандцЖ, но находив-
шихся въ состояніи взаимнаго смѣшенія.
При этомъ оказывается нужнымъ, чтобы ^іно изъ соприкасаю-
щихся тѣлъ обладало способностью заряжаться положительно, а дру-
Двойные слои на изоляторахъ
49
гое — отрицательно. Оба тѣла могутъ обладать способностью заря-
жаться однимъ и тѣмъ же родомъ электричества. Если они обладаютъ
этой способностью въ различной степени, то тѣло, обладающее ею въ
большей степени, будетъ притягивать заряды опредѣленнаго знака съ
большею силою, нежели другое тѣло, и результатъ получится тотъ же.
Если привести стекло въ соприкосновеніе съ шелкомъ, то оно по-
прежнему обнаружитъ наличность положительнаго заряда; шелкъ же
окажется заряженнымъ отрицательно. Но, конечно, здѣсь дѣйствіе
не столь значительно, какъ при употребленіи цинковой амальгамы.
Если же мы приведемъ въ соприкосновеніе эбонитовую пластинку и
шелкъ, то шелкъ наэлектризуется положительно, эбонитъ — отрица-
тельно (рис. 15). Стекло обладаетъ большимъ стремленіемъ къ поло-
жительному заряду, эбонитъ—къ отрицательному. Шелкъ занимаетъ
мѣсто между ними; при этомъ неясно, обладаетъ ли онъ нѣкоторымъ
слабымъ стремленіемъ къ положительнымъ или же къ отрицательнымъ
зарядамъ. Мы можемъ, такимъ образомъ, изслѣдовать каждое тѣло
лишь по сравненію съ нѣкоторымъ другимъ тѣломъ. Можно попы-
таться расположить различныя тѣла въ одинъ рядъ такъ, что каждое
тѣло этого ряда при соприкосновеніи съ однимъ изъ предшествую-
щихъ ему тѣлъ заряжается отрицательно, а при соприкосновеніи съ
однимъ изъ послѣдующихъ тѣлъ положительно. Упомянутыя три
тѣла дадутъ подобный рядъ:
4- стекло, шелкъ, эбонитъ —.
Присущее молекуламъ притяженіе опредѣленнаго рода электри-
чества, наличностью котораго обусловливается появленіе двойного элек-
трическаго слоя, называютъ „электродвижущей силой". Эта сила
принадлежитъ къ числу „силъ, присущихъ матеріи", подъ каковымъ
именемъ разумѣются всѣ такія молекулярныя дѣйствія, о природѣ ко-
торыхъ ничего болѣе неизвѣстно. Имѣетъ смыслъ лишь говорить объ
„электродвижущей силѣ между двумя тѣлами". Мѣрой послѣд-
ней служитъ электрическое напряженіе въ полѣ, возникающемъ въ
интрамолекулярныхъ промежуткахъ у поверхности соприкосновеніе
этихъ тѣлъ и удерживающемъ въ равновѣсіи, какъ мы видѣли, сцлй/
присущія молекуламъ. Но тѣмъ не менѣе еще не найдено ср^Соба
измѣрить это напряженіе, въ случаяхъ, подобныхъ нами ]э^с$отрѣн-
нымъ, когда, по крайней мѣрѣ, одно изъ двухъ соприкасающихся
тѣлъ является изоляторомъ. Съ увѣренностью можцр^шшь сказать,
Ми. Электричество и магнитнзмъ.
4
50
Двойные слои на изоляторахъ
что это напряженіе ничтожно мало въ сравненіи съ напряженіями,
доставляемыми электрической машиной. Но болѣе высокія напряженія
мы получаемъ, если силовыя линіи, имѣющія при соприкосновеніи
двухъ тѣлъ длины молекулярныхъ размѣровъ (около ІО-8 санти-
метра), растянемъ на конечную длину (нѣсколько сантиметровъ). Такъ
какъ напряженіе измѣряется произведеніемъ изъ силы поля на длину
силовой линіи, то оно въ этомъ случаѣ возрастаетъ во столько же разъ,
во сколько растягиваются линіи силъ (приблизительно въ 108 разъ).
Если при этомъ поверхности тѣлъ дѣйствительно были въ полномъ
соприкосновеніи и при разъединеніи ихъ не произошло никакой по-
тери зарядовъ, то можно сдѣлать приблизительную оцѣнку величины
электродвижущей силы, если считать наблюденное напряженіе въ сто
милліоновъ разъ большимъ величины этой силы. Но наши предполо-
женія, во всякомъ случаѣ, недостовѣрны, и столь огромная величина
Рис. 16. Двойной электрическій
слой на изоляторѣ.
въ дѣйствительности не достигается,
даже хотя бы приблизительно. Съ
увѣренностью мы можемъ утверждать
лишь то, что, при такомъ способѣ
возбужденія электрическихъ полей,
вся энергія эѳира получается за счетъ
работы, производимой при удаленіи
обоихъ тѣлъ другъ отъ друга про-
тивъ дѣйствія силъ взаимнаго притя-
женія зарядовъ. Сравнительно съ этой
работой, работа молекулярныхъ про-
цессовъ при установленіи двойного
электрическаго слоя оказывается совершенно исчезающей (рис. 16).
30. Теперь мы можемъ правильно представить себѣ способъ
дѣйствія такъ называемой „электрической машины съ треніемъ". Въ
ней электрическая энергія возбуждается вовсе не треніемъ, какъ это,
къ сожалѣнію, можно заключить изъ ея названія. Работа, идущая^ца
преодолѣніе тренія, для нашей цѣли оказывается совершенно ^про-
павшей, и эѳиру сообщается только та работа, которую мы ^должны
произвести, чтобы положительный зарядъ стекляннаго к^уга удалить
отъ отрицательнаго заряда подушекъ, покрытыхъ цинковой амальгамой.
Отсюда ясно, что машина тренія, весьма неэк^цомна, такъ какъ
большая часть идущей на нее работы уходитъ именно на пре-
одолѣніе тренія. Далѣе ясно, что эта машиндк^цоставляртъ одновре-
Опытъ Вольта
51
менно положительные и отрицательные заряды. Чтобы собрать на
подушкахъ отрицательный зарядъ, слѣдуетъ ихъ, подобно положи-
тельному кондуктору, изолировать на стеклянной подставкѣ и соеди-
нить съ металлическимъ шаромъ, съ котораго удобно снимать за-
рядъ. Если послѣ этого желательно имѣть зарядъ только одного
рода (напримѣръ, только положительный), то слѣдуетъ другой по-
люсъ (напримѣръ, подушки) отвести къ землѣ.
ОПЫТЪ ВОЛЬТА.
31. До сихъ поръ мы предполагали, что, по крайней мѣрѣ,
одно изъ двухъ тѣлъ, на которыхъ мы наблюдаемъ электричество,
вызываемое ихъ соприкосновеніемъ, является изоляторомъ. Предста-
вляется ли это, однако, существеннымъ условіемъ для возникновенія
явленія? Прежде, дѣйствительно, существовалъ такой взглядъ, пока
Вольта (Ѵоііа) въ концѣ XVIII вѣка не показалъ, что при соприко-
сновеніи, напримѣръ, мѣди и цинка, совершенно такъ же возникаетъ
двойной электрическій слой, какъ и при соприкосновеніи стекла и
цинка (или цинковой амальгамы). Но напряженіе, которое получается
при разъединеніи пластинокъ въ этомъ случаѣ, гораздо меньше, и его,
напримѣръ, уже нельзя обнаружить при помощи нашей простой элек-
трической стрѣлки. Но такъ какъ тутъ мы имѣемъ дѣло съ двумя
проводниками, то тѣмъ удобнѣе воспользоваться для обнаруженія по-
лучающагося напряженія электрометромъ. Это примѣненіе электро-
метра было въ сущности единственной новостью, введенной въ изслѣ-
дованіе Вольта; слѣдствіемъ этого нововведенія явились открытія,
поднявшія ученіе объ электричествѣ на неожиданную высоту. Теперь
мы ознакомимся съ основнымъ опытомъ Вольта.
Возьмемъ цинковую и мѣдную пластинки и закрѣпимъ ихъ по-
добно деревяннымъ пластинкамъ съ разными наклейками, которыми мы
пользовались выше, на хорошо изолирующихъ стеклянныхъ ручкахъ.
Каждую пластинку соединяемъ съ однимъ изъ зажимовъ электро-
метра (напримѣръ, Ганкеля). Индикаторъ зарядимъ, соединивъ его &
съ положительнымъ полюсомъ батареи, упомянутой въ § 28,
чемъ отрицательный ея полюсъ отведемъ къ землѣ. Нить элеісгреі-
метра спроектируемъ на экранъ, снабженный масштабомъ, сильно ее
увеличивъ. Первоначально она будетъ стоять на нулѣ. Тепер^мы на-
ложимъ, слегка надавливая, металлическія пластинки другтХ на друга
и вновь разнимемъ ихъ (рис. 17). Электрометръ сейчасъ же дастъ
>7 И
52 Напряженіе при соприкосновеніи двухъ металловъ
отклоненіе; слѣдовательно, между обѣими пластинками дѣйствительно
возникаетъ при соприкосновеніи поле. При этомъ цинковая пластинка
Рис. 17. Опытъ Вольта.
заряжается положительно, а мѣдная — отрицательно, что легко уста-
новить, наблюдая направленія отклоненій нити электрометра.
НАПРЯЖЕНІЕ ПРИ СОПРИКОСНОВЕНІИ ДВУХЪ МЕТАЛЛОВЪ.
32. Опытъ Вольта можно легко видоизмѣнить такимъ образомъ,
чтобы произвести одновременно дѣйствительное измѣреніе напряже-
нія въ электрическомъ двойномъ слоѣ. Для этого обѣ пластинки (ска-
жемъ, цинковую и мѣдную) нужно не доводить до соприкосновенія,
но расположить подобно пластинкамъ конденсатора на небольшомъ,
но все же измѣримомъ, разстояніи другъ отъ друга. Соприкоснове-
ніе ихъ въ этомъ случаѣ достигается при помощи маленькаго острія,
скрѣпленнаго съ одной изъ пластинокъ. Какъ мывидѣли, при этомъ
въ молекулярныхъ промежуткахъ у малой ^поверхности контакта
образуется электрическое поле опредѣленна^ напряженія. Но такъ
Напряженіе при соприкосновеніи двухъ металловъ
53
какъ мы имѣемъ здѣсь дѣло съ проводниками, то вся цинковая пла-
стинка заряжается до постояннаго потенціала; то же происходитъ и
съ мѣдной пластинкой. Слѣдовательно, и въ воздушномъ слоѣ между
пластинками образуется поле, напряженіе котораго тождественно съ
напряженіемъ двойного электрическаго слоя. Это напряженіе такъ
мало, что его трудно было бы обнаружить при помощи нашего
электрометра Ганкеля. Если затѣмъ удалить добавочное остріе, то
напряженіе въ образующемся изъ обѣихъ пластинокъ воздушномъ
конденсаторѣ не измѣнится. Послѣ этого можно раздвинуть пластинки
и тѣмъ повысить напряженіе поля. Если, напримѣръ, первоначальная
толщина воздушнаго слоя равнялась х/10 миллиметра, то при удаленіи
ихъ на разстояніе, равное 1 сантиметру, напряженіе возрастаетъ въ
сто разъ. Поэтому, измѣривъ такимъ образомъ полученное уже вы-
сокое напряженіе и раздѣливъ его величину на число разъ, въ ко-
торое мы увеличили разстояніе между пластинками, мы получимъ на-
пряженіе электрическаго двойного слоя или „электродвижущую силу*
между цинкомъ и мѣдью.
Въ результатѣ подобныхъ измѣреній, величины электродвижущихъ
силъ между двумя металлами должны были бы получиться неожиданно
большими. Если допустить, что первоначально пластинки были сбли-
жены до молекулярнаго разстоянія (около ІО-8 сантиметра), а за-
тѣмъ удалены до измѣримаго разстоянія (около 1 сантиметра), и
если далѣе допустить, что при этой операціи не происходитъ ника-
кой потери зарядовъ, такъ что напряженіе возрастаетъ въ сотни
милліоновъ разъ, то вычисленіе даетъ величину, вѣроятно, соотвѣт-
ствующую колоссальнымъ напряженіямъ грозовыхъ тучъ. Отсюда
ясно, что большая часть заряда, являющагося при соприкосновеніи
пластинокъ, снова теряется при ихъ взаимномъ удаленіи. Въ дѣй-
ствительности, поверхности обѣихъ пластинокъ сильно отличаются
отъ математическихъ плоскостей, и потому невозможно удалять ихъ
другъ отъ друга такъ, чтобы на какой-либо небольшой поверхности ихъ
не возникало снова взаимнаго соприкосновенія, когда онѣ вообще <
уже удалены одна отъ другой на замѣтное разстояніе. Слѣдовательно^
нѣкоторое напряженіе „электродвижущей силы* сохраняется и ^Н^а,
когда ихъ взаимное удаленіе уже достигло замѣтной величины, въ
сотни тысячъ и милліоны разъ превосходящей молекулярныя^разстоянія.
Иначе обстоитъ дѣло въ томъ случаѣ, когда одна^ийъ пласти-
нокъ представляетъ собою изоляторъ. Здѣсь мы имѣемьто неудоб-
54
Напряженіе при соприкосновеніи двухъ металловъ
ство, что пластинки заряжаются только тогда, когда онѣ дѣйстви-
тельно соприкасаются (т. е. сближаются до ІО-8 сантиметра). Такъ
какъ пластинки не являются строго плоскими, то дѣйствительное со-
прикосновеніе, во всякомъ случаѣ, происходитъ лишь на небольшой
части ихъ поверхностей. Легко понять, что выгодно получить воз-
можно большую поверхность соприкосновенія, для чего слѣдуетъ
одно изъ тѣлъ („терку “) сдѣлать изъ мягкаго, гибкаго матеріала и
при соприкосновеніи тѣлъ слегка ихъ потереть другъ о друга. Если
послѣ этого разъединить обѣ пластинки, то потеря заряда будетъ
ничтожна, такъ какъ зарядъ изолятора имъ не проводится. Если
напряженіе становится чрезмѣрнымъ, то между двумя пластинками
возникаютъ маленькіе искровые разряды; ихъ появленіе ставитъ гра-
ницу дальнѣйшему увеличенію напряженія.
Электродвижущія силы при соприкосновеніи изоляторовъ, вѣ-
роятно, имѣютъ величины того же порядка, что и при соприкосно-
веніи металловъ.
Причина, по которой нельзя на практикѣ построить электриче-
скую машину съ треніемъ, у которой и подушка и дискъ были бы
сдѣланы изъ металла, заключается въ томъ, что при дѣйствіи такой
машины образующіеся при соприкосновеніи металловъ электрическіе
заряды будутъ при ихъ взаимномъ удаленіи почти совершенно уни-
чтожаться вслѣдствіе существованія проводящихъ контактовъ между
металлами.
33. Если произвести рядъ вышеописанныхъ измѣреній напряже-
нія между двумя соприкасающимися металлами и при этомъ измѣ-
нять различнымъ образомъ условія опыта — напримѣръ, разстояніе пла-
стинокъ, поверхность соприкосновенія, давленіе при соприкоснове-
ніи,— то тѣмъ не менѣе всегда будетъ получаться одна и та же ве-
личина. Отсюда слѣдуетъ важное заключеніе: напряженіе при со-
прикосновеніи двухъ опредѣленныхъ металловъ есть фи-
зическая постоянная.
Этотъ экспериментальный законъ подтверждаетъ наше право при-
нимать напряженіе за мѣру электродвижущей силы.
Уже Вольта установилъ слѣдующій рядъ металлр^Г^
4-цинкъ, олово, свинецъ, латунь, ртуть, желѣзо, мѣдь, серебро, золото—.
Для этого ряда имѣетъ силу слѣдующее положеніеѵиаиряжені е при
соприкосновеніи двухъ металловъ тѣмъ больше, чѣмъ даль-
ше отстоятъ въ ряду эти металлы друКз^отъ друга.
Законъ напряженій Вольта
55
ЗАКОНЪ НАПРЯЖЕНІЙ ВОЛЬТА.
34. Теперь мы должны поставить себѣ слѣдующій вопросъ:
какъ же разрѣшается противорѣчіе между сейчасъ полученнымъ ре-
зультатомъ, согласно которому между двумя соприкасающимися ме-
таллами должно возникать электрическое поле, и закономъ постоян-
ства потенціала на соединенныхъ проводникомъ металлическихъ тѣ-
лахъ, изложеннымъ въ § 26 и подтвержденнымъ непосредственными
опытами въ § 28? Прежде всего слѣдуетъ замѣтить, что при этихъ
опытахъ мы имѣли напряженіе, гораздо большее, чѣмъ напряженіе
при соприкосновеніи металловъ, и соотвѣтственно этому пользовались
электрометромъ, который, конечно, не могъ бы уже отмѣчать столь
малыхъ разностей потенціаловъ, какъ тѣ, которыя имѣются при явленіи
Вольта. Слѣдовательно, для полученія достовѣрнаго отвѣта на по-
ставленный вопросъ мы должны воспользоваться чувствительнымъ
электрометромъ, напримѣръ, квадрантнымъ. Пользуясь послѣднимъ,
мы направимъ черезъ щель лучъ свѣта на небольшое зеркальце, вер-
тикально расположенное и скрѣпленное съ бисквитообразнымъ инди-
каторомъ. Это зеркальце отразитъ лучъ на горизонтально располо-
женный масштабъ. Помѣщая между зеркальцемъ и масштабомъ линзу,
мы можемъ достигнуть того, что свѣтлое пятно на масштабѣ станетъ
яркимъ и рѣзко очерченнымъ. Если теперь индикаторъ отклонится,
то свѣтлое пятно на масштабѣ передвинется. Индикаторъ мы заря-
димъ при помощи электрической батареи, которую мы уже употре-
бляли для заряженія индикатора электрометра Ганкеля. Поднося къ
металлическому тѣлу, соединенному проводникомъ съ одной парой
квадрантовъ, натертую стеклянную палочку и отводя при этомъ дру-
гую пару квадрантовъ къ землѣ, мы замѣтимъ, въ какую сторону
передвигается свѣтлое пятно при положительномъ заряженіи соотвѣт-
ственной пары квадрантовъ; если теперь сообщить съ нею натертую
эбонитовую палочку, то свѣтлое пятно передвинется въ обратную
сторону. При этомъ мы сразу замѣчаемъ, что инструментъ этотъ
крайне чувствителенъ; для напряженій порядка тѣхъ, которые полу-
чаются въ опытѣ Вольта съ мѣдью и цинкомъ, онъ долженъ датьі?
уже замѣтныя отклоненія. Обѣ пары квадрантовъ нашего инструмента
сдѣланы изъ латуни; мы соединимъ ихъ между собою при ^йомощи
латунной проволоки, вслѣдствіе чего потенціалъ на всей системѣ
• ЕѴт
будетъ постояннымъ и напряженіе между этими двумя ^парами ква-
дрантовъ будетъ равно нулю. Мы получаемъ таким$м§бразомъ нуле-
56
Законъ напряженій Вольта
вую точку нашего инструмента т). Теперь разрѣжемъ латунную про-
волоку и соединимъ одинъ ея конецъ съ цинковой пластинкой, дру-
гой— съ мѣдной пластинкой; обѣ пластинки предварительно изоли-
рованы. Наложимъ одну пластинку на другую; свѣтлое пятно остается,
на нулѣ. Гдѣ же то напряженіе при соприкосновеніи, въ наличности
котораго мы убѣдились изъ опыта Вольта? Помѣстимъ обѣ пластинки
рядомъ и соединимъ ихъ желѣзной полосой или инымъ металломъ;
ничто не измѣняется, и свѣтлое пятно не двигается. Полученный ре-
зультатъ мы можемъ кратко формулировать, если величину напря-
женія, получающагося при соприкосновеніи металловъ А и В, условно
обозначимъ черезъ (Д, В). Согласно нашему опыту,
(латунь, мѣдь) + (мѣдь, цинкъ) -|- (цинкъ, латунь) = О
или же
(латунь, мѣдь) 4" (мѣдь, цинкъ) — (латунь, цинкъ).
Вообще:
(А, В)+ (В, С) + (С,О)=(А, О).
Напряженіе при соприкосновеніи двухъ металловъ оди-
наково въ случаѣ ихъ прямого соприкосновенія и въ томъ
случаѣ, если между ними помѣщены любые иные металлы.
Это — законъ напряженій Вольта.
Изъ него непосредственно слѣдуетъ, что напряженіе между двумя
кондукторами, сдѣланными изъ одного металла, равняется нулю при
совершенно произвольной металлической цѣпи между ними.
Далѣе, если два изолированные кондуктора А{ и Д2, сдѣлан-
ные изъ одного металла Д, соединимъ произвольными металличе-
скими цѣпями соотвѣтственно съ кондукторами Вх и В2, также сдѣ-
ланными изъ одного металла В, то разность потенціаловъ между Вх и В2
будетъ равна разности потенціаловъ между Д1 и Д2. Поэтому по-
мощью квадрантнаго электрометра измѣряется вполнѣ точно напря-
женіе между двумя кондукторами, сдѣланными изъ одного металла,
если только они металлически соединены съ парами квадрантовъ;
при этомъ безразлично, изъ какихъ металловъ составленьи эти со-
единенія. (|у
Изъ равенства Чъ
(Д, О) = (Д, В) + (В, С) + (С, О) ^7
Э Т. е. положеніе свѣтлаго пятна даетъ при этоіѵг|.Цуль шкалы. Прим. пер.
Гальваническія цѣпи
57
слѣдуетъ еще, что достаточно знать величины напряженій при со-
прикосновеніи для каждой пары металловъ, рядомъ расположенныхъ
въ ряду Вольта, чтобы вычислить напряженіе при соприкосновеніи
двухъ металловъ, произвольно удаленныхъ въ этомъ ряду другъ отъ
друга. Для этого достаточно сложить величины напряженій при со-
прикосновеніи для всѣхъ промежуточныхъ паръ.
Всѣ эти напряженія, получающіяся при соприкосновеніи метал-
ловъ, могутъ быть измѣрены при посредствѣ опытовъ, описанныхъ
въ § 32. Но ихъ нельзя измѣрить, прямо прижимая соприкасающіяся
тѣла къ чувствительному электрометру.
ГАЛЬВАНИЧЕСКІЯ ЦЪПИ.
35. Теперь мы введемъ въ область нашихъ изслѣдованій также
и жидкіе проводники. Включимъ въ нашъ квадрантный электро-
метръ вышеописанныя пластинки изъ мѣди и цинка и соединимъ
эти пластинки между собою проводникомъ, но не металлическимъ, а
жидкимъ. Можно, напримѣръ, одновременно приложить по пальцу къ
каждой пластинкѣ (рис. 18), такъ какъ человѣческое тѣло въ силу
большого содержанія въ немъ воды можно отнести къ числу жид-
кихъ проводниковъ. Въ такомъ случаѣ свѣтлое пятно электрометра
не остается на нулѣ, но даетъ замѣтное отклоненіе; при этомъ ока-
зывается, что цинкъ заряжается отрицательно, мѣдь - положительно.
Величины напряженій при соприкосновеніи металла и
жидкаго проводника не слѣдуютъ закону напряженій Вольта.
Вслѣдствіе этого при измѣреніяхъ помощью квадрантнаго элек-
трометра слѣдуетъ всѣ провода дѣлать изъ металловъ. Примѣне-
ніе влажнаго шнура и т. п. повело бы къ большимъ ошибкамъ при
измѣреніяхъ.
36. Уже раньше Вольта итальянскій анатомъ Гальвани (Оаіѵапі,
въ 1780 году въ Болоньѣ) сдѣлалъ наблюденіе, указавшее на налич-
ность электрическаго напряженія при соприкосновеніи металловъ и
жидкихъ проводниковъ. Никакого объясненія этого явленія Галь-^
вани не далъ. Онъ замѣтилъ только, что лягушечья ножка, про-^
ткнутая желѣзнымъ крючкомъ, начинала быстро сокращаться, ,;КоГда
ее клали на серебрянную чашечку. Въ этомъ опытѣ роль д^дКаго
проводника играла лягушечья ножка, соприкасавшаяся съ^двумя ме-
таллами — серебромъ, съ одной стороны, и желѣзомъ,, съ другой.
Такъ какъ серебро и желѣзо, въ свою очередь, срцрикасались, то
58
Гальваническія цѣпи
происходило выравниваніе напряженій, получавшихся вслѣдствіе ихъ
соприкосновенія съ лягушечьей ножкой. На эти „ разряды“ и реаги-
ровали сокращеніями мускулы лягушечьей ножки.
Это наблюденіе Гальвани послужило исходнымъ пунктомъ для
важныхъ изслѣдованій Вольта. Въ память Гальвани всѣ комбинаціи
металловъ (часто и иныхъ твердыхъ проводниковъ) съ жидкими про-
Рис. 18. Электризація при соприкосновеніи металла и жидкаго проводника.
водниками, дающія между двумя металлическими „полюсами^ (соб-
ственно полюсовыми зажимами) электрическое напряжеф^хвѣ теченіе
продолжительнаго времени, по настоящее время называетъ" гальвани-
ческими цѣпями или гальваническими элементами. Изъ двухъ
. • \\ \\ Vх
полюсовъ гальванической цѣпи различаютъ одинцы положительный и
другой- отрицательный. Въ вышеуказанной А^кой цѣпи мѣдь-жид-
Гальваническія цѣпи
59’
кій проводникъ - цинкъ положительнымъ полюсомъ является мѣдь,,
отрицательнымъ - цинкъ.
Гальваническая цѣпь, подобно электрической машинѣ, можетъ
служить для полученія продолжительныхъ электрическихъ зарядовъ.
Это легко можно показать, пользуясь вышеописанною простою цѣпью.
Наложимъ на мѣдную пластинку кружокъ смоченной пропускной бу-
маги, а на него цинковую пластинку и соединимъ обѣ металлическія
пластинки съ квадрантнымъ электрометромъ. При этомъ получается
замѣтное отклоненіе. Если, изолировавъ цинковую пластинку, удалить
ее, отклоненіе замѣтно не измѣнится. Помѣстимъ теперь между двумя
проводами, ведущими къ электрометру, палочку графита, напримѣръ,
изъ обыкновеннаго карандаша. Послѣ этого свѣтлое пятно возвра-
щается на нуль, такъ какъ графитъ относится къ числу металличе-
скихъ проводниковъ. Посредствомъ графитовой палочки обѣ пла-
стинки „разряжаются"; иначе говоря, въ силу того, что черезъ про-
водящую палочку соединяются положительный и отрицательный за-
ряды, они оба постепенно исчезаютъ, пока, наконецъ, квадрантный
электрометръ не укажетъ на полное отсутствіе напряженія. Если те-
перь, оставивъ попрежнему графитовую палочку, мы снова опустимъ
цинковую пластинку на влажную пропускную бумагу, то снова по-
является нѣкоторое напряженіе между парами квадрантовъ, всегда
нѣсколько меньшее, нежели при отсутствіи графитоваго стержня.
Получаются такимъ образомъ два взаимно противоположныя явленія,
дѣйствія которыхъ отчасти взаимно уничтожаются: 1) графитъ уни-
чтожаетъ заряды, вызывающіе отклоненія электрометра; 2) электро-
движущія силы на поверхностяхъ соприкосновенія жидкаго провод-
ника съ металлами стремятся возстановить двойные электрическіе
слои, отчасти уничтожаемые дѣйствіемъ графита. Въ силу взаимо-
дѣйствія этихъ явленій и получается наблюдаемый нами результатъ.
Если сравнить работу гальванической цѣпи съ работой электри-
ческой машины, то мы придемъ къ нижеслѣдующимъ результатамъ. ,
Въ электрической машинѣ съ треніемъ пользуются двойнымъ р
электрическимъ слоемъ металлъ-изоляторъ (цинковая амальгама-стекло^° ?
Въ гальванической цѣпи дѣйствующимъ является двойной} (&гой
между металломъ и жидкимъ проводникомъ.
Въ электрической машинѣ механическимъ перемершемъ со-
прикасающихся тѣлъ мы медленно получаемъ новые и новые заряды.
Гальваническая цѣпь даетъ возможность чрезвычайно быстро
«О
Единица электрическаго напряженія
снять большой зарядъ, если воспользоваться проводимостью ея со-
ставныхъ частей.
Въ силу предыдущаго, для хорошей изоляціи въ электрической
машинѣ нужно пользоваться стекломъ, покрытымъ шеллакомъ или
чѣмъ-либо подобнымъ.
Въ гальваническомъ элементѣ достаточную изоляцію обычно
даютъ дерево, бумага, хлопокъ.
Въ электрической машинѣ электрическая энергія получается,
главнымъ образомъ, какъ результатъ механической работы, дѣйствіемъ
которой сильно удлиняются силовыя линіи между малыми зарядами,
соотвѣтствующими электродвижущимъ силамъ, и тѣмъ достигаются
колоссальныя напряженія.
Въ гальваническомъ элементѣ вся энергія появляется за счетъ
электродвижущихъ силъ, связанныхъ съ матеріею; внутренняя энер-
гія матеріи при этомъ переходитъ въ электрическую. Эти силы даютъ
заряды съ чрезвычайной быстротой, но напряженіе постоянно остается
тождественнымъ тому низкому напряженію, которое получается при
соприкосновеніи.
ЕДИНИЦА ЭЛЕКТРИЧЕСКАГО НАПРЯЖЕНІЯ.
37. Изобрѣтеніе гальваническихъ цѣпей составило въ наукѣ гро-
мадный шагъ впередъ уже потому, что при помощи ихъ мы можемъ
постоянно и съ удобствомъ получать въ эѳирѣ одно и то же на-
пряженіе. А такая возможность представляетъ собою первое условіе
для точныхъ измѣреній силы поля; и дѣйствительно, послѣ этого
изобрѣтенія ученіе объ электричествѣ начало развиваться въ точную
область знанія, допускающую строгія измѣренія.
Для устройства постоянной цѣпи вышеописаннаго состава (§ 35)
наполняютъ стеклянный сосудъ жидкимъ проводникомъ (напримѣръ,
разведенной сѣрной кислотой), вставляютъ въ нее цинковую и мѣд-
ную полосы и снабжаютъ послѣднія винтовыми зажимами для сое-
динительныхъ проводовъ. Однако, скоро обнаруживается, чтрОгёкая
цѣпь не удовлетворяетъ даже весьма скромнымъ требоварЫшъ. На-
пряженіе на зажимахъ ея можетъ имѣть весьма различныя значенія,
при чемъ нельзя точно установить, почему именно ощг имѣетъ то
или иное значеніе. Такую цѣпь называютъ „ непостоянной “; непо-
стоянная цѣпь можетъ лишь весьма неудовлетворительно воспроизво-
дить электрическое напряженіе опредѣленной^ведичины.
Единица электрическаго напряженія
61
Элементы, обычно употребляемые, представляются, наоборотъ,
„постоянными". Вполнѣ постоянный элементъ, который опредѣ-
ляетъ собой единицу напряженія, называется нормальнымъ эле-
ментомъ.
Старѣйшимъ изъ нормальныхъ элементовъ является элементъ
Даніеля (Цапіеіі). Онъ состоитъ также изъ пластинокъ цинковой
(отрицательный полюсъ) и мѣдной (положительный полюсъ), но заклю-
чаетъ въ себѣ два жидкихъ проводника (рис. 19). Цинковая пластинка въ
немъ погружена въ сильно разбавлен-
ный растворъ цинковаго купороса,
къ которому для лучшей проводи-
мости еще прибавляется сѣрная ки-
слота или какая-нибудь щелочная соль;
мѣдная пластинка погружена въ кон-
центрированный растворъ мѣднаго
купороса. Оба раствора должны со-
прикасаться черезъ проводникъ, но
при этомъ ихъ взаимная диффузія
должна быть возможно медленной.
Обычно для достиженія этого въ со-
судъ, содержащій первый растворъ,
вставляется пористый глиняный ци-
линдръ, который и наполняется вто-
рымъ растворомъ. Оба раствора про-
питываютъ пористый цилиндръ и та-
кимъ образомъ приходятъ въ сопри-
косновеніе; диффузія же при этомъ
Рис. 19. Элементъ Даніеля.
получается незначительная. Напряженіе элемента Даніеля отличается
строгимъ постоянствомъ и поэтому оно уже издавна принималось за
единицу напряженія. Эту единицу прежде называли „даніель"; те-
перь она въ честь Вольта переименована въ „вольтъ".
Напряженіе, равное единицѣ, имѣетъ поле, образую-
щееся между полюсными зажимами элемента Даніеля. Эта
единица напряженія носитъ названіе „вольтъ".
Если мы примемъ, что отклоненія квадрантнаго электрометра
пропорціональны приложеннымъ къ нему напряженія^ -фіасто это
такъ и бываетъ), то достаточно только знать отклоненіе,-вызываемое
однимъ элементомъ Даніеля, чтобы быть въ сосдОйніи по любому
62
Единица электрическаго напряженія
иному отклоненію опредѣлить соотвѣтствующее ему напряженіе въ
вольтахъ. Такимъ путемъ электрометръ калибрируется на вольты. Элек-
трометръ, дающій величины напряженій въ вольтахъ, называется также
вольтметромъ.
Но и элементъ Даніеля требованіямъ современной измѣритель-
ной техники не удовлетворяетъ. Поэтому для вполнѣ точнаго вос-
произведенія единицы напряженія были построены другіе нормальные
элементы; наилучшими изъ нихъ оказались элементы, у которыхъ
одинъ изъ металлическихъ полюсовъ ртутный. Чрезвычайно постоян-
нымъ ртутно-цинковымъ элементомъ является нормальный элементъ
Рис. 20. Элементъ Вестона.
Рис. 21. Аккумуляторъ.
Кларка (Сіагк); его напряженіе при 15° равняется 1,433 вольта. Но
его превосходитъ одинъ изъ ртутно-кадміевыхъ элементовъ; при впол-
нѣ опредѣленномъ составѣ послѣдній обладаетъ чрезвычайно важнымъ
для практики свойствомъ: его напряженіе въ зависимости отъ тем-
пературы измѣняется лишь ничтожно мало. Этотъ элементъ подъ
именемъ элемента Вестона (ХѴезіоп) международнымъ догово-
ромъ всѣхъ культурныхъ странъ принятъ за нор^дльный
элементъ. Единица напряженія опредѣляется при помощфэтого эле-
мента слѣдующимъ образомъ: напряженіе элемента Вестона
при 15° равняется 1,0188 вольта. Такое числодіринято потому,
что желательно было оставить въ
ную еще до изобрѣтенія элемента
силѣ единицу^ напряженія, введен-
Ве сто на (рис. 20). При измѣненіи
1
Гальваническая батарея
63
температуры на 1° напряженіе элемента Вестона измѣняется на
0,00003 вольта.
При послѣдующихъ нашихъ опытахъ мы очень часто будемъ
пользоваться еще иною вполнѣ постоянною цѣпью — свинцовымъ
аккумуляторомъ. Эта цѣпь имѣетъ слѣдующій составъ: — сви-
нецъ, разведенная сѣрная кислота, перекись свинца+. Она отли-
чается отъ всѣхъ упомянутыхъ выше цѣпей тѣмъ, что одинъ ея по-
люсъ состоитъ не изъ металла, но изъ металлической перекиси (РЬО2).
Такъ какъ эта перекись является плохимъ проводникомъ и чрезвы-
чайно хрупка, то въ элементъ вводится солидный свинцовый остовъ
или свинцовая пластинка, на которую наносится перекись; эта перекись
вполнѣ покрываетъ части пластинки, погруженныя въ сѣрную кислоту,
такъ что отъ нея свободна часть пластинки, только выступающая на
воздухъ и предназначаемая для помѣщенія полюснаго зажима. Если
присоединить къ аккумулятору нашъ квадрантный электрометръ, то
отклоненіе послѣдняго покажетъ намъ напряженіе, равное 2 воль-
тамъ (рис. 21).
ГАЛЬВАНИЧЕСКАЯ БАТАРЕЯ.
38. Намъ приходится теперь разсмотрѣть вопросъ о томъ, какъ
измѣнится формулированный выше общій законъ постоянства потен-
ціала на проводящихъ поверхностяхъ, если въ цѣпи будутъ нахо-
диться также и жидкіе проводники. Соединивъ отрицательный по-
люсъ аккумулятора съ одною парою квадрантовъ нашего электро-
метра, отведемъ сначала этотъ полюсъ къ землѣ. Если при этомъ и
другая пара квадрантовъ отведена къ землѣ, то мы имѣемъ нулевое
положеніе электрометра; если же вторая пара квадрантовъ соединена
•съ положительнымъ полюсомъ аккумулятора, то мы получаемъ откло-
неніе, соотвѣтствующее + 2 вольтамъ. Соединимъ теперь отрица-
тельный полюсъ аккумулятора съ положительнымъ полюсомъ эле-
мента Даніеля, отрицательный полюсъ котораго отведемъ къ землѣ,
оставляя при этомъ неизмѣннымъ соединеніе между первою парою
квадрантовъ электрометра и отрицательнымъ полюсомъ аккумуля-Г^
тора, являющимся теперь одновременно и положительнымъ полюсо|фѵ
элемента Даніеля. Теперь оказывается, что, если другая пардіква-
дрантовъ отведена къ землѣ, отклоненіе соотвѣтствуетъ —- 1 ^вольту,
если же она соединена съ положительнымъ полюсомъ аккумулятора,
то отклоненіе, какъ и при первоначальномъ опытѣ, соотвѣтствуетъ
Д- 2 вольтамъ. Отсюда слѣдуетъ важное заключеніеО 41'^ напряженіе
64
Гальваническая батарея
между полюсами аккумулятора не зависитъ отъ потенціала его отри-
цательнаго полюса. На этомъ примѣрѣ выясняется справедливость
слѣдующаго общаго положенія:
Если мы зарядимъ до извѣстнаго потенціала какую-либо
часть проводящей системы, составленной изъ различныхъ
проводниковъ, то отъ этого совершенно не измѣнятся на-
пряженія, существующія между отдѣльными частями си-
стемы и вызываемыя дѣйствіемъ электродвижущихъ силъ.
Если мы сообщаемъ опредѣленной части системы нѣ-
который потенціалъ, то каждая другая составная часть этой
системы заряжается до этого самаго потенціала плюсъ на-
пряженіе соприкосновенія между этой частью и упомяну-
той первой частью системы.
Рис. 22. Электрическое
а) при изолированныхъ полюсахъ;
поле гальванической цѣпи:
Ь) когда одинъ полюсъ отведенъ къ землѣ.
Дѣйствительно, потенціалъ отрицательнаго полюса аккумулятора
равнялся при первомъ опытѣ 0, при второмъ Д- 1 вольту, и мы
можемъ давать ему произвольныя иныя значенія, не мѣняя этимъ
результата опыта. Подобнымъ образомъ, конечно, можно изолирйт,
вать отрицательный полюсъ и сообщать произвольный потеші|алъ
положительному полюсу; и въ этомъ случаѣ измѣреніе даетъ ^»йе са-
мое напряженіе между обоими полюсами, равное 4- 2 вольтамъ^рис. 22).
Если мы составимъ рядъ гальваническихъ^цѣпей, при
чемъ у каждой цѣпи одинъ полюсъ соединимъ съ полю-
сомъ предыдущей, а другой — съ полюсс^ъ^послѣдующей,
такъ что свободными окажутся толькой полюсъ пер-
Гальваническая батарея
65
вой цѣпи и второй полюсъ послѣдней цѣпи, то напряже-
ніе между двумя свободными конечными полюсами будетъ
равняться алгебраической суммѣ напряженій всѣхъ соеди-
ненныхъ между собою цѣпей.
Выраженіе „алгебраическая сумма" здѣсь указываетъ на то
обстоятельство, что дѣйствительно складываются всѣ напряженія
только въ томъ случаѣ, если всѣ цѣпи расположены въ одномъ и томъ
же направленіи, такъ что у каждой цѣпи положительный полюсъ со-
единенъ съ отрицательнымъ полюсомъ слѣдующей цѣпи. Если же одна
или нѣсколько цѣпей расположены въ обратномъ направленіи, то ихъ
напряженія вычитаются изъ суммы напряженій прочихъ цѣпей.
Рядъ цѣпей, расположенныхъ въ одномъ и томъ же направленіи,
называютъ столбомъ или батареею. Каждая отдѣльная цѣпь въ
такомъ ряду называется „элементомъ" батареи.
39. Пользуясь батареями, мы можемъ воспроизводить не только
напряженія, присущія отдѣльнымъ цѣпямъ, но также произвольное
число различныхъ другихъ напряженій. Если, напримѣръ, въ нашемъ
распоряженіи находится 100 элементовъ Даніеля, то мы можемъ по
желанію получить любое напряженіе изъ ряда: 1 вольтъ, 2 вольта,
3 вольта и т. д. до 100 вольтъ.
Уже Вольта замѣтилъ важность выше приведеннаго положенія
и построилъ первую „батарею высокаго напряженія". Для этой цѣли
онъ наложилъ другъ на друга рядъ кружковъ: цинкъ, влажный вой-
локъ, мѣдь, цинкъ, влажный войлокъ, мѣдь и т. д. По внѣшнему
виду такой батареи ее назвали Вольтовымъ столбомъ (рис. 23).
Еще и нынѣ употребляется видоизмѣненіе Вольтова столба
такъ называемый столбъ Замбони (ЕатЬопі), составленный изъ круг-
лыхъ листковъ „золотой" и „серебрянной" бумаги (поддѣльнаго ме-
талла). Эти листки соотвѣтствуютъ мѣднымъ и цинковымъ пластинкамъ.
Входящая въ ихъ составъ бумага представляетъ собою жидкій про-
водникъ, такъ какъ листочки поддерживаются въ слегка влажномъ .
состояніи. Для этого столбъ Замбони слѣдуетъ держать въ слегка 4^
влажномъ воздухѣ, напримѣръ, подъ стекляннымъ колоколомъ вмѣстѣ^? °
съ сосудомъ, наполненнымъ водою. Напряженіе, даваемое столбо^^
Замбони, зависитъ отъ влажности воздуха. Подобные столбы^Часто
употребляются для заряженія индикаторовъ электрометровъ^^
Постоянныя напряженія получаются также, если отдѣльные эле-
менты представляютъ собою изолированные сосуды, ііацолненные жид-
Ми. Электричество п Магнитизмъ.
66
Гальваническая батарея
кими проводниками. Очень удобна „параффиновая батарея“; ее можіо
сдѣлать изъ куска параффина, просверливъ въ немъ рядъ углубле-
ній. Эти углубленія наполняютъ водою, соединяютъ попарно поло-
сками изъ цинка и мѣди и вновь заливаютъ параффиномъ. Такая ба-
тарея даетъ вполнѣ постоянное напряженіе (напримѣръ, 200 вольтъ)
въ теченіе многихъ лѣтъ.
Рис. 23. Вольтовъ столбъ.
Рис. 24. Столбъ Замбони.
Еще болѣе удобными являются батареи изъ элементовъ, за-
ключенныхъ въ стаканчики. Ящикъ съ 50 маленькими свинцовыми
аккумуляторами, каждый изъ которыхъ заключенъ въ стеклянной
пробиркѣ (рис. 25), даетъ точное напряженіе въ 100 вольтъ. Мы
можемъ, напримѣръ, соединить полюсы такой батареи^ съ зажи-
мами электрометра Экснера и отмѣтить дѣленіе шкалы, до котораго
отклонится свѣтлое пятно на экранѣ. У этого дѣленія мы можемъ
написать: „100 вольтъ". Сдѣлавъ тоже съ двумя и тремя соединен-
Примѣры электрическихъ напряженій
67
ными между собою такими батареями (200 вольтъ и 300 вольтъ),
мы прокалибрируемъ такимъ образомъ нашъ электрометръ и будемъ
въ состояніи всѣ его послѣ-
дующія показанія выражать
опредѣленными числами.
Въ природѣ встрѣчаются
подобныя электрическія бата-
реи, но не содержащія ме-
талловъ. Электрическіе аппа-
раты, которыми снабжены нѣ-
которые сорта рыбъ (электри-
Рис. 25. Батарея маленькихъ аккумуляторовъ.
ческій угорь, электрическій скатъ) и при помощи которыхъ они мо-
гутъ производить сильные электрическіе удары, представляютъ собою
батареи, составленныя изъ слоевъ различныхъ органическихъ тканей,
подобію Вольтову столбу.
ПРИМѢРЫ ЭЛЕКТРИЧЕСКИХЪ НАПРЯЖЕНІЙ.
40. Здѣсь умѣстно привести нѣсколько опредѣленныхъ число-
выхъ данныхъ, чтобы числа, случайно встрѣчающіяся, не являлись
простымъ балластомъ для памяти:
напряженія обычно употребляемыхъ гальваническихъ элементовъ
по большей части заключаются въ предѣлахъ 1—2 вольтъ;
общеизвѣстныя дѣйствія притяженія легкихъ бумажныхъ обрѣз-
ковъ, шариковъ изъ бузинной сердцевины и т. д. наблю-
даются у тѣлъ, заряженныхъ до 100 и выше вольтъ;
отчетливый искровый разрядъ получается при напряженіяхъ около
1000 вольтъ (длина искры приблизительно равна !/2 милли-
метра) ;
напряженія электрической машины тренія достигаютъ 10000
вольтъ и болѣе;
лучшія электрическія машины (индукціонныя) легко даютъ на*-1^.
пряженія до 100000 вольтъ;
грозовыя напряженія достигаютъ нѣсколькихъ милліоновъ вольтъ^
Если бы можно было образовать двойной электрическій^слой
путемъ совершеннаго соприкосновенія двухъ тѣлъ и е^^иловыя
линіи растянуть на 1 сантиметръ безъ потери электрическихъ заря-
довъ, то можно было бы получить такимъ обра^мъі напряженія
68
Объясненіе опыта Вольта
порядка сотни милліоновъ вольтъ. Однако, образованію такихъ на-
пряженій должны препятствовать уже разряды, необходимо возни-
кающіе при высокихъ напряженіяхъ.
ОБЪЯСНЕНІЕ ОПЫТА ВОЛЬТА.
41. Въ новое время было найдено, что изслѣдованное впервые
Вольта явленіе, именно возникновеніе напряженія при соприкосновеніи
двухъ металловъ, требуетъ довольно сложнаго объясненія. Металли-
ческая полоса всегда имѣетъ, подобно всякому твердому тѣлу вообще,
на своей поверхности оболочку, состоящую изъ сгущенныхъ составныхъ
частей атмосфернаго воздуха. Явленіе сгущенія газовъ твердыми тѣ-
лами носитъ названіе адсорбціи газовъ. Особенно сильно адсорби-
руется водородъ. Этотъ газовый и водяной слой, образующійся на
твердыхъ тѣлахъ въ силу адсорбціи, какъ извѣстно, крайне трудно
удалить. Чтобы этого добиться, нужно нагрѣвать тѣло въ теченіе
большого промежутка времени. Согласно 'произведеннымъ до на-
стоящаго времени опытамъ, можно высказать слѣдующее положеніе:
если произвести опытъ Вольта въ пустотѣ и съ пластин-
ками, лишенными газоваго и водяного слоя, то при ихъ
соприкосновеніи не обнаруживается никакого напряженія.
Явленіе, обнаруженное Вольта, появляется снова, если
вслѣдствіе притока влажнаго воздуха на пластинкахъ
вновь образуется слой воды и газовъ.
Эти факты совершенно легко объясняются, если принять во вни-
маніе, что между металломъ и водяной оболочкой долженъ суще-
ствовать двойной электрическій слой. При выполненіи опыта Вольта
вслѣдствіе давленія и тренія слой, приставшій къ одной пластинкѣ,
приходитъ въ соприкосновеніе со слоемъ, приставшимъ къ другой
пластинкѣ; если при этомъ на нѣкоторой поверхности соприкосно-
венія водяная оболочка сотрется, то металлы придутъ въ непосред-
ственное соприкосновеніе. При этомъ они оба получаютъ одинако-
вый потенціалъ, какъ это слѣдуетъ изъ опытовъ надъ пластинкамщ
лишенными водяной оболочки.
Такъ какъ при этомъ напряженія двойныхъ слоевъ хметаллъ - во-
дяная оболочка не измѣняются, то обѣ водяныя оболочки пріобрѣ-
таютъ различные потенціалы, которые не могут^двыравняться при
контактѣ, вслѣдствіе весьма плохой проводимости^тончайшихъ обо-
лочекъ. Напримѣръ, водяная оболочка цин^а^аряжается положи-
Объясненіе опыта Вольта
69
тельно (такъ какъ цинкъ самъ заряженъ отрицательно), а водяная
оболочка мѣди—отрицательно (такъ какъ самая мѣдь заряжена по-
ложительно). Въ пространствѣ же между обѣими пластинками обра-
зуется поле (рис. 26), общее напряженіе котораго должно равняться
суммѣ напряженій при соприкосновеніи цинка съ жидкимъ провод-
никомъ и жидкаго проводника съ мѣдью; при этомъ цинкъ заря-
жается положительно, мѣдь—отрицательно. Основной опытъ Вольта
Рис. 26 Ь. Оба металла имѣютъ
одинаковый потенціалъ, водяная
оболочка цинка — положитель-
ный, водяная оболочка мѣди--
отрицательный.
Рис. 26 а. Цинкъ имѣетъ отри-
цательный потенціалъ, мѣдь —
положительный, обѣ водяныя обо-
лочки— нуль.
теоріей, что напряженіе при сопри-
что и въ цѣпи цинкъ-жидкій про-
даетъ, дѣйствительно, согласно съ
косновеніи цинка и мѣди то же,
водникъ-мѣдь; цинкъ при этомъ заряжается положительно. (
Послѣ этого легко понять, почему для металловъ имѣетъ сид^
законъ Вольта. Въ каждой проводящей цѣпи самые металлы имѣютъ
всѣ одинаковый потенціалъ. Находящійся же на поверхностяхъ^ихъ
двойной электрическій слой, конечно, измѣняетъ внѣшн^<Споле, но
не имѣетъ никакого вліянія на то, что мы измѣряемъ^ Йнри помощи
электрометра.
70
Измѣреніе электрическаго поля
ИЗМѢРЕНІЕ ЭЛЕКТРИЧЕСКАГО НОЛЯ.
42. До сихъ поръ мы пользовались электрометромъ исключи-
тельно для измѣренія общихъ напряженій электрическихъ полей, воз-
никающихъ между двумя проводниками. Однако, съ помощью элек-
трометра можно также, если это необходимо, измѣрять силу поля
послѣдовательно въ отдѣльныхъ его точкахъ. Для этой цѣли упо-
требляется еще проводящее тЬло, возможно малыхъ размѣровъ, обла-
дающее свойствомъ принимать на себя и въ теченіе продолжитель-
Рис. 27. Измѣреніе электрическаго поля.
наго промежутка времени сохранять на себѣ потенціалъ, имѣющійся
въ той части поля, куда оно помѣщено. Такое тѣло носитъ названіе
электрическаго зонда или же коллектора. Такой коллекторъ
присоединяется къ электрометру.
Очень простой видъ электрическаго зонда представляетъ собою
коллекторъ съ пламенемъ. Онъ состоитъ изъ племени свѣчи, въ
которомъ помѣщена платиновая проволока, соединеідіая съ электро-
метромъ (рис. 27); какъ пламя, такъ и процолб^а хорошо изоли-
руются. Мы уже знаемъ, что газы пламени ^ярляются слегка прово-
водящими. Поэтому пламя всегда само собою принимаетъ средній
Измѣреніе электрическаго поля
71
потенціалъ пространства, въ которомъ оно находится. Дѣйствительно,
если его потенціалъ отличается отъ этого средняго потенціала, то,
въ силу получающейся диссиметріи окружающаго его поля, электри-
ческіе заряды будутъ вмѣстѣ съ газами пламени переноситься, пока
не возстановится первоначальный потенціалъ. Тотъ же потенціалъ
принимаютъ также помѣщенный въ пламени кончикъ платиновой про-
волоки, проводъ, ведущій къ электрометру, и приключенный къ по-
слѣднему зажимъ электрометра. Если другой зажимъ электрометра
отвести къ землѣ, то отклоненіе его дастъ потенціалъ коллектора;
такимъ путемъ мы можемъ опредѣлять потенціалъ поля послѣдова-
тельно во всѣхъ его точкахъ.
Зарядимъ, напримѣръ, большой изолированный металлическій
шаръ при помощи батареи аккумуляторовъ, одинъ полюсъ которой
отведенъ къ землѣ. Если помѣстить коллекторъ съ пламенемъ вблизи
этого шара, то соединенный съ нимъ электрометръ Экснера даетъ
значительное отклоненіе. Если мы станемъ удалять коллекторъ отъ
шара, то отклоненіе электрометра будетъ непрерывно уменьшаться:
потенціалъ измѣняется обратно пропорціонально разстоянію пламени
ютъ центра шара. Если двигать пламя въ обратномъ направленіи, потен-
ціалъ непрерывно возрастаетъ. Если помѣстить руку вблизи простран-
ства, заключеннаго между пламенемъ и шаромъ, отклоненіе электрометра
уменьшается. Рука притягиваетъ къ себѣ силовыя линіи, такъ что
поле между пламенемъ и шаромъ ослабѣваетъ. Если помѣстить между
пламенемъ и шаромъ мѣдный листъ, то электрометръ даетъ нуль:
мѣдный листъ отрѣзаетъ поле отъ пламени. Если листъ убрать, то
напряженіе распространяется попрежнему. Стеклянная или эбонито-
вая пластинка, будучи помѣщена между шаромъ и коллекторомъ,
поля не отрѣзаетъ.
43. Вышеописанный методъ измѣренія поля при помощи кол-
лектора и электрометра является, вообще говоря, единственнымъ
практичнымъ методомъ и дѣлаетъ излишнимъ примѣненіе того тео-
ретически болѣе простого метода, съ которымъ мы познакомились
въ § 19. Однако, помощью этого метода мы узнаемъ лишь пот^р
ціалы; какъ же опредѣлимъ мы самое поле, его направленіе щаріу?
Построимъ вокругъ точки, въ которой измѣряется пол^^.далень-
кую сферу, радіусъ которой равенъ I сантиметрамъ. Величину ра-
діуса I возьмемъ настолько малой, чтобы внутри уклоненіъ
поля отъ средней величины Е было меньше онШ^Окъ, могущихе
72
Измѣреніе электрическаго поля
вкрасться при измѣреніяхъ величины и направленія поля. Подобная
сфера на языкѣ математиковъ обычно называется безконечно малой.
Однако, въ дѣйствительности она можетъ имѣть весьма значительные
размѣры, если поле измѣняется весьма медленно (какъ, напримѣръ,
описываемое ниже поле земли). Положимъ, что опредѣлены вели-
чины потенціала въ центрѣ этой сферы А и въ нѣкоторой точкѣ В,
лежащей на поверхности сферы. Два значенія, найденныя изложен-
нымъ методомъ, назовемъ черезъ Ѵг и Ѵ2. Изъ § 27 намъ извѣстно,
что полное напряженіе эѳира между А и В равняется
ѴАВ=^~
Если уголъ между направленіемъ поля Е и направленіемъ АВ
равенъ у, то, по опредѣленію полнаго напряженія (§ 24), имѣемъ:
Рис. 28. Потенціалъ и сила
поля.
ѴАВ = Е . I. созср; Ѵх Ѵ2= Е . I. соз ср .
Если направленіе АВ совпадаетъ съ направленіемъ поля, то
= 0, соз (р = 1, Ѵх — Ѵ2 = Е . I имѣетъ наибольшее возможное
значеніе, такъ какъ всегда созг/^Е 1.
Направленіе поля совпадаетъ съ направленіемъ наибо-
лѣе быстраго измѣненія потенціала.
Примемъ направленіе поля за ось нашей сферы и расположимъ
ея экваторіальную плоскость перпендикулярно этому направленію.
Если мы за точку В возьмемъ одну изъ
точекъ экваторіальной плоскости, то бу-
демъ имѣть <р = 90°, соз (р = 0 и Ѵх = ІЛ>.
Слѣдовательно, на экваторіальной пло-
скости потенціалъ имѣетъ постоянное
значеніе; направленіе поля перпендику-
лярно къ „поверхности постояннаго по-
тенціала" въ точкѣ А. Отсюда мы по-
лучаемъ простой методъ для опредѣле-
нія направленія поля. Опредѣляема потен-
ціалъ въ возможно большемъ; еислѣ то-
чекъ поля и по этимъ^|ннымъ нахо-
димъ поверхности постояннаго потенціала. Здѣсь преходится посту-
пать такъ же, какъ при построеніи кривыхъ одинаковыхъ давленій
воздуха на картѣ вѣтровъ по барометрическомъ" даннымъ отдѣль-
ныхъ метеорологическихъ станцій. Слѣдовательно, направленіе
Электрическое поле земли
73
электрическихъ силовыхъ линій всегда перпендикулярно къ
поверхностямъ постояннаго потенціала (рис. 28).
Если направленіе поля въ точкѣ А найдено, то мы можемъ
измѣрить разность потенціаловъ въ точкахъ А и В, лежащей на
этомъ направленіи. Если разстояніе АВ равно /, то
^1- ^2= УАВ = Е-1-
Слѣдовательно,
Р __
Сила поля равняется электрическому напряженію эѳира,
разсчитанному на 1 сантиметръ, иначе говоря, равняется
паденію потенціала.
Согласно этому опредѣленію, единица силы электрическаго поля
должна имѣть наименованіе „вольтъ ша сантиметръ". Сила поля равна
единицѣ, напримѣръ, въ плоскомъ конденсаторѣ, обѣ пластинки ко-
тораго сдѣланы изъ одного металла и отстоятъ другъ отъ друга на
1 сантиметръ, когда напряженіе между ними равно 1 вольту.
ЭЛЕКТРИЧЕСКОЕ ПОЛЕ ЗЕМЛИ.
44. Произведенныя съ помощью коллектора
измѣренія въ воздушной оболочкѣ земли показали,
атмосферы повсюду отличается
отъ потенціала земли, т. е. отъ
нуля. По мѣрѣ возвышенія надъ
поверхностью земли потенціалъ
все
и
электрометра
что потенціалъ
отъ
ное
но
болѣе и болѣе удаляется
нуля, сохраняя отрицатель-
значеніе.
Земной шаръ по стоя н-
окруженъ электриче-
скимъ полемъ, при чемъ
твердая оболочка земли
заряжена отрицательнымъ
электричествомъ.
Дальнѣйшія измѣренія по- ™
Рис. 29. Электрическое поле земли/
казали, что паденіе потенціала
или сила поля въ высокихъ областяхъ атмосферы становится незна-
чительнымъ; отсюда приходится заключить, что в^>° высочайшихъ
воздушныхъ слояхъ оно равно нулю. Слѣдователѣно^возбуждаемое
74
Электрическое поле земли
земнымъ шаромъ поле не распространяется въ міровое пространство,
но ограничивается областью ея воздушной оболочки. Силовыя линіи
начинаются внутри послѣдней и заканчиваются на твердой земной
поверхности (рис. 29).
Воздушная оболочка земли является носительницей
пространственно распредѣленныхъ положительныхъ заря-
довъ, которые въ общей сложности (по крайней мѣрѣ, при-
близительно) равны отрицательному заряду твердой земной
поверхности.
Это описаніе соотвѣтствуетъ, конечно, только нормальному со-
стоянію земного поля. При грозахъ могучія поля электрическихъ
облаковъ совершенно уничтожаютъ слабое нормальное поле атмо-
сферы.
ГЛАВА ТРЕТЬЯ
ЭЛЕКТРИЧЕСКІЙ ЗАРЯДЪ
ОПЫТЪ ФАРАДЭЯ СЪ КЛѢТКОЙ.
45. Въ § 6 мы уже отмѣтили, что электрическій зарядъ тѣла
образуетъ двоякую эффективную связь между матеріей и эѳиромъ.
Съ одной стороны, посредствомъ заряда тѣло вызываетъ въ эѳирѣ
электрическое возбужденіе; съ другой стороны, находящійся въ со-
стояніи электрическаго напряженія эѳиръ дѣйствуетъ при посредствѣ
того же заряда съ извѣстною силою на заряженное тѣло. До сихъ
поръ мы пользовались для измѣренія электрическаго поля только
вторымъ изъ этихъ двухъ эффектовъ; именно, мы наблюдали сило-
вое дѣйствіе эѳира на электрически заряженный индикаторъ. Иной,
совершенно независимый отъ этого, методъ опредѣленія степени
электрическаго состоянія эѳира заключается въ томъ, что измѣряется
какимъ-либо способомъ электрическій зарядъ тѣла, вызывающій это
состояніе.
Чтобы найти методъ измѣренія зарядовъ, мы должны предвари-
тельно познакомиться съ распредѣленіемъ заряда на проводникѣ.
Установимъ съ этой цѣлью чувствительный электрометръ внутри
большого металлическаго полаго тѣла. Чтобы электрометръ былъ все
время виденъ, воспользуемся большой проволочной клѣткой съ мѣд-
нымъ дномъ. Полезно оклеить эту клѣтку станіолемъ, оставивъ два
взаимно противоположныя круглыя отверстія, между которыми и
располагается электрометръ такъ, что его возможно проектировати
Сначала мы снимаемъ проволочную клѣтку съ ея основанія^и^со-
единяемъ зажимъ электрометра Экснера проволокой съ $Д>днымъ
дномъ клѣтки, которое хорошо изолировано отъ земли. Другой за-
жимъ электрометра при этомъ изолируется. СоединимъѴбъ мѣднымъ
дномъ клѣтки одинъ полюсъ электрической мащйЙМ, отведя при
76
Опытъ Фарадэя съ клѣткой
этомъ другой ея полюсъ къ землѣ. Достаточно сдѣлать небольшое
движеніе рукояткой машины, какъ электрометръ даетъ значительное
отклоненіе. Но если мы поставимъ проволочную клѣтку на мѣсто,
явленіе измѣнится. Мы можемъ въ такомъ случаѣ вертѣть рукоятку
машины сколько намъ угодно, и электрометръ не дастъ ни малѣй-
шаго слѣда отклоненія. Даже если мы зарядимъ самую клѣтку на-
Земля
Рис. 30. Опытъ Фарадэя съ клѣткой.
проскакивающею между двумя полюсамиэлек-
электрометръ все-таки не дастъ ни ^фІѣйшаго
столько сильно, что она будетъ разряжаться искрою въ нѣсколько
сантиметровъ длины,
трической машины,
отклоненія. Такимъ образомъ, мы приходимъ къ слѣдурпіему заклю-
ченію: если мы сообщимъ нѣкоторой части^проводника
электрическій зарядъ, то другія части егД^лежащія цѣли-
о \ \\
комъ внутри заряженной, остаются незаряженными.
Этотъ результатъ подтверждается впол^^какъ бы мы ни ви-
Опытъ Фарадэя съ клѣткой
17
доизмѣняли опытъ, какою бы тонкою ни была металлическая обо-
лочка, заключающая въ себѣ изслѣдуемые объекты. Первый дока-
залъ это на опытѣ (рис. 30) Фарадэй. Въ качествѣ проводника онъ.
пользовался камерою, въ которую онъ входилъ самъ съ возможно
болѣе чувствительнымъ индикаторомъ. Камера была сдѣлана изъ де-
рева и вокругъ плотно обмотана мѣдными проволоками. Поэтому та-
кой опытъ и называется опытомъ Фарадэя съ клѣткой.
46. Если мы желаемъ разсмотрѣть всѣ слѣдствія, которыя вы-
текаютъ изъ опыта съ клѣткой, то мы должны имѣть въ виду, что
и сплошной металлъ, изъ котораго составлена проводящая система,
весь, за исключеніемъ только весьма тонкаго поверхностнаго слоя,,
находится „внутри". На этомъ основаніи мы изъ опыта Фарадэя
съ клѣткой заключаемъ, что при сообщеніи заряда сплошнымъ,
проводящимъ массамъ онъ распространяется только въ
томъ тонкомъ поверхностномъ слоѣ, внутри котораго за-
ключены всѣ массы.
Слѣдовательно, зарядъ проводника является всегда поверх-
ностнымъ зарядомъ. Если мы говоримъ о плотности заряда на
проводникѣ, то подъ поверхностной плотностью заряда пони-
маемъ зарядъ, приходящійся на 1 кв. сантиметръ. Конечно, тотъ
поверхностный слой, въ которомъ распространяется зарядъ, имѣетъ
извѣстную толщину, вѣроятно, порядка молекулярныхъ измѣреній
(0,1цц=10—8 сантиметровъ), но она, во всякомъ случаѣ такъ мала,
что до сихъ поръ не могла быть установлена.
47. Электрометръ Экснера даетъ отклоненіе не только въ томъ
случаѣ, когда его стержню съ листочками сообщается зарядъ, но
уже и въ томъ случаѣ, когда его только помѣщаютъ въ электриче-
ское поле. Если мы, напримѣръ, приблизимъ къ нему натертую эбо-
нитовую палочку, онъ сейчасъ же даетъ отклоненіе. Если затѣмъ
удалить эбонитовую палочку, а вмѣстѣ съ ней и поле, то листочки
снова сходятся.
Если мы теперь опять помѣстимъ электрометръ Экснера въ
клѣтку, при чемъ оба зажима изолируемъ другъ отъ друга и от^
другихъ тѣлъ, то, при приближеніи къ нему натертой эбонинэшй4
палочки, ни малѣйшаго отклоненія уже не получимъ. Мы можемъ
даже воспользоваться электрической машиной и произвести^^всѣмъ
близко отъ электрометра чрезвычайно сильное поле, оІ?\все-таки
внутри клѣтки не окажется ни малѣйшаго слѣда егОкХ0°
'78
Опытъ Фарадэя съ клѣткой
Въ пространство, вполнѣ окруженное связанными между
♦собою проводниками, не можетъ снаружи проникнуть ни-
какое электрическое поле.
Это положеніе также было провѣрено на опытѣ Фарадэемъ.
Оно представляетъ собою лишь обобщеніе изложеннаго въ § 45 по-
ложенія; въ самомъ дѣлѣ, если во внутреннемъ пространствѣ не мо-
жетъ возникнуть никакое поле, то, очевидно, туда не можетъ про-
никнуть и никакой зарядъ, хотя и возбуждающій поле снаружи.
Рис. 31. Электрометръ съ защитнымъ панциремъ.
Мы имѣли выше случай познакомиться съ явленіемъ, которое на-
ходится въ тѣсной связи съ этимъ положеніемъ. Именно, мы имѣли
• случай убѣдиться въ § 2 и въ § 42, что металлическая пластинку,
отведенная къ землѣ, не пропускаетъ черезъ себя поля, образуемаго
заряженнымъ тѣломъ, или, какъ мы теперь можемъ выразиться^экра-
нируетъ расположенное за ней пространство отъ вліянія Наэлектри-
зованнаго тѣла. Также совершенно обнаруживается это Экранирую-
щее дѣйствіе и въ томъ случаѣ, если пространсдв^защищено отъ
образованнаго около него поля не съ одной только стороны, но со
івсѣхъ сторонъ при помощи металлической к$^т^и.
Проводники и діэлектрики
79
Весьма важное приложеніе этого экранирующаго дѣйствія провод-
никовъ дѣлается при устройствѣ электрометровъ. Такъ какъ къ полю,
образуемому двумя зажимами электрометра, можетъ еще прибавляться
поле, вызываемое внѣшними зарядами, что давало бы невѣрное откло-
неніе, то весь инструментъ заключается въ металлическую оболочку,
въ которой имѣются одно или два стеклянныхъ окошечка для отсче-
та въ (рис. 31). Въ электрометрѣ Экснера, напримѣръ, эта оболочка
состоитъ изъ металлической коробки, которая соединена съ внѣш-
нимъ зажимомъ; ея двѣ открытыя стороны покрыты стеклами, такъ
что листочекъ черезъ нихъ хорошо виденъ. У чувствительнаго ква-
дрантнаго электрометра эта защита должна быть еще болѣе совер-
шенной. Въ этомъ случаѣ, кромѣ узкихъ отверстій для проводовъ,
дѣлается только одно сравнительно большое отверстіе — незначи-
тельныхъ размѣровъ окошечко, позади котораго располагается зер-
кало, служащее для зеркальныхъ отсчетовъ.
ПРОВОДНИКИ И ДІЭЛЕКТРИКИ.
48. Въ качествѣ важнаго слѣдствія изъ опыта съ клѣткой, мы
получаемъ слѣдующее положеніе.
Въ проводникѣ при наличности равновѣсія поле всегда
равно нулю.
Въ силу этого мы можемъ дать такое опредѣленіе:
Проводникъ есть такого рода матерія, въ которой не
можетъ существовать электрическое поле.
Если бы удалось на одно мгновеніе получить въ проводникѣ
электрическое поле, оно тотчасъ бы уничтожилось.
Полупроводникъ есть такого рода матерія, въ которой
электрическое поле можетъ существовать въ теченіе нѣ-
котораго времени, постепенно при этомъ исчезая.
Изоляторъ можетъ быть въ теченіе продолжительнаго
времени носителемъ электрическаго поля.
Поэтому изоляторъ часто называютъ діэлектрикомъ, такъ
какъ онъ можетъ пронизываться электрическимъ полемъ. ! °Л
Только этими опредѣленіями, собственно говоря, и выражается^
правильно сущность электрической проводимости. Такъ какъ провод-
никъ не обладаетъ способностью удерживать поле, и, въ сшіулѣЪго,
поле въ немъ равно нулю, то напряженіе или разность потенціаловъ
между двумя точками его поверхности, естественно, также должна
80
й Индукція
равняться нулю. Поэтому, если поле находится въ равновѣсіи, то
потенціалъ во всѣхъ точкахъ проводящей поверхности имѣетъ по-
стоянное значеніе. Если соединить проводникъ съ другимъ заряжен-
нымъ проводникомъ, то происходитъ измѣненіе въ распредѣленіи си-
ловыхъ линій, продолжающееся до тѣхъ поръ, пока во всѣхъ точ-
кахъ соединенныхъ между собою проводниковъ не установится оди-
наковый потенціалъ (линейный интегралъ напряженія поля, взятый
отъ любой точки поверхности проводниковъ до земли, имѣетъ на нихъ
одинаковое значеніе). При этомъ заряды, сосредоточенные на поверх-
ности проводника, перемѣстятся — „онъ проводитъ электричество
ИНДУКЦІЯ.
49. Если мы внесемъ проводникъ въ электрическое поле, то
силовыя линіи черезъ него не пройдутъ. Поле обрывается при встрѣчѣ
съ одною стороною проводника. Однако, какъ показываетъ опытъ,
если проводникъ изолированъ, то на другой его сторонѣ при
этомъ снова образуется поле.
Мы можемъ легко въ этомъ убѣдиться если разсмотримъ изобра-
женія поля, полученныхъ описаннымъ въ § 20 способомъ на стеклян-
ныхъ пластинкахъ. На рисункѣ 32 мы видимъ, во-первыхъ, кольцо
въ полѣ плоскаго конденсатора и, во-вторыхъ, такое же кольцо въ
полѣ наэлектризованнаго шара. Кольцо въ обоихъ случаяхъ пред-
ставляетъ собою сѣченіе полаго шара. На обоихъ изображеніяхъ
видно, что силовыя линіи кончаются на одной сторонѣ полаго шара
и вновь начинаются на другой его сторонѣ; внутри же полаго шара
рутиловыя опилки лежатъ вполнѣ безпорядочно, т. е. поле здѣсь
равно нулю.
Начало и конецъ силовыхъ линій, какъ мы знаемъ, идентичны
съ отрицательнымъ и положительнымъ зарядами.
Если внести проводникъ въ электрическое поле, то онъ
оказывается заряженнымъ положительно съ одной стороны
и отрицательно съ другой.
Это явленіе носитъ названіе вліянія или индукціи.
Внесемъ въ поле большого положительно заряженнаго шара
проводникъ, состоящій изъ двухъ шариковъ, закрѣпленіяхъ на изо-
лирующихъ ручкахъ и соприкасающихся другъ с^^другомъ (рис. 33).
Если оба шарика внесены въ поле и затѣмъ4 удалены изъ поля
прочь, то помощью электрической стрѣлки ^ѵіьѣ уоѣждаемся, что оыв-
Индукція
81
шій впереди шарикъ зарядился отрицательно, а бывшій сзади — по-
ложительно. Въ дѣйствительности, на передній шарикъ дѣйствовало
поле большого шара, а на заднемъ поле возникло вновь.
Рис. 32а и 32Ь. Полый шаръ въ полѣ плоскаго конденсатора.
Если бы мы зарядили большой шаръ отрицательно, то полу-
чили бы обратные знаки индуктированныхъ зарядовъ.
Если мы подносимъ къ заряженному тѣлу изолирован-
ный проводникъ, то на той части его, кото’рая обращена
къ наэлектризованному тѣлу, индуктируется эле^рйчеств^о
обратнаго знака, а на противоположной части-^электриче-
ство того же знака. ЖЖѵ
Ми. Электричество и магпитизмь.
6
82
Индукція
Примѣромъ индукціи можетъ также служить то притяженіе лег-
кихъ тѣлъ наэлектризованной палочкой, съ котораго мы начали изу-
ченіе электрическихъ явленій въ §1. Чтобы въ этомъ убѣдиться,
подвѣсимъ рядомъ два шарика изъ бузинной сердцевины. При этомъ
одинъ подвѣсимъ на шелковой нити къ стеклянному штативу, а
Рис. 33. Въ силу индукціи
получаются два заряда съ
различными знаками.
другой на металлической нити къ метал-
лическому же штативу. Если теперь къ
этимъ шарикамъ приблизить натертую эбо-
нитовую палочку, то еще при довольно
значительномъ разстояніи ея отъ шариковъ
шарикъ, подвѣшенный къ металлической
нити, уже къ ней притягивается, шарикъ
же, подвѣшенный на шелковой нити, остает-
ся неподвижнымъ. Въ послѣднемъ шарикѣ
индуктируются заряды обоихъ знаковъ, въ
первомъ же - только зарядъ противопо-
ложнаго знака, т. е. положительный, такъ
какъ отрицательный переходитъ по провод-
никамъ на штативъ. Точно такъ же и лег-
кіе кусочки бумаги притягиваются только
въ томъ случаѣ, если они расположены на проводящей поверх-
ности. Это совершенно ясно изъ вышесказаннаго.
ОПЫТЪ ФАРАДЭЯ СЪ ВЕДРОМЪ.
50. Опытъ Фарадэя съ клѣткой показалъ намъ, что внутри
полаго металлическаго сосуда не обнаруживается никакихъ слѣдовъ
тѣхъ полей, которыя возбуждаются и любымъ образомъ измѣняются
внѣ его. Уже самъ Фарадэй произвелъ этотъ опытъ и въ обрат
номъ направленіи, желая разрѣшить такой вопросъ: вліяютъ ли элек-
трическія поля и ихъ измѣненія внутри полаго сосуда на внѣшнее
пространство?
Возьмемъ хорошо изолированную мѣдную банку, з^рЧтую
крышкой, снабженной отверстіемъ, черезъ которое моиш^^вводить
внутрь банки различные предметы и поворачивать ихф^мъ при по-
мощи изолирующихъ ручекъ. Если банка достаточно глубока, то
оказывается почти безразличнымъ, велико и лишало это отверстіе
или же она наглухо закрыта мѣдною крыщкою; у такой банки
Опытъ Фарадэя съ ведромъ
83
можно крышку удалить совершенно, и результаты нашего наблюде-
нія отъ этого не измѣнятся (рис. 34).
Мы можемъ поэтому для нашихъ опытовъ вмѣсто замкнутаго
<о всѣхъ сторонъ сосуда употреблять именно такую банку; ее мы
будемъ называть ведромъ Фарадэя или Фарадэевскимъ сосу-
домъ. Эту мѣдную банку мы помѣщаемъ для изоляціи на трехъ па-
раффиновыхъ ножкахъ и соединяемъ проволокой съ однимъ изъ за-
жимовъ электрометра Ганкеля; другой его зажимъ отводимъ къ землѣ.
Рис. 34. Ведро Фарадэя.
Земля
Мы вносимъ теперь при помощи изолирующей ручки внутрь
банки положительно заряженный металлическій шаръ; внѣ ея возни-
каетъ поле и, какъ мы видимъ, электрометръ даетъ отклоненіе, ука-
зывающее на положительный зарядъ банки. Это можно было пред-
видѣть: въ силу индукціи внутренняя поверхность банки заряжается
отрицательно, внѣшняя — положительно. Если бы металлическій шаръ
былъ заряженъ отрицательно, электрометръ указалъ бы на отри^-
тельный зарядъ.
Будемъ теперь измѣнять положеніе металлическаго^|ііара въ
Фарадэевскомъ сосудѣ, а вмѣстѣ съ тѣмъ и внутреннё^Поле. Бу-
демъ помѣщать шаръ сперва возможно ближе къ сгонкѣ или дну
6
84 Опытъ Фарадэя. — Измѣреніе электрическихъ зарядовъ
сосуда, а затѣмъ вновь удалять его на середину сосуда; отклоне-
ніе электрометра все время будетъ неизмѣннымъ и, слѣдовательно,
всѣ измѣненія, какія мы производимъ со внутреннимъ полемъ, не
оказываютъ никакого вліянія на внѣшнее поле. Если мы вынемъ за-
ряженный шаръ прочь изъ сосуда, электрометръ тотчасъ возвратится
на нуль.
Мы возвратимъ теперь вновь заряженный шаръ въ сосудъ, чтобы
инымъ пріемомъ измѣнить поле. Мы внесемъ въ сосудъ еще одинъ
незаряженный металлическій шаръ, который, какъ мы видѣли (§ 49),
въ силу индукціи долженъ замѣтно измѣнить поле перваго шара.
Но и присутствіе этого незаряженнаго шара ни малѣйшаго вліянія
на отклоненіе электрометра не оказываетъ.
И даже если мы приведемъ оба металлическіе шара въ сопри-
косновеніе, въ силу чего зарядъ равномѣрно распредѣлится по обоимъ,
то все-таки никакого вліянія на отклоненіе электрометра не обна-
ружимъ. Если же мы послѣ этого одинъ изъ шаровъ вынемъ прочь,
отклоненіе электрометра уменьшится; когда мы вынемъ и второй
шаръ, электрометръ возвратится на нуль. Мы видимъ отсюда, что,
дѣйствительно, каждый изъ двухъ шаровъ имѣлъ на себѣ часть того
заряда, который первоначально былъ на одномъ шарѣ.
Результатъ опыта Фарадэя съ ведромъ получается слѣдующій:
Если внести внутрь замкнутаго со всѣхъ сторонъ ме-
таллическаго сосуда изолированное электрически заряжен-
ное тѣло, то возникающее въ силу индукціи внѣшнее поле
зависитъ исключительно отъ введенныхъ количествъ элек-
тричества и совершенно не зависитъ отъ распредѣленія за-
ряда на отдѣльныхъ тѣлахъ внутри сосуда или отъ распо-
ложенія въ немъ силовыхъ линій.
ИЗМѢРЕНІЕ ЭЛЕКТРИЧЕСКИХЪ ЗАРЯДОВЪ.
51. Въ силу всего вышеизложеннаго оказывается возможнымъ
рѣшить задачу, поставленную въ § 45. Для сравненія электрическихъ
зарядовъ пользуются слѣдующими общими опредѣленіями^
Два тѣла или двѣ системы тѣлъ имѣютъ^Дйнаковые
заряды въ томъ случаѣ, если онѣ, будучи помѣщены въ
Фарадэевскомъ сосудѣ, даютъ одинаковой^силы внѣшнее
поле, что устанавливается при помощи электрометра, одинъ
зажимъ котораго соединенъ съ сосудомъ
Законъ сохраненія зарядовъ
85
Зарядъ системы тѣлъ равняется суммѣ зарядовъ отдѣль-
ныхъ тѣлъ системы.
Согласно этимъ опредѣленіямъ, два тѣла имѣютъ одинаковые
заряды различныхъ знаковъ, если они, будучи помѣщены вмѣстѣ въ
Фарадэевскій сосудъ, даютъ зарядъ, равный нулю.
Этотъ методъ сравненія зарядовъ носитъ названіе электро-
метрическаго метода. Электрометрическій методъ очень удобенъ,
но только въ тѣхъ случаяхъ, когда сравниваемые заряды сравни-
тельно малы. Для большихъ зарядовъ мы имѣемъ другой лучшій спо-
собъ, съ которымъ познакомимся ниже.
ЗАКОНЪ СОХРАНЕНІЯ ЗАРЯДОВЪ.
52. Послѣ того, какъ установленъ способъ сравненія зарядовъ,
можно результатъ опыта Фарадэя съ ведромъ выразить прямо въ
формѣ нижеслѣдующаго закона сохраненія электрическихъ
зарядовъ: если нѣкоторая система тѣлъ получаетъ опре-
дѣленный электрическій зарядъ, то этотъ зарядъ остается
неизмѣннымъ, что бы съ системой не происходило и какъ
бы не измѣнялись его носители, если только не совершается
перехода зарядовъ съ какихъ-либо тѣлъ, этой системѣ не
принадлежащихъ.
Это положеніе, являющееся результатомъ Фарадэевскаго опыта
съ ведромъ, позволяетъ получить еще одно важное и весьма общее
слѣдствіе:
При каждомъ процессѣ возбужденія электрическаго
заряда одновременно возникаютъ одинаковыя количества
положительнаго и отрицательнаго электричества.
Если мы внесемъ въ поле большого заряженнаго тѣла два со-
прикасающіеся металлическіе шарика, укрѣпленные на изолирующихъ
ручкахъ, то по удаленіи ихъ изъ поля, какъ это было показано
въ § 49, одинъ шарикъ оказывается заряженнымъ положительно,
гой — отрицательно. Это легко провѣрить при помощи Фарадэев-
скаго сосуда, если въ него внести оба шарика по очереди. Если ж|
мы въ него внесемъ оба шарика вмѣстѣ, то электрометръ останется
на нулѣ.
Весьма интересно убѣдиться въ томъ, что законъо^раненія
зарядовъ имѣетъ силу и для случая возбужденія электричества при
соприкосновеніи. Какъ мы видѣли въ § 29, при соприкрсновеніи сте-
86
Законъ сохраненія зарядовъ
клянной пластинки съ пластинкой, покрытой ртутной амальгамой, воз-
буждаются заряды - положительный на первой пластинкѣ и отрица-
тельный на второй. Если послѣ того, какъ обѣ пластинки слегка по-
терты другъ о друга, поднести ихъ по очереди къ Фарадэевскому сосуду,
то электрометръ дастъ громадныя отклоненія одинъ разъ въ одну, дру-
гой разъ въ другую сторону. Если же внести въ сосудъ обѣ пластинки
вмѣстѣ, то нить электрометра Ганкеля останется неподвижной.
53. Повторимъ еще разъ опытъ Фарадэя съ ведромъ. Опу-
стимъ снова нашъ заряженный металлическій шаръ въ сосудъ и за-
мѣтимъ, насколько отклонится электрометръ. Послѣ этого дотронемся
внезапно шаромъ до стѣнки сосуда. При этомъ ни малѣйшаго измѣ-
ненія въ показаніи электрометра мы не обнаружимъ. Но если мы те-
перь удалимъ шаръ изъ сосуда, то электрометръ уже не возвра-
тится на нуль, но останется при прежнемъ показаніи; слѣдовательно,
зарядъ Фарадэевскаго сосуда не измѣнился при удаленіи шара.
Отсюда мы заключаемъ, что въ моментъ соприкосновенія со
стѣнкой сосуда шаръ потерялъ весь свой зарядъ, такъ какъ только
совершенно лишенное заряда тѣло не оказываетъ никакого дѣйствія
на электрометръ, когда его вносятъ въ сосудъ или удаляютъ изъ него.
Это понятно, такъ какъ изъ опыта съ клѣткою (§ 45) мы знаемъ, что въ
системѣ соприкасающихся металлическихъ массъ части, лежащія все-
цѣло во внутренней полости, должны быть незаряженными. Слѣ-
довательно, зарядъ шара весь перешелъ на сосудъ. Но въ моментъ
этого перехода никакихъ измѣненій въ показаніи электрометра не
произошло. Слѣдовательно, за все время опыта зарядъ наружной
поверхности сосуда не мѣнялся. Отсюда мы получаемъ слѣдующій
выводъ: заряженное тѣло, введенное въ замкнутый со всѣхъ
сторонъ сосудъ, возбуждаетъ на внѣшней его сторонѣ за-
рядъ, въ точности равный своему собственному заряду.
Это положеніе мы можемъ провѣрить еще на слѣдующемъ опытѣ.
Помѣстимъ въ хорошо изолированный Фарадэевскій сосудъ друт'бй
такой же сосудъ меньшихъ размѣровъ (рис. 35) и шаръ ^^йреж-
нимъ зарядомъ внесемъ во внутренній сосудъ. Электром^уъ даетъ
то же отклоненіе, что и при отсутствіи внутренняго ^сосуда. Слѣ-
довательно, внутренній сосудъ при внесеніи шара ,н)|ійбрѣтаетъ на
своей поверхности такой же зарядъ, какой имѣ^рйіаръ.
Найденный выше законъ разъясняетъ намт^рлубокое значеніе ме-
тода измѣреній при помощи Фарадэевскаго^сосуда. Электрическій
Законъ сохраненія зарядовъ
87
зарядъ, согласно нашимъ взглядамъ, есть не что иное, какъ мѣра того
дѣйствія, которое заряженное тѣло оказываетъ на эѳиръ, того элек-
трическаго возбужденія, которое оно вызываетъ. Поэтому мы часто
будемъ называть зарядъ еще полнымъ возбужденіемъ эѳира подъ
дѣйствіемъ заряженнаго тѣла. Въ опытѣ Фарадэя полное возбужде-
ніе, вызываемое нѣкоторымъ произвольнымъ тѣломъ, переходитъ
на твердое нормальное тѣло постоянной формы — на Фарадэевскій
сосудъ, и мы при помощи индикатора наблюдаемъ поле, которое
образуется въ опредѣленномъ мѣстѣ поверхности нормальнаго тѣла,
точнѣе - - на зажимѣ электрометра, соединенномъ съ сосудомъ.
Рис. 35. Два Фарадэевскіе сосуда.
Этотъ методъ вполнѣ аналогиченъ электрометрическому методу
измѣренія полнаго электрическаго напряженія. Пользуясь послѣднимъ,
мы переносимъ полное напряженіе въ поле нормальной формы,
образуемое двумя зажимами электрометра, и опредѣляемъ при помогли^'
индикатора силу поля въ опредѣленномъ мѣстѣ этого нормадьнаЙг
поля.
54. Въ послѣдующемъ мы можемъ также пользоваться аппа-
ратомъ, съ которымъ мы произвели опытъ Фарадэя, ^сакъ измѣри-
тельнымъ приборомъ. Его легко калибрировать, если^ыбрать опре-
дѣленную единицу.
88
Электрическое возбужденіе эѳира
Мы воспользуемся съ этой цѣлью металлическимъ шаромъ въ
6 сантиметровъ діаметромъ на изолирующей ручкѣ, заряженнымъ
посредствомъ соприкосновенія съ проводомъ отъ батареи высокаго
напряженія до 1000 вольтъ. Зарядъ, пріобрѣтаемый при этомъ ша-
ромъ, мы вполнѣ произвольно примемъ за единицу. Мы касаемся этимъ
шаромъ дна Фарадэевскаго сосуда и замѣчаемъ отклоненіе электро-
метра, соотвѣтствующее этому заряду. Послѣ этого заряжаемъ нашъ
шаръ снова, опять сообщаемъ его зарядъ Фарадэевскому цилиндру
и, такимъ образомъ, получаемъ отклоненіе, соотвѣтствующее заряду,
равному двумъ единицамъ. Если мы такимъ образомъ будемъ послѣ-
довательно прибавлять единичный зарядъ, принятый за единицу, къ
имѣющимся уже въ сосудѣ зарядамъ, то мы получимъ всю шкалу инстру-
мента, какъ съ положительной, такъ и съ отрицательной стороны г).
полнымъ возбужденіемъ
Рис. 36. Различныя плотности
заряда.
ЭЛЕКТРИЧЕСКОЕ ВОЗБУЖДЕНІЕ ЭѲИРА.
55. Мы отождествили электрическій зарядъ нѣкотораго тѣла съ
эѳира, вызываемымъ этимъ тѣломъ. Но въ
различныхъ мѣстахъ тѣла это возбужде-
ніе можетъ быть весьма различно. Заря-
димъ, напримѣръ, 8-образно выгнутую
проволочную сѣтку; въ мѣстахъ, соотвѣт-
ствующихъ ея выпуклостямъ, будетъ воз-
буждаться въ эѳирѣ гораздо болѣе силь-
ное поле, чѣмъ въ мѣстахъ, соотвѣт-
ствующихъ ея вогнутостямъ. Это сразу
видно по различнымъ отклоненіямъ, ко-
торыя испытываютъ два шарика изъ бу-
зинной сердцевины, подвѣшенные въ раз-
личныхъ мѣстахъ сѣтки (рис. 36). Легко
указать и иные примѣры, разсматривая
изображенія различныхъ электрическихъ
полей, приведенныя въ § 20.
Если же мы желаемъ, не ограничи-
ваясь общимъ возбужденіемъ ^ѳйра, знать
и распредѣленіе поля по цЙзЙуждающей
поверхности, то мы дблжны заняться
измѣреніемъ поверхностной плотности заряда.
О Въ зависимости отъ того, съ какимъ полю^бйѣ батареи будемъ со-
единять нашъ шаръ. Прим. пер.
Пробный кружокъ
89
Поверхностная плотность заряда проводника, т. е. за-
рядъ, приходящійся на 1 квадратный сантиметръ, есть мѣра
удѣльнаго возбужденія эѳира, въ данномъ мѣстѣ поверх-
ности проводника.
Когда мы впослѣдствіи будемъ кратко упоминать возбужденіе
эѳира, то при этомъ будемъ имѣть въ виду всегда удѣльное воз-
бужденіе.
Разница между двумя понятіями объ удѣльномъ возбужденіи и
полномъ возбужденіи во многихъ отношеніяхъ аналогична разницѣ
.между понятіями о силѣ поля и о полномъ напряженіи.
ПРОБНЫЙ КРУЖОКЪ.
5'6. Для измѣренія поверхностной плотности заряда и вмѣстѣ
съ тѣмъ электрическаго возбужденія эѳира служитъ весьма простой
инструментъ — -пробный кружокъ — маленькій металлическій кру-
жокъ укрѣпленный на изолирующей ручкѣ, площадь котораго тща-
тельно измѣрена. Наложимъ пробный кружокъ въ томъ мѣстѣ, гдѣ
мы желаемъ измѣрить возбужденіе, на заряженную поверхность. Если
кружокъ настолько малъ, что вплотную прилегаетъ къ поверхности,
то онъ просто снимаетъ зарядъ съ покрытой имъ части поверхности.
Этотъ зарядъ мы измѣряемъ на прокалибрированномъ приборѣ и раз-
дѣляемъ полученную величину на площадь кружка; такъ опредѣляется
удѣльное возбужденіе эѳира.
При помощи пробнаго кружка мы легко можемъ убѣдиться въ
существованіи разности возбужденій на выпуклой и вогнутой сторо-
нахъ вышеописанной 8-образной проволочной сѣтки.
Заряженное тѣло, конечно, возбуждаетъ первоначально непо-
средственно прилежащій къ нему слой эѳира, а оттуда возбужденіе
уже распространяется дальше и дальше на все электрическое поле.
Это можно представить себѣ на студнеобразной модели эѳира, опи-
санной въ § 23. Избытокъ или недостатокъ жидкости въ упругихъ
клѣткахъ нѣкоторой области первоначально вызываетъ смѣщеніе не-..^
посредственно окружающихъ эту область слоевъ студня. Но^этѳ
смѣщеніе необходимо вызываетъ въ болѣе удаленныхъ частяхт^сдудня
дальнѣйшія смѣщенія, и такимъ образомъ возникаетъ „полеф>въ на-
шей студнеобразной модели.
Въ силу этого возможно измѣрять электричесюред возбужденіе
эѳира на большомъ разстояніи отъ возбуждающагО^ѣла совершенно
90
Пробный кружокъ
такъ же, какъ и непосредственно на поверхности послѣдняго. И дѣй-
ствительно, если мы помѣстимъ пробный кружокъ въ любое мѣсто
поля и расположимъ его перпендикулярно къ силовымъ линіямъ, то
онъ въ силу индукціи пріобрѣтетъ зарядъ, характеризующій электри-
ческое возбужденіе въ изслѣдуемомъ мѣстѣ. Если кружокъ чрезвы-
чайно тонокъ, то онъ представитъ собою при этомъ просто часть
эквипотенціальной поверхности и совершенно не измѣнитъ направленія
силовыхъ линій. Пучекъ силовыхъ линій только разсѣкается круж-
комъ, ибо внутри металла, какъ мы знаемъ, поле прерывается. Отри-
цательный зарядъ на одной сторонѣ кружка, согласно нашему опре-
дѣленію, равенъ возбужденію всего заканчивающагося здѣсь пучка си-
ловыхъ линій, положительный же зарядъ на другой сторонѣ пред-
ставляетъ собою возбужденіе пучка силовыхъ линій, возникающее
здѣсь вновь съ тою же силой.
Зарядъ, индуктируемый на пробномъ кружкѣ, располо-
женномъ перпендикулярно къ силовымъ линіямъ, разсчи-
танный на 1 квадратный сантиметръ, даетъ намъ удѣльное
возбужденіе эѳира.
Согласно этому опредѣленію, „возбужденіе" является также ве-
личиною векторіальною. Если помѣстить пробный кружокъ парал-
лельно силовымъ линіямъ, то на каждой его сторонѣ возбуждаются
въ нѣкоторомъ количествѣ и положительный зарядъ и отрицательный;
въ общемъ на каждой сторонѣ зарядъ оказывается равнымъ нулю.
Если помѣстить кружокъ наклонно относительно силовыхъ линій, то
получаются на одной сторонѣ положительный зарядъ, на другой -
отрицательный; но оба заряда оказываются меньше по величинѣ, не-
жели при положеніи кружка, перпендикулярномъ къ силовымъ линіямъ.
Направленіе электрическаго возбужденія эѳира совпа-
даетъ съ направленіями нормалей къ пробному кружку
при такой его оріентировкѣ, которая соотвѣтствуетъ мак-
симальному дѣйствію индукціи; при этомъ оно идетъ одѣ^
отрицательной поверхности кружка къ положительной?;/
Можно произвести дѣйствительное измѣреніе эле^рзйцёскаго
напряженія въ эѳирѣ, если воспользоваться двумя вполнѣ/прилегаю-
-у
щими другъ къ другу кружками, снабженными каж^ьШизолирую щей
ручкой. Въ такомъ случаѣ мы имѣемъ дѣло съ дойнымъ круж-
комъ. Если внести двойной кружокъ въ элек^ийёское поле и пра-
вильно его оріентировать, то при взаимноц>^удаленіи двухъ круж-
Пробный кружокъ
91.
ковъ получаются индуктированные заряды — положительный на
одномъ, отрицательный на другомъ. Эти заряды можно измѣрить^
внося ихъ по очереди въ Фарадэевскій сосудъ; полученныя величины
нужно раздѣлить на величину поверхности каждаго кружка.
Численный примѣръ сдѣлаетъ сказанное болѣе яснымъ. Положимъ,,
двойной кружокъ внесенъ въ поле изолированнаго металлическаго,
шара діаметромъ въ 10 сантиметровъ (рис. 37) и установленъ сперва.
Рис. 37. Измѣреніе поля помощью пробной пластинки.
на разстояніи 20
стояніи 30 сантиметровъ. Кружокъ при этомъ
гаться перпендикулярно къ линіи, соединяющей
шара, и долженъ быть какимъ-либо образомъ
можно было точно отмѣривать его разстоянія отъ центрд^шара..
Отклонимъ теперь наружный кружокъ; чтобы своимъ приближеніемъ
не повліять на поле, воспользуемся для этого достаточно длинною
нитью. Для удобства можно изолирующую ііггангу^чНДкоторой за-
сантиметровъ отъ центра шара, затѣмъ — на раз-
долженъ расгюла-г
его съ центро^Ш^
закрѣпленъ,
92
Законъ постоянства электрическаго возбужденія
крѣпленъ этотъ кружокъ, снабдить вращающимся шарниромъ. Нако-
нецъ, мы можемъ одинъ изъ кружковъ приложить къ нѣкоторой
‘части поверхности самаго заряженнаго шара, чтобы найти величину
возбужденія на самой поверхности. При этомъ опытѣ получаются
^слѣдующія количества электричества, выраженныя въ нашихъ про-
извольно установленныхъ единицахъ (§ 54):
разстояніе отъ центра шара: 30 см. 20 см. 10 см.
зарядъ кружка: 0,4 0,9 3,6
Нашъ кружокъ имѣетъ діаметръ, равный 6,2 сантиметрамъ,
*т. е. площадь его равняется 30 квадратнымъ сантиметрамъ. Слѣдо-
вательно, возбужденіе эѳира, которое мы, какъ это принято, будемъ
обозначать черезъ /), на указанныхъ разстояніяхъ г отъ центра шара
равняется:
г = 30 см. 20 см. 10 см.
О = 0,0133 0,03 0,12
Величину /), которую мы здѣсь называемъ удѣльнымъ воз-
бужденіемъ эѳира, Максвеллъ, а вмѣстѣ съ нимъ и другіе
•авторы называютъ электрическимъ смѣщеніемъ.
ЗАКОНЪ ПОСТОЯНСТВА ЭЛЕКТРИЧЕСКАГО ВОЗБУЖДЕНІЯ.
57. На практикѣ при измѣреніяхъ обыкновенно приходится имѣть
дѣло съ полнымъ возбужденіемъ, представляемымъ всѣмъ электриче-
скимъ зарядомъ тѣла. Совершенно такъ же обстоитъ дѣло при измѣре-
ніи силы поля, когда тоже почти исключительно довольствуются опре-
дѣленіемъ полнаго напряженія. Какъ и въ томъ случаѣ (§ 25), такъ
и здѣсь это упрощеніе основывается на важномъ ^общемъ законѣ
^природы.
Возвратимся еще разъ къ опыту Фарадэя съ ведромъ. Если
мы внесемъ въ ведро положительно заряженное тѣло, то, какъ
мы видѣли въ § 53, электрометръ покажетъ положительный заря^>
ведра, въ точности равный заряду внесеннаго въ ведро тѣла. Соеди-
нимъ теперь зажимъ электрометра, соединенный съ ведромъ^ѣа ко-
роткое время съ другимъ зажимомъ электрометра и тѣмъ^самымъ —
съ землею; заряженное тѣло при этомъ оставимъ поррежнему по-^
груженнымъ въ ведро. Какъ можно было предвидѣлъ^ электрометръ
при этомъ возвращается на нуль. Если прервемъ^ соединеніе ведра
съ землей снова и затѣмъ вынемъ заряж^^І тѣло изъ ведра,
Законъ постоянства электрическаго возбужденія
93:
то электрометръ покажетъ отрицательное отклоненіе; при этомъ,
зарядъ ведра, независимо отъ знака, оказывается въ точности рав-
нымъ положительному внѣшнему заряду, наблюденному до соеди-
ненія ведра съ землей, т. е. заряду самаго погруженнаго въ ведро
тѣла. Зарядъ внутренней поверхности той полости, въ которую вне-
сено заряженное тѣло, въ точности равенъ заряду этого тѣла, но
имѣетъ противоположный знакъ; отъ величины же полости онъ со-
вершенно не зависитъ. .
Если заряженное тѣло или система заряженныхъ тѣлъ
окружены замкнутою поверхностью, то полное электри-
ческое возбужденіе на этой поверхности одно и то же,
какъ въ томъ случаѣ, когда поверхность плотно приле-
гаетъ къ заряженнымъ тѣламъ, такъ и тогда, когда она.
охватываетъ значительное пространство. Эта величина въ.
точности равна суммѣ зарядовъ тѣлъ, возбуждающихъ поле.
Этотъ законъ можно высказать также въ формѣ слѣдующаго
положенія: вдали отъ заряженнаго тѣла не происходитъ ни воз-
никновенія, ни потери электрическаго возбужденія. Его можно
сдѣлать болѣе нагляднымъ, если представить поле графически при.
помощи „линій возбужденія", т. е. линій, имѣющихъ повсюду напра-
вленіе вектора „возбужденіе" (вообще этотъ векторъ совпадаетъ,
съ векторомъ „сила поля"), пространственная плотность которыхъ,
пропорціональна величинѣ возбужденія. Линіи возбужденія электри-
ческаго поля не могутъ ни начинаться, ни исчезать въ тѣхъ мѣстахъ,
гдѣ нѣтъ никакихъ электрическихъ зарядовъ. Начало электрической
линіи возбужденія тождественно съ наличностью положительнаго за-
ряда, конецъ — съ наличностью отрицательнаго заряда.
Представимъ себѣ простѣйшій случай электрически заряженнаго>
шара радіуса гх\ положимъ, что зарядъ его есть т. Предположимъ,
что вдали отъ этого шара не находится никакихъ зарядовъ или
проводящихъ тѣлъ, которые могли бы исказить простую центриче-
скую симметрію поля. Такъ какъ зарядъ на шарѣ долженъ бытьг
распредѣленъ при этомъ равномѣрно и поверхность шара равняете^
4лгг*, то возбужденіе въ нѣкоторой точкѣ его поверхности^ рав-
т
няется /)1 = • Представимъ себѣ теперь, что въ окружающемъ
этотъ шаръ пространствѣ построенъ концентрическій шаръ большаго
. . ; х\ .
радіуса гг. Общее возбужденіе на немъ равно также^р^ и, слѣдо--
“94
Студнеобразная модель эѳира
ъательно, возбужденіе въ нѣкоторой точкѣ его поверхности рав-
няется /)2 = • Слѣдовательно, возбужденіе убываетъ обратно
пропорціонально квадрату разстоянія отъ центра шара.
Приведенныя въ предыдущемъ параграфѣ измѣрительныя данныя
подтверждаютъ это заключеніе. Дѣйствительно:
0,12 : 0,03: 0,0133 =
1
900’
: /)2 :
2 . 1 ._1_
Г\ ’ П • гі •
Полное возбужденіе эѳира, вызываемое большимъ заряженнымъ ша-
ромъ, равняется т = 0,12 . 4л . 100 = 151.
СТУДНЕОБРАЗНАЯ МОДЕЛЬ ЭѲИРА.
58. Всѣ разсмотрѣнные вопросы мы можемъ нѣсколько нагляд-
нѣе выяснить, если воспользуемся студнеобразною моделью эѳира,
описанной въ § 23. Прежде всего займемся разысканіемъ механи-
ческой аналогіи электрическому проводнику. Изъ опыта съ клѣт-
кой выяснилось основное свойство, характеризующее всѣ особен-
ности проводника: проводникъ не можетъ удерживать электрическихъ
напряженій. Поэтому на нашей модели проводникъ можетъ быть
представленъ такой частью пространства, въ которой стѣнки клѣто-
чекъ болѣе или менѣе пористы, такъ что черезъ нихъ можетъ про-
никать клѣточная жидкость, не вызывая при этомъ напряженій. Полу-
проводникъ аналогиченъ такой части студня, въ которой стѣнки клѣ-
точекъ, по крайней мѣрѣ, не вездѣ одинаково плотны. Если въ полу-
проводникѣ имѣетъ мѣсто электрическое напряженіе, то стѣнки клѣ-
точекъ постепенно стягиваются обратно изъ напряженнаго положенія
въ нормальное ихъ положеніе, при чемъ жидкость, вызвавшая ихъ
перемѣщеніе, постепенно черезъ нихъ просачивается. Только въ со-
вершенномъ изоляторѣ стѣнки клѣточекъ являются абсолютно плот-
ными. Поэтому легко понять, что электрическій зарядъ провойнйка
сосредоточивается весь на его поверхности. Предположим^чйто въ
проводящей части пространства заключенъ избытокъ ж^(дй>’сти. Вну-
треннія клѣтки, въ силу ихъ пористости, никакихъ ^вмѣненій при
этомъ не потерпятъ. Только клѣтки, граничащія^фь изоляторомъ,
которыя, по крайней мѣрѣ, съ одной стороныо ^дбтно закупорены,
разбухаютъ. Совершенно аналогичное я вле||іеполу чается въ провод-
Студнеобразная модель эѳира
95
никѣ при отрицательномъ его заряженіи, т. е. при нѣкоторомъ умень-
шеніи нормальнаго содержанія въ немъ жидкости. Общій зарядъ про-
водника является мѣрой измѣненія его объема и, слѣдовательно, мѣ-
рой общаго смѣщенія жидкости въ студенистомъ эѳирѣ, изъ него
исходящаго. Величина заряда въ опредѣленномъ мѣстѣ является мѣ-
рой величины смѣщенія, которому подверглась жидкость въ этомъ
именно мѣстѣ Точно такъ же и внутри поля та величина, которую мы
назвали возбужденіемъ, представляется смѣщеніемъ жидкости (рис. 38).
Если мы представимъ себѣ, что въ поле, перпендикулярно къ ли-
ніямъ смѣщенія въ немъ, внесенъ проводящій кружокъ, т. е. кру-
жокъ, стѣнки клѣтокъ котораго проницаемы, то клѣтки, граничащія
Рис. 38. Модель положительно и отрицательно за-
ряженнаго проводника въ студнеобразномъ эѳирѣ.
Рис. 39. Модель проб-
ной пластинки.
сожмутся, а съ дру-
это будетъ соотвѣт-
(рис. 39).
закона
съ изоляторомъ, съ одной стороны нѣсколько
гой — разбухнутъ, и именно настолько, что
ствовать происходящему въ кружкѣ смѣщенію
Наша модель даетъ намъ простое толкованіе закона постоян-
ства электрическаго возбужденія. Дѣйствительно, если во всѣхъ слу-
чаяхъ увеличеніе объема на внѣшней сторонѣ Фарадэевскаго сосуда
въ точности равно введенному въ него избытку жидкости, какъ бы
ни былъ великъ самый сосудъ, то это значитъ только, что напол-
няющая студенистый эѳиръ жидкость и клѣточныя стѣнки абсолютно
несжимаемы. Если бы студенистый эѳиръ былъ сжимаемъ, то внѣш-
нее увеличеніе объема могло бы быть меньше внесеннаго заряже^%® I
нымъ тѣломъ избытка жидкости, вслѣдствіе сжатія во внутренней
полости тѣла. Изъ этого свойства эѳира — его несжимаемости^^слѣ-
дуетъ такъ же и то положеніе, что при возникновеніи ^котораго
положительнаго заряда одновременно возникаетъ иЛфвный ему
отрицательный зарядъ. Л
96
Студнеобразная модель эѳира
Ниже, въ электродинамикѣ, мы увидимъ, что въ эѳирѣ возможны
только поперечныя волны, но не продольныя. Это обстоятельство
также связано съ тѣмъ свойствомъ эѳира, которое мы назвали
„ несжимаемостьюи. Продольныя волны необходимо связаны со спо-
собностью среды къ сгущенію и разрѣженію. Если бы въ эѳирѣ,
существовали продольныя волны, то изъ этого факта слѣдовало бы
заключить, что опытъ Фарадэя съ ведромъ не вполнѣ точенъ;
обратно, если бы точныя измѣренія указали на отклоненія отъ ре-
зультата, полученнаго Фарадэемъ, то пришлось<бы заключить, что
въ эѳирѣ возможны и продольныя колебанія.
Сила электрическаго поля на нашей модели является мѣрой
силы, которая вопреки упругимъ напряженіямъ клѣточныхъ стѣнокъ
вызываетъ смѣщеніе жидкости, разсчитанной на единицу объема.
Если мы просуммируемъ эти силы отъ заряженной поверхности до
поверхности земли, то такая сумма дастъ намъ напряженіе заряжен-
наго тѣла - разность давленій жидкости на заряженномъ тѣлѣ и на
землѣ. Давленіе жидкости аналогично потенціалу, при чемъ ея да-
вленіе на поверхности земли мы принимаемъ за нормальное, за ну-
левую точку шкалы давленій. Подобно тому, какъ сила поля рав-
няется паденію потенціала, такъ же сила смѣщенія, разсчитанная на
единицу объема, равняется на нашей модели паденію давленія. То
обстоятельство, что проводникъ всегда долженъ быть заряженъ до
постояннаго потенціала, находитъ въ нашей модели аналогію въ томъ, что
въ свободно движущейся жидкости давленіе должно быть постояннымъ.
Мы видимъ такимъ образомъ на модели эѳирнаго студня, какъ,
выясняются аналогіи между напряженіемъ и зарядомъ, силой и де-
формаціей.
ЭЛЕКТРОФОРЪ.
59. На индукціи основано устройство современныхъ электриче-
скихъ машинъ. Мы уже видѣли (§ 30), что дѣйствіе электрической:
машины заключается въ томъ, что положительный и отрицательный
заряды, первоначально образующіе „двойной слой“, удаляются другь.
отъ друга и при этомъ растягиваютъ соединяющія ихъ первоначально*
безконечно короткія силовыя линіи на поле конечньп;ъ<размѣровъ..
Чтобы получить этотъ двойной слой, наличность котораго является'
первымъ требованіемъ при построеніи машины, моИфо пользоваться!
не только контактомъ, какъ въ электрической мфринѣ съ треніемъ»,
но и индукціей. ѵХМ
Электрофоръ
97
Это имѣетъ мѣсто, напримѣръ, въ электрофорѣ. На наэлектри-
зованную пластинку изъ изолирующаго матеріала, напримѣръ, на эбо-
нитъ или на канифоль, натертый кошачьимъ мѣхомъ, кладется ме-
таллическій кругъ (рис. 40). Мы будемъ называть пластинку „ли-
стомъ*', а кругъ — „крышкой". Если листъ заряженъ, напримѣръ,
отрицательно, то крышка въ силу индукціи заряжается на нижней сто-
ронѣ положительно, на верхней — отрицательно. Если крышку соеди-
нить проводникомъ съ землею, то ея верхняя сторона теряетъ свой
Рис. 40. Электрофоръ.
отрицательный зарядъ и остается только положительный зарядъ на
нижней ея сторонѣ, образующій съ отрицательными зарядомъ листа
двойной электрическій слой. Послѣ этого крышка поднимается за изо-
лирующую ручку; при этомъ, вслѣдствіе растяженія силовыхъ линій,
ея потенціалъ повышается. Приблизивъ къ ней проводникъ, можно
извлечь изъ нея большую искру. По истощеніи заряда крышки можно^м
повтореніемъ описанныхъ манипуляцій произвольно часто заряж^йр^
ее вновь.
Электрофоръ имѣетъ то преимущество передъ электрцЧёской
машиной съ треніемъ, что въ немъ не происходитъ никакой^ траты
энергіи на треніе. Но операція накладыванія, отведеідя< къ землѣ и
Ми. Электричество и магнитпзмъ. 7
98
Электрофоръ
подниманія настолько медленна и хлопотлива, что употреблять элек-
трофоръ для возбужденія большихъ зарядовъ совершенно невозможно.
Но такъ какъ эти неудобства не связаны съ сущностью самаго про-
цесса полученія электричества, то тотъ же принципъ можетъ быть
примѣненъ къ построенію быстродѣйствующей машины — электро-
форной машины. Въ такой машинѣ вращающійся стеклянный кругъ
снабженъ рядомъ „крышекъ", расположенныхъ по окружности; парал-
лельно вращающемуся кругу расположенъ неподвижный кругъ, имѣю-
щій съ одной стороны положительно заряженный „листъ", съ другой—
отрицательно заряженный. Двѣ діаметрально противоположныя крышки,
Рис. 41. Схема электрофорной машины.
находящіяся какъ разъ противъ положительнаго и отрицательнаго
листовъ, временно соединяются другъ съ другомъ при посредствѣ
неподвижнаго металлическаго стержня, снабженнаго на концахъ метал-
лическими гребенками и щетками (рис. 41); благодаря этому поло-
жительный поверхностный зарядъ одной крышки нейтрализуется отри-
цательнымъ зарядомъ другой крышки. При вращеніи крышка уда-
ляется отъ своего листа и подходитъ къ другому листу, заряжен-
ному одноименно съ ней. Тутъ она приходитъ въ соприкосш^шеніе съ
неподвижнымъ стержнемъ, снабженнымъ также гребенкри|и щеткой
и соединеннымъ съ однимъ изъ „кондукторовъ" м^ийы- Пройдя
мимо кондуктора, крышка вновь приходитъ въ соприкосновеніе съ
нейтрализующимъ стержнемъ, пріобрѣтаетъ затѣм^зарядъ, противо-
положный заряду листа, вновь удаляется от^л^Гста и т. д.
Индукціонная машина
99
ИНДУКЦІОННАЯ МАШИНА.
60. Отъ этой простой электрофорной машины обычно употре-
бляемыя индукціонныя машины отличаются только приспособле-
ніемъ, благодаря которому оба листа самопроизвольно заряжаются
до возможно болѣе высокаго напряженія и сохраняютъ его. Каждый
листъ индукціонной машины состоитъ изъ проводящей накладки,
напримѣръ, бумажной, настолько большой, что передъ нею одно-
временно находятся три крышки. Первая крышка, подходящая отъ
другого листа и потому заряженная одноименно съ тѣмъ листомъ,
къ которому она подходитъ, и до высокаго потенціала, соединяется
Рис. 42. Схема индукціонной электрической машины.
съ этимъ листомъ при помощи металлической щетки, которой она
при прохожденіи касается; въ силу этого зарядъ листа увеличивается,
если его потенціалъ ниже потенціала листа. Вторая крышка, уже
прошедшая мимо этого контакта съ листомъ, приходитъ въ сопри-
косновеніе съ кондукторомъ машины и заряжаетъ его до своего
потенціала. Третья крышка, наконецъ, уже прошедшая и мимо кондук-
тора, соприкасается съ нейтрализующимъ стержнемъ и получаетъ
рядъ, противоположный заряду листа (рис. 42). При дальнѣйшемъ
вращеніи образуемый индукціею двойной слой раздѣляется,/(Крышка,
наконецъ, подходитъ къ другому листу, и здѣсь происходитъ то же,
что и у перваго листа, и т. д.
Такимъ устройствомъ достигается то, что напряженія зарядовъ
7
100
Индукціонная машина
на листахъ, даже если они первоначально были весьма малы (можно
ограничиться при этомъ заряженіемъ одного изъ двухъ листовъ),
непрерывно повышаются, пока, наконецъ, вслѣдствіе несовершенства
изоляціи не прекратится ихъ дальнѣйшее повышеніе.
На практикѣ употребляются индукціонныя машины трехъ типовъ.
Индукціонная машина Гольца (рис. 44) отличается тѣмъ,
что на вращающемся стеклянномъ кругѣ у нея отсутствуютъ „крышки".
Отсутствуютъ у нея также и металлическія щетки. На нейтрализую-
щемъ стержнѣ и на проводникахъ, соединенныхъ съ кондукторами,
Рис. 43. Машина Вимшурста.
имѣются только гребенки. Около нихъ въ силу дѣйствія присущаго
остріямъ (§§ 13, 15) между гребенками и стекляннымъ кругомъ обра-
зуются „крышки" изъ проводящаго воздушнаго слоя. Внѣшней по-
верхностью такой крышки является самая гребенка, внутреннею—нр-^
верхность вращающагося стекляннаго круга. Далѣе, для заряжейія^ли-
стовъ" употребляются въ машинѣ Гольца не щетки, а.^аленькіе
бумажные листки, касающіеся вращающагося стекляннауркруга.
Прежде, чѣмъ пустить машину Гольца въ хрд^^ее слѣдуетъ
зарядить. Для этого одному изъ двухъ листовъ соЬбщаютъ зарядъ,
безразлично положительный или отрицательны^^ °
Индукціонная машина
101
Индукціонная машина Тендера вполнѣ соотвѣтствуетъ тому
типу, описаніе котораго мы дали выше подъ простымъ названіемъ
индукціонной машины. „Крышками“ на ней являются металлическіе
кружки, приклеенные къ вращающемуся стеклянному кругу. Для со-
единеній употребляются металлическія щеточки. При ихъ скольже-
ніи по стеклянному кругу возникаютъ на послѣднемъ небольшіе за-
ряды, достаточные, однако, для возбужденія машины. Слѣдовательно,
машина Теплера не требуетъ никакого особаго возбужденія, какъ
машина Гольца, и является машиной самовозбуждающейся. При та-
комъ самовозбужденіи вообще зависитъ отъ случая, какой листъ
окажется положительнымъ, и какой — отрицательнымъ. При полученіи
помощью такой машины весьма высокихъ напряженій часто наблю-
Рис. 44. Машина Гольца въ качествѣ генератора и машина Теплера въ
качествѣ мотора.
дается нежелательное явленіе ея „деполяризаціи", при которомъ оба
листа самопроизвольно мѣняются знаками своихъ зарядовъ.
Можно распредѣлить „листы" такъ же, какъ и „крышки", и
кондукторъ соединить съ заряжающей щеткой. Если при этомъ оба
круга построить совершенно одинаковыми и къ обѣимъ сторонамъ
присоединить разряжающій стержень, то можно одновременно вра-
щать оба круга въ противоположныхъ направленіяхъ. „Крышка"
одного круга является при этомъ „листомъ" для другого. Машг^|>7
состоящая изъ двухъ вращающихся въ противоположныя стороны
круговъ — стекляннаго и эбонитоваго съ наклеенными на^йЖь ста-
ніолевыми полосами, носитъ названіе машины Вимшур^т^Г(рис. 43).
61. Въ индукціонной машинѣ, какъ и въ машині| съ треніемъ,
электрическая энергія возникаетъ за счетъ работы^ ^производимой
102
Индукціонная машина
при вращеніи противъ силъ электрическаго поля, дѣйствующихъ на
заряды. Можно, наоборотъ, воспользоваться этими силами для полу-
ченія работы. Для этого нужно непрерывно подводить къ машинѣ
электрическіе заряды. Машина въ этомъ случаѣ будетъ уже не „ге-
нераторомъ электричества", но „моторомъ", и заряды вмѣсто того,
чтобы возобновляться въ силу индукціи между „листами" и „крыш-
ками", будутъ при соединеніи послѣднихъ взаимно уничтожаться. Въ
моторѣ, такимъ образомъ, будетъ изъ электрической энергіи полу-
чаться работа.
Описанный опытъ чрезвычайно легко воспроизвести. Если со-
единить проволоками между собою кондукторы двухъ индукціонныхъ
машинъ и пустить въ ходъ одну изъ нихъ въ качествѣ „генера-
тора", то черезъ небольшой промежутокъ времени вторая приходитъ
въ движеніе, представляя собою „моторъ"; приходится только поза-
ботиться о томъ, чтобы треніе въ послѣдней машинѣ не было слиш-
комъ велико. На рисункѣ 44 представлены машина Гольца въ ка-
чествѣ генератора и машина Теплера въ качествѣ мотора; вторая
машина приводится во вращеніе электрической энергіей, возбуждае-
мой первой машиной. Пользуясь такимъ приспособленіемъ, можно пу-
темъ исключительно протекающихъ въ эѳирѣ процессовъ переводить
энергію отъ источника силы къ мѣсту потребленія. Но такой родъ
электрической передачи энергіи крайне не экономенъ и потому на
практикѣ никогда не примѣняется, такъ какъ и для полученія неболь-
шихъ эффектовъ требовались бы очень большія и весьма хрупкія
машины.
ГЛАВА ЧЕТВЕРТАЯ
ЭЛЕКТРИЧЕСКІЯ СВОЙСТВА ИЗОЛЯТОРОВЪ
ПУСТОТА.
62. Мы уже неоднократно проводили аналогію между физикой
эѳира и механикой вѣсомыхъ упругихъ тѣлъ. Упругія измѣненія вѣ-
сомыхъ тѣлъ могутъ быть изучены путемъ изслѣдованія деформаціи
и напряженія. Эти двѣ величины, измѣряемыя одна независимо отъ
другой, находятся, однако, въ тѣсной связи другъ съ другомъ, такъ
что опредѣленному значенію напряженія соотвѣтствуетъ вполнѣ опре-
дѣленное значеніе деформаціи. Связь, о которой здѣсь идетъ рѣчь,
выражается извѣстнымъ закономъ Гука, по которому деформація
пропорціональна напряженію. Поэтому спеціальныя упругія свойства
опредѣленнаго тѣла характеризуются константой — постояннымъ коэф-
фиціентомъ пропорціональности этихъ двухъ величинъ. Его назы-
ваютъ обычно „модулемъ упругости“, если имѣется въ виду дефор-
мація растяженія и „модулемъ сдвига“ —для деформаціи сдвига.
Мы уже видѣли, что электрическое состояніе эѳира также мо-
жетъ быть охарактеризовано двумя независимо другъ отъ друга
измѣряемыми величинами — его напряженіемъ и его возбужденіемъ.
И въ эѳирѣ эти двѣ величины находятся въ тѣсной связи между
собою, такъ что одна изъ нихъ вполнѣ опредѣляется другою. Мы
изучимъ прежде всего электрическія свойства пустоты, т. е. чистаго
мірового эѳира. Такъ какъ мы знаемъ, что присутствіе изолирующаго
газа, напримѣръ, воздуха, вліяетъ едва замѣтно на свойства чистаго^
эѳира, то мы можемъ производить наши опыты просто въ .пр^І
странствѣ, наполненномъ воздухомъ. Произведемъ нижеслѣд^фцХій
простой опытъ: прокалибрировавь электрометръ въ качест^^ измѣ-
рителя напряженій при помощи соотвѣтствующей гальванической
батареи, соединимъ его съ Фарадэевскимъ сосудомъ;<^сли послѣд-
104
Пустота
нему сообщать, какъ это описано въ §54, заряды, равные 1, 2, 3
и т. д., то окажется, что указываемое электрометромъ напряженіе
всегда строго пропорціонально величинѣ внесеннаго въ сосудъ за-
ряда. Изъ этихъ данныхъ, подтверждающихся и при точнѣйшихъ
изслѣдованіяхъ, слѣдуетъ общій законъ природы — законъ Кулона:
сила электрическаго поля въ эѳирѣ всегда пропорціональна
его электрическому возбужденію:
О = К .Е.
Коэффиціентъ пропорціональности К носитъ названіе д{элек-
трической постоянной эѳира.
Этотъ законъ, которому въ механикѣ какъ разъ соотвѣтствуетъ
законъ Гука, я буду всегда называть закономъ Кулона, хотя самъ
Кулонъ формулировалъ свой законъ иначе и при томъ такимъ обра-
зомъ, что истинный смыслъ закона изъ его формулировки уясняется
лишь съ трудомъ.
Діэлектрическая постоянная эѳира соотвѣтствуетъ обратной ве-
личинѣ модуля упругости для вѣсомыхъ тѣлъ, т. е. такъ называемому
„коэффиціенту упругости". Совершенно такъ же, какъ значеніе ко-
эффиціента упругости зависитъ отъ выбора механическихъ единицъ
(силы и деформаціи), и значеніе діэлектрической постоянной эѳира
зависитъ отъ выбора электрическихъ единицъ (напряженія и заряда).
Къ численному ея опредѣленію мы еще возвратимся ниже.
Однако, существуетъ и весьма значительное различіе между за-
конами Гука и Кулона. Законъ Гука является лишь приблизитель-
нымъ закономъ, справедливымъ только для весьма грубыхъ измѣре-
ній; въ дѣйствительности „вполнѣ упругихъ" тѣлъ, которыя строго
слѣдовали бы закону Гука, не существуетъ. Отъ закона же Ку-
лона, какъ уже сказано, не удалось подмѣтить даже малѣйшихъ
отступленій. Этимъ проводится рѣзкая граница между свойствами
эѳира и свойствами вѣсомыхъ тѣлъ. Мы можемъ сказать: эѳиръ
является единственной дѣйствительно идеальной суДгтан-
ціей, абсолютно точно слѣдующей простому закоцуѵ
63. Теперь мы должны разрѣшить сходный вопро^сь:' въ какой
степени увеличивается силовое дѣйствіе, испытываемре^ заряженнымь
тѣломъ въ постоянномъ электрическомъ полѣ, ж^йрГа зарядъ тѣла
возрастаетъ? °
Рѣшается этотъ вопросъ пижеслѣдуюіцшѵгь простымъ опытомъ.
Пустота
105
Беремъ систему произвольно заряженныхъ тѣлъ, изолированныхъ
другъ отъ друга и находящихся на опредѣленныхъ разстояніяхъ
другъ отъ друга. Если теперь опредѣлить величину силы или вра-
щающій моментъ, дѣйствующій на эту неизмѣняемую систему въ
случаѣ, когда внѣ ея на конечномъ разстояніи не находятся возбу-
ждающія поле тѣла, то получается всегда абсолютный нуль. Отсюда
получаемъ слѣдующій основной принципъ:
Сумма всѣхъ силъ и вращательныхъ моментовъ, дѣй-
ствующихъ на отдѣльныя тѣла въ системѣ электрически
заряженныхъ тѣлъ, равняется нулю.
Если мы имѣемъ частный случай двухъ электрически заряжен-
ныхъ тѣлъ, то дѣйствующія на оба тѣла силы равны между собою
и взаимно противоположны; ихъ направленія совпадаютъ съ линіей,
соединяющей точки ихъ приложенія. Въ силу этого выше высказан-
ный принципъ называютъ принципомъ равенства дѣйствія и
противодѣйствія.
Здѣсь же слѣдуетъ замѣтить, что этотъ принципъ въ физикѣ
эѳира, когда рѣчь идетъ о постоянныхъ поляхъ, имѣетъ весьма общее
значеніе, и мы съ нимъ встрѣтимся еще при иныхъ обстоятельствахъ
Принципъ равенства дѣйствія и противодѣйствія даетъ намъ
отвѣтъ на поставленный выше вопросъ. Дѣйствительно, если мы по-
мѣстимъ на опредѣленномъ разстояніи другъ отъ друга двѣ изоли-
рованныя заряженныя частички и будемъ увеличивать зарядъ одной
изъ нихъ, удерживая постояннымъ зарядъ другой, то, согласно за-
кону Кулона, сила, дѣйствующая на вторую частичку, будетъ воз-
растать пропорціонально заряду первой частички. Изъ закона ра-
венства дѣйствія и противодѣйствія прямо слѣдуетъ, что и сила,
дѣйствіе которой испытываетъ первая частичка въ постоянномъ полѣ
второй частички, возрастаетъ пропорціонально ея заряду.
Сила, дѣйствіе которой испытываетъ заряженная ча-
стичка въ постоянномъ полѣ, пропорціональна заряду ча-
стички. о
Если мы за единицу силы примемъ силу, дѣйствіе которо^Р
испытываетъ частица съ зарядомъ, равнымъ 1
то въ общемъ случаѣ
. 1 ВОЛЬТ'Ю
въ полѣ I------г/—— >
сантиметръ
Р = т . Е,
гдѣ Р — сила, дѣйствіе которой испытываетъ
въ полѣ силы Е.
частиц^ъ зарядомъ т
106
Пустота
64. Простой примѣръ, уясняющій эти закономѣрныя зави-
симости, представляетъ случай шара съ зарядомъ т. Какъ мы
знаемъ (§ 57), возбужденіе 7) на разстояніи г отъ центра шара рав-
няется
Такъ какъ 7) = К. Е, по закону Кулона, то сила поля Е въ этомъ
мѣстѣ равняется
р _ гп
“ 4тг/Сг2*
Если мы помѣстимъ на разстояніи г отъ центра шара частичку съ
зарядомъ т , то она будетъ испытывать дѣйствіе силы Р — пі'. Е.
Иначе:
р _ т . т'
и ~ 4-.Ѵ.Т *
Точно такая же сила, но въ обратномъ направленіи, дѣйствуетъ на
шаръ въ полѣ, возбуждаемомъ въ эѳирѣ частицей съ зарядомъ т\
Въ такой именно формѣ и высказалъ Кулонъ свой законъ.
Если извѣстна сила поля въ окружающемъ шаръ пространствѣ,,
то, конечно, можно чисто математическимъ путемъ вычислить напря-
женіе между двумя точками этого поля. Если, какъ это предполагалось
при выводѣ всѣхъ выше приведенныхъ формулъ, шаръ удаленъ отъ
проводниковъ и отъ земной поверхности, то для величины V напря-
женія между шаромъ и землею, т. е. для потенціала шара, получается
выраженіе
V \ —т_____,
АтгК.а
гдѣ а радіусъ шара.
МАТЕРІАЛЬНЫЕ ДІЭЛЕКТРИКИ.
65. Мы переходимъ теперь къ изученію электрическихъ свойствъ
матеріальныхъ изоляторовъ. Для этого мы воспользуемся знакомой
намъ обстановкой опыта съ Фарадэевскимъ сосудомъ. Введезѵ;ъ5въ
Фарадэевскій сосудъ, уже употреблявшійся нами и снабженньш вы-
браннымъ нами за единицу зарядомъ, металлическій шаръ и Замѣтимъ
отклоненіе соединеннаго съ сосудомъ электрометра. ^Іослѣ этого
вновь введемъ шаръ въ тотъ же сосудъ, но наполненный параффи-
новымъ масломъ—особенно хорошо изолирующей^иДК0СТЬЮ- Откло-
неніе электрометра окажется въ точности р^внЦіъ отклоненію, на-
Матеріальные діэлектрики
107
блюденному при пустомъ сосудѣ. При этомъ послѣ удаленія шара:
изъ параффиноваго масла электрометръ точно возвращается на нуль,,
что служитъ доказательствомъ хорошей изоляціи.
Законы сохраненія электрическихъ зарядовъ и по-
стоянства электрическаго возбужденія сохраняютъ полную
силу и въ тѣхъ случаяхъ, когда заряженное тѣло нахо-
дится не въ воздухѣ, но въ иномъ діэлектрикѣ.
И условіе равновѣсія поля сохраняетъ силу, какъ въ<
воздухѣ, такъ и въ другихъ діэлектрикахъ. Это слѣдуетъ уже
изъ основаній, указанныхъ въ § 25; экспериментальная повѣрка
также во всѣхъ случаяхъ это подтверждаетъ. Поэтому мы будемъ,
для случая діэлектрика любого рода такъ же оперировать съ поня-
тіями общаго напряженія и потенціала, какъ и въ случаѣ воздуха.
Теперь мы слегка измѣнимъ опытъ съ Фарадэевскимъ сосудомъ.
При погруженіи металлическаго шара въ пустой сосудъ соединимъ
его тонкой гибкой проводящей проволокой съ полюсомъ батареи,
потенціалъ которой равенъ 1000 вольтъ. Послѣ погруженія шара въ
сосудъ мы соединяемъ послѣдній съ землею, а затѣмъ снова изо-
лируемъ. Если мы теперь удалимъ шаръ, то электрометръ обнару-
житъ зарядъ, равный и обратный по знаку тому, который былъ
индуктированъ на внутренней сторонѣ сосуда. Этотъ зарядъ въ дан-
номъ опытѣ, когда мы поддерживали постояннымъ потенціалъ на
шарѣ, оказывается нѣсколько большимъ, чѣмъ въ томъ случаѣ, когда
мы удерживали на шарѣ зарядъ ' постояннымъ. Это легко понять,
если мы припомнимъ, что Фарадэевскій сосудъ ограждаетъ внѣшнее
пространство отъ силовыхъ линій, исходящихъ изъ шара, и какъ бы
отсѣкаетъ нѣкоторую ихъ часть. Поэтому напряженіе между ша-
ромъ и сосудомъ при постоянномъ зарядѣ должно быть несомнѣнно
меньше напряженія шара относительно земли. Поэтому, если мы под-
держиваемъ напряженіе между шаромъ и сосудомъ равнымъ 1000
вольтъ, какъ это мы дѣлали въ нашемъ опытѣ, то поле, а, слѣдова-
тельно, и зарядъ шара, вслѣдствіе соединенія съ источникомъ элек-
тричества, должны возрасти.
Если мы этотъ опытъ сдѣлаемъ еще разъ, наполнивъ предва^'
рительно сосудъ параффиновымъ масломъ, то получимъ опять ,о^лйч-
ный отъ прежнихъ результатъ. Послѣ удаленія шара ^фйненіе
(отрицательное) электрометра оказывается вдвое большимъ, нежели
при опытѣ съ воздухомъ. Отсюда слѣдуетъ, что въутараффиновомъ.
108
Матеріальные діэлектрики
маслѣ одно и то же напряженіе поля соотвѣтствуетъ вдвое боль-
шему заряду, нежели въ воздухѣ. Мы можемъ также сказать на-
оборотъ: присутствіе параффиноваго масла понижаетъ вдвое напря-
'женіе поля, вызываемаго опредѣленнымъ зарядомъ.
Отсюда съ несомнѣнностью слѣдуетъ, что діэлектрическія свой-
ства параффиноваго масла значительно выше свойствъ воздуха, и
-именно, примѣрно, вдвое.
Рис. 45. Діэлектрическія свойства параффиноваго масла.
Это обстоятельство настолько важно, что мы пояснимъ его еще
‘слѣдующимъ опытомъ. Соединимъ употреблявшійся нами металличе-
скій шаръ съ однимъ изъ зажимовъ электрометра Ганкеля; другой
зажимъ электрометра отведемъ къ землѣ. Соединимъ теперь шаръ
съ полюсомъ батареи низкаго потенціала, чтобы электрометръдавалъ
легко отсчитываемое отклоненіе. Это отклоненіе остается неизмѣннымъ
и тогда, когда мы удалимъ шаръ, предварительно хоррщб изолиро-
ванный, отъ соединенія съ полюсомъ батареи и погрузимъ его въ
широкій пустой стеклянный сосудъ (рис. 45). ^о^если мы этотъ со-
судъ наполнимъ параффиновымъ масломъ, то ^напряженіе возбужда-
емаго шаромъ поля уменьшится приблизительно вдвое тотчасъ послѣ
Силовыя дѣйствія въ жидкихъ діэлектрикахъ
109'
погруженія шара въ масло. Если затѣмъ удалить шаръ изъ сосуда, „
то напряженіе вновь возрастаетъ до прежней величины.
Этотъ опытъ ясно показываетъ, что съ опредѣленнымъ электри-
ческимъ возбужденіемъ въ параффиновомъ маслѣ связано напряженіе,,
приблизительно вдвое меньшее напряженія въ воздухѣ.
СИЛОВЫЯ ДЪЙСТВІЯ ВЪ ЖИДКИХЪ ДІЭЛЕКТРИКАХЪ.
66. Изъ того факта, что діэлектрическія свойства („діэлектрич-
ность“) у различныхъ изоляторовъ различны, мы можемъ извлечь,
спеціальныя слѣдствія относительно силъ, дѣйствующихъ между за-
ряженными тѣлами.
Окружимъ тѣло, имѣющее опредѣленный зарядъ т, изолирую-
щей жидкостью, діэлектричность которой въ к разъ больше діэлек-
тричности чистаго эѳира. Тогда при постоянствѣ заряда сила вызы-
ваемаго имъ въ опредѣленномъ мѣстѣ поля падаетъ отъ величины
ея Во, соотвѣтствующей чистому эѳиру, до величины Е = ~ Ео.
Слѣдовательно, если въ этомъ мѣстѣ мы помѣстимъ частичку съ.
зарядомъ тх, то сила, дѣйствующая на нее и равная въ чистомъ,
эѳирѣ Ро, уменьшится до величины Р — Ро.
Силы, дѣйствующія между двумя тѣлами съ постоян-
нымъ зарядомъ, измѣняются съ измѣненіемъ діэлектрич-
ности среды, являющейся носительницей поля, и притомъ,
обратно пропорціонально этой діэлектричности.
Это устанавливаемое теоретически со всею строгостью положеніе,,
къ сожалѣнію, не можетъ быть прямо демонстрировано на опытѣ,,
такъ какъ большинство жидкостей изолируетъ настолько плохо,
что тѣла теряютъ свои заряды раньше, нежели можно произвести
измѣреніе дѣйствующихъ силъ. Жидкости же, подобныя хорошо изо-
лирующему параффиновому маслу, слишкомъ вязки для того, чтобы
можно было въ нихъ наблюдать слабыя электрическія поля. Однако,
получающійся пробѣлъ вполнѣ заполняется инымъ опытомъ, очень,
легко воспроизводимымъ. °
Соединяя тѣло, возбуждающее поле, съ источникомъ электриче^
ства постояннаго потенціала, можно и въ несовершенныхъ изолято-
рахъ получать долговременное поле. Такъ какъ въ этомъ^лучаѣ
постояннымъ поддерживается не возбужденіе поля, но егсЦцапряже-
ніе, то Е = Ео. Если возбужденіе въ нѣкоторомъ опредѣленномъ.,
мѣстѣ, когда діэлектрикомъ является чистый эѳиръ,х ^зовемъ черезъ.
110
Силовыя дѣйствія въ жидкихъ діэлектрикахъ
то при заполненіи поля жидкостью оно увеличивается и стано*
вится равнымъ О = кО{}. Слѣдовательно, въ жидкости тѣло заря-
жается большимъ зарядомъ, равнымъ т' = кт, если т его зарядъ
при томъ же потенціалѣ въ чистомъ эѳирѣ.
Если бы мы могли удержать постояннымъ и равнымъ тх и за-
рядъ второй частички, то мы наблюдали бы то же силовое дѣйствіе,
•что и въ пустотѣ: Р = Ро.
Если же мы и второе тѣло соединимъ съ источникомъ элек-
тричества постояннаго потенціала, то послѣ внесенія его въ діэлек-
трикъ, его зарядъ также возрастетъ въ к разъ и станетъ тх — ктх.
Слѣдовательно, возрастетъ и сила, дѣйствующая между двумя тѣлами,
и станетъ равной Р = тх Е = к тх Е^ = к Ро.
Силы, дѣйствующія между двумя тѣлами съ постоянными
потенціалами, измѣняются пропорціонально діэлектричности
среды, являющейся носительницей возникающаго между
ними поля.
Этотъ выводъ можно легко подтвердить на опытѣ. Мы возь-
мемъ маленькій квадрантный электрометръ; при помощи воронки и
резиновой трубки на дно электрометра можно легко наливать жид-
кость и вновь удалять ее. Отклоненіе инструмента мы будемъ на-
блюдать, какъ и прежде, пользуясь отраженнымъ отъ его зеркальца
свѣтовымъ лучемъ. Первоначально мы соединяемъ индикаторъ и обѣ
пары квадрантовъ съ точками опредѣленныхъ потенціаловъ, которые
намъ позволяетъ получить маленькая гальваническая батарея, и, оста-
вляя въ электрометрѣ только воздухъ, наблюдаемъ его отклоненіе.
Послѣ этого мы наполняемъ электрометръ какой-либо достаточно
хорошо изолирующей жидкостью, напримѣръ, этиловымъ эѳиромъ,
ничего не измѣняя въ соединеніяхъ. Когда прекратятся колебанія
индикатора, вызванныя токомъ жидкости, и свѣтлое пятно снова
остановится на одномъ мѣстѣ, отклоненіе его окажется значи-
тельно большимъ. Если введенная въ электрометръ жидкостр?^еть
этиловый эѳиръ, то отклоненіе будетъ приблизительно въ 4^г7раза
больше, чѣмъ въ воздухѣ. Слѣдовательно, діэлектричностьд^этиловаго
эѳира въ 4,3 раза больше діэлектричности воздуха.
Мы познакомились здѣсь съ важнымъ методо^ъ^позволяющимъ
измѣрять діэлектричности, по крайней мѣрѣ, жидкихъ изоляторовъ.
Этотъ методъ впервые былъ разработанъ Видовымъ, ученикомъ
Гельмгольца. ѵМ >
Діэлектрическая постоянная
111
ДІЭЛЕКТРИЧЕСКАЯ ПОСТОЯННАЯ.
67. Измѣряя указаннымъ способомъ діэлектричность жидкости
при употребленіи полей различной силы, всегда находятъ одну и
ту же величину. Отсюда мы заключаемъ, что для жидкихъ (также и
газообразныхъ) діэлектриковъ законъ Кулона приложимъ съ боль-
шою точностью. Ниже мы установимъ то же и для твердыхъ діэлек-
триковъ.
Всѣ основные электрическіе законы, въ томъ числѣ за-
конъ Кулона, также хорошо примѣнимы къ матеріальнымъ
діэлектрикамъ, какъ и къ чистому эѳиру. Но діэлектрич-
ность или постоянное отношеніе между возбужденіемъ и
'напряженіемъ поля имѣетъ для матеріальныхъ діэлектри-
ковъ иныя значенія, нежели для чистаго эѳира.
Для отчетливаго различенія діэлектричности чистаго эѳира отъ ді-
электричности какого-либо иного діэлектрика, мы будемъ въ послѣ-
дующемъ обозначать ее всегда черезъ Ко. Отношеніе діэлектричности К
матеріальнаго изолятора къ діэлектричности чистаго эѳира, т. е. ве-
личина к = называется „удѣльной діэлектрической постоянной"
изолятора, въ отличіе отъ абсолютной діэлектрической постоянной К.
Удѣльная діэлектрическая постоянная изолятора рав-
няется величинѣ его діэлектричности, если для эѳира ді-
электричность принята равной единицѣ.
Если извѣстна величина /\0, то по удѣльной діэлектрической
постоянной К мы всегда можемъ опредѣлить и абсолютную діэлек-
трическую постоянную /<:
К = к.К..
насъ всегда интере-
поля (разность по-
ЕМКОСТЬ.
68. При всѣхъ практическихъ измѣреніяхъ
суетъ только полное электрическое напряженіе
тенціаловъ) и полное возбужденіе (зарядъ). Представимъ себѣ отдѣль-
ное тѣло, возбуждающее электрическое поле и заряженное сперваЛ^р
до потенціала , затѣмъ — до потенціала Ѵ2; электрическіе зарядѣ?
его пусть будутъ соотвѣтственно и М2. Въ такомъ случайно
закону Кулона,
7ИІ : Ѵх - М2 : Ѵ2 = С,
гдѣ С есть нѣкоторая константа.
112
Емкость
Отношеніе заряда къ потенціалу тѣла, возбуждающаго
поле, называется емкостью этого тѣла.
Въ силу.этого мы можемъ законъ Кулона формулировать еще
такъ:
При всѣхъ измѣненіяхъ напряженія емкость остается
постоянной.
Отсюда, очевидно, вытекаетъ слѣдующее положеніе: если измѣ-
няется діэлектричность среды, являющейся носительницей
поля, то емкость измѣняется пропорціонально діэлектрич-
ности.
Въ механикѣ матеріальныхъ тѣлъ понятію емкости до нѣкото-
рой степени соотвѣтствуетъ понятіе упругой податливости тѣла.
Напримѣръ, по закону Гука, прогибъ горизонтальнаго стержня, под-
пертаго въ двухъ точкахъ, пропорціоналенъ грузу, подвѣшенному
къ серединѣ стержня. Упругой податливостью стержня мы назовемъ
въ этомъ случаѣ частное отъ дѣленія величины прогиба на вѣсъ
груза. Ясно, что эта величина зависитъ не только отъ упругихъ
свойствъ матеріала стержня, но и отъ его геометрическихъ размѣровъ.
Точно такъ же и емкость зависитъ отъ геометрическихъ раз-
мѣровъ пространства, заполняемаго полемъ. Для доказательства
этого воспользуемся двумя плоско отшлифованными металлическими
пластинками, закрѣпленными параллельно другъ противъ друга, но
такъ, что разстояніе между ними можно измѣнять и измѣрять
(рис. 46). Такой приборъ носитъ названіе измѣрительнаго конден-
сатора. Одну его пластинку соединимъ проволокой съ водопрово-
домъ; она будетъ въ такомъ случаѣ находиться въ электрическомъ
соединеніи съ землею, и ея потенціалъ будетъ все время равняться
нулю. Другая пластинка изолирована отъ земли и будетъ служить
тѣломъ, возбуждающимъ поле. Соединимъ ее съ однимъ изъ зажи-
мовъ электрометра Ганкеля; другой зажимъ электрометра отведемъ
къ землѣ. Послѣ этого заряжаемъ соединенную съ электрометромъ
пластинку и наблюдаемъ его отклоненіе. Если мы будемъ при^&Мъ.
придвигать заряженную пластинку къ пластинкѣ, соединенной съ
землёю, то замѣтимъ, что отклоненіе будетъ становиться все' меньше
и меньше. Это легко понять: если зарядъ остается шейзмѣннымъ-,
то остается неизмѣннымъ и возбужденіе въ пол^.^между обѣими
пластинками, а, слѣдовательно, и сила поля. Нр полное напря-
женіе представляетъ собою произведеніе изъ^илы поля и длины
Емкость
113
силовыхъ линій. Слѣдовательно, укорачивая силовыя линіи, мы тѣмъ
самымъ уменьшаемъ полное напряженіе или потенціалъ. Если мы
отодвинемъ заряженную пластинку обратно въ ея начальное положе-
ніе, то получимъ опять прежнее отклоненіе электрометра; если затѣмъ
мы будемъ ее еще больше удалять отъ пластинки, соединенной съ
землею, то и отклоненіе электрометра все будетъ возрастать, такъ
какъ мы при этомъ, удлинняя силовыя линіи, все будемъ увеличивать
потенціалъ.
Итакъ, емкость этого прибора тѣмъ больше, чѣмъ меньше раз-
стояніе между обѣими пластинками.
Рис. 46. Измѣрительный конденсаторъ.
Этотъ выводъ легко уяснить себѣ, если обратиться къ описан-
ной въ § 58 студнеобразной модели эѳира и въ ней разсмотрѣть
модель нашего конденсатора — двѣ параллельныя пластинки, въ ко-
торыхъ эѳирная жидкость удобоподвижна, и между ними^упругій
слой, соотвѣтствующій діэлектрику. Понятно, что этотъ слой обла-
даетъ тѣмъ большей упругой податливостью, чѣмъ онъ тоньше. о
Мы можемъ обнаружить еще иную зависимость емкости отт^^
размѣровъ поля на другомъ приборѣ, на такъ называемой „электрй^
ческой шторѣ". Этотъ приборъ состоитъ изъ удлиненнаго тфямо-
угольника толстаго станіоля, который, подобно обыкновеі^з^інторѣ,
можетъ наматываться на изолированную отъ земли дере|фную скалку
и, въ свою очередь, съ нея сматываться. Къ нижнеь$^краю шторы
Ми. Электричество и магнитизмъ.
114
Емкость
подвѣшены на проводникахъ два соприкасающіеся бузинные ша-
рика, играющіе роль электроскопа. Зарядимъ намотанную полосу
станіоля до высокаго потенціала; тогда оба шарика далеко другъ отъ
друга отодвинутся. Если мы теперь будемъ развертывать нашу штору,
то оба шарика будутъ спадать, т. е. напряженіе возбуждаемаго што-
рою поля будетъ при этомъ уменьшаться. Если мы снова смотаемъ
станіолевую полосу, то электроскопъ дастъ опять такое же большое
отклоненіе, какъ и раньше (рис. 47). Этотъ результатъ объясняется
тѣмъ, что при постоянномъ зарядѣ электрическая плотность и самое
поле ослабляются съ увеличеніемъ той поверхности, по которой рас-
предѣляется зарядъ. Если же поле становится слабѣе, то, конечно,
его полное напряженіе уменьшается. Изъ этого опыта слѣдуетъ, что
Рис. 47. Электрическая штора.
емкость аппарата увеличивается при увеличеніи той поверхности, по
которой распредѣляется зарядъ.
Резюмируя все, что мы узнали относительно емкости, мы мо-
жемъ высказать слѣдующее:
емкость тѣмъ больше, чѣмъ больше діэлектричность
заполненнаго полемъ пространства, чѣмъ больше поверх-
ность возбуждающаго поле проводника, и чѣмъ меньше
длина исходящихъ изъ послѣдняго силовыхъ линій.
ИЗМѢРЕНІЕ ДІЭЛЕКТРИЧЕСКОЙ ПОСТОЯННОЙ.
69. Тѣло, обладающее большою емкостью, называютъ конден-
саторомъ. Практически конденсаторъ устраивается всегда изъ двухъ
металлическихъ пластинокъ возможно бол^дігб» размѣра, помѣщае-
Измѣреніе діэлектрической постоянной
115
мыхъ параллельно другъ другу съ постояннымъ, по возможности
малымъ, промежуткомъ между ними. Металлическія пластинки мо?
гутъ быть плоскими (плоскій конденсаторъ) или же могутъ пред-
ставлять собою два коаксіальные цилиндра (цилиндрическій конден-
саторъ). Одна изъ двухъ пластинокъ считается обладающей нулевымъ
потенціаломъ; однако, не является необходимымъ, чтобы она не-
премѣнно была соединена съ землею, такъ какъ подъ полнымъ на-
пряженіемъ, вызываемымъ зарядомъ другой пластинки, мы понимаемъ
напряженіе между двумя пластинками, которое и обозначимъ черезъ V.
Если Е есть сила поля между пластинками и сі — ихъ взаимное раз-
стояніе, то V = сі. Е. Если далѣе / есть полная поверхность одной
изъ пластинокъ, т — ея зарядъ, П - удѣльное возбужденіе поля, то
Е = К .Еит = /.Е = / ,К .Е. Емкость плоскаго конденсатора равна,
слѣдовательно, С=К^> т. е. она пропорціональна заряженной по-
верхности и діэлектричности и обратно пропорціональна длинѣ сило-
выхъ линій. Все это вполнѣ согласуется съ общими выводами пре-
дыдущаго параграфа.
Теоретически самый простой способъ измѣренія діэлектрической
постоянной состоитъ въ томъ, что измѣряютъ емкость какого-нибудь
конденсатора сначала съ воздухомъ, а потомъ (при прочихъ неизмѣн-
ныхъ условіяхъ) съ изслѣдуемымъ діэлектрикомъ. Для этой цѣли можно
пользоваться вышеописаннымъ измѣрительнымъ конденсаторомъ, пла-
стинки котораго нужно сдвинуть настолько, чтобы между ними какъ
разъ помѣщалась пластинка изъ изолирующаго вещества, діэлектри-
ческая постоянная котораго опредѣляется. Затѣмъ, какъ и прежде,
одна пластинка соединяется съ землею, другая —съ электрометромъ
Ганкеля. Этой второй пластинкѣ мы сообщаемъ зарядъ и затѣмъ
ее изолируемъ. Если теперь вставить стеклянную пластинку, то откло-
неніе электрометра уменьшается почти въ семь разъ сравнительно
съ первоначальнымъ. Если стеклянную пластинку удалить, получается
опять прежнее отклоненіе. Слѣдовательно, діэлектрическая постоянная
стекла равняется, приблизительно, 7. Если сдѣлать такой же опыт> ^,
съ эбонитовой пластинкой, то ^отклоненіе электрометра уменьшаемой
въ меньшей степени; діэлектрическая постоянная эбонита оказцпЦется
равной 2,5.
Ясно, что такой методъ примѣнимъ какъ къ твердымъ/такъ и
къ жидкимъ діэлектрикамъ. Съ его помощью можно°\акже убѣ-
диться въ томъ, что законъ Кулона въ весьма широкихъ границахъ
ЪМ 8 '
116
Измѣреніе діэлектрической постоянной
остается справедливымъ для всѣхъ матеріальныхъ діэлектриковъ.
(Въ § 92 мы познакомимся съ однимъ явленіемъ въ діэлектрикахъ,
которое не согласуется съ закономъ Кулона).
Въ нижеслѣдующей таблицѣ даны нѣкоторыя важнѣйшія вели-
чины діэлектрическихъ постоянныхъ:
Стекло (въ завис. отъ сорта) 6—7 Эѳиръ.................4,35
Фарфоръ „ „ „ 5,7 -6,8 Бензолъ................2,26
Слюда „ „ „ 5,7 8,4 Шеллакъ.................3,1
Алкоголь................26,0 Канифоль.................2,5
Сѣроуглеродъ.............2,6 Вода....................81,0
Эбонитъ..................2,5 Хлороформъ...............5,2
Параффинъ................2,0 Керосинъ.................2,0
Сѣра.....................4,0 Параффиновое масло . . 2,1
Всѣ эти величины больше 1. То же оказывается и для всѣхъ
прочихъ изоляторовъ. Слѣдовательно, діэлектричность мате-
ріальнаго изолятора всегда больше діэлектричности чистаго
эѳира. Это положеніе, справедливое во всѣхъ случаяхъ безъ исклю-
ченій, будетъ имѣть для насъ большое значеніе, когда мы захотимъ
себѣ составить болѣе опредѣленный взглядъ на природу матеріаль-
ныхъ діэлектриковъ.
Помощью изложеннаго метода можно опредѣлять и діэлектри-
ческія постоянныя газовъ; для этого конденсаторъ помѣщается подъ
колоколомъ воздушнаго насоса; сперва туда впускаютъ изслѣдуемый
газъ, а затѣмъ его выкачиваютъ. Оказывается, что присутствіе газа
всегда немного увеличиваетъ емкость. Діэлектричность большинства
газовъ мало отличается отъ діэлектричности эѳира. Для воздуха при
атмосферномъ давленіи и комнатной температурѣ к= 1,0006. Слѣ-
довательно, можно, какъ мы это уже и дѣлали неоднократно, при
не очень точныхъ измѣреніяхъ, діэлектричность воздуха считать рав-
ной діэлектричности эѳира. Но при точныхъ изслѣдованіяхъ нужно
вводить поправку, принимая во вниманіе указанную величину,
КОНДЕНСАТОРЫ. р
70. Свойства конденсатора въ значительной мѣрѣ^авиСятъ отъ
входящаго въ него діэлектрика; отъ послѣдняго не^фэлько суще-
ственно зависитъ емкость конденсатора, но также^тегіень изоляціи
обѣихъ пластинокъ и напряженіе, которое конденсаторъ можетъ
выдержать. Обычно употребляются конденсаторы воздушные, сте-
клянные, слюдяные, параффиновые, а такж^масляные.
Конденсаторы
117
Старѣйшимъ видомъ конденсатора является стеклянный конден-
саторъ, состоящій изъ длиннаго цилиндрическаго сосуда, оклееннаго
внутри и снаружи проводящими обкладками, напримѣръ, станіолемъ,
при томъ такъ, чтобы оставался широкій изолирующій край (рис. 48).
Такой цилиндрическій стеклянный конденсаторъ называется лейден-
ской банкой, такъ какъ онъ былъ изобрѣтенъ въ Лейденѣ физикомъ
Мушенброкомъ (МизсНепЬгоек); впрочемъ, одновременно съ нимъ,,
въ 1745 году, такую банку устроилъ каноникъ Клейстъ (ѵ. Кіеізі) въ
Камминѣ въ Помераніи. Первоначально лейденская банка представляла
собою стаканъ, въ который было налито немного воды
или ртути; въ жидкость былъ погруженъ гвоздь. Внѣш-
ней обкладкой служила рука экспериментатора; внутрен-
ней—вода или ртуть. Такой примитивный конденсаторъ
заряжали, соединяя гвоздь съ кондукторомъ электриче-
ской машины; при разрядѣ его, когда экспериментаторъ
свободной рукой касался гвоздя, ощущался сильный
(для той эпохи) ударъ. Причина этого, столь удивитель-
наго для того времени, явленія заключается въ томъ,
что при напряженіи, доставляемомъ электрической ма-
шиной съ треніемъ, стеклянный конденсаторъ обладаетъ
уже сравнительно большимъ электрическимъ зарядомъ.
Въ настоящее время обкладки лейденской банки
дѣлаются изъ станіоля, который хорошо прилегаетъ
къ поверхности стекла. Насколько великъ скопляемый
такой банкой зарядъ, мы можемъ видѣть изъ старин-
наго опыта съ „электрическимъ звономъПо обѣ
стороны изолированнаго колокольчика располагаются два другіе ко-
локольчика, соединенные съ землею. Въ обоихъ промежуткахъ между
Рис. 48. Лей-
денская банка.
тремя колокольчиками подвѣшиваются на изолирующихъ нитяхъ
латунные шарики, играющіе роль язычковъ. Зарядимъ лейденскую
банку при помощи маленькой индукціонной машины и соединимъ
внутреннюю обкладку съ среднимъ колокольчикомъ, а внѣшнюю
обкладку банки съ землею. Тогда произойдетъ слѣдующее явленіе:^0
шарики притянутся къ среднему колокольчику, зарядятся, о^то|йР
нутся къ крайнимъ колокольчикамъ, здѣсь разрядятся, притянутая" къ
среднему колокольчику и т. д. При непрерывномъ звонѣ дейденская
банка будетъ все болѣе и болѣе разряжаться. О велй^нѣ заряда
можно судить по продолжительности этого звона.
118
Конденсаторы
То же самое даетъ и другой, давно уже извѣстный опытъ съ
„Франклиновой доской". Эта доска (рис. 49) представляетъ собою
плоскій конденсаторъ, въ которомъ діэлектрикомъ является стеклянная
или эбонитовая пластинка; эта пластинка съ обѣихъ сторонъ имѣетъ
обкладки изъ станіоля. Съ каждой стороны подвѣшенъ бузинный
шарикъ, соединенный проводникомъ со станіолевой обкладкой. Соеди-
нимъ одну обкладку съ землею, прикоснувшись къ ней пальцемъ, а
другую зарядимъ до высокаго положительнаго потенціала, такъ что
бузинный шарикъ далеко отъ нея отклонится. Если мы теперь изо-
лируемъ первую обкладку и отведемъ вторую къ землѣ, то у внутрен-
няго поля въ діэлектрикѣ мы отнимемъ лишь небольшую часть всего
заряда, и напряженіе уменьшится на весьма незначительную вели-
чину; въ силу этого изолированная (первая) обкладка пріобрѣтетъ
отрицательный потенціалъ, почти столь же высокій, какъ и прежній
положительный потенціалъ второй обкладки. При этомъ мы уви-
димъ, что отъ первой обкладки шарикъ отклоняется на значительное
разстояніе. Если мы опять изолируемъ вторую обкладку и дотронемся
до первой, то шарикъ первой упадетъ на обкладку, а шарикъ |та-
рой отклонится. Мы можемъ такимъ образомъ въ теченіе х^лгаго
' по очереди,^пока не
Если желмьйкоснемся
удалимк^есь электри-
рется маленькая
промежутка времени разряжать обѣ обкладки
истощится весь полученный сначала зарядъ,
одновременно обѣихъ обкладокъ, то мы сразу
ческій зарядъ конденсатора. Въ этомъ случаѣ заіѵ^-|у
свѣтлая искра, мы слышимъ рѣзкій звукъ и ощущаемъ непріятный
электрическій ударъ.
Конденсаторы
119
71. Для полученія конденсаторовъ большой емкости, весьма
удобныхъ на практикѣ, соединяютъ большое число отдѣльныхъ кон-
денсаторовъ.
Можно, напримѣръ, сдѣлать это съ нѣкоторымъ числомъ лей-
денскихъ банокъ, соединяя между собою какъ всѣ ихъ внѣшнія
обкладки, такъ и внутреннія. Если теперь между обкладками возбу-
дить поле опредѣленнаго напряженія, то, понятно, общій зарядъ
внутреннихъ обкладокъ равенъ суммѣ зарядовъ, которые находились
бы на каждой отдѣльной обкладкѣ при томъ же потенціалѣ.
При соединеніи нѣсколькихъ конденсаторовъ между
собою общая емкость образуемой ими проводящей си-
стемы равняется суммѣ емкостей отдѣльныхъ конденса-
торовъ.
С ~ С! + С2 -|- • • • 4- Сп,
если С,, С2,..., Сп —^емкости 1-го, 2-го,..., я-аго конденсатора,
а С емкость всей системы.
Систему соединенныхъ между собою лейденскихъ банокъ издавна
называютъ лейденской батареей.
Рис. 51. Стеклянный плоскій
конденсаторъ.
называемое параллельное со-
Описанное соединеніе — такъ
единеніе — гораздо удобнѣе производится съ плоскими конденс^
торами. Въ этомъ случаѣ просто накладываютъ другъ на друг^о^й-"
наковыя пластинки діэлектрика и между каждыми двумя изъ нихѣщро-
кладываютъ листъ станіоля такъ, чтобы оставались достато^рр>Щиро-
кіе изолирующіе края. Отъ этихъ станіолевыхъ листовъ проводятъ по-
перемѣнно на обѣ стороны проволочки или станіолевыя^пЖоски, слегка
120
Единица электрическаго заряда
выступающія изъ изолирующихъ пластинъ. Когда весь конденсаторъ
составленъ, то съ каждой стороны соединяютъ вмѣстѣ всѣ провода,
ведущіе къ станіолевымъ пластинкамъ, такъ что послѣднія образуютъ
двѣ группы, между которыми при заряженіи конденсатора и возбу-
ждается электрическое поле (рис. 50). Такимъ образомъ приготовляются
очень удобные стеклянные конденсаторы (рис. 51), предназначаемые
для высокихъ напряженій, такъ какъ стекло не легко пробивается раз-
рядомъ. Если желательно воспользоваться меньшими напряженіями, то
можно получать значительно большія емкости, употребляя въ каче-
ствѣ діэлектрика тонкіе листки хорошо параффинированной бумаги
или, еще лучше, тонкія пластинки слюды. Въ настоящее время имѣ-
ются въ продажѣ такіе слюдяные конденсаторы, любой емкости, за-
ключенные въ деревянные ящички.
ЕДИНИЦА ЭЛЕКТРИЧЕСКАГО ЗАРЯДА.
72. До сихъ поръ мы все время оставляли неопредѣленной ве-
личину діэлектрической постоянной эѳира Ко и довольствовались
относительными измѣреніями. Къ этому насъ принуждало то обстоя-
тельство, что до сихъ поръ мы не установили никакого точнаго
опредѣленія единицы электрическаго заряда. Опредѣленіе основныхъ
электрическихъ единицъ должно, какъ и опредѣленіе всякой иной
физической единицы, непремѣнно удовлетворять двумъ требованіямъ:
1. Единицы должны воспроизводиться удобно и совершенно
точно.
2. Онѣ должны лежать въ области величинъ, которыя прихо-
дится съ ними сравнивать.
Первое изъ этихъ двухъ требованій вполнѣ удовлетворяется
при выборѣ единицы напряженія съ помощью нормальнаго эле-
мента (§ 37). Но какъ же обстоитъ дѣло съ единицей заряда? Поль-
зуясь Фарадэевскимъ методомъ и его сосудомъ, мы можемъ вполнѣ
точно перенести измѣряемый зарядъ на тѣло постоянной емкости
(именно, на сосудъ Фарадэя) и измѣрить потенціалъ, соотвѣтствую-
щій этому заряду. Такое электрометрическое измѣреніе заряда является
непрямымъ измѣреніемъ, и потому, если бы существовалъ только этотъ
методъ, нельзя было бы прямо опредѣлить единицу зарядд^Ёё пришлось
бы свести къ единицамъ напряженія и емкости. Такимъ именно пу-
темъ мы уже однажды (§54) установили временн^Уединицу заряда,
выбравъ за нормальную емкость — емкость шар-а— въ 6 сантиметровъ
Единица электрическаго заряда
121
діаметромъ. Но эта емкость пригодна лишь для приблизительныхъ
опредѣленій, такъ какъ намъ извѣстно, что емкость шара въ значи-
тельной мѣрѣ зависитъ отъ окружающей его среды. Для точныхъ
измѣреній слѣдовало бы въ качествѣ единицы емкости имѣть кон-
денсаторъ абсолютно постоянный, который слѣдовало бы хранить въ
надежномъ мѣстѣ, можетъ быть, вмѣстѣ съ единицей длины - извѣ-
стнымъ платиновымъ масштабомъ — въ Парижѣ, и съ нимъ слѣдо-
вало бы сравнивать всѣ употребляющіеся на практикѣ конденса-
торы. Въ продажѣ, дѣйствительно, можно получить очень точно про-
калибрированные конденсаторы, употребляющіеся въ качествѣ еди-
ницъ мѣры, т. е. эталоновъ. Однако, эти конденсаторы калибриру-
ются не сравненіемъ ихъ съ нормальнымъ международнымъ конден-
саторомъ, а инымъ способомъ, съ которымъ мы ниже познакомимся
Именно, существуетъ очень про-
стой методъ прямого измѣре-
нія электрическихъ зарядовъ, и
этотъ методъ и послужитъ намъ
для точнаго и прямого опредѣ-
ленія единицы заряда. Но пока
мы примемъ нѣкоторый точно
прокалибрированный продажный
слюдяной конденсаторъ за нор-
мальный. Этотъ конденсаторъ (рис. 52) хорошо изолированъ и за-
щищенъ отъ механическихъ поврежденій: онъ заключенъ въ дере-
вянный ящичекъ съ эбонитовою крышкою; на послѣдней имѣются
два зажима, каждый изъ которыхъ соединенъ проводникомъ съ одной
изъ двухъ системъ пластинокъ. Между этими двумя зажимами имѣется
надпись, опредѣляющая емкость конденсатора: „1 микрофарадъ".
За единицу емкости въ дальнѣйшемъ мы будемъ прини-
мать емкость нормальнаго конденсатора- 1 микрофарадъ.
Этимъ опредѣляется и единица заряда.
Если соединить одну систему пластинокъ нормальнаго
конденсатора съ землею, а другую зарядить до потенціалу,^,
равнаго 1 вольту, то зарядъ ея будетъ представлять собаюѵ
единицу заряда—1 микрокулонъ.
73. Теперь легко понять, какимъ образомъ іюмощьюЧ^ара-
дэевскаго сосуда и пользуясь нормальнымъ конденсаторной* мы мо-
жемъ электрическіе заряды измѣрять прямо въ микрокулонахъ. Соеди-
ЛЧ
122
Единица электрическаго заряда
няемъ внѣшнюю сторону Фарадэевскаго сосуда съ одной системой
пластинъ конденсатора и съ однимъ изъ зажимовъ чувствительнаго
электрометра, прокалибрированнаго на вольты. Другую систему пла-
стинокъ соединяемъ со вторымъ зажимомъ электрометра и съ зем-
лею. Даже при самыхъ точныхъ измѣреніяхъ можно считать емкость
сосуда и зажимовъ исчезающе малой по сравненію съ 1 микрофара-
домъ, и потому емкость всей системы, которой мы сообщаемъ зарядъ,
Рис. 53. Измѣреніе заряда въ микроку-
лонахъ.
вводя его въ сосудъ, можно счи-
тать равной 1 микрофараду. По-
этому если электрометръ ука-
зываетъ напряженіе, равное е
вольтамъ, то введенный въ со-
судъ зарядъ равняется е микро-
кулонамъ (рис. 53). Этимъ элек-
трометрическимъ методомъ мы
можемъ, напримѣръ, опредѣлить
ту величину заряда шара, кото-
рую мы ранѣе совершенно про-
извольно выбрали за единицу
(§ 54). Если мы этотъ заряжен-
ный шаръ внесемъ въ сосудъ и
приведемъ съ нимъ въ сопри-
косновеніе, то шаръ, какъ мы знаемъ, отдастъ сосуду весь свой за-
рядъ. Однако, напряженіе возбуждаемаго при этомъ поля крайне мало.
Если мы повторимъ эту операцію сто разъ, то напряженіе возрастаетъ
до величины, которую уже можно измѣрить; именно электрометръ по-
кажетъ тогда -г вольта. Отсюда слѣдуетъ, что зарядъ, употреоляв-
о
шійся нами прежде въ качествѣ единицы, равняется микрокулона.
Теперь легко всѣ заряды, измѣренные нами въ нашихъ произволь-
ныхъ единицахъ, вычислить въ микрокулонахъ.
ПРАКТИЧЕСКИ ПРИМѢНЯЕМЫЯ ЕДИНИЦЫ.
74. Мы должны теперь обратить вниманіе также н^второе изъ
требованій, указанныхъ въ § 72. Это требованіе отличается тѣмъ
свойствомъ, что оно, вообще говоря, во всѣхъ случаяхъ не выпол-
нимо. Обратимъ вниманіе на простѣйшій случай ^измѣреніе длинъ.
Разстояніе между двумя городами мы выр^Омъ, по понятнымъ
Практически примѣняемыя единицы
123
причинамъ, не въ миллиметрахъ и, съ другой стороны, толщину про-
волоки мы выражаемъ не въ километрахъ. Вообще, мы обыкновенно-
для различныхъ цѣлей употребляемъ различныя, для этихъ цѣлей
пригодныя единицы. Для того же, чтобы переходить, какъ это часто
приходится дѣлать, отъ одной единицы къ другой безъ утомитель-
ныхъ вычисленій, была изобрѣтена извѣстная всѣмъ десятичная си-
стема единицъ. Всѣ единицы выводятся изъ основной единицы
(напримѣръ, метра) умноженіемъ на степени 10 (1 км. = ІО3
1 мм. = 10~3 м., 10—6 л/.). Такая десятичная система, конечно,
употребляется и въ ученіи объ электричествѣ. Мы уже видѣли, что
основная единица напряженія — вольтъ была выбрана такъ, чтобы
черезъ нее удобно выражались напряженія отдѣльныхъ гальваниче-
скихъ цѣпей. Но когда рѣчь идетъ о напряженіяхъ, получающихся
при электрическихъ разрядахъ, то вольтъ является слишкомъ мелкой
единицей, и въ этихъ случаяхъ часто пользуются киловольтомъ, рав-
нымъ 1000 вольтъ. Съ другой стороны, встрѣчаются напряженія и
гораздо меньшихъ величинъ; мы познакомимся, напримѣръ, съ такими
малыми напряженіями въ термическихъ цѣпяхъ. Въ этихъ случаяхъ
1
пользуются милливольтомъ, равнымъ —- вольта.
Такъ же обстоитъ дѣло и съ единицами заряда. Въ электро-
статикѣ выше принятая единица — 1 микрокулонь- является уже ве-
личиной весьма значительной. Но она ничтожно мала въ сравненіи
съ зарядами, которые можно легко получить долгимъ непрерывнымъ
употребленіемъ гальваническихъ цѣпей. Если тѣло емкостью въ
1 микрофарадъ заряжается однимъ элементомъ Даніеля, то отни-
маемая при этомъ у элемента энергія ничтожно мала въ сравненіи съ
тѣми количествами ея, о которыхъ мы имѣемъ ясное представленіе
(напримѣръ, съ 1 килограмметромъ). Если разрядить микрофарадъ, снова
зарядить, опять разрядить и повторить такую операцію нѣсколько
милліоновъ разъ, то тогда только отъ элемента будетъ взято замѣт-
ное для насъ количество энергіи. Но элементъ можетъ дать и еще.
увидимъ, какъ ихъ
гораздо большія количества энергіи. Ниже мы
можно въ дѣйствительности измѣрять. На основаніи этихъ сообра^
женій, принимая вольтъ за основную единицу напряженія и желаз
избѣгнуть слишкомъ малой единицы энергіи, за основную е^цгицу
заряда берутъ милліонъ микрокулоновъ. Эта единица носиЛ^ назва-
ніе кулона. X ѵ
1 микрокулонъ Л 10~6 кулона.
124
Сравненіе емкостей
Соотвѣтственно съ этимъ, емкость, при напряженіи въ 1 вольтъ
имѣющую зарядъ въ 1 кулонъ, слѣдуетъ назвать фарадомъ.
1 микрофарадъ = 10—6 фарада.
Но, тогда какъ кулонъ является дѣйствительно практической
единицей, пригодной къ употребленію при повторныхъ или длитель-
ныхъ разрядахъ гальваническихъ цѣпей, фарадъ оказывается совер-
шенно не практичной единицей емкости. Поэтому при измѣреніяхъ
‘емкостей чаще употребляется микрофарадъ (1 М. Р.).
СРАВНЕНІЕ ЕМКОСТЕЙ.
75. Существуетъ цѣлый рядъ методовъ для сравненія неизвѣ-
стной емкости съ какой-нибудь опредѣленной, напримѣръ, 1 микрофа-
радомъ. Можно было бы сдѣлать такое сравненіе, напримѣръ, соеди-
няя сперва извѣстную, а затѣмъ неизвѣстную емкость съ внѣшней
стороною Фарадэевскаго сосуда описаннымъ въ §73 способомъ и
внося въ обоихъ случаяхъ совершенно тождественный зарядъ въ со-
судъ (напримѣръ, пользуясь выше упомянутымъ металлическимъ ша-
ромъ). Въ обоихъ случаяхъ придется отмѣтить соотвѣтствующія на-
пряженія; при одинаковыхъ зарядахъ напряженія обратно пропор-
ціональны емкостямъ, включая емкости сосуда и частей электрометра.
Фарадей поступалъ иначе: онъ заряжалъ извѣстную емкость
С до потенціала измѣрявшагося электрометромъ, и затѣмъ, при-
соединяя къ ней помощью хорошо изолированной отъ земли метал-
лической проволоки неизвѣстную емкость х, получалъ на электро-
метрѣ новое напряженіе У2. Такъ какъ при этой операціи электри-
ческій зарядъ т остается неизмѣннымъ, то
СѴГ - (С+ х) Ѵ2,
откуда и вычисляется х.
Этотъ и подобные ему методы, называемые электростатическими
методами измѣренія емкостей, удобны, однако, только въ тѣхъфду-
чаяхъ, когда конденсаторы очень хорошо изолированы. Совершенно
подобно тому, какъ въ механикѣ, для опредѣленія модулей упру-
гости употребляются не только статическіе, но и динамическіе ме-
тоды, такъ и при измѣреніяхъ емкостей примѣняются^^кже динами-
ческіе, методы; послѣдніе, вообще говоря, болѣеѴ удобны и болѣе
точны, чѣмъ методы статическіе.
Абсолютная діэлектрическая постоянная эѳира
125.
АБСОЛЮТНАЯ ДІЭЛЕКТРИЧЕСКАЯ ПОСТОЯННАЯ ЭѲИРА.
76. Для опредѣленія абсолютной діэлектрической постоянной
эѳира Ко достаточно сравнить емкость вакуумъ-конденсатора съ микро-
фарадомъ. Уже пользуясь произведеннымъ въ § 73 измѣреніемъ за-
ряда шара, мы можемъ вычислить приблизительно величину
Радіусъ шара у насъ равнялся а = 3 см., потенціалъ возбужденнаго-
имъ поля V = 1000 вольтъ, возбуждающій зарядъ т = ІО 8 ку-
О
лона. Но, какъ мы видѣли въ § 64,
V =.____-___
4ъК0.а
Въ силу этого абсолютная діэлектрическая постоянная чистаго эѳира
(собственно, воздуха) въ легальныхъ единицахъ — кулонахъ и воль-
тахъ равняется
Ко =
-7-^7 = приблиз. 0,9 . 10~13.
опредѣлить емкость плоскаго конденсатора, въ.
между пластинками равняется б/, поверхность
Если тщательно
которомъ разстояніе
пластинокъ равняется / и діэлектрикомъ служитъ пустота, то по фор-
мулѣ
“ Л° сі ’
выведенной въ § 69, мы получаемъ:
К —
Такъ можно опредѣлить значеніе Ко съ весьма большой точностью..
Абсолютная діэлектрическая постоянная чистаго эѳира
при измѣреніи возбужденія въ кулонахъ, напряженія въ.
вольтахъ, длинъ въ сантиметрахъ равняется
Ко = 0,8842 . ІО-18-----кулонъ------
вольтъ. сантиметръ
Это первая важная эѳирная константа, съ которой мы познако-
мились. Мы можемъ уяснить себѣ нѣсколько ея значеніе на слѣдую--
щемъ примѣрѣ. Представимъ себѣ вакуумъ конденсаторъ изъ огроа^Я)
ныхъ металлическихъ пластинъ, равныхъ 1 кв. м.\ пусть разстоянія
между каждыми двумя изъ нихъ равняются 0,8842 мм. (приблизи-
тельно мм.). Положимъ, что конденсаторъ состоитъ изъ^Оф^лемен-
товъ, т. е. изъ 101 пластины съ 100 промежутками. Емкость такого,
конденсатора будетъ равна 10—3 фарада = 1 М.Р.
126
Емкость земли. — Электростатическія единицы
ЕМКОСТЬ ЗЕМЛИ.
77. Съ помощью выше полученной формулы мы можемъ легко
опредѣлить емкость шара, находящагося въ пустотѣ и расположен-
наго на большомъ разстояніи отъ другихъ тѣлъ. Она равняется
т л
С = р = 4дКо . а.
Емкость изолированнаго шара пропорціональна его
радіусу.
По этой формулѣ мы можемъ вычислить емкость земного шара.
За тѣло, обладающее нулевымъ потенціаломъ, въ такомъ случаѣ при-
нимается пустое пространство на большомъ разстояніи отъ земли.
Средній радіусъ земли равенъ
6367 км. = 6367 . ІО5 см.
Подставляя это число въ нашу формулу, получаемъ для емкости
земли величину
С - 707 . ІО"6 фарада - 707 М. Р.
. Это число ясно показываетъ, какую крупную единицу предста-
вляетъ собою микрофарадъ.
ТАКЪ НАЗЫВАЕМЫЯ ЭЛЕКТРОСТАТИЧЕСКІЯ ЕДИНИЦЫ.
78. Кромѣ общепризнанныхъ международныхъ десятичныхъ
единицъ употребляются иногда также единицы, имѣющія истори-
ческое значеніе и часто отличающіяся отъ единицъ десятичной
системы весьма сложными множителями. Эти единицы тоже необхо-
димо знать, чтобы, встрѣчаясь съ ними въ литературѣ, имѣть воз-
можность перевести ихъ на десятичныя единицы. При измѣреніяхъ
длинъ мы встрѣчаемся такимъ образомъ съ футомъ, дюймомъ, лок-
темъ, при электрическихъ измѣреніяхъ, именно при измѣреніяхъ на-
пряженія и заряда,— съ такъ называемыми „электростатическими
единицами", которыя прежде, до введенія нынѣ употребляемой
строго опредѣленной системы измѣреній, спеціально были ^идуманы
для электростатическихъ измѣреній. ।
Электростатическая единица напряженія представляетъ собою
крупное кратное вольта, электростатическая еди^щЙГ заряда—весьма
малую дробь кулона. Спеціальныхъ названій эт^Чстаринныя единицы
не получили; величины, въ этихъ единицахъ выраженныя, отмѣчаютъ
Электростатическія единицы
127
просто значкомъ е8 (еіекіго-зіаіізсѣ), такъ какъ обычно вполнѣ ясно,
идетъ ли рѣчь о напряженіи или же о зарядѣ. Для перевода этихъ
единицъ на нормальныя десятичныя единицы слѣдуетъ пользоваться
слѣдующей таблицей:
напряженіе 1 С8 = 300 вольтъ;
зарядъ 1 е8 = -7} • ІО-9 кулона,
о
Если выразить въ этихъ единицахъ абсолютную діэлектрическую
постоянную чистаго эѳира (сохраняя сантиметръ въ качествѣ единицы
длины), то получится:
Ко - 0,0796 ез.
Это число приблизительно равняется • Поэтому во многихъ
формулахъ въ теоретическихъ сочиненіяхъ и статьяхъ, посвященныхъ
х л 1 1
электростатикѣ, стоятъ множители 4лг или — вмѣсто нашихъ
и А'о. Замѣчательно, что въ теоретическомъ ученіи объ электриче-
ствѣ все еще употребляется старая система измѣреній, на практикѣ
уже давно вытѣсненная системой десятичныхъ мѣръ, производныхъ
отъ вольта и кулона. Но было бы въ высшей степени желательно,
чтобы неудобныя, стоящія внѣ десятичной системы единицы, упо-
треблявшіяся прежде въ ученіи объ электричествѣ, исчезли изъ на-
учныхъ работъ вмѣстѣ со старинными футомъ, дюймомъ и т. д. въ
линейной метрологіи и съ градусами Реомюра и Фаренгейта въ
температурныхъ измѣреніяхъ.
Чрезвычайно наглядна единица емкости въ старой е8 - системѣ.
Если мы подставимъ въ выведенную въ § 17 формулу емкости изо-
лированнаго въ пустотѣ шара С = 4 л:. А'о . а значеніе Ко — то
мы получимъ:
С - а е8.
Итакъ, въ электростатической системѣ измѣреній емкость изоли-
рованнаго шара равняется прямо радіусу шара, измѣренному въ сан-
тиметрахъ. Емкостью 1 обладаетъ изолированный шаръ, радіусъ ко^Ху
тораго равенъ 1 сантиметру. Поэтому и самую электростатичесц|чфу
единицу емкости часто называютъ „1 сантиметръ".
1 см. = 1,11 . 10~12 фарада.
Для тѣхъ же цѣлей, что и электростатическія единицы, могли
бы служить слѣдующія десятичныя единицы:
128
Послѣдовательное соединеніе конденсаторовъ
1 киловольтъ = 1000 вольтъ,
1 миллимикрокулонъ > ІО-9 кулона,
1 минимофарадъ = 10 ,; микрофарада ( = 0,9 см.).
Послѣднее названіе придумано ад Нос и вообще не употре-
бляется.
ПОСЛѢДОВАТЕЛЬНОЕ СОЕДИНЕНІЕ КОНДЕНСАТОРОВЪ.
79. Мы разсмотрѣли въ §71 случай параллельнаго соединенія
конденсаторовъ. ~Но кромѣ этого возможно еще послѣдователь-
ное соединеніе конденсаторовъ. Возьмемъ п хорошо изолирован-
ныхъ другъ отъ друга лейденскихъ банокъ и соединимъ внѣшнюю
обкладку каждой банки съ внутренней обкладкой слѣдующей; только
внутреннюю обкладку первой банки и внѣшнюю послѣдней оставимъ
свободными. Этимъ двумъ обкладкамъ мы сообщимъ то напряженіе,
до котораго мы желаемъ зарядить батарею. Отдѣльные конденса-
торы или элементы батареи, какъ говорятъ, соединены въ этомъ
случаѣ послѣдовательно. Ясно, что такимъ же способомъ можно
соединять послѣдовательно и плоскіе конденсаторы. Зарядимъ теперь
обѣ свободныя обкладки такъ, чтобы напряженіе между ними было V.
Положимъ, что внутренняя обкладка первой банки получитъ при
этомъ зарядъ -|~ т; тогда внѣшняя обкладка этой банки получитъ
зарядъ т. Но такъ какъ послѣдняя обкладка передъ этимъ была
не заряжена и, будучи хорошо изолированной, соединена проводомъ
лишь съ внутренней обкладкой второй банки, то по закону сохра-
ненія зарядовъ внутренняя обкладка второй банки должна получить
зарядъ 4" ту равный заряду внутренней обкладки первой банки.
Такія же разсужденія мы можемъ провести и дальше; всѣ вну-
треннія обкладки должны получить зарядъ 4"всѣ внѣшнія — за-
рядъ т.
Если емкости отдѣльныхъ банокъ суть С\, С.2, ... , Сн, то на-
пряженія ихъ равняются
і г т т г .. т
= Г - ^2= Г’•••’ѵ'1== г •
Но приложенное къ свободнымъ конечнымъ обкладкам^Ййлное на-
пряженіе V "равно суммѣ напряженій въ отдѣльцыхѣ банкахъ:
V = 4- 4- • • • 4- Ѵп. Емкость же батареи, очевидно, равняется
отношенію сообщеннаго заряда, т. е. т, къ полному напряженію,
пі V 1 //4 ' *
т. е. V. Итакъ: С = р; — = • Отсюда ^фмуетъ такой законъ:
Каскадная батарея
129
Если мы соединяемъ послѣдовательно рядъ конденса;
торовъ емкостей С,, С2, ..., Сп, то всѣ они заряжаются оди-
наковымъ зарядомъ и напряженія ихъ складываются; обрат-
ная величина емкости С батареи равняется при этомъ
суммѣ обратныхъ величинъ отдѣльныхъ емкостей, т. е.
С С,^С^ г Сп
Если емкости всѣхъ банокъ равны между собою, т. е.
Сх = Сг = • • • = Сп, то эта формула даетъ: С = С\. Вообще можно
сказать, что емкость батареи, составленной такимъ способомъ, меньше
емкости отдѣльнаго элемента и притомъ тѣмъ меньше, чѣмъ большее
число элементовъ входитъ въ ея составъ.
КАСКАДНАЯ БАТАРЕЯ.
80. Суммированіе напряженій послѣдовательно соединенныхъ
емкостей вполнѣ аналогично суммированію напряженій гальваниче-
скихъ цѣпей (§ 38). И дѣйствительно, гальваническую цѣпь всегда
можно уподобить конденсатору, емкость котораго чрезвычайно ве-
лика, такъ какъ толщина его двойныхъ слоевъ имѣетъ молекуляр-
ные размѣры, т. е. чрезвычайно мала въ сравненіи съ толщинами
двойныхъ слоевъ въ настоящихъ конденсаторахъ, измѣряющимися
большей частью въ миллиметрахъ. Кромѣ того, гальваническая цѣпь
отличается отъ конденсатора еще свойственными ей химическими
процессами, поддерживающими напряженія въ двойныхъ слояхъ по-
стоянными.
Конденсатору въ родѣ лейденской банки мы легко можемъ со-
общить гораздо большія напряженія, нежели тѣ, которыя имѣются
въ гальваническихъ цѣпяхъ, а послѣдовательнымъ соединеніемъ кон-
денсаторовъ мы можемъ еще ихъ значительно повысить. Приспосо-
бленіе, служащее для этой цѣли, носитъ названіе каскадной ба-
тареи. Оно состоитъ изъ нѣкотораго числа одинаковыхъ лейден-
скихъ банокъ, хорошо изолированныхъ. Каждая отдѣльная обкладка^?*
соединена съ хорошо изолированной (напримѣръ, помѣщенной ^въ^
параффинѣ) чашечкой со ртутью. Всѣ эти чашечки расположены въ
въ два^ряда; чашечки одного ряда соединены съ внутренн^м^обклад-
ками банокъ, чашечки другого ряда —съ внѣшними обкладками, при
чемъ каждыя двѣ чашечки, лежащія другъ противъ, Д>у<а, соединены
Ми. Электричество и магннтизмъ. 9
130
Каскадная батарея
съ двумя обкладками одной и той же банки. При помощи спеціаль-
наго приспособленія, соединяющаго чашечки каждаго ряда между со-
бою, можно привести всѣ банки въ параллельное соединеніе и, кромѣ
того, соединить ихъ обкладки съ полюсами индукціонной машины,
служащей для заряженія. Заставляя предварительно возбужденную
машину совершить опредѣленное число оборотовъ, можно заря-
дить обкладки для опредѣленнаго напряженія. Достигнутое напря-
Рис. 54. Каскадная батарея.
женіе можно приблизительно измѣрить помощью искромѣра, оба
шарика котораго можно прямо соединить съ внутренней обклад^й
первой банки и внѣшней обкладкой послѣдней банки (рис. 54). Пер-
воначально мы дѣлаемъ разстояніе, которое должна пройти ігскра, не-
большимъ, устанавливая между шариками искромѣра третій шарикъ
такой величины, чтобы между нимъ и шариками искррмѣра остава-
лись еще маленькіе промежутки. Г
симальное число оборотовъ, при
искры черезъ эти короткіе промежутки. Зарѣ^^увеличимъ искровой
ідимъ индукціонной машинѣ мак-
которомъ еще\н.е проскакиваютъ
Каскадная батарея. — Энергія электрическаго поля
131
промежутокъ, для чего достаточно удалить средній шарикъ. Ясно,
что теперь искра можетъ проскочить лишь въ томъ случаѣ, если
между обоими шариками искромѣра получится весьма высокое напря-
женіе. Такого напряженія мы достигнемъ, если мы замѣнимъ парал-
лельное соединеніе заряженныхъ банокъ послѣдовательнымъ. Для
этого мы вынимаемъ прежній соединитель изъ чашечекъ со ртутью
и замѣняемъ его другимъ соединителемъ, состоящимъ изъ ряда косо
расположенныхъ проволочекъ, соединяющихъ внѣшнюю обкладку
каждой банки съ внутренней обкладкой слѣдующей банки; свобод-
ными остаются только внутренняя обкладка первой банки и внѣшняя
обкладка послѣдней, которыя соединены съ шариками искромѣра.
Какъ только мы установимъ этотъ соединитель, сейчасъ же черезъ
большой искровой промежутокъ проскочитъ искра.
Если напряженіе, полученное помощью индукціонной машины,
есть I/, а число конденсаторовъ равно п, то послѣ описаннаго со-
единенія получается напряженіе, равное п . V.
Мы видѣли выше (§ 39), что для полученія сравнительно высо-
кихъ напряженій можно пользоваться батареями гальваническихъ
элементовъ. Если желательно получить еще болѣе высокія напряже-
нія, то можно пользоваться каскадной батареей. Если мы имѣемъ
въ нашемъ распоряженіи аккумуляторную батарею на 2000 вольтъ
и заряжаемъ ею 10 лейденскихъ банокъ, то при послѣдовательномъ
ихъ соединеніи можемъ получить уже напряженіе въ 20000 вольтъ.
ЭНЕРГІЯ ЭЛЕКТРИЧЕСКАГО ПОЛЯ.
81. Если наблюдать за искрами при описанномъ въ § 80 опытѣ
съ каскадной батареей, то можно замѣтить, что короткія искры,
проскакивающія при параллельномъ соединеніи банокъ, если дать
индукціонной машинѣ слишкомъ большое число оборотовъ, значительно
свѣтлѣе и даютъ болѣе громкій звукъ, нежели длинныя искры, по-
лучающіяся при послѣдовательномъ соединеніи банокъ. Это обстоя-
тельство легко понять. Если зарядъ, получаемый каждой банкой при
напряженіи V равняется /И, то при короткихъ искрахъ разрядъ происхс^
дитъ при зарядѣ п . М, тогда какъ при длинныхъ искрахъ разряжается
лишь зарядъ М. Въ обоихъ случаяхъ въ искрахъ проявляетс^та* же
энергія, которой обладаютъ всѣ лейденскія банки вмѣстѣ^ нр ъъ ко-
роткой искрѣ она сосредоточивается на меньшемъ пространствѣ, нежели
въ длинной искрѣ, и потому вызываетъ болѣе знач шовныя дѣйствія.
9
132
Единица энергіи
Эта энергія происходитъ, слѣдовательно:
1) въ короткихъ искрахъ отъ заряда п.М при напряженіи V;
2) въ длинныхъ искрахъ отъ заряда М при напряженіи п. V.
Слѣдовательно, количество энергіи, заключенной въ батареѣ,
зависитъ отъ двухъ величинъ — напряженія и заряда.
ЕДИНИЦА ЭНЕРГІИ.
82. Прежде, чѣмъ вывести вполнѣ опредѣленное выраженіе для
энергіи конденсатора мы должны, понятно, условиться относительно
единицы энергіи. Въ ученіи объ электричествѣ единица силы выбирается
такъ, чтобы величина силы, дѣйствующей на частицу съ зарядомъ т,
помѣщенную въ полѣ силы Е, равнялась Р — Е. т. При этомъ Е
дается въ вольтахъ на сантиметръ, т въ кулонахъ. Установленная
такимъ образомъ единица силы отлична отъ употребляемыхъ въ
механикѣ единицъ силы (килограммъ, граммъ и т. д.), но не полу-
чила особаго названія, такъ какъ въ этомъ нѣтъ никакой необхо-
димости.
Если мы теперь частичку съ зарядомъ т передвинемъ въ напра-
вленіи силы на маленькій отрѣзокъ, равный 5 сантиметрамъ, то полу-
чимъ энергію въ формѣ работы, такъ какъ электрическая сида способ-
ствуетъ такому движенію. Для измѣренія этой энергіи ѴЕ единица
выбирается такъ, чтобы величина ѴЕ вычислялась по простой фор-
мулѣ ѴЕ — Р8.5, гдѣ Р8 ► - слагающая силы въ направленіи 5. Энер-
гія \Ѵ при движеніи частицы, понятно, была получена отъ эѳира,
въ которомъ вслѣдствіе перемѣщенія заряда т поле измѣнилось та-
кимъ образомъ, что энергія его слегка уменьшилась. Если мы обо-
значимъ полное напряженіе поля вдоль отрѣзка 5 черезъ V, то отня-
тая у поля энергія ІГ можетъ быть вычислена по формулѣ
\Ѵ = Р8 . 8 = т . Е8.8 = т . V' х).
Если т передвигается по линіи конечной длины, вдоль которой
полное напряженіе поля равняется Ѵ12, то мы можемъ, какъ ігХѣ
§ 24, всю линію мысленно раздѣлить на большое число ^малыхъ
отрѣзковъ , $2, и т. д., къ которымъ можно примѣнить ^вьіше вы-
веденную формулу. Въ этомъ случаѣ вся энергія, отнятая^тъ эѳира,
будетъ равна хЗЗ
Ѵ7=т. (Е8і . 5, + Е.,., . 52 + • • •) = XX.
----------------' X
х) Здѣсь Е§—слагающая силы поля Е въ направленіи 5. Прим. пер.
Единица энергіи
133
Положимъ, напримѣръ, что І/12 представляетъ собою напря-
женіе между обкладками конденсатора I и II. Отнимемъ при по-
мощи пробнаго кружка отъ положительно заряженной обкладки I
количество электричества пг, чрезвычайно малое въ сравненіи со
всѣмъ зарядомъ, и перенесемъ его на обкладку II; въ силу этого
отъ поля конденсатора будетъ отнята небольшая часть его энергіи,
которая сообщится въ формѣ работы рукѣ, переносящей пробный
кружокъ. Эта отнятая у поля энергія равняется 117 = т . Ѵ12. Послѣ
описанной операціи напряженіе І712 въ конденсаторѣ должно умень-
шиться на незначительную его часть. Мы можемъ возстановить преж-
нее напряженіе, напримѣръ, при помощи гальванической батареи, и
тѣмъ самымъ вернуть полю потерянную энергію, отнимая ее отъ за-
паса химической энергіи батареи. Если мы повторимъ ту же операцію,
то вновь отнимемъ отъ поля небольшое количество энергіи. Мы мо-
жемъ вновь зарядить конденсаторъ до прежняго напряженія и путемъ
многократнаго повторенія такой операціи перенести отъ одной
обкладки къ другой произвольно большой зарядъ М — Ет. Вмѣстѣ
съ этимъ мы отнимемъ отъ поля произвольно большое количество
энергіи, поддерживая его напряженіе постоянно равнымъ Ѵѵі вслѣд-
ствіе непрерывнаго пополненія отнимаемой энергіи при помощи галь-
ванической батареи. Согласно нашему условію мы можемъ теперь
единицу энергіи опредѣлить слѣдующимъ образомъ:
если мы постепенно переводимъ зарядъ, равный 1 ку-
лону, по пути, вдоль котораго напряженіе поддерживается
равнымъ 1 вольту, то мы при этомъ постепенно отнимаемъ
отъ электрическаго поля количество энергіи, равное еди-
ницѣ. Установленная этимъ для ученія объ электричествѣ
единица энергіи называется джуль.
1 джуль = 1 вольтъ X 1 кулонъ.
Если зарядъ, равный М кулонамъ, будетъ перенесенъ вдоль на-
пряженія въ V вольтъ, то отъ поля будетъ отнята энергія, равная
7И V джулей.
Отношеніе этой новой единицы энергіи къ тѣмъ единицамъ,
которыя употребляются въ механикѣ и въ ученіи о теплотѣ,^. е.
къ килограмметру и къ калоріи, мы установимъ тогда,
комимся съ удобнымъ методомъ измѣренія зарядовъ^
уже выше шла рѣчь (§73). о/С
к^апозна-
которомъ
134
Вычисленіе полной энергіи поля
ВЫЧИСЛЕНІЕ ПОЛНОЙ ЭНЕРГІИ ПОЛЯ.
83. Теперь мы можемъ вычислить въ джуляхъ полную энергію
конденсатора. Будемъ постепенно разряжать конденсаторъ, переводя
при помощи пробнаго кружка малые заряды т отъ одной обкладки
къ другой, пока, послѣ весьма большого числа такихъ операцій,
не удалимъ всего заряда М — Ы . т. При этомъ процессѣ напря-
женіе должно постепенно, начиная отъ своего начальнаго значенія V,
уменьшаться, пока, наконецъ, оно не станетъ равнымъ нулю. Вся отня-
тая при этомъ отъ конденсатора энергія можетъ быть выражена
суммой произведеній т . V, т . V', т . V" и т. д., гдѣ V", V" и т. д.
суть значенія напряженія, которыя оно послѣдовательно принимаетъ
за время разряда до достиженія имъ нулевого значенія. Мы можемъ,
слѣдовательно, написать:
Въ этомъ произведеніи Ы . т ~ М — полному заряду конденсатора,
Ѵ+V'-+0 .
а ------------------есть среднее ариѳметическое всѣхъ значеній
напряженія отъ V до 0. Но такъ какъ, по закону Кулона, напря-
женіе при одинаковыхъ т уменьшается на одинаковыя величи-
ны, то это среднее значеніе въ точности равно ~ V. Поэтому,
полная энергія поля конденсатора равняется
Г = у М . V.
Для примѣра приложимъ эту формулу къ вышеописанной кас-
кадной батареѣ. Если каждая изъ п банокъ имѣетъ зарядъ М и на-
пряженіе Ѵу то энергія батареи равна п • ~ М . V. Если банки со-
единены параллельно, то общій зарядъ батареи равенъ п . М, а на-
пряженіе— V и энергія батареи равна • пМ. V. Если банки со-
единены послѣдовательно, то напряженіе батареи равно п . I/, а за-
рядъ — М и энергія ея равняется у • М . п V. Всѣ три раза энергія
получилась одинаковой.
Если мы заряжаемъ конденсаторъ емкости С до опредѣленнаго на-
пряженія Ѵу то зарядъ его равенъ М— С. V и, значитъ, энергія его равна
1 Ч
ІУ = у С . V2. Слѣдовательно, приданномъ напряженій; энергія кон-
денсатора тѣмъ больше, чѣмъ больше его емкос^ь^Въ силу этого
конденсаторы служатъ для накопленія электрической энергіи при дан-
номъ напряженіи.
Распредѣленіе энергіи въ полѣ
135
Иначе обстоитъ дѣло, когда мы сообщаемъ конденсатору ем-
кости С не опредѣленное напряженіе, но опредѣленный электриче-
скій зарядъ М. Въ этомъ случаѣ конденсаторъ заряжается до по-
Л4 №
тенціала V = и энергія его равняется П/ = Слѣдовательно,
если мы сообщаемъ конденсатору данный зарядъ 7И, то энергія его
тѣмъ меньше, чѣмъ больше его емкость. Примѣромъ здѣсь могутъ
служить двойные слои электрическихъ машинъ, какъ машины съ тре-
ніемъ, такъ и индукціонныхъ машинъ и электрофора. Во всѣхъ этихъ
машинахъ двойные слои получаютъ первоначально нѣкоторый опре-
дѣленный зарядъ, а затѣмъ вслѣдствіе удлиненія силовыхъ линій ихъ
емкость уменьшается, и возрастаютъ напряженіе и энергія полей двой-
ныхъ слоевъ.
РАСПРЕДѢЛЕНІЕ ЭНЕРГІИ ВЪ ПОЛѢ.
84. Подобно тому, какъ теплота въ нагрѣтомъ тѣлѣ обладаетъ
нѣкоторымъ дѣйствительнымъ пространственнымъ распредѣленіемъ,
обладаютъ имъ и энергія движенія стремительнаго ручья и энергія
напряженія согнутаго стержня. Точно такъ же и энергія электриче-
скаго состоянія въ эѳирѣ (или вообще въ діэлектрикѣ) совершенно
опредѣленнымъ образомъ распредѣляется въ пространствѣ. Въ тѣхъ
мѣстахъ, гдѣ поле болѣе интенсивно, должно приходиться боль-
шее количество энергіи на каждый кубическій сантиметръ діэлек-
трика; въ мѣстахъ меньшей интенсивности поля и энергія должна рас-
полагаться менѣе плотно. Чтобы выяснить, какъ измѣняется плот-
ность распредѣленія энергіи съ измѣненіемъ силы поля, мы можемъ
сначала просто энергію поля плоскаго конденсатора, гдѣ она распре-
дѣлена равномѣрно, раздѣлить на заполняемый ею объемъ. Тогда мы
прямо получимъ количество энергіи, приходящееся на одинъ куби-
ческій сантиметръ, т. е. плотность энергіи. Это опредѣленіе совер-
шенно тождественно съ вычисленіемъ массовой плотности нѣкотораго
вещества.
Положимъ, поверхность обкладки есть/, толщина діэлектрика—
тогда объемъ, заполненный полемъ, равенъ т = /. сі. Мы знаемъ
1
лѣе, что полная энергія поля равняется = — М . V; слѣдователь-
но, плотность энергіи равняется
1 М V _ ' п Р джуль^У'
т 2 ’ / ’ а ~ 2 и ѣ нуб.^^
136
Механическія аналогіи
Здѣсь О удѣльное возбужденіе эѳира, выраженное въ куло-
нахъ на кв. сантиметръ, Е — сила поля, выраженная въ вольтахъ
на сантиметръ. Мы можемъ написать выраженіе а еще иначе, вводя
въ формулу К абсолютную діэлектрическую постоянную среды.
Такъ какъ О = К. Е, то
о = . Ег.
Плотность энергіи растетъ пропорціонально второй
степени силы поля.
Эти формулы справедливы, конечно, и въ томъ случаѣ, если
поле не гомогенно, т. е. если плотность энергіи измѣняется въ немъ
отъ одной точки къ другой.
МЕХАНИЧЕСКІЯ АНАЛОГІИ.
85. Не безынтересно отмѣтить, что формулы, выражающія элек-
трическую энергію эѳира, вполнѣ аналогичны формуламъ, служащимъ
для вычисленія энергіи напряженія упруго-деформированнаго тѣла.
Полное напряженіе аналогично полной деформирующей силѣ; возбу-
ждающій зарядъ аналогиченъ полной деформаціи, измѣряемой смѣ-
щеніемъ точки приложенія силы. Аналогомъ силы поля является, ко-
нечно, напряженіе, разсчитанное на 1 квадратный сантиметръ (давле-
ніе), аналогомъ возбужденія въ данномъ мѣстѣ деформація въ дан-
номъ мѣстѣ (напримѣръ, растяженіе на единицу длины). Чтобы сдѣ-
лать эту аналогію болѣе очевидной, я остановлюсь на простомъ при-
мѣрѣ однороднаго растяженія, которое испытываетъ закрѣпленная въ
верхней своей точкѣ проволока при дѣйствіи силы на нижній ея ко-
нецъ. Если эта сила равна Р килограммамъ („полное напряженіе про-
волоки “) и А есть полное удлиненіе, выраженное въ сантиметрахъ
(аналогично „полному возбужденію“), то механика учитъ, что полная
энергія напряженія проволоки равняется
ІГ = Р . а кгр. см.
Въ нашемъ простомъ случаѣ эта энергія равномѣрно распредѣ-
ляется по всей проволокѣ. Если д есть поперечное с^Ченіе послѣд-
ней, / ея длина, то объемъ ея равенъ т = д . /, растяженіе въ дан-
, . Р кгр. . А ' , .
номъ мѣстѣ равняется р = — удлиненіе ъъ данномъ мѣстѣ
Теорія матеріальныхъ діэлектриковъ
137
равняется
Если
по закону
X 4,
8 = у и, слѣдовательно, плотность энергіи равна
1 кгр. см,
б = р , 8 ----
2 Г куб. см,
а есть коэффиціентъ растяженія матеріала проволоки, то,
Гука (Ноок), 8 = а.р и
° = Iп • Р--
Формулы для б остаются вѣрными и въ случаѣ неоднороднаго
растяженія (напримѣръ, при изгибѣ стержня). При сложныхъ дефор-
маціяхъ приходится, конечно, принимать въ расчетъ еще энергію
деформаціи сдвига; формулы при этомъ усложняются, но по суще-
ству дѣла аналогія сохраняется.
И на студнеобразной модели эѳира мы можемъ легко устано-
вить подобныя аналогіи.
ТЕОРІЯ МАТЕРІАЛЬНЫХЪ ДІЭЛЕКТРИКОВЪ.
86. На нашей студнеобразной модели коэффиціентъ упругости,
т. е. отношеніе смѣщенія клѣточки къ приложенному къ ней на-
пряженію, вполнѣ соотвѣтствуетъ діэлектрической постоянной. Раз-
личныя вещества имѣютъ различныя діэлектрическія постоянныя; на
нашей модели мы должны представлять себѣ, что занятыя этими ве-
ществами части эѳира обладаютъ различною упругостью. Выраженіе
„вѣсомые діэлектрики имѣютъ большую діэлектрическую постоян-
ную, нежели чистый эѳиръ“ значитъ: „присутствіе молекулъ дѣлаетъ
эѳиръ болѣе податливымъ “.
Попытку объясненія этого явленія первый далъ Клаузіусъ
(Сіаизіиз). Молекулы будутъ обладать такимъ вліяніемъ, если мы пред-
ставимъ ихъ себѣ въ видѣ проводящихъ частичекъ, изолированныхъ
другъ отъ друга находящимся между ними эѳиромъ. Это легко понять,
представивъ себѣ въ твердомъ студнѣ нашей модели эѳира разсѣян-
ные въ большомъ числѣ маленькіе пузырьки, стѣнки которыхъ снаб-
жены отверстіями. Слой студня, въ которомъ находятся такіе пу-
зырьки, заключаетъ въ себѣ меньше клѣточныхъ перепонокъ, могу^
ЩИХЪ оказать сопротивленіе смѣщенію, нежели слой сплошного
студня; слѣдовательно, напряженіе, соотвѣтствующее опредѣленному
•смѣщенію, для перваго слоя должно быть меньше, нежели для вто-
рого. Совершенно такъ же модуль упругости губчатаго^еталла, на-
полненнаго воздушными пузырьками, меньше модулядупругости мас-
сивнаго металла. •
138
Діэлектрическая поляризація и свободные заряды
ДІЭЛЕКТРИЧЕСКАЯ ПОЛЯРИЗАЦІЯ И СВОБОДНЫЕ ЗАРЯДЫ.
87. Представленіе о строеніи діэлектриковъ, развитое Клаузіу-
сомъ, заставляетъ насъ обратить вниманіе на нѣкоторыя новыя ихъ
свойства. Представимъ себѣ стержень, сдѣланный изъ твердаго діэлек-
трика и подвѣшенный въ электрическомъ полѣ такъ, чтобы его ось была
направлена параллельно силовымъ линіямъ. Если молекулы его предста-
вляютъ собою проводящія частички, то поле индуктируетъ въ каждой
изъ нихъ положительный и отрицательный заряды, т. е. каждая мо-
лекула представляетъ собою при этомъ электрическій диполь, по-
добный маленькой электрической стрѣлкѣ. Внутри стержня сумма всѣхъ
индуктированныхъ зарядовъ равняется нулю, но на поверхностяхъ
его получаются обкладки -положительная съ одной стороны и отри-
цательная съ другой (рис. 55). Такимъ образомъ стержень, сдѣлан-
©©©©©©ф©@@©
©©©©Ф©©@©@©
©©©©©©©©©©©
©©©©©©©©©©©
©©©©©©©©©О©
©©©©©©©Ф©©©
©©©©О©©©©©©
©©©©©©©©©©©
©фф©©фффф©©
©©©©©©©©©©©
Рис. 55. Діэлектрическая
поляризація.
въ направленіи силовыхъ
ный изъ діэлектрика, обнаруживаетъ то же
явленіе, что и проводящій стержень, на ко-
торомъ поле индуктируетъ заряды. Это
свойство діэлектриковъ мы можемъ обна-
ружить, воспользовавшись стержнемъ изъ
весьма хорошаго изолятора (напримѣръ, сур-
гуча или сѣры), подвѣшеннымъ между дву-
мя металлическими пластинками. При отсут-
ствіи поля онъ можетъ быть расположенъ
въ произвольномъ направленіи, но при за-
ряженіи обѣихъ пластинокъ до различныхъ
потенціаловъ онъ явственно устанавливается
линій. Тоже было бы и съ проводникомъ,
только силы, дѣйствующія на проводникъ, были бы больше силъ,
дѣйствующихъ на изолирующій стержень.
Тѣмъ не менѣе мы должны отчетливо различать эти два случая. Въ
совершенномъ изоляторѣ никогда не могутъ индуктироваться заряды.
Если мы внесемъ въ электрическое поле стержень изъ сѣры, разрѣзан-
ный посрединѣ и вновь сложенный въ одно цѣлое, и въ полѣ отдѣлимъ
его части другъ отъ друга, то, пользуясь Фарадэевскимъ сосудамъ, мы,
вопреки тому, что наблюдается для проводниковъ, не за^Ѣймъ ни на
одной изъ его половинъ никакихъ слѣдовъ заряда. Обтрясти стержня
въ полѣ имѣютъ каждая положительный и отрицательной полюсы, дѣй-
ствія которыхъ въ точкѣ соприкосновенія взащро уничтожаются,
такъ что замѣтными оказываются только дваррлюса на концахъ.
Діэлектрическая поляризація и свободные заряды
13$
. Вполнѣ изолирующее тѣло, внесенное въ электрическое
поле, становится насквозь „электрически поляризованнымъ",
но никакихъ дѣйствительныхъ поверхностныхъ зарядовъ не
пріобрѣтаетъ.
Чтобы отмѣтить, что оба электрическіе полюса, возникающіе на
изолирующемъ стержнѣ въ электрическомъ полѣ, появляются потому,,
что на концахъ стержня электрическіе диполи, не нейтрализуемые
прилежащими къ нимъ диполями, остаются свободными, говорятъ, чісь
Рис. 56. Кружокъ изъ діэлектрика въ электрическомъ полѣ.
зарядъ; такой зарядъ противополагается
появляющемуся на проводникѣ въ силу
проводникѣ заряды вліяютъ на поле, въ.
на каждомъ концѣ такого стержня находится свободное электри-
чество или свободный
дѣйствительному заряду,
индукціи.
Индуктированные на
которое онъ внесенъ, стягивая къ нему по обѣимъ сторонамъ сило-
выя линіи (§ 49).
Совершенно такое же вліяніе оказываютъ и свободные заря^Ы^
изолирующаго стержня. Но тогда какъ на поверхности про§^у^ка
поле совершенно прекращается и внутри проводника не замѣчается
и слѣда его, изоляторъ вполнѣ пронизывается полемъ.
Это легко прямо показать помощью описаннагоДвъ § 20 ме-
тола объективнаго воспроизведенія силовыхъ линій.^Для этого помѣ-
140
Дальнѣйшія дополненія теоріи
'сгимъ между двумя мѣдными полосками, наклеенными на стеклян-
ныя пластинки и возбуждающими поле, подобное полю плоскаго
^конденсатора, круглую пластинку изъ хороню изолирующаго янтаря
'(рис. 56). Если насыпать рутиловый порошокъ и возбудить поле, то
при постукиваніи становится видно, какъ линіи силъ, прямыя между
двумя мѣдными полосками, втягиваются въ янтарь, хотя и не въ
такой степени, какъ въ случаѣ проводящаго кружка. Кромѣ того
*видно, что рутиловый порошокъ, лежащій на янтарной пластинкѣ,
также располагается линіями; это служитъ доказательствомъ прони-
зыванія полемъ янтарной пластинки.
ДАЛЬНѢЙШІЯ ДОПОЛНЕНІЯ ТЕОРІИ.
88. Теорія Клаузіуса сводитъ проблему діэлектрика къ про-
блемѣ электрической проводимости. Мы становимся такимъ обра-
зомъ передъ новымъ вопросомъ: какимъ образомъ наличность моле-
кулъ сообщаетъ эѳиру свойства проводника? Или же, если перейти
на языкъ аналогій, то мы должны спросить себя: почему клѣтки
‘Студня въ тѣхъ мѣстахъ, гдѣ находятся молекулы, оказываются по-
ристыми? Разрѣшенію этого вопроса посвящены послѣдующія главы
этой книги. Но для пониманія нижеизложеннаго будетъ полезно ука-
зать здѣсь вкратцѣ на одинъ результатъ описанныхъ въ этихъ гла-
вахъ экспериментальныхъ изслѣдованій. Оказывается, что молекулы и
даже самые атомы состоятъ изъ положительныхъ и отрицательныхъ
элементарныхъ частицъ, обладающихъ всегда постоянными зарядами.
„Атомъ или молекула не заряженыи это значитъ, что въ атомѣ или
въ молекулѣ сумма положительныхъ элементарныхъ зарядовъ равна
суммѣ отрицательныхъ. Электрическая проводимость имѣетъ мѣсто
въ про-
что ча-
должцы
въ томъ случаѣ, если эти заряженныя частички подвижны;
водникѣ энергія и напряженіе поля уничтожаются потому,
стицы подчиняются дѣйствующимъ на нихъ силамъ.
Если мы сопоставимъ это съ теоріей Клаузіуса,
будемъ сказать, что заряды молекулъ существуютъ и
поля, но только при этомъ заряженныя элементарныя
положены совершенно безпорядочно или, по крайней
‘•образомъ, что никакого преобладающаго направленія ^^расположе-
ніи диполей не существуетъ. Если же поле возбуждено, то поло-
жительныя элементарныя частички слегка смѣщаются въ направленіи
тюля, отрицательныя въ обратномъ направленій, такъ что диполи
то мы должцы
при ОТСУТСТВІИ
частицы^ рас-
^гѣрЖ? такимъ
Діэлектрическія свойства кристалловъ
141
располагаются преимущественно въ направленіи силовыхъ линій. Эта*
оріентировка диполей или, какъ говорятъ, „поляризація молекулъ “
выступаетъ тѣмъ явственнѣе, чѣмъ больше сила поля.
ДІЭЛЕКТРИЧЕСКІЯ СВОЙСТВА КРИСТАЛЛОВЪ.
89. Особенныя свойства наблюдаются у кристалловъ, т. е. у
твердыхъ тѣлъ, молекулы которыхъ имѣютъ вполнѣ правильное рас-
предѣленіе по такъ называемой „пространственной рѣшеткѣ". Оказы-
вается, что молекулы кристалловъ въ нѣкоторыхъ опредѣленныхъ,
направленіяхъ поляризуются сильнѣе, чѣмъ въ прочихъ направле-
ніяхъ. Слѣдовательно, діэлектрическія свойства кристалловъ различны;
въ различныхъ направленіяхъ.
Всякій кристаллъ вообще обладаетъ нѣкоторымъ опредѣленнымъ,
направленіемъ I, въ которомъ его діэлектрическая постоянная имѣетъ,
максимальное значеніе; затѣмъ существуетъ опредѣленное направле-
ніе II, перпендикулярное къ первому, въ которомъ діэлектрическая по-
стоянная имѣетъ минимальное значеніе; наконецъ, перпендикулярно*
къ направленіямъ I и II располагается
направленіе III, въ которомъ діэлек-
трическая постоянная имѣетъ „макси-
минимальное" значеніе, т. е. большее,
чѣмъ во всѣхъ прочихъ направле-
ніяхъ плоскости II III, и меньшее,
чѣмъ во всѣхъ прочихъ направленіяхъ
плоскости IIII. Если заставить поле Рис. 57. Кристаллическій шаръ въ.
пронизывать кристаллическую среду электрическомъ полѣ.
въ направленіи, наклонномъ къ главнымъ направленіямъ I, II, III, то*
поляризація молекулъ произойдетъ не въ направленіи, параллельномъ,
направленію поля, какъ въ аморфныхъ тѣлахъ, но ея направленіе-
отклонится въ ту сторону, въ которой молекулы, соотвѣтственно ихъ.
природѣ, поляризуются сильнѣе всего. Поэтому, вообще говоря, элек-
трическое возбужденіе въ кристаллѣ не параллельно силѣ электри- 4^
ческаго поля. Экспериментально обнаружить это, конечно, не легкоу^Ь0
Если бы можно было въ кристаллической пластинкѣ, вполнѣ
рующей и представляющей собою діэлектрикъ плоскаго конденсатора,
сдѣлать нѣсколько очень узкихъ щелей подъ различными^угламш
къ плоскости пластинки и въ нихъ вводить двойной кружокъ ДЛЯ’
измѣренія индукціи, то можно было бы убѣдиті^с^Свъ томъ, что.
3 42 Постоянная поляризація и пироэлектричество
максимумъ индукціи соотвѣтствуетъ вполнѣ опредѣленному наклону
'пробнаго кружка, образующему острый уголъ съ нормалью къ пла-
стинкѣ. Сила же поля, какъ это слѣдуетъ изъ опредѣленія, даннаго
въ § 19, и условій равновѣсія поля, изложенныхъ въ §26, во вся-
комъ случаѣ должна имѣть направленіе, совпадающее съ направле-
ніемъ нормали къ пластинкѣ. Но такого рода измѣренія невыполнимы.
-Удалось, однако, сдѣлать иное наблюденіе, подтверждающее выводы
теоріи. Именно, если изготовить по возможности математически точ-
ный шаръ изъ вполнѣ однороднаго правильно образованнаго кри-
сталла, напримѣръ, кварца или сѣры, и подвѣсить этотъ шаръ на
тонкой нити между двумя пластинками воздушнаго конденсатора, то,
вообще говоря, шаръ долженъ испытывать въ электрическомъ полѣ
дѣйствіе вращающей силы, такъ какъ его диполи располагаются на-
клонно къ направленію поля. Дѣйствительно, наблюденія показываютъ,
что шаръ при этомъ самъ устанавливается въ такомъ направленіи,
въ которомъ діэлектрическая постоянная больше, нежели въ осталь-
ныхъ направленіяхъ плоскости вращенія (рис. 57).
Для примѣра приводимъ три главныя значенія діэлектрической
постоянной для кристалла сѣры:
3,59; 3,85; 4,61.
ПОСТОЯННАЯ ПОЛЯРИЗАЦІЯ И ПИРОЭЛЕКТРИЧЕСТВО.
90. Совершенно особаго характера явленія наблюдаются у такъ
'называемыхъ гемиморфныхь кристалловъ. Эти кристаллы имѣютъ
одно направленіе, у котораго можно различить двѣ стороны, какъ
у вектора. У большинства кристалловъ такого направленія не ока-
зывается; это значитъ, что, если вырѣзать изъ кристалла въ лю-
бомъ направленіи стерженекъ, то ни при какомъ опытѣ поворотъ
его на 180° не дастъ какого-либо измѣненія. Но иначе обстоитъ дѣло
съ гемиморфными кристаллами, классическимъ примѣромъ которыхъ
является турмалинъ (рис. 58).
В. Фогтъ (АѴ. Ѵоі^і) вырѣзалъ изъ одного турмалина н^только
стерженьковъ, продольная ось которыхъ совпадала съ ндп^ІШіеніемъ
гемиморфной главной оси кристалла. Одинъ изъ этихъутерженьковъ
былъ помѣщенъ надъ двумя чашечками со ртутью, срфйненными каж-
дая съ парою квадрантовъ чувствительнаго электрометра, и затѣмъ
разломанъ по заранѣе сдѣланному надрѣзу. ГІло^кости разлома были
сейчасъ же погружены въ чашечки со ртуть^Дігравшія здѣсь роль Фа-
Постоянная поляризація и пироэлектричество
143
радэевскаго сосуда. Фогтъ обнаружилъ при этомъ отклоненіе элек-
трометра и могъ вычислить какъ свободные заряды, такъ и постоян-
ную поляризацію турмалиноваго стерженька. При многократныхъ
разломахъ стерженька положительный зарядъ оказывался всегда на
одной и той же сторонѣ полярной оси и, въ предѣлахъ ошибокъ
вычисленія, зарядъ, разсчитанный на 1 кв. см. сѣченія, оказывался
постояннымъ. Если поверхности разлома оставались въ теченіе нѣ-
котораго времени въ воздухѣ, то онѣ теряли часть своихъ зарядовъ,
такъ какъ при этомъ около нихъ образовался проводящій поверх-
ностный слой.
Этотъ опытъ указываетъ на то, что турмалинъ (и, вѣроятно, каж-
дый иной гемиморфный кристаллъ) въ направленіи своей полярной оси
обладаетъ постоянной діэлектрической поляризаціей. Моле-
кулярные диполи здѣсь при отсутствіи внѣшняго электрическаго на-
пряженія, въ силу присущаго имъ распредѣленія, имѣютъ преиму-
щественное направленіе. Въ силу этого электриче-
ское возбужденіе въ гемиморфномъ кристаллѣ (измѣ-
ряемое величинами свободныхъ зарядовъ, приходя-
щихся на 1 кв. см., непосредственно опредѣленными
Фогтомъ) отлично отъ нуля, хотя сила поля равна
нулю. Если мы обозначимъ это постоянное возбу-
жденіе черезъ По, то напряженію Е будетъ * соот-
вѣтствовать возбужденіе Р, вычисляющееся по фор-
мулѣ Е = 4- К . Е, гдѣ К — абсолютная діэлек- Рис. 58. Кристаллъ
трическая постоянная кристалла. турмалина.
То обстоятельство, что обычно это своеобразное постоянное
возбужденіе не наблюдается, объясняется тѣмъ, что, вслѣдствіе сла-
бой проводимости влажной оболочки на кристаллѣ, присоединяется
еще настоящій электрическій зарядъ, принимающій въ заключеніе
величину Е^ и тогда вполнѣ компенсирующій первоначальный
свободный зарядъ. Надъ этимъ дѣйствіемъ проводящаго водяного слоя
много изслѣдованій сдѣлалъ Рике (Е. Кіеске); при этомъ онъ тщательно.
изучилъ давно извѣстное явленіе, оонаруживающееся при нагрѣва^'Г
кристалла. Именно, оказывается, что постоянная поляризація Ео ^Ѣма
сильно зависитъ отъ температуры; а такъ какъ образованід компен-
сирующаго дѣйствительнаго заряда идетъ весьма медленнаго при
быстрыхъ измѣненіяхъ температуры, т. е. при внезаішомт^нагрѣваніи
или охлажденіи кристалла, наблюдается образова^е^’немъ электри-
144
Піезоэлектричество
ческихъ полюсовъ, какъ на электрической стрѣлкѣ. Это образованіе
электрическихъ полюсовъ вслѣдствіе рѣзкаго измѣненія постояннаго
возбужденія съ измѣненіемъ температуры было извѣстно уже давно
и получило названіе пироэлектричества гемиморфныхъ .кристал-
ловъ. Знаки соотвѣтственныхъ полюсовъ оказываются противопо-
ложными при нагрѣваніи и охлажденіи. Рике нашелъ, что, если по-
мѣстить нагрѣтый кристаллъ въ эксикаторъ, гдѣ н^ немъ не мо-
жетъ образоваться водяная оболочка, то при поддержаніи постоянной
температуры сила полюса остается часами неизмѣнной, и можно
легко такимъ образомъ измѣрять зависимость постояннаго возбужде-
нія О0 отъ температуры.
ПІЕЗОЭЛЕКТРИЧЕС1 ВО.
91. Совершенно такъ же, какъ температура, вліяютъ на постоян-
ное возбужденіе въ направленіи полярной оси и упругія деформаціи
кристалла. Если сжимать помощью маленькаго винтового пресса
кристаллъ турмалина, то обнаруживаются электрическіе полюсы такъ
же хорошо, какъ и при нагрѣваніи кристалла. Это явленіе, впервые
наблюденное Ж. и П. Кюри (Л. и Р. Сигіе), носитъ названіе піезо-
эл ектричества 1).
Піезоэлектричество можно наблюдать на многихъ кристаллахъ,
которые по своей природѣ не могутъ обнаруживать никакихъ пиро-
электрическихъ явленій. Таковы такъ называемые геміэдрическіе кри-
сталлы. Эти кристаллы имѣютъ всегда нѣсколько полярныхъ напра-
вленій, при чемъ всѣ эти направленія равноцѣнны другъ другу и
расположены симметрично, въ силу чего возбужденіе вдоль одной
полярной оси вполнѣ компенсируется по закону сложенія векторовъ
(параллелограммъ векторовъ) возбужденіями вдоль симметрично рас-
положенныхъ осей. Типичнымъ примѣромъ такого кристалла является
кварцъ. Кристаллъ кварца обладаетъ одною не полярною осью сим-
метріи третьяго порядка и тремя перпендикулярными къ ней поляр-
ными направленіями, которыя, въ силу указанной симметріи, эквива-
лентны другъ другу. Въ силу этого кварцъ совершенно не^р&етъ
обнаруживать пироэлектричества. Если нарисовать три равные век-
тора въ трехъ направленіяхъ его полярныхъ осей, т^Срни дадутъ
результирующую, равную нулю.
----------------- ,
Э Гаю и (Найу) наблюдалъ піезоэлектрическія^я^ленія на кристаллѣ
известковаго шпата еще въ 1817 г., за 63 года ^до °опубликованія работъ
Кюри. Прим. пер.
Піезоэлектричество
145
Иное получится, если кварцъ сжимать - напримѣръ, въ напра-
вленіи одной изъ его полярныхъ осей. Въ этомъ случаѣ постоянное
возбужденіе въ ея направленіи измѣнится иначе, нежели въ напра-
вленіяхъ двухъ осей, наклонныхъ къ сжимаемой оси. Въ силу этого
кварцъ обнаружитъ два электрическіе полюса на концахъ оси, со-
впадающей съ направленіемъ сжатія (рис. 59).
П. Кюри воспользовался этимъ явленіемъ для измѣренія малыхъ
электрическихъ зарядовъ. Кварцевый кубъ, одно изъ реберъ кото-
раго параллельно полярной оси, снабжается проводящими обклад-
ками на граняхъ, перпендикулярныхъ къ оси. При помощи различныхъ
нагрузокъ можно вызывать вдоль этой оси произвольное электриче-
ское возбужденіе. Обкладка той поверхности, на которой вызывае-
мый давленіемъ свободный зарядъ имѣетъ знакъ, обратный знаку
Рис. 59. Объясненіе піезоэлектрическихъ свойствъ кварца.
измѣряемаго заряда, соединяется съ хорошо изолированнымъ Фара-
дэевскимъ сосудомъ, въ который вносится измѣряемый зарядъ. На-
грузка кварца повышается до тѣхъ поръ, пока зарядъ Фарадэевскаго
сосуда не будетъ вполнѣ компенсированъ піезоэлектрическимъ возбу-
жденіемъ. Измѣряемая величина, значитъ, прямо сравнивается съ извѣст-
нымъ зарядомъ кварца. Можно было бы возбужденіе опредѣленнаго
кварцеваго куба при вполнѣ опредѣленной нагрузкѣ принять за единицу
заряда; однако, какъ мы ниже увидимъ, есть возможность воспользо-
ваться для опредѣленія этой единицы значительно лучшимъ методомъ. /
Описанный маленькій приборъ, который П. Кюри часто употре- С/
блялъ при изслѣдованіяхъ надъ радіоактивными тѣлами, носитъ нд|р
званіе „піезоэлектрическаго кварца".
Если нагрѣвать кристаллъ кварца, не заботясь о томъ^фтобы
температура была распредѣлена въ немъ равномѣрно, то ^/различ-
ныхъ мѣстахъ онъ расширяется не одинаково и благодаря этому въ
немъ появляются внутреннія напряженія, связанныя,|ъувою очередь,
Мгі. Электричество и магнитизмъ. Ю
146
Діэлектрическое послѣдѣйствіе
съ электрическими возбужденіями. Это образованіе электрическихъ
полюсовъ вслѣдствіе нагрѣванія, наблюдаемое часто и на иныхъ ге-
міэдрическихъ кристаллахъ, прежде часто называли тоже пироэлек-
тричествомъ. Но такъ какъ, въ дѣйствительности, здѣсь мы имѣемъ
дѣло лишь съ піезоэлектрическими явленіями, то теперь его назы-
ваютъ „ложнымъ пироэлектричествомъ".
ДІЭЛЕКТРИЧЕСКОЕ ПОСЛЪДЪЙСТВІЕ.
92. Зарядивъ обыкновенную лейденскую банку до высокаго на-
пряженія, оставимъ ее на нѣкоторое время въ такомъ состояніи, а
затѣмъ разрядимъ помощью металлической дуги; послѣ этого на-
пряженіе между двумя ея обкладками становится равнымъ нулю.
Оставимъ банку теперь опять постоять пять минутъ; если послѣ
этого снова приблизить къ ней разрядникъ, то снова получается
искра. Банка сама собою зарядилась вновь. Это явленіе „электри-
ческаго остатка" стало извѣстнымъ вскорѣ послѣ изобрѣтенія
лейденской банки: уже тогда замѣтили, что, если послѣ ея полнаго
разряженія прикоснуться къ ней вновь, то получаются неожиданные
и потому особенно непріятные удары.
Отсюда приходится заключить, что свойства матеріальныхъ ді-
электриковъ не выражаются исчерпывающимъ образомъ закономъ
Кулона. Аналогично „не вполнѣ упругимъ тѣламъ" существуютъ
также „не вполнѣ діэлектрическіе изоляторы". Было бы въ самомъ
дѣлѣ удивительно, если бы матеріальныя тѣла, ни въ чемъ не обнару-
живающія характера идеальныхъ тѣлъ, подчинялись въ своихъ элек-
трическихъ свойствахъ тому же простому закону, что и міровой эѳиръ.
Разовьемъ дальше сравненіе матеріальныхъ діэлектриковъ съ не
вполнѣ упругими тѣлами. Если подвѣсить грузъ на каучуковой
трубкѣ, то при небольшихъ нагрузкахъ получается растяженіе, про-
порціональное приложенной силѣ, т. е. согласное съ закономъ Гука.
Но если нагрузка будетъ висѣть въ теченіе продолжительнаго времени,
то мы замѣтимъ, что растяженіе трубки все болѣе и болѣе увели-
чивается. Это продолжается въ теченіе нѣсколькихъ часовъ, пока
конецъ трубки постепенно не достигнетъ какой-нибудь тх<йки опоры.
Если теперь удалить нагрузку, тб трубка не сразу принимаетъ свою
первоначальную длину, но сперва остается слегка^ растя ну той и лишь
черезъ продолжительный періодъ времени вновь ^совершенно стяги-
вается. Если видоизмѣнить этотъ опытъ и закрѣпить конецъ рези-
Діэлектрическое послѣдѣйствіе
14^
новой трубки въ томъ мѣстѣ, гдѣ онъ оказывается непосредственно
послѣ разгрузки, то трубка все-таки будетъ стремиться сократиться еще
дальше, и вслѣдствіе этого въ ней вновь будутъ возникать напряженія.
Это явленіе вполнѣ аналогично тому, которое имѣетъ мѣсто въ лей-
денской банкѣ, когда она послѣ своего разряженія вновь пріобрѣ-
таетъ напряженія. Подобнаго рода явленія, объяснимыя лишь тѣмъ,
что свойства вѣсомой матеріи обусловливаются не только ея состоя-
ніемъ въ данный моментъ (какъ это предполагаютъ законъ Гука и
законъ Кулона), но и всей предыдущей исторіей матеріи, извѣ-
Рис. 60. Объясненіе діэлектрическаго гистерезиса.
стны также и въ иныхъ областяхъ физики; ихъ обычно объединяютъ
названіемъ послѣдѣйствій. Въ ученіи объ электричествѣ и магни-
тизмѣ введенъ также спеціальный терминъ „гистерезисъ". Такъ,
явленіе „электрическаго остатка" еще называется „діэлектрическимъ
послѣдѣйствіемъ" и „діэлектрическимъ гистерезисомъ".
Вѣроятно, явленіе это нужно приписать тому, что въ діэлеку?
трикѣ находятся частички, которыя, будучи одинъ разъ сильно
ляризованы, продолжаютъ еще нѣкоторое время оставаться поляризо-
ванными и по удаленіи поля. Въ силу этого на обкладках^/конден-
сатора послѣ его разряда остаются еще заряды, компенсирующіе
остаточное возбужденіе этихъ частицъ (подобно тому, Ѵ/ какъ заряды
водяной оболочки на турмалиновомъ стержнѣ компенсируютъ его
V 10
148
Діэлектрическое послѣдѣйствіе
постоянное возбужденіе). По мѣрѣ исчезновенія остаточнаго возбу-
жденія, между этими двумя компенсирующими зарядами снова возни-
каютъ напряженія. Весьма вѣроятно, что частички, вызывающія оста-
точное возбужденіе, представляютъ собою не молекулы, но неболь-
шія неоднородности, въ которыхъ вещество обладаетъ нѣкоторой
слабой проводимостью (рис. 60). Опытнымъ путемъ вполнѣ рѣшить
этотъ вопросъ, вѣроятно, никогда не удастся. Но въ пользу выска-
заннаго предположенія говоритъ то обстоятельство, что явственнѣе
всего наблюдается послѣдѣйствіе у не вполнѣ опредѣленныхъ, съ
химической точки зрѣнія, тѣлъ, каковы стекло, эбонитъ и т. д.;
чистыя же вещества, какъ, напримѣръ, слюда, даютъ лишь нич-
тожный гистерезисъ. Во многихъ случаяхъ можно опредѣленно ука-
зать на тѣ слабо проводящія неоднородности, которыя являются при-
чиною гистерезиса. Именно это возможно тогда, когда эти неодно-
родности не разсѣяны по діэлектрику, но представляютъ собою
сплошной слой плохого проводника въ изоляторѣ. Такъ, напримѣръ,
замѣтный гистерезисъ вызываетъ клей, которымъ приклеивается ста-
ніолевая обкладка къ стеклянной пластинкѣ или къ слюдяному листу.
Если наклеенную станіолевую обкладку замѣнить слоемъ серебра, то
послѣдѣйствіе тотчасъ уменьшается. Это дѣйствіе слоя клея можно хо-
рошо пояснить простымъ опытомъ. Если взять лейденскую банку, об-
Рис. 61. Разборная Лейденская
банка.
кладки которой представляютъ собою
два металлическіе цилиндра, легко от-
дѣляющіеся отъ стекляннаго цилиндра,
то вмѣсто слоя клея мы будемъ имѣть
дѣло съ тонкимъ слоемъ воздуха, ко-
торый, подъ вліяніемъ неизбѣжныхъ
при большихъ напряженіяхъ тихихъ
разрядовъ, становится плохимъ про-
водникомъ. Зарядимъ теперь эту ^раз-
борную лейденскую банку (рцС-61),
поставимъ ее на изолирующую под-
ставку и вынемъ прочь ^утреннюю
обкладку, стараясь не коснуться при этомъ внѣшнейц^бкладки. За-
тѣмъ удаляемъ также и внѣшнюю обкладку. Такъ какъ мы удаляли
обѣ обкладки рукою, то онѣ, конечно, уже н^имѣютъ зарядовъ и
ихъ можно приложить одну къ другой, не ^получая искры. Теперь
снова соберемъ нашу банку на изолирующей подставкѣ, опять
Діэлектрическое послѣдѣйствіе
149
не дотрагиваясь до обѣихъ обкладокъ (одновременно. Если мы послѣ
этого поднесемъ къ обѣимъ обкладкамъ разрядникъ, то получимъ
искру. Этотъ „остаточный-зарядъ“ объясняется тѣмъ, что часть за-
ряда перешла съ металлическихъ обкладокъ на стеклянныя поверхности
черезъ слабо проводящій воздушный слой. При станіолевой обкладкѣ
слой клея играетъ совершенно такую же роль, какъ здъсь слой
воздуха.
И въ жидкихъ изоляторахъ наблюдаются „остаточные заряды
Здѣсь дѣло обстоитъ почти такъ же, какъ и въ случаѣ твердыхъ
діэлектриковъ. Ни одна жидкость не представляетъ собою вполнѣ
совершеннаго изолятора; поэтому при заряженіи жидкаго конденса-
тора будетъ происходить незначительный переносъ электрическихъ
зарядовъ черезъ діэлектрикъ. Съ другой стороны опыты показываютъ,
что слабый электрическій токъ измѣняетъ проводимость плохого
проводника и именно такимъ образомъ, что образуются слои раз-
личной проводимости. Итакъ, и здѣсь гистерезисъ вполнѣ объясняется
„теоріей слоистаго діэлектрика", изложенной нами, согласно пред-
ставленіямъ Максвелла.
Такимъ образомъ мы приходимъ къ заключенію, что діэлектри-
ческій гистерезисъ, по всей вѣроятности, не представляетъ собою
какого-либо новаго свойства изоляторовъ, но всегда объясняется
присутствіемъ извѣстныхъ неоднородностей въ діэлектрикѣ.
ГЛАВА ПЯТАЯ
ЭЛЕКТРИЧЕСКОЕ ПОЛЕ ВНУТРИ ПРОВОДНИКОВЪ
ЭЛЕКТРИЧЕСКІЙ ТОКЪ.
93. Мы сможемъ глубже познать электрическія свойства вѣсо-
мой матеріи или, что то же самое, природу связей между молеку-
лами и эѳиромъ, когда мы изучимъ также и электрическія свойства
проводниковъ.
Но какъ можно говорить объ электрическихъ свойствахъ про-
водниковъ? Развѣ, на основаніи опыта Фарадэя съ клѣткой, не
исключена вообще возможность возникновенія поля въ проводникѣ?
Это справедливо лишь въ тѣхъ случаяхъ, когда мы соединяемъ
проводникъ только съ однимъ полюсомъ источника электричества;
такъ мы поступали во всѣхъ опытахъ, относящихся къ электро-
статикѣ въ узкомъ смыслѣ слова, изученіемъ которой мы до сихъ
поръ занимались. Возьмемъ для примѣра брусокъ хорошо проводя-
щаго дерева, на которомъ укрѣплены на одинаковыхъ разстояніяхъ
одна отъ другой проволоки, снабженныя каждая двумя свѣшиваю-
щимися бумажными полосками, играющими роль электроскоповъ. Если
мы соединимъ проволокой одинъ изъ полюсовъ индукціонной ма-
шины съ концомъ бруска, то каждая пара бумажныхъ полосъ ра-
зойдется почти одинаково сильно. Какъ и слѣдовало ожидать, весь
брусокъ пріобрѣтаетъ постоянный потенціалъ, равный потенціалущр-
люса индукціонной машины.
Но нѣчто совсѣмъ иное мы получимъ, если одновреі^|Т|Но со-
единимъ проволокой другой конецъ бруска со вторымъ^пблюсомъ
индукціонной машины. Какъ только мы перестанем^ вращать ма-
шину, брусокъ и оба полюса попрежнему окажутся заряженными
до одного и того же потенціала, и именно до цо^нціала, приблизи-
тельно равнаго нулю; всѣ электроскопы на брускѣ спадутъ. Проти-
Электрическій токъ
151
воположные заряды, которые прежде были на полюсахъ, нейтрализу-
ются, соединившись черезъ брусокъ; поле, въ силу этого, сейчасъ же
исчезаетъ. Если же мы будемъ достаточно быстро вращать машину,
то сможемъ удерживать полюсы при различныхъ потенціалахъ, такъ
какъ нейтрализація зарядовъ въ брускѣ требуетъ нѣкотораго времени.
Напряженіе между двумя концами бруска будетъ возрастать до тѣхъ
поръ, пока исчезновеніе поля не будетъ происходить съ такой же
быстротой, съ какой происходитъ возникновеніе новаго поля вслѣд-
ствіе дѣятельности машины. Исчезновеніе поля идетъ тѣмъ быстрѣе,,
чѣмъ выше его напряженіе. Отсюда слѣдуетъ, что чѣмъ бы-
стрѣе мы вращаемъ машину, тѣмъ выше получается напряженіе.
Дѣйствительно, при быстромъ ея вращеніи мы видимъ, что оба элек-
троскопа на концахъ бруска даютъ большое расхожденіе; прибли-
жая къ нимъ натертую эбонитовую палочку, мы можемъ убѣдиться
въ томъ, что одинъ изъ нихъ заряженъ положительно, а другой
отрицательно. Но что же даютъ при этомъ остальные электроскопы?
Тотъ изъ нихъ, который находится какъ разъ посрединѣ бруска,
совершенно не даетъ отклоненія; слѣдовательно, посрединѣ бруска
потенціалъ равенъ нулю. По мѣрѣ удаленія отъ середины все воз-
растающія величины отклоненій электроскоповъ указываютъ на по-
степенное повышеніе потенціала. При этомъ, конечно, съ одной
стороны потенціалы положительны, съ другой отрицательны. Если
мы обозначимъ потенціалъ положительнаго полюса индукціонной ма-
шины черезъ -|- V, отрицательнаго полюса черезъ I/, то мы должны
будемъ сказать: потенціалъ бруска непрерывно измѣняется отъ-|- V
до — V; значитъ, мы, дѣйствительно, имѣемъ въ проводящемъ брускѣ
паденіе потенціала, т. е. наличность электрическаго поля.
Если мы, при помощи достаточно мощнаго источника
электричества, будемъ подводить непрерывно къ одной
точкѣ проводника положительные заряды, а къ другой —
отрицательные, то между этими двумя точками образуется
внутри проводника электрическое поле. Чѣмъ сильнѣе это^
поле, тѣмъ быстрѣе происходитъ его уничтоженіе и
« - „
тѣмъ большей скоростью должны подводиться изъ источ-
ника электричества заряды, чтобы оно сохранялось.
Это явленіе непрерывнаго уничтоженія поля и возобновленія его
при помощи непрерывно дѣйствующаго источника электричества мы
называемъ электрическимъ разрядомъ или же, по основаніямъ, кото-
152
Электрическій токъ
рыя будутъ развиты ниже, электрическимъ токомъ. Поэтому
выше найденный результатъ мы можемъ выразить еще такъ: внутри
проводника, по которому проходитъ электрическій токъ, заключается
электрическое поле.
Поле проводника, по которому проходитъ токъ, мы можемъ сдѣ-
лать видимымъ, пользуясь часто употреблявшимся нами методомъ
примѣненія рутиловаго порошка. Наклеимъ на стеклянную пластинку
рядомъ двѣ полоски бумаги, соединенныя между собою однимъ
концомъ. Эти бумажныя полоски, уже сами по себѣ представляющія
до нѣкоторой степени проводники, можно сдѣлать лучше проводя-
Рис. 62. Силовыя линіи поля проводника съ токомъ.
щими, нанеся по нимъ вдоль краевъ карандашныя чертылКонцы
бумажной полосы соединяемъ съ двумя полюсами небольшой индук-
ціонной машины, которая за все время опыта непрерывно вращается,
вызывая непрерывный электрическій разрядъ. Если теперь насыпап>
на стеклянную пластинку рутиловаго порошка, то при потряхиваніи
рутиловыя частички между обѣими бумажными полосками правильно
выстроятся и укажутъ намъ на наличность электрическаго "поля
(рис. 62). При этомъ поле оказывается очень сильнымъивъ тѣхъ мѣ-
стахъ, которыя непосредственно соединены съ полюсами индукціон-
ной машины, но, по мѣрѣ удаленія отъ этого мѣ<та, все слабѣетъ
и, наконецъ, около мѣста соединенія обѣих;^ полосъ становится едва
Электрическій токъ
153
замѣтнымъ. Слѣдовательно, въ одной изъ точекъ соединенія съ индук-
ціонной машиной проводникъ имѣетъ весьма высокій положительный
потенціалъ, а въ другой—столь же высокій отрицательный потенціалъ.
По мѣрѣ приближенія къ срединѣ проводника, т. е. къ точкѣ со-
единенія бумажныхъ полосъ другъ съ другомъ, величина потенціала съ
обѣихъ сторонъ убываетъ и посрединѣ она равняется нулю. Такимъ
образомъ, вдоль проводника, а, слѣдовательно, и въ самомъ провод-
никѣ возникаетъ приблизительно равномѣрное паденіе потенціала,
т. е. электрическое поле. Силовыя линіи въ самой проводящей по-
лосѣ исходятъ изъ положительнаго полюса проводника, идутъ по
направленію бумажной полосы и заканчиваются у отрицательнаго
полюса. Ихъ, конечно, нельзя прямо демонстрировать при помощи
рутиловаго порошка, но ихъ существованіе и направленіе становятся
вполнѣ очевидными изъ разсмотрѣнія видимыхъ внѣшнихъ полей.
Дерево и бумага, однако, представляютъ собою весьма плохіе
проводники, полупроводники. Но при помощи подходящихъ элек-
трометровъ можно убѣдиться въ существованіи паденія потенціала
и въ дѣйствительныхъ, хорошихъ проводникахъ. Только въ этомъ
случаѣ приходится пользоваться болѣе мощнымъ источникомъ
электричества, нежели электрическая машина, именно — гальвани-
ческой батареей. Натянемъ, для примѣра, тонкую металлическую
проволоку въ 4 м. длиною между двумя неподвижными зажи-
мами (рис. 63). Эти зажимы соединимъ съ большою батареею
аккумуляторовъ, дающей напряженіе въ 72 вольта. Наличность
поля въ этой проволокѣ мы можемъ установить помощью элек-
трометра Ганкеля. Одинъ изъ его зажимовъ соединяемъ со сре-
диной проволоки; къ другому зажиму присоединимъ длинную про-
волоку, которая будетъ намъ служить зондомъ для изслѣдованія
поля. Соединимъ сначала эту проволоку съ однимъ изъ неподвиж-
ныхъ зажимовъ; тогда получится отклоненіе, соотвѣтствующее, при-
близительно, + 36 вольтамъ. Передвигаясь затѣмъ вдоль натяну-
той проволоки, мы увидимъ, что отклоненіе электрометра будетъ Д
все время уменьшаться; на разстояніи 1 м. (х/4 длины) мы б^ѵ
демъ имѣть 4-18 вольтъ, на разстояніи 2 м. (средина) отклоне-
ніе уменьшится до нуля; далѣе оно становится отрицательнымъ,
на разстояніи 3 м. (3/4 длины) даетъ—18 вольтъ и,/^наконецъ,
ца противоположномъ концѣ проволоки мы находимтДДЗб вольтъ.
Слѣдовательно, батарея даетъ столь значительныял^о^ичества элек-
154
Электрическій токъ
тричества, что напряженіе между зажимами на ея полюсахъ не измѣ-
няется замѣтно при соединеніи ихъ проволокой.
Здѣсь мы снова убѣждаемся въ томъ, что въ проволокѣ имѣется
электрическое поле. Далѣе мы видимъ, что разность потенціаловъ между
двумя точками проволоки строго пропорціональна взаимному раз-
стоянію этихъ точекъ. Слѣдовательно, вся проволока заполнена по-
стояннымъ электрическимъ полемъ.
Рис. 63. Напряженія на проволокѣ, по которой проходитъ токъ.
Если, пользуясь мощнымъ источникомъ электричества,
поддерживать двѣ точки проволоки постоянной толщины»
сдѣланной изъ однороднаго матеріала, при различныхъ
потенціалахъ, то внутри проволоки по всей ея длинѣ
между этими точками образуется постоянное поле.
ПОЛУЧЕНІЕ ПРОИЗВОЛЬНЫХЪ НАПРЯЖЕНІЙ.
94. Прежде, чѣмъ идти дальше, мы укажемъ здѣф^на одно
чрезвычайно важное для практики слѣдствіе изъ этого^положенія.
Соединимъ съ различными точками выпіеописаннойДіроволоки про-
водящія тѣла, хорошо изолированныя другъ отъ щруга и отъ земли,
подобно тому, какъ мы это дѣлали въ ОРМѢ, описанномъ въ
Полученіе произвольныхъ напряженій
155
§28 (рис. 14). Если мы будемъ изслѣдовать такое тѣло при по-
мощи нашего зонда, то убѣдимся, что оно имѣетъ во всѣхъ точ-
кахъ одинъ и тотъ же потенціалъ, равный потенціалу той точки
проволоки, съ которой оно соединено. Это можно было предвидѣть,ч
такъ какъ по присоединенному проводнику никакого тока не течетъ,,
и мы уже выше, при описаніи опыта съ проволокой, принимали, какъ
само собою разумѣющееся, что зажимъ электрометра имѣетъ потен-
ціалъ соединенной съ нимъ точки проволоки. Отсюда мы выводимъ.
весьма важное для практики заключеніе, что при помощи натянутой
проволоки, на концахъ которой поддерживается данная разность по-
тенціаловъ, мы можемъ сообщить проводнику любой потенціалъ, зна-
ченіе котораго лежитъ между значеніями потенціала на концахъ про-
волоки. Въ силу этого становится неограниченнымъ примѣненіе галь-
ваническихъ цѣпей для полученія постоянныхъ напряженій. Прежде
мы могли, пользуясь цѣпью, имѣющей напряженіе въ 1 вольтъ, сло-
женіемъ получать 2, 3, 4, 5 и т. д. вольтъ; теперь при помощи
проволоки мы можемъ сверхъ того точно воспроизвести любую пра-
вильную или неправильную дробь вольта.
Это имѣетъ важное примѣненіе въ измѣрительной техникѣ
_при употребленіи такъ называемаго компенсаціоннаго метода
для сравненія напряженій двухъ элементовъ или двухъ батарей.
Натянемъ тонкую проволоку между двумя зажимами, соединенными
посредствомъ толстыхъ мѣдныхъ проволокъ съ полюсами большой ба-
тареи; эти зажимы мы будемъ называть главными зажимами (рис. 64).
Съ отрицательнымъ главнымъ зажимомъ соединимъ помощью про-
волоки отрицательный полюсъ меньшей батареи; потенціалъ этого
зажима назовемъ черезъ Ѵ2. Потенціалъ положительнаго главнаго
зажима пусть будетъ а потенціалъ положительнаго полюса малой
батареи V'. Напряженіе большой батареи равняется, слѣдовательно,
напряженіе малой равняется х=Ѵ'— Ѵ2. Если у больше,
чѣмъ х, какъ мы это предполагаемъ, то величина V' лежитъ между
величинами и Ѵ2. Слѣдовательно, на проволокѣ, натянутой между 4^'
обоими главными зажимами, должна быть точка, потенціалъ въ коъ^>?
торой равенъ V. Мы можемъ найти эту точку, изслѣдуя натяцу^йх
проволоку „зондомъ", т. е. гибкой проволокой, соединец^й' съ
однимъ изъ зажимовъ электрометра. Если другой зажимъ ^электро-
метра соединенъ съ положительнымъ полюсомъ маленькой батареи,
то при соприкосновеніи зонда съ искомой точкцр,4имѣющей по--
156
Полученіе произвольныхъ напряженій
тенціалъ V', электрометръ устанавливается на нулѣ. При движеніи
зонда вправо или влѣво отъ этой точки электрометръ даетъ откло-
неніе въ ту или въ другую сторону. Положимъ, что длина отрѣзка
проволоки между найденной такимъ образомъ точкой и отрицатель-
нымъ главнымъ зажимомъ равна Ь, а длина всей проволоки между
двумя главными зажимами равняется а\ въ такомъ случаѣ, согласно
^закону, изложенному въ § 93, искомое отношеніе будетъ:
х _ Г — Ѵг _ Ь
у ~ Ц — Ц ~ а ’
Если, напримѣръ, Ѵ\ — Ѵ2=72 вольтамъ, а = 4 метрамъ и
опытъ даетъ Ь = 2,5 метровъ, то х = 45 вольтамъ.
Рис. 64. Методъ компенсаціи.
При употребленіи компенсаціоннаго метода, особенно удобнаго
для очень точныхъ измѣреній, нужно всегда обращать|^циманіе на
то, чтобы большее изъ двухъ сравниваемыхъ напряженій было со-
единено съ обоими главными зажимами, между которыми непрерывно
проходитъ электрическій токъ. Источникъ же электричества съ мень-
шимъ напряженіемъ, наоборотъ, остается „^вобрднымъ отъ тока*.
Проблема электрической проводимости
157
ПРОБЛЕМА ЭЛЕКТРИЧЕСКОЙ ПРОВОДИМОСТИ.
95. Первымъ вопросомъ, который мы должны разрѣшить, если
мы желаемъ глубже проникнуть въ природу проводниковъ, является
слѣдующій: какъ это вообще возможно, чтобы присутствіе
вѣсомой матеріи такъ вліяло на эѳиръ, что онъ становится
неспособнымъ удерживать электрическое поле безъ непре-
рывнаго притока энергі <?
Если электрическое поле исчезаетъ, то возбуждающіе его за-
ряды должны претерпѣвать измѣненія; эти измѣненія всегда слѣдуетъ,
представлять себѣ, какъ перемѣщенія зарядовъ въ пространствѣ. Если
мы, напримѣръ, соединяемъ проводникомъ обѣ обкладки лейденской
банки, то заряды передвигаются изъ обкладокъ въ проводникъ, пока
они не смѣшаются и не дадутъ въ суммѣ нуль; тогда и поле вполнѣ
уничтожится. Такой взглядъ является необходимымъ слѣдствіемъ изло-
женныхъ въ § 52 законовъ сохраненія электрическихъ зарядовъ.
Представленіе объ уничтоженіи поля, какъ о нѣкоторомъ пере-
мѣщеніи электрическихъ зарядовъ, можно сдѣлать нѣсколько болѣе
нагляднымъ помощью простого опыта. Возьмемъ двѣ металлическія
изолированныя пластинки и укрѣпимъ ихъ параллельно и другъ про-
тивъ друга въ горизонтальномъ положеніи. На нижнюю пластинку на-
сыплемъ шариковъ, сдѣланныхъ изъ бузинной сердцевины или изъ
пробки. Зарядимъ теперь при помощи индукціонной машины обѣ.
пластинки, образующія вмѣстѣ плоскій конденсаторъ до значительнаго
потенціала и оставимъ ихъ изолированными. Мы замѣтимъ при этомъ,
что шарики между ними будутъ все время двигаться вверхъ и внизъ.
Это происходитъ отъ того, что каждый шарикъ, лежащій на поло-
жительной пластинкѣ, заряжается тотчасъ самъ положительно, оттал-
кивается къ отрицательной пластинкѣ, касается ея, отдаетъ ей свой
зарядъ и заряжается отрицательно, отталкивается къ положительной
пластинкѣ и т. д. Мы видимъ, такимъ образомъ, во-первыхъ, что поло-
жительные заряды переносятся на отрицательную пластинку и отрица-
тельные заряды на положительную пластинку и, во-вторыхъ, что пр^
этомъ поле постепенно уничтожается. Во всѣхъ случаяхъ движеніи
электрически заряженныхъ тѣлъ въ направленіи дѣйствующей^^нихъ
силы, напряженія въ эѳирѣ уменьшаются, такъ какъ тѣла прр ’этомъ
извлекаютъ энергію изъ эѳира. Въ нашемъ примѣрѣ^энергія элек-
трическаго поля, въ концѣ концовъ, обращается віутерлоту, вслѣд-
ствіе тренія шариковъ о воздухъ при ихъ полет^хъѣщ о пластинкц
158
Проблема электрической проводимости
при столкновеніяхъ съ ними. Мы можемъ прямо сказать, что про-
странство между пластинками, вслѣдствіе присутствія въ немъ шари-
ковъ, переносящихъ заряды, принимаетъ характеръ электрическаго
проводника.
Поэтому мы можемъ проблему электрической проводимости фор-
мулировать еще такъ: какимъ образомъ наличность вѣсомой
матеріи дѣлаетъ возможнымъ переносъ электрическихъ
зарядовъ съ одного мѣста на другое?
При такой формулировкѣ ясно выступаетъ трудность про-
блемы. Какъ мы знаемъ, электрическій зарядъ не есть „невѣсомая
жидкость", существующая внѣ вѣсомой матеріи и независимо отъ
нея. Въ §§ 5 и 6 мы видѣли, что выраженіе „электрическій за-
рядъ" тождественно съ выраженіемъ „связь вѣсомыхъ матеріаль-
ныхъ тѣлъ съ міровымъ эѳиромъ". Въ силу этого, совершенно
нельзя представить себѣ электрическаго заряда отдѣльно отъ мате-
ріальнаго тѣла, а потому нельзя представить себѣ и передвиженія
электрическихъ зарядовъ безъ одновременнаго передвиженія ихъ ма-
теріальныхъ носителей. Въ опытѣ съ танцующими шариками можно
было непосредственно глазомъ прослѣдить за движеніемъ матеріаль-
ныхъ частичекъ, связаннымъ съ уничтоженіемъ поля. Но какъ пред-
ставить себѣ, что въ твердой металлической проволокѣ, когда по ней
течетъ электрическій токъ, происходитъ передвиженіе матеріальныхъ
частичекъ ?
Мы стоимъ здѣсь передъ вопросомъ, который въ явномъ или
скрытомъ видѣ смущалъ тысячи умовъ, изъ-за котораго, главнымъ
образомъ, возникло то широко распространенное убѣжденіе, что о
„сущности электричества" вообще невозможно составить'себѣ^яснаго
представленія.
ГЛАВА ШЕСТАЯ
ПРОХОЖДЕНІЕ ЭЛЕКТРИЧЕСТВА ЧЕРЕЗЪ ЭЛЕКТРОЛИТЫ
ЭЛЕКТРОЛИЗЪ.
96. Скорѣе всего мы можемъ надѣяться получить отвѣтъ на нашъ
вопросъ для случая такихъ проводниковъ, въ которыхъ мы наблю-
даемъ какое-либо измѣненіе вещества, когда они въ теченіе нѣкото-
раго времени заполнены уничтожающимся электрическимъ полемъ.
Приведемъ нѣсколько примѣровъ такого явленія. Если пропускать
электрическій токъ черезъ сосудъ съ хорошо проводящей разведен-
ной сѣрной кислотой, въ которую погружены двѣ платиновыя пла-
стинки, соединенныя съ гальванической батареей—такъ называемые
электроды,- то на обоихъ электродахъ можно замѣтить появленіе
пузырьковъ газа. Химическое изслѣдованіе показываетъ, что на элек-
тродѣ, имѣющемъ отрицательный потенціалъ -на катодѣ — по-
является водородъ, а на электродѣ, имѣющемъ положительный по-
тенціалъ- на анодѣ - кислородъ. Подобно разведенной сѣрной ки-
слотѣ, всѣ вообще водные растворы кислотъ, основаній и со-
лей являются болѣе или менѣе хорошими проводниками. Вода
вообще проводитъ лишь благодаря тому, что въ ней всегда бываетъ
растворена, хотя бы въ минимальномъ количествѣ, какая-либо соль.
Для второго примѣра мы можемъ взять растворъ мѣднаго купороса въ
большомъ сосудѣ съ двумя платиновыми электродами. Вскорѣ послѣ
начала пропусканія тока черезъ этотъ растворъ на катодѣ появляется/к?
красный налетъ металлической мѣди. Если мы теперь измѣнимъ со-
единеніе электродовъ съ батареею такъ, чтобы прежній катодт^сталъ
анодомъ, то, понятно, увидимъ, что мѣднымъ налетомъ начинаетъ
покрываться другая пластинка, а на той, которая теперь является
анодомъ, оставшійся отъ предыдущаго пропусканія.тока мѣдный на-
160
Электролизъ
летъ постепенно исчезаетъ. Мы заключаемъ отсюда слѣдующее: если
анодъ состоитъ изъ мѣди, то онъ при прохожденіи электрическаго
тока разъѣдается, на катодѣ же, наоборотъ, мѣдь осаждается. Нако-
нецъ, въ качествѣ третьяго примѣра возьмемъ растворъ свинцоваго
сахара при свинцовыхъ электродахъ. Въ этомъ случаѣ на катодѣ
отлагается свинецъ въ видѣ прекраснаго кристаллическаго образова-
нія, такъ называемаго „свинцоваго дерева" (рис. 65). При этомъ свин-
цовый анодъ постепенно растворяется, въ чемъ можно убѣдиться
взвѣшиваніемъ.
Такихъ примѣровъ можно привести безчисленное множество.
Всѣ растворы кислотъ, основаній или солей въ водѣ даютъ при про-
Къ батареѣ
хожденіи электрическихъ зарядовъ химическія
измѣненія на обоихъ электродахъ. Поэтому
такія вещества носятъ названіе электроли-
товъ. Самое явленіе разложенія при прохо-
жденіи электрическихъ зарядовъ носитъ на-
званіе электролиза. Первый наблюдалъ
явленіе электролиза Вольта.
Уже изъ трехъ вышеприведенныхъ примѣ-
ровъ мы могли бы вывести нижеслѣдующій
законъ, въ дѣйствительности являющійся
вполнѣ общимъ:
при прохожденіи электрическихъ
Рис. 65. Свинцовое дерево, зарядовъ черезъ электролитъ на като-
дѣ осаждаются водородъ или металлъ,
входящій въ составъ растворенной соли, на анодѣ же—
кислородъ или кислотный остатокъ соли, иногда раство-
ряющій въ себѣ металлъ анода.
Такимъ образомъ, на катодѣ всегда имѣетъ мѣсто химическое
„возстановленіе", а на катодѣ „окисленіе". Нужно еще замѣтить,
что при нѣкоторыхъ обстоятельствахъ на катодѣ осаждается не чи-
стый металлъ, а его низшіе окислы, напримѣръ, закись мѣДи изъ.
мѣднаго купороса.
97. Электролитическія явленія нашли многостороннія и важныя
примѣненія въ техникѣ. Здѣсь мы укажемъ только <нд<два старѣйшія
ИЗЪ НИХЪ.
Прежде всего можно отложеніе металла дна катодѣ использо-
вать для покрытія металлическаго предме^аСЧрнкимъ слоемъ иного*
Электролизъ
161
металла, могущаго сообщить покрываемому предмету какія-либо цѣн-
ныя свойства, напримѣръ, предохранить его отъ окисленія или при-
дать ему блескъ или красивый видъ. Покрываемый предметъ предва-
рительно долженъ быть хорошо вычищенъ, при чемъ въ особенности
слѣдуетъ позаботиться объ удаленіи слѣдовъ жира; затѣмъ онъ по-
-ружается въ качествѣ катода въ электролитическую ванну. Легко
сдѣлать такой опытъ съ хорошо вычищенными латунными пластин-
ками. Погрузимъ по одной такой пластинкѣ въ качествѣ катодовъ въ
стаканы съ растворами мѣднаго купороса, сѣрнокислой соли никкеля
и цинковаго купороса. Въ качествѣ анода во всѣхъ случаяхъ возь-
мемъ металлъ соотвѣтственной соли. Тогда при прохожденіи тока на
латунномъ катодѣ будетъ осаждаться соотвѣтственный металлъ, а на
анодѣ онъ будетъ въ такомъ же количествѣ растворяться; растворъ
будетъ все время оставаться неизмѣннымъ. Черезъ нѣкоторое время
первая латунная пластинка покроется красною мѣдью, вторая окажется
никкелированной, третья — матово оцинкованной.
Отрасль техники, посвященная такому способу покрыванія одного
металла тонкимъ слоемъ другого, носитъ названіе гальваностегіи.
При гальваностегіи приходится заботиться о томъ, чтобы ме-
таллическій слой на катодѣ оказался прочно держащимся. Поэтому
покрываемыя металлическія вещи должны быть тщательно очищены
отъ жира, окисловъ и т. д. Другая отрасль техники посвящена какъ
разъ обратной задачѣ- полученію отпечатковъ, которые легко потомъ
отдѣлить отъ электрода. Такая задача представляется въ тѣхъ слу-
чаяхъ, когда желательно получить изъ металла точную копію какого-
либо предмета. Съ этой цѣлью прежде всего приготовляютъ „нега-
тивный оттискъ44 копируемаго предмета изъ воска или изъ другого
матеріала, легко поддающагося формовкѣ. Затѣмъ поверхность, ко-
торая должна быть скопирована, покрываютъ слоемъ графита, при
чемъ между графитомъ и проводниками тока долженъ быть хорошій
электрическій контактъ; весь негативъ погружаютъ въ качествѣ ка-
тода въ растворъ соотвѣтственнаго металла. Графитовый слой при
этомъ сообщается съ отрицательнымъ полюсомъ батареи. Послѣ до-Дд"
статочно продолжительнаго пропусканія тока на графитѣ отлагается^
толстый металлическій слой. Отдѣливъ его отъ воска, мы получаемъ
требуемое воспроизведеніе.
Такой пріемъ воспроизведенія пластическихъ объект(|ігьііомоіцыо
электролиза носитъ названіе гальванопластики.
дгѵ
Ми. Электричество и магнитизмъ. . ДхД 11
162
Первый законъ Фарадэя
ПЕРВЫЙ ЗАКОНЪ ФАРАДЭЯ.
98. Чтобы установить закономѣрную связь между электроли-
зомъ и разрушеніемъ электрическаго поля, которому онъ сопут-
ствуетъ, мы должны, конечно, разыскать количественную зависи-
мость между обоими явленіями.
Весьма простое соотношеніе даетъ намъ слѣдующій опытъ.
Проведемъ отъ одного изъ полюсовъ батареи проволоку къ трой-
ному винтовому зажиму (рис. 66); отъ него проведемъ двѣ прово-
Рис. 66. Первый законъ Фарадэя.
разве-
соеди-
локи къ двумъ электролитическимъ сосудамъ, наполненнымъ
денной сѣрной кислотой. Вторые электроды этихъ сосудовъ
нимъ съ другимъ тройнымъ зажимомъ, отъ котораго проведемъ про-
волоку къ третьему сосуду, также наполненному разведенной сѣр-
ной кислотой; другой электродъ послѣдняго сосуда соединимъ со
вторымъ полюсомъ батареи. Три сосуда, употребляемые при этомъ
опытѣ, для наглядности слѣдуетъ брать по возможности равными.
Удобно придать имъ слѣдующую форму: двѣ достаточно широкія
стеклянныя трубки соединены посредствомъ каучуковой трубки,
такъ что образуется II-образная трубка; ^стеклянная трубка
Первый законъ Фарадэя
163
сверху открыта, другая же закрыта краномъ. Послѣдняя трубка снаб-
жена дѣленіями, позволяющими отсчитывать, начиная отъ крана,
объемъ въ кубическихъ сантиметрахъ. Снизу въ закрытую трубку
впаяны двѣ платиновыя проволоки, заканчивающіяся внутри трубки
двумя платиновыми электродами. Чтобы наполнить сосудъ жидкостью,
«ее вливаютъ черезъ открытую трубку, открывъ предварительно кранъ
въ другой трубкѣ. Когда жидкость заполнитъ послѣднюю до крана,
его запираютъ. Концентрація кислоты можетъ быть во всѣхъ трехъ со-
судахъ любой и различной. При пропусканіи тока на каждомъ катодѣ
выдѣляется водородъ, на каждомъ анодѣ — кислородъ. Смѣсь этихъ
газовъ (гремучій газъ) скопляется въ закрытомъ колѣнѣ и заставляетъ
жидкость переходить въ широкую открытую трубку. По нанесен-
нымъ дѣленіямъ легко отсчитать, сколько кубическихъ сантиметровъ
гремучаго газа образовалось при прохожденіи электрическихъ заря-
довъ. Положимъ, что по истеченіи опредѣленнаго промежутка вре-
мени въ трехъ сосудахъ выдѣлились количества газа, равныя со-
отвѣтственно ѵх, ѵ2, ѵ3. Во всѣхъ случаяхъ при этомъ ока-
зывается соблюденнымъ слѣдующее простое соотношеніе:
ѵх ѵ2 = ѵ.А. Напримѣръ, могутъ получиться такія числа: ѵх — 136,
— 61, — 197 и т. п.
Разберемъ значеніе этого результата. Пока цѣпь была замкнута,
опредѣленное количество электричества 4- т было снято съ положи-
тельнаго полюса батареи и такое же количество — т съ ея отрица-
тельнаго полюса. Эти электрическіе заряды возбуждаются съ боль-
шою скоростью внутри составляющихъ батарею цѣпей, вслѣдствіе
происходящаго подъ дѣйствіемъ электродвижущихъ силъ раздѣле-
нія электричествъ въ двойныхъ слояхъ. Затѣмъ эти заряды, взаимно
•соединяясь въ проводахъ, даютъ нуль. Мы можемъ, напримѣръ, пред-
ставить себѣ, что съ положительнаго полюса снятъ зарядъ т0', а со
стороны отрицательнаго полюса къ нему подведенъ зарядъ — т^', Отно-
сительно каждой изъ величинъ и т” въ отдѣльности мы ничего опре-
дѣленнаго сказать не можемъ, но вмѣстѣ взятыя онѣ даютъ весь исчез-о
нувшій съ положительнаго полюса положительный зарядъ: т =
Переносъ электрическихъ зарядовъ по пути разряда мы должны
ставлять себѣ такъ, что черезъ каждое поперечное сѣченіепрохо-
дитъ количество положительнаго электричества, равное -рМ^по на-
правленію отъ положительнаго полюса къ отрицательному} и коли-
чество отрицательнаго электричества, равное т'\^ъ обратномъ
164
Первый законъ Фарадэя.
направленіи. Каждая изъ величинъ т и т" можетъ измѣняться про-
извольно отъ сѣченія къ сѣченію, но ихъ сумма должна оставаться
постоянной: т'т" = т. Дѣйствительно, если бы въ какомъ-либо
сѣченіи сумма перенесенныхъ зарядовъ т + гі' была бы больше
величины т, то либо изъ этого сѣченія исходило бы больше поло-
жительнаго электричества, нежели его подходитъ отъ положительнаго
полюса, либо въ него вступало бы больше отрицательнаго электри-
чества, нежели его получаетъ положительный полюсъ. Въ обоихъ
случаяхъ по закону сохраненія зарядовъ часть проводника между
положительнымъ полюсомъ и разсматриваемымъ сѣченіемъ должна
была бы зарядиться отрицательно; соотвѣтственно этому, другая
часть проводника должна была бы зарядиться положительно. Обратно
было бы, если бы мы предположими, что т" -}- т" < т. Съ перваго
взгляда можетъ показаться, что это такъ и есть, что проводникъ, по
которому проходить токъ, въ самомъ дѣлѣ пріобрѣтаетъ заряды, такъ
какъ онъ возбуждаетъ внѣ себя электрическое поле (§ 93). Но ниже
мы сейчасъ увидимъ, что даже самые большіе заряды, которые, бу-
дучи перенесены на проводникъ значительной емкости, даютъ сильныя
поля, при прохожденіи ихъ черезъ электролитъ вызываютъ въ немъ
лишь незначительное разложеніе. Иными словами: количество элек-
тричества т, вызвавшее при разрядѣ въ вышеописанномъ опытѣ обра-
зованіе гремучаго газа, въ громадное число разъ больше зарядовъ,
возбуждающихъ поле тока въ проводникѣ. Эти заряды, незначительные
по сравненію съ большимъ количествомъ электричества т, образую-
щимся въ батареѣ и разряжающимся черезъ электролитъ, даже при
точнѣйшихъ измѣреніяхъ могутъ не приниматься во вниманіе. Ихъ
можно считать равными нулю по сравненію съ величиной т. Слѣдо-
вательно, для всякаго сѣченія дѣйствительно должно имѣть мѣсто ра-
венство т + т" == ті гдѣ т — постоянная величина.
Въ проводникѣ электрическаго тока черезъ каждое его
сѣченіе проходитъ одно и то же количество электриче^бИа.
Такимъ образомъ, электрическій токъ до нѣкоторой стед^йи мо-
жетъ быть уподобленъ теченію несжимаемой жидкостномъ трубѣ,
такъ какъ черезъ каждое сѣченіе трубы проходитъ при этомъ одно
и то же количество жидкости. Но существуетъ иСразличіе между
этими двумя явленіями: электрическій токъ сос^фгіъ какъ бы изъ
двухъ частей — тока положительныхъ зарядовъдй тока отрицатель-
ныхъ зарядовъ, направленнаго противоположно^первому току. И только
Первый законъ Фарадэя
165
сумма этихъ обоихъ токовъ должна быть постоянною вдоль всего
проводника.
Если мы назовемъ разрядившееся въ нашемъ опытѣ количество
электричества черезъ т, то во всякомъ случаѣ ясно, что заряды -|-
прошедшіе черезъ электролитическій сосудъ III, удовлетво-
ряютъ условію т3 4- т3" — т3 = т. Между обоими тройными зажи-
мами токъ развѣтвляется; если черезъ сосудъ I разрядилось количе-
ство электричества тхг т” — т}, черезъ II — т2 + = т2, то,
какъ и при теченіи несжимаемой жидкости, должно быть + т2 ~ т
или же тх -|- т2 = т3. Выше найденный законъ, согласно которому.
= ѵз > показываетъ намъ, слѣдовательно, что при разрядѣ одина-
ковыхъ количествъ электричества образуются одинаковыя количества
гремучаго газа, независимо отъ того, происходитъ ли разрядъ черезъ
узкое или широкое пространство, иными словами, независимо отъ
плотности тока. Мы можемъ сосуды Іи II до нѣкоторой степени
уподобить двумъ частямъ одного большого сосуда; вслѣдствіе этого
мы приходимъ къ слѣдующему заключенію: количество образующа-
гося гремучаго газа не зависитъ отъ формы электродовъ и сосу-
довъ. Нетрудно было бы подтвердить это заключеніе, взявъ сосудъ
III совершенно иной формы съ электродами иного вида и расположен-
ными на иномъ растояніи другъ отъ друга; въ результатѣ опыта опять
получилось бы, что т/3 = + ѵ2. Этотъ результатъ, какъ мы видѣли,
не зависитъ отъ того, одинакова или различна концентрація въ трехъ
сосудахъ, одинакова или различна температура ихъ (если только
измѣряемые объемы газа приводить къ одной опредѣленной темпе-
ратурѣ). Короче, во всѣхъ случаяхъ мы имѣемъ одинъ и тотъ же
результатъ: выдѣляющіяся количества гремучаго газа удовлетворяютъ
соотношенію (ѵ1 -|- ѵ2 — ѵ3,
Мы установили здѣсь этотъ законъ только для сосудовъ съ раз-
веденной сѣрной кислотой. Но совершенно то же самое даютъ опыты
съ любымъ инымъ электролитомъ. Такимъ образомъ, мы приходимъ
къ весьма общему закону природы — первому закону Фарадэя:
количество продуктовъ разложенія, образовавшихся при
прохожденіи тока черезъ электролитъ, зависитъ исключи-
тельно отъ количества прошедшихъ черезъ него эле^ьЙфи-
ческихъ зарядовъ. Оно не зависитъ ни отъ плотное^ Тока,
ни отъ скорости разряда, ни отъ формы сосуда,Содержа-
щаго электролитъ, ни отъ формы и взаимнапрлразстоянія
если только тх т2 — т3.
166
Первый законъ Фарадэя
электродовъ, не зависитъ также отъ концентраціи и темпе-
ратуры электролита.
Количественные законы, относящіеся къ электролизу, были
открыты Фарадэемъ. Поэтому они и носятъ его имя.
Сосуды, содержащіе электролитъ и снабженные электродами, ока-
зываются весьма удобными для точнаго измѣренія большихъ электри-
ческихъ зарядовъ. Дѣйствительно, вышеописанный опытъ позволяетъ
еще сдѣлать заключеніе, что зависимость между разрядившимся ко-
личествомъ электричества и количествомъ продуктовъ разложенія
отличается крайнею простотою. Представимъ себѣ, что электрическій
разрядъ происходитъ одновременно черезъ п параллельно соединен-
ныхъ вполнѣ одинаковыхъ электролитическихъ сосудовъ и что про-
вода, которыми они соединены съ источникомъ тока, также вполнѣ
одинаковы. Конечно, мы будемъ наблюдать при этомъ, что во всѣхъ
сосудахъ образуется одно и то же количество гремучаго газа?
ѵг = ѵ2 — ѵ3 = • • • — ѵп. Слѣдовательно, черезъ всѣ сосуды разря-
жается при этомъ одинаковое количество электричества: т2 —
= т3= • • • — тп. Если все количество разрядившагося электричества
равно т = тх + т2 т3 -|- • • • -|- то = т2 = • • • = т.
Если, далѣе, объемъ гремучаго газа, соотвѣтствующій разрядивше-
муся количеству электричества т, равенъ -у, то, по закону Фарадэя,
должно быть ѵ = ѵ1 -|- ѵ2 ѵ3 • • • + ѵПі т. е. ѵ1 = ѵ2 = • • • = ~ ѵ.
Итакъ, если при прохожденіи заряда т образуется количество грему-
чаго газа, равное V, то при прохожденіи заряда -- т образуется
1
количество газа, равное — ѵ.
Количество продуктовъ разложенія, образующихся въ
электролитическомъ сосудѣ, всегда строго пропорціонально
количеству разрядившагося электричества.
ВОЛЬТАМЕТРЪ ИЛИ КУЛОНМЕТРЪ.
99. Совершенно понятно, что электролитическій сосудт^рбдоб-
ный вышеописанному, можно примѣнить къ измѣренію Электриче-
скихъ зарядовъ. Количество образующагося гремучаго,газа прямо
является мѣрою количества разрядившагося электричества. Слѣдуетъ
только опредѣлить, какое количество гремучаго ^газа соотвѣтствуетъ
тому заряду, который принимается за единиц^Энйпримѣръ, 1 кулону
Вольтаметръ или кулонметръ
167
или 1 микрокулону). Электролитическій сосудъ, приспособленный
для измѣренія электрическихъ зарядовъ, былъ названъ Фарадэемъ
вольтаметромъ, въ честь Вольта, открывшаго электролитическіе
процессы. Этотъ терминъ до недавняго времени былъ общеприня-
тымъ; въ настоящее время вмѣсто него начинаетъ употребляться
терминъ кулонметръ, такъ какъ самый приборъ предназначается
для измѣренія электрическихъ зарядовъ, единицей которыхъ является
кулонъ. Конечно, варварскія словообразованія „амперметръ", „вольт-
метръ", „кулонметръ", вмѣсто „измѣритель тока", „измѣритель
напряженія", „измѣритель заряда", не очень красивы, хотя они все
же представляютъ собою далеко не самое скверное въ современномъ
нашемъ языкѣ. Но первые два термина, несомнѣнно, стали уже столь
общеупотребительными, что изгнать ихъ не представляется возмож-
нымъ. Чтобы быть послѣдовательнымъ, приходится принять и тер-
минъ „кулонметръ"; на этомъ основаніи, я его буду ниже употре-
блять вмѣсто слова „вольтаметръ". Такимъ образомъ, тотъ инстру-
ментъ, которымъ мы до сихъ поръ пользовались, представляетъ со-
бою кулонметръ (или вольтаметръ) съ гремучимъ газомъ.
Основанный на электролизѣ методъ измѣренія электрическихъ
зарядовъ я, въ отличіе отъ описаннаго въ § 51 электрометрическаго
метода, буду называть кулонметрическимъ и вольтаметрическимъ.
УЗАКОНЕННАЯ ЕДИНИЦА ЭЛЕКТРИЧЕСКАГО ЗАРЯДА.
100. Газовый кулонметръ является все же не идеальнымъ измѣ-
рительнымъ аппаратомъ. Прежде всего, измѣреніе количества выдѣ-
ляющагося газа помощью калибрированной трубки нѣсколько услож-
няется тѣмъ обстоятельствомъ, что плотность газа весьма значи-
тельно измѣняется съ измѣненіемъ давленія и температуры. Если
желательно произвести точное измѣреніе, то необходимо опредѣлить
температуру и давленіе выдѣлившагося гремучаго газа и изъ вели-
чины послѣдняго вычесть давленіе водяного пара, образующагося
надъ разведенной сѣрной кислотой. Послѣ этого вычисляется объемр^И
который то же количество гремучаго газа занимало бы^тгри
нормальныхъ условіяхъ (0° Цельсія и 760 мм. давленія ртутнаго
столба) и при полномъ отсутствіи
пользуются формулой
въ немъ водяного пара.'Для этого
273 + &
273
760
’0 = ѵ • —
0 Р
168
Узаконенная единица электрическаго заряда
гдѣ ѵ измѣренный объемъ, р —-давленіе (за вычетомъ давленія
водяного пара), і)— температура.
Но и въ этомъ случаѣ газовый вольтаметръ все же не является
точнымъ инструментомъ, такъ какъ не весь кислородъ выдѣляется въ
видѣ О2, но образуется еще немного озона (О3) и перекиси водорода
(Н2О2). Количество этихъ примѣсей вообще незначительно, но при
точныхъ измѣреніяхъ опредѣляется лишь съ трудомъ, такъ какъ оно
зависитъ отъ трудно учитываемыхъ случайностей.
Лучшимъ инструментомъ является мѣдный кулонметръ сосудъ,
наполненный растворомъ мѣднаго купороса, въ которомъ катодъ
анодъ - изъ мѣди. Платиновый катодъ пе-
сдѣланъ изъ платины, а
Рис. 67.Серебряный кулонметръ.
редъ измѣреніемъ долженъ быть тща-
тельно вычищенъ и взвѣшенъ. Послѣ про-
хожденія тока онъ взвѣшивается снова;
разность вѣсовъ даетъ количество отло-
жившейся мѣди, а отсюда легко найти
и величину прошедшаго электрическаго
заряда. Мѣдный кулонметръ весьма упо-
требителенъ, въ особенности для измѣ-
ренія очень большихъ зарядовъ, хотя и
при его употребленіи не удается вполнѣ
избѣжать незначительныхъ погрѣшностей,
зависящихъ отъ трудно учитываемыхъ хи-
мическихъ соединеній, которыя обра-
зуетъ выдѣляющаяся мѣдь. Точнымъ инструментомъ, въ строгомъ
смыслѣ слова, является серебряный кулонметръ (рис. 67). Онъ
состоитъ изъ изолированнаго платиноваго тигля, въ проводящемъ
соединеніи съ которымъ находится винтовой зажимъ, предназначае-
мый для провода. Тигель наполняется растворомъ азотно-серебряной
соли, въ которомъ подвѣшивается серебряная палочка, также соеди-
ненная проводниками съ винтовымъ зажимомъ. Эта палочка служитъ
анодомъ, а платиновый тигель является катодомъ; измѣреніе ведется
такъ же, какъ и съ мѣднымъ вольтаметромъ. оЯ/
Съ помощью серебрянаго кулонметра измѣренія количества элек-
тричества можно производить съ такой чрезвычайно^^ точностью,
что по международному соглашенію узаконенное опредѣле-
ніе единицы электрическаго заряда основано именно на
такихъ измѣреніяхъ. Это опредѣленіе ед/инуцы заряда гласитъ:
Измѣреніе емкости
169
электрическій зарядъ равенъ 1 кулону, если при его раз-
рядѣ черезъ серебряный кулонметръ выдѣляется 1,118 мгр.
серебра.
Если сравнить показаніе серебрянаго кулонметра съ показаніями
мѣднаго кулонметра и кулонметра съ гремучимъ газомъ, одновре-
менно включенныхъ въ одну и ту же цѣпь, то оказывается ниже-
слѣдующее.
Въ мѣдномъ кулонметрѣ при разрядѣ 1 кулона выдѣляется
0,3294 мгр. мѣди.
Въ кулонметрѣ съ гремучимъ газомъ при комнатной темпера-
турѣ (18°) и нормальномъ давленіи воздуха (760 мм.) объемъ выдѣ-
лившагося газа, соотвѣтствующій 1 кулону, равенъ приблизительно
0,19 куб. см. Если произвести болѣе точное вычисленіе съ приве-
деніемъ къ 0° и 760 мм. давленія, какъ это указано выше, то ока-
зывается, что 1 кулону соотвѣтствуетъ 0,174 куб. см. гремучаго
газа при нормальныхъ условіяхъ.
ИЗМѢРЕНІЕ ЕМКОСТИ.
101. Прежде всего воспользуемся кулонметромъ для измѣренія
емкости; мы получимъ, такимъ образомъ, заключеніе изложенныхъ
въ § 72 предварительныхъ опредѣленій. Опредѣливъ предварительно
емкость С нѣкотораго конденсатора путемъ непосредственнаго срав-
ненія съ описаннымъ въ § 72 микрофарадомъ, соединимъ этотъ
конденсаторъ съ ртутнымъ коммутаторомъ такимъ образомъ, чтобы
удобно было поперемѣнно то заряжать его, соединяя съ батареей
высокаго напряженія, то разряжать черезъ газовый кулонметръ
(рис. 68). Какъ мы уже указывали выше, заряды, вызывающіе даже
сильныя электрическія поля, все же малы по сравненію съ 1 ку-
лономъ. Поэтому для измѣренія заряда конденсатора, кулонметру
форму, при которой возможно отсчитывать
газа. Пріемникомъ газа служитъ въ этомъ
нужно придать такую
весьма малые объемы
случаѣ капиллярная трубка, внизу воронкообразно расширенная.
это расширеніе введены электроды—двѣ тонкія изогнутыя стекл^шфыя
трубочки, въ концы которыхъ впаяны тонкія короткія платиновыя
проволочки; трубочки эти наполнены ртутью, образующ^Соедине-
ніе между платиновыми проволочками и двумя погруженному въ ртуть
мѣдными проволоками, ведущими къ выключателю. ' сосудъ, въ
170
Измѣреніе емкости
которомъ помѣщенъ этотъ маленькій кулонметръ, наполнить разве-
денной сѣрной кислотой, то въ моментъ соединенія заряженнаго
конденсатора съ крошечными электродами отъ нихъ отдѣляются
нѣсколько маленькихъ пузырьковъ газа, которые и собираются въ
капиллярной пріемной трубкѣ. Эту трубку удобно закрыть сверху
проволокой, какъ разъ заполняющей сѣченіе трубки и легко пе-
редвигаемой. Въ такомъ случаѣ не только удается заполнить капил-
Рис. 68. Измѣреніе емкости.
ляръ жидкостью, но также можно передвиженіями проволоки до-
биться того, чтобы всѣ газовые пузырьки, гдѣ-либо на путио остано-
вившіеся, собрались наверху трубки. Для измѣренія количествъ вы-
дѣляющагося газа остается только раздѣлить капилляръ^ца кубиче-
скіе миллиметры. Лучше зарядить и разрядить конденсаторъ нѣсколько
разъ подрядъ, чтобы не имѣть дѣла со слишкомъ ^малыми количе-
ствами газа. Такимъ путемъ легко опредѣлитьде^ичину заряда, со-
общающаго 1 микрофараду опредѣленное ^напряженіе, и выразить
Электрическая единица энергіи
171
этотъ зарядъ черезъ кулонъ единицу, опредѣленную въ предыду-
щемъ параграфѣ.
Численный примѣръ пояснитъ это. Положимъ, что емкость слю-
дяного конденсатора оказалось равной С = 2,7 М.Р. Заряжаемъ его
помощью батареи высокаго напряженія до 500 вольтъ и разряжаемъ
черезъ вышеописанный кулонметръ. Повторяемъ эту операцію 20 разъ,
подрядъ. Послѣ этого въ капиллярной трубкѣ оказывается 5,1 куб. мм.
гремучаго газа. Это соотвѣтствуетъ заряду въ 5,1:0,19 = 27 мил-
ликулоновъ; слѣдовательно, при каждомъ отдѣльномъ заряженіи кон-
денсаторъ получалъ 27:20= 1,35 милликулона. Такъ какъ напря-
женіе конденсатора равнялось 500 вольтамъ, то на 1 вольтъ при-
ходится, слѣдовательно, 2,7 . 10~6 кулона. Мы видимъ, такимъ обра-
зомъ, что единица заряда, опредѣленіе которой дано въ § 100,
тождественна съ единицей заряда, которая опредѣлена въ § 72.
Въ дѣйствительности, продажные нормальные конденсаторы въ 1 М.Р.
калибрируются путемъ прямого или косвеннаго измѣренія ихъ заряда
точнымъ (серебрянымъ) кулонметромъ.
Опредѣленіе единицы заряда, данное въ § 100, вмѣстѣ
съ опредѣленіемъ единицы напряженія, даннымъ въ § 37,
подтверждаютъ приведенную въ § 76 величину абсолютной
діэлектрической постоянной эѳира, равную 0,8842 . ІО-13.
ЭЛЕКТРИЧЕСКАЯ ЕДИНИЦА ЭНЕРГІИ.
102. Занимаясь изученіемъ электрическаго поля въ проводникѣ,
мы уже переходимъ за границы электростатики въ тѣсномъ смыслѣ
слова. Въ проводникѣ происходитъ постоянный оборотъ энергіи,
такъ какъ поле въ немъ постоянно разрушается. Проводникъ погло-
щаетъ энергію, подводимую къ нему непрерывно извнѣ и получае-
мую либо при помощи работы, приложенной къ электрической ма-
шинѣ, либо за счетъ внутреннихъ измѣненій въ гальваническихъ цѣ-
пяхъ, поддерживающихъ поле. Прикасаясь къ проводнику, по кото-
рому проходитъ токъ, напримѣръ, къ описанной въ § 93 длинной тонкой 4^'
проволокѣ, мы замѣчаемъ, что онъ нагрѣвается. Слѣдовательно, энергія^0
непрерывно разрушающагося въ немъ поля преобразуется въ теплбуу.
Если бы мы пожелали сравнить этотъ процессъ съ какиАГЬ-либо-
механическимъ процессомъ, то мы могли бы остановиться, ^примѣръ,
на теченіи жидкости съ треніемъ. Въ спокойномъ состояшйжидкость
неспособна испытывать напряженія сдвига, такъ какъ^ёформація ея
172
Электрическая единица энергіи
не связана съ напряженіями. Иначе обстоитъ дѣло, когда жидкость
течетъ такимъ образомъ, что ея частицы непрерывно деформиру-
ются. Въ этомъ случаѣ появляются силы напряженій, пропорціо-
нальныя скорости деформированія. Для поддержанія этихъ напря-
женій должна непрерывно притекать энергія, которая преобразуется
въ „теплоту тренія".
Нагрѣваніе электрическаго проводника удобно использовать для
«сравненія единицы энергіи, связанной съ единицами заряда и напря-
женія, т. е. электрической единицы энергіи, для которой мы въ § 82
ввели терминъ „джуль", съ другими употребительными единицами
энергіи, напримѣръ, съ калоріей.
Если мы отнимемъ отъ источника электричества, имѣющаго
напряженіе, равное V вольтамъ, электрическій зарядъ въ + 7И куло-
новъ, то онъ дастъ намъ, какъ это слѣдуетъ изъ приведенныхъ въ
§82 разсужденій, энергію, равную 714. V джулямъ. Эту энергію по-
• глощаетъ проводникъ, черезъ который происходить разрядъ; она
распредѣляется при этомъ въ проводникѣ такъ, что заключенный
между сѣченіями А и В отрѣзокъ проводника, вдоль котораго
-имѣется напряженіе ѴАВ, поглощаетъ энергію ѴАВ . М.
Такъ какь 2Ѵ^В = V, то, дѣйствительно, сумма количествъ
энергіи, поглощенныхъ отдѣльными частями проводника, равняется
всей энергіи, полученной отъ источника электричества: 2М . ѴАВ =
— М. АВ = Л4. V. Если проводникъ между точками А и В предста-
вляетъ собою проволоку, то дѣло обстоитъ особенно просто. Про-
волока при прохожденіи черезъ нее тока не испытываетъ никакихъ
иныхъ измѣненій, кромѣ нагрѣванія. Слѣдовательно, всю энергію, со-
общенную ей съ помощью эѳира, можно снова получить въ видѣ
„тепла". Какъ говорятъ, въ проводникѣ „электрическая энергія"
преобразуется въ „теплоту". Если количество этой теплоты измѣ-
рить въ калоріяхъ, а затраченную электрическую энергію въ джуляхъ,
то сейчасъ же можно будетъ вычислить отношеніе обѣихъ единицъ
энергіи „электрическій эквивалентъ теплоты".
Вышесказанное мы пояснимъ конкретнымъ примѣромъ. ТонД^іник-
келиновая проволока, которой придана форма спирали, что^іѵможно
'было взять ее достаточно длинной, погружена въ стеклянный сосудъ,
наполненный керосиномъ (рис. 69). Оба конца проволоки соединены
съ измѣрителемъ напряженія, напримѣръ, съ малочувствительнымъ
квадрантнымъ электрометромъ; кромѣ того, од^іт^ сконецъ ея соеди-
Электрическая единица энергіи
173,
йенъ прямо съ однимъ изъ полюсовъ аккумуляторной батареи, а дру-
гой соединенъ черезъ газовый кулонметръ съ другимъ полюсомъ ба-
тареи. Въ керосинъ погруженъ термометръ; при демонстраціяхъ,
удобно пользоваться грубымъ воздушнымъ термометромъ, изображен-
нымъ на рис. 69. Конечно, вся цѣпь должна быть снабжена еще вы-
ключателемъ. Сдѣлавъ отсчетъ на термометрѣ и наполнивъ измѣри-
тельный сосудъ кулонметра до верху разведенной сѣрной кислотой.,
замыкаютъ токъ отъ аккумуляторной батареи и пропускаютъ его»
Рис. 69. Измѣреніе энергіи.
до тѣхъ поръ, пока термометръ не покажетъ нѣкотораго вполнѣ за-
мѣтнаго повышенія температуры; въ продолженіе всего этого времени,
дѣлаются отсчеты напряженія V на электрометрѣ для того, чтобы про-
вѣрить, остается ли оно постояннымъ. По выключеніи тока отсчиты-
ваютъ показаніе кулонметра и вычисляютъ прошедшій зарядъ ЛГ.
Никкелиновая спираль при этомъ получила отъ эѳира количество энер-
гіи, равное
Ѵ7 = V .М джулей. ' -.
Если, далѣе, все количество керосина равнялось Р ки^р^рам^
мамъ, его теплоемкость есть ц, начальная и конечная температурь!
были и #2, то керосинъ получилъ отъ никкелиновой ліроволокн
количество энергіи, равное I
’ ($ = Р .в. ) калорій.
174
Электрическая единица энергіи
Если измѣреніе не должно отличаться особою точностью, то
теплоемкостями никкелиновой проволоки, стекляннаго сосуда и обо-
лочки термометра можно пренебречь. Въ такомъ случаѣ П7 должно
равняться (^, и искомое отношеніе получается въ такой формѣ:
Ѵ.М у .
Р.0.(8г__8|) ДжУлей = 1 кал°р>и-
Положимъ для примѣра, что при такомъ опытѣ постоянное на-
пряженіе между концами никкелиновой проволоки равнялось 36 воль-
тамъ; въ кулонметрѣ послѣ выключенія тока оказалось 142 куб. см.
гремучаго газа; керосинъ нагрѣлся отъ 18° до 47°. При этомъ ке-
росина было взято 0,44 кгр. литра), и его теплоемкость равня-
лась 0,50. Въ такомъ случаѣ, керосинъ получилъ
= 0,44.0,5 . 29 = 6,4 калоріи.
Разрядившееся количество электричества равно
М = 142 : 0,19 = 747 кулонамъ.
Количество энергіи, пріобрѣтенной проволокой, оказывается, такимъ
образомъ, равнымъ
ІГ = 36 . 747 - 26900 джулей.
Мы имѣемъ, слѣдовательно:
26900 джулей = 6,4 калорій,
4200 джулей = 1 калоріи.
Если бы измѣренія производились съ особою тщательностью, то мы
получили бы вмѣсто 4200 мало отличное отъ этого число 4190.
Опредѣленіемъ электрическихъ единицъ напряженія
(вольта) и заряда (кулона) устанавливается единица энергіи
вольтъ X кулонъ == джуль, равная одной 4190-й части боль-
шой калоріи.
Слѣдовательно, 4,19 джулей равняются одной малой калоріи.
А такъ какъ 427 килограмметровъ — 1 калоріи, то
9,81 джулей = 1 килограмметру.
Въ круглыхъ числахъ 1 джуль равенъ одной сотой
Такъ какъ число 9,81 какъ разъ представляетъ
ускоренія силы тяжести въ метрахъ въ секунду, то
зать, что джуль равенъ значенію килограмметра на
ніи отъ центра земли, гдѣ ускореніе силы тяжести [
1 м. въ секунду. Поэтому джуль равняется удвоенгюй кинетической
энергіи, которою обладаетъ масса въ 1 кгр. п]
въ секунду. Обѣ электрическія единицы вольрър кулонъ, —конечно,
і килограмметра. г
. собою величину
। можно еще ска-
_ Я?
такрДъ разстоя-
равряется только
. \\Л'
ірр скорости въ 1 м.
Второй законъ Фарадэя
175
намѣренно выбраны такъ, что получается столь простое значеніе
единицы энергіи.
Скорость въ 1 м. въ секунду примѣрно равняется скорости
очень медленно идущаго человѣка. Слѣдовательно, кинетическая
энергія медленно идущаго человѣка уже достигаетъ примѣрно 100
джулей. Отсюда ясно, насколько мала эта единица энергіи. Въ тех-
никѣ, гдѣ стоимость получаемой энергіи играетъ большую роль, при-
нята поэтому болѣе удобная единица, цѣнность которой выражается
въ цѣлыхъ копейкахъ. Таковою является „киловаттъ-часъ“.
1 киловаттъ - часъ = 3,6 . ІО6 джулей = 3,6 мегаджулей.
Единица энергіи въ выше описанной (§78) „электростатической си-
стемѣ единицъ“ гораздо меньше джуля и равняется
300 вольтъ X 4 • Ю-9 кулона = 10-7 джуля.
о
Эта единица представляетъ собою удвоенную кинетическую энергію
массы въ 1 граммъ, движущейся со скоростью въ 1 см. въ секунду.
Это минимальное количество энергіи называется эргомъ и является
единицей энергіи въ такъ называемой „абсолютной системѣ единицъ".
Слѣдовательно, электростатическія единицы принадлежатъ къ числу
„абсолютныхъ единицъ", что, впрочемъ, не представляетъ никакого
существеннаго преимущества.
ВТОРОЙ ЗАКОНЪ ФАРАДЭЯ.
103. Какъ мы знаемъ, при электролизѣ разведенной сѣрной ки-
слоты образуются водородъ и кислородъ. Легко опредѣлить, въ какомъ
отношеніи между собою находятся количества этихъ двухъ продуктовъ
разложенія. Въ самомъ дѣлѣ, такъ какъ эти газы являются единствен-
ными продуктами разложенія и жидкость всегда остается разведен-
ной сѣрной кислотой, то оба эти газа должны представлять собою
продукты разложенія воды (Н2 О). Двѣ граммъ-молекулы водорода (т. е.
4 гр.) приходятся всегда на одну граммъ-молекулу кислорода (т. е. на
32 гр.). Получающаяся смѣсь при нагрѣваніи даетъ сильный взрывъ,
такъ какъ оба компонента смѣси цѣликомъ вступаютъ въ соедине-
ніе, при чемъ образуется водяной паръ безъ примѣси того и др^<
гого газа. Если мы будемъ пропускать полученный электролизом^|ре-
мучій газъ черезъ мыльный растворъ и будемъ поджигать^образую-
щіеся на поверхности раствора мыльные пузыри, то, дѣйствительно,
будутъ получаться сильные взрывы.
176
Второй законъ Фарадэя
Правильность нашего заключенія можно сдѣлать совершенно
несомнѣнной, если устроить вольтаметръ такъ, чтобы кислородъ и
водородъ собирались отдѣльно. Для этой цѣли берутъ И-образную
трубку, оба колѣна которой сверху снабжены кранами и къ которой
припаяно посрединѣ сгиба третье сверху открытое колѣно. Въ каж-
домъ изъ закрытыхъ колѣнъ впаяна платиновая проволока, къ кото-
рой внутри трубки прикрѣплена платиновая пластинка, служащая элек-
тродомъ. Если, наполнивъ такой аппаратъ разведенной сѣрной кисло-
той, пропустить черезъ него токъ, то въ одномъ колѣнѣ будетъ
собираться кислородъ, въ другомъ водородъ. При этомъ оказывается,
что со стороны катода получается вдвое большій объемъ газа, не-
жели со стороны анода. Если открыть немного кранъ со стороны
катода и поднести къ струѣ вытекающаго газа зажженную спичку,
то газъ загорается и горитъ слабымъ голубоватымъ пламенемъ; это,
дѣйствительно, водородъ. Если немного открыть кранъ со стороны
анода и внести тлѣющую лучинку въ струю газа, то лучинка вспы-
хиваетъ и горитъ яркимъ пламенемъ; здѣсь, дѣйствительно, полу-
чается кислородъ. Теперь нужно обратить вниманіе на два обстоя-
тельства. Во - первыхъ, какъ учитъ насъ химія, оба газа имѣютъ дву-
атомныя молекулы - Н2 и О2. Во-вторыхъ, по закону Авогадро,
одинаковые объемы газовъ содержатъ всегда одинаковое количество
граммъ-молекулъ, и, слѣдовательно, двойной объемъ содержитъ
двойное ихъ число. Поэтому мы можемъ сдѣлать такое заключеніе:
всегда, когда образуется 2 Н2, образуется и 102; когда выдѣляется
1Н, выдѣляется ]/о0. Въ водѣ Н химически одновалентенъ, О —хи-
мически двувалентенъ; атомный вѣсь химическаго элемента (также
молекулярный вѣсъ химическаго радикала, каковы 8О4, КО3), раз-
дѣленный на его валентность, мы называемъ химическимъ экви-
валентомъ вещества; напримѣръ, 1/2О = 8 гр. кислорода предста-
вляетъ собою эквивалентъ кислорода, 1Н = 1 гр водорода пред-
ставляютъ собою эквивалентъ водорода. Поэтому мы можемъ г вы-
разиться еще такъ: при электролизѣ разведенной сѣрной кислоты
получается одинаковое число химическихъ эквивалентовъ^врдорода
и кислорода, т. е. образуются эквивалентныя колщіс^івй обоихъ
газовъ (рис. 70).
Къ этому результату присоединяется еще ^^рутой результатъ.
При обсужденіи перваго закона Фарадэя (§^ мы видѣли, что
количество выдѣляющихся продуктовъ разложенія совершенно не за-
Второй законъ Фарадэя
177
черезъ
то же
катодѣ
виситъ отъ степени концентраціи раствора. Эту закономѣрность мы
можемъ еще болѣе обобщить. Наполнимъ три газовые вольтаметра,
имѣющіе описанные отдѣльные пріемники для обоихъ продуктовъ раз-
ложенія, тремя различными электролитами: одинъ разведенной соля-
ной кислотой (НС1), второй разведенной сѣрной кислотой (Н28О4),
третій разведенной щавелевой кислотой (С2Н2О4). Включимъ всѣ
три аппарата послѣдовательно въ цѣпь галь-
ванической батареи. Въ такомъ случаѣ
каждый изъ нихъ разрядится одно и
количество электричества.
Во всѣхъ трехъ аппаратахъ на
выдѣляется водородъ и во всѣхъ трехъ въ
одинаковомъ количествѣ. Слѣдовательно, это
количество не зависитъ отъ того, въ какое
соединеніе входитъ водородъ въ растворѣ.
Этотъ законъ строго подтверждается при всѣхъ
опытахъ съ веществами, выдѣляющимися при
электролизѣ.
Количество электролитически вы-
дѣленнаго вещества зависитъ только
отъ количества разрядившагося элек-
тричества, но не зависитъ отъ того, въ
какомъ соединеніи входитъ выдѣляю-
щееся вещество въ растворъ, если имѣть
въ виду только тѣ соединенія, въ кото-
рыя оно входитъ съ одною и тою же ва-
лентностью.
Со стороны анода въ первомъ изъ аппа- Къ батареѣ
ратовъ выдѣляется желтоватый газъ —хлоръ Рис- ВтоРой законъ
(С12), въ двухъ остальныхъ — кислородъ (О2). Фарадэя.
Хлоръ одновалентенъ, кислородъ - двувалентенъ. Вслѣдствіе этого
объемъ хлора, выдѣлившійся въ первомъ аппаратѣ, таковъ жеь
какъ объемъ выдѣлившагося водорода, объемъ же кислорода, выдѣ-
лившагося въ остальныхъ двухъ аппаратахъ, вдвое меньше. Т^^жё
количество электричества, которое выдѣляетъ при разрядѣ ^бива-
лентъ водорода, выдѣляетъ также одинъ эквивалентъ хлор^фіГодинъ
эквивалентъ кислорода. Здѣсь мы опятъ имѣемъ вподй^ общій за-
конъ природы. Если, напримѣръ, соединить послѣдовательно четыре
' К • ТГ
Ми. Электричество и магнитизмъ. 12
178
Токи іоновъ
вольтаметра съ платиновыми электродами, наполненные соотвѣтственно
разведенной сѣрной кислотой и растворами сѣрнокислой мѣди, сѣр-
нокислаго цинка и сѣрнокислаго никкеля, то при электрическомъ
разрядѣ выдѣляются на всѣхъ четырехъ анодахъ одинаковыя коли-
чества кислорода, а на катодахъ химически эквивалентныя количества
водорода, мѣди, цинка и никкеля.
Второй законъ Фарадэя: одно и то же количество элек-
тричества при прохожденіи черезъ различные электролиты
всегда выдѣляетъ на электродахъ химически эквивалентныя
количества продуктовъ разложенія.
Электрическій зарядъ, который при прохожденіи черезъ электро-
литъ выдѣляетъ какъ разъ одинъ эквивалентъ вещества, называютъ
эквивалентнымъ зарядомъ. Мы легко можемъ вычислить его въ
кулонахъ. Серебро одновалентно, значитъ, его эквивалентный вѣсъ
равенъ атомному вѣсу, который равняется 107,93. Такъ какъ 1 кулонъ
выдѣляетъ 1,118 мгр. серебра, то 1 эквивалентъ серебра выдѣляетъ
107930
= 96540 кулоновъ.
1,11 о
Эквивалентный зарядъ равняется 96540 кулонамъ.
ТОКИ ІОНОВЪ.
104. Мы подходимъ теперь къ вопросу о томъ, гдѣ образуются
тѣ продукты разложенія, которые мы наблюдаемъ на электродахъ.
Изучить этотъ вопросъ мы можемъ, напримѣръ, на растворѣ мѣд-
наго купороса. Электроды возьмемъ въ видѣ двухъ горизонтальныхъ
мѣдныхъ проволокъ, расположенныхъ одна надъ другой. Когда при-
боръ соединенъ съ батареей, мы видимъ, что отъ катода поднима-
ются струйки жидкости вверхъ. Это указываетъ намъ на то, что
вблизи катода плотность раствора уменьшается. Именно, вслѣдствіе
осажденія мѣди на катодѣ, растворъ мѣди разжижается. Наоборотъ,
у анода замѣчаются струи жидкости, опускающіяся внизъ. Здѣсь рас-
творъ становится болѣе концентрированнымъ, такъ какъ въ фіего
переходитъ мѣдь съ проволоки. Въ пространствѣ между эл^тродамп
растворъ остается неизмѣненнымъ. Первыя точныя изслѣдованія этого
явленія были сдѣланы Гитторфомъ (НіКогІ). Онъ установилъ одинъ
на другомъ нѣсколько сосудовъ, изъ которыхъ только ^нижній имѣлъ
вполнѣ непроницаемое дно. Во всѣхъ остальныхъѴбсудахъ дно пред-
ставляло собою перепонку, черезъ которую растворъ могъ медленно
Токи іоновъ
179
диффундировать. Чтобы измѣреніе не могло вызвать никакихъ возра-
женій, эти перепонки должны быть сдѣланы изъ пористаго вещества,
напримѣръ, изъ глины, одинаково проницаемой и для воды и для іоновъ,
о которыхъ будетъ сказано ниже. Въ верхнемъ и въ нижнемъ сосу-
дахъ помѣщались электроды (рис. 71). Такимъ образомъ можно было
черезъ этотъ аппаратъ пропускать электрическій токъ, при чемъ ме-
ханическое смѣшеніе жидкостей изъ разныхъ отдѣленій было невоз-
можно. Послѣ разряда весь приборъ разбирался на части, и содер-
жимое каждаго сосуда изслѣдовалось отдѣльно. При этомъ рас-
творъ въ среднихъ сосудахъ оказывался тѣмъ же, что и
прежде, но въ крайнихъ сосудахъ, содержавшихъ элек-
троды, онъ оказывался измѣненнымъ. Для наглядности
опишемъ эти измѣненія въ частномъ случаѣ, когда былъ
взятъ растворъ мѣднаго купороса при мѣдныхъ электро-
дахъ. На катодѣ осаждается мѣдь, и въ то же время изъ
раствора въ катодномъ сосудѣ исчезаетъ мѣдный купоросъ.
Эта потеря при выдѣленіи 1 эквивалента мѣди (^Си =
= 31,8 гр.), по опытамъ Гитторфа, равняется 0,7 эквива-
лента сѣрнокислой соли мѣди (0,7 . 1/2Сп8О4 — 55,9 гр.).
Одновременно на анодѣ происходитъ какъ разъ обратное:
электродъ теряетъ 31,8 гр. мѣди, а растворъ около него
пріобрѣтаетъ 55,9 гр. сѣрнокислой соли мѣди. Все явле-
ніе можетъ быть представлено нижеслѣдующей схемой:
Катодный сосудъ Средніе дНОдНЬщ сосудъ
сосуды
Си + эквивалента 0 — 0,3 эквивалента
$О4 -0,7 „ 0 +0,7
Рис. 71. Аппа-
Мы видимъ, такимъ образомъ, что въ анодномъ со-
судѣ исчезла мѣдь (0,3 эквивалента), а въ катодномъ
ратъ Гит-
торфа.
сосудѣ такое же ея количество прибавилось. Далѣе, въ катодномъ
сосудѣ исчезло нѣкоторое количество (0,7 эквивалента) сѣрнокислаго
радикала (8О4), а въ анодномъ сосудѣ такое же его количество^
прибавилось.
Отсюда мы заключаемъ прежде всего, что законъ сохраненія
матеріи, которому учитъ химія, сохраняетъ свою силу и ц|йэлек-
тролизѣ. Но этотъ законъ требуетъ еще, чтобы въ тѣ\ѣ^случаяхъ,
когда вещество въ одномъ мѣстѣ исчезаетъ, а въ друг^м^появляется,
180
Токъ іоновъ
оно при этомъ непрерывно переходило изъ перваго мѣста
во второе. Такимъ образомъ, если мы будемъ основываться на этомъ
фундаментальномъ законѣ всего естествознанія и не будемъ видѣть
въ природѣ фокусничества, то мы должны будемъ изъ этихъ опы-
товъ вывести слѣдующее заключеніе: электрическій разрядъ че-
резъ электролиты сопровождается перемѣщеніемъ вещества.
Въ нашемъ примѣрѣ раствора сѣрнокислой соли мѣди токъ
мѣди движется въ направленіи силовыхъ линій (отъ анода къ ка-
тоду), а токъ сѣрнокислаго радикала идетъ въ обратномъ направле-
ніи. Но не слѣдуетъ это явленіе представлять себѣ такъ, что та са-
мая мѣдь, которая отдѣлилась отъ анода, проходитъ черезъ весь рас-
творъ до катода. Дѣйствительно, въ такомъ случаѣ растворъ сѣр-
нокислой соли мѣди въ промежуточномъ пространствѣ не участво-
валъ бы въ явленіи проводимости, а между тѣмъ онъ, несомнѣнно,
въ немъ участвуетъ, несмотря на то, что онъ не подвергается
измѣненіямъ. Это видно изъ того, что, если помѣстить въ этотъ рас-
творъ слой изолирующей жидкости (напримѣръ, тщательно дистил-
лированной воды), то электрическая проводимость исчезаетъ. Влія-
ніе раствора, находящагося между электродами, на электрическую
проводимость можно установить также, взявъ два различные со-
прикасающіеся раствора, напримѣръ, растворы сѣрнокислыхъ со-
лей мѣди и цинка въ элементѣ Даніеля. Если соединить полюсы
нашей батареи съ полюсами элемента Даніеля такъ, чтобы мѣдь
была анодомъ, а цинкъ - катодомъ, то мѣдь анода переходитъ въ
растворъ, но на катодѣ осаждается не мѣдь, а цинкъ изъ сѣрни-
стой соли цинка. При этомъ обнаруживается также измѣненіе въ
пограничномъ слоѣ между двумя растворами: мѣдный купоросъ нѣ-
сколько передвигается за границу, а цинковый купоросъ слегка отсту-
паетъ назадъ. Это явленіе, какъ и всѣ прочіе вышеописанные факты,
можно объяснить только въ томъ случаѣ, если принять, что одно
изъ двухъ передвигающихся черезъ электролитъ веществъ (Си) ^пе-
редвигается по всему раствору равномѣрно въ направленіи си^офыхъ
линій, т. е. отъ анода къ катоду, а другое (8О4) такъ жС^редви-
гается, но въ противоположномъ направленіи.
Это явленіе мы можемъ уяснить себѣ на простой^одели. Пусть
двѣ цвѣтныя пластинки, какъ разъ покрывающі^^фа другую, пред-
ставляютъ собою два вещества въ водномъ растворѣ, напримѣръ,
красная пусть изображаетъ Си, желтая —Точно наложенныя
Токи іоновъ
181
одна на другую онѣ представляютъ собою Си8О4; пусть при этомъ
полоса шириною въ 1 см. представляетъ собою 1 эквивалентъ. Сдви-
немъ красную пластинку на 0,3 см. въ одну сторону, а желтую на
0,7 см. въ противоположную сторону. Результатъ этого будетъ слѣ-
дующій: средній слой остается неизмѣннымъ (Си 8О4 той же концен-
траціи), съ одного края появляется красная полоса въ 1 см. шири-
ною (выдѣляется 1 эквивалентъ Си), съ другого края появляется та-
кой же ширины желтая полоса (освобождается 1 эквивалентъ 8О4
и растворяетъ 1 эквивалентъ мѣди).
Вещества, передвигающіяся въ электролитѣ при элек-
трическомъ разрядѣ черезъ него, называются іонами. Веще-
ство, передвигающееся по направленію силовыхъ линій
(отъ анода къ катоду), называется катіономъ, а вещество,
перемѣщающееся въ обратномъ направленіи, называется
аніономъ.
За то время, какъ на электродахъ выдѣляется 1 химическій экви-
валентъ продуктовъ разложенія, аніонъ передвигается такимъ обра-
зомъ, что на катодѣ исчезаетъ опредѣленная часть его эквивалента,
появляясь на анодѣ. Эту часть мы обозначимъ черезъ па (для раствора
сѣрнокислой соли мѣди въ нашемъ примѣрѣ па = 0,7). Одновременно
передвигается и катіонъ такъ, что опредѣленная часть его экви-
валента переходитъ отъ анода на катодъ (въ нашемъ примѣрѣ —0,3).
Числа па и пк должны быть связаны равенствомъ па + пк — 1; при
помощи вышеописанной модели легко уяснить себѣ, что при этомъ
на каждомъ изъ электродовъ выдѣлится равно 1 эквивалентъ со-
отвѣтственнаго продукта разложенія.
Эти числа па и пк носятъ названіе чиселъ переноса аніона
и катіона. Ихъ можно всегда опредѣлить путемъ химическаго ана-
лиза растворовъ, взятыхъ въ непосредственной близости отъ элек-
тродовъ. Ихъ опредѣленіе является важной задачей въ области фи-
зико-химическихъ измѣреній, и оно сдѣлано для большого числа
веществъ.
105. Слѣдуетъ замѣтить, что вообще продукты разложенія цС
іоны не оказываются тождественными. Это видно, напримѣръ, ^ъ^
случаѣ электролиза сѣрной кислоты, у которой іоны суть Н и М^$О4,
а продукты разложенія — Н2 и О2. Кислородъ на анодѣ получается
вслѣдствіе разложенія воды. На каждую молекулу 8О4 ,%йфиближаю-
щуюся къ аноду, выдѣляется одинъ атомъ О изъ моде^улы НаО и
182 Токи іоновъ.— Теорія электрической проводимости электролитовъ
въ растворѣ остается Н28О,(. Особенно рѣзко это обнаруживается,
если въ качествѣ электролита взять растворъ какой-либо щелочной
соли, напримѣръ, сѣрнокислой соли калія К28О,(. Наполнимъ раство-
ромъ этой соли, окрашеннымъ въ лиловый цвѣтъ помощью лакмуса,
сосудъ, раздѣленный поперечной перегородкой на два отдѣленія. Въ
перегородкѣ сдѣланъ каналъ, черезъ который оба отдѣленія соединя-
ются. Погрузимъ въ оба отдѣленія въ качествѣ электродовъ платино-
выя проволочки и соединимъ ихъ съ батареей. Тотчасъ мы замѣтимъ
образованіе газа у электродовъ; какъ и при электролизѣ разведен-
ной сѣрной кислоты, образуются водородъ и кислородъ. Но вскорѣ
затѣмъ мы замѣчаемъ еще иныя химическія измѣненія: на анодѣ
растворъ становится свѣтлокраснымъ, вслѣдствіе образованія сѣрной
кислоты, а на катодѣ онъ становится голубымъ, вслѣдствіе обра-
зованія ѣдкаго кали. Если проанализировать растворы, то окажется
слѣдующее:
на анодѣ на катодѣ
выдѣлилось Ч?® 1 Н
освободилось 1/2Н28О4 1 КОН
измѣненіе въ содержаніи соли — 0,3 К28О4 0,2 К28О4
полное измѣненіе К —0,6 эквивалента + 0,6 эквивалента
$О4 +0,4 0,4
разложено 1/2Н2О 1/2Н2О
Слѣдовательно, продуктами разложенія въ этомъ случаѣ явля-
ются кислородъ, сѣрная кислота, водородъ и ѣдкій кали, а іонами
являются К и 8О4 и ихъ числа переноса равны — 0,6 и па = 0,4.
Катіонами всегда являются металлы и водородъ, аніонами
кислотные радикалы и гидроксильная группа (ОН).
ТЕОРІЯ ЭЛЕКТРИЧЕСКОЙ ПРОВОДИМОСТИ ЭЛЕКТРОЛИТОВЪ.
106. До сихъ поръ мы излагали только факты. Но уже теперь
умѣстно поставить вопросъ о сущности связи между электрическимъ
токомъ и переносомъ іоновъ. Такая связь должна существовать, такъ
какъ во всѣхъ случаяхъ безъ исключеній одно изъ этихъ^ явленій
связано съ другимъ. Съ другой стороны, мы привели^йше (§95)
теоретическія соображенія, показывающія, что электрическій токъ
безусловно долженъ быть связанъ съ матеріальными токомъ. Поэтому
мы почти невольно приходимъ къ слѣдующему^заключенію: іоны
сами являются носителями электрическимъ зарядовъ, кото-
Теорія электрической проводимости электролитовъ
183
рые переносятся отъ одного электрода къ другому при
явленіи прохожденія тока черезъ электролитъ.
Это общепризнанное положеніе составляетъ основу теоріи элек-
тролитической проводимости. Согласно ему, электрическій токъ за-
ключается въ томъ, что катіонъ переноситъ положительный за-
рядъ т въ направленіи силовыхъ линій и въ то же время аніонъ пе-
реноситъ отрицательный зарядъ т” въ противоположномъ направленіи.
Числа переноса даютъ намъ отношенія обоихъ частныхъ токовъ къ
' I „ Г1І
общему току т = т + т ; именно, па = —, пк = — • Когда, напри-
мѣръ, количество разрядившагося электричества равно точно 1 экви-
валентному заряду, то отъ положительнаго полюса отнята пк экви-
валентами катіона часть пк положительнаго электричества и подве-
дена къ нему па эквивалентами аніона часть па отрицательнаго элек-
тричества. Аналогичное происходитъ и на отрицательномъ полюсѣ.
На основаніи законовъ Фарадэя, отсюда слѣдуетъ:
Каждый химическій эквивалентъ любого іона, незави-
симо отъ химической природы этого іона, несетъ съ со-
бою одинъ и тотъ же электрическій зарядъ, именно 1 экви-
валентный зарядъ.
Согласно сказанному въ § 103, эквивалентный зарядъ Р рав-
няется 96 540 кулонамъ.
Но въ настоящее время общепризнаннымъ является предста-
вленіе о вѣсомой матеріи, какъ состоящей изъ атомовъ. Слѣдова-
тельно, принявъ во вниманіе, что въ 1 вѣсовомъ эквивалентѣ всегда
содержится одно и то же число Ы атомовъ или атомныхъ комплек-
совъ (напримѣръ, ЫО3) одноатомнаго вещества, или А/" атомовъ дву-
атомнаго вещества, или атомовъ трехатомнаго вещества и т. д.,
мы приходимъ къ такому заключенію:
Каждый одновалентный атомъ и каждый одновалентный
атомный комплексъ (напримѣръ, МО3) въ качествѣ іона х
имѣетъ одинъ и тотъ же электрическій зарядъ. Этотъ зарядъ
называютъ элементарнымъ количествомъ электричества. Каж^^?°
дый двувалентный атомъ (или радикалъ, напримѣръ, 8О4)въ^
качествѣ іона имѣетъ зарядъ, равный двумъ элементарМ|1мъ
количествамъ электричества. Вообще, каждый /г-валжный
л \\ 4 . ѵ •
атомъ или радикалъ въ качествѣ іона имѣетъ заця^'ъ, рав-
ный п элементарнымъ количествамъ электри
184
Теорія электрической проводимости электролитовъ
Согласно этому воззрѣнію, электрическій зарядъ (по крайней
мѣрѣ, въ электролитахъ) также обладаетъ атомнымъ строеніемъ.
Наименьшимъ возможнымъ зарядомъ, никоимъ образомъ далѣе не
раздѣляющимся, является элементарное количество электричества.
Поэтому этотъ зарядъ иногда называютъ еще атомомъ электри-
чества. Величина элементарнаго количества электричества равняется
96540 гт х • гт /т-и * х
8 = —щ— кулоновъ. По новымъ опредѣленіямъ Планка (Ріапск),
7Ѵ, вѣроятно, равняется 0,6175 .ІО21 и, слѣдовательно,
8 = 1,564 . ІО-19 кулона.
Слѣдуетъ упомянуть, что подъ словомъ „іонъ“ иногда разумѣютъ
не измѣримое количество переносящаго электричество вещества, но
отдѣльную электрически заряженную частичку.
107. Мы глубоко проникли теперь въ сущность электролити-
ческой проводимости. Что же представляетъ собою проводникъ, точ-
нѣе — электролитъ? Это -- тѣло, въ которомъ содержатся въ громад-
номъ числѣ положительныя и отрицательныя частички, іоны. Число
іоновъ обоихъ родовъ одинаково, такъ что зарядъ тѣла въ общемъ
равняется нулю. Эти іоны подвижны, такъ что легко поддаются дѣй-
ствію электрическаго поля и уничтожаютъ напряженіе. Энергія поля
при этомъ обращается въ теплоту, такъ какъ іонамъ при ихъ дви-
женіи приходится преодолѣвать сопротивленіе тренія.
Іоны соляного раствора могутъ легко поддаваться дѣйствію
силы поля лишь въ томъ случаѣ, если положительныя и отрицатель-
ныя частички уже раньше отдѣлены другъ отъ друга, иными словами,
если молекулы соли разложены на іоны. Въ случаѣ сѣрнокислой соли
калія (К28О4) мы должны представлять себѣ, что положительно заря-
женные атомы калія и отрицательно заряженные комплексы 8О4 сво-
бодно движутся во всѣ стороны. Кромѣ того, въ растворѣ всегда имѣ-
ются н не-диссоціированныя молекулы К2ЗО4, зарядъ которыхъ равенъ
нулю, но онѣ не играютъ никакой роли въ электрической проводи-
мости. Такое представленіе, съ точки зрѣнія химіи, сначала казалось
непріемлемымъ. Но методы опредѣленія молекулярнаго вѣса?раство-
ровъ (пониженіе точки плавленія и повышеніе точкц^ кипѣнія)
также указываютъ на то, что соли, кислоты и основанія,Гсообщаю-
щія водѣ проводимость, всегда диссоціированны^ВрДа отличается
отъ всѣхъ остальныхъ жидкостей своей особе^ой способностью
расщеплять на іоны эти вещества при ихъ раствореніи. Вполнѣ чи-
Возможна ли іонная теорія матеріи?
185
•стая дестиллированная вода представляетъ собою изоляторъ (или
лишь полупроводникъ); изоляторами являются также водные растворы
сахара и прочихъ индифферентныхъ тѣлъ, которыя, согласно опре-
дѣленіямъ молекулярнаго вѣса, не диссоціируются. Только прибавле-
ніе къ водѣ такого вещества, которое въ ней распадается на іоны,
сообщаетъ ей свойства настоящаго проводника. Въ меньшей степени
то же наблюдается и для всѣхъ другихъ растворителей, напримѣръ,
для алкоголя, этиловаго эѳира, бензола и т. д.
Что же представляетъ собою, въ такомъ случаѣ, изоляторъ?
Вещество безъ свободныхъ іоновъ. Въ изоляторѣ всѣ іоны связаны
въ молекулы, притомъ такъ, что сумма зарядовъ, содержащихся въ
одной молекулѣ, равняется нулю. Въ изоляторѣ іоны не могутъ свободно
передвигаться въ направленіи поля. Но каждая отдѣльная молекула
представляетъ собою небольшой проводникъ, вполнѣ со всѣхъ сто-
ронъ изолированный. Если на молекулу дѣйствуетъ электрическое
поле, то положительныя ея составныя части стремятся по возмож-
ности сдвинуться въ направленіи силовыхъ линій, а отрицательныя
ея части стремятся сдвинуться въ противоположномъ направленіи;
это стремленіе тѣмъ значительнѣе, чѣмъ сильнѣе поле. Такимъ обра-
зомъ молекула образуетъ маленькій электрическій диполь въ напра-
вленіи силовыхъ линій и для насъ становится понятно, почему удѣль-
ная діэлектричность матеріальныхъ изоляторовъ отличается отъ удѣль-
ной діэлектричности эѳира и именно превышаетъ ее.
Полупроводниками являются тѣла съ весьма малымъ числомъ
свободныхъ іоновъ.
ВОЗМОЖНА ЛИ ІОННАЯ ТЕОРІЯ МАТЕРІИ?
108. Какъ мы видимъ, электролитическія явленія приводятъ насъ
къ іонной теоріи матеріи вообще. Можетъ быть, электрическій за-
рядъ является неотъемлемымъ свойствомъ атомовъ, въ силу котораго
они находятся въ неизмѣнной прочной связи съ эѳиромъ, такъ ска-
зать, условіемъ существованія отдѣльнаго атома въ окружающемъ
его пустомъ пространствѣ?
Эти соблазнительныя мысли наталкиваются, однако, на
затрудненія. Одинъ и тотъ же атомъ можетъ встрѣчаться і
ствѣ одновалентнаго и двувалентнаго іона, положительнаго щотрица-
тельнаго; онъ же можетъ встрѣчаться и не заряженнымъ^Атомы мо-
гутъ обмѣниваться своими зарядами, что чаще всегоА случается на
большія
жаче-
186
Химизмъ гальваническихъ цѣпей
электродахъ, гдѣ іонъ, достигая электрода, просто отцаетъ ему свой
зарядъ. И тѣмъ не менѣе при всѣхъ явленіяхъ (по крайней мѣрѣ,
въ электролитахъ) недѣлимый атомъ электричества продолжаетъ су-
ществовать.
Окончательное сужденіе относительно намѣченной здѣсь „элек-
трической теоріи матеріи" мы сможемъ составить, лишь уяснивъ себѣ
также природу иныхъ проводниковъ —газовъ и металловъ, въ осо-
бенности же рѣшивъ вопросъ о томъ, состоятъ ли и въ этихъ слу-
чаяхъ заряды изъ „атомовъ электричества".
ХИМИЗМЪ ГАЛЬВАНИЧЕСКИХЪ ЦЪПЕЙ.
109. Прежде, чѣмъ идти дальше, мы еще немного остановимся
на явленіяхъ электролиза, происходящихъ внутри гальваническихъ
цѣпей. Для того, чтобы составить себѣ о нихъ ясное представленіе,
разсмотримъ элементъ Даніеля. Обратимъ вниманіе сначала на его
положительный мѣдный полюсъ. При разрядѣ отъ него уносится
положительное электричество. Но, какъ мы знаемъ, въ то же время
работа химическихъ силъ, дѣйствующихъ между мѣдью и растворомъ
сѣрнокислой соли мѣди, возстанавливаетъ электрическіе двойные слои,
отъ которыхъ отнимаются заряды. Въ силу этого мѣдь отнимаетъ
отъ раствора положительные заряды или отдаетъ ему отрицательные.
Итакъ, процессъ возстановленія двойного слоя долженъ быть не-
премѣнно связанъ съ процессомъ электролиза, въ которомъ мѣдь
является катодомъ; въ силу этого мѣдь осаждается изъ раствора
сѣрнокислой соли мѣди на мѣдномъ электродѣ. Одновременно про-
исходитъ аналогичный процессъ, но въ обратномъ направленіи,
и на цинковомъ электродѣ. Послѣдній играетъ роль анода въ ра-
створѣ сѣрнистой соли цинка, и въ силу этого въ растворъ перехо-
дитъ цинкъ въ количествѣ, строго эквивалентномъ количеству выдѣ-
лившейся мѣди.
Что этотъ процессъ протекаетъ именно такъ, какъ предсказы-
ваетъ теорія, мы можемъ видѣть на любомъ старомъ элементѣ Да-
ніеля. Чѣмъ дольше онъ находился въ употребленіи, тѣмъ^болѣе
разъѣденъ въ немъ цинкъ. На мѣдномъ электродѣ, напоротъ, за
все это время осаждалась мѣдь.
Энергія, доставляемая гальванической цѣпью, предста-
вляетъ собою энергію химическихъ превращеній, которыми
сопровождается внутри цѣпи процессЖ^црзбужденія элек-
тричества.
Свободная энергія и скрытая энергія
187
Цинкъ представляетъ собою такъ называемый неблагородный
металлъ; онъ легко растворяется, и при этомъ освобождается энергія.
Мѣдь по своимъ химическимъ свойствамъ должна быть отнесена кт>
числу благородныхъ металловъ, всегда стремящихся выдѣляться изъ
раствора съ освобожденіемъ энергіи. Если мы на мгновеніе погру-
зимъ цинковую пластинку въ растворъ мѣднаго купороса, то на ней
осадится бурый слой, по химическомъ изслѣдованіи, оказывающійся1
мѣднымъ. Отъ цинка при этомъ отнимается эквивалентное отложив-
шейся мѣди количество его, что можно констатировать взвѣшива-
ніемъ. При этомъ образовалось нѣкоторое количество цинковаго купо-
роса, а нѣкоторое количество мѣднаго купороса исчезло. Мы имѣемъ
здѣсь тотъ же химическій процессъ, что и въ элементѣ Даніеля, и,
очевидно, онъ связанъ съ освобожденіемъ энергіи. Цинковая пла-
стинка и растворъ слегка нагрѣваются, и образующуюся теплоту
можно измѣрить. Оказывается, что количество образующейся при
этомъ простомъ опытѣ тепловой энергіи весьма близко къ количе-
ству электрической энергіи, отнимаемой отъ элемента Даніеля, когда
въ немъ совершаются количественно тѣ же превращенія.
СВОБОДНАЯ ЭНЕРГІЯ И СКРЫТАЯ ЭНЕРГІЯ-
ПО. Такого рода измѣренія были сдѣланы для цѣлаго ряда
гальваническихъ цѣпей. При этомъ выяснилось, что вообще ихъ
энергія обнаруживается въ двухъ формахъ: во-первыхъ, въ видѣ элек-
трической энергіи, которая отъ цѣпи отнимается, и, во-вторыхъ, въ
видѣ положительнаго или отрицательнаго количества теплоты, кото-
рое элементъ отдаетъ окружающей средѣ или получаетъ изъ нея,
если поддерживать его температуру постоянной. Эта вторая часть
энергіи представляетъ собою родъ скрытой теплоты, съ которой свя-
занъ химическій процессъ, подобно тому, какъ со скрытой теплотой
сжатія связано расширеніе или сжатіе газа, поддерживаемаго при по-
стоянной температурѣ, или со скрытой теплотой парообразованія свя-
зано кипѣніе жидкости при постоянной точкѣ кипѣнія и т. д. Вообще,
въ каждомъ физическомъ или химическомъ процессѣ, протекающе^^?°
при постоянной температурѣ, получающаяся энергія распадается^а
двѣ вполнѣ опредѣленныя части. Первую часть составляетъ та(^нер-
гія, которую при правильномъ теченіи процесса мы можем^полу-
чить въ видѣ работы (или въ видѣ электрической энер'^Х вторую
часть представляетъ собою всегда сопровождающая ^^рцессъ скры-
тая теплота. Эти двѣ составныя части энергіи называютъ, по Гельм-
188
Устройство гальванической цѣпи
гольцу, свободной энергіей и скрытой (или связанной)
энергіей. Сумма этихъ энергій въ гальванической цѣпи равняется
количеству теплоты, которое получается при повтореніи происходя-
щихъ въ цѣпи химическихъ процессовъ въ реактивномъ сосудѣ, когда
часть энергіи не отнимается въ видѣ электричества. Здѣсь лишній
разъ подтверждается, такимъ образомъ, принципъ сохраненія энергіи.
Энергія, получаемая въ видѣ электричества отъ галь-
ванической цѣпи, вообще не равняется всей энергіи, по-
лучающейся вслѣдствіе происходящихъ въ цѣпи химиче-
скихъ превращеній, но представляетъ собою лишь „сво-
бодную энергію".
Гальваническими цѣпями удобно пользоваться для опредѣленія
свободной энергіи, а, слѣдовательно, и обѣихъ частей энергіи въ
отдѣльности. Напримѣръ, въ элементѣ Даніеля скрытая теплота
•очень мала, такъ какъ въ немъ свободная энергія почти равняется,
какъ мы видѣли, всей энергіи, доставляемой химическимъ процессомъ.
УСТРОЙСТВО ГАЛЬВАНИЧЕСКОЙ ЦЪПИ.
111. Такъ какъ на „катодѣ" всегда происходитъ возстановленіе,
а на „анодѣ"- окисленіе, то относительно устройства гальваническихъ
цѣпей можно высказать нижеслѣдующія общія положенія.
1. Отрицательный полюсъ, играющій при дѣйствіи элемента роль
„анода", долженъ состоять изъ неблагороднаго металла, чтобы при
происходящемъ на немъ процессѣ окисленія освобождалась энергія.
Поэтому для него берутся цинкъ, свинецъ или кадмій.
2. Положительный полюсъ, играющій роль „катода", наоборотъ,
долженъ состоять изъ металла, склоннаго къ возстановленію, т. е.
или изъ того благороднаго металла (мѣдь, серебро, ртуть), который
осаждается изъ окружающаго полюсъ раствора, или же изъ высшаго
окисла, возстанавливающагося при дѣйствіи элемента въ низшій оки-
селъ (азотная кислота, хромовая кислота, перекись свинца, перекись
марганца). Если положительный электродъ составленъ изъ т|кдй
перекиси, то въ него обыкновенно вводятъ еще какое-либо нейтраль-
ное тѣло, не принимающее участія въ химическихъ процессахъ, но
•сообщающее электроду лучшую проводимость, напримѣръ, уголь,
платину или свинецъ (въ свинцовыхъ аккумулято^^ъ)?^
3. Въ какой электролитъ погружаются оба ^электрода, обыкно-
венно не имѣетъ значенія. Для большинству ^элементовъ слѣдуетъ
Мѣстные токи
189*
лишь заботиться о томъ, чтобы сопротивленіе прохожденію тока
было по возможности мало (это достигается прибавленіемъ сѣрной
кислоты или концентрированнаго раствора какой-нибудь соли); у
элементовъ, отличающихся особенно постояннымъ напряженіемъ (нор-
мальные элементы) электролиты должны представлять собою, по воз-
можности, чистые растворы металловъ, изъ которыхъ состоятъ элек-
троды, чтобы при отнятіи зарядовъ ни электролиты, ни электроды не
измѣнялись химически.
МЪСТНЫЕ ТОКИ.
Рис. 72. Раствореніе цинка въ .
сѣрной кислотѣ.
112. Въ основѣ всей химіи водныхъ растворовъ лежатъ электро-
химическія свойства іоновъ. Рамки этой книги не позволяютъ долго
на нихъ останавливаться. Мы ограничимся лишь небольшимъ при-
мѣромъ. При погруженіи цинковой палочки въ разведенную сѣрную
кислоту, какъ извѣстно, цинкъ растворяется съ выдѣленіемъ водо-
рода. Но это происходитъ лишь въ томъ случаѣ, если для опыта
берется обыкновенный, не химически чи-
стый цинкъ. Химически чистый цинкъ
вообще не растворяется въ разведенной
сѣрной кислотѣ. Если мы погрузимъ въ
сосудъ съ разведенной сѣрной кислотой
палочки изъ химически чистаго цинка и
мѣди, то ни на одной изъ нихъ не обна-
ружимъ появленія газовыхъ пузырьковъ.
Но если мы сблизимъ ихъ (рис. 72)
такъ, чтобы онѣ касались одна другой,
все равно - въ воздухѣ или внутри сѣрной
кислоты, то сейчасъ же получается бы-
палочкѣ. Газъ, образующійся
На цинковой же палочкѣ ни-
лишь постепенно растворяется
вспомнить, что цинкъ и М'
строе образованіе газа на мѣдной
при этомъ, оказывается водородомъ,
чего подобнаго не замѣчается; она
въ сѣрной кислотѣ.
Это явленіе легко понять, если
въ разведенной сѣрной кислотѣ образуютъ Вольтову цѣпь (§^3.6)_
Если мы соединяемъ металлически полюсы этой цѣпи, то водород-
ные іоны устремляются къ мѣди и образуютъ тамъ водорддшѣій газъ,
а іоны 8О4 устремляются къ цинку и растворяютъ ег^Д^І
Химически нечистый цинкъ растворяется, потому что еодержить въ
190
Мѣстные токи
себѣ постороннія примѣси, напримѣръ, частицы угля, съ которыми онъ
«образуетъ въ разведенной сѣрной кислотѣ „коротко замкнутыя“
гальваническія цѣпи. Пузырьки водорода, образующіеся при раство-
реніи цинка, выдѣляются, такимъ образомъ, не на цинкѣ, но на ча-
стичкахъ угля. Послѣ растворенія такого цинка въ растворѣ замѣ-
чается черный осадокъ угольныхъ частицъ. Если желательно избѣг-
нуть растворенія цинка въ разведенной сѣрной кислотѣ, то слѣдуетъ
наамальгамировать его поверхность. Мягкая цинковая амальгама по-
крываетъ всѣ инородныя тѣла, такъ что вся поверхность, приходящая
въ соприкосновеніе съ разведенной сѣрной кислотой, состоитъ изъ
чистой цинковой амальгамы.
Незначительные электрическіе токи, возникающіе въ нечистомъ
металлѣ около инородныхъ частичекъ, называютъ мѣстными то-
ками. Часто бываетъ полезнымъ разсмотрѣть, будетъ ли дѣйствіе
мѣстныхъ токовъ благопріятнымъ или же вреднымъ. Напримѣръ,
когда впервые стали гальванически покрывать желѣзную проволоку
.другимъ металломъ для предохраненія ея отъ ржавчины, то для этой
цѣли употребляли мѣдь. Оказалось, однако, что такая проволока
подвергалась ржавленію еще скорѣе, нежели непокрытая. Такъ какъ
совершенно избѣжать маленькихъ скважинъ въ оболочкѣ невозможно,
то подъ вліяніемъ проникавшей черезъ нихъ влаги въ проволокѣ
образовывались мѣстные токи, вызывавшіе быстрое окисленіе желѣза.
Въ силу этого желѣзную проволоку стали покрывать цинкомъ и
этимъ, дѣйствительно, удалось избѣгнуть ржавленія. Между цинкомъ
и желѣзомъ мѣстные токи дѣйствуютъ такъ, что окисляется цинкъ,
а на желѣзѣ отлагается водородъ или же при наличности окиси
желѣза она возстановляется. Желѣзо, какъ обычно выражаются,
менѣе неблагородный металлъ, чѣмъ цинкъ, а мѣдь благороднѣе
желѣза.
ЭЛЕКТРОЛИТИЧЕСКАЯ ПОЛЯРИЗАЦІЯ.
113. Такъ какъ электролизъ химически измѣняетъ раствору
вблизи обоихъ электродовъ и притомъ различнымъ образомъ, аиногда
измѣненію подвергаются и самые электроды вслѣдствіе выдѣленія на
нихъ вещества изъ раствора, то электролитическое разлрж^ніе обычно
влечетъ за собою электрическое напряженіе между электродами. Подъ
вліяніемъ электролиза вольтаметръ становится гальванической цѣпью.
Мы можемъ легко доказать это на весьма ^простомъ примѣрѣ.
-Если мы приложимъ къ двумъ платиновымъ^ эД0%тродамъ, погружен-
Электролитическая поляризація
191
нымъ въ разведенную сѣрную кислоту, напряженіе одного элемента
Лекланше (ЬесІапсИё) (немного болѣе 1 вольта), то, несмотря на
соединеніе проводниками обоихъ полюсовъ элемента, никакого выдѣ-
ленія газовъ на электродахъ не замѣчается; слѣдовательно, никакого
разряда при этомъ не происходитъ. Что же является причиной этого?
Въ то мгновеніе, когда къ вольтаметру приложено напряженіе, за-
ряды начинаютъ переходить въ него, но это происходитъ лишь до
тѣхъ поръ, пока вызванное разложеніемъ напряженіе не станетъ
равнымъ напряженію элемента Лекланше. Послѣ этого оба соеди-
нительные провода по всей ихъ длинѣ остаются заряженными до по-
стояннаго потенціала, поле находится въ равновѣсіи, разрядъ пре-
кращается. Иное произойдетъ, если мы удвоимъ приложенное напря-
женіе, соединивъ послѣдовательно два элемента Лекланше. Въ этомъ
случаѣ мы замѣтимъ въ вольтаметрѣ слабое, но непрерывно продол-
жающееся образованіе газа. Сь тройнымъ напряженіемъ (три элемента
Лекланше, соединенные послѣдовательно) мы получаемъ уже зна-
чительный токъ. Напряженіе между электродами въ вольтаметрѣ, оче-
видно, возрастаетъ лишь до опредѣленнаго максимума, послѣ чего
дальнѣйшее разложеніе его уже не повышаетъ. Въ нашемъ примѣрѣ
это максимальное значеніе напряженія равняется, приблизительно, 1,8
вольтъ. Такъ какъ два элемента Лекланше вмѣстѣ даютъ напряже-
ніе выше 2 вольтъ, то ихъ напряженіе превосходитъ указанный
максимумъ примѣрно на 1/2 вольта, чѣмъ и вызывается наблюдаемый
слабый разрядъ. При трехъ элементахъ Лекланше этотъ избытокъ
напряженія доходитъ почти до 2 вольтъ, что и вызываетъ болѣе
сильное образованіе газа.
Это явленіе носитъ названіе электролитической поляриза-
ціи; напряженіе, получающееся въ вольтаметрѣ, называется напря-
женіемъ поляризаціи.
Въ нашемъ примѣрѣ возникновеніе напряженія поляризаціи объ-
ясняется весьма просто. Платиновые электроды поглощаютъ выдѣляю-
щіеся газы - водородъ и кислородъ —и становятся, вслѣдствіе этого,
водороднымъ и кислороднымъ электродами. Самая платина при этомз^
играетъ роль индифферентнаго тѣла, проводящаго электричестдр^къ
электродамъ (водороду и кислороду), вещество которыхъ по
себѣ слабо проводитъ (подобную же роль играетъ уго^^въ эле-
ментѣ Лекланше, см. § 116). Съ возрастаніемъ содержанія/водорода
и кислорода на электродахъ напряженіе цѣпи во^орр^ъ-кислородъ
возрастаетъ, пока платиновые электроды не насытятся газами, послѣ
192
Электролитическая поляризація
чего выдѣляющіеся газы будутъ уже образовывать пузырьки. При
этомъ будетъ достигнутъ максимумъ напряженія 1,8 вольта.
Конечно, напряженіе образующейся такимъ образомъ цѣпи во-
дородъ-кислородъ можно установить и непосредственно. Для этого
платиновые электроды (не слишкомъ малыхъ размѣровъ) соединяемъ*
съ коммутаторомъ, помощью котораго вольтаметръ можно соединять
или съ большой батареей, или съ квадрантнымъ электрометромъ.
Будемъ пропускать черезъ вольтаметръ токъ въ теченіе нѣкотораго
времени. Если теперь „заряженный" вольтаметръ соединить съ
электрометромъ, то послѣдній дастъ отклоненіе, соотвѣтствующее
1,8 вольта. Это отклоненіе исчезаетъ, если соединить проволокой
электроды цѣпи водородъ-кислородъ; въ этомъ случаѣ зарядъ двой-
ныхъ слоевъ выравнивается черезъ эту проволоку. Если оставить
цѣпь замкнутой лишь на короткое время и снова удалить проволоку,
то вскорѣ электрическое напряженіе цѣпи возстанавливается, и элек-
трометръ снова указываетъ напряженіе въ 1,8 вольта. Если же ко-
ротко замкнуть цѣпь на продолжительное время, то она „разряжается",
и электрометръ послѣ прекращенія короткаго соединенія остается на
нулѣ. Это объясняется тѣмъ, что „токъ разряда", въ силу самой природы
явленія, течетъ черезъ газовую цѣпь въ направленіи, противополож-
номъ направленію заряжающаго тока. Вслѣдствіе этого водородный
электродъ окисляется, а кислородный возстановляется. На обоихъ
происходитъ образованіе воды до тѣхъ поръ, пока не исчезнутъ
вполнѣ выдѣлившіеся газы. Тогда напряженіе, понятно, становится
равнымъ нулю. Энергія, доставляемая цѣпью, есть, слѣдовательно, хи-
мическая энергія, освобождающаяся при соединеніи кислорода и во-
дорода въ воду.
Это послѣднее соображеніе приводитъ насъ къ выясненію болѣе
глубокаго значенія поляризаціонныхъ напряженій. Когда мы пропускаемъ
черезъ вышеописанный вольтаметръ „заряжающій токъ", то двойные
слои поглощаютъ энергію, такъ какъ электрическіе заряды прохрдягь
черезъ нихъ противъ дѣйствія электродвижущихъ силъ. Поглощаемая
ими энергія равняется т . V, гдѣ т - прошедшій зарядъ, напря-
женіе поляризаціи. Эта энергія идетъ на поддержані^фймическаго
процесса разложенія электролита, въ нашемъ слу^цф — на разло-
женіе воды на водородъ и кислородъ. Мы можемъ^ слѣдовательно,
придти къ такому заключенію: во всѣхъ случаяхъ, когда элек-
тролизъ связанъ съ химическими изм^еіііями въ электро-
Электрокапиллярныя явленія
193
литахъ или же въ электродахъ, между электродами возни-
каетъ напряженіе поляризаціи, имѣющее направленіе, про-
тивоположное направленію тока. Произведеніе изъ этого
напряженія поляризаціи на количество разрядившагося элек-
тричества равняется свободной энергіи, необходимой для
химическаго разложенія.
Бываютъ случаи, когда электролизъ не вызываетъ дѣйствитель-
наго разложенія. Если мы пропустимъ зарядъ черезъ растворъ сѣр-
нокислой мѣди съ двумя мѣдными электродами, то концентрація сдѣ-
лается неодинаковой въ разныхъ мѣстахъ раствора. Но свободная
энергія, необходимая для возбужденія различій въ концентраціи рас-
твора, чрезвычайно мала. Поэтому въ подобныхъ случаяхъ и напря-
женіе поляризаціи также весьма мало. Два мѣдные электрода въ рас-
творѣ сѣрнокислой мѣди являются примѣромъ неполяризуюіцихся
электродовъ.
ЭЛЕКТРОКАПИЛЛЯРНЫЯ ЯВЛЕНІЯ.
114. Весьма интересное побочное дѣйствіе двойныхъ электри-
ческихъ слоевъ наблюдается на ртутныхъ электродахъ, именно- -
измѣненіе поверхностнаго натяженія.
Вообще, если зарядить нѣкоторое количество жидкости, то элек-
трическіе заряды испытываютъ дѣйствіе силы, стремящейся увели-
чить поверхность этой жидкости. Если мы зарядимъ мыльный пузырь,
то его радіусъ слегка увеличится, и онъ слегка раздувается, при чемъ
энергію для этого доставляетъ эѳиръ благодаря происходящему въ
немъ сокращенію силовыхъ линій. Эта энергія идетъ на преодолѣніе
поверхностнаго натяженія, стремящагося сжать пузырь, какъ упругія
силы стремятся сжать надутый резиновый шаръ. Такимъ образомъ сила,
съ которою эѳиръ дѣйствуетъ на заряды, дѣйствуетъ обратно поверх-
ностному натяженію. Можно сказать, что электрическій зарядъ умень-
шаетъ поверхностное натяженіе, и притомъ это дѣйствіе проявляется
независимо отъ знака заряда.
Весьма извѣстный опытъ красиво иллюстрируетъ это дѣйстві^^
заряда. Разсматривая водяную струю, выходящую изъ маленькагр
отверстія (фонтанъ), мы можемъ замѣтить, что она начинается в^видѣ
длиннаго, гладкаго цилиндрическаго водяного столба, кр^фвій на
нѣкоторой высотѣ сначала становится негладкимъ (появляется пере-
хваты), а затѣмъ распадается на капли (рис. 73). Причиной вызы-
х>/'
Ми. Электричество и магнитизмъ.
194
Электрокапиллярныя явленія
вающей образованіе перехватовъ и въ заключеніе раздробленіе на
капли является поверхностное натяженіе. Если мы осторожно при-
близимъ къ водяной струѣ натертую эбонитовую палочку, то струя
въ силу индукціи заряжается (положительно) и подъ вліяніемъ за-
ряда поверхностное натяженіе ея уменьшается. Водяной столбъ при
этомъ остается сплошнымъ на гораздо большемъ протяженіи, чѣмъ
раньше, и распадается гораздо позже, когда перехваты становятся осо-
бенно сильными, на небольшое число сравнительно крупныхъ капель.
Такъ какъ уменьшеніе поверхностнаго натяженія происходитъ
одинаковымъ образомъ какъ при положительномъ, такъ и при отри-
Рис. 73. Электрическій фонтанъ.
нательномъ зарядѣ, то и электрическіе двойные слои производятъ
то же дѣйствіе. Если мы помѣстимъ большую каплю ртути на пло-
ское часовое стекло и нальемъ на нее разведенной сѣрной кислрты,
въ которую опустимъ кристалликъ двухромокислаго кали, то поверх-
ностное натяженіе капли сильно уменьшится, и она стан6т^°шире,
чѣмъ была въ воздухѣ. Если мы затѣмъ погрузимъ въ я^идѣость же-
лѣзную иголку, то получимъ настоящую гальваническую цѣпь съ
благороднымъ металломъ — ртутью и неблагороднымъ металломъ —
желѣзомъ. Если мы иголку приблизимъ настолько; чтобы она кос-
нулась ртути, то цѣпь замыкается, и полу^е^'я токъ, сейчасъ же
Электрокапиллярныя явленія
195
уменьшающій напряженія двойныхъ слоевъ. Вслѣдствіе этого возра-
стаетъ поверхностное натяженіе, и капля слегка сжимается. Токъ при
этомъ размыкается, скоро возстанавливается прежнее состояніе, ртут-
ная капля вновь расширяется, снова касается желѣзной иголки, и весь
процессъ начинается сначала. Ртутная капля начинаетъ правильно пуль-
сировать и совершаетъ движенія, сходныя съ движеніями живого сердца.
115. Вліяніемъ электролитической поляризаціи на поверхностное
натяженіе пользуются для построенія чувствительнаго капиллярнаго
электрометра. Этотъ приборъ состоитъ изъ слегка наклоненной
стеклянной капиллярной трубки, имѣющей на каждомъ концѣ по
открытому шарообразному стеклянному сосуду (рис. 74). Въ верхній
Рис. 74. Капиллярный электрометръ.
сосудъ сначала наливается немного ртути чтобы ея уровень былъ
ниже отверстія капилляра. На ртуть наливаютъ разведенную сѣрную
кислоту такъ, чтобы она заполнила сосудъ и проникла въ капил-
ляръ. Въ нижній сосудъ наливается ртуть въ такомъ количествѣ,
чтобы она доходила приблизительно до половины капилляра, въ ко-
торомъ находится разведенная сѣрная кислота. Если въ капиллярѣ
•окажутся пузырьки воздуха, то ихъ удаляютъ, наклоняя капилляръ
въ ту или другую сторону. Этотъ электрометръ представляетъ со-
бою, слѣдовательно, не что иное, какъ вольтаметръ съ двумя рту^^г
ными электродами, различающимися другъ отъ друга тѣмъ, чщ^Йо’-
верхность одного приблизительно въ тысячу разъ больше поверх-
ности. другого. Оба эти электрода металлически соединяются^? двумя
винтовыми зажимами. Первоначально эти зажимы соединяются между
собою проволокою; при этомъ наблюдается положеніеконца ртут-
13
196
Электрокапиллярныя явленія
наго столбика на небольшомъ масштабѣ, расположенномъ рядомъ
съ капилляромъ. Это положеніе ртути опредѣляетъ нулевую точку
инструмента. Если приложить къ зажимамъ небольшое напряженіе,
то конецъ ртутнаго столбика передвинется на нѣкоторое разстояніе.
Если (перемѣною зажимовъ) измѣнить знакъ приложеннаго напряже-
нія, то произойдетъ перемѣщеніе конца ртутнаго столбика въ обрат-
номъ направленіи. Въ одномъ случаѣ, слѣдовательно, ртутный ме-
нискъ поднимается, въ другомъ опускается, сравнительно съ его
нулевымъ положеніемъ. Это измѣненіе длины ртутнаго столбика обу-
словливается непосредственно измѣненіемъ поверхностнаго натяженія
въ ртутномъ менискѣ. Чѣмъ больше поверхностное натяженіе, тѣмъ
ниже опускается менискъ. Слѣдовательно, на капиллярномъ элек-
трометрѣ прежде всего наблюдается увеличеніе или уменьшеніе по-
верхностнаго натяженія. Это измѣненіе поверхностнаго натяженія
обусловливается измѣненіемъ напряженія въ двойномъ электриче-
скомъ слоѣ между ртутью и разведенной сѣрной кислотой, разность
потенціаловъ котораго уменьшается или увеличивается, смотря по
направленію приложеннаго напряженія. Весь процессъ въ электро-
метрѣ протекаетъ приблизительно слѣдующимъ образомъ. Тотчасъ
послѣ включенія тока небольшой зарядъ проходитъ черезъ электро-
метръ, и въ силу этого возникаетъ напряженіе поляризаціи, напра-
вленное противоположно приложенному напряженію. Но на большой
ртутной поверхности поляризація ничтожно мала по сравненію съ
поляризаціей въ капиллярѣ, такъ какъ въ капиллярѣ продукты элек-
тролитическаго разложенія приблизительно въ тысячу разъ болѣе
концентрированы, нежели въ широкомъ сосудѣ. Мы можемъ поэтому
принять, что все напряженіе поляризаціи сосредоточено только на
ртутномъ менискѣ въ капиллярѣ. Это напряженіе вызываетъ здѣсь уве-
личеніе или уменьшеніе поверхностнаго натяженія, смотря по тому,
направлено ли оно одинаково съ начальнымъ напряженіемъ двой-
ного слоя, или же противоположно ему. Слѣдовательно, роль двухъ
тѣлъ электрометра (см. § 28) здѣсь играютъ сѣрная кислота оц^гуть
въ капиллярѣ; они еще сначала обладаютъ опредѣленною разностью
потенціаловъ, именно напряженіемъ, вызываемымъ ихъ^соприкосно-
веніемъ. Когда же затѣмъ присоединяется измѣряемое^іапряженіе въ
видѣ поляризаціи, то измѣняется сила, дѣйствующ^уна оба эти тѣла
въ слоѣ ихъ соприкосновенія. Это измѣненіе сильі замѣчается по пе-
ремѣщенію мениска; ртуть играетъ при этймѣ роль индикатора.
Непостоянныя и постоянныя цѣпи
197
Капиллярный электрометръ легко прокалибрировать, прилагая къ нему
различныя извѣстныя напряженія, получаемыя по методу, описанному
въ § 94. Область примѣненія его ограничена опредѣленной высшей
величиной измѣряемаго имъ напряженія, которая равна максималь-
ному напряженію поляризаціи между ртутью и сѣрной кислотой,
т. е. приблизительно 1 вольту. Если приложить къ этому прибору
большее напряженіе, то на обоихъ электродахъ выдѣляется газъ, и
черезъ электрометръ проходитъ постоянный токъ. Вслѣдствіе этого
капиллярный электрометръ служитъ спеціально для точнаго измѣре-
нія малыхъ напряженій; благодаря своей простой конструкціи онъ
оказывается чрезвычайно удобнымъ для этой цѣли. Отъ прочихъ
электрометровъ онъ отличается тѣмъ, что имѣетъ весьма большую
емкость и еще тѣмъ, что его изоляція весьма несовершенна (на-
пряженіе двойного слоя постепенно возвращается къ „нулевому зна-
ченію"). Поэтому его слѣдуетъ употреблять лишь въ тѣхъ случаяхъ,
когда потеря зарядовъ не имѣетъ значенія, напримѣръ, при измѣре-
ніи напряженій гальваническихъ цѣпей.
НЕПОСТОЯННЫЯ И ПОСТОЯННЫЯ ЦѢПИ.
116. Поляризаціонныя явленія играютъ роль также во многихъ
гальваническихъ элементахъ. Если мы, напримѣръ, соединимъ про-
водникомъ полюсы Вольтовой цѣпи (мѣдь разведенная сѣрная ки-
слота - амальгамированный цинкъ), то замѣтимъ выдѣленіе газа на
мѣдной пластинкѣ; газъ этотъ, конечно, водородъ. Это образованіе
газа не остается безъ вліянія на дѣятельность цѣпи, такъ какъ мѣдь,
подобно всѣмъ прочимъ тѣламъ, поглощаетъ газы, хотя и въ не-
большихъ количествахъ. Но насыщенная водородомъ мѣдь оказы-
ваетъ уже иное дѣйствіе, нежели чистая мѣдь. Именно, вслѣдствіе
поглощенія водорода напряженіе цѣпи понижается. Такимъ образомъ
при пользованіи токомъ Вольтовой цѣпи, напряженіе ея падаетъ.
Это легко можно показать при помощи квадрантнаго электрометра.
Если затѣмъ оставить цѣпь въ покоѣ, то, по мѣрѣ того, какъ мѢді>?>Х
теряегь водородъ, напряженіе снова повышается. Элементъ постепенно
возстанавливается.
Всѣ гальваническія цѣпи, напряженіе которыхъ падаетъ при
ихъ употребленіи, называются непостоянными цѣпям^и. Вообще
говоря, непостоянныя цѣпи возстанавливаются, еслц^хъ оставить
198
Непостоянныя и постоянныя цѣпи
на нѣкоторое время въ покоѣ. Примѣрами непостоянныхъ цѣпей
являются слѣдующіе элементы:
Элементъ Бунзена (Випзеп) съ электродами изъ цинка и азот-
ной кислоты (въ пористомъ глиняномъ цилиндрѣ). Электролитомъ въ
немъ служитъ разведенная сърная кислота, ьъ азотную кислоту для
отвода электричества погружается угольная или платиновая (въ эле-
ментѣ Грове) палочка.
Элементъ Грене или хромовокислый элементъ, электродами ко-
тораго являются цинкъ и хромовая кислота. Электролитомъ въ немъ
служитъ разведенная сѣрная кислота, при-
бавляемая къ хромовой кислотѣ. Цинкъ
погружается прямо въ смѣсь сѣрной и
хромовой кислотъ. Для отвода электри-
чества отъ хромовокислаго полюса слу-
житъ палочка угля.
Элементъ Лекланше (рис. 75),
электроды котораго состоятъ изъ цинка
и перекиси марганца. Въ качествѣ элек-
тролита для него берется обыкновенно
растворъ нашатыря. Перекись марганца
для повышенія ея проводимости смѣши-
ваютъ съ угольнымъ порошкомъ и прес-
суютъ затѣмъ въ видѣ палочки.
Всѣ эти элементы при пользованіи
ихъ электрическими разрядами испыты-
ваютъ настолько значительныя химиче-
скія измѣненія (вслѣдствіе возстановленія высшихъ окисловъ), что
напряженіе ихъ падаетъ.
Элементы съ постояннымъ напряженіемъ получаются, если взять
два металлическіе электрода и погрузить каждый изъ нихъ въ рас-
творъ соли, основаніемъ которой является металлъ погружаемаго
электрода. Такимъ образомъ получаются два неполяризующіе&°элек-
трода- -
Типичной постоянной цѣпью является элемецтт/ Даніеля
(рис. 19 на стр. 61) мѣдь въ мѣдномъ купоросѣ, цинкъ въ цинко-
вомъ купоросѣ. Растворъ цинковаго купороса долженъ оыть весьма
слабымъ, если желательно получить возможноМолѣе высокое напря-
женіе. Для лучшей проводимости къ этому раствору прибавляютъ еще
Непостоянныя и постоянныя цѣпи
199
сѣрной кислоты или какой-либо легко растворяющейся соли. Рас-
творъ мѣднаго купороса долженъ быть возможно болѣе крѣпкимъ,
для чего въ него иногда помѣщаютъ твердые кристаллы мѣднаго ку-
пороса (элементъ Мейдингера). Всѣ измѣненія, происходящія при
пользованіи такою цѣпью, сводятся къ повышенію концентраціи рас-
твора цинковаго купороса и убыли концентраціи мѣднаго купороса
(если она не возстанавливается, какъ при наличности твердыхъ кри-
сталловъ мѣднаго купороса). Эти измѣненія имѣютъ лишь незначи-
тельное вліяніе на напряженіе.
Практически элементъ Даніеля неудобенъ тѣмъ, что въ немъ
цинковый и мѣдный купоросы постепенно диффундируютъ другъ въ
друга; когда же мѣдный купоросъ достигаетъ цинка, то на немъ
образуется осадокъ бурой мѣди. Въ силу этого цѣпь постепенно
ослабляется и потому не можетъ служить нормальнымъ элементомъ,
такъ какъ такой элементъ долженъ удовлетворять условію неизмѣн-
ности напряженія при храненіи его въ теченіе большого промежутка
времени. Въ тѣхъ цѣпяхъ, которыя употребляются въ качествѣ
нормальныхъ элементовъ, положительнымъ электродомъ слу-
житъ ртуть.
Въ кадміевомъ элементѣ Вестона (см. рис. 20) ртутный элек-
тродъ покрытъ пастою изъ плохо растворимой сѣрнокислой ртути
(Н^28О4). Такимъ образомъ, электродъ оказывается погруженнымъ
въ весьма слабый и все- таки всегда насыщенный растворъ своей
собственной соли. Жидкостью въ элементѣ является концентриро-
ванный растворъ сѣрнокислаго кадмія, въ который для поддержанія
въ немъ постоянной концентраціи помѣщаются кристаллы той же
соли. Отрицательнымъ электродомъ служитъ кадміевая амальгама.
Элементъ Кларка построенъ совершенно такъ же, какъ элементъ
Вестона, только въ немъ всюду кадмій замѣненъ цинкомъ. Благодаря
чрезвычайно малой растворимости ртутныхъ солей, въ этихъ элемен-
тахъ удается совершенно избѣгнуть недостатка, свойственнаго эле-
менту Даніеля. Съ другой стороны эта плохая растворимость ртут^^
ныхъ солей влечетъ за собою то неудобство, что элементъ може^©^
давать лишь чрезвычайно слабые токи, такъ какъ иначе ртуі^ые
іоны будутъ расходоваться скорѣе, нежели они получаютоСвслѣд-
ствіе растворенія сѣрнокислой закиси ртути, и кадмій Дили цинкъ)
будетъ доходить до металлической ртути. Послѣ этцг^^напряженіе
элемента падаетъ, и нормальная величина напряженья Получается снова
200
Непостоянныя и постоянныя цѣпи
только спустя значительный промежутокъ времени. Поэтому нор-
мальнымъ элементомъ слѣдуетъ пользоваться такъ, чтобы отъ него
отнимались лишь малые заряды. Такими элементами пользуются для
градуировки электрометровъ или для измѣренія напряженій выше-
описаннымъ (§ 94) компенсаціоннымъ методомъ, при чемъ нормальный
элементъ, конечно, помѣщается въ вѣтвь, лишенную тока.
117. Цѣпи постояннаго напряженія по своей природѣ являются
всегда обратимыми цѣпями. Это значитъ, что химическія превраще-
нія, происходящія для полученія электрической энергіи, всегда можно
заставить совершаться въ обратномъ направленіи, затрачивая электри-
ческую энергію. Когда мы получаемъ токъ отъ элемента Даніеля,
то въ немъ растворяется цинкъ и выдѣляется эквивалентное количе-
ство мѣди. Если же, пользуясь инымъ источникомъ электричества,
напримѣръ, аккумуляторомъ, пропустить черезъ элементъ Даніеля
токъ въ обратномъ направленіи, то будетъ растворяться мѣдь, обра-
зуя вновь мѣдный купоросъ, а на другомъ полюсѣ будетъ выдѣляться
эквивалентное количество цинка изъ раствора цинковаго купороса.
Если напряженіе элемента Даніеля есть V (приблизительно 1 вольтъ),
то при первомъ процессѣ на каждый эквивалентъ раствореннаго цинка
(и на каждый эквивалентъ выдѣленной мѣди) получается электриче-
ская энергія V . Е джулей, гдѣ Р эквивалентный зарядъ. При обрат-
номъ процессѣ это же количество электрической энергіи вызываетъ
выдѣленіе 1 эквивалента цинка и раствореніе 1 эквивалента мѣди.
То же можно сказать и про ртутные нормальные элементы, если
имѣть въ виду крайне слабые токи. Конечно, образующіяся вслѣдствіе
растворенія ртути или кадмія количества соли тотчасъ выдѣляются
изъ концентрированнаго раствора, и поэтому въ нихъ растворы со-
лей не испытываютъ ни малѣйшихъ измѣненій въ концентраціи, такъ
что напряженіе на электродахъ сохраняется абсолютно постояннымъ.
Непостоянныя цѣпи характеризуются тѣмъ, что происходящіе въ
нихъ химическіе процессы не могутъ быть непосредственно обращены.
СВИНЦОВЫЙ АККУМУЛЯТОРЪ.
118. Тогда какъ большинство цѣпей, имѣющихъ хцоложитель-
нымъ электродомъ перекись, принадлежитъ къ числу ^постоянныхъ
цѣпей, свинцовый аккумуляторъ, уже описанный^вѣ § 37, положи-
тельнымъ полюсомъ котораго является перекись свинца (РЬО2), пред-
ставляетъ собою достаточно постоянную ц^р^^
Свинцовый аккумуляторъ
201
Если отъ аккумулятора брать токъ, то свинецъ отрицательнаго
электрода, къ которому устремляются іоны 8О4 разведенной сѣрной
кислоты, превращается въ очень трудно растворимый сѣрнокислый
свинецъ РЬ8О4. Перекись же свинца положительнаго электрода, къ
которой устремляются іоны Н, возстанавливается въ окись свинца РЬО
съ образованіемъ воды, что вмѣстѣ съ сѣрной кислотой даетъ опять
воду и сѣрнокислый свинецъ. Такимъ образомъ на обоихъ электро-
дахъ образуется сѣрнокислый свинецъ, при чемъ одновременно рас-
творъ сѣрной кислоты становится менѣе крѣпкимъ. Свободная энергія,
появляющаяся при окисленіи свинца и возстановленіи перекиси свинца,
равняется V . Л ваттамъ на эквивалентъ, гдѣ V — напряженіе акку-
мулятора г). Это напряженіе, почти постоянно и равняется 2 вольтамъ.
Процессъ можетъ протекать и въ обратномъ направленіи. Если
пропустить черезъ использованный аккумуляторъ электрическій за-
рядъ въ обратномъ направленіи, то на свинцовой пластинкѣ свин-
цовый купоросъ снова возстановится въ свинецъ, а на другой пла-
стинкѣ онъ окислится въ перекись свинца, при чемъ связанная сѣр-
ная кислота снова станетъ свободной.
Этому обстоятельству, главнымъ образомъ, аккумуляторъ обя-
занъ своимъ значеніемъ. Въ немъ можно электрическимъ путемъ
накопить химическую энергію, которая въ любой моментъ можетъ
быть использована опять въ видѣ электрической энергіи.
Аккумуляторъ, такимъ образомъ, представляетъ собою обрати-
мую цѣпь; въ связи съ этимъ находится и постоянство его напря-
женія. Но все-таки обратимость его не вполнѣ совершенна, такъ
какъ при зарядѣ его напряженіе равняется Ѵ' = 2,6 вольтъ. Поэтому
при заряженіи его тратится энергія (V'./7 на эквивалентъ), большая
той, которая получается при его употребленіи (Г V на эквивалентъ).
Отношеніе полученной энергіи къ затраченной равняется
V : V' = 2 : 2,6 = 0,77.
Слѣдовательно, „полезный эффектъ" аккумулятора равняется 77%^
Диффузія и внутреннее разложеніе, происходящія въ элементѣ Дду
ніеля, въ аккумуляторѣ невозможны. Единственная опасность^заШію-
чается въ возможности перегрузить аккумуляторъ; тогда пла-
стинки коробятся и крошатся. Поэтому для каждаго аккумулятора
_________________ ж
Э Р здѣсь, какъ и выше, обозначаетъ эквивалентныйЗарядъ. Прим. пер.
202
Свинцовый аккумуляторъ
нужно точно знать, сколько можно брать отъ него кулоновъ въ се-
кунду. Наконецъ, для пластинокъ вредно, если аккумуляторъ долгое
время остается незаряженнымъ.
Такъ какъ разведенная сѣрная кислота является очень хорошимъ
проводникомъ, а пластинки аккумулятора располагаются близко другъ,
отъ друга, то внутреннее сопротивленіе аккумулятора весьма мало;
этимъ онъ отличается отъ всѣхъ прочихъ элементовъ.
Чтобы построить аккумуляторъ, достаточно опустить двѣ свин-
цовыя пластинки въ разведенную сѣрную кислоту и пропустить токъ
Къ батареѣ
Рис. 76. Заряженіе и разряженіе аккумулятора.
черезъ такой вольтаметръ. Тогда анодъ окисляется въ перекись свинца.
Токомъ такого аккумулятора можно питать маленькую лампочку на-
каливанія (рис. 76). Но горѣніе ея продолжается недолго, такъ какъ
накопленная въ аккумуляторѣ энергія скоро истощается. Чтобы сб>?
общить ему большую „емкость", нужно разрыхлить свинцовы^цла-
стинки, дабы химическія измѣненія глубже въ нихъ проникали. Это
дѣлается такимъ образомъ, что устроенный вышеописаішымть спосо-
бомъ аккумуляторъ разряжаютъ, затѣмъ заряжаютъ ^рУобратномъ
направленіи, снова разряжаютъ, заряжаютъ въ первоначальномъ на-
правленіи, опять разряжаютъ и т. д. Если этуоперацію продѣлы-
вать въ теченіе нѣсколькихъ мѣсяцевъ, то д^Жіьность заряженія и
Свинцовый аккумуляторъ
2оа
разряженія все увеличивается и, наконецъ, такимъ путемъ дости-
гается состояніе, при которомъ дѣйствіе оказывается наилучшимъй
Этотъ процессъ носитъ названіе формированія аккумулятора. Онъ.
былъ примѣненъ впервые Планте (Ріапіё), изобрѣтателемъ аккуму-
лятора. Позже научились сокращать продолжительность процесса фор-
мированія. Для этого прибѣгали, напримѣръ, къ заполненію клѣтокъ
свинцовой рѣшетки порошкомъ окиси свинца (процессъ Тюдора) и
формировали получавшіяся такимъ образомъ пластинки (рис. 77). Такъ
какъ окись свинца сама по себѣ уже имѣетъ рыхлую консистенцію^
то формированіе при этомъ идетъ быстрѣе. Въ современныхъ аккуму-
Рис. 77. Положительная и
отрицательная аккумуляторныя пластины.
ляторахъ обычно положительныя пластинки съ перекисью свинца фор-
мируются по методу Планте, а отрицательныя свинцовыя по ме-
тоду Тюдора. Для достиженія возможно большей емкости важно,,
чтобы пластинки имѣли достаточно большія поверхности. Съ этой
цѣлью пластинки, въ особенности положительныя, различнымъ обра-
зомъ и бороздятся.
ЭЛЕКТРОЛИТИЧЕСКІЙ ВЫПРЯМИТЕЛЬ.
119. Если однимъ изъ электродовъ въ вольтаметрѣ служитъ С;
алюминій, то мы получаемъ удивительное явленіе. Въ качествѣ дру^о -
гого электрода возьмемъ свинцовую пластинку, электролитомъ п^т?
будетъ борнокислая или виннокислая соль какого-нибудь щеточнаго
металла; въ этомъ случаѣ интересующее насъ явленіе дѣлаегсй осо-
бенно замѣтнымъ. Оба электрода соединимъ съ электрр^еѣрОмъ Ган-
келя и, кромѣ того, отведемъ отъ нихъ провода іры коммутатору
тока, соединенному съ источникомъ электричества ^РВяженія около
204
Электролитическій выпрямитель
50 вольтъ. Если мы соединимъ этотъ источникъ съ нашимъ вольта-
метромъ такъ, чтобы алюминій былъ катодомъ, то черезъ вольта-
метръ пройдетъ сильный электрическій токъ, и начнетъ выдѣляться
газъ; при этомъ электрометръ даетъ едва замѣтное напряженіе,
что указываетъ на хорошую проводимость вольтаметра. Но какъ
только мы переключимъ токъ и сдѣлаемъ алюминій анодомъ, обра-
зованіе газа почти совершенно прекращается, т. е. и токъ почти
прекращается, а электрометръ показываетъ почти всю величину на-
пряженія источника тока. Такимъ образомъ вольтаметръ становится
изоляторомъ, по крайней мѣрѣ, для напряженій до 50 вольтъ (рис. 78).
Къ батареѣ
Рис. 78. Выпрямитель.
Болѣе точныя изслѣдованія показали, что, когда алюминій служитъ
въ вольтаметрѣ анодомъ, то онъ покрывается весьма тонкимъ, но со-
вершенно сплошнымъ слоемъ нерастворимаго соединенія аллюминій
(напримѣръ, бористаго алюминія); этотъ слой, какъ кажется, въО^вою
очередь, покрывается слоемъ газа (кислорода), образу ющагрвполнѣ
изолирующую преграду между электролитомъ и электродомъ. При
болѣе высокихъ напряженіяхъ происходятъ разряды ^черезъ газовую
оболочку, и она тогда пріобрѣтаетъ характеръ проводника.
Для не очень высокихъ напряженій описанша^ Вольтаметръ мо-
жетъ служить выпрямителемъ, такъ какъ онъупррпускаетъ электри-
Не водные электролитическіе проводники
205
ческій токъ только въ одномъ направленіи. Въ техникѣ такіе выпря-
мители примѣняются въ случаяхъ, когда имѣется лишь перемѣнный
токъ, а требуется постоянный, напримѣръ, для заряженія аккумуля-
Рис. 79. Преобразованіе перемѣннаго тока въ постоянный.
торовъ. Въ такихъ случаяхъ прибѣгаютъ къ установкѣ изъ четырехъ
выпрямителей, изображенной на рис. 70, гдѣ жирныя черты обозна-
чаютъ алюминіевые электроды.
НЕ ВОДНЫЕ ЭЛЕКТРОЛИТИЧЕСКІЕ ПРОВОДНИКИ.
120. Если растворять солеобразныя соединенія не въ водѣ, но
въ иныхъ жидкостяхъ—алкоголѣ, анилинѣ, бензолѣ, этиловомъ эѳирѣ
и т. д., то будутъ также получаться растворы, проводимость которыхъ
лучше проводимости чистыхъ растворителей. Экспериментально уста-
новлено, что во всѣхъ этихъ случаяхъ прохожденіе тока также со-
провождается электролизомъ. Вода, однако, отличается отъ всѣхъ
прочихъ жидкостей тѣмъ, что растворенныя въ ней соли особенно
хорошо распадаются на іоны, тогда какъ въ другихъ жидкостяхъ
образуется относительно малое число іоновъ. Поэтому явленія элек-
тролитической проводимости особенно замѣтны и отчетливы въ водѣ,€
такъ что, обычно, подъ именемъ электролита разумѣютъ именно вод^У
ный растворъ какой-нибудь соли или кислоты.
Но особенно замѣчательно, что существуютъ и тверды^;Тѣла,,
въ которыхъ проводимость электричества несомнѣнно связана съ пе-
редвиженіемъ іоновъ. Примѣромъ такого тѣла можетъ служить стекло,
являющееся при температурѣ около 300° прекра^^мк проводни-
206
Не водные электролитическіе проводники
комъ. Опыты Варбурга (ХѴагЬиг^) показали, что электрическій токъ
въ стеклѣ сопровождается передвиженіемъ заключающихся въ немъ
-атомовъ натрія въ направленіи переноса положительныхъ зарядовъ,
Варбургъ помѣщалъ, напримѣръ, пробирку съ небольшимъ коли-
чествомъ ртути въ болѣе широкій стеклянный сосудъ, также содер-
жавшій въ себѣ ртуть. При нагрѣваніи до 300° и при достаточномъ
напряженіи на анодной сторонѣ, откуда атомы натрія удалялись, по-
лучался слой почти чистаго кварца (кремневой кислоты), отличаю-
щагося весьма плохой проводимостью, и токъ вскорѣ прекращался.
Когда же онъ бралъ въ качествѣ анода не ртуть, а натріевую амаль-
гаму, то токъ поддерживался часами, при чемъ катодъ, состоявшій
первоначально изъ чистой ртути, все болѣе и болѣе обогащался на-
тріемъ. При количественномъ опредѣленіи прошедшаго черезъ сте-
клянную стѣнку къ катоду натрія, получался точно 1 граммъ-атомъ
на эквивалентный зарядъ. Весь проходившій зарядъ измѣрялся вклю-
ченнымъ въ цѣпь серебрянымъ кулонметромъ.
121. Многія тѣла становятся проводниками, если ихъ нагрѣть
.до размягченія или до плавленія. Такъ, въ техникѣ большую роль
играетъ электрическая проводимость расплавленныхъ щелочныхъ се-
лей (напримѣръ, каменной соли и сильвина). При этомъ на катодѣ
выдѣляется чистый щелочной металлъ и такимъ путемъ его можно
получать въ большихъ количествахъ.
Сильное повышеніе проводимости при размягченіи можно очень
хорошо показать на стеклянной палочкѣ, длиною примѣрно въ
2 см., которая зажата между упругими металлическими полосками,
соединенными съ полюсами батареи. При напряженіи батареи около
200 вольтъ ничего особеннаго не замѣчается. Но если нагрѣть сте-
клянную палочку при помощи бунзеновской горѣлки до краснаго
каленія, то по небольшимъ искоркамъ, перескакивающимъ между
металлическими полосками и стеклянной палочкой въ тѣхъ мѣстахъ,
гдѣ онѣ не плотно соприкасаются, ясно видно, что послѣдняя начи-
наетъ становиться проводникомъ. Если продолжать нагрѣваніе далѣе,
то стекло внезапно раскаляется до-бѣла и начинаетъ д^ускать
ослѣпительный свѣтъ. Послѣ этого можно удалить горѣд|<у^и стекло
не охладится, такъ какъ черезъ него проходитъ сильный электри-
ческій токъ, сообщающій ему такое количество у^ергіи, которое
поддерживаетъ его при температурѣ бѣлаго каленія^ При этомъ стекло
проводитъ токъ такъ хорошо, что въ цѣпь ^приходится ввести со-
» г- _ И
Не водные электролитическіе проводники
207
противленіе, дабы оно не расплавилось совершенно и не начало ка-
пать. Если разсмотрѣть палочку послѣ прохожденія черезъ нее та-
кого тока, то окажется, что концы ея весьма различаются другъ отъ
друга по виду и окраскѣ, т. е. что прохожденіе тока сопровожда-
лось электролизомъ.
Нѣчто сходное съ вышеописанной свѣтящейся стеклянной па-
лочкой представляетъ собою лампа Нернста (Иегизі); главной ея
составною частью является стерженекъ изъ окиси магнія. Прохожде-
ніе тока и здѣсь начинается лишь при накаливаніи стерженька: лампу
Нернста нужно зажигать. Это производится спичкою или какимъ-
либо пламенемъ; въ продажныхъ лампахъ Нернста для большого
удобства имѣется электрическій нагрѣватель — проволочная спираль,
накаливаемая токомъ до-красна и нагрѣвающая при этомъ стер-
женекъ магнезіи до тѣхъ поръ, пока онъ не станетъ пропускать
черезъ себя токъ. Въ этотъ моментъ маленькій механизмъ автомати-
чески выключаетъ нагрѣвающую спираль, и токъ идетъ затѣмъ лишь
по стерженьку (рис. 80). Проводимость и здѣсь имѣетъ электролити-
ческій характеръ, при чемъ съ одной стороны выдѣляется кислородъ,
съ другой — магній. Если лампа горитъ на воздухѣ, то магній тот-
часъ же окисляется кислородомъ воздуха, а кислородъ съ другой
стороны уходитъ въ воздухъ, такъ что никакихъ слѣдовъ электро-
лиза при этомъ не замѣчается. Большимъ недостат-
комъ лампы Нернста является ея большая чувстви-
тельность къ колебаніямъ напряженія тока. Если на-
пряженіе немного понижается, то сила тока умень-
шается, и температура падаетъ. Такъ какъ при по-
ниженіи температуры проводимость магнезіи ухуд-
шается, то сила тока, температура и сила свѣта
быстро падаютъ, и лампа можетъ даже совсѣмъ по-
тухнуть. Еще хуже можетъ отозваться повышеніе на-
пряженія. При этомъ сила тока и температура возра-
стаютъ, стерженекъ становится лучшимъ проводни-
комъ, и вслѣдствіе этого небольшому увеличенію на-
пряженія соотвѣтствуетъ весьма значительное усиленіе
тока. Часто стерженекъ оказывается не въ состояніи
перенести такую силу тока, онъ расплавляется, и лампа
какъ никакая электрическая станція не можетъ поддерживать напря-
женіе строго постояннымъ, то приходится ограждать лампу Нернста
Рис. 80. '
Нернс^аи>
по^гиъря. Такъ
208
Не водные электролитическіе проводники
отъ непріятныхъ послѣдствій колебаній напряженія. Съ этой цѣлью
передъ нитью выключается еще тонкая проволока, играющая роль
„предохранительнаго" сопротивленія, свойства которой при измѣне-
ніяхъ температуры измѣняются обратно свойствамъ магнезіи. Этимъ
отчасти устраняется гибельное дѣйствіе колебаній напряженія, и они
становятся неопасными. Предохранительное сопротивленіе поглощаетъ
много энергіи и потому сильно понижаетъ экономичность лампы, хотя
и при его наличности лампа Нернста все-же остается весьма чув-
ствительной къ колебаніямъ напряженія. Предохранительное сопро-
тивленіе и маленькій механизмъ, выключающій нагрѣвающую спираль,
помѣщаются въ небольшомъ цилиндрическомъ футлярѣ, который на-
ходится надъ самою лампою.
ГЛАВА СЕДЬМАЯ
ЭЛЕКТРОПРОВОДНОСТЬ ГАЗОВЪ
СПОСОБЫ ВЫЗВАТЬ ЭЛЕКТРОПРОВОДНОСТЬ ГАЗОВЪ.
122. Какъ уже было указано въ § 13, опредѣленными сред-
ствами можно сдѣлать проводящими и газы, которые сами по себѣ
являются прекрасными изоляторами.
Однимъ изъ такихъ средствъ является, какъ мы видѣли, горѣніе.
Газы, выдѣляющіеся изъ пламени, представляютъ собою проводники
электричества. Такимъ же образомъ вліяетъ на газъ его соприкосно-
веніе съ раскаленнымъ тѣломъ. Если мы поднесемъ къ заряженному
электрометру Экснера тлѣющую лучинку, то окружающій его воз-
духъ становится проводящимъ и листки его спадаютъ. Такимъ пу-
темъ мы удобно можемъ получать проводящіе газы для точнаго изу-
ченія законовъ ихъ проводимости.
Вторую группу средствъ, служащихъ для достиженія той же
цѣли, представляютъ собою разнаго рода лучи. При прохожденіи
черезъ газъ Рентгеновскихъ лучей, онъ становится проводникомъ
электричества; такъ же дѣйствуютъ ультрафіолетовые лучи весьма
малой длины волны. Послѣдніе лучи сильно поглощаются воздухомъ
и другими газами и потому не находятся въ солнечномъ спектрѣ, но
ихъ много въ свѣтѣ Вольтовой дуги, по крайней мѣрѣ, вблизи нея,
когда проходимый лучами воздушный слой невеликъ. Наконецъ, сюда
относятся нѣкоторые роды лучей, съ которыми мы ближе познако-
мимся при изученіи явленій разряда, именно катодные и закатодныеЛ\>
лучи. Подобные лучи имѣются также и въ природѣ: ихъ саморр^^
извольно испускаютъ радіоактивныя тѣла (уранъ, торій, радій ц^д.).
Если, напримѣръ, мы приблизимъ хорошій препаратъ радія^Хъ за-
ряженному электроскопу примѣрно на Ѵ2 метра, то листки электро-
скопа тотчасъ спадутъ, такъ какъ подъ вліяніемъ радія воз-
Ми. Электричество и магнитизмъ. * 14=
210
Непостоянство проводимости
духъ, окружающій электроскопъ, становится проводящимъ и уноситъ
зарядъ электроскопа.
Третье средство сдѣлать газы проводящими заключается въ элек-
трическихъ разрядахъ. Выше (§ 13) мы познакомились съ дѣйствіемъ
разряда на остріи. Подобнымъ образомъ вообще всякій электриче-
скій разрядъ дѣлаетъ газъ около себя проводящимъ. Если мы, на-
примѣръ, зарядимъ пучокъ бумажекъ на стержнѣ настолько, что
бумажки широко разойдутся, и будемъ по близости получать частыя
искры помощью индукціонной машины, то бумажки въ скоромъ вре-
мени спадутъ, такъ какъ окружающій искры воздухъ становится
проводящимъ.
НЕПОСТОЯНСТВО ПРОВОДИМОСТИ.
123. Приступая къ болѣе тщательному изученію природы явле-
ній проводимости въ газахъ, мы прежде всего должны разрѣшить
слѣдующій вопросъ: сообщается ли газу проводимость на долгое
Къ проду
вателю
Къ землѣ
Рис. 81. Уменьшеніе проводимости воздуха.
Къ большой
батареѣ
время или же онъ снова ее теряетъ, когда причина,у^ызывающая еег
прекращаетъ свое дѣйствіе. Для разрѣшенія этогр^ вопроса будемъ
продувать воздухъ, которому сообщены проволяіщя свойства, черезъ
широкую металлическую трубу (рис. 81) Ді ^будемъ при этомъ опре-
Непостоянство проводимости
211
дѣлятъ его проводимость черезъ опредѣленные промежутки времени.
Для этой цѣли черезъ стѣнку металлической трубы введены внутрь
ея хорошо изолированные небольшіе металлическіе стерженьки, рас-
положенные на одинаковыхъ разстояніяхъ одинъ отъ другого; воз-
духъ при продуваніи послѣдовательно проходитъ мимо нихъ всѣхъ.
Эти стерженьки мы соединяемъ одинъ за другимъ съ заряженнымъ
электрометромъ и наблюдаемъ разряжающее дѣйствіе продуваемаго
воздуха. Чтобы сообщить воздуху проводимость, устанавливаемъ
передъ металлической трубой широкую стеклянную трубку, въ кото-
рой помѣщена толстая платиновая проволока, согнутая спиралью.
Къ послѣдней черезъ стѣнку стеклянной трубки подведены металли-
ческіе провода. При продуваніи воздуха черезъ стеклянную трубку
мы пропускаемъ черезъ платиновую спираль сильный электрическій
токъ, доводя ее до бѣлаго каленія. Если мы соединимъ съ электро-
метромъ первый металлическій стерженекъ, то замѣтимъ, что, какъ
только платиновая спираль накалилась до бѣла, зарядъ электрометра
исчезаетъ. Слѣдовательно, воздухъ при этомъ дѣйствительно стано-
вится проводникомъ. Если мы будемъ соединять съ электрометромъ
болѣе удаленные стерженьки, то найдемъ, что по мѣрѣ удаленія отъ
спирали проводимость воздуха оказывается все меньшей и меньшей.
Если воздухъ достигаетъ стерженька лишь черезъ нѣсколько секундъ,
то движеніе листочковъ электрометра становится едва замѣтнымъ.
Слѣдовательно, по прошествіи нѣсколькихъ секундъ проводимость
воздуха почти совершенно исчезаетъ.
Для того, чтобы газъ проводилъ электричество непре-
рывно, его слѣдуетъ непрерывно подвергать вліянію, со-
общающему ему проводимость.
Проводимость газа, вызванная искусственно, во всѣхъ случаяхъ
оказывается весьма малой. Всегда газъ проводитъ, какъ полупровод-
никъ, напримѣръ, шерсть или дерево.
ІОНЫ ВЪ ВОЗДУХЪ.
124. Мы подходимъ теперь къ основному вопросу: какимъ обра&д?
зомъ газъ можетъ становиться проводникомъ? Многими способами
можно показать, что проводящій воздухъ заключаетъ въ себѣопре-
дѣленныя матеріальныя частицы, переносящія заряды. А^ь^осполь-
зуемся въ качествѣ доказательства этого нижеслѣдующему опытомъ.
Къ описанному въ § 123 аппарату присоединяемъ цилиндрическую
212
Іоны въ воздухѣ
металлическую трубу, помѣщая ее между стеклянной трубой съ пла-
тиновой спиралью и металлической трубой, въ которой изслѣдова-
лась проводимость воздуха (рис. 82). Внутренность этой новой трубы
отчасти заполняетъ изолированный отъ нея и скрѣпленный съ ней
концентрически металлическій стержень. ВмѣстѣШь нимъ труба обра-
зуетъ цилиндрическій конденсаторъ. Снаружи >къ этой трубѣ под-
Іоны въ воздухѣ
213
ведены хорошо изолированные провода, одинъ изъ которыхъ про-
ходитъ черезъ нее насквозь до стержня. Такимъ образомъ можно
легко заряжать цилиндрическій конденсаторъ; мы будемъ пользо-
ваться для этого маленькой батареей приблизительно въ 100 вольтъ-
Если мы доведемъ платиновую спираль до бѣлаго каленія и будемъ
затѣмъ продуваемый воздухъ испытывать на его проводимость по-
мощью перваго стерженька, то найдемъ, что онъ оказывается про-
водящимъ лишь въ томъ случаѣ, когда конденсаторъ не заряженъ.
Но какъ только въ конденсаторѣ возбуждается поле, выходящій изъ
него воздухъ становится совершеннымъ изоляторомъ.
Достаточно сильное электрическое поле уничтожаетъ
ихъ пути,
и такимъ
проводимость газа.
Этотъ результатъ прямо указываетъ на то, что проводимость
газа обусловливается присутствіемъ опредѣленныхъ частицъ, которыя
переносятъ на себѣ заряды и которыя удаляются изъ него (подобно
іонамъ) въ электрическомъ полѣ.
125. Мы можемъ даже перехватить эти частички на
когда онѣ переносятъ заряды въ электрическомъ полѣ,
образомъ убѣдиться въ ихъ су-
ществованіи. Помѣстимъ между
пластинками воздушнаго конден-
сатора пламя Бунзеновской го-
рѣлки съ цѣлью непрерывно со-
общать воздуху проводимость
(рис. 83). Обѣ пластинки конден-
сатора соединяемъ съ полюсами
батареи. Въ такомъ случаѣ между
металлическими пластинками про-
ходитъ постоянный, хотя и очень
слабый токъ; при этомъ частич-
ки, дѣлающія воздухъ проводя-
щимъ, извлекаются электриче-
скимъ полемъ изъ пламени. Если
мы теперь помощью стеклянной
трубки будемъ выдувать воз-
духъ изъ пространства, заклю-
ченнаго между пламенемъ и одной изъ пластинокъ, въ направленіи,
перпендикулярномъ къ силовымъ линіямъ, заставляющій проходить
Къ электро-
метру
Рис. 83. Зарядъ воздух^ф?^
214
Токъ насыщенія
въ небольшую металлическую коробку, дно которой сдѣлано изъ
частой проволочной сѣтки, то эта коробка будетъ все болѣе и бо-
лѣе заряжаться, въ чемъ легко убѣдиться, соединивъ ее съ электро-
метромъ. Такимъ образомъ, выдуваемый воздухъ содержитъ въ себѣ
электрическіе заряды; эти заряды оказываются отрицательными на
сторонѣ положительной пластинки и положительными — на сторонѣ
отрицательной пластинки. .Эти заряды принадлежатъ тѣмъ частич-
камъ, которыя поле извлекло изъ пламени. Эти заряженныя частички,
сообщающія воздуху проводимость, мы будемъ, какъ въ случаѣ
электролита, называть іонами или воздушными іонами.
Проводимость газовъ всегда вызывается присутствіемъ
іоновъ.
ТОКЪ НАСЫЩЕНІЯ.
126. Проводящій газъ, какъ содержащій іоны, можно въ извѣ-
стномъ смыслѣ назвать газообразнымъ электролитомъ. Однако, такой
газъ отличается отъ обычныхъ электролитовъ нѣкоторыми особен-
ностями. Напримѣръ, съ растворомъ соли въ водѣ нельзя было бы
произвести опыта, подобнаго тому, который описанъ въ § 124. Съ
тѣмъ фактомъ, что сильное электрическое поле извлекаетъ изъ про-
водящаго газа всѣ заключающіеся въ немъ іоны, связано еще одно
замѣчательное явленіе, наблюдаемое у газовъ съ малой проводи-
мостью.
Будемъ іонизировать 1) воздухъ между двумя пластинками воз-
душнаго конденсатора помощью помѣщеннаго подъ нимъ препарата
радія (рис. 84); пластинки конденсатора соединимъ сь полюсами не-
большой батареи такимъ образомъ, чтобы имѣть возможность удобно
измѣнять число включенныхъ элементовъ и, слѣдовательно, примѣ-
няемое напряженіе. Въ одинъ изъ проводовъ включимъ какой-нибудь
плохой проводникъ, лучше всего II-образную трубку, наполненную
амиловымъ алкоголемъ, смѣшаннымъ съ небольшимъ количествомъ
іодистаго кадмія, въ который въ качествѣ электродовъ опуцщны
кадміевыя проволочки, чтобы по возможности избѣгнуть ^л&йтроли-
тической поляризаціи. Этотъ растворъ іодистаго кадмія (Проводитъ,
какъ обычный электролитъ, правда, гораздо хуже, ^да-мъ водяной
электролитъ, но въ то же время гораздо лучше^ чѣмъ іонизирован-
ный газъ. Далѣе, можно считать вполнѣ установленнымъ, что ско-
Э Т. е. сообщать проводимость, вызывая образованіе іоновъ. Прим. пер.
Токъ насыщенія
215
ростъ разряда въ этомъ растворѣ („сила тока“), какъ во всякомъ
электролитическомъ проводникѣ, тѣмъ больше, чѣмъ выше напряже-
ніе поля въ немъ. Мы можемъ, не дѣлая большой погрѣшности, при-
нять силу тока въ немъ пропорціональной напряженію поля. Оба
конца трубки съ амиловымъ алкоголемъ соединимъ съ зажимами
квадрантнаго электрометра. Напряженіе, которое будетъ намъ ука-
зывать электрометръ, дастъ намъ мѣру скорости разряда. Беря сна-
ІН"- Высокое на-
Къ батареѣ
Рис. 84. Демонстрація тока насыщенія.
чала малыя напряженія — 20 вольтъ, 40 вольтъ и т. д., мы увидимъ,
что скорость разряда возрастаетъ съ возрастаніемъ напряженія,
приблизительно пропорціонально ему. Но при напряженіяхъ въ 80,
100 и болѣе вольтъ, сила тока уже не возрастаетъ столь же°<
быстро и, наконецъ, достигаетъ опредѣленнаго значенія, котор^
далѣе не возрастаетъ, хотя бы напряженіе достигало 200, 300 в^ьтъ
и болѣе. Эту максимальную величину силы тока въ провидящемъ
газѣ называютъ токомъ насыщенія. Кривая, показывающая зави-
симость силы тока отъ напряженія для проводящаго дана на
216
Токъ насыщенія
рис. 85. Въ настоящихъ же электролитахъ сила тока возрастаетъ съ
возрастаніемъ напряженія безпредѣльно, не достигая никогда макси-
мальнаго значенія.
Различіе въ свойствахъ настоящаго электролита и проводящаго
газа основывается въ сущности на томъ, что въ настоящихъ элек-
тролитахъ образуется безчисленное количество свободныхъ іоновъ, и
разрядъ электричества черезъ нихъ не уменьшаетъ замѣтно числа
іоновъ, между тѣмъ какъ въ газахъ іонизирующій агентъ (напри-
мѣръ, излученіе радія) всегда образуетъ лишь ограниченное число
іоновъ, такъ что сильное электрическое поле почти тотчасъ ихъ всѣхъ
извлекаетъ. Но, конечно, изъ газа при разрядѣ не можетъ выйти за
Рис. 85. Кривая силы тока для проводящаго воздуха.
секунду большее число іоновъ, чѣмъ то, которое образуется за это
время подъ дѣйствіемъ іонизирующаго агента. Поэтому сила тока
можетъ возрастать лишь до тѣхъ поръ, пока не будетъ достигнута
эта величина. Такимъ образомъ, мы приходимъ къ слѣдующему объ-
ясненію явленія тока насыщенія: токъ насыщенія, выраженный
въ кулонахъ на секунду, равняется заряду свободныхъ
іоновъ, образующихся подъ дѣйствіемъ іонизирующаго
агента въ каждую секунду въ пространствѣ, заполненномъ
токомъ.
СТЕПЕНЬ ІОНИЗАЦІИ.
127. Такъ какъ помощью сильнаго электрическаго по^Шожно
быстро удалить изъ воздуха всѣ іоны, то легко опредѣлить коли-
чество содержащихся въ немъ іоновъ. Для этого слѣдуетъ лишь
измѣрить отнятый при этомъ процессѣ отъ возбуЖгелей поля за-
рядъ, что можно сдѣлать электрометрическ^ъЛметодомъ. Чтобы
удобно измѣрять это количество, назовемѣСграммъ - эквивален-
Степень іонизаціи
217
томъ іоновъ такое ихъ количество, которое несетъ на себѣ эквива-
лентный зарядъ (+ 96 540 кулоновъ). Это та же самая единица, ко-
торою мы пользовались для измѣренія количества іоновъ въ настоя-
щихъ электролитахъ.
Вышеописаннымъ методомъ Рётгерфордъ (КиШегіогб) нашелъ
въ воздухѣ, подвергавшемся въ теченіе нѣкотораго времени дѣйствію
Рентгеновскихъ лучей средней интенсивности, непосредственно послѣ
прекращенія излученія, одинаковое количество положительныхъ и отри-
цательныхъ іоновъ, выражающееся въ вышеуказанной мѣрѣ числомъ,
равнымъ +3,4.10—18 граммъ-эквивалента на кубическій сантиметръ.
Мы видѣли ранѣе (§107), что помощью извѣстныхъ физико-
химическихъ методовъ (напримѣръ, опредѣленіемъ пониженія точки
плавленія) можно опредѣлить степень іонизаціи соляныхъ растворовъ.
Въ очень хорошо проводящихъ водныхъ растворахъ количество
іоновъ можно принять равнымъ въ круглыхъ числахъ 10“3 граммъ -
эквивалента на куб. сантиметръ. Конечно, число іоновъ въ этомъ
случаѣ зависитъ отъ концентраціи раствора. Мы привели вышеопи-
санное число лишь для того, чтобы показать, какъ велико число
іоновъ, заключенныхъ въ настоящихъ электролитахъ, по сравненію съ
іонизированнымъ воздухомъ; оно больше въ нѣсколько билліоновъ разъ.
Если опредѣлять число іоновъ не только непосредственно послѣ
дѣйствія іонизирующаго агента, но и потомъ черезъ опредѣленные
промежутки времени, то можно установить законъ убыванія іониза-
ціи. Такимъ путемъ было найдено, что скорость, съ которою
самопроизвольно убываетъ іонизація газа, въ каждый мо-
ментъ пропорціональна второй степени, существующей
въ этотъ моментъ степени іонизаціи.
Такимъ образомъ, если въ куб. сантиметрѣ газа содержатся №
положительныхъ и М отрицательныхъ іоновъ, то убыль іонизаціи за
секунду выражается числомъ а. 7Ѵ2, гдѣ а — константа, имѣющая
для каждаго газа вполнѣ опредѣленное значеніе. Исчезновеніе газо-
выхъ іоновъ въ связи съ закономъ сохраненія зарядовъ можетъ быть 4+
объяснено лишь предположеніемъ, что при этомъ происходитъ
единеніе положительныхъ и отрицательныхъ іоновъ въ незаряженныя
частички. Такъ какъ эти іоны раньше образовались вслѣдствіе рас-
щепленія незаряженныхъ частицъ, то а называютъ коэффиціен-
томъ рекомбинаціи іоновъ въ разсматриваемомъ Т^ѣ. Напри-
мѣръ, для сухого воздуха а = 0,98. ІО18.
218
Скорость переноса іоновъ
Если іонизирующее дѣйствіе не прерывается, то непрерывно
образуются новые іоны и, какъ мы видѣли, измѣряя токъ насыщенія,
мы можемъ опредѣлить скорость образованія іоновъ д. Если мы
опять количество іоновъ будемъ выражать въ граммъ-эквивалентахъ,
то д = : (Л. С), гдѣ — токъ насыщенія (или максимальный токъ),
Р— эквивалентный зарядъ, равный 96 540, С равно объему газа въ
кубическихъ сантиметрахъ. По такой формулѣ д вычисляется на 1 куб.
сантиметръ. При употребленіи Рентгеновскихъ лучей, іонизирующее
дѣйствіе которыхъ выражается вышеуказаннымъ числомъ + 3,4 . ІО-18,
Рётгерфордъ нашелъ д равнымъ 11,3. ІО-18.
Постоянная іонизація воздуха при постоянномъ же дѣйствіи
іонизирующаго агента зависитъ отъ того, что прибыль іоновъ д ком-
пенсируется ихъ убылью а . №. Поэтому, если мы обозначимъ остаю-
щееся постояннымъ число іоновъ въ куб. сантиметрѣ черезъ Л^, то
должно имѣть мѣсто равенство:
д=а. ЛѴ-
Эта формула извѣстна подъ именемъ закона диссоціаціи.
Изъ нея мы находимъ: . Для воздуха (а = 0,98 . ІО18)
при д = 11,3. ІО-18 она, дѣйствительно, даетъ вышеприведенное зна-
ченіе 7Ѵ0 = 3,4 . ІО-18.
СКОРОСТЬ ПЕРЕНОСА ІОНОВЪ.
128. Если въ іонизированной средѣ находятся М граммъ-экви-
валентовъ положительныхъ іоновъ на куб. сантиметръ и всѣ эти
іоны двигаются въ опредѣленномъ направленіи со скоростью см.
въ секунду, то въ средѣ проходитъ электрическій токъ въ РІ .Р .ѵх
кулоновъ въ секунду на кв. сантиметръ; здѣсь Р, какъ обычно,
обозначаетъ эквивалентный зарядъ. Если въ то же время отрица-
тельные іоны, которыхъ, допустимъ, также заключается М граммъ-
эквивалентовъ въ куб. сантиметрѣ, двигаются со скоростью ѵ2 къ
противоположномъ направленіи, то они, со своей стороны, даіютъ
электрическій токъ въ Ы.Р.ѵ2 кулоновъ въ секунду на к&ч^ѣнти-
метръ. Оба тока вмѣстѣ образуютъ токъ / = № Р куло-
новъ въ секунду на кв. сантиметръ.
Согласно вышесказанному, электрическій токъ^дкъ мы это уже
видѣли въ случаѣ электролитовъ (§ 106), состоит^ь^изъ тока поло-
жительныхъ іоновъ и тока отрицательныхъ іоцовъ. Если мы возбу-
Скорость переноса іоновъ
219*
димъ въ іонизированной средѣ электрическое поле, то положитель-
ные іоны будутъ двигаться въ направленіи силовыхъ линій, отрица-
тельные—въ обратномъ направленіи; оба явленія связаны съ тратой
энергіи поля.
Если намъ извѣстна іонизація 7Ѵ, то измѣреніемъ силы тока }
мы можемъ опредѣлить сумму скоростей съ которыми дви-
гаются іоны. Сила тока, т. е. количество электричества, разряжаю-
щееся за секунду, опредѣляется для проводящихъ газовъ электро-
метрическимъ методомъ, такъ какъ при этомъ приходится имѣть дѣло»
съ ничтожно малыми зарядами. Такими измѣреніями былъ устано-
вленъ нижеслѣдующій простой законъ, который ниже намъ опять
встрѣтится въ качествѣ „закона Ома“:
Скорость, съ которою переносятся іоны въ іонизиро-
ванномъ газѣ, пропорціональна силѣ поля.
Скорость, которую пріобрѣтаетъ опредѣленный родъ
, . вольтъ
іоновъ при силѣ поля въ 1 --------> называется просто ско-
см.
ростью переноса этихъ іоновъ.
, Если „скорость переноса“ равняется и, сила поля—Е, то дѣй-
ствительная скорость іона равняется ѵ = и.Е. Поэтому, У = . Е. Е
(«! + ^2)-Если измѣрить силу тока У, напряженіе Е и іонизацію Ы*
то можно вычислить сумму обѣихъ скоростей переноса. Напримѣръ*
для сухого воздуха при атмосферномъ давленіи получается этимъ
путемъ: и2= 3,2® •
Но можно измѣрить въ отдѣльности скорости переноса обоихъ
родовъ газовыхъ іоновъ, такъ какъ легко вполнѣ отдѣлить другъ
отъ друга положительные и отрицательные іоны и затѣмъ изслѣдо-
вать ихъ отдѣльно. Чтобы выяснить возможность такихъ опредѣле-
ній, представимъ себѣ, что іонизированію подвергается только огра-
ниченный слой газа передъ поверхностью одного изъ электродовъ;
тогда въ пространствѣ между этимъ слоемъ и другимъ электродомъ
переносъ заряда совершается лишь тѣми іонами, которые однозначны
съ первымъ электродомъ, и различными способами можно опредѣ^^
лить, съ какою скоростью они проходятъ это пространство. Такимъ
путемъ было установлено, что скорость переноса для двухъ судовъ
іоновъ вообще нѣсколько различна. Для сухого воздуха дфМТ атмо-
сферномъ давленіи получилось для положительныхъ (катіо-
новъ) ик = 1,36, для отрицательныхъ іоновъ (аніон^вѣ)ѵд/А = 1,87.
220
Скорость переноса іоновъ
Сумма этихъ величинъ 3,23 оказывается достаточно близкой выше
приведенной величинѣ 3,20.
Такъ какъ тѣ скорости, съ которыми движутся іоны въ не очень
-слабомъ полѣ, легко можно реализовать механическими средствами,
то движеніе іоновъ можно подвергнуть прямому сравненію съ дру-
гимъ движеніемъ. Съ этой цѣлью газъ, черезъ который проходитъ
электрическій токъ, приводятъ въ движеніе помощью раздуваль-
наго мѣха и опредѣляютъ вліяніе этого движенія на токъ іоновъ.
Такъ какъ общее движеніе газа и происходящее въ немъ движеніе
іоновъ складываются по закону параллелограмма ^скоростей, то та-
кимъ путемъ прямо получается отношеніе скорости іоновъ къ ско-
рости движенія газа. А такъ какъ послѣдняя величина, конечно, легко
можетъ быть измѣрена, то такимъ путемъ опредѣляются также и
величины иА и ик. Такими опытами были получены для этихъ вели-
чинъ тѣ же значенія, что и вышеприведенныя.
Подобныя изслѣдованія производились преимущественно въ
лабораторіи Кэвендиша въ Кэмбриджѣ подъ руководствомъ
Дж. Дж. Томсона.
Ниже мы увидимъ, что возможно совершенно сходными мето-
дами измѣрить скорости переноса іоновъ въ жидкихъ электролитахъ.
Въ качествѣ типичнаго примѣра укажемъ здѣсь, что скорость пере-
с м
носа іона калія равняется и = 0,000670 Въ водѣ іоны испыты-
ваютъ громадное сопротивленіе тренія и потому переносятся съ го-
раздо меньшей скоростью, нежели въ воздухѣ.
ДИФФУЗІЯ ІОНОВЪ.
129. Если описанный въ § 123 опытъ видоизмѣнить такимъ
образомъ, чтобы іонизированный воздухъ продувался не черезъ ши-
рокую трубу, но черезъ узкую трубку или, еще лучше, черезъ пу-
чокъ узкихъ металлическихъ трубокъ, то оказывается, что проводи-
мость воздуха при этомъ падаетъ гораздо быстрѣе, нежели это слѣ^
дуетъ по закону рекомбинаціи (§127). Пучокъ металлическихъ тру-
бокъ является какъ-бы поглощающимъ „іонный газъ“, см^ш^нный
съ воздухомъ.
Это явленіе очень легко объясняется тѣмъ, что іоны; подобно
всякимъ электрически заряженнымъ частичкамъ, приближаясь къ ме-
таллическимъ стѣнкамъ, притягиваются ими въ сил^4 дѣйствія индук-
ціи и удерживаются на нихъ. Металлическая Поверхность абсорби-
Диффузія іоновъ
221
руетъ такимъ образомъ іоны, подобно тому, какъ пропитанная сѣр-
ной кислотой поверхность абсорбируетъ водяной паръ. Это дѣйствіе
усиливается, если абсорбирующая поверхность увеличивается, напри-
мѣръ, если труба, по которой долженъ пройти іонизированный воз-
духъ, замѣняется пучкомъ капиллярныхъ трубокъ.
Такъ какъ самый процессъ абсорбціи протекаетъ безконечно
быстро, то скорость, съ которой абсорбируется газъ, зависитъ исклю-
чительно отъ скорости, съ которой онъ диффундируетъ черезъ за-
полняемое имъ пространство къ абсорбирующей поверхности. Пред-
ставимъ себѣ, напримѣръ, стеклянный колоколъ, заполненный влаж-
нымъ воздухомъ, въ которомъ помѣщенъ широкій сосудъ съ сѣрной
кислотой. Непосредственно надъ сѣрной кислотой воздухъ почти со-
вершенно свободенъ отъ влаги, но въ мѣстахъ, болѣе удаленныхъ
отъ поверхности сѣрной кислоты, водяной паръ исчезаетъ лишь,
медленно, диффундируя въ лишенную влаги область и исчезая тамъ..
Совершенно аналогичный процессъ происходитъ и въ іонизирован-
номъ газѣ, теряющемъ свои іоны благодаря присутствію металличе-
ской поверхности. Математическій анализъ этого явленія далъ воз-
можность по величинѣ скорости абсорбціи іоновъ въ пучкѣ метал-
лическихъ капилляровъ вычислить коэффиціенты диффузіи для
обоихъ родовъ іоновъ.
При продуваніи іонизированнаго воздуха черезъ пучокъ метал-
лическихъ капилляровъ сейчасъ же обнаруживается, что выходящій
изъ нихъ воздухъ заряженъ положительно, а металлическіе капил-
ляры пріобрѣтаютъ отрицательный зарядъ. Иными словами, отрица-
тельные іоны быстрѣе абсорбируются капиллярами, нежели положи-
тельные, т. е. они быстрѣе диффундируютъ къ стѣнкамъ.
Въ іонизированномъ воздухѣ коэффиціентъ диффузіи
отрицательныхъ іоновъ немного больше коэффиціента
диффузіи іоновъ положительныхъ.
Убыль обоихъ родовъ іоновъ была тщательно измѣрена Тоун-
сен домъ (Тохѵпзепсі) въ лабораторіи Кэвендиша; имъ были полу-
чены нижеслѣдующія значенія коэффиціента диффузіи для воздуха :|3О
аніоны.............. 0,043; катіоны.......... 0,028. I
XV
Значеніе этихъ чиселъ слѣдующее. Если п есть концентрація
. ... ХЧГ
іоновъ на куб. сантиметръ, §— градіентъ концентраціи,^ т>е. измѣ-
неніе ея на протяженіи 1 см., ѵ—скорость перенос<ціоновъ въ на-
правленіи градіента концентраціи въ сантиметрахъвъсекунду, т. е.
222
Диффузія іоновъ
•если п . ѵ есть сила тока на кв. сантиметръ, то коэффиціентъ диффу-
зіи 7), значенія котораго выше даны, опредѣляется изъ нижеслѣдую-
щаго уравненія:
ѵ = О-$-.
п
При этомъ выборъ единицы количества іоновъ не играетъ роли,
гакъ какъ эта единица входитъ и въ числителя (^) и въ знамена-
теля (я).
Въ тѣхъ же единицахъ (скорость выражена въ сантиметрахъ въ
секунду) коэффиціенты диффузіи въ воздухъ для нѣкоторыхъ дру-
гихъ газовъ имѣютъ слѣдующія величины:
водородъ............ 0,634 углекислота..........0,134
кислородъ............0,178 пары этиловаго эѳира 0,078.
Итакъ, даже крупныя молекулы паровъ этиловаго эѳира диф-
фундируютъ гораздо быстрѣе, нежели іоны. Отсюда мы съ весьма
значительной вѣроятностью можемъ заключить, что воздушные іоны
представляютъ собою крупныя и сложныя образованія.
Въ воздухѣ, которому искусственно сообщена прово-
димость, іоны представляютъ собою скопленія многихъ
молекулъ около электрически заряженнаго ядра.
То же имѣетъ мѣсто и для всѣхъ прочихъ газовъ. Точно такъ
же мы убѣдимся ниже и въ томъ, что іоны жидкихъ электролитовъ
представляютъ собою сравнительно грубыя частицы.
ЗАРЯДЪ ГАЗЮНА.
130. Очевидно, что скорость диффузіи іоновъ должна нахо-
диться въ связи съ ихъ скоростью переноса. Дѣйствительно, въ
обоихъ случаяхъ аніонъ воздуха оказывается болѣе быстрымъ и въ
обоихъ случаяхъ получается приблизительно одно и то же отноше-
ніе скоростей обоихъ іоновъ. По измѣреніямъ Тоунсенда аніону
диффундируетъ въ 1,5 раза скорѣе катіона, а скорость пвр^нка
•аніона приблизительно въ 1,4 раза превышаетъ скорость ^рерВноса
катіона. Очевидно, что^различіе въ этихъ числахъ зав^сугѣ только
ютъ неизбѣжныхъ ошибокъ наблюденій.
Связь между обѣими скоростями въ сущности СВОДИТСЯ къ тому,
•что обѣ находятся въ тѣсной зависимости отъ сопротивленія тренія,
испытываемаго частичками при ихъ поступательномъ движеніи въ
Зарядъ газіона
223
газѣ. Коэффиціентъ диффузіи можетъ быть, согласно простымъ за-
конамъ механики, вычисленъ по величинѣ сопротивленія тренія, ко-
торое испытываетъ опредѣленное количество (напримѣръ, граммъ-
молекула) диффундирующаго газа при его движеніи черезъ другой
газъ. Удѣльное сопротивленіе тренія, приходящееся на граммъ-моле-
кулу при скорости въ 1 см. въ секунду, мы обозначимъ черезъ 117.
Механика газовъ учитъ, что
гдѣ /?—газовая постоянная, равная 8,31 при вычисленіи въ джуляхъ
и градусахъ, Ѳ — абсолютная температура (Ѳ = 290° при 17° С),
О коэффиціентъ диффузіи. Такимъ образомъ получается, что въ
воздухѣ для аніона 117 = 56 000, для катіона ІІ7 = 86 000.
Скорость переноса въ электрическомъ полѣ также зависитъ отъ
величины 117, но, въ отличіе отъ скорости диффузіи, она зависитъ
также и отъ силы, съ которою поле дѣйствуетъ на іоны, иными
словами, отъ электрическаго заряда іоновъ. Такъ какъ мы вычислили
117 по скорости диффузіи, то по скорости переноса мы можемъ
опредѣлить зарядъ іоновъ. Пусть М обозначаетъ общій зарядъ
граммъ-молекулы іоновъ, т. е. общій зарядъ такого числа іоновъ,
которое равняется числу отдѣльныхъ молекулъ, приходящемуся на
1 граммъ-молекулу. Если сила поля есть Е, то вся сила, дѣйствую-
щая на это количество іоновъ, равняется Е. /И. Если они движутся
со скоростью ѵ = Е. и, то испытываемое ими при этомъ сопроти-
вленіе тренія равняется 117. ѵ = 117. Е . и. Сила и треніе должны на-
ходиться въ равновѣсіи, т. е. должно имѣть мѣсто равенство:
Е.М= 117. ѵ= 117,Е.и.
Отсюда 7И—Ц7.«; вычисленіе даетъ какъ для катіоновъ, такъ и для
аніоновъ въ круглыхъ числахъ /14= 1,10. ІО5 кулоновъ. Эта вели-
чина отличается отъ эквивалентнаго заряда, равнаго 0,97. ІО5 куло-
намъ, примѣрно на 14%, что вполнѣ можно отнести на счетъ оши-
бокъ наблюденій. Поэтому мы можемъ результатъ этихъ измѣреній
выразить равенствомъ М = Е, гдѣ Е - эквивалентный зарядъ.\/Готъ
же результатъ дали и измѣренія надъ многими иными газами^
Число отдѣльныхъ газіоновъ, заключающихся въ
\\ V
граммъ - эквивалентѣ, всегда равняется числу отдѣльныхъ
молекулъ, заключающихся въ граммъ-молекулѣ^
224
Газіоны, какъ ядра тумана
Зарядъ отдѣльнаго газіона равняется заряду одно-
валентнаго электролитическаго іона, т. е. элементарному
количеству электричества.
Такимъ образомъ мы пришли къ весьма важному заключенію»
что и въ вопросѣ о проводимости электричества въ газахъ понятіе
элементарнаго количества электричества сохраняетъ свое значеніе.
коэффиціентъ диффузіи 7)
катіоновъ аніоновъ
0,032 0,035.
ГАЗІОНЫ, КАКЪ ЯДРА ТУМАНА.
131. Какъ мы видѣли въ § 129, маленькія электрическія ча-
стички являются въ газахъ ядрами большихъ скопленій молекулъ.
Различныя молекулы обнаруживаютъ въ различной степени склон-
ность группироваться вокругъ электрическаго ядра; особенно велика
эта склонность, напримѣръ, у молекулъ воды. 1
Для воздуха, содержащаго много водяного пара, измѣренія дали
слѣдующія значенія и и О:
скорость переноса и
катіоновъ аніоновъ
1,37 1,51
Если опять вычислить отсюда зарядъ граммъ-молекулы /И, то
получается М — 1,03 . ІО5. Вѣроятно, небольшія отклоненія значеній
М отъ Е зависятъ отъ того, что при обоихъ опредѣленіяхъ (ско-
рости переноса и диффузіи) воздухъ, а, слѣдовательно, и скопленія
іоновъ не были вполнѣ тожественными. Каждый разъ скорость диф-
фузіи оказывается слишкомъ малой.
Еще болѣе интересныя наблюденія могутъ быть произведены,
если внезапно понизить температуру влажнаго воздуха настолько,
чтобы водяной паръ сконденсировался. Такую быструю конденсацію
удобнѣе всего получать путемъ внезапнаго расширенія воздуха. Для
этой цѣли пользуются достаточно большимъ стекляннымъ сосудомъ
(рис. 86); черезъ хорошо закупоривающую пробку въ него про-
пускается широкая стеклянная трубка. Эта трубка снабжена краномъ
съ широкимъ каналомъ. Чтобы насытить воздухъ въ сосуд^йодя-
нымъ паромъ, въ сосудъ наливается немного воды и потряхиваніемъ
достигается увлажненіе всѣхъ стѣнокъ его. Сначала воздухъ въ со-
судѣ слегка сжимаютъ, вдувая еще немного воздуха черезъ боковую
трубку и сейчасъ же запирая ее. Выждавъ затѣей ^ѣкоторое время,
пока температура, слегка повысившаяся при сжатіи, не выравняется
вновь, внезапно открываютъ большой крацѣО Температура момен-
Газіоны, какъ ядра тумана
225
тально понижается, и насыщенный водяной паръ оказывается пере-
охлажденнымъ. Чтобы ясно видѣть, что при этомъ происходитъ въ
сосудѣ, его возможно ярче освѣщаютъ, напримѣръ, помощью про-
экціоннаго фонаря, и разсматриваютъ его на темномъ фонѣ. Если
въ сосудѣ находятся частицы пыли, то онѣ становятся ядрами ту-
мана. Такимъ образомъ, при охлажденіи образуется туманъ, медленно
Рис. 86.
Газіоны, какъ ядра тумана.
дно сосуда. Если повторять опытъ нѣт^;
то постепенно всѣ пылинки опустятсяна
затѣмъ опускающійся на
сколько разъ подъ рядъ,
дно и при дальнѣйшихъ охлажденіяхъ воздухъ сохраняетъ |(;свою
прозрачность, такъ какъ капельки тумана могутъ образовываться
только на болѣе или менѣе крупныхъ частичкахъ, заключающихся
въ воздухѣ. Въ случаѣ отсутствія такихъ частичекъ, |0Дйной паръ,
дѣйствительно, становится переохлажденнымъ или ^пересыщеннымъ.
Ми. Электричество и магнитизмъ.
15
226
Газіоны, какъ ядра тумана
Когда это достигнуто, въ сосудъ вводятся іоны; удобнѣе всего для
этого слегка понизить давленіе въ сосудѣ и затѣмъ дать войти въ
него воздуху, прошедшему мимо накаленной проволоки или тлѣю-
щей лучинки. Если теперь снова, какъ можно быстрѣе, произвести
охлажденіе, то образуется плотный туманъ. Слѣдовательно, іоны, въ
моментъ открытія крана все еще находящіеся въ сосудѣ въ боль-
шомъ количествѣ, образуютъ собою центры сгущенія тумана. Когда
вода осаждается на находящихся въ воздухѣ іонахъ, небольшія мо-
лекулярныя скопленія превращаются въ замѣтныя капельки тумана.
132. Паръ кипящей воды, вырывающійся черезъ узкое отверстіе,
въ моментъ своего выхода изъ него слегка расширяется, такъ какъ
внутри сосуда долженъ быть избытокъ давленія, подъ вліяніемъ ко-
тораго паръ прогоняется черезъ отверстіе. Съ этимъ расширеніемъ
также связано переохлажденіе и, слѣдовательно, образованіе тумана.
Можно и въ такой струѣ пара наблюдать іонный туманъ, если, на-
примѣръ, приблизить къ ней тлѣющую лучину. Туманъ станетъ въ
этомъ случаѣ плотнѣе и бѣлѣе. Еще отчетливѣе выступаетъ это дѣй-
ствіе іоновъ, если въ трубку съ паромъ помѣстить небольшой искро-
мѣръ такъ, чтобы паръ увлекалъ за собою большое число іоновъ,
образующихся въ искрѣ. Интересное явленіе наблюдается при вы-
пусканіи пара черезъ оба противоположныя отверстія Т-образной
трубки, въ которой, какъ разъ въ мѣстѣ ея раздвоенія, помѣщенъ не-
большой искромѣръ (рис. 87). Для полученія искръ удобнѣе всего
воспользоваться машиною, о которой мы еще не говорили и кото-
рая будетъ описана лишь въ послѣдующихъ главахъ этой книги,
именно индукторіемъ. Этотъ аппаратъ доставляетъ при высокомъ
напряженіи большія количества электрическихъ зарядовъ, нежели
электрическая машина; поэтому его употребленіе позволяетъ не за-
ботиться о тщательной изоляціи, которой всегда затруднительно до-
стигнуть при работахъ съ водянымъ паромъ. Для послѣдующаго намъ
пока достаточно знать, что индукторій также имѣетъ положительной
и отрицательный полюсы, и что между ними такъ же проскакиваютъ
искры, какъ и между полюсами электрической машины. Ееди'мы бу-
демъ выпускать паръ изъ обоихъ отверстій Т-образной трубки, то,
пока искры не проскакиваютъ, мы замѣтимъ образованіе слабаго сѣ-
раго тумана. Но какъ только мы приведемъ въ д^йр'віе индукціон-
ный аппаратъ, туманъ становится, благодаря дѣйствію іоновъ, плот-
нымъ и бѣлымъ. У
Газіоны, какъ ядра тумана
227
Если мы тщательно позаботимся о томъ, чтобы водяной паръ
выходилъ при не слишкомъ большомъ давленіи, то мы сможемъ за-
мѣтить, что обѣ струи его выглядятъ не совсѣмъ одинаково. Одна
изъ нихъ даетъ болѣе плотныя туманныя образованія, нежели дру-
гая. Легко убѣдиться въ томъ, что это различіе находится въ зави-
симости отъ различія знаковъ обоихъ искровыхъ электродовъ. Дѣй-
ствительно, если переключить полюсы индукціоннаго аппарата, что
можно съ большою быстротою сдѣлать помощью особаго приспо-
собленія, то струи обмѣниваются своими свойствами. При этомъ
всегда та струя пара, которая выходитъ со стороны положительнаго
искрового электрода, оказывается содержащей болѣе густой туманъ.
Рис. 87. Іоны въ струѣ пара.
Логически необходимымъ выводомъ изъ этого опыта является
заключеніе, что положительные и отрицательные іоны слегка разли-
чаются другъ отъ друга по своей способности образовывать туманъ.
Поле, образующееся вокругъ искровыхъ электродовъ, вызываетъ
частичное раздѣленіе іоновъ. Со стороны положительнаго электрода
получается избытокъ отрицательныхъ іоновъ, съ противоположной
стороны —избытокъ положительныхъ іоновъ. Выше описанный опытъ/, _
показываетъ, что при не очень сильномъ переохлажденіи не всѣ Іоны
становятся центрами туманнаго сгущенія (иначе туманъ должец^былъ
бы одинаково образовываться съ обѣихъ сторонъ), но п^ймуще-
ственно, а можетъ быть и исключительно, отрицательны^Волѣе тща-
15
228
Счетъ іоновъ, находящихся въ воздухѣ
тельныя изслѣдованія привели Вильсона (С. Т. К АѴіІзоп) къ слѣ-
дующему заключенію: при самомъ маломъ переохлажденіи,
которое только вообще можетъ вызвать образованіе ту-
мана, играютъ роль, въ качествѣ центровъ туманнаго сгу-
щенія, лишь отрицательные іоны и притомъ всѣ; при нѣко-
торомъ же вполнѣ опредѣленномъ болѣе значительномъ пе-
реохлажденіи къ нимъ присоединяются и положительные
іоны.
Различіе между положительными и отрицательными іонами вы-
ясняется уже изъ наблюденій надъ скоростями переноса во влажномъ
, • иА 1,87 л .
воздухѣ. Отношеніе — для сухого воздуха равняется- 1,4; для
1,оО
1,51 , , гл
влажнаго же воздуха оно равняется = 1,1. Отсюда ясно видно,
1,0/
что уже въ не переохлажденномъ водяномъ парѣ сначала нагру-
жаются водяными молекулами именно отрицательные іоны.
СЧЕТЪ ІОНОВЪ, НАХОДЯЩИХСЯ ВЪ ВОЗДУХЪ.
133. То обстоятельство, что воздушные іоны являются види-
мыми центрами туманнаго сгущенія, Дж. Дж. Томсонъ использо-
валъ для ихъ счета. Сдѣлать это, конечно, не просто, и Дж. Дж.
Томсонъ долженъ былъ сперва придумать весьма остроумные методы
для такого счета. Здѣсь намъ достаточно знать, что сдѣлать это ему
удалось 2). Для воздуха, іонизированнаго лучами радія, при наимень-
шемъ охлажденіи, которое только вызывало образованіе тумана,
Томсонъ нашелъ, какъ среднее изъ многихъ опредѣленій, что въ
]) Томсонъ сдѣлалъ это опредѣленіе, допустивъ, что каждый іонъ ста-
новится центромъ одной водяной капельки. Поэтому его задачей было со-
считать число образующихся при переохлажденіи капелекъ. Для этой цѣли
онъ опредѣлялъ общую массу всѣхъ капелекъ, т. е. массу всего образовы-
вавшагося облака и массу отдѣльной капельки. Отношеніе этихъ двухъ ве-
личинъ и давало искомое число капелекъ. Общую массу капелекъ онъ могъ
опредѣлить, зная повышеніе температуры воздуха при образованіи тумана,
теплоемкость воздуха при постоянномъ объемѣ и скрытую теплоту ^іспаренія
воды. Массу отдѣльной капельки онъ могъ опредѣлить по веліідіфѣ ея діа-
метра, принимая самую капельку за шаръ. Для опредѣленія послѣдней вели-
чины Томсонъ воспользовался формулой, связывающей величину скорости
паденія тяжелаго шара въ вязкой средѣ съ діаметромъшара и коэффиціен-
томъ вязкости среды. Коэффиціентъ вязкости воздуха ему былъ извѣстенъ,
а скорость паденія капелекъ онъ опредѣлялъ непосредственно, наблюдая за
опусканіемъ верхней границы туманнаго облака/^ Прим. перев.
Счетъ іоновъ, находящихся въ воздухѣ
229
кубическомъ сантиметрѣ содержится 30000 капелекъ тумана; при
болѣе сильномъ охлажденіи ихъ число увеличивается до 65000 въ
куб. сантиметрѣ. Первое число — число отрицательныхъ іоновъ —
оказывается приблизительно вдвое меньшимъ второго — числа всѣхъ
іоновъ. Уже эти числа показываютъ, что ошибки наблюденій мо-
гутъ быть довольно велики. При этомъ можно сказать напередъ,
что получающіяся при такихъ опытахъ числа всегда болѣе или менѣе
превышаютъ истинное число іоновъ. Это становится понятнымъ, если
обратить вниманіе на то, что при процессѣ іонизаціи всегда про-
исходятъ также нѣкоторыя химическія явленія, въ результатѣ кото-
рыхъ образуются въ воздухѣ болѣе крупныя твердыя или жидкія
частички; эти частички, не представляющія собою іоновъ, также
оказываются центрами туманныхъ образованій. Такихъ частичекъ
образуется особенно много при іонизаціи крайними ультрафіолето-
выми лучами; лучи радія, кажется, вызываютъ менѣе значительное
ихъ образованіе. Но, во всякомъ случаѣ, дѣйствительное число всѣхъ
іоновъ должно быть нѣсколько меньше 65000, и, вѣроятно, число
отрицательныхъ іоновъ также меньше 30000.
Измѣреніемъ тока насыщенія была опредѣлена въ томъ же
объемѣ воздуха скорость іонизаціи, вызываемой лучами радія, и эта
скорость была разсчитана на кубич. сантиметръ. Такъ какъ коэф-
фиціентъ рекомбинаціи для воздуха извѣстенъ, то отсюда можно
было вычислить постоянную іонизацію /Ѵо = Опыты Томсона
дали въ электрохимической системѣ мѣръ, которую мы все время
употребляемъ въ этой книгѣ, 7Ѵ0 = 3,6.10^20 , граммъ-эквивалента
положительныхъ іоновъ въ куб. сантиметрѣ и такое же число для
отрицательныхъ.
Отсюда, дѣля 30000 на 3,6.10~20, мы получаемъ число іоновъ
въ одномъ граммъ-эквивалентѣ:
0,833. ІО24.
Согласно сказанному въ § 130, это число М должно предста-
влять собою также и число молекулъ [въ одной граммъ - молекулѣ.
Вычисленія Планка, основанныя на законѣ излученія, дали, какъэтО
уже было выше упомянуто (§ 106) '
0,6175. ІО24.
Поэтому мы можемъ предположить, что изъ 30 000 о ^считан-
ныхъ капелекъ тумана приблизительно четверть образовались не на
іонахъ, а три четверти на отрицательныхъ іонахъ,
230
Атмосферное электричество
АТМОСФЕРНОЕ ЭЛЕКТРИЧЕСТВО.
134. Уже давно было извѣстно, что и обычный атмосферный
воздухъ не представляетъ собою совершеннаго изолятора. Болѣе
точныя данныя по этому вопросу мы имѣемъ благодаря изслѣдова-
ніямъ, произведеннымъ за послѣднее время преимущественно Эль-
стеромъ (Еізіег) и Гейтелемъ (Сеііеі). Эти изслѣдователи соеди-
няли съ хорошо изолированнымъ электрометромъ металлическое
тѣло съ большой поверхностью, которое выставлялось на воздухъ
и притомъ такъ, чтобы оно не касалось никакого другого тѣла (рис. 88).
Рис. 88. Электрометръ Эльстера и Гей теля.
При этихъ условіяхъ электрометръ по прошествіи нѣсколькихъ ча-
совъ терялъ сообщенный ему зарядъ, тогда какъ при отсутствіи ме-
таллическаго тѣла онъ сохранялъ бы постоянное напряженіе,/вѣро-
ятно, въ теченіе цѣлаго дня.
Произведя большое число опытовъ, Эльстеръ и ^й'тель до-
казали, что проводимость обыкновеннаго атмосфернаго/воздуха нужно
приписать тому обстоятельству, что въ немъ всегда/содержится ни-
чтожное количество тѣхъ самыхъ іоновъ, которые образуются въ немъ
въ большихъ количествахъ при примѣнены вписанныхъ въ §122
методовъ. Это содержаніе іоновъ въ воздухѣ отнюдь не является
Атмосферное электричество
231
постояннымъ; оно измѣняется во времени и въ пространствѣ и, въ
виду важности его изученія для метеорологіи, были построены аппа-
раты, позволяющіе измѣрять его примѣрно съ той же степенью точ-
ности, съ какой при помощи гигрометра измѣряютъ содержаніе водяного
пара въ воздухѣ.
Изслѣдованія показали, что въ погребахъ и пещерахъ воздухъ
содержитъ больше іоновъ, нежели въ свободной атмосферѣ; въ по-
слѣдней же всегда заключается нѣсколько большее количество іоновъ,
когда барометръ падаетъ, нежели тогда, когда барометръ повышается.
Послѣднее обстоятельство зависитъ отъ того, что при паденіи да-
вленія воздухъ изъ почвы черезъ небольшія капиллярныя поры и
щели поднимается вверхъ. Ниже мы увидимъ, что это обычно на-
блюдаемое явленіе объясняется постояннымъ образованіемъ въ почвѣ
весьма малыхъ количествъ радіоактивнаго газа, называемаго „эмана-
ціей*', который, смѣшиваясь съ воздухомъ, непрерывно сообщаетъ ему
слабую іонизацію.
Эльстеру и Гейтелю удалось съ іонами, содержащимися въ
обыкновенномъ воздухѣ, воспроизвести почти всѣ вышеописанные
опыты. Такъ, напримѣръ, при продуваніи воздуха черезъ пучокъ
капиллярныхъ трубокъ оказалось, что по выходѣ изъ нихъ воздухъ
обладалъ слабымъ положительнымъ зарядомъ, тогда какъ самые ме-
таллическіе капилляры заряжались отрицательно. Этотъ результатъ,
совпадающій съ полученнымъ въ § 129, весьма важенъ для ученія
объ атмосферномъ электричествѣ. Какъ мы видѣли, воздухъ, подни-
мающійся изъ земныхъ полостей черезъ малыя капиллярныя щели въ
почвѣ, особенно хорошо іонизированъ. Поэтому при переходѣ въ
атмосферу онъ непремѣнно долженъ содержать въ себѣ нѣкоторый
избытокъ положительныхъ іоновъ, тогда какъ земная поверхность
должна при этомъ пріобрѣтать отрицательный зарядъ. Въ этомъ и
заключается причина, по которой земля всегда окружена описаннымъ
въ § 44 электрическимъ полемъ. Понятно, что сила этого поля не
можетъ превзойти опредѣленной предѣльной величины, такъ какъ
подъ вліяніемъ этого поля положительные іоны стремятся вернуться
къ земной поверхности, и, чѣмъ сильнѣе поле, тѣмъ значительнѣе это3
стремленіе.
Къ этимъ явленіямъ присоединяются еще иныя, такж^|діяющія
на электрическое поле въ атмосферѣ. Когда влажный воздухъ ниж-
нихъ слоевъ переносится восходящими токами въ области болѣе низ-
232
Атмосферное электричество
каго давленія, то онъ расширяется и, вслѣдствіе этого, охлаждается;
при этомъ изъ водяного пара образуются водяныя капельки обла-
ковъ и дождя совершенно такъ же, какъ въ опытѣ, описанномъ въ
§131. Центрами сгущенія капелекъ служатъ отчасти частицы пыли,
носящейся въ воздухѣ, отчасти же отрицательные іоны. Поэтому
обычныя дождевыя капли оказываются либо незаряженными, либо
заряженными отрицательно. Это обстоятельство также усиливаетъ
отрицательный зарядъ земли, такъ какъ положительные заряды оста-
ются въ воздухѣ.
135. Иное явленіе происходитъ, однако, въ томъ случаѣ, когда
токъ воздуха поднимается вверхъ съ очень большою скоростью. Такъ
какъ въ этомъ случаѣ, вслѣдствіе быстраго расширенія, охлажденіе
можетъ быть весьма значительнымъ, то и положительные іоны мо-
гутъ оказаться центрами сгущенія капель. Поэтому капли ливней,
образующихся такимъ путемъ при быстромъ подъемѣ воздуха, часто
оказываются заряженными положительно. Такіе быстро поднимаю-
щіеся токи воздуха чаще всего образуются въ лѣтнее время, когда
земля очень сильно нагрѣвается солнечнымъ лучеиспусканіемъ и за-
тѣмъ, подобно печи, доводитъ до высокой температуры прилежащіе
къ ней нижніе слои воздуха, въ то время какъ верхніе его слои
остаются ненагрѣтыми. Такимъ образомъ атмосфера оказывается въ
неустойчивомъ равновѣсіи, и легко можетъ случиться, что весь воз-
душный океанъ въ томъ мѣстѣ, гдѣ образовалось описанное темпе-
ратурное распредѣленіе, такъ сказать, опрокинется, т. е. верхніе хо-
лодные слои воздуха и нижніе горячіе весьма быстро обмѣняются
своими мѣстами. Это могущественное явленіе представляетъ собой
то, что называютъ грозою. Часто „опрокидываніе" начинается около
одного края такой воздушной области съ неустойчивымъ равновѣ-
сіемъ и распространяется оттуда подобно волнѣ. Когда горячій воз-
духъ у земной поверхности, въ нашихъ странахъ всегда содержащій
очень много водяного пара, поднимается, то въ сравнительно низ-
кихъ слояхъ при первоначальномъ его расширеніи и охлажденіи
образуются водяныя капли на отрицательныхъ іонахъ. Подъ вліяніемъ
своего вѣса онѣ отстаютъ отъ потока воздуха, который поднимается
выше уже положительно заряженнымъ. Въ верхнихъ ^слояхъ атмо-
сферы послѣ новаго и болѣе сильнаго, чѣмъ раньше^нёреохлажде-
нія, вода осаждается на положительныхъ іонахъ фрѳдумается поло-
жительно заряженное облако. Извѣстно, что облака, образовавшіяся
Свѣтовыя явленія при іонизаціи
233
путемъ быстраго расширенія—грозовыя тучи —могутъ обладать чрез-
вычайно сильными зарядами. Между двумя облаками, заряженными
разноименными электричествами, или между заряженными облаками
и землею и происходятъ мощные разряды съ молніей и громомъ.
СВЪТОВЫЯ ЯВЛЕНІЯ ПРИ ІОНИЗАЦІИ.
136. Если вблизи газа, іонизируемаго лучами радія или Рент-
геновскими лучами, помѣстить фотографическую пластинку, притомъ
такъ, чтобы она не подвергалась дѣйствію самаго іонизирующаго
агента, то она все-таки почернѣетъ. Спеціальные опыты пока-
зали, что почернѣніе пластинки вызывается свѣтовыми лучами, пре-
имущественно ультрафіолетовыми, которые испускаетъ газъ. Если
іонизирующее дѣйствіе весьма сильно, какъ это бываетъ, напримѣръ,
при іонизаціи лучами радія въ непосредственной близости отъ радіо-
активнаго препарата, то свѣченіе воздуха можно замѣтить и гла-
зомъ. Изслѣдованія спектра свѣтящагося воздуха показали, что испу-
скаемый воздухомъ свѣтъ тождественъ со свѣтомъ, испускаемымъ
Гейсслеровой трубкой, наполненной азотомъ. Эти изслѣдованія
указываютъ на то, что, вѣроятно, всякое явленіе іонизаціи
газа связано со свѣтовыми явленіями.
ГЛАВА ВОСЬМАЯ
ТИХІЙ РАЗРЯДЪ
ІОНИЗАЦІЯ, КАКЪ СЛѢДСТВІЕ СТОЛКНОВЕНІЙ ІОНОВЪ.
137. До сихъ поръ мы изучали электрическій токъ въ газахъ,
іонизируемыхъ спеціальнымъ агентомъ, такъ сказать, извнѣ. Теперь
мы переходимъ къ явленіямъ, обнаруживающимся, когда электриче-
ское напряженіе въ полѣ тока само является причиной, вызывающей
іонизацію. Единственнымъ условіемъ, необходимымъ для того, чтобы
напряженіе поля оказывало такое дѣйствіе, является превышеніе имъ
опредѣленнаго минимальнаго значенія.
Для того, чтобы опытъ, описанный въ § 126, удался, т. е. чтобы
мы получили въ іонизированномъ воздухѣ между двумя металличе-
скими пластинками токъ насыщенія, остающійся постояннымъ при воз-
растаніи напряженія, мы не должны дѣлать напряженіе между этими
пластинками слишкомъ высокимъ. Если же мы его доведемъ до нѣ-
сколькихъ сотъ, наконецъ, до тысячи вольтъ и выше, то мы уви-
димъ, что сила тока сначала медленно, а затѣмъ все быстрѣе и быстрѣе
возрастаетъ, переходя за найденную нами величину тока насыщенія;
наконецъ, она становится настолько значительной, что уже не мо-
жетъ быть измѣрена описаннымъ въ § 126 способомъ. Это ясно
видно изъ кривой силы тока, изображенной на рис. 89. Замѣча-
тельно, что возрастаніе силы тока идетъ тѣмъ быстрѣе, чѣмъ больше
іоновъ вызываетъ внѣшній іонизирующій агентъ (напримѣръ, излу-
ченіе радія) самъ по себѣ.
Ясно, что здѣсь мы имѣемъ дѣло съ іонизирующимъ дѣйствіемъ
самыхъ подвижныхъ іоновъ. Въ самомъ дѣлѣ, это явленіе ненасту-
паетъ, если іоновъ вовсе нѣтъ или если скорость имѣющіф^іоновъ
не перешла извѣстнаго предѣла. Величина этого дѣйсуьІй’ зависитъ,
во-первыхъ, отъ количества іоновъ, приходящагося сч? самаго начала
на кубическій сантиметръ, и, во-вторыхъ, отъ си^ршоля, т. е. отъ
скорости іоновъ. Это новое іонизирующее дѣйствіе проще всего
объясняется, если принять, что іонъ, сталкиваясь, при достаточной
Іонизація, какъ слѣдствіе столкновеній іоновъ
235'
его скорости съ молекулой, можетъ расщепить ее на іоны. Поэтому
такое дѣйствіе называютъ іонизаціей посредствомъ столкнове-
нія іоновъ.
Какъ только при производствѣ вышеописаннаго опыта мы уда-
лимъ іонизирующій агентъ (напримѣръ, лучи радія), токъ прекра-
щается. Хотя при высокихъ напряженіяхъ большая часть іоновъ обра-
Рис. 89. Кривая силы тока при столкновеніяхъ іоновъ.
зовывается вслѣдствіе столкновеній, токъ все же совершенно исче-
заетъ, какъ только прекращается іонизація извнѣ. Для своего раз-
витія токъ нуждается, слѣдовательно, въ томъ сравнительно неболь-
шомъ числѣ іоновъ, которое образуется подъ вліяніемъ первоначаль-
наго іонизирующаго агента.
Но существуютъ также и продолжительные вполнѣ „самостоя-
тельные" разряды черезъ газъ, при которыхъ токъ самъ играетъ
также и роль этого первоначальнаго іонизирующаго агента.
ТИХІЙ РАЗРЯДЪ ВЪ РАЗРѢЖЕННЫХЪ ГАЗАХЪ.
138. Особенности вполнѣ самостоятельнаго разряда удоб^і^рй от-
четливѣе всего можно наблюдать въ разрѣженныхъ газахър Поэтому
мы съ этого случая и начнемъ.
Возьмемъ достаточно широкую стеклянную т^Йку, приблизи-
тельно въ метръ длины, закрытую съ обѣихъ стрронъ. Черезъ оба
236
Тихій разрядъ въ разрѣженныхъ газахъ
ея конца проходятъ внутрь впаянныя платиновыя проволоки, сна-
бженныя снаружи зажимами, а внутри электродами, лучше всего алю-
миніевыми. На рис. 90 представлена такая трубка, при чемъ одинъ
ея электродъ имѣетъ форму пластинки, другой — форму стерженька.
Къ этой широкой трубкѣ должна быть присоединена еще трубка,
ведущая къ воздушному насосу, чтобы можно было достигать тре-
буемаго разрѣженія. Соединимъ теперь электроды съ мощнымъ источ-
никомъ электричества, напримѣръ, съ батареей аккумуляторовъ, имѣю-
щей напряженіе въ нѣсколько тысячъ вольтъ. Между батареей и
однимъ изъ электродовъ слѣдуетъ, кромѣ того, ввести плохой про-
водникъ, напримѣръ, достаточно узкую, наполненную водой трубку-
„жидкое сопротивленіе14, какъ мы будемъ обычно для краткости вы-
ражаться, чтобы сила тока не была чрезмѣрно большой.
Къ воздушному
насосу
Рис. 90. Тихій разрядъ со слоистой свѣтовой колонной.
Если мы теперь соединимъ электроды трубки съ батареей и
приведемъ въ дѣйствіе воздушный насосъ, то при опредѣленной сте-
пени разрѣженія мы внезапно замѣтимъ въ трубкѣ свѣтовое явленіе*
Изъ одной точки анода выходитъ узкій красный пучекъ свѣта, про-
ходящій черезъ всю трубку почти до катода, гдѣ онъ обрывается.
Противъ его конца на катодѣ находится сравнительно широкое го-
лубоватое свѣтлое пятно. Одновременно со свѣтовымъ явленіемъ
происходитъ и электрическій разрядъ, въ которомъ сила тока всегда
оказывается значительно большей, нежели та наибольшая сила тока/
которая можетъ оказаться въ искусственно іонизируемыхъ г§з&хъ.
Части свѣтового явленія, связаннаго съ разрядомъ, называютъ пр/іо-
жительной свѣтовой колонной и отрицательнымъ^тлѣю-
щимъ свѣтомъ. Темное промежуточное пространство мфжду ними
называютъ, въ отличіе отъ другого темнаго простцавфва, съ кото-
рымъ мы познакомимся ниже, внѣшнимъ темньі^ъ простран-
ствомъ или же (по имени открывшаго его ученаго^) темнымъ про-
Тихій разрядъ въ разрѣженныхъ газахъ
237-
странствомъ Фарадэя. Самый разрядъ въ такой формѣ носитъ
названіе тихаго разряда.
Если мы будемъ продолжать эвакуацію трубки, то замѣтимъ
во-первыхъ, что положительная свѣтовая колонна становится шире,
дѣлается болѣе размытой и менѣе яркой, во-вторыхъ, что отрица-
тельный тлѣющій свѣтъ все болѣе и болѣе распространяется по по-
верхности катода, и въ то же время занимаетъ все большее про-
странство и становится расплывчатымъ, въ - третьихъ, что темное
промежуточное пространство между положительной свѣтовой колон-
ной и отрицательнымъ тлѣющимъ свѣтомъ становится все больше и
больше. Когда, наконецъ, давленіе газа опускается примѣрно до
1 мм. ртутнаго столба, то положительная свѣтовая колонна запол-
няетъ трубку по всей ея ширинѣ, отрицательный тлѣющій свѣтъ
окружаетъ весь катодъ, подобно растянутой голубоватой свѣтовой
туманности, а между ними находится большое темное пространство
Фарадэя. Весьма часто при такихъ разрѣженіяхъ положительная
свѣтовая колонна распадается на рядъ отдѣльныхъ сегментовъ, по-
добно позвоночному столбу (рис. 90). Эти отдѣльныя части назы-
ваютъ слоями, и въ этомъ случаѣ говорятъ о слоистой свѣтовой
колоннѣ (или о стратификаціи свѣта). Со стороны, обращенной
къ катоду, слои свѣтлы и рѣзко ограничены, съ другой же стороны:
слабѣе и болѣе размыты; часто они бываютъ искривлены и всегда
при этомъ обращены выпуклостями въ сторону катода.
При изслѣдованіи свѣтовыхъ явленій, сопровождающихъ тихій
• разрядъ, съ помощью спектроскопа, всегда наблюдаются спектры,
характерные для газа, заполняющаго трубку. Эти спектры могутъ
быть разнаго рода; иногда преимущественно выступаетъ полосатый
спектръ, иногда же преобладаютъ линіи линейчатаго спектра. Отсюда
легко понять, почему въ различныхъ мѣстахъ трубки свѣтъ можетъ
имѣть столь разнообразные виды, какъ свѣтовая колонна и тлѣющій
свѣтъ. Но всегда и полосы и линіи, замѣчаемыя въ такомъ спектрѣ,
характерны для газа. Въ силу этого разряды въ разрѣженныхъ га-
захъ имѣютъ весьма большое значеніе для спектроскопіи.
Вспоминая о наблюденіяхъ, описанныхъ въ § 136, мы^рйхо-
димъ къ слѣдующему заключенію: въ тѣхъ мѣстахъ, гдф^газъ
при тихомъ разрядѣ свѣтится, имѣетъ мѣсто сил,тфгдя іони-
зація; въ темныхъ мѣстахъ токъ поддерживался іонами^
переходящими сюда изъ центровъ іонизацьиО°
238
Тихій разрядъ въ разрѣженныхъ газахъ
Тщательное изученіе тихаго разряда стало возможнымъ лишь
послѣ изобрѣтенія ртутныхъ воздушныхъ насосовъ, такъ какъ ста-
рые поршневые воздушные насосы не даютъ достаточнаго разрѣже-
нія. Первый построилъ пригодный для употребленія ртутный воз-
душный насосъ боннскій стеклодувъ Гейсслеръ (Сеіззіег, прибл.
въ 1857 г.); онъ же первый примѣнилъ свой насосъ къ эвакуаціи
'стеклянныхъ трубокъ со впаянными электродами. Въ. его честь сте-
клянные сосуды съ разрѣженными газами называются Гейсслеро-
выми трубками. Но и раньше дѣлались наблюденія надъ тихими
разрядами (прежде всего Фарадэемъ въ 1838 г.), хотя совершенно
•единичныя, вслѣдствіе экспериментальныхъ трудностей.
139. Изслѣдуемъ теперь, что будетъ происходить при сокраще-
ніи пути разряда. Для этой цѣли мы можемъ воспользоваться, какъ
это видно изъ рис. 90, вспомогательными электродами, помѣщае-
мыми между двумя конечными электродами. Если мы будетъ послѣ-
довательно соединять положительный полюсъ батареи съ этими про-
межуточными электродами, пользуясь все время однимъ и тѣмъ же
катодомъ, то мы увидимъ, что тлѣющій свѣтъ вокругъ катода остается
при этомъ совершенно неизмѣннымъ. Лишь положительная свѣтовая
колонна укорачивается на величину разстоянія между первоначаль-
нымъ и новымъ анодомъ. Еще удобнѣе это можно показать, сдѣ-
лавъ какимъ-либо образомъ анодъ подвижнымъ. Если его вдвинуть
въ темное пространство, то положительная свѣтовая колонна исче-
заетъ совершенно. Можно даже придвинуть анодъ къ отрицательному
тлѣющему свѣту, и явленія на катодѣ, по крайней мѣрѣ, тлѣющій
свѣтъ, существенно отъ этого не измѣнятся. Въ такомъ случаѣ мы
получаемъ, наконецъ, тихій разрядъ, обнаруживающій только тлѣю-
щій свѣтъ (рис. 91).
Въ тихомъ электрическомъ разрядѣ необходимыми
являются лишь тѣ процессы въ газѣ, которые обнаружи-
ваются въ отрицательномъ тлѣющемъ свѣтѣ; положитель-
ная же колонна и темное пространство Фарадэя могутъ
•отсутствовать. • •
140. Поэтому мы должны прежде всего тщательнѣе познакомиться
•со свойствами отрицательнаго тлѣющаго свѣта. Разсматривая его
•ближе, мы находимъ, что онъ состоитъ изъ трех^частей. Самая
поверхность катода покрыта плотно прилегающей дъ ней свѣтящейся
оболочкой, которая въ трубкѣ съ воздухом^Сиідѣетъ красноватый
Распространеніе отрицательнаго тлѣющаго свѣта
239
оттѣнокъ. Ее называютъ катоднымъ свѣтовымъ поясомъ. Этотъ
свѣтовой поясъ окруженъ темнымъ слоемъ или внутреннимъ темнымъ
пространствомъ —катоднымъ темнымъ пространствомъ, которое
впервые было замѣчено Гитторфомъ (Ніііогі) и въ его честь на-
зывается Гитторфовымъ темнымъ пространствомъ. Внутреннее
темное пространство снаружи рѣзко ограничивается голубоватой
массой свѣта, распространяющейся на далекое разстояніе; со стороны
катоднаго темнаго пространства она обрывается сразу, съ внѣшней
Рис. 91. Три слоя отрицательнаго тлѣющаго свѣта.
же стороны она постепенно переходитъ въ темноту. Эта обширная
голубоватая свѣтовая масса и представляетъ собою собственно тлѣю-
щій свѣтъ.
Всѣ три части отрицательнаго свѣта достигаютъ тѣмъ большаго
развитія, чѣмъ ниже падаетъ давленіе въ трубкѣ. На рис. 91 пред-
ставленъ его видъ въ трубкѣ, болѣе эвакуированной, нежели въ
случаѣ рис. 90.
РАСПРОСТРАНЕНІЕ ОТРИЦАТЕЛЬНАГО ТЛЪЮЩАГО СВЪТА.
141. Если наблюдать тихій разрядъ въ не слишкомъ сильно
эвакуированномъ пространствѣ и, включая большое водяное сопро-
тивленіе, пропускать * черезъ трубку лишь весьма слабый токъ, то
можно замѣтить, что отрицательный тлѣющій свѣтъ покрываетъ не
весь катодъ, но только образуетъ на катодной поверхности ограни-
ченное голубоватое свѣтлое пятно. Лучше всего при этомъ взять
катодъ цилиндрической формы, напримѣръ, длинный кусокъ алюми-
ніевой проволоки. Въ такомъ случаѣ можно легко установить, что
голубоватый свѣтъ покрываетъ тѣмъ большую часть проволоки, чѣмъ^
сильнѣе проходящій черезъ трубку токъ. Если какимъ-либо
извѣстныхъ методовъ измѣрить количество электричества, разр$|каю-
щееся за секунду, то оказывается, что распространеніе тлѣющаго
свѣта въ точности пропорціонально силѣ тока. Гейсслерову^трубку,
подобную вышеописанной, можно поэтому употреблять для измѣренія
силы тока, что въ нѣкоторыхъ случаяхъ оказывается весьма удобнымъ.
240
Катодное напряженіе
КАТОДНОЕ НАПРЯЖЕНІЕ.
142. Если во внѣшнее темное пространство трубки на границѣ
отрицательнаго тлѣющаго свѣта пропустить запаянную въ стекло
трубки проволоку въ качествѣ зонда и измѣрить электрическое на-
пряженіе между катодомъ и этимъ зондомъ, т. е. темнымъ простран-
ствомъ, то оказывается, что напряженіе мало мѣняется съ измѣне-
ніемъ мѣста зонда: можно его продвинуть далеко въ область тлѣю-
щаго свѣта и измѣряемое напряженіе не уменьшится на замѣтную
величину. Мы заключаемъ отсюда, что въ области тлѣющаго свѣта
электрическое поле весьма слабо и не оказываетъ замѣтнаго вліянія
на измѣряемое напряженіе. Ниже это заключеніе еще подтвердится.
Въ силу этого, мы можемъ просто говорить о напряженіи между
катодомъ и внѣшнимъ тлѣющимъ свѣтомъ.
Напряженіе поля между катодомъ и внѣшнимъ тлѣю-
щимъ свѣтомъ называется катоднымъ напряженіемъ.
Гитторфъ первый показалъ, что, до тѣхъ поръ, пока тлѣющій
свѣтъ не покрываетъ всего катода, катодное напряженіе совершенно
не зависитъ отъ силы тока. Но когда тлѣющій свѣтъ покрываетъ
весь катодъ, катодное напряженіе слегка возрастаетъ съ возрастаніемъ
силы тока.
Постоянная величина катоднаго напряженія при не
вполнѣ покрытомъ тлѣющимъ свѣтомъ катодѣ называется
„нормальнымъ катоднымъ напряженіемъ"; большія значенія
этой величины, которыя получаются при вполнѣ покрытомъ
тлѣющимъ свѣтомъ катодѣ, называются „аномальными ка-
тодными напряженіями".
Особенно тщательныя изслѣдованія надъ нормальнымъ катод-
нымъ напряженіемъ производилъ Варбургъ. Онъ установилъ слѣ-
дующій законъ: нормальное катодное напряженіе совершенно
не зависитъ отъ давленія газа въ Гейсслеровой трубкѣ; рно
зависитъ исключительно отъ химическихъ свойствъ гафа и
катода.
Небольшія примѣси посторонняго газа могутъ сильно повліять
на величину нормальнаго катоднаго напряженія; поэтому при такихъ
изслѣдованіяхъ газы должны быть тщательно
новомъ катодѣ многіе наблюдатели нашли
для нормальнаго катоднаго напряженія^
орирщньі. При плати-
осЛ^дующія величины
Электрическое поле при тихомъ разрядѣ 241
Воз- духъ Водо- родъ Кисло- родъ Азотъ Пары ртути Гелій Водяные пары Аммо- ніакъ
Вольты . . 345 прибл. 300 369 230 340 226 469 582
Въ чистомъ водородѣ изслѣдованіе различныхъ катодныхъ
металловъ дало слѣдующія числа:
Пла- тина Сере- бро Мѣдь Желѣ- зо Цинкъ Алю- миній Маг- ній Нат- рій Калій Калій +натрій
Вольты 300 295 280 230 213 190 168 185 172 169
ЭЛЕКТРИЧЕСКОЕ ПОЛЕ ПРИ ТИХОМЪ РАЗРЯДЪ.
143. Для того, чтобы постепенно точка за точкой изслѣдовать
электрическое поле въ области тихаго разряда, проще всего вос-
пользоваться способомъ зондированія. Это можно сдѣлать, напри-
мѣръ, слѣдующимъ образомъ: черезъ стеклянную оболочку Гейссле-
ровой трубки пропускаютъ рядомъ двѣ проволоки—зонды и дѣлаютъ
оба электрода, соединенные между собою стеклянной полосой, пере-
движными; такимъ образомъ оказывается возможнымъ провести пе-
редъ зондами все поле тихаго разряда. Раздѣливъ напряженіе, полу-
чающееся между зондами, на разстояніе между ними, можно прямо
Рис. 92. Трубка съ зондами для измѣренія поля.
найти силу поля въ вольтахъ на сантиметръ (рис. 92). На рисункахъ
93 и 94 даны кривыя, представляющія собою результаты подобныхъ.
измѣреній. Обѣ кривыя одинаково • указываютъ на то, что въ т^ЙГ"
номъ катодномъ пространствѣ господствуетъ колоссальная силагюля,
которая въ области тлѣющаго свѣта очень быстро понижаетсйіпочти
до нуля и лишь въ области внѣшняго темнаго пространства снова
постепенно возрастаетъ. Отсюда слѣдуетъ, что на внутренней сто-
ронѣ тлѣющаго свѣта происходитъ сильное скопленіе Положительныхъ
зарядовъ (т. е. положительныхъ іоновъ); во всемъСостальномъ заня-
Л/п. Электричество и магніпнзыъ.
16
242
Электрическое поле при тихомъ разрядѣ
томъ тлѣющимъ свѣтомъ пространствѣ также имѣется слабый избы-
токъ положительныхъ зарядовъ, исчезающій постепенно по мѣрѣ
Рис. 93. Поле тихаго разряда съ однородной свѣтовой колонной.
Катодъ и тлѣющій свѣтъ образуютъ двойной электри-
ческій слой, сильное поле котораго пронизываетъ катодное
темное пространство.
Наличность этого двойного электрическаго слоя явля-
ется условіемъ возникновенія тихаг^й^азряда; минималь-
Электрическое поле при тихомъ разрядѣ
243“
ное значеніе, которое можетъ имѣть напряженіе двойного
слоя, представляетъ собою нормальное катодное напря-
женіе.
Слѣдуетъ обратить особенное вниманіе на то обстоятельство,
что до сихъ поръ мы не высказывали никакихъ гипотезъ. О суще-
ствованіи положительнаго электрическаго заряда въ тлѣющемъ свѣтѣ
мы необходимо должны были заключить изъ разсмотрѣнія свойствъ
поля.
Съ такой же достовѣрностью мы можемъ по свойствамъ поля
заключить еще, что на обращенной къ аноду сторонѣ Фарадэ-
евскаго темнаго пространства всегда имѣетъ мѣсто сильное
скопленіе отрицательныхъ іоновъ. Въ неслоистой свѣтовой
колоннѣ между этимъ отрицательнымъ пограничнымъ слоемъ и по-
ложительнымъ зарядомъ анода господствуетъ сильное постоянное
поле. Въ случаѣ существованія слоевъ явленіе можно себѣ пред-
ставить въ слѣдующемъ видѣ: скопляющійся на катодной сторонѣ
слоя отрицательный зарядъ образуетъ собою новый вторичный ка-
тодъ, которому въ слоѣ противолежитъ положительный зарядъ, по-
добно тому, какъ это имѣетъ мѣсто въ отрицательномъ тлѣющемъ
свѣтѣ. Каждый слой представляетъ собою повтореніе отри-
цательнаго тлѣющаго свѣта, а темное промежуточное про-
странство между каждыми двумя слоями представляетъ со-
бою повтореніе Фарадэевскаго темнаго пространства. Но
при этомъ слѣдуетъ имѣть въ виду, что напряженіе двойного элек-
трическаго слоя каждаго слоя свѣтовой колонны несравненно меньше,
нежели напряженіе двойного слоя на катодѣ.
Недалеко отъ анода вообще замѣчается недостатокъ положи-
тельныхъ іоновъ, слѣдствіемъ чего является отрицательный зарядъ
газа и возрастаніе силы поля вблизи анода. Эта область высокой
силы поля часто отдѣляется отъ обычной свѣтовой колонны слабо
развитымъ небольшимъ темнымъ промежуткомъ съ малой силой поля.
Такимъ образомъ, оказывается возможнымъ установить извѣстную о
•аналогію между анодомъ и катодомъ, при чемъ явленія на анож^Жц
обыкновенно весьма слабо развиты и даже не всегда имѣют^та
лицо, такъ какъ положительная свѣтовая колонна, какъ былѳ^уже
указано, можетъ совершенно отсутствовать.
15
244
Напряженіе при сближенныхъ электродахъ
НАПРЯЖЕНІЕ ПРИ СБЛИЖЕННЫХЪ ЭЛЕКТРОДАХЪ.
144. Если въ Гейсслеровой трубкѣ взять въ качествѣ электро-
довъ двѣ алюминіевыя пластинки, заполняющія все сѣченіе трубки,
и помѣстить эти два электрода посреди трубки на небольшомъ раз-
стояніи другъ отъ друга (приблизительно на разстояніи 1 см.), то
тихій разрядъ образуется уже внѣ ихъ, если только разрѣженіе воз-
духа настолько сильно, что ширина темнаго катоднаго пространства
превышаетъ ихъ взаимное разстояніе. Если взять достаточно сильное
напряженіе, то въ обширной части трубки за катодомъ образуется
настоящее катодное свѣченіе со свѣтлымъ поясомъ, темнымъ про-
странствомъ и голубоватымъ тлѣющимъ свѣтомъ (рис. 95). Отъ нѣ-
Рпс. 95. Сильно эвакуированная разрядная трубка съ очень сближенными
пластинчатыми электродами.
которой точки на краю анода распространяется по направленію къ
тлѣющему свѣту положительная свѣтовая колонна, которая свѣтлой
узкой полосой проходить между стеклянной стѣнкой и катодомъ въ
томъ мѣстѣ, гдѣ они не плотно прилегаютъ другъ къ другу. Про-
странство между обоими электродами остается совершенно темнымъ.
Этотъ опытъ весьма ясно доказываетъ, что существеннымъ
условіемъ для наступленія тихаго разряда является возникновеніе
проявляющихся въ видѣ катоднаго свѣченія процессовъ, которые
непрерывно поддерживаютъ двойной электрическій слой на катфіѣ,
и что для нормальнаго развитія явленій на катодѣ требуется
опредѣленный объемъ. Они образуются независимо отѣ) положе-
нія анода тамъ, гдѣ имѣется необходимый для этого 6б>емъ.
Это обстоятельство было впервые замѣчено ^Гитторфомъ и
демонстрировано имъ при помощи Гейсслеровой трубки особенной
формы (рис. 96). Два объемистые стеклянныепіара сообщаются
между собою, во-первыхъ, при помощи короткой трубки, предста-
вляющей кратчайшее соединеніе между ними, и, во-вторыхъ, при по-
Напряженіе при сближенныхъ электродахъ
245
тока оказывается, что весь разрядъ
спиральную трубку. Въ короткой
другъ къ другу, остается полная тем-
Рис. 96. Трубка Гитторфа.
мощи длинной спирально изогнутой трубки. Электродами являются
двѣ алюминіевыя проволоки, проходящія черезъ оба шара и окан-
чивающіяся въ короткой соединительной трубкѣ на весьма маломъ
разстояніи другъ отъ друга. Если воздухъ въ трубкѣ достаточно
разрѣженъ, то при замыканіи
проходитъ черезъ длинную
трубкѣ, гдѣ электроды близки
нота: здѣсь слишкомъ ма-
ло мѣста для развитія ка-
тодныхъ явленій.
Въ связи съ этимъ
самъ собою возникаетъ во-
просъ: что же произой-
детъ въ томъ случаѣ, если
ограничить окружающее
катодъ пространство со
всѣхъ сторонъ такъ, .что-
бы нигдѣ не было доста-
точно мѣста для нормаль-
ныхъ катодныхъ явленій.
Для того, чтобы по-
лучить отвѣтъ на этотъ
вопросъ, возьмемъ корот-
кую Гейсслерову трубку
обычной цилиндрической формы и будемъ ее постепенно эвакуиро-
вать помощью хорошаго ртутнаго насоса. Вмѣстѣ съ тѣмъ мы за-
ставимъ проходить черезъ нее тихій разрядъ и будемъ измѣрять
напряженіе между обоими электродами. По мѣрѣ паденія давленія
воздуха въ трубкѣ катодный тлѣющій свѣтъ и внѣшнее темное про-
странство все увеличиваются. Вмѣстѣ съ тѣмъ напряженіе все болѣе
и болѣе падаетъ, и, наконецъ, одновременно съ совершеннымъ ис-
чезновеніемъ положительной свѣтовой колонны, оно опускается до
величины катоднаго напряженія, которое теперь вообще немногому
выше, нежели нормальное катодное напряженіе. При дальнѣйшей
эвакуаціи напряженіе мѣняется лишь незначительно, пока ищется
еще достаточно мѣста для образованія тлѣющаго свѣт^^р^когда
катодное пространство расширится настолько, что для^ ^нормальнаго
образованія трехъ катодныхъ слоевъ въ трубкѣ не-Лхватитъ мѣста,
246
Катодные лучи
то напряженіе начинаетъ очень быстро возрастать. При дальнѣйшей
эвакуаціи оно очень скоро достигаетъ величины въ нѣсколько ты-
сячъ вольтъ. Наконецъ, для того, чтобы черезъ трубку проходилъ
разрядъ, придется примѣнять напряженія, доставляемыя индукціонной
машиной, которыя даютъ въ атмосферномъ воздухѣ искры въ нѣ-
сколько сантиметровъ длиною.
Наименьшей величиною напряженія между электродами
при тихомъ разрядѣ является величина катоднаго напряженія.
Если ограничить окружающее катодъ пространство на-
столько, чтобы нормальное образованіе катодныхъ явленій
стало невозможнымъ, то необходимо примѣнять громадныя
напряженія для того, чтобы вызвать разрядъ.
КАТОДНЫЕ ЛУЧИ.
145. При производствѣ вышеописаннаго опыта обращаетъ на
себя вниманіе происходящее при этомъ измѣненіе свѣтовыхъ явленій.
Въ то время, какъ съ возрастаніемъ разрѣженія испускаемый заключен-
нымъ въ сосудѣ газомъ свѣтъ становится все блѣднѣе и туманнѣе,
другой свѣтъ становится при большихъ разрѣженіяхъ все интенсив-
нѣе: именно, при этомъ начинаютъ свѣтиться стеклянныя стѣнки Гейс-
слеровой трубки. При сравнительно высокихъ давленіяхъ, около 1 мм.
ртутнаго столба, когда свѣтовое явленіе въ самомъ газѣ очень кра-
сиво, лишь тщательно всматриваясь, можно замѣтить, что очень
близко отъ катода стекло трубки испускаетъ слабый зеленый свѣтъ.
При болѣе сильномъ разрѣженіи, когда для возникновенія разряда
необходимы высокія напряженія, этотъ испускаемый стекломъ свѣтъ
становится болѣе интенсивнымъ. Съ перваго взгляда кажется, что
получается совершенно новое явленіе: газъ почти совершенно теменъ
и представляется въ видѣ очень слабаго сѣро-голубого свѣтлаго тумана,,
а бывшее прежде темнымъ стекло стѣнокъ трубки испускаетъ весьма
интенсивный ярко-зеленый свѣтъ. Тѣмъ не менѣе переходъ отъ одного
явленія къ другому совершается вполнѣ непрерывное мы ско^убѣ-
димся въ томъ, что свѣченіе газа въ трубкѣ при достаточно боль-
шомъ объемѣ и свѣченіе стеклянныхъ стѣнокъ въ случаѣ ^недостатка
мѣста вызываются однимъ и тѣмъ же физическимъ д^^ніемъ. Прежде
всего ясно, что свѣченіе стекла не представляе^ъ^фбою явленія флу-
оресценціи, возбуждаемой ультрафіолетовыми^ дучами свѣтящагося
газа. Правда, и въ отрицательномъ свѣтѣ <|Свъ свѣтѣ положитель-
Катодные лучи
247
ной колонны имѣется много ультрафіолетовыхъ лучей, и стеклодувы
пользуются возбуждаемыми ими явленіями флуоресценціи для устрой-
ства разныхъ игрушекъ. Но эти явленія флуоресценціи, понятно,
тѣмъ ярче, чѣмъ сильнѣе свѣтъ самаго разряда, и они получаются,
слѣдовательно, наиболѣе отчетливо при не слишкомъ сильной эва-
куаціи трубки. Свѣтлозеленое свѣченіе, о которомъ мы теперь го-
воримъ, наоборотъ, становится рѣзкимъ лишь тогда, когда свѣтъ са-
маго разряда становится слабымъ вслѣдствіе очень сильнаго разрѣ-
женія находящагося въ трубкѣ газа.
Простой опытъ показываетъ намъ, что въ дѣйствительности это
яркое свѣченіе стеклянныхъ стѣнокъ вызывается особыми темными
лучами, исходящими прямо изъ катода. Возьмемъ сильно эвакуиро-
ванную трубку, въ которой катодъ имѣетъ форму диска, а проти-
воположная ему стеклянная стѣнка сосуда представляетъ сравнительно
большую, слабо искривленную поверхность; оказывается, что при
разрядѣ эта противолежащая катоду поверхность свѣтится ярче всего.
При этомъ совершенно безразлично, гдѣ находится анодъ; его поло-
женіе и его величина не оказываютъ никакого вліянія на явленіе,
и въ качествѣ анода
можно воспользоваться
впаянной гдѣ-либо въ
сторонѣ проволокой.
Если затѣмъ мы помѣ-
стимъ между катодомъ
и противолежащей ему
поверхностью какое-ли-
бо твердое тѣло, на-
примѣръ, металлическій
крестъ (рис. 97), то
на свѣтящейся поверх-
ности мы увидимъ со-
Рис. 97. Крестъ Крукса.
вершенно рѣзкую тѣнь этого тѣла. Изъ этого опыта съ очевидностью
слѣдуетъ, что желтозеленая флуоресценція стекла вызывается нѣкото%
рымъ агентомъ, исходящимъ изъ катода и распространяющимсд^Кр^
молинейно до стеклянной стѣнки, иными словами, какими-то луцами,
исходящими изъ катода. Въ вышеописанной формѣ опыт^йринадле-
житъ Круксу (Сгоокез); существованіе же катодныхт^уЦей было
задолго до него подобными же опытами доказано^ццдторфомъ.
248
Катодные лучи
Этотъ опытъ указываетъ кромѣ того еще на одну весьма за-
мѣчательную особенность катоднаго излученія. Представимъ себѣ,
что дискъ, которымъ мы выше пользовались въ качествѣ катода,
какимъ-либо способомъ раскаленъ и испускаетъ свѣтъ. Дастъ-ли
этотъ свѣтъ также вполнѣ рѣзкую тѣнь креста на противолежащей
диску стѣнкѣ? Конечно, нѣтъ. Каждая точка свѣтящейся поверхности
испускаетъ свѣтъ во всѣ стороны и потому на каждую точку линіи,
ограничивающей поверхность креста, падаютъ лучи отъ всѣхъ точекъ
свѣтящагося диска; темная тѣнь креста при такихъ условіяхъ будетъ
окружена полутѣнью, постепенно переходящею въ яркую незатѣненную
поверхность. Этой полутѣни катодные лучи совершенно не даютъ. Отсю-
да слѣдуетъ, что отъ каждой точки катода исходитъ катод-
ный лучъ въ одномъ единственномъ направленіи. Это на-
правленіе всегда совпадаетъ съ отрицательнымъ направле-
ніемъ окружающаго катодъ электрическаго поля.
Уже отсюда мы ясно видимъ, что катодные лучи по своей при-
родѣ совершенно отличны отъ свѣтовыхъ лучей; въ дальнѣйшемъ
мы еще лучше убѣдимся въ этомъ.
Вышеуказаннымъ свойствомъ катодныхъ лучей можно восполь-
зоваться для того, чтобы соединить эти лучи въ одной точкѣ—„фо-
кусѣ". Въ этомъ случаѣ придаютъ катоду форму вогнутаго сфериче-
скаго зеркала; такъ какъ электрическое поле имѣетъ направленіе при-
близительно перпендикулярное къ поверхности катода, то всѣ катодные
лучи идутъ по направленіямъ радіусовъ того шара, частью поверхности
котораго является катодъ, и сходятся приблизительно въ его центрѣ.
146. Не только металлы, но и прочія твердыя тѣла непрозрачны
для катодныхъ лучей, если только они не берутся въ формѣ тончайшихъ
пластинокъ. Герцъ (Н. Негіх) первый показалъ, что тонкіе метал-
лическіе листки, толщина которыхъ не превышаетъ 1—2//., оказы-
ваются въ замѣтной степени прозрачными для катодныхъ лучей.
Послѣ этого Ленардъ (РИ. Ьепагсі) произвелъ рядъ опытовъ съ ка-
тодными лучами, выпустивъ ихъ изъ трубки черезъ окошечко^Д-
крытое алюминіевымъ листкомъ. На рис. 98 изображена трубка, по-
строенная по указаніямъ Де-Кудра (ТИ. Эез Соисігез) дляШолученія
сильныхъ „Ленардовыхъ лучей". Это короткая эбонтйоѣая трубка;
съ одной стороны въ ней имѣется катодная пла^фса, къ которой
ведетъ проволока, прочно вдѣланная въ отверс^іе^въ трубкѣ; съ
другой же стороны трубка закрыта металлической крышкой, имѣю-
Катодные лучи
249
щей посрединѣ „окно" изъ тончайшаго алюминія. Эта металлическая
крышка служитъ анодомъ и вмѣстѣ съ тѣмъ сообщена съ землею.
Съ ней проводящимъ образомъ соединена большая желѣзная пла-
стинка, имѣющая посрединѣ круглое отверстіе, въ*Ткоторое вста-
вляется трубка Де-Кудра. Этимъ листомъ, крышкой и окномъ внѣш-
нее пространство, въ которомъ изслѣдуются лучи, вполнѣ защища-
ется отъ дѣйствія поля въ трубкѣ. Такимъ образомъ здѣсь можно
имѣть катодные лучи отдѣльно и независимо отъ явленія разряда.
Ленардъ нашелъ, что всѣ вещества, взятыя въ видѣ очень тон-
кихъ листковъ, прозрачны для катодныхъ лучей. По ослабленію свѣ-
ченія, вызываемаго катодными лучами на флу-
оресцирующемъ экранѣ, онъ могъ приблизи-
тельно опредѣлить поглощеніе, испытываемое
ими при прохожденіи черезъ листокъ. Оказа-
лось, что поглощеніе приблизительно пропор-
ціонально вѣсу листка, разсчитанному на ква-
дратный сантиметръ, совершенно независимо
отъ того, изъ какого химическаго вещества
сдѣланъ листокъ. Тому же закону слѣдуетъ и
поглощеніе въ газахъ; слой воздуха въ 2,1 мм.
поглощаетъ приблизительно такъ же, какъ ли-
стокъ алюминія въ 0,001 мм. Удѣльные вѣса
этихъ веществъ равны соотвѣтственно 0,0012
2 7
и 2,7, такъ что отношеніе ихъ = 2250, Рис.98.ТрубкаДс-Кудра
« „ ’ , для Ленардовыхъ лучей,
дѣйствительно, оказывается примѣрно рав- г 7
нымъ отношенію указанныхъ толщинъ ^одинаково поглощающихъ
2 1
слоевъ = 2100.
147. Какъ мы увидимъ ниже, при поглощеніи катодныхъ лучей
большая часть ихъ энергіи переходитъ въ теплоту. Но*при этомъ
происходятъ еще нѣкоторыя явленія, на которыя тоже тратится нѣ-
которая, хотя и малая часть энергіи катодныхъ лучей. Катодные лучи
вызываютъ химическія измѣненія въ тѣлахъ, которыя ихъ погда-
щаютъ. Напримѣръ, они дѣйствуютъ подобно свѣту на фотографи-
ческую пластинку. Щелочныя соли и стекло, подвергавшіяся истече-
ніе нѣкотораго времени дѣйствію очень сильныхъ катодн|іф> лучей,
принимаютъ коричневую, фіолетовую и иныя окраски^410 указы-
ваетъ на наличность какихъ-то еще хорошо не изс^іффэванныхъ хи-
250
Электрическія и магнитныя свойства катодныхъ лучей
мическихъ измѣненій. Сильная флуоресценція, которую вызываютъ
катодные лучи у большинства химически сложныхъ тѣлъ, предста-
вляетъ собою свѣтовое явленіе, тоже зависящее отъ химическихъ
процессовъ въ тѣлахъ.
Газы подъ вліяніемъ катодныхъ лучей не только химически
измѣняются (напримѣръ, въ воздухѣ при этомъ образуются озонъ и
азотистыя соединенія), но въ то же время весьма сильно іонизиру-
ются. При функціонированіи трубки Де-Кудра въ темнотѣ, когда
катодные лучи выходятъ изъ окошечка, передъ окошечкомъ ясно
видно разсѣянное голубоватое свѣченіе, сопровождающее іонизацію.
Этотъ свѣтъ тождественъ съ голубымъ тлѣющимъ свѣтомъ въ
Гейсслеровой трубкѣ. Связь между тлѣющимъ свѣтомъ и катодными
лучами становится совершенно очевидной, если помѣстить въ Гейс-
слеровой трубкѣ вблизи катода небольшой стерженекъ. Тогда ясно
видно, что этотъ стерженекъ отбрасываетъ тѣнь въ пространство,
занятое отрицательнымъ тлѣющимъ свѣтомъ.
Вблизи катода Гейсслеровой трубки катодные лучи
являются іонизирующимъ агентомъ; отрицательный тлѣю-
щій свѣтъ характеризуетъ пространство, гдѣ происходитъ
іонизація катодными лучами.
ЭЛЕКТРИЧЕСКІЯ И МАГНИТНЫЯ СВОЙСТВА КАТОДНЫХЪ ЛУЧЕЙ.
148. Весьма удобной формой Гейсслеровой трубки для демон-
страціи многихъ свойствъ катодныхъ лучей является трубка Брауна
(Вганп), изображенная на рис. 99. Часть ея, въ которой происхо-
Рис. 99. Трубка Брауна.
дитъ разрядъ, представляетъ собою довольно узкій цилйнЙръ, на
одномъ концѣ котораго помѣщенъ дискообразный ка^рДъ. Помѣ-
щенная на разстояніи приблизительно 25 см. отъ^сатода круглая
діафрагма выдѣляетъ среднюю часть пучка параллельныхъ катод-
ныхъ лучей, исходящихъ отъ катода. Въ ^нѣкОТоромъ разстояніи
отъ этой діафрагмы узкая разрядная труб^персходитъ въ весьма
Электрическія и магнитныя свойства катодныхъ лучей
251
широкій сосудъ, дно котораго покрыто хорошо флуоресцирующимъ,
экраномъ. Трубка очень хорошо эвакуируется и требуетъ для раз-
ряда весьма высокаго напряженія; поэтому въ качествѣ источника
электричества при ея употребленіи лучше всего пользоваться индук-
ціонной электрической машиной. Когда черезъ трубку проходитъ
разрядъ, то на флуоресцирующемъ экранѣ видно свѣтлое, рѣзко-
ограниченное круглое пятно.
Эта трубка очень удобна для наблюденій надъ отклоненіемъ
катоднаго пучка отъ его прямолинейнаго пути. Подобное отклоненіе
имѣетъ мѣсто, если лучи проходятъ черезъ электрическое поле, на-
правленіе котораго перпендикулярно къ направленію лучей. Чтобы
получить такое поле въ трубкѣ Брауна, позади діафрагмы помѣ-
щается небольшой плоскій конденсаторъ, пластинки котораго имѣютъ
форму удлиненныхъ прямоугольниковъ. Помощью впаянныхъ въ стекло-
проволокъ можно эти пластинки соединять съ батареею аккумулято-
ровъ. Какъ только между ними возбуждается электрическое поле,,
тотчасъ же свѣтлое пятно на флуоресцирующемъ экранѣ перемѣ-
щается; если измѣнить направленіе поля на обратное, то и перемѣ-
щеніе пятна происходитъ въ противоположномъ направленіи. Такимъ
образомъ, пучокъ катодныхъ лучей подвергается отклоненію. Легко
можно установить, что онъ отклоняется отъ отрицательной пластинки
конденсатора къ положительной. Такъ какъ мы знаемъ, что электри-
ческое поле дѣйствуетъ лишь на электрически заряженныя тѣла, то
отсюда слѣдуетъ, что катодные лучи имѣютъ матеріальную
природу и что они заряжены отрицательно.
Пучокъ катодныхъ лучей можно, такимъ образомъ, разсматри-
вать какъ отрицательно заряженную нить, обладающую извѣстной
твердостью; поэтому можно сказать, что вышеописанная трубка
Брауна съ плоскимъ конденсаторомъ представляетъ собою не что
иное, какъ разновидность электрометра Ганкеля; отличается трубка
Брауна отъ обыкновеннаго электрометра Ганкеля тѣмъ, что ка-
тодный лучъ подчиняется дѣйствію силы поля дѣйствительно момен<^
тально (гораздо скорѣе, чѣмъ въ билліонную часть секунды), т^гдя
какъ нить электрометра Ганкеля въ лучшемъ случаѣ тратитъ^на это
приблизительно Ѵіооо секунды.
Магнитное состояніе эѳира также дѣйствуетъ на катод^цй пучокъ.
Ниже мы увидимъ, что „магнитное поле" въ эѳирѣ характеризуется, по-
добно электрическому, опредѣленно направленнымиг|йшіями — магнит-
.252
Электрическія и магнитныя свойства катодныхъ лучей
ными силовыми линіями. Въ случаѣ желѣзнаго подковообразнаго магни-
та эти линіи идутъ прямо отъ одного полюса къ другому. Если мы
помѣстимъ такой магнитъ надъ трубкой Брауна, приблизительно
"въ томъ мѣстѣ, гдѣ находится конденсаторъ, такъ, чтобы трубка
приходилась между его полюсами и чтобы магнитное поле пронизы-
вало трубку, то катодные лучи отклонятся. Но въ магнитномъ полѣ
отклоненіе происходитъ такимъ образомъ, что катодный лучъ оги-
'баетъ силовыя линія въ плоскости, къ нимъ перпендикулярной. Это
очень удобно показать, пользуясь трубкой, изображенной на рис. 100,
Рис. 100. Отклоненіе катодныхъ лучей магнитомъ.
ъь которой катодные лучи проходятъ черезъ діафрагму, имѣющую
ъидъ щели, и даютъ слѣдъ на флуоресцирующемъ экранѣ, располо-
женномъ въ направленіи ихъ длины и лишь слегка наклоненномъ къ
направленію лучей. Если мы возбудимъ магнитное поле, перпенди-
кулярное къ плоскости экрана, то увидимъ, какъ слѣдъ катоднаго
пучка изгибается въ томъ пространствѣ, которое пронизывается маг-
нитнымъ полемъ. Въ электродинамикѣ мы увидимъ, что потокъ дви-
жущихся электрическихъ частицъ испытываетъ въ магнитномъ полѣ
отклоненіе, перпендикулярное къ направленію силовыхъ линій, точно
такъ же, какъ катодный пучекъ. При этомъ направленіе отклоненія
^катодныхъ лучей совпадаетъ съ тѣмъ, въ которомъ отклонялся бы
тіотокъ отрицательныхъ частицъ, если бы онъ распространялся въ
томъ же направленіи, что и катодные лучи. Какъ и опытъ надъ
отклоненіемъ въ электрическомъ полѣ, это указываетъ намъ оі^ять
«а то, что катодный лучъ представляетъ собою не что иное^гакъ
потокъ отрицательно заряженныхъ частичекъ. ^§7
Въ этомъ можно убѣдиться также и непосредственідДрДля этого
внутри разрядной трубки противъ катода помѣщаютдметаллическук)
пластинку такимъ образомъ, чтобы на нее падалъ^к^тодный пучекъ,
пропущенный черезъ соотвѣтственную діафрагму^ сПосредствомъ пла-
тиновой проволоки, впаянной въ стекляннуіЮстѣнку трубки, эта
Электрическія и магнитныя свойства катодныхъ лучей 253^
пластинка соединяется съ электрометромъ. Помощью подковообразнаго
желѣзнаго магнита легко отклонять катодный пучекъ такимъ образомъ,,
чтобы онъ по желанію падалъ на металлическую пластинку или же
проходилъ мимо нея. Когда катодные лучи падаютъ на металлъ, то
электрометръ указываетъ на отрицательный зарядъ, постепенно воз-
растающій; когда же они проходятъ мимо пластинки, никакого за-
ряда на ней не оказывается. Для того, чтобы точно измѣрить отри-
цательный зарядъ, несомый катоднымъ пучкомъ, пропускаютъ лучи:
черезъ достаточно широкое отверстіе въ небольшой Фарадэевскій
сосудъ, окруженный отведенной къ землѣ металлической оболочкой,.,
имѣющей отверстіе для пропуска катодныхъ лучей внутрь и предна-
значенной для уничтоженія вліянія внѣшнихъ полей и газа, который ста-
новится проводящимъ благодаря дѣйствію катодныхъ лучей (рис. 101).
Такая установка имѣетъ особенный
отверстіе охранной оболочки мож-
но закрыть очень тонкимъ вполнѣ
непроницаемымъ для воздуха алю-
миніевымъ листкомъ, не препятстуя
этимъ проникновенію внутрь обо-
лочки катодныхъ лучей. Такимъ
образомъ, при помощи катодныхъ лучей оказывается возможнымъ,
ввести электрическіе заряды въ замкнутый со всѣхъ сторонъ метал-
лическій сосудъ черезъ металлическую стѣнку.
Всѣ полученныя нами до сихъ поръ данныя мы можемъ кратко
формулировать въ двухъ нижеслѣдующихъ положеніяхъ:
Катодные лучи представляютъ собою потокъ отрица-.
теоретическій интересъ, такъ какъ.
Электр омеги ,
Рис. 101. Фарадэевскій сосудъ для
катодныхъ лучей.
тельно заряженныхъ частичекъ, переносящихся въ напра-
вленіи, противоположномъ направленію катоднаго поля»,
отъ катода.
Для этихъ частицъ всѣ роды матеріи оказываются про-
ницаемыми; онѣ могутъ проникать, не теряя своего за*
ряда, даже черезъ совершенно лишенные отверстій метал^
лическіе листки.
ИЗМѢРЕНІЯ, ПРОИЗВЕДЕННЫЯ НАДЪ КАТОДНЫМИ ЛУ^МИ.
149. Энергію катодныхъ лучей легко вычислить, есдй^ принять,,
что отрицательно наэлектризованныя частицы, исходя^изъ катода^
проходятъ черезъ все катодное поле и въ силу эт^г^пріобрѣтаютъ.
кинетическую энергію. Если напряженіе на катѳ^ѣ^есть V, зарядъ,.
254
Измѣренія, произведенныя надъ катодными лучами
одной частички^- е, то эта частичка отнимаетъ отъ эѳира энергію V . е.
Если съ другой стороны т есть масса, ѵ - - скорость частички, то ея
кинетическая энергія равняется т . ѵ2; слѣдовательно, должно
имѣть мѣсто равенство V . е — т . ѵ2, если въ обоихъ случаяхъ
энергія измѣряется въ одинаковыхъ единицахъ. Если мы будемъ
производить вычисленія, пользуясь обычными единицами граммомъ
для ш, сантиметромъ въ секунду для г», вольтомъ для V и куло-
номъ для е, то мы получимъ энергію въ одномъ случаѣ въ джуляхъ
и въ другомъ случаѣ въ эргахъ. Отношеніе этихъ единицъ энергіи
равняется ІО7 (§ 102) и, слѣдовательно,
V. е = у т . ѵ2 . 10”7,
или
У = ’ — .ѵз. 10-7.
2 е
Но такъ какъ нельзя быть увѣреннымъ въ томъ, что частица е
прошла въ дѣйствительности черезъ все катодное поле, то мы мо-
жемъ значеніе V разсматривать только, какъ верхній предѣлъ
•отношенія энергіи частицы къ ея заряду:
4- --'У8. 10-7 V.
2 е
Къ счастью, существуетъ возможность найти также и нижній
предѣлъ для величины этого отношенія. Если направить потокъ ка-
тодныхъ лучей на какое-либо тѣло, ихъ поглощающее, то послѣднее
нагрѣвается; достаточно сильное излученіе можетъ довести его до
•бѣлаго каленія. Энергія катоднаго излученія преобразуется такимъ
образомъ — по крайней мѣрѣ, отчасти въ теплоту. Оптика даетъ
намъ средства для измѣренія переходящей въ теплоту энергіи излу-
ченія. Для этой цѣли употребляется болометръ, т. е. тонкая метал-
лическая полоска или же тонкая проволока, которая поглощаетъ гіа-
дающую на нее въ видѣ лучей энергію (въ случаѣ свѣтовыхъ, лучей
О С;/"
она должна быть для этого закопчена) и температура котвой мо-
жетъ быть точно измѣрена. По повышенію температурь!-болометра,
Л*
вызываемому поглощеніемъ лучистой энергіи, можно, ^ользуясь извѣ-
стными методами, вычислить поглощеніе, т. е. поглощаемую за се-
кунду энергію. Одновременно съ этимъ измѣреніемъ должно быть
произведено описанное въ предыдущемъ параграфѣ измѣреніе элек-
Измѣренія, произведенныя надъ катодными лучами
255
трическаго заряда, переносимаго катодными лучами. Если число уча-
ствующихъ въ этомъ переносѣ частичекъ есть IV, перенесенный ими
зарядъ — а, то а=ІѴ. е. Если мы допустимъ, что поглощенная бо-
лометромъ энергія (? джулей представляетъ собою всю энергію по-
глощенныхъ лучей, то
= IV. у . тѵ2. ІО"7
и, слѣдовательно,
.2 = 1. ю-7.
а 2 е
Но такъ какъ при поглощеніи катодныхъ лучей, кромѣ нагрѣ-
ванія, происходятъ еще нѣкоторыя явленія, на которыя, конечно,
тоже расходуется часть энергіи, то вмѣсто написаннаго только-что
равенства, мы имѣемъ неравенство:
- < 4 • - • V2 • Ю-7.
а 2 е
Обозначимъ для краткости черезъ V отношеніе найденныхъ
значеній (2 и а\ въ такомъ случаѣ получаемъ неравенство:
V'— • ѵ?. ю-*^ ІА
2 е
Измѣренія, произведенныя Зейтцемъ (АѴ. Зеііх) показали, что
разности между величинами V и V не превосходятъ ошибокъ на-
блюденій, т. е. неизмѣримо малы. Отсюда мы заключаемъ, во - пер-
выхъ, что частички, составляющія катодные лучи, пріобрѣ-
таютъ свойственную имъ скорость, пройдя все катодное
поле, и, во-вторыхъ, что на процессы, развивающіеся при
поглощеніи катодныхъ лучей металломъ, затрачивается
лишь ничтожно малая часть энергіи лучей, и можно считать,
что вся ихъ энергія переходитъ при этомъ въ теплоту.
Слѣдовательно, можно принять, что
V = 2 • Ю-7 • — • ѵ>-.
2 е
Катодное напряженіе равняется отношенію энергіи ка/
тодной частички къ ея заряду.
Послѣдній выводъ можно формулировать еще такъ: катодное
напряженіе равняется (если не принимать во внц^дціе чи-
сленнаго множителя 0,5 . 10~7) произведенію изъ ^отношенія
(т\ ЛоѴ
массы къ заряду — частички на квадратъ ея ^скорости (т/-).
256
Измѣренія, произведенныя надъ катодными лучами
150. Существуетъ еще иной методъ для опредѣленія отношенія
энергіи къ заряду, имѣющій особенное значеніе въ тѣхъ случаяхъ,
когда лучи, обладающіе всѣми свойствами катодныхъ лучей, возни-
каютъ въ отсутствіи какого-либо электрическаго поля конечныхъ
размѣровъ. Ниже мы познакомимся съ такими лучами. Въ подобныхъ
случаяхъ пользуются отклоненіемъ лучей въ электрическомъ полѣ.
Если поле постоянно и отклоненіе незначительно, то путь луча въ полѣ
почти въ точности имѣетъ
Рис. 102. Радіусъ кривизны
траэкторіи катодныхъ лучей.
форму слабо искривленной дуги круга.
Весьма простыми геометрическими раз-
сужденіями можно по измѣренному откло-
ненію лучей получить величину радіуса
этого круга. При помощи обозначеній,
употребленныхъ на рис. 102, этотъ ра-
2 і) с -р с2
діусъ выразится такъ: о = ---Какъ
извѣстно изъ механики, центробѣжная
сила равняется Эта центробѣжная
сила находится въ равновѣсіи съ силою,
съ которою дѣйствуетъ на частичку элек-
трическое поле. Такъ какъ, согласно сдѣ-
ланному нами предположенію, кривизна
весьма мала, то во всѣхъ точкахъ пути
катодныхъ лучей можно считать напра-
вленіе поля нормальнымъ къ этому пути..
Если напряженіе между пластинками кон-
денсатора равно Ѵ\ и ихъ взаимное разсто-
яніе есть б/, то сила поля равняется Е --
а сила, дѣйствующая на частичку, равна Е . е. Поэтому должно имѣть
мѣсто равенство Е . е —-----, гдѣ т .ѵ2 вычислено въ джуляхъ.
Если принять, какъ выше, массу частички равной т граммамъ, ^ско-
рость ея —равной ѵ сантиметрамъ въ секунду, то придется ѣ^ти
множитель 107. Въ такомъ случаѣ мы можемъ написать^?
Е-0 = --ѵ> . 10-'. зе-
Такимъ образомъ, Е. р = 2 V, гдѣ V напряженіе, которое
сообщаетъ покоющейся частичкѣ скорость ІЛ
Эта связь подтверждена также и экспериментально Зейтцемъ;
V оказалось равнымъ катодному напряженію.
Измѣренія, произведенныя надъ катодными лучами
257
151. Совершенно такое же вычисленіе можно произвести и для
отклоненія въ магнитномъ полѣ. Какъ измѣряется магнитное поле,
пронизывающее трубку, мы укажемъ ниже въ электродинамикѣ. Обо-
значимъ черезъ В „магнитное возбужденіе", выраженное въ той еди-
ницѣ, которую прямо даетъ этотъ методъ измѣренія. Сила, съ ко-
торою дѣйствуетъ поле на частичку, движущуюся со скоростью ѵ
сантиметровъ въ секунду и обладающую зарядомъ въ е кулоновъ,
равняется, какъ мы это увидимъ ниже, произведенію В ,е. ѵ. Слѣ-
довательно,
о т . ѵ2 1 л 7
В .е .ѵ -------ІО-7,
Р
гдѣ р обозначаетъ радіусъ кривизны пути въ магнитномъ полѣ.
Иначе,
В.о = — • ѵ. ІО-7.
е
Обычно магнитное возбужденіе выражается въ иной единицѣ,
составляющей часть той единицы, которую мы употребили здѣсь.
Эта малая единица издавна называется „абсолютной" единицей на-
пряженія поля. Магнитное возбужденіе, выраженное въ этой еди-
ницѣ, мы будемъ обозначать черезъ Н. Слѣдовательно, В = Н. ІО-8 и
т 1 Л*
Н .о — — . ѵ. 10.
4 е
Измѣреніе магнитнаго отклоненія даетъ отношеніе ве-
личины количества движенія т.ѵ къ заряду е или же, что
т
то же, произведеніе отношенія — на скорость ѵ.
Если мы теперь положимъ
2.107. Ѵ = а, Ю7.В.о = ^ =/>,
то будемъ имѣть:
а е а лАА
'Ѵ = — > — = -— • 'XX ,
Ъ т Ь2 о
По величинамъ катоднаго напряженія и магнитнаг^уХ
отклоненія можно вычислить скорость частичекъ въ кард-
номъ лучѣ и отношеніе ихъ заряда къ массѣ. р?
152. Если мы помѣстимъ подковообразный желѣзныірмагнитъ
надъ узкой частью трубки Брауна, въ которой разрядррызывается
помощью равномѣрно вращающейся электрической мшнины, то мы
Ми. Электричество и магнитизмъ. > 17
258 Измѣренія, произведенныя надъ катодными лучами.—Электроны
увидимъ, что свѣтлое пятно цѣликомъ передвигается въ сторону,
оставаясь вполнѣ рѣзкимъ. Иными словами: если напряженіе V (а, слѣ-
довательно, и величина а) постоянно, то и о (и величина Ь) также
остается постояннымъ.
Слѣдовательно, при опредѣленномъ катодномъ напряженіи всѣ
частички, переносящіяся въ катодномъ лучѣ, имѣютъ вполнѣ одина-
ковыя скорости. При изслѣдованіи же катодныхъ лучей, возникшихъ
при различныхъ катодныхъ напряженіяхъ, оказывается, что они тѣмъ
менѣе отклоняются, являются тѣмъ болѣе жесткими, чѣмъ выше со-
отвѣтствующее катодное напряженіе. Чѣмъ больше V и а, тѣмъ
больше () и Ь и тѣмъ жестче лучи. При этомъ былъ найденъ весьма
общій количественный законъ: Ь всегда пропорціонально ]/а, при
чемъ коэффиціентъ пропорціональности во всѣхъ случаяхъ одинъ и
тотъ же и не зависитъ ни отъ природы газа въ трубкѣ, ни отъ ве-
щества электродовъ, ни отъ давленія газа въ трубкѣ, ни отъ какихъ
иныхъ причинъ. А такъ какъ — = то оказывается, что отри-
цательно заряженныя частички, изъ которыхъ состоятъ
катодные лучи, при всевозможныхъ обстоятельствахъ имѣ-
ютъ всегда одинаковое отношеніе заряда къ массѣ.
Отсюда мы съ полнымъ основаніемъ заключаемъ, что всѣ ка-
тодныя частички совершенно одинаковы между собою:
ЭЛЕКТРОНЫ.
153. Одинаковость всѣхъ катодныхъ частичекъ представляетъ
собою фактъ чрезвычайной важности, установленіе котораго очень
сильно повліяло на общепринятые взгляды относительно природы
матеріальныхъ атомовъ. Тогда какъ прежде предполагалось, что изъ
химическаго атома ни при какихъ обстоятельствахъ не можетъ быть
выдѣлена какая-нибудь составная часть, что атомы двухъ различныхъ эле-
ментовъ не имѣютъ между собою ничего общаго, мы познакомились
въ катодной частичкѣ съ такимъ веществомъ, которое заключатся въ
различныхъ химическихъ элементахъ и поэтому должно ^йдставлять
собою продуктъ распада атомовъ.
Что частички, составляющія катодные лучи, д^сДвительно обра-
зуютъ вѣсомую матерію, не подлежитъ сомнѣнію,У потому что на-
личность электрическаго заряда должна быть^непремѣнно связана съ
наличностью вѣсомой матеріи. Катодныя чЛстиМки можно „осязать"
Электроны
259
подобно обычнымъ матеріальнымъ тѣламъ, такъ какъ ихъ можно со-
бирать въ сосудахъ и переносить въ этихъ сосудахъ съ мѣста на
мѣсто; онѣ должны, слѣдовательно, непремѣнно обладать свойствомъ
непроницаемости. Этому не противорѣчитъ фактъ ихъ прохожденія
черезъ тонкіе слои вещества. Многіе газы вѣдь также проходятъ
насквозь черезъ твердыя тѣла, напримѣръ, водородъ черезъ раска-
ленную платину и т. п. Катодныя частички обладаютъ далѣе и свой-
ствомъ инерціи, такъ какъ при криволинейныхъ ихъ движеніяхъ
появляется, какъ мы видѣли, опредѣленная центробѣжная сила; слѣ-
дуетъ еще упомянуть, что въ нѣкоторыхъ опытахъ ихъ движеніе
удалось ускорять или замедлять помощью электрическихъ полей и
что вычисленныя на основаніи этихъ опытовъ значенія для массы
совпадаютъ съ найденными другими путями. Инерція, непроницае-
мость, подвижность являются характерными свойствами матеріальныхъ
тѣлъ, отличающими ихъ отъ пустоты или эѳира, въ приложеніи къ
которому эти понятія, повидимому, вообще не имѣютъ смысла; слѣ-
довательно, катодныя частицы являются матеріальными по своей
природѣ.
Съ другой стороны онѣ не представляютъ собою атомовъ ка-
кого-либо новаго химическаго элемента. Ихъ можно выдѣлять
всевозможныхъ химическихъ атомовъ. Совершенно безразлично, на-
полнена ли разрядная трубка водородомъ, кислородомъ, азотомъ, па-
рами ртути и т. п.; при всѣхъ этихъ газахъ получаются однѣ и тѣ же
катодныя частички, и мы увидимъ ниже, что онѣ могутъ также хо-
рошо выдѣляться и изъ всевозможныхъ твердыхъ веществъ. Поэтому
онѣ, навѣрное, являются составными частями всѣхъ химическихъ
атомовъ. Онѣ оказываются всегда заряженными отрицательно; ни-
когда не удавалось наблюдать ихъ не заряженными и потому при-
нимаютъ, что зарядъ составляетъ ихъ неотъемлемое свойство. Отсюда
прямо слѣдуетъ, что никакое твердое тѣло не можетъ состоять только
изъ этихъ частицъ, такъ какъ ихъ электрическія поля взаимно оттал-
киваются съ большою силою и онѣ не могутъ обладать сцѣпленіемъо.
Входить въ составъ крупныхъ матеріальныхъ массъ онѣ могутѣ^
лишь въ качествѣ частей химическихъ атомовъ, въ которыхъ^ихъ
заряды компенсируются положительными зарядами. І
Частицы, изъ которыхъ состоятъ катодные лучй, назы-
ваютъ электронами; это слово должно, во-первыдъ, указы-
вать на то ихъ существенное свойство, что онХ^обладаютъ
изъ
17
260
Электроны
неизмѣннымъ электрическимъ зарядомъ, и, во-вторыхъ, на
то, что они играютъ при разрядѣ роль іоновъ.
Далѣе является вопросъ о величинѣ заряда электрона. Оказы-
вается ли онъ тождественнымъ съ зарядомъ электролитическаго іона,
одновалентнаго или многовалентнаго, или же онъ составляетъ лишь
часть элементарнаго количества электричества? Существуетъ одно
явленіе, позволяющее съ полной опредѣленностью рѣшить этотъ во-
просъ. Если электроны попадаютъ въ атмосферный воздухъ, что
имѣетъ мѣсто при всѣхъ происходящихъ въ воздухѣ разрядахъ, то
черезъ нѣкоторое время они исчезаютъ, а вмѣсто нихъ появляются
крупные воздушные іоны, о которыхъ шла рѣчь въ §§ 129, 130, 131.
Очевидно, электроны являются въ нихъ центрами скопленія молекулъ.
Поэтому мы должны принять, что зарядъ электрона тождественъ съ
зарядомъ отрицательнаго воздушнаго іона. Какъ мы видѣли въ§ 130,
послѣдній представляетъ собою зарядъ одновалентнаго іона, т. е.
элементарное количество электричества. Впрочемъ, если бы этотъ
фактъ и не былъ извѣстенъ, все же надо было бы, не колеблясь, сдѣ-
лать то же предположеніе, такъ какъ оно сразу и простѣйшимъ
образомъ разрѣшаетъ всѣ трудности проблемы іоннаго заряда и элек-
трической проводимости, о которыхъ была рѣчь въ § 108. Ниже мы
въ этомъ убѣдимся. Вообще общепринятымъ принципомъ научнаго
изслѣдованія является выборъ простѣйшаго предположенія во всѣхъ
тѣхъ случаяхъ, когда необходима нѣкоторая гипотеза для объеди-
ненія извѣстныхъ фактовъ и проложенія новыхъ путей для изслѣдо-
ванія. Приложеніе этого принципа почти всегда приводитъ тотчасъ
къ принятію такого предположенія, которое позже оказывается не-
сомнѣнно справедливымъ.
Въ послѣдующемъ мы будемъ считать несомнѣннымъ,
что зарядъ электрона тождественъ съ элементарнымъ ко-
личествомъ электричества.
Установивъ это, мы можемъ перейти къ опредѣленію „атомнаго
вѣса“ электроновъ. Но оказывается, что гораздо легче былр^уста-
е • /цѵ
новить одинаковость значенія — для различныхъ катодныхъ лучей,
чѣмъ на самомъ дѣлѣ вычислить это значеніе. Для этого прежде
всего нужно точно измѣрить во всѣхъ точкахъ отк^рфГющее магнит-
ное поле, такъ какъ оно въ дѣйствительности отнюдь не является
о V
однороднымъ, какъ мы это приняли для прост^ы въ § 151, и ввести
въ вычисленія соотвѣтствующія поправки.ЛхПрц столь сложныхъ измѣ-
Скорость катодныхъ лучей
261
реніяхъ невозможно совершенно избѣгнуть ошибокъ. Всѣ тщатель-
ныя измѣренія, произведенныя до сихъ поръ, позволяютъ съ увѣрен-
е
ностью утверждать лишь, что искомая величина — заключается меж-
ду 1,7. ІО8 и 1,9. ІО8. По послѣднимъ измѣреніямъ она весьма
близка къ
175 ІО8 кулонъ.
’ ’ граммъ
Такъ какъ электронъ соотвѣтствуетъ одновалентному іону, то
число содержащихся въ граммъ - атомѣ отдѣльныхъ частичекъ рав-
р
няется 7Ѵ ——, гдѣ Е обозначаетъ эквивалентный зарядъ (96 540 ку-
лоновъ). Масса граммъ - атома равняется
М = ІЧ.т = --т = Р:—,
е т
что даетъ
7И = -^2 . 10-8 = 0,00055.
1, / О
Атомный вѣсъ электроновъ равенъ 0,00055, т. е. въ круг-
1
лыхъ числахъ части атомнаго вѣса водорода.
Отсюда слѣдуетъ, что электронъ является весьма малой состав-
ной частью химическаго атома, и это хорошо согласуется съ выше
изложенной теоріей. Съ дальнѣйшими подробностями относительно
строенія атомовъ мы познакомимся ниже.
СКОРОСТЬ КАТОДНЫХЪ ЛУЧЕЙ.
154. Различные роды катодныхъ лучей отличаются другъ отъ
друга только скоростью. Принимая для величину 1,75 . ІО8, мы мо-
жемъ вычислить скорость ѵ по величинѣ катоднаго напряженія Ѵ\
получается слѣдующая формула:
ѵ = 6.107 . Ѵѵ —.
г сек.
При не слишкомъ высокомъ катодномъ напряженіи, равномъ
10 000 вольтъ, получаемъ отсюда ѵ = 6 . ІО9 СМ- = скорости
ССК. о
свѣта. И даже при нормальныхъ катодныхъ напряженіяхъ получа-
ются все же колоссальныя скорости. Если, напримѣръ, взять пла-
тиновый катодъ въ воздухѣ, то У = 345 вольтамъ (см. § 142)П
1,11. 109 -^Ь=1
’ сек. 27
скорость ѵ по величинѣ
рости свѣта, но никогда
намъ придется вернуться
. . X А , ‘"в 11
О X
скорости свѣта. При высокихъ напряженіяхъ
приближается, такимъ образойѣУ къ ско-
ея не достигаетъ; къ этому обстоятельству
еще разъ въ концѣ книгц.$Ѵ<>
262
Скорость катодныхъ лучей. — Вторичные лучи
Колоссальныя величины, вычисленныя нами для скорости ѵ, были
измѣрены также и непосредственно Вихертомъ (АѴіесНегі) по методу,
напоминающему методъ Физо для измѣренія скорости свѣта. Резуль-
таты измѣреній настолько хорошо согласуются съ величинами, получен-
ными вычисленіемъ, что лучшаго, въ виду большихъ эксперимен-
тальныхъ трудностей измѣренія, нельзя и требовать.
Такъ какъ скорость катодныхъ лучей зависитъ исключительно
отъ вызывающаго ихъ напряженія, то для характеристики катодныхъ
лучей обычно указываютъ лишь это напряженіе. Такъ, говорятъ о
катодныхъ лучахъ „10 000 вольтныхъ" и т. п.
Катодные лучи различныхъ скоростей обладаютъ нѣкоторыми
различіями въ своихъ свойствахъ. Что катодные лучи большей ско-
рости въ магнитномъ и электрическомъ поляхъ оказываются менѣе
„гибкими", понятно само собою. Но они оказываются также бо-
лѣе „пронизывающими", т. е. они менѣе быстро поглощаются ма-
теріальными тѣлами, нежели катодные лучи меньшей скорости. Обычно
различаютъ „жесткіе" и „мягкіе" катодные лучи. Жесткіе лучи воз-
никаютъ при высокихъ напряженіяхъ, мягкіе — при болѣе низкихъ.
Параллельно съ болѣе сильнымъ поглощеніемъ обнаруживается и
тотъ фактъ, что мягкіе катодные лучи вызываютъ въ газѣ, черезъ
который они проходятъ, болѣе сильную іонизацію, нежели жесткіе лучи.
ВТОРИЧНЫЕ ЛУЧИ.
155. Если мы будемъ разсматривать хорошо эвакуированную
трубку при прохожденіи черезъ нее заряда, то мы сейчасъ же за-
мѣтимъ, что стекло свѣтится зеленымъ свѣтомъ флуоресценціи не
только въ томъ мѣстѣ, гдѣ на него падаютъ катодные лучи, но что
оно испускаетъ относительно слабый, но все же отчетливо видный
зеленый свѣтъ и во всѣхъ остальныхъ мѣстахъ.
Лучи, вызывающіе это слабое зеленое сіяніе, возникаютъ въ
тѣхъ мѣстахъ, гдѣ настоящіе „катодные" лучи поглощаются тѣлами,
на которыя они падаютъ. Ихъ называютъ поэтому вторичвдми
лучами. Эти лучи по своимъ свойствамъ вполнѣ подобны катсйнймъ, но
они возникаютъ безъ поля, по крайней мѣрѣ, безъ поля^^мѣтныхъ
размѣровъ, каково катодное поле. Эти вторичные лучй^всегда обра-
зующіеся при поглощеніи катодныхъ лучей, многократно подверга-
лись изученію. Они не однородны, т. е. представляютъ собою смѣсь
лучей различныхъ скоростей и именно смѣс^^^ухъ группъ лучей,
Вторичные лучи
263
между которыми имѣется существенная разница. Первая группа со-
стоитъ изъ лучей, скорость которыхъ очень близка къ скорости пер-
вичныхъ лучей и даже достигаетъ ея. Часто эти аучи называютъ
отраженными катодными лучами, при чемъ имѣютъ въ виду диффуз-
ное отраженіе, подобное отраженію свѣта отъ бумаги. Интенсивность
диффузно отраженныхъ катодныхъ лучей независитъ отъ угла паденія
первичныхъ лучей на отражающую поверхность. Вторая группа, обна-
руженная впервые Аустиномъ и Штарке (Ь. Аизііп и Н. Зіагке),
состоитъ изъ весьма мягкихъ лучей. Согласно Фихтбауеру (СНг. ЕйсНі-
Ъаиег), они соотвѣтствуютъ 30 вольтнымъ катоднымъ лучамъ. Ихъ
интенсивность весьма мала при нормальномъ паденіи первичныхъ
лучей и замѣтно возрастаетъ съ возрастаніемъ угла паденія этихъ
лучей.
При прохожденіи катодныхъ лучей черезъ какія-либо тѣла, напри-
мѣръ, черезъ тонкіе металлическіе листки или черезъ газы, они также
постепенно преобразуются въ болѣе мягкіе вторичные лучи и при
этомъ мѣняютъ свое первоначально опредѣленное прямолинейное
распространеніе на диффузно - разсѣянное. Если бы это обстоятель-
ство не было извѣстно изъ прямыхъ опытовъ, его можно было бы
установить просто по виду отрицательнаго тлѣющаго свѣта. Вблизи
катода мы имѣемъ относительно жесткіе первичные лучи, слабо
глощаемые газомъ и потому слабо іонизирующіе. Въ темномъ
тодномъ пространствѣ имѣются почти исключительно эти лучи,
чему въ немъ и отсутствуетъ тлѣющій свѣтъ. Но какъ только
большая доля первичныхъ лучей поглотится, количество возбуждаю-
щихся мягкихъ, сильно іонизирующихъ вторичныхъ лучей очень быстро
возрастаетъ, такъ какъ, когда первые болѣе мягкіе вторичные лучи
поглотятся, тотчасъ возникаютъ „третичные лучи“, поглощающіеся,
по крайней мѣрѣ, столь же быстро, какъ и вторичные лучи, и т. д>
Такимъ образомъ іонизирующее дѣйствіе и сопровождающее его
свѣченіе сразу очень быстро возрастаютъ. Мы видимъ это по отно-
сительно рѣзкому началу катоднаго тлѣющаго свѣта. Во внѣшней
части іонизирующее дѣйствіе убываетъ постепенно, такъ какъ пер-о
вичные лучи постепенно исчезаютъ, а скорость вторичныхъ лучей^
становится все меньше и меньше, въ виду того, что и электрическое
поле въ тлѣющемъ свѣтѣ постепенно ослабѣваетъ (см. § 143)*^йко-
нецъ, лучи теряютъ совершенно способность образовывать^путемъ
столкновеній іоновъ новые іоны; какъ мы видѣли (§ 137д\ля этого
по-
ка-
по-
не-
264
Лучи Рентгена
необходима нѣкоторая опредѣленная
ко внѣшнему темному пространству,
присутствія іоновъ, залетѣвшихъ изъ
ложительной свѣтовой колонны.
скорость. Такъ мы приходимъ
гдѣ проводимость зависитъ отъ
области тлѣющаго свѣта и по-
О катодномъ свѣтовомъ поясѣ мы здѣсь ничего не говорили.
Ниже мы увидимъ, что онъ образуется не катодными лучами.
Совсѣмъ мягкіе, сильно іонизирующіе лучи въ отрицательномъ
тлѣющемъ свѣтѣ были непосредственно наблюдаемы Дж. Дж. Том-
сономъ.
ЛУЧИ РЕНТГЕНА.
156. Кромѣ вторичныхъ лучей, тѣло, на которое падаютъ ка-
тодные лучи, высылаетъ еще иные невидимые лучи, именно Рент-
геновскіе лучи, открытые въ 1895 году Рентгеномъ (Рбпі^еп).
Удобнѣе всего ихъ получать при помощи разрядной трубки съ во-
Рис. 103. Рентге-
новская трубка.
гнутымъ сферическимъ катодомъ (рис. 103). Какъ
мы знаемъ (§ 143), выходящіе изъ вогнутаго катода
катодные лучи сходятся всѣ приблизительно въ
одной точкѣ, лежащей около центра катодной сферы.
Противъ катода, подъ угломъ въ 45° къ среднему
лучу исходящаго изъ катода пучка, помѣщается
толстая металлическая пластинка — антикатодъ,
устанавливаемая, по возможности, въ фокусѣ ка-
тоднаго пучка. Такая установка позволяетъ получить
сильные Рентгеновскіе лучи, исходящіе приблизи-
тельно изъ одной точки — фокуса на антикатодѣ. Для
равномѣрности излученія оказалось еще полезнымъ
пользоваться короткимъ проволочнымъ анодомъ,-
соединеннымъ съ антикатодомъ.
Весьма важно достигнуть въ „Рентгеновской
лампѣ“ опредѣленной степени разрѣженія и под-
держивать ее неизмѣнной. Отъ этого главнымъ обра-
зомъ зависятъ интенсивность и свойства ^Рент-
геновскихъ лучей. Чтобы избѣжать быстрыхъ измѣненій;^ давле-
нія, происходящихъ отъ того, что электрическій рНрядъ всегда
сопровождается образованіемъ и поглощеніемъ гадрРентгеновская
лампа должна имѣть возможно большой объемъ; ей^придаютъ обычно
форму большого шара. Кромѣ того, слѣдуемъ о Заботиться о томъ,
Лучи Рентгена
265
чтобы антикатодъ не слишкомъ нагрѣвался; для этого его дѣлаютъ
массивнымъ. Въ лампахъ же, дающихъ очень сильное излученіе,
устраивается особое охлаждающее приспособленіе: антикатодъ при-
крѣпляется къ металлической трубкѣ, внутренность которой изоли-
рована отъ пустоты и по которой циркулируетъ холодная вода или
холодный воздухъ. Многія Рентгеновскія лампы имѣютъ кромѣ того
особыя приспособленія, позволяющія вводить въ нихъ небольшія ко-
личества газа, такъ какъ вообще при длительныхъ разрядахъ содер-
жаніе газа въ трубкѣ уменьшается.
По тому, какой видъ имѣетъ разрядъ, можно сразу узнать,,
правильно ли эвакуирована лампа. Если въ газѣ замѣтно отчетливое
.голубоватое сіяніе, то эвакуація недостаточна. При очень низкихъ
давленіяхъ газъ кажется совершенно темнымъ по сравненію съ ярко
сіяющими стеклянными стѣнками. Если эвакуація чрезмѣрна, такъ что
напряженіе источника электричества недостаточно для разряда, то
вся трубка остается почти темной. Если давленіе воздуха въ трубкѣ
какъ разъ то, которое нужно, то противъ антикатода на стеклѣ за-
мѣтно ярко зеленое свѣтлое пятно, вызванное вторичными лучами,
которые, конечно, возбуждаются такъ же, какъ и Рентгеновскіе, въ
фокусѣ катодныхъ лучей. Это свѣтлое пятно рѣзко ограничено кри-
вою, лежащей въ одной плоскости съ антикатодомъ, а въ „области
тѣни* стеклянныя стѣнки лишь слегка свѣтятся зеленоватымъ свѣ-
томъ подъ вліяніемъ третичныхъ лучей.
Всѣ тѣла являются для Рентгеновскихъ лучей болѣе или менѣе
прозрачными. При этомъ, какъ и для катодныхъ лучей, поглоща-
тельная способность тѣла тѣмъ выше, чѣмъ больше удѣльный вѣсъ
тѣла. Рентгеновскіе лучи никогда не испытываютъ преломленія, по-
добнаго тому, какое испытываетъ свѣтъ, вступая въ прозрачное тѣло.
Такимъ образомъ, если на пути Рентгеновскихъ лучей помѣстить
какое-нибудь тѣло, то они отбрасываютъ тѣневое его изображеніе,
подобно тому, какъ свѣтъ даетъ изображеніе стеклянной пластинки,
нѣкоторыя мѣста которой состоятъ изъ болѣе или менѣе темныхъ г
участковъ дымчатаго стекла, имѣющаго тотъ же показатель прело^ф)
.ленія. Это тѣневое изображеніе будетъ рѣзкимъ лишь въд^иѣ
случаѣ, если • источникъ излученія имѣетъ очень малые рд|^ѣры.
Чѣмъ большіе размѣры имѣетъ источникъ излученія,^ т^Х болѣе
широкими и размытыми оказываются полутѣни. ПомоЩ^ Рентгенов-
скихъ трубокъ вышеописанной формы, дающихъ ^йочти точечный
266
Лучи Рентгена. — Теорія Рентгеновскихъ лучей
источникъ лучеиспусканія, изображенія получаются необычайно рѣз-
кими. Это очень хорошо видно, если заставить лучи, пройдя черезъ
какой-нибудь объектъ, падать на экранъ, покрытый синеродистымъ
баріемъ; при этомъ на экранѣ получается изображеніе вслѣдствіе
флуоресценціи его подъ вліяніемъ Рентгеновскихъ лучей. Ставя на мѣсто
экрана фотографическую пластинку, мы на ней можемъ получить фо-
тографію изслѣдуемаго объекта.
Характеръ Рентгеновскихъ лучей вполнѣ зависитъ отъ природы
вызывающихъ ихъ катодныхъ лучей. Жесткіе катодные лучи, воз-
никающіе при высокихъ напряженіяхъ, даютъ также жест-
кіе Рентгеновскіе лучи, лишь слабо поглощаемые всѣми
тѣлами; они довольно хорошо проходятъ даже черезъ толстыя ме-
таллическія пластинки, монеты, черезъ плотныя кости (напримѣръ,
черепныя) и т. п. и при этомъ на самыя тѣла оказываютъ также
лишь ничтожное вліяніе. Мягкіе катодные лучи даютъ мягкіе
Рентгеновскіе лучи, сильно поглощаемые всѣми тѣлами; эти
лучи менѣе пригодны для фотографированія. Мягкіе Рентгеновскіе
лучи вызываютъ въ поглощающихъ ихъ тѣлахъ сильныя измѣненія.
Поэтому работать съ очень сильными мягкими Рентгеновскими лу-
чами не безопасно, такъ какъ они могутъ вызвать весьма непріятныя
и даже опасныя для жизни воспаленія въ тѣхъ частяхъ человѣческаго
тѣла, въ которыя они проникаютъ. Съ другой стороны съ интенсив-
ными дѣйствіями ихъ связаны также и цѣлебныя ихъ свойства, ко-
торыми нынѣ пользуются въ медицинѣ.
ТЕОРІЯ РЕНТГЕНОВСКИХЪ ЛУЧЕЙ.
157. Хотя Рентгеновскіе лучи по своимъ дѣйствіямъ на погло-
щающую матерію очень похожи на катодные, они, внѣ всякаго со-
мнѣнія, представляютъ собою нѣчто вполнѣ отличное отъ катодныхъ
лучей. Ниже мы увидимъ, что кажущееся сходство Рентгеновскихъ
лучей съ катодными лучами зависитъ отъ вторичныхъ процессовъ.
Если производить съ Рентгеновскими лучами тѣ опыты, которые
имѣли для насъ основное значеніе при ознакомленіи съ природой
катодныхъ лучей и доказали ихъ тождественность съ потокомъ элек-
трическихъ частицъ (§148), то оказывается, что всѣ эти орьйъі даютъ для
Рентгеновскихъ лучей вполнѣ отрицательные резуль^іы? Поэтому воз-
можны только двѣ теоріи Рентгеновскихъ лучей^і^г одной они пред-
ставляютъ собою потоки незаряженныхъ частицС/эмиссіонная теорія),
Теорія Рентгеновскихъ лучей
267
по другой же они представляютъ собою волнообразные процессы въ
эѳирѣ, какъ и свѣтъ (теорія колебанія).
Теоретическія соображенія очень многое говорятъ въ пользу
второй теоріи. Изъ прочно обоснованныхъ законовъ электродина-
мики, съ которыми мы познакомимся во второй части этой книги,
съ неопровержимой строгостью слѣдуетъ, что при внезапномъ измѣ-
неніи въ движеніи электрической частички, все равно измѣняется ли
при этомъ только направленіе движенія или также и скорость,
въ эѳирѣ возникаетъ волнообразное движеніе. При этомъ такое
излученіе энергіи продолжается до тѣхъ поръ, пока движеніе ча-
стички не сдѣлается опять постояннымъ. Если катодныя частички
падаютъ на поглощающее ихъ тѣло, то онѣ должны въ кратчайшій
промежутокъ времени перейти изъ состоянія чрезвычайно быстраго
движенія въ стаціонарное состояніе покоя. Въ этотъ моментъ непре-
мѣнно долженъ распространиться въ пространство, въ видѣ шаровой
волны, взрывъ энергіи, который можно сравнить со звуковой волной,
возникающей въ воздухѣ при внезапномъ столкновеніи твердаго тѣла
съ твердымъ же препятствіемъ, оказавшимся на его пути. Но ничто
не заставляетъ насъ думать, что электронъ высылаетъ только одну
такую взрывную волну энергіи. Онъ нѣсколько разъ совершаетъ ко-
лебанія въ разныя стороны прежде, чѣмъ прійдетъ въ состояніе по-
коя, и при каждомъ колебаніи получается въ эѳирѣ волна. Такъ какъ
за короткій промежутокъ времени объ антикатодъ ударяется громад-
ное число электроновъ, то отъ него исходитъ хаосъ этихъ корот-
кихъ эѳирныхъ волнъ, подобный тому, который, распространяясь въ
воздухѣ, вызываетъ у насъ ощущеніе шипящаго звука. Эти безпо-
рядочныя волны, возникновеніе которыхъ необходимо должно имѣть
мѣсто, по всей вѣроятности, и представляютъ собою Рентгеновскіе
лучи. Отъ имѣющаго подобный же составъ излученія въ эѳирѣ, ко-
торое мы воспринимаемъ въ качествѣ свѣта, эти колебанія отлича-
ются тѣмъ, что періодъ каждаго изъ составляющихъ ихъ иррегуляр-
ныхъ толчковъ гораздо короче періодовъ свѣтовыхъ колебаній; по
всей вѣроятности, продолжительность толчка въ Рентгеновскихъ лу<-
1 1 .
чахъ составляетъ отъ до періода колебаній въ свѣтовыхъ
лучахъ, и она тѣмъ короче, чѣмъ жестче самые лучи. Если эт^спра-
ведливо, то длина волны Рентгеновскихъ лучей должнау$рггь при-
близительно порядка молекулярныхъ діаметровъ; этимъ^полнѣ объ-
ясняется отсутствіе преломленія и правильнаго отраженія у Рентге-
-'268
Іонизація Рентгеновскими лучами и вторичные лучи
яовскихъ лучей. Молекулы по отношенію къ Рентгеновскимъ лучамъ
являются тѣмъ же, чѣмъ являются маленькія капли тумана по отно-
шенію къ свѣту, т. е. благодаря ихъ присутствію заполняемое ими
"пространство представляетъ собою для Рентгеновскихъ лучей мут-
ную среду.
Имѣются нѣсколько наблюденій и измѣреній, какъ будто под-
тверждающихъ эти теоретическіе выводы. Однако, вслѣдствіе боль-
шихъ экспериментальныхъ трудностей, ихъ нельзя считать вполнѣ
убѣдительными, и потому мы здѣсь ихъ разсматривать не будемъ.
Одно явленіе, которое, по всей вѣроятности, скорѣе всего приведетъ
къ опредѣленнымъ заключеніямъ относительно природы Рентгенов-
скихъ лучей, мы разберемъ подробнѣе въ слѣдующемъ параграфѣ.
ІОНИЗАЦІЯ РЕНТГЕНОВСКИМИ ЛУЧАМИ И ВТОРИЧНЫЕ ЛУЧИ.
158. Тотчасъ же послѣ своего открытія Рентгенъ замѣтилъ,
что его лучи іонизируютъ газъ, черезъ который они проходятъ. Это
можно легко показать помощью заряженнаго электрометра (ср. § 122).
Изъ фактовъ, съ которыми мы познакомились, говоря о газіонахъ,
‘слѣдуетъ, что эта іонизація основана на отщепленіи электроновъ отъ
молекулъ. Такимъ образомъ, Рентгеновскіе лучи вызываютъ въ га-
захъ, ихъ поглощающихъ, образованіе своего рода диффузныхъ ка-
тодныхъ лучей.
Для того, чтобы лучше изучить это явленіе, удобно Рентгенов-
скіе лучи направить на твердое тѣло —лучше всего на металлъ,—
сильно ихъ поглощающее. Въ этомъ случаѣ изъ того мѣста, гдѣ
они поглощаются, распространяется по всѣмъ направленіямъ вторич-
ное излученіе, состоящее изъ двухъ частей. Одну его часть соста-
вляютъ жесткіе катодные лучи, лишь немного болѣе мягкіе, нежели
тѣ лучи, которыми были возбуждены Рентгеновскіе лучи; вторая
часть состоитъ изъ вторичныхъ Рентгеновскихъ лучей, немного б^-
лѣе мягкихъ, нежели первичные.
Такъ какъ Рентгеновскіе лучи при ихъ поглощеніи какимъ-либо
тѣломъ всегда вызываютъ катодное излученіе, то, слѣдовательно, ихъ
. дѣйствіе всегда сводится къ тому, какъ будто бы тѣ^цросто было
подвергнуто дѣйствію катодныхъ лучей, и этимъ .объясняется кажу-
щееся сходство обоихъ родовъ излученій. И
Чѣмъ жестче Рентгеновскіе лучи, тѣмъ жестче и возбуждаемые
Фотоэлектрическія явленія
269*
ими катодные лучи. Скорость возбуждаемыхъ катодныхъ лучей могла
бы прямо служить мѣрою жесткости Рентгеновскихъ. Возможно, что
по ея величинѣ можно также опредѣлить и длину волны Рентгенов-
скихъ лучей, какъ мы это увидимъ въ слѣдующемъ параграфѣ.
ФОТОЭЛЕКТРИЧЕСКІЯ ЯВЛЕНІЯ.
159. Какъ мы видѣли, Рентгеновскіе лучи, вѣроятно, предста-
вляютъ собою волновое излученіе, отличающееся отъ излученія обыч-
наго источника свѣта лишь гораздо меньшей величиной средней
длины волны. Въ пользу этого предположенія говоритъ еще то.
обстоятельство, что кратчайшія волны, заключающіяся въ излученіи
обычнаго источника свѣта, производятъ дѣйствія, позволяющія ихъ.
уподобить Рентгеновскимъ лучамъ.
Крайніе ультрафіолетовые лучи такъ сильно поглощаются воз-
духомъ и всѣми газами, что ихъ можно изслѣдовать только въ пу-
стотѣ. Громадныя экспериментальныя трудности, связанныя съ этимъ.,
обстоятельствомъ, удалось преодолѣть Шуману (V. ЗсНишапп)*
изучившему лучи электрической искры по ихъ фотографическому
дѣйствію. Эти лучи правильно отражаются и преломляются, но въ
другихъ отношеніяхъ уже вполнѣ могутъ быть уподоблены очень,
мягкимъ Рентгеновскимъ лучамъ. Какъ показалъ Ленардъ, они
сильно іонизируютъ воздухъ при поглощеніи.
Обычные ультрафіолетовые лучи, для которыхъ воздухъ прозра-
ченъ и которые поэтому имѣются и въ доходящемъ до насъ солнеч-
номъ свѣтѣ, понятно, не могутъ обладать такимъ дѣйствіемъ. Но ихъ
родство съ Рентгеновскими лучами проявляется, если ихъ заставить,
падать' на металлическія поверхности, которыя ихъ поглощаютъ.
Лучше всего удается такой опытъ съ легко окисляющимися метал-
лами, напримѣръ, съ цинкомъ, который слѣдуетъ слегка наамальга—
мировать, чтобы получить гладкую поверхность. Соединимъ амаль-
гамированную цинковую пластинку съ не слишкомъ чувствительнымъ
гальванометромъ и зарядимъ ее отрицательно (рис. 104). Убѣдимся^
предварительно въ томъ, что электрометръ хорошо изолированій?
показаніе его не измѣняется съ теченіемъ времени. Послѣ^гЬго-
внезапно подвергнемъ пластинку дѣйствію свѣта электрической ду-
говой лампы; отклоненіе электрометра сейчасъ же начнетѣ умень-
шаться и черезъ короткое время становится равным^^ліо. Если мы
повторимъ тотъ же опытъ съ положительнымъ урядомъ, то ни ма—
270
Фотоэлектрическія явленія
лѣйшаго вліянія свѣта не обнаружимъ. Помощью весьма чувстви-
тельнаго электрометра можно убѣдиться въ томъ, что незаряженная
цинковая пластинка, подвергнутая дѣйствію свѣта, отдаетъ отрица-
тельные заряды и съ теченіемъ времени заряжается до нѣкотораго,
правда, довольно низкаго положительнаго потенціала. Если пластинку
помѣстить въ пустотѣ, то можно получить напряженія въ нѣсколько
вольтъ.
Тонъ къ дуггь
Рис. 104. Фотоэлектрическое дѣйствіе.
Что здѣсь мы имѣемъ дѣло именно съ дѣйствіями ультрафіоле-
товыхъ лучей, легко установить, помѣщая передъ цинково|/йластин-
кой кусокъ стекла. Стекло поглощаетъ ультрафіолетовые лучи и
фотоэлектрическій эффектъ исчезаетъ. Если цинковую пластинку за-
мѣнить латунной, то и при дѣйствіи ультрафіолетоваго свѣта мы
едва ли что-нибудь замѣтимъ; такимъ образомъ мы въ самомъ дѣлѣ
наблюдали дѣйствіе ультрафіолетовыхъ луч^й^ цинкъ.
Фотоэлектрическія явленія
271
Это явленіе впервые было точно изучено Гальваксомъ (Наіі-
АѵасИз), но уже Герцъ случайно сдѣлалъ наблюденіе, указавшее на
существованіе фотоэлектрическаго дѣйствія.
Ленардъ изслѣдовалъ фотоэлектрическія явленія въ пустотѣ;
для этой цѣли онъ пропускалъ ультрафіолетовые лучи черезъ квар-
цевое окошечко на помѣщенную въ эвакуированной трубкѣ цинко-
вую пластинку, которая была соединена съ отрицательнымъ полю-
сомъ батареи. Оказалось, что отъ цинковой пластинки распростра-
нялись лучи, вполнѣ тождественные съ катодными лучами. Слѣдова-
тельно, фотоэлектрическій эффектъ заключается ни въ чемъ иномъ,
какъ въ выдѣленіи электроновъ изъ металла. Для проявленія этого
дѣйствія нѣтъ необходимости въ электрическомъ полѣ. Тѣ мѣста,
въ которыхъ металлъ поглощаетъ ультрафіолетовые лучи и при
отсутствіи электрическаго поля, испускаютъ электроны. О скорости
этихъ весьма мягкихъ катодныхъ лучей можно судить по тому, до
какого положительнаго потенціала заряжается незаряженная пластинка,
если откачать воздухъ, который дѣйствуетъ проводящимъ образомъ
подъ вліяніемъ іонизаціи этими мягкими лучами. Величина этого потен-
ціала, по опытамъ Ладенбурга и Маркау (Е. ЬадепЬиг^ и К. Магкаи),
равняется приблизительно 3 вольтамъ.
Жесткость образующихся катодныхъ лучей находится, повиди-
мому, въ закономѣрной зависимости отъ длины волны поглощаемаго
свѣта. По наблюденіямъ Ладенбурга и Маркау, она возрастаетъ
съ убываніемъ длины волны. Вѣроятно, она обратно пропорціональна
длинѣ волны. Такъ какъ жесткость, измѣряемая напряженіемъ въ
3 вольта, соотвѣтствуетъ длинѣ волны въ 230то длина волны
Рентгеновскихъ лучей, вызывающихъ вторичные лучи жесткости въ
9000 вольтъ, получается равной приблизительно 0,077Болѣе
жесткіе Рентгеновскіе лучи должны имѣть меньшую длину волны,
болѣе мягкіе — большую. Однако, въ виду отсутствія точныхъ изслѣ-
дованій, это является пока лишь гипотезой.
Ольстеръ и Гейтель произвели большое число опытовъ надъ^'
фотоэлектрическими свойствами различныхъ металловъ. Они раот^р
дожили металлы въ рядъ по ихъ фотоэлектрическому дѣйствію,/!'. е.
по количеству высылаемыхъ ими электроновъ; оказалось, что^этотъ
рядъ тождественъ съ рядомъ напряженій Вольта (§ ЗЗ^Онъ на-
оД
чинается легко окисляющимися металлами и кончает^грйагородными
металлами. Наиболѣе дѣятельными являются щелрчнйр металлы. Чѣмъ
272
Флуоресценція.— Закатодные лучи
легче металлъ окисляется, тѣмъ выше верхняя граница длины волны
дѣйствующихъ лучей. Натрій и рубидій очень сильно реагируютъ,
даже на желтый и оранжевый свѣтъ.
ФЛУОРЕСЦЕНЦІЯ.
160. Замѣчательно, что тѣ роды лучей, которые отличаются
сильнымъ фотоэлектрическимъ дѣйствіемъ, вмѣстѣ съ тѣмъ являются
и наилучшими возбудителями флуоресценціи. Было изслѣдовано-
большое число жидкостей на ихъ фотоэлектрическія свойства и ока-
залось, что почти всегда оправдывается слѣдующее правило: жид-
кость активна фотоэлектрически только въ томъ случаѣ, если она
флуоресцируетъ. Поэтому свѣтъ флуоресценціи, вѣроятно, можно
разсматривать какъ вторичные свѣтовые лучи, возбуждаемые первич-
нымъ ультрафіолетовымъ свѣтомъ вмѣстѣ съ мягкими катодными
лучами. Такимъ образомъ флуоресценція оказывается вполнѣ анало-
гичной вторичнымъ Рентгеновскимъ лучамъ, возникающимъ при но-
глощеніи первичныхъ Рентгеновскихъ лучей.
ЗАКАТОДНЫЕ ЛУЧИ (КА№Е8ТЯАНЬЕМ).
161. Изучивъ всесторонне катодные лучи, возвратимся теперь
къ изученію тихаго разряда. Мы знаемъ навѣрное, что катодъ вы-
сылаетъ электроны, но мы до сихъ поръ не ставили еще вопроса 0‘
томъ, какимъ образомъ эти электроны выдѣляются изъ газовыхъ
или металлическихъ молекулъ прежде, чѣмъ они приходятъ въ дви-
женіе подъ дѣйствіемъ катоднаго поля.
Прежде всего является весьма вѣроятнымъ, что іонизирующія
дѣйствія, вызывающія выдѣленіе катодныхъ частицъ, обнаруживаются
въ видѣ катоднаго свѣтового пояса, описаннаго въ § 140. Это свѣ-
ченіе впервые тщательно изучилъ Гольдштейнъ (СоМзІеіп). При
своихъ изслѣдованіяхъ онъ пользовался разрядной трубкой, въ кото-
рой за катодомъ находилось еще одно эвакуированное пространство;:
это пространство отдѣлялось отъ разряднаго пространства катрдомъ,
имѣвшимъ видъ пластинки. Въ этой пластинкѣ было сдѣлано одно
или нѣсколько отверстій, представлявшихъ собою „канаДы^, которыми
соединялись между собою оба эвакуированныя пространства (рис.'105).
При этихъ условіяхъ наблюдается, что красный освфтовой поясъ про-
ходитъ черезъ каналы въ катодѣ въ расположенное за нимъ про-
странство въ видѣ длинныхъ полосъ свѣт^^оторыя въ достаточно>
За катодные лучи
273
эвакуированныхъ сосудахъ достигаютъ длины въ 10 — 20 см., при
чемъ въ концѣ онѣ постепенно переходятъ въ диффузное туманное
свѣченіе. Когда эти лучеобразные придатки свѣтового пояса встрѣ-
чаютъ стеклянную стѣнку, то они вызываютъ на послѣдней совер-
шенно такое же флуоресцирующее свѣ-
ченіе, какъ и катодные лучи.
Описанныя свѣтовыя полосы пред-
ставляютъ собою новаго рода лучи, ко-
торые Гольдштейнъ называетъ Капаі-
зігаЫеп *), такъ какъ ихъ можно наблю-
дать, только заставляя ихъ проходить
черезъ каналы въ катодѣ.
Если внести въ катодное темное
пространство твердое тѣло, то оно отбро-
ситъ тѣнь не только въ тлѣющемъ свѣтѣ,
но и въ свѣтовомъ поясѣ, и изъ тѣхъ
отверстій катода, которыя лежатъ въ
тѣни, никакихъ закатодныхъ лучей не
появится. Отсюда можно сдѣлать важное
заключеніе: закатодные лучи возни-
каютъ въ ограничивающемъ катод-
Рис. 105. Закатодные лучи.
ное темное пространство положительно заряженномъ слоѣ
и идутъ черезъ сильное электрическое поле катоднаго про-
странства по направленію къ катоду.
Точныя изслѣдованія надъ закатодными
дены В. Виномъ (\Ѵ. \Ѵіеп). Они показали,
отклоняются какъ въ
трическомъ полѣ, но
тодныхъ лучей. Если
дэевскій сосудъ, то
Отсюда мы заключаемъ, что закатодные лучи состоятъ изъ по-
ложительно заряженныхъ частичекъ, движущихся съ боль-
шою скоростью.
лучами были произве-
что закатодные лучи
полѣ, такъ и въ элек-
сильномъ магнитномъ
въ сторону, противоположную отклоненію ка-
заставить закатодные лучи падать въ Фара-
они ему сообщаютъ положительный зарядъ.
ИЗМѢРЕНІЯ НАДЪ ЗАКАТОДНЫМИ ЛУЧАМИ.
162. Явленія отклоненія для закатодныхъ лучей не та^ъ просты,
какъ для катодныхъ лучей. Даже при вполнѣ постоянномъ катод-
---------------
г) Въ русской научной литературѣ эти лучи обычно называются зака-
тодными, каковымъ названіехмъ мы и будемъ пользоваться. Прим. пер.
Ми. Электричество и магнитизмь.
18
274
Измѣренія надъ закатодными лучами
номъ напряженіи свѣтлое пятно, вызываемое на флуоресцирующемъ
экранѣ прошедшими черезъ діафрагму закатодными лучами, подъ
дѣйствіемъ электрическаго или магнитнаго поля не отклоняется просто
въ сторону, какъ это происходитъ въ случаѣ катодныхъ лучей, но
растягивается въ полосу. Если возбудить одновременно магнитное
и электрическое поля, то получающаяся при этомъ полоса распола-
гается приблизительно по діагонали относительно двухъ полосъ,
образующихся при раздѣльномъ дѣйствіи обоихъ полей. Отсюда
можно заключить, что отношеніе электрическаго и магнитнаго откло-
неній приблизительно постоянно, и, значитъ, какъ это слѣдуетъ изъ
формулъ, данныхъ въ § 151, частички закатодныхъ лучей имѣютъ
всѣ приблизительно одинаковую скорость. Но онѣ существенно раз-
личаются между собою значеніями отношенія В. Винъ нашелъ,
что легче всего произвести изслѣдованіе, когда трубка наполнена
водородомъ, такъ какъ въ этомъ случаѣ пятно флуоресценціи осо-
бенно ярко ’). Въ этомъ случаѣ отношеніе для наиболѣе откло-
ненныхъ частицъ закатодныхъ лучей получалось при многихъ измѣ-
реніяхъ всегда приблизительно равнымъ 100 000 ку-юн--. Это число
г г г граммъ
почти точно соотвѣтствуетъ величинѣ эквивалентнаго заряда (96 540);
слѣдовательно, частицы, къ которымъ оно относится, имѣютъ атом-
ный вѣсъ, равный 1, т. е. представляютъ собою положительно за-
ряженные атомы водорода. Для менѣе отклоненныхъ частицъ
величина-^- получилась меньшей; В. Винъ при своихъ измѣреніяхъ
наблюдалъ всегда также и вовсе не отклоненныя частицы, для кото-
рыхъ, слѣдовательно, отношеніе — равняется нулю.
Эти факты становятся понятными, если принять во вниманіе,
что частицы закатодныхъ лучей обладаютъ массою, весьма значи-
тельною, по сравненію съ массою электрона. Поэтому легко можетъ
случиться, что во время своего движенія такая частичка присоеди-
нитъ къ себѣ электронъ, не претерпѣвая при этомъ уменьшенія
скорости, т. е. не выходя изъ пучка закатодныхъ лучей.Вели это
случается во время прохожденія ея черезъ электрическое и маг-
нитное поля, то такая частица претерпѣваетъ менѣщее отклоненіе,
Э Подробныя изслѣдованія закатодныхъ лучейовъ\ трубкахъ съ различ-
ными газами были сдѣланы въ послѣднее время Дж.дж. Томсономъ.
п?им- пер-
Измѣренія надъ закатодными лучами
275
Это свойство закатодныхъ лучей
именно такое, какое получила бы частица съ зарядомъ, равнымъ
е = е • —, гдѣ --отношеніе пути, пройденнаго безъ электрона ко
всему пройденному пути. По отклоненію такой частицы для нея
€ С
опредѣляется величина — = —
т т
В. Винъ изучилъ еще полнѣе, изслѣдовавъ не отклоненныя частички.
Именно, оказалось, что и не отклоненныя магнитнымъ полемъ ча-
стички также несутъ съ собою положительные заряды. Когда помощью
спеціальной діафрагмы всѣ отклоненныя частички задерживались, и
лучъ, состоящій исключительно изъ не отклоненныхъ частицъ, подвер-
гался дѣйствію новаго магнитнаго поля, то онъ не проходилъ че-
резъ послѣднее неизмѣннымъ, но давалъ на экранѣ полосу совер-
шенно такъ же, какъ и первоначальный лучъ. Отсюда совершенно
ясно слѣдуетъ, что частицы закатодныхъ лучей, то присоединяя къ
себѣ электроны, то отдѣляя ихъ отъ себя, совершаютъ свой путь то
въ видѣ незаряженныхъ, то въ видѣ заряженныхъ атомовъ.
Частицы закатодныхъ лучей представляютъ собою по-
ложительно заряженные химическіе атомы, періодически
теряющіе и возстанавливающіе свой зарядъ, вслѣдствіе при-
соединеній и отдѣленій электроновъ.
Дальнѣйшимъ подтвержденіемъ этой теоріи являются наблюденія
В. Вина, сдѣланныя въ тщательнѣйшимъ образомъ высушенномъ
кислородѣ. Здѣсь, при полномъ отсутствіи водорода, измѣреніе дало
для наиболѣе отклоненныхъ частицъ — = 7500 КУЛОНЪ.. для одно-
т граммъ
атомнаго кислороднаго іона должно было бы получиться число 6030.
Разница въ числахъ вполнѣ объясняется трудностью наблюденій,'
такъ какъ закатодные лучи въ кислородѣ даютъ весьма слабую флуо-
ресценцію. Весьма возможно также, что въ закатодныхъ лучахъ
атомы кислорода являются не только въ видѣ одновалентныхъ и не-
заряженныхъ атомовъ, но иногда въ видѣ двувалентныхъ. Въ такомъ
случаѣ, конечно, должна была получиться большая величина — • Изъ
всѣхъ многочисленныхъ сдѣланныхъ до сихъ поръ наблюденій, во
всякомъ случаѣ, съ большою увѣренностью можно заключить, чт^
положительныхъ электроновъ не существуетъ.
Поэтому іонизацію газа слѣдуетъ представлять себѣ^^ѣдую-
щимъ образомъ: отъ атома отщепляется электронъ (можетъ^ быть,
нѣсколько электроновъ); положительно заряженный имѣетъ
ѴФ 18
276
Явленіе Допплера въ закатодныхъ лучахъ
массу атома, такъ какъ потеря электрона не уменьшаетъ массы за-
мѣтнымъ образомъ.
Приблизительную величину скорости закатодныхъ частицъ можно
вычислить по величинѣ катоднаго напряженія, сообщающаго имъ эту
скорость. Какъ мы видѣли въ § 149,
V = 4- • 10-7. — .
2 е
Если мы обозначимъ черезъ А химическій эквивалентный вѣсъ
и положимъ Р = 96 540 кулоновъ, то будемъ имѣть:
т _ А
е Р
и, слѣдовательно,
V = 1,39 . ІО6 1/? —•
Г А сек.
При катодномъ напряженіи въ 10 000 вольтъ отсюда получается для
водорода ѵ = 13,9 . 107 —для кислорода—ѵ — 3,47 . 107 * •
свк. сек•
ЯВЛЕНІЕ ДОППЛЕРА ВЪ ЗАКАТОДНЫХЪ ЛУЧАХЪ.
163. Описанныя въ §161 свѣтящіяся полосы, распространяю-
щіяся въ пространствѣ за снабженнымъ каналами катодомъ, обра-
зуются не только вслѣдствіе іонизирующаго вліянія закатодныхъ лу-
чей на пронизываемый ими газъ; несомнѣнно, что самые положи-
тельные іоны, перемѣщаясь въ пространствѣ, также свѣтятся. Это
вытекаетъ изъ того факта, что въ свѣтѣ описанныхъ полосъ,
какъ показалъ Штаркъ (3. Зіагк), наблюдается явленіе Допплера.
На рис. 106 воспроизведена
полученная Штаркомъ фо-
тографія спектра закатод-
ныхъ лучей въ водородѣ.
Щель спектральнаго аппарата
была установленао у ^конца
трубки съ закатодными лу-
чами, такъ чтосвѣтъ падалъ,
закатодныхъ? лучей. На ри-
д
Рис. 106. Явленіе Допплера въ закатодныхъ
лучахъ (три линіи водорода).
на нее въ направленіи распространенія
сункѣ изображены лишь синяя и фіолетовая спектра; кромѣ
нѣсколькихъ слабыхъ линій, принадлежащихъ^ обыкновенному тлѣю-
щему свѣту, видны три яркіялиніи водорода /Тр Не. Каждая изъ
Явленіе Допплера въ закатодныхъ лучахъ
277
этихъ линій рѣзко выдѣляется на обычномъ своемъ мѣстѣ въ спектрѣ,
но кромѣ того имѣетъ еще одно изображеніе, слегка смѣщенное въ
сторону болѣе короткихъ волнъ и имѣющее менѣе рѣзкіе края.
Такое смѣщеніе спектральныхъ линій въ сторону болѣе короткихъ
волнъ наблюдается всегда въ тѣхъ случаяхъ, когда источникъ свѣта
движется по направленію къ спектральному аппарату. Это явленіе,
уже давно играющее большую роль въ астрономіи при изученіи соб-
ственныхъ движеній неподвижныхъ звѣздъ т), носитъ названіе явле-
нія Допплера. Если Л есть наблюдаемое измѣненіе длины волны,
А — длина волны при покоющемся источникѣ свѣта, ѵ — скорость
источника свѣта, с = 3 . ІО10 —4- скорость свѣта, то имѣетъ
сек. г
мѣсто уравненіе:
Д ѵ о Д см.
— = — откуда ѵ = 3 . ІО10 ------------
X с > X ск.
Рѣзкія линіи на спектрограммѣ принадлежатъ водороднымъ іонамъ,
образовавшимся въ покоющемся газѣ подъ дѣйствіемъ закатодныхъ
лучей, такъ какъ высылающія ихъ свѣтящіяся частицы неподвижны
или имѣютъ незначительную скорость. Смѣщенныя менѣе рѣзкія ли-
ніи принадлежатъ свѣту самыхъ закатодныхъ лучей. Величину А
легко опредѣлить измѣреніемъ на спектрограммѣ и, такъ какъ вели-
чина А извѣстна, то по выше приведенной формулѣ прямо опредѣ-
ляется ѵ. Размытость краевъ смѣщенныхъ линій указываетъ на то,
что не всѣ закатодныя частички имѣютъ въ точности одну и ту же
скорость. Если взять среднюю величину для Л, то получается для ѵ,
приблизительно, та же величина, которую вычислилъ В. Винъ изъ
своихъ измѣреній, и которая нѣсколько меньше скорости, получа-
емой по формулѣ § 162.
Полосатые спектры, которые всегда даетъ свѣтъ трубокъ съ
закатодными лучами и, вообще, свѣтъ Гейсслеровыхъ трубокъ никогда
не обнаруживаютъ явленія Допплера. Отсюда слѣдуетъ, что поло-
сатые спектры высылаются покоющимися незаряженными молекулами
или атомами. Положительные іоны, получающіеся изъ нихъ при по-
терѣ одного или нѣсколькихъ электроновъ и при быстромъ ихъ де^|^'
женіи образующіе закатодные лучи, даютъ лишь линейчатые спекУры.
Э И во многихъ иныхъ случаяхъ. Прим. пер.
278
Іонизація закатодными лучами
ІОНИЗАЦІЯ ЗАКАТОДНЫМИ ЛУЧАМИ И ВТОРИЧНЫЕ ЛУЧИ.
164. Закатодные лучи всѣми тѣлами поглощаются гораздо силь-
нѣе, нежели катодные лучи. До сихъ поръ не удалось еще наблю-
дать ихъ прохожденія черезъ твердыя тѣла, напримѣръ, черезъ тон-
чайшіе слои металловъ. Газы также поглощаютъ ихъ чрезвычайно
Сильно и въ то же время сильно ими іонизируются. При паденіи
закатодныхъ лучей на металлъ возникаютъ вторичные лучи. Какъ и
въ случаѣ катодныхъ лучей (§ 155), изъ тѣхъ мѣстъ, въ которыхъ
закатодные лучи достигаютъ металла, исходятъ, какъ показалъ
Хр. Фихтбауэръ, двѣ различныя между собою группы вторичныхъ
лучей. Первая группа состоитъ изъ диффузно разсѣянныхъ закатод-
ныхъ лучей, которые, вѣроятно, весьма сходны съ первичными лу-
чами и которые потому можно назвать „ отраженными закатодными
лучами"; вторая группа состоитъ изъ очень мягкихъ катодныхъ лу-
чей, соотвѣтствующихъ напряженію около 30 вольтъ. Очевидно, воз-
никновеніе этихъ мягкихъ катодныхъ лучей въ металлѣ представляетъ
собою по существу тоже явленіе, что и іонизація въ газахъ.
НИЖНІЙ ПРЕДѢЛЪ НАПРЯЖЕНІЯ, ВЫЗЫВАЮЩАГО ІОНИЗАЦІЮ
СТОЛКНОВЕНІЕМЪ ЮНОВЪ.
§137 опыта,
165. Какъ это слѣдуетъ уже изъ
іонизація, вызываемая столкновеніями
описаннаго въ
іоновъ, прекращается, когда
напряженіе поля, вызывающаго движеніе іоновъ, становится мень-
шимъ нѣкотораго опредѣленнаго минимальнаго значенія. Точно такъ
же катодные и закатодные лучи перестаютъ іонизировать газы и
металлы, если вызывающее ихъ напряженіе падаетъ ниже нѣко-
тораго опредѣленнаго предѣла. Минимальная величина напряженія,
при которомъ еще вызывается іонизація газа, для положительныхъ
іоновъ лежитъ гораздо выше, нежели для быстро движущихся элек-
троновъ. Поэтому іонизація газа при тихомъ разрядѣ вызывается
лишь столкновеніями молекулъ съ электронами. Іонизирую щі^зака-
тодные лучи имѣются лишь у катода, гдѣ они освобождаютъ элек-
троны изъ металла и (послѣ „отраженія" отъ металла) тонкомъ
газовомъ слоѣ передъ металломъ (въ катодномъ св^бвомъ поясѣ).
ТЕОР,Я ТИХАГО РАЗРЯДА^
166. Въ газѣ, наполняющемъ разряднуюх трубку, всегда имѣетъ
мѣсто слабая іонизація, вызванная хотя бьцдѣйствіемъ свѣта, падаю-
Теорія тихаго разряда
279
щаго на электроды. Если возбудить между электродами сильное на-
пряженіе, то число іоновъ вслѣдствіе столкновеній увеличивается, и
въ заключеніе на катодѣ получается нижеслѣдующее: такъ какъ отри-
цательныя частички—электроны — отъ него удаляются, а положи-
тельные іоны постоянно къ нему приближаются изъ пространства,
заполненнаго газомъ, то передъ катодомъ получается сильное ско-
пленіе положительныхъ іоновъ и возникаетъ двойной слой, посте-
пенно все усиливающійся. Наконецъ, напряженіе этого двойного слоя
достигаетъ того значенія, при которомъ попадающіе на катодъ по-
ложительные іоны (закатодные лучи) начинаютъ выдѣлять изъ металла
электроны. Эти электроны, двигаясь черезъ поле двойного слоя, обра-
зуютъ собою катодные лучи и сильно іонизируютъ при этомъ окру-
жающій газъ, въ силу чего опять увеличивается количество поло-
жительныхъ іоновъ, двигающихся къ катоду. Такимъ образомъ, оба
эти явленія (закатодные лучи и катодные лучи) взаимно усилива-
ются, вслѣдствіе чего токъ внезапно сильно возрастаетъ и начина-
ется настоящій разрядъ. Разрядъ начинается, слѣдовательно, тогда,
когда напряженіе двойного электрическаго слоя на катодѣ достига-
етъ минимальной величины, необходимой для сообщенія закатоднымь
лучамъ способности отщеплять электроны, и эта величина должна
быть тождественна съ величиной нормальнаго катоднаго напряженія.
Нормальное катодное напряженіе есть наименьшее на-
пряженіе, достаточное для того, чтобы положительные
іоны газа пріобрѣли скорость, достаточную для выдѣленія
электроновъ изъ катоднаго металла.
Отсюда легко понять, почему величина нормальнаго катоднаго
напряженія зависитъ отъ природы газа и металла, но не зависитъ
отъ давленія газа.
То обстоятельство, что явленія около катода занимаютъ тѣмъ боль-
шее пространство, чѣмъ болѣе разрѣженъ газъ, понятно теперь само
собою, такъ какъ въ болѣе разрѣженныхъ газахъ катодные лучи
встрѣчаютъ въ томъ же пространствѣ меньшее число молекулъ и,
слѣдовательно, менѣе поглощаются и менѣе іонизируютъ. Какъ мы:>
видѣли (§ 155), темное катодное пространство, вѣроятно, предс.'^Э
вляетъ собою область, въ которой число столкновеній катодныхъ
частичекъ съ молекулами еще совершенно ничтожно. Чѣм^^ѣзрѣ-
женнѣе газъ, тѣмъ значительнѣе эта область. Если (^кружающее
катодъ пространство настолько мало, что прямой іонизаціи газа ка-
280
Теорія тихаго разряда
тодными лучами въ немъ не происходитъ, и только возникающіе на
стеклянной стѣнкѣ вторичные лучи возбуждаютъ небольшое число
іоновъ, то для возникновенія разряда необходимо большее напря-
женіе, чтобы имѣющіеся въ небольшомъ числѣ положительные іоны
съ большею силою ударялись о катодъ, увеличивая тѣмъ число
свободныхъ электроновъ и сообщая достаточную силу катоднымъ
лучамъ.
Катодные и закатодные лучи всегда являются „ первичнымъ
іонизирующимъ агентомъ“, о которомъ шла рѣчь въ § 137: они
доставляютъ току необходимое первоначальное число іоновъ для
дальнѣйшаго ихъ образованія. На анодѣ ничего подобнаго происхо-
дить не можетъ, такъ какъ изъ твердаго вещества могутъ освобо-
ждаться лишь электроны, но не положительные іоны. Тихій разрядъ
исходитъ изъ катода. Но, съ другой стороны, онъ заключается не
въ однихъ только явленіяхъ, происходящихъ около катода. Въ про-
странствѣ за слоемъ положительныхъ іоновъ, скопляющихся въ отри-
цательномъ тлѣющемъ свѣтѣ, собираются выдѣлившіеся изъ катода
электроны и здѣсь получается избытокъ отрицательнаго заряда, плот-
ность котораго все увеличивается по мѣрѣ приближенія къ аноду.
Это ясно видно по рисункамъ 93 и 94. Если выдѣленіе электро-
новъ на катодѣ достаточно энергично и анодъ расположенъ не слиш-
комъ близко, то это накопленіе отрицательныхъ зарядовъ прини-
маетъ такіе размѣры, что сила поля между ними и анодомъ дости-
гаетъ того минимальнаго значенія, которое необходимо для образо-
ванія іоновъ посредствомъ столкновеній электроновъ съ молекулами.
Эта новая область іонизаціи и есть положительная свѣтовая колонна.
Сила поля, въ области положительной свѣтовой ко-
лонны, представляетъ собою ту минимальную силу поля, при
которой начинается замѣтная іонизація газа посредствомъ
столкновеній электроновъ съ молекулами.
Согласно опытамъ А. Герца (А. Негг) сила поля въ области
положительной свѣтовой колонны измѣняется въ зависимостщотъ
ширины трубки и силы тока. Это указываетъ на то, что «^суще-
ствуетъ никакой опредѣленной границы для скорости, ниже кото-
рой іонизація посредствомъ столкновеній электроновъ ^^ёзапно ста-
новилась бы равной нулю. Вѣроятно, іонизирующее ^^ствіе медленно
движущихся электроновъ убываетъ съ уменьш^л^ъ скорости по-
степенно, становясь, наконецъ, незамѣтно мальвЩ^ Прямыя наблюде-
Теорія тихаго разряда
281
нія Тоунсенда надъ іонизирующей силой движущихся электроновъ
подтверждаютъ это заключеніе.
Чтобы дать представленіе о величинѣ силы поля, при которой,
подъ вліяніемъ столкновеній іоновъ, получается сильное образованіе
іоновъ, приведемъ здѣсь одну изъ таблицъ, данныхъ А. Герцемъ.
Діаметръ трубки 2 см.\ сила поля 1,2 милликулона въ секунду; чистый азотъ.
Давленіе въ мм. ртутн. столба
Сила поля въ вольтахъ на см.
1
29,8
1,5 2 2,5
40,8 51,4 61,5
3 3,5 4 4,5
71,2 80,5 89,3 97,7
Какъ видно отсюда, сила поля, необходимая для того, чтобы
происходила іонизація, возрастаетъ нѣсколько медленнѣе, нежели
давленіе.
Границу внѣшняго темнаго пространства можно разсматривать,
какъ новый катодъ, но электроны, непрерывно вылетающіе изъ этого
„вторичнаго катода“, не освобождаются при помощи особаго про-
цесса, подобнаго закатоднымъ лучамъ, но постоянно проносятся отъ
первичнаго катода черезъ темное пространство. Въ области положи-
тельной свѣтовой колонны необходимо для іонизаціи лишь поле та-
кой силы, при которой столкновенія электроновъ съ молекулами
достаточно энергичны. Отсюда ясно видно, что существованіе поло-
жительной свѣтовой колонны обусловливается процессами на катодѣ,
но не наоборотъ.
Если въ содержащемся въ разрядной трубкѣ газѣ образуются
положительные іоны только одного рода, то въ области положи-
тельной свѣтовой колонны не происходитъ болѣе скопленія какихъ-
либо іоновъ, ея поле однородно, и она равномѣрно свѣтится по всей
своей длинѣ. Если же имѣются различные роды іоновъ съ различ-
ными скоростями, то могутъ возникать неравномѣрности въ распре-
дѣленіи іоновъ, связанныя съ накопленіемъ зарядовъ въ газѣ. Если
и анодомъ,
въ сторону /
ниже пре^д
въ какомъ-нибудь мѣстѣ, между „вторичнымъ катодомъ“
газъ оказывается заряженнымъ положительно, то поле
анода ослабляется и, какъ только сила поля опустится
дѣла, необходимаго для іонизаціи, возникаетъ новое темное^ц^б-
странство. Это темное пространство вполнѣ аналогично Фарадэеуукому
темному пространству; съ другой его стороны образуетсяі с^ттъ новый
„вторичный катодъ", и все это періодически правильно ^повторяется
до анода. Такъ получается стратификація свѣтовой ^колонны.
282
Темный разрядъ
Около анода, конечно, имѣетъ мѣсто убыль положительныхъ
іоновъ, такъ какъ положительные іоны іонизированнаго газа не-
прерывно отъ него удаляются, а изъ металла они не выдѣляются.
Это является причиной образованія въ газѣ вблизи анода отрица-
тельнаго заряда и неравномѣрностей въ полѣ, ясно видныхъ на рис.
93 и 94.
ТЕМНЫЙ РАЗРЯДЪ.
167. Если жидкое сопротивленіе, введенное между источникомъ
электричества и разрядной трубкой, сдѣлать очень большимъ, чтобы
сила тока разряда была очень мала, то, какъ мы уже знаемъ (§ 141),
катодный тлѣющій свѣтъ превращается въ небольшое свѣтлое пятно;
въ то же время положительная свѣтовая колонна начинаетъ свѣтиться
гораздо слабѣе и становится совсѣмъ короткой. Эту особую, отли-
чающуюся слабымъ свѣченіемъ форму тихаго разряда мы для отли-
чія отъ типичной его формы, описанной въ § 138, будемъ называть
темнымъ разрядомъ. Къ сожалѣнію, не было еще сдѣлано ника-
кихъ изслѣдованій надъ свойствами этой формы разряда, весьма
важной для всей теоріи разряда въ газахъ.
Если, уменьшая постепенно жидкое сопротивленіе, мы будемъ
увеличивать силу тока въ темномъ разрядѣ, то свѣтовыя явленія въ
газѣ становятся постепенно болѣе яркими и занимаютъ все большее
пространство и, наконецъ, получается правильный тихій разрядъ.
При возрастаніи силы тока и развитіи свѣтовыхъ явленій электро-
метръ, соединенный съ электродами трубки, показываетъ также воз-
растаніе напряженія между электродами.
При переходѣ отъ темнаго разряда къ типичному ти-
хому разряду, сила тока и напряженіе между электродами
одновременно возрастаютъ.
РАЗРЯДНОЕ ИЛИ ИСКРОВОЕ НАПРЯЖЕНІЕ.
168. Когда сила тока настолько велика, что происходитъ уже
правильный тихій разрядъ съ длинной положительной свѣтовой ко-
лонной, то, при дальнѣйшемъ уменьшеніи жидкаго сопротивленія,
происходитъ нѣчто новое. Отрицательный тлѣющій св^тъ'начинаетъ
увеличиваться въ размѣрахъ и становится болѣедбдестящимъ; въ
то же время катодное напряженіе подымается выше нормальнаго
значенія. По мѣрѣ того, какъ явленія окодо>уф)ицательнаго элек-
Искровое напряженіе
283
трода развиваются, положительная свѣтовая колонна ими оттѣсняется.
Если измѣрять напряженіе между обоими электродами, то оказыва-
ется, что оно теперь убываетъ съ возрастаніемъ силы тока. Этотъ
фактъ тѣснѣйшимъ образомъ связанъ съ тѣмъ, что тихій разрядъ
обусловливается іонизаціей путемъ столкновеній іоновъ. Если въ глав-
номъ центрѣ іонизаціи около катода уже скопилось большое коли-
чество іоновъ, то достаточно небольшого повышенія силы іонизи-
рующаго поля, чтобы остальное разрядное пространство пріобрѣло
такой избытокъ іоновъ, что проводимость значительно улучшается
и притомъ настолько, что въ общемъ вызывающее токъ іоновъ на-
Рис. 107. Кривая напряженія при тихомъ разрядѣ.
пряженіе падаетъ. Нѣчто подобное мы замѣтили выше (§121) у
лампы Нернста; тамъ также іонизація значительно возрастала съ
силой тока вслѣдствіе повышенія температуры.
При типичномъ тихомъ разрядѣ напряженіе на элек-
тродахъ падаетъ съ возрастаніемъ силы тока.
А
Такъ какъ переходъ отъ темнаго разряда къ тихому соверша
ется съ повышеніемъ силы тока вполнѣ непрерывно, то общій хр^ъ
зависимости напряженія на электродахъ отъ силы тока можед^ь|быть
представленъ кривою, подобной кривой, изображенной на^рис. 107.
Характернымъ свойствомъ такой кривой является наличность вполнѣ
опредѣленнаго максимума въ томъ мѣстѣ, которое осоотвѣтствуетъ
началу типичнаго тихаго разряда.
284
Искровое напряженіе
Если для данной разрядной трубки получена эмпирически
такая кривая, то графическимъ путемъ весьма легко опредѣлить,
какого рода разрядъ произойдетъ при данномъ напряженіи Ѵо источ-
ника электричества и данномъ дополнительномъ сопротивленіи /?,
если предположить, что для этого дополнительнаго сопротивленія
имѣетъ силу законъ Ома, по которому напряженіе V между кон-
цами его пропорціонально силѣ тока (Ѵ'=/?7). Обозначимъ черезъ
/0 силу тока, который получился бы, если бы разрядная трубка
была коротко замкнута металлическимъ проводникомъ (І/о = 7?/0).
Наносимъ на ось напряженій значеніе І/о, на ось силъ тока зна-
ченіе и соединяемъ обѣ точки прямою. Точка, въ которой
эта прямая въ первый разъ пересѣкаетъ кривую, даетъ намъ
силу тока У и напряженіе на электродахъ V при тихомъ раз-
рядѣ. Изъ рисунка ясно видно, что Ѵо —Ѵ = а эта величина
равняется какъ разъ напряженію V', которое, согласно закону Ома,
должно существовать между конечными зажимами дополнительнаго
сопротивленія, когда сила тока равна У. Такъ какъ, такимъ обра-
зомъ, Ѵ-\-Ѵ' = Ѵъ, то, согласно §25, при такой силѣ тока напря-
женія въ эѳирѣ находятся въ равновѣсіи.
Начало разряда слѣдуетъ представлять себѣ такъ, какъ это
было уже описано въ § 166. Какъ только образовался двойной слой
у катода и начинается разрядъ, напряженіе на электродахъ, равняв-
шееся до этого Уо, падаетъ и притомъ такъ низко, что электриче-
ское поле выходитъ изъ состоянія равновѣсія. Разрядный токъ, вна-
чалѣ дающій, понятно, темный разрядъ, быстро усиливается, и тихій
разрядъ проходитъ всѣ стадіи, соотвѣтствующія всѣмъ точкамъ кри-
вой рис. 107, пока не достигается первая точка, въ которой выше
построенная прямая пересѣкаетъ кривую. Теперь поле находится въ
равновѣсіи, и сила тока не можетъ падать или возрастать безъ новаго
нарушенія равновѣсія. Отсюда становится яснымъ, что прежде, чѣмъ
наступаетъ типичный тихій разрядъ, разрядъ проходитъ черезъ точкуч
максимальнаго напряженія на электродахъ. Но это возможно только
въ томъ случаѣ, если напряженіе источника электричества^вьшіе
этого максимальнаго напряженія. Произойдетъ ли при этомъ Дѣйстви-
тельно типичный тихій разрядъ или же темный разрядд||5зависитъ,
конечно, кромѣ напряженія источника электричества,^тце и отъ до-
полнительнаго сопротивленія. Если это сопротивленій мало, то мы
получаемъ слѣдующее (рис. 108): прямая линія^Опересѣченіе кото-
5^.^
Искровое напряженіе
285
рой съ кривой разряднаго тока характеризуетъ устанавливающійся-
разрядъ, располагается слегка наклонно къ горизонтальной оси (кт>
оси силъ тока); по мѣрѣ возрастанія напряженія Уо, эта прямая пере-
мѣщается на чертежѣ параллельно самой себѣ. Пока начальная точка
І/о этой кривой лежитъ ниже величины максимальнаго напряженія^
получается темный разрядъ съ весьма малой силой тока (I). Если
довести Ѵо до максимальнаго напряженія, то при дальнѣйшемъ уве-
личеніи І/о прямая скоро придетъ въ такое положеніе, что она бу-
детъ касаться кривой; если напряженіе Ѵо еще немного повысить,
то первая точка пересѣченія будетъ лежать уже не въ началѣ кри-
вой, но въ весьма удаленной ея точкѣ, соотвѣтствующей большой
силѣ тока и лежащей на
нисходящей вѣтви кривой,
соотвѣтствующей типич-
ному тихому разряду (II).
Иными словами, какъ толь-
ко мы перейдемъ черезъ
критическое напряженіе,
лежащее немного выше
максимальнаго напряженія
на электродахъ, характеръ
разряда внезапно измѣня-
ется, при чемъ сила тока
сразу чрезвычайно сильно
увеличивается. Нѣчто по-
добное мы имѣемъ при
Сила тока
Рис. 108. Возникновеніе и прекращеніе тихаго
разряда.
подъемѣ вагона на гору: какъ только достигнута наивысшая точка,,
вагонъ, при небольшомъ движеніи еще впередъ, самъ начинаетъ спу-
скаться съ горы, развивая громадную скорость.
Такой внезапно возникающій при опредѣленномъ напряженіи
сильный электрическій токъ называютъ электрической искрой,,
а иногда и просто электрическимъ разрядомъ. Обычно со слр^
вомъ искра связываютъ представленіе кратковременности, но ^гіо
свойство вовсе не является существеннымъ. Напряженіе, пр^Мйото-
ромъ образуется искра, называется искровымъ напряженіемъ или.
же разряднымъ напряженіемъ.
Если сопротивленіе ведущихъ къ электр,о~дамъ^прово-
довъ ничтожно мало, то^искровое напряжейГе^между этими.
286
Прерывистый тихій разрядъ
электродами тождественно съ максимальной величиной на-
пряженія между электродами при тихомъ разрядѣ.
Когда тихій разрядъ начался, онъ уже не прекращается, даже
если понизить напряженіе Уо. Если прямую сдвинуть изъ ея поло-
женія (II) опять внизъ, то точка, характеризующая тихій разрядъ,
остается на вѣтви типичнаго тихаго разряда, такъ какъ въ такомъ
случаѣ уже однажды установились условія, необходимыя для того,
чтобы онъ происходилъ. И только, когда напряженіе Уо мы пони-
зимъ настолько, что прямая уже болѣе не будетъ пересѣкать этой
вѣтви (III), тихій разрядъ „тухнетъ" такъ же внезапно, какъ онъ
раньше „вспыхнулъ".
ПРЕРЫВИСТЫЙ ТИХІЙ РАЗРЯДЪ.
169. Давно уже извѣстенъ тотъ фактъ, что тихій разрядъ въ
Гейсслеровой трубкѣ очень часто лишь кажется непрерывнымъ, а
въ дѣйствительности состоитъ изъ многочисленныхъ быстро другъ
за другомъ слѣдующихъ отдѣльныхъ разрядовъ съ правильными не-
большими промежутками между ними. Въ этомъ можно весьма просто
убѣдиться, напримѣръ, наблюдая разрядъ во вращающемся зеркалѣ.
Въ этомъ случаѣ свѣтъ разряда представляется не въ видѣ одной
широкой полосы, но въ видѣ ряда узкихъ полосъ, расположенныхъ
на одинаковыхъ разстояніяхъ другъ отъ друга съ темными проме-
жутками между ними. Еще проще воспользоваться для той же цѣли
телефономъ, включивъ его въ цѣпь тока. Ниже, при описаніи теле-
фона, мы увидимъ, что онъ представляетъ собою аппаратъ, откли-
кающійся лишь на прерывающіеся или перемѣнные токи, но не на
постоянный токъ. Поэтому, если во время тихаго разряда телефонъ
молчитъ, то это служитъ указаніемъ на то, что токъ постояненъ,
если же телефонъ звучитъ, то токъ прерывистый.
Прерывистость тока появляется лишь въ томъ случаѣ, если
проводъ, ведущій отъ регулирующаго сопротивленія къ электро^
дамъ, имѣетъ не слишкомъ малую емкость. Если увеличить ^^про-
тивленіе самыхъ электродовъ, сдѣлавъ ихъ изъ очень плох^го^ про-
водящаго матеріала, то получить прерывистый тихій разрядъ/оказы-
вается невозможнымъ. Если же за регулирующимъ сопротивленіемъ
помѣщена значительная емкость, соединенная съ Ыіектродами нич-
тожно малымъ сопротивленіемъ, то эта емкость^ играетъ роль какъ
«бы вторичнаго источника электричества. Как^тодько она зарядится
Прерывистый тихій разрядъ
287
до искрового напряженія, между электродами начнетъ проходить
тихій разрядъ, при чемъ сила тока принимаетъ очень большое зна-
ченіе, вслѣдствіе ничтожной малости сопротивленія между „источ-
никомъ электричества" и электродами. Но большая сила тока тотчасъ
вызываетъ быстрое паденіе напряженія заряженной емкости, такъ
какъ потерянный зарядъ возстанавливается первичнымъ источникомъ
электричества черезъ большое сопротивленіе лишь медленно. Напря-
женіе поэтому падаетъ настолько низко,, что тихій разрядъ затуха-
етъ. Послѣ этого емкость снова заряжается первичнымъ источникомъ
черезъ большое сопротивленіе, и ея напряженіе возрастаетъ. Нако-
нецъ, оно достигаетъ величины искрового напряженія и весь про-
цессъ повторяется снова.
Если, уменьшая регулирующее сопротивленіе, увеличивать силу
разряднаго тока, то введенный въ цѣпь телефонъ, при опредѣленной
силѣ тока, внезапно замолкаетъ и при дальнѣйшемъ возрастаніи силы
тока продолжаетъ молчать. Изъ даннаго выше объясненія преры-
вистаго разряда слѣдуетъ, что онъ можетъ возникнуть лишь въ
томъ случаѣ, если кривая напряженія при тихомъ разрядѣ въ соот-
вѣтствующемъ мѣстѣ опускается внизъ. Какъ видно изъ рис. 107,
наклонъ кривой съ возрастаніемъ силы тока постепенно уменьша-
ется. Изъ того факта, что телефонъ внезапно умолкаетъ, мы должны
заключить, что для существованія прерывистаго разряда не доста-
точно, чтобы кривая вообще опускалась внизъ, но необходимо, чтобы
уголъ наклона превосходилъ опредѣленное, отличное отъ нуля, мини-
мальное значеніе. Причина этого заключается въ томъ, что при уси-
леніи тока появляются противодѣйствующія силы, которыя току при-
ходится преодолѣвать. Съ этими силами мы познакомимся въ электро-
динамикѣ, гдѣ онѣ носятъ общее названіе, „самоиндукціи". Понятно,
что минимальное значеніе наклона кривой, при которомъ появляется
прерывистость, существенно зависитъ отъ емкости электродовъ.
ВЛІЯНІЕ ДАВЛЕНІЯ ГАЗА НА ТИХІИ РАЗРЯДЪ.
о
170. Предположимъ, что химическій составъ заполняющаго ра§^
рядную трубку газа остается неизмѣннымъ, но что мѣняете^^ѣб
плотность, т. е. давленіе. Въ этомъ случаѣ въ явленіи тиха^р^ раз-
ряда обнаруживаются измѣненія троякаго рода: 1) измѣняются раз-
мѣры свѣтовыхъ явленій; 2) измѣняется сила тока; зАйзмѣняется
напряженіе.
288
Тихій разрядъ въ атмосферномъ воздухѣ
Длины катоднаго тлѣющаго свѣта и внѣшняго темнаго про-
странства тѣмъ значительнѣе, чѣмъ меньше давленіе газа. Эти длины
зависятъ, кромѣ того, еще отъ силы тока, какъ это было уже ука-
зано въ § 108. Ниже мы увидимъ, что, для одного и того же газа,
длины, которыя имѣютъ при максимальномъ напряженіи отдѣльные
слои катоднаго тлѣющаго свѣта и темное пространство, вѣроятно,
обратно пропорціональны давленію. Положительная свѣтовая колонна
измѣняетъ не только свою длину, но и ширину. Именно, ея ширина
вообще убываетъ съ уменьшеніемъ давленія газа, если разрядный
сосудъ достаточно обширенъ. Кромѣ того, эта ширина при постоян-
номъ давленіи возрастаетъ съ увеличеніемъ силы тока.
Сила тока въ тихомъ разрядѣ вообще убываетъ при возрастаніи
разрѣженія. До тѣхъ поръ, пока отрицательный тлѣющій свѣтъ не по-
крываетъ еще всего катода, при постоянной величинѣ поверхности
тлѣющаго свѣта, сила тока обратно пропорціональна давленію газа.
Напряженіе между электродами обычно убываетъ съ возраста-
ніемъ разрѣженія. Это происходитъ отъ убыванія длины положитель-
ной свѣтовой колонны и силы тока въ ней. Какъ мы видѣли (§ 144)
при весьма сильныхъ разрѣженіяхъ, послѣ совершеннаго исчезновенія
свѣтовой колонны, напряженіе на электродахъ вновь начинаетъ воз-
растать.
ТИХІЙ РАЗРЯДЪ ВЪ АТМОСФЕРНОМЪ ВОЗДУХѢ.
171. Получить непрерывный тихій разрядъ при высокихъ давле-
ніяхъ, напримѣръ, въ атмосферномъ воздухѣ, весьма затруднительно.
Во-первыхъ, при этомъ требуется токъ настолько большой силы, что
тихій разрядъ легко переходитъ въ описанный ниже дуговой раз-
рядъ. Если, во избѣжаніе этого, включить въ цѣпь большое сопро-
тивленіе, то получаются прерывистые разряды. Приходится увеличи-
вать сопротивленіе самихъ электродовъ.
Если оба полюса индукціонной машины окружить плохими про^
водниками, напримѣръ, деревянными обкладками, то легко можно на-
блюдать ту форму тихаго разряда, которую мы выше назвал^емнымъ
разрядомъ. Типичный непрерывный тихій разрядъ получилъ Теплеръ
(М. Тбріег), воспользовавшись особенно мощнымъ источникомъ элек-
тричества высокихъ напряженій, именно, 60 полоской индукціонной
машиной, и употребивъ въ качествѣ электродсш^ базальтовую пла-
стинку и тонкое металлическое остріе. Нужн^однако, замѣтить, что
Разрядъ съ острія
289
наблюденный Теллеромъ непрерывный тихій разрядъ въ обыкновен-
номъ воздухѣ (который онъ называетъ „пучкообразной дугой")
.отличается, повидимому, въ одномъ отношеніи отъ обычныхъ формъ
такого разряда при низкихъ давленіяхъ; именно, при такомъ раз-
рядѣ могутъ отсутствовать значительныя части свѣтовыхъ явленій.
Ниже мы ближе познакомимся съ „оборваннымъ" тихимъ разрядомъ.
Во всякомъ случаѣ, его образованіе указываетъ на существованіе
особыхъ вліяній, которыя въ болѣе плотныхъ газахъ могутъ видо-
измѣнять разрядъ, а въ разрѣженныхъ газахъ незамѣтны.
РАЗРЯДЪ СЪ ОСТРІЯ.
172. О непрерывномъ разрядѣ съ острія уже часто упоминалось
выше. Издавна было замѣчено, что такой разрядъ сопровождается
замѣтнымъ матеріальнымъ токомъ - электрическимъ вѣтромъ. На-
сколько силенъ этотъ вѣтеръ, можно заключить, напримѣръ, изъ
слѣдующаго: если противъ пламени свѣчи держать иглу, соеди-
ненную съ однимъ изъ полюсовъ мощной индуктивной машины*
то легко можно потушить свѣчу исходящимъ
отъ иглы токомъ воздуха. Такъ какъ этотъ воз-
душный токъ, конечно, вызывается силами, рас-
пространяющимися изъ электрическаго поля иглы, I
то, согласно принципу равенства дѣйствія и проти- !
водѣйствія (§ 63), иголка также должна испытывать |
силовое дѣйствіе въ направленіи, противоположномъ і1
направленію электрическаго вѣтра. Если посрединѣ
8-образной жестяной пластинки съ заостренными
концами сдѣлать небольшое углубленіе и наса- Рис. 109. Элек-
, 1ЛПЧ . . трическое реак-
дить ее на остріе (рис. 109), то подъ вліяніемъ тивное колесо,
„силы противодѣйствія" она начинаетъ вращаться,
какъ только зарядится до достаточно высокаго потенціала.
Если наблюдать остріе, заряженное до высокаго потенціала, въ
темнотѣ, то на немъ видна маленькая свѣтящаяся точка. Это свѣче-о р,
ніе указываетъ, конечно, какъ всегда, на центръ іонизаціи. Если іоны^ѵ
образуются такимъ образомъ лишь непосредственно вблизи ост^й,^
то въ темномъ пространствѣ, гдѣ происходитъ переносъ зарядовъ,
могутъ находиться іоны только одного рода, именно о^ндац'ачные
съ остріемъ, такъ какъ іоны противоположнаго знака тотчасъ из-
влекаются остріемъ изъ центра іонизаціи. Такъ какт^^имъ обра-
Ми. Электричество и магнитизмъ.
19
2 90
Разрядъ съ острія
зомъ, іоны въ темномъ пространствѣ движутся всѣ въ одномъ на-
правленіи прочь отъ острія, то они въ силу тренія должны увле-
кать за собою окружающія массы воздуха. Такимъ образомъ воз-
никаетъ воздушный вихрь, при чемъ въ пространствѣ передъ остріем ь
воздухъ удаляется отъ него, и такъ возникаетъ электрическій вѣтеръ.
Въ узкомъ пространствѣ этотъ большой вихревой потокъ не
можетъ образоваться. Поэтому въ узкомъ замкнутомъ сосудѣ вмѣ-
сто электрическаго вѣтра наблюдается только „электрическое давле-
ніе". Сила тренія іоновъ о воздухъ вызываетъ возрастаніе давленія
по мѣрѣ удаленія отъ острія. Чэттокъ (СЬаііоск) произвелъ рядъ
измѣреній и по измѣненію давленія вычислилъ силу тренія передви-
гающихся іоновъ. Опредѣливъ послѣ этого переносимые ими за се-
кунду заряды, онъ могъ вычислить и ихъ скорость переноса. Изслѣ-
дованія производились какъ при положительномъ, такъ и при отри-
цательномъ зарядѣ острія (рис. 110), и привели къ выводу, что
Рис. ПО. Схема разряда съ острія.
участвующіе въ явленіи разряда съ острія іоны тождественны съ тѣми
скопленіями молекулъ, о которыхъ шла рѣчь въ § 129.
Образующіеся при разрядѣ съ острія въ свѣтящейся
точкѣ элементарные іоны по вступленіи въ темное про-
странство окружаются плотными скопленіями газовыхъ
молекулъ.
Можно считать вполнѣ достовѣрнымъ, что это быстрое превра-
щеніе электроновъ и заряженныхъ атомовъ въ заряженныя молеку-
лярныя скопленія происходитъ только въ плотныхъ газахъ. Въ раз-
рѣженныхъ газахъ іоны остаются даже въ темныхъ частяхъразряд-
наго пространства, по всей вѣроятности, свободными отъънагрузки
молекулами. Кромѣ того, въ плотныхъ газахъ, вѣроятно,' происхо-
дятъ рекомбинаціи іоновъ, играющія при разрядѣ в^разрѣженныхъ
газахъ, повидимому, лишь весьма незначительн^іордль. Надо пред-
полагать, что оба эти явленія и вызываютъ сизмъненія въ харак-
терѣ тихаго разряда въ плотныхъ газахъ
Разрядъ съ острія
291
173. Многочисленныя измѣренія были произведены надъ на-
пряженіемъ, при которомъ происходитъ разрядъ съ острія. Для это-
го противъ острія устанавливаютъ большую металлическую пластинку,
отведенную къ землѣ, и затѣмъ измѣряютъ потенціалъ острія. Раз-
рядъ начинается при опредѣленномъ минимальномъ потенціалѣ, ве-
личина котораго зависитъ отъ заостренности острія и природы газа,
и въ тѣхъ случаяхъ, когда это давленіе выше 1/2 атмосферы, отъ давле-
нія газа, но не зависитъ отъ разстоянія пластинки. Если продолжать
повышать потенціалъ, т. е. давать ему значенія, превышающія ми-
нимальное, то сила тока возрастаетъ. Избытокъ потенціала служитъ
при этомъ, главнымъ образомъ, для уравновѣшенія сопротивленія
газа въ темномъ пространствѣ; онъ зависитъ уже отъ разстоянія
пластинки и отъ давленія газа. Минимальный же потенціалъ пред-
ставляетъ собой, вѣроятно, напряженіе іонизаціи въ центрѣ іониза-
ціи у острія. Для хорошо заостреннаго острія минимальныя величины
потенціала имѣютъ слѣдующія значенія: въ воздухѣ
+ 2750 вольтъ и —2050 вольтъ;
въ чистомъ азотѣ
+ 2840 вольтъ и — 1370 вольтъ.
Слѣдовательно, при положительномъ зарядѣ этотъ минимумъ
лежитъ выше, нежели при отрицательномъ. Это правило имѣетъ си-
лу во всѣхъ случаяхъ. Но и отрицательный минимальный потен-
ціалъ значительно выше нормальнаго катоднаго напряженія. Если
свѣтящуюся точку на остріѣ наблюдать подъ микроскопомъ, то ви-
денъ вполнѣ типичный маленькій тихій разрядъ съ отрицательнымъ
тлѣющимъ свѣтомъ, темнымъ пространствомъ и положительной свѣ-
товой колонной. Замѣчательно въ этомъ случаѣ то обстоятельство,
что здѣсь имѣется только одинъ электродъ, и все явленіе съ проти-
воположной стороны просто обрывается и переходитъ въ воздухѣ
въ обычный несамостоятельный токъ проводимости.
Если, повышая потенціалъ острія при такомъ разрядѣ, значи- +
тельно увеличивать силу тока, то длина положительной свѣтовоф|р
колонны тоже значительно возрастаетъ, такъ что въ воздухѣ рбра-'
зуются одинъ или нѣсколько разрядныхъ каналовъ, начинаірцщхся
у острія, а съ другой стороны внезапно обрывающихся.^ Этотъ уве-
личенный тихій разрядъ съ острія называютъ „пучкообразнымъ раз-
рядомъ".
19
292
Разрядъ съ острія
Если взять въ качествѣ электродовъ два острія, то на обоихъ
возникаютъ подобные оборванные тихіе разряды, снабжающіе про-
межуточное между ними пространство обоими родами іоновъ. Но
во всѣхъ случаяхъ существеннымъ условіемъ для возникновенія ти-
пичныхъ разрядовъ съ острія является наличность высокаго давленія
воздуха (свыше 1/3 атмосферы).
При значительныхъ давленіяхъ типичный тихій разрядъ
въ газѣ можетъ внезапно прекратиться и перейти въ обычный
токъ проводимости. Этотъ особый видъ разряда называютъ
въ зависимости отъ величины свѣтовой колонны „разря-
домъ съ острія" или „пучкообразнымъ разрядомъ". Причи-
на возникновенія оборваннаго тихаго разряда заключается,
вѣроятно, въ большей легкости образованія молекулярныхъ
скопленій въ плотныхъ газахъ.
Пучкообразный разрядъ всегда сопровождается шипящимъ шу-
момъ, что указываетъ на его прерывистость. Такъ какъ преры-
вистость возможна лишь при круто идущей внизъ кривой напряже-
нія тока, то отсюда слѣдуеть, что оборванный разрядъ съ острія
имѣетъ кривую напряженія такую же, какъ и обычный тихій разрядъ
(рис. 107). Первая, поднимающаяся вверхъ часть кривой предста-
вляетъ собою вѣтвь собственно разряда съ острія, вторая, идущая
внизъ часть характеризуетъ пучкообразный разрядъ. Напряженіе на
электродахъ при оборванномъ тихомъ разрядѣ всегда меньше искро-
вого напряженія. Этимъ объясняется тотъ фактъ, что, вращая ин-
дукціонную машину не слишкомъ быстро, весьма часто можно за-
мѣтить, что пучкообразные разряды предшествуютъ искровымъ. На
шарикахъ искромѣра всегда имѣются какія-либо пылинки, играющія
при этомъ роль острія.
174. Съ перваго взгляда разряды съ острія при положитель-
номъ и отрицательномъ потенціалѣ ничѣмъ не отличаются другъ отъ
друга. Но въ дѣйствительности мы имѣемъ при этомъ два различныя
явленія. При отрицательномъ разрядѣ съ острія отсутствуетъ^тблько
анодъ, а катодныя явленія, играющія главную роль въ ^разрядѣ,
могутъ развиться на катодѣ вполнѣ правильно. Наоборотъ/, положи-
тельный разрядъ съ острія весьма существенно отли^ется отъ на-
стоящаго тихаго разряда. Въ этомъ случаѣ катоМѣ^олженъ образо-
ваться въ самомъ газѣ, и возникновеніе электродовъ вызывается уда-
рами положительныхъ іоновъ не о металлъ^но>о газовыя молекулы,
*
Нагрѣваніе и распыленіе катода
293
случайно особенно къ этому приспособленныя. Положительный раз-
рядъ съ острія всегда представляется распространяющимся по весьма
тонкимъ мѣняющимся кана-
ламъ, тогда какъ отрицатель-
ный разрядъ является болѣе
спокойнымъ и имѣетъ широ-
кое основаніе.
Это можно видѣть, по-
мѣщая остріе на изолирую-
щей пластинкѣ, посыпанной
мелкимъ порошкомъ (порош-
комъ ликоподія). Если со-
единить остріе съ заряжен-
ной лейденской банкой, то
произойдетъ непродолжитель-
ный разрядъ, порошокъ бу-
детъ сдутъ съ путей разряда,
и получатся фигуры, изоб- Рис. 111. Положительныя и отрицательныя
раженныя на рисункѣ 111. фигуры Лихтенберга.
Эти такъ называемыя „пыльныя фигуры Лихтенберга" извѣстны
уже болѣе ста лѣтъ, именно въ качествѣ доказательства существен-
наго различія между положительнымъ и отрицательнымъ электриче-
ствомъ. Какъ мы теперь^знаемъ, это различіе заключается въ томъ,
что отрицательные электроны существуютъ, положительные же не
существуютъ.
НАГРѢВАНІЕ И РАСПЫЛЕНІЕ КАТОДА.
175. Если черезъ Гейсслерову трубку пропустить сильный тихій
разрядъ, то она, конечно, нагрѣется. Наиболѣе нагрѣваются при этомъ
тѣ части, на которыя падаютъ сильные катодные или закатодные
лучи. Объ этомъ уже было упомянуто выше (§§ 149, 156). При
типичномъ тихомъ разрядѣ единственными твердыми частями, кото-
рыхъ достигаютъ лучи, являются электроды. Но катодное излучені^^
достигающее анода подъ вліяніемъ аноднаго поля (§143), обладаетъ
энергіей весьма незначительной, по сравненію съ энергіей дадаю-
щаго на катодъ закатоднаго излученія. Понятно, что п^иХтйхомъ
разрядѣ катодъ нагрѣвается сильнѣе и легко можетъ раскалиться и
даже расплавиться.
294
Нагрѣваніе и распыленіе катода
Рядомъ съ нагрѣваніемъ идетъ „распыленіе", которое можно,
напримѣръ, очень отчетливо наблюдать на катодахъ изъ платиновой
проволоки. Стекло трубки вблизи такого катода вскорѣ покрывается
равномѣрно плотнымъ зеркальнымъ слоемъ платины, при чемъ ве-
щество катода выбрасывается изъ него, повидимому, въ направленіи,
перпендикулярномъ къ поверхности проволоки. Такъ какъ такимъ
путемъ можно получать чрезвычайно тонкіе, но все же сплошные и
равномѣрные слои платины (или иного металла), при чемъ можно по-
лучать слой желательной толщины, регулируя силу тока и продолжи-
тельность дѣйствія его, то распыленіемъ катоднаго металла пользуются
на практикѣ, помѣщая тѣло, которое нужно покрыть металломъ, въ
разрядную трубку вблизи катода. Степень распыленія зависитъ какъ
отъ рода металла, такъ и отъ рода газа въ трубкѣ. Алюминій рас-
пыляется только въ аргонѣ и геліи, въ большинствѣ же прочихъ
газовъ его распыленія не замѣчается. По этой причинѣ Гейсслеровы
трубки чаще всего снабжаются алюминіевыми электродами.
ГЛАВА ДЕВЯТАЯ
ДУГОВОЙ РАЗРЯДЪ И ИСКРА
ВЫДѢЛЕНІЕ ЭЛЕКТРОНОВЪ РАСКАЛЕННЫМИ ТѢЛАМИ.
176. Какъ мы уже знаемъ, раскаленное до-бѣла тѣло іонизи-
руетъ окружающій его воздухъ (§ 122). Чтобы изучить спеціально
дѣйствіе такого тѣла, займемся сначала изслѣдованіемъ раскален-
Токъ къ лампѣ
Рис. 112. Раскаленная до-бѣла
угольная нить высылаетъ электрон>^(§Л
наго тѣла, помѣщеннаго въ возможно болѣе эвакуирова^-цЬё про-
странство (пустоту). Мы воспользуемся обыкновенной^мпой на-
каливанія съ угольной нитью; въ этой лампѣ воздухъ долженъ
296
Выдѣленіе электроновъ раскалеными тѣлами
быть сильно разрѣженъ, и въ стекло долженъ быть впаянъ еще пла-
тиновый штифтъ (рис. 112). Концы угольной нити соединимъ по-
мощью выключателя съ полюсами сильной аккумуляторной батареи,
токъ которой раскалитъ нить до-бѣла. Кромѣ того, проведемъ отъ
обоихъ концовъ угольной нити и отъ платиноваго штифта прово-
локи къ коммутатору, при помощи котораго можно соединять пла-
тиновый штифтъ по желанію либо съ положительнымъ концомъ
угольной нити, либо съ отрицательнымъ. Въ проводъ, идущій отъ
платиноваго штифта, включимъ аппаратъ, служащій указателемъ
тока; если мы не пожелаемъ воспользоваться амперметромъ, кото-
рый будетъ описанъ лишь ниже, то можно взять электрометръ, оба
зажима котораго соединены черезъ сопротивленіе, какъ мы это
дѣлали въ § 126 (рис. 84). Если мы повернемъ коммутаторъ
такъ, чтобы платиновый штифтъ былъ соединенъ съ положи-
тельнымъ концомъ раскаленной угольной нити, то указатель обна-
ружитъ замѣтный токъ порядка обычнаго тихаго разряда. Такъ
какъ такой разрядъ возникаетъ лишь въ томъ случаѣ, когда уголь-
ная нить накалена до-бѣла, то ясно, что раскаленная нить является
источникомъ необходимыхъ для проводимости іоновъ, по крайней
мѣрѣ, первичнымъ источникомъ, такъ какъ возможно, что при этомъ
также играютъ роль и столкновенія іоновъ. Но раскаленная нить
дѣлаетъ возможнымъ разрядъ лишь въ томъ случаѣ, когда она, какъ
въ только-что описанномъ опытѣ, служитъ катодомъ; если мы
повернемъ коммутаторъ такъ, чтобы раскаленная угольная нить
стала анодомъ, то сила тока, идущаго къ платинѣ, упадетъ до
нуля. Отсюда слѣдуетъ, во-первыхъ, что пустота въ лампочкѣ явля-
ется совершеннымъ изоляторомъ, и, во-вторыхъ, что раскаленная
до-бѣла угольная нить выдѣляетъ только отрицательные, но не поло-
жительные іоны.
Такой же опытъ можно произвести и съ раскаленными до-бѣла
металлическими проволоками, напримѣръ, съ платиновой; результатъ
получается тотъ же, хотя сила тока можетъ получиться меньшей^не-
жели въ опытѣ съ угольной нитью. Детальное изученіе отрицатель-
ныхъ іоновъ, выдѣляющихся изъ накаленныхъ тѣлъ вовсѣхь слу-
чаяхъ, приводитъ къ заключенію, что они суть электроны.
Раскаленное тѣло выдѣляетъ электр^цдУвъ довольно
большомъ количествѣ.
Газъ, соприкасающійся съ раскаленнымъ тѣломъ, іони-
Выдѣленіе электроновъ раскаленными тѣлами
297
зируется, такимъ образомъ, очень мягкими катодными лу-
чами, выходящими изъ этого тѣла.
Если нагрѣть платиновую проволоку только до желтаго каленія,
то она высылаетъ также и положительные іоны. Но это, несомнѣнно,
вторичное явленіе, такъ какъ оно наблюдается лишь тогда, когда
изъ накаленной платины выдѣляются газы (послѣднее случается,
впрочемъ, почти всегда, такъ какъ платина при низкихъ температу-
рахъ, какъ извѣстно, сильно поглощаетъ газы). Выдѣляемый накален-
ной платиной газъ тотчасъ же расщепляется на іоны катодными лу-
чами, исходящими изъ металла; часть этихъ іоновъ возвращается въ
платину, а часть уходитъ во внѣшнее пространство. При болѣе низкихъ
температурахъ сначала получается даже избытокъ положительныхъ
іоновъ. Но послѣ болѣе продолжительнаго нагрѣванія, во время ко-
тораго проволока постепенно освобождается отъ поглощеннаго газа,
образованіе положительныхъ іоновъ совершенно прекращается. При
болѣе высокихъ температурахъ всегда уже съ самаго начала пре-
обладаютъ электроны, выдѣляющіеся изъ самой платины.
Если накалить катодъ Гейсслеровой
трубки, то катодное напряженіе сильно па-
даетъ. Катодные лучи въ этомъ случаѣ са-
мостоятельно поддерживаются катодомъ, и
бѣдное электронами пространство передъ
нимъ не можетъ образоваться. Закатодные
лучи и катодное напряженіе становятся тѣмъ
слабѣе, чѣмъ сильнѣе раскаленъ катодъ.
Это вліяніе высокой температуры на ка-
тодное напряженіе было замѣчено еще
Гитторфомъ.
177. Венельтъ (А. ХѴейпеІі) открылъ,
что испусканіе электроновъ раскаленнымъ
катодомъ особенно сильно, если его по-
Рис. 113. Трубка Венельта.
верхность покрыта окисью щелочно-земель-
наго металла (кальція, стронція, барія). Въ
„трубкѣ Венельта“ катодъ состоитъ изъ
платиновой пластинки, къ которой ведутъ черезъ стеклянную стѣнку
два толстые провода для нагрѣвающаго тока (рис. 113)хЭта пла'
стинка покрыта окисью кальція. Трубка достаточно сильно эвакуи-
руется, во всякомъ случаѣ ниже 1 мм. Очень сильныеітоки можно
возможно болѣе донкой
298
Выдѣленіе электроновъ раскаленными тѣлами
получать лишь тогда, когда испускаемые раскаленнымъ катодомъ
электроны сильно іонизируютъ газъ, а для этого давленіе должно
быть выше 0,1 мм. Если же работать со слабыми токами, то могутъ
оказаться достаточными первичные электроны и можно еще понизить
давленіе. Катодъ трубки Венельта испускаетъ весьмам ягкіе, но чрез-
вычайно интенсивные катодные лучи, которые могутъ быть исполь-
зованы для многихъ изслѣдованій. Венельтъ опредѣлилъ для нихъ
отношеніе ~ и получилъ приблизительно ту же величину, которая
была указана выше (§§ 149— 153).
Если измѣнить соединеніе такимъ образомъ, чтобы раскаленный
электродъ трубки Венельта былъ соединенъ съ положительнымъ по-
люсомъ батареи аккумуляторовъ, то даже при напряженіяхъ въ
нѣсколько сотъ вольтъ замѣтнаго тока въ трубкѣ не обнаруживается.
Поэтому трубка Венельта можетъ служить прекраснымъ электриче-
скимъ выпрямителемъ для полученія постояннаго тока изъ перемѣн-
наго, подобно описанному въ § 114 электролитическому выпрямителю.
Въ не очень сильно эвакуированной трубкѣ Венельта, благодаря
значительной іонизаціи газа мягкими катодными лучами, высыла-
емыми раскаленнымъ электродомъ, сила тока при разрядѣ можетъ
достигать огромныхъ величинъ. Она можетъ во много тысячъ разъ
превосходить силу тока при тихомъ разрядѣ въ Гейсслеровой трубкѣ;
это доказываетъ, что высокія температуры вызываютъ гораздо болѣе
обильное образованіе іоновъ, чѣмъ закатодные лучи. Токъ можетъ
стать настолько сильнымъ, что анодъ нагрѣвается до бѣлаго каленія.
Во избѣжаніе этого, какъ указано на рис. 113, анодъ дѣлается съ
большой поверхностью. При этомъ катодное напряженіе можетъ
равняться приблизительно 2 вольтамъ, а напряженіе между обоими
электродами - приблизительно 20 вольтамъ.
АНОДНЫЕ ЛУЧИ. .
178. Согласно новѣйшимъ изслѣдованіямъ Герке (Е. О|1цке)
и Рейхенгейма (О. КеісНепНеіт), раскаленныя соли можщѵзаста-
вить образовывать положительные газіоны. Согласно ихъ\ указаніямъ,
въ обыкновенной сильно эвакуированной трубкѣ посѣщается въ
качествѣ анода стержень изъ какой-нибудь соли ^лучще всего іоди-
стой) ; такой стержень изготовляютъ, вливая расплавленную соль, смѣ-
шанную съ графитнымъ порошкомъ, въ конецъ У§крй стеклянной труб-
Анодные лучи
290
ки (рис. 114). Сзади въ соляной стержень вплавляютъ провода, под-
водящіе токъ. Если въ хорошо эвакуированной трубкѣ съ такимъ,
анодомъ вызвать разрядъ, то сначала соль нагрѣвается до плавленія,
и съ этого момента анодъ начинаетъ высы-
лать рѣзко ограниченный пучокъ анодныхъ
лучей.Эти лучи свѣтятся подобно закатоднымъ;
въ спектроскопѣ ихъ свѣтъ даетъ линіи метал-
ла анодной соли. При достаточной дисперсіи
можно наблюдать, какъ и для закатодныхъ лу-
чей, явленіе Допплера и измѣрить такимъ
образомъ скорость положительныхъ іоновъ,
изъ которыхъ эти лучи состоятъ. Если въ
то же время опредѣлить ихъ магнитное откло-
неніе, то оказывается возможнымъ вычислить
Къ воздуш-
ному насосу
Рис. 114. Трубка для
анодныхъ лучей.
е
(ср. § 151) для нихъ отношеніе — • Такія измѣренія всегда давали
съ очень большой точностью атомный вѣсъ металла анодной соли;
такимъ образомъ, не можетъ быть ни малѣйшаго сомнѣнія въ томъ*,
что анодные лучи состоятъ изъ положительно заряженныхъ метал-
лическихъ атомовъ. Скорость ихъ обязана своимъ происхожденіемъ
дѣйствію образующагося около анода поля высокаго напряженія..
Герке и Рейхенгеймъ получали „анодныя напряженія" въ нѣсколько
тысячъ вольтъ, эвакуируя трубку очень сильно и тѣмъ затрудняя
развитіе катодныхъ лучей. Такимъ образомъ, соляной анодъ обла-
даетъ тѣми же свойствами, какими обыкновенно обладаетъ катодъ,,
напряженіе котораго чрезвычайно сильно возрастаетъ, когда оказы-
вается недостатокъ въ положительныхъ частицахъ, составляющихъ
закатодные лучи (§ 166). По всей вѣроятности, явленіе анодныхъ
лучей представляетъ собою точное обращеніе явленія обычныхъ,
катодныхъ лучей; положительные іоны въ этомъ случаѣ освобо-
ждаются не дѣйствіемъ высокой температуры, какъ электроны въ
трубкѣ Венельта, но подъ дѣйствіемъ бомбардировки анода отрица-
тельными частицами.
Необходимо все же имѣть въ виду, что эти своеобразныя^^-
нія получаются только въ томъ случаѣ, когда анодъ состоитъизъ.
соли, дающей при высокихъ температурахъ обильные парьц^ъ этомъ
можно убѣдиться по сильному окрашиванію пламени Вунзеновской
горѣлки, когда въ него эта соль вносится. Особецйо пригодными
300
Дуговой разрядъ
для возбужденія анодныхъ лучей оказываются галоиды щелочныхъ
и щелочноземельныхъ металловъ. Напротивъ, щелочноземельные оки-
слы, которые, согласно Венельту, особенно легко выдѣляютъ элек-
троны, но которые лишь слабо окрашиваютъ пламя Бунзеновской
горѣлки, для полученія анодныхъ лучей совершенно непригодны. От-
сюда можно заключить, что анодные лучи возникаютъ не въ самой
соли, но въ слоѣ металлическихъ паровъ, образующемся у поверх-
ности раскаленнаго соленого анода.
Кажется, можно считать установленнымъ, что твердое тЬло
можетъ высылать непосредственно электроны какъ подъ дѣйствіемъ
закатодныхъ или иныхъ лучей, такъ и подъ вліяніемъ высокихъ
температуръ.
ДУГОВОЙ РАЗРЯДЪ.
179. Соединимъ съ полюсами источника электричества, напря-
женіе котораго должно быть не ниже 50 вольтъ, двѣ угольныя па-
лочки и прикоснемся одной изъ нихъ къ другой. Въ мѣстѣ сопри-
косновенія сопротивленіе очень велико, такъ что, если въ цѣпи нѣтъ
другихъ значительныхъ сопротивленій, тамъ выдѣляется большое ко-
личество теплоты, и палочки накаляются до-бѣла. Если послѣ этого
разъединить раскаленные угли, то электрическій токъ не прекра-
тится, и въ воздухѣ образуется проводящее соединеніе, испускающее
голубоватый свѣтъ, вслѣдствіе своей (часто серповидной) формы, назы-
ваемый свѣтовою дугою1). Эта проводящая дуга поддерживается
въ газѣ между углями все время, пока оба угля остаются накален-
ными до-бѣла. Если прекратить бѣлое каленіе электродовъ, примѣняя
^искусственное охлажденіе или же включая добавочное сопротивленіе
и ослабляя, такимъ образомъ, токъ настолько, что отдаваемая имъ
углямъ энергія оказывается недостаточной для поддержанія темпера-
туры бѣлаго каленія, то и свѣтовая дуга въ тотъ же моментъ исче-
заетъ, и газъ между углями теряетъ свою проводимость.
Дуговымъ разрядомъ называютъ электрическій
проходящій черезъ газъ между двумя ।
тродами, если накаливаніе электродовъ
•особымъ источникомъ энергіи (какъ въ
яельта), но самымъ токомъ разряда.
токъ,
раскаленны лек-
» поддерживается не
> случаѣ^к'атода Ве-
Прим. пер.
Э Весьма часто также Вольтовою дугою
Дуговой разрядъ
30 Р
180. Уже по бѣлому цвѣту высылаемаго раскаленными уголь-
ными электродами свѣта можно заключить, что они поддерживаются
энергіею тока при чрезвычайно высокой температурѣ. Измѣренія по-
казали, что на анодѣ температура въ круглыхъ числахъ достигаетъ
4000°. Температура катода нѣсколько ниже; по Віоллю (ѴѴіоІІе)
она достигаетъ 2700°. Также и въ самой свѣтовой дугѣ тем-
пература весьма высока, какъ въ пламени. Разницу въ темпе-
ратурахъ обоихъ углей можно замѣтить уже при первомъ взглядѣ
на нихъ. Раскаленный участокъ на ано-
дѣ гораздо больше и ярче, нежели на
катодѣ. Далѣе, высокая температура
анода вызываетъ весьма сильное испа-
реніе, и въ немъ образуется впадина,
такъ называемый свѣтовой кратеръ.
На катодѣ также теряется вещество, но
эта потеря отчасти возмѣщается оса-
жденіемъ пара, развившагося на анодѣ.
При этомъ катодъ заостряется. На рис. 115
видно различіе между формами обоихъ Рис. 115. Угольная свѣтовая
электродовъ. Свѣтовая дуга соединяетъ
между собою наиболѣе яркія мѣста электродовъ. Въ ней можно за-
мѣтить „темное пространство1', раздѣляющее дугу на меньшую по-
ложительную и большую отрицательную части. Голубоватая свѣтовая
дуга всегда окружена желтозеленой свѣтовой оболочкой, такъ на-
зываемымъ ореоломъ. Этотъ ореолъ, незамѣтный на рис. 115 вслѣд-
ствіе малой его яркости, представляетъ собою область, въ которой
происходятъ химическія взаимодѣйствія между газами свѣтовой дуги
и воздухомъ и, слѣдовательно, не играетъ существенной роли въ
явленіи разряда.
Если произвести дуговой разрядъ между иными электродами,,
напримѣръ, между двумя металлическими стержнями, то явленіе въ
общихъ чертахъ останется тѣмъ же. Только различіе между обоим^С^1
электродами будетъ не такъ велико, какъ въ случаѣ дуги меи^^ѵ
углями. Часто даже катодъ болѣе раскаляется, чѣмъ анодъ. Эт^/по—
казываетъ, что какъ ни замѣчательно преобладаніе раскаленности на
положительномъ свѣтовомъ кратерѣ у углей, однако, оно\^7имѣетъ,
принципіальнаго значенія при детальномъ изученіи природы дугового,,
разряда. Къ этому вопросу мы еще возвратимся нц^е?>
302
Примѣненія свѣтовой дуги
ПРИМЪНЕНІЯ СВЪТОВОЙ ДУГИ.
181. Важнѣйшимъ примѣненіемъ свѣтовой дуги является дуго-
вая лампа. Въ обычныхъ дуговыхъ лампахъ источникомъ свѣта
является почти исключительно положительный кратеръ. Самая свѣ-
товая дуга и катодъ при этомъ играютъ сравнительно
+ незначительную роль. Поэтому дуговую лампу нужно
всегда помѣщать такъ, чтобы лучи отъ кратера падали
___________на освѣщаемый объектъ. Если лампа виситъ, то по-
ложительный уголь долженъ быть помѣщенъ сверху,
чтобы лучи отъ кратера падали внизъ (рис. 116).
Нормальнымъ напряженіемъ для обыкновенной ду-
говой лампы считается обычно напряженіе въ 55 вольтъ.
Но этого низкаго напряженія, конечно, недостаточно
для возбужденія разряда въ газѣ, когда оба электрода
удалены другъ отъ друга. Для того, чтобы „зажечь"
свѣтовую дугу, обыкновенно приводятъ угли въ сопри-
затѣмъ разъединяютъ ихъ. У лампъ, служащихъ для
Рис. 116. Рас-
положеніе уг-
лей въ обыч-
ной дуговой
лампѣ посто-
яннаго тока.
Рис.
косновеніе, а
освѣщенія, это, конечно, должно дѣлаться автоматически. Надъ круг-
лымъ стекляннымъ колпакомъ такой лампы всегда
можно замѣтить цилиндрическій футляръ, со-
держащій необходимый для этой цѣли механизмъ
(рис. 117). Пока токъ не проходитъ черезъ лам-
пу, угли благодаря дѣйствію пружины касаются
другъ друга. Если же замкнуть токъ, то меха-
низмъ приходитъ въ дѣйствіе и удаляетъ угли
другъ отъ друга до тѣхъ поръ, пока сила тока
не достигнетъ нормальной величины. Во время
горѣнія лампы этотъ механизмъ автоматически
поддерживаетъ постоянной длину свѣтовой дуги
и силу тока. Вслѣдствіе испаренія и образованія
углекислоты подъ дѣйствіемъ кислорода воздуха
обѣ угольныя палочки постепенно укорачиваются
и по истеченіи нѣкотораго времени должны быть
замѣнены новыми. Для того, чтобы оба угля из-
Чу
нашивались одинаково быстро, для ррложительнаго
"электрода берется болѣе толстая палочка, нежели^ляубтрицательнаго.
Угольная дуговая лампа принадлежитъ къущслу довольно эко-
номичныхъ источниковъ свѣта. Во всякомъ случаѣ, полезный эффектъ
117. Дуговая
лампа.
Свѣтовая дуга
303
т. е. отношеніе получаемаго количества свѣта къ затрачиваемой энер-
гіи, у дуговой лампы гораздо больше, чѣмъ у лампъ накаливанія.
Причиною этого является необыкновенно высокая температура свѣ-
тового кратера, температура, которой не могла бы выдержать уголь-
ная нить. Общимъ правиломъ является, что экономичность источника
свѣта тѣмъ значительнѣе, чѣмъ выше его температура; при этомъ
полезный эффектъ чрезвычайно быстро увеличивается съ возвыше-
ніемъ температуры.
182. Высокою температурою угольной свѣтовой дуги пользу-
ется также и химія. Ее примѣняютъ въ „электрическахъ печахъ",
доставляющихъ температуры, которыя никакими иными способами
нельзя поддерживать въ теченіе продолжительнаго времени. Въ этихъ
электрическихъ печахъ производятся теперь такія химическія реакціи,
о которыхъ раньше нельзя было и думать. Такимъ способомъ полу-
чаются, напримѣръ, карбиды—важныя для техники вещества—кар-
бидъ кальція и карбидъ кремнія. Муассанъ (Моіззап) въ электриче-
ской печи искусственно получалъ драгоцѣнные камни и иные мине-
ралы. Очень важная отрасль химической индустріи—алюминіевая ин-
дустрія— пользуется угольными свѣтовыми дугами громадныхъ раз-
мѣровъ для расплавленія алюминіевой руды, изъ которой возстано-
вленіемъ получается металлъ х).
СВѢТОВАЯ ДУГА.
183. Если сильно дуть на свѣтовую дугу, то ее можно „поту-
шить", т. е. прекратить разрядъ. Это прекращеніе тока нельзя объ-
яснить охлажденіемъ электродовъ 'потокомъ воздуха, потому что его
можно направить такъ, чтобы онъ не попадалъ на раскаленныя
мѣста углей, и дуга все же потухнетъ. Причину этого явленія нужно
искать въ увлеченіи дуги воздушнымъ токомъ, при чемъ она изги-
бается и потому удлиняется; это легко замѣтить при производствѣ
опыта. Вслѣдствіе этого сопротивленіе увеличивается, разрядный
токъ въ свѣтовой дугѣ ослабѣваетъ и, наконецъ, оказывается не въ
состояніи поддерживать электроды достаточно горячими.
Увлеченіе свѣтовой дуги токомъ воздуха можно показ^рЙіе
иначе, заставляя ее образовываться между двумя проволоками^лизко
Э Весьма важную роль играетъ также примѣненіе электрическихъ печей
къ добыванію азотной кислоты изъ воздуха. ^Рим' пеР'
304
Свѣтовая дуга
подходящими другъ къ другу и затѣмъ изогнутыми въ противопо-
ложныя стороны. Такія двѣ проволоки имѣютъ видъ пары роговъ,
помѣщенныхъ другъ противъ друга (рис. 118). Соединимъ рога съ
полюсами аккумуляторной батареи высокаго напряженія (около 500
вольтъ). Чтобы зажечь дугу, присоединимъ еще индукціонную ма-
шину, которую будемъ вращать, пока не проскочитъ искра въ про-
странствѣ между наиболѣе сближенными частями роговъ. Проводя-
щее соединеніе, даваемое искрой, тотчасъ становится путемъ, по ко-
торому разряжается аккумуляторная батарея; вслѣдствіе большой
силы тока образуется правильная свѣтовая дуга. Нагрѣваемый этой
дугою воздухъ поднимается вверхъ, а потому и самая дуга подни-
мается вверхъ, такъ что оба края дуги, или точки, въ которыхъ
проволоки раскалены до-бѣла, также движутся вверхъ. Это продол-
жается до тѣхъ поръ, пока длина свѣтовой дуги не станетъ слиш-
комъ большой; тогда токъ ослабѣваетъ и дуга тухнетъ.
Такое приспособленіе находитъ примѣненіе на практикѣ въ
формѣ такъ называемаго „рогообразнаго громоотводаи, служащаго
для защиты электрическихъ проводовъ
• отъ ударовъ молніи. Часто можно видѣть,
что на электрическихъ проводахъ ка-
ждая проволока на опредѣленныхъ раз-
стояніяхъ снабжена рогообразнымъ при-
способленіемъ, противъ котораго уста-
навливается второй „рогъ“, отводимый
КЪ Землѣ. ЕСЛИ ВО Время ГрОЗЫ ПрОВОДЪ Къ землю
гдѣ-либо зарядится до высокаго потен- ~ .
г Рис. 118. Рогообразньш громо-
ціала, то черезъ ближайшій къ этому мѣсту отводъ,
рогообразный громоотводъ проскочитъ искра, и зарядъ, обусловли-
вавшій высокое напряженіе, уйдетъ въ землю прежде, нежели 1 онъ
вызоветъ какое-либо поврежденіе. Послѣ его исчезновенія соединеніе
съ землею прекращается автоматически вышеописаннымъ образомт^
Изъ этихъ опытовъ выясняется, что свѣтовая дуга представля-
етъ собою полоску очень хорошо проводящаго газа, расположённую
въ воздухѣ между электродами. При движеніяхъ возду^^увлекаетъ
за собою эту проводящую полоску, какъ увлекает^онъ,напри-
мѣръ, легкую проволоку. Слѣдуетъ, однако, замѣнить, что прово-
дящая полоска, представляющая собою свѣтовую дугу, весьма
быстро теряетъ проводимость и обращается/§въ обыкновенный
Свѣтовая дуга
305
непроводящій газъ, какъ только токъ прекращается. Это обратное
превращеніе совершается, впрочемъ, не сразу, въ чемъ можно убѣ-
диться, воспользовавшись въ вышеописанномъ опытѣ съ рогообраз-
нымъ громоотводомъ вмѣсто аккумуляторной батареи источникомъ
перемѣннаго тока высокаго напряженія. Хотя при такомъ токѣ на-
пряженіе каждый разъ, черезъ извѣстные промежутки времени, по-
нижается настолько, что свѣтовая дуга должна потухнуть, тѣмъ не
менѣе новая свѣтовая дуга, образующаяся при слѣдующемъ воз-
растаніи напряженія, проходитъ по тому же пути, что и предыдущая,
и явленіе при примѣненіи перемѣннаго тока имѣетъ тотъ же видъ,
что и при примѣненіи постояннаго тока.
Что, дѣйствительно, свѣтовая дуга при перемѣнномъ токѣ пе-
ріодически тухнетъ и вновь загорается благодаря сохраняющейся
проводимости газа, легко можно замѣтить на каждой угольной свѣ-
товой дугѣ, питаемой перемѣннымъ токомъ. Такая дуга всегда из-
даетъ довольно громкій тонъ, число колебаній котораго въ точности
равно удвоенному числу колебаній перемѣннаго тока. Этотъ тонъ
вызывается періодически повторящимися затуханіями и возобновле-
ніями дуги, влекущими за собою охлажденія и нагрѣванія, связан-
ныя, въ свою очередь, съ сжатіемъ и расширеніемъ газа въ дугѣ.
Если мы будемъ быстро двигать палку въ свѣтѣ дуговой лампы
перемѣннаго тока, то вмѣсто непрерывнаго слѣда, получаемаго въ
случаѣ постояннаго источника свѣта, мы увидимъ изображеніе періоди-
чески—то свѣтлое, то темное, дающее впечатлѣніе дрожащаго движенія.
Обыкновенная искра и молнія, какъ мы увидимъ ниже, пред-
ставляютъ собою ни что иное, какъ пути дуговыхъ разрядовъ весьма
короткой продолжительности. Поперечное сѣченіе проводящаго га-
зоваго канала въ этихъ случаяхъ весьма мало. Когда удается наблю-
дать молнію при сильномъ вѣтрѣ, можно часто видѣть нѣсколько
свѣтящихся линій, параллельныхъ другъ, другу. Въ этихъ случаяхъ
по проводящему пути въ воздухѣ, созданному для себя сильнымъ
разрядомъ молніи, слѣдуетъ за нимъ нѣсколько болѣе слабыхъ раз-о
рядовъ; если вѣтеръ перемѣщаетъ этотъ проводящій каналъ, то ока-- ^
зывается, что отдѣльные „частичные разряды" проходятъ рфрйѣ»
другъ съ другомъ. Между двумя послѣдовательными частхфными
разрядами можетъ пройти нѣсколько десятыхъ секундфСіілѣдова-
тельно, въ теченіе такого промежутка времени газъ на°п^ги разря-
да сохраняетъ свойства хорошаго проводника.
Ми. Электричество и магпитизмъ.
20
306
Новыя дуговыя лампы
Химическій составъ газа, составляющаго свѣтовую дугу, легко
установить, наблюдая ее при помощи спектроскопа. Свѣтовая дуга
всегда даетъ спектръ, свойственный веществу электродовъ. Въ этомъ
заключается еще одно отличіе дугового разряда отъ тихаго разряда,
при которомъ проводникомъ становится самый газъ, находящійся
между электродами.
Свѣтовая дуга состоитъ изъ сильно раскаленныхъ, очень
хорошо проводящихъ паровъ вещества электродовъ.
НОВЫЯ ДУГОВЫЯ ЛАМПЫ.
184. Какъ мы уже видѣли, свѣтовая дуга угольной лампы явля-
ется весьма слабо свѣтящей. Она даетъ свѣтъ, подобный свѣту Бун-
зеновской горѣлки. Гораздо ярче свѣтовая дуга при металлическихъ
электродахъ. Но особенно яркой она оказывается, если въ качествѣ
электродовъ взять угли, пропитанные солями щелочныхъ или ще-
лочноземельныхъ металловъ. Такую свѣтовую дугу можно уподо-
Рис. 119.
Расположеніе
углей въ пла-
менной лампѣ.
бить пламени Бунзеновской горѣлки, въ которое вве-
дена соль. Подобное пламя проводитъ лучше, чѣмъ
не свѣтящее пламя Бунзеновской горѣлки, при чемъ хо-
рошая проводимость обусловливается въ этомъ случаѣ
присутствіемъ большого количества положительно за-
ряженныхъ атомовъ металла. Окрашенное пламя до
нѣкоторой степени является подобнымъ электролиту,
напримѣръ, водному соляному раствору. Точно такъ же
и въ случаѣ свѣтовой дуги, образующейся между про-
питанными солью углями, главную роль въ переносѣ
электричества играютъ, вѣроятно, металлическіе іоны.
Такъ какъ такая свѣтовая дуга является гораздо лучшимъ провод-
никомъ, нежели простая угольная дуга, то ее можно гораздо силь-
нѣе растягивать. Въ устраиваемыхъ на практикѣ лампахъ съ пропи-
танными углями оба угля устанавливаются рядомъ и наклонно другъ
къ другу (рис. 119). Въ такой пламенной лампѣ самая дуга тоже
даетъ много свѣта, и потому такая лампа имѣетъ гораздо ^брЛьшій
полезный эффектъ, нежели обыкновенныя угольныя дугрвъія лампы.
Особымъ родомъ дуговой лампы, въ которой пользуются исклю-
чительно свѣтомъ дуги, является ртутная лампа* вітервые построен-
ная Аронсомъ (Агопз). Юиттъ (Неѵѵііі) придалъМй ту форму, въ
которой она обычно примѣняется на практщсѣ^ (рис. 120). Лампа
Юитта состоитъ изъ длинной, достаточію^пшрокой эвакуирован
Новыя дуговыя лампы
307
ной стеклянной трубки, снабженной желѣзнымъ электродомъ вверху
и ртутнымъ электродомъ внизу; вблизи нижняго электрода трубка
имѣетъ значительное расширеніе. Катодомъ долженъ служить непре-
мѣнно ртутный электродъ; изъ какого металла сдѣланъ анодъ—въ
сущности совершенно безразлично. Часто пользуются ртутнымъ
же анодомъ, но удобнѣе твердый желѣзный электродъ. Для зажи-
ганія лампы ее наклоняютъ настолько, чтобы ртуть
коснулась желѣза. Если затѣмъ приводить лампу А
въ ея нормальное положеніе, то между возвращаю- 8
щейся на мѣсто ртутью а анодомъ образуется свѣто-
вая дуга, которая постепенно вытягивается и, нако-
нецъ, заполняетъ всю трубку. Болѣе удобенъ способъ }
зажиганія, придуманный Юиттомъ, при которомъ лам- |І
па остается въ покоѣ, а въ трубкѣ помощью кратко- |
временнаго сильнаго напряженія производится разрядъ, I
приготовляющій проводящій путь для послѣдующаго I
дугового разряда. Кратковременное высокое напряже- V
ніе легко получается помощью такъ называемаго са- У*
моиндукціоннаго дѣйствія, съ которымъ мы ближе позна- |
комимся въ главѣ о самоиндукціи. При достаточно боль- ~ \
шой силѣ тока вся трубка свѣтится мягкимъ, какъ-будто
бѣлымъ свѣтомъ, дающимъ характерный спектръ ртути. Рис. 120.
„ , Ртутная дуго-
Проводникомъ электрическаго тока, слѣдовательно, вая ламва
здѣсь Являются пары ртути. Эти пары образуются на
катодѣ въ томъ мѣстѣ, гдѣ токъ въ него входитъ—въ „базисѣ то-
ка". Это мѣсто имѣетъ видъ яркой бѣлой точки, которая безпо-
койно передвигается во всѣ стороны по поверхности ртути и обра-
зуетъ въ ней небольшое воронкообразное углубленіе. Такимъ обра-
зомъ, въ базисѣ тока ртуть нагрѣта до бѣлаго каленія, и въ немъ
происходитъ столь быстрое парообразованіе, что получается избы-
токъ давленія, вызывающій образованіе углубленія въ поверхности
ртути; получается своего рода „свѣтовой кратеръ". Къ этому яркому
кратеру примыкаетъ свѣтящійся пучокъ, который, однако, отдѣленъ ^3
отъ длинной колонны, собственно представляющей собою дугу,
нымъ пространствомъ почти въ 2 см. ширины. Для правильнаго
дѣйствія лампы нужно, чтобы давленіе наполняющаго ее ^ртутнаго
пара не становилось слишкомъ высокимъ. Съ этой цѣлью\ёго охла-
ждаютъ; въ лампѣ Юитта это охлажденіе происходитъ благодаря
20
308
Катодъ и анодъ
вышеописанному расширенію въ нижней части трубки. Черезъ эту
„охладительную камеру" токъ не проходитъ, поэтому непрерывно
притекающій паръ въ ней не нагрѣвается и конденсируется; та-
кимъ образомъ, давленіе автоматически приводится къ нормальному.
Рѣзкимъ отличіемъ ртутной лампы отъ угольной является второсте-
пенная роль ея анода, который остается все время при сравнительно
низкой температурѣ.
Ртутная лампа изъ всѣхъ искусственныхъ источниковъ свѣта
даетъ наибольшій полезный эффектъ. Поэтому она, конечно, полу-
чила бы широкое распространеніе, если бы только свѣтъ ея былъ дѣй-
ствительно бѣлымъ. Къ сожалѣнію, онъ такимъ только кажется, на са-
момъ же дѣлѣ онъ состоитъ изъ желтаго, зеленаго и синяго цвѣтовъ;
красный цвѣтъ въ немъ отсутствуетъ совершенно. Поэтому въ свѣтѣ
ртутной лампы предметы окрашиваются въ противный сине-зеленый
цвѣтъ. Красные цвѣта кажутся грязно-зелено-бурыми, у людей оказыва-
ются черно-синія губы, сине-зелено-желтый крапчатый цвѣтъ лица и т. д.
КАТОДЪ И АНОДЪ.
185. Обыкновенно при дуговомъ разрядѣ накаливаются оба
электрода, однако, въ нѣкоторыхъ случаяхъ удается получить разряды,
носящіе характеръ чисто дуговыхъ, но съ раскаленнымъ мѣстомъ толь-
ко на катодѣ. Легче всего получается свѣтовая дуга съ холоднымъ
анодомъ при низкихъ давленіяхъ газа; мы только-что видѣли при-
мѣръ такого разряда — разрядъ въ ртутной лампѣ. Но такіе разряды
возможны и при атмосферномъ давленіи. Штаркъ (Л. 8іагк) иКассуто
(Ь. Саззпіо) впервые показали съ полной несомнѣнностью, что и въ
этомъ случаѣ можетъ возникнуть дуговой разрядъ при холодномъ ано-
дѣ, если раскаленъ только катодъ. Обратный случай — дуговой раз-
рядъ при холодномъ катодѣ и горячемъ анодѣ совершенно невозможенъ.
Это обстоятельство представляется тѣмъ болѣе удивительнымъ,
что при обыкновенной, по крайней мѣрѣ, угольной свѣтовой/едугѣ,
анодъ имѣетъ гораздо болѣе высокую температуру. Но и для уголь-
ныхъ электродовъ можно весьма простымъ опытомъ п^азать, что
существеннымъ условіемъ для возникновенія дугового^азряда явля-
ется только раскаленное состояніе катода. Соединилъ двѣ угольныя
палочки черезъ коммутаторъ съ аккумуляторной батареей и попробуемъ
зажечь дугу между ними помощью третьей^гОльной палочки. Съ
этой цѣлью подносимъ свободную угольн^іО^иалочку, которая должна
Катодъ и анодъ
309
быть соединена гибкимъ проводомъ съ однимъ изъ двухъ закрѣплен-
ныхъ углей, сначала къ другому углю, а затѣмъ отводимъ зажжен-
ную такимъ образомъ дугу къ первому углю. Начало дуги перехо-
дитъ на послѣдній въ томъ случаѣ, если другой неподвижный уголь,
у котораго была зажжена дуга, является катодомъ. Такимъ образомъ
отъ горячаго катода къ холодному аноду переходитъ разрядъ, сей-
часъ же раскаляющій этотъ анодъ, такъ что между обоими углями
образуется непрерывно горящая свѣтовая дуга. Наоборотъ, если тотъ
неподвижный уголь, у котораго
была зажжена дуга, служитъ ано-
домъ, то опытъ не удается, дуга
не переходитъ на холодный ка-
тодъ. Такой опытъ (рис. 121) былъ
произведенъ уже въ 1840 году
Флемингомъ (Ріетіп^).
Первымъ условіемъ воз-
никновенія дугового разряда
всегда является раскаленное
состояніе катода. Раскален-
ность анода, по всей вѣроят-
ности, имѣетъ значеніе лишь
постольку, поскольку она спо-
собствуетъ образованію пара
въ количествѣ, достаточномъ
Къ батареѣ
для сильнаго электрическаго Рис. 121. Дуга загорается только
при раскаленномъ катодѣ.
тока.
186. Въ связи съ тѣмъ фактомъ, что въ ртутной лампѣ раска-
леннымъ является лишь катодъ (точнѣе небольшой участокъ катода)
а анодъ остается холоднымъ, находится интересное свойство такой
лампы: она горитъ только при постоянномъ токѣ и только въ томъ
случаѣ, когда ртуть служитъ катодомъ. Послѣднее условіе зависитъ,
конечно, отъ того, что только при раскаленномъ ртутномъ катодѣ про-
исходитъ образованіе необходимыхъ для разряда паровъ ртути. Если
измѣнить направленіе тока такъ, чтобы желѣзный электродъ ста^|Ь
катодомъ, то ртутный электродъ будетъ оставаться холоднымъ, рарѣі
исчезнутъ, и свѣтовая дуга потухнетъ. Если послѣ этого попробо-
вать вновь пустить токъ въ прежнемъ направленіи, то онъ ^ нё смо-
жетъ пройти, такъ какъ катодъ за это время охладил^т Если ртут-
310
Электрическое поле въ свѣтовой дугѣ
ная лампа должна горѣть на перемѣнномъ токѣ, то она должна быть
снабжена двумя
желѣзными электродами, которые соединяются съ
Рис. 122. Ртутная дуговая лампа
для перемѣннаго тока.
обоими полюсами источника тока.
Ртутный электродъ соединяется съ
точкой, потенціалъ которой всегда
представляетъ собой среднее между
потенціалами обоихъ полюсовъ, на-
примѣръ, какъ это указано на рис.
122, съ серединой сопротивленія, со-
единяющаго оба полюса. При такомъ
устройствѣ ртутный электродъ всегда
остается катодомъ, и „свѣтовой кра-
теръ “ не успѣваетъ охлаждаться. Въ
качествѣ анодовъ функціонируютъ
оба желѣзные электрода по очереди.
Въ ртутной лампѣ и въ проводникѣ,
ведущемъ къ ртутному электроду,
электрическій токъ всегда имѣетъ одно
и то же направленіе. Поэтому такая
лампа можетъ употребляться для вы-
прямленія тока, подобно вышеописан-
нымъ выпрямителямъ (§ § 119, 177).
ЭЛЕКТРИЧЕСКОЕ ПОЛЕ ВЪ СВЪТОВОЙ ДУГЪ.
187. Если мы будемъ изслѣдовать помощью зонда и электро-
метра поле свѣтовой дуги, то найдемъ кривую потенціаловъ, подобную
изображенной на рис. 123. Въ средней части свѣтовой дуги имѣется,
какъ въ обыкновенномъ проводникѣ, несущемъ электрическій токъ
(§ 93), постоянное электрическое поле (постоянное паденіе потенціала).
Вблизи обоихъ электродовъ поле рѣзко усиливается. Напряженіе
между электродами и началомъ средняго (постояннаго) поля на-
зываемъ соотвѣтственно катоднымъ напряженіемъ и аноднымъ на-
пряженіемъ. Обѣ эти величины зависятъ до нѣкоторой ^д^пени отъ
силы тока, уменьшаясь съ ея возрастаніемъ. При сре^нй силѣ тока
получаются слѣдующія приблизительныя величины:
Уголь
Анодное напряженіе 23
Катодное „ 9
Желѣзо^?
Цинкъ
12
14
Мѣдь
11 вольтъ.
14 вольтъ.
*
Электрическое поле въ свѣтовой дугѣ
311
Какъ мы уже часто видѣли выше, произведеніе изъ напря-
женія на протекающій въ секунду зарядъ (на силу тока) рав-
няется энергіи, которую эѳиръ доставляетъ въ секунду веществу
проводника. Въ нашемъ случаѣ произведеніе аноднаго и катоднаго
напряженій на силу тока равняется энергіи, употребляемой въ се-
кунду на нагрѣваніе раскаленныхъ анода и катода. Такъ какъ сила
тока съ обѣихъ сторонъ одинакова, то нагрѣваться сильнѣе будетъ
тотъ электродъ, около котораго напряженіе больше. Для угольныхъ
электродовъ числа даютъ крупную разницу, которая уже замѣтна
по внѣшнему виду дуги. Для приведенныхъ въ таблицѣ металличе-
скихъ свѣтовыхъ дугъ такихъ большихъ разностей не оказывается,
напряженіе на катодѣ въ нихъ немного больше, чѣмъ на анодѣ. о
Чтобы составить себѣ представленіе объ энергіи, идущейнаг
нагрѣваніе электродовъ, разсмотримъ свѣтовую угольную ^^угу,
черезъ которую течетъ токъ въ 15 л-- (15 амперъ). Энергія въ
сек' у уСѴ
этомъ случаѣ равняется (нужно принять во вниманіе, что\6личество
312
Теорія дугового разряда
энергіи, равное 4190 джулямъ, равняется 1 калоріи):
на анодѣ приблизительно 15.23 = 345 .^жуль — 0,082
г сек. сек.
на катодѣ приблизительно 15 . 9 = 135 -Ч-Ч = 0,032 л;-л-
г сек. сек.
Небольшое паяльное пламя, употребляемое при обработкѣ стекла
для его размягченія, поглощаетъ приблизительно 7 куб. см. свѣтиль-
наго газа въ секунду. Такъ какъ 1 литръ газа даетъ около 5 кало-
рій, то такое пламя развиваетъ всего около 0,035 кал\ Мы видимъ
сек.
отсюда, что свѣтовая дуга на краяхъ ея, гдѣ она соприкасается съ
электродами, развиваетъ приблизительно ту же энергію, что и паяль-
ное пламя. Единственная разница заключается въ томъ, что эта
энергія получается не за счетъ химическихъ превращеній, но за
счетъ процессовъ въ эѳирѣ, поддерживающихъ электрическій токъ и
іонную бомбардировку на электродахъ.
ТЕОРІЯ ДУГОВОГО РАЗРЯДА.
188. Изъ приведенныхъ фактовъ вытекаетъ, что дуговой раз-
рядъ представляетъ собою въ сущности то же явленіе, что и разрядъ
въ трубкѣ Венельта. Разница заключается только въ томъ, что въ
трубкѣ Венельта катодъ разогрѣвается помощью особаго тока, а въ
свѣтовой дугѣ разрядный токъ самъ производитъ нагрѣваніе, какъ
это только-что выяснено. Катодное напряженіе, необходимое для
вызывающей нагрѣваніе іонной бомбардировки, регулируется вполнѣ
автоматически. Какъ только напряженіе уменьшается, катодъ охла-
ждается, выдѣляетъ меньшее количество электроновъ и такимъ об-
разомъ получается тотчасъ же большой недостатокъ отрицательныхъ
іоновъ передъ катодомъ и, слѣдовательно, повышеніе катоднаго на-
пряженія. Если напряженіе увеличивается, то катодъ нагрѣвается,
выдѣляетъ больше электроновъ, по сравненію съ нормой, и катодное
напряженіе вновь падаетъ.
Точно такъ же и на анодѣ, вслѣдствіе необходимо возникающаго
уменьшенія числа положительныхъ іоновъ, образуется -весьДфЗ>силь-
ное поле (§ 143), и анодъ, подъ вліяніемъ сильной электронной, бом-
бардировки, также накаливается, что можно наблюдатЧи въ труб-
кахъ Венельта. Если накаливаніе настолько сильно,-что анодъ пла-
вится и образуетъ слой пара, то, согласно наблюденіямъ Герке и
Рейхенгейма(§ 178), образуются положительные іоны на его поверх-
Сила тока и напряженіе
313
ности. Вмѣстѣ съ тѣмъ анодное напряженіе достигаетъ своего наи-
большаго значенія и болѣе уже не измѣняется, регулируясь авто-
матически такимъ же путемъ, какъ и катодное напряженіе. Возможно,
что необычайно высокая температура угольнаго анода зависитъ отъ
того, что уголь плавится и испаряется съ большимъ трудомъ, и обра-
зованіе положительныхъ іоновъ у него начинается лишь при весьма
сильномъ бѣломъ каленіи.
Эта теорія объясняетъ, почему при небольшихъ силахъ тока
возможны дуговые разряды съ холоднымъ анодомъ, но не съ хо-
лоднымъ катодомъ.
СИЛА ТОКА И НАПРЯЖЕНІЕ.
189. Такъ какъ въ свѣтовой дугѣ, какъ и въ тихомъ разрядѣ,
іоны образуются самымъ токомъ, то проводимость газа въ дугѣ
весьма сильно возрастаетъ съ увеличеніемъ силы тока. Вслѣдствіе
этого напряженіе между электродами убываетъ, если уменьшеніемъ
сопротивленія во внѣшней цѣпи увеличить силу тока. Убыль напря-
женія настолько значительна, что ее можно легко обнаружить по-
мощью электрометра, соединяя его съ обоими углями обыкновенной
дуговой лампы. Чѣмъ ярче горитъ лампа, тѣмъ меньше отклоненіе
электрометра. Г-жа Айртонъ (Аугіоп) произвела нѣсколько рядовъ
весьма точныхъ измѣреній, при чемъ для каждаго ряда разстояніе
между электродами оставалось постояннымъ; эти измѣренія дали
возможность выяснить зависимость между силой тока и напряжені-
емъ на электродахъ угольной дуги для различныхъ разстояній между
электродами.
Примѣромъ такой зависимости можетъ служить кривая (рис. 124),
выведенная изъ ряда наблюденій, сдѣланныхъ при разстояніи между
электродами въ 3 мм. Она показываетъ, что съ увеличеніемъ силы
тока напряженіе при спокойно горящей дугѣ постепенно падаетъ
приблизительно до 3/4 той величины, которую оно имѣло при наи-
меньшей силѣ тока. Если еще далѣе выключать сопротивленіе, т. е.
увеличивать силу тока, то напряженіе внезапно упадетъ, послѣ чего
уже почти не будетъ измѣняться. Этой второй части кривой сорт-
вѣтствуетъ неспокойная и шипящая дуга. Если произвести рядъна-
блюденій надъ дугой при неизмѣнномъ разстояніи межд^^электро-
дами, то оказывается, что ея базисъ на анодѣ становится^все шире
по мѣрѣ возрастанія силы тока. Въ моментъ, когда начинаетъ
314
Сила тока и напряженіе
переходить за границы кратера, происходитъ внезапное паденіе на-
пряженія на электродахъ, и дуга начинаетъ шипѣть. Такимъ обра-
зомъ, шипящая вольтова дуга не отличается существенно отъ спо-
койной.
Подобно Гейсслеровой трубкѣ и лампѣ Нернста, дуговая лампа,
въ виду сильной зависимости сопротивленія отъ силы тока, крайне
чувствительна къ небольшимъ колебаніямъ напряженія. Поэтому, если
желательно имѣть хотя бы до нѣкоторой степени спокойный свѣтъ,
2 к 6 8 10 12 74 16 18 20 22 2к 26 28 30 Сила
въ амперахъ
Рис. 124. Кривая силы тока и напряженія угольной свѣтовой дуги въ
3 мм. длиною.
то передъ дуговой лампой нужно включить, какъ передъ лампой
Нернста, добавочное сопротивленіе. Обыкновенно въ лампахъ, слу1
жащихъ для освѣщенія, это добавочное сопротивленіе помѣщается
въ томъ футлярѣ (§181), который заключаетъ въ себѣ регулиру-
ющій механизмъ. 4^^
Интересное приложеніе чувствительности дуговой лампы сдИшболь-
шимъ добавочнымъ сопротивленіемъ сдѣлалъ Симонъ (Н. ТПрЗітоп),
соединивъ ламповую цѣпь съ телефонной цѣпью Ѣакимъ обра-
зомъ, что колебанія напряженія въ телефонной ц^|ій^передавались
на ламповую цѣпь. Для этой цѣли удобно примѣнцть^такъ называемое
индуктивное соединеніе, съ которымъ мы познакомимся въ электро-
Прерывистыя свѣтовыя дуги
315-
динамикѣ при изученіи трансформатора. Колебанія напряженія въ
ламповой цѣпи вызываютъ соотвѣтственныя колебанія силы тока, а
послѣднія, какъ это было уже нами указано при описаніи свѣтовой
дуги перемѣннаго тока (§ 183), вызываютъ воздушныя колебанія*,
центромъ которыхъ является дуга. Если мы будемъ говорить или
пѣть въ телефонъ, то дуга будетъ одновременно говорить или пѣть.
Такимъ образомъ, ею можно пользоваться въ качествѣ телефоннаго»
пріемника.
ПРЕРЫВИСТЫЯ СВѢТОВЫЯ ДУГИ.
190. Кривыя напряженія „самостоятельныхъ" разрядовъ въ га-
захъ обнаруживаютъ слѣдующую особенность этихъ разрядовъ: съ.
увеличеніемъ силы тока сопротивленіе убываетъ въ такой мѣрѣ, что-
напряженіе на электродахъ уменьшается съ возрастаніемъ,
силы тока. На этомъ основываются всѣ особенности разрядовъ въ
газахъ, отличающія ихъ отъ электрическихъ токовъ въ обычныхъ.
проводникахъ.
Въ качествѣ такой особенности тихаго разряда, мы познакоми-
лись выше (§ 169) съ прерывистымъ разряднымъ токомъ и видѣли,,
что условіе для возникновенія этого явленія заключается въ до-
статочно крутомъ паденіи кривой. При небольшихъ углахъ наклона
разрядъ постояненъ. Минимальное значеніе наклона кривой, при
которомъ начинаются перерывы, не можетъ быть прямо указано,,
такъ какъ оно зависитъ отъ многихъ, отчасти неизвѣстныхъ величинъ..
Подобно тихому разряду, дуговой разрядъ также часто оказы-
вается прерывистымъ, особенно въ случаѣ металлическихъ электро-
довъ. Напротивъ, угольная дуга обыкновенно горитъ спокойно и
не даетъ никакихъ перерывовъ. „Устойчивость" дугового разряда
существенно зависитъ отъ того, въ какой мѣрѣ температура элек-
тродовъ можетъ слѣдить за колебаніями силы тока. Чѣмъ хуже тепло-
проводность вещества электродовъ, тѣмъ медленнѣе температура ихъ.
можетъ измѣняться и тѣмъ менѣе склоненъ разрядъ къ прерывисто-
сти, тѣмъ болѣе онъ „устойчивъ". Это непосредственно ясно йз|Ь
теоріи дугового разряда. Такъ какъ уголь по сравненію съ метал-
лами обладаетъ плохой теплопроводностью, то угольная дуг^оритъ.
особенно спокойно. Если желательно (при нѣкоторыхъ (^стоятель-
ствахъ это случается) сдѣлать свѣтовую дугу „способной къ пере-
рывамъ" или „неустойчивой", то слѣдуетъ позабЛЖгься о хоро-
316
Переходъ отъ тихаго разряда къ дуговому
шемъ охлажденіи электродовъ. Кромѣ того, какъ и при тихомъ раз-
рядѣ, большое вліяніе на явленіе оказываютъ емкость электродовъ
и сопротивленіе проводниковъ между источникомъ тока и этой
емкостью. Обыкновенную угольную свѣтовую дугу можно сдѣлать
прерывистой, включая параллельно съ ней достаточную емкость; въ
главѣ, посвященной электрическимъ колебаніямъ, мы познакомимся
съ важными приложеніями прерывистой свѣтовой дуги.
ПЕРЕХОДЪ ОТЪ ТИХАГО РАЗРЯДА КЪ ДУГОВОМУ.
191. Если, уменьшая внѣшнее сопротивленіе, мы будемъ увели-
чивать силу тока тихаго разряда между двумя электродами, то элек-
троды будутъ при этомъ нагрѣваться, какъ это уже было указано
въ § 175. Прежде всего сильно нагрѣвается катодъ, и такъ какъ, въ
силу этого, изъ него выдѣляются электроны, то катодное напряженіе по-
нижается, при чемъ одновременно іонизація въ газѣ и сила тока
значительно возрастаютъ: начинается дуговой разрядъ сначала при
холодномъ анодѣ. При дальнѣйшемъ возрастаніи силы тока раска-
ляется и анодъ, и получается настоящій дуговой разрядъ. Переход-
ная форма свѣтовой дуги съ холоднымъ анодомъ наблюдается весьма
рѣдко. На нѣкоторыхъ металлическихъ электродахъ ее констатиро-
вали Арнольдъ (Н. И. АгпоШ) и Кэди (АѴ. 6. Сабу).
Мы можемъ считать переходъ отъ одной формы разряда къ
другой вполнѣ непрерывнымъ и построить одну кривую напряженій
и силы тока для всего разряда. Рис. 125 даетъ приблизительное
представленіе о томъ, каковъ можетъ быть видъ этой кривой. Въ
дѣйствительности, первая ея часть, соотвѣтствующая темному раз-
ряду и тихому разряду, должна была бы быть начерчена еще круче,
съ большими напряженіями и меньшими силами тока. Съ другой сто-
роны, часть, соотвѣтствующая собственно свѣтовой дугѣ, должна
была бы быть растянута еще болѣе въ сторону возрастающихъ силъ
тока, нежели это возможно было сдѣлать въ предѣлахъ рисункд.
Отъ вершины кривой, гдѣ темный разрядъ переходитъ въ тихій раз-
рядъ, до конца тихаго разряда, гдѣ начинается переходъ къ дуговому
разряду, сила тока возрастаетъ, примѣрно, въ тысячу разъ; сйДа тока
дугового разряда, въ свою очередь, въ сто или даже въ^ддгсячу разъ
больше силы тока сильнаго тихаго разряда. Кромѣ ^того, слѣдуетъ
замѣтить, что кривыя напряженія до сихъ поръ извѣстны лишь по
частямъ. Именно извѣстна, во-первыхъ, часть, ^со^твътствующая тем-
Переходъ отъ тихаго разряда къ дуговому
за 7
ному разряду, во-вторыхъ, приблизительно горизонтально идущая
часть собственно тихаго разряда и, въ-третьихъ, такая же часть, со-
отвѣтствующая дуговому разряду. Въ отдѣльныхъ случаяхъ изъ по-
слѣдней части извѣстны двѣ области, соотвѣтствующія холодному и
раскаленному аноду. Переходныя области между указанными неиз-
вѣстны по весьма понятнымъ причинамъ. Это суть тѣ части кривой,,
въ которыхъ она чрезвычайно круто спускается внизъ, т. е. соотвѣт-
ствующія настолько неустойчивому разряду, что его нельзя удержать,
постояннымъ, въ теченіе сколько нибудь значительнаго промежутка
Напряженіе на электродахъ
Свѣтовая дуга съ раскаленнымъ анооомъ
Сила тока
Рис. 125. Кривая силы тока и напряженія для всего разряда.
времени. Въ весьма многихъ случаяхъ часть дугового разряда съ хо-
лоднымъ анодомъ относится еще къ области неустойчиваго перехода
отъ тихаго разряда къ полному дуговому разряду съ двумя раска-
ленными электродами. Поэтому эти неустойчивыя части кривой при-,
ходится проводить наудачу, но общій характеръ кривой переданъ
на рис. 125 несомнѣнно вѣрно.
Разборъ кривой рис. 125 можно сдѣлать совершенно такъ же/
какъ сдѣланъ разборъ кривой рис. 107 въ §§ 168, 169. Въ ч^елѴ
ности ясно, что, при постоянномъ разстояніи между электродамйр ду-
говой разрядъ можно получить только въ томъ случаѣ, есЛ'И? пред-
варительно поднять напряженіе на электродахъ до его л^<сймальнаго
значенія, которое мы назвали въ § 168 разряднымъ или-^искровымъ,
напряженіемъ. Если введенное въ цѣпь сопротивленіе ^весьма мало,
318
Переходъ отъ тихаго разряда къ дуговому
пока не получатся большія
прямо показывающій связь
разрядомъ, былъ придуманъ
между тихимъ разрядомъ
Къ высокому напряженію
Рис. 126. Схема опыта
Лемана.
то разрядъ проходитъ съ большою скоростью всѣ стадіи, начиная
съ наивысшей точки кривой рис. 125,
силы тока дугового разряда.
192. Весьма интересный опытъ,
и дуговымъ
Леманомъ (О. ЬеЬтапп). Гейсслероватруб-
ка соединяется черезъ большія жидкія со-
противленія съ аккумуляторной батареей
высокаго напряженія (рис. 126). При этихъ
условіяхъ въ ней получается обычный не-
прерывный тихій разрядъ. Если затѣмъ, не
измѣняя другихъ условій, соединить еще
электроды съ зажимами плоскаго кон-
денсатора, емкостью въ нѣсколько микро-
фарадъ, то картина совершенно измѣня-
ется. Черезъ трубку начинаютъ проскаки-
вать, слѣдующіе другъ за другомъ черезъ
короткіе промежутки времени, дуговые раз-
ряды („искры"); каждый такой разрядъ
быстро прекращается и, въ промежутки вре-
мени между двумя послѣдовательными раз-
рядами, трубка остается совершенно темной.
Объясненіе этого явленія весьма просто. Разрядъ можетъ прой-
ти черезъ трубку лишь тогда, когда конденсаторъ, включенный парал-
лельно съ трубкой, зарядится до искрового напряженія трубки, что
требуетъ нѣкотораго времени, вслѣдствіе большой величины введен-
наго сопротивленія. Какъ только это напряженіе достигнуто, кон-
денсаторъ разряжается. Такъ какъ между нимъ и трубкой никакого
сопротивленія не помѣщено, то токъ быстро усиливается и скоро
переходитъ въ настоящій дуговой разрядъ; въ то же время напря-
женіе быстро падаетъ. Такимъ образомъ, конденсаторъ за короткое
время разряжается настолько, что его напряженіе оказываетсяічедо-
статочнымъ даже для поддержанія свѣтовой дуги. Дуговоіуразрядъ
поэтому прекращается, конденсаторъ вновь начинаетъ^ заряжаться,
тіо какъ только достигается искровое напряженіе, вг^вь происхо-
дитъ разрядъ.
Вліяніе предшествующей исторіи разряда
319
ВЛІЯНІЕ ПРЕДШЕСТВУЮЩЕЙ ИСТОРІИ РАЗРЯДА.
193. При зажиганіи дуговой лампы всегда замѣчается, что лампа
начинаетъ горѣть ровно и постоянно только по истеченіи нѣкото-
раго времени. Угли сперва должны раскалиться въ частяхъ, окру-
жающихъ конечныя точки свѣтовой дуги, для того, чтобы установи-
лись теплопроводность и температура электродовъ, отъ которой су-
щественно зависитъ разрядъ. Въ началѣ разряда теплопроводность
больше, нежели впослѣдствіи, при спокойно горящей дугѣ; сила тока,
слѣдовательно, сначала меньше.
Отсюда слѣдуетъ, что кривая напряженій не можетъ быть впол-
нѣ однозначной. Для дугового разряда, получающагося въ опытѣ
Лемана, она должна имѣть нѣсколько другой видъ, нежели для не-
прерывно горящей свѣтовой дуги, для которой могутъ быть сдѣланы
измѣренія по методу г-жи Айртонъ. Поэтому въ насъ не должно
вызывать особаго удивленія то обстоятельство, что весьма быстро
протекающій разрядъ (напримѣръ, въ опытѣ Лемана) и выглядитъ
иначе, нежели свѣтовая дуга, горящая продолжительное время.
Примѣръ зависимости вида кривой напряженій отъ предыдущей
исторіи разряда мы имѣли уже въ дугѣ перемѣннаго тока. Хотя
здѣсь свѣтовая дуга черезъ опредѣленные промежутки времени совер-
шенно затухаетъ, она каждый разъ загорается вновь при сравни-
тельно небольшомъ напряженіи источника перемѣннаго тока, благо-
даря тому, что электроды ея за это время не успѣваютъ охладиться,
и газъ потухшей свѣтовой дуги сохраняетъ свою проводимость.
Здѣсь разрядъ, такъ сказать, перескакиваетъ черезъ стадіи тихаго
разряда; приблизительное представленіе о формѣ кривой для дуги,
перемѣннаго тока можно составить себѣ, проведя на рис. 125 пря-
мую линію отъ нулевой точки къ началу дугового разряда съ рас-
каленнымъ анодомъ, и замѣняя этой прямой линіей часть кривой,
соотвѣтствующую высокимъ напряженіямъ тихаго разряда. Симонъ
получилъ помощью методовъ, съ которыми мы познакомимся въо
электродинамикѣ, подобныя кривыя напряженій для свѣтовыхъ дугъ^
перемѣннаго тока; примѣръ такой кривой данъ на рис. 127. На
видно, что кривая, соотвѣтствующая разгорающейся дугѣ, от^й"Чна
отъ кривой, соотвѣтствующей затухающей дугѣ. Именно, ^ъ^фхвремя,
когда дуга разгорается и, слѣдовательно, температура электродовъ
должна повышаться и іонизація газа должна возрастай^напряженіе
320
Вліяніе предшествующей исторіи разряда
выше, чѣмъ тогда, когда дуга тухнетъ, и разряду благопріятствуютъ
высокая температура и значительная степень іонизаціи, сохранившіяся
отъ предыдущей стадіи разряда. Въ общемъ кривая рис. 127 имѣ-
етъ, дѣйствительно, ту форму, которая получается вышеуказаннымъ
пріемомъ изъ кривой рис. 125. Слѣдуетъ лишь замѣтить, что кривыя
изображены на этихъ двухъ рисункахъ въ различныхъ масштабахъ.
Кривыя рис. 127, по сравненію съ кривой рис. 125, сильно растя-
нуты въ направленіи оси напряженій, т. е. въ вертикальномъ напра-
Рис. 127. Кривая силы тока и напряженія для свѣтовой дуги перемѣннаго
тока, при угольныхъ электродахъ. Длина дуги 3 4 мм. Число періодовъ 50.
вленіи, а въ направленіи оси силъ тока, т. е. въ горизонтальномъ
направленіи, сокращены; это сдѣлано для большей ихъ отчетливости.
Мы видимъ, такимъ образомъ, что непосредственно предше-
ствующій дуговой разрядъ чрезвычайно сильно понижаетъ максималь-
ное напряженіе, то напряженіе, при которомъ разрядъ возобновляется
и которое мы могли бы, какъ раньше, назвать „искровымъ напряже-
ніемъ". Такое вліяніе предшествующихъ разрядовъ замѣчается также
и у прерывистыхъ дуговыхъ разрядовъ. Потухшій разрядъ возобно-
вляется, какъ и при перемѣнномъ токѣ, какъ только напряженіе
нѣсколько возросло. Къ особенностямъ дуговой лампы, которая^а-
етъ прерывистый разрядъ, благодаря включенному параллел^о^ съ
ней і
конденсатору, мы возвратимся еще разъ въ электродинамикѣ..
Относительно прерывистаго тихаго разряда точныхъ^ изслѣдова-
еще не существуетъ. Но, несомнѣнно, предшествующій разряды
ній
вызываемымъ имъ образованіемъ іоновъ и связаннымъ съ нимъ рас-
О \\
предѣленіемъ этихъ іоновъ подготовляетъ пуж^ для новаго разряда,,
если послѣдній весьма быстро слѣдуетъ ^^нимѣ. Такимъ образомъ,.
Электрическая искра
321
„искровое напряженіе" въ случаѣ весьма быстро прерывающагося
тихаго разряда, вѣроятно, имѣетъ гораздо меньшее значеніе, нежели
то, при которомъ разрядъ получается въ первый разъ. Кривая на-
пряженій и силъ тока для стаціонарныхъ тихихъ разрядовъ поэтому,
вѣроятно, выглядитъ нѣсколько иначе, нежели для быстро протека-
ющихъ разрядовъ, которыми начинается, напримѣръ, искровой раз-
рядъ въ опытѣ Лемана.
ЭЛЕКТРИЧЕСКАЯ ИСКРА.
194. Подъ „искрой" мы понимаемъ всякій весьма быстро
прекращающійся разрядъ.
Какимъ образомъ возникаетъ искра, ясно изъ опыта, описаннаго
въ §192. Для ея возникновенія всегда необходимо, чтобы „искровой
промежутокъ" былъ соединенъ помощью проводника весьма ма-
лаго сопротивленія съ емкостью, къ которой зарядъ подводится
весьма медленно. Величина необходимой емкости зависитъ отъ
свойствъ искрового промежутка и отъ скорости, съ которою къ ней
подводится зарядъ. Электрическая машина обыкновенно даетъ искро-
вые разряды даже при весьма малой емкости электродовъ (если
только давленіе газа между электродами не является крайне малымъ),
такъ какъ она развиваетъ электрическіе заряды весьма, медленно
(§ 36). Однако, и въ этомъ случаѣ емкость имѣетъ большое вліяніе
на видъ искры. Нужно отличать два существенно различные рода
искры. Во-первыхъ, при весьма малой емкости электродовъ полу-
чаются блѣдно-красныя искры; красноватая свѣтовая нить начинается
на анодѣ и подходитъ вплотную къ катоду, на которомъ около
конца этой нити появляется голубоватое, по большей части, непра-
вильной формы пятно тлѣющаго свѣта. Во-вторыхъ, при большей
емкости электродовъ искра представляетъ собою блестящую бѣлую
свѣтовую нить, оканчивающуюся на каждомъ изъ электродовъ ярко
свѣтящейся точкой. Блѣдно красная искра, очевидно, представляетъ
собою тихій разрядъ весьма короткой продолжительности; онъ по-^°ѵ
лучается въ томъ случаѣ, когда электрическій зарядъ электродсф^
оказывается уже исчерпаннымъ, какъ только разрядъ, перейдя ^ефеѣъ
высшую точку кривой рисунка 125, достигаетъ части кривой,^соот-
вѣтствующей тихому разряду. Бѣлая искра получается когда
разрядъ проходитъ всѣ стадіи тихаго разряда, за которыми слѣду-
/Г у
етъ отчетливая свѣтовая дуга весьма короткой прй^рджительности
Ми. Электричество и ю агнитизмъ.
21
322
Электрическая искра
съ двумя раскаленными до-бѣла исходными точками на электродахъ
(рис. 128). Въ обоихъ случаяхъ свѣтовая нить чрезвычайно тонка;
это указываетъ на то, что всякій разрядъ въ первый моментъ обра-
зуетъ весьма тонкій проводящій каналъ, который расширяется лишь
при продолжительномъ токѣ.
Очень характерный искровой разрядъ можно получить, соединяя
большую лейденскую банку или батарею лейденскихъ банокъ про-
волокою съ одной стороны съ полюсами индукціонной машины, а
съ другой стороны съ двумя изолированными латунными шарами,
расположенными другъ противъ друга на разстояніи нѣсколькихъ
сантиметровъ и образующими, такимъ образомъ, искромѣръ. Если
начать вращать индукціонную машину, то будутъ медленно возни-
а) красноватая искра.
Ь) бѣлая искра.
Рис. 128. Два рода электрическихъ искръ.
кать электрическіе заряды, и получатся какъ разъ условія вышеопи-
саннаго опыта Лемана (см. рис. 126). Какъ только достигается раз-
рядное напряженіе, черезъ искровой промежутокъ проскакиваетъ ослѣ-
пительно-бѣлая искра, сопровождаемая сильнымъ трескомъ. По спек-
тру искры можно заключить, что температура быстро прекращаю-
щагося дугового разряда — искры — гораздо выше, нежели температура
обычнаго стаціонарнаго дугового разряда. Дѣйствительно, за корот-
кое время существованія искры (обыкновенно меньше милліонной
доли секунды) дуговой разрядъ доходитъ до громадной силы тока.
Обращеніе электрической энергіи въ теплоту происходитъ въ теченіе
чрезвычайно короткаго промежутка времени и потому вызываетъ
весьма интенсивныя явленія. Исходныя точки искры на электродахъ
также должны имѣть громадныя температуры, такъ какъ на|нихъ въ
теченіе очень короткаго времени происходитъ интенсивной образо-
ваніе пара; однако, раскаленное состояніе этихъ то^кь исчезаетъ
вмѣстѣ съ искрою въ силу теплопроводности, таісъ^какъ въ общемъ
имѣющіяся здѣсь количества энергіи не великц іѵвызываютъ высо-
кія температуры лишь вслѣдствіе малости^пррмежутка времени и
Электрическая искра
323
пространства. Сильный трескъ указываетъ на колоссальное терми-
ческое расширеніе, моментально происходящее въ искровомъ про-
межуткѣ.
Можно избѣжать громаднаго развитія силы тока и вмѣстѣ съ
тѣмъ увеличить продолжительность разряда, помѣщая между лейден-
ской банкой и искромѣромъ вмѣсто проволоки влажный конопля-
ный шнуръ, имѣющій большое сопротивленіе. Въ такомъ случаѣ
искра оказывается не бѣлой, а желтой, какъ обычная свѣтовая дуга
между латунными электродами, и не трещитъ, а только издаетъ сла-
бый глухой шумъ. Что искра въ этомъ случаѣ образуетъ свѣтовую
дугу, горящую немного болѣе продолжительное время, нежели обык-
новенная искра, слѣдуетъ изъ того, что она не образуетъ тонкой
нити, но представляется, подобно стаціонарной свѣтовой дугѣ, въ
видѣ широкой свѣтящейся полосы.
Весьма интересный опытъ можетъ показать различіе въ про-
должительностяхъ обѣихъ описанныхъ искръ. Возьмемъ искромѣръ,
состоящій изъ сравнительно малыхъ шаровъ, и заполнимъ искровой
промежутокъ обыкновеннымъ чернымъ порохомъ. Интенсивная искра его
не зажигаетъ, такъ какъ подъ вліяніемъ внезапнаго расширенія воздуха
порохъ разлетается, какъ отъ взрыва, во всѣ стороны прежде, неже-
ли онъ успѣваетъ загорѣться. Болѣе продолжительная и болѣе сла-
бая желтая искра, наоборотъ, зажигаетъ порохъ. Мы имѣемъ здѣсь, до
нѣкоторой степени, подобіе „холоднаго" и „горячаго" ударовъ молніи.
Помѣщая между лейденской банкой и искровымъ промежуткомъ
подходящее сопротивленіе, можно удержать разрядъ на любой ста-
діи кривой (рис. 125). Такъ, пользуясь весьма длиннымъ влажнымъ
шнуромъ, мы получимъ уже не желтый дуговой разрядъ, но правильный
тихій разрядъ съ красной положительной свѣтовой колонной и голу-
бымъ пятномъ тлѣющаго свѣта на катодѣ. Что при большихъ коли-
чествахъ электричества, скопляющихся въ лейденской банкѣ, разрядъ
оказывается уже болѣе продолжительнымъ, видно изъ того, что
тлѣющій свѣтъ заполняетъ сравнительно широкое пространство и имѣ-
<етъ совершенно иной видъ, нежели блѣднокрасная искра (рис. 128а^з^'
ИСКРОВОЕ НАПРЯЖЕНІЕ. Э
195. Изъ предшествующаго вполнѣ ясно, что напряженіе, при
которомъ происходитъ разрядъ емкости черезъ искровой^омежутокъ,
должно быть тождественно съ максимальнымъ значеніемъ напряженія
324
Искровое напряженіе
на электродахъ при тихомъ разрядѣ, которое мы въ § 168 называли
разряднымъ напряженіемъ. Точный ходъ кривой рисунка 125 сейчасъ,
за ея высшей точкой не можетъ быть установленъ экспериментально,
такъ какъ разрядъ здѣсь слишкомъ неустойчивъ, но для самой вер-
шины кривой величина напряженія, по крайней мѣрѣ, опредѣляется
очень легко. Для этого опредѣленія достаточно медленно заряжать
соединенный съ искровымъ промежуткомъ конденсаторъ, наблюдая
въ то же время за возрастаніемъ его потенціала и отмѣчая то значеніе
его, при которомъ внезапно возникаетъ искра. Такія измѣренія мо-
гутъ быть произведены, понятно, для любого не слишкомъ большого
искрового промежутка въ любомъ газѣ, при любомъ давленіи газа,
при любомъ матеріалѣ электродовъ; они имѣютъ большое практи-
ческое значеніе, такъ какъ точная таблица искровыхъ напряженій
служитъ прекраснымъ средствомъ для точнаго калибрированія элек-
трометра для высокихъ напряженій. Съ этой цѣлью обычно употре-
бляется искромѣръ, у котораго разстояніе между электродами можно из-
мѣнять и точно измѣрять — такъ называемый искровой микрометръ.
То обстоятельство, что удается опредѣлить важнѣйшую точку кри-
вой напряженій или, по крайней мѣрѣ, ея высоту, имѣетъ, кромѣ
того, конечно, и большое теоретическое значеніе.
Измѣренія, произведенныя Пашеномъ (Разсѣеп) при различ-
ныхъ давленіяхъ и различныхъ длинахъ искръ, привели его къ весьма
простому и общему закону, который по измѣреніямъ другихъ
изслѣдователей примѣнимъ въ еще болѣе широкихъ предѣлахъ.
Этотъ законъ Пашена гласитъ, что длина искры, соотвѣт-
ствующая опредѣленному напряженію въ опредѣленномъ
газѣ, обратно пропорціональна давленію. При этомъ темпе-
ратура принимается за постоянную (комнатная температура). Если
мы обозначимъ разрядное напряженіе черезъ V, давленіе черезъ р
длину искры черезъ /, то законъ Пашена можно выразить еще такъ:
V зависитъ исключительно отъ произведенія рі. Кривыя рисун^а329
даютъ эту зависимость для атмосфернаго воздуха; V нао^нихъ вы-
ражено въ вольтахъ, р — въ мм. ртутнаго столба, I — ^рмм. Изъ
нихъ ясно, что кривая искрового напряженія имѣёТ^> минимумъ;
минимальное значеніе искрового напряженія равняет^Сприблизительно
350 вольтамъ; соотвѣтствующее ему значеніе ^произведенія рі рав-
няется 5,5. Слѣдовательно, длина искры, прикоторой искровое на-
пряженіе имѣетъ наименьшее значеніе, прт0 атмосферномъ давленіи
Искровое напряженіе
325
(760 мм.) равняется 7,25 ц. Если длину искры еще уменьшить, то
искровое напряженіе быстро возрастаетъ. Минимальное значеніе
Рис. 129 а. Искровое напряженіе при очень маломъ искровомъ промежуткѣ
въ воздухѣ.
Рис. 129 Ь. Искровое напряженіе при большомъ искровомъ промежуткѣ
въ воздухѣ. ѵС/"
яяя
искрового напряженія тождественно съ нормальной велич^офкатод-
наго напряженія (§ 142). Слѣдовательно, соотвѣтствующая^ ему дли-
на искры представляетъ собою кратчайшее разстоян||<Гмежду элек-
326
Искровое напряженіе
тродами, при которомъ могутъ нормально развиться катодныя
явленія. При дальнѣйшемъ ихъ сближеніи напряженіе возрастаетъ,
какъ всегда при сближенныхъ электродахъ (§ 144; см. также § 166).
Чтобы получить это явленіе, нужно заключить почти плоскіе элек-
троды въ узкую капсюлю изъ изолирующаго матеріала, такъ какъ
иначе искра выберетъ болѣе длинный путь (какъ въ трубкѣ Гитторфа,
изображенной на рис. 96). Такъ какъ законъ Пашена, какъ пока-
зали спеціальныя изслѣдованія Карра (Сагг), имѣетъ силу и для
весьма малыхъ длинъ искры, то мы можемъ заключить, что явленія
на катодѣ при искровомъ напряженіи (максимальномъ напряженіи на
электродахъ), измѣняясь съ измѣненіемъ давленія, остаются геометри-
чески подобными самимъ себѣ, притомъ длины измѣняются обратно
пропорціонально давленію.
Послѣ минимума искровое напряженіе возрастаетъ сперва весьма
медленно; затѣмъ, начиная отъ опредѣленной точки (въ воздухѣ
400 вольтъ при рі = 9) кривая на значительномъ протяженіи имѣ-
етъ видъ почти прямой линіи. Такимъ образомъ, разрядное напря-
женіе складывается изъ постоянной величины напряженія отъ катода
до начала положительной свѣтовой колонны (400 вольтъ) и напря-
женія самой свѣтовой колонны. Сила поля въ свѣтовой колоннѣ въ
этой области почти постоянна. Такъ какъ приростъ напряженія въ
атмосферномъ воздухѣ на каждый миллиметръ разстоянія между
электродами равенъ, какъ это видно по кривой рис. 129 а, прибли-
зительно 7,5р вольтъ, то сила поля въ свѣтовой колоннѣ, при раз-
__ вольтъ .
рядномъ напряженіи, равняется 75 р —; слѣдовательно, при да-
вленіи въ 1 мм. она равняется 75 вольт^_г Интересно отмѣтить, что
г сантим. г
эта величина гораздо больше силы поля при стаціонарномъ ти- х
хомъ разрядѣ (§ 166).
При большихъ значеніяхъ рі кривая искрового напряженія до-
вольно сильно загибается внизъ. Слѣдовательно, при большихъ дл^ахъ
искръ сила поля въ положительной свѣтовой колоннѣ у анодааиеньше,
нежели 75 р. По измѣреніямъ Пашена, на основаніи которыхъ по-
строена кривая рис. 129 а, при 760 мм. давленія и при длинѣ искры
въ 3 — 4 мм., искровое напряженіе убываетъ лишь/^й 3100 вольтъ
(4,1.760.) на 1 мм. и сила поля положительной ^(свѣтовой колонны
х ошпл вольтъ \\^
вблизи анода равняется 31000---------, тогда^какъ 75р даетъ зна-
г • сантим. ^41
ченіе 57000.
Задержка разряда
327
Все изложенное справедливо лишь въ томъ случаѣ, если элек-
троды настолько незначительно искривлены, что поле передъ разря-
домъ можно считать однороднымъ. Сильно искривленные электроды,
при которыхъ поле передъ разрядомъ оказывается неоднороднымъ,
даютъ меньшія искровыя напряженія.
ЗАДЕРЖКА РАЗРЯДА.
196. Прежде, чѣмъ получится разрядъ, въ искровомъ проме-
жуткѣ долженъ произойти цѣлый рядъ явленій, о которыхъ уже
была рѣчь въ § 166. Прежде всего изъ ничтожнаго числа іоновъ
ПаѣГі
Рис. 130. Задержка разряда.
столкновеній образоваться большое ихъ число, а
должно вслѣдствіе
затѣмъ должны образоваться характерные для тихаго разряда двой-
ные слои. Насколько быстро происходитъ весь процессъ разряда въ
обычной искрѣ при маломъ сопротивленіи, какъ только установился^,
„тихій разрядъ съ максимальнымъ напряженіемъ на электродахъ^^
настолько же медленно могутъ протекать подготовляющія разрядт^явле-
нія.Варбургъ производилъ относящіяся къ этому вопросу изслѣдованія
и нашелъ, что промежутокъ времени, предшествующій разряду— „за-
держку разряда“—можно значительно сократить, еслд искусственно
увеличить начальное содержаніе іоновъ помощью ^лабо іонизирую-
328
Задержка разряда
щаго агента — ультрафіолетовыхъ лучей или лучей радія. Этого
можно было ожидать и на основаніи теоріи разряда. Фактъ этотъ
легко можно демонстрировать на простомъ опытѣ. Соединимъ обѣ
обкладки лейденской банки, какъ обычно, съ индукціонной машиной
и съ небольшимъ искромѣромъ, помѣщеннымъ въ пространство, на-
полненное хорошо высушеннымъ воздухомъ (рис. 130). Для опре-
дѣленія напряженія лейденской банки включимъ въ цѣпь еще элек-
трометръ, приспособленный для измѣренія высокихъ напряженій. Осо-
баго устройства прерыватель позволяетъ соединить искромѣръ съ
лейденской банкой на весьма короткій промежутокъ времени. Замы-
каніе въ этомъ прерывателѣ производится при помощи вращающагося
рычага изъ изолирующаго вещества, имѣющаго на концѣ латунный
шаръ. Сначала рычагъ удерживается неподвижно помощью арретира.
Если его освободить, то онъ быстро поворачивается подъ дѣйствіемъ
сильной пружины, при чемъ латунный шаръ одновременно касается
двухъ другъ отъ друга изолированныхъ латунныхъ проволокъ, обра-
зуя на мгновеніе металлическое соединеніе между ними. Изъ этихъ
латунныхъ проволокъ одна соединяется съ одною изъ обкладокъ
лейденской банки, а другая съ однимъ изъ электродовъ искромѣра.
Другой электродъ послѣдняго постоянно соединенъ съ другой об-
кладкой банки. Такимъ образомъ, латунный шаръ, касаясь проволокъ,
на короткое мгновеніе заряжаетъ электроды искромѣра до напряже-
нія лейденской банки. Сначала находимъ искровое напряженіе, уста-
навливая рычагъ въ положеніи, замыкающемъ токъ черезъ искромѣръ,
на продолжительное время, и замѣчая напряженіе, указываемое элек-
трометромъ въ моментъ разряда. Послѣ этого арретируемъ рычагъ,
снова заряжаемъ лейденскую банку до найденнаго только что напря-
женія или еще выше и спускаемъ рычагъ. Разряда при этомъ не проис-
ходитъ, такъ какъ короткаго промежутка времени замыканія оказы-
вается недостаточно для окончанія предшествующихъ разряду явле-
ній. Если повторить опытъ совершенно такимъ же образомъ, но п^^
вергнуть при этомъ искровой промежутокъ дѣйствію лучей препарата
радія, то искра появляется. Слѣдовательно, іонизація лучамиѴфадія
сокращаетъ продолжительность подготовляющихъ разрядъ^рЪЦессовъ.
Задержка разряда является источникомъ значител^ійхъ погрѣш*
ностей при измѣреніи искровыхъ напряженій. Если^дая этихъ измѣ-
реній примѣнять безъ всякихъ измѣненій методъ, описанный въ § 195,
то почти всегда получается слишкомъ больща^^еличина, такъ какъ
Искры въ жидкостяхъ и въ твердыхъ тѣлахъ
329
искра проскакиваетъ лишь черезъ нѣкоторое время послѣ достиженія
искрового напряженія, когда, слѣдовательно, напряженіе еще нѣсколько
повысилось. Если же іонизировать газъ между электродами, то полу-
чаются вѣрныя болѣе низкія величины. Прежде думали, что искус-
ственной іонизаціей искровое напряженіе дѣйствительно понижается.
Но Варбургъ съ достовѣрностью показалъ, что слабая іонизація
на самое искровое напряженіе совершенно не вліяетъ и только пара-
лизуетъ задержку. Отсюда слѣдуетъ практическое заключеніе, что
для быстраго полученія вѣрныхъ значеній искровыхъ напряженій
всегда слѣдуетъ прибѣгать къ помощи іонизирующаго агента, лучше
всего — лучей радія.
ИСКРЫ ВЪ ЖИДКОСТЯХЪ И ВЪ ТВЕРДЫХЪ ТѢЛАХЪ.
197. Электрическая свѣтовая дуга можетъ горѣть не только въ
газахъ, но и въ жидкостяхъ. Если погрузить въ воду два угольные
электрода, соединенные съ подходящимъ источникомъ электричества,
и привести ихъ въ соприкосновеніе, то можно между ними зажечь
свѣтовую дугу такъ же, какъ и въ воздухѣ. Конечно, въ этомъ слу-
чаѣ дуга горитъ въ водяныхъ парахъ. Только охлажденіе въ жид-
кости всегда больше, нежели въ газѣ, и потому напряженіе, необхо-
димое для какой-нибудь опредѣленной силы тока, въ этомъ случаѣ
тоже нѣсколько больше.
Точно такъ же во всякой жидкости можно получать и искры.
Если помѣстить весьма короткій искровой промежутокъ, соединен-
ный съ лейденской банкой, въ стеклянный сосудъ, наполненный во-
дою, и зарядить лейденскую банку при помощи индукціонной ма-
шины, то при нѣкоторомъ напряженіи, значительно превышающемъ
соотвѣтствующее искровое напряженіе въ воздухѣ, проскакиваетъ
блестящая искра. Если стѣнки сосуда не очень толсты, то онъ раз-
бивается въ дребезги подъ дѣйствіемъ взрывной волны, образу-
ющейся при разрядѣ. Возможность искрового разряда въ жидко-
стяхъ обусловливается тѣмъ, что во всѣхъ жидкостяхъ, не исключая^
и изолирующихъ, постоянно имѣются іоны. Вѣроятно, при высокихъ
напряженіяхъ подъ вліяніемъ столкновеній іоновъ число ихъ^увели-
чивается, и подъ вліяніемъ сильнаго тока температура ^^ъішается
настолько, что на пути разряда развивается паръ, и электроды раска-
ляются; при этихъ условіяхъ становится возможнымъ^ правильный
330
Скользящія искры
искровой разрядъ. Внезапное образованіе пара и высокая темпера-
тура, получающаяся моментально, вызываютъ образованіе интенсив-
ной волны давленія, которая, ударяя о стекло, разрушаетъ его. Нѣчто
подобное можно наблюдать, когда молнія ударяетъ въ ель. Разрядъ
проходитъ черезъ содержащіе жидкость пучки сосудовъ между корой
и деревомъ, и, подъ вліяніемъ подобнаго взрыву дѣйствія, кора раз-
летается во всѣ стороны на разстоянія въ нѣсколько метровъ, такъ
что дерево остается обнаженнымъ.
И въ твердыхъ тѣлахъ можетъ, какъ въ газахъ и жидкостяхъ,
образовываться искра. Помѣстимъ по одну сторону тонкой стеклян-
ной пластинки, по возможности посрединѣ ея, маленькую металличе-
скую пластинку и съ противоположной стороны поднесемъ къ стеклу
металлическое остріе; затѣмъ соединимъ эти электроды, которые
должны быть хорошо изолированы, съ лейденской банкой. Если за-
рядить послѣднюю при помощи индукціонной машины до очень вы-
сокаго напряженія, то черезъ стекло проскакиваетъ искра. При этомъ
она образуетъ въ стеклѣ весьма узкій каналъ, словно сдѣланный
тончайшимъ сверломъ; содержимое этого канала вполнѣ улетучива-
ется подъ вліяніемъ высокой температуры. Для этого опыта необ-
ходимы очень большія напряженія; притомъ, если стеклянная пла-
стинка не очень велика, то разрядъ предпочитаетъ пройти болѣе
длинный путь въ воздухѣ вокругъ краевъ пластинки и не проби-
ваетъ стекла.
СКОЛЬЗЯЩІЯ ИСКРЫ.
198. Очень длинныя искры, которыми удобно пользоваться при
демонстраціяхъ, получаются, если нанести на стеклянную пластинку
слой клея и на него насыпать металлическія опилки. Если такую
пластинку помѣстить между двумя удаленными другъ отъ друга ме-
таллическими шарами, соединенными съ заряженной лейденской бан-
кой, то вдоль покрытой металлическими опилками стеклянной щта-
7^7
стинки проходитъ блестящая искра отъ одного электрода къ Дру-
гому. Металлическія частички служатъ „промежуточными «гэлектро-
77,И
дами“, и, въ силу ихъ присутствія, длина проходимЯго^искрой газо-
ваго слоя уменьшается, такъ что искра проскакиваетъ при болѣе
низкомъ напряженіи, нежели въ свободномъ воз^ух^
Даже присутствіе чистой стеклянной поверхности уже понижа-
етъ разрядное напряженіе. Если зарядить искромѣръ до напряженія,
Скользящія искры
331
немного меньшаго, чѣмъ его искровое напряженіе въ воздухѣ, и
поднести къ его шарикамъ стеклянную полоску, то по стеклянной
поверхности проходитъ почти прямолинейная искра. Такую искру
называютъ скользящей искрой. Ея появленіе можно объяснить
тѣмъ, что слой влаги на стеклянной поверхности дѣйствуетъ, по-
добно металлическимъ опилкамъ въ вышеописанномъ опытѣ.
ГЛАВА ДЕСЯТАЯ
РАДІОАКТИВНОСТЬ
ИЗЛУЧЕНІЯ РАДІОАКТИВНЫХЪ ТѢЛЪ.
199. Въ недавнее время было открыто нѣсколько химическихъ
элементовъ, самопроизвольно испускающихъ особые лучи, подобные
тѣмъ, которые образуются при тихомъ разрядѣ. Раньше всего эти
лучи были открыты Беккерелемъ (Н. Весдиегеі) у элемента урана.
Элементы, обладающіе подобными свойствами, называются радіоак-
тивными элементами. Важнѣйшими изъ нихъ являются уранъ,
торій и открытый г-жею Кюри (Сигіе), благодаря его сильной ак-
тивности, радій; далѣе идутъ два менѣе хорошо изученные эле-
мента, а именно,^полоній и актиній и газообразный элементъ, называ-
емый эманаціей. Наконецъ, существуетъ еще рядъ тѣлъ, которыя
встрѣчаются лишь въ видѣ слѣдовъ, но тѣмъ не менѣе обладаютъ,
какъ мы увидимъ ниже, вполнѣ опредѣленными радіоактивными свой-
ствами, позволяющими отличать ихъ другъ отъ друга и отъ дру-
гихъ элементовъ.
Радіоактивныя тѣла высылаютъ четыре совершенно различные
рода лучей, которые получили названія а-лучей, 0-лучей, у-лучей и
б-лучей.
а-лучи характеризуются слѣдующими свойствами: они сильно
поглощаются воздухомъ и вызываютъ при этомъ сильную іонизацію
его; твердыя тѣла пропускаютъ ихъ, лишь будучи взяты въ тончай-
шихъ слояхъ; на фотографическую пластинку они дѣйствуютъ срав-
нительно слабо; электрическія и магнитныя ихъ свойства таковы же/
какъ у весьма быстрыхъ закатодныхъ лучей. Отсюда можно заклю-
чить, что а-лучи состоятъ изъ потока быстро движущихся „положи-
тельно заряженныхъ частичекъ. Точныя измѣренія попали, что
всѣ эти частички обладаютъ одинаковымъ эквивалентнымъ вѣсомъ
2,0 (Н = 1) и что ихъ скорость лежитъ въ предѣлахъ^между 1 . ІО9
и 2 . ІО9 (отъ до скорости свѣта). Закатодные лучи могли
Излученія радіоактивныхъ тѣлъ
333;
бы пріобрѣсти такія скорости лишь въ поляхъ въ нѣсколько мил-
ліоновъ вольтъ.
Р-лучи болѣе пронизывающи, нежели а-лучи, и потому легко-
могуть быть отъ нихъ отдѣлены. Продажные препараты радія обык-
новенно бываютъ заключены въ плоскія свинцовыя коробочки, на-
крытыя слюдянымъ листкомъ. Черезъ этотъ листокъ а-лучи совер-
шенно не проникаютъ, тогда какъ р-лучи поглощаются имъ лишь незна-
чительно. Іонизирующее дѣйствіе р-лучей можетъ быть обнаружено при
помощи заряженнаго электроскопа даже на разстояніи 30 см. Такъ,
какъ р-лучи менѣе поглощаются воздухомъ и прочими газами, нежели
а-лучи, то и ихъ іонизирующее дѣйствіе гораздо слабѣе; для не-
покрытаго препарата и вблизи отъ него оно можетъ считаться со-
вершенно исчезающимъ, по сравненію съ іонизирующимъ дѣйствіемъ
а-лучей. На фотографическую пластинку Р-лучи дѣйствуютъ весьма
сильно, давая такія же изображенія, какъ весьма мягкіе, слабо про-
низывающіе Рентгеновскіе лучи. Подобно Рентгеновскимъ лучамъ, р-лучи
также вызываютъ флуоресценцію баріевосинеродистаго экрана. Маг-
нитныя и электрическія свойства Р-лучей тождественны съ такими же
свойствами катодныхъ лучей весьма большой скорости, лежащей между
1,5.1010 и 2,9. 1010—(отъ 0,5 до
сек. ѵ
0,97 скорости свѣта). Благодаря такимъ
громаднымъ скоростямъ, изученіе р-лучей
имѣетъ огромное значеніе для теоріи
матеріи; объ этомъ мы еще будемъ го-
ворить въ послѣдней главѣ этой книги.
Т-лучи обладаютъ наибольшей про-
низывающей способностью среди всѣхъ
вообще извѣстныхъ лучей; они прохо-
дятъ даже черезъ желѣзныя и свинцовыя
Рис. 131. Отклоненіе лучей
радіоактивнаго вещества подъ *
дѣйствіемъ магнитнаго поля\^‘
пластинки въ нѣсколько сантиметровъ
толщиною. Обнаруживаются они легче
всего по ихъ флуоресценціоннымъ дѣй-
ствіямъ. Ихъ іонизирующее и фотографическое дѣйствія, вт^ййду
ихъ весьма малой поглощаемости, слабы. Въ магнитномъ и Центри-
ческомъ поляхъ они не отклоняются. Несомнѣнно, что ^^уйи пред-
ставляютъ собою родъ Рентгеновскихъ лучей такой жесткости, ко-
1 • С>ѵ
торая не можетъ быть достигнута искусственно помощью Рентге-
334
Излученія радіоактивныхъ тѣлъ
новскихъ лампъ. Возможно, что у-лучи возбуждаются [3-лучами, по-
добно тому, какъ Рентгеновскіе лучи возбуждаются катодными; во
всякомъ случаѣ, р-лучи и у-лучи всегда встрѣчаются совмѣстно.
б-лучи представляютъ собою мягкіе катодные лучи, которые
сильно поглощаются и которые поэтому обыкновенно приходится
наблюдать вмѣстѣ съ а-лучами. Чтобы получить чистые а-лучи, по-
мѣщаютъ радіоактивный препаратъ между полюсами подковообраз-
наго магнита, д-лучи тогда настолько сильно отклоняются, что,
описавъ краткій путь, возвращаются къ препарату; а-лучи, подобно
закатоднымъ лучамъ, отклоняются отъ прямолинейнаго пути лишь
немного. Вѣроятно, д-лучи являются вторичными лучами, возбужда-
емыми а-лучами при ихъ поглощеніи въ пронизываемыхъ ими мате-
ріальныхъ слояхъ.
На рис. 131 представлены схематически всѣ роды лучей радіо-
активнаго тѣла. Чтобы понять этотъ рисунокъ, нужно вообразить
себѣ магнитное поле, силовыя линіи котораго расположены перпен-
дикулярно къ плоскости рисунка.
Очень сильные радіоактивные препараты, каковы соединенія ра-
дія и полонія, кажутся непрерывно свѣтящимися. Въ дѣйствитель-
ности, свѣтъ высылается непосредственно окружающими препаратъ
слоями воздуха. Спектральный анализъ указываетъ, что этотъ свѣтъ
испускается азотомъ, іонизируемымъ а-лучами (ср. § 136).
СЧЕТЪ а-ЧАСТИЧЕКЪ.
200. Падая на экранъ, покрытый порошкомъ сѣрнистаго цинка,
а-лучи вызываютъ его свѣченіе. Разсматривая свѣтящееся мѣсто эк-
рана при помощи лупы или слабаго микроскопа, можно убѣдиться
въ томъ, что оно состоитъ изъ отдѣльныхъ свѣтящихся точекъ, вспы-
хивающихъ и вновь исчезающихъ. Очевидно, каждая а-частичка, попа-
дая на экранъ, вызываетъ кратковременную вспышку, и такимъ образомъ
можно наблюдать на экранѣ изъ сѣрнистаго цинка дождь а-часті^дъ.
Этимъ явленіемъ Регенеръ (Е. Ре^епег) воспользовался^ Лля
того, чтобы подъ микроскопомъ сосчитать число а-частицъДдыбра-
сываемыхъ радіоактивнымъ препаратомъ. Для небольшого^ррепарата
полонія онъ нашелъ, что это число равно приблизительнаГ800 части-
цамъ въ секунду. При этомъ онъ принялъ (это подтверждено опыт-
нымъ путемъ), что плотность лучей во всѣхъ направленіяхъ одина-
кова и такова же, какъ и въ направленіи къ^фф мѣсту экрана, гдѣ
Счетъ а-частичекъ
335
наблюдалось вспыхиваніе. Кромѣ того, оказалось возможнымъ опре-
дѣлить, какъ и для закатодныхъ лучей, общій зарядъ, переносимый
всѣми а-частицами препарата. Для препарата Регенера этотъ за-
рядъ равнялся приблизительно 0,5 . ІО-15 кулона въ секунду. Отсюда
зарядъ одной а-частицы получается равнымъ 0,5.10~15: 1800 т. е.
приблизительно 2,8. ІО-19 кулона.
Весьма тщательныя и точныя опредѣленія числа а-частицъ
были произведены Рётгерфордомъ и Гейгеромъ (Н. Оеі^ег).
Помимо свѣтящагося экрана они пользовались для счета вылетаю-
щихъ а-частицъ еще инымъ методомъ. Имъ удалось помощью весьма
остроумнаго прибора сдѣлать замѣтной каждую отдѣльную а-частич-
ку по ея іонизирующему дѣйствію. Оба метода дали вполнѣ совпа-
дающіе результаты; именно, оказалось, что граммъ радія выдѣляетъ
за секунду 13,5.1010 а-частицъ. Тщательными измѣреніями тѣ же
авторы установили также величину положительнаго заряда, несомаго
всѣми этими частицами; она оказалась равной 42. ІО-9 кулона. От-
сюда зарядъ отдѣльной а-частички оказывается равнымъ
3,11 . ІО-19 кулона = 2.1,55.10~19 = 2е,
гдѣ е — элементарное количество электричества (ср. § 106; тамъ мы
нашли для е величину 1,56.10~19 кулона). Измѣренія Рётгерфорда
и Гейгера являются съ одной стороны точнѣйшими прямыми измѣ-
реніями элементарнаго количества электричества, во всякомъ случаѣ,
болѣе надежными и точными, нежели описанныя въ § 133 измѣренія
Томсона, а съ другой стороны они позволяютъ съ увѣренностью
заключить, что а-частица заряжена двумя элементарными
количествами электричества.
Изъ предыдущаго слѣдуетъ, что атомный вѣсъ а-частицы равенъ
4,0. Это, какъ разъ, атомный вѣсъ гелія. Какъ мы увидимъ ниже,
радіоктивныя вещества, дѣйствительно, непрерывно образуютъ гелій.
Поэтому съ большою степенью вѣроятности можно высказать слѣ-
дующее положеніе:
а-частицы представляютъ собою атомы гелія, нагру-
женные двумя положительными одновалентными зарядами?
РАДІОАКТИВНЫЯ ПРЕВРАЩЕНІЯ.
201. Не подлежитъ никакому сомнѣнію, что отк^фй г-жею
Кюри радій представляетъ собою совершенно опредѣленны^ химическій
элементъ. Онъ образуетъ кристаллизирующіяся химическія соединенія,
336
Радіоактивныя превращенія
подобныя соединеніямъ щелочноземельныхъ металловъ (въ особенности,
барія), обладаетъ характернымъ спектромъ, который измѣренъ и ока-
зался также сходнымъ со спектрами щелочноземельныхъ металловъ;
его атомный вѣсъ весьма высокъ и достигаетъ 226.
Для радія, какъ и для всѣхъ прочихъ радіоактивныхъ веществъ,,
имѣетъ силу законъ, установленный еще Беккерелемъ для соеди-
неній урана: радіоактивность элемента не зависитъ отъ того, въ ка-
комъ химическомъ соединеніи онъ находится. Опредѣленному коли-
честву радія всегда соотвѣтствуетъ одна и та же интенсивность ра-
діоактивныхъ явленій. Поэтому несомнѣнно, что радіоактивныя
явленія обязаны своимъ происхожденіемъ процессамъ, со-
вершающимся въ самыхъ атомахъ.
Если препаратъ радія, который въ теченіе нѣсколькихъ недѣль
былъ предоставленъ самому себѣ, нагрѣть въ замкнутомъ эвакуиро-
ванномъ пространствѣ, то изъ него выдѣляется газъ. Этотъ газъ
представляетъ собою смѣсь гелія и особаго радіоактивнаго газа, ко-
торый называютъ „эманаціей" или точнѣе „эманаціей радія". Эма-
нація представляетъ собою настоящій газъ; для нея имѣетъ силу за-
конъ Маріотта-Гэй-Люссака; она диффундируетъ въ иные газы
и проходитъ черезъ пористую перегородку съ опредѣленной ско-
ростью; она имѣетъ точно опредѣленную точку конденсаціи (— 150°)
и можетъ быть отдѣлена отъ иныхъ газовъ при помощи ожиженія.
Чистота эманаціи можетъ быть изслѣдуема спектрально-аналитиче-
скимъ путемъ, такъ какъ она имѣетъ характерный спектръ,
отличающій ее отъ всѣхъ прочихъ химическихъ элементовъ. Нѣтъ
никакого сомнѣнія въ томъ, что эманація представляетъ собою
новый газообразный радіоактивный элементъ. Эманація не поддается
вліянію никакихъ химическихъ агентовъ и, вѣроятно, принадлежитъ
къ числу химически инертныхъ элементовъ, какъ гелій, аргонъ и т. п.
Однако, до сихъ .поръ не удалось еще опредѣлить ея атомный вѣсъ,,
такъ какъ не удалось получить такихъ ея количествъ, которыя
но было бы взвѣсить достаточно точно для того, чтобы приложить,
затѣмъ законъ Авогадро1). (Л
Э П. Кюри, Ретгерфордъ и рядъ другихъ у^йыхъ опредѣляли
косвенными путями атомный вѣсъ эманаціи радія и получили величины въ
предѣлахъ отъ 70 до 235. Въ самое послѣднее врем^ірамзай и Грей(Сгау)
помощью микровѣсовъ, построенныхъ Стилемъ $&ей) и Грантомъ (Огапі),
Радіоактивныя превращенія
337
Согласно опытамъ Рамзая (Катзау) и Содди (8ос!с!у) оказа-
лось, что количество эманаціи, окклюдированной солью радія, кото-
рое можно добыть, напримѣръ, прокаливаніемъ, есть величина по-
рядка 1 куб. мм. на каждый граммъ радія при комнатной темпера-
турѣ и атмосферномъ давленіи. Рётгерфордъ рядомъ точнѣйшихъ
опытовъ, при которыхъ были учтены всѣ возможныя погрѣшности,
нашелъ число 0,58 куб. мм. на граммъ радія. Это число, во вся-
комъ случаѣ, весьма близко къ истинному. Измѣренія этого рода
весьма затруднительны, такъ какъ изслѣдователи имѣютъ обыкно-
венно въ своемъ распоряженіи весьма малыя количества радія.
Если, послѣ удаленія изъ радіевой соли всего содержавшагося
въ ней газа посредствомъ нагрѣванія въ пустотѣ, снова предоста-
вить ее самой себѣ на нѣсколько недѣль, то опытъ можно повто-
рить вновь. При этомъ по интенсивности радіоактивныхъ явленій
легко убѣдиться въ томъ, что количество освобождающейся эма-
націи получается опять то же самое, что и въ первый разъ. И снова
вмѣстѣ съ эманаціей выдѣляется и гелій.
На основаніи приведенныхъ данныхъ, можно считать прочно
установленнымъ фактъ образованія изъ атомовъ радія новыхъ ато-
мовъ эманаціи и гелія. Подобное превращеніе химическихъ элемен-
товъ можно констатировать при всѣхъ радіоактивныхъ процессахъ.
Поэтому мы можемъ высказать слѣдующее общее положеніе:
Лучеиспусканіе радіоактивныхъ тѣлъ связано съ ко-
ренными измѣненіями самыхъ атомовъ; эти измѣненія
состоятъ въ томъ, что часть атомовъ (которые прежде счи-
тались недѣлимыми) распадается, и при этомъ получаются
новые химическіе элементы.
Это положеніе было высказано Рётгерфордомъ, который изслѣ-
довалъ радіоактивныя превращенія въ большомъ числѣ случаевъ,
пользуясь придуманными имъ остроумными методами.
202. Какъ указано выше, образующаяся изъ радія эманація
представляетъ собою радіоактивный газъ. Она развиваетъ интенсив-^^
ные а-лучи, которые іонизируютъ самый газъ (а также смѣшащее’
опредѣлили атомный вѣсъ эманаціи радія непосредственнымъ взвѣнуш|иісмъ;
онъ оказался равнымъ 223. Такъ какъ всѣ свойства этого газа ^хорошо из-
вѣстны, то Рамзай и Грей предложили для него особыя назв;а(ф§ и обозна-
ченіе: „нитонъ" — Ыі. пеР-
Ми. Электричество и магнитизмъ. Л
338
Радіоактивныя превращенія
съ эманаціей газы) настолько сильно, что сопровождающее іониза-
цію свѣченіе можно видѣть простымъ глазомъ. Такимъ образомъ,
эманація является, до нѣкоторой степени, фосфоресцирующимъ га-
зомъ, который, однако, испускаетъ свѣтъ самопроизвольно, не нужда-
ясь для этого въ предварительномъ освѣщеніи.
Если изслѣдовать радіоактивность эманаціи въ теченіе нѣсколь-
кихъ дней подрядъ, то оказывается, что она постепенно замѣтно
уменьшается. Отсюда можно заключить, что радіоактивному распаду
подвергается настолько значительная часть атомовъ эманаціи, что
убыль количества эманаціи становится замѣтной уже черезъ нѣсколько
дней. Дѣлая это заключеніе, мы опираемся на слѣдующее общее
положеніе, которое подтверждено во многихъ случаяхъ непосред-
ственно опытнымъ путемъ и выводы изъ котораго также всегда
оказывались правильными:
Эффектъ, производимый радіоактивными процессами,
совершающимися въ опредѣленномъ радіоактивномъ ве-
ществѣ, строго пропорціоналенъ количеству заключаю-
щихся въ немъ атомовъ соотвѣтствующаго радіоактивнаго
элемента.
Поэтому мы можемъ принять общій эффектъ, производимый
излученіемъ эманаціи, за мѣру количества эманаціи. Самый эффектъ
проще всего измѣряется іонизирующимъ дѣйствіемъ испускаемыхъ
эманаціей а-лучей, такъ какъ это дѣйствіе пропорціонально упо-
требленной на него энергіи. Если такимъ путемъ слѣдить за само-
произвольнымъ уменьшеніемъ количества эманаціи, то получается
нижеслѣдующій простой законъ Рётгерфорда, который, какъ по-
казалъ этотъ ученый, примѣнимъ ко всѣмъ сильно-радіоактивнымъ
тѣламъ: самопроизвольная убыль количества радіоактивнаго
вещества протекаетъ всегда такъ, что за одинаковые про-
межутки времени исчезаетъ одинаковая часть имѣющагося
въ наличности количества вещества.
Математически этотъ законъ выражается въ слѣдующем^ѣидѣ:
- 7Ѵ=7Ѵ0.е-х/,
гдѣ Д^о и 7Ѵ— количества вещества въ моменты вре^ёни 0 и і,
X — характерная для даннаго радіоактивнаго вещёс^д^Ѣонстанта, е—
извѣстное число — основаніе натуральныхъ логариѳмовъ, равное
7 1 О /X
Радіоактивныя превращенія
339
Быстро распадающіяся радіоактивныя вещества всегда вполнѣ ха-
рактеризуются присущимъ имъ значеніемъ „коэффиціента распада" X,
такъ что ихъ можно отличать другъ отъ друга и въ тѣхъ слу-
чаяхъ, когда они имѣются въ самыхъ ничтожныхъ количествахъ.
Такимъ образомъ, радіоактивность является вѣрнѣйшей и наиболѣе
чувствительной реакціей по сравненію со всѣми химическими дѣй-
ствіями. Обычно приводится не самая величина X, но связанная съ
ней величина
~ _ 1о§ паі 2 _ 0,693
7 X ~ ~Г" ’
дающая промежутокъ времени, за который количество радіоактивнаго
вещества уменьшается вдвое. Этотъ промежутокъ времени Т носитъ
названіе періода распада (НаІЬіешп&зрегіосІе) соотвѣтствующаго
вещества; для эманаціи радія онъ равенъ 3,8 днямъ. Этимъ эма-
нація радія рѣзко отличается отъ двухъ другихъ радіоактивныхъ
газовъ, образующихся изъ торія и актинія х) и имѣющихъ чрезвы-
чайно короткіе періоды распада.
Законъ Рётгерфорда можно разсматривать, какъ слѣдствіе
высказаннаго выше общаго принципа радіоактивныхъ дѣйствій. Если
дѣйствія, сопровождающія распадъ, пропорціональны имѣющимся въ
наличности количествамъ вещества, то такая же пропорціональность
должна имѣть мѣсто и для самаго распада, т. е. за одинаковые про-
межутки времени должны распадаться одинаковыя части имѣющагося
въ наличности количества вещества.
Исчезновеніе эманаціи наблюдали непосредственно Рамзай и
Содди и позже Рётгерфордъ. Для этого они нѣсколько дней
подъ рядъ изслѣдовали порцію газа, выдѣлившуюся изъ большого
количества бромистаго радія. По спектру можно было видѣть, что
за нѣсколько дней эманація совершенно исчезла; вмѣсто нея обра-
зовалось значительное количество гелія.
Спрашивается, во что же превращается эманація, когда она исче-
заетъ? Изъ вышеописанныхъ опытовъ Рамзая и Содди можно
было бы заключить, что она превращается въ гелій. Однако, гелійф^
при этомъ является, такъ сказать, побочнымъ продуктомъ, выдѣляю-
щимся при радіоактивныхъ процессахъ въ формѣ а-лучей. Тайная
9 Эти газы носятъ названія соотвѣтственно эманаціи торной эманаціи
актинія. Прим. пер.
22
340
Радіоактивныя превращенія
масса эманаціи послѣ превращенія имѣетъ видъ твердаго тѣла, оса-
ждающагося на стѣнкахъ сосуда и на всѣхъ тѣлахъ, съ которыми
находилась въ соприкосновеніи эманація. Этотъ осадокъ весьма
сильно радіоактивенъ и, какъ показали новѣйшія изслѣдованія, со-
стоитъ изъ трехъ тѣлъ, различныхъ въ химическомъ и физическомъ
отношеніяхъ. Всѣ они имѣютъ чрезвычайно короткіе періоды суще-
ствованія, въ силу чего не могли быть изслѣдованы достаточно точно.
Эти три вещества, называемыя радіемъ Л, радіемъ В и радіемъ С,
превращаются одно въ другое въ порядкѣ А, В, С, Ихъ періоды рас-
пада равняются соотвѣтственно 3 минутамъ, 26 минутамъ и 19 ми-
нутамъ. Изъ радія С образуется весьма прочное вещество — радій 23,
который, однако, до сихъ поръ плохо изученъ; изъ него получа-
ются послѣдовательно быстро распадающійся радій Е и радій Е
или полоній, который былъ открытъ г-жею Кюри вмѣстѣ съ ра-
діемъ. Уже вскорѣ послѣ этого открытія г-жа Кюри замѣтила,
что полоній существенно отличается отъ радія тѣмъ, что онъ не
даетъ вполнѣ постояннаго излученія, но излученіе его замѣтнымъ
образомъ падаетъ въ теченіе не очень большого промежутка вре-
мени. Точныя изслѣдованія надъ тщательно химически очищен-
нымъ полоніемъ, дѣйствительно, показали, что періодъ распада по-
лонія равняется 143 днямъ, такъ что замѣтное уменьшеніе его
радіоактивности получается уже въ теченіе нѣсколькихъ недѣль.
203. Періодъ распада радія, несомнѣнно, чрезвычайно великъ.
Его можно оцѣнить на основаніи сдѣланныхъ Рётгерфордомъ
измѣреній количества эманаціи, которое оказывается окклюдирован-
нымъ въ твердомъ препаратѣ радія, если предварительно дать ему
постоять въ теченіе нѣсколькихъ недѣль. Такъ какъ твердая соль
радія при обыкновенной температурѣ совершенно не выдѣляетъ эма-
націи во внѣшнее пространство, то отношеніе между обоими веще-
ствами можетъ оставаться постояннымъ лишь въ томъ случаѣ, если
эманація теряетъ при распадѣ ровно столько же атомовъ, сколько
ихъ образуется вновь изъ радія. Такое равновѣсіе устанавливается,
какъ показываютъ опыты, по истеченіи нѣсколькихъ н^ѣ>іь. Но
скорость распада, т. е. количество распадающагося въМекунду ве-
щества, согласно закону Рётгерфорда, зависитъ двухъ вели-
чинъ. Во-первыхъ, она тѣмъ больше, чѣмъ большіе у имѣющееся въ
наличности количество 2Ѵ распадающагося цеірества; во-вторыхъ,
она тѣмъ больше, чѣмъ меньше періодъ распада Т. Точнѣе говоря,
Радіоактивныя превращенія
341
она пропорціональна величинѣ М и обратно пропорціональна вели-
чинѣ Т. Если мы примемъ, что изъ одного распавшагося атома
радія всегда образуется одинъ атомъ эманаціи, то условіе равно-
вѣсія можно будетъ выразить въ такой формѣ: число распадающихся
въ секунду атомовъ радія равно числу распадающихся въ секунду
атомовъ эманаціи. Математически условіе равновѣсія выражается
.пропорціей:
Л “ Л ’
гдѣ Ту и Т2 — періоды распада радія и эманаціи, —выраженное
въ граммъ-атомахъ количество заключающагося въ соли радія, —
количество окклюдированной солью эманаціи, тоже выраженное въ
граммъ-атомахъ. 1 граммъ-атомъ радія равняется 226 граммамъ; на это
количество приходится, по Рётгерфорду, 226.0,58 — 130 куб. мм.
эманаціи при комнатной температурѣ и атмосферномъ давленіи. По
законамъ газоваго состоянія, 1 граммъ-молекула газа занимаетъ при
указанныхъ условіяхъ объемъ, равный 23 600 куб. см.; слѣдовательно,
количество окклюдированной эманаціи равняется 0,55.10-6 граммъ-
молекулы. Если мы сдѣлаемъ еще предположеніе, что эманація, въ
качествѣ инертнаго газа, подобно гелію, аргону и т. п., одноатомна,
то это количество будетъ равняться 0,55 . ІО-5 граммъ-атома. Со-
гласно условію равновѣсія,
1 0,55.10 5
откуда Ту = 1,8 . ІО5. Т2. Итакъ, періодъ распада радія въ сто
восемьдесятъ тысячъ разъ превышаетъ періодъ распада эманаціи и ра-
венъ 690000 днямъ или, въ круглыхъ числахъ, 1900 годамъ. Это число,
конечно, указываетъ только на порядокъ искомой величины, такъ
какъ, во-первыхъ, измѣренія Рётгерфорда не вполнѣ точны, и, во-
вторыхъ, оба предположенія—что изъ одного атома радія всегда
получается одинъ атомъ эманаціи и что эманація представляетъ со-
бою одноатомный газъ, хотя и вѣроятны, но не достовѣрны. Однако,
опредѣленіе періода распада радія, произведенное Болтвудомъ^р
(Войдѵоосі) по совершенно иному прямому методу, также дало^еМ?
чину, равную 1900 годамъ; поэтому мы можемъ считать сдѣЖнныя
предположенія правильными. ѵШ'"
Періодъ распада радія близокъ къ двумъДтысячамъ
лѣтъ.
** -'• ѵ 4
342
Начало и конецъ радія
НАЧАЛО И КОНЕЦЪ РАДІЯ.
204. Хотя точная величина періода распада радія неизвѣстна,
все же можно съ полною несомнѣнностью вывести одно слѣдствіе
изъ полученнаго приблизительнаго значенія этой величины. Именно,
можно утверждать, что всѣ радіевыя руды, существовавшія при об-
разованіи земли, давно уже должны были безслѣдно исчезнуть.
Содержащійся въ землѣ радій весь образовался за по-
слѣднія тысячелѣтія вслѣдствіе радіоактивнаго распада ка-
кого-то болѣе прочнаго элемента и поэтому можетъ встрѣ-
чаться только въ смѣси со своимъ предшественникомъ.
Дѣйствительно, замѣтныя количества радія всегда обнаружива- •
ются вмѣстѣ съ нѣкоторыми вполнѣ опредѣленными веществами;
именно, уранъ является, повидимому, элементомъ, обусловливающимъ
присутствіе радія. Г-жа Кюри выдѣлила радій изъ урановой смо-
ляной обманки, и съ тѣхъ поръ во всѣхъ урановыхъ рудахъ неиз-
мѣнно обнаруживался радій. Болѣе того, тщательные анализы урано-
выхърудъ изъ различныхъ, мѣсторожденій, выполненные Болтвудомъ,
показали, что во всѣхъ рудахъ отношеніе содержащагося въ
нихъ количества радія къ количеству урана одно и то же.
Этимъ окончательно устанавливается, что радій происходитъ отъ
урана. Отношеніе между ними за многія тысячелѣтія настолько вы-
равнялось, что между ними установилось равновѣсіе, т. е. количе-
ство распадающагося радія всегда равно количеству его, вновь об-
разующемуся изъ урана. Если количества урана и радія равны
и ТѴ2 граммъ-атомамъ и періоды распада обоихъ элементовъ
суть Т1 и Т2, то, какъ мы уже знаемъ, при допущеніи, что изъ
одного распадающагося атома урана образуется всегда одинъ атомъ
радія, должно существовать соотношеніе:
М М
“ г,
ИЛИ о
т, = т'^'
Въ этомъ случаѣ сдѣланное нами предположенье является крайне
вѣроятнымъ уже потому, что атомные вѣса урана и радія равны
239,5 и 226, т. е. различаются только на ІЗ^З^вѣсъ, соотвѣтству-
ющій приблизительно тремъ выдѣлившимсяМгомамъ ' гелія. Отноше-
[ Г • -
•}' -
Начало и конецъ радія
343
ніе извѣстно изъ измѣреній Рётгерфорда и Болтвуда: на 1
граммъ урана приходится 3,8 . ІО-7 грамма радія. Пользуясь выше-
указанными величинами атомныхъ вѣсовъ обоихъ элементовъ, полу-
чаемъ отсюда:
= 2 500 000.
Періодъ распада урана въ 2,5 милліона разъ больше
періода распада радія, т. е. равенъ въ круглыхъ числахъ
5000 милліоновъ лѣтъ.
Если приведенный взглядъ на радій, какъ на продуктъ распада
урана, правиленъ, то должно быть возможно наблюдать такой распадъ
непосредственно, слѣдя въ теченіе многихъ лѣтъ за большимъ коли-
чествомъ урана, тщательно очищеннаго отъ радія.
По величинѣ періода распада можно вычислить, какое коли-
чество радія получалось бы въ теченіе года, если бы радій образовался
непосредственно изъ урана. Опыты показали, однако, что въ тща-
тельно очищенномъ уранѣ образуются лишь ничтожныя количе-
ства радія, менынія тысячной доли вычисленнаго количества. Отсюда
слѣдуетъ, что изъ урана предварительно образуется, по крайней
мѣрѣ, одно неизвѣстное вещество, достаточно устойчивое и весьма
медленно распадающееся съ образованіемъ радія. Что уранъ ведетъ
къ радію не непосредственно, знали уже давно; но раньше было
извѣстно только одно быстро распадающееся вещество, которое
удалось выдѣлить и изслѣдовать, поскольку это возможно было
сдѣлать съ ничтожно малыми его количествами, наличность кото-
рыхъ можно было установить лишь по ихъ радіоактивности. Это
вещество уранъ X съ періодомъ распада, равнымъ 22 днямъ, -какъ
кажется, образуется изъ урана непосредственно и само-по-себѣ не
можетъ замѣтно повліять на продолжительность образованія радія,
такъ какъ само оно распадается сравнительно быстро. Во всякомъ
случаѣ, изъ него предварительно образуется упомянутое выше
радіоактивное вещество съ большою продолжительностью существо-
ванія (можетъ быть получается даже рядъ промежуточныхъ веществъ),
изъ котораго уже выдѣляется радій. Болтвудъ и Рётгерфордъ
давно обнаружили въ урановыхъ рудахъ слѣды новаго радіоактЦІ?
наго элемента, изъ котораго дѣйствительно непрерывно образуется
радій въ замѣтныхъ количествахъ. Этотъ элементъ получиуіъЖазва-
ніе „іонія".
Теперь мы достаточно выяснили происхожденіе^ радія. Меньше
344
Начало и конецъ радія
свѣдѣній мы имѣемъ о томъ, во что онъ въ конечномъ результатѣ
превращается. Достовѣрно извѣстно, во всякомъ случаѣ, что при
радіоактивныхъ процессахъ образуется гелій. Этотъ элементъ встрѣ-
чается даже почти исключительно въ видѣ окклюдированнаго газа
въ урановыхъ рудахъ; поэтому вполнѣ допустимо, что сначала онъ
не находился въ числѣ веществъ, составляющихъ землю. Но нѣтъ
никакого сомнѣнія въ томъ, что гелій образуется только въ видѣ
выдѣляющихся а-частицъ и его можно, значитъ, разсматривать
только, какъ побочный продуктъ. Въ качествѣ собственно продукта
распада радія мы познакомились въ § 202 съ полоніемъ. Полоній
представляетъ собой сравнительно быстро распадающееся вещество и
потому еще недостаточно хорошо изученъ. Но можно, повидимому,
считать установленнымъ, что дальнѣйшихъ радіоактивныхъ веществъ
изъ него не получается. Изъ нерадіоактивныхъ металловъ въ урано-
выхъ рудахъ старыхъ формацій встрѣчается постоянно въ небольшихъ
количествахъ свинецъ. Отсюда возникаетъ предположеніе, что изъ по-
лонія въ конечномъ результатѣ образуется свинецъ. Съ этимъ предпо-
ложеніемъ вполнѣ согласуется то обстоятельство, что атомный вѣсъ
свинца равенъ 206,9. Дѣйствительно, такой атомный вѣсъ долженъ
быть у элемента, который получится, если отъ атома радія отнять
5 атомовъ гелія- какъ разъ столько, сколько есть промежуточныхъ
продуктовъ, выдѣляющихъ а-частицы. По этой теоріи, изъ ура-
новой руды, предоставленной самой себѣ на много билліоновъ лѣтъ,
въ заключеніе получаются лишь свинцовая руда и гелій.
ИЗЛУЧЕНІЯ, СОПРОВОЖДАЮЩІЯ ПРОЦЕССЫ РАСПАДА.
205. Не слѣдуетъ думать, что перечисленные въ § 199 роды лучей
всегда образуются всѣ вмѣстѣ. Кристаллъ соли радія выдѣляетъ, правда,
ихъ всѣ, но только потому, что въ немъ содержатся одновременно всѣ
продукты распада радія. Если же радій тщательно отъ нихъ очи-
стить, то оказывается, что онъ испускаетъ только а-лучи (и балу-
чи). Если излучающій слой имѣетъ значительную толщину^го
эти а-лучи обладаютъ весьма различными скоростями. Ес^іркё на-
нести на металлическую пластинку весьма тонкій слріЦрй'и радія,
то получаются только а-лучи вполнѣ опредѣленной ^Жѳрости. Это
различіе объясняется тѣмъ, что испускаемыя сплошной массой соли
а-частички должны пройти черезъ болѣе илиомёйѣе толстый слой
вещества, отъ чего, какъ показываютъ опы^Ойхъ скорость умень-
Излученія, сопровождающія процессы распада
345
шается, притомъ тѣмъ болѣе, чѣмъ толще пронизываемый ими слой.
Подобнымъ образомъ и всякое иное радіоактивное вещество, взятое
въ весьма тонкомъ слоѣ, высылаетъ или а-лучи опредѣленной ско-
рости, или опредѣленной скорости Р-лучи, или одновременно а-лучи
и Р-лучи; наконецъ, въ нѣкоторыхъ случаяхъ превращеніе не со-
провождается лучеиспусканіемъ. Высылаемая препаратомъ радіація,
точно такъ же, какъ періодъ распада, вполнѣ характеризуетъ этотъ
препаратъ, такъ что ею можно пользоваться вмѣсто химической ре-
акціи для распознаванія радіоактивныхъ веществъ. Принимаютъ, что
измѣненія атомнаго вѣса происходятъ лишь тогда, когда выдѣляются
а-частички. Опыты Брэгга (Вга^) и Клеемана (Кіеетапп) показали,
что вещества, распадающіяся съ выдѣленіемъ а-лучей, высылаютъ
при одинаковыхъ скоростяхъ распада одинаковыя количества а-ча-
стицъ въ единицу времени. Напримѣръ, если радій находится въ
равновѣсіи со своими быстро распадающимися продуктами (до КаС
включительно), то, какъ нашли Брэггъ и. Клееманъ, каждое изъ
четырехъ высылающихъ а-лучи веществъ высылаетъ одно и то же
количество а-частицъ. Такъ какъ общее ихъ число, какъ мы видѣли
въ §200, равняется 13,5. ІО10 на граммъ радія въ секунду, то,_
слѣдовательно, 1 гр. чистаго радія высылаетъ четвертую часть этого
количества, т. е. 3,4. ІО10 частицъ въ секунду. Весьма вѣроятно,
что каждый распадающійся атомъ всегда высылаетъ только одну
а-частичку. Это подтверждается слѣдующимъ разсчетомъ. Если ка-
ждый распадающійся атомъ выбрасываетъ одну- а-частицу, то въ од-
номъ граммъ-атомѣ въ секунду распадается 226.3,4 . ІО10 = 768.1010
атомовъ. Всего въ граммъ-атомѣ содержится 0,6175. ІО24 атомовъ
(см. § 106), значитъ, въ теченіе одной секунды распадается такая
часть радія, которая выражается дробью 1,25.10“п. Отсюда пе-
ріодъ распада получается равнымъ 1800 годамъ, что почти совер-
шенно совпадаетъ съ результатами двухъ другихъ вполнѣ незави-
симыхъ вычисленій (§ 203).
При отщепленіи а-частицы атомный вѣсъ, вѣроятно, уменьша- >
ется приблизительно на 4. Если же высылаются только Р-лучи иди5
не высылаются лучи вовсе, то получается, вѣроятно, элементъ,
атомный вѣсъ котораго лишь ничтожно отличается отъ атомнаго
вѣса исходнаго элемента (примѣрно такъ, какъ различающеймежду
собою атомные вѣса іода и теллура, кобальта и никкел^?
На рис. 132 представлена схематически послѣдовательность
346
Радіоактивныя семейства
всѣхъ продуктовъ распада урана; на немъ
указаны для каждаго вещества періодъ рас-
пада и сопровождающія каждый распадъ из-
лученія.
РАДІОАКТИВНЫЯ СЕМЕЙСТВА.
206. Разсмотрѣнныя до сихъ поръ радіо-
активныя вещества представляютъ характерный
примѣръ „радіоактивнаго семейства". Оно
характеризуется тѣмъ, чтоотъ исходнаго веще-
ства— „родоначальника" — къ продуктамъ рас-
пада—его „отпрыскамъ"—ведетъ одна един-
ственная линія. Но нельзя отрицать возмож-
ности существованія развѣтвленныхъ семействъ,
въ которыхъ исходное вещество образуетъ
одновременно нѣсколько радіоактивныхъ ве-
ществъ. Однако, опредѣленныхъ указаній на
существованіе развѣтвленій радіоактивныхъ
семействъ пока еще не имѣется.
Помимо описаннаго семейства урана из-
вѣстны еще два радіоактивныя семейства,
также развивающіяся въ одну линію — се-
мейство торія и семейство актинія. Мы
ограничимся только ихъ упоминаніемъ, такъ
какъ ихъ изученіе до сихъ поръ не дало
ничего новаго сравнительно съ данными, по-
лученными для семейства урана. Важнымъ
пунктомъ для дальнѣйшихъ изслѣдованій въ
этой области является вопросъ о томъ, не
существуетъ ли какой-либо связи между этщѵіи
тремя семействами. Замѣчательно, что ^ъпри-
родѣ всѣ радіоактивныя вещества п^брльшей
части встрѣчаются совмѣстно. О^нй<о, отсюда
нельзя сдѣлать никакихъ заключеній относи-
тельно связей между ура^о^у торіемъ и ак-
тиніемъ, ' какъ это ‘ былоЛ возможно въ сход-
номъ случаѣ (§204) дл® урана и радія.
4 >
Энергія радіоактивныхъ процессовъ
347
ЭНЕРГІЯ РАДІОАКТИВНЫХЪ ПРОЦЕССОВЪ.
207. Выдѣленіе а-лучей сопровождается громадной тратой энер-
гіи (другіе роды лучей вызываютъ ея расходъ въ гораздо меньшей
мѣрѣ). Величину этой энергіи можно установить непосредственно
по развитію теплоты въ кристаллѣ соли радія. Такъ какъ а-лучи
сильно поглощаются уже тонкими слоями твердыхъ (и жидкихъ)
тѣлъ, то изъ поверхностныхъ слоевъ сколько-нибудь толстаго кри-
сталла радія выходитъ наружу лишь сравнительно небольшая часть
всего числа частицъ, выбрасываемыхъ атомами. Поглощеніе осталь-
ныхъ влечетъ за собою сильное развитіе теплоты въ кристаллѣ, ко-
торый въ силу этого всегда имѣетъ болѣе высокую температуру,
нежели окружающія его тѣла. Если заключить кристаллъ въ капсюлю^
поглощающую всѣ лучи, то можно легко при помощи калориметра
опредѣлить общее количество теплоты, развивающееся за секунду,
т. е. эффектъ всѣхъ совершающихся въ немъ радіоактивныхъ про-
цессовъ. Далѣе, такъ какъ извѣстно (§ 205), какая доля общаго из-
лученія а-частицъ приходится на долю радія и какая — на долю про-
дуктовъ его распада, то возможно также опредѣлить эффектъ, вызы-
ваемый собственно распадомъ радія. А такъ какъ скорость распада
радія также извѣстна, то возможно вычислить, какое количество
теплоты развилось бы при превращеніи 1 граммъ-атома радія въ
1 граммъ-атомъ эманаціи. Получается громадное число—142 мил-
ліона большихъ калорій. Если сравнить это число съ количествами
энергіи, освобождающимися при обычныхъ химическихъ процессахъ,
напримѣръ, при сгораніи 1 граммъ-молекулы водорода и образованіи
1 граммъ-молекулы воды, когда освобождается приблизительно 68
большихъ калорій, то оказывается, что оно является величиною со-
вершенно иного порядка. Освобождаемая при радіоактивныхъ,
процессахъ энергія, разсчитанная на распадъ одного граммъ-
атома, приблизительно въ милліонъ разъ превышаетъ энер-
гі.ю, освобождаемую интенсивнымъ химическимъ процессо^Р
сгоранія, разсчитанную на 1 граммъ-молекулу. Этимъ^Йад-
тверждается, что радіоактивные процессы, при которыхъ превраще-
ніямъ подвергаются самые атомы, представляютъ собою нѣчто, вполнѣ
отличное отъ химическихъ процессовъ въ точномъ СмьГслѣ этого
слова.
•348
Возможна ли алхимія?
ВОЗМОЖНА ЛИ АЛХИМІЯ?.
208. Когда стали извѣстными первыя открытія относительно
радіоактивныхъ превращеній, появилась склонность предполагать,
что въ будущемъ до нѣкоторой степени удастся осуществить мечты
^алхимиковъ о превращеніи одного элемента въ другой. Если бы даже
эти методы не оказались практически выгодными, то это все же не
уменьшило бы ихъ интереса съ научной точки зрѣнія.
Чтобы разрѣшить вопросъ о томъ, насколько основательны
такія ожиданія, мы должны уяснить себѣ, къ чему въ сущности
сводятся всѣ методы химіи. Они всѣ сводятся къ тому, что мы
вліяемъ на ходъ химическихъ реакцій между данными веществами
путемъ измѣненій температуры или давленія, или путемъ примѣненія
электрическаго поля (въ электролизѣ), или даже лучистой энергіи,
наконецъ, путемъ введенія тѣхъ веществъ, которыя должны реаги-
ровать между собою въ формѣ различныхъ соединеній. Иными сло-
вами, всѣ химическіе методы основываются на томъ, что химическіе
процессы зависятъ отъ давленія, температуры, наличности электри-
ческаго поля, отъ дѣйствія лучей, отъ присутствія веществъ, не
входящихъ въ составъ конечныхъ продуктовъ реакціи, и еще отъ
иныхъ обстоятельствъ. Если мы желаемъ направлять по нашему
усмотрѣнію радіоактивные процессы, то мы должны предварительно
выяснить, отъ какихъ вліяній они зависятъ. Замѣчено, что измѣне-
нія температуры и измѣненія аггрегатнаго состоянія оказываютъ
вліяніе на излученіе радіоактивнаго элемента и что это излученіе
зависитъ отъ того, въ какое соединеніе входитъ данное вещество.
Однако, Рётгерфордъ показалъ, что эти вліянія всегда объ-
ясняются либо измѣненіемъ поглощающей способности радіоактив-
наго вещества по отношенію къ идущимъ изъ внутреннихъ частей
препарата лучамъ, либо освобожденіемъ или связываніемъ непрерывно
выдѣляемыхъ имъ продуктовъ распада (напримѣръ, эманаціи)^ §о
коэффиціентъ распада X для каждаго радіоактивнаго элемента явля-
ется во всѣхъ случаяхъ абсолютно постояннымъ числомъ.
Тѣ процессы, которые протекаютъ въ самьгх^атомахъ
радіоактивныхъ тѣлъ и которые ведутъ къ^иХь распаду,
не испытываютъ ни малѣйшихъ вліяній со^Стороны физи-
ческихъ или химическихъ агентовъ.
Эманація въ атмосферѣ
349
Изъ этого положенія, не поколебленнаго до сихъ поръ ни од-
нимъ опытомъ, но непрерывно подтверждаемаго новыми данными*-
слѣдуетъ съ полной очевидностью, что „алхимія", т. е. произволь-
ное превращеніе одного элемента въ другой, невозможна.
Мы не имѣемъ никакихъ средствъ для разложенія ато-
мовъ химическихъ элементовъ; они распадаются лишь
вполнѣ самопроизвольно и мы даже не въ состояніи уско-
рить или замедлить распадъ, не говоря уже о томъ, что-
бы вызвать или прекратить его по нашему желанію.
Единственное измѣненіе, которое мы можемъ вызвать въ атомѣ,
по нашему усмотрѣнію, заключается въ выдѣленіи изъ него элек-
троновъ средствами, описанными въ предыдущихъ главахъ.
ЭМАНАЦІЯ ВЪ АТМОСФЕРЪ.
209. Открытіе радіоактивныхъ веществъ имѣло чрезвычайно^
важное значеніе также для ученія объ атмосферномъ электри-
чествѣ. Въ §§ 134 и 135 мы видѣли, что атмосферный воздухъ
всегда слабо іонизированъ и что изъ этого факта вытекаютъ
важныя слѣдствія. Ольстеръ и Гейтель, которымъ мы обязаны
основными изысканіями въ этой области, доказали, что воздухъ,
всегда содержитъ небольшое количество эманаціи радія. Это коли-
чество оказывается тѣмъ большимъ, чѣмъ сильнѣе іонизація. Врядъ,
ли можно сомнѣваться въ томъ, что агентомъ, непрерывно іонизи-
рующимъ атмосферный воздухъ, является излученіе эманаціи. Мы
знаемъ (§ 202), что эманація за нѣсколько недѣль вполнѣ исчезаетъ,,
если она не образуется вновь. И дѣйствительно, Эльстеръ и Гей-
тель непосредственно наблюдали въ замкнутой массѣ воздуха убы-
ваніе іонизаціи, соотвѣтствующее распаду эманаціи. Слѣдовательно,
долженъ существовать источникъ, непрерывно вновь снабжающій
атмосферу эманаціею. Этимъ источникомъ является почва, содержа-
щая повсюду уранъ и радій. Это содержаніе хотя и ничтожно, но^
можетъ быть отчетливо замѣчено по радіоактивнымъ дѣйствія^ъ|з/?
если пользоваться весьма чувствительнымъ электрометромъ. Э^мъ
объясняется также то обстоятельство (§ 134), что поднимающійся
изъ почвы воздухъ всегда особенно сильно іонизировантД^Эхазалось.
также, что и вода океановъ, подобно земной поверх^тбстй, содер-
житъ замѣтныя количества радія.
350
Электронная теорія матеріи
ЭЛЕКТРОННАЯ ТЕОРІЯ МАТЕРІИ.
210. Всѣ химическіе элементы содержатъ въ себѣ отрицатель-
ные электроны. Отъ каждаго атома можно отдѣлить одинъ или
нѣсколько электроновъ различными искусственными средствами —
ультрафіолетовымъ свѣтомъ, Рентгеновскими лучами, катодными лу-
чами, закатодными лучами, накаливаніемъ до-бѣла. При распадѣ атома
въ радіоактивныхъ тѣлахъ также выдѣляются электроны. Всѣ элек-
троны вполнѣ тождественны между собою, имѣютъ одинаковую массу
1 \
массы атома водорода), заряжены электричествомъ и притомъ
всегда отрицательнымъ элементарнымъ количествомъ электричества.
Если отъ незаряженнаго атома отдѣляется электронъ, то этотъ
атомъ превращается въ положительный іонъ съ зарядомъ, равнымъ
элементарному количеству электричества. Потеря двухъ электроновъ
.даетъ положительный іонъ двойного заряда и т. д. Къ этимъ за-
ключеніямъ мы пришли, основываясь на фактахъ, связанныхъ съ
разрядомъ въ газахъ; пользуясь ими, мы теперь можемъ составить
слѣдующую простую картину атома.
Каждый атомъ состоитъ изъ одного крупнаго положи-
тельнаго заряженнаго ядра, съ которымъ подвижнымъ об-
разомъ соединены нѣсколько отрицательныхъ электроновъ.
Положительный зарядъ ядра представляетъ собою кратное
элементарнаго количества электричества, такъ что онъ
вполнѣ компенсируется соотвѣтствующимъ числомъ присо-
единенныхъ къ ядру электроновъ, когда атомъ не заря-
женъ. Уменьшеніе или увеличеніе числа электроновъ дѣ-
лаетъ изъ атома положительный или отрицательный іонъ.
Такимъ образомъ очень просто объясняется тотъ отмѣченный
въ § 108 фактъ, что атомъ можетъ имѣть различные заряды, но
всегда зарядъ атома есть кратное элементарнаго количества элек-
тричества. Совершенно понятно, что, вслѣдствіе ничтожной величины
массы электрона, убыль или присоединеніе электроновъ неизмѣня-
ютъ замѣтно массы атома. Измѣненія массы на величину Сйорядка
1 4 I ।
массы атома водорода лежатъ за предѣлами т^ности хими-
ческихъ опредѣленій. Кромѣ того, слѣдуетъ им^ть^ѣ виду, что въ
проводникахъ, не заряженныхъ электрически, всегда содержатся оди-
наковые эквивалентные вѣса отрицательныхъ^ и положительныхъ
Электронная теорія матеріи
351
іоновъ, такъ что избытокъ электроновъ въ однихъ компенсируется
недостаткомъ электроновъ въ другихъ; а такъ какъ раздѣлить оба
рода іоновъ невозможно, то при самыхъ точныхъ взвѣшиваніяхъ
положительная погрѣшность и отрицательная погрѣшность вполнѣ
другъ друга покрываютъ.
211. Выше очерченная „электронная теорія атома" влечетъ
за собою новый своеобразный взглядъ на сущность матеріи. Она,
очевидно, приводитъ къ заключенію, что не существуетъ мате-
ріи, лишенной электрическаго заряда. Электрическій зарядъ,
хотя бы отчасти, является сущностью самой матеріи. Это мы мо-
жемъ выразить еще такъ: не существуетъ матеріи внѣ связи
ея съ міровымъ эѳиромъ. Электрическій зарядъ является, такимъ
образомъ, условіемъ существованія матеріи; составныя части атома
въ сущности представляютъ собою ни болѣе ни менѣе, какъ узло-
выя точки электрическихъ напряженій въ эѳирѣ. Дѣло въ томъ, что,
согласно основному закону, изложенному въ §§ 57 и 58, эѳиръ
вообще обладаетъ свойствомъ несжимаемости; это значитъ, что
электрическія силовыя линіи не имѣютъ въ немъ ни начальныхъ, ни
конечныхъ точекъ. Для существованія электрическихъ полей необ-
ходимо должны существовать опредѣленныя области, гдѣ бы міровая
субстанція обладала исключительными свойствами, не подчиняясь
основному закону несжимаемости эѳира. Такія особыя области долж-
ны существовать двухъ родовъ: во-первыхъ, совокупности началь-
ныхъ точекъ электрическихъ силовыхъ линій—это положительно
заряженныя ядра атомовъ; во-вторыхъ, совокупности конечныхъ
точекъ силовыхъ линій, т. е. отрицательно заряженные электроны.
Почему начала и концы полей оказываются совмѣщенными съ малыми
тѣсно ограниченными областями атомовъ и электроновъ, а не рас-
предѣлены по широкимъ областямъ эѳира—этого объяснить точно
нельзя. Во всякомъ случаѣ, должны существовать еще особыя силы,
относительно которыхъ мы ничего не знаемъ, кромѣ того только,
что онѣ препятствуютъ исключительному состоянію перейти за пре;
дѣлы постояннаго объема —объема положительнаго іона или электрона^
Это совершенно еще не изслѣдованное силовое дѣйствіе ми^ѳ-
жемъ охарактеризировать, какъ „силу сцѣпленія узловой з^чки".
Если по какой-либо причинѣ область исключительна^^^стоянія,
которую мы называемъ атомомъ, іономъ или электрономъ^ въ нѣко-
торомъ мѣстѣ а (рис. 133) переходитъ за свою граййЦу, то „сила
352
Электронная теорія матеріи
сцѣпленія“ вызываетъ въ нѣкоторомъ другомъ мѣстѣ Ь соотвѣтству-
ющее перемѣщеніе границы, такъ что объемъ области всегда оста-
ется постояннымъ. Такимъ образомъ атомъ „движетсят. е. узло-
вая точка электрическаго поля перемѣщается въ эѳирѣ. Такое дви-
женіе возникаетъ въ томъ случаѣ, если при смѣщеніи узла, вслѣд-
ствіе сопровождающихъ его измѣненій электрическихъ и иныхъ по-
лей въ эѳирѣ (напримѣръ, поля силы тяжести), энергія полей умень-
шается. Она превращается въ „энергію движеніяи атома, которая,
вѣроятно, представляетъ собою энергію нѣкоторыхъ процессовъ въ
эѳирѣ, сопровождающихъ смѣщеніе узла и о которыхъ мы еще
будемъ говорить въ электродинамикѣ. Иными словами, движенія ато-
мовъ суть только смѣщенія узловъ и перераспредѣленія энергіи въ
эѳирѣ, происходящія въ томъ случаѣ, если условія равновѣсія эѳир-
ныхъ полей, по крайней мѣрѣ, въ нѣкоторыхъ мѣстахъ, не выпол-
нены. Установивъ такимъ образомъ, что понимается въ
• электронной теоріи подъ движеніемъ узловъ эѳирныхъ,
полей, т. е. атомовъ, іоновъ и электроновъ, мы видимъ,
что здѣсь совершенно не можетъ быть рѣчи о движе-
Рис. 133. ніи самаго эѳира. Въ связи съ новыми теоріями эѳира
Движеніе
электриче- ПР° ЭѲИРЪ часто говорятъ, что онъ „абсолютно непод-
скаго узла. виженъ"; правильнѣе было бы сказать: „понятіе движенія
эѳира само-по-себѣ является безсмысленнымъ".
Подобно увеличенію объема узла уменьшеніе его приходится
также считать невозможнымъ. Поэтому однозначные іоны непрони-
цаемы другъ для друга. Совершенно другой вопросъ, возможно ли
взаимное проникновеніе положительнаго и отрицательнаго узловъ.
Многіе факты, на которыхъ мы въ этой книгѣ не можемъ остана-
вливаться, дѣлаютъ весьма вѣроятнымъ предположеніе, что электроны
атома располагаются не внѣ его положительно заряженнаго ядра,
но внутри его и могутъ быть извлечены оттуда лишь при посред-
ствѣ особыхъ вліяній, съ которыми мы познакомились ВЪ послѣд-
нихъ главахъ. Принимаютъ, что діаметры положительнаго ядрд^аТома
и электрона находятся приблизительно въ такомъ же ^^бшеніи,
какъ діаметры земной орбиты и земного шара. Если эт^праведливо,
то внутри положительнаго атомнаго ядра можетъ находиться цѣлая
„планетная система" маленькихъ электроновъ. Но Предстоитъ еще
большой рядъ экспериментальныхъ работъ прд^де^ нежели эти пред-
положенія будутъ выведены за предѣлы чи^ой/гипотезы.
Электронная теорія матеріи
353
Если, какъ это утверждаетъ электронная теорія матеріи, атомы
состоятъ изъ узловъ электрическихъ полей, то законъ сохраненія
электрическихъ зарядовъ (§ 52) оказывается тождественнымъ съ за-
кономъ сохраненія матеріи. Всѣ электрическія поля возникаютъ, слѣ-
довательно, лишь вслѣдствіе взаимнаго удаленія положительныхъ и
отрицательныхъ элементарныхъ частей атомовъ, при чемъ существо-
вавшія уже и раньше, но бывшія неизмѣримо короткими силовыя
линіи растягиваются на измѣримыя разстоянія.
Хотя изложенная теорія кажется съ перваго взгляда очень
трудной и весьма далекой отъ обычныхъ нашихъ представленій о
матеріи, однако, при дальнѣйшемъ размышленіи скоро обнаружива-
ется, что противорѣчіе между старой и новой точкой зрѣнія отнюдь
не является такимъ рѣзкимъ. Это и вообще невозможно, такъ какъ
прогрессъ въ нашихъ теоріяхъ никогда не идетъ такимъ путемъ,
чтобы долго существовавшія и приносившія пользу представленія
вполнѣ упразднялись и замѣнялись совершенно новыми.
Наоборотъ, научныя теоріи развиваются обыкновенно такимъ
путемъ, что старыя представленія, во-первыхъ, освобождаются отъ
такихъ частностей, которыя связаны съ ихъ существеннымъ и не-
измѣннымъ ядромъ не въ силу природы вещей, а въ силу природы
нашей фантазіи, и, во-вторыхъ, становятся болѣе точными. Такъ
обстоитъ дѣло и въ данномъ случаѣ. Прежде матерію опре-
дѣляли, какъ нѣчто дѣйствующее, заполняющее пустое простран-
ство. По электронной теоріи „дѣйствующее" всегда предста-
вляетъ собою „электрическій зарядъ" вмѣстѣ съ окружающимъ
его полемъ, которое является какъ бы органомъ дѣйствія атома и
при помощи котораго атомъ дѣйствуетъ въ удаленныхъ отъ него
мѣстахъ. Однако, ни въ какомъ случаѣ нельзя утверждать, что этимъ
совершенно исчерпано понятіе матеріи. Ея свойства (напримѣръ,
тяготѣніе, инерція), во всякомъ случаѣ, существенно зависятъ еще отъ
природы и свойствъ намъ еще до сихъ поръ совершенно не ясной х
„силы сцѣпленія узловъ". Слѣдовательно, электронная теорія матеріи-^'
пока еще несомнѣнно связана съ неясностями и, можетъ быть, дат^рѵ
нѣйшее изслѣдованіе вызоветъ необходимость нѣкоторыхъ изміше-
ній въ частностяхъ той картины, которую мы сейчасъ набросали.
Но существенная часть ея, по всей вѣроятности, послужитъ надеж-
нымъ фундаментомъ для всѣхъ будущихъ теорій. Эта Существенная
часть заключается въ слѣдующихъ положеніяхъ: ^йучьГ состоятъ
Ми. Электричество и магнитномъ.
23
354 Электронная теорія матеріи
только изъ мѣстъ, въ которыхъ эѳиръ обладаетъ особыми
исключительными свойствами изъ „узловыхъ точекъ" си-
ловыхъ полей; атомы не могутъ быть вообще мыслимы не-
зависимыми отъ эѳира и отъ состояній эѳира, которыя
являются для нихъ какъ бы „органами дѣйствій на раз-
стояніи".
ГЛАВА ОДИННАДЦАТАЯ
МЕТАЛЛИЧЕСКІЕ ПРОВОДНИКИ
СУЩНОСТЬ ПРОВОДИМОСТИ МЕТАЛЛОВЪ.
212. Проблема электрической проводимости (§ 95) можетъ быть
формулирована такъ: требуется найти тѣхъ матеріальныхъ носите-
лей электрическихъ зарядовъ—тѣ „іоны", которые своими перемѣ-
щеніями обусловливаютъ разрушеніе электрическаго поля. Относи-
тельно легко оказалось найти этихъ носителей въ электролитахъ:
электролизъ, какъ мы видѣли, представляетъ собою ни что иное,
какъ перемѣщеніе матеріальныхъ частицъ въ проводникѣ, и можно
•съ увѣренностью сказать, что эти частицы являются искомыми носи-
телями зарядовъ. Въ газахъ заряженныя частички уже не обнару-
живаются такъ легко, однако тщательныя изслѣдованія не только
убѣждаютъ насъ въ ихъ существованіи, но даже позволяютъ вы-
яснить многія ихъ важныя свойства. Открытіе электроновъ явилось
важнѣйшимъ результатомъ изслѣдованій надъ проводимостью газовъ.
Твердые проводники распадаются на двѣ группы. Въ провод-
никахъ первой группы, о которыхъ мы уже говорили въ §§ 120 и 121,
можно наблюдать совершенно такъ же, какъ и въ жидкихъ электро-
литахъ, перемѣщенія опредѣленныхъ химическихъ веществъ, которыя
мы можемъ принять за носителей электрическихъ зарядовъ. Тотъ
фактъ, что внутри твердаго тѣла могутъ совершаться медленныя
передвиженія вещества, подобныя передвиженіямъ воды въ пористыхъ
земляныхъ породахъ, не представляетъ самъ по себѣ ничего новаго.
Всѣ твердыя тѣла поглощаютъ въ большей или меньшей степени
газы; особенно хорошо извѣстно такое свойство платины. Если раз-°2
городить замкнутое помѣщеніе непроницаемой перегородкой, сн|-
бженной платиновымъ окномъ, и одно изъ отдѣленій наполнить водо-
родомъ, то послѣдній проникаетъ въ платину, постепенно диффун-
дируетъ сквозь нее и появляется въ другомъ отдѣленіи^рсобенно
быстро идетъ диффузія черезъ раскаленную платину^^Гйо понять,
что, подобно газамъ, диффундирующимъ сквозь^ твердыя тѣла, и
23.
356
Сущность проводимости металловъ
электрически заряженныя частички также могутъ продвигаться внутри
ихъ подъ вліяніемъ силы электрическихъ полей.
Гораздо труднѣе было понять, еще недавно, процессы, про-
исходящіе въ проводникахъ второй группы, которые характеризу-
ются полнымъ отсутствіемъ химическихъ разложеній при прохожденіи
черезъ нихъ тока. Къ числу проводниковъ этой группы принадле-
жатъ всѣ металлы, уголь и обладающія металлическимъ блескомъ
руды. Для отличія отъ электролитическихъ проводниковъ ихъ крат-
ко называютъ „металлическими проводниками" или „провод-
никами перваго класса", относя электролиты къ числу „провод-
никовъ второго класса".
Металлическіе проводники рѣзко характеризуются тѣмъ,,
что электрическій токъ не вызываетъ въ нихъ ни малѣй-
шихъ матеріальныхъ измѣненій—ни внутри однороднаго
проводника, ни въ пограничномъ слоѣ двухъ соприкаса-
ющихся металлическихъ проводниковъ.
Единственный слѣдъ, оставляемый электрическимъ токомъ въ
металлическомъ проводникѣ, заключается въ температурныхъ измѣ-
неніяхъ, которыя онъ всегда влечетъ за собою.
Частицы, переносящія заряды въ металлическомъ проводникѣ,
не могутъ состоять изъ веществъ, принадлежащихъ одному только
данному проводнику и не встрѣчающихся въ другихъ. Дѣйствитель-
но, если бы это имѣло мѣсто, то, напримѣръ, при переходѣ тока
изъ серебра въ мѣдь характерные для серебра положительные іоны
должны были бы попадать въ мѣдь, а отрицательные іоны мѣди —
въ серебро. Поэтому въ пограничномъ слоѣ оба металла должны
были бы замѣтно измѣниться. Слѣдовательно, частицы, переносящія*
заряды, должны быть одинаковыми во всѣхъ металлическихъ провод-
никахъ. Когда электроны еще не были извѣстны, то эти разсужде-
нія заставляли принять, что существуетъ „невѣсомая" электрическая
жидкость, движеніе которой и представляетъ собою электрическій
токъ въ металлическихъ проводникахъ. Въ настоящее же время^ред-
ставляется вполнѣ несомнѣннымъ, что эта „жидкость" сос^йтъ изъ
отрицательныхъ электроновъ. Дѣйствительно, они являшся общей
составной частью всѣхъ веществъ и всегда электрически заряжены,
они могутъ, какъ мы знаемъ изъ опытовъ надъ угодными лучами
(§146), проникать черезъ всѣ тѣла и, слѣдовательно, могутъ пере-
двигаться въ нихъ подъ вліяніемъ электрическихъ силъ. Нужно еще
Электронная теорія металлическихъ проводниковъ
357
только принять, что въ проводникахъ встрѣчаются электроны, кото-
рые могутъ свободно передвигаться и, слѣдовательно, должны быть
отдѣлены отъ положительныхъ атомныхъ ядеръ.
Металлы суть такіе химическіе элементы, атомы кото-
рыхъ легко самопроизвольно распадаются на положитель-
ные іоны и электроны.
Въ металлическихъ проводникахъ электроны остаются свобод-
ными, въ электролитахъ же они соединяются съ другими атомами
или комплексами атомовъ и образуютъ отрицательные іоны. Въ ме-
таллическихъ проводникахъ передвигаются лишь особенно легкопо-
движные свободные электроны, въ электролитахъ-же подвижность
положительныхъ и отрицательныхъ іоновъ, имѣющихъ приблизи-
тельно одинаковую величину, почти одинакова.
ЭЛЕКТРОННАЯ ТЕОРІЯ МЕТАЛЛИЧЕСКИХЪ ПРОВОДНИКОВЪ.
213. Какъ уже было указано въ §211, общепризнано, что элек-
троны весьма малы по сравненію съ атомами (а, слѣдовательно, и
съ атомными разстояніями). Они заполняютъ поэтому промежутки въ
въ твердомъ остовѣ, составляемомъ положительно заряженными ато-
мами металла подобно тому, какъ газъ заполняетъ малыя поры гли-
няной стѣнки, которыя все же весьма велики по сравненію съ мо-
лекулами газа. Отрицательно заряженный „электронный газъ“ дол-
женъ распространяться въ пористомъ металлѣ по тѣмъ же простымъ
законамъ, по которымъ обыкновенный газъ распространяется въ пори-
стой глинѣ. Ниже мы увидимъ, въ какой мѣрѣ законы электрической
проводимости въ металлахъ подтверждаютъ такое предположеніе.
Если металлъ нагрѣвать, то безпорядочное движеніе электро-
новъ можетъ стать настолько интенсивнымъ, что нѣкоторые изъ
нихъ несмотря на дѣйствіе силъ притяженія со стороны положи-
тельно заряженныхъ атомовъ, вылетятъ изъ сферы ихъ дѣйствія.
Это наблюдается въ дѣйствительности при/ накаливаніи металловъ
(§ 176). Явленіе это совершенно тождественно съ явленіемъ испан
ренія, когда, вслѣдствіе сильнаго движенія молекулъ, нѣкоторыя^ф/
нихъ, преодолѣвая силы сцѣпленія, вылетаютъ за предѣлы жидкости.
Ричардсонъ (РісНапізоп) показалъ, что между количестврдрэ элек-
троновъ, вылетающихъ изъ раскаленной платины, и ^тейпературой
существуетъ приблизительно такая же зависимость^0 окйкъ между
упругостью пара и температурой. ѵ
358
Термоэлектрическія напряженія
ТЕРМОЭЛЕКТРИЧЕСКІЯ НАПРЯЖЕНІЯ
214. Мы видѣли (§ 41), что открытое Вольта напряженіе при
соприкосновеніи двухъ металловъ образуется не въ двойномъ слоѣ ме-
таллъ-металлъ (напримѣръ, цинкъ-мѣдь), но въ двойномъ слоѣ ме-
таллъ-газовая оболочка. Если газовая оболочка удалена, то обык-
новенный электрометръ въ мѣстѣ соприкосновенія двухъ металловъ
даетъ напряженіе, равное нулю. Но, пользуясь исключительно чув-
ствительными измѣрительными приборами, можно замѣтить, что и
при соприкосновеніи двухъ металловъ также возникаютъ напряженія
(т. е. двойные электрическіе слои), конечно, весьма незначительныя
по сравненію съ такъ называемыми Вольтовыми контактными напря-
женіями. Слѣдуетъ имѣть въ виду, что эти спеціально металлическія
контактныя напряженія при постоянной температурѣ также должны
слѣдовать закону напряженій Вольта и потому не могутъ быть об-
наружены при помощи электрометра, соединеннаго съ обоими ме-
таллами, если всѣ части цѣпи находятся при одной и той же тем-
пературѣ. Дѣйствительно, если предположить, что въ этомъ случаѣ
законъ Вольта не имѣетъ силы, то можно было бы изъ различныхъ
металлическихъ проволокъ образовать замкнутую проводящую цѣпь,
по которой непрерывно шелъ бы токъ, такъ какъ сумма контактныхъ
напряженій была бы отлична отъ нуля. Энергію этого тока можно
было бы использовать, напримѣръ, для электролиза или врашенія мо-
• торовъ. Но такъ какъ электрическій токъ въ металлахъ не сопро-
вождается никакими химическими или физическими измѣненіями (за
исключеніемъ температурныхъ), то такимъ образомъ получалась бы
полезная энергія исключительно за счетъ теплоты, притекающей,
напримѣръ, изъ окружающаго воздуха. Такой процессъ, согласно
второму принципу термодинамики, невозможенъ.
Но можно непосредственно наблюдать контактныя напряженія,
если имѣются нѣсколько контактовъ при различныхъ температурдх^.
Мы воспользуемся съ этой цѣлью весьма чувствительнымъ ^прибо-
ромъ— „вольтметромъ", съ которымъ мы познакомимся ниж&у'Пока
намъ достаточно знать, это этотъ приборъ выполняетъ^г^же роль,
что и электрометръ, но легче можетъ быть доведенъ С до высокой
чувствительности.
Соединимъ этотъ инструментъ при помшшп мѣдныхъ прово-
довъ съ концами вилки, образованной двумя?Сй<янными проволоками
Термоэлектрическія напряженія
359
изъ различныхъ металловъ (напримѣръ, желѣза и нейзильбера).
Стрѣлка будетъ стоять на нулѣ, точно такъ же, какъ если бы мы
соединили мѣдные провода непосредствено другъ съ другомъ. Это
является доказательствомъ строгой приложимости закона напряженій
Вольта къ этому случаю. Но если нагрѣть мѣсто спая проволокъ,
хотя бы только подержавъ его между пальцами, стрѣлка инструмента
тотчасъ отклонится отъ нулевого положенія; если спай охладить,
окруживъ его льдомъ, стрѣлка отклонится въ противоположную сто-
рону. Такъ какъ при этомъ контактныя напряженія на концахъ мѣд-
ныхъ проводовъ, гдѣ все осталось попрежнему, не могли измѣниться,
то отсюда слѣдуетъ, что измѣнилось напряженіе въ мѣстѣ спая и
что оно перестало удовлетворять закону напряженій Вольта. Откло-
неніе стрѣлки вольтметра показываетъ, насколько измѣнилось кон-
тактное напряженіе въ мѣстѣ спая съ измѣненіемъ температуры.
Въ мѣстѣ соприкосновенія двухъ металловъ возникаетъ
незначительное контактное напряженіе, измѣняющееся съ
температурой.
Появляющіяся при измѣненіяхъ температуры разности напряженій
называютъ термоэлектрическими напряженіями. Они были от-
крыты въ 1823 году Зеебекомъ (ЗееЬеск). Комбинація изъ двухъ
сваренныхъ или спаянныхъ съ одного конца проволокъ носитъ на-
званіе термоэлемента или термоэлектрической цѣпи.
Величину самаго контактнаго напряженія найти такимъ путемъ,
конечно, нельзя; какъ мы видѣли, вольтметръ даетъ лишь разность
контактныхъ напряженій при двухъ различныхъ температурахъ. По-
этому мы даемъ въ помѣщенной ниже таблицѣ „термоэлектрическія
напряженія" въ видѣ разностей между напряженіями при данной тем-
пературѣ и при нѣкоторой опредѣленной температурѣ (напримѣръ, 0°);
величины самыхъ напряженій пока еще остаются неизвѣстными.
Если мы знаемъ термоэлектрическую разность напряженій для
пары металловъ А и В (напримѣръ, мѣди и свинца) и для пары В
и С (свинца и желѣза), то, пользуясь закономъ напряженій Вольта, г
мы можемъ сейчасъ же найти и разность напряженій для пары А и С.
Именно, должно имѣть мѣсто равенство (Л, С) = (Л, В) 4" (В,^^ѵ
гдѣ (Л, В) и (В, С) означаютъ измѣренныя термоэлектрическ^раз-
ности напржечій, а (Л, С)—искомую. Чтобы уяснить это,предста-
вимъ себѣ два термоэлемента, изъ которыхъ одинъ устррецѣ выше-
описаннымъ образомъ изъ двухъ спаянныхъ концами оразличныхъ
360
Термоэлектрическія напряженія
проволокъ, напримѣръ, желѣзной и мѣдной, а другой имѣетъ между
этими двумя еще третью проволоку, напримѣръ, свинцовую. Если со-
единить съ вольтметромъ сперва первый термоэлементъ, поддерживая
мѣсто спая при опредѣленной температурѣ, а затѣмъ второй, поддержи-
вая оба его спая при той же температурѣ, при которой мы прежде под-
держивали спай желѣза и мѣди, то въ обоихъ случаяхъ отклоненіе
будетъ совершенно одинаковымъ, такъ какъ законъ напряженій
Вольта при одинаковыхъ температурахъ сохраняетъ полную силу.
Поэтому, имѣя таблицу термоэлектрическихъ напряженій, полу-
чающихся въ одномъ спаѣ металловъ съ опредѣленнымъ нормаль-
нымъ металломъ (чаще всего за таковой принимаютъ свинецъ) при
опредѣленной нормальной температурѣ другого спая (обычно 0° Цель-
сія), можно изъ нея опредѣлить также термоэлектрическія напря-
женія для произвольной иной пары металловъ и для произволь-
ныхъ температуръ различныхъ контактовъ.
Дальнѣйшее упрощеніе получается еще благодаря тому, что
здѣсь оказывается примѣнимымъ одинъ эмпирическій законъ. Именно,
зависимость контактнаго напряженія металловъ отъ температуры
весьма точно выражается функціей второй степени; мы имѣемъ, та-
кимъ образомъ, равенство
V- Ѵ0 = а.& + []. {Р,
гдѣ V—контактное напряженіе при температурѣ й°, Уо— неизвѣст-
ное контактное напряженіе при 0°. Если мы имѣемъ два спая, ко-
торые мы поддерживаемъ при температурахъ г/^0 и #2°, то термо-
электрическое напряженіе равно
V, - Ѵ2 = а - і).г) + (#,2 - 1)^).
Если, напримѣръ, таково напряженіе между мѣдью и свинцомъ,
а напряженіе между желѣзомъ и свинцомъ равно
Ѵ1'-Ѵ2' = а'(,91_^) + /9'(І712_1922),
то для пары мѣдь-желѣзо разность У/' -- У2" вычисляется при ^по-
мощи коэффиціентовъ а" = а— а, [У =[] — [}'.
Въ нижеслѣдующей таблицѣ даны коэффиціентное и для
ряда металловъ относительно свинца. Знаки выбраныД^Къ, что элек-
трическія напряженія на обоихъ спаяхъ считались^по направленію
къ свинцу. Знакъ -I- означаетъ, слѣдовательно^0 что положительный
Термоэлектрическія напряженія
361
зарядъ двойного слоя находится на иномъ металлѣ, а отрицатель-
ный на свинцѣ.
а ' 3
Желѣзо + 17,34.10—6 0,0487.10-6
Золото + 2,83.10-6 + 0,0102.10-6
Кадмій + 2,66.10-6 + 0,0429.10-6
Платина твердая + 2,60.10-6 - 0,0075.10-6
Магній + 2,44.10-6 - 0,0095.10-6
Цинкъ + 2,34.10-6 + 0,0240. ІО-6
Серебро + 2,14.10-6 + 0,0150.10-6
Мѣдь + 1,36.10-6 + 0,0095.10-6
Свинецъ 0 0
Ртуть - 0,42. ІО'6 —
Олово - 0,43.10-6 + 0,0055.10-6
Платина мягкая - 0,61 . іо-6 - 0,0110.10-6
Алюминій - 0,77 . ІО-6 + 0,0039. ІО-6
Палладій - 6,25.10-6 - 0,0359.10-6
Никкель - 22,04. ІО-6 0,0512.10-6
Изъ этой таблицы видно, что при
разностяхъ температуръ въ нѣ-
сколько градусовъ получаются напряженія, выражающіяся въ микро-
напряженіе между желѣ-
Нагрттые спаи
Холодные спаи
вольтахъ. При разности температуръ въ 100°
зомъ и мѣдью равно, приблизительно,
1 милливольту, между желѣзомъ и никке-
лемъ 4 милливольтамъ. Это уже очень
большія термоэлектрическія напряженія.
Большія напряженія получаются, правда,
при употребленіи висмута и сурьмы, но эти
металлы во многихъ случаяхъ оказыва-
ются неудобопримѣнимыми изъ-за ихъ
механическихъ свойствъ. Пользуясь этими
металлами и соединяя послѣдовательно
рядъ холодныхъ и теплыхъ спаевъ по
указанной на рис. 134 схемѣ, можно
легко получить „термостолбики", дающіе
напряженіе въ нѣсколько вольтъ и токъ
силою въ нѣсколько амперъ. Нагрѣваніе производится помощью Бун-
зеновскихъ горѣлокъ, въ пламени которыхъ помѣщаетс^Жинъ рядъ
спаевъ. Для того, чтобы поддерживать другіе спаи при низкой темпе-
Къ измѣрителъ напряженія
Рис. 134. Схема термо-
столбика.
I
362
Термоэлектрическія напряженія
ратурѣ, ихъ соединяютъ съ тонкими мѣдными пластинками, которыя
быстро отдаютъ теплоту окружающему ихъ воздуху. Такъ какъ эффектъ,
получаемый отъ такого термостолбика, достигаетъ нѣсколькихъ джу-
лей въ секунду, то его можно часто съ пользою примѣнять, напри-
мѣръ, для маленькаго мотора, вращающаго химическую мѣшалку
(рис. 135) и т. п.
215. Важнѣйшимъ примѣненіемъ термоэлементовъ является ихъ
использованіе для измѣреній температуры, т. е. въ роли термометровъ.
Легко построить термоэлементы, которые, въ отличіе отъ обычныхъ
термометровъ, могутъ употребляться при весьма низкихъ и весьма
высокихъ температурахъ. Термоэлементъ, пригодный для высокихъ
Рис. 135. Термостолбикъ доставляетъ энергію, нужную для вращенія
маленькаго электромотора.
температуръ, можетъ быть изготовленъ изъ платины и сплава пла-
тины съ родіемъ. Обѣ проволоки вмѣстѣ съ мѣстомъ ихъ сварки по-
мѣщаются въ длинной фарфоровой трубкѣ, которая прямо вста-
вляется въ печь, температуру которой нужно опредѣлить. На высту-
пающемъ концѣ трубки помѣщаются два винтовые зажима, соединен-
ье-
ные со свободными концами проволокъ термоэлемента; отъэтихъ
зажимовъ идутъ провода къ вольтметру. Такой платино-родіевый
термометръ очень удобенъ и въ готовомъ къ употребленію видѣ
имѣется въ продажѣ.
Но и независимо отъ измѣреній весьма высокихъ и весьма низ-
° \
кихъ температуръ бываютъ случаи, въ которых^термоэлементъ явля-
Термоэлектрическія напряженія
363
ется технически наиболѣе пригоднымъ приборомъ. Термоэлементъ
по сравненію со всѣми прочими термометрами, обладаетъ тѣмъ огром-
нымъ преимуществомъ, что мѣсту спая
можно придать ничтожно малый объ-
емъ и минимальную теплоемкость.
Поэтому его часто употребляютъ въ
тѣхъ случаяхъ, когда приходится из-
мѣрять температуру въ отдѣльныхъ
точкахъ области съ неравномѣрнымъ
распредѣленіемъ температуры, напри-
мѣръ, при изслѣдованіяхъ надъ тепло-
проводностью и въ тому подобныхъ
вопросахъ.
Малая теплоемкость дѣлаетъ тер-
моэлементъ также весьма пригоднымъ
для измѣренія интенсивности лучи-
стой энергіи. Для этого заставляютъ
падать лучи на зачерненный спай тер-
моэлемента ; при этомъ лучистая энер-
гія поглощается, спай нагрѣвается, и
повышеніе температуры является мѣ-
рою интенсивности лучистой энергіи. Рис. 136. Термостолбикъ для из-
Чувствительность такого измѣрителя мѣренія излученій.
лучистой энергіи или „болометра" х) можно еще значительно повы-
сить, соединяя послѣдовательно нѣсколько термоэлементовъ; одну
половину спаевъ подвергаютъ дѣйствію лучей, другую половину отъ
нихъ защищаютъ (рис. 136).
ЯВЛЕНІЕ ПЕЛЬТЬЕ.
216. Такъ какъ термоэлектрическая цѣпь отдаетъ въ другомъ
видѣ часть энергіи, притекающей къ ней въ формѣ теплоты отъ
источника нагрѣванія, то въ термоэлектрической цѣпи теплота, по-
нятно, должна исчезать. По второму принципу термодинамики т&<
плота можетъ переходить въ полезную работу только въ томъ ^ду-'
чаѣ, если въ поддерживающемъ этотъ переходъ аппаратѣ имѣется
г) Обычно названіе „болометръ" прилагается не къ описываемому здѣсь
термоэлектрическому столбику, а къ прибору, описаніе котораго помѣщена
ниже въ § 267. ' | -г^Прим. пер.
-364
Явленіе Пельтье
разности температуръ; въ термоэлектрической цѣпи таковыя, какъ
мы знаемъ, имѣются. При этомъ въ нагрѣтомъ мѣстѣ аппарата ис-
чезаетъ нѣкоторое количество теплоты а въ охлаждаемомъ мѣстѣ
появляется нѣкоторое количество теплоты ф2. Но исчезающая те-
плота больше появляющейся теплоты ф2; теряющаяся при этомъ
переходѣ отъ теплаго мѣста къ холодному теплота ф,— <22 и пРе“
'вращается въ получаемую отъ аппарата полезную энергію. Эта энер-
гія получается, однако, только въ томъ случаѣ, если термоэлементъ
Рис. 137. Демонстрація явленія Пельтье.
замкнутъ черезъ проводникъ, т. е. если возникаетъ электрическій токъ.
Другими словами, когда черезъ мѣсто спая протекаетъ электриче-
скій токъ, то отъ него отнимается или же къ нему подводится^е-
плота. Которое изъ этихъ двухъ явленій имѣетъ мѣсто, завцс^тѣ не
только отъ температуры разсматриваемаго спая, такъ какд|гіри од-
ной и той же температурѣ спай можетъ быть болѣе ^Д^грѣтымъ. и
и болѣе холоднымъ, чѣмъ другой. Въ этихъ двухъ ріучаяхъ напра-
вленіе электрическаго тока, возникающаго при замыканіи цѣпи, раз-
лично. Отсюда видно, что токъ отнимаетъ т^п-уюТу отъ спая, если
онъ идетъ въ томъ направленіи, которое имѣетъ токъ въ замкнутой
Явленіе Пельтье
365-
термоэлектрической цѣпи, когда мѣсто спая является болѣе нагрѣ-
тымъ; токъ отдаетъ теплоту спаю при обратномъ его направленіи.
Мы можемъ при помощи весьма простого опыта убѣдиться въ.
существованіи этого явленія, наличность котораго предсказывается 4
теоріей. Соединимъ зажимы термостолбика съ выключателемъ, по-
мощью котораго можно термостолбикъ соединять съ полюсами галь-
ванической батареи (съ введеніемъ небольшого сопротивленія) или же
съ инструментомъ для измѣренія тока (рис. 137). Сначала соединя-
емъ термостолбикъ съ батареей. Въ такомъ случаѣ черезъ него про-
ходитъ токъ, отнимающій теплоту отъ одного ряда спаевъ и под-
водящій теплоту къ другому ряду спаевъ. Въ силу этого въ термо-
элементахъ возникаетъ разность температуръ, тогда какъ до
начала опыта температура въ нихъ была повсюду одинакова. Въ.
наличности этой разности температуръ можно убѣдиться по откло-
ненію, даваемому стрѣлкой инструмента, если повернуть выклю-
чатель. При этомъ возбуждаемый разностью температуръ токъ идетъ
въ такомъ направленіи, что онъ отнимаетъ теплоту отъ на-
грѣтыхъ первымъ токомъ спаевъ и нагрѣваетъ спаи, охлажденные
первоначальнымъ токомъ. Иначе говоря, этотъ токъ имѣетъ напра-
вленіе, обратное направленію тока батареи. Если повторить опытъ,
переключивъ полюсы батареи такъ, чтобы „ первичный“ токъ былъ
обратнаго направленія по сравненію съ первымъ опытомъ, то и
знакъ разности температуръ измѣнится, а потому стрѣлка отклонится
въ противоположную сторону.
Разсмотрѣнное явленіе, заключающееся въ томъ, что электри-
ческій токъ, въ зависимости отъ направленія его, отнимаетъ или
подводитъ теплоту къ спаю, впервые наблюдалъ Пельтье (Реіііег),.
почему оно и называется „явленіемъ Пельтье“.
ТЕРМОЭЛЕКТРИЧЕСКІЙ СТОЛБИКЪ, КАКЪ ТЕПЛОВАЯ МАШИНА.
217. Вышеописанный опытъ напоминаетъ заряженіе и разряже-
ніе аккумулятора (§ 118). Токъ, посылаемый первоначально черезъ
термостолбикъ при помощи внѣшняго источника тока, такъ сказат^
заряжаетъ его, накопляетъ въ немъ энергію, которую затѣмъ можно
получить отъ него въ видѣ работы. Явленіе Пельтье оказывается
такимъ образомъ, въ отличіе отъ явленія обычнаго нагрѣванія токомъ,
явленіемъ обратимымъ. Помощью тока разряда можно^б^іло бы по-
лучить обратно всю энергію, подведенную токомъ Даря да, если бы
366
Термоэлектрическій столбикъ, какъ тепловая машина
часть энергіи не терялась на нагрѣваніе проводниковъ токомъ и
если бы не уменьшалась разность температуръ въ силу теплопро-
водности. Въ аккумуляторѣ электрическій эффектъ получается за
счетъ накопленной химической энергіи; въ термоэлектрической цѣпи
этотъ эффектъ получается за счетъ энергіи, запасъ которой можно
возобновлять при ея израсходованіи, просто подводя теплоту. Иными
•словами, термоэлектрическій столбикъ представляетъ собою тепло-
вую машину, подобно паровой машинѣ. Но отъ всѣхъ прочихъ те-
пловыхъ машинъ онъ отличается тѣмъ, что въ немъ всѣ матеріальныя
части находятся въ покоѣ, а работаетъ только эѳиръ. Поэтому онъ
имѣетъ передъ всѣми прочими машинами то преимущество, что въ
немъ должны быть соблюдены изъ механическихъ условій только
условія статической прочности. Если онъ сдѣланъ изъ металловъ,
выдерживающихъ весьма высокія температуры, такъ что часть его
можетъ находиться въ раскаленномъ состояніи, то его можно заста-
вить работать при гораздо большихъ разностяхъ температуръ, не-
жели паровую машину. Кромѣ того, электрическая форма энергіи
является для насъ наиболѣе удобной: ее можно переводить въ дру-
гое мѣсто при помощи проволокъ и, слѣдовательно, можно обходиться
•безъ подвижныхъ трансмиссій; примѣненія ея чрезвычайно много-
образны. Къ сожалѣнію, эта прекрасная машина обладаетъ боль-
шимъ недостаткомъ: большое количество получающейся энергіи те-
ряется въ металлическихъ элементахъ въ силу теплопроводности;
если же понизить теплопроводность, то внутреннее сопротивленіе
столбика сильно возрастаетъ и обусловливаетъ опять большую по-
терю энергіи. Поэтому экономичность такой машины, несмотря на
большія разности температуръ, ничтожна.
ИСТИННЫЯ НАПРЯЖЕНІЯ ПРИ СОПРИКОСНОВЕНІИ МЕТАЛЛОВЪ.
218. Явленіе Пельтье представляетъ собою непосредственное
доказательство того, что между двумя соприкасающимися металлами
имѣется контактное напряженіе. Передвиженіе электроновъ^чірезъ
мѣсто контактовъ обоихъ металловъ можетъ быть связано ^погло-
щеніемъ энергіи изъ эѳира, необходимой для нагрѣваній/ или съ
отдачей энергіи, соотвѣтствующей охлажденію, толькрръ томъ слу-
чаѣ, если въ контактномъ слоѣ имѣется электрическое поле, электри-
ческій двойной слой. Обозначимъ выраженно^е<і^вольтахъ напря-
женіе этого двойного слоя, т. е. контактйбе- напряженіе между
Истинныя напряженія при соприкосновеніи металловъ
367.
двумя металлами черезъ I/, выраженный въ кулонахъ зарядъ, про-
ходящій въ секунду черезъ контактный слой, черезъ У, количество
теплоты, выдѣляемое или поглощаемое въ теченіе секунды, измѣрен-
ное при помощи калориметра и выраженное въ джуляхъ, черезъ Р.
Въ такомъ случаѣ (см. § 102)
Р = V. У.
Эта формула позволяетъ вычислить неизвѣстное намъ до сихъ поръ
контактное напряженіе У, пользуясь явленіемъ Пельтье.
Истинное напряженіе при соприкосновеніи двухъ ме-
талловъ равняется частному отъ дѣленія теплоты Пельтье,
вычисленной въ джуляхъ, на электрическій зарядъ, прохо-
дящій черезъ поверхность контакта, вычисленный въ ку-
лонахъ
ѵ--т-
Такимъ образомъ были опредѣлены величины V для ряда паръ
металловъ. Оказалось, что V всегда очень точно выражается слѣ-
дующей формулой:
Ѵ = (« + 2/9. &). (273 + $),
гдѣ а и /9 суть коэффиціенты, приведенные въ таблицѣ § 214,
?7—температура по шкалѣ Цельсія, 273 + слѣдовательно,— абсо-
лютная температура.
Если мы подставимъ въ эту формулу числа, приведенныя въ ука-
занной таблицѣ, то мы увидимъ, что контактныя напряженія между
металлами не превышаютъ нѣсколькихъ милливольтъ. Это еще разъ
доказываетъ, что Вольта наблюдалъ не напряженіе между двумя
металлами, а напряженіе между металломъ и поверхностной его
оболочкой.
ЯВЛЕНІЕ ТОМСОНА.
219. Если, пользуясь явленіемъ Пельтье, вычислить контактньд^
напряженія пары металловъ при двухъ температурахъ и й2 и найти
разность между этими двумя напряженіями, то получается н^/^а ве-
личина, которую имѣетъ термоэлектрическая разность ^ѢЙфяженій
для обоихъ металловъ, если ихъ спай поддерживается^рц^ темпера-
турѣ , а оба соединенія съ ведущими къ измѣрителю напряженій
368
Явленіе Томсона
мѣдными проводами — при температурѣ &2. Термоэлектрическая раз-
ность напряженій вычисляется (см. § 214) по формулѣ
Разность же контактныхъ напряженій, какъ показываетъ легкое вы-
численіе, равняется
а. (#х - #,) + . (Я,2 - ^2) + 0. [(273 4- #і)2 - (273 + #2)2].
Разность между двумя приведенными выраженіями, т. е. величина
/9. [(273 +^і)2- (273+ ед
можетъ быть объяснена только тѣмъ, что паденіе температуры
вдоль образующихъ термоэлектрическую цѣпь проволокъ связано
съ электрическимъ полемъ, напряженіе котораго въ различныхъ
металлахъ имѣетъ различныя величины. Если это напряженіе въ
одномъ металлѣ равно . [(273 + г^)2 — (273 +$'2)2], а въ другомъ
/?2 . [(273+ $1)2 — (273 + &2)2], то къ разности напряженій на кон-
тактахъ нужно прибавить еще выраженіе
(А - &). [(273 + - (273 + ад;
слѣдовательно, Д — /3.2 есть величина, обозначенная раньше черезъ /9.
Выше мы вычислили контактныя напряженія двухъ металловъ
по теплотѣ, которая выдѣляется или поглощается при прохожденіи
тока черезъ спай этихъ металловъ. Подобнымъ же образомъ мы мо-
жемъ вычислить теперь самые коэффиціенты (до сихъ поръ мы знали
только ихъ разности) и |32, характеризующіе поле, обязанное сво-
имъ происхожденіемъ паденію температуры вдоль проволоки, поль-
зуясь тепловымъ дѣйствіемъ тока, аналогичнымъ явленію Пельтье. Для
того, чтобы уяснить себѣ описанное только-что явленіе, мы можемъ
разсматривать участки одной и той же проволоки, имѣющіе различ-
ныя температуры, какъ различныя по своимъ электрическимъ свой-
ствамъ тѣла, между которыми должно, слѣдовательно, существовать
контактное напряженіе. Если мы теперь пропустимъ токъ по про-
волокѣ, вдоль которой существуетъ паденіе температуры, то между
различно нагрѣтыми частями ея возникаетъ явленіе, аналогичное
явленію Пельтье. Когда токъ идетъ въ одномъ направленіи^црово-
лока нагрѣвается сильнѣе, чѣмъ можно ожидать, принцма^ѣо вни-
маніе ея сопротивленіе; при обратномъ направленіи токд+роисходитъ
меньшее выдѣленіе тепла. Наблюдая разность выт^шощихся коли-
чествъ теплоты, при томъ и другомъ направленіи^тока можно уста-
новить наличность описываемаго явленія. ^Дервый убѣдился тео-
ретически и экспериментально въ этом^ь^ особенномъ дѣйствіи
Электронная теорія термоэлектричества
369
тока Вильямъ Томсонъ (позже лордъ Кельвинъ); поэтому явленіе
это и называется явленіемъ Томсона.
Въ свинцѣ явленіе Томсона не наблюдается. Поэтому и берутъ
въ термоэлектрическихъ таблицахъ свинецъ за исходный металлъ.
ЭЛЕКТРОННАЯ ТЕОРІЯ ТЕРМОЭЛЕКТРИЧЕСТВА.
220. Не трудно набросать въ общихъ чертахъ электронную
картину термоэлектричества. Слѣдуетъ представить себѣ, что элек-
троны свободно могутъ выходить изъ металлическаго атома и вхо-
дить въ него, хотя они испытываютъ дѣйствіе притягательныхъ силъ
со стороны положительнаго ядра атома. Маленькіе электроны обра-
зуютъ какъ бы „паръ" вокругъ крупныхъ „атомныхъ капель" и
электрическая сила притяженія уподобляется силѣ сцѣпленія, стремя-
щейся удержать частицы пара въ каплѣ. Если далѣе этотъ „элек-
тронный паръ" въ различныхъ металлахъ имѣетъ различную упру-
гость, то онъ „дестиллируется" отъ металла, въ которомъ упругость
„электроннаго пара" больше, къ металлу, въ которомъ эта упругость
меньше. Эта дестилляція происходитъ до тѣхъ поръ, пока поле двойно-
го слоя образующагося на поверхности соприкосновенія обоихъ метал-
ловъ не окажется достаточно сильнымъ для того, чтобы воспрепят-
ствовать дальнѣйшему переходу электроновъ. Такимъ образомъ кон-
тактное напряженіе является мѣрою для разности упругостей элек-
троннаго пара въ обоихъ металлахъ. Если предположить, что „упру-
гости электроннаго пара" зависятъ отъ температуры, то контактныя
напряженія также должны зависѣть отъ температуры; кромѣ того, въ
этомъ случаѣ электроны дестиллируются также и внутри однород-
наго металла, въ которомъ имѣются разности температуръ, и это
происходитъ до тѣхъ поръ, пока въ силу смѣщенія электроновъ
въ металлѣ не возникнетъ поле, какъ разъ уничтожающее дестил-
ляцію. Такимъ образомъ просто объясняется существованіе термо-
электрическихъ явленій. Однако, необходимо отмѣтить, что устано-
вленіе точной теоріи этихъ явленій оказывается далеко не простымъ о
дѣломъ, и еще многіе частные вопросы остаются здѣсь неразрѣшенными^^
ВЛІЯНІЕ ФИЗИЧЕСКИХЪ СВОЙСТВЪ МЕТАЛЛА. '
221. Изъ вышеизложеннаго ясно, что изученіе тер^Октри-
ческихъ силъ играетъ огромную роль для пониманія электрическихъ
свойствъ металловъ. Къ сожалѣнію, однако, это изу^еніе^далеко не
Ми. Электричество и магнитизмъ.
24
370
Вліяніе физическихъ свойствъ металла
просто. Сильно затрудняетъ его, прежде всего, то обстоятельство,
что одинъ и тотъ же металлъ, даже химически чистый, можетъ обла-
дать весьма различными электрическими свойствами. Уже электро-
проводность металла зависитъ отъ его обработки (напримѣръ, отъ
того, былъ ли онъ закаленъ или оставленъ мягкимъ); еще больше
отъ этого зависятъ термоэлектрическія силы. Напримѣръ, въ таблицѣ
§ 214 платина встрѣчается два раза съ совершенно различными
коэффиціентами.
Эту зависимость термоэлектрическихъ свойствъ отъ механи-
ческой обработки вещества можно весьма легко демонстрировать.
Соединимъ желѣзную проволоку съ двумя проводами, ведущими къ
гальванометру, и свернемъ часть этой проволоки въ узкую спираль.
Если нагрѣть то мѣсто, въ которомъ спираль переходитъ въ прямо-
линейную часть проволоки, то стрѣлка гальванометра отклоняется.
Можно поступить иначе, прокаливъ часть жесткой проволоки. Если
затѣмъ нагрѣть то мѣсто, въ которомъ прокаленная часть проволоки
переходитъ въ непрокаленную, жесткую, то опять получается
отклоненіе.
Отсюда слѣдуетъ, что углубиться въ сущность термоэлектри-
ческихъ явленій и электрическихъ свойствъ металловъ можно будетъ
лишь тогда, когда будетъ установлены для каждаго отдѣльнаго ма-
теріала по возможности всѣ свойства его, имѣющія вліяніе на эти
явленія.
ЗАКЛЮЧЕНІЕ КЪ ЭЛЕКТРОСТАТИКѢ
ЭЛЕКТРОСТАТИЧЕСКАЯ И ЭЛЕКТРОДИНАМИЧЕСКАЯ ТОЧКИ ЗРѢНІЯ.
222. Въ послѣднихъ главахъ мы въ одномъ отношеніи вышли
изъ области чистой электростатики. Электрическій токъ связанъ съ пере-
носомъ и превращеніями энергіи и потому относится также къ области
динамической. Однако, легко видѣть, что мы его не разсматривали
до сихъ поръ съ точки зрѣнія динамики. Это можно пояснить срав-
неніемъ съ перемѣщеніями матеріальныхъ тѣлъ, которыя также мо-
гутъ быть разсматриваемы съ двухъ точекъ зрѣнія.
Представимъ себѣ, что намъ нужно описать устройство и экс-
плоатацію желѣзнодорожной сѣти. Съ одной стороны, мы должны
обратить вниманіе на самыя перемѣщенія перевозимыхъ товаровъ и
людей и изслѣдовать ихъ возможность, т. е. изучить желѣзнодорож-
ные пути и росписанія, при помощи которыхъ передвиженія могутъ
совершаться безопасно и безпрепятственно. Эту точку зрѣнія мы
назовемъ статической. Съ другой стороны, мы должны обратить
вниманіе также на физическія явленія, благодаря которымъ совер-
шаются перемѣщенія товаровъ и людей. Это суть движенія инерт-
ныхъ массъ желѣзнодорожныхъ поѣздовъ; для возбужденія и пре-
кращенія этихъ движеній необходимы большія силы. Этимъ именно
и занимается динамика.
Въ ученіи объ электричествѣ мы имѣемъ дѣло съ перемѣще-
ніями энергіи при посредствѣ эѳира. Въ главахъ электростатики,
посвященныхъ проводникамъ, только указывается, какимъ обра-
зомъ можетъ происходить въ проводникахъ перемѣщеніе энергіи
въ связи съ электрическимъ токомъ. Именно, возможность
щеній энергіи основывается на томъ, что въ проводникахъ
прерывно разрушается и потомъ возстанавливается вновь подъ^ влі-
яніемъ внѣшнихъ силъ. Разрушеніе поля въ проводниках^фляется
объектомъ изученія статики проводниковъ; мы подробнр^показали,
что оно основывается всегда на передвиженіяхъ подвижныхъ іоновъ
”еРемѣ>
юлене*
372 Электростатическая и электродинамическая точки зрѣнія
и что можно детально прослѣдить за всѣми многоразличными явле-
ніями, совершающимися въ проводникѣ за счетъ вступающей въ
него энергіи. При этомъ принимается просто за фактъ, что поле
всегда продвигается въ образующіеся въ проводникѣ перерывы,
такъ что равновѣсіе напряженій при этомъ сохраняется. Тѣ физи-
ческія явленія, которыя приводятъ къ непрерывному переносу на-
пряженія въ проводникѣ, ближе не разсматриваются въ электро-
статикѣ. Это уже составляетъ предметъ электродинамики. Пер-
вымъ вопросомъ въ ней является вопросъ о природѣ этихъ явленій
и методахъ ихъ изслѣдованія. Въ первыхъ главахъ электродинамики *
мы увидимъ, что переносъ электрическихъ напряженій вызывается
магнитнымъ состояніемъ эѳира. Вторымъ вопросомъ электродинамики
будетъ вопросъ о томъ, чѣмъ обусловливается возникновеніе и пре-
кращеніе этихъ переносящихъ поле магнитныхъ явленій. Для меха-
нической динамики характернымъ является разсмотрѣніе силъ, кото-
рыя не находятся во взаимномъ равновѣсіи и потому вызываютъ
движенія, измѣняютъ и прекращаютъ ихъ. Совершено то же мы
найдемъ и въ электродинамикѣ. Исключительно разсматривавшіяся
нами до сихъ поръ стаціонарныя электрическія напряженія всегда,
даже въ сложнѣйшихъ случаяхъ газовыхъ разрядовъ, удовлетворя-
ютъ условіямъ равновѣсія, изложеннымъ въ § 25, т. е. являются ста-
тическими напряженіями. Во второй половинѣ электродинамики мы
будемъ подробно разсматривать такія поля, въ которыхъ напряженія
эѳира не удерживаются во взаимномъ равновѣсіи. Мы увидимъ, что
эти не находящіяся въ равновѣсіи электродинамическія напря-
женія являются причиной, вызывающей магнитныя явленія, измѣняю-
щей й прекращающей ихъ.
СОДЕРЖАНІЕ I ТОМА
Стр.
Предисловіе редактора.............................. VII
Предисловіе автора .............................. VIII
Часть первая. Электростатика.
Глава I. Общія свойства электрическаго поля..................... 3—19
Признаки электрическаго поля ................................ 3
Носители электрическаго поля................................. 4
Пустота или эѳиръ . •...................................... 6
Электрическій зарядъ, какъ связь между эѳиромъ и матеріей 7
Два рода электрическихъ зарядовъ..................... . 9
Электрическая стрѣлка............................... 11
Проводники и изоляторы........................... 12
Земля, какъ проводникъ . . 14
Жидкіе проводники........................................... 15
Проводящіе газы .... 16
Электрическая машина съ треніемъ............................ 18
Глава II. Электрическое напряженіе .
20—74
Направленіе электрическаго поля.............................. 20
Сила или напряженіе поля . . ...... 21
Изображенія поля................ . ..... 25
Физическое различіе между матеріей и эѳиромъ ... 29
Нѣкоторыя уподобленія........................................ 31
Полное напряженіе................................... ... 34
Равновѣсіе напряженій ... 36
Потенціалъ................................................... 41
Электрометръ ... ............. . . . 42
Двойные слои на изоляторахъ .... .... 46
Опытъ Вольта ... ............. .... 51
Напряженіе при соприкосновенія двухъ металловъ ... 52
Законъ напряженій Вольта..................................... 55
Гальваническія цѣпи . 57
Единица электрическаго напряженія . ............. 60
Гальваническая батарея . 63
Примѣры электрическихъ напряженій............................ 67
Объясненіе опыта Вольта ..................................... 68
Измѣреніе электрическаго поля . ................ 70
Электрическое поле земли..................................... 73
Глава III. Электрическій зарядъ . . .
Опытъ Фарадэя съ клѣткой . . .
Проводники и діэлектрики ....
Индукція...................... .
Опытъ Фарадэя съ ведромъ .
Измѣреніе электрическихъ зарядовъ .
Законъ сохраненія зарядовъ . . .
Электрическое возбужденіе эѳира
Пробный кружокъ................'.
374;
Содержаніе
Стр.
Законъ постоянства электрическаго возбужденія .... 92
Студнеобразная модель эѳира................. ... 94
Электрофоръ................................. ... 96
Индукціонная машина................................. 99
Глава IV. Электрическія свойства изоляторовъ..........103—149
Пустота........................... . . ..................... 103
Матеріальные діэлектрики ........................... . . 106
Силовыя дѣйствія въ жидкихъ діэлектрикахъ . . . . 109
Діэлектрическая постоянная ........................ ... 111
Емкость..................................................... 111
Измѣреніе діэлектрической постоянной......................... 114
Конденсаторы .............................................. 116
Единица электрическаго заряда................................ 120
Практически примѣняемыя единицы ............................. 122
Сравненіе емкостей • • .... . 124
Абсолютная діэлектрическая постоянная эѳира .... 125
Емкость земли • • • • ............... 126
Такъ называемыя электрическія единицы ... . . 126
Послѣдовательное соединеніе конденсаторовъ .... 128
Каскадная батарея • • .... ... 129
Энергія электрическаго поля.................................. 131
Единица энергіи............................................ 132
Вычисленіе полной энергіи поля............................... 134
Распредѣленіе энергіи въ полѣ ............................... 135
Механическія аналогіи • . . . • . 136
Теорія матеріальныхъ діэлектриковъ .......................... 137
Діэлектрическая поляризація и свободные заряды • • 138
Дальнѣйшія дополненія теоріи • • ........ 140
Діэлектрическія свойства кристалловъ......................... 141
Постоянная поляризація и пироэлектричество................... 142
Піезоэлектричество........................................... 144
Діэлектрическое послѣдѣйствіе • 146
Глава V. Электрическое поле внутри проводниковъ • • 150—158
Электрическій токъ........................................... 150
Полученіе произвольныхъ напряженій........................... 154
Проблема электрической проводимости.......................... 157
Глава VI. Прохожденіе электричества черезъ электролиты • 159—208
Электролизъ ..................................
Первый законъ Фарадэя • ...
Вольтаметръ или кулонметръ ......
Узаконенная единица электрическаго заряда
Измѣреніе емкости.............................
Электрическая единица энергіи.................
Второй законъ Фарадэя ........................
Токи іоновъ...................................
Теорія электрической проводимости электролитовъ
Возможна ли іонная теорія матеріи? ....
Химизмъ гальваническихъ цѣпей ...............<
Свободная энергія и скрытая энергія • • • •
Устройство гальванической цѣпи • •
Мѣстные токи............................
159
162
166
1§7
169
,171
175
178
182
185
186
187
188
189
Содержаніе
375
Стр.
Электролитическая поляризація • .... . . 190
Электрокапиллярныя явленія • • 193
Непостоянныя и постоянныя цѣпи.............................. 197
Свинцовый аккумуляторъ..................................... 200
Электролитическій выпрямитель............................... 203
Не водные электролитическіе проводники • 205
Глава VII. Электропроводность газовъ.......................... 209 —233
Способы вызвать электропроводность газовъ.................. 209'
Непостоянство проводимости.................................. 210
Іоны въ воздухѣ .......................................... 211
Токъ насыщенія • • 214
Степень іонизаціи • • .... 216
Скорость переноса іоновъ • • • .... 218
Диффузія іоновъ • .... ................ 220
Зарядъ газіона ........................................... 222
Газіоны, какъ ядра тумана .................................. 224
Счетъ іоновъ, находящихся въ воздухѣ • • ... 228
Атмосферное электричество #.............................. 230
Свѣтовыя явленія при іонизаціи.............................. 233
Глава VIII. Тихій разрядъ ........................... 234—294
Іонизація, какъ слѣдствіе столкновеній іоновъ .... 234
Тихій разрядъ въ разрѣженныхъ газахъ....................... 235
Распространеніе отрицательнаго тлѣющаго свѣта - • • 239
Катодное напряженіе........................................ 240
Электрическое поле при тихомъ разрядѣ...................... 241
Напряженіе при сближенныхъ электродахъ................. 244
Катодные лучи ... ........................ 246
Электрическія и магнитныя свойства катодныхъ лучей • • 250
Измѣренія, произведенныя надъ катодными лучами • • 253
Электроны.............................................. 258
Скорость катодныхъ лучей ................................ 261
Вторичные лучи........................................... 262
Лучи Рентгена................................................ 264
Теорія рентгеновскихъ лучей ................................. 266
Іонизація рентгеновскими лучами и вторичные лучи • • 268
Фотоэлектрическія явленія ................................... 269
Флуоресценція ... . ..................... 272
Закатодные лучи (КапаЫгаІіІеп)............................... 272
Измѣренія надъ закатодными лучами 273
Явленіе Допплера въ закатодныхъ лучахъ ... 276
Іонизація закатодными лучами и вторичные лучи • • 278
Нижній предѣлъ напряженія, вызывающаго іонизацію столк-
новеніемъ іоновъ..................................... 278
Теорія тихаго разряда................................ • 278
Темный разрядъ • • ..................*. . . . 282
Разрядное или искровое напряженіе .......................V \ 282
Прерывистый тихій разрядъ...................................286
Вліяніе давленія газа на тихій разрядъ .... 287
Тихій разрядъ въ атмосферномъ воздухѣ ... ѴѴ • 288
Разрядъ съ острія.............................Л • 289
Нагрѣваніе и распыленіе катода.............• • * * 293
376
Содержаніе
Глава IX. Дуговой разрядъ и искра
Стр.
295—331
Выдѣленіе электроновъ раскаленными тѣлами .... 295
Анодные лучи............................ • ... 298
Дуговой разрядъ .......................................... 300
Примѣненія свѣтовой дуги 302
Свѣтовая дуга....................................... • 303
Новыя дуговыя лампы....................................... 306
Катодъ и анодъ........................................... 308
Электрическое поле въ свѣтовой дугѣ....................... 310
Теорія дугового разряда .................................. 312
Сила тока и напряженіе .... 313
Прерывистыя свѣтовыя дуги................................. 315
Переходъ отъ тихаго разряда къ дуговому................... 316
Вліяніе предшествующей исторіи разряда.................... 319
Электрическая искра .... . ........... 321
Искровое напряженіе....................................... 323
Задержка разряда • • 327
Искры въ жидкостяхъ и въ твердыхъ тѣлахъ .... 329
Скользящія искры......................................... 330
Глава X. Радіоактивность • • 332—354
Излученія радіоактивныхъ тѣлъ 332
Счетъ а-частичекъ ... . .............. 334
Радіоактивныя превращенія.............. .... 335
Начало и конецъ радія .................................... 342
Излученія, сопровождающія процессы распада .... 344
Радіоактивныя семейства........................ 346
Энергія радіоактивныхъ процессовъ • .... 347
Возможна ли алхимія?..................................... 348
Эманація въ атмосферѣ................................ 349
Электронная теорія матеріи........................... 350
Глава XI. Металлическіе проводники......................... 355 -370
Сущность проводимости металловъ................. • 355
Электронная теорія металлическихъ проводниковъ • • • 357
Термоэлектрическія напряженія ... . ..^ . 358
Явленіе Пельтье...................................... 363
Термоэлектрическій столбикъ, какъ тепловая машина • • 365
Истинныя напряженія при соприкосновеніи металловъ • • 366
Явленіе Томсона...................................... 367
Электронная теорія термоэлектричества .................... 369
Вліяніе физическихъ свойствъ металла................. 369
Заключеніе къ электростатикѣ............................... 371—372
Электростатическая и электродинамическая точки зрѣнія • ^^371
КНИГОИЗДАТЕЛЬСТВО ,,МАТЕЗИСЪ“.
Дж. ПОЙТИНГЪ, профессоръ Бирмингамскаго университета.
ДАВЛЕНІЕ СВЪТД.
Переводъ подъ редакціей „Вѣстника Опытной Физики и Элементарной
Математики". 1284-ІІ стр. 16°. Съ 42 рис. 1912. Цѣна 50 к.
Содержаніе. Предисловіе. Главы I—V: Какимъ образомъ свѣтъ про-
изводитъ давленіе.—Опыты надъ давленіемъ свѣта, падающаго нормально къ
поверхности.—Опыты надъ давленіемъ свѣта на источникъ, изъ котораго онъ
исходитъ. Отдача свѣта. —Опыты, иллюстрирующіе переносъ количества дви-
женія пучкомъ свѣтовыхъ лучей.—Давленіе свѣта въ астрономіи.—Нѣкото-
рыя возможныя слѣдствія. Примѣчанія: 1—7. Давленіе свѣта по корпуску-
лярной теоріи.—Давленіе, вызываемое волнами, перпендикулярными къ по-
верхности, изъ которой онѣ исходятъ.—Давленіе лучей, падающихъ перпен-
дикулярно на идеально отражающую поверхность.—Давленіе свѣта у пре-
ломляющей поверхности.—Давленіе солнечнаго свѣта на поглощающій шаръ
въ сравненіи съ ‘ силой тяготѣнія.—Количество матеріи, которое можетъ
быть вытолкнуто давленіемъ солначнаго свѣта.—Сила сопротивленія, дѣйст-
вующая на сферу, обращающуюся вокругъ солнца и излучающую К на кв.
см. въ секунду, и сокращеніе ея орбиты.—Эмиссіонный эффектъ Допплера.
ИЗЪ ОТЗЫВА: „Опытное подтвержденіе этой теоріи [давленія свѣта]
было дано лишь въ самое послѣднее время проф. П. И. Лебедевымъ, Ни-
кольсомъ, Гулломъ, Борлоу и самимъ Понтингомъ. Такое деликатное и из-
ящное явленіе, какъ давленіе свѣта, конечно требуетъ и соотвѣтственной
обстановки опытовъ и инструментовъ. И дѣйствительно, въ смыслѣ дели-
катности, изящности и, въ то же время, точности и убѣдительности опыты
названныхъ ученыхъ представл/потъ верхъ совершенства.
Книжка Пойтинга задается цѣлью сдѣлать понятной для широкой пуб-
лики и объяснить, какъ самую теорію давленія свѣта, такъ и ея опытное
подтвержденіе.
Нужно признать, что эта трудная задача разрѣшена Пойтингомъ въ пол-
ной мѣрѣ. Наглядность изложенія теоретической стороны вопроса, иллю-
страція его чертежами, аналогіями и сравненіями изъ повседневной жизни
не оставляетъ желать большаго.
Достоинства книжки заставляютъ насъ рекомендовать ее всѣмъ, кто
интересуется новѣйшими успѣхами физики, и кому не удавалось вполнѣ
посвятить себя этой наукѣ*. Природа, Сентябрь 1912.
О. ЛОДЖЪ, проф. МІРОВОЙ ЭѲИРЪ.
Переводъ съ англійскаго подъ редакціей прив.-доц. Д. Д. Хмырова.
ѴЦ-216 стр. 16°. Съ 19 рис. 1911 г. Ц. 80 к.
Содержаніе: Введеніе. — Общее и историческое. — Свѣтоносный
эѳиръ и современная теорія свѣта,—Междупланетный эѳиръ, какъ соединя-
ющая среда.—Вліяніе движенія на различныя явленія.—Опыты надъ эѳи-
ромъ.—Особый опытъ надъ вязкостью эѳира.—Плотность эѳира.- Дальнѣй-
шія разъясненія по поводу плотности и энергіи эѳира.—Эѳиръ и матерія.—
Способность эѳира выдерживать натяженіе.—Общая теорія аберраціи.—При-
бавленіе I О тяготѣніи и натяженіи эѳира.—Прибавленіе II. Вычисленія, от-
носящіяся къ плотности эѳира.—Прибавленіе III. Законъ Френеля, какъ част-
ный случай примѣненія повсюду существующей потенціальной функціи.
ИЗЪ ОТЗЫВОВЪ,- „Вопросъ объ эѳирѣ есть одинъ изъ труднѣйшихъ
и важнѣйшихъ вопросовъ современной физики, и въ то время, какъ одни
ученые готовы считать эѳиръ „единственнымъ вешествомъ во всей матері-
альной вселенной*, другіе совсѣмъ отрицаютъ его существованіе. Въ лицф;
Лоджа мы имѣемъ выдающагося и ревностнаго сторонника идеи всеобѣвм-
лющаго значенія эѳира для вселенной. Этотъ „пѣвецъ эѳира* (какъ его на-
звалъ одинъ англійскій ученый) не только кладетъ ѳѳиръ въ основу всѣхъ
матеріальныхъ явленій, но надѣляетъ его психической функціей^ хотя въ
разбираемой теперь нами его работѣ онъ ограничивается чист^фйзической
стороной вопроса... Переводъ, въ общемъ, хорошъ*. (РусскоеБогатство,
сентябрь 1911 г.). \ \
„Несомнѣнно, чтѳ книга знаменитаго англійскаго физика, такъ много по-
работавшаго надъ выясненіемъ свойствъ безграничной космической стихіи,
прочтется каждымъ съ живѣйшимъ интересомъ*;-^ И. Сергѣевъ.
(Физикъ-Любитель, дек. 1911 г.)
Типографія „ТЕХНИКЪ*,
Одесса, Екатеринин., 58.